BookSol.dvi Steven H. Simon The Oxford Solid State Basics, Solution Manual University Press (2015)
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 199 [warning: Documents this large are best viewed by clicking the View PDF Link!]
The Oxford Solid State Basics
Solutions to Exercises
Steven H. Simon
Oxford University
CLARENDON PRESS .OXFORD
2015
iii
These are the solutions to exercises from the Book The Oxford Solid
State Basics by Steven H. Simon, published by Oxford University Press,
2013 edition. Please do everyone a favor and do not circulate these
solutions. Do not post these solutions on your website. Do not put them
on Russian websites. Do not copy them and hand them out to students.
While there is no way for me to enforce these reasonable rules, be assured
that I, being a professor at Hogwarts, am in possession of powerful hexes
which I have used to protect the secrecy of these solutions. Those who
attempt to circulate these solutions unlawfully will activate the hex and
will suffer thirty years of bad luck, including spiders crawling into your
underwear.
Some of these solutions have been tested through use in several years
of courses. Other solutions have not been completely tested. Errors
or ambiguities that are discovered in the exercises will be listed on my
web page. If you think you have found errors in the problems or the
solutions please do let me know, and I will make sure to fix them in the
next version. Doing so will undoubtedly improve your Karma. ,
Steven H Simon
Oxford, United Kingdom
January 2014
Contents
1 About Condensed Matter Physics 1
2 Specific Heat of Solids: Boltzmann, Einstein, and Debye 3
3 Electrons in Metals: Drude Theory 15
4 More Electrons in Metals: Sommerfeld (Free Electron)
Theory 21
5 The Periodic Table 35
6 What Holds Solids Together: Chemical Bonding 39
7 Types of Matter 47
8 One-Dimensional Model of Compressibility, Sound, and
Thermal Expansion 49
9 Vibrations of a One-Dimensional Monatomic Chain 55
10 Vibrations of a One-Dimensional Diatomic Chain 71
11 Tight Binding Chain (Interlude and Preview) 81
12 Crystal Structure 95
13 Reciprocal Lattice, Brillouin Zone, Waves in Crystals 99
14 Wave Scattering by Crystals 111
15 Electrons in a Periodic Potential 125
16 Insulator, Semiconductor, or Metal 135
17 Semiconductor Physics 139
18 Semiconductor Devices 149
19 Magnetic Properties of Atoms: Para- and
Dia-Magnetism 159
vi Contents
20 Spontaneous Magnetic Order: Ferro-, Antiferro-, and
Ferri-Magnetism 167
21 Domains and Hysteresis 175
22 Mean Field Theory 179
23 Magnetism from Interactions: The Hubbard Model 191

About Condensed Matter
Physics 1
There are no exercises for chapter 1.

Specific Heat of Solids:
Boltzmann, Einstein, and
Debye 2
(2.1) Einstein Solid
(a) Classical Einstein (or “Boltzmann”) Solid:
Consider a three dimensional simple harmonic oscilla-
tor with mass mand spring constant k(i.e., the mass
is attracted to the origin with the same spring constant
in all three directions). The Hamiltonian is given in the
usual way by
H=p2
2m+k
2x2
Calculate the classical partition function
Z=Zdp
(2π~)3Zdx e−βH(p,x)
Note: in this problem pand xare three dimensional vec-
tors.
Using the partition function, calculate the heat ca-
pacity 3kB.
Conclude that if you can consider a solid to consist
of Natoms all in harmonic wells, then the heat capac-
ity should be 3NkB= 3R, in agreement with the law of
Dulong and Petit.
(b) Quantum Einstein Solid:
Now consider the same Hamiltonian quantum mechan-
ically.
Calculate the quantum partition function
Z=X
j
e−βEj
where the sum over jis a sum over all eigenstates.
Explain the relationship with Bose statistics.
Find an expression for the heat capacity.
Show that the high temperature limit agrees with
the law of Dulong of Petit.
Sketch the heat capacity as a function of tempera-
ture.
(See also exercise 2.7 for more on the same topic)
(a)
H=p2
2m+k
2x2
Z=Zdp
(2π~)3Zdx e−βH(p,x)
Since, Z∞
−∞
dy e−ay2=pπ/a
in three dimensions, we get
Z=h1/(2π~)pπ/(β/2m)pπ/(βk/2))i3= (~ωβ)−3
with ω=pk/m. From the partition function
U=−(1/Z)∂Z/∂β = 3/β = 3kBT
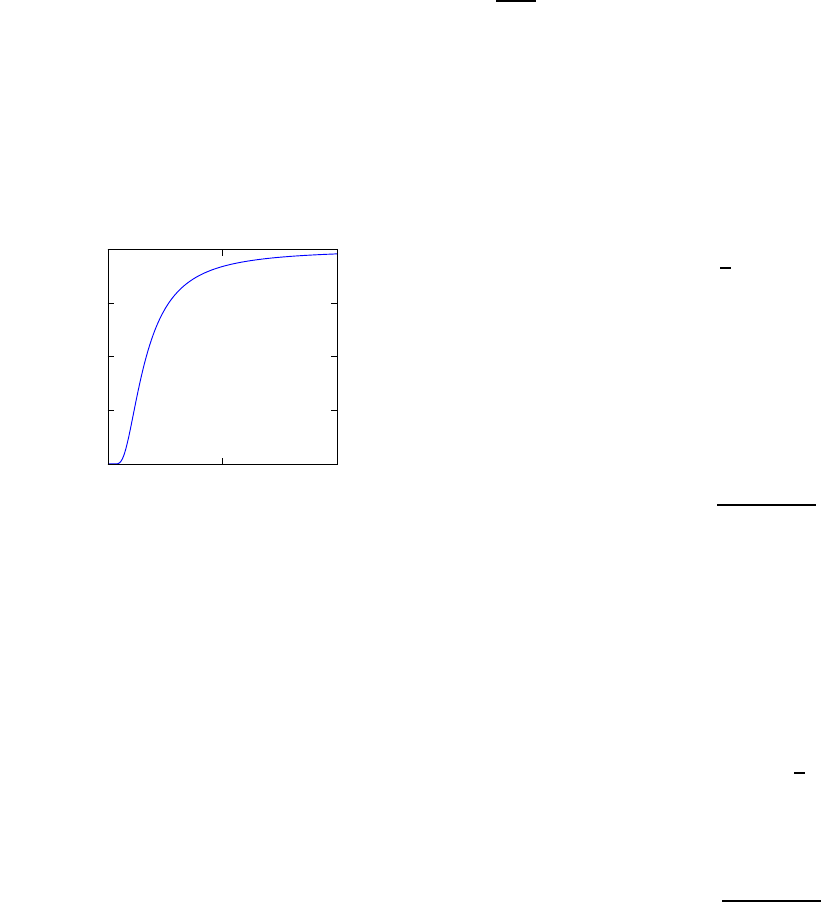
4Specific Heat of Solids: Boltzmann, Einstein, and Debye
Thus the heat capacity ∂U/∂T is 3kB.
(b) Quantum mechanically, for a 1d harmonic oscillator, we have
eigenenergies
En=~ω(n+ 1/2)
with ω=pk/m. The partition function is then
Z1d=X
n≥0
e−β~ω(n+1/2)
=e−β~ω/21/(1 −e−β~ω)
= 1/[2 sinh(β~ω/2)]
The expectation of energy is then
01 2
0
0.25
0.5
0.75
1
Fig. 2.1 Heat capacity in the Einstein
model (per atom) in one dimension.
Units are kbon vertical axis and kbT/ω
on horizontal. In three dimensions, the
heat capacity per atom is three times
as large.
hEi=−(1/Z)∂Z/∂β = (~ω/2) coth(β~ω/2)
=~ω(nB(β~ω) + 1
2)
where nBis the boson occupation factor
nB(x) = 1/(ex−1)
(hence again the relationship with free bosons). The high temperature
limit gives nB(x)→1/(x+x2/2) = 1/x−1/2 so that hEi → kBT. More
generally, we obtain
C=kB(β~ω)2eβ~ω
(eβ~ω−1)2
In 3D,
En1,n2,n3=~ω[(n1+ 1/2) + (n2+ 1/2) + (n3+ 1/2)]
and
Z3d=X
n1,n2,n3≥0
e−βEn1,n2,n3= [Z1d]3
and correspondingly
hEi= 3~ω(nB(β~ω) + 1
2)
So the high temperature limit is hEi → 3kBTand the heat capacity
C=∂hEi/∂T = 3kB. More generally we obtain
C= 3kB(β~ω)2eβ~ω
(eβ~ω−1)2
Plotted this looks like Fig. 2.1.
5
(2.2) Debye Theory I
(a)‡State the assumptions of the Debye model of heat
capacity of a solid.
Derive the Debye heat capacity as a function of
temperature (you will have to leave the final result in
terms of an integral that cannot be done analytically).
From the final result, obtain the high and low tem-
perature limits of the heat capacity analytically.
You may find the following integral to be useful
Z∞
0
dx x3
ex−1=
∞
X
n=1 Z∞
0
x3e−nx = 6
∞
X
n=1
1
n4=π4
15
By integrating by parts this can also be written as
Z∞
0
dx x4ex
(ex−1)2=4π4
15 .
(b) The following table gives the heat capacity Cfor
potassium iodide as a function of temperature.
T(K) C(J K−1mol−1)
0.1 8.5×10−7
1.0 8.6×10−4
5 .12
8 .59
10 1.1
15 2.8
20 6.3
Discuss, with reference to the Debye theory, and
make an estimate of the Debye temperature.
(a) The key assumption of Debye theory is that the dispersion curve
is linear (ω=vk) up to a cut-off frequency ωDebye determined by the
requirement that the total number of vibrational modes is correct.
For a crystal containing Natoms, the low temperature limiting form
is
C=12NkBπ4
5T
TD3
(2.1)
and the high temperature limit is 3N kB. Here, TD=~ωDebye/kB.
The full derivation goes as follows. For oscillators with frequency ω(k)
a system has a full energy
E=L3Zd3k(2π)3~ω(k)[nB(β~ω(k)) + 1/2]
One includes also a factor of 3 out front to account for the three different
sound modes (two transverse and one longitudinal) and we cut off the
integral at some cutoff frequency ωcutof f . We use the assumption that
ω=v|k|although it is not much harder to consider three different
velocities for the three different modes. We thus obtain
E=Zωcutoff
0
dωg(ω)[nB(β~ω) + 1/2]~ω
where
g(ω) = N12πω2
(2π)3nv3=N9ω2
ω3
d
and we have replaced nL3=Nwhere nis the density of atoms. Here
ω3
d= 6π2nv3is the Debye frequency, and ~ωd=kBTDebye defines the
Debye temperature. Note that there is no dependence of g(ω) on the
density n(it cancels). This shows that until the cutoff is imposed, there
6Specific Heat of Solids: Boltzmann, Einstein, and Debye
is actually no knowledge of the underlying lattice — only the overall
volume and sound velocity.
We should choose the cutoff frequency such that we have the right
number of modes in the system, thus we have
3N=Zωcutoff
0
dωg(ω)
performing this integral, we find that the proper value of ωcutof f is
exactly the Debye frequency ωdthat we just defined.
The general heat Debye theory heat capacity will then be
C=dhEi/dT =kB
(kBT)2Zωd
0
dωg(ω)(~ω)2eβ~ω
(eβ~ω−1)2
Defining x=~ω/kBTwe obtain
C=dhEi/dT =NkBT
TDebye 3
9Z~ωd/kBT
0
dxx4ex
(ex−1)2
This integral is known as the Debye integral. In the low temperature
limit, we can extend the integral out to infinity whereupon it just gives
the constant 4π4/15 recovering the above claimed result Eq. 2.1.
In the high temperature limit, the exponents can be expanded such
that the Debye integral becomes
Z~ωd/kBT
0
dxx4ex
(ex−1)2=Z~ωd/kBT
0
dxx2= (1/3)(~ωd/kBT)3
which then recovers the law of Dulong-Petit C= 3NkB
(b) Given the heat capacity and the temperature, in the low Tlimit
we should have (from Eq. 2.1)
TD=12Rπ4T3
5C1/3
The table of heat capacity looks like
T(K) 0.1 1.0 5 8 10 15 20
C(J K −1mol −1) 8.5×10−78.6×10−41.2×10−15.9×10−11.1 2.8 6.3
12Rπ4T3
5C1/3(K) 132 131 127 119 121 132 135
So TDebye is about 130K. The fact that the T3fit is not perfect is a
reflection of (a) that Debye theory is just an approximation (in particular
that phonons have a nonlinear spectrum!) and (b) that one needs to be
in the low Tlimit to obtain perfect T3scaling. (Note that at low enough
T, the T3scaling does indeed work).
7
(2.3) Debye Theory II
Use the Debye approximation to determine the heat
capacity of a two dimensional solid as a function of tem-
perature.
State your assumptions.
You will need to leave your answer in terms of an inte-
gral that one cannot do analytically.
At high T, show the heat capacity goes to a con-
stant and find that constant.
At low T, show that Cv=KT nFind n. Find Kin
terms of a definite integral.
If you are brave you can try to evaluate the integral,
but you will need to leave your result in terms of the
Riemann zeta function.
In 2d there should be 2N modes. So high Theat capacity should be
C= 2kbN(Law of Dulong-Petit).
Assume longitudinal and transverse sound velocities are equal.
2N= 2AZ|k|=kDebye
0
d2k
(2π)2=2(πk2
Debye
(2π)2
with Athe area. So
kDebye =√4πn
with n=N/A the density. So ΘDebye =~kDebyecwith cthe sound
velocity.
Since phonons obey bose statistics we have
E= 2AZ|k|=kDebye
0
d2k
(2π)2ǫknB(βǫk)
= 2AZ|k|=kDebye
0
d2k
(2π)2~ck 1
eβ~ck −1
= 2A2π
(2π)2Z|k|=kDebye
0
k dk ~ck 1
eβ~ck −1
=A
πZΘDebye
0
dǫ
~c
ǫ
~cǫ1
eβǫ −1
Let z=βǫ =ǫ/(kbT) and we get
E=A(kbT)3
π~2c2ZΘDebye /(kbT)
0
z2dz
ez−1
For large T, Θ/T is small so zis small, so
z2dz
ez−1=z
so we get ZΘDebye /(kbT)
0
zdz = (ΘDebye/(kbT))2/2
so in this limit
E=A(kbT)Θ2
Debye
2π~2c2=Ak2
DebyekbT
2π=A(4πN/A)kbT
2π= 2NkbT

8Specific Heat of Solids: Boltzmann, Einstein, and Debye
which gives
C=dE/dT = 2Nkb
as expected.
For small T, the upper limit of the integral goes to infinity and we
have
E=A(kbT)3
π~2c2Z∞
0
z2dz
ez−1
So
Cv=KT 2
where
K=3Ak3
b
π~2c2Z∞
0
z2dz
ez−1
To evaluate the integral we have
Z∞
0
z2dz
ez−1=Z∞
0
z2dz
e
−z∞
X
n=0
e−nz
=
∞
X
n=1 Z∞
0
dzz2e−nz =
∞
X
n=1
2/n3= 2ζ(3)
Thus we obtain
K=6Ak3
bζ(3)
π~2c2
(2.4) Debye Theory III
Physicists should be good at making educated guesses:
Guess the element with the highest Debye temperature.
The lowest? You might not guess the ones with the abso-
lutely highest or lowest temperatures, but you should be
able to get close.
Largest Debye temperature should be the one with the highest speed
of sound which is probably the hardest element (ie., highest spring con-
stant) and/or smallest mass. Diamond is the obvious guess (and indeed
it does have the highest Debye temperature). ΘDebye = 2230K. The
lowest is harder to guess. One presumably wants a soft material of some
sort – also possibly a heavy material.
Material ΘDebye
Neon 75 K
Argon 92 K
Krypton 64 K
Xenon 64 K
Radon 64 K
Mercury 69 K
Potassium 91 K
Rubidium 56 K
Cesium 32 K
Some Low Debye Temperatures
Soft and heavy metals like mercury are good guesses. (in fact mercury
is liquid at room temperature and one has to go to low T to measure
a Debye temperature). Also good guesses are Noble gases where the
spring constant is very low (weak interaction between the atoms). Also
heavy soft group 1 metals are good guesses. Many of these are gas or
liquid at room T and a Debye temeperature can only be measured at
low T.

9
(2.5) Debye Theory IV
From Fig. 2.3 (main text) estimate the Debye temper-
ature of diamond. Why does it not quite match the result
listed in Table 2.2 (main text)?
Extracting the slope from the figure gives C/T 3≈1.9×10−7J/(mol −K4)
Then using the formula
C=12NkBπ4
5T
TD3
We obtain
TD≈2200K
The reason that it does not match the Debye temperature given in
the figure caption has to do with the comment in the caption. Debye
theory predicts the heat capacity at all possible temperatures. The
Debye temperature quoted in the text is chosen so as to give a good fit
over the full temperature range. The Debye temperature measured here
is chosen to give a good fit at the lowest temperatures (where Debye
theory can actually be exact).
(2.6) Debye Theory V*
In the text we derived the low temperature Debye heat
capacity assuming that the longitudinal and transverse
sound velocities are the same and also that the sound ve-
locity is independent of the direction the sound wave is
propagating.
(a) Suppose the transverse velocity is vtand the lon-
gitudinal velocity is vl. How does this change the Debye
result? State any assumptions you make.
(b) Instead suppose the velocity is anisotropic. For ex-
ample, suppose in the ˆx, ˆyand ˆzdirection, the sound ve-
locity is vx, vyand vzrespectively. How does this change
the Debye result?
(a) This is actually quite simple. The derivation of the heat capacity
follows the text (or exercise 2.1). The only difference is in the density
of states. In the isotropic calculation we use
g(ω) = N12πω2
(2π)3nv3
Recall the origin of these factors. Really we had (See Eq. 2.3 of the
main text)
g(ω) = 3L34πω2
(2π)3v3
where the factor of 3 out front is for the three polarizations of the sound
waves. One could just as well have written it as
g(ω) = L34πω2
(2π)31
v3+1
v3+1
v3

10 Specific Heat of Solids: Boltzmann, Einstein, and Debye
separating out the three different polarizations. Now, if the three polar-
izations have three different velocities, we have
g(ω) = L34πω2
(2π)31
v3
1
+1
v3
2
+1
v3
3
this is true since the density of states of the three different excitation
modes simply add. In an isotropic solid, the two transverse mode have
the same velocity vtand the one longitudinal mode has velocity vland
we would have
g(ω) = L34πω2
(2π)32
v3
t
+1
v3
l
The remainder of the derivation is unchanged. Thus, defining ¯vsuch
that 3
¯v3=2
v3
t
+1
v3
l
we obtain the low temperature capacity in the usual form
C=12NkBπ4
5T
TD3
where now
(kBTD)3= 6π2n~3¯v3
.
Note that the high frequency cutoff is different for the two types of modes
(but the kcutoff is the same for both modes).
(b) If instead we have three different sound velocities in three different
directions, the situation is more complicated (and here we neglect the
differences between longitudinal and transverse modes). Here we must
make some assumption about the sound velocity in some arbitrary di-
rection. A reasonable guess would be as follows. If you consider a sound
wave in direction ˆ
k(with ˆ
k=k/|k|a unit vector), we would have
v(ˆ
k) = qv2
xˆ
k2
x+v2
yˆ
k2
y+v2
zˆ
k2
z
Now, following the usual derivation of Debye theory, we start with
hEi= 3 L3
(2π)3Zdkxdkydkz~ω(k)nB(β~ω(k)) + 1
2.
And now
ω(k) = v(ˆ
k)|k|=qv2
xk2
x+v2
yk2
y+v2
zk2
z
Since the system is now not isotropic, we cannot do the usual thing
and convert to spherical polar coordinates directly. Instead, we rescale
the axes first writing (with j=x, y, z)
Kj=kjvj
So that
ω(K) = v(ˆ
k)|k|=qK2
x+K2
y+K2
z
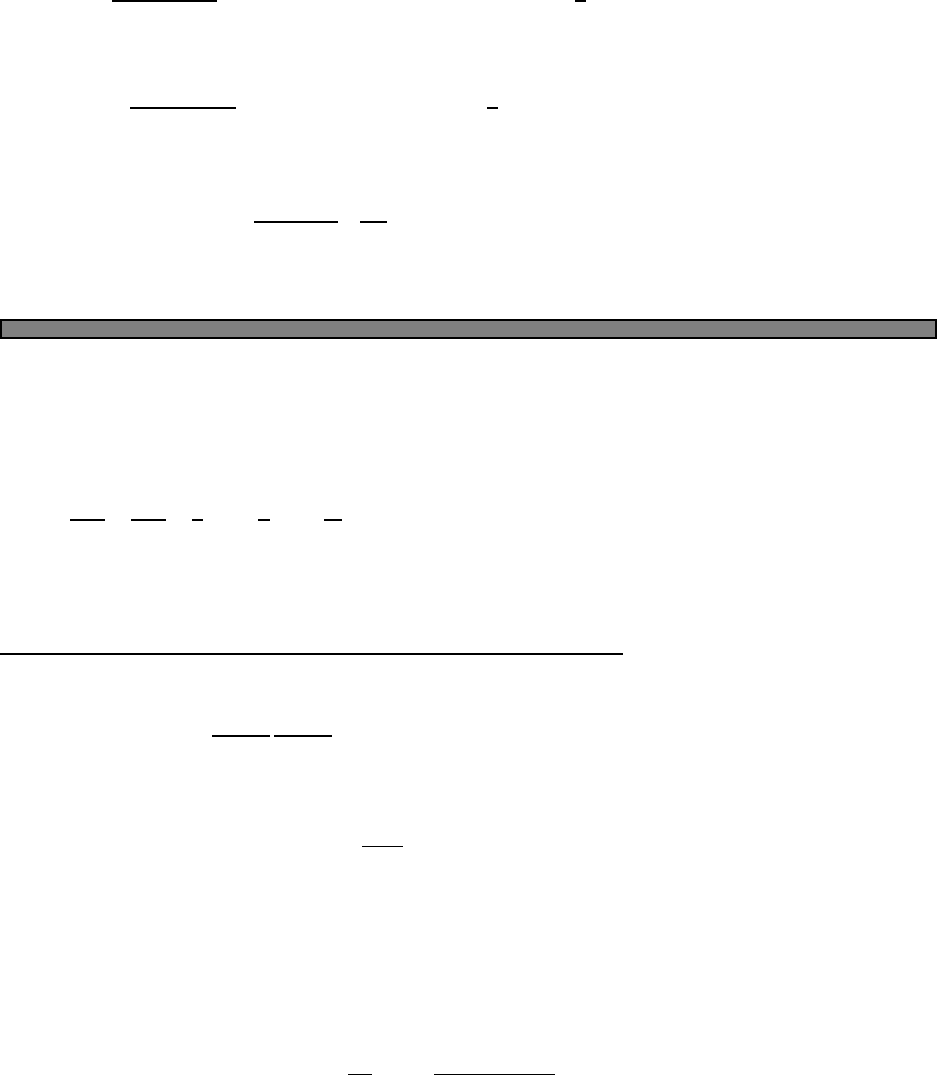
11
and
hEi= 3 L3
(2π)3vxvyvzZdKxdKydKz~ω(K)nB(β~ω(K)) + 1
2.
We can now use spherical symmetry to obtain
hEi= 3 4πL3
(2π)3vxvyvzZ∞
0
ω2dω(~ω)nB(β~ω) + 1
2.
(2.2)
The rest of the derivation follows as usual to give the usual expression
for heat capacity
C=12NkBπ4
5T
TD3
where now
(kBTD)3= 6π2n~3vxvyvz.
(2.7) Diatomic Einstein Solid*
Having studied exercise 2.1, consider now a solid made
up of diatomic molecules. We can (very crudely) model
this as a two particles in three dimensions, connected to
each other with a spring, both in the bottom of a har-
monic well.
H=p12
2m1
+p22
2m2
+k
2x12+k
2x22+K
2(x1−x2)2
Here kis the spring constant holding both particles in the
bottom of the well, and Kis the spring constant holding
the two particles together. Assume that the two particles
are distinguishable atoms.
(For this problem you may find it useful to transform to
relative and center-of-mass coordinates. If you find this
difficult, for simplicity you may assume that m1=m2.)
(a) Analogous to exercise 2.1 above, calculate the clas-
sical partition function and show that the heat capacity
is again 3kBper particle (i.e., 6kBtotal).
(b) Analogous to exercise 2.1 above, calculate the quan-
tum partition function and find an expression for the heat
capacity. Sketch the heat capacity as a function of tem-
perature if K≫k.
(c)** How does the result change if the atoms are in-
distinguishable?
(a) We can write the partition function as
Z=Zdp1
(2π~)3
dp2
(2π~)3Zdx1dx2e−βH
Considering the momentum integrals first, we have
Zdpe−βp2/(2m)=2πm
β3/2
Then the spatial integrals are made simple by transforming
Y=x1−x2
y= (x1+x2)/2
So the spatial integrals are
ZdYdye−β(−ky2−(k/4+K/2)Y2)=π
kβ 3/2π
β(k/4 + K/2)3/2
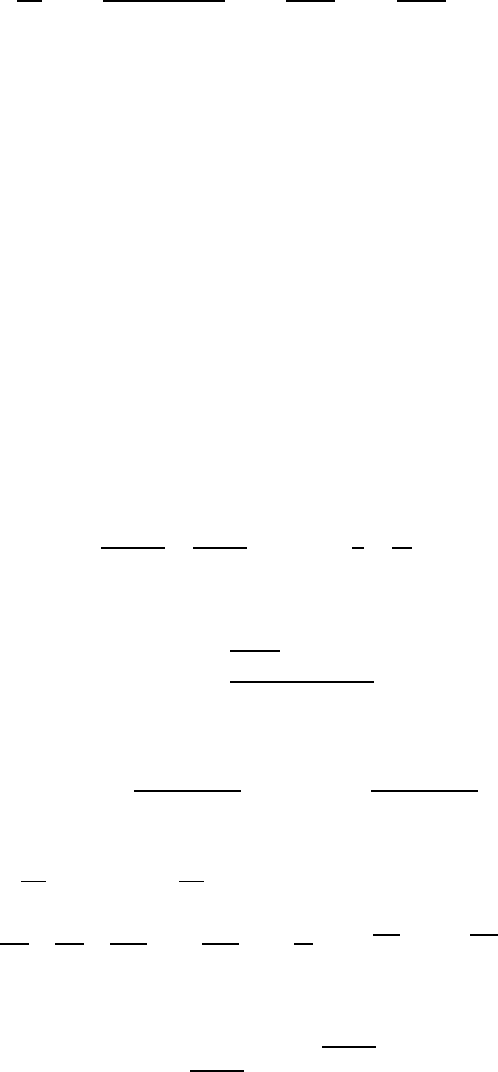
12 Specific Heat of Solids: Boltzmann, Einstein, and Debye
Putting these together we get a partition function
Z=π
kβ 3/2π
β(k/4 + K/2)3/22πm1
β3/22πm2
β3/2
∼β−6
The energy is
hEi=−∂ln Z/∂β = 6/β
So the heat capacity for the two particles is
C=∂hEi/∂T = 6kB
(b) The case where the two masses are identical is fairly simple. Again,
we construct
Y=x1−x2
y= (x1+x2)/2
and correspondingly
Q= (p1−p2)/2
q= (p1+p2)
Note that these two variables are constructed so that [Qj, Yk] = i~δjk
and [qj, yk] = i~δjk and all other commutators are zero (in other words,
these are canonical conjugates). The Hamiltonian is now written as
H=Q2
2(m/2) +q2
2(2m)+kY2+k
4+K
2y2
which comprises two independent three-dimensional harmonic oscillators
with frequencies
ω1=p4k/m
ω2=p(k/2 + K)/(2m)
The heat capacity is then (analogous to 2,1)
C= 3kB(β~ω1)2eβ~ω1
(eβ~ω1−1)2+ 3kB(β~ω2)2eβ~ω2
(eβ~ω2−1)2(2.3)
The case of unequal masses is more tricky. The general method is
similar to the discussion outlined in problem *** below. First, rescale
ri=pi√miand xi=zi/√miso that the Hamiltonian reads
H=r12
2+r22
2+k
2m1
z12+k
2m2
z22+K
2(z1/√m1−z2/√m2)2(2.4)
Note that rand zare canonically conjugate just like pand x. The
potential can be viewed as a matrix which we can write as
(k+K)/m1−K/√m1m2
−K/√m1m2(k+K)/m2

13
We can diagonalize this matrix to define two new decoupled degrees of
freedom representing two independent harmonic oscillators. The fre-
quencies of these oscillaltors squared are the eigenvalues of the above
matrix.
ω1=(k+K)(m1+m2) + p(k+K)2(m1−m2)2+ 4K2m1m2
2m1m2
ω2=(k+K)(m1+m2)−p(k+K)2(m1−m2)2+ 4K2m1m2
2m1m2
And the heat capacity is given by formula 2.3 using these two oscillator
frequencies. A plot is given in Fig. 2.2.
246 8 10 T
1
2
3
4
5
Ck_B
Fig. 2.2 Heat capacity of two einstein
oscillators. Here ω1= 1 and ω2= 10
(d) If the two atoms are indistinguishable then they must obey either
Bose or Fermi statistics depending on the atom type. The center of
mass degree of freedom (yabove) has the same Einstein heat capacity as
calculated before. However, the relative degree of freedom does not. Due
to the statistics, the relative wavefunction must obey Ψ(Y) = ±Ψ(−Y)
with the ±depending on whether we have bosons or fermions. Since
the three dimesional harmonic motion wavefunction can be decomposed
into three one-dimensional wavefunctions Ψ(r) = ψnx(x)ψny(y)ψnz(z),
and ψnis symmetric or antisymmetric depending on whether nis even
or odd, we must have that
nx+ny+nz= even for bosons, odd for fermions
So when we write the partition function for this oscillator, instead of
X
nx,ny,nz≥0
e−β~ω(nx+ny+nz+3/2)
as usual, we instead only include the terms of sum respecting the even/odd
symmetry. This restriction can be handled by writing
X
nx+ny+nz=even/odd →1
2X
nx,ny,nz≥0
(1 ±(−1)nx+ny+nz)
The sum can then be evaluated to give a partition function
Zbose/fermi =e−3
2β~ω2"1
1−e−β~ω2
±1
1 + e−β~ω3#
which then can be differentiated to get the heat capacity. I obtained
C=kb
24e2ω/kbT1 + 2e2ω/kbT+ 5e4ω/kbT
1 + 2e2ω/kbT−3e4ω/kbT2(kbT)2
for the fermi case and
C=kb
24e2ω/kbT5 + 2e2ω/kbT+e4ω/kbT
−3 + 2e2ω/kbT+e4/kbT2(kbT)2
for the bose case. Note that both of these have the correct Dulong-Petit
high temperature limit of 3kb.

14 Specific Heat of Solids: Boltzmann, Einstein, and Debye
(2.8) Einstein Versus Debye*
In both the Einstein model and the Debye model the
high temperature heat capacity is of the form
C=NkB(1 −κ/T 2+...)
For the Einstein model calculate κin terms of the
Einstein temperature.
For the Debye model calculate κin terms of the
Debye temperature.
From your results give an approximate ratio
TEinstein/TDebye. Compare your result to the values for
silver given in Fig. 2.4 (main text). (The ratio you cal-
culate should be close to the ratio stated in the caption
of the Figure. It is not exactly the same though. Why
might it not be?).
Expanding the heat capacity of a single Einstein oscillator
C=kb(β~ω)2eβ~ω
(eβ~ω−1)2
∼kb(β~ω2)1 + β~ω+ (β~ω)2/2
[β~ω+ (β~ω)2/2 + (β~ω)3/6]2
∼kb
1 + β~ω+ (β~ω)2/2
[1 + (β~ω)/2 + (β~ω)2/6]2
∼kb
1 + β~ω+ (β~ω)2/2
[1 + (β~ω)/2 + (7/12)(β~ω)2]
∼kb1 + β~ω+ (β~ω)2/2[1 −(β~ω)/2 + (5/12)(β~ω)2]
∼kb1−(β~ω)2/12 + ...
So κ=T2
Einstein/12.
We can handle the Debye case by realizing that the heat capacity is
just an integration over Einstein oscillators. So
C=ZωD
0
dωg(ω)kb(β~ω)2eβ~ω
(eβ~ω−1)2
∼kbZωD
0
dωg(ω)1−(β~ω)2/12 + ...
where g(ω) = N9ω2/ω3
D. Note that the integration is cut off so that the
integral over 1 gives precisely 3Nkbas it should. Thus we obtain
C∼3kBN1−(β~ωD)2/20 + ...
So κ=T2
Debye/20. Setting T2
Einstein/12 = T2
Debye/20 we would predict
TDebye =p5/3TEinstein ≈1.29TEinstein
In the data from Fig 2.4 the ratio is 215/151 ≈1.42. The reason this
does not match perfectly with our prediction is mainly because TDebye
and TEinstein are likely fit over the full range of the heat capacities
measured, not just in the high temperature limit. If they were fit pa-
rameters for only the high temperature limit, the ratio would come out
as we predicted here.

Electrons in Metals: Drude
Theory 3
(3.1) Drude Theory of Transport in Metals
(a)‡Assume a scattering time τand use Drude theory
to derive an expression for the conductivity of a metal.
(b) Define the resistivity matrix ρ
eas E=ρ
ej. Use
Drude theory to derive an expression for the matrix ρ
efor
a metal in a magnetic field. (You may assume Bparallel
to the ˆzaxis. The under-tilde means that the quantity ρ
e
is a matrix.) Invert this matrix to obtain an expression
for the conductivity matrix σ
e.
(c) Define the Hall coefficient.
Estimate the magnitude of the Hall voltage for a
specimen of sodium in the form of a rod of rectangular
cross-section 5mm by 5mm carrying a current of 1A down
its long axis in a magnetic field of 1T perpendicular to
the long axis. The density of sodium atoms is roughly
1 gram/cm3, and sodium has atomic mass of roughly 23.
You may assume that there is one free electron per sodium
atom (sodium has valence 1).
What practical difficulties would there be in mea-
suring the Hall voltage and resistivity of such a specimen.
How might these difficulties be addressed).
(d) What properties of metals does Drude theory not
explain well?
(e)* Consider now an applied AC field E∼eiωt which
induces an AC current j∼eiωt. Modify the above calcu-
lation (in the presence of a magnetic field) to obtain an
expression for the complex AC conductivity matrix σ
e(ω).
For simplicity in this case you may assume that the metal
is very clean, meaning that τ→ ∞, and you may assume
that E⊥B. You might again find it convenient to as-
sume Bparallel to the ˆzaxis. (This exercise might look
hard, but if you think about it for a bit, it isn’t really
much harder than what you did above!)
At what frequency is there a divergence in the con-
ductivity? What does this divergence mean? (When τis
finite, the divergence is cut off.)
Explain how could one use this divergence (known
as the cyclotron resonance) to measure the mass of the
electron. (In fact, in real metals, the measured mass of
the electron is generally not equal to the well-known value
me= 9.1095×10−31 kg. This is a result of band structure
in metals, which we will explain in Part VI.)
(a) We consider an electron with momentum pat time tand we ask
what momentum it will have at time t+dt. There is a probability dt/τ
that it will scatter to momentum zero. If it does not scatter to momen-
tum zero (with probability 1 −dt/τ) it simply accelerates as dictated by
its usual equations of motion dp/dt =FThus
hp(t+dt)i=1−dt
τ(p(t) + Fdt)
or dp
dt =F−p
τ(3.1)
where here the force Fon the electron is just the Lorentz force
F=−e(E+v×B)
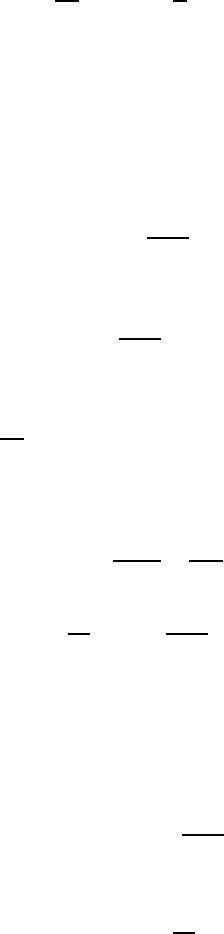
16 Drude Theory
In absence of magnetic field
dp
dt =−eE−p
τ
In steady state, dp/dt = 0 so we have
mv=p=−eτE
with mthe mass of the electron and vits velocity. If there is a density
nof electrons in the metal, and they are all moving at velocity vthen
the electrical current is given by
j=−env=e2τn
mE
or in other words, the conductivity of the metal is
σ=e2τn
m(3.2)
(b) In both an electric and a magnetic field
dp
dt =−e(E+v×B)−p/τ
Again setting this to zero in steady state, and using p=mvand j=
−nev, we obtain an equation for the steady state current
0 = −eE+j×B
n+m
neτ j
or
E=1
nej×B+m
ne2τj
We now define the 3 by 3 resistivity matrix ρ
ewhich relates the current
vector to the electric field vector
E=ρ
ej
We then obtain components of this matrix
ρxx =ρyy =ρzz =m
ne2τ
and if we imagine Boriented in the ˆzdirection, then
ρxy =−ρyx =B
ne
Inverting this equation we obtain a conductivity matrix
σzz =ne2τ/m
σxx =σyy =ρxx/(ρ2
xx +ρ2
xy) = σzz /[1 + (eBτ/m)2]
σyx =−σxy =ρxy/(ρ2
xx +ρ2
xy) = σzz (eBτ/m)/[1 + (eBτ/m)2]

17
with all other entries in the σmatrix being zero.
(c) The Hall coefficient is RH=ρyx/B which is −1/ne in Drude
theory. If sodium n= 1 gm /cm3with atomic mass M= 23, this is then
a density of atoms of
n=NA×n/M = 2.6×1028m−3
hence the same density of electrons assuming one free electron per atom.
The cross section of the rod is Lby Lwith L= 5mm, so the current
density is j=I/L2. The Hall resistivity is ρxy =B/(ne) so the Hall
voltage is jρxyL. So the total Hall voltage is
V=IB
Lne = 4.8×10−8Volts
Some of the problems with making this measurement might be:
•This is a very small voltage: One needs a sensitive voltmeter
•There may be contact resistance: Use a high impedance voltmeter
•Contacts may not be perfectly aligned: Try varying (reversing) the
magnetic field to pick out only the Bdependent part (I.e., measure
(V(B)−V(−B))/2).
•Could have heating
Tutors might also use this problem as an opportunity to discuss how
useful lock-in amplifiers are (which most students do not appear to
know).
(d) Drude theory fails to explain why the electrons do not carry heat
capacity of 3/2kBper electron as a classical gas would. This results in
incorrect predictions of, ex, thermoelectric coefficients. Drude theory
also fails to explain why the sign of the Hall effect can be different in
different samples. Drude theory does not explain why we should only
count valence electrons.
(e) Drude theory at finite frequency. We start with the equation of
motion simplified by setting τ→ ∞
dp
dt =−e(E+v×B)
setting E= ˆxE0
xeiωt and B=Bˆz,
m˙vx=−eE0
xeiωt −evyB
m˙vy=evxB
We can differentiate the first equation to give
m¨vx=−iωeE0
xeiωt −e˙vyB
then plug in the second equation to give
¨vx=−iωe(E0
x/m)eiωt −(eB/m)2vx

18 Drude Theory
which is the equation of a driven harmonic oscillator. We use the ansatz
solution vx=v0
xeiωt so we obtain
−ω2v0
x=−iω(eE0
x/m)−(eB/m)2v0
x
which we solve
v0
x=−iω(eEx/m)
(eB/m)2−ω2
and similarly
v0
y=−(eB/m)(eEx/m)
(eB/m)2−ω2
with the current being j=−env we obtain
σxx =iω(ne2/m)/[(eB/m)2−ω2]
σyx = (eB/m)(ne2/m)/[(eB/m)2−ω2]
The cyclotron frequency eB/m is the natural oscillation frequency of a
particle of charge −eof mass min magnetic field B. This divergent
response is easy to detect experimentally as a strong absorbtion of the
ac electric field at a particular frequency. (Then this obviously can be
converted into a measurement of the mass).
The motion in the z-direction is unaffected by the magnetic field in
the zdirection so that we have
σzz =ne2/(iωm)
and off-diagonal terms including zare zero.
Note, the calculation may look a bit nicer if you set vor equivalently
j, and solve for Eto obtain the finite frequency resistance matrix, and
then invert last. Lets try doing it that way also. Starting with
dp
dt =−e(E+v×B)
Writing E=E0eiωt and j=j0eiωt and also j=n(−e)v=n(−e)p/m
we then have
iωmj0/(n(−e)) = −e[E0+j0×B/(n(−e))]
or
E0=iωm
ne2j0−B×j0/(n(−e))
So assuming Bin the ˆzdirection, we have a resistivity matrix
ρ
e=
iωm
ne2B/(−ne) 0
B/(ne)iωm
ne20
0 0 iωm
ne2
which we invert to get the same result as above.

19
(3.2) Scattering Times
The following table gives electrical resistivities ρ, den-
sities n, and atomic weights wfor the metals silver and
lithium:
ρ(Ωm) n(g/cm3)w
Ag 1.59 ×10810.5 107.8
Li 9.28 ×1080.53 6.94
Given that both Ag and Li are monovalent (i.e.,
have one free electron per atom), calculate the Drude
scattering times for electrons in these two metals.
In the kinetic theory of gas, one can estimate the scat-
tering time using the equation
τ=1
nhviσ
where nis the gas density, hviis the average velocity (see
Eq. 3.4 main text), and σis the cross-section of the gas
molecule—which is roughly πd2with dthe molecule di-
ameter. For a nitrogen molecule at room temperature,
we can use d=.37nm.
Calculate the scattering time for nitrogen gas at
room temperature and compare your result to the Drude
scattering times for electrons in Ag and Li metals.
Note: the table should read 10−8not 108!
We use σ=ρ−1=Ne2τ /m with mthe free electron mass and where
Nhere is the electron density which we calculate by
N=nAvagadro Number
mol-weight in grams/cm3106
Solving for τwe get
τAg = 3.8×10−14sec
τLi = 8.3×10−15sec
The second part should say room temperature and pressure. The
weight of a Nitrogen molecule is about 28 times that of a proton (two
nitrogen atoms of atomic weight 14). So the velocity at 300 K is
hvi=s8kBT
π28mp≈475m/sec
uncoincidentally being close to the speed of sound in air. The density
is given by n=P/RT with Rthe gas constant. At P= 105pascals
and T= 300 K, this gives .025 mol/m3. (This should be the usual 22.4
moles per liter that people remember, but we used 300 K instead of 273
and we approximated the pressure). Multiplying by Avagadro’s number
give the density that we should use in the equation
τ=1
nhviσ≈2×10−10sec
So electrons scatter much much much more often — this is not surprising
considering how much higher their density is than that of the nitrogen
gas.
20 Drude Theory
(3.3) Ionic Conduction and Two Carrier Types
In certain materials, particularly at higher tempera-
ture, positive ions can move throughout the sample in
response to applied electric fields, resulting in what is
known as ionic conduction. Since this conduction is typ-
ically poor, it is mainly observable in materials where
there are no free electrons that would transport cur-
rent. However, occasionally it can occur that a material
has both electrical conduction and ionic conduction of
roughly the same magnitude—such materials are known
as mixed ion–electron conductors.
Suppose free electrons have density neand scattering
time τe(and have the usual electron mass meand charge
−e). Suppose that the free ions have density ni, scatter-
ing time τi, mass miand charge +e. Using Drude theory,
(a) Calculate the electrical resistivity.
(b) Calculate the thermal conductivity.
(c)* Calculate the Hall resistivity.
If we fix the electric field, both species respond to the electric field in-
dependently. So the total conductivity is the sum of the two independent
conductivities
σ=σe+σi=e2neτe
me
+niτi
mi
And thus
ρ=1
e2neτe
me+niτi
mi
The thermal conductivity is similar – both pieces add
κ=κe+κi=4k2
BT
πneτe
me
+niτi
mi
Note that the Weidemann-Franz law continues to hold here in the ratio
of σto κ.
The Hall resistivity is more complicated. To simplify, if we apply
magentic field in the zdirection, we need only keep track of conductivity
in the x, y plane (i.e., we can think of this as a two dimensional problem).
For a single species, we have (See exercise 3.1)
ρ=r BR
−BR r
where r=m/(nq2τ) and R=q/n with qthe charge on the charge
carrier. We define tensors ρeand ρifor the two separate species in
terms of rj=mj/(njq2
jτj) and Rj=qj/njwith j=eor i. The
conductivity tensors are σj=ρ−1
jand then the total conductivity tensor
is σ=σe+σi. Finally this is inverted to give the tensor ρtotal =σ−1.
There is a lot of algebra involved in this. I obtained
ρxx =B2(reR2
i+riR2
e) + rire(re+ri)
B2(Re+Ri)2+ (re+ri)2
ρxy =BB2ReRi(Re+Ri) + Rir2
e+Rer2
i
B2(Re+Ri)2+ (re+ri)2

More Electrons in Metals:
Sommerfeld (Free
Electron) Theory 4
(4.1) Fermi Surface in the Free Electron (Som-
merfeld) Theory of Metals
(a)‡Explain what is meant by the Fermi energy, Fermi
temperature and the Fermi surface of a metal.
(b)‡Obtain an expression for the Fermi wavevector and
the Fermi energy for a gas of electrons (in 3D).
Show that the density of states at the Fermi sur-
face, dN/dEFcan be written as 3N/2EF.
(c) Estimate the value of EFfor sodium [The density
of sodium atoms is roughly 1 gram/cm3, and sodium has
atomic mass of roughly 23. You may assume that there
is one free electron per sodium atom (sodium has valence
one)]
(d) Now consider a two-dimensional Fermi gas. Ob-
tain an expression for the density of states at the Fermi
surface.
(a.i) Fermi Energy EFis chemical potential at T= 0. Note, if there is
a filled band the chemical potential is mid-gap, and this differs from the
conventional intuition that it is the highest filled state at zero tempera-
ture. Note that some books define fermi energy to be chemical potential
as a function of temperature. This is annoying — why define a new
quantity if it is just another name for the old quantity?!
(a.ii) Fermi temperature TF=EF/kbwith kbbeing Boltzmann’s con-
stant.
(a.iii) Fermi surface is the surface in momentum space separating the
filled and unfilled states at zero temperature. (This is ill-defined for the
case of a filled band – but we don’t do band theory until later in the
course). Or the manifold of states having energy EF. Note that it need
not be a sphere, for example, if the effective mass (defined later!) is
anisotropic you get an ellipsoid instead.
(b)
N= 2VZk<kF
dk
(2π)3=2V
(2π)3
4πk3
F
3
Note the factor of 2 out front is for two species of spins. This result
implies
kF= (3π2N/V )1/3

22 Sommerfeld Theory
which gives us the Fermi energy
EF=~2(3π2N/V )2/3
2m(4.1)
with mthe (effective) electron mass.
Here is a short way to show that the density of states at the Fermi
surface is 3N/2EF. We write the density as
EF=C(N)2/3
where Cis a bunch of constants (given in Eq. 4.1, although we actually
don’t care about its actual value). We then have
dEF/dN = (2/3)CN −1/3= (2/3)EF/N
which immediately gives us
dN/dEF= (3/2)N/EF
(c) Sodium had density of 1gm/cc and atomic mass 23. Thus we have
(1gm/cm3)(102cm/m)3(mole/23gm)(6.02 ×1023atoms/mole)
= 2.6×1028atom/m3.
(See also part (c) of problem 3.1.) With 1 free electron per atom, this
gives us the density N/V and we can plug this into Eq. 4.1 yielding
EF= 5 ×10−19J= 3.2eV
dividing by Boltzmann’s constant this gives about 37,000 Kelvin.
(d) For a 2d Fermi gas we have
N= 2AZk<kF
dk
(2π)2=2A
(2π)2πk2
F
where Ais the (2d) area of the system. Thus we obtain
kF= (2πN/A)1/2
The Fermi energy is then
EF=~2(2πN/A)
2m=~2πN/A
m
The density of states is then independent of energy and is given by
dN/dE =Am/(~2π) = N/EF
One can ask the same question in ddimensions and use a similar scheme
to do the calculation.

23
(4.2) Velocities in the Free Electron Theory
(a) Assuming that the free electron theory is applica-
ble: show that the speed vFof an electron at the Fermi
surface of a metal is vF=~
m(3π2n)1/3where nis the
density of electrons.
(b) Show that the mean drift speed vdof an electron
in an applied electric field Eis vd=|σE/(ne)|, where σ
is the electrical conductivity, and show that σis given
in terms of the mean free path λof the electrons by
σ=ne2λ/(mvF).
(c) Assuming that the free electron theory is applicable
to copper:
(i) calculate the values of both vdand vFfor
copper at 300K in an electric field of 1 V m−1
and comment on their relative magnitudes.
(ii) estimate λfor copper at 300K and com-
ment upon its value compared to the mean
spacing between the copper atoms.
You will need the following information: copper is mono-
valent, meaning there is one free electron per atom. The
density of atoms in copper is n= 8.45 ×1028 m−3. The
conductivity of copper is σ= 5.9×107Ω−1m−1at 300K.
(a) As in the previous problem, in 3D, kF= (3π2n)1/3with n=N/V .
Thus pF=~kFand the fermi velocity is vF=~kF/m.
(b) If an electric field Eis applied, a current density j=σEflows, with
σthe conductivity. The electrical current is then given by j=−envd
where −eis the electron charge, nis the density of the electrons, and
vdis the average drift velocity. Thus we obtain
|vd|=|σE/(ne)|
Deriving the conductivity from the mean free path is an exercise in
Drude theory. As in problem 3.1, we have the Drude theory expression
dp
dt =F−p
τ
With F=−eEwe then have the steady state momentum p=−eE/τ
corresponding to the steady state drift velocity vd=−eE/(τm). The
current density is then j=ne2/(τm)Eyielding the usual expression for
the Drude conductivity
σ=ne2τ
m
Now if the typical velocity of an electron is on the order of the Fermi
velocity vF, then in the scattering time τthe distance traveled, i.e., the
mean free path is λ=τvF. Thus we can rewrite the Drude conductivity
as
σ=ne2λ
mvF
(c.i) On the scale of the Fermi temperature, 300K is close to zero
kelvin so we can ignore this temperature.
vF=~(3π2n)1/3
we obtain vF≈1.6×106m/sec. This is about 0.5% of the speed of light.
Very fast.

24 Sommerfeld Theory
The drift velocity is
vd=σE/(ne)
which gives vd≈4.4×10−3m/sec. I.e., very slow.
(c.ii) Use here
λ=vFσm/(ne2)
plugging in numbers this gives λ≈3.9×10−8m, or about 400 angstoms
– roughly 100 lattice spacings.
(4.3) Physical Properties of the Free Electron
Gas
In both (a) and (b) you may always assume that the
temperature is much less than the Fermi temperature.
(a)‡Give a simple but approximate derivation of the
Fermi gas prediction for heat capacity of the conduction
electron in metals.
(b)‡Give a simple (not approximate) derivation of
the Fermi gas prediction for magnetic susceptibility of
the conduction electron in metals. Here susceptibility is
χ=dM/dH =µ0dM/dB at small Hand is meant to
consider the magnetization of the electron spins only.
(c) How are the results of (a) and (b) different from
that of a classical gas of electrons?
What other properties of metals may be different
from the classical prediction?
(d) The experimental specific heat of potassium metal
at low temperatures has the form:
C=γ T +α T 3
where γ= 2.08 mJ mol−1K−2and α=
2.6 mJ mol−1K−4.
Explain the origin of each of the two terms in this
expression.
Make an estimate of the Fermi energy for potassium
metal.
(a) Let the density of states at the Fermi surface be given by D(EF)
(and assume this is a nonzero quantity). At temperature T, electrons
within an energy kbTof the Fermi surface can be excited above the
Fermi energy. Typically if an electron is excited, it will gain an energy
of order kbT. Thus, the electron energy (above the ground state) is
roughly (kbT)2D(EF). Thus the heat capacity is approximately
C=dE/dT ≈2kb(kbT)D(EF)
In a slightly more careful (but still not exact) treatment, one approxi-
mates the smooth fermi function as a simple function as shown here in
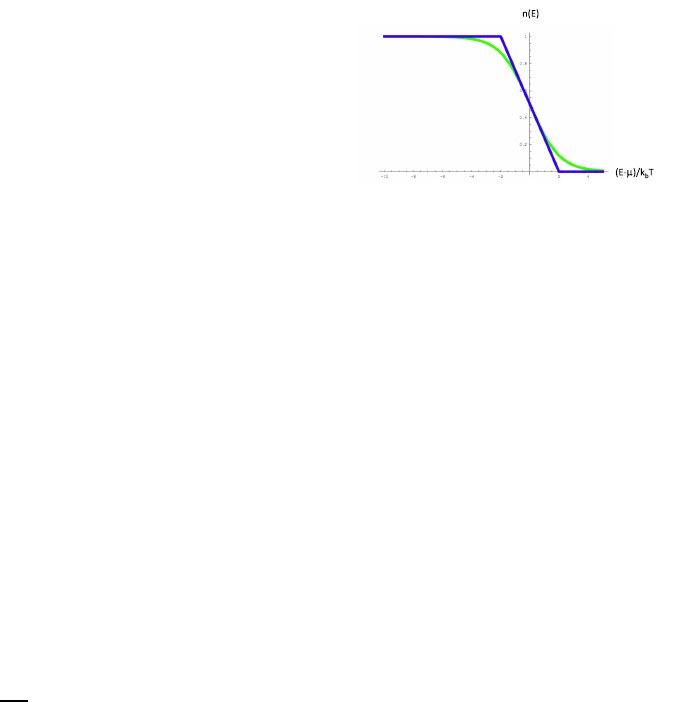
Fig. 4.1.
25
Fig. 4.1 The Fermi function (green)
and a simple approximation to the
fermi function (blue).
In this picture, the approximation to the fermi function is given by
n(E) =
1 (E−µ)/kbT < −2
0 (E−µ)/kbT > 2
1/2−(E−µ)/(4kbT) otherwise
In this approximation, one can calculate that the energy is given by
E(T) = Constant + DZ2/kbT
−2/kbT
dEE(1/2−E/(4kbT))
= Constant + D(kbT)2(4/3)
which results in C= (8/3)kb(kbT)D(EF).
An exact calculation (See Ashcroft+Mermin, or exercise 4.9.b below)
of this result is
C= (π2/3)kb(kbT)D(EF) = N(π2/2)kb(kbT)/EF(4.2)
This calculation is an exercise given as an additional problem.
Note that as discussed above, for a free fermi gas D(EF) = 3N/2EF.
Thus up to constants of order one we have
C∼kbN(kbT/EF)
which is very small since T≪TF.
(b) There are several ways that the electrons can respond to the mag-
netic field. First, we assume that the magnetic field couples only to
the spins of the electron (we ignore orbital effects). The Hamiltonian
(neglecting the Lorentz force of the magnetic field) becomes
H=p2
2m+gµBB·σ
where g= 2 is the g-factor of the electron Bis the externally applied
magnetic field and σis the spin of the electron which takes eigenvalues
±1/2. Here µB≈.67(K/T )/kBthe conventional Bohr magneton. Thus
in the magnetic field the energy of an electron with spin up or down
26 Sommerfeld Theory
(with up meaning it points the same way as the applied field)
ǫ(k,↑) = ~2|k|2
2m+µb|B|
ǫ(k,↓) = ~2|k|2
2m−µb|B|
The spin magnetization of the system in the direction of the applied
magnetic field will then be
M=−1
V
dE
dB =−([# up spins] −[# down spins]) µB/V (4.3)
So when the magnetic field is applied, it is lower energy for the spins to
be pointing down, so more of them will point down.
Let us now calculate the Pauli paramagnetism of the free electron
gas at T= 0. With zero magnetic field applied, both the spin up and
spin down states are filled up to the Fermi energy (i.e, to the Fermi
wavevector). Near the Fermi level the density of states per unit volume
for spin up electrons is g(EF)/2 and similarly the density of states per
unit volume for spin down electrons is g(EF)/2. When Bis applied, the
spin ups will be more costly by an energy µBB. Thus, (assuming that the
chemical potential does not change) we will have (g(EF)/2)µBBfewer
spin ups electrons per unit volume. Similarly, the spin downs will be less
costly by the same amount, so we will have (g(EF)/2)µBBmore spin
downs per unit volume. Note that the total number of electrons in the
system did not change, so our assumption that the chemical potential did
not change is correct. (Recall that chemical potential is always adjusted
so it gives the right total number of electrons in the system). Thus,
using Eq. 4.3 the moment per unit volume is given by
M=g(EF)µ2
BB
and hence the magnetic susceptibility χ=∂M/∂H is given (at T= 0
by)
χP auli =µ0µ2
Bg(EF)
(c) For a classical monatomic gas, the specific heat is given by the
equipartition law C= 3kBNwhich is larger than the result above by
roughly a factor of EF/kbTwhich could be a factor of 100 or more.
Similarly, for a single isolated spin 1/2 we can calculate the partition
function (this calculation was done in stat mech class last year).
Z=eβgµBB/2+e−βgµBB/2
The expectation of the moment (per spin) is then
m=−dlog Z/d(Bβ) = (gµB/2) tanh(βgµBB/2)
For small Bthis is
m= (gµB/2)2(B/kbT)

27
thus the total susceptibility for Nspins (recall susceptibility is measured
per unit volume) is
dM/dH =µ0dM/dB =Nµ0(gµB/2)2(1/kbT)
which, for any T≪TFis much larger than the Pauli susceptibility
calculated above (by a factor of approximately TF/T ).
Other properties that differ from the classical prediction include: Ther-
mopower, Peltier Coefficinent, Average Electron Velocity, Compressibil-
ity, ...
(d) The T3term is clearly from Debye phonon specific heat. The T-
linear term is the specific heat of free electrons. Using the above formula
Eq. 4.2 yields
EF= (π2/2)R(T/Clinear) =≈2×104KkB≈1.7eV
The real value is roughly 2.1 eV.
Another method would be to use the density of potassium and assume
the valence is 1. If you do this, you get something much closer to the
right answer.
(4.4) Another Review of Free Electron Theory
What is the free electron model of a metal.
Define Fermi energy and Fermi temperature.
Why do metals held at room temperature feel cold
to the touch even though their Fermi temperatures are
much higher than room temperature?
(a) A d-dimensional sample with volume Ldcontains
Nelectrons and can be described as a free electron model.
Show that the Fermi energy is given by
EF=~2
2mL2(Nad)2/d
Find the numerical values of adfor d= 1,2, and 3.
(b) Show also that the density of states at the Fermi
energy is given by
g(EF) = Nd
2LdEF
Assuming the free electron model is applicable, es-
timate the Fermi energy and Fermi temperature of a
one-dimensional organic conductor which has unit cell of
length 0.8 nm, where each unit cell contributes one mobile
electron.
(c) Consider relativistic electrons where E=c|p|. Cal-
culate the Fermi energy as a function of the density for
electrons in d= 1,2,3 and calculate the density of states
at the Fermi energy in each case.
The free electron model of a metal describes electrons in a metal as a
noninteracting gas of fermions at some fixed density (usually chosen to
be velectrons per unit cell of the metal where vis the valence).
Fermi Energy EFis chemical potential at T= 0. Note, if there is a
filled band the chemical potential is mid-gap, and this differs from the
conventional intuition that it is the highest filled state at zero tempera-
ture. Note that some books define fermi energy to be chemical potential
as a function of temperature. This is annoying — why define a new
quantity if it is just another name for the old quantity?!
Fermi temperature TF=EF/kbwith kbbeing Boltzmann’s constant.
Due to Pauli exclusion, a metal can have a very high Fermi tempera-

28 Sommerfeld Theory
ture (high chemical potential) even if the material is at zero temperature
— i.e., if the material is in its ground state. When you touch a material
and it feels hot, this is because heat has flowed from the material to you.
If the material is in its ground state (despite having a high fermi temper-
ature) it cannot lower its own energy and therefore cannot transfer heat
to you. Note: Having a high chemical potential DOES mean that the
material might have a tendency to transfer electrons to another body
with fewer electrons (although this might create a charge imbalance that
then prevents further flow of electrons). We discuss physics of this type
in Chapter 18.
(a) In any number of dimensions we can write
N= 2LdZ|k|<kF
ddk
(2π)d
with the 2 accounting for spin. The integration is over a d-dimensional
ball. In 1,2, 3d we obtain
N/Ld=
2kF/π 1d
k2
F/(2π) 2d
k3
F/(3π2) 3d
So that
kF=
(N/L)(π/2) 1d
(N1/2/L)(2π)1/22d
(N1/3/L)(3π2)1/33d
And in any dimension EF=~2k2
F/(2m), so that a1=π/2 and a2= 2π
and a3= 3π2.
(b) We have
EF=Cd/L2N2/d
for some constant Cd. Then
dEF/dN = (2/d)(EF/N)
and
g(EF) = (1/V )(dN/dEF) = (N/Ld)(d/(2EF)).
For a one dimensional system, as noted above EF= (~2/(2m))(π/2)2(N/L)2
where here N/L = 1/(.8nm) This gives me EF= 2.4×10−20Jor
TF=EF/kb= 1700K.
(c) Our above expression for kFstill holds. So
EF=c~|kF|=c~(N1/d/L)ad
So here we have
dEF/dN = (1/d)(EF/N)
and
g(EF) = (1/V )(dN/dEF) = (N/V )(d/EF)

29
(4.5) Chemical Potential of 2D Electrons
Show that for free electron gas in two dimensions, the
chemical potential µis independent of the temperature so
long as T≪µ. Hint: first examine the density of states
in two dimensions.
The key here is to realize that the density of states is independent
of energy. From the previous problem, in 2d, we have EF∼N, and
g(EF)∼N/EFso that the density of states is a constant independent
of temperature. Now, given a fixed density of electrons, the chemical
potential is set by
n=Z∞
0
dEg(E)1
eβ(E−µ)+ 1
where ghere is now constant. The point here is that except for correc-
tions exponentially small in βµ the value of the integral is independent of
β. Therefore the dependence of non µis to a very good approximation
independent of temperature.
To see this in more detail rewrite as
n/g =Z∞
−µ
dx 1
eβx + 1 =Z∞
−µ
dx e−βx
e−βx + 1
=1
βln(eβµ + 1)
Now for large βµ we can expand to get
n/g =µ+O(e−βµ)
so, as claimed, the relationship of nto µis to a good approximation
independent of Tso long as µ≫kbT.
(4.6) Chemical Potential at T= 0
Consider a system of Nnon-interacting electrons. At
T= 0 the Nlowest-energy eigenstates will be filled and
all the higher energy eigenstates will be empty. Show that
at T= 0 the energy of the chemical potential is precisely
half way between the highest energy filled eigenstate and
the lowest-energy unfilled eigenstate.
This is a bit more difficult than it appears as most generally one
should consider the possibility that the highest filled state at energy E1
or lowest unfilled state at energy E2are degenerate – i.e, there is more
than one eigenstate at the given energy. Let us call the degeneracies of
these levels g1and g2respectively. Let us focus on these two energies
only and assume for now (to be justified in retrospect) that we can
ignore any other states in the system with the intuition that any state
with energy below E1is completely filled and can be ignored any any
state with energy above E2is completely empty and can be ignored.

30 Sommerfeld Theory
We take our system (E1with degeneracy g1and E2with degeneracy
g2) and will fill it with exactly g1electrons. (Were we to choose fewer,
the lowest unfilled would move down to E1were we to choose more the
highest filled would move up to E2). Fermi occupation then gives us
N=g1=g1
eβ(E1−µ)+ 1 +g2
eβ(E2−µ)+ 1
Defining x=eβ(E1−µ)and z=e−β(E2−E1)this then becomes
g1=g1
x+ 1 +g2
x/z + 1
Solving for x(and taking the positive root only) gives
x=(g2−g1)z+p(g2−g1)2z2+ 4g1g2z
2g1
Since temperature is small, zbecomes very small, so we can expand this
expression to give
x=√g1g2z
Or equivalently taking log of both sides
β(E1−µ) = 1
2(ln(g1g2)−β(E2−E1))
Taking the limit of small temperature or large β, this becomes
µ= (E1+E2)/2 + ...
(4.7) More Thermodynamics of Free Electrons
(a) Show that the kinetic energy of a free electron gas
in three dimensions is E=3
5EFN.
(b) Calculate the pressure P=−∂E/∂V , and then the
bulk modulus B=−V ∂P/∂V .
(c) Given that the density of atoms in sodium is
2.53×1022 cm−3and that of potassium is 1.33×1022 cm−3,
and given that both of these metals are monovalent (i.e.,
have one free electron per atom), calculate the bulk modu-
lus associated with the electrons in these materials. Com-
pare your results to the measured values of 6.3 GPa and
3.1 GPa respectively.
(a) We begin with the fact that the density of state g(ǫ)∼ǫ1/2. To
see this note that ǫ∼k2so dǫ ∼kdk and dN ∼dk ∼k2dk, so we have
dN/dǫ ∼k∼ǫ1/2. We can thus write g(ǫ) = Cǫ1/2for some constant C
and
N=VZEF
0
dǫg(ǫ) = CV (2/3)E3/2
F
E=VZEF
0
ǫdǫg(ǫ) = CV (2/5)E5/2
F
Thus dividing one by the other we get
E/N = (3/5)EF

31
(b) From exercise 4.4.a or on dimensional grounds EF∼V−2/3, so
E∼V−2/3so the pressure is
P=−∂E
∂VN
=2
3
E
V=2
5
NEF
V
Since P∼V−5/3we then have the bulk modulus
B=−V∂P
∂V =5
3P=10
9
E
V=2EF
3
N
V
(c) From exercise 4.1 or 4.4 we calculate the fermi energy EF= 5.0×
10−19Jand EF= 3.3×10−19 for sodium and potassium respectively.
Thus we obtain B= 8.5 GPa and B= 2.9 GPa respectively. Not too
shabby!!
(4.8) Heat Capacity of a Free Electron Gas*
In Exercise 4.3.a we approximated the heat capacity of
a free electron gas
(a*) Calculate an exact expression for the heat capacity
of a 2d metal at low temperature.
(b**) Calculate an exact expression for the heat capac-
ity of a 3d metal at low temperature.
The following integral may be useful for these calcula-
tions: Z∞
−∞
dx x2ex
(ex+ 1)2=π2
3=ζ(2)/2
Note that for the 3d case you have to worry about the
fact that the chemical potential will shift as a function of
temperature. Why does this not happen (at least for low
T) in the 2d case?
(a) As pointed out in exercise 4.6, in two dimensions µis indepdendent
of temperature — a result of the fact that the density of states is a
constant (the answer to the last part of this question). First we need to
evaluate the value of the density of states. Using the result of 4.4, we
obtain at the fermi energy (and therefore at all energies)
g=m
~2π
We thus have
µ=EF=n/g
We can then write the total energy as
E=VZ∞
0
dǫ ǫ g
eβ(ǫ−µ)+ 1 =V g Z∞
−µ
dx x
eβx + 1 +V g Z∞
−µ
dx µ
eβx + 1
where we have defined x=ǫ−µ. We recognize the second term here
as simply being µN , and as discussed in 4.6, this is independent of
temperature. To evaluate the first term, we integrate by parts to get
E−Nµ =gV x2/2
eβx + 1
∞
−µ−gV Z∞
−µ
dx x2
2−βeβx
(eβx + 1)2

32 Sommerfeld Theory
Assuming βµ is large, to within corrections that are of order of e−βµ
we can throw away the first term and we can extend the integral in
the second term all the way to −∞ (since the argument is peaked near
x= 0 wiht only exponentially small tails). Scaling out the factor of β
and using the integral given we obtain
E−Nµ =V g(kbT)2π2
6+O(e−βµ)
Differentiating to obtan the heat capacity we obtain
C/V =gkb(kbT)π2/3
which is precisely the result claimed above in exercise 4.3 (see Eq. 4.2).
However, here note that up to exponentially small corrections, this is
exact – in other words, there is no subleading Tnwith n > 1 term at
all!
(b) In the more general case where g(E) is not a constant, one must use
the so-called Sommerfeld expansion. This is quite a bit more complex.
First we will quote the key formula and use it to derive our result for
the heat capacity, then we will go back to derive Sommerfeld’s formula.
Defining the Fermi function
nF(ǫ) = 1
eβ(ǫ−µ)+ 1
The Sommerfeld formula is
Z∞
∞
H(ǫ)nF(ǫ)dǫ =Zµ
∞
H(ǫ)dǫ +π
6(kbT)2H′(µ) + O(T4) (4.4)
The intuition behind this formula is that at low temperature the fermi
function is a step function (given by the first term). The finite slope of
the fermi function where it is almost a step creates the small correction
term which is determined by H′. Note that as we determinmed in 4.6
and above, if the argument His constant, then up to exponentially small
terms, there is no correction term at any order in T. One could carry
this expansion to higher order and pick up terms related to H′′ etc as
well.
Expecting that the chemical potential will remain very close to the
Fermi energy at low temperatures, we can conclude
Z∞
∞
H(ǫ)nF(ǫ)dǫ =ZEF
∞
H(ǫ)dǫ + (µ−EF)H(EF) + π
6(kbT)2H′(EF) + ...
Using this equation to write an expression for the density
N
V=Z∞
0
g(ǫ)nF(ǫ)dǫ (4.5)
=ZEF
∞
dǫg(ǫ) + (µ−EF)g(EF) + π
6(kbT)2g′(µ) + ...
=N(T= 0)
V+n(µ−EF)g(EF) + π
6(kbT)2g′(EF)o(4.6)

33
Since we are fixing the density N, the term in brackets must remain
zero for all temperatures (accurate to order T2). This confirms that
µ=EF+O(T2) and confirms our suspicion that it should be very close
to EFat low temperature. Note also that for g′= 0, such as in 2d,
µ=EFindependent of temperature.
We can then write a similar expression for the energy density
E
V=Z∞
0
ǫg(ǫ)nF(ǫ)dǫ
=ZEF
∞
ǫg(ǫ)dǫ +EF(µ−EF)g(EF) + π
6(kbT)2(ǫg(ǫ))′
ǫ=EF+...
=E(T= 0)
V+EFn(µ−EF)g(EF) + π
6(kbT)2g′(EF)o
+π2
6(kbT)2g(EF) + ... (4.7)
Note that in the final equation the term in brackets is the same as the
term in brackets from Eq. 4.6 which we have set to zero in order to keep
the density constant as a function of temperature. Thus we obtain
E
V=E(T= 0)
V+π2
6(kbT)2g(EF) + ...
Which we differentiate to obtain the heat capacity
C/V =π2
3kb(kbT)g(EF)
as claimed.
Finally we return to prove the Sommerfeld formula 4.4. The quantity
we would like to evaluate is
I=Z∞
∞
H(ǫ)nF(ǫ)dǫ
Let us define a function
K(ǫ) = Zǫ
−∞
dǫ′H(ǫ′)
So that, integrating by parts, we have
I=Z∞
∞
K(ǫ)−∂nF(ǫ)
∂ǫ dǫ
there are no boundary terms (to accuracy of O(e−βµ) because ∂nF/∂ǫ
decays very rapidly away from the chemical potential. Note now that
the function ∂nF/∂ǫ is a symmetric (even) function around the chemical
potential. Thus let if expand Kin a taylor series around the chemical
potential only the even terms will have a nonzero contribution, thus we
have
I=Z∞
∞K(µ) + 1
2(ǫ−µ)2K′′(µ) + ...−∂nF(ǫ)
∂ǫ dǫ (4.8)
34 Sommerfeld Theory
Z∞
∞
−∂nF(ǫ)
∂ǫ = 1
the first term in the expansion of Eq. 4.8 is just
K(µ) = Zµ
−∞
H(ǫ)dǫ
as required. The next term gives a prefactor of K′′(µ) = H′(µ) and
requires that we evaluate the integral
Z∞
∞
1
2(ǫ−µ)2−∂nF(ǫ)
∂ǫ dǫ =1
2Z∞
∞
x2eβx
(eβx + 1)2= (kbT)2π2/6
using the given integral. Thus we have obtained the first two terms of
Eq. 4.8. By followin a similar procedure one can evaluate higher terms
in the expansion and in particular we will find that the next term in the
expansion must be proportional to T4.

The Periodic Table 5
(5.1) Madelung’s Rule
Use Madelung’s rule to deduce the atomic shell fill-
ing configuration of the element tungsten (symbol W)
which has atomic number 74.
Element 118 has recently been discovered, and is
expected to be a noble gas, i.e., is in group VIII. (No
real chemistry tests have been performed on the ele-
ment yet, as the nucleus decays very quickly.) Assuming
that Madelung’s rule continues to hold, what should the
atomic number be for the next noble gas after this one?
Angular momentum lorbitals (l= 0 is called s, l= 1 is called p, etc)
contain up to 2(2l+1) electrons. Madulung’s rule fills orbitals according
to the diagram Fig. 5.1: from lowest n+lto highest, and for cases of
the same n+l, fill the lower nfirst. So we have
Tungsten atomic number 74:
1s22s22p63s23p64s23d10 4p65s24d10 5p66s24f14 5d4.
Note that the “exponents” add to 74. Or equivalently we write
[Xe] 4f14 5d4.
Note that the noble gases occur whenever a p-shell has just filled.
Element 118 has a filled 7p shell. Madelung’s rule tells us that we then
have to fill 8s, 5g, 6f, 7d and finally 8p. This brings us to element
168. For entertainment sake (and you can try to prove this) note that
the sequence of nobel gas element numbers 2, 10, 18, 36, 54, 86, 118,
168 has successive differences which are twice the perfect squares each
occurring twice. (10-2)/2 = 4 , (18-10)/2 = 4, (36-18)/2 = 9, (54-36)/2
= 9, (86-54)/2 = 16, (118-86)/2=16, (168-118)/2 = 25, and so forth.
Fig. 5.1 Ordering of filling orbitals in
atoms (Madelung’s rule).
(5.2) Effective Nuclear Charge and Ionization
Energy
(a) Let us approximate an electron in the nth shell
(i.e., principal quantum number n) of an atom as being
like an electron in the nth shell of a hydrogen atom with
an effective nuclear charge Z. Use your knowledge of
the hydrogen atom to calculate the ionization energy of
this electron (i.e., the energy required to pull the electron
away from the atom) as a function of Zand n.
(b) Consider the two approximations discussed in the
text for estimating the effective nuclear charge:
•(Approximation a)
Z=Znuc −Ninside
•(Approximation b)
Z=Znuc −Ninside −(Nsame −1)/2
where Znuc is the actual nuclear charge (or atomic num-
ber), Ninside is the number of electrons in shells inside of n
(i.e., electrons with principal quantum numbers n′< n),
and Nsame is the total number of electrons in the nth
principal shell (including the electron we are trying to
remove from the atom, hence the −1).
36 The Periodic Table
Explain the reasoning behind these two approxima-
tions.
Use these approximations to calculate the ioniza-
tion energies for the atoms with atomic number 1 through
21. Make a plot of your results and compare them to the
actual ionization energies (you will have to look these up
on a table).
Your results should be qualitatively quite good. If you
try this for higher atomic numbers, the simple approxi-
mations begin to break down. Why is this?
Neglecting fine structure, the energy of an electron in the nth shell of
hydrogen is
En=−Ry
n2
where Ry=13.6 eV is the Rydberg constant. For a hydrogenic atom
with nuclear charge Z, the Coulomb interaction is Ztimes as strong
as in hydrogen, resulting in binding energy which is Z2as strong. To
see this in detail, one can solve the Schroedinger equation in detail.
However, without doing this one can get it by a scaling argument as
well. The bound state is a balancing of the kinetic with the potential
energy. So roughly one should be able to estimate the binding energy
by setting these equal to each other. Setting the the length scale to a,
(i.e, define ato be the effective Bohr radius) we have
KE =~2
ma2=P E =Ze2
4πǫ0a
solving for aobtains a∼1/Z and plugging back into P E or KE we
determine that the kinetic energy should scale as Z2.
Fig. 5.2 Ionization Energy (eV) as a
function of atomic number. Exact com-
pared to the two proposed approxima-
tions 0
50
100
150
200
250
0 5 10 15 20 25
Ionization Energies
experiment
"approx1.txt"
"approx2.txt"
The two approximations are plotted here with the exact ionization
energies. Qualitatively they are OK, but quantitatively not so good I
guess.
One can do a bit better (See Fig. 5.3) by assuming that p-shells are
“outside” of s-shells. In other words, a single electron in a p-shell sees
a charge of Z= 1 since the entire s-shell is inside of it. In this case one
gets the following figure (in the two apperoximations discussed above).
In fact, this is getting to be pretty decent. Notice with this second
approximation one obtains a dip in the ionization energy for filled s-
shells (such as atomic numbers 4 and 12) which is seen in the experiment,
although is weaker in reality.

37
0
20
40
60
80
100
120
140
0 5 10 15 20 25
Ionization Energies
experiment
"approx3.txt"
"approx4.txt"
Fig. 5.3 Ionization Energy (eV) as
a function of atomic number. Exact
compared to the two proposed approx-
imations with the modification that p-
shells are declared to be outside of s-
shells.
Once you get to the transition metals, the d-shells really are not very
easily described as being inside or outside of anything. And often when
transition metals ionize, they lose their s-electrons.
(5.3) Exceptions to Madelung’s Rule
Although Madelung’s rule for the filling of electronic
shells holds extremely well, there are a number of excep-
tions to the rule. Here are a few of them:
Cu = [Ar] 4s13d10
Pd = [Kr] 5s04d10
Ag = [Kr] 5s14d10
Au = [Xe] 6s14f145d10
What should the electron configurations be if these
elements followed Madelung’s rule and the Aufbau prin-
ciple?
Explain how the statement “3d is inside of 4s”
might help justify this exception in copper.
Madelung’s rule incorrectly predicts:
Cu = [Ar] 4s23d9
Pd = [Kr] 5s24d8
Ag = [Kr] 5s24d9
Au = [Xe] 6s24f145d9
For copper, the fact that 3d is inside 4s makes the 4s electron less well
bound than you might otherwise expect. Thus the d electrons can fill
preferentially over the s in some cases.
(5.4) Mendeleev’s Nobel Prize
Imagine writing a letter to the Nobel committee nom-
inating Mendeleev, the creator of the periodic table, for
a Nobel Prize. Explain why the periodic table is so im-
portant. Remember that the periodic table (1869) was
devised many years before the structure of the hydrogen
atom was understood. (If you do not already have some
background in chemistry, you may want to read the next
chapter before attempting this exercise.)

38 The Periodic Table
Dear Nobel Committee,
Do I have to smack you upside the head? Do
the right thing and give the prize to Mendeleev for
God sake!
Sincerely,
Professor Steven H. Simon

What Holds Solids
Together: Chemical
Bonding 6
(6.1) Chemical Bonding
(a) Qualitatively describe five different types of chem-
ical bonds and why they occur.
Describe which combinations of what types of
atoms are expected to form which types of bonds (make
reference to location on the periodic table).
Describe some of the qualitative properties of ma-
terials that have these types of bonds.
(Yes, you can just copy the table out of the chapter
summary, but the point of this exercise is to learn the
information in the table!)
(b) Describe qualitatively the phenomenon of van der
Waals forces. Explain why the force is attractive and pro-
portional to 1/R7where Ris the distance between two
atoms.
(a) Just look at the table in the Chapter Summary of chapter 6.
(b) van der Waals forces are from correlated dipole flucuations. If
the electron is a given fixed position, there is a dipole moment p=er
where ris the vector from the electron to the proton. With the electron
“orbiting” (i.e, in an eigenstate), the average dipole moment is zero.
However, if an electric field is applied to the atom, the atom will develop
a polarization (i.e., it will be more likely for the electron to be found on
one side of the nucleus than on the other). We write
p=χE
with χthe polarizability. .
Now, let us suppose we have two such atoms, separated a distance r
in the ˆxdirection. Suppose one atom momentarily has a dipole moment
p1(for definiteness, suppose this dipole moment is in the ˆzdirection).
Then the second atom will feel an electric field
E=p1
4πǫ0r3
in the negative ˆzdirection. The second atom then, due to its polariz-
ability, develops a dipole moment p2=χE whi ch in turn is attracted
to the first atom. The potential energy between these two dipoles is
U=−|p1||p2|
4πǫ0r3=−p1χE
(4πǫ0)r3=−|p1|2χ
(4πǫ0r3)2

40 Chemical Bonding
corresponding to a force which is attractive and proportional to 1/r7.
Note that while for a single isolated atom hpi= 0 the result is propor-
tional instead to h|p|2i ∼ h|r|2i ∼ with rthe position of an electron, is
nonzero. This calculation is done more carefully in problem 6.6 below.
(6.2) Covalent Bonding in Detail*
(a) Linear Combination of Atomic Orbitals:
In Section 6.2.2 we considered two atoms each with a
single atomic orbital. We called the orbital |1iaround nu-
cleus 1 and |2iaround nucleus 2. More generally we may
consider any set of wavefunctions |nifor n= 1,...,N.
For simplicity, let us assume this basis is orthonormal
hn|mi=δn,m (More generally, one cannot assume that
the basis set of orbitals is orthonormal. In Exercise 6.5
we properly consider a non-orthonormal basis.)
Let us write a trial wavefunction for our ground state
as
|Ψi=X
n
φn|ni.
This is known as a linear combination of atomic orbitals,
LCAO, or tight binding (it is used heavily in numerical
simulation of molecules).
We would like to find the lowest-energy wavefunction
we can construct in this form, i.e., the best approxima-
tion to the actual ground-state wavefunction. (The more
states we use in our basis, generally, the more accurate
our results will be.) We claim that the ground state is
given by the solution of the effective Schroedinger equa-
tion
Hφ=Eφ(6.1)
where φis the vector of Ncoefficients φn, and His the
Nby Nmatrix
Hn,m =hn|H|mi
with Hthe Hamiltonian of the full system we are consid-
ering. To prove this, let us construct the energy
E=hψ|H|ψi
hψ|ψi
Show that minimizing this energy with respect to
each φngives the same eigenvalue equation, Eq. 6.1.
(Caution: φnis generally complex! If you are not com-
fortable with complex differentiation, write everything in
terms of real and imaginary parts of each φn.) Similarly,
the second eigenvalue of the effective Schroedinger equa-
tion will be an approximation to the first excited state of
the system.
(b) Two-orbital covalent bond
Let us return to the case where there are only two or-
bitals in our basis. This pertains to a case where we have
two identical nuclei and a single electron which will be
shared between them to form a covalent bond. We write
the full Hamiltonian as
H=p2
2m+V(r−R1) + V(r−R2) = K+V1+V2
where Vis the Coulomb interaction between the electron
and the nucleus, R1is the position of the first nucleus
and R2is the position of the second nucleus. Let ǫbe the
energy of the atomic orbital around one nucleus in the
absence of the other. In other words
(K+V1)|1i=ǫ|1i
(K+V2)|2i=ǫ|2i
Define also the cross-energy element
Vcross =h1|V2|1i=h2|V1|2i
and the hopping matrix element
t=−h1|V2|2i=−h1|V1|2i
These are not typos!
Why can we write Vcross and tequivalently using
either one of the expressions given on the right-hand side?
Show that the eigenvalues of our Schroedinger
equation Eq. 6.1 are given by
E=ǫ+Vcross ± |t|
Argue (perhaps using Gauss’s law) that Vcross
should roughly cancel the repulsion between nuclei, so
that, in the lower eigenstate the total energy is indeed
lower when the atoms are closer together.
This approximation must fail when the atoms get
sufficiently close. Why?
41
(a) writing
|ψi=X
n
φn|ni
E=hψ|H|ψi
hψ|ψi=Pn,m φ∗
nHnmφm
Pn|φn|2(6.2)
We can extremize by differentiating with respect to φ∗
n. Note: When
working with complex quantities we can simplify life by treating φnand
φ∗
nas independent variables. We thus have
0 = ∂E
∂φ∗
n
=PmHnmφm
Pp|φp|2−Pn,m φ∗
nHnmφm
Pn|φn|2φn
Pp|φp|2
0 = X
mHnmφm−Eφn
where we have used Eq. 6.2 to identify E.
(b) The 2 by 2 matrix given by Hin this basis is
ǫ+Vcross t
t∗ǫ+Vcross
which has eigenvalues E=ǫ+Vcross ± |t|. Note that tcan always be
taken as real by simply making a gauge transform on the single particle
wavefunction (i.e., redefining the phase of one of the wavefunctions to
absorb the phase of t).
Here Vcross is the potential felt by the electron on atom 2 due to the
nucleus of atom 1. Since the charge distribution of the electron on atom
2 is roughly spherical we can use Gauss’s law to calculate its interaction
energy with the nucleus of atom 1. If the nucleus of atom 1 is outside
of this spherical distribution of charge of the electron, Gauss’s law tells
us that we can treat the entire spherical distribution of charge as if it is
all at the center of the sphere. In this way, the charge of the electron on
atom 2 exactly cancels the charge of the nucleus of atom 2.
When the two nuclei get close, this argument no longer works, as the
nucleus is then inside much of the distribution of the electron charge. If
the electron charge distribution remains spherical, the nucleus of atom
2 will only see electron charge that is at smaller distances (inside) to
the center of this spherical distribution. When the nuclei are very close
together, the nucleus does not see the electron charge at all, and only
sees the other nucleus. Also, when the atoms get close together, the
assumption of orthogonality of grounds tate orbitals on different sites
breaks down. (One has to choose whether you want orthogonal orbitals
or orbitals that are eigenstates of the single atom Hamiltonian.)
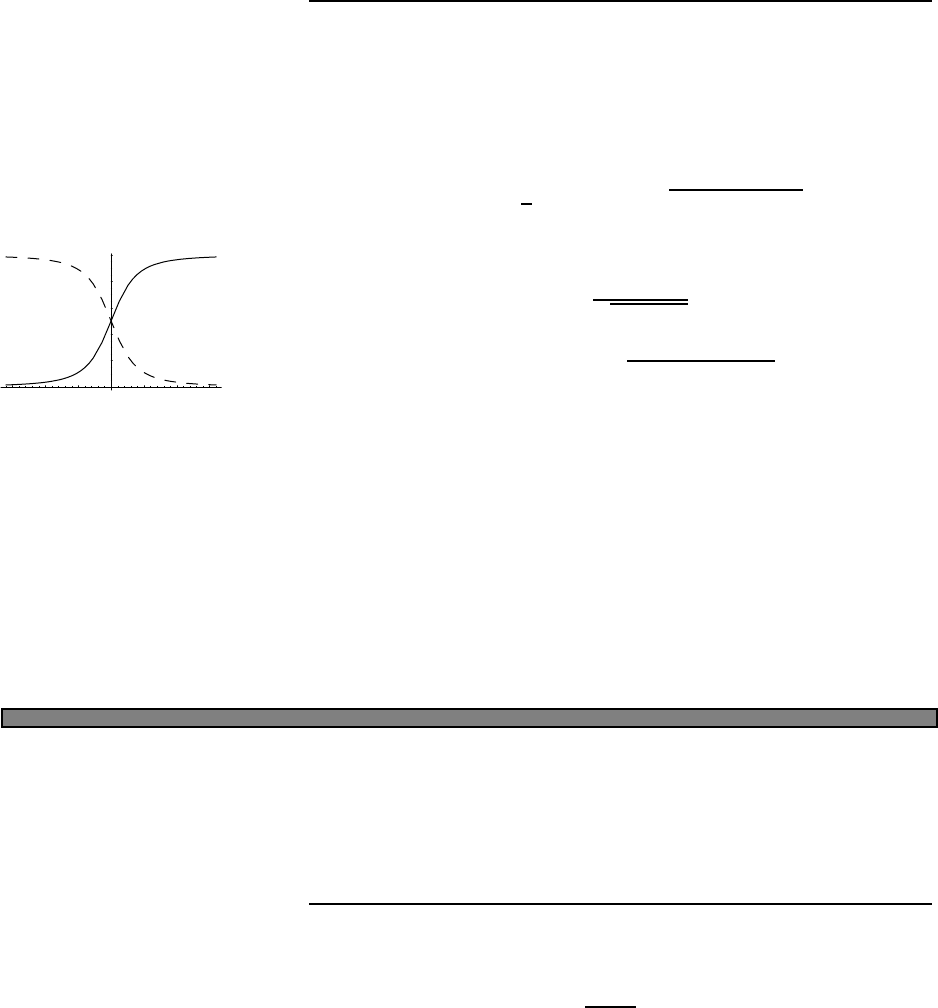
42 Chemical Bonding
(6.3) LCAO and the Ionic–Covalent Crossover
For Exercise 6.2.b consider now the case where the
atomic orbitals |1iand |2ihave unequal energies ǫ0,1and
ǫ0,2. As the difference in these two energies increases
show that the bonding orbital becomes more localized on
the lower-energy atom. For simplicity you may use the
orthogonality assumption h1|2i= 0. Explain how this
calculation can be used to describe a crossover between
covalent and ionic bonding.
Here we have instead, the two by two hamiltonian matrix
ǫ1t
t∗ǫ2
where we have now absorbed Vcross into the values of ǫi. The lower
energy eigenstate is
Eground =1
2n(ǫ1+ǫ2) + p(ǫ1−ǫ2)2+ 4t2o
with normalized eigenvector
ψ=(X, 2t)
√4t2+X2
with
X=E2−E1+p(E2−E1)2+ 4t2
-7.5 -5 -2.5 2.5 5 7.5 HE2 -E1Lt
0.2
0.4
0.6
0.8
1
Probability
Fig. 6.1 Probability (squared ampli-
tude) of ground state wavefunction be-
ing on site 1 (solid) or site 2 (dashed)
as a function of E2−E1.
When E2−E1≫tthen X≫tand all of the wavefunction ends
up on the first atom (i.e., the one with the lower energy). Similarly, if
E1−E2≫tthen conversely all of the weight of the wavefunction ends
up on the second atom. In Fig. 6.1 it is shown how the weight of the
wavefunction moves from towards the lower energy atom as a function
of energy.
When the energies on the two sites are equal, one has an equal shar-
ing of the wavefunction in the ground state (as in the prior problem).
However, as the energy difference is increased, the ground state moves
more towards the lower energy site, until the bond is completely ”ionic“
meaning that the electron is completely transferred from one atom to
the other.
(6.4) Ionic Bond Energy Budget
The ionization energy of a sodium atom is about 5.14
eV. The electron affinity of a chlorine atom is about 3.62
eV. When a single sodium atom bonds with a single chlo-
rine atom, the bond length is roughly 0.236 nm. As-
suming that the cohesive energy is purely Coulomb en-
ergy, calculate the total energy released when a sodium
atom and a chlorine atom come together to form a NaCl
molecule. Compare your result to the experimental value
of 4.26 eV. Qualitatively account for the sign of your er-
ror.
(c) The cohesive energy is (with dthe bond distance)
Ecoh =e2
4πǫ0d= 6.10eV
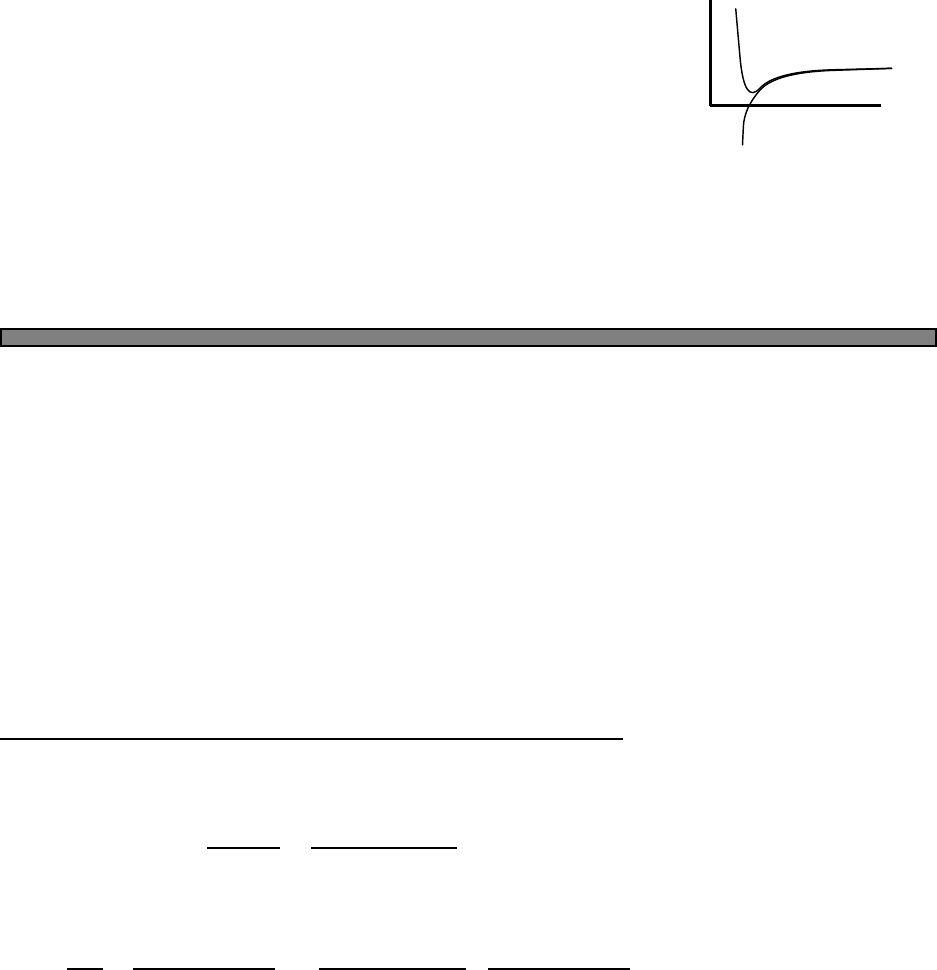
43
Thus the total bonding energy is
E=−5.14eV + 3.62eV + 6.10eV = 4.58eV
which is slightly larger than the experimentally measured bonding en-
ergy. The reason for the discrepancy is that there must be a repulsive
force in addition to the coulomb attractive force which reduces the mag-
nitude of the cohesive (binding) energy.
In the Fig. 6.2 the lower curve is the pure Coulomb energy. The upper
curve includes a short range repulsion. The repulsion must be there, or
there would be no minimum in the curve!
✻
✲
V(x)
x
Fig. 6.2 Probability (squared ampli-
tude) of ground state wavefunction be-
ing on site 1 (solid) or site 2 (dashed)
as a function of E2−E1.
(6.5) LCAO Done Right*
(a)* In Exercise 6.2 we introduced the method of lin-
ear combination of atomic orbitals. In that exercise we
assumed that our basis of orbitals is orthonormal. In this
exercise we will relax this assumption.
Consider now many orbitals on each atom (and poten-
tially many atoms). Let us write
|ψi=
N
X
i=1
φi|ii
for an arbitrary number Nof orbitals. Let us write the
Nby Noverlap matrix Swhose elements are
Si,j =hi|ji
In this case do not assume that Sis diagonal.
Using a similar method as in Exercise 6.2, derive the
new “Schroedinger equation”
Hφ=ESφ(6.3)
with the same notation for Hand φas in Exercise 6.2.
This equation is known as a “generalized eigenvalue prob-
lem” because of the Son the right-hand side.
(b)** Let us now return to the situation with only two
atoms and only one orbital on each atom but such that
h1|2i=S1,26= 0. Without loss of generality we may as-
sume hi|ii= 1 and S1,2is real. If the atomic orbitals
are s-orbitals then we may assume also that tis real and
positive (why?).
Use Eq. 6.3 to derive the eigenenergies of the system.
(a) This is very similar to 6.2.
E=hψ|H|ψi
hψ|ψi=Pn,m φ∗
nHnmφm
Pn,m φ∗
nSnmφm
(6.4)
We can extremize by differentiating with respect to φ∗
nto give
0 = ∂E
∂φ∗
n
=PmHnmφm
Pn,m φ∗
nSnmφm− Pn,m φ∗
nHnmφm
Pn,m φ∗
nSnmφm!Pn,m Snmφm
Pn,m φ∗
nSnmφm
0 = X
mHnmφm−EX
m
Snmφm
where we have used Eq. 6.4 to identify E.
(b) An s-orbital can be taken to be manifestly postive everywhere (no
nodes), so overlaps Sij must be real and positive. Here the easiest thing
44 Chemical Bonding
to do is to just apply S−1to both sides of the equation to give the
eigenvalue problem
SHφ=Eφ
Here, let us write the Hamiltonian as
H=ǫ t
t∗ǫ
where we have absorbed Vcross into ǫ, and
S=1S
S1
with S=S12. The matrix we want to diagonalize is then
S−1H=1
1−S2ǫ−St t −ǫS
t−ǫS ǫ −St
The eigenvalues are easily seen to be
E=1
1−S2([ǫ−St]± |t−ǫS|)
(6.6) Van der Waals Bonding in Detail*
(a) Here we will do a much more precise calculation
of the van der Waals force between two hydrogen atoms.
First, let the positions of the two nuclei be separated by
a vector R, and let the vector from nucleus 1 to electron
1 be r1and let the vector from nucleus 2 to electron 2 be
r2as shown in the following figure.
■✒
++
--
r1r2
✲
R
Let us now write the Hamiltonian for both atoms
(assuming fixed positions of nuclei, i.e., using Born–
Oppenheimer approximation) as
H=H0+H1
H0=p12
2m+p22
2m−e2
4πǫ0|r1|−e2
4πǫ0|r2|
H1=e2
4πǫ0|R|+e2
4πǫ0|R−r1+r2|
−e2
4πǫ0|R−r1|−e2
4πǫ0|R+r2|
Here H0is the Hamiltonian for two non-interacting hy-
drogen atoms, and H1is the interaction between the
atoms.
Without loss of generality, let us assume that Ris in
the ˆxdirection. Show that for large Rand small ri, the
interaction Hamiltonian can be written as
H1=e2
4πǫ0|R|3(z1z2+y1y2−2x1x2) + O(1/R4)
where xi, yi, ziare the components of ri. Show that this
is just the interaction between two dipoles.
(b) Perturbation Theory:
The eigenvalues of H0can be given as the eigen-
values of the two atoms separately. Recall that the
eigenstates of hydrogen are written in the usual nota-
tion as |n, l, miand have energies En=−Ry/n2with
Ry = me4/(32π2ǫ2
0~2) = e2/(8πǫ0a0) the Rydberg (here
l≥0, |m| ≤ land n≥l+ 1). Thus the eigenstates
of H0are written as |n1, ll, m1;n2, l2, m2iwith energies
En1,n2=−Ry(1/n2
1+ 1/n2
2). The ground state of H0is
|1,0,0; 1,0,0i.
Perturbing H0with the interaction H1, show that
to first order in H1there is no change in the ground-state
energy. Thus conclude that the leading correction to the
ground-state energy is proportional to 1/R6(and hence
the force is proportional to 1/R7).
Recalling second-order perturbation theory show
45
that we have a correction to the total energy given by
δE =
X
n1, n2
l1, l2
m1, m2
|<1,0,0; 1,0,0|H1|n1, ll, m1;n2, l2, m2i|2
E0,0−En1,n2
Show that the force must be attractive.
(c)*Bounding the binding energy:
First, show that the numerator in this expression is
zero if either n1= 1 or n2= 1. Thus the smallest En1,n2
that appears in the denominator is E2,2. If we replace
En1,n2in the denominator with E2,2then the |δE|we
calculate will be greater than than the |δE|in the exact
calculation. On the other hand, if we replace En1,n2by
0, then the |δE|will always be less than the δE of the
exact calculation.
Make these replacements, and perform the remain-
ing sum by identifying a complete set. Derive the bound
6e2a5
0
4πǫ0R6≤ |δE| ≤ 8e2a5
0
4πǫ0R6
You will need the matrix element for a hydrogen atom
h1,0,0|x2|1,0,0i=a2
0
where a0= 4πǫ0~2/(me2) is the Bohr radius. (This last
identity is easy to derive if you remember that the ground-
state wavefunction of a hydrogen atom is proportional to
e−r/2a0.)
(a) In fact, this is more or less the definition of dipole interaction! Let
us start by deriving
1
|R−a|=1
Rq1 + 2a·R
R2+a2
R2
=1
R1−a·R
R2+−1
2
a2
R2+3
2
(a·R)2
R4+...(6.5)
Applying this to all the terms in
H1=e2
4πǫ0|R|+e2
4πǫ0|R−r1+r2|
−e2
4πǫ0|R−r1|−e2
4πǫ0|R+r2|
We discover that the first two leading orders completely cancel, thus
leaving us with only the contribution of the terms coming from the
square bracketed terms of Eq. 6.5. We then obtain
H1=e2
4πǫ0Rr2
1+r2
2− |r1−r2|2
2R2+3(R·(r2−r1))2−(R·r1)2−(R·r2)2)
R4
with Rin the ˆxdirection, this simplifies to
H1=e2
4πǫ0R3r1·r2+ 3 (x1−x2)2−x2
1−x2
2
which then simplifies to the desired answer.
(b) The expectation of xor yor zin the ground state of the hydrogen
atom |100iis zero due to the fact that the state is spherically symmetric.
As a result taking the expectation of H1in the ground state gives zero.
Thus the leading correction to the energy occurs at second order in H1
46 Chemical Bonding
and is proportional to 1/R6(assuming it does not vanish, which we will
show next).
Given then the form of the 2nd order perturbation theory, note that
every term has an overall negative sign (numerator is positive, denomi-
nator is negative). Thus the interaction is of the form −C/R6for some
positive constant C(to be calculated), and hence the force is attractive.
(c) As just above, since xor yor zhas zero expectation in the ground
state, this means H1has zero matrix element unless n1>1 and n2>1
(for n= 1 we must have l=m= 0).
First let us consider the quantity
I=X
n1, n2
l1, l2
m1, m2
|<1,0,0; 1,0,0|H1|n1, ll, m1;n2, l2, m2i|2(6.6)
=X
n1, n2
l1, l2
m1, m2
h1,0,0; 1,0,0|H1|n1, ll, m1;n2, l2, m2i(6.7)
× hn1, ll, m1;n2, l2, m2|H1|1,0,0; 1,0,0i(6.8)
We notice the complete set in the middle here, so we do the sum over
the set to obtain
I=h1,0,0; 1,0,0|H2
1|1,0,0; 1,0,0i
=e2
4πǫ0R2hy2
1ihy2
2i+hz2
1ihz2
2i+ 4hx2
1ihx2
2i
with all expectations being in the ground state of the respective hydrogen
atom (each bracket gives a2
0). Thus we obtain
I=e2
4πǫ0R32
6a4
0
Now, the upper bound is defined by setting En1,n2=E2,2whereas
the lower bound is defined by setting En1,n2= 0 so we obtain
I
E0,0
<|δE|<I
E0,0−E2,2
Here using the excitation spectrum of the hydrogen atom, we have
E0,0=-2Ry and E2,2=−Ry/2 so E0,0−E2,2=−(3/2)Ry, and us-
ing the fact that the Rydberg is e2/(8πǫ0a0) we have
W=I/Ry = 12e2a5
0
4πǫ0R6
so our inequality is W
2<|δE|<2W
3
which is the required result.

Types of Matter 7
There are no exercises for chapter 7.
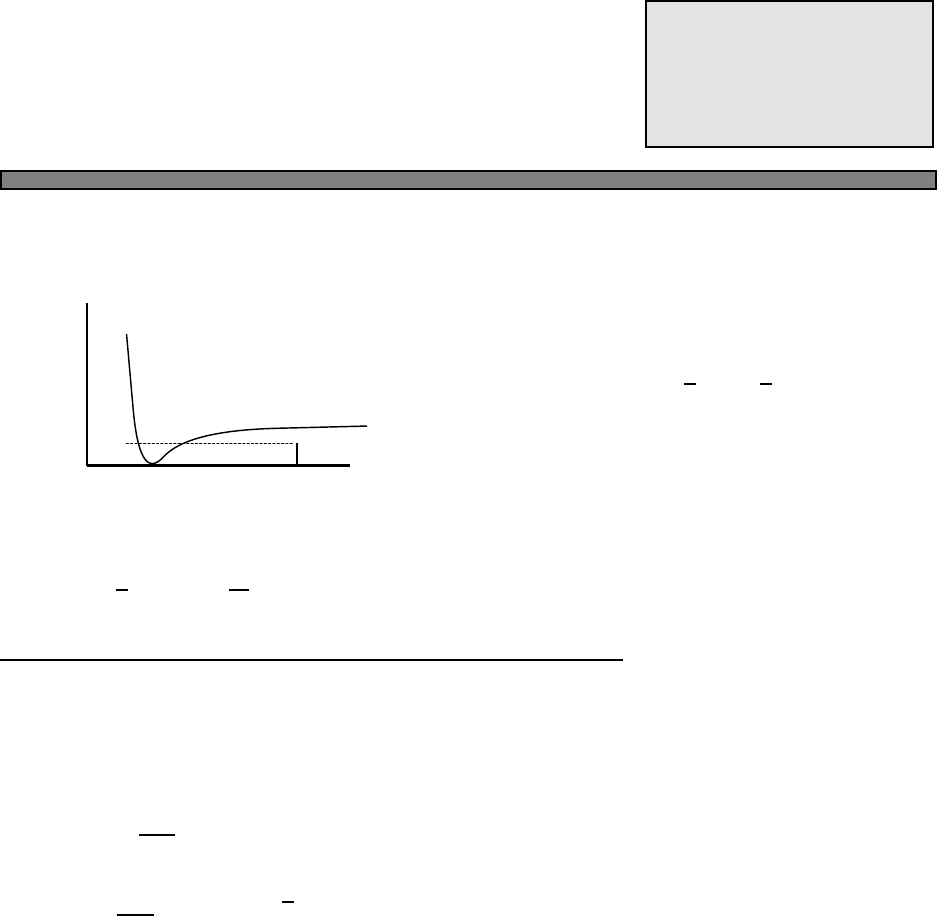
One-Dimensional Model of
Compressibility, Sound,
and Thermal Expansion 8
(8.1) Potentials Between Atoms
As a model of thermal expansion, we study the distance
between two nearest-neighbor atoms in an anharmonic
potential that looks roughly like this
✻
✲
✻
kBT
V(x)
x
x0
where xis the distance between the two neighboring
atoms. This potential can be expanded around its mini-
mum as
V(x) = κ
2(x−x0)2−κ3
3! (x−x0)3+. . . (8.1)
where the minimum is at position x0and κ3>0. For
small energies, we can truncate the series at the cubic
term. (Note that we are defining the energy at the bot-
tom of the well to be zero here.)
A very accurate approximate form for interatomic po-
tentials (particularly for inert atoms such as helium or
argon) is given by the so-called Lennard-Jones potential
V(x) = 4ǫσ
x12 −σ
x6+ǫ(8.2)
where ǫand σare constants that depend on the particular
atoms we are considering.
What is the meaning of the exponent 6 in the sec-
ond term of this expression (i.e., why is the exponent
necessarily chosen to be 6).
By expanding Eq. 8.2 around its minimum, and
comparing to Eq. 8.1, calculate the values of the coef-
ficients x0,κ, and κ3for the Lennard-Jones potential in
terms of the constants ǫand σ. We will need these results
in Exercise 8.3.
The exponent 6 determines the long range behavior of the potential
and is fixed by the form of the Van der Waals interaction.
By setting dV/dx = 0 we find the minimum at x0= 21/6σ.
Taking second and third derivatives at this position
d2V
dx2x=x0
= 36 ×22/3ǫ/σ2=κ≈57ǫ/σ2(8.3)
and d3V
dx3x=x0
=−756√2ǫ/σ3=−κ3≈1069ǫ/σ3(8.4)
50 Compressibility, Sound, and Thermal Expansion
(8.2) Classical Model of Thermal Expansion
(i) In classical statistical mechanics, we write the ex-
pectation of xas
hxiβ=Rdx x e−βV (x)
Rdx e−βV (x)
Although one cannot generally do such integrals for ar-
bitrary potential V(x) as in Eq. 8.1, one can expand the
exponentials as
e−βV (x)=e−βκ
2(x−x0)21 + βκ3
6(x−x0)3+...
and let limits of integration go to ±∞.
Why is this expansion of the exponent and the ex-
tension of the limits of integration allowed?
Use this expansion to derive hxiβto lowest order in
κ3, and hence show that the coefficient of thermal expan-
sion is
α=1
L
dL
dT ≈1
x0
dhxiβ
dT =1
x0
kBκ3
2κ2
with kBBoltzmann’s constant.
In what temperature range is the above expansion
valid?
While this model of thermal expansion in a solid is
valid if there are only two atoms, why is it invalid for the
case of a many-atom chain? (Although actually it is not
so bad as an approximation!)
hxiβ=Rdx x e−βV (x)
Rdx e−βV (x)
with
e−βV (x)=e−βκ
2(x−x0)21 + βκ3
6(x−x0)3+...
Redefine y= (x−x0) so we have
hxiβ=Rdy (y+x0)e−βκ
2y2h1 + βκ3
6y3+...i
Rdye−βκ
2y2h1 + βκ3
6y3+...i
=x0+
βκ3
6Rdy y4e−βκ
2y2
Rdy e−βκ
2y2+...
Using Zdxe−ax2=pπ/a
as a generating function, we have
Zdxx4e−ax2= (d/da)2Zdxe−ax2= (d/da)2pπ/a = (3/4)pπ/a5
gives
hxiT=x0+κ3(kbT)
2κ2+...
Thus 1
x0
dhxiT
dT =1
x0
κ3kb
2κ2
In order for this calculation to be valid, since we have treated the cubic
term perturbatively, this term actually must be small compared to the
leading term.

51
Roughly, if the leading term is most important, we have κ(x−x0)2∼
kbTwhich means that the typical deviation is |x−x0| ∼ pkbT/κ. Then
in order to have the leading term be larger than the cubic term, we have
κ|x−x0|2≫κ3|x−x0|3
or
kbT≫κ3(kbT/κ)3/2
or equivalently
kbT≪κ3/κ2
3
For a many atom chain, one must solve for the normal modes of the
chain. Then at finite temperature one should “occupy” the phonons
thermally and then calculate the effect of the nonlinear terms in this
state. What we have done in this problem is more or less the thermal
expansion of an Boltzmann model of a solid.
(8.3) Properties of Solid Argon
For argon, the Lennard-Jones constants ǫand σfrom
Eq. 8.2 are given by ǫ= 10meV and σ=.34nm. You will
need to use some of the results from Exercise 8.1.
(a) Sound
Given that the atomic weight of argon is 39.9, estimate
the sound wave velocity in solid argon. The actual value
of the longitudinal velocity is about 1600 m/sec.
(b) Thermal Expansion
Using the results of Exercise 8.2, estimate the thermal
expansion coefficient αof argon. Note: You can do this
part even if you couldn’t completely figure out Exercise
8.2!
The actual thermal expansion coefficient of argon is
approximately α= 2 ×10−3/K at about 80K. However,
at lower temperature αdrops quickly. In the next ex-
ercise will use a more sophisticated quantum model to
understand why this is so.
Sound: From the text in one dimension we have
v=qκx2
0/m
where x0is the neighbor distance. From our above problem on Lennard-
Jones, we have
κx2
0= 72ǫ
and the mass m=.0399kg/NA. Which gives
v= 1320m/s
Thermal expansion. Plugging in our above expression for x0,κand
κ3for the Lennard Jones case, we obtain
α=1
x0
κ3kb
2κ2=7kb
48ǫ≈.0012/K

52 Compressibility, Sound, and Thermal Expansion
(8.4) Quantum Model of Thermal Expansion
(a) In quantum mechanics we write a Hamiltonian
H=H0+δV
where
H0=p2
2m+κ
2(x−x0)2(8.5)
is the Hamiltonian for the free Harmonic oscillator, and
δV is the perturbation (see Eq. 8.1)
δV =−κ3
6(x−x0)3+...
where we will throw out quartic and higher terms.
What value of mshould be used in Eq. 8.5?
Using perturbation theory it can be shown that, to
lowest order in κ3the following equation holds
hn|x|ni=x0+Enκ3/(2κ2) (8.6)
where |niis the eigenstate of the Harmonic oscillator
whose energy is
En=~ω(n+1
2) + O(κ3)n≥0
with ω=pκ/m. In (c) we will prove Eq. 8.6. For now,
take it as given.
Note that even when the oscillator is in its ground
state, the expectation of xdeviates from x0. Physically
why is this?
(b)* Use Eq. 8.6 to calculate the quantum expectation
of xat any temperature. We write
hxiβ=Pnhn|x|nie−βEn
Pne−βEn
Derive the coefficient of thermal expansion.
Examine the high temperature limit and show that
it matches that of Exercise 8.2.
In what range of temperatures is our perturbation
expansion valid?
In light of the current quantum calculation, when
is the classical calculation from Exercise 8.2 valid?
Why does the thermal expansion coefficient drop
at low temperature?
(c)** Prove Eq. 8.6 by using lowest-order perturbation
theory.
Hint: It is easiest to perform this calculation by using
raising and lowering (ladder) operators. Recall that one
can define operators aand a†such that [a, a†] = 1 and
a†|ni0=√n+ 1|n+ 1i0
a|ni0=√n|n−1i0.
Note that these are kets and operators for the unper-
turbed Hamiltonian H0. In terms of these operators, we
have the operator x−x0given by
x−x0=r~
2mω (a+a†).
(a) For a system of two atoms, one should use the ”reduced” mass
µ=m1m2/(m1+m2) which for two identical atoms is m/2.
Quantum mechanically the oscillator does not sit in its exact mini-
mum, rather it has “quantum fluctuations” around this minimum . Since
the well is asymmetric around the minimum, the expectation value of
the position is slightly greater than x0even in the ground state.
(b)
hxiβ=Pnhn|x|nie−βEn
Pne−βEn=Pnhn|(x0+Enκ3/(2κ2))|nie−βEn
Pne−βEn
=x0+hEiβκ3
2κ2
where hEiβis the energy expectation of a harmonic oscillator of fre-
quency ωat temperature β= 1/(kbT). As derived above when we
discussed Einstein model, this expectation is
hEiβ= (nB(β~ω) + 1
2)~ω=~ω
2coth(β~ω/2)

53
with nBthe boson occupation factor. Thus we obtain
hxiβ=x0+ (κ3~ω/(4κ2)) coth(β~ω/2)
The coefficient of thermal expansion is then
α=1
x0
dhxiβ
dT =κ3
2x0κ2
dhEi
dT
where C=dhEi/dT is exactly the specific heat of a harmonic oscillator
(recall einstein model). Thus we obtain
α=κ3C
2x0κ2=κ3
2x0κ2kb(β~ω)2eβ~ω
(eβ~ω−1)2
We can see that the thermal expansion drops as modes ”freeze” out,
entirely analogous to the specific heat dropping at low temperature.
In the high Tlimit, the specific heat Cgoes to kb, so we obtain
α= (κ3kb/(2x0κ2))
in agreement with the classical result.
For the classical calculation to be valid, we must have kbT≫~ωso
that quantum mechanics can be replaced by classical mechanics.
(c) First let us consider the unperturbed harmonic oscillator. Recall
the raising and lowering operators
a=rmω
2~[(x−x0) + (i/mω)p]
a†=rmω
2~[(x−x0)−(i/mω)p]
(8.7)
So that the position is given by
x−x0=p~/(2mω)(a+a†)
Write the eigenstates |ni0to mean the eigenstates of the unperturbed
oscillator with energy En=~ω(n+ 1/2). In lowest order perturbation
theory, the perturbed eigenket is given by
|ni=|ni0+−κ3
6~
2mω 3/2X
m|mi00hm|(a+a†)3|ni0
En−Em
So that we have
hn|x−x0|ni=−2κ3
6~
2mω 2X
m
0hn|a+a†|mi0 0hm|(a+a†)3|ni0
En−Em
There are two nonzero terms of the sum, the one where n=m+1 which
gives us a denominator ~ωand a numerator
0hn|a†|n−1i0 0hn−1|a†aa +aa†a+aaa†|ni0
=√n√n(n−1) + n√n+ (n+ 1)√n= 3n2
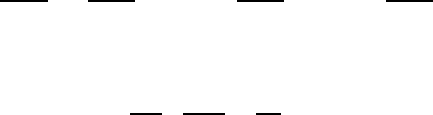
54 Compressibility, Sound, and Thermal Expansion
and also the term with n=m−1 which gives a denominator −~ωand
a numerator
0hn|a|n+ 1i0 0hn+ 1|a†a†a+a†aa†+aa†a†|ni0
=√n+ 1 n√n+ 1 + (n+ 1)√n+ 1 + (n+ 2)√n+ 1= 3(n+ 1)2
Thus we get
hn|x−x0|ni=2κ3
6~
2mω 21
~ω(6n+ 3) = Enκ3/(2κ2)

Vibrations of a
One-Dimensional
Monatomic Chain 9
(9.1) Classical Normal Modes to Quantum
Eigenstates
In Section 9.3 we stated without proof that a classical
normal mode becomes a quantum eigenstate. Here we
prove this fact for a simple diatomic molecule in a poten-
tial well (see Exercise 2.7 for a more difficult case, and see
also Exercise 9.7 where this principle is proven in more
generally).
Consider two particles, each of mass min one dimen-
sion, connected by a spring (K), at the bottom of a poten-
tial well (with spring constant k). We write the potential
energy as
U=k
2(x2
1+x2
2) + K
2(x1−x2)2
Write the classical equations of motion.
Transform into relative xrel = (x1−x2) and center
of mass xcm = (x1+x2)/2 coordinates.
(a) Show that in these transformed coordinates, the
system decouples, thus showing that the two normal
modes have frequencies
ωcm =pk/m
ωrel =p(k+ 2K)/m.
Note that since there are two initial degrees of freedom,
there are two normal modes.
Now consider the quantum-mechanical version of the
same problem. The Hamiltonian is
H=p2
1
2m+p2
2
2m+U(x1, x2)
Again transform into relative and center of mass co-
ordinates.
Define the corresponding momenta prel = (p1−p2)/2
and pcm = (p1+p2).
(b) Show that [pα, xγ] = −i~δα,γ where αand γtake
the values cm or rel.
(c) In terms of these new coordinates show that the
Hamiltonian decouples into two independent harmonic
oscillators with the same eigenfrequencies ωcm and ωrel.
Conclude that the spectrum of this system is
Enrel,ncm =~ωrel(nrel +1
2) + ~ωcm(ncm +1
2)
where ncm and nrel are non-negative integers.
(d) At temperature Twhat is the expectation of the
energy of this system?
(a) The equations of motion are
m¨x1=−kx1−K(x1−x2)
m¨x2=−kx2−K(x2−x1)
Taking the sum and difference of these two equations gives
m¨xcm =−kxcm
m¨xrel =−(k+ 2K)xrel

56 Vibrations of a One-Dimensional Monatomic Chain
which we identify as harmonic oscillators of frequencies
ωcm =pk/m
ωrel =p(k+ 2K)/m
(b) We have [pi, xj] = −i~δij . Defining prel = (p1−p2)/2 and pcm =
p1+p2and xrel =x1−x2and xcm = (x1+x2)/2 we obtain
[prel, xrel] = 1
2([p1, x1]−[p1, x2]−[p2, x1] + [p2, x2])
=1
2(−i~)(1 −0−0 + 1) = −i~
[prel, xcm] = 1
4([p1, x1] + [p1, x2]−[p2, x1]−[p2, x2])
=1
4(−i~)(1 + 0 −0−1) = 0
[pcm, xrel] = ([p1, x1]−[p1, x2] + [p2, x1]−[p2, x2])
= (−i~)(1 + 0 −0−1) = 0
[pcm, xcm] = 1
2([p1, x1] + [p1, x2] + [p2, x1] + [p2, x2])
=1
2(−i~)(1 + 0 + 0 + 1) = −i~
One could alternately dmonstrate that prel =−i~∂/∂xrel etc using ja-
cobians to confirm these commutations.
(c) We have
p1=pcm/2 + prel
p2=pcm/2−prel
x1=xcm +xrel/2
x2=xcm −xrel/2
So the Hamiltonian becomes
H=1
2m(p2
1+p2
2) + k
2(x2
1+x2
2) + K
2(x1−x2)2
=1
2m(p2
cm/2 + 2p2
rel) + k
2(2x2
cm +x2
rel/2) + K
2x2
rel
which decouples into (note the total mass is 2mand the reduced mass
is m/2)
H1=p2
cm
2(2m)+2k
2x2
cm
H2=p2
rel
2(m/2) +(k/2 + K)
2x2
rel
which are two independent harmonic oscilators with frequencies
ωcm =pk/m
ωrel =p(k+ 2K)/m

57
such that the spectrum can be written as
Enrel ,ncm =~ωrel(nrel +1
2) + ~ωcm(ncm +1
2)
At temperature T, the expectation of the energy of this system will
correspondingly be
hEi=~ωrel(nB(β~ωrel) + 1/2) + ~ωcm(nB(β~ωcm) + 1/2)
where nB(x) = 1/(ex−1) is the usual Bose factor.
The purpose of this exercise is not just to do another quantum me-
chanics problem. It is here to point out that coupled deg rees of freedom
act just like a single simple harmonic oscillator once the degrees of free-
dom are “rediagonalized”. This is important motivation for treating
phonons (coupled modes of springs) as individual harmonic oscillators.
(9.2) Normal Modes of a One-Dimensional
Monatomic Chain
(a)‡Explain what is meant by “normal mode” and by
“phonon”.
Explain briefly why phonons obey Bose statistics.
(b)‡Derive the dispersion relation for the longitudinal
oscillations of a one-dimensional mass-and-spring crystal
with Nidentical atoms of mass m, lattice spacing a, and
spring constant κ(motion of the masses is restricted to
be in one dimension).
(c)‡Show that the mode with wavevector khas the
same pattern of mass displacements as the mode with
wavevector k+ 2π/a. Hence show that the dispersion
relation is periodic in reciprocal space (k-space).
How many different normal modes are there.
(d)‡Derive the phase and group velocities and sketch
them as a function of k.
What is the sound velocity?
Show that the sound velocity is also given by vs=
1/√βρ where ρis the chain density and βis the com-
pressibility.
(e) Find the expression for g(ω), the density of states
of modes per angular frequency.
Sketch g(ω).
(f) Write an expression for the heat capacity of this
one-dimensional chain. You will inevitably have an inte-
gral that you cannot do analytically.
(g)* However, you can expand exponentials for high
temperature to obtain a high-temperature approxima-
tion. It should be obvious that the high-temperature
limit should give heat capacity C/N =kB(the law of
Dulong–Petit in one dimension). By expanding to next
non-trivial order, show that
C/N =kB(1 −A/T 2+. . .)
where
A=~2κ
6mk2
B.
(a) A normal mode is a periodic collective motion where all particles
move at the same frequency. A phonon is a quantum of vibration.
[I do not like the definition ”a quantum of vibrational energy”. The
vibration does carry energy, but it carries momentum as well, so why
specify energy only?]
Each classical normal mode of vibration corresponds to a quantum
mode of vibration which can be excited multiple times. A single mode
may be occupied by a single phonon, or it may be occupied with mul-
tiple phonons corresponding to a larger amplitude oscillation. The fact
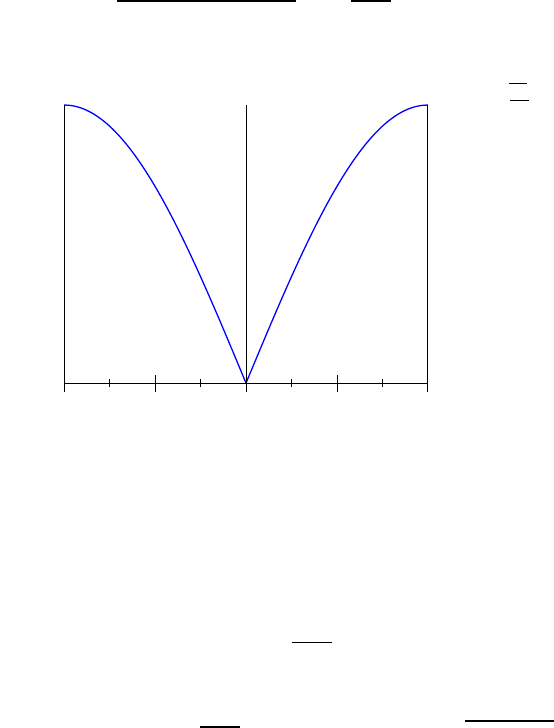
58 Vibrations of a One-Dimensional Monatomic Chain
that the same state may be multiply occupied by phonons means that
phonons must be bosons.
(b) The equation of motion for the nth particle along the chain is given
by
m¨xn=κ(xn+1 −xn) + κ(xn−1−xn) = κ(xn+1 +xn−1−2xn)
note that na is the equilibrium position of the nth particle. Using the
ansatz
xn=Aeiωt−ikna
we obtain
−ω2meiωt−ikna =κeiωt(eik(n+1)a+eik(n−1)a−2eikn)
ω2m= = 2κ(cos(ka)−1)
or
ω=p(2κ/m)(cos(ka)−1) = 2pκ/m |sin(ka/2)|
Fig. 9.1 Dispersion relation for
vibrations of the one-dimensional
monatomic harmonic chain. The
dispersion is periodic in k→k+ 2π/a.
ω
0 k=+π/a k=−π/a
ω = 2√ m
κ
(c)
e−i(k+2π/a)na =e−i(k+2π/a)na =e−ikna
If you assume periodic boundary conditions, then k= 2πm/L but kis
identified with k+ 2π/a so that there are therefore exactly N=L/a
different normal modes.
(d)
vphase =ω(k)/k = 2pκ/m |sin(ka/2)|/k
and
vgroup =dω(k)/dk =pκ/m a cos(|k|a/2) = (a/2)ω0q1−ω2/ω2
0

59
Fig. 9.2 The monatomic harmonic chain. Right: Phase velocity. Left: Group
velocity. Note velocities are signed quantities, to the left of the origin, the velocity
should have negative sign.
where ω0= 2pκ/m. Note that the phase velocity is not periodic in the
Brillouin zone! One can understand this if you think carefully about
aliasing of waves. The phase velocity is the velocity at which the peaks
of waves move. However, the waves are only defined at the position of
the masses along the chain. We write cos(kna) for the positions of the
masses at some time, but this only defines the value of the wave for
integer n. For integer n, we have kis the same as k+ 2π/a. However,
the ”peak” of this function may be between the integer values of n.
However, when we make nnon-integer, then kis no longer the same as
k+ 2π/n.
For sketches see figure 9.2
The sound velocity is the velocity at small k. This is
v=apκ/m
. The density of the chain is ρ=m/a and the compressibility is β=
−(1/L)dL/dF = 1/(κa). Thus we obtain v−2=ρβ
(e) Note first that
(ω(k)/2)2+ (vgroup(k)/a)2=κ/m (9.1)
Density of states is uniform in k. If there are Nsites in the system,
there are Nmodes total. The density of states in kis therefore dN/dk =
Na/(2π) = L/(2π) where Lis the length of the system.
Thus we have
g(ω) = dN/dω = (dN/dk)(dk/dω) = Na
2πvgroup
=N
2πpκ/m cos(|k|a/2)
=2N
2πp(κ/m)−(ω(k)/2)2(9.2)
where we have used Eq. 9.1.

60 Vibrations of a One-Dimensional Monatomic Chain
Fig. 9.3 The one dimensional harmonic chain. Density of states g(ω). Note that the
DOS diverges at ω= 2pk/m where the group velocity goes to zero.
The additional factor of 2 that appears up top is to account for the
fact that for each value of ω > 0 there are actually two values of kwith
that ω. (Note if you integrate over frequency you correctly get back N
degrees of freedom).
(f) The energy stored in the chain is given by
U=Zdωg(ω)~ω(nB(ω) + 1/2)
so the heat capacity is C=∂U/∂T . Note that we can drop the +1/2
since it has no derivative.
(g) To recover the law of Dulong-Petit, one takes the high temperature
limit of nB(ω) = kBT/~ωso th at we have
C=∂
∂T Zdωg(ω)(kBT) = kBZdωg(ω) = kBN
To go further, we use the high temperature expansion (expanding
1/(ex−1) for small x)
nB(ω) + 1/2 = kBT
~ω+1
12
~ω
kBT+...
So that we now have
C=∂U
∂T =kBN−1
T2Zdω~ωg(ω)1
12
~ω
kB
So that the coefficient Adefined in the problem has the values
A=~2
12Nk2
BZdωω2g(ω)
Inserting our expression for g(ω) we obtain
A=~2
12πk2
BZωmax
0
dω ω2
p(κ/m)−(ω/2)2

61
Defining x= (ω/2)pm/κ we obtain
A=~2
12πk2
B
8κ
mZ1
0
dx x2
√1−x2
The integral is evaluated to give π/4 (make the substitution x= sin θ).
Thus we obtain
A=~2
6k2
B
κ
m
as required.
(9.3) More Vibrations
Consider a one-dimensional spring and mass model of
a crystal. Generalize this model to include springs not
only between neighbors but also between second nearest
neighbors. Let the spring constant between neighbors be
called κ1and the spring constant between second neigh-
bors be called κ2. Let the mass of each atom be m.
(a) Calculate the dispersion curve ω(k) for this model.
(b) Determine the sound wave velocity. Show the group
velocity vanishes at the Brillouin zone boundary.
(a) Use the same approach
m¨xn=κ1(xn+1 −xn) + κ1(xn−1−xn) + κ2(xn+2 −xn) + κ1(xn−2−xn)
=κ1(xn+1 +xn−1−2xn) + κ2(xn+2 +xn−2−2xn)
Using the same ansatz
xn=Aeiωt−ikna
we obtain
−mω2= 2κ1(cos(ka)−1) + 2κ2(cos(2ka)−1) (9.3)
so
ω=r2κ1
m(cos(ka)−1) + 2κ2
m(cos(2ka)−1)
(b) To obtain the sound velocity, expand for small kto obtain
ω=r2κ1
m
(ka)2
2+2κ2
m
(2ka)2
2= arκ1+ 4κ2
m!k
Thus the sound velocity is
vs=arκ1+ 4κ2
m
The easiest way to examine ∂ω/∂k at the zone boundary is to differ-
entiate Eq. 9.3 to given
mω∂ω/∂k =−2aκ1sin(ka)−4aκ2sin(2ka)
At the zone boundary k=π/2 both terms on the right hand side are
zero, hence we have zero group velocity.

62 Vibrations of a One-Dimensional Monatomic Chain
(9.4) Decaying Waves
In the dispersion curve of the harmonic chain (Eq. 9.3),
there is a maximum possible frequency of oscillation
ωmax. If a vibration with frequency ω > ωmax is forced
upon the chain (say by a driving force) the “wave” will
not propagate along the chain, but rather will decay as
one moves away from the point where the oscillation is im-
posed (this is sometimes known as an “evanescent” wave).
With ω > ωmax solve Eq. 9.3 for a complex kto determine
the decay length of this evanescent wave. What happens
to this length as ω→ωmax ?
The usual form is
Ω = ω/ωmax =±sin(ka/2)
with ±chosen so Ω is positive. Thus
ka =±2 sin−1Ω
When Ω = 1 then ka =π. When Ω >1 then ka becomes complex
with a real part of π. The complex part gets smaller and vanishes as
Ω approaches 1 from above. The complex part of kgives the inverse
length scale of the wave’s decay (and it can decay left-going or right-
going depending on the ±sign). So as Ω approachs 1 from above, the
length scale of decay grows longer and longer until at 1 it extends over
the entire system and is a nondecaying wave.
See also the solution of 9.6 below, which is quite similar.
To check these properties of the arcsin, consider
y= sin(x) = z−z−1
2i
where z=eix. Multiplying by zwe obtain the quadratic
z2−2izy −1 = 0
Solving this equation gives
z=iy ±p1−y2
Note that for y > 1 we have z=eix along the positive imaginary axis,
which means x=π/2 + real. For y= 1 we have x=π/2 whereas for
y < 1 we obtain a complex valued zwith unti magnitude, thus a real x.
If one is concerned that this solution might not work, one can always
go back to the equations of motion
m¨xn=κ(xn+1 −xn) + κ(xn−1−xn) = κ(xn+1 +xn−1−2xn)
Using the ansatz
xn=Aeiωt−ikna
we obtain
−ω2meiωt−ikna =κeiωt(eik(n+1)a+eik(n−1)a−2eikn)
ω2m= = 2κ(cos(ka)−1)
63
Note that nowhere did we specify that kis real (!) so we can happily
extend into the complex plane. Using double angle formula
ω2=4κ
msin2(ka/2)
The only thing we would need to be careful about is choosing the sign
of the square root.
(9.5) Reflection at an Interface*
Consider a harmonic chain of equally spaced identical
masses of mass mwhere left of the n= 0 mass the spring
constant is κLbut right of the n= 0 mass, the spring
constant is κR, as shown in this figure.
n= 0
a
mmmmmmm
κLκLκLκRκRκR
I
RT
A wave with amplitude Iis incident on this interface
from the left, where it can be either transmitted with
amplitude Tor reflected with amplitude R. Using the
following ansatz form
δxn=T eiωt−ikLna n≥0
Ieiωt−ikRna +Reiωt+ikRna n < 0
derive T/I and R/I given ω,κL,κRand m.
Oops sorry about the typo, it should read
δxn=T eiωt−ikRna n≥0
Ieiωt−ikLna +Reiωt+ikLna n < 0
On both the left and the right, we must have the usual relations
between kL,R and ω
ω= 2qκL,R/m|sin(kL,Ra/2)|
or
kL,R =2
asin−1ω
2qm/κL,R
with these values of k, the ansatz form will then satisfy the equations of
motion except near the boundary.
Near the boundary, we have equations of motion for δx−1and δx0
which involve δx coordinates on both sides of the junction. We write
m¨
δx−1=κL(δx−2+δx0−2δx−1)
m¨
δx0=κL(δx−1−δx0) + κR(δx1−δx0)
64 Vibrations of a One-Dimensional Monatomic Chain
Plugging in the ansatz form of the wavefunction and doing a bit of
algebra gives us
(−mω2+ 2κL)IeikLa+Re−ikLa=κLIeikL2a+Re−ikL2a+T
(−mω2+κL+κR)T=κLIeikLa+Re−ikLa+κRT e−ikRa
(9.4)
The first equation simplifies quite a bit by rewriting the dispersion rela-
tion as
−mω2= 2κL(cos(kLa)−1)
So that
−mω2+ 2κL=κLeikLa+e−ikLa(9.5)
and the first equation becomes simply
I+R=T
which is just extending the wavefunction from the left hand side until
it hits position zero and matching it to the value of the wave from the
right at this position.
Plugging this into the second equation of Eq. 9.4 and solving to obtain
T/I =κL2isin(kLa)
−mω2+κL(1 −e−ikLa) + κR(1 −e−ikRa)
In the denominator we can simplify further applying 9.5 to give us
−mω2/2 + κL(1 −e−ikLa) = iκLsin(kLa)
and similarly for the right hand wave so that we get
T/I =2
1 + κRsin(kRa)
κLsin(kLa)
(9.6) Impurity Phonon Mode*
Consider a harmonic chain where all spring constants
have the same value κand masses have value m, except
for the mass at position n= 0 which instead has value
M < m as shown in this figure:
n= 0
a
mmmMmmm
κκκκκκ
Along with traveling wave solutions, there can be a
standing wave normal mode localized near the impurity.
Use an ansatz of the form
δxn=Aeiωt−q|n|a
with qreal to solve for the frequency of this impurity
mode. Consider your result in the context of Exercise
9.4.

65
Another error here: qneeds to have both real and imaginary parts.
This problem is fairly easy once you have solved 9.4. For 0 < ω <
ωmax the only solution to our equations of motion (except at the impu-
rity site) is for the usual waves
−mω2= 2κ(cos(ka)−1) (9.6)
or equivalently
ω=ωmax|sin(ka/2)|
or
ka = 2 sin−1(ω/ωmax)
with ω > ωmax = 2pκ/m we have decaying solutions of the form given
by the usual where (as shown in Exercise 9.4)
ka =π±iqa
with qhere real. Then on the left we choose + and on the right we
choose −so that the wave decays away from the impurity. So we have
δxn=Aeiωt+iπn+qan n≤0
Aeiωt−iπn−qan n≥0
with q > 0 this solves all of the equations of motion except for the one
at n= 0
M¨
δx0=κ(δx−1+δx1−2δx0)
Plugging in our ansatz, we obtain the three equations
−M ω2=κ(−e−qa −e−qa −2)
Taking this equation with to Eq. 9.6 and eliminating ω2we obtain
M(cosh(qa) + 1) = m(e−qa + 1)
Now, if M=mthe only place the two sides are equal is at q= 0, which
means there is no bound state. Further, since the left hand side grows
with increasing qand the right shrinks with qit is clear that there can
be no solution for M > m. However, for M < m there is one crossing
of the two curves, which finds the qappropriate for the bound state. In
fact, one can go a bit further analytically, writing z=eqa we have
(M/m)((z+z−1)/2 + 1) = z−1+ 1
which is a quadratic equation in z, which we can solve to given
z=eqa =2m
M−1
66 Vibrations of a One-Dimensional Monatomic Chain
Or
qa = log 2m
M−1
which, since we require q > 0 has a solution only for M < m. Finally
to obtain the frequency, one just has to plub back into our dispersion
relation to give
−mω2= 2κ(cos(π+iqa)−1)
which gives a real frequency greater than ωmax
(9.7) General Proof That Normal Modes Be-
come Quantum Eigenstates∗
This proof generalizes the argument given in Exercise
9.1. Consider a set of Nparticles a= 1,...N with masses
mainteracting via a potential
U=1
2X
a,b
xaVa,b xb
where xais the deviation of the position of particle afrom
its equilibrium position and Vcan be taken (without loss
of generality) to be a symmetric matrix. (Here we con-
sider a situation in 1d, however, we will see that to go
to 3d we just need to keep track of three times as many
coordinates.)
(i) Defining ya=√maxa, show that the classical equa-
tions of motion may be written as
¨ya=−X
b
Sa,b yb
where
Sa,b =1
√ma
Va,b
1
√mb
Thus show that the solutions are
y(m)
a=e−iωmts(m)
a
where ωmis the mth eigenvalue of the matrix Swith
corresponding eigenvector s(m)
a. These are the Nnormal
modes of the system.
(ii) Recall the orthogonality relations for eigenvectors
of hermitian matrices
X
a
[s(m)
a]∗[s(n)
a] = δm,n (9.7)
X
m
[s(m)
a]∗[s(m)
b] = δa,b.(9.8)
Since Sis symmetric as well as hermitian, the eigenvec-
tors can be taken to be real. Construct the transformed
coordinates
Y(m)=X
a
s(m)
axa√ma(9.9)
P(m)=X
a
s(m)
apa/√ma(9.10)
show that these coordinates have canonical commutations
[P(m), Y (n)] = −i~δn,m (9.11)
and show that in terms of these new coordinates the
Hamiltonian is rewritten as
H=X
m1
2[P(m)]2+1
2ω2
m[Y(m)]2.
(9.12)
Conclude that the quantum eigenfrequencies of the sys-
tem are also ωm. (Can you derive this result from the
prior two equations?)
Yet another typo, in part (i) it should say −ω2
mis the mth eigenvaluer.
(i) First given the expression for U, differentiate with resepect to xa
to obtain the force on particle a
Fa=−∂U
∂xa
=−X
b
Va,bxb
The equation of motion is then
ma¨xa=−X
b
Va,bxb

67
Now defining xa=ya/√mawe obtain
¨ya=−X
b
1
√ma
Va,b
1
√ma
yb=−X
b
Sa,byb
as required. Using the ansatz ya=e−iωtsawe have
ω2sa=X
b
Sa,bsa(9.13)
which is solved by sabeing the eigenvector of Sand ω2its eigenvalue.
(ii) Given
Y(m)=X
a
s(m)
axa√ma
P(n)=X
b
s(n)
bpb/√mb
we calculate
[P(n), Y (m)] = X
a,b
s(n)
bs(m)
a[pb, xa]pma/mb
Using the canonical commutations
[pb, xa] = −i~δab
we have
[P(n), Y (m)] = −i~X
a
s(m)
as(n)
a=−i~δnm
where we have used the orthogonality of eigenstates.
Next let us look at the terms of the proposed Hamiltonian
X
m
1
2[P(m)]2=X
mX
a,b
1
2s(m)
as(m)
bpapb/√mamb
=X
a
1
2ma
p2
a
where we have used the orthogonality of sto collapse the msum and
generate δab.
Now examining the second term of the proposed Hamiltonian
X
m
1
2ω2
m[Y(m)]2=X
mX
a,b
1
2s(m)
aω2
ms(m)
bxaxb√mamb
But here we can use Eq. 9.13 to replace ω2with the matrix Sgiving us
X
m
1
2ω2
m[Y(m)]2=X
mX
a,b,c
1
2s(m)
aSb,cs(m)
cxaxb√mamb
=X
a,b
1
2Sb,axaxb√mamb=X
a,b
1
2xaVa,bxb
68 Vibrations of a One-Dimensional Monatomic Chain
where we have used the orthogonality of sand taken the sum over mto
give a δac.
Thus the given Hamiltonian is equivalent to the original Hamitlonian
H=X
a
1
2ma
p2
a+X
a,b
1
2xaVa,bxb
The new form of the Hamiltonian in terms of Pand Yhas each m
coordinate completely decoupled. Further the Pand Ysatisfy canonical
commutations for momenta and positon so each mis simply a harmonic
oscillator with frequency ωm.
If one wanted to derive the spectrum from the Hamiltonian, one could
follow the usual procedure of writing
a†=1
√2~P/√ω+i√ωY
to rewrite the Hamiltonian for each decoupled mode as
H=~ω(a†a+ 1/2)
(9.8) Phonons in 2d* Consider a mass and spring model of a two-dimensional
triangular lattice as shown in the figure (assume the lat-
tice is extended infinitely in all directions). Assume that
identical masses mare attached to each of their six neigh-
bors by equal springs of equal length and spring con-
stant κ. Calculate the dispersion curve ω(k). The two-
dimensional structure is more difficult to handle than the
one-dimensional examples given in this chapter. In Chap-
ters 12 and 13 we study crystals in two and three dimen-
sions, and it might be useful to read those chapters first
and then return to try this exercise again.
Ok, this one is pretty hard if you have never seen such a thing before.
Probably it should have two stars.
First of all, one assumes that the crystal starts in equilibrium with
the springs unstretched. Forces on the springs will be proportional to
the amount of stretching. Note however, that if one of the masses is
displaced in a direction perpendicular to one of its attaching springs, to
linear order, the spring is not stretched at all (it is only rotated)! So in
other words, we need only keep track of the stretching in the direction
parallel to the spring.
Let us let the edge have unit length for simplicity of notation. If
we let the position of a sites in equilibrium be called rnand let the
displacements from this equilibrium be called urn. Now let us define
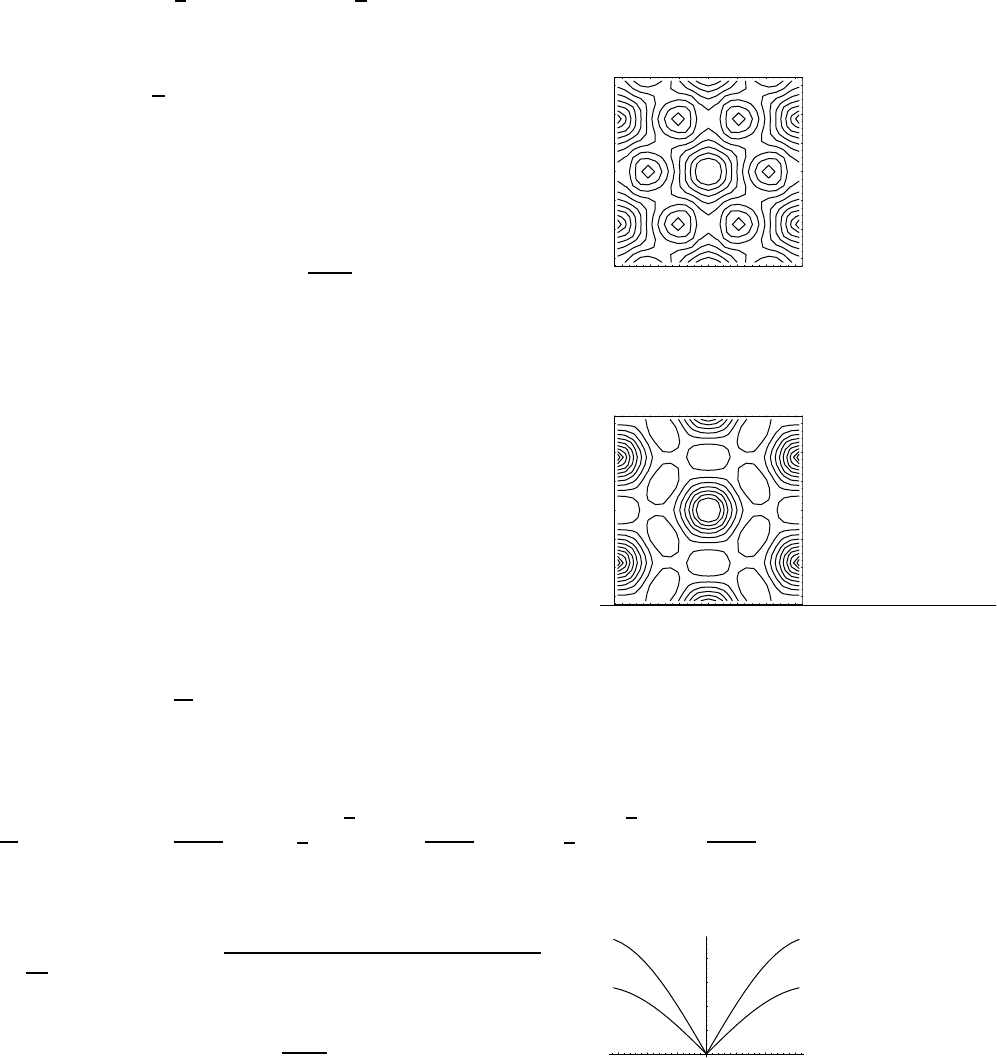
69
three unit vectors aipointing in the three directions of the lattice edges
a1= (1,0),a2= (1/2,√3/2),a2= (−1/2,√3/2). The total potential
energy of the system can then be written as
-6 -4 -2 0 2 46
-6
-4
-2
0
2
4
6
Fig. 9.4 Contour plot of the transverse
mode frequency of the triangular lattice
phonons in kx, kyspace.
U=κ
2X
rn
3
X
j=1 urn−urn+aj·aj2
where here we have included each spring once in the sum and we have
dotted the displacement with its direction so as to only count stretching
of the spring and not rotation. The force on a mass, and hence using
newton’s law we have
-6 -4 -2 0 2 46
-6
-4
-2
0
2
4
6
Fig. 9.5 Contour plot of the longitu-
dinal mode frequency of the triangular
lattice phonons in kx, kyspace.
m¨uα
rn=Fα
rn=−∂U
∂uα
rn
where αis a basis direction (say, xor y). Carefully taking the derivative
we get
m¨uα
rn=−κ
3
X
j=1
aα
j
X
β
[uβ
rn+aj+uβ
rn−ap−2uβ
rn]aβ
j
Using a wave ansatz
uα
rn=Uαeiωt−ik·rn
We obtain the two by two eigenvalue problem
ω2Uα=X
β
Dαβ (k)Uβ
where the so-called dynamical matrix is given by
Dαβ(k) = κ
m
3
X
j=1
aα
jaβ
j(eik·aj+e−ik·aj−2)
Note that this matrix is symmetric in αand β. Plugging in the values
of ajand using some trig identities we gets
D=κ
m 4 0
0 0 sin2(k·a1
2) + 1√3
√3 3 sin2(k·a2
2) + 1−√3
−√3 3 sin2(k·a3
2)
For each kthere will be two eigenvalues which correspond to the longi-
tudinal and transverse phonon modes. The eigenvalues of this becomes
ω2=2κ
mS1+S2+S3±qS2
1+S2
2+S2
3−S1S2−S1S3−S2S3
where
Si= sin2(k·ai
2)
-3 -2 -1 1 2 3
0.5
1
1.5
2
Fig. 9.6 Cut along k= (kx, 0) of
the spectrum of the triangular lattice
phonons.
These spectra are shown in figures 9.4 - 9.6. Note that the spectrum
is periodic in the Brillouin zone – which has the shape of a hexagon.
Vibrations of a
One-Dimensional Diatomic
Chain 10
(10.1) Normal modes of a One-Dimensional Di-
atomic Chain
(a) What is the difference between an acoustic mode
and an optical mode.
Describe how particles move in each case.
(b) Derive the dispersion relation for the longitudi-
nal oscillations of a one-dimensional diatomic mass-and-
spring crystal where the unit cell is of length aand each
unit cell contains one atom of mass m1and one atom of
mass m2connected together by springs with spring con-
stant κ, as shown in the figure (all springs are the same,
and motion of particles is in one dimension only).
a
m1m2
κ κ
(c) Determine the frequencies of the acoustic and op-
tical modes at k= 0 as well as at the Brillouin zone
boundary.
Describe the motion of the masses in each case (see
margin note 4 of this chapter!).
Determine the sound velocity and show that the
group velocity is zero at the zone boundary.
Show that the sound velocity is also given by vs=
pβ−1/ρ where ρis the chain density and βis the com-
pressibility.
(d) Sketch the dispersion in both reduced and extended
zone scheme.
If there are Nunit cells, how many different normal
modes are there?
How many branches of excitations are there? I.e.,
in reduced zone scheme, how many modes are there there
at each k?
(e) What happens when m1=m2?
The following figure depicts a long wavelength acoustic wave: All
atoms in the unit cell move in-phase with a slow spatial modulation.
Acoustic waves ω∼kfor small k.
a
m1m2
κ κ
acoustic
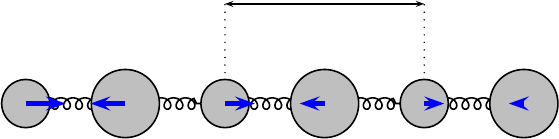
72 Vibrations of a One-Dimensional Diatomic Chain
The following depicts a long wavelength optical wave: The two differ-
ent types of atoms move out of phase, with a slow spatial modulation.
(In general a long wavelength optical mode is any long wavelength mode
where not all atoms in the unit cell are moving in phase). Note that the
amplitude of motion of the different atoms in the cells is generally not
the same. Optical modes have ωnonzero as k→0.
a
m1m2
κ κ
optical
(b) Let xnbe the position of the nth particle of mass m1and ynbe
the position of the nth particle of mass m2. We can assume that the
equilibrium position of xnis given by na and the equilibrium position
of ynis given by na +d.
We write the equations of motion for the deviations from these equi-
librium positions δxnand δyn.
m1¨
δxn=−κ(δxn−δyn−1)−κ(δxn−δyn)
m2¨
δyn=−κ(δyn−δxn)−κ(δyn−δxn+1)
Writing the ans¨atze
δxn=Axeikan−iωt
δyn=Ayeikan−iωt
we obtain the equations
−m1ω2Axeikna =−2κAxeikna +κAy(eikna +eik(n−1)a)
−m2ω2Ayeikna =−2κAyeikna +κAx(eikna +eik(n+1)a)
or
ω2Ax= 2(κ/m1)Ax−(κ/m1)(1 + e−ika)Ay(10.1)
ω2Ay= 2(κ/m2)Ay−(κ/m2)(1 + eika)Ax(10.2)
which is an eigenvalue problem from ω2. Thus we need to find the roots
of the determinant
2(κ/m1)−ω2−(κ/m1)(1 + e−ika)
−(κ/m2)(1 + eika) 2(κ/m2)−ω2

73
which gives the equation
0 = ω4−ω2(2κ(1/m1+ 1/m2)) + κ2
m1m24−(1 + eika)(1 + e−ika)
0 = ω4−ω22(m1+m2)κ
m1m2+κ2
m1m2
(2 −2 cos(ka)))
with the solution (skipping a few steps)
ω2=κ
m1m2m1+m2±qm2
1+m2
2+ 2m1m2cos(ka)
=κ
m1m2m1+m2±q(m1+m2)2−4m1m2sin2(ka/2)
(c) At k= 0, cos(ka) = 1, the acoustic mode has zero energy, whereas
the optical mode has energy
ω=s2κ(m1+m2)
m1m2
At the zone boundary cos(ka) = −1, so the two modes have energy
ω=r2κm1
m1m2
and r2κm2
m1m2
the greater of which is the optical mode, the lesser being the acoustic
mode.
To find the motions corresponding to these modes we need to plug
our frequencies back into Eqs. 10.1 and 10.2 to find the relation between
Axand Ay. For the acoustic mode at k= 0 we obtain Ax=Aywhich
means the two masses move in phae with the same amplitude. For the
optical mode at k= 0 we have Ax=−(m2/m1)Aymeaning that the
two different masses move in opposite directions with the heavier mass
moving with lower amplitude. At the zone boundary the two modes cor-
respond to one of the masses staying still and the other mass moving.
For example, for the lower frequency mode, the higher mass particles
move and the lower mass particle stays fixed. Since we are at the zone
boundary, every other higher mass particle moves in the opposite di-
rection (thus compressing symmetrically around the fixed particle. An
example of a zone boundary mode is shown in the following figure
a
m1m2
κ κ
zone boundary
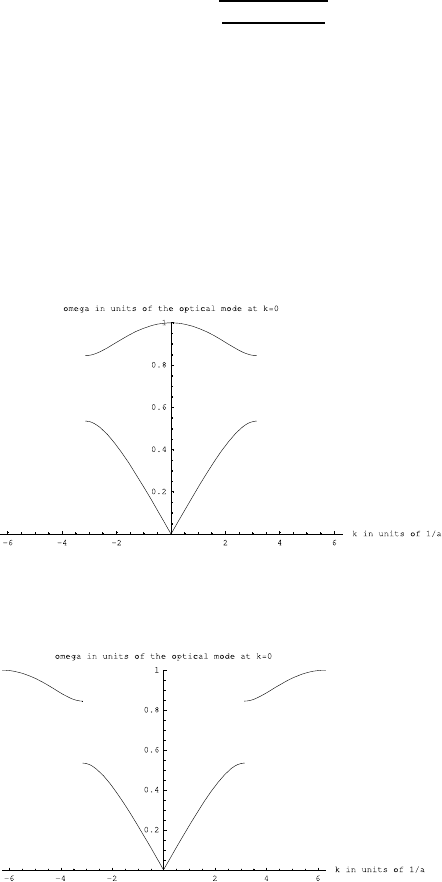
74 Vibrations of a One-Dimensional Diatomic Chain
To find the sound velocity, expand the cos around k= 0, one obtains
the acoustic mode velocity ω=vk with
v=arκ
2(m1+m2)
We check that v−2=ρβ. The density of the chain is ρ= (m1+m2)/a,
the compressibility of two springs in series is κ/2 so the compressibility
of the chain is β=−(1/L)dL/dF = 2/(κa).
Near the zone boundary, since the group velocity is dω/dk and since
dω/d cos(ka) is nonsingular, the group velocity must be zero by using
the chain rule since dcos(ka)/dk =asin(ka) = 0 at the zone boundary
(k=π/a).
Fig. 10.1 Diatomic Chain. Top Reduced Zone Scheme. Bottom Extended Zone
Scheme. Both pictures use m1/m2=.4.
If there are Nunit cells, therefore 2Natoms, there are 2N modes.
There are 2 modes per kin the reduced zone scheme, therefore two
branches.

75
(e) When m1=m2the unit cell is now of size a/2 so the Brillouin
zone is doubled in size. In this limit, the gap at the Brillouin zone
boundary vanishes and the two branches become the single branch of
the monatomic chain (this is most easily described in extended zone
scheme).
(10.2) Decaying Waves
Consider the alternating diatomic chain dispersion as
discussed in the text Eq. 10.6 and shown in Fig. 10.6.
For frequencies above ω+(k= 0) there are no propagat-
ing wave modes, and similarly for frequencies between
ω−(k=π/a) and ω+(k=π/a) there are no propagating
wave modes. As in Exercise 9.4, if this chain is driven at
a frequency ωfor which there are no propagating wave
modes, then there will be a decaying, or evanescent, wave
instead. By solving 10.6 for a complex k, find the length
scale of this decaying wave.
As in problem 9.4, we simply want to analytically extend kto complex
numbers. From the text Eq. 10.6 we can rearrange to obtain
ka = cos−11
2κ1κ2(mω2−κ1−κ2)2−κ2
1−κ2
2
The argument on the right hand size is greater than 1 for ωlarger than
the q= 0 optical mode freuquency, whereas for ωbetween the zone
boundary acoustic and optical model frequencies, the right hand side is
less than −1. The arccos of a number greater than one is pure imaginary
and grows from 0 as the argument increases from unity. Whereas the
arcos of a number less than -1 is π+ imaginary with the imaginary part
growing from zero as the argument decreases from -1. The length scale
of decay is always given by L=a/q with qthe imaginary part of k.
(10.3) General Diatomic Chain*
Consider a general diatomic chain as shown in Fig. 10.1
with two different masses m1and m2as well as two dif-
ferent spring constants κ1and κ2and lattice constant a.
(a) Calculate the dispersion relation for this system.
(b) Calculate the acoustic mode velocity and compare
it to vs=pβ−1/ρ where ρis the chain density and βis
the compressibility.
(a) This is the same approach as the prior cases, just a bit more
algebra to keep track of
m1¨
δxn=−κ1(δxn−δyn−1)−κ2(δxn−δyn)
m2¨
δyn=−κ2(δyn−δxn)−κ1(δyn−δxn+1)
Writing the ans¨atze
δxn=Axeikan−iωt
δyn=Ayeikan−iωt
76 Vibrations of a One-Dimensional Diatomic Chain
we obtain the equations
−m1ω2Axeikna =−(κ1+κ2)eiknaAx+ (κ2eikna +κ1eik(n−1)a)Ay
−m2ω2Ayeikna =−(κ1+κ2)eiknaAy+ (κ2eikna +κ1eik(n+1)a)Ax
or
ω2Ax=κ1+κ2
m1Ax+κ2
m1
+e−ika κ1
m1Ay
ω2Ay=κ1+κ2
m2Ay+κ2
m2
+eika κ1
m2Ax
which is an eigenvalue equation for ω2. The secular equation is then
0 = (κ1+κ2−m1ω2)(κ1+κ2−m2ω2)−κ2
1−κ2
2−2κ1κ2cos(ka)
or
ω4−(κ1+κ2)(m1+m2)
m1m2
ω2−4κ1κ2
m1m2
sin2(ka/2) = 0
with the solution (skipping a few steps)
ω2=(κ1+κ2)(m1+m2)
2m1m2
±1
2s(κ1+κ2)2(m1+m2)2
(m1m2)2−16κ1κ2
m1m2
sin2(ka/2)
(b) Simply taylor expanding the dispersion gives us
ω=rκ1κ2
(κ1+κ2)(m1+m2)ak
or
vs=sa2κ1κ2
(κ1+κ2)(m1+m2)
Now the hydrodynamic approach. The density of the chain is ρ=
(m1+m2)/a, the spring constant of the two springs in series is κ1κ2/(κ1κ2)
so the compressibility of the chain is β=−(1/L)dL/dF = (κ1κ2)/(κ1+
κ2)/. Plugging this into vs=pβ−1/ρ gives the same result.

77
(10.4) Second Neighbor Diatomic Chain* Con-
sider the diatomic chain from Exercise 10.1. In addition
to the spring constant κbetween neighboring masses, sup-
pose that there is also a next nearest-neighbor coupling
with spring constant κ′connecting equivalent masses in
adjacent unit cells. Determine the dispersion relation for
this system. What happens if κ′≫κ?
We write the equations of motion
m1¨
δxn=−κ(δxn−δyn−1)−κ(δxn−δyn)−κ′(δxn−δxn−1)−κ′(δxn−δxn+1)
m2¨
δyn=−κ(δyn−δxn)−κ(δyn−δxn+1)−κ′(δyn−δyn−1)−κ′(δyn−δyn+1)
Writing the usual ans¨atze
δxn=Axeikan−iωt
δyn=Ayeikan−iωt
we obtain the equations
−m1ω2Axeikna =−2(κ+κ′)Axeikna +κAy(eikna +eik(n−1)a) + κ′Ax(eik(n+1)a+eik(n−1)a)
−m2ω2Ayeikna =−2(κ+κ′)Ayeikna +κAx(eikna +eik(n+1)a) + κ′Ay(eik(n+1)a+eik(n−1)a)
or
m1ω2Ax= 2 [(κ+κ′)−κ′cos(ka)] Ax−κ(1 + e−ika)Ay
m2ω2Ay= 2 [(κ+κ′)−κ′cos(ka)] Ay−κ(1 + eika)Ax
which is an eigenvalue problem for ω2. Using some trig identies and
some algebra the secular equation can be reduced to
0 = m1m2ω4−(m1+m2)2κ+ 4κ′sin2(ka/2)ω2+[4κ2+ 16κκ′] sin2(ka/2) + 16κ′2sin4(ka/2)
with the solution
ω2=1
2m1m2(m1+m2)(2κ+ 4κ′sin2(ka/2))
±q(m1+m2)2(2κ+ 4κ′sin2(ka/2))2−4m1m2([4κ2+ 16κκ′] sin2(ka/2) + 16κ′2sin4(ka/2))
=1
m1m2(m1+m2)(κ+ 2κ′sin2(ka/2))
±q4m1m2κ2cos2(ka/2) + 4(m1−m2)2κ′2sin4(ka/2) + κκ′sin2(ka/2)
Note that when κ2= 0 we recover the diatomic chain from Exercise
10.1. When κ′≫κwe get two decoupled monatomic chains (as should
be expected!).
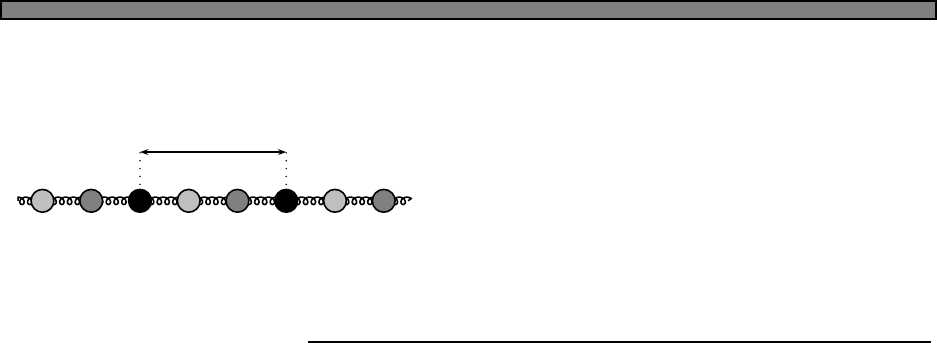
78 Vibrations of a One-Dimensional Diatomic Chain
(10.5) Triatomic Chain*
Consider a mass-and-spring model with three different
masses and three different springs per unit cell as shown
in this diagram.
a
m3m1m2m3m1m2
κ3κ1κ2κ3κ1
As usual, assume that the masses move only in one
dimension.
(a) At k= 0 how many optical modes are there? Cal-
culate the energies of these modes. Hint: You will get a
cubic equation. However, you already know one of the
roots since it is the energy of the acoustic mode at k= 0
(b)* If all the masses are the same and κ1=κ2de-
termine the frequencies of all three modes at the zone
boundary k=π/a. You will have a cubic equation, but
you should be able to guess one root which corresponds
to a particularly simple normal mode.
(c)* If all three spring constants are the same, and
m1=m2determine the frequencies of all three modes at
the zone boundary k=π/a. Again you should be able to
guess one of the roots.
With three particles in the unit cell, in one dimesion there is one
acoustic mode and two optical modes.
Declaring the unit cell to be one set of m1, m2, m3with positions
x, y, z our equations of motion are
m1¨
δxn=−κ3(δxn−δzn−1)−κ1(δxn−δyn)
m2¨
δyn=−κ1(δyn−δxn)−κ2(δyn−δzn)
m3¨
δzn=−κ2(δzn−δyn)−κ3(δzn−δxn+1)
Plugging in the usual wave ansatz gives us the secular determinant
0 =
κ3+κ1−m1ω2κ1κ3e−ika
κ1κ1+κ2−m2ω2κ2
κ3eika κ2κ2+κ3−m3ω2
which multiplied out gives the secular polynomial
0 = m1m2m3ω6
−[κ1(m1+m2)m3+κ3m2(m1+m3) + κ2m1(m2+m3)] ω4
+ [(κ2κ3+κ1κ2+κ3κ1)(m1+m2+m3)] ω2
−[κ1κ2κ3(2 −2 cos(ka))] (10.3)
At k= 0, the final term vanishes and the secular polynomial clearly
has ω= 0 a root. This we could have guessed in advance since we know
the acoustic mode should come down to zero frequency at k= 0. Once
we remove the obvious factor of ω2the remaining polynomial is just
quadratic and we can obtain the two roots in the obvious way.
(b) Setting all the masses the same and κ1=κ2, and setting ka =π
we obtain
0 = m3ω6−2m2(2κ1+κ3)ω4
+(2κ1κ3+κ2
1)(3m)ω2−κ2
1κ3(4)(10.4)

79
Here we have a difficult cubic. However, with some intuition we realize
that there should be a mode at the zone boundary where the κ3spring
does not compress at all – the two masses connected to κ3moving in
unison, but since we are at the zone boundary every other κ3spring
moves in the opposite direction. The two masses moving in unison have
mass 2mand have a restoring force of 2κ1from the two springs on the
two sides. Thus we expect a frequency of ω2=κ1/m. Indeed, this
frequncy solves Eq. 10.4. We can thus factor out this root to obtain a
quadratic which we then solve to get the two other roots at the zone
boundary
ω2=3κ1+ 2κ3±p9κ2
1−4κ1κ3+ 4κ2
3
2m
(c) Setting all of the spring constants the same and m1=m2and
setting ka =πwe obtain
0 = m2
1m3ω6−[2κm1(2m3+m1)] ω4
+(2m1+m3)(3κ2)ω2−4κ3(10.5)
Very similar reasoning suggests a mode at this wavevector with frequency
ω2=κ/m1(which is indeed a solution) which we can then factor out to
give the two additional zone boundary modes
ω2=κ 3m3+ 2m1±p9m2
3−4m1m3+ 4m2
1
2m1m3!

Tight Binding Chain
(Interlude and Preview) 11
(11.1) Monatomic Tight Binding Chain
Consider a one-dimensional tight binding model of elec-
trons hopping between atoms. Let the distance between
atoms be called a, and here let us label the atomic or-
bital on atom nas |nifor n= 1 . . . N (you may assume
periodic boundary conditions, and you may assume or-
thonormality of orbitals, i.e., hn|mi=δnm). Suppose
there is an on-site energy ǫand a hopping matrix element
−t. In other words, suppose hn|H|mi=ǫfor n=mand
hn|H|mi=−tfor n=m±1.
Derive and sketch the dispersion curve for electrons.
(Hint: Use the effective Schroedinger equations of Exer-
cise 6.2a. The resulting equation should look very similar
to that of Exercise 9.2.)
How many different eigenstates are there in this
system?
What is the effective mass of the electron near the
bottom of this band?
What is the density of states?
If each atom is monovalent (it donates a single elec-
tron) what is the density of states at the Fermi surface?
Give an approximation of the heat capacity of the
system (see Exercise 4.3).
What is the heat capacity if each atom is divalent?
Write a general wavefunction as
Ψ = X
n
φn|ni
The schroedinger equation (See problem 6.2a) is
Eφn=ǫφn−t(φn+1 +φn−1)
write the ansatz
φn=eikna
and we obtain
E(k) = ǫ−2tcos(ka)
(I won’t sketch this because it is rather trivial). Note however, for t > 0
the minimum occurs at k= 0 whereas for t < 0 the minimum is at the
zone boundary.
If there are Nsites in the system, the total length of the system (as-
sumed periodic) is Na. Thus kmust be quantized k= 2πm/(N a). Thus
there are exactly Ndifferent values of kwithin the Brillouin zone. This
is to be expected. If we started with a Hilbert space of Ndimensions
(described by states |ni), then we expect that there should be exactly

82 Tight Binding Chain (Interlude and Preview)
Neigenstates. (And one gets twice as many eigenstates if you include
spin).
Expanding around the minimum one obtains
E= const + |t|a2k2
which we set equal to a free particle dispersion
~2k2/(2m∗) = |t|a2k2
yielding an effective mass
m∗=~2/(2|t|a2)
The density of states in kspace is uniform as usual dN/dk =L/(2π) =
Na/(2π) (I have not included spin here yet) so the density of states in
energy
dN/dE = (dN/dk)(dk/dE)
Now using
dE/dk = 2ta sin(ka) = 2|t|aq1−((E−ǫ)/(2t))2
we obtain
dN/dE =N
2π
2∗2
2|t|q1−((E−ǫ)/(2t))2
and, as in exercise 9.2 there is an extra factor of 2 being that one has
two possible kstates for each energy Eand still another factor of 2
to include the 2 spin states. (Note if you integrate over frequency you
correctly get back 2Ndegrees of freedom, now with the factor of 2 for
spin included).
If each atom is monovalent, the band is exactly half filled (since two
electrons can go into each orbital). Thus the density of states is
dN/dE =N
π
1
|t|
The heat capacity is given in terms of the density of states as
CV= ˜γk2
Bg(EF)V T
with ˜γ=π2/6 (the exact number is from a more complicated calculation
that the students are not responsible for). Here g(EF)V=N
π
1
|t|.
If there were two electrons per atom, then the band would be com-
pletely full, and there would be no freedom in the system at all. The
heat capacity would be zero. The spin susceptibility would be zero too.

83
(11.2) Diatomic Tight Binding Chain
We now generalize the calculation of the previous exer-
cise to a one-dimensional diatomic solid which might look
as follows:
−A−B−A−B−A−B−
Suppose that the onsite energy of type Ais different from
the onsite energy of type B. I.e, hn|H|niis ǫAfor nbeing
on a site of type Aand is ǫBfor nbeing on a site of type
B. (All hopping matrix elements −tare still identical to
each other.)
Calculate the new dispersion relation. (This is ex-
tremely similar to Exercise 10.1. If you are stuck, try
studying that exercise again.)
Sketch this dispersion relation in both the reduced
and extended zone schemes.
What happens if ǫA=ǫB?
What happens in the “atomic” limit when tbe-
comes very small.
What is the effective mass of an electron near the
bottom of the lower band?
If each atom (of either type) is monovalent, is the
system a metal or an insulator?
*Given the results of this exercise, explain why LiF
(which has very ionic bonds) is an extremely good insu-
lator.
The unit cell ais now the distance from an A atom to the next A
atom. Let φA
nbe the amplitude of the wavefunction on the nth site of
type Aand φB
nbe the amplitude on the nth site of type B.
The Schroedinger equation becomes
EφA
n=ǫAφA
n−t(φB
n+φB
n−1)
EφB
n=ǫBφB
n−t(φA
n+φA
n+1)
Using the ans¨atz
φA
n=Aeikna
φB
n=Beikna
gives
EA =ǫAA−t(1 + e−ika)B
EB =ǫBB−t(1 + eika)A
again giving a two by two eigenvalue problem, where we solve for the
roots of the determinant
ǫA−E−t(1 + e−ika)
−t(1 + eika)ǫB−E
yielding the secular equation
0 = E2−E(ǫA+ǫB) + (ǫAǫB−t2(2 + 2 cos(ka)))
with the solutions
E±(k) = 1
2ǫA+ǫB±p(ǫA−ǫB)2+ 4t2(2 + 2 cos(ka))
Note that in the limit that ǫA=ǫBwe recover
E=ǫ±2|t|cos(ka/2)
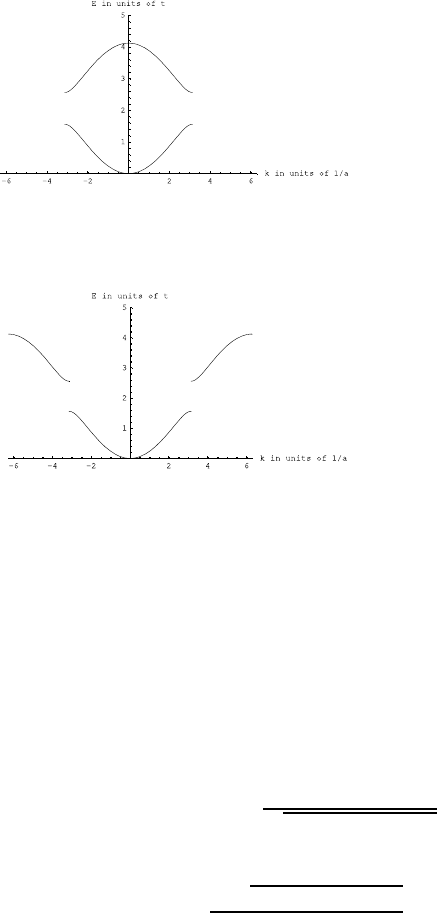
84 Tight Binding Chain (Interlude and Preview)
Fig. 11.1 Diatomic Tight Binding Problem in 1D. Left: Reduced Zone scheme.
Right: Extended Zone scheme. In both pictures we have chosen ǫA= 2.56 and
ǫB= 1.56
which matches the solution of part (a) above, but for the change in the
definition of the size of the unit cell. (See the figure for sketches of the
dispersion)
In the limit of small tthe bands become very flat at energies ǫAand
ǫB.
Expanding around the minimum gives
E= constant + 2t2(ka)2
p(ǫA−ǫB)2+ 16t2
which we set equal to ~2k2/(2m∗) to yield
m∗=~2p(ǫA−ǫB)2+ 16t2
4t2a2
If each atom is monovalent, there are now two electrons per unit cell,
and this fills exactly the lower band (leaving the upper band empty).
The system is therefore an insulator.
If ǫA=ǫBthis becomes a monotonic chain, the gap closes and it
becomes a metal.
For LiF we can expect a much lower energy for electrons on F than
on Li (F high high electron affinity, Li has low ionization energy). So

85
we can set ǫA≪ǫB. What happens in this limit is that the band
are extremely far apart – thus a very good insulator. Further, if we
look a the eigenvectors in the lower band, we will find that they are
almost completely on the lower energy atoms. Thus the free electron is
transferred almost completely from the higher to the lower energy atom.
(11.3) Tight Binding Chain Done Right
Let us reconsider the one-dimensional tight binding
model as in Exercise 11.1. Again we assume an on-site en-
ergy ǫand a hopping matrix element −t. In other words,
suppose hn|H|mi=ǫfor n=mand hn|H|mi=−tfor
n=m±1. However, now, let us no longer assume that or-
bitals are orthonormal. Instead, let us assume hn|mi=A
for n=mand hn|mi=Bfor n=m+ 1 with hn|mi= 0
for |n−m|>1.
Why is this last assumption (the |n−m|>1 case)
reasonable?
Treating the possible non-orthogonality of orbitals here
is very similar to what we did in Exercise 6.5. Go back
and look at that exercise.
Use the effective Schroedinger equation from Ex-
ercise 6.5 to derive the dispersion relation for this one-
dimensional tight binding chain.
One can assume that orbitals far apart have no overlap since the tails
of wavefunctions decay exponentially.
The generalized Schoedinger equation is
X
m
Hnmφm=EX
m
Snmφm
where here
Hnm =ǫ0δnm −t(δn,m+1 +δn,m−1)
Snm =Aδnm +Bδn,m+1 +B∗δn,m−1
(note we did not promise that Bis real!). Plugging in our wave ansatz
φm=eimka into the Schroedinger equation, we obtain
E(A+Beik +B∗e−ik) = ǫ0−2tcos(ka)
or
E=ǫ0−2tcos(ka)
A+Beik +B∗e−ik
(11.4) Two Orbitals per Atom
(a) Consider an atom with two orbitals, Aand Bhav-
ing eigenenergies ǫA
atomic and ǫB
atomic. Now suppose we
make a one-dimensional chain of such atoms and let us
assume that these orbitals remain orthogonal. We imag-
ine hopping amplitudes tAA which allows an electron on
orbital Aof a given atom to hop to orbital Aon the neigh-
boring atom. Similarly we imagine a hopping amplitude
tBB that allows an electron on orbital Bof a given atom
to hop to orbital Bon the neighboring atom. (We as-
sume that V0, the energy shift of the atomic orbital due
to neighboring atoms, is zero).
Calculate and sketch the dispersion of the two re-
sulting bands.
If the atom is diatomic, derive a condition on the
quantities ǫA
atomic −ǫB
atomic, as well as tAA and tBB which

86 Tight Binding Chain (Interlude and Preview)
determines whether the system is a metal or an insulator.
(b)* Now suppose that there is in addition a hopping
term tAB which allows an electron on one atom in orbital
Ato hop to orbital Bon the neighboring atom (and vice
versa). What is the dispersion relation now?
(a) The two orbitals are completely decoupled from each other. So we
get two independent dispersions (we assume t’s real here)
E=ǫA−2tAA cos(ka) (11.1)
and
E=ǫB−2tBB cos(ka) (11.2)
A sketch is given in Fig. 11.2.
-3 -2 -1 1 2 3
-2
-1
1
2
3
4
5
Fig. 11.2 Dispersion in the two orib-
tal tight binding model (Eqs. 11.1 and
11.2). Here, tAA = 1, tBB = 2, ǫA= 0,
ǫB= 4. Horizontal axis is ka.
It should say ”’if the atom is divalent” not diatomic (doh!). If the
atom is divalent, then it will be a metal if the bands overlap and an
insulator (or semiconductor) if the bands do not overlap. A band with
the dispersion as in Eqs. 11.1 has a band which extends from ǫA−2|tAA|
to ǫA+ 2|tAA|(and similar for the other band – this holds even if t’s are
complex). In order for the bands to not overlap we must have either
ǫA+ 2|tAA|< ǫB−2|tBB |
or
ǫB+ 2|tBB |< ǫA−2|tAA|
If neither of these is satisfied the bands must overlap and we have a
metal. Note if we are tricky we can summarize the two above conditions
as one condition which, if satisfied, tells us we have an insulator
|ǫA−ǫB|>2 (|tAA| − |tBB |)
(b) When there is hopping tAB between an Aorbital on one site and a
Borbital on a neighboring site, we have a matrix schroedinger equation
EφA
n=ǫAφA
n−tAAφA
n+1 −t∗
AAφA
n−1−tABφB
n+1 −t∗
ABφB
n−1
EφB
n=ǫBφB
n−tBB φB
n+1 −t∗
BB φB
n−1−tABφA
n+1 −t∗
ABφA
n−1
Using the usual ans¨atz
φA
n=Aeikna
φB
n=Beikna
we obtain
EA =ǫA−tAAeika −t∗
AAe−ikaA+−tABeika −t∗
ABe−ikaB
EB =ǫB−tBB eika −t∗
BB e−ikaB+−tAB eika −t∗
ABe−ikaA
which is an eigenvalue equation for E. Defining
TAA =tAAeika +t∗
AAe−ika = 2Re[tAAeika](11.3)
TBB =tBB eika +t∗
BB e−ika = 2Re[tBBeika] (11.4)
TAB =tABeika +t∗
ABe−ika = 2Re[tAB eika] (11.5)

87
We can write the secular equation as
0 = E2+E(TAA +TBB −ǫA−ǫB)
+ (ǫA−TAA) (ǫB−TBB)−T2
AB (11.6)
which we solve as a quadratic equation to give
E=1
2ǫA+ǫB−TAA −TBB ±q(ǫA−ǫB−TAA +TBB)2−4T2
AB
(11.5) Electronic Impurity State*
Consider the one-dimensional tight binding Hamilto-
nian given in Eq. 11.4. Now consider the situation where
one of the atoms in the chain (atom n= 0) is an impurity
such that it has an atomic orbital energy which differs by
∆ from all the other atomic orbital energies. In this case
the Hamiltonian becomes
Hn,m =ǫ0δn,m −t(δn+1,m +δn−1,m) + ∆δn,mδn,0.
(a) Using an ansatz
φn=Ae−qa|n|
with qreal, and athe lattice constant, show that there
is a localized eigenstate for any negative ∆, and find the
eigenstate energy. This exercise is very similar to Exercise
9.6.
(b) Consider instead a continuum one-dimensional
Hamiltonian with a delta-function potential
H=−~2
2m∗∂2
x+ (a∆)δ(x).
Similarly show that there is a localized eigenstate for any
negative ∆ and find its energy. Compare your result to
that of part (a).
(a) Consider first without the impurity. Propose exponentially decay-
ing or growing solutions
φn=Ae±qa|n|
plugging these in we obtain
E=ǫ0−2tcosh(qa) (11.7)
these give solutions with qreal for (ǫ0−E)/2t > 1, or in other words,
for energies below the bottom of the band. These are analogous to the
evanescent waves discussed in Exercises 9.4 and 10.2.
Now, we can patch together two of these evanescent waves at the
impurity. Examining the schroedinger equation at position zero, we
have
Eφ0= (ǫ0+ ∆)φ0−t(φ1+φ−1)
which gives us
E−ǫ0−∆ = 2te−qa
Then plugging in the value of Ein terms of qfrom Eq. 11.7, we obtain
−∆ = 2 sinh(qa)
recalling that ∆ was negative we have a solution for any value of ∆ <0
with
qa = sinh−1(|∆|/(2t))

88 Tight Binding Chain (Interlude and Preview)
Plugging back into Eq. 11.7 we obtain the bound state energy
E=ǫ0−2tp[∆/(2t)]2+ 1
and note that for ∆ = 0 this gives us the energy at the bottom of the
band.
(b) For the continuum problem we have similarly a decaying waves of
the form e−qx with energies
E=−~2q2
2m∗
Then we need to patch together solutions at zero, we have
∂ψ−−∂ψ+= 2q= (a|∆|)(2m∗)/~2
or
q= (a|∆|m∗)/~2
with energy
E=−a2m∗∆2/(2~2)
To compare to the above tight binding problem, we use the value of
the effective mass m∗=~2/(2ta2) to obtain
q=|∆|/(2t)
which matches our above result for small ∆. Correspondingly the energy
is
E=−∆2/(4t)
which also matches the above result for small ∆ so long as we choose
the bottom of the band to be called zero energy.
(11.6) Reflection from an Impurity*
Consider the tight binding Hamiltonian from the pre-
vious exercise representing a single impurity in a chain.
Here the intent is to see how this impurity scatters a
plane wave incoming from the left with unit amplitude
(this is somewhat similar to Exercise 9.5). Use an ansatz
wavefunction
φn=T e−ikna n≥0
e−ikna +Re+ikna n < 0
to determine the transmission Tand reflection Ras a
function of k.
Use the schroedinger equation at position n=−1
Eφ−1=ǫ0φ−1−t(φ0+φ−2)
and at position zero
Eφ0= (ǫ0+ ∆)φ0−t(φ1+φ−1)
89
and we plug in the ansatz form. The former equation simply tells us
that we must have 1 + R=T(To see this recall that the relationship
between Eand kis fixed by the plane wave away from positon zero.
So this first equation tells us that position φ0must just be the usual
continuation of this wave-front with no changes.) The second equation
then gives us
E T = (ǫ0+ ∆)T−t(T eika +eika +Re−ika)
Using 1 + R=Tas well as using E=ǫ0+ 2tcos(ka) this becomes
T=1
∆
2it sin(ka)+ 1
Note that when ∆ = 0, we have complete transmission T= 1 and
R= 0. With R=T−1, we have |R|2+|T|2= 1 which indicates current
conservation.
(11.7) Transport in One Dimension*
(a) Consider the one-dimensional tight binding chain
discussed in this chapter at (or near) zero temperature.
Suppose the right end of this chain is attached to a reser-
voir at chemical potential µRand the left end of the
chain is attached to a reservoir at chemical potential µL
and let us assume µL> µR. The particles moving to-
wards the left will be filled up to chemical potential µR,
whereas the particles moving towards the right will be
filled up to chemical potential µL, as shown in the bot-
tom of Fig. 11.4, and also diagrammed schematically in
the following figure
µLµR
µR
µL
(i) Argue that the total current of all the particles mov-
ing to the right is
jR=Z∞
0
dk
πv(k)nF(β(E(k)−µL))
with v(k) = (1/~)dǫ(k)/dk the group velocity and nFthe
Fermi occupation factor; and an analogous equation holds
for left moving current.
(ii) Calculate the conductance Gof this wire, defined
as
Jtotal =GV
where Jtotal =jL−jRand eV =µL−µR, and show
G= 2e2/h with hPlanck’s constant. This “quantum” of
conductance is routinely measured in disorder free one-
dimensional electronic systems.
(iii) In the context of Exercise 11.2, imagine that an im-
purity is placed in this chain between the two reservoirs
to create some backscattering. Argue that the conduc-
tance is reduced to G= 2e2|T|2/h. This is known as the
Landauer formula and is a pillar of nano-scale electron-
ics.
(b) Now suppose that the chemical potentials at both
reservoirs are the same, but the temperatures are TLand
TRrespectively.
(i) Argue that the heat current jqof all the particles
moving to the right is
jq
R=Z∞
0
dk
πv(k) (E(k)−µ)nF(βL(E(k)−µ))
and a similar equation holds for left-moving heat current.
(ii) Define the thermal conductance Kto be
Jq=K(TL−TR)
where Jq=jq
L−jq
Rand TL−TRis assumed to be small.
Derive that the thermal conductance can be rewritten as
K=−2
hT Z∞
−∞
dE(E−µ)2∂
∂E nF(β(E−µ)).
Evaluating this expression, confirm the Wiedemann–
Franz ratio for clean one-dimensional systems
K
T G =π2k2
B
3e2
(Note that this is a relationship between conductance and
thermal conductance rather than between conductivity

90 Tight Binding Chain (Interlude and Preview)
and thermal conductivity.) In evaluating the above inte-
gral you will want to use
Z∞
−∞
dx x2∂
∂x
1
ex+ 1 =−π2
3.
If you are very adventurous, you can prove this nasty
identity using the techniques analogous to those men-
tioned in footnote 20 of Chapter 2, as well as the fact that
the Riemann zeta function takes the value ζ(2) = π2/6
which you can prove analogous to the appendix of that
chapter.
(a)(i) Genereally the velocity of a wavepacket is the group velocity
v=dω/dk. Here, ω=Ek/~To find the total right going current, one
integrates over all possible k, the occupancy of that ktimes the group
velocity, to obtain the current. There should be an additional factor of
−eout front to turn this into an electrical current. The integral over
kusually has 2πdownstairs, but the 2 is cancelled by a factor of 2 out
front for two spins. The integral over kalso usually comes with a factor
of volume (or length in this case) out front. To see why this is missing we
have to think carefully about the definition of current – which counts the
number of particles crossing a given point in some unit of time. If one
has a particle in a keigenstate, it is delocalized over the entire system.
Thus the ”probability“ that with velocity vit crosses that given point
in a unit of time is given by v/L.
(ii) We can write the total current as
J=−e
πZ∞
0
dE(k)
dk nF(β(Ek−µR))dk −Z−∞
0
dE(k)
dk nF(β(Ek−µL))dk
=−e
~πZ∞
0
dEnF(β(E−µR)) −Z∞
0
dEnF(β(E−µL))
=−e
~π[µL−µR]
where in the last step we have assumed that µ≫kBTso that the
occupancy at E= 0 is unity — in which case the integral of the Fermi
function simply gives the chemical potential (one can see this by starting
at T= 0 where the Fermi function is just a step function. As we raise
the temperature, the change in the fermi function is symmetric around
the chemical potential, so even though the fermi function gets smaller
below µand larger above µthe integral is unchanged).
Plugging in the expression for voltage
J=−e2
π~V
or G= 2e2/h.
(iii) If the amplitude of transmission through the impurity is Tthen
the probability of transmission is |T|2. The resulting current is then
reduced by the probability that each particle is transmitted. Thus we
obtain
G= 2e2|T|2/h
Note that as we discovered in exercise 11.6, Tis a function of wavevector
and hence energy. Once should use knear kFto calculate T. The
91
reason for this is that all of the net current is coming from near the
Fermi surface. Well below the fermi surface the currents of left and
right movers exactly cancel.
(b) (i) The argument here is quite similar. Here each electron is
moving with velocity v, but is carrying energy E−µ. Here energy is
measured with respect to the chemical potential – this is an appropriate
definition since even at T= 0 the addition of an electron carries the
chemical potential worth of energy. The difference from this T= 0
energy is the excess heat added.
(ii) We take the difference of right moving and left moving energy
currents (the sign gives current moving from left to right)
Jq=−1
πZ∞
0
dE(k)
dk (Ek−µ)nF(βR(Ek−µ))dk −Z−∞
0
dE(k)
dk (Ek−µ)nF(βL(Ek−µL))dk
=−1
~πZ∞
0
dE(E−µ)nF(βR(E−µ)) −Z∞
0
dE(E−µ)nF(βL(E−µ))
=−1
~π(βR−βL)Z∞
0
dE(E−µ)dnF(β(E−µ))
dβ
(11.8)
where we have made the approximation that βR−βLis small to
replace the finite difference with a derivative with respect to β. This
then becomes.
Jq=−1
~πβ (βR−βL)Z∞
0
dE(E−µ)2dnF(β(E−µ))
dE
then using
βR−βL≈TL−TR
kBT2
gives the desired result. Note that the formula also extends the lower
limit of integration to −∞. This is allowed since dnF/dE is strongly
peaked around µ.
Finally scaling out some factors of βwe obtain
K=−2T
hZ∞
−∞
dxx2d
dx
1
ex+ 1 =2π2k2
BT
3h
Thus dividing by the expresion for Gwe obtain
K
GT =π2k2
BT
3he2
which is the Weideman-Franz law.
For completeness, we evaluate the integral. First, note that the inte-

92 Tight Binding Chain (Interlude and Preview)
grand is symmetric around zero so we can write
I=Z∞
−∞
dxx2d
dx
1
ex+ 1 = 2 Z∞
0
dxx2d
dx
1
ex+ 1 =−4Z∞
0
dxx e−x
1 + e−x
= 4 Z∞
0
dxx
∞
X
n=1
(−ex)n= 4
∞
X
n=1
(−1)n
n2
=−4"∞
X
n=1
1
n2−2
∞
X
n=1,evens
1
n2#= 4(1 −2
4)ζ(2) = 2ζ(2)
The method of calculating ζ(2) proceeds similar to the appendix of
Chapter 1. First, consider the function xin the range [−π, π] as a fourier
series. It can be writen as
x=
∞
X
n=1
ansin(nx)
with
an=1
πZπ
−π
xsin(nx) = −2(−1)n/n
The calculate Zπ
−π
dx x2= 2π3/3
but also caculate the same quantity in terms of its fourier transforms
(using percival’s theorem)
Zπ
−π
dx x2=Zπ
−π
dx =
∞
X
n=1 |an|2sin2(nx) =
∞
X
n=1
4
n2π
setting these two expressions equal to each other gives
∞
X
n=1
1
n2=π2
6
(11.8) Peierls Distortion*
Consider a chain made up of all the same type of atom,
but in such a way that the spacing between atoms alter-
nates as long-short-long-short as follows
−A=A−A=A−A=A−
In a tight binding model, the shorter bonds (marked with
=) will have hopping matrix element tshort =t(1 + ǫ)
whereas the longer bonds (marked with −) have hopping
matrix element tlong =t(1 −ǫ). Calculate the tight-
binding energy spectrum of this chain. (The onsite en-
ergy ǫis the same on every atom). Expand your result to
linear order in ǫ. Suppose the lower band is filled and the
upper band is empty (what is the valence of each atom
in this case?). Calculate the total ground-state energy of
the filled lower band, and show it decreases linearly with
increasing ǫ.
Now consider a chain of equally spaced identical A
atoms connected together with identical springs with
spring constant κ. Show that making a distortion
whereby alternating springs are shorter/longer by δx
costs energy proportional to (δx)2. Conclude that for a
chain with the valence as in the first part of this problem,
a distortion of this sort will occur spontaneously. This is
known as a Peierls distortion.

93
OK, I messed up this problem a bit, so bear with me.
First we need to evalulate the spectrum. Consider the unit cell to be
a single unit like this A=A−. Call the left side the A site and the
right site the B site. Set the onsite energy epsilon0to zero for simplicity
and assume tis real (without loss of generality). We then have the
tight-binding schroedinger equation
EφA
n=−t(1 + ǫ)φB
n−t(1 −ǫ)φB
n−1
EφB
n=−t(1 + ǫ)φA
n−t(1 −ǫ)φA
n+1
Using the usual ansatz this gives us
EA =−t(1 + ǫ)B−t(1 −ǫ)Be−ika
EB =−t(1 + ǫ)A−t(1 −ǫ)Aeika
which is an eigenvalue problem with solutions
E(k) = ±|2t[cos(ka/2) + iǫ sin(ka/2)]|=±|2t|pǫ2+ (1 −ǫ2) cos2(ka/2)
To find the total energy of a filled lower band, we need
Etot = 2LZdk
2πE(k)
which is some horrid ellipic integral. Ideally, we just evaluate this horrid
integral and we are done, but this is very difficult analytically (we could
do it numerically though!).
However, all we need to do is to make an estimate of how this changes
to lowest order in ǫ. Near the zone boundary, since the cosine term is
small the effect of epsilon is most pronounced where the energy reduction
in the lower band is −|2tǫ|. As we move away from the zone boundary
the cosine term becomes more important. Define κa =π−ka to be the
distance to the zone boundary (focusing for now on the zone boundary
at ka =π).
For small κwe see that the two term in the square root become roughly
equal when
κa ≈ǫ
And when κa ≫ǫthe cosine term dominates. Let us then split the
integration roughly at this intermediate point κa ≈ǫ. For smaller κ, the
energy reduction can be approximated as −|2tǫ|for each value of κand
integrating then a range of κthat is ǫlarge we get an energy reduction
of ∼L|t|ǫ2, which we are not interested in. For the region further from
the zone boundary, we have roughly
δE ≈ |2tL|Zcutoff
κa=ǫ
dκ hpǫ2+ (κa)2/4−κa/2i
≈ |2tL|Zcutoff
κa=ǫ
dκǫ2
κ≈ |2tL|ǫ2log(ǫ/cutoff)
94 Tight Binding Chain (Interlude and Preview)
here the cutoff is some arbitrary momentum much further from the zone
boundary (it will not matter where we choose the cutoff!). Thus we see
that the energy saving is proportional to ǫ2log ǫ.
(ii) The energy of stretching springs is always quadratic in the stretch-
ing (hookes’ law), hence proportional to ǫ2. For small ǫthe electronic
energy saving ǫ2log ǫalways wins, so the system always distorts sponta-
neously!
(11.9) Tight Binding in 2d*
Consider a rectangular lattice in two dimensions as
shown in the figure. Now imagine a tight binding model
where there is one orbital at each lattice site, and where
the hopping matrix element is hn|H|mi=t1if sites nand
mare neighbors in the horizontal direction and is = t2if
nand mare neighbors in the vertical direction. Calculate
the dispersion relation for this tight binding model. What
does the dispersion relation look like near the bottom of
the band? (The two-dimensional structure is more diffi-
cult to handle than the one-dimensional examples given
in this chapter. In Chapters 12 and 13 we study crys-
tals in two and three dimensions, and it might be useful
to read those chapters first and then return to try this
exercise again.)
t1
t2
This is a lot easier than it looks! Let us label the sites (m,n). Let
the wavefunctions on the sites be φn,m accordingly. The Schroedinger
equation is then
Eφn,m =ǫ0φn,m −t1(φn+1,m +φn−1,m)−t2(φn,m+1 +φn,m−1)
Using an ansatz
φn,m =eikxnax+kymay
where axand ayare the lattice distances in the two directions.
and assuming both t1and t2real
E=ǫ0−2t1cos(kxax)−2t2cos(kyay)
Assuming both t1and t2positive, the minimum occurs at kx=ky= 0.
Near this minimum, we can expand to gets
E≈(ǫ0−2t1−2t2) + 1
2t1(kxax)2+t2(kyay)2
which has equal-Econtours which are ellipses. Thus near the bottom of
the band we have an ellipsoidal bowl.

Crystal Structure 12
(12.1) Crystal Structure of NaCl Consider the
NaCl crystal structure shown in Fig. 12.21. If the lattice
constant is a= 0.563 nm, what is the distance from a
sodium atom to the nearest chlorine? What is the dis-
tance from a sodium atom to the nearest other sodium
atom?
Super easy: The Na-Cl distance is a/2 = .2815 nm whereas the Na-Na
distance is a√2/2 = .398 nm.
(12.2) Neighbors in the Face-Centered Lattice.
(a) Show that each lattice point in an fcc lattice has
twelve nearest neighbors, each the same distance from the
initial point. What is this distance if the conventional
unit cell has lattice constant a?
(b)∗Now stretch the side lengths of the fcc lattice
such that you obtain a face-centered orthorhombic lattice
where the conventional unit cell has sides of length a,b,
and cwhich are all different. What are the distances to
these twelve neighboring points now? How many nearest
neighbors are there?
(a) Given the primitive lattice vectors, one can define the fcc lattice
as being vectors of the form a
2(n, m, l) where n, m, l are either all even
or two odd and one even. Among this sets of possible lattice points, the
closest ones to [0,0,0] are of the form a
2[1,1,0]. Here the two entries that
are 1 could be either ±1 which gives four possibilities. Further the 0 can
be in one of three places. Thus we have 12 possibilities. The distance
from [0,0,0] to any of these points is a√2/2 (analogous to previous
problem).
(b) In units of the three different (unequal) conventional unit cell
lattice constants, the 12 points are still of the form 1
2[1,1,0] and permu-
tations. The distances to these 12 points are then
[±1,±1,0] →d=1
2pa2+b2
[±1,0,±1] →d=1
2pa2+c2
[0,±1,±1] →d=1
2pb2+c2
There are four nearest neighbors corresponding to the smaller two of
a, b, c.
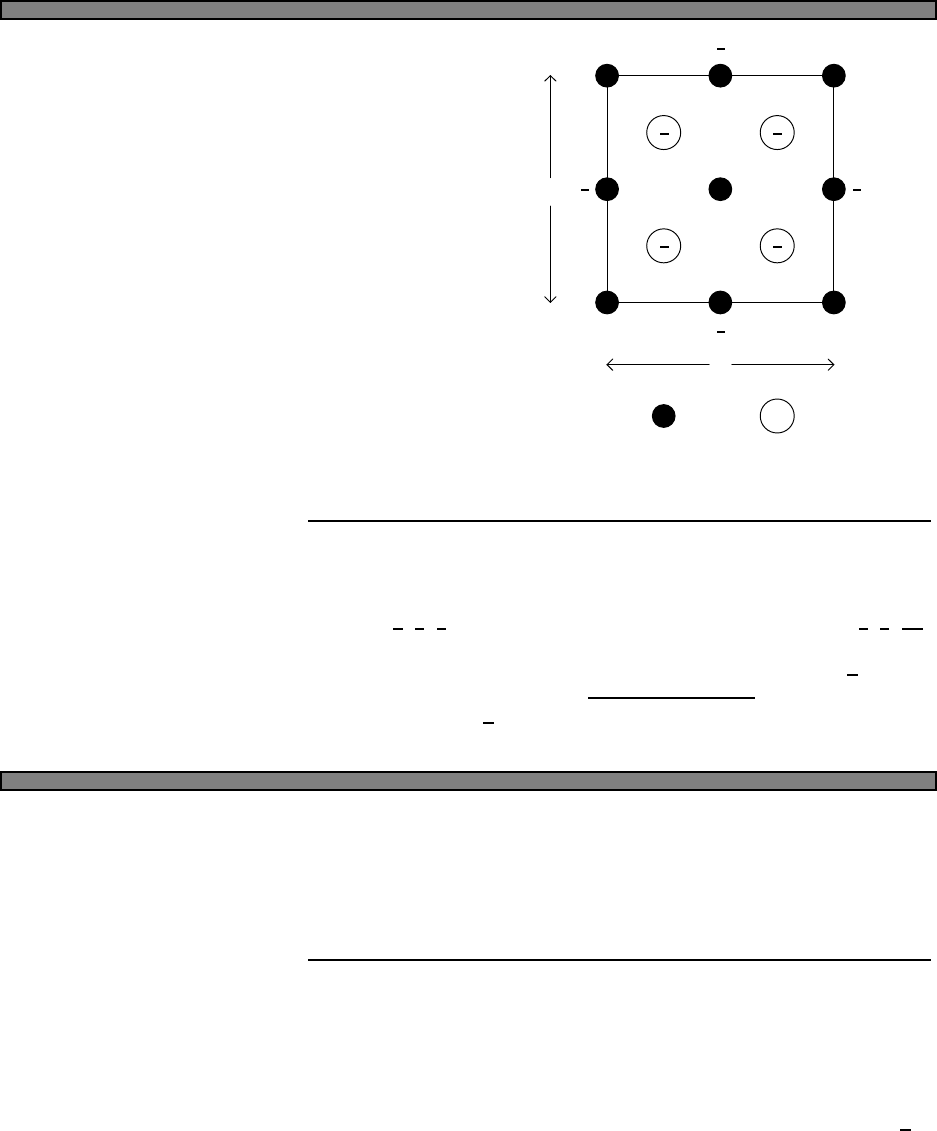
96 Crystal Structure
(12.3) Crystal Structure
The diagram of Fig. 12.22 shows a plan view of a
structure of cubic ZnS (zincblende) looking down the z
axis. The numbers attached to some atoms represent the
heights of the atoms above the z= 0 plane expressed as a
fraction of the cube edge a. Unlabeled atoms are at z= 0
and z=a.
(a) What is the Bravais lattice type?
(b) Describe the basis.
(c) Given that a= 0.541 nm, calculate the nearest-
neighbor Zn–Zn, Zn–S, and S–S distances.
1
4
3
4
3
4
1
4
1
2
1
2
1
2
1
2
a
a
Zn= S =
Fig. 12.23 Plan view of conventional unit cell of
zincblende.
(a) The lattice is FCC (otherwise known as ”cubic F”)
(b) The basis can be described as Zn at position [0,0,0] and S at
position [ 1
4,1
4,3
4] (or equivalently, but less standard notation [1
4,1
4,−1
4]
all in units of the lattice constant.
(c) (just a bit of geometry:) nearest neighbor Zn-Zn is a/√2 = 0.383
nm; nearest neighbor Zn-S is ap1/42+ 1/42+ 1/42= 0.234 nm; nearest
neighbor S-S is a/√2 = 0.383 nm;
(12.4) Packing Fractions
Consider a lattice with a sphere at each lattice point.
Choose the radius of the spheres to be such that neighbor-
ing spheres just touch (see for example, Fig. 12.8. The
packing fraction is the fraction of the volume of all of
space which is enclosed by the union of all the spheres
(i.e., the ratio of the volume of the spheres to the total
volume).
(a) Calculate the packing fraction for a simple cubic
lattice.
(b) Calculate the packing fraction for a bcc lattice.
(c) Calculate the packing fraction for an fcc lattice.
(a) The volume of a conventional unit cell is Vcell =a3. Each cell cor-
responds to a single sphere. The radius of this sphere is a/2 so its volume
is Vsphere = 4π/3(a/2)3. Thus the packing fraction is Vsphere/Vcell =
π/6≈.52.
(b) The volume of a conventional unit cell is Vcell =a3. Each conven-
tional unit cell contains two lattice points which are a distance a√3/2
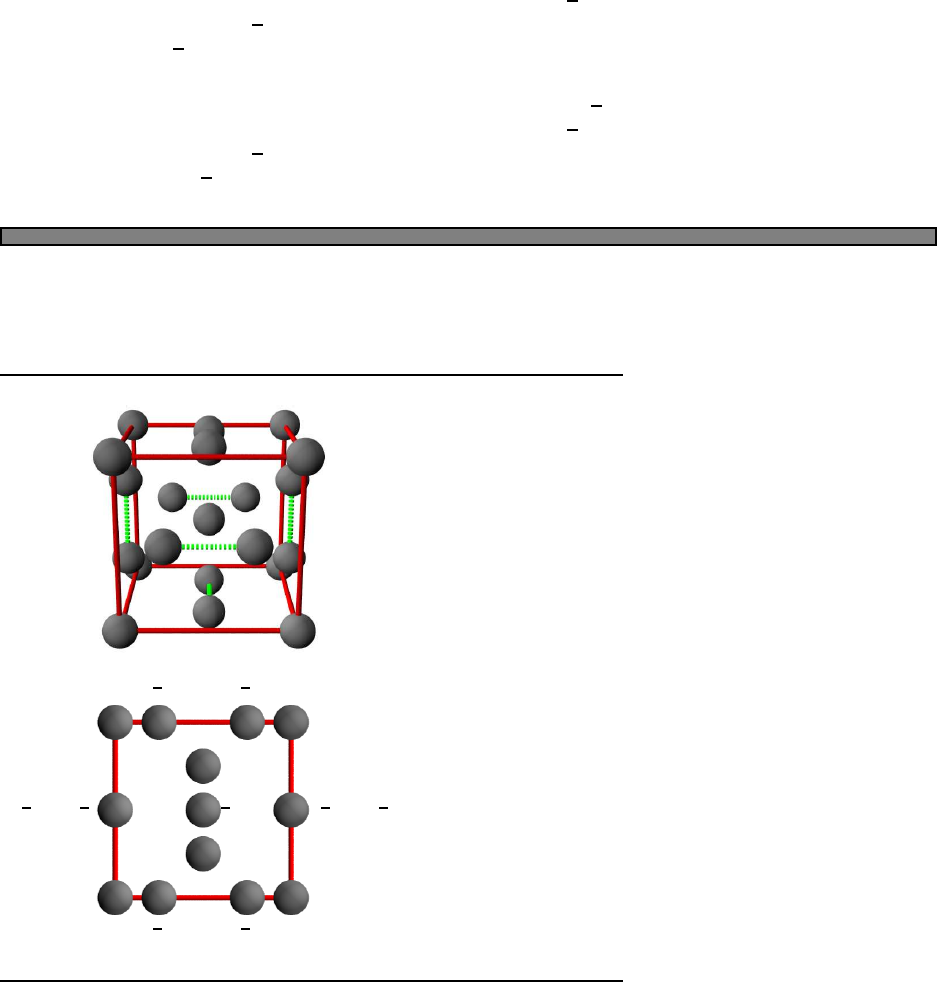
97
apart from each other. Thus the radius of the each sphere is a√3/4 so
has volume Vsphere = 4π(a√3/4)3/3. Thus we have a packing fraction
2Vsphere/Vcell =π√3/8≈.68
(c) The volume of a conventional unit cell is Vcell =a3. Each conven-
tional unit cell contains four lattice points which are a distance a√2/2
apart from each other. Thus the radius of the each sphere is a√2/4 so
has volume Vsphere = 4π(a√2/4)3/3. Thus we have a packing fraction
4Vsphere/Vcell =π/(3√2) ≈.74
(12.5) Fluorine Beta Phase
Fluorine can crystalize into a so-called beta-phase at
temperatures between 45 and 55 Kelvin. Fig. 12.24 shows
the cubic conventional unit cell for beta phase fluorine in
three-dimensional form along with a plan view.
How many atoms are in this conventional unit cell?
What is the lattice and the basis for this crystal?
1
2
1
2
1
2
1
2
1
2
1
4and 3
4
1
4and 3
4
Fig. 12.23 A conventional unit cell for fluorine beta
phase. All atoms in the picture are fluorine. Lines are
drawn for clarity Top: Three-dimensional view. Bottom:
Plan view. Unlabeled atoms are at height 0 and 1 in units
of the lattice constant.
There are 8 atoms in the conventional unit cell. 1 in the corner (8
times 1/8). Each atom on the face counts 1/2. Then there is one in the
center.
The lattice is simple cubic. The basis is
[0,0,0],[0,1/2,1/4],[0,1/2,3/4],[1/4,0,1/2],[3/4,0,1/2],[1/2,1/4,0],[1/2,3/4,0],[1/2,1/2,1/2]

Reciprocal Lattice,
Brillouin Zone, Waves in
Crystals 13
(13.1) Reciprocal Lattice
Show that the reciprocal lattice of a fcc (face-centered
cubic) lattice is a bcc (body-centered cubic) lattice. Cor-
respondingly, show that the reciprocal lattice of a bcc
lattice is an fcc lattice. If an fcc lattice has conventional
unit cell with lattice constant a, what is the lattice con-
stant for the conventional unit cell of the reciprocal bcc
lattice?
Consider now an orthorhombic face-centered lattice
with conventional lattice constants a1, a2, a3. What it
the reciprocal lattice now?
Brief Solution
Say we have an fcc lattice in real space. This can be written as cubic
with a basis R1= [0,0,0], and R2= [1/2,1/2,0] and R3= [1/2,0,1/2]
and R4= [0,1/2,1/2] in units of the lattice constant a. In reciprocal
space, we propose a basis for the reciprocal lattice which is S1= (0,0,0)
and S2= (1/2,1/2,1/2) in units of the reciprocal cubic lattice constant
4π/a. For these to be reciprocal, we must therefore have
ei2πRi·Sj= 1
for all iand jwhich is easy to check is true. Further, we can show that
given the fcc basis there is no third point that can be added to the bcc
basis which would still have the same property. Similarly, given the bcc
basis there is no fifth point we can add to the fcc basis.
For the orthorhombic face centered system one would similarly obtain
a reciprocal lattice which is an orthorhombic body centered systems with
basis vectors 4π/ai.
Detailed Solution
The more straightforward way to find the reciprocal lattice of a direct
lattice is by construction. Let us start with the direct lattice of the BCC
100 Reciprocal Lattice, Brillouin Zone, Waves in Crystals
lattice which has primitive lattice vectors
a1= [1,0,0]a
a2= [0,1,0]a
a3= [1/2,1/2,1/2]a
we then construct the primitive lattice vectors of the reciprocal lattice
via
bi=2πbfaj×ak
a1·a2×a3
with i, j, k cyclic. This gives
b1= (1/2,0,−1/2) 4π
a
b2= (0,1/2,−1/2) 4π
a
b3= (0,0,1) 4π
a
we can then reassemble these vectors to give the standard primitive
lattice vectors for FCC
b′
1=b1+b3= (1/2,0,1/2) 4π
a
b′
2=b2+b3= (0,1/2,1/2) 4π
a
b′
3=b1+b2+b3= (1/2,1/2,0) 4π
a
which shows us tht the fcc lattice has lattice constant 4π/a. NOTE
about making this transformation from binto b′. We are guaranteed
that that bare primitive lattice vectors. We assemble them together
with integer coefficients to make b′. However we must also be able to
reassemble the b′with integer coefficients to get back the bin order for
this to be an allowed transformation from one set of primitive lattice
vectors to another.
Slick Solution
Once one has read chapter 14 on scattering and selection rules, we
simply note that the selection rules on miller indices tell us the form
of the reciprocal lattice. For example, if the direct lattice is BCC, the
selection rule is that h+k+lis even. This means that either all h, k, l
are even or two are odd and one is even. Thus if we write
G(hkl) = 4π
ah
2ˆx+k
2ˆy+l
2ˆz
we must have either all h/2, k/2, l/2 integer or two half-odd integer and
one integer. This is precisely the condition we would use to define an
FCC lattice. The prefactor 4π/a then gives us the lattice constant.
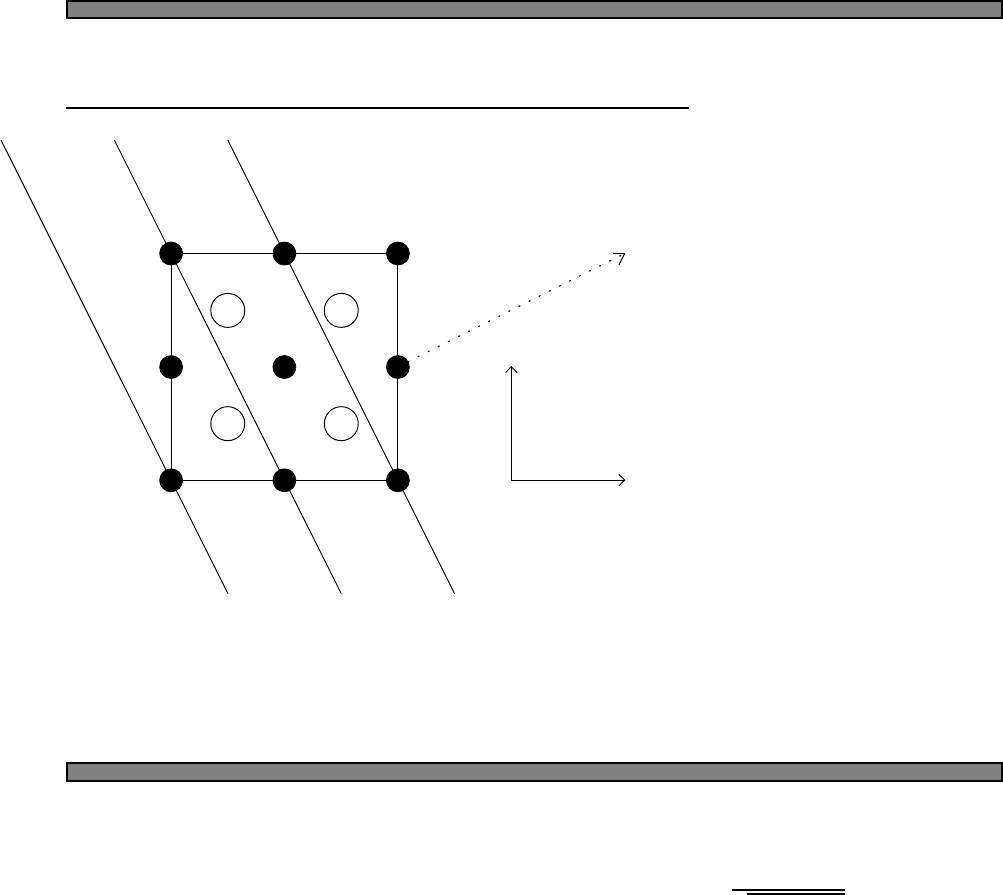
101
Similarly in reverse, if the direct space lattice is FCC, the selection
rule is h, k, l all even or all odd. This means (h/2, k/2, l/2) all integer or
all half-odd integer. This is precisely the condition for defining a BCC
lattice.
The moral of this story is that scattering occurs when (h, k, l) repre-
sents a reciprocal lattice vector. The selection rules tell you when this
is so.
(13.2) Lattice Planes
Consider the crystal shown in Exercise 12.3. Copy this
figure and indicate the [210] direction and the (210) fam-
ily of lattice planes.
x
y
(210) planes
[210]
NOTE: As drawn here this is a family of planes (it is a family of
lattice planes for the corresponding simple cubic). For the FCC to be
a family of lattice planes, it must have half the plane spacing so that it
is called (420) and it cuts though every lattice point. So the question is
not correctly written as it stands.
(13.3) Directions and Spacings of Crystal
Planes
‡Explain briefly what is meant by the terms “crys-
tal planes” and “Miller indices”.
Show that the general direction [hkl] in a cubic
crystal is normal to the planes with Miller indices (hkl).
Is the same true in general for an orthorhombic
crystal?
Show that the spacing dof the (hkl) set of planes
in a cubic crystal with lattice parameter ais
d=a
√h2+k2+l2
What is the generalization of this formula for an
orthorhombic crystal?
102 Reciprocal Lattice, Brillouin Zone, Waves in Crystals
Acrystal plane is a plane which intersects at least three non-colinear
(and therefore an infinite number of) points of the lattice.
Miller indices are a set of three integers which specify a set of parallel
planes (or equivalently specify a vector in reciprocal space). If the axes
of a lattice are mutually orthogonal , the Miller indices (hkl) specifies
the reciprocal lattice vector (2π)(hˆ
x/ax+kˆ
y/ay+lˆ
z/azwhere ax,ayand
azare the length of the three basis vectors. In terms of lattice planes,
one can determine the lattice vectors by picking any given plane from
the family, and finding its intersection points with the three coordinate
axes. These intersection points (kx,0,0) and (0, ky,0) and (0,0, kz) have
the property that they are in the ratios
h:k:l=1
kx
:1
ky
:1
kz
The actual values of h:k:lare then the smallest integer values with
these ratios. By convention note that negative numbers are denoted as
an integer with a bar on top, ex (1,1,¯
1) to denote (1,1,−1).
Let the basis vectors of the lattice be a,band c, assumed to be orthog-
onal. Let the lengths of these three lattice vectors be a, b, c respectively.
The plane (hkl) can be defined as the plane connecting the points a/h,
b/k and c/l. To construct a vector normal to this plane, take any two
(noncolinear) vectors in this plane and take their cross product
n= (a/h −b/k)×(a/h −c/l)
=abc
hkl h
a2a+k
b2b+l
c2c
This is only parallel to the vector [hkl] in the case of the cubic crystal
a=b=c.
Much more succinctly one could also note that for orthogonal axes,
bi= 2π/ai, and the family of lattice planes (hkl) is normal to the cor-
responding reciprocal lattice vector.
The unit normal in this direction is
ˆ
n=1
p(h/a)2+ (k/b)2+ (l/c)2h
a2a+k
b2b+l
c2c
To find the inter-planar spacing, take any vector that connects two ad-
jacent planes and find the component in the direction of the normal to
the plane. For example, the vector a/h connects two adjacent planes,
and we can resolve it parallel to nby taking the dot product with the
unit normal vector ˆ
n. Thus we obtain
dhkl =ˆ
n·a/h =1
p(h/a)2+ (k/b)2+ (l/c)2(13.1)
with the case a=b=cappropriate for cubic crystals.
Note: In cases where the axes are not orthogonal, this formula does
not work.

103
(13.4) ‡Reciprocal Lattice
(a) Define the term Reciprocal Lattice.
(b) Show that if a lattice in 3d has primitive lattice
vectors a1,a2and a3then primitive lattice vectors for
the reciprocal lattice can be taken as
b1= 2πa2×a3
a1·(a2×a3)(13.2)
b2= 2πa3×a1
a1·(a2×a3)(13.3)
b3= 2πa1×a2
a1·(a2×a3)(13.4)
What is the proper formula in 2d?
(c) Define tetragonal and orthorhombic lattices. For an
orthorhombic lattice, show that |bj|= 2π/|aj|. Hence,
show that the length of the reciprocal lattice vector
G=hb1+kb2+lb3is equal to 2π/d, where dis the
spacing of the (hkl) planes (see question 13)
(a) Given a lattice of points (in 3d it would look like R[uvw]=ua1+
va2+wa3with [uvw] integers), the reciprocal lattice is defined by the
set of points in kspace such that
eik·R= 1
for all points Rin the lattice . Note that this set of points forms a lattice
of values of k.
(b) If we take
b1= 2πa2×a3
a1·(a2×a3)
b2= 2πa3×a1
a1·(a2×a3)(13.5)
b3= 2πa1×a2
a1·(a2×a3)
Then we can show the key formula
bi·aj= 2πδij .
If these are our basis vectors for the reciprocal lattice, we then have a
general reciprocal lattice point given by
Ghkl =hb1+kb2+lb3(13.6)
with h, k, l integers. It is trivial to then see that
eiK·R= 1 (13.7)
for any lattice vector Rand any reciprocal lattice vector K. However,
this does not quite prove the desired statement. What it proves is that
vector Kof the form of Eq. 13.6 are in the reciprocal lattice. We need
to show that there are no other vectors in the reciprocal lattice as well
so that b1,b2, and b3can indeed be taken as the basis.

104 Reciprocal Lattice, Brillouin Zone, Waves in Crystals
To show this, consider an arbitrary vector Kof the form of Eq. 13.6
but do not require that h, k, l are integers. Given an arbitrary Ruvw of
the real space lattice, in order that Eq. 13.7 is satisfied, we must have
uk +vh +wl = integer
for this to be true for arbitrary u, v, w which are integers, we can conclude
that k, h, l are integers.
We can derive the 2d analogous formula by setting a3=ˆ
zthe unit
vector normal to the plane, more conveniently written as
b1= 2πa2׈z
ˆ
z·(a1×a2)
b2= 2πˆ
z×a1
ˆ
z·(a1×a2)
(c) A tetragonal lattice is a lattice (in 3d) where all three basis vectors
are normal to each other, and two of them are the same length but the
third is a different length. An orthorhombic lattice is a lattice (in 3d)
where all three basis vectors are normal to each other and all three have
different lengths. (Note: crystals may have orthorhombic or tetragonal
symmetry even if lattice constants in the three directions are all equal.
The symmetry of a crystal has to do with whether it looks the same
under various types of rotations. An orthorhombic crystal does not look
the same under the three 90 degree rotations – this may be the case even
if all three lattice constants are the same).
For an orthorhombic crystal, without loss of generality, let us write
a1=a1ˆ
xand a2=a2ˆ
yand a3=a3ˆ
z. We then just use the above
formula Eq. 13.5 to obtain
b1= 2πa2a3
a1a2a3
ˆ
y׈
z= 2πˆ
x/a1
b2= 2πa2a3
a1a2a3
ˆ
z׈
x= 2πˆ
y/a2
b3= 2πa2a3
a1a2a3
ˆ
x׈
y= 2πˆ
z/a3
So |bi|=2π/|ai|. Thus the length of G=hb1+kb2+lb3is given by
|Ghkl|=ph2|b1|2+k2|b2|2+l2|b3|2=p(2πh/a1)2+ (2πk/a2)2+ (2πl/a3)2= 2π/dhk
as given in Eq. 13.1.
(13.5) More Reciprocal Lattice
A two-dimensional rectangular crystal has a unit cell
with sides a1= 0.468 nm and a2= 0.342 nm.
(a) Draw to scale a diagram of the reciprocal lattice.
Label the reciprocal lattice points for indices in the
range 0 ≤h≤3 and 0 ≤k≤3.
(b) Draw the first and second Brillouin zones using the
Wigner–Seitz construction.
The reciprocal lattice vectors are b1= 2πˆ
x/|a1|, and b2= 2πˆ
y/|a2|.
Their magnitudes are
|b1|= 13.4nm−1|b2|= 18.4nm−1
105
(a) A diagram of the reciprocal lattice is given in the figure.
Fig. 13.1 Figures for problem 13. First Two Brillouin Zones. Red is the 1st Zone.
Blue is the 2nd zone.
To find the Brillouin zones, one first constructs perpendicular bisectors
between the origin and any given lattice point (shown as dotted lines on
the plot). Then starting at the origin, the region one can get to without
crossing a dotted line is the first zone. Crossing only one dotted line
gets one to the second zone. etc.
(13.6) Brillouin Zones
(a) Consider a cubic lattice with lattice constant a.
Describe the first Brillouin zone. Given an arbitrary
wavevector k, write an expression for an equivalent
wavevector within the first Brillouin zone (there are sev-
eral possible expressions you can write).
(b) Consider a triangular lattice in two dimensions
(primitive lattice vectors given by Eqs. 12.3). Find the
first Brillouin zone. Given an arbitrary wavevector k(in
two dimensions), write an expression for an equivalent
wavevector within the first Brillouin zone (again there
are several possible expressions you can write).
(a) The reciprocal lattice of a cubic lattice with lattice constant a
is a cubic lattice with lattice constant 2π/a. The first Brillouin zone
is a cube centered around the origin in reciprocal space (0,0,0), with
side length 2π/a. It spans kx, ky, kz∈[−π/a, π/a]. Given an arbitrary
k= (kx, ky, kz) we can write the equivalent wavevector as (k′
x, k′
y, kz)′
where
k′
j=kj−[[(kj+π/a)/(2π/a)]] ∗2π/a (13.8)
with j=x, y, z and [[ ]] is the floor function – meaning the greatest
integer less than its argument. The point of Eq. 13.8 is that it takes kin
units of the reciprocal lattice constant (2π/a) and returns a number be-
tween -1/2 and +1/2 of the reciprocal lattice constant by appropriately
106 Reciprocal Lattice, Brillouin Zone, Waves in Crystals
adding or subtracting integer units of 2π/a.
(b) Start with the primitive lattice vectors
a1=aˆx
a2= (a/2)ˆx + (a√3/2)ˆy
We need to find vectors b1,b2such that ai·bj= 2πδi,j . One way to
do this is to use the usual 3d formula
b1= 2πa2×a3
a1·(a2×a3)
b2= 2πa3×a1
a1·(a2×a3)
b3= 2πa1×a2
a1·(a2×a3)
then assigning a3=ˆz. The denominator is a2√3/2. Thus we have
b1= 2π[(a√3/2)ˆx −(a/2)ˆy]/(a2√3/2) = (2π/a)[ˆx −(√3/3)ˆy]
b2= 2πˆya/(a2√3/2) = (2π/a)ˆy(2√3/3)
These form the primitive lattice vectors of a triangular lattice in k-space.
The first Brillouin zone is the Wigner-Seitz cell of the reciprocal lattice
— which is a hexagon centered around zero wavevector (see fig 12.6 of
the book).
Two write a formula that translates any kinto the first Brillouin zone,
we first write any kpoint in terms of the primitive lattice vectors
k=α1b1+α2b2
We are going to need to solve for αiin terms of k. To do this we write
k·b1=α1|b1|2+α2b1·b2
k·b2=α1b1·b2+α2|b2|2
and we will want to solve for the αs. In this particular case, things are
quite easy since |b1|2=|b2|2=−2b1·b2= (2π/a)2(4/3). So this
becomes
βk·b1=α1−α2/2
βk·b2=−α1/2 + α2
where we have defined
β=3
4
a2
(2π)2
Solving this system of equations we obtain
α1= (β/3)(2k·b1+k·b2)
α2= (β/3)(k·b1+ 2k·b2)

107
Now to obtain αwithin the first brillouin zone we need to shift both
α’s by integers until they lie in the range [−1/2,1/2]. To do this we
write
α′
j=αj−[[αj+ 1/2]]
again with [[ ]] being the floor function. Once we have α′’s we construct
k′=α′
1b1+α′
2b2
which is now within the first Brillouin zone.
(13.7) Number of States in the Brillouin Zone
A specimen in the form of a cube of side Lhas a primi-
tive cubic lattice whose mutually orthogonal fundamental
translation vectors (primitive lattice vectors) have length
a. Show that the number of different allowed k-states
within the first Brillouin zone equals the number of prim-
itive unit cells forming the specimen. (One may assume
periodic boundary conditions, although it is worth think-
ing about whether this still holds for hard-wall boundary
conditions as well.)
We are given a cubic lattice with lattice constant aand an overall size
Lon a size. The number of atoms in this sample are N= (L/a)3. It
is simplest to assume periodic boundary conditions. Since eikx(x+L)=
eikxxwe must have kx= 2πn/L for nan integer. Thus (considering all
three directions) there is one eigenstate per volume (2π/L)3in k-space.
The first Brillouin zone extends from −π/a ≤kx, ky, kz≤π/a. This
has volume in k-space of (2π/a)3. Dividing this by the volume occupied
by one eigenstate gives a total of (L/a)3states in the first Brillouin zone.
This agreement is not coincidental. If one thinks in a tight-binding or
atomic orbital picture, there should be exactly one orbital per atom per
band when hopping is turned off. Once hopping is turned back on, each
atomic orbital spreads into a band that fills the Brillouin zone, but the
total number of states stays constant.
One can also consider the same problem with hard wall boundary
conditions, although it is less convenient. In this case the eigenstates
are not of the form eikx but are rather sin(kx) where k > 0, so one is
not really talking about pure plane waves. In this case the analogue of
the Brillouin zone goes from 0 ≤kx, ky, kz≤π/a, but the density of
kstates is doubled, k=π/L in each direction, so the total number of
states remains the same as using periodic boundary conditions.

108 Reciprocal Lattice, Brillouin Zone, Waves in Crystals
(13.8) Calculating Dispersions in d > 1*
(a) In Exercises 9.8 and 11.9 we discussed dispersion
relations of systems in two dimensions (if you have not
already solved those exercises, you should do so now).
In Exercise 11.9 describe the Brillouin zone (you
may assume perpendicular lattice vectors with length a1
and a2). Show that the tight-binding dispersion is peri-
odic in the Brillouin zone. Show that the dispersion curve
is always flat crossing a zone boundary.
In Exercise 9.8, describe the Brillouin zone. Show
that the phonon dispersion is periodic in the Brillouin
zone. Show that the dispersion curve is always flat cross-
ing a zone boundary.
(b) Consider a tight binding model on a three-
dimensional fcc lattice where there are hopping matrix
elements −tfrom each site to each of the nearest-neighbor
sites. Determine the energy spectrum E(k) of this model.
Show that near k=0the dispersion is parabolic.
(a) [First see solutions for 9.8 and 11.9]
In Exercise 11.9, for a rectangular lattice with lattice vectors of length
a1and a2the reciprocal lattice is rectangular with lattice vectors of
length b1= (2π)/a1and b2= (2π)/a2. The Brillouin zone is hence a
rectangle extending between kx∈[−π/a1, π/a1] and ky∈[−π/a2, π/a2].
Given the derived dispersion
E=ǫ0−2t1cos(kxa1)−2t2cos(kya2)
at the zone boundary, the cos is at its maximum, and its derivative is
zero. Thus the dispersion is always flat approaching the zone boundary.
In Exercise 9.8 we have a triangular lattice, whose reciprocal lattice is
also triangular and has a Wigner-Seitz cell which is hexagonal (see exer-
cise 13.6.b also). Note also the figures shown in the solution of 9.8 which
clearly show the hexagonal periodicity of the dispersion curve. Note that
the dispersion must be symmetric as kapproaches the zone boundary.
Let the zone boundary wavevector be bi/2 + k⊥where k⊥·bi= 0.
Imagine approaching the zone boundary via k=αbi/2 + k⊥and taking
αto one. Note that the dispersion must be symmetric around α= 1
since (by reflection symmetry of the problem) the frequency at kis the
same as the frequency at k′=−αbi/2 + k⊥. However, one can translate
this by a reciprocal lattice vector to get (2 −α)bi/2 + k⊥which is the
same point reflected around the zone boundary. Thus, so long as the
dispersion does not have a cusp at the zone boundary, it must have zero
derivative.
Recall from Eq. 9.8 that the derived freuquency spectrum is
ω2=2κ
mS1+S2+S3±qS2
1+S2
2+S2
3−S1S2−S1S3−S2S3
where
Si= sin2(k·ai
2)
where aiare three independent vectors along the lattice. In terms of
primitive lattice vectors here we can take a1and a2to be primitive
lattice vector, and then a3=a2−a1.
109
The frequency is an analytic function in kso long as the argument of
the square-root is nonzero. By rewriting the argument as
1
2(S1−S2)2+ (S2−S3)2+ (S3−S1)2
it is clear the argument must be nonzero except at k=0. Thus we can
conclude that the dispersion is analytic and symmetric around the zone
boundary and therefore must have zero slope. This may seem like a bit
of a cheat, but it is perfectly rigorous.
For those who would prefer to see this statment proven a bit more
directly, we take the following approach. Let us start with the primitive
lattice vectors
a1=aˆx
a2= (a/2)ˆx + (a√3/2)ˆy
Recall that the reciprocal lattice vectors (see 13.6.b) are given by
b1= 2π[(a√3/2)ˆx −(a/2)ˆy]/(a2√3/2) = (2π/a)[ˆx −(√3/3)ˆy]
b2= 2πˆya/(a2√3/2) = (2π/a)ˆy(2√3/3)
For simplicity let us imagine approachig the zone boundary
k=αb2/2 + k⊥
(the other zone boundaries will be the same by symmetry). Here the
direction orthogonal to b2is b1+b2/2. So we can write k⊥=β(b1+
b2/2) for some value of β. We then have (using ai·bj= 2πδij for
i, j ∈1,2)
k·a1= (β+α)π
k·a2=β2π
k·a3= (β−α)π
Now let us examine the terms in the dispersion. In particular we are
concerned with the dependence of the dispersion on αnear α= 1. Again
all we need to do is to show that the dispersion is symmetric and analytic
around α= 1. Here S2is independent of αso we are not concerned with
that piece. Using sin2(x/2) = (1 −cos(x))/2 we have that
S1= [1 −cos((β+α)π)]/2
S2= [1 −cos((β−α)π)]/2
The cos is periodic in α→α±2, and reflection of αaround 1 (i.e.,
α→2−α) turns S1into S2, hence leaves the freqeuncy unchanged.
Thus we have the dispersion symmetric and analytic around the zone
boundary, thus having zero slope.
(b) For an fcc lattice, if the conventional unit cell has lattice constant
a, the vectors to the 12 nearest neighbors of a lattice point are given by
110 Reciprocal Lattice, Brillouin Zone, Waves in Crystals
(see exercise 12.2)
[±1,±1,0]a/2
[±1,0,±1]a/2
[0,±1,±1]a/2
Thus we have the schroedinger equation (setting the onsite energy ǫ0to
zero for simplicity)
Eψ(r) = −tX
u
ψ(r+u)
where the sum is over ubeing these 12 vectors. Using the usual ansatz
ψ(r) = Aeik·rwe obtain
E=−tX
α=±1,β=±1heik·[α,β,0]a/2+eik·[α,0,β]a/2+eik·[0,α,β]a/2i
or
E=−4t[cos(kxa/2) cos(kya/2) + cos(kxa/2) cos(kza/2) + cos(kya/2) cos(kza/2)]
Expanding around k= 0 to second order we obtain
E=−12t+tk2
x+k2
y+k2
z(a2) + ...
which is parabolic as claimed.
Wave Scattering by
Crystals 14
(14.1) Reciprocal Lattice and X-ray Scattering
Consider the lattice described in Exercise 13.5 (a two-
dimensional rectangular crystal having a unit cell with
sides a1= 0.468 nm and a2= 0.342 nm). A collimated
beam of monochromatic X-rays with wavelength 0.166 nm
is used to examine the crystal.
(a) Draw to scale a diagram of the reciprocal lattice.
(b) Calculate the magnitude of the wavevectors kand
k′of the incident and reflected X-ray beams, and hence
construct on your drawing the “scattering triangle” cor-
responding to the Laue condition ∆k=Gfor diffraction
from the (210) planes (the scattering triangle includes k,
k′and ∆k).
A diagram of the reciprocal lattice is given in the figure. The scatter-
Fig. 14.1 A picture of the reciprocal Lattice with the scattering triangle for the
(210) reciprocal wavevector.
ing triangle is the triangle such that |k|=|k′|and k+G=|k′|(Note
for fixed Gthere are two such possible triangles).
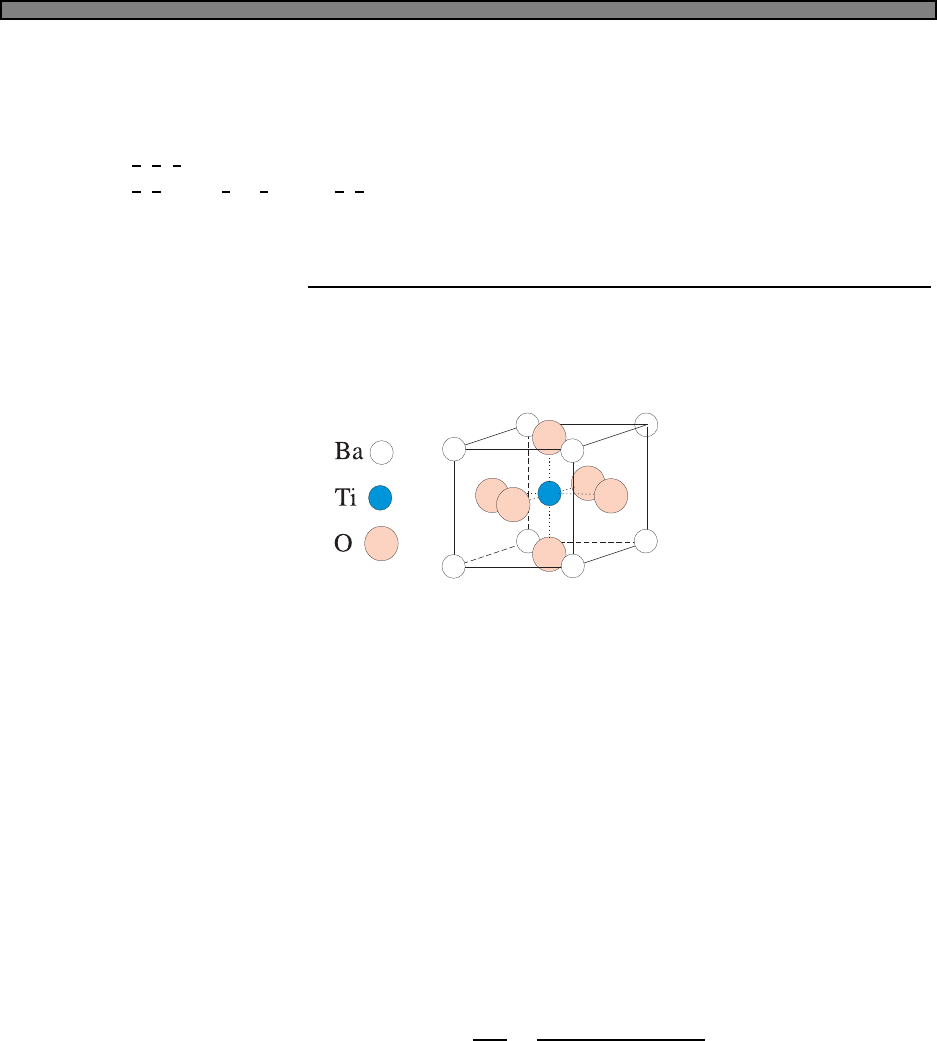
112 Wave Scattering by Crystals
(14.2) ‡X-ray scattering II
BaTiO3has a primitive cubic lattice and a basis with
atoms having fractional coordinates
Ba [0,0,0]
Ti [ 1
2,1
2,1
2]
O [ 1
2,1
2,0], [ 1
2,0,1
2], [0,1
2,1
2]
Sketch the unit cell.
Show that the X-ray structure factor for the (00l)
Bragg reflections is given by
S(hkl)=fBa + (−1)lfT i +h1 + 2(−1)lifO
where fBa is the atomic form factor for Ba, etc.
Calculate the ratio I(002)/I(001), where I(hkl)is the
intensity of the X-ray diffraction from the (hkl) planes.
You may assume that the atomic form factor is propor-
tional to atomic number (Z), and neglect its dependence
on the scattering vector. (ZBa = 56, ZTi = 22, ZO= 8.)
Fig. 14.2 Unit cell of BaTiO3
The X-ray structure factor is given by
S(hkl)=X
d
fdeik(hkl)·Rd=X
d
fde2πi(hxd+kyd+lzd)
where Rd= (xd, yd, zd) are the positions of atom din the unit cell, and
fdit the corresponding form factor (which we take to be proportional
to Zd). If we are interested in (00l) we set h=k= 0 and obtain
S(00l)=fBa + (−1)lfT i + [1 + 2(−1)l]fO
The Bragg peak intensity is proportional to the square of the structure
factor (times a multiplicity factor, but the multiplicity for all (00l) are
the same!), thus we obtain
I002
I001
=(fBa +fT i + 3fO)2
(fBa−fT i −fO)2≈15.4
In reality the form factor depends on the scattering vector, and the
variation is different from each atom, so this is just an approximation.

113
(14.3) ‡X-ray scattering and Systematic Ab-
sences
(a) Explain what is meant by “Lattice Constant” for a
cubic crystal structure.
(b) Explain why X-ray diffraction may be observed in
first order from the (110) planes of a crystal with a body-
centered cubic lattice, but not from the (110) planes of a
crystal with a face-centered cubic lattice.
Derive the general selection rules for which planes
are observed in bcc and fcc lattices.
(c) Show that these selection rules hold independent of
what atoms are in the primitive unit cell, so long as the
lattice is bcc or fcc respectively.
(d) A collimated beam of monochromatic X-rays of
wavelength 0.162 nm is incident upon a powdered sample
of the cubic metal palladium. Peaks in the scattered X-
ray pattern are observed at angles of 42.3◦, 49.2◦, 72.2◦,
87.4◦, and 92.3◦from the direction of the incident beam.
Identify the lattice type.
Calculate the lattice constant and the nearest-
neighbor distance.
If you assume there is only a single atom in the ba-
sis does this distance agree with the known data that the
density of palladium is 12023 kg m−3? (Atomic mass of
palladium = 106.4.)
(e) How could you improve the precision with which
the lattice constant is determined. (For one suggestion,
see Exercise 14.10.)
(a) For a cubic lattice, the lattice constant is the distance between
one lattice point and the nearest neighbor lattice point.
(b) The (110) planes of a body-centred cubic lattice contain all the
lattice points, whereas the (110) planes of a crystal with a face-centred
cubic lattice contain only half the lattice points. The remaining fcc
lattice points lie on a set of planes half-way in between the (110) planes,
and so X-rays reflected from these planes interfere destructively with
X-rays reflected from the (110) planes.
Let us see this more analytically now:
We view both the bcc and fcc lattices as being a cubic lattice with a
basis. For a cubic lattice, we must have khkl = (2π/a)(hˆ
x+kˆ
y+lˆ
z) (or
in other words we consider reciprocal lattice vectors (h, k, l).)
Generally we sum over lattice points Riin a unit cell to get the struc-
ture factor
S(hkl)∼X
Ri
eiRi·k(hkl)
The bcc lattice is a cubic lattice with a basis (0,0,0) and (1/2,1/2,1/2).
So we obtain
Sbcc
(hkl)∼1 + eik(hkl)·[(1/2)ˆ
x+(1/2)ˆ
y+(1/2)ˆ
z]= 1 + (−1)h+k+l
This is only nonzero when h+k+l= even.
The fcc lattice is a cubic lattice with with basis (0,0,0) and (1/2,1/2,0)
and (1/2,0,1/2) and (0,1/2,1/2). Analogously we obtain
Sfcc
(hkl)∼1 + (−1)h+k+ (−1)h+l+ (−1)k+l
This is only nonzero when h, k, l are either all even or all odd.
Note that these selection rules hold for an orthorhombic lattice as
well as for cubic (nowhere did we use the lattice constants in the three

114 Wave Scattering by Crystals
directions!).
(c) This is the general principle that you multiply a lattice by a basis.
Suppose we have a Bravais lattice (either fcc or bcc) and then we have
a basis of matoms which are at positions rj(j= 1,...m) with respect
to the lattice points. These atoms may have scattering form factors fj
as well.
As above, we treat the Bravais lattice as a cubic lattice with a basis
Ri(i=1,2 for bcc and i= 1 ...4 for fcc). So positions of all of the atoms
(2mor 4mof them) in the full cubic unit cell can be written as
Rij =Ri+rj
Writing the structure factor
S(hkl)=X
i,j
fjeik(hkl)Rij =X
j
fj"X
i
eik(hkl)Ri#eik(hkl)rj(14.1)
The factor inside the brackets is exactly the structure factor for the Bra-
vais lattice as calculated above. So if the fcc structure factor vanishes,
then the structure will also vanish for any lattice having an fcc lattice
with any basis.
(d) Note that the angle given is 2θ(the full deflection angle)! We are
given 2θthen we use Bragg’s law λ= 2dsin θto get the distance between
lattice planes. We then examine the ratio’s between these distances.
2θd=λ/(2 sin θ) (dmax/d)2aestimate =d√h2+k2+l2
42.3◦.224 nm 1 .389 nm
49.2◦.195 nm 1.33 .389 nm
72.2◦.137 nm 2.66 .389 nm
87.4◦.117 nm 3.67 .389 nm
92.3◦.112 nm 4.00 .389 nm
we see that the values of 1/d2are in ratios 3:4:8:11:12. Recall (see
problem 13.3) that for a cubic lattice (a2/d2) = h2+k2+l2. So the
observed peaks are of the types (1,1,1), (2,0,0), (2,2,0), (1,1,3), and
(2,2,2). These are all even or all odd, which is characteristic of the fcc
lattice. All measured scattering points give the same estimate of the
lattice constant ato three digits (which is the same number of digits
that the measurement contains... so no higher accuracy estimate can be
made from this data).
m3
12023 kg
.1064 kg
6.022 ×1023 atoms = 1.4682 ×10−29m3/atom
Then for an fcc there are 4 atoms per unit cell, so the volume of the unit
cell is 5.872 ×10−29m3. The cube root of this gives 3.887 nm which is
in good agreement. An equivalent calculation is to calculate the density

115
based on the lattice constant
4∗.1064 kg
6.022 ×1023 atoms 1
.389 ×10−9m3
= 12006 kg/m3
in good agreement.
(e) to improve the precision of the measurement one would need to ob-
tain more “digits” of resolution in the measurement of the angle. There
are several things that will help this. From Bragg’s law d∼1/sin θso
1
d
∂d
∂θ = cot θ
So if there is an error in measurement of θone ends up with a fractional
error in dgiven by
δlog d= (cot θ)(δθ)
As a result, error is minimized if one can work as close as possible to
scattering angle of 90 degrees (See exercise 14.10).
In addition some experimental issues can be listed. A higher bright-
ness source will frequently reduce the noise and make the signal easier to
analyze. Better columnation will make measurements of angle more pre-
cise. At least as important is the calibration of the device that measures
the angles! Defining the wavelength λmore precisely becomes necessary
at some point. Temperature control is necessary since lattice constants
do change as a function of temperature due to thermal expansion.
(14.4) ‡Neutron Scattering
(a) X-ray diffraction from sodium hydride (NaH) estab-
lished that the Na atoms are arranged on a face-centered
cubic lattice.
Why is it difficult to locate the positions of the H
atoms using X-rays?
The H atoms were thought to be displaced from the Na
atoms either by [ 1
4,1
4,1
4] or by [ 1
2,1
2,1
2], to form the ZnS
(zincblende) structure or NaCl (sodium chloride) struc-
ture, respectively. To distinguish these models a neutron
powder diffraction measurement was performed. The in-
tensity of the Bragg peak indexed as (111) was found to
be much larger than the intensity of the peak indexed as
(200).
Write down expressions for the structure factors
S(hkl)for neutron diffraction assuming NaH has
(i) the sodium chloride (NaCl) structure
(ii) the zinc blende (ZnS) structure.
Hence, deduce which of the two structure mod-
els is correct for NaH. (Nuclear scattering length of Na
= 0.363 ×105nm; nuclear scattering length of H =
−0.374 ×105nm.)
(b) How does one produce monochromatic neutrons for
use in neutron diffraction experiments?
What are the main differences between neutrons
and X-rays?
Explain why (inelastic) neutron scattering is well
suited for observing phonons, but X-rays are not.
[This problem is based on a classic experiment by Shull et al, who
later won a Nobel prize for his work on neutron scattering]
Note, the scattering length should be in units of 10−5nm not 105nm.
It doesn’t change the problem much though.
It is difficult to see H atoms with X-rays since the form factor (am-
plitude) of scattering is proportional to the charge of the nucleus (the
atomic number), and the charge of H is very small.

116 Wave Scattering by Crystals
From Eq. 14.1 above we have
S(hkl)= X
i
eik(hkl)Ri!
X
j
bjeik(hkl)rj
where jare the elements of the basis and iare the 4-elements of the fcc
lattice basis when fcc is viewed as a cubic lattice with a basis. Here I have
replaced fjby bjwhich is the conventional notation for the scattering
length (which is analogous to the form factor in X-rays) in neutron
scattering. Note that the first factor in brackets is the scattering from
the fcc lattice which always gives (See problem 14)
Sfcc
hkl = (1 + eiπ(h+k)+eiπ(k+l)+eiπ(h+l))
For the case of the NaCl structure, we have a basis of Na at [0,0,0]
and H at [1/2,1/2,1/2]. So we obtain
S(hkl)= (1 + eiπ(h+k)+eiπ(k+l)+eiπ(h+l))(bNa +bHeiπ(h+k+l))
For the case of the ZnS structure we have a basis of Na at [0,0,0] and
H at [1/4,1/4,1/4] so we obtain
S(hkl)= (1 + eiπ(h+k)+eiπ(k+l)+eiπ(h+l))(bNa +bHei(π/2)(h+k+l))
The powder scattering intensity is proportional to the structure factor
squared times a multiplicity factor that counts how many symmetry re-
lated vectors give the same scattering pattern. The multiplicity of (111)
is 8 (since each factor of 1 could have been ¯
1), whereas the multiplicity
of (200) is 6 since the 2 could be of either sign, and any one of the 3
entries could contain the 2.
Thus we obtain in the NaCl case a ratio of scattering intensities
I(111)
I(200)
=(bNa −bH)2
(bNa +bH)2
8
6= 6000
whereas in the ZnS case we have
I(111)
I(200)
=(b2
Na +b2
H)
(bNa −bH)2
8
6= 0.67
Thus we conclude that NaH has NaCl structure.
(b) Two typical schemes for producing monochromatic neutrons. (1)
time of flight (a ”chopper”) can select a particular velocity (2) Bragg
scattering of a given angle off of a crystal can select a particular wave-
length.
The main things to know about the differences between X-rays and
neutrons are:
X-rays are scattered by electrons. The electromagnetic interaction is
relatively strong, and so X-rays typically penetrate only a few microns
into a sample. The intensity of scattering varies with the atomic form

117
factor f(∆k), which approximately scales with the number of electrons
in the atom.
Neutrons, on the other hand, are electrically neutral, and so interact
weakly with matter. They penetrate typically a few cm into materi-
als. Neutrons may scatter from nuclei (via the strong nuclear force)
or unpaired electrons (via the magnetic dipole-dipole interaction). The
diffraction theory is the same as for X-rays, except that for scattering
from nuclei the atomic form factor f(∆k) is replaced by the nuclear scat-
tering length b, which is independent of ∆k. (Note, we typically make
the approximation that fis independent of ∆k, to make calculations
easier, but it is not really such a good approximation. In the neutron
case, it really is a good approximation because the scattering is essen-
tially off of a point nucleus). The scattering length bvaries irregularly
from nucleus to nucleus so that the scattering from light elements is sim-
ilar in strength to that from heavy elements. Neutrons can thus easily
see small atoms, and can easily distinguish atoms with similar atomic
number.
Magnetic neutron diffraction can also be used to determine magnetic
structures (in which case there is a form factor similar to that for X-
rays).
The reason inelastic scattering of neutrons is more useful than X-rays
for studying phonons is because the X-ray velocity (velocity of light)
is huge. This makes it very difficult to conserve both momentum and
energy in any inelastic process involving light since a very small mo-
mentum change corresponds to a huge energy change. Although with
modern tools measurement of phonons using X-rays is now possible.
(14.5) And More X-ray Scattering
A sample of aluminum powder is put in an Debye–
Scherrer X-ray diffraction device. The incident X-ray ra-
diation is from Cu–Ka X-ray transition (this just means
that the wavelength is λ= .154 nm). The following scat-
tering angles were observed:
19.48◦22.64◦33.00◦39.68◦41.83◦50.35◦57.05◦59.42◦
Given also that the atomic weight of Al is 27, and the
density is 2.7 g/cm3, use this information to calculate
Avagadro′s number. How far off are you? What causes
the error?
Note: The angles listed are θnot 2θhere. If you use 2θby mistake

118 Wave Scattering by Crystals
you will discover that the ratios of dvalues do not make sense!
θ d =λ/(2 sin θ) (dmax/d)2aestimate =d√h2+k2+l2
19.48◦.2309 nm 1 .3999 nm
22.64◦.2000 nm 1.33 .4001 nm
33.00◦.1414 nm 2.67 .3999 nm
39.68◦.1206 nm 3.66 .4000 nm
41.83◦.1155 nm 4.00 .4000 nm
50.35◦.1000 nm 5.33 .4000 nm
57.05◦.0918 nm 6.33 .4000 nm
59.42◦.0894 nm 6.66 .4000 nm
From the third column we see that we have an fcc lattice. From the
final column we conclude the conventional lattice constant is about .4000
nm. There are four atoms per unit cell, so we would predict an atomic
density of 4/(4nm)3= 6.28 ×1028m−3. On the other hand, with atomic
weight of 27 and density 2.7 g/cm3we predict an atomic density of
NA×105m−3with NA= 6.022 ×1023 being Avagadro’s number. (Or
in other words, our slighly inaccurate prediction of Avagadro’s number
is 6.28 ×1023). So we are off by abour 4%. Where does the error come
from? There are a few possible places. First, the atomic mass is not
quite 27, it is actually about 26.982 (depending a bit on isotopic abun-
dances, but this is typical). But this is an error of much less than an
percent. Probably the biggest possible error is that the density changes
as a function of temperature. If the density is measured at one tem-
perature, but the lattice constant is measured at another temperature,
then there can be a substantial disagreement. In fact the linear thermal
expansion coefficient of aluminum is about (22 ×10(−6))K−1which
would give a density different between T= 0 and room temperature of
a few percent (and indeed, the measurements could even be done above
room temperature!). In the literature X-ray measurements of the lattice
constant of alumium give numbers of about .404 nm at room tempera-
ture (which would match the stated density much more closely). Thus I
suspect the data given above was measured at low temperature, hence
the disagreement.
(14.6) More Neutron Scattering
The conventional unit cell dimension for a particular
bcc solid is .24nm. Two orders of diffraction are observed.
What is the minimum energy of the neutrons? At what
temperature would such neutrons be dominant if the dis-
tribution is Maxwell–Boltzmann.
For bcc, the lowest two order diffraction peaks are the (110) and the
(200). The corresponding plane spacings are
d=a/ph2+k2+l2
119
Or d=a/√2 and d=a/2. Using Bragg’s law,
d=λ/(2 sin θ)
the wavelength must be at least as small as 2din order to see a particular
peak. Or in other words λ≤a=.24nm. The corresponding energy of
neutrons is
E=~2k2
2mn
=~2(2π)2
2mnλ2= 2.28 ×10−21J
and
E/kB= 165K
(14.7) Lattice and Basis
Prove that the structure factor for any crystal (de-
scribed with a lattice and a basis) is the product of the
structure factor for the lattice times the structure factor
for the basis (i.e., prove Eq. 14.14).
We have the definition of the structure factor
S(hkl)=X
atoms jin (conventional) unit cell
fje2πi(hxj+kyj+lzj)
When we have a lattice and a basis, all of the positons rjof atoms jin
the unit cell can be written as the sum of a lattice point Raand a basis
vector uα. Thus we can write
rj=Ra+uα
and the sum over jbecomes a sum over aand α. Thus we have
S(hkl)=X
α,a
fαe2πi(h(Rx,a+ux,α )+k(Ry,a +uy,α)+l(Rz,a+uz,α ))
Note that the atom type depends only on the basis vector not on the
lattice point. We split this sum into two
S(hkl)=X
α
fαe2πi(hux,α)+kuy,α +luz,α)X
a
e2πi(hRx,a+kRy,a +lRz,a)
which is simply the product of basis and lattice structure factors
S(hkl)=Sbasis
(hkl)Slattice
(hlk)
120 Wave Scattering by Crystals
(14.8) Cuprous Oxide and Fluorine Beta
(a) The compound Cu2O has a cubic conventional unit
cell with the basis:
O [000] ; [ 1
2,1
2,1
2]
Cu [ 1
4,1
4,1
4] ; [ 1
4,3
4,3
4] ; [ 3
4,1
4,3
4] ; [ 3
4,3
4,1
4]
Sketch the conventional unit cell. What is the lattice
type? Show that certain diffraction peaks depend only
on the Cu form factor fCu and other reflections depend
only on the O form factor fO.
(b) Consider fluorine beta phase as described in exer-
cise 12.5. Calculate the structure factor for this crystal.
What are the selection rules?
(a) the conventional unit cell of Cu2O is shown in Figure 14.3.
The structure factor is
S(hkl)=fO(1 + eiπ(h+k+l))
+fCu heiπ
2(h+k+l)+eiπ
2(h+3k+3l)+eiπ
2(3h+k+3l)+eiπ
2(3h+3k+l)i
Note that sqaure bracketed expression can be simplified to
eiπ
2(h+k+l)h1 + eiπ(k+l)+eiπ(h+l)+eiπ(k+l)i
Note that the coefficient of f0vanishes unless h+k+lis even. Indeed,
Fig. 14.3 Conventional unit cell of
Cu2O. The darker atoms at the corners
and the center are O and the lighter col-
ored atoms are Cu.
this tells us that the oxygens alone form a bcc lattice. The coefficient of
the fCu vanish unless h, k, l are all even or all odd, which tells us that
the Cu alone form an fcc lattice (perhaps less obvious!). Thus peaks
such as (110) depend only on fOwheras peaks such as (111) depend
only on fCu.
(b) From 12.5 the basis of Flourine beta is
[0,0,0],[0,1/2,1/4],[0,1/2,3/4],[1/4,0,1/2],
[3/4,0,1/2],[1/2,1/4,0],[1/2,3/4,0],[1/2,1/2,1/2]
The structure factor is then
1 + eiπk+iπl/2+eiπk+iπ3l/2+eiπl+iπh/2+eiπl+iπ3h/2
+eiπh+iπk/2+eiπh+iπ3k/2+eiπ(h+k+l)
which can be simplified to
1 + (−1)h+k+l+ (−1)k[il+i−l] + (−1)l[ih+i−h] + (−1)h[ik+i−k]
Note that the first two terms cancel if h+k+lis odd and otherwise
give 2. Let us examine the last three terms. Note that
ik+i−k=
0l= odd
2l= 0 mod 4
−2l= 2 mod 4

121
Thus we obtain the following rules for (hkl) where the structure factor
does not vanish
one even two odd if the even one is 2 mod 4
one odd two even if the two even indices are not the same mod 4
all even with either one or all three indices being 2 mod 4
(14.9) Form Factors
(a) Assume that the scattering potential can be written
as the sum over the contributions of the scattering from
each of the atoms in the system. Write the positions of
the atoms in terms of a lattice plus a basis so that
V(x) = X
R,α
Vα(x−R−yα)
where Rare lattice points, αindexes the particles in the
basis and yαis the position of atom αin the basis. Now
use the definition of the structure factor Eq. 14.5 and de-
rive an expression of the form of Eq. 14.8 and hence derive
expression 14.9 for the form factor. (Hint: Use the fact
that an integral over all space can be decomposed into a
sum over integrals of individual unit cells.)
(b) Given the equation for the form factor you just de-
rived (Eq. 14.9), assume the scattering potential from an
atom is constant inside a radius aand is zero outside that
radius. Derive Eq. 14.10.
(c)* Use your knowledge of the wavefunction of an elec-
tron in a hydrogen atom to calculate the X-ray form factor
of hydrogen.
(a) Start with 14.5
S(G) = Zunitcell
dx eiG·xV(x) = X
R,α Zunitcell
dx eiG·xVα(x−R−yα)
we then using eiG·R= 1 we have
S(G) = X
R,α Zunitcell
dx eiG·(x−R)Vα(x−R−yα)
Now we note that the integral dx over a unit cell summed over all
possible unit cells indexed by Ris equivalent to a single integral over all
of space, so we have
S(G) = X
αZdx eiG·xVα(x−yα) = X
αZdx eiG·(x+yα)Vα(x)
=X
α
eiG·yαfα(G)
with
fα(G) = Zdx eiG·xVα(x)
as required.
(b) Assuming the potential is V0inside a radius aand zero outside we
have
fα(G) = V0Zradius=a
0
dx eiG·x= 2πV0Za
0
r2dr Zsin θdθeirGcosθ
122 Wave Scattering by Crystals
where θis the angle between xand G. So we have
fα(G) = 2πV0Za
0
r2dr Z1
−1
dzeirGz = 2πV0Za
0
r2dr 2 sin(rG)
rG
= 4πV0a3sin(x)−xcos(x)
x3
where x=Ga. Now comparing this to 14.10, it looks identical except for
the prefactor. Note however, that the charge of atom is spread out over
a volume 4πa3/3. So setting V04πa3/3 = Zmakes the two equations
match.
(c) The normalized wavefunction for an electron in the ground state
of a hydrogen atom is
ψ=1
√4π
2
a3/2
0
e−r/a0
with a0the Bohr radius. The scattering potential is proportional to the
electron density |ψ|2. Let us call the constant of proportionality K. We
then have (using similar calculation as above)
f(G) = KZdx eiG·x|ψ(r)|2=K2πZ∞
0
r2dr 2 sin(rG)
rG |ψ(r)|2
So we want
f(G) = 2K
a3
0Z∞
0
r2dr 2 sin(rG)
rG e−2r/a0
The integration is not too difficult and gives the result
f(G) = 16K
(a2
0G2+ 4)2
(14.10) Error Analysis
Imagine you are trying to measure the lattice constant
aof some crystal using X-rays. Suppose a diffraction peak
is observed at a scattering angle of 2θ. However, suppose
that the value of θis measured only within some uncer-
tainty δθ. What is the fractional error δa/a in the result-
ing measurement of the lattice constant? How might this
error be reduced? Why could it not be reduced to zero?
See 14.3.e.
(e) From Bragg’s law d∼1/sin θso
1
d
∂d
∂θ = cot θ
So if there is an error in measurement of θone ends up with a fractional
error in dgiven by
δlog d= (cot θ)(δθ)
As a result, error is minimized if one can work as close as possible to
scattering angle of 90 degrees. Although at 90 degrees one could have

123
this expression be exactly zero. However, this does not mean the error
is actually zero. One has only made the error in measurement zero to
lowest order. One also has to worry about higher derivative term
1
d
∂2d
∂θ2= 1 6= 0
at 90 degrees.

Electrons in a Periodic
Potential 15
(15.1) ‡Nearly Free Electron Model
Consider an electron in a weak periodic potential in one
dimension V(x) = V(x+a). Write the periodic potential
as
V(x) = X
G
eiGxVG
where the sum is over the reciprocal lattice G= 2πn/a,
and V∗
G=V−Gassures that the potential V(x) is real.
(a) Explain why for knear to a Brillouin zone bound-
ary (such as knear π/a) the electron wavefunction should
be taken to be
ψ=Aeikx +Bei(k+G)x(15.1)
where Gis a reciprocal lattice vector such that |k|is close
to |k+G|.
(b) For an electron of mass mwith kexactly at a zone
boundary, use the above form of the wavefunction to show
that the eigenenergies at this wavevector are
E=~2k2
2m+V0± |VG|
where Gis chosen so |k|=|k+G|.
Give a qualitative explanation of why these two
states are separated in energy by 2|VG|.
Give a sketch (don’t do a full calculation) of the
energy as a function of kin both the extended and the
reduced zone schemes.
(c) *Now consider kclose to, but not exactly at, the
zone boundary. Give an expression for the energy E(k)
correct to order (δk)2where δk is the wavevector differ-
ence from kto the zone boundary wavevector.
Calculate the effective mass of an electron at this
wavevector.
(a) A periodic lattice can only scatter a wave by a reciprocal lattice
vector (Bragg diffraction). In the nearly free electron picture, the scat-
tering perturbation is weak, so that we can treat the scattered wave in
perturbation theory. In this case, there is an energy denominator which
suppresses mixing of k-vectors which have greatly different unperturbed
energies. Thus, the only mixing that can occur is between two states
with similar energies that are separated by a reciprocal lattice vector.
Degenerate perturbation theory tells us that we should first diagonalize
within the degenerate space spanned by only these two eigenstates.
(b)We have our (variational) trial wavefunction given by
|ψi=A|ki+B|k+Gi(15.2)
or equivalently
ψ= (Aeikx +Bei(k+G)x)/√L
To maintain normalization we can insist that |A|2+|B|2= 1. Taking k
and k+Gboth on a Brillouin zone boundary we have k=nπ/a and k+

126 Electrons in a Periodic Potential
G=−nπ/a, where here we have chosen the nth zone boundary, and we
must have G=−2nπ/a the reciprocal lattice vector. The Hamiltonian
Hin question is the usual Kinetic term plus V(x).
Approach 1: Diagonalize Hwithin the 2d degenerate space
hk|H|ki=~2(nπ/a)2/(2m) + V0
hk+G|H|k+Gi=~2(nπ/a)2/(2m) + V0
hk|H|k+Gi=V2nπ/a
hk+G|H|ki=V−2nπ/a
Diagonalizing this two by two matrix
~2(π/a)2/(2m) + V0V2nπ/a
V−2nπ/a ~2(π/a)2/(2m) + V0
gives eigenstates
E=~2(nπ/a)2
2m+V0± |V2nπ/a|
where we have used VG=V∗
−G. The eigenstates are correspondingly
|ψ±i=|ki+|k+Gi
which are (proportional to) the functions sin(2nπx/a) and cos(2nπx/a).
Interpretation: If we have considered only the V2nπ/a and V−2nπ/a
Fourier modes of the potential then we have V= 2V2nπ/a cos(2nπr/a).
Assuming V2nπ/a >0, then the higher energy state is the ψ= cos(2nπr/a)
which puts the maximum amplitude of the wavefunction exactly at the
maxima of the potential. Similarly, the lower energy wavefunction is the
sin(2nπr/a) which has the minimum amplitude of the wavefunction at
the maximum of the potential. In the case of V2nπ/a <0 the sin is the
higher energy wavefunction.
Approach 2: Variational.
If we simply calculate the expectation value of Hin the trial state
given by Eq. 15.2 we obtain
hψ|H|ψi=~2(nπ/a)2/(2m) + V0+A∗B V ∗
2nπ/a +B∗A V2nπ/a
Using the variational principle, the eigenstate is the trial wavefunction
which minimizes the total energy while preserving the normalization.
One way to do this is to write A= cos(θ) and B=eiχ sin(θ) which is
the most general form we can write while still preserving |A|2+|B|2= 1
(we can arbitrarily choose Ato be real, since that only introduces an
irrelevant overall phase). In terms of these parameters we have
hψ|H|ψi=~2(nπ/a)2/2m+V0+ 2Re[V2nπ/aeiχ sin(θ) cos(θ)]
for V2nπ/a >0 this is minimized for χ=πand θ=π/4 (or equiv-
alently χ= 0 and θ= 3π/4). It gives minimum energy states for
ψ= sin(2nπr/a) as above.
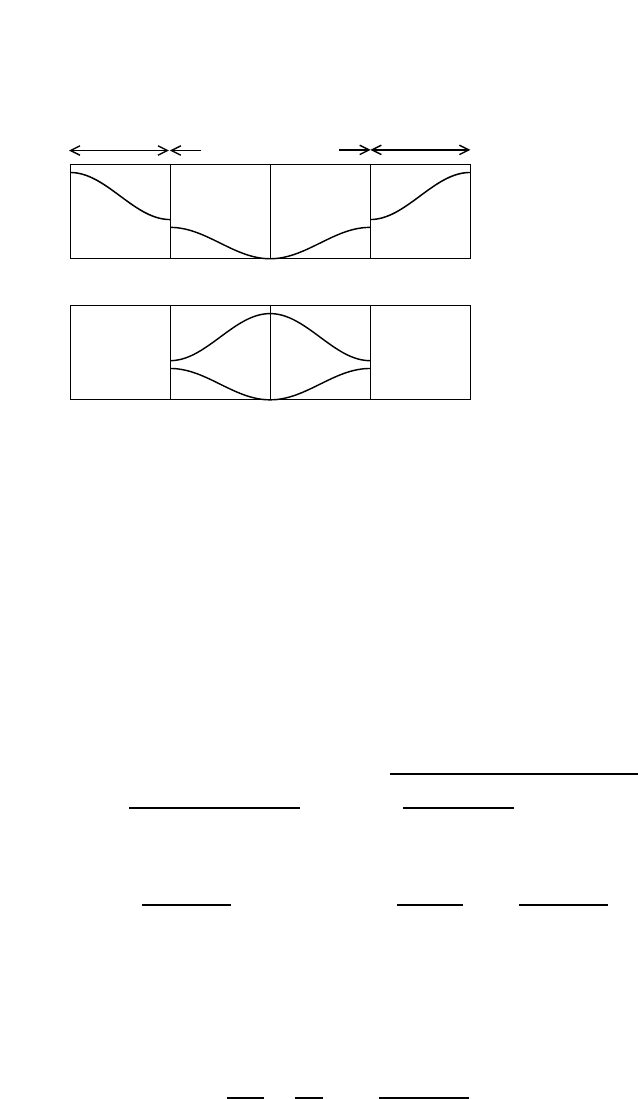
127
See figure 15.1 for a sketch of the bands in the extended zone scheme.
0
0π/a
π/a
−π/a
−π/a
2π/a
2π/a
−2π/a
−2π/a
Reduced
Zone
Scheme
Scheme
Zone
Extended
1st Brillouin Zone
2nd Zone 2nd Zone
Fig. 15.1 Diagram of the dispersion in a nearly free electron model. Top: extended
zone scheme. Bottom: reduced zone scheme. Note that gaps open up at all zone
boundaries
(c) This calculation is entirely analogous to that above, only here we
need to consider knot on the zone boundary. Letting k=nπ/a +δk
and k+G=−nπ/a +δk we have
hk|H|ki=~2(δk +nπ/a)2/(2m) + V0
hk+G|H|k+Gi=~2(δk −nπ/a)2/(2m) + V0
hk|H|k+Gi=V2nπ/a
hk+G|H|ki=V−2nπ/a
which we now need to diagonalize. We obtain
E±=~2[(δk)2+ (nπ/a)2]
2m+V0±s~22(δk)nπ/a
2m2
+|V2nπ/a|2
expanding the square-root we obtain
E±=~2(nπ/a)2
2m+V0± |V2nπ/a|+~2(δk)2
2m1±~2(nπ/a)2
m|V2nπ/a|
which is a quadratic correction as we move away from the Brillouin
zone. Note that for this expansion to remain valid we must have the
bracketed term in the square root two equations up small compared to
the |V2nπ/a|2term.
The effective mass is then obtained by setting
1
2m∗=1
2m1±~2(nπ/a)2
m|V2nπ/a|

128 Electrons in a Periodic Potential
or equivalently
m∗=
m
1±~2(nπ/a)2
m|V2nπ/a |
with the + being for the upper band.
(15.2) Periodic Functions
Consider a lattice of points {R}and a function ρ(x)
which has the periodicity of the lattice ρ(x) = ρ(x+R).
Show that ρcan be written as
ρ(x) = X
G
ρGeiG·x
where the sum is over points Gin the reciprocal lattice.
Generally we can always write ρ(x) in terms of its Fourier transform
ρ(x) = VZdk
(2π)3ρkeik·x
Now by periodicity we know that ρ(x) = ρ(x+R) for any lattice vector
R, so let us take a sum over all Nlattice vectors in the system
ρ(x) = 1
NX
R
ρ(x+R) = V
NX
RZdk
(2π)3ρkeik·(x+R)
=V
NZdk
(2π)3ρkeik·xX
R
eik·R
The sum gives X
R
eik·R=(2π)3
vX
G
δ3(k−G)
where the sum is over all Gwhich are reciprocal lattice vectors and vis
the volume of the unit cell. Letting the delta function act and cancelling
some factors, we then directly obtain
ρ(x) = X
G
eiG·xρG
(15.3) Tight Binding Bloch Wavefunctions
Analogous to the wavefunction introduced in Chapter
11, consider a tight-binding wave ansatz of the form
|ψi=X
R
eik·R|Ri
where the sum is over the points Rof a lattice, and |Ri
is the ground-state wavefunction of an electron bound to
a nucleus on site R. In real space this ansatz can be
expressed as
ψ(r) = X
R
eik·Rϕ(r−R).
Show that this wavefunction is of the form required by
Bloch’s theorem (i.e., show it is a modified plane wave).

129
Start by writing the function ϕin its fourier representation
ϕ(r) = VZdq
(2π)3eiq·rϕq
so that
ψ(r) = X
R
eik·RVZdq
(2π)3eiq·(r−R)ϕq
The sum over Rgives
X
R
ei(k−q)·R=(2π)3
vX
G
δ3(k−q−G)
and we allow the delta function to act, giving
ψ(r) = eik·rV
vX
G
e−iG·rϕk−G
The sum over Gis a function periodic in r→r+R(since eiG·R= 1)
hence this is in Bloch form.
(15.4) *Nearly Free Electrons in Two Dimen-
sions Consider the nearly free electron model for a square
lattice with lattice constant a. Suppose the periodic po-
tential is given by
V(x, y) = 2V10[cos(2πx/a) + cos(2πy/a)]
+ 4V11[cos(2πx/a) cos(2πy/a)]
(a) Use the nearly free electron model to find the energies
of states at wavevector G= (π/a, 0).
(b) Calculate the energies of the states at wavevec-
tor G= (π/a, π/a). (Hint: You should write down a 4
by 4 secular determinant, which looks difficult, but actu-
ally factors nicely. Make use of adding together rows or
columns of the determinant before trying to evaluate it!)
Note, we should not call the points (π/a, 0) and (π/a, π/a) as Gsince
they are not reciprocal lattice vectors!
(a) The first part of this problem is no different from the one di-
mensional problem posed in 15.1! The fourier components V10 couple
(π/a, 0) and (−π/a, 0). The energies of the states are
E=~2(π/a)2/(2m)± |V10|
(b) The second part of the problem is more complicated. Here, all four
points (±π/a, ±π/a) all have the same energy and are coupled together
by the scattering potential. Therefore we must treat all of these states
in degenerate perturbation theory. Let us label the points
|1i= (+π/a, +π/a)
|2i= (+π/a, −π/a)
|3i= (−π/a, −π/a)
|4i= (−π/a, +π/a)

130 Electrons in a Periodic Potential
Writing a general wavefunction within this space as Piφi|iithe Hamil-
tonian matrix within this reduced Hilbert space is
ǫ V10 V11 V10
V10 ǫ V10 V11
V11 V10 ǫ V10
V10 V11 V10 ǫ
where ǫ=~2(π/a)2/m. To find the eigenenergies we would thus like to
solve the determinant equation
0 =
ǫ−E V10 V11 V10
V10 ǫ−E V10 V11
V11 V10 ǫ−E V10
V10 V11 V10 ǫ−E
Adding and subtracting rows and columns leaves the determinant un-
changed. So we can subtract row 3 from row 1 and subtract row 4 from
row 2. Then add column 3 to column 1 and add column 4 to column 2.
The result is
0 =
0 0 V11 −ǫ+E0
0 0 0 V11 −ǫ+E
V11 +ǫ−E2V10 ǫ−E V10
2V10 V11 +ǫ−E V10 ǫ−E
Because of all the zeros, method of minors can then evaluate the deter-
minant easily to given
0 = (V11 −ǫ+E)2(V11 +ǫ−E)2−4V2
10
Thus giving solutions
E=ǫ+V11 (two solutions)
E=ǫ−V11 ±2|V10|
(15.5) Decaying Waves
As we saw in this chapter, in one dimension, a peri-
odic potential opens a band gap such that there are no
plane-wave eigenstates between energies ǫ0(G/2) − |VG|
and ǫ0(G/2) + |VG|with Ga reciprocal lattice vector.
However, at these forbidden energies, decaying (evanes-
cent) waves still exist. Assume the form
ψ(x) = eikx−κx
with 0 < κ ≪kand κreal. Find κas a function of energy
for k=G/2. For what range of VGand Eis your result
valid?
Here, we can think of the wavevector kas taking an imaginary part
(i.e., absorb κinto k)
k=−G/2 + iκ
131
so that
ǫ0(k) = ~2k2
2m=~2((G/2)2−iGκ −κ2)
2m=ǫR−iǫI
ǫ0(k+G) = ~2(k+G)2
2m=~2((G/2)2+iGκ −κ2)
2m=ǫR−iǫI
where we have defined
ǫR=~2((G/2)2−κ2)
2m
ǫI=~2(Gκ)
2m
As worked out in the text (Eq. 15.8), the characteristic equation is
0 = (ǫ0(k)−E) (ǫ0(k+G)−E)− |VG|2
= (ǫR−iǫI−E)(ǫR+iǫI−E)− |VG|2
= (ǫR−E)2+ǫ2
I− |VG|2(15.3)
Thus, we have
E=ǫR±q|VG|2−ǫ2
I
Note here that for |ǫI|>|VG|the energy becomes imaginary and the
solution is not valid. Thus we must have
|VG| ≥ |~2Gκ/(2m)|
In Eq. 15.3 we have a quadratic equation for κ2(there are no lone factors
of κ), which can be solved to then give only one (possibly) positive
solution
~2κ2
2m=−~2(G/2)2
2m−E+r4E~2(G/2)2
2m+|VG|2
In order for this solution to be valid, we must have the right hand side
be positive. We can write this condition as
~2(G/2)2
2m+E2
≤4E~2(G/2)2
2m+|VG|2
Or equivalently
~2(G/2)2
2m−E≤ |VG|
or in other words, that the energy is inside the gap!
(15.6) Kronig–Penney Model*
Consider electrons of mass min a so-called “delta-
function comb” potential in one dimension
V(x) = aU X
n
δ(x−na)

132 Electrons in a Periodic Potential
(a) Argue using the Schroedinger equation that in-
between delta functions, an eigenstate of energy Eis al-
ways of a plane wave form eiqExwith
qE=√2mE/~.
Using Bloch’s theorem conclude that we can write an
eigenstate with energy Eas
ψ(x) = eikx uE(x)
where uE(x) is a periodic function defined as
uE(x) = Asin(qEx) + Bcos(qEx) 0 < x < a
and uE(x) = uE(x+a) defines uoutside of this interval.
(b) Using continuity of the wavefunction at x= 0 de-
rive
B=e−ika[Asin(qEa) + Bcos(qEa)],
and using the Schroedinger equation to fix the disconti-
nuity in slope at x= 0 derive
qEA−eikak[Acos(qEa)−Bsin(qEa)] = 2maUB/~2
Solve these two equations to obtain
cos(ka) = cos(qEa) + mUa
~2qE
sin(qEa)
The left-hand side of this equation is always between −1
and 1, but the right-hand side is not. Conclude that there
must be values of Efor which there are no solutions of the
Schroedinger equation—hence concluding there are gaps
in the spectrum.
(c) For small values of the potential Ushow that this
result agrees with the predictions of the nearly free elec-
tron model (i.e., determine the size of the gap at the zone
boundary).
Oops another error in this problem. Actually this one is really bad.
The first part of the problem should ask you to show that
ψ(x+a) = eikaψ(x)
and it should be ψthat has the form Asin(qx) + Bcos(qx) not u. Then
in the second to last equation there is an extra random factor of kin
front of the brackets, it should be qEnot k. AND the exponent is e−ika.
. Probably too many martinis.
(a) Bloch’s theorem tells us
ψ(x) = eikxu(x)
with uperiodic in the unit cell. This then implies ψ(x+a) = eikaψ(x)
as required.
Between delta functions, there is no potential so the solution must be
plane waves e±iqEx. Since the Hamiltonian is time reversal invariant we
can choose the wavefunction to be real. As a result, we must have ψof
the form Asin(qEx) + Bcos(qEx).
(b) Using ψ(a+) = eikaψ(0) = Beika and ψ(a−) = Asin(qEa) +
Bcos(qEa) gives the required result immediately. The Schroedinger
equation evaluated near x=a
~2
2m∂2
xψ(x) = aUδ(x−a)ψ(x)
is equivalent to
~2
2m∂xψ(a+)−∂xψ(a−)=aUψ(a)
133
Using
ψ(a) = Beika
∂xψ(a+) = eikaqEA
∂xψ(a−) = qE[Acos(qEa)−Bsin(qEa)]
gives the desired result which now reads (after removing errors!)
A−e−ika[Acos(qEa)−Bsin(qEa)] = 2maU B/(qE~2)
The two equations (with errors removed) have the required solution.
(c) First we note that for G=π/a, we have
VG=1
LZdxV (x)eiGx =1
LX
n
Ua =U
Note this is true also at V0=U, so we expect an overall energy shift
of U(from V0) and then a gap of magnitude 2|U|opening at the zone
boundary as well.
Setting k=π/a and qE=k+δwe have
−1 = cos(±π+δa) + mU a
~2(π/a +δ)sin(π+δ)
Expanding for small δand solving to lowest order we get two solutions
δ= 0 or 2mUa
~2π
Substituting back into E=~2(π/a +δ)2/(2m) we obtain
E=E0or E0+ 2U
giving the gap of 2|U|at the zone boundary as expected (and the mid-
point of the gap shifted up by Udue to V0as well).

Insulator, Semiconductor,
or Metal 16
(16.1) Metals and Insulators
Explain the following:
(a) sodium, which has two atoms in a bcc (conventional
cubic) unit cell, is a metal;
(b) calcium, which has four atoms in a fcc (conventional
cubic) unit cell, is a metal;
(c) diamond, which has eight atoms in a fcc (conven-
tional cubic) unit cell with a basis, is an electrical insula-
tor, whereas silicon and germanium, which have similar
structures, are semiconductors. (Try to think up several
possible reasons!)
Why is diamond transparent?
(a) The conventional bcc unit cell contain 2 atoms, but the primitive
unit cell contains only a single atom. Thus sodium, as a monovalent
atom, results in a half-filled 1st BZ – and thus gives a metal.
(b) The conventional fcc unit cell contains 4 atoms, but the primitive
unit cell contains only one atom. So calcium, which is divalent, could
be either a metal or an insulator — depending on the strength of the
periodic potential. The fact that it is a metal tells us that the potential
is not strong enough to make it an insulator.
(c) C,Si, and Ge are group IV elements and are therefore 4-valent.
The fcc unit cell has 4 atoms, but the primitive unit cell has 1 atom,
and therefore 4 electrons. This could therefore constitute 2 completely
filled bands. In the case of C (diamond) this is indeed an insulator with
a large band gap (5.5 eV). For Si and Ge, the band gap is smaller (1.1
eV and .67 eV respectively), hence they are semiconductors.
There are various explanations for this effect. One argument is that
for carbon, the periodic potential is extremely strong (no inner shell
electrons to screen it, and atoms much closer together) therefore it is
an insulator with a large band gap. For Si and Ge, the potential is less
strong, so the gap is smaller. Hence they are semiconductors.
Another argument is given by thinking in the tight binding picture.
Before you bring the atoms together to make a solid, one needs to con-
sider single-electron orbitals. The higher orbitals in an atom are typically
closer together in energy (as they are for hydrogen). For C the valence
electrons are in the 2p shell whereas for Si and Ge, the valence electrons
are 3p and 4p respectively. Hence we expect smaller gaps for Si and Ge.
In a more chemical language, 4 electrons per atom can therefore form
4 covalent bonds with each of the 4 neighbors in the diamond lattice

136 Insulator, Semiconductor, or Metal
structure. The electrons are all therefore tied up in covalent bonds,
making the material an insulator.
Diamond is transparent because it is an insulator with band gap that
is larger than any visible light frequency. Thus light cannot be absorbed
(or reflected) by any electronic transition.
(16.2) Fermi Surface Shapes
(a) Consider a tight binding model of atoms on a (two-
dimensional) square lattice where each atom has a single
atomic orbital. If these atoms are monovalent, describe
the shape of the Fermi surface.
(b) Now suppose the lattice is not square, but is rect-
angular instead with primitive lattice vectors of length
axand ayin the xand ydirections respectively, where
ax> ay. In this case, imagine that the hoppings have
a value −txin the x-direction and a value −tyin the y-
direction, with ty> tx. (Why does this inequality match
ax> ay?)
Write an expression for the dispersion of the elec-
tronic states ǫ(k).
Suppose again that the atoms are monovalent, what
is the shape of the Fermi surface now?
(a) The dispersion of the tight binding model is given by
ǫ(kx, ky) = −2t(cos(kxa) + cos(kya))
A contour plot of this energy is given in the left of Fig. 16.1. If we are
considering a monovalent unit cell, then the Brillouin zone is half filled.
This then gives a Fermi surface in the shape of a diamond, as shown in
the right of Fig. 16.1.
-3 -2 -1 012 3
-3
-2
-1
0
1
2
3
-3 -2 -1 012 3
-3
-2
-1
0
1
2
3
Fig. 16.1 Left: Dispersion of a 2D tight binding model on a square lattice. Right:
the Fermi surface for one electron per unit cell.
(b) If ax> ayone expects the hopping magnitude to be smaller in
the xdirection since the atoms are further apart (although this is not
holy, as the orbitals, such as pxorbitals, may not be isotropic). We then
expect a dispersion of the form
ǫ(kx, ky) = −2txcos(kxax)−2tycos(kyay)

137
As an example, let us choose ty= 2txbut ax=ay=afor simplicity.
A contour plot of the energy is given in the left of Fig. 16.2. If we are
considering a monovalent unit cell, then the Brillouin zone is half filled.
This then gives a Fermi surface in the shape of ... well, i’m not sure
what to call it. But it is shown in the right of Fig. 16.2.
-3 -2 -1 012 3
-3
-2
-1
0
1
2
3
-3 -2 -1 012 3
-3
-2
-1
0
1
2
3
Fig. 16.2 Left: Dispersion of a 2D tight binding model on a square lattice with
anisotropic hoppings. Right: the corresponding Fermi surface for one electron per
unit cell.
(16.3) More Fermi Surface Shapes*
Consider a divalent atom, such as Ca or Sr, that forms
an fcc lattice (with a single atom basis). In the absence
of a periodic potential, would the Fermi surface touch the
Brillouin zone boundary? What fraction of the states in
the first Brillouin zone remain empty?
This is some nasty geometry. First, recall that the reciprocal lattice
of an FCC lattice with lattice constant ais a BCC lattice with lattice
constant 4π/a (See excercise 13.1). The BCC lattice has two lattice
points per conventional unit cell, so the primitive unit cell (or the Bril-
louin zone in this case) has volume 1
2(4π/a)3in k-space. Now since we
have a divalent unit cell in real space, we should have enough electrons
to fill exactly the volume of the Brillouin zone. Thus for electrons in the
absence of a periodic potential we have
4πk3
F
3=1
24π
a3
≈992/a3
or
kF= (24π2)1/3/a ≈6.187/a
We would like to know if this hits the Brillouin zone boundary or not.
For a BCC lattice, the nearest neighbor of the point [0,0,0] is the point

138 Insulator, Semiconductor, or Metal
[1/2,1/2,1/2] in units of the lattice constant. The perpendicular bisector
to this point is thus a distance √3/4. For our reciprocal lattice with
lattice constant 4π/a, the distance to this perpendicular bisector (i.e.,
to the Brillouin zone boundary) is then
dk =π√3/a ≈5.441/a
which is less than the Fermi wavevector, thus telling us that the Fermi
surface hits the Brillouin zone boundary (it is obvious that it must hit
the Brillouin zone boundary since the volume of the fermi surface must
equal the volume of the Brillouin zone and they are not the same shape!).
The Fermi surface thus goes into the 2nd Brillouin zone as a spherical
cap of radius 6.187/a where the Brillouin zone boundary is of radius
5.441/a. Note that the center of this spherical cap is in the Ldirection
(in the language of Brillouin zones, see fig 13.6 of the book). We should
check that the spherical cap remains on the L-face. We can check this
by noting that the angle subtended by this spherical cap is only θ=
cos−1(5.441/6.187) ≈28.425 degrees, which is much smaller than the
angle to say the Kpoint.
The height of the spherical cap is h= 6.187/a −5.441/a = 0.745/a.
A well known geometric formula gives us that the volume of a cap is
V=πh2
3(3r−h) = 10.4/a3
However, note that we have 8 such spherical caps in all of the 8 equivalent
Ldirections, thus giving a total volume of
V= 83/a3
in the 2nd Brillouin zone, compared to the total volume of the fermi
surface which is 992/a3. Thus the caps in the second Brillouin zone
account for roughly 8% of the filled states.
Semiconductor Physics 17
(17.1) Holes
(a) In semiconductor physics, what is meant by a hole
and why is it useful?
(b) An electron near the top of the valence band in a
semiconductor has energy
E=−10−37|k|2
where Eis in Joules and kis in m−1. An electron is re-
moved from a state k= 2 ×108m−1ˆx, where ˆxis the unit
vector in the x-direction. For a hole, calculate (and give
the sign of!)
(i) the effective mass
(ii) the energy
(iii) the momentum
(iv) the velocity.
If there is a density p= 105m−3of such holes all
having almost exactly this same momentum, calculate the
current density and its sign.
(a) A hole is the absence of an electron in an otherwise filled valence
band. This is useful since instead of describing the dynamics of all the
(many) electrons in the band, it is equivalent to describe the dynamics
of just the (few) holes.
(b) Effective mass ~2k2/(2m∗) = (10−37Joule ·meter2)k2. So m∗=
5×10−32 kg or .05 the mass of the electron. This mass is positive in the
usual convention. The energy is E= (10−37Joule·meter2))k2= 4×10−21
J, or about 0.025 eV. This energy is positive (it takes energy to ”push”
the hole down into the fermi sea, like pushing a balloon under water).
Getting the momentum and velocity right are tricky. First, note that
the velocity of an eigenstate is the same whether or not the state is filled
with an electron. It is always true that the velocity of an electron in a
state is ∇kEk/~where Ekis the electron energy. Thus the hole velocity
here is negative v=−~k/m∗=−3.8×105m/s (i.e the velocity is in
the negative ˆx) direction.
For momentum, since a filled band carries no (crystal) momentum,
and for electrons crystal momentum is always ~k, the removal of an
electron leaves the band with net momentum −~kwhich we assign as
the momentum of the hole. Thus we obtain hole momentum −~k=
−2.1×10−26 kg-m/s which is also in the negative ˆxdirection. (this
matches well to the intuition that p=mv with a positive effective mass
for holes). With pthe density of such holes, the total current density is
pev =−6×10−9Amp/m2also in the negative ˆxdirection (noting that
the charge of the hole is positive).
Note that it is typical to define the wavevector of a hole to be negative
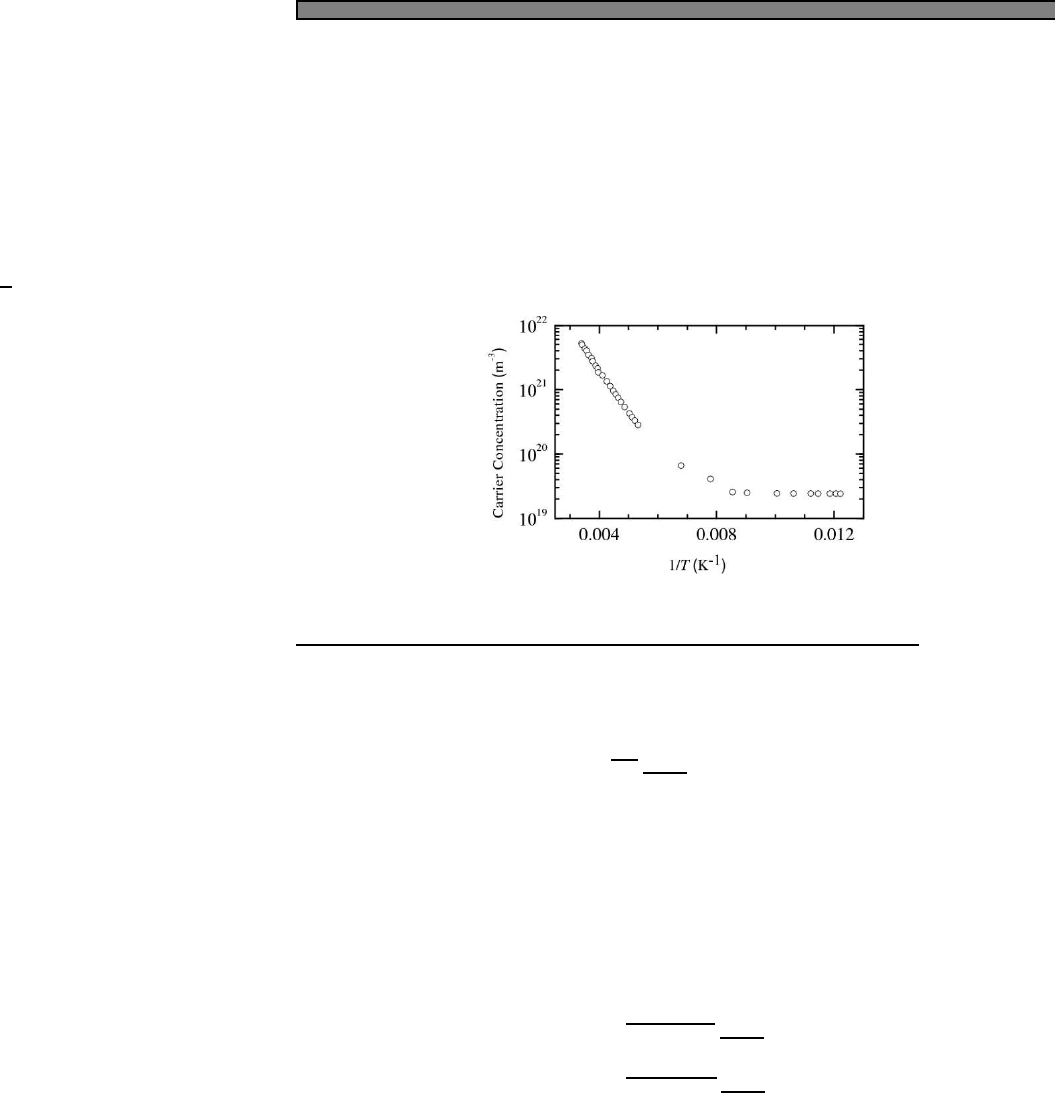
140 Semiconductor Physics
of the wavevector of the missing electron.
(17.2) Law of Mass Action and Doping of Semi-
conductors
(a) Assume that the band-gap energy Egis much
greater than the temperature kBT. Show that in a pure
semiconductor at a fixed T, the product of the number of
electrons (n) and the number of holes (p) depends only on
the density of states in the conduction band and the den-
sity of states in the valence band (through their effective
masses), and on the band-gap energy.
Derive expressions for nfor pand for the product
np. You may need to use the integral R∞
0dx x1/2e−x=
√π/2.
(b) The band gaps of silicon and germanium are 1.1
eV and 0.75 eV respectively. You may assume the ef-
fective masses for silicon and germanium are isotropic,
roughly the same, and are roughly .5 of the bare electron
mass for both electrons and holes. (Actually the effective
masses are not quite the same, and furthermore the effec-
tive masses are both rather anisotropic, but we are just
making a rough estimates here.)
Estimate the conduction electron concentration for
intrinsic (undoped) silicon at room temperature.
Make a rough estimate of the maximum concen-
tration of ionized impurities that will still allow for this
“intrinsic” behavior.
Estimate the conduction electron concentration for
germanium at room temperature.
(c) The graph in Fig. 17.1 shows the relationship be-
tween charge-carrier concentration for a certain n-doped
semiconductor.
Estimate the band gap for the semiconductor and
the concentration of donor ions.
Describe in detail an experimental method by
which these data could have been measured, and suggest
possible sources of experimental error.
Fig. 17.1 Figure for Exercise 17.
(a) The density of states per unit volume of free electron with disper-
sion E=~2k2/(2m) is given by (including spin)
g(E) = √2Em3/2
~3π2
So if the dispersion near the valence band edge and conduction band
edges are
Ee(k) = Ec+~2k2/(2me)
Eh=Ev−~2k2/(2mh)
we obtain density of states for conduction electrons and valence holes
given by
ge(E > Ec) = p2(E−Ec)m3/2
e
~3π2
gh(E < Ev) = p2(Ev−E)m3/2
h
~3π2
141
At fixed chemical potential µand temperature βthe number density of
electrons in the conduction band is
n=Z∞
Ec
ge(E)nF(β(E−µ))dE
where nF(x) = 1/(ex+ 1) is the Fermi occupation factor. Assuming
that µis well below the conduction band (by at least energy kbT), then
x=β(E−µ) is very positive and it is acceptable to replace nF(x) by
the Boltzmann factor e−x, thus we obtain.
n=Z∞
Ec
ge(E)e−β(E−µ)dE
Similarly, the number of holes in valence band is given by
p=ZEv
−∞
gh(E)(1 −nF(β(E−µ))dE
Assuming that µis well above the valence band (by at least energy kbT)
then x=β(E−µ) is very negative and we can replace the fermi factor
1−nF(x) by exresulting in
p=ZEv
−∞
gh(E)eβ(E−µ)dE
It is then clear immediately, that when we multiply np the variable µ
completely vanishes.
A bit more manipulation obtains
n=eβµ√2m3/2
e
~3π2Z∞
Ecp(E−Ec)e−βEdE
redefining variables y=E−Ecand performing the integral, one obtains
n=1
42mekbT
π~23/2
e−β(Ec−µ)(17.1)
and similarly
p=1
42mhkbT
π~23/2
e−β(µ−Ev)(17.2)
Obtaining
np =1
16 2√mhmekbT
π~23
e−β(Ec−Ev)
which depends only on the band gap, Tand the effective masses.
(b) In the undoped case n=p, and we are assuming mh=me=m/2
as well so we have
n=1
42(m/2)kbT
π~23/2
e−β(Eg/2)

142 Semiconductor Physics
with Egthe gap value. Plugging in numbers gives
n= 5.26 ×1015m−3
for Silicon and
n= 4.54 ×1018m−3
for Germanium. When the doping level gets to on the order of the
expected intrinsic level, then you no longer have intrinsic behavior.
(c) The concentration of donor atoms is simply the saturation concen-
tration at low T(which I estimate from the figure to be about 2 ×1019
m−3). Note that at very low temperature one could get carrier freeze-out
where the density drops again.
To estimate the gap, we need to measure the slope of the curve at
high temperature.
Extracting a slope
log n/(m3) = −1500K/T +Constant.
Or equivalently
n∼e−1500K/T
We then set 1500K=Eg/(2kb) and obtain a band gap of about .26 eV.
It might be useful to also mention to the students that Si and Ge
both have valley degeneracies (i.e, multiple equi-energy minima in the
conduction band). These may add an additional factor to the law of
mass action.
The concentration is most likely measured by a Hall effect measure-
ment. Several possible sources of error can occur here. First, when there
are both electrons and holes present, then you measure some (nontriv-
ial) combination of the Hall resistivities weighted by their concentrations
and by their mobilities (in a very nontrivial way).
RH=Reρ2
e+Rhρ2
h
(ρe+ρh)2
(See exercise 17.9). One only gets an accurate absolute measurement of
the electron concentration to the extent that the electron resistivity is
much lower than the hole resistivity.
There are other more obvious sources of experimental error such as
heating when one runs current through a sample to measure it – thus it
requires measuring small voltages accurately. To measure hall resistivity,
without mixing in longitudinal resisitivity, one needs to align contacts
exactly parallel to each other in a hall bar. One has to also make sure
that the voltages being measured are due to the sample and not the
contacts/wires/amplifiers etc.

143
(17.3) Chemical Potential
(a) Show that the chemical potential in an intrinsic
semiconductor lies in the middle of the gap at low tem-
perature.
(b) Explain how the chemical potential varies with tem-
perature if the semiconductor is doped with (i) donors (ii)
acceptors.
(c) A direct-gap semiconductor is doped to produce a
density of 1023 electrons/m3. Calculate the hole density
at room temperature given that the gap is 1.0 eV, and
the effective mass of carriers in the conduction and va-
lence band are 0.25 and 0.4 electron masses respectively.
Hint: use the result of Exercise 17.2.a.
(a) In an intrinsic semiconductor n=pso we can set
n
p= 1
Referrring back to the previous problem we can insert the expressions
Eq. 17.1 and Eq. 17.2 for nand prespectively. Almost all of the nasty
prefactors cancel and we obtains
m3/2
ee−β(Ec−µ)
m3/2
he−β(µ−Ev)= 1
We can solve this trivially to obtain
µ=Ec+Ev
2+3
4(kBT) log(mh/me)
So at low temperature the chemical potential lies mid-gap. (Incidentally,
this is why it is never a good idea to say that the fermi energy is the
energy of the highest filled state. There may be a very large difference
between the highest filled state and the chemical potential!).
(b) Let us assume for a moment we are well above the freezeout tem-
perature, so the doping can be thought of as going directly into the
conduction band. For simplicity let us assume me=mh, so the intrinsic
behavior is then simply that the chemical potential is fixed as a func-
tion of temperature. If the doner density is much higher than nint then
n≈ndopant (i.e., the thermally excited electrons are irrelevant compared
to those that are there from doping). Then looking at Eq. 17.1 fixing n
to be ndopant and solving for µwe have
µ≈Ec−kBTlog
ndopant
1
42mekbT
π~23/2
Similarly for acceptor impurities
µ≈Ev+kBTlog
pacceptor
1
42mhkbT
π~23/2
So at low tempearture, the chemical potential is essentially right at the
conduction (donor) or valence (acceptor) band and moves towards mid-
gap as the temperature is increased. When the intrinsic density exceeds

144 Semiconductor Physics
the dopant density, then one expects to have µgiven by the intrinsic
expression from part a, which is roughly to have the chemical potential
mid-gap with a small slope dependent on the ratio of masses.
Now the story is a bit more complicated if one wants to think about
the very low temperature regime where there is carrier freezeout. At
zero temperature all of the electrons are bound to their dopant nuclei
and one can think of this as being a filled “impurity band” playing the
role of a filled valence band, and the nearby conduction band is empty.
As is usually the case, at zero temperature the chemical potential is
midway between the top of the impurity band and the bottom of the
conduction band. As the temperature is increased, since the real valence
band is very far away compared to the temperature so we can ignore it.
It is then only a matter of figuring out how the chemical potential moves
between the filled impurity band and the empty conduction band. Since
the density of states in the conduction band is larger than the those
in the sparse impurity band, as the temperature is raised, the chemical
potential moves up towards the conduction band.
(c) We first calculate the undoped intrinsic carrier concentration using
the law of mass action with n=p=nintrinsic. At T=293 Kelvin, I
obtained
nintrinsic = 1016m−3
Then since ndopant ≫nintrinsic we can set p=n2
intrinsic/n (from the
law of mass action) to obtain
p= 109m−3
(17.4) Energy Density
Show that the energy density of electrons in the valence
band of a semiconductor is
(ǫc+3
2kBT)n
where nis the density of these electrons and ǫcis the
energy of the bottom of the conduction band.
In short this is just a matter of realizing that the electrons in the
conduction band are essentially classical (are activated with Boltzmann
factors not fermi factors), so classical stat mech applies and one can ap-
ply the equipartition theorem. One obtains ǫcfor each particle excited,
then an extra 3
2kBTfor the translational degrees of freedom as usual in
equipartition theorem.
One can, of course, do the calculation more rigorously writing the
total energy density as (compare problem 17.2)
E/V =Z∞
Ec
Ege(E)nF(β(E−µ))dE
where nF(x) = 1/(ex+ 1) is the Fermi occupation factor. As in 17.2 it

145
is acceptable to replace nF(x) by the Boltzmann factor to get
E/V =Z∞
Ec
Ege(E)e−β(E−µ)dE
The same manipulation obtains
E/V =eβ(µ−Ec)√2m3/2
e
~3π2Z∞
Ec
[(E−Ec) + Ec]p(E−Ec)e−β(E−Ec)dE
Note the second term in brackets, the Ecterm (compare 17.2) gives the
same integral as the above calcualtion of nin 17.2 so we obtain nEc.
To evaluate the remaining term we redefine variables y=E−Ecand
performing the integral, whixh we recognize as being precisely ∂/∂β of
the prior integral from 17.2. Since the prior integral was proportional to
T(3/2) we obtain (3/2)(kBT) times the prior integral and thus a total
of (3/2)(kBT)nproving the result.
(17.5) Semiconductors
Describe experiments to determine the following prop-
erties of a semiconductor sample: (i) sign of the majority
carrier (ii) carrier concentration (assume that one carrier
type is dominant) (iii) band gap (iv) effective mass (v)
mobility of the majority carrier.
(i,ii) Sign of majority carrier and carrier concentration (assuming there
is only one type of carrier) are both easily measured with Hall effect. (iii)
band gap may be measured optically. Or by carrier concentration (es-
sentially conductance) as a function of temperature. (iv) Effective mass
is measured with cyclotron resonance (v) mobility is easily measured via
resistivity once concentration of carriers is known.
(17.6) More Semiconductors
Outline the absorption properties of a semiconductor
and how these are related to the band gap. Explain the
significance of the distinction between a direct and an
indirect semiconductor. What region of the optical spec-
trum would be interesting to study for a typical semicon-
ducting crystal?
Optical absorbtion can occur when a photon is absorbed while exciting
an electron out of the valence band into the conduction band. This
requires a minimum of the gap energy (Small amounts of absorbtion can
occur below the gap for impure semiconductors if there are impurity or
defect states within the gap – also very weak nonlinear processes can
allow multiple photons to be absorbed while exciting a single electron).
In the absorbtion process energy and momentum must both be con-
served. Since photons carry very little momentum given a certain energy

146 Semiconductor Physics
(being that cis very large) one should think of this absorbtion as not
tranferring any momentum to the system. This means that direct gap
absorbtion (where the momentum of the electron does not change) is
highly favored over indirect gap absorbtion. Indirect gap absorbtion
can occur, but it must be assisted by a phonon or some other process
that can account for the necessary momentum.
Semiconductor gaps tend to be in the optical, or infra-red range (some-
where from 400 nm to 3 micron, or roughly 3 eV to .5 eV). Only a very
few wide gap semiconductors reach the optical blue range and UV.
(17.7) Yet More Semiconductors
Outline a model with which you could estimate the en-
ergy of electron states introduced by donor atoms into an
n-type semiconductor. Write down an expression for this
energy, explaining why the energy levels are very close to
the conduction band edge.
One can consider a simple hydrogenic schroedinger equation with an
attractive proton being the ionized donor and the single electron. The
main differences are that the mass of the electron is replaced by the
band electron mass, and ǫ0is multiplied by the dielectric constant ǫrof
the semiconductor. As a result, the Rydberg becomes replaced by an
effective Rydberg
R∗=R0(m∗/m)(1/ǫ2
r)
This gives us a hydrogenic binding energy that can be extremely small
for typical semiconductors, hence the bound states remain very close the
conduction band edge.
(17.8) Maximum Conductivity*
Suppose holes in a particular semiconductor have mo-
bility µhand electrons in this semiconductor have mobil-
ity µe. The total conductivity of the semiconductor will
be
σ=e(n µe+p µh)
with nand pthe densities of electrons in the conduction
band and holes in the valence band. Show that, indepen-
dent of doping, the maximum conductivity that can be
achieved is
σ= 2e nintrinic √µeµh
with nintrinsic the intrinsic carrier density. For what
value of n−pis this conductivity achieved?
Actually this is easy. Using law of mass action np =n2
intrinsic. Thus
we write
σ=en µe+nintrinsic
nµh
Now set dσ/dn = 0 to maximize and solve to obtain
n=nintrinsicpµh/µe
Which correspondingly results in
p=nintrinsicpµe/µh

147
plugging into the original expression for σwith a tiny bit of algebra we
obtain
σ= 2e nintrinic √µeµh
as required, and we also obtain
n−p=nintrinsic pµh/µe−pµe/µh
(17.9) Hall Effect with Both n- and p-Dopants*
Suppose a semiconductor has a density pof holes in
the valence band with mobility µhand a density nof
electrons in the conduction band with mobility µn. Use
Drude theory to calculate the Hall resistivity of this sam-
ple.
See also exercise 3.3c. For a single species, we have (See exercise 3.1)
ρ=r BR
−BR r
where r=nµ and R=q/n with qthe charge on the charge carrier and
nthe carrier density. We define tensors ρeand ρhfor the two species
with re=nµnand rh=pµhand Re=e/n and Rh=−e/p. The
conductivity tensors are σj=ρ−1
jand then the total conductivity tensor
is σ=σe+σi. Finally this is inverted to give the tensor ρtotal =σ−1.
There is a lot of algebra involved in this. I obtained
ρxx =B2(reR2
h+rhR2
e) + rhre(re+rh)
B2(Re+Rh)2+ (re+rh)2
ρxy =BB2ReRh(Re+Rh) + Rhr2
e+Rer2
h
B2(Re+Rh)2+ (re+rh)2

Semiconductor Devices 18
(18.1) Semiconductor Quantum Well
(a) A quantum well is formed from a layer of GaAs
of thickness Lnm, surrounded by layers of Ga1−xAlxAs
(see Fig. 18.2). You may assume that the band gap of the
Ga1−xAlxAs is substantially larger than that of GaAs.
The electron effective mass in GaAs is 0.068 mewhereas
the hole effective mass is 0.45 mewith methe mass of
the electron.
Sketch the shape of the potential for the electrons
and holes.
What approximate value of Lis required if the band
gap of the quantum well is to be 0.1 eV larger than that
of GaAs bulk material?
(b) *What might this structure be useful for?
(a) This is a particle in a box problem. Both electron and holes are
particles in a box of length L. Thus the lowest lying electron in the well
is
Ee=Ec+π
L2~2
2m∗
e
with Ecthe bulk conduction band minimum. Similarly the highest lying
hole state in the well is
Eh=Ev−π
L2~2
2m∗
h
Thus the difference in energy is
Ee−Eh=Ebulkgap +~2
2π
L21
m∗
e−1
m∗
h
Setting Ee−Eh−Ebulkgap to 1eV and solving for Lgives 8 nm.
(b) This type of quantum well device is useful to precisely design a
band gap for example for a laser where one wants to fix the emission
wavelength. If one puts donor impurities outside of the well (on both
sides, say) the donated electrons can reduce their energies by falling
into the well, but the ionized dopants remain behind. This is known as
modulation doping. It is useful because one can obtain extremely high
mobility electrons within the quantum well since there are no ionized
dopants in the well to scatter off of. One uses these structures heavily
for fundamental physics studies of clean (unperturbed) electrons.
150 Semiconductor Devices
(18.2) Density of States for Quantum Wells
(a) Consider a quantum well as described in the previ-
ous exercise. Calculate the density of states for electrons
and holes in the quantum well. Hint: It is a 2D electron
gas, but don’t forget that there are several particle-in-a-
box states.
(b) Consider a so-called “quantum wire” which is a
one-dimensional wire of GaAs embedded in surrounding
AlGaAs. (You can consider the wire cross-section to be a
square with side 30nm.) Describe the density of states for
electrons or holes within the quantum wire. Why might
this quantum wire make a very good laser?
(a) For a 2D electron gas for electrons with mass m, we quickly cal-
cualte the density of states.
N= 2AZkF
0
dk
(2π)2
with Athe area and the factor of 2 out front for spin and ka two
dimensional vector. This can be converted to
n=N/A =k2
F
2π
When the energy of an electron is given by
E=~2k2
2m
we have k2= 2mE/~2and we then have a density of states per unit
volume of
g=dn
dE =m
π~2
This is the correct answer for any E≥0 and the density of states is zero
for any E < 0. We then write more precisely that
g(E) = m
π~2Θ(E)
where Θ is the step function which has value 1 for nonnegative argument
and value 0 for negative argument.
In our quantum well we must make a few minor changes. First of
all, we should use the effective mass rather than the actual mass of
the electron. Secondly the energy of the particle in the quantum well
also includes its particle-in-a-box energy for its motion transverse to the
2D quantum well. Thus for an electron in the conduction band of the
quantum well we have
E=Ec+~2π2
2m∗
e
a2
L2+~2k2
2m∗
e
where Ecis the bulk conduction band bottom, and a= 1,2,3,... is
the transverse quantum number of the particle in the well. Fixing the
transverse quantum number a, the density of states would be
g(E) = m∗
e
π~2ΘE−Ec−~2π2
2m∗
e
a2
L2
151
Now accounting for the fact that there may be many transverse modes
we have
g(E) = m∗
e
π~2X
a>0
ΘE−Ec−~2π2
2m∗
e
a2
L2
and this expression remains true up to an energy where the transverse
modes spill out of the box.
Analogously the density of holes in the valuence band in the quantum
well is
g(E) = m∗
h
π~2X
a>0
ΘEv−~2π2
2m∗
h
a2
L2−E
(b) First we determine the density of states for a one dimensional
electron gas.
N= 2LZkF
−kF
dk
2π
with Lthe Length of the system and the factor of 2 out front for spin.
This can be converted to
n=N/L =2kF
π
using k=√2mE/~we then obtain a density of states
g(E) = dn
dE =√2m
π~E−1/2Θ(E)
Now in the seminconductor quantum wire we must consider the trans-
verse modes. In general the energy of an electron in the wire is then given
by
E=Ec+~2π2
2m∗
e
a2
1+a2
2
L2+~2k2
2m∗
e
where a1and a2are the mode indices (integers greater than zero) in the
two transverse directions. Adding the density of states associated with
all of these modes we obtain
g(E) = √2m∗
e
π~X
a1,a2>0E−Ec−~2π2
2m∗
e
a2
1+a2
2
L2−1/2
ΘE−Ec−~2π2
2m∗
e
a2
1+a2
2
L2
and similarly in the valence band
g(E) = p2m∗
h
π~X
a1,a2>0Ev−~2π2
2m∗
h
a2
1+a2
2
L2−E−1/2
ΘEv−~2π2
2m∗
h
a2
1+a2
2
L2−E
(18.3) p-nJunction*
Explain the origin of the depletion layer in an abrupt
p-njunction and discuss how the junction causes rectifca-
tion to occur. Stating your assumptions, show that the
total width wof the depletion layer of a p-njunction is:
w=wn+wp
152 Semiconductor Devices
where
wn=2ǫrǫ0NAφ0
eND(NA+ND)1/2
and a similar expression for wpHere ǫris the relative
permittivity and NAand NDare the acceptor and donor
densities per unit volume, while φ0is the difference in
potential across the p-njunction with no applied voltage.
You will have to use Poisson’s equation to calculate the
form of φgiven the presence of the ion charges in the
depletion region.
Calculate the total depletion charge and infer how
this changes when an additional voltage Vis applied.
What is the differential capacitance of the diode
and why might it be useful to use a diode as a capacitor
in an electronic circuit?
Let us set the position xto be zero, where we have an ndoped region
to the left (negative x) and a pdoped region to the right (positive x).
Let the depletion widths be wnand wprespectively, and the doping
densitities be NDand NArespectively. Within the depletion widths
there is a net charge built up (see Fig 18.4 of the book for example).
We must solve the Poisson equation ∂2
xφ=ρ/(ǫ0ǫr) where ρis the local
charge density (which is constant in each region). Setting φ(x= 0) = 0
for simplicity, we immediately obtain
φ(x) = −eND
2ǫ0ǫr
x2+CDx x < 0
φ(x) = eNA
2ǫ0ǫr
x2+CAx x > 0
where CDand CDare constants to be fixed here. We have additional
boundary conditions that the electric field must go to zero at the edge
of the depletion region, so we have ∂xφ(x=−wn) = ∂x(x=wa) = 0.
This fixes the constants so that we now have
φ(x) = −eND
2ǫ0ǫrx2+ 2wnxx < 0
φ(x) = eNA
2ǫ0ǫrx2−2waxx > 0
The total potential drop across both regions is then
φ0=φ(−wn)−φ(wa) = e
2ǫ0ǫrNDw2
n+NAw2
a(18.1)
We also note that the total charge in the two depletion regions must sum
to zero (since the depletion occurs by annihilation of opposite charges)
so we have
waNA=wnND(18.2)
Plugging Eq. 18.2 into Eq. 18.1 and solving for wnyields the desired
expression.
wn=2ǫrǫ0NAφ0
eND(NA+ND)1/2
and similarly
wa=2ǫrǫ0NDφ0
eNA(NA+ND)1/2
153
When an additional voltage is added, it simply shifts φ0to φ0+eV .
The total depletion charge per unit cross sectional area is then
q=wnND=waNA=2ǫrǫ0NDNA(φ0+eV )
e(NA+ND)1/2
The differential capacitance per unit cross sectional area is
C=∂q
∂V =ǫrǫ0NDNA
2e(NA+ND)1/2
(φ0+eV )−1/2
This provides a useful circuit element as it allows one to control a ca-
pacitance by applying a DC voltage.
(18.4) Single Heterojunction*
Consider an abrupt junction between an n-doped semi-
conductor with minimum conduction band energy ǫc1and
an undoped semiconductor with minimum conduction
band energy ǫc2where ǫc1< ǫc2. Describe qualitatively
how this structure might result in a two-dimensional elec-
tron gas at the interface between the two semiconductors.
Sketch the electrostatic potential as a function of position.
It should say, ǫc1> ǫc2.
In this problem, nothing interesting happens in the valence band — so
we only draw the conduction band. The situation is quite similar to the
p-n junction. Before the two semiconductors are brought together, there
are electrons in the conduction band on the left (or in dopant orbitals
slightly below the conduction band as shown in the figure), but empty
states on the right at lower energy because the conduction band energy
is lower. This situation is shown in figure 18.1
Fig. 18.1 Before electrons are allowed to flow between
the two seminconductors, there are electrons on the left
at higher energy than empty states on the right. The
blue lines indicate the conduction band minima. The
dotted line is the fermi energy (slighly below the conduc-
tion band assuming that electrons are bound to dopants).
As in the p-n junction, electrons want to flow between the two semi-
conductors in order to lower their energies, but in so doing charge builds
up (a postive charge is left on the left and negative charged electrons
accumulate on the right. When equilibrium is established the electro-
chemical potential is as shown in figure 18.2. The electrons are back
154 Semiconductor Devices
attracted to the positive charges they left behind, thus accumulating in
a roughly triangular well that forms near the interface. If the confine-
ment is sufficiently strong, this becomes a particle in a box problem and
the electrons in the well may become restricted to a single transverse
wavefunction — thus becoming a strictly two dimensional electron gas.
Fig. 18.2 Electrochemical potential of a semiconductor
heterostructure. There is net postive charge on the left
where electrons have left their donor atoms behind and
net negative charge on the right where electrons have
accumulated without positively charged nuclei.
(18.5) Diode Circuit
Design a circuit using diodes (and any other simple
circuit elements you need) to convert an AC (alternating
current) signal into a DC (direct current) signal.
*Can you use this device to design a radio reciever?
For the purpose of this problem we will make the crude assumption
that a diode (arrow in a circuit diagram) is an ideal circuit element that
allows current flow one way but no current flow the other way.
Fig. 18.3 A half-wave rectifier.
The circuit shown in Fig. 18.3 is known as “half-wave rectifier”. If the
source voltage is sinusoidal, V=V0sin(ωt), the voltage across the load
155
resistor is then
V=V0sin(ωt)Θ(sin(ωt))
where Θ is the Heaviside step function. I.e., the current goes to zero
instead of going negative. Now instead of giving a true DC output, this
gives an output that is nonnegative. In order to smooth the nonnegative
(but fluctuating) voltage into a smooth DC voltage one inserts a capac-
itor into the circuit to act as a “battery” as shown in Fig. 18.4. This
effectively damps the high frequency components of the signal leaving
only the low frequency DC component. One should choose a capacitor
such that RloadC≫1/ω in which case the non-dc component of the
resultant signal is of magnitude VAC ≈V0/(ωRC) .
Fig. 18.4 A half-wave rectifier with a smoothing capac-
itor.
One can do a bit better in circuit design by using more diodes to
construct a “Full wave rectifier” as shown in Figure 18.5.
Fig. 18.5 A full-wave rectifier.
In this case, in the absence of the smoothing capacitor, the voltage
156 Semiconductor Devices
across the load is given by
V=|V0sin(ωt)|
a smoothing capacitor can be used as above. This scheme has the advan-
tage that the resulting DC voltage ends up being of higher magnitude
than that of the half-wave, and the fluctuating DC component ends up
being smaller.
In order to design a radio, we must first think about how radios
encode information. The simplest encoding system is AM or amplitude
modulation. In this case a signal A(t) (for simplicity let us assume the
signal is everywhere positive) is multiplied by a high frequency carrier
wave sin(ωt) and the product A(t) sin(ωt) is transmitted and then re-
ceived by an antenna. To convert the received signal back into A(t) one
simply puts it through a rectifier. If one wants to do a slightly bet-
ter job, one wants to recieve only signals where the carrier frequency is
very close to some given frequency ω0. To do this, one needs to build
a resonant (LC) circuit which will respond only to frequencies near its
resonance. A sample 1-diode radio circuit (often known as a “crystal”
radio after the fact that the diode was often made of a small crystal)
is shown in Fig. 18.6. In this figure the right hand side (D1,C3,E1) is
just a half-wave rectifier as discussed above. Here E1 is the “earphone”
or output load of the circuit. The middle of the circuit L2,C2 is the
resonant LC circuit, which is inductively coupled to the incoming signal
from the antenna. Note that the capacitors are made tunable here so
that the resonance frequencies can be modified. Many other designs are
possible as well.
Fig. 18.6 A radio circuit. Here E1 is the “earphone”
or output load of the circuit. The incoming antenna is
on the far left. A very crude radio could be made by
with only the rectifier (D1,C3) attached directly to an
incoming antenna and an outgoing earphone E1.
157
(18.6) CMOS Circuit*
Design a circuit made of one n-MOSFET and one p-
MOSFET (and some voltage sources etc.) which can act
as a latch—meaning that it is stable in two possible states
and can act a single bit memory (i.e., when it is turned
on it stays on by itself, and when it is turned off it stays
off by itself).
A simple (and very rough) CMOS latch circuit (also known as an
SCR or silicon-controlled rectified) is shown in Fig. 18.7. When the
switch (S1) is closed no current flows. The reason for this is that there
is no voltage on either of the two gates, so both transistors are “off”
meaning they prevent current flow (and therefore prevent voltage from
being transmitted). However, when a voltage is momentarily applied
to the ON input, then this activates the P-MOSFET, allowing current
to flow to the gate of the N-MOSFET, which then activates it, allowing
current to flow to the gate of the P-MOSFET even when the ON voltage
is removed. Thus the circuit is latched in the “On” state. To put
the circuit back in the “Off” state, one must disconnect the switch S1
momentarily.
Fig. 18.7 A CMOS latch circuit.
Magnetic Properties of
Atoms: Para- and
Dia-Magnetism 19
(19.1) ‡Atomic Physics and Magnetism
(a) Explain qualitatively why some atoms are param-
agnetic and others are diamagnetic with reference to the
electronic structure of these materials.
(b) Use Hund’s rules and the Aufbau principle to de-
termine L,S, and Jfor the following isolated atoms:
(i) Sulfur (S) atomic number = 16
(ii) Vanadium (V), atomic number = 23
(iii) Zirconium (Zr), atomic number = 40
(iv) Dysprosium (Dy), atomic number = 66
(a) To a first approximation, paramagnetic atoms have net moment
J6= 0 which can be re-aligned, whereas the typical diamagnetic atoms
have no moment.
If an atom has completely filled shells (say, the noble gases), then J=
L=S= 0, and the atom is diamagnetic due to Larmor Diamagnetism.
If an atom has a net moment J6= 0, from unfilled shells, then it is
paramagnetic. This is almost all other atoms.
However (more advanced answer): it is also possible to have J= 0
while having Land Snonzero. In this case, the atom can either be para-
magnetic or diamagnetic. Both para and dia terms are weak and either
one can win in this case. This can occur for atoms that are one electron
short of half-filled shells. (Known as Van Vleck Paramagnetism).
In metals one can have Pauli paramagnetism associated with re-orientation
of the spins of the conduction electron. One can also have Landau dia-
magnetism (beyond the scope of the course) which is the diamagnetic
response of the orbital motion of the conduction electrons. Pauli para-
magnetism in a metal is much weaker than Curie paramagnetism and
can be roughly the same size as diamagnetic effects.
(b) Shells are filled in the order
1s,2s,2p,3s,3p,4s,3d,4p,5s,4d ...
with s,p,d shells containing 2,6,10 electrons respectively.
(i) 16S: [Ne]3s23p4
(ii) 23V: [Ar]4s23d3
(iii) 40Zr: [Kr]5s24d2

160 Magnetic Properties of Atoms: Para- and Dia-Magnetism
(iv) 54Xe: [Xe] (All filled shells)
(v) 66Dy: [Xe]6s24f10
Where filled shell configurations [Ne] contains 10 electrons, [Ar] con-
tains 18, [Kr] contains 36 and [Xe] contains 54.
Thus
(i) Sulfer has 4 electrons in a p-shell, these fill lz=−1,0,1 with spin
up and lz= 1 with spin down. Thus L= 1 and S= 1, and since the
shell is more than half full J=L+S= 2.
(ii) Vanadium has 3 electrons in a d-shell, these fill lz= 2,1,0 with
spin up giving L= 3 and S= 3/2. Since the shell is less than half filled
J=L−S= 3/2.
(iii) Zirconium has 2 electrons in a d-shell, these fill lz= 2,1 with
spin up giving L= 3 and S= 1. Since the shell is less than half filled
J=L−S= 2.
(iv) Xenon is a noble gas, meaning all shells are filled, so J=L=
S= 0.
(v) Dysprosium has 10 electrons in an f-shell, these fill all the spin up
state (7 of them) and lz= 3,2,1 for spin down giving L= 6 and S= 2.
Since the shell is more than half filled J=L+S= 8.
Note that none of these atoms violate the Madelung rule which dic-
tates the filling order or violates Hund’s rules when the atoms are iso-
lated. (Violations do sometimes occur but these atoms work as they are
supposed to).
(19.2) More Atomic Physics
(a) In solid erbium (atomic number=68), one electron
from each atom forms a delocalized band so each Er atom
has eleven felectrons on it. Calculate the Land´e g-factor
for the eleven electrons (the localized moment) on the Er
atom.
(b) In solid europium (atomic number =63), one elec-
tron from each atom forms a delocalized band so each Eu
atom has seven felectrons. Calculate the Land´e g-factor
for the seven electrons (the localized moment) on the Eu
atom.
Er typically is in a +3 state. 2 of those are from the core s-orbitals.
1 is from the f orbital.
(a) For 11 electrons in an f-shell, using Hund’s first rule we obtain
S= 3/2 and Hund’s second rule we have L= 6. Since the shell is more
than half filled, Jis given by the sum J= 6 + 3/2 = 15/2. Using the
formula for the Lande gfactor (with g= 2) we have
˜g=1
2(g+ 1) + 1
2(g−1) S(S+ 1) −L(L+ 1)
J(J+ 1) = 6/5
This is almost exactly right.
(b) The counting here is messed up. There are 7 electrons before
losing one. For 7 electrons in an f-shell, L= 0 and S= 7/2 and J=S.
is purely spin, so ˜g=g= 2 (it also comes out of the above formula as

161
well). In fact, we should have 6 electrons when one is lost, and we get
L= 3 = Sand J= 0. However, This is a van-vleck ion, so in fact the
result is not what is predicted here.
(19.3) Hund’s Rules*
Suppose an atomic shell of an atom has angular mo-
mentum l(l= 0 means an s-shell, l= 1 means a p-shell
etc, with an lshell having 2l+ 1 orbital states and two
spin states per orbital.). Suppose this shell is filled with
nelectrons. Derive a general formula for S,L, and Jas
a function of land nbased on Hund’s rules.
The shell has 2l+1 orbital states and 2 spin states per orbital. Hund’s
first rule tells us that
S(n, l) =
n
20≤n≤2l+ 1
4l+2−n
22l+ 1 ≤n≤4l+ 2
The second rule tells us that for n≤2l+ 1 we have
L(n, l) =
x=l
X
x=l−n+1
x
We can do this sum to obtain
L(n, l) = 1
2n(2l+ 1 −n)
For 2l+ 1 ≤n≤4l+ 2 we can consider only the electrons in addition
to the L= 0 half-filled shell, so L(n, l) = L(n−(2l+ 1), l) So we have
in all,
L(n, l) =
1
2n(2l+ 1 −n) 0 ≤n≤2l+ 1
1
2(n−2l−1)(4l+ 2 −n) 2l+ 1 ≤n≤4l+ 2
And thus we have (using Hund’s third rule) J=L−Sfor less than half
filled and J=L+Sfor more than half filled so
J(n, l) =
1
2n(2l−n) 0 ≤n < 2l+ 1
1
2(n−2l)(4l+ 2 −n) 2l+ 1 ≤n≤4l+ 2
‡(19.4) Para and Diamagnetism
Manganese (Mn, atomic number=25) forms an atomic
vapor at 2000K with vapor pressure 105Pa. You can
consider this vapor to be an ideal gas.
(a) Determine L, S, and Jfor an isolated manganese
atom. Determine the paramagnetic contribution to the
(Curie) susceptibility of this gas at 2000K.
(b) In addition to the Curie susceptibility, the man-
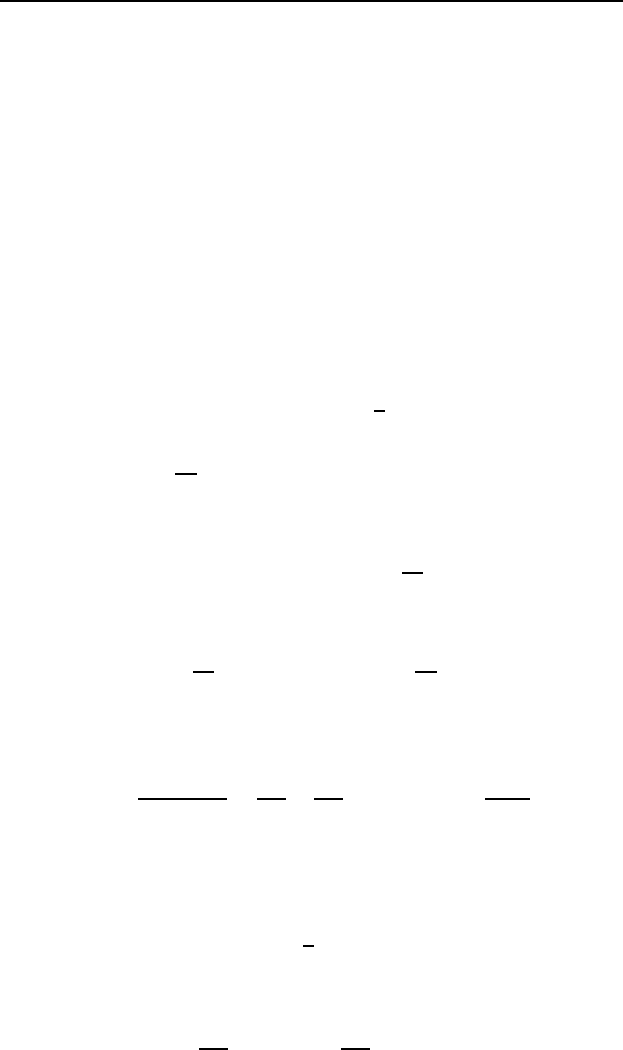
162 Magnetic Properties of Atoms: Para- and Dia-Magnetism
ganese atom will also have some diamagnetic susceptibil-
ity due to its filled core orbitals. Determine the Larmor
diamagnetism of the gas at 2000K. You may assume the
atomic radius of an Mn atom is one ˚
Angstrom.
Make sure you know the derivations of all the formulas
you use!
Using the ideal gas law, the density of Mn atoms is n=P/(kBT). We
will use this below.
(a) Atomic Mn has orbital configuration 25Mn: [Ar]4s23d5, meaning
a half filled d-shell. This then has L= 0 and S= 5/2. Since this is
purely spin moment the g-factor is 2.
Now we need to determine the paramagnetic susceptibility of a spin
S= 5/2. Let us write the partition function
Z=
5/2
X
m=−5/2
e−βgµBBm
Since we will be concerned with small B, it is probably simplest to
expand the partition function directly
Z≈
5/2
X
m=−5/21−(βgµBBm) + 1
2(βgµBBm)2+...
= 6 + 35
4(βgµBB)2
Calculating the moment
moment = −∂(kBTlog Z)/∂B =35
12β(gµB)2B
Yielding a susceptibility of the gas
χ=∂M/∂H =nµ0
35
12β(gµB)2= [P/(kBT)2]35
3µ0µ2
B= 1.6×10−7
(b) Diamagnetism is understood from the schroedinger equation and
expanding for small magnetic field
H=(p+eA)2
2m=p2
2m+1
2m(p·A+Ap) + e2A2
2m
The middle term is a L·B, and has zero expectation if there is a filled
shell such that hLi= 0. The final term is the source of diamagnetism.
One can write in circular gauge
A=1
2r×B
and the final term ends up being
e2
8m|B|2(r⊥)2=e2
6m|B|2r2

163
where we have used the spherical symmetry of the atom so that x2+y2=
(2/3)r2. We thus have the susceptibility
χ=−µ0dE2/dB2=−µ0
ρe2
6mhr2i
where here ρis the density of electrons. Since there are 20 core electrons
per atom, we have ρ= 20nwith nthe gas density (using 25 here would
also be sensible). Using 1 angstrom for rwe thus obtain
χ=−4.3×10−9
which is much much smaller than the paramagnetic contribution, even
at 2000K!
‡(19.5) Diamagnetism
(a) Argon is a noble gas with atomic number 18 and
atomic radius of about .188 nm. At low temperature it
forms an fcc crystal. Estimate the magnetic susceptibility
of solid argon.
(b) The wavefunction of an electron bound to an im-
purity in n-type silicon is hydrogenic in form. Estimate
the impurity contribution to the diamagnetic susceptibil-
ity of a Si crystal containing 1020 m−3donors given that
the electron effective mass m∗= 0.4meand the relative
permittivity is ǫr= 12. How does this value compare to
the diamagnetism of the underlying silicon atoms? Si has
atomic number 14, atomic weight 28.09, and density 2.33
g/cm3.
(a) First we establish the density of Argon. The radius of the avrgon
atom is r=.188 nm. For an fcc crystal, the nearest neighbor distance is
r=a/(2√2) We then have four atoms per conventional unit cell for an
overall atomic density of 4/a3= 1/(4√2r3). The number of electrons is
18 times the number of atoms, so we have (see 19.4 for derivation)
χ=−µ0
ρe2
6mhr2i=−µ018 e2
(4√2r3)6mhr2i=−µ0
3
4√2
e2
mr =−1×10−4
This number is actually a bit too big because the average hr2iis smaller
than this number since most of the electrons are further inside the atom
than the full atomic radius. Measurement gives us a suscpetability about
10−5, which would correspond to phr2i ≈ r/3.
(b) For a hydrogenic orbital (recall ψ∼e−r/a0) it is easy to calcualte
that hr2i= 3a2
0. We need only calculate the Bohr radius of an impurity
in a silicon atom. Recalling that the expression for the Bohr radius is
a0=4πǫ0~2
me2
we see that the Bohr radius in silicon should be rescaled by
aSi
0=a0ǫrm/m∗=a0∗12/.4 = 1.6nm.
Again using the result of the prior problem (and using m∗rather than
m)
χ=−µ0
ρe2
6m∗hr2i ≈ −10−11
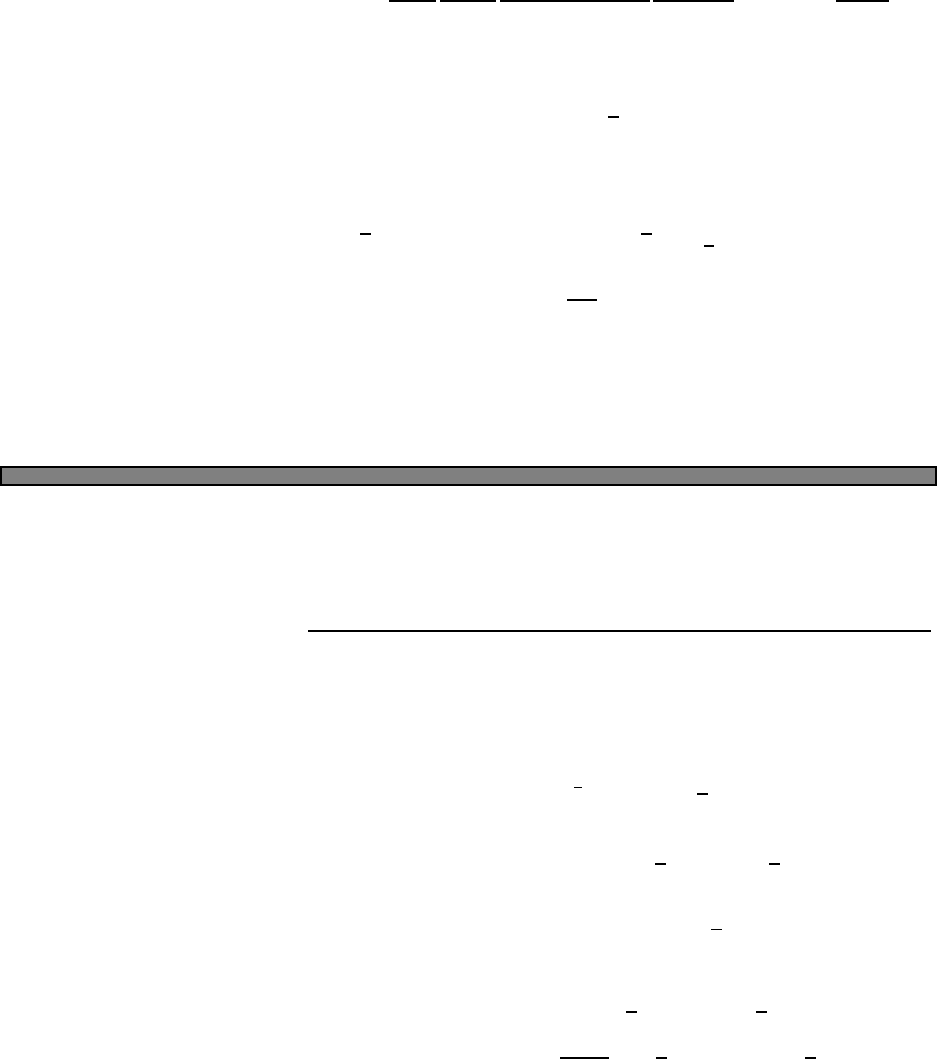
164 Magnetic Properties of Atoms: Para- and Dia-Magnetism
Finally we would like to compare this to the diamagnetism of the pure
silicon. First let us calculate the density of atoms in the system
n=2.33g
cm3
mol
28.09g
6.02 ×1023atoms
mol
(100cm)3
m3= 5 ×1028 atoms
m3
Now we need to determine the atomic radius of silicon from the data
given. If we didn’t know the crystal structure, we might guess roughly
that
r=1
2n−1/3
which would be exact for a simple cubic lattice. However, we know that
Si is diamond structure with 8 atoms per conventional unit cell, so the
density is n= 8/a3with athe lattice constant so a= 2n−1/3. The
nearest neighbor distance is from [0,0,0] to [a/4, a/4, a/4] or a distance
of a√3/4, so the atomic radius is a√3/8 = 1
4n−1/3= 1.17 Angstrom.
We then have
χ=−µ0
ρe2
6mhr2i ≈ −4×10−6
This is much much greater than the diamagnetism of the few impurities.
(Note: I think the table value is almost exactly this, however, this is
fortuitous as the table value is usually given in cgs which differs from
the SI version by a factor of 4 pi. Again the error is in the estimate of
r2. )
‡(19.6) Paramagnetism
Consider a gas of monatomic atoms with spin S= 1/2
(and L= 0) in a magnetic field B. The gas has density
n.
(a) Calculate the magnetization as a function of Band
T. Determine the susceptibility.
(b) Calculate the contribution to the specific heat of
this gas due to the spins. Sketch this contribution as a
function of µBB/kBT.
“Monatomic atoms” ? What was I smoking when I wrote this? It
should say monovalent. Doh! I should have also specified the g-factor
(as usual we can take it to be 2).
(a) Same calculation as we have done a million times.
Z=e+βgµB1
2B+e−βgµB
1
2B
F=−kBTlog Z
m=−∂F/∂B =gµB
1
2tanh(βgµB
1
2B)
M=mn
χ= lim
B→0µ0∂M/∂B =µ0n(1
2gµB)2β
(b) Similarly, we have
U=∂log Z/∂β =gµB
1
2Btanh(βgµB
1
2B)
C=∂U/∂T =1
kBT2(gµB
1
2B)2sech2(βgµB
1
2B)

165
(19.7) Spin JParamagnet*
Given the Hamiltonian for a system of non-interacting
spin-Jatoms
H= ˜gµBB·J
(a)* Determine the magnetization as a function of Band
T.
(b) Show that the susceptibility is given by
χ=nµ0(˜gµB)2
3
J(J+ 1)
kBT
where nis the density of spins. (You can do this part
of the exercise without having a complete closed-form ex-
pression for part a!)
(a) The eigenenergies of a single spin are
Em= ˜gµBBm m =−J, −J+ 1 ,−J+ 2 ,...J −1, J
So the canonical partition function of the single spin is
Z=
J
X
m=−J
e−βgµBBm =eβ˜gµbBJ
2J
X
p=0
e−β˜gµBp
=eβ˜gµbBJ 1−e−β˜gµBB(2J+1)
1−e−β˜gµBB=eβ˜gµBB(2J+1)/2−e−β˜gµBB(2J+1)/2
eβ˜gµBB/2−e−β˜gµBB/2
=sinh(β˜gµBB(2J+ 1)/2)
sinh(β˜gµBB/2)
we construct the free energy per spin F/N =−kBTlog Zand then get
the magnetic moment per spin
m=−∂(F/N)
∂B = (˜gµB/2) [(2J+ 1) coth(β˜gµBB(2J+ 1)/2) −coth(β˜gµBB/2)]
and the total magnetizaton is then the moment per spin times the density
of spins n, so
M=n(˜gµB/2) [(2J+ 1) coth(β˜gµBB(2J+ 1)/2) −coth(β˜gµBB/2)]
(b) To obtain the susceptibility, we want
χ= lim
B→0µ0
∂M
∂B
To take this limit we take the argument of the coth to be small and we
use the expansion
lim
x→0coth x=1
x+x
3
Note that the two 1/x terms cancel when subtracted leaving
M∼n(˜gµB/2) (2J+ 1)2β˜gµBB/6−β˜gµBB/6
So we have
χ=nµ0(˜gµB)2
3
J(J+ 1)
kBT
as required.
166 Magnetic Properties of Atoms: Para- and Dia-Magnetism
Note, the question claims that part (b) may be achieved without com-
pleting part (a). To do this, note that we only concerned with small B
so we can expand the partition function directly for small B.
Z=
J
X
m=−J
e−β˜gµBBm =
J
X
m=−J
1−β˜gµBBm +1
2(β˜gµBB)2m2+...
The first term in the sum gives (2J+ 1) and the second term gives 0 by
symmetry. The third term is the only hard one. I claim that
G[J] =
J
X
m=−J
=1
3(2J+ 1)(J+ 1)J(19.1)
I will derive this below, but for now let us assume it is correct. So we
have
Z= (2J+ 1)[1 + 1
6(β˜gµBB)2J(J+ 1) + ...]
Using the free energy per spin is F/N =−kBTlog Z, since Bis small
we have
F/N =−kBTlog(2J+ 1) −1
6kBT(˜gµBB)2J(J+ 1)
And the magnetic moment per site is
m=−∂(F/N)
∂B =(˜gµB)2BJ(J+ 1)
3kBT
which multiplying by the density of spins nto give the magnetization,
gives the same result as above.
Finally we turn to derive Eqn. 19.1. The result of this sum must be
some polynomial in J. Further, approximating it as an integral, it must
have a maximum power of J3, and the coefficient of the J0term must
be zero since G[0] = 0. Thus we propose
G[J] = aJ3+bJ2+cJ
Then we can also write the difference of two successive sums as just the
new ad
G[J+ 1] −G[J] = 2(J+ 1)2
which we multiply out to give
a(3J2+ 3J+ 1) + b(2J+ 1) + c= 2(J+ 1)2
matching coefficients then gives the values of a, b, c which proves Eq. 19.1.
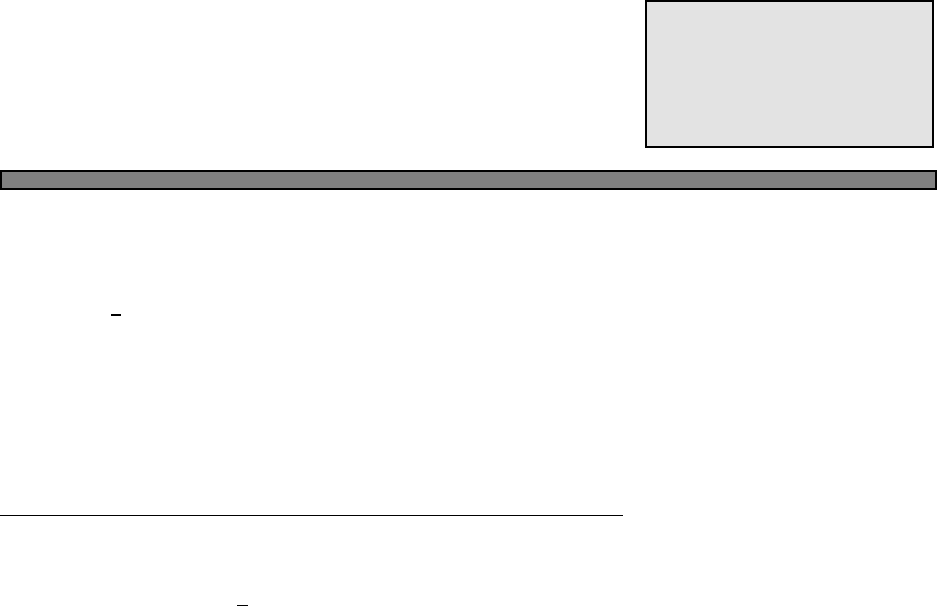
Spontaneous Magnetic
Order: Ferro-, Antiferro-,
and Ferri-Magnetism 20
(20.1) Ferromagnetic vs Antiferromagnetic
States
Consider the Heisenberg Hamiltonian
H=−1
2X
hi,ji
JSi·Sj+X
i
gµBB·Si(20.1)
and for this exercise set B= 0.
(a) For J > 0, i.e., for the case of a ferromagnet, in-
tuition tells us that the ground state of this Hamiltonian
should simply have all spins aligned. Consider such a
state. Show that this is an eigenstate of the Hamiltonian
Eq. 20.1 and find its energy.
(b) For J < 0, the case of an antiferromagnet on a cu-
bic lattice, one might expect that (at least for B= 0) the
state where spins on alternating sites point in opposite
directions might be an eigenstate. Unfortunately, this is
not precisely true. Consider such a state of the system.
Show that the state in question is not an eigenstate of the
Hamiltonian.
Although the intuition of alternating spins on alter-
nating sites is not perfect, it becomes reasonable for sys-
tems with large spins S. For smaller spins (like spin 1/2)
one needs to consider so-called “quantum fluctuations”
(which is much more advanced, so we will not do that
here).
It is useful here to recall that
Si·Sj=1
2(S+
iS−
j+S−
iS+
j) + Sz
iSz
j
(Indeed, students often need to be reminded of this! Maybe it is worth
giving this as a hint!)
(a) If each spin is aligned in the ˆzdirection (it has Sz= 1), then the
energy is −gµbBper spin and for each bond we have energy −JSi·Sj=
−JSz
iSz
j=−JS2since S+on the spins all give zero. The system is in
an energy eigenstate with energy
E=−NgµB|B| − NzJS2/2
with zthe number of neighbors of each site (=6 for a cubic lattice).
(b) Assuming an antiferromagnetic configuration, the key here is to
note that there are terms S+
iS−
jwhich do not vanish (where S+is ap-
plied to a down spin, and S−is applied to an up spin). This means
that when the hamiltonian is applied to the proposed antiferromagnetic
ground states, it generates other spin configurations. Hence this is not
an eigenstate.

168 Spontaneous Magnetic Order: Ferro-, Antiferro-, and Ferri-Magnetism
(20.2) Frustration
Consider the Heisenberg Hamiltonian as in Exercise 20
with J < 0, and treat the spins as classical vectors.
(a) If the system consists of only three spins arranged
in a triangle (as in Fig. 20.2), show that the ground state
has each spin oriented 120◦from its neighbor.
(b) For an infinite triangular lattice, what does the
ground state look like?
Probably here I should have stated explicitly that all three spins have
the same |S|(might be interesting to consider a case where they don’t
all have the same spin!).
(a) The Hamiltonian is
H=J(S1·S2+S1·S3+S2·S3)
Since Si·Si=S2is a constant we can write
H= (J/2)(S1+S2+S3)2+ constant
To minimize the energy, we must have
S1+S2+S3= 0
which implies that the spins are at 120 degree angles from each other –
but can lie in any plane.
(b) For a triangular lattice, each triangle must have three spins each
at 120 degree angles from its neighbors. So choose three directions all
at 120 degree angles from each other in any given plane. Call these
three directions A, B, C. Now we must assign each site on the triangular
lattice one of the three values A, B, or C in such a way that all triangles
contain one site of type A, one of type B, and one of type C. One can
think of this as being now a crystal whose unit cell has three times the
area of the original unit cell, and now contains one spin of each type A,
B, C.
(20.3) Spin Waves*
For the spin-Sferromagnet particularly for large S, our
“classical” intuition is fairly good and we can use simple
approximations to examine the excitation spectrum above
the ground state.
First recall the Heisenberg equations of motion for any
operator
i~dˆ
O
dt = [ ˆ
O, H]
with Hthe Hamiltonian (Eq. 20.1 with Sibeing a spin S
operator).
(a) Derive equations of motion for the spins in the
Hamiltonian Eq. 20.1. Show that one obtains
~dSi
dt =Si× JX
j
Sj−gµbB!(20.2)
where the sum is over sites jthat neighbor i.
In the ferromagnetic case, particularly if Sis large, we
can treat the spins as not being operators, but rather as
being classical variables. In the ground state, we can set
all Si= ˆzS (Assuming Bis in the −ˆzdirection so the
ground state has spins aligned in the ˆzdirection). Then
to consider excited states, we can perturb around this
169
solution by writing
Sz
i=S− O((δS)2/S)
Sx
i=δSx
i
Sy
i=δSy
i
where we can assume δSxand δSyare small compared to
S. Expand the equations of motion (Eq. 20.2) for small
perturbation to obtain equations of motion that are linear
in δSxand δSy
(b) Further assume wavelike solutions
δSx
i=Axeiωt−ik·r
δSy
i=Ayeiωt−ik·r
This ansatz should look very familiar from our prior con-
sideration of phonons.
Plug this form into your derived equations of motion.
Show that Sx
iand Sy
iare out of phase by π/2.
What does this mean?
Show that the dispersion curve for “spin-waves” of
a ferromagnet is given by ~ω=|F(k)|where
F(k) = gµb|B|
+JS(6 −2[cos(kxa) + cos(kya) + cos(kza)])
where we assume a cubic lattice.
How might these spin waves be detected in an ex-
periment?
(c) Assume the external magnetic field is zero. Given
the spectrum you just derived, show that the specific heat
due to spin wave excitations is proportional to T3/2.
(a) We need the angular momentum algebra
[Sx, Sy] = iSz
and cyclic permutations of this. We then have the Heisenberg equations
i~dSx
i
dt = [Sx
i,H]
The only terms that this does not commute with are those containing
Sy
iand Sz
i. Thus we have
i~dSx
i
dt = [Sx
i, gµb(BySy
i+BzSz
i)−JX
j
(Sy
jSy
i+Sz
jSz
i)]
with the sum over jbeing over neighbors of i. Thus we obtain
i~dSx
i
dt =i
(gµb)(BySz
i−BzSy
i)−JX
j
(Sy
jSz
i−Sz
jSy
i)
and similar for the other two components of the spin. Thus we conclude
~dSi
dt =Si×
JX
j
Sj−gµbB
Writing
Si= ˆzS +δSi
we obtain
~dδSi
dt =JS ˆz×X
j
δSj+δSi×(JZS ˆz+gµb|B|)
where Zis the number of neighbors of a site.

170 Spontaneous Magnetic Order: Ferro-, Antiferro-, and Ferri-Magnetism
(b) Plugging in the wave ansatz (for a cubic lattice) we obtain
i~ωAx=F(k)Ay
i~ωAy=−F(k)Ax
where
F(k) = JS(6 −2[cos(kxa) + cos(kya) + cos(kza)]) + gµb|B|
This system of equations can be solved immediately to give dispersion
~ω=|F(k)|
Spin waves are typically detected by inelastic neutron scattering. This
is like scattering from phonons except that one uses (spin-polarized)
neutrons in order to couple to the spin.
(c) For small k=|k|, and hence small energy, the energy spectrum is
quadratic
E=JSa2k2
We will also need
k= (E/JSa2)1/2
and
dk =dE/(2(EJSa2)1/2)
Calculating the total energy stored in spin waves, we have
U=VZBZ
dk
(2π)3E(k)nB(E(k)) ≈V
2π2Z∞
0
dkk2E(k)nB(E(k))
with nBthe usual Bose factor and the approximation accurate for low
temperatures. We rewrite this as
U=V
4π2(JSa2)3/2Z∞
0
dEE3/2nB(E)
=V(kbT)5/2
4π2(JSa2)3/2Z∞
0
dx x5/2
ex−1
which we differentiate to get the heat capacity
C=dU/dT =kb
5
2
V(kbT)3/2
4π2(JSa2)3/2Z∞
0
dx x5/2
ex−1
(one does not really need to carry all of the constants to see how it
scales!). For those who are interested though, the integral can be eval-
uated in the usual way
Z∞
0
dx x5/2
ex−1=
∞
X
n=1 Z∞
0
dxx5/2e−nx =
∞
X
n=1
1
n7/2Z∞
0
dyy5/2e−y= Γ(7/2)ζ(7/2)
where Γ(7/2) = 15√π/8 and ζ(7/2) ≈1.1267 ....

171
(20.4) Small Heisenberg Models
(a) Consider a Heisenberg model containing a chain of
only two spins, so that
H=−JS1·S2.
Supposing these spins have S= 1/2, calculate the en-
ergy spectrum of this system. Hint: Write 2S1·S2=
(S1+S2)2−S12−S12.
(b) Now consider three spins forming a triangle (as
shown in Fig. 20.2). Again assuming these spins are
S= 1/2, calculate the spectrum of the system. Hint:
Use the same trick as in part (a)!
(c) Now consider four spins forming a tetrahedron.
Again assuming these spins are S= 1/2, calculate the
spectrum of the system.
Note the obvious typo, it should read 2S1·S2= (S1+S2)2−S12−S22.
(a)
H=−(J/2)[(S1+S2)2−S2
1−S2
2]
Since (S)2=S(S+ 1) for spin-1/2 we have (S)2= 3/4. Further, when
two spin 1/2’s are added they can form either a spin-0 singlet or a spin-
1 triplet (three Szstates). So (S1+S2)2takes the values 0 for the
singlet or S(S+ 1) = 2 for the S= 1 triplet. Thus the Hamiltonian has
eigenstates 3J/4 for the singlet (one eigensate) and −J/4 for the triplet
(three eigenstates).
(b) Similarly
H=−(J/2)[(S1+S2+S3)2−S2
1−S2
2−S2
3]
Here, again for spin 1/2 we have (S)2= 3/4. When adding three spin-
1/2s, we can obtain spin-1/2 in two ways and spin-3/2 in one way. (To
see this, think about adding the first two spin-1/2 to get spin-0 or spin-
1. Now adding a spin-1/2 the spin-0 gives spin-1/2 and adding spin-1/2
to the spin-1 gives either spin-1/2 or spin-3/2. Note that counting the
total nbumber of eigenstates we should get 8 since each spin-1/2 has
two possible Szstates. Each of the two possible spin-1/2’s can take two
possible Szstates and the spin-3/2 can take 4 possible Szstates, which
gives a total of 8 possible Szstates.
In the case that the three spins add to spin-1/2, we obtain energy
3J/4 (four eigenstates) whereas if the three spins add to spin-3/2, S2=
S(S+ 1) = 15/4, so the energy is −3J/4 (four eigenstates).
(c) Same story
H=−(J/2)[(S1+S2+S3+S4)2−S2
1−S2
2−S2
3−S2
4]
The sum of the four spins can give spin 0 in two ways, spin 1 in 3 ways,
and spin 2 in one way. Again we should add up the total number of
eigenstates to check that it is 24= 16. We have 2 spin 0’s + 3 states for
spin 1 in 3 ways + 5 states in spin 2. So we have 2+9+5 = 16. The spin-
0 singlets (two eigenstates) have energy (−J/2)[0 −4(3/4)] = 3J/2. The
three spin-1 triplets (9 eigenstates) have energy (−J/2)[2 −4(3/4)] =
J/2 and the spin-2 fiveplets (5 eigenstates) have energy (−J/2)[2 ×3−
4(3/4)] = −3J/2

172 Spontaneous Magnetic Order: Ferro-, Antiferro-, and Ferri-Magnetism
(20.5) One-Dimensional Ising Model with B= 0
(a) Consider the one-dimensional Ising model with spin
S= 1. We write the Hamiltonian for a chain of Nspins
in zero magnetic field as
H=−J
N−1
X
i=1
σiσi+1
where each σitakes the value ±1. The partition function
can be written as
Z=X
σ1,σ2,...σN
e−βH .
Using the transformation Ri=σiσi+1 rewrite the parti-
tion function as a sum over the Rvariables, and hence
evaluate the partition function.
Show that the free energy has no cusp or disconti-
nuity at any temperature, and hence conclude that there
is no phase transition in the one-dimensional Ising model.
(b) *At a given temperature T, calculate an expres-
sion for the probability that Mconsecutive spins will be
pointing in the same direction. How does this probability
decay with Mfor large M? What happens as Tbecomes
small? You may assume N≫M.
(a) The first spin can be either in the spin-up or spin down state, so
we leave σ1as a variable to be summed over. The remaining spins are
defined by Rifor i= 1,...N −1 where each Rcan take the values ±1.
The Hamitonian in terms of the Rvariables is
H=−J
N−1
X
i=1
Ri
So the partition function is
Z= 2(e−βJ +eβJ )N−1= 2(2 cosh(βJ))N−1
with the factor of 2 out front being the sum over the first spin. The free
energy is thus
F=−kBTlog Z=−kBT N log 2 −kbT N log cosh(βJ)
which is a completely continuous function with no cusps or discontinu-
ities at finite β.
(b) The probability that a given Ris in the +1 state is
P(R= +1) = eβJ
eβJ +e−βJ =1
e−2βJ + 1
Having Rin the +1 state tells us that two consecutive spins are pointing
in the same direction. Looking at M−1 consecutive values of R, the
probability that all of these are +1 is then
P(M) = 1
e−2βJ + 1 M−1
which would put Mconsecutive spins in the same direction. This prob-
ability decays exponentially with M. To see this, rewrite
P(M) = exp[−(M−1) log(e−2βJ + 1)]

173
so the decay length is 1/log(e−2βJ + 1). In the low tempearture limit
P(R+ 1) becomes close to unity, and the decay length becomes long.
Actually, we can see that for very large βwe have log(e−2βJ +1) ≈e−2βJ ,
so the decay length is e2βJ lattice sites and is exponentially long.
(20.6) One-Dimensional Ising Model with B6= 0*
Consider the one-dimensional Ising model with spin
S= 1. We write the Hamiltonian (Eq. ??) for a chain of
Nspins in magnetic field Bas
H=
N
X
i=1 Hi(20.3)
where
H1=hσ1
Hi=−Jσiσi−1+hσifor i > 1
where each σitakes the value ±1 and we have defined
h=gµBBfor simplicity of notation.
Let us define a partial partition function for the first M
spins (the first Mterms in the Hamiltonian sum Eq. 20.3)
given that the Mth spin is in a particular state. I.e.,
Z(M, σM) = X
σ1,...,σM−1
e−βPM
i=1 Hi
so that the full partition function is Z=Z(N, +1) +
Z(N, −1).
(a) Show that these partial partition functions satisfy
a recursion relation
Z(M, σM) = X
σM−1
TσM,σM−1Z(M−1, σM−1)
where Tis a 2 by 2 matrix, and find the matrix T. (Tis
known as a “transfer matrix”).
(b) Write the full partition function in terms of the
matrix Traised to the (N−1)th power.
(c) Show that the free energy per spin, in the large N
limit, can be written as
F/N ≈ −kBTlog λ+
where λ+is the larger of the two eigenvalues of the matrix
T.
(d) From this free energy, derive the magnetization,
and show that the susceptibility per spin is given by
χ∝βe2βJ
which matches the Curie form at high T.
(a) The transfer matrix takes the form
T=e−βH(+,+) e−βH(+,−)
e−βH(−,+) e−βH(−,−)=e−β(−J+h)e−β(J−h)
e−β(J+h)e−β(−J−h)
(b) The full partition function is then
Z=vT N−1vT
where v= (1,1). Although Tis not hermitian, it can still be brought to
diagonal form via a Jordon decomposition
T=JΛJ−1
where Λ is a diagonal matrix of the eigenvalues of Tand Jis a matrix
made of the eigenvectors of T(these are no longer orthonormal!). (c)
Assuming these two eigenvalues are not degenerate, we then have for
large Nthat
Z∼λN−1
+

174 Spontaneous Magnetic Order: Ferro-, Antiferro-, and Ferri-Magnetism
where λ+is the larger of the two eigenvalues. Thus the free energy per
site is
F/N ∼ −kBTlog λ+
For the record, the value of the larger eigenvalue is
λ+=e−β(h+J)
21 + e2βh +p1−2e2βh +e4βh + 4e4β(h+J)
Just to check that this agrees with the previous problem, note that
setting h= 0 we correctly obtain
λ+=e−βJ +eβJ
(d) Probably we want to derive the magnetic moment per spin which is
m=−∂(F/N)
∂B =gµBkbT∂log λ+
∂h
The result is a bit of a mess. Then once we have this, we want the
susceptibility per spin
χ=µ0∂m/∂B
which one evaluates at B= 0. It is much easier to make expansions for
small hsince this is all we will need. In the end we will obtain
χ=g2µ2
Bµ0kbT∂2log λ+
∂h2=g2µ2
Bµ0βe−2βJ
as claimed.

Domains and Hysteresis 21
(21.1) Domain Walls and Geometry
Suppose a ferromagnet is made up of a density ρof
spins each with moment µB.
(a) Suppose a piece of this material forms a long cir-
cular rod of radius rand length L≫r. In zero external
magnetic field, if all of the moments are aligned along the
L-direction of the rod, calculate the magnetic energy of
this ferromagnet. (Hint: a volume of aligned magnetic
dipoles is equivalent to a density of magnetic monopoles
on its surface.)
(b) Suppose now the material is shaped such that
r≫L. What is the magnetic energy now?
(c) If a domain wall is introduced into the material,
where might it go to minimize the magnetic energy in the
two different geometries. Estimate how much magnetic
energy is saved by the introduction of the domain wall.
(d) Suppose the spins in this material are arranged in
a cubic lattice, and the exchange energy between nearest
neighbors is denoted Jand the anisotropy energy is very
large. How much energy does the domain wall cost? Com-
paring this energy to the magnetic energy, what should
we conclude about which samples should have domain
walls?
(e) Note that factors of the lattice constant aare often
introduced in quoting exchange and anisotropy energies
to make them into energies per unit length or unit vol-
ume. For magnetite, a common magnetic material, the
exchange energy is JS2/a = 1.33 ×10−11 J/m and the
anisotropy energy is κS2/a3= 1.35×104J/m3. Estimate
the width of the domain wall and its energy per unit area.
Make sure you know the derivation of any formulas you
use!
(a) Following the hint, the magnetic energy between two monopoles
of charge qmand q′
mseparated by distance ris given by
E=µ0
4π
qmq′
m
r
Here we have charge of magnitude qm=µBAρ where A=πr2is the
area of the end. Check that this has the right dimensions, recall that
a dipole is a charge times a length, so qmcorrectly has dimension of a
charge.
Thus the energy is
µ0
4π
(µBρ(πr2))2
L
(b) This problem, on the other hand is analogous to the energy of a
capacitor. The energy stored in a capacitor is q2/(2C) where electrically
the capacitance is ǫ0A/d with Athe area and dthe spacing. The analogy
here is thus A/(dµ0). Thus the total energy stored is
E=q2
mµ0d/(2A) = µ0(µBρ)2(πr2)L
2
(c) First, let us consider a domain wall that cuts Lin half (i.e., a plane
parallel to the Asurface). This puts two magnetic charges of the same

176 Domains and Hysteresis
sign right next to each other and is therefore energetically unfavorable.
Now consider a domain wall perpendicular to this plane — i.e., that runs
along the Laxis. In the (a) case we can view this as, instead of having a
single charge at each end of the rod, now we have two opposite charges
along each end of the rod (each with charge ±qm/2). This completely
kills the leading energy cost and now we have instead some sort of dipolar
interaction between the two ends — with energy typically on the much
smaller order
E=µ0
4π
(µBρ(πr2/2))2r2
L3
Similarly with the capacitor configuration of part (b), we can convert
“charge” energy to “dipole” energy by placing a domain wall in the
diraction along the axis (in the direction of L). However, here we will
not be able to consider the system “dipolar” until the size of the domains
dis smaller than L. Once we do this, the energy will again drop as in
the (a) case proportional to d6/L3
(d) Since the lattice spacing will be a=ρ−1/3, the energy of intro-
ducing a domain wall of area Ais AJρ2/3= 2LrJρ2/3. In the (a) case,
for large enough L, the magnetic energy is not very large to begin with,
so introducing an energy cost proportional to Lis not a very good idea.
Now let us consider the (b) case. Let us consider introducing a domain
wall network spaced by d. The number of domains is πr2/d2and the
total aread of the walls will be πr2L/d and their total domain wall en-
ergy will be πr2LJρ2/3/d. As a function of d, as discussed in part (c)
then magnetic energy drops strongly when d < L. Thus, there will be
some happy medium which optimizes the total energy.
(e) As mentioned in the text, the width of a domain wall should be
pJ/κ which here is 3100 lattice spacings. The energy per unit area is
then √Jκ = 4 ×107Joules per a2area.
(21.2) Critical Field for Crystallite
(a) Given that the energy of a crystallite in a magnetic
field is given by
E/V =E0− |M||B|cos θ−κ′|M|2(cos θ)2
show that for |B|< Bcrit there is a local energy minimum
where the magnetization points opposite the applied field,
and find Bcrit.
(b)* In part (a) we have assumed Bis aligned with the
anisotropy direction of the magnetization. Describe what
can occur if these directions are not aligned.
(c) For small B, roughly how large (in energy per unit
volume) is the activation barrier for the system to get
from the local minimum to the global minimum.
(d) Can you make an estimate (in terms of actual num-
bers) of how big this activation barrier would be for a fer-
romagnetic crystal of magnetite that is a sphere of radius
1 nm ? You may use the parameters given in Exercise
31.1.e (you may need to estimate some other parameters
as well).
(a) Let cos θ=z. The function E(z) is an upside-down parabola
with maxium at z=−B/(2κ′|M|)<0. If this parameter is z > −1
then there are two minima, one at θ= 0 and the other at θ=π. The
absolute minium is always at θ= 0.
(b) Let us consider Bagain pointing in the ˆzdirection and the anisotropy
direction oriented at an angle φfrom ˆz. In this case we have an energy

177
functional
E/V =E0− |M||B|cos θ−κ′|M|2[cos(θ−φ)]2
If y=κ|M|/(2B) is small, then the minimum will always be close to 0. If
this parameter is greater than 1/2, then there may be a metastable min-
imum as well, although for yclose to 1/2 then there is only a metastable
minimum if φis close to zero. If yis large, then the metastable minima
always exist near to φand φ+π.
(c) Consider small B, so zis close to zero. In this case, Emin =
E0−κ|M|2and Emax =E0. So the activation barrier is κ|M|2.
(d) The activation barrier is just the total anisotropy energy. This is
1.35 ×104J/m3and the size is (4/3)π×1nm3≈10−26m3, so we have a
total energy of about 10−22J≈10Kelvin activation energy.
(21.3) Exact Domain Wall Solution*
The approximation used in Section 21.1.1 of the en-
ergy of the anisotropy (κ) term is annoyingly crude. To
be more precise, we should instead write κS2(cos θi)2and
then sum over all spins i. Although this makes things
more complicated, it is still possible to solve the problem
so long as the spin twists slowly so that we can replace
the finite difference δθ with a derivative, and replace the
sum over sites with an integral. In this case, we can write
the energy of the domain wall as
E=Zdx
a(JS2a2
2dθ(x)
dx 2
−κS2[cos θ(x)]2)
with athe lattice constant.
(a) Using calculus of variations show that this energy
is minimized when
(Ja2/κ)d2θ/dx2−sin(2θ) = 0
(b) Verify that this differential equation has the solu-
tion
θ(x) = 2 tan−1exp √2(x/a)rκ
J
thus demonstrating the same L∼pJ/κ scaling.
(c) Show that the total energy of the domain wall be-
comes Etot/(A/a2) = 2√2S2√Jκ.
It is better to write the first equation as + sin2instead of −cos2.
These differ only by a constant, but in the former case, the background
energy is zero whereas as written the background energy is finite.
(a) This is a trivial exercise in calculus of variations. To clarify it,
write θ=θ0+δθ and expand to linear order in δθ. Isolating the terms
inside the integral linear in δθ, and then integrating by parts to remove
the derivatives gives
−JS2a2d2θ(x)
dx2+ 2κS2cos θ(x) sin θ(x)δθ(x)
Setting this variation to zero immediately gives the desired result.
(b) This is an exercise in nasty algebra. First write b=√2(1/a)pκ
J
so that we have
θ(x) = 2 tan−1(ebx)
178 Domains and Hysteresis
From this we obtain on the left of the equation
dθ/dx = 2bebx
1 + e2bx =b
cosh(bx)(21.1)
d2θ/dx2=−b2sinh(bx)
cosh2(bx)(21.2)
On the right of the equation we need to evaluate
sin 2θ= 2 sin θcos θ= 4 sin θ
2cos θ
2(cos2θ
2−sin2θ
2)(21.3)
We have θ/2 = tan−1(ebx) so ebx = tan θ
2so we have 1 + e2bx = sec2θ
2
so
cos θ
2=1
√1 + e2bx
sin θ
2=ebx
√1 + e2bx
Plugging these results into the prior expression for sin 2θthe gives
sin 2θ= 4 ebx
1 + e2bx
1−e2bx
1 + e2bx =−2 sinh(bx)
cosh2(bx)
Comparing this result to Eq. 21.2 along with the expression for bimme-
diately confirms the desired solution.
(c) Starting with
E=Zdx
a(JS2a2
2dθ(x)
dx 2
+κS2[sin θ(x)]2)
we have dθ/dx =b
cosh(bx)and
sin θ= 2 cos θ/2 sin θ/2 = 2ebx
1 + e2bx = 1/cosh(bx)
This then naturally gives
E=Zdx
a(JS2a2
2b
cosh(bx)2
+κS21
cosh2(bx))
Plugging in the value of bthis simplifies to
E= 2κS2Zdx
a
1
cosh2bx =2κS2
ab Zdx 1
cosh x
plug in the value of bto get a prefactor of S2√2κJ and the integral of
sech2is tanh thus giving a factor of 2, yielding the desired result.

Mean Field Theory 22
(22.1) ‡Weiss Mean Field Theory of a Ferromag-
net
Consider the spin-1/2 ferromagnetic Heisenberg Hamil-
tonian on the cubic lattice:
H=−J
2X
hi,ji
Si·Sj+gµBBX
i
Si(22.1)
Here, J > 0, with the sum indicated with hi, jimeans
summing over iand jbeing neighboring sites of the cu-
bic lattice, and Bis the externally applied magnetic field,
which we will assume is in the ˆzdirection for simplicity.
The factor of 1/2 out front is included so that each pair of
spins is counted only once. Each site iis assumed to have
a spin Siof spin S= 1/2. Here µBis the conventional
Bohr magneton defined to be positive. The fact that the
final term has a + sign out front is from the fact that the
electron charge is negative, therefore the magnetic mo-
ment opposes the spin direction. If one were to assume
that these were nuclear spins the sign would be reversed
(and the magnitude would be much smaller due to the
larger nuclear mass).
(a) Focus your attention on one particular spin Si, and
write down an effective Hamiltonian for this spin, treat-
ing all other variables Sjwith j6=ias expectations hSji
rather than operators.
(b) Calculate hSiiin terms of the temperature and the
fixed variables hSjito obtain a mean-field self-consistency
equation. Write the magnetization M=|M|in terms of
hSiand the density of spins.
(c) At high temperature, find the susceptibility χ=
dM/dH =µ0dM/dB in this approximation.
(d) Find the critical temperature in this approxima-
tion.
Write the susceptibility in terms of this critical tem-
perature.
(e) Show graphically that in zero external field (B= 0),
below the critical temperature, there are solutions of the
self-consistency equation with M6= 0.
(f) Repeat parts (a)–(d) but now assuming there is an
S= 1 spin on each site (meaning that Sztakes the values
−1,0,+1).
(a) The effective Hamiltonian for one spin-1/2 is
Hi=Si·
−JX
jhSji+gµbB
= +Si·gµbBi,ef f
where
gµbBi,ef f =gµbB−JX
jhSji
with the sums being over sites jneighboring site i. (Note the factor of
1/2 out front is now missing).
(b)Assuming Baligned with ˆztells us that hSkishould be aligned
with −ˆzif nonzero. Thus we can treat these quantities as scalars rather
than vectors. We then have the usual calculation
Zi= exp(βgµbBi,eff (1/2)) + exp(−βgµbBi,eff (1/2)) (22.2)
hSz
ii=−1
2tanh[βg ˜µbBeff (1/2)]

180 Mean Field Theory
which gives us the self consistency equation
hSzi=−1
2tanh[β(gµbB−JzhSzi)(1/2)] (22.3)
where zis the number of neighboring spins for each site (which is z= 6
for a cubic lattice).
(c) At high Tthe magnetization is zero in the absence of a field. Thus
for small field we can expand the tanh for small argument to obtain.
hSzi=−1
2[β(gµbB−JzhSzi)(1/2)]
or
hSzi=(−1/4)β(gµbB)
1−βJz/4
The moment per site is thus
m=−gµbhSzi=(1/4)(gµb)2B
kbT−Jz/4
giving the susceptibility
χ=(µ0/4)(gµb)2N
kbT−Jz/4=(1/4)(gµb)2N
kb(T−Tc)(22.4)
refWeissMeanFerro where Nis the density of spins.
(d) the critical temperature is the point where the susceptibility di-
verges, or kbTc=Jz/4.
(e) Graphically we plot the right and left sides of Eq. 22.3 as shown
roughly in Fig. 22.1. The horizontal axis is −hSi. The left side of the
equation is a straight line, the right side is a tanh. At high enough T,
these intersect only at hSi= 0, however at T < Tcthey intersect as well
at a finite value of hSi. Note that the point at which the curves are
tangent is the critical temperature. We will show in the next problem
that below Tcthe solution with hSi= 0 is unstable.
(f) The procedure is the same for S= 1. In this case, the partition
function Eq. 22.2 is replaced by
Zi= exp(βgµbBi,eff ) + 1 + exp(−βgµbBi,ef f )(22.5)
leading to
hSz
ii=−2 sinh(x)
2 cosh(x) + 1
with x=βgµbBeff =β(gµbB−JzhSz
ii). At high Twe expand for small
xwe obtain the equation
hSzi=−2x
3=−2
3β(gµbB−JzhSzi)
which then gives us
hSzi=(−2/3)βgµbB
1−2
3βJz

181
Fig. 22.1 graphical solution of Eq. 22.3
or a susceptibility of
χ=(2/3)µ0(gµb)2N
kbT−2
3Jz
and a critical temperature of kbTc= (2/3)Jz (where Nis the density of
spins).
(22.2) Bragg-Williams Approximation
This exercise provides a different approach to obtain-
ing the Weiss mean-field equations. For simplicity we will
again assume spin 1/2 variables on each site.
Assume there are Nlattice sites in the system. Let
the average spin value be hSz
ii=s. Thus the probability
of a spin being an up spin is P↑= 1/2 + swhereas the
probability of a spin being a down spin is P↓= 1/2−s.
The total number of up spins or down spins is then NP↑
and NP↓respectively where there are Ntotal lattice sites
in the system.
(a) Consider first a case where sites do not interact
with each other. In the micro-canonical ensemble, we can
count the number of configurations (microstates) which
have the given number of spin-ups and spin-downs (de-
termined by s). Using S=kBln Ω, calculate the entropy
of the system in the large Nlimit.
(b) Assuming all sites have independent probabilities
P↑and P↓of pointing up and down respectively, calculate
the probability that two neighboring sites will point in the
same direction and the probability that two neighboring
sites will point in opposite directions.
Use this result to calculate an approximation to the
expectation of the Hamiltonian. Note: This is not an ex-
act result, as in reality, sites that are next to each other
will have a tendency to have the same spin because that
will lower their energies, but we have ignored this effect
here.
(c) Putting together the results of (a) and (b) above,
derive the approximation to the free energy
F=E−T S
=NkBT(1
2+s) log( 1
2+s)
+ ( 1
2−s) log( 1
2−s)
+gµBBzNs −JNzs2/2
where zis the number of neighbors each spin has, and we
have assumed the external field Bto be in the ˆzdirec-
tion. (Again we assume the spin is electron spin so that

182 Mean Field Theory
the energy of a spin interacting with the external field is
+gµbB·S.)
(d) Extremize this expression with respect to the vari-
able sto obtain the Weiss mean field equations.
Below the critical temperature note that there are
three solutions of the mean field equations.
By examining the second derivative of Fwith re-
spect to s, show that the s= 0 solution is actually a
maximum of the free energy rather than a minimum.
Sketch F(s) both above and below the critical tem-
perature for B= 0. At non-zero B?
(a) The number of configurations is
Ω = N
N↑=N!
(N(1/2 + s))!(N(1/2−s))!
giving the entropy (using Stirling’s approximation)
S=kbln Ω = −kbN(1
2+s) log( 1
2+s) + (1
2−s) log( 1
2−s)
(b) The expected energy per bond is −J(1/2)2times the probability of
having like spins on neighboring sites plus J(1/2)2times the probability
of having unlike spins. We thus have
E/bond =−(J/4)[P↑P↑+P↓P↓]+2(J/4)P↑P↓=−(J/4)(P↑−P↓)2=−Js2
If there are N z/2 bonds in the whole system (with zbeing the number
of neighbors of each site) we thus obtain a total energy
E=−JN zs2/2
We must add to this the coupling to the external field which is simply
NgµBs. Adding these terms together F=E−T S gives us the desired
result.
(c)
1
N
dF
ds =gµbB−sJz +kbTlog( 1
2+s)−log( 1
2−s)
Setting this to zero we obtain
β(−gµbB+sJz) = log( 1
2+s)−log( 1
2−s)
defining the left to be x, we exponentiate both sides to get
ex=1/2 + s
1/2−s
which we rearrange to
s=1
2
ex−1
ex+ 1 =1
2tanh(x/2) = 1
2tanh(β(−gµbB+sJz)/2)
which is the same self-consistency condition.
183
(d) Look at the second derivative
1
N
d2F
ds2=−Jz +kbT1
1/2 + s+1
1/2−s
Now examine this at s= 0, we obtain
1
N
d2F
ds2m=0
=−Jz + 4kbT
Note that this changes sign exactly at the critical temperature! Thus
below Tcthe s= 0 solution becomes a maximum of the free energy rather
than a minimum as it is as above Tc. The free energy as a function of s
is plotted in Fig. 22.2.
Fig. 22.2 Free energy (vertical axis) as a function of s(horizontal axis), at, and
below Tc. Left: in zero applied B. Right: In gµbB= 0.02Tc
(22.3) Spin SMean Field Theory
Using the result of Exercise 19.7 use mean field the-
ory to calculate the critical temperature for a spin Sfer-
romagnet with a given g-factor g, having coordination
number zand nearest-neighbor exchange coupling Jex.
(It may be useful to re-solve Exercise 19.7 if you don’t
remember how this is done.)

184 Mean Field Theory
From Exercise 19.7, in a field Bthe resulting hSiper site (for small
perturbation B) is given by
hSi=S(S+ 1)
3βgµBB
And in mean field theory, the effective field seen from neighboring spins
is
gµBBef f =JexzhSi
Thus we have at the crtical point
hSi=S(S+ 1)
3βJexzhSi
which has the solution for the critical temperature
kbTc=S(S+ 1)
3Jexz
(22.4) Low-Temperature Mean Field Theory
Consider the S= 1/2 ferromagnet mean field calcula-
tion from Exercise 22.1. At zero temperature, the magnet
is fully polarized.
(a) Calculate the magnetization in the very low temper-
ature limit. Show that the deviation from fully polarized
becomes exponentially small as Tgoes to zero.
(b)* Now consider a spin Sferromagnet. Determine
the magnetization in the low Tlimit. You can express
your result conveniently in terms of the result of Exercise
22.3.
(c)* In fact this exponential behavior is not observed
experimentally! The reason for this has to do with spin-
waves, which are explored in Exercise 20.3, but are not
included in mean field theory. Using some results from
that exercise, determine (roughly) the low-temperature
behavior of the magnetization of a ferromagnet.
(a) In absence of external field, using the results of 22.1, the self
consistency equation is
Sz=1
2tanh(βJzSz/2)
For large argument xwe have
tanh x=1−e−2x
1 + e−2x≈1−2e−2x
So at low temperature we have
Sz≈1
2−e−βJzSz
Since at low temperature, Szis very close to 1/2, this becomes
Sz≈1
2−e−βJz/2
185
Another way to see this is to note that, if all the neighbors are aligned,
then gµBef f =Jz 1
2. Thus the energy for flipping a given spin in this
effective field is Jz/2. So the activated deviation from fully aligned is
e−βJz/2.
(b) Probably the easiest way to do this one is to use the final comment
of part (a). If all the spins are aligned to extremize Sz, the effective field
is gµBef f =JzS. The low energy excitations excite Szby a single step
at activation energy JzS, thus we obtain
Sz=S−e−βJzS
I have no idea what the comment about expressing the answer in terms
of 22.3!
(c) As noted in problem 20.3 the low energy spectrum of spin waves
(in absence of external field) is given by
~ω=JSa2|k|2
Each excitation reduces the magnetization by one step. The total num-
ber of spins is V /(a3) and the number of excitations (the number of lost
steps) at finite Tis
VZdk
(2π)3nB(~ωk)
with nBthe bose factor. Thus, for each spin the reduction in magneti-
zation is
a34π
(2π)3Z∞
0
dkk21
eβJS2a2k2−1=1
2π2kbT
JS23/2Z∞
0
dx x2
ex−1
and the final integral gives 2ζ(3) ≈2.4.
(22.5) Mean Field Theory for the Antiferromag-
net
For this Exercise we use the molecular field (Weiss
mean field) approximation for the spin-1/2 antiferromag-
netic model on a three-dimensional cubic lattice. The
full Hamiltonian is exactly that of Eq. 22.1, except that
now we have J < 0, so neighboring spins want to point
in opposite directions (compared to a ferromagnet where
J > 0 and neighboring spins want to point in the same
direction). For simplicity let us assume that the external
field points in the ˆzdirection.
At mean field level, the ordered ground state of this
Hamiltonian will have alternating spins pointing up and
down respectively. Let us call the sublattices of alternat-
ing sites, sublattice Aand sublattice Brespectively (i.e,
Asites have lattice coordinates (i, j, k) with i+j+kodd
whereas Bsites have lattice coordinates with i+j+k
even).
In mean field theory the interaction between neighbor-
ing spins is replaced by an interaction with an average
spin. Let sA=hSziAbe the average value of the spins
on sublattice A, and sB=hSziBbe the average value of
the spins on sublattice B(we assume that these are also
oriented in the ±ˆzdirection).
(a) Write the mean field Hamiltonian for a single site
on sublattice Aand the mean field Hamiltonian for a sin-
gle site on sublattice B.
(b) Derive the mean-field self-consistency equations
sA=1
2tanh(β[JZsB−gµBB]/2)
sB=1
2tanh(β[JZsA−gµBB]/2)
with β= 1/(kBT). Recall that J < 0.
(c) Let B= 0. Reduce the two self-consistency equa-
tions to a single self-consistency equation. (Hint: Use
symmetry to simplify! Try plotting sAversus sB.)

186 Mean Field Theory
(d) Assume sA,B are small near the critical point and
expand the self-consistency equations. Derive the critical
temperature Tcbelow which the system is antiferromag-
netic (i.e., sA,B become non-zero).
(e) How does one detect antiferromagnetism experi-
mentally?
(f) In this mean-field approximation, the magnetic sus-
ceptibility can be written as
χ=−(N/2)gµ0µBlim
B→0
∂(sA+sB)
∂B
(why the factor of 1/2 out front?).
Derive this susceptibility for T > Tcand write it in
terms of Tc.
Compare your result with the analogous result for
a ferromagnet (Exercise 22). In fact, it was this type of
measurement that first suggested the existence of antifer-
romagnets!
(g)* For T < Tcshow that
χ=(N/4)µ0(gµb)2(1 −(2s)2)
kBT+kBTc(1 −(2s)2)
with sthe staggered moment (ie, s(T) = |sA(T)|=
|sB(T)|).
Compare this low Tresult with that of part f.
Give a sketch of the susceptibility at all T.
This follows very much problem 22 (a)
Hi,A =Si·
−JX
jhSjBi+gµbB
Hi,B =Si·
−JX
jhSjAi+gµbB
(b) solving as above gives the desired self-consistency equations.
(c) For B= 0 we have
sA=1
2tanh(βJZsB/2)
sB=1
2tanh(βJZsA/2)
These are solved by
sA=−sB=1
2tanh(βJZsB/2) = −1
2tanh(βJZsA/2)
Recall that J < 0. (Since tanh is an odd function these are the only
possible solutions for J < 0, which one can check graphically by plotting
sAversus sB).
Thus the problem is reduced to
sA=−1
2tanh(βJZsA/2) = 1
2tanh(β|J|ZsA/2)
which is identical to the relation we obtained in the ferromagnetic case.
(d) As in the ferromagnet kbTc=z|J|/4.
(e) This staggered moment is most easily observed with neutron scat-
tering where the scattering will be spin-dependent. Going into the anti-
ferromagnetic phase there is a new unit cell of lattice constant 2a, thus
one sees new diffraction peaks at k=n2π/(2a) (with nodd) which are
not present above Tc.

187
(f)The factor of 1/2 is because we have only N/2 A sites or B sites.
Expanding the self consistency equations for high Twe obtain
sA=β[JZsB−gµbB]/4)
sB=β[JZsA−gµbB]/4)
One can solve this system of two equations in two unknowns to obtain
sA=sB=−βgµbB
4−βJz
Thus giving
χ=(1/4)µ0(gµb)2N
kb(T+Tc)
compare to the T−Tcfactor in Eq. 22.4.
(g) This required implicit differentiation. Differentiating our two self-
consistency equations gives
∂sA
∂B B=0
=βJZ
4
∂sB
∂B B=0 −βgµb
4sech2(βJZsB/4)
∂sB
∂B B=0
=βJZ
4
∂sA
∂B B=0 −βgµb
4sech2(βJZsA/4)
Noting that sA=−sB=sso both sech terms are the same, we add
both equations together to get
∂(sA+sB)
∂B h=0
=βJZ
4
∂(sA+sB)
∂B B=0 −βgµb
2sech2(βJZs/4)
Making note that sech2+ tanh2= 1, we then have
sech2(βJZs/4) = 1 −tanh2(βJZm/4) = 1 −(2s)2
where we have used the self-consistency equation to replace the tanh by
s. We thus have
∂(sA+sB)
∂B B=0
=βJZ
4
∂(sA+sB)
∂B B=0 −βgµb
2(1 −(2s)2)
This then can be rearranged into
∂(sA+sB)
∂B B=01−βJZ(1 −(2s)2)/4=−(βgµb/2)(1 −(2s)2)
or
χ=(N/4)µ0(gµb)2(1 −(2s)2)
kbT+kbTc(1 −(2s)2)
with sthe staggered moment (with Nthe density of spins). Above Tc,
we have s= 0 and we have the same behavior as part f above. Below
Tc, the factor 1 −(2s)2goes quickly down to zero, and the susceptibility
drops rapidly. At Tcthere is a cusp. This behavior is illustrated in the
figure 22.3
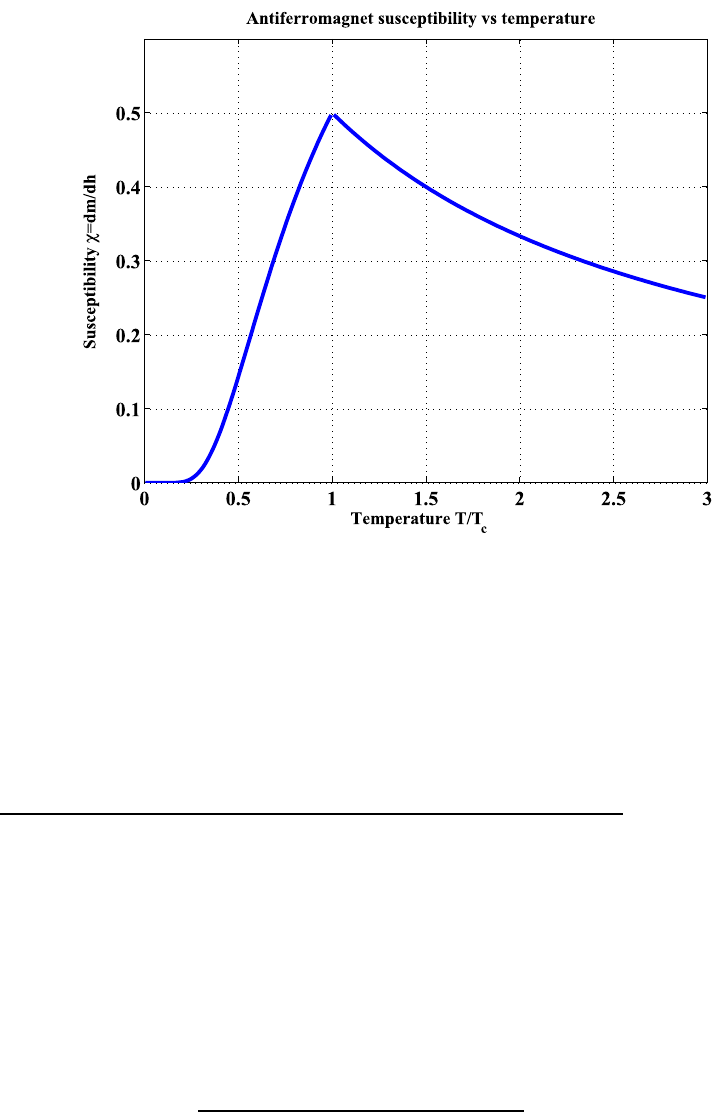
188 Mean Field Theory
Fig. 22.3 Susceptibility of an Antiferromagnet.
(22.6) Correction to Mean Field*
Consider the spin-1/2 Ising ferromagnet on a cubic lat-
tice in ddimensions. When we consider mean field theory,
we treat exactly a single spin σiand the z= 2dneigh-
bors on each side will be considered to have an average
spin hσi. The critical temperature you calculate should
be kBTc=Jz/4.
To improve on mean field theory, we can instead treat
a block of two connected spins σiand σi′where the neigh-
bors outside of this block are assumed to have the average
spin hσi. Each of the spins in the block has 2d−1 such
averaged neighbors. Use this improved mean field the-
ory to write a new equation for the critical temperature
(it will be a transcendental equation). Is this improved
estimate of the critical temperature higher or lower than
that calculated in the more simple mean-field model?
We have to consider four configurations in our partition function:
(↑,↑),(↑,↓),(↓,↑),(↓,↓)
Correspondingly, the partition function is
Z=e−β(Jhσi(z−1)+gµBB)−βJ/4+ 2eβJ/4+eβ(Jhσi(z−1)+gµBB)−βJ/4
From this we calculate the magnetization per site (note that this parti-
tion function represents two sites), and then setting Bto zero we obtain
m=hσi=e−βJ/4sinh(β(Jhσi(z−1))
2e−βJ/4cosh(β(Jhσi(z−1)) + 2eβJ/4

189
Expanding for small hσiwe find equality (which finds Tc) when
kBT=J(z−1)
4e−βJ/4
cosh(βJ/4)
The final factor in brackets is always less than unity, so this expression
always gives a lower prediction for Tcthan our prior mean field theory.

Magnetism from
Interactions: The Hubbard
Model 23
(23.1) Itinerant Ferromagnetism
(a.i) Review 1: For a three-dimensional tight binding
model on a cubic lattice, calculate the effective mass in
terms of the hopping matrix element tbetween nearest
neighbors and the lattice constant a.
(a.ii) Review 2: Assuming the density nof electrons
in this tight binding band is very low, one can view the
electrons as being free electrons with this effective mass
m∗. For a system of spinless electrons show that the total
energy per unit volume (at zero temperature) is given by
E/V =nEmin +Cn5/3
where Emin is the energy of the bottom of the band.
Calculate the constant C.
(b) Let the density of spin-up electrons be n↑and the
density of spin-down electrons be n↓. We can write these
as
n↑= (n/2)(1 + α)(23.1)
n↓= (n/2)(1 −α) (23.2)
where the total net magnetization of the system is given
by
M=−µbnαB.
Using the result of part (a), fixing the total density of
electrons in the system n,
calculate the total energy of the system per unit
volume as a function of α.
Expand your result to fourth order in α.
Show that α= 0 gives the lowest possible energy.
Argue that this remains true to all orders in α
(c) Now consider adding a Hubbard interaction term
HHubbard =UX
i
Ni
↑Ni
↓
with U≥0 where Ni
σis the number of electrons of spin
σon site i.
Calculate the expectation value of this interaction term
given that the up and down electrons form Fermi seas
with densities n↑and n↓as given by Eqns. 23.1 and 23.2.
Write this energy in terms of α.
(d) Adding together the kinetic energy calculated in
part b with the interaction energy calculated in part c,
determine the value of Ufor which it is favorable for αto
become non-zero.
For values of Unot too much bigger than this value,
calculate the magnetization as a function of U.
Explain why this calculation is only an approxima-
tion.
(e) Consider now a two-dimensional tight binding
model on a square lattice with a Hubbard interaction.
How does this alter the result of part (d)?
(a.i) The tight binding spectrum is
E=E0−2t[cos(kxa) + cos(kya) + cos(kza)]
which we expand to get
E=Emin +ta2|k|2
192 Magnetism from Interactions: The Hubbard Model
where Emin =E0−6tis the bottom of the band. We thus have
ta2|k|2=~2|k|2/(2m∗)
or
m∗=~2
2ta2
(a.ii) As we have calculated many times (note we are considering spin
polarized electrons here, so there is no factor of 2 out front)
N=V
(2π)3Zkf
0
dk =V
(2π)3Zkf
0
4πk2dk =V
(2π)3
4πk3
f
3
or
kf= (6π2n)1/3
The total energy is given by
E−EminN=V
(2π)3Zkf
0
~2k2
2m∗dk =V
(2π)3Zkf
0
~2k2
2m∗4πk2dk
=V
(2π)3
~2
2m∗
4πk5
f
5=V
20π2
~2
m∗k5
f
Thus we have
E/V =Eminn+Cn5/3
with
C=1
20π2
~2
m∗(6π2)5/3=ta2
10π2(6π2)5/3
(b) Note that nremains fixed. So we have
E/V −Eminn= +Chn5/3
↑+n5/3
↓i
=C(n/2)5/3h(1 + α)5/3+ (1 −α)5/3i
Taylor expanding here, note that the odd terms of the expansion cancel
leaving only even terms
E/V −Eminn= 2C(n/2)5/31 + (1/2!)(5/3)(2/3)α2+
(1/4!)(5/3)(2/3)(−1/3)(−4/3)α4+...
= 2C(n/2)5/31 + (5/9)α2+ (5/243)α4+...
Note that successive terms of the expansion always have positive coeffi-
cient.
(c) The expected number of electrons per unit site is na3and simi-
larly n↑a3and n↓a3are the expected number of spin up and spin down
electrons per site. Thus, the expectation of the hubbard interaction per
unit volume is
Ehubbard/V = (U/a3)(n↑a3)(n↓a3) = Ua3n↑n↓
=Ua3(n/2)2(1 + α)(1 −α) = U a3(n/2)2(1 −α2)

193
(d) We thus obtain a total energy given by
Etotal/V = constant+α2h2C(5/9)(n/2)5/3−Ua3(n/2)2i+α4h2C(n/2)5/3(5/243)i+...
(23.3)
And taking the limit of small αwe see that α= 0 is the solution only
for
U≤2C(5/9)(n/2)−1/3
For Unot too much bigger than this, we can use the quartic form of the
energy given in Eq. 23.3. Minimizing with respect to αgives
α=s−2C(5/9)(n/2)5/3+U a3(n/2)2
4C(n/2)5/3(5/243)
and M=−µbnα.
(e) In the 2d case, the key here is that N∼k2
fand ǫ∼E2
F, so
E/V ∼n2. As a result, we have the kinetic term given by
E=˜
C[(1 + α)2+ (1 −α2)] = 2 ˜
C[1 + α2]
and there is no quartic term. Thus, we have a total energy of the form
Etotal = const + α2(˜
C−˜
KU )
Once Ubecomes large enough that α= 0 is not the lowest energy
solution, then αimmediately goes to its maximum possible value 1.
Thus, the transition is discontinuous going suddenly from unpolarized
spins to fully polarized spins.
(23.2) Antiferromagnetism in the Hubbard
Model
Consider a tight binding model with hopping tand a
strong Hubbard interaction
HHubbard =UX
i
Ni
↑Ni
↓.
(a) If there is one electron per site, if the interaction term
Uis very strong, explain qualitatively why the system
must be an insulator.
(b) On a square lattice, with one electron per site,
and large U, use second-order perturbation theory to de-
termine the energy difference between the ferromagnetic
state and the antiferromagnetic state. Which one is lower
energy?
(a) If Uis strong enough, there must always be one electron per site.
This makes a traffic jam of electrons where no one can move (so long as
there is no doping).
(b) For the antiferromagnet, each spin can make a virtual excursion
to each of the neighboring sites, at an energy cost of U. If the hopping
is tat 2nd order in perturbation theory, this gives a reduction in the
ground state energy, per site, of
−2zt2/U
where zis the number of neighbors. For a ferromagnet, no excursion is
allowed by the Pauli principle, so it is higher energy.