TEOS 10 Manual

User Manual:

Open the PDF directly: View PDF .
Page Count: 210 [warning: Documents this large are best viewed by clicking the View PDF Link!]

Thermodynamic_Manual_16Oct10_1st_part.pdf
- Appendix C: Publications describing the TEOS-10 thermodynamic
- descriptions of seawater, ice and moist air ……...………..…..…. 130
  - A.1.1 Definition
  - A.1.2 ITS-90 temperature scale
Thermodynamic_Manual_17Oct10_2nd_part.pdf
Thermodynamic_Manual_16Oct10_3rd_part.pdf
- Manual on Aquatic Cyanobacteria – A photo guide and a synopsis of their toxicology. 2006. 106 pp. (English)

The international thermodynamic

equation of seawater – 2010:

Calculation and use of thermodynamic properties

Manuals and Guides 56

Intergovernmental Oceanographic Commission

ManualsandGuides56

IntergovernmentalOceanographicCommission

Theinternationalthermodynamic

equationofseawater–2010:

Calculation and use of thermodynamic properties



The authors are responsible for the choice and the presentation of the facts contained in this publication

and for the opinions expressed therein, which are not necessarily those of UNESCO, SCOR or IAPSO and

do not commit those Organizations.

The photograph on the front cover of a CTD and lowered ADCP hovering just below the sea surface was

taken south of Timor from the Southern Surveyor in August 2003 by Ann Gronell Thresher.

For bibliographic purposes, this document should be cited as follows:

IOC,SCORandIAPSO,2010:Theinternationalthermodynamicequationofseawater–2010:Calculationand

useofthermodynamicproperties.IntergovernmentalOceanographicCommission,ManualsandGuidesNo.

56,UNESCO(English),196pp.

Printed by UNESCO

(IOC/2010/MG/56)

iii

IOC Manuals and Guides No. 56

Table of contents

Acknowledgements ……………………………………………………………………... vii

Foreword ……………………………………………………………………………….…… viii

Abstract ………………………………………………………………………………...……… 1

1. Introduction ………………………………………………………………….…..… 2

1.1 Oceanographic practice 1978 - 2009 ……………………………………………………. 2

1.2 Motivation for an updated thermodynamic description of seawater ………….… 2

1.3 SCOR/IAPSO WG127 and the approach taken ………………....……………….… 3

1.4 A guide to this TEOS-10 manual ………………………………………………………. 6

1.5 A remark on units …………………………………………………………………..…… 7

1.6 Recommendations …………………………………………………………………..…… 7

2. Basic Thermodynamic Properties ……………….………………..…. 9

2.1 ITS-90 temperature ………………………………...…..…………………………..……. 9

2.2 Sea pressure ………………………………….…………………..……….……………. 9

2.3 Practical Salinity …………………………..…………………………………………..… 9

2.4 Reference Composition and the Reference-Composition Salinity Scale …..……. 10

2.5 Absolute Salinity ………………………………………………………………………. 11

2.6 Gibbs function of seawater .…….………………………………………………… 15

2.7 Specific volume ………….…….……………………….…….……………………… 18

2.8 Density ………...…………………...……………………………………………….… 18

2.9 Chemical potentials ……..………………………………..………………………… 19

2.10 Entropy …………………………………………………….............................……… 20

2.11 Internal energy …………………………………………………..............….……… 20

2.12 Enthalpy ………..………………………………………………………….…...…… 20

2.13 Helmholtz energy ….…………………………………………………….....……… 21

2.14 Osmotic coefficient ….………………………………………………….….........… 21

2.15 Isothermal compressibility ..…….………………………………………………... 21

2.16 Isentropic and adiabatic compressibility …..…………….……………………… 22

2.17 Sound speed ……………………….……………………………………………..… 22

2.18 Thermal expansion coefficients ……...………………………………………….... 22

2.19 Saline contraction coefficients ……………………………………………….…… 23

2.20 Isobaric heat capacity ………..…………………………………………………… 24

2.21 Isochoric heat capacity ……….…………………………………………………… 24

2.22 Adiabatic lapse rate ………..……………………………………………………… 25

IOC Manuals and Guides No. 56

3. Derived Quantities …………………………………..……….………………. 26

3.1 Potential temperature …………………………………………………………………. 26

3.2 Potential enthalpy ………………………………………....………………………… 27

3.3 Conservative Temperature ……………….………………….………………………. 27

3.4 Potential density ……………………………………………….……………………… 28

3.5 Density anomaly …………………….………………………….…………………… 28

3.6 Potential density anomaly ………….…………………………….…………………… 29

3.7 Specific volume anomaly ………………………………………….…………………. 29

3.8 Thermobaric coefficient ………….……………………………………………………. 30

3.9 Cabbeling coefficient ………….…………………………………………………....…. 31

3.10 Buoyancy frequency ……….…………………………………………….……..….… 32

3.11 Neutral tangent plane …….……………………………………………………..…. 32

3.12 Geostrophic, hydrostatic and “thermal wind” equations …….………………. 33

3.13 Neutral helicity …………….…………………………………………………..….…. 34

3.14 Neutral Density ….…………………………………………………………..….…….. 35

3.15 Stability ratio …..………………………………………………………………...…. 36

3.16 Turner angle ….………………………………………………………………………. 36

3.17 Property gradients along potential density surfaces …………………………… 36

3.18 Slopes of potential density surfaces and neutral tangent planes compared ..… 37

3.19 Slopes of in situ density surfaces and specific volume anomaly surfaces …..… 37

3.20 Potential vorticity …………………………………….………………………………. 38

3.21 Vertical velocity through the sea surface …….…………………………………… 39

3.22 Freshwater content and freshwater flux …………………………………………. 40

3.23 Heat transport …………………….………………………………………………….. 40

3.24 Geopotential ………….……………………………………………………………….. 41

3.25 Total energy …………….…………………………………………………………….. 41

3.26 Bernoulli function ……….…………………………………………………………… 42

3.27 Dynamic height anomaly …………………………………………………………… 42

3.28 Montgomery geostrophic streamfunction ………….…………………………… 43

3.29 Cunningham geostrophic streamfunction ……….……………………………… 44

3.30 Geostrophic streamfunction in an approximately neutral surface ….………… 45

3.31 Pressure-integrated steric height ……..…………………………………………… 45

3.32 Pressure to height conversion …….………………………………………………… 46

3.33 Freezing temperature ……….…………………………………………………….….. 46

3.34 Latent heat of melting ….…………………………………………..………….…… 48

3.35 Sublimation pressure …………………………………………………………….… 49

3.36 Sublimation enthalpy …………………………………………………………….… 50

3.37 Vapour pressure ……………………………………………………………….…… 52

3.38 Boiling temperature ……….……………………………………….…………….… 53

3.39 Latent heat of evaporation ………………………………………………………… 53

3.40 Relative humidity and fugacity …………………………………………………… 55

3.41 Osmotic pressure …………………………………………………………………… 58

3.42 Temperature of maximum density …….….……………………………………… 59

4. Conclusions ………………………………………….……..……………………… 60

IOC Manuals and Guides No. 56

Appendix A: Background and theory underlying the use of the

Gibbs function of seawater ………………..……………...... 62

A.1 ITS-90 temperature …………………………………………………………………... 62

A.2 Sea pressure, gauge pressure and absolute pressure …………………………….... 66

A.3 Reference Composition and the Reference-Composition Salinity Scale …….…... 67

A.4 Absolute Salinity ……………………………………………….……………………... 69

A.5 Spatial variations in seawater composition ……………………………….………... 75

A.6 Gibbs function of seawater ………………………………….…………….……..…... 78

A.7 The fundamental thermodynamic relation ………………………………….……... 79

A.8 The “conservative” and “isobaric conservative” properties ……………….…..…. 79

A.9 The “potential” property ……………….……….………………………………...... 82

A.10 Proof that

()

A,S

θη

= and

(

)

A,S

Θ=Θ .…………………….…………………... 84

A.11 Various isobaric derivatives of specific enthalpy ……………...…..…………… 84

A.12 Differential relationships between ,,

and A

S …………...……...….………. 86

A.13 The First Law of Thermodynamics ………………….……………………...…...... 87

A.14 Advective and diffusive “heat” fluxes ………………….………………..……...... 90

A.15 Derivation of the expressions for ,,

θθ

βα

and

………………….……….. 92

A.16 Non-conservative production of entropy ………………………...……………...... 94

A.17 Non-conservative production of potential temperature ………………….……... 97

A.18 Non-conservative production of Conservative Temperature ………………….. 99

A.19 Non-conservative production of density and of potential density ………….. 102

A.20 Therepresentationofsalinityinnumericaloceanmodels………………........... 103

A.21 The material derivatives of *,S A,S R

S and

in a turbulent ocean ……….... 108

A.22 The material derivatives of density and of locally-referenced

potential density; the dianeutral velocity e

 …………….……............................ 112

A.23 The water-mass transformation equation …………….…….................................. 113

A.24 Conservation equations written in potential density coordinates ………..……. 114

A.25 The vertical velocity through a general surface …………….………………….... 116

A.26 The material derivative of potential density ………………………..….……..... 116

A.27 The diapycnal velocity of layered ocean models (without rotation

of the mixing tensor) ……………………………………………….….….……..... 117

A.28 The material derivative of orthobaric density ………………………..….……..... 118

A.29 The material derivative of Neutral Density …………………………….……..... 119

A.30 Computationally efficient 25-term expressions for the density

of seawater in terms of

and

………………………..…………………….. 120

Appendix B: Derivation of the First Law of Thermodynamics ….…….…… 123

Appendix C: Publications describing the TEOS-10 thermodynamic

descriptions of seawater, ice and moist air ……...………..…..…. 130

Appendix D: Fundamental constants …….…………………..……………………... 133

IOC Manuals and Guides No. 56

Appendix E: Algorithm for calculating Practical Salinity ……….…………….. 137

E.1 Calculation of Practical Salinity in terms of K15 ….……........................................... 137

E.2 Calculation of Practical Salinity at oceanographic temperature and pressure ..... 137

E.3 Calculation of conductivity ratio R for a given Practical Salinity .......................... 138

E.4 Evaluating Practical Salinity using ITS-90 temperatures ......................................... 139

E.5 Towards SI-traceability of the measurement procedure for Practical Salinity

and Absolute Salinity .................................................................................................. 139

Appendix F: Coefficients of the IAPWS-95 Helmholtz function of

fluid water (with extension down to 50K) …………...………...… 142

Appendix G: Coefficients of the pure liquid water Gibbs function

of IAPWS-09 ………………………...……………………….…...………. 145

Appendix H: Coefficients of the saline Gibbs function for seawater

of IAPWS-08 ………………………………………………..…….………. 146

Appendix I: Coefficients of the Gibbs function of ice Ih of IAPWS-06 …... 147

Appendix J: Coefficients of the Helmholtz function of moist air

of IAPWS-10 ……………………………..…….………………………… 149

Appendix K: Coefficients of 25-term expressions for the density

of seawater in terms of

and of

…….……………………....... 153

Appendix L: Recommended nomenclature, symbols and

units in oceanography ………………………………………………… 156

Appendix M: Seawater-Ice-Air (SIA) library of computer software ……….. 162

Appendix N: Gibbs-SeaWater (GSW) Oceanographic Toolbox ..................... 173

Appendix O: Checking the Gibbs function of seawater against the

original thermodynamic data ……………………….………….…… 175

Appendix P: Thermodynamic properties based on

(

)( )

,, , , , ,gS tp hS p



()

A,,hS p

 and

(

)

ˆ,,hS pΘ …………………….…………………... 178

References ……………………………..……………………………….………….…….… 182

Index ……………………………………..……………………………….…………….….… 191

vii

IOC Manuals and Guides No. 56

Acknowledgements



ThisTEOS‐10ManualreviewsandsummarizestheworkoftheSCOR/IAPSOWorking

Group127ontheThermodynamicsandEquationofStateofSeawater.DrJohnGouldand

ProfessorPaolaMalanotte‐Rizzoliplayedpivotalrolesintheestablishmentofthe

WorkingGroupandwehaveenjoyedrock‐solidscientificsupportfromtheofficersof

SCOR,IAPSOandIOC.TJMcDwishestoacknowledgefruitfuldiscussionswithDrs

JürgenWillebrandandMichaelMcIntyreregardingthecontentsofappendixB.Wehave

benefitedfromextensivecommentsondraftsofthismanualbyDrStephenGriffiesandDr

AllynClarke.DrHarryBrydenisthankedforvaluableandtimelyadviceonthe

treatmentofsalinityinoceanmodels.LouiseBellofCSIROprovidedmuchappreciated

adviceonthelayoutofthisdocument.TJMcDandDRJwishtoacknowledgepartial

financialsupportfromtheWealthfromOceansNationalFlagship.Thisworkcontributes

totheCSIROClimateChangeResearchProgram.Thisdocumentisbasedonwork

partiallysupportedbytheU.S.NationalScienceFoundationtoSCORunderGrantNo.

OCE‐0608600.FJMwishestoacknowledgetheOceanographicSectionoftheNational

ScienceFoundationandtheNationalOceanicandAtmosphericAdministrationfor

supportinghiswork.



ThisdocumenthasbeenwrittenbythemembersofSCOR/IAPSOWorkingGroup127,

TrevorJ.McDougall,(chair),CSIRO,Hobart,Australia

RainerFeistel,Leibniz‐InstitutfuerOstseeforschung,Warnemuende,Germany

DanielG.Wright+,BedfordInstituteofOceanography,Dartmouth,Canada

RichPawlowicz,UniversityofBritishColumbia,Vancouver,Canada

FrankJ.Millero,UniversityofMiami,Florida,USA

DavidR.Jackett,CSIRO,Hobart,Australia

BrianA.King,NationalOceanographyCentre,Southampton,UK

GilesM.Marion,DesertResearchInstitute,Reno,USA

SteffenSeitz,Physikalisch‐TechnischeBundesanstalt(PTB),Braunschweig,Germany

PetraSpitzer,Physikalisch‐TechnischeBundesanstalt(PTB),Braunschweig,Germany

C‐T.ArthurChen,NationalSunYat‐SenUniversity,Taiwan,R.O.C.



March2010



+deceased,8thJuly2010.



viii

IOC Manuals and Guides No. 56

Foreword



ThisdocumentdescribestheInternationalThermodynamicEquationOfSeawater–2010

(TEOS‐10forshort).Thisdescriptionofthethermodynamicpropertiesofseawaterand

oficeIhhasbeenadoptedbytheIntergovernmentalOceanographicCommissionatits

25thAssemblyinJune2009toreplaceEOS‐80astheofficialdescriptionofseawaterand

icepropertiesinmarinescience.

FundamentaltoTEOS‐10aretheconceptsofAbsoluteSalinityandReference

Salinity.Thesevariablesaredescribedindetailhere,emphasisingtheirrelationshipto

PracticalSalinity.

ThescienceunderpinningTEOS‐10hasbeendescribedinaseriesofpapers

publishedintherefereedliterature(seeappendixC).Thepresentdocumentmaybe

calledthe“TEOS‐10Manual”andactsasaguidetothosepublishedpapersand

concentratesonhowthethermodynamicpropertiesobtainedfromTEOS‐10aretobe

usedinoceanography.

Inadditiontothethermodynamicpropertiesofseawater,TEOS‐10alsodescribesthe

thermodynamicpropertiesoficeandofhumidair,andthesepropertiesaresummarised

inthisdocument.TheTEOS‐10computersoftware,thisTEOS‐10Manualandother

documentsmaybeobtainedfromwww.TEOS‐10.org.

WhenreferringtotheuseofTEOS‐10,itisthepresentdocumentthatshouldbe

referencedasIOCetal.(2010)[IOC,SCORandIAPSO,2010:Theinternational

thermodynamicequationofseawater–2010:Calculationanduseofthermodynamicproperties.

IntergovernmentalOceanographicCommission,ManualsandGuidesNo.56,UNESCO

(English),196pp.].



ThisversionoftheTEOS‐10Manualincludescorrectionsupto16thOctober2010.



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Abstract

Thisdocumentoutlineshowthethermodynamicpropertiesofseawaterareevaluated

usingtheInternationalThermodynamicEquationOfSeawater–2010(TEOS‐10).This

thermodynamicdescriptionofseawaterisbasedonaGibbsfunctionformulationfrom

whichthermodynamicpropertiessuchasentropy,potentialtemperature,enthalpyand

potentialenthalpyarecalculateddirectly.WhendeterminedfromtheGibbsfunction,

thesequantitiesarefullyconsistentwitheachother.Entropyandenthalpyarerequired

foranaccuratedescriptionoftheadvectionanddiffusionofheatintheoceaninteriorand

forquantifyingtheocean’sroleinexchangingheatwiththeatmosphereandwithice.The

GibbsfunctionisafunctionofAbsoluteSalinity,temperatureandpressure.Incontrastto

PracticalSalinity,AbsoluteSalinityisexpressedinSIunitsanditincludestheinfluenceof

thesmallspatialvariationsofseawatercompositionintheglobalocean.AbsoluteSalinity

istheappropriatesalinityvariablefortheaccuratecalculationofhorizontaldensity

gradientsintheocean.AbsoluteSalinityisalsotheappropriatesalinityvariableforthe

calculationoffreshwaterfluxesandforcalculationsinvolvingtheexchangeoffreshwater

withtheatmosphereandwithice.Potentialfunctionsareincludedforiceandformoist

air,leadingtoaccurateexpressionsfornumerousthermodynamicpropertiesoficeandair

includingfreezingtemperatureandlatentheatsofmeltingandofevaporation.This

TEOS‐10Manualdescribeshowthethermodynamicpropertiesofseawater,iceandmoist

airareusedinordertoaccuratelyrepresentthetransportofheatintheoceanandthe

exchangeofheatwiththeatmosphereandwithice.

2 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

1. Introduction



1.1 Oceanographic practice 1978 - 2009

ThePracticalSalinityScale,PSS‐78,andtheInternationalEquationofStateofSeawater

(Unesco(1981))whichexpressesthedensityofseawaterasafunctionofPracticalSalinity,

temperatureandpressure,haveservedtheoceanographiccommunityverywellforthirty

years.TheJointPanelonOceanographicTablesandStandards(JPOTS)(Unesco(1983))

alsopromulgatedtheMillero,PerronandDesnoyers(1973)algorithmforthespecificheat

capacityofseawateratconstantpressure,theChenandMillero(1977)expressionforthe

soundspeedofseawaterandtheMilleroandLeung(1976)formulaforthefreezingpoint

temperatureofseawater.ThreeotheralgorithmssupportedundertheauspicesofJPOTS

concernedtheconversionbetweenhydrostaticpressureanddepth,thecalculationofthe

adiabaticlapserate,andthecalculationofpotentialtemperature.Theexpressionsforthe

adiabaticlapserateandforpotentialtemperaturecouldinprinciplehavebeenderived

fromtheotheralgorithmsoftheEOS‐80set,butinfacttheywerebasedontheformulasof

Bryden(1973).Weshallrefertoallthesealgorithmsjointlyas‘EOS‐80’forconvenience

becausetheyrepresentoceanographicbestpracticefromtheearly1980sto2009.

1.2 Motivation for an updated thermodynamic description of seawater

Inrecentyearsthefollowingaspectsofthethermodynamicsofseawater,iceandmoistair

havebecomeapparentandsuggestthatitistimelytoredefinethethermodynamic

propertiesofthesesubstances.

• SeveralofthepolynomialexpressionsoftheInternationalEquationofStateof

Seawater(EOS‐80)arenottotallyconsistentwitheachotherastheydonotexactly

obeythethermodynamicMaxwellcross‐differentiationrelations.Thenew

approacheliminatesthisproblem.

• Sincethelate1970samoreaccurateandmorebroadlyapplicablethermodynamic

descriptionofpurewaterhasbeendevelopedbytheInternationalAssociationfor

thePropertiesofWaterandSteam,andhasappearedasanIAPWSRelease(IAPWS‐

95).Alsosincethelate1970ssomemeasurementsofhigheraccuracyhavebeen

madeofseveralpropertiesofseawatersuchas(i)heatcapacity,(ii)soundspeedand

(iii)thetemperatureofmaximumdensity.Thesecanbeincorporatedintoanew

thermodynamicdescriptionofseawater.

• Theimpactonseawaterdensityofthevariationofthecompositionofseawaterin

thedifferentoceanbasinshasbecomebetterunderstood.Inordertofurther

progressthisaspectofseawater,astandardmodelofseawatercompositionis

neededtoserveasagenerallyrecognisedreferencefortheoreticalandchemical

investigations.

• Theincreasingemphasisontheoceanasbeinganintegralpartoftheglobalheat

enginepointstotheneedforaccurateexpressionsfortheentropy,enthalpyand

internalenergyofseawatersothatheatfluxescanbemoreaccuratelydeterminedin

theoceanandacrosstheinterfacesbetweentheoceanandtheatmosphereandice

(entropy,enthalpyandinternalenergywerenotavailablefromEOS‐80).

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

• Theneedforathermodynamicallyconsistentdescriptionoftheinteractionsbetween

seawater,iceandmoistair;inparticular,theneedforaccurateexpressionsforthe

latentheatsofevaporationandfreezing,bothattheseasurfaceandinthe

atmosphere.

• ThetemperaturescalehasbeenrevisedfromIPTS‐68toITS‐90andrevisedIUPAC

(InternationalUnionofPureandAppliedChemistry)valueshavebeenadoptedfor

theatomicweightsoftheelements(Wieser(2006)).



1.3 SCOR/IAPSO WG127 and the approach taken

In2005SCOR(ScientificCommitteeonOceanicResearch)andIAPSO(International

AssociationforthePhysicalSciencesoftheOcean)establishedWorkingGroup127onthe

“ThermodynamicsandEquationofStateofSeawater”(henceforthreferredtoasWG127).

Thisgrouphasnowdevelopedacollectionofalgorithmsthatincorporateourbest

knowledgeofseawaterthermodynamics.Thepresentdocumentsummarizestheworkof

SCOR/IAPSOWorkingGroup127.

Tocomputeallthermodynamicpropertiesofseawateritissufficienttoknowoneofits

so‐calledthermodynamicpotentials(Fofonoff1962,Feistel1993,Alberty2001).ItwasJ.W.

Gibbs(1873)whodiscoveredthat“anequationgivinginternalenergyintermsofentropyand

specificvolume,ormoregenerallyanyfiniteequationbetweeninternalenergy,entropyandspecific

volume,foradefinitequantityofanyfluid,maybeconsideredasthefundamentalthermodynamic

equationofthatfluid,asfromit…maybederivedallthethermodynamicpropertiesofthefluid(so

farasreversibleprocessesareconcerned).”

TheapproachtakenbyWG127hasbeentodevelopaGibbsfunctionfromwhichall

thethermodynamicpropertiesofseawatercanbederivedbypurelymathematical

manipulations(suchasdifferentiation).Thisapproachensuresthatthevarious

thermodynamicpropertiesareself‐consistent(inthattheyobeytheMaxwellcross‐

differentiationrelations)andcomplete(inthateachofthemcanbederivedfromthegiven

potential).

TheGibbsfunction(orGibbspotential)isafunctionofAbsoluteSalinityA

S(rather

thanofPracticalSalinityP

S),temperatureandpressure.AbsoluteSalinityistraditionally

definedasthemassfractionofdissolvedmaterialinseawater.TheuseofAbsolute

SalinityasthesalinityargumentfortheGibbsfunctionandforallotherthermodynamic

functions(suchasdensity)isamajordeparturefrompresentpractice(EOS‐80).Absolute

SalinityispreferredoverPracticalSalinitybecausethethermodynamicpropertiesof

seawateraredirectlyinfluencedbythemassofdissolvedconstituentswhereasPractical

Salinitydependsonlyonconductivity.Considerforexampleexchangingasmallamount

ofpurewaterwiththesamemassofsilicateinanotherwiseisolatedseawatersampleat

constanttemperatureandpressure.Sincesilicateispredominantlynon‐ionic,the

conductivity(andthereforePracticalSalinityP

S)isalmostunchangedbuttheAbsolute

Salinityisincreased,asisthedensity.Similarly,ifasmallmassofsayNaClisaddedand

thesamemassofsilicateistakenoutofaseawatersample,themassfractionabsolute

salinitywillnothavechanged(andsothedensityshouldbealmostunchanged)butthe

PracticalSalinitywillhaveincreased.

Thevariationsintherelativeconcentrationsofseawaterconstituentscausedby

biogeochemicalprocessesactuallycausecomplicationsinevendefiningwhatexactlyis

meantby“absolutesalinity”.Theseissueshavenotbeenwellstudiedtodate,butwhatis

knownissummarizedinsection2.5andappendicesA.4,A.5andA.20.Hereitis

sufficienttopointoutthattheAbsoluteSalinityA

Swhichisthesalinityargumentofthe

TEOS‐10Gibbsfunctionistheversionofabsolutesalinitythatprovidesthebestestimate

ofthedensityofseawater;anothernameforA

Sis“DensitySalinity”.

4 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

TheGibbsfunctionofseawater,publishedasFeistel(2008),hasbeenendorsedbythe

InternationalAssociationforthePropertiesofWaterandSteamastheReleaseIAPWS‐08.

Thisthermodynamicdescriptionofseawaterproperties,togetherwiththeGibbsfunction

oficeIh,IAPWS‐06,hasbeenadoptedbytheIntergovernmentalOceanographic

Commissionatits25thAssemblyinJune2009toreplaceEOS‐80astheofficialdescription

ofseawaterandicepropertiesinmarinescience.Thethermodynamicpropertiesofmoist

airhavealsorecentlybeendescribedusingaHelmholtzfunction(Feisteletal.(2010a),

IAPWS(2010))soallowingtheequilibriumpropertiesattheair‐seainterfacetobemore

accuratelyevaluated.Thenewapproachtothethermodynamicpropertiesofseawater,of

iceIhandofhumidairisreferredtocollectivelyasthe“InternationalThermodynamic

EquationOfSeawater–2010”,or“TEOS‐10”forshort.AppendixCliststhepublications

whichliebehindTEOS‐10.

AnotabledifferenceofTEOS‐10comparedwithEOS‐80istheadoptionofAbsolute

Salinitytobeusedinjournalstodescribethesalinityofseawaterandtobeusedasthe

salinityargumentinalgorithmsthatgivethevariousthermodynamicpropertiesof

seawater.Thisrecommendationdeviatesfromthecurrentpracticeofworkingwith

PracticalSalinityandtypicallytreatingitasthebestestimateofAbsoluteSalinity.This

practiceisinaccurateandshouldbecorrected.Notehoweverthatwestrongly

recommendthatthesalinitythatisreportedtonationaldatabasesremainPractical

SalinityasdeterminedonthePracticalSalinityScaleof1978(suitablyupdatedtoITS‐90

temperaturesasdescribedinappendixEbelow).

TherearethreeverygoodreasonsforcontinuingtostorePracticalSalinityratherthan

AbsoluteSalinityinsuchdatarepositories.First,PracticalSalinityisan(almost)directly

measuredquantitywhereasAbsoluteSalinityisgenerallyaderivedquantity.Thatis,we

calculatePracticalSalinitydirectlyfrommeasurementsofconductivity,temperatureand

pressure,whereastodatewederiveAbsoluteSalinityfromacombinationofthese

measurementsplusothermeasurementsandcorrelationsthatarenotyetwellestablished.

PracticalSalinityispreferredovertheactuallymeasuredinsituconductivityvalue

becauseofitsconservativenaturewithrespecttochangesoftemperatureorpressure,or

dilutionwithpurewater.Second,itisimperativethatconfusionisnotcreatedinnational

databaseswhereachangeinthereportingofsalinitymaybemishandledatsomestage

andlaterbemisinterpretedasarealincreaseintheocean’ssalinity.Thissecondpoint

arguesstronglyfornochangeinpresentpracticeinthereportingofPracticalSalinityP

S

innationaldatabasesofoceanographicdata.Thirdly,thealgorithmsfordeterminingthe

ʺbestʺ estimateofAbsoluteSalinityofseawaterwithnon‐standardcompositionare

immatureandwillundoubtedlychangeinthefuture,sowecannotrecommendstoring

AbsoluteSalinityinnationaldatabases.Storageofamorerobustintermediatevalue,the

ReferenceSalinity,R

S(definedasdiscussedinappendixA.3togivethebestestimateof

AbsoluteSalinityofStandardSeawater)wouldalsointroducethepossibilityofconfusion

inthestoredsalinityvalueswithoutprovidinganyrealadvantageoverstoringPractical

Salinitysowealsoavoidthispossibility.ValuesofReferenceSalinityobtainedfrom

suitableobservationaltechniques(forexamplebydirectmeasurementofthedensityof

StandardSeawater)shouldbeconvertedtocorrespondingnumbersofPracticalSalinity

forstorage,asdescribedinsections2.3‐2.5.

Notethatthepracticeofstoringonetypeofsalinityinnationaldatabases(Practical

Salinity)butusingadifferenttypeofsalinityinpublications(AbsoluteSalinity)isexactly

analogoustoourpresentpracticewithtemperature;insitutemperaturetisstoredindata

bases(sinceitisthemeasuredquantity)butthetemperaturevariablethatisusedin

publicationsisacalculatedquantity,beingeitherpotentialtemperature

or

ConservativeTemperatureΘ.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

InordertoimprovethedeterminationofAbsoluteSalinityweneedtobegincollecting

andstoringvaluesofthesalinityanomalyAAR

SSS

−basedonmeasuredvaluesof

density(suchascanbemeasuredwithavibratingtubedensimeter,Kremling(1971)).The

4‐letterGF3code(IOC(1987))DENSiscurrentlydefinedforinsitumeasurementsor

computedvaluesfromEOS‐80.Itisrecommendedthatthedensitymeasurementsmade

withavibratingbeamdensimeterbereportedwiththeGF3codeDENSalongwiththe

laboratorytemperature(TLABinC°)andlaboratorypressure(PLAB,theseapressurein

thelaboratory,usually0dbar).FromthisinformationandthePracticalSalinityofthe

seawatersample,theabsolutesalinityanomalyAAR

SSS

−canbecalculatedusingan

inversionoftheTEOS‐10equationfordensitytodetermineA.SForcompleteness,itis

advisabletoalsoreportA

underthenewGF3codeDELS.

ThethermodynamicdescriptionofseawaterandoficeIhasdefinedinIAPWS‐08and

IAPWS‐06hasbeenadoptedastheofficialdescriptionofseawaterandoficeIhbythe

IntergovernmentalOceanographicCommissioninJune2009.Thesenewinternational

standardswereadoptedwhilerecognizingthatthetechniquesforestimatingAbsolute

Salinitywilllikelyimproveoverthecomingdecades,andthealgorithmforevaluating

AbsoluteSalinityintermsofPracticalSalinity,latitude,longitudeandpressurewillbe

updatedfromtimetotime,afterrelevantappropriatelypeer‐reviewedpublicationshave

appeared,andthatsuchanupdatedalgorithmwillappearonthewww.TEOS‐10.orgweb

site.Usersofthissoftwareshouldalwaysstateintheirpublishedworkwhichversionof

thesoftwarewasusedtocalculateAbsoluteSalinity.

ThemoreprominentadvantagesofTEOS‐10comparedwithEOS‐80are

• TheGibbsfunctionapproachallowsthecalculationofinternalenergy,entropy,

enthalpy,potentialenthalpyandthechemicalpotentialsofseawateraswellasthe

freezingtemperature,andthelatentheatsoffreezingandofevaporation.These

quantitieswerenotavailablefromtheInternationalEquationofState1980butare

essentialfortheaccurateaccountingof“heat”intheoceanandfortheconsistent

andaccuratetreatmentofair‐seaandice‐seaheatfluxes.Forexample,anew

temperaturevariable,ConservativeTemperature,canbedefinedasbeing

proportionaltopotentialenthalpyandisavaluablemeasureofthe“heat”content

perunitmassofseawaterforuseinphysicaloceanographyandinclimatestudies,

asitisapproximatelytwoordersofmagnitudemoreconservativethanpotential

temperature.

• Forthefirsttimetheinfluenceofthespatiallyvaryingcompositionofseawatercan

systematicallybetakenintoaccountthroughtheuseofAbsoluteSalinity.Inthe

openocean,thishasanon‐trivialeffectonthehorizontaldensitygradientcomputed

fromtheequationofstate,andtherebyontheoceanvelocitiesandheattransports

calculatedviathe“thermalwind”relation.

• Thethermodynamicquantitiesavailablefromthenewapproacharetotally

consistentwitheachother.

• Thenewsalinityvariable,AbsoluteSalinity,ismeasuredinSIunits.Moreoverthe

treatmentoffreshwaterfluxesinoceanmodelswillbeconsistentwiththeuseof

AbsoluteSalinity,butisonlyapproximatelysoforPracticalSalinity.

• TheReferenceCompositionofstandardseawatersupportsmarinephysicochemical

studiessuchasthesolubilityofseasaltconstituents,thealkalinity,thepHandthe

oceanacidificationbyrisingconcentrationsofatmosphericCO2.



6 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

1.4 A guide to this TEOS-10 manual

Theremainderofthismanualbeginsbylisting(insection2)thedefinitionsofvarious

thermodynamicquantitiesthatfollowdirectlyfromtheGibbsfunctionofseawaterby

simplemathematicalprocessessuchasdifferentiation.Thesedefinitionsarethen

followedinsection3bythediscussionofseveralderivedquantities.Thecomputer

softwaretoevaluatethesequantitiesisavailablefromtwoseparatelibraries,theSeawater‐

Ice‐Air(SIA)libraryandtheGibbs‐SeaWater(GSW)OceanographicToolbox,asdescribed

inappendicesMandN.ThefunctionsintheSIAlibraryaregenerallyavailableinbasic‐SI

units(1

kg kg−,kelvinandPa),bothfortheirinputparametersandfortheoutputsofthe

algorithms.SomeadditionalroutinesareincludedintheSIAlibraryintermsofother

commonlyusedunitsfortheconvenienceofusers.TheSIAlibrarytakessignificantly

morecomputertimetoevaluatemostquantities(approximatelyafactorof65more

computertimeformanyquantities,comparingoptimizedcodeinbothcases)and

providessignificantlymorepropertiesthandoestheGSWToolbox.TheSIAlibraryuses

theworld‐widestandardforthethermodynamicdescriptionofpurewatersubstance

(IAPWS‐95).Sincethisisdefinedoverextendedrangesoftemperatureandpressure,the

algorithmsarelongandtheirevaluationtime‐consuming.TheGSWToolboxusesthe

GibbsfunctionofFeistel(2003)(IAPWS‐09)toevaluatethepropertiesofpurewater,and

sincethisisvalidonlyovertherestrictedrangesoftemperatureandpressureappropriate

fortheocean,thealgorithmsareshorterandtheirexecutionisfaster.TheGSW

OceanographicToolboxisnotascomprehensiveastheSIAlibrary;forexample,the

propertiesofmoistairareonlyavailableintheSIAlibrary.Inaddition,acomputationally

efficientexpressionfordensity

intermsofConservativeTemperature(ratherthanin

termsofinsitutemperature)involvingjust25coefficientsisalsoavailableandisdescribed

inappendixA.30andappendixK.

TheinputandoutputparametersoftheGSWOceanographicToolboxareinunits

whichoceanographerswillfindmorefamiliarthanbasicSIunits.Weexpectthat

oceanographerswillmostlyusethisGSWToolboxbecauseofitsgreatersimplicityand

computationalefficiency,andbecauseofthemorefamiliarunitscomparedwiththeSIA

library.ThenameGSW(Gibbs‐SeaWater)hasbeenchosentobesimilarto,butdifferent

fromtheexisting“sw”(SeaWater)librarywhichisalreadyinwidecirculation.Boththe

SIAandGSWlibraries,togetherwiththisTEOS‐10Manualareavailablefromthewebsite

www.TEOS‐10.org.InitiallytheSIAlibraryisbeingmadeavailableinVisualBasicand

FORTRANwhiletheGSWlibraryisavailablemainlyinMATLAB.

Afterthesedescriptionsinsections2and3ofhowtodeterminethethermodynamic

quantitiesandvariousderivedquantities,weendwithsomeconclusions(section4).

AdditionalinformationonPracticalSalinity,theGibbsfunction,ReferenceSalinity,

compositionanomalies,AbsoluteSalinity,andsomefundamentalthermodynamic

propertiessuchastheFirstLawofThermodynamics,thenon‐conservativenatureofmany

oceanographicvariables,alistofrecommendedsymbols,andsuccinctlistsof

thermodynamicformulaearegivenintheappendices.Muchofthisworkhasappeared

elsewhereinthepublishedliteraturebutiscollectedhereinacondensedformforthe

usersʹconvenience.



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

1.5 A remark on units

Themostconvenientvariablesandunitsinwhichtoconductthermodynamic

investigationsareAbsoluteSalinityA

Sinunitsofkgkg‐1,AbsoluteTemperatureT(K),

andAbsolutePressure

inPa.ThesearetheparametersandunitsusedintheSIA

softwarelibrary.Oceanographicpracticetodatehasusednon‐basic‐SIunitsformany

variables,inparticular,temperatureisusuallymeasuredontheCelsius(C°)scale,

pressureisseapressurequotedindecibarsrelativetothepressureofastandard

atmosphere(10.1325dbar),whilesalinityhashaditsownoceanography‐specificscale,the

PracticalSalinityScaleof1978.IntheGSWOceanographicToolboxweadoptC°forthe

temperatureunit,pressureisseapressureindbarandAbsoluteSalinityA

Sisexpressed

inunitsofgkg−1sothatittakesnumericalvaluesclosetothoseofPracticalSalinity.

Adoptingthesenon‐basic‐SIunitsdoesnotcomewithoutapenaltyastherearemany

thermodynamicformulaethataremoreconvenientlymanipulatedwhenexpressedinSI

units.Asanexample,thefreshwaterfractionofseawateriswrittencorrectlyas

()

1S−,

butitisclearthatinthisinstanceAbsoluteSalinitymustbeexpressedin1

kg kg−notin

gkg .

−TherearealsocaseswithintheGSWToolboxinwhichSIunitsarerequiredand

thismayoccasionallycausesomeconfusion.Acommonexampleofthisissueariseswhen

avariableisdifferentiatedorintegratedwithrespecttopressure.Nevertheless,formany

applicationsitisdeemedimportanttoremainclosetopresentoceanographicpracticeeven

thoughitmeansthatonehastobevigilanttodetectthoseexpressionsthatneedavariable

tobeexpressedintheless‐familiarSIunits.



1.6 Recommendations

InaccordancewithresolutionXXV‐7oftheIntergovernmentalOceanographic

Commissionatits25thAssemblyinJune2009,andtheseveralReleasesandGuidelinesof

theInternationalAssociationforthePropertiesofWaterandSteam,theTEOS‐10

thermodynamicdescriptionofseawater,oficeandofmoistairisrecommendedforuseby

oceanographersinplaceoftheInternationalEquationOfState–1980(EOS‐80).The

softwaretoimplementthischangeisavailableatthewebsitewww.TEOS‐10.org.

UnderTEOS‐10itisrecognizedthatthecompositionofseawatervariesaroundthe

worldoceanandthatthethermodynamicpropertiesofseawateraremoreaccurately

representedasfunctionsofAbsoluteSalinityA

SthanofPracticalSalinityP

S.Itisuseful

tothinkofthetransitionfromPracticalSalinitytoAbsoluteSalinityintwosteps.Inthe

firststepaseawatersampleiseffectivelytreatedasthoughitisStandardSeawaterandits

ReferenceSalinityR

Siscalculated;ReferenceSalinitymaybetakentobesimply

proportionaltoPracticalSalinity.ReferenceSalinityhasSIunits(forexample,1

gkg

−)and

isthenaturalstartingpointtoconsidertheinfluenceofanyvariationincomposition.In

thesecondsteptheAbsoluteSalinityAnomalyisevaluatedusingoneofseveral

techniques,theeasiestofwhichisviaacomputeralgorithmthateffectivelyinterpolates

betweenaspatialatlasofthesevalues.ThenAbsoluteSalinityisestimatedasthesumof

ReferenceSalinityandAbsoluteSalinityAnomaly.Ofthefourpossibleversionsof

absolutesalinity,theonethatisusedastheargumentfortheTEOS‐10Gibbsfunctionis

designedtoprovideaccurateestimatesofthedensityofseawater.

Itisrecognizedthatourknowledgeofhowtoestimateseawatercomposition

anomaliesandtheireffectonthermodynamicpropertiesislimited.Nevertheless,we

shouldnotcontinuetoignoretheinfluenceofthesecompositionvariationsonseawater

propertiesandonoceandynamics.Asmoreknowledgeisgainedinthisareaoverthe

comingdecadeorso,andaftersuchknowledgehasbeendulypublishedinthescientific

8 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

literature,anyupdatedalgorithmtoevaluatetheAbsoluteSalinityAnomalywillbe

available(withitsversionnumber)fromwww.TEOS‐10.org.

ThestorageofsalinityinnationaldatabasesshouldcontinuetooccurasPractical

Salinity,asthiswillmaintaincontinuityofthisimportanttimeseries.Oceanographic

databaseslabelstored,processedorexportedparameterswiththeGF3codePSALfor

PracticalSalinityandSSALforsalinitymeasuredbefore1978(IOC,1987).Inorderto

avoidpossibleconfusionindatabasesbetweendifferenttypesofsalinityitisvery

stronglyrecommendedthatundernocircumstancesshouldeitherReferenceSalinityor

AbsoluteSalinitybestoredinnationaldatabases.

Inordertoaccuratelycalculatethethermodynamicpropertiesofseawater,Absolute

SalinitymustbecalculatedbyfirstcalculatingReferenceSalinityandthenaddingonthe

AbsoluteSalinityAnomaly.BecauseAbsoluteSalinityistheappropriatesalinityvariable

forusewiththeequationofstate,AbsoluteSalinityshouldbethesalinityvariablethatis

publishedinoceanographicjournals.Theversionnumberofthesoftware,ortheexact

formula,thatwasusedtoconvertReferenceSalinityintoAbsoluteSalinityshouldalways

bestatedinpublications.Nevertheless,theremaybesomeapplicationswherethelikely

futurechangesinthealgorithmthatrelatesReferenceSalinitytoAbsoluteSalinity

presentsaconcern,andfortheseapplicationsitmaybepreferabletopublishgraphsand

tablesinReferenceSalinity.Forthesestudiesorwhereitisclearthattheeffectof

compositionalvariationsareinsignificantornotofinterest,theGibbsfunctionmaybe

calledwithR

SratherthanA

S,thusavoidingtheneedtocalculatetheAbsoluteSalinity

Anomaly.Whenthisisdone,itshouldbeclearlystatedthatthesalinityvariablethatis

beinggraphedisReferenceSalinity,notAbsoluteSalinity.

TheTEOS‐10approachofusingthermodynamicpotentialstodescribetheproperties

ofseawater,iceandmoistairmeansthatitispossibletoderivemanymore

thermodynamicpropertiesthanwereavailablefromEOS‐80.Theseawaterproperties

entropy,internalenergy,enthalpyandparticularlypotentialenthalpywerenotavailable

fromEOS‐80butarecentraltoaccuratelycalculatingthetransportof“heat”intheocean

andhencetheair‐seaheatfluxinthecoupledclimatesystem.

UnderEOS‐80theobservedvariables

(

)

P,,Stpwerefirstusedtocalculatepotential

temperature

andthenwatermasseswereanalyzedontheP

−

diagram.Curved

contoursofpotentialdensitycouldalsobedrawnonthissameP

−

diagram.Under

TEOS‐10,sincedensityandpotentialdensityarenownotfunctionsofPracticalSalinityP

S

butratherarefunctionsofAbsoluteSalinityA

S,itisnownotpossibletodrawisolinesof

potentialdensityonaP

−diagram.Rather,becauseofthespatialvariationsof

seawatercomposition,agivenvalueofpotentialdensitydefinesanareaontheP

−

diagram,notacurvedline.UnderTEOS‐10,theobservedvariables

(

)

P,,Stp,together

withlongitudeandlatitude,areusedtofirstformAbsoluteSalinityA

SandConservative

Temperature.ΘOceanographicwatermassesarethenanalyzedontheA

S−Θdiagram,

andpotentialdensitycontourscanalsobedrawnonthisA

−

Θdiagram,while

PreformedSalinity*

Sisthenaturalsalinityvariabletobeusedinapplicationssuchas

numericalmodellingwhereitisimportantthatthesalinityvariablebeconservative.

WhendescribingtheuseofTEOS‐10,itisthepresentdocument(theTEOS‐10Manual)

thatshouldbereferencedasIOCetal.(2010)[IOC,SCORandIAPSO,2010:The

internationalthermodynamicequationofseawater–2010:Calculationanduseofthermodynamic

properties.IntergovernmentalOceanographicCommission,ManualsandGuidesNo.56,

UNESCO(English),196pp]. 



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

2.BasicThermodynamicProperties



2.1ITS‐90temperature



In1990theInternationalPracticalTemperatureScale1968(IPTS‐68)wasreplacedbythe

InternationalTemperatureScale1990(ITS‐90).Therearetwomainmethodstoconvert

betweenthesetwotemperaturescales;Rusby’s(1991)8thorderfitvalidoverawiderange

oftemperatures,andSaunders’(1990)1.00024scalingwidelyusedintheoceanographic

community.Thetwomethodsareformallyindistinguishableintheoceanographic

temperaturerangebecausetheydifferbylessthaneithertheuncertaintyin

thermodynamictemperature(oforder1mK),orthepracticalapplicationoftheIPTS‐68

andITS‐90scales.ThedifferencesbetweentheSaunders(1990)andRusby(1991)

formulaearelessthan1mKthroughoutthetemperaturerange‐2°Cto40°Candlessthan

0.03mKinthetemperaturerangebetween‐2°Cand10°C.Hencewerecommendthatthe

oceanographiccommunitycontinuestousetheSaundersformula

()

(

)

68 90

/ C = 1.00024 / C .tt°°(2.1.1)

Oneapplicationofthisformulaisintheupdatedcomputeralgorithmforthecalculationof

PracticalSalinity(PSS‐78)intermsofconductivityratio.ThealgorithmsforPSS‐78

require68

tasthetemperatureargument.Inordertousethesealgorithmswith90

tdata,

tmaybecalculatedusing(2.1.1).

Anextendeddiscussionofthedifferenttemperaturescales,theirinherentuncertainty

andthereasoningforourrecommendationof(2.1.1)canbefoundinappendixA.1.



2.2Seapressure



SeapressurepisdefinedtobetheAbsolutePressure

lesstheAbsolutePressureofone

standardatmosphere,0101 325Pa;P≡thatis

0.pPP

≡

−(2.2.1)

Itiscommonoceanographicpracticetoexpressseapressureindecibars(dbar).Another

commonpressurevariablethatarisesnaturallyinthecalibrationofsea‐boardinstruments

isgaugepressuregauge

pwhichisAbsolutePressurelesstheAbsolutePressureofthe

atmosphereatthetimeoftheinstrument’scalibration(perhapsinthelaboratory,or

perhapsatsea).Becauseatmosphericpressurechangesinspaceandtime,seapressurep

ispreferredasathermodynamicvariableasitisunambiguouslyrelatedtoAbsolute

Pressure.TheseawaterGibbsfunctionintheGSWToolboxisexpressedasafunctionof

seapressurep(functionallyequivalenttotheuseofAbsolutePressure

intheIAPWS

ReleasesandintheSIAlibrary);thatis,

isafunctionofp,itisnotafunctionofgauge

p.



2.3PracticalSalinity



PracticalSalinityP

SisdefinedonthePracticalSalinityScaleof1978(Unesco(1981,1983))

intermsoftheconductivityratio15

Kwhichistheelectricalconductivityofthesampleat

temperature68

t=15°Candpressureequaltoonestandardatmosphere(p=0dbarand

absolutepressure

equalto101325Pa),dividedbytheconductivityofastandard

10 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

potassiumchloride(KCl)solutionatthesametemperatureandpressure.Themass

fractionofKCl(i.e.,themassofKClpermassofsolution)inthestandardsolutionis

32.4356 10−

×.When15

K=1,thePracticalSalinityP

Sisbydefinition35.Notethat

PracticalSalinityisaunit‐lessquantity.Thoughsometimesconvenient,itistechnically

incorrecttoquotePracticalSalinityin“psu”;ratheritshouldbequotedasacertain

PracticalSalinity“onthePracticalSalinityScalePSS‐78”.Theformulaforevaluating

PracticalSalinitycanbefoundinappendixEalongwiththesimplechangethatmustbe

madetotheUnesco(1983)formulaesothatthealgorithmforPracticalSalinitycanbe

calledwithITS‐90temperatureasaninputparameterratherthantheolder68

t

temperatureinwhichthePSS‐78algorithmsweredefined.Thereaderisalsodirectedto

theCDIACchapteron“Methodforsalinity(conductivityratio)measurement”which

describesbestpracticeinmeasuringtheconductivityratioofseawatersamples(Kawano

(2009)).

PracticalSalinityisdefinedonlyintherangeP

242.S

<PracticalSalinitiesbelow2

orabove42computedfromconductivity,asmeasuredforexampleincoastallagoons,

shouldbeevaluatedbythePSS‐78extensionsofHilletal.(1986)andPoissonand

Gadhoumi(1993).SamplesexceedingaPracticalSalinityof50mustbedilutedtothevalid

salinityrangeandthemeasuredvalueshouldbeadjustedbasedontheaddedwatermass

andtheconservationofseasaltduringthedilutionprocess.Thisisdiscussedfurtherin

appendixE.

Datastoredinnationalandinternationaldatabasesshould,asamatterofprinciple,be

measuredvaluesratherthanderivedquantities.Consistentwiththis,werecommend

continuingtostorethemeasured(insitu)temperatureratherthanthederivedquantity,

potentialtemperature.SimilarlywestronglyrecommendthatPracticalSalinityP

S

continuetobethesalinityvariablethatisstoredinsuchdatabasessinceP

Sisclosely

relatedtothemeasuredvaluesofconductivity.Thisrecommendationhasthevery

importantadvantagethatthereisnochangetothepresentpracticeandsothereisless

chanceoftransitionalerrorsoccurringinnationalandinternationaldatabasesbecauseof

theadoptionofAbsoluteSalinityinoceanography.



2.4ReferenceCompositionandtheReference‐CompositionSalinityScale



ThereferencecompositionofseawaterisdefinedbyMilleroetal.(2008a)astheexactmole

fractionsgiveninTableD.3ofappendixDbelow.Thiscompositionwasintroducedby

Milleroetal.(2008a)astheirbestestimateofthecompositionofStandardSeawater,being

seawaterfromthesurfacewatersofacertainregionoftheNorthAtlantic.Theexact

locationforthecollectionofbulkmaterialforthepreparationofStandardSeawaterisnot

specified.ShipsgatheringthisbulkmaterialaregivenguidancenotesbytheStandard

SeawaterService,requestingthatwaterbegatheredbetweenlongitudes50°Wand40°W,

indeepwater,duringdaylighthours.Reference‐CompositionSalinityR

S(orReference

Salinityforshort)wasdesignedbyMilleroetal.(2008b)tobethebestestimateofthe

mass‐fractionAbsoluteSalinityA

SofStandardSeawater.Independentofaccuracy

considerations,itprovidesaprecisemeasureofdissolvedmaterialinStandardSeawater

andisthecorrectsalinityargumenttobeusedintheTEOS‐10GibbsfunctionforStandard

Seawater.

FortherangeofsalinitieswherePracticalSalinitiesaredefined(thatis,intherange

242S<<)Milleroetal.(2008a)showthat

RPSP

SuS≈where 1

PS (35.165 04 35) g kgu

−

≡.(2.4.1)

IntherangeP

242S<<,thisequationexpressestheReferenceSalinityofaseawatersample

ontheReference‐CompositionSalinityScale(Milleroetal.(2008a)).Forpractical

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

purposes,thisrelationshipcanbetakentobeanequalitysincetheapproximatenatureof

thisrelationonlyreflectstheextenttowhichPracticalSalinity,asdeterminedfrom

measurementsofconductivityratio,temperatureandpressure,varieswhenaseawater

sampleisheated,cooledorsubjectedtoachangeinpressurebutwithoutexchangeof

masswithitssurroundings.ThePracticalSalinityScaleof1978wasdesignedtosatisfy

thispropertyasaccuratelyaspossiblewithintheconstraintsofthepolynomial

approximationsusedtodetermineChlorinity(andhencePracticalSalinity)intermsofthe

measuredconductivityratio.

FromEqn.(2.4.1),aseawatersampleofReferenceCompositionwhosePractical

SalinityP

Sis35hasaReferenceSalinityR

Sof1

35.165 04 g kg

−

.Milleroetal.(2008a)

estimatethattheabsoluteuncertaintyinthisvalueis1

0.007 g kg

−

±.Thedifference

betweenthenumericalvaluesofReferenceandPracticalSalinitiescanbetracedbackto

theoriginalpracticeofdeterminingsalinitybyevaporationofwaterfromseawaterand

weighingtheremainingsolidmaterial.Thisprocessalsoevaporatedsomevolatile

componentsandmostofthe1

0.165 04 g kg

−

salinitydifferenceisduetothiseffect.

MeasurementsofthecompositionofStandardSeawaterataPracticalSalinityP

Sof35

usingmassspectrometryand/orionchromatographyareunderwayandmayprovide

updatedestimatesofboththevalueofthemassfractionofdissolvedmaterialinStandard

Seawateranditsuncertainty.AnyupdateofthisvaluewillnotchangetheReference‐

CompositionSalinityScaleandsowillnotaffectthecalculationofReferenceSalinitynor

ofAbsoluteSalinityascalculatedfromReferenceSalinityplustheAbsoluteSalinity

Anomaly.

Oceanographicdatabaseslabelstored,processedorexportedparameterswiththeGF3

codePSALforPracticalSalinityandSSALforsalinitymeasuredbefore1978(IOC,1987).

Inordertoavoidpossibleconfusionindatabasesbetweendifferenttypesofsalinityitis

verystronglyrecommendedthatundernocircumstancesshouldeitherReferenceSalinity

orAbsoluteSalinitybestoredinnationaldatabases.

DetailedinformationonReferenceCompositionandReferenceSalinitycanbefound

inMilleroetal.(2008a).Fortheuserʹsconvenienceabriefsummaryofinformationfrom

Milleroetal.(2008a),includingtheprecisedefinitionofReferenceSalinityisgivenin

appendixA.3andinTableD3ofappendixD.



2.5AbsoluteSalinity



AbsoluteSalinityistraditionallydefinedasthemassfractionofdissolvedmaterialin

seawater.ForseawaterofReferenceComposition,ReferenceSalinitygivesourcurrent

bestestimateofAbsoluteSalinity.Todealwithcompositionanomaliesinseawater,we

needanextensionoftheReference‐CompositionSalinityR

Sthatprovidesauseful

measureofsalinityoverthefullrangeofoceanographicconditionsandagreesprecisely

withReferenceSalinitywhenthedissolvedmaterialhasReferenceComposition.When

compositionanomaliesarepresent,nosinglemeasureofdissolvedmaterialcanfully

representtheinfluencesonseawaterpropertiesonallthermodynamicproperties,soitis

clearthateitheradditionalinformationwillberequiredorcompromiseswillhavetobe

made.Inaddition,wewouldliketointroduceameasureofsalinitythatistraceabletothe

SI(Seitzetal.,2010b)andmaintainsthehighaccuracyofPSS‐78necessaryfor

oceanographicapplications.TheintroductionofʺDensitySalinityʺ dens

Saddressesbothof

theseissues;itisthistypeofabsolutesalinitythatinTEOS‐10parlanceislabeledA

Sand

calledAbsoluteSalinity.InthissectionweexplainhowA

Sisdefinedandevaluated,but

firstweoutlineotherchoicesthatareavailableforthedefinitionofabsolutesalinityinthe

presenceofcompositionvariationsinseawater.

12 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Themostobviousdefinitionofabsolutesalinityis“themassfractionofdissolvednon‐

H2Omaterialinaseawatersampleatitstemperatureandpressure”.Thisseemingly

simpledefinitionisactuallyfarmoresubtlethanitfirstappears.Notably,thereare

questionsaboutwhatconstituteswaterandwhatconstitutesdissolvedmaterial.Perhaps

themostobviousexampleofthisissueoccurswhenCO2isdissolvedinwatertoproducea

mixtureofCO2,H2CO3,HCO3‐,CO32‐,H+,OH‐andH2O,withtherelativeproportions

dependingondissociationconstantsthatdependontemperature,pressureandpH.Thus,

thedissolutionofagivenmassofCO2inpurewateressentiallytransformssomeofthe

waterintodissolvedmaterial.Achangeinthetemperatureandevenanadiabaticchange

inpressureresultsinachangeinabsolutesalinitydefinedinthiswayduetothe

dependenceofchemicalequilibriaontemperatureandpressure.Pawlowiczetal.(2010)

andWrightetal.(2010b)addressthissecondissuebydefining“SolutionAbsolute

Salinity”(usuallyshortenedto“SolutionSalinity”),soln

S,asthemassfractionofdissolved

non‐H2Omaterialafteraseawatersampleisbroughttotheconstanttemperature25 Ct=°

andthefixedseapressure0dbar(fixedAbsolutePressureof101325Pa).

Anothermeasureofabsolutesalinityisthe“Added‐MassSalinity”add

SwhichisR

S

plusthemassfractionofmaterialthatmustbeaddedtoStandardSeawatertoarriveatthe

concentrationsofallthespeciesinthegivenseawatersample,afterchemicalequilibrium

hasbeenreached,andafterthesampleisbroughttotheconstanttemperature25 Ct=°

andthefixedseapressureof0dbar.Theestimationofabsolutesalinityadd

Sisnot

straightforwardforseawaterwithanomalouscompositionbecausewhilethefinal

equilibriumstateisknown,onemustiterativelydeterminethemassofanomaloussolute

priortoanychemicalreactionswithReference‐Compositionseawater.Pawlowiczetal.

(2010)provideanalgorithmtoachievethis,atleastapproximately.Thisdefinitionof

absolutesalinity,add

S,isusefulforlaboratorystudiesofartificialseawateranditdiffers

fromsoln

Sbecauseofthechemicalreactionsthattakeplacebetweentheseveralspeciesof

theaddedmaterialandthecomponentsofseawaterthatexistinStandardSeawater.

Added‐MassSalinitymaybethemostappropriateformofsalinityforaccurately

accountingforthemassofsaltdischargedbyriversandhydrothermalventsintothe

ocean.

“PreformedAbsoluteSalinity”(usuallyshortenedto“PreformedSalinity”),*

S,isa

differenttypeofabsolutesalinitywhichisspecificallydesignedtobeascloseaspossible

tobeingaconservativevariable.Thatis,*

Sisdesignedtobeinsensitiveto

biogeochemicalprocessesthataffecttheothertypesofsalinitytovaryingdegrees.

PreformedSalinity*

Sisformedbyfirstestimatingthecontributionofbiogeochemical

processestooneofthesalinitymeasuresA

S,soln

S,oradd

S,andthensubtractingthis

contributionfromtheappropriatesalinityvariable.InthiswayPreformedSalinity*

Sis

designedtobeaconservativesalinityvariablewhichisindependentoftheeffectsofthe

non‐conservativebiogeochemicalprocesses. *

Swillfindaprominentroleinocean

modeling.Thethreetypesofabsolutesalinitysoln

S,add

Sand*

Sarediscussedinmore

detailinappendicesA.4andA.20,whereapproximaterelationshipsbetweenthese

variablesanddens

SS≡arepresented,basedontheworkofPawlowiczetal.(2010)and

Wrightetal.(2010b).NotethatforasampleofStandardSeawater,allofthefivesalinity

variablesR

S,A

S,soln

S,add

Sand*

Sandareequal.

Thereisnosimplemeanstomeasureeithersoln

Soradd

Sforthegeneralcaseofthe

arbitraryadditionofmanycomponentstoStandardSeawater.Henceamorepreciseand

easilydeterminedmeasureoftheamountofdissolvedmaterialinseawaterisrequired

andTEOS‐10adopts“DensitySalinity”forthispurpose.“DensitySalinity”dens

Sis

definedasthevalueofthesalinityargumentoftheTEOS‐10expressionfordensitywhich

givesthesample’sactualmeasureddensityatthetemperature25 Ct

°andatthesea

pressurep=0dbar.Whenthereisnoriskofconfusion,“DensitySalinity”isalsocalled

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

AbsoluteSalinitywiththelabelA

S,thatisdens

SS≡.Usuallywedonothaveaccurate

measurementsofdensitybutratherwehavemeasurementsofPracticalSalinity,

temperatureandpressure,andinthiscase,AbsoluteSalinitymaybecalculatedusing

PracticalSalinityandthecomputeralgorithmofMcDougall,JackettandMillero(2010a)

whichprovidesanestimateofAAR

SSS

−.Thiscomputerprogramwasformedas

follows.

Inaseriesofpapers(Milleroetal.(1976a,1978,2000,2008b),McDougalletal.(2010a)),

accuratemeasurementsofthedensityofseawatersamples,alongwiththePractical

Salinityofthosesamples,gaveestimatesofAAR

SSS

−frommostofthemajorbasinsof

theworldocean.Thiswasdonebyfirstcalculatingthe“ReferenceDensity”fromthe

TEOS‐10equationofstateusingthesample’sReferenceSalinityasthesalinityargument

(thiscalculationessentiallyassumesthattheseawatersamplehasthecompositionof

StandardSeawater).Thedifferencebetweenthemeasureddensityandthe“Reference

Density”wasthenusedtoestimatetheAbsoluteSalinityAnomalyAAR

SSS

=−(Millero

etal.(2008a)).TheMcDougalletal.(2010a)algorithmisbasedontheobservedcorrelation

betweenthisAR

SS−dataandthesilicateconcentrationoftheseawatersamples(Millero

etal.,2008a),withthesilicateconcentrationbeingestimatedbyinterpolationofaglobal

atlas(GouretskiandKoltermann(2004)).

ThealgorithmforAbsoluteSalinitytakestheform

(

)

ARAAP

,,, ,SSSSS p

δφλ

=+ = (2.5.1)

Where

islatitude(degreesNorth),

islongitude(degreeseast,rangingfrom0°Eto

360°E)whilepisseapressure.

HeuristicallythedependenceofAAR

SSS

−onsilicatecanbethoughtofas

reflectingthefactthatsilicateaffectsthedensityofaseawatersamplewithout

significantlyaffectingitsconductivityoritsPracticalSalinity.Inpracticethisexplains

about60%oftheeffectandtheremainderisduetothecorrelationofothercomposition

anomalies(suchasnitrate)withsilicate.IntheMcDougalletal.(2010a)algorithmthe

BalticSeaistreatedseparately,followingtheworkofMilleroandKremling(1976)and

Feisteletal.(2010c,2010d),becausesomeriversflowingintotheBalticareunusuallyhigh

incalciumcarbonate.



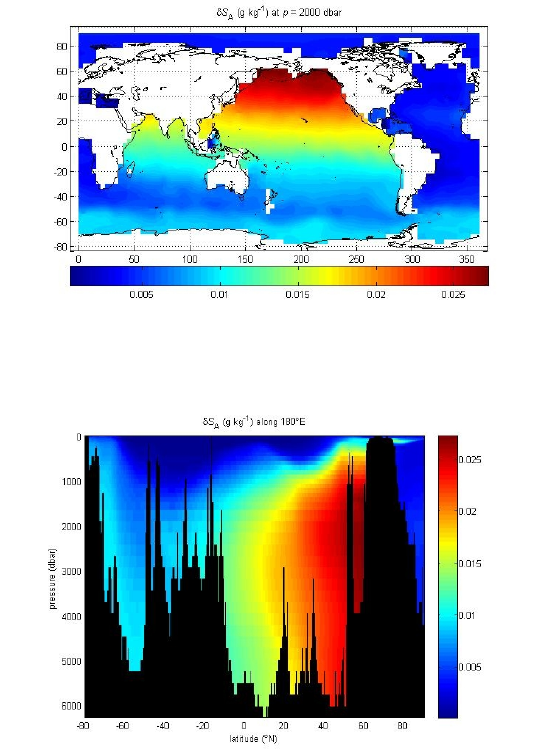
Figure1.Asketchindicatinghowthermodynamicquantities

suchasdensityarecalculatedasfunctionsofAbsoluteSalinity.

AbsoluteSalinityisfoundbyaddinganestimateofthe

AbsoluteSalinityAnomalyA

totheReferenceSalinity.



14 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56



Sincethedensityofseawaterisrarelymeasured,werecommendtheapproach

illustratedinFigure1asapracticalmethodtoincludetheeffectsofcomposition

anomaliesonestimatesofAbsoluteSalinityanddensity.Whencompositionanomalies

arenotknown,thealgorithmofMcDougalletal.(2010a)maybeusedtoestimateAbsolute

SalinityintermsofPracticalSalinityandthespatiallocationofthemeasurementinthe

worldoceans.

ThedifferencebetweenAbsoluteSalinityandReferenceSalinity,asestimatedbythe

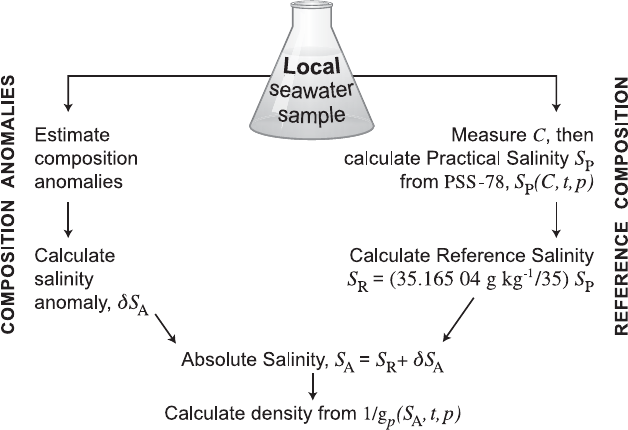
McDougalletal.(2010a)algorithm,isillustratedinFigure2(a)atapressureof2000dbar,

andinaverticalsectionthroughthePacificOceaninFigure2(b).

Oftheapproximately800samplesofseawaterfromtheworldoceanthathavebeen

examinedtodateforAAR

SSS

=−thestandarderror(squarerootofthemeansquared

value)ofAAR

SSS

=−is0.0107gkg‐1.Thatis,the“typical”valueofAAR

SSS

=−ofthe

811samplestakentodateis0.0107gkg‐1.Thestandarderrorofthedifferencebetweenthe

measuredvaluesofAAR

SSS

=−andthevaluesevaluatedfromthecomputeralgorithm

ofMcDougalletal.(2010a)is0.0048gkg‐1.ThemaximumvaluesofAAR

SSS

=−of

approximately0.025gkg‐1occurintheNorthPacific.



Figure2(a).AbsoluteSalinityAnomalyA

atp=2000dbar.



Figure2(b).AverticalsectionofAbsoluteSalinity

AnomalyA

along180oEinthePacificOcean.



The thermodynamic description of seawater and of ice Ih as defined in IAPWS-08 and

IAPWS-06 has been adopted as the official description of seawater and of ice Ih by the

Intergovernmental Oceanographic Commission in June 2009. These thermodynamic

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

descriptions of seawater and ice were endorsed recognizing that the techniques for

estimating Absolute Salinity will likely improve over the coming decades. The algorithm

for evaluating Absolute Salinity in terms of Practical Salinity, latitude, longitude and

pressure, will likely be updated from time to time, after relevant appropriately peer-

reviewed publications have appeared, and such an updated algorithm will appear on the

www.TEOS-10.org web site. Users of this software should state in their published work

which version of the software was used to calculate Absolute Salinity. 

ThepresentcomputersoftwarewhichevaluatesAbsoluteSalinityA

Sgiventheinput

variablesPracticalSalinity P

S,longitude

,latitude

andpressureisavailableat

www.TEOS‐10.org.AbsoluteSalinityisalsoavailableastheinversefunctionofdensity

()

A,,STP

intheSIAlibraryofcomputeralgorithmsasthealgorithmsea_sa_si(see

appendixM)andintheGSWToolboxasthealgorithmgsw_SA_from_rho.



2.6Gibbsfunctionofseawater



TheGibbsfunctionofseawater

(

)

A,,

Stpisrelatedtothespecificenthalpyhand

entropy,

by

()

hTt

=− + where0273.15KT

istheCelsiuszeropoint.TEOS‐10

definestheGibbsfunctionofseawaterasthesumofapurewaterpartandthesalinepart

(IAPWS‐08)

()

(

)

(

)

,, , ,,

S tp g tp g S tp=+ .(2.6.1)

ThesalinepartoftheGibbsfunction,S,

isvalidovertheranges0<A

S<42gkg–1,

–6.0°C<t<40°C,and4

0< 10 dbarp<,althoughitsthermalandcolligativeproperties

arevaliduptot=80°CandA

S=120gkg–1atp=0.

Thepure‐waterpartoftheGibbsfunction,W,

canbeobtainedfromtheIAPWS‐95

Helmholtzfunctionofpure‐watersubstancewhichisvalidfromthefreezingtemperature

orfromthesublimationtemperatureto1273K.Alternatively,thepure‐waterpartofthe

GibbsfunctioncanbeobtainedfromtheIAPWS‐09Gibbsfunctionwhichisvalidinthe

oceanographicrangesoftemperatureandpressure,fromlessthanthefreezing

temperatureofseawater(atanypressure),upto40 C°(specificallyfrom

()

(2.65 0.0743 MPa ) CpP −

−++× °

to40°C),andinthepressurerange4

0 < 10 dbarp<.

ForpracticalpurposesinoceanographyitisexpectedthatIAPWS‐09willbeusedbecause

itexecutesapproximatelytwoordersofmagnitudefasterthantheIAPWS‐95codefor

purewater.Howeverifoneisconcernedwithtemperaturesbetween40 C°and80 C°

thenonemustusetheIAPWS‐95versionofW

(expressedintermsofabsolute

temperature(K)andabsolutepressure(Pa))ratherthantheIAPWS‐09version.

ThethermodynamicpropertiesderivedfromtheIAPWS‐95(theReleaseprovidingthe

Helmholtzfunctionformulationforpurewater)andIAPWS‐08(theReleaseendorsingthe

Feistel(2008)Gibbsfunction)combinationareavailablefromtheSIAsoftwarelibrary,

whilethatderivedfromtheIAPWS‐09(theReleaseendorsingthepurewaterpartof

Feistel(2003))andIAPWS‐08combinationareavailablefromtheGSWOceanographic

Toolbox.TheGSWToolboxisrestrictedtotheoceanographicstandardrangein

temperatureandpressure,howeverthevalidityofresultsextendsatp=0toAbsolute

Salinityuptomineralsaturationconcentrations(Marionetal.2009).Specificvolume

(whichisthepressurederivativeoftheGibbsfunction)ispresentlyanextrapolated

quantityoutsidetheNeptunianrange(i.e.theoceanographicrange)oftemperatureand

AbsoluteSalinityatp=0,andexhibitserrorsthereofupto3%.Weemphasizethat

modelsofseawaterpropertiesthatuseasinglesalinityvariable,A,Sasinputrequire

approximatelyfixedchemicalcompositionratios(e.g.,Na/Cl,Ca/Mg,Cl/HCO3,etc.).As

seawaterevaporatesorfreezes,eventuallymineralssuchasCaCO3willprecipitate.Small

anomaliesarereasonablyhandledbyusingA

Sastheinputvariable(seesection2.5)but

16 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

precipitationmaycauselargedeviationsfromthenearlyfixedratiosassociatedwith

standardseawater.Underextremeconditionsofprecipitation,modelsofseawaterbased

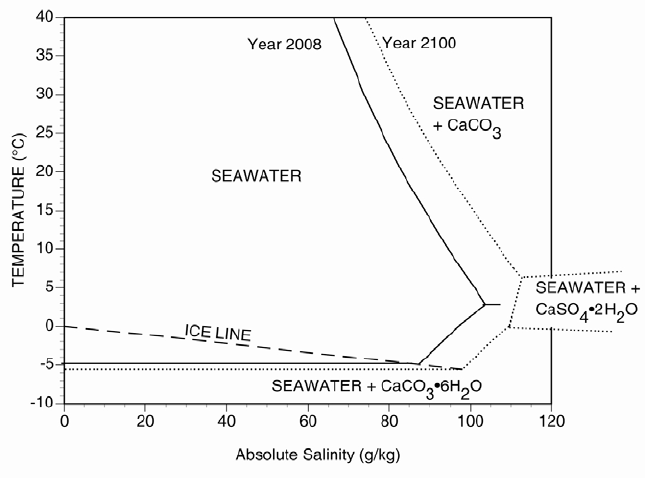
ontheMilleroetal.(2008a)ReferenceCompositionwillnolongerbeapplicable.Figure3

illustratesA

St−boundariesofvalidity(determinedbytheonsetofprecipitation)for2008

(pCO2=385atm

)and2100(pCO2=550atm

)(fromMarionetal.(2009)).



Figure3.TheboundariesofvalidityoftheMilleroetal.(2008a)

compositionatp=0inYear2008(solidlines)andpotentially

inYear2100(dashedlines).Athighsalinity,calciumcarbonate

saturatesfirstandcomesoutofsolution;thereafterthe

ReferenceCompositionofStandardSeawaterofMilleroetal.

(2008a)doesnotapply.



TheGibbsfunction(2.6.1)containsfourarbitraryconstantsthatcannotbedetermined

byanysetofthermodynamicmeasurements.Thesearbitraryconstantsmeanthatthe

Gibbsfunction(2.6.1)isunknownandunknowableuptothearbitraryfunctionof

temperatureandAbsoluteSalinity(where0

TistheCelsiuszeropoint,273.15K)

()

(

)

120 340 A

aaTt aaTtS

⎡⎤⎡⎤

+++++

⎣⎦⎣⎦

(2.6.2)

(seeforexampleFofonoff(1962)andFeistelandHagen(1995)).Thefirsttwocoefficients

aand2

aarearbitraryconstantsofthepurewaterGibbsfunction

()

tpwhilethe

secondtwocoefficients3

aand4

aarearbitrarycoefficientsofthesalinepartoftheGibbs

function

()

A,, .

StpFollowinggenerallyacceptedconvention,thefirsttwocoefficients

arechosentomaketheentropyandinternalenergyofliquidwaterzeroatthetriplepoint

(

)

,0tp

(2.6.3)

and

(

)

,0utp

(2.6.4)

asdescribedinIAPWS‐95andinmoredetailinFeisteletal.(2008a)fortheIAPWS‐95

Helmholtzfunctiondescriptionofpurewatersubstance.Whenthepure‐waterGibbs

function

()

tpof(2.6.1)istakenfromthefittedGibbsfunctionofFeistel(2003),thetwo

arbitraryconstants1

aand2

aare(intheappropriatenon‐dimensionalform)00

and10



ofthetableinappendixGbelow.Thesevaluesof00

and10

arenotidenticaltothe

valuesinFeistel(2003)becausethepresentvalueshavebeentakenfromIAPWS‐09and

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

havebeenchosentomostaccuratelyachievethetriple‐pointconditions(2.6.3)and(2.6.4)

asdiscussedinFeisteletal.(2008a).

Theremainingtwoarbitraryconstants3

aand4

aof(2.6.2)aredeterminedbyensuring

thatthespecificenthalpyhandspecificentropy

ofasampleofstandardseawaterwith

standard‐oceanproperties1

SO SO SO

( , , ) (35.165 04 g kg , 0 C, 0 dbar)Stp −

=°arebothzero,

thatisthat

()

SO SO SO

,, 0hS t p

(2.6.5)

and

()

SO SO SO

,, 0.Stp

(2.6.6)

Inmoredetail,theseconditionsareactuallyofficiallywrittenas(Feistel(2008),IAPWS‐08)

(

)

(

)

(

)

SWW

SO SO SO t t SO SO

,, , ,hS t p u tp h t p=− (2.6.7)

and

(

)

(

)

(

)

SWW

SO SO SO t t SO SO

,, , ,Stp tp tp

ηηη

=− .(2.6.8)

Writteninthisway,(2.6.7)and(2.6.8)usepropertiesofthepurewaterdescription(the

right‐handsides)toconstrainthearbitraryconstantsinthesalineGibbsfunction.While

thefirsttermsontheright‐handsidesoftheseequationsarezero(see(2.6.3)and(2.6.4)),

theseconstraintsonthesalineGibbsfunctionarewrittenthiswaysothattheyare

independentofanysubsequentchangeinthearbitraryconstantsinvolvedinthe

thermodynamicdescriptionofpurewater.Whilethetwoslightlydifferent

thermodynamicdescriptionsofpurewater,namelyIAPWS‐95andIAPWS‐09,both

achievezerovaluesoftheinternalenergyandentropyatthetriplepointofpurewater,

thevaluesassignedtotheenthalpyandentropyofpurewateratthetemperatureand

pressureofthestandardocean,

(

)

SO SO

,htpand

(

)

SO SO

,tp

ontheright‐handsidesof

(2.6.7)and(2.6.8),areslightlydifferentinthetwocases.Forexample

()

SO SO

,htpis

3.3 10x−1

Jkg

−fromIAPWS‐09(asdescribedinthetableofappendixG)comparedwith

theround‐offerrorof8

210x−1

Jkg

−

whenusingIAPWS‐95withdouble‐precision

arithmetic.Thisissuesisdiscussedinmoredetailinsection3.3.

ThepolynomialformandthecoefficientsforthepurewaterGibbsfunction

()

tp

fromFeistel(2003)andIAPWS‐09aregiveninappendixG,whilethecombined

polynomialandlogarithmicformandthecoefficientsforthesalinepartoftheGibbs

function

()

A,,

Stp(fromFeistel(2008)andIAPWS‐08)arereproducedinappendixH.

SCOR/IAPSOWorkingGroup127hasindependentlycheckedthattheGibbsfunctions

ofFeistel(2003)andofFeistel(2008)doinfactfittheunderlyingdataofvarious

thermodynamicquantitiestotheaccuracyquotedinthosetwofundamentalpapers.This

checkingwasperformedbyGilesM.Marion,andissummarizedinappendixO.Further

checkingoftheseGibbsfunctionshasoccurredintheprocessleadinguptoIAPWS

approvingtheseGibbsfunctionformulationsastheReleasesIAPWS‐08andIAPWS‐09.

DiscussionsofhowwelltheGibbsfunctionsofFeistel(2003)andFeistel(2008)fitthe

underlying(laboratory)dataofdensity,soundspeed,specificheatcapacity,temperature

ofmaximumdensityetcmaybefoundinthosepapers,alongwithcomparisonswiththe

correspondingalgorithmsofEOS‐80.TheIAPWS‐09releasediscussestheaccuracyto

whichtheFeistel(2003)Gibbsfunctionfitstheunderlyingthermodynamicpotentialof

IAPWS‐95;insummary,forthevariablesdensity,thermalexpansioncoefficientand

specificheatcapacity,thermsmisfitbetweenIAPWS‐09andIAPWS‐95,intheregionof

validityofIAPWS‐09,areafactorofbetween20and100lessthanthecorrespondingerror

inthelaboratorydatatowhichboththermodynamicpotentialswerefitted.Hence,inthe

oceanographicrangeofparameters,IAPWS‐09andIAPWS‐95mayberegardedasequally

accuratethermodynamicdescriptionsofpureliquidwater.

TheGibbsfunction

hasunitsof1

Jkg

−

inboththeSIAandGSWsoftwarelibraries.



18 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

2.7Specificvolume



ThespecificvolumeofseawatervisgivenbythepressurederivativeoftheGibbs

functionatconstantAbsoluteSalinityA

Sandinsitutemperature,tthatis

()

,, .

PST

vvStpg gP===∂∂(2.7.1)

NoticethatspecificvolumeisafunctionofAbsoluteSalinityA

SratherthanofReference

SalinityR

SorPracticalSalinityP.STheimportanceofthispointisdiscussedinsection

2.8.Whenderivativesaretakenwithrespecttoinsitutemperature,oratconstantinsitu

temperature,thesymboltisavoidedasitcanbeconfusedwiththesamesymbolfortime.

Rather,weuseTinplaceoftintheexpressionsforthesederivatives.

Formanytheoreticalandmodelingpurposesinoceanographyitisconvenientto

regardtheindependenttemperaturevariabletobepotentialtemperature

or

ConservativeTemperatureΘratherthaninsitutemperature.tWenoteherethatthe

specificvolumeisequaltothepressurederivativeofspecificenthalpyatfixedAbsolute

Salinitywhenanyoneof,

orΘisalsoheldconstant,asfollows(fromappendixA.11)

AA A

,, ,

SS S

hP hP hP v

ηθ

∂∂ =∂∂ =∂∂ = (2.7.2)

Theuseof

intheseequationsemphasizesthatitmustbeinPa notdbar. Specific

volumevhasunitsof31

mkg

−inboththeSIAandGSWsoftwarelibraries.



2.8Density



Thedensityofseawater

isthereciprocalofthespecificvolume.Itisgivenbythe

reciprocalofthepressurederivativeoftheGibbsfunctionatconstantAbsoluteSalinityA

S

andinsitutemperature,tthatis

()()

(

)

,, .

PST

Stp g gP

ρρ

−

===∂∂(2.8.1)

NoticethatdensityisafunctionofAbsoluteSalinityA

SratherthanofReferenceSalinity

SorPracticalSalinityP.SThisisanextremelyimportantpointbecauseAbsolute

SalinityA

Sinunitsof1

gkg

−isnumericallygreaterthanPracticalSalinitybybetween

0.1651

gkg

−and0.1951

gkg

−intheopenoceansothatifPracticalSalinitywere

inadvertentlyusedasthesalinityargumentforthedensityalgorithm,asignificantdensity

errorofbetween3

0.12 kg m−and3

0.15 kg m

−

wouldresult.

Formanytheoreticalandmodelingpurposesinoceanographyitisconvenientto

regarddensitytobeafunctionofpotentialtemperature

orConservativeTemperature

Θratherthanofinsitutemperature.tThatis,itisconvenienttoformthefollowingtwo

functionalformsofdensity,

()

(

)

,, , , ,Sp Sp

ρρ θ ρ

==Θ

(2.8.2)

where

andΘarerespectivelypotentialtemperatureandConservativeTemperature,

bothreferencedtor0dbar.p=Wewilladopttheconvention(seeTableL.2inappendix

L)thatwhenenthalpy,hspecificvolumevordensity

aretakentobefunctionsof

potentialtemperaturetheyattractanover‐tildeasinv

or,

andwhentheyaretakento

befunctionsofConservativeTemperaturetheyattractacaretasinˆ

vandˆ.

Withthis

convention,expressionsinvolvingpartialderivativessuchas(2.7.2)canbewrittenmore

compactlyas(fromappendixA.11)

PPP

hhh v

−

== ==



(2.8.3)

sincetheothervariablesaretakentobeconstantduringthepartialdifferentiation.

AppendixPlistsexpressionsformanythermodynamicvariablesintermsofthe

thermodynamicpotentials

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

()

A,,hhS p



,

(

)

A,,hhS p

=and

(

)

ˆ,, .

hhS p=Θ

(2.8.4)

Density

hasunitsof3

kg m−inboththeSIAandGSWsoftwarelibraries.

Computationallyefficientexpressionsfor

(

)

ˆ,,

Θand

(

)

A,,Sp

ρθ

involving25

coefficientsareavailable(McDougalletal.(2010b))andaredescribedinappendixA.30

andappendixK.Theseexpressionscanbeintegratedwithrespecttopressuretoprovide

closedexpressionsfor

(

)

ˆ,,

hS pΘand

(

)

A,,hS p

(seeEqn.(A.30.6)).



2.9Chemicalpotentials



Asforanytwo‐componentthermodynamicsystem,theGibbsenergy,,Gofaseawater

samplecontainingthemassofwaterW

mandthemassofsaltS

mattemperaturetand

pressurepcanbewrittenintheform(LandauandLifshitz(1959),Alberty(2001),Feistel

(2008))

()

WS W S

,,,Gm m tp m m

=+(2.9.1)

wherethechemicalpotentialsofwaterinseawaterW

andofsaltinseawaterS

are

definedbythepartialderivatives

W,,mTp

∂

=∂,and

S,,

mTp

∂

=∂(2.9.2)

Identifyingabsolutesalinitywiththemassfractionofsaltdissolvedinseawater,

()

AS WS

/Smmm=+(Milleroetal.(2008a)),thespecificGibbsenergy

isgivenby

() ()

()

WSW SW

AAAA

,, 1

gS tp S S S

μμμ μμ

==−+=+−

+(2.9.3)

andisindependentofthetotalmassofthesample.Notethatthisexpressionfor

asthe

sumofawaterpartandasalinepartisnotthesameasthepurewaterandthesalinesplit

in(2.6.1)(W

isthechemicalpotentialofwaterinseawater;itdoesnotcorrespondtoa

purewatersampleasW

does).ThisGibbsenergy

isusedasthethermodynamic

potentialfunction(Gibbsfunction)forseawater.Theabovethreeequationscanbeusedto

writeexpressionsforW

andS

intermsoftheGibbsfunction

as

() ()

WS A

WAWA

,, Tp Tp

mTp

mmg gS g

gm m gS

mSmS

⎡⎤

∂+ ∂∂ ∂

⎣⎦

==++=−

∂∂∂∂

(2.9.4)

andforthechemicalpotentialofsaltinseawater,

() () ()

WS A

SASA

Tp Tp

mTp

mmg gS g

gm m g S

mSmS

⎡⎤

∂+ ∂∂ ∂

⎣⎦

==++=+−

∂∂∂∂

(2.9.5)

Therelativechemicalpotential

(commonlycalledthe“chemicalpotentialofseawater”)

followsfrom(2.9.4)and(2.9.5)as

μμμ

∂

=− =

∂(2.9.6)

anddescribesthechangeintheGibbsenergyofaparcelofseawateroffixedmassifa

smallamountofwaterisreplacedbysaltatconstanttemperatureandpressure.Also,

fromthefundamentalthermodynamicrelation(Eqn.(A.7.1)inappendixA.7)itfollows

thatthechemicalpotentialofseawater

describesthechangeofenthalpydhifat

constantpressureandentropy,asmallmassfractionofwaterisreplacedbysalt,A

d.S

Equations(2.9.4)–(2.9.6)servetodefinethethreechemicalpotentialsintermsofthe

20 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Gibbsfunction

ofseawater.NotethattheweightsofthesumsthatappearinEqns.

(2.9.1)–(2.9.5)arestrictlythemassfractionsofsaltandofpurewaterinseawater,sothat

foraseawatersampleofanomalouscompositionthesemassfractionswouldbemore

accuratelygivenintermsofsoln

Sthanbydens

SS≡.Inthisregard,theGibbsenergyin

Eqn.(2.9.1)shouldstrictlybetheweightedsumofthechemicalpotentialsofallthe

constituentsinseawater.However,practicallyspeaking,thevapourpressure,thelatent

heatandthefreezingtemperatureareallratherweaklydependentonsalinity,andhence

theuseofA

Sinthissectionisrecommended.

TheSIAcomputersoftwarelibrary(appendixM)predominantlyusesbasicSIunits,so

thatA

Shasunitsof1

kg kg−andS

,,g

andW

allhaveunitsof1

Jkg .

−IntheGSW

OceanographicToolbox(appendixN)A

Shasunitsof1

gkg

−

whileS

andW

allhave

unitsof1

Jg .

−Thisadoptionofoceanographic(i.e.non‐basic‐SI)unitsforA

Smeansthat

specialcareisneededinevaluatingequationssuchas(2.9.3)and(2.9.5)whereintheterm

()

1S−itisclearthatA

Smusthaveunitsof1

kg kg

−

.Theadoptionofnon‐basic‐SIunits

iscommoninoceanography,butoftencausessomedifficultiessuchasthis.



2.10Entropy



Thespecificentropyofseawater

isgivenby

()

,, .

TSp

Stp g gT

ηη

==−=−∂∂(2.10.1)

Whentakingderivativeswithrespecttoinsitutemperature,thesymbolTwillbeusedfor

temperatureinorderthatthesederivativesnotbeconfusedwithtimederivatives.

Entropy

hasunitsof11

Jkg K

−−

inboththeSIAandGSWsoftwarelibraries.



2.11Internalenergy



Thespecificinternalenergyofseawateruisgivenby(where0

TistheCelsiuszeropoint,

273.15Kand0101 325PaP=isthestandardatmospherepressure)

()()() () ()

A000 0

,, .

Sp ST

uuStp gTt pPv gTt pP

∂∂

==++−+=−+−+

∂∂

(2.11.1)

Thisexpressionisanexamplewheretheuseofnon‐basicSIunitspresentsaproblem,

becauseintheproduct

()

pPv−+ ,

(

)

pP P

=mustbeinPaifspecificvolumehasits

regularunitsof31

mkg

−:‐hencehereseapressurepmustbeexpressedinPa .Also,the

pressurederivativeinEqn.(2.11.1)mustbedonewithrespecttopressureinPa .

Specificinternalenergyuhasunitsof1

Jkg

−

inboththeSIAandGSWsoftware

libraries.



2.12Enthalpy



Thespecificenthalpyofseawaterhisgivenby

()() ()

A00

,, .

hhStp gTt gTtT

∂

==++=−+

∂(2.12.1)

Specificenthalpyhhasunitsof1

Jkg

−

inboththeSIAandGSWsoftwarelibraries.



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

2.13Helmholtzenergy



ThespecificHelmholtzenergyofseawater

isgivenby

( ) () ()

A00

,, .

f fStp g pPv g pP P

∂

==−+=−+

∂(2.13.1)

Thisexpressionisanotherexamplewheretheuseofnon‐basicSIunitspresentsaproblem,

becauseintheproduct

()

pPv−+ ,pmustbeinPaifspecificvolumehasitsregularunitsof

mkg .

−ThespecificHelmholtzenergy

hasunitsof1

Jkg

−

inboththeSIAandGSW

computersoftwarelibraries.



2.14Osmoticcoefficient



Theosmoticcoefficientofseawater

isgivenby

() ()

()

AASW0

,, .

Stp g S mRT t

φφ

−

⎛⎞

∂

⎜⎟

==−− +

⎜⎟

∂

⎝⎠

(2.14.1)

Theosmoticcoefficientofseawaterdescribesthechangeofthechemicalpotentialofwater

permoleofaddedsalt,expressedasmultiplesofthethermalenergy,

()

RT t+(Millero

andLeung(1976),FeistelandMarion(2007),Feistel(2008)),

()

(

)

(

)

ASW0

0, , , ,tp S tp m RT t

μφ

=++.(2.14.2)

Here,R=8.31447211

Jmol K

−−

istheuniversalmolargasconstant.ThemolalitySW

mis

thenumberofdissolvedmolesofsolutes(ions)oftheReferenceCompositionasdefined

byMilleroetal.(2008a),perkilogramofpurewater.Notethatthemolalityofseawater

maytakedifferentvaluesifneutralmoleculesofsaltratherthanionsarecounted(seethe

discussiononpage519ofFeistelandMarion(2007)).Thefreezing‐pointlowering

equations(3.33.1,3.33.2)orthevapour‐pressureloweringcanbecomputedfromthe

osmoticcoefficientofseawater(seeMilleroandLeung(1976),Bromleyetal.(1974)).



2.15Isothermalcompressibility



ThethermodynamicquantitiesdefinedsofarareallbasedontheGibbsfunctionitselfand

itsfirstderivatives.Theremainingquantitiesdiscussedinthissectionallinvolvehigher

orderderivatives.

Theisothermalandisohalinecompressibilityofseawatert

isdefinedby

()

ST ST

Stp v

κκ ρ

−−

∂∂

===−=−

∂∂ (2.15.1)

wherethesecondderivativeof

istakenwithrespecttopressure(inPa )atconstantA

S

and.tTheuseof

inthepressurederivativesinEqn.(2.15.1)servestoemphasizethat

thesederivativesmustbetakenwithrespecttopressureinPa notindbar .The

isothermalcompressibilityofseawatert

producedbyboththeSIAandGSWcomputer

softwarelibraries(appendicesMandN)hasunitsof1

Pa .

−





22 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

2.16Isentropicandisohalinecompressibility



WhentheentropyandAbsoluteSalinityareheldconstantwhilethepressureischanged,

theisentropicandisohalinecompressibility

isobtained:

()

AAAA

1111

,,,,

SSSS

TP TT PP

PTT

Stp v

PPPP

ggg

ηηθ

ρρρ

κκ ρ ρ ρ

−−−−

∂∂∂∂

== =−= =

∂∂∂∂

−

(2.16.1)

Theisentropicandisohalinecompressibility

issometimescalledsimplytheisentropic

compressibility(orsometimesthe“adiabaticcompressibility”),ontheunstated

understandingthatthereisalsonotransferofsaltduringtheisentropicoradiabatic

changeinpressure.Theisentropicandisohalinecompressibilityofseawater

produced

byboththeSIAandGSWsoftwarelibraries(appendicesMandN)hasunitsof1

Pa .

−



2.17Soundspeed



Thespeedofsoundinseawatercisgivenby

() ()

(

)

,, .

PTT TP TTPP

ccStp P gg g gg

ρρκ

−

==∂∂== −

(2.17.1)

NotethatintheseexpressionsinEqn.(2.17.1),sincesoundspeedisin1

−anddensity

hasunitsof3

kg m−itfollowsthatthepressureofthepartialderivativesmustbeinPaand

theisentropiccompressibility

musthaveunitsof1

−

.Thesoundspeedcproduced

byboththeSIAandtheGSWsoftwarelibraries(appendicesMandN)hasunitsof1

−.



2.18Thermalexpansioncoefficients



Thethermalexpansioncoefficientt

withrespecttoinsitutemperature,tis

()

,, .

tt TP

Sp Sp

Stp TvT g

αα ρ

∂∂

==−==

∂∂ (2.18.1)

Thethermalexpansioncoefficient

withrespecttopotentialtemperature,

is(see

appendixA.15)

()

(

)

,, , ,

PTT

Sp Sp

gS p

Stpp vgg

θθ

αα ρθ θ

∂∂

==−==

∂∂ (2.18.2)

wherer

pisthereferencepressureofthepotentialtemperature.TheTT

derivativeinthe

numeratorisevaluatedat

()

,,Sp

whereastheotherderivativesareallevaluatedat

()

A,, .Stp

Thethermalexpansioncoefficient

withrespecttoConservativeTemperature,Θis

(seeappendixA.15)

() ()

,, .

PTT

Sp Sp

Stp vgTg

αα ρθ

ΘΘ ∂∂

==−==−

∂Θ ∂Θ + (2.18.3)

NotethatConservativeTemperature

isdefinedonlywithrespecttoareference

pressureof0dbarsothatthe

inEqn.(2.18.3)isthepotentialtemperaturewith

0dbar.

p=Allthederivativesontheright‐handsideofEqn.(2.18.3)areevaluatedat

()

A,, .StpTheconstant0

cisdefinedinEqn.(3.3.3)below.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

2.19Salinecontractioncoefficients



Thesalinecontractioncoefficientt

(sometimesalsocalledthehalinecontraction

coefficient)atconstantinsitutemperature,tis

()

,, .

Tp Tp

Stp SvS g

ββ ρ

∂∂

===−=−

∂∂ (2.19.1)

Thesalinecontractioncoefficient

atconstantpotentialtemperature,

is(see

appendixA.15)

()

AA A

,, ,

TP ST ST TT SP

PTT

Stpp SvS

gg gg

gSp

θθ

ββ ρ

∂∂

===−

∂∂

⎡⎤

−−

⎣⎦

(2.19.2)

wherer

pisthereferencepressureof.

OneoftheA

derivativesinthenumeratoris

evaluatedat

()

,,Sp

whereasalltheotherderivativesareevaluatedat

()

A,, .Stp

Thesalinecontractioncoefficient

atconstantConservativeTemperature,Θis(see

appendixA.15)

()

() ( )

AA A

,,0

TP S T S TT S P

PTT

Stp SvS

gg gg

gT S

ββ ρ

θθ

ΘΘ

−

∂∂

===−

∂∂

⎡⎤

−+ −

⎣⎦

(2.19.3)

NotethatConservativeTemperature

isdefinedonlywithrespecttoareference

pressureof0dbarasindicatedinthisequation.TheA

derivativeinthenumeratoris

evaluatedat

()

A,,0S

whereasalltheotherderivativesareevaluatedat

()

A,, .Stp

IntheSIAcomputersoftware(appendixM)allthreesalinecontractioncoefficientsare

producedinunitsof1

kg kg−whileintheGSWOceanographicToolbox(appendixN)all

threesalinecontractioncoefficientsareproducedinunitsof1

kg g

−

consistentwiththe

preferredoceanographicunitforA

SintheGSWToolboxbeing1

gkg .

−





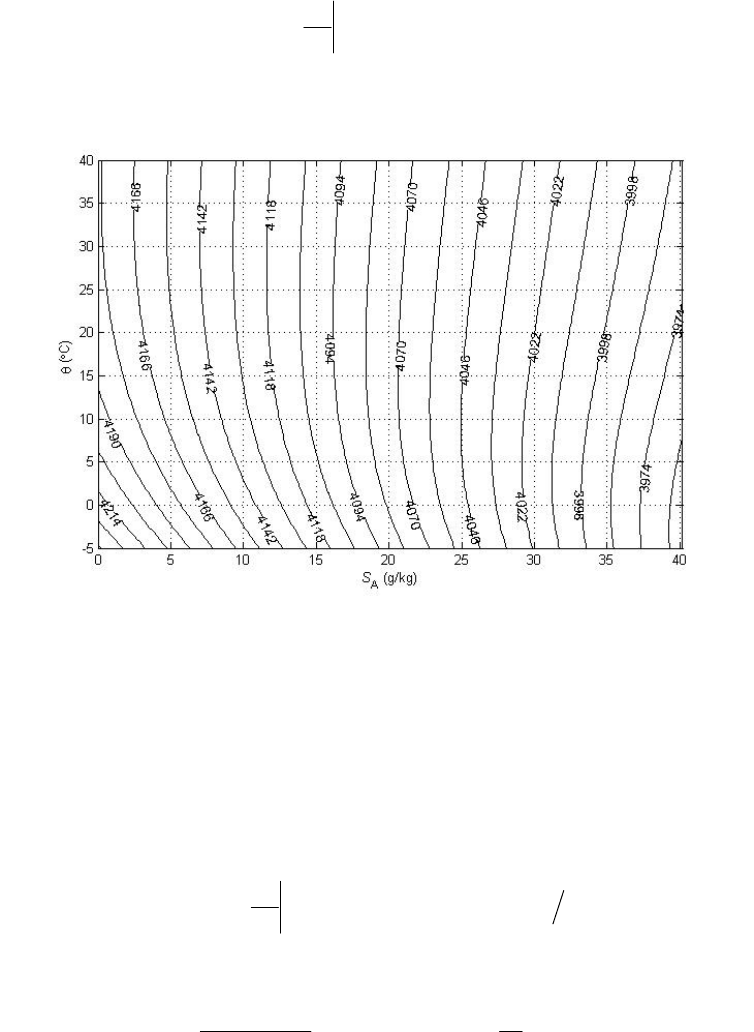
24 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

2.20Isobaricheatcapacity



Thespecificisobaricheatcapacityp

cistherateofchangeofspecificenthalpywith

temperatureatconstantAbsoluteSalinityA

Sandpressure,psothat

() ()

,, .

pp TT

ccStp Ttg

∂

===−+

∂(2.20.1)

Theisobaricheatcapacityp

cvariesovertheA

−

Θplaneatp=0byapproximately5%,

asillustratedinFigure4.



Figure4.Contoursofisobaricspecificheatcapacityp

cofseawater

(in 11

Jkg K

−−

),Eqn.(2.20.1),atp=0.



Theisobaricheatcapacityp

chasunitsof11

Jkg K

−

−inboththeSIAandGSW

computersoftwarelibraries.



2.21Isochoricheatcapacity



Thespecificisochoricheatcapacityv

cistherateofchangeofspecificinternalenergyu

withtemperatureatconstantAbsoluteSalinityA

Sandspecificvolume,,vsothat

() ()

()

,, .

v v TT PP TP PP

ccStp Ttgg g g

∂

===−+−

∂(2.21.1)

Notethattheisochoricandisobaricheatcapacitiesarerelatedby

()

vp t

ρκ

=− andby .

=(2.21.2)

Theisochoricheatcapacityv

chasunitsof11

Jkg K

−

−inboththeSIAandGSW

computersoftwarelibraries.



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

2.22Theadiabaticlapserate



TheadiabaticlapserateΓisthechangeofinsitutemperaturewithpressureatconstant

entropyandAbsoluteSalinity,sothat(McDougallandFeistel(2003))

()

(

)

() () () ()

()

AA A

,, ,

00 00

00 0

,,0

TT p

SS Sp

pp p

Sp S

tt ghv

Stp PP g P c

TTTT

PcS

cc c

ηη ρ

θθθαθα

ρθ

∂∂ ∂ ∂

Γ=Γ = = = − = = =

∂∂ ∂∂∂

++++

∂∂

====

∂Θ ∂Θ∂

(2.22.1)

Theadiabatic(andisohaline)lapserateiscommonly(andincorrectly)explainedasbeing

proportionaltotheworkdoneonafluidparcelasitsvolumechangesinresponsetoan

increaseinpressure.Accordingtothisexplanationtheadiabaticlapseratewouldincrease

withbothpressureandthefluid’scompressibility,butthisisnotthecase.Rather,the

adiabaticlapserateisproportionaltothethermalexpansioncoefficientandis

independentofthefluid’scompressibility.Indeed,theadiabaticlapseratechangessignat

thetemperatureofmaximumdensitywhereasthecompressibilityandtheworkdoneby

compressionisalwayspositive.McDougallandFeistel(2003)showthattheadiabatic

lapserateisindependentoftheincreaseintheinternalenergythataparcelexperiences

whenitiscompressed.Rather,theadiabaticlapseraterepresentsthatchangein

temperaturethatisrequiredtokeeptheentropy(andalso

and

)ofaseawaterparcel

constantwhenitspressureischangedinanadiabaticandisohalinemanner.Thereference

pressureofthepotentialtemperature

thatappearsinthelastfourexpressionsinEqn.

(2.22.1)isr0dbar.p=

TheadiabaticlapserateΓoutputofboththeSIAandtheGSWcomputersoftware

librariesisinunitsof1

K Pa−.



26 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

3.DerivedQuantities



3.1Potentialtemperature



Theveryusefulconceptofpotentialtemperaturewasappliedtotheatmosphereoriginally

byHelmholtz(1888),firstunderthenameof‘heatcontent’,andlaterrenamed‘potential

temperature’(Bezold(1888)).Theseconceptsweretransferredtooceanographyby

Helland‐Hansen(1912).Potentialtemperatureisthetemperaturethatafluidparcel

wouldhaveifitspressurewerechangedtoafixedreferencepressurer

pinanisentropic

andisohalinemanner.Thephrase“isentropicandisohaline”isusedrepeatedlyinthis

document.Tothesetwoqualifiersweshouldreallyalsoadd“withoutdissipationof

mechanicalenergy”.Aprocessthatobeysallthreerestrictionsisathermodynamically

reversibleprocess.Notethatoneoften(falsely)readsthattherequirementofareversible

processisthattheprocessoccursatconstantentropy.Howeverthisstatementis

misleadingbecauseitispossibleforafluidparceltoexchangesomeheatandsomesalt

withitssurroundingsinjusttherightratiosoastokeepitsentropyconstant,butthe

processesisnotreversible(seeEqn.(A.7.1)).

Potentialtemperaturereferredtoreferencepressurer

pisoftenwrittenasthepressure

integraloftheadiabaticlapserate(Fofonoff(1962),(1985))

()

[]

()

Ar AA

,, , , ,, , , .

S tpp t S S tpp p dP

θθ θ

′

′′

==+Γ

∫(3.1.1)

NotethatthispressureintegralneedstobedonewithrespecttopressureexpressedinPa 

notdbar .

ThealgorithmthatisusedwiththeTEOS‐10Gibbsfunctionapproachtoseawater

equatesthespecificentropiesoftwoseawaterparcels,onebeforeandtheotherafterthe

isentropicandisohalinepressurechange.Inthisway,

isevaluatedusingaNewton‐

Raphsoniterativesolutiontechniquetosolvethefollowingequationfor



()

(

)

Ar A

,, ,, ,Sp Stp

ηθ η

=(3.1.2)

or,intermsoftheGibbsfunction,,



()

(

)

Ar A

,, ,, .

Sp gStp

−=−(3.1.3)

ThisrelationisformallyequivalenttoEqn.(3.1.1).IntheGSWOceanographicToolbox



isfoundtomachineprecision(14

10 C

−°∼)intwoiterationsofamodifiedNewton‐Raphson

method,usingasuitableinitialvalueasdescribedbyMcDougalletal.(2010b)..

Notethatthedifferencebetweenthepotentialandinsitutemperaturesisnotdueto

theworkdoneincompressingafluidparcelongoingfromonepressuretoanother:‐the

signofthisworkisofteninthewrongsenseandthemagnitudeisoftenwrongbyafew

ordersofmagnitude(McDougallandFeistel(2003)).Rather,thedifferencebetweenthese

temperaturesiswhatisrequiredtokeeptheentropyconstantduringtheadiabaticand

isohalinepressurechange.Thepotentialtemperature

outputoftheSIAsoftwareisin

unitsofKwhiletheoutputfromtheGSWToolboxisinC°.



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

3.2Potentialenthalpy



Potentialenthalpy0

histheenthalpythatafluidparcelwouldhaveifitspressurewere

changedtoafixedreferencepressurer

pinanisentropicandisohalinemanner.Because

heatfluxesintoandoutoftheoceanoccurmostlyneartheseasurface,thereference

pressureforpotentialenthalpyisalwaystakentober

p=0dbar(thatis,atzerosea

pressure).Potentialenthalpycanbeexpressedasthepressureintegralofspecificvolume

as(fromMcDougall(2003)andseethediscussionbelowEqn.(2.8.2))

()()()()

[]

()

() ( )

AA AA AA

,, , ,0 , ,, , ,, , ,

,, , ,

,, , , ,

h S tp hS h S hS tp vS S tpp p dP

hS tp vS p dP

θθ θ

′′ ′

=== −

′′

=−

′′

=−

′′

=−Θ

∫







(3.2.1)

andweemphasizethatthepressureintegralsheremustbedonewithrespecttopressure

expressedinPa ratherthandbar. IntermsoftheGibbsfunction,potentialenthalpy0

his

evaluatedas

()( )

(

)

(

)

(

)

AA A0A

,, ,,0 ,,0 ,,0.

hStp hS gS T gS

θθθθ

== −+ (3.2.2)



3.3ConservativeTemperature



ConservativeTemperatureΘisdefinedtobeproportionaltopotentialenthalpy

accordingto

()()

(

)

(

)

0000

AAA A

,, , ,, ,

Stp S hStpc hS c

θθ

Θ=Θ= =



(3.3.1)

wherethevaluethatischosenfor0

cismotivatedintermsofpotentialenthalpyevaluated

atanAbsoluteSalinityof1

SO PS

35 35.165 04 g kgSu

−

== andat25 C

°by

()()

SO SO 11

,25 C,0 ,0 C,0 3991.867 957 119 63 J kg K ,

(25 K)

hS hS

−

⎡⎤

°− °

⎣⎦

≈(3.3.2)

notingthat

()

SO ,0 C,0dbarhS °iszeroaccordingtothewaytheGibbsfunctionisdefined

in(2.6.5).Infactweadopttheexactdefinitionfor0

ctobethe15‐digitvaluein(3.3.2),so

that

011

3991.867 957 119 63 J kg K .

−

≡(3.3.3)

WhenIAPWS‐95isusedforthepurewaterpartoftheGibbsfunction,

()

SO ,0 C,0SΘ°and

()

SO ,25 C,0SΘ°differfrom0°Cand25°Crespectivelybytheround‐offamountof

510 C.

−

×°WhenIAPWS‐09(whichisbasedonthepaperofFeistel(2003),seeappendix

G)isusedforthepurewaterpartoftheGibbsfunction,

(

)

SO ,0 C,0SΘ°differsfrom0°C

by8

8.25 10 C

−

−× °and

()

SO ,25 C,0SΘ°differsfrom25°Cby6

9.3 10 C.

−

°Overthe

temperaturerangefrom0C°to40 C°thedifferencebetweenConservativeTemperature

usingIAPWS‐95andIAPWS‐09asthepurewaterpartisnomorethan5

1.5 10 C

−

±× °,a

temperaturedifferencethatwillbeignored.

Thevalueof0

cin(3.3.3)isveryclosetotheaveragevalueofthespecificheatcapacity

cattheseasurfaceoftoday’sglobalocean.Thisvalueof0

calsocausestheaverage

valueof

−Θattheseasurfacetobeveryclosetozero.Since0

cissimplyaconstantof

proportionalitybetweenpotentialenthalpyandConservativeTemperature,itistotally

28 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

arbitrary,andweseenoreasonwhyitsvaluewouldneedtochangefrom(3.3.3)even

wheninfuturedecadesanimprovedGibbsfunctionofseawaterisagreedupon.

AppendixA.18outlineswhyConservativeTemperaturegetsitsname;itis

approximatelytwoordersofmagnitudemoreconservativecomparedwitheither

potentialtemperatureorentropy.

TheSIAandGSWsoftwarelibrariesbothincludeanalgorithmfordetermining

ConservativeTemperatureΘfromvaluesofAbsoluteSalinityA

Sandpotential

temperature

referencedto0dbarp=.Theselibrariesalsohaveanalgorithmfor

evaluatingpotentialtemperature(referencedto0 dbar )fromA

SandΘ.Thisinverse

algorithm,

()

ˆ,S

Θ,hasaninitialseedbasedonarationalfunctionapproximationand

findspotentialtemperaturetomachineprecision(14

10 C

−°∼)inoneandahalfiterationsof

amodifiedNewton‐Raphsontechnique(McDougalletal.(2010b)).



3.4Potentialdensity



Potentialdensity

isthedensitythatafluidparcelwouldhaveifitspressurewere

changedtoafixedreferencepressurer

pinanisentropicandisohalinemanner.Potential

densityreferredtoreferencepressurer

pcanbewrittenasthepressureintegralofthe

isentropiccompressibilityas

()()

[]

()

[]

()

Ar A AA AA

,, , ,, , ,, , , , ,, , , .

Stpp Stp S Stpp p S Stpp pdP

ρρρθ κθ

′

′′′′

∫(3.4.1)

ThesimplerexpressionforpotentialdensityintermsoftheGibbsfunctionis

()

[

]

()

[

]

(

)

Ar AArr AArr

,, , , ,, , , , ,, , , .

Stpp S Stpp p g S Stpp p

ρρθ θ

−

== (3.4.2)

Usingeitherofthefunctionalforms(2.8.2)forinsitudensity,thatis,either

()

A,,Sp

ρρ θ

=or

()

ˆ,, ,Sp

ρρ

=Θpotentialdensitywithrespecttoreferencepressure

p(e.g.1000dbar)canbeeasilyevaluatedas

(

)

(

)

(

)

(

)

(

)

A r A r Ar Ar A r

,, , ,, , , , , , , , ,S tpp S tpp S p S p S p

ρρρηρθρ

====Θ



(3.4.3)

wherewenotethatthepotentialtemperature

inthethirdexpressionisthepotential

temperaturewithrespectto0dbar.Oncethereferencepressureisfixed,potentialdensity

isafunctiononlyofAbsoluteSalinityandConservativeTemperature(orequivalently,of

AbsoluteSalinityandpotentialtemperature).Notethatitisequallycorrecttolabel

potentialdensityas

or

Θ(orindeedas

)because

,

and

areconstantduring

theisentropicandisohalinepressurechangefromptor

p;thatis,thesevariablesposses

the“potential”propertyofappendixA.9.

FollowingthediscussionafterEqn.(2.8.2)above,potentialdensitymayalsobe

expressedintermsofthepressurederivativeoftheexpressions

()

A,,hhS p

=and

()

ˆ,,hhS p=Θ

forenthalpyas(seealsoappendixP)

()()( ) ( )

Ar Ar A r A r

,, , ,, , , , , , .

Stpp Stpp hS pp hS pp

ρρ θ

−

⎡

⎤

⎡⎤

====Θ=

⎣⎦

⎣

⎦

(3.4.4)



3.5Densityanomaly



Densityanomalyt

isanold‐fashioneddensitymeasurethatisnowseldomused.Itis

thedensityevaluatedattheinsitutemperaturebutatzeroseapressure,minus1000

kg m ,

−thatis,

()()

(

)

31 3

AA A

,, ,,0 1000kgm ,,0 1000kgm .

Stp St g St

σρ

−

−−

=− = − (3.5.1)

wasusedasanapproximationto

whichavoidedthecomputationaldemandof

evaluating

.Densityanomalyt

isnotprovidedintheTEOS‐10softwarelibraries.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

3.6Potentialdensityanomaly



Potentialdensityanomaly,

or,

issimplypotentialdensityminus1000kgm–3,

()()

(

)

()

[]

()

Ar Ar Ar

AA rr

,, , ,, , ,, , 1000kgm

,, , 1000kgm

,,,,, 1000kgm.

Stpp Stpp Stpp

Stpp

gS Stppp

θθ

σσρ

Θ−

−

==−

=−

(3.6.1)

Notethatitisequallycorrecttolabelpotentialdensityanomalyas

or

Θbecauseboth

andΘareconstantduringtheisentropicandisohalinepressurechangefromptor.p



3.7Specificvolumeanomaly



Thespecificvolumeanomaly

isdefinedasthedifferencebetweenthespecificvolume

andagivenfunctionofpressure.Traditionally

hasbeendefinedas

(

)( )

(

)

AASO

,, ,, ,0C,Stp vStp vS p

=−°(3.7.1)

(wherethetraditionalvalueofPracticalSalinityof35hasbeenupdatedtoanAbsolute

Salinityof1

SO 35 35.16504 g kg

−

== inthepresentformulation).Notethatthesecond

term,

()

SO ,0 C, ,vS p°isafunctiononlyofpressure.Inordertohaveasurfaceofconstant

specificvolumeanomalymoreaccuratelyapproximateneutraltangentplanes(seesection

3.11),itisadvisabletoreplacetheargumentsSO

Sand0C°withmoregeneralvaluesA





andt



thatarecarefullychosen(assaythemedianvaluesofAbsoluteSalinityand

temperaturealongthesurface)sothatthemoregeneraldefinitionofspecificvolume

anomalyis

()()

(

)

()

(

)

AAA A A

,, ,, , , ,, , , .

Stp vStp vStp g Stp gStp

=−= −



(3.7.2)

ThelasttermsinEqns.(3.7.1)and(3.7.2)aresimplyfunctionsofpressureandonehas

thefreedomtochooseanyotherfunctionofpressureinitsplaceandstillretainthe

dynamicalpropertiesofspecificvolumeanomaly.Inparticular,onecanconstructspecific

volumeandenthalpytobefunctionsofConservativeTemperature(ratherthaninsitu

temperature)as

()

ˆ,,vS pΘand

(

)

ˆ,,hS pΘandwriteaslightlydifferentdefinitionof

specificvolumeanomalyas

()()

(

)

()

(

)

AAA A A

ˆˆ

,, ,, ,, ,, ,, .

SpvSpvSphSphSp

Θ= Θ− Θ= Θ− Θ

 

  (3.7.3)

Thesamecanalsobedonewithpotentialtemperaturesothatintermsofthespecific

volume

()

A,,vS p

andenthalpy

(

)

A,,hS p

wecanwriteanotherformofthespecific

volumeanomalyas

()()

(

)

()

(

)

AAA A A

,, ,, ,, ,, ,, .

S p vS pvS p hS phS p

δθ θ θ θ θ

=−= −









 (3.7.4)

Theseexpressionsexploitthefactthat(seeappendixA.11)

AA A

,, ,

SS S

hP hP hP v

ηθ

∂∂ =∂∂ =∂∂ = (3.7.5)



30 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

3.8Thermobariccoefficient



Thethermobariccoefficientquantifiestherateofvariationwithpressureoftheratioofthe

thermalexpansioncoefficientandthesalinecontractioncoefficient.Withrespectto

potentialtemperature

thethermobariccoefficientis(McDougall(1987b))

()

bbA

TTStp PP P

θθ θθθ

θθ θ

αβ ααβ

ββ

∂∂∂

== =−

∂∂ ∂

(3.8.1)

Thisexpressionforthethermobariccoefficientismostreadilyevaluatedbydifferentiating

anexpressionfordensityexpressedasafunctionofpotentialtemperatureratherthanin

situtemperature,thatis,withdensityexpressedinthefunctionalform

()

A,, .Sp

ρρ θ

=

WithrespecttoConservativeTemperature

thethermobariccoefficientis

()

bbA

TTStp PP P

αβ ααβ

ββ

ΘΘ ΘΘΘ

ΘΘ Θ

∂∂∂

== =−

∂∂ ∂

(3.8.2)

Thisexpressionforthethermobariccoefficientismostreadilyevaluatedbydifferentiating

anexpressionfordensityexpressedasafunctionofConservativeTemperatureratherthan

insitutemperature,thatis,withdensityexpressedinthefunctionalform

()

ˆ,, .Sp

ρρ

=Θ

Thethermobariccoefficiententersvariousquantitiestodowiththepath‐dependent

natureofneutraltrajectoriesandtheill‐definednatureofneutralsurfaces(see(3.13.1)–

(3.13.7)).Thethermobaricdianeutraladvectionassociatedwiththelateralmixingofheat

andsaltalongneutraltangentplanesisgivenbyTb 2

bnn

egNKT P

−

=− ∇ ⋅∇ or

Tb 2

bnn

egNKT P

−Θ

=− ∇Θ⋅∇ wheren

∇

andn

∇

Θarethetwo‐dimensionalgradientsof

eitherpotentialtemperatureorConservativeTemperaturealongtheneutraltangent

plane,n

∇isthecorrespondingepineutralgradientofabsolutepressureandKisthe

epineutraldiffusioncoefficient.Notethatthethermobaricdianeutraladvectionis

proportionaltothemesoscaleeddyfluxof“heat”alongtheneutraltangentplane,

cK−∇Θandisindependentoftheamountofsmall‐scale(dianeutral)turbulentmixing

andhenceisalsoindependentofthedissipationofmechanicalenergy

(Klockerand

McDougall(2010a)).ItisshowninappendixA.14belowthatwhiletheepineutral

diffusivefluxesn

−∇andn

K−∇Θaredifferent,theproductofthesefluxeswiththeir

respectivethermobariccoefficientsisthesame,thatis,bb

∇

=∇ΘHencethe

thermobaricdianeutraladvectionTb

eisthesamewhetheritiscalculatedas

bnn

NKT P

−

−∇⋅∇oras2

NKT P

−Θ

−∇Θ⋅∇Expressionsfor

and

TΘintermsof

enthalpyinthefunctionalforms

(

)

A,,hS p

and

(

)

ˆ,,hS pΘcanbefoundinappendixP.

Interestingly,forgivenmagnitudesoftheepineutralgradientsofpressureand

ConservativeTemperature,thedianeutraladvection,Tb 2

bnn

egNKT P

−Θ

−∇Θ⋅∇,of

thermobaricityismaximizedwhenthesegradientsareparallel,whileneutralhelicityis

maximizedwhenthesegradientsareperpendicular,sinceneutralhelicityisproportional

to

()

bnn

Θ∇×∇Θ⋅k(seeEqn.(3.13.2)).

Thisthermobaricverticaladvectionprocess,Tb

e,isabsentfromstandardlayered

oceanmodelsinwhichtheverticalcoordinateisafunctiononlyofA

SandΘ(suchas2,



potentialdensityreferencedto2000dbar).AsdescribedinappendixA.27below,the

isopycnaldiffusionofheatandsaltintheselayeredmodels,causedbybothparameterized

diffusionalongthecoordinateandbyeddy‐resolvedmotions,doesgiverisetothe

cabbelingadvectionthroughthecoordinatesurfacesbutdoesnotallowthethermobaric

velocityTb

ethroughthesesurfaces(KlockerandMcDougall(2010a)).

InboththeSIAandGSWcomputersoftwarelibrariesthethermobaricparameteris

outputinunitsof11

K Pa

−

−.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

3.9Cabbelingcoefficient



Thecabbelingcoefficientquantifiestherateatwhichdianeutraladvectionoccursasa

resultofmixingofheatandsaltalongtheneutraltangentplane.Withrespecttopotential

temperature

thecabbelingcoefficientis(McDougall(1987b))

()

bbA

,, ,

,2 .

Sp p p

CCStp SS

θθθθθ

θθ

ααααβ

θββ

⎛⎞

∂∂ ∂

==+ −

⎜⎟

∂∂ ∂

⎝⎠ (3.9.1)

Thisexpressionforthecabbelingcoefficientismostreadilyevaluatedbydifferentiatingan

expressionfordensityexpressedasafunctionofpotentialtemperatureratherthaninsitu

temperature,thatis,withdensityexpressedinthefunctionalform

()

A,, .Sp

ρρ θ

=

WithrespecttoConservativeTemperature

thecabbelingcoefficientis

()

bbA

,, ,

,2 .

Sp p p

CCStp SS

ααααβ

ββ

ΘΘΘΘΘ

ΘΘ

⎛⎞

∂∂ ∂

==+ −

⎜⎟

∂Θ ∂ ∂

⎝⎠ (3.9.2)

Thisexpressionforthecabbelingcoefficientismostreadilyevaluatedbydifferentiatingan

expressionfordensityexpressedasafunctionofConservativeTemperatureratherthanin

situtemperature,thatis,withdensityexpressedinthefunctionalform

()

ˆ,, .Sp

ρρ

=Θ

Thecabbelingdianeutraladvectionassociatedwiththelateralmixingofheatandsalt

alongneutraltangentplanesisgivenbyCab 2

bnn

egNKC

−Θ

−∇Θ⋅∇Θ(orlessaccuratelyby

Cab 2

bnn

egNKC

−

≈− ∇ ⋅∇ )wheren

∇

andn

∇

Θarethetwo‐dimensionalgradientsof

eitherpotentialtemperatureorConservativeTemperaturealongtheneutraltangentplane

andKistheepineutraldiffusioncoefficient.Thecabbelingdianeutraladvectionis

proportionaltothemesoscaleeddyfluxof“heat”alongtheneutraltangentplane,

K−∇Θandisindependentoftheamountofsmall‐scale(dianeutral)turbulentmixing

andhenceisalsoindependentofthedissipationofmechanicalenergy(Klockerand

McDougall(2010a)).ItisshowninappendixA.14thatbbnn n n

θθ

∇

⋅∇ ≠ ∇ Θ⋅∇ Θso

thattheestimateofthecabbelingdianeutraladvectionisdifferentwhencalculatedusing

potentialtemperaturethanwhenusingConservativeTemperature.Theestimateusing

potentialtemperatureisslightlylessaccuratebecauseofthenon‐conservativenatureof

potentialtemperature.

Whenthecabbelingandthermobaricityprocessesareanalyzedbyconsideringthe

mixingoftwofluidparcelsonefindsthatthedensitychangeisproportionaltothesquare

oftheproperty(Θand/orp)contrastsbetweenthetwofluidparcels(forthecabbeling

case,seeEqn.(A.19.4)inappendixA.19).Thisleadstothethoughtthatifanoceanfrontis

splitupintoaseriesofmanysmallerfrontsthentheeffectsofcabbelingand

thermobaricitymightbereducedbyperhapsthesquareofthenumberofsuchfronts.This

isnotthecase.Rather,thetotaldianeutraltransportacrossafrontalregiondependson

theproductofthelateralfluxofheatpassingthroughthefrontandthecontrastin

temperatureand/orpressureacrossthefront,butisindependentofthesharpnessofthe

front(KlockerandMcDougall(2010a)).Thiscanbeunderstoodbynotingfromabovethat

thedianeutralvelocityduetocabbeling,Cab 2

egNKC

−Θ

−∇Θ⋅∇Θisproportionaltothe

scalarproductoftheepineutralfluxofheat0

−

∇Θandtheepineutraltemperature

gradientn

∇Θ.Spatiallyintegratingthisproductovertheareaofthefrontalregion,one

findsthatthetotaldianeutraltransportisproportionaltothelateralheatfluxtimesthe

differenceintemperatureacrossthefrontalregion(inthecaseofcabbeling)orthe

differenceinpressureacrossthefrontalregion(inthecaseofthermobaricity).

InboththeSIAandGSWsoftwarelibrariesthecabbelingparameterisoutputinunits

of2

K−.Expressionsfor

and

intermsofenthalpyinthefunctionalforms

()

A,,hS p

and

()

ˆ,,hS pΘcanbefoundinappendixP.

32 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

3.10Buoyancyfrequency



Thesquareofthebuoyancyfrequency(sometimescalledtheBrunt‐Väisäläfrequency)2

N

isgivenintermsoftheverticalgradientsofdensityandpressure,orintermsofthe

verticalgradientsofpotentialtemperatureandAbsoluteSalinity(orintermsofthe

verticalgradientsofConservativeTemperatureandAbsoluteSalinity)by(the

onthe

left‐handsideisthegravitationalacceleration,andx,yandzarethespatialCartesian

coordinates)

(

)

12 1 1 2

zz zz

zxy

NPPc

θθ

ρρ κ ρ ρ

αθ β

αβ

−− −

ΘΘ

=− + =− −

=−∂∂

=Θ−∂∂

(3.10.1)

Fortwoseawaterparcelsseparatedbyasmalldistance

inthevertical,anequally

accuratemethodofcalculatingthebuoyancyfrequencyistobringbothseawaterparcels

adiabaticallyandwithoutexchangeofmattertotheaveragepressureandtocalculatethe

differenceindensityofthetwoparcelsafterthischangeinpressure.Inthiswaythe

potentialdensityofthetwoseawaterparcelsarebeingcomparedatthesamepressure.

ThiscommonprocedurecalculatesthebuoyancyfrequencyNaccordingto

NzP

ρρ

ΘΘ

ΔΔ

=− =

ΔΔ

(3.10.2)

where

Δisthedifferencebetweenthepotentialdensitiesofthetwoseawaterparcels

withthereferencepressurebeingtheaverageofthetwooriginalpressuresoftheseawater

parcels.ThelastpartofEqn.(3.10.2)hasusedthehydrostaticrelationz

=− .



3.11Neutraltangentplane



Theneutralplaneisthatplaneinspaceinwhichthelocalparcelofseawatercanbemoved

aninfinitesimaldistancewithoutbeingsubjecttoaverticalbuoyantrestoringforce;itis

theplaneofneutral‐orzero‐buoyancy.Thenormalvectortotheneutraltangentplanen

isgivenby

(

)

12 1 1 2

NPPc

θθ

ρρκ ρ ρ

αθβ

αβ

−− −

ΘΘ

=− ∇ + ∇ =− ∇ −∇

=∇−∇

=∇Θ−∇

(3.11.1)

Asdefined,nisnotquiteaunitnormalvector,ratheritsverticalcomponentisexactly,k

thatis,itsverticalcomponentisunity.ItisclearthatA

θθ

αθβ

∇

−∇isexactlyequalto

A.S

αβ

ΘΘ

∇Θ − ∇ Interestingly,both

∇

andA

∇

areindependentofthefour

arbitraryconstantsoftheGibbsfunction(seeEqn.(2.6.2))whileboth

Θ∇Θ andA

Θ∇

containanidenticaladditionalarbitrarytermproportionalto3A

∇

;termsthatexactly

cancelintheirdifference,A,S

αβ

ΘΘ

∇Θ − ∇ inEqn.(3.11.1).

Expressingthetwo‐dimensionalgradientofpropertiesintheneutraltangentplaneby

∇thepropertygradientsinaneutraltangentplaneobey

(

)

112

nn nn

θθ

ρρκ ρ ρ

αθβ

αβ

−−

ΘΘ

−∇+∇ =− ∇−∇

=∇−∇

=∇Θ−∇

(3.11.2)

Heren

∇isanexampleofaprojectednon‐orthogonalgradient

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

rxy

ττ

∂∂

∇≡ + +ijk(3.11.3)

thatiswidelyusedinoceanicandatmospherictheoryandmodelling.Horizontal

distancesaremeasuredbetweentheverticalplanesofconstantlatitudexandlongitudey

whilethevaluesoftheproperty

areevaluatedonthersurface(e.g.anisopycnal

surface,orinthecaseofn

∇,aneutraltangentplane).Thiscoordinatesystemisdescribed

bySutcliffe(1947),Bleck(1978),McDougall(1987b),McDougall(1995)andGriffies(2004).

Notethatr

∇hasnoverticalcomponent;itisnotdirectedalongthersurface,butrather

itpointsinexactlythehorizontaldirection.

FinitedifferenceversionsofEqn.(3.11.2)suchasA0S

αβ

ΘΘ

Θ− Δ ≈ arealsovery

accurate.Here

Θand

Θarethevaluesofthesecoefficientsevaluatedattheaverage

valuesofA

,SΘandpoftwoparcels

(

)

A11

,,SpΘand

(

)

A22

,,SpΘona“neutralsurface”

andΔΘ andA

SΔarethepropertydifferencesbetweenthetwoparcels.Theerror

involvedwiththisfiniteamplitudeversionofEqn.(3.11.2),namely

()

,TPPd

−−Θ

∫(3.11.4)

isdescribedinsection2andappendixA(c)ofJackettandMcDougall(1997).Anequally

accuratefiniteamplitudeversionofEqn.(3.11.2)istoequatethepotentialdensitiesofthe

twofluidparcels,eachreferencedtotheaveragepressure

(

)

0.5 .ppp=+



3.12Geostrophic,hydrostaticand“thermalwind”equations



Thegeostrophicapproximationtothehorizontalmomentumequations((B9)below)

equatestheCoriolistermtothehorizontalpressuregradientz

∇

sothatthegeostrophic

equationis

×=−∇ku or 1.

=×∇vk (3.12.1)

whereuisthethreedimensionalvelocityand

(

)

−× ×vkkuisthehorizontalvelocity

wherekistheverticalunitvector(pointingupwards)and

istheCoriolisparameter.

Thehydrostaticequationisanapproximationtotheverticalmomentumequation(see

Eqn.(B9)),namely

−(3.12.2)

Theuseof

intheseequationsratherthanpservestoremindusthatinordertoretain

theusualunitsforheight,densityandthegravitationalacceleration,pressureinthese

dynamicalequationsmustbeexpressedinPa notdbar. 

Thesocalled“thermalwind”equationisanequationfortheverticalgradientofthe

horizontalvelocityunderthegeostrophicapproximation.VerticallydifferentiatingEqn.

(3.12.1),usingthehydrostaticequationEqn.(3.12.2)andignoringthetinyterminz



(whichisofBoussinesqmagnitude),thethermalwindcanbewrittenas

()

zzz z n

ρρρ

=×∇ =−×∇= ×∇vk k k(3.12.3)

wherez

∇isthegradientoperatorintheexactlyhorizontaldirectionalonggeopotentials,

andthelastpartofthisequationrelatesthe“thermalwind”tothepressuregradientinthe

neutraltangentplane,thatis,effectivelytotheslopeoftheneutraltangentplane(see

McDougall(1995)).



34 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

3.13Neutralhelicity



Neutraltangentplanes(whichdoexist)donotlinkupinspacetoformawell‐defined

neutralsurfaceunlesstheneutralhelicityn

Hiseverywherezeroonthesurface.Neutral

helicityisdefinedasthescalarproductofthevectorA

αβ

ΘΘ

∇

Θ− ∇ withitscurl,

()

(

)

HS S

αβ αβ

ΘΘ ΘΘ

≡∇Θ−∇⋅∇×∇Θ−∇(3.13.1)

andthisisproportionaltothethermobariccoefficient

oftheequationofstate

accordingto

()

zpp

HTPS

PT S

gNT P

ΘΘ

−Θ

=∇⋅∇×∇Θ

=∇×∇Θ⋅

≈∇×∇Θ⋅

(3.13.2)

wherez

issimplytheverticalgradientofpressure(1

Pa m

−

)andn

∇

Θandp

∇Θ

arethe

two‐dimensionalgradientsofΘintheneuraltangentplaneandinthehorizontalplane

(actuallytheisobaricsurface)respectively.Thegradientsa

∇

anda

∇

Θaretakeninan

approximatelyneutralsurface.SinceA

θθ

αθβ

∇

−∇andA

αβ

ΘΘ

∇

Θ− ∇ areexactly

equal,neutralhelicitycanbedefinedinEqn.(3.13.1)asthescalarproductofthisvector

withitscurlbasedoneitherformulation,sothat(fromthethirdlineofEqn.(3.13.2),and

bearinginmindthatn

∇Θandn

∇areparallelvectors)weseethatbb

θθ

∇= ∇Θa

resultthatweuseinsection3.8andinappendixA.14.Neutralhelicityhasunitsof3

−

Becauseofthenon‐zeroneutralhelicityintheocean,lateralmotionfollowingneutral

tangentplaneshasthecharacterofhelicalmotion.Thatis,ifweignoretheeffectsof

diapycnalmixingprocesses(aswellasignoringcabbelingandthermobaricity),themean

flowaroundoceangyresstillpassesthroughanywell‐defined“density”surfacebecause

ofthehelicalnatureofneutraltrajectories,causedinturnbythenon‐zeroneutralhelicity.

Thisdia‐surfaceflowisexpressedinEqns.(A.25.4)and(A.25.6)intermsofthe

appropriatemeanhorizontalvelocityandthedifferencebetweentheslopeoftheneutral

tangentplaneandtheslopeofawell‐defined“density”surface.

Neutralhelicityisproportionaltothecomponentoftheverticalshearofthe

geostrophicvelocity(,

vthe“thermalwind”)inthedirectionofthetemperaturegradient

alongtheneutraltangentplane,

∇Θsince,fromEqn.(3.12.3)andthethirdlineof(3.13.2)

wefindthat

HTf

=⋅∇Θv(3.13.3)

Intheevolutionequationofpotentialvorticitydefinedwithrespecttopotential

density

thereisthebaroclinicproductionterm2p

ρρ ρ

−

∇

⋅∇ ×∇ (Straub(1999))and

thefirstterminaTaylorseriesexpansionforthisbaroclinicproductiontermis

proportionaltoneutralhelicityandisgivenby(McDougallandJackett(2007))

(

)

PPH

ρρ ρ

−∇⋅∇×∇≈ − (3.13.4)

wherer

isthereferencepressureofthepotentialdensity.Similarly,thecurlina

potentialdensitysurfaceofthehorizontalpressuregradientterminthehorizontal

momentumequation,

()

σρ

∇× ∇ isgivenby(McDougallandKlocker(2010))

()

1r.

zPHPPz

σρ

−

⎛⎞

∂

∇× ∇ ⋅ = − −

⎜⎟

∂

⎝⎠

k(3.13.5)

Thefactthatthiscurlisnonzeroprovesthatageostrophicstreamfunctiondoesnotexistin

apotentialdensitysurface.

Neutralhelicityn

Halsoarisesinthecontextoffindingaclosedexpressionforthe

meanvelocityintheocean.Thecomponentofthehorizontalvelocityinthedirection

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

alongacontourofΘinaneutraltangentplane,namelythevelocitycomponent

⋅×∇Θ∇Θvk isgivenby(McDougall(1995),Zikaetal.(2010a,2010b))

φρ

⊥

∇Θ −

⋅× = +

∇Θ ∇Θ

vk (3.13.6)

sothatthefullexpressionforthehorizontalvelocityis

zn n

Hv v

φρ

⊥⊥

⎧⎫

∇

Θ∇Θ

−

⎪⎪

=+×+

⎨⎬

∇

Θ∇Θ

∇Θ

⎪⎪

⎩⎭

(3.13.7)

Herez

istherateofspiraling(radianspermeter)intheverticaloftheΘcontourson

neutraltangentplanes,andv⊥isthevelocitycomponentacrosstheΘcontouronthe

neutraltangentplane(avelocitycomponentthatresultsfromirreversiblemixing

processes).Neutralhelicityarisesinthiscontextbecauseitisproportionaltothe

componentofthethermalwindvectorz

vinthedirectionacrosstheΘcontouronthe

neutraltangentplane(see(3.13.3)).Thisequation(3.13.7)fortheisopycnally‐averaged

velocityvshowsthatintheabsenceofmixingprocesses(sothat0

⊥⊥

=)andsolong

as(i)theepineutral

contoursspiralintheverticaland(ii)n

∇

Θisnotzero,thenneutral

helicityn

Hisrequiredtobenon‐zerointheoceanwhenevertheoceanisnotmotionless.

Interestingly,forgivenmagnitudesoftheepineutralgradientsofpressureand

ConservativeTemperature,neutralhelicityismaximizedwhenthesegradientsare

perpendicularsinceneutralhelicityisproportionalto

(

)

bnn

∇

×∇ Θ ⋅k(seeEqn.

(3.13.2)),whilethedianeutraladvectionofthermobaricity,Tb 2

bnn

egNKT P

−Θ

−∇Θ⋅∇,is

maximizedwhenn

∇Θandn

∇areparallel(seesection3.8).



3.14NeutralDensity



NeutralDensityisthenamegiventoadensityvariablethatresultsfromthecomputer

softwaredescribedinJackettandMcDougall(1997).NeutralDensityisgiventhesymbol

butitisnotathermodynamicvariableasitisafunctionnotonlyofsalinity,

temperatureandpressure,butalsooflatitudeandlongitude.Becauseofthenon‐zero

neutralhelicityn

Hintheoceanitisnotpossibletoformsurfacesthatareeverywhere

osculatewithneutraltangentplanes(McDougallandJackett(1988)).NeutralDensity

surfacesminimizeinsomesensetheglobaldifferencesbetweentheslopesoftheneutral

tangentplaneandtheNeutralDensitysurface.Thisslopedifferenceisgivenby

(

)

na a a

zzgN S

βα

−Θ Θ

=∇ −∇ = ∇ − ∇Θs(3.14.1)

wheren

∇istheslopeoftheneutraltangentplane,a

∇

istheslopeoftheapproximately

neutralsurfaceanda

∇isthetwo‐dimensionalgradientoperatorintheapproximately

neutralsurface(ofwhichaNeutralDensitysurfaceisoneexample).Theverticalvelocity

throughanapproximatelyneutralsurfaceduetolateralmotionalonganeutraltangent

planeisthescalarproduct⋅vswherevisthehorizontalvelocity(seeEqn.(A.25.4)).

SinceNeutralDensityisnotathermodynamicvariable,itwillnotbedescribedmorefully

inthismanual.



36 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

3.15Stabilityratio



ThestabilityratioR

istheratiooftheverticalcontributionfromConservative

TemperaturetothatfromAbsoluteSalinitytothestaticstability2

Nofthewatercolumn.

From(3.10.1)abovewefind

() ()

RSS

ρθ

ααθ

ββ

=≈

(3.15.1)



3.16Turnerangle



TheTurnerangleTu ,namedafterJ.StewartTurner,isdefinedasthefour‐quadrant

arctangent(Ruddick(1983)andMcDougalletal.(1988),particularlytheirFigure1)

(

)

(

)

()

() ()

()

tan ,

Tu S S

θθ θθ

αβ αβ

αθ β αθ β

−Θ Θ Θ Θ

−

=Θ+ Θ−

≈+ − (3.16.1)

wherethefirstofthetwoargumentsofthearctangentfunctionisthe“y”‐argumentand

thesecondonethe“x”‐argument,thisbeingthecommonorderoftheseargumentsin

FortranandMATLAB.TheTurnerangleTu isquotedindegreesofrotation.Turner

anglesbetween45°and90°representthe“salt‐finger”regimeofdouble‐diffusive

convection,withthestrongestactivitynear90°.Turneranglesbetween−45°and−90°

representthe“diffusive”regimeofdouble‐diffusiveconvection,withthestrongestactivity

near−90°.Turneranglesbetween−45°and45°representregionswherethestratificationis

stablystratifiedinbothΘandA.STurneranglesgreaterthan90°orlessthan−90°

characterizeastaticallyunstablewatercolumninwhich20.N

Asacheckonthe

calculationoftheTurnerangle,notethat

(

)

tan 45 .RTu

−+°

TheTurnerangleandthe

stabilityratioareavailableintheGSWOceanographicToolboxfromthefunction

gsw_Turner_Rsubrho_CT25.



3.17Propertygradientsalongpotentialdensitysurfaces



Thetwo‐dimensionalgradientofascalar

alongapotentialdensitysurface

∇is

relatedtothecorrespondinggradientintheneutraltangentplanen

∇

by

[

]

ϕϕ

−

∇=∇+ ∇Θ

Θ⎡⎤

−

⎣⎦

(3.17.1)

(fromMcDougall(1987a)),whereristheratiooftheslopeontheA

−

Θdiagramofan

isolineofpotentialdensitywithreferencepressurer

ptotheslopeofapotentialdensity

surfacewithreferencepressurep,andisdefinedby

(

)

(

)

()()

Ar Ar

,, ,,

Sp Sp

rSp Sp

αβ

ΘΘ

=ΘΘ

.(3.17.2)

Substituting

Θinto(3.17.1)givesthefollowingrelationbetweenthe(parallel)

isopycnalandepineutralgradientsof



rR G

⎡⎤

−

⎣⎦

∇Θ= ∇Θ= ∇Θ

⎡⎤

−

⎣⎦

(3.17.3)

wherethe“isopycnaltemperaturegradientratio”

GRr

⎡

⎤

−

⎣

⎦

≡

⎡

⎤

−

⎣

⎦

(3.17.4)

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

hasbeendefinedasashorthandexpressionforfutureuse.ThisratioGΘisavailablein

theGSWToolboxfromthealgorithmgsw_isopycnal_vs_ntp_CT_ratio_CT25,whilethe

ratiorofEqn.(3.17.2)isavailablethereasgsw_isopycnal_slope_ratio_CT25.

SubstitutingA

=intoEqn.(3.17.1)givesthefollowingrelationbetweenthe(parallel)

isopycnalandepineutralgradientsofA

S

AAA

SSS

⎡⎤

−

⎣⎦

∇= ∇= ∇

⎡⎤

−

⎣⎦

(3.17.5)



3.18Slopesofpotentialdensitysurfacesandneutraltangentplanescompared



Thetwo‐dimensionalslopeofasurfaceisdefinedasthetwo‐dimensionalgradientof

heightzofthatsurface.Thetwo‐dimensionalslopeofasurfaceisanexactlyhorizontal

gradientvector;ithasnoverticalcomponent.Theslopedifferencebetweentheneutral

tangentplaneandapotentialdensitysurfacewithreferencepressurer

pisgivenby

(McDougall(1988))

[]

()

[

]

nnn

nzzz z

Rr Rr

zz G

Rr rR

ρ ρ

σσ

ρ ρ

−−

∇Θ ∇Θ ∇Θ−∇Θ ∇Θ

∇−∇ = = − = =

ΘΘΘ Θ

⎡⎤ ⎡⎤

−−

⎣⎦ ⎣⎦

(3.18.1)

Whilepotentialdensitysurfaceshavebeenthemostcommonlyusedsurfaceswith

whichtoseparate“isopycnal”mixingprocessesfromverticalmixingprocesses,many

othertypesofdensitysurfacehavebeenused.Thelistincludesspecificvolumeanomaly

surfaces,patchedpotentialdensitysurfaces(ReidandLynn(1971)),NeutralDensity

surfaces(JackettandMcDougall(1997)),orthobaricdensitysurfaces(deSzoekeetal.

(2000))andsomepolynomialfitsofNeutralDensityasfunctionofonlysalinityandeither

orΘ(EdenandWillebrand(1999),McDougallandJackett(2005b)).Themostrecent

methodforformingapproximatelyneutralsurfacesisthatofKlockeretal.(2009a,b).This

methodisrelativelycomputerintensivebuthasthebenefitthattheremnantmis‐match

betweenthefinalsurfaceandtheneutraltangentplaneateachpointisdueonlytothe

neutralhelicityofthedatathroughwhichthesurfacepasses.Therelativeskillofallthese

surfacesatapproximatingtheneutraltangentplaneslopeateachpointhasbeen

summarizedintheequationsandhistogramplotsinthepapersofMcDougall(1989,1995),

McDougallandJackett(2005a,2005b),andKlockeretal.(2009a,b).

WhenlateralmixingwithisopycnaldiffusivityKisimposedalongpotentialdensity

surfacesratherthanalongneutraltangentplanes,afictitiousdiapycnaldiffusivityarises

whichisoftenlabeledthe“Veroniseffect”afterVeronis(1975)(whoconsideredtheill

effectsofexactlyhorizontalversusisopycnalmixing).Thisfictitiousdiapycnaldiffusivity

ofdensityisequaltoKtimesthesquareoftheslopeerror,Eqn.(3.18.1)(Klockeretal.

(2009a)).



3.19Slopesofinsitudensitysurfacesandspecificvolumeanomalysurfaces



Thevectorslopeofaninsitudensitysurface,,

∇

isdefinedtobetheexactlyhorizontal

vector

ρρρ

∂∂

∇= + +ijk(3.19.1)

representingthe“dip”ofthesurfaceinbothhorizontaldirections(notethatheight

is

definedpositiveupwards).Thisvectorslopecanberelatedtothe(verysmall)slopeof

isobaricsurfaceby(

hereisthegravitationalacceleration)(McDougall(1989))

38 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

()

pnp

zz zz N

−

⎡

⎤

∇−∇ =∇−∇ +

⎢

⎥

⎣

⎦(3.19.2)

wherecisthespeedofsoundandNisthebuoyancyfrequency.Intheupperwater

columnwherethesquareofthebuoyancyfrequencyissignificantlylargerthan

22 52

4.3 10

cxs

−−

≈,theinsitudensitysurfacehasasimilarslopetotheneutraltangent

plane.

∇Inthedeepocean2

Nisonlyabout1%of22

candsothesurfacesof

constantinsitudensityhaveaslopeofonly1%oftheslopeoftheneutraltangentplane.

Atapressureofabout1000dbarwhere252

10 sN

−

≈,theslopeofaninsitudensitysurface

isonlyaboutonefifththatoftheneutraltangentplane.Neutrallybuoyantfloatsinthe

oceanareusuallymetalcylindersthataremuchlesscompressiblethanseawater.These

floatshaveaconstantmassandanalmostconstantvolume.Hencethesefloatshavean

almostconstantinsitudensityandtheirmotionapproximatelyoccursonsurfacesof

constantinsitudensitywhichatmiddepthintheoceanaremuchclosertobeingisobaric

surfacesthanbeinglocally‐referencedpotentialdensitysurfaces.Thisiswhythesefloats

aresometimesdescribedas“isobaricfloats”.

Theslopeofaspecificvolumeanomalysurface,,

∇

canbeexpressedas

()

22 22

pnp

gc gc

zz zz NN

−

⎡

⎤

∇−∇ =∇−∇ + −

⎢

⎥

⎣

⎦



(3.19.3)

wherec



isthesoundspeedofthereferenceparcel

(

)

A,S



atpressure.pThisexpression

confirmsthatwherethelocalseawaterpropertiesareclosetothoseofthereferenceparcel,

thespecificvolumeanomalysurfacecancloselyapproximatetheneutraltangentplane.

ThesquarebracketinEqn.(3.19.3)isequalto2

ρδ

−

∂

∂(fromsection7ofMcDougall

(1989)where

isspecificvolumeanomaly).



3.20Potentialvorticity



PlanetarypotentialvorticityistheCoriolisparameter

timestheverticalgradientofa

suitablevariable.Potentialdensityissometimesusedforthatvariablebutusingpotential

density(i)involvesaninaccurateseparationbetweenlateralanddiapycnaladvection

becausepotentialdensitysurfacesarenotagoodapproximationtoneutraltangentplanes

and(ii)incursthenon‐conservativebaroclinicproductiontermofEqn.(3.13.4).Using

approximatelyneutralsurfaces,“ans”,(suchasNeutralDensitysurfaces)providesan

optimalseparationbetweentheeffectsoflateralanddiapycnalmixinginthepotential

vorticityequation.Inthiscasethepotentialvorticityvariableisproportionaltothe

reciprocalofthethicknessbetweenapairofcloselyspacedapproximatelyneutral

surfaces.ThisplanetarypotentialvorticityvariableiscalledNeutral‐Surface‐Potential‐

Vorticity(NSPV forshort)andisrelatedto2

Nby

(

)

{

}

1n 2 22

ans

exp .

zaPa

NSPV g f fN g N T P d

ργ ρ

−−Θ

≡− ≈ − ∇Θ−Θ ∇ ⋅

∫l(3.20.1)

TheexponentialexpressionwasderivedbyMcDougall(1988)(hisequation(47))andis

approximatebecausethevariationofthesalinecontractioncoefficient

Θwithpressure

wasneglectedincomparisonwiththelargerproportionalchangeinthethermalexpansion

coefficient

Θwithpressure.TheintegralinEqn.(3.20.1)istakenalonganapproximately

neutralsurfacefromalocationwhereNSPV isequalto2.

NInterestinglythe

combinationaPa

∇Θ−Θ∇ issimplytheisobaricgradientofConservativeTemperature,

∇Θwhichisalmostthesameasthehorizontalgradient,.

∇

ΘAmoreaccurateversion

ofthisequationwhichdoesnotignorethevariationofthesalinecontractioncoefficient

canbeshowntobe

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

(

)

{

}

{}

1n 2 2 2

ans

222

ans

exp ( ) ( )

exp ( ) .

zPPPP

NSPV g f fN g N S d

fN g N d

ργ ρα ρβ

ρκ

−−ΘΘ

−

≡− = − ∇ Θ− ∇ ⋅

=∇⋅

∫

l(3.20.2)

TheexponentialfactorinEqn.(3.20.2)isapproximatelytheintegratingfactorb,defined

asn()

lll

ρρρ

≡∇ ⋅∇ ∇ ⋅∇ whereA

()

ρρβ α

ΘΘ

∇

≡∇−∇Θ,whichallowsspatialintegrals

ofn

()

bS b

βα ργ

ΘΘ

∇− ∇Θ=∇≈∇tobeapproximatelyindependentofpathfor

“verticalpaths”,thatis,forpathsinsurfaceswhosenormalhaszeroverticalcomponent.

Thegradienta

∇of2

NisrelatedtothatofNSPV by(fromEqns.(3.20.2)and(3.20.1))

()

(

)

22222

ln ln ( ) .

aa P aPa

NNSPVgN gNT P

ρκ ρ

−−Θ

∇−∇ =−∇≈ ∇Θ−Θ∇(3.20.3)

Thedeficienciesof2

Nasaformofplanetarypotentialvorticityhavenotbeenwidely

appreciated.Eveninalake,andalsointhesimplesituationwheretemperaturedoesnot

varyalongadensitysurface(a

∇Θ=0),theuseof2

Nasplanetarypotentialvorticityis

inaccuratesincetheright‐handsideof(3.20.3)isthenapproximately

NT P T P

ρα

−Θ Θ

−

Θ∇ = ∇

⎡⎤

−

⎣⎦

,(3.20.4)

andthemerefactthatthedensitysurfacehasaslope(i.e.aP

∇

≠0)meansthatthe

contoursof2

NwillnotbeparalleltocontoursofNSPV onthedensitysurface.(Inthis

situation(wherea

∇Θ=0)thecontoursofNSPV alongapproximatelyneutralsurfaces

coincidewiththoseofisopycnal‐potential‐vorticity(

PV ),thepotentialvorticitydefined

withrespecttotheverticalgradientofpotentialdensityby1z

IPV fg

−

=− ).

PV isrelatedto2

Nby(McDougall(1988))

()

1rr

111

zRr

IPV g

fN N p p G G

ββ

ρρ

ββ

ΘΘ

−Θ

ΘΘΘΘ

⎡⎤

−

−⎣⎦

≡= = ≈

⎡⎤

−

⎣⎦

(3.20.5)

sothattheratioofNSPV to

PV plottedonanapproximatelyneutralsurfaceisgivenby

()

{}

ans

1exp ( ) .

NSPV

IPV pRr

βρκ

Θ−

⎡⎤

−

⎣⎦

=∇⋅

⎡⎤

−

⎣⎦

∫l(3.20.6)

YouandMcDougall(1991)showthatbecauseofthehighlydifferentiatednatureof

potentialvorticity,isolinesof

PV andNSPV donotcoincideevenatthereference

pressurer

pofthepotentialdensityvariable(seeequations(14)–(16)andFigure14of

thatpaper). NSPV ,2

Nand

PV havetheunits3

−

Theratio2

PV fN isavailablein

theGSWOceanographicToolboxasthefunctiongsw_IPV_vs_fNsquared_ratio_CT25.



3.21Verticalvelocitythroughtheseasurface



Therehasbeenconfusionregardingtheexpressionthatrelatesthenetevaporationatthe

seasurfacetotheverticalvelocityintheoceanthroughtheseasurface.Sincethese

expressionshaveofteninvolvedthesalinity(throughthefactor

(

)

1S−)andsoappearto

bethermodynamicexpressions,herewepresentthecorrectequationwhichwewillseeis

merelykinematics,notthermodynamics.Let

(

)

WEP

−betheverticalmassfluxthrough

theair‐seainterfaceontheatmosphericsideoftheinterface(where

(

)

−

isthenotional

verticalvelocityoffreshwaterthroughtheair‐seainterfacewithdensityW

;thisdensity

beingthatofpurewaterattheseasurfacetemperatureandatatmosphericpressure).The

samemassflux

(

)

WEP

−mustflowthroughtheair‐seainterfaceontheoceansideof

theinterfacewherethedensityis

(

)

A,,0.St

ρρ

=Theverticalvelocitythroughan

arbitrarysurfacewhoseheightis

(

)

xyt

=canbeexpressedasH

−⋅∇−∂∂V

(wherewistheverticalvelocitythroughthegeopotentialsurface,seesection3.24,and

40 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

notethattistimeinthiscontext)andthemassfluxassociatedwiththisdia‐surface

verticalvelocitycomponentisthisverticalvelocitytimesthedensityoftheseawater,.



Byequatingthetwomassfluxesoneithersideoftheair‐seainterfacewearriveatthe

verticaloceanvelocitythroughtheair‐seainterfaceas(Griffies(2004),Warren(2009))

(

)

1W .

wtEP

ηη ρρ

−

−⋅∇−∂∂= −V(3.21.1)



3.22Freshwatercontentandfreshwaterflux



Oceanographerstraditionallycallthepurewaterfractionofseawaterthe“freshwater

fraction”orthe“freshwatercontent”.Thiscancauseconfusionbecauseinsomescience

circles“freshwater”isusedtodescribewateroflowbutnon‐zerosalinity.Nevertheless,

hereweretaintheoceanographicuseof“freshwater”asbeingsynonymouswithpure

water(i.e.A0S=,thispurewaterbeinginliquid,gaseousorsolidiceforms).The

freshwatercontentofseawateris

(

)

(

)

110.001/(gkg).SS

−

−=− Thefirstexpression

hereclearlyrequiresthatAbsoluteSalinityisexpressedinkgofseasaltperkgofsolution.

NotethatthefreshwatercontentisnotbasedonPracticalSalinity,thatis,itisnot

()

1 0.001 .S−

Theadvectivefluxofmassperunitareaisu

whereuisthefluidvelocitythrough

thechosenareaelementwhiletheadvectivefluxofseasaltisA.Su

Theadvectivefluxof

freshwaterperunitareaisthedifferenceofthesetwomassfluxes,namely

()

1.Su

−As

outlinedinsection2.5andappendicesA.4andA.20,forwaterofanomalouscomposition

therearefourtypesofabsolutesalinitythatmightberelevanttothisdiscussionof

freshwaterfluxes;DensitySalinitydens

SS≡,SolutionSalinitysoln

S,Added‐MassSalinity

add

S,andPreformedSalinity*

S.SincePreformedSalinityisdesignedtobeaconservative

variablewithazerofluxair‐seaboundarycondition,probablythebestformoffreshwater

content,atleastinthecontextofanoceanmodel,is

(

)

(

)

1 1 0.001 / (g kg ) .SS

−

−=− 



3.23Heattransport



Afluxofheatacrosstheseasurfaceataseapressureof0dbarisidenticaltothefluxof

potentialenthalpywhichinturnisexactlyequalto0

ctimesthefluxofConservative

TemperatureΘ,where0

cisgivenby(3.3.3).Bycontrast,thesameheatfluxacrossthe

seasurfacechangespotentialtemperature

ininverseproportionto

()

A,,0

andthis

heatcapacityvariesby5%attheseasurface,dependingmainlyonsalinity.

TheFirstLawofThermodynamics,namelyEqn.(A.13.1)ofappendixA.13,canbe

approximatedas

0RQ

ρρερ

Θ≈−∇⋅ −∇⋅ + +

FF S(3.23.1)

withanerrorinΘthatisapproximatelyonepercentoftheerrorincurredbytreating

either0

or

()

A,,0

asthe“heatcontent”ofseawater(seeMcDougall(2003)and

appendicesA.13andA.18).Equation(3.23.1)isexactat0dbarwhileatgreatdepthinthe

oceantheerrorwiththeapproximation(3.23.1)isnolargerthantheneglectofthe

dissipationofmechanicalenergyterm

inthisequation(seeappendixA.21).

Becausetheleft‐handsideoftheFirstLawofThermodynamics,Eqn.(3.23.1),canbe

writtenasdensitytimesthematerialderivativeof0

itfollowsthat

canbetreatedas

aconservativevariableintheoceanandthat0

istransportedbyadvectionandmixed

byturbulentepineutralanddianeutraldiffusionasthoughitisthe“heatcontent”of

seawater.Forexample,theadvectivemeridionalfluxof“heat”istheareaintegralof

vh vc

ρρ

=Θ(herevisthenorthwardvelocity).Theerrorincomparingthisadvective

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

meridional“heatflux”withtheair‐seaheatfluxisapproximately1%oftheerrorinso

interpretingtheareaintegralofeither0

or

(

)

A,,0

vc S

θθ

.Similarly,turbulent

diffusivefluxesof“heat”areaccuratelygivenbyaturbulentdiffusivitytimesthespatial

gradientof0

cΘbutarelessaccuratelyapproximatedbythesameturbulentdiffusivity

timesthespatialgradientof0

(seeappendixA.14foradiscussionofthispoint).

Warren(1999,2006)hasarguedthatbecauseenthalpyisunknownuptoalinear

functionofsalinity,itisonlypossibletotalkofafluxof“heat”throughanoceansectionif

thefluxesofmassandsaltthroughtheoceansectionarebothzero.Thisopinionseemsto

bewidelyheld,butitisincorrect.Becauseenthalpyisunknownandunknowableuptoa

linearfunctionofA

S(i.e.uptothearbitraryfunction13A

aaS

intermsoftheconstants

definedinEqn.(2.6.2)),theleft‐handsideofEqn.(3.23.1)isunknowabletotheextent

dd.aSt

ItisshowninappendixBthatthetermsA

−∇⋅ +FSontheright‐hand

sideofEqn.(3.23.1)arealsounknowabletothesameextentsothattheeffectof3

acancels

fromEqn.(3.23.1).Hencethefactthat0

isunknowableuptoalinearfunctionofA

S

doesnotaffecttheusefulnessof0

hor0

asmeasuresof“heatcontent”.Similarly,the

differencebetweenthemeridionalfluxesof0

acrosstwolatitudesisequaltothearea‐

integratedair‐seaandgeothermalheatfluxesbetweentheselatitudes(afterallowingfor

anyunsteadyaccumulationof0

cΘinthevolume),irrespectiveofwhethertherearenon‐

zerofluxesofmassorsaltacrossthesections.Thispowerfulresultfollowsdirectlyfrom

thefactthat0

cΘisaconservativevariable,obeyingthesimpleconservationstatement

Eqn.(3.23.1).Thisissueisdiscussedatgreaterlengthinsection6ofMcDougall(2003).



3.24Geopotential



ThegeopotentialΦisthegravitationalpotentialenergyperunitmasswithrespecttothe

height

=0.Allowingthegravitationalaccelerationtobeafunctionof

,Φisgivenby

()

zdz

′

Φ=∫(3.24.1)

Ifthegravitationalaccelerationistakentobeconstant

issimply.

zNotethatheight

andΦarenegativequantitiesintheoceansincetheseasurface(orthegeoid)istakenas

thereferenceheightand

ismeasuredupwardfromthissurface.InSIunitsΦis

measuredin122

Jkg m s .

−−

=Iftheoceanisassumedtobeinhydrostaticbalancesothat

=− (or

dz vdP

′

−= )thenthegeopotentialEqn.(3.24.1)maybeexpressedasthe

verticalpressureintegralofthespecificvolumeinthewatercolumn,

()

Pvp dP

′

Φ=Φ−∫(3.24.2)

where0

Φisthevalueofthegeopotentialatzeroseapressure,thatis,thegravitational

accelerationtimestheheightofthefreesurfaceabovethegeoid.Notethatthe

gravitationalaccelerationhasnotbeenassumedtobeconstantinEqn.(3.24.2).



3.25Totalenergy



Thetotalenergy

isthesumofspecificinternalenergy,ukineticenergyperunitmass

0.5 ⋅uu(whereuisthethree‐dimensionalvelocityvector)andthegeopotential,Φ

2.u

+Φ+ ⋅uu

(3.25.1)

Totalenergy

isnotafunctionofonly

(

)

A,,Stpandsoisnotathermodynamic

quantity.

42 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

3.26Bernoullifunction



TheBernoullifunctionisthesumofspecificenthalpy,hkineticenergyperunitmass

0.5 ⋅uu,andthegeopotential,Φ

2.h=+Φ+ ⋅uu

(3.26.1)

Usingtheexpression(3.2.1)thatrelatesenthalpyandpotentialenthalpy,togetherwith

Eqn.(3.24.2)for,ΦtheBernoullifunction(3.26.1)maybewrittenas

() ( )

2ˆ,, .

hvpvSpdP

′

′′

=+Φ+⋅− − Θ

∫

(3.26.2)

Thepressureintegraltermhereisaversionofthedynamicheightanomaly(3.27.1),this

timeforaspecificvolumeanomalydefinedwithrespecttotheAbsoluteSalinityand

ConservativeTemperature(orequivalently,withrespecttotheAbsoluteSalinityand

potentialtemperature)oftheseawaterparcelinquestionatpressure

.Thispressure

integralisequaltotheCunninghamgeostrophicstreamfunction,Eqn.(3.29.2).

TheBernoullifunction

isnotafunctionofonly

(

)

A,,Stpandsoisnota

thermodynamicquantity.

TheBernoullifunctionisdominatedbythecontributionofenthalpyhto(3.26.1)and

bythecontributionofpotentialenthalpy0

hto(3.26.2).Thevariationofkineticenergyor

thegeopotentialfollowingafluidparcelistypicallyseveralthousandtimeslessthanthe

variationofenthalpyorpotentialenthalpyfollowingthefluidmotion.

ThedefinitionofspecificvolumeanomalygiveninEqn.(3.7.3)hasbeenusedby

Saunders(1995)towrite(3.26.2)as(withthedynamicheightanomalyΨdefinedin

(3.27.1))

()()

()()()()

00 1SO A

00 1SO SO A A

ˆˆ

,0 C, , ,

ˆˆˆˆ

,0 C, ,0 C,0 , , , ,0 .

hvSpvSpdP

hhSphShSphS

′′′

=+Φ+Ψ+ ⋅− ° − Θ

=+Φ+Ψ+ ⋅− ° + ° + Θ − Θ

∫

(3.26.3)

Notethat

()

ˆ,,0 p

hS cΘ=Θand

()

ˆ,0 C,0 0hS °=

.



3.27Dynamicheightanomaly



ThedynamicheightanomalyΨ,givenbytheverticalintegral

[][]

()

A,, ,

PSptppdP

′

′′ ′

Ψ=−∫(3.27.1)

isthegeostrophicstreamfunctionfortheflowatpressure

withrespecttotheflowatthe

seasurfaceand

isthespecificvolumeanomaly.Thusthetwo‐dimensionalgradientof

Ψinthe

pressuresurfaceissimplyrelatedtothedifferencebetweenthehorizontal

geostrophicvelocityvat

andattheseasurface 0

vaccordingto

f×∇ Ψ = −kvv(3.27.2)

ThedefinitionEqn.(3.27.1)ofdynamicheightanomalyappliestoallchoicesofthe

referencevaluesA

and,t



orˆ

inthedefinitionEqns.(3.7.1–3.7.4)ofthespecific

volumeanomaly.

Also,

inEqn.(3.27.1)canbereplacedwithspecificvolumev

withoutaffectingtheisobaricgradientoftheresultingstreamfunction.Thatis,this

substitutiondoesnotaffectEqn.(3.27.2)becausetheadditionaltermisafunctiononlyof

pressure.Traditionallyitwasimportanttousespecificvolumeanomalyinpreferenceto

specificvolumeasitwasmoreaccuratewithcomputercodewhichworkedwithsingle‐

precisionvariables.Sincecomputersnowregularlyemploydouble‐precision,thisissue

hasbeenovercomeandconsequentlyeither

orvcanbeusedintheintegrandofEqn.

(3.27.1),somakingiteitherthe“dynamicheightanomaly”orthe“dynamicheight”.Asin

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

thecaseofEqn.(3.24.2),soalsothedynamicheightanomalyEqn.(3.27.1)hasnotassumed

thatthegravitationalaccelerationisconstantandsoEqn.(3.27.2)appliesevenwhenthe

gravitationalaccelerationistakentovaryinthevertical.

Thedynamicheightanomaly

shouldbequotedinunitsof22

m s

−.Thesearethe

unitsinwhichtheGSWToolbox(appendixN)outputsdynamicheightanomalyinthe

functiongsw_geo_strf_dyn_height.NotethattheintegrationinEqn.(3.27.1)ofspecific

volumeanomalywithpressureindbar wouldyielddynamicheightanomalyinunitsof

m kg dbar

−,andtheuseoftheseunitsinEqn.(3.27.2)wouldnotgivetheresultant

horizontalgradientintheusualunits,beingtheproductoftheCoriolisparameter(unitsof

s−)andthevelocity(unitsof1

m s

−

).Thisisthereasonwhythepressureintegrationis

donewithpressureinPa anddynamicheightanomalyisoutputin22

m s

−.



3.28Montgomerygeostrophicstreamfunction



TheMontgomery“accelerationpotential”

definedby

()

[][]

()

PSptppdP

πδδ

′

′′ ′

=− −

∫(3.28.1)

isthegeostrophicstreamfunctionfortheflowinthespecificvolumeanomalysurface

()

,,Stp

=relativetotheflowat0

(thatis,at0dbarp

).Thusthetwo‐

dimensionalgradientof

inthe1

specificvolumeanomalysurfaceissimplyrelatedto

thedifferencebetweenthehorizontalgeostrophicvelocityvinthe1

surfaceandat

theseasurface 0

vaccordingto

×∇ = −kvv

or

(

)

10.ff

δπ

∇=−×−kvv

(3.28.2)

Thedefinition,Eqn.(3.28.1),oftheMontgomerygeostrophicstreamfunctionappliestoall

choicesofthereferencevaluesA



andt



inthedefinition,Eqn.(3.7.2),ofthespecific

volumeanomaly.

Bycarefullychoosingthesereferencevaluesthespecificvolume

anomalysurfacecanbemadetocloselyapproximatetheneutraltangentplane

(McDougallandJackett(2007)).

ItisnotuncommontoreadofauthorsusingtheMontgomerygeostrophic

streamfunction,Eqn.(3.28.1),asageostrophicstreamfunctioninsurfacesotherthan

specificvolumeanomalysurfaces.Thisincurserrorsthatshouldberecognized.For

example,thegradientoftheMontgomerygeostrophicstreamfunction,Eqn.(3.28.1),ina

neutraltangentplanebecomes(insteadofEqn.(3.28.2)inthe1

surface)

(

)

(

)

00nn

ff PP

∇=−× − +−∇kvv ,(3.28.3)

wherethelasttermrepresentsanerrorarisingfromusingtheMontgomery

streamfunctioninasurfaceotherthanthesurfaceforwhichitwasderived.

ZhangandHogg(1992)subtractedanarbitrarypressureoffset,

()

P−,from

()

P−inthefirstterminEqn.(3.28.1),sodefiningthemodifiedMontgomery

streamfunction

()

[][]

()

Z-H

A,, .

PSptppdP

πδδ

′

′′ ′

=− −

∫(3.28.4)

ThegradientofZ-H

inaneutraltangentplanebecomes

(

)

(

)

Z-H

ff PP

∇=−×−+−∇kvv (3.28.5)

wherethelasttermcanbemadesignificantlysmallerthanthecorrespondingterminEqn.

(3.28.3)bychoosingtheconstantpressure

tobeclosetotheaveragepressureonthe

surface.

Thistermcanbefurtherminimizedbysuitablychoosingtheconstantreferencevalues



andΘ



inthedefinition,Eqn.(3.7.3),ofspecificvolumeanomaly



sothatthissurface

44 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

morecloselyapproximatestheneutraltangentplane(McDougall(1989)).This

improvementisavailablebecauseitcanbeshownthat

()

(

)

(

)

,, ,, .

nnbn

Sp SpPT P

ρδ κ κ

⎡⎤

∇=− Θ− Θ ∇≈ Θ−Θ∇

⎢⎥

⎣⎦

 

  (3.28.6)

ThelastterminEqn.(3.28.5)isthenapproximately

()

(

)

()

nbn

PTPP

δρ

−Θ

−∇ ≈ Θ−Θ∇ −



(3.28.7)

andhencesuitablechoicesof

,A



and



canreducethelastterminEqn.(3.28.5)that

representstheerrorininterpretingtheMontgomerygeostrophicstreamfunction,Eqn.

(3.28.4),asthegeostrophicstreamfunctioninasurfacethatismoreneutralthanaspecific

volumeanomalysurface.

TheMontgomerygeostrophicstreamfunctionshouldbequotedinunitsof22

m s

−

.

ThesearetheunitsinwhichtheGSWToolbox(appendixN)outputstheMontgomery

geostrophicstreamfunctioninthefunctiongsw_geo_strf_Montgomery.



3.29Cunninghamgeostrophicstreamfunction



Cunningham(2000)andAldersonandKillworth(2005),followingSaunders(1995)and

Killworth(1986),suggestedthatasuitablestreamfunctiononadensitysurfaceina

compressibleoceanwouldbethedifferencebetweentheBernoullifunction

and

potentialenthalpy0.hSincethekineticenergyperunitmass,0.5 ⋅uu,isatiny

componentoftheBernoullifunction,itwasignoredandCunningham(2000)essentially

proposedthestreamfunction0

Π+Φ (seehisequation(12)),where

()

AA A

(,,) (,,0) (),(), .

hS p hS vS p p p dP

Π≡ − − ⋅−Φ

=− +Φ−Φ

′

′′ ′

=Θ−Θ− Θ

∫

(3.29.1)

Thelastlineofthisequationhasusedthehydrostaticequationz

=− toexpress

zΦ≈ intermsoftheverticalpressureintegralofspecificvolumeandtheheightofthe

seasurfacewherethegeopotentialis0.



Thedefinitionofpotentialenthalpy,Eqn.(3.2.1),isusedtorewritethelastlineofEqn.

(3.29.1),showingthatCunningham’s

isalsoequalto

()()

ˆˆ

(), (), ,, .

PvS p p p vS p dP

′

′′ ′ ′

Π=− Θ − Θ

∫(3.29.2)

Inthisformitappearsverysimilartotheexpression,Eqn.(3.27.1),fordynamicheight

anomaly,theonlydifferencebeingthatinEqn.(3.27.1)thepressure‐independentvalues

ofAbsoluteSalinityandConservativeTemperaturewereSO

Sand0C°whereasherethey

arethelocalvaluesonthesurface,A

Sand

.WhiletheselocalvaluesofAbsolute

SalinityandConservativeTemperatureareconstantduringthepressureintegralinEqn.

(3.29.2),theydovarywithlatitudeandlongitudealongany“density”surface.

Thegradientof

alongtheneutraltangentplaneis

{

}

()

0b0

nz n

PTPP

ρρ

−Θ

∇

Π≈ ∇ −∇Φ − − ∇Θ(3.29.3)

(fromMcDougallandKlocker(2010))sothattheerrorinn

∇

ΠinusingΠasthe

geostrophicstreamfunctionisapproximately

()

1b0

TPP

−Θ

−

−∇Θ

.Whenusingthe

CunninghamstreamfunctionΠinapotentialdensitysurface,theerrorin

∇Πis

approximately

()

(

)

1b0r0

22TPP PPP

−Θ

−−−−∇Θ

.TheCunninghamgeostrophic

streamfunctionshouldbequotedinunitsof22

m s

−

andisavailableintheGSW

OceanographicToolbox(appendixN)asthefunctiongsw_geo_strf_Cunningham.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

3.30Geostrophicstreamfunctioninanapproximatelyneutralsurface



Inordertoevaluatearelativelyaccurateexpressionforthegeostrophicstreamfunctionin

anapproximatelyneutralsurface(suchasan

‐surfaceofKlockeretal.(2009a,b)ora

NeutralDensitysurfaceofJackettandMcDougall(1997))asuitablereferenceseawater

parcel

()

A,,SpΘ







isselectedfromtheapproximatelyneutralsurfacethatoneisconsidering,

andthespecificvolumeanomaly



isdefinedasin(3.7.3)above.Theapproximate

geostrophicstreamfunctionisgivenby(fromMcDougallandKlocker(2010))

()

(

)

(

)

AAb

212

,, ,, .

Sp PPSp T PP dP

ϕδρ δ

−Θ ′

Θ= − Θ− Θ−Θ−−

∫











(3.30.1)

Thisexpressionisveryaccuratewhenthevariationofconservativetemperaturewith

pressurealongtheapproximatelyneutralsurfaceiseitherlinearorquadratic.Thatis,in

thesesituations

(

)

n100

∇≈∇−∇Φ=−×−kvvtoaverygoodapproximation.In

Eqn.(3.30.1)1

−Θ

istakentobetheconstantvalue15 1 2 2 2

2.7 10 K (Pa) m sx

−

−−−

.This

McDougall‐KlockergeostrophicstreamfunctionisavailablefromtheGSWOceanographic

Toolboxasthefunctiongsw_geo_strf_McD_Klocker.



3.31Pressure‐integratedstericheight



Thedepth‐integratedmassfluxofthegeostrophicEulerianflowbetweentwofixed

pressurelevelscanalsoberepresentedbyastreamfunction.Usingthehydrostatic

relation,

=− andassumingthegravitationalaccelerationtobeindependentof

height,thedepth‐integratedmassfluxdz

∫visgivenby1

−

−∫vandthismotivates

takingthepressureintegraloftheDynamicHeightAnomaly

(fromEqn.(3.27.1))to

formthePressure‐Integrated‐Steric‐Height

ISH (alsocalledDepth‐IntegratedSteric

Height

ISH byGodfrey(1989)),

()

[][]

()

[][]

()

000

=,,

,, .

PPP

ISH g p dP g S p t p p dP dP

g PP SptppdP

′′

−−

−

′′′′′ ′′′′′′

Ψ= Ψ =−

′′′′′

=− −

∫∫∫

∫

(3.31.1)

Thetwo‐dimensionalgradientof

′

isrelatedtothedepth‐integratedmassfluxofthe

velocitydifferencewithrespecttothevelocityatzeroseapressure,0,vaccordingto

()

zP P

pzP P

zdzgfpdP

−

′′′′′

⎡⎤ ⎡ ⎤

×∇ Ψ = − = −

⎣⎦ ⎣ ⎦

∫∫

kvvvv(3.31.2)

Thedefinition,Eqn.(3.31.1),of

ISH appliestoallchoicesofthereferencevaluesAA

,SS







and,t





orΘ



inthedefinitions,Eqns.(3.7.2–3.7.4),ofthespecificvolumeanomaly.

Sincethevelocityatdepthintheoceanisgenerallymuchsmallerthanatthesea

surface,itiscustomarytotakethereferencepressuretobesomeconstant(deep)pressure

sothatEqn.(3.27.1)becomes

[][]

()

A,,

PSptppdP

′

′′ ′

Ψ= ∫(3.31.3)

and

ISH ,reflectingthedepth‐integratedhorizontalmasstransportfromtheseasurface

topressure1

,relativetotheflowat1

,is

46 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

()

[][]

()

[][]

()

[][]

()

111

1A0

=,,

,, .

PPP

ISH g p dP g S p t p p dP dP

gPPSptppdP

gSptppdPP

−−

′′

−

′

′′ ′′ ′ ′ ′ ′ ′′

Ψ= Ψ =

′′′′′

=−

′′′ ′

=−

∫∫∫

∫

(3.31.4)

Thetwo‐dimensionalgradientof

′

isnowrelatedtothedepth‐integratedmassfluxof

thevelocitydifferencewithrespecttothevelocityat 1

,1,vaccordingto

()

zP P

pzP P

zdzgfpdP

−

′

′′ ′ ′

⎡⎤ ⎡ ⎤

×∇ Ψ = − = −

⎣⎦ ⎣ ⎦

∫∫

kvvvv(3.31.5)

Thespecificvolumeanomaly

inEqns.(3.31.1),(3.31.3)and(3.31.4)canbereplacedwith

specificvolumevwithoutaffectingtheisobaricgradientoftheresultingstreamfunction.

Thatis,thissubstitutionin′

ΨdoesnotaffectEqn.(3.31.2)orEqn.(3.31.5),asthe

additionaltermisafunctiononlyofpressure.Withspecificvolumeinplaceofspecific

volumeanomaly,Eqn.(3.31.4)becomesthedepth‐integratedgravitationalpotential

energyofthewatercolumn(plusaverysmalltermthatispresentbecausethe

atmosphericpressureisnotzero,McDougalletal.(2003)).

ISH shouldbequotedinunitsof2

kg s

−

sothatitstwo‐dimensionalgradienthasthe

sameunitsasthedepth‐integratedfluxof

(

)

′

⎡

⎤

−

⎣

⎦

vvtimestheCoriolisfrequency.



3.32Pressuretoheightconversion



Whenverticallyintegratingthehydrostaticequationz

−inthecontextofanocean

modelwhereAbsoluteSalinityA

SandConservativeTemperatureΘ(orpotential

temperature

)arepiecewiseconstantinthevertical,thegeopotential(Eqn.(3.24.2))

()

Pvp dP

′

Φ=Φ−∫(3.32.1)

canbeevaluatedasaseriesofexactdifferences.Ifthereareaseriesoflayersofindexi

separatedbypressuresi

pand1i

(with1ii

+>)thentheintegralcanbeexpressed

(makinguseof(3.7.5),namelyA,

hhv

=)asasumovernlayersofthedifferences

inspecificenthalpysothat

()

()()

001

ˆˆ

,, ,, .

Pniii iii

Pvp dP hS p hS p

−+

⎡

⎤

′′

Φ=Φ− =Φ− Θ − Θ

⎣

⎦

∑

∫(3.32.2)



3.33Freezingtemperature



Freezingoccursatthetemperaturef

tatwhichthechemicalpotentialofwaterinseawater

equalsthechemicalpotentialoficeIh

.Thus,f

tisfoundbysolvingtheimplicit

equation

()

(

)

WIh

Af f

,, ,Stp tp

μμ

=(3.33.1)

orequivalently,intermsofthetwoGibbsfunctions,

()

(

)

(

)

Af A Af f

,, ,, , .

Stp S Stp g tp−=(3.33.2)

TheGibbsfunctionforiceIh,

(

)

Ih ,,

tp isdefinedbyIAPWS‐06(IAPWS(2009a))and

FeistelandWagner(2006)andissummarizedinappendixIbelow.Inthespecialcaseof

zerosalinity,thechemicalpotentialofwaterinseawaterreducestotheGibbsfunctionof

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

purewater,

() ()

0, , , .tp g tp

=Asimplecorrelationfunctionforthemeltingpressure

asafunctionoftemperatureisavailablefromIAPWS(2008b)andhasbeenimplemented

intheSIAlibrary.

Attheoceansurface,p=0dbar,fromEqn.(3.33.1)theTEOS‐10freezingpointofpure

wateris

()

f0gkg , 0dbart−=0.002519°Cwithanuncertaintyofonly2μK,notingthatthe

triplepointtemperatureofwaterisexactly273.16KbydefinitionoftheITS‐90

temperaturescale.Thefreezingtemperatureofthestandardoceanis

()

fSO

,0dbartS =

‐1.919°Cwithanuncertaintyof2mK.NotethatEqn.(3.33.1)isvalidforair‐free

water/seawater.Dissolutionofairinwaterlowersthefreezingpointslightly;saturation

withairlowersthefreezingtemperaturesbyabout2mK .

Toestimatetheeffectsofsmallchangesinthepressureorsalinityonthefreezing

temperature,itisconvenienttoconsiderapowerseriesexpansionof(3.33.1).Theresultin

thelimitofaninfinitesimalpressurechangeatfixedsalinitygivesthepressurecoefficient

offreezingpointlowering,as(Clausius‐Clapeyronequation,Feisteletal.(2010a)),

()

AIh

pSpp

pTSTT

Sg g

tSp

Sg g

−−

∂==−

∂−−

(3.33.3)

Itsvalues,evaluatedfromTEOS‐10,varyonlyweaklywithsalinitybetween

()

0gkg , 0dbar

−=–0.7429mK/dbar forpurewaterand

(

)

SO ,0dbar

=–0.7483

mK/dbar forthestandardocean.TEOS‐10isconsistentwiththemostaccurate

measurementofp

anditsexperimentaluncertaintyof0.0015mK/dbar (Feisteland

Wagner(2005),(2006)).Sincethevalueofp

alwaysexceedsthatoftheadiabaticlapse

rateΓ,coldseawatermayfreezeanddecomposeintoiceandbrineduringadiabatic

upliftbutthiscanneverhappentoasinkingparcel.

InthelimitofinfinitesimalchangesinAbsoluteSalinityatfixedpressure,weobtain

thesalinecoefficientoffreezingpointlowering,as(Raoult’slaw),

()

AIh

STSTT

tSp

SgSg g

∂==

∂−−

(3.33.4)

Typicalnumericalvaluesare

()

0gkg , 0dbar

−=–59.21

mK/(g kg )

−

forpurewaterand

()

SO ,0dbar

=–56.91

mK/(g kg )

−forseawater.

Asarawpracticalestimate,Eqn.(3.33.4)canbeexpandedintopowersofsalinity,

usingonlytheleadingtermoftheTEOS‐10salineGibbsfunction,S

SA A

RTS S≈,which

stemsfromPlanck’sideal‐solutiontheory(Planck(1888)).Here,SS

RRM

=264.7599

Jkg–1K–1isthespecificgasconstantofseasalt,Ristheuniversalmolargasconstant,and

=31.40382gmol–1isthemolarmassofseasaltwithReferenceComposition.The

denominatorofEqn.(3.33.4)isproportionaltothemeltingheatSI

L,Eqn.(3.34.7).The

convenientresultobtainedwiththesesimplificationsis

()

59 mK/(g kg )

tTt

−

∂≈− + ≈−

∂.(3.33.5)

wherewehaveusedf2Ct=− andSI

= 3301

Jkg

−

asapproximationsthatareappropriate

forthestandardocean.Thissimpleresultisonlyweaklydependentonthesechoicesand

isinreasonableagreementwiththeexactvaluesfromEqn.(3.33.4)andwithMilleroand

Leung(1976).Thefreezingtemperatureofseawaterisalwayslowerthanthatofpure

water.

Whensea‐iceisformed,itoftencontainsremnantsofseawaterincludedinbrine

pockets.Atequilibrium,thesalinityinthesepocketsdependsonlyontemperatureand

pressure,ratherthan,forexample,onthepocketvolume,andcanbecomputedinthe

functionalform

(

)

A,StpasanimplicitsolutionofEqn.(3.33.1).Measuredvaluesforthe

brinesalinityofAntarcticseaiceagreeverywellwiththosecomputedofEqn.(3.33.1)up

48 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

tothesaturationconcentrationofabout1101

gkg

−

atsurfacepressure(Feisteletal.

(2010b)).Athighpressures,thevalidityoftheGibbsfunctionofseawater,andtherefore

ofthecomputedfreezingpointorbrinesalinity,too,islimitedtoonly501

gkg

−.

Wenotethatinthefirstapproximation,asinferredfromPlanck’stheoryofideal

solutions,theabovepropertiesdependonthenumberofdissolvedparticlesregardlessof

theparticlesizes,massesorcharges.Inotherwords,theydependmainlyonthemolar

ratherthanonthemassdensityofthesolute,incontrasttopropertiessuchasthedensity

ofseawaterandpropertiesderivedfromit.Thepropertiesconsideredintheremainderof

thissection(3.33‐3.42)whichsharethisattributearereferredtoasthecolligative

propertiesofseawater.



3.34Latentheatofmelting



Themeltingprocessoficeinpurewatercanbeconductedbysupplyingheatatconstant

pressure.Ifthisisdoneslowlyenoughthatequilibriumismaintained,thenthe

temperaturewillalsoremainconstant.Theheatrequiredpermassofmolteniceisthe

latentheat,orenthalpy,ofmelting,WI

L.Itisfoundasthedifferencebetweenthespecific

enthalpyofwater,W,handthespecificenthalpyofice,Ih ,h(Kirchhoff’slaw,Curryand

Webster(1999)):

()

(

)

(

)

WI W Ih

,,.

phtphtp=− (3.34.1)

Here,

()

tpisthefreezingtemperatureofwater,section3.33.TheenthalpiesW

handIh

h

areavailablefromIAPWS‐95(IAPWS(2009b))andIAPWS‐06(IAPWS(2009a)),

respectively.

Inthecaseofseawater,themeltwaterwilladditionallymixwiththeambientbrine,

thuschangingthesalinityandthefreezingtemperatureoftheseawater.Consequently,

theenthalpyrelatedtothisphasetransitionwilldependontheparticularconditions

underwhichthemeltingoccurs.

Here,wedefinethelatentheatofmeltingastheenthalpyincreaseperinfinitesimal

massofmolteniceofacompositesystemconsistingoficeandseawater,whenthe

temperatureisincreasedatconstantpressureandatconstanttotalmassesofwaterand

salt,inexcesstotheheatneededtowarmuptheseawaterandicephasesindividually

(FeistelandHagen(1998),Feisteletal.(2010b)).Massconservationofbothwaterandsalt

duringthisthermodynamicprocessisessentialtoensuretheindependenceofthelatent

heatformulafromtheunknownabsoluteenthalpiesofsaltandwaterthatotherwise

wouldaccompanyanymassexchange.

Theenthalpyofseaice,SI ,hisadditivewithrespecttoitsconstituentsice,Ih ,hwith

themassfractionIh ,wandseawater,,hwiththeliquidmassfraction

(

)

1:w−

()

(

)

(

)

SI Ih Ih Ih

1,, ,h w hS tp wh tp=− + .(3.34.2)

Uponwarming,themassofmeltwaterchangestheicefractionIh

wandthebrinesalinity

A.STherelatedtemperaturederivativeofEqn.(3.34.2)is

() () ()

SI Ih Ih

Ih Ih Ih Ih

Sp p

ppp

hh hShw

ww whh

TT STT T

∂∂ ∂∂∂∂

=− +− + + −

∂∂ ∂∂∂ ∂

.(3.34.3)

TherateofbrinesalinitychangewithtemperatureisgivenbythereciprocalofEqn.

(3.33.4)andisrelatedtotheisobaricmeltingrate,Ih /p

−

∂∂,bytheconservationofthe

totalsalt,

()

1wS−=const,intheform

SSw

∂∂

−.(3.34.4)

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Usingthisrelation,Eqn.(3.34.3)takesthesimplifiedform

()

SI Ih

Ih Ih Ih SI

1ppp

wc wc L

∂∂

=− + −

∂∂

.(3.34.5)

Thecoefficientinfrontofthemeltingrate,

()

SI Ih

LSp hS h

∂

=− −

∂,(3.34.6)

providesthedesiredexpressionforisobaricmeltingenthalpy,namelythedifference

betweenthepartialspecificenthalpiesofwaterinseawaterandofice.Asisphysically

requiredforanymeasurablethermodynamicquantity,thearbitraryabsoluteenthalpiesof

ice,waterandsaltcancelintheformula(3.34.6),providedthatthereferencestate

conditionsfortheiceandseawaterformulationsarechosenconsistently(Feisteletal.

(2008a)).Notethatbecauseof

(

)

hg Tt

=+ + andEqn.(3.33.2),thelatentheatcanalso

bewrittenintermsofentropies

ratherthanenthalpies,hintheform

()( )

SI Ih

A0fA

LSp T t S S

ηη

⎛⎞

∂

⎜⎟

=+×− −

⎜⎟

∂

⎝⎠

.(3.34.7)

Againtheresultisindependentofunknown(andunknowable)constants.

Thelatentheatofmeltingdependsonlyweaklyonsalinityandonpressure.Atthe

surfacepressure,thecomputedvalueis

(

)

(

)

SI WI

0,0 0

LL==333426.5Jkg–1forpurewater,

and

()

SO ,0

LS =329928.5Jkg–1forthestandardocean,withadifferenceofabout1%due

tothedissolvedsalt.Atapressureof1000dbar,thesevaluesreduceby0.6%to

()()

SI WI

0,1000dbar 1000dbar

LL==331528Jkg–1and

(

)

SO ,1000dbar

LS =328034Jkg–1.

TEOS‐10isconsistentwiththemostaccuratemeasurementsofWI

Landtheirexperimental

uncertaintiesof200Jkg–1,or0.06%(FeistelandWagner(2005),(2006)).



3.35Sublimationpressure



Thesublimationpressureoficesubl

isdefinedastheabsolutepressure

ofwater

vapourinequilibriumwithiceatagiventemperaturet,atorbelowthefreezing

temperature.ItisfoundbyequatingthechemicalpotentialofwatervapourV

withthe

chemicalpotentialoficeIh ,

soitisfoundbysolvingtheimplicitequation

()

(

)

Vsubl Ihsubl

,,,tP tP

μμ

=(3.35.1)

orequivalently,intermsofthetwoGibbsfunctions,

()

(

)

Vsubl Ihsubl

,,.gtP gtP=(3.35.2)

TheGibbsfunctionforiceIh,

(

)

Ih ,

tP isdefinedbyIAPWS‐06andFeistelandWagner

(2006)andissummarizedinappendixIbelow.Notethatheretheabsolutepressure



ratherthantheseapressurepisusedbecausethesublimationpressureoficeatambient

conditionsismuchlowerthantheatmosphericpressure.

TheGibbsfunctionofvapour,

(

)

tP ,isavailablefromtheHelmholtzfunctionof

fluidwater,asdefinedbyIAPWS‐95;fordetailsseeforexampleFeisteletal.(2008a),

(2010a),(2010b).Thehighestpossiblesublimationpressureisfoundatthetriplepointof

water.TheTEOS‐10valueofthemaximumsublimationpressure(i.e.,thetriplepoint

pressure)computedfromEqn.(3.35.1)issubl

=611.655Paandhasanuncertaintyof

0.01Pa(IAPWS‐06,Feisteletal.(2008a)).

Reliabletheoreticalvaluesforthesublimationpressureareavailabledownto20K

(FeistelandWagner(2007));asimplecorrelationfunctionforthesublimationpressure

downto50KisprovidedbyIAPWS(2008b)andisincludedasafunctionintheSIA

50 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

library.TheIAPWS‐95functionV

requiredforEqn.(3.35.1)isonlyvalidabove130K.

Anextensionto50KwasdevelopedforTEOS‐10(Feisteletal.(2010a))andisavailableas

thedefaultoptionintheSIAlibrary.Innature,vapourcannotreasonablybeexpectedto

existbelow50Ksinceithasextremelylowdensity,evenintheinterstellarvacuum.For

thisreason,theiceofcometsdoesnotevaporatefarfromthesun.Thelowest

temperaturesestimatedfortheterrestrialpolaratmospheredonotgobelow130K.

Inthepresenceofair,iceisunderhighertotalpressurethanjustitsownsublimation

pressure.Thepartialpressureofvapourinhumidair,vap

xP=,iscomputedfromthe

totalabsolutepressure

andthemolefractionofvapour,V.

Similartotheabsolute

salinityA

Sofseawater,thevariable

describesthemassfractionofdryairpresentin

humidair.Given,

themolefractionofvapouriscomputedfrom

()

11 /

xAMM

−

=−− ,(3.35.3)

whereA

isthemolarmassofdryairandW

isthemolarmassofwater.

Thesublimationpressure,

(

)

subl sat

tP x P=,oficeinequilibriumwithhumidairisthe

partialpressureofvapourinsaturatedair.Tocomputesat

fromEqn.(3.35.3),the

requiredairfractionatsaturation,

(

)

sat ,,

AtP=isfoundbyequatingthechemical

potentialofwatervapourinhumidairAV

withthechemicalpotentialoficeIh ,

sothat

itisfoundbysolvingtheimplicitequation

()

AV sat Ih

W,, , ,

tP tP

μμ

=(3.35.4)

orequivalently,intermsofthetwoGibbsfunctions,

()

(

)

()

AV sat sat AV sat Ih

,, ,, ,

AtPAg AtPgtP−=.(3.35.5)

TheGibbsfunctionofhumidair,

()

AV ,,

AtP ,isdefinedbyFeisteletal.(2010a).

Att=0°Candatmosphericpressure,thesublimationpressureoficehasthevalue

subl

(0°C,101325Pa)=613.745Pa,computedbysolvingEqn.(3.35.4)forsat ,

thenusing

(3.35.3)todeterminethecorrespondingmolefractionandmultiplyingtheatmospheric

pressurebythisquantity.Similarly,atthefreezingpointofthestandardoceanthe

sublimationpressureissubl

(‐1.919°C,101325Pa)=523.436Pa.

Thedifferencebetweenobservedormodelledpartialvapourpressuresandthe

sublimationpressurecomputedfromTEOS‐10isanappropriatequantityforusein

parameterizationsofthemassfluxbetweeniceandtheatmosphere.



3.36Sublimationenthalpy



Thesublimationprocessthatoccurswheniceisincontactwithpurewatervapourcanbe

conductedbysupplyingheatatconstanttandP,withtatorbelowthefreezing

temperature.Theheatrequiredpermassevaporatedfromtheiceisthelatentheat,or

enthalpy,ofsublimation,VI

L.Itisfoundasthedifferencebetweenthespecificenthalpy

ofwatervapour,V,handthespecificenthalpyofice,Ih :h

()

(

)

(

)

VI V subl Ih subl

,,.

Lt htP htP=− (3.36.1)

Here,

()

subl

tisthesublimationpressureoficeatthetemperature,tsection3.35.The

enthalpiesV

handIh

hareavailablefromIAPWS‐95andIAPWS‐06,respectively.Reliable

valuesforthesublimationenthalpyaretheoreticallyavailabledownto20Kfromasimple

correlationfunction(FeistelandWagner(2007)).Atthetriplepointofwater,theTEOS‐10

sublimationenthalpyis

()

VI 0.01 C

L°=2834359Jkg–1withanuncertaintyof1000Jkg–1,or

0.03%.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Inthecasewhenairispresent,thevapourresultingfromthesublimationwilladdto

thegasphase,thusincreasingthemolefractionofvapoursat

.Ifforexamplethetotal

pressure

isheldconstant,thepartialpressuresat

Pwillrise,andtheicemustget

warmertomaintainequilibriumatthemodifiedsublimationpressuresubl sat

xP=

Consequently,theenthalpyrelatedtothisphasetransitionwilldependontheparticular

conditionsunderwhichthesublimationprocessoccurs.Theseeffectsaresmallunder

ambientconditionsbutmayberelevantathigherairdensities.

Here,wedefinethelatentheatofsublimationastheenthalpyincreaseper

infinitesimalmassofsublimatediceofacompositesystemconsistingoficeandhumidair,

whenthetemperatureisincreasedatconstantpressureandatconstanttotalmassesof

wateranddryair,inexcessoftheenthalpyincreaseneededtowarmuptheiceandhumid

airphasesindividually(Feisteletal.(2010a)).Massconservationofbothtotalwaterand

dryairduringthisthermodynamicprocessisessentialtoensuretheindependenceofthe

latentheatformulafromtheunknownabsoluteenthalpiesofairandwaterthatotherwise

wouldaccompanyanymassexchange.

Theenthalpyoficeair,AI ,hisadditivewithrespecttoitsconstituentsice,Ih ,hwith

themassfractionIh ,wandhumidair,AV ,hwiththegasfraction

(

)

1:w−

()

(

)

(

)

AI Ih AV Ih Ih

1,, ,h w h Atp wh tp=− + .(3.36.2)

Uponwarming,themassofvapourproducedbysublimationreducestheicefractionIh

w

andincreasesthehumidity,thatis,decreasestherelativedry‐airfraction

ofthegas

phase.TherelatedtemperaturederivativeofEqn.(3.36.2)is

() () ()

AI AV AV Ih Ih

Ih Ih Ih Ih AV

pApTpp p

hh hAh w

ww whh

TT ATT T

∂∂ ∂∂∂ ∂

=− +− + + −

∂∂ ∂∂∂ ∂

.(3.36.3)

Theair‐fractionchangeisrelatedtotheisobaricsublimationrate,Ih /p

−

∂∂,bythe

conservationofthedryair,

()

1wA−=const,intheform

AAw

∂∂

−.(3.36.4)

Usingthisrelation,Eqn.(3.36.3)takesthesimpleform

()

AI Ih

Ih AV Ih Ih AI

ppp

wc wc L

∂∂

=− + −

∂∂

(3.36.5)

Thecoefficientinfrontofthesublimationrate,

()

AI AV Ih

LAp h A h

∂

=− −

∂,(3.36.6)

providesthedesiredexpressionforisobaricsublimationenthalpy,namelythedifference

betweenthepartialspecificenthalpiesofvapourinhumidairandofice.Intheideal‐gas

approximationsforairandforvapour,thepartialspecificenthalpyofvapourinhumid

air,AV AV

hAh−,equalsthespecificenthalpyofvapour,

(

)

ht,asafunctionofonlythe

temperature,independentofthepressureandofthepresenceofair(Feisteletal.(2010a)).

Inthiscase,Eqn.(3.36.6)coincidesformallywithEqn.(3.36.1),exceptthatthetwoare

evaluatedatthedifferentpressures

andsubl ,Prespectively.Asisphysicallyrequired

foranymeasurablethermodynamicquantity,thearbitraryabsoluteenthalpiesofice,

vapourandaircancelintheformula(3.36.6),providedthatthereferencestateconditions

fortheiceandhumidairformulationsarechosenconsistently(Feisteletal.(2008a),

(2010a)).Thelatentheatofsublimationdependsonlyweaklyontheairfractionandon

thepressure.

52 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Forsaturatedairoverseaice,theairfractionsat

A=canbecomputedfromthebrine

salinity,orfromtheseasurfacesalinityinthecaseoffloatingice,section3.38.Atthe

absolutesurfacepressureSO

=101325Paandthefreezingpointf

t=‐1.919°Cofthe

standardocean,theTEOS‐10valueforsaturatedairwith

(

)

sat

SO f SO

AtP==0.99678is

()

SO SO

LAP=2833006Jkg–1.Therelatedsublimationpressureis

()

subl

fSO

tP =523.436

Pa,seesection3.35.

Observationaldatashowthattheambientairovertheoceansurfaceissub‐saturated

intheclimatologicalmean.Ratherthanbeingsaturated,valuesforAthatcorrespondtoa

relativehumidityof75%–82%(seesection3.40)maybeamorerealisticestimateforthe

marineatmosphere(Dai(2006));thesevaluesrepresentnon‐equilibriumconditionsthat

resultinnetevaporationaspartoftheglobalhydrologicalcycle.



3.37Vapourpressure



Thevapourpressureofseawater

(

)

vap

Stisdefinedastheabsolutepressure

of

watervapourinequilibriumwithseawateratagiventemperaturetandsalinityA.SItis

foundbyequatingthechemicalpotentialofvapourV

withthechemicalpotentialof

waterinseawater W

sothatitisfoundbysolvingtheimplicitequation

(

)

(

)

V vap W vap

,,,tP S tP

μμ

=,(3.37.1)

orequivalently,intermsofthetwoGibbsfunctions,

()

(

)

(

)

V vap vap vap

AAA

,,, ,,

gtP gStP Sg StP=− .(3.37.2)

Notethathereweusetheabsolutepressure

ratherthantheseapressurep;sincethe

vapourpressureofwateratambientconditionsismuchlowerthantheatmospheric

pressure,thecorrespondingseapressure(Pvap–101325Pa)wouldbenegativeandnear

‐105Pa.TheGibbsfunctionsofvapourandseawater,

(

)

tP andA

(,,),

StPare

availablefromtheHelmholtzfunctionoffluidwater,asdefinedbyIAPWS‐95,andthe

Gibbsfunctionofseawater,IAPWS‐08orIAPWS‐09(IAPWS(2009c)).

Inthecaseofpurewater,A0,S

thesolutionofEqn.(3.37.1)istheso‐called

saturationcurveinthetP−diagramofwater,whichconnectsthetriplepointwiththe

criticalpoint.Thelowestpossiblevapourpressureofpureliquidwaterisfoundatthe

triplepointofwater.TheTEOS‐10valueofthisminimumvapourpressure,computed

fromEqn.(3.37.1),isvap

(0,0.01°C)=t

=611.655Pawithanuncertaintyof0.01Pa

(IAPWS‐95,Feisteletal.(2008a)).Forcomparison,thevapourpressureofthestandard

oceanisvap

(SO ,S0°C)=599.907Pa.Atlaboratorytemperaturetherelatedvaluesare

vap

(0,25°C)=3169.93Paandvap

(SO ,S25°C)=3110.57Pa.

Therelativelysmallvapourpressureloweringcausedbythepresenceofdissolvedsalt

canbecomputedfromtheisothermalsalinityderivativeofEqn.(3.37.1)intheform

(Raoult’slaw)

vap A

SP P

Sg g

∂=

∂−−

.(3.37.3)

Asarawpracticalestimate,thisequationcanbeexpandedintopowersofsalinity,using

onlytheleadingtermoftheTEOS‐10salineGibbsfunction,S

SA A

RTS S≈,whichstems

fromPlanck’sideal‐solutiontheory.Here,SS

RRM

=264.7599Jkg–1K–1isthespecific

gasconstantofseasalt,Ristheuniversalmolargasconstant,andS

=31.40382gmol–1

isthemolarmassofseasaltwithReferenceComposition.Thespecificvolumeof

seawater,,

isneglectedincomparisontothatofvapour.Thelatterisapproximately

consideredasanidealgas,

(

)

Vvap

gRTMP≈,whereW

=18.015268gmol–1isthe

molarmassofwater.Theconvenientresultobtainedwiththesesimplificationsis

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

vap

vap vap

0.57

∂≈− ≈− ×

∂.(3.37.4)

Thevapourpressureofseawaterisalwayslowerthanthatofpurewater.

Inthepresenceofair,seawaterisunderahigherpressure

thanunderitsvapour

pressurevap .PInthiscase,thevapourpressureofseawater

(

)

vap

A,,

StPisdefinedasthe

partialpressureofwatervapourinhumidairthatisinequilibriumwithseawaterata

givenpressure,

temperaturetandsalinityA.SItisfoundbyequatingthechemical

potentialofvapourinhumidairV

withthechemicalpotentialofwaterinseawater

sothatitisfoundbysolvingtheimplicitequation

()

Vcond W

AV A

,, ,,

tP S tP

μμ

=(3.37.5)

for

()

cond

A,,

StP,orequivalently,intermsofthetwoGibbsfunctions,

()

(

)

() ()

AV cond cond AV cond

AAA

,, ,, ,, ,,

A tP A g A tP gS tP S g S tP−=−.(3.37.6)

Sincethevapourpressureisloweredinthepresenceofseasalt(Eqn.(3.37.4)),atvapour

pressuresabovethecondensationpointvapourcondensesoutoftheairattheseasurface,

evenbeforethesaturationpoint(thatis,relativehumidityof100%)isreached,tomaintain

localequilibriumwiththeseawater.Thelargerscaleequilibrationprocessmayinvolve

downwarddiffusionofwatervapourtotheseasurfaceratherthanprecipitationofdewor

fog.Fromthecalculatedsub‐saturatedairfractionofthecondensationpoint,cond

,the

molefractionofvapourcond

(3.53.2),andinturnthevapourpressure

()

vap cond

StP x P=areavailablefromstraightforwardcalculations.TheGibbsfunction

ofhumidairAV

isavailablefromFeisteletal.(2010a)andisalsoplannedtobemade

availableasthedocumentIAPWS(2010).

TheTEOS‐10valuecomputedfromEqn.(3.37.5)isvap

(0,0°C,PSO)=613.760Pafor

purewateratsurfaceairpressure;thevapourpressureofthestandardoceanis

vap

(SO ,S0°C,SO

)=602.403Pa.Atlaboratorytemperaturetherelatedvaluesare

vap

(0,25°C,SO

)=3183.73Paandvap

(SO ,S25°C,SO

)=3124.03Pa.



3.38Boilingtemperature



Theboilingtemperatureofwaterorseawaterisdefinedasthetemperature

()

boil

A,tSPat

whichthevapourpressure(ofsection3.37)equalsagivenpressure.

Itisfoundby

equatingthechemicalpotentialofvapourV

withthechemicalpotentialofwaterin

seawater W

sothatitisfoundbysolvingtheimplicitequation

()

(

)

Vboil W boil

,,,,tP StP

μμ

=(3.38.1)

forboil

(,)tSP,orequivalentlyintermsofthetwoGibbsfunctions,

(

)( )

(

)

V boil boil boil

AAA

,,, ,,.

tP gStPSgStP=− (3.38.2)

TheTEOS‐10boilingtemperatureofpurewateratatmosphericpressureis

()

boil

0,tP=

99.974°C.Thistemperatureisoutsidethevalidityrangeofupto80°CoftheTEOS‐10

Gibbsfunctionforseawater.



3.39Latentheatofevaporation



Theevaporationprocessofpureliquidwaterincontactwithpurewatervapourcanbe

conductedbysupplyingheatatconstanttand.

Theheatrequiredpermassevaporated

fromtheliquidisthelatentheat,orenthalpy,ofevaporation,VW

L.Itisfoundasthe

54 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

differencebetweenthespecificenthalpyofwatervapour,V,handthespecificenthalpyof

liquidwater,W:h

()

(

)

(

)

VW V vap W vap

Lt htP htP=−.(3.39.1)

Here,vap ()

tisthevapourpressureofwateratthetemperaturet(section3.37).The

enthalpiesV

handW

hareavailablefromIAPWS‐95.Atthetriplepointofwater,the

TEOS‐10evaporationenthalpyis

(

)

VW 0.01 C

L°=2500915Jkg–1.

Inthecaseofseawaterincontactwithair,thevapourresultingfromtheevaporation

willaddtothegasphase,thusincreasingthemolefractionofvapour,whiletheliquid

waterlosswillincreasethebrinesalinity,andcauseachangetotheseawaterenthalpy.

Consequently,theenthalpyrelatedtothisphasetransitionwilldependontheparticular

conditionsunderwhichtheevaporationprocessoccurs.

Here,wedefinethelatentheatofevaporationastheenthalpyincreaseper

infinitesimalmassofevaporatedwaterofacompositesystemconsistingofseawaterand

humidair,whenthetemperatureisincreasedatconstantpressureandatconstanttotal

massesofwater,saltanddryair,inexcessoftheenthalpyincreaseneededtowarmupthe

seawaterandhumidairphasesindividually(Feisteletal.(2010a)).Massconservation

duringthisthermodynamicprocessisessentialtoensuretheindependenceofthelatent

heatformulafromtheunknownabsoluteenthalpiesofair,saltandwaterthatotherwise

wouldaccompanyanymassexchange.

Theenthalpyofseaair,SA ,hisadditivewithrespecttoitsconstituents,seawater,,h

withthemassfractionSW ,wandhumidair,AV ,hwiththegasfraction

(

)

1:w−

()

(

)

(

)

SA SW AV SW

1,, ,,hwhAtpwhStp=− + .(3.39.2)

Uponwarming,themassofwatertransferredfromtheliquidtothegasphaseby

evaporationreducestheseawatermassfractionSW ,wincreasesthebrinesalinityA

Sand

increasesthehumidity,withacorrespondingdecreaseinthedry‐airfraction

ofthegas

phase.TherelatedtemperaturederivativeofEqn.(3.39.2)is

() ()

()

SA AV AV

SW SW

SW SW AV

pApTp

Sp p

Tp p

hh hA

TT AT

hhS w

ww hh

TST T

∂∂ ∂∂

=− +−

∂∂ ∂∂

∂∂∂ ∂

++ +−

∂∂∂ ∂

(3.39.3)

TheisobaricevaporationrateSW /p

wT−∂ ∂ isrelatedtotheair‐fractionchangebythe

conservationofthedryair,

()

1wA−=const,intheform

AAw

∂∂

−,(3.39.4)

andtothechangeofsalinitybytheconservationofthesalt,SW

wS=const,intheform

SW .

SSw

∂∂

=−

∂∂

(3.39.5)

Usingtheserelations,Eqn.(3.39.3)takesthesimplifiedform

()

SA SW

SW AV SW SA

1ppp

wc wcL

∂∂

=− + −

∂∂

.(3.39.6)

Thecoefficientinfrontoftheevaporationrate,

()

SA AV

,,, ,

LAStp h A hS

∂∂

=− −+

∂∂

(3.39.7)

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

providesthedesiredexpressionforisobaricevaporationenthalpy,namelythedifference

betweenthepartialspecificenthalpiesofvapourinhumidair(thefirsttwoterms)andof

waterinseawater(thelasttwoterms).Intheideal‐gasapproximationsforairandfor

vapour,thepartialspecificenthalpyofvapourinhumidair,AV AV

hAh−,equalsthe

specificenthalpyofvapour,

()

ht,asafunctionofonlythetemperature,independentof

thepressureandofthepresenceofair(Feisteletal.(2010a)).Asisphysicallyrequiredfor

anymeasurablethermodynamicquantity,thearbitraryabsoluteenthalpiesofwater,salt

andaircancelintheformula(3.39.7),providedthatthereferencestateconditionsforboth

theseawaterandthehumid‐airformulationarechosenconsistently(Feisteletal.(2008a),

(2010a)).Thelatentheatofevaporationdependsonlyweaklyonsalinityandonair

fraction,andisanalmostlinearfunctionofthetemperatureandofthepressure.

Selectedrepresentativevaluesfortheairfractionatcondensation,cond ,Aandthelatent

heatofevaporation,SA

,aregiveninTable3.39.1.



Table3.39.1:Selectedvaluesfortheequilibriumairfraction,cond ,Acomputed

fromEqn.(3.37.6),andthelatentheatofevaporation,SA

,

computedfromEqn.(3.39.7),fordifferentsea‐surfaceconditions.

NotethattheTEOS‐10formulationforhumid‐airisvalidupto5

MPa,i.e.,almost500dbarseapressure.



ConditionA

S

gkg–1

t

°C

p

dbar

cond



%



Jkg–1

Purewater00 0 99.62231 2499032

Brackishwater100 0 99.62427 2499009

Standardocean35.16504 0 0 99.62931 2498510

Tropicalocean35.16504 25 098.05933 2438971

Highpressure35.16504 0400 99.98943 2443759



InthederivationofEqn.(3.39.7),thevalueof

isindirectlyassumedtobecomputed

fromtheequilibriumcondition(3.37.6)betweenhumidairandseawater,

=cond .AAt

thishumiditytheairisstillsub‐saturated,cond sat ,

A>butitsvapourstartscondensingat

theseasurface.Thevaluesofcond

andsat

coincideonlybelowthefreezingpointof

seawater,oratvanishingsalinity,seealsothefollowingsection3.40.

Theevaporationrate,SW /p

wT−∂ ∂ ,canbecomputedfromEqn.(3.37.6),the

equilibriumconditionbetweenhumidairandseawater,atchangingtemperatureand

constantpressure(Feisteletal.(2010a)).Incontrast,thederivationofSA

LusingEqns.

(3.39.2)‐(3.39.7)isamereconsiderationofmassandenthalpybalances;noequilibrium

conditionisactuallyinvolved.Hence,itisphysicallyevidentthatEqn.(3.39.7)canalsobe

appliedtosituationsinwhich

takesanygivenvaluedifferentfromcond ,Athatis,itcan

beappliedregardlessofwhetherornotthehumidairisactuallyatequilibriumwiththe

seasurface.



3.40Relativehumidityandfugacity



Parameterisedformulasforthefluxofwaterandheatthroughtheoceansurfaceare

usuallyexpressedintermsofagivenrelativehumidityoftheairincontactwithseawater.

Inthissectionweprovidetheformulasfortherelativehumidityandthefugacityfromthe

TEOS‐10potentialfunctionsforseawaterandhumidair,andweexplainwhytherelative

fugacitywithrespecttocondensationratherthanwithrespecttosaturationshouldbe

usedforoceanographicfluxestimates(Feisteletal.(2010a)).Nearthesaturationpoint,the

56 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

twofluxformulasmayevenexhibitdifferentsigns(differentfluxdirections)since

condensationoccursattheseasurfaceatsub‐saturatedvaluesofrelativehumidity.

Relativehumidityisnotuniquelydefinedintheliterature,butthecommondefinitions

givethesameresultsintheideal‐gaslimitofhumidair.Alsointhisapproximation,

relativehumidityisonlyapropertyoffluidwateratgiventemperatureandpressureof

thevapourphase,independentofthepresenceofair.

TheCCT1definitionofrelativehumidityisintermsofmolefraction:“Atgiven

pressureandtemperature,[therelativehumidityisdefinedas]theratio,expressedasa

percent,ofthemolefractionofwatervapourtothevapourmolefractionwhichthemoist

gaswouldhaveifitweresaturatedwithrespecttoeitherwateroriceatthesamepressure

andtemperature.”ConsistentwithCCT,IUPAC2definesrelativehumidity“astheratio,

oftenexpressedasapercentage,ofthepartialpressureofwaterintheatmosphereatsome

observedtemperature,tothesaturationvapourpressureofpurewateratthis

temperature”(Calvert(1990),IUPAC(1997)).Thisdefinitionoftherelativehumidity

takestheform

CCT sat

=(3.40.1)

withregardtothemolefractionofvapour

(

)

AEqn.(3.35.3),andthesaturatedair

fraction

() ( )

sat cond

,0,,

AtP A tP== eitherfromEqn.(3.37.6)withrespecttoliquidwater,

attabovethefreezingpointofpurewater,orfromEqn.(3.35.5)withrespecttoice,att

belowthefreezingpointofpurewater.Here,

(

)

cond

A,,

StPistheairfractionofhumid

airatequilibriumwithseawater,Eqn.(3.37.5),whichissubsaturatedforA0.S>

TheWMO3definitionoftherelativehumidityis(PruppacherandKlett(1997),

Jacobson(2005)),

WMO sat sat

1/ 1

RH rA

−

(3.40.2)

where

()

1/rAA=− isthehumidityratio.Ifrissmall,wecanestimateVAW

rM M≈

(fromEqn.(3.35.3))andthereforeWMO CCT

RH RH

≈

,thatis,wefindapproximate

consistencybetweenEqns.(3.40.1)and(3.40.2).

Sometimes,especiallywhenconsideringphaseorchemicalequilibria,itismore

convenienttousethefugacity(oractivity)ratherthanpartialpressureratio(IUPAC

(1997)).Thefugacityofvapourinhumidairisdefinedas

()

VV, id

,, exp .fATP xP RT

μμ

⎧

⎫

−

⎪

⎨

⎬

⎪

⎩⎭

(3.40.3)

Here,WW

RRM=isthespecificgasconstantofwater,

(

)

VAVAV

TP g Ag

=− isthe

chemicalpotentialofvapourinhumidair,and

(

)

V, id ,,

isitsideal‐gaslimitwhichis

equaltothetruechemicalpotentialinthelimitofverylowpressure,

() ()

V, id V V,id V

,, 1 'd' ln

AT P g c T T R T

⎛⎞

=+ − +

⎜⎟

⎝⎠

∫.(3.40.4)

ThevaluesofV

,V

andV

TofV,id

mustbechosenconsistentlywiththeadjustable

constantsofAV

(Feisteletal.(2010a)).Theideal‐gasheatcapacityofvapour

()

V, id

cTis

availablefromIAPWS‐95.Intheideal‐gaslimitofinfinitedilution,V

convergestothe

partialpressureofvapour(Glasstone(1947)),

(

)

vap

lim , , .

PfATP xP P

→==(3.40.5)

1CCT:ConsultativeCommitteeforThermometry,www.bipm.org/en/committees/cc/cct/

2IUPAC:InternationalUnionofPureandAppliedChemistry,www.iupac.org

3WMO:WorldMeteorologicalOrganisation,www.wmo.int

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Thesaturationfugacityisdefinedbytheequilibriumbetweenliquidwater(orice)and

vapourinair,

()()

,, 0,,

TP TP

μμ

=,thatis,

()

(

)

WV,idsat

sat sat

0, , , ,

exp ,

TP A TP

fxP RT

μμ

⎧

⎫

−

⎪

⎨

⎬

⎪

⎩⎭

(3.40.6)

where

()

W0, ,

=isthechemicalpotentialofliquidwater(orthechemicalpotential

ofice,Ih

).Therelativefugacity

ofhumidairisthendefined,dividingEqn.(3.40.3)by

Eqn.(3.40.6)andmakinguseofEqn.(3.40.4),as

()()

sat

,, 0,,

exp .

AT P T P

μμ

⎧

⎫

−

⎪

⎨

⎬

⎪

⎩⎭

(3.40.7)

Intheideal‐gaslimit, VV, id

μμ

=andusing(3.40.3)weseethattherelativefugacity



coincideswiththerelativehumidity,Eqn.(3.40.1).

TakingEqn.(3.40.7)atthecondensationpoint,cond ,AA=Eqn.(3.37.5),itfollowsthat

therelativefugacityofhumidairatequilibriumwithseawater(“seaair”forshort)is

()()

SA V

sat

,, 0,,

exp .

STP TP

μμ

⎧

⎫

−

⎪

⎨

⎬

⎪

⎩⎭

(3.40.8)

Thechemicalpotentialdifferenceintheexponentisproportionaltotheosmoticcoefficient

ofseawater,,

whichiscomputedfromthesalinepartoftheGibbsfunctionas(Feistel

andMarion(2007),Feistel(2008)),

()

SW A ,

,, ,

STP g S

mRT S

⎡

⎤

∂

⎢

⎥

=− − ∂

⎢

⎥

⎣

⎦

(3.40.9)

whereSW

misthemolalityofseawater(Milleroetal.(2008a)),

()

mSM

=−(3.40.10)

Fromthechemicalpotentialofwaterinseawater,A

gSg=− ,andEqns.(3.40.8)‐

(3.40.10)weinferfortherelativefugacityofseaairthesimpleformula

(

)

SW W

exp ,mM

=− (3.40.11)

whichisidenticaltotheactivityW

aofwaterinseawater.Similartotheidealgas

approximation,therelativefugacityofseaairisindependentofthepresenceorthe

propertiesofair.InEqn.(3.40.11),therelativefugacitySA 1

≤

expressesthefactthatthe

vapourpressureofseawaterislowerthanthatofpurewater,i.e.,thathumidairin

equilibriumwithseawateraboveitsfreezingtemperatureisalwayssub‐saturated.

Asarawpracticalestimate,usingaseriesexpansionofEqns.(3.40.10)and(3.40.11)

withrespecttosalinity,wecanobtainfromthemolality2

SW A S A

/()mSMOS=+andthe

osmoticcoefficient

()

1OS

=+ thelinearrelation

SA W

≈− (3.40.12)

i.e.,Raoult’slawforthevapour‐pressureloweringofseawater,Eqn.(3.37.4).

Belowthefreezingtemperatureofpurewateratagivenpressure,thesaturationof

vapourisdefinedbythechemicalpotentialoficeratherthanliquidwater,i.e.by

()

(

)

Ih V,id sat

sat sat

,,,

exp ,

TP A TP

fxP RT

μμ

⎧⎫

−

⎪⎪

=⎨⎬

⎪⎪

⎩⎭

(3.40.13)

ratherthanEqn.(3.40.6).Then,therelativefugacityofseaairis

58 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

()()

WIh

SA V

sat

,, ,

exp .

STP TP

μμ

⎧

⎫

−

⎪

⎨

⎬

⎪

⎩⎭

(3.40.14)

Whenthetemperatureisloweredfurthertothefreezingpointofseawater,theexponentof

(3.40.14)vanishesandseaairissaturated,SA 1,

forsea‐iceairatanylowertemperature.

Thermodynamicfluxesinnon‐equilibriumstatesaredrivenbyOnsagerforcessuchas

thegradientof/T

(DeGrootandMazur(1984)).Attheseasurface,assumingthesame

temperatureandpressureonbothsidesofthesea‐airinterface,thedimensionlessOnsager

force

()

SA A

,,,XASTPdrivingthetransferofwateristhedifferencebetweenthechemical

potentialsofwaterinhumidairandinseawater,

(

)

(

)

AV A

WW W

,, ,, .

TP S TP

XRT RT RT

μμ

⎛⎞

=Δ = −

⎜⎟

⎝⎠ (3.40.15)

Thisdifferencevanishesatthecondensationpoint,

(

)

cond

A,, ,

ASTP=Eqn.(3.37.5),

ratherthanatsaturation. SA

Xcanalsobeexpressedintermsoffugacities,Eqns.(3.40.7),

(3.40.8)and(3.40.11),intheform

(

)

() ()

SA SW W

ln ln .

XmMA

ϕφϕ

==+(3.40.16)

Ratherthantherelativehumidity,Eqns.(3.40.1),(3.40.2),thesea‐airOnsagerforceSA ,Xin

conjunctionwiththeformula(3.39.7),isrelevantfortheparameterizationofnon‐

equilibriumlatentheatfluxesacrosstheseasurface.Inthespecialcaseoflimnological

applications,orbelowthefreezingpointofseawater,itreducesto

()

SA lnXA

=,which

correspondstotherelativehumidity,

(

)

CCT

ln RH ,intheideal‐gasapproximation.All

propertiesrequiredforthecalculationoftheformula(3.40.16)areavailablefromthe

TEOS‐10thermodynamicpotentialsforseawater,ice,andhumidair.



3.41Osmoticpressure



Ifpurewaterisseparatedfromseawaterbyasemi‐permeablemembranewhichallows

watermoleculestopassbutnotsaltparticles,waterwillpenetrateintotheseawater,thus

dilutingitandpossiblyincreasingitspressure,untilthechemicalpotentialofwaterin

bothboxesbecomesthesame(orthepurewaterreservoirisexhausted).Intheusual

modelconfiguration,thetwosamplesarethermallycoupledbutmaypossessdifferent

pressures;theresultingpressuredifferencerequiredtomaintainequilibriumisthe

osmoticpressureofseawater.Anexampleofapracticalapplicationisdesalinationby

reverseosmosis;ifthepressureonseawaterinavesselexceedsitsosmoticpressure,

freshwatercanbe“squeezed”outofsolutionthroughsuitablemembranewalls

(Sherwoodetal.(1967)).Theosmoticpressureofseawaterisveryimportantformarine

organisms;itisconsideredresponsibleforthesmallnumberofspeciesthatcansurvivein

brackishenvironments.

Thedefiningconditionfortheosmoticequilibriumisequalityofthechemical

potentialsofpurewateratthepressureW

pandofwaterinseawateratthepressure,p

()

,,, .

gtp gStp SS

∂

=−

∂(3.41.1)

Thesolutionofthisimplicitrelationfortheosmoticpressureis

(

)

osm W

A,, .

Stp P P=− (3.41.2)

TheTEOS‐10valuefortheosmoticpressureofthestandardoceanis

()

osm

SO ,0 C,0dbarPS°=

2354684Pa,computedfromEqn.(3.41.1).



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

3.42Temperatureofmaximumdensity



Atabout4°Candatmosphericpressure,purewaterhasadensitymaximumbelowwhich

thethermalexpansioncoefficientandtheadiabaticlapseratechangetheirsigns(Röntgen

(1892),McDougallandFeistel(2003)).Atsalinitieshigherthan23.8gkg–1thetemperature

ofmaximumdensityMD

tisbelowthefreezingpointf

t(Table3.42.1).Theseasonaland

spatialinterplaybetweendensitymaximumandfreezingpointishighlyimportantforthe

stratificationstabilityandtheseasonaldeepconvectionforbrackishestuarieswith

permanentverticalandlateralsalinitygradientssuchastheBalticSea(Feisteletal.

(2008b),LeppärantaandMyrberg(2009),Reissmannetal.(2009)).

ThetemperatureofmaximumdensityMD

tiscomputedfromtheconditionof

vanishingthermalexpansioncoefficient,thatis,fromthesolutionoftheimplicitequation

forMD A

(,)tSp,

(

)

AMD

,, 0.

gSt p

(3.42.1)

ThetemperatureofmaximumdensityisavailableintheGSWOceanographicToolboxas

functiongsw_temps_maxdensity.Thisfunctionalsoreturnsthepotentialtemperature

andtheConservativeTemperatureatthismaximumdensitypoint.SelectedTEOS‐10

valuescomputedfromEqn.(3.42.1)aregiveninTable3.42.1.



Table3.42.1:Freezingtemperaturef

tandtemperatureofmaximumdensityMD

t

forair‐freebrackishseawaterwithabsolutesalinitiesA

Sbetween0

and1

25 g kg−,computedatthesurfacepressurefromTEOS‐10.

ValuesofMD

tinparenthesesarelessthanthefreezingtemperature.



g kg–1

°C

t

°C

g kg–1

°C

t

°C

g kg–1

°C

t

°C

0 +0.003 3.978 8.5 –0.456 2.128 17 –0.912 0.250

0.5 –0.026 3.868 9 –0.483 2.019 17.5 –0.939 0.139

1 –0.054 3.758 9.5 –0.509 1.909 18 –0.966 0.027

1.5 –0.081 3.649 10 –0.536 1.800 18.5 –0.994 –0.085

2 –0.108 3.541 10.5 –0.563 1.690 19 –1.021 –0.196

2.5 –0.135 3.432 11 –0.590 1.580 19.5 –1.048 –0.308

3 –0.162 3.324 11.5 –0.616 1.470 20 –1.075 –0.420

3.5 –0.189 3.215 12 –0.643 1.360 20.5 –1.102 –0.532

4 –0.216 3.107 12.5 –0.670 1.249 21 –1.130 –0.644

4.5 –0.243 2.999 13 –0.697 1.139 21.5 –1.157 –0.756

5 –0.269 2.890 13.5 –0.724 1.028 22 –1.184 –0.868

5.5 –0.296 2.782 14 –0.750 0.917 22.5 –1.212 –0.980

6 –0.323 2.673 14.5 –0.777 0.807 23 –1.239 –1.092

6.5 –0.349 2.564 15 –0.804 0.696 23.5 –1.267 –1.204

7 –0.376 2.456 15.5 –0.831 0.584 24 –1.294 (–1.316)

7.5 –0.403 2.347 16 –0.858 0.473 24.5 –1.322 (–1.428)

8 –0.429 2.238 16.5 –0.885 0.362 25 –1.349 (–1.540)



60 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

4.Conclusions



TheInternationalThermodynamicEquationofSeawater–2010(TEOS‐10)allowsallthe

thermodynamicpropertiesofpurewater,iceIh,seawaterandmoistairtobeevaluatedin

aninternallyself‐consistentmanner.IceIhisthenaturallyabundantformofice,having

hexagonalcrystals.Forthefirsttimetheeffectsofthesmallvariationsinseawater

compositionaroundtheworldoceancanbeincluded,especiallytheireffectsonthedensity

ofseawater(whichcanbeequivalenttotentimestheprecisionofourPracticalSalinity

measurementsatsea).

PerhapsthemostapparentchangecomparedtotheInternationalEquationofStateof

seawater(EOS‐80)istheadoptionofAbsoluteSalinityA

SinsteadofPracticalSalinityP

S

(PSS‐78)asthesalinityargumentforthethermodynamicpropertiesofseawater.

Importantly,PracticalSalinityisretainedasthesalinityvariablethatisstoredindata

basesbecausePracticalSalinityisvirtuallythemeasuredvariable(whereasAbsolute

Salinityisacalculatedvariable)andalsosothatnationaldatabasesdonotbecome

corruptedwithincorrectlylabeledandstoredsalinitydata.

TheadoptionofAbsoluteSalinityastheargumentforallthealgorithmsusedto

evaluatethethermodynamicpropertiesofseawatermakessensesimplybecausethe

thermodynamicpropertiesofseawaterdependonA

SratherthanonP

S;seawaterparcels

thathavethesamevaluesoftemperature,pressureandofP

Sdonothavethesame

densityunlesstheparcelsalsosharethesamevalueofA

S.AbsoluteSalinityismeasured

inSIunitsandthecalculationofthefreshwaterconcentrationandoffreshwaterfluxes

followsnaturallyfromAbsoluteSalinity,butnotfromPracticalSalinity.

AbsoluteSalinityiscalculatedinatwo‐stageprocess.FirstReferenceSalinityis

calculatedfrommeasurementsofPracticalSalinityusingEqn.(2.4.1).ThentheAbsolute

SalinityAnomalyisestimatedfromthecomputeralgorithmofMcDougalletal.(2010a)or

byothermeans,andAbsoluteSalinityisformedasthesumofReferenceSalinityandthe

AbsoluteSalinityAnomaly.Therearesubtleissuesindefiningwhatisexactlymeantby

“absolutesalinity”andatleastfourdifferentdefinitionsarepossiblewhencompositional

anomaliesarepresent.Wehavechosenthedefinitionthatyieldsthemostaccurate

estimatesofseawaterdensitysincetheoceancirculationissensitivetorathersmall

gradientsofdensity.ThealgorithmthatestimatesAbsoluteSalinityAnomalyrepresents

thestateoftheartasat2010,butthisareaofoceanographyisrelativelyimmature.Itis

likelythattheaccuracyofthisalgorithmwillimproveasmoreseawatersamplesfrom

aroundtheworldoceanhavetheirdensityaccuratelymeasured.Aftersuchfuturework

ispublishedandtheresultsdistilledintoarevisedalgorithmforAbsoluteSalinity

Anomaly,suchanalgorithmwillbeservedfromwww.TEOS‐10.org.Oceanographers

shouldpublishtheversionnumberofthissoftwarethatisusedtoobtainthermodynamic

propertiesintheirmanuscripts.

BecauseAbsoluteSalinityistheappropriatesalinityvariableforusewiththeequation

ofstate,AbsoluteSalinityisthesalinityvariablethatshouldbepublishedin

oceanographicjournals.Theversionnumberofthesoftwarethatisusedtoconvert

ReferenceSalinityR

SintoAbsoluteSalinityA

Sshouldalwaysbestatedinpublications.

Nevertheless,theremaybesomeapplicationswherethelikelyfuturechangesinthe

algorithmthatrelatesReferenceSalinitytoAbsoluteSalinitypresentsaconcern,andfor

theseapplicationsitmaybepreferabletopublishgraphsandtablesinReferenceSalinity.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Forthesestudiesorwhereitisclearthattheeffectofcompositionalvariationsare

insignificantornotofinterest,theGibbsfunctionmaybecalledwithR

SratherthanA

S,

thusavoidingtheneedtocalculatetheAbsoluteSalinityAnomaly.Whenthisisdone,it

shouldbeclearlystatedthatthesalinityvariablethatisbeinggraphedisReference

Salinity,notAbsoluteSalinity.

ThetreatmentofsalinityinoceanmodelsisdiscussedinappendixA.20.The

recommendedapproachistocarrybothPreformedSalinity*

SandAbsoluteSalinity

AnomalyA

asmodelvariablessothatDensitySalinitycanbecalculatedateachtime

stepofthemodelandusedtoaccuratelyevaluatedensity.

Potentialtemperaturehasbeenusedinoceanographyasthoughitisaconservative

variable,andyetthespecificheatofseawatervariesby5%attheseasurface,andpotential

temperatureisnotconservedwhenseawaterparcelsmix.TheFirstLawof

Thermodynamicscanbeveryaccuratelyregardedasthestatementthatpotentialenthalpy

isaconservativevariableintheocean.This,togetherwiththeknowledgethattheair‐sea

heatfluxisexactlytheair‐seafluxofpotentialenthalpy(i.e.theair‐seafluxof0

)

meansthatpotentialenthalpycanbetreatedasthe“heatcontent”ofseawaterandfluxes

ofpotentialenthalpyintheoceancanbetreatedas“heatfluxes”.Justasitisperfectly

validtotalkofthefluxofsalinityanomaly,A

(constant)S

−

,acrossanoceansectioneven

whenthemassfluxacrossthesectionisnon‐zero,soitisperfectlyvalidtotreatthefluxof

cΘacrossanoceansectionasthe“heatflux”acrossthesectionevenwhenthefluxesof

massandofsaltacrossthesectionarenon‐zero.

Thetemperaturevariableinoceanmodelsiscommonlyregardedasbeingpotential

temperature,butsincethenon‐conservativesourcetermsthatarepresentintheevolution

equationforpotentialtemperaturearenotincludedinmodels,itisapparentthatthe

interiorofoceanmodelsalreadytreattheprognostictemperaturevariableasConservative

Temperature.ΘTocompletethetransitionto

inoceanmodeling,modelsshouldbe

initializedwithΘratherthan

,theoutputtemperaturemustbecomparedtoobserved

Θdataratherthanto

data,andduringthemodelrun,anyair‐seafluxesthatdependon

thesea‐surfacetemperature(SST)mustbecalculatedateachmodeltimestepusing

()

ˆ,.

θθ

=ΘThefinalingredientneededforanoceanmodelisacomputationally

efficientformofdensityintermsofConservativeTemperature,thatis

()

ˆ,, ,

ρρ

=Θ

suchasthatdescribedinappendixA.30andappendixKofthisTEOS‐10Manual.

UnderEOS‐80theobservedvariables

(

)

P,,Stpwerefirstusedtocalculatepotential

temperature

andthenwatermasseswereanalyzedontheP

−

diagram.Curved

contoursofpotentialdensitycouldalsobedrawnonthissameP

−

diagram.Under

TEOS‐10,sincedensityandpotentialdensityarenownotfunctionsofPracticalSalinityP

S

butratherarefunctionsofAbsoluteSalinityA

S,itisnownotpossibletodrawisolinesof

potentialdensityonaP

−diagram.Rather,becauseofthespatialvariationsof

seawatercomposition,agivenvalueofpotentialdensitydefinesanareaontheP

−

diagram,notacurvedline.UnderTEOS‐10,theobservedvariables

(

)

P,,Stp,together

withlongitudeandlatitude,areusedtofirstformAbsoluteSalinityA

SandConservative

Temperature.ΘOceanographicwatermassesarethenanalyzedontheA

S−Θdiagram,

andpotentialdensitycontourscanalsobedrawnonthisA

−

Θdiagram,while

PreformedSalinity*

Sisthenaturalsalinityvariabletobeusedinapplicationssuchas

numericalmodellingwhereitisimportantthatthesalinityvariablebeconservative.

WhendescribingtheuseofTEOS‐10,itisthepresentdocument(theTEOS‐10Manual)

thatshouldbereferencedasIOCetal.(2010)[IOC,SCORandIAPSO,2010:The

internationalthermodynamicequationofseawater–2010:Calculationanduseofthermodynamic

properties.IntergovernmentalOceanographicCommission,ManualsandGuidesNo.56,

UNESCO(English),196pp]. 

62 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

APPENDIXA:

Backgroundandtheoryunderlying

theuseoftheGibbsfunctionofseawater



A.1 ITS-90 temperature

Inordertounderstandthelimitationsofconversionbetweendifferenttemperaturescales,

itishelpfultoreviewthedefinitionsoftemperatureandoftheinternationalscaleson

whichitisreported.



A.1.1Definition

Whenconsideringtemperature,thefundamentalphysicalquantityisthermodynamic

temperature,symbolT.Theunitfortemperatureisthekelvin.Thenameoftheunithasa

lowercasek.ThesymbolfortheunitisuppercaseK.Onekelvinis1/273.16ofthe

thermodynamictemperatureofthetriplepointofwater.(Arecentevolutionofthe

definitionhasbeentospecifytheisotopiccompositionofthewatertobeusedasthatof

ViennaStandardMeanOceanWater,VSMOW.)TheCelsiustemperature,symbol,tis

definedbyC K 273.15,tT°= − and1°Cisthesamesizeas1K.



A.1.2ITS‐90temperaturescale

ThedefinitionoftemperaturescalesistheresponsibilityoftheConsultativeCommittee

forThermometry(CCT)whichreportstotheInternationalCommitteeforWeightsand

Measures(oftenreferredtoasCIPMforitsnameintheFrenchlanguage).Overthelast40

years,twotemperaturescaleshavebeenused;theInternationalPracticalTemperature

Scale1968(IPTS‐68),followedbytheInternationalTemperatureScale1990(ITS‐90).These

aredefinedbyBarber(1969)andPreston‐Thomas(1990).Forinformationaboutthe

InternationalTemperatureScalesof1948and1927thereaderisreferredtoPreston‐

Thomas(1990).

Intheoceanographicrange,temperaturesaredeterminedusingaplatinumresistance

thermometer.Thetemperaturescalesaredefinedasfunctionsoftheratio,Wnamelythe

ratioofthethermometerresistanceatthetemperaturetobemeasured

()

Rttothe

resistanceatareferencetemperature0.RInIPTS‐68,0

Ris

(

)

0C,R°whileinITS‐900

Ris

()

0.01 C .R°Thedetailsofthesetemperaturescalesandthedifferencesbetweenthetwo

scalesarethereforedefinedbythefunctionsofWusedtocalculate.TForITS‐90,andin

therange0°C<90

t<968.71°C,90

tisdescribedbyapolynomialwith10coefficientsgiven

byTable4ofPreston‐Thomas(1990).

WenoteinpassingthattheconversionsfromWtoTandfromTtoWareboth

definedbypolynomialsandthesearenotperfectinversesofoneanother.Preston‐

Thomaspointsoutthattheinversesareequivalenttowithin0.13mK.Infacttheinverses

haveadifferenceof0.13mKat861°C,andamaximumerrorintherange0°C<90

t<40°C

of0.06mKat31°C.ThattheCCTallowedthisdiscrepancybetweenthetwopolynomials

immediatelyprovidesanindicationoftheabsoluteuncertaintyinthedetermination,and

indeedinthedefinition,oftemperature.

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

AseconduncertaintyintheabsoluterealizationofITS‐90arisesfromwhatisreferred

toassub‐rangeinconsistency.Thepolynomialreferredtoabovedescribesthebehaviour

ofan‘ideal’thermometer.Anypracticalthermometerhassmalldeviationsfromthisideal

behaviour.ITS‐90allowsthedeviationstobedeterminedbymeasuringtheresistanceof

thethermometeratuptofivefixedpoints:thetriplepointofwaterandthefreezingpoints

oftin,zinc,aluminiumandsilver,coveringtherange0.01°C<90

t<961.78°C.Ifnotallof

thesepointsaremeasured,thenitispermissibletoestimatethedeviationfromasmanyof

thosepointsasaremeasured.ThemeltingpointofGallium(90

t=29.7646°C)andthe

triplepointofMercury(90

t=‐38.8344°C)mayalsobeusedifthethermometeristo

operateoverasmallertemperaturerange.Hencethemannerinwhichthethermometer

maybeusedtointerpolatebetweenthepointsisnotunique.Ratheritdependsonwhich

fixedpointsaremeasured,andthereareseveralpossibleoutcomes,allequallyvalid

withinthedefinition.Sections3.3.2and3.3.3ofPreston‐Thomas(1990)giveprecise

detailsoftheformulationofthedeviationfunction.Thedifferencebetweenthedeviation

functionsderivedfromdifferentsetsoffixedpointswilldependonthethermometer,soit

notpossibletostateanupperboundonthisnon‐uniqueness.Commonpracticein

oceanographicstandardslaboratoriesistoestimatethedeviationfunctionfrom

measurementsatthetriplepointofwaterandthemeltingpointofGallium(90

t=29.7646

°C).Thisallowsalineardeviationfunctiontobedetermined,butnohigherorderterms.

Insummary,thereisnon‐uniquenessinthedefinitionofITS‐90,inadditiontoany

imperfectionsofmeasurementbyanypracticalthermometer(RudtschandFischer(2008),

Feisteletal.(2008a)).Itisthereforenotpossibletoseekauniqueandperfectconversion

betweenIPTS‐68andITS‐90.

GoldbergandWeir(1992)andMaresandKalova(2008)havediscussedthe

proceduresneededtoconvertmeasuredthermophysicalquantities(suchasspecificheat)

fromonetemperaturedefinitiontoanother.Whenmechanicalorelectricalenergyisused

inalaboratorytoheatacertainsample,thisenergycanbemeasuredinelectricalor

mechanicalunitsbyappropriateinstrumentssuchasanamperemeter,independentof

anydefinitionofatemperaturescale.Itisobviousfromthefundamentalthermodynamic

relation(atconstantAbsoluteSalinity),dd d,uT Pv

+thatthesameenergydifference

resultsindifferentvaluesfortheentropy,

dependingonthenumberreadforT

fromathermometercalibratedonthe1990comparedwithonecalibratedonthe1968

scale.Asimilardependenceisfoundfornumbersderivedfromentropy,forexample,for

theheatcapacity,

A,.

=

Douglas(1969)listedasystematicconsiderationofthequantitativerelationsbetweenthe

measuredvaluesofvariousthermalpropertiesandtheparticulartemperaturescaleused

inthelaboratoryatthetimethemeasurementwasconducted.Conversionformulasto

ITS‐90ofreadingsonobsoletescalesareprovidedbyGoldbergandWeir(1992)andWeir

andGoldberg(1996).

Anythermalexperimentaldatathatenteredtheconstructionofthethermodynamic

potentialsthatformTEOS‐10werecarefullyconvertedbytheserules,inadditiontothe

conversionbetweenthevariousolderdefinitionsofforexamplecaloriesandjoules.This

mustbeborneinmindwhenpropertiescomputedfromTEOS‐10arecombinedwith

historicalmeasurementsfromtheliterature.



64 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

A.1.3TheoreticalconversionbetweenIPTS‐68andITS‐90

HavingunderstoodthattheconversionbetweenIPTS‐68andITS‐90isnotuniquely

defined,wereviewthesourcesofuncertainty,orevenflexibility,intheconversion

between90

tand68.t

Considerfirstwhy90

tand68

ttemperaturesdiffer:

1)ThefixedpointshavenewtemperaturedefinitionsinITS‐90,duetoimprovementsin

determiningtheabsolutethermodynamictemperaturesofthemelting/freezingphysical

statesrelativetothetriplepointofwater.

2)ForsomegivenresistanceratioWthetwoscaleshavedifferentalgorithmsfor

interpolatingbetweenthefixedpoints.



Nowconsiderwhythereisnon‐uniquenessintheconversion:

3)InsomerangeofITS‐90,theconversionofWto90

tcanbeundertakenwithachoiceof

coefficientsthatismadebytheuser(Preston‐Thomas(1990)Sections3.3.2.1to3.3.3),

referredtoassub‐rangeinconsistency.

4)TheimpactoftheITS‐90deviationfunctionontheconversionisnon‐linear.Therefore

thesizeofthecoefficientsinthedeviationfunctionwillaffectthedifference,90 68.tt−

Theformalconversionisdifferentforeachactualthermometerthathasbeenusedto

acquiredata.

ThegroupresponsiblefordevelopingITS‐90waswellawareofthenon‐uniqueness

oftheconversion.Table6ofPreston‐Thomas(1990)givesdifferences

()

90 68

tt−witha

resolutionof1mK,because

(a)thetruethermodynamictemperatureTwasknowntohaveuncertaintiesoforder

1mKorlargerinsomeranges,

(b)thesub‐rangeinconsistencyofITS‐90usingthesamecalibrationdatagavean

uncertaintyofseveraltenthsof1mK.

Thereforetoattempttodefineagenericconversionof

(

)

90 68

tt−witharesolutionofsay

0.1mKwouldprobablybemeaninglessandpossiblymisleadingasthereisn’taunique

genericconversionfunction.



A.1.4PracticalconversionbetweenIPTS‐68andITS‐90

Rusby(1991)publishedan8thorderpolynomialthatwasafittoTable6ofPreston‐

Thomas(1990).Thisfitisvalidintherange73.15Kto903.89K(‐200°Cto630.74°C).He

reportsthatthepolynomialfitsthetabletowithin1mK,commensuratewiththenon‐

uniquenessofIPTS‐68.

Rusby’s8thorderpolynomialisineffectthe‘officialrecommended’conversion

betweenIPTS‐68andITS‐90.ThispolynomialhasbeenusedtoconverthistoricalIPTS‐68

datatoITS‐90forthepreparationofthenewthermodynamicpropertiesofseawaterthat

arethemainsubjectofthismanual.

Asaconvenientconversionvalidinanarrowertemperaturerange,Rusby(1991)also

proposed

(

)

(

)

90 68 68

/K = - 0.00025 / K - 273.15TT T−(A.1.1)

intherange260Kto400K(‐13°Cto127°C).Rusby(1991)alsoexplicitlyremindsreaders

(seehispage1158)thatcompoundquantitiesthatinvolvetemperatureintervalssuchas

heatcapacityandthermalconductivityareaffectedbytheirdependenceonthederivative

()

90 68 68

/.dT T dT−AboutthesametimethatRusbypublishedhisconversionfrom68

tto

90 ,tSaunders(1990)madearecommendationtooceanographersthatinthecommon

oceanographictemperaturerange‐2°C<68

t<40°C,conversioncouldbeachievedusing

()

(

)

90 68

/ C = / C 1.00024.tt°° (A.1.2)

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

ThedifferencebetweenSaunders(1990)andRusby(1991)arisesfromthebestslopebeing

1.00024near0°Cand1.00026near100°C(recallthat68

tfortheboilingpointofwaterwas

100°Cwhileits90

tis99.974°C).ThusRusby(1991)chose1.00025overthewiderrangeof

0°Cto100°C.

Inconsideringwhatisa‘reasonable’conversionbetweenthetwotemperaturescales,

wemustrecallthattheuncertaintyinconversionbetweenmeasuredresistanceandeither

temperaturescaleisoforderafewtenthsofmK,andtheuncertaintyintheabsolute

thermodynamictemperatureTisprobablyatleastaslarge,andmaybelargerthan1mK

insomepartsoftheoceanographicrange.Forallpracticalpurposesdataconvertedusing

Saunders’1.00024cannotbeimprovedupon;conversionsusingRusby’s(1991)8thorderfit

arefullyconsistentwithSaunders’1.00024intheoceanographictemperaturerangewithin

thelimitationsofthetemperaturescales.



A.1.5Recommendationregardingtemperatureconversion

TheITS‐90scalewasintroducedtocorrectdifferencesbetweentruethermodynamic

temperature,TandtemperaturesreportedinIPTS‐68.

Thereareremainingimperfectionsandresidualsin90

−

(Rusby,pers.comm.),

whichmaybeashighasacoupleofmKintheregionofinterest.Thisisbeing

investigatedbytheConsultativeCommitteeforThermometry(CCT).Atameetingin

2000(RusbyandWhite(2003))theCCTconsideredintroducinganewtemperaturescale

toincorporatetheknownimperfections,referredtoatthattimeasITS‐XX.Further

considerationbyCCTWG1hasmovedthinkingawayfromthedesirabilityofanewscale.

Thefieldofthermometryisundergoingrapidadvancesatpresent.Insteadofanew

temperaturescale,theknownlimitationsoftheITS‐90canbeaddressedinlargepart

throughtheITS‐90TechnicalAnnex,anddocumentationfromtimetotimeofanyknown

differencesbetweenthermodynamictemperatureandITS‐90(Rippleetal.(2008)).

ThetwomainconversionscurrentlyinuseareRusby’s8thorderfitvalidoverawide

rangeoftemperatures,andSaunders’1.00024scalingwidelyusedintheoceanographic

community.Theyareformallyindistinguishablebecausetheydifferbylessthanboththe

uncertaintyinthermodynamictemperature,andtheuncertaintyinthepractical

applicationoftheIPTS‐68andITS‐90scales.NeverthelesswenotethatRusby(1991)

suggestsalinearfitwithslope1.00025intherange‐13°Cto127°C,andthatSaunders’

slope1.00024isabetterfitintherange‐2°Cto40°CwhileRusby’s8thorderfitismore

robustfortemperaturesoutsidetheoceanographicrange.Thedifferencebetween

Saunders(1990)andRusby(1991)islessthan1mKeverywhereintherange‐2°Cto40°C

andlessthan0.03mKintherange‐2°Cto10°C.

Inconclusion,thealgorithmsforPSS‐78require68

tasthetemperatureargument.In

ordertousethesealgorithmswith90

tdata,68

tmaybecalculatedusingEqn.(A.1.3)thus

()

(

)

68 90

/ C = 1.00024 / C .tt°°(A.1.3)



66 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

A.2 Sea pressure, gauge pressure and absolute pressure

SeapressurepisdefinedtobetheAbsolutePressure

lesstheAbsolutePressureofone

standardatmosphere,0101 325Pa;P≡thatis

0.pPP

≡

−(A.2.1)

Also,itiscommonoceanographicpracticetoexpressseapressureindecibars(dbar).

Anothercommonpressurevariablethatarisesnaturallyinthecalibrationofsea‐board

instrumentsisgaugepressuregauge

pwhichisAbsolutePressurelesstheAbsolute

Pressureoftheatmosphereatthetimeoftheinstrument’scalibration(perhapsinthe

laboratory,orperhapsatsea).Becauseatmosphericpressurechangesinspaceandtime,

seapressurepispreferredasathermodynamicvariableasitisunambiguouslyrelatedto

AbsolutePressure.TheseawaterGibbsfunctionisnaturallyafunctionofseapressurep

(orfunctionallyequivalently,ofAbsolutePressure

);itisnotafunctionofgauge

pressure.



TableA.2.1Pressureunitconversiontable





Pascal

(Pa)



decibar

(dbar)



bar

(bar)



Technical

atmosphere

(at)



atmosphere

(atm)



torr

(Torr)

pound‐

forceper

square

inch

(psi)

1Pa≡1N/m210−410−510.197×10−69.8692×10−67.5006×10−3145.04×10−6

1dbar104≡105dyn/cm20.10.1019798.692×10−375.0061.45037744

1bar10000010≡106dyn/cm21.01970.98692750.0614.5037744

1at98066.59.806650.980665≡1kgf/cm20.967841735.5614.223

1atm10132510.13251.013251.0332≡1atm76014.696

1torr133.3221.3332×10−21.3332×10−31.3595×10−31.3158×10−3≡1Torr19.337×10−3

1psi6894.7570.6894868.948×10−370.307×10−368.046×10−351.715≡1lbf/in2



Example:1Pa=1N/m2=10−4dbar=10−5bar=10.197×10−6at=9.8692×10−6atm,etc.



Thedifferencebetweenseapressureandgaugepressureisquitesmallandprobably

insignificantformanyoceanographicapplications.Neverthelessitwouldbebestpractice

toensurethattheCTDpressurethatisusedintheseawaterGibbsfunctioniscalibrated

ondecktoreadtheatmosphericpressureasreadfromtheship’sbridgebarometer,less

theabsolutepressureofonestandardatmosphere,0101 325Pa.P

≡

(WhentheCTDis

loweredfromtheseasurface,themonitoringsoftwaremaywelldisplaygaugepressure,

indicatingthedistancefromthesurface.)

Sincethereareavarietyofdifferentunitsusedtoexpressatmosphericpressure,we

presentatable(TableA.2.1)toassistinconvertingbetweenthesedifferentunitsof

pressure(seeISO(1993)).Notethatonedecibar(1dbar)isexactly0.1bar,andthat1

mmHgisverysimilarto1torrwiththeactualrelationshipbeing1mmHg=1.000000142

466321...torr.Thetorrisdefinedasexactly1/760oftheAbsolutePressureofone

standardatmosphere,sothatonetorrisexactlyequalto(101325/760)Pa.



TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

A.3 Reference Composition and the Reference-Composition Salinity Scale

Asmentionedinthemaintext,theReferenceCompositionofseawaterisdefinedby

Milleroetal.(2008a)astheexactmolefractionsgiveninTableD.3ofappendixDbelow.

Thiscompositionmodelwasdeterminedfromthemostaccuratemeasurementsavailable

ofthepropertiesofStandardSeawater,whichisfilteredseawaterfromthesurfacewaters

oftheNorthAtlanticasmadeavailablebytheIAPSOStandardSeawaterService.The

ReferenceCompositionisperfectlyconsistentwithchargebalanceofoceanwatersandthe

mostrecentatomicweightestimates(Wieser(2006)).Forseawaterwiththisreference

compositiontheReference‐CompositionSalinityR

Sasdefinedbelowprovidesourbest

estimateoftheAbsoluteSalinity.

TheReferenceCompositionincludesallimportantcomponentsofseawaterhaving

massfractionsgreaterthanabout0.0011

gkg

−

(i.e.1.01

mg kg

−

)thatcansignificantly

affecteithertheconductivityorthedensityofseawaterhavingaPracticalSalinityof35.

ThemostsignificantionsnotincludedareLi

(~0.181

mg kg

−

)andRb+(~0.121

mg kg

−

).

Dissolvedgases2

N(~161

mg kg−)and2

O(upto81

mg kg

−

intheocean)arenotincluded

asneitherhaveasignificanteffectondensityoronconductivity.Inaddition,2

Nremains

withinafewpercentofsaturationatthemeasuredtemperatureinalmostalllaboratory

andinsituconditions.However,thedissolvedgas2

CO (~0.71

mg kg

−

),andtheionOH

−



(~0.081

mg kg−)areincludedintheReferenceCompositionbecauseoftheirimportantrole

intheequilibriumdynamicsofthecarbonatesystem.ChangesinpH whichinvolve

conversionof2

CO toandfromionicformsaffectconductivityanddensity.

Concentrationsofthemajornutrients4

Si(OH) ,3

−

and3

−

areassumedtobe

negligibleinStandardSeawater;theirconcentrationsintheoceanrangefrom0‐16

mg kg−,0‐21

mg kg

−

,and0‐0.21

mg kg

−

respectively.TheReferenceCompositiondoes

notincludeorganicmatter.ThecompositionofDissolvedOrganicMatter(DOM)is

complexandpoorlyknown.DOMistypicallypresentatconcentrationsof0.5‐21

mg kg

−



intheocean.

Reference‐CompositionSalinityisdefinedtobeconservativeduringmixingor

evaporationthatoccurswithoutremovalofseasaltfromsolution.Becauseofthis

property,theReference‐CompositionSalinityofanyseawatersamplecanbedefinedin

termsofproductsdeterminedfromthemixtureorseparationoftwopreciselydefinedend

members.PurewaterandKCl‐normalizedseawateraredefinedforthispurpose.Purewater

isdefinedasViennaStandardMeanOceanWater,VSMOW,whichisdescribedinthe

2001GuidelineoftheInternationalAssociationforthePropertiesofWaterandSteam

(IAPWS(2005),BIPM(2005));itistakenasthezeroreferencevalue.KCl‐normalized

seawater(ornormalizedseawaterforshort)isdefinedtocorrespondtoaseawatersample

withaPracticalSalinityof35.Thus,anyseawatersamplethathasthesameelectrical

conductivityasasolutionofpotassiumchloride(KCl)inpurewaterwiththeKClmass

fractionof32.4356gkg‐1whenbothareattheITS‐90temperaturet=14.996°Candone

standardatmospherepressure,

=101325Paisreferredtoasnormalizedseawater.

Here,KClreferstothenormalisotopicabundancesofpotassiumandchlorineasdescribed

bytheInternationalUnionofPureandAppliedChemistry(Wieser(2006)).Asdiscussed

below,anynormalizedseawatersamplehasaReference‐CompositionSalinityof

35.165041

gkg .

−

SinceReference‐CompositionSalinityisdefinedtobeconservativeduringmixing,ifa

seawatersampleofmass1

mandReference‐CompositionSalinityR1

Sismixedwith

anotherseawatersampleofmass2

mandReference‐CompositionSalinityR2,Sthefinal

Reference‐CompositionSalinityR12

Softhissampleis

1R1 2R2

R12

mS mS

Smm

=+.(A.3.1)

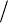
68 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Negativevaluesof1

mand2,mcorrespondingtotheremovalofseawaterwiththe

appropriatesalinityarepermitted,solongas

(

)

(

)

1R12R2

110mSmS

−

+−>.Inparticular,if

R2 0S=(purewater)and2

misthemassofpurewaterneededtonormalizetheseawater

sample(thatis,2

misthemassneededtoachieveR12

S=35.16504gkg−1),thentheoriginal

Reference‐CompositionSalinityofsample1isgivenby

-1

R1 2 1

[1 ( / )] 35.16504 g kgSmm=+ × .(A.3.2)

ThedefinitionsandproceduresaboveallowonetodeterminetheReferenceSalinityof

anyseawatersampleattheITS‐90temperaturet=14.996°Candonestandard

atmospherepressure.Tocompletethedefinition,wenotethattheReference‐Composition

SalinityofaseawatersampleatgiventemperatureandpressureisequaltotheReference‐

CompositionSalinityofthesamesampleatanyothertemperatureandpressureprovided

thetransitionprocessisconductedwithoutexchangeofmatter,inparticular,without

evaporation,precipitationordegassingofsubstancefromthesolution.Notethatthis

propertyissharedbyPracticalSalinitytotheaccuracyofthealgorithmsusedtodefine

thisquantityintermsoftheconductivityratio15.R

WenotedabovethataPracticalSalinityof35isassociatedwithaReferenceSalinityof

35.165041

gkg .

−ThisvaluewasdeterminedbyMilleroetal.(2008a)usingthereference

compositionmodel,themostrecentatomicweights(Wieser(2006))andtherelationS=

1.80655Cl /1

(g kg )

−whichwasusedintheoriginaldefinitionofPracticalSalinityto

convertbetweenmeasuredChlorinityvaluesandPracticalSalinity.Sincetherelation

betweenPracticalSalinityandconductivityratiowasdefinedusingthesameconservation

relationassatisfiedbyReferenceSalinity,theReferenceSalinitycanbedeterminedtothe

sameaccuracyasPracticalSalinitywhereverthelatterisdefined(thatis,intherange

242S<<),as

RPSP

SuS≈where 1

PS (35.165 04 35) g kgu

−

≡.(A.3.3)

Forpracticalpurposes,thisrelationshipcanbetakentobeanequalitysincethe

approximatenatureofthisrelationonlyreflectstheaccuracyofthealgorithmsusedinthe

definitionofPracticalSalinity.ThisfollowsfromthefactthatthePracticalSalinity,like

ReferenceSalinity,isintendedtobepreciselyconservativeduringmixingandalsoduring

changesintemperatureandpressurethatoccurwithoutexchangeofmasswiththe

surroundings.

TheReference‐CompositionSalinityScaleisdefinedsuchthataseawatersample

whosePracticalSalinityP

Sis35hasaReference‐CompositionSalinityR

Sofprecisely

35.165 04 g kg−.Milleroetal.(2008a)estimatethattheabsoluteuncertaintyassociated

withusingthisvalueasanestimateoftheAbsoluteSalinityofReferenceComposition

Seawateris1

0.007 g kg−

±.ThusthenumericaldifferencebetweentheReferenceSalinity

expressedin1

gkg

−andPracticalSalinityisabout24timeslargerthanthisestimateof

uncertainty.ThedifferenceisalsolargecomparedtoourabilitytomeasurePractical

Salinityatsea(whichcanbeaspreciseas0.002

).Understandinghowthisdiscrepancy

wasintroducedrequiresconsiderationofsomehistoricaldetailsthatinfluencedthe

definitionofPracticalSalinity.ThedetailsarepresentedinMilleroetal.(2008a)andin

Millero(2010)andarebrieflyreviewedbelow.

Therearetwoprimarysourcesoferrorthatcontributetothisdiscrepancy.First,and

mostsignificant,intheoriginalevaporationtechniqueusedbySørensenin1900(Forchet

al.1902)toestimatesalinity,somevolatilecomponentsofthedissolvedmaterialwerelost

sotheamountofdissolvedmaterialwasunderestimated.Second,theapproximate

relationdeterminedbyKnudsen(1901)todetermine

(

)

‰Sfrommeasurementsof

()

‰Cl 

wasbasedonanalysisofonlyninesamples(onefromtheRedSea,onefromtheNorth

Atlantic,onefromtheNorthSeaandsixfromtheBalticSea).Boththeerrorsinestimating

absoluteSalinitybyevaporationandthebiastowardsBalticSeaconditions,wherestrong

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

compositionanomaliesrelativetoNorthAtlanticconditionsarefound,arereflectedin

Knudsenʹsformula,

()

(

)

K‰0.031.805 ‰.SCl=+ (A.3.4)

WhenthePracticalSalinityScalewasdecideduponinthelate1970sitwasknownthat

thisrelationincludedsignificanterrors,butitwasdecidedtomaintainnumerical

consistencywiththisaccepteddefinitionofsalinityfortypicalmid‐oceanconditions

(Millero(2010)).Toachievethisconsistencywhilehavingsalinitydirectlyproportionalto

Chlorinity,theJointPanelforOceanographicTablesandStandards(JPOTS)decidedto

determinetheproportionalityconstantfromKnudsenʹsformulaatK

S=35‰(Cl =

19.3740‰),(Woosteretal.,1969).Thisresultedintheconversionformula

()

(

)

‰ 1.80655 ‰SCl=(A.3.5)

beingusedinthedefinitionofthepracticalsalinityscaleasifitwereanidentity,thus

introducingerrorsthathaveeitherbeenoverlookedoracceptedforthepast30years.We

nowbreakwiththistraditioninordertodefineasalinityscalebasedonacomposition

modelforStandardSeawaterthatwasdesignedtogiveamuchimprovedestimateofthe

mass‐fractionsalinityforStandardSeawaterandforReference‐CompositionSeawater.

Theintroductionofthissalinityscaleprovidesamorephysicallymeaningfulmeasureof

salinityandsimplifiesthetaskofsystematicallyincorporatingtheinfluenceofspatial

variationsofseawatercompositionintotheprocedureforestimatingAbsoluteSalinity.

Finally,wenotethattodefinetheReference‐CompositionSalinityScalewehave

introducedthequantityPS

uinEqn.(A.3.3),definedby1

PS (35.165 04 35) g kgu−

≡.This

valuewasdeterminedbytherequirementthattheReference‐CompositionSalinitygives

thebestestimateofthemass‐fractionAbsoluteSalinity(thatis,themass‐fractionofnon‐

H2Omaterial)ofReference‐CompositionSeawater.However,theuncertaintyinusingR

S

toestimatetheAbsoluteSalinityofReferenceCompositionSeawaterisatleast0.007

gkg

−atS=35(Milleroetal.(2008b)).Thus,althoughPS

uispreciselyspecifiedinthe

definitionoftheReference‐CompositionSalinityScale,itmustbenotedthatusingthe

resultingdefinitionoftheReferenceSalinitytoestimatetheAbsoluteSalinityofReference

CompositionSeawaterdoeshaveanon‐zerouncertaintyassociatedwithit.Thisand

relatedissuesarediscussedfurtherinthenextsubsection.



A.4 Absolute Salinity

Milleroetal.(2008a)listthefollowingsixadvantagesofadoptingReferenceSalinityR

S

andAbsoluteSalinityA

SinpreferencetoPracticalSalinity P.S



1. ThedefinitionofPracticalSalinityP

SonthePSS‐78scaleisseparatefromthe

systemofSIunits(BIPM(2006)).ReferenceSalinitycanbeexpressedintheunit

(g kg )

−asameasureofAbsoluteSalinity.AdoptingAbsoluteSalinityand

ReferenceSalinitywillterminatetheongoingcontroversiesintheoceanographic

literatureabouttheuseof“PSU”or“PSS”andmakeresearchpapersmore

readabletotheoutsidescientificcommunityandconsistentwithSI.

2. Thefreshwatermassfractionofseawaterisnot(1–0.001P

S).Rather,itis

(1–0.001A

S/( 1

gkg

−)),whereA

SistheAbsoluteSalinity,definedasthemass

fractionofdissolvedmaterialinseawater.ThevaluesofA

S/( 1

gkg

−)andP

Sare

knowntodifferbyabout0.5%.Thereseemstobenogoodreasonforcontinuing

toignorethisknowndifference,forexampleinoceanmodels.

3. PSS‐78islimitedtotherange2<P

S<42.Forasmoothcrossoverononesideto

purewater,andontheothersidetoconcentratedbrinesuptosaturation,asfor

70 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

exampleencounteredinseaiceatverylowtemperatures,salinitiesbeyondthese

limitsneedtobedefined.WhilethisposesachallengeforP,SitistrivialforR.S

4. ThetheoreticalDebye‐Hückellimitinglawsofseawaterbehavioratlowsalinities,

usedforexampleinthedeterminationoftheGibbsfunctionofseawater,canonly

becomputedfromachemicalcompositionmodel,whichisavailableforR

Sbut

notforP.S

5. ForartificialseawaterofReferenceComposition,R

Shasafixedrelationto

Chlorinity,independentofconductivity,salinity,temperature,orpressure.

6. StoichiometricanomaliescanbespecifiedaccuratelyrelativetoReference‐

CompositionSeawaterwithitsknowncomposition,butonlyuncertainlywith

respecttoIAPSOStandardSeawaterwithitsunknowncomposition.These

variationsinthecompositionofseawatercausesignificant(afewpercent)

variationsinthehorizontaldensitygradient.



Regardingpointnumber2,PracticalSalinityP

Sisadimensionlessnumberofthe

orderof35intheopenocean;nounitsortheirmultiplesarepermitted.Thereishowever

morefreedominchoosingtherepresentationofAbsoluteSalinityA

Ssinceitisdefinedas

themassfractionofdissolvedmaterialinseawater.Forexample,allthefollowing

quantitiesareequal(seeISO(1993)andBIPM(2006)),

34g/kg=34mg/g=0.034kg/kg=0.034=3.4%=34000ppm=34000mg/kg.

Inparticular,itisstrictlycorrecttowritethefreshwaterfractionofseawateraseither

(1–0.001A

S/( 1

gkg

−

))oras(1–A

S)butitwouldbeincorrecttowriteitas(1–0.001A

S).

ClearlyitisessentialtoconsidertheunitsusedforAbsoluteSalinityinanyparticular

application.Ifthisisdone,thereshouldbenodangerofconfusion,buttomaintainthe

numericalvalueofAbsoluteSalinityclosetothatofPracticalSalinityP

Sweadoptthefirst

optionabove,namely1

gkg

−asthepreferredunitforA,S(asinA

S=35.16504gkg−1).

TheReferenceSalinity,R,Sisdefinedtohavethesameunitsandfollowsthesame

conventionsasA.SSalinity“S‰”measuredpriortoPSS‐78availablefromtheliterature

orfromdatabasesisusuallyreportedin‰orppt(partperthousand)andisconvertedto

theReferenceSalinity,RPS

‰,SuS=bythenumericalfactorPS

ufrom(A.3.3).

Regardingpointnumber5,ChlorinityCl istheconcentrationvariablethatwasused

inthelaboratoryexperimentsforthefundamentaldeterminationsoftheequationofstate

andotherproperties,buthasseldombeenmeasuredinthefieldsincethedefinitionof

PSS‐78(Millero,2010).Sincetherelation1.806 55SCl

forStandardSeawaterwasused

inthedefinitionofPracticalSalinitythismaybetakenasanexactrelationforStandard

SeawateranditisalsoourbestestimateforReferenceCompositionSeawater.Thus,

Chlorinityexpressedin‰canbeconvertedtoReference‐CompositionSalinitybythe

relation, RCl

,SuCl=withthenumericalfactorCl PS

1.806 55 .uu

Theseconstantsare

recommendedfortheconversionofhistorical(pre1900)data.Theprimarysourceoferror

inusingthisrelationwillbethepossiblepresenceofcompositionanomaliesinthe

historicaldatarelativetoStandardSeawater.

Regardingpointnumber6,thecompositionofdissolvedmaterialinseawaterisnot

constantbutvariesalittlefromoneoceanbasintoanother,andthevariationiseven

strongerinestuaries,semi‐enclosedorevenenclosedseas.BrewerandBradshaw(1975)

andMillero(2000)pointoutthatthesespatialvariationsintherelativecompositionof

seawaterimpacttherelationshipbetweenPracticalSalinity(whichisessentiallyameasure

oftheconductivityofseawateratafixedtemperatureandpressure)anddensity.Allthe

thermophysicalpropertiesofseawateraswellasothermulticomponentelectrolyte

solutionsaredirectlyrelatedtotheconcentrationsofthemajorcomponents,notthe

salinitydeterminedbyconductivity;notethatsomeofthevariablenonelectrolytes(e.g.,

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

Si (OH) ,2

CO anddissolvedorganicmaterial)donothaveanappreciableconductivity

signal.ItisforthisreasonthatthenewTEOS‐10thermodynamicdescriptionofseawater

(Milleroetal.(2008a),Millero(2010))hastheGibbsfunction

ofseawaterexpressedasa

functionofAbsoluteSalinityas

(

)

A,,

StpratherthanasafunctionofPracticalSalinity

SorofReferenceSalinity,R.STheissueofthespatialvariationinthecompositionof

seawaterisdiscussedmorefullyinappendixA.5.

Regardingpointnumber2,wenotethatitisperhapsdebatablewhichof

(1–0.001dens

S/( 1

gkg

−)),(1–0.001soln

S/( 1

gkg

−

)),(1–0.001add

S/( 1

gkg

−))or

(1–0.001*

S/( 1

gkg

−

))isthemostappropriatemeasureofthefreshwatermassfraction.

(Thesedifferentversionsofabsolutesalinityaredefinedinsection2.5andalsolaterinthis

appendix.)ThisisaminorpointcomparedwiththepresentuseofP

Sinthiscontext,and

thechoiceofwhichoftheseexpressionsmaydependontheuseforthefreshwatermass

fraction.Forexample,inthecontextofoceanmodelling,if*

Sisthesalinityvariablethat

istreatedasaconservativevariableinanoceanmodel,then(1–0.001*

S/( 1

gkg

−))is

probablythemostappropriateversionoffreshwatermassfraction.

ItshouldbenotedthatthequantityA

Sappearingasanargumentofthefunction

()

A,,

StpistheAbsoluteSalinity(the“DensitySalinity”dens

SS≡)measuredonthe

Reference‐CompositionSalinityScale.ThisisimportantsincetheGibbsfunctionhasbeen

fittedtolaboratoryandfieldmeasurementswiththeAbsoluteSalinityvaluesexpressed

onthisscale.Thus,forexample,itispossiblethatsometimeinthefutureitwillbe

determinedthatanimprovedestimateofthemassfractionofdissolvedmaterialin

StandardSeawatercanbeobtainedbymultiplyingR

Sbyafactorslightlydifferentfrom1

(uncertaintiespermitvaluesintherange1

0.002).WeemphasizethatsincetheGibbs

functionisexpressedintermsoftheAbsoluteSalinityexpressedontheReference‐

CompositionSalinityScale,useofanyotherscale(evenonethatgivesmoreaccurate

estimatesofthetruemassfractionofdissolvedsubstancesinStandardSeawater)will

reducetheaccuracyofthethermodynamicpropertiesdeterminedfromtheGibbs

function.Inpartforthisreason,werecommendthattheReference‐CompositionSalinity

continuetobemeasuredonthescaledefinedbyMilleroetal.(2008a)evenifnewresults

indicatethatimprovedestimatesofthetruemassfractioncanbeobtainedusinga

modifiedscale.Thatis,werecommendthatthevalueofPS

uusedin(A.3.3)notbe

updated.Ifamoreaccuratemassfractionestimateisrequiredforsomepurposeinthe

future,sucharevisedestimateshoulddefinitelynotbeusedasanargumentofthe

TEOS‐10Gibbsfunction.

Finally,wenoteasecondreasonforrecommendingthatthevalueassignedtoPS

unot

bemodifiedwithoutverycarefulconsideration.WorkingGroup127isrecommending

thatthepracticeofexpressingsalinityasPracticalSalinityinpublicationsbephasedoutin

favourofusingAbsoluteSalinityforthispurpose.Itiscriticallyimportantthatthisnew

measureofsalinityremainstableintothefuture.Inparticular,wenotethatanychangein

thevalueofPS

uusedinthedeterminationofReferenceSalinitywouldresultinachange

inreportedsalinityvaluesthatwouldbeunrelatedtoanyrealphysicalchange.For

example,achangeinPS

ufrom35.16504/35to(35.16504/35)x1.001forexample,would

resultinchangesofthereportedsalinityvaluesoforder0.0351

gkg

−

whichismorethan

tentimeslargerthantheprecisionofmodernsalinometers.Thuschangesassociatedwith

aseriesofimprovedestimatesofPS

u(asameasureofthemassfractionofdissolvedsalts

inStandardSeawater)couldcauseveryseriousconfusionforresearcherswhomonitor

salinityasanindicatorofclimatechange.Basedonthisconcernandthefactthatthe

GibbsfunctionisexpressedasafunctionofAbsoluteSalinitymeasuredontheReference‐

CompositionSalinityScaleasdefinedbyMilleroetal.(2008a),westronglyrecommend

thattheReference‐CompositionSalinitycontinuetobeexpressedonthisscale;nochanges

inthevalueofPS

ushouldbeintroduced.

72 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

ForseawaterofReferenceComposition,ReferenceSalinityR

Sisthebestavailable

estimateofthemass‐fractionofnon‐H2Omaterialinseawater.Asdiscussedinsections

2.4and2.5,underTEOS‐10R

Swasdeterminedtoprovidethebestavailableestimateof

themass‐fractionofnon‐H2OmaterialinStandardSeawaterbyMilleroetal.(2008a).

Subsequently,Pawlowicz(2010)hasarguedthattheDICcontentoftheReference

Compositionisprobablyabout1171

mol kg

−

lowforSSWandalsofortheNorthAtlantic

surfacewaterfromwhichitwasprepared.ThisdifferenceinDICcausesanegligible

effectonbothconductivityanddensity,andhenceonReferenceSalinityandDensity

Salinity.TheinfluenceonSolutionSalinityisnearlyafactorof10larger(Pawlowiczetal.,

2010)butat0.00551

gkg

−itisstilljustbelowtheuncertaintyof0.0071

gkg

−assignedto

theestimatedAbsoluteSalinitybyMilleroetal.(2008a).Infact,thelargestuncertaintiesin

ReferenceSalinityasameasureoftheAbsoluteSalinityofSSWareassociatedwith

uncertaintiesinthemassfractionsofotherconstituentssuchassulphate,whichmaybeas

largeas0.051

gkg

−(Seitzetal.,2010a).Nevertheless,itseemsthatthesulphatevalueof

Reference‐CompositionSeawaterlieswithinthe95%uncertaintyrangeofthebest

laboratory‐determinedestimatesofSSW’ssulphateconcentration,sothereisno

justificationforanupdateoftheReferenceCompositionatthistime.

WhenthecompositionofseawaterdiffersfromthatofStandardSeawater,thereare

severalpossibledefinitionsoftheabsolutesalinityofaseawatersample,asdiscussedin

section2.5.Conceptuallythesimplestdefinitionis“themassfractionofdissolvednon‐

HOmaterialinaseawatersampleatitstemperatureandpressure”.Onedrawbackof

thisdefinitionisthatbecausetheequilibriumconditionsbetween2

HOandseveralcarbon

compoundsdependsontemperatureandpressure,thismass‐fractionwouldchangeasthe

temperatureandpressureofthesampleischanged,evenwithouttheadditionorlossof

anymaterialfromthesample.Thisdrawbackcanbeovercomebyfirstbringingthe

sampletotheconstanttemperature25 Ct

°andthefixedseapressure0dbar,andwhen

thisisdone,theresultingmass‐fractionofnon‐2

HOmaterialiscalled“SolutionAbsolute

Salinity”(usuallyshortenedto“SolutionSalinity”),soln

S.Anothermeasureofabsolute

salinityisthe“Added‐MassSalinity”add

SwhichisR

Splusthemassfractionofmaterial

thatmustbeaddedtoStandardSeawatertoarriveattheconcentrationsofallthespecies

inthegivenseawatersample,afterchemicalequilibriumhasbeenreached,andafterthe

samplehasbeenbroughtto25 Ct=°andp

0dbar.

Anotherformofabsolutesalinity,“PreformedAbsoluteSalinity”(usuallyshortened

to“PreformedSalinity”),*

S,hasbeendefinedbyPawlowiczetal.(2010)andWrightetal.

(2010b).PreformedSalinity*

Sisdesignedtobeascloseaspossibletobeinga

conservativevariable.Thatis,*

Sisdesignedtobeinsensitivetobiogeochemical

processesthataffecttheothertypesofsalinitytovaryingdegrees. *

Sisformedbyfirst

estimatingthecontributionofbiogeochemicalprocessestooneofthesalinitymeasures

S,soln

S,oradd

S,andthensubtractingthiscontributionfromtheappropriatesalinity

variable.Becauseitisdesignedtobeaconservativeoceanographicvariable,*

Swillfinda

prominentroleinoceanmodeling.

Thereisstillnosimplemeanstomeasureeithersoln

Soradd

Sforthegeneralcaseofthe

arbitraryadditionofmanycomponentstoStandardSeawater.Henceamorepreciseand

easilydeterminedmeasureoftheamountofdissolvedmaterialinseawaterisrequired

andTEOS‐10adopts“DensitySalinity”dens

Sforthispurpose.“DensitySalinity”dens

Sis

definedasthevalueofthesalinityargumentoftheTEOS‐10expressionfordensitywhich

givesthesample’sactualmeasureddensityatthetemperature25 Ct

°andatthesea

pressurep=0dbar.Whenthereisnoriskofconfusion,“DensitySalinity”isalsocalled

AbsoluteSalinitywiththelabelA

S,thatisdens

SS≡.Therearetwoclearadvantagesof

dens

SS≡overbothsoln

Sandadd

S.First,itispossibletomeasurethedensityofa

seawatersampleveryaccuratelyandinanSI‐traceablemanner,andsecond,theuseof

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

dens

SS≡yieldsthebestavailableestimatesofthedensityofseawater.Thisisimportant

becauseinthefieldofphysicaloceanography,itisdensitythatneedstobeknowntothe

highestrelativeaccuracy.

Pawlowiczetal.(2010)andWrightetal.(2010b)foundthatwhilethenatureofthe

ocean’scompositionvariationschangesfromoneoceanbasintoanother,thefivedifferent

salinitymeasuresR

S,dens

S,soln

S,add

Sand*

Sareapproximatelyrelatedbythefollowing

simplelinearrelationships,(obtainedbycombiningequations(55)–(57)and(62)of

Pawlowiczetal.(2010))

 dens

0.35SS S

∗−≈− ,(A.4.1)

dens dens

AR R

1.0SS S

−≡ ,(A.4.2)

soln dens

AR R

1.75 δSSS−≈ ,(A.4.3)

add dens

AR R

0.78SS S

−≈ .(A.4.4)

Eqn.(A.4.2)issimplythedefinitionoftheAbsoluteSalinityAnomaly,

dens dens

ARAR

SSSS

δδ

≡≡−.NotethatinmanyTEOS‐10publications,thesimplernotation

isusedfordens dens

RAR

SSS

≡−,asalinitydifferenceforwhichaglobalatlasis

available(McDougalletal.(2010a)).Inthecontextofoceanmodelling,itismore

convenienttocastthesesalinitydifferenceswithrespecttothePreformedSalinityS∗as

follows(usingtheaboveequations)

dens

0.35SS S

∗

−≈ ,(A.4.5)

dens dens

1.35SS S

∗

−≈ ,(A.4.6)

 soln dens

A* R

2.1SS S

−≈ ,(A.4.7)

add dens

1.13SS S

∗

−≈ .(A.4.8)

TheserelationshipsareillustratedonthenumberlineofsalinityinFigureA.4.1.ForSSW,

allfivesalinityvariablesR

S,dens

S,soln

S,add

Sand*

Sareequal.Itshouldbenotedthat

thesimplerelationshipsofEqns.(A.4.1)–(A.4.8)arederivedfromsimplelinearfitsto

modelcalculationsthatshowmorecomplexvariations.However,thevariationabout

theserelationshipsisnotlargerthanthetypicaluncertaintyofoceanmeasurements.

Theselinearrelationshipsprovideawaybywhichtheeffectsofanomalousseawater

compositionmaybeaddressedinoceanmodels(seeappendixA.20).



FigureA.4.1.Numberlineofsalinity,illustratingthedifferences

betweenvariousformsofsalinityforseawaterwhose

compositiondiffersfromthatofStandardSeawater.



IfmeasurementsareavailableoftheTotalAlkalinity,DissolvedInorganicCarbon,and

thenitrateandsilicateconcentrations,butnotofdensityanomalies,thenalternative

formulaeareavailableforthefoursalinitydifferencesthatappearontheleft‐handsidesof

74 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Eqns.(A.4.1)–(A.4.8).Pawlowiczetal.(2010)haveusedachemicalmodelofconductivity

anddensitytoestimatehowthemanysalinitydifferencesintroducedabovedependon

themeasuredpropertiesofseawater.ThefollowingequationscorrespondtoEqns.(A.4.1)

–(A.4.4)above,andcomefromequations(51)–(54)and(59)ofPawlowiczetal.(2010).

Theseequationsarewrittenintermsofthevaluesofthenitrateandsilicateconcentrations

intheseawatersample(measuredin1

mol kg

−

),thedifferencebetweentheTotalAlkalinity

(TA )andDissolvedInorganicCarbon(DIC )ofthesampleandthecorrespondingvalues

ofourbestestimatesofTA andDIC inStandardSeawater,TA

andDICΔ,both

measuredin1

mol kg

−

.ForStandardSeawaterourbestestimatesofTAandDICare

0.0023 ( 35)S1

mol kg−andP

0.00208 ( 35)S1

mol kg

−

respectively(seePawlowicz(2010),

Pawlowiczetal.(2010)andthediscussionofthisaspectofSSWversusRCSWinWrightet

al.(2010b))).

()

1 1

*R 3 4

/ (g kg ) 18.1 TA 7.1 DIC 43.0 NO 0.1 Si(OH) (mol kg )SS −−−

−=−Δ−Δ−+ ,(A.4.9)

() ( )

dens 1 1

AR 3 4

/ (g kg ) 55.6 TA 4.7 DIC +38.9 NO 50.7 Si(OH) (mol kg )SS −−−

−=Δ+Δ + ,(A.4.10)

() ( )

soln 1 1

AR 3 4

/ (g kg ) 7.2 TA 47.0 DIC+ 36.5 NO 96.0 Si(OH) (mol kg )SS −−−

−=Δ+Δ + ,(A.4.11)

() ( )

add 1 1

AR 3 4

/ (g kg ) 25.9 TA 4.9 DIC +16.1NO 60.2 Si(OH) (mol kg )SS −−−

−=Δ+Δ + .(A.4.12)

ThestandarderrorofthemodelfitsinEqns.(A.4.9)–(A.4.11)aregivenbyPawlowiczet

al.(2010)atlessthan43

10 kg m

−−

(intermsofdensity)whichisequivalenttoafactorof20

smallerthantheaccuracytowhichPracticalSalinitycanbemeasuredatsea.Itisclear

thatifmeasurementsofTA,DIC,nitrateandsilicateareavailable(andrecognizingthat

thesemeasurementswillcomewiththeirownerrorbars),theseexpressionswilllikely

givemoreaccurateestimatesofthesalinitydifferencesthantheapproximatelinear

expressionspresentedinEqns.(A.4.1)–(A.4.8).ThecoefficientsinEqn.(A.4.10)are

reasonablysimilartothecorrespondingexpressionofBrewerandBradshaw(1975)(as

correctedbyMilleroetal.(1976a)):‐ whenexpressedasthesalinityanomalydens

SS−

ratherthanasthecorrespondingdensityanomalyR

−,theirexpressioncorresponding

toEqn.(A.4.10)hadthecoefficients71.4,‐12.8,31.9and59.9comparedwiththe

coefficients55.6,4.7,38.9and50.7respectivelyinEqn.(A.4.10).

ThesalinitydifferencesexpressedwithrespecttoPreformedSalinity*

Swhich

correspondtoEqns.(A.4.5)–(A.4.8)canbefoundbylinearcombinationsofEqns.(A.4.9)–

(A.4.12)asfollows

()

1 1

R* 3 4

/ (g kg ) 18.1 TA 7.1 DIC 43.0 NO 0.1 Si(OH) (mol kg )SS −−−

−=Δ+Δ+− ,(A.4.13)

() ( )

dens 1 1

A* 3 4

/ (g kg ) 73.7 TA 11.8 DIC +81.9 NO 50.6 Si(OH) (mol kg )SS −−−

−=Δ+Δ + ,(A.4.14)

() ( )

soln 1 1

A* 3 4

/ (g kg ) 25.3 TA 54.1 DIC +79.5 NO 95.9 Si(OH) (mol kg )SS −−−

−=Δ+Δ + ,(A.4.15)

() ( )

add 1 1

A* 3 4

/ (g kg ) 44.0 TA 12.0 DIC+59.1NO 60.1 Si(OH) (mol kg )SS −−−

−=Δ+Δ + .(A.4.16)



TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

A.5 Spatial variations in seawater composition

WhentheoceanographicdataneededtoevaluateEqn.(A.4.10)fordens

SS−isnot

available,thelook‐uptablemethodofMcDougalletal.(2010a)isrecommendedto

evaluatedens dens

AR AR

SS SS

δδ

≡≡−.Thefollowingparagraphsdescribehowthismethod

wasdeveloped.

InaseriesofpapersMilleroetal.(1976a,1978,2000,2008b)andMcDougalletal.

(2010a)havereportedondensitymeasurementsmadeinthelaboratoryonsamples

collectedfromaroundtheworld’soceans.EachsamplehashaditsPracticalSalinity

measuredinthelaboratoryaswellasitsdensity(measuredwithavibratingtube

densimeterat25°Candatmosphericpressure).ThePracticalSalinityyieldsaReference

SalinityR

SaccordingtoEqn.(A.3.3),whilethedensitymeasurementmeas

impliesan

AbsoluteSalinitydens

SS≡byusingtheequationofstateandtheequality

()

meas dens

A,25 C,0dbarS

ρρ

=°.Thedifferencedens

SS−betweenthesetwosalinity

measuresistakentobeduetothecompositionofthesamplebeingdifferenttothatof

StandardSeawater.InthesepapersMilleroestablishedthatthesalinitydifferenceAR

SS−

couldbeestimatedapproximatelyfromknowledgeofjustthesilicateconcentrationofthe

fluidsample.Thereasonfortheexplainingpowerofsilicatealoneisthoughttobethat(a)

itisitselfsubstantiallycorrelatedwithotherrelevantvariables(e.g.totalalkalinity,nitrate

concentration,DIC[oftencalledtotalcarbondioxide]),(b)itaccountsforasubstantial

fraction(about0.6)ofthetypicalvariationsinconcentrations1

(g kg )

−oftheabovespecies

and(c)beingessentiallynon‐ionic;itspresencehaslittleeffectonconductivitywhile

havingadirecteffectondensity.

WhentheexistingdataonA

,basedonlaboratorymeasurementsofdensity,was

regressedagainstthesilicateconcentrationoftheseawatersamples,McDougalletal.

(2010a)foundthesimplerelation

(

)

11 1

AAR 4

/(gkg ) ( )/(gkg ) 98.24 Si(OH) /(mol kg )SSS

−− −

=− = .Global(A.5.1)

Thisregressionwasdoneoverallavailabledensitymeasurementsfromtheworldocean,

andthestandarderrorinthefitwas0.0054gkg‐1.

ThedependenceofA

onsilicateconcentrationisobservedtobedifferentineach

oceanbasin,andthisaspectwasexploitedbyMcDougalletal.(2010a)toobtainamore

accuratedependenceofA

onlocationinspace.FordataintheSouthernOceansouthof

30oSthebestsimplefitwasfoundtobe

()

/(gkg ) 74.884 Si(OH) /(mol kg )S

−−

=,SouthernOcean(A.5.2)

andtheassociatedstandarderroris0.0026gkg‐1.

Thedatanorthof30oSineachofthePacific,IndianandAtlanticOceanswastreated

separately.Ineachofthesethreeregionsthefitwasconstrainedtomatch(A.5.2)at30oS

andtheslopeofthefitwasallowedtovarylinearlywithlatitude.Theresultingfitswere

(forlatitudesnorthof30oS,thatisfor30

≥− °)

[

]

()

(

)

1 1

/ (g kg ) 74.884 1 0.3622 / 30 1 Si(OH) / (mol kg )S

δλ

− −

=+ °+ ,Pacific(A.5.3)

[

]

()

(

)

1 1

/ (g kg ) 74.884 1 0.3861 / 30 1 Si(OH) / (mol kg )S

δλ

− −

=+ °+ ,Indian(A.5.4)

[

]

()

(

)

1 1

/ (g kg ) 74.884 1 1.0028 / 30 1 Si(OH) / (mol kg ) .S

δλ

− −

=+ °+ Atlantic(A.5.5)

TheserelationshipsbetweentheAbsoluteSalinityAnomalyAAR

SSS

−andsilicate

concentrationhavebeenusedbyMcDougall,JackettandMillero(2010a)inacomputer

algorithmthatusesanexistingglobaldatabaseofsilicate(GouretskiandKoltermann

(2004))andprovidesanestimateofAbsoluteSalinitywhengivenaseawatersample’s

76 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

PracticalSalinityaswellasitsspatiallocationintheworldocean.Thiscomputer

algorithmaccountsforthelatestunderstandingofAbsoluteSalinityintheBalticSea,butit

issilentontheinfluenceofcompositionalvariationsinothermarginalseas.TheAbsolute

SalinityAnomalyintheBalticSeahasbeenquitevariableoverthepastfewdecadesof

observation(Feisteletal.(2010c)).ThecomputeralgorithmofMcDougalletal.(2010a)

usestherelationshipfoundbyFeisteletal.(2010c)thatappliesintheyears2006‐2009,

namely

()

AR RSO

0.087 g kg 1SS SS

−

−= ×− ,(A.5.6)

whereSO

S=35.16504gkg–1isthestandard‐oceanReferenceSalinitythatcorrespondsto

thePracticalSalinityof35.

Inordertogaugetheimportanceofthespatialvariationofseawatercomposition,the

northwardgradientofdensityatconstantpressureisshowninFig.A.5.1forthedataina

worldoceanhydrographicatlasdeeperthan1000m.Theverticalaxisinthisfigureisthe

magnitudeofthedifferencebetweenthenorthwarddensitygradientatconstantpressure

whentheTEOS‐10algorithmfordensityiscalledwithdens

SS≡(asitshouldbe)

comparedwithcallingthesameTEOS‐10densityalgorithmwithR

Sasthesalinity

argument.FigureA.5.1showsthatthe“thermalwind”ismisestimatedbymorethan2%

for58%ofthedataintheworldoceanbelowadepthof1000miftheeffectsofthevariable

seawatercompositionareignored.



FigureA.5.1.Thenorthwarddensitygradientatconstantpressure(thehorizontalaxis)

fordataintheglobaloceanatlasofGouretskiandKoltermann(2004)for

 1000p>dbar.Theverticalaxisisthemagnitudeofthedifference

betweenevaluatingthedensitygradientusingA

SversusR

Sasthe

salinityargumentintheTEOS‐10expressionfordensity.



TheimportanceofthespatialvariationsinseawatercompositionillustratedinFig.

A.5.1canbecomparedwiththecorrespondingimprovementachievedbytheTEOS‐10

GibbsfunctionforStandardSeawatercomparedwithusingEOS‐80.Thisisdoneby

ignoringspatialvariationsinseawatercompositioninboththeevaluationofTEOS‐10and

inEOS80bycallingTEOS‐10withR

SandEOS‐80withP

S.FigureA.5.2showsthe

magnitudeoftheimprovementinthe“thermalwind”inthepartoftheoceanthatis

deeperthan1000 m throughtheadoptionofTEOS‐10butignoringtheinfluenceof

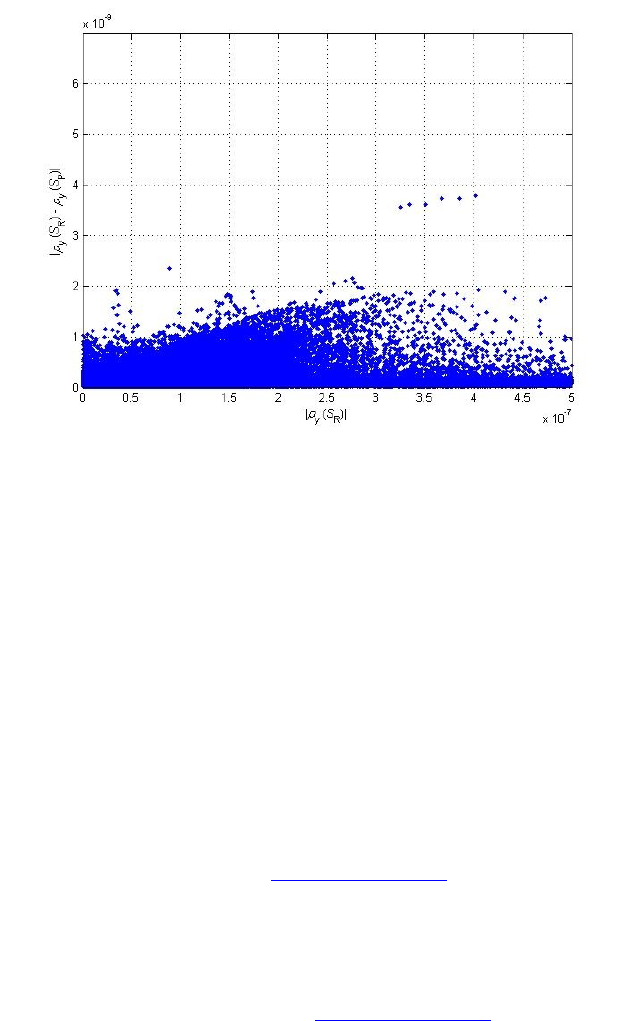
TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

compositionalvariations.BycomparingFigs.A.5.1andA.5.2itisseenthatthemain

benefitthatTEOS‐10deliverstotheevaluationofthe“thermalwind”isthroughthe

incorporationofspatialvariationsinseawatercomposition;thegreateraccuracyofTEOS‐

10overEOS‐80forStandardSeawaterisonly18%aslargeastheimprovementgainedby

theincorporationofcompositionalvariationsintoTEOS‐10(i.e.thermsvalueofthe

verticalaxisinFig.A.5.2is18%ofthatoftheverticalaxisofFig.A.5.1).IftheAtlantic

wereexcludedfromthiscomparison,therelativeimportanceofcompositionalvariations

wouldbeevenlarger.



FigureA.5.2.Thenorthwarddensitygradientatconstantpressure(thehorizontalaxis)

fordataintheglobaloceanatlasofGouretskiandKoltermann(2004)for

 1000 dbarp>.Theverticalaxisisthemagnitudeofthedifference

betweenevaluatingthedensitygradientusingR

Sasthesalinity

argumentintheTEOS‐10expressionfordensitycomparedwithusingP

S

intheEOS‐80algorithmfordensity.



ThethermodynamicdescriptionofseawaterandoficeIhasdefinedinIAPWS‐08and

IAPWS‐06hasbeenadoptedastheofficialdescriptionofseawaterandoficeIhbythe

IntergovernmentalOceanographicCommissioninJune2009.TheadoptionofTEOS‐10

hasrecognizedthatthistechniqueofestimatingAbsoluteSalinityfromreadilymeasured

quantitiesisperhapstheleastmatureaspectoftheTEOS‐10thermodynamicdescriptionof

seawater.Thepresentcomputersoftware,inbothFORTRANandMATLAB,whichevaluates

AbsoluteSalinityA

SgiventheinputvariablesPracticalSalinity P

S,longitude

,latitude

andseapressurepisavailableatwww.TEOS‐10.org.Itisexpected,asnewdata

(particularlydensitydata)becomeavailable,thatthedeterminationofAbsoluteSalinity

willimproveoverthecomingdecades,andthealgorithmforevaluatingAbsoluteSalinity

intermsofPracticalSalinity,latitude,longitudeandpressure,willbeupdatedfromtime

totime,afterrelevantappropriatelypeer‐reviewedpublicationshaveappeared,andsuch

anupdatedalgorithmwillappearonthewww.TEOS‐10.orgwebsite.Usersofthis

softwareshouldstateintheirpublishedworkwhichversionofthesoftwarewasusedto

calculateAbsoluteSalinity.



78 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

A.6 Gibbs function of seawater

TheGibbsfunctionofseawater

()

A,,

StpisdefinedasthesumoftheGibbsfunctionfor

purewater

()

tpandthesalinepartoftheGibbsfunction

(

)

A,,

Stpsothat

()

(

)

(

)

,, , ,, .

S tp g tp g S tp=+ (A.6.1)

InthiswayatzeroAbsoluteSalinity,thethermodynamicpropertiesofseawaterareequal

tothoseofpurewater.ThisconsistencyisalsomaintainedwithrespecttotheGibbs

functionforicesothatthepropertiesalongtheequilibriumcurvecanbeaccurately

determined(suchasthefreezingtemperatureasafunctionofAbsoluteSalinityand

pressure).Thecarefulalignmentofthethermodynamicpotentialsofpurewater,iceIh

andseawaterisdescribedinFeisteletal.(2008a).

Theinternationallyacceptedthermodynamicdescriptionofthepropertiesofpure

water(IAPWS‐95)istheofficialpure‐waterbasisuponwhichtheGibbsfunctionof

seawaterisbuiltaccordingto(A.6.1).This

()

tpGibbsfunctionofliquidwaterisvalid

overextendedrangesoftemperatureandpressurefromthefreezingpointtothecritical

point(–22°C<t<374°Cand600Pa<p+P0<1000MPa)howeveritisacomputationally

expensivealgorithm.PartofthereasonforthiscomputationalintensityisthattheIAPWS‐

95formulationisintermsofaHelmholtzfunctionwhichhasthepressureasafunctionof

temperatureanddensity,sothataniterativeprocedureisneedtofortheGibbsfunction

()

tp(seeforexample,Feisteletal.(2008a))

Forpracticaloceanographicuseintheoceanographicrangesoftemperatureand

pressure,fromlessthanthefreezingtemperatureofseawater(atanypressure),upto

40 C°(specificallyfrom

()

2.65 0.0743 MPa CpP −

⎡⎤

−++× °

⎣⎦

to40°C),andinthepressure

range4

0 < 10 dbarp<wealsorecommendtheuseofthepurewaterpartoftheGibbs

functionofFeistel(2003)whichhasbeenapprovedbyIAPWSastheSupplementary

Release,IAPWS‐09.TheIAPWS‐09releasediscussestheaccuracytowhichtheFeistel

(2003)GibbsfunctionfitstheunderlyingthermodynamicpotentialofIAPWS‐95;in

summary,forthevariablesdensity,thermalexpansioncoefficientandspecificheat

capacity,thermsmisfitbetweenIAPWS‐09andIAPWS‐95,intheregionofvalidityof

IAPWS‐09,areafactorofbetween20and100lessthanthecorrespondingerrorinthe

laboratorydatatowhichIAPWS‐95wasfitted.Hence,intheoceanographicrangeof

parameters,IAPWS‐09andIAPWS‐95mayberegardedasequallyaccurate

thermodynamicdescriptionsofpureliquidwater.

AllofthethermodynamicpropertiesofseawaterthataredescribedinthisManualare

availableasbothFORTRANandMATLABimplementations.Theseimplementationsare

availablefor

()

tpbeingIAPWS‐95andIAPWS‐09,bothbeingequallyaccurate

relativetothelaboratory‐determinedknownproperties,butwiththecomputercodebased

onIAPWS‐09beingapproximatelyafactorof65fasterthanthatbasedonIAPWS‐95.

Mostoftheexperimentalseawaterdatathatwerealreadyusedfortheconstructionof

EOS‐80wereexploitedagainfortheIAPWS‐08formulationaftertheircarefuladjustment

tothenewtemperatureandsalinityscalesandtheimprovedpure‐waterreference

IAPWS‐95.Additionally,IAPWS‐08wassignificantlyimproved(comparedwithEOS‐80)

bymakinguseoftheoreticalrelationssuchastheideal‐solutionlawandtheDebye‐

Hückellimitinglaw,aswellasbyincorporatingadditionalaccuratemeasurementssuch

asthetemperaturesofmaximumdensity,vapourpressuresandmixingheats,and

implicitlybytheenormousbackgrounddatasetwhichhadenteredthedeterminationof

IAPWS‐95(WagnerandPruß(2002),Feistel(2003,2008)).Forexample,MilleroandLi

(1994)concludedthatthepure‐waterpartoftheEOS‐80sound‐speedformulaofChenand

Millero(1977)wasresponsibleforadeviationof0.51

−

fromDelGrosso’s(1974)

formulaforseawaterathighpressuresandtemperaturebelow5oC.ChenandMillero

(1977)onlymeasuredthedifferencesinthesoundspeedsofseawaterandpurewater.The

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

newGibbsfunctioninwhichweuseIAPWS‐95forthepure‐waterpartaswellassound

speedsfromDelGrosso(1974),isperfectlyconsistentwithChenandMillero’s(1976)

densitiesandBradshawandSchleicher’s(1970)thermalexpansiondataathighpressures.

Theaccuracyofhigh‐pressureseawaterdensitieshasincreasedwiththeuseofIAPWS‐95,

directlyasthepure‐waterpart,andindirectlybycorrectingearlierseawater

measurements,makingthemʺnewʺ seawaterdata.Inthismannertheknownsound‐

speedinconsistencyofEOS‐80hasbeenresolvedinanaturalmanner.



A.7 The fundamental thermodynamic relation

Thefundamentalthermodynamicrelationforasystemcomposedofasolvent(water)and

asolute(seasalt)relatesthetotaldifferentialsofthermodynamicquantitiesforthecase

wherethetransitionsbetweenequilibriumstatesarereversible.Thisrestrictionissatisfied

forinfinitesimallysmallchangesofaninfinitesimallysmallseawaterparcel.The

fundamentalthermodynamicrelationis

(

)

dd d dhvP Tt S

ημ

−=++ .(A.7.1)

AderivationofthefundamentalthermodynamicrelationcanbefoundinWarren(2006)

(hisequation(8)).Theleft‐handsideofEqn.(A.7.1)isoftenwrittenas

()

ddupPv++ 

where

()

pP+istheabsolutepressure.Herehisthespecificenthalpy(i.e.enthalpyper

unitmassofseawater),uisthespecificinternalenergy,1

−

=isthespecificvolume,

()

Tt+istheabsolutetemperature,

isthespecificentropyand

istherelative

chemicalpotential.Influiddynamicsweusuallydealwithmaterialderivatives,ddt,that

is,derivativesdefinedfollowingthefluidmotion,ddtt

∂∂ + ⋅∇uwhereuisthefluid

velocity.Intermsofthistypeofderivative,andassuminglocalthermodynamic

equilibrium(i.e.thatlocalthermodynamicequilibriumismaintainedduringthetemporal

change),thefundamentalthermodynamicrelationis

()

d1d d d

dd d d

hP S

tt tt

−=++ (A.7.2)

Notethattheconstancyofentropydoesnotimplytheabsenceofirreversibleprocesses

because,forexample,therecanbeirreversiblechangesofbothsalinityandenthalpyat

constantpressureinjusttherightratiosoastohaveequaleffectsinEqns.(A.7.1)or(A.7.2)

sothatthechangeofentropyintheseequationsiszero.



A.8 The “conservative” and “isobaric conservative” properties

AthermodynamicvariableCissaidtobe“conservative”ifitsevolutionequation(thatis,

itsprognosticequation)hastheform

() ( )

ρρρ

+∇⋅ = = −∇⋅uF(A.8.1)

Forsucha“conservative”property,intheabsenceoffluxesC

Fattheboundaryofa

controlvolume,thetotalamountofC‐stuffisconstantinsidethecontrolvolume.The

middlepartofEqn.(A.8.1)hasusedthecontinuityequation(whichistheequationforthe

conservationofmass)

(

)

,, 0.

xyz

ρρ

∂∂ +∇⋅ =u(A.8.2)

Inthespecialcasewhenthematerialderivativeofapropertyiszero(thatis,themiddle

partofEqn.(A.8.1)iszero)thepropertyissaidtobe“materiallyconserved”.

Theonlyquantitythatcanberegardedas100%conservativeintheoceanismass

[equivalenttotaking1C=andC

F0inEqn.(A.8.1)].Infact,lookingaheadto

80 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

appendicesA.20andA.21,ifwestrictlyinterpret

uasthemassfluxperunitareaof

pureseawater(i.e.ofonlypurewaterplusdissolvedmaterial)andspecifically,that

u

excludesthefluxofparticulatematter,thentheright‐handsideofthecontinuityequation

(A.8.2)shouldbeA

S,thenon‐conservativesourceofmassduetobiogeochemical

processes.ItcanbeshownthattheinfluenceofthissourcetermA

Sinthecontinuity

equationontheevolutionequationforAbsoluteSalinityislessimportantbythefactor

()

ˆˆ

1SS−thanthesamesourcetermthatappearsinthisevolutionequationfor

AbsoluteSalinity,Eqn.(A.21.8).Hencethecurrentpracticeofassumingthatthenon‐

particulatepartoftheoceanobeystheconservativeform(A.8.2)ofthecontinuityequation

isconfirmedeveninthepresenceofbiogeochemicalprocesses.

Twoothervariables,totalenergy0.5u

+⋅+Φuu

(seeEqn.(B.15))and

ConservativeTemperatureΘ(orequivalently,potentialenthalpy0

h)arenotcompletely

conservative,buttheerrorinassumingthemtobeconservativeisnegligible(seeappendix

A.21).OthervariablessuchasReferenceSalinityR,SAbsoluteSalinityA,Spotential

temperature,

enthalpy,hinternalenergy,uentropy,

density,

potentialdensity

specificvolumeanomaly

andtheBernoullifunction0.5h

+⋅+Φuu

(seeEqn.

(B.17))arenotconservativevariables.

WhilebothAbsoluteSalinityandReferenceSalinityareconservativeunderthe

turbulentmixingprocess,bothareaffectedinanon‐conservativewaybythe

remineralizationprocess.Becausethedominantvariationsofthecompositionofseawater

areduetospecieswhichdonothaveastrongsignatureinconductivity,insomesituations

itmaybesufficientlyaccuratetotakeReferenceSalinityR

Stobeaconservativevariable.

However,wenotethattheerrorinvolvedwithassumingthatR

Sisaconservative

variableisafactorofapproximately40larger(intermsofitseffectsondensity)thanthe

errorinassumingthatΘisaconservativevariable.PreformedSalinity*

Sisconstructed

sothatitcontainsnosignatureofthebiogeochemicalprocessesthatcausethespatial

variationofseawatercomposition.Inthisway*

Sisspecificallydesignedtobea

conservativeoceanicsalinityvariable.Havingsaidthat,theaccuracywithwhichwecan

constructPreformedSalinity*

Sfromoceanobservationsispresentlylimitedbyour

knowledgeofthebiogeochemicalprocesses(seeappendicesA.4andA.5andPawlowiczet

al.(2010)).

Summarizingthisdiscussionthusfar,thequantitiesthatcanbeconsidered

conservativeintheoceanare(indescendingorderofaccuracy)(i)mass,(ii)totalenergy

0.5u=+ ⋅+Φuu

,(iii)ConservativeTemperature

,and(iv)PreformedSalinity*

S.

Adifferentformof“conservation”attribute,namely“isobaricconservation”occurs

whenthetotalamountofthequantityisconservedwhentwofluidparcelsaremixedat

constantpressurewithoutexternalinputofheatormatter.This“isobaricconservative”

propertyisaveryvaluableattributeforanoceanographicvariable.Any“conservative”

variableisalso“isobaricconservative”,thusthefourconservativevariableslistedabove,

namelymass,ConservativeTemperature

,PreformedSalinity*

S,andtotalenergy



are“isobaricconservative”.Inaddition,theBernoullifunction

andspecificenthalpyh

arealso“isobaricconservative”(seeEqn.(B.17)andthediscussionthereafter).

Somevariablesthatarenot“isobaricconservative”includepotentialtemperature,



internalenergy,uentropy,

density,

potentialdensity,

andspecificvolume

anomaly.

EnthalpyhandConservativeTemperature

arenotexactly“isobaric

conservative”becauseenthalpyincreaseswhenthekineticenergyoffluidmotionis

dissipatedbymolecularviscosityinsidethecontrolvolumeandwhenthereisasalinity

sourcetermduetotheremineralizationofparticulatematter.However,thesearetiny

effectsintheFirstLawofThermodynamics(seeappendixA.21)andtraditionallywe

regardenthalpyhasan“isobaricconservative”variable.Notethatwhilehis“isobaric

conservative”,itisnota“conservative”variable.

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

AppendicesA.18andA.21showthatforallpracticalpurposeswecantreatΘand0

h

asbeing“conservative”variables(andhencealso“isobaricconservative”variables);doing

soignoresthedissipationofmechanicalenergy

andothertermsofsimilarorsmaller

magnitude.Henceforallpracticalpurposesinoceanographywehavemassandthe

followingthreeothervariablesthatare“conservative”and“isobaricconservative”;

(1)ConservativeTemperature,

(andpotentialenthalpy0

h),

(2)PreformedSalinity*

S,and

(3)totalenergy

.



Herewecommentbrieflyonthelikelyerrorsinvolvedwithassumingvariablesother

than*

SandΘtobeconservativevariablesinoceanmodels.IfonetookAbsoluteSalinity

Sasanoceanmodel’ssalinityvariableandtreateditasbeingconservative,thesalinity

errorwould(afteralongspin‐uptime)beapproximatelyaslargeastheAbsoluteSalinity

Anomaly(asshowninFigure2),whichislargerthan1

0.025 g kg

−

intheNorthPacific,

implyingdensityerrorsof3

0.020 kg m

−

.Asameasureoftheimportanceofthistypeof

densityerror,wenotethatiftheequationofstateinanoceanmodelwerecalledwithR

S

insteadofwithA

S,thenorthwarddensitygradientatfixedpressure(i.e.thethermal

wind)wouldbemisestimatedbymorethan2%formorethan58%ofthedatabelowa

pressureof1000dbarintheworldocean.Itisclearlydesirabletonothavethistypeof

systematicerrorinthedynamicalequationsoftheoceancomponentofcoupledclimate

models.AppendixA.20discussespracticalwaysofincludingtheeffectsofthenon‐

conservativeremineralizationsourceterminoceanmodels.Therecommendedoptionis

thatoceanmodelscarryPreformedSalinity*

Sasthemodel’sconservativesalinitymodel

variable,andthattheyalsocarryanevolutionequationforanAbsoluteSalinityAnomaly

asdescribedinsectionA.20.1andEqns.(A.20.3)–(A.20.5).

Theerrorsincurredinoceanmodelsbytreatingpotentialtemperature

asbeing

conservativehavenotyetbeenthoroughlyinvestigated,butMcDougall(2003)and

Tailleux(2010)havemadeastartonthistopic.McDougall(2003)foundthattypicalerrors

in

are0.1 C±°whileinisolatedregionssuchaswherethefreshAmazonwater

dischargesintotheocean,theerrorcanbeaslargeas1.4 C°.Thecorrespondingerrorin

themeridionalheatfluxappearstobeabout0.005PW(orarelativeerrorof0.4%).The

useofConservativeTemperature

inoceanmodelsreducestheseerrorsbyalmosttwo

ordersofmagnitude.

Iftheoceanwereinthermodynamicequilibrium,itstemperaturewouldbethesame

everywhereaswouldthechemicalpotentialsofwaterandofeachdissolvedspecies,while

theentropyandtheconcentrationsofeachspecieswouldbefunctionsofpressure.

Turbulentmixingactsinthecomplementarydirection,tendingtomakesalinityand

entropyconstantbutintheprocesscausinggradientsintemperatureandthechemical

potentialsasfunctionsofpressure.Thatis,turbulentmixingactstomaintainanon‐

equilibriumstate.Thisdifferencebetweentherolesofmolecularversusturbulentmixing

resultsfromthesymmetrybreakingroleofthegravityfield;forexample,inalaboratory

withoutgravity,turbulentandmolecularmixingwouldhaveindistinguishableeffects.

NotethatthemolecularfluxofsaltS

Fisgivenbyequation(58.11)ofLandauand

Lifshitz(1959)andbyEqn.(B.23)below. S

Fconsistsnotonlyoftheproductoftheusual

moleculardiffusivityandA

−∇ ,butalsocontainstwoothertermsthatareproportional

tothegradientsoftemperatureandpressurerespectively.Itisthesetermsthatcausethe

equilibriumverticalgradientsofthedissolvedsolutesinanon‐turbulentoceantobe

differentandnon‐zero;thelasttermbeingcalledthebaro‐diffusioneffect.Thepresence

ofturbulentmixingintherealoceanrendersthisprocessmootasturbulencetendsto

homogenizetheoceanandmaintainsarelativelyconstantsea‐saltcomposition.

Notethatthedescription“conservationequation”ofaparticularquantityisoften

usedfortheequationthatdescribeshowthisquantitychangesinresponsetothe

82 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

divergenceofvariousfluxesofthequantityandtonon‐conservative“source”terms.For

example,itisusualtorefertothe“conservationequation”forentropyorfor“potential

temperature”.Sincethesevariablesarenotconservativevariablesitseemsunnaturalto

refertotheirevolutionequationsas“conservationequations”.Henceherewewillusethe

term“conservationequation”onlyforavariablethatis(forallpracticalpurposes)

conserved.Forothervariableswewillrefertotheir“evolutionequation”ortheir

“prognosticequation”ortheir“localbalanceequation”.



A.9 The “potential” property

Anythermodynamicpropertyofseawaterthatremainsconstantwhenaparcelof

seawaterismovedfromonepressuretoanotheradiabatically,withoutexchangeofmass

andwithoutinteriorconversionbetweenitsturbulentkineticandinternalenergies,issaid

topossessthe“potential”property,orinotherwords,tobea“potential”variable.Prime

examplesof“potential”variablesareentropy

andalltypesofsalinity.Theconstancyof

entropy

canbeseenfromtheFirstLawofThermodynamicsinEqn.(B.19)below;with

theright‐handsideofEqn.(B.19)beingzero,andwithnochangeinAbsoluteSalinity,it

followsthatentropyisalsoconstant.Anythermodynamicpropertythatisafunctionof

onlyAbsoluteSalinityandentropyalsoremainsunchangedbythisprocedureandissaid

tohavethe“potential”property.Thermodynamicpropertiesthatpossesthe“potential”

attributeincludepotentialtemperature,

potentialenthalpy0,hConservative

TemperatureΘandpotentialdensity

(nomatterwhatfixedreferencepressureis

chosen).Somethermodynamicpropertiesthatdonotpossesthepotentialpropertyare

temperature,tenthalpy,hinternalenergy,uspecificvolume,vdensity,

specific

volumeanomaly,

totalenergy

andtheBernoullifunction.

FromEqn.(B.17)we

noticethatintheabsenceofmolecularfluxesandthesourcetermofAbsoluteSalinity,the

Bernoullifunction

isconstantfollowingthefluidflowonlyifthepressurefieldis

steady;ingeneralthisisnotthecase.Thenon‐potentialnatureof

isexplainedinthe

discussionfollowingEqn.(B.17).

Someauthorshaveusedtheterm“quasi‐material”todescribeavariablethathasthe

“potential”property.Thename“quasi‐material”derivesfromtheideathatthevariable

onlychangesasaresultofirreversiblemixingprocessesanddoesnotchangeinresponse

toadiabaticandisohalinechangesinpressure.

Theword“adiabatic”istraditionallytakentomeanaprocessduringwhichthereisno

exchangeofheatbetweentheenvironmentandthefluidparceloneisconsidering.With

thisdefinitionof“adiabatic”itisstillpossiblefortheentropy

,thepotentialtemperature

andtheConservativeTemperature

ofafluidparceltochangeduringanisohaline

andadiabaticprocess.Thisisbecausethedissipationofmechanicalenergy

causes

increasesin

,

andΘ(seetheFirstLawofThermodynamics,Eqns.(A.13.3)‐(A.13.5)).

Whilethedissipationofmechanicalenergyisasmalltermwhoseinfluenceisroutinely

neglectedintheFirstLawofThermodynamicsinoceanography,itseemsadvisableto

modifythemeaningoftheword“adiabatic”inoceanographysothatouruseoftheword

moreaccuratelyreflectsthepropertieswenormallyassociatewithanadiabaticprocess.

Accordinglyweproposethattheword“adiabatic”inoceanographybetakentodescribea

processoccurringwithoutexchangeofheatandalsowithouttheinternaldissipationof

mechanicalenergy.Withthisdefinitionof“adiabatic”,aprocessthatisbothisohalineand

adiabaticdoesimplythattheentropy

,potentialtemperature

andConservative

TemperatureΘareallconstant.

Usingthismorerestrictivedefinitionoftheword“adiabatic”wecanrestatethe

definitionofa“potential”propertyasfollows;anythermodynamicpropertyofseawater

thatremainsconstantwhenaparcelofseawaterismovedfromonepressuretoanother

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

“adiabatically”andwithoutexchangeofmass,issaidtopossessthe“potential”property,

orinotherwords,tobea“potential”variable.

InappendixA.8aboveweconcludedthatonlymass,andthethreevariables

,*

S

andΘ(approximately)are“conservative”(andhencealso“isobaricconservative”).Since

doesnotpossesthe“potential”property,wenowconcludethatonlymassandthetwo

variables*

Sand

possesallthreehighlydesiredproperties,namelythattheyare

“conservative”,“isobaricconservative”andare“potential”variables.Inthecaseof

ConservativeTemperature,Θits“conservative”(andthereforeits“isobaric

conservative”)natureisapproximate:‐ while

isnota100%conservativevariable,itis

approximatelytwoordersofmagnitudeclosertobeingatotallyconservativevariable

thanareeitherpotentialtemperatureorentropy.Similarly,PreformedSalinity*

Sisin

principle100%conservative,butourabilitytoevaluate*

Sfromhydrographic

observationsislimited(forexample,bytheapproximaterelations(A.4.1)or(A.4.9)).



TableA.9.1The“potential”,“conservative”,“isobaricconservative”and

thefunctionalnatureofvariousoceanographicvariables

Variable “potential”? “conservative”? “isobaric conservative”? function of

()

A,,Stp?

S x

S x 1 x 1

,SS

x 1 x 1 x

t x x x

x x

h x x 2

,hΘ 3 3

u x x x

x x 4 x

x 4 4 x

x x x

x x

x x x

x x x 5

x x x x



1TheremineralizationoforganicmatterchangesR

SlessthanitchangesA.S

2Taking

andtheeffectsofremineralizationtobenegligible.

3Taking

andothertermsofsimilarsizetobenegligible(seethediscussion

followingEqn.(A.21.13)).

4Takingtheeffectsofremineralizationtobenegligible.

5Oncethereferencesoundspeedfunction

(

)

0,cp

hasbeendecidedupon.



InTableA.9.1variousoceanographicvariablesarecategorizedaccordingtowhetherthey

possesthe“potential”property,whethertheyare“conservative”variables,whetherthey

are“isobaricconservative”variables,andwhethertheyarefunctionsofonly

()

A,,Stp.

84 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

NotethatΘistheonlyvariablethatachievefour“ticks”inthistable,whilePreformed

Salinity*

Shasticksinthefirstthreecolumns,butnotinthelastcolumnsinceitisa

functionnotonlyof

()

A,,Stpbutalsoofthecompositionofseawater.HenceΘisthe

most“ideal”thermodynamicvariable.Ifitwerenotforthenon‐conservationofAbsolute

Salinity,ittoowouldbean“ideal”thermodynamicvariable,butinthissense,Preformed

SalinityissuperiortoAbsoluteSalinity.ConservativeTemperatureΘandPreformed

Salinity*

Saretheonlytwovariablesinthistabletobeboth“potential”and

“conservative”.ThelastfourrowsofTableA.9.1areforpotentialdensity,

(seesection

3.4),specificvolumeanomaly,

(seesection3.7),orthobaricdensity,v

(seeappendix

A.28)andNeutralDensityn

(seesection3.14andappendixA.29).



A.10 Proof that

()

A,S

θη

= and

(

)

A,S

Θ=Θ

Considerchangesoccurringattheseasurface,(specificallyatp

0dbar)wherethe

temperatureisthesameasthepotentialtemperaturereferencedto0dbarandthe

incrementofpressuredpiszero.Regardingspecificenthalpyhandchemicalpotential

tobefunctionsofentropy

(inplaceoftemperaturet),thatis,consideringthe

functionalformofhand

tobe

(

)

A,,hhS p



and

(

)

A,, ,Sp

μμ η



itfollowsfromthe

fundamentalthermodynamicrelation(Eqn.(A.7.1))that

() ()

(

)

(

)

AAA0AA

,,0d ,,0 d d ,,0d ,

hS h S S T S S

ηη η θημη

+=++



(A.10.1)

whichshowsthatspecificentropy

issimplyafunctionofAbsoluteSalinityA

Sand

potentialtemperature,

thatis

(

)

A,S

ηθ

=,withnoseparatedependenceonpressure.

Itfollowsthat

(

)

A,.S

θη

=

Similarly,fromthedefinitionofpotentialenthalpyandConservativeTemperaturein

Eqns.(3.2.1)and(3.3.1),at0p=dbaritcanbeseenthatthefundamentalthermodynamic

relation(A.7.1)implies

()

(

)

0AA

dd,,0d.

cT SS

θη μ θ

Θ= + +(A.10.2)

ThisshowsthatConservativeTemperatureisalsosimplyafunctionofAbsoluteSalinity

andpotentialtemperature,

()

A,S

Θ=Θ ,withnoseparatedependenceonpressure.Itthen

followsthatΘmayalsobeexpressedasafunctionofonlyA

Sand.

Itfollowsthat



hasthe“potential”property.



A.11 Various isobaric derivatives of specific enthalpy

Becauseofthecentralroleofenthalpyinthetransportandtheconservationof“heat”in

theocean,thederivativesofspecificenthalpyatconstantpressureareherederivedwith

respecttoAbsoluteSalinityandwithrespecttothethree“temperature‐like”variables

andΘaswellasinsitutemperature.t

Webeginbynotingthatthethreestandardderivativesof

()

A,,hhStp=whenin

situtemperature tistakenasthe“temperature‐like”variableare

()

(

)

(

)

AA0A

,,, ,, ,

hS Stp T t Stp

μμ

∂∂ = − + (A.11.1)

()

(

)

(

)

AA0A

,,, ,, ,

hT c Stp T t Stp

∂∂ = = + (A.11.2)

and

()

(

)

(

)

AA0A

,,, ,, .

h P vS tp T tv S tp∂∂ = − + (A.11.3)

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

Nowconsideringspecificenthalpytobeafunctionofentropy(ratherthanof

temperaturet),thatis,taking

(

)

A,, ,hhS p



thefundamentalthermodynamicrelation

(A.7.1)becomes

()

AA0 A

dd dd

hhSTt S

ηημ

+=++



while

A,,

hP v

∂

∂=



(A.11.4)

sothat

()

,Sp

hTt

∂∂ = +



and A,.

∂

∂=



(A.11.5)

Nowtakingspecificenthalpytobeafunctionofpotentialtemperature(ratherthanof

temperaturet),thatis,taking

(

)

A,, ,hhS p

=thefundamentalthermodynamicrelation

(A.7.1)becomes

()

AA0 A

dd dd

hhSTt S

θθημ

+=++

 while

A,.

hP v

∂

∂=

(A.11.6)

Toevaluatetheh

partialderivative,itisfirstwrittenintermsofthederivativewith

respecttoentropyas

()

AA0

,,,

Sp Sp

hh Tt

θθηθ

ηη

==+



(A.11.7)

where(A.11.5)hasbeenused.Thisequationcanbeevaluatedat0p

whenitbecomes

(thepotentialtemperatureusedhereisreferencedtor0p

)

()

(

)

AA0

,0 ,,0 .

hcS T

θθ

ηθ

===+

(A.11.8)

Thesetwoequationsareusedtoarriveatthedesiredexpressionforh

namely

()

(

)

()

,,0 .

hcST

(A.11.9)

ToevaluatetheA

partialderivative,wefirstwritespecificenthalpyinthefunctional

form

()

,,,hhS S p

ηθ



andthendifferentiateit,finding

AA A

,,,

SS S

ppSp

hhh

θηη



(A.11.10)

ThepartialderivativeofspecificentropyT

−(Eqn.(2.10.1))withrespecttoAbsolute

Salinity,AA

SST

=− isalsoequaltoT

−

sincechemicalpotentialisdefinedbyEqn.

(2.9.6)asA

=.SincethepartialderivativeofentropywithrespecttoA

Sin(A.11.10)is

performedatfixedpotentialtemperature(ratherthanatfixedinsitutemperature),thisis

equaltoT

−evaluatedat0.p=Substitutingbothpartsof(A.11.5)into(A.11.10)we

havethedesiredexpressionforA

namely

()

(

)

(

)

AA0A

,,, , ,0.

hStpTtS

μμθ

=−+

(A.11.11)

Noticethatthisexpressioncontainssomethingsthatareevaluatedatthegeneralpressure

pandoneevaluatedatthereferencepressurer0.p



NowconsideringspecificenthalpytobeafunctionofConservativeTemperature

(ratherthanoftemperaturet),thatis,taking

(

)

ˆ,, ,hhS p

=Θthefundamental

thermodynamicrelation(A.7.1)becomes

()

AA0 A

ˆˆ

dd dd

hhSTt S

ημ

ΘΘ+ = + + while

ˆ.

hP v

∂

∂=(A.11.12)

Thepartialderivativeˆ

hΘfollowsdirectlyfromthisequationas

() ()

ˆ.

Sp S

hTt Tt

ηη

ΘΘΘ

=+ =+ (A.11.13)

At0p=thisequationreducesto

()

ˆ,

hcT

θη

ΘΘ

===+ (A.11.14)

andcombiningthesetwoequationsgivesthedesiredexpressionforˆ

namely

86 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

(

)

()

ˆ.

=+(A.11.15)

ToevaluatetheA

ˆS

hpartialderivativewefirstwritehinthefunctionalform

()

,,,hhS S p

=Θ



andthendifferentiateit,finding(usingbothpartsofEqn.(A.11.5))

()()

ˆ,, .

hStpTt

μη

Θ=++(A.11.16)

ThedifferentialexpressionEqn.(A.11.12)canbeevaluatedat0p

wheretheleft‐hand

sideissimply0d

cΘsothatfromEqn.(A.11.12)wefindthat

(

)

()

,,0,

μθ

ηθ

Θ=− +(A.11.17)

sothatthedesiredexpressionforA

ˆS

his

()

(

)

()

ˆ,, , ,0.

hStp S

μμθ

=−

+(A.11.18)

Theaboveboxedexpressionsforfourdifferentisobaricderivativesofspecificenthalpyare

importantastheyareintegraltoformingtheFirstLawofThermodynamicsintermsof

potentialtemperatureandintermsofConservativeTemperature.



A.12 Differential relationships between ,,

and A

Evaluatingthefundamentalthermodynamicrelationintheforms(A.11.6)and(A.11.12)

andusingthefourboxedequationsinappendixA.11,wefindtherelations

() () ()

()

() ( ) ( ) ()

()

() () ()

()

0A 0A

dd 0d 0d

d0d.

Tt pS c p Tt S

Tt Tt

cp S

ημ θ μ μ

μμ

θθ

+⎡⎤

++ = + −+

⎣⎦

⎡⎤

=Θ+−

⎢⎥

⎣⎦

(A.12.1)

Thequantity

()

dpS

isnowsubtractedfromeachofthesethreeexpressionsandthe

wholeequationisthenmultipliedby

(

)

(

)

TTt

+obtaining

() ()

(

)

(

)

(

)

00AA

d0d 0dd0d.

pTp

TcT Sc S

θη θ θμ μ

+= −+ =Θ− (A.12.2)

Fromthisfollowsallthefollowingpartialderivativesbetween,,

andA,S



()

A,,0 ,

ScS c

θθ

Θ= 

(

)

(

)

(

)

A0A

,,0 ,,0 ,

STp

STSc

θμθ θμ θ

⎡⎤

Θ= −+

⎣⎦

(A.12.3)



()

STc

Θ=+ 

(

)

A,,0 ,

μθ

Θ= (A.12.4)



()

(

)

A0A

,,0,

STcS

θθθ

=+ 

(

)

(

)

(

)

A0A A

,,0 ,,0,

STp

TScS

θθμθθ

=+ (A.12.5)

()

A,,0,

SccS

θθ

Θ=

(

)

(

)

(

)( )

AA0A A

,,0 ,,0 ,,0,

STp

STScS

θμθ θμθ θ

Θ⎡⎤

=− − +

⎣⎦

(A.12.6)



()()

AA0

,,0 ,

ScS T

θθ

=+

(

)

AA,,0,

ημθ

=− (A.12.7)



()

ScT

Θ=+

(

)

(

)

AA0

,,0 .

SST

μθ θ

Θ=− + (A.12.8)

Thethreesecondorderderivativesof

(

)

ˆ,S

arelistedinEqns.(P.14)and(P.15)of

appendixP.Thecorrespondingderivativesof

()

ˆ,S

,namelyˆ

,A

ˆS

,ˆ

ΘΘ ,A

ˆS

Θand

ˆSS

canalsobederivedusingEqn.(P.13),obtaining

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

Θ=Θ

, A

ˆS

=−Θ



,

()

θθ

ΘΘ

=− Θ



,

() ()

A23

ˆSS

θθ

ΘΘ

=− +

ΘΘ





,(A.12.9a,b,c,d)

and AA A A A

ˆ2

SS S S S

θθ θ θ

⎛⎞

ΘΘΘΘ

=− + −

⎜⎟

ΘΘΘΘΘ

⎝⎠







,(A.12.10)

intermsofthepartialderivatives

,A

,

,A

andAA

whichcanbeobtained

bydifferentiatingthepolynomial

(

)

A,S

fromtheTEOS‐10Gibbsfunction.



A.13 The First Law of Thermodynamics

Thelawoftheconservationofenergyforthermodynamicequilibriumstateswas

discoveredinthe19thcenturybyGibbs(1873)andotherearlypioneers.Itwasformulated

asabalancebetweeninternalenergy,heatandwork,similartothefundamentalequation

(A.7.1),andreferredtoastheFirstLawofThermodynamics(Thomson(1851),Clausius

(1876),Alberty(2001)).Undertheweakerconditionofalocalthermodynamicequilibrium

(GlansdorffandPrigogine(1971)),theoriginalthermodynamicconceptscanbesuitably

generalizedtodescribeirreversibleprocessesoffluiddynamicswhicharesubjectto

molecularfluxesandmacroscopicmotion(LandauandLifshitz(1959),DeGrootand

Mazur(1984)).

Insomecirclesthe“FirstLawofThermodynamics”isusedtodescribetheevolution

equationfortotalenergy,beingthesumofinternalenergy,potentialenergyandkinetic

energy.HerewefollowthemorecommonpracticeofregardingtheFirstLawof

Thermodynamicsasthedifferencebetweentheconservationequationoftotalenergyand

theevolutionequationforkineticenergypluspotentialenergy,leavingwhatmight

looselybetermedtheevolutionequationof“heat”,Eqn.(A.13.1)(LandauandLifshitz

(1959),McDougall(2003),Griffies(2004)).

TheFirstLawofThermodynamicscanthereforebewrittenas(seeEqn.(B.19)andthe

otherEqns.(A.13.3),(A.13.4)and(A.13.5)ofthisappendix;alloftheseequationsare

equallyvalidincarnationsoftheFirstLawofThermodynamics)

d1d ,

hP h

ρρερ

⎛⎞

−=−∇⋅−∇⋅++

⎜⎟

⎝⎠

FF S(A.13.1)

whereR

FisthesumoftheboundaryandradiativeheatfluxesandQ

Fisthesumofall

moleculardiffusivefluxesofheat,beingthenormalmolecularheatfluxdirecteddownthe

temperaturegradientplusatermproportionaltothemolecularfluxofsalt(theDufour

Effect,seeEqn.(B.24)below).Lastly,

istherateofdissipationofmechanicalenergyper

unitmass,transformedintointernalenergyandA

Sistherateofincreaseof

enthalpyduetotheinteriorsourcetermofAbsoluteSalinitycausedbyremineralization.

Thederivationof(A.13.1)issummarizedinappendixBbelow,wherewealsodiscussthe

relatedevolutionequationsfortotalenergyandfortheBernoullifunction.

FollowingFofonoff(1962)wenotethatanimportantconsequenceof(A.13.1)isthat

whentwofinitesizedparcelsofseawateraremixedatconstantpressureandunderideal

conditions,thetotalamountofenthalpyisconserved.Toseethisonecombines(A.13.1)

withthecontinuityequation

(

)

ρρ

∂∂+∇⋅ =utofindthefollowingdivergenceformof

theFirstLawofThermodynamics,

() ()

ht h h

ρρ ρερ

∂∂+∇⋅ −=−∇⋅−∇⋅++uFFS(A.13.2)

Onethenintegratesoverthevolumethatencompassesbothfluidparcelswhileassuming

theretobenoradiative,boundaryormolecularfluxesacrosstheboundaryofthecontrol

volume.Thiscontrolvolumemaychangewithtimeasthefluidmoves(atconstant

88 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

pressure),mixesandcontracts.Thedissipationofmechanicalenergybyviscousfriction

andthesourcetermduetotheproductionofAbsoluteSalinityarealsocommonlyignored

duringsuchmixingprocessesbutinfactthesetermsdocauseasmallincreaseinthe

enthalpyofthemixturewithrespecttothatofthetwooriginalparcels.Apartfromthese

non‐conservativesourceterms,undertheseassumptionsEqn.(A.13.2)reducestothe

statementthatthevolumeintegratedamountofh

isthesameforthetwoinitialfluid

parcelsasforthefinalmixedparcel,thatis,thetotalamountofenthalpyisunchanged.

Thisresultofnon‐equilibriumthermodynamicsisoftheutmostimportancein

oceanography.Thefactthatenthalpyisconservedwhenfluidparcelsmixatconstant

pressureisthecentralresultuponwhichallofourunderstandingof“heatfluxes”andof

“heatcontent”intheoceanrests.Theimportanceofthisresultcannotbeoveremphasized;

itmustformpartofallourintroductorycoursesonoceanographyandclimatedynamics.

Asimportantasthisresultis,itdoesnotfollowthatenthalpyisthebestvariableto

represent“heatcontent”intheocean.Enthalpyisaverypoorrepresentationof“heat

content”intheoceanbecauseitdoesnotpossesthe“potential”property.Itwillbeseen

thatpotentialenthalpy0

h(referencedtozeroseapressure)isthebestthermodynamic

variabletorepresent“heatcontent”intheocean.

TheFirstLawofThermodynamics(A.13.1)canbewritten(usingEqn.(A.7.2))asan

evolutionequationforentropyasfollows

()

dd .

Tt h

ρμ ρερ

⎛⎞

++ =−∇⋅−∇⋅++

⎜⎟

⎝⎠

FF S(A.13.3)

TheFirstLawofThermodynamics(A.13.1)canalsobewrittenintermsofpotential

temperature

(withrespecttoreferencepressurer

p)bysubstitutingEqns.(A.11.9)and

(A.11.11)intoEqn.(A.13.1)as(fromBaconandFofonoff(1996)andMcDougall(2003))

()

() () ( ) ( )

r0r

Tt S

cp p T t p

Tt t

ρμμ

ρε ρ

⎛⎞

+⎡⎤

+−+ =

⎜⎟

⎣⎦

⎜⎟

⎝⎠

−∇⋅ −∇⋅ + +FF S

(A.13.4)

where0

TistheCelsiuszeropoint(0

Tisexactly273.15K),whileintermsofConservative

TemperatureΘ,theFirstLawofThermodynamicsis(fromMcDougall(2003),usingEqns.

(A.11.15)and(A.11.18)above)

()

() () ()

()

Tt Tt S

Tt T t

ρμμ

θθ

ρε ρ

⎛⎞

⎡⎤

Θ+− =

⎜⎟

⎢⎥

⎜⎟

⎢⎥

⎣⎦

⎝⎠

−∇⋅ −∇⋅ + +FF S

(A.13.5)

where0

cisthefixedconstantdefinedbytheexact15‐digitnumberinEqn.(3.3.3).

InappendicesA.16,A.17andA.18thenon‐conservativeproductionofentropy,

potentialtemperatureandConservativeTemperaturearequantified,bothasTaylorseries

expansionswhichidentifytherelevantnon‐linearthermodynamictermsthatcausethe

productionofthesevariables,andalsoontheA

−

Θdiagramwherevariablesare

contouredwhichgraphicallyillustratethenon‐conservationofthesevariables.Inother

words,appendicesA.16,A.17andA.18quantifythenon‐idealnatureoftheleft‐handsides

ofEqns.(A.13.3)‐(A.13.5).Thatis,theseappendicesquantifythedeviationsoftheleft‐

handsidesoftheseequationsfrombeingproportionaltoddt

,ddt

andddt

Θ.

Aquickrankingofthesethreevariables,,



and,

fromtheviewpointofthe

amountoftheirnon‐conservation,canbegleanedbyexaminingtherangeoftheterms(at

fixedpressure)thatmultiplythematerialderivativesontheleft‐handsidesoftheabove

Eqns.(A.13.3),(A.13.4)and(A.13.5).Theoceancirculationmaybeviewedasaseriesof

adiabaticandisohalinemovementsofseawaterparcelsinterruptedbyaseriesofisolated

turbulentmixingevents.Duringanyoftheadiabaticandisohalinetransportstagesevery

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

“potential”propertyisconstant,soeachoftheabovevariables,entropy,potential

temperatureandConservativeTemperatureare100%idealduringtheseadiabaticand

isohalineadvectionstages.Theturbulentmixingeventsoccuratfixedpressuresothe

non‐conservativeproductionofsayentropydependsontheextenttowhichthe

coefficients

()

Tt+and

inEqn.(A.13.3)varyatfixedpressure.Similarlythenon‐

conservativeproductionofpotentialtemperaturedependsontheextenttowhichthe

coefficients

()

(

)( )

r0 0p

cpT t T

++and

(

)

(

)

(

)

0rT

pTt p

μμ

⎡

⎤

−+

⎣

⎦inEqn.(A.13.4)varyat

fixedpressure,whilethenon‐conservativeproductionofConservativeTemperature

dependsontheextenttowhichthecoefficients

(

)( )

TtT

++and

() ()( )( )

0pTtT

μθ

⎡⎤

−++

⎣⎦

inEqn.(A.13.5)varyatfixedpressure.

Accordingtothiswayoflookingattheseequationswenotethatthematerial

derivativeofentropyappearsinEqn.(A.13.3)multipliedbytheabsolutetemperature

()

Tt+whichvariesbyabout15%attheseasurface(

(

)

273.15 40 273.15 1.146+≈),the

termthatmultipliesddt

in(A.13.4)isdominatedbythevariationsintheisobaric

specificheat

()

cStpwhichismainlyafunctionofA

Sandwhichvariesby5%atthe

seasurface(seeFigure4),whilethematerialderivativeofConservativeTemperature

ddtΘinEqn.(A.13.5)ismultipliedbytheproductofaconstant“heatcapacity”0

cand

thefactor

()

(

)

TtT

++whichvariesverylittleintheocean,especiallywhenone

realizesthatitisonlythevariationofthisratioateachpressurelevelthatisofconcern.

Thisfactorisunityattheseasurfaceandisalsoveryclosetounityinthedeepocean.



FigureA.13.1.Contours(inC°)ofthedifference

−

Θbetweenpotential

temperature

andConservativeTemperature

atthe

seasurfaceoftheannually‐averagedatlasofGouretski

andKoltermann(2004).



Fortunately,ConservativeTemperatureisnotonlymuchmoreaccuratelyconserved

intheoceanthanpotentialtemperaturebutitisalsorelativelyeasytousein

oceanography.BecauseConservativeTemperaturealsopossessesthe“potential”

property,itisaveryaccuraterepresentationofthe“heatcontent”ofseawater.The

difference

−Θbetweenpotentialtemperature

andConservativeTemperatureΘat

theseasurfaceisshowninFigureA.13.1(afterMcDougall,2003).Ifanoceanmodelis

90 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

writtenwithpotentialtemperatureastheprognostictemperaturevariableratherthan

ConservativeTemperature,andisrunwiththesameconstantvalueoftheisobaricspecific

heatcapacity(0

casgivenbyEqn.(3.3.3)),theneglectofthenon‐conservativesource

termsthatshouldappearintheprognosticequationfor

meansthatsuchanocean

modelincurserrorsinthemodeloutput.Theseerrorswilldependonthenatureofthe

surfaceboundarycondition;forfluxboundaryconditionstheerrorsareasshownin

FigureA.13.1.

Thisappendixhaslargelydemonstratedthebenefitsofpotentialenthalpyand

ConservativeTemperaturefromtheviewpointofconservationequations,butthebenefits

canalsobeprovenbythefollowingparcel‐basedargument.First,theair‐seaheatflux

needstoberecognizedasafluxofpotentialenthalpywhichisexactly0

ctimesthefluxof

ConservativeTemperature.Second,theworkofappendixA.18showsthatwhileitisthe

insituenthalpythatisconservedwhenparcelsmix,anegligibleerrorismadewhen

potentialenthalpyisassumedtobeconservedduringmixingatanydepth.Third,note

thattheoceancirculationcanberegardedasaseriesofadiabaticandisohalinemovements

duringwhichΘisabsolutelyunchanged(becauseofits“potential”nature)followedbya

seriesofturbulentmixingeventsduringwhich

isalmosttotallyconserved.Henceitis

clearthatΘisthequantitythatisadvectedanddiffusedinanalmostconservativefashion

andwhosesurfacefluxisexactlyproportionaltotheair‐seaheatflux.



A.14 Advective and diffusive “heat” fluxes

Insection3.23andappendicesA.8andA.13theFirstLawofThermodynamicsisshownto

bepracticallyequivalenttotheconservationequation(A.21.15)forConservative

Temperature.ΘWehaveemphasizedthatthismeansthattheadvectionof“heat”isvery

accuratelygivenastheadvectionof0.

Inthisway0

canberegardedasthe“heat

content”perunitmassofseawaterandtheerrorinvolvedwithmakingthisassociationis

approximately1%oftheerrorinassumingthateither0

or

(

)

A,,0dbar

isthe

“heatcontent”perunitmassofseawater(seealsoappendixA.21foradiscussionofthis

point).

Theconservativeform(A.21.15)impliesthattheturbulentdiffusivefluxofheatshould

bedirecteddownthemeangradientofConservativeTemperatureratherthandownthe

meangradientofpotentialtemperature.Inthisappendixwequantifythedifference

betweenthesemeantemperaturegradients.

Considerfirsttherespectivetemperaturegradientsalongtheneutraltangentplane.

FromEqn.(3.11.2)wefindthat

()

(

)

nn n

θθ

αβ θ αβ

ΘΘ

∇=∇ = ∇Θ(A.14.1)

sothattheepineutralgradientsof

and

arerelatedbytheratiosoftheirrespective

thermalexpansionandsalinecontractioncoefficients,namely

(

)

()

θθ

αβ

θαβ

ΘΘ

∇= ∇Θ(A.14.2)

Thisproportionalityfactorbetweentheparalleltwo‐dimensionalvectorsn

∇andn

∇Θis

readilycalculatedandillustratedgraphically.Beforedoingsowenotetwoother

equivalentexpressionsforthisproportionalityfactor.

Theepineutralgradientsof

,

andA

Sarerelatedby(using

()

ˆ,S

θθ

Θ)

ˆˆ

nnSn

θθ θ

∇=∇Θ+ ∇ (A.14.3)

andusingtheneutralrelationship

(

)

Ann

αβ

ΘΘ

∇

=∇Θwefind

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

()

ˆˆ

nSn

θθ αβθ

ΘΘ

Θ⎡⎤

∇= + ∇Θ

⎣⎦ (A.14.4)

Also,insection3.13wefoundthat,

bn bn

∇

=∇Θsothatwecanwritetheequivalent

expressions

()

ˆˆ

nbS

θθ

αβ

αβθ

αβ

ΘΘ ΘΘΘ

∇⎡⎤

===+

⎣⎦

∇Θ (A.14.5)

anditcanbeshownthatˆ

αθ

=and

(

)

ˆˆ

βαβθθ

ΘΘΘ

⎡⎤

⎣⎦ ,thatis,

ˆˆ

βαθθ

ΘΘ

=+ Thepartialderivativesˆ

andA

ˆS

inthelastpartofEqn.(A.14.5)

arebothindependentofpressurewhile

Θisafunctionofpressure.Thisratio,Eqn.

(A.14.5),oftheepineutralgradientsof

and

isshowninFigureA.14.1at0p=,

indicatingthattheepineutralgradientofpotentialtemperatureissometimesmorethat1%

differenttothatofConservativeTemperature.Thisrationn

∇

∇Θisonlyaweak

functionofpressure.Thisratio,nn

∇

∇Θ(i.e.Eqn.(A.14.5)),isavailableintheGSW

OceanographicToolboxasfunctiongsw_ntp_pt_vs_CT_ratio_CT25.

SimilarlytoEqn.(A.14.3),theverticalgradientsarerelatedby

ˆˆ

zzS

θθ θ

=Θ+ (A.14.6)

andusingthedefinition,Eqn.(3.15.1),ofthestabilityratiowefindthat

ˆˆ

αβθ

−ΘΘ

Θ⎡⎤

=+⎣⎦

Θ(A.14.7)

Forvaluesofthestabilityratio

closetounity,theratiozz

isclosetothevaluesof

∇∇ΘshowninFigureA.14.1.ForothervaluesofR

,Eqn.(A.14.7)canbe

calculatedandplotted.



FigureA.14.1.Contoursof

()

1100%

∇∇Θ−× at0p

,showingthepercentage

differencebetweentheepineutralgradientsof

andΘ.Thebluedots

arefromtheoceanatlasofGouretskiandKoltermann(2004)at0p=.



Asnotedinsection3.8thedianeutraladvectionofthermobaricityisthesamewhen

quantifiedintermsofpotentialtemperatureaswhendoneintermsofConservative

Temperature.Thesameisnottrueofthedianeutralvelocitycausedbycabbeling.Theratio

ofthecabbelingdianeutralvelocitycalculatedusingpotentialtemperaturetothatusing

ConservativeTemperatureisgivenby

(

)

(

)

bbnn n n

θθθ

∇

⋅∇ ∇ Θ⋅∇ Θ (seesection3.9)which

canbeexpressedas

92 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

()

bbbbb

bbbb

ˆˆ

CCCTC

CCTC

θθθθ

θθ

αβ

θθαβθ

αβ

ΘΘ ΘΘΘ

ΘΘΘ

⎛⎞

∇⎡⎤

===+

⎜⎟ ⎣⎦

∇Θ ⎝⎠ (A.14.8)

andthisiscontouredinFig.A.14.2.WhiletheratioofEqn.(A.14.8)isnotexactlyunity,it

variesrelativelylittleintheoceanographicrange,indicatingthatthedianeutraladvection

duetocabbelingestimatedusing

or

arewithinhalfapercentofeachotherat0p=.



FigureA.14.2.Contoursofthepercentagedifferenceof

(

)()

bbnn

θθ

∇

∇Θ 

fromunityat0p

dbar.



A.15 Derivation of the expressions for ,,

θθ

βα

and

ThisappendixderivestheexpressionsinEqns.(2.18.2)–(2.18.3)and(2.19.2)–(2.19.3)for

thethermalexpansioncoefficients

and

andthehalinecontractioncoefficients



and.

Θ

InordertoderiveEqn.(2.18.2)for

wefirstneedanexpressionforA,.

∂∂ This

isfoundbydifferentiatingwithrespecttoinsitutemperaturetheentropyequality

()

[

]

()

AAArr

,, , ,, , ,Stp S Stpp p

ηηθ

=whichdefinespotentialtemperature,obtaining

(

)

()

(

)

()

Ar Ar

,, ,, .

,, ,,

TTT

Stp g Stp

TSpgSp

ηθ θ

∂==

∂(A.15.1)

ThisisthenusedtoobtainthedesiredexpressionEqn.(2.18.2)for

asfollows

()

AAA

AAr

,,,

,, , ,

11 .

,, ,,

TP TT

PTT

Sp Sp Sp

Stpg S p

v v T T g S tp g S tp

αθ

−

⎛⎞

∂∂∂

== =

⎜⎟

∂∂∂

⎝⎠

(A.15.2)

InordertoderiveEqn.(2.18.3)for

wefirstneedanexpressionforA,.

t∂Θ ∂ This

isfoundbydifferentiatingwithrespecttoinsitutemperaturetheentropyequality

()

[

]

()

AAA

,, , ,,

Stp S Stp

ηη

=Θ obtaining

() ()( )

A0A

,, ,, ,

TTTp

Sp S

Stp T g Stpc

ηθ

∂Θ ∂Θ

==−+

∂∂ (A.15.3)

wherethesecondpartofthisequationhasusedEqn.(A.12.4)for

ΘThisisthenused

toobtainthedesiredexpressionEqn.(2.18.3)for

asfollows

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

()

()( )

AAA

A0 A

,,,

11 .

,, ,,

PTT

Sp Sp Sp

gStp

vvTT gStpTgStp

αθ

−

Θ⎛⎞

∂∂∂Θ

== =−

⎜⎟

∂Θ ∂ ∂ +

⎝⎠

(A.15.4)

InordertoderiveEqn.(2.19.2)for

wefirstneedanexpressionforA,.

∂∂ This

isfoundbydifferentiatingwithrespecttoAbsoluteSalinitytheentropyequality

()

[

]

()

AAArr

,, , ,, , ,Stp S Stpp p

ηηθ

=whichdefinespotentialtemperature,obtaining

()( )

()

()()

()()()

AAr

Ar A

AArAr

,, , ,

,, ,,

,, ,, ,, ,

ST ST TT

Stp S p

TSp Stp

cS p

Stp g S p g S p

θθη η θ

θμθ μ

θθ

∂⎡⎤

=−

⎣⎦

∂

+⎡⎤

=−

⎣⎦

⎡⎤

=−

⎣⎦

(A.15.5)

whereEqns.(A.12.5)and(A.12.7)havebeenusedwithageneralreferencepressurer

p

ratherthanwithr0.p=Bydifferentiating

[

]

(

)

AA r

,,,,,SStppp

ρρ θ

=withrespectto

AbsoluteSalinityitcanbeshownthat(Gill(1982),McDougall(1987a))

AAA

,,,

11 ,

pTpTp

SSS

θθ

ρρθ

βα

ρρ

∂∂∂

== +

∂∂∂

(A.15.6)

andusingEqn.(A.15.5)wearriveatthedesiredexpressionEqn.(2.19.2)for



()

()()( )

()()

AAA Ar

AAA

,, ,, , ,

,, .

,, ,, ,,

TP S T S T

PPTT

gStp Stp S p

gStp

g S tp g S tpg S tp

θθ

⎡

⎤

−

⎣

⎦

=− + (A.15.7)

NotethatthetermsinthenaturallogarithmofthesquarerootofAbsoluteSalinitycancel

fromthetwopartsofthesquarebracketsinEqns.(A.15.5)and(A.15.7).

InordertoderiveEqn.(2.19.3)for

wefirstneedanexpressionforA,.

S∂Θ ∂ 

ThisisfoundbydifferentiatingwithrespecttoAbsoluteSalinitytheentropyequality

()

[

]

()

AAA

,, , ,,Stp S Stp

ηη

=Θ obtaining(usingEqns.(A.12.4)and(A.12.8))

()

()()()

A0A

A0 A

,,0 ,,

,,0 ,, .

SSTp

Stp

STStpc

STgStpc

ηηη

μθ θμ

θθ

∂Θ ⎡⎤

=Θ −

⎣⎦

∂

⎡⎤

=−+

⎣⎦

⎡⎤

=−+

⎣⎦

(A.15.8)

Differentiating

[]

(

)

ˆ,,,,SStpp

ρρ

=Θ withrespecttoAbsoluteSalinityleadsto

AAA

,,,

11 ,

pTpTp

SSS

ρρ

βα

ρρ

ΘΘ

∂∂∂Θ

==+

∂∂∂

(A.15.9)

andusingEqn.(A.15.8)wearriveatthedesiredexpression(2.19.3)for

Θnamely

()

()()()()

()()

AAAA0

AAA

,, ,, , ,0

,, .

,, ,, ,,

TP S T S

PPTT

gStp Stp S T

gStp

g S tp g S tpg S tp

θθ

⎡

⎤

−+

⎣

⎦

=− + (A.15.10)

NotethatthetermsinthenaturallogarithmofthesquarerootofAbsoluteSalinitycancel

fromthetwopartsofthesquarebracketsinEqns.(A.15.8)and(A.15.10).



94 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

A.16 Non-conservative production of entropy

Inthisandthefollowingthreeappendices(A.16–A.19)thenon‐conservativenatureof

severalthermodynamicvariables(entropy,potentialtemperature,Conservative

Temperatureandpotentialdensity)willbequantifiedbyconsideringthemixingofpairs

ofseawaterparcelsatfixedpressure.Themixingistakentobecompletesothattheend

stateisaseawaterparcelthatishomogeneousinAbsoluteSalinityandentropy.Thatis,

wewillbeconsideringmixingtocompletionbyaturbulentmixingprocess.Inappendix

A.20thenon‐conservativeproductionofAbsoluteSalinitybytheremineralizationof

particulateorganicmatterisconsidered.Thisprocessisnotbeingconsideredin

appendicesA.16–A.19.Thenon‐conservativeproductionwhichisquantifiedin

appendicesA.16–A.19occursintheabsenceofanyvariationinseawatercomposition.

FollowingFofonoff(1962),considermixingtwofluidparcels(parcels1and2)that

haveinitiallydifferenttemperaturesandsalinities.Themixingprocessoccursatpressure

.pThemixingisassumedtohappentocompletionsothatinthefinalstateAbsolute

Salinity,entropyandalltheotherpropertiesareuniform.Assumingthatthemixing

happenswithavanishinglysmallamountofdissipationofmechanicalenergy,the

term

canbedroppedfromtheFirstLawofThermodynamics,(A.13.1),thisequationbecoming

() ( )

ρρ

+∇⋅ = −∇⋅ −∇⋅uFFatconstantpressure(A.16.1)

Notethatthisequationhastheform(A.8.1)andsohisconservedduringmixingat

constantpressure,thatis,his“isobaricconservative”.Inthecaseweareconsideringof

mixingthetwoseawaterparcels,thesystemisclosedandtherearenoradiative,boundary

ormolecularheatfluxescomingthroughtheoutsideboundarysotheintegraloverspace

andtimeoftheright‐handsideofEqn.(A.16.1)iszero.Thesurfaceintegralof

()

u

throughtheboundaryisalsozero.Henceitisapparentthatthevolumeintegralofh

is

thesameatthefinalstateasitisattheinitialstate,thatis,enthalpyisconserved.Hence

duringthemixingprocessthemass,saltcontentandenthalpyareconserved,thatis

12 ,mmm

=(A.16.2)

1A1 2A2 A

,mS mS mS+=(A.16.3)

11 2 2 ,mh mh mh+=(A.16.4)

whilethenon‐conservativenatureofentropymeansthatitobeystheequation,

11 2 2 .mm mm

ηδηη

++=(A.16.5)

HereA,Shand

arethevaluesofAbsoluteSalinity,enthalpyandentropyofthefinal

mixedfluidand

istheproductionofentropy,thatis,theamountbywhichentropyis

notconservedduringthemixingprocess.Entropy

isnowregardedasthefunctional

form

()

A,,Shp

ηη

=andisexpandedinaTaylorseriesofA

Sandhaboutthevaluesof

Sandhofthemixedfluid,retainingtermstosecondorderin

[

]

A2 A1 A

SS S

−

=Δ andin

[]

21 .hh h−=ΔThen1

and2

areevaluatedand(A.16.4)and(A.16.5)usedtofind

() ( )

{

}

AAA

1AA

222.

hh hS S S

mm hhS S

δη η η η

=− Δ + Δ Δ + Δ

  (A.16.6)

Towardstheendofthissectiontheimplicationsoftheproduction(A.16.6)ofentropy

willbequantified,butfornowweaskwhatconstraintstheSecondLawof

ThermodynamicsmightplaceontheformoftheGibbsfunction

(

)

A,,

Stpofseawater.

TheSecondLawofThermodynamicstellsusthattheentropyexcess

mustnotbe

negativeforallpossiblecombinationsofthedifferencesinenthalpyandsalinitybetween

thetwofluidparcels.From(A.16.6)thisrequirementimpliesthefollowingthree

inequalities,

 0,

(A.16.7)

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

AA 0,

(A.16.8)

()

AAA

hS hh S S

ηηη



(A.16.9)

wherethelastrequirementreflectstheneedforthediscriminantofthequadraticin

(A.16.6)tobenegative.SinceentropyisalreadyafirstderivativeoftheGibbsfunction,

theconstraintswouldseemtobethreedifferentconstraintsonvariousthirdderivativeof

theGibbsfunction.Infact,wewillseethattheyamounttoonlytworatherwell‐known

constraintsonsecondorderderivativesoftheGibbsfunction.

Fromthefundamentalthermodynamicrelation(A.7.1)wefindthat(whereTisthe

absolutetemperature,0

TT t=+)



hSp

−

∂

(A.16.10)

∂

==−

∂

(A.16.11)

andfromtheserelationsthefollowingexpressionsforthesecondorderderivativesof



canbefound,

212

hh p

Sp Sp

−−

∂∂ −

== =

∂

(A.16.12)

(

)

Sh pT

pSp

hS h c T

ημ

∂−

∂⎛⎞

== =−

⎜⎟

∂∂ ∂ ⎝⎠

(A.16.13)

and

(

)

(

)

,,,

hp Tp S p

ShS

TcT

μμ

∂− ∂−

∂∂

== −

∂∂∂

∂

⎡⎤

⎛⎞

=− − ⎢⎥

⎜⎟

⎝⎠

⎣⎦



(A.16.14)

ThelastequationcomesfromregardingA

as

[

]

(

)

,,,,.

ShStpp

ηη

 

Theconstraint(A.16.7)that0

simplyrequires(from(A.16.12))thattheisobaric

heatcapacityp

cispositive,orthat0.

Theconstraint(A.16.8)thatAA 0,



requires(from(A.16.14))that

SS pT

gcT

⎡

⎤

⎛⎞

>−

⎢

⎥

⎜⎟

⎝⎠

⎣

⎦(A.16.15)

thatis,thesecondderivativeoftheGibbsfunctionwithrespecttoAbsoluteSalinityAA

g

mustexceedsomenegativenumber.Theconstraint(A.16.9)that

()

AAA

hS hh S S

ηηη





requiresthat(substitutingfrom(A.16.12),(A.16.13)and(A.16.14))

30,

Tc >(A.16.16)

andsincetheisobaricheatcapacitymustbepositive,thisrequirementisthatAA 0,

g>

andsoismoredemandingthan(A.16.15).

Weconcludethatwhiletherearethethreerequirements(A.16.7)to(A.16.9)onthe

functionalformofentropy

()

A,,Shp

ηη

=inordertosatisfytheconstraintoftheSecond

LawofThermodynamicsthatentropybeproducedwhenwaterparcelsmix,thesethree

constraintsaresatisfiedbythefollowingtwoconstraintsontheformoftheGibbsfunction

()

A,,

Stp,

(A.16.17)

and

AA 0.

g>(A.16.18)

96 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

TheSecondLawofThermodynamicsdoesnotimposeanyadditionalrequirementonthe

crossderivativesA

noronanythirdorderderivativesoftheGibbsfunction.

Theconstraint(A.16.18)canbeunderstoodbyconsideringthemoleculardiffusionof

saltwhichisknowntobedirecteddownthegradientofchemicalpotential

()

A,,Stp



(LandauandLifshitz(1959)).Thatis,themolecularfluxofsaltisproportionalto.

−∇ 

Expanding

−∇ intermsofgradientsofAbsoluteSalinity,oftemperature,andof

pressure,onefindsthatthefirsttermisAASS

−

∇andinordertoavoidanunstable

explosionofsaltonemusthaveAAA

SSS

>Sotheconstraint(A.16.18)amountsto

therequirementthatthemoleculardiffusivityofsaltispositive.

Thetwoconstraints(A.16.17)and(A.16.18)ontheGibbsfunctionarewellknownin

thethermodynamicsliterature.LandauandLifshitz(1959)derivethemonthebasisofthe

contributionofmolecularfluxesofheatandsalttotheproductionofentropy(their

equations58.9and58.13).Alternatively,Planck(1935)aswellasLandauandLifshitz

(1980)intheir§96(thisis§98ineditionsbeforethe1976extensionmadebyLifshitzand

Pitayevski)inferredsuchinequalitiesfromthermodynamicstabilityconsiderations.Itis

pleasingtoobtainthesameconstraintsontheseawaterGibbsfunctionfromtheabove

Non‐EquilibriumThermodynamicsapproachofmixingfluidparcelssincethisapproach

involvesturbulentmixingwhichisthetypeofmixingthatdominatesintheocean;

(moleculardiffusionhasthecomplementaryroleofdissipatingtracervariance).

InadditiontotheSecondLawrequirements(A.16.17)and(A.16.18)thereareother

constraintswhichtheseawaterGibbsfunctionmustobey.Oneisthattheadiabatic(and

isohaline)compressibilitymustbepositiveforotherwisethefluidwouldexpandin

responsetoanincreaseinpressurewhichisanunstablesituation.Taking0

g>(since

specificvolumeneedstobepositive)therequirementthattheadiabatic(andisohaline)

compressibilitybepositiveimposesthefollowingtwoconstraints(from(2.16.1))

(A.16.19)

and

()

TP PP TT

gg<(A.16.20)

recognizingthatTT

isnegative(TP

may,anddoes,takeeithersign).Equation(A.16.20)

ismoredemandingof

thanis(A.16.19),requiring

tobelessthananegative

numberratherthansimplybeinglessthanzero.Thislastinequalitycanalsoberegarded

asaconstraintonthethermalexpansioncoefficientt

,implyingthatitssquaremustbe

lessthan2

PP TT

−orotherwisetherelevantcompressibility(

)wouldbenegativeand

thesoundspeedcomplex.

TheconstraintsontheseawaterGibbsfunction

(

)

A,,

Stp

thathavebeendiscussed

abovearesummarizedas

g> AA 0

g>, 0,

0,

and

()

TP PP TT

gg<(A.16.21)

Wereturnnowtoquantifythenon‐conservativeproductionofentropyintheocean.

Whenthemixingprocessoccursat0,p

theexpression(A.16.6)fortheproductionof

entropycanbeexpressedintermsofConservativeTemperature

(sinceΘissimply

proportionaltohat0p=)asfollows(nowentropyistakentobethefunctionalform

()

ˆ,S

ηη

=Θ)

() ( )

{

}

AAA

1AA

22ˆˆ ˆ

SSS

mm SS

δη η η η

ΘΘ Θ

=− ΔΘ + ΔΘΔ + Δ (A.16.22)

Themaximumproductionoccurswhenparcelsofequalmassaremixedsothat

mmm

−=andweadoptthisvalueinwhatfollows.Toillustratethemagnitudeof

thisnon‐conservationofentropywefirstscaleentropybyadimensionalconstantsothat

theresultingvariable(“entropictemperature”)hasthevalue25 C°at

()( )

ASO

,,25CSSΘ= ° andthenΘissubtracted.TheresultiscontouredinA

S−Θspace

inFigureA.16.1.

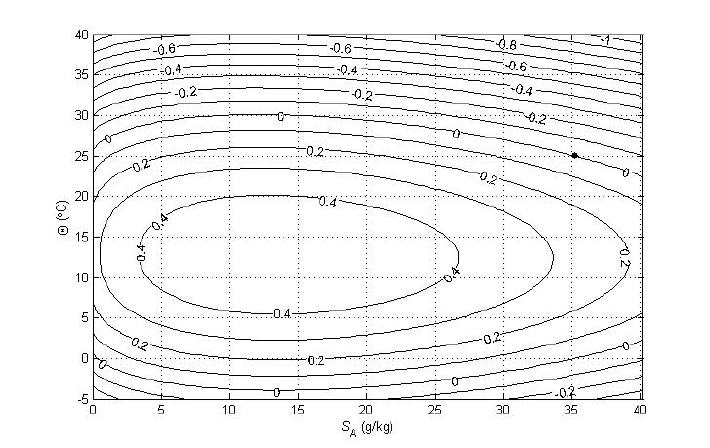
TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

FigureA.16.1.Contours(inC°)ofavariablewhichillustratesthenon‐conservative

productionofentropy

intheocean.



ThefactthatthevariableinFigureA.16.1isnotzerooverthewholeA

S−Θplaneis

becauseentropyisnotaconservativevariable.Thenon‐conservativeproductionof

entropycanbereadoffthisfigurebyselectingtwoseawatersamplesandmixingalong

thestraightlinebetweentheseparcelsandthenreadingofftheproduction(inC°)of

entropyfromthefigure.Takingthemostextremesituationwithoneparcelat

()

A,0gkg,0CS−

Θ= ° andtheotheratthewarmestandsaltiestcornerofthefigure,the

non‐conservativeproductionof

onmixingparcelsofequalmassisapproximately

0.9 C°.

Sinceentropycanbeexpressedindependentlyofpressureasafunctionofonly

AbsoluteSalinityandConservativeTemperature

(

)

ˆ,S

ηη

Θ,andsinceatanypressure

intheoceanbothA

SandΘmaybeconsideredconservativevariables(seeappendixA.18

below),itisclearthatthenon‐conservativeproductiongivenby(A.16.22)andillustrated

inFigureA.16.1isequivalenttotheslightlymoreaccurateexpression(A.16.6)which

appliesatanypressure.Theonlydiscrepancybetweentheproductionofentropy

calculatedfrom(A.16.22)andthatfrom(A.16.6)isduetotheverysmallnon‐conservative

productionofΘatpressuresotherthanzero(aswellasthefactthatbothexpressions

containonlythesecondordertermsinaninfiniteTaylorseries).



A.17 Non-conservative production of potential temperature

Whenfluidparcelsundergoirreversibleandcompletemixingatconstantpressure,the

thermodynamicquantitiesthatareconservedduringthemixingprocessaremass,

AbsoluteSalinityandenthalpy.AsinsectionA.16weagainconsidertwoparcelsbeing

mixedwithoutexternalinputofheatormassandthethreeequationsthatrepresentthe

conservationofthesequantitiesareagainEqns.(A.16.2)–(A.16.4).Potentialtemperature

isnotconservedduringthemixingprocessandtheproductionofpotential

temperatureisgivenby

11 2 2 .mmm m

θδθ θ

++=(A.17.1)

Enthalpyinthefunctionalform

(

)

A,,hhS p

=isexpandedinaTaylorseriesofA

Sand

aboutthevaluesA

Sand

ofthemixedfluid,retainingtermstosecondorderin

98 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

[]

A2 A1 A

SS S−=Δandin

[]

21 .

θθ

−=ΔThen1

hand2

hareevaluatedandEqns.(A.16.4)

and(A.17.1)usedtofind

() ()

AAA

1AA

222.

SSS

mm SS

hh h

θθ

θθ θ

δθ θ θ

⎧⎫

⎪⎪

=Δ+ΔΔ+Δ

⎨⎬

⎪⎪

⎩⎭





 

(A.17.2)

Themaximumproductionoccurswhenparcelsofequalmassaremixedsothat

.mmm

−=The“heatcapacity”h

isnotastrongfunctionof

butisamuch

strongerfunctionofA

SsothefirstterminthecurlybracketsinEqn.(A.17.2)isgenerally

smallcomparedwiththesecondterm.Also,thethirdterminEqn.(A.17.2)whichcauses

theso‐called“dilutionheating”,isusuallysmallcomparedwiththesecondterm.A

typicalvalueofA

isapproximately–5.411 11

Jkg K (gkg )

−

−−−

(seethedependenceof

isobaricheatcapacityonA

SinFigure4ofsection2.20)sothatanapproximateexpression

fortheproductionofpotentialtemperature

is

()

1AA

43.4 10 / [g kg ] .

hSh x S

θθ

−−

≈Δ ≈− Δ

 (A.17.3)

Sincepotentialtemperature

(

)

ˆ,S

θθ

Θcanbeexpressedindependentlyofpressure

asafunctionofonlyAbsoluteSalinityandConservativeTemperature,andsinceduring

turbulentmixingbothA

SandΘmaybeconsideredconservativevariables(seesection

A.18below),itisclearthatthenon‐conservativeproductiongivenby(A.17.2)canbe

approximatedbythecorrespondingproductionofpotentialtemperaturethatwouldoccur

ifthemixinghadoccurredat0p=,namely

() ()

AAA

1AA

222SSS

mm SS

θθ

θθ θ

δθ θ θ

ΘΘ

⎧⎫

=Δ+ΔΔ+Δ

⎨⎬

ΘΘ Θ

⎩⎭

,(A.17.4)

wheretheexactproportionalitybetweenpotentialenthalpyandConservative

Temperature00

hc≡Θhasbeenexploited.Themaximumproductionoccurswhenparcels

ofequalmassaremixedsothat2

mmm

−

andweadoptthisvalueinwhatfollows.

Equations(A.17.2)or(A.17.4)maybeusedtoevaluatethenon‐conservative

productionofpotentialtemperatureduetomixingapairoffluidparcelsacrossafrontat

whichthereareknowndifferencesinsalinityandtemperature.Thetemperature

difference

−ΘiscontouredinFigureA.17.1andcanbeusedtoillustrateEqn.(A.17.4).

canbereadoffthisfigurebyselectingtwoseawatersamplesandmixingalongthe

straightlinebetweentheseparcels(alongwhichbothAbsoluteSalinityandConservative

Temperatureareconserved)andthencalculatingtheproduction(inC°)of

fromthe

contouredvaluesof

−Θ.Takingthemostextremesituationwithoneparcelat

()

A,0gkg,0CS−

Θ= ° andtheotheratthewarmestandsaltiestcornerofFigureA.17.1,

thenon‐conservativeproductionof

onmixingparcelsofequalmassisapproximately‐

0.55C°.Thisistobecomparedwiththecorrespondingmaximumproductionofentropy,

asdiscussedaboveinconnectionwithFigureA.16.1,ofapproximately0.9C°.

IfFigureA.17.1weretobeusedtoquantifytheerrorsinoceanographicpractice

incurredbyassumingthat

isaconservativevariable,onemightselectproperty

contraststhatweretypicalofaprominentoceanicfrontanddecidethatbecause

is

smallatthisonefront,thattheissuecanbeignored(seeforexample,Warren(2006)).But

theobservedpropertiesintheoceanresultfromalargeandindeterminatenumberofsuch

priormixingeventsandthenon‐conservativeproductionof

accumulatesduringeachof

thesemixingevents,ofteninasign‐definitefashion.Howcanwepossiblyestimatethe

errorthatismadebytreatingpotentialtemperatureasaconservativevariableduringall

oftheseunknowablymanypastindividualmixingevents?Thisseeminglydifficultissue

ispartiallyresolvedbyconsideringwhatisactuallydoneinoceanmodelstoday.These

modelscarryatemperatureconservationequationthatdoesnothavenon‐conservative

sourceterms,sothatthemodel’stemperaturevariableisbestinterpretedasbeingΘ.This

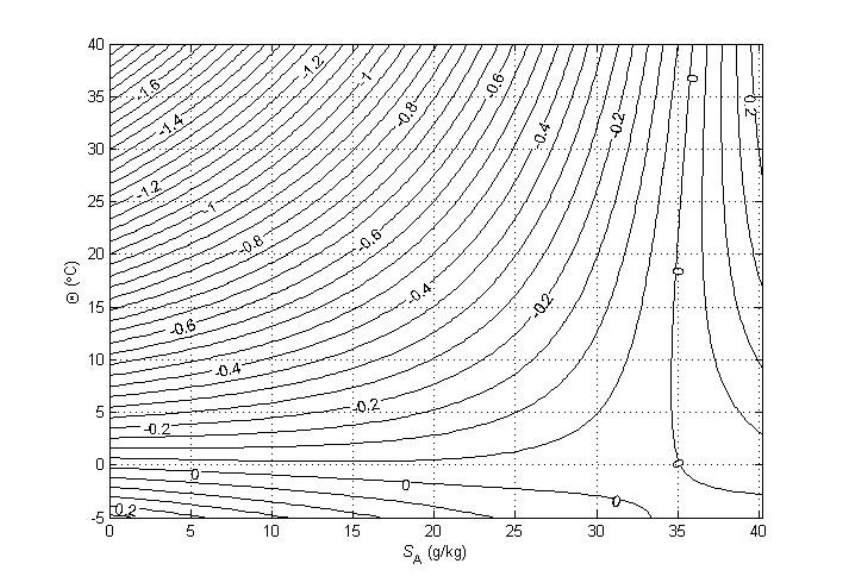
TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

beingthecase,thetemperaturedifferencecontouredinFigureA.17.1illustratestheerror

thatismadebyinterpretingthemodeltemperatureasbeing

.Thatis,thevalues

contouredinFiguresA.16.1andA.17.1arerepresentativeoftheerror,expressedinC°,

associatedwithassumingthat

and

respectivelyareconservativevariables.These

contouredvaluesoftemperaturedifferenceencapsulatetheaccumulatednon‐conservative

productionthathasoccurredduringallthemanymixingprocessesthathaveleadtothe

ocean’spresentstate.Themaximumsucherrorfor

isapproximately‐1.0C°(from

FigureA.16.1)whilefor

themaximumerrorisapproximately‐1.8C°(fromFigure

A.17.1).Onepercentofthedataattheseasurfaceoftheworldoceanhavevaluesof

−Θ

thatlieoutsidearangethatis0.25C°wide(McDougall(2003)),implyingthatthisisthe

magnitudeoftheerrorincurredbyoceanmodelswhentheytreat

asaconservative

quantity.FromthecurvatureoftheisolinesonFigureA.17.1itisclearthatthenon‐

conservativeproductionofpotentialtemperaturetakesbothpositiveandnegativesigns.



FigureA.17.1.Contours(inC°)ofthedifferencebetweenpotentialtemperature

andConservativeTemperature

−

Θ.Thisplotillustratesthenon‐

conservativeproductionofpotentialtemperature

intheocean.



A.18 Non-conservative production of Conservative Temperature

Whenfluidparcelsundergoirreversibleandcompletemixingatconstantpressure,the

thermodynamicquantitiesthatareconservedduringthemixingprocessaremass,

AbsoluteSalinityandenthalpy.AsinsectionsA.16andA.17weconsidertwoparcels

beingmixedwithoutexternalinputofheatormassandthethreeequationsthatrepresent

theconservationofthesequantitiesareagainEqns.(A.16.2)–(A.16.4).Potentialenthalpy

handConservativeTemperature

arenotexactlyconservedduringthemixingprocess

andtheproductionofΘisgivenby

100 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

11 2 2 .mmmm

Θ+ Θ+ Θ= Θ(A.18.1)

Enthalpyinthefunctionalform

(

)

ˆ,,hhS p=Θ

isexpandedinaTaylorseriesofA

Sand



aboutthevaluesA

SandΘofthemixedfluid,retainingtermstosecondorderin

[]

A2 A1 A

SS S−=Δ

andin

[]

21 .Θ−Θ =ΔΘThen1

hand2

hareevaluatedandEqns.(A.16.4)

and(A.18.1)areusedtofind

() ()

AAA

1AA

ˆˆ

ˆˆ ˆ

SSS

mm SS

mhh h

ΘΘ

ΘΘ Θ

⎧⎫

⎪⎪

Θ= ΔΘ + ΔΘΔ + Δ

⎨⎬

⎪⎪

⎩⎭

(A.18.2)

Inordertoevaluatethesepartialderivatives,wefirstwriteenthalpyintermsofpotential

enthalpy(i.e.0

cΘ)usingEqn.(3.2.1),as

() ( )

ˆˆ

,, ,, .

hhSpc vSpdP

′

=Θ=Θ+ Θ

∫(A.18.3)

Thisisdifferentiatedwithrespectto

giving

ˆ.

Sp P

hhc dP

αρ

ΘΘ

′

==+

∫(A.18.4)

Theright‐handsideofEqn.(A.18.4)scalesas

(

)

cPP

−

+− whichismorethan0

c

byonlyabout0

0.0015 p

cfor

()

P−of7

410×Pa(4,000dbar).Hence,toaverygood

approximation,ˆ

hΘinEqn.(A.18.2)maybetakentobesimply0

c.Itisinterestingto

examinewhythisapproximationissoaccuratewhenthedifferencebetweenenthalpy,,h

andpotentialenthalpy,0,hasgivenbyEqns.(3.2.1)and(A.18.3),scalesas1

−whichis

aslargeastypicalvaluesofpotentialenthalpy.ThereasonisthattheintegralinEqns.

(3.2.1)or(A.18.3)isdominatedbytheintegralofthemeanvalueof1,

−socausinga

significantoffsetbetweenhand0

hasafunctionofpressurebutnotaffectingthepartial

derivativeˆ

hΘwhichistakenatfixedpressure.Eventhedependenceofdensityon

pressurealonedoesnotaffectˆ.hΘ

Thesecondorderderivativesofˆ

hareneededinEqn.(A.18.2),andthesecanbe

estimatedintermsofthestrengthofcabbelingasfollows.Equation(A.18.4)is

differentiatedwithrespecttoConservativeTemperature,giving

(

)

ˆˆ,

h v dP dP

αρ

ΘΘ ΘΘ Θ

′

∫∫ (A.18.5)

sothatwemaywriteEqn.(A.18.2)approximatelyas(assuming12

)

(

)() ( )

{

}

AAA

0ˆˆ ˆ

8SSS

PP vvSvS

ΘΘ Θ

−

Θ≈ ΔΘ + ΔΘΔ + Δ (A.18.6)

ThedominantterminEqn.(A.18.6)isusuallytheterminˆ

Θwhichisapproximately

2ˆ

−ΘΘ

−,andfromEqn.(A.19.4)belowweseethat

isapproximatelyproportionalto

thenon‐conservativeproductionofdensityatfixedpressure,oftenreferredtolooselyas

“cabbeling”(McDougall,1987b),thatis,

()

(

)()

(

)

000

00220

ˆ.

ppp

PP PP PP

ccc

δρ

ρρ

ΘΘ

−−−

Θ ≈ ΔΘ ≈ − ΔΘ ≈ (A.18.7)

TheproductionofΘcausesanincreaseintemperatureandaconsequentdecreasein

densityof

αδ

−Θ.Theratioofthischangeindensity(usingEqn.(A.18.6))tothat

causedbycabbeling(fromEqn.(A.19.4))is

(

)

−− whichisabout0.0015fora

valueof

()

P−of40MPa.Henceitisclearthatcabbelinghasamuchlargereffecton

densitythandoesthenon‐conservationof.

Nevertheless,fromEqn.(A.18.6)wesee

thatthenon‐conservativeproductionof

isapproximatelyproportionaltotheproductof

seapressureandthestrengthofcabbeling.

ThefirstterminthebracketinEqn.(A.18.6)isusuallyaboutafactoroftenlargerthan

theothertwoterms(McDougall(1987b)),sotheproductionofConservativeTemperature

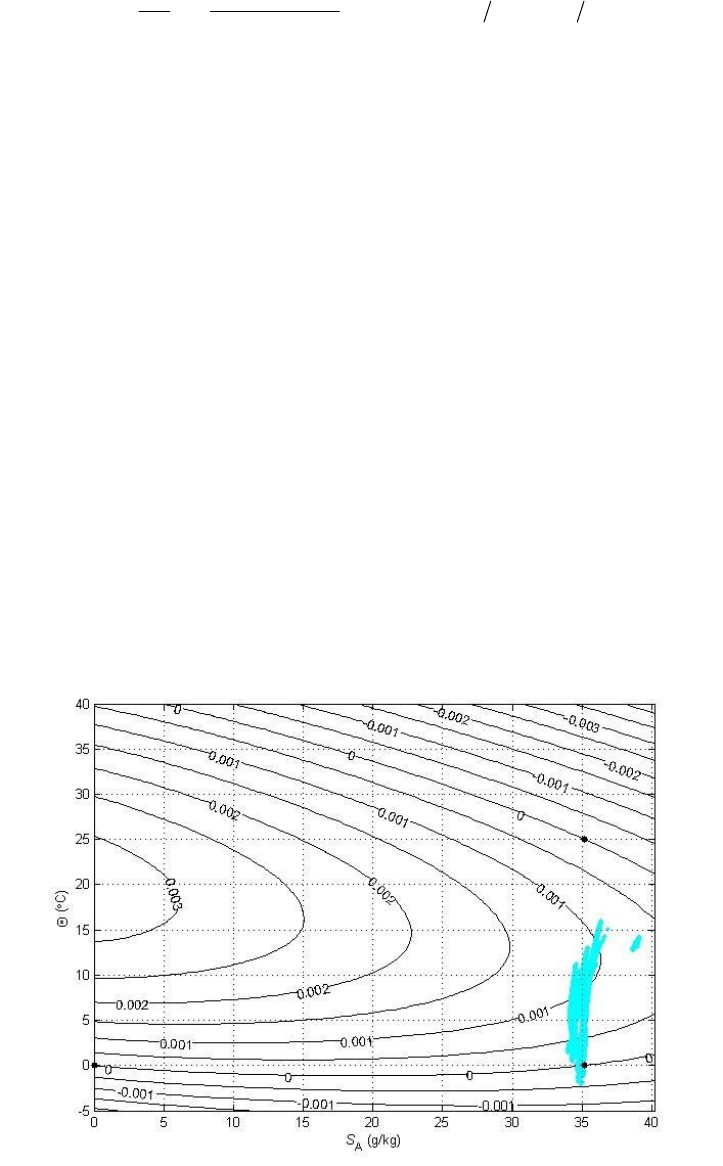
TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

101

ΘasaratioofthecontrastinConservativeTemperature21

Θ=Θ −Θmaybe

approximatedas(since21

ρρα

−−Θ

ΘΘ ΘΘ Θ

≈− ≈ )

() ()()

03.3 10 dbar K .

PP p

Θ−

−ΔΘ

Θ≈≈×ΔΘ

ΔΘ (A.18.8)

where

Θhasbeentakentobe52

1.1 10 K

−

×(McDougall,1987b).

AttheseasurfaceConservativeTemperature

istotallyconserved(0

Θ= ).The

non‐conservativeproductionofConservativeTemperature,,

increaseslinearlywith

pressure(seeEqn.(A.18.6))butatlargerpressuretherangeoftemperatureandsalinityin

theoceandecreases,andfromtheaboveequationsitisclearthatthemagnitudeof



decreasesproportionallytothesquareofthetemperatureandsalinitycontrasts.

McDougall(2003)concludedthattheproduction

betweenextremeseawaterparcelsat

eachpressureislargestat600dbar,andthemagnitudeofthenon‐conservative

productionofConservativeTemperature,,

isillustratedinFigureA.18.1fordataat

thispressure.ThequantitycontouredonthisfigureisthedifferencebetweenΘandthe

followingtotallyconservativequantityat600p

dbar.Thisconservativequantitywas

constructedbytakingtheconservativepropertyenthalpyhatthispressureandadding

thelinearfunctionofA

Swhichmakestheresultequaltozeroat

(

)

A0, 0 CS

Θ= ° andat

()

A35.165 04 g kg , 0 C .S−

=Θ=°Thisquantityisthenscaledsothatitbecomes25 C°at

()

A35.165 04 g kg , 25 C .S−

=Θ=°InthismannerthequantitythatiscontouredinFigure

A.18.1hasunitsofC°andrepresentstheamountbywhichConservativeTemperature



isnotatotallyconservativevariableatapressureof600dbar.Themaximumamountof

productionbymixingseawaterparcelsattheboundariesofFigureA.18.1isabout

410 C

−

×°althoughtherangeofvaluesencounteredintherealoceanatthispressureis

actuallyquitesmall,asindicatedinFigureA.18.1.McDougall(2003)concludesthatthe

maximumnon‐conservationofΘintherealoceanisafactorofapproximatelyahundred

lessthanthemaximumnon‐conservativeproductionofpotentialtemperature.



FigureA.18.1.Contours(inC°)ofavariablethatisusedtoillustratethenon‐

conservativeproductionofConservativeTemperatureΘat

600p

dbar.Thecloudofpointsshowwheremostofthe

oceanicdataresideat600p

dbar.Thethreepointsthatare

forcedtobezeroareshownwithblackdots.

102 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

FromthecurvatureoftheisolinesonFigureA.18.1itisclearthatthenon‐conservative

productionofConservativeTemperatureat600p

dbarispositive,sothatanocean

modelthatignoresthisproductionofConservativeTemperaturewillslightly

underestimateΘ.FromEqn.(A.18.2)oneseesthenon‐conservativeproductionof

ConservativeTemperatureisalwayspositiveifˆ0hΘΘ >,AA

ˆ0

h>andAAA

ˆˆˆ

()

SSS

hhh

ΘΘΘ

<

everywhere,anditcanbeshownthattheserequirementsareinfactmet.

FromEqns.(A.18.8)and(A.17.3)wecanwritetheratiooftheproductionof

ConservativeTemperaturetotheproductionofpotentialtemperaturewhentwoseawater

parcelsmixastheapproximateexpression

()()

()

10 dbar K / [g kg ] .pS

δθ

−

−−

Θ≈− ΔΘ Δ (A.18.9)

Takingatypicalratiooftemperaturedifferencestosalinitydifferencesinthedeepocean

tobe1

10 K / [g kg ]

−,Eqn.(A.18.9)becomes

(

)

10 dbar .p

δδθ

−

Θ≈− Atapressureof4000

dbarthisratiois0.4

δθ

Θ≈−implyingthatConservativeTemperatureisalmostasnon‐

conservativeasispotentialtemperature.Whilethisisthecase,thetemperatureand

salinitycontrastsinthedeepoceanaresmall,sothenon‐conservationofbothtypesof

temperatureamounttoverysmalltemperatureincrementsofboth

and.

ΘThe

largestnon‐conservativeincrementofConservativeTemperature

seemstooccurata

pressureofabout600dbar(McDougall(2003))andthisvalueof

isapproximatelytwo

ordersofmagnitudelessthanthemaximumvalueof

whichoccursattheseasurface.

ThematerialinappendicesA.16‐A.18hascloselyfollowedthepaperofMcDougall

(2003).



A.19 Non-conservative production of density and of potential density

Forthepurposeofcalculatingthenon‐conservativeproductionofdensitywetakeboth

AbsoluteSalinityA

SandConservativeTemperature

tobe100%conservative(see

appendixA.18above).Densityiswritteninthefunctionalform

(

)

ˆ,,Sp

ρρ

=Θ(A.19.1)

andthesamemixingprocessbetweentwofluidparcelsisconsideredasintheprevious

appendices.MassandAbsoluteSalinityareconservedduringtheturbulentmixing

process(Eqns.(A.16.2)and(A.16.3))asisConservativeTemperature,thatis

11 22 ,mm mΘ+ Θ= Θ(A.19.2)

whilethenon‐conservativenatureofdensitymeansthatitobeystheequation,

11 2 2 .mm mm

ρδρρ

++=(A.19.3)

DensityisexpandedinaTaylorseriesofA

Sand

aboutthevaluesofA

SandΘofthe

mixedfluid,retainingtermstosecondorderin

[

]

A2 A1 A

SS S

−

=Δ andin

[]

21 .Θ−Θ =ΔΘ

Then1

and2

areevaluatedand(A.19.3)isusedtofind

() ( )

{

}

AAA

1AA

22ˆˆ ˆ

SSS

mm SS

δρ ρ ρ ρ

ΘΘ Θ

=− ΔΘ + ΔΘΔ + Δ (A.19.4)

Thenon‐conservativeproductionofdensity

ofEqn.(A.19.4)isillustratedinFigure

A.19.1formixingat0p=dbar.Thatis,thisfigureshowstheproduction

of

potentialdensity

(notethatthesymbol

couldequallywellbeusedforpotential

density).Thequantitycontouredonthisfigureisformedasfollows.Firstthelinear

functionofA

Sisfoundthatisequalto

at

(

)

A0, 0 CS

Θ= ° andat

()

A35.165 04 g kg , 0 C .S−

=Θ=°ThislinearfunctionofA

Sissubtractedfrom

andthe

resultisscaledtoequal25 C°at

(

)

A35.165 04 g kg , 25 C .S−

Θ= ° Thevariablethatis

contouredinFigureA.19.1isthedifferencebetweenthisscaledlinearcombinationof



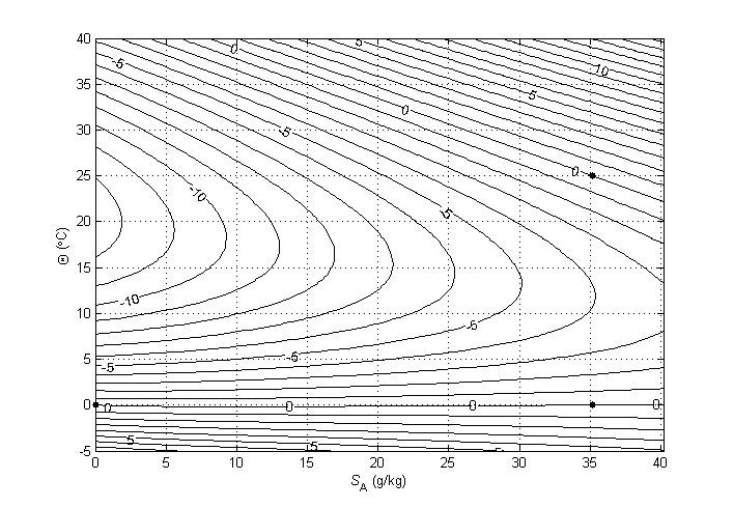
TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

103

andA

S,andConservativeTemperature.Thisfigureallowsthenon‐conservativenature

ofdensitytobeunderstoodintemperatureunits.Themixingofextremefluidparcelson

FigureA.19.1causesthesameincreaseindensityasacoolingofapproximately10 C.°

FromFigureA.18.1itisseenthatthe(tiny)non‐conservativenatureofΘisafactorof

approximately4000smallerthanthis.

FigureA.19.1.Contours(inC°)ofavariablethatisusedtoillustratethenon‐

conservativeproductionofpotentialdensity.

Thethree

pointsthatareforcedtobezeroareshownwithblackdots.



A.20 The representation of salinity in numerical ocean models

Oceanmodelsneedtoevaluatesalinityateverytimestepasanecessarypreludetousing

theequationofstatetodeterminedensityanditsderivativesforuseinthehydrostatic

relationshipandfrequentlyinneutralmixingalgorithms.Thecurrentpracticein

numericalmodelsistotreatsalinityasaperfectlyconservedquantityintheinteriorofthe

ocean;salinitychangesatthesurfaceandatcoastalboundariesduetoevaporation,

precipitation,brinerejection,icemeltandriverrunoffandsatisfiesanadvection‐diffusion

equationawayfromtheseboundaries.Theinclusionofcompositionanomalies

necessitatesseveralchangestothisapproach.Thesechangescanbedividedintotwo

broadcategories.First,inadditiontofreshwaterinputsandbrinerejection,allsourcesof

dissolvedmaterialenteringthroughthesurfaceandcoastalboundariesofthemodel

shouldbeconsideredaspossiblesourcesofcompositionanomalies.Second,withinthe

interiorofthemodel,changesduetothegrowth,decayandremineralizationofbiological

materialmustbeconsidered.Here,wefocusonthissecondissue.Whiletheultimate

resolutionoftheseissueswillinvolvebiogeochemicalmodels,inthisappendixwediscuss

somepracticalwaysforwardbasedontheapproximaterelations(A.4.5)and(A.4.6)

betweenthesalinityvariablesR*

,SSanddens

SS=thatwerediscussedinsectionA.4.At

thetimeofwriting,thesuggestedapproachesherehavenotbeentested,soitmustbe

acknowledgedthatthetreatmentofseawatercompositionanomaliesinoceanmodelsis

currentlyaworkinprogress.

WebeginbyrestatingEqns.(A.4.5)and(A.4.6),namely

dens

R1R

SSrS

∗

−≈ ,(A.20.1)

104 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

dens dens

A1R

(1 )SS rS

∗

−≈+ ,(A.20.2)

where1

rwillbetakentobetheconstant0.35basedontheworkofPawlowiczetal.(2010),

andinthissectiontheseapproximaterelationswillbetakentobeexact.TheAbsolute

SalinityAnomalydens dens

RA R

SS S

≡−isthesalinitydifferencethatcanbedirectlymeasured

fromseawatersamplesusingavibratingbeamdensimeterandknowledgeofthesample’s

PracticalSalinity,andagloballook‐uptableexistsforthisquantity(McDougalletal.

(2010a)).Becausethisparticularsalinitydifferenceisbasedondirectmeasurements,itis

thenaturalmeasureoftheanomalouscompositionofseawatertouseindevelopingthe

followingoptionsfornumericalmodelingofcompositionanomalies.



A.20.1UsingPreformedSalinity*

Sastheconservativesalinityvariable

BecausePreformedAbsoluteSalinity*

S(henceforthreferredtobytheshortenedname,

PreformedSalinity)isdesignedtobeaconservativesalinityvariable,blindtotheeffectsof

biogeochemicalprocesses,itsevolutionequationwillbeintheconservativeform(A.8.1).

Whenthistypeofconservationequationisaveragedintheappropriatemanner(see

appendixA.21)theconservationequationforPreformedSalinitybecomes(fromEqn.

(A.21.7)),

()

ˆˆ

dˆ.

dnn

hK S D

⎛⎞

∂

=∇⋅ ∇ +

⎜⎟

∂

⎝⎠

(A.20.3)

AsexplainedinappendixA.21,theover‐tildeof*

Sindicatesthatthisvariableisthe

thickness‐weightedaveragePreformedSalinity,havingbeenaveragedbetweenapairof

closelyspacedneutraltangentplanes.Thematerialderivativeontheleft‐handsideof

Eqn.(A.20.3)iswithrespecttothesumoftheEulerianandquasi‐Stokesvelocitiesof

heightcoordinates(equivalenttothedescriptioninappendixA.21intermsofthe

thickness‐weightedaveragehorizontalvelocityandthemeandianeutralvelocity),while

theright‐handsideofthisequationisthestandardnotationindicatingthat*

Sisbeing

diffusedalongneutraltangentplaneswiththediffusivityKandintheverticaldirection

withthediapycnaldiffusivityD(andhhereistheaveragethicknessbetweentwoclosely

spacedneutraltangentplanes).

Inordertoevaluatedensityduringtherunningofanoceanmodel,DensitySalinity

mustbeevaluated.ThiscanbedonefromEqn.(A.20.2)asthesumofthemodel’ssalinity

variable*

Sanddens

(1 )rS

+.Thiscouldbedonebysimplyaddingtothemodel’s

salinityvariable1

(1 )r

timesthefixedspatialmapof

()

dens

RobsS

asobservedtoday(and

asisavailablefromthecomputeralgorithmofMcDougalletal.(2010a)).However

experiencehasshownthatevenasmoothfieldofdensityerrorscanresultinsignificant

anomaliesindiagnosticmodelcalculations,primarilyduetothemisalignmentofthe

densityerrorsandthemodelbottomtopography.Indeed,evenifthecorrectmean

densitycouldsomehowbedetermined,approximationsassociatedwiththespecification

ofthemodelbottomtopographywouldresultinsignificanterrorsinbottompressure

torquesthatcandegradethemodelsolution.Onewaytominimizesucherrorsistoallow

somedynamicaladjustmentofthespecifieddensityfieldsothat,forexample,density

contourstendtoalignwithbottomdepthcontourswheretheflowisconstrainedtofollow

bottomtopography.Thissimpleideaisthekeytothesuccessoftherobustdiagnostic

approach(SarmientoandBryan(1982)).ToallowdynamicaladjustmentoftheAbsolute

SalinityAnomaliesdens

R(, , )Sxyp

whilenotpermittingthemtodeveloplargedifferences

fromtheobservedvaluesdens

R(obs)S

,werecommendcarryinganevolutionequationfor

dens

sothatitbecomesanextramodelvariablewhichevolvesaccordingto

() ()

dens dens

dens 1 dens dens

1RRR

d(obs) .

dnn

hK S D S S

δδ

δτδδ

−

⎛⎞

∂

=∇⋅ ∇ + + −

⎜⎟

∂

⎝⎠ (A.20.4)

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

105

Herethemodelvariabledens

wouldbeinitializedbasedonobservations,dens

R(obs)S

,

andadvectedanddiffusedlikeanyothertracer,butinaddition,thereisanon‐

conservativesourceterm

()

1 dens dens

(obs)SS

τδ δ

−−whichservestorestorethemodel

variabledens

towardstheobservedvaluewitharestoringtime

thatcanbechosento

suitparticularmodelingneeds.Itshouldbeatleast30daystopermitsignificant

adjustment,butitmightproveappropriatetoallowamuchlongeradjustmentperiod(up

toseveralyears)ifdriftfromobservationsissufficientlyslow.Thelowerboundisbased

onaveryroughestimateofthetimerequiredforthedensityfieldtobealignedwith

topographybyadvectiveprocesses.Theupperboundissetbytherequirementtohave

therestoringtimerelativelyshortcomparedtoverticalandbasin‐scalehorizontal

redistributiontimes.

Ideallyonewouldlikethenon‐conservativesourcetermtoreflecttheactualphysical

andchemicalprocessesresponsibleforremineralizationintheoceaninterior,butuntilour

knowledgeoftheseprocessesimprovessuchthatthisispossible,theapproachofEqn.

(A.20.4)providesawayforward.Anindicationofhowthisapproachmightbeimproved

inthefuturecanbegleanedfromlookingatEqn.(A.4.14)fordens

∗

−(takenfrom

Pawlowiczetal.(2010)).Ifabiogeochemicalmodelproducedestimatesofthequantities

ontheright‐handsideofthisequation,itcouldbeimmediatelyintegratedintoanocean

modeltodiagnosetheeffectsoftheincludedbiogeochemicalprocessesonthemodelʹs

densityanditscirculation.

Insummary,theapproachsuggestedherecarriestheevolutionEqns.(A.20.3)and

(A.20.4)for*

Sanddens

,whiledens

Siscalculatedbythemodelateachtimestep

accordingto

dens dens

A1R

ˆˆ

(1 )SS rS

∗

=++ ,(A.20.5)

withourbestpresentestimateof1

(1 )r

being1.35 .Themodelisinitializedwithvalues

ofPreformedSalinityusingEqn.(A.20.1)(namelydens

R1 R

ˆˆ

SSrS

∗=− )basedon

observationsofReferenceSalinityandontheglobaldatabaseof

()

dens

RobsS

from

McDougalletal.(2010a).



A.20.2IncludingasourcetermintheevolutionequationforAbsoluteSalinity

Anequivalentprocedureistocarrythefollowingevolutionequation(A.20.6)forAbsolute

Salinity,whichmorespecifically,iscalledDensitySalinity,dens

.SS≡Oninspectionof

Eqn.(A.20.2),dens dens

A1R

(1 )SS rS

∗

−≈+ ,andrecognizingthatS

∗

isaconservativevariable,

itisclearthatthenon‐conservativeproductionofdens

Smustoccurattherate1

(1 )r+

timestherateatwhichthesamenon‐conservativeprocessesaffecttheAbsoluteSalinity

Anomalydens

.Since(fromEqn.(A.20.4))thenon‐conservativesourcetermfordens

is

()

1 dens dens

(obs)SS

τδ δ

−−,wefindthattheevolutionequationforDensitySalinitytobe

()

dens dens

dens 1 dens dens

1A1RR

dens

dens A

ˆˆ

dˆ1(obs)

ˆˆ

hK S D r S S

hK S D z

τδ δ

−

⎛⎞

∂

=∇⋅ ∇ + ++ −

⎜⎟

∂

⎝⎠

⎛⎞

∂

=∇⋅ ∇ + +

⎜⎟

∂

⎝⎠

(A.20.6)

Alternatively,thisequationcanbederivedbysummingEqn.(A.20.3)plus1

(1 )r+times

Eqn.(A.20.4).Herethenon‐conservativesourcetermintheevolutionequationfor

DensitySalinityhasbeengiventhelabelA

ˆS

Sforlateruse.

Inthisapproachtheevolutionequation(A.20.4)fordens

isalsocarriedandthe

model’ssalinityvariable,dens

S,isuseddirectlyastheargumentoftheequationofstate

andotherthermodynamicfunctionsinthemodel.Themodelwouldbeinitializedwith

valuesofDensitySalinityusingEqn.(A.4.2)(namelydens dens

ARR

ˆˆ

SSS

=+ )basedon

106 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

observationsofReferenceSalinityandontheglobaldatabaseof

()

dens

RobsS

from

McDougalletal.(2010a).

ThisapproachshouldgiveidenticalresultstothatdescribedinsectionA.20.1using

PreformedSalinity.OnedisadvantageofhavingDensitySalinityasthemodel’ssalinity

variableisthatitsevolutionequation(A.20.6)isnotintheconservativeformsothat,for

example,itisnotpossibletoperformeasyglobalbudgetsofsalinitytotestforthe

numericalintegrityofthemodelcode.Anotherdisadvantageisthattheair‐seafluxof

carbondioxideandothergasesmayneedtobetakenintoaccountasthesurfaceboundary

conditionofDensitySalinity.Suchair‐seafluxesdonotaffectPreformedSalinity.



A.20.3IncludingasourcetermintheevolutionequationforReferenceSalinity

Anequivalentprocedureistocarrythefollowingevolutionequation(A.20.7)for

ReferenceSalinity.OninspectionofEqn.(A.20.1),dens

R1R

SSrS

∗

−≈ ,andrecognizing

thatS∗isaconservativevariable,itisclearthatthenon‐conservativeproductionofR

S

mustoccurattherate1

rtimestherateatwhichthesamenon‐conservativeprocesses

affecttheAbsoluteSalinityAnomalydens

.Since(fromEqn.(A.20.4))thenon‐

conservativesourcetermfordens

is

(

)

1 dens dens

(obs)SS

τδ δ

−−,theevolutionequationfor

ReferenceSalinityis

()

1 dens dens

1R1RR

ˆˆ

dˆ(obs)

ˆˆ

hK S D r S S

hK S D zr

τδ δ

−

⎛⎞

∂

=∇⋅ ∇ + + −

⎜⎟

∂

⎝⎠

⎛⎞

∂

=∇⋅ ∇ + +

⎜⎟

∂+

⎝⎠

,(A.20.7)

wherethenon‐conservativesourcetermis11

(1 )rr

timesthecorrespondingsourceterm

intheevolutionequationforDensitySalinityinEqn.(A.20.6).

InthisapproachtheevolutionEqns.(A.20.7)and(A.20.4)forR

Sanddens

are

carriedbytheoceanmodel,whiledens

Siscalculatedbythemodelateachtimestep

accordingtoEqn.(A.4.2),namely

dens dens

ARR

ˆˆ

SSS

=+ .(A.20.8)

Thisapproach,likethatofsectionA.20.2shouldgiveidenticalresultstothatdescribed

insectionA.20.1usingPreformedSalinityexceptforthemorecomplicatedair‐seaflux

boundaryconditionforReferenceSalinitythanforPreformedSalinity.Itdoesseemthat

theconservativenatureofEqn.(A.20.3)forPreformedSalinityisasignificantadvantage,

andsothisapproachislikelytobepreferredbyoceanmodelers.



A.20.4Discussionoftheconsequencesifremineralizationisignored

IfanoceanmodeldoesnotcarrytheevolutionequationforAbsoluteSalinityAnomaly

(Eqn.(A.20.4))andthemodel’ssalinityevolutionequationdoesnotcontainthe

appropriatenon‐conservativesourceterm,istherethenanypreferencetoinitializingand

interpretingthemodel’ssalinityvariableaseitherPreformedSalinity,AbsoluteSalinityor

ReferenceSalinity?Thatis,thesimplestmethodofdealingwiththesesalinityissuesisto

continuethegeneralapproachthathasbeentakenforthepastseveraldecadesofsimply

takingonetypeofsalinityinthemodelandthatsalinityistakentobeconservative.

Underthisapproximationthesalinitythatisusedintheequationofstatetocalculate

densityinthemodelisthesameasthesalinitythatobeysanormalconservationequation

oftheformEqn.(A.20.3).Inthisapproachthereisstillachoiceofhowtoinitializethe

salinityinamodel,andherewediscusstherelativevirtuesoftheseoptions.

IfthemodelisinitializedwithadatasetofestimatedPreformedSalinity*

S,then*

S

shouldevolvecorrectly,since*

SisaconservativevariableanditsevolutionequationEqn.

(A.20.3)containsnonon‐conservativesourceterms.Inthisapproachtheequationofstate

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

107

willbecalledwith*

Sratherthandens

S,andthesesalinitiesdifferbyapproximately

dens

(1 )rS

+.Thelikelyerrorswiththisapproachcanbeestimatedusingthesimple

exampleofFigureA.5.1.Theverticalaxisinthisfigureisthedifferencebetweenthe

northwarddensitygradientatconstantpressurewhentheequationofstateiscalledwith

dens

SandwithR

S.ThefigureshowsthatwhenusingR

S,forallthedataintheworld

oceanbelowadepthof1000m,58%ofthisdataisinerrorbymorethan2%.Ifthisgraph

werere‐donewith*

SasthesalinityargumentratherthanR

S,theerrorswouldbelarger

intheratio1

(1 ) 1.35r+≈ .Thatis,for58%ofthedataintheworldoceandeeperthan1000

m,the“thermalwind”relationwouldbemisestimatedby2.7%

≈

if*

Sisusedinplaceof

dens

Sasthesalinityargumenttotheequationofstate.Also,thesepercentageerrorsin

“thermalwind”arelargerinthePacificOcean.

Anotherchoiceofthesalinitydatatoinitializethemodelisdens

S.Thischoicehasthe

advantagethatforaninitialperiodoftimeafterinitializationtheequationofstateiscalled

withthecorrectsalinityvariable.Howeveratlatertimes,theneglectofthenon‐

conservativesourceterminEqn.(A.20.6)meansthatthemodel’ssalinityvariablewill

departfromrealityanderrorswillcreepinduetothelackoftheselegitimatenon‐

conservativesourceterms.Howlongmightitbeacceptabletointegratesuchamodel

beforetheerrorsapproachedthosedescribedinthepreviousparagraph?Onecould

imaginethatintheupperoceantheinfluenceofthesedifferentsalinityvariablesis

dwarfedbyotherphysicssuchasairseainteractionandactivegyralmotions.Ifone

consideredadepthof1000masbeingadepthwheretheinfluenceofthedifferent

salinitieswouldbebothapparentandwouldmakeasignificantimpactonthethermal

windequation,thenonemightguessthatitwouldtakeseveraldecadesfortheneglectof

thenon‐conservativesourcetermsintheevolutionequationforDensitySalinitytobegin

tobeimportant.Thisisnottosuggestthattherelaxationtimescale

shouldbechosento

beaslongasthis,ratherthisisanestimateofhowlongitwouldtakefortheneglectofthe

non‐conservativesourcetermA

ˆS

SinEqn.(A.20.6)tobecomesignificant.

AthirdchoiceistoinitializethemodelwithReferenceSalinity,R

S.Thischoiceincurs

theerrorsdisplayedinFigureA.5.1rightfromthestartofanynumericalsimulation.

Thereafter,onsomeunknowntimescale,furthererrorswillarisebecausetheconservation

equationforReferenceSalinityismissingthelegitimatenon‐conservativesourceterms

thatrepresenttheeffectsofbiogeochemistryonconductivityandR

S.Hencethischoiceis

theleastdesiredofthethreeconsideredinthissubsection.Notethatthischoiceis

basicallytheapproachthathasbeenusedtodateinoceanmodelingstudiessincewehave

routinelyinitializedmodelswithobservationsofPracticalSalinityandhavetreateditas

thoughitwereaconservativevariableandhaveuseditasthesalinityargumentforthe

equationofstate.

Inprinciple,thereareothercombinationsofoptionswheretheevolutionequationfor

AbsoluteSalinityAnomaly(A.20.4)iscarriedbyanoceanmodel,butsomeoptionother

thanthosediscussedinsubsectionsA.20.1–A.20.3ispursued.Wedonotconsiderthese

variousoptionshere,sinceifonegoestothetroubleofcarryingtheevolutionequationfor

AbsoluteSalinityAnomaly,thenoneshouldbesufficientlycarefultoimplementoneof

theoptionsdiscussedinsubsectionsA.20.1–A.20.3.



A.20.5Discussionoftheoptionsforincludingremineralization

TheapproachesofsubsectionsA.20.1–A.20.3ofthisappendixcaneachaccountforthe

non‐conservativeeffectsofremineralizationif1

risaconstantandsolongasthe

appropriateboundaryconditionsareimposed.Theadvantageofusing*

Sisthatitobeys

astandardconservativeevolutionequation(A.20.3)withnosourcetermontheright‐hand

side.Since*

Sisdesignedtobeaconservativesalinityvariable,itwouldappeartobethe

mostappropriatesalinityvariableforhavingasanaxisofthetraditional“S

−diagram”,

108 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

whichwouldthenbecomethe*

S−Θdiagram.Similarly,*

Swouldalsobethebestchoice

forthesalinityvariableinaninversestudy.

IfanoceanmodelweretoberunwithoutcarryingtheevolutionequationforAbsolute

SalinityAnomaly(A.20.4)andhencewithouttheabilitytoincorporatetheappropriate

non‐conservativesourcetermsineitherEqns.(A.20.6)or(A.20.7),thenthemodelmust

resorttocarryingonlyonesalinityvariable,andthissalinityvariablemustbetreatedasa

conservativevariableintheoceanmodel.Inthiscircumstance,weadvisethattheocean’s

salinityvariablebeinterpretedasDensitySalinity,andinitializedassuch.Inthisway,the

errorsinthethermalwindequationwilldeveloponlyslowlyoveratimescaleofseveral

decadesormoreinthedeepocean.

Itshouldbenotedthateachofthemodellingapproachesdescribedinsubsections

A.20.1–A.20.3arerelatedtotoday’sestimateofthe

()

dens

RobsS

field.Thisfieldwill

changenotonlyastheobservationaldatabaseimprovesbutalsoastheoceancomposition

evolveswithtime.



A.21 The material derivatives of *,S A,S R

S and

in a turbulent ocean

PreformedSalinity*

Sisdesignedtobeaconservativevariablewhichobeysthefollowing

instantaneousconservationequation(basedonEqn.(A.8.1))

() ( )

ρρρ

+∇⋅ = = −∇⋅uF(A.21.1)

ThereareseveraldifferentcontributionstothemolecularfluxofsaltS

F,expressionsfor

whichcanbeseenatequation(58.11)ofLandauandLifshitz(1959)andinEqn.(B.23)

below.Forcompleteness,werepeatthecontinuityequation(A.8.2)hereas

(

)

ρρ

+∇⋅ =u(A.21.2)

TemporallyaveragingthisequationinCartesiancoordinates(i.e.atfixed,,

yz)gives

(

)

ρρ

+∇⋅ =u(A.21.3)

whichwechoosetowriteinthefollowingform,afterdivisionbyaconstantdensity0



(usuallytakentobe3

1035 kg m−,seeGriffies(2004))

(

)

ρρ

+∇⋅ =u

where 0.

≡uu

(A.21.4)

Thisvelocityu

isactuallyproportionaltotheaveragemassfluxofseawaterperunitarea.

TheconservationequationforPreformedSalinity(A.21.1)isnowaveragedinthe

correspondingmannerobtaining(McDougalletal.2002)

()()

()

00 00

*11

** * *

SS S S

ρρ ρ

ρρ

ρρ ρρ

∂′′ ′′

+∇⋅ = + ⋅∇ = − ∇⋅ − ∇⋅

∂

uu Fu

 (A.21.5)

HerethePreformedSalinityhasbeendensity‐weightedaveraged,thatis,**

≡,

andthedoubleprimedquantitiesaredeviationsoftheinstantaneousquantityfromits

density‐weightedaveragevalue.Sincetheturbulentfluxesaremanyordersofmagnitude

largerthanmolecularfluxesintheocean,themolecularfluxofsaltishenceforthignored.

TheaveragingprocessinvolvedinEqn.(A.21.5)hasnotinvokedthetraditional

Boussinesqapproximation.Theaboveaveragingprocessisbestviewedasanaverage

overmanysmall‐scalemixingprocessesoverseveralhours,butnotovermesoscaletime

andspacescales.Thislateraveragingovertheenergeticmesoscaleeddiesisnotalways

necessary,dependingonthescaleofthepieceofoceanoroceanmodelthatisunder

investigation.Thetwo‐stageaveragingprocesses,withoutinvokingtheBoussinesq

approximation,overfirstsmall‐scalemixingprocesses(severalmeters)followedby

averagingoverthemesoscale(oforder100km)hasbeenperformedbyGreatbatchand

McDougall(2003),yieldingtheprognosticequationforPreformedSalinity

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

109

() ()()

()

000000

*** *

ˆˆ

ˆˆˆ ˆ

ˆˆ

ˆ.

SSeS Se

hK S D z

ρρρρρρ

∂∂

+∇ ⋅ + = + ⋅∇ +

∂∂

⎛⎞

∂

=∇⋅ ∇ +

⎜⎟

∂

⎝⎠





(A.21.6)

Heretheover‐caretmeansthatthevariable(e.g.*

S)hasbeenaveragedinathickness‐and‐

density‐weightedmannerbetweenapairof“neutralsurfaces”asmalldistancehapartin

thevertical,ˆ

visthethickness‐and‐density‐weightedhorizontalvelocity,eisthe

dianeutralvelocity(theverticalvelocitythatpenetratesthroughtheneutraltangentplane)

ande

isthetemporalaverageofeonthe“neutralsurface”(thatis,e

isnotthickness‐

weighted).TheturbulentfluxesareparameterizedbytheepineutraldiffusivityKandthe

dianeutral(orvertical)diffusivity.

Thedensityvalue

isthedensitywhoseaverage

heightistheheightatwhichtheequationisevaluated.Theissuesofaveraginginvolved

inEqns.(A.21.5)and(A.21.6)aresubtle,andarenotcentraltoourpurposeinthis

thermodynamicmanual.HenceweproceedwiththemorestandardBoussinesq

approach,butretaintheover‐caretstoremindthereaderofthethickness‐weightednature

ofthevariables.

Havingderivedthisevolutionequation(A.21.6)forPreformedSalinitywithout

invokingtheBoussinesqapproximation,wenowfollowcommonpracticeandinvokethis

approximation,findingthesimplerexpression

()

** *

ˆˆ ˆ

ˆˆ

ˆ.

nnn

SS S

Se hKS D

tz z

⎛⎞

∂∂ ∂

+⋅∇ + =∇⋅ ∇ +

⎜⎟

∂∂ ∂

⎝⎠

v(A.21.7)

Theleft‐handsideisthematerialderivativeofthethickness‐weightedPreformedSalinity

withrespecttothethickness‐weightedhorizontalvelocityˆ

vandthetemporallyaveraged

dianeutralvelocitye

ofdensitycoordinates.Theright‐handsideisthedivergenceofthe

turbulentfluxesofPreformedSalinity;thefactthatthelateraldiffusiontermisthe

divergenceofafluxcanbeseenwhenitistransformedtoCartesiancoordinates.The

sameconservationstatementEqn.(A.21.7)canbederivedwithoutmakingtheBoussinesq

approximationbyasimplereinterpretationoftheverticalcoordinateasbeingpressure,

andthisinterpretationisnowbecomingcommoninoceanmodelling(seeBleck(1978),

Huangetal.(2001),deSzoekeandSamelson(2002),Loschetal.(2004)andGriffies(2004)).

WenowproceedtodevelopthecorrespondingevolutionequationforAbsolute

SalinityA.SNotethatA

SistheconvenientgenericsymbolforDensitySalinitydens

S;

unlessthereisroomforconfusionwiththeothermeasuresofabsolutesalinity,soln

Sand

add

S,itprovesconvenienttousethesimplersymbolA

Sratherthandens

Sandtousethe

descriptionAbsoluteSalinityratherthanDensitySalinity.

AbsoluteSalinityobeystheinstantaneousevolutionequation(basedonEqn.(A.8.1))

() ( )

ρρρ ρ

+∇⋅ = = −∇⋅ +uFS(A.21.8)

ThesourcetermA

SisdescribedinappendixA.20(seeeqn.(A.20.6)).Thisnon‐

conservativesourcetermisduetobiogeochemicalprocesses,forexample,the

remineralizationofbiologicalmaterial;theturningofparticulatematterintodissolved

seasalt.Whenthisequationisdensity‐weightedaveraged,wefind

()()

()

00 0

AA A

SS S

ρρ ρ

ρρ

ρρ ρ

∂

+∇⋅ = + ⋅∇

∂

′′ ′′

=− ∇⋅ − ∇⋅ +



(A.21.9)

whichcorrespondstoEqn.(A.21.5)above.Whenaveragedoverthemesoscalethe

prognosticequationforAbsoluteSalinitybecomes

110 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

() ()()

()

000000

AAA A

ˆˆ

ˆˆˆ ˆ

ˆˆ

ˆ,

SSeS Se

hK S D z

ρρρρρρ

∂∂

+∇ ⋅ + = + ⋅∇ +

∂∂

⎛⎞

∂

=∇⋅ ∇ + +

⎜⎟

∂

⎝⎠







(A.21.10)

andwhentheBoussinesqapproximationismadewefindthesimplerexpression

()

AA A

ˆˆ ˆ

ˆˆ

ˆ.

nnn

n z

SS S

Se hKS D

tz z

⎛⎞

∂∂ ∂

+⋅∇ + =∇⋅ ∇ + +

⎜⎟

∂∂ ∂

⎝⎠

vS(A.21.11)

Theleft‐handsideisthematerialderivativeofthethickness‐weightedAbsoluteSalinity

withrespecttothethickness‐weightedhorizontalvelocityˆ

vandthetemporallyaveraged

dianeutralvelocitye

ofdensitycoordinates.Apartfromthenon‐conservativesource

termA

ˆS

S,theright‐handsideisthedivergenceoftheturbulentfluxesofAbsolute

Salinity.

ThecorrespondingturbulentevolutionequationforReferenceSalinityis

()

RR R1

ˆˆ ˆ

ˆˆ

ˆ.

nnn

n z

SS Sr

Se hKS D

tz zr

⎛⎞

∂∂ ∂

+⋅∇ + =∇⋅ ∇ + +

⎜⎟

∂∂ ∂+

⎝⎠

vS(A.21.12)

Thenon‐conservativesourcetermhereisjustifiedinsubsectionA.20.3ofappendixA.20.

AsdiscussedinappendicesA.4andA.20,givenourratherelementaryknowledgeofthe

wayvariationsinseawatercompositionaffectconductivity,werecommendthat1

rbe

takentobetheconstant10.35.r=HenceweseethatReferenceSalinityisaffectedby

biogeochemicalprocessesatabout0.26(0.35/ 1.35

≈

)ofthecorrespondinginfluenceof

biogeochemistryonDensitySalinity.

WeturnnowtoconsiderthematerialderivativeofConservativeTemperatureina

turbulentocean.FromEqns.(A.13.5)and(A.21.8)theinstantaneousmaterialderivativeof

Θis,withoutapproximation,

(

)

()

() ()

()

0RQ

tTt

ρρερ

θμμ ρ

Θ=−∇⋅−∇⋅++

⎡⎤

−−−∇⋅+

⎢⎥

⎣⎦

(A.21.13)

Thefactthattheright‐handsideofEqn.(A.21.13)isnotthedivergenceofafluxmeans

thatΘisnota100%conservativevariable.However,thefinite‐amplitudeanalysisof

mixingpairsofseawaterparcelsinappendixA.18hasshownthatthenonconstant

coefficientsofthedivergencesofthemolecularfluxesofheatQ

−

∇⋅FandsaltS

−∇⋅ F

appearingontheright‐handsideofEqn.(A.21.13)areofnopracticalconsequenceasthey

causeanerrorinConservativeTemperatureofnomorethan1.2mK (seeFigureA.18.1).

Thesenon‐idealtermsontheright‐handsideofEqn.(A.21.13)arenolargerthanthe

dissipationterm

whichisalsojustifiablyneglectedinoceanography(McDougall

(2003)).ThesourcetermA

Swasnotconsideredinthemixingofseawaterparcelsin

appendixA.18,andwenowshowthatthesetermsalsomakenegligiblecontributionsto

Eqn.(A.21.13).

ThepartialderivativeofenthalpywithrespecttoAbsoluteSalinity,A,

hthatappears

inEqn.(A.21.13)isabout1

65 J g

−

−(i.e.65

−

111

Jkg (gkg )

−

−−

)atatemperatureof10 C°.

ThisvaluecanbededucedfromFigureA.17.1andalsofromFigure30(c)andTable12of

Feistel(2003),albeitfortheGibbsfunctionofseawaterthatimmediatelypredatedthe

TEOS‐10salineGibbsfunctionofFeistel(2008)andIAPWS(2008).Thespatialintegralof

thesourcetermA

SfromtheNorthAtlantictotheNorthPacificissufficienttocausea

changeinAbsoluteSalinityof0.0251

gkg

−

,sothemaximumcontributiontoanerrorin



TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

111

fromthesourceterm

()

(

)

A00

hTTt

ρθ

+SinEqn.(A.21.13),whenintegratedoverthe

wholeocean,isapproximately

(

)

(

)

01 1 1

( ) 65 J g 0.025 g kg 0.4 mK

c−− −

≈.Theothertermin

SinEqn.(A.21.13)ismultipliedbythesquarebracketwhichfromequation(27)of

McDougall(2003)isequalto

()

(

)

TTt

++timesapproximately1

Θ−

−,sothatthis

squarebracketisapproximately301

−

(i.e.30 111

Jkg (gkg )

−

−−

)atapressurepof4000

dbar(40MPa)sothecontributionofthistermislessthanhalfthatoftheterminA

Sin

thefirstlineofEqn.(A.21.13).ThisconfirmsthatthepresenceofthetwotermsinA

S

intheFirstLawofThermodynamicshaslessimpactthaneventhenon‐idealnatureofthe

molecularfluxdivergencetermsinEqn.(A.21.13)andthedissipationofmechanical

energyinthisequation.

Hencewithnegligibleerror,theright‐handsideofEqn.(A.21.13)mayberegardedas

thesumoftheidealmolecularfluxofheattermQ

−

∇⋅Fandthetermduetotheboundary

andradiativeheatfluxes,

()

(

)

.TTt

−+∇⋅ +FAttheseasurfacethepotential

temperature

andinsitutemperaturetareequalsothatthistermissimplyR

−∇⋅Fso

thattherearenoapproximationswithtreatingtheair‐seasensible,latentandradiative

heatfluxesasbeingfluxesof0.

cΘThereisanissueattheseafloorwheretheboundary

heatflux(thegeothermalheatflux)affectsConservativeTemperaturethroughthe“heat

capacity”

()()

00p

TtcT

++ratherthansimply0.

cThatis,theinputofacertain

amountofgeothermalheatwillcausealocalchangein

asthoughtheseawaterhadthe

“specificheatcapacity”

()

(

)

00p

TtcT

++ratherthan0.

cThesetwospecificheat

capacitiesdifferfromeachotherbynomorethan0.15%atapressureof4000dbar.Ifthis

smallpercentagechangeintheeffective“specificheatcapacity”waseverconsidered

important,itcouldbecorrectedbyartificiallymultiplyingthegeothermalheatfluxatthe

seafloorby

()()

TTt

++.

WeconcludethatitissufficientlyaccuratetoassumethatConservativeTemperature

isinfactconservativeandthattheinstantaneousconservationequationis

() ( )

00 0 RQ

pp p

cc c

ρρρ

Θ + ∇⋅ Θ = = −∇⋅ − ∇⋅uFF(A.21.14)

Nowweperformthesametwo‐stageaveragingprocedureasoutlinedaboveinthecaseof

PreformedSalinity.TheBoussinesqformofthemesoscale‐averagedequationis

(analogoustoEqn.(A.21.7))

()( )

bound

ˆˆ

ˆˆˆ

ˆ.

nnnz

ehKDF

∂Θ ∂Θ

+ ⋅∇Θ+ = ∇ ⋅ ∇Θ + Θ−

∂∂

v(A.21.15)

Asinthecaseofthe*

Sequation(A.21.7),themolecularfluxofheathasbeenignoredin

comparisonwiththeturbulentfluxesofConservativeTemperature.Theair‐seafluxesof

sensibleandlatentheat,theradiativeandthegeothermalheatfluxesremaininEqn.

(A.21.15)intheverticalheatflux

ound

Fwhichisthesumoftheseboundaryheatfluxes

dividedby0

Anyconservativevariable,,Cobeysaconservationequationidentical

informtoEqns.(A.21.7)and(A.21.15),withˆ

Csimplyreplacing*

Sorˆ

Θinthese

equations,andofcoursewiththeboundaryfluxbeingtheboundaryfluxofpropertyC.

Theerrorsincurredinoceanmodelsbytreatingpotentialtemperature

asbeing

conservativehavenotyetbeenthoroughlyinvestigated,butMcDougall(2003)and

Tailleux(2010)havemadeastartonthistopic.McDougall(2003)foundthattypicalerrors

in

are0.1 C±°whileinisolatedregionssuchaswherethefreshAmazonwater

dischargesintotheocean,theerrorcanbeaslargeas1.4 C°.Thecorrespondingerrorin

themeridionalheatfluxappearstobeabout0.005PW(orarelativeerrorof0.4%).The

useofConservativeTemperatureΘinoceanmodelsreducestheseerrorsbytwoordersof

magnitude.

Itispossibletoderiveanevolutionequationforpotentialtemperaturewhich

resemblesEqn.(A.21.15)butwhichcontainsadditionalnon‐conservativesourcetermson

112 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

theright‐handsideoftheequation.However,thereseemslittlepointindoingsohere,as

itismuchmoreconvenienttoinsteadadopttheConservativeTemperaturevariable.Note

thattheconsequencesfordynamicaloceanographyofignoringthenon‐conservative

sourcetermsinthepotentialtemperatureevolutionequationareaslargeasignoringthe

variationsinseawatercomposition;a

rangeof0.2 C°correspondstoadensityrangeof

0.04 kg m−whichistwiceaslargeasthedensityerrorduetoignoringthemaximum

valueofAR

SS−of1

0.025 g kg−.

TheevolutionequationsofPreformedSalinity(A.21.7)andConservativeTemperature

(A.21.15)aretheunderpinningconservationequationsforthesevariablesinocean

models.Animportantissueforoceanmodelsishowtorelateˆ

vtotheEulerian‐mean

horizontalvelocityv.Thisareaofresearchinvolvestemporal‐residual‐meantheoryand

thequasi‐Stokesstreamfunction(GentandMcWilliams(1990),Gentetal.(1995),

McDougallandMcIntosh(2001)andGriffies(2004)).Wewillnotdiscussthistopichere.

SufficeittosaythatthemeanadvectioncanbeexpressedinCartesiancoordinates,with

forexample,Eqn.(A.21.15)becoming

()( )

* bound

dˆˆˆ ˆˆ

ˆ,

dtzznn z

zwhKDF

Θ=Θ + ⋅∇Θ+ Θ = ∇ ⋅ ∇Θ + Θ −v(A.21.16)

wheretheverticalvelocity*

wisrelatedtoe

by

*ˆ.

wz ze=+⋅∇+v(A.21.17)



A.22 The material derivatives of density and of locally-referenced

potential density; the dianeutral velocity e



RegardingdensitytobeafunctionofConservativeTemperature(i.e.

()

ˆ,,Sp

ρρ

=Θ)and

takingthematerialderivativeofthenaturallogarithmofdensityfollowingthemesoscale‐

thickness‐weighted‐averagedmeanflow(asinEqns.(A.21.15)or(A.21.16)),wehave

ˆˆ

dddd

ˆ,

dddd

tttt

ρβακ

−ΘΘ

=−+

(A.22.1)

whereˆ

isthethickness‐weightedaveragevalueofdensity.Onecancontinueto

considerthematerialderivativeofinsitudensity,andinsodoing,onecarriesalongthe

lastterminEqn.(A.22.1),dP dt

,butitismorerelevantandmoreinterestingtoconsider

thematerialderivativeofthelogarithmofthelocally‐referencedpotentialdensity,ˆ,

since

thisvariableislocallyconstantintheneutraltangentplane.Thematerialderivativeofˆl



isgivenby

11 A

ˆˆ

ddddd

ˆˆ .

ddddd

lPS

ttttt

ρρ

ρρκβα

−− ΘΘ

=−= −(A.22.2)

SubstitutingfromEqns.(A.21.11)and(A.21.15)above,andnotingthatboththetemporal

andthelateralgradientsofˆl

vanishalongtheneutraltangentplane(thatis,

ˆˆ

αβ

ΘΘ

∇Θ− ∇ =0andA

ˆˆ

tnn

αβ

ΘΘ

Θ− =),thematerialderivativeofˆl

amounts

tothefollowingequationforthedianeutralvelocitye

(notethattheboundaryheatflux

ound

Falsoneedstobeincludedforfluidvolumesthatabuttheseasurface)

()

(

)

(

)

() ( )

ˆˆ ˆ ˆ

ˆˆ .

znnnn

zzz

eShhKhhKS

DDS

αβ α β

αβ β

Θ Θ Θ− Θ−

ΘΘ Θ

Θ− = ∇⋅ ∇Θ− ∇⋅ ∇

+Θ− −



S(A.22.3)

Theleft‐handsideisequalto12

eg N

−

andthefirsttwotermsontherighthandside

wouldsumtozeroiftheequationofstatewerelinear.Thisequationcanberewrittenas

thefollowingequationforthetemporallyaveragedverticalvelocitythroughtheneutral

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

113

tangentplaneatagivenlongitudeandlatitude(fromMcDougall(1987b),andseeEqns.

(3.8.2)and(3.9.2)forthedefinitionsof

and

)

()

(

)

(

)

bb A

ˆˆ ˆ ˆ ˆ .

nn nn z

eg N K C T p D DS

αβ β

−Θ Θ ΘΘΘ

=− ∇Θ⋅∇Θ+ ∇Θ⋅∇ + Θ − −

S(A.22.4)

Thecabbelingnonlinearity(the

CΘterm)alwayscauses“densification”,thatis,italways

causesanegativedianeutralvelocity,e

,whilethethermobaricnonlinearity(the

TΘterm)

cancauseeitherdiapycnalupwellingordownwelling.

TosummarizethisappendixA.22;wehavefoundthatthematerialderivativeofin

situdensityEqn.(A.22.1),whenadjustedforthedynamicallypassivecompressibility

term,becomesthematerialderivativeoflocally‐referencedpotentialdensityEqn.(A.22.2)

whichcanbeinterpretedasanexpressionEqn.(A.22.4)for,e

thetemporally‐averaged

verticalvelocitythroughthelocalneutraltangentplane.Thisdianeutralvelocitye

isnot

aseparatemixingprocess,butratherisadirectresultofmixingprocessessuchas(i)

small‐scaleturbulentmixingasparameterizedbythediffusivity,

and(ii)lateral

turbulentmixingofheatandsaltalongtheneutraltangentplane(asparameterizedbythe

lateralturbulentdiffusivityK)actinginconjunctionwiththecabbelingandthermobaric

nonlinearitiesoftheequationofstate.Notethatacommondiapycnalmixingmechanism,

double‐diffusiveconvection(whichactuallycomesintwoseparateflavours,asalt‐

fingeringtypeanda“diffusive”typeofdouble‐diffusiveconvection)isomittedfromthe

conservationequations(A.21.11)and(A.21.15)andalsofromthemeandianeutralvelocity

equation(A.22.4).Itishoweverstraight‐forwardtoincludetheseprocessesinthese

conservationequations(seeforexampleMcDougall(1994,1997b)).



A.23 The water-mass transformation equation

ItisinstructivetosubstituteEqn.(A.22.4)fore

intotheexpression(A.21.15)forthe

materialderivativeofˆ

Θ,thuseliminatinge

andobtainingthefollowingequationforthe

temporalandspatialevolutionofˆ

Θalongtheneutraltangentplane(McDougall(1984))

() ( )

()

1bb

23 A

ˆˆˆˆˆˆˆ

ˆˆ

ˆ,

ˆ1

n n n z nn nn

hK KgN C T p

DgN dR

βα

−Θ Θ

Θ−

∂Θ + ⋅∇ Θ = ∇ ⋅ ∇ Θ + Θ ∇ Θ⋅∇ Θ + ∇ Θ⋅∇

∂

+Θ+

Θ−

(A.23.1)

where

isthestabilityratioofthewatercolumn,A

ˆˆ

αβ

ΘΘ

=Θ Theterminvolving

hasbeenwrittenasproportionaltothecurvatureoftheA

ˆˆ

−

Θdiagramofavertical

cast;thistermcanalsobewrittenas

(

)

ˆˆ ˆ ˆ .

zz z

zzz

DgN S S

Θ−

Θ−ΘTheformofEqn.(A.23.1)

illustratesthatwhenanalyzedindensitycoordinates,ConservativeTemperature(and

AbsoluteSalinity)(i)areaffectednotonlybytheexpectedlateraldiffusionprocessalong

densitysurfacesbutalsobythenonlineardianeutraladvectionprocesses,cabbelingand

thermobaricity,(ii)areaffectedbydiapycnalturbulentmixingonlytotheextentthatthe

verticalA

ˆˆ

S−Θdiagramisnotlocallystraight,and(iii)arenotinfluencedbythevertical

variationof

sincez

doesnotappearinthisequation.

Equations(A.21.11)and(A.21.15)arethefundamentalconservationequationsof

salinityandConservativeTemperatureinaturbulentocean,andthepairofequations

(A.22.4)and(A.23.1)aresimplyderivedaslinearcombinationsofEqns.(A.21.11)and

(A.21.15).The“density”conservationequation(A.22.4)andthe“water‐mass

transformation”equation(A.23.1)areinsomesensethe“normalmodes”ofEqns.

(A.21.11)and(A.21.15).Thatis,Eqn.(A.22.4)expresseshowmixingprocessescontribute

tothemeanverticalvelocitye

throughtheneutraltangentplane,while(A.23.1)expresses

114 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

howthetracercalled“ConservativeTemperaturemeasuredalongtheneutraldirection”is

affectedbymixingprocesses;thisequationdoesnotcontain.e



Forcompleteness,thewater‐massconservationequationforAbsoluteSalinitythat

correspondstoEqn.(A.23.1)is

() ( )

()

AAAbb

23 A

ˆˆˆˆˆˆˆ

ˆˆ

ˆ,

ˆ1

nnn nnnn

SShKSKgNSC Tp

DgN dR

−Θ Θ

Θ−

∂+ ⋅∇ = ∇ ⋅ ∇ + ∇ Θ⋅∇ Θ + ∇ Θ⋅∇

∂

+Θ+

Θ−

(A.23.2)

anditeasytoshowthat

Θtimestheright‐handsideofEqn.(A.23.1)isequalto

Θtimes

theright‐handsideofEqn.(A.23.2).

Toconstructthewater‐masstransformationequationofaconservativetracer,Cthe

meandianeutralvelocitye

iseliminatedfromtheˆ

Cconservationequation(A.24.1)using

Eqn.(A.22.4)giving(fromMcDougall(1984))

() ( )

()

1bb

223 2

A22

ˆˆˆˆˆˆˆ

ˆˆ ˆ ˆ

ˆˆˆ

ˆˆ ˆ

n n n z nn nn

zzz

CChKCKgNCC Tp

dC C dS

DS D gN CgN

dS S d

αβ

−Θ Θ

Θ− −Θ

∂+ ⋅∇ = ∇ ⋅ ∇ + ∇Θ⋅∇Θ+ ∇Θ⋅∇

∂

++Θ+

(A.23.3)

Thisequationshowsthatverticalturbulentmixingprocessesaffectthetraceronneutral

tangentplanesaccordingtothecurvaturesofverticalcastsasdisplayedonboththe

ˆˆ

SC−andtheA

ˆˆ

−

Θcurves.Thetermsinvolving

canalsobewrittenas

()

() ()

223 A

A22

AAA AAA

ˆˆ ˆ

ˆˆ

ˆˆ ˆ

ˆˆ ˆ ˆ ˆ ˆ ˆˆ ˆˆ ˆ

zz z zz z z

zz z z z zz

dC C dS

DS D gN

dS S d

SC S C S DC gN S S S

Θ−

+Θ=

−+Θ−Θ

(A.23.4)



A.24 Conservation equations written in potential density coordinates

ThematerialderivativeofaquantityCcanbeexpressedwithrespecttotheCartesian

referenceframe,theneutraltangentplane,orapotentialdensityreferenceframesothat

theconservationequationofaconservativevariablecanbewrittenas(seeEqn.(A.21.16),

()()

* d

ˆˆˆ ˆ

ˆˆˆˆˆ

ˆˆˆ

ˆˆ

znzz

nn z

CCC C

Cw CeC CeC

tzt t

hK C DC

∂∂∂ ∂

+⋅∇+ = +⋅∇+ = +⋅∇ +

∂∂∂ ∂

=∇⋅ ∇ +

vvv



(A.24.1)

whered

isthemeanverticalcomponentofthetotaltransportvelocitythatmoves

throughthepotentialdensitysurface.AnyfluxofCacrosstheoceanboundaries

ound

F

(e.g.,theseasurface)wouldneedtobeaddedastheextraterm

ound

F−onthelastlineof

Eqn.(A.24.1).Noticethatthelateraldiffusionoccursalongtheneutraltangentplane.In

thissectionweconsiderwhattermsareneglectedifthislateralmixingtermisinstead

regardedasdiffusionoccurringalongpotentialdensitysurfaces.

ThetemporalandlateralgradientsofAbsoluteSalinityandConservative

Temperatureinapotentialdensitysurfacearerelatedby(McDougall(1991))

() ()

rrA

ˆˆ

ppS

σσ

αβ

ΘΘ

Θ− =and

(

)

(

)

rrA

ˆˆ

ppS

σσ

αβ

ΘΘ

∇

Θ− ∇ =0,(A.24.2)

where

()

Θand

()

Θareshorthandnotationsfor

(

)

ˆˆ

,,Sp

ΘΘand

()

ˆˆ

,,Sp

ΘΘ

respectively,andr

pisthereferencepressureofthepotentialdensity.UsingEqns.(3.17.1)

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

115

to(3.17.5)whichrelatethegradientsofpropertiesinapotentialdensitysurfacetothosein

aneutraltangentplane,thefollowingformoftheconservationequation(A.21.15)for

ConservativeTemperaturecanbederived(seeequation(26)ofMcDougall(1991))

()()

()

ˆˆ

ˆˆˆ

ˆˆ

ehKD

GhK

GG K

σσσ

ΘΘ

∂Θ ∂Θ

+ ⋅∇Θ+ = ∇ ⋅ ∇Θ + Θ

∂∂

⎡⎤

−∇⋅ − ∇Θ

⎣⎦

⎛⎞

∇Θ⋅∇Θ

⎡⎤

−−

⎜⎟

⎣⎦

⎜⎟

⎝⎠

v

(A.24.3)

wherethe“isopycnaltemperaturegradientratio”G

isdefinedas(fromEqn.(3.17.4))

1GrR Rr

ρρ

Θ⎡⎤⎡⎤

=− −

⎣⎦⎣⎦

andrisdefinedinEqn.(3.17.2)astheratioof/

ΘΘ

atthein

situpressureptothatevaluatedatthereferencepressurer.pThecorresponding

equationforAbsoluteSalinityis

()()

AAA

ˆˆ ˆ

ˆˆˆ

ˆˆ

Se hKS DS

GhK S

SG GK

σσσ

ΘΘ

∂∂

+⋅∇ + = ∇⋅ ∇ + +

∂∂

⎛⎞

⎡⎤

−∇⋅ − ∇

⎜⎟

⎢⎥

⎜⎟

⎣⎦

⎝⎠

⎛⎞

∇Θ⋅∇

⎡⎤

−−

⎜⎟

⎣⎦

⎜⎟

⎝⎠

vS

(A.24.4)

ThetermsinthesecondandthirdlinesofEqns.(A.24.3)and(A.24.4)arisebecauseinthe

firstlineoftheseequations,thelateraldiffusioniswrittenasbeingalongpotentialdensity

surfacesratherthanalongneutraltangentplanes.AsexplainedinMcDougall(1991),

thesetermsarenonzeroevenatthereferencepressureofthepotentialdensityvariable.

MultiplyingEqn.(A.24.4)by

(

)

Θandsubtracting

(

)

ΘtimesEqn.(A.24.3)we

findthecorrespondingexpressionforthediapycnalvelocityd

(followingMcDougall

(1991))

()

(

)

()

(

)

()

()( )

()

() ()

()

d11

rAr

rA r r

1ˆˆ

ˆˆ

1ˆ

ˆˆ ˆ

nn nn

nn n

ephKSphK

pDS pD p

pr hK p Kr

pGGK

pGKC T

σσ

σσ σσ

βα

βαβ

αα

ββ

ΘΘ

ΘΘΘ

ΘΘ

ΘΘΘ

ΘΘΘΘ

∂= ∇⋅∇− ∇⋅∇Θ

∂

+−Θ+

+−∇⋅∇Θ+ ∇⋅∇Θ

⎛⎞ ∇Θ⋅∇Θ

⎡⎤

−−

⎜⎟

⎣⎦

⎜⎟ Θ

⎝⎠

⎡⎤

−−∇Θ⋅∇Θ+∇

⎢⎥

⎣⎦



()

npΘ⋅∇

(A.24.5)

Allthetermsinthelastthreelinesofthisequationoccurbecausethefirstlinehaslateral

mixingalongpotentialdensitysurfacesratherthanalongneutraltangentplanes.Evenat

thereferencepressurewhere1Gr

=theselastthreelinesdonotreducetozerobut

rathertobˆ

TK p

Θ∇Θ⋅∇ showingthatthethermobariceffectremains.

Insummary,thissectionhaswrittendowntheexpressionsforthematerialderivatives

ofConservativeTemperature,AbsoluteSalinityandpotentialdensityinaformwhereone

canidentifythemanyrathernastytermsthatareneglectedifoneassumesthattheocean

mixeslaterallyalongpotentialdensitysurfacesinsteadofthephysicallycorrectneutral

tangentplanes.Itisnotedinpassingthatthefirstlineoftheright‐handsideofEqn.

(A.24.5)canalsobewrittenas

()

br ˆˆ

CpK

σσ

∇

Θ⋅∇ Θ(c.f.thelastlineofEqn.(A.27.2)below).

116 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

A.25 The vertical velocity through a general surface

Considerageneralsurfacewhichweidentifywiththelabel“a”(forexample,thiscould

standfor“approximatelyneutralsurface”).Thematerialderivativeontheleft‐handsides

oftheconservationequations(A.21.11)and(A.21.15)forAbsoluteSalinityand

ConservativeTemperaturearenowwrittenwithrespecttothisgeneral“a”coordinateas

()

AA A

ˆˆ ˆ

ˆˆ

ˆ,

ann

a z

SS S

Se hKS D

tz z

⎛⎞

∂∂ ∂

+⋅∇ + =∇⋅ ∇ + +

⎜⎟

∂∂ ∂

⎝⎠

vS(A.25.1)

and

()()

ˆˆ

ˆˆˆ

ˆ.

annz

ehKD

∂Θ ∂Θ

+⋅∇Θ+ =∇⋅ ∇Θ+ Θ

∂∂

v(A.25.2)

Cross‐multiplyingtheseequationsby

(

)

ˆˆ

,,Sp

ββ

ΘΘ

=Θand

()

ˆˆ

,,Sp

αα

ΘΘ

=Θand

subtractinggivesthefollowingequationfortheverticalvelocitythroughthe

approximatelyneutralsurface,

()

() ( )

()

ˆˆ ˆ

ˆˆ

ˆ.

ann nn

zzz

egNKC T p

gN D DS gN

gN S gN tt

αβ β

βα β α

−Θ Θ

−Θ Θ −Θ

−Θ Θ −Θ Θ

=− ∇Θ⋅∇Θ+ ∇Θ⋅∇

+Θ− −

⎡

⎤

∂∂Θ

⎡⎤

+⋅∇−∇Θ+ −

⎢

⎥

⎣⎦

∂∂

⎢

⎥

⎣

⎦



S(A.25.3)

Thetermsinthethirdlineofthisequationrepresentthedeviationofthe“a”coordinate

fromneutralityandthesetermscanbeshowntobe(fromKlockerandMcDougall(2010b)

andfromEqn.(3.14.1)above,assumingthesurfacesarenotvertical)

()

ˆˆ

ˆˆˆˆ

aa na

gN S z z

βα ρ

−Θ Θ ∇

⎡⎤

⋅∇−∇Θ=−⋅ =⋅∇−∇=⋅

⎣⎦

vvvvs(A.25.4)

and

ˆˆ

tatt

lna

Nzz

βα ρ

−Θ Θ

⎡⎤

∂∂Θ

−=−=−

⎢⎥

∂∂

⎢⎥

⎣⎦

(A.25.5)

whereˆl

isthe(thickness‐weighted)locally‐referencedpotentialdensity.

CombiningtheseresultswithEqn.(A.22.4)wehavetherathersimplekinematicresult

that

ˆ,

att

ee zz=+⋅+ −vs

 (A.25.6)

showingthattheverticalvelocitythroughageneral“a”surface,,

isthatthroughthe

neutraltangentplanee

plusthatduetothe“a”surfacehavingadifferentslopeinspace

totheneutraltangentplane,ˆ,

⋅vs

plusthatduetothe“a”surfacemovingverticallyin

time(atfixedlatitudeandlongitude)atadifferentratethantheneutraltangentplane,

z−



A.26 The material derivative of potential density

Thematerialderivativeofthenaturallogarithmofpotentialdensityis

()

Θtimesthe

materialderivativeEqn.(A.21.11)ofAbsolutesalinityminus

(

)

Θtimesthematerial

derivativeEqn.(A.21.15)ofConservativeTemperature.UsingtherelationshipsEqn.

(A.24.2)thatrelatethegradientsofAbsoluteSalinityandConservativeTemperaturein

potentialdensitysurfaces,andtakingthematerialderivativeofpotentialdensitywith

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

117

respecttopotentialdensitysurfaces,onefindsthatthetemporalandisopycnalgradient

termscancelleavingonlytheterminthemeandiapycnalvelocityd

asfollows

()

d11

rAr

rA r r

1ˆˆ

ˆˆ ,

nn nn

e p hK S p hK

pDS pD p

ρβα

βαβ

ΘΘΘ

∂= ∇⋅∇ − ∇⋅∇Θ

∂

+−Θ+



(A.26.1)

wherethefollowingexactexpressionfortheverticalgradientofpotentialdensityhasbeen

used,

() ()

rA r

1ˆˆ

ˆzz

pS p

ρβα

ΘΘΘ

∂=−Θ

∂(A.26.2)

Equation(A.26.1)canbewrittenmoreinformativelyas(followingMcDougall,1991)

()

() () ()

{}

()

[]

()

rrArA

ˆˆ

1ˆ

ˆˆ

ˆˆˆˆ

ˆˆ ˆ ,

zS z S

nn nn

Dp pS pS

pr hK

pKC T p

ρρ

αα β

ΘΘ

ΘΘ Θ

ΘΘΘ

⎛⎞

∂∂

⎜⎟

∂∂

⎝⎠

+Θ+Θ−

+−∇⋅∇Θ

+ ∇ Θ⋅∇ Θ + ∇ Θ⋅∇

S

(A.26.3)

whererisdefinedinEqn.(3.17.2)astheratioof/

Θattheinsitupressureptothat

evaluatedatthereferencepressurer.pIftheequationofstatewerelinear,onlythefirst

twotermswouldbepresentontherightofEqn.(A.26.3).



A.27 The diapycnal velocity of layered ocean models (without rotation of the

mixing tensor)

Layeredmodelsoftheoceancirculationhaveapotentialdensityvariable(usuallywitha

referencepressurer

pof2000dbar)astheirverticalcoordinate.Todatethesemodelshave

notrotatedthedirectionoflateralmixingtoalignwiththeneutraltangentplanebut

ratherhavemixedlaterallyalongthepotentialdensitycoordinatedirection.The

diapycnalvelocityd_model

inthisclassofmodelobeystheequation(c.f.Eqn.(A.26.1)

above)

()

d_model 11

rAr

rA r r

1ˆˆ

ˆˆ ,

ephKSphK

pDS pD p

σσ

σσ σσ

ρβα

βαβ

ΘΘΘ

∂

∇⋅ ∇ − ∇⋅ ∇Θ

∂

+−Θ+



(A.27.1)

where

∇isthegradientoperatoralongthepotentialdensitycoordinate,K

isthelateral

diffusivityalongthelayersandh

isthethicknessbetweenapairofpotentialdensity

surfacesinthevertical.Thisequationcanberewrittenas

()

() () ()

{}

()

d_model

rrArA

ˆˆ

1ˆ

ˆˆ

ˆˆˆˆ

ˆˆ

zS z S

Dp pS pS

KC p

σσσ

ρρ

αα β

ΘΘ

ΘΘ Θ

⎛⎞

∂∂

⎜⎟

∂∂

⎝⎠

+Θ+Θ−

+∇Θ⋅∇Θ

S

(A.27.2)

Thetermsintheverticalturbulentdiffusivity

areidenticaltothoseinthecorrect

equation(A.26.3)whilethediapycnalvelocityduetocabbelingisquitesimilartothatin

thecorrectexpressionEqn.(A.26.3);thedifferencemostlybeingthatthecabbeling

coefficientishereevaluatedatthereferencepressureinsteadofattheinsitupressure,and

118 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

thatthelateraltemperaturegradientishereevaluatedalongthepotentialdensitysurface

ratherthanalongtheneutraltangentplane(thesegradientsareproportionaltoeachother

viatherelation(3.17.3)).Anotherdifferenceisthattheterm

()

[]

()

rˆ

1nn

pr h hK

Θ−

−

∇⋅ ∇Θ

inEqn.(A.26.3)ismissingfromEqn.(A.27.2).Thistypeofdifferenceistobeexpected

sincethedirectionofthelateralmixingisdifferent.

NoticetheabsenceofthethermobaricdiapycnaladvectionfromEqn.(A.27.2);thatis,

thetermproportionaltobˆ

KT p

Θ∇Θ⋅∇ inEqn.(A.26.3)isabsentfromEqn.(A.27.2),as

firstremarkedonbyIudiconeetal.(2008).Thethermobaricdiapycnaladvectionis

probablysignificantintheSouthernOcean(KlockerandMcDougall(2010a))andthis

wouldarguefortherotationofthelateralmixingtensorinlayeredmodelstothelocal

directionoftheneutraltangentplane,asisdoneinheight‐coordinateoceanmodels.Also

missingfromlayeredoceanmodelsisthemeanverticaladvectionˆ

⋅

vsduetothehelical

natureofneutraltrajectoriesintheocean(seesection3.13,Eqn.(A.25.4)andKlockerand

McDougall(2010b)).



A.28 The material derivative of orthobaric density

Orthobaricdensity

()

hasbeendefinedbydeSzoekeetal.(2000)asapressure

correctedformofinsitudensity.Theconstructionoforthobaricdensityrequiresthe

isentropiccompressibilitytobeapproximatedasafunctionofpressureandinsitudensity.

Whileorthobaricdensityhastheadvantageofbeingathermodynamicvariable,

orthobaricdensitysurfacesareoftennotparticularlygoodapproximationstoneutral

tangentplanes(seeMcDougallandJackett(2005a)andKlockeretal.(2009a,b)).The

materialderivativeofv

canbeexpressedwithrespecttoorthobaricdensitysurfacesas

ˆ,

vvv

vee

tzz

ρρ

∂∂∂

+⋅∇ + =

∂∂∂

v

(A.28.1)

wherethetemporallyaveragedverticalvelocitythroughthev

surfaceisgivenby(from

McDougallandJackett(2005a))

()

(

)

Aˆ

egN S p pp

αβ ψ

−Θ Θ

=Θ−+−+⋅∇v



(A.28.2)

where(fromdeSzoekeetal.(2000))

() ()

223 2 2

0b0

12 ,,gN c c gT N p

ρρ

−− Θ−

⎡

⎤

−≈ Δ≈− Θ−Θ

⎣

⎦(A.28.3)

andcΔisthedifferencebetweenthereferencesoundspeedfunction

()

0,cp

andthe

soundspeedofseawaterwhichcanbeexpressedinthefunctionalform

()

,, .cp

ΘThis

differenceinthesoundspeedisequivalenttothedifferencebetweentheactual

ConservativeTemperatureofawaterparcelandthereferencevalue

(

)

0,.p

ΘHereA

is

shorthandforthematerialderivativeofA

Sandisexpressedintermsofmixingprocesses

bytheright‐handsideofEqn.(A.21.11);

issimilarlyshorthandforthematerial

derivativeofˆ

Θandisgivenbytheright‐handsideofEqn.(A.21.15).

ThefirsttermontherightofEqn.(A.28.2)representstheeffectsofirreversiblemixing

processesontheflowthroughorthobaricdensitysurfaces,andthiscontributiontov

is

exactlythesameastheflowthroughneutraltangentplanes,e

(Eqn.(A.22.4)).Thesecond

terminEqn.(A.28.2)arisesfromthenon‐quasi‐material(non‐potential)natureof

orthobaricdensity.Thisverticaladvectionarisesfromtheseeminglyinnocuoussliding

motionalongtheslopingorthobaricdensitysurfaceandfromtheverticalheavingofthese

surfaces.



TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

119

A.29 The material derivative of Neutral Density

NeutralDensityn

isnotathermodynamicfunctionsinceitdependsonlatitudeand

longitude.TheNeutralDensityalgorithmfindsthedatapointinapre‐labeledreference

datasetthathasthesamepotentialdensityasthedatapointthatisbeinglabeled;the

referencepressureofthispotentialdensityistheaverageofthepressuresofthetwo

parcels.Thematerialderivativeofn

canbeexpressedas

nn n

ˆ,

γγ

∂+⋅∇ + =

∂v

(A.29.1)

wherethetemporallyaveragedverticalvelocitythroughthen

surfaceisgivenby(from

McDougallandJackett(2005b))

()

Aref

ref ref

ref 1

ref ref

ref

ref ref

ref

() () ˆ

() ()

()

ˆˆ

1ˆ

()

() ()

2( 1)

() ()

ppS

eppS

ppp

ppS

γγ

γγγ

αβ

ψαβ

ΘΘ

−

ΘΘ

Θ−

≈+⋅

Θ−

+− +⋅∇

⎛⎞

−

+− ⋅∇ − ⋅∇Θ

⎜⎟

Θ−Θ

⎝⎠

Θ−

+− Θ−

+−⋅







(A.29.2)

HereA

isshorthandforthematerialderivativeofA

Sfollowingtheappropriatemean

velocityandisexpressedintermsofmixingprocessesbytheright‐handsideofEqn.

(A.21.11),Θ

issimilarlyshorthandforthematerialderivativeofˆ

andisgivenbyEqn.

(A.21.15),and

()

−isdefinedby

()

2ref

2 2 ref ref ref

ref b b

()

() ()

NgT gTPP

ψρ

ΘΘ

−Θ−Θ

−=

⎡⎤

+Θ−Θ+ −Θ

⎣⎦

(A.29.3)

Here2

ref

Nisthesquareofthebuoyancyfrequencyofthepre‐labelledreferencedataset.

Equation(A.29.3)showsthat

()

−

isnonzerototheextentthatthereisawatermass

contrastref

()Θ−Θ betweentheseawaterparcelthatisbeinglabeledandthedataonthe

pre‐labeledreferencedatasetthatcommunicatesneutrallywiththeseawatersample.For

reasonablevaluesofref

()Θ−Θ andref

()pp−thedenominatorinEqn.(A.29.3)iscloseto

ref

Nand

()

−issmall.Intheseexpressionsthethermalexpansioncoefficient

()

Θ

andsalinecontractioncoefficient

(

)

Θareevaluatedattheaverageofthepropertiesof

theparcelbeinglabeledandtheparcelinthereferencedatasettowhichitisneutrally

related,thatis,

()

Θand

()

Θareshorthandfor

(

)

A,,Sp

ΘΘand

()

A,, .Sp

ΘΘ

ThefirstterminEqn.(A.29.2)isexpectedasNeutralDensitychangesinresponseto

theirreversiblemixingprocessesΘ

andS

.ThenextterminEqn.(A.29.2),ref

ˆ,⋅

vs isalso

expected;itisthemeanverticalmotionthroughthen

surfaceduetothehelicalmotion

ofneutraltrajectoriesinthereferencedataset,causedinturnbythenon‐zeroneutral

helicityofthereferencedataset.TheremainingtermsinthelastfourlinesofEqn.(A.29.2)

arisebecauseofthenon‐quasi‐material(non‐potential)natureofNeutralDensity.The

secondlineofEqn.(A.29.2)representsthecontributiontoe

arisingfromtheseemingly

innocuousslidingmotionalongtheslopingn

surfaceandfromtheverticalheavingof

thesesurfaces.Thelateralgradientsofpropertiesinthereferencedatasetalsoaffectthe

meanflowe

throughthen

surface.Notethatas

(

)

ref

Θ−Θ tendstozero,

()

−also

tendstozerosothatthethirdlineofEqn.(A.29.2)iswell‐behavedandbecomes

proportionalto1ref ref

() .

ppp

−−⋅∇Θv

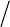
120 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

A.30 Computationally efficient 25-term expressions for the density of seawater

in terms of Θ and

Oceanmodelstodatehavetreatedtheirsalinityandtemperaturevariablesasbeing

PracticalSalinityP

Sandpotentialtemperature

.AsthefullimplicationsofTEOS‐10are

incorporatedintooceanmodelstheywillneedtocarryPreformedSalinity*

Sand

ConservativeTemperatureΘasconservativevariables(asdiscussedinappendicesA.20

andA.21),andacomputationallyefficientexpressionfordensityintermsofAbsolute

SalinityA

SandConservativeTemperature

willbeneeded.

FollowingtheworkofMcDougalletal.(2003)andJackettetal.(2006),theTEOS‐10

density

hasbeenapproximatedbyarationalfunctionofthesameformasinthose

papers.Thefittedexpressionistheratiooftwopolynomialsof

(

)

A,,SpΘ

25 25

num denom

ρρ

≈= .(A.30.1)

Thedensitydatahasbeenfittedina“funnel”ofdatapointsin

(

)

A,,Stpspacewhichis

describedinmoredetailinMcDougalletal.(2010b).The“funnel”extendstoapressureof

8000dbar .Attheseasurfacethe“funnel”coversthefullrangeoftemperatureand

salinitywhileforpressuresgreaterthan5500dbar,themaximumtemperatureofthefitted

datais12 C°andtheminimumAbsoluteSalinityis1

PS 30 g kgu

−

.Thatis,thefithasbeen

performedoveraregionofparameterspacewhichincludeswaterthatisapproximately

10 C°warmerand1

5gkg

−fresherinthedeepoceanthanexistsinthepresentocean(see

Figure1ofJackettetal.(2006)).TableK.1ofappendixKcontainsthe25coefficientsofthe

expression(A.30.1)fordensityintermsof

(

)

A,,SpΘ.

AsoutlinedinappendixK,this25‐termrational‐functionexpressionfor

yieldsthe

thermalexpansionandhalinecontractioncoefficients,

and

,thatareessentiallyas

accurateasthosederivedfromthefullTEOS‐10Gibbsfunctionfordatainthe

“oceanographicfunnel”.Thesamecannotbeclaimedforthesoundspeedderivedby

differentiatingEqn.(A.30.1)withrespecttopressure;thissoundspeedhasanrmserrorin

the“funnel”ofalmost1

0.25 m s−whereasTEOS‐10fitstheavailablesoundspeeddata

withanrmserrorofonly1

0.035 m s

−

.

Indynamicaloceanographyitisthethermalexpansionandhalinecontraction

coefficients

Θand

Θwhicharethemostimportantaspectsoftheequationofstate

sincethe“thermalwind”isproportionaltoApp

αβ

ΘΘ

∇Θ− ∇ andtheverticalstatic

stabilityisgivenintermsofthebuoyancyfrequencyNby12

()

gN S

αβ

−ΘΘ

=Θ− .

Hencefordynamicaloceanographywemaytakethe25‐termrationalfunctionexpression

fordensity,Eqn.(A.30.1),asessentiallyreflectingthefullaccuracyofTEOS‐10.Thisis

confirmedinFig.A.30.1wheretheerrorinusingthe25‐termexpressionfordensityto

calculatetheisobaricnorthwarddensitygradientisshown.Theverticalaxisonthisfigure

isthemagnitudeofthedifferenceinthenorthwardisobaricdensitygradientintheworld

oceanbelow1000 m whenevaluatedusingEqn.(A.30.1)versususingthefullTEOS‐10

Gibbsfunction.Thescalesoftheaxesofthisfigurehavebeenchosentobethesameas

thoseofFig.A.5.1ofappendixA.5sothatthesmallnessoftheerrorsassociatedwithusing

the25‐termdensityexpressioncanbeappreciated.TheerrorsrepresentedinFig.A.30.1

representperhapshalfoftheremaininguncertaintyinourknowledgeofseawater

properties,andbycomparingFigs.A.30.1andA.5.1itisclearthatthemuchmore

importantissueistoproperlyrepresenttheeffectsofseawatercompositiononseawater

density.ThermsvalueoftheverticalaxisinFig.A.30.1is11.4%ofthatofFig.A.5.1.

McDougalletal.(2010b)havealsoprovideda25‐termrational‐functionexpressionfor

densityintermsof

(

)

A,,Sp

.The25coefficientscanbefoundinTableK.2ofappendix

K.Asanapproximationtodensity,this25‐termrationalfunctionisapproximatelyas

accurateastheonedescribedaboveintermsof

(

)

A,,SpΘ.Itmustbeemphasizedthough

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

121

thatanoceanmodelthattreatedpotentialtemperatureasaconservativevariablewould

makeerrorsinitstreatmentofheatfluxes,asdescribedinappendicesA.13,A.14andA.17,

andasillustratedinFiguresA.13.1,A.14.1andA.17.1.



FigureA.30.1.Thenorthwarddensitygradientatconstantpressure(thehorizontal

axis)fordataintheworldoceanatlasofGouretskiandKoltermann

(2004)for1000 dbarp>.Theverticalaxisisthemagnitudeofthe

differencebetweenevaluatingthedensitygradientusingthe25‐term

expressionEqn.(A.30.1)insteadofusingthefullTEOS‐10expression,

usingAbsoluteSalinityA

Sasthesalinityargumentinbothcases.



AppendixPdescribeshowanexpressionfortheenthalpyofseawaterintermsof

ConservativeTemperature,specificallythefunctionalform

(

)

ˆ,,hS pΘ,togetherwithan

expressionforentropyintheform

(

)

ˆ,S

,canbeusedasanalternativethermodynamic

potentialtotheGibbsfunction

(

)

A,,

Stp.Theneedforthefunctionalform

(

)

ˆ,,hS pΘ

alsoarisesinsection3.32andinEqns.(3.26.3)and(3.29.1).The25‐termexpression,Eqn.

(A.30.1),for

()

25 25

ˆ,,Sp

ρρ

=Θcanbeusedtofindaclosedexpressionfor

(

)

ˆ,,hS pΘby

integratingthereciprocalof

()

ˆ,,Sp

Θwithrespecttopressure(inPa ),since

ˆP

−

== (seeEqn.(2.8.3)).

The25‐termexpressionforspecificvolume,Eqn.(A.30.1),isfirstwrittenexplicitlyas

theratiooftwopolynomialsinseapressurep(indbar )as

25 01 2 3

25 2

01 2

ˆˆ2

aapapap

vbbpbp

++ +

== ++ ,(A.30.2)

wherethecoefficients0

ato3

aand0

bto2

barethefollowingfunctionsofA

SandΘ

() ()

1.5 1.5

234 3 2

0 14 15 16 17 18 A 19 A 20 A 21 A 22 A

1acccccScScScScS=+ Θ+ Θ+ Θ+ Θ+ + Θ+ Θ+ + Θ,

123

ac=,

224

ac=Θ,

325

ac=Θ,

()

012 3 4 5A6A 7A

bcccccScScS=+Θ+Θ+Θ+ + Θ+ ,

()

18910A

0.5bcccS=+Θ+,

21112

bc c=+Θ,

andthenumberedcoefficients1

cto25

caresoidentifiedinTableK.1(notethat13 1c=).

ItisnotdifficulttorearrangeEqn.(A.30.2)intotheform

122 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

()

25 25 31 32

A22

2012

ˆˆ ,, ,

ab aaNMp

vvS p p

bbbpbp

⎛⎞ +

=Θ=−++

⎜⎟ ++

⎝⎠ (A.30.3)

whereNand

aregivenby

301 20

abb ab

Na b

=+ − and 1

330 21

ab ab ab

Ma bb

=+ − − .(A.30.4)

ThepressureintegralofthelastterminEqn.(A.30.3)iswellknown(seeforexample

section2.103ofGradshteynandRyzhik(1980))andisdependentonthesignofthe

discriminantofthedenominator.Inourcaseitcanbeshownthat2

102

bbb>overthe

domainofthe“funnel”andalsothatboth0

band1

barepositive,while2

bisnegativeand

boundedawayfromzero.Theindefiniteintegral,withrespecttoseapressuremeasured

inPa ,ofthelastterminEqn.(A.30.3)is(with *4

10NN=and*4

M=)

***

21102

221

01 2

222

01 2 21 02 2 1 1 02

ln 2 ln

bp b b bb

NMp M NbMb

dP b b p b p

bbpbp b b bb b p b b bb

∫+− −

+−

′=+++

++ −++−

,(A.30.5)

Theenthalpy

()

ˆ,,

hS pΘisthedefiniteintegralofEqn.(A.30.3)from0

to

,plus0

,

beingthevalueofenthalpyat0

(i.e.at0dbarp

).Hencethefullexpressionfor

()

ˆ,,

hS pΘis(with2

1102

bbbb=− − and2

1102

Bb b bb=+ − )

()

25 0 4 4 2

31 32

12 2

200 2

ˆ,, 10 10

ln 1 ln 1 .

pab a

hS p c p p

NM BA

Mbb bb

pp p

bbb BA ABbp

⎛⎞

Θ=Θ+ − +

⎜⎟

⎝⎠

−⎛⎞

−

⎛⎞

++++ +

⎜⎟

−+

⎝⎠ ⎝⎠

(A.30.6)

Thefactorof4

10 thatappearshereandin*

Nand*

effectivelyservestoconvertthe

unitsoftheintegrationvariablefromdbar toPa sothat

()

ˆ,,

hS pΘhasunitsof1

Jkg .

−



IntheseequationsA

Sisin1

gkg

−,

inC°andpisindbar. Theargumentsofthetwo

naturallogarithmsinEqn.(A.30.6)arealwaysgreaterthan1,andinfacttheyarebetween

1and1.2evenforpaslargeas4

10 dbar (notethatboth2

band

arenegative).Also,

whentheenthalpydifferenceatthesamevaluesofA

Sand

butatdifferentpressures

(seeEqn.(3.32.2))isevaluatedusingEqn.(A.30.6),theexpressioncanalsobearrangedto

containonlytwologarithmterms.

FollowingYoung(2010),thedifferencebetweenspecificenthalpyand0

cΘmaybe

called“dynamicenthalpy”andcanbereadilycalculatedfromEqn.(A.30.6),recognizing

thatthisequationisbasedonthecomputationallyefficient25‐termexpressionfordensity

ofMcDougalletal.(2010b)ratherthanbeingevaluatedfromthefullTEOS‐10Gibbs

function.Similarly,thepartialderivativesof

()

ˆ,,

hS pΘwithrespecttoAbsolute

SalinityA

SandwithrespecttoConservativeTemperature

canbecalculatedeitherby

algebraicdifferentiationofEqn.(A.30.6)orbyfirstalgebraicallydifferentiatingEqn.

(A.30.1)andthennumericallyintegratingthisexpressionwithrespecttopressure(this

secondprocedureismotivatedbytakingtheappropriateA

Sor

derivativesofEqn.

(3.2.1);seeEqns.(A.18.4)and(A.18.5)).

Anexpression

()

A,,hS p

forenthalpyasafunctionofpotentialtemperature

can

befoundinasimilarmannertothatoutlinedabove,butwiththecoefficientsofthe25‐

termrational‐functionexpressionfordensitynowbeingtakenfromTableK.2,andwith

thefirsttermbeingexpressedastheexactpolynomialexpressionfor

(

)

A,,0hS

insteadof

as0

cΘ.

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

123

AppendixB:

DerivationoftheFirstLawofThermodynamics



Motivation



Forapurefluidinwhichthereisnodissolvedmaterial(suchaspurewaterwithzero

AbsoluteSalinity)thederivationoftheFirstLawofThermodynamicsusuallystartswitha

discussionofhowtheinternalenergyUofafixedmassoffluidischangedunderthe

influenceofitbeing“heated”bytheamountQ

anditsvolumeVbeingchanged.The

infinitesimalchangeintheinternalenergyoftheparceliswrittenas

()

ddUQpPV

=−+ 

where

()

0dpP V−+ isthemechanicalworkdoneonthefluidbythepressureatthe

movingboundariesofthefluidparcel.Thisrelationshipcanbewrittenintermsofthe

specific(i.e.perunitmass)enthalpy,hthedensity,

andQ

perunitvolume,,q

as

d1d .

ddd

hPq

ttt

ρρ

⎛⎞

−=

⎜⎟

⎝⎠

forpurewater(B.1)

Itisrecognizedthattheright‐handsideof(B.1)isnotthedivergenceofa“heat”flux,and

thetermthatcausesthiscomplicationisthedissipationofmechanicalenergyinto“heat”,

whichcontributes

totheright‐handsideof(B.1).Apartfromthisfamiliardissipation

term,theright‐handsideisminusthedivergenceofthesumoftheboundaryand

radiativeheatfluxes,R

F,andminusthedivergenceofthemolecularfluxofheat

kT=− ∇F(whereT

kisthemoleculardiffusivityofheat),sothattheFirstLawof

Thermodynamicsforpurewateris

()

d1d .

ddd

hPq kT

ttt

ρε

⎛⎞

−==−∇⋅+∇⋅∇+

⎜⎟

⎝⎠ Fforpurewater(B.2)

NowconsiderseawaterinwhichtheAbsoluteSalinityanditsgradientsarenon‐zero.

ThesametraditionaldiscussionoftheFirstLawofThermodynamicsinvolvingthe

“heating”,theapplicationofcompressionworkandthechangeofsalinitytoafluidparcel

showsthatthechangeofenthalpyofthefluidparcelisgivenby(seeequations6band17b

ofWarren(2006))

[

]

(

)

dd d,

HVP Q Tt MS

δμ μ

−=+−+ (B.3)

where

isthemassofthefluidparcel.Whenwrittenintermsofthespecificenthalpy

,handQ

perunitvolume,q

,thisequationbecomes(usingA

dd S

=−∇⋅F)

[]

()

d1d

ddd T

hPq Tt

ttt

ρμμ

⎛⎞

−=−−+∇⋅

⎜⎟

⎝⎠ F.(B.4)

Doesthishelpwiththetaskofconstructinganexpressionfortheright‐handsideof

(B.4)intermsofthedissipationofmechanicalenergyandthemolecular,radiativeand

boundaryfluxesof“heat”andsalt?Ifthe“heating”termdqt

in(B.4)werethesameas

inthepurewatercase(B.2)thenwewouldhavesuccessfullyderivedtheFirstLawof

Thermodynamicsinasalineoceanviathisroute.However,wewillnowshowthatdqt



in(B.4)isnotthesameasthatinthepurewatercase,(B.2).

Substitutingtheexpressionfordqt

from(B.2)intotheright‐handsideof(B.4)we

findthattheright‐handsideisnotthesameastheFirstLawofThermodynamics(B.19)

whichwederivebelow(thiscomparisoninvolvesusingthecorrectexpression(B.24))for

124 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

themolecularfluxQ

F).ThetwoversionsoftheFirstLawofThermodynamicsare

differentby

[]

()

[

]

Tt b k

μμ μ

⎡

⎤

⎛⎞

−−+ ∇⋅+∇⋅ +

⎢

⎥

⎜⎟

⎢

⎥

⎝⎠

⎣

⎦

FF.(B.5)

Thisinconsistencymeansthattheratherpoorlydefined“rateofheating”dqt

mustbe

differentinthesalinecasethaninthepurewatersituationbythisamount.Weknowof

nowayofjustifyingthisdifferenceandintheabsenceofnewinspirationwhichwehave

notfoundintheliterature,wetentativelyconcludethatanyattempttoderivetheFirst

LawofThermodynamicsviathisrouteinvolvingthelooselydefined“rateofheating”

dqt

isdoomedtofailure.

SincethereappearstobenowayofderivingtheFirstLawofThermodynamicsthat

involvesthe“heating”termdqt

,wefollowLandauandLifshitz(1959)andderivethe

FirstLawviathefollowingcircuitousroute.Ratherthanattemptingtoguesstheformof

themolecularforcingtermsinthisequationdirectly,wefirstconstructaconservation

equationforthetotalenergy,beingthesumofthekinetic,gravitationalpotentialand

internalenergies.Itisinthisequationthatweinsertthemolecularfluxesofheatand

momentumandtheradiativeandboundaryfluxesofheat.Weknowthattheevolution

equationfortotalenergymusthavetheconservativeform,andsoweinsistthatthe

forcingtermsinthisequationappearasthedivergenceoffluxes.

Havingformedtheconservationequationfortotalenergy,theknownevolution

equationsfortwoofthetypesofenergy,namelythekineticandgravitationalpotential

energies,aresubtracted,leavingaprognosticequationfortheinternalenergy,thatis,the

FirstLawofThermodynamics.

Westartbydevelopingtheevolutionequationsforgravitationalpotentialenergyand

forkineticenergy(viathemomentumequation).Thesumofthesetwoevolution

equationsisnoted.Wethenstepbackalittleandconsiderthesimplifiedsituationwhere

therearenomolecularfluxesofheatandsaltandnoeffectsofviscosityandnoradiative

orboundaryheatfluxes.Inthis“adiabatic”limitweareabletodeveloptheconservation

equationfortotalenergy,beingthesumofinternalenergy,kineticenergyand

gravitationalpotentialenergy.Tothisequationweintroducethemolecular,radiativeand

boundaryfluxdivergences.FinallytheFirstLawofThermodynamicsisfoundby

subtractingfromthistotalenergyequationtheconservationstatementforthesumofthe

kineticandgravitationalpotentialenergies.



Thefundamentalthermodynamicrelation



Recallthefundamentalthermodynamicrelation(A.7.1)repeatedhereintheform(A.7.2)

intermsofmaterialderivativesfollowingtheinstantaneousmotionofafluidparcel

dd ,

xyz

tt=∂ ∂ + ⋅∇u

() ()

d1d d d d d

ddd d d d

hPu v S

pP T t

ttt t tt

−=++=++ (B.6)

Theuseofthesamesymboltfortimeandforinsitutemperaturein°Cisnotedbut

shouldnotcauseconfusion.Themiddleexpressionin(B.6)usesthefactthatspecific

enthalpyhandspecificinternalenergyuarerelatedby

()

huPvu pPv=+ =+ + where

visthespecificvolume.



TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

125

Gravitationalpotentialenergy



Ifthegravitationalaccelerationistakentobeconstantthegravitationalpotentialenergy

perunitmasswithrespecttotheheight

=0issimply.

zAllowingthegravitational

accelerationtobeafunctionofheightmeansthatthegravitationalpotentialenergyper

unitmassΦwithrespecttosomefixedheight0

zisdefinedby

()

zdz

′

Φ=∫(B.7)

AtafixedlocationinspaceΦisindependentoftimewhileitsspatialgradientisgivenby

∇Φ = kwherekistheunitvectorpointingupwardsintheverticaldirection.The

evolutionequationforΦisthenreadilyconstructedas

() ( )

ρρρρ

Φ+∇⋅ Φ = =u(B.8)

Wherewistheverticalcomponentofthethree‐dimensionalvelocity,thatis.w=⋅uk

(Clearlyinthissection

isthegravitationalacceleration,nottheGibbsfunction).Note

thatthislocalbalanceequationforgravitationalpotentialenergyisnotintheform(A.8.1)

requiredofaconservativevariablesincetheright‐handsideof(B.8)isnotminusthe

divergenceofaflux.



Momentumevolutionequation



ThemomentumevolutionequationisderivedinmanytextbooksincludingLandauand

Lifshitz(1959),Batchelor(1970),Gill(1982)andGriffies(2004).Themolecularviscosity

appearsintheexactmomentumevolutionequationintherathercomplicatedexpressions

appearinginequations(3.3.11)and(3.3.12)ofBatchelor(1970).Weignorethetermthat

dependsontheproductofthesocalleddynamicviscosityvisc

vandthevelocity

divergence∇⋅u(followingGill(1982)),soarrivingat

(

)

visc

dfPgv

ρρρρ

+×=−∇− +∇⋅ ∇

uku k u

(B.9)

Where

istheCoriolisfrequency,visc

vistheviscosityand

∇

uistwicethesymmetrized

velocityshear,

(

)

ij ji

ux u x∇=∂ ∂ +∂ ∂uUnderthesameassumptionasaboveofignoring

thevelocitydivergence,thepressurepthatenters(B.9)canbeshowntobeequivalentto

theequilibriumpressurethatisrightlythepressureargumentoftheequationofstate

(Batchelor(1970).Thecentripetalaccelerationassociatedwiththecoordinatesystembeing

onarotatingplanetcanbetakenintoaccountbyanadditiontothegravitational

accelerationin(B.9)(Griffies(2004)).



Kineticenergyevolutionequation



ThekineticenergyevolutionequationisfoundbytakingthescalarproductofEqn.(B.9)

withugiving

()

[]

()

[]

()

visc 1

dd ,

tPgwv

ρρ

ρρ ρε

⋅+∇⋅ ⋅

=⋅=−⋅∇−+∇⋅∇⋅−

uu u uu

uu u uu (B.10)

wherethedissipationofmechanicalenergy

isthepositivedefinitequantity

(

)

visc

2.v

≡∇⋅∇uu(B.11)



126 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Evolutionequationforthesumofkineticandgravitationalpotentialenergies



Theevolutionequationfortotalmechanicalenergy0.5

⋅

+Φuu isfoundbyaddingEqns.

(B8)and(B10)giving

()()

()

[]

()

visc 1

dd .

tPv

ρρ

ρρε

⎡⎤ ⎡⎤

⋅+Φ +∇⋅ ⋅+Φ

⎣⎦ ⎣⎦

= ⋅ +Φ = − ⋅∇ +∇⋅ ∇ ⋅ −

uu u uu

uu u uu (B.12)

Noticethattheterm

whichhastheroleofexchangingenergybetweenthekinetic

andgravitationalpotentialformshascancelledwhenthesetwoevolutionequationswere

added.



Conservationequationfortotalenergy

intheabsenceofmolecularfluxes



Intheabsenceofmolecularorotherirreversibleprocesses(suchasradiationofheat),andin

theabsenceofthenon‐conservativesourcetermforAbsoluteSalinitythatisassociatedwith

remineralization,boththespecificentropy

andtheAbsolutesalinityA

Sofeachfluid

parcelisconstantfollowingthefluidmotionsothattheright‐handsideof(B.6)iszeroand

thematerialderivativeofinternalenergysatisfies

(

)

dd ddut pP vt=− + sothattheinternal

energychangesonlyasaresultoftheworkdoneincompressingthefluidparcel.Realizing

that1

−

=andusingthecontinuityEqn.(A.8.1)intheformdd 0,t

∇⋅ =uddutcan

beexpressedinthissituationofnomolecular,radiativeorboundaryfluxesas

()

dd .ut pP

−

=− + ∇⋅uAddingthisequationtotheinviscid,non‐dissipativeversionof

(B.12)gives

() ( )

[

]

(

)

ttpP

ρρρ

+∇⋅ = = −∇⋅ +uu

EEE

,nomolecularfluxes(B.13)

wherethetotalenergy

u=+ ⋅+Φuu

(B.14)

isdefinedasthesumoftheinternal,kineticandgravitationalpotentialenergies.



Conservationequationfortotalenergyinthepresenceofmolecularfluxesand

remineralization



Now,followingsection49LandauandLifshitz(1959)weneedtoconsiderhowmolecular

fluxesofheatandsaltandtheradiationofheatwillalterthesimplifiedconservation

equationoftotalenergy(B.14).Themolecularviscositygivesrisetoastressinthefluid

representedbythetensor,σandtheinteriorfluxofenergyduetothisstresstensoris

⋅uσsothatthereneedstobetheadditionalterm

(

)

−

∇⋅ ⋅u

addedtotheright‐handside

ofthetotalenergyconservationequation.ConsistentwithEqn.(B.9)abovewetakethe

stresstensortobe

visc

=− ∇uσsothattheextratermis

[]

(

)

visc 1

2.v

∇⋅ ∇ ⋅uu Alsoheat

fluxesattheoceanboundariesandbyradiationR

FandmoleculardiffusionQ

F

necessitatetheadditionaltermsRQ

−∇⋅ − ∇ ⋅FF.Atthisstagewehavenotspecifiedthe

formofthemoleculardiffusivefluxofheatQ

Fintermsofgradientsoftemperatureand

AbsoluteSalinity;thisisdonebelowineq(B.24).Thenon‐conservativeproductionof

AbsoluteSalinitybytheremineralizationofsinkingparticulatematter,A

S,introduces

asourceofenergybecausethespecificinternalenergyandthespecificenthalpyofseasalt

arenotthesameasforpurewater.Thetotalenergyconservationequationinthepresence

ofmolecular,radiativeandboundaryfluxes,aswellastheinteriorsourceofsalinityis

() ( )

[

]

(

)

[]

()

visc 1

tpP

ρρρ

ρρ

+∇⋅ = = −∇⋅ + −∇⋅ −∇⋅

+∇⋅ ∇ ⋅ +

uuFF

uu S

EEE

(B.15)

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

127

where

()

A0ST

hTt

=− + (seeEqn.(A.11.1))isthepartialderivativeofspecificenthalpy

withrespecttoAbsoluteSalinityatfixedtemperatureandpressure.ThislastterminEqn.

(B.15)ismorereadilyjustifiedinEqn.(B.17)below,whichisarearrangedformofEqn.

(B.15).

Ifitwerenotfortheremineralizationsourceterm,A

S,theright‐handsideof

the

conservationequation(B.15)wouldbethedivergenceofaflux,ensuringthattotal

energy

wouldbebotha“conservative”variableandan“isobaricconservative”

variable(seeappendixA.8forthedefinitionofthesecharacteristics).



Twoalternativeformsoftheconservationequationfortotalenergy



Anotherwayofexpressingthetotalenergyequation(B.15)istowriteitinaquasi‐

divergenceform,withthetemporalderivativebeingof

(

)

ρρ

+⋅+Φuu

whilethe

divergencepartoftheleft‐handsideisbasedonadifferentquantity,namelytheBernoulli

function 1

2.h=+ ⋅+Φuu

Thisformofthetotalenergyequationis

() ( )

[

]

(

)

RQ visc

tvh

ρρ ρ ρ

+∇⋅ =−∇⋅ −∇⋅ +∇⋅ ∇ ⋅ +uFF uuS

(B.16)

Inanoceanmodellingcontext,itisratherstrangetocontemplatetheenergyvariablethat

isadvectedthroughthefaceofamodelgrid,

,tobedifferenttotheenergyvariablethat

ischangedinthegridcell,

.Hencethisformofthetotalenergyequationhasnot

provedpopular.

Athirdwayofexpressingthetotalenergyequation(B.15)istowritetheleft‐handside

intermsofonlytheBernoullifunction1

+⋅+Φuu

sothattheprognosticequation

fortheBernoullifunctionis

() ( )

[

]

(

)

RQ visc

dd .

ttP v h

ρρρ ρ ρ

+∇⋅ = = −∇⋅ −∇⋅ +∇⋅ ∇ ⋅ +uFFuu

BBB

S(B.17)

ThesourcetermA

SofAbsoluteSalinitycausedbytheremineralizationofparticulate

matteraffectsenthalpyattherate

(

)

A0ST

hTt

=− + andcanbethoughtofasreplacing

someseasaltinplaceofwatermolecules,occurringatfixedpressureandtemperature,as

mightoccurthroughtwosyringesintheinteriorofaseawaterparcel,onesupplyingpure

saltandtheotherextractingpurewater,atthesametemperatureandpressure.The

influenceofthesalinityincrementcausedbythissourcetermonenthalpy(andtherefore

ontheBernoullifunction

)issimilartothewayanincrementofAbsoluteSalinity

entersEqn.(B.3).Whentheflowissteady,andinparticular,whenthepressurefieldis

timeinvariantateverypointinspace,thisBernoulliformofthetotalenergyequationhas

thedesirablepropertythat

isconservedfollowingthefluidmotionintheabsenceof

radiative,boundaryandmolecularfluxesandintheabsenceofnon‐conservativesalinity

production.Subjecttothissteady‐stateassumption,andintheabsenceofA

Sthe

Bernoullifunction

possessesthe“potential”property.Thenegativeaspectofthis



evolutionequation(B.17)isthatinthemoregeneralsituationwheretheflowisunsteady,

thepresenceofthet

termmeansthattheBernoullifunctiondoesnotbehaveasa

conservativevariablebecausetheright‐handsideof(B.17)isnotthedivergenceofaflux.

Inthisgeneralnon‐steadysituation

is“isobaricconservative”butisnota

“conservative”variablenordoesitpossesthe“potential”property.

Notingthatthetotalenergy

isrelatedtotheBernoullifunctionby

()

=−+

andcontinuingtotakethewholeoceantobeinasteadystateand

withA0

=S,sothat

hasthe“potential”property,itisclearthat

doesnothave

the“potential”propertyinthissituation.Thatis,ifaseawaterparcelmovesfromsay

2000dbarto0dbarwithoutexchangeofmaterialorheatwithitssurroundingsandwith

P=everywhere,then

remainsconstantwhiletheparcel’stotalenergy

changes

bythedifferenceinthequantity

(

)

−+ betweenthetwolocations.Hencewe

concludethateveninasteadyocean

doesnotpossesthe“potential”property.

128 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

ObtainingtheFirstLawofThermodynamicsbysubtraction



Theevolutionequation(B.12)forthesumofkineticandgravitationalpotentialenergiesis

nowsubtractedfromthetotalenergyconservationequation(B.15)giving

() ( )

(

)

dd .

uuutpP h

ρρρ ρερ

+∇⋅ = = − + ∇⋅ −∇⋅ −∇⋅ + +uuFFS(B.18)

Usingthecontinuityequationintheformddvt

∇⋅uandthefundamental

thermodynamicrelation(A.7.2),thisequationcanbewrittenas

() ()

d1d d d d d

dd d d d d

hP u v S

pP T t

tt t t tt

ρρ ρμ

ρε ρ

⎛⎞

⎛⎞⎛ ⎞

−=++=++

⎜⎟

⎜⎟⎜ ⎟

⎝⎠⎝ ⎠

⎝⎠

=−∇⋅ −∇⋅ + +FF S

,(B.19)

whichistheFirstLawofThermodynamics.Thecorrespondingevolutionequationfor

AbsoluteSalinityis(Eqn.(A.21.8))

() ( )

SSS

ρρ ρ ρ

= +∇⋅ = −∇⋅ +uFS(B.20)

whereS

FisthemolecularfluxofsaltandA

Sisthenon‐conservativesourceof

AbsoluteSalinityduetotheremineralizationofparticulatematter.Formanypurposesin

oceanographytheexactdependenceofthemolecularfluxesofheatandsaltonthe

gradientsofAbsoluteSalinity,temperatureandpressureisunimportant,nevertheless,

Eqns.(B.23)and(B.24)belowlistthesemolecularfluxesintermsofthespatialgradientsof

thesequantities.

AtfirstsightEqn.(B.19)haslittletorecommendit;therearetwonon‐conservative

sourceterms

andA

Sontheright‐handsideandtheleft‐handsideisnot



timesthematerialderivativeofanyquantityasisrequiredofaconservationequationofa

conservativevariable.Equation(B.19)correspondstoequation(57.6)ofLandauand

Lifshitz(1959)andisrepeatedatEqns.(A.13.1)and(A.13.3)above.

TheapproachusedheretodeveloptheFirstLawofThermodynamicsseemsrather

convolutedinthattheconservationequationfortotalenergyisfirstformed,andthenthe

evolutionequationsforkineticandgravitationalpotentialenergiesaresubtracted.

Moreover,themolecular,radiativeandboundaryfluxeswereincludedintothetotal

energyconservationequationasseparatedeliberatefluxdivergences,ratherthancoming

fromanunderlyingbasicconservationequation.ThisistheapproachofLandauand

Lifshitz(1959)anditisadoptedforthefollowingreasons.Firstthisapproachensuresthat

themolecular,radiativeandboundaryfluxesdoenterthetotalenergyconservation

equation(B.15)asthedivergenceoffluxessothatthetotalenergyisguaranteedtobea

conservativevariable(apartfromthesalinitysourceterm).Thisisessential;totalenergy

canonlybeallowedtospontaneouslyappearordisappearwhenthereisabonafide

interiorsourcetermsuchasA

S.Second,itisratherunclearhowonewould

otherwisearriveatthemolecularfluxesofheatandsaltontheright‐handsideoftheFirst

LawofThermodynamicssincethedirectapproachwhichwasattemptedatthebeginning

ofthisappendixinvolvedthepoorlydefined“rateofheating”dqt

anddidnotleadus

totheFirstLaw.Forcompleteness,themolecularfluxesQ

FandS

Farenowwrittenin

termsofthegradientsofAbsoluteSalinity,temperatureandpressure.

LandauandLifshitz(1959)(theirsection58)showthatthemolecularfluxesQ

Fand

Faregivenintermsofthechemicalpotential

andthegradientsoftemperatureandof

chemicalpotentialby



TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

129

S,abT

=− ∇ − ∇F(B.21)

and

() ,bT t T

μγ μ

=− + ∇ − ∇ +FF(B.22)

where,aband

arethreeindependentcoefficients.Notethesymmetrybetweensome

ofthecross‐diffusiontermsinthatthesamecoefficientbappearsinbothequations.

WhenwrittenintermsofthegradientsofAbsoluteSalinity,temperatureandpressure

theseexpressionsforthemolecularfluxesQ

FandS

Fbecome

SSt

kS bT P

ρμ β

ρμμ

⎛⎞

=− ∇ − + ∇ + ∇

⎜⎟

⎝⎠

F(B.23)

(usingtherelationtp

ρμ

=− thatfollowsfromthedefinitionofbotht

and

interms

oftheGibbsfunction)and

()

bkT

μρ

⎛⎞

=+ −∇

⎜⎟

⎝⎠

FF(B.24)

Theseexpressionsinvolvethepuremoleculardiffusivitiesoftemperatureandsalinity(T

k

andS

k)andthesingleparameterbthatappearsinpartofboththecross‐diffusionofsalt

downthetemperaturegradientandpartofthecross‐diffusionof“heat”downthe

gradientofAbsoluteSalinity.Theotherparametersintheseequationsfollowdirectly

fromtheGibbsfunctionofseawater.Thelasttermin(B.23)represents“barodiffusion”as

itcausesafluxofsaltdownthegradientofpressure.Themiddletermin(B.23)isafluxof

saltduetothegradientofinsitutemperatureandiscalledtheSoreteffectwhilethefirst

termin(B.24)isafluxof“heat”causedbythemolecularfluxofsalt,S

F,andthisiscalled

theDufoureffect.

Themolecularfluxofsaltisindependentofthefourarbitraryconstants(Fofonoff

(1962))thatappearintheGibbsfunctionofseawater(seeEqn.(2.6.2)).SinceT

contains

thearbitraryadditionalconstant4,athefactthatS

Fcontainsnoarbitraryconstants

impliesthatthecross‐diffusioncoefficientbinEqns.(B.21)–(B.24)isarbitrarytothe

extentA

−.

Themolecularfluxof“heat”Q

FisunknowabletotheextentS

aF(since

is

arbitrarytotheextent

()

340

aaTt++andthepresenceofbinEqn.(B.24)cancelsthe

influenceof4

a).ThismeansthattheQ

−

∇⋅FtermontherightoftheFirstLawEqn.

(B.19)isunknowabletotheextentS

3.a

−

∇⋅FTheleft‐handsideofEqn.(B.19)is

unknowabletotheextent3A

ddaSt

(sincespecificenthalpyhcontainsthearbitrary

component13A

aaS+).ThelastterminEqn.(B.19)containsthearbitrarytermA

S

(sinceA

hisarbitrarybytheamount3

a).Thesethreearbitrary,unknowable

contributionstotheFirstLawofThermodynamicsEqn.(B.19)sumto3

atimesthe

evolutionequation(B.20)forAbsoluteSalinity.Thisallowsthesearbitrarytermstobe

subtractedfromEqn.(B.19),confirmingthatthefourarbitraryunknowableconstantsof

Eqn.(2.6.2)havenomeasureableconsequencesontheFirstLawofThermodynamics.

RegardingEqns.(B.21)–(B.24),itisnotedthatstrictlyspeakingthegradientofthe

chemicalpotential

mustbereplacedbythegradientsofthechemicalpotentialsofthe

individualconstituentsofseasalt,andthediffusioncoefficientsinfrontofthesemany

gradientsaredifferentforeachconstituent,sincethereisnouniformmoleculardiffusion

ofthemixtureʺseasaltʺ.Whenadditionalprocessesacttokeepthecomposition

approximatelyfixed,theuseofonlyonechemicalpotentialforseasaltispermittedin

non‐equilibriumsituations.TheseprocessesaremainlyionrelaxationbyCoulombforces,

whichintheformofambipolardiffusionpreventanylocalelectricalchargeseparation,

andsecondly,turbulentmixingwhichhasthesametransportcoefficientforeachspecies

andwhosefluxesareproportionaltotheconcentrationgradientsof“potential”quantities

(seeappendixA.9)ratherthantothegradientsoftheindividualchemicalpotentials.

130 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

AppendixC:

PublicationsdescribingtheTEOS‐10thermodynamic

descriptionsofseawater,iceandmoistair



Primarystandarddocuments



Harvey,A.H.andP.H.Huang,2007:First‐PrinciplesCalculationoftheAir–WaterSecond

VirialCoefficient.Int.J.Thermophys.,28,556–565.

Hyland,R.W.andA.Wexler,1983:Formulationsforthethermodynamicpropertiesofdryair

from173.15to473.15K,andofsaturatedmoistairfrom173.15to372.15K,atpressures

upto5Mpa.ASHRAETransact.89,520–535.

IAPWS,2008a:ReleaseontheIAPWSFormulation2008fortheThermodynamicPropertiesof

Seawater.TheInternationalAssociationforthePropertiesofWaterandSteam.Berlin,

Germany,September2008,availablefromhttp://www.iapws.org.ThisReleaseisreferred

tointhetextasIAPWS‐08.

IAPWS,2009a:RevisedReleaseontheEquationofState2006forH2OIceIh.TheInternational

AssociationforthePropertiesofWaterandSteam.Doorwerth,TheNetherlands,

September2009,availablefromhttp://www.iapws.org.ThisrevisedReleaseisreferredto

inthetextasIAPWS‐06.

IAPWS,2009b:RevisedReleaseontheIAPWSFormulation1995fortheThermodynamic

PropertiesofOrdinaryWaterSubstanceforGeneralandScientificUse.TheInternational

AssociationforthePropertiesofWaterandSteam.Doorwerth,TheNetherlands,

September2009,availablefromhttp://www.iapws.org.ThisrevisedReleaseisreferredto

inthetextasIAPWS‐95.

IAPWS,2009c:SupplementaryReleaseonaComputationallyEfficientThermodynamic

FormulationforLiquidWaterforOceanographicUse.TheInternationalAssociationfor

thePropertiesofWaterandSteam.Doorwerth,TheNetherlands,September2009,

availablefromhttp://www.iapws.org.ThisReleaseisreferredtointhetextasIAPWS‐09.

IAPWS,2010:GuidelineonanEquationofStateforHumidAirinContactwithSeawaterand

Ice,ConsistentwiththeIAPWSFormulation2008fortheThermodynamicPropertiesof

Seawater.TheInternationalAssociationforthePropertiesofWaterandSteam.Niagara

Falls,Canada,July2010,availablefromhttp://www.iapws.org.ThisGuidelineisreferred

tointhetextasIAPWS‐10.

Lemmon,E.W.,R.T.Jacobsen,S.G.PenoncelloandD.G.Friend,2000:Thermodynamic

propertiesofairandmixturesofnitrogen,argonandoxygenfrom60to2000Kat

pressuresto2000MPa.J.Phys.Chem.Ref.Data,29,331–362.

Millero,F.J.,R.Feistel,D.G.Wright,andT.J.McDougall,2008a:ThecompositionofStandard

SeawaterandthedefinitionoftheReference‐CompositionSalinityScale,Deep‐SeaRes.I,

55,50‐72.



Secondarystandarddocuments



IOC,SCORandIAPSO,2010:Theinternationalthermodynamicequationofseawater–2010:

Calculationanduseofthermodynamicproperties.IntergovernmentalOceanographic

Commission,ManualsandGuidesNo.56,UNESCO(English),196pp,Paris.Available

fromhttp://www.TEOS‐10.org[thepresentdocument,calledtheTEOS‐10manual]

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

131

Tertiarystandarddocuments



McDougall,T.J.,D.R.JackettandF.J.Millero,2010a:AnalgorithmforestimatingAbsolute

Salinityintheglobalocean.submittedtoOceanScience,apreliminaryversionisavailable

atOceanSci.Discuss.,6,215‐242.http://www.ocean‐sci‐discuss.net/6/215/2009/osd‐6‐215‐

2009‐print.pdfandthecomputersoftwareisavailablefromhttp://www.TEOS‐10.org



Backgroundpaperstothedeclaredstandards



Feistel,R.,2003:AnewextendedGibbsthermodynamicpotentialofseawater.Progr.

Oceanogr.,58,43‐114.

Feistel,R.,2008:AGibbsfunctionforseawaterthermodynamicsfor−6to80°Candsalinityup

to120gkg–1.Deep‐SeaRes.I,55,1639‐1671.

Feistel,R.andW.Wagner,2006:ANewEquationofStateforH2OIceIh.J.Phys.Chem.Ref.

Data,35,2,1021‐1047.

Feistel,R.,S.Weinreben,H.Wolf,S.Seitz,P.Spitzer,B.Adel,G.Nausch,B.SchneiderandD.

G.Wright,2010c:DensityandAbsoluteSalinityoftheBalticSea2006–2009.Ocean

Science,6,3–24.http://www.ocean‐sci.net/6/3/2010/os‐6‐3‐2010.pdf

Feistel,R.,D.G.Wright,H.‐J.Kretzschmar,E.Hagen,S.HerrmannandR.Span,2010a:

Thermodynamicpropertiesofseaair.OceanScience,6,91–141.http://www.ocean‐

sci.net/6/91/2010/os‐6‐91‐2010.pdf

Feistel,R.,D.G.Wright,K.Miyagawa,A.H.Harvey,J.Hruby,D.R.Jackett,T.J.McDougall

andW.Wagner,2008:Mutuallyconsistentthermodynamicpotentialsforfluidwater,ice

andseawater:anewstandardforoceanography.OceanScience,4,275‐291.

http://www.ocean‐sci.net/4/275/2008/os‐4‐275‐2008.html

McDougall,T.J.,2003:Potentialenthalpy:Aconservativeoceanicvariableforevaluatingheat

contentandheatfluxes.JournalofPhysicalOceanography,33,945‐963.

Marion,G.M.,F.J.Millero,andR.Feistel,2009:Precipitationofsolidphasecalcium

carbonatesandtheireffectonapplicationofseawaterA

STP

−

−models,OceanSci.,5,

285‐291.www.ocean‐sci.net/5/285/2009/

Millero,F.J.,2000.Effectofchangesinthecompositionofseawateronthedensity‐salinity

relationship.Deep‐SeaRes.I47,1583‐1590.

Millero,F.J.,2010:Historyoftheequationofstateofseawater.Oceanography,23,18‐33.

Millero,F.J.,F.Huang,N.Williams,J.WatersandR.Woosley,2009:Theeffectofcomposition

onthedensityofSouthPacificOceanwaters,Mar.Chem.,114,56‐62.

Millero,F.J.,J.Waters,R.Woosley,F.Huang,andM.Chanson,2008b:Theeffectof

compositiononthedensityofIndianOceanwaters,Deep‐SeaRes.I,55,460‐470.

Pawlowicz,R.,2010:Amodelforpredictingchangesintheelectricalconductivity,Practical

Salinity,andAbsoluteSalinityofseawaterduetovariationsinrelativechemical

composition.OceanScience,6,361–378.http://www.ocean‐sci.net/6/361/2010/os‐6‐361‐

2010.pdf

Pawlowicz,R.,D.G.WrightandF.J.Millero,2010:Theeffectsofbiogeochemicalprocesseson

oceanicconductivity/salinity/densityrelationshipsandthecharacterizationofreal

seawater.OceanScienceDiscussions,7,773–836.

http://www.ocean‐sci‐discuss.net/7/773/2010/osd‐7‐773‐2010‐print.pdf

Seitz,S.,R.Feistel,D.G.Wright,S.Weinreben,P.SpitzerandP.deBievre,2010b:Metrological

TraceabilityofOceanographicSalinityMeasurementResults.OceanScienceDiscussions,7,

1303–1346.http://www.ocean‐sci‐discuss.net/7/1303/2010/osd‐7‐1303‐2010‐print.pdf

Wagner,W.andPruß,A.,2002:TheIAPWSformulation1995forthethermodynamic

propertiesofordinarywatersubstanceforgeneralandscientificuse.J.Phys.Chem.Ref.

Data,31,387‐535.

Wright,D.G.,R.Pawlowicz,T.J.McDougall,R.FeistelandG.M.Marion,2010b:Absolute

Salinity,“DensitySalinity”andtheReference‐CompositionSalinityScale:presentand

futureuseintheseawaterstandardTEOS‐10.OceanSci.Discuss.,7,1559‐1625.

http://www.ocean‐sci‐discuss.net/7/1559/2010/osd‐7‐1559‐2010‐print.pdf



132 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Papersdescribingcomputersoftware



Feistel,R.,D.G.Wright,D.R.Jackett,K.Miyagawa,J.H.Reissmann,W.Wagner,U.Overhoff,

C.Guder,A.FeistelandG.M.Marion,2010b:Numericalimplementationand

oceanographicapplicationofthethermodynamicpotentialsofliquidwater,water

vapour,ice,seawaterandhumidair‐Part1:Backgroundandequations.OceanScience,6,

633‐677.http://www.ocean‐sci.net/6/633/2010/os‐6‐633‐2010.pdfandhttp://www.ocean‐

sci.net/6/633/2010/os‐6‐633‐2010‐supplement.pdf

Wright,D.G.,R.Feistel,J.H.Reissmann,K.Miyagawa,D.R.Jackett,W.Wagner,U.Overhoff,

C.Guder,A.FeistelandG.M.Marion,2010a:Numericalimplementationand

oceanographicapplicationofthethermodynamicpotentialsofliquidwater,water

vapour,ice,seawaterandhumidair‐Part2:Thelibraryroutines.OceanScience,6,695‐

718.http://www.ocean‐sci.net/6/695/2010/os‐6‐695‐2010.pdfandhttp://www.ocean‐

sci.net/6/695/2010/os‐6‐695‐2010‐supplement.pdf

McDougallT.J.,D.R.Jackett,P.M.Barker,C.Roberts‐Thomson,R.FeistelandR.W.Hallberg,

2010b:Acomputationallyefficient25‐termexpressionforthedensityofseawaterin

termsofConservativeTemperature,andrelatedpropertiesofseawater.submittedto

OceanScienceDiscussions.Computersoftwareisavailablefromhttp://www.TEOS‐10.org

McDougall,T.J.,D.R.JackettandF.J.Millero,2010a:AnalgorithmforestimatingAbsolute

Salinityintheglobalocean.submittedtoOceanScience,apreliminaryversionisavailable

atOceanSci.Discuss.,6,215‐242.



TEOS‐10website



SCOR/IAPSOWorkingGroup127hascreatedthewebsitewww.TEOS‐10.orgwhichserves

manyoftheTEOS‐10papers,thisTEOS‐10manualaswellastheSIA(SeawaterIceAir)

andGSW(GibbsSeaWater)librariesofoceanographiccomputersoftware.TheGSW

MATLABOceanographicToolboxcontainsmanyhelpfiles,includingonecalled“Getting

startedwiththeGibbsSeaWater(GSW)OceanographicToolboxofTEOS‐10”whichserves

asasuccinctintroductiontotheuseofTEOS‐10inphysicaloceanography.



NotethatseveralofthepaperslistedinthisappendixareappearinginOceanScienceinthe

specialissue“ThermophysicalPropertiesofSeawater”.



TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

133

AppendixD:Fundamentalconstants



FollowingtherecommendationofIAPWS(2005),thevaluesofthefundamentalconstants

weretakenfromCODATA2006(Mohretal.(2008)),aslistedinTableD.1.Selected

propertiesofpurewaterweretakenfromIAPWS(1996,1997,2005,2006)aslistedinTable

D.2.ThechemicalReferenceCompositionofseawaterfromMilleroetal.(2008a)isgiven

inTableD.3.SelectedseawaterconstantsderivedfromtheReferenceCompositionare

listedinTableD.4.Theexactvalueoftheisobaric“heatcapacity”0

cisgiveninTable

D.5.



TableD.1.FundamentalconstantsfromCODATA2006(Mohretal.(2008))andISO(1993).

SymbolValueUncertaintyUnitComment

R8.3144720.000015Jmol–1K–1molargasconstant

101325exactPanormalpressure

T273.15exactKCelsiuszeropoint



TableD.2.SelectedpropertiesofliquidwaterfromIAPWS(1996,1997,2005,2006)

andFeistel(2003).



SymbolValueUncertaintyUnitComment

18.0152680.000002gmol–1molarmass

t3.9781210.04°Cmaximumdensity,temperature

999.974950.00084kgm–3maximumdensityat0



999.84310.001kgm–3densityat0

Tand0

,00

1/v

=

(

)

∂∂6.774876×10–20.06×10–2kgm–3K–1

(

)

∂∂ at0

Tand0



T273.16exactKtriplepointtemperature

611.6570.01Patriplepointpressure

999.7930.01kgm–3triplepointdensity

0exactJkg–1K–1triplepointentropy

u0exactJkg–1triplepointinternalenergy

T273.1525190.000002Kfreezingpointat0



134 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

TableD.3.Theseasaltcompositiondefinitionforreferencesalinityofthestandardocean.

Thestandardoceanisat25°Cand101325Pa.X–molefractions,Z–valences,

W–massfractions(Milleroetal.2008a).MolarmassesMfromWieser(2006)

withtheiruncertaintiesgiveninthebrackets.Themassfractionsarewith

respecttothemassofsolutionratherthanthemassofpurewaterinsolution.



Solute j Zj Mj

g mol–1

10–7 Xj × Zj

10–7 Wj

Na+ +1 22.989 769 28(2) 4188071 4188071

0.3065958

Mg2+ +2 24.305 0(6) 471678 943356

0.0365055

Ca2+ +2 40.078(4) 91823 183646

0.0117186

K+ +1 39.098 3(1) 91159 91159

0.0113495

Sr2+ +2 87.62(1) 810 1620

0.0002260

Cl– –1 35.453(2) 4874839 –4874839

0.5503396

SO4

2– –2 96.062 6(50) 252152 –504304

0.0771319

HCO3

– –1 61.016 84(96) 15340 –15340

0.0029805

Br– –1 79.904(1) 7520 –7520

0.0019134

CO3

2– –2 60.008 9(10) 2134 –4268

0.0004078

B(OH)4

– –1 78.840 4(70) 900 –900

0.0002259

F– –1 18.998 403 2(5) 610 –610

0.0000369

OH– –1 17.007 33(7) 71 –71

0.0000038

B(OH)3 0 61.833 0(70) 2807 0

0.0005527

CO2 0 44.009 5(9) 86 0

0.0000121

Sum 1 000 000 0 0 1.0

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

135

TableD.4.SelectedpropertiesoftheKCl‐normalisedreferenceseawater

(Milleroetal.2008a),andproposalsofWG127(2006).



Symbol Value Uncertainty Unit Comment

31.403 8218 0.001 g mol–1

referencesalinitymolarmass

XM=

∑

1.245 2898 exacta -

referencesalinityvalencefactor

XZ=

∑

N 6.022 141 79 × 1023 3 × 1016 1

mol

−

Avogadroconstant

N 1.917 6461 × 1022 6 × 1017 g–1 referencesalinityparticlenumber

SAS

/NNM

u 1.004 715… exacta g kg–1 unitconversionfactor,

≡

35.165 04 g kg–1 / 35

SSO 35.165 04 exacta g kg–1 standardoceanreferencesalinity,

35 PS

TSO 273.15 exactK standardoceantemperature

TSO = T0

tSO 0 exact°C standardoceantemperature

tSO = TSO – T0

PSO 101 325 exactPa standardoceansurfacepressure

PSO = P0

p 0 exactPa standardoceansurfaceseapressure

p = PSO – P0

hSO 0 exactJ kg–1 standardoceansurfaceenthalpy

hSO = ut

SO 0 exactJ kg–1 K–1 standardoceansurfaceentropy

SO =

Su 40.188 617… exacta g kg–1 unit‐relatedscalingconstant,

40 PS

tu 40 exact°C unit‐relatedscalingconstant

pu 108 exactPa unit‐relatedscalingconstant

gu 1 exactJ kg–1 unit‐relatedscalingconstant

a bydefinitionofReferenceSalinityandreferencecomposition

TableD.5.Theexactdefinitionoftheisobaric“heatcapacity”thatrelates

potentialenthalpytoConservativeTemperature.



Symbol Value Uncertainty Unit Comment

c 3991.867 957 119 63 exact J kg–1 K–1 See Eqn. (3.3.3)



136 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56



TableD.6.ChemicalcompositionofdryairwithafixedCO2level.

MolefractionsarefromPicardetal.(2008)exceptfor2

N

whichwasadjustedbysubtractingallothermole

fractionsfrom1(Picardetal.(2008)).Uncertaintiesof

themolarmasses(Wieser(2006))aregiveninbrackets.



Gas Mole

fraction

Mass

fraction

Molar mass

g mol–1

N2 0.780 847 9 0.755 184 73 28.013 4(3)

O2 0.209 390 0 0.231 318 60 31.998 8(4)

Ar 0.009 332 0 0.012 870 36 39.948 (1)

CO2 0.000 400 0 0.000 607 75 44.009 5(9)

Ne 0.000 018 2 0.000 012 68 20.179 7(6)

He 0.000 005 2 0.000 000 72 4.002 602(2)

CH4 0.000 001 5 0.000 000 83 16.042 46(81)

Kr 0.000 001 1 0.000 003 18 83.798 (2)

H2 0.000 000 5 0.000 000 03 2.015 88(10)

N2O 0.000 000 3 0.000 000 46 44.012 8(4)

CO 0.000 000 2 0.000 000 19 28.010 1(9)

Xe 0.000 000 1 0.000 000 45 131.293 (6)

Air 1.000 000 0 0.999 999 98 28.965 46(33)



CoriolisParameter

TherotationrateoftheearthΩis(inradianspersecond)

7.292 1150 10 sx

−

Ω= ,(D.1)

(Groten(2004))andtheCoriolisparameterfis(inradianspersecond)

2 sin 1.458 423 00 10 sin sfx

φφ

−

=Ω = ,(D.2)

where

islatitude(

hasoppositesignsinthetwohemispheres).



GravitationalAcceleration

Thegravitationalacceleration

intheoceancanbetakentobethefollowingfunctionof

latitude

andseapressurep,orheight

relativetothegeoid,

()

(

)

()

232627

32 54 7

(m s ) 9.780 327 1 5.3024 10 sin 5.8 10 sin 2 1 2.26 10 (m)

9.780 327 1 5.2792 10 sin 2.32 10 sin 1 2.26 10 (m)

9.780 327 1 5.2792 10 sin 2.32 10 sin 1 2.22 10 (dbar) .

gxxxz

xx xz

xx xp

φφ

−−−−

−− −

=+ − −

=+ + −

≈+ + +

(D.3)

ThedependenceonlatitudeinEqn.(D.3)isfromMoritz(2000)andisthegravitational

accelerationonthesurfaceofanellipsoidwhichapproximatesthegeoid.Thevariationof

with

andpintheoceaninEqn.(D.3)isderivedinMcDougalletal.(2010b).The

height

abovethegeoidisnegativeintheocean.Notethat

increaseswithdepthin

theoceanatabout71.85%oftherateatwhichitdecreaseswithheightintheatmosphere.

Atalatitudeof45 N°andat0p

,2

9.8062 m s ,g

−

=whichisavaluecommonlyused

inoceanmodels.Thevalueof

averagedovertheearth’ssurfaceis2

9.7976 m s ,g

−

=

whilethevalueaveragedoverthesurfaceoftheoceanis2

9.7963 m sg

−

=(Griffies(2004)).

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

137

AppendixE:

AlgorithmforcalculatingPracticalSalinity



E.1 Calculation of Practical Salinity in terms of K15

PracticalsalinityP

SisdefinedonthePracticalSalinityScaleof1978(Unesco(1981,1983))

intermsoftheconductivityratio15

Kwhichistheelectricalconductivityofthesampleat

temperature68

t=15°Candpressureequaltoonestandardatmosphere(p=0dbarand

absolutepressurePequalto101325Pa),dividedbytheconductivityofastandard

potassiumchloride(KCl)solutionatthesametemperatureandpressure.Themass

fractionofKClinthestandardsolutionis32.4356x10‐3(massofKClpermassofsolution).

When15

K=1,thePracticalSalinityP

Sisbydefinition35.NotethatPracticalSalinityisa

unit‐lessquantity.Thoughsometimesconvenient,itistechnicallyincorrecttoquote

PracticalSalinityin“psu”;ratheritshouldbequotedasacertainPracticalSalinity“on

thePracticalSalinityScalePSS‐78”.When15

Kisnotunity,P

Sand15

Karerelatedby

(Unesco,1981,1983)thePSS‐78equation

()

P15

SaK

=∑where

(

)

()

P68

,15C,0

35, 15 C,0

CS t

KCt

=°

==° (E.1.1)

andthecoefficientsi

aaregiveninthefollowingtable.Notethatthesumofthesixi

a

coefficientsisprecisely35,whilethesumofthesixi

bcoefficientsispreciselyzero.

Equation(E.1.1)isvalidintherangeP

242.S

<



i i

a i

b i

c i

d i

0 0.0080 0.0005 6.766097 x 10-1

1 - 0.1692 - 0.0056 2.00564 x 10-2 3.426 x 10-2 2.070 x 10-5

2 25.3851 - 0.0066 1.104259 x 10-4 4.464 x 10-4 - 6.370 x10-10

3 14.0941 - 0.0375 - 6.9698 x 10-7 4.215 x 10-1 3.989 x10-15

4 - 7.0261 0.0636 1.0031 x 10-9 - 3.107 x 10-3

5 2.7081 - 0.0144

E.2 Calculation of Practical Salinity at oceanographic temperature and pressure

ThefollowingformulaefromUnesco(1983)arevalidovertherange2C 35Ct−° ≤ ≤ °

and0 10 000dbar.

p≤≤ Measurementsofsalinityinthefieldgenerallymeasurethe

conductivityratioR

()

(

)

()

(

)

()

P68 P68 P68 68

68 P 68 68 68

,, ,, ,,0 35,,0

35, 15 C,0 , ,0 35, ,0 35, 15 C,0

CS t p CS t p CS t C t

RCt CSt Ct Ct

=° =° (E.2.1)

whichhasbeenexpressedin(E.2.1)astheproductofthreefactors,whicharelabeled

andt

rasfollows

()

P68

,, .

35, 15 C,0 ptt

CS t p

RRRr

=° (E.2.2)

138 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Thelastfactort

rhasbeenfittedtoexperimentaldataasthepolynomialintemperature

(68

t)

()

rct

∑(E.2.3)

andthefactorp

Rhasbeenfittedtoexperimentaldataasafunctionof,p68

tandRas

()() ()

1 68 2 68 3 4 68

1/C /C /C

dt dt Rd dt

⎡

⎤

+°+°++°

⎣

⎦

∑

(E.2.4)

ThusforanysamplemeasurementofRitispossibletoevaluatet

randp

Randhence

calculate

RRr

=(E.2.5)

Atatemperatureof68 15 C,t=°t

Rissimply15

KandPracticalSalinityP

Scanbe

determinedform(E.1.1).Fortemperaturesotherthan68 15 Ct

°,PracticalSalinityP

Sis

givenbythefollowingfunctionoft

Rwith0.0162,k



()

(

)

()

/C 15 .

1/C15

it it

SaR bR

°−

⎡⎤

+°−

⎣⎦

∑∑

(E.2.6)

Equations(E.1.1)and(E.2.6)arevalidonlyintherangeP

242.S

<Outsidethis

rangeP

Scanbedeterminedbydilutionwithpurewaterorevaporationofaseawater

sample.PracticalSalinityP

ScanalsobeestimatedfromtheextensionsofthePractical

SalinityScaleproposedbyHilletal.(1986)forP

02S

<andbyPoissonandGadhoumi

(1993)forP

42 50.S<< ThevaluesofPracticalSalinityP

Sestimatedinthismannermay

thenbeusedinEqn.(2.4.1),namelyRPSP

SuS

≈

toestimateReferenceSalinityR.S

ThetemperaturesinEqns.(E.2.1)to(E.2.6)areallontheIPTS‐68scale.Thefunctions

andcoefficientshavenotbeenrefittedtoITS‐90temperatures.Thereforeinorderto

calculatePracticalSalinityfromconductivityratioatameasuredpressureand90

t

temperature,itisnecessaryfirsttoconvertthetemperatureto68

tusing68 90

1.00024tt=

asdescribedEqn.(A.1.3)ofappendixA.1.Thisisdoneasthefirstlineofthecomputer

codedescribedintheGSWOceanographicToolbox(appendixN).Furtherremarkson

theimplicationsofthedifferenttemperaturescalesonthedefinitionandcalculationof

PracticalSalinitycanbefoundinappendixE.4below.



E.3 Calculation of conductivity ratio R for a given Practical Salinity

WhenPracticalSalinityisknownandonewantstodeducetheconductivityratioR

associatedwiththisvalueofPracticalSalinityatagiventemperature,aNewton‐Raphson

iterativeinversionofEqn.(E.2.6)isfirstperformedtoevaluatet

R.Becauset

risa

functiononlyoftemperature,atthisstagebotht

Randt

rareknownsothatEqn.(E.2.4)

canbewrittenasaquadraticinRwithknowncoefficientswhichissolvedtoyield .R

ThisprocedureisoutlinedinmoredetailinUnesco(1983)andisalsoavailableinthe

GSWOceanographicToolboxasthefunctiongsw_cndr_from_SP.Notethatthisiterative

inverseprocedureisdoneintermsof68

t;thecodeaccepts90

tastheinputand

immediatelyconvertsthistoa68

ttemperaturebeforeperformingtheaboveiterative

procedure.TheiterationisstoppedwhenthePracticalSalinitycorrespondingtothe

outputconductivityratiodiffersfromtheinputPracticalSalinitybylessthan10

10−.



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

139

E.4 Evaluating Practical Salinity using ITS-90 temperatures

WefirstconsidertheconsequenceofthechangefromIPTS‐68toITS‐90forthedefinition

ofPracticalSalinityasafunctionof15

KandthedefiningmassfractionofKCl.Suppose

PracticalSalinityP

Sweretobeevaluatedusingthepolynomial(E.1.1)butusing15 90

−



insteadof15

K,where15 90

K−isdefined

(

)

()

P90

15 90

,15C,0

35, 15 C,0

CS t

KCt

−

=°

==° (E.4.1)

Themagnitudeofthedifference15 90 15

−

canbecalculatedandisfoundtobeless

than6.8x10‐7everywhereintherangeP

242.S

<Furthercalculationshowsthat

P15

41SK∂∂ <everywhereinthevalidrangeofPracticalSalinity,sothattheconsequence

ofusing15 90

K−in(E.1.1)insteadof15

KincursachangeinPracticalSalinityoflessthan

3x10‐5.Thisisnearlytwoordersofmagnitudebelowthemeasurementaccuracyofa

sample,andanorderofmagnitudesmallerthantheerrorcausedbytheuncertaintyin

thedefinitionofthemassfractionofKCl.Ifalltheoriginalmeasurementsthatformthe

basisofthePracticalSalinityScalewereconvertedtoITS‐90,andtheanalysisrepeatedto

determinetheappropriatemassfractiontogivetherequiredconductivityat90 15 C,t=°

thesamemassfraction32.4356x10‐3wouldbederived.

Notwithstandingtheinsensitivityofthisconductivityratiotosuchasmall

temperaturedifference,followingMilleroetal.(2008a)thedefinitionofPracticalSalinity

canberestatedwithreferencetotheITS‐90scalebynotingthatthe15

KratioinEqn.

(E.1.1)canequivalentlyrefertoaratioofconductivitiesat90 14.996 C.t

°

Thefactthattheconductivityratiot

Risratherweaklydependentonthetemperature

atwhichtheratioisdeterminedisimportantforthepracticaluseofbenchsalinometers.

Itisimportantthatsamplesandseawaterstandardsshouldberunatthesame

temperature,stableatorder1mK.Thisisachievedbytheuseofalargewaterbathinthe

instrument.However,itisnotcriticaltoknowthestablebathtemperaturetoanybetter

than10or20mK.

Theratios,

andt

rthatunderliethetemperature‐dependentexpression(E.2.6)

forPracticalSalinityaremoresensitivetothedifferencebetweenIPTS‐68andITS‐90

temperaturesandthisisthereasonwhywerecommendretainingtheoriginalcomputer

algorithmsfortheseratios,andtosimplyconverttheinputtemperature(whichthese

daysisontheITS‐90temperaturescale)intothecorrespondingIPTS‐68temperature

using68 90

1.00024tt=asthefirstoperationinthesoftware.Thereafterthesoftware

proceedsaccordingto(E.2.1)–(E.2.6).



E.5 Towards SI-traceability of the measurement procedure for Practical Salinity

and Absolute Salinity

Theobservationofclimatechangetakingplaceintheworldoceanonaglobalscaleover

decadesorcenturiesrequiresmeasurementtechniquesthatpermitthehighestaccuracy

currentlyavailable,long‐termstabilityandworld‐widecomparabilityofthemeasured

values.Thehighestreliabilityforthispurposecanbeensuredonlybytraceabilityof

thesemeasurementresultstotheprimarystandardsoftheInternationalSystemofUnits

(SI),supportedbytheNationalMetrologicalInstitutessuchastheNIST(National

InstituteofStandardsandTechnology)intheUS,theNPL(NationalPhysicalLaboratory)

intheUK,orthePTB(Physikalisch‐TechnischeBundesanstalt)inGermany.

Inordertocomputethethermodynamicpropertiesofaseawatersamplewith

standardcomposition,threeindependentparametersmustbemeasured.Sincethe

introductionofthePracticalSalinityScaleof1978asaninternationalstandardfor

oceanography,thesethreepropertieshavebeenelectrolyticconductivity,temperature

140 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

andpressure,fromwhichsalinity,densityandotherpropertiesarecomputedinturnby

standardalgorithms.Thetraceabilityoftemperatureandpressuremeasurementresults,

forexamplebyCTDsensors,isensuredduetoestablishedcalibrationprocedurescarried

outbythemanufacturerorotherlaboratoriesandwillnotbeconsideredhereanyfurther.

Theobservationoftheocean’ssalinityisamorecomplicatedtask(Milleroetal.

(2008a)).Eventhoughoverthelastcenturydifferentandpermanentlyimprovedmethods

weredevelopedandintroducedinoceanography,traceabilityofsalinitymeasurement

resultstoSIunitshasnotyetbeenachieved(Seitzetal.2008andSeitzetal.(2010b)).This

impliestheriskthatreadingstakentodaymaypossessanenlargeduncertaintywhen

beingcomparedwithobservationstakenahundredyearsfromnow,acircumstancethat

willreducetheaccuracyoflong‐termtrendanalysesperformedinthefuture.

Aquantity,quitegenerally,isa“propertyofaphenomenon,bodyorsubstance,

wherethepropertyhasamagnitudethatcanbeexpressedasanumber”(ISO/IEC,2007).

Theprocesstoobtainthisnumberiscalledmeasurement.Thevalueoftheindicated

number(thequantityvalue)isdeterminedbyacalibrationofthemeasuringsystemwith

areferencehavingaknownquantityvalueofthesamekind.Inturn,thequantityvalue

ofthereferenceisassignedinasuperiormeasurementprocedure,whichislikewise

calibratedwithareferenceandsoon.Thiscalibrationhierarchyendsinaprimary

referenceprocedureusedtoassignaquantityvalueandaunittoaprimarystandardfor

thatkindofquantity.Thus,theunitofameasuredquantityvalueexpressesitslink(its

metrologicaltraceability)tothequantityvalueofthecorrespondingprimarystandard.

Obviously,quantityvaluesmeasuredatdifferenttimesorlocations,bydifferentpersons

withdifferentdevicesormethodscanbecomparedwitheachotheronlyiftheyare

linkedtothesamereferencestandard,whosecorrespondingquantityvaluemustbe

reproduciblewithahighdegreeofreliability.

Concerningcomparabilityofmeasuredquantityvaluesasecondaspectisof

importance.Thequantityvalueofaprimarystandardcanonlyberealisedwithan

inevitableuncertainty.Thesameholdsforeverymeasurementandcalibration.A

measurementresultthereforealwayshastoindicatethemeasuredquantityvalueandits

uncertainty.Obviously,thelatterincreaseswitheverycalibrationstepdownthe

calibrationhierarchy.Measuredquantityvaluescanevidentlyonlybeassumed

equivalentiftheirdifferenceissmallerthantheirmeasurementuncertainty

(compatibility).Ontheotherhandtheycanonlybeassumedreliablydifferent,ifthe

differenceislargerthantheuncertainty.

Toensurecomparabilityinpractice,theInternationalSystemofUnits(SI)was

established.NationalMetrologicalInstitutes(NMIs)havedevelopedprimaryreference

procedurestorealisetheSIunitsintheformofprimarystandards.Extensive(ongoing)

effortsaremadetolinktheseunitstofundamentalandphysicalconstantsinorderto

achievethehighestdegreeofreproducibility.Moreover,theNMIsperiodicallyconduct

internationalcomparisonmeasurementsundertheumbrellaoftheInternationalBureau

ofWeightsandMeasures,inordertoensurethecompatibilityofthequantityvaluesof

nationalstandards.

PSS‐78,andsimilarlythenewReference‐CompositionSalinityScale(Milleroetal.

(2008a)),computethesalinityvaluefromameasuredconductivityratiowithrespectto

the15

KconductivityratioofIAPSOStandardSeawater(SSW,CulkinandRidout(1998)

andBaconetal.(2007)),whichplaystheroleofaprimarystandard.Theproduction

procedureifIAPSOStandardSeawater,andinparticulartheadjustmentofits

conductivitytothatofapotassiumchloride(KCl)solutionofdefinitepurityandthe

correspondingassignmentofthe15

Kratio,canbeseenasaprimaryreferenceprocedure.

HoweverbothofthesesolutionsareartefactslyingoutsidetheSIsystem;theyarenot

subjecttoregularinternationalinter‐comparisons;theirsufficientlyprecisereplicability

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

141

byarbitraryindependentlaboratoriesisneitherknownnorevengranted.Aslowdriftof

artefactpropertiescannotrigorouslybeexcluded,similarinprincipletothe

“evaporation”ofmassfromthekilogramprototypestoredinParis.Itisimpossibleto

foreseeeffectsthatmightaffecttheconductivityofSSWsolutiononeday.Thus,with

respecttodecadalorcenturytimescales,thereisanuncertaintyofits15

Kratio,whicha

prioricannotbequantifiedandputslongtermcomparabilityofsalinitymeasurement

resultsatrisk.

Thisfundamentalproblem,whichisrelatedtoanyartificialreferencestandard,can,

atleastinprinciple,beavoidediftheconductivityofseawaterismeasuredtraceableto

primarySIstandards(“absolute”conductivity)ratherthanrelyingonaconductivity

ratio.Unfortunatelytherelateduncertaintyofabsoluteconductivitymeasurementswith

present‐daystate‐of‐the‐arttechnologyisoneorderofmagnitudelargerthanthatofthe

relativemeasurementspresentlyusedfortheoceanobservationsystem(Seitzetal.

(2008)).

Awayoutofthispracticaldilemmaisthemeasurementofadifferentseawater

quantitythatistraceabletoSIstandardsandpossessesthedemandedsmalluncertainty,

andfromwhichthesalinitycanbecomputedviaanempiricalrelationthatisvery

preciselyknown(Seitzetal.(2010b)).Amongthepotentialcandidatesforthispurpose

arethesoundspeed,therefractiveindex,chemicalanalysis(e.g.bymassspectroscopy)of

thesea‐saltconstituents,inparticularchlorine,anddirectdensitymeasurements.The

latterhasthreeimportantadvantages,i)SI‐traceabledensitymeasurementsofseawater

canbecarriedoutwitharelativeuncertaintyof1ppm(Wolf(2008)),whichperfectly

meetstheneedsofoceanobservation,ii)arelationexistsbetweendensityandthe

AbsoluteSalinityofseawaterisavailablewitharelativeuncertaintyof4ppmintheform

oftheTEOS‐10Gibbsfunction,iii)themeasurand,density,isofimmediaterelevancefor

oceanography,incontrasttootheroptions.

Itisimportanttonotethattheactualmeasuringprocedureforaquantityvalueis

irrelevantforitstraceability.Tomeasuretheweightofaperson,amassbalancecanbe

used,aspringoramagneticcoil;itisthequantityvaluethatistraceable,notthemethod

toachievethisvalue.Themethodinuseisnotintrinsicallyimportantexceptinsofaras

itisresponsiblefortheuncertaintyofthequantityvalue.Hence,wemaymeasurethe

densityofseawaterwithaCTDconductivitysensor,providedthissensorisproperly

calibratedwithrespecttoanSI‐traceabledensityreferencestandard.Inpractice,thiswill

meanthatthesensorcalibrationinoceanographiclabsmustbedonewithstandard

seawatersamplesofcertifieddensityratherthancertifiedPracticalSalinity.Thedensity

valuereturnedfromtheCTDreadingatseaisthenconvertedintoanAbsoluteSalinity

valuebymeansoftheequationofstateofseawater,andeventuallyintoaPractical

Salinitynumberforstorageindatacentres.Thelatterstepmayincludesome

modificationregardinglocalseasaltcompositionanomalies.Storingasalinityvalue

ratherthantherelateddensityreadinghastheadvantageofconservativitywithrespect

todilutionorchangesoftemperatureorpressure.

ThisconceptualproposalofWG127isstillimmatureandneedstobeworkedoutin

moredetailinthefollowingyears.Althoughitmayimplyonlyminorchangesinthe

practicaluseofaCTDorsimilardevices,thenewconceptisverypromisingregarding

thelong‐termreliabilityofobservationsmadeinthenearfutureforclimatictrend

analysestobeperformedbythecominggenerations.Animmediateconsequenceofthis

proposalistohavethedensity(atagiventemperatureandpressure)ofseveralsamples

ofeachbatchofIAPSOStandardSeawatermeasuredwhentheyareproducedandhave

thesedensitiesmadeavailableasreferencevaluesforeachbatch.



142 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

AppendixF:

CoefficientsoftheIAPWS‐95Helmholtzfunction

offluidwater(withextensiondownto50K)



ThespecificHelmholtzenergyforfluid(gaseousandliquid)waterisgivenbytherevised

IAPWSRelease,IAPWS(2009b),whichisbasedmainlyontheworkofWagnerandPruß

(2002).ThisrevisedreleaseisstillreferredtoasIAPWS‐95.ThespecificHelmholtz

energyofIAPWS‐95isdefinedby

()

(

)

(

)

flu V,id res

,, ,fT f T RT

ρϕτδ

=+ , (F.1)

where

()

V,id ,fT

istheideal‐gaspart,(F.2),W

R=461.51805Jkg–1K–1isthespecificgas

constantofwaterusedinIAPWS‐95,and

(

)

res ,

τδ

isthedimensionlessresidualpart

consistingof56terms,availablefrom(F.5)andTablesF.2‐F.4.Notethatthegasconstant

usedherediffersfromthemostrecentvalue,W

RRM==461.52364Jkg–1K–1,where

=18.015268gmol–1isthemolarmassofwater(IAPWS(2005)).

Theideal‐gaspart,

()

V,id ,,fT

ofthespecificHelmholtzenergyforwatervapour

is(fromIAPWS(2009b),WagnerandPruß(2002),Feisteletal.(2010a))

() () ()

V,id 0 ex

,,.fT RT

ϕτδ ϕ τ

⎡

⎤

⎣

⎦ (F.2)

Notethattheterm

()

hasbeenaddedbyFeisteletal.(2010a)inordertoextendthe

formulationtoextraterrestrialapplications,andbecausesublimationpressurevaluesare

nowavailabledownto50KfromFeistelandWagner(2007)andIAPWS(2008b);an

extremerangewherenorelatedexperimentshavebeenperformed.Thistermis

additionaltothespecificHelmholtzenergyofIAPWS(2009b)andWagnerandPruß

(2002).Thefunction

()

τδ

wasobtainedfromanequationforthespecificisobaricheat

capacityofvapourandreads

()

(

)

00000

12 3

,ln ln ln1

nn n n e

ϕτδ δ τ τ

−

=+++ + −

∑. (F.3)

The“reduceddensity”c

ρρ

=and“reducedtemperature”c/TT

arespecifiedby

c322 kg m

−

=,c647.096 K.T

Thecoefficientsof(F.3)areavailablefromTableF.1.The

IAPWS‐95referencestateconditionsdefinetheinternalenergyandtheentropyofliquid

watertobezeroatthetriplepoint.Ahighlyaccuratenumericalimplementationofthese

conditionsgavethefollowingvaluesroundedto16digitsfortheadjustablecoefficients

18.320 446 483 749 693n=−

and26.683 210 527 593 226.n=

Thesearethevaluesusedin

TEOS‐10(IAPWS(2009b),Feisteletal.(2008a)).

ThetemperatureTismeasuredontheITS‐90scale.Therangeofvalidityis130–

2000Kwithouttheextension(F.4),thatiswith

(

)

ex 0.

ϕτ

Therangecanbeextendedto

includetheregion50–130Kwiththefollowingcorrectionfunction

()

addedto(F.2)

inthistemperaturerange,

() ()

223

13 99

τττ

ϕτ τε

τεε

εε

⎛⎞

=×− − + − + +

⎜⎟

⎝⎠

, for50 K ≤ T ≤ 130 K, (F.4)

whereE

T=130K,E=0.278296458178592,andcE

/TT

.At,



()

iszero,as

wellasitsfirst,second,thirdandfourthtemperaturederivatives.Thiscorrectionhas

beendeterminedsuchthatwhenappliedtotheformulausedinIAPWS‐95,itresultsina

fittotheheatcapacitydataofWoolley(1980)between50and130Kwithanr.m.s.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

143

deviationof4

610

−

×inPW

.cR Thisextensionformulahasbeendevelopedparticularly

forimplementationinTEOS‐10(Feisteletal.(2010a)),itisconsistentwiththecorrelation

functiongiveninIAPWS(2008b),butithasnotyetbeenendorsedbyIAPWS.

Theresidualpartof(F.1)hastheform

()

()()

()

751

res

54 56

52 55

exp

ii ii i

ii i

dt dt c

dt b

iiiiii

ϕδτδτδ

ταδεβτγ δψ

=+ −

+−−−−+Δ

∑∑

(F.5)

withtheabbreviations

21−+=Δ

δθ

, i

δτθ

11 −+−= ,and

() ()

(

)

exp 1 1 .

ψδτ

=−−− −(F.6)

Thecoefficientsof(F.5)areavailablefromTablesF.2–F.4.



TableF.1.CoefficientsappearinginEqn.(F.3).Notethattheoriginallypublishedvalues

(WagnerandPruß(2002))oftheadjustablecoefficients1

nand2

nareslightlydifferent

fromthoseofTEOS‐10givenhere(Feisteletal.(2008a)).



i 0

n 0

1 –8.32044648374969

2 6.68321052759323

3 3.00632

4 0.012436 1.28728967

5 0.97315 3.53734222

6 1.2795 7.74073708

7 0.96956 9.24437796

8 0.24873 27.5075105



TableF.2.Coefficientsoftheresidualpart(F.5).



i ci d

i t

i n

1 0 1 –0.5 0.012533547935523

2 0 1 0.875 7.8957634722828

3 0 1 1 –8.7803203303561

4 0 2 0.5 0.31802509345418

5 0 2 0.75 –0.26145533859358

6 0 3 0.375 –7.8199751687981× 10–3

7 0 4 1 8.8089493102134× 10–3

8 1 1 4 –0.66856572307965

9 1 1 6 0.20433810950965

10 1 1 12 –6.6212605039687× 10–5

11 1 2 1 –0.19232721156002

12 1 2 5 –0.25709043003438

13 1 3 4 0.16074868486251

14 1 4 2 –0.040092828925807

15 1 4 13 3.9343422603254× 10–7

16 1 5 9 –7.5941377088144× 10–6

17 1 7 3 5.6250979351888× 10–4

18 1 9 4 –1.5608652257135× 10–5

19 1 10 11 1.1537996422951× 10–9

20 1 11 4 3.6582165144204× 10–7

21 1 13 13 –1.3251180074668× 10–12

22 1 15 1 –6.2639586912454× 10–10

144 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

23 2 1 7 –0.10793600908932

24 2 2 1 0.017611491008752

25 2 2 9 0.22132295167546

26 2 2 10 –0.40247669763528

27 2 3 10 0.58083399985759

28 2 4 3 4.9969146990806× 10–3

29 2 4 7 –0.031358700712549

30 2 4 10 –0.74315929710341

31 2 5 10 0.4780732991548

32 2 6 6 0.020527940895948

33 2 6 10 –0.13636435110343

34 2 7 10 0.014180634400617

35 2 9 1 8.3326504880713× 10–3

36 2 9 2 –0.029052336009585

37 2 9 3 0.038615085574206

38 2 9 4 –0.020393486513704

39 2 9 8 –1.6554050063734× 10–3

40 2 10 6 1.9955571979541× 10–3

41 2 10 9 1.5870308324157× 10–4

42 2 12 8 –1.638856834253× 10–5

43 3 3 16 0.043613615723811

44 3 4 22 0.034994005463765

45 3 4 23 –0.076788197844621

46 3 5 23 0.022446277332006

47 4 14 10 –6.2689710414685× 10–5

48 6 3 50 –5.5711118565645× 10–10

49 6 6 44 –0.19905718354408

50 6 6 46 0.31777497330738

51 6 6 50 –0.11841182425981



TableF.3.Coefficientsoftheresidualpart(F.5).



i di t

i n

i αi βi γi εi

52 3 0 –31.306260323435 20 150 1.21 1

53 3 1 31.546140237781 20 150 1.21 1

54 3 4 –2521.3154341695 20 250 1.25 1



TableF.4.Coefficientsoftheresidualpart(F.5).



i ai b

i B

i n

i C

i D

i A

i βi

55 3.5 0.85 0.2 –0.14874640856724 28 700 0.32 0.3

56 3.5 0.95 0.2 0.31806110878444 32 800 0.32 0.3



Equation(F.1)isvalidbetween50and1273Kandforpressuresupto1000MPainthe

stablesingle‐phaseregionoffluidwater.Uncertaintyestimatesareavailablefrom

IAPWS(2009b)andWagnerandPruß(2002).



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

145

AppendixG:Coefficientsofthepureliquid

waterGibbsfunctionofIAPWS‐09



ThepureliquidwaterpartoftheGibbsfunctionofFeistel(2003)hasbeenapprovedby

IAPWS(IAPWS(2009c))asanalternativethermodynamicdescriptionofpurewaterto

IAPWS‐95intheoceanographicrangesoftemperatureandpressure.Thepurewater

specificGibbsenergy

()

tpisthefollowingfunctionoftheindependentvariablesITS‐

90Celsiustemperature,u

tt y=×,andseapressure,u

pp z

×

(, )

Wjk

tp g g yz

=∑∑ ,(G.1)

withthereducedtemperatureu

ytt

andthereduced(dimensionless)pressure

pp=.Theunit‐relatedconstantsuu

,tpandu

aregiveninTableD4ofappendixD

(e.g.84

10 Pa 10 dbar

p== ).Coefficientsnotcontainedinthetablebelowhavethevalue

=0.Twoofthese41parameters(00

and10

)arearbitraryandarecomputedfrom

thereference‐stateconditionsofvanishingspecificentropy,,

andspecificinternal

energy,,uofliquidH2Oatthetriplepoint,

()

,0,Tp

=and

(

)

,0.uT p

(G.2)

Notethatthevaluesof00

and10

inthetablebelowaretakenfromFeisteletal.(2008a)

andIAPWS(2009),andarenotidenticaltothevaluesinFeistel(2003).Themodified

valueshavebeenchosentomostaccuratelyachievethetriple‐pointconditions(G.2)(see

Feisteletal.(2008a)foradiscussionofthispoint).

j k gjk j k gjk

0 0

0.101 342 743 139 674 × 103 3 2

0.499 360 390 819 152 × 103

0 1

0.100 015 695 367 145 × 106 3 3

–0.239 545 330 654 412 × 103

0 2

–0.254 457 654 203 630 × 104 3 4

0.488 012 518 593 872 × 102

0 3

0.284 517 778 446 287 × 103 3 5

–0.166 307 106 208 905 × 10

0 4

–0.333 146 754 253 611 × 102 4 0

–0.148 185 936 433 658 × 103

0 5

0.420 263 108 803 084 × 10 4 1

0.397 968 445 406 972 × 103

0 6 –0.546 428 511 471 039 4 2 –0.301 815 380 621 876 × 103

1 0

0.590 578 347 909 402 × 10 4 3

0.152 196 371 733 841 × 103

1 1

–0.270 983 805 184 062 × 103 4 4

–0.263 748 377 232 802 × 102

1 2

0.776 153 611 613 101 × 103 5 0

0.580 259 125 842 571 × 102

1 3

–0.196 512 550 881 220 × 103 5 1

–0.194 618 310 617 595 × 103

1 4

0.289 796 526 294 175 × 102 5 2

0.120 520 654 902 025 × 103

1 5

–0.213 290 083 518 327 × 10 5 3

–0.552 723 052 340 152 × 102

2 0

–0.123 577 859 330 390 × 105 5 4

0.648 190 668 077 221 × 10

2 1

0.145 503 645 404 680 × 104 6 0

–0.189 843 846 514 172 × 102

2 2

–0.756 558 385 769 359 × 103 6 1

0.635 113 936 641 785 × 102

2 3

0.273 479 662 323 528 × 103 6 2

–0.222 897 317 140 459 × 102

2 4

–0.555 604 063 817 218 × 102 6 3

0.817 060 541 818 112 × 10

2 5

0.434 420 671 917 197 × 10 7 0

0.305 081 646 487 967 × 10

3 0

0.736 741 204 151 612 × 103 7 1

–0.963 108 119 393 062 × 10

3 1

–0.672 507 783 145 070 × 103

146 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

AppendixH:Coefficientsofthesaline

GibbsfunctionforseawaterofIAPWS‐08



Non‐zerocoefficientsijk

ofthesalinespecificGibbsenergy

(

)

A,,

Stp

asafunctionof

theindependentvariablesabsolutesalinity,Au

²SSx

×,ITS‐90Celsiustemperature,

tt y=×,andseapressure,u

pp z=×:

Au1

(,,) ln ijk

jk ijk

jk i

Stp g g x x gx yz

⎧⎫

⎨⎬

⎩⎭

∑∑

. (H.1)

Theunit‐relatedconstantsuu

St pandu

aregiveninTableD4ofappendixD(e.g.

10 Pa 10 dbar

p== ).Coefficientswithk>0areadoptedfromFeistel(2003).Pure‐

watercoefficientswithi=0donotoccurinthesalinecontribution.Thecoefficients200



and210

weredeterminedtoexactlyachieveEqns.(2.6.7)and(2.6.8)whenthepurewater

GibbsfunctionwasthatofIAPWS‐95.



i j k gijk i j k gijk i j k gijk

1 0 0 5812.81456626732 2 5 0 –21.6603240875311 3 2 2 –54.1917262517112

1 1 0 851.226734946706 4 5 0 2.49697009569508 2 3 2 –204.889641964903

2 0 0 1416.27648484197 2 6 0 2.13016970847183 2 4 2 74.7261411387560

3 0 0 –2432.14662381794 2 0 1 –3310.49154044839 2 0 3 –96.5324320107458

4 0 0 2025.80115603697 3 0 1 199.459603073901 3 0 3 68.0444942726459

5 0 0 –1091.66841042967 4 0 1 –54.7919133532887 4 0 3 –30.1755111971161

6 0 0 374.601237877840 5 0 1 36.0284195611086 2 1 3 124.687671116248

7 0 0 –48.5891069025409 2 1 1 729.116529735046 3 1 3 –29.4830643494290

2 1 0 168.072408311545 3 1 1 –175.292041186547 2 2 3 –178.314556207638

3 1 0 –493.407510141682 4 1 1 –22.6683558512829 3 2 3 25.6398487389914

4 1 0 543.835333000098 2 2 1 –860.764303783977 2 3 3 113.561697840594

5 1 0 –196.028306689776 3 2 1 383.058066002476 2 4 3 –36.4872919001588

6 1 0 36.7571622995805 2 3 1 694.244814133268 2 0 4 15.8408172766824

2 2 0 880.031352997204 3 3 1 –460.319931801257 3 0 4 –3.41251932441282

3 2 0 –43.0664675978042 2 4 1 –297.728741987187 2 1 4 –31.6569643860730

4 2 0 –68.5572509204491 3 4 1 234.565187611355 2 2 4 44.2040358308000

2 3 0 –225.267649263401 2 0 2 384.794152978599 2 3 4 –11.1282734326413

3 3 0 –10.0227370861875 3 0 2 –52.2940909281335 2 0 5 –2.62480156590992

4 3 0 49.3667694856254 4 0 2 –4.08193978912261 2 1 5 7.04658803315449

2 4 0 91.4260447751259 2 1 2 –343.956902961561 2 2 5 –7.92001547211682

3 4 0 0.875600661808945 3 1 2 83.1923927801819

4 4 0 –17.1397577419788 2 2 2 337.409530269367

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

147

AppendixI:CoefficientsoftheGibbsfunction

oficeIhofIAPWS‐06



TheGibbsenergyoficeIh,thenaturallyabundantformofice,havinghexagonalcrystals,

isafunctionoftemperature(ITS‐90)andseapressure,

(

)

Ih ,.

tp ThisGibbsfunctionhas

beenderivedbyFeistelandWagner(2006)andwasadoptedasanIAPWSReleasein2006

andrevisedin2009(IAPWS(2009a)),herereferredtoasIAPWS‐06.Thisequationofstate

foriceIhisgivenbyEqn.(I.1)asafunctionoftemperature,withtwoofitscoefficients

beingpolynomialfunctionsofseapressurep(0

pPP

−)

() ( )( )( )( )

()

00t t

,Relnln2ln

kk k k k kk

gtp g sT T rt t t t t t t

gp g P

rp r P

τττττ

⎡

⎤

=− ⋅+ − −++ +− −

⎢

⎥

⎣

⎦

⎛⎞

=⋅

⎜⎟

⎝⎠

⎛⎞

=⋅

⎜⎟

⎝⎠

∑

(I.1)

withthereducedtemperature

(

)

TtT

=+ andt

Tandt

aregiveninTableI.1.Ifthe

seapressurepisexpressedindbar thent

mustalsobegivenintheseunitsas

t0.061 1657 dbarP=.Therealconstants00

to04

and0

,thecomplexconstants1

t,1

r,

t,and20

rto22

rarelistedinTableI.2.



TABLEI.1SpecialconstantsandvaluesusedintheiceIhGibbsfunction.



Quantity Symbol Value Unit

Experimental triple-point pressure t

611.657 Pa

Numerical triple-point pressure num

P 611.654 771 007 894 Pa

Normal pressure 0

101325 Pa

Triple-point temperature t

T 273.16 K



148 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

TABLEI.2Coefficientsoftheequationofstate(Gibbspotentialfunction)oficeIh

asgivenbyEqn.(I.1).



Coefficient Real part Imaginary part Unit

g00 – 0.632 020 233 335 886 × 106 J kg–1

g01 0.655 022 213 658 955 J kg–1

g02 – 0.189 369 929 326 131 × 10-7 J kg–1

g03 0.339 746 123 271 053 × 10-14 J kg–1

g04 – 0.556 464 869 058 991 × 10-21 J kg–1

s0 (absolute) 0.189 13 × 103 J kg–1 K–1

s0 (IAPWS-95) – 0.332 733 756 492 168 × 104 J kg–1 K–1

t1 0.368 017 112 855 051 × 10-1 0.510 878 114 959 572 ×10-1

r1 0.447 050 716 285 388 × 102 0.656 876 847 463 481 × 102 J kg–1 K–1

t2 0.337 315 741 065 416 0.335 449 415 919 309

r20 – 0.725 974 574 329 220 × 102 – 0.781 008 427 112 870 × 102 J kg–1 K–1

r21 – 0.557 107 698 030 123 × 10-4 0.464 578 634 580 806 × 10-4 J kg–1 K–1

r22 0.234 801 409 215 913 × 10-10 – 0.285 651 142 904 972 × 10-10 J kg–1 K–1



Thenumericaltriplepointpressurenum

PlistedinTableI.1wasderivedinFeisteletal.

(2008a)astheabsolutepressureatwhichthethreephasesofwaterwerein

thermodynamicequilibriumatthetriplepointtemperature,usingthemathematical

descriptionsofthethreephasesasgivenbyIAPWS‐95andIAPWS‐06.Thecomplex

logarithm

()

ismeantastheprincipalvalue,i.e.itevaluatestoimaginarypartsinthe

interval

(

)

Im ln z

⎡⎤

−< ≤+

⎣⎦ .Thecomplexnotationusedherehasnodirectphysical

basisbutservesforconvenienceofanalyticalpartialderivativesandforcompactnessof

theresultingformulae,especiallyinprogramcode.Complexdatatypesaresupportedby

scientificcomputerlanguageslikeFortran(asCOMPLEX*16)orC++(ascomplex

<double>),thusallowinganimmediateimplementationoftheformulaegiven,without

theneedforpriorconversiontomuchmorecomplicatedrealfunctions,orforexperience

incomplexcalculus.

Theresidualentropycoefficients0isgiveninTableI.2intheformoftwoalternative

values.Its‘IAPWS‐95’versionisrequiredforphaseequilibriastudiesbetweeniceand

fluidwaterandseawater.Thisisthevalueof0

usedintheTEOS‐10algorithms.Inthe

ʹabsoluteʹversion,0

isthestatisticalnon‐zeroentropyicepossessesatthezeropoint(0

K)resultingfromthemultiplicityofitsenergeticallyequivalentcrystalconfigurations(for

details,seeFeistelandWagner(2005)).

Thevalueof00

listedintableI.2isthevalueintherevisedIAPWS‐2006IceIh

Release(IAPWS(2009a))whichimprovesthenumericalconsistency(Feisteletal.(2008a))

withtheIAPWS‐1995Releaseforthefluidphaseofwater.



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

149

AppendixJ:

CoefficientsoftheHelmholtzfunctionof

moistairofIAPWS‐10



Theequationofstateofhumidairdescribedhere(Feisteletal.(2010a),IAPWS(2010)[an

IAPWSGuideline,inpreparation])isrepresentedintermsofaHelmholtzfunctionwhich

expressesthespecificHelmholtzenergyasafunctionofdry‐airmassfraction,

absolute

temperatureTandhumid‐airmassdensity,,

andtakestheform

()()

(

)

(

)

(

)

AV VV AAmix

,, 1 , , ,,fAT AfT AfT fAT

ρρ ρ

=− + + . (J.1)

ThevapourpartisgivenbytheIAPWS‐95Helmholtzfunctionforfluidwater(IAPWS

(2009b)),

()

(

)

VV fluV

,,,fT f T

ρρ

≡ (J.2)

iscomputedatthevapourdensity,

(

)

=− ,andisdefinedinEqn.(F.1)ofappendix

F.Thedry‐airpart,

()

,,fT

iscomputedatthedry‐airdensity,A,

=andis

definedbyEqn.(J.3).Theair‐watercross‐overpartmix

isdefinedbyEqn.(J.8).



TableJ.1.Specialconstantsandvaluesusedinthisappendix.Notethatthe

molargasconstantusedherediffersfromthemostrecentvalue

(IAPWS(2005)),andthemolarmassofdryairusedherediffersfrom

themostrecentvalue(Picardetal.(2008)),TableD6.



Quantity Symbol Value Unit Reference

Molar gas constant L

R 8.314 51 J mol–1 K–1 Lemmon et al. (2000)

Molar gas constant R 8.314 472 J mol–1 K–1 IAPWS (2005)

Molar mass of dry air MA 28.958 6 g mol–1 Lemmon et al. (2000)

Molar mass of dry air MA 28.965 46 g mol–1 IAPWS (2010)

Molar mass of water MW 18.015 268 g mol–1 IAPWS (2005)

Celsius zero point T0 273.15 K Preston-Thomas (1990)

Normal pressure 0

101 325 Pa ISO(1993)



ThespecificHelmholtzenergyfordryairis(Lemmonetal.(2000)),

()

() ()

AA id res

,,,

fT M

ατδ α τδ

⎡

⎤

⎣

⎦. (J.3)

ThevaluestobeusedformolarmassA

ofdryair,andforthemolargasconstantL

R

aregiveninTableJ.1.Thefunction

(

)

id ,

τδ

istheideal‐gaspart,

150 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

()

() ()

id 0 4 0 1.5 0 0 0

67 8 11

000 0

91210 13

,ln lnln1exp

ln 1 exp ln 2 / 3 exp

nnnn n

nnn n

τδ δ τ τ τ τ

ττ

−

⎡

⎤

=+ + + + −−

⎣

⎦

⎡⎤⎡ ⎤

+−−+ +

⎣⎦⎣ ⎦

∑ (J.4)

and

()

res ,

τδ

istheresidualpart,

()

10 19

res

111

,exp.

kk kk k

ij ij l

ατδ δτ δτ δ

=+ −

∑∑ (J.5)

The“reducedvariables”inEqns.(J.3)‐(J.5)are*

A/TT

=withthereducingtemperature

A132.6312 KT=,andA*

ρρ

=withthereducingdensity*3

10.4477 mol dm

−

=×.

isgiveninTableJ.1.ThecoefficientsofEqns.(J.4)and(J.6)aregiveninTablesJ.2

andJ.3.

Twooftheparameters(0

nand0

n)listedinTableJ.2arearbitraryandarecomputed

herefromthereference‐stateconditionsofvanishingspecificentropy,A,

andspecific

enthalpy,A,hofdryairatthetemperature0

Tandthenormalpressure0,

asgivenin

TableJ.1,

(

)

,0,TP

(J.6)

(

)

,0.hTP

(J.7)

TheHelmholtzfunctionmix

inEqn.(J.1)describesthewater‐airinteractionandis

definedby

()

() () () () ()

mix AW AAW AWW

AW A W

,, 2 .

AART A

fAT BT C T C T

MM M M

ρρ

⎧⎫

⎡

⎤

−−

⎪⎪

=++

⎨⎬

⎢

⎥

⎪⎪

⎣

⎦

⎩⎭

(J.8)

Thevaluesusedforthemolargasconstant,Rthemolarmassofdryair,A,

andthe

molarmassofwater,W,MaregiveninTableJ.1.

Thesecondcross‐virialcoefficient,

(

)

AW ,BTisgivenbyHarveyandHuang(2007)as

() * .

BT b c

=∑ (J.9)

ThecoefficientsofEqn.(J.9)aregiveninTableJ.4.

Thethirdcross‐virialcoefficients

(

)

AAW

CTand

(

)

AWW

CTaredefinedinHylandand

Wexler(1983),intheform

()

AAW

CTca

−

=∑ (J.10)

and

()

AWW

*exp i

CT c b

−

⎧

⎫

=−

⎨

⎬

⎩⎭

∑. (J.11)

Thecoefficientsi

aandi

bofEqns.(J.10)and(J.11)aregiveninTableJ.4.



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

151

TableJ.2.Dimensionlesscoefficientsandexponentsfortheideal‐gaspart,

Eqn.(J.4),fordryair(Lemmonetal.(2000)).InTEOS‐10,thecoefficients

nand0

narere‐adjustedtothereferencestateconditions,Eqns.(J.6,J.7),

anddeviatefromtheoriginallypublishedvaluesofLemmonetal.(2000).



i 0

n i 0

1 0.605 719 400 000 000 × 10–7 8 0.791 309 509 000 000

2 –0.210 274 769 000 000 × 10–4 9 0.212 236 768 000 000

3 –0.158 860 716 000 000 × 10–3 10 –0.197 938 904 000 000

4 0.974 502 517 439 480 × 10 11 0.253 636 500 000 000 × 102

5 0.100 986 147 428 912 × 102 12 0.169 074 100 000 000 × 102

6 –0.195 363 420 000 000 × 10–3 13 0.873 127 900 000 000 × 102

7 0.249 088 803 200 000 × 10



TableJ.3.Coefficientsandexponentsfortheresidualpart,Eqn.(J.5),

fordryair(Lemmonetal.(2000)).



k ik j

k l

k n

1 1 0 0 0.118 160 747 229

2 1 0.33 0 0.713 116 392 079

3 1 1.01 0

–0.161 824 192 067 × 10

4 2 0 0

0.714 140 178 971 × 10–1

5 3 0 0

–0.865 421 396 646 × 10–1

6 3 0.15 0 0.134 211 176 704

7 4 0 0

0.112 626 704 218 × 10–1

8 4 0.2 0

–0.420 533 228 842 × 10–1

9 4 0.35 0

0.349 008 431 982 × 10–1

10 6 1.35 0

0.164 957 183 186 × 10–3

11 1 1.6 1 –0.101 365 037 912

12 3 0.8 1 –0.173 813 690 970

13 5 0.95 1

–0.472 103 183 731 × 10–1

14 6 1.25 1

–0.122 523 554 253 × 10–1

15 1 3.6 2 –0.146 629 609 713

16 3 6 2

–0.316 055 879 821 × 10–1

17 11 3.25 2

0.233 594 806 142 × 10–3

18 1 3.5 3

0.148 287 891 978 × 10–1

19 3 15 3

–0.938 782 884 667 × 10–2



152 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

TableJ.4.Coefficientsofthecross‐virialcoefficients

(

)

AW ,

T

()

AAW

CT and

(

)

AWW ,CT Eqns.(J.9)‐(J.11).Thereducingfactorsare63 1

*10mmolb−−

=

and66 2

*10mmol,c−−

=the“reducedtemperature”is

()

/100KT

=.



i ai b

i c

i d

0 0.482 737 × 10–3 –0.107 288 76 × 102

1 0.105 678 × 10–2 0.347 802 00 × 102 0.665 687 × 102 –0.237

2 –0.656 394 × 10–2 –0.383 383 00 × 102 –0.238 834 × 103 –1.048

3 0.294 442 × 10–1 0.334 060 00 × 102 –0.176 755 × 103 –3.183

4 –0.319 317 × 10–1



Theequationofstate,Eqn.(J.1),isvalidforhumidairwithinthetemperatureand

pressurerange

193K ≤T≤473Kand10nPa≤

≤5MPa.(J.12)

Thepressureiscomputedfrom2AV

.Pf

=Allvalidityregionsoftheformulas

combinedinEqn.(J.1),includingtheHelmholtzfunctionsofwatervapourandofdryair,

aswellasthecross‐virialcoefficients,overlaponlyinthisrange.Theseparaterangesof

validityoftheindividualcomponentsarewider;someofthemsignificantlywider.

Therefore,Eqn.(J.1)willprovidereasonableresultsoutsideoftheTP−rangegiven

aboveundertheconditionthatacertaincomponentdominatesnumericallyinEqn.(J.1)

andisevaluatedwithinitsparticularrangeofvalidity.

Theairfraction

cantakeanyvaluebetween0and1providedthatthepartial

vapourpressure,vap

xP=,(V

isthemolefractionofvapour,Eqn.(3.35.3))doesnot

exceeditssaturationvalue,i.e.,

01A≤≤ and

(

)

sat ,.

TP A≤(J.13)

Theexactvalueoftheairfraction

(

)

sat ,

TP ofsaturatedhumidairisgivenbyequal

chemicalpotentialsofwatervapourinhumidairandofeitherliquidwater,Eqn.(3.37.5),

ifthetemperatureisabovethefreezingpoint,orofice,Eqn.(3.35.4),ifthetemperatureis

belowthefreezingpoint.Atlowdensity,thesaturationvapourpressuresat

ofhumid

aircanbeestimatedbythecorrelationfunctionforeitherthevapourpressure,

()

liq ,

Tof

purewater(IAPWS(2007)),orforthesublimationpressure,

(

)

subl ,

Tofice(IAPWS

(2008b)),toobtain

()

sat sat sat

,/1/,ATP PP PP M M

⎡

⎤

=− − −

⎣

⎦fromEqn.(3.35.3)asa

practicallysufficientapproximation.



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

153

AppendixK:Coefficientsof25‐termexpressions

forthedensityofseawaterintermsofΘandof





TheTEOS‐10Gibbsfunctionofseawater

(

)

A,,

Stp

iswrittenasapolynomialinterms

ofinsitutemperaturet,whileforoceanmodels,densityneedstobeexpressedasa

computationallyefficientexpressionintermsofeitherConservativeTemperatureΘor

potentialtemperature

(referencedtor0p

dbar).McDougalletal.(2010b)havefitted

theTEOS‐10valuesofdensity

toA,S

andpina“funnel”ofdatapointsin

(

)

A,,Stpspace.Thefittedexpressionisintheformofarationalfunction,beingtheratio

oftwopolynomialsof

(

)

A,,SpΘ

25 25

num denom

ρρ

=.(K.1)

The“funnel”ofdatapointsin

(

)

A,,StpspaceisdescribedinmoredetailinMcDougallet

al.(2010b);attheseasurfaceitcoversthefullrangeoftemperatureandsalinitywhilefor

pressuregreaterthan5500dbar,themaximumtemperatureofthefitteddatais12 C°and

theminimumAbsoluteSalinityis1

PS 30 g kgu

−

.Themaximumpressureofthe“funnel”

is8000dbar .TableK.1containsthe25coefficientsoftheexpression(K.1)fordensityin

termsof

(

)

A,,SpΘ.Thecoefficients112

−

inthistablehaveunitsof3

kg m−andthe

coefficients13 25

cc−aredimensionless,andthenormalizingvaluesofA,SΘandpare

takentobe1

1g kg

−,1Kand1dbarrespectively.

Thermserrorofthis25‐termapproximationtotheTEOS‐10densityislessthan

0.0015 kg m−overthe“funnel”;thiscanbecomparedwiththermsuncertaintyof

0.004 kg m−oftheunderlyinglaboratorydensitydatatowhichtheTEOS‐10Gibbs

functionwasfitted(seethefirsttworowsofTableO.1ofappendixO).Similarly,the

appropriatethermalexpansioncoefficient,

αρ

Θ∂

=− ∂Θ ,(K.2)

ofthe25‐termequationofstateisdifferentfromthesamethermalexpansioncoefficient

evaluatedfromTEOS‐10withanrmserrorinthe“funnel”oflessthan61

0.3 10 Kx−−

,

comparedwiththermserrorofthethermalexpansioncoefficientofthelaboratorydata

towhichtheFeistel(2008)Gibbsfunctionwasfittedof61

0.6 10 Kx

−

−(seerowsixofTable

O.1ofappendixO).Intermsoftheevaluationofdensitygradients,thehalinecontraction

coefficientevaluatedfromEqn.(K.1)ismoreaccuratethanthethermalexpansion

coefficient.Hencewemayconsiderthe25‐termrationalfunctionexpressionfordensity,

Eqn.(K.1),tobeequallyasaccurateasthefullTEOS‐10expressionsfordensity,the

thermalexpansioncoefficientandthesalinecontractioncoefficientfordatathatreside

insidethe“oceanographicfunnel”.

Thesoundspeedevaluatedfromthe25‐termrationalfunctionEqn.(K.1),hasanrms

erroroverthe“funnel”ofalmost0.251

−

whichisapproximatelyfivetimestherms

erroroftheunderlyingsoundspeeddatathatwasincorporatedintotheFeistel(2008)

Gibbsfunction(seerows7to9ofTableO.1ofappendixO).Hence,the25‐term

expressionfordensityisnotaparticularlyaccurateexpressionforthesoundspeedin

seawater,eveninthe“funnel”.Butfordynamicaloceanographywhere

Θand

Θare

theaspectsoftheequationofstatethat,togetherwithspatialgradientsofA

Sand



driveoceancurrentsandaffectthecalculationofthebuoyancyfrequency,wemaytake

154 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

the25‐termrational‐functionexpressionfordensity,Eqn.(K.1),asessentiallyreflecting

thefullaccuracyofTEOS‐10.



num

Coefficients 25

denom

Coefficients

c 9.998 438 029 070 821 4 x 102 13

c 1.0

c Θ 7.118 809 067 894 091 0 x 100 14

7.054 768 189 607 157 6 x 10-3

c 2

Θ -1.945 992 251 337 968 7 x 10-2 15

-1.175 369 560 585 864 7 x 10-5

c 3

Θ 6.174 840 445 587 464 1 x 10-4 16

5.921 980 948 827 490 3 x 10-7

c A

S 2.892 573 154 127 765 3 x 100 17

3.488 790 222 801 251 9 x 10-10

c A

SΘ 2.147 149 549 326 832 4 x 10-3 18

S 2.077 771 608 561 845 8 x 10-3

()

S 1.945 753 175 118 305 9 x 10-3 19

-2.221 085 729 372 299 8 x 10-8

c p 1.193 068 181 853 174 8 x 10-2 20

-3.662 814 106 789 528 2 x 10-10

c 2

pΘ 2.696 914 801 183 075 8 x 10-7 21

()

1.5

S 3.468 821 075 791 734 0 x 10-6

c A

pS 5.935 568 592 503 565 3 x 10-6 22

()

1.5 2

8.019 054 152 807 065 5 x 10-10

c 2

p -2.594 338 980 742 903 9 x 10-8 23

cp 6.831 462 955 412 332 4 x 10-6

c 22

pΘ -7.273 411 171 282 270 7 x 10-12 24

c23

-8.529 479 483 448 544 6 x 10-17

-9.227 532 514 503 807 0 x 10-18

TABLEK.1Coefficients of the polynomials

(

)

num A ,,

Θ and

(

)

denom A ,,

Θ that

define the 25-term rational-function Eqn. (K.1) for density.



ThesameprocedurehasbeenusedbyMcDougalletal.(2010b)tofitarational

functionoftheformofEqn.(K.1)butwherethepolynomialsinthenumeratorand

denominatorarefunctionsof

(

)

A,,Sp

ratherthanof

(

)

A,,SpΘ.Thisformofthe25‐

termrationalfunctionexpressionfordensityisofapproximatelythesameaccuracyas

thatdescribedabove,andthe25coefficientsofthisexpressionaregiveninTableK.2.

Thecoefficients112

−

inthistablehaveunitsof3

kg m

−

andthecoefficients13 25

cc−are

dimensionless,andthenormalizingvaluesofA,S

andparetakentobe1

1g kg

−,1K

and1dbarrespectively.



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

155

num

Coefficients 25

denom

Coefficients

c 9.998 427 704 040 868 8 x 102 13

c 1.0

7.353 990 725 780 200 0 x 100 14

7.288 277 317 994 539 7 x 10-3

c 2

-5.272 502 484 658 053 7 x 10-2 15

-4.427 042 357 570 579 5 x 10-5

c 3

5.105 140 542 790 050 1 x 10-4 16

4.821 816 757 416 573 2 x 10-7

c A

S 2.837 207 495 416 299 4 x 100 17

1.966 643 777 649 954 1 x 10-10

c A

-5.746 287 373 866 898 5 x 10-3 18

S 2.019 220 131 573 115 6 x 10-3

()

S 2.016 582 840 401 100 5 x 10-3 19

-7.838 666 741 074 767 1 x 10-6

c p 1.150 668 012 876 069 5 x 10-2 20

-2.749 397 117 121 584 4 x 10-10

c 2

1.202 602 702 900 458 1 x 10-7 21

()

1.5

S 4.661 419 029 016 429 3 x 10-6

c A

pS 5.536 190 936 504 846 6 x 10-6 22

()

1.5 2

1.518 271 263 728 829 5 x 10-9

c 2

p -2.756 315 640 465 192 8 x 10-8 23

cp 6.414 629 356 742 288 6 x 10-6

c 22

-5.883 476 945 993 336 4 x 10-12 24

c23

-9.536 284 588 639 736 0 x 10-17

-9.623 745 548 627 732 0 x 10-18



TABLEK.2Coefficients of the polynomials

(

)

num A ,,

and

(

)

denom A ,,

that

define the 25-term rational-function Eqn. (K.1) for density.



156 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

AppendixL:Recommendednomenclature,

symbolsandunitsinoceanography



L.1 Recommended nomenclature

ThestrictSIunitsofAbsoluteSalinity,temperatureandpressureare1

kg kg−,Absolute

TemperatureinKandAbsolutePressure

inPa.Thesearetheunitspredominantly

adoptedintheSIAcomputersoftwarefortheinputandoutputvariables.If

oceanographersweretoadoptthispracticeofusingstrictlySIquantitiesitwould

simplifymanythermodynamicexpressionsatthecostofusingunfamiliarunits.

TheGSWOceanographicToolbox(appendixN)adoptsasfaraspossiblethe

currentlyusedoceanographicunits,sothattheinputvariablesforallthecomputer

algorithmsareAbsoluteSalinityinA

Sin1

gkg ,

−

temperatureinC°andpressureassea

pressureindbar.Theoutputsofthefunctionsarealsogenerallyconsistentwiththis

choiceofunits,butsomevariablesaremorenaturallyexpressedinSIunits.

Itseemsimpracticaltorecommendthatthefieldofoceanographyfullyadoptstrict

basicSIunits.Itishoweververyvaluabletohavethefieldadoptuniformsymbolsand

units,andintheinterestsofachievingthisuniformitywerecommendthefollowing

symbolsandunits.ThesearethesymbolsandunitswehaveadoptedintheGSW

OceanographicToolbox.



TableL.1.RecommendedSymbolsandUnitsinOceanography

Quantity Symbol Units Comments

Chlorinity Cl g kg–1 WG127 is recommending that Chlorinity be

defined in terms of a mass fraction as

0.328 523 4 times the ratio of the mass of pure

silver required to precipitate all dissolved chloride,

bromide and iodide in seawater to the mass of

seawater. Hence WG127 recommends that mass

fraction units are used for Chlorinity.

Standard Ocean

Reference Salinity SO

S g kg–1 35.165 04 g kg–1 being exactly PS

35 u,

corresponding to the standard ocean Practical

Salinity of 35.

Freezing temperatures ff

,,tθ

ºC In situ, potential and conservative values, each as a

function of A

S and p.

Absolute pressure P Pa When absolute pressure is used it should always be

in Pa, not in Mpa nor in dbar.

Sea pressure. Sea

pressure is the pressure

argument to all software

in the GSW Toolbox.

p dbar Equal to 0

−

and usually expressed in dbar not

Pa.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

157

Gauge pressure. Gauge

pressure (also called

applied pressure) is

sometimes reported from

ship-born instruments.

gauge

p dbar Equal to the absolute pressure P minus the local

atmospheric pressure at the time of the instrument

calibration, and expressed in dbar not Pa. Sea

pressure p is preferred over gauge pressure gauge ,p

as p is the argument to the seawater Gibbs

function.

Reference pressure r

p dbar The value of the sea pressure p to which potential

temperature and/or potential density are

referenced.

One standard atmosphere 0

Pa exactly 101 325 Pa (= 10.1325 dbar)

Isopycnal slope ratio r 1

(

)

(

)

() ()

αβ

ΘΘ

Stability ratio R

(

)

(

)

RS S

θθ

αβ αθβ

ΘΘ

=Θ ≈

Isopycnal temperature

gradient ratio

GΘ 1 1GrR Rr

ρρ

⎡

⎤⎡ ⎤

−−

⎣

⎦⎣ ⎦

; n

∇

Θ= ∇Θ

Practical Salinity P

S 1 Defined in the range P

242S

< by PSS-78 based

on measured conductivity ratios.

Reference Salinity R

S g kg-1 Reference-Composition Salinity (or Reference

Salinity for short) is the Absolute Salinity of

seawater samples that have Reference

Composition. At P

S = 35, R

S is exactly PS P

while in the range P

242S

< RPSP

.SuS≈

Absolute Salinity

(This is the salinity

argument to all the

GSW Toolbox functions.)

dens

SS=g kg-1 AR A PSP A

SS S uS S

=+ ≈ +

Absolute Salinity is the sum of R

S on the Millero

et al. (2008a) Reference-Salinity Scale and the

Absolute Salinity Anomaly. The full symbol for

S is dens

S as it is the type of absolute salinity

which delivers the best estimate of density when

used as the salinity argument of the TEOS-10

Gibbs function. Another name for dens

SS= is

“Density Salinity”.

Absolute Salinity

Anomaly A

g kg-1 AAR

SSS

=−

, the difference between Absolute

Salinity, dens

,SS= and Reference-Composition

Salinity. An algorithm to evaluate A

available (McDougall et al. (2010a)). In terms of

the full nomenclature of Pawlowicz et al. (2010),

Wright et al. (2010b) and appendix A.4 herein, the

Absolute Salinity Anomaly A

is dens

“Preformed Absolute

Salinity”,

often shortened to

“Preformed Salinity”

S g kg-1 Preformed Absolute Salinity *

S is a salinity

variable that is designed to be as conservative as

possible, by removing the estimated

biogeochemical influences on the seawater

composition from other forms of salinity (see

Pawlowicz et al. (2010), Wright et al. (2010b) and

appendix A.4 herein).

“Solution Absolute

Salinity”, often shortened

to “Solution Salinity”

soln

S g kg-1 The mass fraction of non-H2O constituents in

seawater after it has been brought to chemical

equilibrium at t = 25 C° and p = 0 dbar (see

Pawlowicz et al. (2010), Wright et al. (2010b) and

appendix A.4 herein).

“Added-Mass Salinity” add

S g kg-1 add

−

is the estimated mass fraction of non-

H2O constituents needed as ingredients to be added

to Standard Seawater which when mixed and

brought to chemical equilibrium at t = 25 C° and

p = 0 dbar results in the observed seawater

composition.

158 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Temperature t ºC

Absolute Temperature T K

(

)

(

)

/ K / K / C 273.15 / CTT t t

≡

+°= +°

temperature derivatives T K When a quantity is differentiated with respect to in

situ temperature, the symbol T is used in order to

distinguish this variable from time.

Celsius zero point 0

T K 0273.15 KT

≡

Potential temperature

ºC Defined implicitly by Eqn. (3.1.3)

Conservative Temperature Θ ºC Defined in Eqn. (3.3.1) as exactly potential

enthalpy divided by 0

A constant “specific

heat”, for use with

Conservative Temperature

c J kg–1 K–1 011

3991.867 957 119 63 J kg K .

c−−

≡ This 15-digit

number is defined to be the exact value of 0

Combined standard

uncertainty

uc Varies

Enthalpy H J

Specific enthalpy h J kg–1

(

)

0.hu pPv=+ +

Here p and 0

must be in Pa not dbar.

Specific potential

enthalpy

h0 J kg–1 Specific enthalpy referenced to zero sea pressure,

[

]

(

)

AA r r

,,,,0,0hhS Stpp p

Specific isobaric heat

capacity

c J kg–1 K–1

pSp

chT=∂ ∂

Internal energy U J

Specific internal energy u J kg–1

Specific isochoric heat

capacity v

c J kg–1 K–1

vSv

cuT=∂ ∂

Gibbs function

(Gibbs energy)

G J

Specific Gibbs function

(Gibbs energy)

g J kg–1

Specific Helmholtz

Energy

f J kg–1

Unit conversion factor for

salinities PS

u g kg–1 11

PS (35.16504 35) g kg 1.004 715... g kgu

−

≡≈

The first part of this expression is exact. This

conversion factor is an important and invariant

constant of the 2008 Reference-Salinity Scale

(Millero et al. (2008a)).

Entropy Σ J K–1

Specific entropy

J kg–1 K–1 In many other publications the symbol s is used for

specific entropy.

Density

kg m–3

Density anomaly t

kg m–3

(

)

A,,0St

– 1000 kg m–3

Potential density anomaly

referenced to a sea

pressure of 1000 dbar

kg m–3

[

]

(

)

AA rr

,,,,,SStppp

ρθ

– 1000 kg m-3 where

r1000 dbarp

Potential density anomaly

referenced to a sea

pressure of 4000 dbar

kg m–3

[

]

(

)

AA rr

,,,,,SStppp

ρθ

– 1000 kg m-3 where

r4000 dbarp

Thermal expansion

coefficient with respect to

in situ temperature

K–1 AA

Sp Sp

vvT T

ρρ

−−

∂∂ =− ∂ ∂

Thermal expansion

coefficient with respect to

potential temperature

K–1 AA

Sp Sp

θρρθ

−−

∂∂ =− ∂ ∂

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

159

Thermal expansion

coefficient with respect to

Conservative Temperature

Θ K–1 AA

Sp Sp

ρρ

−−

∂∂Θ =− ∂ ∂Θ

Saline contraction

coefficient at constant in

situ temperature

kg g–1

A, A,

Tp Tp

vvS S

ρρ

−−

−∂∂ = ∂∂

Note that the units for t

are consistent with SA

being in g kg-1.

Saline contraction

coefficient at constant

potential temperature

kg g–1

A, A,

vvS S

ρρ

−−

−∂∂ = ∂∂

Note that the units for

are consistent with SA

being in g kg-1.

Saline contraction

coefficient at constant

Conservative Temperature

Θ kg g–1

A, A,

vvS S

ρρ

−−

ΘΘ

−∂∂ =+∂∂

Note that the units for

are consistent with SA

being in g kg-1.

Isothermal

compressibility

Pa–1

Isentropic and isohaline

compressibility

Pa–1

Chemical potential of

water in seawater

J g–1

Chemical potential of sea

salt in seawater

J g–1

Relative chemical

potential of (sea salt and

water in) seawater

J g–1

(

)

A,tp

∂∂ = −

Dissipation rate of kinetic

energy per unit mass

J kg–1 s–1

= m2 s–3

Adiabatic lapse rate Γ K Pa–1

AAA

,,,SSS

ttt

PPP

∂∂∂

Γ= = =

∂∂∂

Sound speed c m s–1

Specific volume v m3 kg–1 1

−

Specific volume anomaly

m3 kg–1

Thermobaric coefficient

based on

KPa

−

(

)

b,S

θθθθ

βαβ

=∂ ∂

Thermobaric coefficient

based on Θ

TΘ 11

KPa

−

(

)

b,S

βαβ

ΘΘΘΘ

=∂ ∂

Cabbeling coefficient

based on

−

bAA

,, ,

Sp p p

CSS

θθ

θθ θ θ

αα

ββ

αθ α β

⎛⎞

=∂ ∂ + ∂ ∂ − ∂ ∂

⎜⎟

⎝⎠

Cabbeling coefficient

based on Θ

CΘ 2

−

bAA

,, ,

Sp p p

CSS

αα

ββ

αα β

ΘΘ

ΘΘ Θ Θ

ΘΘ

⎛⎞

=∂ ∂Θ + ∂ ∂ − ∂ ∂

⎜⎟

⎝⎠

Buoyancy frequency N 1

−

(

)

(

)

Ng S g S

θθ

αβ αθβ

ΘΘ

=Θ− = −

Neutral helicity n

H 3

−

Defined by Eqns. (3.13.1) and (3.13.2)

Neutral Density n

kg m–3 A density variable whose iso-surfaces are designed

to be approximately neutral, i. e.

A.S

γγ

αβ

ΘΘ

∇Θ≈ ∇

Neutral-Surface-Potential-

Vorticity

NSPV 3

−

SPV g f

−

=− where f is the Coriolis

parameter.

Dynamic height anomaly ′

Φ 22

−

31 22

Pa m kg m s

−

Montgomery geostrophic

streamfunction

−

31 22

Pa m kg m s

−

160 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

PISH (Pressure-Integrated

Steric Height)

′

Ψ kg s-2 Streamfunction for f times the depth-integrated

relative mass flux, see Eqns. (3.31.1) – (3.31.5).

Coriolis parameter

−

1.458 42 10 sin sx

−

−, where

is latitude

Molality

mol kg–1

()

==−

∑ where S

is the

mole-weighted average atomic weight of the

elements of sea salt,

S0.031 403 821 8 kg molM−

=…

Ionic strength

mol kg–1

()

0.622 644 9

622.644 9 mol kg

31.403 821 8 1

ImZ mz

−

≈−

∑

Osmotic coefficient

()

(

)

(

)

()

SW 0

0, , , ,

tp S tp

STp mRT t

−

where the molar gas constant,

R = 8.314 472 J mol–1 K–1. See also Eqn. (3.40.9)

for an equivalent definition of .



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

161

L.2 Suggested Symbols when variables are functions of ,

and Θ

Notethatwhetherusingstandardnotationorvariantsfromit,allvariablesshouldbe

explicitlydefinedinpublicationswhenfirstused.Standardnotationshouldbe

consideredasanadditionalaidtoimprovereadability,notasareplacementforexplicit

definitions.

Notethatoxygenshouldbereportedinμmol/kgandnotcm3dm–3,ml/lorμmol/l

(thisreflectsadesireforconsistencywithreportingofotherquantitiesandwillavoid

problemsassociatedwithconversionbetweenmolesandmlusingthegasequations).

Whenthermodynamicvariablesaretakentobefunctionsofvariablesotherthanthe

standardcombination

()

A,,Stpitisconvenienttoindicatethisbyamarkingonthe

variable.Thisgreatlysimplifiesthenomenclatureforpartialderivatives.TableL.2lists

thesuggestedmarkingsonthevariablesthatarisecommonlyinthiscontext.The

thermodynamicvariablesarerelatedtothethermodynamicpotentials

()

A,,hhS p



,

()

A,,hhS p

=and

()

ˆ,,

hhS p=ΘbytheexpressionsinappendixP.



TableL.2.SuggestedSymbolswhenvariablesarefunctionsof,

andΘ

quantity function of symbol for this

functional form

enthalpy,h

specificvolume,v

density,



entropy,



(

)

A,,Stp

(

)

A,,hhStp=

(

)

A,,vvStp=

(

)

A,,Stp

ρρ

(

)

A,,Stp

ηη

enthalpy,h

specificvolume,v

density,



potentialtemperature,



(

)

A,,Sp

(

)

A,,hhS p



(

)

A,,vvS p



(

)

A,,Sp

ρρ η



(

)

A,S

θη



enthalpy,h

specificvolume,v

density,



entropy,



(

)

A,,Sp

(

)

A,,hhS p

=

(

)

A,,vvS p

=

(

)

A,,Sp

ρρ θ

=

(

)

A,S

ηθ

=

enthalpy,h

specificvolume,v

density,



entropy,



(

)

A,,SpΘ

(

)

ˆ,,

hhS p=Θ

(

)

ˆ,,

vvS p=Θ

(

)

ˆ,,

ρρ

=Θ

(

)

ˆ,

ηη

162 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

AppendixM:

Seawater‐Ice‐Air(SIA)libraryofcomputersoftware



Thissoftwarelibrary,theSeawater‐Ice‐Airlibrary(theSIAlibraryforshort),containsthe

TEOS‐10subroutinesforevaluatingawiderangeofthermodynamicpropertiesofpure

water(usingIAPWS‐95),seawater(usingIAPWS‐08forthesalinepart),iceIh(using

IAPWS‐06)andformoistair(usingFeisteletal.(2010a),IAPWS(2010)).Itisdividedinto

sixlevels(levels0through5)witheachsuccessivelevelbuildingonthefunctional

capabilitiesintroducedatlowerlevels.Briefly,

• level0definesfundamentalconstants,setsoptionsusedthroughoutthelibraryand

providesroutinestoconvertbetweenPracticalSalinityandAbsoluteSalinity

• level1definesacompletesetofindependentandconsistentelementsthatarebased

onpreviousworkandformtheessentialbuildingblocksfortherestofthelibrary

routines

• level2providesaccesstoasetofpropertiesforindividualmediums(liquidorvapour

water,ice,seawateranddryorhumidair)thatcanbecalculatedfromthelevel0and

1routineswithoutadditionalapproximations

• level3introducesadditionalfunctionsthatrequirenumericalsolutionofequations.

Mostimportantly,itisatthislevelthatthedensityofpurefluidwaterisdetermined

fromtemperatureandpressureinformation.ThispermitsthedefinitionofGibbs

functionsforpurewaterandseawaterthatmakeuseoftheIAPWS‐95Helmholtz

functionasafundamentalbuildingblock

• level4dealswithafairlybroad(butnotexhaustive)selectionofequilibrium

propertiesinvolvingfluidwater,seawater,iceandair;and

• level5includesasetofroutinesthatbuildontheSIAroutinesbutviolateprincipals

adheredtothroughoutlevels0though4.Inparticular,non‐basicSIunitsare

permittedatthislevelasdiscussedbelow.



Asageneralrule,theinputsandtheoutputsofthealgorithmsintheSIAlibraryare

inbasicSIunits.HencethesalinityisAbsoluteSalinityA

Sinunitsof1

kg kg−(sothatfor

examplestandardoceanReferenceSalinityisinputtoSIAfunctionsas0.03516504

kg kg−)ratherthan35.165 04 (1

gkg

−

),insitutemperatureisinputasAbsolute

TemperatureTinK,andpressureisinputasAbsolutePressure

inPa.Useofthese

basicSIunitssimplifiesthecalculationoftheoreticalexpressionsinthermodynamics.

TheonlyexceptionstothisrulefortheunitsoftheinputsandoutputsintheSIAlibrary

areasfollows.

• ThefunctionAAP

(,,,)SSS P

=thatcalculatesAbsoluteSalinity(inkgkg‐1)when

givenPracticalSalinityP

S(whichisunitlessandtakesnumberslike35not0.035)as

itssalinityinputvariable,alongwithlocationintheformoflongitude

(°E)latitude

(°N)andAbsolutePressure

(Pa).Locationisrequiredinthisroutinetoaccount

fortheinfluenceofcompositionanomaliesthroughalookuptableadoptedfromthe

GSWOceanographicToolbox.

• Theinversefunction

()

PPA

,,, .SSS P

φλ

=Thisandthepreviousroutinearefoundat

level0sinceAbsoluteSalinityisrequiredasaninputtomanyofthehigherlevel

libraryroutines.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

163

• Generalpurposeroutinesthatallowforconversionsbetweenabroadrangeof

pressure,temperatureandsalinityunitsthatareincommonusageareprovidedat

level5.Thenumericalinputvalueanditsunitareprovidedbytheuserandresults

arereturnedinaspecifiedoutputunit.

• Algorithmsareincludedatlevel5thatusenon‐basicSIunitsasinputandasoutput.

MostnoteworthyistheGSWlibrarymodulethatusestheSIAroutinestomimic

manyoftheroutinesintheGSWOceanographicToolbox.Theseroutinesuse

IAPWS‐09forpurewaterinplaceofIAPWS‐95toprovideimprovedcomputational

efficiency.Theyhavebeenusedtoprovideindependentchecksonthe

correspondingroutinesintheGSWOceanographicToolbox.



BecausetheIAPWS‐95descriptionofpurewatersubstance(bothliquidandvapour)

istheworld‐widestandardforpurewatersubstance,theSIAlibraryistheofficial

descriptionofseawater,althoughitshouldbenotedthatthecomputersoftwaredoesnot

comewithanywarranty.RatheritistheunderlyingpapersaslistedinappendixCthat

aretheofficiallywarranteddescriptions.

TheSIAlibrarybenefitsfromthefullrangeofapplicabilityoftheIAPWS‐95

Helmholtzfunctionforpurewater,0kgm‐3<

<1200kgm‐3,130K<T<1273K,plus

anextensiondownto50KintroducedbyFeisteletal.(2010a).Itdoeshoweverhavetwo

disadvantagesasfarasthefieldofoceanographyisconcerned.First,becauseIAPWS‐95

isvalidoververywiderangesoftemperatureandpressure,itisnecessarilyanextensive

seriesofpolynomialsandexponentialswhichisnotasfastcomputationallyasthe

equationofstateEOS‐80withwhichoceanographersarefamiliar.Second,theIAPWS‐95

thermodynamicpotentialisaHelmholtzfunctionwhichexpressesthermodynamic

propertiesintermsofdensityandtemperatureratherthanpressureandtemperatureas

normallyusedinoceanography.SinceIAPWS‐95describesnotonlyliquidwaterbutalso

watervapour,thisHelmholtzformofthethermodynamicpotentialisnatural.Although

thelibraryalsoincludesaGibbsfunctionformulationwithtemperatureandpressureas

independentvariables,thecoreroutinesimplementthisformulationbyfirstsolving

2(, )PfT

=for

andthenusingIAPWS‐95,whichisacomputationallyexpensive

procedure.

IntheGSWOceanographicToolbox(appendixN)wepresentanalternative

thermodynamicdescriptionofseawaterpropertiesbasedontheIAPWS‐09descriptionof

thepureliquidwaterpartasaGibbsfunction.TheGSWformulationislimitedtothe

Neptunianrange(i.e.theoceanographicrange)oftemperatureandpressureanddeals

onlywithliquidwater,butitisfarmorecomputationallyefficientsincethelimitedrange

ofvalidityallowsequivalentaccuracywithfewertermsandtheGibbsfunction

formulationavoidstheneedtoinverttherelation 2(, )PfT

=.Thisformulationis

alsoimplementedatlevel5oftheSIAlibraryasacross‐checkontheGSWroutinesand

fortheconvenienceofSIAlibraryusersworkingonapplicationsrequiringincreased

computationalefficiency.NotehoweverthatsomeofroutinesintheSIAimplementation

oftheGSWroutinesarenotasfullyoptimizedasthecorrespondingroutinesintheGSW

OceanographicToolbox.

Thepresenceofdissolvedsaltsinseawaterreducestherangeofapplicabilityofthe

SIAandGSWseawaterroutinesincomparisonwiththeIAPWS‐95rangeofapplicability

forpurefluidwater,whetherornottheIAPWS‐09Gibbsformulationisusedtorepresent

purewaterproperties.Thisisbecausetherangeofapplicabilityofthesalinecomponent

oftheGibbsfunctionislimitedto0kgkg‐1≤ A

S≤0.12kgkg‐1,262K≤T≤353K,and

100Pa≤P≤ 8

10 Pa.

Sincethismanualfocusesonseawater,wereferthereadertoFeisteletal.(2010b)and

Wrightetal.(2010a)fordetailsontheiceandaircomponentsoftheSIAlibrary.

164 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

However,below,wediscussafewfeaturesofthelibrarythatrelatetotheseadditional

components.First,wenotethatthethermodynamicpotentialsofpurewater,ice,the

salinepartoftheseawaterGibbsfunctionandtheGibbsfunctionofmoistairhavebeen

carefullyadjustedtomakethemfullycompatiblewitheachother(Feisteletal.(2008a)).

Onlybysodoingcantheequilibriumpropertiesofcoincidentphasesbeaccurately

evaluated(forexample,thefreezingtemperatureofpurewaterandofseawater).Many

functionsinvolvingequilibriumpropertiesofwater,vapour,ice,seawateranddryor

humidairareimplementedinlevel4oftheSIAlibrary.Toprovideanindicationofthe

rangeoffunctionsavailable,wehavelistedtheroutinenamesinTableM.1below.This

tablecomesfromTable3.1ofWrightetal.(2010a);werefertheinterestedreadertoFeistel

etal.(2010b))andWrightetal.(2010a))fordetailedinformation.Wrightetal.(2010a)

provideasupplementarytablethatiscross‐referencedtotheirTable3.1togivedetailson

theusageofeachroutineandeachtableintheirsupplementreferencesinturnthe

relevantsectionsofFeisteletal.(2010b)foradditionalbackgroundinformation.

DuetothefactthateachleveloftheSIAlibrarybuildsonlowerlevelsandthefact

thatmultiplephasesmaybeinvolvedintheequilibriumcalculations,thedetermination

oftherangesofvalidityoftheroutinesintheSIAlibrarycanbecomeratherinvolved.To

dealwiththisissue,aprocedurehasbeenimplementedinthelibrarytoreturnanerror

codeforfunctionevaluationsthatdependonresultsfromanyofthebasicbuildingblock

routinesfromoutsideoftheirindividualrangesofvalidity.Numericalcheckvaluesare

providedwitheachoftheroutinesinthelibraryandauxiliaryroutinesareprovidedto

assistusersinthevalidationoflocalimplementations.

FurtherdetailsoftheSIAsoftwarelibraryareprovidedinthepapersFeisteletal.

(2010b))andWrightetal.(2010a))andthesoftwareisservedfromthewww.TEOS‐10.org

website.



TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

165

TableM.1.TheSIAlibrarycontents.Modulenamesareinboldanduser‐accessible

routinesareinplaintype.EachofthePublicRoutinescanbeaccessedby

users.Theunderlinedroutinesarethermodynamicpotentialfunctions

includingfirstandsecondderivatives.Thebracketednumberspreceding

mostmodulenamesgivetherelatedtablenumbersinthesupplementto

Wrightetal.(2010a)wheredetailedinformationontheuseofeachfunctionis

provided.

Level 0 routines

Constants_0

Public Parameter Values

celsius_temperature_si

check_limits

cp_chempot_si

cp_density_si

cp_pressure_si

cp_temperature_si

dry_air_dmax

dry_air_dmin

dry_air_tmax

dry_air_tmin

errorreturn

flu_dmax

flu_dmin

flu_tmax

flu_tmin

gas_constant_air_si

gas_constant_air_L2000

gas_constant_molar_si

gas_constant_molar_L2000

gas_constant_h2O_si

gas_constant_h2O_iapws95

ice_pmax

ice_pmin

ice_tmax

ice_tmin

isextension2010

isok

Constants_0 (Cont'd)

Parameter Values (cont'd)

mix_air_dmax

mix_air_dmin

mix_air_tmax

mix_air_tmin

molar_mass_air_si

molar_mass_air_l2000

molar_mass_h2o_si

molar_mass_seasalt_si

sal_pmax

sal_pmin

sal_smax

sal_smin

sal_tmax

sal_tmin

sealevel_pressure_si

so_salinity_si

so_temperature_si

so_pressure_si

tp_density_ice_iapws95_si

tp_density_liq_iapws95_si

tp_density_vap_iapws95_si

tp_enthalpy_ice_si

tp_enthalpy_vap_si

tp_pressure_exp_si

tp_pressure_iapws95_si

tp_temperature_si

Maths_0

Uses

constants_0

Public Routines

get_cubicroots

matrix_solve

(S2) Convert_0

Uses

constants_0

Public Routines

air_massfraction_air_si

air_massfraction_vap_si

air_molar_mass_si

air_molfraction_air_si

air_molfraction_vap_si

asal_from_psal

psal_from_asal

Level 1 routines

(S3) Flu_1 (IAPWS95)

Uses

constants_0

Public Routines

chk_iapws95_table6

chk_iapws95_table7

flu_f_si

(S4) Ice_1 (IAPWS06)

Uses

constants_0

Public Routines

chk_iapws06_table6

ice_g_si

(S5) Sal_1 (IAPWS08)

Uses

constants_0

Public Routines

sal_g_term_si

(S6) Air_1

Uses

constants_0

Public Routines

air_baw_m3mol

air_caaw_m6mol2

air_caww_m6mol2

dry_f_si

dry_init_clear

dry_init_Lemmon2000

166 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Level 2 routines

(S7) Flu_2

Uses

constants_0, flu_1

Public Routines

flu_cp_si

flu_cv_si

flu_enthalpy_si

flu_entropy_si

flu_expansion_si

flu_gibbs_energy_si

flu_internal_energy_si

flu_kappa_s_si

flu_kappa_t_si

flu_lapserate_si

flu_pressure_si

flu_soundspeed_si

((S8) Ice_2

Uses

constants_0, ice_1

Public Routines

ice_chempot_si

ice_cp_si

ice_density_si

ice_enthalpy_si

ice_entropy_si

ice_expansion_si

ice_helmholtz_energy_si

ice_internal_energy_si

ice_kappa_s_si

ice_kappa_t_si

ice_lapserate_si

ice_p_coefficient_si

ice_specific_volume_si

(S9) Sal_2

Uses

constants_0, sal_1

Public Routines

sal_act_coeff_si

sal_act_potential_si

sal_activity_w_si

sal_chem_coeff_si

sal_chempot_h2o_si

sal_chempot_rel_si

sal_dilution_si

sal_g_si

sal_mixenthalpy_si

sal_mixentropy_si

sal_mixvolume_si

sal_molality_si

sal_osm_coeff_si

sal_saltenthalpy_si

sal_saltentropy_si

sal_saltvolume_si

(S10) Air_2

Uses

constants_0, flu_1, air_1

Public Routines

air_f_si

air_f_cp_si

air_f_cv_si

air_f_enthalpy_si

air_f_entropy_si

air_f_expansion_si

air_f_gibbs_energy_si

air_f_internal_energy_si

air_f_kappa_s_si

air_f_kappa_t_si

air_f_lapserate_si

air_f_mix_si

air_f_pressure_si

air_f_soundspeed_si

chk_iapws10_table

Level 3 routines

(S11) Flu_3a

Uses

constants_0, convert_0,

maths_0, flu_1

Public Routines

get_it_ctrl_density

liq_density_si

liq_g_si

set_it_ctrl_density

vap_density_si

vap_g_si

(S12) Sea_3a

Uses

constants_0, sal_1, sal_2,

flu_3a (convert_0, maths_0,

flu_1)

Public Routines

chk_iapws08_table8a

chk_iapws08_table8b

chk_iapws08_table8c

sea_chempot_h2o_si

sea_chempot_rel_si

sea_cp_si

sea_density_si

sea_enthalpy_si

sea_entropy_si

sea_g_si

sea_g_contraction_t_si

sea_g_expansion_si

sea_gibbs_energy_si

sea_internal_energy_si

sea_kappa_s_si

sea_kappa_t_si

sea_lapserate_si

sea_osm_coeff_si

sea_soundspeed_si

sea_temp_maxdensity_si

(S13) Air_3a

Uses

constants_0, convert_0,

maths_0, air_1, air_2 (flu_1)

Public Routines

air_density_si

air_g_si

get_it_ctrl_airdensity

set_it_ctrl_airdensity

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

167

(S14) Flu_3b

Uses

constants_0, flu_2, flu_3a

(convert_0, maths_0,

flu_1)

Public Routines

liq_cp_si

liq_cv_si

liq_enthalpy_si

liq_entropy_si

liq_expansion_si

liq_gibbs_energy_si

liq_internal_energy_si

liq_kappa_s_si

liq_kappa_t_si

liq_lapserate_si

liq_soundspeed_si

vap_cp_si

vap_cv_si

vap_enthalpy_si

vap_entropy_si

vap_expansion_si

vap_gibbs_energy_si

vap_internal_energy_si

vap_kappa_s_si

vap_kappa_t_si

vap_lapserate_si

vap_soundspeed_si

(S15) Sea_3b

Uses

constants_0, sal_2, flu_3a,

sea_3a (convert_0, maths_0,

flu_1, sal_1)

Public Routines

sea_h_si

sea_h_contraction_h_si

sea_h_contraction_t_si

sea_h_contraction_theta_si

sea_h_expansion_h_si

sea_h_expansion_t_si

sea_h_expansion_theta_si

sea_potdensity_si

sea_potenthalpy_si

sea_pottemp_si

sea_temperature_si

set_it_ctrl_pottemp

(S16) Air_3b

Uses

constants_0, convert_0,

air_1, air_2, air_3a (maths_0,

flu_1)

Public Routines

air_g_chempot_vap_si

air_g_compressibility

factor_si

air_g_contraction_si

air_g_cp_si

air_g_cv_si

air_g_density_si

air_g_enthalpy_si

air_g_entropy_si

air_g_expansion_si

air_g_gibbs_energy_si

air_g_internal_energy_si

air_g_kappa_s_si

air_g_kappa_t_si

air_g_lapserate_si

air_g_soundspeed_si

chk_lemmon_etal_2000

(S17) Sea_3c

Uses

constants_0, sea_3a, sea_3b

(convert_0, maths_0, flu_1,

sal_1, sal_2, flu_3a)

Public Routines

sea_eta_contraction_h_si

sea_eta_contraction_t_si

sea_eta_contraction_theta_si

sea_eta_density_si

sea_eta_entropy_si

sea_eta_expansion_h_si

sea_eta_expansion_t_si

sea_eta_expansion_theta_si

sea_eta_potdensity_si

sea_eta_pottemp_si

sea_eta_temperature_si

set_it_ctrl_entropy_si

(S18) Air_3c

Uses

constants_0, convert_0,

air_2, air_3a, air_3b

(maths_0, air_1, flu_1)

Public Routines

air_h_si

air_potdensity_si

air_potenthalpy_si

air_pottemp_si

air_temperature_si

set_it_ctrl_air_pottemp

(S19) Sea_3d

Uses

constants_0, sal_2, flu_3a

(convert_0, maths_0, flu_1,

sal_1)

Public Routines

sea_sa_si

set_it_ctrl_salinity

168 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Level 4 routines

(S20) Liq_Vap_4

Uses

constants_0, maths_0, flu_1,

flu_2, flu_3a (Convert_0)

Public Routines

chk_iapws95_table8

liq_vap_boilingtemperature_si

liq_vap_chempot_si

liq_vap_density_liq_si

liq_vap_density_vap_si

liq_vap_enthalpy_evap_si

liq_vap_enthalpy_liq_si

liq_vap_enthalpy_vap_si

liq_vap_entropy_evap_si

liq_vap_entropy_liq_si

liq_vap_entropy_vap_si

liq_vap_pressure_liq_si

liq_vap_pressure_vap_si

liq_vap_temperature_si

liq_vap_vapourpressure_si

liq_vap_volume_evap_si

set_liq_vap_eq_at_p

set_liq_vap_eq_at_t

set_it_ctrl_liq_vap

(S21) Ice_Vap_4

Uses

constants_0, maths_0, flu_1,

flu_2, ice_1, ice_2

Public Routines

ice_vap_chempot_si

ice_vap_density_ice_si

ice_vap_density_vap_si

ice_vap_enthalpy_ice_si

ice_vap_enthalpy_subl_si

ice_vap_enthalpy_vap_si

ice_vap_entropy_ice_si

ice_vap_entropy_subl_si

ice_vap_entropy_vap_si

ice_vap_pressure_vap_si

ice_vap_sublimationpressure_si

ice_vap_sublimationtemp_si

ice_vap_temperature_si

ice_vap_volume_subl_si

set_ice_vap_eq_at_p

set_ice_vap_eq_at_t

set_it_ctrl_ice_vap

(S22) Sea_Vap_4

Uses

constants_0, maths_0, flu_1,

sal_1, sal_2, flu_3a, sea_3a,

flu_3b (convert_0, flu_2)

Public Routines

sea_vap_boilingtemperature_si

sea_vap_brinefraction_seavap_si

sea_vap_brinesalinity_si

sea_vap_cp_seavap_si

sea_vap_density_sea_si

sea_vap_density_seavap_si

sea_vap_density_vap_si

sea_vap_enthalpy_evap_si

sea_vap_enthalpy_sea_si

sea_vap_enthalpy_seavap_si

sea_vap_enthalpy_vap_si

sea_vap_entropy_sea_si

sea_vap_entropy_seavap_si

sea_vap_entropy_vap_si

sea_vap_expansion_seavap_si

sea_vap_g_si

sea_vap_kappa_t_seavap_si

sea_vap_pressure_si

sea_vap_salinity_si

sea_vap_temperature_si

sea_vap_vapourpressure_si

sea_vap_volume_evap_si

set_it_ctrl_sea_vap

set_sea_vap_eq_at_s_p

set_sea_vap_eq_at_s_t

set_sea_vap_eq_at_t_p

(S23) Ice_Liq_4

Uses

constants_0, maths_0, flu_1,

ice_1, flu_2, ice_2

Public Routines

ice_liq_chempot_si

ice_liq_density_ice_si

ice_liq_density_liq_si

ice_liq_enthalpy_ice_si

ice_liq_enthalpy_liq_si

ice_liq_enthalpy_melt_si

ice_liq_entropy_ice_si

ice_liq_entropy_liq_si

ice_liq_entropy_melt_si

ice_liq_meltingpressure_si

ice_liq_meltingtemperature_si

ice_liq_pressure_liq_si

ice_liq_temperature_si

ice_liq_volume_melt_si

set_ice_liq_eq_at_p

set_ice_liq_eq_at_t

set_it_ctrl_ice_liq

(S24) Sea_Liq_4

Uses

constants_0, flu_1, sal_1, flu_2,

sal_2, flu_3a (convert_0,

maths_0)

Public Routines

sea_liq_osmoticpressure_si

set_sea_liq_eq_at_s_t_p

set_it_ctrl_sea_liq

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

169

(S25) Sea_Ice_4

Uses

constants_0, convert_0,

maths_0, flu_1, ice_1, sal_1,

ice_2, sal_2, flu_3a, sea_3a,

flu_3b (flu_2)

Public Routines

sea_ice_brinefraction_seaice_si

sea_ice_brinesalinity_si

sea_ice_cp_seaice_si

sea_ice_density_ice_si

sea_ice_density_sea_si

sea_ice_density_seaice_si

sea_ice_dtfdp_si

sea_ice_dtfds_si

sea_ice_enthalpy_ice_si

sea_ice_enthalpy_melt_si

sea_ice_enthalpy_sea_si

sea_ice_enthalpy_seaice_si

sea_ice_entropy_ice_si

sea_ice_entropy_sea_si

sea_ice_entropy_seaice_si

sea_ice_expansion_seaice_si

sea_ice_freezingtemperature_si

sea_ice_g_si

sea_ice_kappa_t_seaice_si

sea_ice_meltingpressure_si

sea_ice_pressure_si

sea_ice_salinity_si

sea_ice_temperature_si

sea_ice_volume_melt_si

set_it_ctrl_sea_ice

set_sea_ice_eq_at_s_p

set_sea_ice_eq_at_s_t

set_sea_ice_eq_at_t_p

(S26) Sea_Air_4

Uses

constants_0, convert_0,

maths_0, flu_1, sal_1, air_1,

flu_2, sal_2, air_2, flu_3a,

sea_3a, air_3a, air_3b,

liq_vap_4, liq_air_4a

Public Routines

sea_air_chempot_evap_si

sea_air_condense_temp_si

sea_air_density_air_si

sea_air_density_vap_si

sea_air_enthalpy_evap_si

sea_air_entropy_air_si

sea_air_massfraction_air_si

sea_air_vapourpressure_si

set_it_ctrl_sea_air

set_sea_air_eq_at_s_a_p

set_sea_air_eq_at_s_t_p

170 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

(S27) Liq_Ice_Air_4

Uses

constants_0, convert_0,

maths_0, flu_1, ice_1, air_1,

flu_2, ice_2, air_2, air_3b,

ice_liq_4 (air_3a)

Public Routines

liq_ice_air_airfraction_si

liq_ice_air_density_si

liq_ice_air_dryairfraction_si

liq_ice_air_enthalpy_si

liq_ice_air_entropy_si

liq_ice_air_ifl_si

liq_ice_air_iml_si

liq_ice_air_liquidfraction_si

liq_ice_air_pressure_si

liq_ice_air_solidfraction_si

liq_ice_air_temperature_si

liq_ice_air_vapourfraction_si

set_liq_ice_air_eq_at_a

set_liq_ice_air_eq_at_p

set_liq_ice_air_eq_at_t

set_liq_ice_air_eq_at

_wa_eta_wt

set_liq_ice_air_eq_at

_wa_wl_wi

set_it_ctrl_liq_ice_air

(S28) Sea_Ice_Vap_4

Uses

constants_0, maths_0, flu_1,

ice_1, sal_1, sal_2

Public Routines

sea_ice_vap_density_vap_si

sea_ice_vap_pressure_si

sea_ice_vap_salinity_si

sea_ice_vap_temperature_si

set_it_ctrl_sea_ice_vap

set_sea_ice_vap_eq_at_p

set_sea_ice_vap_eq_at_s

set_sea_ice_vap_eq_at_t

(S29) Liq_Air_4a

Uses

constants_0, convert_0,

maths_0, flu_1, air_1, flu_2,

air_2, flu_3a, air_3a, air_3b,

liq_vap_4

Public Routines

liq_air_a_from_rh_cct_si

liq_air_a_from_rh_wmo_si

liq_air_condensationpressure_si

liq_air_density_air_si

liq_air_density_liq_si

liq_air_density_vap_si

liq_air_dewpoint_si

liq_air_enthalpy_evap_si

liq_air_entropy_air_si

liq_air_icl_si

liq_air_ict_si

liq_air_massfraction_air_si

liq_air_pressure_si

liq_air_rh_cct_from_a_si

liq_air_rh_wmo_from_a_si

liq_air_temperature_si

set_it_ctrl_liq_air

set_liq_air_eq_at_a_eta

set_liq_air_eq_at_a_p

set_liq_air_eq_at_a_t

set_liq_air_eq_at_t_p

(S30) Ice_Air_4a

Uses

constants_0, convert_0,

maths_0, air_1, ice_1, ice_2,

air_2, air_3a, air_3b, ice_vap_4

(flu_1, flu_2)

Public Routines

ice_air_a_from_rh_cct_si

ice_air_a_from_rh_wmo_si

ice_air_condensationpressure_si

ice_air_density_air_si

ice_air_density_ice_si

ice_air_density_vap_si

ice_air_enthalpy_subl_si

ice_air_frostpoint_si

ice_air_icl_si

ice_air_ict_si

ice_air_massfraction_air_si

ice_air_pressure_si

ice_air_rh_cct_from_a_si

ice_air_rh_wmo_from_a_si

ice_air_sublimationpressure_si

ice_air_temperature_si

set_ice_air_eq_at_a_eta

set_ice_air_eq_at_a_p

set_ice_air_eq_at_a_t

set_ice_air_eq_at_t_p

set_it_ctrl_ice_air

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

171

(S31) Liq_Air_4b

Uses

constants_0, flu_3a, air_3a,

liq_air_4a (convert_0,

maths_0, flu_1, air_1, flu_2,

air_2, air_3b, liq_vap_4)

Public Routines

liq_air_g_si

liq_air_g_cp_si

liq_air_g_density_si

liq_air_g_enthalpy_si

liq_air_g_entropy_si

liq_air_g_expansion_si

liq_air_g_kappa_t_si

liq_air_g_lapserate_si

liq_air_liquidfraction_si

liq_air_vapourfraction_si

(S32) Ice_Air_4b

Uses

constants_0, convert_0, ice_1,

air_3a, ice_air_4a (maths_0,

flu_1, air_1, flu_2, ice_2, air_2,

air_3b, ice_vap_4)

Public Routines

ice_air_g_si

ice_air_g_cp_si

ice_air_g_density_si

ice_air_g_enthalpy_si

ice_air_g_entropy_si

ice_air_g_expansion_si

ice_air_g_kappa_t_si

ice_air_g_lapserate_si

ice_air_solidfraction_si

ice_air_vapourfraction_si

(S33) Liq_Air_4c

Uses

constants_0, air_3a, ice_liq_4,

liq_air_4a, liq_air_4b

(convert_0, maths_0, flu_1,

ice_1, air_1, flu_2, ice_2 air_2,

flu_3a, air_3b, liq_vap_4)

Public Routines

liq_air_h_si

liq_air_h_cp_si

liq_air_h_density_si

liq_air_h_kappa_s_si

liq_air_h_lapserate_si

liq_air_h_temperature_si

liq_air_potdensity_si

liq_air_potenthalpy_si

liq_air_pottemp_si

set_it_ctrl_liq_air_pottemp

(S34) Ice_Air_4c

Uses

constants_0, convert_0,

ice_liq_4, ice_air_4b (maths_0,

flu_1, ice_1, air_1, flu_2, ice_2,

air_2, air_3a, air_3b,

ice_air_4a, ice_vap_4)

Public Routines

ice_air_h_si

ice_air_h_cp_si

ice_air_h_density_si

ice_air_h_kappa_s_si

ice_air_h_lapserate_si

ice_air_h_temperature_si

ice_air_potdensity_si

ice_air_potenthalpy_si

ice_air_pottemp_si

set_it_ctrl_ice_air_pottemp

172 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Level 5 routines

(S35) Flu_IF97_5

Uses

constants_0

Public Routines

chk_iapws97_table

fit_liq_density_if97_si

fit_liq_g_if97_si

fit_vap_density_if97_si

fit_vap_g_if97_si

(S36) Ice_Flu_5

Uses

constants_0

Public Routines

fit_ice_liq_pressure_si

fit_ice_liq_temperature_si

fit_ice_vap_pressure_si

(S37) Sea_5a

Uses

constants_0, sea_3a,

sea_3b, sea_3c (convert_0,

maths_0, flu_1, sal_1, sal_2,

flu_3a)

Public Routines

sea_alpha_ct_si

sea_alpha_pt0_si

sea_alpha_t_si

sea_beta_ct_si

sea_beta_pt0_si

sea_beta_t_si

sea_cabb_ct_si

sea_cabb_pt0_si

sea_ctmp_from_ptmp0_si

sea_ptmp0_from_ctmp_si

sea_thrmb_ct_si

sea_thrmb_pt0_si

(S38) Air_5

Uses

constants_0,

air_3b, liq_air_4a

(convert_0,

maths_0, flu_1,

flu_2, flu_3a, air_1,

air_2, air_3a,

liq_vap_4)

Public Routines

air_lapserate_moist

_c100m

(S39) Liq_F03_5

Uses

constants_0

Public Routines

chk_iapws09_table6

fit_liq_cp_f03_si

fit_liq_density_f03_si

fit_liq_expansion_f03_si

fit_liq_g_f03_si

fit_liq_kappa_t_f03_si

fit_liq_soundspeed_f03_si

(S40) OS2008_5

Uses

flu_1, flu_2,

flu_3a, ice_1, liq_vap_4,

sal_1, sal_2 (constants_0,

convert_0, maths_0)

Public Routines

chk_os2008_table

(S41) GSW_Library_5

Uses

constants_0, maths_0,

liq_f03_5, flu_1, flu_3a,

sal_1, sal_2, sea_3a,

sea_3b, sea_5a (convert_0)

Public Routines

gsw_alpha_ct

gsw_alpha_pt0

gsw_alpha_t

gsw_asal_from_psal

gsw_beta_ct

gsw_beta_pt0

gsw_beta_t

gsw_cabb_ct

gsw_cabb_pt0

gsw_cp

gsw_ctmp_from_ptmp0

gsw_dens

gsw_enthalpy

gsw_entropy

gsw_g

gsw_kappa

gsw_kappa_t

gsw_pden

gsw_psal_from_asal

gsw_ptmp

gsw_ptmp0_from_ctmp

gsw_specvol

gsw_svel

gsw_thrmb_ct

gsw_thrmb_pt0

(S42) Convert_5

Uses

constants_0,

convert_0

Public Routines

cnv_pressure

cnv_salinity

cnv_temperature

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

173

AppendixN:

Gibbs‐SeaWater(GSW)OceanographicToolbox



ThisGibbs‐SeaWater(GSW)OceanographicToolbox(the“GSWToolbox”forshort),

containstheTEOS‐10subroutinesforevaluatingthethermodynamicpropertiesofpure

water(usingIAPWS‐09)andseawater(usingIAPWS‐08forthesalinepart).TheGSW

OceanographicToolboxdoesnotprovidepropertiesoficeorofmoistair(these

propertiescanbefoundintheSIAlibrary).ThisGSWOceanographicToolboxdoesnot

adheretostrictbasic‐SIunitsbutratheroceanographicunitsareadopted.Whileitis

comfortableforoceanographerstoadoptthesefamiliarnon‐basicSIunits,doingso

comesataprice,sincemanyofthethermodynamicexpressionsdemandthatvariablesbe

expressedinbasic‐SIunits.Thesimplestexampleisthepurewaterfraction(theso‐called

“freshwaterfraction”)whichis

()

1S−onlywhenAbsoluteSalinityA

Sisinbasic‐SI

units.Thepricethatonepaysforadoptingcomfortableunitsisthatonemustbevigilant

whenevaluatingthermodynamicexpressions;therearetrapsfortheunwary,particularly

concerningtheunitsofAbsoluteSalinityandofpressure.

ThisGSWOceanographicToolboxhasinputsin“oceanographic”units,namely

AbsoluteSalinityA

Sin1

gkg

−(sothatforexample,standardoceanreferencesalinitySO

S

is35.165041

gkg

−[not0.035165041

kg kg

−

]),insitutemperaturetin°Candpressureas

seapressurepindbar.

TheGSWOceanographicToolboxisdesignedasasuccessortotheSeawaterlibrary

ofoceanographicMATLABroutineswhichhasbeenwidelyusedbyoceanographersinthe

pastfifteenyears;seehttp://www.cmar.csiro.au/datacentre/ext_docs/seawater.htmMany

ofthenon‐thermodynamicsubroutinesoftheSeawaterlibraryhavebeenretainedor

updatedintheGSWToolbox(forexample,afunctiontocalculatethesquareofthe

buoyancyfrequency,andfunctionstocalculateaselectionofdifferentgeostrophic

streamfunctions).ThepaperbyMcDougalletal.(2010b)describeshowmanyofthese

functionsarecalculated.

Thethermodynamicvariablesdensityandenthalpy,andseveralthermodynamic

variablesderivedfromdensityandenthalpy,areavailableintheGSWToolboxintwo

forms.OneformusesthefullTEOS‐10Gibbsfunction(beingthesumofIAPWS‐09and

IAPWS‐08)whiletheotherformisbasedona25‐termcomputationallyefficient

expressionfordensityasafunctionofAbsoluteSalinity,ConservativeTemperatureand

pressure(seeappendixA.30andappendixK).Bothformsgivevaluesofdensity,the

thermalexpansioncoefficientetc.withintheaccuracyoflaboratory‐determinedvalues

forthesequantities,sothatforoceanographicpurposesthetwoformscanberegardedas

equallyaccurate.Certainly,thepresentuncertaintyinaccountingforthespatial

variationsinseawatercompositionhasalargerimpactondensityetc.thanthesmall

differenceincurredbyusingthecomputationallyefficient25‐termversionfordensity.

Version1oftheGSWToolboxwasreleasedinJanuary2009andversion2.0in

October2010.Thisversion2.0oftheGSWToolboxisavailabletodateonlyinMATLAB

(version1isalsoavailableinFORTRAN)fromthewebsiteatwww.TEOS‐10.org.Aquick

introductiontoTEOS‐10isavailableontheTEOS‐10website(www.TEOS‐10.org)asthe

shortdocumentcalled“GettingstartedwiththeGibbsSeaWater(GSW)Oceanographic

ToolboxofTEOS‐10”.SomeofthefunctionnamesintheGSWOceanographicToolbox

aregiveninthefollowingtable.

174 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

TableN.1.Aselectionoffunctionsinversion2.0oftheGSWOceanographicToolbox.

Thermodynamic

Property

Functionname

(inMATLAB)

Remarks

AbsoluteSalinity A

Sgsw_SA_from_SP theMcDougall,JackettandMillero(2010a)

algorithmforA

Susingalook‐uptableforA



PreformedSalinity*

Sgsw_Sstar_from_SP PreformedSalinity*

SfromPracticalSalinityP

S

Conservative

TemperatureΘgsw_CT_from_t ConservativeTemperatureΘ,from

()

A,,Stp

Gibbsfunction

andits

1stand2ndderivatives gsw_gibbs thesumoftheIAPWS‐09andIAPWS‐08Gibbs

functions,andthederivativesofthissum

specificvolumevgsw_specvol

(

)

A,,vS tpspecificvolumeusinggsw_gibbs

density

gsw_rho

(

)

A,,Stp

insitudensityusinggsw_gibbs

potentialdensity

Θgsw_pot_rho

(

)

,, ,Stpp

Θusinggsw_gibbs

density

,and

potentialdensity

Θ gsw_rho_CT25

(

)

ˆ,,Sp

Θ,insitudensityusingthe25‐term

expressionfordensityintermsofConservative

Temperature(CTforshort),Θ.Potentialdensity

withrespecttopressurer

p,usingthis25‐term

expression,isobtainedbysimplycalling

gsw_rho_CT25withthispressure,obtaining

()

ˆ,,

ρρ

Θ=Θ.

specificentropy

gsw_entropy

(

)

A,,Stp

usinggsw_gibbs

specificenthalpyh gsw_enthalpy

(

)

A,,hS tpusinggsw_gibbs

firstorderderivativesof

enthalpywithrespectto

ConservativeTemperature

gsw_enthalpy_first_derivati

ves

andA

ˆS

husinggsw_gibbs(seeEqns.(A.11.15)

and(A.11.18))

secondorderderivativesof

enthalpywithrespectto

ConservativeTemperature

gsw_enthalpy_second_deri

vatives A

ˆˆ

ΘΘ Θ andAA

ˆSS

husinggsw_gibbs

soundspeedcgsw_sound_speed

(

)

A,,cS tpusinggsw_gibbs

Conservative

TemperatureΘgsw_CT_from_pt

(

)

A,S

Θ,founddirectlyfromgsw_gibbs.

Here

ispotentialtemperaturewithr

p=0.

potentialtemperature

gsw_pt_from_t

(

)

,, ,Stpp

foundbyusinggsw_gibbsandby

equatingtwovaluesofentropy

potentialtemperature

gsw_pt0_from_t

(

)

A,,Stp

,acomputationallyfasterversionof

gsw_pt_from_twhenr0p

dbar.

potentialtemperature

gsw_pt_from_CT

(

)

A,S

,foundbyNewton_Raphsoniteration,

beingtheinversefunctionofgsw_CT_from_pt

thermalexpansion

coefficientwithrespectto

Conservative

Temperature

Θ

gsw_alpha_wrt_CT

()

A,,Stp

Θusinggsw_gibbs

salinecontraction

coefficientatconstant

Conservative

TemperatureΘ

gsw_beta_const_CT

()

A,,Stp

Θusinggsw_gibbs

density,thermal

expansionandsaline

contractioncoefficient

gsw_rho_alpha_beta_CT25

(

)

ˆ,,Sp

Θ,

()

ˆ,,

ΘΘand

()

ˆ,,

ΘΘ

usingthe25‐termexpressionfordensityinterms

ofConservativeTemperatureΘ

dynamicheightanomalygsw_geo_strf_dyn_height geostrophicstreamfunctioninanisobaricsurface

McDougall‐Klocker

geostrophicstreamfunctiongsw_geo_strf_McD_Klocker geostrophicstreamfunctioninanapproximately

neutralsurface,seeEqn.(3.30.1)

Montgomerygeostrophic

streamfunction gsw_geo_strf_Montgomery geostrophicstreamfunctioninaspecificvolume

anomalysurface,seeEqn.(3.28.1)

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

175

AppendixO:

CheckingtheGibbsfunctionofseawater

againsttheoriginalthermodynamicdata



OneofthetasksundertakenbySCOR/IAPSOWorkingGroup127wastoverifythe

accuracyoftheFeistel(2003)andFeistel(2008)Gibbsfunctionsagainsttheunderlying

laboratorydatatowhichtheseGibbsfunctionswerefitted.Thischeckingwasperformed

byGilesM.Marion,andisreportedhere.



VerificationoftheFeistel(2003)Gibbsfunction

Table9ofFeistel(2003)includedarootmeansquare(r.m.s.)estimateofthefitofthe

Gibbsfunctiontotheoriginalexperimentaldata.InTableO.1here,thisestimateisthe

columnlabeled“Resultingr.m.s.”.AllthedatainTableO.1arefromFeistel(2003)except

forthelastcolumn,whereGilesM.Marionhasestimatedanindependent“Verifying

r.m.s.”.

TheseawaterpropertiesthatwereusedtodeveloptheFeistel(2003)Gibbsfunction

(seeColumn1ofTableO.1)includeddensity

,isobaricspecificheatcapacityp

c,

thermalexpansioncoefficientt

,soundspeed,cspecificvolume,vfreezing

temperaturef

tmixingheat.hΔThisdatasetincluded1834observations.Column2of

TableO.1arethedatasourcesthatarelistedinthereferences.Ther.m.s.valueswere

calculatedwiththeequation:

()

0.5

r.m.s F03 - expt.datum

⎡⎤

=⎢⎥

⎣⎦

∑(O.1)

whereF03referstooutputoftheFORTRANcodethatimplementsFeistel’s(2003)Gibbs

function.Inmanycases,theexperimentaldatahadtobeadjustedtobringthisdatainto

conformitywithrecentdefinitionsoftemperatureandthethermalpropertiesofpure

water(seeFeistel(2003)forthespecificsofthedatasetsusedandtheinternal

assumptionsinvolvedindevelopingtheGibbsfunction).

Comparisonsofthe“Resulting”(Feistel)and“Verifying”(Marion)columnsinTable

O.1showthattheyareinexcellentagreement.Thesmalldifferencesbetweenthetwo

r.m.s.columnsarelikelydueto(1)thenumberofdigitsusedinthecalculations,(2)small

variationsintheexactequationsusedforthecalculations,or(3)smallerrorsinmodel

inputs.Inanycase,thesesmalldifferencesareinsignificant.

ThereweretwotypographicalerrorsintheoriginalTable9ofFeistel(2003)inthe

“Resultingr.m.s.”column.TheoriginalvalueforthePG93datasetwaslistedas11.3

ppm,whichisslightlydifferentfromtheverifyingvalueof11.9ppm.Asubsequent

checkindicatedthatthisvalueshouldhavebeenlistedas12.0ppm,whichisinexcellent

agreementwiththevalueof11.9ppm.Similarly,theoriginal“Resultingr.m.s.”valuefor

theBDSW70datasetwaslistedas0.54J/(kgK),whichissignificantlyatvariancefromthe

verifyingestimateof1.43J/(kgK).Asubsequentcheckindicatedthatthisvalueshould

havebeenlistedas1.45J/(kgK),whichisinexcellentagreementwiththeindependent

estimateof1.43J/(KgK).

TherewerethreeminorerrorsbetweentheoriginalliteraturedataandtheFeistel

(2003)compilationofthisdata.IntheBS70dataset,twoP

Scolumnsweremislabeledas

176 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

30.504and30.502,wherethecorrectordershouldhavebeen30.502and30.504.Inthe

CM76dataset,thecorrectvalueatP

S=20.062,t=25°C,andp=588.0barsshouldhave

been0.9643933

kg m

−

,not0.9643833

kg m

−

.Theseminorerrorsareinsignificant.The

independentcomparisonsinTableO.1verifytheaccuracyoftheFeistel(2003)Gibbs

function.



VerificationoftheFeistel(2008)salinepartoftheGibbsfunctionofseawater

ThesalineGibbsfunctionFeistel(2008)wasdesignedtoincreasethetemperature

rangeupto80°Candthesalinityrangeupto1201

gkg

−

(Feistel,2008).Table7ofFeistel

(2008)includedarootmeansquare(r.m.s.)estimateofthemodelfittotheoriginal

experimentaldata(seethecolumn“Resultingr.m.s.”intheattachedTableO.2).Allthe

datainthistablearefromtheFeistel(2008)paperexceptforthelastcolumn,whereGiles

M.Marionhasestimatedanindependent“Verifyingr.m.s.”.

ThenewseawatersalinitydatabasesthatwereusedtodeveloptheFeistel(2008)

Gibbsfunction(seeColumn1ofTableO.2)includedisobaricspecificheatcapacity

c,

mixingheathΔ,freezingpointdepressionf

twatervapourpressurevap ,pandthe

Debye‐Hückellimitinglaw.

Thissalinitydatasetincluded602observations.

Column2ofTableO.2arethedatasourcesthatarelistedinthereferences.Inmany

cases,theexperimentaldatahadtobeadjustedtobringthisdataintoconformitywith

recentdefinitionsoftemperatureandthethermalpropertiesofpurewater(seeFeistel

(2008)forthespecificsonthedatasetsusedandtheinternalassumptionsinvolvedin

modeldevelopment).

Comparisonsofthe“Resulting”(Feistel)and“Verifying”(Marion)“r.m.s.”columns

showthattheyareinexcellentagreement.Themostlikelyexplanationforthefewsmall

differencesisthenumberofdigitsusedinthecalculations.Ingeneral,thegreaterthe

numberofdigitsusedinthesecalculations,themoreaccuratethecalculations.

Thisindependentcheckrevealsthattherearenosignificantdifferencesbetweenthe

FeistelandMarionestimationsofr.m.s.valuesforthesecomparisons(TableO.2),which

verifiestheaccuracyoftheFeistel(2008).



VerificationofthePureWaterpartoftheFeistel(2003)Gibbsfunction

ThepurewaterpartoftheFeistel(2003)GibbsfunctionwasitselfafittotheIAPWS‐

95Helmholtzfunctionofpurewatersubstance.TheaccuracyofthisfittoIAPWS‐95in

theoceanographicrangesoftemperatureandpressurehasbeencheckedindependently

bytwomembersoftheSCOR/IAPSOWorkingGroup127(DanG.WrightandDavidR.

Jackett).TheaccuracyofthispurewaterpartoftheFeistel(2003)Gibbsfunctionhasalso

beencheckedbyanevaluationcommitteeofIAPWSintheprocessofapprovingthe

Feistel(2003)GibbsfunctionasanIAPWSRelease(IAPWS‐09).InIAPWS‐09itisshown

thatthepurewaterpartoftheFeistel(2003)GibbsfunctionfitstheIAPWS‐95properties

morepreciselythantheuncertaintyofthedatathatunderliesIAPWS‐95.Hencewecan

betotallycomfortablewiththeuseoftheFeistel(2003)Gibbsfunctiontorepresentthe

propertiesofpureliquidwaterintheoceanographicrangesoftemperatureandpressure.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

177

Table O.1. Summary of data used in the regression to determine the coefficients of the Feistel

(2003) Gibbs potential.

Quantity

Source

()

AgkgS−

t /°C

P/MPa

Points

Required

r.m.s.

Resulting

r.m.s.

Verifying

r.m.s.

MGW76c 0.5-40 0-40 0 122 4 ppm 4.1 ppm 4.2 ppm

PBB80 5-42 0-30 0 345 4 ppm 4.0 ppm 4.2 ppm

PG93 34-50 15-30 0 81 10 ppm 12.0i ppm 11.9 ppm

cp BDSW70 10-50 0-40 0 25 2 J/(kg K) 1.45ii J/(kg K) 1.43 J/(kg K)

cp MPD73 1-40 5-35 0 48 0.5 J/(kg K) 0.52 J/(kg K) 0.45 J/(kg K)

C78 10-30 -6-1 0.7-33 31 0.6x10-6 K-1 0.73x10-6 K-1 0.74x10-6 K-1

c D74(I-III) 29-43 0-35 0-2 92 5 cm/s 1.7 cm/s 1.6 cm/s

c D74(IVa-d) 29-43 0-30 0.1-5 32 5 cm/s 1.2 cm/s 1.2 cm/s

c D74(V-VI) 33-37 0-5 0-100 128 5 cm/s 3.5 cm/s 3.5 cm/s

v CM76 5-40 0-40 0-100 558 10 ppm 11.0 ppm 11.2 ppm

vS BS70 30-40 -2-30 1-100 221 4 ppm 2.6 ppm 2.6 ppm

t DK74 4-40 -2-0 0 32 2 J/kg 1.8 J/kg 1.9 J/kg

h B68 0-33 25 0 24 4 J 2.4 J 2.4 J

h MHH73 1-41 0-30 0 95 0.4 J/kg 0.5 J/kg 0.5 J/kg

i TheoriginalvalueinTable9ofFeistel(2003)of11.3ppmreferstothespecificvolume.

ii TheoriginalvalueinTable9ofFeistel(2003)was0.54J/(kgK),whichapparentlywasa

typographicalerror.

Table O.2. Summary of extra datasets used in the regression to determine the coefficients of

the Feistel (2008) Gibbs potential.

Quantity

Source

()

AgkgS−

t /°C

P/MPa

Points

Resulting

r.m.s.

Verifying

r.m.s.

cp BDCW67 11-117 2-80 0 221 3.46 J/(kg K) 3.46 J/(kg K)

c MPD73 1-40 5-35 0 48 0.57 J/(kg K) 0.57 J/(kg K)

cp MP05 1-35 10-40 0 41 1.30 J/(kg K) 1.30 J/(kg K)

h B68 0-97 25 0 33 0.75 J/kg 0.75 J/kg

h C70 35-36 2-25 0 19 7.2 J/kg 7.1 J/kg

h MHH73 1-35 0-30 0 120 3.3 J/kg 3.3 J/kg

t DK74 4-40 -0.2-(-2.2) 0 32 1.6 mK 1.6 mK

t FM07 5-109 -0.3-(-6.9) 0 22 1.2 mK 1.0 mK

pvap R54 18-40 25 0 13 2.8 J/kg 2.8 J/kg

oil

t BSRSR74 6-70 60-80 0 32 9.1 J/kg 9.3 J/kg

gLL F08 35 -5-95 0 21 0.091 J/kg 0.092 J/kg

178 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

AppendixP:Thermodynamicproperties

basedon

(

)

(

)

(

)

AA A

,, , , , , , ,gS tp hS p hS p

ηθ



and

(

)

ˆ,,hS pΘ



ThethermodynamicpotentialonwhichTEOS‐10isbasedistheGibbsfunctionof

seawater.BeingaGibbsfunction,

(

)

A,,

StpisnaturallyafunctionofAbsoluteSalinity,

insitutemperatureandpressure.Thereareotherchoicesforathermodynamicpotential.

OnesuchchoiceisenthalpyhasafunctionofAbsoluteSalinity,entropyandpressure,

andwegivethisfunctionalformforenthalpyaboomerangoverthehsothat

()

A,, .hhS p



Itprovestheoreticallyconvenienttoconsidertheadditionalfunctional

forms

()

A,,hhS p

=and

()

ˆ,,hhS p=Θ

forenthalpy.Thesetwofunctionalformsdonot

constituteacompletethermodynamicdescriptionofseawaterbutwhensupplementedby

theexpressions

()

A,S

ηθ

=and

(

)

ˆ,S

ηη

Θforentropy,theydoformcomplete

thermodynamicpotentials.Intheexpressions

(

)

A,,hhS p

=and

()

A,S

ηθ

=itis

possibletochooseanyfixedreferencepressurer

pforthedefinitionofpotential

temperature,

.Howeverthereisnoadvantagetochoosingthereferencepressuretobe

differentfromr0p

anditisthisvaluethatistakeninTableP.1andthroughoutthis

appendix.TableP.1listsexpressionsforsomecommonthermodynamicquantitiesin

termsofthesepotentialfunctions(theresultsinthistablefor

(

)

A,,hS p



mostlycome

fromFeistel(2008)andFeisteletal.(2010b)).Notethatthereferencepressurer

pthat

appearsinthelastthreecolumnsofthe

rowofTableP.1isthereferencepressureof

potentialdensity,notof

,whereasintheGibbsfunctioncolumn,thisgeneralreference

pressuremustalsobeusedtoevaluate

.

InadditiontoTableP.1wehavethefollowingexpressionsforthethermobaricand

cabbelingcoefficients(ofEqns.(3.8.1)–(3.9.2))

AA A

PPS PS PS

PP P P P

PS P S

hh vv

Tvvv

θθθ θθ θθ

ρρ

ρρρ

=− =− =−+



 





 

 (P.1)

AA A

ˆˆ ˆ

ˆˆˆ

ˆˆ ,

ˆˆˆ ˆˆˆ

ˆˆˆ

PPS PS PS

PP P P P

PPSP

hh vv

Tvvv

hhh

ρρ

ρρρ

ΘΘΘ ΘΘ ΘΘ

=− =− =−+ (P.2)

AAA AAA

AAA

PS PS S S S S

PP P

PS P PS P

SSS

hh vv

hh h vv v

Cvvv v v

hh h h

θθ

θθθ θ θ θθ θ θ

θθ θ θ

ρρ

ρρ ρ

ρρρρ ρ

⎛⎞ ⎛⎞

=− + =− +

⎜⎟ ⎜⎟

⎜⎟

⎜⎟ ⎝⎠

⎝⎠

⎛⎞

=− + −

⎜⎟

⎝⎠



  

 

     



 

  

(P.3)

AAA AAA

AAA

ˆˆ

ˆˆ ˆ ˆˆ

ˆˆ ˆ

ˆˆˆ ˆ ˆ ˆˆˆˆ ˆ

ˆˆ

ˆˆ ˆ

ˆˆˆ ˆ ˆ

PS PSS S SS

PP P

PPSP PS P

SSS

hh vv

hh h vv v

Cvvvv v

hhh h h

ρρ

ρρ ρ

ρρρ ρ ρ

ΘΘ

ΘΘΘ Θ Θ ΘΘ Θ Θ

ΘΘ Θ Θ

⎛⎞ ⎛⎞

⎜⎟

=− + =− +

⎜⎟

⎜⎟ ⎝⎠

⎝⎠

⎛⎞

=− + −⎜⎟

⎜⎟

⎝⎠

(P.4)

HerefollowssomeinterestingexpressionsthatcanbegleanedfromTableP.1.

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

179

() ()

0ˆ

00 ,

chc

θθ

ΘΘ

==Θ=−



()

+= 

(

)

()

Tt hh

Tch

+∂

+∂(P.5)

() ()

ˆˆ

ˆ,

ˆ0

Sp S p

ηθη

θθ α

θηα

ΘΘ ΘΘ

∂∂

====− =− = =

∂Θ ∂Θ Θ

(P.6)

() ()

ˆˆ

μθη

=− = − + (P.7)

()

AA A

010

AA A

ˆˆ

ˆ.

SpS S

SS S c

ηθη

θθ

θη

−

ΘΘ

ΘΘ Θ

Θ+

∂

∂∂

= = =− =− = = −

∂∂ ∂



(P.8)

SeealsoEqn.(A.12.6)foranalternativeexpressionforA

ˆS

.Equation(P.8)canalsobe

writtenas

()

ˆ.

−

∂+ =

∂(P.9)

NowweconsiderhowallthetermsinthelastcolumnofTableP.1maybeevaluated

intermsoftheexpression

()

ˆ,,hS pΘofEqn.(A.30.6);thisbeingtheexpressionfor

specificenthalpythatfollowsfromthe25‐termexpressionfordensityasafunctionof

()

A,,SpΘasdescribedinEqn.(K.1)andTableK.1.Thesuperscript“25”isaddedto

()

ˆ,,hS pΘtoemphasizethatthisisanapproximateexpressionforspecificenthalpy.

Thefirststepistoevaluate

exactlyfromthefollowingimplicitexpressionforΘin

termsoftheGibbsfunctionat0p=(seeEqn.(2.12.1)),asdiscussedinsection3.3,

()

(

)

(

)

(

)

AA0A

,,0 ,,0 ,,0

chSt gSt TgSt

θθθθ

Θ= = = = − + = .(P.10)

Next,weremindourselvesthatweknowthefunctionalformsof

(

)

A,S

,

()

A,S

and

()

A,,0S

μθ

intermsofthecoefficientsoftheGibbsfunctionofseawaterastheexact

polynomialandlogarithmtermsgivenby(fromEqns.(2.10.1)and(2.9.6))

() ( )

,,,0

SgSt

ηθ θ

=− =

,

(

)

(

)

,,0 , ,0

SgSt

μθ θ

,(P.11a,b)

andEqn.(P.10)isrepeatedhereemphasizingthefunctionalformoftheleft‐handside,

()( )

(

)

(

)

AA 0A

,,,0 ,,0

cS gSt T gSt

θθθθ

Θ==−+ =

.(P.12)

Thepartialderivativeswithrespectto

andwithrespectto

,bothatconstantA

S

andp,andthepartialderivativeswithrespecttoA

S,arerelatedby

Sp Sp

θθ

∂∂

∂Θ ∂

,and A

AA ,

∂∂ ∂

=−

∂∂ ∂



.(P.13a,b)

Useoftheseexpressions,actingonentropyyields(with0p

everywhere,andusing

Eqn.(P.7)[orEqn.(A.12.8b)]andEqn.(P.8))

()

ˆp

Θ=≡



,

()

ˆp

ΘΘ =−Θ+

,

(

)

()

,,0

ˆS

μθ

ηθ

=− +



,(P.14a,b,c)

()

ˆSp

=Θ+



,and

()

(

)

()

,,0

ˆS

μθ

ηθ

=− −

+Θ+



,(P.15a,b)

intermsofthepartialderivativesoftheexactpolynomialexpressions(P.11b)and(P.12).

AllofthethermodynamicvariablesofthelastcolumnofTableP.1cannowbe

evaluatedusingthepartialderivativesof

()

ˆ,,hS pΘandtheexactexpressions(P.14)

and(P.15)whicharewrittenintermsofpotentialtemperature

whichisfoundfromthe

exactimplicitequation(P.10).Thiscompletesthediscussionofhow

()

ˆ,,hS pΘcanbe

usedasanalternativethermodynamicpotentialofseawater.Thepartialderivativesof

entropyinEqns.(P.14)and(P.15)areavailableintheGSWToolboxfromthefunctions

gsw_entropy_first_derivativesandgsw_entropy_second_derivatives.



180 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Table P.1. Expressions for various thermodynamic variables based on four different thermodynamic potentials

Expressionsbasedon

()

A,,

Stp

Expressionsbasedon

(

)

A,,hS p



Expressionsbasedon

()

A,,hS p

and

(

)

A,S



Expressionsbasedon

(

)

ˆ,,hS pΘand

(

)

ˆ,S

t t

(

)

Tt h



()

Tt h



(

)

0ˆˆ

Tt h

(

)( )

Ar A

,, ,,

SpgStp

=

[thisisanimplicitequationfor

]

(

)

(

)

00Th



()

(

)

;0Th

θη



(

)

0ˆ

(

)( )

(

)

A0A

,,0 ,,0

gS T g S

θθθ

−+

Θ=

(

)

hcΘ=



(

)

hcΘ= 

(

)

hcΘΘ=

()

A,,

gS tp=

=−



gh h

=−



ˆˆ

gh h

=−

(

)

A,S

ηθ

=

(

)

ˆ,S

ηη

()

hgTtg=− +

(

)

A,,hhS p



(

)

A,,hhS p

=

(

)

ˆ,,hhS p=Θ

vg=

vh=



vh= ˆ

vh=

()

−

(

)

−



(

)

−

=

(

)

ˆP

−

= A



ηη

=−



ˆˆ

ηη

=−

(

)( )

00TP

ugTtg pPg=− + − +

(

)

uh pPh=− +



(

)

uh pPh=− +



(

)

ˆˆ

uh pPh=− +

()

gpPg=−+

(

)

hh pPh

=− − +





(

)

hh pPh

θθ

ηη

=− − +

 



(

)

ˆˆ ˆ

ˆˆ

hh pPh

ηη

ΘΘ

=− − +

()

0pTT

cTtg=− + p

chh

ηη



(

)

ch hh

θθθθθθθ

ηη η

=−



 

(

)

ˆˆˆ

ˆˆ ˆ

ch h h

ηη η

ΘΘΘΘΘΘΘ

=−

()()()

A0A

,,0 ,,0

hgS T gS

θθθ

=−+

(

)

00hh=



(

)

00hh=

(

)

ˆ0p

hh c

=Θ

()

gS p

ρθ

−

⎡⎤

=⎣⎦

()

−

⎡

⎤

⎣

⎦



()

−

⎡

⎤

⎣

⎦



()

ˆP

ρρ

−

⎡

⎤

⎣

⎦

−

=−

PPP P

hh h h

−−

=− +



 



()

11tP

PPP P

hh h hh

θθ

θθ θθ θ

−−

=− − −



 



()

ˆˆ

ˆˆ ˆ

ˆˆ

PPP P

hh h

−−

ΘΘ

ΘΘ ΘΘ Θ

=− − −

PPP P

gg g

−−

=− + 1

−

=−



−

=− 1

ˆˆ

−

=−

TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

181

Table P.1. (cont’d) Expressions for various thermodynamic variables based on four different thermodynamic potentials

Expressionsbasedon

()

A,,

Stp

Expressionsbasedon

(

)

A,,hS p



Expressionsbasedon

()

A,,hS p

and

(

)

A,S



Expressionsbasedon

(

)

ˆ,,hS pΘand

(

)

ˆ,S

()

TT TP TT PP

cgg g gg=−

ch h=−



ch h=−



ˆˆ

ch h=−

Γ TP TT

=−

Γ=



Γ=  ˆˆ

Γ=

tTP

= 1

−



()

hh hh

θθ θθ θ

−

=− −





()

1ˆ

ˆˆ

−Θ

ΘΘ ΘΘ Θ

=− −

()

PTT

()

ηη

−



 1

−

=

ˆˆ

hh c

−Θ

=−

()

αθ

Θ=− +

()

hh h

Θ−

=



()

hh h

Θ−

=

 1

ˆˆ

Θ−

−

=− A

PPS

hh h

−

=−







()

PPS

hh hh

θθθ

θθθ θθθ

ηη

−

=−

−

+−



()

ˆˆ

PPS

ηη

−

ΘΘΘ

−Θ

ΘΘΘ ΘΘΘ

=−

−

+−

()

PPS

TP ST ST

PTT

gSp

−

=−

⎡⎤

−

⎣⎦

()

PPS

hh h

ηη

−

=−





 A

−

=− A

ˆˆ ˆˆ

PPS PP

hh hh

θη

βη

−−

=− +

()( )

,,0

PPS

TP S T S

PTT

gT S

θθ

Θ−

−

=−

⎡

⎤

−+

⎣

⎦

()

PPS

hh h

Θ−

−

=−







(

)

()

PPS PP

hh hh h

Θ− −

=− +



 

 A

ˆˆ

Θ−

=−

182 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

References



Alberty,R.A.,2001:UseofLegendretransformsinchemicalthermodynamics.PureAppl.

Chem.,73,1349–1380.

Alderson,S.G.andP.D.Killworth,2005:Apreoperationalschemeforcalculatingseasurface

heightbyBernoulliinverseofAgrofloatdataintheNorthAtlantic.J.Atmos.Oceanic

Tech.,22,1416‐1422.

Bacon,S.,F.Culkin,N.HiggsandP.Ridout,2007:IAPSOStandardSeawater:Definitionofthe

uncertaintyinthecalibrationprocedure,andstabilityofrecentbatches.JAtmos.Oceanic

Technol.24,1785‐1799.

Bacon,S.andNFofonoff,1996:Oceanicheatfluxcalculation.JAtmos.OceanicTechnol.13,

1327‐1329.

Barber,C.R.,1969:TheInternationalTemperatureScaleof1968.Metrologia,5,35‐44.

Batchelor,G.K.,1970:AnIntroductiontoFluidDynamics.CambridgeUniversityPress,615pp.

Bezold,W.v.,1888:ZurThermodynamikderAtmosphaere.PotentielleTemperatur.Verticaler

Temperaturgradient.ZusammengesetzteConvection.SitzungsberichtederKoeniglich

PreussischenAkademiederWissenschaftenzuBerlin,46,1189‐1206.

http://bibliothek.bbaw.de/bibliothek‐

digital/digitalequellen/schriften/anzeige/index_html?band=10‐sitz/1888‐2&seite:int=530

BIPM,2005:Clarificationofthedefinitionofthekelvin,unitofthermodynamictemperature

RECOMMENDATION2(CI‐2005)TheInternationalCommitteeforWeightsand

Measures(CIPM),http://www.bipm.org/cc/CIPM/Allowed/94/CIPM‐Recom2CI‐2005‐EN.pdf

BIPM,2006:TheInternationalSystemofUnits(SI),8thedition.BureauInternationaldesPoidset

Mesures,OrganisationIntergouvernementaledelaConventionduMètre,Sèvres,France.

http://www.bipm.fr/utils/common/pdf/si_brochure_8_en.pdf

Bleck,R.,1978:Finitedifferenceequationsingeneralizedverticalcoordinates,I,Totalenergy

conservation.Contrib.Atmos.Phys.,51,360‐372.

Bradshaw,A.andK.E.Schleicher,1970:Directmeasurementsofthermalexpansionofsea

waterunderpressure.Deep‐SeaRes.,17,691‐706.

Brewer,P.G.,andA.Bradshaw,1975.Theeffectofnon‐idealcompositionofseawateron

salinityanddensity.J.Mar.Res.33,157‐175.

Bromley,L.A.,1968:Relativeenthalpiesofseasaltsolutionsat25°C.JournalofChemicaland

EngineeringData,13,399‐402.

Bromley,L.A.,V.A.Desaussure,J.C.Clipp,andJ.S.Wright,1967:Heatcapacitiesofsea

watersolutionsatsalinitiesof1to12%andtemperaturesof2°to80°.JournalofChemical

andEngineeringData,12,202‐206.

Bromley,L.A.,A.E.Diamond,E.Salami,andD.G.Wilkins,1970:Heatcapacitiesand

enthalpiesofseasaltsolutionsto200°C.JournalofChemicalandEngineeringData,15,246‐

253.

Bromley,L.A.,D.Singh,P.Ray,S.Sridhar,andS.M.Read,1974:Thermodynamicproperties

ofseasaltsolutions.AIChEJournal,20,326‐335.

Bryden,H.L.,1973:Newpolynomialsforthermalexpansion,adiabatictemperaturegradient

andpotentialtemperatureofseawater.Deep‐SeaRes.,20,401‐408.

Caldwell,D.R.,1978:Themaximumdensitypointsofpureandsalinewater.Deep‐Sea

Research,25,175‐181.

Calvert,J.G.,1990:Glossaryofatmosphericchemistryterms(Recommendations1990),Pure&

App.Chem.,62,2167‐2219.

Chen,C.‐T.andF.J.Millero,1976:Thespecificvolumeofseawaterathighpressures.Deep‐Sea

Res.23,595‐612.

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

183

Chen,C.‐T.andF.J.Millero,1977:Soundspeedofseawaterathighpressures.J.Acoust.Soc.

Am.,62,1129‐1135.

Clausius,R.,1876:DieMechanischeWärmetheorie.FriedrichViewegundSohn,

Braunschweig.

Culkin,F.andP.S.Ridout,1998:StabilityofIAPSOStandardSeawater,J.Atmos.Oceanic.

Technol.,15,1072–1075.

Cunningham,S.A.,2000:CirculationandvolumefluxoftheNorthAtlanticusingsynoptic

hydrographicdatainaBernoulliinverse.J.MarineRes.,58,1‐35.

Curry,J.A.andP.J.Webster,1999:Thermodynamicsofatmospheresandoceans.AcademicPress,

SanDiego,USA.

Dai,A.,2006:RecentClimatology,Variability,andTrendsinGlobalSurfaceHumidity.J.

Climate,19,3589‐3605.

DeGroot,S.R.andP.Mazur,1984:Non‐equilibriumthermodynamics.DoverPublications,Inc.,

NewYork.

DelGrosso,V.A.,1974:Newequationforthespeedofsoundinnaturalwaters(with

comparisontootherequations).J.Acoust.Soc.Am.,56,1084‐1091.

deSzoeke,R.A.,2000:EquationsofMotionUsingThermodynamicCoordinates.Journalof

PhysicalOceanography,30,2814‐2829.

deSzoeke,R.A.andR.M.Samelson,2002:ThedualitybetweentheBoussinesqandnon‐

Boussinesqhydrostaticequationsofmotion.JournalofPhysicalOceanography,32,2194‐

2203.

deSzoeke,R.A.,S.R.SpringerandD.M.Oxilia,2000:Orthobaricdensity:Athermodynamic

variableforoceancirculationstudies.J.Phys.Oceanogr.,30,2830‐2852.

Douglas,T.B.,1969:Conversionofexistingcalorimetricallydeterminedthermodynamic

propertiestothebasesoftheInternationalPracticalScaleof1968.Jour.ofRes.NBS‐A:

PhysicsandChemistry,73A,451–470.

Eden,C.andJ.Willebrand,1999:Neutraldensityrevisited.Deep‐SeaRes.II,46,33‐54.

Feistel,R.,1993:Equilibriumthermodynamicsofseawaterrevisited,Progr.Oceanogr.,31,101‐

179.

Feistel,R.,2003:AnewextendedGibbsthermodynamicpotentialofseawater,Progr.

Oceanogr.,58,43‐114.

Feistel,R.,2008:AGibbsfunctionforseawaterthermodynamicsfor−6to80°Candsalinityup

to120gkg–1,Deep‐SeaRes.I,55,1639‐1671.

Feistel,R.andE.Hagen,1995:OntheGIBBSthermodynamicpotentialofseawater.Prog.in

Oceanogr.,36,249‐327.

Feistel,R.andE.Hagen,1998:AGibbsthermodynamicpotentialofseaice,ColdRegionsSci.

Technol.,28,83‐142,1998.

Feistel,R.andG.M.Marion,2007:AGibbs‐Pitzerfunctionofhigh‐salinityseawater

thermodynamics.ProgressinOceanography,74,515‐539.

Feistel,R.,G.M.Marion,R.PawlowiczandD.G.Wright,2010d:Thermophysicalproperty

anomaliesofBalticseawater.OceanScienceDiscussions,7,1103‐1208.http://www.ocean‐

sci‐discuss.net/7/1103/2010/osd‐7‐1103‐2010‐print.pdf

Feistel,R.,G.Nausch,N.Wasmund(Eds),2008b:StateandEvolutionoftheBalticSea,1952‐

2005.ADetailed50‐YearSurveyofMeteorologyandClimate,Physics,Chemistry,

Biology,andMarineEnvironment.JohnWiley&Sons,Inc.,Hoboken.

Feistel,R.andW.Wagner,2005.High‐pressurethermodynamicGibbsfunctionsoficeandsea

ice.JournalofMarineResearch,63,95‐139.

Feistel,R.andW.Wagner,2006:ANewEquationofStateforH2OIceIh.J.Phys.Chem.Ref.

Data,35,2,1021‐1047.

Feistel,R.andW.Wagner,2007:SublimationpressureandsublimationenthalpyofH2OiceIh

between0and273.16K,Geochim.Cosmochim.Acta,71,36–45,2007.

Feistel,R.,S.Weinreben,H.Wolf,S.Seitz,P.Spitzer,B.Adel,G.Nausch,B.SchneiderandD.

G.Wright,2010c:DensityandAbsoluteSalinityoftheBalticSea2006–2009.Ocean

Science,6,3–24.http://www.ocean‐sci.net/6/3/2010/os‐6‐3‐2010.pdf

184 TEOS-10 Manual: Calculation and use of the thermodynamic properties of seawater

IOC Manuals and Guides No. 56

Feistel,R.,D.G.Wright,K.Miyagawa,A.H.Harvey,J.Hruby,D.R.Jackett,T.J.McDougall

andW.Wagner,2008a:Mutuallyconsistentthermodynamicpotentialsforfluidwater,ice

andseawater:anewstandardforoceanography.OceanScience,4,275‐291.

http://www.ocean‐sci.net/4/275/2008/os‐4‐275‐2008.pdf

Feistel,R.,D.G.Wright,D.R.Jackett,K.Miyagawa,J.H.Reissmann,W.Wagner,U.Overhoff,

C.Guder,A.FeistelandG.M.Marion,2010b:Numericalimplementationand

oceanographicapplicationofthethermodynamicpotentialsofliquidwater,water

vapour,ice,seawaterandhumidair‐Part1:Backgroundandequations.OceanScience,6,

633‐677.http://www.ocean‐sci.net/6/633/2010/os‐6‐633‐2010.pdfandhttp://www.ocean‐

sci.net/6/633/2010/os‐6‐633‐2010‐supplement.pdf

Feistel,R.,D.G.Wright,H.‐J.Kretzschmar,E.Hagen,S.HerrmannandR.Span,2010a:

Thermodynamicpropertiesofseaair.OceanScience,6,91–141.http://www.ocean‐

sci.net/6/91/2010/os‐6‐91‐2010.pdf

Fofonoff,N.P.,1962:Physicalpropertiesofseawater.TheSea,Vol.1,MNHill,Ed.,Wiley‐

Interscience,3‐30.

Fofonoff,N.P.,1985:Physicalpropertiesofseawater:Anewsalinityscaleandequationof

stateforseawater.J.Geophys.Res.,90,3322–3342.

Gent,P.R.andJ.C.McWilliams,1990:Isopycnalmixinginoceancirculationmodels.Journalof

PhysicalOceanography,20,150‐155.

Gent,P.R.,J.Willebrand,T.J.McDougallandJ.C.McWilliams,1995:Parameterizingeddy‐

inducedtracertransportsinoceancirculationmodels.JournalofPhysicalOceanography,25,

463‐474.

Gibbs,J.W.,1873:Graphicalmethodsinthethermodynamicsoffluids,Trans.Connecticut

Acad.ArtsandSci.,2,309‐342.

Gill,A.E.,1982:Atmosphere‐OceanDynamics.AcademicPress,662pp.

Glasstone,S.,1947:ThermodynamicsforChemists,D.vanNostrandCompany,Inc.,Princeton,

NewJersey,USA.

Godfrey,J.S.,1989:ASverdrupmodelofthedepth‐integratedflowfortheworldocean

allowingforislandcirculations.GeophysicalandAstrophysicalFluidDynamics.45,89‐119.

Goldberg,R.N.andR.D.Weir,1992:Conversionoftemperaturesandthermodynamic

propertiestothebasisoftheInternationalTemperatureScaleof1990.Pure&Applied

Chemistry,64,1545‐1562.

Gouretski,V.V.andK.P.Koltermann,2004:WOCEglobalhydrographicclimatology.Berichte

desBundesamtesfürSeeschifffahrtundHydrographieTech.Rep.35/2004,49pp.

Gradshteyn,I.S.andI.M.Ryzhik,1980:TablesofIntegrals,SeriesandProducts.AcademicPress,

1160pp.

Greatbatch,R.J.andT.J.McDougall,2003:Thenon‐BoussinesqTemporal‐Residual‐Mean.

JournalofPhysicalOceanography,33,1231‐1239.

Griffies,S.M.,2004:FundamentalsofOceanClimateModels.Princeton,NJ:PrincetonUniversity

Press,518pp+xxxiv.

Groten,E.,2004:FundamentalParametersandCurrent(2004)BestEstimatesoftheParameters

ofCommonRelevancetoAstronomy,Geodesy,andGeodynamics.JournalofGeodesy,77,

724‐797.

Harvey,A.H.andP.H.Huang,2007:First‐PrinciplesCalculationoftheAir–WaterSecond

VirialCoefficient.Int.J.Thermophys.,28,556–565.

Helland‐Hansen,B.,1912:TheOceanWaters.Intern.Rev.Hydrobiol.Hydrog.,Hydrog.Supp.

Ser.1No.2,Leipzig.

Helmholtz,H.v.,1888:UeberatmosphaerischeBewegungen.SitzungsberichtederKoeniglich

PreussischenAkademiederWissenschaftenzuBerlin,46,647–663.

http://bibliothek.bbaw.de/bibliothek‐

digital/digitalequellen/schriften/anzeige/index_html?band=10‐sitz/1888‐1&seite:int=665

Hill,K.D.,T.M.DauphineeandD.J.Woods,1986:TheextensionofthePracticalSalinityScale

1978tolowsalinities,IEEEJ.OceanicEng.,11,109–112.

Huang,R.X.,X.JinandX.Zhang,2001:Anoceanicgeneralcirculationmodelinpressure

coordinates.AdvancesinAtmosphericPhysics,18,1‐22.

TEOS-10 Manual: Calculation and Use of the Thermodynamic Properties of Seawater

IOC Manuals and Guides No. 56

185

Hyland,R.W.andA.Wexler,1983:Formulationsforthethermodynamicpropertiesofdryair

from173.15to473.15K,andofsaturatedmoistairfrom173.15to372.15K,atpressures

upto5Mpa.ASHRAETransact.89,520–535.

IAPWS,2005:GuidelineontheUseofFundamentalPhysicalConstantsandBasicConstantsof

Water.TheInternationalAssociationforthePropertiesofWaterandSteam.Gaithersburg,

Maryland,USA,September2001.RevisedJuly2005,availableat:http://www.iapws.org

IAPWS,2007:RevisedReleaseontheIAPWSIndustrialFormulation1997forthe

ThermodynamicPropertiesofWaterandSteam,Lucerne,Switzerland,August2007,

availablefromwww.iapws.org

IAPWS,2008a:ReleaseontheIAPWSFormulation2008fortheThermodynamicPropertiesof

Seawater.TheInternationalAssociationforthePropertiesofWaterandSteam.Berlin,

Germany,September2008,availablefromwww.iapws.org.ThisReleaseisreferredtoin

thetextasIAPWS‐08.

IAPWS,2008b:RevisedReleaseonthePressurealongtheMeltingandSublimationCurvesof

OrdinaryWaterSubstance.TheInternationalAssociationofthePropertiesofWaterand

Steam,Berlin,Germany,September2008,availablefromhttp://www.iapws.org.

IAPWS,2009a:RevisedReleaseontheEquationofState2006forH2OIceIh.TheInternational

AssociationforthePropertiesofWaterandSteam.Doorwerth,TheNetherlands,

September2009,availablefromhttp://www.iapws.org.ThisReleaseisreferredtointhe

textasIAPWS‐06.

IAPWS,2009b:RevisedReleaseontheIAPWSFormulation1995fortheThermodynamic

PropertiesofOrdinaryWaterSubstanceforGeneralandScientificUse.TheInternational

AssociationforthePropertiesofWaterandSteam.Doorwerth,TheNetherlands,

September2009,availablefromhttp://www.iapws.org.ThisReleaseisreferredtointhe

textasIAPWS‐95.