The Data Science Design Manual

The%20Data%20Science%20Design%20Manual

User Manual:

Open the PDF directly: View PDF .
Page Count: 453 [warning: Documents this large are best viewed by clicking the View PDF Link!]

Preface
Contents
What is Data Science?
Mathematical Preliminaries
Data Munging
Scores & Rankings
Statistical Analysis
Visualizing Data
Mathematical Models
Linear Algebra
Linear & Logistic Regression
Distance & Network Methods
Machine Learning
Big Data - achieving Scale
Coda
Biblio
Index

Steven S. Skiena

The Data Science Design Manual

Steven S. Skiena

Computer Science Department

Stony Brook University

Stony Brook, NY

USA

ISSN 1868-0941 ISSN 1868-095X (electronic)

Texts in Computer Science

ISBN 978-3-319-55443-3 ISBN 978-3-319-55444-0 (eBook)

DOI 10.1007/978-3-319-55444-0

Library of Congress Control Number: 2017943201

This Springer imprint is published by Springer Nature

The registered company is Springer International Publishing AG

The registered company address is: Gewerbestrasse 11, 6330 Cham, Switzerland

Preface

Making sense of the world around us requires obtaining and analyzing data from

our environment. Several technology trends have recently collided, providing

new opportunities to apply our data analysis savvy to greater challenges than

ever before.

Computer storage capacity has increased exponentially; indeed remembering

has become so cheap that it is almost impossible to get computer systems to for-

get. Sensing devices increasingly monitor everything that can be observed: video

streams, social media interactions, and the position of anything that moves.

Cloud computing enables us to harness the power of massive numbers of ma-

chines to manipulate this data. Indeed, hundreds of computers are summoned

each time you do a Google search, scrutinizing all of your previous activity just

to decide which is the best ad to show you next.

The result of all this has been the birth of data science, a new ﬁeld devoted

to maximizing value from vast collections of information. As a discipline, data

science sits somewhere at the intersection of statistics, computer science, and

machine learning, but it is building a distinct heft and character of its own.

This book serves as an introduction to data science, focusing on the skills and

principles needed to build systems for collecting, analyzing, and interpreting

data.

My professional experience as a researcher and instructor convinces me that

one major challenge of data science is that it is considerably more subtle than it

looks. Any student who has ever computed their grade point average (GPA) can

be said to have done rudimentary statistics, just as drawing a simple scatter plot

lets you add experience in data visualization to your resume. But meaningfully

analyzing and interpreting data requires both technical expertise and wisdom.

That so many people do these basics so badly provides my inspiration for writing

this book.

To the Reader

I have been gratiﬁed by the warm reception that my book The Algorithm Design

Manual [Ski08] has received since its initial publication in 1997. It has been

recognized as a unique guide to using algorithmic techniques to solve problems

that often arise in practice. The book you are holding covers very diﬀerent

material, but with the same motivation.

In particular, here I stress the following basic principles as fundamental to

becoming a good data scientist:

•Valuing doing the simple things right: Data science isn’t rocket science.

Students and practitioners often get lost in technological space, pursuing

the most advanced machine learning methods, the newest open source

software libraries, or the glitziest visualization techniques. However, the

heart of data science lies in doing the simple things right: understanding

the application domain, cleaning and integrating relevant data sources,

and presenting your results clearly to others.

Simple doesn’t mean easy, however. Indeed it takes considerable insight

and experience to ask the right questions, and sense whether you are mov-

ing toward correct answers and actionable insights. I resist the temptation

to drill deeply into clean, technical material here just because it is teach-

able. There are plenty of other books which will cover the intricacies of

machine learning algorithms or statistical hypothesis testing. My mission

here is to lay the groundwork of what really matters in analyzing data.

•Developing mathematical intuition: Data science rests on a foundation of

mathematics, particularly statistics and linear algebra. It is important to

understand this material on an intuitive level: why these concepts were

developed, how they are useful, and when they work best. I illustrate

operations in linear algebra by presenting pictures of what happens to

matrices when you manipulate them, and statistical concepts by exam-

ples and reducto ad absurdum arguments. My goal here is transplanting

intuition into the reader.

But I strive to minimize the amount of formal mathematics used in pre-

senting this material. Indeed, I will present exactly one formal proof in

this book, an incorrect proof where the associated theorem is obviously

false. The moral here is not that mathematical rigor doesn’t matter, be-

cause of course it does, but that genuine rigor is impossible until after

there is comprehension.

•Think like a computer scientist, but act like a statistician: Data science

provides an umbrella linking computer scientists, statisticians, and domain

specialists. But each community has its own distinct styles of thinking and

action, which gets stamped into the souls of its members.

In this book, I emphasize approaches which come most naturally to com-

puter scientists, particularly the algorithmic manipulation of data, the use

of machine learning, and the mastery of scale. But I also seek to transmit

the core values of statistical reasoning: the need to understand the appli-

cation domain, proper appreciation of the small, the quest for signiﬁcance,

and a hunger for exploration.

No discipline has a monopoly on the truth. The best data scientists incor-

porate tools from multiple areas, and this book strives to be a relatively

neutral ground where rival philosophies can come to reason together.

Equally important is what you will not ﬁnd in this book. I do not emphasize

any particular language or suite of data analysis tools. Instead, this book pro-

vides a high-level discussion of important design principles. I seek to operate at

a conceptual level more than a technical one. The goal of this manual is to get

you going in the right direction as quickly as possible, with whatever software

tools you ﬁnd most accessible.

To the Instructor

This book covers enough material for an “Introduction to Data Science” course

at the undergraduate or early graduate student levels. I hope that the reader

has completed the equivalent of at least one programming course and has a bit

of prior exposure to probability and statistics, but more is always better than

less.

I have made a full set of lecture slides for teaching this course available online

at http://www.data-manual.com. Data resources for projects and assignments

are also available there to aid the instructor. Further, I make available online

video lectures using these slides to teach a full-semester data science course. Let

me help teach your class, through the magic of the web!

Pedagogical features of this book include:

•War Stories: To provide a better perspective on how data science tech-

niques apply to the real world, I include a collection of “war stories,” or

tales from our experience with real problems. The moral of these stories is

that these methods are not just theory, but important tools to be pulled

out and used as needed.

•False Starts: Most textbooks present methods as a fait accompli, ob-

scuring the ideas involved in designing them, and the subtle reasons why

other approaches fail. The war stories illustrate my reasoning process on

certain applied problems, but I weave such coverage into the core material

as well.

•Take-Home Lessons: Highlighted “take-home” lesson boxes scattered

through each chapter emphasize the big-picture concepts to learn from

each chapter.

•Homework Problems: I provide a wide range of exercises for home-

work and self-study. Many are traditional exam-style problems, but there

are also larger-scale implementation challenges and smaller-scale inter-

view questions, reﬂecting the questions students might encounter when

searching for a job. Degree of diﬃculty ratings have been assigned to all

problems.

In lieu of an answer key, a Solution Wiki has been set up, where solutions to

all even numbered problems will be solicited by crowdsourcing. A similar

system with my Algorithm Design Manual produced coherent solutions,

or so I am told. As a matter of principle I refuse to look at them, so let

the buyer beware.

•Kaggle Challenges: Kaggle (www.kaggle.com) provides a forum for data

scientists to compete in, featuring challenging real-world problems on fas-

cinating data sets, and scoring to test how good your model is relative to

other submissions. The exercises for each chapter include three relevant

Kaggle challenges, to serve as a source of inspiration, self-study, and data

for other projects and investigations.

•Data Science Television: Data science remains mysterious and even

threatening to the broader public. The Quant Shop is an amateur take

on what a data science reality show should be like. Student teams tackle

a diverse array of real-world prediction problems, and try to forecast the

outcome of future events. Check it out at http://www.quant-shop.com.

A series of eight 30-minute episodes has been prepared, each built around

a particular real-world prediction problem. Challenges include pricing art

at an auction, picking the winner of the Miss Universe competition, and

forecasting when celebrities are destined to die. For each, we observe as a

student team comes to grips with the problem, and learn along with them

as they build a forecasting model. They make their predictions, and we

watch along with them to see if they are right or wrong.

In this book, The Quant Shop is used to provide concrete examples of

prediction challenges, to frame discussions of the data science modeling

pipeline from data acquisition to evaluation. I hope you ﬁnd them fun, and

that they will encourage you to conceive and take on your own modeling

challenges.

•Chapter Notes: Finally, each tutorial chapter concludes with a brief notes

section, pointing readers to primary sources and additional references.

Dedication

My bright and loving daughters Bonnie and Abby are now full-blown teenagers,

meaning that they don’t always process statistical evidence with as much alacrity

as I would I desire. I dedicate this book to them, in the hope that their analysis

skills improve to the point that they always just agree with me.

And I dedicate this book to my beautiful wife Renee, who agrees with me

even when she doesn’t agree with me, and loves me beyond the support of all

creditable evidence.

Acknowledgments

My list of people to thank is large enough that I have probably missed some.

I will try to do enumerate them systematically to minimize omissions, but ask

those I’ve unfairly neglected for absolution.

First, I thank those who made concrete contributions to help me put this

book together. Yeseul Lee served as an apprentice on this project, helping with

ﬁgures, exercises, and more during summer 2016 and beyond. You will see

evidence of her handiwork on almost every page, and I greatly appreciate her

help and dedication. Aakriti Mittal and Jack Zheng also contributed to a few

of the ﬁgures.

Students in my Fall 2016 Introduction to Data Science course (CSE 519)

helped to debug the manuscript, and they found plenty of things to debug. I

particularly thank Rebecca Siford, who proposed over one hundred corrections

on her own. Several data science friends/sages reviewed speciﬁc chapters for

me, and I thank Anshul Gandhi, Yifan Hu, Klaus Mueller, Francesco Orabona,

Andy Schwartz, and Charles Ward for their eﬀorts here.

I thank all the Quant Shop students from Fall 2015 whose video and mod-

eling eﬀorts are so visibly on display. I particularly thank Jan (Dini) Diskin-

Zimmerman, whose editing eﬀorts went so far beyond the call of duty I felt like

a felon for letting her do it.

My editors at Springer, Wayne Wheeler and Simon Rees, were a pleasure to

work with as usual. I also thank all the production and marketing people who

helped get this book to you, including Adrian Pieron and Annette Anlauf.

Several exercises were originated by colleagues or inspired by other sources.

Reconstructing the original sources years later can be challenging, but credits

for each problem (to the best of my recollection) appear on the website.

Much of what I know about data science has been learned through working

with other people. These include my Ph.D. students, particularly Rami al-Rfou,

Mikhail Bautin, Haochen Chen, Yanqing Chen, Vivek Kulkarni, Levon Lloyd,

Andrew Mehler, Bryan Perozzi, Yingtao Tian, Junting Ye, Wenbin Zhang, and

postdoc Charles Ward. I fondly remember all of my Lydia project masters

students over the years, and remind you that my prize oﬀer to the ﬁrst one who

names their daughter Lydia remains unclaimed. I thank my other collaborators

with stories to tell, including Bruce Futcher, Justin Gardin, Arnout van de Rijt,

and Oleksii Starov.

I remember all members of the General Sentiment/Canrock universe, partic-

ularly Mark Fasciano, with whom I shared the start-up dream and experienced

what happens when data hits the real world. I thank my colleagues at Yahoo

Labs/Research during my 2015–2016 sabbatical year, when much of this book

was conceived. I single out Amanda Stent, who enabled me to be at Yahoo

during that particularly diﬃcult year in the company’s history. I learned valu-

able things from other people who have taught related data science courses,

including Andrew Ng and Hans-Peter Pﬁster, and thank them all for their help.

If you have a procedure with ten parameters, you probably missed

some.

– Alan Perlis

Caveat

It is traditional for the author to magnanimously accept the blame for whatever

deﬁciencies remain. I don’t. Any errors, deﬁciencies, or problems in this book

are somebody else’s fault, but I would appreciate knowing about them so as to

determine who is to blame.

Steven S. Skiena

Department of Computer Science

Stony Brook University

Stony Brook, NY 11794-2424

http://www.cs.stonybrook.edu/~skiena

skiena@data-manual.com

May 2017

Contents

1 What is Data Science? 1

1.1 Computer Science, Data Science, and Real Science . . . . . . . . 2

1.2 Asking Interesting Questions from Data . . . . . . . . . . . . . . 4

1.2.1 The Baseball Encyclopedia . . . . . . . . . . . . . . . . . 5

1.2.2 The Internet Movie Database (IMDb) . . . . . . . . . . . 7

1.2.3 GoogleNgrams........................ 10

1.2.4 New York Taxi Records . . . . . . . . . . . . . . . . . . . 11

1.3 PropertiesofData .......................... 14

1.3.1 Structured vs. Unstructured Data . . . . . . . . . . . . . 14

1.3.2 Quantitative vs. Categorical Data . . . . . . . . . . . . . 15

1.3.3 Big Data vs. Little Data . . . . . . . . . . . . . . . . . . . 15

1.4 Classiﬁcation and Regression . . . . . . . . . . . . . . . . . . . . 16

1.5 Data Science Television: The Quant Shop . . . . . . . . . . . . . 17

1.5.1 Kaggle Challenges . . . . . . . . . . . . . . . . . . . . . . 19

1.6 About the War Stories . . . . . . . . . . . . . . . . . . . . . . . . 19

1.7 War Story: Answering the Right Question . . . . . . . . . . . . . 21

1.8 ChapterNotes ............................ 22

1.9 Exercises ............................... 23

2 Mathematical Preliminaries 27

2.1 Probability .............................. 27

2.1.1 Probability vs. Statistics . . . . . . . . . . . . . . . . . . . 29

2.1.2 Compound Events and Independence . . . . . . . . . . . . 30

2.1.3 Conditional Probability . . . . . . . . . . . . . . . . . . . 31

2.1.4 Probability Distributions . . . . . . . . . . . . . . . . . . 32

2.2 Descriptive Statistics . . . . . . . . . . . . . . . . . . . . . . . . . 34

2.2.1 Centrality Measures . . . . . . . . . . . . . . . . . . . . . 34

2.2.2 Variability Measures . . . . . . . . . . . . . . . . . . . . . 36

2.2.3 Interpreting Variance . . . . . . . . . . . . . . . . . . . . 37

2.2.4 Characterizing Distributions . . . . . . . . . . . . . . . . 39

2.3 Correlation Analysis . . . . . . . . . . . . . . . . . . . . . . . . . 40

2.3.1 Correlation Coeﬃcients: Pearson and Spearman Rank . . 41

2.3.2 The Power and Signiﬁcance of Correlation . . . . . . . . . 43

2.3.3 Correlation Does Not Imply Causation! . . . . . . . . . . 45

2.3.4 Detecting Periodicities by Autocorrelation . . . . . . . . . 46

2.4 Logarithms .............................. 47

2.4.1 Logarithms and Multiplying Probabilities . . . . . . . . . 48

2.4.2 Logarithms and Ratios . . . . . . . . . . . . . . . . . . . . 48

2.4.3 Logarithms and Normalizing Skewed Distributions . . . . 49

2.5 War Story: Fitting Designer Genes . . . . . . . . . . . . . . . . . 50

2.6 ChapterNotes ............................ 52

2.7 Exercises ............................... 53

3 Data Munging 57

3.1 Languages for Data Science . . . . . . . . . . . . . . . . . . . . . 57

3.1.1 The Importance of Notebook Environments . . . . . . . . 59

3.1.2 Standard Data Formats . . . . . . . . . . . . . . . . . . . 61

3.2 CollectingData............................ 64

3.2.1 Hunting............................ 64

3.2.2 Scraping............................ 67

3.2.3 Logging ............................ 68

3.3 CleaningData ............................ 69

3.3.1 Errors vs. Artifacts . . . . . . . . . . . . . . . . . . . . . 69

3.3.2 Data Compatibility . . . . . . . . . . . . . . . . . . . . . . 72

3.3.3 Dealing with Missing Values . . . . . . . . . . . . . . . . . 76

3.3.4 Outlier Detection . . . . . . . . . . . . . . . . . . . . . . . 78

3.4 War Story: Beating the Market . . . . . . . . . . . . . . . . . . . 79

3.5 Crowdsourcing ............................ 80

3.5.1 The Penny Demo . . . . . . . . . . . . . . . . . . . . . . . 81

3.5.2 When is the Crowd Wise? . . . . . . . . . . . . . . . . . . 82

3.5.3 Mechanisms for Aggregation . . . . . . . . . . . . . . . . 83

3.5.4 Crowdsourcing Services . . . . . . . . . . . . . . . . . . . 84

3.5.5 Gamiﬁcation ......................... 88

3.6 ChapterNotes ............................ 90

3.7 Exercises ............................... 90

4 Scores and Rankings 95

4.1 The Body Mass Index (BMI) . . . . . . . . . . . . . . . . . . . . 96

4.2 Developing Scoring Systems . . . . . . . . . . . . . . . . . . . . . 99

4.2.1 Gold Standards and Proxies . . . . . . . . . . . . . . . . . 99

4.2.2 Scores vs. Rankings . . . . . . . . . . . . . . . . . . . . . 100

4.2.3 Recognizing Good Scoring Functions . . . . . . . . . . . . 101

4.3 Z-scores and Normalization . . . . . . . . . . . . . . . . . . . . . 103

4.4 Advanced Ranking Techniques . . . . . . . . . . . . . . . . . . . 104

4.4.1 EloRankings ......................... 104

4.4.2 Merging Rankings . . . . . . . . . . . . . . . . . . . . . . 108

4.4.3 Digraph-based Rankings . . . . . . . . . . . . . . . . . . . 109

4.4.4 PageRank...........................111

4.5 War Story: Clyde’s Revenge . . . . . . . . . . . . . . . . . . . . . 111

4.6 Arrow’s Impossibility Theorem . . . . . . . . . . . . . . . . . . . 114

4.7 War Story: Who’s Bigger? . . . . . . . . . . . . . . . . . . . . . . 115

4.8 ChapterNotes ............................118

4.9 Exercises ............................... 119

5 Statistical Analysis 121

5.1 Statistical Distributions . . . . . . . . . . . . . . . . . . . . . . . 122

5.1.1 The Binomial Distribution . . . . . . . . . . . . . . . . . . 123

5.1.2 The Normal Distribution . . . . . . . . . . . . . . . . . . 124

5.1.3 Implications of the Normal Distribution . . . . . . . . . . 126

5.1.4 Poisson Distribution . . . . . . . . . . . . . . . . . . . . . 127

5.1.5 Power Law Distributions . . . . . . . . . . . . . . . . . . . 129

5.2 Sampling from Distributions . . . . . . . . . . . . . . . . . . . . . 132

5.2.1 Random Sampling beyond One Dimension . . . . . . . . . 133

5.3 Statistical Signiﬁcance . . . . . . . . . . . . . . . . . . . . . . . . 135

5.3.1 The Signiﬁcance of Signiﬁcance . . . . . . . . . . . . . . . 135

5.3.2 The T-test: Comparing Population Means . . . . . . . . . 137

5.3.3 The Kolmogorov-Smirnov Test . . . . . . . . . . . . . . . 139

5.3.4 The Bonferroni Correction . . . . . . . . . . . . . . . . . . 141

5.3.5 False Discovery Rate . . . . . . . . . . . . . . . . . . . . . 142

5.4 War Story: Discovering the Fountain of Youth? . . . . . . . . . . 143

5.5 Permutation Tests and P-values . . . . . . . . . . . . . . . . . . . 145

5.5.1 Generating Random Permutations . . . . . . . . . . . . . 147

5.5.2 DiMaggio’s Hitting Streak . . . . . . . . . . . . . . . . . . 148

5.6 Bayesian Reasoning . . . . . . . . . . . . . . . . . . . . . . . . . 150

5.7 ChapterNotes ............................151

5.8 Exercises ............................... 151

6 Visualizing Data 155

6.1 Exploratory Data Analysis . . . . . . . . . . . . . . . . . . . . . . 156

6.1.1 Confronting a New Data Set . . . . . . . . . . . . . . . . 156

6.1.2 Summary Statistics and Anscombe’s Quartet . . . . . . . 159

6.1.3 Visualization Tools . . . . . . . . . . . . . . . . . . . . . . 160

6.2 Developing a Visualization Aesthetic . . . . . . . . . . . . . . . . 162

6.2.1 Maximizing Data-Ink Ratio . . . . . . . . . . . . . . . . . 163

6.2.2 Minimizing the Lie Factor . . . . . . . . . . . . . . . . . . 164

6.2.3 Minimizing Chartjunk . . . . . . . . . . . . . . . . . . . . 165

6.2.4 Proper Scaling and Labeling . . . . . . . . . . . . . . . . 167

6.2.5 Eﬀective Use of Color and Shading . . . . . . . . . . . . . 168

6.2.6 The Power of Repetition . . . . . . . . . . . . . . . . . . . 169

6.3 ChartTypes ............................. 170

6.3.1 TabularData.........................170

6.3.2 Dot and Line Plots . . . . . . . . . . . . . . . . . . . . . . 174

6.3.3 ScatterPlots .........................177

6.3.4 Bar Plots and Pie Charts . . . . . . . . . . . . . . . . . . 179

6.3.5 Histograms ..........................183

6.3.6 DataMaps ..........................187

6.4 Great Visualizations . . . . . . . . . . . . . . . . . . . . . . . . . 189

6.4.1 Marey’s Train Schedule . . . . . . . . . . . . . . . . . . . 189

6.4.2 Snow’s Cholera Map . . . . . . . . . . . . . . . . . . . . . 191

6.4.3 New York’s Weather Year . . . . . . . . . . . . . . . . . . 192

6.5 ReadingGraphs............................192

6.5.1 The Obscured Distribution . . . . . . . . . . . . . . . . . 193

6.5.2 Overinterpreting Variance . . . . . . . . . . . . . . . . . . 193

6.6 Interactive Visualization . . . . . . . . . . . . . . . . . . . . . . . 195

6.7 War Story: TextMapping the World . . . . . . . . . . . . . . . . 196

6.8 ChapterNotes ............................198

6.9 Exercises ............................... 199

7 Mathematical Models 201

7.1 Philosophies of Modeling . . . . . . . . . . . . . . . . . . . . . . . 201

7.1.1 Occam’s Razor . . . . . . . . . . . . . . . . . . . . . . . . 201

7.1.2 Bias–Variance Trade-Oﬀs . . . . . . . . . . . . . . . . . . 202

7.1.3 What Would Nate Silver Do? . . . . . . . . . . . . . . . . 203

7.2 A Taxonomy of Models . . . . . . . . . . . . . . . . . . . . . . . 205

7.2.1 Linear vs. Non-Linear Models . . . . . . . . . . . . . . . . 206

7.2.2 Blackbox vs. Descriptive Models . . . . . . . . . . . . . . 206

7.2.3 First-Principle vs. Data-Driven Models . . . . . . . . . . . 207

7.2.4 Stochastic vs. Deterministic Models . . . . . . . . . . . . 208

7.2.5 Flat vs. Hierarchical Models . . . . . . . . . . . . . . . . . 209

7.3 BaselineModels............................210

7.3.1 Baseline Models for Classiﬁcation . . . . . . . . . . . . . . 210

7.3.2 Baseline Models for Value Prediction . . . . . . . . . . . . 212

7.4 Evaluating Models . . . . . . . . . . . . . . . . . . . . . . . . . . 212

7.4.1 Evaluating Classiﬁers . . . . . . . . . . . . . . . . . . . . 213

7.4.2 Receiver-Operator Characteristic (ROC) Curves . . . . . 218

7.4.3 Evaluating Multiclass Systems . . . . . . . . . . . . . . . 219

7.4.4 Evaluating Value Prediction Models . . . . . . . . . . . . 221

7.5 Evaluation Environments . . . . . . . . . . . . . . . . . . . . . . 224

7.5.1 Data Hygiene for Evaluation . . . . . . . . . . . . . . . . 225

7.5.2 Amplifying Small Evaluation Sets . . . . . . . . . . . . . 226

7.6 War Story: 100% Accuracy . . . . . . . . . . . . . . . . . . . . . 228

7.7 Simulation Models . . . . . . . . . . . . . . . . . . . . . . . . . . 229

7.8 War Story: Calculated Bets . . . . . . . . . . . . . . . . . . . . . 230

7.9 ChapterNotes ............................233

7.10Exercises ............................... 234

8 Linear Algebra 237

8.1 The Power of Linear Algebra . . . . . . . . . . . . . . . . . . . . 237

8.1.1 Interpreting Linear Algebraic Formulae . . . . . . . . . . 238

8.1.2 Geometry and Vectors . . . . . . . . . . . . . . . . . . . . 240

8.2 Visualizing Matrix Operations . . . . . . . . . . . . . . . . . . . . 241

8.2.1 Matrix Addition . . . . . . . . . . . . . . . . . . . . . . . 242

8.2.2 Matrix Multiplication . . . . . . . . . . . . . . . . . . . . 243

8.2.3 Applications of Matrix Multiplication . . . . . . . . . . . 244

8.2.4 Identity Matrices and Inversion . . . . . . . . . . . . . . . 248

8.2.5 Matrix Inversion and Linear Systems . . . . . . . . . . . . 250

8.2.6 MatrixRank .........................251

8.3 Factoring Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . 252

8.3.1 Why Factor Feature Matrices? . . . . . . . . . . . . . . . 252

8.3.2 LU Decomposition and Determinants . . . . . . . . . . . 254

8.4 Eigenvalues and Eigenvectors . . . . . . . . . . . . . . . . . . . . 255

8.4.1 Properties of Eigenvalues . . . . . . . . . . . . . . . . . . 255

8.4.2 Computing Eigenvalues . . . . . . . . . . . . . . . . . . . 256

8.5 Eigenvalue Decomposition . . . . . . . . . . . . . . . . . . . . . . 257

8.5.1 Singular Value Decomposition . . . . . . . . . . . . . . . . 258

8.5.2 Principal Components Analysis . . . . . . . . . . . . . . . 260

8.6 War Story: The Human Factors . . . . . . . . . . . . . . . . . . . 262

8.7 ChapterNotes ............................263

8.8 Exercises ............................... 263

9 Linear and Logistic Regression 267

9.1 LinearRegression........................... 268

9.1.1 Linear Regression and Duality . . . . . . . . . . . . . . . 268

9.1.2 Error in Linear Regression . . . . . . . . . . . . . . . . . . 269

9.1.3 Finding the Optimal Fit . . . . . . . . . . . . . . . . . . . 270

9.2 Better Regression Models . . . . . . . . . . . . . . . . . . . . . . 272

9.2.1 Removing Outliers . . . . . . . . . . . . . . . . . . . . . . 272

9.2.2 Fitting Non-Linear Functions . . . . . . . . . . . . . . . . 273

9.2.3 Feature and Target Scaling . . . . . . . . . . . . . . . . . 274

9.2.4 Dealing with Highly-Correlated Features . . . . . . . . . . 277

9.3 War Story: Taxi Deriver . . . . . . . . . . . . . . . . . . . . . . . 277

9.4 Regression as Parameter Fitting . . . . . . . . . . . . . . . . . . 279

9.4.1 Convex Parameter Spaces . . . . . . . . . . . . . . . . . . 280

9.4.2 Gradient Descent Search . . . . . . . . . . . . . . . . . . . 281

9.4.3 What is the Right Learning Rate? . . . . . . . . . . . . . 283

9.4.4 Stochastic Gradient Descent . . . . . . . . . . . . . . . . . 285

9.5 Simplifying Models through Regularization . . . . . . . . . . . . 286

9.5.1 Ridge Regression . . . . . . . . . . . . . . . . . . . . . . . 286

9.5.2 LASSO Regression . . . . . . . . . . . . . . . . . . . . . . 287

9.5.3 Trade-Oﬀs between Fit and Complexity . . . . . . . . . . 288

9.6 Classiﬁcation and Logistic Regression . . . . . . . . . . . . . . . 289

9.6.1 Regression for Classiﬁcation . . . . . . . . . . . . . . . . . 290

9.6.2 Decision Boundaries . . . . . . . . . . . . . . . . . . . . . 291

9.6.3 Logistic Regression . . . . . . . . . . . . . . . . . . . . . . 292

9.7 Issues in Logistic Classiﬁcation . . . . . . . . . . . . . . . . . . . 295

9.7.1 Balanced Training Classes . . . . . . . . . . . . . . . . . . 295

9.7.2 Multi-Class Classiﬁcation . . . . . . . . . . . . . . . . . . 297

9.7.3 Hierarchical Classiﬁcation . . . . . . . . . . . . . . . . . . 298

9.7.4 Partition Functions and Multinomial Regression . . . . . 299

9.8 ChapterNotes ............................300

9.9 Exercises ............................... 301

10 Distance and Network Methods 303

10.1 Measuring Distances . . . . . . . . . . . . . . . . . . . . . . . . . 303

10.1.1 Distance Metrics . . . . . . . . . . . . . . . . . . . . . . . 304

10.1.2 The LkDistance Metric . . . . . . . . . . . . . . . . . . . 305

10.1.3 Working in Higher Dimensions . . . . . . . . . . . . . . . 307

10.1.4 Dimensional Egalitarianism . . . . . . . . . . . . . . . . . 308

10.1.5 Points vs. Vectors . . . . . . . . . . . . . . . . . . . . . . 309

10.1.6 Distances between Probability Distributions . . . . . . . . 310

10.2 Nearest Neighbor Classiﬁcation . . . . . . . . . . . . . . . . . . . 311

10.2.1 Seeking Good Analogies . . . . . . . . . . . . . . . . . . . 312

10.2.2 k-Nearest Neighbors . . . . . . . . . . . . . . . . . . . . . 313

10.2.3 Finding Nearest Neighbors . . . . . . . . . . . . . . . . . 315

10.2.4 Locality Sensitive Hashing . . . . . . . . . . . . . . . . . . 317

10.3 Graphs, Networks, and Distances . . . . . . . . . . . . . . . . . . 319

10.3.1 Weighted Graphs and Induced Networks . . . . . . . . . . 320

10.3.2 Talking About Graphs . . . . . . . . . . . . . . . . . . . . 321

10.3.3 Graph Theory . . . . . . . . . . . . . . . . . . . . . . . . 323

10.4PageRank...............................325

10.5Clustering............................... 327

10.5.1 k-means Clustering . . . . . . . . . . . . . . . . . . . . . . 330

10.5.2 Agglomerative Clustering . . . . . . . . . . . . . . . . . . 336

10.5.3 Comparing Clusterings . . . . . . . . . . . . . . . . . . . . 341

10.5.4 Similarity Graphs and Cut-Based Clustering . . . . . . . 341

10.6 War Story: Cluster Bombing . . . . . . . . . . . . . . . . . . . . 344

10.7ChapterNotes ............................ 345

10.8Exercises ............................... 346

11 Machine Learning 351

11.1NaiveBayes..............................354

11.1.1 Formulation..........................354

11.1.2 Dealing with Zero Counts (Discounting) . . . . . . . . . . 356

11.2 Decision Tree Classiﬁers . . . . . . . . . . . . . . . . . . . . . . . 357

11.2.1 Constructing Decision Trees . . . . . . . . . . . . . . . . . 359

11.2.2 Realizing Exclusive Or . . . . . . . . . . . . . . . . . . . . 361

11.2.3 Ensembles of Decision Trees . . . . . . . . . . . . . . . . . 362

11.3 Boosting and Ensemble Learning . . . . . . . . . . . . . . . . . . 363

11.3.1 Voting with Classiﬁers . . . . . . . . . . . . . . . . . . . . 363

11.3.2 Boosting Algorithms . . . . . . . . . . . . . . . . . . . . . 364

11.4 Support Vector Machines . . . . . . . . . . . . . . . . . . . . . . 366

11.4.1 LinearSVMs .........................369

11.4.2 Non-linear SVMs . . . . . . . . . . . . . . . . . . . . . . . 369

11.4.3 Kernels ............................371

11.5 Degrees of Supervision . . . . . . . . . . . . . . . . . . . . . . . . 372

11.5.1 Supervised Learning . . . . . . . . . . . . . . . . . . . . . 372

11.5.2 Unsupervised Learning . . . . . . . . . . . . . . . . . . . . 372

11.5.3 Semi-supervised Learning . . . . . . . . . . . . . . . . . . 374

11.5.4 Feature Engineering . . . . . . . . . . . . . . . . . . . . . 375

11.6DeepLearning ............................ 377

11.6.1 Networks and Depth . . . . . . . . . . . . . . . . . . . . . 378

11.6.2 Backpropagation . . . . . . . . . . . . . . . . . . . . . . . 382

11.6.3 Word and Graph Embeddings . . . . . . . . . . . . . . . . 383

11.7 War Story: The Name Game . . . . . . . . . . . . . . . . . . . . 385

11.8ChapterNotes ............................ 387

11.9Exercises ............................... 388

12 Big Data: Achieving Scale 391

12.1WhatisBigData? .......................... 392

12.1.1 Big Data as Bad Data . . . . . . . . . . . . . . . . . . . . 392

12.1.2 TheThreeVs......................... 394

12.2 War Story: Infrastructure Matters . . . . . . . . . . . . . . . . . 395

12.3 Algorithmics for Big Data . . . . . . . . . . . . . . . . . . . . . . 397

12.3.1 Big Oh Analysis . . . . . . . . . . . . . . . . . . . . . . . 397

12.3.2 Hashing............................399

12.3.3 Exploiting the Storage Hierarchy . . . . . . . . . . . . . . 401

12.3.4 Streaming and Single-Pass Algorithms . . . . . . . . . . . 402

12.4 Filtering and Sampling . . . . . . . . . . . . . . . . . . . . . . . . 403

12.4.1 Deterministic Sampling Algorithms . . . . . . . . . . . . . 404

12.4.2 Randomized and Stream Sampling . . . . . . . . . . . . . 406

12.5Parallelism .............................. 406

12.5.1 One, Two, Many . . . . . . . . . . . . . . . . . . . . . . . 407

12.5.2 Data Parallelism . . . . . . . . . . . . . . . . . . . . . . . 409

12.5.3 GridSearch..........................409

12.5.4 Cloud Computing Services . . . . . . . . . . . . . . . . . . 410

12.6MapReduce .............................. 410

12.6.1 Map-Reduce Programming . . . . . . . . . . . . . . . . . 412

12.6.2 MapReduce under the Hood . . . . . . . . . . . . . . . . . 414

12.7 Societal and Ethical Implications . . . . . . . . . . . . . . . . . . 416

12.8ChapterNotes ............................ 419

12.9Exercises ............................... 419

13 Coda 423

13.1GetaJob!...............................423

13.2 Go to Graduate School! . . . . . . . . . . . . . . . . . . . . . . . 424

13.3 Professional Consulting Services . . . . . . . . . . . . . . . . . . 425

14 Bibliography 427

Chapter 1

What is Data Science?

The purpose of computing is insight, not numbers.

– Richard W. Hamming

What is data science? Like any emerging ﬁeld, it hasn’t been completely deﬁned

yet, but you know enough about it to be interested or else you wouldn’t be

reading this book.

I think of data science as lying at the intersection of computer science, statis-

tics, and substantive application domains. From computer science comes ma-

chine learning and high-performance computing technologies for dealing with

scale. From statistics comes a long tradition of exploratory data analysis, sig-

niﬁcance testing, and visualization. From application domains in business and

the sciences comes challenges worthy of battle, and evaluation standards to

assess when they have been adequately conquered.

But these are all well-established ﬁelds. Why data science, and why now? I

see three reasons for this sudden burst of activity:

•New technology makes it possible to capture, annotate, and store vast

amounts of social media, logging, and sensor data. After you have amassed

all this data, you begin to wonder what you can do with it.

•Computing advances make it possible to analyze data in novel ways and at

ever increasing scales. Cloud computing architectures give even the little

guy access to vast power when they need it. New approaches to machine

learning have lead to amazing advances in longstanding problems, like

computer vision and natural language processing.

•Prominent technology companies (like Google and Facebook) and quan-

titative hedge funds (like Renaissance Technologies and TwoSigma) have

proven the power of modern data analytics. Success stories applying data

to such diverse areas as sports management (Moneyball [Lew04]) and elec-

tion forecasting (Nate Silver [Sil12]) have served as role models to bring

data science to a large popular audience.

2CHAPTER 1. WHAT IS DATA SCIENCE?

This introductory chapter has three missions. First, I will try to explain how

good data scientists think, and how this diﬀers from the mindset of traditional

programmers and software developers. Second, we will look at data sets in terms

of the potential for what they can be used for, and learn to ask the broader

questions they are capable of answering. Finally, I introduce a collection of

data analysis challenges that will be used throughout this book as motivating

examples.

1.1 Computer Science, Data Science, and Real

Science

Computer scientists, by nature, don’t respect data. They have traditionally

been taught that the algorithm was the thing, and that data was just meat to

be passed through a sausage grinder.

So to qualify as an eﬀective data scientist, you must ﬁrst learn to think like

a real scientist. Real scientists strive to understand the natural world, which

is a complicated and messy place. By contrast, computer scientists tend to

build their own clean and organized virtual worlds and live comfortably within

them. Scientists obsess about discovering things, while computer scientists in-

vent rather than discover.

People’s mindsets strongly color how they think and act, causing misunder-

standings when we try to communicate outside our tribes. So fundamental are

these biases that we are often unaware we have them. Examples of the cultural

diﬀerences between computer science and real science include:

•Data vs. method centrism: Scientists are data driven, while computer

scientists are algorithm driven. Real scientists spend enormous amounts

of eﬀort collecting data to answer their question of interest. They invent

fancy measuring devices, stay up all night tending to experiments, and

devote most of their thinking to how to get the data they need.

By contrast, computer scientists obsess about methods: which algorithm

is better than which other algorithm, which programming language is best

for a job, which program is better than which other program. The details

of the data set they are working on seem comparably unexciting.

•Concern about results: Real scientists care about answers. They analyze

data to discover something about how the world works. Good scientists

care about whether the results make sense, because they care about what

the answers mean.

By contrast, bad computer scientists worry about producing plausible-

looking numbers. As soon as the numbers stop looking grossly wrong,

they are presumed to be right. This is because they are personally less

invested in what can be learned from a computation, as opposed to getting

it done quickly and eﬃciently.

1.1. COMPUTER SCIENCE, DATA SCIENCE, AND REAL SCIENCE 3

•Robustness: Real scientists are comfortable with the idea that data has

errors. In general, computer scientists are not. Scientists think a lot about

possible sources of bias or error in their data, and how these possible prob-

lems can eﬀect the conclusions derived from them. Good programmers use

strong data-typing and parsing methodologies to guard against formatting

errors, but the concerns here are diﬀerent.

Becoming aware that data can have errors is empowering. Computer

scientists chant “garbage in, garbage out” as a defensive mantra to ward

oﬀ criticism, a way to say that’s not my job. Real scientists get close

enough to their data to smell it, giving it the sniﬀ test to decide whether

it is likely to be garbage.

•Precision: Nothing is ever completely true or false in science, while every-

thing is either true or false in computer science or mathematics.

Generally speaking, computer scientists are happy printing ﬂoating point

numbers to as many digits as possible: 8/13 = 0.61538461538. Real

scientists will use only two signiﬁcant digits: 8/13 ≈0.62. Computer

scientists care what a number is, while real scientists care what it means.

Aspiring data scientists must learn to think like real scientists. Your job is

going to be to turn numbers into insight. It is important to understand the why

as much as the how.

To be fair, it beneﬁts real scientists to think like data scientists as well. New

experimental technologies enable measuring systems on vastly greater scale than

ever possible before, through technologies like full-genome sequencing in biology

and full-sky telescope surveys in astronomy. With new breadth of view comes

new levels of vision.

Traditional hypothesis-driven science was based on asking speciﬁc questions

of the world and then generating the speciﬁc data needed to conﬁrm or deny

it. This is now augmented by data-driven science, which instead focuses on

generating data on a previously unheard of scale or resolution, in the belief that

new discoveries will come as soon as one is able to look at it. Both ways of

thinking will be important to us:

•Given a problem, what available data will help us answer it?

•Given a data set, what interesting problems can we apply it to?

There is another way to capture this basic distinction between software en-

gineering and data science. It is that software developers are hired to build

systems, while data scientists are hired to produce insights.

This may be a point of contention for some developers. There exist an

important class of engineers who wrangle the massive distributed infrastructures

necessary to store and analyze, say, ﬁnancial transaction or social media data

4CHAPTER 1. WHAT IS DATA SCIENCE?

on a full Facebook or Twitter-level of scale. Indeed, I will devote Chapter 12

to the distinctive challenges of big data infrastructures. These engineers are

building tools and systems to support data science, even though they may not

personally mine the data they wrangle. Do they qualify as data scientists?

This is a fair question, one I will ﬁnesse a bit so as to maximize the poten-

tial readership of this book. But I do believe that the better such engineers

understand the full data analysis pipeline, the more likely they will be able to

build powerful tools capable of providing important insights. A major goal of

this book is providing big data engineers with the intellectual tools to think like

big data scientists.

1.2 Asking Interesting Questions from Data

Good data scientists develop an inherent curiosity about the world around them,

particularly in the associated domains and applications they are working on.

They enjoy talking shop with the people whose data they work with. They ask

them questions: What is the coolest thing you have learned about this ﬁeld?

Why did you get interested in it? What do you hope to learn by analyzing your

data set? Data scientists always ask questions.

Good data scientists have wide-ranging interests. They read the newspaper

every day to get a broader perspective on what is exciting. They understand that

the world is an interesting place. Knowing a little something about everything

equips them to play in other people’s backyards. They are brave enough to get

out of their comfort zones a bit, and driven to learn more once they get there.

Software developers are not really encouraged to ask questions, but data

scientists are. We ask questions like:

•What things might you be able to learn from a given data set?

•What do you/your people really want to know about the world?

•What will it mean to you once you ﬁnd out?

Computer scientists traditionally do not really appreciate data. Think about

the way algorithm performance is experimentally measured. Usually the pro-

gram is run on “random data” to see how long it takes. They rarely even look

at the results of the computation, except to verify that it is correct and eﬃcient.

Since the “data” is meaningless, the results cannot be important. In contrast,

real data sets are a scarce resource, which required hard work and imagination

to obtain.

Becoming a data scientist requires learning to ask questions about data, so

let’s practice. Each of the subsections below will introduce an interesting data

set. After you understand what kind of information is available, try to come

up with, say, ﬁve interesting questions you might explore/answer with access to

this data set.

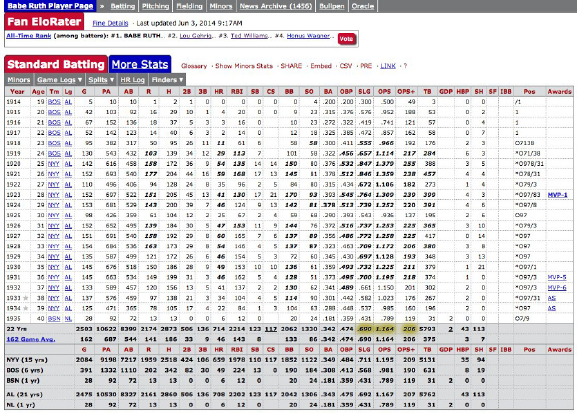
1.2. ASKING INTERESTING QUESTIONS FROM DATA 5

Figure 1.1: Statistical information on the performance of Babe Ruth can be

found at http://www.baseball-reference.com.

The key is thinking broadly: the answers to big, general questions often lie

buried in highly-speciﬁc data sets, which were by no means designed to contain

them.

1.2.1 The Baseball Encyclopedia

Baseball has long had an outsized importance in the world of data science. This

sport has been called the national pastime of the United States; indeed, French

historian Jacques Barzun observed that “Whoever wants to know the heart and

mind of America had better learn baseball.” I realize that many readers are not

American, and even those that are might be completely disinterested in sports.

But stick with me for a while.

What makes baseball important to data science is its extensive statistical

record of play, dating back for well over a hundred years. Baseball is a sport of

discrete events: pitchers throw balls and batters try to hit them – that naturally

lends itself to informative statistics. Fans get immersed in these statistics as chil-

dren, building their intuition about the strengths and limitations of quantitative

analysis. Some of these children grow up to become data scientists. Indeed, the

success of Brad Pitt’s statistically-minded baseball team in the movie Moneyball

remains the American public’s most vivid contact with data science.

This historical baseball record is available at http://www.baseball-reference.

com. There you will ﬁnd complete statistical data on the performance of every

player who even stepped on the ﬁeld. This includes summary statistics of each

season’s batting, pitching, and ﬁelding record, plus information about teams

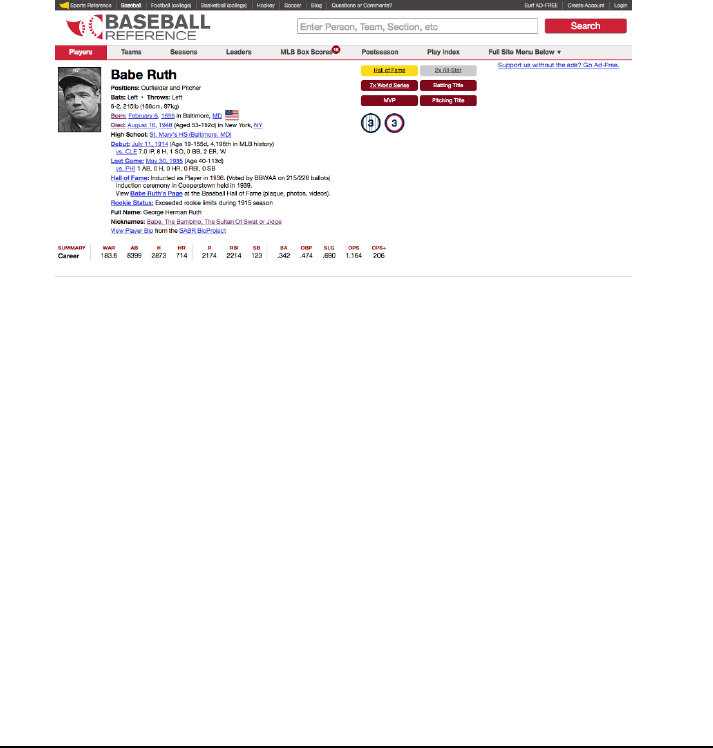
6CHAPTER 1. WHAT IS DATA SCIENCE?

Figure 1.2: Personal information on every major league baseball player is avail-

able at http://www.baseball-reference.com.

and awards as shown in Figure 1.1.

But more than just statistics, there is metadata on the life and careers of all

the people who have ever played major league baseball, as shown in Figure 1.2.

We get the vital statistics of each player (height, weight, handedness) and their

lifespan (when/where they were born and died). We also get salary information

(how much each player got paid every season) and transaction data (how did

they get to be the property of each team they played for).

Now, I realize that many of you do not have the slightest knowledge of or

interest in baseball. This sport is somewhat reminiscent of cricket, if that helps.

But remember that as a data scientist, it is your job to be interested in the

world around you. Think of this as chance to learn something.

So what interesting questions can you answer with this baseball data set?

Try to write down ﬁve questions before moving on. Don’t worry, I will wait here

for you to ﬁnish.

The most obvious types of questions to answer with this data are directly

related to baseball:

•How can we best measure an individual player’s skill or value?

•How fairly do trades between teams generally work out?

•What is the general trajectory of player’s performance level as they mature

and age?

•To what extent does batting performance correlate with position played?

For example, are outﬁelders really better hitters than inﬁelders?

These are interesting questions. But even more interesting are questions

about demographic and social issues. Almost 20,000 major league baseball play-

1.2. ASKING INTERESTING QUESTIONS FROM DATA 7

ers have taken the ﬁeld over the past 150 years, providing a large, extensively-

documented cohort of men who can serve as a proxy for even larger, less well-

documented populations. Indeed, we can use this baseball player data to answer

questions like:

•Do left-handed people have shorter lifespans than right-handers? Handed-

ness is not captured in most demographic data sets, but has been diligently

assembled here. Indeed, analysis of this data set has been used to show

that right-handed people live longer than lefties [HC88]!

•How often do people return to live in the same place where they were

born? Locations of birth and death have been extensively recorded in this

data set. Further, almost all of these people played at least part of their

career far from home, thus exposing them to the wider world at a critical

time in their youth.

•Do player salaries generally reﬂect past, present, or future performance?

•To what extent have heights and weights been increasing in the population

at large?

There are two particular themes to be aware of here. First, the identiﬁers

and reference tags (i.e. the metadata) often prove more interesting in a data set

than the stuﬀ we are supposed to care about, here the statistical record of play.

Second is the idea of a statistical proxy, where you use the data set you have

to substitute for the one you really want. The data set of your dreams likely

does not exist, or may be locked away behind a corporate wall even if it does.

A good data scientist is a pragmatist, seeing what they can do with what they

have instead of bemoaning what they cannot get their hands on.

1.2.2 The Internet Movie Database (IMDb)

Everybody loves the movies. The Internet Movie Database (IMDb) provides

crowdsourced and curated data about all aspects of the motion picture industry,

at www.imdb.com. IMDb currently contains data on over 3.3 million movies and

TV programs. For each ﬁlm, IMDb includes its title, running time, genres, date

of release, and a full list of cast and crew. There is ﬁnancial data about each

production, including the budget for making the ﬁlm and how well it did at the

box oﬃce.

Finally, there are extensive ratings for each ﬁlm from viewers and critics.

This rating data consists of scores on a zero to ten stars scale, cross-tabulated

into averages by age and gender. Written reviews are often included, explaining

why a particular critic awarded a given number of stars. There are also links

between ﬁlms: for example, identifying which other ﬁlms have been watched

most often by viewers of It’s a Wonderful Life.

Every actor, director, producer, and crew member associated with a ﬁlm

merits an entry in IMDb, which now contains records on 6.5 million people.

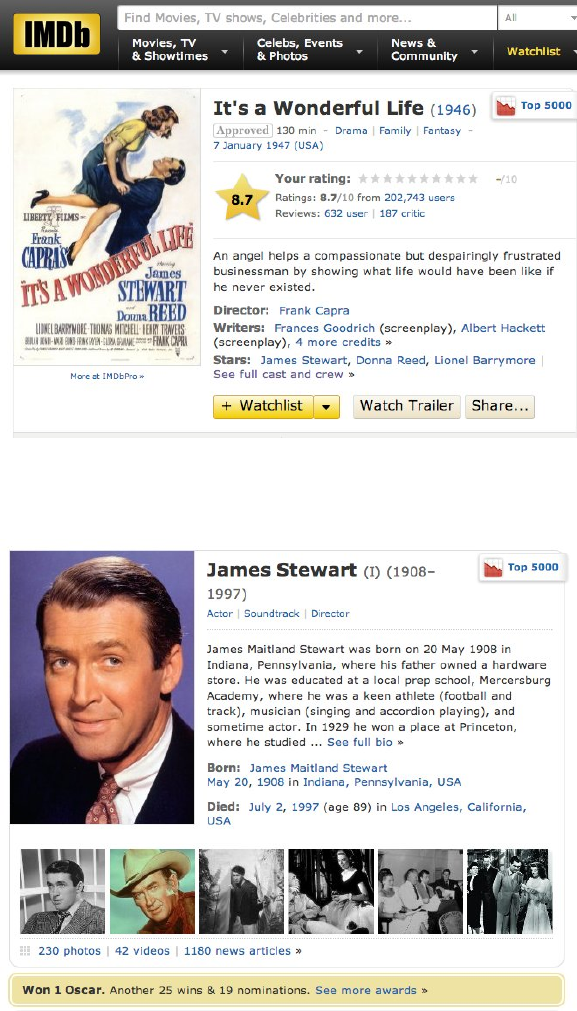
8CHAPTER 1. WHAT IS DATA SCIENCE?

Figure 1.3: Representative ﬁlm data from the Internet Movie Database.

Figure 1.4: Representative actor data from the Internet Movie Database.

1.2. ASKING INTERESTING QUESTIONS FROM DATA 9

These happen to include my brother, cousin, and sister-in-law. Each actor

is linked to every ﬁlm they appeared in, with a description of their role and

their ordering in the credits. Available data about each personality includes

birth/death dates, height, awards, and family relations.

So what kind of questions can you answer with this movie data?

Perhaps the most natural questions to ask IMDb involve identifying the

extremes of movies and actors:

•Which actors appeared in the most ﬁlms? Earned the most money? Ap-

peared in the lowest rated ﬁlms? Had the longest career or the shortest

lifespan?

•What was the highest rated ﬁlm each year, or the best in each genre?

Which movies lost the most money, had the highest-powered casts, or got

the least favorable reviews.

Then there are larger-scale questions one can ask about the nature of the

motion picture business itself:

•How well does movie gross correlate with viewer ratings or awards? Do

customers instinctively ﬂock to trash, or is virtue on the part of the cre-

ative team properly rewarded?

•How do Hollywood movies compare to Bollywood movies, in terms of rat-

ings, budget, and gross? Are American movies better received than foreign

ﬁlms, and how does this diﬀer between U.S. and non-U.S. reviewers?

•What is the age distribution of actors and actresses in ﬁlms? How much

younger is the actress playing the wife, on average, than the actor playing

the husband? Has this disparity been increasing or decreasing with time?

•Live fast, die young, and leave a good-looking corpse? Do movie stars live

longer or shorter lives than bit players, or compared to the general public?

Assuming that people working together on a ﬁlm get to know each other,

the cast and crew data can be used to build a social network of the movie

business. What does the social network of actors look like? The Oracle of

Bacon (https://oracleofbacon.org/) posits Kevin Bacon as the center of

the Hollywood universe and generates the shortest path to Bacon from any

other actor. Other actors, like Samuel L. Jackson, prove even more central.

More critically, can we analyze this data to determine the probability that

someone will like a given movie? The technique of collaborative ﬁltering ﬁnds

people who liked ﬁlms that I also liked, and recommends other ﬁlms that they

liked as good candidates for me. The 2007 Netﬂix Prize was a $1,000,000 com-

petition to produce a ratings engine 10% better than the proprietary Netﬂix

system. The ultimate winner of this prize (BellKor) used a variety of data

sources and techniques, including the analysis of links [BK07].

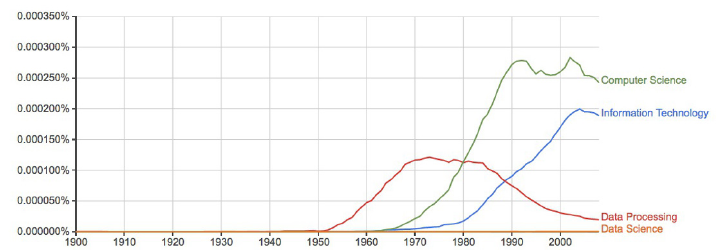
10 CHAPTER 1. WHAT IS DATA SCIENCE?

Figure 1.5: The rise and fall of data processing, as witnessed by Google Ngrams.

1.2.3 Google Ngrams

Printed books have been the primary repository of human knowledge since

Gutenberg’s invention of movable type in 1439. Physical objects live somewhat

uneasily in today’s digital world, but technology has a way of reducing every-

thing to data. As part of its mission to organize the world’s information, Google

undertook an eﬀort to scan all of the world’s published books. They haven’t

quite gotten there yet, but the 30 million books thus far digitized represent over

20% of all books ever published.

Google uses this data to improve search results, and provide fresh access

to out-of-print books. But perhaps the coolest product is Google Ngrams, an

amazing resource for monitoring changes in the cultural zeitgeist. It provides

the frequency with which short phrases occur in books published each year.

Each phrase must occur at least forty times in their scanned book corpus. This

eliminates obscure words and phrases, but leaves over two billion time series

available for analysis.

This rich data set shows how language use has changed over the past 200

years, and has been widely applied to cultural trend analysis [MAV+11]. Figure

1.5 uses this data to show how the word data fell out of favor when thinking

about computing. Data processing was the popular term associated with the

computing ﬁeld during the punched card and spinning magnetic tape era of the

1950s. The Ngrams data shows that the rapid rise of Computer Science did not

eclipse Data Processing until 1980. Even today, Data Science remains almost

invisible on this scale.

Check out Google Ngrams at http://books.google.com/ngrams. I promise

you will enjoy playing with it. Compare hot dog to tofu,science against religion,

freedom to justice, and sex vs. marriage, to better understand this fantastic

telescope for looking into the past.

But once you are done playing, think of bigger things you could do if you

got your hands on this data. Assume you have access to the annual number

of references for all words/phrases published in books over the past 200 years.

1.2. ASKING INTERESTING QUESTIONS FROM DATA 11

Google makes this data freely available. So what are you going to do with it?

Observing the time series associated with particular words using the Ngrams

Viewer is fun. But more sophisticated historical trends can be captured by

aggregating multiple time series together. The following types of questions

seem particularly interesting to me:

•How has the amount of cursing changed over time? Use of the four-

letter words I am most familiar with seem to have exploded since 1960,

although it is perhaps less clear whether this reﬂects increased cussing or

lower publication standards.

•How often do new words emerge and get popular? Do these words tend

to stay in common usage, or rapidly fade away? Can we detect when

words change meaning over time, like the transition of gay from happy to

homosexual?

•Have standards of spelling been improving or deteriorating with time,

especially now that we have entered the era of automated spell check-

ing? Rarely-occurring words that are only one character removed from a

commonly-used word are likely candidates to be spelling errors (e.g. al-

gorithm vs. algorthm). Aggregated over many diﬀerent misspellings, are

such errors increasing or decreasing?

You can also use this Ngrams corpus to build a language model that captures

the meaning and usage of the words in a given language. We will discuss word

embeddings in Section 11.6.3, which are powerful tools for building language

models. Frequency counts reveal which words are most popular. The frequency

of word pairs appearing next to each other can be used to improve speech

recognition systems, helping to distinguish whether the speaker said that’s too

bad or that’s to bad. These millions of books provide an ample data set to build

representative models from.

1.2.4 New York Taxi Records

Every ﬁnancial transaction today leaves a data trail behind it. Following these

paths can lead to interesting insights.

Taxi cabs form an important part of the urban transportation network. They

roam the streets of the city looking for customers, and then drive them to their

destination for a fare proportional to the length of the trip. Each cab contains

a metering device to calculate the cost of the trip as a function of time. This

meter serves as a record keeping device, and a mechanism to ensure that the

driver charges the proper amount for each trip.

The taxi meters currently employed in New York cabs can do many things

beyond calculating fares. They act as credit card terminals, providing a way

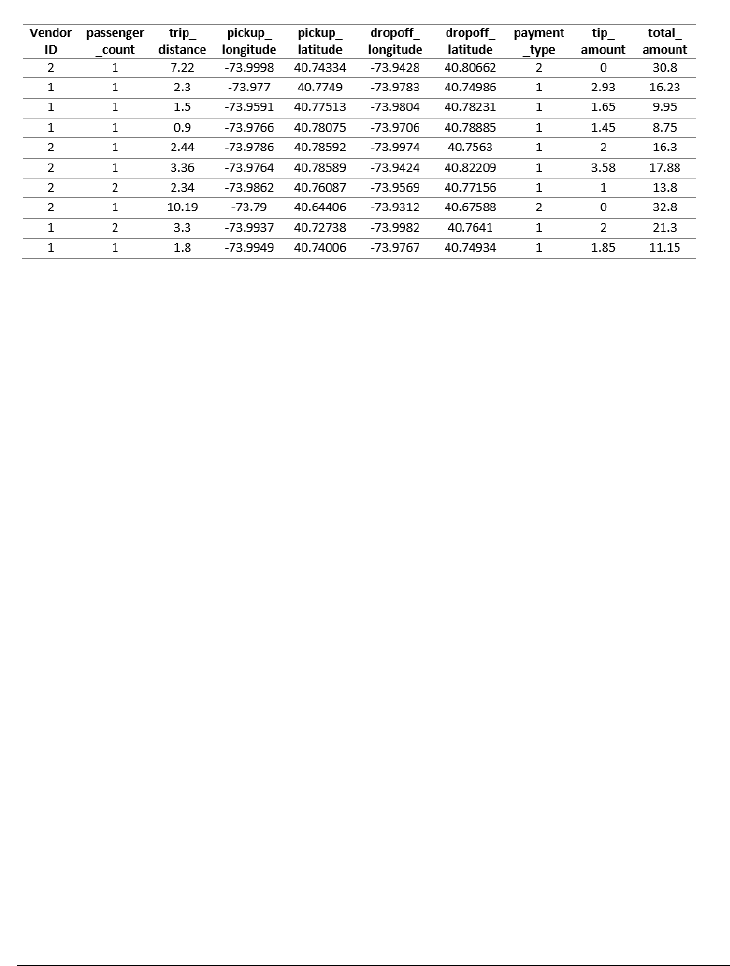
12 CHAPTER 1. WHAT IS DATA SCIENCE?

Figure 1.6: Representative ﬁelds from the New York city taxi cab data: pick up

and dropoﬀ points, distances, and fares.

for customers to pay for rides without cash. They are integrated with global

positioning systems (GPS), recording the exact location of every pickup and

drop oﬀ. And ﬁnally, since they are on a wireless network, these boxes can

communicate all of this data back to a central server.

The result is a database documenting every single trip by all taxi cabs in

one of the world’s greatest cities, a small portion of which is shown in Figure

1.6. Because the New York Taxi and Limousine Commission is a public agency,

its non-conﬁdential data is available to all under the Freedom of Information

Act (FOA).

Every ride generates two records: one with data on the trip, the other with

details of the fare. Each trip is keyed to the medallion (license) of each car

coupled with the identiﬁer of each driver. For each trip, we get the time/date

of pickup and drop-oﬀ, as well as the GPS coordinates (longitude and latitude)

of the starting location and destination. We do not get GPS data of the route

they traveled between these points, but to some extent that can be inferred by

the shortest path between them.

As for fare data, we get the metered cost of each trip, including tax, surcharge

and tolls. It is traditional to pay the driver a tip for service, the amount of which

is also recorded in the data.

So I’m talking to you. This taxi data is readily available, with records of

over 80 million trips over the past several years. What are you going to do with

it?

Any interesting data set can be used to answer questions on many diﬀerent

scales. This taxi fare data can help us better understand the transportation

industry, but also how the city works and how we could make it work even

better. Natural questions with respect to the taxi industry include:

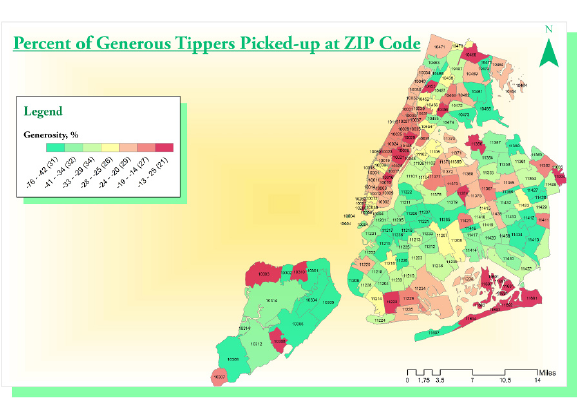
1.2. ASKING INTERESTING QUESTIONS FROM DATA 13

Figure 1.7: Which neighborhoods in New York city tip most generously? The

relatively remote outer boroughs of Brooklyn and Queens, where trips are

longest and supply is relatively scarce.

•How much money do drivers make each night, on average? What is the

distribution? Do drivers make more on sunny days or rainy days?

•Where are the best spots in the city for drivers to cruise, in order to pick

up proﬁtable fares? How does this vary at diﬀerent times of the day?

•How far do drivers travel over the course of a night’s work? We can’t

answer this exactly using this data set, because it does not provide GPS

data of the route traveled between fares. But we do know the last place

of drop oﬀ, the next place of pickup, and how long it took to get between

them. Together, this should provide enough information to make a sound

estimate.

•Which drivers take their unsuspecting out-of-town passengers for a “ride,”

running up the meter on what should be a much shorter, cheaper trip?

•How much are drivers tipped, and why? Do faster drivers get tipped

better? How do tipping rates vary by neighborhood, and is it the rich

neighborhoods or poor neighborhoods which prove more generous?

I will confess we did an analysis of this, which I will further describe in

the war story of Section 9.3. We found a variety of interesting patterns

[SS15]. Figure 1.7 shows that Manhattanites are generally cheapskates

relative to large swaths of Brooklyn, Queens, and Staten Island, where

trips are longer and street cabs a rare but welcome sight.

14 CHAPTER 1. WHAT IS DATA SCIENCE?

But the bigger questions have to do with understanding transportation in

the city. We can use the taxi travel times as a sensor to measure the level of

traﬃc in the city at a ﬁne level. How much slower is traﬃc during rush hour

than other times, and where are delays the worst? Identifying problem areas is

the ﬁrst step to proposing solutions, by changing the timing patterns of traﬃc

lights, running more buses, or creating high-occupancy only lanes.

Similarly we can use the taxi data to measure transportation ﬂows across

the city. Where are people traveling to, at diﬀerent times of the day? This tells

us much more than just congestion. By looking at the taxi data, we should

be able to see tourists going from hotels to attractions, executives from fancy

neighborhoods to Wall Street, and drunks returning home from nightclubs after

a bender.

Data like this is essential to designing better transportation systems. It is

wasteful for a single rider to travel from point ato point bwhen there is another

rider at point a+who also wants to get there. Analysis of the taxi data enables

accurate simulation of a ride sharing system, so we can accurately evaluate the

demands and cost reductions of such a service.

1.3 Properties of Data

This book is about techniques for analyzing data. But what is the underlying

stuﬀ that we will be studying? This section provides a brief taxonomy of the

properties of data, so we can better appreciate and understand what we will be

working on.

1.3.1 Structured vs. Unstructured Data

Certain data sets are nicely structured, like the tables in a database or spread-

sheet program. Others record information about the state of the world, but in

a more heterogeneous way. Perhaps it is a large text corpus with images and

links like Wikipedia, or the complicated mix of notes and test results appearing

in personal medical records.

Generally speaking, this book will focus on dealing with structured data.

Data is often represented by a matrix, where the rows of the matrix represent

distinct items or records, and the columns represent distinct properties of these

items. For example, a data set about U.S. cities might contain one row for each

city, with columns representing features like state, population, and area.

When confronted with an unstructured data source, such as a collection of

tweets from Twitter, our ﬁrst step is generally to build a matrix to structure

it. A bag of words model will construct a matrix with a row for each tweet, and

a column for each frequently used vocabulary word. Matrix entry M[i, j] then

denotes the number of times tweet icontains word j. Such matrix formulations

will motivate our discussion of linear algebra, in Chapter 8.

1.3. PROPERTIES OF DATA 15

1.3.2 Quantitative vs. Categorical Data

Quantitative data consists of numerical values, like height and weight. Such data

can be incorporated directly into algebraic formulas and mathematical models,

or displayed in conventional graphs and charts.

By contrast, categorical data consists of labels describing the properties of

the objects under investigation, like gender, hair color, and occupation. This

descriptive information can be every bit as precise and meaningful as numerical

data, but it cannot be worked with using the same techniques.

Categorical data can usually be coded numerically. For example, gender

might be represented as male = 0 or f emale = 1. But things get more com-

plicated when there are more than two characters per feature, especially when

there is not an implicit order between them. We may be able to encode hair

colors as numbers by assigning each shade a distinct value like gray hair = 0,

red hair = 1, and blond hair = 2. However, we cannot really treat these val-

ues as numbers, for anything other than simple identity testing. Does it make

any sense to talk about the maximum or minimum hair color? What is the

interpretation of my hair color minus your hair color?

Most of what we do in this book will revolve around numerical data. But

keep an eye out for categorical features, and methods that work for them. Clas-

siﬁcation and clustering methods can be thought of as generating categorical

labels from numerical data, and will be a primary focus in this book.

1.3.3 Big Data vs. Little Data

Data science has become conﬂated in the public eye with big data, the analysis of

massive data sets resulting from computer logs and sensor devices. In principle,

having more data is always better than having less, because you can always

throw some of it away by sampling to get a smaller set if necessary.

Big data is an exciting phenomenon, and we will discuss it in Chapter 12. But

in practice, there are diﬃculties in working with large data sets. Throughout

this book we will look at algorithms and best practices for analyzing data. In

general, things get harder once the volume gets too large. The challenges of big

data include:

•The analysis cycle time slows as data size grows: Computational opera-

tions on data sets take longer as their volume increases. Small spreadsheets

provide instantaneous response, allowing you to experiment and play what

if? But large spreadsheets can be slow and clumsy to work with, and

massive-enough data sets might take hours or days to get answers from.

Clever algorithms can permit amazing things to be done with big data,

but staying small generally leads to faster analysis and exploration.

•Large data sets are complex to visualize: Plots with millions of points on

them are impossible to display on computer screens or printed images, let

alone conceptually understand. How can we ever hope to really understand

something we cannot see?

16 CHAPTER 1. WHAT IS DATA SCIENCE?

•Simple models do not require massive data to ﬁt or evaluate: A typical

data science task might be to make a decision (say, whether I should oﬀer

this fellow life insurance?) on the basis of a small number of variables:

say age, gender, height, weight, and the presence or absence of existing

medical conditions.

If I have this data on 1 million people with their associated life outcomes, I

should be able to build a good general model of coverage risk. It probably

wouldn’t help me build a substantially better model if I had this data

on hundreds of millions of people. The decision criteria on only a few

variables (like age and martial status) cannot be too complex, and should

be robust over a large number of applicants. Any observation that is so

subtle it requires massive data to tease out will prove irrelevant to a large

business which is based on volume.

Big data is sometimes called bad data. It is often gathered as the by-product

of a given system or procedure, instead of being purposefully collected to answer

your question at hand. The result is that we might have to go to heroic eﬀorts

to make sense of something just because we have it.

Consider the problem of getting a pulse on voter preferences among presi-

dential candidates. The big data approach might analyze massive Twitter or

Facebook feeds, interpreting clues to their opinions in the text. The small data

approach might be to conduct a poll, asking a few hundred people this speciﬁc

question and tabulating the results. Which procedure do you think will prove

more accurate? The right data set is the one most directly relevant to the tasks

at hand, not necessarily the biggest one.

Take-Home Lesson: Do not blindly aspire to analyze large data sets. Seek the

right data to answer a given question, not necessarily the biggest thing you can

get your hands on.

1.4 Classiﬁcation and Regression

Two types of problems arise repeatedly in traditional data science and pattern

recognition applications, the challenges of classiﬁcation and regression. As this

book has developed, I have pushed discussions of the algorithmic approaches

to solving these problems toward the later chapters, so they can beneﬁt from a

solid understanding of core material in data munging, statistics, visualization,

and mathematical modeling.

Still, I will mention issues related to classiﬁcation and regression as they

arise, so it makes sense to pause here for a quick introduction to these problems,

to help you recognize them when you see them.

•Classiﬁcation: Often we seek to assign a label to an item from a discrete

set of possibilities. Such problems as predicting the winner of a particular

1.5. DATA SCIENCE TELEVISION: THE QUANT SHOP 17

sporting contest (team Aor team B?) or deciding the genre of a given

movie (comedy, drama, or animation?) are classiﬁcation problems, since

each entail selecting a label from the possible choices.

•Regression: Another common task is to forecast a given numerical quan-

tity. Predicting a person’s weight or how much snow we will get this year

is a regression problem, where we forecast the future value of a numerical

function in terms of previous values and other relevant features.

Perhaps the best way to see the intended distinction is to look at a variety

of data science problems and label (classify) them as regression or classiﬁcation.

Diﬀerent algorithmic methods are used to solve these two types of problems,

although the same questions can often be approached in either way:

•Will the price of a particular stock be higher or lower tomorrow? (classi-

ﬁcation)

•What will the price of a particular stock be tomorrow? (regression)

•Is this person a good risk to sell an insurance policy to? (classiﬁcation)

•How long do we expect this person to live? (regression)

Keep your eyes open for classiﬁcation and regression problems as you en-

counter them in your life, and in this book.

1.5 Data Science Television: The Quant Shop

I believe that hands-on experience is necessary to internalize basic principles.

Thus when I teach data science, I like to give each student team an interesting

but messy forecasting challenge, and demand that they build and evaluate a

predictive model for the task.

These forecasting challenges are associated with events where the students

must make testable predictions. They start from scratch: ﬁnding the relevant

data sets, building their own evaluation environments, and devising their model.

Finally, I make them watch the event as it unfolds, so as to witness the vindi-

cation or collapse of their prediction.

As an experiment, we documented the evolution of each group’s project

on video in Fall 2014. Professionally edited, this became The Quant Shop, a

television-like data science series for a general audience. The eight episodes of

this ﬁrst season are available at http://www.quant-shop.com, and include:

•Finding Miss Universe – The annual Miss Universe competition aspires

to identify the most beautiful woman in the world. Can computational

models predict who will win a beauty contest? Is beauty just subjective,

or can algorithms tell who is the fairest one of all?

18 CHAPTER 1. WHAT IS DATA SCIENCE?

•Modeling the Movies – The business of movie making involves a lot of

high-stakes data analysis. Can we build models to predict which ﬁlm will

gross the most on Christmas day? How about identifying which actors

will receive awards for their performance?

•Winning the Baby Pool – Birth weight is an important factor in assessing

the health of a newborn child. But how accurately can we predict junior’s

weight before the actual birth? How can data clarify environmental risks

to developing pregnancies?

•The Art of the Auction – The world’s most valuable artworks sell at auc-

tions to the highest bidder. But can we predict how many millions a

particular J.W. Turner painting will sell for? Can computers develop an

artistic sense of what’s worth buying?

•White Christmas – Weather forecasting is perhaps the most familiar do-

main of predictive modeling. Short-term forecasts are generally accurate,

but what about longer-term prediction? What places will wake up to a

snowy Christmas this year? And can you tell one month in advance?

•Predicting the Playoﬀs – Sports events have winners and losers, and book-

ies are happy to take your bets on the outcome of any match. How well can

statistics help predict which football team will win the Super Bowl? Can

Google’s PageRank algorithm pick the winners on the ﬁeld as accurately

as it does on the web?

•The Ghoul Pool – Death comes to all men, but when? Can we apply

actuarial models to celebrities, to decide who will be the next to die?

Similar analysis underlies the workings of the life insurance industry, where

accurate predictions of lifespan are necessary to set premiums which are

both sustainable and aﬀordable.

Figure 1.8: Exciting scenes from data science television: The Quant Shop.

1.6. ABOUT THE WAR STORIES 19

•Playing the Market – Hedge fund quants get rich when guessing right

about tomorrow’s prices, and poor when wrong. How accurately can we

predict future prices of gold and oil using histories of price data? What

other information goes into building a successful price model?

I encourage you to watch some episodes of The Quant Shop in tandem with

reading this book. We try to make it fun, although I am sure you will ﬁnd

plenty of things to cringe at. Each show runs for thirty minutes, and maybe

will inspire you to tackle a prediction challenge of your own.

These programs will certainly give you more insight into these eight speciﬁc

challenges. I will use these projects throughout this book to illustrate important

lessons in how to do data science, both as positive and negative examples. These

projects provide a laboratory to see how intelligent but inexperienced people not

wildly unlike yourself thought about a data science problem, and what happened

when they did.

1.5.1 Kaggle Challenges

Another source of inspiration are challenges from Kaggle (www.kaggle.com),

which provides a competitive forum for data scientists. New challenges are

posted on a regular basis, providing a problem deﬁnition, training data, and

a scoring function over hidden evaluation data. A leader board displays the

scores of the strongest competitors, so you can see how well your model stacks

up in comparison with your opponents. The winners spill their modeling secrets

during post-contest interviews, to help you improve your modeling skills.

Performing well on Kaggle challenges is an excellent credential to put on your

resume to get a good job as a data scientist. Indeed, potential employers will

track you down if you are a real Kaggle star. But the real reason to participate

is that the problems are fun and inspiring, and practice helps make you a better

data scientist.

The exercises at the end of each chapter point to expired Kaggle challenges,

loosely connected to the material in that chapter. Be forewarned that Kaggle

provides a misleading glamorous view of data science as applied machine learn-

ing, because it presents extremely well-deﬁned problems with the hard work

of data collection and cleaning already done for you. Still, I encourage you to

check it out for inspiration, and as a source of data for new projects.

1.6 About the War Stories

Genius and wisdom are two distinct intellectual gifts. Genius shows in discover-

ing the right answer, making imaginative mental leaps which overcome obstacles

and challenges. Wisdom shows in avoiding obstacles in the ﬁrst place, providing

a sense of direction or guiding light that keeps us moving soundly in the right

direction.

20 CHAPTER 1. WHAT IS DATA SCIENCE?

Genius is manifested in technical strength and depth, the ability to see things

and do things that other people cannot. In contrast, wisdom comes from ex-

perience and general knowledge. It comes from listening to others. Wisdom

comes from humility, observing how often you have been wrong in the past and

ﬁguring out why you were wrong, so as to better recognize future traps and

avoid them.

Data science, like most things in life, beneﬁts more from wisdom than from

genius. In this book, I seek to pass on wisdom that I have accumulated the hard

way through war stories, gleaned from a diverse set of projects I have worked

on:

•Large-scale text analytics and NLP: My Data Science Laboratory at Stony

Brook University works on a variety of projects in big data, including sen-

timent analysis from social media, historical trends analysis, deep learning

approaches to natural language processing (NLP), and feature extraction

from networks.

•Start-up companies: I served as co-founder and chief scientist to two

data analytics companies: General Sentiment and Thrivemetrics. General

Sentiment analyzed large-scale text streams from news, blogs, and social

media to identify trends in the sentiment (positive or negative) associated

with people, places, and things. Thrivemetrics applied this type of analysis

to internal corporate communications, like email and messaging systems.

Neither of these ventures left me wealthy enough to forgo my royalties

from this book, but they did provide me with experience on cloud-based

computing systems, and insight into how data is used in industry.

•Collaborating with real scientists: I have had several interesting collab-

orations with biologists and social scientists, which helped shape my un-

derstanding of the complexities of working with real data. Experimental

data is horribly noisy and riddled with errors, yet you must do the best

you can with what you have, in order to discover how the world works.

•Building gambling systems: A particularly amusing project was building

a system to predict the results of jai-alai matches so we could bet on them,

an experience recounted in my book Calculated Bets: Computers, Gam-

bling, and Mathematical Modeling to Win [Ski01]. Our system relied on

web scraping for data collection, statistical analysis, simulation/modeling,

and careful evaluation. We also have developed and evaluated predictive

models for movie grosses [ZS09], stock prices [ZS10], and football games

[HS10] using social media analysis.

•Ranking historical ﬁgures: By analyzing Wikipedia to extract meaningful

variables on over 800,000 historical ﬁgures, we developed a scoring func-

tion to rank them by their strength as historical memes. This ranking

does a great job separating the greatest of the great (Jesus, Napoleon,

Shakespeare, Mohammad, and Lincoln round out the top ﬁve) from lesser

1.7. WAR STORY: ANSWERING THE RIGHT QUESTION 21

mortals, and served as the basis for our book Who’s Bigger?: Where His-

torical Figures Really Rank [SW13].

All this experience drives what I teach in this book, especially the tales that

I describe as war stories. Every one of these war stories is true. Of course, the

stories improve somewhat in the retelling, and the dialogue has been punched

up to make them more interesting to read. However, I have tried to honestly

trace the process of going from a raw problem to a solution, so you can watch

how it unfolded.

1.7 War Story: Answering the Right Question

Our research group at Stony Brook University developed an NLP-based system

for analyzing millions of news, blogs and social media messages, and reducing

this text to trends concerning all the entities under discussion. Counting the

number of mentions each name receives in a text stream (volume) is easy, in

principle. Determining whether the connotation of a particular reference is

positive or negative (sentiment analysis) is hard. But our system did a pretty

good job, particularly when aggregated over many references.

This technology served as the foundation for a social media analysis company

named General Sentiment. It was exciting living through a start-up starting up,

facing the challenges of raising money, hiring staﬀ, and developing new products.

But perhaps the biggest problem we faced was answering the right question.

The General Sentiment system recorded trends about the sentiment and volume

for every person, place, and thing that was ever mentioned in news, blogs, and

social media: over 20 million distinct entities. We monitored the reputations of

celebrities and politicians. We monitored the fates of companies and products.

We tracked the performance of sports teams, and the buzz about movies. We

could do anything!

But it turns out that no one pays you to do anything. They pay you to do

something, to solve a particular problem they have, or eliminate a speciﬁc pain

point in their business. Being able to do anything proves to be a terrible sales

strategy, because it requires you to ﬁnd that need afresh for each and every

customer.

Facebook didn’t open up to the world until September 2006. So when Gen-

eral Sentiment started in 2008, we were at the very beginning of the social media

era. We had lots of interest from major brands and advertising agencies which

knew that social media was ready to explode. They knew this newfangled thing

was important, and that they had to be there. They knew that proper analysis

of social media data could give them fresh insights into what their customers

were thinking. But they didn’t know exactly what it was they really wanted to

know.

One aircraft engine manufacturer was very interested in learning how much

the kids talked about them on Facebook. We had to break it to them gently

that the answer was zero. Other potential customers demanded proof that we

22 CHAPTER 1. WHAT IS DATA SCIENCE?

were more accurate than the Nielsen television ratings. But of course, if you

wanted Nielsen ratings then you should buy them from Nielsen. Our system

provided diﬀerent insights from a completely diﬀerent world. But you had to

know what you wanted in order to use them.

We did manage to get substantial contracts from a very diverse group of

customers, including consumer brands like Toyota and Blackberry, governmental

organizations like the Hawaii tourism oﬃce, and even the presidential campaign

of Republican nominee Mitt Romney in 2012. Our analysts provided them

insights into a wide variety of business issues:

•What did people think about Hawaii? (Answer: they think it is a very

nice place to visit.)

•How quickly would Toyota’s sentiment recover after news of serious brake

problems in their cars? (Answer: about six months.)

•What did people think about Blackberry’s new phone models? (Answer:

they liked the iPhone much better.)

•How quickly would Romney’s sentiment recover after insulting 47% of the

electorate in a recorded speech? (Answer: never.)

But each sale required entering a new universe, involving considerable eﬀort

and imagination on the part of our sales staﬀ and research analysts. We never

managed to get two customers in the same industry, which would have let us

beneﬁt from scale and accumulated wisdom.

Of course, the customer is always right. It was our fault that we could not

explain to them the best way to use our technology. The lesson here is that the

world will not beat a path to your door just for a new source of data. You must

be able to supply the right questions before you can turn data into money.

1.8 Chapter Notes

The idea of using historical records from baseball players to establish that left-

handers have shorter lifespans is due to Halpern and Coren [HC88, HC91],

but their conclusion remains controversial. The percentage of left-handers in

the population has been rapidly growing, and the observed eﬀects may be a

function of survivorship bias [McM04]. So lefties, hang in there! Full disclosure:

I am one of you.

The discipline of quantitative baseball analysis is sometimes called sabermet-

rics, and its leading light is a fellow named Bill James. I recommend budding

data scientists read his Historical Baseball Abstract [Jam10] as an excellent ex-

ample of how one turns numbers into knowledge and understanding. Time

Magazine once said of James: “Much of the joy of reading him comes from the

extravagant spectacle of a ﬁrst-rate mind wasting itself on baseball.” I thank

http://sports-reference.com for permission to use images of their website

in this book. Ditto to Amazon, the owner of IMDb.

1.9. EXERCISES 23

The potential of ride-sharing systems in New York was studied by Santi et.

al. [SRS+14], who showed that almost 95% of the trips could have been shared

with no more than ﬁve minutes delay per trip.

The Lydia system for sentiment analysis is described in [GSS07]. Methods

to identify changes in word meaning through analysis of historical text corpora

like Google Ngram are reported in [KARPS15].

1.9 Exercises

Identifying Data Sets

1-1. [3] Identify where interesting data sets relevant to the following domains can be

found on the web:

(a) Books.

(b) Horse racing.

(d) Risks of diseases.

(e) Colleges and universities.

(f) Crime rates.

(g) Bird watching.

For each of these data sources, explain what you must do to turn this data into

a usable format on your computer for analysis.

1-2. [3] Propose relevant data sources for the following The Quant Shop prediction

challenges. Distinguish between sources of data that you are sure somebody must

have, and those where the data is clearly available to you.

(a) Miss Universe.

(b) Movie gross.

(d) Art auction price.

(e) White Christmas.

(f) Football champions.

(g) Ghoul pool.

(h) Gold/oil prices.

1-3. [3] Visit http://data.gov, and identify ﬁve data sets that sound interesting to

you. For each write a brief description, and propose three interesting things you

might do with them.

Asking Questions

1-4. [3] For each of the following data sources, propose three interesting questions

you can answer by analyzing them:

(a) Credit card billing data.

24 CHAPTER 1. WHAT IS DATA SCIENCE?

(b) Click data from http://www.Amazon.com.

1-5. [5] Visit Entrez, the National Center for Biotechnology Information (NCBI)

portal. Investigate what data sources are available, particularly the Pubmed

and Genome resources. Propose three interesting projects to explore with each

of them.

1-6. [5] You would like to conduct an experiment to establish whether your friends

prefer the taste of regular Coke or Diet Coke. Brieﬂy outline a design for such

a study.

1-7. [5] You would like to conduct an experiment to see whether students learn better

if they study without any music, with instrumental music, or with songs that

have lyrics. Brieﬂy outline the design for such a study.

1-8. [5] Traditional polling operations like Gallup use a procedure called random digit

dialing, which dials random strings of digits instead of picking phone numbers

from the phone book. Suggest why such polls are conducted using random digit

dialing.

Implementation Projects

1-9. [5] Write a program to scrape the best-seller rank for a book on Amazon.com.

Use this to plot the rank of all of Skiena’s books over time. Which one of these

books should be the next item that you purchase? Do you have friends for whom

they would make a welcome and appropriate gift? :-)

1-10. [5] For your favorite sport (baseball, football, basketball, cricket, or soccer)

identify a data set with the historical statistical records for all major partici-

pants. Devise and implement a ranking system to identify the best player at

each position.

Interview Questions

1-11. [3] For each of the following questions: (1) produce a quick guess based only on

your understanding of the world, and then (2) use Google to ﬁnd supportable

numbers to produce a more principled estimate from. How much did your two

estimates diﬀer by?

(a) How many piano tuners are there in the entire world?

(b) How much does the ice in a hockey rink weigh?

(d) How many people ﬂy in and out of LaGuardia Airport every day?

(e) How many gallons of ice cream are sold in the United States each year?

(f) How many basketballs are purchased by the National Basketball Associa-

tion (NBA) each year?

(g) How many ﬁsh are there in all the world’s oceans?

(h) How many people are ﬂying in the air right now, all over the world?

(i) How many ping-pong balls can ﬁt in a large commercial jet?

(j) How many miles of paved road are there in your favorite country?

1.9. EXERCISES 25

(k) How many dollar bills are sitting in the wallets of all people at Stony Brook

University?

(l) How many gallons of gasoline does a typical gas station sell per day?

(m) How many words are there in this book?

(n) How many cats live in New York city?

(o) How much would it cost to ﬁll a typical car’s gas tank with Starbuck’s

coﬀee?

(p) How much tea is there in China?

(q) How many checking accounts are there in the United States?

1-12. [3] What is the diﬀerence between regression and classiﬁcation?

1-13. [8] How would you build a data-driven recommendation system? What are the

limitations of this approach?

1-14. [3] How did you become interested in data science?

1-15. [3] Do you think data science is an art or a science?

Kaggle Challenges

1-16. Who survived the shipwreck of the Titanic?

https://www.kaggle.com/c/titanic

1-17. Where is a particular taxi cab going?

https://www.kaggle.com/c/pkdd-15-predict-taxi-service-trajectory-i

1-18. How long will a given taxi trip take?

https://www.kaggle.com/c/pkdd-15-taxi-trip-time-prediction-ii

Chapter 2

Mathematical Preliminaries

A data scientist is someone who knows more statistics than a com-

puter scientist and more computer science than a statistician.

– Josh Blumenstock

You must walk before you can run. Similarly, there is a certain level of mathe-

matical maturity which is necessary before you should be trusted to do anything

meaningful with numerical data.

In writing this book, I have assumed that the reader has had some degree

of exposure to probability and statistics, linear algebra, and continuous math-

ematics. I have also assumed that they have probably forgotten most of it, or

perhaps didn’t always see the forest (why things are important, and how to use

them) for the trees (all the details of deﬁnitions, proofs, and operations).

This chapter will try to refresh your understanding of certain basic math-

ematical concepts. Follow along with me, and pull out your old textbooks if

necessary for future reference. Deeper concepts will be introduced later in the

book when we need them.

2.1 Probability

Probability theory provides a formal framework for reasoning about the likeli-

hood of events. Because it is a formal discipline, there are a thicket of associated

deﬁnitions to instantiate exactly what we are reasoning about:

•An experiment is a procedure which yields one of a set of possible out-

comes. As our ongoing example, consider the experiment of tossing two

six-sided dice, one red and one blue, with each face baring a distinct inte-

ger {1,...,6}.

•Asample space Sis the set of possible outcomes of an experiment. In our

28 CHAPTER 2. MATHEMATICAL PRELIMINARIES

dice example, there are 36 possible outcomes, namely

S={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),

(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),

(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}.

•An event Eis a speciﬁed subset of the outcomes of an experiment. The

event that the sum of the dice equals 7 or 11 (the conditions to win at

craps on the ﬁrst roll) is the subset

E={(1,6),(2,5),(3,4),(4,3),(5,2),(6,1),(5,6),(6,5)}.

•The probability of an outcome s, denoted p(s) is a number with the two

properties:

–For each outcome sin sample space S, 0 ≤p(s)≤1.

–The sum of probabilities of all outcomes adds to one: Ps∈Sp(s) = 1.

If we assume two distinct fair dice, the probability p(s) = (1/6) ×(1/6) =

1/36 for all outcomes s∈S.

•The probability of an event Eis the sum of the probabilities of the out-

comes of the experiment. Thus

p(E) = X

s∈E

p(s).

An alternate formulation is in terms of the complement of the event ¯

the case when Edoes not occur. Then

P(E)=1−P(¯

E).

This is useful, because often it is easier to analyze P(¯

E) than P(E) di-

rectly.

•Arandom variable Vis a numerical function on the outcomes of a proba-

bility space. The function “sum the values of two dice” (V((a, b)) = a+b)

produces an integer result between 2 and 12. This implies a probabil-

ity distribution of the values of the random variable. The probability

P(V(s) = 7) = 1/6, as previously shown, while P(V(s) = 12) = 1/36.

•The expected value of a random variable Vdeﬁned on a sample space S,

E(V) is deﬁned

E(V) = X

s∈S

p(s)·V(s).

All this you have presumably seen before. But it provides the language we

will use to connect between probability and statistics. The data we see usually

comes from measuring properties of observed events. The theory of probability

and statistics provides the tools to analyze this data.

2.1. PROBABILITY 29

2.1.1 Probability vs. Statistics

Probability and statistics are related areas of mathematics which concern them-

selves with analyzing the relative frequency of events. Still, there are funda-

mental diﬀerences in the way they see the world:

•Probability deals with predicting the likelihood of future events, while

statistics involves the analysis of the frequency of past events.

•Probability is primarily a theoretical branch of mathematics, which studies

the consequences of mathematical deﬁnitions. Statistics is primarily an

applied branch of mathematics, which tries to make sense of observations

in the real world.

Both subjects are important, relevant, and useful. But they are diﬀerent, and

understanding the distinction is crucial in properly interpreting the relevance

of mathematical evidence. Many a gambler has gone to a cold and lonely grave

for failing to make the proper distinction between probability and statistics.

This distinction will perhaps become clearer if we trace the thought process

of a mathematician encountering her ﬁrst craps game:

•If this mathematician were a probabilist, she would see the dice and think

“Six-sided dice? Each side of the dice is presumably equally likely to land

face up. Now assuming that each face comes up with probability 1/6, I

can ﬁgure out what my chances are of crapping out.”

•If instead a statistician wandered by, she would see the dice and think

“How do I know that they are not loaded? I’ll watch a while, and keep

track of how often each number comes up. Then I can decide if my ob-

servations are consistent with the assumption of equal-probability faces.

Once I’m conﬁdent enough that the dice are fair, I’ll call a probabilist to

tell me how to bet.”

In summary, probability theory enables us to ﬁnd the consequences of a

given ideal world, while statistical theory enables us to measure the extent to

which our world is ideal. This constant tension between theory and practice is

why statisticians prove to be a tortured group of individuals compared with the

happy-go-lucky probabilists.

Modern probability theory ﬁrst emerged from the dice tables of France in

1654. Chevalier de M´er´e, a French nobleman, wondered whether the player or

the house had the advantage in a particular betting game.1In the basic version,

the player rolls four dice, and wins provided none of them are a 6. The house

collects on the even money bet if at least one 6 appears.

De M´er´e brought this problem to the attention of the French mathematicians

Blaise Pascal and Pierre de Fermat, most famous as the source of Fermat’s Last

Theorem. Together, these men worked out the basics of probability theory,

1He really shouldn’t have wondered. The house always has the advantage.

30 CHAPTER 2. MATHEMATICAL PRELIMINARIES

A\B

A B

A[B

Figure 2.1: Venn diagrams illustrating set diﬀerence (left), intersection (middle),

and union (right).

along the way establishing that the house wins this dice game with probability

p= 1 −(5/6)4≈0.517, where the probability p= 0.5 would denote a fair game

where the house wins exactly half the time.

2.1.2 Compound Events and Independence

We will be interested in complex events computed from simpler events Aand B

on the same set of outcomes. Perhaps event Ais that at least one of two dice

be an even number, while event Bdenotes rolling a total of either 7 or 11. Note

that there exist certain outcomes of Awhich are not outcomes of B, speciﬁcally

A−B={(1,2),(1,4),(2,1),(2,2),(2,3),(2,4),(2,6),(3,2),(3,6),(4,1),

(4,2),(4,4),(4,5),(4,6),(5,4),(6,2),(6,3),(6,4),(6,6)}.

This is the set diﬀerence operation. Observe that here B−A={}, because

every pair adding to 7 or 11 must contain one odd and one even number.

The outcomes in common between both events Aand Bare called the in-

tersection, denoted A∩B. This can be written as

A∩B=A−(S−B).

Outcomes which appear in either Aor Bare called the union, denoted A∪B.

With the complement operation ¯

A=S−A, we get a rich language for combining

events, shown in Figure 2.1. We can readily compute the probability of any of

these sets by summing the probabilities of the outcomes in the deﬁned sets.

The events Aand Bare independent if and only if

P(A∩B) = P(A)×P(B).

This means that there is no special structure of outcomes shared between events

Aand B. Assuming that half of the students in my class are female, and half

the students in my class are above average, we would expect that a quarter of

my students are both female and above average if the events are independent.

2.1. PROBABILITY 31

Probability theorists love independent events, because it simpliﬁes their cal-

culations. But data scientists generally don’t. When building models to predict

the likelihood of some future event B, given knowledge of some previous event

A, we want as strong a dependence of Bon Aas possible.

Suppose I always use an umbrella if and only if it is raining. Assume that

the probability it is raining here (event B) is, say, p= 1/5. This implies the

probability that I am carrying my umbrella (event A) is q= 1/5. But even

more, if you know the state of the rain you know exactly whether I have my

umbrella. These two events are perfectly correlated.

By contrast, suppose the events were independent. Then

P(A|B) = P(A∩B)

P(B)=P(A)P(B)

P(B)=P(A)

and whether it is raining has absolutely no impact on whether I carry my pro-

tective gear.

Correlations are the driving force behind predictive models, so we will discuss

how to measure them and what they mean in Section 2.3.

2.1.3 Conditional Probability

When two events are correlated, there is a dependency between them which

makes calculations more diﬃcult. The conditional probability of Agiven B,

P(A|B) is deﬁned:

P(A|B) = P(A∩B)

P(B)

Recall the dice rolling events from Section 2.1.2, namely:

•Event Ais that at least one of two dice be an even number.

•Event Bis the sum of the two dice is either a 7 or an 11.

Observe that P(A|B) = 1, because any roll summing to an odd value must

consist of one even and one odd number. Thus A∩B=B, analogous to the

umbrella case above. For P(B|A), note that P(A∩B)=9/36 and P(A) =

25/36, so P(B|A)=9/25.

Conditional probability will be important to us, because we are interested in

the likelihood of an event A(perhaps that a particular piece of email is spam)

as a function of some evidence B(perhaps the distribution of words within the

document). Classiﬁcation problems generally reduce to computing conditional

probabilities, in one way or another.

Our primary tool to compute conditional probabilities will be Bayes theorem,

which reverses the direction of the dependencies:

P(B|A) = P(A|B)P(B)

P(A)

Often it proves easier to compute probabilities in one direction than another, as

in this problem. By Bayes theorem P(B|A) = (1·9/36)/(25/36) = 9/25, exactly

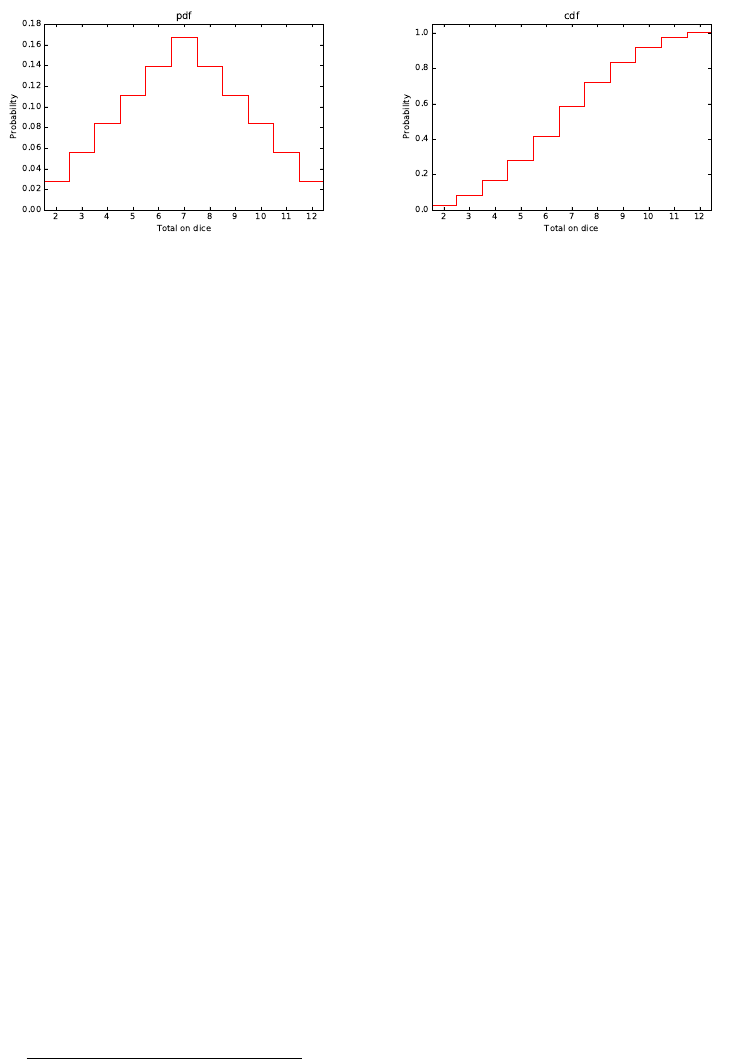
32 CHAPTER 2. MATHEMATICAL PRELIMINARIES

Figure 2.2: The probability density function (pdf) of the sum of two dice con-

tains exactly the same information as the cumulative density function (cdf), but

looks very diﬀerent.

what we got before. We will revisit Bayes theorem in Section 5.6, where it will

establish the foundations of computing probabilities in the face of evidence.

2.1.4 Probability Distributions

Random variables are numerical functions where the values are associated with

probabilities of occurrence. In our example where V(s) the sum of two tossed

dice, the function produces an integer between 2 and 12. The probability of a

particular value V(s) = Xis the sum of the probabilities of all the outcomes

which add up to X.

Such random variables can be represented by their probability density func-

tion, or pdf. This is a graph where the x-axis represents the range of values

the random variable can take on, and the y-axis denotes the probability of that

given value. Figure 2.2 (left) presents the pdf of the sum of two fair dice. Ob-

serve that the peak at X= 7 corresponds to the most frequent dice total, with

a probability of 1/6.

Such pdf plots have a strong relationship to histograms of data frequency,

where the x-axis again represents the range of value, but ynow represents the

observed frequency of exactly how many event occurrences were seen for each

given value X. Converting a histogram to a pdf can be done by dividing each

bucket by the total frequency over all buckets. The sum of the entries then

becomes 1, so we get a probability distribution.

Histograms are statistical: they reﬂect actual observations of outcomes. In

contrast, pdfs are probabilistic: they represent the underlying chance that the

next observation will have value X. We often use the histogram of observations

h(x) in practice to estimate the probabilities2by normalizing counts by the total

2A technique called discounting oﬀers a better way to estimate the frequency of rare events,

and will be discussed in Section 11.1.2.

2.1. PROBABILITY 33

Figure 2.3: iPhone quarterly sales data presented as cumulative and incremental

(quarterly) distributions. Which curve did Apple CEO Tim Cook choose to

present?

number of observations:

P(k=X) = h(k=X)

Pxh(x=X)

There is another way to represent random variables which often proves use-

ful, called a cumulative density function or cdf. The cdf is the running sum of

the probabilities in the pdf; as a function of k, it reﬂects the probability that

X≤kinstead of the probability that X=k. Figure 2.2 (right) shows the

cdf of the dice sum distribution. The values increase monotonically from left

to right, because each term comes from adding a positive probability to the

previous total. The rightmost value is 1, because all outcomes produce a value

no greater than the maximum.

It is important to realize that the pdf P(V) and cdf C(V) of a given random

variable Vcontain exactly the same information. We can move back and forth

between them because:

P(k=X) = C(X≤k+δ)−C(X≤k),

where δ= 1 for integer distributions. The cdf is the running sum of the pdf, so

C(X≤k) = X

x≤k

P(X=x).

Just be aware of which distribution you are looking at. Cumulative distribu-

tions always get higher as we move to the right, culminating with a probability

of C(X≤ ∞) = 1. By contrast, the total area under the curve of a pdf equals

1, so the probability at any point in the distribution is generally substantially

less.

34 CHAPTER 2. MATHEMATICAL PRELIMINARIES

An amusing example of the diﬀerence between cumulative and incremental

distributions is shown in Figure 2.3. Both distributions show exactly the same

data on Apple iPhone sales, but which curve did Apple CEO Tim Cook choose to

present at a major shareholder event? The cumulative distribution (red) shows

that sales are exploding, right? But it presents a misleading view of growth

rate, because incremental change is the derivative of this function, and hard to

visualize. Indeed, the sales-per-quarter plot (blue) shows that the rate of iPhone

sales actually had declined for the last two periods before the presentation.

2.2 Descriptive Statistics

Descriptive statistics provide ways of capturing the properties of a given data

set or sample. They summarize observed data, and provide a language to talk

about it. Representing a group of elements by a new derived element, like

mean, min, count, or sum reduces a large data set to a small summary statistic:

aggregation as data reduction.

Such statistics can become features in their own right when taken over natu-

ral groups or clusters in the full data set. There are two main types of descriptive

statistics:

•Central tendency measures, which capture the center around which the

data is distributed.

•Variation or variability measures, which describe the data spread, i.e. how

far the measurements lie from the center.

Together these statistics tell us an enormous amount about our distribution.

2.2.1 Centrality Measures

The ﬁrst element of statistics we are exposed to in school are the basic centrality

measures: mean, median, and mode. These are the right place to start when

thinking of a single number to characterize a data set.

•Mean: You are probably quite comfortable with the use of the arithmetic

mean, where we sum values and divide by the number of observations:

µX=1

i=1

We can easily maintain the mean under a stream of insertions and dele-

tions, by keeping the sum of values separate from the frequency count,

and divide only on demand.

The mean is very meaningful to characterize symmetric distributions with-

out outliers, like height and weight. That it is symmetric means the num-

ber of items above the mean should be roughly the same as the number

2.2. DESCRIPTIVE STATISTICS 35

below. That it is without outliers means that the range of values is rea-

sonably tight. Note that a single MAXINT creeping into an otherwise

sound set of observations throws the mean wildly oﬀ. The median is a

centrality measure which proves more appropriate with such ill-behaved

distributions.

•Geometric mean: The geometric mean is the nth root of the product of n

values:

i=1

ai!1/n

√a1a2. . . an

The geometric mean is always less than or equal to the arithmetic mean.

For example, the geometric mean of the sums of 36 dice rolls is 6.5201, as

opposed to the arithmetic mean of 7. It is very sensitive to values near

zero. A single value of zero lays waste to the geometric mean: no matter

what other values you have in your data, you end up with zero. This is

somewhat analogous to having an outlier of ∞in an arithmetic mean.

But geometric means prove their worth when averaging ratios. The ge-

ometric mean of 1/2 and 2/1 is 1, whereas the mean is 1.25. There is

less available “room” for ratios to be less than 1 than there is for ratios

above 1, creating an asymmetry that the arithmetic mean overstates. The

geometric mean is more meaningful in these cases, as is the arithmetic

mean of the logarithms of the ratios.

•Median: The median is the exact middle value among a data set; just as

many elements lie above the median as below it. There is a quibble about

what to take as the median when you have an even number of elements.

You can take either one of the two central candidates: in any reasonable

data set these two values should be about the same. Indeed in the dice

example, both are 7.

A nice property of the median as so deﬁned is that it must be a genuine

value of the original data stream. There actually is someone of median

height to you can point to as an example, but presumably no one in the

world is of exactly average height. You lose this property when you average

the two center elements.

Which centrality measure is best for applications? The median typically

lies pretty close to the arithmetic mean in symmetrical distributions, but

it is often interesting to see how far apart they are, and on which side of

the mean the median lies.

The median generally proves to be a better statistic for skewed distribu-

tions or data with outliers: like wealth and income. Bill Gates adds $250

to the mean per capita wealth in the United States, but nothing to the

median. If he makes you personally feel richer, then go ahead and use the

mean. But the median is the more informative statistic here, as it will be

for any power law distribution.

36 CHAPTER 2. MATHEMATICAL PRELIMINARIES

3000

P(H)

3000

Hours Hours

P(H)

0.01

Figure 2.4: Two distinct probability distributions with µ= 3000 for the lifespan

of light bulbs: normal (left) and with zero variance (right).

•Mode: The mode is the most frequent element in the data set. This is 7

in our ongoing dice example, because it occurs six times out of thirty-six

elements. Frankly, I’ve never seen the mode as providing much insight

as centrality measure, because it often isn’t close to the center. Samples

measured over a large range should have very few repeated elements or

collisions at any particular value. This makes the mode a matter of hap-

penstance. Indeed, the most frequently occurring elements often reveal

artifacts or anomalies in a data set, such as default values or error codes

that do not really represent elements of the underlying distribution.

The related concept of the peak in a frequency distribution (or histogram)

is meaningful, but interesting peaks only get revealed through proper buck-

eting. The current peak of the annual salary distribution in the United

States lies between $30,000 and $40,000 per year, although the mode pre-

sumably sits at zero.

2.2.2 Variability Measures

The most common measure of variability is the standard deviation σ, which

measures sum of squares diﬀerences between the individual elements and the

mean:

σ=sPn

i=1(ai−¯a)2

n−1

A related statistic, the variance V, is the square of the standard deviation,

i.e. V=σ2. Sometimes it is more convenient to talk about variance than

standard deviation, because the term is eight characters shorter. But they

measure exactly the same thing.

As an example, consider the humble light bulb, which typically comes with

an expected working life, say µ= 3000 hours, derived from some underlying dis-

tribution shown in Figure 2.4. In a conventional bulb, the chance of it lasting

longer than µis presumably about the same as that of it burning out quicker,

and this degree of uncertainty is measured by σ. Alternately, imagine a “printer

2.2. DESCRIPTIVE STATISTICS 37

cartridge bulb,” where the evil manufacturer builds very robust bulbs, but in-

cludes a counter so they can prevent it from ever glowing after 3000 hours of

use. Here µ= 3000 and σ= 0. Both distributions have the same mean, but

substantially diﬀerent variance.

The sum of squares penalty in the formula for σmeans that one outlier value

dunits from the mean contributes as much to the variance as d2points each

one unit from the mean, so the variance is very sensitive to outliers.

An often confusing matter concerns the denominator in the formula for stan-

dard deviation. Should we divide by nor n−1? The diﬀerence here is technical.

The standard deviation of the full population divides by n, whereas the standard

deviation of the sample divides by n−1. The issue is that sampling just one

point tells us absolutely nothing about the underlying variance in any popu-

lation, where it is perfectly reasonable to say there is zero variance in weight

among the population of a one-person island. But for reasonable-sized data sets

n≈(n−1), so it really doesn’t matter.

2.2.3 Interpreting Variance

Repeated observations of the same phenomenon do not always produce the

same results, due to random noise or error. Sampling errors result when our

observations capture unrepresentative circumstances, like measuring rush hour

traﬃc on weekends as well as during the work week. Measurement errors reﬂect

the limits of precision inherent in any sensing device. The notion of signal

to noise ratio captures the degree to which a series of observations reﬂects a

quantity of interest as opposed to data variance. As data scientists, we care

about changes in the signal instead of the noise, and such variance often makes

this problem surprisingly diﬃcult.

I think of variance as an inherent property of the universe, akin to the speed

of light or the time-value of money. Each morning you weigh yourself on a scale

you are guaranteed to get a diﬀerent number, with changes reﬂecting when you

last ate (sampling error), the ﬂatness of the ﬂoor, or the age of the scale (both

measurement error) as much as changes in your body mass (actual variation).

So what is your real weight?

Every measured quantity is subject to some level of variance, but the phe-

nomenon cuts much deeper than that. Much of what happens in the world is

just random ﬂuctuations or arbitrary happenstance causing variance even when

the situation is unchanged. Data scientists seek to explain the world through

data, but distressingly often there is no real phenomena to explain, only a ghost

created by variance. Examples include:

•The stock market: Consider the problem of measuring the relative “skill”

of diﬀerent stock market investors. We know that Warren Buﬀet is much

better at investing than we are. But very few professional investors prove

consistently better than others. Certain investment vehicles wildly out-

perform the market in any given time period. However, the hot fund one

38 CHAPTER 2. MATHEMATICAL PRELIMINARIES

Figure 2.5: Sample variance on hitters with a real 30% success rate results in a

wide range of observed performance even over 500 trials per season.

year usually underperforms the market the year after, which shouldn’t

happen if this outstanding performance was due to skill rather than luck.

The fund managers themselves are quick to credit proﬁtable years to their

own genius, but losses to unforeseeable circumstances. However, several

studies have shown that the performance of professional investors is es-

sentially random, meaning there is little real diﬀerence in skill. Most

investors are paying managers for previously-used luck. So why do these

entrail-readers get paid so much money?

•Sports performance: Students have good semesters and bad semesters, as

reﬂected by their grade point average (GPA). Athletes have good and bad

seasons, as reﬂected by their performance and statistics. Do such changes

reﬂect genuine diﬀerences in eﬀort and ability, or are they just variance?

In baseball, .300 hitters (players who hit with a 30% success rate) represent

consistency over a full season. Batting .275 is not a noteworthy season,

but hit .300 and you are a star. Hit .325 and you are likely to be the

batting champion.

Figure 2.5 shows the results of a simple simulation, where random numbers

were used to decide the outcome of each at-bat over a 500 at-bats/season.

Our synthetic player is a real .300 hitter, because we programmed it to

report a hit with probability 300/1000 (0.3). The results show that a real

.300 hitter has a 10% chance of hitting .275 or below, just by chance.

Such a season will typically be explained away by injuries or maybe the

inevitable eﬀects of age on athletic performance. But it could just be

natural variance. Smart teams try to acquire a good hitter after a lousy

season, when the price is cheaper, trying to take advantage of this variance.

Our .300 hitter also has a 10% chance of batting above .325, but you

2.2. DESCRIPTIVE STATISTICS 39

can be pretty sure that they will ascribe such a breakout season to their

improved conditioning or training methods instead of the fact they just

got lucky. Good or bad season, or lucky/unlucky: it is hard to tell the

signal from the noise.

•Model performance: As data scientists, we will typically develop and eval-

uate several models for each predictive challenge. The models may range

from very simple to complex, and vary in their training conditions or

parameters.

Typically the model with the best accuracy on the training corpus will

be paraded triumphantly before the world as the right one. But small

diﬀerences in the performance between models is likely explained by sim-

ple variance rather than wisdom: which training/evaluation pairs were

selected, how well parameters were optimized, etc.

Remember this when it comes to training machine learning models. In-

deed, when asked to choose between models with small performance dif-

ferences between them, I am more likely to argue for the simplest model

than the one with the highest score. Given a hundred people trying to

predict heads and tails on a stream of coin tosses, one of them is guar-

anteed to end up with the most right answers. But there is no reason to

believe that this fellow has any better predictive powers than the rest of

us.

2.2.4 Characterizing Distributions

Distributions do not necessarily have much probability mass exactly at the

mean. Consider what your wealth would look like after you borrow $100 million,

and then bet it all on an even money coin ﬂip. Heads you are now $100 million

in clear, tails you are $100 million in hock. Your expected wealth is zero, but

this mean does not tell you much about the shape of your wealth distribution.

However, taken together the mean and standard deviation do a decent job

of characterizing any distribution. Even a relatively small amount of mass

positioned far from the mean would add a lot to the standard deviation, so a

small value of σimplies the bulk of the mass must be near the mean.

To be precise, regardless of how your data is distributed, at least (1 −

(1/k2))th of the mass must lie within ±kstandard deviations of the mean.

This means that at least 75% of all the data must lie within 2σof the mean,

and almost 89% within 3σfor any distribution.

We will see that even tighter bounds hold when we know the distribution is

well-behaved, like the Gaussian or normal distribution. But this is why it is a

great practice to report both µand σwhenever you talk about averages. The

average height of adult women in the United States is 63.7±2.7 inches, meaning

µ= 63.7 and σ= 2.7. The average temperature in Orlando, Fl is 60.3 degrees

Fahrenheit. However, there have been many more 100 degree days at Disney

World than 100 inch (8.33 foot) women visiting to enjoy them.

40 CHAPTER 2. MATHEMATICAL PRELIMINARIES

Take-Home Lesson: Report both the mean and standard deviation to charac-

terize your distribution, written as µ±σ.

2.3 Correlation Analysis

Suppose we are given two variables xand y, represented by a sample of npoints

of the form (xi, yi), for 1 ≤i≤n. We say that xand yare correlated when the

value of xhas some predictive power on the value of y.

The correlation coeﬃcient r(X, Y ) is a statistic that measures the degree

to which Yis a function of X, and vice versa. The value of the correlation

coeﬃcient ranges from −1 to 1, where 1 means fully correlated and 0 implies

no relation, or independent variables. Negative correlations imply that the

variables are anti-correlated, meaning that when Xgoes up, Ygoes down.

Perfectly anti-correlated variables have a correlation of −1. Note that nega-

tive correlations are just as good for predictive purposes as positive ones. That

you are less likely to be unemployed the more education you have is an example

of a negative correlation, so the level of education can indeed help predict job

status. Correlations around 0 are useless for forecasting.

Observed correlations drives many of the predictive models we build in data

science. Representative strengths of correlations include:

•Are taller people more likely to remain lean? The observed correlation

between height and BMI is r=−0.711, so height is indeed negatively

correlated with body mass index (BMI).3

•Do standardized tests predict the performance of students in college? The

observed correlation between SAT scores and freshmen GPA is r= 0.47,

so yes, there is some degree of predictive power. But social economic

status is just as strongly correlated with SAT scores (r= 0.42).4

•Does ﬁnancial status aﬀect health? The observed correlation between

household income and the prevalence of coronary artery disease is r=

−0.717, so there is a strong negative correlation. So yes, the wealthier

you are, the lower your risk of having a heart attack.5

•Does smoking aﬀect health? The observed correlation between a group’s

propensity to smoke and their mortality rate is r= 0.716, so for G-d’s

sake, don’t smoke.6

3https://onlinecourses.science.psu.edu/stat500/node/60

4https://research.collegeboard.org/sites/default/files/publications/2012/9/

researchreport-2009-1-socioeconomic-status-sat-freshman-gpa-analysis-data.pdf

5http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3457990/.

6http://lib.stat.cmu.edu/DASL/Stories/SmokingandCancer.html.

2.3. CORRELATION ANALYSIS 41

•Do violent video games increase aggressive behavior? The observed cor-

relation between play and violence is r= 0.19, so there is a weak but

signiﬁcant correlation.7

This section will introduce the primary measurements of correlation. Fur-

ther, we study how to appropriately determine the strength and power of any

observed correlation, to help us understand when the connections between vari-

ables are real.

2.3.1 Correlation Coeﬃcients: Pearson and Spearman Rank

In fact, there are two primary statistics used to measure correlation. Mercifully,

both operate on the same −1 to 1 scale, although they measure somewhat

diﬀerent things. These diﬀerent statistics are appropriate in diﬀerent situations,

so you should be aware of both of them.

The Pearson Correlation Coeﬃcient

The more prominent of the two statistics is Pearson correlation, deﬁned as

r=Pn

i=1(Xi−¯

X)(Yi−¯

qPn

i=1(Xi−¯

X)2qPn

i=1(Yi−¯

Y)2

=Cov(X, Y )

σ(X)σ(Y)

Let’s parse this equation. Suppose Xand Yare strongly correlated. Then

we would expect that when xiis greater than the mean ¯

X, then yishould be

bigger than its mean ¯

Y. When xiis lower than its mean, yishould follow. Now

look at the numerator. The sign of each term is positive when both values are

above (1 ×1) or below (−1×−1) their respective means. The sign of each term

is negative ((−1×1) or (1 ×−1)) if they move in opposite directions, suggesting

negative correlation. If Xand Ywere uncorrelated, then positive and negative

terms should occur with equal frequency, oﬀsetting each other and driving the

value to zero.

The numerator’s operation determining the sign of the correlation is so useful

that we give it a name, covariance, computed:

Cov(X, Y ) =

i=1

(Xi−¯

X)(Yi−¯

Y).

Remember covariance: we will see it again in Section 8.2.3.

The denominator of the Pearson formula reﬂects the amount of variance in

the two variables, as measured by their standard deviations. The covariance

between Xand Ypotentially increases with the variance of these variables, and

this denominator is the magic amount to divide it by to bring correlation to a

−1 to 1 scale.

7http://webspace.pugetsound.edu/facultypages/cjones/chidev/Paper/Articles/

Anderson-Aggression.pdf.

42 CHAPTER 2. MATHEMATICAL PRELIMINARIES

Figure 2.6: The function y=|x|does not have a linear model, but seems like it

should be easily ﬁtted despite weak correlations.

The Spearman Rank Correlation Coeﬃcient

The Pearson correlation coeﬃcient deﬁnes the degree to which a linear predictor

of the form y=m·x+bcan ﬁt the observed data. This generally does a good job

measuring the similarity between the variables, but it is possible to construct

pathological examples where the correlation coeﬃcient between Xand Yis zero,

yet Yis completely dependent on (and hence perfectly predictable from) X.

Consider points of the form (x, |x|), where xis uniformly (or symmetrically)

sampled from the interval [−1,1] as shown in Figure 2.6. The correlation will

be zero because for every point (x, x) there will be an oﬀsetting point (−x, x),

yet y=|x|is a perfect predictor. Pearson correlation measures how well the

best linear predictors can work, but says nothing about weirder functions like

absolute value.

The Spearman rank correlation coeﬃcient essentially counts the number of

pairs of input points which are out of order. Suppose that our data set contains

points (x1, y1) and (x2, y2) where x1< x2and y1< y2. This is a vote that

the values are positively correlated, whereas the vote would be for a negative

correlation if y2< y1.

Summing up over all pairs of points and normalizing properly gives us Spear-

man rank correlation. Let rank(xi) be the rank position of xiin sorted order

among all xi, so the rank of the smallest value is 1 and the largest value n. Then

ρ= 1 −6Pd2

n(n2−1)

where di=rank(xi)−rank(yi).

The relationship between our two coeﬃcients is better delineated by the

example in Figure 2.7. In addition to giving high scores to non-linear but

monotonic functions, Spearman correlation is less sensitive to extreme outlier

elements than Pearson. Let p= (x1, ymax) be the data point with largest value

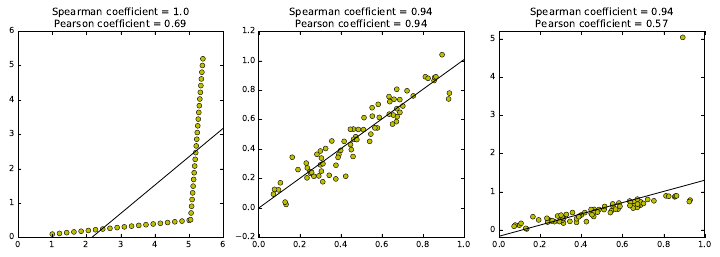
2.3. CORRELATION ANALYSIS 43

Figure 2.7: A monotonic but not linear point set has a Spearman coeﬃcient

r= 1 even though it has no good linear ﬁt (left). Highly-correlated sequences

are recognized by both coeﬃcients (center), but the Pearson coeﬃcient is much

more sensitive to outliers (right).

of yin a given data set. Suppose we replace pwith p0= (x1,∞). The Pearson

correlation will go crazy, since the best ﬁt now becomes the vertical line x=x1.

But the Spearman correlation will be unchanged, since all the points were under

p, just as they are now under p0.

2.3.2 The Power and Signiﬁcance of Correlation

The correlation coeﬃcient rreﬂects the degree to which xcan be used to predict

yin a given sample of points S. As |r| → 1, these predictions get better and

better.

But the real question is how this correlation will hold up in the real world,

outside the sample. Stronger correlations have larger |r|, but also involve sam-

ples of enough points to be signiﬁcant. There is a wry saying that if you want

to ﬁt your data by a straight line, it is best to sample it at only two points.

Your correlation becomes more impressive the more points it is based on.

The statistical limits in interpreting correlations are presented in Figure 2.8,

based on strength and size:

•Strength of correlation: R2: The square of the sample correlation coef-

ﬁcient r2estimates the fraction of the variance in Yexplained by Xin

a simple linear regression. The correlation between height and weight is

approximately 0.8, meaning it explains about two thirds of the variance.

Figure 2.8 (left) shows how rapidly r2decreases with r. There is a pro-

found limit to how excited we should get about establishing a weak corre-

lation. A correlation of 0.5 possesses only 25% of the maximum predictive

power, and a correlation of r= 0.1 only 1%. Thus the predictive value of

correlations decreases rapidly with r.

What do we mean by “explaining the variance”? Let f(x) = mx+cbe the

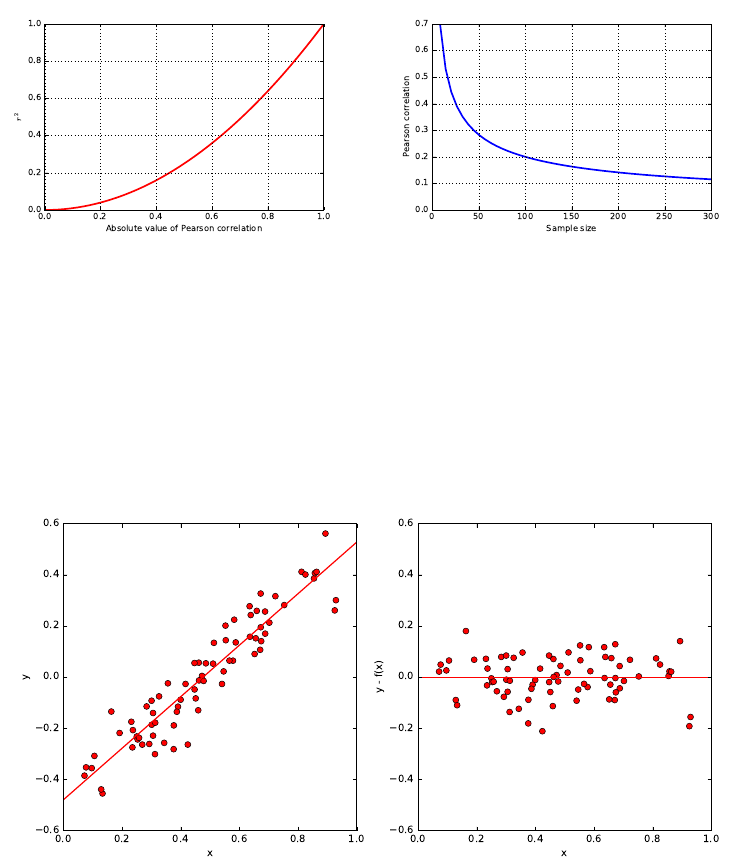
44 CHAPTER 2. MATHEMATICAL PRELIMINARIES

Figure 2.8: Limits in interpreting signiﬁcance. The r2value shows that weak

correlations explain only a small fraction of the variance (left). The level of cor-

relation necessary to be statistically signiﬁcance decreases rapidly with sample

size n(right).

Figure 2.9: Plotting ri=yi−f(xi) shows that the residual values have lower

variance and mean zero. The original data points are on the left, with the

corresponding residuals on the right.

2.3. CORRELATION ANALYSIS 45

predictive value of yfrom x, with the parameters mand ccorresponding

to the best possible ﬁt. The residual values ri=yi−f(xi) will have mean

zero, as shown in Figure 2.9. Further, the variance of the full data set

V(Y) should be much larger than V(r) if there is a good linear ﬁt f(x).

If xand yare perfectly correlated, there should be no residual error, and

V(r) = 0. If xand yare totally uncorrelated, the ﬁt should contribute

nothing, and V(y)≈V(r). Generally speaking, 1 −r2=V(r)/V (y).

Consider Figure 2.9, showing a set of points (left) admitting a good linear

ﬁt, with correlation r= 0.94. The corresponding residuals ri=yi−f(xi)

are plotted on the right. The variance of the yvalues on the left V(y) =

0.056, substantially greater than the variance V(r)=0.0065 on the right.

Indeed,

1−r2= 0.116 ←→ V(r)/V (y)=0.116.

•Statistical signiﬁcance: The statistical signiﬁcance of a correlation depends

upon its sample size nas well as r. By tradition, we say that a correlation

of npoints is signiﬁcant if there is an α≤1/20 = 0.05 chance that we

would observe a correlation as strong as rin any random set of npoints.

This is not a particularly strong standard. Even small correlations become

signiﬁcant at the 0.05 level with large enough sample sizes, as shown in

Figure 2.8 (right). A correlation of r= 0.1 becomes signiﬁcant at α=

0.05 around n= 300, even though such a factor explains only 1% of the

variance.

Weak but signiﬁcant correlations can have value in big data models involving

large numbers of features. Any single feature/correlation might explain/predict

only small eﬀects, but taken together a large number of weak but independent

correlations may have strong predictive power. Maybe. We will discuss signiﬁ-

cance again in greater detail in Section 5.3.

2.3.3 Correlation Does Not Imply Causation!

You have heard this before: correlation does not imply causation:

•The number of police active in a precinct correlate strongly with the local

crime rate, but the police do not cause the crime.

•The amount of medicine people take correlates with the probability they

are sick, but the medicine does not cause the illness.

At best, the implication works only one way. But many observed correlations

are completely spurious, with neither variable having any real impact on the

other.

Still, correlation implies causation is a common error in thinking, even among

those who understand logical reasoning. Generally speaking, few statistical tools

are available to tease out whether Areally causes B. We can conduct controlled

experiments, if we can manipulate one of the variables and watch the eﬀect on

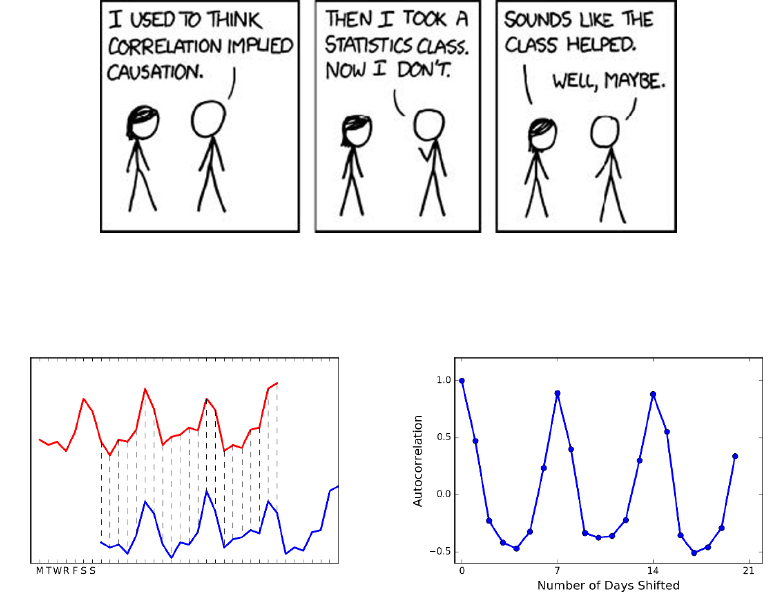
46 CHAPTER 2. MATHEMATICAL PRELIMINARIES

Figure 2.10: Correlation does not imply causation. (Source https://www.xkcd.

com/552.)

Figure 2.11: Cyclic trends in a time series (left) are revealed through correlating

it against shifts of itself (right) .

the other. For example, the fact that we can put people on a diet that makes

them lose weight without getting shorter is convincing evidence that weight does

not cause height. But it is often harder to do these experiments the other way,

e.g. there is no reasonable way to make people shorter other than by hacking

oﬀ limbs.

2.3.4 Detecting Periodicities by Autocorrelation

Suppose a space alien was hired to analyze U.S. sales at a toy company. Instead

of a nice smooth function showing a consistent trend, they would be astonished

to see a giant bump every twelfth month, every year. This alien would have

discovered the phenomenon of Christmas.

Seasonal trends reﬂect cycles of a ﬁxed duration, rising and falling in a reg-

ular pattern. Many human activities proceed with a seven-day cycle associated

with the work week. Large populations of a type of insect called a cicada emerge

on a 13-year or 17-year cycle, in an eﬀort to prevent predators from learning to

2.4. LOGARITHMS 47

eat them.

How can we recognize such cyclic patterns in a sequence S? Suppose we

correlate the values of Siwith Si+p, for all 1 ≤i≤n−p. If the values are in sync

for a particular period length p, then this correlation with itself will be unusually

high relative to other possible lag values. Comparing a sequence to itself is called

an autocorrelation, and the series of correlations for all 1 ≤k≤n−1 is called

the autocorrelation function. Figure 2.11 presents a time series of daily sales,

and the associated autocorrelation function for this data. The peak at a shift of

seven days (and every multiple of seven days) establishes that there is a weekly

periodicity in sales: more stuﬀ gets sold on weekends.

Autocorrelation is an important concept in predicting future events, because

it means we can use previous observations as features in a model. The heuristic

that tomorrow’s weather will be similar to today’s is based on autocorrelation,

with a lag of p= 1 days. Certainly we would expect such a model to be

more accurate than predictions made on weather data from six months ago (lag

p= 180 days).

Generally speaking, the autocorrelation function for many quantities tends

to be highest for very short lags. This is why long-term predictions are less accu-

rate than short-term forecasts: the autocorrelations are generally much weaker.

But periodic cycles do sometimes stretch much longer. Indeed, a weather fore-

cast based on a lag of p= 365 days will be much better than one of p= 180,

because of seasonal eﬀects.

Computing the full autocorrelation function requires calculating n−1 diﬀer-

ent correlations on points of the time series, which can get expensive for large n.

Fortunately, there is an eﬃcient algorithm based on the fast Fourier transform

(FFT), which makes it possible to construct the autocorrelation function even

for very long sequences.

2.4 Logarithms

The logarithm is the inverse exponential function y=bx, an equation that can

be rewritten as x= logby. This deﬁnition is the same as saying that

blogby=y.

Exponential functions grow at a very fast rate: consider b={21,22,23,24, . . .}.

In contrast, logarithms grow a very slow rate: these are just the exponents of

the previous series {1,2,3,4, . . .}. They are associated with any process where

we are repeatedly multiplying by some value of b, or repeatedly dividing by b.

Just remember the deﬁnition:

y= logbx←→ by=x.

Logarithms are very useful things, and arise often in data analysis. Here

I detail three important roles logarithms play in data science. Surprisingly,

only one of them is related to the seven algorithmic applications of logarithms

48 CHAPTER 2. MATHEMATICAL PRELIMINARIES

I present in The Algorithm Design Manual [Ski08]. Logarithms are indeed very

useful things.

2.4.1 Logarithms and Multiplying Probabilities

Logarithms were ﬁrst invented as an aide to computation, by reducing the prob-

lem of multiplication to that of addition. In particular, to compute the product

p=x·y, we could compute the sum of the logarithms s= logbx+ logbyand

then take the inverse of the logarithm (i.e. raising bto the sth power) to get p,

because:

p=x·y=b(logbx+logby).

This is the trick that powered the mechanical slide rules that geeks used in the

days before pocket calculators.

However, this idea remains important today, particularly when multiplying

long chains of probabilities. Probabilities are small numbers. Thus multiplying

long chains of probability yield very small numbers that govern the chances of

very rare events. There are serious numerical stability problems with ﬂoating

point multiplication on real computers. Numerical errors will creep in, and will

eventually overwhelm the true value of small-enough numbers.

Summing the logarithms of probabilities is much more numerically stable

than multiplying them, but yields an equivalent result because:

i=1

pi=bP, where P=

i=1

logb(pi).

We can raise our sum to an exponential if we need the real probability, but

usually this is not necessary. When we just need to compare two probabilities

to decide which one is larger we can safely stay in log world, because bigger

logarithms correspond to bigger probabilities.

There is one quirk to be aware of. Recall that the log2(1

2) = −1. The

logarithms of probabilities are all negative numbers except for log(1) = 0. This

is the reason why equations with logs of probabilities often feature negative

signs in strange places. Be on the lookout for them.

2.4.2 Logarithms and Ratios

Ratios are quantities of the form a/b. They occur often in data sets either as

elementary features or values derived from feature pairs. Ratios naturally occur

in normalizing data for conditions (i.e. weight after some treatment over the

initial weight) or time (i.e. today’s price over yesterday’s price).

But ratios behave diﬀerently when reﬂecting increases than decreases. The

ratio 200/100 is 200% above baseline, but 100/200 is only 50% below despite

being a similar magnitude change. Thus doing things like averaging ratios is

committing a statistical sin. Do you really want a doubling followed by a halving

to average out as an increase, as opposed to a neutral change?

2.4. LOGARITHMS 49

Figure 2.12: Plotting ratios on a scale cramps the space allocated to small ratios

relative to large ratios (left). Plotting the logarithms of ratios better represents

the underlying data (right).

One solution here would have been to use the geometric mean. But better is

taking the logarithm of these ratios, so that they yield equal displacement, since

log22 = 1 and log2(1/2) = −1. We get the extra bonus that a unit ratio maps

to zero, so positive and negative numbers correspond to improper and proper

ratios, respectively.

A rookie mistake my students often make involves plotting the value of ratios

instead of their logarithms. Figure 2.12 (left) is a graph from a student paper,

showing the ratio of new score over old score on data over 24 hours (each red

dot is the measurement for one hour) on four diﬀerent data sets (each given a

row). The solid black line shows the ratio of one, where both scores give the

same result. Now try to read this graph: it isn’t easy because the points on the

left side of the line are cramped together in a narrow strip. What jumps out at

you are the outliers. Certainly the new algorithm does terrible on 7UM917 in

the top row: that point all the way to the right is a real outlier.

Except that it isn’t. Now look at Figure 2.12 (right), where we plot the

logarithms of the ratios. The space devoted to left and right of the black line

can now be equal. And it shows that this point wasn’t really such an outlier at

all. The magnitude of improvement of the leftmost points is much greater than

that of the rightmost points. This plot reveals that new algorithm generally

makes things better, only because we are showing logs of ratios instead of the

ratios themselves.

2.4.3 Logarithms and Normalizing Skewed Distributions

Variables which follow symmetric, bell-shaped distributions tend to be nice as

features in models. They show substantial variation, so they can be used to

discriminate between things, but not over such a wide range that outliers are

overwhelming.

But not every distribution is symmetric. Consider the one in Figure 2.13

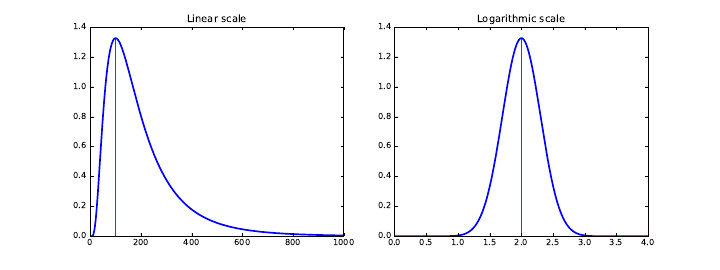
50 CHAPTER 2. MATHEMATICAL PRELIMINARIES

Figure 2.13: Hitting a skewed data distribution (left) with a log often yields a

more bell-shaped distribution (right).

(left). The tail on the right goes much further than the tail on the left. And

we are destined to see far more lopsided distributions when we discuss power

laws, in Section 5.1.5. Wealth is representative of such a distribution, where

the poorest human has zero or perhaps negative wealth, the average person

(optimistically) is in the thousands of dollars, and Bill Gates is pushing $100

billion as of this writing.

We need a normalization to convert such distributions into something easier

to deal with. To ring the bell of a power law distribution we need something

non-linear, that reduces large values to a disproportionate degree compared to

more modest values.

The logarithm is the transformation of choice for power law variables. Hit

your long-tailed distribution with a log and often good things happen. The

distribution in Figure 2.13 happened to be the log normal distribution, so taking

the logarithm yielded a perfect bell-curve on right. Taking the logarithm of

variables with a power law distribution brings them more in line with traditional

distributions. For example, as an upper-middle class professional, my wealth is

roughly the same number of logs from my starving students as I am from Bill

Gates!

Sometimes taking the logarithm proves too drastic a hit, and a less dramatic

non-linear transformation like the square root works better to normalize a dis-

tribution. The acid test is to plot a frequency distribution of the transformed

values and see if it looks bell-shaped: grossly-symmetric, with a bulge in the

middle. That is when you know you have the right function.

2.5 War Story: Fitting Designer Genes

The word bioinformatician is life science speak for “data scientist,” the prac-

titioner of an emerging discipline which studies massive collections of DNA

sequence data looking for patterns. Sequence data is very interesting to work

2.5. WAR STORY: FITTING DESIGNER GENES 51

with, and I have played bioinformatician in research projects since the very

beginnings of the human genome project.

DNA sequences are strings on the four letter alphabet {A, C, G, T }. Proteins

form the stuﬀ that we are physically constructed from, and are composed of

strings of 20 diﬀerent types of molecular units, called amino acids. Genes are

the DNA sequences which describe exactly how to make speciﬁc proteins, with

the units each described by a triplet of {A, C, G, T }s called codons.

For our purposes, it suﬃces to know that there are a huge number of possible

DNA sequences describing genes which could code for any particular desired

protein sequence. But only one of them is used. My biologist collaborators and

I wanted to know why.

Originally, it was assumed that all of these diﬀerent synonymous encodings

were essentially identical, but statistics performed on sequence data made it

clear that certain codons are used more often than others. The biological con-

clusion is that “codons matter,” and there are good biological reasons why this

should be.

We became interested in whether “neighboring pairs of codon matter.” Per-

haps certain pairs of triples are like oil and water, and hate to mix. Certain

letter pairs in English have order preferences: you see the bigram gh far more

often than hg. Maybe this is true of DNA as well? If so, there would be pairs

of triples which should be underrepresented in DNA sequence data.

To test this, we needed a score comparing the number of times we actually

see a particular triple (say x=CAT ) next to another particular triple (say

y=GAG) to what we would expect by chance. Let F(xy) be the frequency

of xy, number of times we actually see codon xfollowed by codon yin the

DNA sequence database. These codons code for speciﬁc amino acids, say a

and brespectively. For amino acid a, the probability that it will be coded by

xis P(x) = F(x)/F (a), and similarly P(y) = F(y)/F (b). Then the expected

number of times of seeing xy is

Expected(xy) = F(x)

F(a)F(y)

F(b)F(ab)

Based on this, we can compute a codon pair score for any given hexamer xy

as follows:

CP S(xy) = ln Observed(xy)

Expected(xy)= ln 



F(xy)

F(x)F(y)

F(a)F(b)F(ab)



Taking the logarithm of this ratio produced very nice properties. Most im-

portantly, the sign of the score distinguished over-represented pairs from under-

represented pairs. Because the magnitudes were symmetric (+1 was just as

impressive as −1) we could add or average these scores in a sensible way to give

a score for each gene. We used these scores to design genes that should be bad

for viruses, which gave an exciting new technology for making vaccines. See the

chapter notes (Section 2.6) for more details.

52 CHAPTER 2. MATHEMATICAL PRELIMINARIES

Figure 2.14: Patterns in DNA sequences with the lowest codon pair scores

become obvious on inspection. When interpreted in-frame, the stop symbol

TAG is substantially depleted (left). When interpreted in the other two frames,

the most avoided patterns are all very low complexity, like runs of a single base

(right)

Knowing that certain pairs of codons were bad did not explain why they were

bad. But by computing two related scores (details unimportant) and sorting

the triplets based on them, as shown in Figure 2.14, certain patterns popped

out. Do you notice the patterns? All the bad sequences on the left contain

T AG, which turns out to be a special codon that tells the gene to stop. And

all the bad sequences on the right consist of Cand Gin very simple repetitive

sequences. These explain biologically why patterns are avoided by evolution,

meaning we discovered something very meaningful about life.

There are two take-home lessons from this story. First, developing numerical

scoring functions which highlight speciﬁc aspects of items can be very useful

to reveal patterns. Indeed, Chapter 4 will focus on the development of such

systems. Second, hitting such quantities with a logarithm can make them even

more useful, enabling us to see the forest for the trees.

2.6 Chapter Notes

There are many excellent introductions to probability theory available, including

[Tij12, BT08]. The same goes for elementary statistics, with good introductory

texts including [JWHT13, Whe13]. The brief history of probability theory in

this chapter is based on Weaver [Wea82].

In its strongest form, the eﬃcient market hypothesis states that the stock

market is essentially unpredictable using public information. My personal advice

is that you should invest in index funds that do not actively try to predict the

direction of the market. Malkiel’s A Random Walk Down Wall Street [Mal99]

2.7. EXERCISES 53

is an excellent introduction to such investment thinking.

The Fast Fourier Transform (FFT) provides an O(nlog n) time algorithm to

compute the full autocorrelation function of an n-element sequence, where the

straightforward computation of ncorrelations takes O(n2). Bracewell [Bra99]

and Brigham [Bri88] are excellent introductions to Fourier transforms and the

FFT. See also the exposition in Press et.al. [PFTV07].

The comic strip in Figure 2.10 comes from Randall Munroe’s webcomic xkcd,

speciﬁcally https://xkcd.com/552, and is reprinted with permission.

The war story of Section 2.5 revolves around our work on how the phe-

nomenon of codon pair bias aﬀects gene translation. Figure 2.14 comes from

my collaborator Justin Gardin. See [CPS+08, MCP+10, Ski12] for discussions

of how we exploited codon pair bias to design vaccines for viral diseases like

polio and the ﬂu.

2.7 Exercises

Probability

2-1. [3] Suppose that 80% of people like peanut butter, 89% like jelly, and 78% like

both. Given that a randomly sampled person likes peanut butter, what is the

probability that she also likes jelly?

2-2. [3] Suppose that P(A) = 0.3 and P(B) = 0.7.

(a) Can you compute P(Aand B) if you only know P(A) and P(B)?

(b) Assuming that events Aand Barise from independent random processes:

•What is P(Aand B)?

•What is P(Aor B)?

•What is P(A|B)?

2-3. [3] Consider a game where your score is the maximum value from two dice.

Compute the probability of each event from {1,...,6}.

2-4. [8] Prove that the cumulative distribution function of the maximum of a pair of

values drawn from random variable Xis the square of the original cumulative

distribution function of X.

2-5. [5] If two binary random variables Xand Yare independent, are ¯

X(the com-

plement of X) and Yalso independent? Give a proof or a counterexample.

Statistics

2-6. [3] Compare each pair of distributions to decide which one has the greater

mean and the greater standard deviation. You do not need to calculate the

actual values of µand σ, just how they compare with each other.

(a) i. 3,5,5,5,8,11,11,11,13.

ii. 3,5,5,5,8,11,11,11,20.

(b) i. −20,0,0,0,15,25,30,30.

ii. −40,0,0,0,15,25,30,30.

54 CHAPTER 2. MATHEMATICAL PRELIMINARIES

ii. 20,22,24,26,28,30.

(d) i. 100,200,300,400,500.

ii. 0,50,300,550,600.

2-7. [3] Construct a probability distribution where none of the mass lies within one

σof the mean.

2-8. [3] How does the arithmetic and geometric mean compare on random integers?

2-9. [3] Show that the arithmetic mean equals the geometric mean when all terms

are the same.

Correlation Analysis

2-10. [3] True or false: a correlation coeﬃcient of −0.9 indicates a stronger linear

relationship than a correlation coeﬃcient of 0.5. Explain why.

2-11. [3] What would be the correlation coeﬃcient between the annual salaries of

college and high school graduates at a given company, if for each possible job

title the college graduates always made:

(a) $5,000 more than high school grads?

(b) 25% more than high school grads?

2-12. [3] What would be the correlation between the ages of husbands and wives if

men always married woman who were:

(a) Three years younger than themselves?

(b) Two years older than themselves?

2-13. [5] Use data or literature found in a Google search to estimate/measure the

strength of the correlation between:

(a) Hits and walks scored for hitters in baseball.

(b) Hits and walks allowed by pitchers in baseball.

2-14. [5] Compute the Pearson and Spearman Rank correlations for uniformly drawn

samples of points (x, xk). How do these values change as a function of increasing

Logarithms

2-15. [3] Show that the logarithm of any number less than 1 is negative.

2-16. [3] Show that the logarithm of zero is undeﬁned.

2-17. [5] Prove that

x·y=b(logbx+logby)

2-18. [5] Prove the correctness of the formula for changing a base-blogarithm to base-

a, that

loga(x) = logb(x)/logb(a).

2.7. EXERCISES 55

Implementation Projects

2-19. [3] Find some interesting data sets, and compare how similar their means and

medians are. What are the distributions where the mean and median diﬀer on

the most?

2-20. [3] Find some interesting data sets and search all pairs for interesting correla-

tions. Perhaps start with what is available at http://www.data-manual.com/

data. What do you ﬁnd?

Interview Questions

2-21. [3] What is the probability of getting exactly kheads on ntosses, where the

coin has a probability of pin coming up heads on each toss? What about kor

more heads?

2-22. [5] Suppose that the probability of getting a head on the ith toss of an ever-

changing coin is f(i). How would you eﬃciently compute the probability of

getting exactly kheads in ntosses?

2-23. [5] At halftime of a basketball game you are oﬀered two possible challenges:

(a) Take three shots, and make at least two of them.

(b) Take eight shots, and make at least ﬁve of them.

Which challenge should you pick to have a better chance of winning the game?

2-24. [3] Tossing a coin ten times resulted in eight heads and two tails. How would

you analyze whether a coin is fair? What is the p-value?

2-25. [5] Given a stream of nnumbers, show how to select one uniformly at random

using only constant storage. What if you don’t know nin advance?

2-26. [5] Ak-streak starts at toss iin a sequence of ncoin ﬂips when the outcome of the

ith ﬂip and the next k−1 ﬂips are identical. For example, sequence HTTTHH

contains 2-streaks starting at the second, third, and ﬁfth tosses. What are the

expected number of k-streaks that you will see in ntosses of a fair coin ?

2-27. [5] A person randomly types an eight-digit number into a pocket calculator.

What is the probability that the number looks the same even if the calculator

is turned upside down?

2-28. [3] You play a dice rolling game where you have two choices:

(a) Roll the dice once and get rewarded with a prize equal to the outcome

number (e.g, $3 for number “3”) and then stop the game.

(b) You can reject the ﬁrst reward according to its outcome and roll the dice

a second time, and get rewarded in the same way.

Which strategy should you choose to maximize your reward? That is, for what

outcomes of the ﬁrst roll should you chose to play the second game? What is

the statistical expectation of reward if you choose the second strategy?

2-29. [3] What is A/B testing and how does it work?

2-30. [3] What is the diﬀerence between statistical independence and correlation?

2-31. [3] We often say that correlation does not imply causation. What does this

mean?

56 CHAPTER 2. MATHEMATICAL PRELIMINARIES

2-32. [5] What is the diﬀerence between a skewed distribution and a uniform one?

Kaggle Challenges

2-33. Cause–eﬀect pairs: correlation vs. causation.

https://www.kaggle.com/c/cause-effect-pairs

2-34. Predict the next “random number” in a sequence.

https://www.kaggle.com/c/random-number-grand-challenge

2-35. Predict the fate of animals at a pet shelter.

https://www.kaggle.com/c/shelter-animal-outcomes

Chapter 3

Data Munging

On two occasions I have been asked, “Pray, Mr. Babbage, if you put

into the machine wrong ﬁgures, will the right answers come out?”

. . . I am not able rightly to apprehend the kind of confusion of ideas

that could provoke such a question.

– Charles Babbage

Most data scientists spend much of their time cleaning and formatting data.

The rest spend most of their time complaining that there is no data available

to do what they want to do.

In this chapter, we will work through some of the basic mechanics of com-

puting with data. Not the high-faluting stuﬀ like statistics or machine learning,

but the grunt work of ﬁnding data and cleaning it that goes under the moniker

of data munging.

While practical questions like “What is the best library or programming

language available?” are clearly important, the answers change so rapidly that

a book like this one is the wrong place to address them. So I will stick at the

level of general principles, instead of shaping this book around a particular set

of software tools. Still, we will discuss the landscape of available resources in

this chapter: why they exist, what they do, and how best to use them.

The ﬁrst step in any data science project is getting your hands on the right

data. But this is often distressingly hard. This chapter will survey the richest

hunting grounds for data resources, and then introduce techniques for cleaning

what you kill. Wrangling your data so you that can safely analyze it is critical

for meaningful results. As Babbage himself might have said more concisely,

“garbage in, garbage out.”

3.1 Languages for Data Science

In theory, every suﬃciently powerful programming language is capable of ex-

pressing any algorithm worth computing. But in practice, certain programming

58 CHAPTER 3. DATA MUNGING

languages prove much better than others at speciﬁc tasks. Better here might

denote easier for the programmer or perhaps more computationally eﬃcient,

depending upon the mission at hand.

The primary data science programming languages to be aware of are:

•Python: This is today’s bread-and-butter programming language for data

science. Python contains a variety of language features to make basic

data munging easier, like regular expressions. It is an interpreted lan-

guage, making the development process quicker and enjoyable. Python

is supported by an enormous variety of libraries, doing everything from

scraping to visualization to linear algebra and machine learning.

Perhaps the biggest strike against Python is eﬃciency: interpreted lan-

guages cannot compete with compiled ones for speed. But Python compil-

ers exist in a fashion, and support linking in eﬃcient C/assembly language

libraries for computationally-intensive tasks. Bottom line, Python should

probably be your primary tool in working through the material we present

in this book.

•Perl: This used to be the go to language for data munging on the web,

before Python ate it for lunch. In the TIOBE programming language pop-

ularity index (http://www.tiobe.com/tiobe-index), Python ﬁrst ex-

ceeded Perl in popularity in 2008 and hasn’t looked back. There are several

reasons for this, including stronger support for object-oriented program-

ming and better available libraries, but the bottom line is that there are

few good reasons to start projects in Perl at this point. Don’t be surprised

if you encounter it in some legacy project, however.

•R: This is the programming language of statisticians, with the deepest

libraries available for data analysis and visualization. The data science

world is split between R and Python camps, with R perhaps more suit-

able for exploration and Python better for production use. The style of

interaction with R is somewhat of an acquired taste, so I encourage you

to play with it a bit to see whether it feels natural to you.

Linkages exist between R and Python, so you can conveniently call R

library functions in Python code. This provides access to advanced statis-

tical methods, which may not be supported by the native Python libraries.

•Matlab: The Mat here stands for matrix, as Matlab is a language de-

signed for the fast and eﬃcient manipulation of matrices. As we will see,

many machine learning algorithms reduce to operations on matrices, mak-

ing Matlab a natural choice for engineers programming at a high-level of

abstraction.

Matlab is a proprietary system. However, much of its functionality is

available in GNU Octave, an open-source alternative.

3.1. LANGUAGES FOR DATA SCIENCE 59

•Java and C/C++: These mainstream programming languages for the

development of large systems are important in big data applications. Par-

allel processing systems like Hadoop and Spark are based on Java and

C++, respectively. If you are living in the world of distributed comput-

ing, then you are living in a world of Java and C++ instead of the other

languages listed here.

•Mathematica/Wolfram Alpha: Mathematica is a proprietary system pro-

viding computational support for all aspects of numerical and symbolic

mathematics, built upon the less proprietary Wolfram programming lan-

guage. It is the foundation of the Wolfram Alpha computational knowl-

edge engine, which processes natural language-like queries through a mix

of algorithms and pre-digested data sources. Check it out at http://www.

wolframalpha.com.

I will confess a warm spot for Mathematica.1It is what I tend to reach

for when I am doing a small data analysis or simulation, but cost has

traditionally put it out of the range of many users. The release of the

Wolfram language perhaps now opens it up to a wider community.

•Excel: Spreadsheet programs like Excel are powerful tools for exploratory

data analysis, such as playing with a given data set to see what it contains.

They deserve our respect for such applications.

Full featured spreadsheet programs contain a surprising amount of hidden

functionality for power users. A student of mine who rose to become a

Microsoft executive told me that 25% of all new feature requests for Excel

proposed functionality already present there. The special functions and

data manipulation features you want probably are in Excel if you look

hard enough, in the same way that a Python library for what you need

probably will be found if you search for it.

3.1.1 The Importance of Notebook Environments

The primary deliverable for a data science project should not be a program. It

should not be a data set. It should not be the results of running the program

on your data. It should not just be a written report.

The deliverable result of every data science project should be a computable

notebook tying together the code, data, computational results, and written

analysis of what you have learned in the process. Figure 3.1 presents an excerpt

from a Jupyter/IPython notebook, showing how it integrates code, graphics,

and documentation into a descriptive document which can be executed like a

program.

The reason this is so important is that computational results are the product

of long chains of parameter selections and design decisions. This creates several

problems that are solved by notebook computing environments:

1Full disclosure: I have known Stephen Wolfram for over thirty years. Indeed, we invented

the iPad together [Bar10, MOR+88].

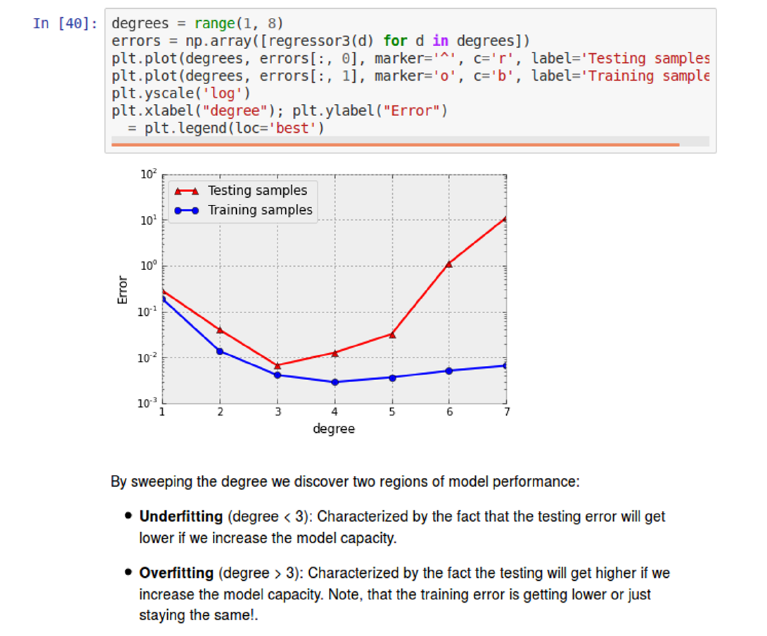
60 CHAPTER 3. DATA MUNGING

Figure 3.1: Jupyter/IPython notebooks tie together code, computational re-

sults, and documentation.

3.1. LANGUAGES FOR DATA SCIENCE 61

•Computations need to be reproducible. We must be able to run the same

programs again from scratch, and get exactly the same result. This means

that data pipelines must be complete: taking raw input and producing the

ﬁnal output. It is terrible karma to start with a raw data set, do some

processing, edit/format the data ﬁles by hand, and then do some more

processing – because what you did by hand cannot be readily done again

on another data set, or undone after you realize that you may have goofed

up.

•Computations must be tweakable. Often reconsideration or evaluation will

prompt a change to one or more parameters or algorithms. This requires

rerunning the notebook to produce the new computation. There is nothing

more disheartening to be given a big data product without provenance and

told that this is the ﬁnal result and you can’t change anything. A notebook

is never ﬁnished until after the entire project is done.

•Data pipelines need to be documented. That notebooks permit you to

integrate text and visualizations with your code provides a powerful way

to communicate what you are doing and why, in ways that traditional

programming environments cannot match.

Take-Home Lesson: Use a notebook environment like IPython or Mathematica

to build and report the results of any data science project.

3.1.2 Standard Data Formats

Data comes from all sorts of places, and in all kinds of formats. Which represen-

tation is best depends upon who the ultimate consumer is. Charts and graphs

are marvelous ways to convey the meaning of numerical data to people. Indeed,

Chapter 6 will focus on techniques for visualizing data. But these pictures are

essentially useless as a source of data to compute with. There is a long way

from printed maps to Google Maps.

The best computational data formats have several useful properties:

•They are easy for computers to parse: Data written in a useful format is

destined to be used again, elsewhere. Sophisticated data formats are often

supported by APIs that govern technical details ensuring proper format.

•They are easy for people to read: Eyeballing data is an essential operation

in many contexts. Which of the data ﬁles in this directory is the right one

for me to use? What do we know about the data ﬁelds in this ﬁle? What

is the gross range of values for each particular ﬁeld?

These use cases speak to the enormous value of being able to open a data

ﬁle in a text editor to look at it. Typically, this means presenting the

data in a human-readable text-encoded format, with records demarcated

by separate lines, and ﬁelds separated by delimiting symbols.

62 CHAPTER 3. DATA MUNGING

•They are widely used by other tools and systems: The urge to invent

proprietary data standard beats ﬁrmly in the corporate heart, and most

software developers would rather share a toothbrush than a ﬁle format.

But these are impulses to be avoided. The power of data comes from

mixing and matching it with other data resources, which is best facilitated

by using popular standard formats.

One property I have omitted from this list is conciseness, since it is generally

not a primary concern for most applications running on modern computing

systems. The quest to minimize data storage costs often works against other

goals. Cleverly packing multiple ﬁelds into the higher-order bits of integers saves

space, but at the cost of making it incompatible and unreadable.

General compression utilities like gzip prove amazingly good at removing the

redundancy of human-friendly formatting. Disk prices are unbelievably cheap:

as I write this you can buy a 4TB drive for about $100, meaning less than the

cost of one hour of developer time wasted programming a tighter format. Unless

you are operating at the scale of Facebook or Google, conciseness does not have

nearly the importance you are liable to think it does.2

The most important data formats/representations to be aware of are dis-

cussed below:

•CSV (comma separated value) ﬁles: These ﬁles provide the simplest, most

popular format to exchange data between programs. That each line repre-

sents a single record, with ﬁelds separated by commas, is obvious from in-

spection. But subtleties revolve around special characters and text strings:

what if your data about names contains a comma, like “Thurston Howell,

Jr.” The csv format provides ways to escape code such characters so they

are not treated as delimiters, but it is messy. A better alternative is to

use a rarer delimiter character, as in tsv or tab separated value ﬁles.

The best test of whether your csv ﬁle is properly formatted is whether

Microsoft Excel or some other spreadsheet program can read it without

hassle. Make sure the results of every project pass this test as soon as the

ﬁrst csv ﬁle has been written, to avoid pain later.

•XML (eXtensible Markup Language): Structured but non-tabular data

are often written as text with annotations. The natural output of a

named-entity tagger for text wraps the relevant substrings of a text in

brackets denoting person, place, or thing. I am writing this book in La-

Tex, a formatting language with bracketing commands positioned around

mathematical expressions and italicized text. All webpages are written in

HTML, the hypertext markup language which organizes documents using

bracketing commands like <b> and </b> to enclose bold faced text.

XML is a language for writing speciﬁcations of such markup languages. A

proper XML speciﬁcation enables the user to parse any document comply-

ing with the speciﬁcation. Designing such speciﬁcations and fully adhering

2Indeed, my friends at Google assure me that they are often slovenly about space even at

the petabyte scale.

3.1. LANGUAGES FOR DATA SCIENCE 63

to them requires discipline, but is worthwhile. In the ﬁrst version of our

Lydia text analysis system, we wrote our markups in a “pseudo-XML,”

read by ad hoc parsers that handled 99% of the documents correctly but

broke whenever we tried to extend them. After a painful switch to XML,

everything worked more reliably and more eﬃciently, because we could

deploy fast, open-source XML parsers to handle all the dirty work of en-

forcing our speciﬁcations.

•SQL (structured query language) databases: Spreadsheets are naturally

structured around single tables of data. In contrast, relational databases

prove excellent for manipulating multiple distinct but related tables, using

SQL to provide a clunky but powerful query language.

Any reasonable database system imports and exports records as either csv

or XML ﬁles, as well as an internal content dump. The internal represen-

tation in databases is opaque, so it really isn’t accurate to describe them

as a data format. Still, I emphasize them here because SQL databases

generally prove a better and more powerful solution than manipulating

multiple data ﬁles in an ad hoc manner.

•JSON (JavaScript Object Notation): This is a format for transmitting data

objects between programs. It is a natural way to communicate the state of

variables/data structures from one system to another. This representation

is basically a list of attribute-value pairs corresponding to variable/ﬁeld

names, and the associated values:

{"employees":[

{"firstName":"John", "lastName":"Doe"},

{"firstName":"Anna", "lastName":"Smith"},

{"firstName":"Peter", "lastName":"Jones"}

]}

Because library functions that support reading and writing JSON objects

are readily available in all modern programming languages, it has become

a very convenient way to store data structures for later use. JSON objects

are human readable, but are quite cluttered-looking, representing arrays of

records compared to CSV ﬁles. Use them for complex structured objects,

but not simple tables of data.

•Protocol buﬀers: These are a language/platform-neutral way of serializing

structured data for communications and storage across applications. They

are essentially lighter weight versions of XML (where you deﬁne the format

of your structured data), designed to communicate small amounts of data

across programs like JSON. This data format is used for much of the inter-

machine communication at Google. Apache Thrift is a related standard,

used at Facebook.

64 CHAPTER 3. DATA MUNGING

3.2 Collecting Data

The most critical issue in any data science or modeling project is ﬁnding the

right data set. Identifying viable data sources is an art, one that revolves around

three basic questions:

•Who might actually have the data I need?

•Why might they decide to make it available to me?

•How can I get my hands on it?

In this section, we will explore the answers to these questions. We look at

common sources of data, and what you are likely to be able to ﬁnd and why.

We then review the primary mechanisms for getting access, including APIs,

scraping, and logging.

3.2.1 Hunting

Who has the data, and how can you get it? Some of the likely suspects are

reviewed below.

Companies and Proprietary Data Sources

Large companies like Facebook, Google, Amazon, American Express, and Blue

Cross have amazing amounts of exciting data about users and transactions,

data which could be used to improve how the world works. The problem is that

getting outside access is usually impossible. Companies are reluctant to share

data for two good reasons:

•Business issues, and the fear of helping their competition.

•Privacy issues, and the fear of oﬀending their customers.

A heartwarming tale of what can happen with corporate data release oc-

curred when AOL provided academics with a data set of millions of queries to

its search engine, carefully stripped of identifying information. The ﬁrst thing

the academics discovered was that the most frequently-entered queries were des-

perate attempts to escape to other search engines like Google. This did nothing

to increase public conﬁdence in the quality of AOL search.

Their second discovery was that it proved much harder to anonymize search

queries than had previously been suspected. Sure you can replace user names

with id numbers, but it is not that hard to ﬁgure out who the guy on Long Island

repeatedly querying Steven Skiena,Stony Brook, and https://twitter.com/

search?q=Skiena&src=sprv is. Indeed, as soon as it became publicized that

people’s identities had been revealed by this data release, the responsible party

was ﬁred and the data set disappeared. User privacy is important, and ethical

issues around data science will be discussed in Section 12.7.

3.2. COLLECTING DATA 65

So don’t think you are going to sweet talk companies into releasing conﬁden-

tial user data. However, many responsible companies like The New York Times,

Twitter, Facebook, and Google do release certain data, typically by rate-limited

application program interfaces (APIs). They generally have two motives:

•Providing customers and third parties with data that can increase sales.

For example, releasing data about query frequency and ad pricing can

encourage more people to place ads on a given platform.

•It is generally better for the company to provide well-behaved APIs than

having cowboys repeatedly hammer and scrape their site.

So hunt for a public API before reading Section 3.2.2 on scraping. You won’t

ﬁnd exactly the content or volume that you dream of, but probably something

that will suﬃce to get started. Be aware of limits and terms of use.

Other organizations do provide bulk downloads of interesting data for oﬀ-

line analysis, as with the Google Ngrams, IMDb, and the taxi fare data sets

discussed in Chapter 1. Large data sets often come with valuable metadata,

such as book titles, image captions, and edit history, which can be re-purposed

with proper imagination.

Finally, most organizations have internal data sets of relevance to their busi-

ness. As an employee, you should be able to get privileged access while you

work there. Be aware that companies have internal data access policies, so you

will still be subject to certain restrictions. Violating the terms of these policies

is an excellent way to become an ex-employee.

Government Data Sources

Collecting data is one of the important things that governments do. Indeed,

the requirement that the United States conduct a census of its population is

mandated by our constitution, and has been running on schedule every ten

years since 1790.

City, state, and federal governments have become increasingly committed

to open data, to facilitate novel applications and improve how government can

fulﬁll its mission. The website http://Data.gov is an initiative by the federal

government to centrally collect its data sources, and at last count points to over

100,000 data sets!

Government data diﬀers from industrial data in that, in principle, it belongs

to the People. The Freedom of Information Act (FOI) enables any citizen to

make a formal request for any government document or data set. Such a request

triggers a process to determine what can be released without compromising the

national interest or violating privacy.

State governments operate under ﬁfty diﬀerent sets of laws, so data that is

tightly held in one jurisdiction may be freely available in others. Major cities

like New York have larger data processing operations than many states, again

with restrictions that vary by location.

66 CHAPTER 3. DATA MUNGING

I recommend the following way of thinking about government records. If

you cannot ﬁnd what you need online after some snooping around, ﬁgure out

which agency is likely to have it. Make a friendly call to them to see if they

can help you ﬁnd what you want. But if they stonewall you, feel free to try for

a FOI act request. Preserving privacy is typically the biggest issue in deciding

whether a particular government data set can be released.

Academic Data Sets

There is a vast world of academic scholarship, covering all that humanity has

deemed worth knowing. An increasing fraction of academic research involves

the creation of large data sets. Many journals now require making source data

available to other researchers prior to publication. Expect to be able to ﬁnd

vast amounts of economic, medical, demographic, historical, and scientiﬁc data

if you look hard enough.

The key to ﬁnding these data sets is to track down the relevant papers.

There is an academic literature on just about any topic of interest. Google

Scholar is the most accessible source of research publications. Search by topic,

and perhaps “Open Science” or “data.” Research publications will typically

provide pointers to where its associated data can be found. If not, contacting

the author directly with a request should quickly yield the desired result.

The biggest catch with using published data sets is that someone else has

worked hard to analyze them before you got to them, so these previously mined

sources may have been sucked dry of interesting new results. But bringing fresh

questions to old data generally opens new possibilities.

Often interesting data science projects involve collaborations between re-

searchers from diﬀerent disciplines, such as the social and natural sciences.

These people speak diﬀerent languages than you do, and may seem intimidating

at ﬁrst. But they often welcome collaboration, and once you get past the jargon

it is usually possible to understand their issues on a reasonable level without

specialized study. Be assured that people from other disciplines are generally

not any smarter than you are.

Sweat Equity

Sometimes you will have to work for your data, instead of just taking it from

others. Much historical data still exists only in books or other paper documents,

thus requiring manual entry and curation. A graph or table might contain

information that we need, but it can be hard to get numbers from a graphic

locked in a PDF (portable document format) ﬁle.

I have observed that computationally-oriented people vastly over-estimate

the amount of eﬀort it takes to do manual data entry. At one record per minute,

you can easily enter 1,000 records in only two work days. Instead, computational

people tend to devote massive eﬀorts trying to avoid such grunt work, like

hunting in vain for optical character recognition (OCR) systems that don’t make

3.2. COLLECTING DATA 67

a mess of the ﬁle, or spending more time cleaning up a noisy scan than it would

take to just type it in again fresh.

A middle ground here comes in paying someone else to do the dirty work for

you. Crowdsourcing platforms like Amazon Turk and CrowdFlower enable you

to pay for armies of people to help you extract data, or even collect it in the

ﬁrst place. Tasks requiring human annotation like labeling images or answering

surveys are particularly good use of remote workers. Crowdsourcing will be

discussed in greater detail in Section 3.5.

Many amazing open data resources have been built up by teams of contrib-

utors, like Wikipedia, Freebase, and IMDb. But there is an important concept

to remember: people generally work better when you pay them.

3.2.2 Scraping

Webpages often contain valuable text and numerical data, which we would like

to get our hands on. For example, in our project to build a gambling system

for the sport of jai-alai, we needed to feed our system the results of yesterday’s

matches and the schedule of what games were going on today. Our solution

was to scrape the websites of jai-alai betting establishments, which posted this

information for their fans.

There are two distinct steps to make this happen, spidering and scraping:

•Spidering is the process of downloading the right set of pages for analysis.

•Scraping is the ﬁne art of stripping this content from each page to prepare

it for computational analysis.

The ﬁrst thing to realize is that webpages are generally written in simple-to-

understand formatting languages like HTML and/or JavaScript. Your browser

knows these languages, and interprets the text of the webpage as a program

to specify what to display. By calling a function that emulates/pretends to

be a web browser, your program can download any webpage and interpret the

contents for analysis.

Traditionally, scraping programs were site-speciﬁc scripts hacked up to look

for particular HTML patterns ﬂanking the content of interest. This exploited the

fact that large numbers of pages on speciﬁc websites are generated by programs

themselves, and hence highly predictable in their format. But such scripts tend

to be ugly and brittle, breaking whenever the target website tinkers with the

internal structure of its pages.

Today, libraries in languages like Python (see BeautifulSoup) make it easier

to write robust spiders and scrapers. Indeed, someone else probably has already

written a spider/scraper for every popular website and made it available on

SourceForge or Github, so search before you code.

Certain spidering missions may be trivial, for example, hitting a single URL

(uniform resource locator) at regular time intervals. Such patterns occur in mon-

itoring, say, the sales rank of this book from its Amazon page. Somewhat more

sophisticated approaches to spidering are based on the name regularity of the

68 CHAPTER 3. DATA MUNGING

underlying URLs. If all the pages on a site are speciﬁed by the date or product

ID number, for example http://www.amazon.com/gp/product/1107041376/,

iterating through the entire range of interesting values becomes just a matter

of counting.

The most advanced form of spidering is web crawling, where you systemat-

ically traverse all outgoing links from a given root page, continuing recursively

until you have visited every page on the target website. This is what Google does

in indexing the web. You can do it too, with enough patience and easy-to-ﬁnd

web crawling libraries in Python.

Please understand that politeness limits how rapidly you should spider/crawl

a given website. It is considered bad form to hit a site more than once a second,

and indeed best practices dictate that providers block access to the people who

are hammering them.

Every major website contains a terms of service document that restricts what

you can legally do with any associated data. Generally speaking, most sites will

leave you alone provided you don’t hammer them, and do not redistribute any

data you scrape. Understand that this is an observation, not a legal opinion.

Indeed, read about the Aaron Schwartz case, where a well-known Internet ﬁg-

ure was brought up on serious criminal charges for violating terms of services

in spidering/scraping journal articles, and literally hounded to death. If you

are attempting a web-scraping project professionally, be sure that management

understands the terms of service before you get too creative with someone else’s

property.

3.2.3 Logging

If you own a potential data source, treat it like you own it. Internal access to

a web service, communications device, or laboratory instrument grants you the

right and responsibility to log all activity for downstream analysis.

Amazing things can be done with ambient data collection from weblogs

and sensing devices, soon destined to explode with the coming “Internet of

Things.” The accelerometers in cell phones can be used to measure the strength

of earthquakes, with the correlation of events within a region suﬃcient to ﬁlter

out people driving on bumpy roads or leaving their phones in a clothes dryer.

Monitoring the GPS data of a ﬂeet of taxi cabs tracks traﬃc congestion on

city streets. Computational analysis of image and video streams opens the

door to countless applications. Another cool idea is to use cameras as weather

instruments, by looking at the color of the sky in the background of the millions

of photographs uploaded to photo sites daily.

The primary reason to instrument your system to collect data is because

you can. You might not know exactly what to do with it now, but any well-

constructed data set is likely to become of value once it hits a certain critical

mass of size.

Current storage costs make clear just how low a barrier it is to instrument a

system. My local Costco is currently selling three terabyte disk drive for under

$100, which is Big O of nothing. If each transaction record takes 1 kilobyte (one

3.3. CLEANING DATA 69

thousand characters), this device in principle has room for 3 billion records,

roughly one for every two people on earth.

The important considerations in designing any logging system are:

•Build it to endure with limited maintenance. Set it and forget it, by

provisioning it with enough storage for unlimited expansion, and a backup.

•Store all ﬁelds of possible value, without going crazy.

•Use a human-readable format or transactions database, so you can un-

derstand exactly what is in there when the time comes, months or years

later, to sit down and analyze your data.

3.3 Cleaning Data

“Garbage in, garbage out” is the fundamental principle of data analysis. The

road from raw data to a clean, analyzable data set can be a long one.

Many potential issues can arise in cleaning data for analysis. In this section,

we discuss identifying processing artifacts and integrating diverse data sets. Our

focus here is the processing before we do our real analysis, to make sure that

the garbage never gets in in the ﬁrst place.

Take-Home Lesson: Savvy painting restorers only do things to the original that

are reversible. They never do harm. Similarly, data cleaning is always done

on a copy of the original data, ideally by a pipeline that makes changes in a

systematic and repeatable way.

3.3.1 Errors vs. Artifacts

Under ancient Jewish law, if a suspect on trial was unanimously found guilty

by all judges, then this suspect would be acquitted. The judges had noticed

that unanimous agreement often indicates the presence of a systemic error in

the judicial process. They reasoned that when something seems too good to be

true, a mistake has likely been made somewhere.

If we view data items as measurements about some aspect of the world,

data errors represent information that is fundamentally lost in acquisition. The

Gaussian noise blurring the resolution of our sensors represents error, precision

which has been permanently lost. The two hours of missing logs because the

server crashed represents data error: it is information which cannot be recon-

structed again.

By contrast, artifacts are generally systematic problems arising from pro-

cessing done to the raw information it was constructed from. The good news is

that processing artifacts can be corrected, so long as the original raw data set

remains available. The bad news is that these artifacts must be detected before

they can be corrected.

70 CHAPTER 3. DATA MUNGING

Figure 3.2: What artifacts can you ﬁnd in this time series, counting the number

of author’s names ﬁrst appearing in the scientiﬁc literature each year?

The key to detecting processing artifacts is the “sniﬀ test,” examining the

product closely enough to get a whiﬀ of something bad. Something bad is usually

something unexpected or surprising, because people are naturally optimists.

Surprising observations are what data scientists live for. Indeed, such insights

are the primary reason we do what we do. But in my experience, most surprises

turn out to be artifacts, so we must look at them skeptically.

Figure 3.2 presents computational results from a project where we investi-

gated the process of scientiﬁc publication. It shows a time series of the 100,000

most proliﬁc authors, binned according to the year of their ﬁrst paper appearing

in Pubmed, an essentially complete bibliography of the biomedical literature.

Study this ﬁgure closely, and see if you can discover any artifacts worth

commenting on. I see at least two of them. Extra credit will be awarded if you

can ﬁgure out what caused the problem.

The key to ﬁnding artifacts is to look for anomalies in the data, that con-

tradict what you expect to see. What should the distribution in the number of

virgin authors look like, and how should it change over time? First, construct

a prior distribution of what you expect to see, so that you can then properly

evaluate potential anomalies against it.

My intuition says that the distribution of new top scientists should be pretty

ﬂat, because new stars are born with every successive class of graduate students.

I would also guess that there may be a gradual drift upward as population

expands, and more people enter the scientiﬁc community. But that’s not what

I see in Figure 3.2. So try to enumerate what the anomalies/potential artifacts

are. . .

I see two big bumps when I look at Figure 3.2: a left bump starting around

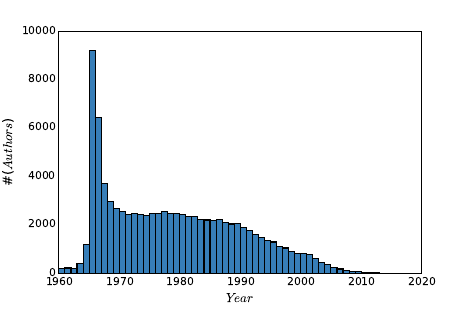
3.3. CLEANING DATA 71

Figure 3.3: The cleaned data removes these artifacts, and the resulting distri-

bution looks correct.

1965, and a peak which explodes in 2002. On reﬂection, the leftmost bump

makes sense. This left peak occurs the year when Pubmed ﬁrst started to

systematically collect bibliographic records. Although there is some very in-

complete data from 1960–1964, most older scientists who had been publishing

papers for several years would “emerge” only with the start of systematic records

in 1965. So this explains the left peak, which then settles down by 1970 to what

looks like the ﬂat distribution we expected.

But what about that giant 2002 peak? And the decline in new authors to

almost zero in the years which precede it? A similar decline is also visible to

the right of the big peak. Were all the world’s major scientists destined to be

born in 2002?

A careful inspection of the records in the big peak revealed the source of

the anomaly: ﬁrst names. In the early days of Pubmed, authors were identiﬁed

by their initials and last names. But late in 2001, SS Skiena became Steven S.

Skiena, so it looked like a new author emerging from the heavens.

But why the declines to nothingness to the left and right of this peak? Recall

that we limited this study to the 100,000 most proliﬁc scientists. A scientiﬁc

rock star emerging in 1998 would be unlikely to appear in this ranking because

their name was doomed to change a few years later, not leaving enough time

to accumulate a full career of papers. Similar things happen at the very right

of the distribution: newly created scientists in 2010 would never be able to

achieve a full career’s work in only a couple of years. Both phenomena are

neatly explained by this ﬁrst name basis.

Cleaning this data to unify name references took us a few iterations to get

right. Even after eliminating the 2002 peak, we still saw a substantial dip in

prominent scientists starting their careers in the mid 1990s. This was because

many people who had a great half career pre-ﬁrst names and a second great

half career post-ﬁrst names did not rise to the threshold of a great full career

72 CHAPTER 3. DATA MUNGING

in either single period. Thus we had to match all the names in the full before

identifying who were the top 100,000 scientists.

Figure 3.3 shows our ﬁnal distribution of authors, which matches the pla-

tonic ideal of what we expected the distribution to be. Don’t be too quick to

rationalize away how your data looks coming out of the computer. My collabo-

rators were at one point ready to write oﬀ the 2002 bump as due to increases in

research funding or the creation of new scientiﬁc journals. Always be suspicious

of whether your data is clean enough to trust.

3.3.2 Data Compatibility

We say that a comparison of two items is “apples to apples” when it is fair com-

parison, that the items involved are similar enough that they can be meaning-

fully stood up against each other. In contrast, “apples to oranges” comparisons

are ultimately meaningless. For example:

•It makes no sense to compare weights of 123.5 against 78.9, when one is

in pounds and the other is in kilograms.

•It makes no sense to directly compare the movie gross of Gone with the

Wind against that of Avatar, because 1939 dollars are 15.43 times more

valuable than 2009 dollars.

•It makes no sense to compare the price of gold at noon today in New York

and London, because the time zones are ﬁve hours oﬀ, and the prices

aﬀected by intervening events.

•It makes no sense to compare the stock price of Microsoft on February 17,

2003 to that of February 18, 2003, because the intervening 2-for-1 stock

split cut the price in half, but reﬂects no change in real value.

These types of data comparability issues arise whenever data sets are merged.

Here I hope to show you how insidious such comparability issues can be, to

sensitize you as to why you need to be aware of them. Further, for certain

important classes of conversions I point to ways to deal with them.

Take-Home Lesson: Review the meaning of each of the ﬁelds in any data set

you work with. If you do not understand what’s in there down to the units of

measurement, there is no sensible way you can use it.

Unit Conversions

Quantifying observations in physical systems requires standard units of measure-

ment. Unfortunately there exist many functionally equivalent but incompatible

systems of measurement. My 12-year old daughter and I both weigh about 70,

but one of us is in pounds and the other in kilograms.

3.3. CLEANING DATA 73

Disastrous things like rocket explosions happen when measurements are en-

tered into computer systems using the wrong units of measurement. In par-

ticular, NASA lost the $125 million Mars Climate Orbiter space mission on

September 23, 1999 due to a metric-to-English conversion issue.

Such problems are best addressed by selecting a single system of measure-

ments and sticking to it. The metric system oﬀers several advantages over the

traditional English system. In particular, individual measurements are naturally

expressed as single decimal quantities (like 3.28 meters) instead of incomparable

pairs of quantities (5 feet, 8 inches). This same issue arises in measuring angles

(radians vs. degrees/seconds) and weight (kilograms vs. pounds/oz).

Sticking to the metric system does not by itself solve all comparability is-

sues, since there is nothing to prevent you from mixing heights in meters and

centimeters. But it is a good start.

How can you defend yourself against incompatible units when merging data

sets? Vigilance has to be your main weapon. Make sure that you know the

intended units for each numerical column in your data set, and verify compat-

ibility when merging. Any column which does not have an associated unit or

object type should immediately be suspect.

When merging records from diverse sources, it is an excellent practice to

create a new “origin” or “source” ﬁeld to identify where each record came from.

This provides at least the hope that unit conversion mistakes can be corrected

later, by systematically operating on the records from the problematic source.

A partially-automated procedure to detect such problems can be devised

from statistical signiﬁcance testing, to be discussed in Section 5.3. Suppose we

were to plot the frequencies of human heights in a merged data set of English

(feet) and metric (meter) measurements. We would see one peak in the distri-

bution around 1.8 and a second around 5.5. The existence of multiple peaks in a

distribution should make us suspicious. The p-value resulting from signiﬁcance

testing on the two input populations provides a rigorous measurement of the

degree to which our suspicions are validated.

Numerical Representation Conversions

Numerical features are the easiest to incorporate into mathematical models.

Indeed, certain machine learning algorithms such as linear regression and sup-

port vector machines work only with numerically-coded data. But even turning

numbers into numbers can be a subtle problem. Numerical ﬁelds might be rep-

resented in diﬀerent ways: as integers (123), as decimals (123.5), or even as

fractions (123 1/2). Numbers can even be represented as text, requiring the

conversion from “ten million” to 10000000 for numerical processing.

Numerical representation issues can take credit for destroying another rocket

ship. An Ariane 5 rocket launched at a cost of $500 million on June 4, 1996

exploded forty seconds after lift-oﬀ, with the cause ultimately ascribed to an

unsuccessful conversion of a 64-bit ﬂoating point number to a 16-bit integer.

The distinction between integers and ﬂoating point (real) numbers is impor-

tant to maintain. Integers are counting numbers: quantities which are really

74 CHAPTER 3. DATA MUNGING

discrete should be represented as integers. Physically measured quantities are

never precisely quantiﬁed, because we live in a continuous world. Thus all mea-

surements should be reported as real numbers. Integer approximations of real

numbers are sometimes used in a misbegotten attempt to save space. Don’t do

this: the quantiﬁcation eﬀects of rounding or truncation introduces artifacts.

In one particularly clumsy data set we encountered, baby weights were rep-

resented as two integer ﬁelds (pounds and the remaining ounces). Much better

would have been to combine them into a single decimal quantity.

Name Uniﬁcation

Integrating records from two distinct data sets requires them to share a common

key ﬁeld. Names are frequently used as key ﬁelds, but they are often reported

inconsistently. Is Jos´e the same fellow as Jose? Such diacritic marks are banned

from the oﬃcial birth records of several U.S. states, in an aggressive attempt to

force them to be consistent.

As another case in point, databases show my publications as authored by the

Cartesian product of my ﬁrst (Steve,Steven, or S.), middle (Sol,S., or blank),

and last (Skiena) names, allowing for nine diﬀerent variations. And things get

worse if we include misspellings. I can ﬁnd myself on Google with a ﬁrst name

of Stephen and last names of Skienna and Skeina.

Unifying records by key is a very ugly problem, which doesn’t have a magic

bullet. This is exactly why ID numbers were invented, so use them as keys if

you possibly can.

The best general technique is uniﬁcation: doing simple text transformations

to reduce each name to a single canonical version. Converting all strings to

lower case increases the number of (usually correct) collisions. Eliminating

middle names or at least reducing them to an abbreviation creates even more

name matches/collisions, as does mapping ﬁrst names to canonical versions (like

turning all Steves into Stevens).

Any such transformation runs the risk of creating Frankenstein-people, single

records assembled from multiple bodies. Applications diﬀer in whether the

greater danger lies in merging too aggressively or too timidly. Figure out where

your task sits on this spectrum and act accordingly.

An important concern in merging data sets is character code uniﬁcation.

Characters in text strings are assigned numerical representations, with the map-

ping between symbols and number governed by the character code standard.

Unfortunately, there are several diﬀerent character code standards in common

usage, meaning that what you scrape from a webpage might not be in the same

character code as assumed by the system which will process it.

Historically, the good old 7-bit ASCII code standard was expanded to the

8-bit IS0 8859-1 Latin alphabet code, which adds characters and punctuation

marks from several European languages. UTF-8 is an encoding of all Unicode

characters using variable numbers of 8-bit blocks, which is backwards compatible

with ASCII. It is the dominant encoding for web-pages, although other systems

remain in use.

3.3. CLEANING DATA 75

Correctly unifying character codes after merging is pretty much impossible.

You must have the discipline to pick a single code as a standard, and check the

encoding of each input ﬁle on preprocessing, converting it to the target before

further work.

Time/Date Uniﬁcation

Data/time stamps are used to infer the relative order of events, and group events

by relative simultaneity. Integrating event data from multiple sources requires

careful cleaning to ensure meaningful results.

First let us consider issues in measuring time. The clocks from two computers

never exactly agree, so precisely aligning logs from diﬀerent systems requires a

mix of work and guesswork. There are also time zone issues when dealing with

data from diﬀerent regions, as well as diversities in local rules governing changes

in daylight saving time.

The right answer here is to align all time measurements to Coordinated Uni-

versal Time (UTC), a modern standard subsuming the traditional Greenwich

Mean Time (GMT). A related standard is UNIX time, which reports an event’s

precise time in terms of the number of elapsed seconds since 00:00:00 UTC on

Thursday, January 1, 1970.

The Gregorian calendar is common throughout the technology world, al-

though many other calendar systems are in use in diﬀerent countries. Subtle

algorithms must be used to convert between calendar systems, as described in

[RD01]. A bigger problem for date alignment concerns the proper interpretation

of time zones and the international date line.

Time series uniﬁcation is often complicated by the nature of the business

calendar. Financial markets are closed on weekends and holidays, making for

questions of interpretation when you are correlating, say, stock prices to local

temperature. What is the right moment over the weekend to measure tempera-

ture, so as to be consistent with other days of the week? Languages like Python

contain extensive libraries to deal with ﬁnancial time series data to get issues

like this correct. Similar issues arise with monthly data, because months (and

even years) have diﬀerent lengths.

Financial Uniﬁcation

Money makes the world go round, which is why so many data science projects

revolve around ﬁnancial time series. But money can be dirty, so this data

requires cleaning.

One issue here is currency conversion, representing international prices using

a standardized ﬁnancial unit. Currency exchange rates can vary by a few percent

within a given day, so certain applications require time-sensitive conversions.

Conversion rates are not truly standardized. Diﬀerent markets will each have

diﬀerent rates and spreads, the gap between buying and selling prices that cover

the cost of conversion.

76 CHAPTER 3. DATA MUNGING

The other important correction is for inﬂation. The time value of money

implies that a dollar today is (generally) more valuable than a dollar a year

from now, with interest rates providing the right way to discount future dollars.

Inﬂation rates are estimated by tracking price changes over baskets of items,

and provide a way to standardize the purchasing power of a dollar over time.

Using unadjusted prices in a model over non-trivial periods of time is just

begging for trouble. A group of my students once got very excited by the

strong correlation observed between stock prices and oil prices over a thirty-

year period, and so tried to use stock prices in a commodity prediction model.

But both goods were priced in dollars, without any adjustment as they inﬂated.

The time series of prices of essentially any pair of items will correlate strongly

over time when you do not correct for inﬂation.

In fact, the most meaningful way to represent price changes over time is

probably not diﬀerences but returns, which normalize the diﬀerence by the initial

price:

ri=pi+1 −pi

This is more analogous to a percentage change, with the advantage here that

taking the logarithm of this ratio becomes symmetric to gains and losses.

Financial time series contain many other subtleties which require cleaning.

Many stocks give scheduled dividends to the shareholder on a particular date

every year. Say, for example, that Microsoft will pay a $2.50 dividend on Jan-

uary 16. If you own a share of Microsoft at the start of business that day, you

receive this check, so the value of the share then immediately drops by $2.50

the moment after the dividend is issued. This price decline reﬂects no real loss

to the shareholder, but properly cleaned data needs to factor the dividend into

the price of the stock. It is easy to imagine a model trained on uncorrected

price data learning to sell stocks just prior to its issuing dividends, and feeling

unjustly proud of itself for doing so.

3.3.3 Dealing with Missing Values

Not all data sets are complete. An important aspect of data cleaning is iden-

tifying ﬁelds for which data isn’t there, and then properly compensating for

them:

•What is the year of death of a living person?

•What should you do with a survey question left blank, or ﬁlled with an

obviously outlandish value?

•What is the relative frequency of events too rare to see in a limited-size

sample?

Numerical data sets expect a value for every element in a matrix. Setting

missing values to zero is tempting, but generally wrong, because there is always

some ambiguity as to whether these values should be interpreted as data or not.

3.3. CLEANING DATA 77

Is someone’s salary zero because he is unemployed, or did he just not answer

the question?

The danger with using nonsense values as not-data symbols is that they

can get misinterpreted as data when it comes time to build models. A linear

regression model trained to predict salaries from age, education, and gender will

have trouble with people who refused to answer the question.

Using a value like −1 as a no-data symbol has exactly the same deﬁciencies

as zero. Indeed, be like the mathematician who is afraid of negative numbers:

stop at nothing to avoid them.

Take-Home Lesson: Separately maintain both the raw data and its cleaned

version. The raw data is the ground truth, and must be preserved intact for

future analysis. The cleaned data may be improved using imputation to ﬁll in

missing values. But keep raw data distinct from cleaned, so we can investigate

diﬀerent approaches to guessing.

So how should we deal with missing values? The simplest approach is to

drop all records containing missing values. This works just ﬁne when it leaves

enough training data, provided the missing values are absent for non-systematic

reasons. If the people refusing to state their salary were generally those above

the mean, dropping these records will lead to biased results.

But typically we want to make use of records with missing ﬁelds. It can be

better to estimate or impute missing values, instead of leaving them blank. We

need general methods for ﬁlling in missing values. Candidates include:

•Heuristic-based imputation: Given suﬃcient knowledge of the underlying

domain, we should be able to make a reasonable guess for the value of

certain ﬁelds. If I need to ﬁll in a value for the year you will die, guessing

birth year+80 will prove about right on average, and a lot faster than

waiting for the ﬁnal answer.

•Mean value imputation: Using the mean value of a variable as a proxy

for missing values is generally sensible. First, adding more values with

the mean leaves the mean unchanged, so we do not bias our statistics by

such imputation. Second, ﬁelds with mean values add a vanilla ﬂavor to

most models, so they have a muted impact on any forecast made using

the data.

But the mean might not be appropriate if there is a systematic reason

for missing data. Suppose we used the mean death-year in Wikipedia to

impute the missing value for all living people. This would prove disastrous,

with many people recorded as dying before they were actually born.

•Random value imputation: Another approach is to select a random value

from the column to replace the missing value. This would seem to set us up

for potentially lousy guesses, but that is actually the point. Repeatedly

selecting random values permits statistical evaluation of the impact of

imputation. If we run the model ten times with ten diﬀerent imputed

78 CHAPTER 3. DATA MUNGING

values and get widely varying results, then we probably shouldn’t have

much conﬁdence in the model. This accuracy check is particularly valuable

when there is a substantial fraction of values missing from the data set.

•Imputation by nearest neighbor: What if we identify the complete record

which matches most closely on all ﬁelds present, and use this nearest

neighbor to infer the values of what is missing? Such predictions should

be more accurate than the mean, when there are systematic reasons to

explain variance among records.

This approach requires a distance function to identify the most similar

records. Nearest neighbor methods are an important technique in data

science, and will be presented in greater detail in Section 10.2.

•Imputation by interpolation: More generally, we can use a method like

linear regression (see Section 9.1) to predict the values of the target col-

umn, given the other ﬁelds in the record. Such models can be trained over

full records and then applied to those with missing values.

Using linear regression to predict missing values works best when there is

only one ﬁeld missing per record. The potential danger here is creating

signiﬁcant outliers through lousy predictions. Regression models can easily

turn an incomplete record into an outlier, by ﬁlling the missing ﬁelds in

with unusually high or low values. This would lead downstream analysis

to focus more attention on the records with missing values, exactly the

opposite of what we want to do.

Such concerns emphasize the importance of outlier detection, the ﬁnal step

in the cleaning process that will be considered here.

3.3.4 Outlier Detection

Mistakes in data collection can easily produce outliers that can interfere with

proper analysis. An interesting example concerns the largest dinosaur vertebra

ever discovered. Measured at 1500 millimeters, it implies an individual that was

188 feet long. This is amazing, particularly because the second largest specimen

ever discovered comes in at only 122 feet.

The most likely explanation here (see [Gol16]) is that this giant fossil never

actually existed: it has been missing from the American Museum of Natural

History for over a hundred years. Perhaps the original measurement was taken

on a conventionally-sized bone and the center two digits accidentally transposed,

reducing the vertebra down to 1050 millimeters.

Outlier elements are often created by data entry mistakes, as apparently was

the case here. They can also result from errors in scraping, say an irregularity

in formatting causing a footnote number to be interpreted as a numerical value.

Just because something is written down doesn’t make it correct. As with the

dinosaur example, a single outlier element can lead to major misinterpretations.

3.4. WAR STORY: BEATING THE MARKET 79

General sanity checking requires looking at the largest and smallest values

in each variable/column to see whether they are too far out of line. This can

best be done by plotting the frequency histogram and looking at the location of

the extreme elements. Visual inspection can also conﬁrm that the distribution

looks the way it should, typically bell-shaped.

In normally distributed data, the probability that a value is kstandard de-

viations from the mean decreases exponentially with k. This explains why there

are no 10-foot basketball players, and provides a sound threshold to identify

outliers. Power law distributions are less easy to detect outliers in: there really

is a Bill Gates worth over 10,000 times as much as the average individual.

It is too simple to just delete the rows containing outlier ﬁelds and move

on. Outliers often point to more systematic problems that one must deal with.

Consider a data set of historical ﬁgures by lifespan. It is easy to ﬁnger the

biblical Methuselah (at 969 years) as an outlier, and remove him.

But it is better to ﬁgure out whether he is indicative of other ﬁgures that we

should consider removing. Observe that Methuselah had no ﬁrmly established

birth and death dates. Perhaps the published ages of anybody without dates

should be considered suspicious enough to prune. By contrast, the person with

the shortest lifespan in Wikipedia (John I, King of France) lived only ﬁve days.

But his birth (November 15) and death (November 20) dates in 1316 convinces

me that his lifespan was accurate.

3.4 War Story: Beating the Market

Every time we met, my graduate student Wenbin told me we were making

money. But he sounded less and less conﬁdent every time I asked.

Our Lydia sentiment analysis system took in massive text feeds of news and

social media, reducing them to daily time series of frequency and sentiment

for the millions of diﬀerent people, places, and organizations mentioned within.

When somebody wins a sports championship, many articles get written describ-

ing how great an athlete they are. But when this player then gets busted on drug

charges, the tone of the articles about them immediately changes. By keeping

count of the relative frequency of association with positive words (“victorious”)

vs. negative words (“arrested”) in the text stream, we can construct sentiment

signals for any news-worthy entity.

Wenbin studied how sentiment signals could be used to predict future events

like the gross for a given movie, in response to the quality of published reviews

or buzz. But he particularly wanted to use this data to play the stock market.

Stocks move up and down according to news. A missed earnings report is bad

news for a company, so the price goes down. Food and Drug Administration

(FDA) approval of a new drug is great news for the company which owns it, so

the price goes up. If Wenbin could use our sentiment signal to predict future

stock prices, well, let’s just say I wouldn’t have to pay him as a research assistant

anymore.

So he simulated a strategy of buying the stocks that showed the highest

80 CHAPTER 3. DATA MUNGING

sentiment in that day’s news, and then shorting those with the lowest sentiment.

He got great results. “See,” he said. “We are making money.”

The numbers looked great, but I had one quibble. Using today’s news re-

sults to predict current price movements wasn’t really fair, because the event

described in the article may have already moved the price before we had any

chance to read about it. Stock prices should react very quickly to important

news.

So Wenbin simulated the strategy of buying stocks based on sentiment from

the previous day’s news, to create a gap between the observed news and price

changes. The return rate went down substantially, but was still positive. “See,”

he said. “We are still making money.”

But I remained a little uncomfortable with this. Many economists believe

that the ﬁnancial markets are eﬃcient, meaning that all public news is instantly

reﬂected in changing prices. Prices certainly changed in response to news, but

you would not be able to get in fast enough to exploit the information. We had

to remain skeptical enough to make sure there were no data/timing problems

that could explain our results.

So I pressed Wenbin about exactly how he had performed his simulation. His

strategy bought and sold at the closing price every day. But that left sixteen

hours until the next day’s open, plenty of time for the world to react to events

that happened while I slept. He switched his simulated purchase to the opening

price. Again, the return rate went down substantially, but was still positive.

“See,” he said. “We are still making some money.”

But might there still be other artifacts in how we timed our data, giving

us essentially tomorrow’s newspaper today? In good faith, we chased down all

other possibilities we could think of, such as whether the published article dates

reﬂected when they appeared instead of when they were written. After doing

our best to be skeptical, his strategies still seemed to show positive returns from

news sentiment.

Our paper on this analysis [ZS10] has been well received, and Wenbin has

gone on to be a successful quant, using sentiment among other signals to trade

in the ﬁnancial markets. But I remain slightly queasy about this result. Clean-

ing our data to precisely time-stamp each news article was very diﬃcult to do

correctly. Our system was originally designed to produce daily time series in a

batch mode, so it is hard to be sure that we did everything right in the millions

of articles downloaded over several years to now perform ﬁner-scale analysis.

The take-home lesson is that cleanliness is important when there is money

on the line. Further, it is better to design a clean environment at the beginning

of analysis instead of furiously washing up at the end.

3.5 Crowdsourcing

No single person has all the answers. Not even me. Much of what passes for

wisdom is how we aggregate expertise, assembling opinions from the knowledge

and experience of others.

3.5. CROWDSOURCING 81

Figure 3.4: Guess how many pennies I have in this jar? (left) The correct answer

was determined using precise scientiﬁc methods (right).

Crowdsourcing harnesses the insights and labor from large numbers of people

towards a common goal. It exploits the wisdom of crowds, that the collective

knowledge of a group of people might well be greater than that of the smartest

individual among them.

This notion began with an ox. Francis Galton, a founder of statistical science

and a relative of Charles Darwin, attended a local livestock fair in 1906. As part

of the festivities, villagers were invited to guess the weight of this particular ox,

with the person whose guess proved closest to the mark earning a prize. Almost

800 participants took a whack at it. No one picked the actual weight of 1,178

pounds, yet Galton observed that the average guess was amazingly close: 1,179

pounds! Galton’s experiment suggests that for certain tasks one can get better

results by involving a diverse collection of people, instead of just asking the

experts.

Crowdsourcing serves as an important source of data in building models, es-

pecially for tasks associated with human perception. Humans remain the state-

of-the-art system in natural language processing and computer vision, achieving

the highest level of performance. The best way to gather training data often

requires asking people to score a particular text or image. Doing this on a large

enough scale to build substantial training data typically requires a large number

of annotators, indeed a crowd.

Social media and other new technologies have made it easier to collect and

aggregate opinions on a massive scale. But how can we separate the wisdom of

crowds from the cries of the rabble?

3.5.1 The Penny Demo

Let’s start by performing a little wisdom of crowds experiment of our own.

Figure 3.4 contains photos of a jar of pennies I accumulated in my oﬃce over

many years. How many pennies do I have in this jar? Make your own guess

now, because I am going to tell you the answer on the next page.

82 CHAPTER 3. DATA MUNGING

To get the right answer, I had my biologist-collaborator Justin Garden weigh

the pennies on a precision laboratory scale. Dividing by the weight of a single

penny gives the count. Justin can be seen diligently performing his task in

Figure 3.4 (right).

So I ask again: how many pennies do you think I have in this jar? I performed

this experiment on students in my data science class. How will your answer

compare to theirs?

I ﬁrst asked eleven of my students to write their opinions on cards and

quietly pass them up to me at the front of the room. Thus these guesses were

completely independent of each other. The results, sorted for convenience, were:

537, 556, 600, 636, 1200, 1250, 2350, 3000, 5000, 11,000, 15,000.

I then wrote then wrote these numbers on the board, and computed some

statistics. The median of these guesses was 1250, with a mean of 3739. In

fact, there were exactly 1879 pennies in the jar. The median score among my

students was closer to the right amount than any single guess.

But before revealing the actual total, I then asked another dozen students

to guess. The only diﬀerence was that this cohort had seen the guesses from

the ﬁrst set of students written on the board. Their choices were:

750, 750, 1000, 1000, 1000, 1250, 1400, 1770, 1800, 3500, 4000, 5000.

Exposing the cohort to other people’s guesses strongly conditioned the dis-

tribution by eliminating all outliers: the minimum among the second group was

greater than four of the previous guesses, and the maximum less than or equal

to three of the previous round. Within this cohort, the median was 1325 and

the mean 1935. Both happen to be somewhat closer to the actual answer, but

it is clear that group-think had settled in to make it happen.

Anchoring is the well-known cognitive bias that people’s judgments get ir-

rationally ﬁxated on the ﬁrst number they hear. Car dealers exploit this all the

time, initially giving an inﬂated cost for the vehicle so that subsequent prices

sound like a bargain.

I then did one ﬁnal test before revealing the answer. I allowed my students

to bid on the jar, meaning that they had to be conﬁdent enough to risk money

on the result. This yielded exactly two bids from brave students, at 1500 and

2000 pennies respectively. I pocketed $1.21 from the sucker with the high bid,

but both proved quite close. This is not a surprise: people willing to bet their

own money on an event are, by deﬁnition, conﬁdent in their selection.

3.5.2 When is the Crowd Wise?

According to James Surowiecki in his book The Wisdom of Crowds [Sur05],

crowds are wise when four conditions are satisﬁed:

3.5. CROWDSOURCING 83

•When the opinions are independent: Our experiment highlighted how

easy it is for a group to lapse into group-think. People naturally get

inﬂuenced by others. If you want someone’s true opinion, you must ask

them in isolation.

•When crowds are people with diverse knowledge and methods: Crowds

only add information when there is disagreement. A committee composed

of perfectly-correlated experts contributes nothing more than you could

learn from any one of them. In the penny-guessing problem, some people

estimated the volume of the container, while others gauged the sag of my

arm as I lifted the heavy mass. Alternate approaches might have estimated

how many pennies I could have accumulated in twenty years of occasionally

emptying my pockets, or recalled their own hoarding experiences.

•When the problem is in a domain that does not need specialized knowledge:

I trust the consensus of the crowd in certain important decisions, like

which type of car to buy or who should serve as the president of my

country (gulp). But when it comes to deciding whether my tumor sample

is cancerous or benign, I will trust the word of one doctor over a cast of

1,000 names drawn at random from the phone book.

Why? Because the question at hand beneﬁts greatly from specialized

knowledge and experience. There is a genuine reason why the doctor

should know more than all the others. For simpler perceptual tasks the

mob rules, but one must be careful not to ask the crowd something they

have no way of knowing.

•Opinions can be fairly aggregated: The least useful part of any mass

survey form is the open response ﬁeld “Tell us what you think!”. The

problem here is that there is no way to combine these opinions to form

a consensus, because diﬀerent people have diﬀerent issues and concerns.

Perhaps these texts could be put into buckets by similarity, but this is

hard to do eﬀectively.

The most common use of such free-form responses are anecdotal. People

cherry-pick the most positive-sounding ones, then put them on a slide to

impress the boss.

Take-Home Lesson: Be an incomparable element on the partial order of life.

Diverse, independent thinking contributes the most wisdom to the crowd.

3.5.3 Mechanisms for Aggregation

Collecting wisdom from a set of responses requires using the right aggrega-

tion mechanism. For estimating numerical quantities, standard techniques like

plotting the frequency distribution and computing summary statistics are ap-

propriate. Both the mean and median implicitly assume that the errors are

84 CHAPTER 3. DATA MUNGING

symmetrically distributed. A quick look at the shape of the distribution can

generally conﬁrm or reject that hypothesis.

The median is, generally speaking, a more appropriate choice than the mean

in such aggregation problems. It reduces the inﬂuence of outliers, which is a

particular problem in the case of mass experiments where a certain fraction of

your participants are likely to be bozos. On our penny guessing data, the mean

produced a ghastly over-estimate of 3739, which reduced to 2843 after removing

the largest and smallest guess, and then down to 2005 once trimming the two

outliers on each end (recall the correct answer was 1879).

Removing outliers is a very good strategy, but we may have other grounds

to judge the reliability of our subjects, such as their performance on other tests

where we do know the answer. Taking a weighted average, where we give more

weight to the scores deemed more reliable, provides a way to take such conﬁdence

measures into account.

For classiﬁcation problems, voting is the basic aggregation mechanism. The

Condorcet jury theorem justiﬁes our faith in democracy. It states that if the

probability of each voter being correct on a given issue is p > 0.5, the probability

that a majority of the voters are correct (P(n)) is greater than p. In fact, it is

exactly:

P(n) =

i=(n+1)/2n

ipi(1 −p)n−i

Large voter counts give statistical validity even to highly contested elections.

Suppose p= 0.51, meaning the forces of right are a bare majority. A jury of 101

members would reach the correct decision 57% of the time, while P(1001) = 0.73

and P(10001) = 0.9999. The probability of a correct decision approaches 1 as

n→ ∞.

There are natural limitations to the power of electoral systems, however.

Arrow’s impossibility theorem states that no electoral system for summing per-

mutations of preferences as votes satisﬁes four natural conditions for the fairness

of an election. This will be discussed in Section 4.6, in the context of scores and

rankings.

3.5.4 Crowdsourcing Services

Crowdsourcing services like Amazon Turk and CrowdFlower provide the oppor-

tunity for you to hire large numbers of people to do small amounts of piecework.

They help you to wrangle people, in order to create data for you to wrangle.

These crowdsourcing services maintain a large stable of freelance workers,

serving as the middleman between them and potential employers. These work-

ers, generally called Turkers, are provided with lists of available jobs and what

they will pay, as shown in Figure 3.5. Employers generally have some ability to

control the location and credentials of who they hire, and the power to reject a

worker’s eﬀorts without pay, if they deem it inadequate. But statistics on em-

ployers’ acceptance rates are published, and good workers are unlikely to labor

for bad actors.

3.5. CROWDSOURCING 85

Figure 3.5: Representative tasks on Mechanical Turk.

The tasks assigned to Turkers generally involve simple cognitive eﬀorts that

cannot currently be performed well by computers. Good applications of Turkers

include:

•Measuring aspects of human perception: Crowdsourcing systems pro-

vide eﬃcient ways to gather representative opinions on simple tasks. One

nice application was establishing linkages between colors in red-green-blue

space, and the names by which people typically identify them in a lan-

guage. This is important to know when writing descriptions of products

and images.

So where is the boundary in color space between “blue” and “light blue,”

or “robin’s egg blue” and “teal”? The right names are a function of

culture and convention, not physics. To ﬁnd out, you must ask people,

and crowdsourcing permits you to easily query hundreds or thousands of

diﬀerent people.

•Obtaining training data for machine learning classiﬁers: Our primary

interest in crowdsourcing will be to produce human annotations that serve

as training data. Many machine learning problems seek to do a particular

task “as well as people do.” Doing so requires a large number of training

instances to establish what people did, when given the chance.

For example, suppose we sought to build a sentiment analysis system ca-

pable of reading a written review and deciding whether its opinion of a

product is favorable or unfavorable. We will need a large number of re-

views labeled by annotators to serve as testing/training data. Further, we

need the same reviews labeled repeatedly by diﬀerent annotators, so as to

86 CHAPTER 3. DATA MUNGING

identify any inter-annotator disagreements concerning the exact meaning

of a text.

•Obtaining evaluation data for computer systems:A/B testing is a stan-

dard method for optimizing user interfaces: show half of the judges version

Aof a given system and the other half version B. Then test which group

did better according to some metric. Turkers can provide feedback on how

interesting a given app is, or how well a new classiﬁer is performing.

One of my grad students (Yanqing Chen) used CrowdFlower to evaluate

a system he built to identify the most relevant Wikipedia category for a

particular entity. Which category better describes Barack Obama: Presi-

dents of the United States or African-American Authors? For $200, he got

people to answer a total of 10,000 such multiple-choice questions, enough

for him to properly evaluate his system.

•Putting humans into the machine: There still exist many cognitive tasks

that people do much better than machines. A cleverly-designed interface

can supply user queries to people sitting inside the computer, waiting to

serve those in need.

Suppose you wanted to build an app to help the visually impaired, enabling

the user to snap a picture and ask someone for help. Maybe they are in

their kitchen, and need someone to read the label on a can to them. This

app could call a Turker as a subroutine, to do such a task as it is needed.

Of course, these image-annotation pairs should be retained for future anal-

ysis. They could serve as training data for a machine learning program to

take the people out of the loop, as much as possible.

•Independent creative eﬀorts: Crowdsourcing can be used to commission

large numbers of creative works on demand. You can order blog posts

or articles on demand, or written product reviews both good and bad.

Anything that you might imagine can be created, if you just specify what

you want.

Here are two silly examples that I somehow ﬁnd inspiring:

–The Sheep Market (http://www.thesheepmarket.com) commissioned

10,000 drawings of sheep for pennies each. As a conceptual art piece,

it tries to sell them to the highest bidder. What creative endeavors

can you think of that people will do for you at $0.25 a pop?

–Emoji Dick (http://www.emojidick.com) was a crowdsourced ef-

fort to translate the great American novel Moby Dick completely

into emoji images. Its creators partitioned the book into roughly

10,000 parts, and farmed out each part to be translated by three

separate Turkers. Other Turkers were hired to select the best one of

these to be incorporated into the ﬁnal book. Over 800 Turkers were

involved, with the total cost of $3,676 raised by the crowd-funding

site Kickstarter.

3.5. CROWDSOURCING 87

•Economic/psychological experiments: Crowdsourcing has proven a boon

to social scientists conducting experiments in behavioral economics and

psychology. Instead of bribing local undergraduates to participate in their

studies, these investigators can now expand their subject pool to the entire

world. They get the power to harness larger populations, perform inde-

pendent replications in diﬀerent countries, and thus test whether there are

cultural biases of their hypotheses.

There are many exciting tasks that can be proﬁtably completed using crowd-

sourcing. However, you are doomed to disappointment if you employ Turkers

for the wrong task, in the wrong way. Bad uses of crowdsourcing include:

•Any task that requires advanced training: Although every person possesses

unique skills and expertise, crowdsourcing workers come with no speciﬁc

training. They are designed to be treated as interchangeable parts. You do

not establish a personal relationship with these workers, and any sensible

gig will be too short to allow for more than a few minutes training.

Tasks requiring speciﬁc technical skills are not reasonably crowdsourced.

However, they might be reasonably subcontracted, in traditional longer-

term arrangements.

•Any task you cannot specify clearly: You have no mechanism for back-

and-forth communication with Turkers. Generally speaking, they have no

way to ask you questions. Thus the system works only if you can specify

your tasks clearly, concisely, and unambiguously.

This is much harder than it looks. Realize that you are trying to program

people instead of computers, with all the attendant bugs associated with

“do as I say” trumping “do what I mean.” Test your speciﬁcations out

on local people before opening up your job to the masses, and then do

a small test run on your crowdsourcing platform to evaluate how it goes

before cutting loose with the bulk of your budget. You may be in for

some cultural surprises. Things that seem obvious to you might mean

something quite diﬀerent to a worker halfway around the world.

•Any task where you cannot verify whether they are doing a good job: Turk-

ers have a single motivation for taking on your piecework: they are trying

to convert their time into money as eﬃciently as possible. They are look-

ing out for jobs oﬀering the best buck for their bang, and the smartest ones

will seek to complete your task as quickly and thoughtlessly as possible.

Crowdsourcing platforms permit employers to withhold payment if the

contracted work is unacceptable. Taking advantage of this requires some

eﬃcient way to check the quality of the product. Perhaps you should

ask them to complete certain tasks where you already know the correct

answer. Perhaps you can compare their responses to that of other inde-

pendent workers, and throw out their work if it disagrees too often from

the consensus.

88 CHAPTER 3. DATA MUNGING

It is very important to employ some quality control mechanism. Some

fraction of the available workers on any platform are bots, looking for

multiple-choice tasks to attack through randomness. Others may be peo-

ple with language skills wholly inadequate for the given task. You need

to check and reject to avoid being a sucker.

However, you cannot fairly complain about results from poorly speciﬁed

tasks. Rejecting too high a fraction of work will lower your reputation,

with workers and the platform. It is particularly bad karma to refuse to

pay people but use their work product anyway.

•Any illegal task, or one too inhuman to subject people to: You are not

allowed to ask a Turker to do something illegal or unethical. The clas-

sic example is hiring someone to write bad reviews of your competitor’s

products. Hiring a hit man makes you just as guilty of murder as the guy

who ﬁred the shots. Be aware that there are electronic trails that can be

followed from the public placement of your ad directly back to you.

People at educational and research institutions are held to a higher stan-

dard than the law, through their institutional review board or IRB. The

IRB is a committee of researchers and administrative oﬃcials who must

approve any research on human subjects before it is undertaken. Be-

nign crowdsourcing applications such as the ones we have discussed are

routinely approved, after the researchers have undergone a short online

training course to make sure they understand the rules.

Always realize that there is a person at the other end of the machine.

Don’t assign them tasks that are oﬀensive, degrading, privacy-violating,

or too stressful. You will probably get better results out of your workers

if you treat them like human beings.

Getting people to do your bidding requires proper incentives, not just clear

instructions. In life, you generally get what you pay for. Be aware of the

currently prevailing minimum hourly wage in your country, and price your tasks

accordingly. This is not a legal requirement, but it is generally good business.

The sinister glow that comes from hiring workers at $0.50 per hour wears

oﬀ quickly once you see the low quality of workers that your tasks attract. You

can easily eat up all your savings by the need to rigorously correct their work

product, perhaps by paying multiple workers do it repeatedly. Higher paying

tasks ﬁnd workers much more quickly, so be prepared to wait if you do not pay

the prevailing rate. Bots and their functional equivalents are happier to accept

slave wages than the workers you really want to hire.

3.5.5 Gamiﬁcation

There is an alternative to paying people to annotate or transcribe your data.

Instead, make things so much fun that people will work for you for free!

Games with a purpose (GWAP) are systems which disguise data collection

as a game people want to play, or a task people themselves want done. With

3.5. CROWDSOURCING 89

the right combination of game, motive, and imagination, amazing things can be

done. Successful examples include:

•CAPTCHAs for optical character recognition (OCR): CAPTCHAs are

those distorted text images you frequently encounter when creating an

account on the web. They demand that you type in the contents of text

strings shown in the image to prove that you are a human, thus enabling

them to deny access to bots and other programmed systems.

ReCAPTCHAs were invented to get useful data from the over 100 million

CAPTCHAs displayed each day. Two text strings are displayed in each,

one of which the system checks in order to grant entry. The other rep-

resents a hard case for an OCR system that is digitizing old books and

newspapers. The answers are mapped back to improve the digitization of

archival documents, transcribing over 40 million words per day.

•Psychological/IQ testing in games/apps: Psychologists have established

ﬁve basic personality traits as important and reproducible aspects of per-

sonality. Academic psychologists use multiple-choice personality tests to

measure where individuals sit along personality scales for each of the big

ﬁve traits: openness, conscientiousness, extroversion, agreeableness, and

neuroticism.

By turning these surveys into game apps (“What are your personality

traits?”) psychologists have gathered personality measurements on over

75,000 diﬀerent people, along with other data on preferences and behavior.

This has created an enormous data set to study many interesting issues

in the psychology of personality.

•The FoldIt game for predicting protein structures: Predicting the struc-

tures formed by protein molecules is one of the great computational chal-

lenges in science. Despite many years of work, what makes a protein fold

into a particular shape is still not well understood.

FoldIt (https://fold.it) is a game challenging non-biologists to design

protein molecules that fold into a particular shape. Players are scored as

to how closely their design approaches the given target, with the highest

scoring players ranked on a leader board. Several scientiﬁc papers have

been published on the strength of the winning designs.

The key to success here is making a game that is playable enough to become

popular. This is much harder than it may appear. There are millions of free

apps in the app store, mostly games. Very few are ever tried by more than

a few hundred people, which is nowhere near enough to be interesting from a

data collection standpoint. Adding the extra constraint that the game generate

interesting scientiﬁc data while being playable makes this task even harder.

Motivational techniques should be used to improve playability. Keeping

score is an important part of any game, and the game should be designed so that

performance increases rapidly at ﬁrst, in order to hook the player. Progress bars

90 CHAPTER 3. DATA MUNGING

provide encouragement to reach the next level. Awarding badges and providing

leader boards seen by others encourages greater eﬀorts. Napoleon instituted

a wide array of ribbons and decorations for his soldiers, observing that “it is

amazing what men will do for a strip of cloth.”

The primary design principle of games such as FoldIt is to abstract the

domain technicality away, into the scoring function. The game is conﬁgured

so players need not really understand issues of molecular dynamics, just that

certain changes make the scores go up while others make them go down. The

player will build their own intuition about the domain as they play, resulting in

designs which may never occur to experts skilled in the art.

3.6 Chapter Notes

The Charles Babbage quote from the start of this chapter is from his book

Passages from the Life of a Philosopher [Bab11]. I recommend Padua’s graphic

novel [Pad15] for an amusing but meaningful (albeit ﬁctitious) introduction to

his work and relationship with Ada Lovelace.

Many books deal with hands-on practical matters of data wrangling in par-

ticular programming languages. Particularly useful are the O’Reilly books for

data science in Python, including [Gru15, McK12].

The story of our jai-alai betting system, including the role of website scrap-

ing, is reported in my book Calculated Bets [Ski01]. It is a quick and fun overview

of how to build simulation models for prediction, and will be the subject of the

war story of Section 7.8.

The failure of space missions due to numerical computing errors has been

well chronicled in popular media. See Gleick [Gle96] and Stephenson et al.

[SMB+99] for discussions of the Ariane 5 and Mars Climate Orbiter space mis-

sions, respectively.

The clever idea of using accelerometers in cell phones to detect earthquakes

comes from Faulkner et al. [FCH+14]. Representative studies of large sets of

Flickr images includes Kisilevich et al. [KKK+10].

Kittur [KCS08] reports on experiences with crowdsourcing user studies on

Amazon Turk. Our use of CrowdFlower to identify appropriate descriptions

of historical ﬁgures was presented in [CPS15]. Methods for gamiﬁcation in

instruction are discussed in [DDKN11, Kap12]. Recaptchas are introduced in

Von Ahn, et al. [VAMM+08]. The large-scale collection of psychological trait

data via mobile apps is due to Kosinski, et al. [KSG13].

3.7 Exercises

Data Munging

3-1. [3] Spend two hours getting familiar with one of the following programming

languages: Python, R, MatLab, Wolfram Alpha/Language. Then write a brief

paper with your impressions on its characteristics:

3.7. EXERCISES 91

•Expressibility.

•Runtime speed.

•Breadth of library functions.

•Programming environment.

•Suitability for algorithmically-intensive tasks.

•Suitability for general data munging tasks.

3-2. [5] Pick two of the primary data science programming languages, and write

programs to solve the following tasks in both of them. Which language did you

ﬁnd most suitable for each task?

(a) Hello World!

(b) Read numbers from a ﬁle, and print them out in sorted order.

(d) Read a text ﬁle, and count the total number of distinct words.

(e) Read a ﬁle of numbers, and plot a frequency histogram of them.

(f) Download a page from the web, and scrape it.

3-3. [3] Play around for a little while with Python, R, and Matlab. Which do you

like best? What are the strengths and weaknesses of each?

3-4. [5] Construct a data set of nhuman heights, with p% of them recording in En-

glish (feet) and the rest with metric (meter) measurements. Use statistical tests

to test whether this distribution is distinguishable from one properly recorded

in meters. What is the boundary as a function of nand pwhere it becomes

clear there is a problem?

Data Sources

3-5. [3] Find a table of storage prices over time. Analyze this data, and make a

projection about the cost/volume of data storage ﬁve years from now. What

will disk prices be in 25 or 50 years?

3-6. [5] For one or more of the following The Quant Shop challenges, ﬁnd relevant

data sources and assess their quality:

•Miss Universe.

•Movie gross.

•Baby weight.

•Art auction price.

•Snow on Christmas.

•Super Bowl/college champion.

•Ghoul pool?

•Future gold/oil price?

Data Cleaning

92 CHAPTER 3. DATA MUNGING

3-7. [3] Find out what was weird about September 1752. What special steps might

the data scientists of the day have had to take to normalize annual statistics?

3-8. [3] What types of outliers might you expect to occur in the following data sets:

(a) Student grades.

(b) Salary data.

3-9. [3] A health sensor produces a stream of twenty diﬀerent values, including blood

pressure, heart rate, and body temperature. Describe two or more techniques

you could use to check whether the stream of data coming from the sensor is

valid.

Implementation Projects

3-10. [5] Implement a function that extracts the set of hashtags from a data frame

of tweets. Hashtags begin with the “#” character and contain any combination

of upper and lowercase characters and digits. Assume the hashtag ends where

there is a space or a punctuation mark, like a comma, semicolon, or period.

3-11. [5] The laws governing voter registration records diﬀer from state to state in the

United States. Identify one or more states with very lax rules, and see what you

must do to get your hands on the data. Hint: Florida.

Crowdsourcing

3-12. [5] Describe how crowdsourced workers might have been employed to help gather

data for The Quant Shop challenges:

•Miss Universe.

•Movie gross.

•Baby weight.

•Art auction price.

•Snow on Christmas.

•Super Bowl/college champion.

•Ghoul pool.

•Future gold/oil price?:

3-13. [3] Suppose you are paying Turkers to read texts and annotate them based on

the underlying sentiment (positive or negative) that each passage conveys. This

is an opinion task, but how can we algorithmically judge whether the Turker was

answering in a random or arbitrary manner instead of doing their job seriously?

Interview Questions

3-14. [5] Suppose you built a system to predict stock prices. How would you evaluate

it?

3-15. [5] In general, how would you screen for outliers, and what should you do if you

ﬁnd one?

3-16. [3] Why does data cleaning play a vital role in analysis?

3.7. EXERCISES 93

3-17. [5] During analysis, how do you treat missing values?

3-18. [5] Explain selection bias. Why is it important? How can data management

procedures like handling missing data make it worse?

3-19. [3] How do you eﬃciently scrape web data?

Kaggle Challenges

3-20. Partially sunny, with a chance of hashtags.

https://www.kaggle.com/c/crowdflower-weather-twitter

3-21. Predict end of day stock returns, without being deceived by noise.

https://www.kaggle.com/c/the-winton-stock-market-challenge

3-22. Data cleaning and the analysis of historical climate change.

https://www.kaggle.com/berkeleyearth/climate-change-earth-surface-temperature-data

Chapter 4

Scores and Rankings

Money is a scoreboard where you can rank how you’re doing against

other people.

– Mark Cuban

Scoring functions are measures that reduce multi-dimensional records to a single

value, highlighting some particular property of the data. A familiar example

of scoring functions are those used to assign student grades in courses such as

mine. Students can then be ranked (sorted) according to these numerical scores,

and later assigned letter grades based on this order.

Grades are typically computed by functions over numerical features that

reﬂect student performance, such as the points awarded on each homework and

exam. Each student receives a single combined score, often scaled between 0

and 100. These scores typically come from a linear combination of the input

variables, perhaps giving 8% weight to each of ﬁve homework assignments, and

20% weight to each of three exams.

There are several things to observe about such grading rubrics, which we

will use as a model for more general scoring and ranking functions:

•Degree of arbitrariness: Every teacher/professor uses a diﬀerent trade-oﬀ

between homework scores and exams when judging their students. Some

weigh the ﬁnal exam more than all the other variables. Some normalize

each value to 100 before averaging, while others convert each score to a Z-

score. They all diﬀer in philosophy, yet every teacher/professor is certain

that their grading system is the best way to do things.

•Lack of validation data: There is no gold standard informing instruc-

tors of the “right” grade that their students should have received in the

course. Students often complain that I should give them a better grade,

but self-interest seems to lurk behind these requests more than objectiv-

ity. Indeed, I rarely hear students recommend that I lower their grade.

96 CHAPTER 4. SCORES AND RANKINGS

Without objective feedback or standards to compare against, there is no

rigorous way for me to evaluate my grading system and improve it.

•General Robustness: And yet, despite using widely-disparate and totally

unvalidated approaches, diﬀerent grading systems generally produce simi-

lar results. Every school has a cohort of straight-A students who monopo-

lize a sizable chunk of the top grades in each course. This couldn’t happen

if all these diﬀerent grading systems were arbitrarily ordering student per-

formance. C students generally muddle along in the middle-to-lower tiers

of the bulk of their classes, instead of alternating As and Fs on the way

to their ﬁnal average. All grading systems are diﬀerent, yet almost all are

defensible.

In this chapter, we will use scoring and ranking functions as our ﬁrst foray

into data analysis. Not everybody loves them as much as I do. Scoring func-

tions often seem arbitrary and ad hoc, and in the wrong hands can produce

impressive-looking numbers which are essentially meaningless. Because their

eﬀectiveness generally cannot be validated, these techniques are not as scientif-

ically sound as the statistical and machine learning methods we will present in

subsequent chapters.

But I think it is important to appreciate scoring functions for what they

are: useful, heuristic ways to tease understanding from large data sets. A

scoring function is sometimes called a statistic, which lends it greater dignity

and respect. We will introduce several methods for getting meaningful scores

from data.

4.1 The Body Mass Index (BMI)

Everybody loves to eat, and our modern world of plenty provides numerous

opportunities for doing so. The result is that a sizable percentage of the popu-

lation are above their optimal body weight. But how can you tell whether you

are one of them?

The body mass index (BMI) is a score or statistic designed to capture whether

your weight is under control. It is deﬁned as

BM I =mass

height2

where mass is measured in kilograms and height in meters.

As I write this, I am 68 inches tall (1.727 meters) and feeling slightly pudgy

at 150 lbs (68.0 kg). Thus my BMI is 68.0/(1.7272) = 22.8. This isn’t so terrible,

however, because commonly accepted BMI ranges in the United States deﬁne:

•Underweight: below 18.5.

•Normal weight: from 18.5 to 25.

•Overweight: from 25 to 30.

4.1. THE BODY MASS INDEX (BMI) 97

Figure 4.1: Height–weight scatter plot, for 1000 representative Americans. Col-

ors illustrate class labels in the BMI distribution.

•Obese: over 30.

Thus I am considered to be in normal range, with another dozen pounds

to gain before I oﬃcially become overweight. Figure 4.1 plots where a repre-

sentative group of Americans sit in height–weight space according to this scale.

Each point in this scatter plot is a person, colored according to their weight

classiﬁcation by BMI. Regions of seemingly solid color are so dense with people

that the dots overlap. Outlier points to the right correspond to the heaviest

individuals.

The BMI is an example of a very successful statistic/scoring function. It

is widely used and generally accepted, although some in the public health ﬁeld

quibble that better statistics are available.

The logic for the BMI is almost sound. The square of height should be pro-

portional to area. But mass should grow proportional to the volume, not area,

so why is it not mass/height3? Historically, BMI was designed to correlate with

the percentage of body fat in an individual, which is a much harder measure-

ment to make than height and weight. Experiments with several simple scoring

functions, including m/l and m/l3revealed that BMI works best.

It is very interesting to look at BMI distributions for extreme populations.

Consider professional athletes in American football (NFL) and basketball (NBA):

•Basketball players are notoriously tall individuals. They also have to run

up and down the court all day, promoting superior ﬁtness.

•American football players are notoriously heavy individuals. In particular,

linemen exist only to block or move other linemen, thus placing a premium

on bulk.

Let’s look at some data. Figure 4.2 shows the BMI distributions of basketball

and football players, by sport. And indeed, almost all of the basketball players

98 CHAPTER 4. SCORES AND RANKINGS

Figure 4.2: BMI distributions of professional basketball (left) and football

(right) players.

Figure 4.3: Position in basketball (left) and football (right) is largely determined

by size.

have normal BMI despite their very abnormal heights. And the football players

are almost uniformly animals, with most scored as obese despite the fact that

they are also well-conditioned athletes. These football players are generally

optimized for strength, instead of cardiovascular ﬁtness.

In Chapter 6, we will discuss visualization techniques to highlight the presen-

tation of data, but let’s start to develop our aesthetic here. We use scatter plots

to show each individual as a point in height–weight space, with labels (weight

class or player position) shown as colors.

The breakdown of BMI by position is also revealing, and shown in Figure

4.3. In basketball, the guards are quick and sleek while the centers are tall and

intimidating. So all of these positions segregate neatly by size. In football, the

skill players (the quarterbacks, kickers, and punters) prove to be considerably

smaller than the sides of beef on the line.

4.2. DEVELOPING SCORING SYSTEMS 99

4.2 Developing Scoring Systems

Scores are functions that map the features of each entity to a numerical value

of merit. This section will look at the basic approaches for building eﬀective

scoring systems, and evaluating them.

4.2.1 Gold Standards and Proxies

Historically, paper currencies were backed with gold, meaning that one paper

dollar could always be traded in for $1 worth of gold. This was why we knew

that our money was worth more than the paper it was printed on.

In data science, a gold standard is a set of labels or answers that we trust to

be correct. In the original formulation of BMI, the gold standard was the body

fat percentages carefully measured on a small number of subjects. Of course,

such measurements are subject to some error, but by deﬁning these values to be

the gold standard for ﬁtness we accept them to be the right measure. In gold

we trust.

The presence of a gold standard provides a rigorous way to develop a good

scoring system. We can use curve-ﬁtting technique like linear regression (to be

discussed in Section 9.1) to weigh the input features so as to best approximate

the “right answers” on the gold standard instances.

But it can be hard to ﬁnd real gold standards. Proxies are easier-to-ﬁnd data

that should correlate well with the desired but unobtainable ground truth. BMI

was designed to be a proxy for body fat percentages. It is easily computable

from just height and weight, and does a pretty good job correlating with body

fat. This means it is seldom necessary to test buoyancy in water tanks or “pinch

an inch” with calipers, more intrusive measures that directly quantify the extent

of an individual’s ﬂab.

Suppose I wanted to improve the grading system I use for next year’s data

science course. I have student data from the previous year, meaning their scores

on homework and tests, but I don’t really have a gold standard on what grades

these students deserved. I have only the grade I gave them, which is meaningless

if I am trying to improve the system.

I need a proxy for their unknown “real” course merit. A good candidate for

this might be each student’s cumulative GPA in their other courses. Generally

speaking, student performance should be conserved across courses. If my scor-

ing system hurts the GPA of the best students and helps the lower tier, I am

probably doing something wrong.

Proxies are particularly good when evaluating scoring/ranking systems. In

our book Who’s Bigger? [SW13] we used Wikipedia to rank historical ﬁgures by

“signiﬁcance.” We did not have any gold standard signiﬁcance data measuring

how important these people really were. But we used several proxies to evaluate

how we were doing to keep us honest:

•The prices that collectors will pay for autographs from celebrities should

generally correlate with the celebrity’s signiﬁcance. The higher the price

people are willing to pay, the bigger the star.

100 CHAPTER 4. SCORES AND RANKINGS

•The statistics of how good a baseball player is should generally correlate

with the player’s signiﬁcance. The better the athlete, the more important

they are likely to be.

•Published rankings appearing in books and magazines list the top pres-

idents, movie stars, singers, authors, etc. Presidents ranked higher by

historians should generally be ranked higher by us. Such opinions, in ag-

gregate, should generally correlate with the signiﬁcance of these historical

ﬁgures.

We will discuss the workings of our historical signiﬁcance scores in greater

detail in Section 4.7.

4.2.2 Scores vs. Rankings

Rankings are permutations ordering nentities by merit, generally constructed by

sorting the output of some scoring system. Popular examples of rankings/rating

systems include:

•Football/basketball top twenty: Press agencies generally rank the top

college sports teams by aggregating the votes of coaches or sportswriters.

Typically, each voter provides their own personal ranking of the top twenty

teams, and each team gets awarded more points the higher they appear

on the voter’s list. Summing up the points from each voter gives a total

score for each team, and sorting these scores deﬁnes the ranking.

•University academic rankings: The magazine U.S News and World Report

publishes annual rankings of the top American colleges and universities.

Their methodology is proprietary and changes each year, presumably to

motivate people to buy the new rankings. But it is generally a score

produced from statistics like faculty/student ratio, acceptance ratio, the

standardized test scores of its students and applicants, and maybe the

performance of its football/basketball teams :-). Polls of academic experts

also go into the mix.

•Google PageRank/search results: Every query to a search engine triggers

a substantial amount of computation, implicitly ranking the relevance of

every document on the web against the query. Documents are scored on

the basis of how well they match the text of the query, coupled with ratings

of the inherent quality of each page. The most famous page quality metric

here is PageRank, the network-centrality algorithm that will be reviewed

in Section 10.4.

•Class rank: Most High Schools rank students according to their grades,

with the top ranked student honored as class valedictorian. The scor-

ing function underlying these rankings is typically grade-point average

(GPA), where the contribution of each course is weighted by its number

of credits, and each possible letter grade is mapped to a number (typically

4.2. DEVELOPING SCORING SYSTEMS 101

A= 4.0). But there are natural variants: many schools choose to weigh

honors courses more heavily than lightweight classes like gym, to reﬂect

the greater diﬃculty of getting good grades.

Generally speaking, sorting the results of a scoring system yields a numerical

ranking. But thinking the other way, each item’s ranking position (say, 493th

out of 2196) yields a numerical score for the item as well.

Since scores and rankings are duals of each other, which provides a more

meaningful representation of the data? As in any comparison, the best answer

is that it depends, on issues like:

•Will the numbers be presented in isolation? Rankings are good at pro-

viding context for interpreting scores. As I write this, Stony Brook’s

basketball team ranks 111th among the nation’s 351 college teams, on the

strength of our RPI (ratings percentage index) of 39.18. Which number

gives you a better idea of whether we have a good or bad team, 111th or

39.18?

•What is the underlying distribution of scores? By deﬁnition, the top

ranked entity has a better score than the second ranked one, but this tells

you nothing about the magnitude of the diﬀerence between them. Are

they virtually tied, or is #1 crushing it?

Diﬀerences in rankings appear to be linear: the diﬀerence between 1 and 2

seems the same as the diﬀerence between 111 and 112. But this is not gen-

erally true in scoring systems. Indeed, small absolute scoring diﬀerences

can often yield big ranking diﬀerences.

•Do you care about the extremes or the middle? Well-designed scoring sys-

tems often have a bell-shaped distribution. With the scores concentrated

around the mean, small diﬀerences in score can mean large diﬀerences in

rank. In a normal distribution, increasing your score from the mean by

one standard deviation (σ) moves you from the 50th percentile to the 84th

percentile. But the same sized change from 1σto 2σtakes you only from

the 84th to 92.5th percentile.

So when an organization slips from ﬁrst to tenth, heads should roll. But

when Stony Brook’s team slides from 111th to 120th, it likely represents

an insigniﬁcant diﬀerence in score and should be discounted. Rankings

are good at highlighting the very best and very worst entities among the

group, but less so the diﬀerences near the median.

4.2.3 Recognizing Good Scoring Functions

Good scoring functions are good because they are easily interpretable and gen-

erally believable. Here we review the properties of statistics which point in these

directions:

102 CHAPTER 4. SCORES AND RANKINGS

•Easily computable: Good statistics can be easily described and presented.

BMI is an excellent example: it contains only two parameters, and is eval-

uated using only simple algebra. It was found as the result of a search

through all simple functional forms on a small number of easily obtained,

relevant variables. It is an excellent exercise to brainstorm possible statis-

tics from a given set of features on a data set you know well, for practice.

•Easily understandable: It should be clear from the description of the

statistics that the ranking is relevant to the question at hand. “Mass

adjusted by height” explains why BMI is associated with obesity. Clearly

explaining the ideas behind your statistic is necessary for other people to

trust it enough to use.

•Monotonic interpretations of variables: You should have a sense of how

each of the features used in your scoring function correlate with the ob-

jective. Mass should correlate positively with BMI, because being heavy

requires that you weigh a lot. Height should correlate negatively, because

tall people naturally weigh more than short people.

Generally speaking, you are producing a scoring function without an ac-

tual gold standard to compare against. This requires understanding what

your variables mean, so your scoring function will properly correlate with

this mushy objective.

•Produces generally satisfying results on outliers: Ideally you know enough

about certain individual points to have a sense of where they belong in

any reasonable scoring system. If I am truly surprised by the identity

of the top entities revealed by the scoring system, it probably is a bug,

not a feature. When I compute the grades of the students in my courses,

I already know the names of several stars and several bozos from their

questions in class. If my computed grades do not grossly correspond to

these impressions, there is a potential bug that needs to be tracked down.

If the data items really are completely anonymous to you, you probably

should spend some time getting to know your domain better. At the very

least, construct artiﬁcial examples (“Superstar” and “Superdork”) with

feature values so that they should be near the top and bottom of the

ranking, and then see how they ﬁt in with the real data.

•Uses systematically normalized variables: Variables drawn from bell-

shaped distributions behave sensibly in scoring functions. There will be

outliers at the tails of either end which correspond to the best/worst items,

plus a peak in the middle of items whose scores should all be relatively

similar.

These normally-distributed variables should be turned into Z-scores (see

Section 4.3) before adding them together, so that all features have compa-

rable means and variance. This reduces the scoring function’s dependence

on magic constants to adjust the weights, so no single feature has too

dominant an impact on the results.

4.3. Z-SCORES AND NORMALIZATION 103

µB= 21.9σB= 1.92

µZ= 0 σZ= 1

B 19 22 24 20 23 19 21 24 24 23

Z−1.51 0.05 1.09 −0.98 0.57 −1.51 −0.46 1.09 1.09 0.57

Figure 4.4: Taking the Z-scores of a set of values Bnormalizes them to have

mean µ= 0 and σ= 1.

Generally speaking, summing up Z-scores using the correct signs (plus for

positively correlated variables and minus for negative correlations) with

uniform weights will do roughly the right thing. A better function might

weigh these variables by importance, according to the strength of the

correlation with the target. But it is unlikely to not make much diﬀerence.

•Breaks ties in meaningful ways: Ranking functions are of very limited

value when there are bunches of ties. Ranking the handiness of people by

how many ﬁngers they have won’t be very revealing. There will be a very

select group with twelve, a vast majority tied with ten, and then small

groups of increasingly disabled accident victims until we get down to zero.

In general, scores should be real numbers over a healthy range, in order to

minimize the likelihood of ties. Introducing secondary features to break

ties is valuable, and makes sense provided these features also correlate

with the property you care about.

4.3 Z-scores and Normalization

An important principle of data science is that we must try to make it as easy

as possible for our models to do the right thing. Machine learning techniques

like linear regression purport to ﬁnd the line optimally ﬁtting to a given data

set. But it is critical to normalize all the diﬀerent variables to make their

range/distribution comparable before we try to use them to ﬁt something.

Z-scores will be our primary method of normalization. The Z-score transform

is computed:

Zi= (ai−µ)/σ

where µis the mean of the distribution and σthe associated standard deviation.

Z-scores transform arbitrary sets of variables to a uniform range. The Z-

scores of height measured in inches will be exactly the same as that of the

height measured in miles. The average value of a Z-score over all points is zero.

Figure 4.4 shows a set of integers reduced to Z-scores. Values greater than the

mean become positive, while those less than the mean become negative. The

standard deviation of the Z-scores is 1, so all distributions of Z-scores have

similar properties.

Transforming values to Z-scores accomplishes two goals. First, they aid in

visualizing patterns and correlations, by ensuring that all ﬁelds have an identical

104 CHAPTER 4. SCORES AND RANKINGS

mean (zero) and operate over a similar range. We understand that a Z-score of

3.87 must represent basketball-player level height in a way that 79.8 does not,

without familiarity with the measurement unit (say inches). Second, the use

of Z-scores makes it easier on our machine learning algorithms, by making all

diﬀerent features of a comparable scale.

In theory, performing a linear transformation like the Z-score doesn’t really

do anything that most learning algorithms couldn’t ﬁgure out by themselves.

These algorithms generally ﬁnd the best coeﬃcient to multiply each variable

with, which is free to be near σif the algorithm really wants it to be.

However, the realities of numerical computation kick in here. Suppose we

were trying to build a linear model on two variables associated with U.S. cities,

say, area in square miles and population. The ﬁrst has a mean of about 5 and a

max around 100. The second has a mean about 25,000 and a max of 8,000,000.

For the two variables to have a similar eﬀect on our model, we must divide the

second variable by a factor of 100,000 or so.

This causes numerical precision problems, because a very small change in the

value of the coeﬃcient causes a very large change in how much the population

variable dominates the model. Much better would be to have the variables be

grossly the same scale and distribution range, so the issue is whether one feature

gets weighted, say, twice as strongly as another.

Z-scores are best used on normally distributed variables, which, after all, are

completely described by mean µand standard deviation σ. But they work less

well when the distribution is a power law. Consider the wealth distribution in the

United States, which may have a mean of (say) $200,000, with a σ= $200,000.

The Z-score of $80 billion dollar Bill Gates would then be 4999, still an incredible

outlier given the mean of zero.

Your biggest data analysis sins will come in using improperly normalized

variables in your analysis. What can we do to bring Bill Gates down to size?

We can hit him with a log, as we discussed in Section 2.4.

4.4 Advanced Ranking Techniques

Most bread-and-butter ranking tasks are solved by computing scores as linear

combinations of features, and then sorting them. In the absence of any gold

standard, these methods produce statistics which are often revealing and infor-

mative.

That said, several powerful techniques have been developed to compute rank-

ings from speciﬁc types of inputs: the results of paired comparisons, relationship

networks, and even assemblies of other rankings. We review these methods here,

for inspiration.

4.4.1 Elo Rankings

Rankings are often formed by analyzing sequences of binary comparisons, which

arise naturally in competitions between entities:

4.4. ADVANCED RANKING TECHNIQUES 105

•Sports contest results: Typical sporting events, be they football games or

chess matches, pit teams Aand Bagainst each other. Only one of them

will win. Thus each match is essentially a binary comparison of merit.

•Votes and polls: Knowledgeable individuals are often asked to compare

options and decide which choice they think is better. In an election, these

comparisons are called votes. A major component of certain university

rankings come from asking professors: which school is better, Aor B?

In the movie The Social Network, Facebook’s Mark Zuckerberg is shown

getting his start with FaceMash, a website showing viewers two faces and

asking them to pick which one is more attractive. His site then ranked all

the faces from most to least attractive, based on these paired comparisons.

•Implicit comparisons: From the right vantage point, feature data can be

meaningfully interpreted as pairwise comparisons. Suppose a student has

been accepted by both universities Aand B, but opts for A. This can be

taken as an implicit vote that Ais better than B.

What is the right way to interpret collections of such votes, especially where

there are many candidates, and not all pairs of players face oﬀ against each

other? It isn’t reasonable to say the one with the most wins wins, because (a)

they might have competed in more comparisons than other players, and (b) they

might have avoided strong opponents and beaten up only inferior competition.

The Elo system starts by rating all players, presumably equally, and then

incrementally adjusts each player’s score in response to the result of each match,

according to the formula:

r0(A) = r(A) + k(SA−µA),

where

•r(A) and r0(A) represent the previous and updated scores for player A.

•kis a ﬁxed parameter reﬂecting the maximum possible score adjustment

in response to a single match. A small value of kresults in fairly static

rankings, while using too large a kwill cause wild swings in ranking based

on the latest match.

•SAis the scoring result achieved by player Ain the match under consid-

eration. Typically, SA= 1 if Awon, and SA=−1 if Alost.

•µAwas the expected result for Awhen competing against B. If Ahas

exactly the same skill level as B, then presumably µA= 0. But suppose

that Ais a champion and Bis a beginner or chump. Our expectation is

that Ashould almost certainly win in a head-to-head matchup, so µA>0

and is likely to be quite close to 1.

106 CHAPTER 4. SCORES AND RANKINGS

Figure 4.5: The shape of the logit function, for three diﬀerent values for c.

All is clear here except how to determine µA. Given an estimate of the

probability that Abeats B(PA>B ), then

µA= 1 ·PA>B + (−1) ·(1 −PA>B ).

This win probability clearly depends on the magnitude of the skill diﬀerence

between players Aand B, which is exactly what is supposed to be measured by

the ranking system. Thus x=r(A)−r(B) represents this skill diﬀerence.

To complete the Elo ranking system, we need a way to take this real variable

xand convert it to a meaningful probability. This is an important problem we

will repeatedly encounter in this book, solved by a bit of mathematics called

the logit function.

The Logit Function

Suppose we want to take a real variable −∞ < x < ∞and convert it to a

probability 0 ≤p≤1. There are many ways one might imagine doing this, but

a particularly simple transformation is p=f(x), where

f(x) = 1

1 + e−cx

The shape of the logit function f(x) is shown in Figure 4.5. Particularly

note the special cases at the mid and endpoints:

•When two players are of equal ability, x= 0, and f(0) = 1/2, reﬂects that

both players have an equal probability of winning.

•When player Ahas a vast advantage, x→ ∞, and f(∞) = 1, deﬁning

that Ais a lock to win the match.

4.4. ADVANCED RANKING TECHNIQUES 107

Garry Kasparov

2851

Steven Skiena

1200

Judit Polgar Magnus Carlsen

2735 2882

Steven Skiena Judit Polgar

K = 2771

S = 1280

P = 2790

C = 2827

Judit Polgar

P = 2790

S = 1280

Figure 4.6: Changes in ELO scores as a consequence of an unlikely chess tour-

nament.

•When player Bhas a vast advantage, x→ −∞, and f(−∞) = 0, denoting

that Bis a lock to win the match.

These are exactly the values we want if xmeasures the skill diﬀerence between

the players.

The logit function smoothly and symmetrically interpolates between these

poles. The parameter cin the logit function governs how steep the transition

is. Do small diﬀerences in skill translate into large diﬀerences in the probability

of winning? For c= 0, the landscape is as ﬂat as a pancake: f(x) = 1/2 for all

x. The larger cis, the sharper the transition, as shown in Figure 4.5. Indeed,

c=∞yields a step function from 0 to 1.

Setting c= 1 is a reasonable start, but the right choice is domain speciﬁc.

Observing how often a given skill-diﬀerence magnitude results in an upset (the

weaker party winning) helps specify the parameter. The Elo Chess ranking

system was designed so that r(A)−r(B) = 400 means that Ahas ten times the

probability of winning than B.

Figure 4.6 illustrates Elo computations, in the context of a highly unlikely

tournament featuring three of the greatest chess players in history, and one low-

ranked patzer. Here k= 40, implying a maximum possible scoring swing of 80

points as a consequence of any single match. The standard logit function gave

Kasparov a probability of 0.999886 of beating Skiena in the ﬁrst round, but

through a miracle akin to raising Lazarus the match went the other way. As a

consequence, 80 points went from Kasparov’s ranking to mine.

On the other side of the bracket two real chess champions did battle, with the

more imaginable upset by Polgar moving only 55 points. She wiped the ﬂoor

with me the ﬁnal round, an achievement so clearly expected that she gained

essentially zero rating points. The Elo method is very eﬀective at updating

ratings in response to surprise, not just victory.

108 CHAPTER 4. SCORES AND RANKINGS

Figure 4.7: Borda’s method for constructing the consensus ranking of

{A, B, C, D, E}from a set of four input rankings, using linear weights.

4.4.2 Merging Rankings

Any single numeric feature f, like height, can seed n

2pairwise comparisons

among nitems, by testing whether f(A)> f(B) for each pair of items Aand

B. We could feed these pairs to the Elo method to obtain a ranking, but this

would be a silly way to think about things. After all, the result of any such

analysis would simply reﬂect the sorted order of f.

Integrating a collection of rankings by several diﬀerent features makes for a

more interesting problem, however. Here we interpret the sorted order of the

ith feature as deﬁning a permutation Pion the items of interest. We seek the

consensus permutation P, which somehow best reﬂects all of the component

permutations P1, . . . , Pk.

This requires deﬁning a distance function to measure the similarity between

two permutations. A similar issue arose in deﬁning the Spearman rank corre-

lation coeﬃcient (see Section 2.3.1), where we compared two variables by the

measure of agreement in the relative order of the elements.1

Borda’s method creates a consensus ranking from multiple other rankings by

using a simple scoring system. In particular, we assign a cost or weight to each

of the npositions in the permutation. Then, for each of the nelements, we sum

up the weights of its positions over all of the kinput rankings. Sorting these n

scores determines the ﬁnal consensus ranking.

All is now clear except for the mapping between positions and costs. The

simplest cost function assign ipoints for appearing in the ith position in each

permutation, i.e. we sum up the ranks of the element over all permutations.

This is what we do in the example of Figure 4.7. Item Agets 3 ·1 + 1 ·2=5

points on the strength of appearing ﬁrst in three rankings and second in one.

Item Cﬁnishes with 12 points by ﬁnishing 2, 3, 3, and 4. The ﬁnal consensus

ranking of {A, B, C, D, E}integrates all the votes from all input rankings, even

though the consensus disagrees at least in part with all four input rankings.

But it is not clear that using linear weights represents the best choice,

because it assumes uniform conﬁdence in our accuracy to position elements

1Observe the diﬀerence between a similarity measure and a distance metric. In correlation,

the scores get bigger as elements get more similar, while in a distance function the diﬀerence

goes to zero. Distance metrics will be discussed more thoroughly in Section 10.1.1.

4.4. ADVANCED RANKING TECHNIQUES 109

Figure 4.8: Equally-spaced values by the normal distribution are closer in the

middle than the ends, making appropriate weights for Borda’s method.

throughout the permutation. Typically, we will know the most about the mer-

its of our top choices, but will be fairly fuzzy about exactly how those near the

middle order among themselves. If this is so, a better approach might be to

award more points for the distinction between 1st and 2nd than between 110th

and 111th.

This type of weighting is implicitly performed by a bell-shaped curve. Sup-

pose we sample nitems at equal intervals from a normal distribution, as shown

in Figure 4.8. Assigning these xvalues as the positional weights produces more

spread at the highest and lowest ranks than the center. The tail regions really

are as wide as they appear for these 50 equally-spaced points: recall that 95%

of the probability mass sits within 2σof the center.

Alternately, if our conﬁdence is not symmetric, we could sample from the

half-normal distribution, so the tail of our ranks is weighted by the peak of

the normal distribution. This way, there is the greatest separation among the

highest-ranked elements, but little distinction among the elements of the tail.

Your choice of weighting function here is domain dependent, so pick one that

seems to do a good job on your problem. Identifying the very best cost function

turns out to be an ill-posed problem. And strange things happen when we try

to design the perfect election system, as will be shown in Section 4.6.

4.4.3 Digraph-based Rankings

Networks provide an alternate way to think about a set of votes of the form “A

ranks ahead of B.” We can construct a directed graph/network where there is

a vertex corresponding to each entity, and a directed edge (A, B) for each vote

that Aranks ahead of B.

The optimal ranking would then be a permutation Pof the vertices which

110 CHAPTER 4. SCORES AND RANKINGS

B C

Figure 4.9: Consistently ordered preferences yield an acyclic graph or DAG

(left). Inconsistent preferences result in directed cycles, which can be broken by

deleting small sets of carefully selected edges, here shown dashed (right).

violates the fewest number of edges, where edge (A, B) is violated if Bcomes

before Ain the ﬁnal ranking permutation P.

If the votes were totally consistent, then this optimal permutation would

violate exactly zero edges. Indeed, this is the case when there are no directed

cycles in the graph. A directed cycle like (A, C), (C, E), (E, A) represents

an inherent contradiction to any rank order, because there will always be an

unhappy edge no matter which order you choose.

A directed graph without cycles is called a directed acyclic graph or DAG.

An alert reader with a bit of algorithms background will recall that ﬁnding

this optimal vertex order is called topologically sorting the DAG, which can

be performed eﬃciently in linear time. Figure 4.9 (left) is a DAG, and has

exactly two distinct orders consistent with the directed edges: {A, B, C, D, E}

and {A, C, B, D, E}.

However, it is exceedingly unlikely that a real set of features or voters will

all happen to be mutually consistent. The maximum acyclic subgraph problem

seeks to ﬁnd the smallest number of edges to delete to leave a DAG. Removing

edge (E, A) suﬃces in Figure 4.9 (right). Unfortunately, the problem of ﬁnding

the best ranking here is NP-complete, meaning that no eﬃcient algorithm exists

for ﬁnding the optimal solution.

But there are natural heuristics. A good clue as to where a vertex vbelongs

is the diﬀerence dvbetween its in-degree and its out-degree. When dvis highly

negative, it probably belongs near the front of the permutation, since it domi-

nates many elements but is dominated by only a few. One can build a decent

ranking permutation by sorting the vertices according to these diﬀerences. Even

better is incrementally inserting the most negative (or most positive) vertex v

into its logical position, deleting the edges incident on v, and then adjusting the

counts before positioning the next best vertex.

4.5. WAR STORY: CLYDE’S REVENGE 111

4.4.4 PageRank

There is a diﬀerent and more famous method to order the vertices in a network

by importance: the PageRank algorithm underpinning Google’s search engine.

The web is constructed of webpages, most of which contain links to other

webpages. Your webpage linking to mine is an implicit endorsement that you

think my page is pretty good. If it is interpreted as a vote that “you think my

page is better than yours,” we can construct the network of links and treat it

as a maximum acyclic-subgraph problem, discussed in the previous subsection.

But dominance isn’t really the right interpretation for links on the web.

PageRank instead rewards vertices which have the most in-links to it: if all

roads lead to Rome, Rome must be a fairly important place. Further, it weighs

these in-links by the strength of the source: a link to me from an important

page should count for more than one from a spam site.

The details here are interesting, but I will defer a deeper discussion to Section

10.4, when we discuss network analysis. However, I hope this brief introduction

to PageRank helps you appreciate the following tale.

4.5 War Story: Clyde’s Revenge

During my sophomore year of high school, I had the idea of writing a program to

predict the outcome of professional football games. I wasn’t all that interested

in football as a sport, but I observed several of my classmates betting their

lunch money on the outcome of the weekend football games. It seemed clear to

me that writing a program which accurately predicted the outcome of football

games could have signiﬁcant value, and be a very cool thing to do besides.

In retrospect, the program I came up with now seems hopelessly crude. My

program would average the points scored by team xand the points allowed by

team yto predict the number of points xwill score against y.

Px=((points scored by team x) + (points allowed by team y))

2×(games played)

Py=((points scored by team y) + (points allowed by team x))

2×(games played)

I would then adjust these numbers up or down in response to other factors,

particularly home ﬁeld advantage, round the numbers appropriately, and call

what was left my predicted score for the game.

This computer program, Clyde, was my ﬁrst attempt to build a scoring

function for some aspect of the real world. It had a certain amount of logic

going for it. Good teams score more points than they allow, while bad teams

allow more points than they score. If team xplays a team ywhich has given up

a lot of points, then xshould score more points against ythan it does against

112 CHAPTER 4. SCORES AND RANKINGS

teams with better defenses. Similarly, the more points team xhas scored against

the rest of the league, the more points it is likely to score against y.

Of course, this crude model couldn’t capture all aspects of football reality.

Suppose team xhas been playing all stiﬀs thus far in the season, while team y

has been playing the best teams in the league. Team ymight be a much better

team than xeven though its record so far is poor. This model also ignores

any injuries a team is suﬀering from, whether the weather is hot or cold, and

whether the team is hot or cold. It disregards all the factors that make sports

inherently unpredictable.

And yet, even such a simple model can do a reasonable job of predicting

the outcome of football games. If you compute the point averages as above,

and give the home team an additional three points as a bonus, you will pick

the winner in almost two-thirds of all football games. Compare this to the even

cruder model of ﬂipping a coin, which predicts only half the games correctly.

That was the ﬁrst major lesson Clyde taught me:

Even crude mathematical models can have real predictive power.

As an audacious 16 year-old, I wrote to our local newspaper, The New

Brunswick Home News, explaining that I had a computer program to predict

football game results and was ready to oﬀer them the exclusive opportunity to

publish my predictions each week. Remember that this was back in 1977, well

before personal computers had registered on the public consciousness. In those

days, the idea of a high school kid actually using a computer had considerable

gee-whiz novelty value. To appreciate how much times have changed, check out

the article the paper published about Clyde and I in Figure 4.10.

I got the job. Clyde predicted the outcome of each game in the 1977 National

Football League. As I recall, Clyde and I ﬁnished the season with the seemingly

impressive record of 135–70. Each week, they would compare my predictions

against those of the newspaper’s sportswriters. As I recall, we all ﬁnished within

a few games of each other, although most of the sportswriters ﬁnished with

better records than the computer.

The Home News was so impressed by my work that they didn’t renew me

the following season. However, Clyde’s picks for the 1978 season were published

in the Philadelphia Inquirer, a much bigger newspaper. I didn’t have the col-

umn to myself, though. Instead, the Inquirer included me among ten amateur

and professional prognosticators, or touts. Each week we had to predict the

outcomes of four games against the point spread.

The point spread in football is a way of handicapping stronger teams for

betting purposes. The point spread is designed to make each game a 50/50

proposition, and hence makes predicting the outcome of games much harder.

Clyde and I didn’t do very well against the spread during the 1978 National

Football League season, and neither did most of the other Philadelphia Inquirer

touts. We predicted only 46% of our games correctly against the spread, a

performance good (or bad) enough to ﬁnish 7th out of the ten published prog-

nosticators. Picking against the spread taught me a second major life lesson:

4.5. WAR STORY: CLYDE’S REVENGE 113

Figure 4.10: My ﬁrst attempt at mathematical modeling.

114 CHAPTER 4. SCORES AND RANKINGS

Crude mathematical models do not have real predictive power when

there is real money on the line.

So Clyde was not destined to revolutionize the world of football prognosti-

cation. I pretty much forgot about it until I assigned the challenge of predicting

the Super Bowl as a project in my data science class. The team that got the

job was made up of students from India, meaning they knew much more about

cricket than American football when they started.

Still, they rose to the challenge, becoming fans as they built a large data

set on the outcome of every professional and college game played over the past

ten years. They did a logistic regression analysis over 142 diﬀerent features

including rushing, passing, and kicking yardage, time of possession, and number

of punts. They then proudly reported to me the accuracy of their model: correct

predictions on 51.52% of NFL games.

“What!” I screamed, “That’s terrible!” “Fifty percent is what you get by

ﬂipping a coin. Try averaging the points scored and yielded by the two teams,

and give three points to the home team. How does that simple model do?”

On their data set, this Clyde-light model picked 59.02% of all games cor-

rectly, much much better than their sophisticated-looking machine learning

model. They had gotten lost in the mist of too many features, which were

not properly normalized, and built using statistics collected over too long a

history to be representative of the current team composition. Eventually the

students managed to come up with a PageRank-based model that did a little

bit better (60.61%), but Clyde did almost as well serving as a baseline model.

There are several important lessons here. First, garbage in, garbage out.

If you don’t prepare a clean, properly normalized data set, the most advanced

machine learning algorithms can’t save you. Second, simple scores based on a

modest amount of domain-speciﬁc knowledge can do surprisingly well. Further,

they help keep you honest. Build and evaluate simple, understandable baselines

before you invest in more powerful approaches. Clyde going baseline left their

machine learning model defenseless.

4.6 Arrow’s Impossibility Theorem

We have seen several approaches to construct rankings or scoring functions from

data. If we have a gold standard reporting the “right” relative order for at least

some of the entities, then this could be used to train or evaluate our scoring

function to agree with these rankings to the greatest extent possible.

But without a gold standard, it can be shown that no best ranking system

exists. This is a consequence of Arrow’s impossibility theorem, which proves

that no election system for aggregating permutations of preferences satisﬁes the

following desirable and innocent-looking properties:

•The system should be complete, in that when asked to choose between

alternatives Aand B, it should say (1) Ais preferred to B, (2) Bis

preferred to A, or (3) there is equal preference between them.

4.7. WAR STORY: WHO’S BIGGER? 115

Voter Red Green Blue

x 1 2 3

y 2 3 1

z 3 1 2

Figure 4.11: Preference rankings for colors highlighting the loss of transitivity.

Red is preferred to green and green preferred to blue, yet blue is preferred to

red.

•The results should be transitive, meaning if Ais preferred to B, and Bis

preferred to C, then Amust be preferred to C.

•If every individual prefers Ato B, then the system should prefer Ato B.

•The system should not depend only upon the preferences of one individual,

a dictator.

•The preference of Acompared to Bshould be independent of preferences

for any other alternatives, like C.

Figure 4.11 captures some of the ﬂavor of Arrow’s theorem, and the non-

transitive nature of “rock-paper-scissors” type ordering. It shows three voters

(x,y, and z) ranking their preferences among colors. To establish the preference

among two colors aand b, a logical system might compare how many permuta-

tions rank abefore bas opposed to bbefore a. By this system, red is preferred

to green by xand y, so red wins. Similarly, green is preferred to blue by xand

z, so green wins. By transitivity, red should be preferred to blue by implication

on these results. Yet yand z, prefer blue to red, violating an inherent property

we want our election system to preserve.

Arrow’s theorem is very surprising, but does it mean that we should give up

on rankings as a tool for analyzing data? Of course not, no more than Arrow’s

theorem means that we should give up on democracy. Traditional voting systems

based on the idea that the majority rules generally do a good job of reﬂecting

popular preferences, once appropriately generalized to deal with large numbers

of candidates. And the techniques in this chapter generally do a good job of

ranking items in interesting and meaningful ways.

Take-Home Lesson: We do not seek correct rankings, because this is an ill-

deﬁned objective. Instead, we seek rankings that are useful and interesting.

4.7 War Story: Who’s Bigger?

My students sometimes tell me that I am history. I hope this isn’t true quite

yet, but I am very interested in history, as is my former postdoc Charles Ward.

Charles and I got to chatting about who the most signiﬁcant ﬁgures in history

116 CHAPTER 4. SCORES AND RANKINGS

were, and how you might measure this. Like most people, we found our answers

in Wikipedia.

Wikipedia is an amazing thing, a distributed work product built by over

100,000 authors which somehow maintains a generally sound standard of accu-

racy and depth. Wikipedia captures an astonishing amount of human knowledge

in an open and machine-readable form.

We set about using the English Wikipedia as a data source to base historical

rankings on. Our ﬁrst step was to extract feature variables from each person’s

Wikipedia page that should clearly correlate with historical signiﬁcance. This

included features like:

•Length: Most signiﬁcant historical ﬁgures should have longer Wikipedia

pages than lesser mortals. Thus article length in words provides a natural

feature reﬂecting historical wattage, to at least some degree.

•Hits: The most signiﬁcant ﬁgures have their Wikipedia pages read more

often than others, because they are of greater interest to a larger number

of people. My Wikipedia page gets hit an average of twenty times per day,

which is pretty cool. But Issac Newton’s page gets hit an average of 7700

times per day, which is a hell of a lot better.

•PageRank: Signiﬁcant historical ﬁgures interact with other signiﬁcant

historical ﬁgures, which get reﬂected as hyperlink references in Wikipedia

articles. This deﬁnes a directed graph where the vertices are articles, and

the directed edges hyperlinks. Computing the PageRank of this graph will

measure the centrality of each historical ﬁgure, which correlates well with

signiﬁcance.

All told, we extracted six features for each historical ﬁgure. Next, we normal-

ized these variables before aggregating, essentially by combining the underlying

rankings with normally-distributed weights, as suggested in Section 4.4.2. We

used a technique called statistical factor analysis related to principal component

analysis (discussed in Section 8.5.2), to isolate two factors that explained most

of the variance in our data. A simple linear combination of these variables gave

us a scoring function, and we sorted the scores to determine our initial ranking,

something we called fame.

The top twenty ﬁgures by our fame score are shown in Figure 4.12 (right).

We studied these rankings and decided that it didn’t really capture what we

wanted it to. The top twenty by fame included pop musicians like Madonna

and Michael Jackson, and three contemporary U.S. presidents. It was clear that

contemporary ﬁgures ranked far higher than we thought they should: our scoring

function was capturing current fame much more than historical signiﬁcance.

Our solution was to decay the scores of contemporary ﬁgures to account

for the passage of time. That a current celebrity gets a lot of Wikipedia hits

is impressive, but that we still care about someone who died 300 years ago is

much more impressive. The top twenty ﬁgures after age correction are shown

in Figure 4.12 (left).

4.7. WAR STORY: WHO’S BIGGER? 117

Signif Name

1 Jesus

2 Napoleon

3 William Shakespeare

4 Muhammad

5 Abraham Lincoln

6 George Washington

7 Adolf Hitler

8 Aristotle

9 Alexander the Great

10 Thomas Jeﬀerson

11 Henry VIII

12 Elizabeth I

13 Julius Caesar

14 Charles Darwin

15 Karl Marx

16 Martin Luther

17 Queen Victoria

18 Joseph Stalin

19 Theodore Roosevelt

20 Albert Einstein

Fame Person

1 George W. Bush

2 Barack Obama

3 Jesus

4 Adolf Hitler

5 Ronald Reagan

6 Bill Clinton

7 Napoleon

8 Michael Jackson

9 W. Shakespeare

10 Elvis Presley

11 Muhammad

12 Joseph Stalin

13 Abraham Lincoln

14 G. Washington

15 Albert Einstein

16 John F. Kennedy

17 Elizabeth II

18 John Paul II

19 Madonna

20 Britney Spears

Figure 4.12: The top 20 historical ﬁgures, ranked by signiﬁcance (left) and

contemporary fame (right).

Now this was what we were looking for! We validated the rankings using

whatever proxies for historical signiﬁcance we could ﬁnd: other published rank-

ings, autograph prices, sports statistics, history textbooks, and Hall of Fame

election results. Our rankings showed a strong correlation against all of these

proxies.

Indeed, I think these rankings are wonderfully revealing. We wrote a book

describing all kinds of things that could be learned from them [SW13]. I proudly

encourage you to read it if you are interested in history and culture. The more

we studied these rankings, the more I was impressed in their general soundness.

That said, our published rankings did not meet with universal agreement.

Far from it. Dozens of newspaper and magazine articles were published about

our rankings, many quite hostile. Why didn’t people respect them, despite our

extensive validation? In retrospect, most of the ﬂack we ﬁelded came for three

diﬀerent reasons:

•Diﬀering implicit notions of signiﬁcance: Our methods were designed

to measure meme-strength, how successfully these historical ﬁgures were

propagating their names though history. But many readers thought our

methods should capture notions of historical greatness. Who was most

important, in terms of changing the world? And do we mean world or

just the English-speaking world? How can there be no Chinese or Indian

118 CHAPTER 4. SCORES AND RANKINGS

ﬁgures on the list when they represent over 30% of the world’s population?

We must agree on what we are trying to measure before measuring it.

Height is an excellent measure of size, but it does not do a good job of

capturing obesity. However, height is very useful to select players for a

basketball team.

•Outliers: Sniﬀ tests are important to evaluating the results of an analysis.

With respect to our rankings, this meant checking the placement of people

we knew, to conﬁrm that they fell in reasonable places.

I felt great about our method’s ranking of the vast majority of historical

ﬁgures. But there were a few people who our method ranked higher than

any reasonable person would, speciﬁcally President George W. Bush (36)

and teenage TV star Hilary Duﬀ (1626). One could look at these out-

liers and dismiss the entire thing. But understand that we ranked almost

850,000 historical ﬁgures, roughly the population of San Francisco. A few

cherry-picked bad examples must be put in the proper context.

•Pigeonhole constraints: Most reviewers saw only the rankings of our top

100 ﬁgures, and they complained about exactly where we placed people

and who didn’t make the cut. The women’s TV show The View com-

plained we didn’t have enough women. I recall British articles complain-

ing we had Winston Churchill (37) ranked too low, South African articles

that thought we dissed Nelson Mandela (356), Chinese articles saying we

didn’t have enough Chinese, and even a Chilean magazine whining about

the absence of Chileans.

Some of this reﬂects cultural diﬀerences. These critics had a diﬀerent

implicit notion of signiﬁcance than reﬂected by English Wikipedia. But

much of it reﬂects the fact that there are exactly one hundred places in

the top 100. Many of the ﬁgures they saw as missing were just slightly

outside the visible horizon. For every new person we moved into the top

hundred, we had to drop somebody else out. But readers almost never

suggested names that should be omitted, only those who had to be added.

What is the moral here? Try to anticipate the concerns of the audience for

your rankings. We were encouraged to explicitly call our measure meme-strength

instead of signiﬁcance. In retrospect, using this less-loaded name would have

permitted our readers to better appreciate what we were doing. We probably

also should have discouraged readers from latching on to our top 100 rankings,

and instead concentrate on relative orderings within groups of interest: who

were the top musicians, scientists, and artists? This might have proved less

controversial, better helping people build trust in what we were doing.

4.8 Chapter Notes

Langville and Meyer [LM12] provide a through introduction to most of the

ranking methods discussed here, including Elo and PageRank.

4.9. EXERCISES 119

One important topic not covered in this chapter is learning to rank methods,

which exploit gold standard ranking data to train appropriate scoring functions.

Such ground truth data is generally not available, but proxies can sometimes be

found. When evaluating search engines, the observation that a user clicked the

(say) fourth item presented to them can be interpreted as a vote that it should

have been higher ranked than the three placed above it. SVMrank [Joa02]

presents a method for learning ranking functions from such data.

The heuristic proposed minimizing edge conﬂicts in a vertex order is due

to Eades et. al. [ELS93]. My presentation of Arrow’s impossibility theorem is

based on notes from Watkins [Wat16].

The war stories of this chapter were drawn very closely from my books

Calculated Bets and Who’s Bigger? Don’t sue me for self-plagiarism.

4.9 Exercises

Scores and Rankings

4-1. [3] Let Xrepresent a random variable drawn from the normal distribution de-

ﬁned by µ= 2 and σ= 3. Suppose we observe X= 5.08. Find the Z-score of x,

and determine how many standard deviations away from the mean that xis.

4-2. [3] What percentage of the standard normal distribution (µ= 0, σ= 1) is found

in each region?

(a) Z > 1.13.

(b) Z < 0.18.

(d) |Z|<0.5.

4-3. [3] Amanda took the Graduate Record Examination (GRE), and scored 160 in

verbal reasoning and 157 in quantitative reasoning. The mean score for verbal

reasoning was 151 with a standard deviation of 7, compared with mean µ= 153

and σ= 7.67 for quantitative reasoning. Assume that both distributions are

normal.

(a) What were Amanda’s Z-scores on these exam sections? Mark these scores

on a standard normal distribution curve.

(b) Which section did she do better on, relative to other students?

4-4. [3] Identify three successful and well-used scoring functions in areas of personal

interest to you. For each, explain what makes it a good scoring function and

how it is used by others.

4-5. [5] Find a data set on properties of one of the following classes of things:

(a) The countries of the world.

(b) Movies and movie stars.

120 CHAPTER 4. SCORES AND RANKINGS

(d) Universities.

Construct a sensible ranking function reﬂecting quality or popularity. How well

is this correlated with some external measure aiming at a similar result?

4-6. [5] Produce two substantially diﬀerent but sensible scoring functions on the same

set of items. How diﬀerent are the resulting rankings? Does the fact that both

have to be sensible constrain rankings to be grossly similar?

4-7. [3] The scoring systems used by professional sports leagues to select the most

valuable player award winner typically involves assigning positional weights to

permutations speciﬁed by voters. What systems do they use in professional

baseball, basketball, and football? Are they similar? Do you think they are

sensible?

Implementation Projects

4-8. [5] Use Elo ratings to rank all the teams in a sport such as baseball, football,

or basketball, which adjusts the rating in response to each new game outcome.

How accurately do these Elo ratings predict the results of future contests?

4-9. [5] Evaluate the robustness of Borda’s method by applying krandom swaps to

each of mdistinct copies of the permutation p={1,2,...,n}. What is the

threshold where Borda’s method fails to reconstruct p, as a function of n,k,

and m?

Interview Questions

4-10. [5] What makes a data set a gold standard?

4-11. [5] How can you test whether a new credit risk scoring model works?

4-12. [5] How would you forecast sales for a particular book, based on Amazon public

data?

Kaggle Challenges

4-13. Rating chess players from game positions.

https://www.kaggle.com/c/chess

4-14. Develop a ﬁnancial credit scoring system.

https://www.kaggle.com/c/GiveMeSomeCredit

4-15. Predict the salary of a job from its ad.

https://www.kaggle.com/c/job-salary-prediction

Chapter 5

Statistical Analysis

It is easy to lie with statistics, but easier to lie without them.

– Frederick Mosteller

I will confess that I have never had a truly satisfying conversation with a statis-

tician. This is not completely for want of trying. Several times over the years

I have taken problems of interest to statisticians, but always came back with

answers like “You can’t do it that way” or “But it’s not independent,” instead

of hearing “Here is the way you can handle it.”

To be fair, these statisticians generally did not appreciate talking with me,

either. Statisticians have been thinking seriously about data for far longer than

computer scientists, and have many powerful methods and ideas to show for it.

In this chapter, I will introduce some of these important tools, like the deﬁnitions

of certain fundamental distributions and tests for statistical signiﬁcance. This

chapter will also introduce Baysian analysis, a way to rigorously assess how new

data should aﬀect our previous estimates of future events.

Population

Sample

Probability

Inferential Statistics

Descriptive

Statistics

Figure 5.1: The central dogma of statistics: analysis of a small random sample

enables drawing rigorous inferences about the entire population.

122 CHAPTER 5. STATISTICAL ANALYSIS

Figure 5.1 illustrates the process of statistical reasoning. There is an un-

derlying population of possible things that we can potentially observe. Only a

relatively small subset of them are actually sampled, ideally at random, mean-

ing that we can observe properties of the sampled items. Probability theory

describes what properties our sample should have, given the properties of the

underlying population. But statistical inference works the other way, where we

try to deduce what the full population is like given analysis of the sample.

Ideally, we will learn to think like a statistician: enough so as to remain

vigilant and guard against overinterpretation and error, while retaining our

conﬁdence to play with data and take it where it leads us.

5.1 Statistical Distributions

Every variable that we observe deﬁnes a particular frequency distribution, which

reﬂects how often each particular value arises. The unique properties of variables

like height, weight, and IQ are captured by their distributions. But the shapes

of these distributions are themselves not unique: to a great extent, the world’s

rich variety of data appear only in a small number of classical forms.

These classical distributions have two nice properties: (1) they describe

shapes of frequency distributions that arise often in practice, and (2) they can

often be described mathematically using closed-form expressions with very few

parameters. Once abstracted from speciﬁc data observations, they become prob-

ability distributions, worthy of independent study.

Familiarity with the classical probability distributions is important. They

arise often in practice, so you should be on the look out for them. They give us

a vocabulary to talk about what our data looks like. We will review the most

important statistical distributions (binomial, normal, Poisson, and power law)

in the sections to follow, emphasizing the properties that deﬁne their essential

character.

Note that your observed data does not necessarily arise from a particular

theoretical distribution just because its shape is similar. Statistical tests can

be used to rigorously prove whether your experimentally-observed data reﬂects

samples drawn from a particular distribution.

But I am going to save you the trouble of actually running any of these tests.

I will state with high conﬁdence that your real-world data does not precisely ﬁt

any of the famous theoretical distributions.

Why is that? Understand that the world is a complicated place, which makes

measuring it a messy process. Your observations will probably be drawn from

multiple sample populations, each of which has a somewhat diﬀerent underlying

distribution. Something funny generally happens at the tails of any observed

distribution: a sudden burst of unusually high or low values. Measurements will

have errors associated with them, sometimes in weird systematic ways.

But that said, understanding the basic distributions is indeed very impor-

tant. Each classical distribution is classical for a reason. Understanding these

reasons tells you a lot about observed data, so they will be reviewed here.

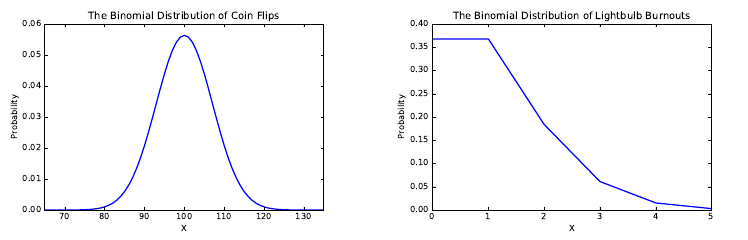
5.1. STATISTICAL DISTRIBUTIONS 123

Figure 5.2: The binomial distribution can be used to model the distribution of

heads in 200 coin tosses with p= 0.5 (left), and the number of blown lightbulbs

in 1000 events with failure probability p= 0.001 (right).

5.1.1 The Binomial Distribution

Consider an experiment consisting of identical, independent trials which have

two possible outcomes P1and P2, with the respective probabilities of pand

q= (1−p). Perhaps your experiment is ﬂipping fair coins, where the probability

of heads (p= 0.5) is the same as getting tails (q= 0.5). Perhaps it is repeatedly

turning on a light switch, where the probability of suddenly discovering that

you must change the bulb (p= 0.001) is much less than that of seeing the light

(q= 0.999).

The binomial distribution reports the probability of getting exactly x P1

events in the course of nindependent trials, in no particular order. Independence

is important here: we are assuming the probability of failure of a bulb has no

relation to how many times it has previously been used. The pdf for the binomial

distribution is deﬁned by:

P(X=x) = n

xpx(1 −p)(n−x)

There are several things to observe about the binomial distribution:

•It is discrete: Both arguments to the binomial distribution (nand x) must

be integers. The smoothness of Figure 5.2 (left) is an illusion, because

n= 200 is fairly large. There is no way of getting 101.25 heads in 200

coin tosses.

•You probably can explain the theory behind it: You ﬁrst encountered the

binomial distribution in high school. Remember Pascal’s triangle? To end

up with exactly xheads in nﬂips in a particular sequence occurs with

probability px(1 −p)(n−x), for each of the n

xdistinct ﬂip sequences.

•It is sort of bell-shaped: For a fair coin (p= 0.5), the binomial distribution

is perfectly symmetrical, with the mean in the middle. This is not true

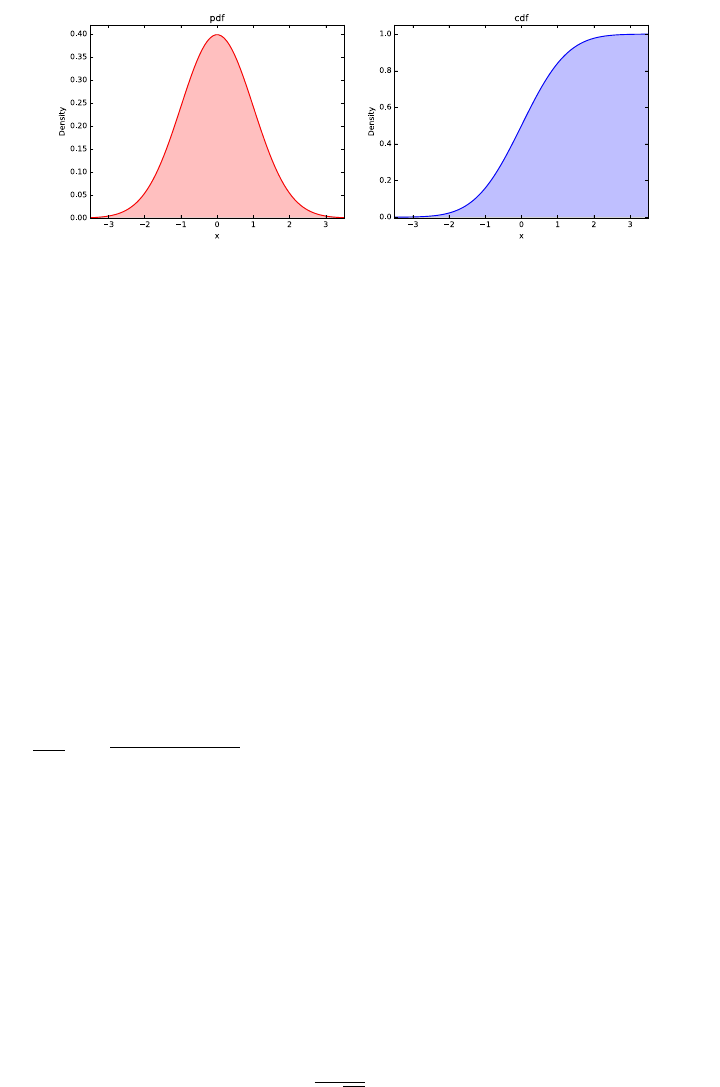
124 CHAPTER 5. STATISTICAL ANALYSIS

Figure 5.3: The probability density function (pdf) of the normal distribution

(left) with its corresponding cumulative density function (cdf) on right.

in the lightbulb case: if we only turn on the bulb n= 1000 times, the

most likely number of failures will be zero. This rings just half the bell

in Figure 5.2. That said, as n→ ∞ we will get a symmetric distribution

peaking at the mean.

•It is deﬁned using only two parameters: All we need are values of pand

nto completely deﬁne a given binomial distribution.

Many things can be reasonably modeled by the binomial distribution. Recall

the variance in the performance of a p= 0.300 hitter discussed in Section 2.2.3.

There the probability of getting a hit with each trial was p= 0.3, with n= 500

trials per season. Thus the number of hits per season are drawn from a binomial

distribution.

Realizing that it was a binomial distribution meant that we really didn’t have

to use simulation to construct the distribution. Properties like the expected

number of hits µ=np = 500 ×0.3 = 150 and its standard deviation σ=

√npq =√500 ×0.3×0.7 = 10.25 simply fall out of closed-form formulas that

you can look up when needed.

5.1.2 The Normal Distribution

A great many natural phenomenon are modeled by bell-shaped curves. Mea-

sured characteristics like height, weight, lifespan, and IQ all ﬁt the same basic

scheme: the bulk of the values lie pretty close to the mean, the distribution is

symmetric, and no value is too extreme. In the entire history of the world, there

has never been either a 12-foot-tall man or a 140-year-old woman.

The mother of all bell-shaped curves is the Gaussian or normal distribution,

which is completely parameterized by its mean and standard deviation:

P(x) = 1

σ√2πe−(x−µ)2/2σ2

5.1. STATISTICAL DISTRIBUTIONS 125

Figure 5.3 shows the pdf and cdf of the normal distribution. There are

several things to note:

•It is continuous: The arguments to the normal distribution (mean µand

standard deviation σ) are free to arbitrary real numbers, with the lone

constraint that σ > 0.

•You probably can’t explain where it comes from: The normal distribution

is a generalization of the binomial distribution, where n→ ∞ and the

degree of concentration around the mean is speciﬁed by the parameter σ.

Take your intuition here from the binomial distribution, and trust that

Gauss got his calculations right: the great mathematician worked out

the normal distribution for his Ph.D. dissertation. Or consult any decent

statistics book if you are really curious to see where it comes from.

•It truly is bell-shaped: The Gaussian distribution is the platonic exam-

ple of a bell-shaped curve. Because it operates on a continuous variable

(like height) instead of a discrete count (say, the number of events) it

is perfectly smooth. Because it goes inﬁnitely in both directions, there

is no truncation of the tails at either end. The normal distribution is a

theoretical construct, which helps explain this perfection.

•It is also deﬁned using only two parameters: However, these are diﬀerent

parameters than the binomial distribution! The normal distribution is

completely deﬁned by its central point (given by the mean µ) and its

spread (given by the standard deviation σ). They are the only knobs we

can use to tweak the distribution.

What’s Normal?

An amazing number of naturally-occurring phenomenon are modeled by the

normal distribution. Perhaps the most important one is measurement error.

Every time you measure your weight on a bathroom scale, you will get a some-

what diﬀerent answer, even if your weight has not changed. Sometimes the scale

will read high and other times low, depending upon room temperature and the

warping of the ﬂoor. Small errors are more likely than big ones, and slightly

high is just as likely as slightly low. Experimental error is generally normally

distributed as Gaussian noise.

Physical phenomenon like height, weight, and lifespan all have bell-shaped

distributions, by similar arguments. Yet the claim that such distributions are

normal is usually made too casually, without precisely specifying the underlying

population. Is human height normally distributed? Certainly not: men and

women have diﬀerent mean heights and associated distributions. Is male height

normally distributed? Certainly not: by including children in the mix and

shrinking senior citizens you again have the sum of several diﬀerent underlying

distributions. Is the height of adult males in the United States normal? No,

probably not even then. There are non-trivial populations with growth disorders

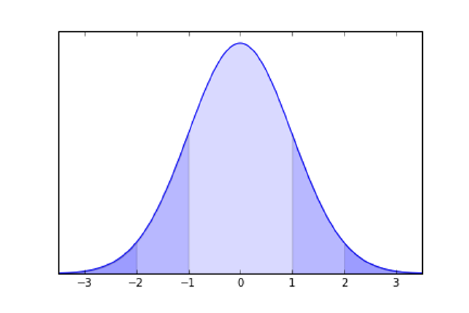
126 CHAPTER 5. STATISTICAL ANALYSIS

Figure 5.4: The normal distribution implies tight bounds on the probability of

lying far from the mean. 68% of the values must lie within one sigma of the

mean, and 95% within 2σ, and 99.7% within 3σ.

like dwarﬁsm and acromegaly, that leave bunches of people substantially shorter

and taller than could be explained by the normal distribution.

Perhaps the most famous bell-shaped but non-normal distribution is that

of daily returns (percentage price movements) in the ﬁnancial markets. A big

market crash is deﬁned by a large percentage price drop: on October 10, 1987,

the Dow Jones average lost 22.61% of its value. Big stock market crashes occur

with much greater frequency than can be accurately modeled by the normal dis-

tribution. Indeed, every substantial market crash wipes out a certain number of

quants who assumed normality, and inadequately insured against such extreme

events. It turns out that the logarithm of stock returns proves to be normally

distributed, resulting in a distribution with far fatter tails than normal.

Although we must remember that bell-shaped distributions are not always

normal, making such an assumption is a reasonable way to start thinking in the

absence of better knowledge.

5.1.3 Implications of the Normal Distribution

Recall that the mean and standard deviation together always roughly charac-

terize any frequency distribution, as discussed in Section 2.2.4. But they do a

spectacularly good job of characterizing the normal distribution, because they

deﬁne the normal distribution.

Figure 5.4 illustrates the famous 68%–95%–99% rule of the normal distribu-

tion. Sixty-eight percent of the probability mass must lie within the region ±1σ

of the mean. Further, 95% of the probability is within 2σ, and 99.7% within

3σ.

This means that values far from the mean (in terms of σ) are vanishingly

rare in any normally distributed variable. Indeed the term six sigma is used to

5.1. STATISTICAL DISTRIBUTIONS 127

connote quality standards so high that defects are incredibly rare events. We

want plane crashes to be six sigma events. The probability of a 6σevent on the

normal distribution is approximately 2 parts per billion.

Intelligence as measured by IQ is normally distributed, with a mean of 100

and standard deviation σ= 15. Thus 95% of the population lies within 2σof

the mean, from 70 to 130. This leaves only 2.5% of people with IQs above 130,

and another 2.5% below 70. A total of 99.7% of the mass lies within 3σof the

mean, i.e. people with IQs between 55 and 145.

So how smart is the smartest person in the world? If we assume a population

of 7 billion people, the probability of a randomly-selected person being smartest

is approximately 1.43 ×10−10. This is about the same probability of a single

sample lying more than 6.5σfrom the mean. Thus the smartest person in the

world should have an IQ of approximately 197.5, according to this reckoning.

The degree to which you accept this depends upon how strongly you believe

that IQ really is normally distributed. Such models are usually in grave danger

of breaking down at the extremes. Indeed, by this model there is almost the

same probability of there being someone dumb enough to earn a negative score

on an IQ test.

5.1.4 Poisson Distribution

The Poisson distribution measures the frequency of intervals between rare events.

Suppose we model human lifespan by a sequence of daily events, where there

is a small but constant probability 1 −pthat one happens to stop breathing

today. A lifespan of exactly ndays means successfully breathing for each of

the ﬁrst n−1 days and then forever breaking the pattern on the nth day. The

probability of living exactly ndays is given by P r(n) = pn−1(1 −p), yielding

an expected lifespan

µ=

∞

k=0

k·P r(k).

The Poisson distribution basically follows from this analysis, but takes a

more convenient argument than p. Instead it is based on µ, the average value of

the distribution. Since each pdeﬁnes a particular value of µ, these parameters

are in some sense equivalent, but the average is much easier to estimate or

measure. The Poisson distribution yields the very simple closed form:

P r(x) = e−µµx

Once you start thinking the right way, many distributions begin to look

Poisson, because they represent intervals between rare events.

Recall the binomial distribution lightbulb model from the previous section.

This made it easy to compute the expected number of changes in Figure 5.2

(right), but not the lifespan distribution, which is Poisson. Figure 5.5 plots the

associated Poisson distribution for µ= 1/p = 1000, which shows that we should

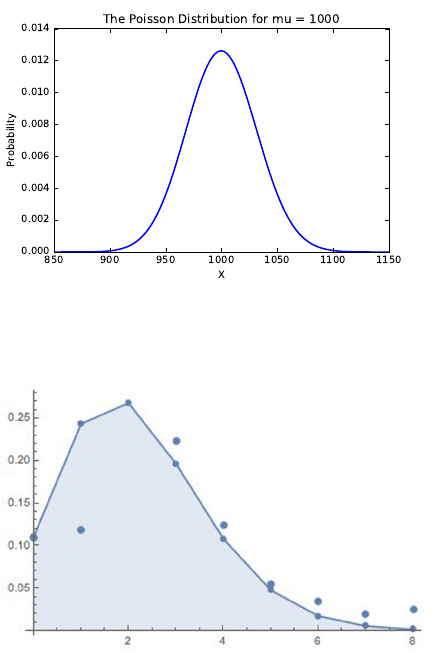
128 CHAPTER 5. STATISTICAL ANALYSIS

Figure 5.5: The lifespan distribution of lightbulbs with an expected life of µ=

1000 hours, as modeled by a Poisson distribution.

Figure 5.6: The observed fraction of families with xkids (isolated points) is

accurately modeled by Poisson distribution, deﬁned by an average of µ= 2.2

children per family (polyline).

expect almost all bulbs to glow for between 900 and 1100 hours before the dying

of the light.

Alternately, suppose we model the number of children by a process where

the family keeps having children until after one too many tantrums, bake sales,

or loads of laundry, a parent ﬁnally cracks. “That’s it! I’ve had enough of this.

No more!”

Under such a model, family size should be modeled as a Poisson distribution,

where every day there is a small but non-zero probability of a breakdown that

results in shutting down the factory.

How well does the “I’ve had it” model work to predict family size? The

polygonal line in Figure 5.6 represents the Poisson distribution with the param-

eter λ= 2.2, meaning families have an average of 2.2 kids. The points represent

the fraction of families with kchildren, drawn from the 2010 U.S. General Social

5.1. STATISTICAL DISTRIBUTIONS 129

50 100 150 200 250 300

200 000

400 000

600 000

1 5 10 50 100

1×105

5×105

1×106

5×106

1×107

Figure 5.7: The population of U.S. cities by decreasing rank (left). On the right

is the same data, now including the very largest cities, but plotted on a log-log

scale. That they sit on a line is indicative of a power law distribution.

Survey (GSS).

There is excellent agreement over all family sizes except k= 1, and frankly,

my personal experience suggests there are more singleton kids than this data

set represents. Together, knowing just the mean and the formula for Poisson

distribution enables us to construct a reasonable estimate of the real family-size

distribution.

5.1.5 Power Law Distributions

Many data distributions exhibit much longer tails than could be possible under

the normal or Poisson distributions. Consider, for example, the population of

cities. There were exactly 297 U.S. cities in 2014 with populations greater than

100,000 people, according to Wikipedia. The population of the kth largest city,

for 1 ≤k≤297 is presented in Figure 5.7 (left). It shows that a relatively

small number of cities have populations wildly dominating the rest. Indeed, the

seventeen largest cities have populations so large they have been clipped oﬀ this

plot so that we can see the rest.

These cities have a mean population of 304,689, with a ghastly standard

deviation of 599,816. Something is wrong when the standard deviation is so

large relative to the mean. Under a normal distribution, 99.7% of the mass lies

within 3σof the mean, thus making it unlikely that any of these cities would

have a population above 2.1 million people. Yet Houston has a population of

2.2 million people, and New York (at 8.4 million people) is more than 13σabove

the mean! City populations are clearly not normally distributed. In fact, they

observe a diﬀerent distribution, called a power law.

130 CHAPTER 5. STATISTICAL ANALYSIS

For a given variable Xdeﬁned by a power law distribution,

P(X=x) = cx−α

This is parameterized by two constants: the exponent αand normalization

constant c.

Power law distributions require some thinking to properly parse. The total

probability deﬁned by this distribution is the area under the curve:

A=Z∞

x=−∞

cx−α=cZ∞

x=−∞

x−α

The particular value of Ais deﬁned by the parameters αand c. The normal-

ization constant cis chosen speciﬁcally for a given αto make sure that A= 1,

as demanded by the laws of probability. Other than that, cis of no particular

importance to us.

The real action happens with α. Note that when we double the value of the

input (from xto 2x), we decrease the probability by a factor of f= 2−α. This

looks bad, but for any given αit is just a constant. So what the power law is

really saying is that the probability of a 2x-sized event is 2αtimes less frequent

than an x-sized event, for all x.

Personal wealth is well modeled by a power law, where f≈0.2=1/5. This

means that over a large range, if Zpeople have xdollars, then Z/5 people have

2xdollars. One ﬁfth as many people have $200,000 than have $100,000. If there

are 625 people in the world worth $5 billion, then there should be approximately

125 multi-billionaires each worth $10 billion. Further, there should be 25 super-

billionaires each worth $20 billion, ﬁve hyper-billionaires at the $40 billion level,

and ﬁnally a single Bill Gates worth $80 billion.

Power laws deﬁne the “80/20” rules which account for all the inequality of

our world: the observation that the top 20% of the Agets fully 80% of the

B. Power laws tend to arise whenever the rich get richer, where there is an

increasing probability you will get more based on what you already have. Big

cities grow disproportionately large because more people are attracted to cities

when they are big. Because of his wealth, Bill Gates gets access to much better

investment opportunities than I do, so his money grows faster than mine does.

Many distributions are deﬁned by such preferential growth or attachment

models, including:

•Internet sites with xusers: Websites get more popular because they have

more users. You are more likely to join Instagram or Facebook because

your friends have already joined Instagram or Facebook. Preferential at-

tachment leads to a power law distribution.

•Words used with a relative frequency of x: There is a long tail of millions

of words like algorist or defenestrate1that are rarely used in the English

1Defenestrate means “to throw someone out a window.”

5.1. STATISTICAL DISTRIBUTIONS 131

language. On the other hand, a small set of words like the are used wildly

more often than the rest.

Zipf’s law governs the distribution of word usage in natural languages, and

states that the kth most popular word (as measured by frequency rank)

is used only 1/kth as frequently as the most popular word. To gauge how

well it works, consider the ranks of words based on frequencies from the

English Wikipedia below:

It should be convincing that frequency of use drops rapidly with rank:

recall that grandmom is only a slang form of grandma, not the real McCoy.

Why is this a power law? A word of rank 2xhas a frequency of F2x∼

F1/2x, compared to Fx∼F1/x. Thus halving the rank doubles the fre-

quency, and this corresponds to the power law with α= 1.

What is the mechanism behind the evolution of languages that lead to this

distribution? A plausible explanation is that people learn and use words

because they hear other people using them. Any mechanism that favors

the already popular leads to a power law.

•Frequency of earthquakes of magnitude x: The Richter scale for measuring

the strength of earthquakes is logarithmic, meaning a 5.3 quake is ten times

stronger than a 4.3 scale event. Adding one to the magnitude multiplies

the strength by a factor of ten.

With such a rapidly increasing scale it makes sense that bigger events

are rarer than smaller ones. I cause a 0.02 magnitude quake every time

I ﬂush a toilet. There are indeed billions of such events each day, but

larger quakes get increasingly rare with size. Whenever a quantity grows

in a potentially unbounded manner but the likelihood it does diminishes

exponentially, you get a power law. Data shows this is as true of the energy

released by earthquakes as it is with the casualties of wars: mercifully the

number of conﬂicts which kill xpeople decreases as a power law.

Learn to keep your eyes open for power law distributions. You will ﬁnd them

everywhere in our unjust world. They are revealed by the following properties:

•Power laws show as straight lines on log value, log frequency plots: Check

out the graph of city populations in Figure 5.7 (right). Although there are

some gaps at the edges where data gets scarce, by and large the points lie

Rank Word Count

1the 25131726

110 even 415055

212 men 177630

312 least 132652

412 police 99926

514 quite 79205

614 include 65764

714 knowledge 57974

816 set 50862

916 doctor 46091

Rank Word Count

1017 build 41890

2017 essential 21803

3018 sounds 13867

4018 boards 9811

5018 rage 7385

6019 occupied 5813

7020 continually 4650

8020 delay 3835

9021 delayed 3233

10021 glances 2767

Rank Word Count

10021 glances 2767

20026 ecclesiastical 881

30028 zero-sum 405

40029 excluded 218

50030 sympathizes 124

60034 capon 77

70023 ﬁbs 49

80039 conventionalized 33

90079 grandmom 23

100033 slum-dwellers 17

132 CHAPTER 5. STATISTICAL ANALYSIS

neatly on a line. This is the main characteristic of a power law. By the

way, the slope of this line is determined by α, the constant deﬁning the

shape of the power law distribution.

•The mean does not make sense: Bill Gates alone adds about $250 to the

wealth of the average person in the United States. This is weird. Under a

power law distribution there is a very small but non-zero probability that

someone will have inﬁnite wealth, so what does this do to the mean? The

median does a much better job of capturing the bulk of such distributions

than the observed mean.

•The standard deviation does not make sense: In a power law distribution,

the standard deviation is typically as large or larger than the mean. This

means that the distribution is very poorly characterized by µand σ, while

the power law provides a very good description in terms of αand c.

•The distribution is scale invariant: Suppose we plotted the populations

of the 300th through 600th largest U.S. cities, instead of the top 300 as

in Figure 5.7 (left). The shape would look very much the same, with the

population of the 300th largest city towering over the tail. Any exponential

function is scale invariant, because it looks the same at any resolution.

This is a consequence of it being a straight line on a log-log plot: any

subrange is a straight line segment, which has the same parameters in its

window as the full distribution.

Take-Home Lesson: Be on the lookout for power law distributions. They reﬂect

the inequalities of the world, which means that they are everywhere.

5.2 Sampling from Distributions

Sampling points from a given probability distribution is a common operation,

one which it is pays to know how to do. Perhaps you need test data from a power

law distribution to run a simulation, or to verify that your program operates

under extreme conditions. Testing whether your data in fact ﬁts a particular

distribution requires something to compare it against, and that should generally

be properly-generated synthetic data drawn from the canonical distribution.

There is a general technique for sampling from any given probability distri-

bution, called inverse transform sampling. Recall that we can move between

the probability density function Pand the cumulative density function Cby

integration and diﬀerentiation. We can move back and forth between them

because:

P(k=X) = C0(k) = C(X≤k+δ)−C(X≤k), and

5.2. SAMPLING FROM DISTRIBUTIONS 133

Figure 5.8: The inverse transform sampling method enables us to convert a

random number generated uniformly from [0,1] (here 0.729) to a random sample

drawn from any distribution, given its cdf.

C(X≤k) = Zk

x=−∞

P(X=x).

Suppose I want to sample a point from this possibly very complicated distri-

bution. I can use a uniform random number generator to select a value pin the

interval [0,...,1]. We can interpret pas a probability, and use it as an index

on the cumulative distribution C. Precisely, we report the exact value of xsuch

that C(X≤x) = p.

Figure 5.8 illustrates the approach, here sampling from the normal distri-

bution. Suppose p= 0.729 is the random number selected from our uniform

generator. We return the xvalue such that y= 0.729, so x= 0.62 as per this

cdf.

If you are working with a popular probability distribution in a well-supported

language like Python, there is almost certainly a library function to generate

random samples already available. So look for the right library before you write

your own.

5.2.1 Random Sampling beyond One Dimension

Correctly sampling from a given distribution becomes a very subtle problem

once you increase the number of dimensions. Consider the task of sampling

points uniformly from within a circle. Think for a moment about how you

might do this before we proceed.

134 CHAPTER 5. STATISTICAL ANALYSIS

Figure 5.9: Randomly generating 10,000 points by angle-radius pairs clearly

oversamples near the origin of the circle (left). In contrast, Monte Carlo sam-

pling generates points uniformly within the circle (right).

The clever among you may hit upon the idea of sampling the angle and

distance from the center independently. The angle that any sampled point

must make with respect to the origin and positive x-axis varies between 0 and

2π. The distance from the origin must be a value between 0 and r. Select these

coordinates uniformly at random and you have a random point in the circle.

This method is clever, but wrong. Sure, any point so created must lie within

the circle. But the points are not selected with uniform frequency. This method

will generate points where half of them will lie within a distance of at most r/2

from the center. But most of the area of the circle is farther from the center

than that! Thus we will oversample near the origin, at the expense of the mass

near the boundary. This is shown by Figure 5.9 (left), a plot of 10,000 points

generated using this method.

A dumb technique that proves correct is Monte Carlo sampling. The xand

ycoordinates of every point in the circle range from −rto r, as do many points

outside the circle. Thus sampling these values uniformly at random gives us

a point which lies in a bounding box of the circle, but not always within the

circle itself. This can be easily tested: is the distance from (x, y) to the origin

at most r, i.e. is px2+y2≤r? If yes, we have found a random point in the

circle. If not, we toss it out and try again. Figure 5.9 (right) plots 10,000 points

constructed using this method: see how uniformly they cover the circle, without

any obvious places of over- or under-sampling.

The eﬃciency here depends entirely upon the ratio of the desired region

volume (the area of the circle) to the volume of the bounding box (the area of

a square). Since 78.5% of this bounded box is occupied by the circle, less than

two trials on average suﬃce to ﬁnd each new circle point.

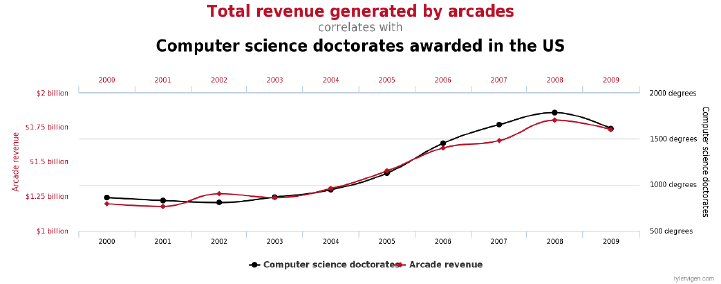
5.3. STATISTICAL SIGNIFICANCE 135

Figure 5.10: Correlation vs. causation: the number of Computer Science Ph.Ds

awarded each year in the United States strongly correlates with video/pinball

arcade revenue. (from [Vig15])

5.3 Statistical Signiﬁcance

Statisticians are largely concerned with whether observations on data are signiﬁ-

cant. Computational analysis will readily ﬁnd a host of patterns and correlations

in any interesting data set. But does a particular correlation reﬂect a real phe-

nomena, as opposed to just chance? In other words, when is an observation

really signiﬁcant?

Suﬃciently strong correlations on large data sets may seem to be “obviously”

meaningful, but the issues are often quite subtle. For one thing, correlation does

not imply causation. Figure 5.10 convincingly demonstrates that the volume of

advanced study in computer science correlates with how much video games are

being played. I’d like to think I have driven more people to algorithms than

Nintendo, but maybe this is just the same thing? The graphs of such spurious

correlations literally ﬁll a book [Vig15], and a very funny one at that.

The discipline of statistics comes into its own in making subtle distinctions

about whether an observation is meaningful or not. The classical example comes

from medical statistics, in determining the eﬃcacy of drug treatments. A phar-

maceutical company conducts an experiment comparing two drugs. Drug A

cured 19 of 34 patients. Drug Bcured 14 of 21 patients. Is drug Breally better

than drug A? FDA approval of new drugs can add or subtract billions from the

value of drug companies. But can you be sure that a new drug represents a real

improvement? How do you tell?

5.3.1 The Signiﬁcance of Signiﬁcance

Statistical signiﬁcance measures our conﬁdence that there is a genuine diﬀerence

between two given distributions. This is important. But statistical signiﬁcance

does not measure the importance or magnitude of this diﬀerence. For large

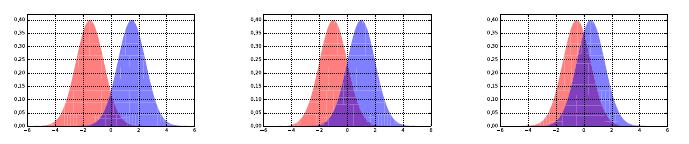
136 CHAPTER 5. STATISTICAL ANALYSIS

Figure 5.11: Pairs of normal distributions with the same variance, but decreasing

diﬀerence in their means from left to right. As the means get closer, the greater

overlap between the distributions makes it harder to tell them apart.

enough sample sizes, extremely small diﬀerences can register as highly signiﬁcant

on statistical tests.

For example, suppose I get suckered into betting tails on a coin which comes

up heads 51% of the time, instead of the 50% we associate with a fair coin. After

100 tosses of a fair coin, I would expect to see 51% or more heads 46.02% of

the time, so I have absolutely no grounds for complaint when I do. After 1,000

tosses, the probability of seeing at least 510 heads falls to 0.274. By 10,000

tosses, the probability of seeing so many heads is only 0.0233, and I should

start to become suspicious of whether the coin is fair. After 100,000 tosses, the

probability of fairness will be down to 1.29 ×10−10, so small that I must issue

a formal complaint, even if I thought my opponent to be a gentleman.

But here is the thing. Although it is now crystal clear that I had been tricked

into using a biased coin, the consequences of this act are not substantial. For

almost any issue in life worth ﬂipping over, I would be willing to take the short

side of the coin, because the stakes are just not high enough. At $1 bet per ﬂip,

my expected loss even after 100,000 tosses would only be $1,000 bucks.

Signiﬁcance tells you how unlikely it is that something is due to chance, but

not whether it is important. We really care about eﬀect size, the magnitude

of diﬀerence between the two groups. We informally categorize a medium-level

eﬀect size as visible to the naked eye by a careful observer. On this scale, large

eﬀects pop out, and small eﬀects are not completely trivial [SF12]. There are

several statistics which try to measure the eﬀect size, including:

•Cohen’s d: The importance of the diﬀerence between two means µand

µ0depends on the absolute magnitude of the change, but also the natural

variation of the distributions as measured by σor σ0. This eﬀect size can

be measured by:

d= (|µ−µ0|)/σ.

A reasonable threshold for a small eﬀect size is >0.2, medium eﬀect >0.5,

and large eﬀect size >0.8.

•Pearson’s correlation coeﬃcient r: Measures the degree of linear relation-

ship between two variables, on a scale from −1 to 1. The thresholds for

eﬀect sizes are comparable to the mean shift: small eﬀects start at ±0.2,

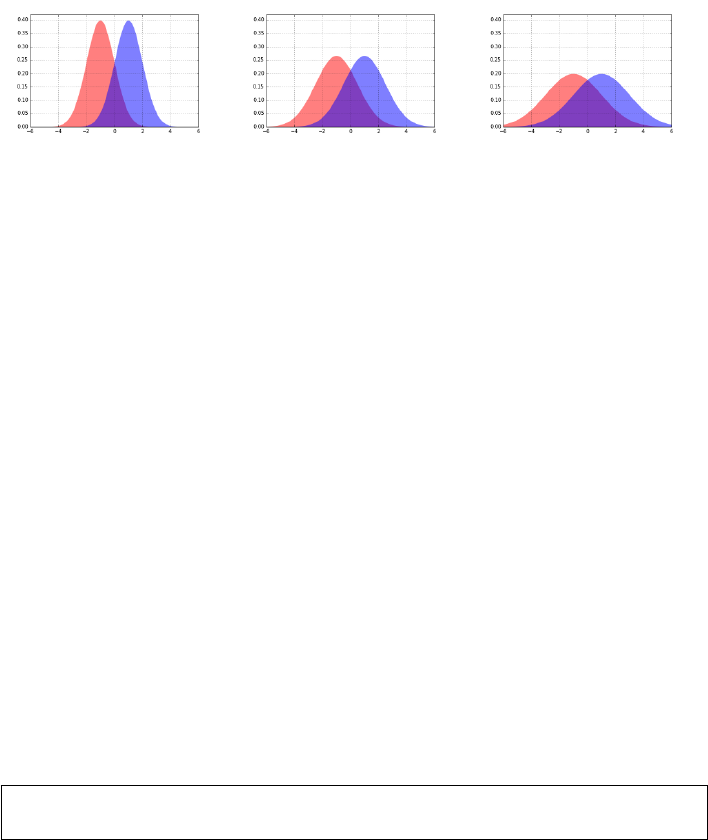
5.3. STATISTICAL SIGNIFICANCE 137

Figure 5.12: Pairs of normal distributions with the same diﬀerence in their

means but increasing variance, from left to right. As the variance increases,

there becomes greater overlap between the distributions, making it harder to

tell them apart.

medium eﬀects about ±0.5, and large eﬀect sizes require correlations of

±0.8.

•The coeﬃcient of variation r2: The square of the correlation coeﬃcient

reﬂects the proportion of the variance in one variable that is explained by

the other. The thresholds follow from squaring those above. Small eﬀects

explain at least 4% of the variance, medium eﬀects ≥25% and large eﬀect

sizes at least 64%.

•Percentage of overlap: The area under any single probability distribu-

tion is, by deﬁnition, 1. The area of intersection between two given dis-

tributions is a good measure of their similarity, as shown in Figure 5.11.

Identical distributions overlap 100%, while disjoint intervals overlap 0%.

Reasonable thresholds are: for small eﬀects 53% overlap, medium eﬀects

67% overlap, and large eﬀect sizes 85% overlap.

Of course, any sizable eﬀect which is not statistically signiﬁcant is inherently

suspect. The CS study vs. video game play correlation in Figure 5.10 was so

high (r= 0.985) that the eﬀect size would be huge, were the number of sample

points and methodology sound enough to support the conclusion.

Take-Home Lesson: Statistical signiﬁcance depends upon the number of sam-

ples, while the eﬀect size does not.

5.3.2 The T-test: Comparing Population Means

We have seen that large mean shifts between two populations suggest large eﬀect

sizes. But how many measurements do we need before we can safely believe that

the phenomenon is real. Suppose we measure the IQs of twenty men and twenty

women. Does the data show that one group is smarter, on average? Certainly

the sample means will diﬀer, at least a bit, but is this diﬀerence signiﬁcant?

The t-test evaluates whether the population means of two samples are dif-

ferent. This problem commonly arises in AB testing, associated with evaluating

138 CHAPTER 5. STATISTICAL ANALYSIS

whether a product change makes a diﬀerence in performance. Suppose you show

one group of users version A, and another group version B. Further, suppose

you measure a system performance value for each user, such as the number of

times they click on ads or the number of stars they give it when asked about

the experience. The t-test measures whether the observed diﬀerence between

the two groups is signiﬁcant.

Two means diﬀer signiﬁcantly if:

•The mean diﬀerence is relatively large: This makes sense. One can con-

clude that men weigh more than women on average fairly easily, because

the eﬀect size is so large. According to the Center for Disease Control2

the average American male weighed 195.5 pounds in 2010, whereas the

average American woman weighted 166.2 pounds. This is huge. Proving

that a much more subtle diﬀerence, like IQ, is real requires much more

evidence to be equally convincing.

•The standard deviations are small enough: This also makes sense. It is

easy to convince yourself that men and women have, on average, the same

number of ﬁngers because the counts we observe are very tightly bunched

around the mean: {10,10,10,10,9,10 . . .}. The equal-ﬁnger count hypoth-

esis would require much more evidence if the numbers jumped around a

lot. I would be reluctant to commit to a true distributional average of

µ= 10 if I what I observed was {3, 15, 6, 14, 17, 5}.

•The number of samples are large enough: This again makes sense. The

more data I see, the more solidly I become convinced that the sample will

accurately represent its underlying distribution. For example, men un-

doubtedly have fewer ﬁngers on average than women, as a consequence of

more adventures with power tools.3But it would require a very large num-

ber of samples to observe and validate this relatively rare phenomenon.

The t-test starts by computing a test statistic on the two sets of observations.

Welch’s t-statistic is deﬁned as

t=¯x1−¯x2

qσ12

n1+σ22

where ¯xi,σi, and niare the mean, standard deviation, and population size of

sample i, respectively.

Let us parse this equation carefully. The numerator is the diﬀerence between

the means, so the bigger this diﬀerence, the bigger the value of the t-statistic.

The standard deviations are in the denominator, so the smaller that σiis, the

bigger the value of the t-statistic. If this is confusing, recall what happens when

you divide xby a number approaching zero. Increasing the sample sizes ni

2http://www.cdc.gov/nchs/fastats/obesity-overweight.htm

3This observation alone may be suﬃcient to resolve the gender–IQ relationship, without

the need for additional statistical evidence.

5.3. STATISTICAL SIGNIFICANCE 139

also makes the denominator smaller, so the larger niis, the bigger the value of

the t-statistic. In all cases, the factors that make us more conﬁdent in there

being a real diﬀerence between the two distributions increases the value of the

t-statistic.

Interpreting the meaning of a particular value of the t-statistic comes from

looking up a number in an appropriate table. For a desired signiﬁcance level

αand number of degrees of freedom (essentially the sample sizes), the table

entry speciﬁes the value vthat the t-statistic tmust exceed. If t > v, then the

observation is signiﬁcant to the αlevel.

Why Does This Work?

Statistical tests like the t-test often seem like voodoo to me, because we look

up a number from some magic table and treat it like gospel. The oracle has

spoken: the diﬀerence is signiﬁcant! Of course there is real mathematics behind

signiﬁcance testing, but the derivation involves calculus and strange functions

(like the gamma function Γ(n), a real numbered generalization of factorials).

These complex calculations are why the convention arose to look things up in a

precomputed table, instead of computing it yourself.

You can ﬁnd derivations of the relevant formulae in any good statistics book,

if you are interested. These tests are based on ideas like random sampling. We

have seen how the mean and standard deviation constrain the shape of any

underlying probability distribution. Getting a sample average very far from the

mean implies bad luck. Randomly picking values several standard deviations

away from the population mean is very unlikely, according to the theory. This

makes it more likely that observing such a large diﬀerence is the result of drawing

from a diﬀerent distribution.

Much of the technicality here is a consequence of dealing with subtle phe-

nomenon and small data sets. Historically, observed data was a very scarce

resource, and it remains so in many situations. Recall our discussion of drug

eﬃcacy testing, where someone new must die for every single point we collect.

The big data world you will likely inhabit generally features more observations

(everybody visiting our webpage), lower stakes (do customers buy more when

you show them a green background instead of a blue background?), and per-

haps smaller eﬀect sizes (how big an improvement do we really need to justify

changing the background color?).

5.3.3 The Kolmogorov-Smirnov Test

The t-test compares two samples drawn from presumably normal distribu-

tions according to the distance between their respective means. Instead, the

Kolmogorov-Smirnov (KS) test compares the cumulative distribution functions

(cdfs) of the two sample distributions and assesses how similar they are.

This is illustrated in Figure 5.13. The cdfs of the two diﬀerent samples are

plotted on the same chart. If the two samples are drawn from the same dis-

tribution, the ranges of xvalues should largely overlap. Further, since both

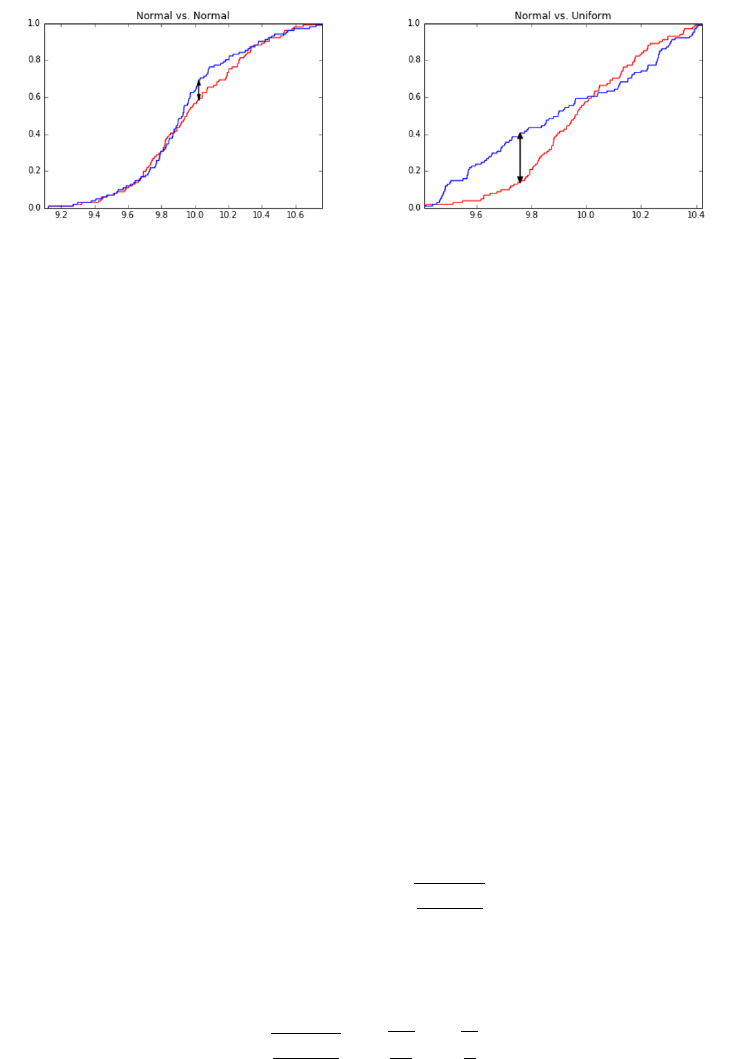
140 CHAPTER 5. STATISTICAL ANALYSIS

Figure 5.13: The Kolmogorov-Smirnov test quantiﬁes the diﬀerence between

two probability distributions by the maximum y-distance gap between the two

cumulative distribution functions. On the left, two samples from the same

normal distribution. On the right, comparison of samples from uniform and

normal distributions drawn over the same x-range.

distributions are represented as cdfs, the y-axis represents cumulative probabil-

ity from 0 to 1. Both functions increase monotonically from left to right, where

C(x) is the fraction of the sample ≤x.

We seek to identify the value of xfor which the associated yvalues of the

two cdfs diﬀer by as much as possible. The distance D(C1, C2) between the

distributions C1and C2is the diﬀerence of the yvalues at this critical x, formally

stated as

D(C1, C2) = max

−∞≤x≤∞ |C1(x)−C2(x)|

The more substantially that two sample distributions diﬀer at some value,

the more likely it is that they were drawn from diﬀerent distributions. Figure

5.13 (left) shows two independent samples from the same normal distribution.

Note the resulting tiny gap between them. In contrast, Figure 5.13 (right)

compares a sample drawn from a normal distribution against one drawn from

the uniform distribution. The KS-test is not fooled: observe the big gaps near

the tails, where we would expect to see it.

The KS-test compares the value of D(C1, C2) against a particular target,

declaring that two distributions diﬀer at the signiﬁcance level of αwhen:

D(C1, C2)> c(α)rn1+n2

n1n2

where c(α) is a constant to look up in a table.

The function of the sample sizes has some intuition behind it. Assume for

simplicity that both samples have the same size, n. Then

rn1+n2

n1n2

=r2n

n2=r2

5.3. STATISTICAL SIGNIFICANCE 141

The quantity √narises naturally in sampling problems, such as the standard

deviation of the binomial distribution. The expected diﬀerence between the

number of heads and tails in ncoin ﬂips is on the order of √n. In the context

of the KS-test, it similarly reﬂects the expected deviation when two samples

should be considered the same. The KS-test reﬂects what is happening in the

meat of the distribution, where a robust determination can be made.

I like the Kolmogorov-Smirnov test. It provides pictures of the distributions

that I can understand, that identify the weakest point in the assumption that

they are identical. This test has fewer technical assumptions and variants than

the t-test, meaning we are less likely to make a mistake using it. And the

KS-test can be applied to many problems, including testing whether points are

drawn from a normal distribution.

Normality Testing

When plotted, the normal distribution yields a bell-shaped curve. But not every

bell-shaped distribution is normal, and it is sometimes important to know the

diﬀerence.

There exist specialized statistical tests for testing the normality of a given

distributional samples f1. But we can use the general KS-test to do the job,

provided we can identify a meaningful f2to compare f1to.

This is exactly why I introduced random sampling methods in Section 5.2.

Using the cumulative distribution method we described, statistically-sound ran-

dom samples of npoints can be drawn from any distribution that you know

the cdf of, for any n. For f2, we should pick a meaningful number of points to

compare against. We can use n2=n1, or perhaps a somewhat larger sample

if n1is very small. We want to be sure that we are capturing the shape of the

desired distribution with our sample.

So if we construct our random sample for f2from the normal distribution,

the KS-test should not be able to distinguish f1from f2if f1also comes from

a normal distribution on the same µand σ.

One word of caution. A suﬃciently-sensitive statistical test will probably

reject the normality of just about any observed distribution. The normal distri-

bution is an abstraction, and the world is a complicated place. But looking at

the plot of the KS-test shows you exactly where the deviations are happening.

Are the tails too fat or too lean? Is the distribution skewed? With this under-

standing, you can decide whether the diﬀerences are big enough to matter to

you.

5.3.4 The Bonferroni Correction

It has long been the convention in science to use α= 0.05 as the cutoﬀ between

statistical signiﬁcance and irrelevance. A statistical signiﬁcance of 0.05 means

there is a probability of 1/20 that this result would have come about purely by

chance.

142 CHAPTER 5. STATISTICAL ANALYSIS

This is not an unreasonable standard when collecting data to test a chal-

lenging hypothesis. Betting on a horse at 20 to 1 odds and winning your bet is a

noteworthy accomplishment. Unless you simultaneously placed bets on millions

of other horses. Then bragging about the small number of 20-1 bets where you

actually won would be misleading, to say the least.

Thus ﬁshing expeditions which test millions of hypotheses must be held

to higher standards. This is the fallacy that created the strong but spurious

correlation between computer science Ph.Ds and video game activity in Figure

5.10. It was discovered in the course of comparing thousands of time series

against each other, and retaining only the most amusing-sounding pairs which

happened to show a high correlation score.

The Bonferroni correction4provides an important balance in weighing how

much we trust an apparently signiﬁcant statistical result. It speaks to the fact

that how you found the correlation can be as important as the strength of the

correlation itself. Someone who buys a million lottery tickets and wins once has

much less impressive mojo going than the fellow who buys a single ticket and

wins.

The Bonferroni correction states that when testing ndiﬀerent hypotheses

simultaneously, the resulting p-value must rise to a level of α/n, in order to be

considered as signiﬁcant at the αlevel.

As with any statistical test, there lurk many subtleties in properly applying

the correction. But the big principle here is important to grasp. Computing

people are particularly prone to running large-scale comparisons of all things

against all things, or hunting for unusual outliers and patterns. After all, once

you’ve written the analysis program, why not run it on all your data? Presenting

only the best, cherry-picked results makes it easy to fool other people. The

Bonferroni correction is the way to prevent you from fooling yourself.

5.3.5 False Discovery Rate

The Bonferroni correction safeguards us from being too quick to accept the sig-

niﬁcance of a lone successful hypothesis among many trials. But often when

working with large, high-dimensional data we are faced with a diﬀerent prob-

lem. Perhaps all mof the variables correlate (perhaps weakly) with the target

variable. If nis large enough, many of these correlations will be statistically

signiﬁcant. Have we really made so many important discoveries?

The Benjamini-Hochberg procedure for minimizing false discovery rate (FDR)

procedure gives a very simple way to draw the cutoﬀ between interesting and

uninteresting variables based on signiﬁcance. Sort the variables by the strength

of their p-value, so the more extreme variables lie on the left, and the least

signiﬁcant variables on the right. Now consider the ith ranked variable in this

ordering. We accept the signiﬁcance of this variable at the αlevel if

∀i

j=1 (pj≤j

mα)

4I have always thought that “The Bonferroni Correction” would make a fabulous title for

an action movie. Dwayne Johnson as Bonferroni?

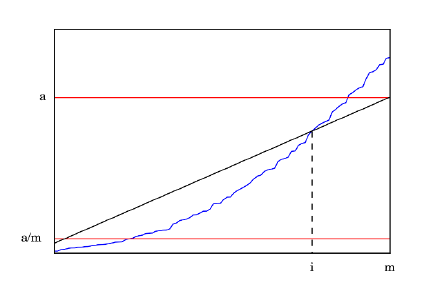
5.4. WAR STORY: DISCOVERING THE FOUNTAIN OF YOUTH? 143

Figure 5.14: The Benjamini-Hochberg procedure minimizes false discovery rate,

by accepting p-values only when pi≤αi/m. The blue curve shows the sorted p-

values, and the diagonal deﬁnes the cutoﬀ for when such a p-value is signiﬁcant.

The situation is illustrated in Figure 5.14. The p-values are sorted in increas-

ing order from left to right, as denoted by the irregular blue curve. If we were

accepting all p-values less than α, we accept too many. This is why Bonferroni

developed his correction. But requiring all p-values to meet the standard of the

Bonferroni correction (where the curve crosses α/m) is too stringent.

The Benjamini-Hochberg procedure recognizes that if many values are really

signiﬁcant to a certain standard, a certain fraction of them should be signiﬁcant

to a much higher standard. The diagonal line in Figure 5.14 appropriately

enforces this level of quality control.

5.4 War Story: Discovering the Fountain of Youth?

It had been a beautiful wedding. We were very happy for Rachel and David, the

bride and groom. I had eaten like a king, danced with my lovely wife, and was

enjoying a warm post-prime rib glow when it hit me that something was oﬀ. I

looked around the room and did a double-take. Somehow, for the ﬁrst time in

many years, I had become younger than most of the people in the crowd.

This may not seem like a big deal to you, but that is because you the reader

probably are younger than most people in many settings. But trust me, there

will come a time when you notice such things. I remember when I ﬁrst realized

that I had been attending college at the time when most of my students were

being born. Then they started being born when I was in graduate school.

Today’s college students were not only born after I became a professor, but

after I got tenure here. So how could I be younger than most of the people at

this wedding?

There were two possibilities. Either it was by chance that so many older

144 CHAPTER 5. STATISTICAL ANALYSIS

people entered the room, or there was a reason explaining this phenomenon,

This is why statistical signiﬁcance tests and p-values were invented, to aid in

distinguishing something from nothing.

So what was the probability that I, then at age 54, would have been younger

than most of the 251 people at Rachel’s wedding? According to Wolfram Al-

pha (more precisely, the 2008–2012 American Community Survey ﬁve-year es-

timates), there were 309.1 million people in the United States, of whom 77.1

million were age 55 or older. Almost exactly 25% of the population is older than

I am as I write these words.

The probability that the majority of 251 randomly selected Americans would

be older than 55 years is thus given by:

251

i=126 251

i(1 −.75)i(0.75)(251−i)= 8.98 ×10−18

This probability is impossibly small, comparable to pulling a fair coin out of

your pocket and having it come up heads 56 times in a row. This could not have

been the result of a chance event. There had to be a reason why I was junior

to most of this crowd, and the answer wasn’t that I was getting any younger.

When I asked Rachel about it, she mentioned that, for budgetary reasons,

they decided against inviting children to the wedding. This seemed like it could

be a reasonable explanation. After all, this rule excluded 73.9 million people

under the age of eighteen from attending the wedding, thus saving billions of

dollars over what it would have cost to invite them all. The fraction fof people

younger than me who are not children works out to f= 1 −(77.1/(309.1−

73.9)) = 0.672. This is substantially larger than 0.5, however. The probability

of my being younger than the median in a random sample drawn from this

cohort is:

251

i=126 251

i(1 −.0672)i(0.672)(251−i)= 9.118 ×10−9

Although this is much larger than the previous p-value, it is still impossibly

small: akin to tossing oﬀ 27 straight heads on your fair coin. Just forbidding

children was not nearly powerful enough to make me young again.

I went back to Rachel and made her fess up. It turns out her mother had an

unusually large number of cousins growing up, and she was exceptionally good at

keeping in touch with all of them. Recall Einstein’s Theory of Relativity, where

E=mc2denotes that everyone is my mother’s cousin, twice removed. All of

these cousins were invited to the wedding. With Rachel’s family outpopulating

the groom’s unusually tiny clan, this cohort of senior cousins came to dominate

the dance ﬂoor.

Indeed, we can compute the number of the older-cousins (c) that must be

invited to yield a 50/50 chance that I would be younger than the median guest,

assuming the rest of the 251 guests were selected at random. It turns out that

5.5. PERMUTATION TESTS AND P-VALUES 145

Figure 5.15: Permutation tests reveal the signiﬁcance of the correlation between

gender and the height (left). A random assignment of gender to height (center)

results in a substantially diﬀerent distribution of outcomes when sorted (right),

validating the signiﬁcance of the original relationship.

c= 65 single cousins (or 32.5 married pairs) suﬃce, once the children have been

excluded (f= 0.672).

The moral here is that it is important to compute the probability of any

interesting observation before declaring it to be a miracle. Never stop with a

partial explanation, if it does not reduce the surprise to plausible levels. There

likely is a genuine phenomenon underlying any suﬃciently rare event, and fer-

reting out what it is makes data science exciting.

5.5 Permutation Tests and P-values

Traditional statistical signiﬁcance tests prove quite eﬀective at deciding whether

two samples are in fact drawn from the same distribution. However, these tests

must be properly performed in order to do their job. Many standard tests have

subtleties like the issues of one- vs. two-sided tests, distributional assumptions,

and more. Performing these tests correctly requires care and training.

Permutation tests allow a more general and computationally idiot-proof way

to establish signiﬁcance. If your hypothesis is supported by the data, then

146 CHAPTER 5. STATISTICAL ANALYSIS

Figure 5.16: Permutation tests score signiﬁcance by the position of the score on

actual data against a distribution of scores produced by random permutations.

A position on the extreme tail (left) is highly signiﬁcant, but one within the

body of the distribution (left) is uninteresting.

randomly shuﬄed data sets should be less likely to support it. By conducting

many trials against randomized data, we can establish exactly how unusual the

phenomenon is that you are testing for.

Consider Figure 5.15, where we denote the independent variable (gender:

male or female) and dependent variable (say, height) using colors. The orig-

inal outcome color distribution (left) looks starkly diﬀerent between men and

women, reﬂective of the genuine diﬀerences in height. But how unusual is this

diﬀerence? We can construct a new data set by randomly assigning gender

to the original outcome variables (center). Sorting within each group makes

clear that the pseudo-male/female distribution of outcomes is now much more

balanced than in the original data (right). This demonstrates that gender was

indeed a signiﬁcant factor in determining height, a conclusion we would come

to believe even more strongly after it happens again and again over 1,000 or

1,000,000 trials.

The rank of the test statistic on the real data among the distribution of

statistic values from random permutations determines the signiﬁcance level or

p-value. Figure 5.16 (left) shows what we are looking for. The real value lies

on the very right of the distribution, attesting to signiﬁcant. In the ﬁgure on

right, the real value lies in the squishy middle of the distribution, suggesting no

eﬀect.

Permutation tests require that you develop a statistic which reﬂects your

hypothesis about the data. The correlation coeﬃcient is a reasonable choice

if you want to establish an important relationship between a speciﬁc pair of

variables. Ideally the observed correlation in the real data will be stronger than

in any random permutation of it. To validate the gender–height connection,

perhaps our statistic could be the diﬀerence in the average heights of men and

women. Again, we hope this proves larger in the real data than in most random

permutations of it.

Be creative in your choice of statistic: the power of permutation tests is

5.5. PERMUTATION TESTS AND P-VALUES 147

that they can work with pretty much anything you can come up with to prove

your case. It is best if your statistic minimizes the chance of ties, since you are

honor-bound to count all ties against your hypothesis.

Take-Home Lesson: Permutation tests give you the probability of your data

given your hypothesis, namely that the statistic will be an outlier compared to

the random sample distribution. This is not quite the same as proving your

hypothesis given the data, which is the traditional goal of statistical signiﬁcance

testing. But it is much better than nothing.

The signiﬁcance score or p-value of a permutation test depends upon how

many random tries are run. Always try to do at least 1,000 random trials, and

more if it is feasible. The more permutations you try, the more impressive your

signiﬁcance p-value can be, at least up to a point. If the given input is in fact

the best of all k! permutations, the most extreme p-value you can get is 1/k!,

no matter how many random permutations you try. Oversampling will inﬂate

your denominator without increasing your true conﬁdence one bit.

Take-Home Lesson: P-values are computed to increase your conﬁdence that an

observation is real and interesting. This only works when you do the permuta-

tion test honestly, by performing experiments that can provide a fair measure

of surprise.

5.5.1 Generating Random Permutations

Generating random permutations is another important sampling problem that

people often botch up. The two algorithms below both use sequences of random

swaps to scramble up the initial permutation {1,2, . . . , n}.

But ensuring that all n! permutations are generated uniformly at random is

a tricky business. Indeed only one of these algorithms gets it right. Is it this

one,

for i= 1 to ndo a[i] = i;

for i= 1 to n−1 do swap[a[i], a[Random[i, n]];

or is it this:

for i= 1 to ndo a[i] = i;

for i= 1 to n−1 do swap[a[i], a[Random[1, n]];

Think about this carefully: the diﬀerence here is very subtle. It is so subtle

you might not even notice it in the code. The critical diﬀerence is the 1 or iin

the call to Random. One of these algorithms is right and one of these algorithms

is wrong. If you think you can tell, convincingly explain why one works and the

other one doesn’t.

If you really must know, the ﬁrst algorithm is the correct one. It picks

a random element from 1 to nfor the ﬁrst position, then leaves it alone and

148 CHAPTER 5. STATISTICAL ANALYSIS

Figure 5.17: The generation frequency of all 4! = 24 permutations using two

diﬀerent algorithms. Algorithm 1 generates them with uniform frequency, while

algorithm 2 is substantially biased.

recurs on the rest. It generates permutations uniformly at random. The second

algorithm gives certain elements a better chance to end up ﬁrst, showing that

the distribution is not uniform.

But if you can’t prove this theoretically, you can use the idea of a permu-

tation test. Implement both of the algorithms, and perform 1,000,000 runs of

each, constructing random permutations of, say, n= 4 elements. Count how

often each algorithm generates each one of the 4! = 24 distinct permutations.

The results of such an experiment are shown in Figure 5.17. Algorithm 1 proves

incredibly steady, with a standard deviation of 166.1 occurrences. In contrast,

there is an eight-fold diﬀerence between the most and least frequent permuta-

tions under algorithm 2, with σ= 20,923.9.

The moral here is that random generation can be very subtle. And that

Monte Carlo-type experiments like permutation tests can eliminate the need for

subtle reasoning. Verify, then trust.

5.5.2 DiMaggio’s Hitting Streak

One of baseball’s most amazing records is Joe DiMaggio’s 56-game hitting

streak. The job of a batter is to get hits, and they receive perhaps four chances

every game to get one. Even very good hitters often fail.

But back in 1941, Joe DiMaggio succeeded in getting hits in 56 straight

games, a truly amazing accomplishment. No player in the seventy-ﬁve years

since then has come close to this record, nor any one before him.

But how unusual was such a long streak in the context of his career? DiMag-

5.5. PERMUTATION TESTS AND P-VALUES 149

Figure 5.18: The distribution of longest hitting streaks, over 100,000 simulated

careers. DiMaggio’s actual 56-game hitting streak stands at the very tail of this

distribution, thus demonstrating the diﬃculty of this feat.

gio played 1736 games, with 2214 hits in 6821 at bats. Thus he should get hits

in roughly 1 −(1 −(2214/6821))4= 79.2% of his games with four at bats.

What is the probability that someone with his skill level could manage such a

consecutive game streak in the course of their career?

For those of you tired of my baseball analogies, let’s put this in another

context. Suppose you are a student who averages a grade of 90 on tests. You

are a very good student to be sure, but not perfect. What are the chances you

could have a hot streak where you scored above 90 on ten straight tests? What

about twenty straight? Could you possibly ace 56 tests in a row?5If such a long

streak happened, would that mean that you had taken your studies to another

level, or did you just get lucky?

So when DiMaggio had his hitting streak, was it just an expected conse-

quence of his undisputed skills and consistency, or did he just get lucky? He

was one of the very best hitters of his or any time, an all-star every season of

his thirteen-year career. But we also know that DiMaggio got lucky from time

to time. After all, he was married to the movie star Marilyn Monroe.

To resolve this question, we used random numbers to simulate when he

got hits over a synthetic “career” of 1736 games. Each game, the simulated

Joe received four chances to hit, and succeeded with a probability of p=

(2214/6821) = 0.325. We could then identify the longest hitting streak over

the course of this simulated career. By simulating 100,000 DiMaggio careers,

we get a frequency distribution of streaks that can put the rarity of his accom-

plishment in context, getting a p-value in the process.

The results are shown in Figure 5.18. In only 44 of 100,000 simulated careers

(p= 0.00044) did DiMaggio manage a streak of at least 56 games. Thus the

length is quite out of line with what would be expected from him. The second

5Not if you are taking one of my classes, I tell you.

150 CHAPTER 5. STATISTICAL ANALYSIS

Figure 5.19: Bayes’ Theorem in action.

longest streak of any major league hitter is only 44 games, so it is out of line

with everyone else as well. But he also once hit in 61 straight games at a lower

level of competition, so he seems to have had an extraordinary capacity for

consistency.

Hitting streaks can be thought of as runs between games without hits, and so

can be modeled using a Poisson distribution. But Monte Carlo simulations pro-

vide answers without detailed mathematics. Permutation tests give us insight

with minimal knowledge and intellectual eﬀort.

5.6 Bayesian Reasoning

The conditional probability P(A|B) measures the likelihood of event Agiven

knowledge that event Bhas occurred. We will rely on conditional probability

throughout this book, because it lets us update our conﬁdence in an event in

response to fresh evidence, like observed data.

Bayes’ Theorem is an important tool for working with conditional probabil-

ities, because it lets us turn the conditionals around:

P(A|B) = P(B|A)P(A)

P(B)

With Bayes theorem, we can convert the question of P(outcome|data) to

P(data|outcome), which is often much easier to compute. In some sense, Bayes’

theorem is just a consequence of algebra, but it leads to a diﬀerent way of

thinking about probability.

Figure 5.19 illustrates Bayes’ theorem in action. The event space consists of

picking one of four blocks. The complex events Aand Brepresent sub-ranges

of blocks, where P(A) = 3/4 and P(B) = 2/4 = 1/2. By counting blocks from

the ﬁgure, we can see that P(A|B)=1/2 and P(B|A)=1/3. These also follow

5.7. CHAPTER NOTES 151

directly from Bayes’ theorem:

P(A|B) = P(B|A)P(A)

P(B)=(1/3) ·(3/4)

(1/2) = 1/2

P(B|A) = P(A|B)P(B)

P(A)=(1/2) ·(1/2)

(3/4) = 1/3

Bayesian reasoning reﬂects how a prior probability P(A) is updated to give

the posterior probability P(A|B) in the face of a new observation B, according

to the ratio of the likelihood P(B|A) and the marginal probability P(B). The

prior probability P(A) reﬂects our initial assumption about the world, to be

revised based on the additional evidence B.

Bayesian reasoning is an important way to look at the world. Walking into

Rachel and David’s wedding, my prior assumption was that the age distribution

would reﬂect that of the world at large. But my conﬁdence weakened with every

elderly cousin I encountered, until it ﬁnally crumbled.

We will use Bayesian reasoning to build classiﬁers in Section 11.1. But keep

this philosophy in mind as you analyze data. You should come to each task with

a prior conception of what the answers should be, and then revise in accordance

with statistical evidence.

5.7 Chapter Notes

Every data scientist should take a good elementary statistics course. Represen-

tative texts include Freedman [FPP07] and James et al. [JWHT13]. Wheelan

[Whe13] is a gentler introduction, with Huﬀ [Huf10] the classic treatise on how

best to lie with statistics.

Donoho [Don15] presents a fascinating history of data science from the van-

tage point of a statistician. It makes an eﬀective case that most of the major

principles of today’s data science were originally developed by statisticians, al-

though they were not quickly embraced by the discipline at large. Modern

statisticians have begun having much more satisfying conversations with com-

puter scientists on these matters as interests have mutually converged.

Vigen [Vig15] presents an amusing collection of spurious correlations drawn

from a large number of interesting time series. Figure 5.10 is representative,

and is reprinted with permission.

It has been demonstrated that the size of American families is reasonably well

ﬁt by a Poisson distribution. In fact, an analysis of household size distributions

from 104 countries suggests that the “I’ve had enough” model works around the

world [JLSI99].

5.8 Exercises

Statistical Distributions

152 CHAPTER 5. STATISTICAL ANALYSIS

5-1. [5] Explain which distribution seems most appropriate for the following phe-

nomenon: binomial, normal, Poisson, or power law?

(a) The number of leaves on a fully grown oak tree.

(b) The age at which people’s hair turns grey.

(d) The number of people who have been hit by lightning xtimes.

(e) The number of miles driven before your car needs a new transmission.

(f) The number of runs a batter will get, per cricket over.

(g) The number of leopard spots per square foot of leopard skin.

(h) The number of people with exactly xpennies sitting in drawers.

(i) The number of apps on people’s cell phones.

(j) The daily attendance in Skiena’s data science course.

5-2. [5] Explain which distribution seems most appropriate for the following The

Quant Shop phenomenon: binomial, normal, Poisson, or power law?

(a) The beauty of contestants at the Miss Universe contest.

(b) The gross of movies produced by Hollywood studios.

(d) The price of art works at auction.

(e) The amount of snow New York will receive on Christmas.

(f) The number of teams that will win xgames in a given football season.

(g) The lifespans of famous people.

(h) The daily price of gold over a given year.

5-3. [5] Assuming that the relevant distribution is normal, estimate the probability

of the following events:

(a) That there will be 70 or more heads in the next hundred ﬂips of a fair

coin?

(b) That a randomly selected person will weight over 300 lbs?

5-4. [3] The average on a history exam was 85 out of 100 points, with a standard

deviation of 15. Was the distribution of the scores on this exam symmetric?

If not, what shape would you expect this distribution to have? Explain your

reasoning.

5-5. [5] Facebook data shows that 50% of Facebook users have a hundred or more

friends. Further, the average user’s friend count is 190. What do these ﬁndings

say about the shape of the distribution of number of friends of Facebook users?

Signiﬁcance Testing

5-6. [3] Which of the following events are likely independent and which are not?

(a) Coin tosses.

5.8. EXERCISES 153

(b) Basketball shots.

5-7. [5] The 2010 American Community Survey estimates that 47.1% of women aged

15 years and over are married.

(a) Randomly select three women between these ages. What is the probability

that the third woman selected is the only one that is married?

(b) What is the probability that all three women are married?

a married woman? What is the standard deviation?

(d) If the proportion of married women was actually 30%, how many women

would you expect to sample before selecting a married woman? What is

the standard deviation?

(e) Based on your answers to parts (c) and (d), how does decreasing the prob-

ability of an event aﬀect the mean and standard deviation of the wait time

until success?

Permutation Tests and P-values

5-8. [5] Prove that the permutation generation algorithm of page 147 generates per-

mutations correctly, meaning uniformly at random.

5-9. [5] Obtain data on the heights of mmen and wwomen.

(a) Use a t-test to establish the signiﬁcance of whether the men are on average

taller than the women.

(b) Perform a permutation test to establish the same thing: whether the men

are on average taller than the women.

Implementation Projects

5-10. [5] In sporting events, good teams tend to come back and win. But is this

because they know how to win, or just because after a long-enough game the

better team will generally prevail? Experiment with a random coin ﬂip model,

where the better team has a probability of p > 0.5 of outplaying the other over

a single period.

For games of nperiods, how often does the better team win, and how often

does it come from behind, for a given probability p? How does this compare to

statistics from real sports?

5-11. [8] February 2 is Groundhog Day in the United States, when it is said that six

more weeks of winter follows if the groundhog sees its shadow. Taking whether

it is sunny on February 2 as a proxy for the groundhog’s input, is there any

predictive power to this tradition? Do a study based on weather records, and

report the accuracy of the beast’s forecasts along with its statistical signiﬁcance

Interview Questions

5-12. [3] What is conditional probability?

5-13. [3] What is Bayes Theorem? And why is it useful in practice?

154 CHAPTER 5. STATISTICAL ANALYSIS

5-14. [8] How would you improve a spam detection algorithm that uses a naive Bayes

classiﬁer?

5-15. [5] A coin is tossed ten times and the results are two tails and eight heads. How

can you tell whether the coin is fair? What is the p-value for this result?

5-16. [8] Now suppose that ten coins are each tossed ten times, for a total of 100

tosses. How would you test whether the coins are fair?

5-17. [8] An ant is placed on an inﬁnitely long twig. The ant can move one step

backward or one step forward with the same probability, during discrete time

steps. What is the probability that the ant will return to its starting point after

2nsteps?

5-18. [5] You are about to get on a plane to Seattle. Should you bring an umbrella?

You call three random friends of yours who live there and ask each independently

whether it is raining. Each of friends has a 2/3 chance of telling you the truth

and a 1/3 chance of lying. All three friends tell you that it is raining. What is

the probability that it is actually raining in Seattle?

Kaggle Challenges

5-19. Decide whether a car bought at an auction is a bad buy.

https://www.kaggle.com/c/DontGetKicked

5-20. Forecast the demand of a product in a given week.

https://www.kaggle.com/c/grupo-bimbo-inventory-demand

5-21. How much rain we will get in the next hour?

https://www.kaggle.com/c/how-much-did-it-rain

Chapter 6

Visualizing Data

At their best, graphics are instruments for reasoning.

– Edward Tufte

Eﬀective data visualization is an important aspect of data science, for at least

three distinct reasons:

•Exploratory data analysis: What does your data really look like? Getting

a handle on what you are dealing with is the ﬁrst step of any serious

analysis. Plots and visualizations are the best way I know of to do this.

•Error detection: Did you do something stupid in your analysis? Feeding

unvisualized data to any machine learning algorithm is asking for trouble.

Problems with outlier points, insuﬃcient cleaning, and erroneous assump-

tions reveal themselves immediately when properly visualizing your data.

Too often a summary statistic (77.8% accurate!) hides what your model

is really doing. Taking a good hard look what you are getting right vs.

wrong is the ﬁrst step to performing better.

•Communication: Can you present what you have learned eﬀectively to

others? Meaningful results become actionable only after they are shared.

Your success as a data scientist rests on convincing other people that

you know what you are talking about. A picture is worth 1,000 words,

especially when you are giving a presentation to a skeptical audience.

You have probably been making graphs and charts since grade school. Ubiq-

uitous software makes it easy to create professional-looking images. So what is

so hard about data visualization?

To answer, I oﬀer a parable. A terrible incident during my youth concerned

an attack on an ice skating champion. A thug hit her on the knee with a stick,

hoping to knock her out of the upcoming Olympic games. Fortunately, he missed

the knee, and the skater went on to win the silver medal.

156 CHAPTER 6. VISUALIZING DATA

But upon getting to know his client, the thug’s lawyer came up with an

interesting defense. This crime, he said, was clearly too complex for his client

to have conceived on his own. This left an impression on me, for it meant that

I had underestimated the cognitive capacity necessary to rap someone on the

leg with a stick.

My intended moral here is that many things are more complicated than

they look. In particular, I speak of the problem of plotting data on a graph to

capture what it is saying. An amazingly high fraction of the charts I have seen

in presentations are terrible, either conveying no message or misconveying what

the data actually showed. Bad charts can have negative value, by leading you

in the wrong direction.

In this section, we will come to understand the principles that make standard

plot designs work, and show how they can be misleading if not properly used.

From this experience, we will try to develop your sense of when graphs might

be lying, and how you can construct better ones.

6.1 Exploratory Data Analysis

The advent of massive data sets is changing in the way science is done. The

traditional scientiﬁc method is hypothesis driven. The researcher formulates a

theory of how the world works, and then seeks to support or reject this hy-

pothesis based on data. By contrast, data-driven science starts by assembling a

substantial data set, and then hunts for patterns that ideally will play the role

of hypotheses for future analysis.

Exploratory data analysis is the search for patterns and trends in a given data

set. Visualization techniques play an important part in this quest. Looking

carefully at your data is important for several reasons, including identifying

mistakes in collection/processing, ﬁnding violations of statistical assumptions,

and suggesting interesting hypotheses.

In this section, we will discuss how to go about doing exploratory data

analysis, and what visualization brings to the table as part of the process.

6.1.1 Confronting a New Data Set

What should you do when encountering a new data set? This depends somewhat

upon why you are interested in it in the ﬁrst place, but the initial steps of

exploration prove almost application-independent.

Here are some basic steps that I encourage doing to get acquainted with any

new data set, which I illustrate in exploring the body measurement data set

NHANES, available at https://www.statcrunch.com/app/index.php?dataid=

1406047. This is tabular data, but the general principles here are applicable to

a broader class of resources:

•Answer the basic questions: There are several things you should know

about your data set before you even open the ﬁle. Ask questions like:

6.1. EXPLORATORY DATA ANALYSIS 157

–Who constructed this data set, when, and why? Understanding how

your data was obtained provides clues as to how relevant it is likely

to be, and whether we should trust it. It also points us to the right

people if we need to know more about the data’s origin or provenance.

With a little digging, I discovered that it came from the National

Health and Nutrition Examination Survey 2009–2010, and who was

responsible for posting it.

–How big is it? How rich is the data set in terms of the number of ﬁelds

or columns? How large is it as measured by the number of records or

rows? If it is too big to explore easily with interactive tools, extract

a small sample and do your initial explorations on that. This data

set has 4978 records (2452 men and 2526 women), each with seven

data ﬁelds plus gender.

–What do the ﬁelds mean? Walk through each of the columns in your

data set, and be sure you understand what they are. Which ﬁelds are

numerical or categorical? What units were the quantities measured

in? Which ﬁelds are IDs or descriptions, instead of data to com-

pute with? A quick review shows that the lengths and weights here

were measured using the metric system, in centimeters and kilograms

respectively.

•Look for familiar or interpretable records: I ﬁnd it extremely valuable to

get familiar with a few records, to the point where I know their names.

Records are generally associated with a person, place, or thing that you

already have some knowledge about, so you can put it in context and

evaluate the soundness of the data you have on it. But if not, ﬁnd a

few records of special interest to get to know, perhaps the ones with the

maximum or minimum values of the most important ﬁeld.

If familiar records do not exist, it sometimes pays to create them. A

clever developer of a medical records database told me that he had used

the top 5000 historical names from Who’s Bigger to serve as patient names

while developing the product. This was a much more inspired idea than

making up artiﬁcial names like “Patient F1253.” They were fun enough

to encourage playing with the system, and memorable enough that outlier

cases could be ﬂagged and reported: e.g. “There is something seriously

wrong with Franz Kafka.”

•Summary statistics: Look at the basic statistics of each column. Tukey’s

ﬁve number summary is a great start for numerical values, consisting of

the extreme values (max and min), plus the median and quartile elements.

Applied to the components of our height/weight data set, we get:

158 CHAPTER 6. VISUALIZING DATA

Min 25% Median 75% Max

Age 241 418 584 748 959

Weight 32.4 67.2 78.8 92.6 218.2

Height 140 160 167 175 204

Leg Length 23.7 35.7 38.4 41 55.5

Arm Length 29.5 35.5 37.4 39.4 47.7

Arm Circumference 19.5 29.7 32.8 36.1 141.1

Waist 59.1 87.5 97.95 108.3 172

This is very informative. First, what’s the deal that the median age is 584?

Going back to the data, we learn that age is measured in months, meaning

the median is 48.67 years. Arm and leg length seem to have about the same

median, but leg length has much greater variability. I never knew that.

But suddenly I realize that people are more often described as long/short

legged than long/short armed, so maybe this is why.

For categorical ﬁelds, like occupation, the analogous summary would be a

report on how many diﬀerent label types appear in the column, and what

the three most popular categories are, with associated frequencies.

•Pairwise correlations: A matrix of correlation coeﬃcients between all

pairs of columns (or at least the columns against the dependent variables

of interest) gives you an inkling of how easy it will be to build a successful

model. Ideally, we will have several features which strongly correlate with

the outcome, while not strongly correlating with each other. Only one

column from a set of perfectly correlated features has any value, because

all the other features are completely deﬁned from any single column.

Leg Arm Arm

Age Weight Height Length Length Circum Waist

Age 1.000

Weight 0.017 1.000

Height −0.105 0.443 1.000

Leg Len −0.268 0.238 0.745 1.000

Arm Len 0.053 0.583 0.801 0.614 1.000

Arm Circ 0.007 0.890 0.226 0.088 0.444 1.000

Waist 0.227 0.892 0.181 −0.029 0.402 0.820 1.000

These pairwise correlations are quite interesting. Why is height negatively

correlated with age? The people here are all adults (241 months = 20.1

years), so they are all fully grown. But the previous generation was shorter

than the people of today. Further, people shrink when they get older, so

together this probably explains it. The strong correlation between weight

and waist size (0.89) reﬂects an unfortunate truth about nature.

•Class breakdowns: Are there interesting ways to break things down by

major categorical variables, like gender or location? Through summary

6.1. EXPLORATORY DATA ANALYSIS 159

Figure 6.1: The array of dot plots of variable pairs provides quick insight into

the distributions of data values and their correlations.

statistics, you can gauge whether there is a diﬀerence among the distribu-

tions when conditioned on the category. Look especially where you think

there should be diﬀerences, based on your understanding of the data and

application.

The correlations were generally similar by gender, but there were some

interesting diﬀerences. For example, the correlation between height and

weight is stronger for men (0.443) than women (0.297).

•Plots of distributions: This chapter focuses on visualization techniques

for data. Use the chart types we will discuss in Section 6.3 to eyeball the

distributions, looking for patterns and outliers. What is the general shape

of each distribution? Should the data be cleaned or transformed to make

it more bell-shaped?

Figure 6.1 shows the power of a grid of dot plots of diﬀerent variables. At

a glance we see that there are no wild outliers, which pairs are correlated,

and the nature of any trend lines. Armed with this single graphic, we are

now ready to apply this data set to whatever is the challenge at hand.

6.1.2 Summary Statistics and Anscombe’s Quartet

There are profound limits to how well you can understand data without visu-

alization techniques. This is best depicted by Anscombe’s quartet: four two-

dimensional data sets, each with eleven points and shown in Figure 6.2. All four

160 CHAPTER 6. VISUALIZING DATA

I II III IV

x y x y x y x y

10.0 8.04 10.0 9.14 10.0 7.46 8.0 6.58

8.0 6.95 8.0 8.14 8.0 6.77 8.0 5.76

13.0 7.58 13.0 8.74 13.0 12.74 8.0 7.71

9.0 8.81 9.0 8.77 9.0 7.11 8.0 8.84

11.0 8.33 11.0 9.26 11.0 7.81 8.0 8.47

14.0 9.96 14.0 8.10 14.0 8.84 8.0 7.04

6.0 7.24 6.0 6.13 6.0 6.08 8.0 5.25

4.0 4.26 4.0 3.10 4.0 5.39 19.0 12.50

12.0 10.84 12.0 9.31 12.0 8.15 8.0 5.56

7.0 4.82 7.0 7.26 7.0 6.42 8.0 7.91

5.0 5.68 5.0 4.74 5.0 5.73 8.0 6.89

Mean 9.0 7.5 9.0 7.5 9.0 7.5 9.0 7.5

Var. 10.0 3.75 10.0 3.75 10.0 3.75 10.0 3.75

Corr. 0.816 0.816 0.816 0.816

Figure 6.2: Four data sets with identical statistical properties. What do they

look like?

data sets have identical means for the xand yvalues, identical variances for the

xand yvalues, and the exact same correlation between the xand yvalues.

These data sets must all be pretty similar, right? Study the numbers for a

little while so you can get an idea of what they look like.

Got it? Now peak at the dot plots of these data sets in Figure 6.3. They all

look diﬀerent, and tell substantially diﬀerent stories. One trends linear, while a

second looks almost parabolic. Two others are almost perfectly linear modulo

outliers, but with wildly diﬀerent slopes.

The point here is that you can instantly appreciate these diﬀerences with

a glance at the scatter plot. Even simple visualizations are powerful tools for

understanding what is going on in a data set. Any sensible data scientist strives

to take full advantage of visualization techniques.

6.1.3 Visualization Tools

An extensive collection of software tools are available to support visualization.

Generally speaking, visualization tasks fall into three categories, and the right

choice of tools depends upon what your mission really is:

•Exploratory data analysis: Here we seek to perform quick, interactive

explorations of a given data set. Spreadsheet programs like Excel and

notebook-based programming environments like iPython, R, and Mathe-

matica are eﬀective at building the standard plot types. The key here is

hiding the complexity, so the plotting routines default to doing something

reasonable but can be customized if necessary.

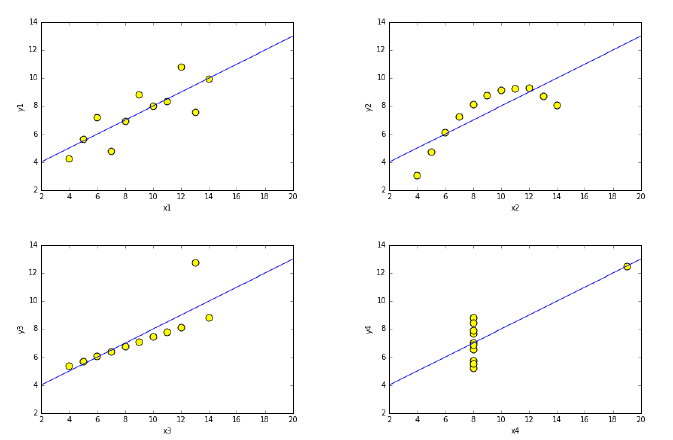
6.1. EXPLORATORY DATA ANALYSIS 161

Figure 6.3: Plots of the Ascombe quartet. These data sets are all dramatically

diﬀerent, even though they have identical summary statistics.

•Publication/presentation quality charts: Just because Excel is very pop-

ular does not mean it produces the best possible graphs/plots. The best

visualizations are an interaction between scientist and software, taking full

advantage of the ﬂexibility of a tool to maximize the information content

of the graphic.

Plotting libraries like MatPlotLib or Gnuplot support a host of options

enabling your graph to look exactly like you want it to. The statistical lan-

guage R has a very extensive library of data visualizations. Look through

catalogs of the plot types supported by your favorite library, to help you

ﬁnd the best representation for your data.

•Interactive visualization for external applications: Building dashboards

that facilitate user interaction with proprietary data sets is a typical task

for data science-oriented software engineers. The typical mission here is

to build tools that support exploratory data analysis for less technically-

skilled, more application-oriented personnel.

Such systems can be readily built in programming languages like Python,

using standard plotting libraries. There is also a class of third-party

systems for building dashboards, like Tableau. These systems are pro-

grammable at a higher-level than other tools, supporting particular inter-

action paradigms and linked-views across distinct views of the data.

162 CHAPTER 6. VISUALIZING DATA

Figure 6.4: Which painting do you like better? Forming intelligent preferences

in art or visualizations depend upon having a distinctive visual aesthetic.

6.2 Developing a Visualization Aesthetic

Sensible appreciation of art or wine requires developing a particular taste or

aesthetic. It isn’t so much about whether you like something, but ﬁguring out

why you like it. Art experts talk about the range of a painter’s palate, use of

light, or the energy/tension of a composition. Wine connoisseurs testify to the

fragrance, body, acidity, and clarity of their favorite plonk, and how much oak

or tannin it contains. They always have something better to say than “that

tastes good.”

Distinguishing good/bad visualizations requires developing a design aes-

thetic, and a vocabulary to talk about data representations. Figure 6.4 presents

two famous landmarks in Western painting. Which one is better? This question

is meaningless without a sense of aesthetics and a vocabulary to describe it.

My visual aesthetic and vocabulary is largely derived from the books of

Edward Tufte [Tuf83, Tuf90, Tuf97]. He is an artist: indeed I once got to meet

him at his former art gallery across from Chelsea Piers in Manhattan. He has

thought long and hard about what makes a chart or graph informative and

beautiful, basing a design aesthetic on the following principles:

•Maximize data-ink ratio: Your visualization is supposed to show oﬀ your

data. So why is so much of what you see in charts the background grids,

shading, and tic-marks?

•Minimize the lie factor: As a scientist, your data should reveal the truth,

ideally the truth you want to see revealed. But are you being honest with

your audience, or using graphical devices that mislead them into seeing

something that isn’t really there?

•Minimize chartjunk: Modern visualization software often adds cool visual

eﬀects that have little to do with your data set. Is your graphic interesting

because of your data, or in spite of it?

•Use proper scales and clear labeling: Accurate interpretation of data de-

pends upon non-data elements like scale and labeling. Are your descriptive

6.2. DEVELOPING A VISUALIZATION AESTHETIC 163

Figure 6.5: Three-dimensional monoliths casting rendered shadows (l) may look

impressive. But they really are just chartjunk, which serves to reduce the clarity

and data-ink ratio from just showing the data (r).

materials optimized for clarity and precision?

•Make eﬀective use of color: The human eye has the power to discriminate

between small gradations in hue and color saturation. Are you using color

to highlight important properties of your data, or just to make an artistic

statement?

•Exploit the power of repetition: Arrays of similar graphics with diﬀerent

but related data elements provide a concise and powerful way to enable

visual comparisons. Are your chart multiples facilitating comparisons, or

merely redundant?

Each of these principles will be detailed in the subsections below.

6.2.1 Maximizing Data-Ink Ratio

In any graphic, some of the ink is used to represent the actual underlying data,

while the rest is employed on graphic eﬀects. Generally speaking, visualizations

should focus on showing the data itself. We deﬁne the data-ink ratio to be:

Data-Ink Ratio = Data-Ink

Total ink used in graphic

Figure 6.5 presents average salary by gender (Bureau of Labor Statistics,

2015), and helps clarify this notion. Which data representation do you pre-

fer? The image on the left says “Cool, how did you make those shadows and

that three-dimensional perspective eﬀect?” The image on the right says “Wow,

women really are underpaid at all points on the income spectrum. But why is

the gap smallest for counselors?”

Maximizing the data-ink ratio lets the data talk, which is the entire point

of the visualization exercise in the ﬁrst place. The ﬂat perspective on the right

permits a fairer comparison of the heights of the bars, so the males do not look

164 CHAPTER 6. VISUALIZING DATA

like pipsqueaks to the women. The colors do a nice job enabling us to compare

apples-to-apples.

There are more extreme ways to increase the data-ink ratio. Why do we

need bars at all? The same information could be conveyed by plotting a point

of the appropriate height, and would clearly be an improvement were we plotting

much more than the eight points shown here. Be aware that less can be more

in visualizing data.

6.2.2 Minimizing the Lie Factor

A visualization seeks to tell a true story about what the data is saying. The

baldest form of lie is to fudge your data, but it remains quite possible to report

your data accurately, yet deliberately mislead your audience about what it is

saying. Tufte deﬁnes the lie factor of a chart as:

lie factor = (size of an eﬀect in the graphic)

(size of the eﬀect in the data)

Graphical integrity requires minimizing this lie factor, by avoiding the tech-

niques which tend to mislead. Bad practices include:

•Presenting means without variance: The data values {100,100,100,100,100}

and {200,0,100,200,0}tell diﬀerent stories, even though both means are

100. If you cannot plot the actual points with the mean, at least show

the variance, to make clear the degree to which the mean reﬂects the

distribution.

•Presenting interpolations without the actual data: Regression lines and

ﬁtted curves are eﬀective at communicating trends and simplifying large

data sets. But without showing the data points it is based on, it is im-

possible to ascertain the quality of the ﬁt.

•Distortions of scale: The aspect ratio of a ﬁgure can have a huge eﬀect on

how we interpret what we are seeing. Figure 6.6 presents three renderings

of a given ﬁnancial time series, identical except for the aspect ratio of the

chart.

In the bottom rendering, the series looks ﬂat: there is nothing to worry

about here. On the right, proﬁts have fallen oﬀ a cliﬀ: the sky is falling!

The left corner plot presents a serious decline, but with signs of an autumn

rebound.

Which plot is right? People are generally used to seeing plots presented

according to the Golden ratio, implying that the width should be about 1.6

times the height. Give this shape to them, unless you have well-developed

reasons why it is inappropriate. Psychologists inform us that 45 degree

lines are the most readily interpretable, so avoid shapes that substantially

amplify or mute lines from this objective.

6.2. DEVELOPING A VISUALIZATION AESTHETIC 165

Figure 6.6: Three renderings of the same ﬁnancial time series. Which most

accurately represents the situation?

•Eliminating tick labels from numerical axes: Even the worst scale dis-

tortions can be completely concealed by not printing numerical reference

labels on axes. Only with the numerical scale markings can the actual

data values be reconstructed from the plot.

•Hide the origin point from the plot: The implicit assumption in most

graphs is that the range of values on the y-axis goes from zero to ymax. We

lose the ability to visually compare magnitudes if the y-range instead goes

from ymin −to ymax. The largest value suddenly looks many times larger

than the smallest value, instead of being scaled to the proper proportion.

If Figure 6.5 (right) were drawn with a tight y-range [900,2500], the mes-

sage would be that counselors were starving, instead of earning salaries as

close to teachers as software developers are to pharmacists. Such decep-

tions can be recognized provided the scales are marked on the axis, but

are hard to catch.

Despite Tufte’s formula, the lie factor cannot be computed mechanically,

because it requires understanding the agenda that is behind the distortion. In

reading any graph, it is important to know who produced it and why. Under-

standing their agenda should sensitize you to potentially misleading messages

encoded in the graphic.

6.2.3 Minimizing Chartjunk

Extraneous visual elements distract from the message the data is trying to tell.

In an exciting graphic, the data tells the story, not the chartjunk.

166 CHAPTER 6. VISUALIZING DATA

Figure 6.7: A monthly time series of sales. How can we improve/simplify this

bar chart time series?

Figure 6.7 presents a monthly time series of sales at a company beginning

to encounter bad times. The graphic in question is a bar plot, a perfectly sound

way to represent time series data, and is drawn using conventional, perhaps

default, options using a reasonable plotting package.

But can we simplify this plot by removing elements to make the data stand

out better? Think about this for a minute before peeking at Figure 6.8, which

presents a series of four successive simpliﬁcations to this chart. The critical

operations are:

•Jailbreak your data (upper left): Heavy grids imprison your data, by visu-

ally dominating the contents. Often graphs can be improved by removing

the grid, or at least lightening it.

The potential value of the data grid is that it facilitates more precise

interpretation of numerical quantities. Thus grids tend to be most useful

on plots with large numbers of values which may need to be accurately

quoted. Light grids can adequately manage such tasks.

•Stop throwing shade (upper right): The colored background here con-

tributes nothing to the interpretation of the graphic. Removing it in-

creases the data-ink ratio, and makes it less obtrusive.

•Think outside the box (lower left): The bounding box does not really

contribute information, particularly the upper and rightmost boundaries

which do not deﬁne axes. Take them out, and let more air into your plots.

•Make missing ink work for you (lower right): The eﬀect of the reference

grid can be recovered by removing lines from the bars instead of adding

elements. This makes it easier to compare the magnitude of biggest num-

bers, by focusing attention on big changes in the relatively small top piece,

instead of small changes in the long bar.

6.2. DEVELOPING A VISUALIZATION AESTHETIC 167

Figure 6.8: Four successive simpliﬁcations of Figure 6.7, by removing extraneous

non-data elements.

The architect Mies van der Rohe famously said that “less is more.” Remov-

ing elements from plots often improves them far more than adding things. Make

this part of your graphical design philosophy.

6.2.4 Proper Scaling and Labeling

Deﬁciencies in scaling and labeling are the primary source of intentional or ac-

cidental misinformation in graphs. Labels need to report the proper magnitude

of numbers, and scale needs to show these numbers to the right resolution, in a

way to facilitate comparison. Generally speaking, data should be scaled so as

to ﬁll the space allotted to it on the chart.

Reasonable people can diﬀer as to whether to scale the axes over the full

theoretical range of the variable, or cut it down to reﬂect only the observed

values. But certain decisions are clearly unreasonable.

Figure 6.9 (left) was produced by a student of mine, presenting the cor-

relation between two variables for almost a hundred languages. Because the

correlation ranges between [−1,1], he forced the plot to respect this interval.

The vast sea of white in this plot captures only the notion that we might have

done better, by getting the correlation closer to 1.0. But the chart is otherwise

unreadable.

Figure 6.9 (right) presents exactly the same data, but with a truncated scale.

Now we can see where there are increases in performance as we move from left

to right, and read oﬀ the score for any given language. Previously, the bars

168 CHAPTER 6. VISUALIZING DATA

Figure 6.9: Scaling over the maximum possible range (left) is silly when all

it shows is white space. Better scaling permits more meaningful comparisons

(right).

were so far removed from the labels that it was diﬃcult to make the name–bar

correspondence at all.

The biggest sin of truncated scales comes when you do not show the whole

of each bar, so the length of the bar no longer reﬂects the relative value of the

variable. We show the y= 0 line here, helping the reader to know that each bar

must be whole. Getting the data out of its prison grid would also have helped.

6.2.5 Eﬀective Use of Color and Shading

Colors are increasingly assumed as part of any graphical communication. In-

deed, I was pleased to learn that my publisher’s printing costs are now identical

for color and black-and-white, so you the reader are not paying any more to see

my color graphics here.

Colors play two major roles in charts, namely marking class distinctions and

encoding numerical values. Representing points of diﬀerent types, clusters, or

classes with diﬀerent colors encodes another layer of information on a conven-

tional dot plot. This is a great idea when we are trying to establish the extent

of diﬀerences in the data distribution across classes. The most critical thing is

that the classes be easily distinguishable from each other, by using bold primary

colors.

It is best when the colors are selected to have mnemonic values to link nat-

urally to the class at hand. Losses should be printed in red ink, environmental

causes associated with green, nations with their ﬂag colors, and sports teams

with their jersey colors. Coloring points to represent males as blue and females

as red oﬀers a subtle clue to help the viewer interpret a scatter plot, as shown

in Figure 9.17.

Selecting colors to represent a numerical scale is a more diﬃcult problem.

Rainbow color maps are perceptually non-linear, meaning it is not obvious to

anyone whether purple lies before or after green. Thus while plotting numbers in

rainbow colors groups similar numbers in similar colors, the relative magnitudes

are imperceptible without explicitly referencing the color scale. Figure 6.10

presents several color scales from Python’s MatPlotLib, for comparison.

6.2. DEVELOPING A VISUALIZATION AESTHETIC 169

Figure 6.10: Color scales from Python’s MatPlotLib, varying hue, saturation,

and brightness. Rainbow color maps are perceptually non-linear, making it

diﬃcult to recognize the magnitudes of diﬀerences.

Much better are color scales based on a varying either brightness or satura-

tion. The brightness of a color is modulated by blending the hue with a shade

of gray, somewhere between white and black. Saturation is controlled by mixing

in a fraction of gray, where 0 produces the pure hue, and 1 removes all color.

Another popular color scale features distinct positive/negative colors (say,

blue and red, as in the seismic color scale of Figure 6.10) reﬂected around a white

or gray center at zero. Thus hue tells the viewer the polarity of the number,

while brightness/saturation reﬂects magnitude. Certain color scales are much

better for color-blind people, particularly those avoiding use of red and green.

As a general rule, large areas on plots should be shown with unsaturated

colors. The converse is true for small regions, which stand out better with

saturated colors. Color systems are a surprisingly technical and complicated

matter, which means that you should always use well established color scales,

instead of inventing your own.

6.2.6 The Power of Repetition

Small multiple plots and tables are excellent ways to represent multivariate data.

Recall the power of grids showing all bivariate distributions in Figure 6.1.

There are many applications of small multiple charts. We can use them to

break down a distribution by classes, perhaps plotting separate but comparable

charts by region, gender, or time period. Arrays of plots facilitate comparisons:

what has changed between diﬀerent distributions.

Time series plots enable us to compare the same quantities at diﬀerent cal-

endar points. Even better is to compare multiple time series, either as lines on

the same plot, or multiple plots in a logical array reﬂecting their relationship.

170 CHAPTER 6. VISUALIZING DATA

6.3 Chart Types

In this section, we will survey the rationale behind the primary types of data

visualizations. For each chart, I present best practices for using them, and

outline the degrees of freedom you have to make your presentation as eﬀective

as possible.

Nothing says “Here’s a plot of some data” like a thoughtlessly-produced

graphic, created using the default settings of some software tool. My students

present me with such undigested data products way too often, and this section

is somewhat of a personal reaction against it.

Take-Home Lesson: You have the power and responsibility to produce mean-

ingful and interpretable presentations of your work. Eﬀective visualization

involves an iterative process of looking at the data, deciding what story it is

trying to tell, and then improving the display to tell the story better.

Figure 6.11 presents a handy decision tree to help select the right data rep-

resentation, from Abela [Abe13]. The most important charts will be reviewed

in this section, but use this tree to better understand why certain visualizations

are more appropriate in certain contexts. We need to produce the right plot for

a given data set, not just the ﬁrst thing that comes to mind.

6.3.1 Tabular Data

Tables of numbers can be beautiful things, and are very eﬀective ways to present

data. Although they may appear to lack the visual appeal of graphic presenta-

tions, tables have several advantages over other representations, including:

•Representation of precision: The resolution of a number tells you some-

thing about the process of how it was obtained: an average salary of

$79,815 says something diﬀerent than $80,000. Such subtleties are gener-

ally lost on plots, but nakedly clear in numerical tables.

•Representation of scale: The digit lengths of numbers in a table can be

likened to bar charts, on a logarithmic scale. Right-justifying numbers

best communicates order-of-magnitude diﬀerences, as (to a lesser extent)

does scanning the leading digits of numbers in a column.

left center right

1 1 1

10 10 10

100 100 100

1000 1000 1000

Left justifying numbers prevents such comparisons, so always be sure to

right justify them.

6.3. CHART TYPES 171

www.ExtremePresentation.com

200

. Abela —

a.v.abela@gm

ail.

com

Chart Suggestions—A  ought-Starter

Circular Area Chart

Line Chart

Column Chart

Line Chart

Scatter Chart

3D Area Chart

Pie Chart

Waterfall Chart

Stacked 100% Column Chart

with Subcomponents

Stacked Area Chart

Stacked 100%

Area Chart

Stacked

Column Chart

Stacked 100%

Column Chart

Bubble Chart

Scatter Chart

Variable Width

Column Chart

Table or Table with

Embedded Charts

Bar Chart

Column Chart

Column Histogram

Line Histogram

 ree

Variables

Two

Variables

Single

Variable

Many Periods

Few Periods

Two Variables

per Item

Many

Categories

One Variable per Item

Among Items

What would you

like to show?

Many Items

Few Categories

Few Items

Many Periods

Cyclical Data

Non-Cyclical Data

Few Periods

Single or Few Categories

Many Categories

Over Time

Comparison

Distribution

Few

Data

Points

Many

Data

Points

Two

Variables

 ree

Variables

Relationship

Composition

Simple Share

of Total

Accumulation or

Subtraction to Total

Components

of Components

Static

Only Relative

Diﬀ erences Matter

Relative and Absolute

Diﬀ erences Matter

Only Relative

Diﬀ erences Matter

Relative and Absolute

Diﬀ erences Matter

Changing

Over Time

Figure 6.11: A clever decision tree to help identify the best visual representation

for representing data. Reprinted with permission from Abela [Abe13].

172 CHAPTER 6. VISUALIZING DATA

•Multivariate visualization: Geometry gets complicated to understand

once we move beyond two dimensions. But tables can remain manage-

able even for large numbers of variables. Recall Babe Ruth’s baseball

statistics from Figure 1.1, a table of twenty-eight columns which is readily

interpretable by any knowledgeable fan.

•Heterogeneous data: Tables generally are the best way to present a mix

of numerical and categorical attributes, like text and labels. Glyphs like

emojis can even be used to represent the values of certain ﬁelds.

•Compactness: Tables are particularly useful for representing small num-

bers of points. Two points in two dimensions can be drawn as a line, but

why bother? A small table is generally better than a sparse visual.

Presenting tabular data seems simple to do (“just put it in a table”), akin to

rapping a leg with a stick. But subtleties go into producing the most informative

tables. Best practices include:

•Order rows to invite comparison: You have the freedom to order the rows

in a table any way you want, so take advantage of it. Sorting the rows

according to the values of an important column is generally a good idea.

Thus grouping the rows is valuable to facilitate comparison, by putting

likes with likes.

Sorting by size or date can be more revealing than the name in many

contexts. Using a canonical order of the rows (say, lexicographic by name)

can be helpful for looking up items by name, but this is generally not a

concern unless the table has many rows.

•Order columns to highlight importance, or pairwise relationships: Eyes

darting from left-to-right across the page cannot make eﬀective visual com-

parisons, but neighboring ﬁelds are easy to contrast. Generally speaking,

columns should be organized to group similar ﬁelds, hiding the least im-

portant ones on the right.

•Right-justify uniform-precision numbers: Visually comparing 3.1415 with

39.2 in a table is a hopeless task: the bigger number has to look bigger.

Best is to right justify them, and set all to be the same precision: 3.14 vs.

39.20.

•Use emphasis,font, or color to highlight important entries: Marking

the extreme values in each column so they stand out reveals important

information at a glance. It is easy to overdo this, however, so strive for

subtlety.

•Avoid excessive-length column descriptors: White ribbons in tables are

distracting, and usually result from column labels that are longer than the

values they represent. Use abbreviations or multiple-line word stacking to

minimize the problem, and clarify any ambiguity in the caption attached

to the table.

6.3. CHART TYPES 173

To help illustrate these possible sins, here is a table recording six properties

of ﬁfteen diﬀerent nations, with the row and column orders given at random.

Do you see any possible ways of improving it?

Country Area Density Birthrate Population Mortality GDP

Russia 17075200 8.37 99.6 142893540 15.39 8900.0

Mexico 1972550 54.47 92.2 107449525 20.91 9000.0

Japan 377835 337.35 99.0 127463611 3.26 28200.0

United Kingdom 244820 247.57 99.0 60609153 5.16 27700.0

New Zealand 268680 15.17 99.0 4076140 5.85 21600.0

Afghanistan 647500 47.96 36.0 31056997 163.07 700.0

Israel 20770 305.83 95.4 6352117 7.03 19800.0

United States 9631420 30.99 97.0 298444215 6.5 37800.0

China 9596960 136.92 90.9 1313973713 24.18 5000.0

Tajikistan 143100 51.16 99.4 7320815 110.76 1000.0

Burma 678500 69.83 85.3 47382633 67.24 1800.0

Tanzania 945087 39.62 78.2 37445392 98.54 600.0

Tonga 748 153.33 98.5 114689 12.62 2200.0

Germany 357021 230.86 99.0 82422299 4.16 27600.0

Australia 7686850 2.64 100.0 20264082 4.69 29000.0

There are many possible orderings of the rows (countries). Sorting by any

single column is an improvement over random, although we could also group

them by region/continent. The order of the columns can be made more un-

derstandable by putting like next to like. Finally, tricks like right-justifying

numbers, removing uninformative digits, adding commas, and highlighting the

biggest value in each column makes the data easier to read:

Birth

Country Population Area Density Mortality GDP Rate

Afghanistan 31,056,997 647,500 47.96 163.07 700 36.0

Australia 20,264,082 7,686,850 2.64 4.69 29,000 100.0

Burma 47,382,633 678,500 69.83 67.24 1,800 85.3

China 1,313,973,713 9,596,960 136.92 24.18 5,000 90.9

Germany 82,422,299 357,021 230.86 4.16 27,600 99.0

Israel 6,352,117 20,770 305.83 7.03 19,800 95.4

Japan 127,463,611 377,835 337.35 3.26 28,200 99.0

Mexico 107,449,525 1,972,550 54.47 20.91 9,000 92.2

New Zealand 4,076,140 268,680 15.17 5.85 21,600 99.0

Russia 142,893,540 17,075,200 8.37 15.39 8,900 99.6

Tajikistan 7,320,815 143,100 51.16 110.76 1,000 99.4

Tanzania 37,445,392 945,087 39.62 98.54 600 78.2

Tonga 114,689 748 153.33 12.62 2,200 98.5

United Kingdom 60,609,153 244,820 247.57 5.16 27,700 99.0

United States 298,444,215 9,631,420 30.99 6.50 37,800 97.0

174 CHAPTER 6. VISUALIZING DATA

Figure 6.12: Many of the line chart styles that we have seen are supported by

Python’s MatPlotLib package.

6.3.2 Dot and Line Plots

Dot and line plots are the most ubiquitous forms of data graphic, providing a

visual representation of a function y=f(x) deﬁned by a set of (x, y) points.

Dot plots just show the data points, while line plots connect them or interpolate

to deﬁne a continuous function f(x). Figure 6.12 shows several diﬀerent styles

of line plots, varying in the degree of emphasis they give the points vs. the

interpolated curve. Advantages of line charts include:

•Interpolation and ﬁtting: The interpolation curve derived from the points

provides a prediction for f(x) over the full range of possible x. This enables

us to sanity check or reference other values, and make explicit the trends

shown in the data.

Overlaying a ﬁtted or smoothed curve on the same graph as the source

data is a very powerful combination. The ﬁt provides a model explaining

what the data says, while the actual points enable us to make an educated

judgment of how well we trust the model.

•Dot plots: A great thing about line plots is that you don’t actually have to

show the line, resulting in a dot plot. Connecting points by line segments

(polylines) proves misleading in many situations. If the function is only

deﬁned at integer points, or the x-values represent distinct conditions,

then it makes no sense at all to interpolate between them.

Further, polylines dramatically swing out of their way to capture outliers,

thus visually encouraging us to concentrate on exactly the points we should

most ignore. High frequency up-and-down movement distracts us from

6.3. CHART TYPES 175

seeing the broader trend, which is the primary reason for staring at a

chart.

Best practices with line charts include:

•Show data points, not just ﬁts: It is generally important to show the

actual data, instead of just the ﬁtted or interpolated lines.

The key is to make sure that one does not overwhelm the other. To

represent large numbers of points unobtrusively, we can (a) reduce the

size of the points, possibly to pinpricks, and/or (b) lighten the shade of

the points so they sit in the background. Remember that there are ﬁfty

shades of gray, and that subtlety is the key.

•Show the full variable range if possible: By default, most graphic software

plots from xmin to xmax and ymin to ymax, where the mins and maxes are

deﬁned over the input data values. But the logical min and max are

context speciﬁc, and it can reduce the lie factor to show the full range.

Counts should logically start from zero, not ymin.

But sometimes showing the full range is uninformative, by completely

ﬂattening out the eﬀect you are trying to illustrate. This was the case in

Figure 6.9. One possible solution is to use a log scale for the axis, so as to

embed a wider range of numbers in a space eﬃcient way. But if you must

truncate the range, make clear what you are doing, by using axis labels

with tick marks, and clarifying any ambiguity in the associated caption.

•Admit uncertainty when plotting averages: The points appearing on a line

or dot plot are often obtained by averaging multiple observations. The

resulting mean better captures the distribution than any single observa-

tion. But means have diﬀering interpretations based on variance. Both

{8.5,11.0,13.5,7.0,10.0}and {9.9,9.6,10.3,10.1,10.1}average to be 10.0,

but the degree to which we trust them to be precise diﬀers substantially.

There are several ways to confess the level of measurement uncertainty in

our plots. My favorite simply plots all the underlying data values on the

same graph as the means, using the same x-value as the associated mean.

These points will be visually unobtrusive relative to the heavier trend line,

provided they are drawn as small dots and lightly shaded, but they are

now available for inspection and analysis.

A second approach plots the standard deviation σaround yas a whisker,

showing the interval [y−σ, y +σ]. This interval representation is honest,

denoting the range with 68% of the values under a normal distribution.

Longer whiskers means you should be more suspicious of the accuracy of

the means, while short whiskers implies greater precision.

Box plots concisely record the range and distribution of values at a point

with a box. This box shows the range of values from the quartiles (25%

and 75%), and is cut at the median (50th percentile). Typically whiskers

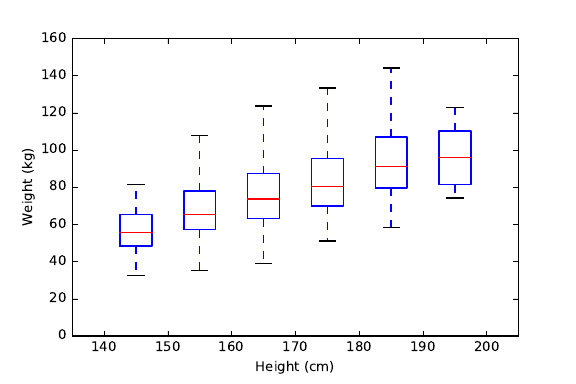
176 CHAPTER 6. VISUALIZING DATA

Figure 6.13: Box and whisker plots concisely show the range/quartiles (i.e.

median and variance) of a distribution.

(hairs) are added to show the range of the highest and lowest values.

Figure 6.13 shows a box-and-whisker plot of weight as a function of height

in a population sample. The median weight increases with height, but

not the maximum, because fewer points in the tallest bucket reduces the

chance for an outlier maximum value.

Real scientists seem to love box-and-whisker plots, but I personally ﬁnd

them to be overkill. If you really can’t represent the actual data points,

perhaps just show the contour lines ﬂanking your mean/median at the

25th and 75th percentiles. This conveys exactly the same information as

the box in the box plot, with less chartjunk.

•Never connect points for categorical data: Suppose you measure some

variable (perhaps, median income) for several diﬀerent classes (say, the

ﬁfty states, from Alabama to Wyoming). It might make sense to display

this as a dot plot, with 1 ≤x≤50, but it would be silly and misleading

to connect the points. Why? Because there is no meaningful adjacency

between state iand state i+ 1. Indeed, such graphs are better oﬀ thought

of as bar charts, discussed in Section 6.3.4

Indeed, connecting points by polylines is very often chartjunk. Trend or

ﬁt lines are often more revealing and informative. Try to show the raw

data points themselves, albeit lightly and unobtrusively.

•Use color and hatching to distinguish lines/classes: Often we are faced

representing the same function f(x) drawn over two or more classes, per-

haps income as a function of schooling, separately for men and women.

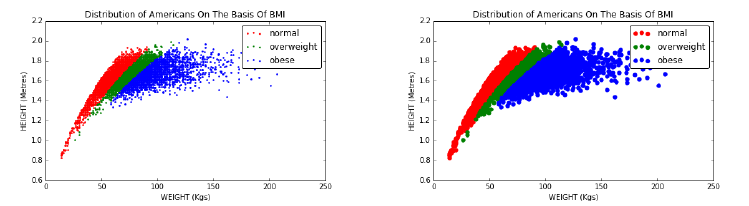
6.3. CHART TYPES 177

Figure 6.14: Smaller dots on scatter plots (left) reveal more detail than the

default dot size (right).

These are best handled by assigning distinct colors to the line/points for

each class. Line hatchings (dotted, dashed, solid, and bold) can also be

used, but these are often harder to distinguish than colors, unless the

output media is black and white. In practice, two to four such lines can

be distinguished on a single plot, before the visual collapses into a mess.

To visualize a large number of groups, partition them into logical clusters

and use multiple line plots, each with few enough lines to be uncluttered.

6.3.3 Scatter Plots

Massive data sets are a real challenge to present in an eﬀective manner, because

large numbers of points easily overwhelm graphic representations, resulting in

an image of the black ball of death. But when properly drawn, scatter plots are

capable of showing thousands of bivariate (two-dimensional) points in a clear

understandable manner.

Scatter plots show the values of every (x, y) point in a given data set. We

used scatter plots in Section 4.1 to represent the body mass status of individuals

by representing them as points in height–weight space. The color of each point

reﬂected their classiﬁcation as normal, overweight, or obese. Best practices

associated with scatter plots include:

•Scatter the right-sized dots: In the movie Oh G-d, George Burns as the

creator looks back on the avocado as his biggest mistake. Why? Because

he made the pit too large. Most people’s biggest mistake with scatter

plots is that they make the points too large.

The scatter plots in Figure 6.14 show the BMI distribution for over 1,000

Americans, with two diﬀerent sizes of dots. Observe how the smaller dots

show ﬁner structure, because they are less likely to overlap and obscure

other data points.

Now we see a ﬁne structure of a dense core, while still being able to detect

the light halo of outliers. The default dot size for most plotting programs

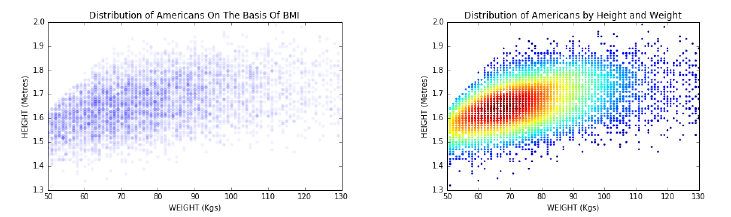
178 CHAPTER 6. VISUALIZING DATA

Figure 6.15: Overlapping dots can obscure scatter plots, particularly for large

data sets. Reducing the opacity of the dots (left) shows some of the ﬁne struc-

ture of the data (left). But a colored heatmap more dramatically reveals the

distribution of the points (right).

is appropriate for about ﬁfty points. But for larger data sets, use smaller

dots.

•Color or jiggle integer points before scatter-plotting them: Scatter plots

reveal grid patterns when the xand yvalues have integer values, because

there are no smooth gradations between them. These scatter plots look

unnatural, but even worse tend to obscure data because often multiple

points will share exactly the same coordinates.

There are two reasonable solutions. The ﬁrst is to color each point based

on its frequency of occurrence. Such plots are called heatmaps, and concen-

tration centers become readily visible provided that a sensible color scale

is used. Figure 6.15 shows a heatmap of height–weight data, which does

a much better job of revealing point concentrations than the associated

simple dot plot.

A related idea is to reduce the opacity (equivalently, increase the trans-

parency) of the points we scatter plot. By default, points are generally

drawn to be opaque, yielding a mass when there are overlapping points.

But now suppose we permit these points to be lightly shaded and trans-

parent. Now the overlapping points show up as darker than singletons,

yielding a heatmap in multiple shades of gray.

The second approach is to add a small amount of random noise to each

point, to jiggle it within a sub-unit radius circle around its original po-

sition. Now we will see the full multiplicity of points, and break the

distracting regularity of the grid.

•Project multivariate data down to two dimensions, or use arrays of pair-

wise plots: Beings from our universe ﬁnd it diﬃcult to visualize data sets

in four or more dimensions. Higher-dimensional data sets can often be

projected down to two dimensions before rendering them on scatter plots,

using techniques such as principal component analysis and self-organizing

6.3. CHART TYPES 179

maps. A pretty example appears a few chapters ahead in Figure 11.16,

where we project a hundred dimensions down to two, revealing a very

coherent view of this high-dimensional data set.

The good thing about such plots is that they can provide eﬀective views of

things we couldn’t otherwise see. The bad thing is that the two dimensions

no longer mean anything. More speciﬁcally, the new dimensions do not

have variable names that can convey meaning, because each of the two

“new” dimensions encodes properties of all the original dimensions.

An alternative representation is to plot a grid or lattice of all pairwise

projections, each showing just two of the original dimensions. This is a

wonderful way to get a sense of which pairs of dimensions correlate with

each other, as we showed in Figure 6.1.

•Three-dimensional-scatter plots help only when there is real structure to

show: TV news stories about data science always feature some researcher

gripping a three-dimensional point cloud and rotating it through space,

striving for some important scientiﬁc insight. They never ﬁnd it, because

the view of a cloud from any given direction looks pretty much the same

as the view from any other direction. There generally isn’t a vantage point

where it suddenly becomes clear how the dimensions interact.

The exception is when the data was actually derived from structured three-

dimensional objects, such as laser scans of a given scene. Most of the

data we encounter in data science doesn’t ﬁt this description, so have

low expectations for interactive visualization. Use the grid of all two-

dimensional projections technique, which essentially views the cloud from

all orthogonal directions.

•Bubble plots vary color and size to represent additional dimensions: Mod-

ulating the color, shape, size, and shading of dots enables dot plots to

represent additional dimensions, on bubble plots. This generally works

better than plotting points in three dimensions.

Indeed Figure 6.16 neatly shows four dimensions (GDP, life expectancy,

population, and geographic region) using x,y, size, and color, respectively.

There is much to read into such a bubble chart: it clearly reveals the

correlation between GDP and health (by the straight line ﬁt, although

note that the x-values are not linearly-spaced), the new world is generally

richer than the old world, and that the biggest countries (China and India)

generally sit in the middle of the pack. Certain rich but sick nations are

doing abysmally by their people (e.g. South Africa), while countries like

Cuba and Vietnam seem to be punching above their weight.

6.3.4 Bar Plots and Pie Charts

Bar plots and pie charts are tools for presenting the relative proportions of

categorical variables. Both work by partitioning a geometric whole, be it a

180 CHAPTER 6. VISUALIZING DATA

DATA SOURCES—INCOME: World Bank’s GDP per capita, PPP (2011 international $). Income of Syria & Cuba are Gapminder estimates. X-axis uses log-scale to make a doubling income show same distance on all levels. POPULATION: Data from UN Population Division. LIFE EXPECTANCY: IHME GBD-2015, as of Oct 2016.

ANIMATING GRAPH: Go to www.gapminder.org/tools to see how this graph changed historically and compare 500 other indicators. LICENSE:

Our charts are freely available under Creative Commons Attribution License. Please copy, share, modify, integrate and even sell them, as long as you mention: ”Based on a free chart from www.gapminder.org”.

$1 000 $2 000 $16 000$4 000 $8 000 $32 000 $64 000 $128 000

LEVEL 2

LEVEL 1 LEVEL 3 LEVEL 4INCOME LEVELS

50 60

55 7065 8075 85

INCOME

POOR RICH

version 15

apminder World 2015

India

Japan

Indonesia

Spain

Vietnam

Ethiopia

Congo

Dem. Rep.

Czech Rep.

South Africa

Sudan

Tanzania

Switzerland

Mali

Burkina Faso

Madagascar

Slovak Rep.

Uganda

Kenya

Norway

Cameroon

Guinea

Ghana

Zimbabwe

Niger

Cote d'Ivoire

Bosnia & Herz.

Senegal

Burundi

Rwanda

Moldova

Benin

Sierra Leone

Chad

Lao

Papua N. G.

Malawi

Tajikistan

Togo

Maced F.

Dominican R.

Eritrea

Nicaragua

Liberia

Honduras

Congo, Rep.

Mauritania

Oman

Trinidad & Tobago

Singapore

Gabon

Palestine

Guyana

Monten.

Luxembourg

Gambia

Fiji

Comoros

Equatorial

Guinea

Kuwait

Solomon Isl.

Djibouti

Kiribati

Micronesia

Brunei

Seychelles

Mars. Isl.

Andorra

United Arab Em.

Central African Rep.

Somalia

Guinea-Bissau

Mozambique

Afghanistan

Lesotho

Haiti

North Korea

Timor-Leste

Nepal

Bangladesh

Kyrgyz Rep.

Cambodia

Swaziland

Pakistan

Nigeria

USA

Saudi Arabia

Russia

Egypt

Philippines

Italy

France

Australia

Sweden

Ireland

Netherlands

Germany

Austria

Belgium

Denm.

Finl.

N. Zeal.

South Korea

Sloven.

Greece

Portugal

Israel

Malta

Cyprus

Iceland

Algeria

Brazil

Mexico

Argentina

Malaysia

Azerbaijan

Suriname

Belarus

Costa Rica

Maldives

South Sudan

Zambia

Vanuatu

Myanmar

Syria

Sao T & P

Uzbekistan

Tonga

Samoa

Bolivia

Cape Verde

Georgia

Guatemala

Bhutan

Ukraine

Belize

St.V&G

Grenada

Morocco Armenia

El Salvador Jamaica

Paraguay

St. Lucia

Dominica

Ecuador

Sri Lanka

Albania

Tunisia

Jordan

Colombia

Peru

Serbia

Barbados

Lebanon

Turkey

Thailand Iran

Venezuela Bulgaria

Libya

Mauritius

Romania

Latvia Lithuania

Bahamas

Kazakhastan

Iraq

Namibia

Mongolia

Uruguay

Croatia

Panama

Cuba

Chile

Poland

Hungary

Estonia

Antig.& B.

Puerto

Rico

Bahrain

Aruba

Angola

Qatar

Turkmenistan

Canada

Bermuda

Yemen

China

COLOR BY REGION

SIZE BY POPULATION

www.gapminder.org

100

1 000

million

This graph compares

Life Expectancy & GDP per capita

for all 182 nations

recognized by the UN.

a free fact-based worldview

HEALTH & INCOME

OF NATIONS

IN 2015

HEALTH

SICK HEALTHY

Life expectancy (years)

GDP per capita ($ adjusted for price differences, PPP 2011)

Figure 6.16: Adding size and color to a scatter plot leads to natural four-

dimensional visualizations, here illustrating properties of the world’s nations.

Based on a free chart from http://www.gapminder.org.

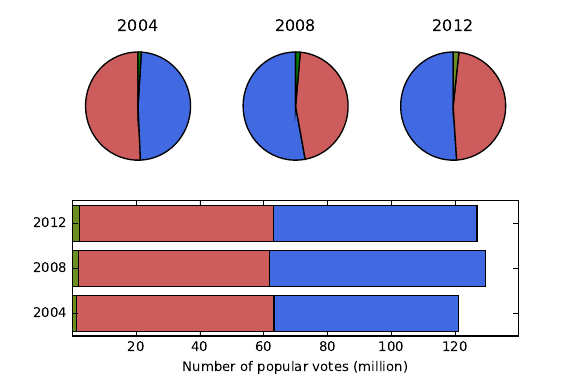
6.3. CHART TYPES 181

Figure 6.17: Voter data from three U.S. presidential elections. Bar plots and

pie charts display the frequency of proportion of categorical variables. Relative

magnitudes in a time series can be displayed by modulating the area of the line

or circle.

bar or a circle, into areas proportional to the frequency of each group. Both

elements are eﬀective in multiples, to enable comparisons. Indeed, partitioning

each bar into pieces yields the stacked bar chart.

Figure 6.17 shows voter data from three years of U.S. presidential elections,

presented as both pie and bar charts. The blue represents Democratic votes, the

red Republican votes. The pies more clearly shows which side won each elections,

but the bars show the Republican vote totals have stayed fairly constant while

the Democrats were generally growing. Observe that these bars can be easily

compared because they are left-justiﬁed.

Certain critics get whipped into an almost religious fever against pie charts,

because they take up more space than necessary and are generally harder to

read and compare. But pie charts are arguably better for showing percentages

of totality. Many people seem to like them, so they are probably harmless in

small quantities. Best practices for bar plots and pie charts include:

•Directly label slices of the pie: Pie charts are often accompanied by legend

keys labeling what each color slice corresponds to. This is very distracting,

because your eyes must move back and forth between the key and the pie

to interpret this.

Much better is to label each slice directly, inside the slice or just beyond

the rim. This has a secondary beneﬁt of discouraging the use of too many

slices, because slivers generally become uninterpretable. It helps to group

the slivers into a single slice called other, and then perhaps present a

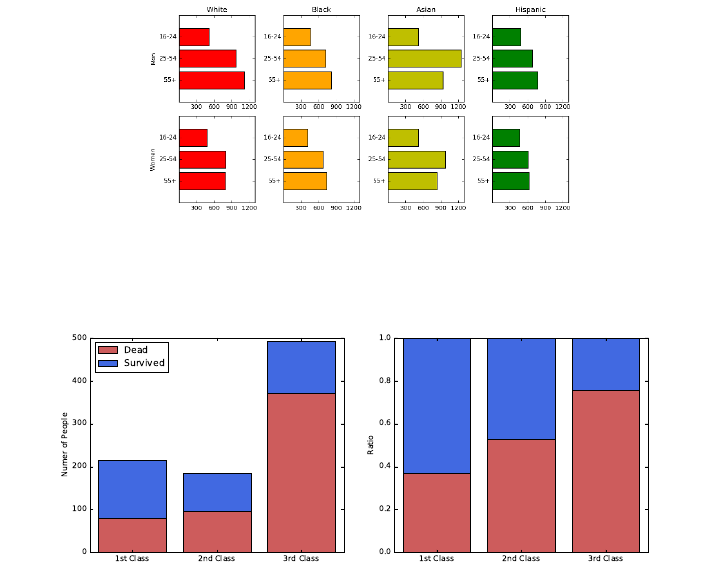
182 CHAPTER 6. VISUALIZING DATA

Figure 6.18: Small multiple bar plots/tables are excellent ways to represent

multivariate data for comparison.

Figure 6.19: Stacked bar charts illustrating the survivorship rate on the doomed

ship Titanic, by ticket class. The histogram (left) informs us of the size of each

class, but scaled bars (right) better capture proportions. Primary conclusion:

you were better oﬀ not to be traveling steerage (third class).

second pie chart decomposed into the major other components.

•Use bar charts to enable precise comparisons: When anchored on a ﬁxed

line, arrays of bars make it easy to identify the minimum and maximum

values in a series, and whether a trend is increasing or decreasing.

Stacked bar charts are concise, but harder to use for such purposes. Pre-

senting an array of small bar charts, here one for each gender/ethnic group,

empowers us to make such ﬁne comparisons, as shown in Figure 6.18.

•Scale appropriately, depending upon whether you seek to highlight absolute

magnitude or proportion: Pie charts exist to represent fractions of the

whole. In presenting a series of pie or bar charts, your most critical decision

is whether you want to show the size of the whole, or instead the fractions

of each subgroup.

Figure 6.19 shows two stacked bar charts presenting survivorship statistics

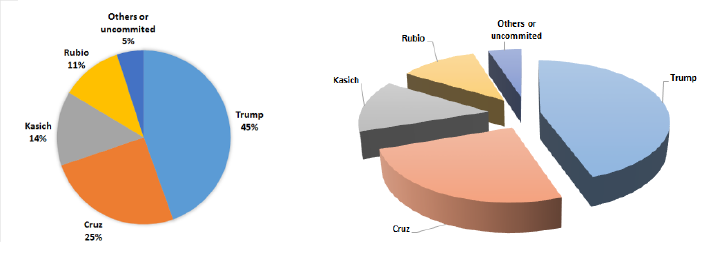
6.3. CHART TYPES 183

Figure 6.20: Pie charts of delegates to the 2016 Republican convention by can-

didate. Which one is better and why?

on the doomed ship Titanic, reported by ticket class. The histogram (left)

precisely records the sizes of each class and the resulting outcomes. The

chart with equal length bars (right) better captures how the mortality rate

increased for lower classes.

Pie charts can also be used to show changes in magnitude, by varying the

area of the circle deﬁning the pie. But it is harder for the eye to calculate

area than length, making comparisons diﬃcult. Modulating the radius to

reﬂect magnitude instead of area is even more deceptive, because doubling

the radius of a circle multiplies the area by four.

Bad Pie Charts

Figure 6.20 shows two pie charts reporting the distribution of delegates to the

2016 Republican convention, by candidate. The left pie is two-dimensional,

while the chart on right has thick slices neatly separated to show oﬀ this depth.

Which one is better at conveying the distribution of votes?

It should be clear that the three-dimensional eﬀects and separation are pure

chartjunk, that only obscures the relationship between the size of the slices. The

actual data values disappeared as well, perhaps because there wasn’t enough

space left for them after all those shadows. But why do we need a pie chart at

all? A little table of labels/colors with an extra column with percentages would

be more concise and informative.

6.3.5 Histograms

The interesting properties of variables or features are deﬁned by their underlying

frequency distribution. Where is the peak of the distribution, and is the mode

near the mean? Is the distribution symmetric or skewed? Where are the tails?

Might it be bimodal, suggesting that the distribution is drawn from a mix of

two or more underlying populations?

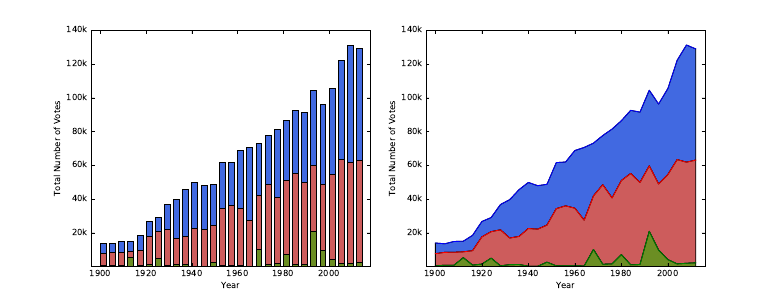
184 CHAPTER 6. VISUALIZING DATA

Figure 6.21: Time series of vote totals in U.S. presidential elections by party en-

able us to see the changes in magnitude and distribution. Democrats are shown

in blue, and Republicans in red. It is hard to visualize changes, particularly in

the middle layers of the stack.

Often we are faced with a large number of observations of a particular vari-

able, and seek to plot a representation for them. Histograms are plots of the

observed frequency distributions. When the variable is deﬁned over a large

range of possible values relative to the nobservations, it is unlikely we will ever

see any exact duplication. However, by partitioning the value range into an ap-

propriate number of equal-width bins, we can accumulate diﬀerent counts per

bin, and approximate the underlying probability distribution.

The biggest issue in building a histogram is deciding on the right number of

bins to use. Too many bins, and there will be only a few points in even the most

popular bucket. We turned to binning to solve exactly this problem in the ﬁrst

place. But use too few bins, and you won’t see enough detail to understand the

shape of the distribution.

Figure 6.22 illustrates the consequences of bin size on the appearance of a

histogram. The plots in the top row bin 100,000 points from a normal distri-

bution into ten, twenty, and ﬁfty buckets respectively. There are enough points

to ﬁll ﬁfty buckets, and the distribution on right looks beautiful. The plots in

the bottom row bin have only 100 points, so the thirty-bucket plot on right is

sparse and scraggy. Here seven bins (shown on the left) seems to produce the

most representative plot.

It is impossible to give hard and fast rules to select the best bin count bfor

showing oﬀ your data. Realize you will never be able to discriminate between

more than a hundred bins by eye, so this provides a logical upper bound. In

general, I like to see an average of 10 to 50 points per bin to make things

smooth, so b=dn/25egives a reasonable ﬁrst guess. But experiment with

diﬀerent values of b, because the right bin count will work much better than the

others. You will know it when you see it.

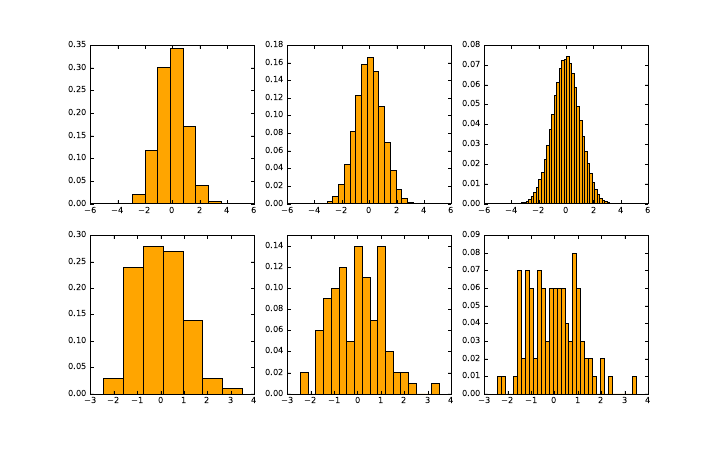
6.3. CHART TYPES 185

Figure 6.22: Histograms of a given distribution can look wildly diﬀerent de-

pending on the number of bins. A large data set beneﬁts from many bins (top).

But the structure of a smaller data set is best shown when each bin a non-trivial

number of element.

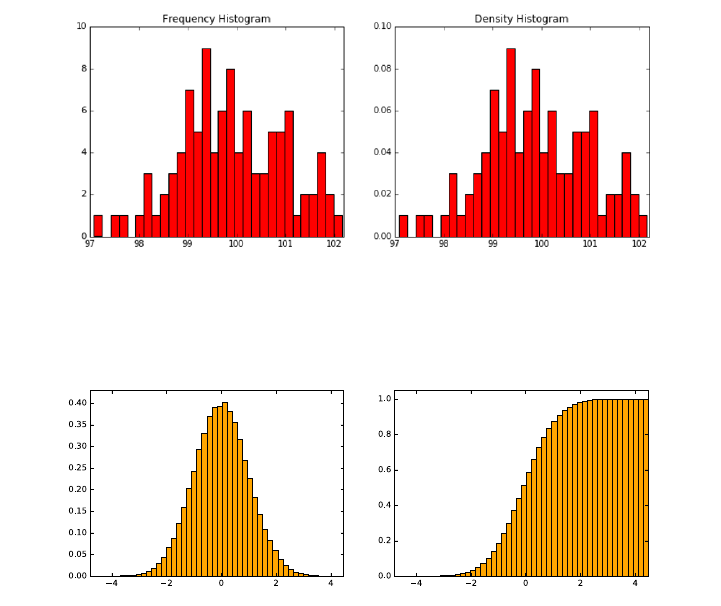
186 CHAPTER 6. VISUALIZING DATA

Figure 6.23: Dividing counts by the total yields a probability density plot, which

is more generally interpretable even though the shapes are identical.

Figure 6.24: Generally speaking, histograms are better for displaying peaks in

a distribution, but cdfs are better for showing tails.

Best practices for histograms include:

•Turn your histogram into a pdf: Typically, we interpret our data as

observations that approximate the probability density function (pdf) of

an underlying random variable. If so, it becomes more interpretable to

label the y-axis by the fraction of elements in each bucket, instead of the

total count. This is particularly true in large data sets, where the buckets

are full enough that we are unconcerned about the exact level of support.

Figure 6.23 shows the same data, plotted on the right as a pdf instead of a

histogram. The shape is exactly the same in both plots: all that changes

is the label on the y-axis. Yet the result is easier to interpret, because it

is in terms of probabilities instead of counts.

•Consider the cdf: The cumulative density function (cdf) is the integral of

the pdf, and the two functions contain exactly the same information. So

consider using a cdf instead of a histogram to represent your distribution,

6.3. CHART TYPES 187

Figure 6.25: Maps summarizing the results of the 2012 U.S. presidential election.

The recipient of each state’s electoral votes is eﬀectively presented on a data

map (left), while a cartogram making the area of each state proportional to

the number of votes (right) better captures the magnitude of Obama’s victory.

Source: Images from Wikipedia.

as shown in Figure 6.24.

One great thing about plotting the cdf is that it does not rely on a bin

count parameter, so it presents a true, unadulterated view of your data.

Recall how great the cdfs looked in the Kolmogorov-Smirnov test, Figure

5.13. We draw a cdf as a line plot with n+ 2 points for nobservations.

The ﬁrst and last points are (xmin −, 0) and (xmax +, 1). We then sort

the observations to yield S={s1, . . . , sn}, and plot (si, i/n) for all i.

Cumulative distributions require slightly more sophistication to read than

histograms. The cdf is monotonically increasing, so there are no peaks

in the distribution. Instead, the mode is marked by the longest vertical

line segment. But cdfs are much better at highlighting the tails of a

distribution. The reason is clear: the small counts at the tails are obscured

by the axis on a histogram, but accumulate into visible stuﬀ in the cdf.

6.3.6 Data Maps

Maps use the spatial arrangement of regions to represent places, concepts, or

things. We have all mastered skills for navigating the world through maps, skills

which translate into understanding related visualizations.

Traditional data maps use color or shading to highlight properties of the

regions in the map. Figure 6.25 (left) colors each state according to whether

they voted for Barack Obama (blue) or his opponent Mitt Romney (red) in the

2012 U.S. presidential election. The map makes clear the country’s political

divisions. The northeast and west coasts are as solidly blue as the Midwest and

south are red.

188 CHAPTER 6. VISUALIZING DATA

Figure 6.26: The periodic table maps the elements into logical groupings, re-

ﬂecting chemical properties. Source:http://sciencenotes.org

Maps are not limited to geographic regions. The most powerful map in the

history of scientiﬁc visualization is chemistry’s periodic table of the elements.

Connected regions show where the metals and Nobel gases reside, as well as

spots where undiscovered elements had to lie. The periodic table is a map with

enough detail to be repeatedly referenced by working chemists, yet is easily

understood by school children.

What gives the periodic table such power as a visualization?

•The map has a story to tell: Maps are valuable when they encode infor-

mation worth referencing or assimilating. The periodic table is the right

visualization of the elements because of the structure of electron shells,

and their importance on chemical properties and bonding. The map bears

repeated scrutiny because it has important things to tell us.

Data maps are fascinating, because breaking variables down by region

so often leads to interesting stories. Regions on maps generally reﬂect

cultural, historical, economic, and linguistic continuities, so phenomena

deriving from any of these factors generally show themselves clearly on

data maps.

•Regions are contiguous, and adjacency means something: The continu-

ity of regions in Figure 6.26 is reﬂected by its color scheme, grouping

elements sharing similar properties, like the alkali metals and the Nobel

gases. Two elements sitting next to each other usually means that they

share something important in common.

6.4. GREAT VISUALIZATIONS 189

•The squares are big enough to see: A critical decision in canonizing the

periodic table was the placement of the Lanthanide (elements 57–71) and

Actinide metals (elements 89–103). They are conventionally presented as

the bottom two rows, but logically belong within the body of the table in

the unlabeled green squares.

However, the conventional rendering avoids two problems. To do it “right,”

these elements would either be compressed into hopelessly thin slivers, or

else the table would need to become twice as wide to accommodate them.

•It is not too faithful to reality: Improving reality for the sake of better

maps is a long and honorable tradition. Recall that the Mercator projec-

tion distorts the size of landmasses near the poles (yes, Greenland, I am

looking at you) in order to preserve their shape.

Cartograms are maps distorted such that regions reﬂect some underlying

variable, like population. Figure 6.25 (right) plots the electoral results of

2012 on a map where the area of each state is proportional to its popu-

lation/electoral votes. Only now does the magnitude of Obama’s victory

become clear: those giant red Midwestern states shrink down to an ap-

propriate size, yielding a map of more blue than red.

6.4 Great Visualizations

Developing your own visualization aesthetic gives you a language to talk about

what you like and what you don’t like. I now encourage you to apply your

judgment to assess the merits and demerits of certain charts and graphs.

In this section, we will look at a select group of classic visualizations which

I consider great. There are a large number of terrible graphics I would love to

contrast them against, but I was taught that it is not nice to make fun of people.

This is especially true when there are copyright restrictions over the use of

such images in a book like this. However, I strongly encourage you to visit

http://wtfviz.net/ to see a collection of startling charts and graphics. Many

are quite amusing, for reasons you should now be able to articulate using the

ideas in this chapter.

6.4.1 Marey’s Train Schedule

Tufte points to E.J. Marey’s railroad schedule as a landmark in graphical design.

It is shown in Figure 6.27. The hours of the day are represented on the x-axis.

Indeed, this rectangular plot is really a cylinder cut at 6AM and laid down

ﬂat. The y-axis represents all the stations on the Paris to Lyon line. Each line

represents the route of a particular train, reporting where it should be at each

moment in time.

Normal train schedules are tables, with a column for each train, a row for

each station, and entry (i, j) reporting the time train jarrives at station i. Such

tables are useful to tell us what time to arrive to catch our train. But Marey’s

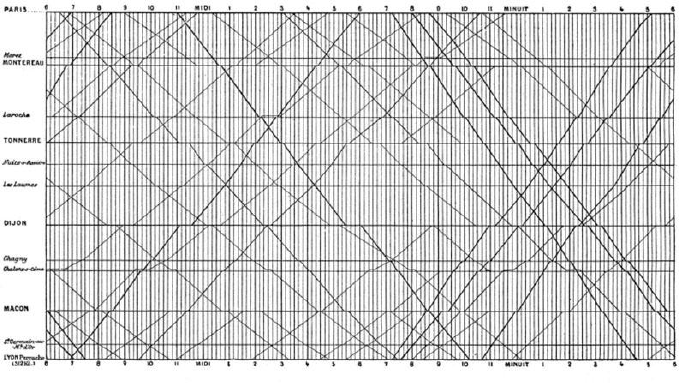
190 CHAPTER 6. VISUALIZING DATA

Figure 6.27: Marey’s train schedule plots the position of each train as a function

of time.

design provides much more information. What else can you see here that you

cannot with conventional time tables?

•How fast is the train moving? The slope of a line measures how steep it

is. The faster the train, the greater the absolute slope. Slower trains are

marked by ﬂatter lines, because they take more time to cover the given

ground.

A special case here is identifying periods when the train is idling in the

station. At these times, the line is horizontal, indicating no movement

down the line.

•When do trains pass each other? The direction of a train is given by the

slope of the associated line. Northbound trains have a positive slope, and

southbound trains a negative slope. Two trains pass each other at the

intersection points of two lines, letting passengers know when to look out

the window and wave.

•When is rush hour? There is a concentration of trains leaving both Paris

and Lyon around 7PM, which tells me that must have been the most

popular time to travel. The trip typically took around eleven hours, so

this must have been a sleeper train, where travelers would arrive at their

destination bright and early the next day.

The departure times for trains at a station are also there, of course. Each

station is marked by a horizontal line, so look for the time when trains cross

your station in the proper direction.

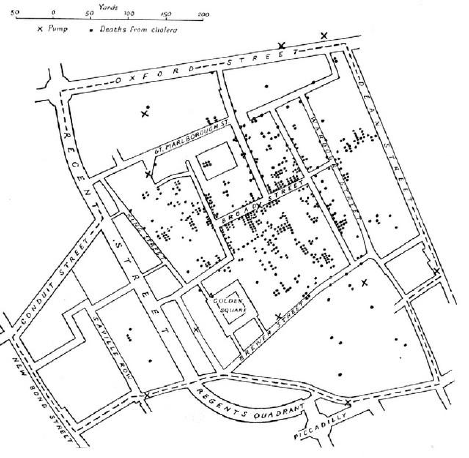
6.4. GREAT VISUALIZATIONS 191

Figure 6.28: Cholera deaths center around a pump on Broad street, revealing

the source of the epidemic.

My only quibble here is that it would have been even better with a lighter

data grid. Never imprison your data!

6.4.2 Snow’s Cholera Map

A particularly famous data map changed the course of medical history. Cholera

was a terrible disease which killed large numbers of people in 19th-century cities.

The plague would come suddenly and strike people dead, with the cause a

mystery to the science of the day.

John Snow plotted cholera cases from an epidemic of 1854 on a street map

of London, hoping to see a pattern. Each dot in Figure 6.28 represented a

household struck with the disease. What do you see?

Snow noticed a cluster of the cases centered on Broad Street. Further, at the

center of the cluster was a cross, denoting a well where the residents got their

drinking water. The source of the epidemic was traced to the handle of a single

water pump. They changed the handle, and suddenly people stopped getting

sick. This proved that cholera was an infectious disease caused by contaminated

water, and pointed the way towards preventing it.

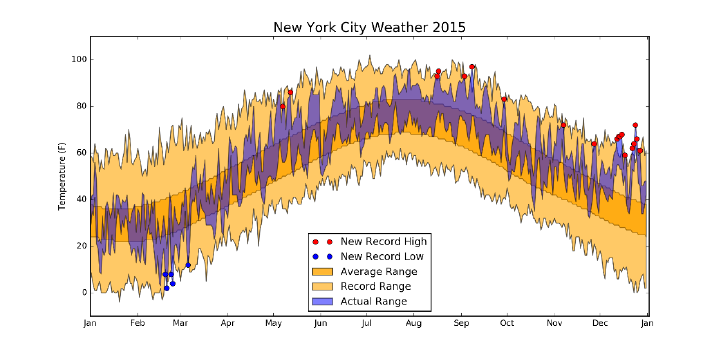
192 CHAPTER 6. VISUALIZING DATA

Figure 6.29: This weather year in review displays a clear story in over 2000

numbers.

6.4.3 New York’s Weather Year

It is almost worth enduring a New York winter to see a particular graphic which

appears in The New York Times each January, summarizing the weather of the

previous year. Figure 6.29 presents an independent rendition of the same data,

which captures why this chart is exciting. For every day of the year, we see

the high and low temperature plotted on a graph, along with historical data to

put it in context: the average daily high and low, as well as the highest/lowest

temperatures ever recorded for that date.

What is so great about that? First, it shows 6 ×365 = 2190 numbers in a

coherent manner, which facilitates comparisons on the sine curve of the seasons:

•We can tell when there were hot and cold spells, and how long they lasted.

•We can tell what days had big swings in temperature, and when the ther-

mometer hardly moved at all.

•We can tell whether the weather was unusual this year. Was it an unusu-

ally hot or cold year, or both? When were record high/lows set, and when

did they get close to setting them?

This single graphic is rich, clear, and informative. Be inspired by it.

6.5 Reading Graphs

What you see isn’t always what you get. I have seen many graphs brought to

me by my students over the years. Some have been amazing, and most others

good enough to get the job done.

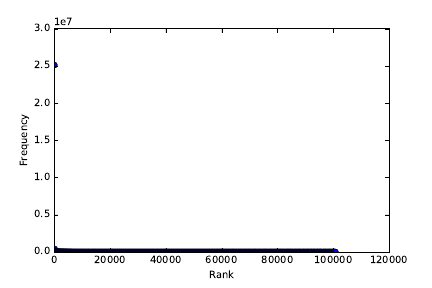
6.5. READING GRAPHS 193

Figure 6.30: A dotplot of word frequency by rank. What do you see?

But I also repeatedly see plots with the same basic problems. In this section,

for a few of my pet peeves, I present the original plot along with the way to

remedy the problem. With experience, you should be able to identify these

kinds of problems just by looking at the initial plot.

6.5.1 The Obscured Distribution

Figure 6.30 portrays the frequency of 10,000 English words, sorted by frequency.

It doesn’t look very exciting: all you can see is a single point at (1,2.5). What

happened, and how can you ﬁx it?

If you stare at the ﬁgure long enough, you will see there are actually a lot

more points. But they all sit on the line y= 0, and overlap each other to the

extent that they form an undiﬀerentiated mass.

The alert reader will realize that this single point is in fact an outlier, with

magnitude so large as to shrink all other totals toward zero. A natural reaction

would delete the biggest point, but curiously the remaining points will look

much the same.

The problem is that this distribution is a power law, and plotting a power

law on a linear scale shows nothing. The key here is to plot it on log scale, as in

Figure 6.31 (left). Now you can see the points, and the mapping from ranks to

frequency. Even better is plotting it on a log-log scale, as in Figure 6.31 (right).

The straight line here conﬁrms that we are dealing with a power law.

6.5.2 Overinterpreting Variance

In bioinformatics, one seeks to discover how life works by looking at data. Figure

6.32 (left) presents a graph of the folding energy of genes as a function of their

length. Look at this graph, and see if you can make a discovery.

It is pretty clear that something is going on in there. For gene lengths above

1500, the plot starts jumping around, producing some very negative values. Did

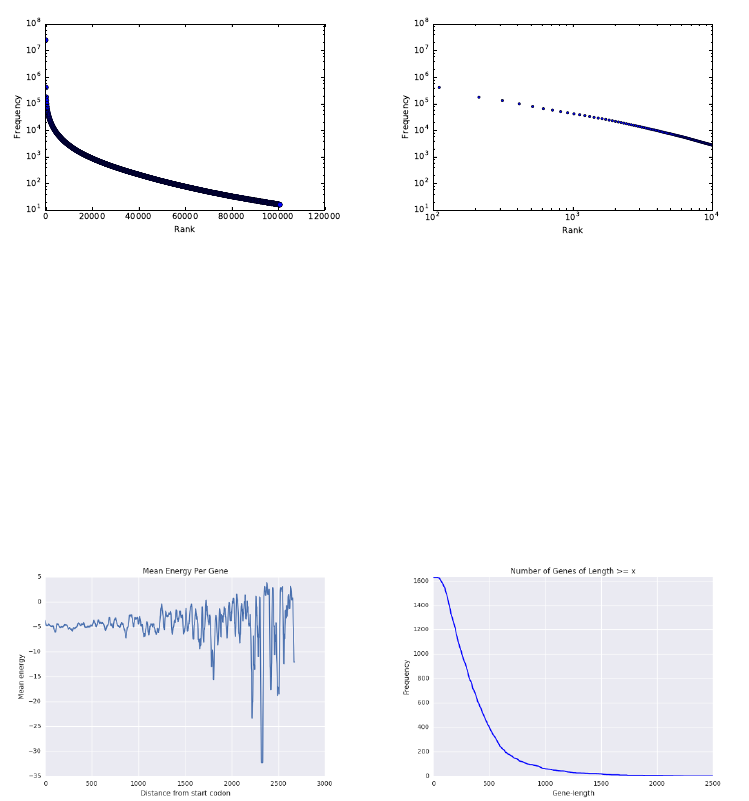
194 CHAPTER 6. VISUALIZING DATA

Figure 6.31: Frequency of 10,000 English words. Plotting the word frequencies

on a log scale (left), or even better on a log-log scale reveals that it is power law

(right).

Figure 6.32: Folding energy of genes as a function of their length. Mistak-

ing variance for signal: the extreme values in the left ﬁgure are artifacts from

averaging small numbers of samples.

6.6. INTERACTIVE VISUALIZATION 195

we just discover that energy varies inversely with gene length?

No. We just overinterpreted variance. The ﬁrst clue is that what looked

very steady starts to go haywire as the length increases. Most genes are very

short in length. Thus the points on the right side of the left plot are based on

very little data. The average of a few points is not as robust as the average of

many points. Indeed, a frequency plot of the number of genes by length (on

right) shows that the counts drop oﬀ to nothing right where it starts jumping.

How could we ﬁx it? The right thing to do here is to threshold the plot by

only showing the values with enough data support, perhaps at length 500 or a

bit more. Beyond that, we might bin them by length and take the average, in

order to prove that the jumping eﬀect goes away.

6.6 Interactive Visualization

The charts and graphs we have discussed so far were all static images, designed

to be studied by the viewer, but not manipulated. Interactive visualization

techniques are becoming increasingly important for exploratory data analysis.

Mobile apps, notebooks, and webpages with interactive visualization widgets

can be especially eﬀective in presenting data, and disseminating it to larger

audiences to explore. Providing viewers with the power to play with the actual

data helps ensure that the story presented by a graphic is the true and complete

story.

If you are going to view your data online, it makes sense to do so using

interactive widgets. These are generally extensions of the basic plots that we

have described in this chapter, with features like oﬀering pop-ups with more

information when the user scrolls over points, or encouraging the user to change

the scale ranges with sliders.

There are few potential downsides to interactive visualization. First, it is

harder to communicate exactly what you are seeing to others, compared with

static images. They might not be seeing exactly the same thing as you. Screen-

shots of interactive systems generally cannot compare to publication-quality

graphics optimized on traditional systems. The problem with what you see is

what you get (WYSIWYG) systems is that, generally, what you see is all you

get. Interactive systems are best for exploration, not presentation.

There are also excesses which tend to arise in interactive visualization.

Knobs and features get added because they can, but the visual eﬀects they

add can distract rather than add to the message. Rotating three-dimensional

point clouds always looks cool, but I ﬁnd them hard to interpret and very seldom

ﬁnd such views insightful.

Making data tell a story requires some insight into how to tell stories.

Films and television represent the state-of-the-art in narrative presentation.

Like them, the best interactive presentations show a narrative, such as moving

through time or riﬂing through alternative hypotheses. For inspiration, I en-

courage you to watch the late Han Rosling’s TED talk1using animated bubble

1https://www.ted.com/talks/hans_rosling_shows_the_best_stats_you_ve_ever_seen

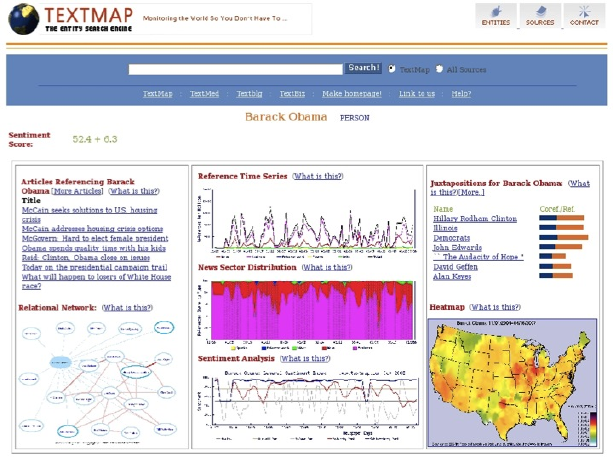
196 CHAPTER 6. VISUALIZING DATA

Figure 6.33: The TextMap dashboard for Barack Obama, circa 2008.

charts to present the history of social and economic development for all the

world’s nations.

Recent trends in cloud-based visualization encourage you to upload your

data to a site like Google Charts https://developers.google.com/chart/,

so you can take advantage of interactive visualization tools and widgets that

they provide. These tools produce very nice interactive plots, and are easy to

use.

The possible sticking point is security, since you are giving your data to a

third party. I hope and trust that the CIA analysts have access to their own in-

house solutions which keep their data conﬁdential. But feel free to experiment

with these tools in less sensitive situations.

6.7 War Story: TextMapping the World

My biggest experience in data visualization came as a result of our large scale

news/sentiment analysis system. TextMap presented a news analysis dashboard,

for every entity whose name appeared in news articles of the time. Barack

Obama’s page is shown in Figure 6.33. Our dashboard was made up of a variety

of subcomponents:

•Reference time series: Here we reported how often the given entity ap-

peared in the news, as a function of time. Spikes corresponded to more

important news events. Further, we partitioned these counts according

6.7. WAR STORY: TEXTMAPPING THE WORLD 197

to appearances in each section of the newspaper: news, sports, entertain-

ment, or business.

•News sector distribution: This graph contains exactly the same data as

in the reference time series, but presented as a stacked area plot to show

the fraction of entity references in each section of the paper. Obama

clearly presents as a news ﬁgure. But other people exhibited interesting

transitions, such as Arnold Schwarzenegger when he shifted from acting

to politics.

•Sentiment analysis: Here we present a time series measuring the senti-

ment of the entity, by presenting the normalized diﬀerence of the number

of positive news mentions to total references. Thus zero represented a

neutral reputation, and we provided a central reference line to put the

placement into perspective. Here Obama’s sentiment ebbs and ﬂows with

events, but generally stays on the right side of the line.

It was nice to see bad things happen to bad people, by watching their news

sentiment drop. As I recall, the lowest news sentiment ever achieved was

by a mom who achieved notoriety by cyberbullying one of her daughter’s

social rivals into committing suicide.

•Heatmap: Here we presented a data map showing the relative reference

frequency of the entity. Obama’s great red patch around Illinois is because

he was serving as a senator from there at the time he ﬁrst ran for president.

Many classes entities showed strong regional biases, like sports ﬁgures and

politicians, but less so entertainment ﬁgures like movie stars and singers.

•Juxtapositions and relational network: Our system built a network on

news entities, by linking two entities whenever they were mentioned in

the same article. The strength of this relationship could be measured by

the number of articles linking them together. The strongest of these asso-

ciations are reported as juxtapositions, with their frequency and strength

shown by a bar chart on a logarithmic scale.

We have not really talked so far about network visualization, but the

key idea is to position vertices so neighbors are located near each other,

meaning the edges are short. Stronger friendships are shown by thicker

lines.

•Related articles: We provided links to representative news articles men-

tioning the given entity.

One deﬁciency of our dashboard was that it was not interactive. In fact, it

was anti-interactive: the only animation was a gif of the world spinning forlornly

in the upper-left corner. Many of the plots we rendered required large amounts

of data access from our clunky database, particularly the heatmap. Since it

could not be rendered interactively, we precomputed these maps oﬄine and

showed them on demand.

198 CHAPTER 6. VISUALIZING DATA

After Mikhail updated our infrastructure (see the war story of Section 12.2),

it became possible for us to support some interactive plots, particularly time

series. We developed a new user interface called TextMap Access that let users

play with our data.

But when General Sentiment licensed the technology, the ﬁrst thing it dis-

posed of was our user interface. It didn’t make sense to the business analysts

who were our customers. It was too complicated. There is a substantial diﬀer-

ence between surface appeal and the real eﬀectiveness of an interface for users.

Look carefully at our TextMap dashboard: it had “What is this?” buttons

in several locations. This was a sign of weakness: if our graphics were really

intuitive enough we would not have needed them.

Although I grumbled about the new interface, I was undoubtedly wrong.

General Sentiment employed a bunch of analysts who used our system all day

long, and were available to talk to our developers. Presumably the interface

evolved to serve them better. The best interfaces are built by a dialog between

developers and users.

What are the take-home lessons from this experience? There is a lot I still

ﬁnd cool about this dashboard: the presentation was rich enough to really expose

interesting things about how the world worked. But not everyone agreed. Dif-

ferent customers preferred diﬀerent interfaces, because they did diﬀerent things

with them.

One lesson here is the power of providing alternate views of the same data.

The reference time series and news sector distribution were exactly the same

data, but provided quite diﬀerent insights when presented in diﬀerent ways.

All songs are made from the same notes, but how you arrange them makes for

diﬀerent kinds of music.

6.8 Chapter Notes

I strongly recommend Edward Tufte’s books [Tuf83, Tuf90, Tuf97] to anyone

interested in the art of scientiﬁc visualization. You don’t even have to read

them. Just look at the pictures for eﬀective contrasts between good and bad

graphics, and plots that really convey stories in data.

Similarly good books on data visualization are Few [Few09] and far between.

Interesting blogs about data visualization are http://flowingdata.com and

http://viz.wtf. The ﬁrst focuses on great visualizations, the second seeking

out the disasters. The story of Snow’s cholera map is reported in Johnson

[Joh07].

The chartjunk removal example from Section 6.2.3 was inspired by an ex-

ample by Tim Bray at http://www.tbray.org. Anscombe’s quartet was ﬁrst

presented in [Ans73]. The basic architecture of our Lydia/TextMap news analy-

sis system is reported in Lloyd et al. [LKS05], with additional papers describing

heatmaps [MBL+06] and the Access user interface [BWPS10].

6.9. EXERCISES 199

6.9 Exercises

Exploratory Data Analysis

6-1. [5] Provide answers to the questions associated with the following data sets,

available at http://www.data-manual.com/data.

(a) Analyze the movie data set. What is the range of movie gross in the United

States? Which type of movies are most likely to succeed in the market?

Comedy? PG-13? Drama?

(b) Analyze the Manhattan rolling sales data set. Where in Manhattan is the

most/least expensive real estate located? What is the relationship between

sales price and gross square feet?

ship between a country’s population and the number of medals it wins?

What can you say about the relationship between the ratio of female and

male counts and the GDP of that country?

(d) Analyze the GDP per capita data set. How do countries from Europe, Asia,

and Africa compare in the rates of growth in GDP? When have countries

faced substantial changes in GDP, and what historical events were likely

most responsible for it?

6-2. [3] For one or more of the data sets from http://www.data-manual.com/data,

answer the following basic questions:

(a) Who constructed it, when, and why?

(b) How big is it?

(d) Identify a few familiar or interpretable records.

(e) Provide Tukey’s ﬁve number summary for each column.

(f) Construct a pairwise correlation matrix for each pair of columns.

(g) Construct a pairwise distribution plot for each interesting pair of columns.

Interpreting Visualizations

6-3. [5] Search your favorite news websites until you ﬁnd ten interesting charts/plots,

ideally half good and half bad. For each, please critique along the following

dimensions, using the vocabulary we have developed in this chapter:

(a) Does it do a good job or a bad job of presenting the data?

(b) Does the presentation appear to be biased, either deliberately or acciden-

tally?

(d) Are the axes labeled in a clear and informative way?

(e) Is the color used eﬀectively?

(f) How can we make the graphic better?

200 CHAPTER 6. VISUALIZING DATA

6-4. [3] Visit http://www.wtfviz.net. Find ﬁve laughably bad visualizations, and

explain why they are both bad and amusing.

Creating Visualizations

6-5. [5] Construct a revealing visualization of some aspect of your favorite data set,

using:

(a) A well-designed table.

(b) A dot and/or line plot.

(d) A heatmap.

(e) A bar plot or pie chart.

(f) A histogram.

(g) A data map.

6-6. [5] Create ten diﬀerent versions of line charts for a particular set of (x, y) points.

Which ones are best and which ones worst? Explain why.

6-7. [3] Construct scatter plots for sets of 10, 100, 1000, and 10,000 points. Experi-

ment with the point size to ﬁnd the most revealing value for each data set.

6-8. [5] Experiment with diﬀerent color scales to construct scatter plots for a par-

ticular set of (x, y, z) points, where color is used to represent the zdimension.

Which color schemes work best? Which are the worst? Explain why.

Implementation Projects

6-9. [5] Build an interactive exploration widget for your favorite data set, using

appropriate libraries and tools. Start simple, but be as creative as you want to

be.

6-10. [5] Create a data video/movie, by recording/ﬁlming an interactive data explo-

ration. It should not be long, but how interesting/revealing can you make it?

Interview Questions

6-11. [3] Describe some good practices in data visualization?

6-12. [5] Explain Tufte’s concept of chart junk.

6-13. [8] How would you to determine whether the statistics published in an article

are either wrong or presented to support a biased view?

Kaggle Challenges

6-14. Analyze data from San Francisco Bay Area bike sharing.

https://www.kaggle.com/benhamner/sf-bay-area-bike-share

6-15. Predict whether West Nile virus is present in a given time and place.

https://www.kaggle.com/c/predict-west-nile-virus

6-16. What type of crime is most likely at a given time and place?

https://www.kaggle.com/c/sf-crime

Chapter 7

Mathematical Models

All models are wrong, but some models are useful.

– George Box

So far in this book, a variety of tools have been developed to manipulate and

interpret data. But we haven’t really dealt with modeling, which is the process of

encapsulating information into a tool which can forecast and make predictions.

Predictive models are structured around some idea of what causes future

events to happen. Extrapolating from recent trends and observations assumes

a world view that the future will be like the past. More sophisticated models,

such as the laws of physics, provide principled notions of causation; fundamental

explanations of why things happen.

This chapter will concentrate on designing and validating models. Eﬀectively

formulating models requires a detailed understanding of the space of possible

choices.

Accurately evaluating the performance of a model can be surprisingly hard,

but it is essential for knowing how to interpret the resulting predictions. The

best forecasting system is not necessarily the most accurate one, but the model

with the best sense of its boundaries and limitations.

7.1 Philosophies of Modeling

Engineers and scientists are often leery of the p-word (philosophy). But it pays

to think in some fundamental way about what we are trying to do, and why.

Recall that people turn to data scientists for wisdom, instead of programs.

In this section, we will turn to diﬀerent ways of thinking about models to

help shape the way we build them.

7.1.1 Occam’s Razor

Occam’s razor is the philosophical principle that “the simplest explanation is

202 CHAPTER 7. MATHEMATICAL MODELS

the best explanation.” According to William of Occam, a 13th-century theolo-

gian, given two models or theories which do an equally accurate job of making

predictions, we should opt for the simpler one as sounder and more robust. It

is more likely to be making the right decision for the right reasons.

Occam’s notion of simpler generally refers to reducing the number of assump-

tions employed in developing the model. With respect to statistical modeling,

Occam’s razor speaks to the need to minimize the parameter count of a model.

Overﬁtting occurs when a model tries too hard to achieve accurate performance

on its training data. This happens when there are so many parameters that the

model can essentially memorize its training set, instead of generalizing appro-

priately to minimize the eﬀects of error and outliers.

Overﬁt models tend to perform extremely well on training data, but much

less accurately on independent test data. Invoking Occam’s razor requires that

we have a meaningful way to evaluate how accurately our models are performing.

Simplicity is not an absolute virtue, when it leads to poor performance. Deep

learning is a powerful technique for building models with millions of parameters,

which we will discuss in Section 11.6. Despite the danger of overﬁtting, these

models perform extremely well on a variety of complex tasks. Occam would have

been suspicious of such models, but come to accept those that have substantially

more predictive power than the alternatives.

Appreciate the inherent trade-oﬀ between accuracy and simplicity. It is

almost always possible to “improve” the performance of any model by kludging-

on extra parameters and rules to govern exceptions. Complexity has a cost, as

explicitly captured in machine learning methods like LASSO/ridge regression.

These techniques employ penalty functions to minimize the features used in the

model.

Take-Home Lesson: Accuracy is not the best metric to use in judging the

quality of a model. Simpler models tend to be more robust and understandable

than complicated alternatives. Improved performance on speciﬁc tests is often

more attributable to variance or overﬁtting than insight.

7.1.2 Bias–Variance Trade-Oﬀs

This tension between model complexity and performance shows up in the sta-

tistical notion of the bias–variance trade-oﬀ:

•Bias is error from incorrect assumptions built into the model, such as

restricting an interpolating function to be linear instead of a higher-order

curve.

•Variance is error from sensitivity to ﬂuctuations in the training set. If our

training set contains sampling or measurement error, this noise introduces

variance into the resulting model.

Errors of bias produce underﬁt models. They do not ﬁt the training data as

tightly as possible, were they allowed the freedom to do so. In popular discourse,

7.1. PHILOSOPHIES OF MODELING 203

I associate the word “bias” with prejudice, and the correspondence is fairly apt:

an apriori assumption that one group is inferior to another will result in less

accurate predictions than an unbiased one. Models that perform lousy on both

training and testing data are underﬁt.

Errors of variance result in overﬁt models: their quest for accuracy causes

them to mistake noise for signal, and they adjust so well to the training data

that noise leads them astray. Models that do much better on testing data than

training data are overﬁt.1

Take-Home Lesson: Models based on ﬁrst principles or assumptions are likely

to suﬀer from bias, while data-driven models are in greater danger of overﬁt-

ting.

7.1.3 What Would Nate Silver Do?

Nate Silver is perhaps the most prominent public face of data science today. A

quantitative fellow who left a management consulting job to develop baseball

forecasting methods, he rose to fame through his election forecast website http:

//www.fivethirtyeight.com. Here he used quantitative methods to analyze

poll results to predict the results of U.S. presidential elections. In the 2008

election, he accurately called the winner of 49 of the 50 states, and improved

in 2012 to bag 50 out of 50. The results of the 2016 election proved a shock

to just about everyone, but alone among public commentators Nate Silver had

identiﬁed a substantial chance of Trump winning the electoral college while

losing the popular vote. This indeed proved to be the case.

Silver wrote an excellent book The Signal and the Noise: Why so many

predictions fail – but some don’t [Sil12]. There he writes sensibly about state-

of-the-art forecasting in several ﬁelds, including sports, weather and earthquake

prediction, and ﬁnancial modeling. He outlines principles for eﬀective modeling,

including:

•Think probabilistically: Forecasts which make concrete statements are

less meaningful than those that are inherently probabilistic. A forecast

that Trump has only 28.3% chance of winning is more meaningful than

one that categorically states that he will lose.

The real world is an uncertain place, and successful models recognize this

uncertainty. There are always a range of possible outcomes that can occur

with slight perturbations of reality, and this should be captured in your

model. Forecasts of numerical quantities should not be single numbers, but

instead report probability distributions. Specifying a standard deviation

σalong with the mean prediction µsuﬃces to describe such a distribution,

particularly if it is assumed to be normal.

1To complete this taxonomy, models that do better on testing data than the training data

are said to be cheating.

204 CHAPTER 7. MATHEMATICAL MODELS

Several of the machine learning techniques we will study naturally provide

probabilistic answers. Logistic regression provides a conﬁdence along with

each classiﬁcation it makes. Methods that vote among the labels of the

knearest neighbors deﬁne a natural conﬁdence measure, based on the

consistency of the labels in the neighborhood. Collecting ten of eleven

votes for blue means something stronger than seven out of eleven.

•Change your forecast in response to new information: Live models are

much more interesting than dead ones. A model is live if it is contin-

ually updating predictions in response to new information. Building an

infrastructure that maintains a live model is more intricate than that of a

one-oﬀ computation, but much more valuable.

Live models are more intellectually honest than dead ones. Fresh informa-

tion should change the result of any forecast. Scientists should be open to

changing opinions in response to new data: indeed, this is what separates

scientists from hacks and trolls.

Dynamically-changing forecasts provide excellent opportunities to evalu-

ate your model. Do they ultimately converge on the correct answer? Does

uncertainty diminish as the event approaches? Any live model should track

and display its predictions over time, so the viewer can gauge whether

changes accurately reﬂected the impact of new information.

•Look for consensus: A good forecast comes from multiple distinct sources

of evidence. Data should derive from as many diﬀerent sources as possible.

Ideally, multiple models should be built, each trying to predict the same

thing in diﬀerent ways. You should have an opinion as to which model is

the best, but be concerned when it substantially diﬀers from the herd.

Often third parties produce competing forecasts, which you can monitor

and compare against. Being diﬀerent doesn’t mean that you are wrong,

but it does provide a reality check. Who has been doing better lately?

What explains the diﬀerences in the forecast? Can your model be im-

proved?

Google’s Flu Trends forecasting model predicted disease outbreaks by

monitoring key words on search: a surge in people looking for aspirin or

fever might suggest that illness is spreading. Google’s forecasting model

proved quite consistent with the Center for Disease Control’s (CDC) statis-

tics on actual ﬂu cases for several years, until they embarrassingly went

astray.

The world changes. Among the changes was that Google’s search interface

began to suggest search queries in response to a user’s history. When of-

fered the suggestion, many more people started searching for aspirin after

searching for fever. And the old model suddenly wasn’t accurate any-

more. Google’s sins lay in not monitoring its performance and adjusting

over time.

7.2. A TAXONOMY OF MODELS 205

Certain machine learning methods explicitly strive for consensus. Boosting

algorithms combine large numbers of weak classiﬁers to produce a strong

one. Ensemble decision tree methods build many independent classiﬁers,

and vote among them to make the best decision. Such methods can have

a robustness which eludes more single-track models.

•Employ Baysian reasoning: Bayes’ theorem has several interpretations,

but perhaps most cogently provides a way to calculate how probabilities

change in response to new evidence. When stated as

P(A|B) = P(B|A)P(A)

P(B)

it provides a way to calculate how the probability of event Achanges in

response to new evidence B.

Applying Bayes’ theorem requires a prior probability P(A), the likelihood

of event Abefore knowing the status of a particular event B. This might

be the result of running a classiﬁer to predict the status of Afrom other

features, or background knowledge about event frequencies in a popula-

tion. Without a good estimate for this prior, it is very diﬃcult to know

how seriously to take the classiﬁer.

Suppose Ais the event that person xis actually a terrorist, and Bis

the result of a feature-based classiﬁer that decides if xlooks like a terror-

ist. When trained/evaluated on a data set of 1,000 people, half of whom

were terrorists, the classiﬁer achieved an enviable accuracy of, say, 90%.

The classiﬁer now says that Skiena looks like a terrorist. What is the

probability that Skiena really is a terrorist?

The key insight here is that the prior probability of “xis a terrorist” is

really, really low. If there are a hundred terrorists operating in the United

States, then P(A) = 100/300,000,000 = 3.33 ×10−7. The probability of

the terrorist detector saying yes, P(B) = 0.5, while the probability of the

detector being right when it says yes P(B|A)=0.9. Multiplying this out

gives a still very tiny probability that I am a bad guy,

P(A|B) = P(B|A)P(A)

P(B)=(0.9)(3.33 ×10−7)

(0.5) = 6 ×10−7

although admittedly now greater than that of a random citizen.

Factoring in prior probabilities is essential to getting the right interpreta-

tion from this classiﬁer. Bayesian reasoning starts from the prior distribu-

tion, then weighs further evidence by how strongly it should impact the

probability of the event.

7.2 A Taxonomy of Models

Models come in, well, many diﬀerent models. Part of developing a philosophy

of modeling is understanding your available degrees of freedom in design and

206 CHAPTER 7. MATHEMATICAL MODELS

implementation. In this section, we will look at model types along several diﬀer-

ent dimensions, reviewing the primary technical issues which arise to distinguish

each class.

7.2.1 Linear vs. Non-Linear Models

Linear models are governed by equations that weigh each feature variable by a

coeﬃcient reﬂecting its importance, and sum up these values to produce a score.

Powerful machine learning techniques, such as linear regression, can be used to

identify the best possible coeﬃcients to ﬁt training data, yielding very eﬀective

models.

But generally speaking, the world is not linear. Richer mathematical descrip-

tions include higher-order polynomials, logarithms, and exponentials. These

permit models that ﬁt training data much more tightly than linear functions

can. Generally speaking, it is much harder to ﬁnd the best possible coeﬃcients

to ﬁt non-linear models. But we don’t have to ﬁnd the best possible ﬁt: deep

learning methods, based on neural networks, oﬀer excellent performance despite

inherent diﬃculties in optimization.

Modeling cowboys often sneer in contempt at the simplicity of linear models.

But linear models oﬀer substantial beneﬁts. They are readily understandable,

generally defensible, easy to build, and avoid overﬁtting on modest-sized data

sets. Occam’s razor tells us that “the simplest explanation is the best explana-

tion.” I am generally happier with a robust linear model, yielding an accuracy

of x%, than a complex non-linear beast only a few percentage points better on

limited testing data.

7.2.2 Blackbox vs. Descriptive Models

Black boxes are devices that do their job, but in some unknown manner. Stuﬀ

goes in and stuﬀ comes out, but how the sausage is made is completely impen-

etrable to outsiders.

By contrast, we prefer models that are descriptive, meaning they provide

some insight into why they are making their decisions. Theory-driven models are

generally descriptive, because they are explicit implementations of a particular

well-developed theory. If you believe the theory, you have a reason to trust the

underlying model, and any resulting predictions.

Certain machine learning models prove less opaque than others. Linear

regression models are descriptive, because one can see exactly which variables

receive the most weight, and measure how much they contribute to the resulting

prediction. Decision tree models enable you to follow the exact decision path

used to make a classiﬁcation. “Our model denied you a home mortgage because

your income is less than $10,000 per year, you have greater than $50,000 in

credit card debt, and you have been unemployed over the past year.”

But the unfortunate truth is that blackbox modeling techniques such as

deep learning can be extremely eﬀective. Neural network models are generally

completely opaque as to why they do what they do. Figure 7.1 makes this

7.2. A TAXONOMY OF MODELS 207

Figure 7.1: Synthetic images that are mistakenly recognized as objects by state-

of-the-art Deep Learning neural networks, each with a conﬁdence greater than

99.6%. Source: [NYC15].

clear. It shows images which were very carefully constructed to fool state-of-

the-art neural networks. They succeeded brilliantly. The networks in question

had ≥99.6% conﬁdence that they had found the right label for every image in

Figure 7.1.

The scandal here is not that the network got the labels wrong on these

perverse images, for these recognizers are very impressive systems. Indeed, they

were much more accurate than dreamed possible only a year or two before. The

problem is that the creators of these classiﬁers had no idea why their programs

made such terrible errors, or how they could prevent them in the future.

A similar story is told of a system built for the military to distinguish images

of cars from trucks. It performed well in training, but disastrously in the ﬁeld.

Only later was it realized that the training images for cars were shot on a sunny

day and those of trucks on a cloudy day, so the system had learned to link the

sky in the background with the class of the vehicle.

Tales like these highlight why visualizing the training data and using descrip-

tive models can be so important. You must be convinced that your model has

the information it needs to make the decisions you are asking of it, particularly

in situations where the stakes are high.

7.2.3 First-Principle vs. Data-Driven Models

First-principle models are based on a belief of how the system under investi-

gation really works. It might be a theoretical explanation, like Newton’s laws

of motion. Such models can employ the full weight of classical mathematics:

calculus, algebra, geometry, and more. The model might be a discrete event

simulation, as will be discussed in Section 7.7. It might be seat-of-the-pants

reasoning from an understanding of the domain: voters are unhappy if the

economy is bad, therefore variables which measure the state of the economy

should help us predict who will win the election.

208 CHAPTER 7. MATHEMATICAL MODELS

In contrast, data-driven models are based on observed correlations between

input parameters and outcome variables. The same basic model might be used

to predict tomorrow’s weather or the price of a given stock, diﬀering only on the

data it was trained on. Machine learning methods make it possible to build an

eﬀective model on a domain one knows nothing about, provided we are given a

good enough training set.

Because this is a book on data science, you might infer that my heart lies

more on the side of data-driven models. But this isn’t really true. Data science is

also about science, and things that happen for understandable reasons. Models

which ignore this are doomed to fail embarrassingly in certain circumstances.

There is an alternate way to frame this discussion, however. Ad hoc models

are built using domain-speciﬁc knowledge to guide their structure and design.

These tend to be brittle in response to changing conditions, and diﬃcult to

apply to new tasks. In contrast, machine learning models for classiﬁcation

and regression are general, because they employ no problem-speciﬁc ideas, only

speciﬁc data. Retrain the models on fresh data, and they adapt to changing

conditions. Train them on a diﬀerent data set, and they can do something

completely diﬀerent. By this rubric, general models sound much better than ad

hoc ones.

The truth is that the best models are a mixture of both theory and data. It

is important to understand your domain as deeply as possible, while using the

best data you can in order to ﬁt and evaluate your models.

7.2.4 Stochastic vs. Deterministic Models

Demanding a single deterministic “prediction” from a model can be a fool’s

errand. The world is a complex place of many realities, with events that gener-

ally would not unfold in exactly the same way if time could be run over again.

Good forecasting models incorporate such thinking, and produce probability

distributions over all possible events.

Stochastic is a fancy word meaning “randomly determined.” Techniques

that explicitly build some notion of probability into the model include logistic

regression and Monte Carlo simulation. It is important that your model observe

the basic properties of probabilities, including:

•Each probability is a value between 0 and 1: Scores that are not con-

strained to be in this range do not directly estimate probabilities. The

solution is often to put the values through a logit function (see Section

4.4.1) to turn them into probabilities in a principled way.

•That they must sum to 1: Independently generating values between 0

and 1 does not mean that they together add up to a unit probability, over

the full event space. The solution here is to scale these values so that

they do, by dividing each by the partition function. See Section 9.7.4.

Alternately, rethink your model to understand why they didn’t add up in

the ﬁrst place.

7.2. A TAXONOMY OF MODELS 209

•Rare events do not have probability zero: Any event that is possible must

have a greater than zero probability of occurrence. Discounting is a way

of evaluating the likelihood of unseen but possible events, and will be

discussed in Section 11.1.2.

Probabilities are a measure of humility about the accuracy of our model,

and the uncertainty of a complex world. Models must be honest in what they

do and don’t know.

There are certain advantages of deterministic models, however. First-principle

models often yield only one possible answer. Newton’s laws of motion will tell

you exactly how long a mass takes to fall a given distance.

That deterministic models always return the same answer helps greatly in

debugging their implementation. This speaks to the need to optimize repeata-

bility during model development. Fix the initial seed if you are using a random

number generator, so you can rerun it and get the same answer. Build a re-

gression test suite for your model, so you can conﬁrm that the answers remain

identical on a given input after program modiﬁcations.

7.2.5 Flat vs. Hierarchical Models

Interesting problems often exist on several diﬀerent levels, each of which may

require independent submodels. Predicting the future price for a particular

stock really should involve submodels for analyzing such separate issues as (a)

the general state of the economy, (b) the company’s balance sheet, and (c) the

performance of other companies in its industrial sector.

Imposing a hierarchical structure on a model permits it to be built and

evaluated in a logical and transparent way, instead of as a black box. Certain

subproblems lend themselves to theory-based, ﬁrst-principle models, which can

then be used as features in a general data-driven model. Explicitly hierarchical

models are descriptive: one can trace a ﬁnal decision back to the appropriate

top-level subproblem, and report how strongly it contributed to making the

observed result.

The ﬁrst step to build a hierarchical model is explicitly decomposing our

problem into subproblems. Typically these represent mechanisms governing the

underlying process being modeled. What should the model depend on? If data

and resources exist to make a principled submodel for each piece, great! If

not, it is OK to leave it as a null model or baseline, and explicitly describe the

omission when documenting the results.

Deep learning models can be thought of as being both ﬂat and hierarchical,

at the same time. They are typically trained on large sets of unwashed data, so

there is no explicit deﬁnition of subproblems to guide the subprocess. Looked

at as a whole, the network does only one thing. But because they are built from

multiple nested layers (the deep in deep learning), these models presume that

there are complex features there to be learned from the lower level inputs.

I am always reluctant to believe that machine learning models prove better

than me at inferring the basic organizing principles in a domain that I un-

210 CHAPTER 7. MATHEMATICAL MODELS

derstand. Even when employing deep learning, it pays to sketch out a rough

hierarchical structure that likely exists for your network to ﬁnd. For example,

any image processing network should generalize from patches of pixels to edges,

and then from boundaries to sub-objects to scene analysis as we move to higher

layers. This inﬂuences the architecture of your network, and helps you validate

it. Do you see evidence that your network is making the right decisions for the

right reasons?

7.3 Baseline Models

A wise man once observed that a broken clock is right twice a day. As modelers

we strive to be better than this, but proving that we are requires some level of

rigorous evaluation.

The ﬁrst step to assess the complexity of your task involves building baseline

models: the simplest reasonable models that produce answers we can compare

against. More sophisticated models should do better than baseline models, but

verifying that they really do and, if so by how much, puts its performance into

the proper context.

Certain forecasting tasks are inherently harder than others. A simple base-

line (“yes”) has proven very accurate in predicting whether the sun will rise

tomorrow. By contrast, you could get rich predicting whether the stock mar-

ket will go up or down 51% of the time. Only after you decisively beat your

baselines can your models really be deemed eﬀective.

7.3.1 Baseline Models for Classiﬁcation

There are two common tasks for data science models: classiﬁcation and value

prediction. In classiﬁcation tasks, we are given a small set of possible labels

for any given item, like (spam or not spam), (man or woman), or (bicycle, car,

or truck). We seek a system that will generate a label accurately describing a

particular instance of an email, person, or vehicle.

Representative baseline models for classiﬁcation include:

•Uniform or random selection among labels: If you have absolutely no

prior distribution on the objects, you might as well make an arbitrary

selection using the broken watch method. Comparing your stock market

prediction model against random coin ﬂips will go a long way to showing

how hard the problem is.

I think of such a blind classiﬁer as the monkey, because it is like asking

your pet to make the decision for you. In a prediction problem with twenty

possible labels or classes, doing substantially better than 5% is the ﬁrst

evidence that you have some insight into the problem. You ﬁrst have to

show me that you can beat the monkey before I start to trust you.

•The most common label appearing in the training data: A large training

set usually provides some notion of a prior distribution on the classes.

7.3. BASELINE MODELS 211

Selecting the most frequent label is better than selecting them uniformly

or randomly. This is the theory behind the sun-will-rise-tomorrow baseline

model.

•The most accurate single-feature model: Powerful models strive to exploit

all the useful features present in a given data set. But it is valuable to

know what the best single feature can do. Building the best classiﬁer on

a single numerical feature xis easy: we are declaring that the item is in

class 1 if x≥t, and class 2 if otherwise. To ﬁnd the best threshold t,

we can test all npossible thresholds of the form ti=xi+, where xiis

the value of the feature in the ith of ntraining instances. Then select the

threshold which yields the most accurate classiﬁer on your training data.

Occam’s razor deems the simplest model to be best. Only when your

complicated model beats all single-factor models does it start to be inter-

esting.

•Somebody else’s model: Often we are not the ﬁrst person to attempt a

particular task. Your company may have a legacy model that you are

charged with updating or revising. Perhaps a close variant of the problem

has been discussed in an academic paper, and maybe they even released

their code on the web for you to experiment with.

One of two things can happen when you compare your model against

someone else’s work: either you beat them or you don’t. If you beat

them, you now have something worth bragging about. If you don’t, it is

a chance to learn and improve. Why didn’t you win? The fact that you

lost gives you certainty that your model can be improved, at least to the

level of the other guy’s model.

•Clairvoyance: There are circumstances when even the best possible model

cannot theoretically reach 100% accuracy. Suppose that two data records

are exactly the same in feature space, but with contradictory labels. There

is no deterministic classiﬁer that could ever get both of these problems

right, so we’re doomed to less than perfect performance. But the tighter

upper bound from an optimally clairvoyant predictor might convince you

that your baseline model is better than you thought.

The need for better upper bounds often arises when your training data is

the result of a human annotation process, and multiple annotators evaluate

the same instances. We get inherent contradictions whenever two anno-

tators disagree with each other. I’ve worked on problems where 86.6%

correct was the highest possible score. This lowers expectations. A good

bit of life advice is to expect little from your fellow man, and realize you

will have to make do with a lot less than that.

212 CHAPTER 7. MATHEMATICAL MODELS

7.3.2 Baseline Models for Value Prediction

In value prediction problems, we are given a collection of feature-value pairs

(fi, vi) to use to train a function Fsuch that F(vi) = vi. Baseline models for

value prediction problems follow from similar techniques to what were proposed

for classiﬁcation, like:

•Mean or median: Just ignore the features, so you can always output

the consensus value of the target. This proves to be quite an informative

baseline, because if you can’t substantially beat always guessing the mean,

either you have the wrong features or are working on a hopeless task.

•Linear regression: We will thoroughly cover linear regression in Section

9.1. But for now, it suﬃces to understand that this powerful but simple-to-

use technique builds the best possible linear function for value prediction

problems. This baseline enables you to better judge the performance of

non-linear models. If they do not perform substantially better than the

linear classiﬁer, they are probably not worth the eﬀort.

•Value of the previous point in time: Time series forecasting is a common

task, where we are charged with predicting the value f(tn, x) at time

tngiven feature set xand the observed values f0(ti) for 1 ≤i < n.

But today’s weather is a good guess for whether it will rain tomorrow.

Similarly, the value of the previous observed value f0(tn−1) is a reasonable

forecast for time f(tn). It is often surprisingly diﬃcult to beat this baseline

in practice.

Baseline models must be fair: they should be simple but not stupid. You

want to present a target that you hope or expect to beat, but not a sitting

duck. You should feel relieved when you beat your baseline, but not boastful or

smirking.

7.4 Evaluating Models

Congratulations! You have built a predictive model for classiﬁcation or value

prediction. Now, how good is it?

This innocent-looking question does not have a simple answer. We will

detail the key technical issues in the sections below. But the informal sniﬀ test

is perhaps the most important criteria for evaluating a model. Do you really

believe that it is doing a good job on your training and testing instances?

The formal evaluations that will be detailed below reduce the performance

of a model down to a few summary statistics, aggregated over many instances.

But many sins in a model can be hidden when you only interact with these

aggregate scores. You have no way of knowing whether there are bugs in your

implementation or data normalization, resulting in poorer performance than it

should have. Perhaps you intermingled your training and test data, yielding

much better scores on your testbed than you deserve.

7.4. EVALUATING MODELS 213

Predicted Class

Yes No

Actual Yes True Positives (TP) False Negatives (FN)

Class No False Positives (FP) True Negatives (TN)

Figure 7.2: The confusion matrix for binary classiﬁers, deﬁning diﬀerent classes

of correct and erroneous predictions.

To really know what is happening, you need to do a sniﬀ test. My personal

sniﬀ test involves looking carefully at a few example instances where the model

got it right, and a few where it got it wrong. The goal is to make sure that

I understand why the model got the results that it did. Ideally these will be

records whose “names” you understand, instances where you have some intuition

about what the right answers should be as a result of exploratory data analysis

or familiarity with the domain.

Take-Home Lesson: Too many data scientists only care about the evaluation

statistics of their models. But good scientists have an understanding of whether

the errors they are making are defensible, serious, or irrelevant.

Another issue is your degree of surprise at the evaluated accuracy of the

model. Is it performing better or worse than you expected? How accurate do

you think you would be at the given task, if you had to use human judgment.

A related question is establishing a sense of how valuable it would be if the

model performed just a little better. An NLP task that classiﬁes words correctly

with 95% accuracy makes a mistake roughly once every two to three sentences.

Is this good enough? The better its current performance is, the harder it will

be to make further improvements.

But the best way to assess models involves out-of-sample predictions, results

on data that you never saw (or even better, did not exist) when you built the

model. Good performance on the data that you trained models on is very

suspect, because models can easily be overﬁt. Out of sample predictions are

the key to being honest, provided you have enough data and time to test them.

This is why I had my Quant Shop students build models to make predictions of

future events, and then forced them to watch and see whether they were right

or not.

7.4.1 Evaluating Classiﬁers

Evaluating a classiﬁer means measuring how accurately our predicted labels

match the gold standard labels in the evaluation set. For the common case of

two distinct labels or classes (binary classiﬁcation), we typically call the smaller

and more interesting of the two classes as positive and the larger/other class as

negative. In a spam classiﬁcation problem, the spam would typically be positive

and the ham (non-spam) would be negative. This labeling aims to ensure that

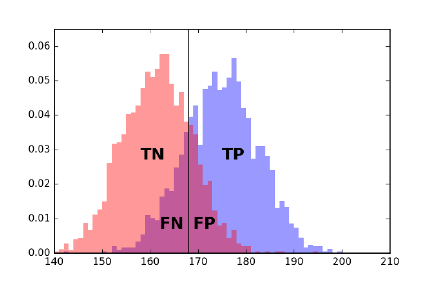
214 CHAPTER 7. MATHEMATICAL MODELS

Figure 7.3: What happens if we classify everyone of height ≥168 centimeters as

male? The four possible results in the confusion matrix reﬂect which instances

were classiﬁed correctly (TP and TN) and which ones were not (FN and FP).

identifying the positives is at least as hard as identifying the negatives, although

often the test instances are selected so that the classes are of equal cardinality.

There are four possible results of what the classiﬁcation model could do

on any given instance, which deﬁnes the confusion matrix or contingency table

shown in Figure 7.2:

•True Positives (TP): Here our classiﬁer labels a positive item as positive,

resulting in a win for the classiﬁer.

•True Negatives (TN): Here the classiﬁer correctly determines that a mem-

ber of the negative class deserves a negative label. Another win.

•False Positives (FP): The classiﬁer mistakenly calls a negative item as a

positive, resulting in a “type I” classiﬁcation error.

•False Negatives (FN): The classiﬁer mistakenly declares a positive item

as negative, resulting in a “type II” classiﬁcation error.

Figure 7.3 illustrates where these result classes fall in separating two distri-

butions (men and women), where the decision variable is height as measured

in centimeters. The classiﬁer under evaluation labels everyone of height ≥168

centimeters as male. The purple regions represent the intersection of both male

and female. These tails represent the incorrectly classiﬁed elements.

Accuracy, Precision, Recall, and F-Score

There are several diﬀerent evaluation statistics which can be computed from the

true/false positive/negative counts detailed above. The reason we need so many

statistics is that we must defend our classiﬁer against two baseline opponents,

the sharp and the monkey.

7.4. EVALUATING MODELS 215

The sharp is the opponent who knows what evaluation system we are using,

and picks the baseline model which will do best according to it. The sharp will

try to make the evaluation statistic look bad, by achieving a high score with a

useless classiﬁer. That might mean declaring all items positive, or perhaps all

negative.

In contrast, the monkey randomly guesses on each instance. To interpret our

model’s performance, it is important to establish by how much it beats both

the sharp and the monkey.

The ﬁrst statistic measures the accuracy of classiﬁer, the ratio of the number

of correct predictions over total predictions. Thus:

accuracy =T P +T N

T P +T N +F N +F P

By multiplying such fractions by 100, we can get a percentage accuracy score.

Accuracy is a sensible number which is relatively easy to explain, so it is

worth providing in any evaluation environment. How accurate is the monkey,

when half of the instances are positive and half negative? The monkey would

be expected to achieve an accuracy of 50% by random guessing. The same

accuracy of 50% would be achieved by the sharp, by always guessing positive,

or (equivalently) always guessing negative. The sharp would get a diﬀerent half

of the instances correct in each case.

Still, accuracy alone has limitations as an evaluation metric, particularly

when the positive class is much smaller than the negative class. Consider the

development of a classiﬁer to diagnose whether a patient has cancer, where

the positive class has the disease (i.e. tests positive) and the negative class is

healthy. The prior distribution is that the vast majority of people are healthy,

p=|positive|

|positive|+|negative|1

The expected accuracy of a fair-coin monkey would still be 0.5: it should get

an average of half of the positives and half the negatives right. But the sharp

would declare everyone to be healthy, achieving an accuracy of 1 −p. Suppose

that only 5% of the test takers really had the disease. The sharp could brag

about her accuracy of 95%, while simultaneously dooming all members of the

diseased class to an early death.

Thus we need evaluation metrics that are more sensitive to getting the pos-

itive class right. Precision measures how often this classiﬁer is correct when it

dares to say positive:

precision =T P

(T P +F P )

Achieving high precision is impossible for either a sharp or a monkey, because

the fraction of positives (p= 0.05) is so low. If the classiﬁer issues too many

positive labels, it is doomed to low precision because so many bullets miss

their mark, resulting in many false positives. But if the classiﬁer is stingy with

positive labels, very few of them are likely to connect with the rare positive

216 CHAPTER 7. MATHEMATICAL MODELS

Monkey

predicted class

yes no

yes (pn)q(pn)(1 −q)

no ((1 −p)n)q((1 −p)n)(1 −q)

Balanced Classiﬁer

predicted class

yes no

yes (pn)q(pn)(1 −q)

no ((1 −p)n)(1 −q) ((1 −p)n)q

Figure 7.4: The expected performance of a monkey classiﬁer on ninstances,

where p·nare positive and (1 −p)·nare negative. The monkey guesses positive

with probability q(left). Also, the expected performance of a balanced classiﬁer,

which somehow correctly classiﬁes members of each class with probability q

(right).

Monkey Sharp Balanced Classiﬁer

q0.05 0.5 0.0 1.0 0.5 0.75 0.9 0.99 1.0

accuracy 0.905 0.5 0.95 0.05 0.5 0.75 0.9 0.99 1.

precision 0.05 0.05 — 0.05 0.05 0.136 0.321 0.839 1.

recall 0.05 0.5 0. 1. 0.5 0.75 0.9 0.99 1.

F score 0.05 0.091 — 0.095 0.091 0.231 0.474 0.908 1.

Figure 7.5: Performance of several classiﬁers, under diﬀerent performance mea-

sures.

instances, so the classiﬁer achieves low true positives. These baseline classiﬁers

achieve precision proportional to the positive class probability p= 0.05, because

they are ﬂying blind.

In the cancer diagnosis case, we might be more ready to tolerate false posi-

tives (errors where we scare a healthy person with a wrong diagnosis) than false

negatives (errors where we kill a sick patient by misdiagnosing their illness).

Recall measures how often you prove right on all positive instances:

recall =T P

(T P +F N )

A high recall implies that the classiﬁer has few false negatives. The easiest

way to achieve this declares that everyone has cancer, as done by a sharp always

answering yes. This classiﬁer has high recall but low precision: 95% of the test

takers will receive an unnecessary scare. There is an inherent trade-oﬀ between

precision and recall when building classiﬁers: the braver your predictions are,

the less likely they are to be right.

But people are hard-wired to want a single measurement describing the

performance of their system. The F-score (or sometimes F1-score) is such a

combination, returning the harmonic mean of precision and recall:

F= 2 ·precision ·recall

precision + recall

F-score is a very tough measure to beat. The harmonic mean is always less

than or equal to the arithmetic mean, and the lower number has a dispropor-

7.4. EVALUATING MODELS 217

tionate large eﬀect. Achieving a high F-score requires both high recall and high

precision. None of our baseline classiﬁers manage a decent F-score despite high

accuracy and recall values, because their precision is too low.

The F-score and related evaluation metrics were developed to evaluate mean-

ingful classiﬁers, not monkeys or sharps. To gain insight in how to interpret

them, let’s consider a class of magically balanced classiﬁers, which somehow

show equal accuracy on both positive and negative instances. This isn’t usually

the case, but classiﬁers selected to achieve high F-scores must balance precision

and recall statistics, which means they must show decent performance on both

positive and negative instances.

Figure 7.5 summarizes the performance of both baseline and balanced classi-

ﬁers on our cancer detection problem, benchmarked on all four of our evaluation

metrics. The take away lessons are:

•Accuracy is a misleading statistic when the class sizes are substantially

diﬀerent: A baseline classiﬁer mindlessly answering “no” for every in-

stance achieved an accuracy of 95% on the cancer problem, better even

than a balanced classiﬁer that got 94% right on each class.

•Recall equals accuracy if and only if the classiﬁers are balanced: Good

things happen when the accuracy for recognizing both classes is the same.

This doesn’t happen automatically during training, when the class sizes

are diﬀerent. Indeed, this is one reason why it is generally a good practice

to have an equal number of positive and negative examples in your training

set.

•High precision is very hard to achieve in unbalanced class sizes: Even a

balanced classiﬁer that gets 99% accuracy on both positive and negative

examples cannot achieve a precision above 84% on the cancer problem.

This is because there are twenty times more negative instances than pos-

itive ones. The false positives from misclassifying the larger class at a 1%

rate remains substantial against the background of 5% true positives.

•F-score does the best job of any single statistic, but all four work together to

describe the performance of a classiﬁer: Is the precision of your classiﬁer

greater than its recall? Then it is labeling too few instances as positives,

and so perhaps you can tune it better. Is the recall higher than the

precision? Maybe we can improve the F-score by being less aggressive in

calling positives. Is the accuracy far from the recall? Then our classiﬁer

isn’t very balanced. So check which side is doing worse, and how we might

be able to ﬁx it.

A useful trick to increase the precision of a model at the expense of recall

is to give it the power to say “I don’t know.” Classiﬁers typically do better on

easy cases than hard ones, with the diﬃculty deﬁned by how far the example is

from being assigned the alternate label.

Deﬁning a notion of conﬁdence that your proposed classiﬁcation is correct is

the key to when you should pass on a question. Only venture a guess when your

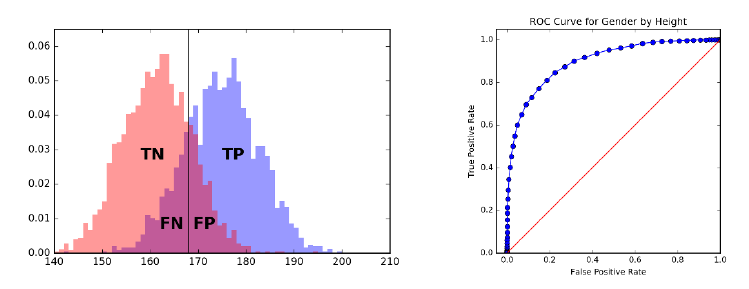
218 CHAPTER 7. MATHEMATICAL MODELS

Figure 7.6: The ROC curve helps us select the best threshold to use in a clas-

siﬁer, by displaying the trade-oﬀ between true positives and false positive at

every possible setting. The monkey ROCs the main diagonal here.

conﬁdence is above a given threshold. Patients whose test scores are near the

boundary would generally prefer a diagnosis of “borderline result” to “you’ve

got cancer,” particularly if the classiﬁer is not really conﬁdent in its decision.

Our precision and recall statistics must be reconsidered to properly accom-

modate the new indeterminate class. There is no need to change the precision

formula: we evaluate only on the instances we call positive. But the denom-

inator for recall must explicitly account for all elements we refused to label.

Assuming we are accurate in our conﬁdence measures, precision will increase at

the expense of recall.

7.4.2 Receiver-Operator Characteristic (ROC) Curves

Many classiﬁers come with natural knobs that you can tweak to alter the trade-

oﬀ between precision and recall. For example, consider systems which compute

a numerical score reﬂecting “in classness,” perhaps by assessing how much the

given test sample looks like cancer. Certain samples will score more positively

than others. But where do we draw the line between positive and negative?

If our “in classness” score is accurate, then it should generally be higher for

positive items than negative ones. The positive examples will deﬁne a diﬀerent

score distribution than the negative instances, as shown in Figure 7.6 (left).

It would be great if these distributions were completely disjoint, because then

there would be a score threshold tsuch that all instances with scores ≥tare

positive and all < t are negative. This would deﬁne a perfect classiﬁer.

But it is more likely that the two distributions will overlap, to at least some

degree, turning the problem of identifying the best threshold into a judgment

call based on our relative distaste towards false positives and false negatives.

The Receiver Operating Characteristic (ROC) curve provides a visual repre-

sentation of our complete space of options in putting together a classiﬁer. Each

7.4. EVALUATING MODELS 219

point on this curve represents a particular classiﬁer threshold, deﬁned by its

false positive and false negative rates.2These rates are in turn deﬁned by the

count of errors divided by the total number of positives in the evaluation data,

and perhaps multiplied by one hundred to turn into percentages.

Consider what happens as we sweep our threshold from left to right over

these distributions. Every time we pass over another example, we either increase

the number of true positives (if this example was positive) or false positives (if

this example was in fact a negative). At the very left, we achieve true/false

positive rates of 0%, since the classiﬁer labeled nothing as positive at that cutoﬀ.

Moving as far to the right as possible, all examples will be labeled positively, and

hence both rates become 100%. Each threshold in between deﬁnes a possible

classiﬁer, and the sweep deﬁnes a staircase curve in true/false positive rate space

taking us from (0%,0%) to (100%,100%).

Suppose the score function was deﬁned by a monkey, i.e. an arbitrary ran-

dom value for each instance. Then as we sweep our threshold to the right, the

label of the next example should be positive or negative with equal probability.

Thus we are equally likely to increase our true positive rate as false, and the

ROC curve should cruise along the main diagonal.

Doing better than the monkey implies an ROC curve that lies above the

diagonal. The best possible ROC curve shoots up immediately from (0%,0%)

to (0%,100%), meaning it encounters all positive instances before any negative

ones. It then steps to the right with each negative example, until it ﬁnally

reaches the upper right corner.

The area under the ROC curve (AUC) is often used as a statistic measuring

the quality of scoring function deﬁning the classiﬁer. The best possible ROC

curve has an area of 100% ×100% →1, while the monkey’s triangle has an area

of 1/2. The closer the area is to 1, the better our classiﬁcation function is.

7.4.3 Evaluating Multiclass Systems

Many classiﬁcation problems are non-binary, meaning that they must decide

among more than two classes. Google News has separate sections for U.S. and

world news, plus business, entertainment, sports, health, science, and technol-

ogy. Thus the article classiﬁer which governs the behavior of this site must

assign each article a label from eight diﬀerent classes.

The more possible class labels you have, the harder it is to get the classiﬁ-

cation right. The expected accuracy of a classiﬁcation monkey with dlabels is

1/d, so the accuracy drops rapidly with increased class complexity.

This makes properly evaluating multiclass classiﬁers a challenge, because low

success numbers get disheartening. A better statistic is the top-ksuccess rate,

which generalizes accuracy for some speciﬁc value of k≥1. How often was the

right label among the top kpossibilities?

This measure is good, because it gives us partial credit for getting close to

the right answer. How close is good enough is deﬁned by the parameter k. For

2The strange name for this beast is a legacy of its original application, in tuning the

performance of radar systems.

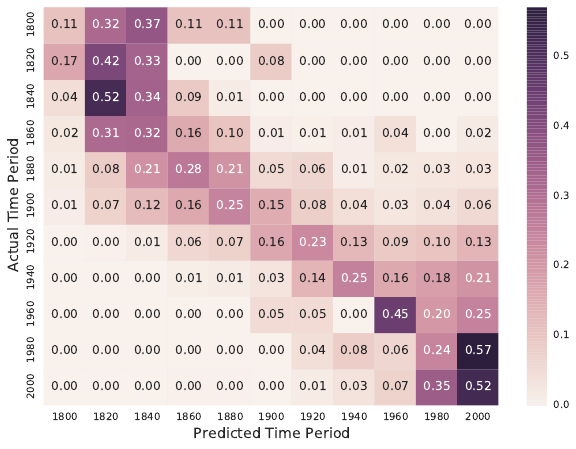
220 CHAPTER 7. MATHEMATICAL MODELS

Figure 7.7: Confusion matrix for a document dating system: the main diagonal

reﬂects accurate classiﬁcation.

k= 1, this reduces to accuracy. For k=d,any possible label suﬃces, and

the success rate is 100% by deﬁnition. Typical values are 3, 5, or 10: high

enough that a good classiﬁer should achieve an accuracy above 50% and be

visibly better than the monkey. But not too much better, because an eﬀective

evaluation should leave us with substantial room to do better. In fact, it is a

good practice to compute the top krate for all kfrom 1 to d, or at least high

enough that the task becomes easy.

An even more powerful evaluation tool is the confusion matrix C, a d×d

matrix where C[x, y] reports the number (or fraction) of instances of class x

which get labeled as class y.

How do we read a confusion matrix, like the one shown in Figure 7.7? It

is taken from the evaluation environment we built to test a document dating

classiﬁer, which analyzes texts to predict the period of authorship. Such docu-

ment dating will be the ongoing example on evaluation through the rest of this

chapter.

The most important feature is the main diagonal, C[i, i], which counts how

many (or what fraction of) items from class iwere correctly labeled as class i.

We hope for a heavy main diagonal in our matrix. Ours in a hard task, and

Figure 7.7 shows a strong but not perfect main diagonal. There are several

places where documents are more frequently classiﬁed in the neighboring period

than the correct one.

But the most interesting features of the confusion matrix are the large counts

7.4. EVALUATING MODELS 221

C[i, j] that do not lie along the main diagonal. These represent commonly

confused classes. In our example, the matrix shows a distressingly high number

of documents (6%) from 1900 classiﬁed as 2000, when none are classiﬁed as

1800. Such asymmetries suggest directions to improve the classiﬁer.

There are two possible explanations for class confusions. The ﬁrst is a bug in

the classiﬁer, which means that we have to work harder to make it distinguish i

from j. But the second involves humility, the realization that classes iand jmay

overlap to such a degree that it is ill-deﬁned what the right answer should be.

Maybe writing styles don’t really change that much over a twenty-year period?

In the Google News example, the lines between the science and technology

categories is very fuzzy. Where should an article about commercial space ﬂights

go? Google says science, but I say technology. Frequent confusion might suggest

merging the two categories, as they represent a diﬀerence without a distinction.

Sparse rows in the confusion matrix indicate classes poorly represented in

the training data, while sparse columns indicate labels which the classiﬁer is

reluctant to assign. Either indication is an argument that perhaps we should

consider abandoning this label, and merge the two similar categories.

The rows and columns of the confusion matrix provide analogous perfor-

mance statistics to those of Section 7.4.1 for multiple classes, parameterized by

class. Precisioniis the fraction of all items declared class ithat were in fact of

class i:

precisioni=C[i, i]/

j=1

C[j, i].

Recalliis the fraction of all members of class ithat were correctly identiﬁed as

such:

recalli=C[i, i]/

j=1

C[i, j].

7.4.4 Evaluating Value Prediction Models

Value prediction problems can be thought of as classiﬁcation tasks, but over

an inﬁnite number of classes. However, there are more direct ways to evaluate

regression systems, based on the distance between the predicted and actual

values.

Error Statistics

For numerical values, error is a function of the diﬀerence between a forecast y0=

f(x) and the actual result y. Measuring the performance of a value prediction

system involves two decisions: (1) ﬁxing the speciﬁc individual error function,

and (2) selecting the statistic to best represent the full error distribution.

The primary choices for the individual error function include:

•Absolute error: The value ∆ = y0−yhas the virtue of being simple

and symmetric, so the sign can distinguish the case where y0> y from

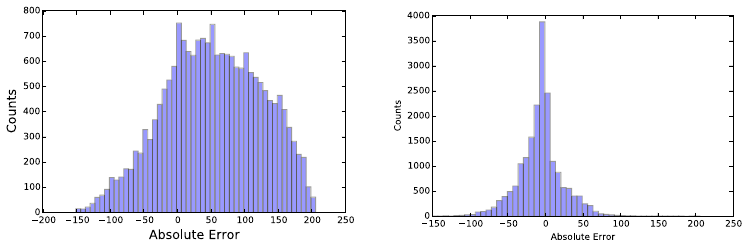
222 CHAPTER 7. MATHEMATICAL MODELS

Figure 7.8: Error distribution histograms for random (left) and naive Bayes

classiﬁers predicting the year of authorship for documents (right).

y > y0. The problem comes in aggregating these values into a summary

statistic. Do oﬀsetting errors like −1 and 1 mean that the system is

perfect? Typically the absolute value of the error is taken to obliterate

the sign.

•Relative error: The absolute magnitude of error is meaningless without a

sense of the units involved. An absolute error of 1.2 in a person’s predicted

height is good if it is measured in millimeters, but terrible if measured in

miles.

Normalizing the error by the magnitude of the observation produces a

unit-less quantity, which can be sensibly interpreted as a fraction or (mul-

tiplied by 100%) as a percentage: = (y−y0)/y. Absolute error weighs

instances with larger values of yas more important than smaller ones, a

bias corrected when computing relative errors.

•Squared error: The value ∆2= (y0−y)2is always positive, and hence

these values can be meaningfully summed. Large errors values contribute

disproportionately to the total when squaring: ∆2for ∆ = 2 is four times

larger than ∆2for ∆ = 1. Thus outliers can easily come to dominate the

error statistic in a large ensemble.

It is a very good idea to plot a histogram of the absolute error distribution

for any value predictor, as there is much you can learn from it. The distribution

should be symmetric, and centered around zero. It should be bell-shaped, mean-

ing small errors are more common than big errors. And extreme outliers should

be rare. If any of the conditions are wrong, there is likely a simple way to im-

prove the forecasting procedure. For example, if it is not centered around zero,

adding an constant oﬀset to all forecasts will improve the consensus results.

Figure 7.8 presents the absolute error distributions from two models for pre-

dicting the year of authorship of documents from their word usage distribution.

On the left, we see the error distribution for the monkey, randomly guessing a

7.4. EVALUATING MODELS 223

Performance Statistics

Error Distributions

Confusion Matrices

Evaluation

Environment

Model

Validation

Data

Figure 7.9: Block diagram of a basic model evaluation environment.

year from 1800 to 2005. What do we see? The error distribution is broad and

bad, as we might have expected, but also asymmetric. Far more documents

produced positive errors than negative ones. Why? The test corpus apparently

contained more modern documents than older ones, so (year −monkey year) is

more often positive than negative. Even the monkey can learn something from

seeing the distribution.

In contrast, Figure 7.8 (right) presents the error distribution for our naive

Bayes classiﬁer for document dating. This looks much better: there is a sharp

peak around zero, and much narrower tails. But the longer tail now resides to

the left of zero, telling us that we are still calling a distressing number of very

old documents modern. We need to examine some of these instances, to ﬁgure

out why that is the case.

We need a summary statistic reducing such error distributions to a single

number, in order to compare the performance of diﬀerent value prediction mod-

els. A commonly-used statistic is mean squared error (MSE), which is computed

MSE(Y, Y 0) = 1

i=1

(y0

i−yi)2

Because it weighs each term quadratically, outliers have a disproportionate ef-

fect. Thus median squared error might be a more informative statistic for noisy

instances.

Root mean squared (RMSD) error is simply the square root of mean squared

error:

RMSD(Θ) = pMSE(Y, Y 0).

The advantage of RMSD is that its magnitude is interpretable on the same

scale as the original values, just as standard deviation is a more interpretable

quantity than variance. But this does not eliminate the problem that outlier

elements can substantially skew the total.

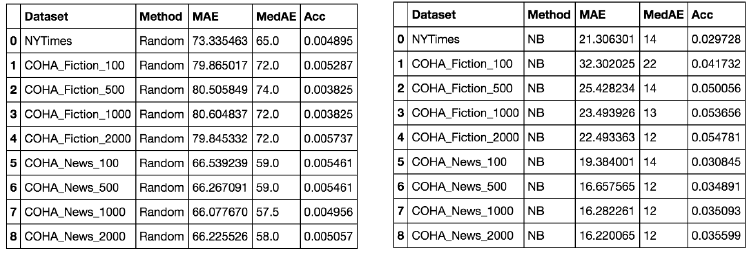
224 CHAPTER 7. MATHEMATICAL MODELS

Figure 7.10: Evaluation environment results for predicting the year of author-

ship for documents, comparing the monkey (left) to a naive Bayes classiﬁer

(right).

7.5 Evaluation Environments

A substantial part of any data science project revolves around building a reason-

able evaluation environment. In particular, you need a single-command program

to run your model on the evaluation data, and produce plots/reports on its ef-

fectiveness, as shown in Figure 7.9.

Why single command? If it is not easy to run, you won’t try it often enough.

If the results are not easy to read and interpret, you will not glean enough

information to make it worth the eﬀort.

The input to an evaluation environment is a set of instances with the associ-

ated output results/labels, plus a model under test. The system runs the model

on each instance, compares each result against this gold standard, and outputs

summary statistics and distribution plots showing the performance it achieved

on this test set.

A good evaluation system has the following properties:

•It produces error distributions in addition to binary outcomes: how close

your prediction was, not just whether it was right or wrong. Recall Figure

7.8 for inspiration.

•It produces a report with multiple plots about several diﬀerent input dis-

tributions automatically, to read carefully at your leisure.

•It outputs the relevant summary statistics about performance, so you can

quickly gauge quality. Are you doing better or worse than last time?

As an example, Figure 7.10 presents the output of our evaluation environ-

ment for the two document-dating models presented in the previous section.

Recall that the task is to predict the year of authorship of a given document

from word usage. What is worth noting?

7.5. EVALUATION ENVIRONMENTS 225

•Test sets broken down by type: Observe the the evaluation environment

partitioned the inputs into nine separate subsets, some news and some

ﬁction, and of lengths from 100 to 2000 words. Thus at a glance we could

see separately how well we do on each.

•Logical progressions of diﬃculty: It is obviously harder to make age

determination from shorter documents than longer ones. By separating

the harder and smaller cases, we better understand our source of errors.

We see a big improvement in naive Bayes as we move from 100 to 500

words, but these gains saturate before 2000 words.

•Problem appropriate statistics: We did not print out every possible error

metric, only mean and median absolute error and accuracy (how often did

we get the year exactly right?). These are enough for us to see that news

is easier than ﬁction, that our model is much better than the monkey,

and that our chances of identifying the actual year correctly (measured by

accuracy) are still too small for us to worry about.

This evaluation gives us the information we need to see how we are doing,

without overwhelming us with numbers that we won’t ever really look at.

7.5.1 Data Hygiene for Evaluation

An evaluation is only meaningful when you don’t fool yourself. Terrible things

happen when people evaluate their models in an undisciplined manner, losing

the distinction between training, testing, and evaluation data.

Upon taking position of a data set with the intention of building a predictive

model, your ﬁrst operation should be to partition the input into three parts:

•Training data: This is what you are completely free to play with. Use

it to study the domain, and set the parameters of your model. Typically

about 60% of the full data set should be devoted to training.

•Testing data: Comprising about 20% of the full data set, this is what

you use to evaluate how good your model is. Typically, people experiment

with multiple machine learning approaches or basic parameter settings,

so testing enables you to establish the relative performance of all these

diﬀerent models for the same task.

Testing a model usually reveals that it isn’t performing as well as we would

like, thus triggering another cycle of design and reﬁnement. Poor perfor-

mance on test data relative to how it did on the training data suggests a

model which has been overﬁt.

•Evaluation data: The ﬁnal 20% of the data should be set aside for a

rainy day: to conﬁrm the performance of the ﬁnal model right before it

goes into production. This works only if you never opened the evaluation

data until it was really needed.

226 CHAPTER 7. MATHEMATICAL MODELS

The reason to enforce these separations should be obvious. Students would

do much better on examinations if they were granted access to the answer key

in advance, because they would know exactly what to study. But this would

not reﬂect how much they actually had learned. Keeping testing data separate

from training enforces that the tests measure something important about what

the model understands. And holding out the ﬁnal evaluation data to use only

after the model gets stable ensures that the speciﬁcs of the test set have not

leaked into the model through repeated testing iterations. The evaluation set

serves as out-of-sample data to validate the ﬁnal model.

In doing the original partitioning, you must be careful not to create unde-

sirable artifacts, or destroy desirable ones. Simply partitioning the ﬁle in the

order it was given is dangerous, because any structural diﬀerence between the

populations of the training and testing corpus means that the model will not

perform as well as it should.

But suppose you were building a model to predict future stock prices. It

would be dangerous to randomly select 60% of the samples over all history

as the training data, instead of all the samples over the ﬁrst 60% of time.

Why? Suppose your model “learned” which would be the up and down days in

the market from the training data, and then used this insight to make virtual

predictions for other stocks on these same days. This model would perform far

better in testing than in practice. Proper sampling techniques are quite subtle,

and discussed in Section 5.2.

It is essential to maintain the veil of ignorance over your evaluation data for

as long as possible, because you spoil it as soon as you use it. Jokes are never

funny the second time you hear them, after you already know the punchline. If

you do wear out the integrity of your testing and evaluation sets, the best solu-

tion is to start from fresh, out-of-sample data, but this is not always available.

Otherwise, randomly re-partition the full data set into fresh training, testing,

and evaluation samples, and retrain all of your models from scratch to reboot

the process. But this should be recognized as an unhappy outcome.

7.5.2 Amplifying Small Evaluation Sets

The idea of rigidly partitioning the input into training, test, and evaluation sets

makes sense only on large enough data sets. Suppose you have 100,000 records at

your disposal. There isn’t going to be a qualitative diﬀerence between training

on 60,000 records instead of 100,000, so it is better to facilitate a rigorous

evaluation.

But what if you only have a few dozen examples? As of this writing, there

have been only 45 U.S. presidents, so any analysis you can do on them represents

very small sample statistics. New data points come very slowly, only once every

four years or so. Similar issues arise in medical trials, which are very expensive to

run, potentially yielding data on well under a hundred patients. Any application

where we must pay for human annotation means that we will end up with less

data for training than we might like.

What can you do when you cannot aﬀord to give up a fraction of your data

7.5. EVALUATION ENVIRONMENTS 227

for testing? Cross-validation partitions the data into kequal-sized chunks, then

trains kdistinct models. Model iis trained on the union of all blocks x6=i,

totaling (k−1)/kth of the data, and tested on the held out ith block. The

average performance of these kclassiﬁers stands in as the presumed accuracy

for the full model.

The extreme case here is leave one out cross-validation, where ndistinct

models are each trained on diﬀerent sets of n−1 examples, to determine whether

the classiﬁer was good or not. This maximizes the amount of training data, while

still leaving something to evaluate against.

A real advantage of cross validation is that it yields a standard deviation

of performance, not only a mean. Each classiﬁer trained on a particular subset

of the data will diﬀer slightly from its peers. Further, the test data for each

classiﬁer will diﬀer, resulting in diﬀerent performance scores. Coupling the mean

with the standard deviation and assuming normality gives you a performance

distribution, and a better idea of how well to trust the results. This makes

cross-validation very much worth doing on large data sets as well, because you

can aﬀord to make several partitions and retrain, thus increasing conﬁdence

that your model is good.

Of the kmodels resulting from cross validation, which should you pick as

your ﬁnal product? Perhaps you could use the one which performed best on its

testing quota. But a better alternative is to retrain on all the data and trust

that it will be at least as good as the less lavishly trained models. This is not

ideal, but if you can’t get enough data then you must do the best with what

you’ve got.

Here are a few other ideas that can help to amplify small data sets for

training and evaluation:

•Create negative examples from a prior distribution: Suppose one wanted

to build a classiﬁer to identify who would be qualiﬁed to be a candidate

for president. There are very few real examples of presidential candidates

(positive instances), but presumably the elite pool is so small that a ran-

dom person will almost certainly be unqualiﬁed. When positive examples

are rare, all others are very likely negative, and can be so labeled to provide

training data as necessary.

•Perturb real examples to create similar but synthetic ones: A useful trick

to avoid overﬁtting creates new training instances by adding random noise

to distort labeled examples. We then preserve the original outcome label

with the new instance.

For example, suppose we are trying to train an optical character recogni-

tion (OCR) system to recognize the letters of some alphabet in scanned

pages. An expensive human was originally given the task of labeling a

few hundred images with the characters that were contained in them. We

can amplify this to a few million images by adding noise at random, and

rotating/translating/dilating the region of interest. A classiﬁer trained on

228 CHAPTER 7. MATHEMATICAL MODELS

this synthetic data should be far more robust than one restricted to the

original annotated data.

•Give partial credit when you can: When you have fewer training/testing

examples than you want, you must squeeze as much information from each

one as possible.

Suppose that our classiﬁer outputs a value measuring its conﬁdence in its

decision, in addition to the proposed label. This conﬁdence level gives

us additional resolution with which to evaluate the classiﬁer, beyond just

whether it got the label right. It is a bigger strike against the classiﬁer

when it gets a conﬁdent prediction wrong, than it is on an instance where

it thought the answer was a tossup. On a presidential-sized problem,

I would trust a classiﬁer that got 30 right and 15 wrong with accurate

conﬁdence values much more than one with 32 right and 13 wrong, but

with conﬁdence values all over the map.

7.6 War Story: 100% Accuracy

The two businessmen looked a little uncomfortable at the university, out of

place with their dark blue suits to our shorts and sneakers. Call them Pablo

and Juan. But they needed us to make their vision a reality.

“The business world still works on paper,” Pablo explained. He was the one

in the darker suit. “We have a contract to digitize all of Wall Street’s ﬁnancial

documents that are still printed on paper. They will pay us a fortune to get a

computer to do the scanning. Right now they hire people to type each document

in three times, just to make sure they got it absolutely right.”

It sounded exciting, and they had the resources to make it happen. But

there was one caveat. “Our system cannot make any errors. It can say ‘I don’t

know’ sometimes. But whenever it calls a letter it has to be 100% correct.”

“No problem.” I told them. “Just let me say I don’t know 100% of the time,

and I can design a system to meet your speciﬁcation.”

Pablo frowned. “But that will cost us a fortune. In the system we want to

build, images of the I don’t knows will go to human operators for them to read.

But we can’t aﬀord to pay them to read everything.”

My colleagues and I agreed to take the job, and in time we developed a

reasonable OCR system from scratch. But one thing bothered me.

“These Wall Street guys who gave you the money are smart, aren’t they?,”

I asked Pablo one day.

“Smart as a whip,” he answered.

“Then how could they possibly believe it when you said you could build an

OCR system that was 100% accurate.”

“Because they thought that I had done it before,” he said with a laugh.

It seems that Pablo’s previous company had built a box that digitized price

data from the television monitors of the time. In this case, the letters were

exact patterns of bits, all written in exactly the same font and the same size.

7.7. SIMULATION MODELS 229

The TV signal was digital, too, with no error at all from imaging, imperfectly-

formed blobs of printers ink, dark spots, or folds in the paper. It was trivial

to test for an exact match between a perfect pattern of bits (the image) and

another perfect pattern of bits (the character in the device’s font), since there is

no source of uncertainty. But this problem had nothing to do with OCR, even

if both involved reading letters.

Our reasonable OCR system did what it could with the business documents

it was given, but of course we couldn’t get to 100%. Eventually, the Wall Street

guys took their business back to the Philippines, where they paid three people to

type in each document and voted two out of three if there was any disagreement.

We shifted direction and got into the business of reading handwritten survey

forms submitted by consumers, lured by the promise of grocery store coupons.

This problem was harder, but the stakes not as high: they were paying us a

crummy $0.22 a form and didn’t expect perfection. Our competition was an

operation that used prison labor to type in the data. We caught a break when

one of those prisoners sent a threatening letter to an address they found on

a survey form, which then threw the business to us. But even our extensive

automation couldn’t read these forms for less than $0.40 a pop, so the contract

went back to prison after we rolled belly up.

The fundamental lesson here is that no pattern recognition system for any

reasonable problem will bat 100% all the time. The only way never to be wrong

is to never make a prediction. Careful evaluation is necessary to measure how

well your system is working and where it is making mistakes, in order to make

the system better.

7.7 Simulation Models

There is an important class of ﬁrst-principle models which are not primarily data

driven, yet which prove very valuable for understanding widely diverse phenom-

ena. Simulations are models that attempt to replicate real-world systems and

processes, so we can observe and analyze their behavior.

Simulations are important for demonstrating the validity of our understand-

ing of a system. A simple simulation which captures much of the behavioral

complexity of a system must explain how it works, by Occam’s razor. Famous

physicist Richard Feynman said, “What I cannot create, I do not understand.”

What you cannot simulate, and get some level of accuracy in the observed re-

sults, you do not understand.

Monte Carlo simulations use random numbers to synthesize alternate reali-

ties. Replicating an event millions of times under slightly perturbed conditions

permits us to generate a probability distribution on the set of outcomes. This

was the idea behind permutation tests for statistical signiﬁcance. We also saw

(in Section 5.5.2) that random coin ﬂips could stand in for when a batter got hits

or made out, so we could simulate an arbitrary number of careers and observe

what happened over the course of them.

The key to building an eﬀective Monte Carlo simulation is designing an

230 CHAPTER 7. MATHEMATICAL MODELS

appropriate discrete event model. A new random number is used by the model

to replicate each decision or event outcome. You may have to decide whether

to go left or go right in a transportation model, so ﬂip a coin. A health or

insurance model may have to decide whether a particular patient will have a

heart attack today, so ﬂip an appropriately weighted coin. The price of a stock

in a ﬁnancial model can either go up or down at each tick, which again can be

a coin ﬂip. A basketball player will hit or miss a shot, with a likelihood that

depends upon their shooting skill and the quality of their defender.

The accuracy of such a simulation rests on the probabilities that you assign

to heads and tails. This governs how often each outcome occurs. Obviously, you

are not restricted to using a fair coin, meaning 50/50. Instead, the probabilities

need to reﬂect assumptions of the likelihood of the event given the state of the

model. These parameters are often set using statistical analysis, by observing

the distribution of events as they occurred in the data. Part of the value of

Monte Carlo simulations is that they let us play with alternate realities, by

changing certain parameters and seeing what happens.

A critical aspect of eﬀective simulation is evaluation. Programming errors

and modeling inadequacies are common enough that no simulation can be ac-

cepted on faith. The key is to hold back one or more classes of observations

of the system from direct incorporation in your model. This provides behavior

that is out of sample, so we can compare the distribution of results from the

simulation with these observations. If they don’t jibe, your simulation is just

jive. Don’t let it go live.

7.8 War Story: Calculated Bets

Where there is gambling there is money, and where there is money there will be

models. During our family trips to Florida as a kid, I developed a passion for

the sport of jai-alai. And, as I learned how to build mathematical models as a

grown-up, I grew obsessed with developing a proﬁtable betting system for the

sport.

Jai-alai is a sport of Basque origin where opposing players or teams alternate

hurling a ball against the wall and catching it, until one of them ﬁnally misses

and loses the point. The throwing and catching is done with an enlarged basket

or cesta, the ball or pelota is made of goat skin and hard rubber, and the wall is of

granite or concrete; ingredients which lead to fast and exciting action captured

in Figure 7.11. In the United States, jai-alai is most associated with the state

of Florida, which permits gambling on the results of matches.

What makes jai-alai of particular interest is its unique and very peculiar

scoring system. Each jai-alai match involves eight players, named 1 through 8

to reﬂect their playing order. Each match starts with players 1 and 2 playing,

and the rest of the players waiting patiently in line. All players start the game

with zero points each. Each point in the match involves two players; one who

will win and one who will lose. The loser will go to the end of the line, while

the winner will add to his point total and await the next point, until he has

7.8. WAR STORY: CALCULATED BETS 231

Figure 7.11: Jai-alai is a fast, exciting ball game like handball, but you can bet

on it.

accumulated enough points to claim the match.

It was obvious to me, even as a kid, that this scoring system would not

be equally fair to all the diﬀerent players. Starting early in the queue gave you

more chances to play, and even a kludge they added to double the value of points

later in the match couldn’t perfectly ﬁx it. But understanding the strength of

these biases could give me an edge in betting.

My quest to build a betting system for jai-alai, started by simulating this

very peculiar scoring system. A jai-alai match consists of a sequence of discrete

events, described by the following ﬂow structure:

Initialize the current players to 1 and 2.

Initialize the queue of players to {3,4,5,6,7,8}.

Initialize the point total for each player to zero.

So long as the current winner has less than 7 points:

Pick a random number to decide who wins the next point.

Add one (or if beyond the seventh point, two) to the

total of the simulated point winner.

Put the simulated point loser at the end of the queue.

Get the next player oﬀ the front of the queue.

End So long as.

Identify the current point winner as the winner of the match.

The only step here which needs more elaboration is that of simulating a

point between two players. If the purpose of our simulation is to see how biases

in the scoring system aﬀect the outcome of the match, it makes the most sense

to consider the case in which all players are equally skillful. To give every player

a 50/50 chance of winning each point he is involved in, we can ﬂip a simulated

coin to determine who wins and who loses.

I implemented the jai-alai simulation in my favorite programming language,

and ran it on 1,000,000 jai-alai games. The simulation produced a table of

statistics, telling me how often each betting outcome paid oﬀ, assuming that all

the players were equally skillful. Figure 7.12 reports the number of simulated

232 CHAPTER 7. MATHEMATICAL MODELS

Simulated Observed

Position Wins % Wins Wins % Wins

1 162675 16.27% 1750 14.1%

2 162963 16.30% 1813 14.6%

3 139128 13.91% 1592 12.8%

4 124455 12.45% 1425 11.5%

5 101992 10.20% 1487 12.0%

6 102703 10.27% 1541 12.4%

7 88559 8.86% 1370 11.1%

8 117525 11.75% 1405 11.3%

1,000,000 100.00% 12,383 100.0%

Figure 7.12: Win biases observed in the jai-alai simulations match well with

results observed in actual matches.

wins for each of the eight starting positions. What insights can we draw from

this table?

•Positions 1 and 2 have a substantial advantage over the rest of the ﬁeld.

Either of the initial players are almost twice as likely to come ﬁrst, second,

or third than the poor shlub in position 7.

•Positions 1 and 2 win at essentially the same frequency. This is as it

should be, since both players start the game on the court instead of in the

queue. The fact that players 1 and 2 have very similar statistics increases

our conﬁdence in the correctness of the simulation.

•Positions 1 and 2 do not have identical statistics because we simulated

“only” one million games. If you ﬂip a coin a million times, it almost

certainly won’t come up exactly half heads and half tails. However, the

ratio of heads to tails should keep getting closer to 50/50 the more coins

we ﬂip.

The simulated gap between players 1 and 2 tells us something about the

limitations on the accuracy of our simulation. We shouldn’t trust any

conclusions which depends upon such small diﬀerences in the observed

values.

To validate the accuracy of the simulation, we compared our results to statis-

tics on the actual outcomes of over 12,000 jai-alai matches, also in Figure 7.12.

The results basically agree with the simulation, subject to the limits of the small

sample size. Post positions 1 and 2 won most often in real matches, and position

7 least often.

Now we knew the probability that each possible betting opportunity in jai-

alai paid oﬀ. Were we now ready to start making money? Unfortunately not.

7.9. CHAPTER NOTES 233

Even though we have established that post position is a major factor in deter-

mining the outcome of jai-alai matches, perhaps the dominant one, we still had

several hurdles to overcome before we could bet responsibly:

•The impact of player skills: Obviously, a good player is more likely to win

than a bad one, regardless of their post positions. It is clear that a better

model for predicting the outcome of jai-alai matches would factor relative

skills into the queuing model.

•The sophistication of the betting public: Many people had noticed the

impact of post-position bias before I did. Indeed, data analysis revealed

the jai-alai betting public had largely factored the eﬀect of post position

in the odds. Fortunately for us, however, largely did not mean completely.

•The house cut – Frontons keep about 20% of the betting pool as the house

percentage, and thus we had to do much better then the average bettor

just to break even.

My simulation provided information on which outcomes were most likely. It

did not by itself identify which are the best bets. A good bet depends both upon

the likelihood of the event occurring and the payoﬀ when it occurs. Payoﬀs are

decided by the rest of the betting public. To ﬁnd the best bets to make, we had

to work a lot harder:

•We had to analyze past match data to determine who were the better play-

ers. Once we knew who was better, we could bias the simulated coin tosses

in their favor, to make our simulation more accurate for each individual

match.

•We had to analyze payoﬀ data to build a model of other bettor’s prefer-

ences. In jai-alai, you are betting against the public, so you need to be

able to model their thinking in order to predict the payoﬀs for a particular

bet.

•We had to model the impact of the house’s cut on the betting pool. Certain

bets, which otherwise might have been proﬁtable, go into the red when

you factor in these costs.

The bottom line is that we did it, with 544% returns on our initial stake.

The full story of our gambling system is reported in my book Calculated Bets

[Ski01]. Check it out: I bet you will like it. It is fun reading about successful

models, but even more fun to build them.

7.9 Chapter Notes

Silver [Sil12] is an excellent introduction to the complexities of models and

forecasting in a variety of domains. Textbooks on mathematical modeling issues

include Bender [Ben12] and Giordano [GFH13].

234 CHAPTER 7. MATHEMATICAL MODELS

The Google Flu Trends project is an excellent case study in both the power

and limitation of big data analysis. See Ginsberg et al. [GMP+09] for the

original description, and Lazer et al. [LKKV14] for a fascinating post-mortem

on how it all went wrong.

Technical aspects of the OCR system presented in Section 7.6 is reported in

Sazaklis et. al. [SAMS97]. The work on year of authorship detection (and as-

sociated evaluation environment example) is from my students Vivek Kulkarni,

Parth Dandiwala, and Yingtao Tian [KTDS17].

7.10 Exercises

Properties of Models

7-1. [3] Quantum physics is much more complicated than Newtonian physics. Which

model passes the Occam’s Razor test, and why?

7-2. [5] Identify a set of models of interest. For each of these, decide which properties

these models have:

(a) Are they discrete or continuous?

(b) Are they linear or non-linear?

(d) Are they general or ad hoc?

(e) Are they data driven or ﬁrst principle?

7-3. [3] Give examples of ﬁrst-principle and data-driven models used in practice.

7-4. [5] For one or more of the following The Quant Shop challenges, discuss whether

principled or data-driven models seem to be the more promising approach:

•Miss Universe.

•Movie gross.

•Baby weight.

•Art auction price.

•Snow on Christmas.

•Super Bowl/college champion.

•Ghoul pool.

•Future gold/oil price.

7-5. [5] For one or more of the following The Quant Shop challenges, partition the

full problem into subproblems that can be independently modeled:

•Miss Universe.

•Movie gross.

•Baby weight.

•Art auction price.

7.10. EXERCISES 235

•Snow on Christmas.

•Super Bowl/college champion.

•Ghoul pool.

•Future gold/oil price.

Evaluation Environments

7-6. [3] Suppose you build a classiﬁer that answers yes on every possible input. What

precision and recall will this classiﬁer achieve?

7-7. [3] Explain what precision and recall are. How do they relate to the ROC curve?

7-8. [5] Is it better to have too many false positives, or too many false negatives?

Explain.

7-9. [5] Explain what overﬁtting is, and how you would control for it.

7-10. [5] Suppose f≤1/2 is the fraction of positive elements in a classiﬁcation. What

is the probability pthat the monkey should guess positive, as a function of f,

in order to maximize the speciﬁc evaluation metric below? Report both pand

the expected evaluation score the monkey achieves.

(a) Accuracy.

(b) Precision.

(d) F-score.

7-11. [5] What is cross-validation? How might we pick the right value of kfor k-fold

cross validation?

7-12. [8] How might we know whether we have collected enough data to train a model?

7-13. [5] Explain why we have training, test, and validation data sets and how they

are used eﬀectively?

7-14. [5] Suppose we want to train a binary classiﬁer where one class is very rare.

Give an example of such a problem. How should we train this model? What

metrics should we use to measure performance?

7-15. [5] Propose baseline models for one or more of the following The Quant Shop

challenges:

•Miss Universe.

•Movie gross.

•Baby weight.

•Art auction price.

•Snow on Christmas.

•Super Bowl/college champion.

•Ghoul pool.

•Future gold/oil price.

Implementation Projects

236 CHAPTER 7. MATHEMATICAL MODELS

7-16. [5] Build a model to forecast the outcomes of one of the following types of betable

events, and rigorously analyze it through back testing:

(a) Sports like football, basketball, and horse racing.

(b) Pooled bets involving multiple events, like soccer pools or the NCAA bas-

ketball tournament.

(d) Election forecasts for local and congressional elections.

(e) Stock or commodity price prediction/trading.

Rigorous testing will probably conﬁrm that your models are not strong enough

for proﬁtable wagering, and this is 100% ok. Be honest: make sure that you

are using fresh enough prices/odds to reﬂect betting opportunities which would

still be available at the time you place your simulated bet. To convince me that

your model is in fact genuinely proﬁtable, send me a cut of the money and then

I will believe you.

7-17. [5] Build a general model evaluation system in your favorite programming lan-

guage, and set it up with the right data to assess models for a particular prob-

lem. Your environment should report performance statistics, error distributions

and/or confusion matrices as appropriate.

Interview Questions

7-18. [3] Estimate prior probabilities for the following events:

(a) The sun will come up tomorrow.

(b) A major war involving your country will start over the next year.

(d) Today you will meet the person whom you will marry.

(e) The Chicago Cubs will win the World Series this year.

7-19. [5] What do we mean when we talk about the bias–variance trade-oﬀ?

7-20. [5] A test has a true positive rate of 100% and false positive rate of 5%. In this

population 1 out of 1000 people have the condition the test identiﬁes. Given a

positive test, what is the probability this person actually has the condition?

7-21. [5] Which is better: having good data or good models? And how do you deﬁne

good?

7-22. [3] What do you think about the idea of injecting noise into your data set to

test the sensitivity of your models?

7-23. [5] How would you deﬁne and measure the predictive power of a metric?

Kaggle Challenges

7-24. Will a particular grant application be funded?

https://www.kaggle.com/c/unimelb

7-25. Who will win the NCAA basketball tournament?

https://www.kaggle.com/c/march-machine-learning-mania-2016

7-26. Predict the annual sales in a given restaurant.

https://www.kaggle.com/c/restaurant-revenue-prediction

Chapter 8

Linear Algebra

We often hear that mathematics consists mainly of “proving theo-

rems.” Is a writer’s job mainly that of “writing sentences?”

– Gian-Carlo Rota

The data part of your data science project involves reducing all of the relevant

information you can ﬁnd into one or more data matrices, ideally as large as pos-

sible. The rows of each matrix represent items or examples, while the columns

represent distinct features or attributes.

Linear algebra is the mathematics of matrices: the properties of arrange-

ments of numbers and the operations that act on them. This makes it the lan-

guage of data science. Many machine learning algorithms are best understood

through linear algebra. Indeed algorithms for problems like linear regression

can be reduced to a single formula, multiplying the right chain of matrix prod-

ucts to yield the desired results. Such algorithms can simultaneously be both

simple and intimidating, trivial to implement and yet hard to make eﬃcient and

robust.

You presumably took a course in linear algebra at some point, but perhaps

have forgotten much of it. Here I will review most of what you need to know:

the basic operations on matrices, why they are useful, and how to build an

intuition for what they do.

8.1 The Power of Linear Algebra

Why is linear algebra so powerful? It regulates how matrices work, and matrices

are everywhere. Matrix representations of important objects include:

•Data: The most generally useful representation of numerical data sets

are as n×mmatrices. The nrows represent objects, items, or instances,

while the mcolumns each represent distinct features or dimensions.

238 CHAPTER 8. LINEAR ALGEBRA

•Geometric point sets: An n×mmatrix can represent a cloud of points in

space. The nrows each represent a geometric point, while the mcolumns

deﬁne the dimensions. Certain matrix operations have distinct geometric

interpretations, enabling us to generalize the two-dimensional geometry

we can actually visualize into higher-dimensional spaces.

•Systems of equations: A linear equation is deﬁned by the sum of variables

weighted by constant coeﬃcients, like:

y=c0+c1x1+c2x2+. . . cm−1xm−1.

A system of nlinear equations can be represented as an n×mmatrix,

where each row represents an equation, and each of the mcolumns is

associated with the coeﬃcients of a particular variable (or the constant

“variable” 1 in the case of c0). Often it is necessary to represent the y

value for each equation as well. This is typically done using a separate

n×1 array or vector of solution values.

•Graphs and networks: Graphs are made up of vertices and edges, where

edges are deﬁned as ordered pairs of vertices, like (i, j). A graph with n

vertices and medges can be represented as an n×nmatrix M, where

M[i, j] denotes the number (or weight) of edges from vertex ito vertex

j. There are surprising connections between combinatorial properties and

linear algebra, such as the relationship between paths in graphs and matrix

multiplication, and how vertex clusters relate to the eigenvalues/vectors

of appropriate matrices.

•Rearrangement operations: Matrices can do things. Carefully designed

matrices can perform geometric operations on point sets, like translation,

rotation, and scaling. Multiplying a data matrix by an appropriate permu-

tation matrix will reorder its rows and columns. Movements can be deﬁned

by vectors, the n×1 matrices powerful enough to encode operations like

translation and permutation.

The ubiquity of matrices means that a substantial infrastructure of tools

has been developed to manipulate them. In particular, the high-performance

linear algebra libraries for your favorite programming language mean that you

should never implement any basic algorithm by yourself. The best library im-

plementations optimize dirty things like numerical precision, cache-misses, and

the use of multiple cores, right down to the assembly-language level. Our job

is to formulate the problem using linear algebra, and leave the algorithmics to

these libraries.

8.1.1 Interpreting Linear Algebraic Formulae

Concise formulas written as products of matrices can provide the power to do

amazing things, including linear regression, matrix compression, and geometric

8.1. THE POWER OF LINEAR ALGEBRA 239

transformations. Algebraic substitution coupled with a rich set of identities

yields elegant, mechanical ways to manipulate such formulas.

However, I ﬁnd it very diﬃcult to interpret such strings of operations in

ways that I really understand. For example, take the “algorithm” behind least

squares linear regression, which is:

c= (ATA)−1ATb

where the n×msystem is Ax =band wis the vector of coeﬃcients of the best

ﬁtting line.

One reason why I ﬁnd linear algebra challenging is the nomenclature. There

are many diﬀerent terms and concepts which must be grokked to really follow

what is going on. But a bigger problem is that most of the proofs are, for

good reason, algebraic. To my taste, algebraic proofs generally do not carry

intuition about why things work the way they do. Algebraic proofs are easier

to verify step-by-step in a mechanical way, rather than by understanding the

ideas behind the argument.

I will present only one formal proof in this text. And by design both the

theorem and the proof are incorrect.

Theorem 1. 2=1.

Proof.

a=b

a2=ab

a2−b2=ab −b2

(a+b)(a−b) = b(a−b)

a+b=b

2b=b

2=1

If you have never seen such a proof before, you might ﬁnd it convincing,

even though I trust you understand on a conceptual level that 2 6= 1. Each

line follows from the one before it, through direct algebraic substitution. The

problem, as it turns out, comes when canceling (a−b), because we are in fact

dividing by zero.

What are the lessons from this proof? Proofs are about ideas, not just

algebraic manipulation. No idea means no proof. To understand linear algebra,

your goal should be to ﬁrst validate the simplest interesting case (typically two

dimensions) in order to build intuition, and then try to imagine how it might

generalize to higher dimensions. There are always special cases to watch for, like

division by zero. In linear algebra, these cases include dimensional mismatches

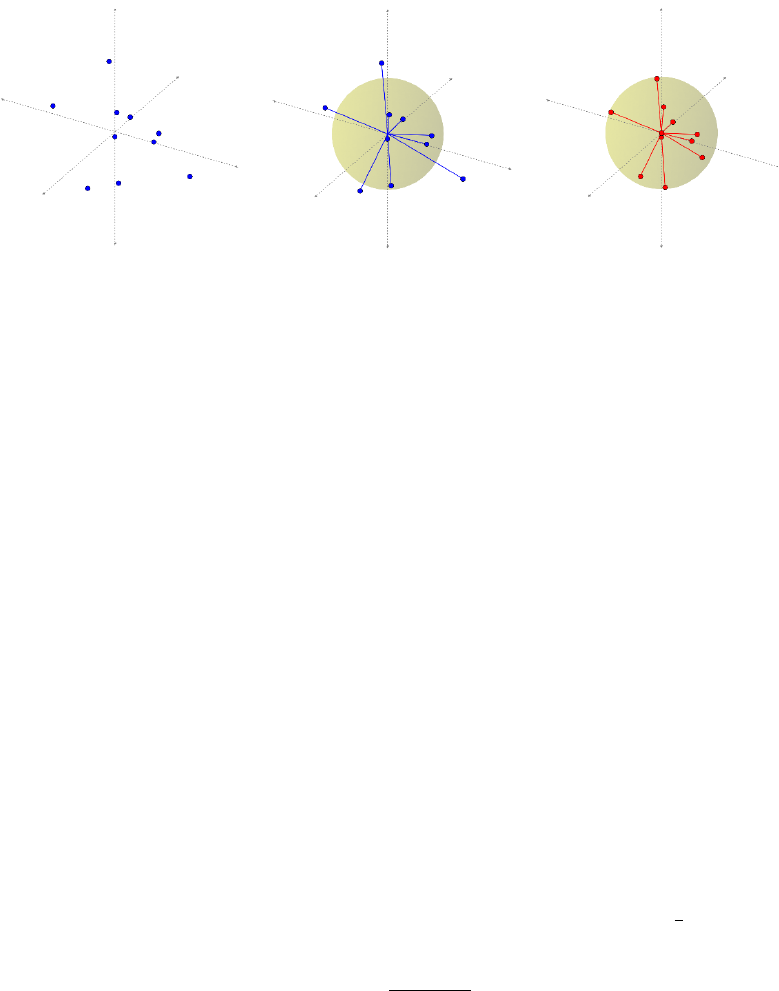
240 CHAPTER 8. LINEAR ALGEBRA

Figure 8.1: Points can be reduced to vectors on the unit sphere, plus magnitudes.

and singular (meaning non-invertible) matrices. The theory of linear algebra

works except when it doesn’t work, and it is better to think in terms of the

common cases rather than the pathological ones.

8.1.2 Geometry and Vectors

There is a useful interpretation of “vectors,” meaning 1 ×dmatrices, as vectors

in the geometric sense, meaning directed rays from the origin through a given

point in ddimensions.

Normalizing each such vector vto be of unit length (by dividing each coor-

dinate by the distance from vto the origin) puts it on a d-dimensional sphere,

as shown in Figure 8.1: a circle for points in the plane, a real sphere for d= 3,

and some unvisualizable hypersphere for d≥4.

This normalization proves a useful thing to do. The distances between points

become angles between vectors, for the purposes of comparison. Two nearby

points will deﬁne a small angle between them through the origin: small distances

imply small angles. Ignoring magnitudes is a form of scaling, making all points

directly comparable.

The dot product is a useful operation reducing vectors to scalar quantities.

The dot product of two length-nvectors Aand Bis deﬁned:

A·B=

i=1

AiBi

We can use the dot product operation to compute the angle θ=6AOB

between vectors Aand B, where Ois the origin:

cos(Θ) = A·B

||A|| ||B||

Let’s try to parse this formula. The ||V|| symbol means “the length of V.”

For unit vectors, this is, by deﬁnition, equal to 1. In general, it is the quantity

by which we must divide Vby to make it a unit vector.

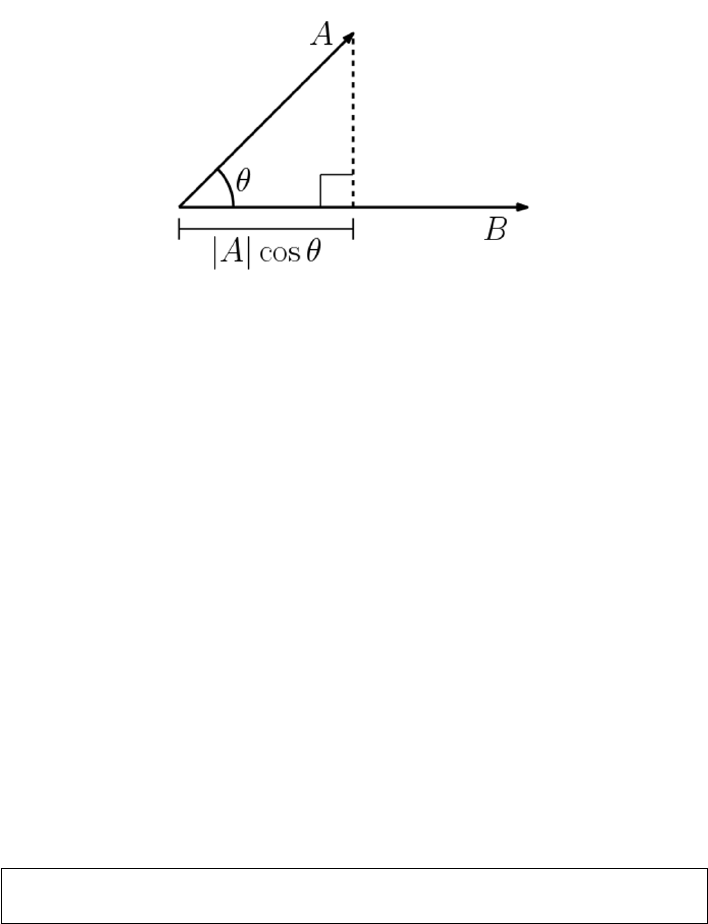
8.2. VISUALIZING MATRIX OPERATIONS 241

Figure 8.2: The dot product of two vectors deﬁnes the cosine of the angle

between them.

But what is the connection between dot product and angle? Consider the

simplest case of an angle deﬁned between two rays, Aat zero degrees and

B= (x, y). Thus the unit ray is A= (1,0). In this case, the dot product

is 1 ·x+ 0 ·y=x, which is exactly what cos(θ) should be if Bis a unit

vector. We can take it on faith that this generalizes for general B, and to higher

dimensions.

So a smaller angle means closer points on the sphere. But there is another

connection between things we know. Recall the special cases of the cosine func-

tion, here given in radians:

cos(0) = 1,cos(π/2) = 0,cos(π) = −1.

The values of the cosine function range from [−1,1], exactly the same range as

that of the correlation coeﬃcient. Further, the interpretation is the same: two

identical vectors are perfectly correlated, while antipodal points are perfectly

negatively correlated. Orthogonal points/vectors (the case of Θ = π/2) have as

little to do with each other as possible.

The cosine function is exactly the correlation of two mean-zero variables.

For unit vectors, ||A|| =||B|| = 1, so the angle between Aand Bis completely

deﬁned by the dot product.

Take-Home Lesson: The dot product of two vectors measures similarity in

exactly the same way as the Pearson correlation coeﬃcient.

8.2 Visualizing Matrix Operations

I assume that you have had some previous exposure to the basic matrix opera-

tions of transposition, multiplication, and inversion. This section is intended as

a refresher, rather than an introduction.

242 CHAPTER 8. LINEAR ALGEBRA

Figure 8.3: Matrix image examples: Lincoln (left) and his memorial (right).

The center image is a linear combination of left and right, for α= 0.5.

But to provide better intuition, I will represent matrices as images rather

than numbers, so we can see what happens when we operate on them. Figure

8.3 shows our primary matrix images: President Abraham Lincoln (left) and

the building which serves as his memorial (right). The former is a human face,

while the latter contains particularly strong rows and columns.

Be aware that we will be quietly rescaling the matrix between each operation,

so the absolute color does not matter. The interesting patterns come in the

diﬀerences between light and dark, meaning the smallest and biggest numbers

in the current matrix. Also, note that the origin element of the matrix M[1,1]

represents the upper left corner of the image.

8.2.1 Matrix Addition

Matrix addition is a simple operation: for matrices Aand B, each of dimensions

n×m,C=A+Bimplies that:

Cij =Aij +Bij ,for all 1 ≤i≤nand 1 ≤j≤m.

Scalar multiplication provides a way to change the weight of every element

in a matrix simultaneously, perhaps to normalize them. For any matrix Aand

number c,A0=c·Aimplies that

ij =cAij ,for all 1 ≤i≤nand 1 ≤j≤m.

Combining matrix addition with scalar multiplication gives us the power to

perform linear combinations of matrices. The formula α·A+ (1 −α)·Benables

us to fade smoothly between A(for α= 1) and B(for α= 0), as shown in

Figure 8.3. This provides a way to morph the images from Ato B.

The transpose of a matrix Minterchanges rows and columns, turning an

a×bmatrix into a b×amatrix MT, where

ij =Mji for all 1 ≤i≤nand 1 ≤j≤m.

The transpose of a square matrix is a square matrix, so Mand MTcan safely

be added or multiplied together. More generally, the transpose is an operation

that is used to orient a matrix so it can be added to or multiplied by its target.

8.2. VISUALIZING MATRIX OPERATIONS 243

Figure 8.4: Lincoln (left) and its transposition (right). The sum of a matrix

and its transposition is symmetric along its main diagonal (right).

The transpose of a matrix sort of “rotates” it by 180 degrees, so (AT)T=A.

In the case of square matrices, adding a matrix to its transpose is symmetric,

as shown in Figure 8.4 (right). The reason is clear: C=A+ATimplies that

Cij =Aij +Aji =Cji.

8.2.2 Matrix Multiplication

Matrix multiplication is an aggregate version of the vector dot or inner product.

Recall that for two n-element vectors, Xand Y, the dot product X·Yis deﬁned:

X·Y=

i=1

XiYi

Dot products measure how “in sync” the two vectors are. We have already seen

the dot product when computing the cosine distance and correlation coeﬃcient.

It is an operation that reduces a pair of vectors to a single number.

The matrix product XY Tof these two vectors produces a 1 ×1 matrix

containing the dot product X·Y. For general matrices, the product C=AB

is deﬁned by:

Cij =

i=1

Aik ·Bkj

For this to work, Aand Bmust share the same inner dimensions, implying that

if Ais n×kthen Bmust have dimensions k×m. Each element of the n×m

product matrix Cis a dot product of the ith row of Awith the jth column of

The most important properties of matrix multiplication are:

•It does not commute:Commutativity is the notation that order doesn’t

matter, that x·y=y·x. Although we take commutativity for granted

when multiplying integers, order does matter in matrix multiplication. For

any pair of non-square matrices Aand B, at most one of either AB or BA

244 CHAPTER 8. LINEAR ALGEBRA

has compatible dimensions. But even square matrix multiplication does

not commute, as shown by the products below:

1 1

0 1·1 1

1 0=2 1

1 06=1 1

1 0·1 1

0 1=1 2

1 1

and the covariance matrices of Figure 8.5.

•Matrix multiplication is associative:Associativity grants us the right to

parenthesize as we wish, performing operations in the relative order that

we choose. In computing the product ABC, we have a choice of two op-

tions: (AB)Cor A(BC). Longer chains of matrices permit even more

freedom, with the number of possible parenthesizations growing exponen-

tially in the length of the chain. All of these will return the same answer,

as demonstrated here:

1 2

4 41 0

0 2!3 2

1 0=1 4

3 83 2

1 0=7 2

17 6

1 2

3 4 1 0

0 23 2

1 0!=1 2

3 43 2

2 0=7 2

17 6

There are two primary reasons why associativity matters to us. In an

algebraic sense, it enables us to identify neighboring pairs of matrices in a

chain and replace them according to an identity, if we have one. But the

other issue is computational. The size of intermediate matrix products can

easily blow up in the middle. Suppose we seek to calculate ABCD, where

Ais 1×n,Band Care n×n, and Dis n×1. The product (AB)(CD) costs

only 2n2+noperations, assuming the conventional nested-loop matrix

multiplication algorithm. In contrast, (A(BC))Dweighs in at n3+n2+n

operations.

The nested-loop matrix multiplication algorithm you were taught in high

school is trivially easy to program, and indeed appears on page 398. But don’t

program it. Much faster and more numerically stable algorithms exist in the

highly optimized linear algebra libraries associated with your favorite program-

ming language. Formulating your algorithms as matrix products on large arrays,

instead of using ad hoc logic is counter-intuitive to most computer scientists.

But this strategy can produce very big performance wins in practice.

8.2.3 Applications of Matrix Multiplication

On the face of it, matrix multiplication is an ungainly operation. When I

was ﬁrst exposed to linear algebra, I couldn’t understand why we couldn’t just

multiply the numbers on a pairwise basis, like matrix addition, and be done

with it.

The reason we care about matrix multiplication is that there are many things

we can do with it. We will review these applications here.

8.2. VISUALIZING MATRIX OPERATIONS 245

Figure 8.5: The Lincoln memorial M(left) and its covariance matrices. The big

block in the middle of M·MT(center) results from the similarity of all rows

from the middle stripe of M. The tight grid pattern of MT·M(right) reﬂects

the regular pattern of the columns on the memorial building.

Covariance Matrices

Multiplying a matrix Aby its transpose ATis a very common operation. Why?

For one thing, we can multiply it: if Ais an n×dmatrix, then ATis a d×

nmatrix. Thus it is always compatible to multiply AAT. They are equally

compatible to multiply the other way, i.e. ATA.

Both of these products have important interpretations. Suppose Ais an

n×dfeature matrix, consisting of nrows representing items or points, and d

columns representing the observed features of these items. Then:

•C=A·ATis an n×nmatrix of dot products, measuring the “in sync-

ness” among the points. In particular Cij is a measure of how similar item

iis to item j.

•D=AT·Ais a d×dmatrix of dot products, measuring the “in sync-ness”

among columns or features. Now Dij represents the similarity between

feature iand feature j.

These beasts are common enough to earn their own name, covariance ma-

trices. This term comes up often in conversations among data scientists, so

get comfortable with it. The covariance formula we gave when computing the

correlation coeﬃcient was

Cov(X, Y ) =

i=1

(Xi−¯

X)(Yi−¯

Y).

so, strictly speaking, our beasts are covariance matrices only if the rows or

columns of Ahave mean zero. But regardless, the magnitudes of the matrix

product captures the degree to which the values of particular row or column

pairs move together.

Figure 8.5 presents the covariance matrices of the Lincoln memorial. Darker

spots deﬁne rows and columns in the image with the greatest similarity. Try to

understand where the visible structures in these covariance matrices come from.

246 CHAPTER 8. LINEAR ALGEBRA

Figure 8.5 (center) presents M·MT, the covariance matrix of the rows. The

big dark box in the middle represents the large dot products resulting from any

two rows cutting across all the memorial’s white columns. These bands of light

and dark are strongly correlated, and the intensely dark regions contribute to

a large dot product. The light rows corresponding to the sky, pediment, and

stairs are equally correlated and coherent, but lack the dark regions to make

their dot products large enough.

The right image presents MT·M, which is the covariance matrix of the

columns. All the pairs of matrix columns strongly correlate with each other,

either positively or negatively, but the matrix columns through the white build-

ing columns have low weight and hence a small dot product. Together, they

deﬁne a checkerboard of alternating dark and light stripes.

Matrix Multiplication and Paths

Square matrices can be multiplied by themselves without transposition. Indeed,

A2=A×Ais called the square of matrix A. More generally Akis called the

kth power of the matrix.

The powers of matrix Ahave a very natural interpretation, when Arep-

resents the adjacency matrix of a graph or network. In an adjacency matrix,

A[i, j] = 1 when (i, j) is an edge in the network. Otherwise, when iand jare

not direct neighbors, A[i, j] = 0.

For such 0/1 matrices, the product A2yields the number of paths of length

two in A. In particular:

A2[i, j] =

k=1

A[i, k]·A[k, j].

There is exactly one path of length two from ito jfor every intermediate vertex

ksuch that (i, k) and (k, j) are both edges in the graph. The sum of these path

counts is computed by the dot product above.

But computing powers of matrices makes sense even for more general matri-

ces. It simulates the eﬀects of diﬀusion, spreading out the weight of each element

among related elements. Such things happen in Google’s famous PageRank al-

gorithm, and other iterative processes such as contagion spreading.

Matrix Multiplication and Permutations

Matrix multiplication is often used just to rearrange the order of the elements

in a particular matrix. Recall that high-performance matrix multiplication rou-

tines are blindingly fast, enough so they can often perform such operations faster

than ad hoc programming logic. They also provide a way to describe such op-

erations in the notation of algebraic formulae, thus preserving compactness and

readability.

The most famous rearrangement matrix does nothing at all. The identity

matrix is an n×nmatrix consisting of all zeros, except for the ones all along

8.2. VISUALIZING MATRIX OPERATIONS 247

P=





0010

1000

0001

0100







M=





11 12 13 14

21 22 23 24

31 32 33 34

41 42 43 44







P M =





31 32 33 34

11 12 13 14

41 42 43 44

21 22 23 24







Figure 8.6: Multiplying a matrix by a permutation matrix rearranges its rows

and columns.

Figure 8.7: Multiplying the Lincoln matrix Mby the reverse permutation matrix

r(center). The product r·Mﬂips Lincoln upside down (left), while M·rparts

his hair on the other side of his head (right).

the main diagonal. For n= 4,

I=





1000

0100

0010

0001







Convince yourself that AI =IA =A, meaning that multiplication by the

identity matrix commutes.

Note that each row and column of Icontains exactly one non-zero element.

Matrices with this property are called permutation matrices, because the non-

zero element in position (i, j) can be interpreted as meaning that element iis

in position jof a permutation. For example, the permutation (2,4,3,1) deﬁnes

the permutation matrix:

P(2431) =





0001

1000

0010

0100







Observe that the identity matrix corresponds to the permutation (1,2, . . . , n).

The key point here is that we can multiply Aby the appropriate permutation

matrix to rearrange the rows and columns, however we wish. Figure 8.7 shows

what happens when we multiply our image by a “reverse” permutation matrix

248 CHAPTER 8. LINEAR ALGEBRA

r, where the ones lie along the minor diagonal. Because matrix multiplication is

not generally commutative, we get diﬀerent results for A·rand r·A. Convince

yourself why.

Rotating Points in Space

Multiplying something by the right matrix can have magical properties. We

have seen how a set of npoints in the plane (i.e. two dimensions) can be

represented by an (n×2)-dimensional matrix S. Multiplying such points by the

right matrix can yield natural geometric transformations.

The rotation matrix Rθperforms the transformation of rotating points about

the origin through an angle of θ. In two dimensions, Rθis deﬁned as

Rθ=cos(θ)−sin(θ)

sin(θ) cos(θ)

In particular, after the appropriate multiplication/rotation, point (x, y) goes to

x0

y0=Rθx

y=xcos(θ)−ysin(θ)

xsin(θ) + ycos(θ)

For θ= 180◦=πradians, cos(θ) = −1 and sin(θ) = 0, so this reduces to

(−x, −y), doing the right thing by putting the point in the opposing quadrant.

For our (n×2)-dimensional point matrix S, we can use the transpose function

to orient the matrix appropriately. Check to conﬁrm that

S0= (RθST)T

does exactly what we want to do.

Natural generalizations of Rθexist to rotate points in arbitrary dimensions.

Further, arbitrary sequences of successive transformations can be realized by

multiplying chains of rotation, dilation, and reﬂection matrices, yielding a com-

pact description of complex manipulations.

8.2.4 Identity Matrices and Inversion

Identity operations play a big role in algebraic structures. For numerical addi-

tion, zero is the identity element, since 0 + x=x+ 0 = x. The same role is

played by one for multiplication, since 1 ·x=x·1 = x.

In matrix multiplication, the identity element is the identity matrix, with all

ones down the main diagonal. Multiplication by the identity matrix commutes,

so IA =AI =A.

The inverse operation is about taking an element xdown to its identity

element. For numerical addition, the inverse of xis (−x), because x+(−x) = 0.

The inverse operation for multiplication is called division. We can invert a

number by multiplying it by its reciprocal, since x·(1/x) = 1.

People do not generally talk about dividing matrices. However, they very

frequently go about inverting them. We say A−1is the multiplicative inverse

8.2. VISUALIZING MATRIX OPERATIONS 249

Figure 8.8: The inverse of Lincoln does not look much like the man (left) but

M·M−1produces the identity matrix, modulo small non-zero terms due to

numerical precision issues.

of matrix Aif A·A−1=I, where Iis the identity matrix. Inversion is an

important special case of division, since A·A−1=Iimplies A−1=I/A. They

are in fact equivalent operations, because A/B =A·B−1.

Figure 8.8 (left) shows the inverse of our Lincoln picture, which looks pretty

much like random noise. But multiplying it by the image yields the thin main

diagonal of the identity matrix, albeit superimposed on a background of numeri-

cal error. Floating point computations are inherently imprecise, and algorithms

like inversion which perform repeated additions and multiplications often accu-

mulate error in the process.

How can we compute the inverse of a matrix? A closed form exists for ﬁnding

the inverse A−1of a 2 ×2 matrix A, namely:

A−1=a b

c d−1

ad −bcd−b

−c a 

More generally, there is an approach to inverting matrices by solving a linear

system using Gaussian elimination.

Observe that this closed form for inversion divides by zero whenever the

products of the diagonals are equal, i.e. ad =bc. This tells us that such

matrices are not invertible or singular, meaning no inverse exists. Just as we

cannot divide numbers by zero, we cannot invert singular matrices.

The matrices we can invert are called non-singular, and life is better when

our matrices have this property. The test of whether a matrix is invertible is

whether its determinant is not zero. For 2 ×2 matrices, the determinant is the

diﬀerence between the product of its diagonals, exactly the denominator in the

inversion formula.

Further, the determinant is only deﬁned for square matrices, so only square

matricies are invertible. The cost of computing this determinant is O(n3), so

it is expensive on large matricies, indeed as expensive as trying to invert the

matrix itself using Gaussian elimination.

250 CHAPTER 8. LINEAR ALGEBRA

[A|I] = 



6 4 1 1 0 0

1072010

5 3 1 0 0 1 

=



11010−1

01001−2

5 3 1 0 0 1 



=



1001−1 1

0 1 0 0 1 −2

5 3 1 0 0 1 

=



100 1−1 1

0 1 0 0 1 −2

001−5 2 2 



→A−1=



1−1 1

0 1 −2

−5 2 2 



Figure 8.9: The inverse of a matrix can be computed by Gaussian elimination.

8.2.5 Matrix Inversion and Linear Systems

Linear equations are deﬁned by the sum of variables weighted by constant co-

eﬃcients:

y=c0+c1x1+c2x2+. . . cm−1xm−1.

Thus the coeﬃcients deﬁning a system of nlinear equations can be represented

as an n×mmatrix C. Here each row represents an equation, and each of the

mcolumns the coeﬃcients of a distinct variable.

We can neatly evaluate all nof these equations on a particular m×1 input

vector X, by multiplying C·X. The result will be an n×1 vector, reporting

the value fi(X) for each of the nlinear equations, 1 ≤i≤n. The special case

here is the additive term c0. For proper interpretation, the associated column

in Xshould contain all ones.

If we generalize Xto be an m×pmatrix containing pdistinct points, our

product C·xresults in an n×pmatrix, evaluating every point against every

equation in a single matrix multiplication.

But the primary operation on systems of nequations is to solve them, mean-

ing to identify the Xvector necessary to yield a target Yvalue for each equation.

Give the n×1 vector of solution values Yand coeﬃcient matrix C, we seek X

such that C·X=Y.

Matrix inversion can be used to solve linear systems. Multiplying both sides

of CX =Yby the inverse of C yields:

(C−1C)X=C−1Y−→ X=C−1Y.

Thus the system of equations can be solved by inverting Cand then multiplying

C−1by Y.

Gaussian elimination is another approach to solving linear systems, which I

trust you have seen before. Recall that it solves the equations by performing

row addition/subtraction operations to simplify the equation matrix Cuntil it

reduces to the identity matrix. This makes it trivial to read oﬀ the values of the

8.2. VISUALIZING MATRIX OPERATIONS 251

variables, since every equation has been reduced to the form Xi=Y0

i, where Y0

is the result of applying these same row operations to the original target vector

Computing the matrix inverse can be done in the same fashion, as shown in

Figure 8.9. We perform row operations to simplify the coeﬃcient matrix to the

identity matrix Iin order to create the inverse. I think of this as the algorithm

of Dorian Gray: the coeﬃcient matrix Cbeautiﬁes to the identity matrix, while

the target Iages into the inverse.1

Therefore we can use matrix inversion to solve linear systems, and linear

system solvers to invert matrices. Thus the two problems are in some sense

equivalent. Computing the inverse makes it cheap to evaluate multiple Yvectors

for a given system C, by reducing it to a single matrix multiplication. But this

can be done even more eﬃciently with LU-decomposition, discussed in Section

8.3.2. Gaussian elimination proves more numerically stable than inversion, and

is generally the method of choice when solving linear systems.

8.2.6 Matrix Rank

A system of equations is properly determined when there are nlinearly inde-

pendent equations and nunknowns. For example, the linear system

2x1+ 1x2= 5

3x1−2x2= 4

is properly determined. The only solution is the point (x1= 2, x2= 1).

In contrast, systems of equations are underdetermined if there are rows (equa-

tions) that can be expressed as linear combinations of other rows. The linear

system

2x1+ 1x2= 5

4x1+ 2x2= 10

is underdetermined, because the second row is twice that of the ﬁrst row. It

should be clear that there is not enough information to solve an undetermined

system of linear equations.

The rank of a matrix measures the number of linearly independent rows. An

n×nmatrix should be rank nfor all operations to be properly deﬁned on it.

The rank of the matrix can be computed by running Gaussian elimination.

If it is underdetermined, then certain variables will disappear in the course of

row-reduction operations. There is also a connection between underdetermined

systems and singular matrices: recall that they were identiﬁed by having a

determinant of zero. That is why the diﬀerence in the cross product here (2 ·

2−4·1) equals zero.

1In Oscar Wilde’s novel The Picture of Dorian Gray, the protagonist remains beautiful,

while his picture ages horribly over the years.

252 CHAPTER 8. LINEAR ALGEBRA

Feature matrices are often of lower rank than we might desire. Files of

examples tend to contain duplicate entries, which would result in two rows of

the matrix being identical. It is also quite possible for multiple columns to be

equivalent: imagine each record as containing the height measured in both feet

and meters, for example.

These things certainly happen, and are bad when they do. Certain algo-

rithms on our Lincoln memorial image failed numerically. It turned out that

our 512 ×512 image had a rank of only 508, so not all rows were linearly inde-

pendent. To make it a full-rank matrix, you can add a small amount of random

noise to each element, which will increase the rank without serious image dis-

tortion. This kludge might get your data to pass through an algorithm without

a warning message, but it is indicative of numerical trouble to come.

Linear systems can be “almost” of lower rank, which results in a greater

danger of precision loss due to numerical issues. This is formally captured by a

matrix invariant called the condition number, which in the case of a linear system

measures how sensitive the value of Xis to small changes of Yin Y=AX.

Be aware of the vagaries of numerical computation when evaluating your

results. For example, it is a good practice to compute AX for any purported

solution X, and see how well AX really compares to Y. In theory the diﬀerence

will be zero, but in practice you may be surprised how rough the calculation

really is.

8.3 Factoring Matrices

Factoring matrix Ainto matrices Band Crepresents a particular aspect of

division. We have seen that any non-singular matrix Mhas an inverse M−1,

so the identity matrix Ican be factored as I=MM−1. This proves that

some matrices (like I) can be factored, and further that they might have many

distinct factorizations. In this case, every possible non-singular Mdeﬁnes a

diﬀerent factorization.

Matrix factorization is an important abstraction in data science, leading

to concise feature representations and ideas like topic modeling. It plays an

important part in solving linear systems, through special factorizations like LU-

decomposition.

Unfortunately, ﬁnding such factorizations is problematic. Factoring integers

is a hard problem, although that complexity goes away when you are allowed

ﬂoating point numbers. Factoring matrices proves harder: for a particular ma-

trix, exact factorization may not be possible, particularly if we seek the factor-

ization M=XY where Xand Yhave prescribed dimensions.

8.3.1 Why Factor Feature Matrices?

Many important machine learning algorithms can be viewed in terms of factoring

a matrix. Suppose we are given an n×mfeature matrix Awhere, as per the

8.3. FACTORING MATRICES 253

..........

...

..........

...

..........

≈

Figure 8.10: Factoring a feature matrix A≈BC yields Bas a more concise

representation of the items and Cas a more concise representations of the

features AT.

usual convention, rows represent items/examples and columns represent features

of the examples.

Now suppose that we can factor matrix A, meaning express it as the product

A≈B·C, where Bis an n×kmatrix and Cak×mmatrix. Presuming that

k < min(n, m), as shown in Figure 8.10, this is a good thing for several reasons:

•Together, Band Cprovide a compressed representation of matrix A: Fea-

ture matrices are generally large, ungainly things to work with. Factoriza-

tion provides a way to encode all the information of the large matrix into

two smaller matrices, which together will be smaller than the original.

•Bserves as a smaller feature matrix on the items, replacing A: The

factor matrix Bhas nrows, just like the original matrix A. However, it

has substantially fewer columns, since k < m. This means that “most” of

the information in Ais now encoded in B. Fewer columns mean a smaller

matrix, and less parameters to ﬁt in any model built using these new

features. These more abstract features may also be of interest to other

applications, as concise descriptions of the rows of the data set.

•CTserves as a small feature matrix on the features, replacing AT: Trans-

posing the feature matrix turns columns/features into rows/items. The

factor matrix CThas mrows and kcolumns of properties representing

them. In many cases, the moriginal “features” are worth modeling in

their own right.

Consider a representative example from text analysis. Perhaps we want to

represent ndocuments, each a tweet or other social message post, in terms

of the vocabulary it uses. Each of our mfeatures will correspond to a distinct

vocabulary word, and A[i, j] will record how often vocabulary word wj(say, cat)

appeared in message number i. The working vocabulary in English is large with

a long tail, so perhaps we can restrict it to the m= 50,000 most frequently used

words. Most messages will be short, with no more than a few hundred words.

Thus our feature matrix Awill be very sparse, riddled with a huge number of

zeros.

Now suppose that we can factor A=BC, where the inner dimension kis

relatively small. Say k= 100. Now each post will be represented by a row of

254 CHAPTER 8. LINEAR ALGEBRA

Bcontaining only a hundred numbers, instead of the full 50,000. This makes

it much easier to compare the texts for similarity in a meaningful way. These

kdimensions can be thought of as analogous to the “topics” in the documents,

so all the posts about sports should light up a diﬀerent set of topics than those

about relationships.

The matrix CTcan now be thought of as containing a feature vector for

each of the vocabulary words. This is interesting. We would expect words that

apply in similar contexts to have similar topic vectors. Color words like yellow

and red are likely to look fairly similar in topic space, while baseball and sex

should have quite distant relationships.

Note that this word–topic matrix is potentially useful in any problem seeking

to use language as features. The connection with social message posts is largely

gone, so it would be applicable to other domains like books and news. Indeed,

such compressed word embeddings prove a very powerful tool in natural language

processing (NLP), as will be discussed in Section 11.6.3.

8.3.2 LU Decomposition and Determinants

LU decomposition is a particular matrix factorization which factors a square

matrix Ainto lower and upper triangular matrices Land U, such that A=L·U.

A matrix is triangular if it contains all zero terms either above or below the

main diagonal. The lower triangular matrix Lhas all non-zero terms below the

main diagonal. The other factor, U, is the upper triangular matrix. Since the

main diagonal of Lconsists of all ones, we can pack the entire decomposition

into the same space as the original n×nmatrix.

The primary value of LU decomposition is that it proves useful in solving

linear systems AX =Y, particularly when solving multiple problems with the

same Abut diﬀerent Y. The matrix Lis what results from clearing out all

of the values above the main diagonal, via Gaussian elimination. Once in this

triangular form, the remaining equations can be directly simpliﬁed. The ma-

trix Ureﬂects what row operations have occurred in the course of building L.

Simplifying Uand applying Lto Yrequires less work than solving Afrom

scratch.

The other importance of LU decomposition is in yielding an algorithm to

compute the determinant of a matrix. The determinant of Ais the product of

the main diagonal elements of U. As we have seen, a determinant of zero means

the matrix is not of full rank.

Figure 8.11 illustrates the LU decomposition of the Lincoln memorial. There

is a distinct texture visible to the two triangular matrices. This particular LU

decomposition function (in Mathematica) took advantage of the fact that the

equations in a system can be permuted with no loss of information. The same

does not hold true for images, but we see accurate reconstructions of the white

columns of the memorial, albeit out of position.

8.4. EIGENVALUES AND EIGENVECTORS 255

Figure 8.11: The LU decomposition of the Lincoln memorial (left), with the

product L·U(center). The rows of the LU matrix were permuted during

calculation, but when properly ordered fully reconstructed the image (right).

8.4 Eigenvalues and Eigenvectors

Multiplying a vector Uby a square matrix Acan have the same eﬀect as multi-

plying it by a scalar l. Consider this pair of examples. Indeed, check them out

by hand:

−5 2

2−2·2

−1=−62

−1

−5 2

2−2·1

2=−11

2

Both of these equalities feature products with the same 2 ×1 vector Uon the

left as on the right. On one side Uis multiplied by a matrix A, and on the other

by a scalar λ. In cases like this, when AU =λU, we say that λis an eigenvalue

of matrix A, and Uis its associated eigenvector.

Such eigenvector–eigenvalue pairs are a curious thing. That the scalar λcan

do the same thing to Uas the entire matrix Atells us that they must be special.

Together, the eigenvector Uand eigenvalue λmust encode a lot of information

about A.

Further, there are generally multiple such eigenvector–eigenvalue pairs for

any matrix. Note that the second example above works on the same matrix A,

but yields a diﬀerent Uand λ.

8.4.1 Properties of Eigenvalues

The theory of eigenvalues gets us deeper into the thicket of linear algebra than I

am prepared to do in this text. Generally speaking, however, we can summarize

the properties that will prove important to us:

•Each eigenvalue has an associated eigenvector. They always come in pairs.

•There are, in general, neigenvector–eigenvalue pairs for every full rank

n×nmatrix.

256 CHAPTER 8. LINEAR ALGEBRA

•Every pair of eigenvectors of a symmetric matrix are mutually orthogonal,

the same way that the xand y-axes in the plane are orthogonal. Two

vectors are orthogonal if their dot product is zero. Observe that (0,1) ·

(1,0) = 0, as does (2,−1) ·(1,2) = 0 from the previous example.

•The upshot from this is that eigenvectors can play the role of dimensions

or bases in some n-dimensional space. This opens up many geometric in-

terpretations of matrices. In particular, any matrix can be encoded where

each eigenvalue represents the magnitude of its associated eigenvector.

8.4.2 Computing Eigenvalues

The ndistinct eigenvalues of a rank-nmatrix can be found by factoring its

characteristic equation. Start from the deﬁning equality AU =λU. Convince

yourself that this remains unchanged when we multiply by the identity matrix

I, so

AU =λIU →(A−λI)U= 0.

For our example matrix, we get

A−λI =−5−λ2

2−2−λ

Note that our equality (A−λI)U= 0 remains true if we multiply vector U

by any scalar value c. This implies that there are an inﬁnite number of solutions,

and hence the linear system must be underdetermined.

In such a situation, the determinant of the matrix must be zero. With a

2×2 matrix, the determinant is just the cross product ad −bc, so

(−5−λ)(−2−λ)−2·2 = λ2+ 7λ+ 6 = 0.

Solving for λwith the quadratic formula yields λ=−1 and λ=−6. More

generally, the determinant |A−λI|is a polynomial of degree n, and hence the

roots of this characteristic equation deﬁne the eigenvalues of A.

The vector associated with any given eigenvalue can be computed by solving

a linear system. As per our example, we know that

−5 2

2−2·u1

u2=λu1

u2

for any eigenvalue λand associated eigenvector U=u1

u2. Once we ﬁx the

value of λ, we have a system of nequations and nunknowns, and thus can solve

for the values of U. For λ=−1,

−5u1+ 2u2=−1u1−→ −4u1+ 2u2= 0

2u1+−2u2=−1u2−→ 2u1+−1u2= 0

which has the solution u1= 1, u2= 2, yielding the associated eigenvector.

8.5. EIGENVALUE DECOMPOSITION 257

For λ=−6, we get

−5u1+ 2u2=−6u1−→ 1u1+ 2u2= 0

2u1+−2u2=−6u2−→ 2u1+ 4u2= 0

This system is underdetermined, so u1= 2, u2=−1 and any constant multiple

of this qualiﬁes as an eigenvector. This makes sense: because Uis on both sides

of the equality AU =λU, for any constant c, the vector U0=c·Uequally

satisﬁes the deﬁnition.

Faster algorithms for eigenvalue/vector computations are based on a matrix

factorization approach called QR decomposition. Other algorithms try to avoid

solving the full linear system. For example, an alternate approach repeatedly

uses U0= (AU)/λ to compute better and better approximations to Uuntil it

converges. When conditions are right, this can be much faster than solving the

full linear system.

The largest eigenvalues and their associated vectors are, generally speaking,

more important that the rest. Why? Because they make a larger contribution

to approximating the matrix A. Thus high-performance linear algebra systems

use special routines for ﬁnding the klargest (and smallest) eigenvalues and then

iterative methods to reconstruct the vectors for each.

8.5 Eigenvalue Decomposition

Any n×nsymmetric matrix Mcan be decomposed into the sum of its n

eigenvector products. We call the neigenpairs (λi, Ui), for 1 ≤i≤n. By

convention we sort by size, so λi≥λi−ifor all i.

Since each eigenvector Uiis an n×1 matrix, multiplying it by its transpose

yields an n×nmatrix product, UiUiT. This has exactly the same dimensions

as the original matrix M. We can compute the linear combination of these

matrices weighted by its corresponding eigenvalue. In fact, this reconstructs

the original matrix, since:

i=1

λiUiUiT

This result holds only for symmetric matrices, so we cannot use it to encode

our image. But covariance matrices are always symmetric, and they encode the

basic features of each row and column of the matrix.

Thus the covariance matrix can be represented by its eigenvalue decompo-

sition. This takes slightly more space than the initial matrix: neigenvectors of

length n, plus neigenvalues vs. the n(n+ 1)/2 elements in the upper triangle

of the symmetric matrix plus main diagonal.

However, by using only the vectors associated with the largest eigenvalues

we get a good approximation of the matrix. The smaller dimensions contribute

very little to the matrix values, and so they can be excluded with little resulting

error. This dimension reduction method is very useful to produce smaller, more

eﬀective feature sets.

258 CHAPTER 8. LINEAR ALGEBRA

Figure 8.12: The Lincoln memorial’s biggest eigenvector suﬃces to capture much

of the detail of its covariance matrix.

Figure 8.13: Error in reconstructing the Lincoln memorial from the one, ﬁve,

and ﬁfty largest eigenvectors.

Figure 8.12 (left) shows the reconstruction of the Lincoln memorial’s covari-

ance matrix Mfrom its single largest eigenvector, i.e. U1·UT

1, along with its

associated error matrix M−U1·UT

1. Even a single eigenvector does a very

respectable job at reconstruction, restoring features like the large central block.

The plot in Figure 8.12 (right) shows that the errors occur in patchy regions,

because more subtle detail requires additional vectors to encode. Figure 8.13

shows the error plot when using the one, ﬁve, and ﬁfty largest eigenvectors.

The error regions get smaller as we reconstruct ﬁner detail, and the magnitude

of the errors smaller. Realize that even ﬁfty eigenvectors is less than 10% of

the 512 necessary to restore a perfect matrix, but this suﬃces for a very good

approximation.

8.5.1 Singular Value Decomposition

Eigenvalue decomposition is a very good thing. But it only works on symmetric

matrices. Singular value decomposition is a more general matrix factorization

approach, that similarly reduces a matrix to the sum of other matrices deﬁned

by vectors.

The singular value decomposition of an n×mreal matrix Mfactors it into

three matrices U,D, and V, with dimensions n×n,n×m, and m×mrespec-

8.5. EIGENVALUE DECOMPOSITION 259

Figure 8.14: Singular value matrices in the decomposition of Lincoln, for 50

singular values.

tively. This factorization is of the form2

M=UDV T

The center matrix Dhas the property that it is a diagonal matrix, meaning all

non-zero values lie on the main diagonal like the identity matrix I.

Don’t worry about how we ﬁnd this factorization. Instead, let’s concentrate

on what it means. The product U·Dhas the eﬀect of multiplying U[i, j] by

D[j, j], because all terms of Dare zero except along the main diagonal. Thus

Dcan be interpreted as measuring the relative importance of each column of

U, or through D·VT, the importance of each row of VT. These weight values

of Dare called the singular values of M.

Let Xand Ybe vectors, of dimensionality n×1 and 1×m, respectively. The

matrix outer product P=XNYis the n×mmatrix where P[j, k] = X[j]Y[k].

The traditional matrix multiplication C=A·Bcan be expressed as the sum of

these outer products, namely:

C=A·B=X

AkOBT

where Akis the vector deﬁned by the kth column of A, and BT

kis the vector

deﬁned by the kth row of B.

Putting this together, matrix Mcan be expressed as the sum of outer prod-

ucts of vectors resulting from the singular value decomposition, namely (UD)k

and (VT)kfor 1 ≤k≤m. Further, the singular values Ddeﬁne how much con-

tribution each outer product makes to M, so it suﬃces to take only the vectors

associated with the largest singular values to get an approximation to M.

2Should Mcontain convex numbers, then this generalizes to M=U DV ∗, where V∗means

the conjugate transpose of V.

260 CHAPTER 8. LINEAR ALGEBRA

Figure 8.15: Lincoln’s face reconstructed from 5 (left) and 50 (center) singular

values, with the error for k= 50 (right).

Figure 8.14 (left) presents the vectors associated with the ﬁrst ﬁfty singular

values of Lincoln’s face. If you look carefully, you can see how the ﬁrst ﬁve to

ten vectors are considerably more blocky than subsequent ones, indicating that

the early vectors rough out the basic structure of the matrix, with subsequent

vectors adding greater detail. Figure 8.14 (right) shows how the mean squared

error between the matrix and its reconstruction shrinks as we add additional

vectors.

These eﬀects become even more vivid when we look at the reconstructed

images themselves. Figure 8.15 (left) shows Lincoln’s face with only the ﬁve

strongest vectors, which is less than 1% of what is available for perfect recon-

struction. But even at this point you could pick him out of a police lineup.

Figure 8.15 (center) demonstrates the greater detail when we include ﬁfty vec-

tors. This looks as good as the raw image in print, although the error plot

(Figure 8.15 (right)) highlights the missing detail.

Take-Home Lesson: Singular value decomposition (SVD) is a powerful tech-

nique to reduce the dimensionality of any feature matrix.

8.5.2 Principal Components Analysis

Principal components analysis (PCA) is a closely related technique for reducing

the dimensionality of data sets. Like SVD, we will deﬁne vectors to represent

the data set. Like SVD, we will order them by successive importance, so we can

reconstruct an approximate representation using few components. PCA and

SVD are so closely related as to be indistinguishable for our purposes. They do

the same thing in the same way, but coming from diﬀerent directions.

The principal components deﬁne the axes of an ellipsoid best ﬁtting the

points. The origin of this set of axes is the centroid of the points. PCA starts

by identifying the direction to project the points on to so as to explain the

maximum amount of variance. This is the line through the centroid that, in

some sense, best ﬁts the points, making it analogous to linear regression. We

can then project each point onto this line, with this point of intersection deﬁn-

ing a particular position on the line relative to the centroid. These projected

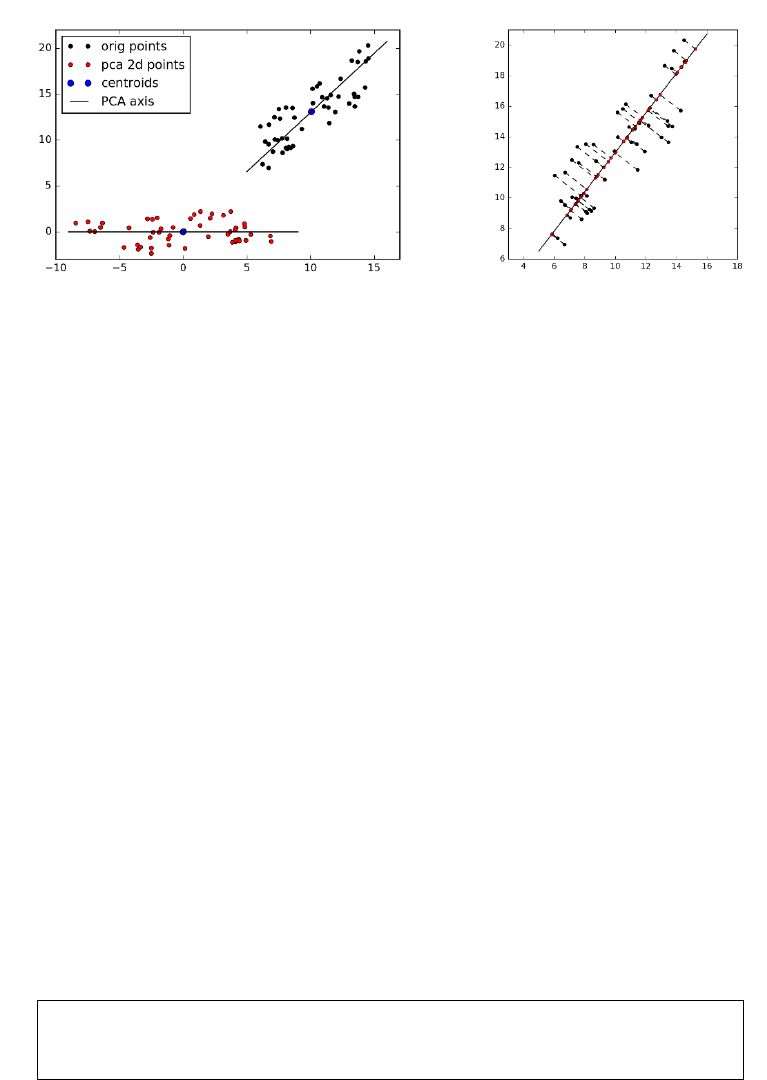
8.5. EIGENVALUE DECOMPOSITION 261

Figure 8.16: PCA projects the black points onto orthogonal axis, rotated to

yield the alternate representation in red (left). The values of each component

are given by projecting each point onto the appropriate axis (right).

positions now deﬁne the ﬁrst dimension (or principal component) of our new

representation, as shown in Figure 8.16.

For each subsequent component, we seek the line lk, which is orthogonal to

all previous lines and explains the largest amount of the remaining variance.

That each dimension is orthogonal to each other means they act like coordinate

axes, establishing the connection to eigenvectors. Each subsequent dimension is

progressively less important than the ones before it, because we chose the most

promising directions ﬁrst. Later components contribute only progressively ﬁner

detail, and hence we can stop once this is small enough.

Suppose that dimensions xand yare virtually identical. We would expect

that the regression line will project down to y=xon these two dimensions, so

they could then largely be replaced by a single dimension. PCA constructs new

dimensions as linear combinations of the original ones, collapsing those which

are highly correlated into a lower-dimensional space. Statistical factor analysis

is a technique which identiﬁes the most important orthogonal dimensions (as

measured by correlation) that explain the bulk of the variance.

Relatively few components suﬃce to capture the basic structure of the point

set. The residual that remains is likely to be noise, and is often better oﬀ

removed from the data. After dimension reduction via PCA (or SVD), we

should end up with cleaner data, not merely a smaller number of dimensions.

Take-Home Lesson: PCA and SVD are essentially two diﬀerent approaches to

computing the same thing. They should serve equally well as low-dimensional

approximations of a feature matrix.

262 CHAPTER 8. LINEAR ALGEBRA

8.6 War Story: The Human Factors

I ﬁrst came to be amazed by the power of dimension reduction methods like

PCA and SVD in the course of our analysis of historical ﬁgures for our book

Who’s Bigger. Recall (from the war story of Section 4.7) how we analyzed the

structure and content of Wikipedia, ultimately extracting a half-dozen features

like PageRank and article length for each of the 800,000+ articles about people

in the English edition. This reduced each of these people to a six-dimensional

feature vector, which we would analyze to judge their relative signiﬁcance.

But things proved not as straightforward as we thought. Wildly diﬀerent

people were ranked highest by each particular variable. It wasn’t clear how to

interpret them.

“There is so much variance and random noise in our features,” my co-author

Charles observed. “Let’s identify the major factors underlying these observed

variables that really show what is going on.”

Charles’ solution was factor analysis, which is a variant of PCA, which is in

turn a variant of SVD. All of these techniques compress feature matrices into a

smaller set of variables or factors, with the goal that these factors explain most

of the variance in the full feature matrix. We expected factor analysis would

extract a single underlying factor deﬁning individual signiﬁcance. But instead,

our input variables yielded two independent factors explaining the data. Both

explained roughly equal proportions of the variance (31% and 28%), meaning

that these latent variables were approximately of equal importance. But the

cool thing is what these factors showed.

Factors (or singular vectors, or principle components) are just linear combi-

nations of the original input features. They don’t come with names attached to

them, so usually you would just describe them as Factor 1 and Factor 2. But

our two factors were so distinctive that Charles gave them the names gravitas

and celebrity, and you can see why in Figure 8.17.

Our gravitas factor largely comes from (or “loads on,” in statistical par-

lance) the two forms of PageRank. Gravitas seems to accurately capture no-

tions of achievement-based recognition. In contrast, the celebrity factor loads

more strongly on page hits, revisions, and article length. The celebrity fac-

tor better captures the popular (some might say vulgar) notions of reputation.

The wattage of singers, actors, and other entertainers are better measured by

celebrity then gravitas.

To get a feel for the distinction between gravitas and celebrity, compare

our highest ranked ﬁgures for each factor, in Figure 8.17. The high gravitas

ﬁgures on the left are clearly old-fashioned heavyweights, people of stature and

accomplishment. They are philosophers, kings, and statesmen. Those names

listed in Figure 8.17 (right) are such complete celebrities that the top four walk

this earth with only one name. They are professional wrestlers, actors, and

singers. It is quite telling that the only two ﬁgures here showing any gravitas

on our celebrity-gravitas meter are Britney Spears (1981– ) [566] and Michael

Jackson (1958–2009) [136], both among the Platonic ideals of modern celebrity.

I ﬁnd it amazing that these unsupervised methods were able to tease apart

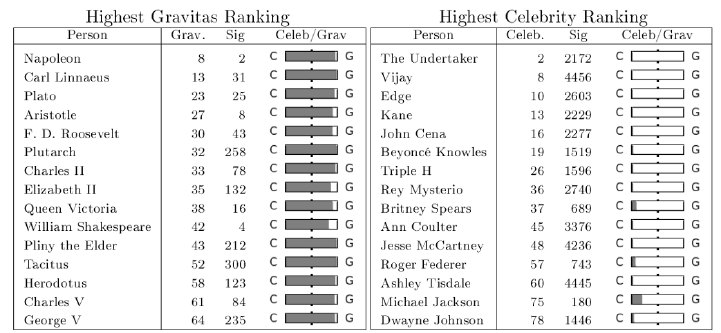
8.7. CHAPTER NOTES 263

Figure 8.17: The gravitas and celebrity factors do an excellent job partitioning

two types of famous people.

two distinct types of fame, without any labeled training examples or even a

preconception of what they were looking for. The factors/vectors/components

simply reﬂected what was there in the data to be found.

This celebrity-gravitas continuum serves as an instructive example of the

power of dimension reduction methods. All the factors/vectors/components all

must, by deﬁnition, be orthogonal to each other. This means that they each

measure diﬀerent things, in a way that two correlated input variables do not.

It pays to do some exploratory data analysis on your main components to try

to ﬁgure out what they really mean, in the context of your application. The

factors are yours to name as you wish, just like a cat or a dog, so choose names

you will be happy to live with.

8.7 Chapter Notes

There are many popular textbooks providing introductions to linear algebra, in-

cluding [LLM15, Str11, Tuc88]. Klein [Kle13] presents an interesting introduc-

tion to linear algebra for computer science, with an emphasis on programming

and applications like coding theory and computer graphics.

8.8 Exercises

Basic Linear Algebra

8-1. [3] Give a pair of square matrices Aand Bsuch that:

(a) AB =BA (it commutes).

(b) AB 6=BA (does not commute).

264 CHAPTER 8. LINEAR ALGEBRA

In general, matrix multiplication is not commutative.

8-2. [3] Prove that matrix addition is associative, i.e. that (A+B)+C=A+(B+C)

for compatible matrices A,Band C.

8-3. [5] Prove that matrix multiplication is associative, i.e. that (AB)C=A(BC)

for compatible matrices A,Band C.

8-4. [3] Prove that AB =BA, if Aand Bare diagonal matrices of the same order.

8-5. [5] Prove that if AC =CA and BC =CB, then

C(AB +BA) = (AB +BA)C.

8-6. [3] Are the matrices MM Tand MTMsquare and symmetric? Explain.

8-7. [5] Prove that (A−1)−1=A.

8-8. [5] Prove that (AT)−1= (A−1)Tfor any non-singular matrix A.

8-9. [5] Is the LU factorization of a matrix unique? Justify your answer.

8-10. [3] Explain how to solve the matrix equation Ax =b?

8-11. [5] Show that if Mis a square matrix which is not invertible, then either Lor

Uin the LU-decomposition M=L·Uhas a zero in its diagonal.

Eigenvalues and Eigenvectors

8-12. [3] Let M=2 1

0 2. Find all eigenvalues of M. Does Mhave two linearly

independent eigenvectors?

8-13. [3] Prove that the eigenvalues of Aand ATare identical.

8-14. [3] Prove that the eigenvalues of a diagonal matrix are equal to the diagonal

elements.

8-15. [5] Suppose that matrix Ahas an eigenvector vwith eigenvalue λ. Show that v

is also an eigenvector for A2, and ﬁnd the corresponding eigenvalue. How about

for Ak, for 2 ≤k≤n?

8-16. [5] Suppose that Ais an invertible matrix with eigenvector v. Show that vis

also an eigenvector for A−1.

8-17. [8] Show that the eigenvalues of MMTare the same as that of MTM. Are

their eigenvectors also the same?

Implementation Projects

8-18. [5] Compare the speed of a library function for matrix multiplication to your

own implementation of the nested loops algorithm.

•How much faster is the library on products of random n×nmatricies, as

a function of nas ngets large?

•What about the product of an n×mand m×nmatrix, where nm?

•By how much do you improve the performance of your implementation to

calculate C=A·Bby ﬁrst transposing Binternally, so all dot products

are computed along rows of the matrices to improve cache performance?

8-19. [5] Implement Gaussian elimination for solving systems of equations, C·X=Y.

Compare your implementation against a popular library routine for:

8.8. EXERCISES 265

(a) Speed: How does the run time compare, for both dense and sparse coeﬃ-

cient matrices?

(b) Accuracy: What are the size of the numerical residuals CX −Y, partic-

ularly as the condition number of the matrix increases.

almost singular matrices, created by adding a little random noise to a

singular matrix?

Interview Questions

8-20. [5] Why is vectorization considered a powerful method for optimizing numerical

code?

8-21. [3] What is singular value decomposition? What is a singular value? And what

is a singular vector?

8-22. [5] Explain the diﬀerence between “long” and “wide” format data. When might

each arise in practice?

Kaggle Challenges

8-23. Tell what someone is looking at from analysis of their brain waves.

https://www.kaggle.com/c/decoding-the-human-brain

8-24. Decide whether a particular student will answer a given question correctly.

https://www.kaggle.com/c/WhatDoYouKnow

8-25. Identify mobile phone users from accelerometer data.

https://www.kaggle.com/c/accelerometer-biometric-competition

Chapter 9

Linear and Logistic

Regression

An unsophisticated forecaster uses statistics as a drunken man uses

lamp posts – for support rather than illumination.

– Andrew Lang

Linear regression is the most representative “machine learning” method to build

models for value prediction and classiﬁcation from training data. It oﬀers a

study in contrasts:

•Linear regression has a beautiful theoretical foundation yet, in practice,

this algebraic formulation is generally discarded in favor of faster, more

heuristic optimization.

•Linear regression models are, by deﬁnition, linear. This provides an op-

portunity to witness the limitations of such models, as well as develop

clever techniques to generalize to other forms.

•Linear regression simultaneously encourages model building with hundreds

of variables, and regularization techniques to ensure that most of them will

get ignored.

Linear regression is a bread-and-butter modeling technique that should serve

as your baseline approach to building data-driven models. These models are

typically easy to build, straightforward to interpret, and often do quite well in

practice. With enough skill and toil, more advanced machine learning techniques

might yield better performance, but the possible payoﬀ is often not worth the

eﬀort. Build your linear regression models ﬁrst, then decide whether it is worth

working harder to achieve better results.

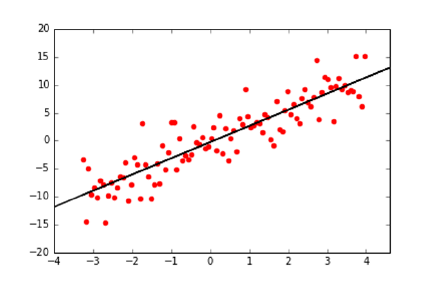
268 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

Figure 9.1: Linear regression produces the line which best ﬁts a set of points.

9.1 Linear Regression

Given a collection of npoints, linear regression seeks to ﬁnd the line which best

approximates or ﬁts the points, as shown in Figure 9.1. There are many reasons

why we might want to do this. One class of goals involves simpliﬁcation and

compression: we can replace a large set of noisy data points in the xy-plane

by a tidy line that describes them, as shown in Figure 9.1. This regression

line is useful for visualization, by showing the underlying trend in the data and

highlighting the location and magnitude of outliers.

However, we will be most interested in regression as a method for value fore-

casting. We can envision each observed point p= (x, y) to be the result of a

function y=f(x), where xrepresents the feature variables and ythe indepen-

dent target variable. Given a collection of nsuch points {p1, p2, . . . , pn}, we

seek the f(x) which best explains these points. This function f(x) interpolates

or models the points, providing a way to estimate the value y0associated with

any possible x0, namely that y0=f(x0).

9.1.1 Linear Regression and Duality

There is a connection between regression and solving linear equations, which is

interesting to explore. When solving linear systems, we seek the single point

that lies on ngiven lines. In regression, we are instead given npoints, and

we seek the line that lies on “all” points. There are two diﬀerences here: (a)

the interchange of points for lines and (b) ﬁnding the best ﬁt under constraints

verses a totally constrained problem (“all” vs. all).

The distinction between points and lines proves trivial, because they both

are really the same thing. In two-dimensional space, both points (s, t) and lines

y=mx +bare deﬁned by two parameters: {s, t}and {m, b}, respectively.

Further, by an appropriate duality transformation, these lines are equivalent to

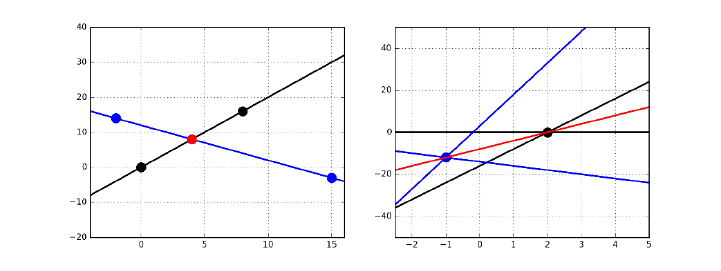
9.1. LINEAR REGRESSION 269

Figure 9.2: Points are equivalent to lines under a duality transform. The point

(4,8) in red (left) maps to the red line y= 4x−8 on right. Both sets of three

collinear points on the left correspond to three lines passing through the same

point on right.

points in another space. In particular, consider the transform that

(s, t)←→ y=sx −t.

Now any set of points that lie on a single line get mapped to a set of lines which

intersect a singular point – so ﬁnding a line that hits all of a set of points is

algorithmically the same thing as ﬁnding a point that hits all of a set of lines.

Figure 9.2 shows an example. The point of intersection in Figure 9.2 (left)

is p= (4,8), and it corresponds to the red line y= 4x−8 on the right. This

red point pis deﬁned by the intersection of black and blue lines. In the dual

space, these lines turn into black and blue points lying on the red line. Three

collinear points on left (red with either two black or two blue) map to three

lines passing through a common point on the right: one red and two of the

same color. This duality transformation reverses the roles of points and lines in

a way that everything makes sense.

The big diﬀerence in deﬁning linear regression is that we seek a line that

comes as close as possible to hitting all the points. We must be careful about

measuring error in the proper way in order to make this work.

9.1.2 Error in Linear Regression

The residual error of a ﬁtted line f(x) is the diﬀerence between the predicted

and actual values. As shown in Figure 9.3, for a particular feature vector xi

and corresponding target value yi, the residual error riis deﬁned:

ri=yi−f(xi).

This is what we will care about, but note that it is not the only way that

error might have been deﬁned. The closest distance to the line is in fact deﬁned

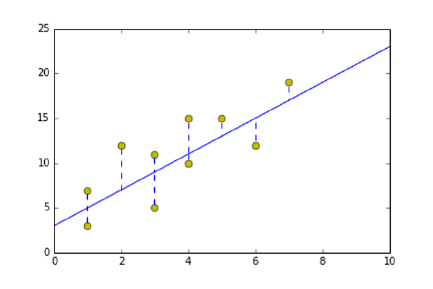
270 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

Figure 9.3: The residual error in least squares is the projection of yi−f(X)

down to X, not the shortest distance between the line and the point.

by the perpendicular-bisector through the target point. But we are seeking to

forecast the value of yifrom xi, so the residual is the right notion of error for

our purposes.

Least squares regression minimizes the sum of the squares of the residuals

of all points. This metric has been chosen because (1) squaring the residual

ignores the signs of the errors, so positive and negative residuals do not oﬀset

each other, and (2) it leads to a surprisingly nice closed form for ﬁnding the

coeﬃcients of the best-ﬁtting line.

9.1.3 Finding the Optimal Fit

Linear regression seeks the line y=f(x) which minimizes the sum of the squared

errors over all the training points, i.e. the coeﬃcient vector wthat minimizes

i=1

(yi−f(xi))2, where f(x) = w0+

m−1

i=1

wixi

Suppose we are trying to ﬁt a set of npoints, each of which is mdimensional.

The ﬁrst m−1 dimensions of each point is the feature vector (x1, . . . , xm−1),

with the last value y=xmserving as the target or dependent variable.

We can encode these nfeature vectors as an n×(m−1) matrix. We can

make it an n×mmatrix Aby prepending a column of ones to the matrix. This

column can be thought of as a “constant” feature, one that when multiplied by

the appropriate coeﬃcient becomes the y-intercept of the ﬁtted line. Further,

the ntarget values can be nicely represented in an n×1 vector b.

The optimal regression line f(x) we seek is deﬁned by an m×1 vector of

coeﬃcients w={w0, w1, . . . , wm−1}. Evaluating this function on these points

is exactly the product A·w, creating an n×1 vector of target value predictions.

Thus (b−A·w) is the vector of residual values.

9.1. LINEAR REGRESSION 271

How can we ﬁnd the coeﬃcients of the best ﬁtting line? The vector wis

given by:

w= (ATA)−1ATb.

First, let’s grok this before we try to understand it. The dimensions of the

term on the right are

((m×n)(n×m))(m×n)(n×1) →(m×1).

which exactly matches the dimensions of the target vector w, so that is good.

Further, (ATA) deﬁnes the covariance matrix on the columns/features of the

data matrix, and inverting it is akin to solving a system of equations. The term

ATbcomputes the dot products of the data values and the target values for each

of the mfeatures, providing a measure of how correlated each feature is with

the target results. We don’t understand why this works yet, but it should be

clear that this equation is made up of meaningful components.

Take-Home Lesson: That the least squares regression line is deﬁned by

w= (ATA)−1ATbmeans that solving regression problems reduces to invert-

ing and multiplying matrices. This formula works ﬁne for small matrices, but

the gradient descent algorithm (see Section 9.4) will prove more eﬃcient in

practice.

Consider the case of a single variable x, where we seek the best-ﬁtting line

of the form y=w0+w1x. The slope of this line is given by

w1=

i=1

(xi−¯x)(yi−¯y)

i=1 (xi−¯x)2=rxy

σx

σy

with w0= ¯y−w1¯x, because of the nice observation that the best-ﬁtting line

passes through (¯x, ¯y).

The connection with the correlation coeﬃcient (rxy ) here is clear. If xwere

uncorrelated with y(rxy = 0), then w1should indeed be zero. Even if they were

perfectly correlated (rxy = 1), we must scale xto bring it into the right size

range of y. This is the role of σy/σx.

Now, where does the linear regression formula come from? It should be

clear that in the best-ﬁtting line, we cannot change any of the coeﬃcients w

and hope to make a better ﬁt. This means that the error vector (b−Aw) has

to be orthogonal with the vector associated with each variable xi, or else there

would be a way to change the coeﬃcient to ﬁt it better.

Orthogonal vectors have dot products of zero. Since the ith column of AT

has a zero dot product with the error vector, (AT)(b−Aw) = ¯

0, where ¯

0 is a

vector of all zeros. Straightforward algebra then yields

w= (ATA)−1ATb.

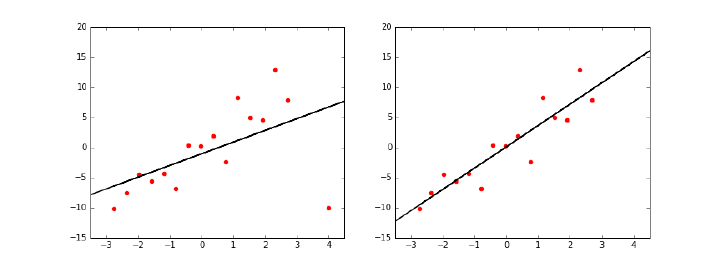
272 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

Figure 9.4: Removing outlier points (left) can result in much more meaningful

ﬁts (right).

9.2 Better Regression Models

Given a matrix Aof npoints, each of m−1 dimensions, and an n×1 target

array b, we can invert and multiply the appropriate matrices to get the desired

coeﬃcient matrix w. This deﬁnes a regression model. Done!

However, there are several steps one can take which can lead to better re-

gression models. Some of these involve manipulating the input data to increase

the likelihood of an accurate model, but others require more conceptual issues

of what our model should look like.

9.2.1 Removing Outliers

Linear regression seeks the line y=f(x) which minimizes the sum of the squared

errors over all training points, i.e. the coeﬃcient vector wthat minimizes

i=1

(yi−f(xi))2, where f(x) = w0+

m−1

i=1

wixi

Because of the quadratic weight of the residuals, outlying points can greatly

aﬀect the ﬁt. A point at a distance 10 from its prediction has 100 times the

impact on training error than a point only 1 unit from the ﬁtted line. One might

argue that this is appropriate, but it should be clear that outlier points have a

big impact in the shape of the best-ﬁtting line. This creates a problem when

the outlier points reﬂect noise rather than signal, because the regression line

goes out of its way to accommodate the bad data instead of ﬁtting the good.

We ﬁrst encountered this problem back in Figure 6.3, with the Anscombe

quartet, a collection of four small data sets with identical summary statistics

and regression lines. Two of these point sets achieved their magic because of

solitary outlier points. Remove the outliers, and the ﬁt now goes through the

heart of the data.

9.2. BETTER REGRESSION MODELS 273

Figure 9.4 shows the best-ﬁtting regression line with (left) and without

(right) an outlier point in the lower right. The ﬁt on the right is much bet-

ter: with an r2of 0.917 without the outlier, compared to 0.548 with the outlier.

Therefore identifying outlying points and removing them in a principled

way can yield a more robust ﬁt. The simplest approach is to ﬁt the entire set of

points, and then use the magnitude of the residual ri= (yi−f(xi))2to decide

whether point piis an outlier. It is important to convince yourself that these

points really represent errors before deleting them, however. Otherwise you will

be left with an impressively linear ﬁt that works well only on the examples you

didn’t delete.

9.2.2 Fitting Non-Linear Functions

Linear relationships are easier to understand than non-linear ones, and grossly

appropriate as a default assumption in the absence of better data. Many phe-

nomena are linear in nature, with the dependent variable growing roughly pro-

portionally with the input variables:

•Income grows roughly linearly with the amount of time worked.

•The price of a home grows roughly linearly with the size of the living area

it contains.

•People’s weight increases roughly linearly with the amount of food eaten.

Linear regression does great when it tries to ﬁt data that in fact has an

underlying linear relationship. But, generally speaking, no interesting function

is perfectly linear. Indeed, there is an old statistician’s rule that states if you

want a function to be linear, measure it at only two points.

We could greatly increase the repertoire of shapes we can model if we move

beyond linear functions. Linear regression ﬁts lines, not high-order curves. But

we can ﬁt quadratics by adding an extra variable with the value x2to our data

matrix, in addition to x. The model y=w0+w1x+w2x2is quadratic, but note

that it is a linear function of its non-linear input values. We can ﬁt arbitrarily-

complex functions by adding the right higher-order variables to our data matrix,

and forming linear combinations of them. We can ﬁt arbitrary polynomials and

exponentials/logarithms by explicitly including the right component variables

in our data matrix, such as √x, lg(x), x3, and 1/x.

Extra features can also be used to capture non-linear interactions between

pairs of input variables. The area of a rectangle Ais computed length ×width,

meaning one cannot get an accurate approximation of Aas a linear combination

of length and width. But, once we add an area feature to our data matrix, this

non-linear interaction can be captured with a linear model.

However, explicit inclusion of all possible non-linear terms quickly becomes

intractable. Adding all powers xifor 1 ≤i≤kwill blow up the data matrix by a

factor of k. Including all product pairs among nvariables is even worse, making

the matrix n(n+ 1)/2 times larger. One must be judicious about which non-

linear terms to consider for a role in the model. Indeed, one of the advantages

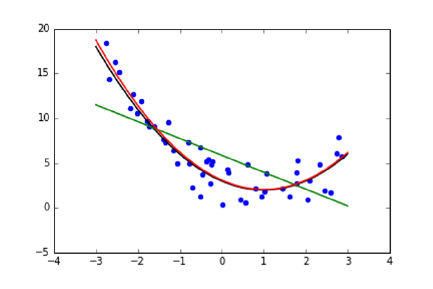
274 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

Figure 9.5: Higher-order models (red) can lead to better ﬁts than linear models

(green).

of more powerful learning methods, like support vector machines, will be that

they can incorporate non-linear terms without explicit enumeration.

9.2.3 Feature and Target Scaling

In principle, linear regression can ﬁnd the best linear model ﬁtting any data set.

But we should do whatever we can to help it ﬁnd the right model. This generally

involves preprocessing the data to optimize for expressibility, interpretability,

and numerical stability. The issue here is that features which vary over wide

numerical ranges require coeﬃcients over similarly wide ranges to bring them

together.

Suppose we wanted to build a model to predict the gross national product

of countries in dollars, as a function of their population size x1and literacy rate

x2. Both factors seem like reasonable components of such a model. Indeed,

both factors may well contribute equally to the amount of economic activity.

But they operate on entirely diﬀerent scales: national populations vary from

tens of thousands to over a billion people, while the fraction of people who can

read is, by deﬁnition, between zero and one. One might imagine the resulting

ﬁtted model as looking somewhat like this:

GDP = $10,000x1+ $10,000,000,000,000x2.

This is very bad, for several reasons:

•Unreadable coeﬃcients: Quick, what is the coeﬃcient of x2in the above

equation? It is hard for us to deal with the magnitude of such numbers

(it is 10 trillion), and hard for us to tell which variable makes a more

important contribution to the result given their ranges. Is it x1or x2?

•Numerical imprecision: Numerical optimization algorithms have trouble

when values range over many orders of magnitude. It isn’t just the fact

9.2. BETTER REGRESSION MODELS 275

that ﬂoating point numbers are represented by a ﬁnite number of bits.

More important is that many machine learning algorithms get parame-

terized by constants that must hold simultaneously for all variables. For

example, using ﬁxed step sizes in gradient descent search (to be discussed

in Section 9.4.2) might cause it to wildly overshoot in certain directions

while undershooting in others.

•Inappropriate formulations: The model given above to predict GDP is

silly on the face of it. Suppose I decide to form my own country, which

would have exactly one person in it, who could read. Do we really think

that Skienaland should have a GDP of $10,000,000,010,000?

A better model might be something like:

GDP = $20,000x1x2

which can be interpreted as each of the x1people creating wealth at a

rate modulated by their literacy. This generally requires seeding the data

matrix with the appropriate product terms. But there is a chance that

with proper (logarithmic) target scaling, this model might fall directly out

from linear regression.

We will now consider three diﬀerent forms of scaling, which address these

diﬀerent types of problems.

Feature Scaling: Z-Scores

We have previously discussed Z-scores, which scale the values of each feature

individually, so that the mean is zero and the ranges are comparable. Let µbe

the mean value of the given feature, and σthe standard deviation. Then the

Z-score of xis Z(x)=(x−µ)/σ.

Using Z-scores in regression addresses the question of interpretability. Since

all features will have similar means and variances, the magnitude of the co-

eﬃcients will determine the relative importance of these factors towards the

forecast. Indeed, in proper conditions, these coeﬃcients will reﬂect the corre-

lation coeﬃcient of each variable with the target. Further, that these variables

now range over the same magnitude simpliﬁes the work for the optimization

algorithm.

Sublinear Feature Scaling

Consider a linear model for predicting the number of years of education ythat

a child will receive as a function of household income. Education levels can

vary between 0 and 12 + 4 + 5 = 19 years, since we consider up to the possible

completion of a Ph.D. A family’s income level xcan vary between 0 and Bill

Gates. But observe that no model of the form

y=w1x+w0

276 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

can possibly give sensible answers for both my kids and Bill Gates’ kids. The

real impact of income on education level is presumably at the lower end: children

below the poverty line may not, on average, go beyond high school, while upper-

middle-class kids generally go to college. But there is no way to capture this in

a linearly-weighted variable without dooming the Gates children to hundreds or

thousands of years at school.

An enormous gap between the largest/smallest and median values means

that no coeﬃcient can use the feature without blowup on big values. Income

level is power law distributed, and the Z-scores of such power law variables

can’t help, because they are just linear transformations. The key is to re-

place/augment such features xwith sublinear functions like log(x) and √x.

Z-scores of these transformed variables will prove much more meaningful to

build models from.

Sublinear Target Scaling

Small-scale variables need small-scale targets, in order to be realized using small-

scale coeﬃcients. Trying to predict GDP from Z-scored variables will require

enormously large coeﬃcients. How else could you get to trillions of dollars from

a linear combination of variables ranging from −3 to +3?

Perhaps scaling the target value from dollars to billions of dollars here would

be helpful, but there is a deeper problem. When your features are normally dis-

tributed, you can only do a good job regressing to a similarly distributed target.

Statistics like GDP are likely power law distributed: there are many small poor

countries compared to very few large rich ones. Any linear combination of

normally-distributed variables cannot eﬀectively realize a power law-distributed

target.

The solution here is that trying to predict the logarithm (logc(y)) of a power

law target yis usually better than predicting yitself. Of course, the value cf(x)

can then be used to estimate y, but the potential now exists to make meaningful

predictions over the full range of values. Hitting a power law function with a

logarithm generally produces a better behaved, more normal distribution.

It also enables us to implicitly realize a broader range of functions. Suppose

the “right” function to predict gross domestic product was in fact

GDP = $20,000x1x2.

This could never be realized by linear regression without interaction variables.

But observe that

log(GDP ) = log($20,000x1x2) = log($20,000) + log(x1) + log(x2).

Thus the logarithms of arbitrary interaction products could be realized, provided

the feature matrix contained the logs of the original input variables as well.

9.3. WAR STORY: TAXI DERIVER 277

9.2.4 Dealing with Highly-Correlated Features

A ﬁnal pitfall we will discuss is the problem of highly-correlated features. It is

great to have features that are highly correlated with the target: these enable

us to build highly-predictive models. However, having multiple features which

are highly correlated with each other can be asking for trouble.

Suppose you have two perfectly-correlated features in your data matrix, say

the subject’s height in feet (x1) as well as their height in meters (x2). Since

1 meter equals 3.28084 feet, these two variables are perfectly correlated. But

having both of these variables can’t really help our model, because adding a

perfectly correlated feature provides no additional information to make predic-

tions. If such duplicate features really had value for us, it would imply that we

could build increasingly accurate models simply by making additional copies of

columns from any data matrix!

But correlated features are harmful to models, not just neutral. Suppose

our dependent variable is a function of height. Note that equally good models

can be built dependent only on x1, or only on x2, or on any arbitrary linear

combination of x1and x2. Which is the right model to report as the answer?

This is confusing, but even worse things can happen. The rows in the co-

variance matrix will be mutually dependent, so computing w= (ATA)−1ATb

now requires inverting a singular matrix! Numerical methods for computing the

regression are liable to fail.

The solution here is to identify feature pairs which correlate excessively

strongly, by computing the appropriate covariance matrix. If they are lurking,

you can eliminate either variable with little loss of power. Better is to elimi-

nate these correlations entirely, by combining the features. This is one of the

problems solved by dimension reduction, using techniques like singular value

decomposition that we discussed in Section 8.5.1.

9.3 War Story: Taxi Deriver

I am proud of many things in my life, but perhaps most so of being a New

Yorker. I live in the most exciting city on earth, the true center of the universe.

Astronomers, at least the good ones, will tell you that each new year starts

when the ball drops in Times Square, and then radiates out from New York at

the speed of light to the rest of the world.

New York cab drivers are respected around the world for their savvy and

street smarts. It is customary to tip the driver for each ride, but there is no

established tradition of how much that should be. In New York restaurants,

the “right” amount to tip the waiter is to double the tax, but I am unaware of

any such heuristic for taxi tipping. My algorithm is to round up to the nearest

dollar and then toss in a couple of bucks depending upon how fast he got me

there. But I have always felt unsure. Am I a cheapskate? Or maybe a sucker?

The taxi data set discussed in Section 1.2.4 promised to hold the answer.

It contained over 80 million records, with ﬁelds for date, time, pickup and

278 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

drop oﬀ locations, distance traveled, fare, and of course tip. Do people pay

disproportionately for longer or shorter trips? Late at night or on weekends?

Do others reward fast drivers like I do? It should all be there in the data.

My student, Oleksii Starov, rose to the challenge. We added appropriate

features to the data set to capture some of these notions. To explicitly capture

conditions like late night and weekends, we set up binary indicator variables,

where 1 would denote that the trip was late night and 0 at some other time of

day. The coeﬃcients of our ﬁnal regression equation was:

variable LR coeﬃcient

(intercept) 0.08370835

duration 0.00000035

distance 0.00000004

fare 0.17503086

tolls 0.06267343

surcharge 0.01924337

weekends −0.02823731

business day 0.06977724

rush hour 0.01281997

late night 0.04967453

# of passengers −0.00657358

The results here can be explained simply. Only one variable really matters:

the fare on the meter. This model tips 17.5% of the total fare, with very minor

adjustments for other things. A single parameter model tipping 18.3% of each

fare proved almost as accurate as the ten-factor model.

There were very strong correlations between the fare and both distance trav-

eled (0.95) and trip duration (0.88), but both of these factors are part of the

formula by which fares are calculated. These correlations with fare are so strong

that neither variable can contribute much additional information. To our disap-

pointment, we couldn’t really tease out an inﬂuence of time of day or anything

else, because these correlations were so weak.

A deeper look at the data revealed that every single tip in the database

was charged to a credit card, as opposed to being paid by cash. Entering

the tip amount into the meter after each cash transaction is tedious and time

consuming, particularly when you are hustling to get as many fares as possible

on each 12 hour shift. Further, real New York cabbies are savvy and street-smart

enough not to want to pay taxes on tips no one else knows about.

I always pay my fares with cash, but the people who pay by credit card are

confronted with a menu oﬀering them the choice of what tip to leave. The data

clearly showed most of them mindlessly hitting the middle button, instead of

modulating their choice to reﬂect the quality of service.

Using 80 million fare records to ﬁt a simple linear regression on ten variables

is obscene overkill. Better use of this data would be to construct hundreds or

even thousands of diﬀerent models, each designed for a particular class of trips.

Perhaps we could build a separate model for trips between each pair of city zip

9.4. REGRESSION AS PARAMETER FITTING 279

codes. Indeed, recall our map of such tipping behavior, presented back in Figure

1.7.

It took several minutes for the solver to ﬁnd the best ﬁt on such a large data

set, but that it ﬁnished at all meant some algorithm faster and more robust

than matrix inversion had to be involved. These algorithms view regression as

a parameter ﬁtting problem, as we will discuss in the next section.

9.4 Regression as Parameter Fitting

The closed form formula for linear regression, w= (ATA)−1ATb, is concise and

elegant. However, it has some issues which make it suboptimal for computation

in practice. Matrix inversion is slow for large systems, and prone to numerical

instability. Further, the formulation is brittle: the linear algebra magic here is

hard to extend to more general optimization problems.

But there is an alternate way to formulate and solve linear regression prob-

lems, which proves better in practice. This approach leads to faster algorithms,

more robust numerics, and can be readily adapted to other learning algorithms.

It models linear regression as a parameter ﬁtting problem, and deploys search

algorithms to ﬁnd the best values that it can for these parameters.

For linear regression, we seek the line that best ﬁts the points, over all pos-

sible sets of coeﬃcients. Speciﬁcally, we seek the line y=f(x) which minimizes

the sum of the squared errors over all training points, i.e. the coeﬃcient vector

wthat minimizes

i=1

(yi−f(xi))2, where f(x) = w0+

m−1

i=1

wixi

For concreteness, let us start with the case where we are trying to model

yas a linear function of a single variable or feature x, so y=f(x) means

y=w0+w1x. To deﬁne our regression line, we seek the parameter pair (w0, w1)

which minimizes error or cost or loss, namely the sum of squares deviation

between the point values and the line.

Every possible pair of values for (w0, w1) will deﬁne some line, but we really

want the values that minimize the error or loss function J(w0, w1), where

J(w0, w1) = 1

i=1

(yi−f(xi))2

i=1

(yi−(w0+w1xi))2

The sum of squares errors should be clear, but where does the 1/(2n) come

from? The 1/n turns this into an average error per row, and the 1/2 is a

common convention for technical reasons. But be clear that the 1/(2n) in no

way eﬀects the results of the optimization. This multiplier will be the same for

each (w0, w1) pair, and so has no say in which parameters get chosen.

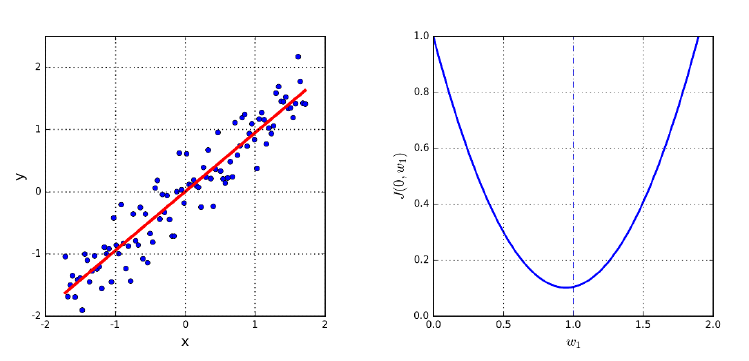
280 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

Figure 9.6: The best possible regression line y=w1x(left) can be found by

identifying the w1that minimizes the error of the ﬁt, deﬁned by the minima of

a convex function.

So how can we ﬁnd the right values for w0and w1? We might try a bunch of

random value pairs, and keep the one which scores best, i.e. with minimum loss

J(w0, w1). But it seems very unlikely to stumble on the best or even a decent

solution. To search more systematically, we will have to take advantage of a

special property lurking within the loss function.

9.4.1 Convex Parameter Spaces

The upshot of the above discussion is that the loss function J(w0, w1) deﬁnes a

surface in (w0, w1)-space, with our interest being in the point in this space with

smallest zvalue, where z=J(w0, w1).

Let’s start by making it even simpler, forcing our regression line to pass

through the origin by setting w0= 0. This leaves us only one free parameter to

ﬁnd, namely the slope of the line w1. Certain slopes will do a wildly better job

of ﬁtting the points shown in Figure 9.6 (left) than others, with the line y=x

clearly being the desired ﬁt.

Figure 9.6 (right) shows how the ﬁtting error (loss) varies with w1. The

interesting thing is that the error function is shaped sort of like a parabola. It

hits a single minimum value at the bottom of the curve. The x-value of this

minimum point deﬁnes the best slope w1for the regression line, which happens

to be w1= 1.

Any convex surface has exactly one local minima. Further, for any convex

search space it is quite easy to ﬁnd this minima: just keep walking in a downward

direction until you hit it. From every point on the surface, we can take a small

step to a nearby point on the surface. Some directions will take us up to a

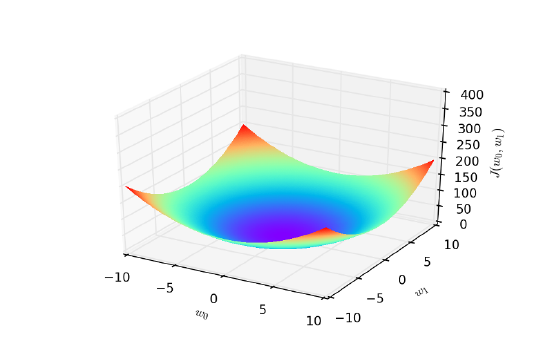
9.4. REGRESSION AS PARAMETER FITTING 281

Figure 9.7: Linear regression deﬁnes a convex parameter space, where each point

represents a possible line, and the minimum point deﬁnes the best ﬁtting line.

higher value, but others will take us down. Provided that we can identify which

step will take us lower, we will move closer to the minima. And there always is

such direction, except when we are standing on the minimal point itself!

Figure 9.7 shows the surface we get for the full regression problem in (w0, w1)-

space. The loss function J(w0, w1) looks like a bowl with a single smallest z-

value, which deﬁnes the optimal values for the two parameters of the line. The

great thing is that this loss function J(w0, w1) is again convex, and indeed it

remains convex for any linear regression problem in any number of dimensions.

How can we tell whether a given function is convex? Remember back to when

you took calculus in one variable, x. You learned how to take the derivative

f0(x) of a function f(x), which corresponds to the value of the slope of the

surface of f(x) at every point. Whenever this derivative was zero, it meant

that you had hit some point of interest, be it a local maxima or a minima.

Recall the second derivative f00(x), which was the derivative function of the

derivative f0(x). Depending upon the sign of this second derivative f00(x), you

could identify whether you hit a maxima or minima.

Bottom line: the analysis of such derivatives can tell us which functions

are and are not convex. We will not delve deeper here. But once it has been

established that our loss function is convex, we know that we can trust a proce-

dure like gradient descent search, which gets us to the global optima by walking

downward.

9.4.2 Gradient Descent Search

We can ﬁnd the minima of a convex function simply by starting at an arbitrary

point, and repeatedly walking in a downward direction. There is only one point

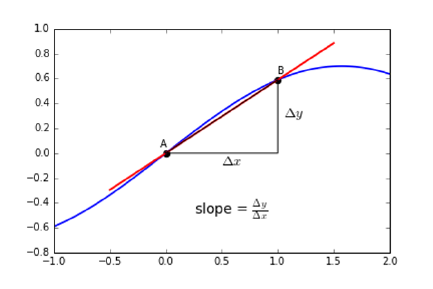
282 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

Figure 9.8: The tangent line approximates the derivative at a point.

where there is no way down: the global minima itself. And it is this point that

deﬁnes the parameters of the best ﬁtting regression line.

But how can we ﬁnd a direction that leads us down the hill? Again, let’s

consider the single variable case ﬁrst, so we seek the slope w1of the best-ﬁtting

line where w0= 0. Suppose our current slope candidate is x0. In this restrictive

one-dimensional setting, we can only move to the left or to the right. Try a

small step in each direction, i.e. the values x0−and x0+. If the value

of J(0, x0−)< J(0, x0), then we should move to the left to go down. If

J(0, x0+)< J(0, x0), then we should move to the right. If neither is true,

it means that we have no place to go to reduce J, so we must have found the

minima.

The direction down at f(x0) is deﬁned by the slope of the tangent line at

this point. A positive slope means that the minima must lie on the left, while

a negative slope puts it on the right. The magnitude of this slope describes the

steepness of this drop: by how much will J(0, x0−) diﬀer from J(0, x0)?

This slope can be approximated by ﬁnding the unique line which passes

through points (x0, J(0, x0)) and (x0, J(0, x0−)), as shown in Figure 9.8. This

is exactly what is done in computing the derivative, which at each point speciﬁes

the tangent to the curve.

As we move beyond one dimension, we gain the freedom to move in a greater

range of directions. Diagonal moves let us cut across multiple dimensions at

once. But in principle, we can get the same eﬀect by taking multiple steps, along

each distinct dimension in an axis-oriented direction. Think of the Manhattan

street grid, where we can get anywhere we want by moving in a combination of

north–south and east–west steps. Finding these directions requires computing

the partial derivative of the objective function along each dimension, namely:

9.4. REGRESSION AS PARAMETER FITTING 283

Gradient descent search in two dimensions

Repeat until convergence {

wt+1

0:= wt

0−α∂

∂w0

Jwt

0, wt

1

wt+1

1:= wt

1−α∂

∂w1

Jwt

0, wt

1

}

Figure 9.9: Pseudocode for regression by gradient descent search. The variable

tdenotes the iteration number of the computation.

∂

∂wj

i=1

(f(xi)−bi)2

∂wj

i=1

(w0+ (w1xi)−bi)2

But zig-zagging along dimensions seems slow and clumsy. Like Superman,

we want to leap buildings in a single bound. The magnitude of the partial

derivatives deﬁnes the steepness in each direction, and the resulting vector (say

three steps west for every one step north) deﬁnes the fastest way down from

this point.

9.4.3 What is the Right Learning Rate?

The derivative of the loss function points us in the right direction to walk towards

the minima, which speciﬁes the parameters to solve our regression problem. But

it doesn’t tell us how far to walk. The value of this direction decreases with

distance. It is indeed true that the fastest way to drive to Miami from New York

is to head south, but at some point you will need more detailed instructions.

Gradient descent search operates in rounds: ﬁnd the best direction, take a

step, and then repeat until we hit the target. The size of our step is called the

learning rate, and it deﬁnes the speed with which we ﬁnd the minima. Taking

tiny baby steps and repeatedly consulting the map (i.e. partial derivatives) will

indeed get us there, but only very slowly.

However, bigger isn’t always better. If the learning rate is too high, we might

jump past the minima, as shown in Figure 9.10 (right). This might mean slow

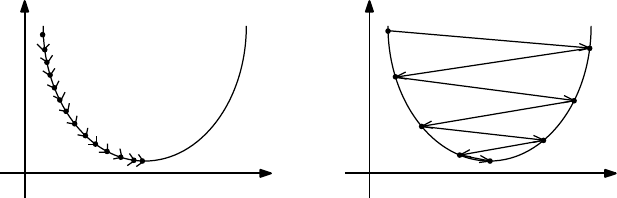
284 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

θ1θ1

I(θ1)I(θ1)

Figure 9.10: The eﬀect of learning rate/step size. Taking too small a step size

requires many iterations to converge, while too large a step size causes us to

overshoot the minima.

progress towards the hole as we bounce past it on each step, or even negative

progress as we end up at a value of J(w) higher than where we were before.

In principle, we want a large learning rate at the beginning of our search, but

one which decreases as we get closer to our goal. We need to monitor the value

of our loss function over the course of the optimization. If progress becomes

too slow, we can increase the step size by a multiplicative factor (say 3) or give

up: accepting the current parameter values for our ﬁtting line as good enough.

But if the value of J(w) increases, it means that we have overshot our goal.

Thus our step size was too large, so we should decrease the learning rate by a

multiplicative factor: say by 1/3.

The details of this are messy, heuristic, and ad hoc. But fortunately library

functions for gradient descent search have built-in algorithms for adjusting the

learning rate. Presumably these algorithms have been highly tuned, and should

generally do what they are supposed to do.

But the shape of the surface makes a big diﬀerence as to how successfully

gradient descent search ﬁnds the global minimum. If our bowl-shaped surface

was relatively ﬂat, like a plate, the truly lowest point might be obscured by a

cloud of noise and numerical error. Even if we do eventually ﬁnd the minima,

it might take us a very long time to get there.

However, even worse things happen when our loss function is not convex,

meaning there can be many local minima, as in Figure 9.11. Now this can’t

be the case for linear regression, but does happen for many other interesting

machine learning problems we will encounter.

Local optimization can easily get stuck in local minima for non-convex func-

tions. Suppose we want to reach the top of a ski slope from our lodge in the

valley. If we start by walking up to the second ﬂoor of the lodge, we will get

trapped forever, unless there is some mechanism for taking steps backwards to

free us from the local optima. This is the value of search heuristics like sim-

ulated annealing, which provides a way out of small local optima to keep us

advancing towards the global goal.

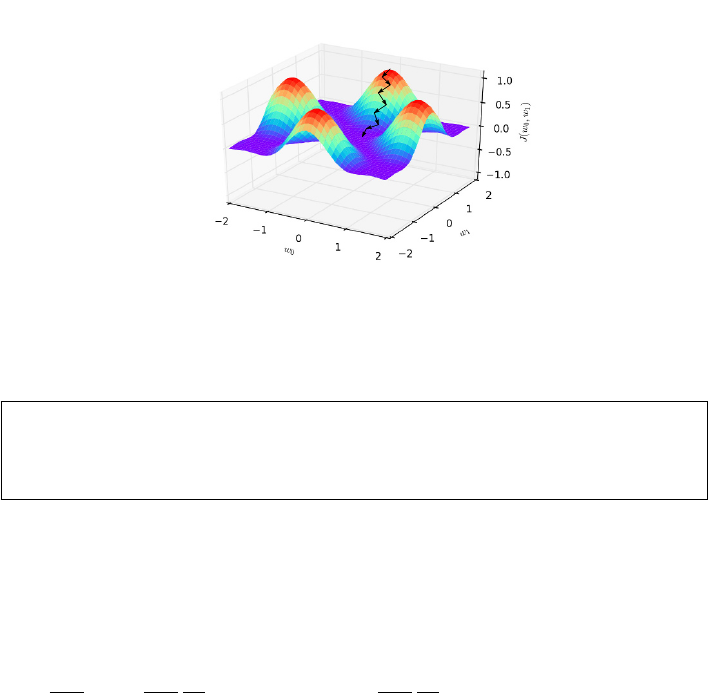
9.4. REGRESSION AS PARAMETER FITTING 285

Figure 9.11: Gradient descent search ﬁnds local minima for non-convex surfaces,

but does not guarantee a globally optimum solution.

Take-Home Lesson: Gradient descent search remains useful in practice for non-

convex optimization, although it no longer guarantees an optimal solution.

Instead, we should start repeatedly from diﬀerent initialization points, and use

the best local minima we ﬁnd to deﬁne our solution.

9.4.4 Stochastic Gradient Descent

The algebraic deﬁnition of our loss function hides something very expensive

going on:

∂

∂wj

i=1

(f(xi)−bi)2=2

∂wj

i=1

(w0+ (w1xi)−bi)2

It’s that summation. To compute the best direction and rate of change for

each dimension j, we must cycle through all nof our training points. Evaluating

each partial derivative takes time linear in the number of examples, for each

step! For linear regression on our lavish taxicab data set, this means 80 million

squared-diﬀerence computations just to identify the absolute best direction to

advance one step towards the goal.

This is madness. Instead, we can try an approximation that uses only a small

number of examples to estimate the derivative, and hopes that the resulting

direction indeed points down. On average it should, since every point will

eventually get to vote on direction.

Stochastic gradient descent is an optimization approach based on sampling

a small batch of training points, ideally at random, and using them to estimate

the derivative at our current position. The smaller the batch size we use, the

faster the evaluation is, although we should be more skeptical that the estimated

direction is correct. Optimizing the learning rate and the batch size for gradient

286 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

descent leads to very fast optimization for convex functions, with the details

blessedly concealed by a call to a library function.

It can be expensive to make random choices at every step of the search. Bet-

ter is to randomize the order of the training examples once, to avoid systematic

artifacts in how they are presented, and then build our batches by simply march-

ing down the list. This way we can insure that all nof our training instances

eventually do contribute to the search, ideally several times as we repeatedly

sweep through all examples over the course of optimization.

9.5 Simplifying Models through Regularization

Linear regression is happy to determine the best possible linear ﬁt to any collec-

tion of ndata points, each speciﬁed by m−1 independent variables and a given

target value. But the “best” ﬁt may not be what we really want.

The problem is this. Most of the m−1 possible features may be uncorrelated

with the target, and thus have no real predictive power. Typically, these will

show as variables with small coeﬃcients. However, the regression algorithm

will use these values to nudge the line so as to reduce least square error on the

given training examples. Using noise (the uncorrelated variables) to ﬁt noise

(the residual left from a simple model on the genuinely correlated variables) is

asking for trouble.

Representative here is our experience with the taxi tipping model, as detailed

in the war story. The full regression model using ten variables had a mean

squared error of 1.5448. The single-variable regression model operating only

on fare did slightly worse, with an error of 1.5487. But this diﬀerence is just

noise. The single variable model is obviously better, by Occam’s or anybody

else’s razor.

Other problems arise when using unconstrained regression. We have seen

how strongly correlated features introduce ambiguity into the model. If features

Aand Bare perfectly correlated, using both yields the same accuracy as using

either one, resulting in more complicated and less interpretable models.

Providing a rich set of features to regression is good, but remember that “the

simplest explanation is best.” The simplest explanation relies on the smallest

number of variables that do a good job of modeling the data. Ideally our regres-

sion would select the most important variables and ﬁt them, but the objective

function we have discussed only tries to minimize sum of squares error. We need

to change our objective function, through the magic of regularization.

9.5.1 Ridge Regression

Regularization is the trick of adding secondary terms to the objective function

to favor models that keep coeﬃcients small. Suppose we generalize our loss

function with a second set of terms that are a function of the coeﬃcients, not

9.5. SIMPLIFYING MODELS THROUGH REGULARIZATION 287

the training data:

J(w) = 1

i=1

(yi−f(xi))2+λ

j=1

In this formulation, we pay a penalty proportional to the sum of squares

of the coeﬃcients used in the model. By squaring the coeﬃcients, we ignore

sign and focus on magnitude. The constant λmodulates the relative strength

of the regularization constraints. The higher λis, the harder the optimization

will work to reduce coeﬃcient size, at the expense of increased residuals. It

eventually becomes more worthwhile to set the coeﬃcient of an uncorrelated

variable to zero, rather than use it to overﬁt the training set.

Penalizing the sum of squared coeﬃcients, as in the loss function above, is

called ridge regression or Tikhonov regularization. Assuming that the depen-

dent variables have all been properly normalized to mean zero, their coeﬃcient

magnitude is a measure of their value to the objective function.

How can we optimize the parameters for ridge regression? A natural exten-

sion to the least squares formulation does the job. Let Γ be our n×n“coeﬃcient

weight penalty” matrix. For simplicity, let Γ = I, the identity matrix. The sum-

of-squares loss function we seek to minimize then becomes

||Aw −b||2+||λΓw||2

The notation ||v|| denotes the norm of v, a distance function on a vector or

matrix. The norm of ||Γw||2is exactly the sum of squares of the coeﬃcients

when Γ = I. Seen this way, the closed form to optimize for wis believable as

w= (ATA+λΓTΓ)−1ATb.

Thus the normal form equation can be generalized to deal with regular-

ization. But, alternately, we can compute the partial derivatives of this loss

function and use gradient descent search to do the job faster on large matri-

ces. In any case, library functions for ridge regression and its cousin LASSO

regression will be readily available to use on your problem.

9.5.2 LASSO Regression

Ridge regression optimizes to select small coeﬃcients. Because of sum-of-squares

cost function, it particularly punishes the largest coeﬃcients. This makes it

great to avoid models of the form y=w0+w1x1, where w0is a large positive

number and w1an oﬀsetting large negative number.

Although ridge regression is eﬀective at reducing the magnitude of the co-

eﬃcients, this criteria does not really push them to zero and totally eliminate

the variable from the model. An alternate choice here is to try to minimize the

sum of the absolute values of the coeﬃcients, which is just as happy to drive

down the smallest coeﬃcients as the big ones.

288 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

LASSO regression (for “Least Absolute Shrinkage and Selection Operator”)

meets this criteria: minimizing the L1metric on the coeﬃcients instead of the

L2metric of ridge regression. With LASSO, we specify an explicit constraint t

as to what the sum of the coeﬃcients can be, and the optimization minimizes

the sum of squares error under this constraint:

J(w, t) = 1

i=1

(yi−f(xi))2subject to

j=1 |wj| ≤ t.

Specifying a smaller value of ttightens the LASSO, further constraining the

magnitudes of the coeﬃcients w.

As an example of how LASSO zeros out small coeﬃcients, observe what it

did to the taxi tipping model for a particular value of t:

variable LR coeﬃcient LASSO

(intercept) 0.08370835 0.079601141

duration 0.00000035 0.00000035

distance 0.00000004 0.00000004

fare 0.17503086 0.17804921

tolls 0.06267343 0.00000000

surcharge 0.01924337 0.00000000

weekends −0.02823731 0.00000000

business day 0.06977724 0.00000000

rush hour 0.01281997 0.00000000

late night 0.04967453 0.00000000

# of passengers −0.00657358 0.00000000

As you can see, LASSO zeroed out most of the coeﬃcients, resulting in

a simpler and more robust model, which ﬁts the data almost as well as the

unconstrained linear regression.

But why does LASSO actively drive coeﬃcients to zero? It has to do with

the shape of the circle of the L1metric. As we will see in Figure 10.2, the

shape of the L1circle (the collection of points equidistant from the origin) is

not round, but has vertices and lower-dimensional features like edges and faces.

Constraining our coeﬃcients wto lie on the surface of a radius-t L1circle means

it is likely to hit one of these lower-dimensional features, meaning the unused

dimensions get zero coeﬃcients.

Which works better, LASSO or ridge regression? The answer is that it de-

pends. Both methods should be supported in your favorite optimization library,

so try each of them and see what happens.

9.5.3 Trade-Oﬀs between Fit and Complexity

How do we set the right value for our regularization parameter, be it λor

t? Using a small-enough λor a large-enough tprovides little penalty against

selecting the coeﬃcients to minimize training error. By contrast, using a very

large λor very small tensures small coeﬃcients, even at the cost of substantial

9.6. CLASSIFICATION AND LOGISTIC REGRESSION 289

modeling error. Tuning these parameters enables us to seek the sweet spot

between over and under-ﬁtting.

By optimizing these models over a large range of values for the appropriate

regularization parameter t, we get a graph of the evaluation error as a function

of t. A good ﬁt to the training data with few/small parameters is more robust

than a slightly better ﬁt with many parameters.

Managing this trade-oﬀ is largely a question of taste. However, several met-

rics have been developed to help with model selection. Most prominent are

the Akaike Information Criteria (AIC) and the Baysian Information Criteria

(BIC). We will not delve deeper than their names, so it is fair for you to think of

these metrics as voodoo at this point. But your optimization/evaluation system

may well output them for the ﬁtted models they produce, providing a way to

compare models with diﬀerent numbers of parameters.

Even though LASSO/ridge regression punishes coeﬃcients based on magni-

tude, they do not explicitly set them to zero if you want exactly kparameters.

You must be the one to remove useless variables from your model. Automatic

feature-selection methods might decide to zero-out small coeﬃcients, but ex-

plicitly constructing models from all possible subsets of features is generally

computationally infeasible.

The features to be removed ﬁrst should be those with (a) small coeﬃcients,

(b) low correlation with the objective function, (c) high correlation with another

feature in the model, and (d) no obvious justiﬁable relationship with the target.

For example, a famous study once showed a strong correlation between the

U.S. gross national product and the annual volume of butter production in

Bangladesh. The sage modeler can reject this variable as ridiculous, in ways

that automated methods cannot.

9.6 Classiﬁcation and Logistic Regression

We are often faced with the challenge of assigning items the right label according

to a predeﬁned set of classes:

•Is the vehicle in the image a car or a truck? Is a given tissue sample

indicative of cancer, or is it benign?

•Is a particular piece of email spam, or personalized content of interest to

the user?

•Social media analysis seeks to identify properties of people from associated

data. Is a given person male or female? Will they tend to vote Democrat

or Republican?

Classiﬁcation is the problem of predicting the right label for a given input

record. The task diﬀers from regression in that labels are discrete entities, not

continuous function values. Trying to pick the right answer from two possibilities

might seem easier than forecasting open-ended quantities, but it is also a lot

easier to get dinged for being wrong.

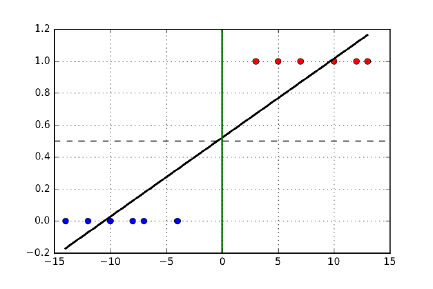
290 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

Figure 9.12: The optimal regression line cuts through the classes, even though

a perfect separator line (x= 0) exists.

In this section, approaches to building classiﬁcation systems using linear

regression will be developed, but this is just the beginning. Classiﬁcation is

a bread-and-butter problem in data science, and we will see several other ap-

proaches over the next two chapters.

9.6.1 Regression for Classiﬁcation

We can apply linear regression to classiﬁcation problems by converting the class

names of training examples to numbers. For now, let’s restrict our attention to

two class problems, or binary classiﬁcation. We will generalize this to multi-class

problems in Section 9.7.2.

Numbering these classes as 0/1 works ﬁne for binary classiﬁers. By conven-

tion, the “positive” class gets 0 and the “negative” one 1:

•male=0 / female=1

•democrat=0 / republican=1

•spam=1 / non-spam=0

•cancer=1 / benign=0

The negative/1 class generally denotes the rarer or more special case. There

is no value judgment intended here by positive/negative: indeed, when the

classes are of equal size the choice is made arbitrarily.

We might consider training a regression line f(x) for our feature vector x

where the target values are these 0/1 labels, as shown in Figure 9.12. There

is some logic here. Instances similar to positive training examples should get

lower scores than those closer to negative instances. We can threshold the value

returned by f(x) to interpret it as a label: f(x)≤0.5 means that xis positive.

When f(x)>0.5 we instead assign the negative label.

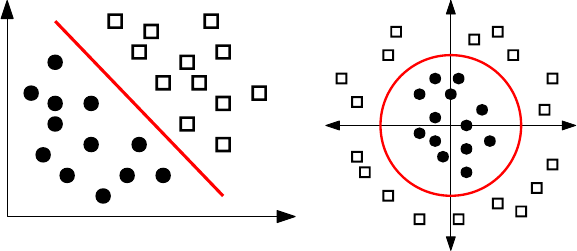
9.6. CLASSIFICATION AND LOGISTIC REGRESSION 291

Figure 9.13: A separating line partitions two classes in feature space (left).

However, non-linear separators are better at ﬁtting certain training sets (right).

But there are problems with this formulation. Suppose we add a number

of “very negative” examples to the training data. The regression line will tilt

towards these examples, putting the correct classiﬁcation of more marginal ex-

amples at risk. This is unfortunate, because we would have already properly

classiﬁed these very negative points, anyway. We really want the line to cut

between the classes and serve as a border, instead of through these classes as a

scorer.

9.6.2 Decision Boundaries

The right way to think about classiﬁcation is as carving feature space into

regions, so that all the points within any given region are destined to be assigned

the same label. Regions are deﬁned by their boundaries, so we want regression

to ﬁnd separating lines instead of a ﬁt.

Figure 9.13 (left) shows how training examples for binary classiﬁcation can be

viewed as colored points in feature space. Our hopes for accurate classiﬁcation

rest on regional coherence among the points. This means that nearby points

tend to have similar labels, and that boundaries between regions tend to be

sharp instead of fuzzy.

Ideally, our two classes will be well-separated in feature space, so a line can

easily partition them. But more generally, there will be outliers. We need to

judge our classiﬁer by the “purity” of the resulting separation, penalizing the

misclassiﬁcation of points which lie on the wrong side of the line.

Any set of points can be perfectly partitioned, if we design a complicated-

enough boundary that swerves in and out to capture all instances with a given

label. See Figure 9.14. Such complicated separators usually reﬂect overﬁtting

the training set. Linear separators oﬀer the virtue of simplicity and robustness

and, as we will see, can be eﬀectively constructed using logistic regression.

More generally, we may be interested in non-linear but low-complexity de-

cision boundaries, if they better separate the class boundaries. The ideal sep-

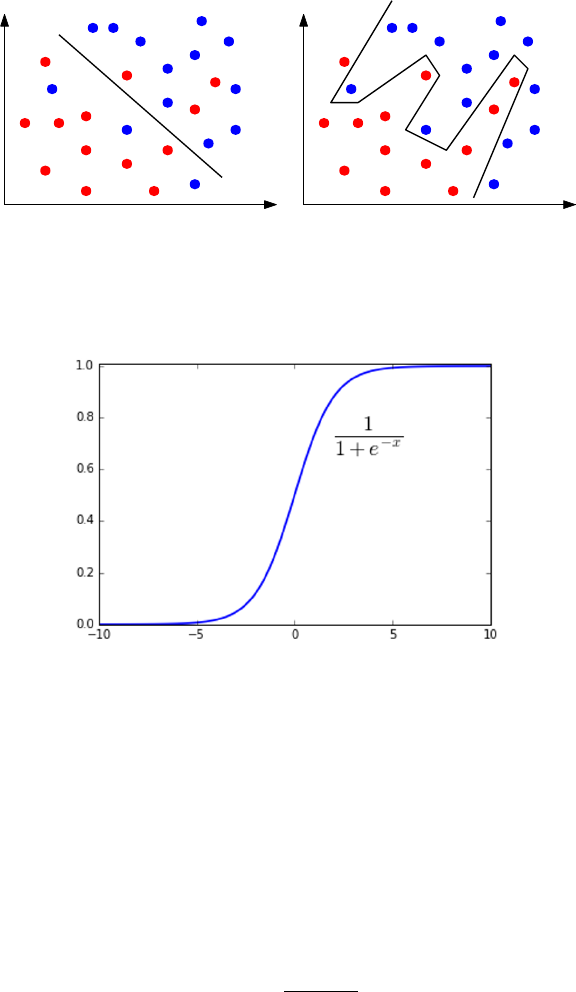
292 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

Figure 9.14: Linear classiﬁers cannot always separate two classes (left). How-

ever, perfect separation achieved using complex boundaries usually reﬂects over-

ﬁtting more than insight (right).

Figure 9.15: The logit function maps a score to a probability.

arating curve in Figure 9.13 (right) is not a line, but a circle. However, it can

be found as a linear function of quadratic features like x2

1and x1x2. We can

use logistic regression to ﬁnd non-linear boundaries if the data matrix is seeded

with non-linear features, as discussed in Section 9.2.2.

9.6.3 Logistic Regression

Recall the logit function f(x), which we introduced back in Section 4.4.1:

f(x) = 1

1 + e−cx

This function takes as input a real value −∞ ≤ x≤ ∞, and produces a value

ranging over [0,1], i.e. a probability. Figure 9.15 plots the logit function f(x),

which is a sigmoidal curve: ﬂat at both sides but a steep rise in the middle.

9.6. CLASSIFICATION AND LOGISTIC REGRESSION 293

The shape of the logit function makes it particularly suited to the interpre-

tation of classiﬁcation boundaries. In particular, let xbe a score that reﬂects

the distance that a particular point plies above/below or left/right of a line l

separating two classes. We want f(x) to measure the probability that pdeserves

a negative label.

The logit function maps scores into probabilities using only one parameter.

The important cases are those at the midpoint and endpoints. Logit says that

f(0) = 1/2, meaning that the label of a point on the boundary is essentially a

coin toss between the two possibilities. This is as it should be. More unam-

biguous decisions can be made the greater our distance from this boundary, so

f(∞) = 1 and f(−∞) = 0.

Our conﬁdence as a function of distance is modulated by the scaling constant

c. A value of cnear zero makes for a very gradual transition from positive to

negative. In contrast, we can turn the logit into a staircase by assigning a large

enough value to c, meaning that small distances from the boundary translate

into large increases in conﬁdence of classiﬁcation.

We need three things to use the logit function eﬀectively for classiﬁcation:

•Extending f(x) beyond a single variable, to a full (m−1)-dimensional

input vector x.

•The threshold value tsetting the midpoint of our score distribution (here

zero).

•The value of the scaling constant cregulating the steepness of the transi-

tion.

We can achieve all three by ﬁtting a linear function h(x, w) to the data,

where

h(x, w) = w0+

m−1

i=1

wi·xi

which can then be plugged into the logistic function to yield the classiﬁer:

f(x) = 1

1 + e−h(x,w)

Note that the coeﬃcients of h(x, w) are rich enough to encode the threshold (t=

w0) and steepness (cis essentially the average of w1through wn−1) parameters.

The only remaining question is how to ﬁt the coeﬃcient vector wto the

training data. Recall that we are given a zero/one class label yifor each input

vector xi, where 1 ≤i≤n. We need a penalty function that ascribes appropriate

costs to returning f(xi) as the probability that the class yiis positive, i.e. yi= 1.

Let us ﬁrst consider the case where yireally is 1. Ideally f(xi) = 1 in this

case, so we want to penalize it for being smaller than 1. Indeed, we want to

punish it aggressively when f(yi)→0, because that means that the classiﬁer is

stating that element ihas little chance of being in class-1, when that actually

is the case.

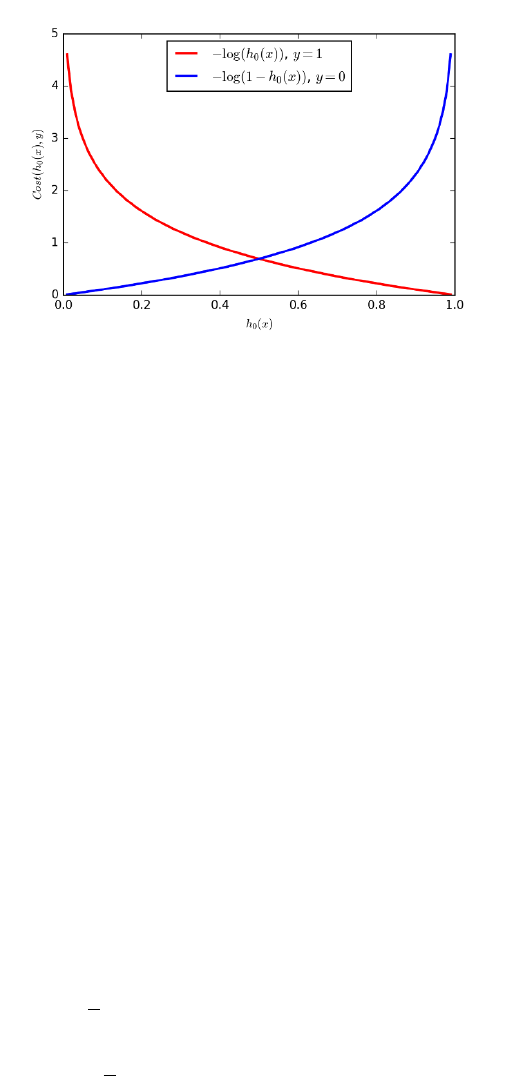
294 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

Figure 9.16: Cost penalties for positive (blue) and negative (right) elements.

The penalty is zero if the correct label is assigned with probability 1, but in-

creasing as a function of misplaced conﬁdence.

The logarithmic function cost(xi,1) = −log(f(xi)) turns out to be a good

penalty function when yi= 1. Recall the deﬁnition of the logarithm (or inverse

exponential function) from Section 2.4, namely that

y= logbx→by=x.

As shown in Figure 9.16, log(1) = 0 for any reasonable base, so zero penalty is

charged when f(xi) = 1, which is as it should be for correctly identifying yi= 1.

Since blogbx=x, log(x)→ −∞ as x→0. This makes cost(xi,1) = −log(f(xi))

an increasingly severe penalty the more we misclassify yi.

Now consider the case where yi= 0. We want to punish the classiﬁer for

high values of f(xi), i.e. more as f(xi)→1. A little reﬂection should convince

you that the right penalty is now cost(xi,0) = −log(1 −f(xi)).

To tie these together, note what happens when we multiply cost(xi,1) times

yi. There are only two possible values, namely yi= 0 or yi= 1. This has the

desired eﬀect, because the penalty is zeroed out in the case where it does not

apply. Similarly, multiplying by (1 −yi) has the opposite eﬀect: zeroing out the

penalty when yi= 1, and applying it when yi= 0. Multiplying the costs by the

appropriate indicator variables enables us to deﬁne the loss function for logistic

regression as an algebraic formula:

J(w) = 1

i=1

cost(f(xi, w), yi)

=−1

i=1

yilog f(xi, w) + (1 −yi) log(1 −f(xi, w))]

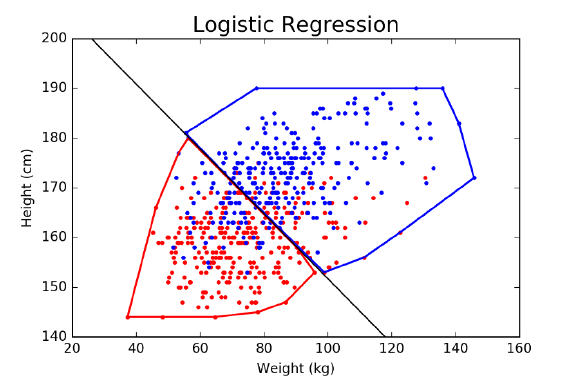
9.7. ISSUES IN LOGISTIC CLASSIFICATION 295

Figure 9.17: The logistic regression classiﬁer best separating men and women

in weight–height space. The red region contains 229 women and only 63 men,

while the blue region contains 223 men to 65 women.

The wonderful thing about this loss function is that it is convex, meaning

that we can ﬁnd the parameters wwhich best ﬁt the training examples using

gradient descent. Thus we can use logistic regression to ﬁnd the best linear

separator between two classes, providing a natural approach to binary classiﬁ-

cation.

9.7 Issues in Logistic Classiﬁcation

There are several nuances to building eﬀective classiﬁers, issues which are rel-

evant both to logistic regression and the other machine learning methods that

we will explore over the next two chapters. These include managing unbalanced

class sizes, multi-class classiﬁcation, and constructing true probability distribu-

tions from independent classiﬁers.

9.7.1 Balanced Training Classes

Consider the following classiﬁcation problem, which is of great interest to law

enforcement agencies in any country. Given the data you have on a particular

person p, decide whether pis a terrorist or is no particular threat.

The quality of the data available to you will ultimately determine the ac-

curacy of your classiﬁer, but regardless, there is something about this problem

that makes it very hard. It is the fact that there are not enough terrorists

available in the general population.

296 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

In the United States, we have been blessed with general peace and security.

It would not surprise me if there were only 300 or so genuine terrorists in the

entire country. In a country of 300 million people, this means that only one out

of every million people are active terrorists.

There are two major consequences of this imbalance. The ﬁrst is that any

meaningful classiﬁer is doomed to have a lot of false positives. Even if our

classiﬁer proved correct an unheard of 99.999% of the time, it would classify

3,000 innocent people as terrorists, ten times the number of bad guys we will

catch. Similar issues were discussed in Section 7.4.1, concerning precision and

recall.

But the second consequence of this imbalance is that there cannot be many

examples of actual terrorists to train on. We might have tens of thousands

of innocent people to serve as positive/class-0 examples, but only a few dozen

known terrorists to be negative/class-1 training instances.

Consider what the logistic classiﬁer is going to do in such an instance. Even

misclassifying all of the terrorists as clean cannot contribute too much to the

loss function, compared with the cost of how we treat the bigger class. It is

more likely to draw a separating line to clear everybody than go hunting for

terrorists. The moral here is that it is generally best to use equal numbers of

positive and negative examples.

But one class may be hard to ﬁnd examples for. So what are our options to

produce a better classiﬁer?

•Force balanced classes by discarding members of the bigger class: This

is the simplest way to realize balanced training classes. It is perfectly

justiﬁed if you have enough rare-class elements to build a respectable

classiﬁer. By discarding the excess instances we don’t need, we create a

harder problem that does not favor the majority class.

•Replicate elements of the smaller class, ideally with perturbation: A sim-

ple way to get more training examples is to clone the terrorists, inserting

perfect replicas of them into the training set under diﬀerent names. These

repeated examples do look like terrorists, after all, and adding enough of

them will make the classes balanced.

This formulation is brittle, however. These identical data records might

create numerical instabilities, and certainly have a tendency towards over-

ﬁtting, since moving one extra real terrorist to the right side of the bound-

ary moves all her clones as well. It might be better to add a certain amount

of random noise to each cloned example, consistent with variance in the

general population. This makes the classiﬁer work harder to ﬁnd them,

and thus minimizes overﬁtting.

•Weigh the rare training examples more heavily than instances of the bigger

class: The loss function for parameter optimization contains a separate

term for the error of each training instance. Adding a coeﬃcient to ascribe

more weight to the most important instances leaves a convex optimization

problem, so it can still be optimized by stochastic gradient descent.

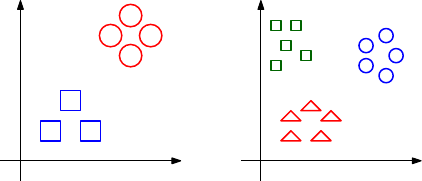
9.7. ISSUES IN LOGISTIC CLASSIFICATION 297

Binary classiﬁcation

Multi-class classiﬁcation

Figure 9.18: Multi-class classiﬁcation problems are a generalization of binary

classiﬁcation.

The problem with all three of these solutions is that we bias the classiﬁer, by

changing the underlying probability distribution. It is important for a classiﬁer

to know that terrorists are extremely rare in the general population, perhaps

by specifying a Baysian prior distribution.

Of course the best solution would be to round up more training examples

from the rarer class, but that isn’t always possible. These three techniques are

about the best we can muster as an alternative.

9.7.2 Multi-Class Classiﬁcation

Often classiﬁcation tasks involve picking from more than two distinct labels.

Consider the problem of identifying the genre of a given movie. Logical possi-

bilities include drama,comedy,animation,action,documentary, and musical.

A natural but misguided approach to represent k-distinct classes would add

class numbers beyond 0/1. In a hair-color classiﬁcation problem, perhaps we

could assign blond = 0, brown = 1, red = 2, black = 4, and so on until we

exhaust human variation. Then we could perform a linear regression to predict

class number.

But this is generally a bad idea. Ordinal scales are deﬁned by either increas-

ing or decreasing values. Unless the ordering of your classes reﬂects an ordinal

scale, the class numbering will be a meaningless target to regress against.

Consider the hair-color numbering above. Should red hair lie between brown

and black (as currently deﬁned), or between blond and brown? Is grey hair a

lighter shade of blond, say class −1, or is it an incomparable condition due

principally to aging? Presumably the features that contribute to grey hair (age

and the number of teen-age children) are completely orthogonal to those of

blond hair (hair salon exposure and Northern European ancestry). If so, there

is no way a linear regression system ﬁtting hair color as a continuous variable

would be destined to separate these colors out from darker hair.

Certain sets of classes are properly deﬁned by ordinal scales. For example,

consider classes formed when people grade themselves on survey questions like

“Skiena’s class is too much work” or “How many stars do you give this movie?”

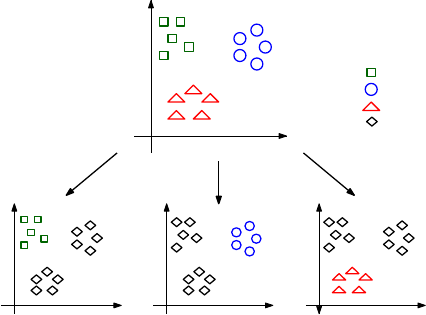
298 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

Class 1:

Class 2:

Class 3:

Others:

Figure 9.19: Voting among multiple one-vs.-rest classiﬁers is generally the best

way to do multi-class classiﬁcation.

Completely Agree ↔Mostly Agree ↔Neutral ↔Mostly Disagree ↔Completely Disagree

Four stars ↔Three stars ↔Two stars ↔One stars ↔Zero stars

Classes deﬁned by such Likert scales are ordinal, and hence such class num-

bers are a perfectly reasonable thing to regress against. In particular, mistak-

enly assigning an element to an adjacent class is much less of a problem than

assigning it to the wrong end of the scale.

But generally speaking, class labels are not ordinal. A better idea for multi-

class discrimination involves building many one-vs.-all classiﬁers, as shown in

Figure 9.19. For each of the possible classes Ci, where 1 ≤i≤c, we train a

logistic classiﬁer to distinguish elements of Ciagainst the union of elements from

all other classes combined. To identify the label associated with a new element

x, we test it against all cof these classiﬁers, and return the label iwhich has

the highest associated probability.

This approach should seem straightforward and reasonable, but note that

the classiﬁcation problem gets harder the more classes you have. Consider the

monkey. By ﬂipping a coin, a monkey should be able to correctly label 50% of

the examples in any binary classiﬁcation problem. But now assume there are

a hundred classes. The monkey will only guess correctly 1% of the time. The

task is now very hard, and even an excellent classiﬁer will have a diﬃcult time

producing good results on it.

9.7.3 Hierarchical Classiﬁcation

When your problem contains a large number of classes, it pays to group them

into a tree or hierarchy so as to improve both accuracy and eﬃciency. Suppose

9.7. ISSUES IN LOGISTIC CLASSIFICATION 299

we built a binary tree, where each individual category is represented by a leaf

node. Each internal node represents a classiﬁer for distinguishing between the

left descendants and the right descendants.

To use this hierarchy to classify a new item x, we start at the root. Running

the root classiﬁer on xwill specify it as belonging to either the left or right

subtree. Moving down one level, we compare xwith the new node’s classiﬁer

and keep recurring until we hit a leaf, which deﬁnes the label assigned to x.

The time it takes is proportional to the height of the tree, ideally logarithmic

in the number of classes c, instead of being linear in cif we explicitly compare

against every class. Classiﬁers based on this approach are called decision trees,

and will be discussed further in Section 11.2.

Ideally this hierarchy can be built from domain knowledge, ensuring that

categories representing similar classes are grouped together. This has two ben-

eﬁts. First, it makes it more likely that misclassiﬁcations will still produce

labels from similar classes. Second, it means that intermediate nodes can deﬁne

higher-order concepts, which can be more accurately recognized. Suppose that

the one hundred categories in a image classiﬁcation problem included “car,”

“truck,” “boat,” and “bicycle”. When all of these categories are descendants of

an intermediate node called “vehicle,” we can interpret the path to this node as

a lower-resolution, higher-accuracy classiﬁer.

There is another, independent danger with classiﬁcation that becomes more

acute as the number of classes grows. Members of certain classes (think “college

students”) are much more plentiful than others, like “rock stars.” The relative

disparity between the size of the largest and smallest classes typically grows

along with number of classes.

For this example, let’s agree that “rock stars” tend to be sullen, grungy-

looking males, providing useful features for any classiﬁer. However, only a

small fraction of sullen, grungy-looking males are rock stars, because there are

extremely few people who have succeeded in this demanding profession. Clas-

siﬁcation systems which do not have a proper sense of the prior distribution on

labels are doomed having many false positives, by assigning rare labels much

too frequently.

This is the heart of Baysian analysis: updating our current (prior) under-

standing of the probability distribution in the face of new evidence. Here, the

evidence is the result is from a classiﬁer. If we incorporate a sound prior distri-

bution into our reasoning, we can ensure that items require particularly strong

evidence to be assigned to rare classes.

9.7.4 Partition Functions and Multinomial Regression

Recall that our preferred means of multi-class classiﬁcation involved training

independent single-class vs. all logistic classiﬁers Fi(x), where 1 ≤i≤cand c

is the number of distinct labels. One minor issue remains. The probabilities we

get from logistic regression aren’t really probabilities. Turning them into real

probabilities requires the idea of a partition function.

300 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

For any particular item x, summing up the “probabilities” over all possible

labels for xshould yield T= 1, where

i=1

Fi(x).

But should doesn’t mean is. All of these classiﬁers were trained independently,

and hence there is nothing forcing them to sum to T= 1.

A solution is to divide all of these probabilities by the appropriate constant,

namely F0(x) = F(x)/T . This may sound like a kludge, because it is. But this

is essentially what physicists do when they talk about partition functions, which

serve as denominators turning something proportional to probabilities into real

probabilities.

Multinomial regression is a more principled method of training independent

single-class vs. all classiﬁers, so that the probabilities work out right. This

involves using the correct partition function for log odds ratios, which are com-

puted with exponentials of the resulting values. More than this I will not say,

but it is reasonable to look for a multinomial regression function in your favorite

machine learning library and see how it does when faced with a multi-class re-

gression problem.

A related notion to the partition function arises in Baysian analysis. We are

often faced with a challenge of identifying the most likely item label, say A, as

a function of evidence E. Recall that Bayes’ theorem states that

P(A|E) = P(E|A)P(A)

P(E)

Computing this as a real probability requires knowing the denominator P(E),

which can be a murky thing to compute. But comparing P(A|E) to P(B|E) in

order to determine whether label Ais more likely than label Bdoes not require

knowing P(E), since it is the same in both expressions. Like a physicist, we can

waive it away, mumbling about the “partition function.”

9.8 Chapter Notes

Linear and logistic regression are standard topics in statistics and optimization.

Textbooks on linear/logistic regression and its applications include [JWHT13,

Wei05].

The treatment of the gradient descent approach to solving regression here

was inspired by Andrew Ng, as presented in his Coursera machine learning

course. I strongly recommend his video lectures to those interested in a more

thorough treatment of the subject.

The discovery that butter production in Bangladesh accurately forecasted

the S&P 500 stock index is due to Leinweber [Lei07]. Unfortunately, like most

spurious correlations it broke down immediately after its discovery, and no

longer has predictive power.

9.9. EXERCISES 301

9.9 Exercises

Linear Regression

9-1. [3] Construct an example on n≥6 points where the optimal regression line is

y=x, even though none of the input points lie directly on this line.

9-2. [3] Suppose we ﬁt a regression line to predict the shelf life of an apple based on

its weight. For a particular apple, we predict the shelf life to be 4.6 days. The

apples residual is −0.6 days. Did we over or under estimate the shelf-life of the

apple? Explain your reasoning.

9-3. [3] Suppose we want to ﬁnd the best-ﬁtting function y=f(x) where y=w2x+

wx. How can we use linear regression to ﬁnd the best value of w?

9-4. [3] Suppose we have the opportunity to pick between using the best ﬁtting

model of the form y=f(x) where y=w2xor y=wx, for constant coeﬃcient

w. Which of these is more general, or are they identical?

9-5. [5] Explain what a long-tailed distribution is, and provide three examples of rel-

evant phenomena that have long tails. Why are they important in classiﬁcation

and regression problems?

9-6. [5] Using a linear algebra library/package, implement the closed form regression

solver w= (ATA)−1ATb. How well does it perform, relative to an existing

solver?

9-7. [3] Establish the eﬀect that diﬀerent values for the constant cof the logit function

have on the probability of classiﬁcation being 0.01, 1, 2, and 10 units from the

boundary.

Experiments with Linear Regression

9-8. [5] Experiment with the eﬀects of ﬁtting non-linear functions with linear regres-

sion. For a given (x, y) data set, construct the best ﬁtting line where the set

of variables are {1, x, . . . , xk}, for a range of diﬀerent k. Does the model get

better or worse over the course of this process, both in terms of ﬁtting error and

general robustness?

9-9. [5] Experiment with the eﬀects of feature scaling in linear regression. For a

given data set with at least two features (dimensions), multiply all the values

of one feature by 10k, for −10 ≤k≤10. Does this operation cause a loss of

numerical accuracy in ﬁtting?

9-10. [5] Experiment with the eﬀects of highly correlated features in linear regression.

For a given (x, y) data set, replicate the value of xwith small but increasing

amounts of random noise. What is returned when the new column is perfectly

correlated with the original? What happens with increasing amounts of random

noise?

9-11. [5] Experiment with the eﬀects of outliers on linear regression. For a given (x, y)

data set, construct the best ﬁtting line. Repeatedly delete the point with the

largest residual, and reﬁt. Is the sequence of predicted slopes relatively stable

for much of this process?

9-12. [5] Experiment with the eﬀects of regularization on linear/logistic regression.

For a given multi-dimensional data set, construct the best ﬁtting line with (a)

302 CHAPTER 9. LINEAR AND LOGISTIC REGRESSION

no regularization, (b) ridge regression, and (c) LASSO regression; the latter two

with a range of constraint values. How does the accuracy of the model change

as we reduce the size and number of parameters?

Implementation Projects

9-13. [5] Use linear/logistic regression to build a model for one of the following The

Quant Shop challenges:

(a) Miss Universe.

(b) Movie gross.

(d) Art auction price.

(e) White Christmas.

(f) Football champions.

(g) Ghoul pool.

(h) Gold/oil prices.

9-14. [5] This story about predicting the results of the NCAA college basketball

tournament is instructive:

http://www.nytimes.com/2015/03/22/opinion/sunday/making-march-madness-easy.

html.

Implement such a logistic regression classiﬁer, and extend it to other sports like

football.

Interview Questions

9-15. [8] Suppose we are training a model using stochastic gradient descent. How do

we know if we are converging to a solution?

9-16. [5] Do gradient descent methods always converge to the same point?

9-17. [5] What assumptions are required for linear regression? What if some of these

assumptions are violated?

9-18. [5] How do we train a logistic regression model? How do we interpret its coeﬃ-

cients?

Kaggle Challenges

9-19. Identify what is being cooked, given the list of ingredients.

https://www.kaggle.com/c/whats-cooking

9-20. Which customers are satisﬁed with their bank?

https://www.kaggle.com/c/santander-customer-satisfaction

9-21. What does a worker need access to in order to do their job?

https://www.kaggle.com/c/amazon-employee-access-challenge

Chapter 10

Distance and Network

Methods

When a measure becomes a target, it ceases to be a measure.

– Charles Goodhart (Goodhart’s Law)

An n×ddata matrix, consisting of nexamples/rows each deﬁned by dfea-

tures/columns, naturally deﬁnes a set of npoints in a d-dimensional geometric

space. Interpreting examples as points in space provides a powerful way to

think about them – like the stars in the heavens. Which stars are the closest

to our sun, i.e. our nearest neighbors? Galaxies are natural groupings of stars

identiﬁed by clustering the data. Which stars share the Milky Way with our

sun?

There is a close connection between collections of points in space and vertices

in networks. Often we build networks from geometric point sets, by connecting

close pairs of points by edges. Conversely, we can build point sets from networks,

by embedding the vertices in space, so that pairs of connected vertices are

located near each other in the embedding.

Several of the important problems on geometric data readily generalize to

network data, including nearest neighbor classiﬁcation and clustering. Thus

we treat both topics together in this chapter, to better exploit the synergies

between them.

10.1 Measuring Distances

The most basic issue in the geometry of points pand qin ddimensions is how

best to measure the distance between them. It might not be obvious that there

is any issue here to speak of, since the traditional Euclidean metric is obviously

304 CHAPTER 10. DISTANCE AND NETWORK METHODS

how you measure distances. The Euclidean matrix deﬁnes

d(p, q) = v

i=1 |pi−qi|2

But there are other reasonable notions of distance to consider. Indeed, what

is a distance metric? How does it diﬀer from an arbitrary scoring function?

10.1.1 Distance Metrics

Distance measures most obviously diﬀer from similarity scores, like the correla-

tion coeﬃcient, in their direction of growth. Distance measures get smaller as

items become more similar, while the converse is true of similarity functions.

There are certain useful mathematical properties we assume of any reason-

able distance measure. We say a distance measure is a metric if it satisﬁes the

following properties:

•Positivity:d(x, y)≥0 for all xand y.

•Identity:d(x, y) = 0 if and only if x=y.

•Symmetry:d(x, y) = d(y, x) for all xand y.

•Triangle inequality:d(x, y)≤d(x, z) + d(z, y) for all x,y, and z.

These properties are important for reasoning about data. Indeed, many algo-

rithms work correctly only when the distance function is a metric.

The Euclidean distance is a metric, which is why these conditions seem

so natural to us. However, other equally-natural similarity measures are not

distance metrics:

•Correlation coeﬃcient: Fails positivity because it ranges from −1 to 1.

Also fails identity, as the correlation of a sequence with itself is 1.

•Cosine similarity/dot product: Similar to correlation coeﬃcient, it fails

positivity and identity for the same reason.

•Travel times in a directed network: In a world with one-way streets, the

distance from xto yis not necessarily the same as the distance from yto

•Cheapest airfare: This often violates the triangle inequality, because the

cheapest way to ﬂy from xto ymight well involve taking a detour through

z, due to bizarre airline pricing strategies.

By contrast, it is not immediately obvious that certain well-known distance

functions are metrics, such as edit distance used in string matching. Instead of

making assumptions, prove or disprove each of the four basic properties, to be

sure you understand what you are working with.

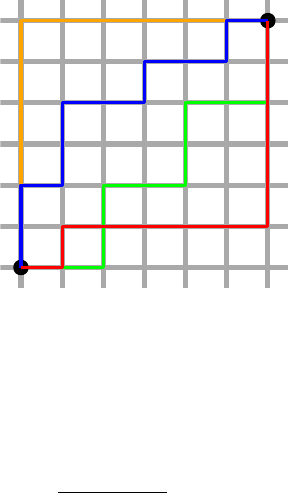
10.1. MEASURING DISTANCES 305

Figure 10.1: Many diﬀerent paths across a grid have equal Manhattan (L1)

distance.

10.1.2 The LkDistance Metric

The Euclidean distance is just a special case of a more general family of distance

functions, known as the Lkdistance metric or norm:

dk(p, q) = k

i=1 |pi−qi|k= (

i=1 |pi−qi|k)1/k

The parameter kprovides a way to trade oﬀ between the largest and the total

dimensional diﬀerences. The value for kcan be any number between 1 and ∞,

with particularly popular values including:

•Manhattan distance (k= 1): If we ignore exceptions like Broadway,

all streets in Manhattan run east–west and all avenues north–south, thus

deﬁning a regular grid. The distance between two locations is then the

sum of this north–south diﬀerence and the east–west diﬀerence, since tall

buildings prevent any chance of shortcuts.

Similarly, the L1or Manhattan distance is the total sum of the deviations

between the dimensions. Everything is linear, so a diﬀerence of 1 in each

of two dimensions is the same as a diﬀerence of 2 in only one dimension.

Because we cannot take advantage of diagonal short-cuts, there are typi-

cally many possible shortest paths between two points, as shown in Figure

10.1.

•Euclidean distance (k= 2): This is the most popular distance metric,

oﬀering more weight to the largest dimensional deviation without over-

whelming the lesser dimensions.

•Maximum component (k=∞): As the value of kincreases, smaller

dimensional diﬀerences fade into irrelevance. If a>b, then akbk.

Taking the kth root of ak+bkapproaches aas bk/ak→0.

306 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.2: The shape of circles deﬁning equal distances changes with k.

Consider the distance of points p1= (2,0) and p2= (2,1.99) from the

origin:

–For k= 1, the distances are 2 and 3.99, respectively.

–For k= 2, they are 2 and 2.82136.

–For k= 1000, they are 2 and 2.00001.

–For k=∞, they are 2 and 2.

The L∞metric returns the largest single dimensional diﬀerence as the

distance.

We are comfortable with Euclidean distance because we live in a Euclidean

world. We believe in the truth of the Pythagorean theorem, that the sides of

a right triangle obey the relationship that a2+b2=c2. In the world of Lk

distances, the Pythagorean theorem would be ak+bk=ck.

We are similarly comfortable with the notion that circles are round. Recall

that a circle is deﬁned as the collection of points which are at a distance rfrom

an origin point p. Change the deﬁnition of distance, and you change the shape

of a circle.

The shape of an Lk“circle” governs which points are equal neighbors about

a center point p. Figure 10.2 illustrates how the shape evolves with k. Under

Manhattan distance (k= 1), the circle looks like a diamond. For k= 2, it is

the round object we are familiar with. For k=∞, this circle stretches out to

an axis-oriented box.

There is smooth transition from the diamond to the box as we vary 1 ≤k≤

∞. Selecting the value of kis equivalent to choosing which circle best ﬁts our

domain model. The distinctions here become particularly important in higher

dimensional spaces: do we care about deviations in all dimensions, or primarily

the biggest ones?

Take-Home Lesson: Selecting the right value of kcan have a signiﬁcant eﬀect on

the meaningfulness of your distance function, particularly in high-dimensional

spaces.

10.1. MEASURING DISTANCES 307

Taking the kth root of the sum of kth-power terms is necessary for the

resulting “distance” values to satisfy the metric property. However, in many

applications we will be only using the distances for comparison: testing whether

d(x, p)≤d(x, q) as opposed to using the values in formulas or isolation.

Because we take the absolute value of each dimensional distance before rais-

ing it to the kth power, the summation within the distance function always

yields a positive value. The kth root/power function is monotonic, meaning

that for x, y, k ≥0

(x>y)→(xk> yk).

Thus the order of distance comparison is unchanged if we do not take the kth

root of the summation. Avoiding the kth root calculation saves time, which

can prove non-trivial when many distance computations are performed, as in

nearest neighbor search.

10.1.3 Working in Higher Dimensions

I personally have no geometric sense about higher-dimensional spaces, anything

where d > 3. Usually, the best we can do is to think about higher-dimensional

geometries through linear algebra: the equations which govern our understand-

ing of two/three-dimensional geometries readily generalize for arbitrary d, and

that is just the way things work.

We can develop some intuition about working with a higher-dimensional data

set through projection methods, which reduce the dimensionality to levels we

can understand. It is often helpful to visualize the two-dimensional projections

of the data by ignoring the other d−2 dimensions entirely, and instead study

dot plots of dimensional pairs. Through dimension reduction methods like prin-

ciple component analysis (see Section 8.5.2), we can combine highly correlated

features to produce a cleaner representation. Of course, some details are lost in

the process: whether it is noise or nuance depends upon your interpretation.

It should be clear that as we increase the number of dimensions in our data

set, we are implicitly saying that each dimension is a less important part of

the whole. In measuring the distance between two points in feature space,

understand that large dmeans that there are more ways for points to be close

(or far) from each other: we can imagine them being almost identical along all

dimensions but one.

This makes the choice of distance metric most important in high-dimensional

data spaces. Of course, we can always stick with L2distance, which is a safe

and standard choice. But if we want to reward points for being close on many

dimensions, we prefer a metric leaning more towards L1. If instead things are

similar when there are no single ﬁelds of gross dissimilarity, we perhaps should

be interested in something closer to L∞.

One way to think about this is whether we are more concerned about random

added noise to our features, or exceptional events leading to large artifacts. L1

is undesirable in the former case, because the metric will add up the noise

from all dimensions in the distance. But artifacts make L∞suspect, because a

308 CHAPTER 10. DISTANCE AND NETWORK METHODS

substantial error in any single column will come to dominate the entire distance

calculation.

Take-Home Lesson: Use your freedom to select the best distance metric. Eval-

uate how well diﬀerent functions work to tease out the similarity of items in

your data set.

10.1.4 Dimensional Egalitarianism

The Lkdistance metrics all implicitly weigh each dimension equally. It doesn’t

have to be this way. Sometimes we come to a problem with a domain-speciﬁc

understanding that certain features are more important for similarity than oth-

ers. We can encode this information using a coeﬃcient cito specify a diﬀerent

weight to each dimension:

dk(p, q) = k

i=1

ci|pi−qi|k= (

i=1

ci|pi−qi|k)1/k

We can view the traditional Lkdistance as a special case of this more general

formula, where ci= 1 for 1 ≤i≤d. This dimension-weighted distance still

satisﬁes the metric properties.

If you have ground-truth data about the desired distance between certain

pairs of points, then you can use linear regression to ﬁt the coeﬃcients cito best

match your training set. But, generally speaking, dimension-weighted distance

is often not a great idea. Unless you have a genuine reason to know that certain

dimensions are more important than others, you are simply encoding your biases

into the distance formula.

But much more serious biases creep in if you do not normalize your variables

before computing distances. Suppose we have a choice of reporting a distance

in either meters or kilometers. The contribution of a 30 meter diﬀerence in the

distance function will either be 302= 900 or 0.03=0.0009, literally a million-fold

diﬀerence in weight.

The correct approach is to normalize the values of each dimension by Z-

scores before computing your distance. Replace each value xiby its Z-score

z= (x−µi)/σi, where µiis the mean value of dimension iand σiits standard

deviation. Now the expected value of xiis zero for all dimensions, and the

spread is tightly controlled if they were normally distributed to start with.

More stringent eﬀorts must be taken if a particular dimension is, say, power law

distributed. Review Section 4.3 on normalization for relevant techniques, like

ﬁrst hitting it with a logarithm before computing the Z-score.

Take-Home Lesson: The most common use of dimension-weighted distance

metrics is as a kludge to mask the fact that you didn’t properly normalize your

data. Don’t fall into this trap. Replace the original values by Z-scores before

computing distances, to ensure that all dimensions contribute equally to the

result.

10.1. MEASURING DISTANCES 309

10.1.5 Points vs. Vectors

Vectors and points are both deﬁned by arrays of numbers, but they are concep-

tually diﬀerent beasts for representing items in feature space. Vectors decouple

direction from magnitude, and so can be thought of as deﬁning points on the

surface of a unit sphere.

To see why this is important, consider the problem of identifying the nearest

documents from word–topic counts. Suppose we have partitioned the vocabulary

of English into ndiﬀerent subsets based on topics, so each vocabulary word sits

in exactly one of the topics. We can represent each article Aas a bag of words, as

a point pin n-dimensional space where piequals the number of words appearing

in article Athat come from topic i.

If we want a long article on football to be close to a short article on football,

the magnitude of this vector cannot matter, only its direction. Without nor-

malization for length, all the tiny tweet-length documents will bunch up near

the origin, instead of clustering semantically in topic space as we desire.

Norms are measures of vector magnitude, essentially distance functions in-

volving only one point, because the second is taken to be the origin. Vectors

are essentially normalized points, where we divide the value of each dimension

of pby its L2-norm L2(p), which is the distance between pand the origin O:

L2(p) = v

i=1

After such normalization, the length of each vector will be 1, turning it into a

point on the unit sphere about the origin.

We have several possible distance metrics to use in comparing pairs of vec-

tors. The ﬁrst class is deﬁned by the Lkmetrics, including Euclidean distance.

This works because points on the surface of a sphere are still points in space.

But we can perhaps more meaningfully consider the distance between two vec-

tors in terms of the angle deﬁned between them. We have seen that the cosine

similarity between two points pand qis their dot product divided by their

L2-norms:

cos(p, q) = p·q

||p|| ||q||

For previously normalized vectors, these norms equal 1, so all that matters is

the dot product.

The cosine function here is a similarity function, not a distance measure,

because larger values mean higher similarity. Deﬁning a cosine distance as

1− |cos(p, q)|does yield distance measure that satisﬁes three of the metric

properties, all but the triangle inequality. A true distance metric follows from

310 CHAPTER 10. DISTANCE AND NETWORK METHODS

angular distance, where

d(p, q)=1−arccos(cos(p, q))

Here arccos() is the inverse cosine function cos−1(), and πis the largest angle

range in radians.

10.1.6 Distances between Probability Distributions

Recall the Kolmogorov-Smirnov test (Section 5.3.3), which enabled us to deter-

mine whether two sets of samples were likely drawn from the same underlying

probability distribution.

This suggests that we often need a way to compare a pair of distributions and

determine a measure of similarity or distance between them. A typical appli-

cation comes in measuring how closely one distribution approximates another,

providing a way to identify the best of a set of possible models.

The distance measures that have been described for points could, in princi-

ple, be applied to measure the similarity of two probability distributions Pand

Qover a given discrete variable range R.

Suppose that Rcan take on any of exactly dpossible values, say R=

{r1, . . . , rd}. Let pi(qi) denote the probability that X=riunder distribu-

tion P(Q). Since Pand Qare both probability distributions, we know that

i=1

pi=

i=1

qi= 1

The spectrum of piand qivalues for 1 ≤i≤dcan be thought of as d-dimensional

points representing Pand Q, whose distance could be computed using the Eu-

clidean metric.

Still, there are more specialized measures, which do a better job of assessing

the similarity of probability distributions. They are based on the information-

theoretic notion of entropy, which deﬁnes a measure of uncertainty for the value

of a sample drawn from the distribution. This makes the concept mildly analo-

gous to variance.

The entropy H(P) of a probability distribution Pis given by

H(P) =

i=1

pilog2(1

) = −

i=1

pilog2(pi).

Like distance, entropy is always a non-negative quantity. The two sums above

diﬀer only in how they achieve it. Because piis a probability, it is generally less

than 1, and hence log(pi) is generally negative. Thus either taking the reciprocal

of the probabilities before taking the log or negating each term suﬃces to make

H(P)≥0 for all P.

Entropy is a measure of uncertainty. Consider the distribution where p1=

1 and pi= 0, for 2 ≤i≤d. This is like tossing a totally loaded die, so

10.2. NEAREST NEIGHBOR CLASSIFICATION 311

despite having dsides there is no uncertainty about the outcome. Sure enough,

H(P) = 0, because either pior log2(1) zeros out every term in the summation.

Now consider the distribution where qi= 1/d for 1 ≤i≤d. This represents

fair dice roll, the maximally uncertain distribution where H(Q) = log2(d) bits.

The ﬂip side of uncertainty is information. The entropy H(P) corresponds

to how much information you learn after a sample from Pis revealed. You learn

nothing when someone tells you something you already know.

The standard distance measures on probability distributions are based on

entropy and information theory. The Kullback-Leibler (KL) divergence measures

the uncertainty gained or information lost when replacing distribution Pwith

Q. Speciﬁcally,

KL(P||Q) =

i=1

pilog2

Suppose P=Q. Then nothing should be gained or lost, and KL(P, P )=0

because lg(1) = 0. But the worse a replacement Qis for P, the larger KL(P||Q)

gets, blowing up to ∞when pi> qi= 0.

The KL divergence resembles a distance measure, but is not a metric, be-

cause it is not symmetric (KL(P||Q)6=KL(Q||P)) and does not satisﬁes the

triangle inequality. However, it forms the basis of the Jensen-Shannon diver-

gence JS(P, Q):

JS(P, Q) = 1

2KL(P||M) + 1

2KL(Q||M)

where the distribution Mis the average of Pand Q, i.e. mi= (pi+qi)/2.

JS(P, Q) is clearly symmetric while preserving the other properties of KL

divergence. Further pJS(P, Q) magically satisﬁes the triangle inequality, turn-

ing it into a true metric. This is the right function to use for measuring the

distance between probability distributions.

10.2 Nearest Neighbor Classiﬁcation

Distance functions grant us the ability to identify which points are closest to

a given target. This provides great power, and is the engine behind nearest

neighbor classiﬁcation. Given a set of labeled training examples, we seek the

training example which is most similar to an unlabeled point p, and then take

the class label for pfrom its nearest labeled neighbor.

The idea here is simple. We use the nearest labeled neighbor to a given query

point qas its representative. If we are dealing with a classiﬁcation problem, we

will assign qthe same label as it nearest neighbor(s). If we are dealing with a

regression problem, assign qthe mean/median value of its nearest neighbor(s).

These forecasts are readily defensible assuming (1) the feature space coherently

captures the properties of the elements in question, and (2) the distance function

meaningfully recognizes similar rows/points when they are encountered.

The Bible exhorts us to love thy neighbor. There are three big advantages

to nearest neighbor methods for classiﬁcation:

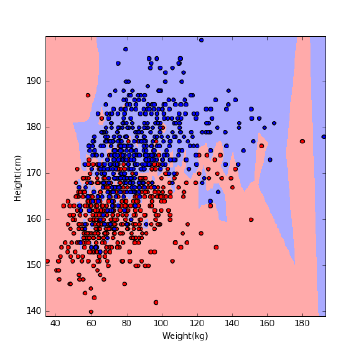
312 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.3: The decision boundary of nearest-neighbor classiﬁers can be non-

linear.

•Simplicity: Nearest neighbor methods are not rocket science; there is no

math here more intimidating than a distance metric. This is important,

because it means we can know exactly what is going on and avoid being

the victim of bugs or misconceptions.

•Interpretability: Studying the nearest-neighbors of a given query point

qexplains exactly why the classiﬁer made the decision it did. If you

disagree with this outcome, you can systematically debug things. Were

the neighboring points incorrectly labeled? Did your distance function fail

to pick out the items which were the logical peer group for q?

•Non-linearity: Nearest neighbor classiﬁers have decision boundaries which

are piecewise-linear, but can crinkle arbitrarily following the training ex-

ample herd, as shown in Figure 10.3. From calculus we know that piecewise-

linear functions approach smooth curves once the pieces get small enough.

Thus nearest neighbor classiﬁers enable us to realize very complicated de-

cision boundaries, indeed surfaces so complex that they have no concise

representation.

There are several aspects to building eﬀective nearest neighbor classiﬁers,

including technical issues related to robustness and eﬃciency. But foremost

is learning to appreciate the power of analogy. We discuss these issues in the

sections below.

10.2.1 Seeking Good Analogies

Certain intellectual disciplines rest on the power of analogies. Lawyers don’t

reason from laws directly as much as they rely on precedents: the results of

10.2. NEAREST NEIGHBOR CLASSIFICATION 313

previously decided cases by respected jurists. The right decision for the current

case (I win or I lose) is a function of which prior cases can be demonstrated to

be most fundamentally similar to the matter at hand.

Similarly, much of medical practice rests on experience. The old country

doctor thinks back to her previous patients to recall cases with similar symptoms

to yours that managed to survive, and then gives you the same stuﬀ she gave

them. My current physician (Dr. Learner) is now in his eighties, but I trust

him ahead of all those young whipper-snappers relying only on the latest stuﬀ

taught in medical school.

Getting the greatest beneﬁts from nearest neighbor methods involves learn-

ing to respect analogical reasoning. What is the right way to predict the price of

a house? We can describe each property in terms of features like the area of the

lot and the number of bedrooms, and assign each a dollar weight to be added

together via linear regression. Or we can look for “comps,” seeking comparable

properties in similar neighborhoods, and forecast a price similar to what we see.

The second approach is analogical reasoning.

I encourage you to get hold of a data set where you have domain knowledge

and interest, and do some experiments with ﬁnding nearest neighbors. One re-

source that always inspires me is http://www.baseball-reference.com, which

reports the ten nearest neighbors for each player, based on their statistics to

date. I ﬁnd these analogies amazingly evocative: the identiﬁed players often ﬁll

similar roles and styles which should not be explicitly captured by the statistics.

Yet somehow they are.

Try to do this with another domain you care about: books, movies, music, or

whatever. Come to feel the power of nearest neighbor methods, and analogies.

Take-Home Lesson: Identifying the ten nearest neighbors to points you know

about provides an excellent way to understand the strengths and limitations of

a given data set. Visualizing such analogies should be your ﬁrst step in dealing

with any high-dimensional data set.

10.2.2 k-Nearest Neighbors

To classify a given query point q, nearest neighbor methods return the label

of q0, the closest labeled point to q. This is a reasonable hypothesis, assuming

that similarity in feature space implies similarity in label space. However, this

classiﬁcation is based on exactly one training example, which should give us

pause.

More robust classiﬁcation or interpolation follows from voting over multiple

close neighbors. Suppose we ﬁnd the kpoints closest to our query, where kis

typically some value ranging from 3 to 50 depending upon the size of n. The

arrangement of the labeled points coupled with the choice of kcarves the feature

space into regions, with all the points in a particular given region assigned the

same label.

Consider Figure 10.4, which attempts to build a gender classiﬁer from data

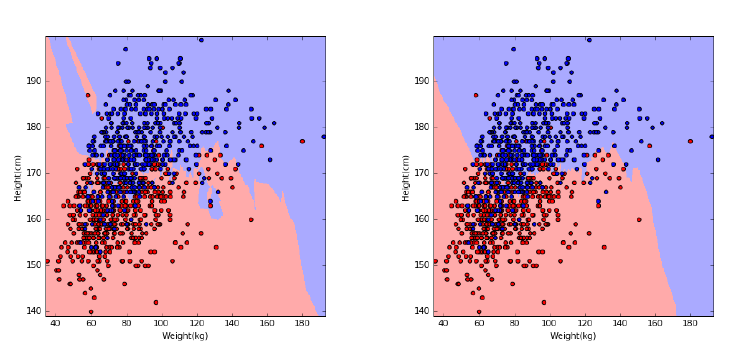
314 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.4: The eﬀect of kon the decision boundary for gender classiﬁcation

using k-NN. Compare k= 3 (left) and k= 10 (right) with k= 1 in Figure 10.3.

on height and weight. Generally speaking, women are shorter and lighter than

men, but there are many exceptions, particularly near the decision boundary. As

shown in Figure 10.4, increasing ktends to produce larger regions with smoother

boundaries, representing more robust decisions. However, the larger we make

k, the more generic our decisions are. Choosing k=nis simply another name

for the majority classiﬁer, where we assign each point the most common label

regardless of its individual features.

The right way to set kis to assign a fraction of labeled training examples as

an evaluation set, and then experiment with diﬀerent values of the parameter

kto see where the best performance is achieved. These evaluation values can

then be thrown back into the training/target set, once khas been selected.

For a binary classiﬁcation problem, we want kto be an odd number, so the

decision never comes out to be a tie. Generally speaking, the diﬀerence between

the number of positive and negative votes can be interpreted as a measure of

our conﬁdence in the decision.

There are potential asymmetries concerning geometric nearest neighbors.

Every point has a nearest neighbor, but for outlier points these nearest neighbors

may not be particular close. These outlier points in fact can have an outsized

role in classiﬁcation, deﬁning the nearest neighbor to a huge volume of feature

space. However, if you picked your training examples properly this should be

largely uninhabited territory, a region in feature space where points rarely occur.

The idea of nearest neighbor classiﬁcation can be generalized to function

interpolation, by averaging the values of the knearest points. This is presumably

done by real-estate websites like www.zillow.com, to predict housing prices from

nearest neighbors. Such averaging schemes can be generalized by non-uniform

10.2. NEAREST NEIGHBOR CLASSIFICATION 315

Figure 10.5: Data structures for nearest neighbor search include Voronoi dia-

grams (left) and kd-trees (right).

weights, valuing points diﬀerently according to distance rank or magnitude.

Similar ideas work for all classiﬁcation methods.

10.2.3 Finding Nearest Neighbors

Perhaps the biggest limitation of nearest neighbor classiﬁcation methods is their

runtime cost. Comparing a query point qin ddimensions against nsuch training

points is most obviously done by performing nexplicit distance comparisons, at

a cost of O(nd). With thousands or even millions of training points available,

this search can introduce a notable lag into any classiﬁcation system.

One approach to speeding up the search involves the use of geometric data

structures. Popular choices include:

•Voronoi diagrams: For a set of target points, we would like to partition

the space around them into cells such that each cell contains exactly one

target point. Further, we want each cell’s target point to be the nearest

target neighbor for all locations in the cell. Such a partition is called a

Voronoi diagram, and is illustrated in Figure 10.5 (left).

The boundaries of Voronoi diagrams are deﬁned by the perpendicular

bisectors between pairs of points (a, b). Each bisector cuts the space in

half: one half containing aand the other containing b, such that all points

on a’s half are closer to athan b, and visa versa.

Voronoi diagrams are a wonderful tool for thinking about data, and have

many nice properties. Eﬃcient algorithms for building them and searching

them exist, particularly in two dimensions. However, these procedures

rapidly become more complex as the dimensionality increases, making

them generally impractical beyond two or three dimensions.

•Grid indexes: We can carve up space into d-dimensional boxes, by divid-

ing the range of each dimension into rintervals or buckets. For example,

316 CHAPTER 10. DISTANCE AND NETWORK METHODS

012345

Figure 10.6: A grid index data structure provides fast access to nearest neighbors

when the points are uniformly distributed, but can be ineﬃcient when points in

certain regions are densely clustered.

consider a two-dimensional space where each axis was a probability, thus

ranging from 0 to 1. This range can be divided into requal-sized intervals,

such that the ith interval ranges between [(i−1)/r, i/r].

These intervals deﬁne a regular grid over the space, so we can associate

each of the training points with the grid cell where it belongs. Search now

becomes the problem of identifying the right grid cell for point qthrough

array lookup or binary search, and then comparing qagainst all the points

in this cell to identify the nearest neighbor.

Such grid indexes can be eﬀective, but there are potential problems. First,

the training points might not be uniformly distributed, and many cells

might be empties, as in Figure 10.6. Establishing a non-uniform grid might

lead to a more balanced arrangement, but makes it harder to quickly ﬁnd

the cell containing q. But there is also no guarantee that the nearest

neighbor of qactually lives within the same cell as q, particularly if qlies

very close to the cell’s boundary. This means we must search neighboring

cells as well, to ensure we ﬁnd the absolute nearest neighbor.

•Kd-trees: There are a large class of tree-based data structures which par-

tition space using a hierarchy of divisions that facilitates search. Starting

from an arbitrary dimension as the root, each node in the kd-tree deﬁnes

median line/plane that splits the points equally according to that dimen-

sion. The construction recurs on each side using a diﬀerent dimension,

and so on until the region deﬁned by a node contains just one training

point.

10.2. NEAREST NEIGHBOR CLASSIFICATION 317

This construction hierarchy is ideally suited to support search. Starting

at the root, we test whether the query point qis to the left or right of the

median line/plane. This identiﬁes which side qlies on, and hence which

side of the tree to recur on. The search time is log n, since we split the

point set in half with each step down the tree.

There are a variety of such space-partition search tree structures avail-

able, with one or more likely implemented in your favorite programming

language’s function library. Some oﬀer faster search times on problems

like nearest neighbor, with perhaps a trade-oﬀ of accuracy for speed.

Although these techniques can indeed speed nearest neighbor search in mod-

est numbers of dimensions (say 2 ≤d≤10), they get less eﬀective as the di-

mensionality increases. The reason is that the number of ways that two points

can be close to each other increases rapidly with the dimensionality, making

it harder to cut away regions which have no chance of containing the nearest

neighbor to q. Deterministic nearest neighbor search eventually reduces to linear

search, for high-enough dimensionality data.

10.2.4 Locality Sensitive Hashing

To achieve faster running times, we must abandon the idea of ﬁnding the exact

nearest neighbor, and settle for a good guess. We want to batch up nearby

points into buckets by similarity, and quickly ﬁnd the most appropriate bucket

Bfor our query point q. By only computing the distance between qand the

points in the bucket, we save search time when |B|  n.

This was the basic idea behind the grid index, described in the previous

section, but the search structures become unwieldy and unbalanced in practice.

A better approach is based on hashing.

Locality sensitive hashing (LSH) is deﬁned by a hash function h(p) that takes

a point or vector as input and produces a number or code as output such that

it is likely that h(a) = h(b) if aand bare close to each other, and h(a)6=h(b)

if they are far apart.

Such locality sensitive hash functions readily serve the same role as the grid

index, without the fuss. We can simply maintain a table of points bucketed by

this one-dimensional hash value, and then look up potential matches for query

point qby searching for h(q).

How can we build such locality sensitive hash functions? The idea is easiest

to understand at ﬁrst when restricting to vectors instead of points. Recall that

sets of d-dimensional vectors can be thought of as points on the surface of a

sphere, meaning a circle when d= 2.

Let us consider an arbitrary line l1through the origin of this circle, which

cuts the circle in half, as in Figure 10.7. Indeed, we can randomly select l1by

simply picking a random angle 0 ≤θ1<2π. This angle deﬁnes the slope of a

line passing through the origin O, and together θ1and Ocompletely specify l1.

If randomly chosen, l1should grossly partition the vectors, putting about half

of them on the left and the remainder on the right.

318 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.7: Nearby points on the circle generally lie on the same side of random

lines through the origin. Locality-sensitive hash codes for each point can be

composed as a sequence of sidedness tests (left or right) for any speciﬁc sequence

of lines.

Now add a second random divider l2, which should share the same properties.

This then partitions all the vectors among four regions, {LL, LR, RL, RR},

deﬁned by their status relative to these dividers l1and l2.

The nearest neighbor of any vector vshould lie in the same region as v,

unless we got unlucky and either l1or l2separated them. But the probability

p(v1, v2) that both v1and v2are on the same side of ldepends upon the angle

between v1and v2. Speciﬁcally p(v1, v2)=1−θ(v1, v2)/π.

Thus we can compute the exact probability that near neighbors are preserved

for npoints and mrandom planes. The pattern of Land Rover these mplanes

deﬁnes an m-bit locality-sensitive hash code h(v) for any vector v. As we move

beyond the two planes of our example to longer codes, the expected number of

points in each bucket drops to n/2m, albeit with an increased risk that one of

the mplanes separates a vector from its true nearest neighbor.

Note that this approach can easily be generalized beyond two dimensions.

Let the hyperplane be deﬁned by its normal vector r, which is perpendicular

in direction to the plane. The sign of s=v·rdetermines which side a query

vector vlies on. Recall that the dot product of two orthogonal vectors is 0, so

s= 0 if vlies exactly on the separating plane. Further, sis positive if vis above

this plane, and negative if vis below it. Thus the ith hyperplane contributes

exactly one bit to the hash code, where hi(q) = 0 iﬀ v·ri≤0.

Such functions can be generalized beyond vectors to arbitrary point sets.

Further, their precision can be improved by building multiple sets of code words

for each item, involving diﬀerent sets of random hyperplanes. So long as q

shares at least one codeword with its true nearest neighbor, we will eventually

10.3. GRAPHS, NETWORKS, AND DISTANCES 319

encounter a bucket containing both of these points.

Note that LSH has exactly the opposite goal from traditional hash functions

used for cryptographic applications or to manage hash tables. Traditional hash

functions seek to ensure that pairs of similar items result in wildly diﬀerent hash

values, so we can recognize changes and utilize the full range of the table. In

contrast, LSH wants similar items to recieve the exact same hash code, so we

can recognize similarity by collision. With LSH, nearest neighbors belong in the

same bucket.

Locality sensitive hashing has other applications in data science, beyond

nearest neighbor search. Perhaps the most important is constructing compressed

feature representations from complicated objects, say video or music streams.

LSH codes constructed from intervals of these streams deﬁne numerical values

potentially suitable as features for pattern matching or model building.

10.3 Graphs, Networks, and Distances

Agraph G= (V, E) is deﬁned on a set of vertices V, and contains a set of

edges Eof ordered or unordered pairs of vertices from V. In modeling a road

network, the vertices may represent the cities or junctions, certain pairs of

which are directly connected by roads/edges. In analyzing human interactions,

the vertices typically represent people, with edges connecting pairs of related

souls.

Many other modern data sets are naturally modeled in terms of graphs or

networks:

•The Worldwide Web (WWW): Here there is a vertex in the graph for each

webpage, with a directed edge (x, y) if webpage xcontains a hyperlink to

webpage y.

•Product/customer networks: These arise in any company that has many

customers and types of products: be it Amazon, Netﬂix, or even the corner

grocery store. There are two types of vertices: one set for customers

and another for products. Edge (x, y) denotes a product ypurchased by

customer x.

•Genetic networks: Here the vertices represent the diﬀerent genes/proteins

in a particular organisms. Think of this as a parts list for the beast.

Edge (x, y) denotes that there are interactions between parts xand y.

Perhaps gene xregulates gene y, or proteins xand ybind together to

make a larger complex. Such interaction networks encode considerable

information about how the underlying system works.

Graphs and point sets are closely related objects. Both are composed of

discrete entities (points or vertices) representing items in a set. Both of them en-

code important notions of distance and relationships, either near–far or connected–

independent. Point sets can be meaningfully represented by graphs, and graphs

by point sets.

320 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.8: The pairwise distances between a set of points in space (left) deﬁne

a complete weighted graph (center). Thresholding by a distance cutoﬀ removes

all long edges, leaving a sparse graph that captures the structure of the points

(right).

10.3.1 Weighted Graphs and Induced Networks

The edges in graphs capture binary relations, where each edge (x, y) represents

that there is a relationship between xand y. The existence of this relationship is

sometimes all there is to know about it, as in the connection between webpages

or the fact of someone having purchased a particular product.

But there is often an inherent measure of the strength or closeness of the

relationship. Certainly we see it in road networks: each road segment has a

length or travel time, which is essential to know for ﬁnding the best route to

drive between two points. We say that a graph is weighted if every edge has a

numerical value associated with it.

And this weight is often (but not always) naturally interpreted as a distance.

Indeed one can interpret a data set of npoints in space as a complete weighted

graph on nvertices, where the weight of edge (x, y) is the geometric distance

between points xand yin space. For many applications, this graph encodes all

the relevant information about the points.

Graphs are most naturally represented by n×nadjacency matrices. Deﬁne a

non-edge symbol x. Matrix Mrepresents graph G= (V, E) when M[i, j]6=xif

and only if vertices i, j ∈Vare connected by an edge (i, j)∈E. For unweighted

networks, typically the edge symbol is 1 while x= 0. For distance weighted

graphs, the weight of edge (i, j) is the cost of travel between them, so setting

x=∞denotes the lack of any direct connection between iand j.

This matrix representation for networks has considerable power, because we

can introduce all our tools from linear algebra to work with them. Unfortunately,

it comes with a cost, because it can be hopelessly expensive to store n×n

matrices once networks get beyond a few hundred vertices. There are more

eﬃcient ways to store large sparse graphs, with many vertices but relatively few

pairs connected by edges. I will not discuss the details of graph algorithms here,

but refer you with conﬁdence to my book The Algorithm Design Manual [Ski08]

for you to learn more.

Pictures of graphs/networks are often made by assigning each vertex a point

in the plane, and drawing lines between these vertex-points to represent edges.

Such node-ink diagrams are immensely valuable to visualize the structure of

10.3. GRAPHS, NETWORKS, AND DISTANCES 321

the networks you are working with. They can be algorithmically constructed

using force-directed layout, where edges act like springs to bring adjacent pairs

of vertices close together, and non-adjacent vertices repel each other.

Such drawings establish the connection between graph structures and point

positions. An embedding is a point representation of the vertices of a graph

that captures some aspect of its structure. Performing a feature compression

like eigenvalue or singular value decomposition (see Section 8.5) on the the

adjacency matrix of a graph produces a lower-dimensional representation that

serves as a point representation of each vertex. Other approaches to graph

embeddings include DeepWalk, to be discussed in Section 11.6.3.

Take-Home Lesson: Point sets can be meaningfully represented by

graphs/distance matrices, and graphs/distance matrices meaningfully repre-

sented by point sets (embeddings).

Geometric graphs deﬁned by the distances between points are representative

of a class of graphs I will call induced networks, where the edges are deﬁned in

a mechanical way from some external data source. This is a common source of

networks in data science, so it is important to keep an eye out for ways that

your data set might be turned into a graph.

Distance or similarity functions are commonly used to construct networks

on sets of items. Typically we are interested in edges connecting each vertex to

its kclosest/most similar vertices. We get a sparse graph by keeping kmodest,

say k≈10, meaning that it can be easily worked with even for large values of

But there are other types of induced networks. Typical would be to connect

vertices xand ywhenever they have a meaningful attribute in common. For

example, we can construct an induced social network on people from their re-

sumes, linking any two people who worked at the same company or attended the

same school in a similar period. Such networks tend to have a blocky structure,

where there are large subsets of vertices forming fully connected cliques. After

all, if xgraduated from the same college as y, and ygraduated from the same

college as z, then this implies that (x, z) must also be an edge in the graph.

10.3.2 Talking About Graphs

There is a vocabulary about graphs that is important to know for working

with them. Talking the talk is an important part of walking the walk. Several

fundamental properties of graphs impact what they represent, and how we can

use them. Thus the ﬁrst step in any graph problem is determining the ﬂavors

of the graphs you are dealing with:

•Undirected vs. Directed: A graph G= (V, E) is undirected if edge (x, y)∈

Eimplies that (y, x) is also in E. If not, we say that the graph is directed.

Road networks between cities are typically undirected, since any large road

has lanes going in both directions. Street networks within cities are almost

322 CHAPTER 10. DISTANCE AND NETWORK METHODS

undirected directed

unweighted

weighted

simple non−simple

sparse dense

embedded topological

unlabeled labeled

Figure 10.9: Important properties/ﬂavors of graphs

always directed, because there are at least a few one-way streets lurking

somewhere. Webpage graphs are typically directed, because the link from

page xto page yneed not be reciprocated.

•Weighted vs. Unweighted: As discussed in Section 10.3.1, each edge (or

vertex) in a weighted graph Gis assigned a numerical value, or weight.

The edges of a road network graph might be weighted with their length,

drive-time, or speed limit, depending upon the application. In unweighted

graphs, there is no cost distinction between various edges and vertices.

Distance graphs are inherently weighted, while social/web networks are

generally unweighted. The diﬀerence determines whether the feature vec-

tors associated with vertices are 0/1 or numerical values of importance,

which may have to be normalized.

•Simple vs. Non-simple: Certain types of edges complicate the task of

working with graphs. A self-loop is an edge (x, x), involving only one

vertex. An edge (x, y) is a multiedge if it occurs more than once in the

graph.

Both of these structures require special care in preprocessing for feature

generation. Hence any graph that avoids them is called simple. We often

seek to remove both self-loops and multiedges at the beginning of analysis.

•Sparse vs. Dense: Graphs are sparse when only a small fraction of

the total possible vertex pairs (n

2for a simple, undirected graph on n

vertices) actually have edges deﬁned between them. Graphs where a large

fraction of the vertex pairs deﬁne edges are called dense. There is no

oﬃcial boundary between what is called sparse and what is called dense,

10.3. GRAPHS, NETWORKS, AND DISTANCES 323

but typically dense graphs have a quadratic number of edges, while sparse

graphs are linear in size.

Sparse graphs are usually sparse for application-speciﬁc reasons. Road

networks must be sparse graphs because of road junctions. The most

ghastly intersection I’ve ever heard of was the endpoint of only nine dif-

ferent roads. k-nearest neighbor graphs have vertex degrees of exactly

k. Sparse graphs make possible much more space eﬃcient representations

than adjacency matrices, allowing the representation of much larger net-

works.

•Embedded vs. Topological – A graph is embedded if the vertices and edges

are assigned geometric positions. Thus, any drawing of a graph is an

embedding, which may or may not have algorithmic signiﬁcance.

Occasionally, the structure of a graph is completely deﬁned by the geom-

etry of its embedding, as we have seen in the deﬁnition of the distance

graph where the weights are deﬁned by the Euclidean distance between

each pair of points. Low-dimensional representations of adjacency matri-

ces by SVD also qualify as embeddings, point representations that capture

much of the connectivity information of the graph.

•Labeled vs. Unlabeled – Each vertex is assigned a unique name or identiﬁer

in a labeled graph to distinguish it from all other vertices. In unlabeled

graphs no such distinctions are made.

Graphs arising in data science applications are often naturally and mean-

ingfully labeled, such as city names in a transportation network. These

are useful as identiﬁers for representative examples, and also to provide

linkages to external data sources where appropriate.

10.3.3 Graph Theory

Graph theory is an important area of mathematics which deals with the fun-

damental properties of networks and how to compute them. Most computer

science students get exposed to graph theory through their courses in discrete

structures or algorithms.

The classical algorithms for ﬁnding shortest paths, connected components,

spanning trees, cuts, matchings and topological sorting can be applied to any

reasonable graph. However, I have not seen these tools applied as generally in

data science as I think they should be. One reason is that the graphs in data

science tend to be very large, limiting the complexity of what can be done with

them. But a lot is simply myopia: people do not see that a distance or similarity

matrix is really just a graph than can take advantage of other tools.

I take the opportunity here to review the connections of these fundamental

problems to data science, and encourage the interested reader to deepen their

understanding through my algorithm book [Ski08].

324 CHAPTER 10. DISTANCE AND NETWORK METHODS

•Shortest paths: For a distance “matrix” m, the value of m[i, j] should

reﬂect the minimum length path between vertices iand j. Note that

independent estimates of pairwise distance are often inconsistent, and do

not necessarily satisfy the triangle inequality. But when m0[i, j] reﬂects

the shortest path distance from ito jin any matrix mit must satisfy the

metric properties. This may well present a better matrix for analysis than

the original.

•Connected components: Each disjoint piece of a graph is called a con-

nected component. Identifying whether your graph consists of a single

component or multiple pieces is important. First, any algorithms you run

will achieve better performance if you deal with the components indepen-

dently. Separate components can be independent for sound reasons, e.g.

there is no road crossing between the United States and Europe because

of an ocean. But separate components might indicate trouble, such as

processing artifacts or insuﬃcient connectivity to work with.

•Minimum spanning trees: A spanning tree is the minimal set of edges

linking all the vertices in a graph, essentially a proof that the graph is

connected. The minimum weight spanning tree serves as the sparsest

possible representation of the structure of the graph, making it useful for

visualization. Indeed, we will show that minimum spanning trees have an

important role in clustering algorithms in Section 10.5.

•Edge cuts: A cluster in a graph is deﬁned by a subset of vertices c,

with the property that (a) there is considerable similarity between pairs

of vertices within c, and (b) there is weak connectivity between vertices

in cand out of c. The edges (x, y) where x∈cand y6∈ cdeﬁne a cut

separating the cluster from the rest of the graph, making ﬁnding such cuts

an important aspect of cluster analysis.

•Matchings: Marrying oﬀ each vertex with a similar, loyal partner can be

useful in many ways. Interesting types of comparisons become possible

after such a matching. For example, looking at all close pairs that diﬀer in

one attribute (say gender) might shed light on how that variable impacts

a particular outcome variable (think income or lifespan). Matchings also

provide ways to reduce the eﬀective size of a network. By replacing each

matched pair with a vertex representing its centroid, we can construct a

graph with half the vertices, but still representative of the whole.

•Topological sorting: Ranking problems (recall Chapter 4) impose a peck-

ing order on a collection of items according to some merit criteria. Topo-

logical sorting ranks the vertices of a directed acyclic graph (DAG) so edge

(i, j) implies that iranks above jin the pecking order. Given a collection

of observed constraints of the form “ishould rank above j,” topological

sorting deﬁnes an item-order consistent with these observations.

10.4. PAGERANK 325

10.4 PageRank

It is often valuable to categorize the relative importance of vertices in a graph.

Perhaps the simplest notion is based on vertex degree, the number of edges

connecting vertex vto the rest of the graph. The more connected a vertex is,

the more important it probably is.

The degree of vertex vmakes a good feature to represent the item associated

with v. But even better is PageRank [BP98], the original secret sauce behind

Google’s search engine. PageRank ignores the textual content of webpages,

to focus only on the structure of the hyperlinks between pages. The more

important pages (vertices) should have higher in-degree than lesser pages, for

sure. But the importance of the pages that link to you also matter. Having a

large stable of contacts recommending you for a job is great, but it is even better

when one of them is currently serving as the President of the United States.

PageRank is best understood in the context of random walks along a net-

work. Suppose we start from an arbitrary vertex and then randomly select an

outgoing link uniformly from the set of possibilities. Now repeat the process

from here, jumping to a random neighbor of our current location at each step.

The PageRank of vertex vis a measure of probability that, starting from a ran-

dom vertex, you will arrive at vafter a long series of such random steps. The

basic formula for the PageRank of v(P R(v)) is:

P Rj(v) = X

(u,v)∈E

P Rj−1(u)

out −degree(u)

This is a recursive formula, with jas the iteration number. We initialize

P R0(vi) = 1/n for each vertex viin the network, where 1 ≤i≤n. The

PageRank values will change in each iteration, but converge surprisingly quickly

to stable values. For undirected graphs, this probability is essentially the same as

each vertex’s in-degree, but much more interesting things happen with directed

graphs.

In essence, PageRank relies on the idea that if all roads lead to Rome, Rome

must be a pretty important place. It is the paths to your page that counts.

This is what makes PageRank hard to game: other people must link to your

webpage, and whatever shouting you do about yourself is irrelevant.

There are several tweaks one can make to this basic PageRank formula to

make the results more interesting. We can allow the walk to jump to an arbitrary

vertex (instead of a linked neighbor) to allow faster diﬀusion in the network.

Let pbe the probability of following a link in the next step, also known as the

damping factor. Then

P Rj(v) = X

(u,v)∈E

(1 −p)

n+pP Rj−1(u)

out-degree(u)

where nis the number of vertices in the graph. Other enhancements involve

making changes to the network itself. By adding edges from every vertex to a

326 CHAPTER 10. DISTANCE AND NETWORK METHODS

PageRank PR1 (all pages)

1 Napoleon

2 George W. Bush

3 Carl Linnaeus

4 Jesus

5 Barack Obama

6 Aristotle

7 William Shakespeare

8 Elizabeth II

9 Adolf Hitler

10 Bill Clinton

PageRank PR2 (only people)

1 George W. Bush

2 Bill Clinton

3 William Shakespeare

4 Ronald Reagan

5 Adolf Hitler

6 Barack Obama

7 Napoleon

8 Richard Nixon

9 Franklin D. Roosevelt

10 Elizabeth II

Table 10.1: Historical individuals with the highest PageRank in the 2010 English

Wikipedia, drawn over the full Wikipedia graph (left) and when restricted to

links to other people (right).

single super-vertex, we ensure that random walks cannot get trapped in some

small corner of the network. Self-loops and parallel edges (multiedges) can be

deleted to avoid biases from repetition.

There is also a linear algebraic interpretation of PageRank. Let Mbe a

matrix of vertex-vertex transition probabilities, so Mij is the probability that

our next step from iwill be to j. Clearly Mij = 1/out-degree(i) if there is a

directed edge from ito j, and zero if otherwise. The jth round estimate for the

PageRank vector P Rjcan be computed as

P Rj=M·P Rj−1

After this estimate converges, P R =M·P R, or λU =M U where λ=

1 and Urepresents the PageRank vector. This is the deﬁning equation for

eigenvalues, so the n×1 vector of PageRank values turns out to be the principle

eigenvector of the transition probability matrix deﬁned by the links. Thus

iterative methods for computing eigenvectors and fast matrix multiplication

leads to eﬃcient PageRank computations.

How well does PageRank work at smoking out the most central vertices? To

provide some intuition, we ran PageRank on the link network from the English

edition of Wikipedia, focusing on the pages associated with people. Table 10.1

(left) lists the ten historical ﬁgures with the highest PageRank.

These high-PageRank ﬁgures are all readily recognized as very signiﬁcant

people. The least familiar among them is probably Carl Linnaeus (1707–1778)

[46], biology’s “father of taxonomy” whose Linnaean system (Genus species;

e.g., Homo sapiens) is used to classify all life on earth. He was a great scientist,

but why is he so very highly regarded by PageRank? The Wikipedia pages of

all the plant and animal species he ﬁrst classiﬁed link back to him, so thousands

of life forms contribute prominent paths to his page.

The Linnaeus example points out a possible weakness of PageRank: do we

really want plants and other inanimate objects voting on who the most promi-

10.5. CLUSTERING 327

Figure 10.10: PageRank graphs for Barack Obama, over all Wikipedia pages

(left) and when restricted only to people (right)

nent people are? Figure 10.10 (left) shows a subset of the full PageRank graph

for Barack Obama [91]. Note, for example, that although the links associated

with Obama seem very reasonable, we can still reach Obama in only two clicks

from the Wikipedia page for Dinosaurs. Should extinct beasts contribute to the

President’s centrality?

Adding and deleting sets of edges from a given network gives rise to diﬀerent

networks, some of which better reveal underlying signiﬁcance using PageRank.

Suppose we compute PageRank (denoted PR2) using only the Wikipedia edges

linking people. This computation would ignore any contribution from places,

organizations, and lower organisms. Figure 10.10 (right) shows a sample of the

PageRank graph for Barack Obama [91] when we restrict it to only people.

PageRank on this graph favors a slightly diﬀerent cohort of people, shown in

Table 10.1 (right). Jesus, Linnaeus and Aristotle (384–322 B.C.)[8] are now gone,

replaced by three recent U.S. presidents – who clearly have direct connections

from many important people. So which version of PageRank is better, PR1 or

PR2? Both seem to capture reasonable notions of centrality with a substan-

tial but not overwhelming correlation (0.68), so both make sense as potential

features in a data set.

10.5 Clustering

Clustering is the problem of grouping points by similarity. Often items come

from a small number of logical “sources” or “explanations”, and clustering is

a good way to reveal these origins. Consider what would happen if an alien

species were to come across height and weight data for a large number of hu-

mans. They would presumably ﬁgure out that there seem to be two clusters

representing distinct populations, one consistently bigger than the other. If

the aliens were really on the ball, they might call these populations ‘men” and

“women”. Indeed, the two height-weight clusters in Figure 10.11 are both highly

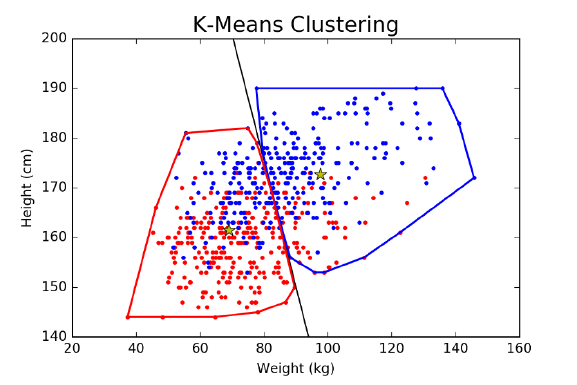
328 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.11: Clustering people in weight-height space, using 2-means cluster-

ing. The left cluster contains 240 women and 112 men, while the right cluster

contains 174 men to 54 women. Compare this to the logistic regression classiﬁer

trained on this same data set, in Figure 9.17.

concentrated in one particular gender.

Patterns on a two-dimensional dot plot are generally fairly easy to see, but we

often deal with higher-dimensional data that humans cannot eﬀectively visual-

ize. Now we need algorithms to ﬁnd these patterns for us. Clustering is perhaps

the ﬁrst thing to do with any interesting data set. Applications include:

•Hypothesis development: Learning that there appear to be (say) four dis-

tinct populations represented in your data set should spark the question

as to why they are there. If these clusters are compact and well-separated

enough, there has to be a reason and it is your business to ﬁnd it. Once

you have assigned each element a cluster label, you can study multiple

representatives of the same cluster to ﬁgure out what they have in com-

mon, or look at pairs of items from diﬀerent clusters and identify why they

are diﬀerent.

•Modeling over smaller subsets of data: Data sets often contain a very

large number of rows (n) relative to the number of feature columns (m):

think the taxi cab data of 80 million trips with ten recorded ﬁelds per

trip. Clustering provides a logical way to partition a large single set of

records in a (say) a hundred distinct subsets each ordered by similarity.

Each of these clusters still contains more than enough records to ﬁt a

forecasting model on, and the resulting model may be more accurate on

this restricted class of items then a general model trained over all items.

Making a forecast now involves identifying the appropriate cluster your

10.5. CLUSTERING 329

query item qbelongs to, via a nearest neighbor search, and then using the

appropriate model for that cluster to make the call on q.

•Data reduction: Dealing with millions or billions of records can be over-

whelming, for processing or visualization. Consider the computational

cost of identifying the nearest neighbor to a given query point, or trying

to understand a dot plot with a million points. One technique is to cluster

the points by similarity, and then appoint the centroid of each cluster to

represent the entire cluster. Such nearest neighbor models can be quite

robust because you are reporting the consensus label of the cluster, and it

comes with a natural measure of conﬁdence: the accuracy of this consensus

over the full cluster.

•Outlier detection: Certain items resulting from any data collection pro-

cedure will be unlike all the others. Perhaps they reﬂect data entry errors

or bad measurements. Perhaps they signal lies or other misconduct. Or

maybe they result from the unexpected mixture of populations, a few

strange apples potentially spoiling the entire basket.

Outlier detection is the problem of ridding a data set of discordant items,

so the remainder better reﬂects the desired population. Clustering is a

useful ﬁrst step to ﬁnd outliers. The cluster elements furthest from their

assigned cluster center don’t really ﬁt well there, but also don’t ﬁt better

anywhere else. This makes them candidates to be outliers. Since invaders

from another population would tend to cluster themselves together, we

may well cast suspicions on small clusters whose centers lie unusually far

from all the other cluster centers.

Clustering is an inherently ill-deﬁned problem, since proper clusters depend

upon context and the eye of the beholder. Look at Figure 10.12. How many

diﬀerent clusters do you see there? Some see three, other see nine, and others

vote for pretty much any number in between.

How many clusters you see depends somewhat upon how many clusters you

want to see. People can be clustered into two groups, the lumpers and the

splitters, depending upon their inclination to make ﬁne distinctions. Splitters

look at dogs, and see poodles, terriers, and cocker spaniels. Lumpers look at

dogs, and see mammals. Splitters draw more exciting conclusions, while lumpers

are less likely to overﬁt their data. Which mindset is most appropriate depends

upon your task.

Many diﬀerent clustering algorithms have been developed, and we will review

the most prominent methods (k-means, agglomerative clustering, and spectral

clustering) in the sections below. But it is easy to get too caught up in the

diﬀerences between methods. If your data exhibits strong-enough clusters, any

method is going to ﬁnd something like it. But when an algorithm returns

clusters with very poor coherence, usually your data set is more to blame than

the algorithm itself.

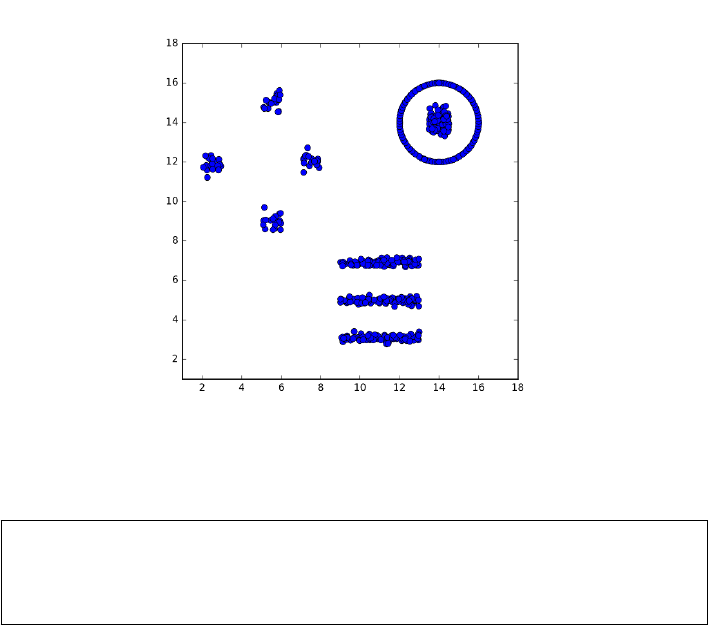
330 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.12: How many clusters do you see here?

Take-Home Lesson: Make sure you are using a distance metric which accu-

rately reﬂects the similarities that you are looking to ﬁnd. The speciﬁc choice

of clustering algorithm usually proves much less important than the similar-

ity/distance measure which underlies it.

10.5.1 k-means Clustering

We have been somewhat lax in deﬁning exactly what a clustering algorithm

should return as an answer. One possibility is to label each point with the

name of the cluster that it is in. If there are kclusters, these labels can be the

integers 1 through k, where labeling point pwith imeans it is in the ith cluster.

An equivalent output representation might be kseparate lists of points, where

list irepresents all the points in the ith cluster.

But a more abstract notion reports the center point of each cluster. Typically

we think of natural clusters as compact, Gaussian-like regions, where there is an

ideal center deﬁning the location where the points “should” be. Given the set

of these centers, clustering the points becomes easy: simply assign each point p

to the center point Ciclosest to it. The ith cluster consists of all points whose

nearest center is Ci.

k-means clustering is a fast, simple-to-understand, and generally eﬀective

approach to clustering. It starts by making a guess as to where the cluster

centers might be, evaluates the quality of these centers, and then reﬁnes them

to make better center estimates.

10.5. CLUSTERING 331

K-means clustering

Select kpoints as initial cluster centers C1, . . . , Ck.

Repeat until convergence {

For 1 ≤i≤n, map point pito its nearest cluster center Cj

Compute centroid C0

jof the points nearest Cj,for 1 ≤j≤k

For all 1 ≤j≤k, set Cj=C0

}

Figure 10.13: Pseudocode for the k-means clustering algorithm.

The algorithm starts by assuming that there will be exactly kclusters in

the data, and then proceeds to pick initial centers for each cluster. Perhaps

this means randomly selecting kpoints from the set of npoints Sand calling

them centers, or selecting krandom points from the bounding box of S. Now

test each of the npoints against all kof the centers, and assign each point in

Sto its nearest current center. We can now compute a better estimate of the

center of each cluster, as the centroid of the points assigned to it. Repeat until

the cluster assignments are suﬃciently stable, presumably when they have not

changed since the previous generation. Figure 10.13 provides pseudocode of this

k-means procedure.

Figure 10.14 presents an animation of k-means in action. The initial guesses

for the cluster centers are truly bad, and the initial assignments of points to

centers splits the real clusters instead of respecting them. But the situation

rapidly improves, with the centroids drifting into positions that separates the

points in the desired way. Note that the k-means procedure does not necessar-

ily terminate with the best possible set of kcenters, only at a locally-optimal

solution that provides a logical stopping point. It is a good idea to repeat the

entire procedure several times with diﬀerent random initializations and accept

the best clustering found over all. The mean squared error is the sum of squares

of the distance between each point Piand its center Cj, divided by the number

of points n. The better of two clusterings can be identiﬁed as having lower mean

squared error, or some other reasonable error statistic.

Centers or Centroids?

There are at least two possible criteria for computing a new estimate for the

center point as a function of the set S0of points assigned to it. The centroid C

of a point set is computed by taking the average value of each dimension. For

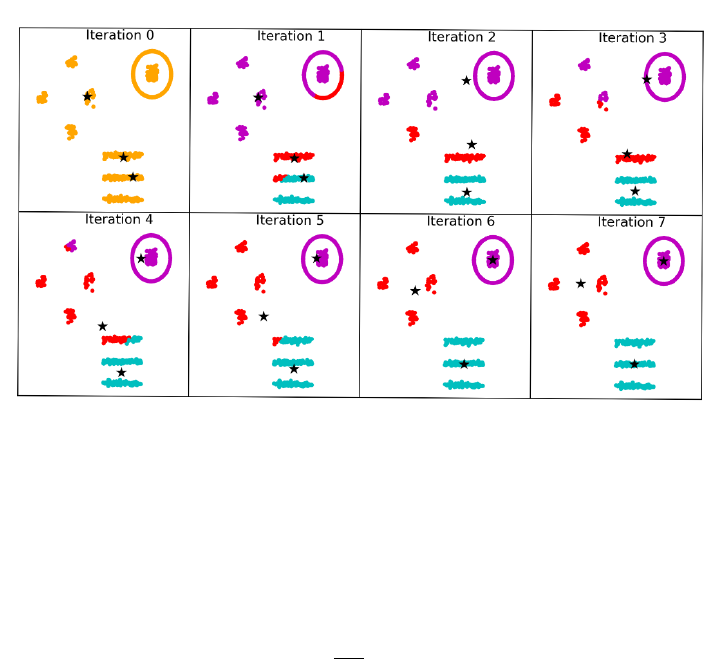
332 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.14: The iterations of k-means (for k= 3) as it converges on a stable

and accurate clustering. Fully seven iterations are needed, because of the un-

fortunate placement of the three initial cluster centers near the logical center.

the dth dimension,

Cd=1

|S0|X

p∈S0

p[d]

The centroid serves as the center of mass of S0, the place where the vectors

deﬁned through this point sum to zero. This balance criteria deﬁnes a natural

and unique center for any S0. Speed of computation is another nice thing about

using the centroid. For n d-dimensional points in S0, this takes O(nd) time,

meaning linear in the input size of the points.

For numerical data points, using the centroid over an appropriate Lkmetric

(like Euclidean distance) should work just ﬁne. However, centroids are not well

deﬁned when clustering data records with non-numerical attributes, like cate-

gorical data. What is the centroid of 7 blonds, 2 red-heads, and 6 gray-haired

people? We have discussed how to construct meaningful distance functions over

categorical records. The problem here is not so much measuring similarity, as

constructing a representative center.

There is a natural solution, sometimes called the k-mediods algorithm. Sup-

pose instead of the centroid we deﬁne the centermost point Cin S0to be the

cluster representative. This is the point which minimizes the sum of distances

10.5. CLUSTERING 333

to all other points in the cluster:

C= arg min

c∈S0

i=1

d(c, pi)

An advantage of using a centerpoint to deﬁne the cluster is that it gives the

cluster a potential name and identity, assuming the input points correspond to

items with identiﬁable names.

Using the centermost input example as center means we can run k-means

so long as we have a meaningful distance function. Further, we don’t lose very

much precision by picking the centermost point instead of the centroid. Indeed,

the sum of distances through the centermost point is at most twice that of the

centroid, on numerical examples where the centroid can be computed. The big

win of the centroid is that it can be computed faster than the centermost vertex,

by a factor of n.

Using center vertices to represent clusters permits one to extend k-means

naturally to graphs and networks. For weighted graphs, it is natural to employ a

shortest path algorithm to construct a matrix Dsuch that D[i, j] is the length of

the shortest path in the graph from vertex ito vertex j. Once Dis constructed,

k-means can proceed by reading the distances oﬀ this matrix, instead of calling a

distance function. For unweighted graphs, a linear time algorithm like breadth-

ﬁrst search can be eﬃciently used to compute graph distances on demand.

How Many Clusters?

Inherent to the interpretation of k-means clustering is the idea of a mixture

model. Instead of all our observed data coming from a single source, we presume

that our data is coming from kdiﬀerent populations or sources. Each source

is generating points to be like its center, but with some degree of variation or

error. The question of how many clusters a data set has is fundamental: how

many diﬀerent populations were drawn upon when selecting the sample?

The ﬁrst step in the k-means algorithm is to initialize k, the number of

clusters in the given data set. Sometimes we have a preconception of how many

clusters we want to see: perhaps two or three for balance or visualization, or

maybe 100 or 1000 as a proxy for “many” when partitioning a large input ﬁle

into smaller sets for separate modeling.

But generally speaking this is a problem, because the “right” number of

clusters is usually unknown. Indeed, the primary reason to cluster in the ﬁrst

place is our limited understanding of the structure of the data set.

The easiest way to ﬁnd the right kis to try them all, and then pick the best

one. Starting from k= 2 to as high as you feel you have time for, perform

k-means and evaluate the resulting clustering according to the mean squared

error (MSE) of the points from their centers. Plotting this yields an error curve,

as shown in Figure 10.16. The error curve for random centers is also provided.

Both error curves show the MSE of points from their centers decreasing as

we allow more and more cluster centers. But the wrong interpretation would

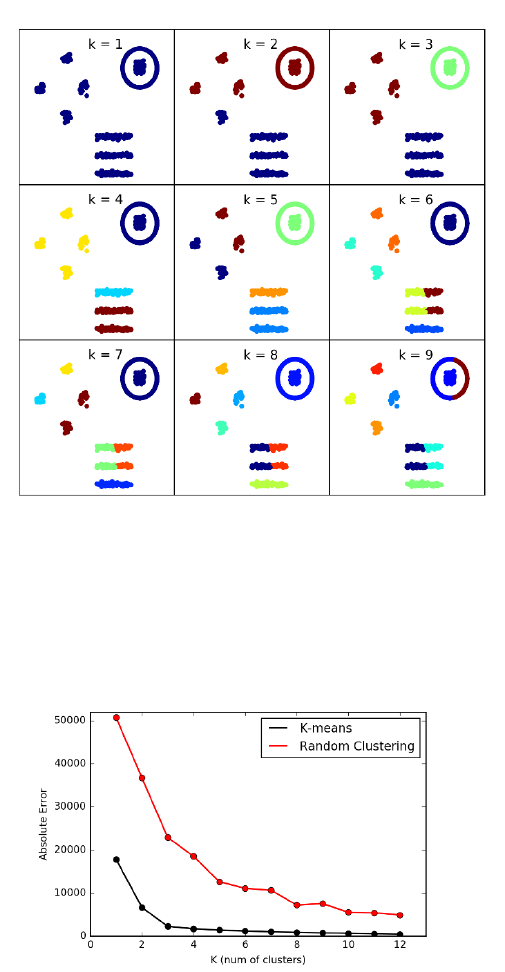
334 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.15: Running k-means for k= 1 to k= 9. The “right” clustering is

found for k= 3, but the algorithm is unable to properly distinguish between

nested circular clusters and long thin clusters for large k.

Figure 10.16: The error curve for k-means clustering on the point set of Figure

10.12, showing a bend in the elbow reﬂecting the three major clusters in the

data. The error curve for random cluster centers is shown for comparison.

10.5. CLUSTERING 335

be to suggest we need kas large as possible, because the MSE should decrease

when allowing more centers. Indeed, inserting a new center at a random position

rinto a previous k-means solution can only decrease the mean squared error,

by happening to land closer to a few of the input points than their previous

center. This carves out a new cluster around r, but presumably an even better

clustering would have been found running by k-means from scratch on (k+ 1)

centers.

What we seek from the error curve in Figure 10.16 is the value kwhere the

rate of decline decreases, because we have exceeded number of true sources, and

so each additional center is acting like a random point in the previous discussion.

The error curve should look something like an arm in typing position: it slopes

down rapidly from shoulder to elbow, and then slower from the elbow to the

wrist. We want kto be located exactly at the elbow. This point might be easier

to identify when compared to a similar MSE error plot for random centers, since

the relative rate of error reduction for random centers should be analogous to

what we see past the elbow. The slow downward drift is telling us the extra

clusters are not doing anything special for us.

Each new cluster center adds dparameters to the model, where dis the

dimensionality of the point set. Occam’s razor tells us that the simplest model

is best, which is the philosophical basis for using the bend in the elbow to select

k. There are formal criterias of merit which incorporate both the number of

parameters and the prediction error to evaluate models, such as the Akaike

information criterion (AIC). However, in practice you should feel conﬁdent in

making a reasonable choice for kbased on the shape of the error curve.

Expectation Maximization

The k-means algorithm is the most prominent example of a class of learning

algorithms based on expectation maximization (EM). The details require more

formal statistics than I am prepared to delve into here, but the principle can

be observed in the two logical steps of the k-means algorithm: (a) assigning

points to the estimated cluster center that is closest to them, and (b) using

these point assignments to improve the estimate of the cluster center. The

assignment operation is the expectation or E-step of the algorithm, while the

centroid computation is the parameter maximization or M-step.

The names “expectation” and “maximization” have no particular resonance

to me in terms of the k-means algorithm. However, the general form of an itera-

tive parameter-ﬁtting algorithm which improves parameters in rounds based on

the errors of the previous models does seem a sensible thing to do. For example,

perhaps we might have partially labeled classiﬁcation data, where there are rel-

atively few training examples conﬁdently assigned to the correct class. We can

build classiﬁers based on these training examples, and use them to assign the

unlabeled points to candidate classes. This presumably deﬁnes larger training

sets, so we should be able to ﬁt a better model for each class. Now reassigning

the points and iterating again should converge on a better model.

336 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.17: Agglomerative clustering of gene expression data.

10.5.2 Agglomerative Clustering

Many sources of data are generated from a process deﬁned by an underlying

hierarchy or taxonomy. Often this is the result of an evolutionary process: In

the Beginning there was one thing, which repeatedly bifurcated to create a rich

universe of items. All animals and plant species are the result of an evolutionary

process, and so are human languages and cultural/ethic groupings. To a lesser

but still real extent, so are products like movies and books. This book can be

described as a “Data Science Textbook”, which is an emerging sub-genre split oﬀ

from “Computer Science Textbook”, which logically goes back to “Engineering

Textbook”, to “Textbook”, to “Non-Fiction” eventually back to the original

source: perhaps “Book”.

Ideally, in the course of clustering items we will reconstruct these evolution-

ary histories. This goal is explicit in agglomerative clustering, a collection of

bottom-up methods that repeatedly merge the two nearest clusters into a big-

ger super-cluster, deﬁning a rooted tree whose leaves are the individual items

and whose root deﬁnes the universe.

Figure 10.17 illustrates agglomerative clustering applied to gene expression

data. Here each column represents a particular gene, and each row the results

of an experiment measuring how active each gene was in a particular condition.

As an analogy, say each of the columns represented diﬀerent people, and one

particular row assessed their spirits right after an election. Fans of the winning

party would be more excited than usual (green), while voters for the losing team

would be depressed (red). Most of the rest of the world wouldn’t care (black).

As it is with people, so it is with genes: diﬀerent things turn them on and oﬀ,

and analyzing gene expression data can reveal what makes them tick.

So how do we read Figure 10.17? By inspection it is clear that there are

blocks of columns which all behave similarly, getting turned on and turned oﬀ in

similar conditions. The discovery of these blocks are reﬂected in the tree above

the matrix: regions of great similarity are associated with small branchings.

Each node of the tree represents the merging of two clusters. The height of

the node is proportional to the distance between the two clusters being merged.

The taller the edge, the more dodgy the notion that these clusters should be

merged. The columns of the matrix have been permuted to reﬂect this tree

10.5. CLUSTERING 337

organization, enabling us to visualize hundreds of genes quantiﬁed in fourteen

dimensions (with each row deﬁning a distinct dimension).

Biological clusterings are often associated with such dendograms or phylo-

genic trees, because they are the result of an evolutionary process. Indeed, the

clusters of similar gene expression behavior seen here are the results of the or-

ganism evolving a new function, that changes the response of certain genes to

a particular condition.

Using Agglomerative Trees

Agglomerative clustering returns a tree on top of the groupings of items. After

cutting the longest edges in this tree, what remains are the disjoint groups

of items produced by clustering algorithms like k-means. But this tree is a

marvelous thing, with powers well beyond the item partitioning:

•Organization of clusters and subclusters: Each internal node in the tree

deﬁnes a particular cluster, comprised of all the leaf-node elements be-

low it. But the tree describes hierarchy among these clusters, from the

most reﬁned/speciﬁc clusters near the leaves to the most general clusters

near the root. Ideally, nodes of a tree deﬁne nameable concepts: natural

groupings that a domain expert could explain if asked. These various lev-

els of granularity are important, because they deﬁne structural concepts

we might not have noticed prior to doing clustering.

•Visualization of the clustering process: A drawing of this agglomeration

tree tells us a lot about the clustering process, particularly if the drawing

reﬂects the cost of each merging step. Ideally there will be very long edges

near the root of the tree, showing that the highest-level clusters are well

separated and belong in distinct groupings. We can tell if the groupings are

balanced, or whether the high level groupings are of substantially diﬀerent

sizes. Long chains of merging small clusters into a big cluster is generally

a bad sign, although the choice of merging criteria (to be discussed below)

can bias the shape of the tree. Outliers show up nicely on a phylogenic

tree, as singleton elements or small clusters that connect near the root

through long edges.

•Natural measure of cluster distance: An interesting property of any tree

Tis that there is exactly one path in Tbetween any two nodes xand

y. Each internal vertex in an agglomerative clustering tree has a weight

associated with it, the cost of merging together the two subtrees below it.

We can compute a “cluster distance” between any two leaves by the sum

of the merger costs on the path between them. If the tree is good, this

can be more meaningful than the Euclidean distance between the records

associated with xand y.

•Eﬃcient classiﬁcation of new items: One important application for clus-

tering is classiﬁcation. Suppose have agglomeratively clustered the prod-

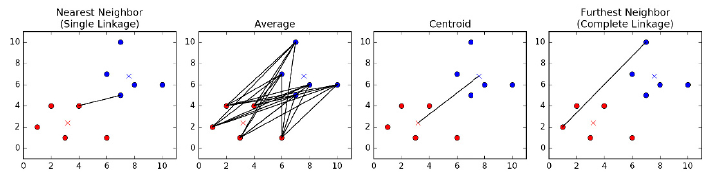
338 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.18: Four distance measures for identifying the nearest pair of clusters.

ucts in a store, to build a taxonomy of clusters. Now a new part comes

along. What category should it be classiﬁed under?

For k-means, each of the cclusters are categorized by their centroid, so

classifying a new item qreduces to computing the distance between qand

all ccentroids to identify the nearest cluster. A hierarchical tree provides a

potentially faster method. Suppose we have precomputed the centroids of

all the leaves on the left and right subtrees beneath each node. Identifying

the right position in the hierarchy for a new item qstarts by comparing

qto the centroids of the root’s left and right subtrees. The nearest of the

two centroids to qdeﬁnes the appropriate side of the tree, so we resume

the search there one level down. This search takes time proportional to

the height of the tree, instead of the number of leaves. This is typically

an improvement from nto log n, which is much better.

Understand that binary merging trees can be drawn in many diﬀerent ways

that reﬂect exactly the same structure, because there is no inherent notion of

which is the left child and which is the right child. This means that there are

2n−1distinct permutations of the nleaves possible, by ﬂipping the direction of

any subset of the n−1 internal nodes in the tree. Realize this when trying to

read such a taxonomy: two items which look far away in left-right order might

well have been neighbors had this ﬂipping been done in a diﬀerent way. And

the rightmost node of the left subtree might be next to the leftmost node in the

right subtree, even though they are really quite far apart in the taxonomy.

Building Agglomerative Cluster Trees

The basic agglomerative clustering algorithm is simple enough to be described

in two sentences. Initially, each item is assigned to its own cluster. Merge the

two closest clusters into one by putting a root over them, and repeat until only

one cluster remains.

All that remains is to specify how to compute the distance between clusters.

When the clusters contain single items, the answer is easy: use your favorite

distance metric like L2. But there are several reasonable answers for the distance

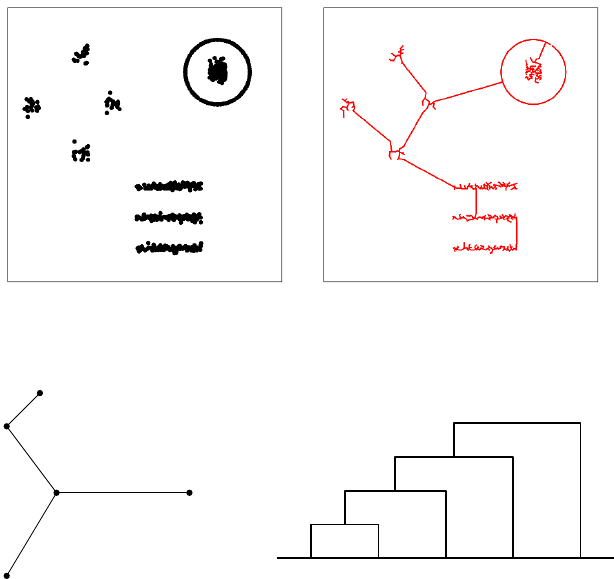
10.5. CLUSTERING 339

Figure 10.19: Single linkage clustering is equivalent to ﬁnding the minimum

spanning tree of a network.

v3v5

v1v2v3v4v5

Figure 10.20: Kruskal’s algorithm for minimum spanning tree is indeed single-

linkage agglomerative clustering, as shown by the cluster tree on right.

between two non-trivial clusters, which lead to diﬀerent trees on the same input,

and can have a profound impact on the shape of the resulting clusters. The

leading candidates, illustrated in Figure 10.18, are:

•Nearest neighbor (single link): Here the distance between clusters C1and

C2is deﬁned by the closest pair of points spanning them:

d(C1, C2) = min

x∈C1,y∈C2||x−y||

Using this metric is called single link clustering, because the decision to

merge is based solely on the single closest link between the clusters.

The minimum spanning tree of a graph Gis tree drawn from the edges

of Gconnecting all vertices at lowest total cost. Agglomerative clustering

with the single link criteria is essentially the same as Kruskal’s algorithm,

which creates the minimum spanning tree (MST) of a graph by repeatedly

adding the lowest weight edge remaining which does not create a cycle in

the emerging tree.

340 CHAPTER 10. DISTANCE AND NETWORK METHODS

The connection between the MST (with nnodes and n−1 edges) and

the cluster tree (with nleaves, n−1 internal nodes, and 2n−2 edges) is

somewhat subtle: the order of insertion edges in the MST from smallest

to largest describes the order of merging in the cluster tree, as shown in

Figure 10.20.

The Platonic ideal of clusters are as compact circular regions, which gen-

erally radiate out from centroids, as in k-means clustering. By contrast,

single-link clustering tends to create relatively long, skinny clusters, be-

cause the merging decision is based only on the nearness of boundary

points. Single link clustering is fast, but tends to be error prone, as out-

lier points can easily suck two well-deﬁned clusters together.

•Average link: Here we compute distance between all pairs of cluster-

spanning points, and average them for a more robust merging criteria

than single-link:

d(C1, C2) = 1

|C1||C2|X

x∈C1X

y∈C2

||x−y||

This will tend to avoid the skinny clusters of single-link, but at a greater

computational cost. The straightforward implementation of average link

clustering is O(n3), because each of the nmerges will potentially require

touching O(n2) edges to recompute the nearest remaining cluster. This is

ntimes slower than single link clustering, which can be implemented in

O(n2) time.

•Nearest centroid: Here we maintain the centroid of each cluster, and

merge the cluster-pair with the closest centroids. This has two main ad-

vantages. First, it tends to produce clusters similar to average link, be-

cause outlier points in a cluster get overwhelmed as the cluster size (num-

ber of points) increases. Second, it is much faster to compare the centroids

of the two clusters than test all |C1||C2|point-pairs in the simplest imple-

mentation. Of course, centroids can only be computed for records with all

numerical values, but the algorithm can be adapted to use the centermost

point in each cluster (medioid) as a representative in the general case.

•Furthest link: Here the cost of merging two clusters is the farthest pair

of points between them:

d(C1, C2) = max

x∈C1,y∈C2||x−y||

This sounds like madness, but this is the criteria which works hardest to

keep clusters round, by penalizing mergers with distant outlier elements.

Which of these is best? As always in this business, it depends. For very

large data sets, we are most concerned with using the fastest algorithms , which

are typically single linkage or nearest centroid with appropriate data structures.

For small to modest-sized data sets, we are most concerned with quality, making

more robust methods attractive.

10.5. CLUSTERING 341

10.5.3 Comparing Clusterings

It is a common practice to try several clustering algorithms on the same data

set, and use the one which looks best for our purposes. The clusterings produced

by two diﬀerent algorithms should be fairly similar if both algorithms are doing

reasonable things, but it is often of interest to measure exactly how similar

they are. This means we need to deﬁne a similarity or distance measure on

clusterings.

Every cluster is deﬁned by a subset of items, be they points or records. The

Jaccard similarity J(s1, s2) of sets s1and s2is deﬁned as the ratio of their

intersection and union:

J(s1, s2) = |s1∩s2|

|s1∪s2|

Because the intersection of two sets is always no bigger than the union of their

elements, 0 ≤J(s1, s2)≤1. Jaccard similarity is a generally useful measure to

know about, for example, in comparing the similarity of the knearest neighbors

of a point under two diﬀerent distance metrics, or how often the top elements

by one criteria match the top elements by a diﬀerent metric.

This similarity measure can be turned into a proper distance metric d(s1, s2)

called the Jaccard distance, where

d(s1, s2)=1−J(s1, s2)

This distance function only takes on values between 0 and 1, but satisﬁes all of

the properties of a metric, including the triangle inequality.

Each clustering is described by a partition of the universal set, and may

have many parts. The Rand index is a natural measure of similarity between

two clusterings c1and c2. If the clusterings are compatible, then any pair of

items in the same subset of c1should be in the same subset of c2, and any pairs

in diﬀerent clusters of c1should be separated in c2. The Rand index counts the

number of such consistent pairs of items, and divides it by the total number of

pairs n

2to create a ratio from 0 to 1, where 1 denotes identical clusterings.

10.5.4 Similarity Graphs and Cut-Based Clustering

Recall our initial discussion of clustering, where I asked asked how many clusters

you saw in the point set repeated in Figure 10.21. To come up with the reason-

able answer of nine clusters, your internal clustering algorithm had to manage

tricks like classifying a ring around a central blob as two distinct clusters, and

avoid merging two lines that move suspiciously close to each other. k-means

doesn’t have a chance of doing this, as shown in Figure 10.21 (left), because

it always seeks circular clusters and is happy to split long stringy clusters. Of

the agglomerative clustering procedures, only single-link with exactly the right

threshold might have a chance to do the right thing, but it is easily fooled into

merging two clusters by a single close point pair.

Clusters are not always round. Recognizing those that are not requires a

high-enough density of points that are suﬃciently contiguous that we are not

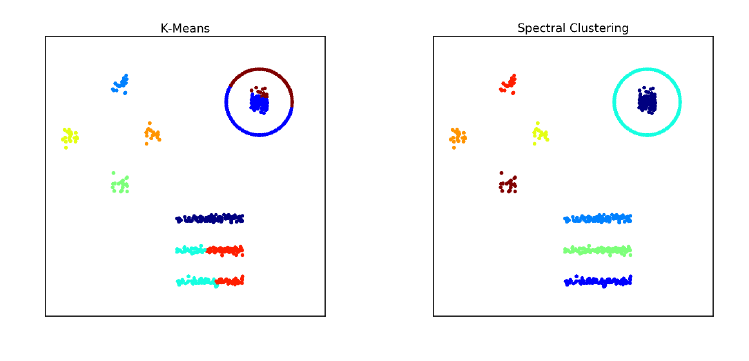
342 CHAPTER 10. DISTANCE AND NETWORK METHODS

Figure 10.21: The results of k-means (left) and cut-based spectral clustering

(right) on our 9-cluster example. Spectral clustering correctly ﬁnds connected

clusters here that k-means cannot.

tempted to cut a cluster in two. We seek clusters that are connected in an

appropriate similarity graph.

An n×nsimilarity matrix Sscores how much alike each pair of elements pi

and pjare. Similarity is essentially the inverse of distance: when piis close to

pj, then the item associated with pimust be similar to that of pj. It is natural

to measure similarity on a scale from 0 to 1, where 0 represents completely

diﬀerent and 1 means identical. This can be realized by making S[i, j] an inverse

exponential function of distance, regulated by a parameter β:

S[i, j] = e−β||pi−pj||

This works because e0= 1 and e−x= 1/ex→0 as x→ ∞.

Asimilarity graph has a weighted edge (i, j) between each pair of vertices i

and jreﬂecting the similar of piand pj. This is exactly the similarity matrix

described above. However, we can make this graph sparse by setting all small

terms (S[i, j]≤tfor some threshold t) to zero. This greatly reduces the number

of edges in the graph. We can even turn it into an unweighted graph by setting

the weight to 1 for all S[i, j]> t.

Cuts in Graphs

Real clusters in similarity graphs have the appearance of being dense regions

which are only loosely connected to the rest of graph. A cluster Chas a weight

which is a function of the edges within the cluster:

W(C) = X

x∈CX

y∈C

S[i, j]

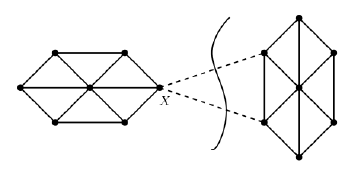
10.5. CLUSTERING 343

Figure 10.22: Low weight cuts in similarity graphs identify natural clusters.

The edges connecting Cto the rest of the graph deﬁne a cut, meaning the set of

edges who have one vertex in Cand the other in the rest of the graph (V−C).

The weight of this cut W0(C) is deﬁned:

W0(C) = X

x∈CX

y∈V−C

S[i, j]

Ideally clusters will have a high weight W(C) but a small cut W0(C), as shown

in Figure 10.22. The conductance of cluster Cis the ratio of cut weight over

internal weight (W0(C)/W (C)), with better clusters having lower conductance.

Finding low conductance clusters is a challenge. Help comes, surprisingly,

from linear algebra. The similarity matrix Sis a symmetric matrix, meaning

that it has an eigenvalue decomposition as discussed in Section 8.5. We saw

that the leading eigenvector results in a blocky approximation to S, with the

contribution of additional eigenvectors gradually improving the approximation.

Dropping the smallest eigenvectors removes either details or noise, depending

upon the interpretation.

Note that the ideal similarity matrix is a blocky matrix, because within each

cluster we expect a dense connection of highly-similar pairs, with little cross talk

to vertices of other clusters. This suggests using the eigenvectors of Sto deﬁne

robust features to cluster the vertices on. Performing k-means clustering on this

transformed feature space will recover good clusters.

This approach is called spectral clustering. We construct an appropriately

normalized similarity matrix called the Laplacian, where L=D−Sand D

is the degree-weighted identity matrix, so D[i, i] = PjS[i, j]. The kmost

important eigenvectors of Ldeﬁne an n×kfeature matrix. Curiously, the most

valuable eigenvectors for clustering here turn out to have the smallest non-zero

eigenvalues, due to special properties of the Laplacian matrix. Performing k-

means clustering in this feature space generates highly connected clusters.

344 CHAPTER 10. DISTANCE AND NETWORK METHODS

Take-Home Lesson: What is the right clustering algorithm to use for your data?

There are many possibilities to consider, but your most important decisions are:

•What is the right distance function to use?

•What are you doing to properly normalize your variables?

•Do your clusters look sensible to you when appropriately visualized? Un-

derstand that clustering is never perfect, because the algorithm can’t read

your mind. But is it good enough?

10.6 War Story: Cluster Bombing

My host at the research labs of a major media/tech company during my sabbat-

ical was Amanda Stent, the leader of their natural language processing (NLP)

group. She is exceptionally eﬃcient, excessively polite, and generally imper-

turbable. But with enough provocation she can get her dander up, and I heard

the exasperation in her voice when she muttered “Product people!”

Part of her mission at the lab was to interface with company product groups

which needed expertise in language technologies. The oﬀenders here were with

the news product, responsible for showing users recent articles of interest to

them. The article clustering module was an important part of this eﬀort, because

it grouped together all articles written about the same story/event. Users did

not want to read ten diﬀerent articles about the same baseball game or Internet

meme. Showing users repeated stories from a single article cluster proved highly

annoying, and chased them away from our site.

But article clustering only helps when the clusters themselves are accurate.

“This is the third time they have come to me complaining about the clus-

tering. They never give me speciﬁc examples of what is wrong, just complaints

that the clusters are not good enough. They keep sending me links to postings

they ﬁnd on Stack Overﬂow about new clustering algorithms, and ask if we

should be using these instead.”

I agreed to talk to them for her.

First, I made sure that the product people understood that clustering is an

ill-deﬁned problem, and that no matter what algorithm they used, there were

going to be occasional mistakes that they would have to live with. This didn’t

mean that there wasn’t any room for improvement over their current clustering

algorithm, but that they would have to temper any dreams of perfection.

Second, I told them that we could not hope to ﬁx the problem until we

were given clear examples of what exactly was going wrong. I asked them for

twenty examples of article pairs which were co-clustered by the algorithm, but

should not have been. And another twenty examples of article pairs which

naturally belonged in the same cluster, yet this similarity was not recognized

by the algorithm.

10.7. CHAPTER NOTES 345

This had the desired eﬀect. They readily agreed that my requests were

sensible, and necessary to diagnose the problem. They told me they would get

right on top of it. But this required work from their end, and everyone is busy

with too many things. So I never heard back from them again, and was left to

spend the rest of my sabbatical in a productive peace.

Months later, Amanda told me she had again spoken with the product peo-

ple. Someone had discovered that their clustering module was only using the

words from the headlines as features, and ignoring the entire contents of the

actual article. There was nothing wrong with the algorithm per-se, only with

the features, and it worked much better soon as it was given a richer feature

set.

What are the morals of this tale? A man has got to know his limitations,

and so does a clustering algorithm. Go to Google News right now, and carefully

study the article clusters. If you have a discerning eye you will ﬁnd several small

errors, and maybe something really embarrassing. But the more amazing thing

is how well this works in the big picture, that you can produce an informative,

non-redundant news feed algorithmically from thousands of diﬀerent sources.

Eﬀective clustering is never perfect, but can be immensely valuable.

The second moral is that feature engineering and distance functions matter

in clustering much more than the speciﬁc algorithmic approach. Those prod-

uct people dreamed of a high-powered algorithm which would solve all their

problems, yet were only clustering on the headlines. Headlines are designed to

attract attention, not explain the story. The best newspaper headlines in his-

tory, such as “Headless Body Found in Topless Bar” and “Ford to City, Drop

Dead” would be impossible to link to more sober ledes associated with the same

stories.

10.7 Chapter Notes

Distance computations are a basis of the ﬁeld of computational geometry, the

study of algorithms and data structures for manipulating point sets. Excellent

introductions to computational geometry include [O’R01, dBvKOS00].

Samet [Sam06] is the best reference on kd-trees and other spatial data struc-

tures for nearest neighbor search. All major (and many minor) variants are de-

veloped in substantial detail. A shorter survey [Sam05] is also available. Indyk

[Ind04] ably surveys recent results in approximate nearest neighbor search in

high dimensions, based on random projection methods.

Graph theory is the study of the abstract properties of graphs, with West

[Wes00] serving as an excellent introduction. Networks represent empirical

connections between real-world entities for encoding information about them.

Easley and Kleinberg [EK10] discuss the foundations of a science of networks in

society.

Clustering, also known as cluster analysis, is a classical topic in statistics and

computer science. Representative treatments include Everitt et al. [ELLS11] and

James et al. [JWHT13].

346 CHAPTER 10. DISTANCE AND NETWORK METHODS

10.8 Exercises

Distance Metrics

10-1. [3] Prove that Euclidean distance is in fact a metric.

10-2. [5] Prove that Lpdistance is a metric, for all p≥1.

10-3. [5] Prove that dimension-weighted Lpdistance is a metric, for all p≥1.

10-4. [3] Experiment with data to convince yourself that (a) cosine distance is not a

true distance metric, and that (b) angular distance is a distance metric.

10-5. [5] Prove that edit distance on text strings deﬁnes a metric.

10-6. [8] Show that the expected distance between two points chosen uniformly and

independently from a line of length 1 is 1/3. Establish convincing upper and

lower bounds on this expected distance for partial credit.

Nearest Neighbor Classiﬁcation

10-7. [3] What is the maximum number of nearest neighbors that a given point pcan

have in two dimensions, assuming the possibility of ties?

10-8. [5] Following up on the previous question, what is the maximum number of

diﬀerent points that can have a given point pas its nearest neighbor, again in

two dimensions?

10-9. [3] Construct a two-class point set on n≥10 points in two dimensions, where

every point would be misclassiﬁed according to its nearest neighbor.

10-10. [5] Repeat the previous question, but where we now classify each point according

to its three nearest neighbors (k= 3).

10-11. [5] Suppose a two-class, k= 1 nearest-neighbor classiﬁer is trained with at least

three positive points and at least three negative points.

(a) Might it possible this classiﬁer could label all new examples as positive?

(b) What if k= 3?

Networks

10-12. [3] Give explanations for what the nodes with the largest in-degree and out-

degree might be in the following graphs:

(a) The telephone graph, where edge (x, y) means xcalls y.

(b) The Twitter graph, where edge (x, y) means xfollows y.

10-13. [3] Power law distributions on vertex degree in networks usually result from

preferential attachment, a mechanism by which new edges are more likely to

connect to nodes of high degree. For each of the following graphs, suggest what

their vertex degree distribution is, and if they are power law distributed describe

what the preferential attachment mechanism might be.

(a) Social networks like Facebook or Instagram.

(b) Sites on the World Wide Web (WWW).

10.8. EXERCISES 347

(d) Product/customer networks like Amazon or Netﬂix.

10-14. [5] For each of the following graph-theoretic properties, give an example of a

real-world network that satisﬁes the property, and a second network which does

not.

(a) Directed vs. undirected.

(b) Weighted vs. unweighted.

(d) Sparse vs. dense.

(e) Embedded vs. topological.

(f) Labeled vs. unlabeled.

10-15. [3] Prove that in any simple graph, there are always an even number of vertices

with odd vertex degree.

10-16. [3] Implement a simple version of the PageRank algorithm, and test it on your

favorite network. Which vertices get highlighted as most central?

Clustering

10-17. [5] For a data set with points at positions (4,10), (7,10) (4,8), (6,8), (3,4),

(2,2), (5,2), (9,3), (12,3), (11,4), (10,5), and (12,6), show the clustering that

results from

(a) Single-linkage clustering

(b) Average-linkage clustering

10-18. [3] For each of the following The Quant Shop prediction challenges, propose

available data that might make it feasible to employ nearest-neighbor/analogical

methods to the task:

(a) Miss Universe.

(b) Movie gross.

(d) Art auction price.

(e) White Christmas.

(f) Football champions.

(g) Ghoul pool.

(h) Gold/oil prices.

10-19. [3] Perform k-means clustering manually on the following points, for k= 2:

S={(1,4),(1,3),(0,4),(5,1),(6,2),(4,0)}

Plot the points and the ﬁnal clusters.

348 CHAPTER 10. DISTANCE AND NETWORK METHODS

10-20. [5] Implement two versions of a simple k-means algorithm: one of which uses

numerical centroids as centers, the other of which restricts centers to be input

points from the data set. Then experiment. Which algorithm converges faster

on average? Which algorithm produces clusterings with lower absolute and

mean-squared error, and by how much?

10-21. [5] Suppose s1and s2are randomly selected subsets from a universal set with

nitems. What is the expected value of the Jaccard similarity J(s1, s2)?

10-22. [5] Identify a data set on entities where you have some sense of natural clusters

which should emerge, be it on people, universities, companies, or movies. Cluster

it by one or more algorithms, perhaps k-means and agglomerative clustering.

Then evaluate the resulting clusters based on your knowledge of the domain.

Did they do a good job? What things did it get wrong? Can you explain why

the algorithm did not reconstruct what was in your head?

10-23. [5] Assume that we are trying to cluster n= 10 points in one dimension, where

point pihas a position of x=i. What is the agglomerative clustering tree for

these points under

(a) Single-link clustering

(b) Average-link clustering

10-24. [5] Assume that we are trying to cluster n= 10 points in one dimension, where

point pihas a position of x= 2i. What is the agglomerative clustering tree for

these points under

(a) Single-link clustering

(b) Average-link clustering

Implementation Projects

10-25. [5] Do experiments studying the impact of merging criteria (single-link, cen-

troid, average-link, furthest link) on the properties of the resulting cluster tree.

Which leads to the tallest trees? The most balanced? How do their running

times compare? Which method produces results most consistent with k-means

clustering?

10-26. [5] Experiment with the performance of diﬀerent algorithms/data structures for

ﬁnding the nearest neighbor of a query point qamong npoints in ddimensions.

What is the maximum dfor which each method remains viable? How much

faster are heuristic methods based on LSH than methods that guarantee the

exact nearest neighbor, at what loss of accuracy?

Interview Questions

10-27. [5] What is curse of dimensionality? How does it aﬀect distance and similarity

measures?

10-28. [5] What is clustering? Describe an example algorithm that performs clustering.

How can we know whether it produced decent clusters on our data set?

10-29. [5] How might we be able to estimate the right number of clusters to use with

a given data set?

10.8. EXERCISES 349

10-30. [5] What is the diﬀerence between unsupervised and supervised learning?

10-31. [5] How can you deal with correlated features in your data set by reducing the

dimensionality of the data.

10-32. [5] Explain what a local optimum is. Why is it important in k-means clustering?

Kaggle Challenges

10-33. Which people are most inﬂuential in a given social network?

10-34. Who is destined to become friends in an online social network?

https://www.kaggle.com/c/socialNetwork

10-35. Predict which product a consumer is most likely to buy.

https://www.kaggle.com/c/coupon-purchase-prediction

https://www.kaggle.com/c/predict-who-is-more-influential-in-a-social-network

Chapter 11

Machine Learning

Any suﬃciently advanced form of cheating is indistinguishable from

learning.

– Jan Schaumann

For much of my career, I was highly suspicious of the importance of machine

learning. I sat through many talks over the years, with grandiose claims and very

meager results. But it is clear that the tide has turned. The most interesting

work in computer science today revolves around machine learning, both powerful

new algorithms and exciting new applications.

This revolution has occurred for several reasons. First, the volume of data

and computing power available crossed a magic threshold where machine learn-

ing systems started doing interesting things, even using old approaches. This

inspired greater activity in developing methods that scale better, and greater

investment in data resources and system development. The culture of open

source software deserves to take a bow, because new ideas turn into available

tools amazingly quickly. Machine learning today is an exploding ﬁeld with a

great deal of excitement about it.

We have so far discussed two ways of building models based on data, linear

regression and nearest neighbor approaches, both in fairly extensive detail. For

many applications, this is all you will need to know. If you have enough labeled

training data, all methods are likely to produce good results. And if you don’t,

all methods are likely to fail. The impact of the best machine learning algorithm

can make a diﬀerence, but generally only at the margins. I feel that the purpose

of my book is to get you from crawling to walking, so that more specialized books

can teach you how to run.

That said, a slew of interesting and important machine learning algorithms

have been developed. We will review these methods here in this chapter, with

the goal of understanding the strengths and weaknesses of each, along several

relevant dimensions of performance:

352 CHAPTER 11. MACHINE LEARNING

•Power and expressibility: Machine learning methods diﬀer in the richness

and complexity of the models they support. Linear regression ﬁts linear

functions, while nearest neighbor methods deﬁne piecewise-linear sepa-

ration boundaries with enough pieces to approximate arbitrary curves.

Greater expressive power provides the possibility of more accurate mod-

els, as well as the dangers of overﬁtting.

•Interpretability: Powerful methods like deep learning often produce mod-

els that are completely impenetrable. They might provide very accurate

classiﬁcation in practice, but no human-readable explanation of why they

are making the decisions they do. In contrast, the largest coeﬃcients

in a linear regression model identify the most powerful features, and the

identities of nearest neighbors enable us to independently determine our

conﬁdence in these analogies.

I personally believe that interpretability is an important property of a

model, and am generally happier to take a lesser-performing model I un-

derstand over a slightly more accurate one that I don’t. This may not

be a universally shared opinion, but you have a sense whether you really

understand your model and its particular application domain.

•Ease of use: Certain machine learning methods feature relatively few

parameters or decisions, meaning they work right out of the box. Both

linear regression and nearest neighbor classiﬁcation are quite simple in

this regard. In contrast, methods like support vector machines (SVMs)

provide much greater scope to optimize algorithm performance with the

proper settings. My sense is that the available tools for machine learning

will continue to get better: easier to use and more powerful. But for now,

certain methods allow the user enough rope to hang themselves if they

don’t know what they are doing.

•Training speed: Methods diﬀer greatly in how fast they ﬁt the neces-

sary parameters of the model, which determines how much training data

you can aﬀord to use in practice. Traditional linear regression methods

can be expensive to ﬁt for large models. In contrast, nearest neighbor

search requires almost no training time at all, outside that of building the

appropriate search data structure.

•Prediction speed: Methods diﬀer in how fast they make classiﬁcation de-

cisions on a new query q. Linear/logistic regression is fast, just computing

a weighted sum of the ﬁelds in the input records. In contrast, nearest

neighbor search requires explicitly testing qagainst a substantial amount

of the training test. In general there is a trade-oﬀ with training speed:

you can pay me now or pay me later.

Figure 11.1 presents my subjective ratings of roughly where the approaches

discussed in this chapter ﬁt along these performance dimensions. These ratings

are not the voice of G-d, and reasonable people can have diﬀerent opinions.

353

Figure 11.1: Subjective rankings of machine learning approaches along ﬁve di-

mensions, on a 1 to 10 scale with higher being better.

Hopefully they survey the landscape of machine learning algorithms in a useful

manner. Certainly no single machine learning method dominates all the others.

This observation is formalized in the appropriately named no free lunch theorem,

which proves there does not exist a single machine learning algorithm better

than all the others on all problems.

That said, it is still possible to rank methods according to priority of use for

practitioners. My ordering of methods in this book (and Figure 11.1) starts with

the ones that are easy to use/tune, but have lower discriminative power than the

most advanced methods. Generally speaking, I encourage you to start with the

easy methods and work your way down the list if the potential improvements

in accuracy really justify it.

It is easy to misuse the material I will present in this chapter, because there

is a natural temptation to try all possible machine learning algorithms and

pick whichever model gives the highest reported accuracy or F1 score. Done

naively through a single library call, which makes this easy, you are likely to

discover that all models do about the same on your training data. Further,

any performance diﬀerences between them that you do ﬁnd are more likely

attributable to variance than insight. Experiments like this is what statistical

signiﬁcance testing was invented for.

The most important factor that will determine the quality of your models

is the quality of your features. We talked a lot about data cleaning in Chapter

3, which concerns the proper preparation of your data matrix. We delve more

deeply into feature engineering in Section 11.5.4, before discussing deep learning

methods that strive to engineer their own features.

One ﬁnal comment. Data scientists tend to have a favorite machine learning

approach, which they advocate for in a similar manner to their favorite pro-

gramming language or sports team. A large part of this is experience, meaning

that because they are most familiar with a particular implementation it works

best in their hands. But part of it is magical thinking, the fact that they noticed

one library slightly outperforming others on a few examples and inappropriately

generalized.

Power of Ease of Ease of Training Prediction

Method Expression Interpretation Use Speed Speed

Linear Regression 59999

Nearest Neighbor 598102

Naive Bayes 48798

Decision Trees 88779

Support Vector Machines 86677

Boosting 96666

Graphical Models 98344

Deep Learning 10 3 4 3 7

354 CHAPTER 11. MACHINE LEARNING

Don’t fall into this trap. Select methods which best ﬁt the needs of your

application based on the criteria above, and gain enough experience with their

various knobs and levers to optimize performance.

11.1 Naive Bayes

Recall that two events Aand Bare independent if p(Aand B) = p(A)·p(B).

If Ais the event that “my favorite sports team wins today” and Bis “the stock

market goes up today,” then presumably Aand Bare independent. But this is

not true in general. Consider the case if Ais the event that “I get an A in Data

Science this semester” and Bis “I get an A in a diﬀerent course this semester.”

There are dependencies between these events: renewed enthusiasms for either

study or drinking will aﬀect course performance in a correlated manner. In the

general case,

p(Aand B) = p(A)·p(B|A) = p(A) + P(B)−p(Aor B).

If everything was independent, the world of probability would be a much

simpler place. The naive Bayes classiﬁcation algorithm crosses its ﬁngers and

assumes independence, to avoid the need to compute these messy conditional

probabilities.

11.1.1 Formulation

Suppose we wish to classify the vector X= (x1,...xn) into one of mclasses

C1, . . . , Cm. We seek to compute the probability of each possible class given X,

so we can assign Xthe label of the class with highest probability. By Bayes

theorem,

p(Ci|X) = p(Ci)·p(X|Ci)

p(X)

Let’s parse this equation. The term p(Ci) is the prior probability, the probabil-

ity of the class label without any speciﬁc evidence. I know that you the reader

are more likely to have black hair than red hair, because more people in the

world have black hair than red hair.1

The denominator P(X) gives the probability of seeing the given input vector

Xover all possible input vectors. Establishing the exact value of P(X) seems

somewhat dicey, but mercifully is usually unnecessary. Observe that this de-

nominator is the same for all classes. We only seek to establish a class label for

X, so the value of p(X) has no eﬀect on our decision. Selecting the class with

highest probability means

C(X) = arg max

i=1,...,m

p(Ci)·p(X|Ci)

p(X)= arg max

i=1,...,m

p(Ci)·p(X|Ci).

1Wikipedia claims that only 1–2% of the world’s population are redheads.

11.1. NAIVE BAYES 355

Day Outlook Temp Humidity Beach?

1 Sunny High High Yes

2 Sunny High Normal Yes

3 Sunny Low Normal No

4 Sunny Mild High Yes

5 Rain Mild Normal No

6Rain High High No

7 Rain Low Normal No

8 Cloudy High High No

9 Cloudy High Normal Yes

10 Cloudy Mild Normal No

P(X|Class) Probability in Class

Outlook Beach No Beach

Sunny 3/4 1/6

Rain 0/4 3/6

Cloudy 1/4 2/6

Temperature Beach No Beach

High 3/4 2/6

Mild 1/4 2/6

Low 0/4 2/6

Humidity Beach No Beach

High 2/4 2/6

Normal 2/4 4/6

P(Beach Day) 4/10 6/10

Figure 11.2: Probabilities to support a naive Bayes calculation on whether

today is a good day to go to the beach: tabulated events (left) with marginal

probability distributions (right).

The remaining term p(X|Ci) is the probability of seeing input vector Xgiven

that we know the class of the item is Ci. This also seems somewhat dicey. What

is the probability someone weighs 150 lbs and is 5 foot 8 inches tall, given that

they are male? It should be clear that p(X|Ci) will generally be very small:

there is a huge space of possible input vectors consistent with the class, only

one of which corresponds to the given item.

But now suppose we lived where everything was independent, i.e. the prob-

ability of event Aand event Bwas always p(A)·p(B). Then

p(X|Ci) =

j=1

p(xj|Ci).

Now anyone who really believes in a world of independent probabilities is quite

naive, hence the name naive Bayes. But such an assumption really does make

the computations much easier. Putting this together:

C(X) = arg max

i=1,...,m

p(Ci)·p(X|Ci) = arg max

i=1,...,m

p(Ci)

j=1

p(xj|Ci).

Finally, we should hit the product with a log to turn it to a sum, for better

numerical stability. The logs of probabilities will be negative numbers, but less

likely events are more negative than common ones. Thus the complete naive

Bayes algorithm is given by the following formula:

C(X) = arg max

i=1,...,m

(log(p(Ci)) +

j=1

log(p(xj|Ci))).

How do we calculate the p(xj|Ci), the probability of observation xjgiven

class label i? This is easy from the training data, particularly if xjis a cate-

gorical variable, like “has red hair.” We can simply select all class iinstances

356 CHAPTER 11. MACHINE LEARNING

in the training set, and compute the fraction of them which have property xj.

This fraction deﬁnes a reasonable estimate of p(xj|Ci). A bit more imagination

is needed when xjis a numerical variable, like “age=18” or “the word dog oc-

curred six times in the given document,” but in principle is computed by how

often this value is observed in the training set.

Figure 11.2 illustrates the naive Bayes procedure. On the left, it presents a

table of ten observations of weather conditions, and whether each observation

proved to be a day to go to the beach, or instead stay home. This table has been

broken down on the right, to produce conditional probabilities of the weather

condition given the activity. From these probabilities, we can use Bayes theorem

to compute:

P(Beach|(Sunny,Mild,High))

= (P(Sunny|Beach) ×P(Mild|Beach) ×P(High|Beach) ×P(Beach)

= (3/4) ×(1/4) ×(2/4) ×(4/10) = 0.0375

P(No Beach|(Sunny,Mild,High))

= (P(Sunny|No) ×P(Mild|No) ×P(High|No)) ×P(No)

= (1/6) ×(2/6) ×(2/6) ×(6/10) = 0.0111

Since 0.0375 >0.0111, naive Bayes is telling us to hit the beach. Note that

it is irrelevant that this particular combination of (Sunny,Mild,High) appeared

in the training data. We are basing our decision on the aggregate probabilities,

not a single row as in nearest neighbor classiﬁcation.

11.1.2 Dealing with Zero Counts (Discounting)

There is a subtle but important feature preparation issue particularly associated

with the naive Bayes algorithm. Observed counts do not accurately capture the

frequency of rare events, for which there is typically a long tail.

The issue was ﬁrst raised by the mathematician Laplace, who asked: What

is the probability the sun will rise tomorrow? It may be close to one, but it

ain’t exactly 1.0. Although the sun has risen like clockwork each morning for

the 36.5 million mornings or so since man started noticing such things, it will

not do so forever. The time will come where the earth or sun explodes, and so

there is a small but non-zero chance that tonight’s the night.

There can always be events which have not yet been seen in any ﬁnite data

set. You might well have records on a hundred people, none of whom happen

to have red hair. Concluding that the probability of red hair is 0/100 = 0 is

potentially disastrous when we are asked to classify someone with red hair, since

the probability of them being in each and every class will be zero. Even worse

would be if there was exactly one redhead in the entire training set, say labeled

11.2. DECISION TREE CLASSIFIERS 357

with class C2. Our naive Bayes classiﬁer would decide that every future redhead

just had to be in class C2, regardless of other evidence.

Discounting is a statistical technique to adjust counts for yet-unseen events,

by explicitly leaving probability mass available for them. The simplest and most

popular technique is add-one discounting, where we add one to the frequency all

outcomes, including unseen. For example, suppose we were drawing balls from

an urn. After seeing ﬁve reds and three greens, what is the probability we will

see a new color on the next draw? If we employ add-one discounting,

P(red) = (5 + 1)/((5 + 1) + (3 + 1) + (0 + 1)) = 6/11,and

P(green) = (3 + 1)/((5 + 1) + (3 + 1) + (0 + 1)) = 4/11,

leaving the new color a probability mass of

P(new-color) = 1/((5 + 1) + (3 + 1) + (0 + 1)) = 1/11.

For small numbers of samples or large numbers of known classes, the dis-

counting causes a non-trivial damping of the probabilities. Our estimate for the

probability of seeing a red ball changes from 5/8 = 0.625 to 6/11 = 0.545 when

we employ add-one discounting. But this is a safer and more honest estimate,

and the diﬀerences will disappear into nothingness after we have seen enough

samples.

You should be aware that other discounting methods have been developed,

and adding one might not be the best possible estimator in all situations. That

said, not discounting counts is asking for trouble, and no one will be ﬁred for

using the add-one method.

Discounting becomes particularly important in natural language processing,

where the traditional bag of words representation models a document as a word

frequency count vector over the language’s entire vocabulary, say 100,000 words.

Because word usage frequency is governed by a power law (Zipf’s law), words

in the tail are quite rare. Have you ever seen the English word defenestrate

before?2Even worse, documents of less than book length are too short to

contain 100,000 words, so we are doomed to see zeros wherever we look. Add-

one discounting turns these count vectors into sensible probability vectors, with

non-zero probabilities of seeing rare and so far unencountered words.

11.2 Decision Tree Classiﬁers

Adecision tree is a binary branching structure used to classify an arbitrary input

vector X. Each node in the tree contains a simple feature comparison against

some ﬁeld xi∈X, like “is xi≥23.7?” The result of each such comparison is

either true or false, determining whether we should proceed along to the left or

right child of the given node. These structures are sometimes called classiﬁcation

and regression trees (CART) because they can be applied to a broader class of

problems.

2It means to throw someone out the window.

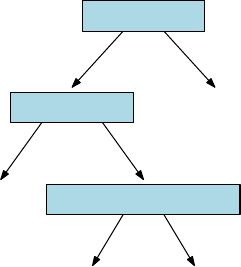
358 CHAPTER 11. MACHINE LEARNING

Yes No

Survived

0.73 35%

Died

0.17 61%

Died

0.05 2%

Survived

0.89 2%

Is sex male?

Is age >9.5?

More than two siblings?

Figure 11.3: Simple decision tree for predicting mortality on the Titanic.

The decision tree partitions training examples into groups of relatively uni-

form class composition, so the decision then becomes easy. Figure 11.3 presents

an example of a decision tree, designed to predict your chances of surviving

the shipwreck of the Titanic. Each row/instance travels a unique root-to-leaf

path to classiﬁcation. The root test here reﬂects the naval tradition of women

and children ﬁrst: 73% of the women survived, so this feature alone is enough

to make a prediction for women. The second level of the tree reﬂects children

ﬁrst: any male 10 years or older is deemed out of luck. Even the younger ones

must pass one ﬁnal hurdle: they generally made it to a lifeboat only if they had

brothers and sisters to lobby for them.

What is the accuracy of this model on the training data? It depends upon

what faction of the examples end on each leaf, and how pure these leaf samples

are. For the example of Figure 11.3, augmented with coverage percentage and

survival fraction (purity) at each node, the classiﬁcation accuracy Aof this tree

is:

A= (0.35)(73%) + (0.61)(83%) + (0.02)(95%) + (0.02)(89%) = 78.86%.

An accuracy of 78.86% is not bad for such a simple decision procedure. We

could have driven it up to 100% by completing the tree so each of the 1317

passengers had a leaf to themselves, labeling that node with their ultimate

fate. Perhaps 23-year-old second-class males were more likely to survive than

either 22- or 24-year-old males, an observation the tree could leverage for higher

training accuracy. But such a complicated tree would be wildly overﬁt, ﬁnding

structure that isn’t meaningfully there. The tree in Figure 11.3 is interpretable,

robust, and reasonably accurate. Beyond that, it is every man for himself.

Advantages of decision trees include:

•Non-linearity: Each leaf represents a chunk of the decision space, but

reached through a potentially complicated path. This chain of logic per-

mits decision trees to represent highly complicated decision boundaries.

11.2. DECISION TREE CLASSIFIERS 359

•Support for categorical variables: Decision trees make natural use of

categorical variables, like “if hair color = red,” in addition to numerical

data. Categorical variables ﬁt less comfortably into most other machine

learning methods.

•Interpretability: Decision trees are explainable; you can read them and

understand what their reasoning is. Thus decision tree algorithms can tell

you something about your data set that you might not have seen before.

Also, interpretability lets you vet whether you trust the decisions it will

make: is it making decisions for the right reasons?

•Robustness: The number of possible decision trees grows exponentially

in the number of features and possible tests, which means that we can

build as many as we wish. Constructing many random decision trees

(CART) and taking the result of each as a vote for the given label increases

robustness, and permits us to assess the conﬁdence of our classiﬁcation.

•Application to regression: The subset of items which follow a similar

path down a decision tree are likely similar in properties other than just

label. For each such subset, we can use linear regression to build a special

prediction model for the numerical values of such leaf items. This will

presumably perform better than a more general model trained over all

instances.

The biggest disadvantage of decision trees is a certain lack of elegance.

Learning methods like logistic regression and support vector machines use math.

Advanced probability theory, linear algebra, higher-dimensional geometry. You

know, math.

By contrast, decision trees are a hacker’s game. There are many cool knobs

to twist in the training procedure, and relatively little theory to help you twist

them in the right way.

But the fact of the matter is that decision tree models work very well in

practice. Gradient boosted decision trees (GBDTs) are currently the most fre-

quently used machine learning method to win Kaggle competitions. We will

work through this in stages. First decision trees, then boosting in the subse-

quent section.

11.2.1 Constructing Decision Trees

Decision trees are built in a top-down manner. We start from a given collection

of training instances, each with nfeatures and labeled with one of mclasses

C1, . . . , Cm. Each node in the decision tree contains a binary predicate, a logic

condition derived from a given feature.

Features with a discrete set of values vican easily be turned into binary

predicates through equality testing: “is feature xi=vij ?” Thus there are

|vi|distinct predicates associated with xi. Numerical features can be turned

into binary predicates with the addition of a threshold t: “is feature xi≥t?”

360 CHAPTER 11. MACHINE LEARNING

The set of potentially interesting thresholds tare deﬁned by the gaps between

the observed values that xitakes on in the training set. If the complete set

of observations of xiare (10,11,11,14,20), the meaningful possible values for

t∈(10,11,14) or perhaps t∈(10.5,11.5,17). Both threshold sets produce the

same partitions of the observations, but using the midpoints of each gap seems

sounder when generalizing to future values unseen in training.

We need a way to evaluate each predicate for how well it will contribute to

partitioning the set Sof training examples reachable from this node. An ideal

predicate pwould be a pure partition of S, so that the class labels are disjoint.

In this dream all members of Sfrom each class Ciwill appear exclusively on one

side of the tree, however, such purity is not usually possible. We also want pred-

icates that produce balanced splits of S, meaning that the left subtree contains

roughly as many elements from Sas the right subtree. Balanced splits make

faster progress in classiﬁcation, and also are potentially more robust. Setting

the threshold tto the minimum value of xipicks oﬀ a lone element from S,

produces a perfectly pure but maximally imbalanced split.

Thus our selection criteria should reward both balance and purity, to max-

imize what we learn from the test. One way to measure the purity of an item

subset Sis as the converse of disorder, or entropy. Let fidenote the fraction of

Swhich is of class Ci. Then the information theoretic entropy of S,H(S), can

be computed:

H(S) = −

i=1

filog2fi

The negative sign here exists to make the entire quantity positive, since the

logarithm of a proper fraction is always negative.

Let’s parse this formula. The purest possible contribution occurs when all

elements belong to a single class, meaning fj= 1 for some class j. The contri-

bution of class jto H(S) is 1 log2(1) = 0, identical to that of all other classes:

0·log2(0) = 0. The most disordered version is when all mclasses are represented

equally, meaning fi= 1/m. Then H(S) = log2(m) by the above deﬁnition. The

smaller the entropy, the better the node is for classiﬁcation.

The value of a potential split applied to a tree node is how much it reduces

the entropy of the system. Suppose a Boolean predicate ppartitions Sinto two

disjoint subsets, so S=S1∪S2. Then the information gain of pis deﬁned

IGp(S) = H(S)−

j=1

|Si|

|S|H(Si)

We seek the predicate p0which maximizes this information gain, as the best

splitter for S. This criteria implicitly prefers balanced splits since both sides of

the tree are evaluated.

Alternate measures of purity have been deﬁned and are used in practice.

The Gini impurity is based on another quantity (fi(1 −fi)), which is zero in

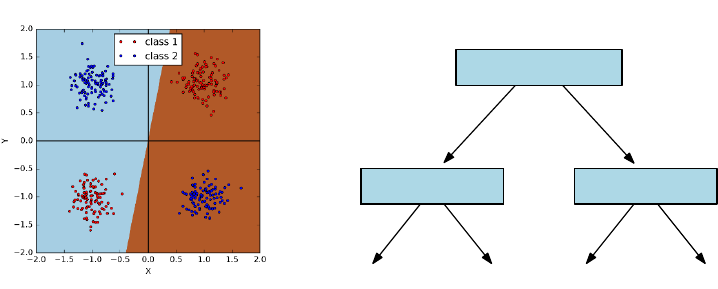
11.2. DECISION TREE CLASSIFIERS 361

Yes No

class 1

x>0

y>0y >0

class 1class 2 class 2

Figure 11.4: The exclusive OR function cannot be ﬁt by linear classiﬁers. On

the left, we present four natural clusters in x−yspace. This demonstrates

the complete inability of logistic regression to ﬁnd a meaningful separator, even

though a small decision tree easily does the job (right).

both cases of pure splits, fi= 0 or fi= 1:

IG(f) =

i=1

fi(1 −fi) =

i=1

(fi−f2

i) =

i=1

fi−

i=1

i= 1 −

i=1

Predicate selection criteria to optimize Gini impurity can be similarly deﬁned.

We need a stopping condition to complete the heuristic. When is a node

pure enough to call it a leaf? By setting a threshold on information gain, we

stop dividing when the reward of another test is less than .

An alternate strategy is to build out the full tree until all leaves are com-

pletely pure, and then prune it back by eliminating nodes which contribute the

least information gain. It is fairly common that a large universe may have no

good splitters near the root, but better ones emerge as the set of live items gets

smaller. This approach has the beneﬁt of not giving up too early in the process.

11.2.2 Realizing Exclusive Or

Some decision boundary shapes can be hard or even impossible to ﬁt using a

particular machine learning approach. Most notoriously, linear classiﬁers cannot

be used to ﬁt certain simple non-linear functions like eXclusive OR (XOR). The

logic function A⊕Bis deﬁned as

A⊕B= (Aor ¯

B) or ( ¯

Aor B).

For points (x, y) in two dimensions, we can deﬁne predicates such that A

means “is x≥0?” and Bmeans the “is y≥0?”. Then there are two distinct

regions where A⊕Btrue, opposing quadrants in this xy-plane shown in Figure

362 CHAPTER 11. MACHINE LEARNING

11.4 (left). The need to carve up two regions with one line explains why XOR

is impossible for linear classiﬁers.

Decision trees are powerful enough to recognize XOR. Indeed, the two-level

tree in Figure 11.4 (right) does the job. After the root tests whether Ais true

or false, the second level tests for Bare already conditioned on A, so each of

the four leaves can be associated with a distinct quadrant, allowing for proper

classiﬁcation.

Although decision trees can recognize XOR, that doesn’t mean it is easy to

ﬁnd the tree that does it. What makes XOR hard to deal with is that you can’t

see yourself making progress toward better classiﬁcation, even if you pick the

correct root node. In the example above, choosing a root node of “is x > 0?”

causes no apparent enrichment of class purity on either side. The value of this

test only becomes apparent if we look ahead another level, since the information

gain is zero.

Greedy decision tree construction heuristics fail on problems like XOR. This

suggests the value of more sophisticated and computationally expensive tree

building procedures in diﬃcult cases, which look-ahead like computer chess

programs, evaluating the worth of move pnot now, but how it looks several

moves later.

11.2.3 Ensembles of Decision Trees

There are an enormous number of possible decision trees which can be built

on any training set S. Further, each of them will classify all training examples

perfectly, if we keep reﬁning until all leaves are pure. This suggests building

hundreds or even thousands of diﬀerent trees, and evaluating a query item q

against each of them to return a possible label. By letting each tree cast its

own independent vote, we gain conﬁdence that the most commonly seen label

will be the right label.

For this to avoid group-think, we need the trees to be diverse. Repeatedly

using a deterministic construction procedure that ﬁnds the best tree is worthless,

because they will all be identical. Better would be to randomly select a new

splitting dimension at each tree node, and then ﬁnd the best possible threshold

for this variable to deﬁne the predicate.

But even with random dimension selection, the resulting trees often are

highly correlated. A better approach is bagging, building the best possible trees

on relatively small random subsets of items. Done properly, the resulting trees

should be relatively independent of each other, providing a diversity of classiﬁers

to work with, facilitating the wisdom of crowds.

Using ensembles of decision trees has another advantage beyond robustness.

The degree of consensus among the trees oﬀers a measure of conﬁdence for any

classiﬁcation decision. There is a big diﬀerence in the majority label appearing

in 501 of 1000 trees vs. 947 of them.

This fraction can be interpreted as a probability, but even better might be

to feed this number into logistic regression for a better motivated measure of

conﬁdence. Assuming we have a binary classiﬁcation problem, let fidenote the

11.3. BOOSTING AND ENSEMBLE LEARNING 363

fraction of trees picking class C1on input vector Xi. Run the entire training

set through the decision tree ensemble. Now deﬁne a logistic regression problem

where fiis input variable and the class of Xithe output variable. The resulting

logit function will determine an appropriate conﬁdence level, for any observed

fraction of agreement.

11.3 Boosting and Ensemble Learning

The idea of aggregating large numbers of noisy “predictors” into one stronger

classiﬁer applies to algorithms as well as crowds. It is often the case that many

diﬀerent features all weakly correlate with the dependent variable. So what is

the best way we can combine them into one stronger classiﬁer?

11.3.1 Voting with Classiﬁers

Ensemble learning is the strategy of combining many diﬀerent classiﬁers into one

predictive unit. The naive Bayes approach of Section 11.1 has a little of this

ﬂavor, because it uses each feature as a separate relatively weak classiﬁer, then

multiplies them together. Linear/logistic regression has a similar interpretation,

in that it assigns a weight to each feature to maximize the predictive power of

the ensemble.

But more generally, ensemble learning revolves on the idea of voting. We saw

that decision trees can be more powerful in aggregate, by constructing hundreds

or thousands of them over random subsets of examples. The wisdom of crowds

comes from the triumph of diversity of thought over the individual with greatest

expertise.

Democracy rests on the principle of one man, one vote. Your educated,

reasoned judgment of the best course of action counts equally as the vote of

that loud-mouthed idiot down the hall. Democracy makes sense in terms of the

dynamics of society: shared decisions generally aﬀect the idiot just as much as

they do you, so equality dictates that all people deserve an equal say in the

matter.

But the same argument does not apply to classiﬁers. The most natural way

to use multiple classiﬁers gives each a vote, and takes the majority label. But

why should each classiﬁer get the same vote?

Figure 11.5 captures some of the complexity of assigning weights to classi-

ﬁers. The example consists of ﬁve voters, each classifying ﬁve items. All voters

are pretty good, each getting 60% correct, with the exception of v1, who batted

80%. The majority option proves no better than the worst individual classiﬁer,

however, at 60%. But a perfect classiﬁer results if we drop voters v4and v5and

weigh the remainders equally. What makes v2and v3valuable is not their over-

all accuracy, but their performance on the hardest problems (Dand especially

E).

There seem to be three primary ways to assign weights to the classiﬁer/voters.

The simplest might be to give more weight to the votes of classiﬁers who have

364 CHAPTER 11. MACHINE LEARNING

Item/voter V1V2V3V4V5Majority Best weights

A * * * * * *

B * * * * * *

C * * * * * *

D * * *

E * * *

% correct 80% 60% 60% 60% 60% 60% 100%

best weight 1/3 1/3 1/3 0 0

Figure 11.5: Uniform weighting of votes does not always produce the best pos-

sible classiﬁer, even when voters are equally accurate, because some problem

instances are harder than others (here, Dand E). The “*” denotes that the

given voter classiﬁed the given item correctly.

proven accurate in the past, perhaps assigning vithe multiplicative weight ti/T ,

where tiis the number of times viclassiﬁed correctly and T=Pc

i=1 ti. Note

that this weighting scheme would do no better than majority rule on the example

of Figure 11.5.

A second approach could be to use linear/logistic regression to ﬁnd the best

possible weights. In a binary classiﬁcation problem, the two classes would be

denoted as 0 and 1, respectively. The 0-1 results from each classiﬁer can be

used as a feature to predict the actual class value. This formulation would ﬁnd

non-uniform weights that favor classiﬁers correlated with the correct answers,

but do not explicitly seek to maximize the number of correct classiﬁcations.

11.3.2 Boosting Algorithms

The third idea is boosting. The key point is to weigh the examples according

to how hard they are to get right, and reward classiﬁers based on the weight of

the examples they get right, not just the count.

To set the weights of the classiﬁer, we will adjust the weights of the training

examples. Easy training examples will be properly classiﬁed by most classiﬁers:

we reward classiﬁers more for getting the hard cases right.

A representative boosting algorithm is AdaBoost, presented in Figure 11.6.

We will not stress the details here, particularly the speciﬁcs of the weight ad-

justments in each round. We presume our classiﬁer will be constructed as the

union of non-linear classiﬁers of the form “is (vi≥ti)?”, i.e. using thresholded

features as classiﬁers.

The algorithm proceeds in Trounds, for t={0, . . . , T }. Initially all train-

ing examples (points) should be of equal weight, so wi,0= 1/n for all points

x1, . . . , xn. We consider all possible feature/threshold classiﬁers, and identify

the fi(x) which minimizes t, the sum of the weights of the misclassiﬁed points.

The weight αtof the new classiﬁer depends upon how accurate it is on the

11.3. BOOSTING AND ENSEMBLE LEARNING 365

AdaBoost

For tin 1 . . . T :

•Choose ft(x):

•Find weak learner ht(x) that minimizes t, the weighted sum

error for misclassiﬁed points t=Piwi,t

•Choose αt=1

2ln 1−t

t

•Add to ensemble:

•Ft(x) = Ft−1(x) + αtht(x)

•Update weights:

•wi,t+1 = (wi,t)e−yiαtht(xi)for all i

•Renormalize wi,t+1 such that Piwi,t+1 = 1

Figure 11.6: Pseudocode for the AdaBoost algorithm.

current point set, as measured by

αt=1

2ln(1−t

t

)

The point weights are normalized so Pn

i=1 wi= 1, so there must always be a

classiﬁer with error t≤0.5.3

In the next round, the weights of the misclassiﬁed points are boosted to

make them more important. Let ht(xi) be the class (−1 or 1) predicted for xi,

and yithe correct class or that point. The sign of ht(xi)·yreﬂects whether

the classes agree (positive) or disagree (negative). We then adjust the weights

according to

i,t+1 =wi,te−yiαtht(xi)

before re-normalizing all of them so they continue to sum to 1, i.e.

i=1

i,t+1,and wi,t+1 =w0

i,t+1/C.

The example in Figure 11.7 shows a ﬁnal classiﬁer as the linear sum of three

thresholded single-variable classiﬁers. Think of them as the simplest possible

3Consider two classiﬁers, one which calls class C0if xi≥ti, the other of which calls class

C1if xi≥ti. The ﬁrst classiﬁer is right exactly when the second one is wrong, so one of these

two must be at least 50%.

366 CHAPTER 11. MACHINE LEARNING

0.42 + 0.65 + 0.92

Figure 11.7: The ﬁnal classiﬁer is a weighted ensemble that correctly classiﬁes

all points, despite errors in each component classiﬁer which are highlighted in

red.

decision trees, each with exactly one node. The weights assigned by AdaBoost

are not uniform, but not so crazily skewed in this particular instance that they

behave diﬀerent than a majority classiﬁer. Observe the non-linear decision

boundary, resulting from the discrete nature of thresholded tests/decision trees.

Boosting is particularly valuable when applied to decision trees as the el-

ementary classiﬁers. The popular gradient boosted decision trees (GBDT) ap-

proach typically starts with a universe of small trees, with perhaps four to ten

nodes each. Such trees each encode a simple-enough logic that they do not

overﬁt the data. The relative weights assigned to each of these trees follows

from a training procedure, which tries to ﬁt the errors from the previous rounds

(residuals) and increases the weights of the trees that correctly classiﬁed the

harder examples.

Boosting works hard to classify every training instance correctly, meaning

it works particularly hard to classify the most diﬃcult instances. There is an

adage that “hard cases make bad law,” suggesting that diﬃcult-to-decide cases

make poor precedents for subsequent analysis. This is an important argument

against boosting, because the method would seem prone to overﬁtting, although

it generally performs well in practice.

The danger of overﬁtting is particularly severe when the training data is

not a perfect gold standard. Human class annotations are often subjective and

inconsistent, leading boosting to amplify the noise at the expense of the signal.

The best boosting algorithms will deal with overﬁtting though regularization.

The goal will be to minimize the number of non-zero coeﬃcients, and avoid

large coeﬃcients that place too much faith in any one classiﬁer in the ensemble.

Take-Home Lesson: Boosting can take advantage of weak classiﬁers in an ef-

fective way. However, it can behave in particularly pathological ways when a

fraction of your training examples are incorrectly annotated.

11.4 Support Vector Machines

Support vector machines (SVMs) are an important way of building non-linear

classiﬁers. They can be viewed as a relative of logistic regression, which sought

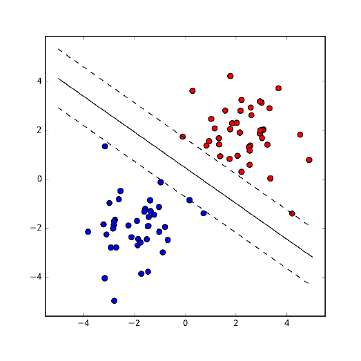
11.4. SUPPORT VECTOR MACHINES 367

Figure 11.8: SVMs seek to separate the two classes by the largest margin,

creating a channel around the separating line.

the line/plane lbest separating points with two classes of labels. Logistic re-

gression assigned a query point qits class label depending upon whether qlay

above or below this line l. Further, it used the logit function to transform the

distance from qto linto the probability that qbelongs in the identiﬁed class.

The optimization consideration in logistic regression involved minimizing

the sum of the misclassiﬁcation probabilities over all the points. By contrast,

support vector machines work by seeking maximum margin linear separators

between the two classes. Figure 11.8(left) shows red and blue points separated

by a line. This line seeks to maximize the distance dto the nearest training

point, the maximum margin of separation between red and blue. This a natural

objective in building a decision boundary between two classes, since the larger

the margin, the farther any of our training points are from being misclassiﬁed.

The maximum margin classiﬁer should be the most robust separator between

the two classes.

There are several properties that help deﬁne the maximum margin separator

between sets of red and blue points:

•The optimal line must be in the midpoint of the channel, a distance d

away from both the nearest red point and the nearest blue point. If this

were not so, we could shift the line over until it did bisect this channel,

thus enlarging the margin in the process.

•The actual separating channel is deﬁned by its contact with a small num-

ber of the red and blue points, where “a small number” means at most

twice the number of dimensions of the points, for well-behaved point sets

avoiding d+ 1 points lying on any d-dimensional face. This is diﬀerent

than with logistic regression, where all the points contribute to ﬁtting the

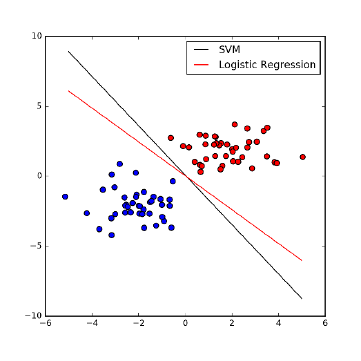
368 CHAPTER 11. MACHINE LEARNING

Figure 11.9: Both logistic regression and SVMs produce separating lines between

point sets, but optimized for diﬀerent criteria.

best position of the line. These contact points are the support vectors

deﬁning the channel.

•Points inside the convex hull of either the red or blue points have absolutely

no eﬀect on the maximum margin separator, since we need all same-colored

points to be on the same side of the boundary. We could delete these

interior points or move them around, but the maximum margin separator

will not change until one of the points leaves the hull and enters the

separating strip.

•It is not always possible to perfectly separate red from blue by using a

straight line. Imagine a blue point sitting somewhere within the convex

hull of the red points. There is no way to carve this blue point away from

the red using only a line.

Logistic regression and support vector machines both produce separating

lines between point sets. These are optimized for diﬀerent criteria, and hence

can be diﬀerent, as shown in Figure 11.9. Logistic regression seeks the separator

which maximizes the total conﬁdence in our classiﬁcation summed over all the

points, while the wide margin separator of SVM does the best it can with

the closest points between the sets. Both methods generally produce similar

classiﬁers.

11.4. SUPPORT VECTOR MACHINES 369

11.4.1 Linear SVMs

These properties deﬁne the optimization of linear support vector machines. The

separating line/plane, like any other line/plane, can be written as

w·x−b= 0

for a vector of coeﬃcients wdotted with a vector of input variables x. The

channel separating the two classes will be deﬁned by two lines parallel to this

and equidistant on both sides, namely w·x−b= 1 and w·x−b= 1.

The actual geometric separation between the lines depends upon w, namely

2/||w||. For intuition, think about the slope in two dimensions: these lines will

be distance 2 apart for horizontal lines but negligibly far apart if they are nearly

vertical. This separating channel must be devoid of points, and indeed separate

red from blue points. Thus we must add constraints. For every red (class 1)

point xi, we insist that

w·x−b≥1,

while every blue (class −1) point ximust satisfy

w·x−b≤ −1,

If we let yi∈[−1,1] denote the class of xi, then these can be combined to yield

the optimization problem

max ||w||,where yi(w·xi−b)≥1 for all 1 ≤i≤n.

This can be solved using techniques akin to linear programming. Note that

the channel must be deﬁned by the points making contact with its boundaries.

These vectors “support” the channel, which is where the provocative name sup-

port vector machines comes from. The optimization algorithm of eﬃcient solvers

like LibLinear and LibSVM search through the relevant small subsets of support

vectors which potentially deﬁne separating channels to ﬁnd the widest one.

Note that there are more general optimization criteria for SVMs, which

seek the line that deﬁnes a wide channel and penalizes (but does not forbid)

points that are misclassiﬁed. This sort of dual-objective function (make the

channel wide while misclassifying few points) can be thought of as a form of

regularization, with a constant to trade oﬀ between the two objectives. Gradient

descent search can be used to solve these general problems.

11.4.2 Non-linear SVMs

SVMs deﬁne a hyperplane which separates the points from the two classes.

Planes are lines in higher dimensions, readily deﬁned using linear algebra. So

how can this linear method produce a non-linear decision boundary?

For a given point set to have a maximum margin separator, the two colors

must ﬁrst be linearly separable. But as we have seen this is not always the case.

Consider the pathological case of Figure 11.10 (left), where the cluster of red

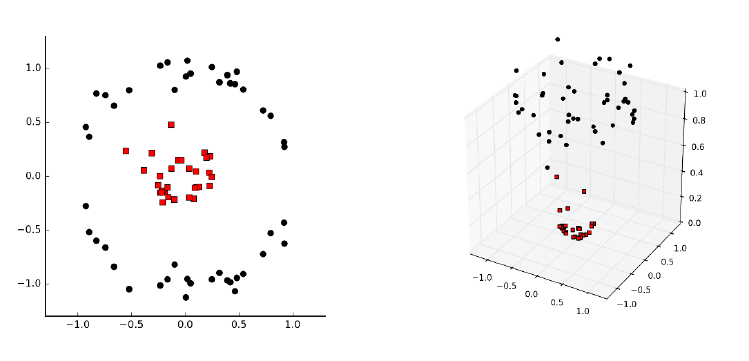
370 CHAPTER 11. MACHINE LEARNING

Figure 11.10: Projecting points to higher dimensions can make them linearly

separable.

points is surrounded by a ring-shaped cluster of black points. How might such

a thing arise? Suppose we partition travel destinations into day trips or long

trips, depending upon whether they are close enough to our given location. The

longitude and latitudes of each possible destination will yield data with exactly

the same structure as Figure 11.10 (left).

The key idea is that we can project our d-dimensional points into a higher-

dimensional space, where there will be more possibilities to separate them. For

nred/blue points along a line in one dimension, there are only n−1 potentially

interesting ways to separate them, speciﬁcally with a cut between the ith and

(i+ 1)st points for 1 ≤i<n. But this blows up to approximately n

2ways

as we move to two dimensions, because there is more freedom to partition as

we increase dimensionality. Figure 11.10 (right) demonstrates how lifting points

through the transformation (x, y)→(x, y, x2+y2) puts them on a paraboloid,

and makes it possible to linearly separate classes which were inseparable in the

original space.

If we jack the dimensionality of any two-class point set high enough, there

will always be a separating line between the red and black points. Indeed, if

we put the npoints in ndimensions through a reasonable transform, they will

always be linearly separable in a very simple way. For intuition, think about the

special case of two points (one red and one blue) in two dimensions: obviously

there must be a line separating them. Projecting this separating plane down to

the original space results in some form of curved decision boundary, and hence

the non-linearity of SVMs depends upon exactly how the input was projected

to a higher-dimensional space.

One nice way to turn npoints in ddimensions into npoints in ndimensions

11.4. SUPPORT VECTOR MACHINES 371

might be to represent each point by its distances to all ninput points. In

particular, for each point piwe can create a vector visuch that vij =dist(i, j),

the distance from pito pj. The vector of such distances should serve as a

powerful set of features for classifying any new point q, since the distances to

members of the actual class should be small compared to those of the other

class.

This feature space is indeed powerful, and one can readily imagine writing

a function to turn the original n×dfeature matrix into a new n×nfeature

matrix for classiﬁcation. The problem here is space, because the number of

input points nis usually vastly larger than the dimension dthat they sit in.

Such a transform would be feasible to construct only for fairly small point sets,

say n≤1000. Further, working with such high-dimensional points should be

very expensive, since every single distance evaluation now takes time linear in

the number of points n, instead of the data dimension d. But something amazing

happens. . .

11.4.3 Kernels

The magic of SVMs is that this distance-feature matrix need not actually be

computed explicitly. In fact, the optimization inherent in ﬁnding the maximum

margin separator only performs the dot products of points with other points

and vectors. Thus we could imagine performing the distance expansion on the

ﬂy, when the associated point is being used in a comparison. Hence there would

be no need to precompute the distance matrix: we can expand the points from

dto ndimensions as needed, do the distance computation, and then throw the

expansions away.

This would work to eliminate the space bottleneck, but we would still pay

a heavy price in computation time. The really amazing thing is that there are

functions, called kernels, which return what is essentially the distance compu-

tation on the larger vector without ever constructing the larger vector. Doing

SVMs with kernels gives us the power of ﬁnding the best separator over a variety

of non-linear functions without much additional cost. The mathematics moves

beyond the scope of what I’d like to cover here, but:

Take-Home Lesson: Kernel functions are what gives SVMs their power to sep-

arate project d-dimensional points to ndimensions, so they can be separated

without spending more that dsteps on the computation.

Support vector machines require experience to use eﬀectively. There are

many diﬀerent kernel functions available, beyond the distance kernel I presented

here. Each have advantages on certain data sets, so there is a need to futz with

the options of tools like LibSVM to get the best performance. They work best

on medium-sized data sets, with thousands but not millions of points.

372 CHAPTER 11. MACHINE LEARNING

11.5 Degrees of Supervision

There is a natural distinction between machine learning approaches based on

the degree and nature of the supervision employed in amassing training and

evaluation data. Like any taxonomy, there is some fuzziness around the margins,

making it an unsatisfying exercise to try to label exactly what a given system

is and is not doing. However, like any good taxonomy it gives you a frame to

guide your thinking, and suggests approaches that might lead to better results.

The methods discussed so far in this chapter assume that we are given train-

ing data with class labels or target variables, leaving our task as one to train

classiﬁer or regression systems. But getting to the point of having labeled data

is usually the hard part. Machine learning algorithms generally perform better

the more data you can give them, but annotation is often diﬃcult and expen-

sive. Modulating the degree of supervision provides a way to raise the volume

so your classiﬁer can hear what is going on.

11.5.1 Supervised Learning

Supervised learning is the bread-and-butter paradigm for classiﬁcation and re-

gression problems. We are given vectors of features xi, each with an associated

class label or target value yi. The annotations yirepresent the supervision,

typically derived from some manual process which limits the potential amount

of training data.

In certain problems, the annotations of the training data come from obser-

vations in interacting with the world, or at least a simulation of it. Google’s

AlphaGo program was the ﬁrst computer program to beat the world champion

at Go. A position evaluation function is a scoring function that takes a board

position and computes a number estimating how strong it is. AlphaGo’s posi-

tion evaluation function was trained on all published games by human masters,

but much more data was needed. The solution was, essentially, to build a po-

sition evaluator by training against itself. Position evaluation is substantially

enhanced by search – looking several moves ahead before calling the evaluation

function on each leaf. Trying to predict the post-search score without the search

produces a stronger evaluation function. And generating this training data is

just a result of computation: the program playing against itself.

This idea of learning from the environment is called reinforcement learn-

ing. It cannot be applied everywhere, but it is always worth looking for clever

approaches to generate mechanically-annotated training data.

11.5.2 Unsupervised Learning

Unsupervised methods try to ﬁnd structure in the data, by providing labels

(clusters) or values (rankings) without any trusted standard. They are best

used for exploration, for making sense of a data set otherwise untouched by

human hands.

11.5. DEGREES OF SUPERVISION 373

The mother of all unsupervised learning methods is clustering, which we

discussed extensively in Section 10.5. Note that clustering can be used to provide

training data for classiﬁcation even in the absence of labels. If we presume that

the clusters found represent genuine phenomenon, we can then use the cluster

ID as a label for all the elements in the given cluster. These can now serve as

training data to build a classiﬁer to predict the cluster ID. Predicting cluster

IDs can be useful even if these concepts do not have a name associated with

them, providing a reasonable label for any input record q.

Topic Modeling

Another important class of unsupervised methods is topic modeling, typically

associated with documents drawn over a given vocabulary. Documents are writ-

ten about topics, usually a mix of topics. This book is partitioned into chapters,

each of which is about a diﬀerent topic, but it also touches on subjects ranging

from baseball to weddings. But what is a topic? Typically each topic is associ-

ated with a particular set of vocabulary words. Articles about baseball mention

hits,pitchers,strikeouts,bases, and slugging.Married,engaged,groom,bride,

love, and celebrate are words associated with the topic of wedding. Certain

words can represent multiple topics. For example love is also associated with

tennis, and hits with gangsters.

Once one has a set of topics (t1, . . . , tk) and the words which deﬁne them, the

problem of identifying the speciﬁc topics associated with any given document

dseems fairly straightforward. We count the number of word occurrences of d

in common with ti, and report success whenever this is high enough. If given

a set of documents manually labeled with topics, it seems reasonable to count

the frequency of each word over every topic class, to construct the list of words

most strongly associated with each topic.

But that is all very heavily supervised. Topic modeling is an unsupervised

approach that infers the topics and the word lists from scratch, just given un-

labeled documents. We can represent these texts by a w×dfrequency matrix

F, where wis the vocabulary size and dthe number of documents and F[i, j]

reﬂects how many times work iappears in document j. Suppose we factor F

into F≈W×D, where Wis a w×tword–topic matrix and Dis a t×dtopic–

document matrix. The largest entries in the ith row of Wreﬂect the topics

word wiis most strongly linked to, while the largest entries in the jth column

of Dreﬂect the topics best represented in document dj.

Such a factorization would represent a completely unsupervised form of

learning, with the exception of specifying the desired number of topics t. It

seems a messy process to construct such an approximate factorization, but there

are a variety of approaches to try to do so. Perhaps the most popular method

for topic modeling is an approach called latent Dirichlet allocation (LDA), which

produces a similar set of matrices Wand D, although not strictly produced by

factorization.

Figure 11.5.2 presents a toy example of LDA in action. Three excellent

books were analyzed, with the goal of seeing how they were organized among

374 CHAPTER 11. MACHINE LEARNING

Figure 11.11: Illustration of topic modeling (LDA). The three books are rep-

resented by their distribution of topics (left). Each topic is represented by a

list of words, with the weight a measure of its importance to the topic (right).

Documents are made up of words: the magic of LDA is that it simultaneously

infers the topics and word assignments in an unsupervised manner.

three latent topics. The LDA algorithm deﬁned these topics in an unsupervised

way, by assigning each word weights for how much it contributes to each topic.

The results here are generally eﬀective: the concept of each topic emerges from

its most important words (on the right). And the word distribution within each

book can then be readily partitioned among the three latent topics (on the left).

Note that this factorization mindset can be applied beyond documents, to

any feature matrix F. The matrix decomposition approaches we have previously

discussed, like singular value decomposition and principle components analysis,

are equally unsupervised, inducing structure inherent in the data sets without

our lead in ﬁnding it.

11.5.3 Semi-supervised Learning

The gap between supervised and unsupervised learning is ﬁlled by semi-supervised

learning methods, which amplify small amounts of labeled training data into

more. Turning small numbers of examples into larger numbers is often called

bootstrapping, from the notion of “pulling yourself up from your bootstraps.”

Semi-supervised approaches personify the cunning which needs be deployed to

build substantive training sets.

We assume that we are given a small number of labeled examples as (xi, yi)

pairs, backed by a large number of inputs xjof unknown label. Instead of

directly building our model from the training set, we can use it to classify the

mass of unlabeled instances. Perhaps we use a nearest neighbor approach to

classify these unknowns, or any of the other approaches we have discussed here.

But once we classify them, we assume the labels are correct and retrain on the

larger set.

Such approaches beneﬁt strongly from having a reliable evaluation set. We

need to establish that the model trained on the bootstrapped examples performs

better than one trained on what we started with. Adding billions of training

examples is worthless if the labels are garbage.

There are other ways to generate training data without annotations. Often

it seems easier to ﬁnd positive examples than negative examples. Consider the

Text T1T2T3

The Bible 0.73 0.01 0.26

Data Sci Manual 0.05 0.83 0.12

Who’s Bigger? 0.08 0.23 0.69

T1T2T3

Term Wei ght Term Weight Term Weight

God 0.028 CPU 0.021 past 0.013

Jesus 0.012 computer 0.010 history 0.011

pray 0.006 data 0.005 old 0.006

Israel 0.003 program 0.003 war 0.004

Moses 0.001 math 0.002 book 0.002

11.5. DEGREES OF SUPERVISION 375

problem of training a grammar corrector, meaning it distinguishes proper bits

of writing from ill-formed stuﬀ. It is easy to get a hold of large amounts of

proper examples of English: whatever gets published in books and newspapers

generally qualiﬁes as good. But it seems harder to get a hold of a large corpora

of incorrect writing. Still, we can observe that randomly adding, deleting, or

substituting arbitrary words to any text almost always makes it worse.4By

labeling all published text as correct and all random perturbations as incorrect,

we can create as large a training set as we desire without hiring someone to

annotate it.

How can we evaluate such a classiﬁer? It is usually feasible to get enough

genuine annotated data for evaluation purposes, because what we need for eval-

uation is typically much smaller than that for training. We can also use our

classiﬁer to suggest what to annotate. The most valuable examples for the anno-

tator to vet are those that our classiﬁer makes mistakes on: published sentences

marked incorrect or random mutations that pass the test are worth passing to

a human judge.

11.5.4 Feature Engineering

Feature engineering is the ﬁne art of applying domain knowledge to make it

easier for machine learning algorithms to do their intended job. In the context

of our taxonomy here, feature engineering can be considered an important part

of supervised learning, where the supervision applies to the feature vectors xi

instead of the associated target annotations yi.

It is important to ensure that features are presented to models in a way that

the model can properly use them. Incorporating application-speciﬁc knowledge

into the data instead of learning it sounds like cheating, to amateurs. But the

pros understand that there are things that cannot be learned easily, and hence

are better explicitly put into the feature set.

Consider a model to price art at auctions. Auction houses make their money

by charging a commission to the winning bidder, on top of what they pay

the owner. Diﬀerent houses charge diﬀerent rates, but they can amount to a

substantial bill. Since the total cost to the winner is split between purchase

price and commission, higher commissions may well lower the purchase price,

by cutting into what the bidder can aﬀord to pay the owner.

So how can you represent the commission price in an art pricing model? I can

think of at least three diﬀerent approaches, some of which can have disastrous

outcomes:

•Specify the commission percentage as a feature: Representing the house

cut (say 10%) as a column in the feature set might not be usable in a

linear model. The hit taken by the bidder is the product of the tax rate

and the ﬁnal price. It has a multiplicative eﬀect, not an additive eﬀect,

4Give it a try someplace on this page. Pick a word at random and replace it by red. Then

again with the. And ﬁnally with defenestrate. Is my original text clearly better written than

what you get after such a change?

376 CHAPTER 11. MACHINE LEARNING

and hence cannot be meaningfully exploited if the price range for the art

spans from $100 to $1,000,000.

•Include the actual commission paid as a feature: Cheater. . . If you include

the commission ultimately paid as a feature, you pollute the features with

data not known at the time of the auction. Indeed, if all paintings were

faced with a 10% tax, and the tax paid was a feature, a perfectly accurate

(and completely useless) model would predict the price as ten times the

tax paid!

•Set the regression target variable to be the total amount paid: Since the

house commission rates and add-on fees are known to the buyer before

they make the bid, the right target variable should be the total amount

paid. Any given prediction of the total purchase price can be broken down

later into the purchase price, commission, and taxes according to the rules

of the house.

Feature engineering can be thought of as a domain-dependent version of data

cleaning, so the techniques discussed in Section 3.3 all apply here. The most

important of them will be reviewed here in context, now that we have ﬁnally

reached the point of actually building data-driven models:

•Z-scores and normalization: Normally-distributed values over compara-

ble numerical ranges make the best features, in general. To make the

ranges comparable, turn the values into Z-scores, by subtracting oﬀ the

mean and dividing by the standard deviation, Z= (x−µ)/σ. To make a

power law variable more normal, replace xin the feature set with log x.

•Impute missing values: Make sure there are no missing values in your

data and, if so, replace them by a meaningful guess or estimate. Recording

that someone’s weight equals −1 is an eﬀortless way to mess up any model.

The simplest imputation method replaces each missing value by the mean

of the given column, and generally suﬃces, but stronger methods train

a model to predict the missing value based on the other variables in the

record. Review Section 3.3.3 for details.

•Dimension reduction: Recall that regularization is a way of forcing mod-

els to discard irrelevant features to prevent overﬁtting. It is even more

eﬀective to eliminate irrelevant features before ﬁtting your models, by re-

moving them from the data set. When is a feature xlikely irrelevant for

your model? Poor correlation with the target variable y, plus the lack of

any qualitative reason you can give for why xmight impact yare both

excellent indicators.

Dimension reduction techniques like singular-value decomposition are ex-

cellent ways to reduce large feature vectors to more powerful and concise

representations. The beneﬁts include faster training times, less overﬁtting,

and noise reduction from observations.

11.6. DEEP LEARNING 377

•Explicit incorporation of non-linear combinations: Certain products or

ratios of feature variables have natural interpretations in context. Area

or volume are products of length, width, and height, yet cannot be part

of any linear model unless explicitly made a column in the feature ma-

trix. Aggregate totals, like career points scored in sports or total dollars

earned in salary, are usually incomparable between items of diﬀerent age

or duration. But converting totals into rates (like points per game played

or dollars per hour) usually make more meaningful features.

Deﬁning these products and ratios requires domain-speciﬁc information,

and careful thought during the feature engineering process. You are much

more likely to know the right combinations than your non-linear classiﬁer

is to ﬁnd it on its own.

Don’t be shy here. The diﬀerence between a good model and a bad model

usually comes down to quality of its feature engineering. Advanced machine

learning algorithms are glamorous, but it is the data preparation that produces

the results.

11.6 Deep Learning

The machine learning algorithms we have studied here do not really scale well to

huge data sets, for several reasons. Models like linear regression generally have

relatively few parameters, say one coeﬃcient per column, and hence cannot

really beneﬁt from enormous numbers of training examples. If the data has a

good linear ﬁt, you will be able to ﬁnd it with a small data set. And if doesn’t,

well, you didn’t really want to ﬁnd it anyway.

Deep learning is an incredibly exciting recent development in machine learn-

ing. It is based on neural networks, a popular approach from the 1980s which

then fell substantially out of style. But over the past ﬁve years something hap-

pened, and suddenly multi-layer (deep) networks began wildly out-performing

traditional approaches on classical problems in computer vision and natural

language processing.

Exactly why this happened remains somewhat of a mystery. It doesn’t seem

that there was a fundamental algorithmic breakthrough so much as that data

volume and computational speeds crossed a threshold where the ability to ex-

ploit enormous amounts of training data overcame methods more eﬀective at

dealing with a scarce resource. But infrastructure is rapidly developing to lever-

age this advantage: new open source software frameworks like Google’s Tensor-

Flow make it easy to specify network architectures to special-purpose processors

designed to speed training by orders of magnitude.

What distinguishes deep learning from other approaches is that it generally

avoids feature engineering. Each layer in a neural network generally accepts

as its input the output of its previous layer, yielding progressively higher-level

features as we move up towards the top of the network. This serves to deﬁne

a hierarchy of understanding from the raw input to the ﬁnal result, and indeed

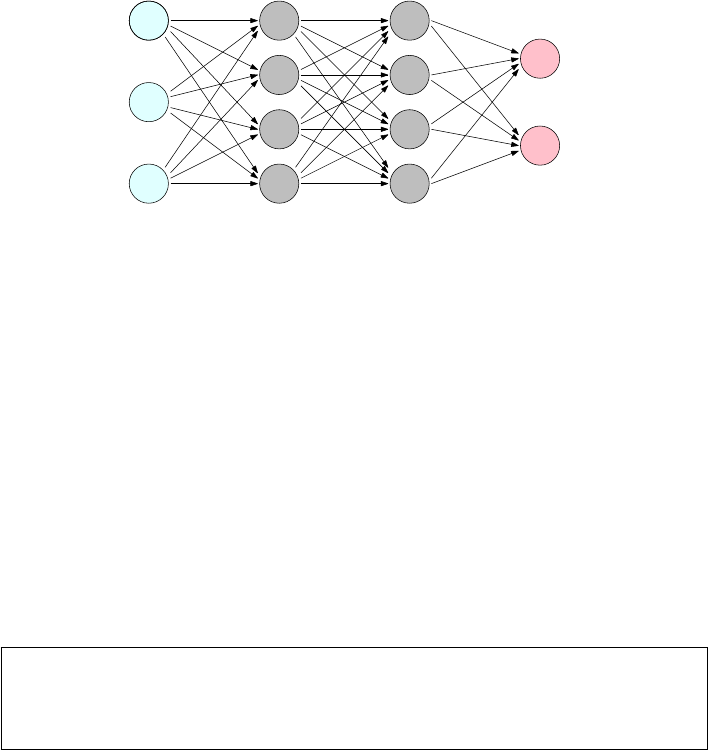
378 CHAPTER 11. MACHINE LEARNING

layer 1 layer 2 layer 3 layer 4

Figure 11.12: Deep learning networks have hidden layers of parameters.

the penultimate level of a network designed for one task often provides useful

high-level features for related tasks.

Why are neural networks so successful? Nobody really knows. There are

indications that for many tasks the full weight of these networks are not really

needed; that what they are doing will eventually be done using less opaque

methods. Neural networks seem to work by overﬁtting, ﬁnding a way to use

millions of examples to ﬁt millions of parameters. Yet they generally manage

to avoid the worst behavior of overﬁtting, perhaps by using less precise ways to

encode knowledge. A system explicitly memorizing long strings of text to split

out on demand will seem brittle and overﬁt, while one representing such phrases

in a looser way is liable to be more ﬂexible and generalizable.

This is a ﬁeld which is advancing rapidly, enough so that I want to keep

my treatment strictly at the idea level. What are the key properties of these

networks? Why have they suddenly become so successful?

Take-Home Lesson: Deep learning is a very exciting technology that has legs,

although it is best suited for domains with enormous amounts of training data.

Thus most data science models will continue to be built using the traditional

classiﬁcation and regression algorithms that we detailed earlier in this chapter.

11.6.1 Networks and Depth

Figure 11.12 illustrates the architecture of a deep learning network. Each node

xrepresents a computational unit, which computes the value of a given sim-

ple function f(x) over all inputs to it. For now, perhaps view it as a simple

adder that adds all the inputs, then outputs the sum. Each directed edge (x, y)

connects the output of node xto the input of a node yhigher in the network.

Further, each such edge has an associated multiplier coeﬃcient wx,y . The value

actually passed to yis the wx,y ·f(x), meaning node ycomputes a weighted

sum of its inputs.

The left column of Figure 11.12 represents a set of input variables, the values

of which change whenever we ask the network to make a prediction. Think of this

11.6. DEEP LEARNING 379

as the interface to the network. Links from here to the next level propagate out

this input value to all the nodes which will compute with it. On the right side are

one or more output variables, presenting the ﬁnal results of this computation.

Between these input and output layers sit hidden layers of nodes. Given the

weights of all the coeﬃcients, the network structure, and the values of input

variables, the computation is straightforward: compute the values of the lowest

level in the network, propagate them forward, and repeat from the next level

until you hit the top.

Learning the network means setting the weights of the coeﬃcient parameters

wx,y. The more edges there are, the more parameters we have to learn. In prin-

ciple, learning means analyzing a training corpus of (xi, yi) pairs, and adjusting

weights of the edge parameters so that the output nodes generate something

close to yiwhen fed input xi.

Network Depth

The depth of the network should, in some sense, correspond to the conceptual

hierarchy associated with the objects being modeled. The image we should have

is the input being successively transformed, ﬁltered, boiled down, and banged

into better and better shape as we move up the network. Generally speaking,

the number of nodes should progressively decrease as we move up to higher

layers.

We can think of each layer as providing a level of abstraction. Consider a

classiﬁcation problem over images, perhaps deciding whether the image contains

a picture of a cat or not. Thinking in terms of successive levels of abstraction, im-

ages can be said to be made from pixels, neighborhood patches, edges, textures,

regions, simple objects, compound objects, and scenes. This is an argument that

at least eight levels of abstraction could potentially be recognizable and usable

by networks on images. Similar hierarchies exist in document understanding

(characters, words, phrases, sentences, paragraphs, sections, documents) and

any other artifacts of similar complexity.

Indeed, deep learning networks trained for speciﬁc tasks can produce valu-

able general-purpose features, by exposing the outputs of lower levels in the

network as powerful features for conventional classiﬁers. For example, Imagenet

is a popular network for object recognition from images. One high-level layer of

1000 nodes measures the conﬁdence that the image contains objects of each of

1000 diﬀerent types. The patterns of what objects light up to what degree are

generally useful for other tasks, such as measuring image similarity.

We do not impose any real vision of what each of these levels should repre-

sent, only to connect them so that the potential to recognize such complexity

exists. Neighborhood patches are functions of small groups of connected pixels,

while regions will be made up of small numbers of connected patches. Some

sense of what we are trying to recognize goes into designing this topology, but

the network does what it feels it has to do during training to minimize training

error, or loss.

The disadvantages of deeper networks is that they become harder to train

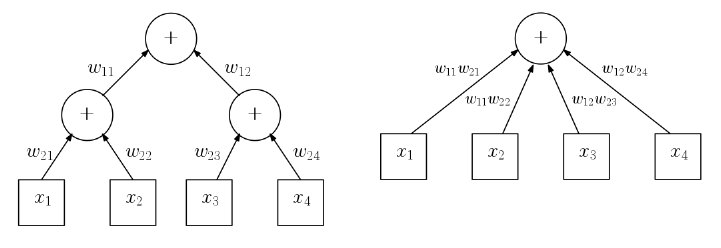
380 CHAPTER 11. MACHINE LEARNING

Figure 11.13: Addition networks do not beneﬁt from depth. The two layer

network (left) computes exactly the function as the equivalent one layer network

(right).

the larger and deeper they get. Each new layer adds a fresh set of edge-weight

parameters, increasing the risks of overﬁtting. Properly ascribing the eﬀect of

prediction errors to edge-weights becomes increasingly diﬃcult, as the number

of intervening layers grows between the edge and the observed result. However,

networks with over ten layers and millions of parameters have been success-

fully trained and, generally speaking, recognition performance increases with

the complexity of the network.

Networks also get more computationally expensive to make predictions as

the depth increases, since the computation takes time linear in the number of

edges in the network. This is not terrible, especially since all the nodes on any

given level can be evaluated in parallel on multiple cores to reduce the prediction

time. Training time is where the real computational bottlenecks generally exist.

Non-linearity

The image of recognizing increasing levels of abstraction up the hidden layers

of a network is certainly a compelling one. It is fair to ask if it is real, however.

Do extra layers in a network really give us additional computational power to

do things we can’t with less?

The example of Figure 11.13 seems to argue the converse. It shows addition

networks built with two and three layers of nodes, respectively, but both com-

pute exactly the same function on all inputs. This suggests that the extra layer

was unnecessary, except perhaps to reduce the engineering constraint of node

degree, the number of edges entering as input.

What it really shows is that we need more complicated, non-linear node ac-

tivation functions φ(v) to take advantage of depth. Non-linear functions cannot

be composed in the same way that addition can be composed to yield addition.

This nonlinear activation function φ(vi) typically operates on a weighted sum

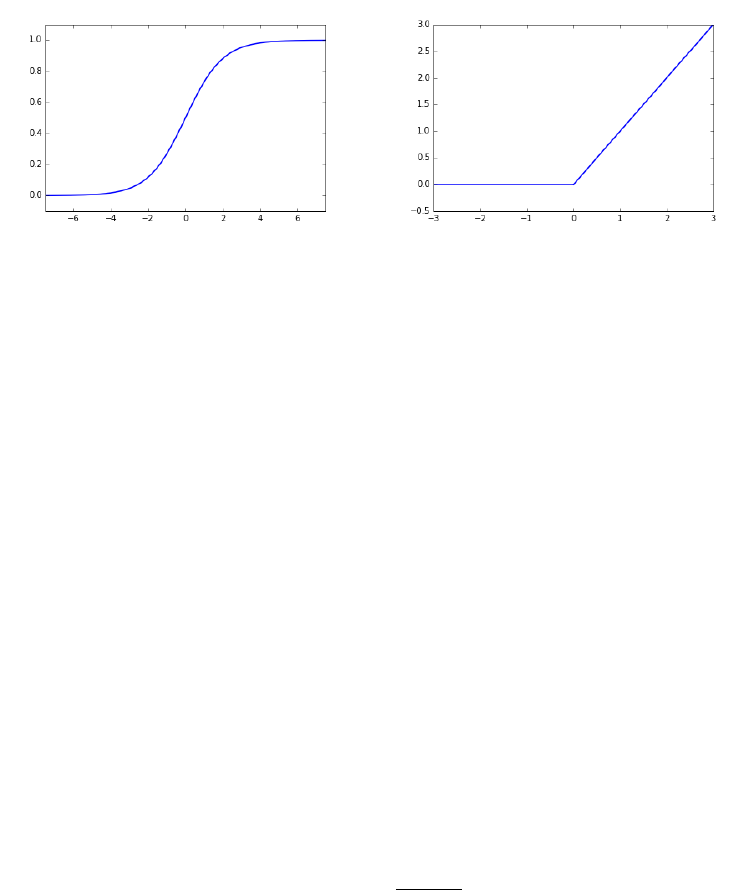
11.6. DEEP LEARNING 381

Figure 11.14: The logistic (left) and ReLU (right) activation functions for nodes

in neural networks.

of the inputs x, where

vi=β+X

wixi.

Here βis a constant for the given node, perhaps to be learned in training. It

is called the bias of the node because it deﬁnes the activation in the absence of

other inputs.

That computing the output values of layer linvolves applying the activation

function φto weighted sums of the values from layer l−1 has an important

implication on performance. In particular, neural network evaluation basically

just involves one matrix multiplication per level, where the weighted sums are

obtained by multiplying an |Vl|×|Vl−1|weight matrix Wby an |Vl−1|×1 output

vector Vl−1. Each element of the resulting |Vl| × 1 vector is then hit with the

φfunction to prepare the output values for that layer. Fast libraries for matrix

multiplication can perform the heart of this evaluation very eﬃciently.

A suite of interesting, non-linear activation functions have been deployed in

building networks. Two of the most prominent, shown in Figure 11.14, include:

•Logit: We have previously encountered the logistic function or logit, in

our discussion of logistic regression for classiﬁcation. Here

f(x) = 1

1 + e−x

This unit has the property that the output is constrained to the range

[0,1], where f(0) = 1/2. Further, the function is diﬀerentiable, so back-

propagation can be used to train the resulting network.

•Rectiﬁed linear units (ReLU): A rectiﬁer or diode in an electrical circuit

lets current ﬂow in only one direction. Its response function f(x) is linear

when xis positive, but zero when xis negative, as shown in Figure 11.14

382 CHAPTER 11. MACHINE LEARNING

(right).

f(x) = xwhen x≥0

= 0 when x < 0

This kink at x= 0 is enough to remove the linearity from the function,

and provides a natural way to turn oﬀ the unit by driving it negative. The

ReLU function remains diﬀerentiable, but has quite a diﬀerent response

than the logit, increasing monotonically and being unbounded on one side.

I am not really aware of a theory explaining why certain functions should

perform better in certain contexts. Speciﬁc activation functions presumably

became popular because they worked well in experiments, with the choice of unit

being something you can change if you don’t feel your network is performing as

well as it should.

Generally speaking, adding one hidden layer adds considerable power to the

network, with additional layers suﬀering from diminishing returns. The theory

shows that networks without any hidden layers have the power to recognize

linearly separable classes, but we turned to neural nets to build more powerful

classiﬁers.

Take-Home Lesson: Start with one hidden layer with a number of nodes be-

tween the size of the input and output layers, so they are forced to learn

compressed representations that make for powerful features.

11.6.2 Backpropagation

Backpropagation is the primary training procedure for neural networks, which

achieves very impressive results by ﬁtting large numbers of parameters incre-

mentally on large training sets. It is quite reminiscent of stochastic gradient

descent, which we introduced in Section 9.4.

Our basic problem is this. We are given a neural network with preliminary

values for each parameter wl

ij , meaning the multiplier that the output of node

vl−1

jgets before being added to node vl

i. We are also given a training set

consisting of ninput vector-output value pairs (xa, ya), where 1 ≤a≤n. In

our network model, the vector xirepresents the values to be assigned to the

input layer v1, and yithe desired response from the output layer vl. Evaluating

the current network on xiwill result in an output vector vl. The error Elof the

network at layer lcan be measured, perhaps as

El=||yi−vl||2=X

(φ(β+X

ij vl−1

ij )−yij )2

We would like to improve the values of the weight coeﬃcients wl

ij so they

better predict yiand minimize El. This equation above deﬁnes the loss Elas

a function of the weight coeﬃcients, since the input values from the previous

11.6. DEEP LEARNING 383

Source 1 2 3 4 5

Apple iPhone iPad apple MacBook iPod

apple apples blackberry Apple iphone fruit

car cars vehicle automobile truck Car

chess Chess backgammon mahjong checkers tournaments

dentist dentists dental orthodontist dentistry Dentist

dog dogs puppy pet cat puppies

Mexico Puerto Peru Guatemala Colombia Argentina

red blue yellow purple orange pink

running run ran runs runing start

write writing read written tell Write

Figure 11.15: Nearest neighbors in word embeddings capture terms with similar

roles and meaning.

layer vl−1is ﬁxed. As in stochastic gradient descent, the current value of the

ij deﬁnes a point pon this error surface, and the derivative of Elat this point

deﬁnes the direction of steepest descent reducing the errors. Walking down a

distance din this direction deﬁned by the current step size or learning rate yields

updated values of the coeﬃcients, whose vldoes a better job predicting yafrom

xa.

But this only changes coeﬃcients in the output layer. To move down to the

previous layer, note that the previous evaluation of the network provided an

output for each of these nodes as a function of the input. To repeat the same

training procedure, we need a target value for each node in layer l−1 to play

the role of yafrom our training example. Given yaand the new weights to

compute vl, we can compute values for the outputs of these layers which would

perfectly predict yi. With these targets, we can modify the coeﬃcient weights

at this level, and keep propagating backwards until we hit the bottom of the

network, at the input layer.

11.6.3 Word and Graph Embeddings

There is one particular unsupervised application of deep learning technology

that I have found readily applicable to several problems of interest. This has

the extra beneﬁt of being accessible to a broader audience with no familiarity

with neural networks. Word embeddings are distributed representations of what

words actually mean or do.

Each word is denoted by a single point in, say, 100-dimensional space, so that

words which play similar roles tend to be represented by nearby points. Figure

11.15 presents the ﬁve nearest neighbors of several characteristic English words

according to the GloVe word embedding [PSM14], and I trust you will agree

that they capture an amazing amount of each word’s meaning by association.

The primary value of word embeddings is as general features to apply in

384 CHAPTER 11. MACHINE LEARNING

speciﬁc machine learning applications. Let’s reconsider the problem of distin-

guishing spam from meaningful email messages. In the traditional bag of words

representation, each message might be represented as a sparse vector b, where

b[i] might report the number of times vocabulary word wiappears in the mes-

sage. A reasonable vocabulary size vfor English is 100,000 words, turning binto

a ghastly 100,000-dimensional representation that does not capture the similar-

ity between related terms. Word vector representations prove much less brittle,

because of the lower dimensionality.

We have seen how algorithms like singular value decomposition (SVD) or

principle components analysis can be used to compress an n×mfeature matrix

Mto an n×kmatrix M0(where km) in such a way that M0retains most

of the information of M. Similarly, we can think of word embeddings as a

compression of a v×tword–text incidence matrix M, where tis the number of

documents in corpus, and M[i, j] measures the relevance of word ito document

j. Compressing this matrix to v×kwould yield a form of word embedding.

That said, neural networks are the most popular approach to building word

embeddings. Imagine a network where the input layer accepts the current em-

beddings of (say) ﬁve words, w1, . . . , w5, corresponding to a particular ﬁve word

phrase from our document training corps. The network’s task might be to pre-

dict the embedding of the middle word w3from the embeddings of the ﬂanking

four words. Through backpropagation, we can adjust the weights of the nodes

in the network so it improves the accuracy on this particular example. The key

here is that we continue the backpropagation past the lowest level, so that we

modify the actual input parameters! These parameters represented the embed-

dings for the words in the given phrase, so this step improves the embedding

for the prediction task. Repeating this on a large number of training examples

yields a meaningful embedding for the entire vocabulary.

A major reason for the popularity of word embeddings is word2vec, a ter-

riﬁc implementation of this algorithm, which can rapidly train embeddings for

hundreds of thousands of vocabulary words on gigabytes of text in a totally un-

supervised manner. The most important parameter you must set is the desired

number of dimensions d. If dis too small, the embedding does not have the

freedom to fully capture the meaning of the given symbol. If dis too large,

the representation becomes unwieldy and overﬁt. Generally speaking, the sweet

spot lies somewhere between 50 and 300 dimensions.

Graph Embeddings

Suppose we are given an n×npairwise similarity matrix Sdeﬁned over a

universe of nitems. We can construct the adjacency matrix of similarity graph G

by declaring an edge (x, y) whenever the similarity of xand yin Sis high enough.

This large matrix Gmight be compressed using singular value decomposition

(SVD) or principle components analysis (PCA), but this proves expensive on

large networks.

Programs like word2vec do an excellent job constructing representations from

sequences of symbols in a training corpus. The key to applying them in new

11.7. WAR STORY: THE NAME GAME 385

domains is mapping your particular data set to strings over an interesting vo-

cabulary. DeepWalk is an approach to building graph embeddings, point repre-

sentations for each vertex such that “similar” vertices are placed close together

in space.

Our vocabulary can be chosen to be the set of distinct vertex IDs, from 1 to

n. But what is the text that can represent the graph as a sequence of symbols?

We can construct random walks over the network, where we start from an

arbitrary vertex and repeatedly jump to a random neighbor. These walks can

be thought of as “sentences” over our vocabulary of vertex-words. The resulting

embeddings, after running word2vec on these random walks, prove very eﬀective

features in applications.

DeepWalk is an excellent illustration of how word embeddings can be used

to capture meaning from any large-scale corpus of sequences, irrespective of

whether they are drawn from a natural language. The same idea plays an

important role in the following war story.

11.7 War Story: The Name Game

My brother uses the name Thor Rabinowitz whenever he needs an alias for a

restaurant reservation or online form. To understand this war story, you ﬁrst

have to appreciate why this is very funny.

•Thor is the name of an ancient Norse god, and more recent super-hero

character. There are a small but not insigniﬁcant number of people in the

world named Thor, the majority of whom presumably are Norwegian.

•Rabinowitz is a Polish-Jewish surname, which means “son of the rabbi.”

There are a small but not insigniﬁcant number of people in the world

named Rabinowitz, essentially none of whom are Norwegian.

The upshot is that there has never been a person with that name, a fact

you can readily conﬁrm by Googling “Thor Rabinowitz”. Mentioning this name

should trigger cognitive dissonance in any listener, because the two names are

so culturally incompatible.

The specter of Thor Rabinowitz hangs over this tale. My colleague Yifan

Hu was trying to ﬁnd a way to prove that a user logging in from a suspicious

machine was really who they said they were. If the next login attempt to my

account suddenly comes from Nigeria after many years in New York, is it really

me or a bad guy trying to steal my account?

“The bad guy won’t know who your friends are,” Yifan observed. “What if

we challenge you to recognize the names of two friends from your email contact

list in a list of fake names. Only the real owner will know who they are.”

“How are you going to get the fake names?” I asked. “Maybe use the names

of other people who are not contacts of the owner?”

“No way,” said Yifan. “Customers will get upset if we show their names to

the bad guy. But we can just make up names by picking ﬁrst and last names

and sticking them together.”

386 CHAPTER 11. MACHINE LEARNING

“But Thor Rabinowitz wouldn’t fool anybody,” I countered, explaining the

need for cultural compatibility.

We needed a way to represent names so as to capture subtle cultural aﬃnities.

He suggested something like a word embedding could do the job, but we needed

training text be that would encode this information.

Yifan rose to the occasion. He obtained a data set composed of the names

of the most important email contacts for over 2 million people. Contact lists for

representative individuals5might be:

•Brad Pitt: Angelina Jolie, Jennifer Aniston, George Clooney, Cate Blanchett,

Julia Roberts.

•Donald Trump: Mike Pence, Ivanika Trump, Paul Ryan, Vladimir Putin,

Mitch McConnell.

•Xi Jinping: Hu Jintao, Jiang Zemin, Peng Liyuan, Xi Mingze, Ke Lingling.

We could treat each email contact list as a string of names, and then con-

catenate these strings to be sentences in a 2 million-line document. Feeding this

to word2vec would train embeddings for each ﬁrst/last name token appearing

in the corpus. Since certain name tokens like John could appear either as ﬁrst

or last names, we created separate symbols to distinguish the cases of John/1

from John/2.

Word2vec made short work of the task, creating a one hundred-dimensional

vector for each name token with marvelous locality properties. First names

associated with the same gender clustered near each other. Why? Men generally

have more male friends in their contact list than women, and visa versa. These

co-locations pulled the genders together. Within each gender we see clusterings

of names by ethnic groupings: Chinese names near Chinese names and Turkish

names near other Turkish names. The principle that birds of a feather ﬂock

together (homophily) holds here as well.

Names regularly go in and out of fashion. We even see names clustering by

age of popularity. My daughter’s friends all seem to have names like Brianna,

Brittany,Jessica, and Samantha. Sure enough, these name embeddings clus-

ter tightly together in space, because they do so in time: these kids tend to

communicate most often with peers of similar age.

We see similar phenomena with last name tokens. Figure 11.16 presents

a map of the 5000 most frequent last names, drawn by projecting our one

hundred-dimensional name embeddings down to two dimensions. Names have

been color-coded according to their dominant racial classiﬁcation according to

U.S. Census data. The cutouts in Figure 11.16 highlight the homogeneity of

regions by cultural group. Overall the embedding clearly places White, Black,

Hispanic, and Asian names in large contiguous regions. There are two distinct

5Great care was taken throughout this project to preserve user privacy. The names of the

email account owners were never included in the data, and all uncommon names were ﬁltered

out. To prevent any possible misinterpretation here, the examples shown are not really the

contact lists for Brad Pitt, Donald Trump, and Xi Jinping.

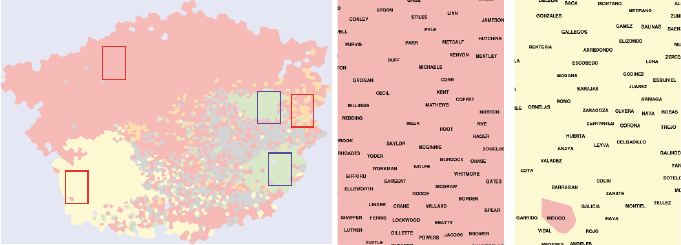
11.8. CHAPTER NOTES 387

Figure 11.16: Visualization of the name embedding for the most frequent 5000

last names from email contact data, showing a two-dimensional projection view

of the embedding (left). Insets from left to right highlight British (center), and

Hispanic (right) names.

Asian regions in the map. Figure 11.17 presents insets for these two regions,

revealing that one cluster consists of Chinese names and the other of Indian

names.

With very few Thors corresponding with very few Rabinowitzes, these corre-

sponding name tokens are destined to lie far apart in embedding space. But the

ﬁrst name tokens popular within a given demographic are likely to lie near the

last names from the same demographic, since the same close linkages appear in

individual contact lists. Thus the nearest last name token yto a speciﬁc ﬁrst

name token xis likely to be culturally compatible, making xy a good candidate

for a reasonable-sounding name.

The moral of this story is the power of word embeddings to eﬀortlessly

capture structure latent in any long sequence of symbols, where order matters.

Programs like word2vec are great fun to play with, and remarkably easy to use.

Experiment with any interesting data set you have, and you will be surprised

at the properties it uncovers.

11.8 Chapter Notes

Good introductions to machine learning include Bishop [Bis07] and Friedman

et al. [FHT01]. Deep learning is currently the most exciting area of machine

learning, with the book by Goodfellow, Bengio, and Courville [GBC16] serving

as the most comprehensive treatment.

Word embeddings were introduced by Mikolov et al. [MCCD13], along with

their powerful implementation of word2vec. Goldberg and Levy [LG14] have

shown that word2vec is implicitly factoring the pointwise mutual information

matrix of word co-locations. In fact, the neural network model is not really

fundamental to what it is doing. Our DeepWalk approach to graph embeddings

is described in Perozzi et al. [PaRS14].

INFO

CORPORATION

SUPPORT

SMITH

AND

JOHNSON

WILLIAMS JONES

BROWN

NOREPLY

MILLER

COM

GARCIA

SERVICE

CASUALTY

DAVIS

GROUP

RODRIGUEZ

CUSTOMERSERVICE

ONE

AIRLINES

LEE

MARTINEZ

WILSON

THOMAS

ANDERSON

GONZALEZ

FARGO

SILVA

TAYLOR

LOPEZ

MARTIN

HERNANDEZ

MOORE

THOMPSON

HOME

WHITE

SANTOS

JACKSON

PEREZ

CUSTOMER

HARRIS

VAN

MARIA

BRANDS

SANCHEZ

ENTERTAINMENT

SECRET

AMAZON

LEWIS

CLARK

ROBINSON

WALKER

YOUNG

OLIVEIRA

SCOTT

GAMBLE

ALLEN

KING

TORRES

SOFTWARE

NOBLE

HALL

ANN

CARLOS

HILL

WRIGHT

GREEN

STEWART

RAMIREZ

YORK

ADAMS

PATEL

NEWSLETTER

CAMPBELL

NGUYEN

BAKER

BANK

NELSON

SINGH

RIVERA

FLORES

JAMES

DIAZ

CRUZ

MITCHELL

ROBERTS

GOMEZ

VIA

KUMAR

CLEARING

EVANS

RAMOS

LTD

RODRIGUES

FERREIRA

EDWARDS

PARKER

PHILLIPS

CARTER

KELLY

KHAN

PEREIRA

TURNER

SOUZA

MURPHY

ALVES

ANTONIO

CARD

COLLINS

MARIE

MORRIS

REYES

CELL

CRISTINA

MORALES

EXPRESS

MORGAN

CASTRO

MEDIA

AMERICA

COOK

LIMA

BELL

COSTA

COOPER

FERNANDEZ

LUIS

ROGERS

ORTIZ

NEWS

ALI

STORE

ALVAREZ

DEL

BAILEY

RUIZ

ROSE

WATSON

WOOD

GOMES

WARD

DAVID

PETERSON

ROSS

WALGREEN

GUTIERREZ

MEMBER

GRAY

DONOTREPLY

BENNETT

HOWARD

UNION

RICHARDSON

ALEXANDER

COX

CASTILLO

ALBERTO

HEALTH

HUGHES

ROMERO

RIBEIRO

DANIEL

CLUB

SHAH

REED

MARTINS

WIRELESS

ITA

PAULA

BROOKS

PRICE

FOSTER

MORENO

VARGAS

JOSE

SULLIVAN

WONG

LONG

SERVICING

PERRY

FERNANDES

MENDOZA

POWELL

JOHN

MURRAY

GRAHAM

KIM

RUSSELL

HAMILTON

WORK

DEPOT

FORD

WEST

JIMENEZ

LOANS

MYERS

FISHER

JORDAN

BUTLER

LAKES

PAUL

GORDON

COLE

CREDIT

HERRERA

SANDERS

BARNES

HENRY

AHMED

MEDINA

RYAN

HENDERSON

JENKINS

GEORGE

WALLACE

ELLIS

CARVALHO

ALMEIDA

SHARMA

ANDRADE

OFFICE

TRAVEL

KENNEDY

ONLINE

COLEMAN

SIMMONS

ROCHA

PATTERSON

MARSHALL

HAYES

RIVER

LOPES

CAMPOS

JOSEPH

HARRISON

REYNOLDS

HOUSE

MANUEL

MEYER

MIRANDA

MCDONALD

TEAM

ROJAS

GIBSON

SHAW

STEVENS

SERVICES

NETWORK

BLACK

GRIFFIN

FERNANDO

STONE

CARE

SOARES

AGUILAR

CHEN

FOX

TRAN

BRYANT

LOVE

EDUARDO

GRANT

WAGNER

CHAVEZ

HUNTER

PALMER

WOODS

SIMPSON

CHAN

WELLS

SCHMIDT

PERMANENTE

BURNS

LYNN

RAY

DIAS

MASON

DIXON

ROBERTSON

PHARMACY

FAMILY

MILLS

RICHARDS

CRAWFORD

ROSA

WEBB

VIEIRA

WASHINGTON

GONZALES

FREEMAN

ANGEL

HOLMES

BARBOSA

PORTER

PETERS

LAWRENCE

WARREN

JEAN

HUNT

TUCKER

SALES

SANTANA

REID

SALAZAR

CLARKE

KNIGHT

OWENS

LEISURE

FERGUSON

MENDEZ

HENRIQUE

VASQUEZ

DOS

SANTIAGO

OBRIEN

NEW

HART

SOTO

BOYD

LANE

AUTO

ANDREWS

MARQUES

CANADA

MICHAEL

VEGA

MACHADO

DUNN

VAZQUEZ

LLC

CENTER

BANKS

MATTHEWS

OLSON

ARAUJO

GARDNER

ANNE

ELENA

HICKS

JOHNSTON

WANG

DANIELS

BURKE

SNYDER

LUCAS

RICE

COHEN

PAYNE

STUDIOS

DELGADO

WALSH

GUZMAN

STEPHENS

SPENCER

ROBERTO

ARMSTRONG

BERRY

MORRISON

ARNOLD

CHAPMAN

HAWKINS

WEBMASTER

CUNNINGHAM

MAY

HANSEN

UNIVERSITY

GREENE

HUDSON

RIOS

LUIZ

PARK

BRADLEY

MOM

JACOBS

ORTEGA

PATRICIA

RILEY

CARROLL

MOREIRA

ELLIOTT

SECURITY

CAROLINA

LYNCH

GMAIL

MOLINA

HOFFMAN

MAIL

DAY

SCHNEIDER

FRANCO

DEAN

SPORTS

DOUGLAS

FRANCIS

WEBER

YAHOO

DUNCAN

LIMITED

CARR

KELLEY

OLIVER

AUSTIN

ALVARADO

WEAVER

NICHOLS

NUNES

ACOSTA

DUARTE

CESAR

MENDES

INSURANCE

NAVARRO

HARPER

WILLIS

HARVEY

GUERRERO

PERKINS

PIERCE

DAVIDSON

FROM

BARRETT

AUGUSTO

GUPTA

JOS

ELIZABETH

HELP

CARDOSO

WHEELER

LUCIA

ANTHONY

FREITAS

JENSEN

NASCIMENTO

FRANCISCO

DIRECT

SIMON

FRANKLIN

PARTS

CHARLES

GILBERT

MALDONADO

BECKER

GONALVES

CARLSON

CONTRERAS

REIS

CARPENTER WATKINS

WILLIAMSON

GARZA

BISHOP

LUNA

LARSON

SUAREZ

MARY

DOMINGUEZ

KLEIN

LITTLE

WALTERS

NEWMAN

INTERNATIONAL

PACHECO

APARECIDA

TAN

JAVIER

MARA

FIGUEROA

MELO

LIU

GARCA

AVILA

AIRWAYS

DAD

LIFE

FOR

THE

GABRIEL

LAWSON

BURTON

BILLING

GUERRA

DEPARTMENT

BATISTA

SANDOVAL

RICHARD

FRANK

CHRISTIAN

ESTRADA

PEARSON

FULLER

LEON

SYSTEMS

BORGES

HOLLAND

MCCARTHY

CABRERA

MONTGOMERY

HOWELL

GONZLEZ

CORREA

KAY

SAN

LPEZ

HANSON

LAMBERT

CRAIG

LAURA

BECK

KELLER

TEIXEIRA

SCHULTZ

CHANG

COLLEGE

CURTIS

BER

ANDREA

SOUSA

BLOCK

FONSECA

MILES

WARNER

GAMING

PAULO

DEBT

SIMS

OCONNOR

JOBS

FOWLER

WELCH

MEJIA

PATRICK

LEONARD

SCHWARTZ

FITCH

LAW

LOWE

LIM

MIGUEL

CHAMBERS

MCCOY

ALEJANDRO

PADILLA

ORLANDO

WADE

HOTEL

MUOZ

MUNOZ

HASSAN

GARRETT

BENSON

DENNIS

GREGORY

BOWMAN

ISABEL

TERRY

GILL

MARQUEZ

ENRIQUE

MORAN

JANE

YANG

FLEMING

DAWSON

RICARDO

ROY

ROBERT

QUINN

FUENTES

MIKE

LARA

HOPKINS

MARK

TECHNOLOGY

DOYLE

VALDEZ

LIVRE

MUSIC

JUNIOR

BARKER

AHMAD

WOLF

BARNETT

SHOP

FERNANDA

PAGE

BATES

MANN

LIN

CITY

POWERS

TODD

WATTS

FINANCE

ARIAS

JENNINGS

FIELDS

STANLEY

PABLO

RODRGUEZ

AGUIRRE

BLAKE

MONTEIRO

CENTRAL

LYONS

FISCHER

ESPINOZA

CROSS

ADMISSIONS

AYALA

FLETCHER

STEELE

HIGGINS

SUTTON

HUSSAIN

BARROS

TIM

NEAL

BREWER

ANDRES

HARDY

PENA

BRASIL

MORA

NATIONAL

BRITO

PINTO

SCHOOL

JAIN

REGINA

FELIPE

PHAM

HERNNDEZ

CALDWELL

RIVAS

FITZGERALD

MANAGER

DAVIES

LAM

RHODES

UPDATE

ESCOBAR

PIERRE

BARBER

MOHAMED

SERRANO

PARKS

NORRIS

LLOYD

DURAN

BALL

BALDWIN

BAUER

WOLFE

WHITNEY

HAYNES

ROWE

SAUNDERS

BETH

MOSS

MEDEIROS

BLAIR

FRIEND

BRADY CUMMINGS

JOBROYALTY

WEBSTER

HOLT

CAMACHO

CARRILLO

GALLAGHER

BOWEN

JOE

ROMAN

LEAL

NEWTON

ZHANG

MAN

PREZ

BYRD

SOSA

MCLAUGHLIN

MICHELLE

MACDONALD

MAXWELL

MORAES

ENERGY

SCRIPTS

GRACE

MARTNEZ

BLANCO

OUTLET

FRAZIER

ZIMMERMAN

ALONSO

REEVES

BRUNO

MATOS

VALENCIA

BRYAN

CHURCH

HALE

SHELTON

LINDA

CHANDLER

HORTON

MOURA

BHAI

CALDERON

JUAREZ

GRIFFITH

GOODMAN

BUSH

MANNING

CARDENAS

WEISS

STEVENSON

ADMIN

ROBLES

MUELLER

CAMERON

MERCADO

VAUGHN

SHARP

VINCENT

TAVARES

THORNTON

SUE

BRUCE

GRAVES

SWANSON

FLYNN

LEVY

BEATRIZ

BERNARD

PINEDA

ALEJANDRA

CORTEZ

DAS

BURGESS

GROSS

CASEY

PHOTO

AMP

RODGERS

MACK

HERTZ

TYLER

LOZANO

LANG

SHERMAN

MARIN

FINANCIAL

JOHNS

SALINAS

DESK

NUNEZ

ROBBINS

CASA

HAMMOND

COMMUNICATIONS

SOLIS

OPINIONS

HUANG

VERA

CURRY

NICOLE

OWEN

MCKENZIE

WALTER

TERESA

CRUISE

NORMAN

BABY

GUY

SNCHEZ

UNITED

CECILIA

MALONE

WATERS

BARTON

CORTES

FRENCH

MCDANIEL

ERICKSON

BUSINESS

JORGE

KRAMER

MOHAMMED

ENGLISH

CUNHA

GOODWIN

OCHOA

GABRIELA

LOGAN

ROTH

MONTOYA

SALAS

POTTER

JOYCE

REDDY

HARRINGTON

BARRY

WALTON

KAUR

JOY

WISE

CHRISTENSEN

ELLEN

GARNER

MOBILE

VILLA

RAMSEY

RESOURCES

EUGENIA

HOGAN

ANA

MARSH

RAHMAN

SCHROEDER

PINHEIRO

HELENA

MAG

NOGUEIRA

CANNON

SEATS

MCGEE

MAMA

TOWNSEND

ONEILL

RAO

WILLIAM

RUSSO

VELASQUEZ

REESE

VILLANUEVA

ROSSI

PARSONS

ROSALES

CLAUDIA

GIBBS HINES

INTERNET

RAFAEL

PAZ

COELHO

BENJAMIN

MCKINNEY

USA

JOB

FELIX

VELEZ

IBRAHIM

BUCHANAN

ORG

CAREY

TATE

BEST

FARRELL

BRAVO

CHRIS

BRENNAN

WILKINSON

BAUTISTA

VON

ACEVEDO

OSBORNE

BRAGA

NORTON

SOLOMON

RANGEL

MCGUIRE

SILVEIRA

LOU

PONCE

VICTOR

PEA

KARMA

HARMON

PRIMA

ESPINOSA

RESEARCH

MOODY

KANE

PIRES

SAMUEL

GIL

ATKINSON

FARMER

MEHTA

POPE

MORTON

NASH

END

INGRAM

FLOWERS

HUBBARD

PRADO

LOAN

LEITE

TRUJILLO

BEAN

ALEX

RICH

HOUSTON

BOWERS

MCLEAN

COLON

OROZCO

KERR

PATTON

AMARAL

NICHOLSON

GLOVER

NEVES

OLSEN

YATES

COBB

ZAMORA

HODGES

LAU

HAMPTON

STREET

CLAYTON

WALL

PRATT

SHEPHERD

BOND

STOKES

PETERSEN

BARRETO

BURNETT

BASS

STEIN

HARTMAN

BRIGGS

JUAN

CHUNG

ABRAHAM

VELAZQUEZ

SWEENEY

FLOYD

CAIN

CARSON

ROSARIO

AZEVEDO

SUN

DRAKE

MOON

BILL

FARIAS

STATE

CHIN

CHENG

MCBRIDE

MICHEL

CABRAL

MCCORMICK

TRUST

ADVISOR

CAROL

MARCELO

CHASE

FOLEY

KEITH

DEE

MEYERS

LISA

XAVIER

LUZ

FRIENDFINDER

COUNTY

MENEZES

CONNER

VILLARREAL

GUEVARA

FREIGHT

MATERNITY

WILKINS

FOOTBALL

STRICKLAND

PALACIOS

KENT

VICTORIA

DAIRY

BARRERA

VIDAL

SMALL

KOCH

LAMB

PRINCE

SAVAGE

BONILLA

PEDRO

ALLISON

MARKS

KAREN

ABREU

GLENN

MATHEWS

LARSEN

HESS

POWER

GOV

GERMANY

PETER

AID

ASHLEY

POOLE

AIRBNB

MAX

ELIAS

STEPHENSON

BEACH

DESAI

HOOD

ABBOTT

AUTHORIZED

SPARKS

HARDWARE

MONTES

LOUIS

BERGER

MULLER

BALLARD

BAXTER

MUHAMMAD

MULLINS

CHAVES

OMAR

ZENDESK

SUMMERS

VILLEGAS

RIGHTS

RUBIO

GOLDEN

IBARRA

BEN

KIRBY

BROCK

SHANNON

HUTCHINSON

ALEXANDRE

LUIZA

GAMES

PARRA

SALGADO

MARCOS

GMEZ

MORNING

ARAJO

MANAGEMENT

KIRK

GLASS

MAIA

BRADFORD

COMPANY

RAYMOND

BUENO

LINDSEY

MARCELA

ANDREW

MELENDEZ

CERVANTES

WILCOX

BERG

DAVILA

ALBERT

COLLIER

MARIO

STEVE

BAY

ODONNELL

ALFONSO

FRASER

QUINTERO

BOB

FASHION

EDU

DILLON

MAE

JEFFERSON

GATES

SIERRA

MONROE

TOM

MASSEY

RANDALL

JACOB

TECH

TOOMEY

BENITEZ

HORN

STUART

TAPIA

BARATO

NOLAN

NORTH

LAKE

VALENZUELA

MAYER

LUISA

ROMANO

SHORT

PAT

MORROW

ACCOUNT

SANTA

DAN

NET

BERNAL

VELASCO

REILLY

KEMP

DONOVAN

GREER

JAY

JOSHI

AQUINO

LEVINE

NUEZ

KATZ

ARROYO

JESUS

HERMAN

HOLLOWAY

PERALTA

RODRIGO

SWEEPSTAKES

BOOTH

CONWAY

FOOD

BOONE

FRIEDMAN

DAVENPORT

RUTH

SKINNER

MOTA

TANG

SHIELDS

SEGUROS

PRIMO

VIANA

DAVE

DENTAL

ABDUL

ADRIAN

MCKAY

FARIA

MELLO

CLAY

MALIK

MEZA

AGUIAR

CASE

COPELAND

COCHRAN

GOLD

FRANCE

SINGLETON

ADKINS

PHONE

DECKER

MACEDO

SRL

HEATH

ATKINS

HANCOCK

SNOW

CAMARGO

REAL

STRONG

CASH

WHITAKER

BOWLING

DYER

LEBLANC

MCINTYRE

VALLE

GUSTAVO

ADRIANA

TEST

TOLEDO

CALLAHAN

CHRISTOPHER

LIBRE

GIRL

BELTRAN

MCINTOSH

MADISON

HANNA

BRIDGES

BOYLE

PRESTON

FROST

MURILLO

FORBES

MACIEL

DALTON

NOEL

DALE

ZAPATA

HODGE

EAGLE

SUPPLY

MACIAS

UNDERWOOD

CANO

WORLD

FASHIONS

BUCKLEY

QUEIROZ

SMART

DUFFY

NIELSEN

BIRD

IQBAL

BARR

JIM

BLUE

MCGRATH

SHAFFER

DAZ

REWARDS

HUGO

FERNNDEZ

STARK

AMORIM

TANNER

MCDOWELL

CARMEN

MCMAHON

COMFORT

SAWYER

GALLEGOS

HARDING

STAR

AZIZ

WARE

GILES

ALFREDO

SIS

MORAIS

DESIGN

MAHONEY

LEUNG

HOOVER

BOYER

EATON

SCHAEFER

FITZPATRICK

CAR

JACK

BARRIOS

KAPLAN

RECRUITMENT

CONLEY

GUADALUPE

ALEXANDRA

FITNESS

MEDICAL

OSORIO

VENTURA

PITTMAN

HONG

MARKETING

ALICE

CUEVAS

SOLUTIONS

GOLDSTEIN

AUSTRALIA

PAOLA

CABALLERO

GILMORE

VIVO

ORR

HOBBS

HUFF

GENERAL

COOKE

ADAM

PAREDES

BARRON

CLINE

NANCY

MUNIZ

BRANCH

SPENCE

GOLDBERG

BARTLETT

HEAD

JARAMILLO

ANGELES

MAGAZINE

WYATT

ROBERSON

PAIVA

WIGGINS

MCCLURE

MOSES

LIST

HOWE

INDIA

ARTHUR

BRAZIL

IVAN

CHOI

MCLEOD

SINCLAIR

MARINO

CHU

MARINA

PRASAD

BYRNE

INES

JACOBSON

HUMPHREY

KNOX

KIDS

BRAUN

HUYNH

BEARD

PROPERTY

OCONNELL

MATHIS

THOMSON

LINDSAY

CONTROL

HURST

LINE

STAFFORD

LANDRY

PHELPS

ROSAS

DICKSON

ARCHER

BRADSHAW

NAIR

RAMREZ

MIDDLETON

TRACY

ANNA

WILEY

LUGO

HAIR

LESTER

WERNER

BUCK

DIEGO

SWEET

GARRISON

GARY

SAM

MCCALL

VARELA

ANGELA

GOOD

IGNACIO

CHARTERED

HURLEY

HAHN

MATA

MARKET

SIQUEIRA

MCMILLAN

ANDRE

WINTER

GOULD

ALFARO

CORDERO

GRIMES

GILLESPIE

AMIN

MERRITT

VAUGHAN

HARRELL

LAI

BENDER

WAYNE

RELATIONS

SLOAN

MCCULLOUGH

PACE

CONRAD

COMMUNITY

VICENTE

DANTAS

DIGITAL

ERIC

BLACKWELL

CONVERSE

WINTERS

FREDERICK

DALY

ARTURO

CEL

SANDRA

MAURICIO

RUSH

ABBAS

DELA

HAYDEN

WHITEHEAD

TREVINO

BEASLEY

ROACH

PARRISH

ENTERPRISES

SCHMITT

GUIMARES

BENTLEY

RITA

ANDERSEN

MAC

SHIRLEY

BOY

BELLO

MEADOWS

CARDONA

HIGH

COMBS

SUSAN

HENDRICKS

ARELLANO

KRAUSE

GALVAN

GALINDO

DIANE

CALL

MCKEE

HUBER

SAMPSON

SUTHERLAND

MORSE

MULLEN

BRO

DONNELLY

BROWNING

FIGUEIREDO

CRANE

DONALDSON

HULL

PITTS

VALENTINE

PEARCE

DICKERSON

HAAS

KNAPP

LESLIE

ISMAIL

NIXON

LEACH

NAVY

INVESTMENT

BRANDT

FREIRE

PLUS

ABU

MICRO

NOVAK

KAUFMAN

ROCK

FRY

BLANCHARD

SHAIKH

DADDY

KLINE

LIVINGSTON

PIMENTEL

CORDOVA

CORREIA

HIDALGO

SHEA

LEO

LINK

CASTELLANOS

HEBERT

CARRASCO

LEMOS

DURHAM

DUKE

DIANA

BRIAN

CLARO

CONTABILIDADE

CHEUNG

STUDENT

KAISER

VANCE

ONEAL

NIEVES

PECK

MCDERMOTT

PALMA

DORSEY

CONTACT

LEONARDO

ARTS

TRADING

MONICA

MELTON

DANIELA

WEEKS

CHRISTINE

HUFFMAN

VERMA

GAINES

LORENA

MCCANN

ORDERS

WOODWARD

SHEPPARD

KATHY

MCPHERSON

GALLO

BULLOCK

ELLISON

CONNOR

WOODARD

ONEIL

MCCONNELL

ADMINISTRATOR

BRANDON

HASAN

CONNOLLY

CORDEIRO

LANGE

EVERETT

RANDOLPH

SERGIO

GONCALVES

BAIRD

PERSONAL

ART

BASTOS

BRIGHT

DINIZ

GUEDES

BEZERRA

QUINTANA

POTTS

REZENDE

KEVIN

ISAAC

MARCUS

VASCONCELOS

CAROLINE

MADDEN

TAX

SEBASTIAN

AVERY

STOUT

COSTELLO

CHOW

ENRIQUEZ

BROWNE

JENNIFER

BURGOS

RIVERS

GALLARDO

HOPE MCCLAIN

HORNE

CALHOUN

WILKERSON

DENISE

CASTANEDA

HEWITT

BARN

RAJ

JULIE

HENSON

MOSLEY

AMOR

GENTRY

RICHMOND

DIAMOND

NETO

BLACKBURN

HALEY

VALLEY

CARLA

GODOY

BOARD

TOURS

ZAVALA

POLLARD

RAMON

PUGH

EDWARD

DAILY

CARNEIRO

RENEE

CLEMENTS

CREATIVE

GRUPO

MALONEY

HUERTA

HURTADO

JARVIS

HICKMAN

VILLALOBOS

DOHERTY

DON

MILENA

NIETO

GORMAN

SILVIA

ALAM

ARMANDO

POST

DOUGHERTY

FLANAGAN

MCKENNA

ARORA

CHONG

IRWIN

RED

LILIANA

AGUILERA

ISLAM

CROSBY

LEARNING

BARBARA

ELECTRIC

TONY

SILVER

CARNEY

FIELD

PHAN

EDUCATION

SHARPE

ACADEMY

KEY

CHERRY

MATHEW

YEE

FERRARI

SAMPAIO

CAMP

HOANG

NGO

BUSTAMANTE

STANTON

LOUISE

HOOPER

COWAN

VOGEL

SANDY

KRUEGER

ROWLAND

CIV

SINGER

PORTO

SELLERS

HILLS

CSAR

STUDIO

DELANEY

DEALS

MORIN

DAWN

SPEARS

BURCH

JUDY

SEGURA

CHACON

GAY

ABDULLAH

ZAMBRANO

SLATER

SISTER

JEFF

JAN

PENNINGTON

PROPERTIES

GOLDMAN

HERBERT

STARR

BUY

CLAUDIO

BARLOW

MONTERO

REALTY

ROSEN

HOLDEN

WALLER

CONSUMER

TRUONG

POP

KNOWLES

MAYO

COTTON

SEARS

MAHER

GUILLERMO

ARGENTINA

MCGOWAN

FILHO

WORLDWIDE

ERNESTO

SAMUELS

SHAPIRO

SANFORD

EVE

TREJO

TOVAR

HOLDER

RITTER

BAEZ

MCNEIL

TRAVIS

VENDAS

HAYS

SAENZ

OLX

AGARWAL

DUDLEY

MERCER

PAYMENTS

RICHTER

CROWLEY

ROSENBERG

REY

SHEPARD

BENTON

HENSLEY

AIR

KUHN

CISNEROS

BRAY

NICOLAS

SARAH

SHEEHAN

SOLANO

AARON

DUBOIS

MCFARLAND

NAVA

CANTU

OJEDA

MAYNARD

AYERS

RUBIN

SIR

DUNLAP

FAULKNER

BECERRA

NICHOLAS

PRIETO

MENA

BERMUDEZ

ALUMNI

GUEST

ANTUNES

EVENTS

MIHAI

OTERO

MISHRA

SHARON

LEIGH

BOLTON

GLOBAL

VERGARA

MAYS

RASMUSSEN

CORBETT

CORONA

DONNA

FREY

URIBE

CLARA

PRUITT

DALEY

ESQUIVEL

DWYER

WELSH

GALLOWAY

SALVADOR

PLACE

OCAMPO

PROCTOR

FERRER

FARLEY

LUTZ

CREEK

WILLS

MCKNIGHT

MCCABE

LOBO

WEB

RAE

MARIANO

FONG

POPA

EMMANUEL

VALDES

SON

ROSADO

VANESSA

MOONEY

STERN

SPRINGER

POSTMASTER

HICKEY

GUIMARAES

DOWNS

FRITZ

DEVELOPMENT

MCNAMARA

ONG

LORD

LAND

FELDMAN

WALLS

DELEON

JULIA

CASSIDY

LANCASTER

LARRY

BOURKE

CARMONA

CLIENT

JIMNEZ

PRO

ALICIA

JASON

ZUNIGA

GODFREY

GEE

GLORIA

COMERCIAL

REALTYTRAC

FRANA

SAAD

HARTLEY

RAZA

PATIL

ELDER

FARM

DOLAN

ESTHER

LOWERY

HINTON

DEPT

CAREERS

LUCERO

CAVALCANTE

AMAYA

EMERSON

ARCE

HILTON

HERRING

ESPOSITO

GIBBONS

MOYER

DREW

ROLLINS

HARDIN

COUNTRY

CURRAN

STAFF

MAIN

RIO

APPLICATIONS

LEANDRO

KESSLER

LEVIN

CLEMENT

GRIFFITHS

TALBOTS

RANA

KENNY

CRISTIAN

DODSON

DANG

SEXTON

MOSER

KENDALL

KORS

SCHULZ

VERONICA

NEWELL

MCCARTY

CORRETORA

LIRA

DRIVER

HAN

EWING

MERRILL

HOMES

BUI

DICKINSON

BRAND

QUIROZ

WIFE

WILDLIFE

CHRISTIE

BACON

LYON

FINLEY

SARMIENTO

APARTMENTS

CHAMBERLAIN

VINICIUS

OSCAR

VITAMIN

STEPHEN

ICE

BLOOM

MEIER

DUTRA

COMPTON

LORENZO

FINCH

SAEED

SWAN

RICO

DONAHUE

BRITT

RIVERO

JACQUES

HYDE

MONTENEGRO

PROGRAM

ANGELICA

EGAN

MADDOX

ENGLAND

ALAN

CLIFFORD

LONDON

ASSIS

MARGARITA

MARINHO

BENAVIDES

BOOKER

HESTER

ALLAN

BONNER

TOMLINSON

HENDRIX

CLAIMS

SCHMITZ

OLIVA

LEHMAN

BOSS

SKY

SOCIAL

HOFFMANN

CROWE

STERLING

QUEEN

FRYE

BOGDAN

SORIANO

FISH

CRESPO

MARIANA

ESTES

TAM

GREENBERG

ISRAEL

MERCEDES

GMBH

WESLEY

CLEVELAND

FULTON

COFFEY

CRAFT

ANDREI

CACERES

DODD

SENIOR

BOYCE

BLANKENSHIP

RESERVATIONS

ALBUQUERQUE

WEBBER

MCALLISTER

KARINA

BERNARDO

HUMBERTO

MASTERS

GROVE

FABIAN

PARIS

KENNEL

SAAVEDRA

RITCHIE

WESTON

ABRAMS

PETTY

MATTOS

MACKEY

MIHAELA

FIRST

FREE

WITT

ACCOUNTS

KIDD

JAIME

MCGILL

OLIVARES

KAMAL

VILA

FINK

REYNA

CAMILO

AMY

GRECO

YOU

GAL

AREVALO

MAGALHES

POPESCU

COURTNEY

RAUL

ODOM

KERN

SEED

SYKES

TRAINING

VALENTIN

BRITTON

SYED

IMVEIS

GREENWOOD

INS

MATIAS

PHOTOGRAPHY

YADAV

SIMMS

MACKENZIE

ALCANTARA

OTTO

SALEH

JULIO

RIGGS

FALCON

TYSON

MILTON

DANCE

ORELLANA

ABEL

TAXI

HASTINGS

BARON

DOWNING

MADRID

ROBIN

ROLAND

SENA

BETTY

BROTHERS

DEMPSEY

MICHAELS

LOCKE

RIZZO

ABD

PAPA

SAID

GUILLEN

HEALTHCARE

HELLER

DEBBIE

GAGNON

INVESTMENTS

JESSICA

TERRELL

BRENT

DSOUZA

HAINES

WOLFF

KENNEY

DRISCOLL

HOLMAN

GUTHRIE

CONSTRUCTION

DICK

SOUTH

MAGEE

CHILDS

RESPUESTA

ROQUE

STAFFING

OSBORN

SIMONS

BINTI

BYERS

SIEGEL

FRIDAY

DENTON

ENGEL

WILDER

LOW

RUTHERFORD

COOLEY

ESTEBAN

STEFAN

SWIFT

SANDERSON

CASTAEDA

MCFADDEN

PHILIPPINES

WARRANTY

RAQUEL

MEXICO

KINNEY

ZIEGLER

MELISSA

RANKIN

CULLEN

MOTTA

STELLA

RENE

WITHIN

SELF

ESPARZA

GUNN

ATENDIMENTO

JUSTICE

GARRIDO

ASSOCIATES

BUTT

WHITFIELD

BEAR

DONALD

CHO

BEAUTY

SNIDER

BATTLE

BABU

COUTO

COUTINHO

ENG

PORTILLO

JOYNER

YODER

RIDDLE

HOLLEY

SEYMOUR

FINANCEIRO

DEAL

ALARCON

CALIFORNIA

IGLESIAS

RASHID

DAUGHERTY

SHERIDAN

KROGER

WILL

BOX

JUNG

SCHWAB

AVALOS

HELPDESK

REZA

LANGLEY

MARCO

SCHUMACHER

JANSEN

MATTHEW

TOYOTA

HATFIELD

MODAS

MAHMOOD

DAILEY

MEDRANO

LADY

LOCKHART

LUKE

LAB

ANGELO

PRINTING

LACERDA

FRANKS

SHOEMAKER

VAZ

PIZZA

CRAMER

BIN

ALFORD

HEALY

GAUTHIER

MAR

DEVINE

LARKIN

STEINER

AMOS

SARGENT

RICK

HOTELS

WYNN

GOFF

ALERTS

BURT

FEDERAL

BENOIT

INNOVATION

FERRELL

SONG

HANEY

DAVISON

KIRKLAND

MAJOR

JERRY

DENIS

CASAS

MONTALVO

GAMBOA

CLAUDE

BROTHER

HUMANOS

INTERACTIVE

REGAN

PURCELL

HOTMAIL

LUCIANO

CARUSO

HELMS

PREMIER

AMADOR

ELISA

MOTORS

HAY

MUSTAFA

CARVER

BETANCOURT

HATCHER

WORKFORCE

SIDDIQUI

FORREST

GRANADOS

LIGHT

FRANCOIS

DUNBAR

ADVANTAGE

DOWNEY

GANDHI

WAY

KIRKPATRICK

DARIO

ROCHE

PRITCHARD

MAHMOUD

MOYA

OTT

RON

DRUMMOND

KHALID

HOSPITAL

MOHAN

SORENSEN

AVILES

BERMAN

FAN

RADU

WINKLER

LING

HERRON

SIMONE

AMANDA

GUTIRREZ

CONSULTING

CLIENTES

CANTRELL

MENDONA

NAVARRETE

PICKETT

ALEXIS

VALLEJO

FELICIANO BRENDA

ALSTON

EMERY

GODWIN

KEARNEY

MOHAMMAD

PATE

PARDO

CHANEY

OHARA

HADDAD

CANALES

DILLARD

CATHERINE

CLAIRE

VIRTUAL

KYLE

ROGER

EDGE

ALEXANDRU

CANCER

CINDY

MASTER

MAI

MINOR

ARRUDA

EAST

BINGHAM

LINARES

STEVEN

RIDGE

REHMAN

THORPE

LUDWIG

FATIMA

PLUMMER

MARIUS

KANG

CARVAJAL

OSMAN

BEATTY

ROE

LEDESMA

PIKE

TALLEY

CASTLE

VILLAGE

TEMPLE

OLEARY

FOODS

PHILIP

READ

PUBLISHING

BOUCHER

MEEKS

TORO

MOHD

RINCON

ROYAL

CONNELLY

BUSTOS

KENDRICK

MATT

VIRGINIA

MCMANUS

ACKERMAN

PRYOR

ZHOU

QUINONES

FERRAZ

GERMAN

CHANDRA

KRAFT

PAN

SALCEDO

OLVERA

DUQUE

GOLF

HANNAH

URBAN

ODELL

ENGINEERING

TILLMAN

NAME

FAJARDO

BOWDEN

EVANGELISTA

CARTWRIGHT

SERRA

CORBIN

NOVO

CARRANZA

KEENAN

MEREDITH

INCORPORATED

CONNELL

DOE

RUCKER

PRESS

BURRELL

PIPER

ROLDAN

PERERA

WHALEN

HOLLIS

GRADY

DEWITT

VISION

KARIM

MAILER

RUTLEDGE

SONI

BERNSTEIN

GERARDO

NAGY

FOREMAN

PIERSON

POLLOCK

BURGER

BARNARD

ASH

DRAPER

HELEN

SWAIN

ELAINE

PAEZ

ROMO SOLEDAD

CHIU

OLIVIER

GLEASON

BARAJAS

BIG

SARA

LOTT

STRATTON

HENDRICKSON

EARL

HHONORS

GORE

STEPHANIE

ANWAR

FIX

MCGINNIS

MAURO

SEPULVEDA

MARCIA

PANDEY

LUND

LCIA

MARTA

CAHILL

HUSBAND

LOWRY

GROVES

JULIAN

BEE

COTE

COVINGTON

WOODRUFF

PLAZA

BROUSSARD

CALVO

MCCAULEY

EVENTOS

TRIBUNE

YOUR

LEN

GUILHERME

HUTCHISON

KURTZ

GAYLE

ARANDA

JARRETT

TIRE

CORNEJO

WINSTON

EDGAR

WHITLEY

DARLING

SCHAFER

MCCORMACK

COKER

HAMMER

GILLIAM

MOBLEY

GREGG

COORDINATOR

ZEPEDA

IRENE

BERTRAND

KIMBALL

ESCALANTE

EDMONDS

HATCH

ASHRAF

GARLAND

PEACOCK

DYE

HOSSAIN

CARRERA

PLATT

ROUSE

DOTSON

PASSOS

WOOTEN

SUSANA

MAYFIELD

WOMACK

MARION

BIGGS

ALBA

TIME

FINN

ANDR

MAGUIRE

VIEW

GOSS

QUICK

SWARTZ

PARENT

BAPTIST

BIANCHI

MARRERO

TUTTLE

LEA

QURESHI

JOAN

METZGER

DODGE

KULKARNI

MAGALHAES

LEONE

HAND

WORKMAN

CROCKER

BURKS

RAI

JANET

VERNON

SALEEM

HORNER

ARIEL

FABIO

PARTNERS

SANDS

COATES

BERGERON

CROW

PAL

RAM

UNCLE

ANDREEA

CRONIN

KOENIG

BLEVINS

GALVEZ

FARRIS

HOLCOMB

HOPPER

CUELLAR

KRISHNA

MONEY

STINSON

PAIGE

BRANDO

BELCHER

CHUA

VELA

TOTH

GAS

VALE

RESTREPO

WALDEN

HAGEN

EDDY

JOEL

STANFORD

CAMARA

JEFFREY

OMALLEY

BLAND

CHAPPELL

HSU

PENN

TONG

RECRUITING

PASTOR

KEN

JEFFRIES

WITH

DIRECTOR

SEWELL

MESQUITA

DOBSON

TURISMO

LUCA

STAHL

MEAD

LAURENT

DUONG

ANSARI

CORONADO

SLAUGHTER

CARMICHAEL

GIORDANO

PEDERSEN

QUEZADA

CHAU

KONG

SHAFER

MENESES

PAM

WEIR

HIRSCH

SALMON

GUSTAFSON

DUKES

TOPS

CARLTON

HARDEN

ADLER

LTDA

ROBISON

JAMISON

MAURER

PHIPPS

CLIFTON

ROBSON

ANIMAL

DOOLEY

TEAGUE

BLUM

APONTE

BUTCHER

PEIXOTO

MLLER

REDMOND

VERDE

VALENTE

CROUCH

MCCLELLAN

BAIN

MCHUGH

FLORIN

ELDRIDGE

THORNE

LETICIA

NOWAK

MICHELE

MARINE

FACTORY

MOUNTAIN

CAETANO

MCCRAY

FUNK

KAYE

LACY

SALEM

PAGAN

HERITAGE

NEUMANN

FOURNIER

JEWELL

SAMSON

SHERWOOD

GROSSMAN

NARANJO

LABEL

FAGAN

DAHL

CUMMINS

GERBER

HAMM

GALE

FAIR

AGRAWAL

PHILIPPE

SECRETARY

HUTCHINS

MELL

RESENDE

ASSISTANT

MCNEILL

ORDER

HUGGINS

HEREDIA

REECE

MONROY

NATHAN

VINSON

STACY

DANIELLE

BOWER

RUDOLPH

MAILBOX

TINA

MARC

YAN

FURTADO

HEART

LOTS

APARECIDO

TOBIN

CURRIE

JACKIE

CLINIC

COAST

ERWIN

CHI

RENATO

INN

CARL

NIX

FERRIS

POOL

DANA

ZHAO

CORRA

ZARATE

KATE

IRELAND

ROONEY

MARIAN

GREY

MCKINLEY

GAMA

GEIGER

GASTON

METZ

BACA

SADLER

RAINEY

DOAN

LILLY

SERNA

ANAND

MCELROY

CORP

SCHWARZ

DICKEY

MACKAY

TAMAYO

ROSENTHAL

PAYROLL

HIPOTECARIO

WHITTAKER

LEONG

SCHAFFER

LOJA

BURRIS

COYLE

CONDE

WORLEY

GIRALDO

RACHEL

SIM

SILVERMAN

PULIDO

LOMBARDI

COUCH

MARGARET

VARGHESE

ZONE

HARRY

NEELY

CHAUHAN

ANDRS

GRIGGS

TOMPKINS

CHERYL

KRUSE

STUBBS

VOGT

QUIROGA

BRIDAL

LAUREN

ARTEAGA

VIDEO

CAPITAL

TATUM

TECHNICAL

MCGHEE

TELLEZ

STROUD VICKERS

SYLVESTER

METCALF

ELMORE

QUIZ

KEATING

MANLEY

MERCHANT

PRAKASH

POLK

CEBALLOS

LOCKWOOD

BERGMAN

HINOJOSA

WEI

CONTI

BURROWS

FINE

MESA

CLIENTE

DUNHAM

BARROSO

WATT

ARAGON

BOSWELL

ALDRIDGE

SINGLE

KOEHLER

VOSS

IVEY

HUSSEIN

MCDONOUGH

BHATT

POINT

HANLEY

HEARD

ROPER

PAINTER

VASILE

FARR

CHRISTINA

AMES

SHELDON

YEAGER

BOUTIQUE

STRAUSS

LEYVA

JACOBSEN

BOO

TRAVELS

STEWARD

CHRISTY

GIMENEZ

ALEMAN

SORIA

NOVA

USER

PELLETIER

KAPOOR

DUMAS

KAHN

GARG

PUBLIC

NATION

GARDEN

FAY

TROTTER

PARTY

HOLBROOK

EDITH

EVELYN

LEIVA

BODY

DARBY

KITCHEN

CREWS

PASCUAL

NEGRON

ARREDONDO

VALVERDE

WINN

SPORTSMANS

LIANG

BAUM

GREG

ERNST

CAVALCANTI

OREILLY

SCHREIBER

ERVIN

JOO

DUGAN

WOO

MCGREGOR

LYN

STOVER

SANCHES

NETWORKS

DAFITI

RICCI

SHERRY

COLBERT

OSULLIVAN

BREWSTER

COULTER

MADRIGAL

INFORMATION

NOT

CHILDERS

LUJAN

BOGGS

TRINDADE

AGENCY

PERES

BASSETT

KRISHNAN

RATLIFF

SAUCEDO

SALIM

SUPER

SOL

LONGO

WILLARD

BOSTON

KRAUS

HAGAN

THI

GRIMM

SHEIKH

STORY

BUSCH

LEMUS

GIVENS

SRIVASTAVA

SHRESTHA

FUNG

HACKETT

MCMULLEN

LIZ

WEINSTEIN

HOSKINS

PADGETT

BUCKNER

DOMINGO

OKEEFE

MARTHA

VENTAS

CONNORS

OGDEN

MCRAE

LANGFORD

TREE

SCHUSTER

PET

HINDS

KHALIL

CONSTANTIN

MAYES

SCOUTS

GROVER

MCGRAW

HOLLIDAY

LACEY

LOMBARDO

SALAH

COLOMBIA

URBINA

PAPPAS

IONESCU

VITOR

SFPPDRAFTAUTHORIZATION

WILHELM

PUCKETT

SOFIA

CHAGAS

BILLINGS

GOODE

WESTBROOK

ANAYA

NANCE

TIPTON

MEADE

DELIA

GAIL

TOUR

CORNELL

ARAYA

SMILEY

WHYTE

ZHU

LOVELL

MILLIGAN

AKERS

REA

HABIB

HONDA

FRED

VIP

ACCOUNTING

CATHY

WADDELL

BRENNER

RECIPIENTS

PONTES

COFFMAN

MARTINO

SNELL

MALCOLM

ADAMSON

BALANCE

ALBRIGHT

PIMENTA

WAITE

CONKLIN

HAWK

MCGOVERN

ALBRECHT

CONROY

WAN

LAY

KEYS

GILLIS

BARRIENTOS

JOLLY

MARI

HADLEY

PENNY

YEUNG

ANGULO

ARENAS

HUI

TOLBERT

CROCKETT

NUGENT

CHILDRESS

VISA

CARLISLE

FRIENDS

CAREER

DUBAI

CODY

LAYTON

ULLAH

NORWOOD

BELEN

MINER

DINH

WALDRON

STOCK

ABDEL

RUBEN

PERSAUD

AMBROSE

AURELIO

VENEGAS

TIWARI

FORTE

UDDIN

TIA

CAO

TALBOT

TODAY

LANIER

GARAY

FAGUNDES

BULLARD

HAYWARD

RENTALS

REES

KRUGER

YARBROUGH

GRAF

WEINER

LORI

THURMAN

BHATIA

MELVIN

ANITA

CENTRE

SHEN

CARO

PESSOA

ESCOBEDO

MURDOCK

ANTNIO

HUTTON

CONCEPCION

GIRARD

SCHULTE

ALVARENGA

BENEDICT

FERRARO

DENNY

LOURDES

LYMPHOMA

HEATHER

MOHR

LINCOLN

CROWDER

DOLORES

SWENSON

CRABTREE

QUIGLEY

GERARD

RUEDA

HAWLEY

BEAL

EVA

LATHAM

POE

PINA

RUSS

MALAYSIA

HOLLINGSWORTH

ULLOA

BRAGG

BATEMAN

MCWILLIAMS

CLEMENTE

TREMBLAY

ASSESSORIA

TECHNOLOGIES

BARBOZA

CENTENO

AUGUSTINE

KOHLER

SHEFFIELD

HINSON

NEFF

ROWLEY

PAI

MCFARLANE

FLOOD

LIVE

DORAN

WISEMAN

PORRAS

STACEY

BOWLES

FERRO

CORCORAN

ATLANTA

JARA

HANDY

NEWSOME

FRESHDESK

TUDOR

OROURKE

MARROQUIN

REPORTS

ROCIO

BLANTON

GARDINER

MANSFIELD

PAR

OVIEDO

VANDER

CLEARY

REEDER

MAYA

NUMBER

MCQUEEN

BARROW

BARTH

COLVIN

DESIGNS

WATER

GENTILE

DELUCA

DIETRICH

HECTOR

MCDONNELL

QUINTANILLA

PROF

GASPAR

CHRISTIANSEN

BEYER

LINS

ROB

RIDER

RADIO

CHOWDHURY

ESTEVES

GIFFORD

FLORENCE

CLEMONS

ALENCAR

SPA

SOCCER

STILES

ESCOLA

CHAMPION

VILELA

ALINA

BAR

MONTIEL

FURNITURE

ELKINS

VZQUEZ

JORGENSEN

KOWALSKI

LUCY

BELLA

FRIAS

FONTANA

VANG

COE

BETTS

DAWKINS

IMRAN

TALENT

FACUL

FONTES

EMILIO

FRAGA

ADRIANO

SPRAGUE

DOMINGUES

SANTAMARIA

FLAHERTY

SHETTY

BLISS

DOG

ELECTRONICS

TRIPP

BULL

WHITING

HAMID

ADDISON

DOWLING

SALDANA

SHEARER

GOLDSMITH

ROXANA

RAINES

DUMITRU

PEARL

NEIL

MORRISSEY

CRUMP

HILLIARD

LUCIO

GUNTER

DUFF

CORNELIUS

IOANA

RECORDS

ADOLFO

TEEN

HOYT

GODDARD

MANCINI

HENLEY

ANTOINE

FENTON

SINHA

LOOK

ZIMMER

GANNON

MOSELEY

MUSA

LAZAR

PAYTON

TOLENTINO

CORMIER

PACK

RAJA

DOBBS

HOBSON

BLACKMON

MEEHAN

ECKERT

DENT

CASANOVA

HATHAWAY

BOOK

CHAVARRIA

BLOUNT

HUMAN

DOLL

STAN

INSTITUTE

SOTELO

CALVERT

MILLAN

BABCOCK

INMAN

CLINTON

PAULINO

PINO

CEZAR

NARVAEZ

AMARO

COUTURE

GOYAL

POLANCO

ASHBY

ADAIR

BRANTLEY

TRINH

BARRAGAN

CHADWICK

ROMANIA

SPIVEY

FONTAINE

HUNG

AGENT

JUDD

NAYLOR

GERALDO

SANABRIA

REGISTRATION

BARCLAY

CAMPO

NORIEGA

CENTRO

SHUKLA

PETTIT

QUESADA

JNIOR

COLES

YAP

EPSTEIN

SUMNER

TEJADA

PARIKH

LAIRD

WILKES

NOOR

FOUNTAIN

MOTT

OAKLEY

JAVED

SCHERER

RENDON

GRANGER

VIGIL

FAYE

REYNOSO

JONATHAN

CARON

YOST

HENRIQUEZ

BELLAMY

KEEN

HINKLE

IRVING

TRINIDAD

BAUMANN

KWAN

VITALE

RALPH

BAHIA

DIEHL

YOUTH

HURT

DOSS

MONTANO

SMYTH

HYATT

LISBOA

ZELAYA

CRUISES

LOS

PAULSON

BAUMAN

PARTNER

CHESTER

PALACIO

HUMPHRIES

BALLESTEROS

ADEL

HAM

LAN

COLOMBO

GHOSH

STALEY

MENENDEZ

GRACIELA

FOOTE

GRANDE

ANTON

USMAN

BARONE

MAGNO

FEEDBACK

HIGHTOWER

CORDOBA

PERDOMO

CARRINGTON

HOFF

TOBIAS

CARLO

LORENZ

BEAVER

DUTTON

DUPONT

MAIER

CHEVROLET

LOZADA

MCKINNON

ASHTON

MOTOR

BAPTISTE

HERNAN

AKHTAR

KAUFFMAN

LYNNE

TIDWELL

PARR

STAPLETON

MICHAUD

SEGOVIA

OAKES

SOLORZANO

FUCHS

ROOT

DIALLO

DANGELO

LAGOS

NICK

COPE

BRIONES

DURAND

SONIA

GONZAGA

HAWTHORNE

JENNY

SCHMID

SHIPLEY

CARDOZO

YOLANDA

TELES

ARRINGTON

HOUSER

SHEETS

BEVERLY

HELTON

HAIDER

HORVATH

MED

HURD

KILGORE

SAINI

BOUTIQE

SIMES

PARA

URBANO

HODGSON

MARIS

BOTELHO

PUTNAM

RENNER

WRAY

DIETZ

DUGGAN

MCNALLY

HUNTERS

EPPS

AMERICAN

COREY

SULTAN

CERQUEIRA

ION

RING

JIANG

ADM

BAER

MACRI

RYDER

ESTELA

BANDA

ROS

WHALEY

HAMLIN

ORDOEZ

TARGET

DOW

LANDERS

BACH

HARMAN

GOODRICH

LINTON

SHOES

CAVANAUGH

SADE

NATALIA

AKBAR

BLACKMAN

MORELAND

ESTRELLA

GOINS

WHITMAN

BARTLEY

CONSULTORIA

PRESCOTT

OLIVERA

MULLIGAN

COUGHLIN

ROBERTA

HAUSER

PARRY

CHANCE

TRENT

CLOUD

MUIR

NAGEL

GAMEZ

STRINGER

BUTTS

ISAACS

BOUCHARD

DALLAS

DICKENS

ZUIGA

HAYWOOD

BRYSON

MARCIO

JEN

VALDIVIA

MADSEN

AYRES

HARTMANN

LINHAS

CUZ

MEMBERSHIP

TIERNEY

IYER

DOCTOR

SAPP

SAYED

PETIT

FERRARA

BERRIOS

STEINBERG

BOLDEN

ALTAMIRANO

MESSINA

BURKETT

MALLORY

CRAVEN

STAPLES

MOREAU

MARX

SHIPPING

SHELLEY

VALERIA

LIVING

SALTER

PURDY

STEEL

MCCRACKEN

TERRA

JUDITH

GAVIN

EUBANKS

ANDY

YANEZ

HWANG

AFONSO

GUIDRY

MARTN

MEI

HILFIGER

ALTMAN

ORANGE

VIAJES

DELLA

ORNELAS

LANDIS

MCCAIN

CUTLER

COURT

NEWSLETTERS

BREEN

BARNHART

FRANZ

SAINT

COUSIN

EMANUEL

DEJESUS

MONTE

ESCAMILLA

BURROUGHS

WENDY

COMPRAS

BUNCH

CASINO

IRVIN

FOUNDATION

AWAD

HENNING

MCCLENDON

PEDRAZA

TRANSPORT

PHILLIP

THAKUR

ELEMENTARY

HAGER

TIMMONS

ROMEO

ALONZO

ANDERS

PEREYRA

BRUNNER

HOUSING

VELOSO

YUSUF

RAMEY

FEDERICO

PEOPLES

POIRIER

RICKS

RICKETTS

GHEORGHE

STOREY

YUEN

APARICIO

TITUS

MISTRY

KAMINSKI

THACKER

SANTORO

CONOSCO

MUTUAL

NACIONAL

CLOTHING

ROA

CADENA

JEROME

GRAPHICS

ENNIS

ENGENHARIA

GREGORIO

FAROOQ

PASCAL

SARAIVA

LOURENO

WING

PICKERING

CASILLAS

FAITH

MCCORD

VIDA

CONNIE

CHEW

SAMS

ELIZONDO

VALLADARES

SHORE

PORTAL

COLIN

RASHEED

BOLAND

SANTO

MNDEZ

EASON

WELLER

HERNDON

GUZMN

LOVETT

CHISHOLM

BARB

MENSAH

GRAYSON

CONSULTANTS

SHAHID

SOLAR

DONOHUE

OVERTON

WAKEFIELD

COACH

LAWTON

SEVILLA

FELTON

ALLEY

JUSTIN

BIRCH

CORLEY

LEGAL

MAM

ULRICH

REAGAN

MUNRO

EASTMAN

MORLEY

CONTE

MATHUR

MARTINI

BERNARDES

FONTENOT

OAKS

TOMA

PENDLETON

JON

BAPTISTA

DILL

MENON

ENGLE

LAWLER

CYCLES

RESORT

ASLAM

MCNULTY

RENATA

JARDIM

DAMICO

PRODUCTS

LANGSTON

LEROY

ESPERANZA

MANSOUR

SCHILLING

COUNCIL

LAL

RUBY

IONUT

CHOICE

TSANG

HARGROVE

FLOREZ

WILD

MOSTAFA

AUCTIONS

SAC

BOURGEOIS

COMPUTER

CHING

MOJICA

MUNSON

MERINO

IRM

GRUBER

VEIGA

POLO

ALDANA

PRINTER

PUENTE

CROFT

NISSAN

TATIANA

STORM

GARZON

ALINE

RAMSAY

AGUSTIN

HANKINS

CRENSHAW

MESSER

ACUA

KEENE

STARKS

MAYORGA

CHILD

IVY

YOUNGBLOOD

JEFFERS

HAMEED

WHITTINGTON

SPAULDING

ARRIAGA

TOWN

PRITCHETT

THIAGO

COONEY

ROUSSEAU

CROWELL

RODAS

JANSSEN

FORRESTER

HOOKER

DEMARCO

TRACEY

MIMS

DOWD

GEORGES

BOCK

PFEIFFER

DAVEY

WASHBURN

BOSCO

CARRIER

WHITLOCK

PIA

RAHIM

MANZANO

VARNER

SAUER

FLINT

CERDA

LIND

AMIGA

CAPUTO

SCHULER

CABLE

REARDON

WORTHINGTON

HERRMANN

LEMON

DAGOSTINO

HILLMAN

BLANK

DOUGLASS

LADD

POSEY

MCNEAL

VALERIO

TAMMY

EMILIA

ROWAN

ASSISTANCE

TROY

VILLAR

GOULART

ARANGO

LASER

SHIN

BRAZ

RUSHING

PATERSON

MALHOTRA

MCNAIR

SAMIR

ZHENG

PARISH

CHUN

ETIENNE

ROBB

MONIQUE

BUSBY

PERRIN

SONS

CATALIN

LEVI

KEYES

CORRIGAN

OSPINA

RENTERIA

MIRZA

WETZEL

BENTO

WHELAN

CORONEL

YOUSSEF

MALLOY

KEANE

MARKETPLACE

BANSAL

LAUGHLIN

HARE

TRIVEDI

MAK

STONER

LINO

MACLEOD

JILL

BAYER

BURNHAM

HOLLY

BANCO

NAIK

IRIZARRY

FREECYCLE

THOMASON

PARKINSON

DUVALL

ROBLEDO

THAYER

PAMELA

HARLEY

DUNNE

CANDIDO

RUFF

CONTATO

SALON

FIERRO

FAUST

CRAIN

REPAIR

CRANDALL

MATHIEU

DEVLIN

ARIF

CHOU

LACKEY

FOOT

GODINEZ

PTE

NAPIER

RICHEY

CLANCY

BIANCO

LEARY

HUMPHREYS

FEITOSA

REBECCA

JUNE

GALICIA

CAROLYN

WALLIS

SALE

ANSWER

LEASING

IRIS

SOMMER

NANA

JONAS

TSAI

LEHMANN

KEARNS

VACATION

CHECK

PAK

HUBERT

SURVEY

MCCOLLUM

OSHEA

WHITMORE

CEPEDA

JOSHUA

MEHMOOD

GREENFIELD

NICOLAE

DELL

FALCO

SANTANDER

ABAD

SPRING

GIPSON

ISLAND

DOVE

RAPP

TELLO

AMATO

LUNDY

CULVER

WOODY

LAZO

SHELL

SNEED

FRANCES

RANSOM

ANG

CORRALES

AKINS

CIFUENTES

BAIG

DES

LILIA

EARLY

DOMINGOS

SPICER

BOURNE

JOHNSTONE

PATRICIO

WAREHOUSE

SCHRADER

BARTHOLOMEW

YBARRA

DOTY

FLOR

VIVIANA

HOUGH

PEGGY

LODGE

FARRAR

MAS

LANCE

FABER

PARMAR

LEAHY

ALDRICH

CATES

MONAHAN

JIN

HELM

BORDEN

ALFRED

JULIANA

LYLE

DEB

SLADE

CHAUDHARY

SEGURO

LENTZ

DOMINIQUE

JOINER

RESTAURANT

PATIO

MCLAIN

MATHIAS

SCHUBERT

ABBASI

STALLINGS

KOVACS

AUNT

SQUIRES

OSWALD

CASTING

HEARN

BISPO

CAMILA

SPANGLER

EBERT

REPRESENTAES

SKELTON

KHANNA

ALL

DASH

APPLE

NUNN

HAIRSTON

WOODALL

BURR

CARBAJAL

TRIMBLE

PERSON

PRESLEY

WELLINGTON

SHEILA

BARRAZA

BRISCOE

IRVINE

CHEEK

SCHOFIELD

LAURIE

SANDER

LAWS

YOGA

YONG

DELONG

DAMIAN

KATHERINE

MARTENS

HUTSON

STOVALL

ALAIN

RHOADES

GRAFF

ZIMMERMANN

LAYNE

BRICE

NADEAU

PEPPER

SPRINGS

GIRON

IMOVEIS

BARAHONA

TAHIR

LAS

TEACHER

GRILL

LEDBETTER

KWOK

JESS

RACING

CHAMPAGNE

HYMAN

REGIONAL

RAMALHO

EMMA

GAGE

HEIN

COMER

CATALINA

TOMAS

OBAMA

PENG

CONCURSOS

SHAHZAD

ARTE

NESBITT

RAJU

AHMADI

STRANGE

NOW

DUVAL

DARNELL

OTOOLE

ELITE

DAIGLE

MARCEL

BRODERICK

PETE

COYNE

TILLEY

DELIVERY

TEXAS

MONCADA

CROOK

THURSTON

SANTILLAN

SMALLS

WOODSON

KISER

MONGE

SOURCE

SPAIN

BAGLEY

ATWOOD

BGOSH

CAT

KILPATRICK

FORTIN

FREEDMAN

NOBRE

BELANGER

DAUGHTER

MARVIN

ESTER

COLEY

KELLOGG

PAES

VITAL

CARABALLO

RUDD

GOUVEIA

SANDHU

WINNER

DURANT

NUEVO

BONNIE

ABERNATHY

SHAVER

UNGER

PRATER

THAKKAR

REN

KIMBLE

KINCAID

SHI

KARLA

BECKY

UNDERGRADUATE

NERI

DEVRIES

GOODSON

BLEDSOE

BITTENCOURT

SALLES

RADER

PANG

SALERNO

BYNUM

KINSEY

OUELLETTE

FORMAN

PATHAK

LUU

EMILY

MERCIER

LUCENA

YAO

TINSLEY

DAMASCENO

NOONAN

REICH

ERIKA

CELIA

MOE

LINN

KNOTT

BROOKE

WINSLOW

ISSA

RATE

DONATO

FACULDADE

ESPINO

ZARAGOZA

CONDON

BRANNON

CALDERN

HUMMEL

MALL

GILCHRIST

KEEGAN

POLICE

THERESA

CALLAWAY

LAVOIE

COTTRELL

MUNICIPAL

CLASS

FALK

MACLEAN

TONEY

EUGENIO

PIZARRO

KNUTSON

PANDYA

VLAD

CARIBBEAN

DEVI

GARVEY

HASKINS

JULIEN

RAPHAEL

CHVEZ

GYM

WILLOUGHBY

BORJA

GAMAL

TOTAL

FORSTER

ADMINISTRATION

MICROSOFT

LUTHER

DORIS

PYLE

DION

ALLRED

PREMIUM

ROWELL

PALUMBO

CORRAL

EASTON

VICK

TADEU

DUMONT

ELY

NORMA

ARENA

MATEO

DUPREE

JAMIESON

STAUFFER

SEAMAN

DESMOND

CAFE

CYNTHIA

COLLAZO

MENARD

MORTGAGE

CAVAZOS

MOCK

GAFFNEY

QUEVEDO

XIONG

RUFFIN

STACK

JAMAL

REDDING

NEVILLE

PRIEST

MAGDALENA

COSMETICS

AGGARWAL

SYLVIA

GRIER

BACK

ROOM

FALLON

SAS

BRUNSON

BOYKIN

ROD

PANTOJA

FIORE

PULSE

TIO

HEDRICK

CYR

SHULTZ

ARNDT MILLARD

HAKIM

SAMPLES

HOROWITZ

MARCH

SAGE

TARIQ

RINALDI

SIMOES

SHOOK

THAI

PRINGLE

FARAH

JAEGER

ARGUETA

BARBOUR

SCHAEFFER

PAQUETTE

BENEFITS

PRESIDENT

BINDER

CLEMENS

MIRIAM

ASIF

SHANE

MEANS

SOLER

STARKEY

DUBE

KELSEY

WAHL

DOZIER

MOELLER

WORTH

COHN

INFANTE

HOUGHTON

COTA

JAMESON

HARWOOD

BHATTI

CRUM

MILNER

SUREZ

CARRION

HONEY

IRMA

TENORIO

SWANN

HUSTON

FINNEY

LYLES

ANTONIA

DIGGS

UPTON

NOEMI

VYAS

LEFEBVRE

BECKMAN

MARKHAM

TEJEDA

SIMONA

MYLES

FORTUNE

BOSCH

HUDDLESTON

SECRETARIA

GRFICA

PRODUCTIONS

ROBINS

GILLETTE

HENRIQUES

DERRICK

PARADISE

PARRIS

DELACRUZ

DAI

GAME

ESTEVEZ

ELLIOT

ARSHAD

SHIPMAN

SAXENA

REDMAN

KAMARA

MOSQUERA

LAWYER

RANDY

HITCHCOCK

SGT

LERNER

HOOK

LENNON

FLORA

CALDAS

FOSS

LUONG

PARENTS

TEODORO

PARHAM

MOB

OLIVIA

PEACE

COMUNICAO

EMPLOYMENT

HORACIO

NEZ

NOTIFICATION

IMMIGRATION

APPAREL

VANN

HANKS

BIS

OLDHAM

ISABELLE

CHURCHILL

DELGADILLO

LOCKETT

SOPHIE

BRINK

CORNWELL

CHAND

PICKENS

KENYON

LEVESQUE

HADI

JEFFERY

GUO

AMIR

MILLAR

HAQUE

HECK

BABA

FLORIDA

BONE

GOETZ

MCCLELLAND

SHAWN

SALMAN

TIRADO

PERDUE

FAISAL

RABELO

PURVIS

PHELAN

CAPPS

SMALLWOOD

SALAM

HERMANN

NOE

FANG

ECHOLS

MATEUS

WENDT

BURNETTE

GYMBOREE

IOAN

NICHOLLS

HUT

LAST

DYSON

YEN

WILDE

CARNES

NICOLETA

CARY

PARADA

CUNHADA

MOREL

MARTEL

SCRUGGS

AMIGO

SHETH

REAVES

BASHIR

HOLIDAY

GOH

MOSHER

SOUTO

CHAO

RANDLE

MCCALLUM

NASIR

SIZEMORE

JUDGE

NICKERSON

MONK

HAPPY

STEARNS

LIDIA

KELLEHER

VIANNA

RENAUD

BRUNER

VALADEZ

TABOR

MEU

CARBONE

CRYSTAL

MODI

HYLTON

LOGISTICS

GUIDO

BOUDREAU

BRIDGE

BANDEIRA

NERY

SRINIVASAN

RAJAN

PARISI

LENZ

WHEATLEY

CIA

CHIANG

CECIL

SLACK

PILLAI

JERNIGAN

MUKHERJEE

JIMMY

JHA

THANH

BOUDREAUX

SEGAL

TEMPLETON

MASTERSON

GRACIA

COATS

SEE

DIEZ

COON

MCCARTNEY

WELDON

CINTRON

AREA

SEN

MCARTHUR

TIFFANY

SAMSUNG

STODDARD

COTTER

CARLIN

BADER

RADFORD

SHANKAR

JANICE

SPORT

OANA

NINA

TRIPLETT

LAING

LOUIE

FIRE

ASHER

TAHA

TOP

LOVELACE

BURNER

CLARKSON

DOUG

KRIEGER

SERVIOS

NATHALIE

NAWAZ

LATIF

CROOKS

EDMONDSON

ASSOCIATION

YIP

DORMAN

CONFIRMATION

SCANLON

VIERA

YOON

LONGORIA

RENT

FISCAL

JOAO

HANLON

TERAN

SALA

AJAYI

HARMS

MANCUSO

MEEK

MONDRAGON

RAND

SEALS

WYLIE

TEE

LUI

HEATON

ANCA

LOBATO

PATTY

AKRAM

LAUER

CBN

COOL

ALCALA

LUNSFORD

HOLGUIN

NURSE

HALIM

EDSON

DONG

AUGUSTIN

HERZOG

TSE

ABDALLAH

ANH

SORENSON

BEAUCHAMP

HONEYCUTT

ALANIZ

SCHELL

JAIRO

GUILLORY

GROGAN

SALLY

ARNETT

OFFICER

TESTA

MOLNAR

GINA

KENNETH

SPEAR

ROJO

HOOKS

GARVIN

WHITTEN

BARBA

BERLIN

ROYER

BEAM

BELLE

LEWANDOWSKI

ASKEW

PALERMO

SAHA

YVONNE

FESTAS

MARR

GALLANT

ARMOUR

DASILVA

KEMPER

ANGIE

BRANCO

GALLEGO

NASSER

TRABAJO

FABIANO

BUS

BECKETT

PANCHAL

DAO

SQUARE

JAMIL

SELL

CAN

HOGUE

SALOMON

CONNECTION

HATTON

YANCEY

CREW

BILAL

HIGGS

STEEN

CHEE

KOPP

CONNECT

TURNBULL

CALLOWAY

PORTELA

ENTERPRISE

RENTAL

OWUSU

JOHANNA

BEATTIE

JURADO

MAGANA

GALVIN

VILLALBA

ESPINAL

FABIOLA

WEINBERG

STEFFEN

LAMAR

VISTA

PALOMINO

SALISBURY

GALARZA

DIN

SOMERS

VIOLA

PROMOTIONS

EYE

SCARBOROUGH

COBURN

ALERTER

MEDLEY

STYLES

SAFETY

RIDLEY

MAIS

SAYLOR

ECHEVERRIA

REGIS

MATTSON

MCAFEE

BROUGHTON

SUZANNE

PITT

JOHANSEN

VANEGAS

FEENEY

SEAN

FAIRCHILD

AKA

GOUGH

POINTE

POSTAL

SAUL

WILES

SZABO

ARANA

DARDEN

DOBBINS

BOWIE

GLEN

MAZZA

SPEED

OPERATIONS

MWANGI

JAIMES

CHARLTON

SOMMERS

PEREA

NORA

HEALEY

PAREKH

CURLEY

FENNELL

MILAN

BURK

BIBLE

CHOPRA

FUN

CAVE

BASSO

BRETT

MIN

KARL

HARDER

NOLASCO

BACHMAN

HENNESSY

SPECIAL

KOHN

WILLEY

WITHERS

CASPER

MOHAMAD

MONACO

SOUTHERN

MAHAN

EASLEY

JEWELRY

NAVAS

WINCHESTER

ZAMAN

KOLB

SILVESTRE

FOREST

MAYBERRY

CARMO

MATEI

BURDICK

GLYNN

HAMEL

FLAVIA

HILDEBRAND

WISNIEWSKI

LAURENCE

CONN

FENG

GALVO

HANNON

SHANK

GARBER

CONCEIO

MARILYN

PELLEGRINO

ANDINO

CAGLE

PRATHER

AGNEW

RONALD

WHARTON

COSGROVE

SEQUEIRA

RODOLFO

HUBBY

RAMONA

MING

TAI

WENZEL

BEJARANO

RETAIL

REINHARDT

FORSYTHE

RESORTS

REITER

BEEBE

NAEEM

MARES

BROWER

KINGSLEY

FIT

ROCA

JEANNE

COOMBS

RESOURCE

IVERSON

CORNETT

NVC

CREATIONS

DUTTA

DAL

ELAM

KOH

VALERIE

QUINLAN

GILMAN

ROGERIO

WEATHERS

GOEL

CASTELLANO

THOM

GONSALVES

INQUIRY

LINDER

MAHARAJ

GRAND

KEEFE

SEAY

MIDDLE

BAUMGARTNER

LEDFORD

MANI

SETHI

EUGENE

MULLIN

PADRON

BERNIER

CHAPA

FAHEY

LACROIX

DURBIN

RAVI

REWARD

FRANTZ

FORT

SABINO

CAICEDO

SATO

DIABETES

KEE

LEGGETT

SABRINA

ALLARD

GANT

TOSCANO

ALERT

MARLENE

JETER

PARROTT

PESSOAL

RUST

AIKEN

CAUDILL

BABE

GAO

PICARD

FOY

OLGA

JOANNE

HIGGINBOTHAM

LIBRARY

TAIT

BIANCA

ELLSWORTH

JADHAV

WHITEHOUSE

SOLIMAN

VAL

ROAD

FORSYTH

RHOADS

FISHMAN

FRANCA

SHOESOURCE

KROLL

CULP

WINE

ELETRO

STILL

CHRISTOPHE

CON

DEBORAH

SORIN

ENQUIRIES

NAYAK

NIGERIA

PEOPLE

MABEL

ANNIE

DIZON

GARCES

NELLY

GALAN

LUC

CARTAGENA

PSYCHICS

SUBRAMANIAN

BEAULIEU

FRESH

VIVAS

MAHON

ILIE

POLLACK

BRASWELL

WILBURN

SOCIETY

HOFMANN

HORAN

PEDERSON

NADEEM

ADI

NYE

SHANAHAN

MART

RODNEY

MOTHER

NEWBERRY

BUITRAGO

POSADA

PEPE

COLLECTION

WAUGH

BARBIERI

HEINZ

WISDOM

MAT

KIMBERLY

CORPORATE

CRIS

PALM

WASHINGTON

FIELD

HARDY

FRAZIER

MAC

EFFERSON

GAINES

NDOLPH

CCLAIN

LEY

TERRELL

BATTLE

YNE

INOR

LLMAN

REMA

AIGE

SLAUGHTE

AMISON

MCCRAY

MELL

HEARD

STEWARD

COLBER

OOD

AYTON

LDEN

HILFIGER

MCCLENDON

TARK

LUNDY

RANSOM

AIRSTO

PER

MALL

REN

FFI

ZIE

LYLE

GGS

VANN

LOC

KET

KEN

SMALLWOOD

EAL

CALLOWAY

DARDEN

LEGGETT

NZALE

LUNA

PENA

JUAREZ

ALINA

VIDAL

ERVANTE

ELASC

GALLEGO

ELE

OSAS

ALIND

HUERT

TRE

AEN

NAVA

ESQUIVE

ELEO

MEXICO

ESPARZA

ARRID

MEDRAN

LVERA

BARAJAS

ZEPEDA

ENESES

ZARATE

TELLEZ

LEYVA

ARREDONDO

ANAYA

SCO

BED

NTIEL

TEL

BARRA

NTAN

GAME

ANE

RNELA

ILLA

ELIZ

COLI

ARRIAGA

VALERI

RENTERIA

GODINEZ

ALI

ZARAGOZ

DEL

ADILL

VALADEZ

ROJO

ACOBS

OWER

WOLF

ATHEWS

GATES

HAFFER

ATON

NLE

ENTLEY

RAN

DER

HAMBERLAI

FFE

MICHAELS

ODE

ENT

BEATTY

IKE

MCGINNIS

TUTTLE

DODGE

RKMAN

HUTCHINS

FERRI

ETCAL

LOCKWOO

LBROO

WILLARD

MCG

ILLIN

NKLI

OCK

IFF

TILE

HEARE

PARR

ROOT

STORM

WORTHINGTON

OUG

WHITM

BORDEN

RHOADES

LINN

THER

PYLE

EDDIN

AME

GILLETT

NWELL

KENY

PURVI

PEAR

AYL

LINDER

RTH

NYE

AIRLINE

ARGO

GAMBLE

NGUYE

STOR

PERMANENTE

LIU

YAN

LIN

PHAM

LAM

ZHAN

HUAN

RUIS

HLEY

LEUN

HUYNH

CHO

ENEE

PHAN

HAN

TAM

SONG

INTERACTIV

INT

FAN

MAI

PAN

YAN

LIANG

YEUNG

DINH

HEN

TRINH

IAN

DALL

HEN

MAK

WOK

PENG

LUU

GUO

HIAN

YIP

LUI

MIN

ENG

KHAN

SHARM

UPT

USS

JAIN

MEHTA

MALIK

BAL

AMIN

HAIKH

VERMA

AROR

GARWA

RANA

SYE

ADA

AHM

OOD

IDDIQU

ANDH

HALID

ONI

PANDEY

RAI

ALEEM

RAWAL

ANAND

PRAKA

OOR

HEIKH

SRIVASTAVA

HRE

THA

TIWAR

RAJA

PARIKH

AVE

SMA

AKHTAR

SAIN

IYER

MISTRY

FAR

OOQ

ALH

TRA

BAN

ARIF

DHAR

KHANNA

TAHIR

THAKKAR

PATHAK

BHATT

RSHA

AXENA

HETH

BASHI

NAWAZ

PAREKH

SETHI

NAYAK

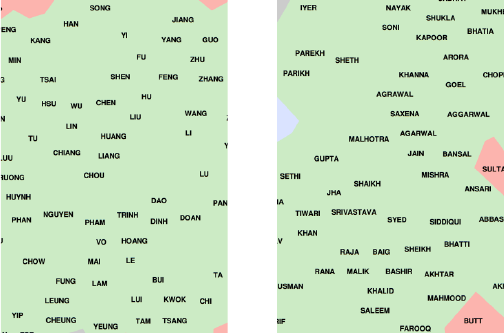
388 CHAPTER 11. MACHINE LEARNING

Figure 11.17: The two distinct Asian clusters in name space reﬂect diﬀerent

cultural groups. On the left, an inset showing Chinese/South Asian names. On

the right, an inset from the cluster of Indian family names.

The Titanic survival examples are derived from the Kaggle competition

https://www.kaggle.com/c/titanic. The war story on fake name genera-

tion is a result of work with Shuchu Han, Yifan Hu, Baris Coskun, and Meizhu

Liu at Yahoo labs.

11.9 Exercises

Classiﬁcation

11-1. [3] Using the naive Bayes classiﬁer of Figure 11.2, decide whether (Cloudy,High,

Normal) and (Sunny,Low,High) are beach days.

11-2. [8] Apply the naive Bayes technique for multiclass text classiﬁcation. Specif-

ically, use The New York Times Developer API to fetch recent articles from

several sections of the newspaper. Then, using the simple Bernoulli model for

word presence, implement a classiﬁer which, given the text of an article from

The New York Times, predicts which section the article belongs to.

11-3. [3] What is regularization, and what kind of problems with machine learning

does it solve?

Decision Trees

11-4. [3] Give decision trees to represent the following Boolean functions:

(a) Aand ¯

(b) Aor (Band C).

11.9. EXERCISES 389

11-5. [3] Suppose we are given an n×dlabeled classiﬁcation data matrix, where each

item has an associated label class A or class B. Give a proof or a counterexample

to each of the statements below:

(a) Does there always exist a decision tree classiﬁer which perfectly separates

Afrom B?

(b) Does there always exist a decision tree classiﬁer which perfectly separates

Afrom Bif the nfeature vectors are all distinct?

arates Afrom B?

(d) Does there always exist a logistic regression classiﬁer which perfectly sep-

arates Afrom Bif the nfeature vectors are all distinct?

11-6. [3] Consider a set of nlabeled points in two dimensions. Is it possible to build a

ﬁnite-sized decision tree classiﬁer with tests of the form “is x > c?”, “is x < c?”,

“is y > c?”, and “is y < c?” which classiﬁes each possible query exactly like a

nearest neighbor classiﬁer?

Support Vector Machines

11-7. [3] Give a linear-time algorithm to ﬁnd the maximum-width separating line in

one dimension.

11-8. [8] Give an O(nk+1) algorithm to ﬁnd the maximum-width separating line in k

dimensions.

11-9. [3] Suppose we use support vector machines to ﬁnd a perfect separating line

between a given set of nred and blue points. Now suppose we delete all the

points which are not support vectors, and use SVM to ﬁnd the best separator

of what remains. Might this separating line be diﬀerent than the one before?

Neural Networks

11-10. [5] Specify the network structure and node activation functions to enable a

neural network model to implement linear regression.

11-11. [5] Specify the network structure and node activation functions to enable a

neural network model to implement logistic regression.

Implementation Projects

11-12. [5] Find a data set involving an interesting sequence of symbols: perhaps text,

color sequences in images, or event logs from some device. Use word2vec to

construct symbol embeddings from them, and explore through nearest neighbor

analysis. What interesting structures do the embeddings capture?

11-13. [5] Experiment with diﬀerent discounting methods estimating the frequency of

words in English. In particular, evaluate the degree to which frequencies on

short text ﬁles (1000 words, 10,000 words, 100,000 words, and 1,000,000 words)

reﬂect the frequencies over a large text corpora, say, 10,000,000 words.

Interview Questions

11-14. [5] What is deep learning? What are some of the characteristics that distinguish

it from traditional machine learning

390 CHAPTER 11. MACHINE LEARNING

11-15. [5] When would you use random forests vs. SVMs, and why?

11-16. [5] Do you think ﬁfty small decision trees are better than a large one? Why?

11-17. [8] How would you come up with a program to identify plagiarism in documents?

Kaggle Challenges

11-18. How relevant are given search results to the user?

https://www.kaggle.com/c/crowdflower-search-relevance

11-19. Did a movie reviewer like or dislike the ﬁlm?

https://www.kaggle.com/c/sentiment-analysis-on-movie-reviews

11-20. From sensor data, determine which home appliance is currently in use.

https://www.kaggle.com/c/belkin-energy-disaggregation-competition

Chapter 12

Big Data: Achieving Scale

A change in quantity also entails a change in quality.

– Friedrich Engels

I was once interviewed on a television program, and asked the diﬀerence between

data and big data. After some thought, I gave them an answer which I will still

hold to today: “size.”

Bupkis is a marvelous Yiddish word meaning “too small to matter.” Used

in a sentence like “He got paid bupkis for it,” it is a complaint about a paltry

sum of money. Perhaps the closest analogy in English vernacular would be the

word “peanuts.”

Generally speaking, the data volumes we have dealt with thus far in this

book all amount to bupkis. Human annotated training sets run in the hundreds

to thousands of examples, but anything you must pay people to create has a

hard time running into the millions. The log of all New York taxi rides for

several years discussed in Section 1.6 came to 80 million records. Not bad, but

still bupkis: you can store this easily on your laptop, and make a scan through

the ﬁle to tabulate statistics in minutes.

The buzzword big data is perhaps reaching its expiration date, but presumes

the analysis of truly massive data sets. What big means increases with time,

but I will currently draw the starting line at around 1 terabyte.

This isn’t as impressive as it may sound. After all, as of this writing a

terabyte-scale disk will set you back only $100, which is bupkis. But acquiring

a meaningful data set to ﬁll it will take some initiative, perhaps privileged access

inside a major internet company or large volumes of video. There are plenty of

organizations wrestling with petabytes and even exabytes of data on a regular

basis.

Big data requires a larger scale of infrastructure than the projects we have

considered to date. Moving enormous volumes of data between machines re-

quires fast networks and patience. We need to move away from sequential

processing, even beyond multiple cores to large numbers of machines ﬂoating

392 CHAPTER 12. BIG DATA: ACHIEVING SCALE

in the clouds. These computations scale to the point where we must consider

robustness, because of the near certainty that some hardware component will

fail before we get our answer.

Working with data generally gets harder with size. In this section, I will try

to sensitize you to the general issues associated with massive data sets. It is

important to understand why size matters, so you will be able to contribute to

projects that operate at that scale.

12.1 What is Big Data?

How big is big? Any number I give you will be out of date by the time I

type it, but here are some 2016 statistics I stumbled across, primarily at http:

//www.internetlivestats.com/ :

•Twitter: 600 million tweets per day.

•Facebook: 600 terabytes of incoming data each day, from 1.6 billion active

users.

•Google: 3.5 billion search queries per day.

•Instagram: 52 million new photos per day.

•Apple: 130 billion total app downloads.

•Netﬂix: 125 million hours of TV shows and movies streamed daily.

•Email: 205 billion messages per day.

Size matters: we can do amazing things with this stuﬀ. But other things

also matter. This section will look at some of the technical and conceptual

complexities of dealing with big data.

Take-Home Lesson: Big data generally consists of massive numbers of rows

(records) over a relatively small number of columns (features). Thus big data

is often overkill to accurately ﬁt a single model for a given problem. The value

generally comes from ﬁtting many distinct models, as in training a custom

model personalized for each distinct user.

12.1.1 Big Data as Bad Data

Massive data sets are typically the result of opportunity, instead of design. In

traditional hypothesis-driven science, we design an experiment to gather exactly

the data we need to answer our speciﬁc question. But big data is more typi-

cally the product of some logging process recording discrete events, or perhaps

distributed contributions from millions of people over social media. The data

12.1. WHAT IS BIG DATA? 393

scientist generally has little or no control of the collection process, just a vague

charter to turn all those bits into money.

Consider the task of measuring popular opinion from the posts on a social

media platform, or online review site. Big data can be a wonderful resource.

But it is particularly prone to biases and limitations that make it diﬃcult to

draw accurate conclusions from, including:

•Unrepresentative participation: There are sampling biases inherent in any

ambient data source. The data from any particular social media site does

not reﬂect the people who don’t use it – and you must be careful not to

overgeneralize.

Amazon users buy far more books than shoppers at Walmart. Their polit-

ical aﬃliations and economic status diﬀers as well. You get equally-biased

but very diﬀerent views of the world if analyzing data from Instagram (too

young), The New York Times (too liberal), Fox News (too conservative),

or The Wall Street Journal (too wealthy).

•Spam and machine-generated content: Big data sources are worse than

unrepresentative. Often they have been engineered to be deliberately mis-

leading.

Any online platform large enough to generate enormous amounts of data

is large enough for there to be economic incentives to pervert it. Armies of

paid reviewers work each day writing fake and misleading product reviews.

Bots churn out mechanically written tweets and longer texts in volume,

and even are the primary consumers of it: a sizable fraction of the hits

reported on any website are from mechanical crawlers, instead of people.

Fully 90% of all email sent over networks is spam: the eﬀectiveness of

spam ﬁlters at several stages of the pipeline is the only reason you don’t

see more of it.

Spam ﬁltering is an essential part of the data cleaning process on any

social media analysis. If you don’t remove the spam, it will be lying to

you instead of just misleading you.

•Too much redundancy: Many human activities follow a power law distri-

bution, meaning that a very small percentage of the items account for a

large percentage of the total activity. News and social media concentrates

heavily on the latest missteps of the Kardashian’s and similar celebrities,

covering them with articles by the thousands. Many of these will be al-

most exact duplicates of other articles. How much more does the full set

of them tell you than any one of them would?

This law of unequal coverage implies that much of the data we see through

ambient sources is something we have seen before. Removing this duplica-

tion is an essential cleaning step for many applications. Any photo sharing

site will contain thousands of images of the Empire State Building, but

none of the building I work in. Training a classiﬁer with such images will

394 CHAPTER 12. BIG DATA: ACHIEVING SCALE

produce fabulous features for landmarks, that may or may not be useful

for more general tasks.

•Susceptibility to temporal bias: Products change in response to competi-

tion and changes in consumer demand. Often these improvements change

the way people use these products. A time series resulting from ambient

data collection might well encode several product/interface transitions,

which make it hard to distinguish artifact from signal.

A notorious example revolves around Google Flu Trends, which for sev-

eral years successfully forecast ﬂu outbreaks on the basis of search engine

queries. But then the model started performing badly. One factor was

that Google added an auto-complete mechanism, where it suggests rele-

vant queries during your search process. This changed the distribution of

search queries suﬃciently to make time series data from before the change

incomparable with the data that follows.

Some of these eﬀects can be mitigated through careful normalization, but

often they are baked so tightly into the data to prevent meaningful longi-

tudinal analysis.

Take-Home Lesson: Big data is data we have. Good data is data appropriate

to the challenge at hand. Big data is bad data if it cannot really answer the

questions we care about.

12.1.2 The Three Vs

Management consulting types have latched onto a notion of the three Vs of big

data as a means of explaining it: the properties of volume,variety, and velocity.

They provide a foundation to talk about what makes big data diﬀerent. The

Vs are:

•Volume: It goes without saying that big data is bigger than little data.

The distinction is one of class. We leave the world where we can represent

our data in a spreadsheet or process it on a single machine. This re-

quires developing a more sophisticated computational infrastructure, and

restricting our analysis to linear-time algorithms for eﬃciency.

•Variety: Ambient data collection typically moves beyond the matrix to

amass heterogeneous data, which often requires ad hoc integration tech-

niques.

Consider social media. Posts may well include text, links, photos, and

video. Depending upon our task, all of these may be relevant, but text

processing requires vastly diﬀerent techniques than network data and mul-

timedia. Even images and videos are quite diﬀerent beasts, not to be pro-

cessed using the same pipeline. Meaningfully integrating these materials

into a single data set for analysis requires substantial thought and eﬀort.

12.2. WAR STORY: INFRASTRUCTURE MATTERS 395

•Velocity: Collecting data from ambient sources implies that the system is

live, meaning it is always on, always collecting data. In contrast, the data

sets we have studied to date have generally been dead, meaning collected

once and stuﬀed into a ﬁle for later analysis.

Live data means that infrastructures must be built for collecting, index-

ing, accessing, and visualizing the results, typically through a dashboard

system. Live data means that consumers want real-time access to the

latest results, through graphs, charts, and APIs.

Depending upon the industry, real-time access may involve updating the

state of the database within seconds or even milliseconds of actual events.

In particular, the ﬁnancial systems associated with high-frequency trading

demand immediate access to the latest information. You are in a race

against the other guy, and you proﬁt only if you win.

Data velocity is perhaps the place where data science diﬀers most substan-

tially from classical statistics. It is what stokes the demand for advanced

system architectures, which require engineers who build for scale using the

latest technologies.

The management set sometimes deﬁnes a fourth V: veracity, a measure for

how much we trust the underlying data. Here we are faced with the problem

of eliminating spam and other artifacts resulting from the collection process,

beyond the level of normal cleaning.

12.2 War Story: Infrastructure Matters

I should have recognized the depth of Mikhail’s distress the instant he lifted his

eyebrow at me.

My Ph.D. student Mikhail Bautin is perhaps the best programmer I have

ever seen. Or you have ever seen, probably. Indeed, he ﬁnished in 1st place at

the 12th International Olympiad in Informatics with a perfect score, marking

him as the best high school-level programmer in the world that year.

At this point, our Lydia news analysis project had a substantial infrastruc-

ture, running on a bunch of machines. Text spidered from news sources around

the world was normalized and passed through a natural language processing

(NLP) pipeline we had written for English, and the extracted entities and their

sentiment were identiﬁed from the text and stored in a big database. With a

series of SQL commands this data could be extracted to a format where you

could display it on a webpage, or run it in a spreadsheet.

I wanted us to study the degree to which machine translation preserved

detectable sentiment. If so, it provided an easy way to generalize our sentiment

analysis to languages beyond English. It would be low-hanging fruit to stick

some third-party language translator into our pipeline and see what happened.

I thought this was a timely and important study, and indeed, our subsequent

paper [BVS08] has been cited 155 times as of this writing. So I gave the project

396 CHAPTER 12. BIG DATA: ACHIEVING SCALE

to my best Ph.D. student, and even oﬀered him the services of a very able mas-

ters student to help with some of the technical issues. Quietly and obediently,

he accepted the task. But he did raise his eyebrow at me.

Three weeks later he stepped into my oﬃce. The infrastructure my lab had

developed for maintaining the news analysis in our database was old-fashioned

and crufty. It would not scale. It oﬀended his sense of being. Unless I let him

rewrite the entire thing from scratch using modern technology, he was leaving

graduate school immediately. He had used his spare time during these three

weeks to secure a very lucrative job oﬀer from a world-class hedge fund, and

was stopping by to say farewell.

I can be a very reasonable man, once things are stated plainly enough. Yes,

his dissertation could be on such an infrastructure. He turned around and

immediately got down to work.

The ﬁrst thing that had to go was the central MYSQL database where all

our news and sentiment references were stored. It was a bottleneck. It could not

be distributed across a cluster of machines. He was going to store everything in

a distributed ﬁle system (HDFS) so that there was no single bottleneck: reads

and writes could happen all over our cluster.

The second thing that had to go was our jury-rigged approach to coordinat-

ing the machines in our cluster on their various tasks. It was unreliable. There

was no error-recovery mechanism. He was going to rewrite all our backend

processing as MapReduce jobs using Hadoop.

The third thing that had to go was the ad hoc ﬁle format we used to repre-

sent news articles and their annotations. It was buggy. There were exceptions

everywhere. Our parsers often broke on them for stupid reasons. This is why

G-d had invented XML, to provide a way to rigorously express structured data,

and eﬃcient oﬀ-the-shelf tools to parse it. Any text that passed through his

code was going to pass an XML validator ﬁrst. He refused to touch the disease-

ridden Perl scripts that did our NLP analysis, but isolated this code completely

enough that the infection could be contained.

With so many moving parts, even Mikhail took some time to get his infras-

tructure right. Replacing our infrastructure meant that we couldn’t advance on

any other project until it was complete. Whenever I fretted that we couldn’t

get any experimental analysis done until he was ready, he quietly reminded me

about the standing oﬀer he had from the hedge fund, and continued right on

with what he was doing.

And of course, Mikhail was right. The scale of what we could do in the lab

increased ten-fold with the new infrastructure. There was much less downtime,

and scrambling to restore the database after a power-glitch became a thing of

the past. The APIs he developed to regulate access to the data powered all our

application analysis in a convenient and logical way. His infrastructure cleanly

survived a porting to the Amazon Cloud environment, running every night to

keep up with the world’s news.

The take-home lesson here is that infrastructure matters. Most of this book

talks about higher-level concepts: statistics, machine learning, visualization –

and it is easy to get hoity-toity about what is science and what is plumbing.

12.3. ALGORITHMICS FOR BIG DATA 397

But civilization does not run right without eﬀective plumbing. Infrastructures

that are clean, eﬃcient, scalable, and maintainable, built using modern software

technologies, are essential to eﬀective data science. Operations that reduce tech-

nical debt like refactoring, and upgrading libraries/tools to currently supported

versions are not no-ops or procrastinating, but the key to making it easier to do

the stuﬀ you really want to do.

12.3 Algorithmics for Big Data

Big data requires eﬃcient algorithms to work on it. In this section, we will delve

brieﬂy into the basic algorithmic issues associated with big data: asymptotic

complexity, hashing, and streaming models to optimize I/O performance in large

data ﬁles.

I do not have the time or space here to provide a comprehensive introduction

to the design and analysis of combinatorial algorithms. However, I can conﬁ-

dently recommend The Algorithm Design Manual [Ski08] as an excellent book

on these matters, if you happen to be looking for one.

12.3.1 Big Oh Analysis

Traditional algorithm analysis is based on an abstract computer called the Ran-

dom Access Machine or RAM. On such a model:

•Each simple operation takes exactly one step.

•Each memory operation takes exactly one step.

Hence counting up the operations performed over the course of the algorithm

gives its running time.

Generally speaking, the number of operations performed by any algorithm

is a function of the size of the input n: a matrix with nrows, a text with n

words, a point set with npoints. Algorithm analysis is the process of estimating

or bounding the number of steps the algorithm takes as a function of n.

For algorithms deﬁned by for-loops, such analysis is fairly straightforward.

The depth of the nesting of these loops deﬁnes the complexity of the algorithm.

A single loop from 1 to ndeﬁnes a linear-time or O(n) algorithm, while two

nested loops deﬁnes a quadratic-time or O(n2) algorithm. Two sequential for-

loops that do not nest are still linear, because n+n= 2nsteps are used instead

of n×n=n2such operations.

Examples of basic loop-structure algorithms include:

•Find the nearest neighbor of point p: We need to compare pagainst

all npoints in a given array a. The distance computation between p

and point a[i] requires subtracting and squaring dterms, where dis the

dimensionality of p. Looping through all npoints and keeping track of

the closest point takes O(d·n) time. Since dis typically small enough to

be thought of as a constant, this is considered a linear-time algorithm.

398 CHAPTER 12. BIG DATA: ACHIEVING SCALE

•The closest pair of points in a set: We need to compare every point a[i]

against every other point a[j], where 1 ≤i6=j≤n. By the reasoning

above, this takes O(d·n2) time, and would be considered a quadratic-time

algorithm.

•Matrix multiplication: Multiplying an x×ymatrix times a y×zmatrix

results in an x×zmatrix, where each of the x·zterms is the dot product

of two y-length vectors:

C = numpy.zeros((x, z))

for i in range(0,x-1):

for j in range(0, z-1):

for k in range(0, y-1):

C[i][j] += A[i][k] * B[k][j]

This algorithm takes x·y·zsteps. If n= max(x, y, z), then this takes at

most O(n3) steps, and would be considered a cubic-time algorithm.

For algorithms which are deﬁned by conditional while loops or recursion,

the analysis often requires more sophistication. Examples, with very concise

explanations, include:

•Adding two numbers: Very simple operations might have no conditionals,

like adding two numbers together. There is no real value of nhere, only

two, so this takes constant time or O(1).

•Binary search: We seek to locate a given search key kin a sorted ar-

ray A, containing nitems. Think about searching for a name in the

telephone book. We compare kagainst the middle element A[n/2], and

decide whether what we are looking for lies in the top half or the bottom

half. The number of halvings until we get down to 1 is log2(n), as we

discussed in Section 2.4. Thus binary search runs in O(log n) time.

•Mergesort: Two sorted lists with a total of nitems can be merged into

a single sorted list in linear time: take out the smaller of the two head

elements as ﬁrst in sorted order, and repeat. Mergesort splits the nele-

ments into two halves, sorts each, and then merges them. The number of

halvings until we get down to 1 is again log2(n) (do see Section 2.4), and

merging all elements at all levels yields an O(nlog n) sorting algorithm.

This was a very fast algorithmic review, perhaps too quick for comprehen-

sion, but it did manage to provide representatives of six diﬀerent algorithm

complexity classes. These complexity functions deﬁne a spectrum from fastest

to slowest, deﬁned by the following ordering:

O(1) O(log n)O(n)O(nlog n)O(n2)O(n3).

12.3. ALGORITHMICS FOR BIG DATA 399

Take-Home Lesson: Algorithms running on big data sets must be linear or

near-linear, perhaps O(nlog n). Quadratic algorithms become impossible to

contemplate for n > 10,000.

12.3.2 Hashing

Hashing is a technique which can often turn quadratic algorithms into linear-

time algorithms, making them tractable for dealing with the scale of data we

hope to work with.

We ﬁrst discussed hash functions in the context of locality-sensitive hashing

(LSH) in Section 10.2.4. A hash function htakes an object xand maps it to a

speciﬁc integer h(x). The key idea is that whenever x=y, then h(x) = h(y).

Thus we can use h(x) as an integer to index an array, and collect all similar

objects in the same place. Diﬀerent items are usually mapped to diﬀerent places,

assuming a well-designed hash function, but there are no guarantees.

Objects that we seek to hash are often sequences of simpler elements. For

example, ﬁles or text strings are just sequences of elementary characters. These

elementary components usually have a natural mapping to numbers: character

codes like Unicode by deﬁnition map symbols to numbers, for example. The

ﬁrst step to hash xis to represent it as a sequence of such numbers, with no

loss of information. Let us assume each of the n=|S|character numbers of x

are integers between 0 and α−1.

Turning the vector of numbers into a single representative number is the job

of the hash function h(x). A good way to do this is to think of the vector as a

base-αnumber, so

h(x) =

n−1

i=0

αn−(i+1)xi(mod m).

The mod function (xmod m) returns the remainder of xdivided by m, and so

yields a number between 0 and m−1. This n-digit, base-αnumber is doomed

to be huge, so taking the remainder gives us a way to get a representative code

of modest size. The principle here is the same as a roulette wheel for gambling:

the ball’s long path around the wheel ultimately ends in one of m= 38 slots, as

determined by the remainder of the path length divided by the circumference

of the wheel.

Such hash functions are amazingly useful things. Major applications include:

•Dictionary maintenance: A hash table is an array-based data structure

using h(x) to deﬁne the position of object x, coupled with an appropriate

collision-resolution method. Properly implemented, such hash tables yield

constant time (or O(1)) search times in practice.

This is much better than binary search, and hence hash tables are widely

used in practice. Indeed, Python uses hashing below the hood to link

variable names to the values they store. Hashing is also the fundamental

400 CHAPTER 12. BIG DATA: ACHIEVING SCALE

idea behind distributed computing systems like MapReduce, which will be

discussed in Section 12.6.

•Frequency counting: A common task in analyzing logs is tabulating

the frequencies of given events, such as word counts or page hits. The

fastest/easiest approach is to set up a hash table with event types as the

key, and increment the associated counter for each new event. Properly

implemented, this algorithm is linear in the total number of events being

analyzed.

•Duplicate removal: An important data cleaning chore is identifying du-

plicate records in a data stream and removing them. Perhaps these are

all the email addresses we have of our customers, and want to make sure

we only spam each of them once. Alternately, we may seek to construct

the complete vocabulary of a given language from large volumes of text.

The basic algorithm is simple. For each item in the stream, check whether

it is already in the hash table. If not insert it, if so ignore it. Properly im-

plemented, this algorithm takes time linear in the total number of records

being analyzed.

•Canonization: Often the same object can be referred to by multiple diﬀer-

ent names. Vocabulary words are generally case-insensitive, meaning that

“The” is equivalent to “the.” Determining the vocabulary of a language

requires unifying alternate forms, mapping them to a single key.

This process of constructing a canonical representation can be interpreted

as hashing. Generally speaking, this requires a domain-speciﬁc simpliﬁ-

cation function doing such things as reduction to lower case, white space

removal, stop word elimination, and abbreviation expansion. These canon-

ical keys can then be hashed, using conventional hash functions.

•Cryptographic hashing: By constructing concise and uninvertible repre-

sentations, hashing can be used to monitor and constrain human behavior.

How can you prove that an input ﬁle remains unchanged since you last

analyzed it? Construct a hash code or checksum for the ﬁle when you

worked on it, and save this code for comparison with the ﬁle hash at any

point in the future. They will be the same if the ﬁle is unchanged, and

almost surely diﬀer if any alterations have occurred.

Suppose you want to commit to a bid on a speciﬁc item, but not reveal

the actual price you will pay until all bids are in. Hash your bid us-

ing a given cryptographic hash function, and submit the resulting hash

code. After the deadline, send your bid in again, this time without en-

cryption. Any suspicious mind can hash your now open bid, and conﬁrm

the value matches your previously submitted hash code. The key is that

it be diﬃcult to produce collisions with the given hash function, meaning

you cannot readily construct another message which will hash to the same

code. Otherwise you could submit the second message instead of the ﬁrst,

changing your bid after the deadline.

12.3. ALGORITHMICS FOR BIG DATA 401

12.3.3 Exploiting the Storage Hierarchy

Big data algorithms are often storage-bound or bandwidth-bound rather than

compute-bound. This means that the cost of waiting around for data to arrive

where it is needed exceeds that of algorithmically manipulating it to get the

desired results. It still takes half an hour to just to read 1 terabyte of data

from a modern disk. Achieving good performance can rest more on smart data

management than sophisticated algorithmics.

To be available for analysis, data must be stored somewhere in a computing

system. There are several possible types of devices to put it on, which diﬀer

greatly in speed, capacity, and latency. The performance diﬀerences between

diﬀerent levels of the storage hierarchy is so enormous that we cannot ignore it

in our abstraction of the RAM machine. Indeed, the ratio of the access speed

from disk to cache memory is roughly the same (106) as the speed of a tortoise

to the exit velocity of the earth!

The major levels of the storage hierarchy are:

•Cache memory: Modern computer architectures feature a complex sys-

tem of registers and caches to store working copies of the data actively

being used. Some of this is used for prefetching: grabbing larger blocks of

data around memory locations which have been recently accessed, in antic-

ipation of them being needed later. Cache sizes are typically measured in

megabytes, with access times between ﬁve and one hundred times faster

than main memory. This performance makes it very advantageous for

computations to exploit locality, to use particular data items intensively

in concentrated bursts, rather than intermittently over a long computa-

tion.

•Main memory: This is what holds the general state of the computation,

and where large data structures are hosted and maintained. Main memory

is generally measured in gigabytes, and runs hundreds to thousands of

times faster than disk storage. To the greatest extent possible, we need

data structures that ﬁt into main memory and avoid the paging behavior

of virtual memory.

•Main memory on another machine: Latency times on a local area net-

work run into the low-order milliseconds, making it generally faster than

secondary storage devices like disks. This means that distributed data

structures like hash tables can be meaningfully maintained across net-

works of machines, but with access times that can be hundreds of times

slower than main memory.

•Disk storage: Secondary storage devices can be measured in terabytes,

providing the capacity that enables big data to get big. Physical devices

like spinning disks take considerable time to move the read head to the

position where the data is. Once there, it is relatively quick to read a

large block of data. This motivates pre-fetching, copying large chunks of

ﬁles into memory under the assumption that they will be needed later.

402 CHAPTER 12. BIG DATA: ACHIEVING SCALE

Latency issues generally act like a volume discount: we pay a lot for the ﬁrst

item we access, but then get a bunch more very cheaply. We need to organize

our computations to take advantage of this, using techniques like:

•Process ﬁles and data structures in streams: It is important to access

ﬁles and data structures sequentially whenever possible, to exploit pre-

fetching. This means arrays are better than linked structures, because

logically-neighboring elements sit near each other on the storage device.

It means making entire passes over data ﬁles that read each item once, and

then perform all necessary computations with it before moving on. Much

of the advantage of sorting data is that we can jump to the appropriate

location in question. Realize that such random access is expensive: think

sweeping instead of searching.

•Think big ﬁles instead of directories: One can organize a corpus of doc-

uments such that each is in its own ﬁle. This is logical for humans but

slow for machines, when there are millions of tiny ﬁles. Much better is to

organize them in one large ﬁle to eﬃciently sweep through all examples,

instead of requiring a separate disk access for each one.

•Packing data concisely: The cost of decompressing data being held in

main memory is generally much smaller than the extra transfer costs for

larger ﬁles. This is an argument that it pays to represent large data ﬁles

concisely whenever you can. This might mean explicit ﬁle compression

schemes, with small enough ﬁle sizes so that they can be expanded in

memory.

It does mean designing ﬁle formats and data structures to be concisely

encoded. Consider representing DNA sequences, which are long strings

on a four-letter alphabet. Each letter/base can be represented in 2 bits,

meaning that four bases can be represented in a single 8-bit byte and

thirty-two bases in a 64-bit word. Such data-size reductions can greatly

reduce transfer times, and are worth the computational eﬀort to pack and

unpack.

We have previously touted the importance of readability in ﬁle formats

in Section 3.1.2, and hold to that opinion here. Minor size reductions are

likely not worth the loss of readability or ease of parsing. But cutting a

ﬁle size in half is equivalent to doubling your transfer rate, which may

matter in a big data environment.

12.3.4 Streaming and Single-Pass Algorithms

Data is not necessarily stored forever. Or even at all. In applications with a

very high volume of updates and activity, it may pay to compute statistics on

the ﬂy as the data emerges so we can then throw the original away.

In a streaming or single-pass algorithm, we get only one chance to view each

element of the input. We can assume some memory, but not enough to store the

12.4. FILTERING AND SAMPLING 403

bulk of the individual records. We need to decide what to do with each element

when we see it, and then it is gone.

For example, suppose we seek to compute the mean of a stream of numbers

as it passes by. This is not a hard problem: we can keep two variables: s

representing the running sum to date, and nthe number of items we have seen

so far. For each new observation ai, we add it to sand increment n. Whenever

someone needs to know the current mean µ=¯

Aof the stream A, we report the

value of s/n.

What about computing the variance or standard deviation of the stream?

This seems harder. Recall that

V(A) = σ2=Pn

i=1(ai−¯

A)2

n−1

The problem is that the sequence mean ¯

Acannot be known until we hit the

end of the stream, at which point we have lost the original elements to subtract

against the mean.

But all is not lost. Recall that there is an alternate formula for the variance,

the mean of the square minus the square of the mean:

V(a) = ( 1

i=1

(ai)2)−(¯

A)2

Thus by keeping track of a running sum of squares of the elements in addition to

nand s, we have all the material we need to compute the variance on demand.

Many quantities cannot be computed exactly under the streaming model.

An example would be ﬁnding the median element of a long sequence. Suppose

we don’t have enough memory to store half the elements of the full stream. The

ﬁrst element that we chose to delete, whatever it is, could be made to be the

median by a carefully-designed stream of elements yet unseen. We need to have

all the data simultaneously available to us to solve certain problems.

But even if we cannot compute something exactly, we can often come up with

an estimate that is good enough for government work. Important problems of

this type include identifying the most frequent items in a stream, the number

of distinct elements, or even estimating element frequency when we do not have

enough memory to keep an exact counter.

Sketching involves using what storage we do have to keep track of a partial

representation of the sequence. Perhaps this is a frequency histogram of items

binned by value, or a small hash table of values we have seen to date. The quality

of our estimate increases with the amount of memory we have to store our sketch.

Random sampling is an immensely useful tool for constructing sketches, and is

the focus of Section 12.4.

12.4 Filtering and Sampling

One important beneﬁt of big data is that with suﬃcient volume you can aﬀord

to throw most of your data away. And this can be quite worthwhile, to make

404 CHAPTER 12. BIG DATA: ACHIEVING SCALE

your analysis cleaner and easier.

I distinguish between two distinct ways to throw data away, ﬁltering and

sampling. Filtering means selecting a relevant subset of data based on a speciﬁc

criteria. For example, suppose we wanted to build a language model for an

application in the United States, and we wanted to train it on data from Twitter.

English accounts for only about one third of all tweets on Twitter, so ﬁltering

out all other languages leaves enough for meaningful analysis.

We can think of ﬁltering as a special form of cleaning, where we remove data

not because it is erroneous but because it is distracting to the matter at hand.

Filtering away irrelevant or hard-to-interpret data requires application-speciﬁc

knowledge. English is indeed the primary language in use in the United States,

making the decision to ﬁlter the data in this way perfectly reasonable.

But ﬁltering introduces biases. Over 10% of the U.S. population speaks

Spanish. Shouldn’t they be represented in the language model, amigo? It is

important to select the right ﬁltering criteria to achieve the outcome we seek.

Perhaps we might better ﬁlter tweets based on location of origin, instead of

language.

In contrast, sampling means selecting an appropriate size subset in an arbi-

trary manner, without domain-speciﬁc criteria. There are several reasons why

we may want to subsample good, relevant data:

•Right-sizing training data: Simple, robust models generally have few pa-

rameters, making big data unnecessary to ﬁt them. Subsampling your

data in an unbiased way leads to eﬃcient model ﬁtting, but is still repre-

sentative of the entire data set.

•Data partitioning: Model-building hygiene requires cleanly separating

training, testing, and evaluation data, typically in a 60%, 20%, and 20%

mix. Constructing these partitions in an unbiased manner is necessary for

the veracity of this process.

•Exploratory data analysis and visualization: Spreadsheet-sized data sets

are fast and easy to explore. An unbiased sample is representative of the

whole while remaining comprehensible.

Sampling nrecords in an eﬃcient and unbiased manner is a more subtle task

than it may appear at ﬁrst. There are two general approaches, deterministic

and randomized, which detailed in the following sections.

12.4.1 Deterministic Sampling Algorithms

Our straw man sampling algorithm will be sampling by truncation, which simply

takes the ﬁrst nrecords in the ﬁle as the desired sample. This is simple, and

has the property that it is readily reproducible, meaning someone else with the

full data ﬁle could easily reconstruct the sample.

However, the order of records in a ﬁle often encodes semantic information,

meaning that truncated samples often contain subtle eﬀects from factors such

as:

12.4. FILTERING AND SAMPLING 405

•Temporal biases: Log ﬁles are typically constructed by appending new

records to the end of the ﬁle. Thus the ﬁrst nrecords would be the oldest

available, and will not reﬂect recent regime changes.

•Lexicographic biases: Many ﬁles are sorted according to the primary key,

which means that the ﬁrst nrecords are biased to a particular population.

Imagine a personnel roster sorted by name. The ﬁrst nrecords might

consist only of the As, which means that we will probably over-sample

Arabic names from the general population, and under-sample Chinese

ones.

•Numerical biases: Often ﬁles are sorted by identity numbers, which may

appear to be arbitrarily deﬁned. But ID numbers can encode meaning.

Consider sorting the personnel records by their U.S. social security num-

bers. In fact, the ﬁrst ﬁve digits of social security numbers are generally

a function of the year and place of birth. Thus truncation leads to a

geographically and age-biased sample.

Often data ﬁles are constructed by concatenating smaller ﬁles together,

some of which may be far more enriched in positive examples than others.

In particularly pathological cases, the record number might completely

encode the class variable, meaning that an accurate but totally useless

classiﬁer may follow from using the class ID as a feature.

So truncation is generally a bad idea. A somewhat better approach is uni-

form sampling. Suppose we seek to sample n/m records out of nfrom a given

ﬁle. A straightforward approach is to start from the ith record, where iis some

value between 1 and m, and then sample every mth record starting from i.

Another way of saying this is that we output the jth record if j(mod m) = i.

Such uniform sampling provides a way to balance many concerns:

•We obtain exactly the desired number of records for our sample.

•It is quick and reproducible by anyone given the ﬁle and the values of i

and m.

•It is easy to construct multiple disjoint samples. If we repeat the process

with a diﬀerent oﬀset i, we get an independent sample.

Twitter uses this method to govern API services that provide access to

tweets. The free level of access (the spritzer hose) rations out 1% of the stream

by giving every 100th tweet. Professional levels of access dispense every tenth

tweet or even more, depending upon what you are willing to pay for.

This is generally better than truncation, but there still exist potential peri-

odic temporal biases. If you sample every mth record in the log, perhaps every

item you see will be associated with an event from a Tuesday, or at 11PM each

night. On ﬁles sorted by numbers, you are in danger of ending up with items

with the same lower order digits. Telephone numbers ending in “000” or repeat

406 CHAPTER 12. BIG DATA: ACHIEVING SCALE

digits like “8888” are often reserved for business use instead of residential, thus

biasing the sample. You can minimize the chances of such phenomenon by forc-

ing mto be a large-enough prime number, but the only certain way to avoid

sampling biases is to use randomization.

12.4.2 Randomized and Stream Sampling

Randomly sampling records with a probability presults in a selection of an

expected p·nitems, without any explicit biases. Typical random number gen-

erators return a value between 0 and 1, drawn from a uniform distribution. We

can use the sampling probability pas a threshold. As we scan each new record,

generate a new random number r. When r≤p, we accept this record into our

sample, but when r > p we ignore it.

Random sampling is a generally sound methodology, but it comes with cer-

tain technical quirks. Statistical discrepancies ensure that certain regions or

demographics will be over-sampled relative to population, however in an unbi-

ased manner and to a predictable extent. Multiple random samples will not be

disjoint, and random sampling is not reproducible without the seed and random

generator.

Because the ultimate number of sampled records depends upon randomness,

we may end up with slightly too many or too few items. If we need exactly k

items, we can construct a random permutation of the items and truncate it after

the ﬁrst k. Algorithms for constructing random permutations were discussed

in Section 5.5.1. These are simple, but require large amounts of irregular data

movement, making them potentially bad news for large ﬁles. A simpler approach

is to append a new random number ﬁeld to each record, and sort with this as

the key. Taking the ﬁrst krecords from this sorted ﬁle is equivalent to randomly

sampling exactly krecords.

Obtaining a ﬁxed size random sample from a stream is a trickier problem,

because we cannot store all the items until the end. Indeed, we don’t even know

how big nwill ultimately be.

To solve this problem, we will maintain a uniformly selected sample in an

array of size k, updated as each new element arrives from the stream. The

probability that the nth stream element belongs in the sample is k/n, and so

we will insert it into our array if random number r≤k/n. Doing so must kick

a current resident out of the table, and selecting which current array element is

the victim can be done with another call to the random number generator.

12.5 Parallelism

Two heads are better than one, and a hundred heads better than two. Com-

puting technology has matured in ways that make it increasingly feasible to

commandeer multiple processing elements on demand for your application. Mi-

croprocessors routinely have 4 cores and beyond, making it worth thinking about

parallelism even on individual machines. The advent of data centers and cloud

12.5. PARALLELISM 407

computing has made it easy to rent large numbers of machines on demand,

enabling even small-time operators to take advantage of big distributed infras-

tructures.

There are two distinct approaches to simultaneously computing with multi-

ple machines, namely parallel and distributed computing. The distinction here

is how tightly coupled the machines are, and whether the tasks are CPU-bound

or memory/IO-bound. Roughly:

•Parallel processing happens on one machine, involving multiple cores and/or

processors that communicate through threads and operating system re-

sources. Such tightly-coupled computation is often CPU-bound, limited

more by the number of cycles than the movement of data through the

machine. The emphasis is solving a particular computing problem faster

than one could sequentially.

•Distributed processing happens on many machines, using network com-

munication. The potential scale here is enormous, but most appropriate

to loosely-coupled jobs which do not communicate much. Often the goal

of distributed processing involves sharing resources like memory and sec-

ondary storage across multiple machines, more so than exploiting multiple

CPUs. Whenever the speed of reading data from a disk is the bottleneck,

we are better oﬀ having many machines reading as many diﬀerent disks

as possible, simultaneously.

In this section, we introduce the basic principles of parallel computing,

and two relatively simple ways to exploit it: data parallelism and grid search.

MapReduce is the primary paradigm for distributed computing on big data, and

will be the topic of Section 12.6.

12.5.1 One, Two, Many

Primitive cultures were not very numerically savvy, and supposedly only counted

using the words one,two, and many. This is actually a very good way to think

about parallel and distributed computing, because the complexity increases very

rapidly with the number of machines:

•One: Try to keep all the cores of your box busy, but you are working on

one computer. This isn’t distributed computing.

•Two: Perhaps you will try to manually divide the work between a few

machines on your local network. This is barely distributed computing,

and is generally managed through ad hoc techniques.

•Many: To take advantage of dozens or even hundreds of machines, per-

haps in the cloud, we have no choice but to employ a system like MapRe-

duce that can eﬃciently manage these resources.

408 CHAPTER 12. BIG DATA: ACHIEVING SCALE

Complexity increases hand-in-hand with the number of agents being coor-

dinated towards a task. Consider what changes as social gatherings scale in

size. There is a continual trend of making do with looser coordination as size

increases, and a greater chance of unexpected and catastrophic events occurring,

until they become so likely that the unexpected must be expected:

•1person: A date is easy to arrange using personal communication.

•>2persons: A dinner among friends requires active coordination.

•>10 persons: A group meeting requires that there be a leader in charge.

•>100 persons: A wedding dinner requires a ﬁxed menu, because the

kitchen cannot manage the diversity of possible orders.

•>1000 persons: At any community festival or parade, no one knows the

majority of attendees.

•>10,000 persons: After any major political demonstration, somebody

is going to spend the night in the hospital, even if the march is peaceful.

•>100,000 persons: At any large sporting event, one of the spectators

will presumably die that day, either through a heart attack [BSC+11] or

an accident on the drive home.

If some of these sound unrealistic to you, recall that the length of a typical

human life is 80 years ×365 days/year = 29,200 days. But perhaps this sheds

light on some of the challenges of parallelization and distributed computing:

•Coordination: How do we assign work units to processors, particularly

when we have more work units than workers? How do we aggregate or

combine each worker’s eﬀorts into a single result?

•Communication: To what extent can workers share partial results? How

can we know when all the workers have ﬁnished their tasks?

•Fault tolerance: How do we reassign tasks if workers quit or die? Must we

protect against malicious and systematic attacks, or just random failures?

Take-Home Lesson: Parallel computing works when we can minimize commu-

nication and coordination complexity, and complete the task with low proba-

bility of failure.

12.5. PARALLELISM 409

12.5.2 Data Parallelism

Data parallelism involves partitioning and replicating the data among multiple

processors and disks, running the same algorithm on each piece, and then col-

lecting the results together to produce the ﬁnal results. We assume a master

machine divvying out tasks to a bunch of slaves, and collecting the results.

A representative task is aggregating statistics from a large collection of ﬁles,

say, counting how often words appear in a massive text corpus. The counts for

each ﬁle can be computed independently as partial results towards the whole,

and the task of merging these resulting count ﬁles easily computed by a single

machine at the end. The primary advantage of this is simplicity, because all

counting processes are running the same program. The inter-processor com-

munication is straightforward: moving the ﬁles to the appropriate machine,

starting the job, and then reporting the results back to the master machine.

The most straightforward approach to multicore computing involves data

parallelism. Data naturally forms partitions established by time, clustering

algorithms, or natural categories. For most aggregation problems, records can

be partitioned arbitrarily, provided all subproblems will be merged together at

the end, as shown in Figure 12.1.

For more complicated problems, it takes additional work to combine the

results of these runs together later. Recall the k-means clustering algorithm

(Section 10.5.1), which has two steps:

1. For each point, identiﬁes which current cluster center is closest to it.

2. Computes the new centroid of the points now associated with it.

Assuming the points have been spread across multiple machines, the ﬁrst step

requires the master to communicate all current centers to each machine, while

the second step requires each slave to report back to the master the new centroids

of the points in its partition. The master then appropriately computes the

averages of these centroids to end the iteration.

12.5.3 Grid Search

A second approach to exploit parallelism involves multiple independent runs

on the same data. We have seen that many machine learning methods involve

parameters which impact the quality of the ultimate result, such as selecting the

right number of clusters kfor k-means clustering. Picking the best one means

trying them all, and each of these runs can be conducted simultaneously on

diﬀerent machines.

Grid search is the quest for the right meta-parameters in training. It is diﬃ-

cult to predict exactly how varying the learning rate or batch size in stochastic-

gradient descent aﬀects the quality of the ﬁnal model. Multiple independent

ﬁts can be run in parallel, and in the end we take the best one according to our

evaluation.

Eﬀectively searching the space over kdiﬀerent parameters is diﬃcult because

of interactions: identifying the best value single of each parameter separately

410 CHAPTER 12. BIG DATA: ACHIEVING SCALE

does not necessarily produce the best parameter set when combined. Typically,

reasonable minimum and maximum values for each parameter piare established

by the user, as well as the number of values tifor this parameter to be tested

at. Each interval is partitioned into equally-spaced values governed by this ti.

We then try all parameter sets which can be formed by picking one value per

interval, establishing the grid in grid search.

How much should we believe that the best model in a grid search is really

better than the others? Often there is simple variance that explains the small

diﬀerences in performance on a given test set, turning grid search into cherry-

picking for the number which makes our performance sound best. If you have

the computational resources available to conduct a grid search for your model,

feel free to go ahead, but recognize the limits of what trial-and-error can do.

12.5.4 Cloud Computing Services

Platforms such as Amazon AWS, Google Cloud, and Microsoft Azure make

it easy to rent large (or small) numbers of machines for short-term (or long-

term) jobs. They provide you with the ability to get access to exactly the right

computing resources when you need them, provided that you can pay for them,

of course.

The cost models for these service providers are somewhat complicated, how-

ever. They will typically be hourly charges for each virtual machine, as a

function of the processor type, number of cores, and main memory involved.

Reasonable machines will rent for between 10 and 50 cents/hour. You will pay

for the amount of long-term storage as a function of gigabyte/months, with dif-

ferent cost tiers depending upon access patterns. Further, you pay bandwidth

charges covering the volume of data transfer between machines and over the

web.

Spot pricing and reserved instances can lead to lower hourly costs for special

usage patterns, but with extra caveats. Under spot pricing, machines go to the

highest bidder, so your job is at risk of being interrupted if someone else needs it

more than you do. With reserved instances, you pay a certain amount up front

in order to get a lower hourly price. This makes sense if you will be needing

one computer 24/7 for a year, but not if you need a hundred computers each

for one particular day.

Fortunately, it can be free to experiment. All the major cloud providers

provide some free time to new users, so you can play with the setup and decide

on their dime whether it is appropriate for you.

12.6 MapReduce

Google’s MapReduce paradigm for distributed computing has spread widely

through open-source implementations like Hadoop and Spark. It oﬀers a simple

programming model with several beneﬁts, including straightforward scaling to

12.6. MAPREDUCE 411

Work

Result

W1W2W3

F1F2F3

worker 2 worker 3worker 1

Figure 12.1: Divide and conquer is the algorithmic paradigm of distributed

computing.

hundreds or even thousands of machines, and fault tolerance through redun-

dancy.

The level of abstraction of programming models steadily increases over time,

as reﬂected by more powerful tools and systems that hide implementation details

from the user. If you are doing data science on a multiple-computer scale,

MapReduce computing is probably going on under the hood, even if you are

not explicitly programming it.

An important class of large-scale data science tasks have the following basic

structure:

•Iterate over a large number of items, be they data records, text strings,

or directories of ﬁles.

•Extract something of interest from each item, be it the value of a particular

ﬁeld, frequency counts of each word, or the presence/absence of particular

patterns in each ﬁle.

•Aggregate these intermediate results over all items, and generate an ap-

propriate combined result.

Representatives of these class of problems include word frequency count-

ing, k-means clustering, and PageRank computations. All are solvable through

straightforward iterative algorithms, whose running times scale linearly in the

size of the input. But this can be inadequate for inputs of massive size, where the

ﬁles don’t naturally ﬁt in the memory of a single machine. Think about web-

scale problems, like word-frequency counting over billions of tweets, k-means

clustering on hundred of millions of Facebook proﬁles, and PageRank over all

websites on the Internet.

The typical solution here is divide and conquer. Partition the input ﬁles

among mdiﬀerent machines, perform the computations in parallel on each of

them, and then combine the results on the appropriate machine. Such a solution

412 CHAPTER 12. BIG DATA: ACHIEVING SCALE

works, in principle, for word counting, because even enormous text corpora will

ultimately reduce to relatively small ﬁles of distinct vocabulary words with as-

sociated frequency counts, which can then be readily added together to produce

the total counts.

But consider a PageRank computation, where for each node vwe need to

sum up the PageRank from all nodes xwhere xpoints to v. There is no way

we can cut the graph into separate pieces such that all these xvertices will sit

on the same machine as v. Getting things in the right place to work with them

is at the heart of what MapReduce is all about.

12.6.1 Map-Reduce Programming

The key to distributing such computations is setting up a distributed hash table

of buckets, where all the items with the same key get mapped to the same bucket:

•Word count: For counting the total frequency of a particular word w

across a set of ﬁles, we need to collect the frequency counts for all the ﬁles

in a single bucket associated with w. There they can be added together

to produce the ﬁnal total.

•k-means clustering: The critical step in k-means clustering is updating

the new centroid c0of the points closest to the current centroid c. After

hashing all the points pclosest to cto a single bucket associated with c,

we can compute c0in a single sweep through this bucket.

•PageRank: The new PageRank of vertex vis the sum of old PageRank

for all neighboring vertices x, where (x, v) is a directed edge in the graph.

Hashing the PageRank of xto the bucket for all adjacent vertices vcollects

all relevant information in the right place, so we can update the PageRank

in one sweep through them.

These algorithms can be speciﬁed through two programmer-written func-

tions, map and reduce:

•Map: Make a sweep through each input ﬁle, hashing or emitting key-

value pairs as appropriate. Consider the following pseudocode for the

word count mapper:

Map(String docid, String text):

for each word w in text:

Emit(w, 1);

•Reduce: Make a sweep through the set of values vassociated with a

speciﬁc key k, aggregating and processing accordingly. Pseudocode for

the word count reducer is:

12.6. MAPREDUCE 413

do your duty

do be do

be do

be there when

duty calls

Map

do: 1

your: 1

duty: 1

do: 3

be: 2

be: 1

there: 1

when: 1

duty: 1

calls: 1

Reduce

do: 4

duty: 2

there: 1

calls: 1

your: 1

be: 3

when: 1

Figure 12.2: Word count in action. Count combination has been performed

before mapping to reduce the size of the map ﬁles.

Reduce(String term, Iterator<Int>values):

int sum = 0;

for each v in values:

sum += v;

The eﬃciency of a MapReduce program depends upon many things, but one

important objective is keeping the number of emits to a minimum. Emitting a

count for each word triggers a message across machines, and this communication

and associated writes to the bucket prove costly in large quantities. The more

stuﬀ that is mapped, the more that must eventually be reduced.

The ideal is to combine counts from particular input streams locally before,

and then emit only the total for each distinct word per ﬁle. This could be

done by adding extra logic/data structures to the map function. An alternate

idea is to run mini-reducers in memory after the map phase, but before inter-

processor communication, as an optimization to reduce network traﬃc. We note

that optimization for in-memory computation is one of the major performance

advantages of Spark over Hadoop for MapReduce-style programming.

Figure 12.2 illustrates the ﬂow of a MapReduce job for word counting, using

three mappers and two reducers. Combination has been done locally, so the

counts for each word used more than once in an input ﬁle (here doc and be)

have been tabulated prior to emitting them to the reducers.

One problem illustrated by Figure 12.2 is that of mapping skew, the natural

imbalance in the amount of work assigned to each reduce task. In this toy

example, the top reducer has been assigned map ﬁles with 33% more words and

60% larger counts than its partner. For a task with a serial running time of

T, perfect parallelization with nprocessors would yield a running time of T/n.

But the running time of a MapReduce job is determined by the largest, slowest

piece. Mapper skew dooms us to a largest piece that is often substantially higher

than the average size.

414 CHAPTER 12. BIG DATA: ACHIEVING SCALE

One source of mapper skew is the luck of the draw, that it is rare to ﬂip n

coins and end up with exactly as many heads as tails. But a more serious prob-

lem is that key frequency is often power law distributed, so the most frequent

key will come to dominate the counts. Consider the word count problem, and

assume that word frequency observes Zipf’s law from Section 5.1.5. Then the

frequency of the most popular word (the) should be greater than the sum of the

thousand words ranked from 1000 to 2000. Whichever bucket the ends up in is

likely to prove the hardest one to digest.1

12.6.2 MapReduce under the Hood

All this is ﬁne. But how does a MapReduce implementation like Hadoop ensure

that all mapped items go to the right place? And how does it assign work to

processors and synchronize the MapReduce operations, all in a fault-tolerant

way?

There are two major components: the distributed hash table (or ﬁle system),

and the run-time system handling coordination and managing resources. Both

of these are detailed below.

Distributed File Systems

Large collections of computers can contribute their memory space (RAM) and

local disk storage to attack a job, not just their CPUs. A distributed ﬁle system

such as the Hadoop Distributed File System (HDFS) can be implemented as

a distributed hash table. After a collection of machines register their available

memory with the coordinating runtime system, each can be assigned a certain

hash table range that it will be responsible for. Each process doing mapping

can then ensure that the emitted items are forwarded to the appropriate bucket

on the appropriate machine.

Because large numbers of items might be mapped to a single bucket, we

may choose to represent buckets as disk ﬁles, with the new items appended to

the end. Disk access is slow, but disk throughput is reasonable, so linear scans

through ﬁles are generally manageable.

One problem with such a distributed hash table is fault tolerance: a single

machine crash could lose enough values to invalidate the entire computation.

The solution is to replicate everything for reliability on commodity hardware.

In particular, the run-time system will replicate each item on three diﬀerent

machines, to minimize the chances of losing data in a hardware failure. Once the

runtime system senses that a machine or disk is down, it gets to work replicating

the lost data from these copies to restore the health of the ﬁle system.

1This is one of the reasons the most frequent words in a language are declared stop words,

and often omitted as features in text analysis problems.

12.6. MAPREDUCE 415

MapReduce Runtime System

The other major component of MapReduce environments for Hadoop or Spark

is their runtime system, the layer of software which regulates such tasks as:

•Processor scheduling: Which cores get assigned to running which map

and reduce tasks, and on which input ﬁles? The programmer can help by

suggesting how many mappers and reducers should be active at any one

time, but the assignment of jobs to cores is up to the runtime system.

•Data distribution: This might involve moving data to an available proces-

sor that can deal with it, but recall that typical map and reduce operations

require simple linear sweeps through potentially large ﬁles. Thus moving

a ﬁle might be more expensive than just doing the computation we desire

locally.

Thus it is better to move processes to data. The runtime system should

have conﬁguration of which resources are available on which machine, and

the general layout of the network. It can make an appropriate decision of

which processes should run where.

•Synchronization: Reducers can’t run until something has been mapped to

them, and can’t complete until after the mapping is done. Spark permits

more complicated work ﬂows, beyond synchronized rounds of map and

reduce. It is the runtime system that handles this synchronization.

•Error and fault tolerance: The reliability of MapReduce requires recov-

ering gracefully from hardware and communications failures. When the

runtime system detects a worker failure, it attempts to restart the com-

putation. When this fails, it transfers the uncompleted tasks to other

workers. That this all happens seamlessly, without the involvement of

the programmer, enables us to scale computations to large networks of

machines, on the scale where hiccups become likely instead of rare events.

Layers upon Layers

Systems like HDFS and Hadoop are merely layers of software that other systems

can build on. Although Spark can be thought of as a competitor for Hadoop,

in fact it can leverage the Hadoop distributed ﬁle system and is often most

eﬃcient when doing so. These days, my students seem to spend less time writing

low-level MapReduce jobs, because they instead use software layers working at

higher levels of abstraction.

The full big data ecosystem consists of many diﬀerent species. An important

class are NoSQL databases, which permit the distribution of structured data

over a distributed network of machines, enabling you to combine the RAM and

disk from multiple machines. Further, these systems are typically designed so

you can add additional machines and resources as you need them. The cost of

this ﬂexibility is that they usually support simpler query languages than full

SQL, but still rich enough for many applications.

416 CHAPTER 12. BIG DATA: ACHIEVING SCALE

The big data software ecosystem evolves much more rapidly than the foun-

dational matters discussed in this book. Google searches and a scan of the

O’Reilly book catalog should reveal the latest technologies when you are ready

to get down to business.

12.7 Societal and Ethical Implications

Our ability to get into serious trouble increases with size. A car can cause a

more serious accident than a bicycle, and an airplane more serious carnage than

an automobile.

Big data can do great things for the world, but it also holds the power to

hurt individuals and society at large. Behaviors that are harmless on a small

scale, like scraping, become intellectual property theft in the large. Describing

the accuracy of your model in an excessively favorable light is common for Pow-

erPoint presentations, but has real implications when your model then governs

credit authorization or access to medical treatment. Losing access to your email

account is a bonehead move, but not properly securing personal data for 100

million customers becomes potentially criminal.

I end this book with a brief survey of common ethical concerns in the world

of big data, to help sensitize you to the types of things the public worries about

or should worry about:

•Integrity in communications and modeling: The data scientist serves

as the conduit between their analysis and their employer or the general

public. There is a great temptation to make our results seem stronger

than they really are, by using a variety of time-tested techniques:

–We can report a correlation or precision level, without comparing it

to a baseline or reporting a p-value.

–We can cherry pick among multiple experiments, and present only the

best results we get, instead of presenting a more accurate picture.

–We can use visualization techniques to obscure information, instead

of reveal it.

Embedded within every model are assumptions and weaknesses. A good

modeler knows what the limitations of their model are: what they trust

it to be able to do and where they start to feel less certain. An honest

modeler communicates the full picture of their work: what they know and

what they are not so sure of.

Conﬂicts of interest are a genuine concern in data science. Often, one

knows what the “right answer” is before the study, particularly the result

that the boss wants most to hear. Perhaps your results will be used to

inﬂuence public opinion, or appear in testimony before legal or govern-

mental authorities. Accurate reporting and dissemination of results are

essential behavior for ethical data scientists.

12.7. SOCIETAL AND ETHICAL IMPLICATIONS 417

•Transparency and ownership: Typically companies and research organi-

zations publish data use and retention policies to demonstrate that they

can be trusted with their customer’s data. Such transparency is impor-

tant, but has proven to be subject to change just as soon as the commercial

value of the data becomes apparent. It is often easier to get forgiveness

than to get permission.

To what extent do users own the data that they have generated? Own-

ership means that they should have the right to see what information

has been collected from them, and the ability to prevent the future use of

this material. These issues can get diﬃcult, both technically and ethically.

Should a criminal be able to demand all references to their crime be struck

from a search engine like Google? Should my daughter be able to request

removal of images of her posted by others without her permission?

Data errors can propagate and harm individuals, without allowing a mech-

anism to people to access and understand what information has been col-

lected about them. Incorrect or incomplete ﬁnancial information can ruin

somebody’s credit rating, but credit agencies are forced by law to make

each person’s record available to them and provide a mechanism to cor-

rect errors. However, data provenance is generally lost in the course of

merging ﬁles, so these updates do not necessarily get back to all derivative

products which were built from defective data. Without it, how can your

customers discover and ﬁx the incorrect information that you have about

them?

•Uncorrectable decisions and feedback loops: Employing models as hard

screening criteria can be dangerous, particularly in domains where the

model is just a proxy for what you really want to measure. Correlation

is not causation. But consider a model suggesting that it is risky to hire

a particular job candidate because people like him who live in lower-class

neighborhoods are more likely to be arrested. If all employers use such

models, these people simply won’t get hired, and are driven deeper into

poverty through no fault of their own.

These problems are particularly insidious because they are generally un-

correctable. The victim of the model typically has no means of appeal.

And the owner of the model has no way to know what they are miss-

ing, i.e. how many good candidates were screened away without further

consideration.

•Model-driven bias and ﬁlters: Big data permits the customization of

products to best ﬁt each individual user. Google, Facebook, and others

analyze your data so as to show you the results their algorithms think you

most want to see.

But these algorithms may contain inadvertent biases picked up from ma-

chine learning algorithms on dubious training sets. Perhaps the search

engine will show good job opportunities to men much more often than to

women, or discriminate on other criteria.

418 CHAPTER 12. BIG DATA: ACHIEVING SCALE

Showing you exactly what you say you want to see may prevent you from

seeing information that you really need to see. Such ﬁlters may have some

responsibility for political polarization in our society: do you see opposing

viewpoints, or just an echo chamber for your own thoughts?

•Maintaining the security of large data sets: Big data presents a bigger

target for hackers than a spreadsheet on your hard drive. We have declared

ﬁles with 100 million records to be bupkis, but that might represent per-

sonal data on 30% of the population of the United States. Data breaches

of this magnitude occur with distressing frequency.

Making 100 million people change their password costs 190 man-years of

wasted eﬀort, even if each correction takes only one minute. But most

information cannot be changed so readily: addresses, ID numbers, and

account information persist for years if not a lifetime, making the damage

from batch releases of data impossible to ever fully mitigate.

Data scientists have obligations to fully adhere to the security practices

of their organizations and identify potential weaknesses. They also have

a responsibility to minimize the dangers of security breaches through en-

cryption and anonymization. But perhaps most important is to avoid

requesting ﬁelds and records you don’t need, and (this is absolutely the

most diﬃcult thing to do) deleting data once your project’s need for it has

expired.

•Maintaining privacy in aggregated data: It is not enough to delete names,

addresses, and identity numbers to maintain privacy in a data set. Even

anonymized data can be eﬀectively de-anonymized in clever ways, by us-

ing orthogonal data sources. Consider the taxi data set we introduced in

Section 1.6. It never contained any passenger identiﬁer information in the

ﬁrst place. Yet it does provide pickup GPS coordinates to a resolution

which might pinpoint a particular house as the source, and a particu-

lar strip joint as the destination. Now we have a pretty good idea who

made that trip, and an equally good idea who might be interested in this

information if the bloke were married.

A related experiment identiﬁed particular taxi trips taken by celebrities,

so as to ﬁgure out their destination and how well they tipped [Gay14].

By using Google to ﬁnd paparazzi photographs of celebrities getting into

taxis and extracting the time and place they were taken, it was easy to

identify the record corresponding to that exact pickup as containing the

desired target.

Ethical issues in data science are serious enough that professional organiza-

tions have weighed in on best practices, including the Data Science Code of Pro-

fessional Conduct (http://www.datascienceassn.org/code-of-conduct.html)

of the Data Science Association and the Ethical Guidelines for Statistical Prac-

tices (http://www.amstat.org/about/ethicalguidelines.cfm) of the Amer-

ican Statistical Association.

12.8. CHAPTER NOTES 419

I encourage you to read these documents to help you develop your sense of

ethical issues and standards of professional behavior. Recall that people turn to

data scientists for wisdom and consul, more than just code. Do what you can

to prove worthy of this trust.

12.8 Chapter Notes

There exist no shortage of books on the topic of big data analysis. Leskovec,

Rajarman and Ullman [LRU14] is perhaps the most comprehensive of these,

and a good place to turn for a somewhat deeper treatment of the topics we

discuss here. This book and some companion videos are available at http:

//www.mmds.org.

My favorite hands-on resources on software technologies are generally books

from O’Reilly Media. In the context of this chapter, I recommend their books

on data analytics with Hadoop [BK16] and Spark [RLOW15].

O’Neil [O’N16] provides a thought-provoking look at the social dangers of

big data analysis, emphasizing the misuse of opaque models relying on proxy

data sources that create feedback loops which exacerbate the problems they are

trying to solve.

The analogy of disk/cache speeds to tortoise/escape velocity is due to Michael

Bender.

12.9 Exercises

Parallel and Distributed Processing

12-1. [3] What is the diﬀerence between parallel processing and distributed process-

ing?

12-2. [3] What are the beneﬁts of MapReduce?

12-3. [5] Design MapReduce algorithms to take large ﬁles of integers and compute:

•The largest integer.

•The average of all the integers.

•The number of distinct integers in the input.

•The mode of the integers.

•The median of the integers.

12-4. [3] Would we expect map skew to be a bigger problem when there are ten

reducers or a hundred reducers?

12-5. [3] Would we expect the problem of map skew to increase or decrease when we

combine counts from each ﬁle before emitting them?

12-6. [5] For each of the following The Quant Shop prediction challenges dream up

the most massive possible data source that might reasonably exist, who might

have it, and what biases might lurk in its view of the world.

420 CHAPTER 12. BIG DATA: ACHIEVING SCALE

(a) Miss Universe.

(b) Movie gross.

(d) Art auction price.

(e) White Christmas.

(f) Football champions.

(g) Ghoul pool.

(h) Gold/oil prices.

Ethics

12-7. [3] What are ﬁve practical ways one can go about protecting privacy in big data?

12-8. [3] What do you consider to be acceptable boundaries for Facebook to use the

data it has about you? Give examples of uses which would be unacceptable to

you. Are these forbidden by their data usage agreement?

12-9. [3] Give examples of decision making where you would trust an algorithm to

make as good or better decisions as a person. For what tasks would you trust

human judgment more than an algorithm? Why?

Implementation Projects

12-10. [5] Do the stream sampling methods we discussed really produce uniform random

samples from the desired distribution? Implement them, draw samples, and run

them through the appropriate statistical test.

12-11. [5] Set up a Hadoop or Spark cluster that spans two or more machines. Run a

basic task like word counting. Does it really run faster than a simple job on one

machine? How many machines/cores do you need in order to win?

12-12. [5] Find a big enough data source which you have access to, that you can justify

processing with more than a single machine. Do something interesting with it.

Interview Questions

12-13. [3] What is your deﬁnition of big data?

12-14. [5] What is the largest data set that you have processed? What did you do, and

what were the results?

12-15. [8] Give ﬁve predictions about what will happen in the world over the next

twenty years?

12-16. [5] Give some examples of best practices in data science.

12-17. [5] How might you detect bogus reviews, or bogus Facebook accounts used for

bad purposes?

12-18. [5] What do the map function and the reduce function do, under the Map-Reduce

paradigm? What do the combiner and partitioner do?

12-19. [5] Do you think that the typed login/password will eventually disappear? How

might they be replaced?

12-20. [5] When a data scientist cannot draw any conclusion from a data set, what

should they say to their boss/customer?

12.9. EXERCISES 421

12-21. [3] What are hash table collisions? How can they be avoided? How frequently

do they occur?

Kaggle Challenges

12-22. Which customers will become repeat buyers?

https://www.kaggle.com/c/acquire-valued-shoppers-challenge

12-23. Which customers are worth sending junk mail to?

https://www.kaggle.com/c/springleaf-marketing-response

12-24. Which hotel should you recommend to a given traveler?

https://www.kaggle.com/c/expedia-hotel-recommendations

Chapter 13

Coda

“Begin at the beginning,” the King said, gravely, “and go on till you

come to the end: then stop.”

– Lewis Carroll

Hopefully you the reader have been at least partially enlightened by this book,

and remain excited by the power of data. The most common path to employing

these skills is to take a job in industry. This is a noble calling, but be aware

there are also other possibilities.

13.1 Get a Job!

There are very rosy predictions of the job prospects for future data scientists.

The McKinsey Global Institute projects that demand for “deep analytical talent

in the United States could be 50% to 60% greater than its projected supply by

2018.” The job placement site www.glassdoor.com informs me that as of today,

the average data scientist salary is precisely $113,436. Harvard Business Review

declared that being a data scientist is “the sexiest job of the 21st century”

[DP12]. That sounds like the place where I want to be!

But all this testimony would be much more convincing if there was some

widely shared understanding of what exactly a data scientist is. It is less obvious

to me that there are ever destined to be vast numbers of jobs with the oﬃcial

title of data scientist the way there are for, say software engineer or computer

programmer. But don’t panic.

It is fair to say that there are several diﬀerent types of jobs that relate to

data science, distinguished by the relative importance of applications knowledge

and technical strength. I see the following basic career tracks related to data

science:

•Software engineering for data science: A substantial fraction of high-end

software development positions are at big data companies like Google,

424 CHAPTER 13. CODA

Facebook, and Amazon, or data-centric companies in the ﬁnancial sector,

like banks and hedge funds. These jobs revolve around building large-

scale software infrastructures for managing data, and generally require a

degree in computer science to acquire the necessary technical skills and

experience.

•Statistician/data scientists: There has always been a diverse job market

for trained statisticians, especially in health care, manufacturing, busi-

ness, education, and the government/non-proﬁt sectors. This world will

continue to grow and thrive, although I suspect it will demand stronger

computational skills than in the past. These computational-oriented sta-

tistical analysts will have training or experience in data science, building

on a strong foundation in statistics.

•Quantitative business analysts: A large cohort of business professionals

work in marketing, sales, advertising, and management, providing essen-

tial functions at any product-based or consulting company. These careers

require a greater degree of business domain knowledge than the previous

two categories, but increasingly expect quantitative skills. They may be

hiring you to work in marketing, but demand a background or experience

in data science/analytics. Or they hire you to work in human resources,

but expect you to be able to develop metrics for job performance and

satisfaction.

The material covered in this book is essential for all three of these career

tracks, but obviously you have more to learn. The careers which are easiest to

train for also prove to be the quickest to saturate, so keep developing your skills

through coursework, projects, and practice.

13.2 Go to Graduate School!

If you ﬁnd the ideas and methods presented in this book interesting, perhaps

you are the kind of person who should think about going to graduate school.1

Technical skills age quickly without advanced training, and it can be diﬃcult to

ﬁnd the time for professional training after joining the working world.

Graduate programs in data science are rapidly emerging from host depart-

ments of computer science, statistics, business, applied mathematics, and the

like. Which type of program is most appropriate for you depends upon your un-

dergraduate training and life experiences. Depending upon their focus, data sci-

ence programs will diﬀer wildly in the computational and statistical background

they expect. Generally speaking, the technically-hardest programs in terms of

programming, machine learning, and statistics provide the best preparation for

the future. Be aware of grandiose claims from programs which minimize these

demands.

1Good for you if you are already there!

13.3. PROFESSIONAL CONSULTING SERVICES 425

Most of these programs are at the masters level, but outstanding students

who are able to make the life commitment should consider the possibility of un-

dertaking a Ph.D degree. Graduate study in computer science, machine learn-

ing, or statistics involves courses in advanced topics that build upon what you

learned as an undergraduate, but more importantly you will be doing new and

original research in the area of your choice. All reasonable American doctoral

programs will pay tuition and fees for all accepted Ph.D students, plus enough

of a stipend to live comfortably if not lavishly.

If you have a strong computer science background and the right stuﬀ, I

would encourage you to continue your studies, ideally by coming to work with

us at Stony Brook! My group does research in a variety of interesting topics

in data science, as you can tell from the war stories. Please check us out at

http://www.data-manual.com/gradstudy.

13.3 Professional Consulting Services

Algorist Technologies is a consulting ﬁrm that provides its clients with short-

term, expert help in data science and algorithm design. Typically, an Algorist

consultant is called in for one to three days worth of intensive on site discussion

and analysis with the client’s own development staﬀ. Algorist has built an

impressive record of performance improvements with several companies and

applications, as well as expert witness services and longer-term consulting.

Visit www.algorist.com/consulting for more information on the services

provided by Algorist Technologies.

Bibliography

[Abe13] Andrew Abela. Advanced Presentations by Design: Creating Communi-

cation that Drives Action. Pfeiﬀer, 2nd edition, 2013.

[Ans73] Francis J Anscombe. Graphs in statistical analysis. The American Statis-

tician, 27(1):17–21, 1973.

[Bab11] Charles Babbage. Passages from the Life of a Philosopher. Cambridge

University Press, 2011.

[Bar10] James Barron. Apple’s new device looks like a winner. From 1988. The

New York Times, January 28, 2010.

[Ben12] Edward A Bender. An Introduction to Mathematical Modeling. Courier

Corporation, 2012.

[Bis07] Christopher Bishop. Pattern Recognition and Machine Learning (Infor-

mation Science and Statistics. Springer, New York, 2007.

[BK07] Robert M. Bell and Yehuda Koren. Lessons from the Netﬂix prize chal-

lenge. ACM SIGKDD Explorations Newsletter, 9(2):75–79, 2007.

[BK16] Benjamin Bengfort and Jenny Kim. Data Analytics with Hadoop: An

Introduction for Data Scientists. O’Reilly Media, Inc., 2016.

[BP98] Serge Brin and Larry Page. The Anatomy of a Large-Scale Hypertex-

tual Web Search Engine. In Proc. 7th Int. Conf. on World Wide Web

(WWW), pages 107–117, 1998.

[Bra99] Ronald Bracewell. The Fourier Transform and its Applications.

McGraw-Hill, 3rd edition, 1999.

[Bri88] E. Oran Brigham. The Fast Fourier Transform. Prentice Hall, Engle-

wood Cliﬀs NJ, facimile edition, 1988.

[BSC+11] M. Borjesson, L. Serratosa, F. Carre, D. Corrado, J. Drezner, D. Dug-

more, H. Heidbuchel, K. Mellwig, N. Panhuyzen-Goedkoop, M. Pa-

padakis, H. Rasmusen, S. Sharma, E. Solberg, F. van Buuren, and

A. Pelliccia. Consensus document regarding cardiovascular safety at

sports arenas. European Heart Journal, 32:2119–2124, 2011.

[BT08] Dimitri Bertsekas and John Tsitsklis. Introduction to Probability. Athena

Scientiﬁc, 2nd edition, 2008.

428 CHAPTER 14. BIBLIOGRAPHY

[BVS08] Mikhail Bautin, Lohit Vijayarenu, and Steven Skiena. International Sen-

timent Analysis for News and Blogs. In Proceedings of the International

Conference on Weblogs and Social Media, Seattle, WA, April 2008.

[BWPS10] Mikhail Bautin, Charles B Ward, Akshay Patil, and Steven S Skiena.

Access: news and blog analysis for the social sciences. In Proceedings

of the 19th International Conference on World Wide Web, pages 1229–

1232. ACM, 2010.

[CPS+08] J Robert Coleman, Dimitris Papamichail, Steven Skiena, Bruce Futcher,

Eckard Wimmer, and Steﬀen Mueller. Virus attenuation by genome-scale

changes in codon pair bias. Science, 320(5884):1784–1787, 2008.

[CPS15] Yanqing Chen, Bryan Perozzi, and Steven Skiena. Vector-based similar-

ity measurements for historical ﬁgures. In International Conference on

Similarity Search and Applications, pages 179–190. Springer, 2015.

[dBvKOS00] Mark de Berg, Mark van Kreveld, Mark Overmars, and Otfried

Schwarzkopf. Computational Geometry: Algorithms and Applications.

Springer, 2nd edition, 2000.

[DDKN11] Sebastian Deterding, Dan Dixon, Rilla Khaled, and Lennart Nacke. From

game design elements to gamefulness: deﬁning gamiﬁcation. In Proceed-

ings of the 15th International Academic MindTrek Conference: Envi-

sioning future media environments, pages 9–15. ACM, 2011.

[Don15] David Donoho. 50 years of data science. Tukey Centennial Workshop,

Princeton NJ, 2015.

[DP12] Thomas H Davenport and DJ Patil. Data scientist. Harvard Business

Review, 90(5):70–76, 2012.

[EK10] David Easley and Jon Kleinberg. Networks, Crowds, and Markets: Rea-

soning about a highly connected world. Cambridge University Press, 2010.

[ELLS11] Brian Everitt, Sabine Landau, Mmorven Leese, and Daniel Stahl. Cluster

Analysis. Wiley, 5th edition, 2011.

[ELS93] Peter Eades, X. Lin, and William F. Smyth. A fast and eﬀective heuristic

for the feedback arc set problem. Information Processing Letters, 47:319–

323, 1993.

[FCH+14] Matthew Faulkner, Robert Clayton, Thomas Heaton, K Mani Chandy,

Monica Kohler, Julian Bunn, Richard Guy, Annie Liu, Michael Olson,

MingHei Cheng, et al. Community sense and response systems: Your

phone as quake detector. Communications of the ACM, 57(7):66–75,

2014.

[Few09] Stephen Few. Now You See It: simple visualization techniques for quan-

titative analysis. Analytics Press, Oakland CA, 2009.

[FHT01] Jerome Friedman, Trevor Hastie, and Robert Tibshirani. The Elements

of Statistical Learning. Springer, 2001.

[FPP07] David Freedman, Robert Pisani, and Roger Purves. Statistics. WW

Norton & Co, New York, 2007.

[Gay14] C. Gayomali. NYC taxi data blunder reveals which celebs don’t tip

and who frequents strip clubs. http://www.fastcompany.com/3036573/,

October 2. 2014.

429

[GBC16] Ian Goodfellow, Yoshua Bengio, and Aaron Courville. Deep Learning.

MIT Press, 2016.

[GFH13] Frank R. Giordano, William P. Fox, and Steven B. Horton. A First

Course in Mathematical Modeling. Nelson Education, 2013.

[Gle96] James Gleick. A bug and a crash: sometimes a bug is more than a

nuisance. The New York Times Magazine, December 1, 1996.

[GMP+09] Jeremy Ginsberg, Matthew H Mohebbi, Rajan S Patel, Lynnette Bram-

mer, Mark S Smolinski, and Larry Brilliant. Detecting inﬂuenza epi-

demics using search engine query data. Nature, 457(7232):1012–1014,

2009.

[Gol16] David Goldenberg. The biggest dinosaur in history may never have ex-

isted. FiveThirtyEight, http://ﬁvethirtyeight.com/features/the-biggest-

dinosaur-in-history-may-never-have-existed/, January 11, 2016.

[Gru15] Joel Grus. Data Science from Scratch: First principles with Python.

O’Reilly Media, Inc., 2015.

[GSS07] Namrata Godbole, Manja Srinivasaiah, and Steven Skiena. Large-scale

sentiment analysis for news and blogs. Int. Conf. Weblogs and Social

Media, 7:21, 2007.

[HC88] Diane F Halpern and Stanley Coren. Do right-handers live longer? Na-

ture, 333:213, 1988.

[HC91] Diane F Halpern and Stanley Coren. Handedness and life span. N Engl

J Med, 324(14):998–998, 1991.

[HS10] Yancheng Hong and Steven Skiena. The wisdom of bookies? sentiment

analysis vs. the NFL point spread. In Int. Conf. on Weblogs and Social

Media, 2010.

[Huf10] Darrell Huﬀ. How to Lie with Statistics. WW Norton & Company, 2010.

[Ind04] Piotr Indyk. Nearest neighbors in high-dimensional spaces. In J. Good-

man and J. O’Rourke, editors, Handbook of Discrete and Computational

Geometry, pages 877–892. CRC Press, 2004.

[Jam10] Bill James. The New Bill James Historical Baseball Abstract. Simon and

Schuster, 2010.

[JLSI99] Vic Jennings, Bill Lloyd-Smith, and Duncan Ironmonger. Household

size and the Poisson distribution. J. Australian Population Association,

16:65–84, 1999.

[Joa02] Thorsten Joachims. Optimizing search engines using clickthrough data.

In Proceedings of the Eighth ACM SIGKDD International Conference on

Knowledge Discovery and Data Mining, pages 133–142. ACM, 2002.

[Joh07] Steven Johnson. The Ghost Map: The story of London’s most terrifying

epidemic – and how it changed science, cities, and the modern world.

Riverhead Books, 2007.

[JWHT13] Gareth James, Daniela Witten, Trevor Hastie, and Robert Tibshirani.

An Introduction to Statistical Learning. Springer-Verlag, sixth edition,

2013.

[Kap12] Karl M Kapp. The Gamiﬁcation of Learning and Instruction: Game-

based methods and strategies for training and education. Wiley, 2012.

430 CHAPTER 14. BIBLIOGRAPHY

[KARPS15] Vivek Kulkarni, Rami Al-Rfou, Bryan Perozzi, and Steven Skiena. Sta-

tistically signiﬁcant detection of linguistic change. In Proceedings of

the 24th International Conference on World Wide Web, pages 625–635.

ACM, 2015.

[KCS08] Aniket Kittur, Ed H Chi, and Bongwon Suh. Crowdsourcing user studies

with mechanical turk. In Proceedings of the SIGCHI Conference on

Human Factors in Computing Systems, pages 453–456. ACM, 2008.

[KKK+10] Slava Kisilevich, Milos Krstajic, Daniel Keim, Natalia Andrienko, and

Gennady Andrienko. Event-based analysis of people’s activities and be-

havior using ﬂickr and panoramio geotagged photo collections. In 2010

14th International Conference Information Visualisation, pages 289–296.

IEEE, 2010.

[Kle13] Phillip Klein. Coding the Matrix: Linear Algebra through Computer

Science Applications. Newtonian Press, 2013.

[KSG13] Michal Kosinski, David Stillwell, and Thore Graepel. Private traits and

attributes are predictable from digital records of human behavior. Proc.

National Academy of Sciences, 110(15):5802–5805, 2013.

[KTDS17] Vivek Kulkarni, Yingtao Tian, Parth Dandiwala, and Steven Skiena.

Dating documents: A domain independent approach to predict year of

authorship. Submitted for publication, 2017.

[Lei07] David J. Leinweber. Stupid data miner tricks: overﬁtting the S&P 500.

The Journal of Investing, 16(1):15–22, 2007.

[Lew04] Michael Lewis. Moneyball: The art of winning an unfair game. WW

Norton & Company, 2004.

[LG14] Omer Levy and Yoav Goldberg. Neural word embedding as implicit ma-

trix factorization. In Advances in Neural Information Processing Sys-

tems, pages 2177–2185, 2014.

[LKKV14] David Lazer, Ryan Kennedy, Gary King, and Alessandro Vespignani.

The parable of Google ﬂu: traps in big data analysis. Science,

343(6176):1203–1205, 2014.

[LKS05] Levon Lloyd, Dimitrios Kechagias, and Steven Skiena. Lydia: A system

for large-scale news analysis. In SPIRE, pages 161–166, 2005.

[LLM15] David Lay, Steven Lay, and Judi McDonald. Linear Algebra and its

Applications. Pearson, 5th edition, 2015.

[LM12] Amy Langville and Carl Meyer. Who’s #1? The Science of Rating and

Ranking. Princeton Univ. Press, 2012.

[LRU14] Jure Leskovec, Anand Rajaraman, and Jeﬀrey David Ullman. Mining of

Massive Datasets. Cambridge University Press, 2014.

[Mal99] Burton Gordon Malkiel. A Random Walk Down Wall Street: Including

a life-cycle guide to personal investing. WW Norton & Company, 1999.

[MAV+11] J. Michel, Y. Shen A. Aiden, A. Veres, M. Gray, Google Books Team,

J. Pickett, D. Hoiberg, D. Clancy, P. Norvig, J. Orwant, S. Pinker,

M. Nowak, and E. Aiden. Quantitative analysis of culture using millions

of digitized books. Science, 331:176–182, 2011.

431

[MBL+06] Andrew Mehler, Yunfan Bao, Xin Li, Yue Wang, and Steven Skiena.

Spatial Analysis of News Sources. In IEEE Trans. Vis. Comput. Graph.,

volume 12, pages 765–772, 2006.

[MCCD13] Tomas Mikolov, Kai Chen, Greg Corrado, and Jeﬀrey Dean. Eﬃ-

cient estimation of word representations in vector space. arXiv preprint

arXiv:1301.3781, 2013.

[McK12] Wes McKinney. Python for Data Analysis: Data wrangling with Pandas,

NumPy, and IPython. O’Reilly Media, Inc., 2012.

[McM04] Chris McManus. Right Hand, Left Hand: The origins of asymmetry in

brains, bodies, atoms and cultures. Harvard University Press, 2004.

[MCP+10] Steﬀen Mueller, J Robert Coleman, Dimitris Papamichail, Charles B

Ward, Anjaruwee Nimnual, Bruce Futcher, Steven Skiena, and Eckard

Wimmer. Live attenuated inﬂuenza virus vaccines by computer-aided

rational design. Nature Biotechnology, 28(7):723–726, 2010.

[MOR+88] Bartlett W Mel, Stephen M Omohundro, Arch D Robison, Steven S

Skiena, Kurt H. Thearling, Luke T. Young, and Stephen Wolfram.

Tablet: personal computer of the year 2000. Communications of the

ACM, 31(6):638–648, 1988.

[NYC15] Anh Nguyen, Jason Yosinski, and Jeﬀ Clune. Deep neural networks are

easily fooled: High conﬁdence predictions for unrecognizable images. In

Computer Vision and Pattern Recognition (CVPR), 2015 IEEE Confer-

ence on, pages 427–436. IEEE, 2015.

[O’N16] Cathy O’Neil. Weapons of Math Destruction: How big data increases

inequality and threatens democracy. Crown Publishing Group, 2016.

[O’R01] Joseph O’Rourke. Computational Geometry in C. Cambridge University

Press, New York, 2nd edition, 2001.

[Pad15] Sydney Padua. The Thrilling Adventures of Lovelace and Babbage: The

(mostly) true story of the ﬁrst computer. Penguin, 2015.

[PaRS14] Bryan Perozzi, Rami al Rfou, and Steven Skiena. Deepwalk: Online

learning of social representations. In Proceedings of the 20th ACM

SIGKDD International Conference on Knowledge Discovery and Data

Mining, pages 701–710. ACM, 2014.

[PFTV07] William Press, Brian Flannery, Saul Teukolsky, and William T. Vetter-

ling. Numerical Recipes: The art of scientiﬁc computing. Cambridge

University Press, 3rd edition, 2007.

[PSM14] Jeﬀrey Pennington, Richard Socher, and Christopher D. Manning.

Glove: Global vectors for word representation. In Empirical Methods

in Natural Language Processing (EMNLP), pages 1532–1543, 2014.

[RD01] Ed Reingold and Nachum Dershowitz. Calendrical Calculations: The

Millennium Edition. Cambridge University Press, New York, 2001.

[RLOW15] Sandy Ryza, Uri Laserson, Sean Owen, and Josh Wills. Advanced An-

alytics with Spark: Patterns for Learning from Data at Scale. O’Reilly

Media, Inc., 2015.

[Sam05] H. Samet. Multidimensional spatial data structures. In D. Mehta and

S. Sahni, editors, Handbook of Data Structures and Applications, pages

16:1–16:29. Chapman and Hall/CRC, 2005.

432 CHAPTER 14. BIBLIOGRAPHY

[Sam06] Hanan Samet. Foundations of Multidimensional and Metric Data Struc-

tures. Morgan Kaufmann, 2006.

[SAMS97] George N Sazaklis, Esther M Arkin, Joseph SB Mitchell, and Steven S

Skiena. Geometric decision trees for optical character recognition. In

Proceedings of the 13th Annual Symposium on Computational Geometry,

pages 394–396. ACM, 1997.

[SF12] Gail M. Sullivan and Richard Feinn. Using eﬀect size: or why the pvalue

is not enough. J. Graduate Medical Education, 4:279282, 2012.

[Sil12] Nate Silver. The Signal and the Noise: Why so many predictions fail-but

some don’t. Penguin, 2012.

[Ski01] S. Skiena. Calculated Bets: Computers, Gambling, and Mathematical

Modeling to Win. Cambridge University Press, New York, 2001.

[Ski08] S. Skiena. The Algorithm Design Manual. Springer-Verlag, London,

second edition, 2008.

[Ski12] Steven Skiena. Redesigning viral genomes. Computer, 45(3):0047–53,

2012.

[SMB+99] Arthur G Stephenson, Daniel R Mulville, Frank H Bauer, Greg A Duke-

man, Peter Norvig, Lia S LaPiana, Peter J Rutledge, David Folta, and

Robert Sackheim. Mars climate orbiter mishap investigation board phase

i report. NASA, Washington, DC, page 44, 1999.

[SRS+14] Paolo Santi, Giovanni Resta, Michael Szell, Stanislav Sobolevsky,

Steven H Strogatz, and Carlo Ratti. Quantifying the beneﬁts of ve-

hicle pooling with shareability networks. Proceedings of the National

Academy of Sciences, 111(37):13290–13294, 2014.

[SS15] Oleksii Starov and Steven Skiena. GIS technology supports taxi tip

prediction. Esri Map Book, 2014 User Conference, July 14-17, San Diego,

2015.

[Str11] Gilbert Strang. Introduction to Linear Algebra. Wellesley-Cambridge

Press, 2011.

[Sur05] James Surowiecki. The wisdom of crowds. Anchor, 2005.

[SW13] Steven S. Skiena and Charles B. Ward. Who’s Bigger?: Where Historical

Figures Really Rank. Cambridge University Press, 2013.

[Tij12] Henk Tijms. Understanding Probability. Cambridge University Press,

2012.

[Tuc88] Alan Tucker. A Uniﬁed Introduction to Linear Algebra: Models, methods,

and theory. Macmillan, 1988.

[Tuf83] Edward R Tufte. The Visual Display of Quantitative Information.

Graphics Press, Cheshire, CT, 1983.

[Tuf90] Edward R Tufte. Envisioning Information. Graphics Press, Cheshire,

CT, 1990.

[Tuf97] Edward R Tufte. Visual Explanations. Graphics Press, Cheshire, CT,

1997.

[VAMM+08] Luis Von Ahn, Benjamin Maurer, Colin McMillen, David Abraham, and

Manuel Blum. recaptcha: Human-based character recognition via web

security measures. Science, 321(5895):1465–1468, 2008.

433

[Vig15] Tyler Vigen. Spurious Correlations. Hatchette Books, 2015.

[Wat16] Thayer Watkins. Arrow’s impossibility theorem for ag-

gregating individual preferences into social preferences.

http://www.sjsu.edu/faculty/watkins/arrow.htm, 2016.

[Wea82] Warren Weaver. Lady Luck. Dover Publications, 1982.

[Wei05] Sanford Weisberg. Applied linear regression, volume 528. Wiley, 2005.

[Wes00] Doug West. Introduction to Graph Theory. Prentice-Hall, Englewood

Cliﬀs NJ, second edition, 2000.

[Whe13] Charles Wheelan. Naked Statistics: Stripping the dread from the data.

WW Norton & Company, 2013.

[ZS09] Wenbin Zhang and Steven Skiena. Improving movie gross prediction

through news analysis. In Proceedings of the 2009 IEEE/WIC/ACM

International Joint Conference on Web Intelligence and Intelligent Agent

Technology-Volume 01, pages 301–304. IEEE Computer Society, 2009.

[ZS10] Wenbin Zhang and Steven Skiena. Trading strategies to exploit blog and

news sentiment. In Proc. Int. Conf. Weblogs and Social Media (ICWSM),

2010.

Index

A/B testing, 86

Aaron Schwartz case, 68

AB testing, 137

academic data, 66

accuracy, 215, 228

activation function, 380

AdaBoost, 364

add-one discounting, 357

agglomerative cluster trees, 338

aggregation mechanisms, 83

Akaike information criterion, 289,

335

algorithm analysis, 397

Amazon Turk, 67, 84

tasks assigned, 85

Turkers, 84

American basketball players, 97

analogies, 312

anchoring, 82

angular distance, 310

Anscombe’s Quartet, 159

AOL, 64

API, 65

Apple iPhone sales, 34

application program interfaces, 65

area under the ROC curve, 219

Aristotle, 326, 327

Arrow’s impossibility theorem, 84,

114

artifacts, 69

Ascombe quartet, 272

asking interesting questions, 4

associativity, 244

autocorrelation, 46

average link, 340

Babbage, Charles, 57, 90

backpropagation, 382

Bacon, Kevin, 9

bag of words, 14

bagging, 362

balanced training classes, 295

bar charts, 179

best practices, 181

stacked, 181

Barzun, Jacques, 5

baseball encyclopedia, 5

baseline models, 210

for classiﬁcation, 210

for value prediction, 212

Bayes’ theorem, 150, 205, 299

Baysian information criteria, 289

bell-shaped, 123, 141

distribution, 101

bias, 202, 417

lexicographic, 405

numerical, 405

temporal, 405

bias–variance trade-oﬀ, 202

big data, 391

algorithms, 397

bad data, 392

statistics, 392

big data engineer, 4

big oh analysis, 397

binary relations, 320

binary search, 398

binomial distribution, 123

436 INDEX

bioinformatician, 50

Blumenstock, Josh, 27

Body Mass Index, 96, 177

Bonferroni correction, 141

boosting, 363, 364

algorithms, 364

bootstrapping, 374

Borda’s method, 108

box plots, 175

Box, George, 201

box-and-whisker plots, 176

bubble plots, 179

bupkis, 391

Bush, George W., 326

C–language, 59

cache memory, 401

canonical representation, 400

canonization, 400

CAPTCHAs, 89

Carroll, Lewis, 423

cartograms, 189

Center for Disease Control, 204

center of mass, 332

centrality measures, 34

centroids, 331

character code uniﬁcation, 74

characteristic equation, 256

characterizing distributions, 39

chart types, 170

bar charts, 179

data maps, 187

dot and line plots, 174

histograms, 183

pie charts, 179

scatter plots, 177

tabular data, 170

cicada, 46

classiﬁcation, 16, 210, 289

binary, 290, 314

multi-class, 297

regression, 290

classiﬁcation and regression trees,

357

classiﬁers

balanced, 217

evaluating, 213

one-vs.-all, 298

perfect, 218

Clinton, Bill, 326

Clinton, Bill], 326

closest pair of points, 398

cloud computing services, 410

cluster

conductance, 343

distance, 337

clustering, 327, 373

agglomerative, 336

applications, 328

biological, 337

cut-based, 341

k-means, 330

single link, 339

visualization of, 337

clusters

number of, 333

organization of, 337

Clyde, 111, 112

coeﬃcient vector, 270

Cohen’s d, 136

collaborative ﬁltering, 9

communication, 408, 416

commutativity, 243

company data, 64

computer scientist, 2

conditional probability, 30, 31

Condorcet jury theorem, 84

confusion matrix, 214, 220

connected components, 324

contingency table, 214

convex, 280

convex hull, 368

coordination, 408

correlation

analysis, 40

interpretation, 43

signiﬁcance, 45

correlation and causation, 45, 135

cosine similarity, 309

cross validation, 227

advantages, 227

CrowdFlower, 67, 84, 86

INDEX 437

crowdsourcing, 67, 80

bad uses, 87

crowdsourcing services, 84

cryptographic hashing, 400

CSV ﬁles, 62

cumulative density function, 33,

132, 186

currency conversion, 75

cut, 343

damping factor, 325

Darwin, Charles, 81

data, 237, 391

quantitative vs. categorical, 15

big vs. little, 15

cleaning, 69

collecting, 64

compatibility, 72

errors, 69

for evaluation, 225

for testing, 225

for training, 225

logging, 68

properties, 14

scraping, 67

structured, 14

types, 14

unstructured, 14

visualizing, 155

data analysis, 404

data centrism, 2

data cleaning, 376

data errors, 417

data formats, 61

data hygiene

evaluation, 225

data munging, 57

data parallelism, 409

data partition, 404

data processing, 10

data reduction, 329

data science, 1

languages, 57

models, 210

data science television, 17

data scientist, 2

data sources, 64

data visualization, 155

data-driven, 156

models, 207

de M´er´e, Chevalier, 29

decision boundaries, 291

decision tree classiﬁers, 299, 357

decision trees, 357

advantages, 358

construction, 359

ensembles of, 362

deep learning, 202, 352, 377

models, 209

network, 378

DeepWalk, 385

degree of vertex, 325

depth, 378

derivative, 281

partial, 282

second, 281

descriptive statistics, 34

deterministic sampling algorithms,

404

developing scoring systems, 99

dictionary maintenance, 399

DiMaggio, 148

dimension reduction, 277, 376

dimensional egalitarianism, 308

dimensions, 384

dinosaur vertebra, 78

directed acyclic graph, 110

directed graph, 321

discounting, 209, 356

disk storage, 401

distance methods, 303

distance metrics, 304

Lk, 305

euclidean, 305

manhattan distance, 305

maximum component, 305

distances, 319

measuring, 303

distributed ﬁle system, 396

distributed processing, 407

divide and conquer, 411

DNA sequences, 402

438 INDEX

dot product, 241

duality, 268

duplicate removal, 400

E-step, 335

edge cuts, 324

edges, 319

eﬀect size, 136

eigenvalues, 255

computation, 256

decomposition, 257

properties of, 255

Elizabeth II, 326

Elo rankings, 104

embedded graph, 323

embedding, 321

Emoji Dick, 86

Engels, Friedrich, 391

ensemble learning, 363

entropy, 310

equations

determined, 251

underdetermined, 251

error, 202, 221

absolute, 221

detection, 155

mean squared, 223, 331

relative, 222

residual, 269

root mean squared, 223

squared, 222

statistics, 221

errors vs. artifacts, 69

ethical implications, 416

Euclidean metric, 303

evaluation

environments, 224

statistics, 214

event, 28

Excel, 59

exclusive or, 361

exercises, 23, 53, 90, 119, 151, 199,

234, 263, 301, 346, 388,

419

expectation maximization, 335

expected value, 28

experiment, 27

exploratory data analysis, 155, 156

visualization, 160

F-score, 216

Facebook, 21

false negatives, 214

false positives, 214

fast Fourier transform, 47

fault tolerance, 408

feature engineering, 375

feature scaling, 274

sublinear, 275

z-scores, 275

features

highly-correlated, 277

Fermat, Pierre de, 30

Feynman, Richard, 229

FFT, 47

ﬁltering, 403

ﬁnancial market, 126

ﬁnancial uniﬁcation, 75

ﬁt and complexity, 288

FoldIt, 89

football, 111

American players, 97

game prediction, 111

forecasting

time series, 212

formulation, 354

Freedom of Information Act, 12, 65

frequency counting, 400

frequency distributions, 184

furthest link, 340

Galton, Francis, 81

games with a purpose, 88

gamiﬁcation, 88

garbage in, garbage out, 3, 69

Gates, Bill, 130

Gaussian

elimination, 250

Gaussian distribution, 124

Gaussian noise, 125

General Sentiment, 20

genius, 19

INDEX 439

geometric mean, 35

geometric point sets, 238

geometry, 240

Gini impurity, 360

Global Positioning System, 12

gold standards, 99

good scoring functions, 101

Goodhart’s law, 303

Goodhart, Charles, 303

Google

AlphaGo, 372

TensorFlow, 377

Google Flu Trends, 394

Google News, 219

Google Ngrams, 10

Google Scholar, 66

government data, 65

gradient boosted decision trees,

359, 366

gradient descent search, 281

graph embeddings, 384

graph theory, 323

graphs, 238, 319, 321

cuts, 342

dense, 322

directed, 321

embedded, 323

labeled, 323

non-simple, 322

simple, 322

sparse, 322

topological, 323

undirected, 321

unlabeled, 323

unweighted, 322

weighted, 320, 322

Gray, Dorian, 251

grid indexes, 315

grid search, 409

Hadoop distributed ﬁle system, 414

Hamming, Richard W., 1

hash functions, 399

applications, 399

hashing, 399

heatmaps, 178

hedge fund, 1

hierarchy, 298

higher dimensions, 307, 370

histograms, 32, 183, 222

best practices, 186

bin size, 184

Hitler, Adolf, 326

HTML, 67

hypothesis development, 328

hypothesis driven, 156, 392

Imagenet, 379

IMDb, 7

imputation

by interpolation, 78

by mean value, 77

by nearest neighbor, 78

by random value, 77

heuristic-based, 77

independence, 30, 123, 354

inﬂation rates, 76

information gain, 360

information theoretic entropy, 360

infrastructure, 396

inner product, 243

institutional review board, 88

Internet Movie Database, 7

Internet of Things, 68

inverse transform sampling, 132

IPython, 61

IQ testing, 89

Jaccard distance, 341

Jaccard similarity, 341

Jackson, Michael [136], 262

Java, 59

Jesus, 326

JSON, 63

k-means clustering, 343, 409

k-mediods algorithm, 332

k-nearest neighbors, 313

Kaggle, viii

kd-trees, 316

kernels, 371

Kolmogorov-Smirnov test, 139

440 INDEX

Kruskal’s algorithm, 339

Kullback-Leibler divergence, 311

labeled graphs, 323

Lang, Andrew, 267

Laplace, 356

Laplacian, 343

large-scale question, 9

latent Dirichlet allocation, 373

learning rate, 283, 383

learning to rank, 119

least squares regression, 270

lie factor, 164

Lincoln, Abraham, 242

line charts, 174

advantages, 174

best practices, 175

line hatchings, 177

linear algebra, 237

power of, 237

linear algebraic formulae

interpretation, 238

linear equation, 238

linear programming, 369

linear regression, 212, 267

error, 269

solving, 270

linear support vector machines, 369

linear systems, 250

Linnaeus, Carl, 326

live data, 395

locality, 401

locality sensitive hashing, 317

logarithm, 47

logistic classiﬁcation

issues, 295

logistic function, 381

logistic regression, 366

logit, 381

logit function, 106, 292

loss function, 280, 294

LU decomposition, 254

lumpers, 329

M-step, 335

machine learning, 351

algorithms, 375

classiﬁers, 85

models, 208

main memory, 401

major league baseball, 6

MapReduce, 407, 410

programming, 412

MapReduce runtime system, 415

matchings, 324

Mathematica, 59, 61

Matlab, 58

matrix, 14, 237, 270, 373

addition, 242

adjacency, 246, 320

covariance, 245, 257, 271

determinant, 249, 254

eigenvalues, 255

eigenvectors, 255

factoring, 252

identity, 246, 248

inversion, 248

linear combinations of, 242

multiplication, 243

multiplicative inverse of, 249

non-singular, 249

permutation, 247

rank, 251

reasons for factoring, 252

rotation, 248

singular, 249

transpose of, 242

triangular, 254

underdetermined, 256

matrix multiplication, 243, 398

applications, 244

matrix operations

visualizing, 241

maximum margin separator, 367

mean, 34, 83, 125, 132, 138, 212,

227, 403

arithmetic, 35

geometric, 35

measurement error, 125

median, 35, 83, 132, 212, 403

mergesort, 398

metadata, 7

INDEX 441

method centrism, 2

metric, 304

identity, 304

positivity, 304

symmetry, 304

triangle inequality, 304

minima

global, 284

local, 284

minimum spanning tree, 324, 339

missing values, 76, 376

mixture model, 333

Moby Dick, 86

mode, 36

model-driven, 417

modeling, 201, 328, 416

philosophies of, 201

principles for eﬀectiveness, 203

models

ad hoc, 208

baseline, 210

blackbox, 206

data science, 210

data-driven, 207

deep learning, 209

descriptive, 206

deterministic, 208

evaluating, 212

ﬁrst-principle, 207

ﬂat, 209

Google’s forecasting, 204

hierarchical, 209

linear, 206

live, 204

machine learning, 208

neural network, 206

non-linear, 206

overﬁt, 203

simplifying, 286

simulation, 229

stochastic, 208

taxonomy of, 205

underﬁt, 202

Moneyball, 5

monkey, 215

monotonic, 307

Monte Carlo

sampling, 134

simulations, 229

Mosteller, Frederick, 121

multiclass systems

evaluating, 219

multiedge, 322

multinomial regression, 299

multiplying probabilities, 48

naive Bayes, 354, 363

name uniﬁcation, 74

Napoleon, 326

NASA, 73

National Football League, 112

natural language processing, 20

nearest centroid, 340

nearest neighbor, 339, 397

nearest neighbor classiﬁcation, 311

advantages, 311

nearest neighbors

ﬁnding, 315

negative class, 213

Netﬂix prize, 9

network

depth, 379

network methods, 303

networks, 109, 238, 319, 378

induced, 320

learning, 379

neural networks, 377

new data set, 156

New York, 277

Nixon, Richard, 326

NLP-based system, 21

no free lunch theorem, 353

node

bias of, 381

non-linear classiﬁers, 366

non-linear functions

ﬁtting, 273

non-linear support vector

machines, 369

non-linearity, 358, 377, 380

norm, 287

normal, 125

442 INDEX

normal distribution, 79, 109, 124,

141

implications, 126

normality testing, 141

normalization, 103, 376

normalizing skewed distribution, 49

norms, 309

NoSQL databases, 415

notebook environments, 59

numerical conversions, 73

Obama, Barack, 326

Obama, Barack [91], 327

Obama, Barack], 326

Occam’s razor, 201, 211, 286

Occam, William of, 202

Oh G-d, 177

optimization

local, 284

Oracle of Bacon, 9

outlier, 118

detection, 78

outlier detection, 329

outliers

removing, 272

overﬁtting, 202, 296

overlap percentage, 137

ownership, 417

p-values, 145

packing data, 402

PageRank, 100, 111, 325

pairwise correlations, 158

parallel processing, 407

parallelism, 406

parameter ﬁtting, 279

parameter spaces

convex, 280

partition function, 299

Pascal’s triangle, 123

Pascal, Blaise, 30

paths, 246

Pearson correlation coeﬃcient, 41,

136

penalty function, 293

performance of models, 39

periodic table, 188

Perl, 58

permutation, 246

randomly generating, 147

tests, 145

personal wealth, 130

pie charts, 179

bad examples, 183

best practices, 181

point spread, 112

points

rotating, 248

points vs. vectors, 309

Poisson distribution, 127

position evaluation function, 372

positive class, 213

power law distribution, 129

power law function, 276

precision, 3, 215, 221

prefetching, 401

principal components, 260

analysis, 260

prior probability, 354

privacy, 418

probabilistic, 203

probability, 27, 29, 354

probability density function, 32,

132, 186

probability distribution, 32

probability of an event, 28

probability of an outcome, 28

probability vs. statistics, 29

program ﬂow graph, 322

programming languages, 57

protocol buﬀers, 63

proxies, 99

psychologists, 89

Pubmed, 70

pure partition, 360

Pythagorean theorem, 306

Python, 58, 67

Quant Shop, 17

R, 58

Rand index, 341

INDEX 443

random access machine, 397

random sampling, 403, 406

random variable, 28

ranking systems

class rank, 100

search results, 100

top sports teams, 100

university rankings, 100

rankings, 95

digraph-based, 109

historical, 117

merging, 108

techniques, 104

ratio, 48

ray

unit, 241

Reagan, Ronald, 326

rearrangement operations, 238

recall, 216, 221

receiver-operator characteristic

curve, 218

rectiﬁed linear units, 381

rectiﬁer, 381

redundancy, 393

regression, 16

application, 359

for classiﬁcation, 290

LASSO, 287

logistic, 289, 292

ridge, 286

regression models, 272

removing outliers, 272

regularization, 286, 376

reinforcement learning, 372

Richter scale, 131

right-sizing training data, 404

road network, 322

robustness, 3, 96, 359

Roosevelt, Franklin D., 326

Rota, Gian-Carlo, 237

sabermetrics, 22

sample space, 27

sampling, 132, 403, 404

beyond one dimension, 133

by truncation, 404

scalar

multiplication, 242

scale invariant, 132

scales

Likert, 298

ordinal, 297

scaling constant, 293

scatter plots, 98, 177

best practices, 177

three-dimensional, 179

Schaumann, Jan, 351

scientist, 2

scores, 95

threshold, 218

scores vs. rankings, 100

scoring functions, 95

security, 418

self-loop, 322

semi-supervised learning, 374

Shakespeare, William, 326

sharp, 215

Sheep Market, 86

shortest paths, 324

signal to noise ratio, 37

signiﬁcance level, 139

Silver, Nate, 203

similarity graphs, 341

similarity matrix, 342

simple graph, 322

single-command program, 224

single-pass algorithm, 402

singular value decomposition, 258

sketching, 403

skew, 413

Skiena, Len, ix

small evaluation set, 226

social media, 392

analysis, 21

data, 394

Social Network–movie, 105

spam, 393

spam ﬁltering, 393

Spearman rank correlation

coeﬃcient, 42, 108

Spears, Britney [566], 262

spectral clustering, 343

444 INDEX

spidering, 67

splitters, 329

sports performance, 38

SQL databases, 63

standard deviation, 36, 125, 132,

138, 227, 403

statistical analysis, 121, 230

statistical distributions, 122

statistical proxy, 7

statistical signiﬁcance, 135

statistics, 29

stochastic gradient descent, 285,

296, 382

stock market, 37, 79, 126

Stony Brook University, 20

stop words, 414

storage hierarchy, 401

streaming, 402

summary statistics, 157, 159

supervised learning, 372

supervision, 372

degrees of, 372

support vector machines, 352, 366

support vectors, 368

Surowiecki, James, 82

sweat equity, 66

T-test, 137

tangent line, 282

target scaling, 274

sublinear, 276

taxi

records from New York, 11

tipping model, 286

tipping rate, 13, 277

taxi driver, 277

test statistic, 138

text analysis, 253

theory of relativity, 144

Tikhonov regularization, 287

time uniﬁcation, 75

Titanic, 183, 358

top-k success rate, 219

topic modeling, 373

topological graph, 323

topological sorting, 110, 324

transparency, 417

tree, 298, 336

trees

agglomerative, 337

true negatives, 214

true positives, 214

truncation, 405

Tufte, Edward, 155, 162

Twitter, 392, 404, 405

U.S. presidential elections, 187, 203

uncertainty, 175

undirected graph, 321

uniform distribution, 406

uniform sampling, 405

uninvertible, 400

unit conversions, 72

UNIX time, 75

unlabeled graphs, 323

unrepresentative participation, 393

unsupervised learning, 372

unweighted graph, 322

urban transportation network, 11

validation data, 95

value prediction, 210

value prediction models

evaluating, 221

variability measures, 36

variance, 36, 202, 403

interpretation, 37

variation coeﬃcient, 137

variety, 394

vectors, 240

unit, 240

velocity, 394

veracity, 395

vertex, 319

vertices, 319

visualization, 404

chart types, 170

critiquing, 189

interactive, 195

tools, 160

visualization aesthetic, 162

INDEX 445

chartjunk, 162, 165

colors, 163, 168

data-ink ratio, 162, 163

lie factor, 162, 164

repetition, 163, 169

scaling and labeling, 162, 167

volume, 394

Voronoi diagrams, 315

voting, 363

with classiﬁers, 363

web crawling, 68

weighted average, 84

weighted graph, 322

Welch’s t-statistic, 138

Wikipedia, 20, 79, 116, 326

wisdom, 19

wisdom of crowds, 81

Wolfram Alpha, 59, 144

word embeddings, 254, 383

word2vec, 384

XML, 62

Z-score, 103, 308, 376

Zipf’s law, 131, 357

The Data Science Design Manual

The%20Data%20Science%20Design%20Manual

Navigation menu

Versions of this User Manual:

Views

Navigation