Theory Manual

User Manual:

Open the PDF directly: View PDF .
Page Count: 59

List of Abbreviations
VTOL sizing: Overview
- The nature of VTOL sizing
  - Iterative convergence
  - Constrained optimziation
Drag models
Rotor and Wing Performance Models
- Rotor performance model
  - Momentum Theory
  - Blade Element Momentum Theory (BEMT)
- Wing performance model
Weight models
Cantilever beam dynamics

HYDRA: Rotorcraft Conceptual Sizing

Authors

Ananth Sridharan

Bharath Govindarajan

This is the user manual for the rotorcraft conceptual sizing analysis HYDRA -HYbrid

Design and Rotorcraft Analysis, developed and evolved over several years at the Uni-

versity of Maryland, with inspiration drawn from the AHS Student Design Com-

petition challenges. This manual contains a description of the theory and various

operations performed by the sizing code for both conventional and novel Vertical-

Lift platforms. The key features of HYDRA are ﬂexibility,speed and reliance on

only open-source tools. With the majority of the code written in an interpreted

language, i.e., Python, modules can be prototyped and added quickly. Subsequently

select parts of the code can be ported to Fortran or C(i.e., compiled languages) and

wrapped for execution sppeed. Using a combination of OpenMP,MPI and algorithmic

acceleration, up to 2000 designs can be generated per second on a desktop worksta-

tion. The use of Pythonenables powerful built-in text parsing abilities, resulting in

more intuitive interfaces.

Another advantage of HYDRA is the ability to set up input decks and call higher

ﬁdelity models (BEMT, FEA for airframe and wings) and the comprehensive anal-

ysis PRASADUM, and through the comprehensive analysis, the Maryland Free Wake

(MFW). These higher-ﬁdelity tools are integrated into the sizing loop to provide ac-

curate estimates of rotor performance and component weights, and may be invoked

as required.

Contents

List of Abbreviations iii

1 VTOL sizing: Overview 1

1.1 The nature of VTOL sizing . . . . . . . . . . . . . . . . . . . . . . . 2

1.1.1 Iterative convergence . . . . . . . . . . . . . . . . . . . . . . . 3

1.1.2 Constrained optimziation . . . . . . . . . . . . . . . . . . . . . 10

2 Drag models 11

2.1 Fuselage and empennage drag . . . . . . . . . . . . . . . . . . . . . . 11

2.2 Edgewise rotor hub drag . . . . . . . . . . . . . . . . . . . . . . . . . 12

2.3 Spinnerdrag................................ 12

2.4 Momentum drag for engine air intakes . . . . . . . . . . . . . . . . . 12

2.5 Landinggeardrag............................. 13

2.6 Coolingdrag................................ 14

2.7 Mast fairing drag for coaxial rotors . . . . . . . . . . . . . . . . . . . 14

2.8 Protrusiondrag.............................. 14

3 Rotor and Wing Performance Models 14

3.1 Rotor performance model . . . . . . . . . . . . . . . . . . . . . . . . 14

3.1.1 MomentumTheory........................ 15

3.1.2 Blade Element Momentum Theory (BEMT) . . . . . . . . . . 15

3.2 Wing performance model . . . . . . . . . . . . . . . . . . . . . . . . . 18

4 Weight models 19

4.1 Engines, fuel and batteries . . . . . . . . . . . . . . . . . . . . . . . . 19

4.1.1 Engines .............................. 19

4.1.2 Fuel, tank and fuel handling systems . . . . . . . . . . . . . . 21

4.1.3 Batterymodels .......................... 23

4.1.4 Electric motor weights . . . . . . . . . . . . . . . . . . . . . . 25

4.2 Electric Transmissions . . . . . . . . . . . . . . . . . . . . . . . . . . 25

4.3 Wireweights ............................... 27

4.4 Physics based model for rotor blades . . . . . . . . . . . . . . . . . . 28

4.4.1 Skinsizing............................. 29

4.4.2 Leading edge weight . . . . . . . . . . . . . . . . . . . . . . . 29

4.4.3 Spar caps and shear web sizing . . . . . . . . . . . . . . . . . 30

4.4.4 Root ﬁtting sizing . . . . . . . . . . . . . . . . . . . . . . . . . 34

4.4.5 Torsion frequency check . . . . . . . . . . . . . . . . . . . . . 34

4.5 Flightcontrols............................... 35

4.5.1 Rotorcontrols........................... 35

4.5.2 Fixed wing controls . . . . . . . . . . . . . . . . . . . . . . . . 36

4.5.3 Tiltactuators........................... 36

4.6 Motormountmass ............................ 36

4.7 Wingweightmodel............................ 38

4.7.1 AFDD wing weight model . . . . . . . . . . . . . . . . . . . . 38

4.7.2 Frequency tuning: bending loads . . . . . . . . . . . . . . . . 38

4.7.3 Hover: shear loads . . . . . . . . . . . . . . . . . . . . . . . . 39

4.8 Airframe Weight Model . . . . . . . . . . . . . . . . . . . . . . . . . . 40

4.8.1 Statistical weight model . . . . . . . . . . . . . . . . . . . . . 40

4.8.2 Component build-up model . . . . . . . . . . . . . . . . . . . 41

4.8.3 Physics-based weight model: load-bearing airframe components 42

4.9 Weightmargin .............................. 46

4.10Fixedweightgroups ........................... 46

4.11 Comparison of weights vs. NDARC . . . . . . . . . . . . . . . . . . . 47

A Cantilever beam dynamics 49

A.1 Potentialenergy.............................. 51

A.2 Kineticenergy............................... 52

A.3 Frequencytuning ............................. 53

A.4 Validation ................................. 54

A.4.1 Case 1: cantilever beam . . . . . . . . . . . . . . . . . . . . . 54

A.4.2 Case 2: distributed non-structural mass . . . . . . . . . . . . . 56

A.4.3 Case 3: half-wing with lumped masses . . . . . . . . . . . . . 56

iii

1 VTOL sizing: Overview

The objective of rotorcraft sizing is to obtain a consistent combination of

weights and performance for the various components in a VTOL platform. The

interdependent nature of the design of various parts (e.g., engine, rotors, transmis-

sion, fuselage) necessitates methods that capture these dependencies to the required

accuracy; otherwise components might be over-designed and heavier/bulkier than

required (performance penalty) or under-designed, requiring a costly sequence of

redesign operations for all parts in the detailed design phase.

Sizing for vertical-lift aircraft is not a new ﬁeld; the fundamental methods

have been adapted from ﬁxed-wing sizing and augmented with VTOL-speciﬁc com-

ponents, and reﬁned over several decades. A notable example of a VTOL sizing

algorithm is the method of Prof. Marat Tishchenko (MIL design bureau) and Dr.

V.T. Nagaraj; this combination of component sizing laws and the iterative sizing

sequence is one of the cornerstones of HYDRA.

Recent work by Dr. Wayne Johnson at NASA Ames produced several it-

erations of a continuously updated NASA code called NDARC. This code can size

conventional and unconventional VTOL platforms, as well as a range of ﬁxed-wing

aircraft. Additionally, each major helicopter manufacturer has built up a database

of manufactured part weights and performance, and have developed their respective

in-house sizing tools. These sizing tools were originally developed for single main

rotor helicopters powered by gas turbine engines, and have been gradually adapted

to include eVTOLs (electric Vertical TakeOﬀ and Landing platforms) and conﬁgu-

rations with hybrid powerplants featuring Distributed Electric Propulsion (DEP).

1.1 The nature of VTOL sizing

Table 1: Conceptual sizing: drivers for group mass

Group name Mass depends on

Fixed wing Aspect ratio, wing loading →take-oﬀ mass

Rotors Radius, solidity, RPM, torque, thrust →take-oﬀ mass

Empennage Tail loading, pitch/yaw stability and control authority

Propeller Vehicle drag →take-oﬀ mass

Fuselage Dimensions, take-oﬀ mass

Landing gear Take-oﬀ mass

Flight controls Blade geometry, wing area, wing loading →take-oﬀ mass

Deicing Wing area, rotor blade area →take-oﬀ mass

Battery C-rating, speciﬁc energy, rotor power →take-oﬀ mass

Motor Maximum torque/power →take-oﬀ mass

Avionics Fixed mass group

Power wire Layout of rotors and motor power limits →take-oﬀ mass

Signal wire Layout of controls and sensors

To illustrate the interdependent nature of sizing laws for various components,

consider the dominant drivers for the weights of various vehicle components in an

eVTOL, shown in Table 1. The list of dependencies is illustrative and not exhaus-

tive, but suﬃcient to highlight the key point: determination of take-oﬀ mass

requires solving for several cyclic dependencies, i.e., the total take-oﬀ mass

depends on itself. Two well-known methods have been successfully used to solve

this class of problems with simultaneous nonlinear equations:

1. Iterative convergence

2. Optimization with compatibility constraints

The implementations of both approaches in HYDRA are detailed in the following

sections.

1.1.1 Iterative convergence

Iterative convergence is a popular technique that is used to solve several classes

of problems. It has been successfully applied to nonlinear algebraic equations in

several variables, where analytical solutions are unavailable. The overall approach

is shown in Fig. 1. Four primary types of models are required for conceptual sizing:

1. Weight

2. Performance

3. Sizing and geometry

4. Energy storage

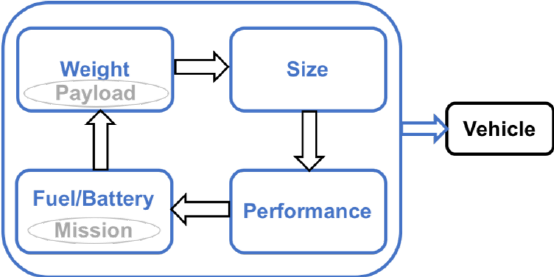
Figure 1: Iterative sizing: the classical approach

Typically, low-ﬁdelity models are used to represent each group for conceptual

sizing, because ﬁne-grained resolution of each component is not possible at this

stage due to the unavailability of design details. For VTOL sizing in particular,

sizing operations can be executed in a particular sequence to obtain answers rapidly

with fewer sizing iterations. One such sequence is shown in Fig. 2.

Each block shown in Fig. 2 consists of further sub-modules that are assembled

together in the implementation. The key inputs for sizing are the three green blocks

that feed information to the sizing of the vehicle: aircraft layout,mission proﬁle

and model calibration data.

The aircraft layout is perhaps the most signiﬁcant assumption required to

initiate sizing. Figure 3 shows a few candidate eVTOL conﬁgurations, with diﬀerent

permutations and combinations of rotor and wing technologies, as shown in Fig. 4.

In HYDRA, the constituent rotor and wing technologies are deﬁned as primitive types.

Based on user inputs, these technology combinations are superimposed in HYDRA to

obtain the appropriate conﬁguration.

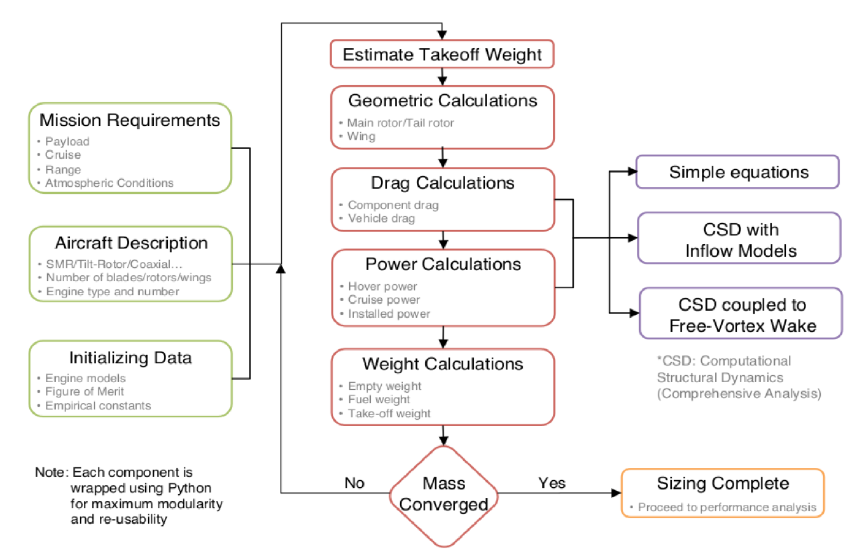
Figure 2: Iterative sizing: detailed breakdown of operations

Figure 3: Variety in electric VTOL aircraft

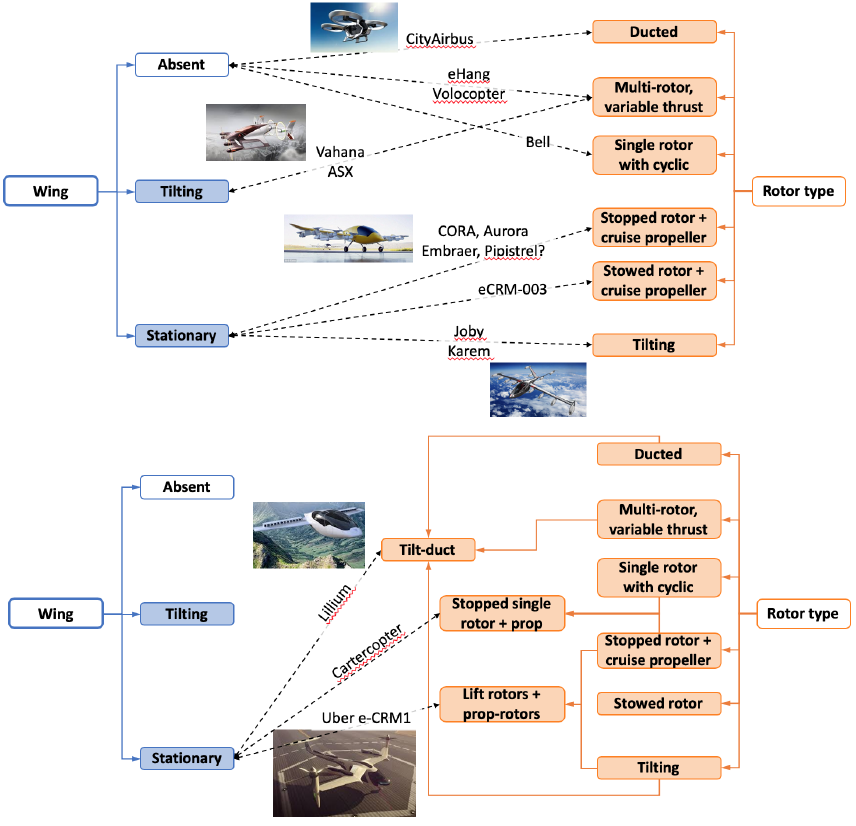
Figure 4: Assembling eVTOLs from rotor and wing technologies

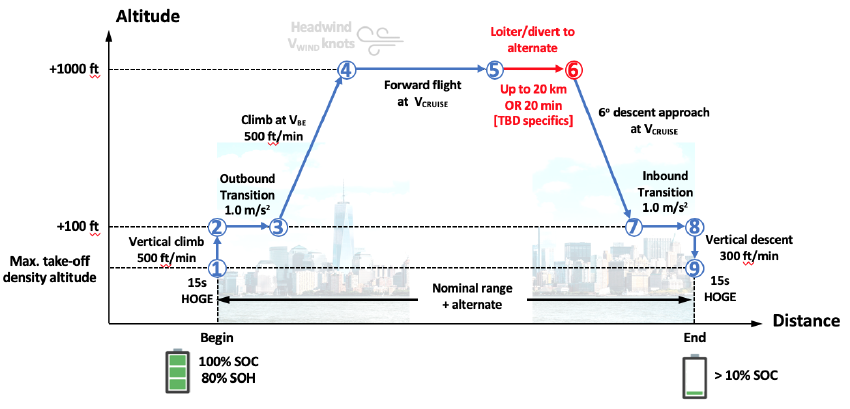
Figure 5: An example mission proﬁle

The mission proﬁle is speciﬁed as a sequence of hover and cruise segments.

Cruise segments are deﬁned through a speciﬁed airspeed and distance/time, while

hover segments are deﬁned through duration. Climb and descent segments are

deﬁned as cruise segments with diﬀerent start and end altitudes. An example mission

proﬁle is shown in Fig. 5.

Finally, the model calibration data refers to calibration constants for para-

metric models of rotor performance, turboshaft engine performance, electric motors,

fuselage drag vs. weight curve ﬁts, and several other assumptions. Typically, up

to 30 constants are required to calibrate diﬀerent low-ﬁdelity models accurately,

deﬁned in the defaults.yaml input ﬁle. In HYDRA, several parametric models have

been systematically replaced with higher-ﬁdelity counterparts and so lift the speciﬁc

assumptions made to arrive at those constants.

Accelerated convergence

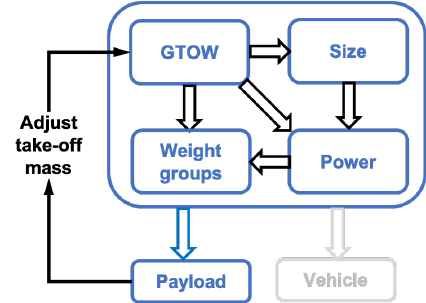
Figure 6: Accelerated convergence for iterative sizing

The implementation of iterative sizing shown in Fig. 1 requires several iterations (up

to 30) to converge take-oﬀ mass to the required tolerance. An alternate approach

is implemented in HYDRA, resulting in signiﬁcantly faster convergence for no loss in

accuracy. This accelerated convergence technique is shown in Fig. 6.

In this method, the “inner loop” is executed in ﬁxed take-oﬀ mass mode, and

the constituent weight groups are evaluated. Finally, the remaining mass (take-oﬀ

mass minus empty weight, minus energy storage) is assigned to payload mass, i.e.,

mpay =M−mempty −mbattery −mfuel (1)

Here, Mrepresents the take-oﬀ mass. Usually, mission proﬁles are speciﬁed

together with the target payload mtarget. However, the “inner loop” described above

runs once to calculate the payload mass mpay for a given take-oﬀ mass M. Therefore,

the take-oﬀ mass needs to be continuously adjusted to ensure that the “calculated”

payload matches the target payload. One update scheme for the take-oﬀ mass (used

in HYDRA) is

Mi+1 =Mi−dM

dmpay

(mpay −mtarget)(2)

The slope dM

dmpay is initially set to 3.0, and subsequently updated based on a ﬁnite-

diﬀerence approximation as iterations proceed. This method usually converges in 3

– 5 updates for take-oﬀ mass (vs. 30 iterations for the baseline technique), resulting

in 5 – 6 times faster convergence for no reduction in accuracy.

1.1.2 Constrained optimziation

The other technique that lends itself to VTOL conceptual sizing is constrained

optimization. The primary advantage of this technique is that it allows for simulta-

neous minimization of a cost function (e.g. vehicle operating cost) while satisfying

compatibility constraints (e.g., payload matching and landing footprint). If only

sizing is required, the design variables are fed as prescribed inputs and compatibil-

ity constraints are speciﬁed as nonlinear algebraic constraints. The take-oﬀ weight

is provided as a design variable and the payload is calculated as an output. The

condition that the calculated payload (mpay) be at least the target mission payload

(mtarget) is enforced as a nonlinear inequality constraint.

In HYDRA, two diﬀerent optimizers are used for constrained minimization of

the vehicle hourly operating cost: gradient-based optimization, and diﬀerential evo-

lution. The constraints are landing footprint (based on wing span and fuselage

length) and payload matching. For concentual sizing, gradient-based optimiza-

tion requires an accurate initial condition to ensure that global minima (and not

local minima) are identiﬁed at the end of optimization. In HYDRA, the gradient-

based optimizer is initialized from several starting conditions, each of which are

obtained from a parametric sweep over the available high-level design variables. For

diﬀerential evolution, compatibility constraints are implemented indirectly as a

“death penalty” - an analog of exterior penalty functions. The cost function is in-

creased by a large number (1e6) for designs that violate any of the user-speciﬁed

constraints. Additionally, HYDRA is programmed to automatically add and remove

design variables based on the number of rotor and wing groups in the vehicle.

The optimizer in HYDRA is invoked after basic sizing over a limited parametric

sweep is carried out. Both optimization techniques - gradient based and diﬀer-

ential evolution - are used to minimize vehicle operating costs, and the resulting

optimized designs are checked for uniqueness. These unique designs (obtained from

optimization with diﬀerent starting conditions) are ranked by operating cost, weight,

battery/fuel or rated power based on a user-selected criterion. Further details are

provided in the appropriate section later on in the documentation.

2 Drag models

2.1 Fuselage and empennage drag

The fuselage is modeled as a slender body of revolution with its length set by

user inputs, and an equivalent diameter based on body width and height (also set by

the user). The procedure to calculate skin friction drag and base drag are identical

to those documented in NASA CR-3083: Rotary-Wing Aerodynamics: Volume II

by C.N. Keys. Similiarly, the approach for estimating the drag of horizontal and

vertical tail surfaces, as documented in NASA CR-3083, is implemented in HYDRA.

2.2 Edgewise rotor hub drag

The ﬂat-plate area of each edgewise rotor hub is estimated based on a modiﬁed

procedure outlined in NASA CR-3083, as follows:

fhub = 1.2R2(0.0006 + 0.00222Nb)(3)

2.3 Spinner drag

The spinner is assumed to be a rotating body with a hemispherical nose and

blunt base. As shown in Fig. 7, the drag coeﬃcient of such a shape is 0.2 (refer-

enced to cross-sectional area πd2/4), for a length-to-diameter ratio of 2.5. For the

calculations presented in this paper, a drag coeﬃcient of 0.36 is assumed, to account

for additional blockage from the airframe, vertical ﬁns and interference eﬀects. The

radius of the spinner is 15% of the rotor radius.

2.4 Momentum drag for engine air intakes

For turboshaft engines operating at cruise speeds above 160 knots, the addi-

tional momentum drag is 0.3 ft2per intake.

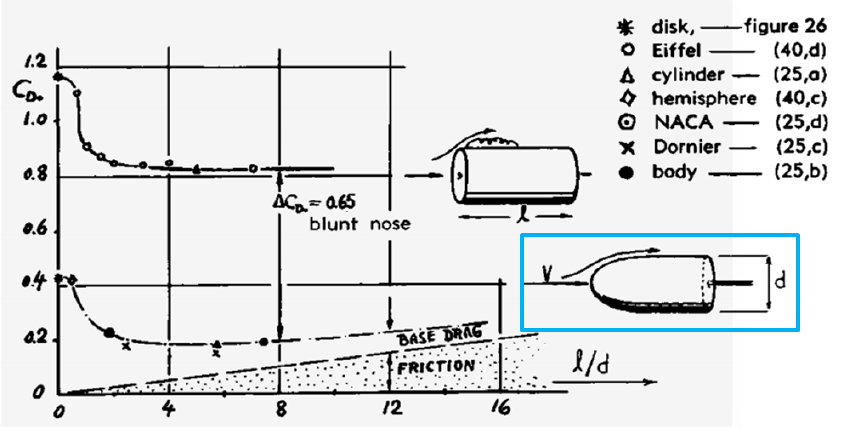
Figure 7: Spinner nose cone:drag coeﬃcient, from Fluid Dynamic Drag, Hoerner

2.5 Landing gear drag

The drag of landing gear is modeled with a parametric representation (obtained

from NASA CR-3083) as follows:

logefLG =y0+mloge(0.001W)(4)

Here, fLG is in square feet, and Wis in lbs. The constants y0and mare set

based on the type of landing gear.

1. Retracted gear:fLG = 0

2. Wheeled gear:y0= 0.5755. The slope m= 0.443 for W ≥1000 lb, and zero

for W ≤1000 lb.

3. Skid gear:y0=-0.11626. The slope m= 0.4979 for W ≥1000 lb, and zero

for W ≤1000 lb.

2.6 Cooling drag

The cooling systems required to regulate engine temperatures creates addi-

tional drag, which is estimated using a parametric model given in NASA CR-3083.

fcool(ft2) = 10−4Pins(hp)(5)

2.7 Mast fairing drag for coaxial rotors

The fairing for the exposed length of the rotor shaft between the upper and

lower rotors of a coaxial system incurs an additional drag penalty, given by

fmast(ft2) = 0.0322R2(6)

2.8 Protrusion drag

The drag of protrusions is modeled as an additional 10% of the accumulated

parasitic drag of all wetted surfaces.

3 Rotor and Wing Performance Models

3.1 Rotor performance model

Two performance models are used to calculate rotor power required in hover

and axial ﬂight. The ﬁrst model is based on momentum theory, and the second

model is based on blade element momentum theory.

3.1.1 Momentum Theory

For momentum theory-based predictions, rotor power is calculated based on

assumed aerodynamic eﬃciency factors in hover and cruise. Imperial units (foot,

pounds of force and horsepower) are assumed for these expressions. In hover, rotor

power is given by

Phover(hp) = T1.5

550√2ρA FM (7)

Here, Tis the thrust required in hover from each rotor, and is calculated assuming

the segment weight is equally divided between all rotors. A vertical download factor

(conﬁguration-dependent) is included in the estimation of rotor thrust. The rotor

disk area is A(ft2), ρis the ambient air density (slug/ft3) and FM is the rotor ﬁgure

of merit in hover.

In cruise, the power required by each rotor when operating in axial ﬂight is

Pcruise(hp) = D

V∞

550ηp

(8)

Here, Dis the total vehicle drag in lbs when operating at a forward ﬂight

speed of V∞ft/s, which is overcome by each of the NRrotors operating at a propeller

eﬃciency of ηp.

3.1.2 Blade Element Momentum Theory (BEMT)

Certain conﬁgurations like the tilt-rotor or tilt-wing ﬂy such that the rotors

operate predominantly in axial ﬂight. Therefore, the Blade Element Momentum

Theory (BEMT) is used as a higher-ﬁdelity replacement for momentum theory-based

predictions. Though BEMT can resolve ﬁner details like angle of attack variations

along the span, it requires detailed inputs, namely airfoil tables and distribution

of blade chord and twist along the span. These details are populated as described

below.

The rotor is assumed to be constructed from multiple user-speciﬁed airfoils.

The lift and drag characteristics for each airfoil may be Reynolds-tabulated or mach-

tabulated. Several combinations of blade chord and twist distribution are generated

assuming linear taper and bilinear twist. The design variables for blade geometry

are:

1. Blade taper ratio (1:1, 2:1 and 3:1)

2. Blade bilinear twist junction (30% – 70% span)

3. Twist at bilinear junction (-5 deg to -20 deg)

4. Twist at tip (-5 deg to -35 deg)

The rotor RPM in cruise (speciﬁed as a fraction of hover RPM) is added as a siz-

ing variable. The BEMT analysis calculates the rotor power required for a given

thrust, for all mission segments, exploring a parameter space of 360 designs (com-

binations of blade twist and taper distribution). The rotor geometry for minimum

energy consumption over the mission is identiﬁed from the parametric sweep, and

the aerodynamic eﬃciencies (ﬁgure of merit F M in hover and propeller eﬃciency

ηpin cruise) are calculated for each mission segment.

Minimizing the energy required at the rotor ensures reduced fuel consumption,

but not necessarily a good overall design. A cruise-dominated mission results in a

prop-rotor with a potentially degraded hover ﬁgure of merit while achieving good

aerodynamic cruise eﬃciency. Therefore, installed power (and therefore, engine and

transmission weights) may increase, resulting in a lower payload fraction. To prevent

unchecked increases in powerplant weights, another condition is introduced in the

BEMT analysis: designs are considered “valid" if the hover ﬁgure of merit is greater

than a user-speciﬁed threshold (e.g., 0.72), and only these valid designs are ranked

to determine the “best” rotor eﬃciencies.

When BEMT is included in the sizing iterations, sizing proceeds in 3 steps:

1. Perform sizing with momentum theory and assumed eﬃciency factors in hover

and cruise (F M=0.75, ηp=0.82)

2. If the design satisﬁes all constraints, perform BEMT analysis to calculate aero-

dynamic eﬃciencies for each segment based on thrust requirements; extract

hover or cruise eﬃciencies (FM, ηp).

3. Perform sizing with momentum theory, using the calculated rotor aerodynamic

eﬃciencies obtained in Step 2.

Figure 8 shows the comparison of thrust and power obtained from BEMT

predictions with airfoil tables vs. sub-scale experiments for a variable-pitch and

variable-RPM sub-scale prop-rotor. Good predictions were obtained at various

cruise speeds ranging from 3 m/s to 15 m/s. For these cases, BEMT was found

to be suﬃcient for accurate performance predictions.

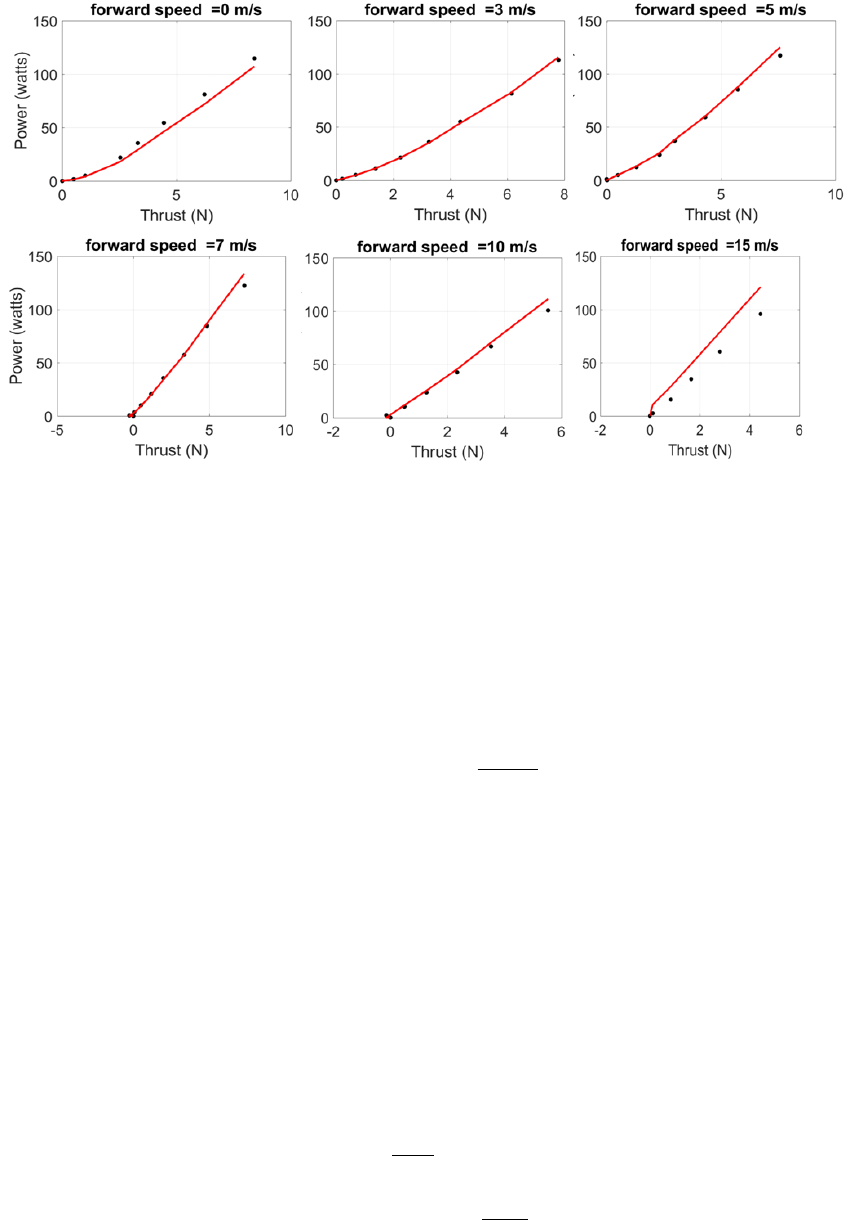
Figure 8: Comparison of BEMT predictions to experiments

3.2 Wing performance model

The drag coeﬃcient of a ﬁxed wing is given by

CD=CDo +1

πAReC2

L(9)

The lift coeﬃcient CLand aspect ratio AR are sizing design variables. The proﬁle

drag coeﬃcient CDo is an assumed value, usually 0.014 (including protrusions and

interference). The Oswald eﬃciency eis calculated as

e= (Q+P πAR)−1

P= 0.38 ×0.02

Q=1.01

s= 1 −2dfus

bwing 2

The parameters are dfus = equivalent fuselage diameter, and bwing = wing span.

4 Weight models

There are three main contributors to vehicle take-oﬀ mass:

1. Energy storage - battery and/or fuel weight. This component may be

traded-oﬀ against payload for mission ﬂexibility, depending on available vol-

ume.

2. Empty weight - this weight group represents the airframe, wings, rotors, en-

gines, transmission, motors, seats, avionics and other non-removable systems.

3. Payload - usually speciﬁed with the mission deﬁnition.

4.1 Engines, fuel and batteries

Though engines strictly belong in the empty weight category, the calculation

of fuel weights are inextricably linked to the evaluation of engine performance and

engine weights. Therefore, engine models are described in this section.

4.1.1 Engines

HYDRA has built-in models for fuel-burning engines of two types: gas turbine

engines, and reciprocating engines (piston engines and aero-diesel engines).

Turboshaft engines

Based on statistical data for various production engines, a trend line was ﬁtted

with good accuracy (R2= 0.92) for the variation of engine weight Wengine (lb) with

installed power Pins (hp). The ﬁtted engine weight model is given by

Wengine (lb) = 7.3874 P0.552

ins (10)

Another ﬁt is shown in Fig. 9, in SI units with engines manufactured over the last

ﬁfty years.

The variation of engine Speciﬁc Fuel Consumption (SFC) at peak eﬃciency

with installed power is

sfcbase (lb/hp-hr) = 1.549 P−0.161

ins (11)

Engines operating at sub-optimal conditions (i.e. at power settings lower than design

power output) suﬀer from higher speciﬁc fuel consumption. This eﬀect is modeled

using a power law as

sfc =sfcbase Preq

Pins −0.256

(12)

Here, Preq is the power output required from the engine to produce a thrust T

during a mission segment. Finally, the variation of available power (relative to

installed power) with ambient temperature and pressure is given by

Pavail =Pins [1 −KT(θ−1)] [1 + KD(δ−1)] (13)

The terms θand δare ratios of ambient temperature and ambient pressure to their

corresponding values at mean sea level (ISA). The constants KTand KDare ob-

tained from curve ﬁts of detailed engine performance curves.

Piston engines

The treatment of piston engine weights is similar to that followed for turboshaft

engines. The variation of engine weight with installed power is given by

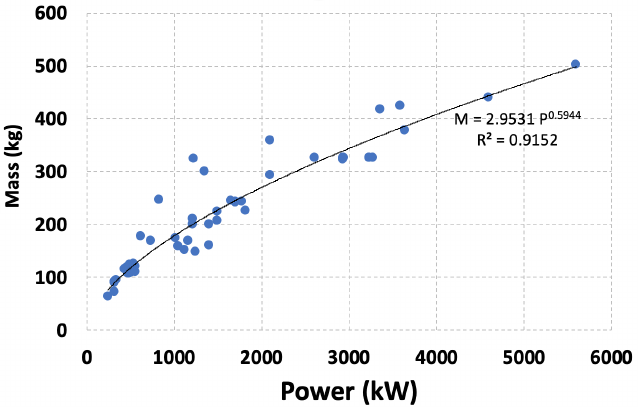
Figure 9: Statistics: turboshaft engine mass vs. installed power

Wengine (lb)=2.367 Pins (hp)0.916 35 ≤Pins (hp) ≤1000 (14)

Another ﬁt is shown in Fig. 10, in SI units with a larger sample size, including less

eﬃcient engines. The variation of engine SFC at its peak eﬃciency is

sfcbase (lb/hp-hr) = 0.42,Pins (hp) ≤4

= 0.594 −0.0046 Pins (hp),4≤Pins ≤56

= 0.52 Pins (hp)−0.0972,56 ≤Pins ≤1000

4.1.2 Fuel, tank and fuel handling systems

After calculating the engine power required, the mission proﬁle (ﬂight segment

duration) is used with engine power requirement and SFC estimates to calculate the

fuel weight as

mfuel =ΣNSEG

i=1 sfc(i)Peng(i) + munusable (15)

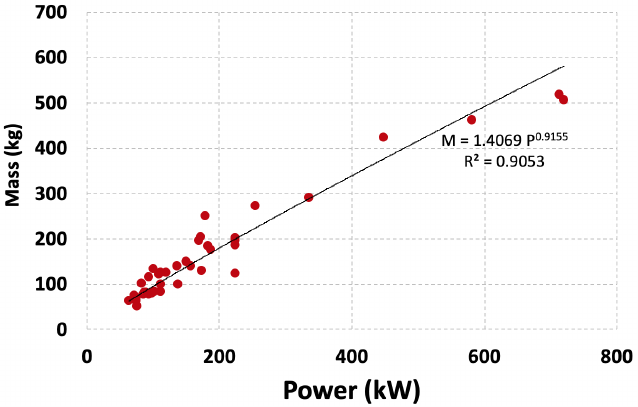
Figure 10: Statistics: reciprocating engine mass vs. installed power

An average density of 6.7 lb/gal is used for both turbine engine fuel and aviation

gasoline. The fuel tank and plumbing mass is estimated from fuel volume using

AFDD models as

Wtank = 0.4341 V0.7717

tank N0.5897

tank fcw f1.9491

bt (16)

The terms used in the equations are

Vtank is the tank volume in U.S. gallons (1 gal = 3.7.8 liters)

Ntank is the number of internal tanks

fcw is the crashworthiness mark-up factor, usually 1.31

fbt is the ballistic survivability mark-up factor (1.2 for military, 1.0 for civilian)

The weight of plumbing systems used for regulating fuel ﬂow from tanks to

engines is modeled as follows:

k0plumb =max(0.022M, 120)

k1plumb = 0.025k0

Wplumb =k0plumb +k1plumb(0.01 ∗Ntank + 0.06 ∗Nengine)˙

V0.866

Vis the peak fuel ﬂow rate to the powerplant in lb/hr and the plumbing system

weight is in pounds. Mis the take-oﬀ mass in kg - the mixing of units and con-

ventions is a result of AFDD models being speciﬁed in FPS units, while HYDRA is

implemented in SI units.

For small-scale powerplants, the trendlines predict an over-estimate of fuel

handling system weight. To handle these special cases, a maximum limiter is placed

on the fuel system weights, with the limit set to 50% of fuel weight.

4.1.3 Battery models

Battery weights are accurately represented using a very simple statistical

model. Figure 11 shows the variation of battery weight with rated energy capacity

for commercially available small-scale batteries, where each data point represents a

manufactured unit. Arguably, a battery density of 158 W-hr/kg is quite low and

improvements can be made; this “conservative” design is typical of commercially

available battery packs including the safety casing.

For full-scale platforms used in commercial operations, several conservative

assumptions are used to incorporate various margins in sizing the battery.

1. The minimum depth of discharge is 7.5% of total energy capacity

2. The maximum state of charge near end of life for the battery is 80%, i.e., after

cycling, the usable battery capacity is at most 80% of the rated energy. Thus,

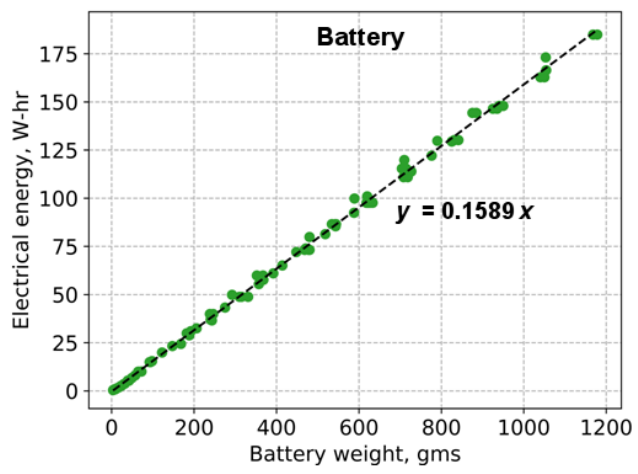
Figure 11: Small-scale batteries: weight statistics

the eﬀective usable energy for battery sizing is 72.5% of the rated capacity.

3. The average discharge eﬃciency of the battery reduces by 4% for every unit

increase in average C-rating.

4. A speciﬁc energy of 240 Wh/kg is used to estimate the mass of the cells.

5. A pack integration factor of 0.75 (deﬁned as battery mass to cell mass) is used

to estimate the weight of battery management systems and casing.

6. A curve ﬁt of temperature rise vs. C-rating (obtained from experimental

data) is used to track the rise of cell temperature over the mission duration. A

maximum limit of of 70oC is used to iteratively add cells until thermal limits

are satisﬁed.

4.1.4 Electric motor weights

Though electric motor weights are strictly driven by peak torque requirements,

the data correlation between weight and peak rated power is also very good as shown

in Fig. 12. For small-scale motors, the speed controller is sized based on the current

drawn by the system assuming a 12 Volt source. The masses of several large-scale

motors with controllers are plotted against rated power in Fig. 13. Motor + speed

controller eﬃciencies range from 85% to 92% depending on the design point and

operating RPM range. Motor and speed controller weights are estimated as

Wmotor(lb) = 0.74 P P ≤13.4hp

WESC (lb) = 1.047 P P ≤13.4hp

Wmotor +WESC (lb) = 1.489 P0.783 13.4hp <P≤350 hp

4.2 Electric Transmissions

Generators for electric transmissions are sized in a manner identical to electric

drive motors. The components of an electric transmission are shown in Fig. 14.

The advantage of this hybrid system is that a mechanical transmission is not

required for power transmission to the rotors; further the hybrid system can serve

as a long-range drop-in upgrade for short-range battery-powered variants. The dis-

advantage of a turboshaft-electric hybrid system is that each additional component

introduces additional points of failure. Adding redundancy and fail-safe architec-

tures can incur a signiﬁcant empty weight penalty.

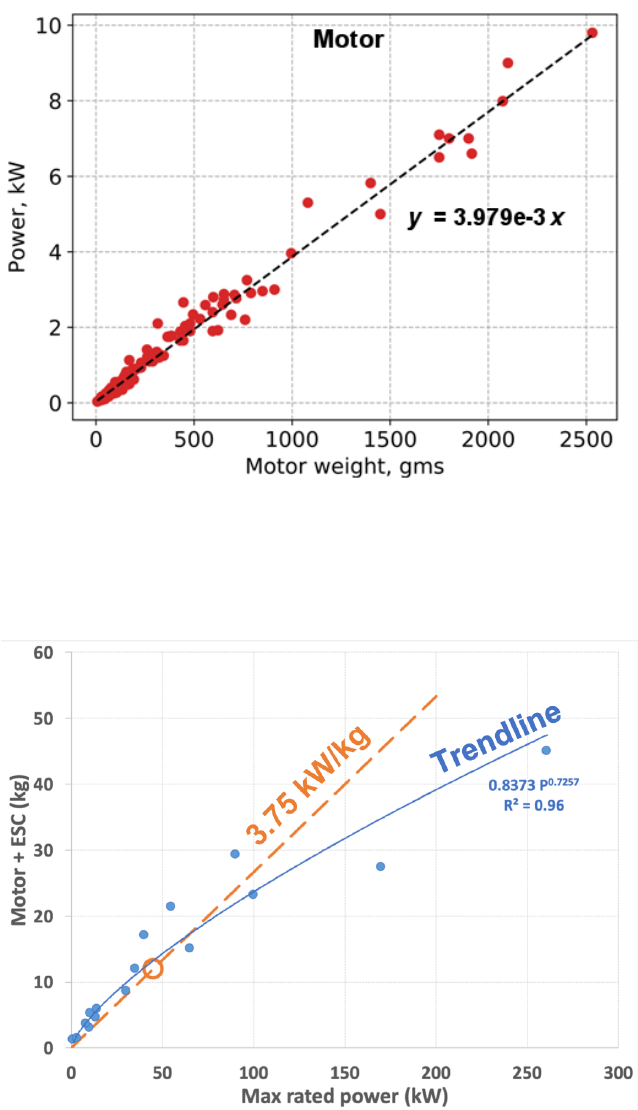
Figure 12: Statistics: weight of small BLDC motors

Figure 13: Statistics: large-scale DC motor + controller mass vs. installed power.

Manufacturing technology in 2018 can achieve 3.75 kW/kg of power density.

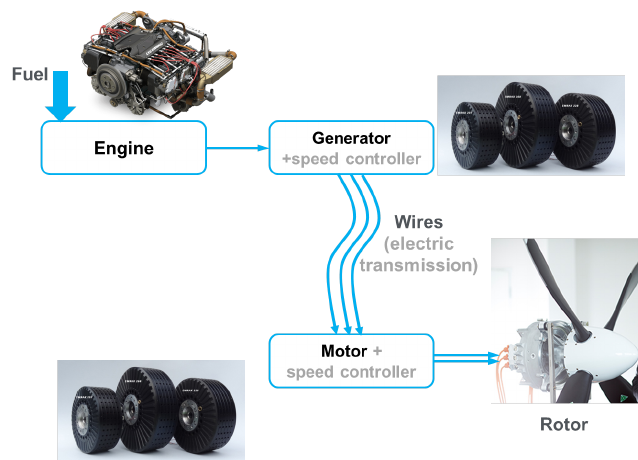
Figure 14: Turbine-generator hybrid powerplant for electric motor. 98% wire trans-

mission eﬃciency, 92% generator eﬃciency

4.3 Wire weights

Two types of wires are considered in the sizing analysis: power cables and signal

wires. The weights of electrical power cables are estimated from the vehicle rotor

layout using a wire mass per unit length per unit power of 0.0057 kg/kW/m. Signal

wires are calculated using a linear mass density of 0.17 kg/m and a knowledge of

the rotor layout, together with an estimate of channel counts. Based on user inputs,

doubly/triply redundant power cables and signal wires are automatically added to

the appropriate weight groups for estimating vehicle empty mass.

At full-scale, a key driver of vehicle weight is the rotor design parameter set

(tip speed, solidity, disk loading/radius, ﬁrst rotating ﬂap frequency). One such em-

Figure 15: Blade cross-section

pirical parameter is the ﬂap natural frequency. In the legacy approach for estimating

rotor blade weight, the designer had to prescribe this parameter to perform sizing.

However, underlying data for the ﬂap frequency is restricted to articulated and hin-

geless rotors, and plentiful data is not available for stiﬀer rotors (νβ≥1.08/rev). For

small-scale VTOL with very stiﬀ rotor systems (νβ≥1.4/rev), extrapolation of the

trend line beyond the range of available data for νβmay yield erroneous estimates

for rotor blade weight. For eVTOLs, a physics-based approach is implemented and

used in HYDRA.

4.4 Physics based model for rotor blades

A schematic of the rotor airfoil is shown in Fig. 15. The cross-section consists

of two categories of materials: non-structural masses, and load-bearing components.

The non-structural masses are:

1. Paint: 0.15 mm thickness, density 1800 kg/cu.m, applied on surface

2. Glue: 0.25 mm thickness, density 1800 kg/cu.m, applied on skin, shear webs

3. Core: density of 52 kg/cu.m, encompasses cross-section area of 0.49 t

cc

4. Leading edge protection: 1.14mm thickness, density 8900 kg/cu.m, from lead-

ing edge to 25% chord on upper and lower surfaces.

Here, t

cis the airfoil thickness-to-chord ratio, usually 0.1 to 0.12 and cis the blade

airfoil chord. For the paint and glue, the chordwise location of the component center

of gravity is 0.5c. For the leading edge protection strip and core, the component

chordwise center of gravity locations are 12.5% chord and 57% chord, respectively.

4.4.1 Skin sizing

The skin is sized to withstand a total torsion moment equivalent to an airfoil

cm=0.2 at the maximum rated rotor speed. The total root pitching moment in hover

Mx=1

6ρV 2

TIPc2cmR

The skin thickness is given by

tskin =nMx

2Acsτskin

Here, Acs is the cross-section area of the airfoil, and τskin is the maximum allowable

shear stress in the skin. The factor naccounts for additional overload and safety

factors to account for for contingency conditions and fatigue margins.

4.4.2 Leading edge weight

The section chordwise center of gravity for the non-structural components

(paint, leading edge protection and core) along with the skin is obtained from the

respective weights and component centroid locations. If this center of gravity is

behind the blade quarter-chord, a leading edge weight is added to avoid torsional

divergence and ﬂutter for the blade.

The CG of the non-structural components and skin is given by

c=mLEP0.125 + mskin0.5 + mcore0.57 + mpaint0.5 + mglue0.5

mLEP +mskin +mcore +mpaint +mglue

If x1

cis greater than 0.25, then a leading edge mass is added, equal to

mLE = (mLEP +mskin +mcore +mpaint +mglue)4x1

c−1

4.4.3 Spar caps and shear web sizing

The spar is placed so that the neutral axis and CG both lie at quarter-chord.

A NACA-0012 section is used to estimate The elements that support shear and

bending moment due to lift and drag and bending loads are the spar webs (shear

and lag bending moment) and spar caps (ﬂap bending moment and tension due to

the centrifugal load).

The limit load for eVTOL rotor blades is determined from the trim thrust

required under OMI (One Motor Inoperative) conditions. For the “conventional”

tilt-wing conﬁguration (6 rotors on main wing, 2 rotors on horizontal tail) and the

tandem tilt-wing conﬁguration (4 rotors each on canard and wing), the maximum

thrust scaling factor is approximately 150% the hover thrust. With rotor radius

R, rotor speed Ωand peak torque at the blade root Qbdetermined from the rotor

geometry, the vertical force on the blade is obtained by dividing the maximum

expected thrust level by the total number of blades as

Fz=W

NRNb

nz(17)

Figure 16: Blade spanwise segment

The terms nzis a load factor that can incorporate safety margins, dynamic over-

shoot/landing and fatigue factors for blade loads. The lift distribution along the

span is assumed to be quadratic (a structurally conservative loading proﬁle - the

optimum hovering rotor features a linear spanwise lift distribution, discounting tip

loss eﬀects). The blade is assumed to constructed with a pre-cone angle βpto alle-

viate root bending moments, and then subdivided into N= 5 equal span segments.

One such segment is shown in Fig. 16.

The dominant loads on the outboard end of the segment, that are carried by

the spar caps, are the centrifugal force (from all segments outboard of the present

one) and a ﬂap bending moment due to (i) distributed lift on segments outboard of

the present one, and (ii) a combination of pre-cone and centrifugal load on segments

outboard of the present one. The blade spanwise segments are successively sized

starting from the tip segment and ending in the root segment. A schematic of the

rotor blade segment and cross-section is shown in Fig. 17.

The total centrifugal load and ﬂap bending moment at the inboard end of the

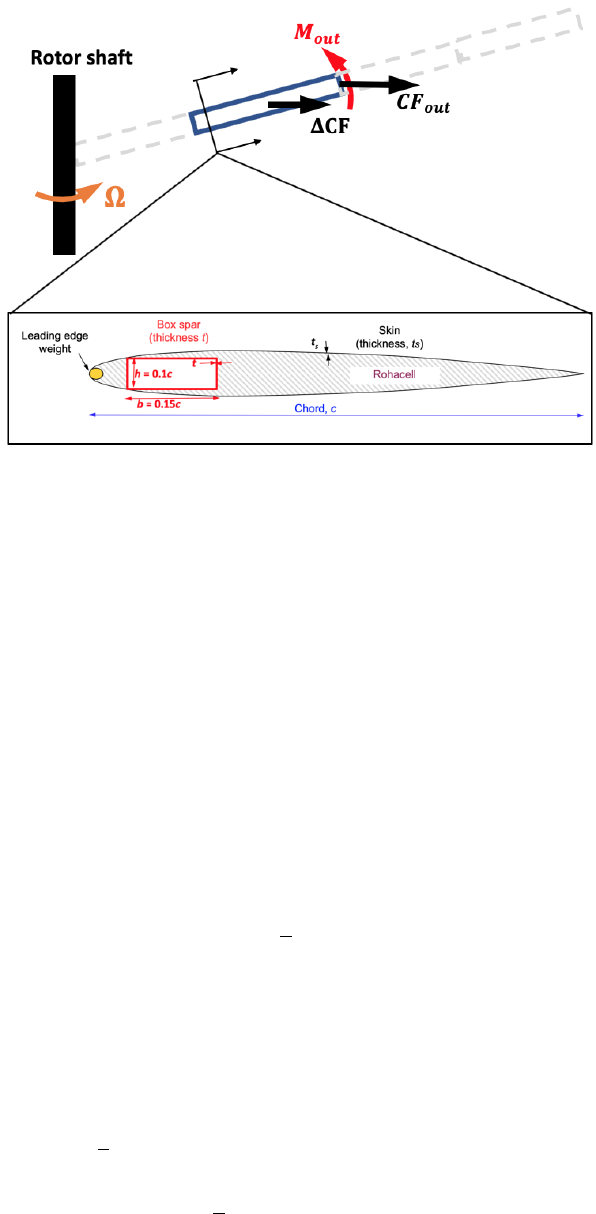
Figure 17: Rotor blade segment sizing: schematic

segment is

CF (xin) = CF (xout) + ∆CF (18)

M(xin) = M(xout) + ∆M(19)

The ﬂap bending moment distribution due to lift, along the non-dimensional span

coordinate x(0 at root, 1 at tip) is

Mlift(x) = 1

4FzR(x4−4x+ 3) (20)

The additional centrifugal load and ﬂap bending moment due to loads on the present

segment are

∆CF =1

2(ms+mns)V2

TIP (x)out2−x2

in)

∆M=−(CFout +1

2∆CF )∆Rβp+Mlift(xin)−Mlift(xout)

The spar mass per unit span is ms)and the non-structural mass per unit span is

mns. The maximum axial stress in the spar caps at the inboard end of the present

segment is

σxx(xin) = CF

Aspar

+M(xin)h

2

2bt h

22

The term Aspar is the area of the spar, given by 2(b+h)t. The individual

expressions can be rearranged to solve for the spar cap thickness t, as

t=RHS

LHS

LHS =1

nσmax +1

2V2

TIP(x2

out −x2

in)ρspar ∆Rβp

b+h

bh −1

RHS =1

2(b+h)CF (xout) + 1

2mnsV2

TIP(x2

out −x2

in)+Mlift(xin)

bh M(xout)−∆RβpCF (xout) + 1

2∆CF 

This formulation avoids iterative convergence inner loops for the rotor blade

structure during sizing, improving computational eﬃciency.

After sizing the spar, the shear webs thickness is determined from the vertical

bending load at the inboard end, given by

tweb = max 1.5nVz

hσskin

, tweb

Here, Vzis the vertical shear due to blade lift integrated from the inboard end of

the segment (x=xin) to the blade tip (x=1). After sizing one spanwise segment,

the total axial load and ﬂap bending moment at the inboard end of the segment

are calculated using Eqns. 18,19 respectively. The loads at the inboard end of the

present segment are then assigned as tip loads for the next segment, and the process

is repeated for all segments in succession.

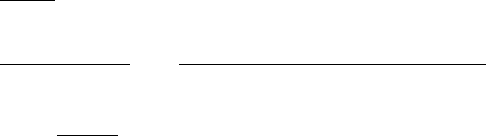
4.4.4 Root ﬁtting sizing

The root ﬁtting for the blade is assumed to extend from the shaft (x=0) to

10% of the blade span (x=0.1), and is made of 7075 Aluminum. The density is 2800

kg/cu.m, and a limiting axial stress of 20 MPa is used based on a fatigue life of 108

cycles. The construction of the root ﬁtting is shown in Fig. 18.

The tube radius is assumed to be equal to 4×the airfoil thickness, and the

thickness tRoot is evaluated to ensure that the maximum tensile stress in the ma-

terial does not exceed the limiting stress (20 MPa). The tube thickness is solved

analytically, using a formulation similar to the approach used for spar sizing. The

expression for tube thickness is

tRoot =RHS

LHS

RHS =CF (x= 0.1)

2πrRootσlimit

+Mlift(x= 0.1) −MCF(x= 0.1)

3πr2

Rootσlimit

LHS = 1 −ρ

2σlimit

Ω2(0.1R)

The root ﬁtting thickness is set to the larger of minimum gauge tmin or the calculated

thickness above, whichever is larger.

4.4.5 Torsion frequency check

The skin thickness is used to calculate the ﬁrst elastic torsion frequency for the

rotating blade and ensure that it is above 3.3/rev at the hover RPM. If the torsion

frequency is too low, then additional skin thickness is added until this requirement

is satisﬁed, preserving the same spar design.

Figure 18: Blade root ﬁtting

4.5 Flight controls

Two categories of actuators are modeled: ﬁxed-wing, and rotary-wing.

4.5.1 Rotor controls

Unlike large rotorcraft, some eVTOLs feature low-bandwidth collective actu-

ators and no cyclic or swashplate. In such designs, the collective pitch (e.g., for

prop-rotors) is usually scheduled with airspeed, and RPM is used for feedback con-

trol. Sizing laws for these collective actuators are therefore markedly diﬀerent from

those used for full-scale helicopter controls. The rotor hub mass and collective pitch

actuator masses scale with tip speed VTIP (and blade chord cfor the actuator) as

Mhub (kg) = 4.84 VTIP

171 2c

0.082(21)

Mact (kg) = 1.47 VTIP

171 2c

0.082(22)

The tip speed VTIP is in m/s and mean blade chord cis in meters.

4.5.2 Fixed wing controls

Fixed wing ﬂap and actuator weights are obtained from the AFDD model as

Wﬂaps (lb) = 0.01735W0.644S0.41

wing (23)

For this model, the weights are in lbs, including the take-oﬀ weight W. The term

Swing is the total plan-form area of all ﬁxed wings, and the actuator weights Wﬂaps

includes all actuators on all ﬁxed wings.

4.5.3 Tilt actuators

For tilt-rotors and tilt-wing conﬁgurations, the masses of tilt actuators are

estimated as the larger of 15.5% of wing mass, and 3.61% of the total mass being

tilted by that actuator. For tilt-wings, both metrics are applicable; for tilt-rotors,

the tilt actuator weight is set to 10% of the masses being tilted.

Mtilt−wing = max(0.155Mwing,0.0361Mtilt)(24)

Mtilt−rotor = 0.10(Mhub +Mact +Mblades +Mmotor)(25)

4.6 Motor mount mass

The motor mount structure refers to the overhang beam connecting the motor

and rotor hub, to a wing (or fuselage). For the Vahana tilt-wing conﬁguration, the

motor mount structure is the overhang beam used to oﬀset the rotor hub ahead of the

wing leading edge, as shown in Fig. 19. The motor mount is modeled as a cantilever

beam of length Lwith a tip mass equal to the mass of the rotor hub, blades and

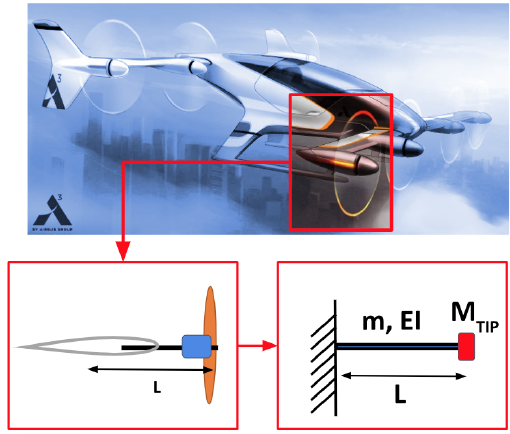
Figure 19: Motor mount model

motor. This structure is sized by a natural frequency requirement, i.e., the ﬁrst

cantilever bending mode for this beam with a tip mass must be suﬃciently

large so that the structural dynamics do not interact with ﬂight dynamics (0 - 4

Hz). For eVTOLs, a target ﬁrst bending frequency of 8.5 – 10 Hz is used to size the

motor mount beam. The overhang length is set to the sum of wing three-quarter

chord and one rotor radius.

For conﬁgurations such as CityAirbus (quad-ducted-coaxial rotors) with no

ﬁxed wings, the rotors are mounted directly on the fuselage using support arms.

The support arms are treated as “motor mounts”, and the beam length is set to

120% rotor radius. Appendix A provides an analytical solution for sizing a cantilever

beam with several lumped non-structural masses, distributed structural and non-

structural masses based on a target frequency.

4.7 Wing weight model

Three models are available to estimate the weight of a ﬁxed wing:

4.7.1 AFDD wing weight model

The weight of a ﬁxed wing is estimated as

Wwing = 5.6641Lw

1000 0.847 n0.4

zS0.21

wingAR0.5

t

c0.0936

The wing weight is in lbs, Lwis the wing design lift in lbs, nzis the design ultimate

load factor, Swing is the wing plan-form area in sq. ft, AR is the wing aspect ratio

and t

cis the wing thickness to chord ratio.

4.7.2 Frequency tuning: bending loads

The wing spar is idealized as a cantilever beam with lumped non-structural

masses (rotor blades, hub and collective actuator assembly and motor), distributed

non-structural masses (skin, ribs) and a hollow circular spar. A schematic of one

half-wing is shown in Fig. 20.

The wing taper ratio λ=cTIP

cROOT is a design parameter with a default value of

0.75. A tapered wing shifts the non-structural skin mass inboard while strengthening

the root, resulting in increased ﬁrst bending frequency for the same mass. The skin

thickness is set to include three layers of carbn ﬁber (45/0/45), resulting in an areal

mass density of ≈4.9 kg/sq.m. During sizing, the rotor assembly mass and motor

mass are used to calculate the wing spar thickness required to achieve a target ﬁrst

bending frequency using the Rayleigh-Ritz approximation detailed in Appendix A.

Figure 20: Wing structure: layout

To decouple wing structural dynamics from vehicle ﬂight dynamics, a target ﬁrst

bending frequency of at least 4 Hz is desirable (for a take oﬀ mass of 2000 kg).

Larger aircraft feature progressively relaxed natural frequency constraints, because

the ﬂight dynamic frequencies are lower for larger vehicles with correspondingly

larger moments inertia.

4.7.3 Hover: shear loads

After determining the spar thickness based on natural frequency requirements,

the wing structure is analyzed with static loads in hover with the tapered beam.

Rotor thrusts are applied at the motor mount locations and the static bending

stresses and shear stresses are calculated at ﬁve points between nodes (nodes are

located at the root and motor mount locations). A load factor of 3.8 and safety

margin of 1.5 are applied to ensure that the spar can support the loads in hover.

This hover loading condition is more limiting than cruise ﬂight with the same load

factors and safety factors, because the bending moments due to distributed lift are

lower than the corresponding bending moments in hover. The shear loading is used

to estimate the number of ±45 deg layers of carbon ﬁber, while the bending loads

are supported by layers of uniaxial carbon ﬁber.

4.8 Airframe Weight Model

4.8.1 Statistical weight model

The AFDD82 fuselage weight model for helicopter is given by

wfuselage =wbasic +wpress +wcw (26)

where wbasic is the basic weight of the fuselage, wpress is the weight from any pressur-

ization constraints (set to none for the sample mission in this work) and wcw is the

weight addition for crashworthiness, which is assumed to be 6% of the basic weight

as per AFDD standards. The basic weight is given by

wbasic = 5.896framp WGTOW

1000 0.4908

n0.1323

zS0.2544

body l0.61 (27)

where framp is the factor for a retractable ramp, nzis the load factor, Sbody is the wet-

ted area of the fuselage (sq. ft) and lis the length of the fuselage (feet). While these

terms can be deﬁned for full-scale helicopters/tiltrotor, their deﬁnitions become in-

creasingly challenging to interpret in the context of unconventional conﬁgurations

such as an eVTOL, with very diﬀerent load paths compared to helicopters.

4.8.2 Component build-up model

Another approach to estimate fuselage mass is to consider the constituent

components in the airframe, and estimate the weight of each part based on the

design limit loads carried by that part. These parts are

1. Skin: using fuselage dimensions and an assumed uniform skin thickness, the

skin mass is calculated using the wetted area of the skin. This wetted area is

estimated as

Swet = 4π(lfhf)1.6+ (bflf)1.6+ (bfhf)1.6

31

1.6

(28)

The skin consists of paint, core, glue and carbon ﬁber. The mass of the fuselage

skin is therefore

Mskin = (ρcarbontcarbon +ρgluetglue +ρcoretcore +ρpainttpaint)(29)

2. Canopy: When a canopy is included, the wetted area of the canopy is assumed

to be 8% of the fuselage wetted area, and the canopy mass is calculated as

mcanopy =ρcanopytcanopyScanopy (30)

3. Bulkhead: 4 bulkheads (elliptical cross-sections) are placed along the length

of the fuselage. Bulkhead mass is calculated assuming no cut-outs, as

mbulkhead = 4 πbh

4tbulkheadρcarbon (31)

4. Keel beam: The keel beam mass is estimated based on strength requirements,

and sized to carry the following loads: (1) bending moment due to tail lift at

a load factor of 3.8 and safety factor of 1.5 (2) torsion moment in the airframe

due to diﬀerential wing lift of 25% vehicle weight, and a moment arm of half-

span; and ﬁnally (3) Combined vertical and lateral shear load during a 3.5 nz

landing.

4.8.3 Physics-based weight model: load-bearing airframe components

A physics-based model is used to estimate the weights of load-bearing compo-

nents that transmit rotor hub forces and wing lift and drag to the vehicle center of

mass. The airframe is subdivided into 3-D beam elements, each with bending, axial

and torsion degrees of freedom. Rotor hub loads and wing lift/drag are modeled

as point loads at the motor points, and distributed uniformly over the wing span,

respectively. The external loads corresponding to each mission phase are applied

on the structure, (rotor thrust, torque, wing lift and wing drag) and the resulting

stresses and deﬂections are calculated and stored at all the nodes. Subsequently,

the cross-section dimensions of the beams are iteratively resized to ensure; (i) Min-

imum factor of safety of 1.5 (based on Von-Mises stress) at a load factor of 3.5,

(ii) A maximum deﬂection of 10% for any node (relative to its distance from the

vehicle center). The cross-sections of all beam elements are assumed to be hollow

circles with wall thickness equal to 15% outer radius. The only design parameter

for a beam element is the outer radius of the cross-section. Beam cross-section radii

for all elements are updated iteratively until the 3 design criteria are satisﬁed, and

the weight of the airframe members is calculated using material density and ﬁnal

dimensions. The ﬁnite element analysis iterations are performed within the sizing

Figure 21: Quad-rotor biplane tail-sitter: layout to ﬁnite element representation

loop. The parameterization for a quad-rotor layout is shown in Fig. 21.

Integration of FEA into sizing: workﬂow

The overall process is depicted in a ﬂowchart shown in Fig. 22 and proceeds as

follows

1. Initialize: A geometric layout of the airframe is chosen, and beam elements

are deﬁned. The present work assumes the beam cross section to be simple

shapes such as a hollow cylinder or a solid square.

2. Inner FEA loop: Point forces and moments are applied to the structure

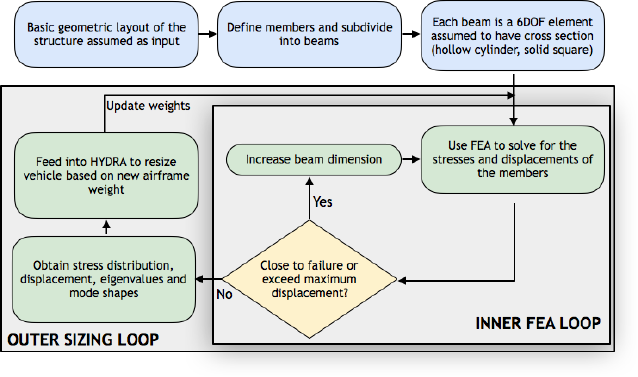
Figure 22: Workﬂow for including physics-based airframe weight model in sizing

based on rotor and wing loads, such as rotor thrust, rotor torque and wing lift.

The von-Mises stress (σVM), the corresponding factor of safety and deﬂection

of the various nodes are computed as

σVM = [(σxx −σyy)2+ (σyy −σzz)2(32)

+ (σzz −σxx)2+ 6(σ2

yz +σ2

xy +σ2

xz)]1/2

where σij are components of the stress tensor and the factor-of-safety (FOS)

FOS = min(σV M )i/σyield ∀i∈N(33)

where Nis the total number of beam elements.

3. Update cross-section dimensions: The mathematical constraints im-

posed for convergence are

|FOStar −∆FOS| ≤ min(FOS) (34)

where FOStar is the target FOS, set to 1.5 and ∆FOS is the allowable band,

set to 0.1. The axial and bending deﬂections of each node are normalized by

the distance of the node from the vehicle center of gravity. These normalized

deﬂections must not exceed a pre-determined fraction (0.08) to ensure struc-

tural rigidity. Depending on the type of condition encountered, two types of

cross-section updates are calculated:

(a) The beam cross-section is scaled up by the term (FOS/FOStar)1/3) if the

factor of safety is not suﬃciently large. The cube root in the expression

stems from the fact that stress is inversely proportional to cross-section

dimension under static load.

(b) If the deﬂection of any one node is too large, the dimensions of all cross-

sections are increased by 10%. Increasing the sizes of all the member

cross-sections is required because adding stiﬀness to the root end of a

longer beam may be more eﬀective than stiﬀening an outboard member

(in the present workﬂow, no apriori assumptions are made about the

load path, and so to guarantee deﬂections are restricted, all members are

stiﬀened).

The larger of the two calculated dimensions for each structural member is

provided to the FEA for the next iteration. The stresses and deﬂections are

recalculated, and members resized until the structure achieves the required

factor of safety and deﬂection limits.

The airframe weight is computed by multiplying the total volume of all the

beam elements with the material density (Aluminum, 2,700 kg/m3or carbon,

1650 kg/m3). This converged airframe weight from static ﬁnite element analy-

sis replaces the fuselage weight from the AFDD empty weight formulae in the

iterative sizing process.

The structural analysis used in in sizing the airframe structure also provides esti-

mates of the natural frequencies and the mode-shapes. This information can be used

in advanced stages of design to ensure suﬃcient separation between the airframe,

blade natural frequencies and operating RPM range of the rotor(s).

4.9 Weight margin

A weight margin is included in the analysis to admit additional expansion of

component performance (and therefore weight) at later stages of design. Therefore,

10% of the vehicle empty weight is allocated for a weight margin.

4.10 Fixed weight groups

Fixed empty weight groups consist of mission-speciﬁc components and do not

scale with vehicle dimensions or system performance during sizing. These ﬁxed

weight groups are

1. Carpets, cabin trim and noise insulation

2. Avionics, sensors and ﬂight computers

3. Airconditioning and heaters

4. Seats

5. Low voltage battery, anti-collision lights, air data systems

6. High voltage bus and power distributors

4.11 Comparison of weights vs. NDARC

To validate the convergence technique, individual weight models and perfor-

mance models in HYDRA, the vehicle weight breakdown was obtained for a single

main rotor helicopter with gas turbine engines and a mechanical transmission, and

compared to values obtained from NDARC (a NASA sizing code). Table 2 shows

that less than 1% error is obtained for most groups, while fuel is slight over-predicted

by 2.8%.

Table 2: Helicopter weight breakdown: HYDRA vs. NDARC

Group weight (lb) HYDRA prediction NDARC prediction % diﬀerence

Gross weight 14230 14243 0.1%

Payload 2500 2500 –

Fuel 1702 1752 2.9%

Empty weight 9252 9267 0.16%

Engine + accessories 1038 1024 1.3%

Transmission 1316 1292 -1.82%

Fuel system (pump, tank) 508 505 -0.6%

Airframe 1304 1301 -0.2%

Alighting gear 461 463 0.4%

Rotor system 1098 1100 0.2%

Empennage 184 179 2.7%

Flt. control, deicing + hydraulics 1013 1013 –

A Cantilever beam dynamics

Consider an eVTOL wing with multiple electric motors and rotors mounted

along the spar, shown in Fig. 23. The wing structure is idealized as a cantilever

beam with non-structural lumped masses placed along the span, shown in Fig. 24.

Figure 23: Rotor layout for an example eVTOL wing

Figure 24: Idealization of eVTOL wing structure

To expand the generality of the analysis, consider a tapered circular spar

running along the length of the wing. The cross-section of the spar is shown in

Figure 25: Linearly tapered circular spar

Fig. 25. The tube thickness is equal to t, and is uniform along the spar length. The

radius of the circular cross-section varies from r1at the root of the beam to r2at

the tip. The mass per unit span and bending stiﬀness of the spar is given by

m(x) = 2πρr(x)t

EIyy(x) = Eπr(x)3t

The ﬁrst bending natural frequency is estimated using a Rayleigh-Ritz approx-

imation, with a mode shape set by the static deﬂection of the cantilever due to a

tip-load, i.e.,

w00(x) = P(L−x)(35)

Integrate twice along the span and apply the cantilever boundary condition to obtain

the deﬂected bending slope as

w0(x) = P

Eπt a2

r(x)2+a1

r(x)+a0(36)

The constants are

a2=−L

2r0−r1

2r02

a1=−1

r02

a0=L

2r0r2

1−1

2r02r1

Integrate the bending slope along the span to obtain the deﬂected mode shape as

w(x) = P

Eπt b0+b1x+bm

r(x)+blloger(x)(37)

The constants are

b0=−a2

r1r0−a1

r0loge(r1)

b1=a0

bm=−a2

bl=a1

A.1 Potential energy

The maximum potential energy is given by

U=1

2ZL

P2(L−x)2

EIyy(x)dx

Substitute for the bending stiﬀness to obtain

U=1

Eπt[A+B+C](λ)

The term λis the spar taper ratio, given by

λ=r2

(38)

The sum A+B+Cis well-represented by a cubic polynomial in λas

A+B+C≈(1.6261 −0.4826λ+ 2.1197λ2−0.5957λ3)1

The constant Kis the inverse of the spar aspect ratio, given by

K=2( t

ARwing

(39)

Here, t

cis the wing thickness to chord ratio, and ARwing is the wing aspect ratio.

A.2 Kinetic energy

The maximum kinetic energy of the beam has contributions from three types

of masses:

1. Structural masses: This term deals with the kinetic energy of the spar

structure. This contribution to kinetic energy is

KEs=ZL

22πr(x)tρ w(x)2ω2

ndx =P2

E2πtρω2

n(RHS)

The term RHS is a function of the taper ratio λ, length Land spar taper ratio

inverse Konly. Further, the dependence on wing taper λcan be approximated

using a cubic polynomial in λ. Thus, the kinetic energy coeﬃcient RHS is

approximated as

RHS ≈L2

K5(0.04823 + 0.269λ+ 0.15178λ2+ 0.36917λ3)

2. Non-structural distributed masses: This term deals with the kinetic en-

ergy due to the skin and other components (e.g., wires) that do not contribute

signiﬁcantly to bending stiﬀness. The kinetic energy term is

KENS =ZL

2mNS(x)w(x)2ω2

ndx

The non-structural mass due to wing skin is given by

mNS(x) = 2MNS

A(t

c)r(x)

The term MNS

Ais the non-structural mass per unit plan-form area of the skin.

Deﬁne an intermediate quantity βgiven by

β=MNS

A(t

The expression for kinetic energy of non-structural masses simpliﬁes to

KENS =βP2ω2

E2π2t2RHS

3. Non-structural lumped mass: This term refers to the kinetic energy of

the electric motor/speed controller unit, rotor hubs and rotor blades. These

discrete lumped masses are mounted along the wing spar, and the kinetic

energy of these masses is given by

KElump =ΣNM

2Miw(xi)2=P2ω2

E2π2t2∆RHS

The coeﬃcient ∆RHS is

∆RHS =ΣNM

2b0+b1xi+blloger(xi) + bm

r(xi)2

A.3 Frequency tuning

The goal is to determine the spar mass by setting a target ﬁrst natural fre-

quency ωnfor the cantilever beam with distributed and lumped non-structural

masses. Equating the maximum total kinetic energy and maximum potential energy

for the ﬁrst bending mode, we obtain

E2πt LHS =ω2

nP2

E2t(RHS) + P2

E2π2t2β(RHS) + P2

E2π2t2∆RHS(40)

Solve for spar thickness as

t=Eπ

2ω2

LHS −ρπRHS−1

[β(RHS) + ∆RHS]

The total spar mass is therefore

Mspar =πρ t(1 + λ)r1(41)

For validation of the Rayleigh-Ritz solution, several cases were evaluated with

and without lumped non-structural masses.

A.4 Validation

A.4.1 Case 1: cantilever beam

Consider a cantilever beam with a hollow circular cross-section of constant wall

thickness, and the cross-section radius is linearly tapered from root to tip, with a

taper ratio of λvarying from 0.5 to 1.2. The beam length is 2.9 m, mean tube radius

is 0.1411 m. The ﬁrst bending natural frequency predictions from the Rayleigh-Ritz

approximation are compared against a beam Finite Element Method analysis. These

two frequencies are plotted in Fig. 26. The Rayleigh-Ritz approximation exhibits

about 2% over-prediction, but otherwise captures the trends accurately. In this

example, no non-structural masses were considered.

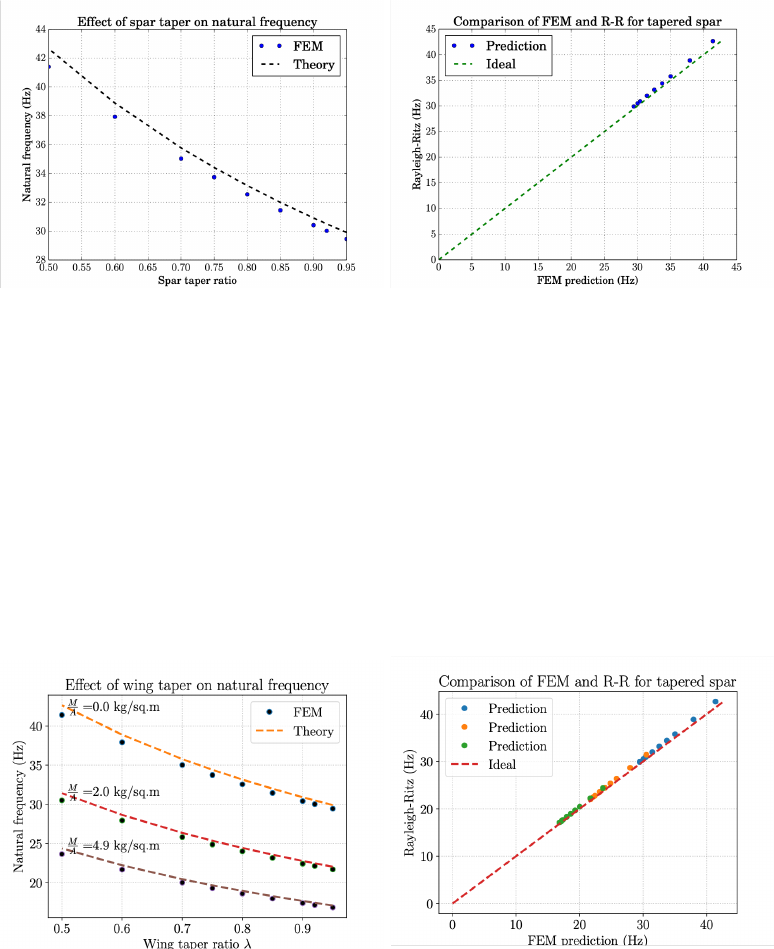
(a) Natural frequency vs. taper ratio (b) Rayleigh-Ritz vs. FEM

Figure 26: Natural frequency: Rayleigh-Ritz vs. FEM predicted natural frequencies

for a tapered cantilever beam

(a) Natural frequency vs. taper ratio (b) Rayleigh-Ritz vs. FEM

Figure 27: Natural frequency: Rayleigh-Ritz vs. FEM for a tapered cantilever beam

with distributed non-structural masses

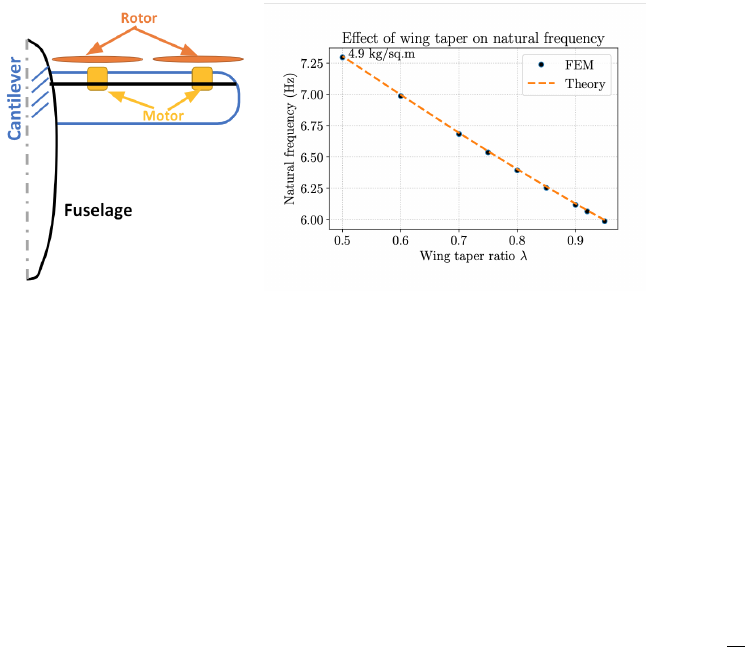
(a) Layout of eVTOL wing (b) Rayleigh-Ritz vs. FEM

Figure 28: Natural frequency: Rayleigh-Ritz vs. FEM for an example eVTOL wing

A.4.2 Case 2: distributed non-structural mass

This case is representative of an aircraft half-wing with skin, and no lumped

masses. The non-structural masses are represented as a mass per unit area, i.e., M

kg/m2. Three diﬀerent values of the non-structural mass per unit wing area were

evaluated: 0, 2.0 and 4.9 kg/m2. The resulting natural frequencies were calculated

from both Rayleigh-Ritz and FEM, and are plotted in Fig. 27. Excellent agreement

is obtained.

A.4.3 Case 3: half-wing with lumped masses

This case is representative of an eVTOL wing. The dimensions of the beam

are the same as in the previous examples, and the distributed skin mass per unit

area is 4.9 kg/m2. Two lumped masses (21.3 kg, 27 kg) are placed along the beam

at 0.5Land L, respectively. The wing layout and natural frequencies are shown in

Fig. 28.

Theory Manual

Navigation menu

Versions of this User Manual:

Views

Navigation