ISMT11_C01_A Thomas' Calculus 11th Edition Solution Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 1057 [warning: Documents this large are best viewed by clicking the View PDF Link!]
CHAPTER 1 PRELIMINARIES
1.1 REAL NUMBERS AND THE REAL LINE
1. Executing long division, 0.1, 0.2, 0.3, 0.8, 0.9
"
99999
2389
œœœœœ
2. Executing long division, 0.09, 0.18, 0.27, 0.81, 0.99
"
11 11 11 11 11
23911
œœœœœ
3. NT = necessarily true, NNT = Not necessarily true. Given: 2 < x < 6.
a) NNT. 5 is a counter example.
b) NT. 2 < x < 6 2 2 < x 2 < 6 2 0 < x 2 < 2.ÊÊ
c) NT. 2 < x < 6 2/2 < x/2 < 6/2 1 < x < 3.ÊÊ
d) NT. 2 < x < 6 1/2 > 1/x > 1/6 1/6 < 1/x < 1/2.ÊÊ
e) NT. 2 < x < 6 1/2 > 1/x > 1/6 1/6 < 1/x < 1/2 6(1/6) < 6(1/x) < 6(1/2) 1 < 6/x < 3.ÊÊÊ Ê
f) NT. 2 < x < 6 x < 6 (x 4) < 2 and 2 < x < 6 x > 2 x < 2 x + 4 < 2 (x 4) < 2.ÊÊ ÊÊÊ Ê
The pair of inequalities (x 4) < 2 and (x 4) < 2 | x 4 | < 2.Ê
g) NT. 2 < x < 6 2 > x > 6 6 < x < 2. But 2 < 2. So 6 < x < 2 < 2 or 6 < x < 2.ÊÊ
h) NT. 2 < x < 6 1(2) > 1(x) < 1(6) 6 < x < 2ÊÊ
4. NT = necessarily true, NNT = Not necessarily true. Given: 1 < y 5 < 1.
a) NT. 1 < y 5 < 1 1 + 5 < y 5 + 5 < 1 + 5 4 < y < 6. Ê Ê
b) NNT. y = 5 is a counter example. (Actually, never true given that 4 y 6)
c) NT. From a), 1 < y 5 < 1, 4 < y < 6 y > 4. Ê Ê
d) NT. From a), 1 < y 5 < 1, 4 < y < 6 y < 6. Ê Ê
e) NT. 1 < y 5 < 1 1 + 1 < y 5 + 1 < 1 + 1 0 < y 4 < 2. Ê Ê
f) NT. 1 < y 5 < 1 (1/2)( 1 + 5) < (1/2)(y 5 + 5) < (1/2)(1 + 5) 2 < y/2 < 3. Ê Ê
g) NT. From a), 4 < y < 6 1/4 > 1/y > 1/6 1/6 < 1/y < 1/4.ÊÊ
h) NT. 1 < y 5 < 1 y 5 > 1 y > 4 y < 4 y + 5 < 1 (y 5) < 1. Ê Ê Ê Ê Ê
Also, 1 < y 5 < 1 y 5 < 1. The pair of inequalities (y 5) < 1 and (y 5) < 1 | y 5 | < 1. Ê Ê
5. 2x 4 x 2 Ê
6. 8 3x 5 3x 3 x 1 x
1
Ê Ê Ÿ ïïïïïïïïïñqqqqqqqqp
7. 5x 3x 8x 10 x $Ÿ( Ê Ÿ Ê Ÿ 5
4
8. 3(2 x) 2(3 x) 6 3x 6 2x Ê
0 5x 0 x x
0
Ê Ê ïïïïïïïïïðqqqqqqqqp
9. 2x 7x 5x Ê
""
##
77
66
x or x Ê
""
56 3
10
ˆ‰
10. 12 2x 12x 16
6x 3x4
42
Ê
28 14x 2 x x
2
Ê Ê qqqqqqqqqðïïïïïïïïî
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
2 Chapter 1 Preliminaries
11. (x 2) (x 6) 12(x 2) 5(x 6)
4
53
Ê
"
12x 24 5x 30 7x 6 or x Ê Ê
6
7
12. (4x 20) 24 6xŸ ÊŸ
x 5 12 3x
24
44 10x x x
22/5
Ê Ÿ Ê Ÿ qqqqqqqqqñïïïïïïïïî
22
5
13. y 3 or y 3œœ
14. y 3 7 or y 3 7 y 10 or y 4œ œÊ œ œ
15. 2t 5 4 or 2t 4 2t 1 or 2t 9 t or t œ &œ Ê œ œ Ê œ œ
"
##
9
16. 1 t 1 or 1 t 1 t or t 2 t 0 or t 2œ œ Êœ! œ Ê œ œ
17. 8 3s or 8 3s 3s or 3s s or sœ œÊœ œ Êœ œ
99725725
266###
18. 1 1 or 1 1 2 or s 4 or s 0
ss ss
## ##
œ œÊ œ œ!Ê œ œ
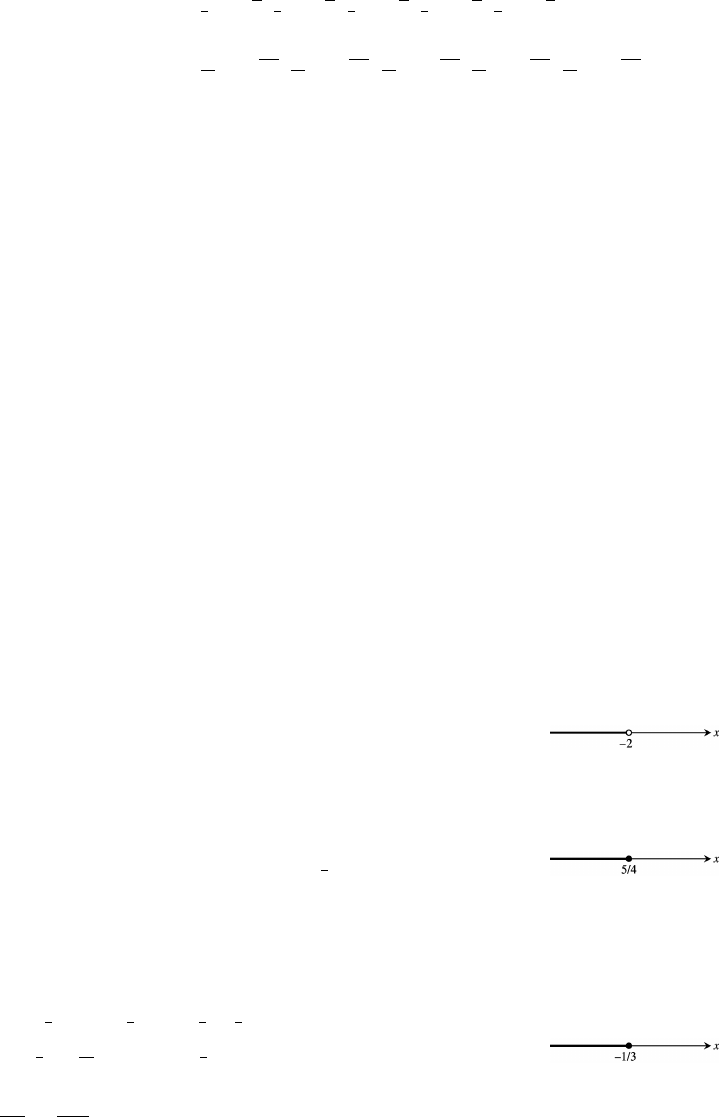
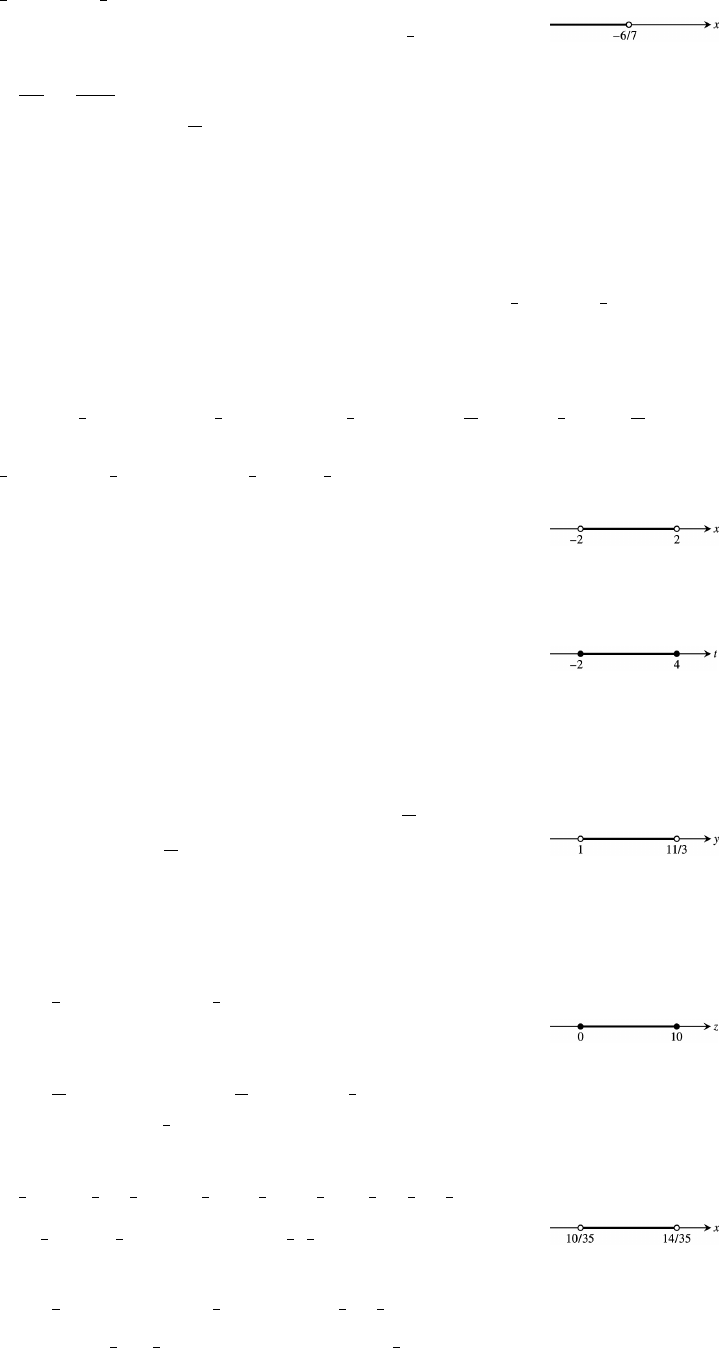
19. 2 x 2; solution interval ( 2 2) ß
20. 2 x 2; solution interval [ 2 2] x
22
Ÿ Ÿ ß qqqqñïïïïïïïïñqqqqp
21. 3 t 1 3 2 t 4; solution interval [ 2 4] Ÿ Ÿ ÊŸŸ ß
22. 1 t 2 1 3 t 1; Ê
solution interval ( 3 1) t
31
ß qqqqðïïïïïïïïðqqqqp
23. 3y 7 4 3 3y 11 1 y ;% Ê Ê 11
3
solution interval 1
ˆ‰
ß11
3
24. 1 2y 5 6 2y 4 3 y 2; "Ê Ê
solution interval ( 3 2) y
32
ß qqqqðïïïïïïïïðqqqqp
25. 1 1 1 0 2 0 z 10;ŸŸ Ê Ÿ Ÿ Ê ŸŸ
zz
55
solution interval [0 10] ß
26. 2 1 2 1 3 z 2; Ÿ Ÿ Ê Ÿ Ÿ Ê Ÿ Ÿ
3z 3z 2
3##
solution interval 2 z
2/3 2
‘
ß qqqqñïïïïïïïïñqqqqp
2
3
27. 3 Ê Ê
""" " "
### ###xxx
7575
x ; solution interval Ê ß
22 22
75 75
ˆ‰
28. 3 4 3 1 1Ê(Ê
22x
xx 7#"
2 x x 2; solution interval 2 x
2/7 2
Ê Ê ß qqqqðïïïïïïïïðqqqqp
22 2
77 7
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 1.1 Real Numbers and the Real Line 3
29. 2s 4 or 2s 4 s 2 or s 2;Ê Ÿ
solution intervals ( 2] [2 ) _ß ß _
30. s 3 or (s 3) s or s Ê
""
####
57
s or s ;Ê Ÿ
57
##
solution intervals s
7/2 5/2
‘‰ˆ
_ß ß _ ïïïïïïñqqqqqqñïïïïïïî
75
##
31. 1 x 1 or ( x) 1 x 0 or x 2 " Ê
x 0 or x 2; solution intervals ( ) (2 ) Ê _ß!ß_
32. 2 3x 5 or (2 3x) 5 3x 3 or 3x 7 Ê
x 1 or x ;Ê
7
3
solution intervals ( 1) x
17/3
_ß ß _ ïïïïïïðqqqqqqðïïïïïïî
ˆ‰
7
3
33. 1 or 1 r 1 2 or r 1 2
rr1"
##
Ê Ÿ
ˆ‰
r 1 or r 3; solution intervals ( 3] [1 ) Ê Ÿ _ßß_
34. or
3r 2 3r 2
555 5
" "
ˆ‰
or r or r 1Ê Ê
3r 7 3r 3 7
55 5 5 3
solution intervals ( ) r
17/3
_ß " ß _ ïïïïïïðqqqqqqðïïïïïïî
ˆ‰
7
3
35. x x 2 2 x 2 ;
## Ê Ê kk ÈÈ È
solution interval 2 2 x
Š‹
ÈÈ ÈÈ
ß qqqqqqðïïïïïïðqqqqqqp
# #
36. 4 x 2 x x 2 or x 2;ŸÊŸ Ê Ÿ
#kk
solution interval ( 2] [2 ) r
22
_ß ß _ ïïïïïïñqqqqqqñïïïïïïî
37. 4 x 9 2 x 3 2 x 3 or 2 x 3Ê Ê
#kk
2 x 3 or 3 x 2;Ê
solution intervals ( 3 2) (2 3) x
3223
ß ß qqqqðïïïïðqqqqðïïïïðqqqp
38. x x x or x
""" """" "
####943 3 3
Ê Ê kk
x or x ;Ê
""" "
##33
solution intervals x
1/2 1/3 1/3 1/2
ˆ‰ˆ‰
ß ß qqqqðïïïïðqqqqðïïïïðqqqp
"" ""
##33
39. (x 1) 4 x 1 2 2 x 1 2 Ê Ê
#kk
1 x 3; solution interval ( ) x
13
Ê "ß $ qqqqqqðïïïïïïïïðqqqqp
40. (x 3) x 3 2#Ê
#kk
È
2 x 3 2 or 3 2 x 3 2 ;Ê
ÈÈÈ È
solution interval 3 2 3 2 x
33
Š‹
ÈÈ ÈÈ
ß qqqqqqðïïïïïïïïðqqqqp
# #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
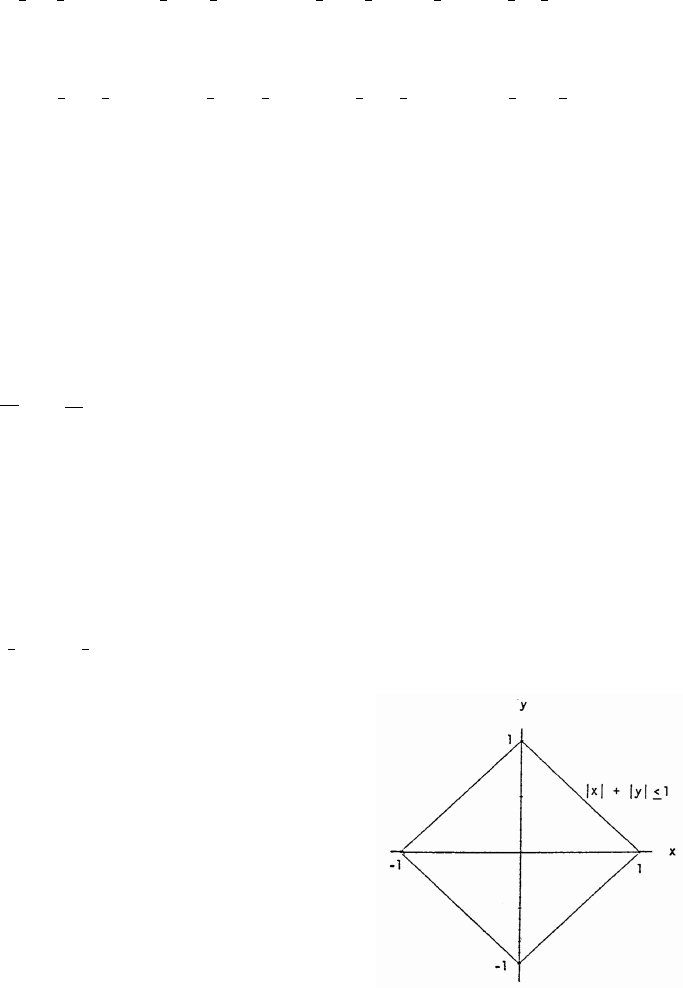
4 Chapter 1 Preliminaries
41. x x 0 x x + < x < x < < x < 0 < x < 1.
##
Ê Ê Ê Ê Ê
11 1 1 1 1 1 11
44 2 4 2 2 2 22
2
ˆ‰ ¹¹
So the solution is the interval (0 1)ß
42. x x 2 0 x x + x x or x x 2 or x 1.
##
Ê Ê Ê Ê Ÿ
19 1 3 13 1 3
44 2 2 22 2 2
¹¹ ˆ‰
The solution interval is ( 1] [2 ) _ß ß _
43. True if a 0; False if a 0.
44. x 1 1 x (x 1) 1 x 1 x 0 x 1kk k kœÍ œÍÍŸ
45. (1) a b (a b) or a b (a b);kk kkœ œ
both squared equal (a b)#
(2) ab ab a b Ÿœkk kkkk
(3) a a or a a, so a a ; likewise, b bkk kk kk kkœœœ œ
##
##
(4) x y implies x y or x y for all nonnegative real numbers x and y. Let x a b and
## ##
ŸŸŸ œ
ÈÈkk
y a b so that a b a b a b a b .œ Ÿ ÊŸkkkk kka bkkkkkkkk kk
##
46. If a 0 and b 0, then ab 0 and ab ab a b . œœkk kkkk
If a 0 and b 0, then ab 0 and ab ab ( a)( b) a b . œ œœkk kkkk
If a 0 and b 0, then ab 0 and ab (ab) (a)( b) a b . Ÿ œœœkk kkkk
If a 0 and b 0, then ab 0 and ab (ab) ( a)(b) a b . Ÿ œœœkk kkkk
47. 3 x 3 and x x 3.Ÿ Ÿ Ê Ÿ
""
##
48. Graph of x y 1 is the interiorkk kkŸ
of “diamond-shaped" region.
49. Let be a real number > 0 and f(x) = 2x + 1. Suppose that | x 1 | < . Then | x 1 | < 2| x 1 | < 2 $$$$ÊÊ
| 2x | < 2 | (2x + 1) 3 | < 2 | f(x) f(1) | < 2# Ê Ê $$$
50. Let > 0 be any positive number and f(x) = 2x + 3. Suppose that | x 0 | < /2. Then 2| x 0 | < and%%%
| 2x + 3 3 | < . But f(x) = 2x + 3 and f(0) = 3. Thus | f(x) f(0) | < .%%
51. Consider: i) a > 0; ii) a < 0; iii) a = 0.
i) For a > 0, | a | a by definition. Now, a > 0 a < 0. Let a = b. By definition, | b | b. Since b = a,œÊœ
| a | ( a) a and | a | | a | a.œœ œœ
ii) For a < 0, | a | a. Now, a < 0 a > 0. Let a b. By definition, | b | b and thus | a| a. So againœ Ê œ œ œ
| a | | a|.œ
iii) By definition | 0 | 0 and since 0 0, | 0 | 0. Thus, by i), ii), and iii) | a | | a | for any real number.œœœ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 1.2 Lines, Circles and Parabolas 5
52. i) Prove | x | > 0 x > a or x < a for any positive number, a.Ê
For x 0, | x | x. | x | > a x > a.œ Ê
For x < 0, | x | x. | x | > a x > a x < a.œ Ê Ê
ii) Prove x > a or x < a | x | > 0 for any positive number, a.Ê
a > 0 and x > a | x | x. So x > a | x | > a.Êœ Ê
For a > 0, a < 0 and x < a x < 0 | x | x. So x < a x > a | x | > a.ÊÊœÊÊ
53. a) 1 = 1 | 1 | = 1 b bÊÊœÊ œÊœÊœ
¹ ¹ ¹¹¹¹ ¹¹
††
"" "
ll ll
ll llbb bb b
bb
b b
b b b b
¹¹¹¹ ¹¹
¹¹ ¹¹¹¹ ¹¹
†
†
b"
b) a a a
ll ll
ll ll ll
""
aa
bb b bb
œœ œ œ
¹ ¹ ¹¹ ¹¹ ¹¹
†† †
"
54. Prove S a a for any real number a and any positive integer n.
nnn
œœkk kk
a a a, so S is true. Now, assume that S a a is true form some positive integer .k k kk kk
¸¸
"" "
œœ œœ 5
kkk
Since a a and a a , we have a a a a a a a a . Thus,k k kk kk k k kk kk kk
¸¸ ¸ ¸ ¸ ¸ ¸¸
"" " " " " "
œœ œ†œœœ
kk k k k k k+
S a a is also true. Thus by the Principle of Mathematical Induction, S a a
k n
kk+ nn
" " "
œ œ œl lœl l
¸¸kk
is true for all n positive integers.
1.2 LINES, CIRCLES, AND PARABOLAS
1. x 1 ( 3) 2, y 2 2 4; d ( x) ( y) 4 16 2 5?? ??œ œ œ œ œ œ œ
ÈÈÈ
##
2. x ( 1) 2, y 2 ( 2) 4; d ( 2) 4 2 5??œ$ œ œ œ œ œ
ÈÈ
##
3. x 8.1 ( 3.2) 4.9, y 2 ( 2) 0; d ( 4.9) 0 4.9??œ œ œ œ œ œ
È##
4. x 0 2 2, y 1.5 4 2.5; d 2 ( 2.5) 8.25??œ œ œ œ œ œ
ÈÈ È
ÊŠ‹ È
##
5. Circle with center ( ) and radius 1. 6. Circle with center ( ) and radius 2.!ß ! !ß ! È
7. Disk (i.e., circle together with its interior points) with center ( ) and radius 3.!ß ! È
8. The origin (a single point).
9. m 3 10. mœœ œ œœ œ
? ?
? ?
y y
x2(1) x2(2) 4
12 3 #"
perpendicular slope perpendicular slopeœ œ
"
3 3
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

6 Chapter 1 Preliminaries
11. m 0 12. m ; no slopeœœ œ œœ
? ?
? ?
y y
x12 x ()
33 0#
# #
perpendicular slope does not exist perpendicular slope 0œ
13. (a) x 1 14. (a) x 2 15. (a) x 0 16. (a) xœ œ œ œ
È1
(b) y (b) y 1.3 (b) y 2 (b) y 0œœœœ
4
3È
17. P( 1 1), m 1 y 1 1 x ( 1) y x ß œ Ê œ Ê œab
18. P(2 3), m y ( 3) (x 2) y x 4ß œ Ê œ Ê œ
"""
###
19. P(3 4), Q( 2 5) m y 4 (x 3) y xß ß Ê œ œ œ Ê œ Ê œ
?
?
y
x23 5 5 5 5
54 23" " "
20. P( 8 0), Q( 1 3) m y 0 x ( 8) y xß ß Ê œ œ œ Ê œ Ê œ
?
?
y
x1(8)7 7 7 7
30 3 3 3 24
ab
21. m , b 6 y x 6 22. m , b 3 y x 3œ œ Ê œ œ œ Ê œ
55
44 ""
##
23. m 0, P( 12 9) y 9 24. No slope, P xœßÊœ ß%Êœ
ˆ‰
""
33
25. a 1, b 4 (0 4) and ( 0) are on the line m 4 y 4x 4œ œ Ê ß "ß Ê œ œ œ Ê œ
?
?
y
x10
04
26. a 2, b 6 (2 0) and ( 6) are on the line m 3 y 3x 6œœÊß !ß Êœœ œÊœ
?
?
y
x02
60
27. P(5 1), L: 2x 5y 15 m parallel line is y ( 1) (x 5) y x 1ß œ Ê œ Ê œ Ê œ
L222
555
28. P 2 2 , L: 2x 5y 3 m parallel line is y 2 x 2 y x
Š‹ Š ‹
ÈÈ È
ÈŠ‹
ß œ Ê œÊ œ Êœ
LÈÈÈ
222
5555
8
29. P(4 10), L: 6x 3y 5 m 2 m perpendicular line is y 10 (x 4) y x 12ß œÊ œÊ œÊ œ Êœ
L¼"""
###
30. P( 1), L: 8x 13y 13 m m perpendicular line is y x 1!ß œ Ê œ Ê œ Ê œ
L813 13
13 8 8
¼
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.2 Lines, Circles and Parabolas 7
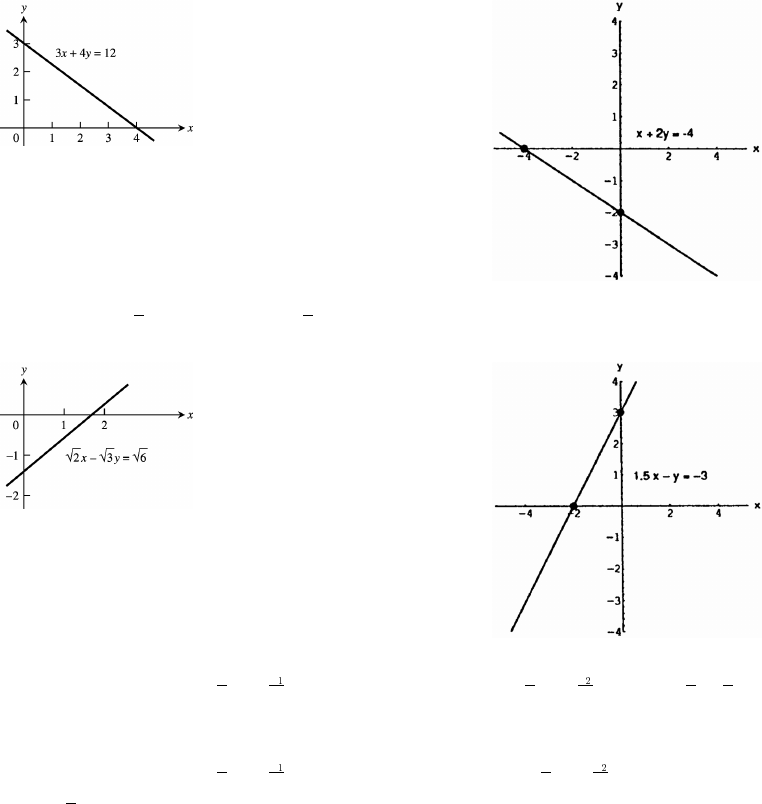
31. x-intercept 4, y-intercept 3 32. x-intercept 4, y-intercept 2œ œ œ œ
33. x-intercept 3, y-intercept 2 34. x-intercept 2, y-intercept 3œœ œœ
ÈÈ
35. Ax By C y x and Bx Ay C y x . Since 1 is the œ Íœ œ Íœ œ
"#
ABAB
BB AA BA
CC
ˆ‰ˆ‰
product of the slopes, the lines are perpendicular.
36. Ax By C y x and Ax By C y x . Since the lines have the sameœ Íœ œ Íœ
"#
AA
BB BB
CC
slope , they are parallel.A
B
37. New position x x y y ( 3 ( 6)) ( 3).œ ß œ#&ß œ$ßab
old old
??
38. New position x x y y (6 ( 6) 0 0) (0 0).œ ß œßœßab
old old
??
39. x 5, y 6, B(3 3). Let A (x y). Then x x x 5 3 x x 2 and?? ?œœß œß œÊœÊœ
#"
y y y 6 3 y y 9. Therefore, A ( 9).?œ ʜʜ œ#ß
#"
40. x , y??œ""œ! œ!!œ!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
8 Chapter 1 Preliminaries
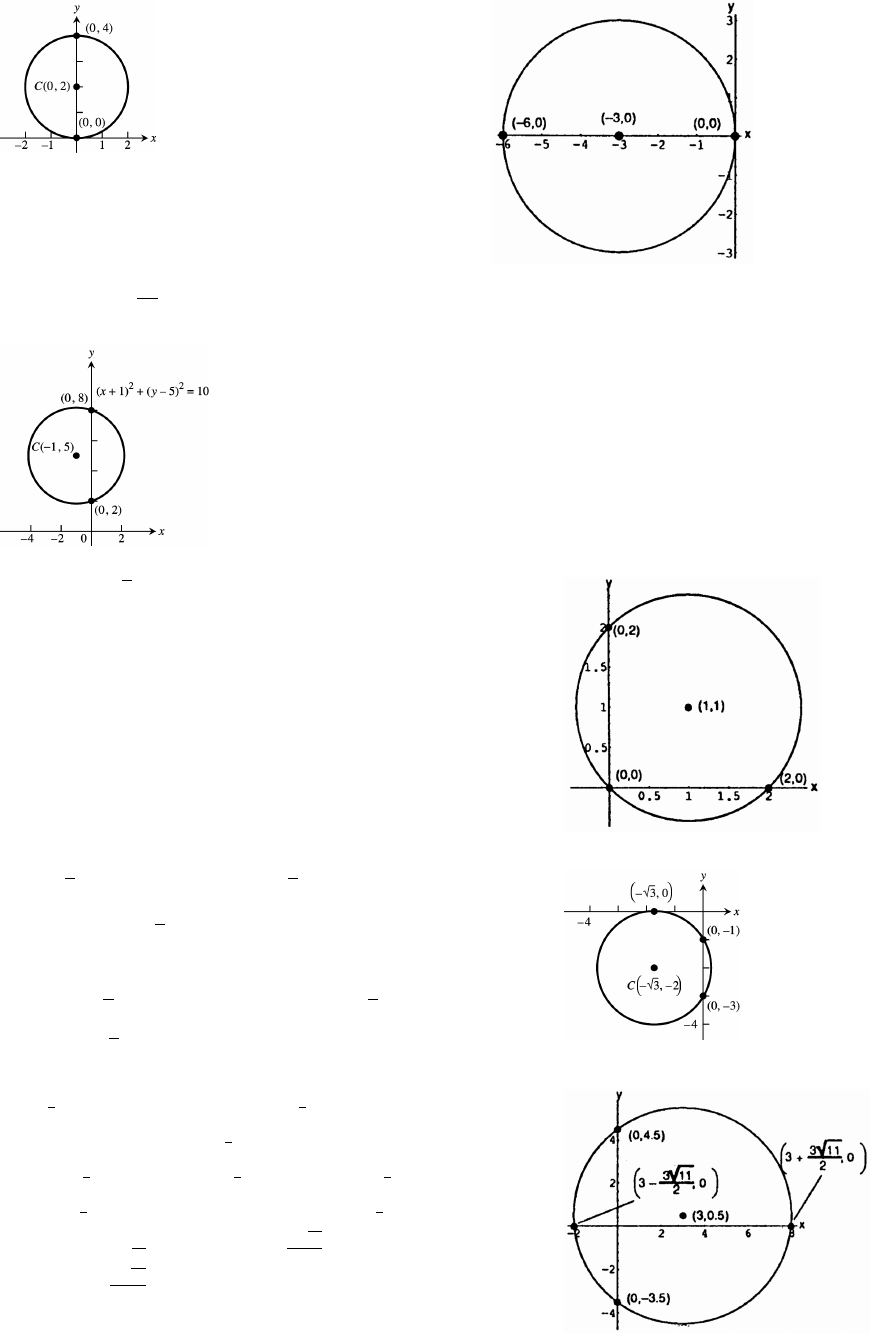
41. C( 2), a 2 x (y 2) 4 42. C( 0), a 3 (x 3) y 9!ß œ Ê œ $ß œ Ê œ
## ##
43. C( 1 5), a 10 (x 1) (y 5) 10ß œ Ê œ
È##
44. C( ), a 2 (x 1) (y 1) 2"ß " œ Ê œ
È##
x 0 (0 1) (y 1) 2 (y 1) 1œÊ œÊ œ
## #
y 1 1 y 0 or y 2.Êœ„Êœ œ
Similarly, y 0 x 0 or x 2œÊœ œ
45. C 3 2 , a 2 x 3 (y 2) 4,
Š‹ Š‹
ÈÈ
ß œÊ œ
##
x 0 0 3 (y 2) 4 (y 2) 1œÊ œÊ œ
Š‹
È###
y 2 1 y 1 or y 3. Also, y 0Êœ„Êœ œ œ
x 3 (0 2) 4 x 3 0Ê œÊ œ
Š‹ Š‹
ÈÈ
##
#
x3ʜ
È
46. C 3 , a 5 (x 3) y 25, so
ˆ‰ ˆ ‰
ߜʜ
""
##
##
x 0 (0 3) y 25œÊ œ
#"
#
#
ˆ‰
y 16 y 4 yÊ œÊœ„Êœ
ˆ‰
""
###
#9
or y . Also, y 0 (x 3) 0 25œ œ Ê œ
7
##
#"#
ˆ‰
(x 3) x 3Ê œ Êœ„
##
99
4
311
È
x3Êœ„
311
È
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.2 Lines, Circles and Parabolas 9
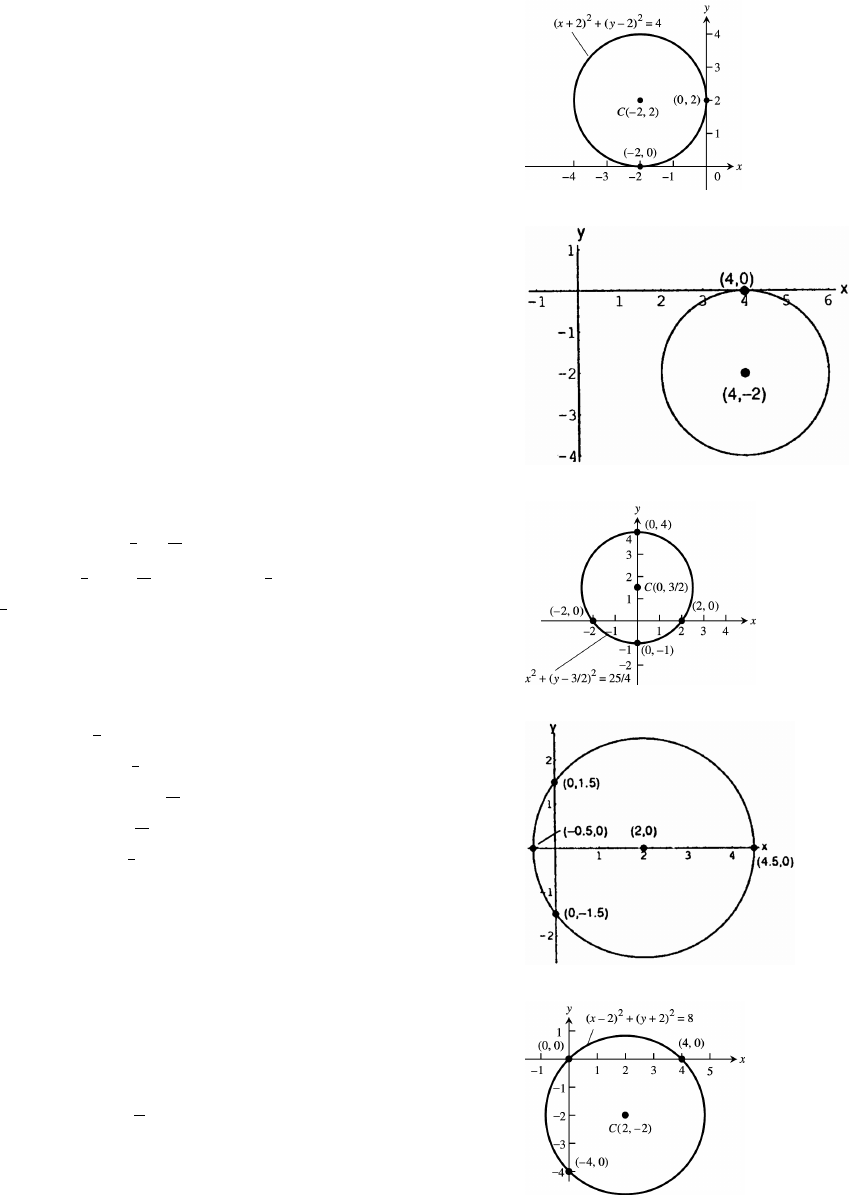
47. x y 4x 4y 0
##
%œ
x y 4y 4Ê%Bœ
##
x 4x4y 4y4 4ʜ
##
(x 2) (y 2) 4 C ( 2 2), a 2.Ê œÊœß œ
##
48. x y 8x 4y 16 0
##
œ
x 8x y 4y 16ʜ
##
x 8x16y 4y4 4Ê œ
##
(x 4) (y 2) 4Ê œ
##
C ( 2), a 2.Êœ%ß œ
49. x y 3y 4 0 x y 3y 4
## ##
œÊ œ
xy3yʜ
## 925
44
xy C0,Ê œ Êœß
###
#
ˆ‰ ˆ‰
325 3
4
a.œ5
#
50. x y 4x 0
##
œ
9
4
x4xyʜ
##
9
4
x 4x4yʜ
##
25
4
(x 2) yʜ
##
25
4
C(20), a .Êœß œ
5
#
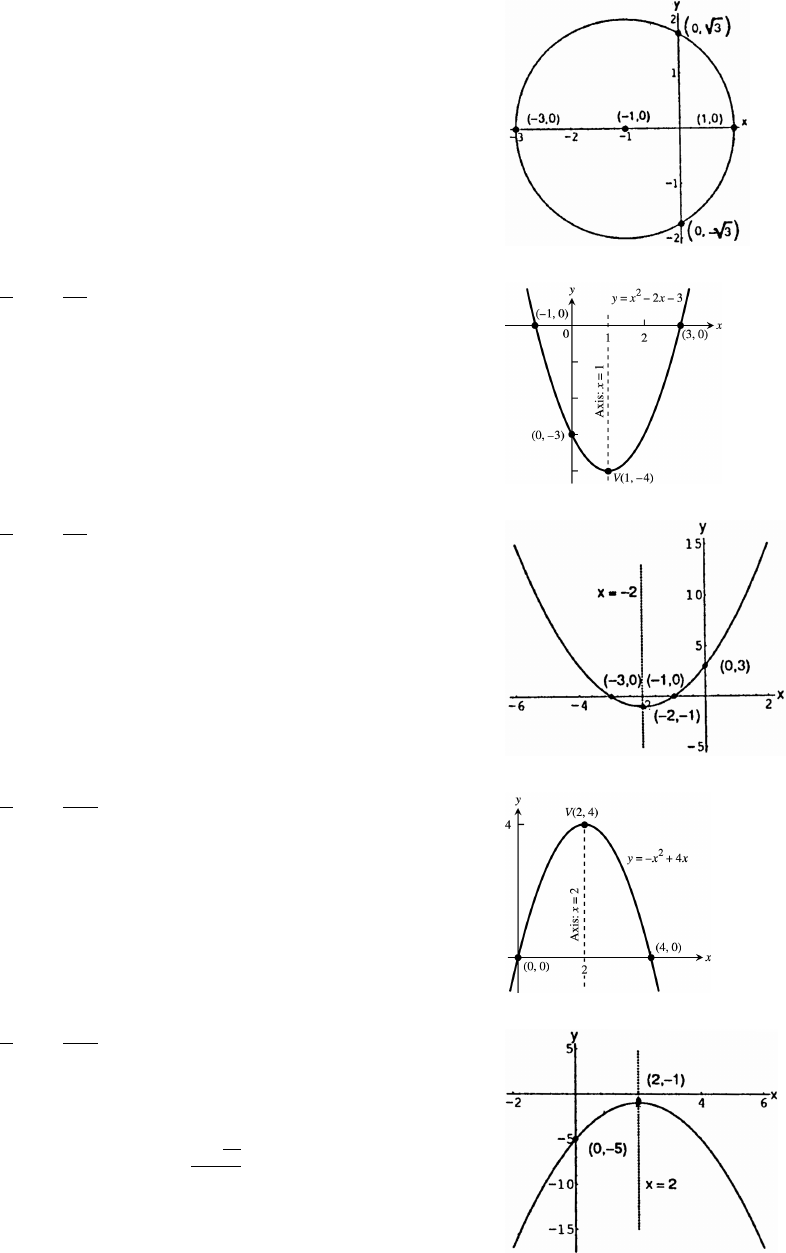
51. x y 4x 4y 0
##
œ
x 4x y 4y 0ʜ
##
x 4x4y 4y4 8ʜ
##
(x 2) (y 2) 8Ê œ
##
C(2 2), a 8.Êßœ
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
10 Chapter 1 Preliminaries
52. x y 2x 3
##
œ
x 2x1y 4ʜ
##
(x 1) y 4ʜ
##
C ( 1 0), a 2.Êœß œ
53. x 1œ œ œ
b2
a2(1)#
y (1) 2(1) 3 4Êœ œ
#
V ( 4). If x 0 then y 3.Êœ"ß œ œ
Also, y 0 x 2x 3 0œÊ œ
#
(x 3)(x 1) 0 x 3 orÊ œÊœ
x 1. Axis of parabola is x 1.œ œ
54. x 2œ œ œ
b4
a2(1)#
y ( 2) 4( 2) 3 1Ê œ œ
#
V ( 2 1). If x 0 then y 3.Êœß œ œ
Also, y 0 x 4x 3 0œÊ œ
#
(x 1)(x 3) 0 x 1 orÊ œÊœ
x 3. Axis of parabola is x 2.œ œ
55. x 2œ œ œ
b4
a2(1)#
y (2) 4(2) 4Êœ œ
#
V (2 4). If x 0 then y 0.Êœß œ œ
Also, y0 x 4x0œÊ œ
#
x(x 4) 0 x 4 or x 0.Ê œ Ê œ œ
Axis of parabola is x 2.œ
56. x 2œ œ œ
b4
a2(1)#
y (2) 4(2) 5 1Êœ œ
#
V (2 1). If x 0 then y 5.Êœß œ œ
Also, y 0 x 4x 5 0œÊ œ
#
x 4x 5 0 xʜʜ
#„
#
44
È
no x intercepts. Axis of parabola is x 2.ʜ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.2 Lines, Circles and Parabolas 11
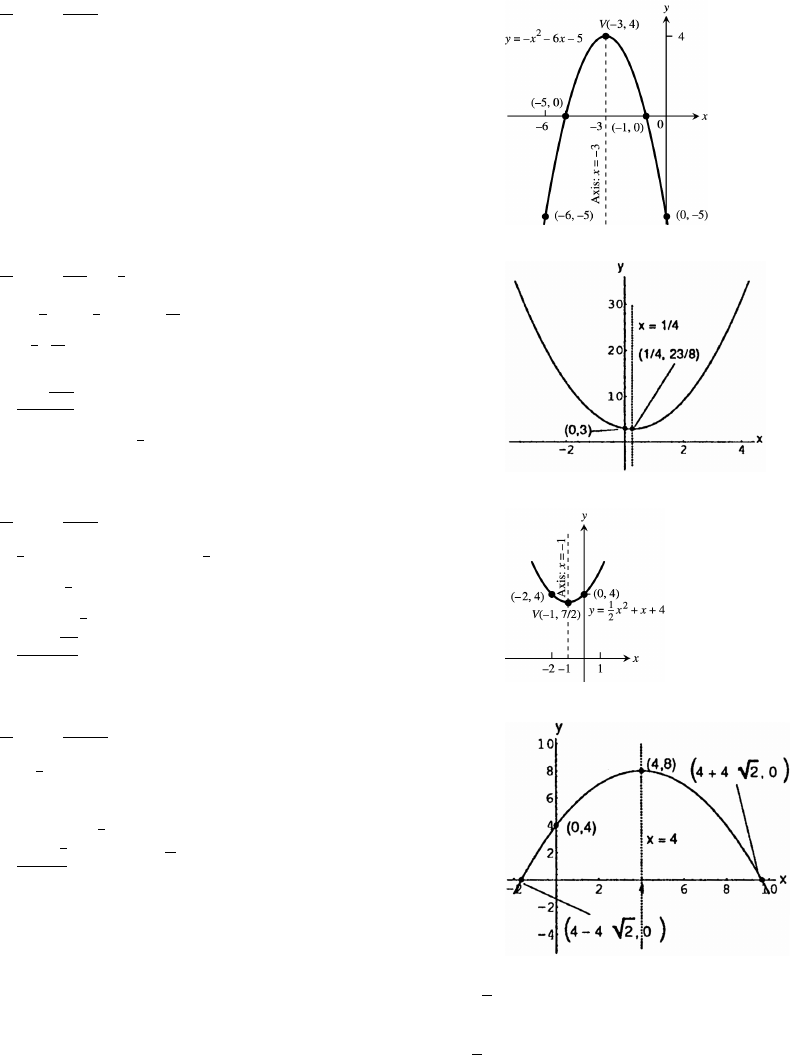
57. x 3œ œ œ
b6
a2(1)#
y ( 3) 6( 3) 5 4Ê œ œ
#
V ( 3 ). If x 0 then y 5.Êœß% œ œ
Also, y 0 x 6x 5 0œÊ œ
#
(x 5)(x 1) 0 x 5 orÊ œÊœ
x 1. Axis of parabola is x 3.œ œ
58. x œ œ œ
b1
a2(2)4#"
y2 3Êœ œ
ˆ‰
""
#
44 8
23
V . If x 0 then y 3.Êœß œ œ
ˆ‰
"
48
23
Also, y 0 2x x 3 0œÊ œ
#
x no x intercepts.Êœ Ê
123
4
„
È
Axis of parabola is x .œ"
4
59. x 1œ œ œ
b1
a2(1/2)#
y ( 1) ( 1) 4Êœ œ
"
##7
2
V . If x 0 then y 4.Êœ"ß œ œ
ˆ‰
7
2
Also, y0 x x40œÊ œ
"
##
x no x intercepts.Êœ Ê
„ 17
1
È
Axis of parabola is x 1.œ
60. x 4œ œ œ
b2
a2(1/4)#
y (4) 2(4) 4 8Êœ œ
"#
4
V (4 8) . If x 0 then y 4.Êœß œ œ
Also, y 0 x 2x 4 0œÊ œ
"#
4
x 4 4 2.Êœ œ„
„
28
1/2
ÈÈ
Axis of parabola is x 4.œ
61. The points that lie outside the circle with center ( 0) and radius 7.!ß È
62. The points that lie inside the circle with center ( 0) and radius 5.!ß È
63. The points that lie on or inside the circle with center ( 0) and radius 2."ß
64. The points lying on or outside the circle with center ( 2) and radius 2.!ß
65. The points lying outside the circle with center ( 0) and radius 1, but inside the circle with center ( 0),!ß !ß
and radius 2 (i.e., a washer).
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
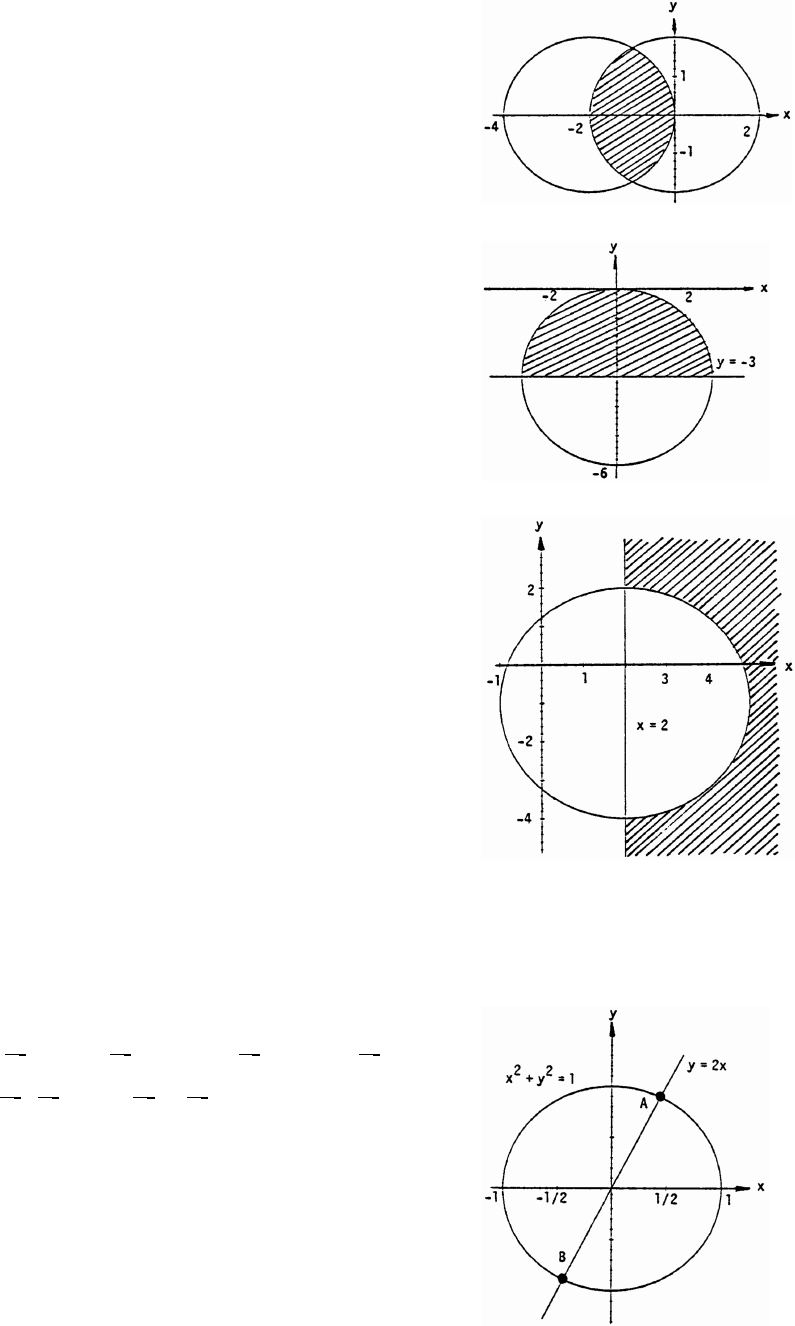
12 Chapter 1 Preliminaries
66. The points on or inside the circle centered
at ( ) with radius 2 and on or inside the!ß !
circle centered at ( 2 0) with radius 2.ß
67. x y 6y 0 x (y 3) 9.
## # #
Ê
The interior points of the circle centered at
( 3) with radius 3, but above the line!ß
y3.œ
68. x y 4x 2y 4 (x 2) (y 1) 9.
## # #
Ê
The points exterior to the circle centered at
(2 1) with radius 3 and to the right of theß
line x 2.œ
69. (x 2) (y 1) 6 70. (x 4) (y 2) 16
## ##
71. x y 2, x 1 72. x y 4, (x 1) (y 3) 10
## ## # #
Ÿ
73. x y 1 and y 2x 1 x 4x 5x
## # # #
œ œ Êœ œ
x and y or x and y .Êœ œ œ œ
Š‹Š ‹
""
ÈÈ È È
55 5 5
22
Thus, A , B are the
Š‹Š ‹
""
ÈÈ È È
55 5 5
22
ßß
points of intersection.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.2 Lines, Circles, and Parabolas 13
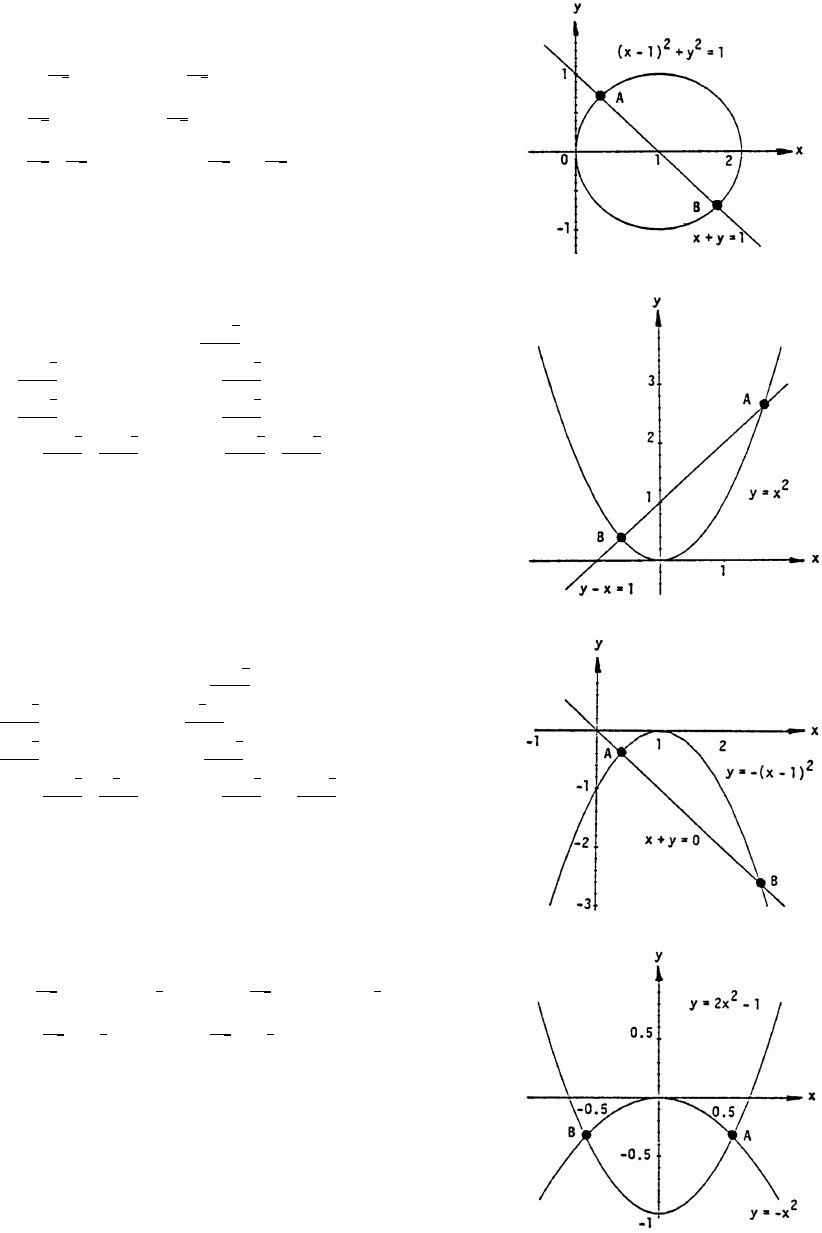
74. x y 1 and (x 1) y 1œ œ
##
1 ( y) y 2yÊœ œ
## #
y and x orÊœ œ"
Š‹
""
ÈÈ
22
y and x 1 . Thus,
Š‹
œ œ
""
ÈÈ
22
A and B 1
Š‹Š ‹
" ß ß
"" " "
ÈÈ È È
22 2 2
are intersection points.
75. y x 1 and y x x x 1œ œ Ê œ
##
xx10 x .ʜʜ
#„
#
15
È
If x, then yx1.œ œœ
15 35
##
ÈÈ
If x, then yx1.œ œœ
15 35
##
ÈÈ
Thus, A and B
Š‹Š‹
1535 1535
## ##
ÈÈ ÈÈ
ßß
are the intersection points.
76. y x and (x 1) (x 1) xœ Cœ Ê œ
##
x 3x 0 x . IfÊ"œÊœ
#„
#
35
È
x , then y x . Ifœœœ
35 53
##
ÈÈ
x , then y x .œœœ
35 35
##
ÈÈ
Thus, A and B
Š‹Š ‹
35 53 35 35
## # #
ÈÈ È È
ßß
are the intersection points.
77. y 2x 1 x 3x 1œœÊ œ
###
x and y or x and y .Ê œ œ œ œ
""" "
ÈÈ
33
33
Thus, A and B are the
Š‹Š ‹
"" ""
ÈÈ
33
33
ß ß
intersection points.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
14 Chapter 1 Preliminaries
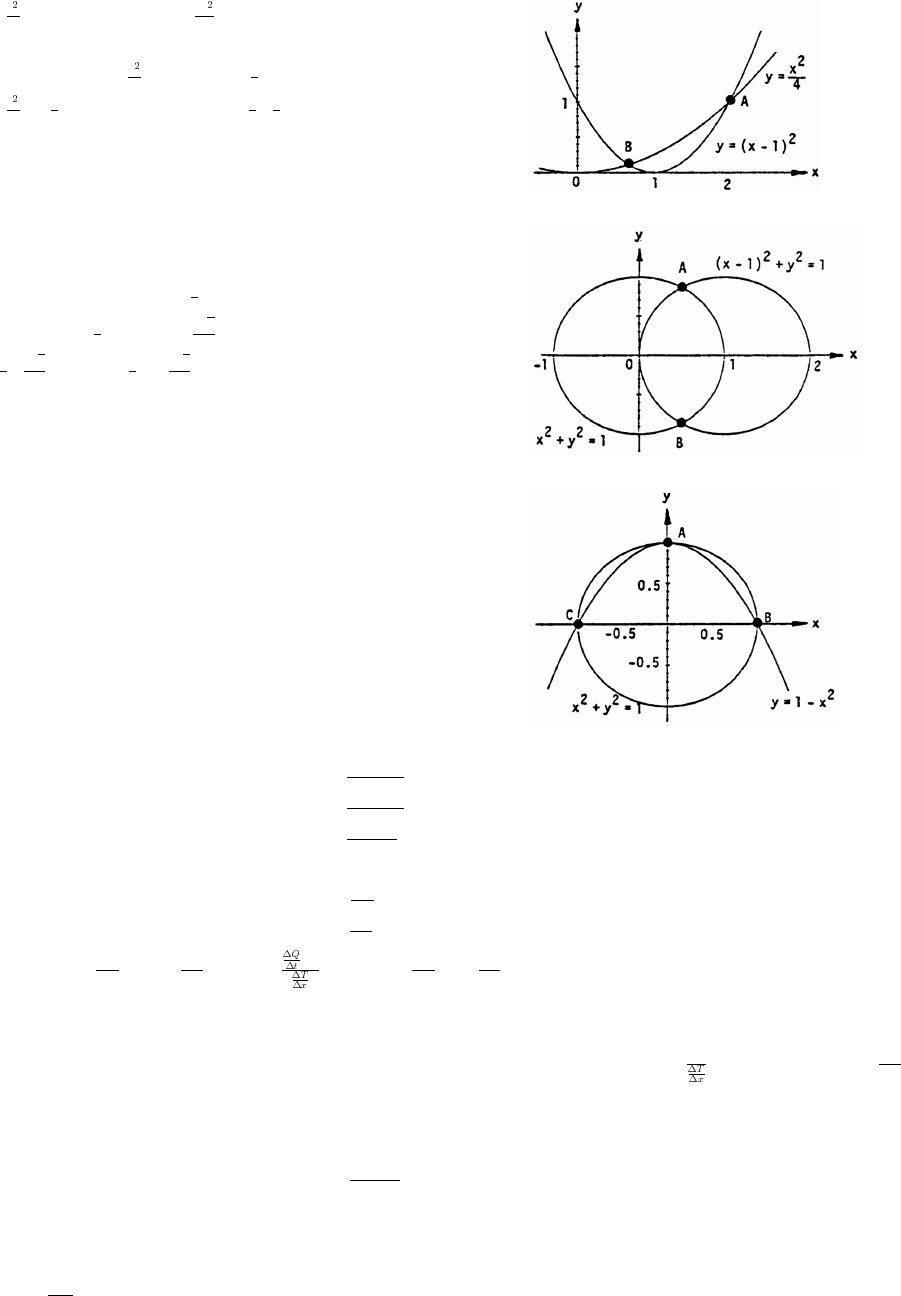
78. y (x 1) 0 2x 1œœ Êœ
x3x
44
#
0 3x 8x 4 (3x 2)(x 2)Êœ œ
#
x 2 and y 1, or x andÊœ œ œ œ
x2
43
y . Thus, A(2 1) and Bœœ ß ß
x2
49 39
""
ˆ‰
are the intersection points.
79. x y 1 (x 1) y
## ##
œœ
x (x 1) x 2x 1Êœœ
###
0 2x 1 x . Henceʜʜ
"
#
y x or y . Thus,
##
#
œ" œ œ „
3
4
3
È
A and B are the
Š‹Š ‹
""
## # #
ßß
ÈÈ
33
intersection points.
80. x y 1 x y y y
## # #
œœÊ œ
y(y 1) 0 y 0 or y 1.ʜʜ œ
If y 1, then x y 0 or x 0.œœ"œœ
##
If y 0, then x 1 y 1 or x 1.œœœœ„
##
Thus, A(0 1), B( 0), and C( 1 0) are theß"ß ß
intersection points.
81. (a) A (69° 0 in), B (68° .4 in) m 2.5°/in.¸ß ¸ß Êœ ¸
68° 69°
.4 0
(b) A (68° .4 in), B (10° 4 in) m 16.1°/in.¸ß ¸ß Êœ ¸
10° 68°
4 .4
(c) A (10° 4 in), B (5° 4.6 in) m 8.3°/in.¸ß ¸ß Êœ ¸
5° 10°
4.6 4
82. The time rate of heat transfer across a material, , is directly proportional to the cross-sectional area, A, of the mate
?
?
U
>rial,
to the temperature gradient across the material, (the slopes from the previous problem), and to a constant characteristic
?
?
X
B
of the material. -kA k = . Note that and are of opposite sign because heat flow is toward lower
??
?? ??
??
UU
>B >B
XX
Î
œÊ
A
temperature. So a small value of k corresponds to low heat flow through the material and thus the material is a good
insulator.Since all three materials have the same cross section and the heat flow across each is the same (temperatures are
not changing), we may define another constant, K, characteristics of the material: K Using the values of fromœ Þ
"X
B
?
?
the prevous problem, fiberglass has the smallest K at 0.06 and thus is the best insulator. Likewise, the wallboard is the
poorest insulator, with K 0.4.œ
83. p kd 1 and p 10.94 at d 100 k 0.0994. Then p 0.0994d 1 is the diver'sœ œ œ Êœ œ œ
10.94
100
"
pressure equation so that d 50 p (0.0994)(50) 1 5.97 atmospheres.œÊœ œ
84. The line of incidence passes through ( 1) and ( 0) The line of reflection passes through ( 0) and ( )!ß "ß Ê "ß #ß "
m 1 y 0 1(x 1) y x 1 is the line of reflection.Ê œ œ Ê œ Ê œ
10
1
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.2 Lines, Circles, and Parabolas 15
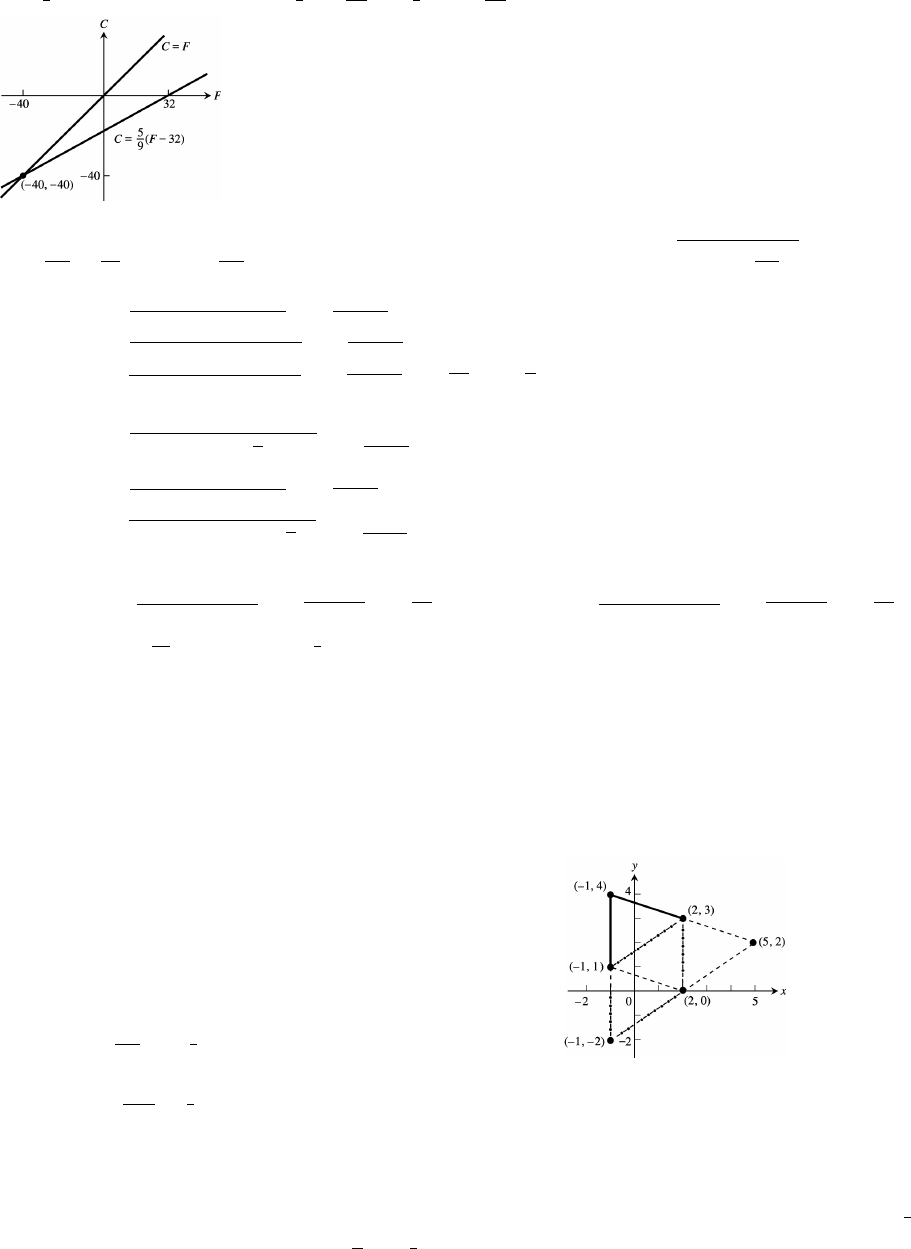
85. C (F 32) and C F F F F or F 40° gives the same numerical reading.œ œÊœÊœ œ
5 5 160 4 160
99999
86. m x . Therefore, distance between first and last rows is (14) 40.25 ft.œœÊœ ¸
37.1 14 14 14
100 x .371 .371??Ɉ‰
##
87. length AB (5 1) (5 2) 16 9 5œœ œ
ÈÈ
##
length AC (4 1) ( ) 9 16 5œ##œœ
ÈÈ
##
length BC (4 5) ( 5) 1 49 50 5 2 5œ#œœœÁ
ÈÈÈÈ
##
88. length AB (1 0) 3 0 1 3 2œ œœ
ÊŠ‹
ÈÈ
##
length AC (2 0) (0 0) 4 0 2œœœ
ÈÈ
##
length BC (2 1) 0 3 1 3 2œ œœ
ÊŠ‹
ÈÈ
##
89. Length AB ( x) ( y) 1 4 17 and length BC ( x) ( y) 4 1 17.œœœ œœœ
ÈÈ
ÈÈ
ÈÈ
?? ??
#### ####
Also, slope AB and slope BC , so AB BC. Thus, the points are vertices of a square. The coordinateœœ¼
4
14
"
increments from the fourth vertex D(x y) to A must equal the increments from C to B 2 x x 4 andßÊœœ?
1 y y x 2 and y 2. Thus D( 2) is the fourth vertex. œ œ" Ê œ œ #ß?
90. Let A (x 2) and C (9 y) B (x y). Then 9 x AD and 2 y DC 2(9 x) 2(2 y) 56œß œß Ê œß œ œ Ê œkk kk
and 9 x 3(2 y) 2(3(2 y)) 2(2 y) 56 y 5 9 x 3(2 ( 5)) x 12.œ Ê œ Ê œÊ œ Ê œ
Therefore, A ( 12 2), C (9 5), and B ( 12 5).œ ß œ ß œ ß
91. Let A( ), B( ), and C(2 ) denote the points."ß " #ß $ ß !
Since BC is vertical and has length BC 3, letkkœ
D ( 4) be located vertically upward from A and
""ß
D ( 2) be located vertically downward from A so
#"ß
that BC AD AD 3. Denote the pointkkkkkkœœœ
"#
D (x y). Since the slope of AB equals the slope of
$ß
CD we have 3y 9 x 2 or
$
"
y3
x2 3
œ Ê œ
x 3y 11. Likewise, the slope of AC equals the slopeœ
of BD so that 3y 2x 4 or 2x 3y 4.
$
y 0
x 2 3
2
œÊ œ œ
Solving the system of equations we find x 5 and y 2 yielding the vertex D (5 ).
x3y
2x 3y 4
œ""
œ œœ ß#
$
92. Let x, y , x and/or y be a point on the coordinate plane. The slope, m, of the segment to x, y is . A 90ab ababÁ! Á! !ß! y
x‰
rotation gives a segment with slope m . If this segment has length equal to the original segment, its endpoint
w"
œ œ
my
x
will be y, x or y, x , the first of these corresponds to a counter-clockwise rotation, the latter to a clockwiseabab
rotation.
(a) ( 4); (b) (3 2); (c) (5 2); (d) (0 x);"ß ß ß ß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
16 Chapter 1 Preliminaries
(e) ( y 0); (f) ( y x); (g) (3 10)ß ß ß
93. 2x ky 3 has slope and 4x y 1 has slope 4. The lines are perpendicular when ( 4) 1 orœ œ œ
2 2
k k
k 8 and parallel when 4 or k .œ œ œ
2
k
"
#
94. At the point of intersection, 2x 4y 6 and 2x 3y 1. Subtracting these equations we find 7y 7 orœ œ œ
y 1. Substitution into either equation gives x 1 (1 1) is the intersection point. The line through (1 1)œœÊß ß
and ( ) is vertical with equation x 1."ß # œ
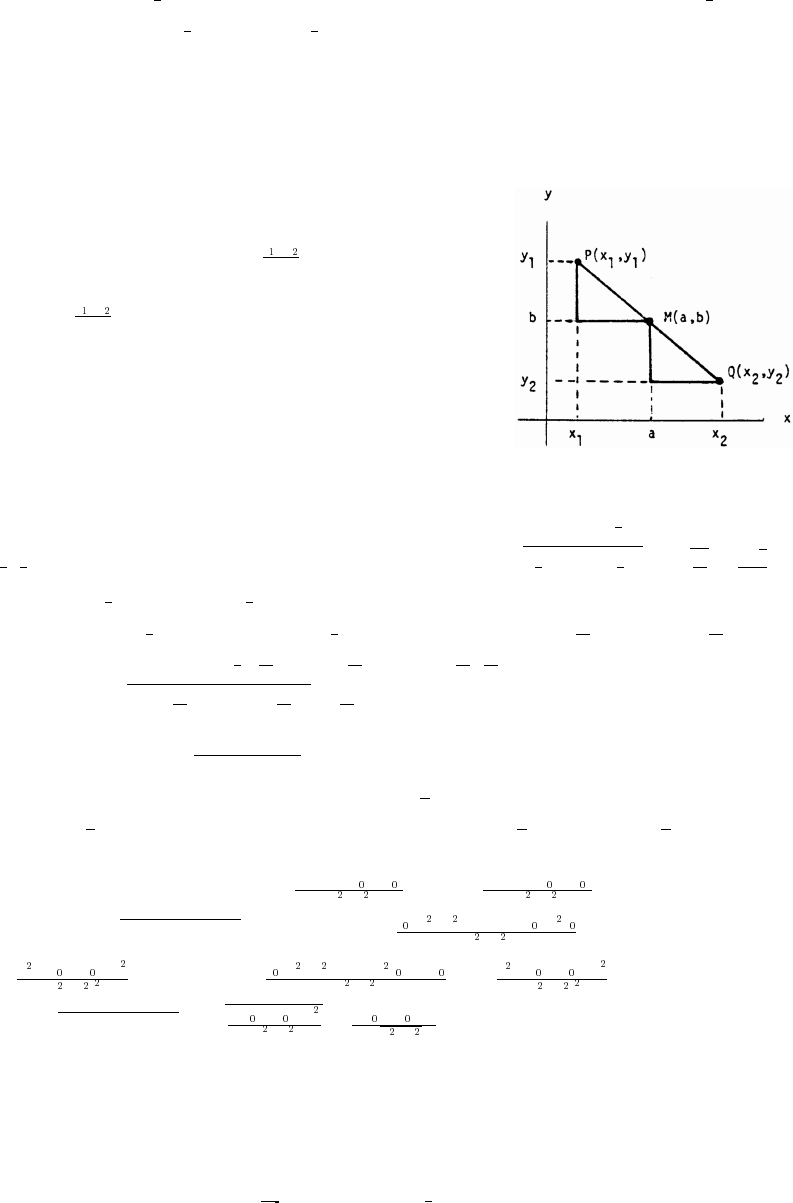
95. Let M(a b) be the midpoint. Since the two trianglesß
shown in the figure are congruent, the value a must
lie midway between x and x , so a .
"#
#
œxx
Similarly, b .œyy
#
96. (a) L has slope 1 so M is the line through P(2 1) with slope 1; or the line y x 3. At the intersectionß œ
point, Q, we have equal y-values, y x 2 x 3. Thus, 2x 1 or x . Hence Q has coordinatesœœ œ œ
"
#
. The distance from P to L the distance from P to Q .
ˆ‰ ˆ‰ˆ‰
ÉÉ
"
## ## #
##
ßœœœœ
53318
4
32
È
(b) L has slope so M has slope and M has the equation 4y 3x 12. We can rewrite the equations ofœ
43
34
the lines as L: x y 3 and M: y 4. Adding these we get y 7 so y . Substitutionœ Bœ œ œ
3 4 25 84
4 3 12 25
into either equation gives x 4 so that Q is the point of intersection. The distanceœœ ß
484 12 1284
325 25 2525
ˆ‰ ˆ ‰
from P to L 4 6 .œœ
Ɉ‰ˆ‰
12 84 22
25 25 5
##
(c) M is a horizontal line with equation y b. The intersection point of L and M is Q( b). Thus, theœ"ß
distance from P to L is (a 1) 0 a 1 .
Èkkœ
##
(d) If B 0 and A 0, then the distance from P to L is x as in (c). Similarly, if A 0 and B 0, theœÁ œÁ
¸¸
C
A!
distance is y . If both A and B are 0 then L has slope so M has slope . Thus,
¸¸
CAB
BBA
Á
!
L: Ax By C and M: Bx Ay Bx Ay . Solving these equations simultaneously we find theœ œ
!!
point of intersection Q(x y) with x and y . The distance fromßœ œ
AC B Ay Bx BC A Ay Bx
AB AB
ab ab
P to Q equals ( x) ( y) , where ( x)
ÈŠ‹
?? ?
## #
#
œ
xA B ACABy Bx
AB
ab
, and ( y) .œœ œ
AAxByC yAB BCAyABx BAxByC
AB AB
AB
ab ab ab
ab ab
#
#
?Š‹
Thus, ( x) ( y) .
ÈÉ
??
##
œ œ
ab
kk
È
Ax By C
AB
Ax By C
AB
1.3 FUNCTIONS AND THEIR GRAPHS
1. domain ( ); range [1 ) 2. domain [0 ); range ( 1]œ_ß_œß_ œß_œ_ß
3. domain ( ); y in range y , t 0 y and y y can be any positive real numberœ!ß_ Ê œ Ê œ !Ê
""
#
Ètt
range ( ).Ê œ !ß _
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 1.3 Functions and Their Graphs 17
4. domain [0 ); y in range y , t 0. If t 0, then y 1 and as t increases, y becomes a smallerœß_ Ê œ œ œ
"
1t
È
and smaller positive real number range (0 1].Êœß
5. 4 z (2 z)(2 z) 0 z [ 2 2] domain. Largest value is g(0) 4 2 and smallest value isœ Í−ßœ œ œ
#È
g( 2) g(2) 0 0 range [0 2].œ œ œ Ê œß
È
6. domain ( 2 2) from Exercise 5; smallest value is g(0) and as 0 z increases to 2, g(z) gets larger andœß œ
"
#
larger (also true as z 0 decreases to 2) range .Êœß_
‰"
#
7. (a) Not the graph of a function of x since it fails the vertical line test.
(b) Is the graph of a function of x since any vertical line intersects the graph at most once.
8. (a) Not the graph of a function of x since it fails the vertical line test.
(b) Not the graph of a function of x since it fails the vertical line test.
9. y x 1 and x . So,œ "Ê "!Ê Ÿ !
Ɉ‰
""
xx
(a) No (x ; (b) No; division by undefined;!Ñ !
(c) No; if x , ; (d) " "Ê "! Ð!ß"Ó
""
xx
10. y x x x and x . x x and x x So, x .œ # Ê# !Ê ! Ÿ# !Ê ! Ÿ# Ê Ÿ%Þ !Ÿ Ÿ%
ÉÈÈÈ ÈÈ È
(a) No; (b) No; (c) Ò!ß %Ó
11. base x; (height) x height x; area is a(x) (base)(height) (x) x x ;œœÊœ œ œ œ
## #
#####
#""
ˆ‰ Š‹
x333
4
ÈÈÈ
perimeter is p(x) x x x 3x.œœ
12. s side length s s d s ; and area is a s a dœÊœÊœ œÊœ
## # # #
"
#
d
2
È
13. Let D diagonal of a face of the cube and the length of an edge. Then D d and (by Exercise 10)œjœjœ
###
D 2 3 d . The surface area is 6 2d and the volume is .
## ## # # $ $Î#
œj Ê jœ Êjœ jœ œ jœ œ
d6d dd
333
33
È È
Š‹
14. The coordinates of P are x x so the slope of the line joining P to the origin is m (x 0). Thus,
ˆ‰
È
ßœœ
È
È
x
xx
"
x, x , .
ˆ‰ˆ‰
Ȝ""
mm
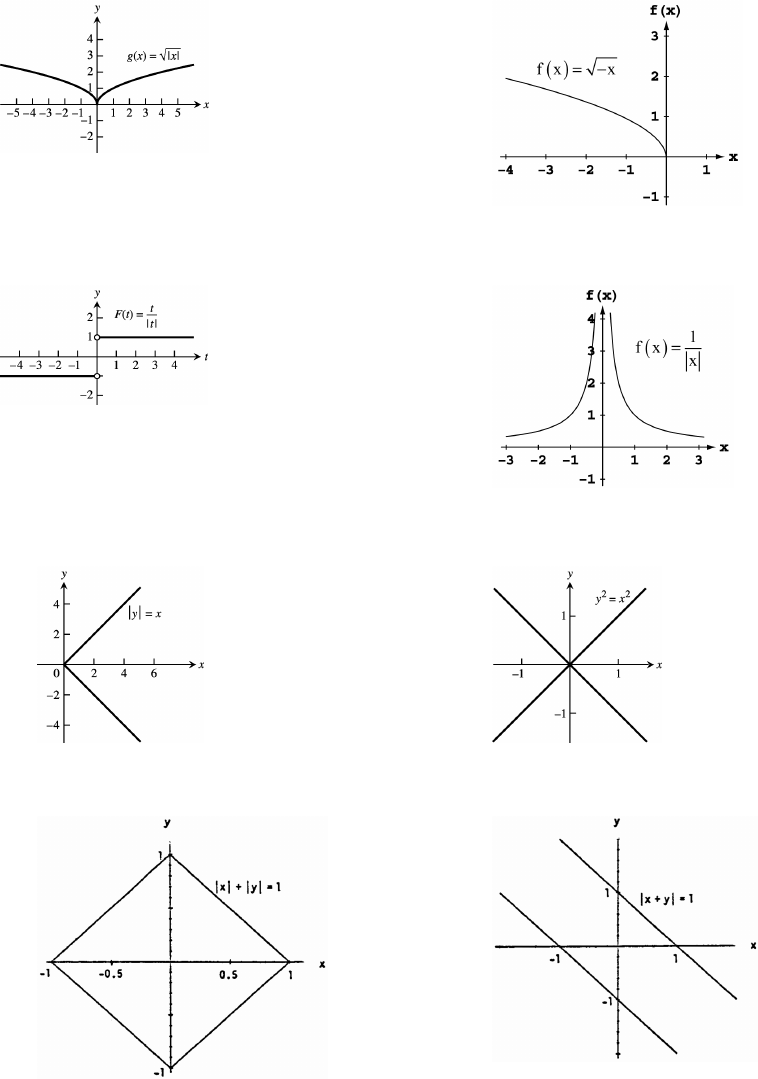
15. The domain is . 16. The domain is .ab ab_ß _ _ß _
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
18 Chapter 1 Preliminaries
17. The domain is . 18. The domain is .ab_ß _ Ð_ß !Ó
19. The domain is . 20. The domain is .abab abab_ß! !ß_ _ß! !ß_
21. Neither graph passes the vertical line test
(a) (b)
22. Neither graph passes the vertical line test
(a) (b)
x y 1
xy y1x
or or
xy y x
kk ÚÞÚÞ
ÛßÛß
ÜàÜà
œÍ Í
œ" œ
œ" œ"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.3 Functions and Their Graphs 19
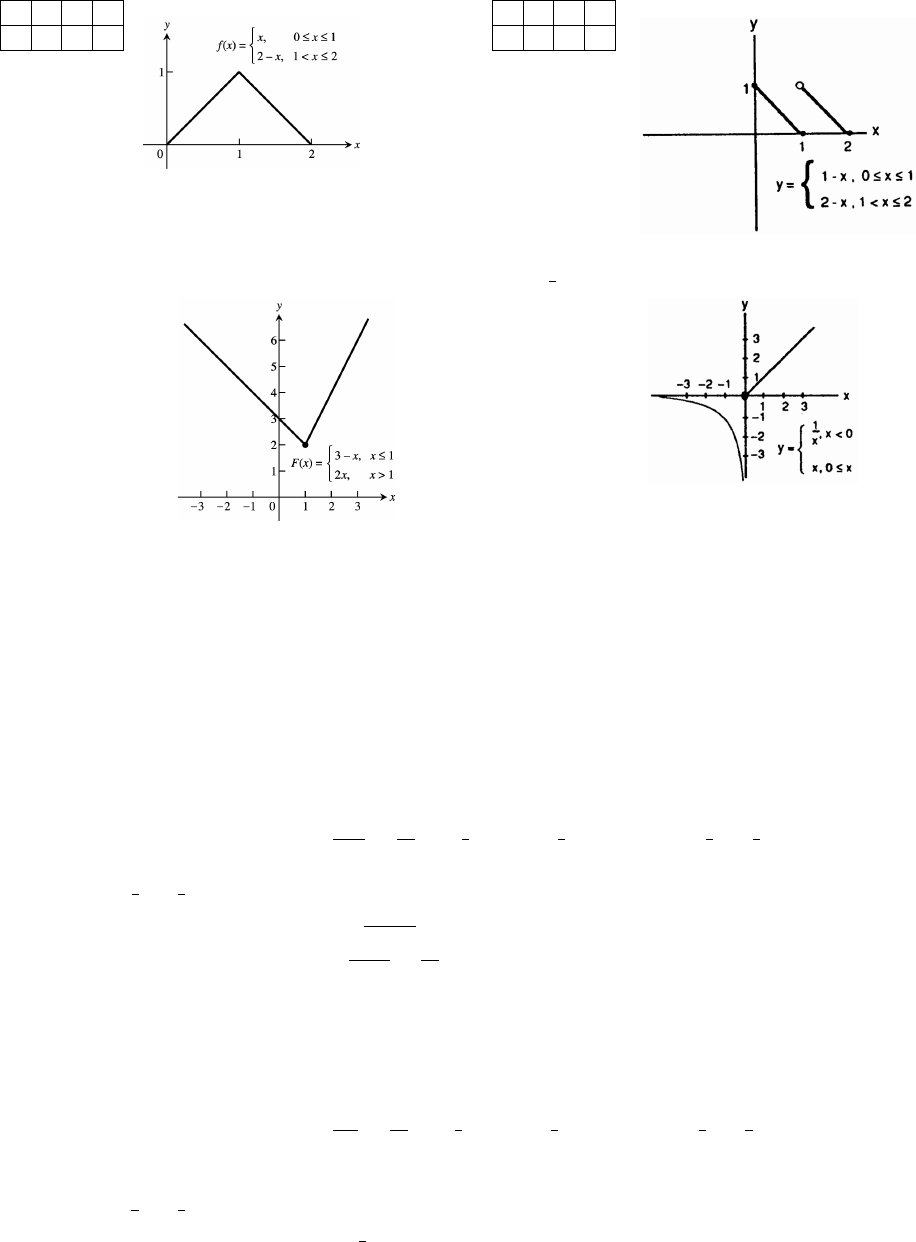
23. x012 24. x012
y010 y100
25. y 26. y
3 x, x 1
2x, 1 x
, x 0
x, 0 x
œœ
Ÿ
Ÿ
œœ
"
x
27. (a) Line through and : y x abab!ß ! "ß " œ
Line through and : y x 2abab"ß " #ß ! œ
f(x)
x, 0 x 1
x 2, 1 x 2
œŸŸ
Ÿ
œ
(b) f(x)
2, x
x
2x
x
œ
!Ÿ "
!ß " Ÿ #
ß#Ÿ$
!ß $ Ÿ Ÿ %
Ú
Ý
Ý
Û
Ý
Ý
Ü
28. (a) Line through 2 and : y x 2 abab!ß #ß ! œ
Line through 2 and : m , so y x 2 xabab a bß " &ß ! œ œ œ œ " œ
!" " " " " &
&# $ $ $ $ $
f(x)
x, 0x
x, x
œ# Ÿ#
#Ÿ&
œ"&
$$
(b) Line through and : m , so y x abab"ß ! !ß $ œ œ $ œ $ $
$!
!Ð"Ñ
Line through and : m , so y xaba b!ß $ #ß " œ œ œ # œ # $
"$ %
#! #
f(x)
x, x
x, x
œ$ $ " Ÿ !
# $ ! Ÿ #
œ
29. (a) Line through and : y x abab"ß " !ß ! œ
Line through and : yabab!ß " "ß " œ "
Line through and : m , so y x xabab a b"ß" $ß! œ œ œ œ " "œ
!" " " " " $
$" # # # # #
f(x)
xx
x
xx
œ
"Ÿ!
"!Ÿ"
"$
Ú
Û
Ü"$
##
(b) Line through and : y x abab#ß" !ß! œ"
#
Line through and : y xabab!ß # "ß ! œ # #
Line through and : yabab"ß " $ß " œ "
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
20 Chapter 1 Preliminaries
f(x)
xx
xx
x
œ
# Ÿ Ÿ !
# # ! Ÿ "
" " Ÿ $
Ú
Û
Ü
"
#
30. (a) Line through and T : m , so y x 0 x
ˆ‰ ˆ ‰
ab
TT
TT T T T#Î##
"! # # #
ß! ß" œ œ œ œ "
ab
f(x)
, 0 x
x, xT
œ!ŸŸ
" Ÿ
T
T
T#
#
#
(b) f(x)
A, x
AxT
A T x
AxT
œ
!Ÿ
ß Ÿ
ߟ
ß Ÿ Ÿ#
Ú
Ý
Ý
Ý
Û
Ý
Ý
Ý
Ü
T
T
T
T
#
#$
#
$
#
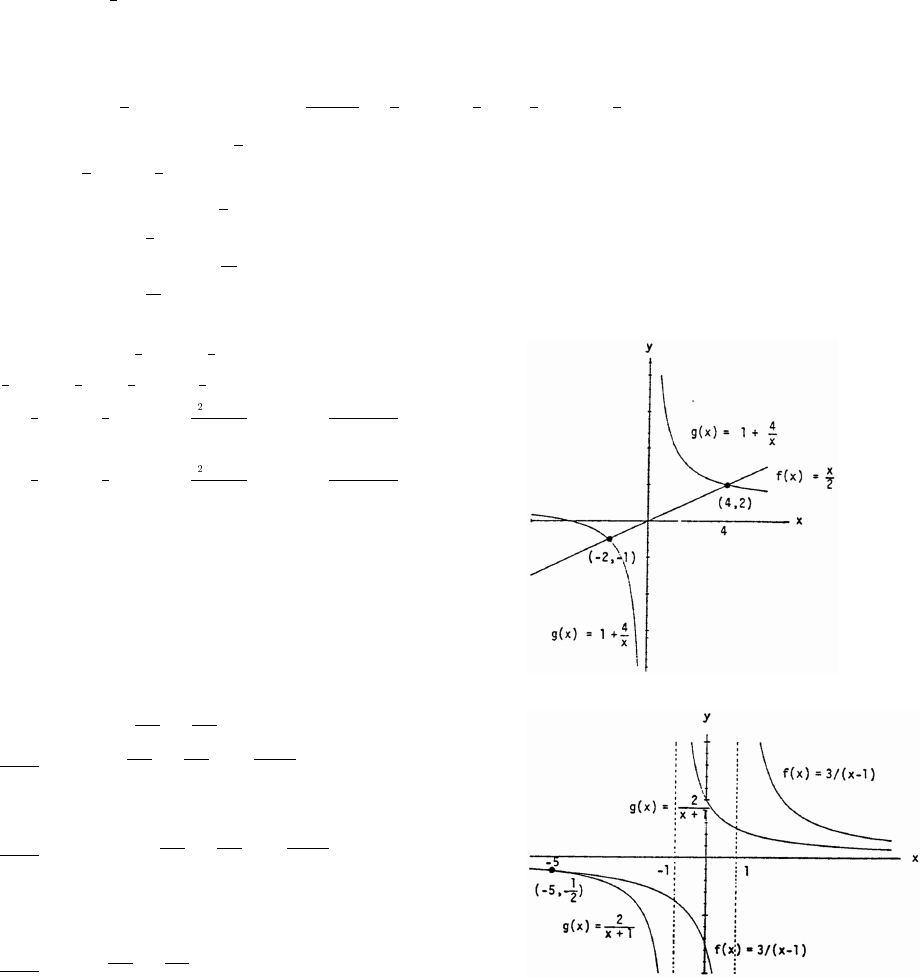
31. (a) From the graph, 1 x ( 2 0) ( )
x4
x# Ê −ß %ß_
(b) 1 1 0
x4x4
xx##
Ê
x 0: 1 0 0 0Ê Ê
x4 x2x8
x2x x
(x 4)(x 2)
##
x 4 since x is positive;Ê
x 0: 1 0 0 0Ê Ê
x4 x2x8
2x 2x x
(x 4)(x 2)
#
x 2 since x is negative;Ê
sign of (x 4)(x 2)
2
ïïïïïðïïïïïðïïïïî
%
Solution interval: ( 0) ( )#ß %ß _
32. (a) From the graph, x ( 5) ( 1 1)
32
x1 x1
Ê−_ßß
(b) x 1: 2Case Ê
32
x1 x1 x1
3(x 1)
3x 3 2x 2 x 5.ÊÊ
Thus, x ( 5) solves the inequality.− _ß
1x1: 2Case Ê
32
x1 x1 x1
3(x 1)
3x 3 2x 2 x 5 which is trueÊÊ
if x 1. Thus, x ( 1 1) solves the − ß
inequality.
1 x: 3x 3 2x 2 x 5Case ÊÊ
32
x1 x1
which is never true if 1 x, so no solution
here.
In conclusion, x ( 5) ( 1 1).−_ß ß
33. (a) x 0 for x [0 1) (b) x 0 for x ( 1 0]ÚÛœ − ß ÜÝœ − ß
34. x x only when x is an integer.ÚÛœÜÝ
35. For any real number x, n x n , where n is an integer. Now: n x n n x n. ByŸ Ÿ " Ÿ Ÿ "ÊÐ "ÑŸ Ÿ
definition: x n and x n x n. So x x for all x .Ü Ýœ Ú Ûœ ÊÚ Ûœ Ü ÝœÚ Û −d
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
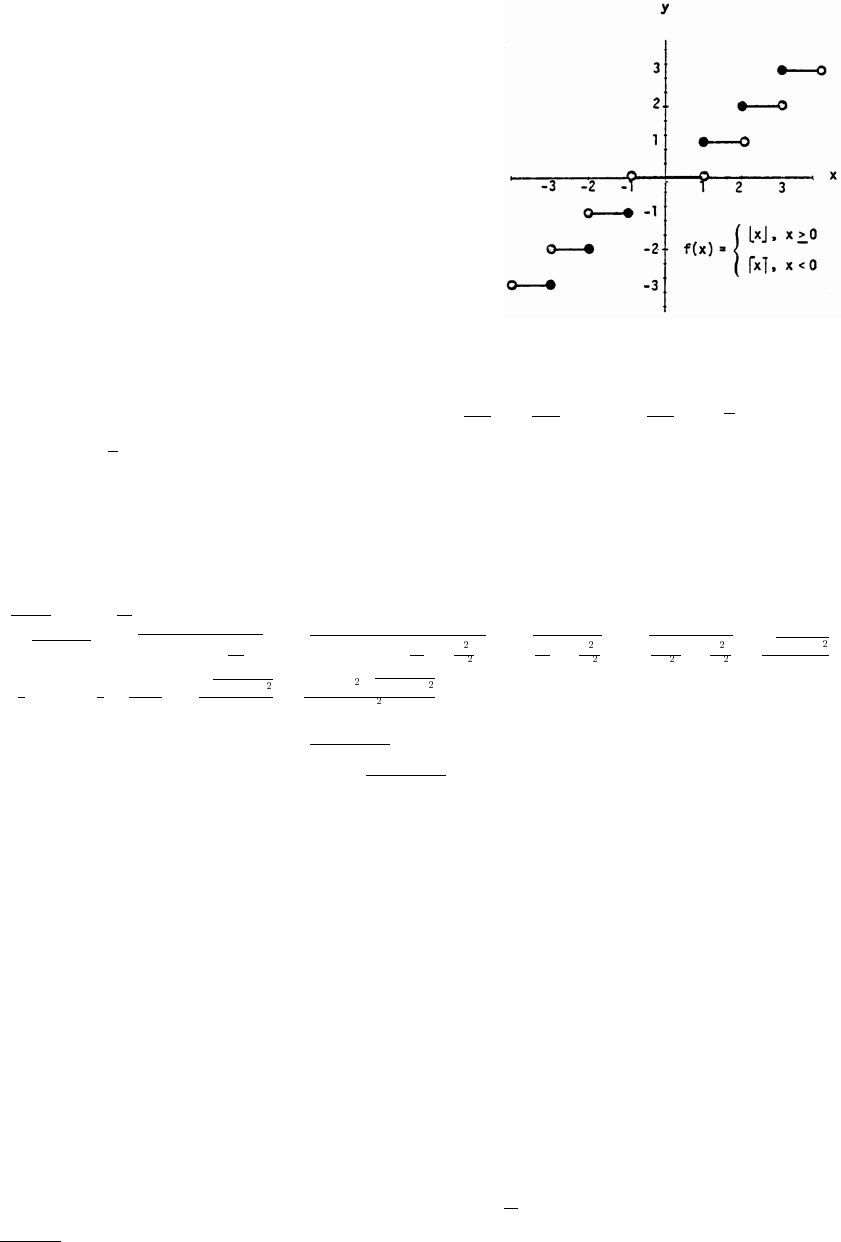
Section 1.3 Functions and Their Graphs 21
36. To find f(x) you delete the decimal or
fractional portion of x, leaving only
the integer part.
37. v f(x) x 2x 22 2x x 72x x; x 7œ œ Ð"% ÑÐ Ñ œ % $!) ! Þ
$#
38. (a) Let h height of the triangle. Since the triangle is isosceles, AB AB 2 AB 2 So,œœÊœÞ
### È
h 2 h B is at slope of AB The equation of AB is
## #
" œ Ê œ"Ê !ß" Ê œ"Ê
Š‹
Èab
y f(x) ; x .œ œ B " − Ò!ß "Ó
(b) A x 2x y 2x x 2x x; x .Ð Ñœ œ Ð "Ñœ # −Ò!ß "Ó
#
39. (a) Because the circumference of the original circle was and a piece of length x was removed.)1
(b) r œœ%
)
##
1
11
xx
(c) h r 16œ "' œ "' % œ "' œ œ œ
ÈɈ‰ ˆ ‰
ÉÉÉ
##%%%%#
#"' "'
x4xx4xxxx
xx
11111111
11
È
(d) V r hœœ † œ
"")
$$# # #%
##"' ) "'
11
ˆ‰
1
11 1
111
xx x xx x
Èab
È
40. (a) Note that 2 mi = 10,560 ft, so there are x feet of river cable at $180 per foot and x feet of land
Èab)!! "!ß &'!
##
cable at $100 per foot. The cost is C x x x .ab a b
È
œ ")! )!! "!! "!ß &'!
##
(b) C $ab! œ "ß #!!ß !!!
C$ab&!! ¸ "ß "(&ß )"#
C$ab"!!! ¸ "ß ")'ß &"#
C$ab"&!! ¸ "ß #"#ß !!!
C$ab#!!! ¸ "ß #%$ß ($#
C$ab#&!! ¸ "ß #()ß %(*
C$ab$!!! ¸ "ß $"%ß )(!
Values beyond this are all larger. It would appear that the least expensive location is less than 2000 feet from the
point P.
41. A curve symmetric about the x-axis will not pass the vertical line test because the points x, y and x, y lie on the samab a be
vertical line. The graph of the function y f x is the x-axis, a horizontal line for which there is a single y-value, ,œœ! !ab
for any x.
42. Pick 11, for example: , the original number.""&œ"'Ä#†"'œ$#Ä$#'œ#'Ä œ"$Ä"$#œ""
#'
#
f x x, the number you started with.abœ#œ
#&'
#
abx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
22 Chapter 1 Preliminaries
1.4 IDENTIFYING FUNCTIONS; MATHEMATICAL MODELS
1. (a) linear, polynomial of degree 1, algebraic. (b) power, algebraic.
(c) rational, algebraic. (d) exponential.
2. (a) polynomial of degree 4, algebraic. (b) exponential.
(c) algebraic. (d) power, algebraic.
3. (a) rational, algebraic. (b) algebraic.
(c) trigonometric. (d) logarithmic.
4. (a) logarithmic. (b) algebraic.
(c) exponential. (d) trigonometric.
5. (a) Graph h because it is an even function and rises less rapidly than does Graph g.
(b) Graph f because it is an odd function.
(c) Graph g because it is an even function and rises more rapidly than does Graph h.
6. (a) Graph f because it is linear.
(b) Graph g because it contains .ab!ß "
(c) Graph h because it is a nonlinear odd function.
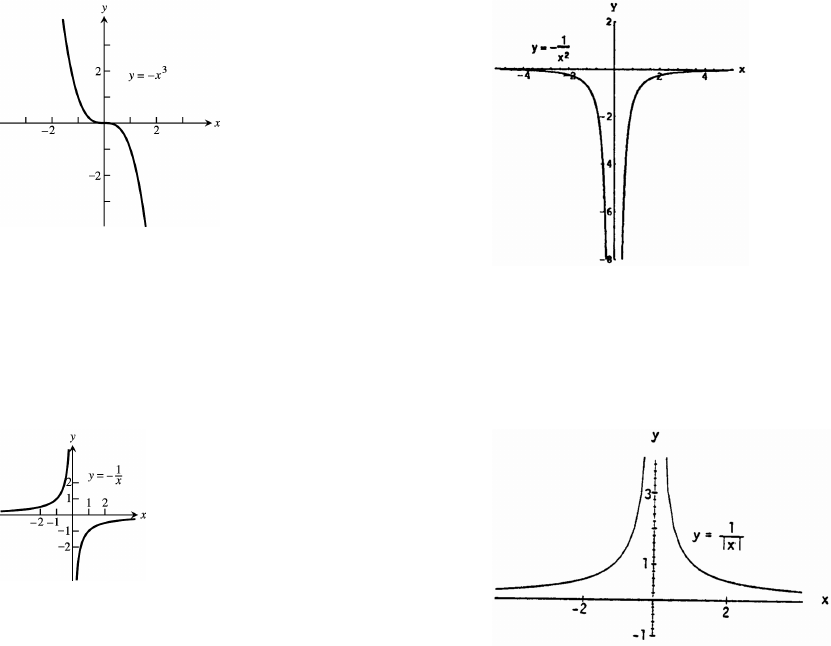
7. Symmetric about the origin 8. Symmetric about the y-axis
Dec: x Dec: x_ _ _ !
Inc: nowhere Inc: x! _
9. Symmetric about the origin 10. Symmetric about the y-axis
Dec: nowhere Dec: x! _
Inc: x Inc: x_ ! _ !
x! _
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.4 Identifying Functions; Mathematical Models 23
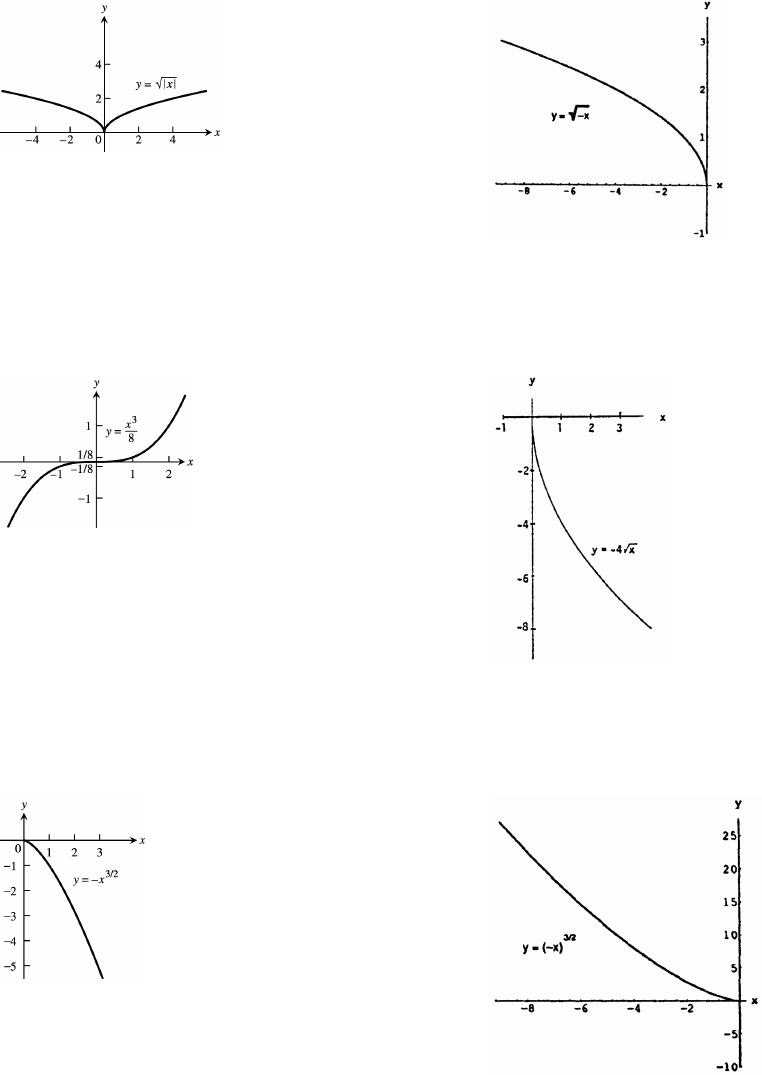
11. Symmetric about the y-axis 12. No symmetry
Dec: x Dec: x_ Ÿ ! _ Ÿ !
Inc: x Inc: nowhere! _
13. Symmetric about the origin 14. No symmetry
Dec: nowhere Dec: x!Ÿ _
Inc: x Inc: nowhere_ _
15. No symmetry 16. No symmetry
Dec: x Dec: x!Ÿ _ _ Ÿ!
Inc: nowhere Inc: nowhere
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

24 Chapter 1 Preliminaries
17. Symmetric about the y-axis 18. Symmetric about the y-axis
Dec: x Dec: x_Ÿ! !Ÿ_
Inc: x Inc: x! _ _ !
19. Since a horizontal line not through the origin is symmetric with respect to the y-axis, but not with respect to the origin, the
function is even.
20. f x x and f x x f x . Thus the function is odd.ab abab ab
ˆ‰
œ œ œ œ œ œ
& """
&
xx
x
ab
21. Since f x x x f x . The function is even.ab a b abœ "œ "œ
##
22. Since f x x x f x x x and f x x x f x x x the function is neither even norÒ œ ÓÁÒ œ Ó Ò œ ÓÁÒ œ Óab a b a b ab ab ab
##
##
odd.
23. Since g x x x, g x x x x x g x . So the function is odd.ab a b a b abœ œœœ
$$$
24. g x x x x x g x thus the function is even.ab ab ab abœ$"œ$ "œß
%# %#
25. g x g x . Thus the function is even.ab a bœœ œ
""
" "
x x
ab
26. g x ; g x g x . So the function is odd.ab ab abœœœ
xx
x x
" "
27. h t ; h t ; h t . Since h t h t and h t h t , the function is neither even nor odd.ab a b ab ab ab ab a bœœœ Á Á
"""
" " "t t t
28. Since t | t |, h t h t and the function is even.lœl œ
$$
ab ab ab
29. h t 2t , h t 2t . So h t h t . h t 2t , so h t h t . The function is neither even norab a b ab a b ab ab abœ " œ " Á œ " Á
odd.
30. h t 2 t and h t 2 t 2 t . So h t h t and the function is even.ab a b ab a bœ l l" œ l l"œ l l" œ
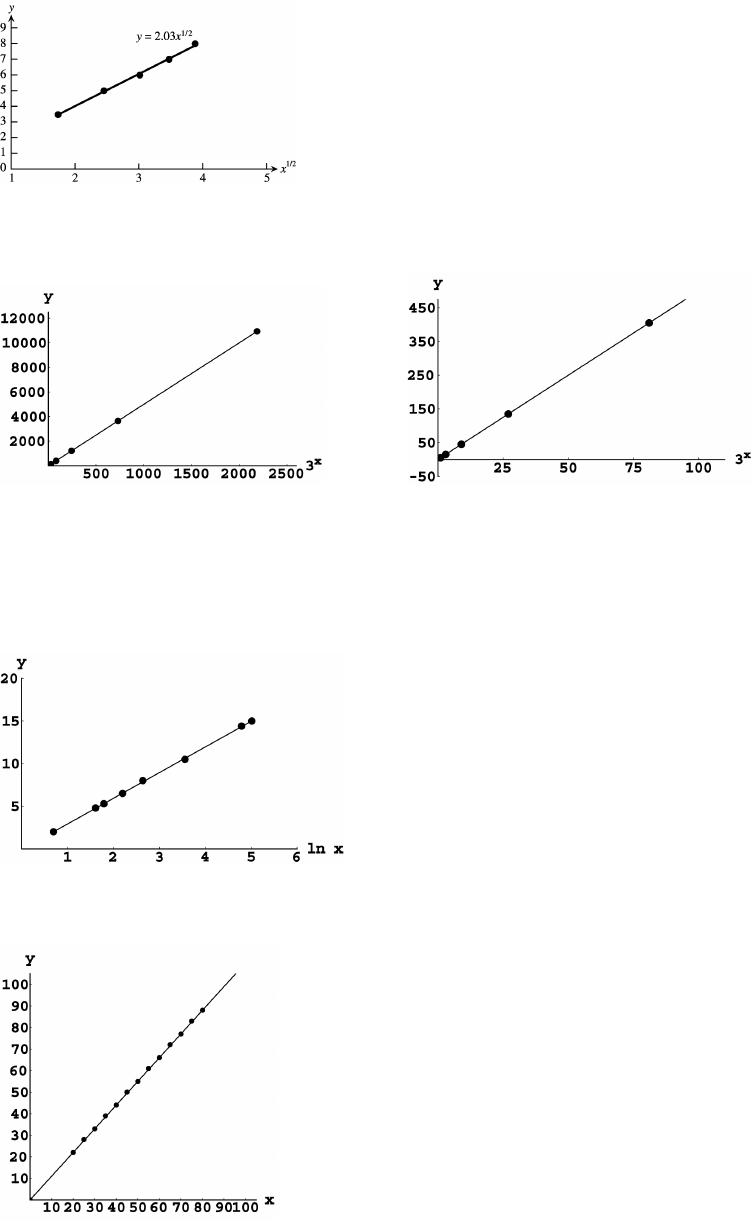
31. (a) The graph supports the assumption that y is proportional to x. The
constant of proportionality is estimated from the slope of the
regression line, which is 0.166.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.4 Identifying Functions; Mathematical Models 25
(b) The graph supports the assumption that y is proportional to x .
"Î#
The constant of proportionality is estimated from the slope of the
regression line, which is 2.03.
32. (a) Because of the wide range of values of the data, two graphs are needed to observe all of the points in relation to the
regression line.
The graphs support the assumption that y is proportional to . The constant of proportionality is estimated from the$x
slope of the regression line, which is 5.00.
(b) The graph supports the assumption that y is proportional to ln x. The constant of proportionality is extimated from
the slope of the regression line, which is 2.99.
33. (a) The scatterplot of y reaction distance versus x speed isœœ
Answers for the constant of proportionality may vary. The constant of proportionality is the slope of the line, which is
approximately 1.1.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
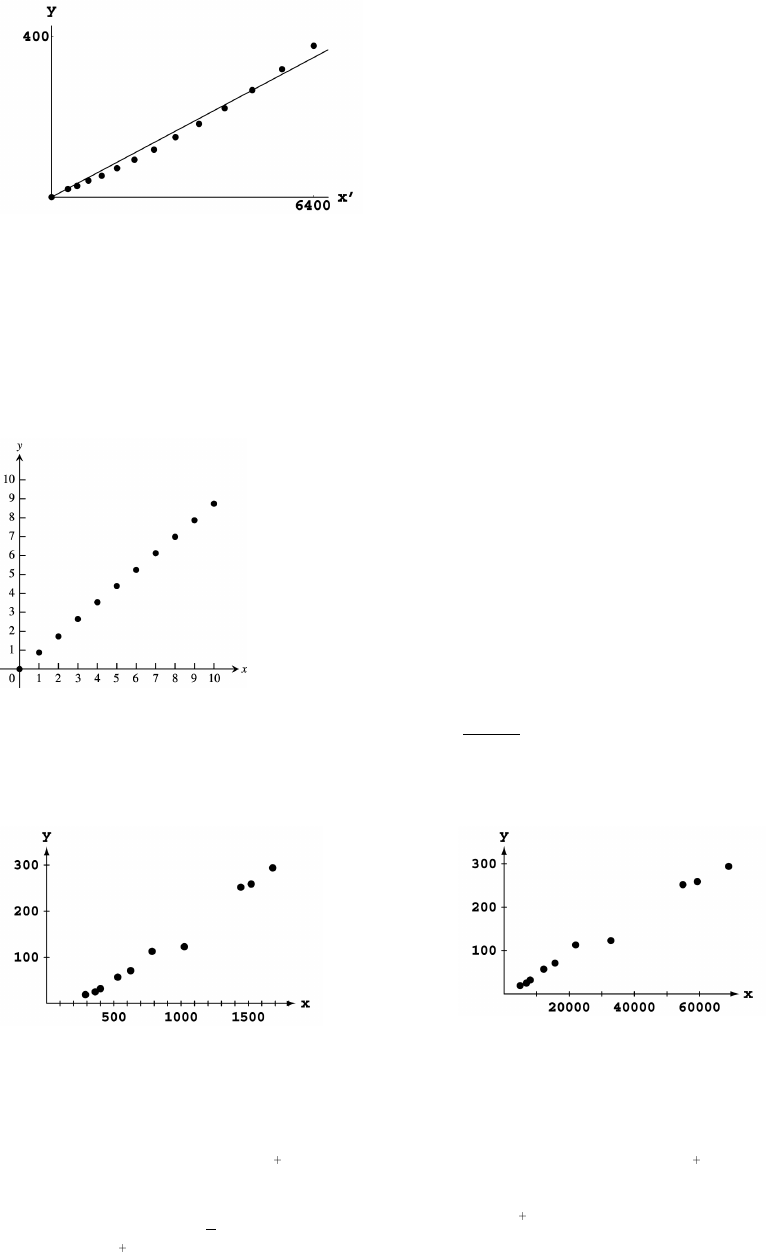
26 Chapter 1 Preliminaries
(b) Calculate x speed squared. The scatterplot of x versus y braking distance is:
ww
œœ
Answers for the constant of proportionality may vary. The constant of proportionality is the slope of the line, which
is approximately 0.059.
34. Kepler's 3rd Law is T days R , R in millions of miles. "Quaoar" is 4 miles from Earth, or aboutabœ!Þ%" ‚"!
$Î# *
4 miles from the sun. Let R 4000 (millions of miles) and‚ "! *$ ‚ "! ¸ % ‚ "! œ
*'*
T days days.œ !Þ%" %!!! ¸ "!$ß (#$abab
$Î#
35. (a)
The hypothesis is reasonable.
(b) The constant of proportionality is the slope of the line in./unit mass in./unit mass.¸ œ !Þ)(%
)Þ(%" !
"!!
(c) y(in.) in./unit mass unit mass in.œ !Þ)( "$ œ ""Þ$"abab
36. (a) (b)
Graph (b) suggests that y k x is the better model. This graph is more linear than is graph (a).œ$
1.5 COMBINING FUNCTIONS; SHIFTING AND SCALING GRAPHS
1. D : x , D : x 1 D D : x 1. R : y , R : y 0, R : y 1, R : y 0
f g fg fg f g fg fg
_ _ Ê œ _ _
2. D : x 1 0 x 1, D : x 1 0 x 1. Therefore D D : x 1.
fg fgfg
Ê Ê œ
R R : y 0, R : y 2, R : y 0
fg fg fg
œ
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 1.5 Combining Functions; Shifting and Scaling Graphs 27
3. D : x , D : x D : x since g(x) 0 for any x; D : x
fg fg gf
_ _ _ _ Ê _ _ Á _ _
since f(x) 0 for any x. R : y 2, R : y 1, R : 0 y 2, R : yÁœŸ
fgfg gfÎ"
#
4. D : x , D : x 0 D : x 0 since g(x) 0 for any x 0; D : x 0 since f(x) 0
fgfg gf
_ _ Ê Á Á
for any x 0. R : y 1, R : y 1, R : 0 y 1, R : yœŸ "
fgfg gfÎ
5. (a) f(g(0)) f( 3) 2œ œ
(b) g(f(0)) g(5) 22œœ
(c) f(g(x)) f(x 3) x 3 5 x 2œœœ
## #
(d) g(f(x)) g(x 5) (x 5) 3 x 10x 22œ œ œ
##
(e) f(f( 5)) f(0) 5œ œ
(f) g(g(2)) g(1) 2œœ
(g) f(f(x)) f(x 5) (x 5) 5 x 10œ œœ
(h) g(g(x)) g(x 3) (x 3) 3 x 6x 6œœœ
###%#
6. (a) f g f
ˆ‰ˆ‰ˆ‰
""
#œœ
2
33
(b) g f g 2
ˆ‰ˆ‰ˆ‰
""
##
œœ
(c) f(g(x)) f 1œœœ
ˆ‰
""
x1 x1 x1
x
(d) g(f(x)) g(x 1)œœ œ
""
(x 1) 1 x
(e) f(f(2)) f(1) 0œœ
(f) g(g(2)) gœœœ
ˆ‰
""
34
3
4
3
(g) f(f(x)) f(x 1) (x 1) 1 x 2œ œœ
(h) g(g(x)) g (x 1 and x 2)œœœÁÁ
ˆ‰
"""
#
x1 x
1
x
x1
7. (a) u(v(f(x))) u v u 4 5 5œœœœ
ˆ‰ˆ‰ˆ‰ˆ‰
"""
#
xxx x
4
(b) u(f(v(x))) u f x u 4 5 5œœœœabab ˆ‰ ˆ‰
#""
xx x
4
(c) v(u(f(x))) v u v 4 5 5œœœ
ˆ‰ˆ ‰ˆ‰ˆ‰ ˆ‰
"" #
xxx
4
(d) v(f(u(x))) v(f(4x 5)) vœœ œ
ˆ‰ˆ‰
""
#
4x 5 4x 5
(e) f(u(v(x))) f u x f 4 x 5œœœaba bab ab
## "
4x 5
(f) f(v(u(x))) f(v(4x 5)) f (4x 5)œœœab
#"
(4x 5)
8. (a) h(g(f(x))) h g x h 4 8 x 8œœœœ
ˆ‰ˆ‰
ÈÈ
Š‹ Š‹
ÈÈ
xx
44
(b) h(f(g(x))) h f h 4 8 2 x 8œœœœ
ˆ‰ˆ‰ˆ‰ ÈÈ È
xxx
444
(c) g(h(f(x))) g h x g 4 x 8 x 2œœœœ
ˆ‰ˆ ‰ˆ‰
ÈÈ È
4x8
4
È
(d) g(f(h(x))) g(f(4x 8)) g 4x 8œœ œ œ
Š‹
ÈÈÈ
4x 8
4
x2
#
(e) f(g(h(x))) f(g(4x 8)) f f(x 2) x 2œœ œœ
ˆ‰ È
4x 8
4
(f) f(h(g(x))) f h f 4 8 f(x 8) x 8œœœœ
ˆ‰ˆ ‰ˆ‰ ˆ‰ È
xx
44
9. (a) y f(g(x)) (b) y j(g(x))œœ
(c) y g(g(x)) (d) y j(j(x))œœ
(e) y g(h(f(x))) (f) y h(j(f(x)))œœ
10. (a) y f(j(x)) (b) y h(g(x)) g(h(x))œœœ
(c) y h(h(x)) (d) y f(f(x))œœ
(e) y j(g(f(x))) (f) y g(f(h(x)))œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
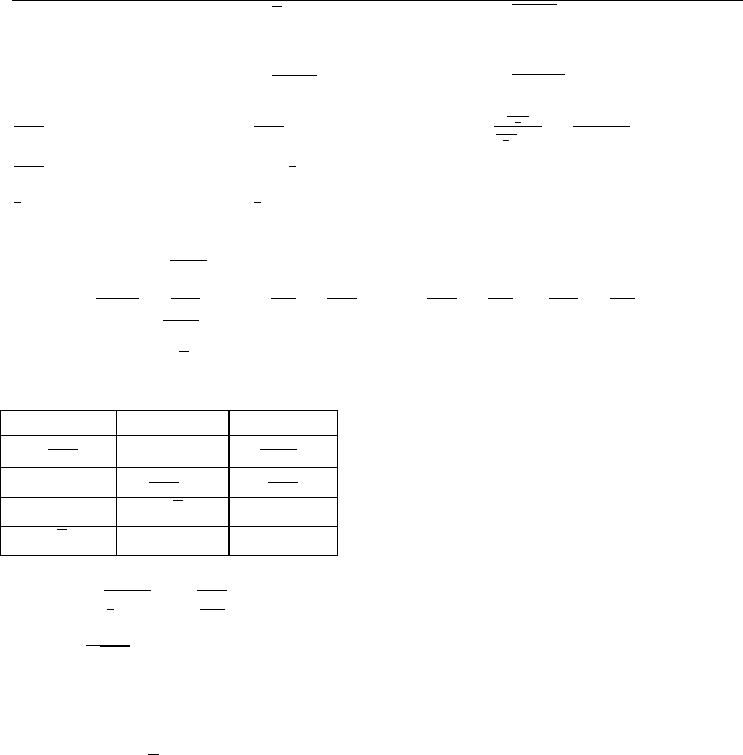
28 Chapter 1 Preliminaries
11. g(x) f(x) (f g)(x)‰
(a) x 7 x x 7
ÈÈ
(b) x2 3x 3(x2) 3x6œ
(c) x x 5 x 5
##
ÈÈ
(d) x
xx x
x1 x1 1 x(x1)
x
x1
x
x1 œœ
(e) 1 x
""
x1 x
(f) x
""
xx
12. (a) f g x g x .a bab ab‰œllœ
"
l"lx
(b) f g x so g x x .a bab ab‰ œ œÊ"œÊ"œÊœß œ"
gx
gx x gx x x gx x gx
xxx
ab
ab ab ab ab
"
" " " "
""""
(c) Since f g x g x x , g x x .a bab ab ab
È
‰œ œll œ
#
(d) Since f g x f x x , f x x . (Note that the domain of the composite is .)a bab ab
ˆ‰
È
‰œ œllœ Ò!ß_Ñ
#
The completed table is shown. Note that the absolute value sign in part (d) is optional.
g x f x f g x
x
x
xxx
xx x
ab ab a bab
È
È
‰
ll
"
ll
ll
""
" l "l
"
"
#
#
xx
xx
xx
13. (a) f g x 1abab ÉÉ
œœ
11x
xx
gfx ababœ1
x1
È
(b) Domain f g : 0, , domain g f : 1, ab ab‰ Ð _Ñ ‰ Ð _Ñ
(c) Range f g : 1, , range g f : 0, ab ab‰ Ð _Ñ ‰ Ð _Ñ
14. (a) f g x 1 2 x xabab È
œ
gfx 1 x ab kkabœ
(b) Domain f g : 0, , domain g f : 0, ab ab‰ Ð _Ñ ‰ Ð _Ñ
(c) Range f g : 0, , range g f : , 1ab ab‰ Ð _Ñ ‰ Ð_ Ñ
15. (a) y (x 7) (b) y (x 4)œ œ
# #
16. (a) y x 3 (b) y x 5œ œ
# #
17. (a) Position 4 (b) Position 1 (c) Position 2 (d) Position 3
18. (a) y (x 1) 4 (b) y (x 2) 3 (c) y (x 4) 1 (d) y (x 2)œ œ œ œ
## # #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.5 Combining Functions; Shifting and Scaling Graphs 29
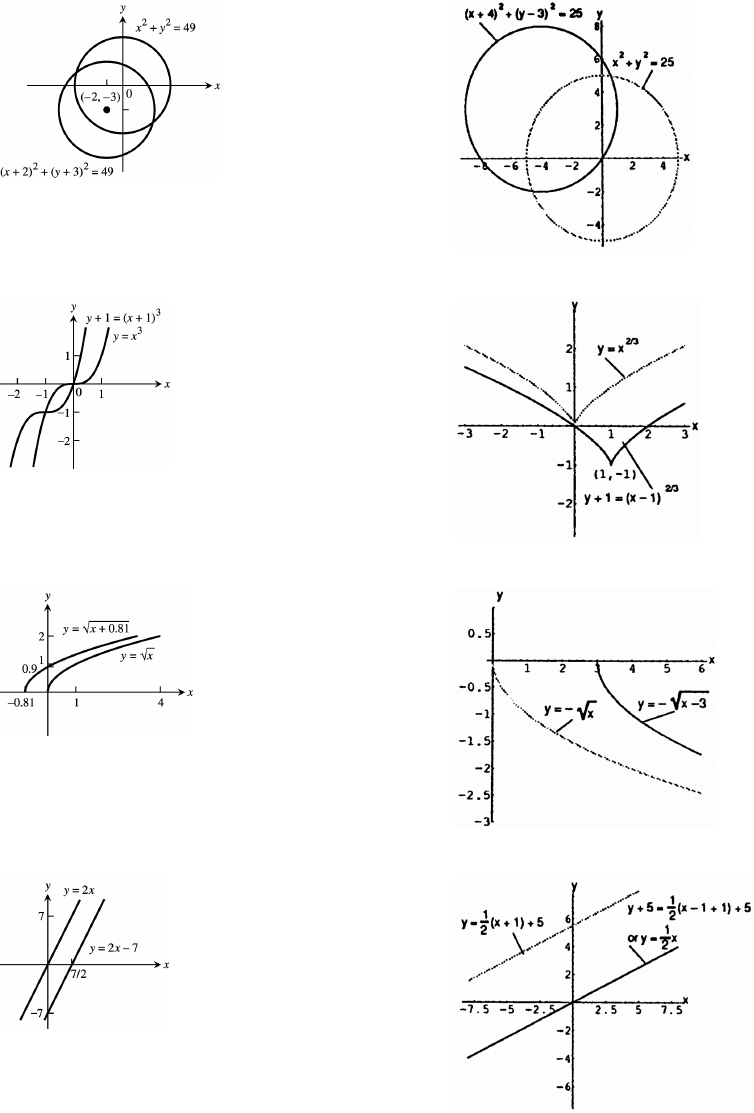
19. 20.
21. 22.
23. 24.
25. 26.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
30 Chapter 1 Preliminaries
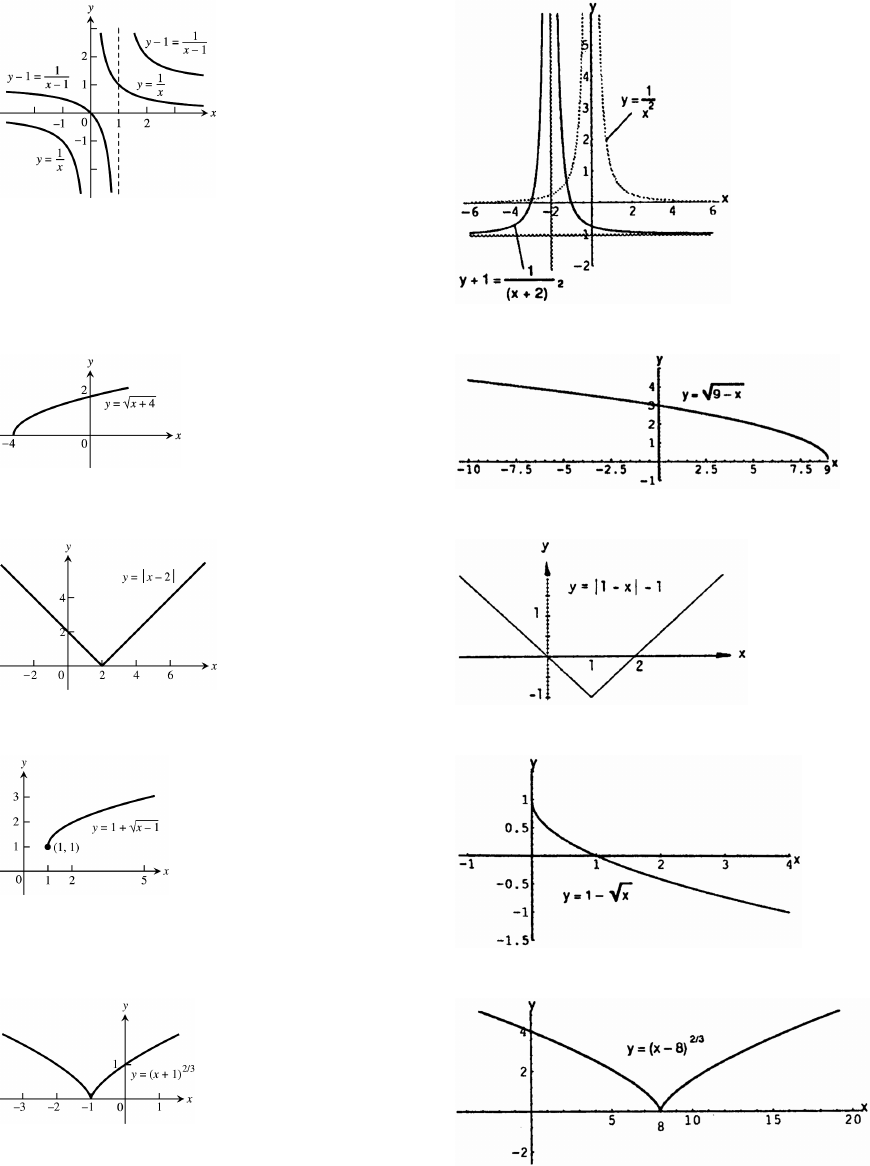
27. 28.
29. 30.
31. 32.
33. 34.
35. 36.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
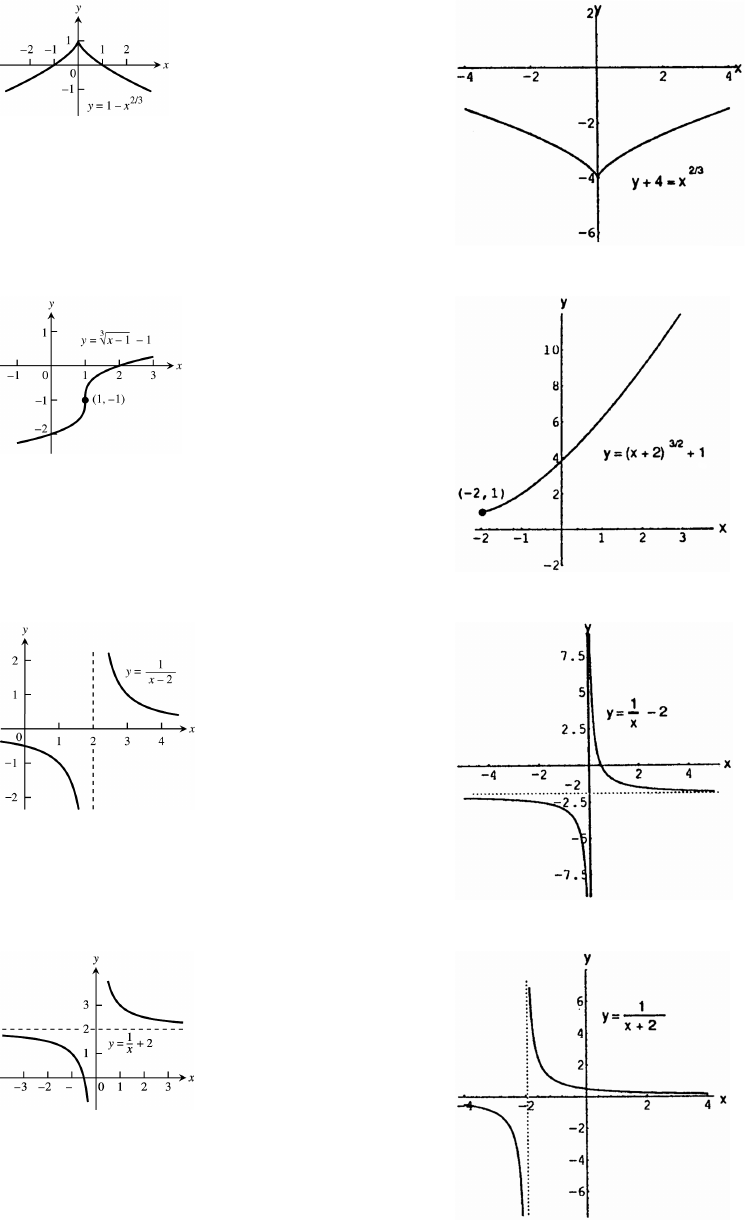
Section 1.5 Combining Functions; Shifting and Scaling Graphs 31
37. 38.
39. 40.
41. 42.
43. 44.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
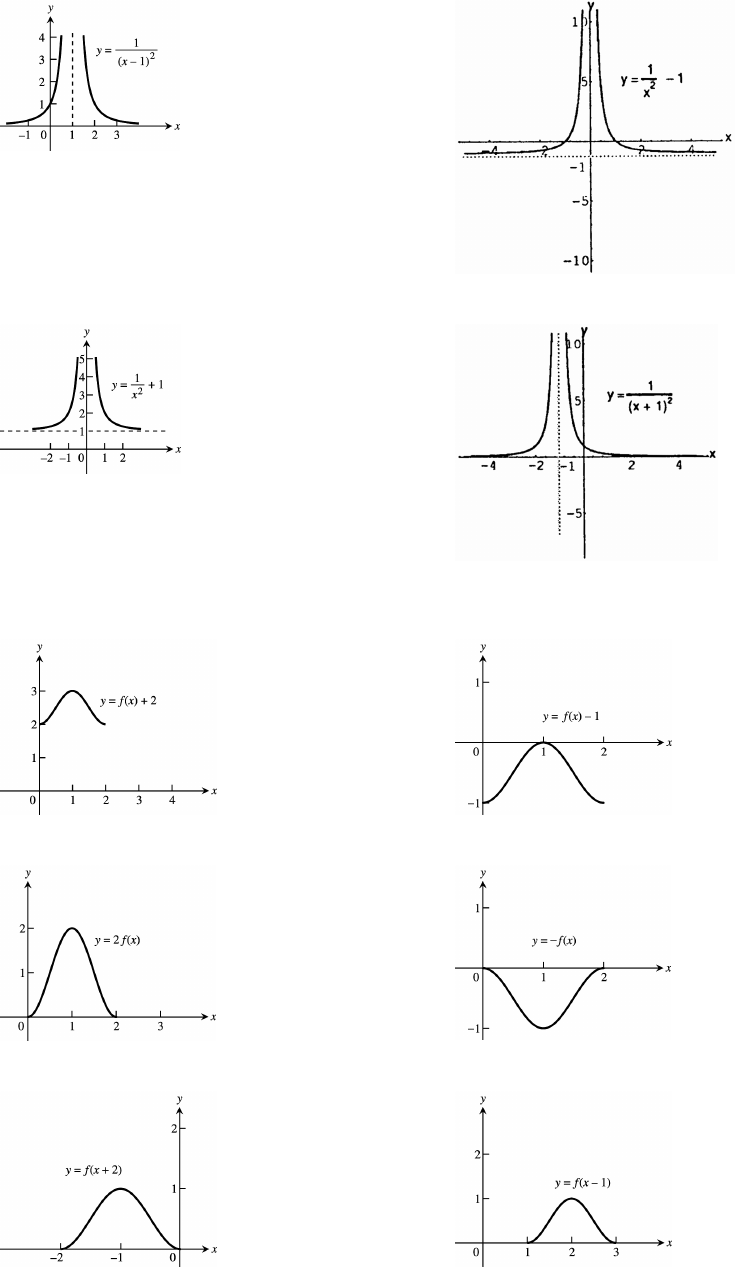
32 Chapter 1 Preliminaries
45. 46.
47. 48.
49. (a) domain: [0 2]; range: [ ] (b) domain: [0 2]; range: [ 1 0]ß#ß$ ßß
(c) domain: [0 2]; range: [0 2] (d) domain: [0 2]; range: [ 1 0]ßß ßß
(e) domain: [ 2 0]; range: [ 1] (f) domain: [1 3]; range: [ ]ß !ß ß !ß"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
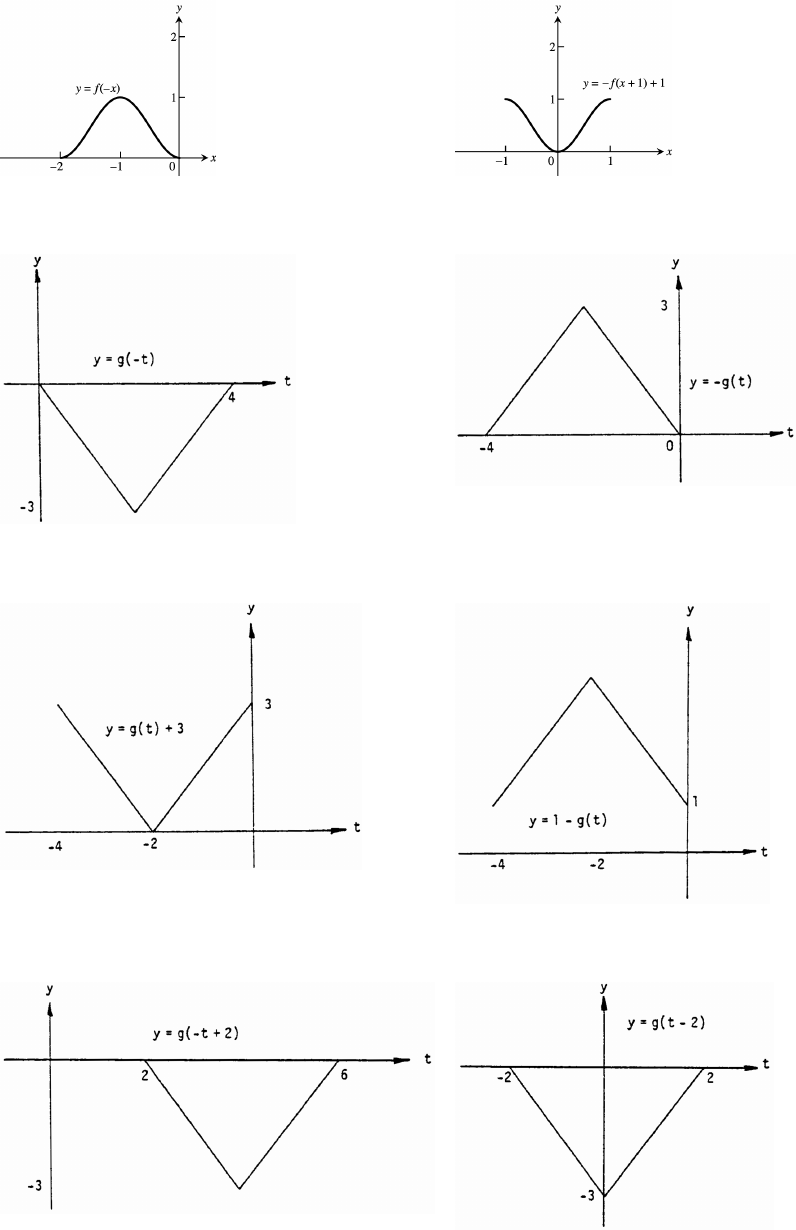
Section 1.5 Combining Functions; Shifting and Scaling Graphs 33
(g) domain: [ 2 0]; range: [ ] (h) domain: [ 1 1]; range: [ ]ß !ß" ß !ß"
50. (a) domain: [0 4]; range: [ 3 0] (b) domain: [ 4 0]; range: [ ]ßß ß!ß$
(c) domain: [ 4 0]; range: [ ] (d) domain: [ 4 0]; range: [ ]ß !ß$ ß "ß%
(e) domain: [ 4]; range: [ 3 0] (f) domain: [ 2 2]; range: [ 3 0]#ß ß ß ß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

34 Chapter 1 Preliminaries
(g) domain: [ 5]; range: [ 3 0] (h) domain: [0 4]; range: [0 3]"ß ß ß ß
51. y 3x 3œ
#
52. y 2x 1 x 1œœ%ab
##
53. y œ" œ
""""
###
ˆ‰
xx
54. y 1 1œ œ
"*
Î$abxx
55. y x 1œ%
È
56. y 3 x 1œ
È
57. y 16 xœ% œ
Ɉ‰ È
x
##
#"#
58. y xœ%
"
$#
È
59. y 3x 27xœ" œ"ab
$$
60. y œ" œ"
ˆ‰
xx
#)
$
61. Let y x f x and let g x x , h x x , i x x , andœ # "œ œ œ œ #
Èab ab ab ab
ˆ‰ ˆ‰
È
"Î# ""
##
"Î# "Î#
j x x f . The graph of h x is the graph of g x shifted left unit; the graph of i x is the graphab ab ab ab ab
’“
Ȉ‰
œ # œ B
" "
# #
"Î#
of h x stretched vertically by a factor of ; and the graph of j x f x is the graph of i x reflected across the x-axis.ab ab ab ab
È#œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
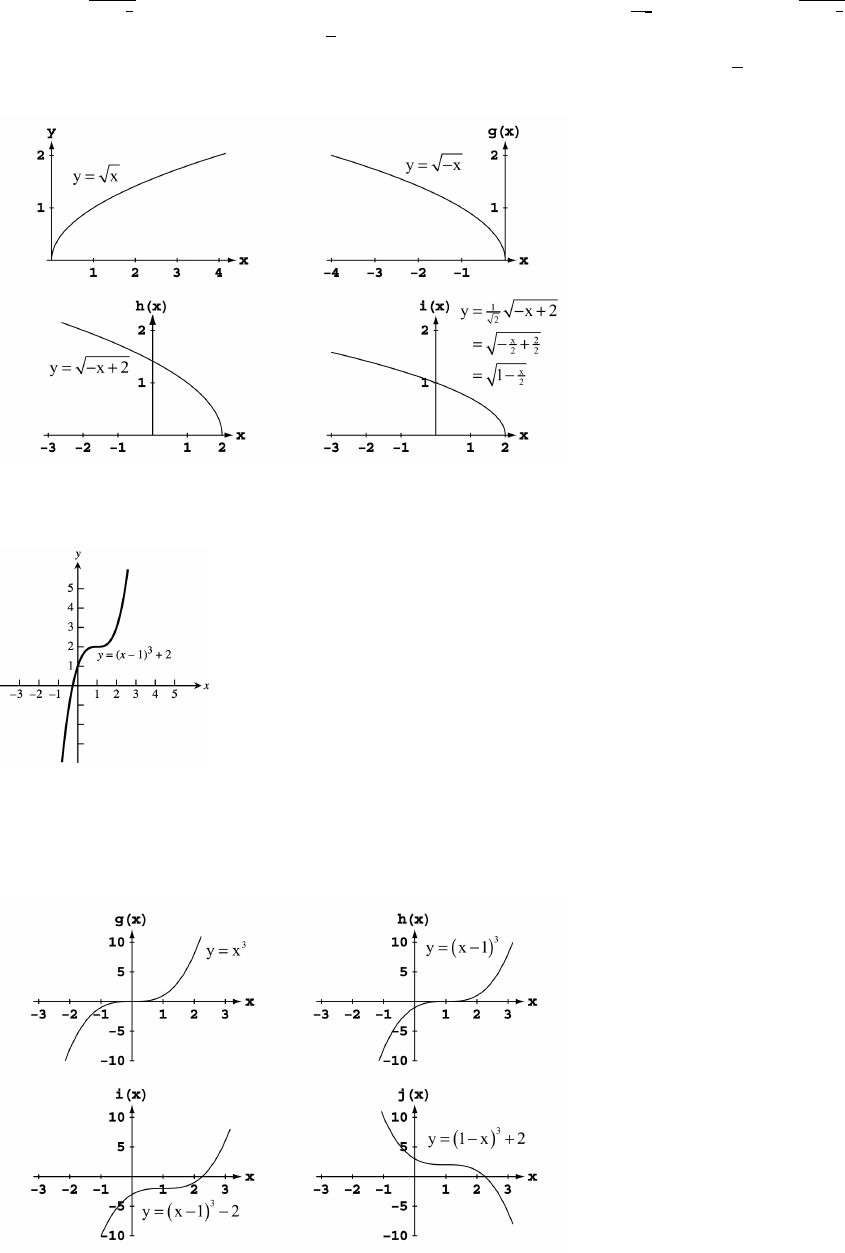
Section 1.5 Combining Functions; Shifting and Scaling Graphs 35
62. Let y f x Let g x x , h x x , and i x x f xœ " œ Þ œ œ# œ # œ " œ Þ
È È
ab ab a b ab a b ab a b ab
x x
# #
"Î# "Î# "Î#
"
#
È
The graph of g x is the graph of y x reflected across the x-axis. The graph of h x is the graph of g x shifted rightab ab ab
È
œ
two units. And the graph of i x is the graph of h x compressed vertically by a factor of .ab ab È#
63. y f x x . Shift f x one unit right followed by a shift two units up to get g x x .œœ œ"#ab ab ab a b
$3
64. y x f x . Let g x x , h x x , i x x , andœ "B #œÒ " # Óœ œ œ " œ " #a b a b a b ab ab ab a b ab a b a b
$$ $$
$
j x x . The graph of h x is the graph of g x shifted right one unit; the graph of i x is the graph ofab a b a b ab ab abœÒ " #Ó
$
h x shifted down two units; and the graph of f x is the graph of i x reflected across the x-axis.ab ab ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
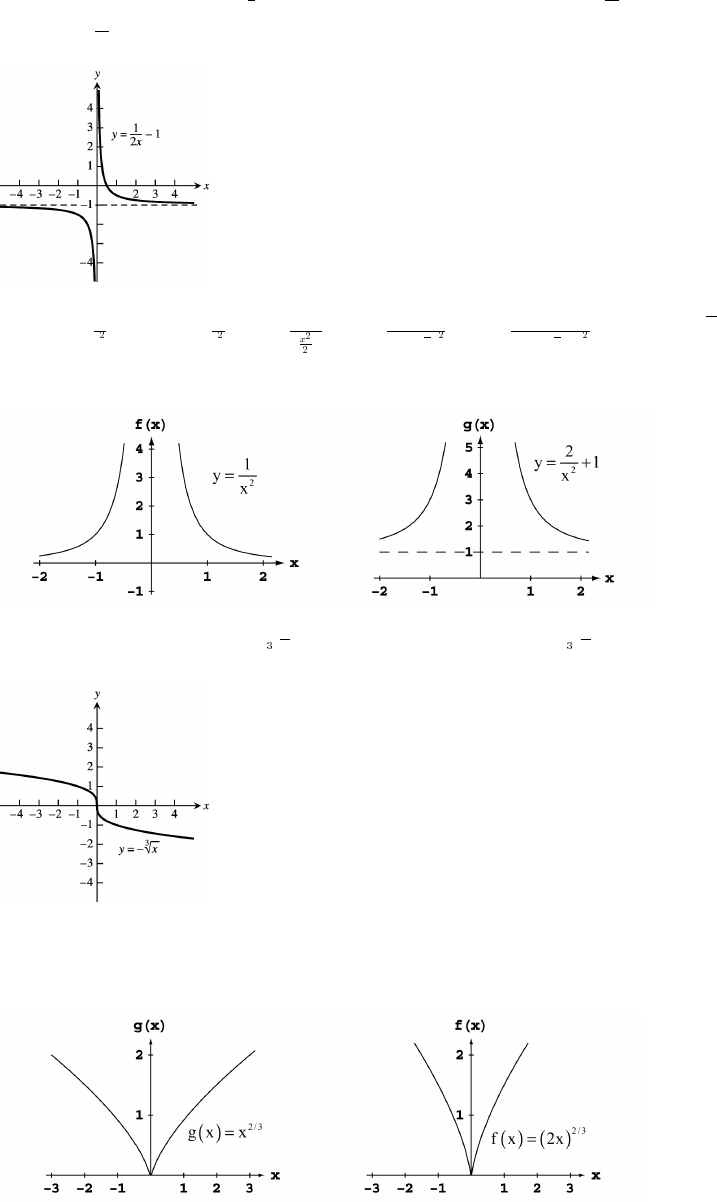
36 Chapter 1 Preliminaries
65. Compress the graph of f x horizontally by a factor of 2 to get g x . Then shift g x vertically down 1 unit toab ab abœœ
""
#xx
get h x .abœ"
"
#x
66. Let f x and g x Since , we see that the graph ofab ab È
œ œ " œ " œ " œ "Þ # ¸ "Þ%
"#"" "
Î# "Î#B
xx x
Š‹ Š‹ ’Š‹“
ÈÈ
f x stretched horizontally by a factor of 1.4 and shifted up 1 unit is the graph of g x .ab ab
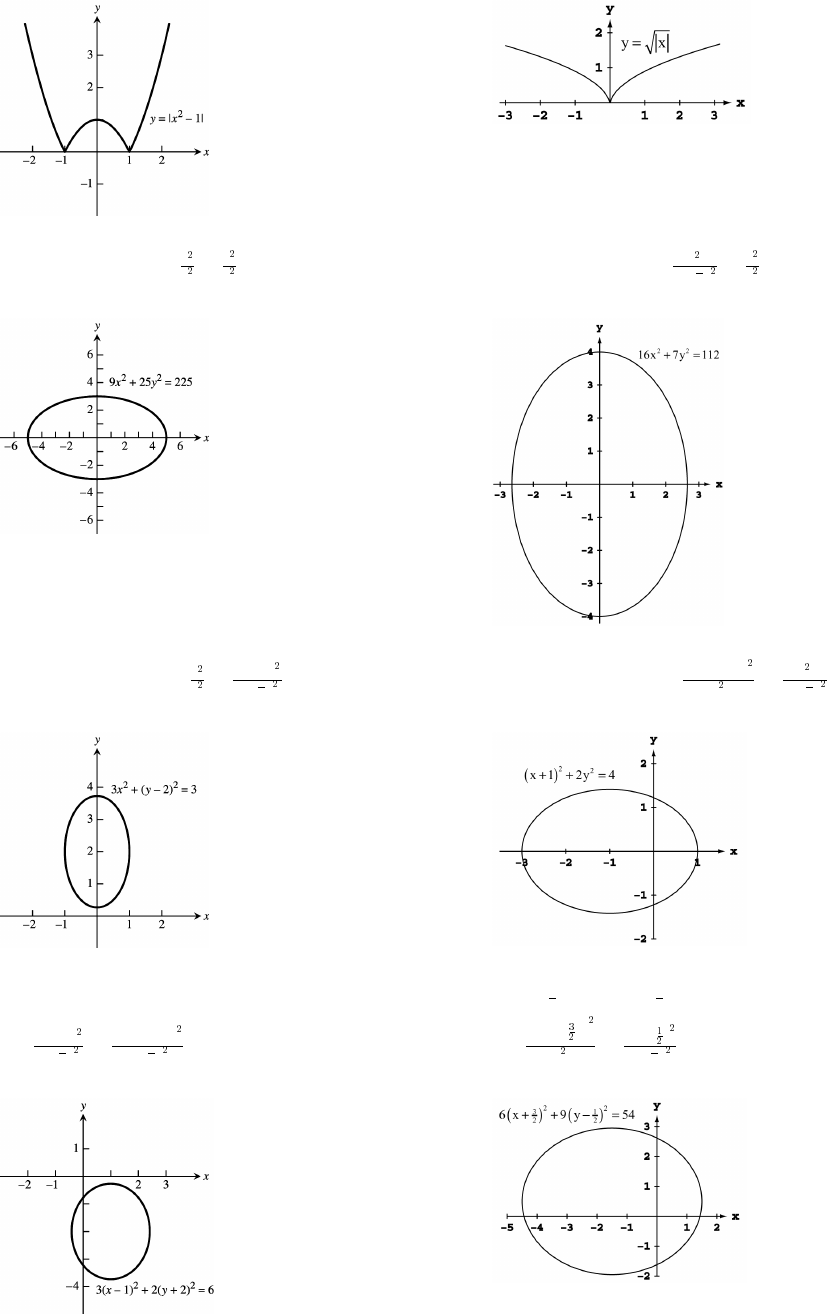
67. Reflect the graph of y f x x across the x-axis to get g x x.œœ œab ab
ÈÈ
68. y f x x x x x . So the graph of f x is the graph of g x xœ œ # œ Ò " # Ó œ " # œ # œab a b a bab a b a b a b ab ab
#Î$ #Î$ #Î$ #Î$
#Î$ #Î$
compressed horizontally by a factor of 2.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.5 Combining Functions; Shifting and Scaling Graphs 37
69. 70.
71. x y 72. x y* #& œ ##& Ê œ " "' ( œ ""# Ê œ "
## ##
&$ %
(
x x
y y
Š‹
È
73. x y 74. x y$ # œ$Ê œ" " # œ%Ê œ"
# #
## #
" #
$ #
"
ab ab
xy x y
ab
Š‹ Š‹
È È
‘
ab
75. x y 76. x y$"##œ' ' * œ&%abab ˆ‰ˆ‰
## $"
##
##
Ê œ" Ê œ"
ab
Š‹ Š‹ Š‹
ÈÈ
‘
ab ’“
ˆ‰ ˆ‰
È
x y xy
"
#$ '
#
$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
38 Chapter 1 Preliminaries
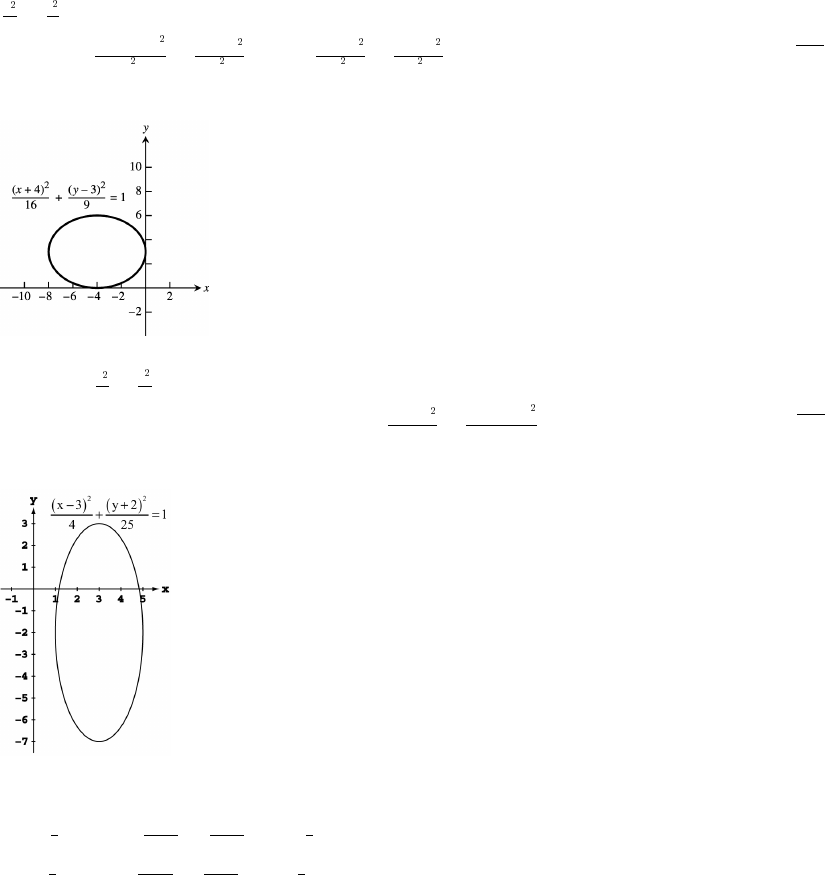
77. has its center at . Shiftinig 4 units left and 3 units up gives the center at h, k . So the
xy
"' *
œ " !ß ! œ %ß $ab aba b
equation is . Center, C, is , and major axis, AB, is the segment
‘
ab ab abab
x 4
43 43
y 3 x y
%$
œ"Êœ" %ß$ab
from to .abab)ß $ !ß $
78. The ellipse has center h, k . Shifting the ellipse 3 units right and 2 units down produces an ellipse
xy
%#&
œ " œ !ß !abab
with center at h, k and an equation . Center, C, is 3 , and AB, the segment fromabab abœ $ß# œ" ß#
ab‘
ab
x 3 y
%#&
#
to is the major axis.aba b$ß $ $ß (
79. (a) (fg)( x) f( x)g( x) f(x)( g(x)) (fg)(x), oddœ œ œ
(b) ( x) (x), odd
Š‹ Š‹
ff
gg(x)g(x)g
f( x) f(x)
œœœ
(c) ( x) (x), odd
ˆ‰ ˆ‰
gg(x)g(x)g
ff(x)f(x)f
œœœ
(d) f ( x) f( x)f( x) f(x)f(x) f (x), even
##
œ œ œ
(e) g ( x) (g( x)) ( g(x)) g (x), even
####
œ œ œ
(f) (f g)( x) f(g( x)) f( g(x)) f(g(x)) (f g)(x), even‰œ œ œ œ‰
(g) (g f)( x) g(f( x)) g(f(x)) (g f)(x), even‰œ œ œ ‰
(h) (f f)( x) f(f( x)) f(f(x)) (f f)(x), even‰œ œ œ‰
(i) (g g)( x) g(g( x)) g( g(x)) g(g(x)) (g g)(x), odd‰ œ œ œ œ ‰
80. Yes, f(x) 0 is both even and odd since f( x) 0 f(x) and f( x) 0 f(x).œœœœœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.6 Trigonometric Functions 39
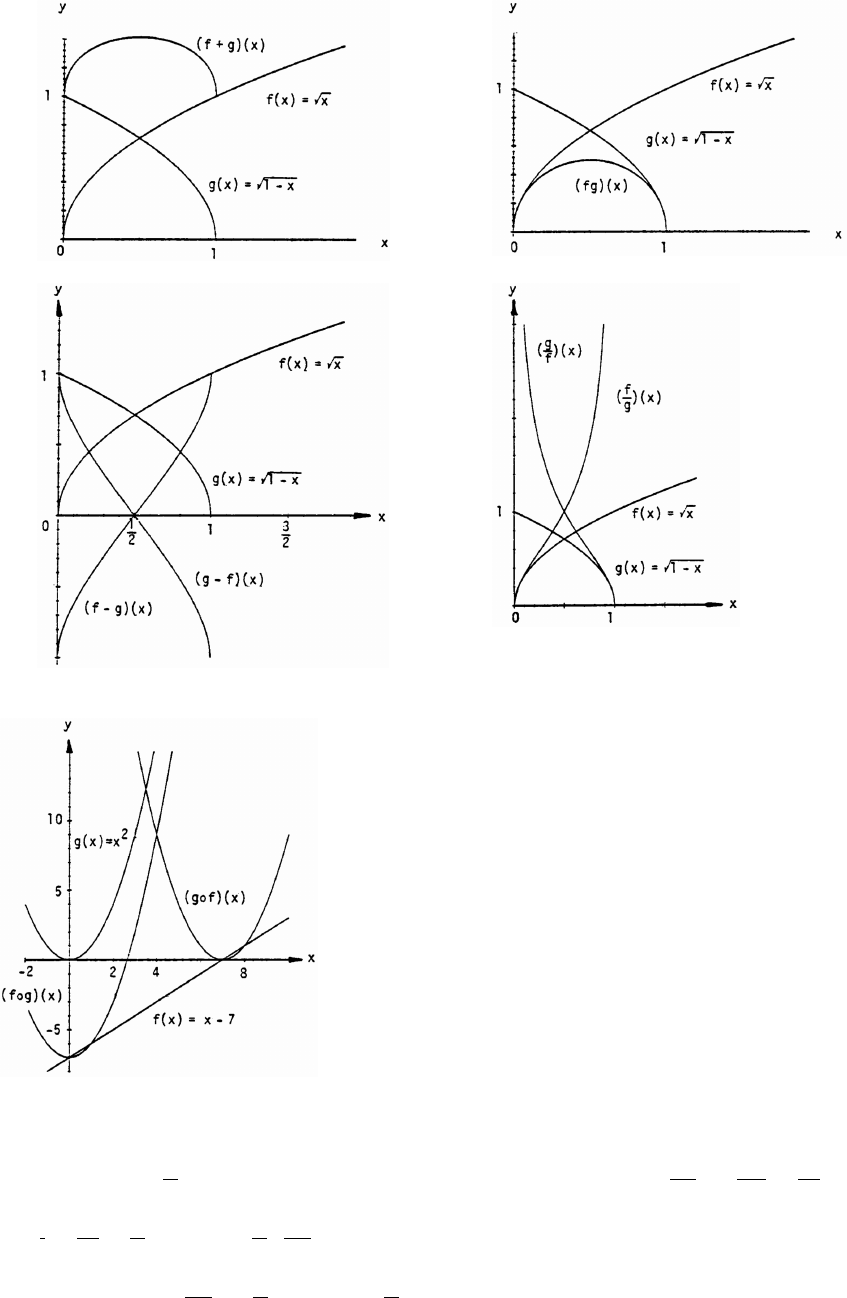
81. (a) (b)
(c) (d)
82.
1.6 TRIGONOMETRIC FUNCTIONS
1. (a) s r (10) 8 m (b) s r (10)(110°) mœœ œ œœ œ œ)1 )
ˆ‰ ˆ ‰
4110 55
5180° 18 9
1111
2. radians and 225°)œœ œ œ
s 10 5 5 180°
r8 4 4
11 1
1
ˆ‰
3. 80° 80° s (6) 8.4 in. (since the diameter 12 in. radius 6 in.)))œÊœ œÊœ œ œ Ê œ
ˆ‰ ˆ‰
11 1
180° 9 9
44
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
40 Chapter 1 Preliminaries
4. d 1 meter r 50 cm 0.6 rad or 0.6 34°œÊœÊœœœ ¸)s 30 180°
r50 ˆ‰
1
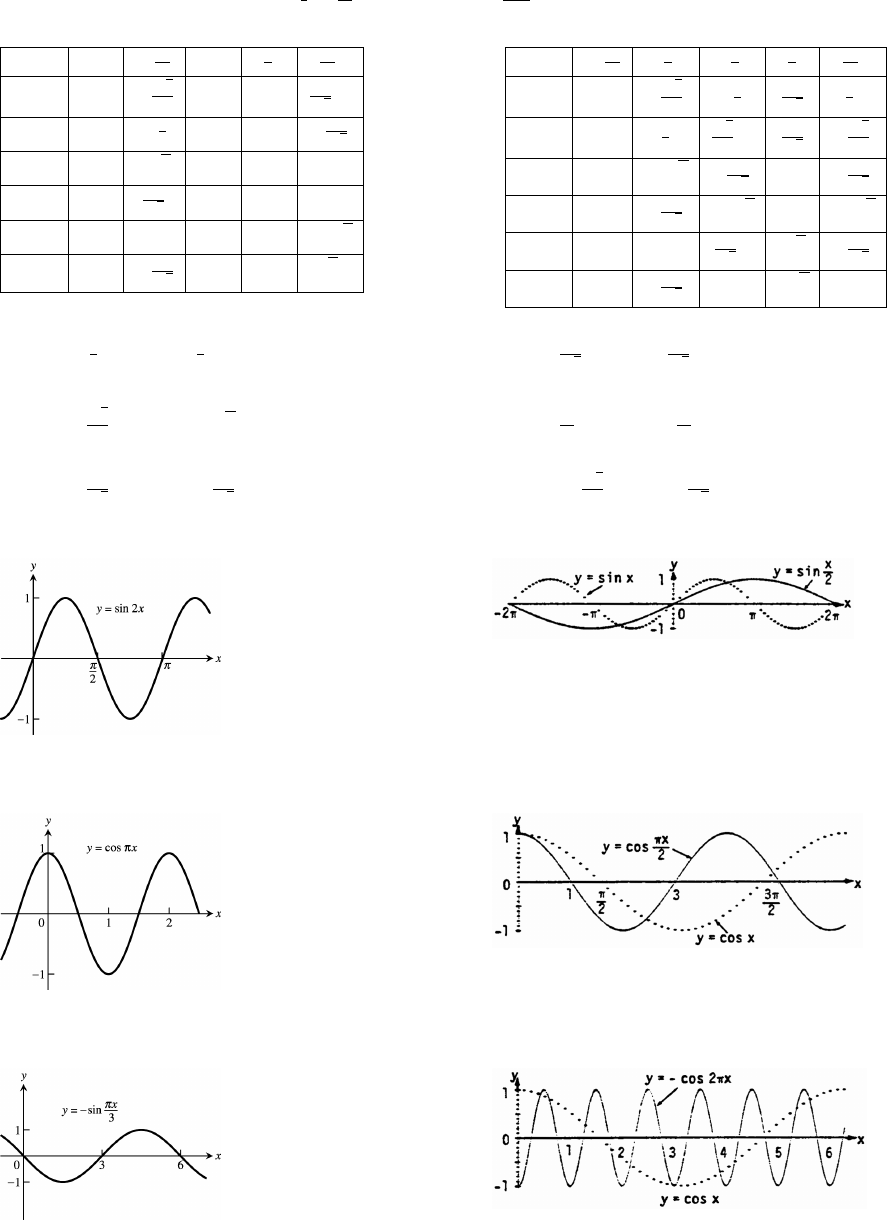
5. 0 6
sin 0 0
cos 1 0
tan 0 3 0 und.
cot und. und. 0 1
sec 1 und. 2
csc und. und. 2
)1
)
)
)
)
)
)
"
"
"
#"
"
23
34
3
2
2
3
2
3
111
#
#
"
""
#
"
ÈÈ
È
È
È
È
È
È
.
sin
cos
tan und. 3
cot 3 3
sec und. 2
csc
)
)
)
)
)
)
)
"
!
"
! "
#
" #
3
3
3
2
33
2
33
3
22
33
2
3
11 1 1 1
#'%'
&
## #
"" "
""
## #
""
"
ÈÈ
ÈÈ
È
ÈÈ
È
ÈÈ
È
È
ÈÈ
È
È2#
7. cos x , tan x 8. sin x , cos xœ œ œ œ
43 2
54 55
ÈÈ
"
9. sin x , tan x 8 10. sin x , tan xœ œ œ œ
È8
313 5
12 12
È
11. sin x , cos x 12. cos x , tan xœ œ œ œ
" "
#
ÈÈ È
È
55 3
23
13. 14.
period period 4œœ11
15. 16.
period 2 period 4œœ
17. 18.
period 6 period 1œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.6 Trigonometric Functions 41
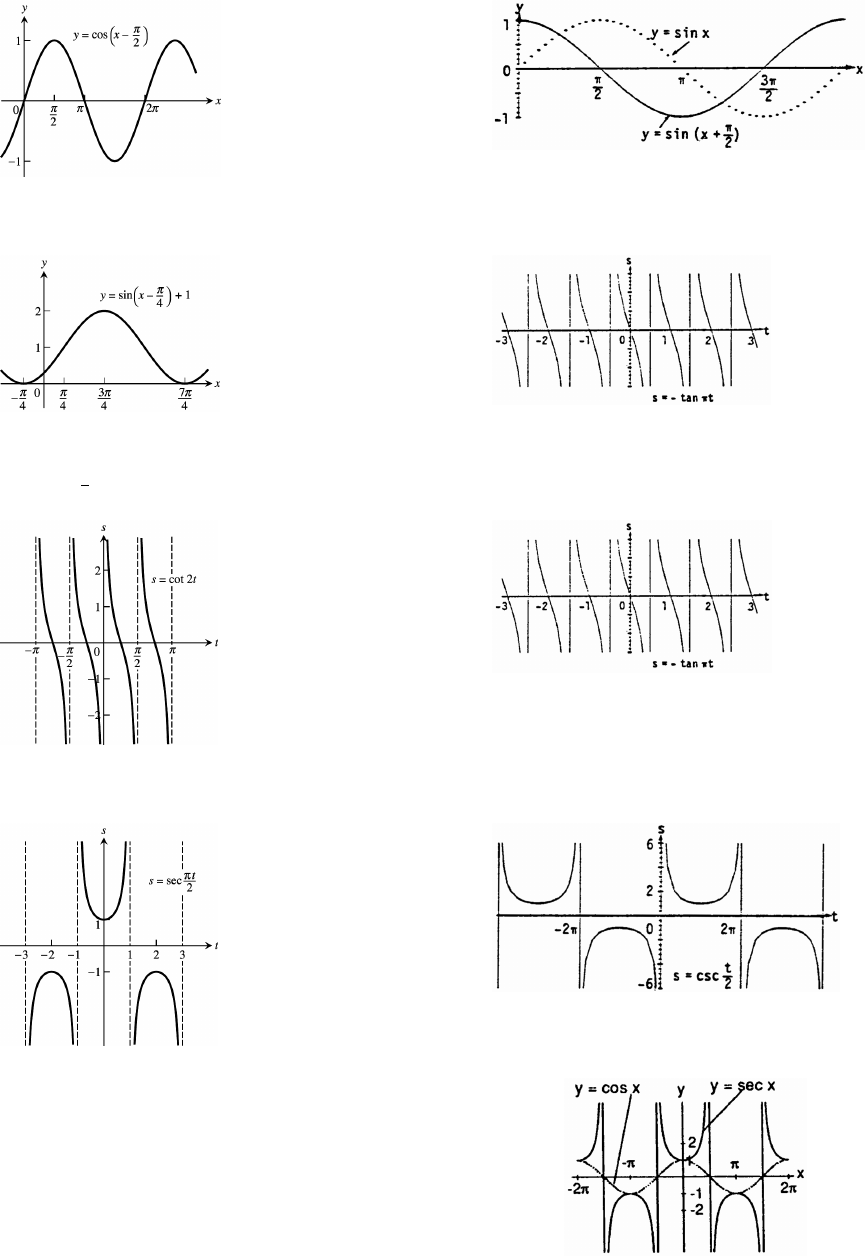
19. 20.
period 2 period 2œœ11
21. 22.
period 2 period 2œœ11
23. period , symmetric about the origin 24. period 1, symmetric about the originœœ
1
#
25. period 4, symmetric about the y-axis 26. period 4 , symmetric about the originœœ1
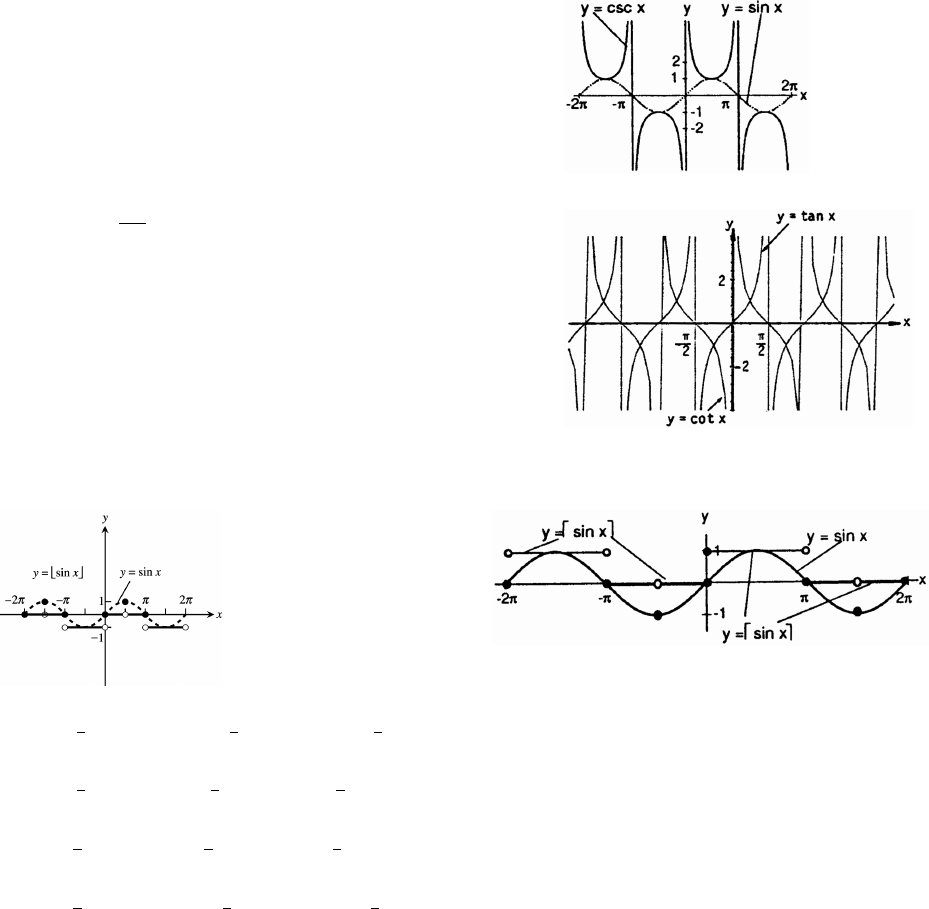
27. (a) Cos x and sec x are positive in QI and QIV and
negative in QII and QIII. Sec x is undefined when
cos x is 0. The range of sec x is ( 1] [ );_ß "ß_
the range of cos x is [ 1]."ß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
42 Chapter 1 Preliminaries
(b) Sin x and csc x are positive in QI and QII and
negative in QIII and QIV. Csc x is undefined when
sin x is 0. The range of csc x is ( 1] [1 );_ß ß _
the range of sin x is [ ]."ß "
28. Since cot x , cot x is undefined when tan x 0œœ
"
tan x
and is zero when tan x is undefined. As tan x approaches
zero through positive values, cot x approaches infinity.
Also, cot x approaches negative infinity as tan x
approaches zero through negative values.
29. D: x ; R: y 1, 0, 1 30. D: x ; R: y 1, 0, 1_ _ œ _ _ œ
31. cos x cos x cos sin x sin (cos x)(0) (sin x)( 1) sin x
ˆ ‰ ˆ‰ ˆ‰
œ œ œ
111
###
32. cos x cos x cos sin x sin (cos x)(0) (sin x)(1) sin x
ˆ ‰ ˆ‰ ˆ‰
œ œ œ
111
###
33. sin x sin x cos cos x sin (sin x)(0) (cos x)(1) cos x
ˆ ‰ ˆ‰ ˆ‰
œœœ
111
###
34. sin x sin x cos cos x sin (sin x)(0) (cos x)( 1) cos x
ˆ ‰ ˆ‰ ˆ‰
œ œ œ
111
###
35. cos (A B) cos (A ( B)) cos A cos ( B) sin A sin ( B) cos A cos B sin A ( sin B)œ œ œ
cos A cos B sin A sin Bœ
36. sin (A B) sin (A ( B)) sin A cos ( B) cos A sin ( B) sin A cos B cos A ( sin B)œ œ œ
sin A cos B cos A sin Bœ
37. If B A, A B 0 cos (A B) cos 0 1. Also cos (A B) cos (A A) cos A cos A sin A sin AœœÊ œ œ œ œ
cos A sin A. Therefore, cos A sin A 1.œ œ
## ##
38. If B 2 , then cos (A 2 ) cos A cos 2 sin A sin 2 (cos A)(1) (sin A)(0) cos A andœœœœ1111
sin (A 2 ) sin A cos 2 cos A sin 2 (sin A)(1) (cos A)(0) sin A. The result agrees with theœœœ111
fact that the cosine and sine functions have period 2 .1
39. cos ( x) cos cos sin sin x ( 1)(cos x) (0)(sin x) cos x111œ B œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 1.6 Trigonometric Functions 43
40. sin (2 x) sin 2 cos ( x) cos (2 ) sin ( x) (0)(cos ( x)) (1)(sin ( x)) sin x11 1œ œ œ
41. sin x sin cos ( x) cos sin ( x) ( 1)(cos x) (0)(sin ( x)) cos x
ˆ ‰ ˆ‰ ˆ‰
33 311 1
## #
œ œ œ
42. cos x cos cos x sin sin x (0)(cos x) ( 1)(sin x) sin x
ˆ ‰ ˆ‰ ˆ‰
33 311 1
## #
œ œ œ
43. sin sin sin cos cos sin
7
1434343 4
22
362
111 1111
#####
"
œœœ œ
ˆ‰ ˆ‰
Š‹ Š‹Š‹
ÈÈÈÈ
È
44. cos cos cos cos sin sin
11 2 2 2
1434343 4
22
326
111 1111
#####
"
œœ œ œ
ˆ‰ ˆ‰
Š‹ Š‹Š‹
ÈÈÈÈ
È
45. cos cos cos cos sin sin
1111111
12 3 4 3 4 3 4
22
313
22
œœ œ œ
ˆ ‰ ˆ‰ ˆ‰ˆ‰
Š‹Š‹Š ‹
"
## # #
ÈÈÈ È
È
46. sin sin sin cos cos sin
52 2 2
134 3 4 34
313
22
22
111 1 1 11
### # #
"
œœœœ
ˆ ‰ ˆ‰ ˆ ‰ ˆ‰ ˆ ‰ ˆ ‰
Š‹Š‹ Š ‹
ÈÈ È È
È
47. cos 48. cos
# #
## ###
1 1
84 1 4
1cos 1 1cos 1
22 23
œœœ œœœ
ˆ‰ ˆ‰
È È
2 2
8 1
23
49. sin 50. sin
# #
## # # #
1 1
14 84
1cos 1 1cos 1
23 22
œœœ œœœ
ˆ‰ ˆ‰
È È
2 2
1 8
32
51. tan (A B)œ œ œ
sin (A B)
cos (A B) cos A cos B sin A sin B
sin A cos B cos A cos B
sin A cos B cos A sin B
cos A cos B cos A cos B
cos A cos B sin A sin B
cos A cos B cos A cos B
œtan A tan B
1tan A tan B
52. tan (A B)œ œ œ
sin (A B)
cos (A B) cos A cos B sin A sin B
sin A cos B cos A cos B
sin A cos B cos A sin B
cos A cos B cos A cos B
cos A cos B sin A sin B
cos A cos B cos A cos B
œtan A tan B
1tan A tan B
53. According to the figure in the text, we have the following: By the law of cosines, c a b 2ab cos
###
œ )
1 1 2 cos (A B) 2 2 cos (A B). By distance formula, c (cos A cos B) (sin A sin B)œ œ œ
## ###
cos A 2 cos A cos B cos B sin A 2 sin A sin B sin B 2 2(cos A cos B sin A sin B). Thusœ œ
####
c 2 2 cos (A B) 2 2(cos A cos B sin A sin B) cos (A B) cos A cos B sin A sin B.
#œ œ Ê œ
54. (a) cos A B cos A cos B sin A sin Babœ
sin cos and cos sin))))œ œ
ˆ‰ ˆ‰
11
##
Let A B)œ
sin A B cos A B cos A B cos A cos B sin A sin Bab ab
’“’“
ˆ‰ ˆ‰ ˆ‰
œ œ œ
1111
####
sin A cos B cos A sin Bœ
(b) cos A B cos A cos B sin A sin Babœ
cos A B cos A cos B sin A sin Ba b ab abab œ
cos A B cos A cos B sin A sin B cos A cos B sin A sin BÊœ œ a b ab ab a b
cos A cos B sin A sin Bœ
Because the cosine function is even and the sine functions is odd.
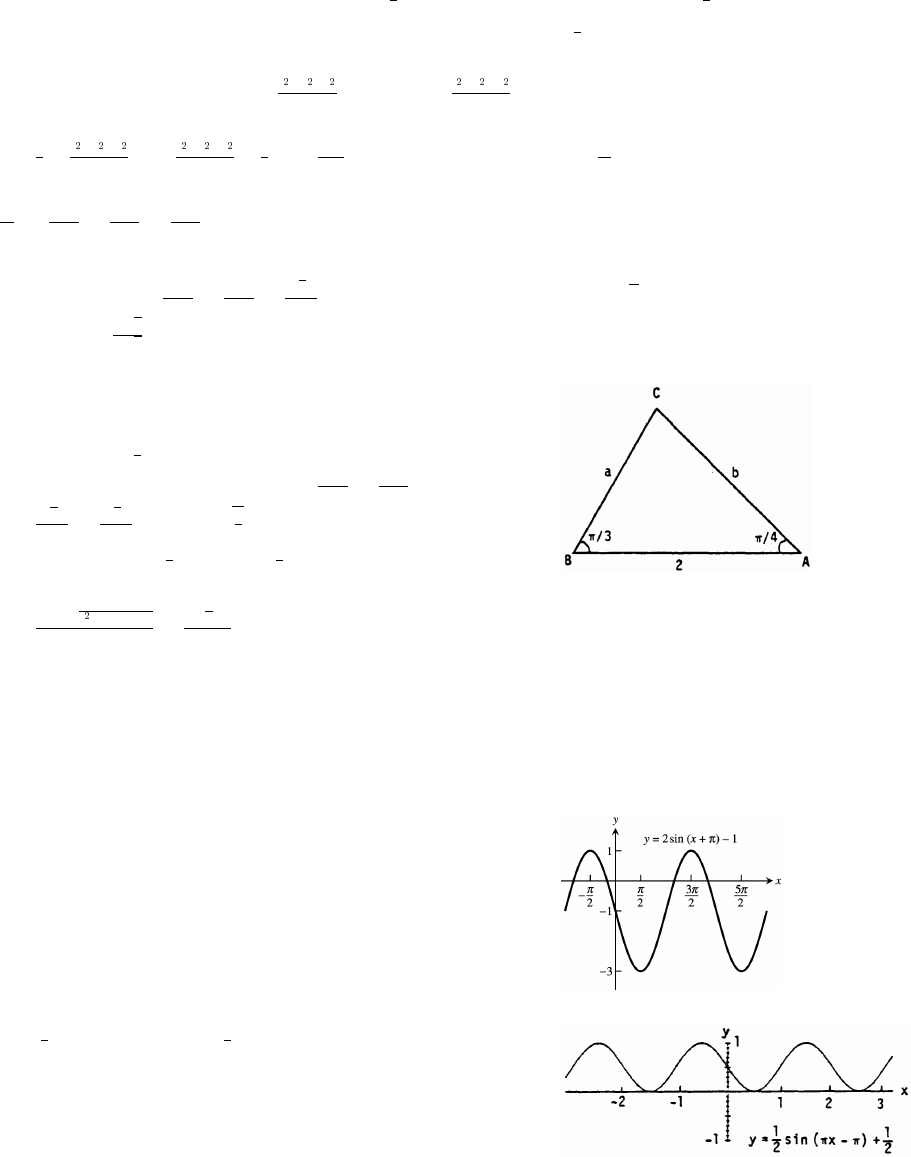
55. c a b 2ab cos C 2 3 2(2)(3) cos (60°) 4 9 12 cos (60°) 13 12 7.
### ## "
#
œ œ œ œ œ
ˆ‰
Thus, c 7 2.65.œ¸
È
56. c a b 2ab cos C 2 3 2(2)(3) cos (40°) 13 12 cos (40°). Thus, c 13 12 cos 40° 1.951.
### ##
œ œ œ œ ¸
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
44 Chapter 1 Preliminaries
57. From the figures in the text, we see that sin B . If C is an acute angle, then sin C . On the other hand,œœ
hh
cb
if C is obtuse (as in the figure on the right), then sin C sin ( C) . Thus, in either case,œœ1h
b
h b sin C c sin B ah ab sin C ac sin B.œœ Êœ œ
By the law of cosines, cos C and cos B . Moreover, since the sum of theœœ
abc acb
2ab 2ac
interior angles of a triangle is , we have sin A sin ( (B C)) sin (B C) sin B cos C cos B sin C11œœœ
2a b c c b ah bc sin A.œœœÊœ
ˆ‰ ˆ‰ ˆ ‰
’“’“ ab
h abc acb h h ah
c 2ab 2ac b 2abc bc
#####
Combining our results we have ah ab sin C, ah ac sin B, and ah bc sin A. Dividing by abc givesœœ œ
.
h sin A sin C sin B
bc a c b
œœœ
ðóóóóóóóñóóóóóóóò
law of sines
58. By the law of sines, . By Exercise 55 we know that c 7.
sin A sin B
3c
3/2
#œœ œ
ÈÈ
Thus sin B 0.982.Ϧ
33
27
È
È
59. From the figure at the right and the law of cosines,
b a 2 2(2a) cos B
###
œ
a44a a2a4.œ œ
##
"
#
ˆ‰
Applying the law of sines to the figure, sin A sin B
ab
œ
b a. Thus, combining results,ʜʜ
ÈÈ
2/2
ab
3/2 3
É#
a 2a 4 b a 0 a 2a 4
####
##
"
œœ Êœ
3
0 a 4a 8. From the quadratic formula and the fact that a 0, we haveʜ
#
a 1.464.œœ¶
##
4 4 4(1)( 8) 434
ÈÈ
60. (a) The graphs of y sin x and y x nearly coincide when x is near the origin (when the calculatorœœ
is in radians mode).
(b) In degree mode, when x is near zero degrees the sine of x is much closer to zero than x itself. The
curves look like intersecting straight lines near the origin when the calculator is in degree mode.
61. A 2, B 2 , C , D 1œ œ œ œ11
62. A , B 2, C 1, Dœœœœ
""
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
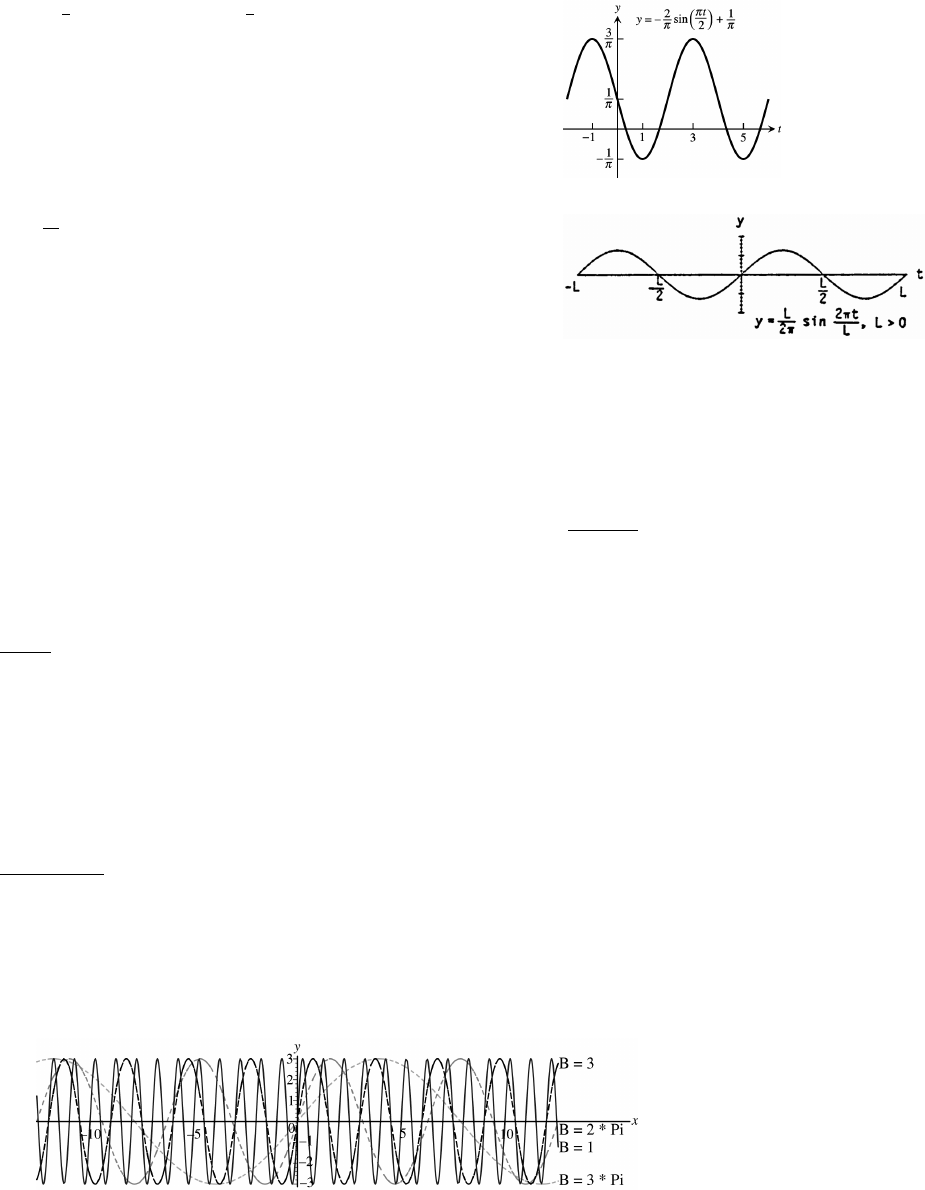
Section 1.6 Trigonometric Functions 45
63. A , B 4, C 0, Dœ œ œ œ
2
11
"
64. A , B L, C 0, D 0œœœœ
L
21
65. (a) amplitude A 37 (b) period B 365œœ œœkk kk
(c) right horizontal shift C 101 (d) upward vertical shift D 25œœ œœ
66. (a) It is highest when the value of the sine is 1 at f(101) 37 sin (0) 25 62° F.œœ
The lowest mean daily temp is 37( 1) 25 12° F. œ
(b) The average of the highest and lowest mean daily temperatures 25° F.œœ
62° ( 12)°
#
The average of the sine function is its horizontal axis, y 25.œ
67-70. Example CAS commands:
Maple
f := x -> A*sin((2*Pi/B)*(x-C))+D1;
A:=3; C:=0; D1:=0;
f_list := [seq( f(x), B=[1,3,2*Pi,5*Pi] )];
plot( f_list, x=-4*Pi..4*Pi, scaling=constrained,
color=[red,blue,green,cyan], linestyle=[1,3,4,7],
legend=["B=1","B=3","B=2*Pi","B=3*Pi"],
title="#67 (Section 1.6)" );
Mathematica
Clear[a, b, c, d, f, x]
f[x_]:=a Sin[2 /b (x c)] + d1
Plot[f[x]/.{a 3, b 1, c 0, d 0}, {x, 4 , 4 }]ÄÄÄÄ 11
67. (a) The graph stretches horizontally.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
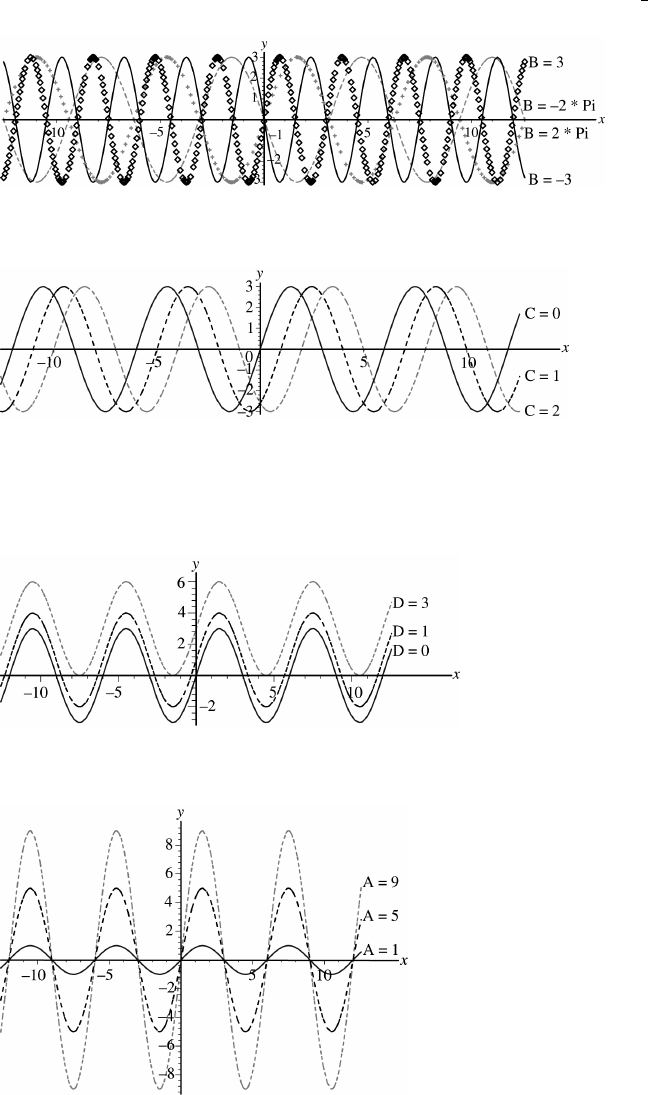
46 Chapter 1 Preliminaries
(b) The period remains the same: period B . The graph has a horizontal shift of period.œl l "
#
68. (a) The graph is shifted right C units.
(b) The graph is shifted left C units.
(c) A shift of one period will produce no apparent shift. C „ l lœ'
69. The graph shifts upwards D units for D and down D units for Dll ! ll !Þ
70. (a) The graph stretches A units.ll
(b) For A , the graph is inverted.!
1.7 GRAPHING WITH CALCULATORS AND COMPUTERS
1-4. The most appropriate viewing window displays the maxima, minima, intercepts, and end behavior of the graphs and
has little unused space.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 1.7 Graphing with Calculators and Computers 47
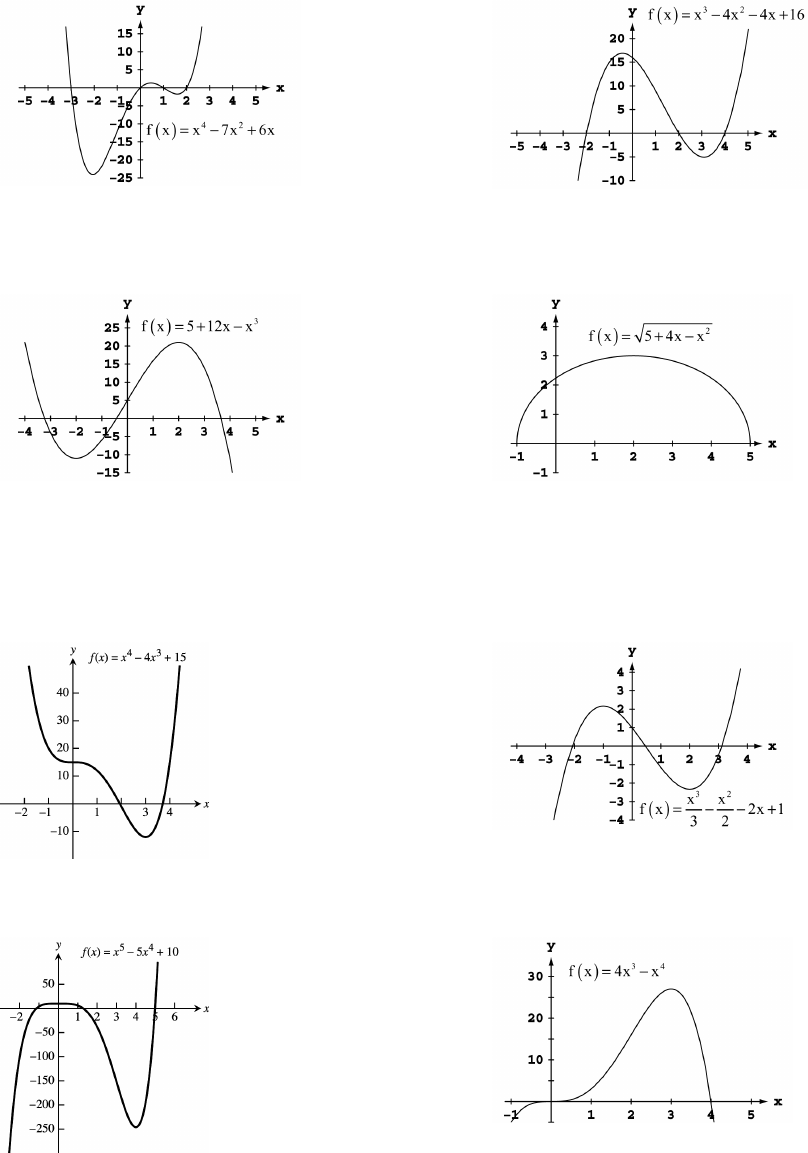
1. d. 2. c.
3. d. 4. b.
5-30. For any display there are many appropriate display widows. The graphs given as answers in Exercises 5 30
are not unique in appearance.
5. 2 5 by 15 40 6. 4 4 by 4 4Ò ß Ó Ò ß Ó Ò ß Ó Ò ß Ó
7. 2 6 by 250 50 8. 1 5 by 5 30Ò ß Ó Ò ß Ó Ò ß Ó Ò ß Ó
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
48 Chapter 1 Preliminaries
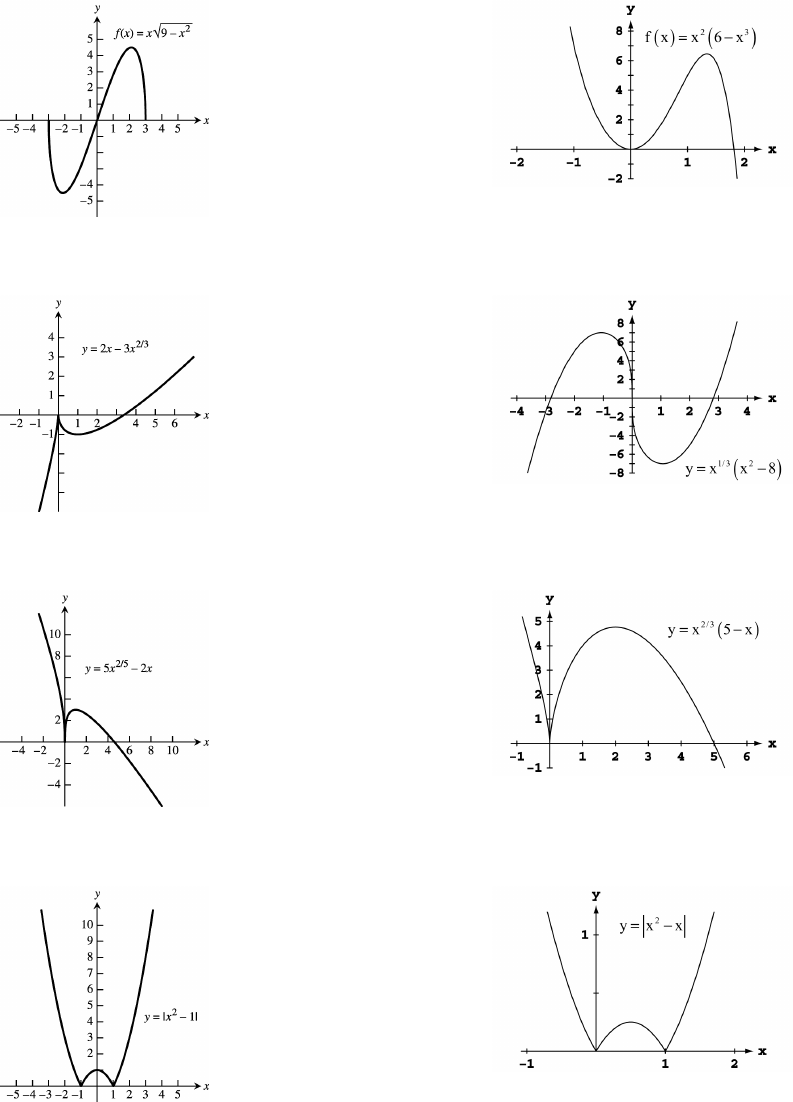
9. 4 4 by 5 5 10. 2 2 by 2 8Ò ß Ó Ò ß Ó Ò ß Ó Ò ß Ó
11. 2 6 by 5 4 12. 4 4 by 8 8Ò ß Ó Ò ß Ó Ò ß Ó Ò ß Ó
13. by 14. by Ò"ß 'Ó Ò"ß %Ó Ò"ß 'Ó Ò"ß &Ó
15. 3 3 by 16. by Ò ß Ó Ò!ß "!Ó Ò"ß #Ó Ò!ß "Ó
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
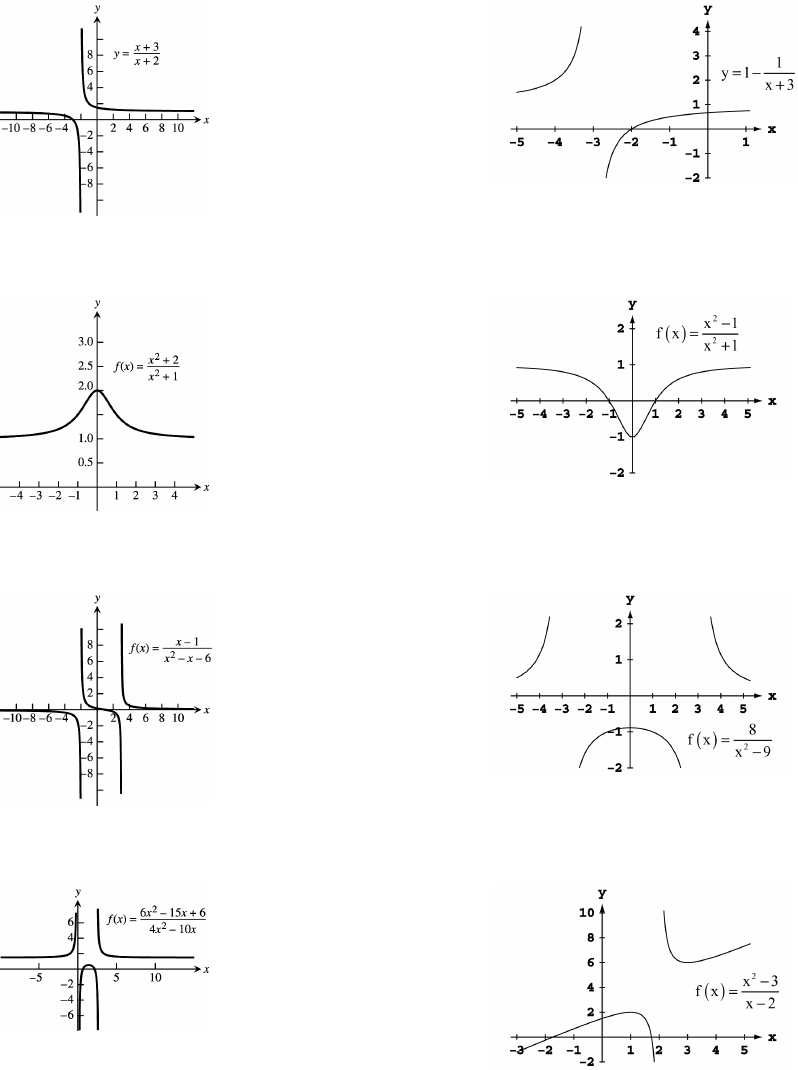
Section 1.7 Graphing with Calculators and Computers 49
17. by 18. by Ò&ß "Ó Ò&ß &Ó Ò&ß "Ó Ò#ß %Ó
19. by 20. by Ò%ß %Ó Ò!ß $Ó Ò&ß &Ó Ò#ß #Ó
21. by 22. by Ò"!ß "!Ó Ò'ß 'Ó Ò&ß &Ó Ò#ß #Ó
23. by 24. by Ò'ß "!Ó Ò'ß 'Ó Ò$ß &Ó Ò#ß "!Ó
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
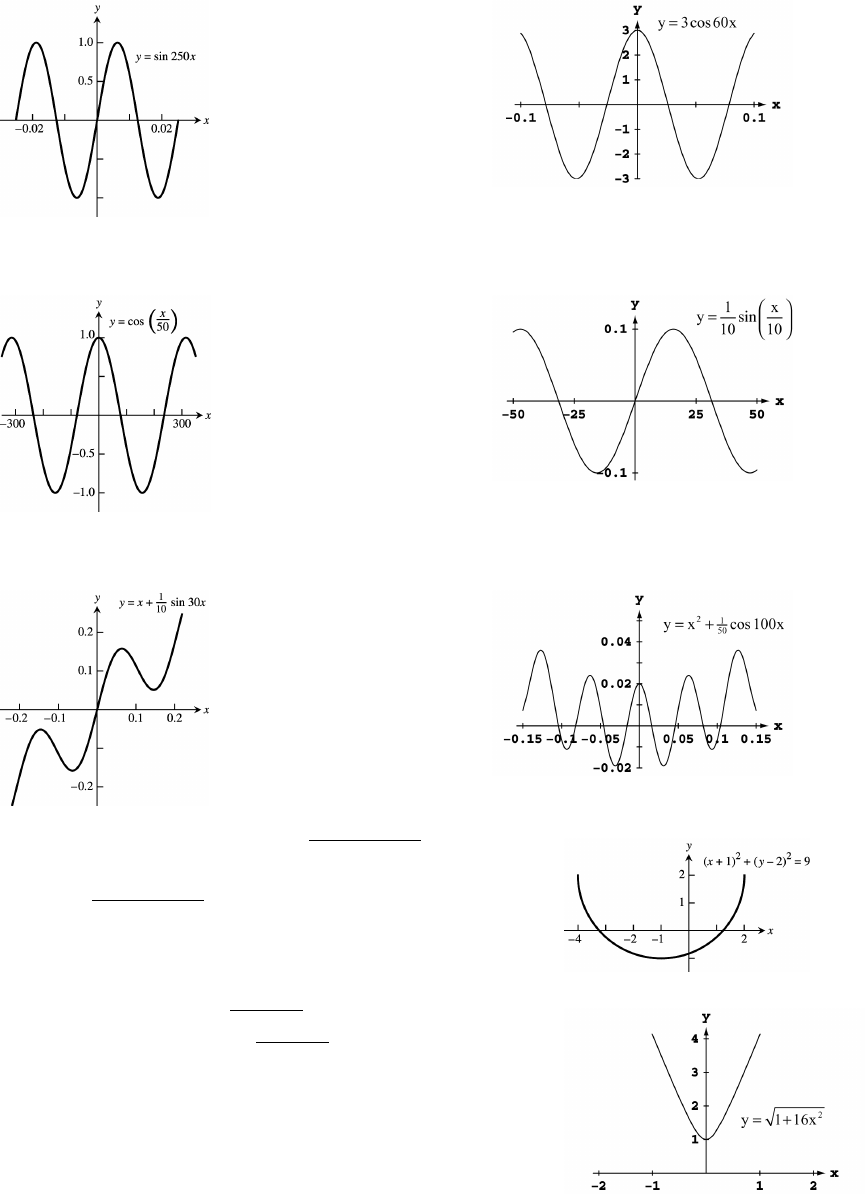
50 Chapter 1 Preliminaries
25. by 26. by Ò!Þ!$ß !Þ!$Ó Ò"Þ#&ß "Þ#&Ó Ò!Þ"ß !Þ"Ó Ò$ß $Ó
27. by 28. by Ò$!!ß $!!Ó Ò"Þ#&ß "Þ#&Ó Ò&!ß &!Ó Ò!Þ"ß !Þ"Ó
29. by 30. by Ò!Þ#&ß !Þ#&Ó Ò!Þ$ß !Þ$Ó Ò!Þ"&ß !Þ"&Ó Ò!Þ!#ß !Þ!&Ó
31. x x y y y x x .
##
#
# œ%% Ê œ#„ # )
È
The lower half is produced by graphing
yxx.œ# # )
È#
32. y x y x . The upper branch
## #
"' œ"Ê œ „ ""'
È
is produced by graphing y x .œ""'
È#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
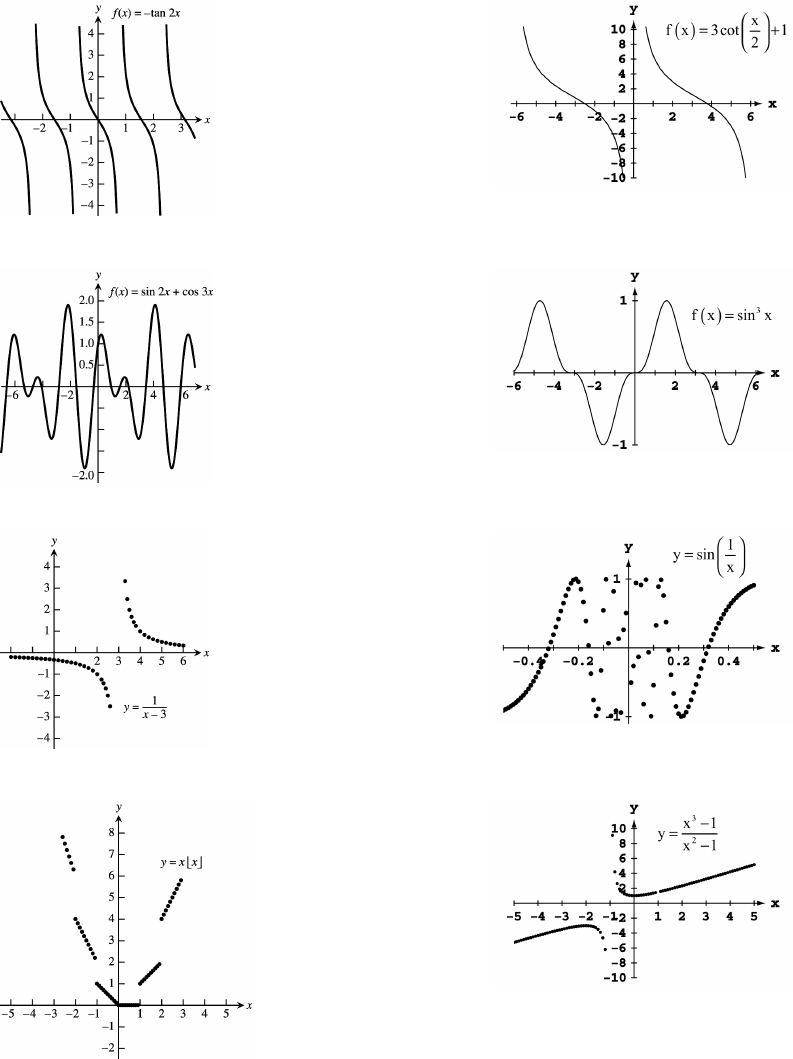
Section 1.7 Graphing with Calculators and Computers 51
33. 34.
35. 36.
37. 38 Þ
39. 40.
41. (a) y xœ "!&*Þ"% #!(%*(#
(b) m dollars/year, which is the yearly increase in compensation.œ "!&*Þ"%
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
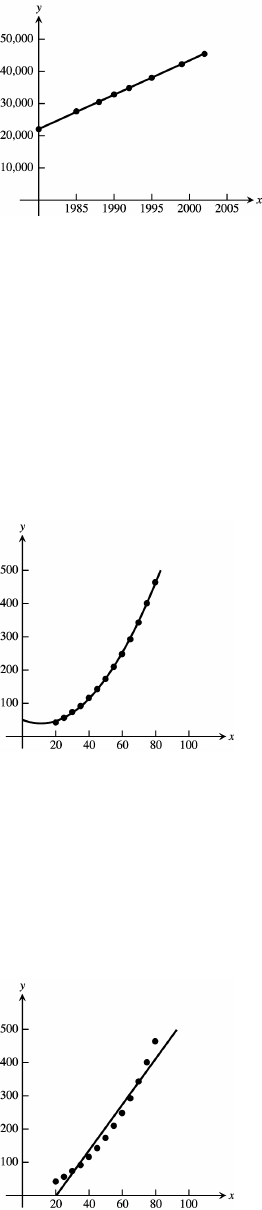
52 Chapter 1 Preliminaries
(c)
(d) Answers may vary slightly. y 14 $ 899œ "!&*Þ #!"! #!(%*(# œ &$ßabab
42. (a) Let C cost and x year.œœ
Cxœ (*'!Þ(" "Þ' ‚ "!ab (
(b) Slope represents increase in cost per year
(c) C xœ #'$(Þ"% &Þ# ‚ "!ab '
(d) The median price is rising faster in the northeast (the slope is larger).
43. (a) Let x represent the speed in miles per hour and d the stopping distance in feet. The quadratic regression function is
dxx.œ !Þ!)'' "Þ*( &!Þ"
#
(b)
(c) From the graph in part (b), the stopping distance is about feet when the vehicle is mph and it is about feet$(! (# &#&
when the speed is mph.)&
Algebraically: d ft.
quadraticab ab ab(# œ !Þ!)'' (# "Þ*( (# &!Þ" œ $'(Þ'
#
d ft.
quadraticab ab ab)& œ !Þ!)'' )& "Þ*( )& &!Þ" œ &##Þ)
#
(d) The linear regression function is d x d ft andœ 'Þ)* "%!Þ% Ê (# œ 'Þ)* (# "%!Þ% œ $&&Þ(
linearab ab
d ft. The linear regression line is shown on the graph in part (b). The quadratic
linearab ab)& œ 'Þ)* )& "%!Þ% œ %%&Þ#
regression curve clearly gives the better fit.
44. (a) The power regression function is y x .œ %Þ%%'%( !Þ&""%"%
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 1 Practice Exercises 53
(b)
(c) 15 2 km/hÞ
(d) The linear regression function is y x and it is shown on the graph in part (b). The linearœ !Þ*"$'(& %Þ")**('
regession function gives a speed of km/h when y m. The power regression curve in part (a) better fits the"%Þ# œ ""
data.
CHAPTER 1 PRACTICE EXERCISES
1. 2x x x ( $ Ê # %Ê #
2. 3x x x "! Ê qqqqqqqqðïïïïïïïî
"!
$"!
$
3. x x x x
""
&%
abab abab" #Ê%"&#
xx xÊ% %& "!Ê'
4. x x x
xx$ %
#$ "
&
Ê $ $ # % qqqqqqqqñïïïïïïïîab ab
xxxxÊ$*)#Ê&"Ê
"
&
5. x x or x x or xl "lœ(Ê "œ( " œ(Ê œ' œ)ab
6. y y yl $l%Ê % $%Ê" (
7. or or x or x
¹¹
" Ê " " Ê Ê & "
xxxxx
## ## ## ####
$$$&"
x or xÊ& "
8. 1 x 1 22 x 8 x
¹¹
#( #(
$$
xx
Ÿ&Ê &Ÿ Ÿ&Ê &Ÿ# (Ÿ &Ê Ÿ# Ÿ Ê""Ÿ Ÿ%
9. Since the particle moved to the y-axis, x x 2. Since y 3 x 6, the new coordinates# œ ! Ê œ œ œ?? ??
are (x x y y) ( ) (0 11). ß œ ##ß&' œ ß??
10. (a)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
54 Chapter 1 Preliminaries
(b) line slope
AB
10 1 9 3
28 6
#
œœ
BC
10 6 4 2
2(4) 6 3
œœ
CD
6(3)
26
93
% #
œœ
DA
1(3)
82 6 3
42
œœ
CE 0
66
% 14
3
œ
BD is vertical and has no slope
(c) Yes; A, B, C and D form a parallelogram.
(d) Yes. The line AB has equation y 1 (x 8). Replacing x by gives y 8œ œ "
314314
33##
ˆ‰
1 5 1 6. Thus, E 6 lies on the line AB and the points A, B and E are collinear.œ œœ ß
310 14
33#ˆ‰ ˆ‰
(e) The line CD has equation y 3 (x 2) or y x. Thus the line passes through the origin.œ œ
33
##
11. The triangle ABC is neither an isosceles triangle nor is it a right triangle. The lengths of AB, BC and AC are
53, 72 and 65, respectively. The slopes of AB, BC and AC are , 1 and , respectively.
ÈÈ È 7
8#
"
12. P(x 3x 1) is a point on the line y 3x 1. If the distance from P to ( 0) equals the distance from P toß œ !ß
( ), then x (3x 1) (x 3) (3 3x) x 9x 6x 1 x 6x 9 9 18x 9x$ß% œ Ê œ
###### # #
18x 17 or x y 3x 1 3 1 . Thus the point is P .Êœ œÊœœ œ ß
17 17 23 17 23
18 18 6 18 6
ˆ‰ ˆ ‰
13. y x y xœ$ " ' Ê œ$ *abab
14. y x y xœ " #Ê œ
""$
###
ab
15. x œ!
16. m y x y xœ œ œ#Ê œ# $ 'Ê œ#
#' )
" $ %ab ab
17. y œ#
18. m y x y xœ œ œ Ê œ $ $Ê œ
&$ # # # # #"
#$ & & & & &
ab
19. y xœ$ $
20. Since x y is equivalent to y x , the slope of the given line (and hence the slope of the desired line) is 2.# œ# œ##
yx yxœ# " "Ê œ# &ab
21. Since x y is equivalent to y x , the slope of the given line (and hence the slope of the desired line) is%$œ"# œ %
%
$
. y x 4 2 y xœ"Êœ
%% %#!
$$ $$
ab
22. Since x y is equivalent to y x , the slope of the given line is and the slope of the perpendicular line is$&œ" œ
$" $
&& &
. y x y xœ#$Êœ
55 5
$$ $$
"*
ab
23. Since x y is equivalent to y x , the slope of the given line is and the slope of the perpendicular line
"" $ $
#$ # #
œ" œ$
is . y x y x
## #)
$$ $$
œ"#Êœab
24. The line passes through and . m y xabab!ß & $ß ! œ œ Ê œ &
! &
$! $ $
&&
ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Chapter 1 Practice Exercises 55
25. The area is A r and the circumference is C r. Thus, r A .œœ#œÊœœ111
#
##%
#
CCC
111
ˆ‰
26. The surface area is S r r . The volume is V r r . Substitution into the formula forœ% Ê œ œ Ê œ11
#$
%$%
"Î# %$
ˆ‰ É
SV
11
surface area gives S r .œ% œ%11
#$
%
#Î$
ˆ‰
V
1
27. The coordinates of a point on the parabola are x x . The angle of inclination joining this point to the origin satisfiesabß#)
the equation tan x. Thus the point has coordinates x x tan tan .)))œœ ß œ ß
x
xaba b
##
28. tan h tan ft.))œ œ Ê œ &!!
rise h
run &!!
29. 30.
Symmetric about the origin. Symmetric about the y-axis.
31. 32.
Neither Symmetric about the y-axis.
33. y x x x y x . Even.abab abœ "œ "œ
##
34. y x x x x x x x y x . Odd.abab ab ab abœœœ
&$ &$
35. y x cos x cos x y x . Even.ab ab abœ" œ" œ
36. y x sec x tan x sec x tan x y x . Odd.ab abab ab œ œ œ œ œ
sin x
cos x cos x
sin x
ab
ab
37. y x y x . Odd.ab abœ œ œ œ
ab
ab ab
"
#
" "
# #
x
xx
xx
xx xx
38. y x sin x sin x. Neither even nor odd.ab abœ" œ"
39. y x x cos x x cos x. Neither even nor odd.ab abœ œ
40. y x x x y x . Even.ab ab ab
ÉÈ
œ "œ "œ
%%
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

56 Chapter 1 Preliminaries
41. (a) The function is defined for all values of x, so the domain is .ab_ß _
(b) Since x attains all nonnegative values, the range is .l l Ò#ß _Ñ
42. (a) Since the square root requires x , the domain is ." ! Ð_ß "Ó
(b) Since x attains all nonnegative values, the range is .
È" Ò#ß _Ñ
43. (a) Since the square root requires x , the domain is ."' ! Ò%ß %Ó
#
(b) For values of x in the domain, x , so x . The range is .! Ÿ "' Ÿ "' ! Ÿ "' Ÿ % Ò!ß %Ó
##
È
44. (a) The function is defined for all values of x, so the domain is .ab_ß _
(b) Since attains all positive values, the range is .$"ß_
#xab
45. (a) The function is defined for all values of x, so the domain is .ab_ß _
(b) Since e attains all positive values, the range is .# $ß _
xab
46. (a) The function is equivalent to y tan x, so we require x for odd integers k. The domain is given by x forœ# #Á Á
kk11
#%
odd integers k.
(b) Since the tangent function attains all values, the range is .ab_ß _
47. (a) The function is defined for all values of x, so the domain is .ab_ß _
(b) The sine function attains values from to , so sin x and hence sin x . The" " #Ÿ# $ Ÿ# $Ÿ# $ "Ÿ"ab ab11
range is 3 1 .Ò ß Ó
48. (a) The function is defined for all values of x, so the domain is .ab_ß _
(b) The function is equivalent to y x , which attains all nonnegative values. The range is .œ Ò!ß _Ñ
È#
49. (a) The logarithm requires x , so the domain is . $ ! $ß _ab
(b) The logarithm attains all real values, so the range is .ab_ß _
50. (a) The function is defined for all values of x, so the domain is .ab_ß _
(b) The cube root attains all real values, so the range is .ab_ß _
51. (a) The function is defined for x , so the domain is .% Ÿ Ÿ % Ò%ß %Ó
(b) The function is equivalent to y x , x , which attains values from to for x in the domain. Theœll%ŸŸ% !#
È
range is .Ò!ß #Ó
52. (a) The function is defined for x , so the domain is .# Ÿ Ÿ # Ò#ß #Ó
(b) The range is .Ò"ß "Ó
53. First piece: Line through and . m y x xabab!ß" "ß! œ œ œ"Ê œ "œ"
!" "
"! "
Second piece: Line through and . m y x x xabab a b"ß" #ß! œ œ œ"Ê œ " "œ #œ#
!" "
#" "
fx x, x
x, x
ab œ
œ" !Ÿ "
# "Ÿ Ÿ#
54. First piece: Line through and 2 5 . m y xabab!ß ! ß œ œ Ê œ
55 5
22 2
!
!
Second piece: Line through 2 5 and 4 . m y x 2 5 x 10 10abab a bß ß! œ œ œ Ê œ œ œ
!
55 5 5 5 5x
42 2 2 2 2 2
f x (Note: x 2 can be included on either piece.)
x, x 2
10 ,2x4
ab
œœ
!Ÿ
ŸŸ
5
2
5x
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
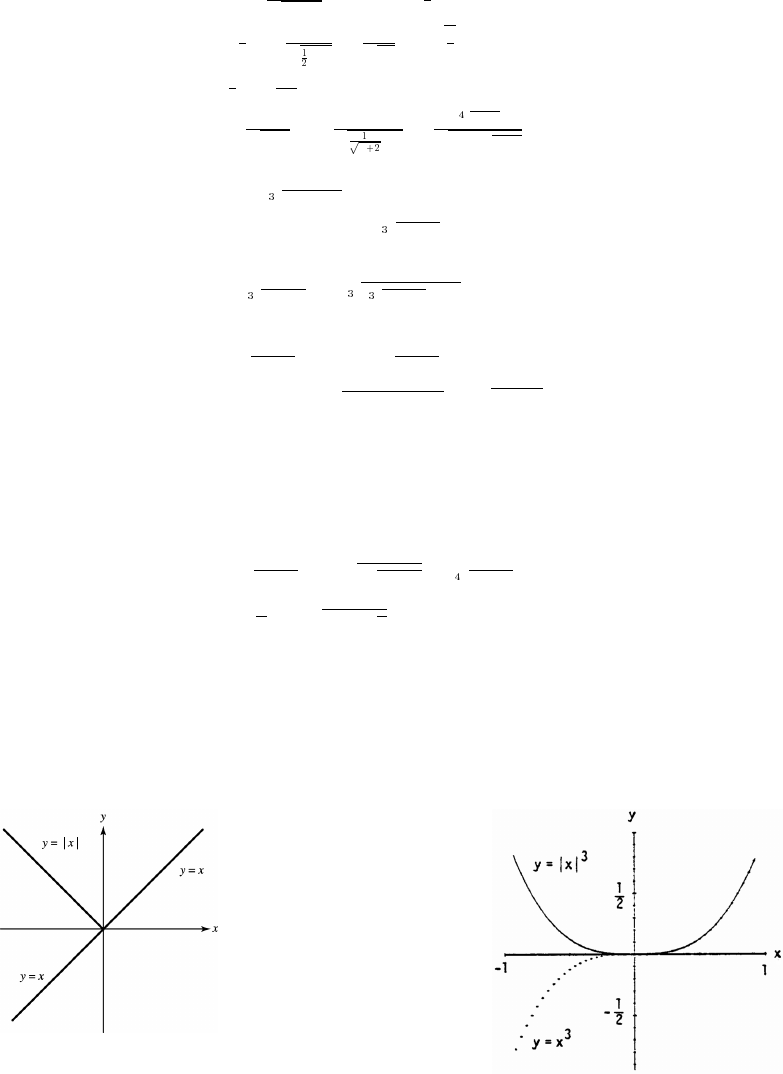
Chapter 1 Practice Exercises 57
55. (a) f g f g f fababa b abab Š‹
‰ "œ " œ œ "œ œ"
""
"# "
È
(b) g f g f g or abab abab ˆ‰ É
‰#œ #œ œ œ
"" " #
# #Þ& &2ÉÈ
(c) f f x f f x f x, xabab abab ˆ‰
‰œ œœœÁ!
""
"Îxx
(d) g g x g g x gabababab Š‹
‰œ œ œ œ
""
# #
#
"# #
ÈÉÉ
ÈÈ
x
x
x
x
56. (a) f g f g f fababa b abab ˆ‰
È
‰ "œ " œ ""œ !œ#!œ#
(b) g f f g g ga bab a b a b abab È
‰#œ #œ##œ!œ !"œ"
(c) f f x f f x f x x xabababab abab‰ œ œ # œ# # œ
(d) g g x g g x g x xabababab ˆ‰
ÈÈ
É
‰ œ œ " œ ""
57. (a) f g x f g x f x x x, x .ababa bab ˆ‰ˆ‰
ÈÈ
‰ œ œ # œ# # œ #
#
gfxfgxgx x xabababababab ÈÈ
‰œ œ#œ##œ%
###
(b) Domain of f g: ‰ Ò#ß _ÑÞ
Domain of g f: ‰ Ò#ß #ÓÞ
(c) Range of f g: ‰ Ð_ß #ÓÞ
Range of g f: ‰ Ò!ß #ÓÞ
58. (a) f g x f g x f x x x.ababa bab Š‹
ÈÈÈ
É
‰œ œ"œ"œ"
gf x fgx g x xabababab ˆ‰
ÈÈ
É
‰œ œ œ"
(b) Domain of f g: ‰ Ð_ß "ÓÞ
Domain of g f: ‰ Ò!ß "ÓÞ
(c) Range of f g: ‰ Ò!ß _ÑÞ
Range of g f: ‰ Ò!ß "ÓÞ
59. 60.
The graph of f (x) f x is the same as the The graph of f (x) f x is the same as the
#" #"
œœab abkk kk
graph of f (x) to the right of the y-axis. The graph of f (x) to the right of the y-axis. The
" "
graph of f (x) to the left of the y-axis is the graph of f (x) to the left of the y-axis is the
# #
reflection of y f (x), x 0 across the y-axis. reflection of y f (x), x 0 across the y-axis.œ œ
" "
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
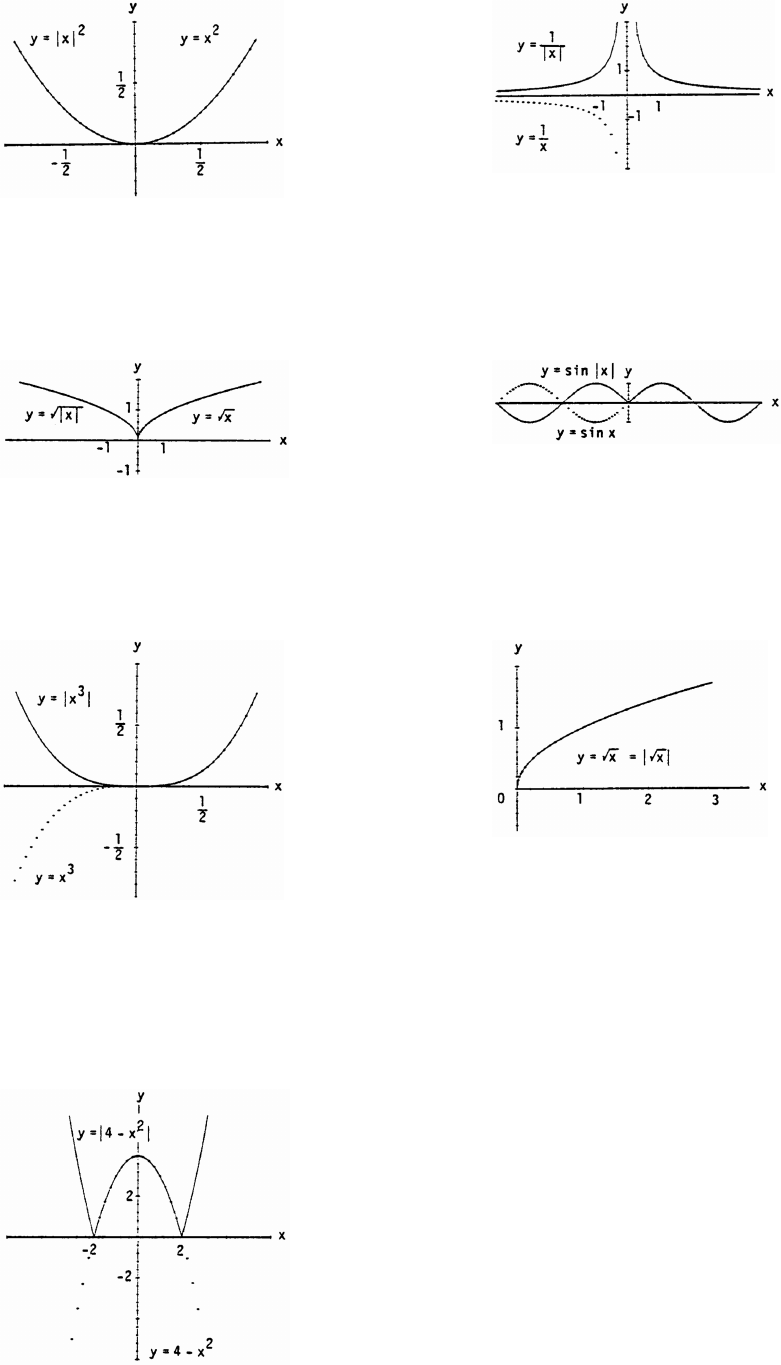
58 Chapter 1 Preliminaries
61. 62.
It does not change the graph. The graph of f (x) f x is the same as the
#"
œabkk
graph of f (x) to the right of the y-axis. The
"
graph of f (x) to the left of the y-axis is the
#
reflection of y f (x), x 0 across the y-axis.œ
"
63. 64.
The graph of f (x) f x is the same as the The graph of f (x) f x is the same as the
#" #"
œœab abkk kk
graph of f (x) to the right of the y-axis. The graph of f (x) to the right of the y-axis. The
" "
graph of f (x) to the left of the y-axis is the graph of f (x) to the left of the y-axis is the
# #
reflection of y f (x), x 0 across the y-axis. reflection of y f (x), x 0 across the y-axis.œ œ
" "
65. 66.
Whenever g (x) is positive, the graph of y g (x) It does not change the graph.
"#
œ
g (x) is the same as the graph of y g (x).œœkk
""
When g (x) is negative, the graph of y g (x) is
"#
œ
the reflection of the graph of y g (x) across theœ"
x-axis.
67. Whenever g (x) is positive, the graph of y g (x) g (x) is
"#"
œœkk
the same as the graph of y g (x). When g (x) is negative, theœ""
graph of y g (x) is the reflection of the graph of y g (x)œœ
#"
across the x-axis.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
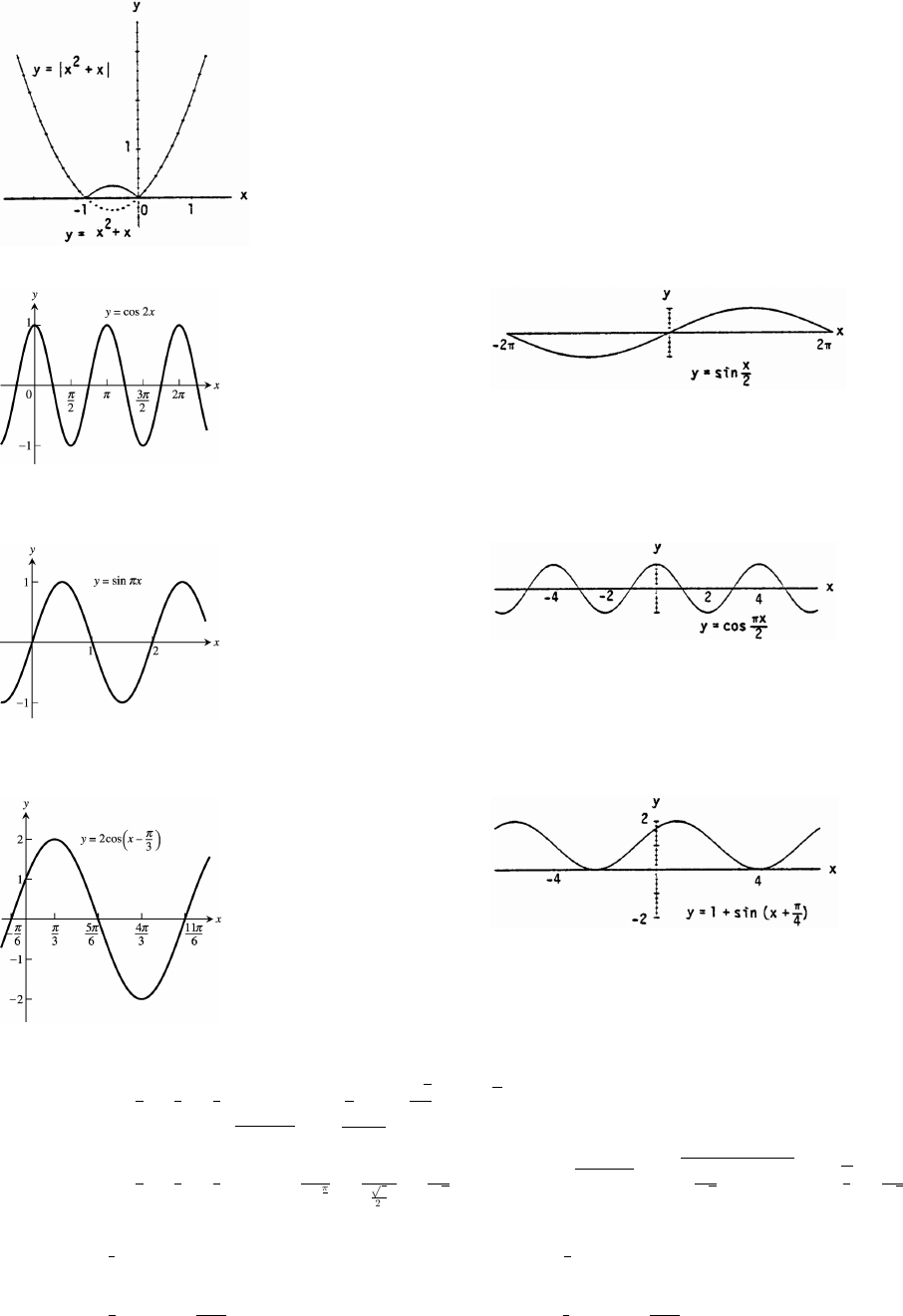
Chapter 1 Practice Exercises 59
68. Whenever g (x) is positive, the graph of y g (x) g (x) is
"#"
œœkk
the same as the graph of y g (x). When g (x) is negative, theœ""
graph of y g (x) is the reflection of the graph of y g (x)œœ
#"
across the x-axis.
69. 70.
period period 4œœ11
71. 72.
period 2 period 4œœ
73. 74.
period 2 period 2œœ11
75. (a) sin B sin b 2 sin 2 3. By the theorem of Pythagoras,œœœÊœ œ œ
11
3c 3
bb 3
##
Š‹È
È
abc a cb 431.
### ##
œ Êœ œ œ
ÈÈ
(b) sin B sin c . Thus, a c b (2) .œœœÊœœœ œœ œœ
1
3cc sin 3
b2 2 2 4 4 4 2
333
33
Š‹ ÈÈÈ
ÈÊŠ‹ É
## #
#
76. (a) sin A a c sin A (b) tan A a b tan AœÊœ œÊœ
a a
c b
77. (a) tan B a (b) sin A cœÊœ œÊœ
bb aa
atan B csin A
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
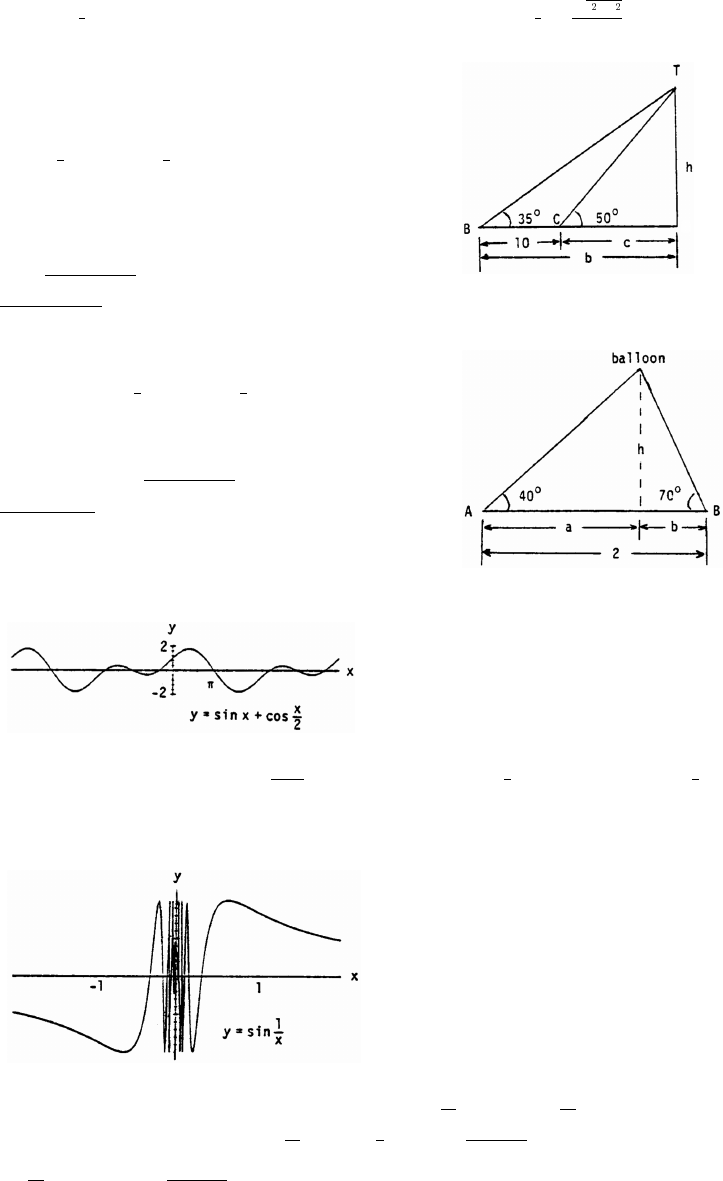
60 Chapter 1 Preliminaries
78. (a) sin A (c) sin Aœœœ
a a
ccc
cb
È
79. Let h height of vertical pole, and let b and c denote theœ
distances of points B and C from the base of the pole,
measured along the flatground, respectively. Then,
tan 50° , tan 35° , and b c 10.œœœ
hh
cb
Thus, h c tan 50° and h b tan 35° (c 10) tan 35°œœœ
c tan 50° (c 10) tan 35°Êœ
c (tan 50° tan 35°) 10 tan 35°Êœ
c h c tan 50°Êœ Êœ
10 tan 35°
tan 50° tan 35°
16.98 m.œ¸
10 tan 35° tan 50°
tan 50° tan 35°
80. Let h height of balloon above ground. From the figure atœ
the right, tan 40° , tan 70° , and a b 2. Thus,œœœ
hh
ab
h b tan 70° h (2 a) tan 70° and h a tan 40°œÊœ œ
(2 a) tan 70° a tan 40° a(tan 40° tan 70°)Ê œ Ê
2 tan 70° a h a tan 40°œÊœ Êœ
2 tan 70°
tan 40° tan 70°
1.3 km.œ¸
2 tan 70° tan 40°
tan 40° tan 70°
81. (a)
(b) The period appears to be 4 .1
(c) f(x 4 ) sin (x 4 ) cos sin (x 2 ) cos 2 sin x cos œ œ œ 11 1 1
ˆ‰ ˆ ‰
x4 x x
###
1
since the period of sine and cosine is 2 . Thus, f(x) has period 4 .11
82. (a)
(b) D ( 0) ( ); R [ 1 1]œ_ß !ß_ œß
(c) f is not periodic. For suppose f has period p. Then f kp f sin 2 0 for all
ˆ‰ˆ‰
""
##11
œ œ œ1
integers k. Choose k so large that kp 0 . But then
"" "
#11 1
Ê
(1/2 ) kp 1
f kp sin 0 which is a contradiction. Thus f has no period, as claimed.
ˆ‰
Š‹
""
##11
œ
(1/ ) kp
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
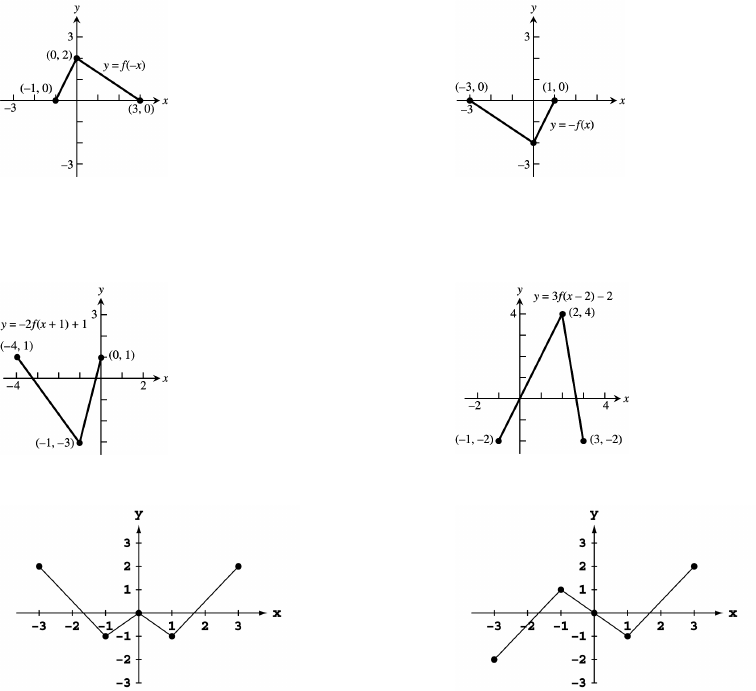
Chapter 1 Additional and Advanced Exercises 61
CHAPTER 1 ADDITIONAL AND ADVANCED EXERCISES
1. (a) The given graph is reflected about the y-axis. (b) The given graph is reflected about the x-axis.
(c) The given graph is shifted left 1 unit, stretched (d) The given graph is shifted right 2 units, stretched
vertically by a factor of 2, reflected about the vertically by a factor of 3, and then shifted
x-axis, and then shifted upward 1 unit. downward 2 units.
2. (a) (b)
3. There are (infinitely) many such function pairs. For example, f(x) 3x and g(x) 4x satisfyœœ
f(g(x)) f(4x) 3(4x) 12x 4(3x) g(3x) g(f(x)).œœœœœœ
4. Yes, there are many such function pairs. For example, if g(x) (2x 3) and f(x) x , thenœ œ
$ "Î$
(f g)(x) f(g(x)) f (2x 3) (2x 3) 2x 3.‰œ œ œ œabab
$$
"Î$
5. If f is odd and defined at x, then f( x) f(x). Thus g( x) f( x) 2 f(x) 2 whereasœ œœ
g(x) (f(x) 2) f(x) 2. Then g cannot be odd because g( x) g(x) f(x) 2 f(x) 2 œ œ œ Ê œ
4 0, which is a contradiction. Also, g(x) is not even unless f(x) 0 for all x. On the other hand, if f isÊœ œ
even, then g(x) f(x) 2 is also even: g( x) f( x) 2 f(x) 2 g(x).œ œœœ
6. If g is odd and g(0) is defined, then g(0) g( 0) g(0). Therefore, 2g(0) 0 g(0) 0.œœ œ Ê œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

62 Chapter 1 Preliminaries
7. For (x y) in the 1st quadrant, x y 1 xßœkk kk
x y 1 x y 1. For (x y) in the 2ndÍ œ Í œ ß
quadrant, x y x1 xy x1kk kk œ Íœ
y 2x 1. In the 3rd quadrant, x y x 1Íœ œkk kk
x y x 1 y 2x 1. In the 4thÍœ Í œ
quadrant, x y x 1 x ( y) x 1kk kkœÍœ
y 1. The graph is given at the right.͜
8. We use reasoning similar to Exercise 7.
(1) 1st quadrant: y y x xœkk kk
2y 2x y x.͜͜
(2) 2nd quadrant: y y x xœkk kk
2y x ( x) 0 y 0.ÍœœÍœ
(3) 3rd quadrant: y y x xœkk kk
y ( y) x ( x) 0 0͜ ͜
points in the 3rd quadrantÊall
satisfy the equation.
(4) 4th quadrant: y y x xœkk kk
y ( y) 2x 0 x. Combining͜ ͜
these results we have the graph given at the
right:
9. By the law of sines, b 2.
sin
3
sin A sin B
abb sin(/3)
sin 3 sin ( /4) 3
34
2
3
ÈÈÈŠ‹
œœœ Êœ œ œ
1
1È
10. By the law of sines, sin B sin .
sin
4ab3 444 8
sin A sin B sin B 3 3 232
4œœœ Ê œ œ œ
1Š‹
ÈÈ
#
11. By the law of cosines, a b c 2bc cos A cos A .
###
œ Ê œ œ œ
bca 232 3
2bc 2(2)(3) 4
12. By the law of cosines, c a b 2ab cos C 2 3 (2)(2)(3) cos 4 9 12
### ##
#
œ œ œ
1
4
2
Š‹
È
13 6 2 c 13 6 2 , since c 0.œ Êœ
ÈÈ
É
13. By the law of cosines, b a c 2ac cos B cos B
###
#
œ Ê œ œ œ
a c b 2 4 3 4169
ac (2)(2)(4) 16
. Since 0 B , sin B 1 cos B 1 .œœœœœ
11 121
16 256 16 16
135 3 15
1ÈÉ
#ÈÈ
14. By the law of cosines, c a b 2ab cos C cos C
###
œ Ê œ œ œ
a b c 2 4 5 41625
2ab (2)(2)(4) 16
. Since 0 C , sin C 1 cos C 1 .œ œ œ œ
525
16 256 16
231
1ÈÉ
#È
15. (a) sin x cos x 1 sin x 1 cos x (1 cos x)(1 cos x) (1 cos x)
## # #
œÊ œœ Êœ
sin x
1cos x
ʜ
1cos x sin x
sin x 1 cos x
(b) Using the definition of the tangent function and the double angle formulas, we have
tan .
#
#
ˆ‰
x1cos x
sin
cos 1cos x
œœ œ
ˆ‰
ˆ‰
x
x
cos 2 x
cos 2 x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 1 Additional and Advanced Exercises 63
16. The angles labeled in the accompanying figure are#
equal since both angles subtend arc CD. Similarly, the
two angles labeled are equal since they both subtend!
arc AB. Thus, triangles AED and BEC are similar which
implies
ac 2a cos b
bac
œ)
(a c)(a c) b(2a cos b)Ê œ )
a c 2ab cos bʜ
## #
)
c a b 2ab cos .Ê œ
### )
17. As in the proof of the law of sines of Section P.5, Exercise 57, ah bc sin A ab sin C ac sin Bœœœ
the area of ABC (base)(height) ah bc sin A ab sin C ac sin B.Êœœœœœ
"""""
#####
18. As in Section P.5, Exercise 57, (Area of ABC) (base) (height) a h a b sin C
# # ######
"""
œœœ
444
a b cos C . By the law of cosines, c a b 2ab cos C cos C .œ " œ Ê œ
"
## # # # #
42ab
abc
ab
Thus, (area of ABC) a b cos C a b
### # ##
""
#
#
œ"œ " œ"
44ab44ab
abc ab abc
abŒ
Š‹ Š ‹
ab
4a b a b c 2ab a b c 2ab a b cœ œ
""
## ### ### ###
#
16 16
Š‹
abc dabababab
(a b) c c (a b) ((a b) c)((a b) c)(c (a b))(c (a b))œ œ
""
### #
16 16
cdc dabab
s(s a)(s b)(s c), where s .œœœ
‘ˆ‰ˆ ‰ˆ‰ˆ‰
abc abc abc abc abc
#### #
Therefore, the area of ABC equals s(s a)(s b)(s c) .
È
19. 1. b c (a c) b a, which is positive since a b. Thus, a c b c. œ
2. b c (a c) b a, which is positive since a b. Thus, a c b c. œ
3. c 0 and a b c 0 c and b a are positive (b a)c bc ac is positive ac bc.Êœ Êœ Ê
4. a b and c 0 b a and c are positive (b a)( c) ac bc is positive bc ac.Ê Êœ Ê
5. Since a 0, a and are positive 0.Ê
""
aa
6. Since 0 a b, both and are positive. By (3), a b and 0 a b or 1 Ê
"" " " "
ab a a a a
b
ˆ‰ ˆ‰
1 by (3) since 0 .Ê Ê
ˆ‰ ˆ‰
"" " ""
bab b ba
b
7. a b 0 and are both negative, i.e., 0 and 0. By (4), a b and 0 b a Ê Ê
"" " " " " "
ab a b a a a
ˆ‰ ˆ‰
1 1 by (4) since 0 .ÊÊ Ê
bb
abab bba
ˆ‰ ˆ‰
"" " ""
20. (a) If a 0, then 0 a b b 0 0 a b . Since a a a a a andœœÍÁÍœ œœœkk kk kk kk kk kkkk k k
## # ##
b b we obtain a b . If a 0 then a 0 and a b a b . On the other hand,kk kk kk kk
#### ##
œÁÊ
if a b then a a b b 0 b a b a b a . Since b a 0
## # #
## ##
œœÊœ kkkk kkkkabababkk kk kk kk kk kk
and the product b a b a is positive, we must have b a 0 b a . Thusabab ab kkkkkk kk kk kk kk kk Ê
ab ab.kk kkÍ
##
(b) ab ab ab 2 ab by Exercise 19(4) above a 2ab b a 2 a b b , sinceŸÊ Ê kk kk kk kkkkkk
##
##
a a and b b . Factoring both sides, (a b) a b a b a b , by part (a).kk kk abkkkkkk kk kk kk
## #
## #
œœ Ê
21. The fact that a a a a a a holds for n 1 is obvious. It also holds fork k kk kk kk
"# " #
á Ÿ á œ
nn
n 2 by the triangle inequality. We now show it holds for all positive integers n, by induction.œ
Suppose it holds for n k 1: a a a a a a (this is the inductionœ á Ÿ ák k kk kk kk
"# " #kk
hypothesis). Then a a a a a a a a a a a akkk kkkkkab
"# "# "#
á œ á Ÿ á
kk1 k k1 k k1
(by the triangle inequality) a a a a (by the induction hypothesis) and theŸákk kk kk k k
"# kk1
inequality holds for n k 1. Hence it holds for all n by induction.œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

64 Chapter 1 Preliminaries
22. The fact that a a a a a a holds for n 1 is obvious. It holds for n 2k k kk kk kk
"# " #
á á œ œ
nn
by Exercise 21(b), since a a a ( a ) a a a a a a .k k k k k k k k kk kkkk k k kk kk
"# " # " # "# "#
œ œ
We now show it holds for all positive integers n by induction.
Suppose the inequality holds for n k 1. Then a a a a a a (this isœ á ák k kk kk kk
"# " #kk
the induction hypothesis). Thus a a a a a akkk kabab
""
á œ á
kk1 k k1
a a a (by Exercise 21(b)) a a a a a a á œ á á kkkkkkkkkkkk kkkkab
"""kk1 kk1 kk1
a a a a (by the induction hypothesis). Hence the inequality holds for allákk kk kk k k
"# kk1
n by induction.
23. If f is even and odd, then f( x) f(x) and f( x) f(x) f(x) f(x) for all x in the domain of f.œ œ Ê œ
Thus 2f(x) 0 f(x) 0.œÊ œ
24. (a) As suggested, let E(x) E( x) E(x) E is anœÊœ œœÊ
f(x) f( x) f( x) f( ( x)) f(x) f( x)
###
even function. Define O(x) f(x) E(x) f(x) . Thenœ œ œ
f(x) f( x) f(x) f( x)
##
O( x) O(x) O is an odd functionœ œ œ œ Ê
f( x) f( ( x)) f( x) f(x) f(x) f( x)
## #
Š‹
f(x) E(x) O(x) is the sum of an even and an odd function.ʜ
(b) Part (a) shows that f(x) E(x) O(x) is the sum of an even and an odd function. If alsoœ
f(x) E (x) O (x), where E is even and O is odd, then f(x) f(x) 0 E (x) O (x)œ œœ
"" " " ""
ab
(E(x) O(x)). Thus, E(x) E (x) O (x) O(x) for all x in the domain of f (which is the same as the œ
""
domain of E E and O O ). Now (E E )( x) E( x) E ( x) E(x) E (x) (since E and E are œœ
"" " " " "
even) (E E )(x) E E is even. Likewise, (O O)( x) O ( x) O( x) O (x) ( O(x))œ Ê œ œ
"" " " "
(since O and O are odd) (O (x) O(x)) (O O)(x) O O is odd. Therefore, E E and
"" "" "
œ œ Ê
O O are both even and odd so they must be zero at each x in the domain of f by Exercise 23. That is,
"
E E and O O, so the decomposition of f found in part (a) is unique.
""
œœ
25. y ax bx c a x x c a x cœ œ œ
## #
Š‹ˆ‰
bb b b b
a4a 4a 2a 4a
(a) If a 0 the graph is a parabola that opens upward. Increasing a causes a vertical stretching and a shift
of the vertex toward the y-axis and upward. If a 0 the graph is a parabola that opens downward.
Decreasing a causes a vertical stretching and a shift of the vertex toward the y-axis and downward.
(b) If a 0 the graph is a parabola that opens upward. If also b 0, then increasing b causes a shift of the
graph downward to the left; if b 0, then decreasing b causes a shift of the graph downward and to the
right.
If a 0 the graph is a parabola that opens downward. If b 0, increasing b shifts the graph upward
to the right. If b 0, decreasing b shifts the graph upward to the left.
(c) Changing c (for fixed a and b) by c shifts the graph upward c units if c 0, and downward c????
units if c 0.?
26. (a) If a 0, the graph rises to the right of the vertical line x b and falls to the left. If a 0, the graphœ
falls to the right of the line x b and rises to the left. If a 0, the graph reduces to the horizontalœ œ
line y c. As a increases, the slope at any given point x x increases in magnitude and the graphœœkk !
becomes steeper. As a decreases, the slope at x decreases in magnitude and the graph rises or fallskk !
more gradually.
(b) Increasing b shifts the graph to the left; decreasing b shifts it to the right.
(c) Increasing c shifts the graph upward; decreasing c shifts it downward.
27. If m 0, the x-intercept of y mx 2 must be negative. If m 0, then the x-intercept exceeds œ "
#
0 mx 2 and x x 0 m 4.Êœ ÊœÊ
""
##
2
m
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
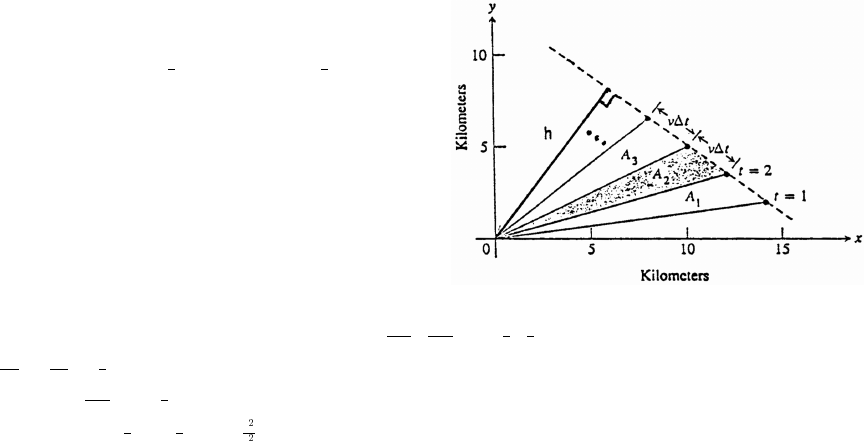
Chapter 1 Additional and Advanced Exercises 65
28. Each of the triangles pictured has the same base
b v t v(1 sec). Moreover, the height of eachœœ?
triangle is the same value h. Thus (base)(height) bh
""
##
œ
A A A . In conclusion, the object sweepsœœœœá
"#$
out equal areas in each one second interval.
29. (a) By Exercise #95 of Section 1.2, the coordinates of P are . Thus the slope
ˆ‰ˆ‰
a0 b0 a b
## ##
ßœß
of OP .œœœ
?
?
y
xa/2a
b/2 b
(b) The slope of AB . The line segments AB and OP are perpendicular when the productœœ
b0 b
0a a
of their slopes is . Thus, b a a b (since both are positive). Therefore, AB" œ œ œ Ê œ
ˆ‰ˆ ‰
bb b
aa a ##
is perpendicular to OP when a b.œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
66 Chapter 1 Preliminaries
NOTES:
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
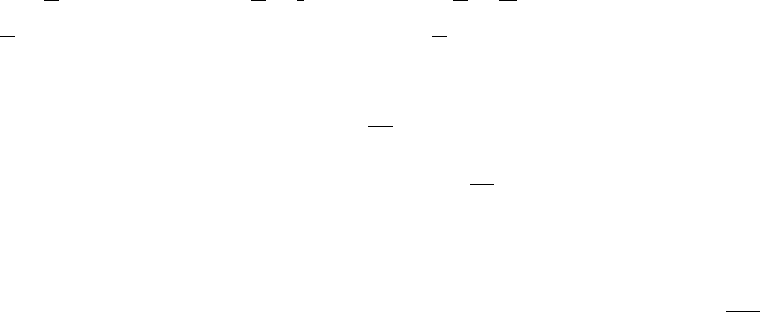
CHAPTER 2 LIMITS AND CONTINUITY
2.1 RATES OF CHANGE AND LIMITS
1. (a) Does not exist. As x approaches 1 from the right, g(x) approaches 0. As x approaches 1 from the left, g(x)
approaches 1. There is no single number L that all the values g(x) get arbitrarily close to as x 1.Ä
(b) 1
(c) 0
2. (a) 0
(b) 1
(c) Does not exist. As t approaches 0 from the left, f(t) approaches 1. As t approaches 0 from the right, f(t)
approaches 1. There is no single number L that f(t) gets arbitrarily close to as t 0.Ä
3. (a) True (b) True (c) False
(d) False (e) False (f) True
4. (a) False (b) False (c) True
(d) True (e) True
5. lim does not exist because 1 if x 0 and 1 if x 0. As x approaches 0 from the left,
x0Ä
xxxxx
xxxxxkk kk kk
œœ œ œ
approaches 1. As x approaches 0 from the right, approaches 1. There is no single number L that all
xx
xxkk kk
the function values get arbitrarily close to as x 0.Ä
6. As x approaches 1 from the left, the values of become increasingly large and negative. As x approaches 1
"
x1
from the right, the values become increasingly large and positive. There is no one number L that all the
function values get arbitrarily close to as x 1, so lim does not exist.Äx1Ä
"
x1
7. Nothing can be said about f(x) because the existence of a limit as x x does not depend on how the functionÄ!
is defined at x . In order for a limit to exist, f(x) must be arbitrarily close to a single real number L when
!
x is close enough to x . That is, the existence of a limit depends on the values of f(x) for x x , not on the
! !
near
definition of f(x) at x itself.
!
8. Nothing can be said. In order for lim f(x) to exist, f(x) must close to a single value for x near 0 regardless of
x0Ä
the value f(0) itself.
9. No, the definition does not require that f be defined at x 1 in order for a limiting value to exist there. If f(1)œ
is defined, it can be any real number, so we can conclude nothing about f(1) from lim f(x) 5.
x1Ĝ
10. No, because the existence of a limit depends on the values of f(x) when x is near 1, not on f(1) itself. If
lim f(x) exists, its value may be some number other than f(1) 5. We can conclude nothing about lim f(x),
x1 x1Ä Ä
œ
whether it exists or what its value is if it does exist, from knowing the value of f(1) alone.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
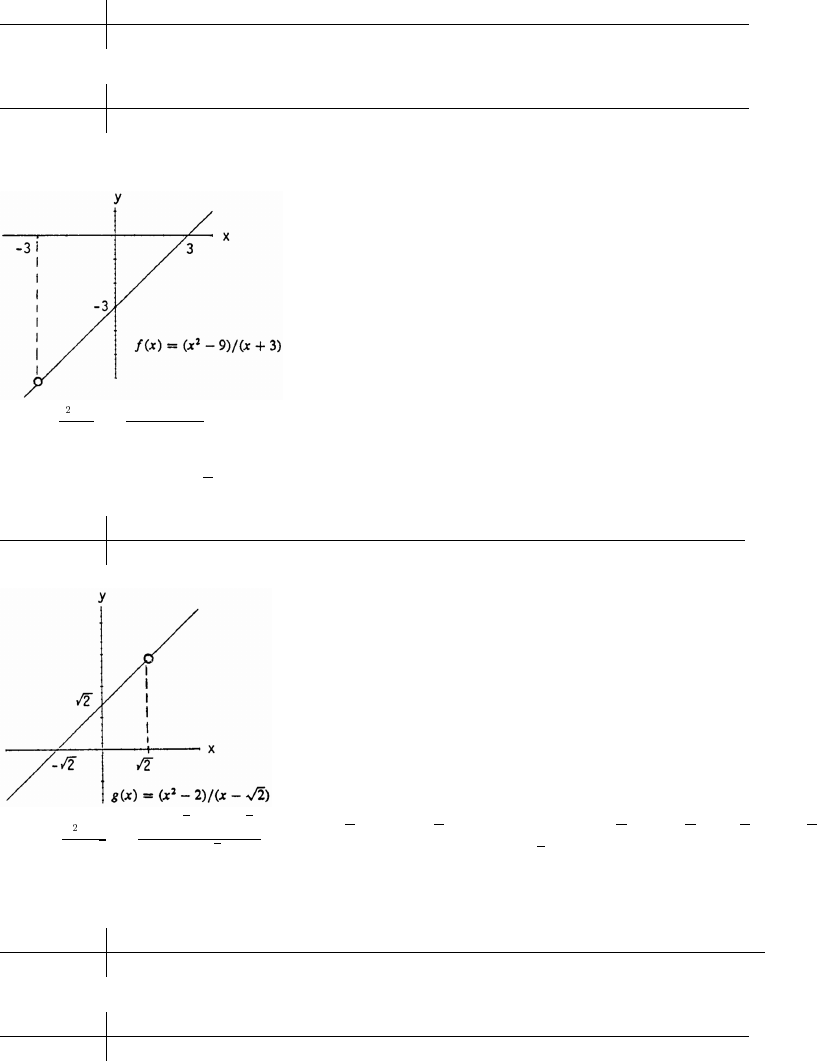
68 Chapter 2 Limits and Continuity
11. (a) f(x) x /(x 3)œ*ab
#
x 3.1 3.01 3.001 3.0001 3.00001 3.000001
f(x) 6.1 6.01 6.001 6.0001 6.00001 6.000001
x 2.9 2.99 2.999 2.9999 2.99999 2.999999
f(x) 5.9 5.99 5.999 5.9999 5.99999 5.999999
The estimate is lim f(x) 6.
xÄ$ œ
(b)
(c) f(x) x 3 if x 3, and lim (x 3) 3 3 6.œ œ œ Á œ œ
x9
x3 x3
(x 3)(x 3)
xÄ$
12. (a) g(x) x / x 2œ# ab
Š‹
È
#
x 1.4 1.41 1.414 1.4142 1.41421 1.414213
g(x) 2.81421 2.82421 2.82821 2.828413 2.828423 2.828426
(b)
(c) g(x) x 2 if x 2, and lim x 2 2 2 2 2.œ œ œ Á œœ
x2
x2
x2x2
x2
ÈŠ‹Š‹
ÈÈ
Š‹
ÈÈÈ ÈÈÈÈ
Š‹
xÄ#
È
13. (a) G(x) (x 6)/ x 4x 12œ ab
#
x 5.9 5.99 5.999 5.9999 5.99999 5.999999
G(x) .126582 .1251564 .1250156 .1250015 .1250001 .1250000
x 6.1 6.01 6.001 6.0001 6.00001 6.000001
G(x) .123456 .124843 .124984 .124998 .124999 .124999
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
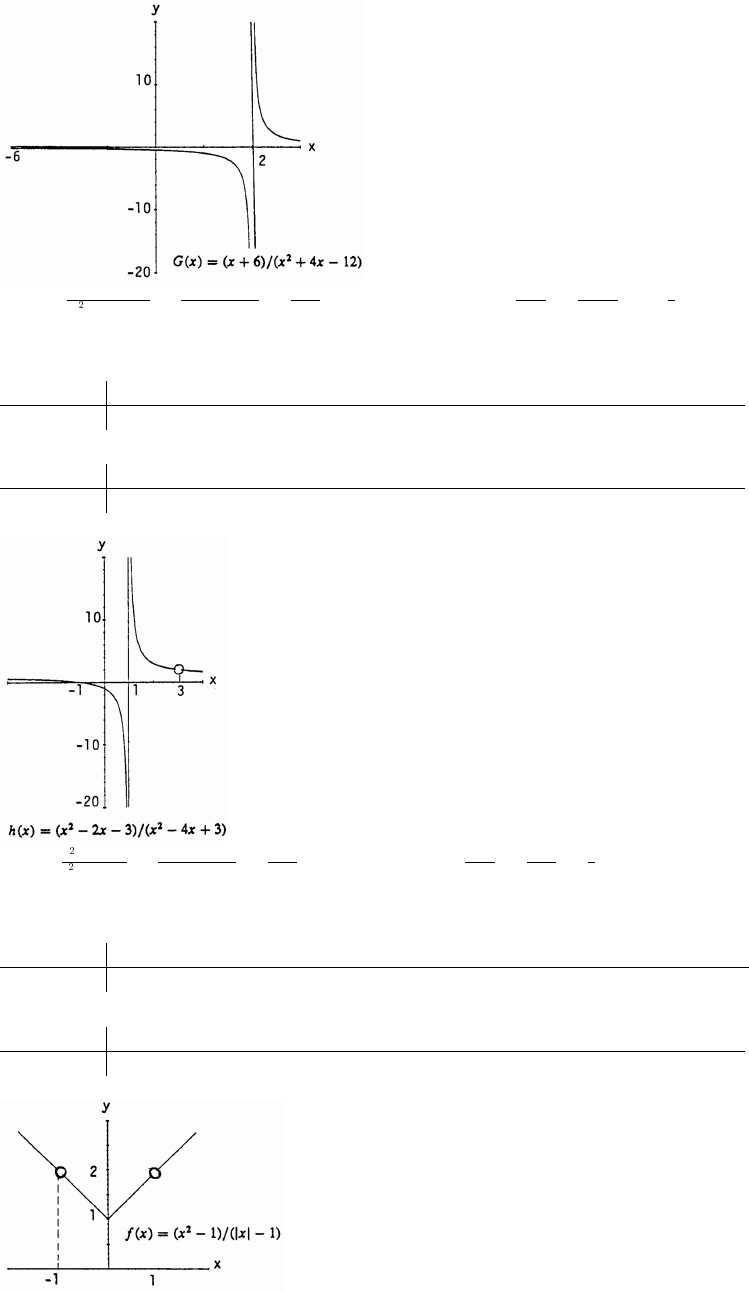
Section 2.1 Rates of Change and Limits 69
(b)
(c) G(x) if x 6, and lim 0.125.œ œ œ Á œ œ œ
x6 x6
x 4x12 (x6)(x2) x x2 2 8
" """
# 'ab xÄ'
14. (a) h(x) x 2x 3 / x 4x 3œ abab
##
x 2.9 2.99 2.999 2.9999 2.99999 2.999999
h(x) 2.052631 2.005025 2.000500 2.000050 2.000005 2.0000005
x 3.1 3.01 3.001 3.0001 3.00001 3.000001
h(x) 1.952380 1.995024 1.999500 1.999950 1.999995 1.999999
(b)
(c) h(x) if x 3, and lim 2.œœ œÁ œœœ
x 2x3 x1 x1 31 4
x 4x3 (x3)(x1) x1 x1 31
(x 3)(x 1)
#
xÄ$
15. (a) f(x) x 1 / x 1œ ababkk
#
x 1.1 1.01 1.001 1.0001 1.00001 1.000001
f(x) 2.1 2.01 2.001 2.0001 2.00001 2.000001
x .9 .99 .999 .9999 .99999 .999999
f(x) 1.9 1.99 1.999 1.9999 1.99999 1.999999
(b)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
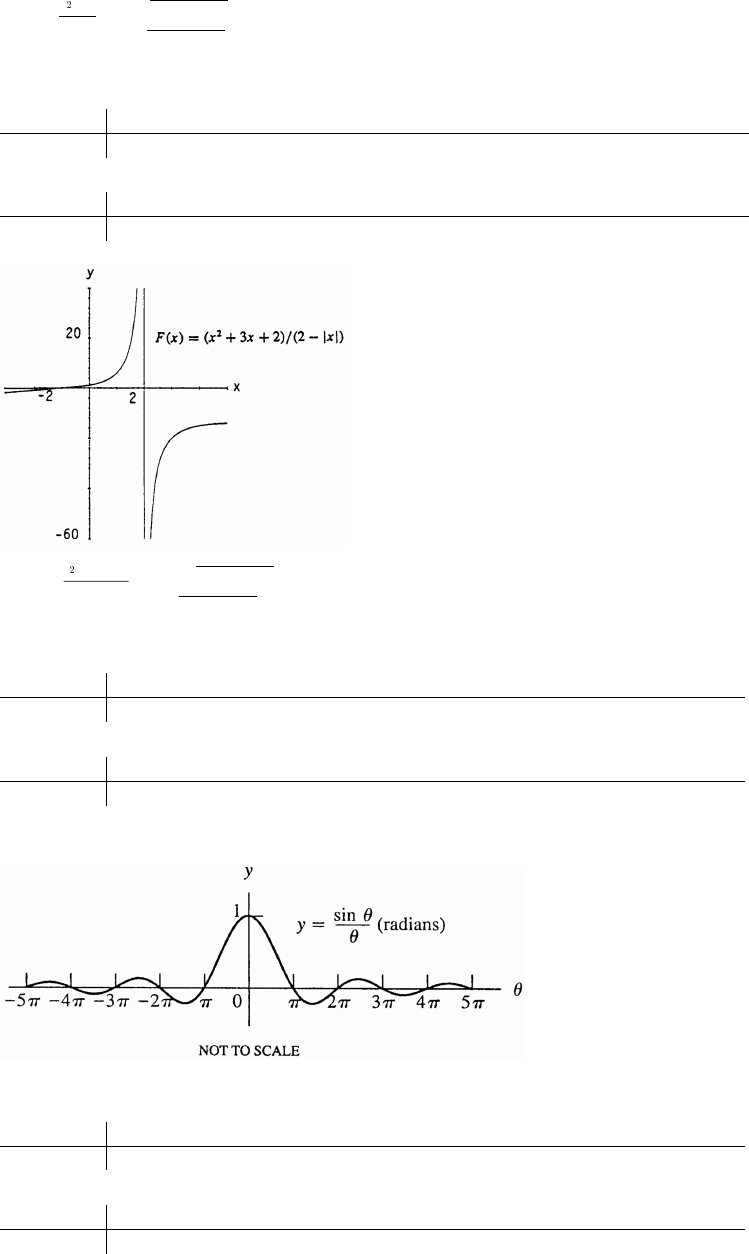
70 Chapter 2 Limits and Continuity
(c) f(x) , and lim (1 x) 1 ( 1) 2.
x 1, x 0 and x 1
1 x, x 0 and x 1
œœ œœ
œ Á
œ Á
x
x1
(x 1)(x 1)
x1
(x 1)(x 1)
(x 1)
"
kk x1Ä
16. (a) F(x) x 3x 2 / 2 xœ ababkk
#
x 2.1 2.01 2.001 2.0001 2.00001 2.000001
F(x) 1.1 1.01 1.001 1.0001 1.00001 1.000001
x 1.9 1.99 1.999 1.9999 1.99999 1.999999
F(x) .9 .99 .999 .9999 .99999 .999999
(b)
(c) F(x) , and lim (x 1) 2 1
, x 0
x 1, x 0 and x 2
œœ œœ
œ Á
x3x2
2x
(x 2)(x 1)
x
(x 2)(x )
2x
#
"
kk xÄ# 1.
17. (a) g( ) (sin )/)))œ
.1 .01 .001 .0001 .00001 .000001
g( ) .998334 .999983 .999999 .999999 .999999 .999999
)
)
.1 .01 .001 .0001 .00001 .000001
g( ) .998334 .999983 .999999 .999999 .999999 .999999
)
)
lim g( ) 1
)Ä!
)œ
(b)
18. (a) G(t) (1 cos t)/tœ #
t .1 .01 .001 .0001 .00001 .000001
G(t) .499583 .499995 .499999 .5 .5 .5
t .1 .01 .001 .0001 .00001 .000001
G(t) .499583 .499995 .499999 .5 .5 .5
lim G(t) 0.5
tÄ! œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
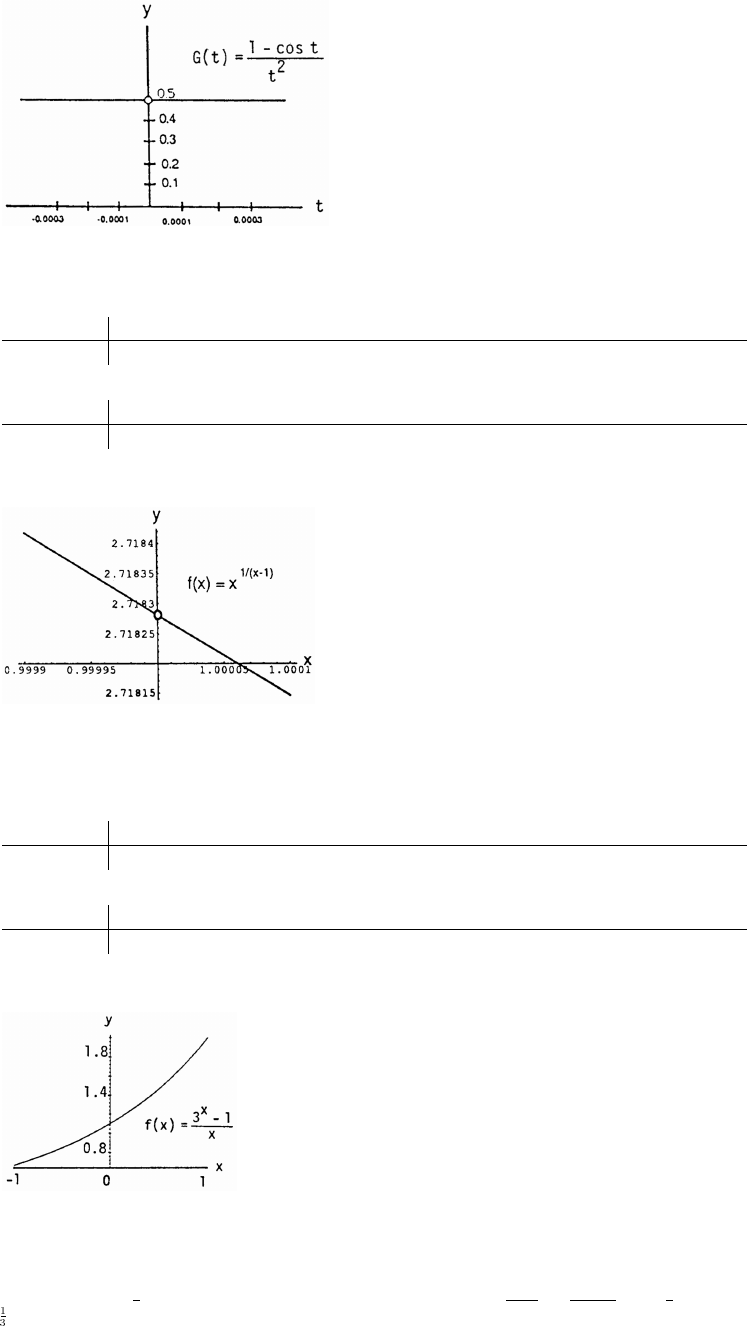
Section 2.1 Rates of Change and Limits 71
(b)
Graph is NOT TO SCALE
19. (a) f(x) xœ"ÎÐ" Ñx
x .9 .99 .999 .9999 .99999 .999999
f(x) .348678 .366032 .367695 .367861 .367877 .367879
x 1.1 1.01 1.001 1.0001 1.00001 1.000001
f(x) .385543 .369711 .368063 .367897 .367881 .367878
lim f(x) 0.36788
x1ĸ
(b)
Graph is NOT TO SCALE. Also the intersection of the axes is not the origin: the axes intersect at the point
(1 2.71820).ß
20. (a) f(x) 3 1 /xœab
x
x .1 .01 .001 .0001 .00001 .000001
f(x) 1.161231 1.104669 1.099215 1.098672 1.098618 1.098612
x .1 .01 .001 .0001 .00001 .000001
f(x) 1.040415 1.092599 1.098009 1.098551 1.098606 1.098611
lim f(x) 1.0986
xÄ! ¸
(b)
21. lim 2x 2(2) 4 22. lim 2x 2(0) 0
xxÄ# Ä!
œœ œœ
23. lim (3x 1) 3 1 0 24. lim
xx1
ÄÄ
œ œ œ œ
ˆ‰
"""
#3 3x 1 3(1) 1
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
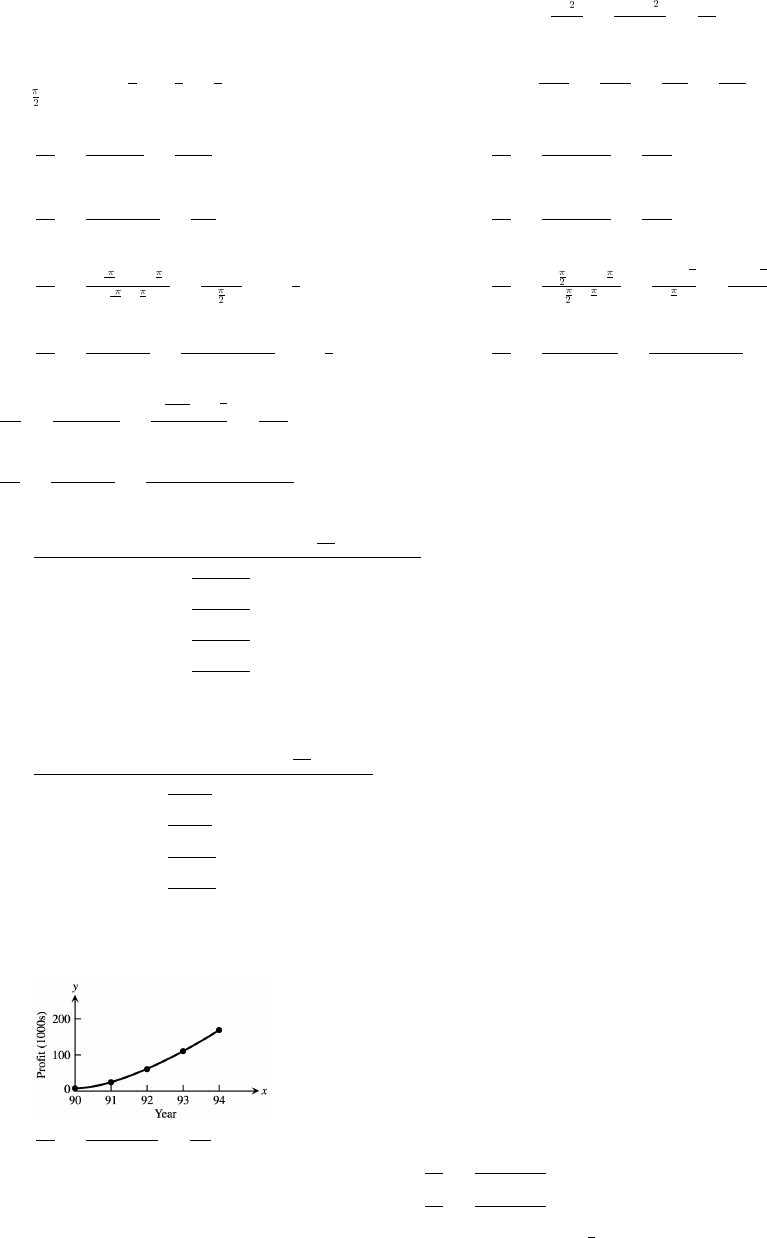
72 Chapter 2 Limits and Continuity
25. lim 3x(2x 1) 3( 1)(2( 1) 1) 9 26. lim 1
xx1
Ä Ä
"œ œ œ œ œ
3x 3
2x1 2(1)1 3
3( 1)
27. lim x sin x sin 28. lim
xx
ÄÄ
œœ œœœ
111 1
1111###
" "
1
cos x cos
111 1
29. (a) 19 (b) 1
??
??
f289 f 20
x3 1 x1(1)
f(3) f(2) f(1) f( )
œœœ œ œœ
"
# #
30. (a) 0 (b) 2
??
??
g g(1) g( 1) g g(0) g( 2)
x1(1) 2 x0(2)
11 0 4
œœœ œœœ
#
31. (a) (b)
??
?1?1
h114 h
t t
hh hh 03 33
œœœ œœœ
ˆ‰ ˆ‰ ÈÈ
ˆ‰ ˆ‰
3
44
3
44
6
63
32. (a) (b) 0
?1 ?11
?1 1 1 ?11 1
g g( ) g(0) (2 1) (2 1) g g( ) g( ) (2 1) (2 )
t0 0 t()
2
œœ œ œ œ œ
"
#
33. 1
?
?)
R3
R(2) R(0)
20
81 1
œœ œœ
##
"
ÈÈ
34. 2 2 0
?
?)
PP(2) P(1) (8 16 10) ( )
21 1
œ œ œœ
"%&
35. (a) Q Slope of PQ œ?
?
p
t
Q (10 225) 42.5 m/sec
"
ߜ
650 225
20 10
Q (14 375) 45.83 m/sec
#
ߜ
650 375
20 14
Q (16.5 475) 50.00 m/sec
$
ߜ
650 475
20 16.5
Q (18 550) 50.00 m/sec
%
ߜ
650 550
20 18
(b) At t 20, the Cobra was traveling approximately 50 m/sec or 180 km/h.œ
36. (a) Q Slope of PQ œ?
?
p
t
Q (5 20) 12 m/sec
"
ߜ
80 20
10 5
Q (7 39) 13.7 m/sec
#
ߜ
80 39
10 7
Q (8.5 58) 14.7 m/sec
$
ߜ
80 58
10 8.5
Q (9.5 72) 16 m/sec
%
ߜ
80 72
10 9.5
(b) Approximately 16 m/sec
37. (a)
(b) 56 thousand dollars per year
?
?
p
t 1994 1992
174 62 112
œœœ
#
(c) The average rate of change from 1991 to 1992 is 35 thousand dollars per year.
?
?
p
t 1992 1991
62 27
œœ
The average rate of change from 1992 to 1993 is 49 thousand dollars per year.
?
?
p
t 1993 1992
111 62
œœ
So, the rate at which profits were changing in 1992 is approximatley 35 49 42 thousand dollars per year.
"
#abœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 2.1 Rates of Change and Limits 73
38. (a) F(x) (x 2)/(x 2)œ
x 1.2 1.1 1.01 1.001 1.0001 1
F(x) 4.0 3.4 3.04 3.004 3.0004 3
5.0; 4.4;
??
??
FF
x1.21 x1.11
4.0 ( 3) 3.4 ( 3)
œœ œœ
4.04; 4. ;
??
??
FF
x1.011 x1.0011
3.04 ( 3) 3.004 ( 3)
œ œ œ œ !!%
4. ;
?
?
F
x 1.0001 1
3. ( 3)
œ œ !!!%
!!!%
(b) The rate of change of F(x) at x 1 is 4.œ
39. (a) 0.414213 0.449489
??
??
g g(2) g(1) 2 g g(1.5) g(1)
x21 1 x1.51 0.5
1.5
œœ¸ œ œ¸
"
#
"
ÈÈ
?
?
g g(1 h) g(1)
x(1h)1 h
1h
œœ
"
È
(b) g(x) xœÈ
1 h 1.1 1.01 1.001 1.0001 1.00001 1.000001
1 h 1.04880 1.004987 1.0004998 1.0000499 1.000005 1.0000005
1 h 1 /h 0.4880 0.4987 0.4998 0.499 0.5
È
Š‹
È0.5
(c) The rate of change of g(x) at x 1 is 0.5.œ
(d) The calculator gives lim .
hÄ! œ
È1h
h
" "
#
40. (a) i) f(3) f(2)
32 1 1 6
"
œœœ
36
ii) , T 2
f(T) f(2)
TTTT(T2)T(2T)T
2T 2T
# # # # # #
"
œœ œ œ œÁ
TTT
2T
(b) T 2.1 2.01 2.001 2.0001 2.00001 2.000001
f(T) 0.476190 0.497512 0.499750 0.4999750 0.499997 0.499999
f(T) f(2) / T 2 0.2381 0.2488 0.2abab500 0.2500 0.2500 0.2500
(c) The table indicates the rate of change is 0.25 at t 2.œ
(d) lim
TÄ#ˆ‰
""
#T4
œ
41-46. Example CAS commands:
:Maple
f := x -> (x^4 16)/(x 2);
x0 := 2;
plot( f(x), x x0-1..x0+1, color black,œœ
title "Section 2.1, #41(a)" );œ
limit( f(x), x x0 );œ
In Exercise 43, note that the standard cube root, x^(1/3), is not defined for x<0 in many CASs. This can be
overcome in Maple by entering the function as f := x -> (surd(x+1, 3) 1)/x.
: (assigned function and values for x0 and h may vary)Mathematica
Clear[f, x]
f[x_]:=(x x 5x 3)/(x 1)
32 2
x0= 1; h = 0.1;
Plot[f[x],{x, x0 h, x0 h}]
Limit[f[x], x x0]Ä
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

74 Chapter 2 Limits and Continuity
2.2 CALCULATING LIMITS USING THE LIMIT LAWS
1. lim (2x 5) 2( 7) 5 14 5 9 2. lim (10 3x) 10 3(12) 10 36 26
xx1
Ä( Ä#
œœœ œ œœ
3. lim x 5x2 (2) 5(2)2 41024
xÄ#ab œ œ œ
##
4. lim x 2x 4x8 (2) 2(2) 4(2)8 8888 16
xÄ#ab
$# $ #
œ œ œ
5. lim 8(t 5)(t 7) 8(6 5)(6 7) 8 6. lim 3s(2s 1) 3 2 1 2 1
ts
Ä' Ä
œ œ œ œ œ
ˆ‰ ‘ ˆ ‰ˆ‰
22 4 2
33 3 3
7. lim 8. lim 2
xxÄ# Ä&
x3 23 5 4 4 4
x6 26 8 x7 57
#
œœ œœœ
9. lim
yÄ&
y(5)
5y 5(5) 10
25 5
#
œœœ
10. lim
yÄ#
y2
y5y6 (2)5()6 4106 0 5
22 4 4
# #
"
œœœœ
11. lim 3(2x 1) 3(2( 1) 1) 3( 3) 27
xÄ"œ œœ
###
12. lim (x 3) ( 4 3) ( 1) 1
xÄ% œœœ
"*)% "*)% "*)%
13. lim (5 y) [5 ( 3)] (8) (8) 2 16
yÄ$ œœ œ œœ
%Î$ %Î$ %Î$ "Î$ %
%
ˆ‰
14. lim (2z 8) (2(0) 8) ( 8) 2
zÄ! œœœ
"Î$ "Î$ "Î$
15. lim
hÄ!
3333
3h11 3(0) 1 1 11 2
ÈÈ È
œœœ
16. lim
hÄ!
5555
5h42 5(0) 4 2 44
ÈÈ È
#
œœœ
17. lim lim lim lim lim
h0 h0 h0 h0 h0ÄÄ ÄÄÄ
ÈÈÈ
È È
ab
Š‹ Š‹
ÈÈ
3h1 3h1 3h11 3h 1
hh
3h11 3h 1
h 3h1 h 3h1
3h 3
" " "
"
" "
œ†œœœ
œœ
3
È""
$
#
18. lim lim lim lim lim
h0 h0 h0 h0 h0ÄÄ ÄÄÄ
ÈÈÈ
È È
ab
Š‹ Š‹
ÈÈ
5h42 5h42 5h42 5h4 4
hh
5h42 5h42
h 5h42 h 5h42
5h 5
œ†œœœ
œœ
55
42 4
È
19. lim lim lim
xx xÄ& Ä& Ä&
x5 x5 1
x 25 (x5)(x5) x5 55 10
""
œœœœ
20. lim lim lim
xx xÄ$ Ä$ Ä$
x3 x3 1
x 4x3 (x3)(x1) x1 31 2
""
œœœœ
21. lim lim lim (x 2) 7
xx xÄ& Ä& Ä&
x3x0
x5 x5
(x 5)(x 2)
"
œœœ&#œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 2.2 Calculating Limits Using the Limit Laws 75
22. lim lim lim (x 5) 2 5 3
xx xÄ# Ä# Ä#
x7x0
xx2
(x 5)(x 2)
"
#
œ œ œœ
23. lim lim lim
tt tÄ" Ä" Ä"
tt2 t2123
t 1 (t 1)(t 1) t 1 1 1
(t 2)(t 1)
#
œœœœ
24. lim lim lim
tt tÄ" Ä" Ä"
t 3t2 t2 12 1
t t2 (t2)(t1) t2 12 3
(t 2)(t 1)
œœœœ
25. lim lim lim
xx xÄ# Ä# Ä#
2x 4 2 2 1
x2x x(x2) x 4 2
2(x 2)
œœœœ
26. lim lim lim
y0 yy
ÄÄ! Ä!
5y 8y y (5y 8) 5y 8
3y 16y y3y16 3y16 16
8
#
"
œœœœ
ab
27. lim lim lim
u1 u1 u1ÄÄ Ä
u 4
u 1 u u1(u1) u u1 111 3
u(u1)(u1) u(u1)
(1 1)(1 1)
"
" "
œœœœ
ab ab
ab
28. lim lim lim
vv vÄ# Ä# Ä#
v 8 v 2v4 444 12 3
v16
(v 2) v 2v 4
(v 2)(v 2) v 4 (v 2) v 4 (4)(8) 32 8
œœœœœ
ab
ab ab
29. lim lim lim
xx xÄ* Ä* Ä*
ÈÈ
ˆ‰ˆ‰
ÈÈ È È
x3 x3
x9 6
x3 x3 x3 93
"""
œœœœ
30. lim lim lim lim x 2 x 4(2 2) 16
xx x xÄ% Ä% Ä% Ä%
4x x
2x 2x 2x
x(4 x) x2 x 2 x
ÈÈ È
ˆ‰ˆ‰
ÈÈ
œœ œœœ
ˆ‰
È
31. lim lim lim lim x 3
x1 x1 x1 x1ÄÄ Ä Ä
x1
x32 x3 x3
(x1) x32 (x1) x3
(x 3) 4
# #
#
ÈÈÈ
ˆ‰ ˆ‰
ÈÈ
ˆ‰ˆ‰
œœœ#
Š‹
È
424œœ
È
32. lim lim lim
xx x1
Ä Ä Ä
""
œœ
ÈŠ‹Š‹
ÈÈ
Š‹ Š‹
ÈÈ
ab
x83
x1
x8 x8
(x 1) x 8 (x 1) x 8
x8
$ $
$ $
*
lim lim œœœœ
x1 x1Ä Ä
(x 1)(x 1)
(x 1) x
x1 2
x33 3
)$
"
)$
Š‹
ÈÈ
33. lim lim lim
x2 x2 x2ÄÄ Ä
ÈŠ‹Š‹
ÈÈ
Š‹ Š‹
ÈÈ
ab
x124
x2
x124 x124
(x 2) x 12 4 (x 2) x 12 4
x1216
œœ
lim lim œœœœ
x2 x2ÄÄ
(x 2)(x 2)
(x 2) x 12 4
x2 4
x124 16 4 2
"
Š‹
ÈÈÈ
34. lim lim lim
x2 x2 x2Ä Ä Ä
x2
x53
x2 x 53 x2 x 53
x53 x53 x59
Èab ab
Š‹ Š‹
ÈÈ
Š‹Š‹
ÈÈ ab
œœ
lim lim œœœœ
x2 x2Ä Ä
ab
Š‹
ÈÈÈ
x2 x 53
(x 2)(x 2) x 2 4 2
x53 93 3
35. lim lim lim
x3 x3 x3Ä Ä Ä
2x5
x3
2x52x5
(x 3) 2 x 5 (x 3) 2 x 5
4x5
ÈŠ‹Š‹
ÈÈ
Š‹ Š‹
ÈÈ
ab
œœ
lim lim lim œœœœœ
x3 x3 x3Ä Ä Ä
9x 3x 6 3
(x 3) 2 x 5 (x 3) 2 x 5
(3 x)(3 x)
2x5 24 2
Š‹ Š‹
ÈÈ
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

76 Chapter 2 Limits and Continuity
36. lim lim lim
x4 x4 x4ÄÄ Ä
4x
5x9
4x5 x 9 4x5 x 9
5x95x9 25 x 9
Èab ab
Š‹ Š‹
ÈÈ
Š‹Š‹
ÈÈ ab
œœ
lim lim lim œœ œœœ
x4 x4 x4ÄÄÄ
ab ab
Š‹ Š‹
ÈÈ
ÈÈ
4x5 x 9 4x5 x 9
16 x (4 x)(4 x) 4 x 8 4
5x9 525 5
37. (a) quotient rule
(b) difference and power rules
(c) sum and constant multiple rules
38. (a) quotient rule
(b) power and product rules
(c) difference and constant multiple rules
39. (a) lim f(x) g(x) lim f(x) lim g(x) (5)( 2) 10
xc xc xcÄÄÄ
œœœ
’“’“
(b) lim 2f(x) g(x) 2 lim f(x) lim g(x) 2(5)( 2) 20
xc xc xcÄÄÄ
œœœ
’“’“
(c) lim [f(x) 3g(x)] lim f(x) 3 lim g(x) 5 3( 2) 1
xc xc xcÄÄÄ
œ œœ
(d) lim
xcÄ
f(x)
f(x) g(x) lim f(x) lim g(x) 5 ( 2) 7
lim f(x) 55
œœœ
xc
xc xc
40. (a) lim [g(x) 3] lim g(x) lim 3
xxxÄ% Ä% Ä%
œ œ$$œ!
(b) lim xf(x) lim x lim f(x) (4)(0) 0
xxxÄ% Ä% Ä%
œœœ†
(c) lim [g(x)] lim g(x) [ 3] 9
xxÄ% Ä%
##
#
œœœ
’“
(d) lim 3
xÄ%
g(x)
f(x) 1 lim f(x) lim 1 0 1
lim g(x) 3
œœœ
x
xx
41. (a) lim [f(x) g(x)] lim f(x) lim g(x) 7 ( 3) 4
xb xb xbÄÄÄ
œ œœ
(b) lim f(x) g(x) lim f(x) lim g(x) (7)( 3) 21
xb xb xbÄÄÄ
†œœœ
’“’“
(c) lim 4g(x) lim 4 lim g(x) (4)( 3) 12
xb xb xbÄÄÄ
œœœ
’“’ “
(d) lim f(x)/g(x) lim f(x)/ lim g(x)
xb xb xbÄÄÄ
œœœ
77
33
42. (a) lim [p(x) r(x) s(x)] lim p(x) lim r(x) lim s(x) 4 0 ( 3) 1
xxxxÄ# Ä# Ä# Ä#
œ œœ
(b) lim p(x) r(x) s(x) lim p(x) lim r(x) lim s(x) (4)(0)( 3) 0
xxxxÄ# Ä# Ä# Ä#
†† œœœ
’“’“’“
(c) lim [ 4p(x) 5r(x)]/s(x) 4 lim p(x) 5 lim r(x) lim s(x) [ 4(4) 5(0)]/ 3
xxxxÄ# Ä# Ä# Ä#
œ œ œ
’“
‚"6
3
43. lim lim lim lim (2 h) 2
hh hhÄ! Ä! Ä! Ä!
(1 h) 1 h(2 h)
hhh
12hh 1
œœœœ
44. lim lim lim lim (h 4) 4
hhhhÄ! Ä! Ä! Ä!
(2 h) (2) h(h 4)
hhh
44hh 4
œœœœ
45. lim lim 3
hhÄ! Ä!
[3(2 h) 4] [3(2) 4]
hh
3h
œœ
46. lim lim lim lim
hhhhÄ! Ä! Ä! Ä!
ˆ‰ˆ‰
h2h
2
"
#
"
h 2h 2h( h) h(4 2h) 4
2(2h) h
œœ œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
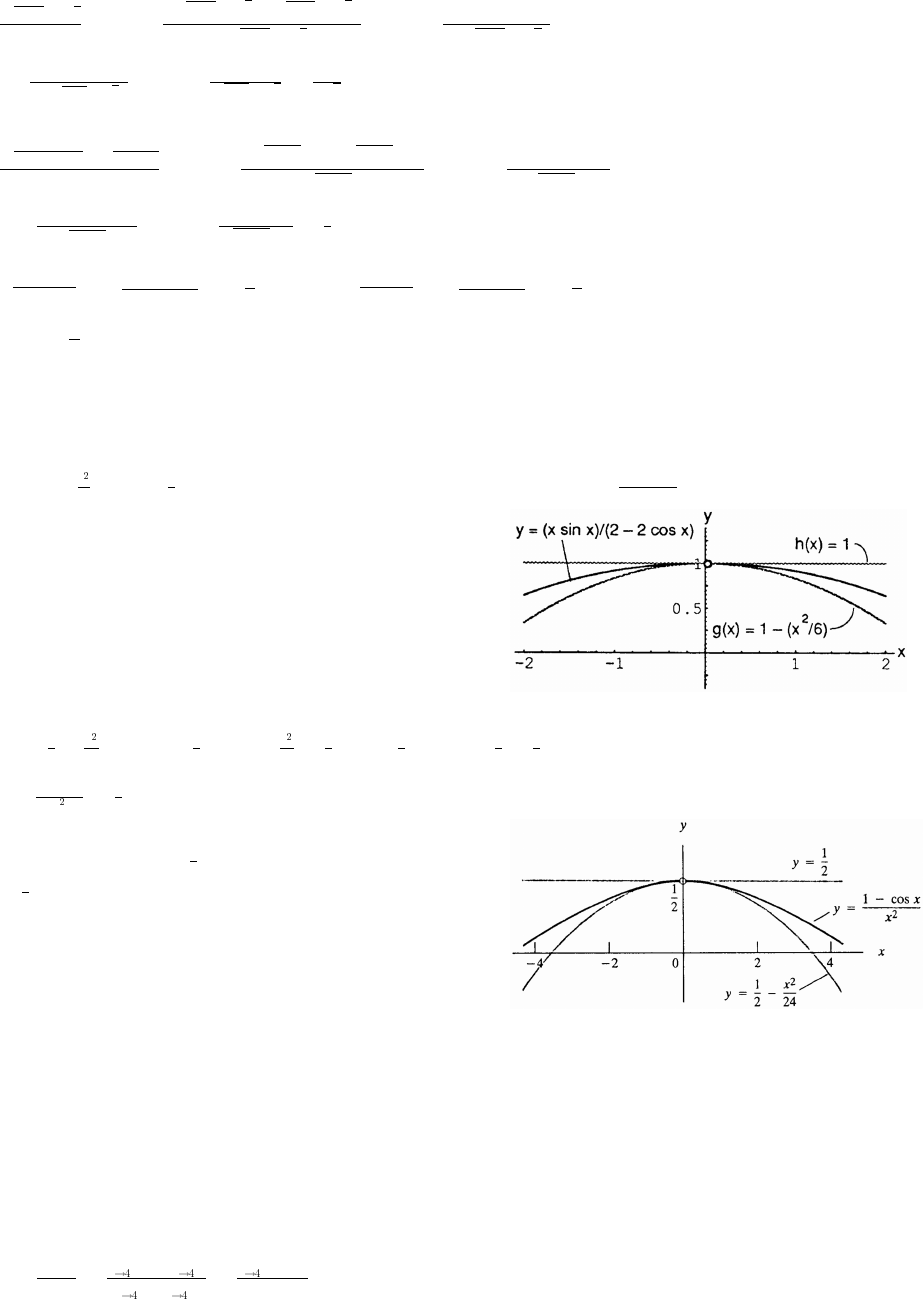
Section 2.2 Calculating Limits Using the Limit Laws 77
47. lim lim lim
hh hÄ! Ä! Ä!
ÈÈŠ‹Š‹
ÈÈ
ÈÈ
Š‹ Š‹
ÈÈ
ÈÈ
7h 7
h
7h 7 7h 7
h7h 7 h7h 7
(7 h) 7
œœ
lim lim œœœ
hhÄ! Ä!
h
h7h7 7h 7 7
Š‹
ÈÈÈÈÈ
""
#
48. lim lim lim
hh hÄ! Ä! Ä!
ÈÈ Š‹Š‹
ÈÈ
Š‹ Š ‹
ÈÈ
3(0 h) 1 3(0) 1
h
3h 1 3h 1
h 3h1 h 3h11
(3h 1)
" "
"
"
œœ
lim lim œœœ
hhÄ! Ä!
3h 3 3
h3h1 3h11
Š‹
ÈÈ
" #
49. lim 5 2x 5 2(0) 5 and lim 5 x 5 (0) 5; by the sandwich theorem,
xxÄ! Ä!
ÈÈ
ÈÈ
ÈÈ
œ œ œ œ
## ##
lim f(x) 5
xÄ! œÈ
50. lim 2 x 2 0 2 and lim 2 cos x 2(1) 2; by the sandwich theorem, lim g(x) 2
xx xÄ! Ä! Ä!
ab œœ œ œ œ
#
51. (a) lim 1 1 1 and lim 1 1; by the sandwich theorem, lim 1
xx xÄ! Ä! Ä!
Š‹
œœ œ œ
x0 x sin x
66 22 cos x
(b) For x 0, y (x sin x)/(2 2 cos x)Áœ
lies between the other two graphs in the
figure, and the graphs converge as x 0.Ä
52. (a) lim lim lim 0 and lim ; by the sandwich theorem,
xxx xÄ! Ä! Ä! Ä!
Š‹
"""""
#######
œ œœ œ
x1x
24 4
lim .
xÄ!
1cos x
x
"
#
œ
(b) For all x 0, the graph of f(x) (1 cos x)/xÁœ
#
lies between the line y and the parabolaœ"
#
y x /24, and the graphs converge as x 0.œ Ä
"
#
#
53. lim f(x) exists at those points c where lim x lim x . Thus, c c c 1 c 0
xc xc xcÄÄÄ
%#%###
œœÊœab
c 0, 1, or 1. Moreover, lim f(x) lim x 0 and lim f(x) lim f(x) 1.Êœ œ œ œ œ
xx x1 x1
Ä! Ä! Ä Ä
#
54. Nothing can be concluded about the values of f, g, and h at x 2. Yes, f(2) could be 0. Since theœ
conditions of the sandwich theorem are satisfied, lim f(x) 5 0.
xÄ# œ Á
55. 1 lim lim f(x) 5 2(1) lim f(x) 2 5 7.œ œ œ Ê œ Ê œœ
xxxÄ% Ä% Ä%
f(x) 5
x 2 lim x lim 2
lim f(x) lim 5 lim f(x) 5
%#
xx x
xx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
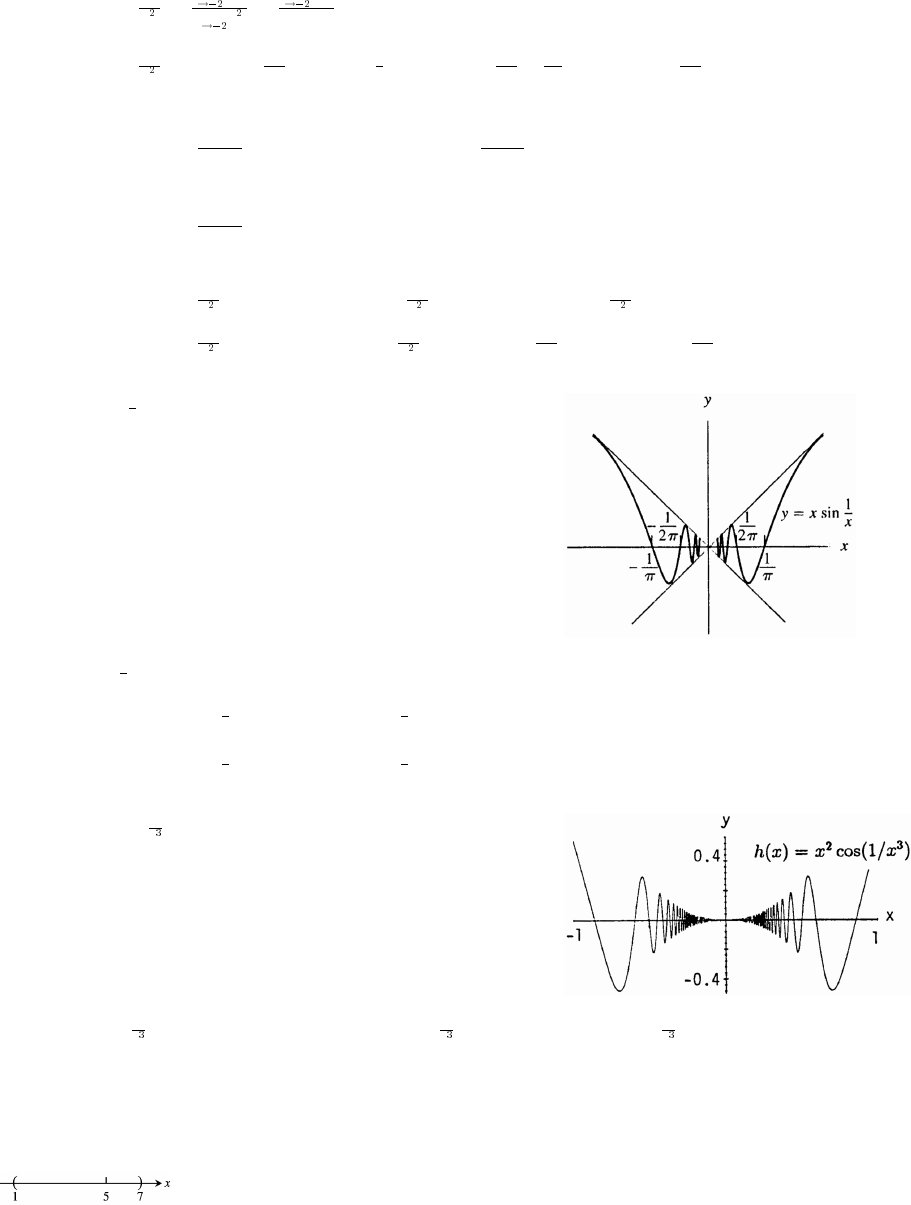
78 Chapter 2 Limits and Continuity
56. (a) 1 lim lim f(x) 4.œœœÊ œ
xxÄ# Ä#
f(x)
x lim x
lim f(x) lim f(x)
xx
x%
(b) 1 lim lim lim lim lim 2.œœ œ Ê œ
xxxx xÄ# Ä# Ä# Ä# Ä#
f(x) f(x) f(x) f(x)
xxxx x
’“’“’“
ˆ‰
""
#
57. (a) 0 3 0 lim lim (x 2) lim (x 2) lim [f(x) 5] lim f(x) 5œ œ œ œ œ †’“’“’ “Š‹
xx x x xÄ# Ä# Ä# Ä# Ä#
f(x) 5 f(x) 5
xx
# #
lim f(x) 5.ʜ
xÄ#
(b) 0 4 0 lim lim (x 2) lim f(x) 5 as in part (a).œœ Ê œ†’“’“
xx xÄ# Ä# Ä#
f(x) 5
x
#
58. (a) 0 1 0 lim lim x lim lim x lim x lim f(x). That is, lim f(xœœ œ œ œ††
’“’“’“’“’“
xx xxx x xÄ! Ä! Ä! Ä! Ä! Ä! Ä!
f(x) f(x) f(x)
xxx
### )0.œ
(b) 0 1 0 lim lim x lim x lim . That is, lim 0.œœ œ œ œ††
’“’“’“
xxx x xÄ! Ä! Ä! Ä! Ä!
f(x) f(x) f(x) f(x)
xxxx
59. (a) lim x sin 0
xÄ!
"
xœ
(b) 1 sin 1 for x 0:Ÿ Ÿ Á
"
x
x 0 x x sin x lim x sin 0 by the sandwich theorem;ÊŸ ŸÊ œ
""
xx
xÄ!
x 0 x x sin x lim x sin 0 by the sandwich theorem.Ê Ê œ
""
xx
xÄ!
60. (a) lim x cos 0
xÄ!
#"
ˆ‰
xœ
(b) 1 cos 1 for x 0 x x cos x lim x cos 0 by the sandwichŸ Ÿ Á Ê Ÿ Ÿ Ê œ
ˆ‰ ˆ‰ ˆ‰
"""
## # #
xxx
xÄ!
theorem since lim x 0.
xÄ!
#œ
2.3 PRECISE DEFINITION OF A LIMIT
1.
Step 1: x5 x5 5x 5kk Ê Ê$$ $$ $
Step 2: 5 7 2, or 5 1 4.$$$$œ Ê œ œ Ê œ
The value of which assures x 5 1 x 7 is the smaller value, 2.$$ $kkÊ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
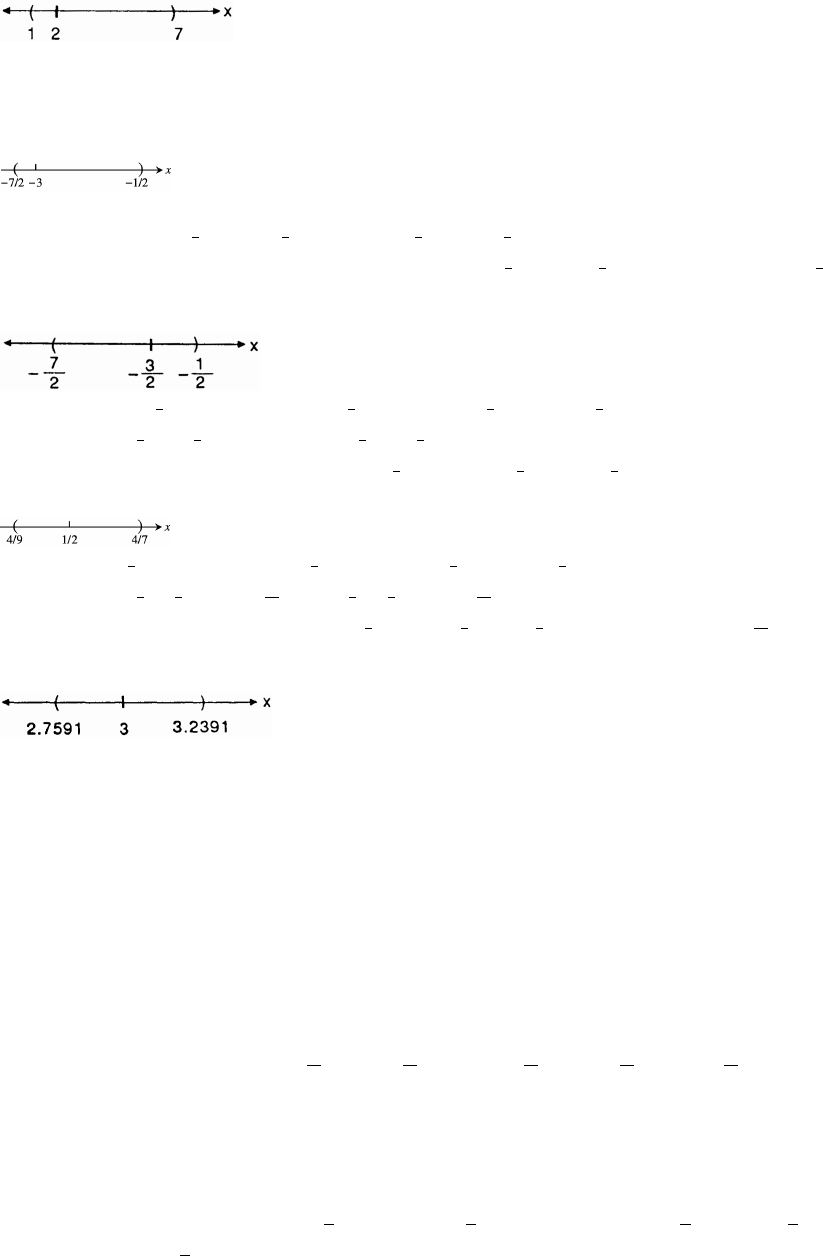
Section 2.3 Precise Definition of a Limit 79
2.
Step 1: x2 x2 x 2kk Ê Ê # $$ $$ $
Step 2: 2 1 1, or 2 7 5.œÊœ œÊœ$$$$
The value of which assures x 2 1 x 7 is the smaller value, 1.$$ $kkÊ œ
3.
Step 1: x ( 3) x 3 x 3kkÊ$Ê$$ $$ $
Step 2: 3 , or . œ Ê œ $œ Ê œ$$$$
75
## ##
""
The value of which assures x ( 3) x is the smaller value, .$$ $kk Ê œ
7
## #
""
4.
Step 1: x x x
¸¸ˆ‰
Ê Ê
3333
####
$$ $$ $
Step 2: , or 1. œ Ê œ# œ Ê œ$$$$
37 3
## ##
"
The value of which assures x x is the smaller value, .$$ $
¸¸ˆ‰
Ê œ"
37
###
"
5.
Step 1: x x x
¸¸
ÊÊ
""""
####
$$ $$ $
Step 2: , or .œÊœ œÊœ$$$$
""""
##
44
918 714
The value of which assures x x is the smaller value, .$$ $
¸¸
Ê œ
""
#
44
97 18
6.
Step 1: x3 x3 3x 3kk Ê Ê$$ $$ $
Step 2: 2.7591 0.2409, or 3.2391 0.2391.$œ Ê œ $œ Ê œ$$$$
The value of which assures x 3 2.7591 x 3.2391 is the smaller value, 0.2391.$$ $kkÊ œ
7. Step 1: x 5 x 5 5 x 5kk Ê Ê$$ $$ $
Step 2: From the graph, 5 4.9 0.1, or 5 5.1 0.1; thus 0.1 in either case.œÊœ œÊœ œ$$$$$
8. Step 1: x ( 3) x 3 3 x 3kk Ê Ê$$ $$ $
Step 2: From the graph, 3 3.1 0.1, or 3 2.9 0.1; thus 0.1. œ Ê œ œ Ê œ œ$$$$$
9. Step 1: x 1 x 1 1 x 1kk Ê Ê$$ $$ $
Step 2: From the graph, 1 , or 1 ; thus .œÊœ œÊœ œ$$$$$
97 259 7
16 16 16 16 16
10. Step 1: x 3 x 3 3 x 3kk Ê Ê$$ $$ $
Step 2: From the graph, 3 2.61 0.39, or 3 3.41 0.41; thus 0.39.œÊœ œÊœ œ$$$$$
11. Step 1: x 2 x 2 2 x 2kk Ê Ê$$ $$ $
Step 2: From the graph, 2 3 2 3 0.2679, or 2 5 5 2 0.2361;œÊœ¸ œÊœ¸$$ $$
ÈÈ ÈÈ
thus 5 2.$œ
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
80 Chapter 2 Limits and Continuity
12. Step 1: x ( 1) x 1 1 x 1kk Ê Ê$$ $$ $
Step 2: From the graph, 1 0.1180, or 1 0.1340; œ Ê œ ¸ œ Ê œ ¸$$ $$
ÈÈ È È
552 323
## ##
thus .$œÈ52
#
13. Step 1: x ( 1) x 1 1 x 1kk Ê Ê$$ $$ $
Step 2: From the graph, 1 0.77, or 1 0.36; thus 0.36. œ Ê œ ¸ œ Ê œ œ œ$$$ $
16 7 16 9 9
9 9 25 25 25
14. Step 1: x x x
¸¸
ÊÊ
""""
####
$$ $$ $
Step 2: From the graph, 0.00248, or 0.00251;œÊœ¸ œÊœ¸$$ $$
""" "
## # #
11 1 1
2.01 2 .01 1.99 1.99
thus 0.00248.$œ
15. Step 1: (x 1) 5 0.01 x 4 0.01 0.01 x 4 0.01 3.99 x 4.01kk kk Ê Ê Ê
Step 2: x 4 x 4 4 x 4 0.01.kk Ê Ê Ê œ$$ $$ $ $
16. Step 1: (2x 2) ( 6) 0.02 2x 4 0.02 0.02 2x 4 0.02 4.02 2x 3.98kkkk Ê Ê Ê
2.01 x 1.99Ê
Step 2: x ( 2) x 2 2 x 2 0.01.kk Ê Ê Ê œ$$ $$ $ $
17. Step 1: x 1 0.1 0.1 x 1 0.1 0.9 x 1 1.1 0.81 x 1 1.21
¹¹
ÈÈÈ
"Ê"ÊÊ
0.19 x 0.21Ê
Step 2: x 0 x . Then, or ; thus, 0.19.kk Ê œ !Þ"* Ê œ !Þ"* œ !Þ#" œ$$ $ $ $ $ $
18. Step 1: x 0.1 0.1 x 0.1 0.4 x 0.6 0.16 x 0.36
¸¸
ÈÈÈ
Ê Ê Ê
""
##
Step 2: x x .
¸¸
Ê Ê B
""""
4444
$$ $$ $
Then, 0.16 0.09 or 0.36 0.11; thus 0.09.œÊœ œÊœ œ$$$$$
""
44
19. Step 1: 19 x 19 x 1 2 19 x 4 19 x 16
¹¹
ÈÈÈ
$"Ê" $ Ê %Ê
x 19 16 15 x 3 or 3 x 15Ê% Ê
Step 2: x 10 x 10 10 x 10.kkÊÊ$$ $$ $
Then 10 3 7, or 10 15 5; thus 5. œ Ê œ œ Ê œ œ$$$ $$
20. Step 1: x 7 4 1 x 7 1 3 x 7 5 9 x 7 25 16 x 32
¹¹
ÈÈÈ
Ê" %Ê Ê Ê
Step 2: x 23 x 23 23 x 23.kkÊÊ$$ $$ $
Then 23 16 7, or 23 32 9; thus 7.œÊœ œÊœ œ$$$$$
21. Step 1: 0.05 0.05 0.05 0.2 0.3 x or x 5.
¸¸
"" "" "
#x4 x4 x 3 3
10 10 10
Ê Ê Ê
Step 2: x 4 x 4 4 x 4.kk Ê Ê$$ $$ $
Then or , or 4 5 or 1; thus .%œ œ œ œ œ$$$$$
10 2 2
33 3
22. Step 1: x 3 .1 0.1 x 3 0.1 2.9 x 3.1 2.9 x 3.1kk ÈÈ
###
!Ê Ê Ê
Step 2: x 3 x 3 3 x 3.
¹¹
ÈÈÈÈ
ÊÊ$$ $$ $
Then 3 2.9 3 2.9 0.0291, or 3 3.1 3.1 3 0.0286;œÊœ¸ œÊœ¸$$ $$
ÈÈ ÈÈ ÈÈ È È
thus 0.0286.$œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 2.3 Precise Definition of a Limit 81
23. Step 1: x 4 0.5 0.5 x 4 0.5 3.5 x 4.5 3.5 x 4.5 4.5 x 3.5,kk kk
ÈÈÈÈ
###
Ê Ê Ê Ê
for x near 2.
Step 2: x ( 2) x 2 x 2.kk Ê Ê#$$ $$ $
Then 4.5 4.5 0.1213, or 3.5 3.5 0.1292; #œ Ê œ #¸ #œ Ê œ# ¸$$ $$
ÈÈ È È
thus 4.5 2 0.12.$œ¸
È
24. Step 1: ( 1) 0.1 0.1 1 0.1 x or x .
¸¸
"""
x x 10x10119911
11 910101010
Ê Ê Ê
Step 2: x ( 1) x 1 x .kk Ê Ê " "$$ $$ $
Then , or ; thus . "œ Ê œ "œ Ê œ œ$$$$$
10 10
9 9 11 11 11
"""
25. Step 1: x 5 11 x 16 1 x 16 1 15 x 17 15 x 17.kkkkab ÈÈ
## ##
"Ê Ê" Ê Ê
Step 2: x4 x4 x .kk Ê Ê % %$$ $$ $
Then 15 15 0.1270, or 17 17 0.1231; %œ Ê œ% ¸ %œ Ê œ %¸$$ $$
ÈÈ ÈÈ
thus 17 4 0.12.$œ¸
È
26. Step 1: 5 1 4 6 30 x 20 or 20 x 30.
¸¸
120 120 120 x
x x x 4 120 6
"Ê" & Ê Ê Ê
""
Step 2: x 24 x 24 24 x 24.kkÊÊ$$ $$ $
Then 24 20 4, or 24 30 6; thus 4.œÊœ œÊœ Êœ$$$$$
27. Step 1: mx 2m 0.03 0.03 mx 2m 0.03 0.03 2m mx 0.03 2m kk Ê Ê Ê
2x2.
0.03 0.03
mm
Step 2: x2 x2 x .kk Ê Ê # #$$ $$ $
Then , or . In either case, .#œ# Ê œ #œ# Ê œ œ$$$$ $
0.03 0.03 0.03 0.03 0.03
mm mm m
28. Step 1: mx 3m c c mx 3m c c 3m mx c 3m 3 x 3kk ÊÊ Ê
cc
mm
Step 2: x3 x3 .kk Ê Ê $B $$$ $$ $
Then , or . In either case, .$œ$ Ê œ $œ$ Ê œ œ$$$$ $
cc cc c
mm mm m
29. Step 1: (mx b) b c mx c c mx c x .
¸¸ˆ‰
-Ê Ê Ê
mmmmcc
mm######
""
Step 2: x x x.
¸¸
ÊÊ
""""
####
$$ $$ $
Then , or . In either case, .œ Ê œ œ Ê œ œ$$$$ $
"" ""
## ##
cc cc c
mm mm m
30. Step 1: (mx b) (m b) 0.05 0.05 mx m 0.05 0.05 m mx 0.05 mkk Ê Ê
1x .Ê "
0.05 0.05
mm
Step 2: x1 x1 x .kk Ê Ê " "$$ $$ $
Then , or . In either case, ."œ" Ê œ "œ" Ê œ œ$$$$ $
0.05 0.05 0.05 0.05 0.05
mm mm m
31. lim (3 2x) 3 2(3) 3
x3Äœ œ
Step 1: 3 2x ( 3) 0.02 0.02 6 2x 0.02 6.02 2x 5.98 3.01 x 2.99 orkkab Ê Ê Ê
2.99 x 3.01.
Step 2: 0 x 3 x 3 x . Ê Ê $ $kk$$ $$ $
Then 2.99 0.01, or 3.01 0.01; thus 0.01.$œ Ê œ $œ Ê œ œ$$$$$
32. lim ( 3x ) ( 3)( 1) 2 1
x1Ä #œœ
Step 1: ( 3x 2) 1 0.03 0.03 3x 3 0.03 0.01 x 1 0.01 1.01 x 0.99.kk Ê Ê Ê
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

82 Chapter 2 Limits and Continuity
Step 2: x ( 1) x 1 x 1.kk Ê Ê"$$ $$ $
Then 1.01 0.01, or 0.99 0.01; thus 0.01. "œ Ê œ "œ Ê œ œ$$$$$
33. lim lim lim (x 2) 4, x 2
xx xÄ# Ä# Ä#
x4
x(x2)
(x 2)(x 2)
#
œœœ##œÁ
Step 1: 4 0.05 0.05 0.05 3.95 x 2 4.05, x 2
¹¹Š‹
x4
x2 (x2)
(x 2)(x 2)
Ê % Ê Á
1.95 x 2.05, x 2.Ê Á
Step 2: x2 x2 x 2.kk Ê Ê # $$ $$ $
Then 1.95 0.05, or 2.05 0.05; thus 0.05.#œ Ê œ #œ Ê œ œ$$$$$
34. lim lim lim (x 1) 4, x 5.
xx xÄ& Ä& Ä&
x6x5
x5 (x5)
(x 5)(x 1)
œœœÁ
Step 1: ( 4) 0.05 0.05 4 0.05 4.05 x 1 3.95, x 5
¹¹Š‹
x6x5
x5 (x5)
(x 5)(x )
"
Ê Ê Á
5.05 x 4.95, x 5.Ê Á
Step 2: x ( 5) x 5 x .kk Ê Ê & &$$ $$ $
Then 5.05 0.05, or 4.95 0.05; thus 0.05. &œ Ê œ &œ Ê œ œ$$$$$
35. lim 1 5x 1 5( 3) 16 4
xÄ$ÈÈ
È
œ œ œ
Step 1: 1 5x 4 0.5 0.5 1 5x 4 0.5 3.5 1 5x 4.5 12.25 1 5x 20.25
¹¹
ÈÈÈ
ÊÊÊ
11.25 5x 19.25 3.85 x 2.25.ÊÊ
Step 2: x ( 3) x 3 x .kk Ê Ê $ $$$ $$ $
Then 3.85 0.85, or 2.25 0.75; thus 0.75. $œ Ê œ $œ Ê œ$$$ $
36. lim 2
xÄ#
44
xœœ
#
Step 1: 2 0.4 0.4 2 0.4 1.6 2.4 x or x .
¸¸
4 4 4 10x10 10 105 5
x x x 16424 4 6 3 2
Ê Ê Ê Ê
Step 2: x2 x2 x .kk Ê Ê # #$$ $$ $
Then , or ; thus .#œ Ê œ #œ Ê œ œ$$$$$
55
33 3
"""
##
37. Step 1: (9 x) 5 4 x 4 x 4 x 4 x 4 .kk ÊÊÊ%Ê%%% %% % % % % %
Step 2: x4 x4 x .kk Ê Ê % %$$ $$ $
Then 4 4 , or . Thus choose . œ Ê œ %œ %Ê œ œ$ % $% $ % $% $%
38. Step 1: (3x 7) 2 3x 9 9 3x 3 x 3 .kkÊ Ê *Ê%% % % % %%
33
Step 2: x 3 x 3 3 x 3.kk Ê Ê$$ $$ $
Then 3 , or 3 3 . Thus choose .œ$ Ê œ œ Ê œ œ$$$$ $
%% %% %
33 33 3
39. Step 1: x 5 2 x 5 x 5 ( ) x 5 ( )
¹¹
ÈÈ È
Ê # Ê# # Ê# #%% % % % % %
##
() x()5.Ê#&#%%
##
Step 2: x 9 x 9 9 x 9.kk Ê Ê$$ $$ $
Then , or . Thus choose *œ % * Ê œ% *œ % * Ê œ% $%% $%%$%% $%%
####
the smaller distance, .$%%œ% #
40. Step 1: 4 x 2 4 x 4 x ( ) x ( )
¹¹
ÈÈ È
Ê # Ê# # Ê# %#%% % % % % %
##
()x4() () x().Ê # # Ê # % # %%%%%
####
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 2.3 Precise Definition of a Limit 83
Step 2: x 0 x .kkÊ$$ $
Then ( ) 4 , or ( ) 4 4 . Thus choose œ# œ % Ê œ% œ# œ $% %%$%%$% %%
## # # #
the smaller distance, 4 .$%%œ
#
41. Step 1: For x 1, x 1 x x 1 x 1Á Ê "Ê" "Ê kk kk
ÈÈ
## #
%% % % % % %
x 1 near .Ê " Bœ"
ÈÈ
%%
Step 2: x1 x1 x .kk Ê Ê " "$$ $$ $
Then 1 1 , or 1 1. Choose"œ Êœ" œ"Êœ"$%$%$%$%
ÈÈ
ÈÈ
min 1 1 , that is, the smaller of the two distances.$%%œ"ß"
š›
ÈÈ
42. Step 1: For x 2, x 4 x 4 4 x 4 4 x 4Á Ê Ê Ê kk kk
ÈÈ
## #
%% % % % % %
4 x 4 near 2.Ê Bœ
ÈÈ
%%
Step 2: x ( 2) x 2 2 x 2.kk Ê Ê$$ $$ $
Then 2 , or . Choose œ % Ê œ % # #œ % Ê œ# %$%$%$%$%
ÈÈ ÈÈ
min .$% %œ % #ß# %
š›
ÈÈ
43. Step 1: 1 x .
¸¸
"" """
xx x11
Ê " Ê" " Ê %% % % % %%
Step 2: x1 x1 x .kk Ê Ê" "$$ $ $ $
Then , or ." œ Ê œ" œ " œ Ê œ "œ$$ $$
"" ""
" " " " " "%%%%%%
%%
Choose , the smaller of the two distances.$œ%
%"
44. Step 1: x
¸¸
"" "" " " " " $
"$ "$
#
x3 x3 3 x 3 3 x 3
13 1 3 3
ÊÊÊ Ê %% % % % %%
%%
x , or x for x near .Ê $
ÉÉ
kk ÉÉ
È
3333
1$ "$ "$ "$%%%%
Step 2: x3 x3 3 x 3.
¹¹
ÈÈÈÈ
ÊÊ$$ $ $ $
Then 3 3 , or 3 3.
ÈÈÈ È
ÉÉ
ÉÉ
œ Ê œ œ Ê œ $$ $$
3333
"$ "$ "$ "$%%%%
Choose min 3 3 .$ϧ
š›
ÈÈ
ÉÉ
33
"$ "$%%
45. Step 1: ( 6) (x 3) 6 , x 3 x 3 x .
¹¹Š‹
x
x3
*
Ê Á Ê Ê $ $%% % % %% %
Step 2: x ( 3) x 3 x 3.kk Ê Ê$$$ $$ $
Then , or . Choose . $œ $ Ê œ $œ $ Ê œ œ$ % $% $ % $% $%
46. Step 1: 2 (x 1) 2 , x 1 x .
¹¹Š‹
x1
x1
Ê ÁÊ""%% % % %
Step 2: x1 x1 x .kk Ê Ê" "$$ $ $ $
Then , or . Choose ." œ" Ê œ " œ" Ê œ œ$ % $% $ % $% $%
47. Step 1: x 1: (4 2x) 2 2 2x since x 1 Thus, 1 x ;l lÊ! Þ !%% %
#
x 1: (6x 4) 2 6x 6 since x 1. Thus, x 1 .llÊ!Ÿ "Ÿ%% %
6
Step 2: x1 x1 x1 .kk Ê Ê"$$ $ $ $
Then 1 , or 1 . Choose . œ" Ê œ " œ Ê œ œ$$$$ $
%% %% %
## 66 6
48. Step 1: x : 2x 0 2x x 0;! Ê !Ê kk%% %
#
x0: x .!Ê!Ÿ#
¸¸
x
#%%
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

84 Chapter 2 Limits and Continuity
Step 2: x 0 x .kkÊ$$ $
Then , or . Choose .œ Ê œ œ# Ê œ# œ$ $ $% $% $
%% %
## #
49. By the figure, x x sin x for all x 0 and x x sin x for x 0. Since lim ( x) lim x 0,Ÿ Ÿ œ œ
""
xx
xxÄ! Ä!
then by the sandwich theorem, in either case, lim x sin 0.
xÄ!
"
xœ
50. By the figure, x x sin x for all x except possibly at x 0. Since lim x lim x 0, thenŸ Ÿ œ œ œ
## # # #
"
xxxÄ! Ä!
ab
by the sandwich theorem, lim x sin 0.
xÄ!
#"
xœ
51. As x approaches the value 0, the values of g(x) approach k. Thus for every number 0, there exists a %$!
such that x 0 g(x) k .!Ê kk k k$%
52. Write x h c. Then x c x c , x c h c c , h c cœ !l l Í Á Í Á$$ $ $ $ab
h, h h .Í Á!Í!l !l$$ $
Thus, f x L for any , there exists such that f x L whenever x clim
xcÄab abœ Í ! ! l l !l l%$ % $
f h c L whenever h f h c L.Íl l !l !l Í œab ab%$lim
hÄ!
53. Let f(x) x . The function values do get closer to 1 as x approaches 0, but lim f(x) 0, not 1. Theœœ
#
xÄ!
function f(x) x never gets to 1 for x near 0.œ
#arbitrarily close
54. Let f(x) sin x, L , and x 0. There exists a value of x (namely, x ) for which sin x for anyœœ œ œ
" "
# #
!
1
6¸¸
%
given 0. However, lim sin x 0, not . The wrong statement does not require x to be arbitrarily close to%œ
xÄ!
"
#
x . As another example, let g(x) sin , L , and x 0. We can choose infinitely many values of x near 0
!!
""
#
œœ œ
x
such that sin as you can see from the accompanying figure. However, lim sin fails to exist. The
"" "
#x x
œxÄ!
wrong statement does not require values of x arbitrarily close to x 0 to lie within 0 of L . Againall !"
#
œœ%
you can see from the figure that there are also infinitely many values of x near 0 such that sin 0. If we
"
xœ
choose we cannot satisfy the inequality sin for all values of x sufficiently near x 0.%%œ
"""
#!
4x
¸¸
55. A 0.01 0.01 9 0.01 8.99 9.01 (8.99) x (9.01)kk ˆ‰
*ŸÊŸ ŸÊŸŸÊ ŸŸ1xx44
4#
##
1
11
2 x 2 or 3.384 x 3.387. To be safe, the left endpoint was rounded up and the rightÊŸŸ ŸŸ
ÉÉ
8.99 9.01
11
endpoint was rounded down.
56. V RI I 5 0.1 0.1 5 0.1 4.9 5.1 œÊœÊŸ ÊŸŸ Ê ŸŸ ÊÊ
V V 120 120 10 R 10
R R R R 49 1 0 51
¸¸ #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 2.3 Precise Definition of a Limit 85
R 23.53 R 24.48.
(120)(10) (120)(10)
51 49
ŸŸ Ê ŸŸ
To be safe, the left endpoint was rounded up and the right endpoint was rounded down.
57. (a) x 1 0 x 1 f(x) x. Then f(x) 2 x 2 2 x 2 1 1. That is, Ê" Ê œ œ œœ$$ kkkk
f(x) 2 1 no matter how small is taken when x 1 lim f(x) 2.kk "Ê Á
"
#$$
x1Ä
(b) 0 x 1 x f(x) x 1. Then f(x) 1 (x 1) 1 x x 1. That is, Ê"" Ê œ œ œ œ$$ kkk kkk
f(x) 1 1 no matter how small is taken when x lim f(x) 1.kk ""Ê Á$$
x1Ä
(c) x 1 x 1 f(x) x. Then f(x) 1.5 x 1.5 1.5 x 1.5 1 0.5.!Ê"Ê œ œ œœ$$ kkkk
Also, x 1 1 x f(x) x 1. Then f(x) 1.5 (x 1) 1.5 x 0.5! Ê " Ê œ œ œ $$ kkk kkk
x 0.5 0.5 0.5. Thus, no matter how small is taken, there exists a value of x such thatœ " œ $
x 1 but f(x) 1.5 lim f(x) 1.5. Ê Á$$kk
"
#x1Ä
58. (a) For 2 x 2 h(x) 2 h(x) 4 2. Thus for 2, h(x) 4 whenever 2 x 2 no Ê œ Ê œ $%%$kk kk
matter how small we choose 0 lim h(x) 4.$Ê Á
xÄ#
(b) For 2 x 2 h(x) 2 h(x) 3 1. Thus for 1, h(x) 3 whenever 2 x 2 no Ê œ Ê œ $%%$kk kk
matter how small we choose 0 lim h(x) 3.$Ê Á
xÄ#
(c) For 2 x 2 h(x) x so h(x) 2 x 2 . No matter how small 0 is chosen, x is close to 4 Ê œ œ $$
## #
kkkk
when x is near 2 and to the left on the real line x 2 will be close to 2. Thus if 1, h(x) 2Ê kk k k
#%%
whenever 2 x 2 no mater how small we choose 0 lim h(x) 2. Ê Á$$
xÄ#
59. (a) For 3 x 3 f(x) 4.8 f(x) 4 0.8. Thus for 0.8, f(x) 4 wheneverÊ Ê $%%kk kk
3 x 3 no matter how small we choose 0 lim f(x) 4. Ê Á$$
xÄ$
(b) For 3 x 3 f(x) 3 f(x) 4.8 1.8. Thus for 1.8, f(x) 4.8 whenever 3 x 3 Ê Ê $%%$kk kk
no matter how small we choose 0 lim f(x) 4.8.$Ê Á
xÄ$
(c) For 3 x 3 f(x) 4.8 f(x) 3 1.8. Again, for 1.8, f(x) 3 whenever x 3 Ê Ê $$%%$kk kk
no matter how small we choose 0 lim f(x) 3.$Ê Á
xÄ$
60. (a) No matter how small we choose 0, for x near 1 satisfying x , the values of g(x) are$$$""
near 1 g(x) 2 is near 1. Then, for we have g(x) 2 for some x satisfyingÊ œ kk kk%""
##
x , or x 1 lim g(x) 2."" !Ê Á$$ $kk x1Ä
(b) Yes, lim g(x) 1 because from the graph we can find a such that g(x) 1 if x ( 1) .
x1Ä œ!!$%$kk kk
61-66. Example CAS commands (values of del may vary for a specified eps):
:Maple
f := x -> (x^4-81)/(x-3);x0 := 3;
plot( f(x), x=x0-1..x0+1, color=black, # (a)
title="Section 2.3, #61(a)" );
L := limit( f(x), x=x0 ); # (b)
epsilon := 0.2; # (c)
plot( [f(x),L-epsilon,L+epsilon], x=x0-0.01..x0+0.01,
color=black, linestyle=[1,3,3], title="Section 2.3, #61(c)" );
q := fsolve( abs( f(x)-L ) = epsilon, x=x0-1..x0+1 ); # (d)
delta := abs(x0-q);
plot( [f(x),L-epsilon,L+epsilon], x=x0-delta..x0+delta, color=black, title="Section 2.3, #61(d)" );
s in [0.1, 0.005, 0.001 ] do # (e)for ep
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

86 Chapter 2 Limits and Continuity
q := fsolve( abs( f(x)-L ) = eps, x=x0-1..x0+1 );
delta := abs(x0-q);
head := sprintf("Section 2.3, #61(e)\n epsilon = %5f, delta = %5f\n", eps, delta );
print(plot( [f(x),L-eps,L+eps], x=x0-delta..x0+delta,
color=black, linestyle=[1,3,3], title=head ));
end do:
(assigned function and values for x0, eps and del may vary):Mathematica
Clear[f, x]
y1: L eps; y2: L eps; x0 1;œ œ œ
f[x_]: (3x (7x 1)Sqrt[x] 5)/(x 1)œ
2
Plot[f[x], {x, x0 0.2, x0 0.2}]
L: Limit[f[x], x x0]π
eps 0.1; del 0.2;œœ
Plot[{f[x], y1, y2},{x, x0 del, x0 del}, PlotRange {L 2eps, L 2eps}] Ä
2.4 ONE-SIDED LIMITS AND LIMITS AT INFINITY
1. (a) True (b) True (c) False (d) True
(e) True (f) True (g) False (h) False
(i) False (j) False (k) True (l) False
2. (a) True (b) False (c) False (d) True
(e) True (f) True (g) True (h) True
(i) True (j) False (k) True
3. (a) lim f(x) , lim f(x)
xx
Ä# Ä#
œ "œ# œ$#œ"
2
#
(b) No, lim f(x) does not exist because lim f(x) lim f(x)
xx
x
Ä# Ä#
Ä# Á
(c) lim f(x) 1 3, lim f(x)
xx
Ä% Ä%
œœ œ"œ$
44
##
(d) Yes, lim f(x) 3 because 3 lim f(x) lim f(x)
xx
x
Ä% Ä% Ä%
œœœ
4. (a) lim f(x) 1, lim f(x) , f(2) 2
xx
Ä# Ä#
œ œ œ$#œ" œ
2
#
(b) Yes, lim f(x) 1 because lim f(x) lim f(x)
xx
x
Ä# Ä#
Ä#
œ"œ œ
(c) lim f(x) 3 ( 1) 4, lim f(x) 3 ( 1) 4
xx
Ä" Ä"
œœ œœ
(d) Yes, lim f(x) 4 because 4 lim f(x) lim f(x)
xx
x
Ä" Ä" Ä"
œœ œ
5. (a) No, lim f(x) does not exist since sin does not approach any single value as x approaches 0
xÄ! ˆ‰
"
x
(b) lim f(x) lim 0 0
xxÄ! Ä!
œœ
(c) lim f(x) does not exist because lim f(x) does not exist
xx
Ä! Ä!
6. (a) Yes, lim g(x) 0 by the sandwich theorem since x g(x) x when x 0Yes, lim g(x) 0
xx Ä!!Ä œœŸŸ
ÈÈ
(b) No, lim g(x) does not exist since x is not defined for x 0
xÄ! È
(c) No, lim g(x) does not exist since lim g(x) does not exist
xxÄ! Ä!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
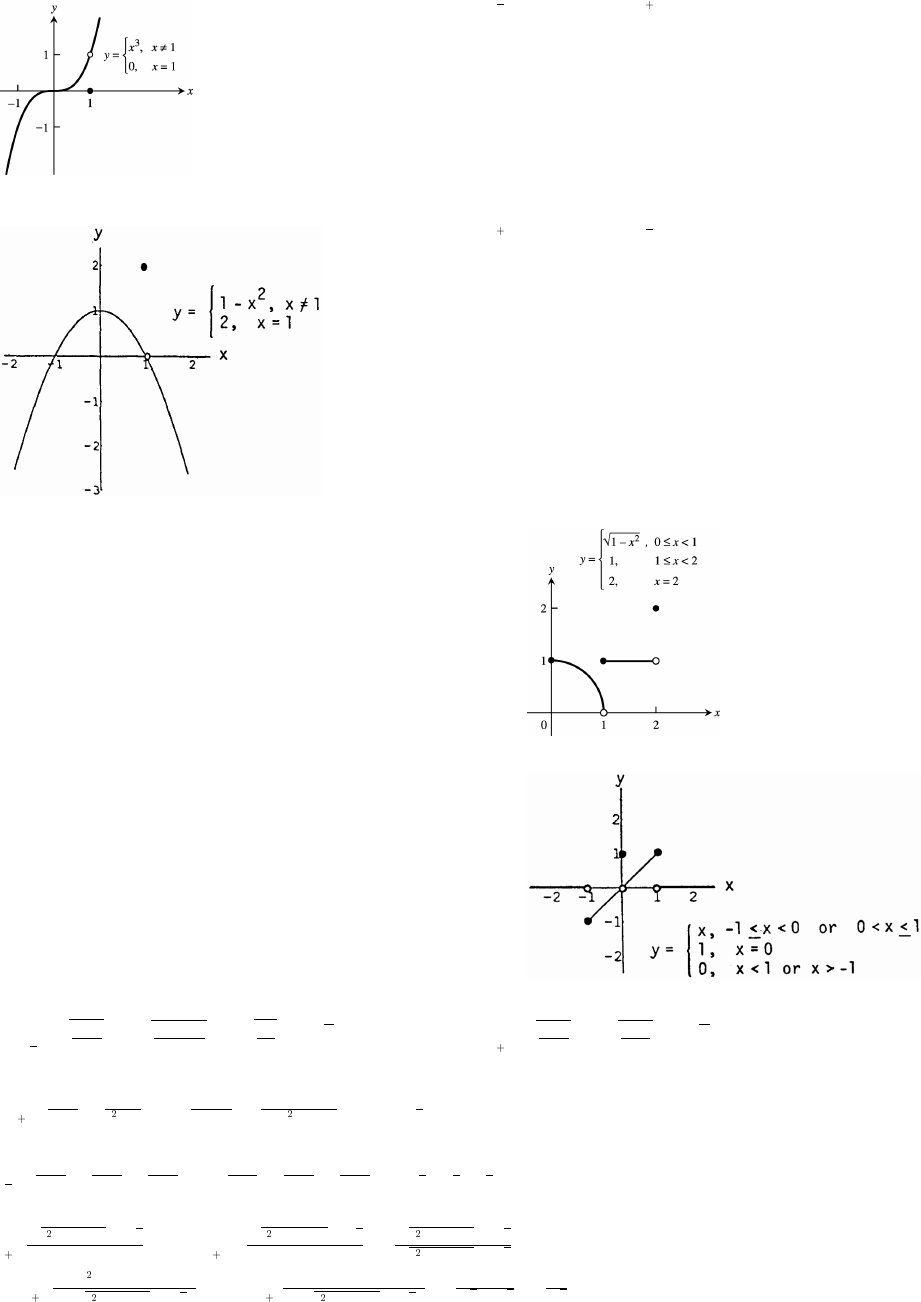
Section 2.4 One-Sided Limits and Limits at Infinity 87
7. (a Ñ(b) lim f(x) lim f(x)
x1 x1
ÄÄ
œ"œ
(c) Yes, lim f(x) 1 since the right-hand and left-hand
x1Ĝ
limits exist and equal 1
8. (a) (b) lim f(x) 0 lim f(x)
x1 x1
ÄÄ
œœ
(c) Yes, lim f(x) 0 since the right-hand and left-hand
x1Ĝ
limits exist and equal 0
9. (a) domain: 0 x 2ŸŸ
range: 0 y 1 and y 2Ÿ œ
(b) lim f(x) exists for c belonging to
xcÄ
(0 1) ( )ß "ß #
(c) x 2œ
(d) x 0œ
10. (a) domain: x_ _
range: y 1" Ÿ Ÿ
(b) lim f(x) exists for c belonging to
xcÄ
( 1)( )( )_ß "ß " "ß _
(c) none
(d) none
11. lim 3 12. lim 0
xx1
Ä!Þ& Ä
ÉÉÉ
ÉÈÈ
É
x2 0.52 3/2 x 11
x1 0.51 1/2 x
"
# "#
œœœ œœœ!
13. lim (2) 1
xÄ# ˆ‰ˆ‰ˆ ‰ ˆ‰
Š‹
x2x5 2
x1 x x ( ) (2)
2( 2) 5
#" # #
"
œœœ
14. lim 1
x1Ĉ‰ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰
" " "
#x1 x 7 11 1 7 1 7
x6 3x 16 31 7 2
œœœ
15. lim lim
hhÄ! Ä!
ÈÈÈ
ÈÈÈ
ÈÈ
h4h5 5 h4h5 5 h4h5 5
hh
h4h5 5
œŠ‹Š‹
lim lim œœœœ
hhÄ! Ä!
ab
Š‹Š‹
ÈÈ
ÈÈ
ÈÈ È
h4h55
hh4h5 5 hh4h5 5
h(h 4) 04 2
55 5
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
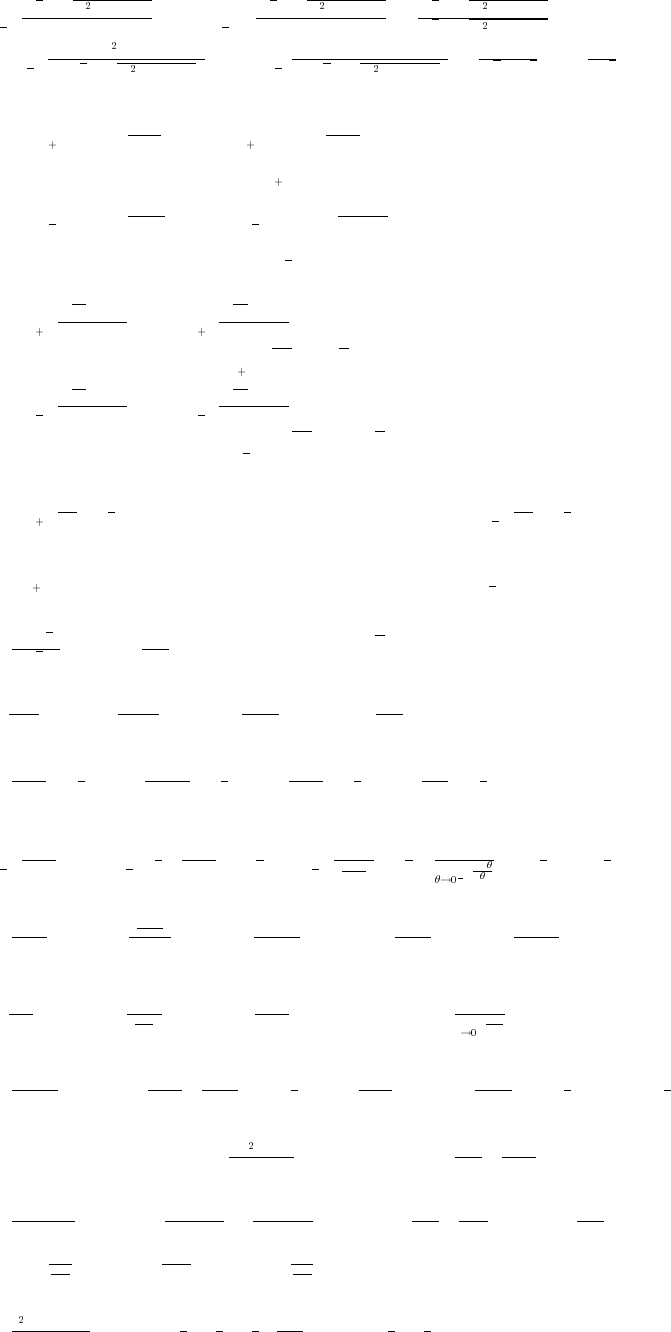
88 Chapter 2 Limits and Continuity
16. lim lim
hhÄ! Ä!
ÈÈÈ
ÈÈÈ
ÈÈ
6 5h 11h 6 6 5h 11h 6 6 5h 11h 6
hh
6 5h 11h 6
œŠ‹Š‹
lim lim œœœœ
hhÄ! Ä!
6 5h 11h 6
h 6 5h 11h 6 h 6 5h 11h 6
h(5h 11) (0 11)
66 26
11
ab
Š‹Š‹
ÈÈ
ÈÈ
ÈÈ È
17. (a) lim (x 3) lim (x 3) x 2 x 2 for x 2
xxÄ# Ä#
œ œ
kkx2
x2 (x )
(x 2)
#
abkk
lim (x 3) ( 2) 3 1œœœ
xÄ#
(b) lim (x 3) lim (x 3) x 2 (x 2) for x 2
xxÄ# Ä#
œ œ
kkx2
x2 (x )
(x 2)
#
’“ abkk
lim (x 3)( 1) ( 2 3) 1œœœ
xÄ#
18. (a) lim lim x 1 x 1 for x 1
x1 x1ÄÄ
ÈÈ
kk
2x (x 1) 2x (x 1)
x1 (x1)
œœabkk
lim 2x 2œœ
x1ÄÈÈ
(b) lim lim x 1 (x 1) for x 1
x1 x1ÄÄ
ÈÈ
kk
2x (x 1) 2x (x 1)
x1 (x1)
œœabkk
lim 2x 2œœ
x1ÄÈÈ
19. (a) lim 1 (b) lim
))
Ä$ Ä$
ÚÛ ÚÛ) )
) )
œœ œ
3 2
3 3
20. (a) lim t t 4 4 0 (b) lim t t 4 3 1
tt
Ä% Ä%
ab abÚÛœœ ÚÛœœ
21. lim lim 1 (where x 2 )
)Ä! Ä!
sin 2
2
sin x
x
È
È)
)œœ œ
xÈ)
22. lim lim lim k lim k 1 k (where kt)
ttÄ! Ä! Ä! Ä!
sin kt k sin kt k sin sin
tkt
œœœ œœ œ
))
))
))
†)
23. lim lim lim lim (where 3y)
yy yÄ! Ä! Ä! Ä!
sin 3y 3 sin 3y sin 3y
4y 4 3y 4 3y 4 4
33sin 3
œœœœ œ
"
)
)
))
24. lim lim lim 1 (where 3h)
hh hÄ! Ä! Ä!
h3h
sin 3h 3 sin 3h 3 3 3 3
lim
œœœœœœ
ˆ‰ Œ
"""""""
††
ˆ‰
sin 3h
3h
sin )
25. lim lim lim lim lim 1 2 2
xx x x xÄ! Ä! Ä! Ä! Ä!
tan 2x sin 2x 2 sin 2x
x x x cos 2x cos 2x x
œœ œ œœ
ˆ‰
sin 2x
cos 2x Š‹Š ‹
"
#†
26. lim 2 lim 2 lim 2 lim cos t 2 2
tt t tÄ! Ä! Ä! Ä!
2t t t cos t
tan t sin t lim
œœœ œ""œ
ˆ‰
sin t sin t
cos t t
Š‹
Œ
"
t
††
27. lim lim lim lim 1 (1)
xx xxÄ! Ä! Ä! Ä!
x csc 2x x 2x
cos 5x sin 2x cos 5x sin 2x cos 5x
œœ œœ
ˆ‰ ˆ‰
Š‹Š‹
††
"" "" "
###
28. lim 6x (cot x)(csc 2x) lim lim 3 cos x 3 1 3
xxxÄ! Ä! Ä!
#œœ œ"œ
6x cos x x 2x
sin x sin 2x sin x sin 2x
ˆ‰
†† ††
29. lim lim lim lim
xx x xÄ! Ä! Ä! Ä!
x x cos x x x cos x x x
sin x cos x sin x cos x sin x cos x sin x cos x sin x
"
œœ
ˆ‰ˆ‰
†
lim lim lim (1)(1) 1 2œœœ
xx xÄ! Ä! Ä!
Š‹ Š‹
ˆ‰
"" "
sin x sin x
xx
†cos x
30. lim lim 0 (1) 0
xxÄ! Ä!
x x sin x x sin x
xx
"" ""
# ### ##
œ œœ
ˆ‰ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 2.4 One-Sided Limits and Limits at Infinity 89
31. lim lim 1 since 1 cos t 0 as t 0
tÄ! Ä!
sin(1 cos t)
1cos t
sin
œœœÄÄ
)
)
))
32. lim lim 1 since sin h 0 as h 0
hÄ! Ä!
sin (sin h)
sin h
sin
œœœÄÄ
)
)
))
33. lim lim lim 1 1
)) )Ä! Ä! Ä!
sin sin 2 sin 2
sin 2 sin 2 sin 2
))) ))
))) ))
œœ œœ
ˆ‰ ˆ ‰
††††
## # #
"""
34. lim lim lim 1 1
xx xÄ! Ä! Ä!
sin 5x sin 5x 4x 5 5 sin 5x 4x 5 5
sin 4x sin 4x 5x 4 4 5x sin 4x 4 4
œœ œœ
ˆ‰ˆ‰
†† † ††
35. lim lim lim
xx xÄ! Ä! Ä!
tan 3x sin 3x sin 3x 8x 3
sin 8x cos 3x sin 8x cos 3x sin 8x 3x 8
œœ
ˆ‰ˆ ‰
††††
""
lim 1 1 1œœœ
3 sin 3x 8x 3 3
8 cos 3x 3x sin 8x 8 8
xÄ! ˆ‰ˆ‰ˆ‰
"†††
36. lim lim lim
yy yÄ! Ä! Ä!
sin 3y cot 5y sin 3y sin 4y cos 5y sin 3y sin 4y cos 5y 3
y cot 4y y cos 4y sin 5y y cos 4y sin 5y
œœ
Š‹Š‹Š‹Š‹
††
††
45y
345y
lim 1111œœœ
yÄ! Š‹Š‹Š‹Š‹
ˆ‰
sin 3y sin 4y 5y cos 5y
3y 4y sin 5y cos 4y 5 5 5
3 4 12 12†††††
Note: In these exercises we use the result lim 0 whenever 0. This result follows immediately from
xĄ_
"
x
m
n
mn œ
Example 6 and the power rule in Theorem 8: lim lim lim 0 0.
xx xĄ_ Ą_ Ą_
ˆ‰ ˆ‰ Š‹
"" "
xx x
mn œœ œœ
mn mn mn
37. (a) 3 (b) 3
38. (a) (b) 11
39. (a) (b)
" "
# #
40. (a) (b)
" "
8 8
41. (a) (b)
5 5
3 3
42. (a) (b)
3 3
4 4
43. lim 0 by the Sandwich TheoremŸ Ÿ Ê œ
""
xxx x
sin 2x sin 2x
xÄ_
44. lim 0 by the Sandwich TheoremŸ Ÿ Ê œ
""
333 3
cos cos
))) )
))
)Ä_
45. lim lim 1
ttÄ_ Ä_
2tsin t 010
tcos t 10
1
1
œœœ
2sin t
tt
cos t
t
ˆ‰
ˆ‰
46. lim lim lim
rr rÄ_ Ä_ Ä_
rsin r 10
2r75 sin r 200
1
25
"
#
œœœ
ˆ‰
ˆ‰
sin r
r
7sin r
rr
47. (a) lim lim (b) (same process as part (a))
xxÄ_ Ä_
2x 3 2 2
5x 7 5 5
2
5
œœ
3
x
7
x
48. (a) lim lim 2
xxÄ_ Ä_
2x 7
xxx7
2
1
œœ
Š‹
7
x
xxx
7
(b) 2 (same process as part (a))
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
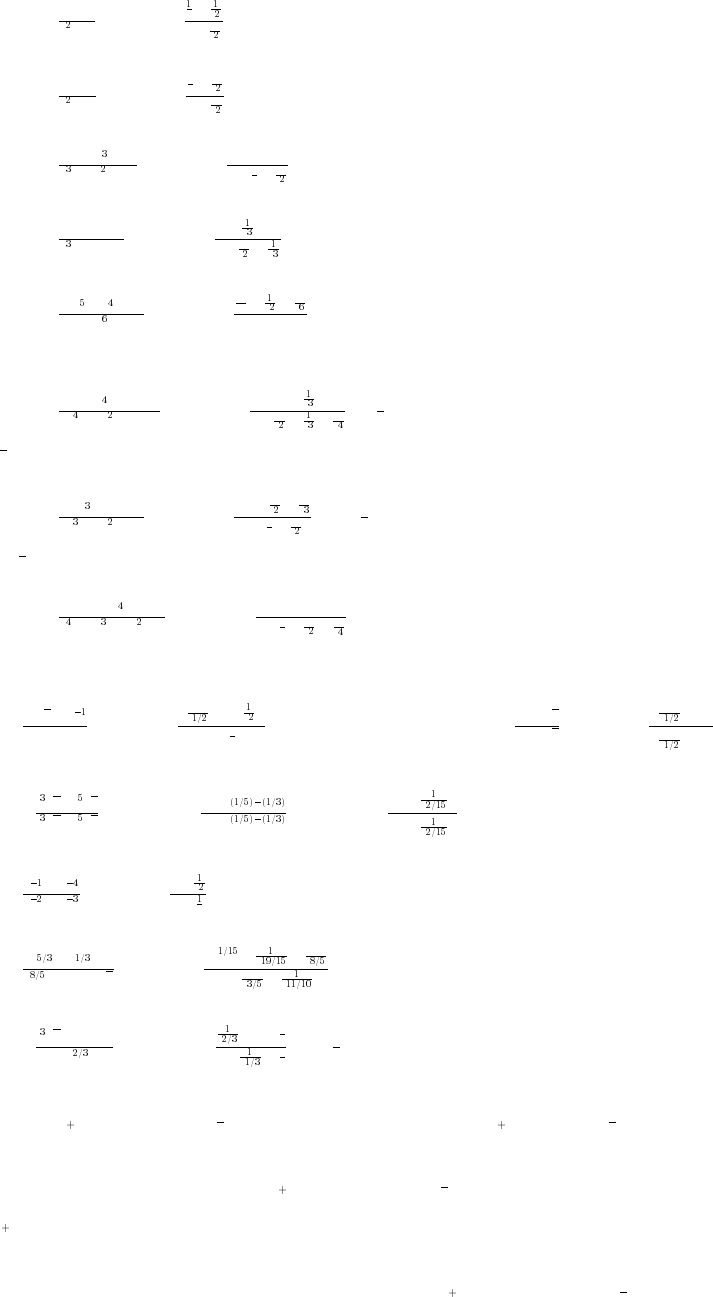
90 Chapter 2 Limits and Continuity
49. (a) lim lim 0 (b) 0 (same process as part (a))
xxÄ_ Ä_
x1
x3 1
œœ
xx
3
x
50. (a) lim lim 0 (b) 0 (same process as part (a))
xxÄ_ Ä_
3x 7
x2 1
œœ
37
xx
2
x
51. (a) lim lim (b) 7 (same process as part (a))
xxÄ_ Ä_
7x 7
x3x6x 1
œœ(
36
xx
52. (a) lim lim (b) 0 (same process as part (a))
xxÄ_ Ä_
"
x4x1 1
œœ!
x
4
xx
53. (a) lim lim 0
xxÄ_ Ä_
10xx31
x1
œœ
10 31
xxx
(b) 0 (same process as part (a))
54. (a) lim lim
xxÄ_ Ä_
9x x 9
2x 5x x 6
9
2
#
œœ
x
56
xxx
(b) (same process as part (a))
9
#
55. (a) lim lim
xxÄ_ Ä_
2x 2x 3 2
3x 3x 5x 3
2
3
œœ
23
xx
35
xx
(b) (same process as part (a))2
3
56. (a) lim lim 1
xxÄ_ Ä_
"
x
x7x7x9 1
œœ
77 9
xxx
(b) 1 (same process as part (a))
57. lim lim 0 58. lim lim 1
xx xxÄ_ Ä_ Ä_ Ä_
2xx 2 x
3x 7 32x 1
È È
Š‹Š‹ Š‹
ÈŠ‹
"
œœ œœ
2 2
x x
x
7
x2
x
59. lim lim lim 1
xx xÄ_ Ä_ Ä_
ÈÈ
ÈÈ Š‹
Š‹
xx
xx
1x
1x
1
1
œœœ
x
x
60. lim lim
xxÄ_ Ä_
xx
xx
x
1
œœ_
x
x
61. lim lim
xxÄ_ Ä_
2xx7
x3xx 1
2x
Èœœ_
xx
7
3
xx
62. lim lim
xxÄ_ Ä_
Èx5x3
2x x 4
5
2
5
#
œœ
x
3
x
x
4
x
63. Yes. If lim f(x) L lim f(x), then lim f(x) L. If lim f(x) lim f(x), then lim f(x) does not exi
xa xa
xa xa
xa xa
ÄÄ
ÄÄ
ÄÄ
œœ œ Á st.
64. Since lim f(x) L if and only if lim f(x) L and lim f(x) L, then lim f(x) can be found by calculating
xc xc
xc xc
Ä Ä
ÄÄ
œœœ
lim f(x).
xcÄ
65. If f is an odd function of x, then f( x) f(x). Given lim f(x) 3, then lim f(x) .œ œ œ$
xx
Ä! Ä!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 2.4 One-Sided Limits and Limits at Infinity 91
66. If f is an even function of x, then f( x) f(x). Given lim f(x) 7 then lim f(x) 7. However, nothingœ œ œ
xx
Ä# Ä#
can be said about lim f(x) because we don't know lim f(x).
xx
Ä# Ä#
67. Yes. If lim 2 then the ratio of the polynomials' leading coefficients is 2, so lim 2 as well.
x xÄ_ Ä_
f(x) f(x)
g(x) g(x)
œœ
68. Yes, it can have a horizontal or oblique asymptote.
69. At most 1 horizontal asymptote: If lim L, then the ratio of the polynomials' leading coefficients is L, so
xÄ_
f(x)
g(x) œ
lim L as well.
xÄ_
f(x)
g(x) œ
70. lim x x x x lim x x x x lim
xx xÄ_ Ä_ Ä_
ÈÈ
ÈÈ
’“’“
## ##
œ œ†ÈÈ
ÈÈ
ÈÈ
abab
xx xx
xx xx xx xx
xx xx
lim lim 1œœœœ
xxÄ_ Ä_
2x 2 2
xx xx 1111
ÈÈÉÉ
xx
71. For any 0, take N 1. Then for all x N we have that f(x) k k k 0 .%%œ œœkkkk
72. For any 0, take N 1. Then for all y N we have that f(x) k k k 0 .% % œ œœkkkk
73. I (5 5 ) 5 x . Also, x 5 x 5 x . Choose œß Ê & Ê Ê & œ$$%%%$%
È## #
lim x 5 0.ʜ
xÄ& È
74. I ( ) x 4. Also, x x x . Choose œ % ß% Ê % % Ê % Ê % œ$$ % % %$%
È## #
lim x 0.Ê%œ
xÄ% È
75. As x 0 the number x is always negative. Thus, ( 1) 1 0 which is alwaysÄÊÊ
¹¹¸¸
xx
xxkk %%%
true independent of the value of x. Hence we can choose any 0 with x lim 1.$$!Ê œ
xÄ!
x
xkk
76. Since x we have x 2 and x 2 x 2. Then, 0Ä# œ " œ " Ê
kk ¹¹
¸¸
x2 x2
x2 x2kk %%
which is always true so long as x . Hence we can choose any , and thus x# ! # #$$
. Thus, lim 1.Ê" œ
¹¹
x2 x2
x2 x2
kk kk
%
xÄ#
77. (a) lim x 400. Just observe that if 400 x 401, then x 400. Thus if we choose , we have for any
xÄ %!! ÚÛœ ÚÛœ œ"$
number that 400 x 400 x 400 400 400 .%$ %! ÊlÚ Û lœl lœ!
(b) lim x 399. Just observe that if 399 x 400 then x 399. Thus if we choose , we have for any
xÄ %!! ÚÛœ ÚÛœ œ"$
number that 400 x 400 x 399 399 399 .%$ %! ÊlÚ Û lœl lœ!
(c) Since lim x lim x we conclude that lim x does not exist.
xxx
Ä %!! Ä %!! Ä %!!
ÚÛÁ ÚÛ ÚÛ
78. (a) lim f(x) lim x 0 0; x 0 x x for x positive. Choose
xxÄ! Ä!
œ œ œ Ê Ê! œ
ÈÈ È
ȸ¸
%% % % $%
##
lim f(x) 0.ʜ
xÄ!
(b) lim f(x) lim x sin 0 by the sandwich theorem since x x sin x for all x 0.
xxÄ! Ä!
œœ ŸŸÁ
####
""
ˆ‰ ˆ‰
xx
Since x 0 x 0 x whenever x , we choose and obtain x sin 0kkk k kk
Èȸ¸ˆ‰
### #"
œœ œ %%$% %
x
if x 0. $
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

92 Chapter 2 Limits and Continuity
(c) The function f has limit 0 at x 0 since both the right-hand and left-hand limits exist and equal 0.
!œ
79. lim x sin lim sin 1, 80. lim lim 1,
x0x
Ä„_ ÄÄ!
Ä_
"" " " "
xx 11x
cos
1
cos
œœœ œœœœ
))
) )
)
)) )
ˆ‰ ˆ‰
x
x
81. lim lim lim , t
xx
t0
Ä„_ Ä„_ Ä
3x 4 3 4t 3
2x 5 2 5t x
3
2
"
#
œœœœ
4
x
5
xˆ‰
82. lim lim z 1, z
xz
Ä_ Ä!
ˆ‰ ˆ ‰
""
"Î
xx
xz
œœœ
83. lim 3 cos lim (3 2 )(cos ) (3)(1) 3,
x0
Ä„_ Ä
ˆ‰ˆ‰ ˆ‰
œœœœ
2
xx x
""
)
)) )
84. lim cos 1 sin lim 3 cos (1 sin ) (0 1)(1 0) 1,
xÄ_ Ä!
ˆ‰ˆ‰ ˆ‰
ab
3
xx x x
œ œœœ
"" "
#
)
)) ) )
2.5 INFINITE LIMITS AND VERTICAL ASYMPTOTES
1. lim 2. lim
xx
Ä! Ä!
"
3x positive 2x negative
positive positive
5
œ_ œ_
Š‹ Š‹
3. lim 4. lim
xx
Ä# Ä$
3
x 2 negative x 3 positive
positive positive
"
œ_ œ_
Š‹ Š‹
5. lim 6. lim
xx
Ä) Ä&
2x 3x
x 8 positive 2x 10 negative
negative negative
œ_ œ_
Š‹ Š‹
7. lim 8. lim
xx
Ä( Ä!
4
(x 7) positive x (x 1) positive positive
positive negative
"
œ_ œ_
Š‹ Š ‹
†
9. (a) lim (b) lim
xx
Ä! Ä!
2 2
3x 3x
œ_ œ_
10. (a) lim (b) lim
xx
Ä! Ä!
2 2
x x
œ_ œ_
11. lim lim 12. lim lim
xx xxÄ! Ä! Ä! Ä!
44
x x
x x
œœ_ œœ_
ab ab
""
13. lim tan x 14. lim sec x
xx
ÄÄ
ˆ‰ ˆ‰
œ_ œ_
15. lim (1 csc )
)Ä! œ_)
16. lim (2 cot ) and lim (2 cot ) , so the limit does not exist
))
Ä! Ä!
œ_ œ_))
17. (a) lim lim
xxÄ# Ä#
"" "
x 4 (x 2)(x 2) positive positive
œœ_ Š‹
†
(b) lim lim
xxÄ# Ä#
"" "
x 4 (x 2)(x 2) positive negative
œœ_ Š‹
†
(c) lim lim
xxÄ# Ä#
"" "
x 4 (x 2)(x 2) positive negative
œœ_ Š‹
†
(d) lim lim
xxÄ# Ä#
"" "
x 4 (x 2)(x 2) negative negative
œœ_ Š‹
†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 2.5 Infinite Limits and Vertical Asymptotes 93
18. (a) lim lim
xxÄ" Ä"
xx
x 1 (x 1)(x 1) positive positive
positive
œœ_ Š‹
†
(b) lim lim
xxÄ" Ä"
xx
x 1 (x 1)(x 1) positive negative
positive
œœ_ Š‹
†
(c) lim lim
xxÄ" Ä"
xx
x 1 (x 1)(x 1) positive negative
negative
œœ_ Š‹
†
(d) lim lim
xxÄ" Ä"
xx
x 1 (x 1)(x 1) negative negative
negative
œœ_ Š‹
†
19. (a) lim 0 lim
xxÄ! Ä!
x
x x negative
#
"" "
œ œ_ Š‹
(b) lim 0 lim
xxÄ! Ä!
x
x x positive
#
"" "
œ œ_ Š‹
(c) lim 2 2 0
x2ÄÈ
x2
x
##
""
#
"Î$ "Î$
œœœ
(d) lim
x1Ä
x3
x1
###
"" "
œ œ
ˆ‰
20. (a) lim (b) lim
xx
Ä# Ä#
x1 x1
2x 4 positive 2x 4 negative
positive positive
œ_ œ_
Š‹ Š‹
(c) lim lim 0
xxÄ" Ä"
x1 20
2x 4 2x 4 4
(x 1)(x 1)
#
œœœ
†
(d) lim
xÄ!
x1
2x 4 4
"
œ
21. (a) lim lim
xxÄ! Ä!
x3x2
x 2x x (x 2) positive negative
(x 2)(x 1) negative negative
œœ_ Š‹
†
†
(b) lim lim lim , x 2
xx xÄ# Ä# Ä#
x 3x2 x1
x2x x(x2) x 4
(x 2)(x 1)
"
œœœÁ
(c) lim lim lim , x 2
xx xÄ# Ä# Ä#
x 3x2 x1
x2x x(x2) x 4
(x 2)(x 1)
"
œœœÁ
(d) lim lim lim , x 2
xx xÄ# Ä# Ä#
x 3x2 x1
x2x x(x2) x 4
(x 2)(x 1)
"
œœœÁ
(e) lim lim
xxÄ! Ä!
x3x2
x 2x x (x 2) positive negative
(x 2)(x 1) negative negative
œœ_ Š‹
†
†
22. (a) lim lim lim
xx xÄ# Ä# Ä#
x3x2
x 4x x(x )(x 2) x(x ) (4) 8
(x 2)(x ) (x 1)
" "
###
"
œœœœ
(b) lim lim lim
xx xÄ# Ä# Ä#
x3x2
x 4x x(x )(x 2) x(x ) negative positive
(x 2)(x ) (x 1) negative
##
"
œœœ_ Š‹
†
(c) lim lim lim
x0 xx
ÄÄ! Ä!
x3x2
x 4x x(x )(x 2) x(x ) negative positive
(x 2)(x ) (x 1) negative
##
"
œœœ_ Š‹
†
(d) lim lim lim 0
xx xÄ" Ä" Ä"
x3x2 0
x 4x x(x )(x 2) x(x ) (1)(3)
(x 2)(x ) (x 1)
##
"
œœœœ
(e) lim
xÄ!
x
x(x ) positive positive
negative
"
# œ_ Š‹
†
and lim
xÄ!
x
x(x ) negative positive
negative
"
# œ_ Š‹
†
so the function has no limit as x 0.Ä
23. (a) lim 2 (b) lim 2
tt
Ä! Ä!
‘ ‘
œ_ œ_
3 3
t t
24. (a) lim 7 (b) lim 7
tt
Ä! Ä!
‘ ‘
" "
t t
œ_ œ_
25. (a) lim (b) lim
xx
Ä! Ä!
’“ ’“
" "
x(x1) x(x1)
2 2
œ_ œ_
(c) lim (d) lim
xx
Ä" Ä"
’“ ’“
" "
x(x1) x(x1)
2 2
œ_ œ_
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
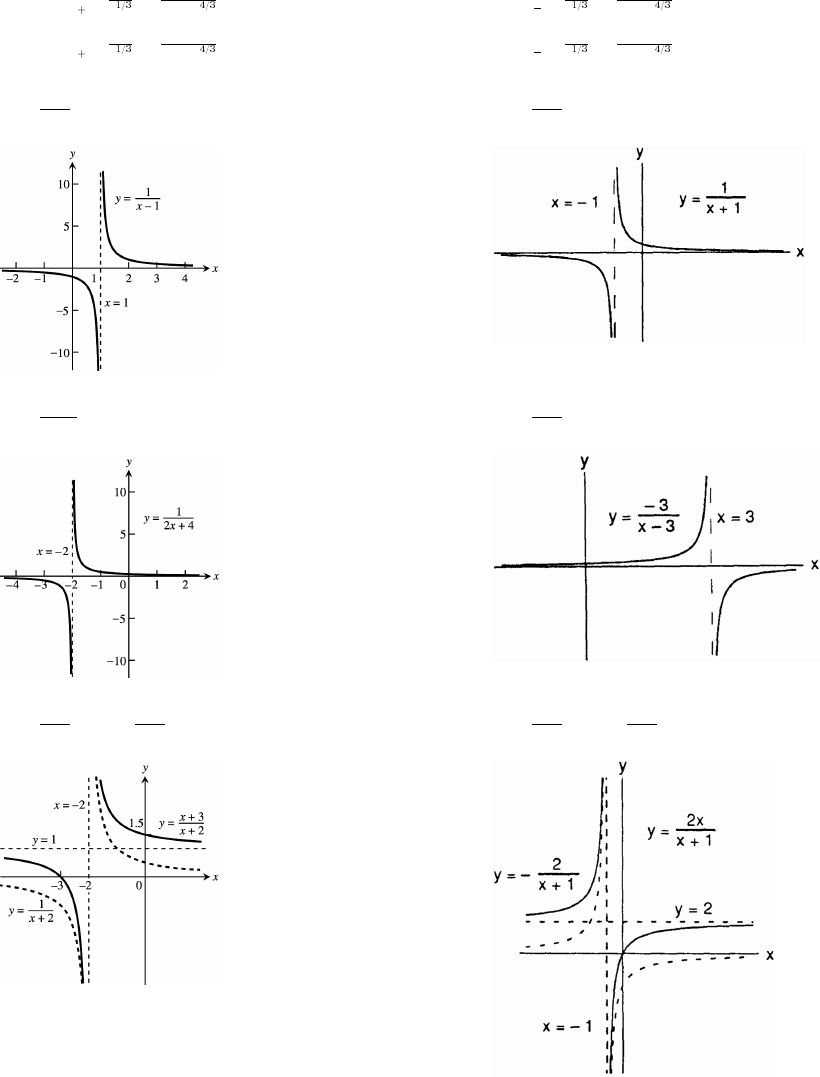
94 Chapter 2 Limits and Continuity
26. (a) lim (b) lim
xx
Ä! Ä!
’“ ’“
" "
x(x1) x(x1)
1 1
œ_ œ_
(c) lim (d) lim
xx
Ä" Ä"
’“ ’“
" "
x(x1) x(x1)
1 1
œ_ œ_
27. y 28. yœœ
" "
x1 x1
29. y 30. yœœ
"
# x4 x3
3
31. y 1 32. yœœ œœ#
x3 2x 2
x2 x x1 x1
"
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
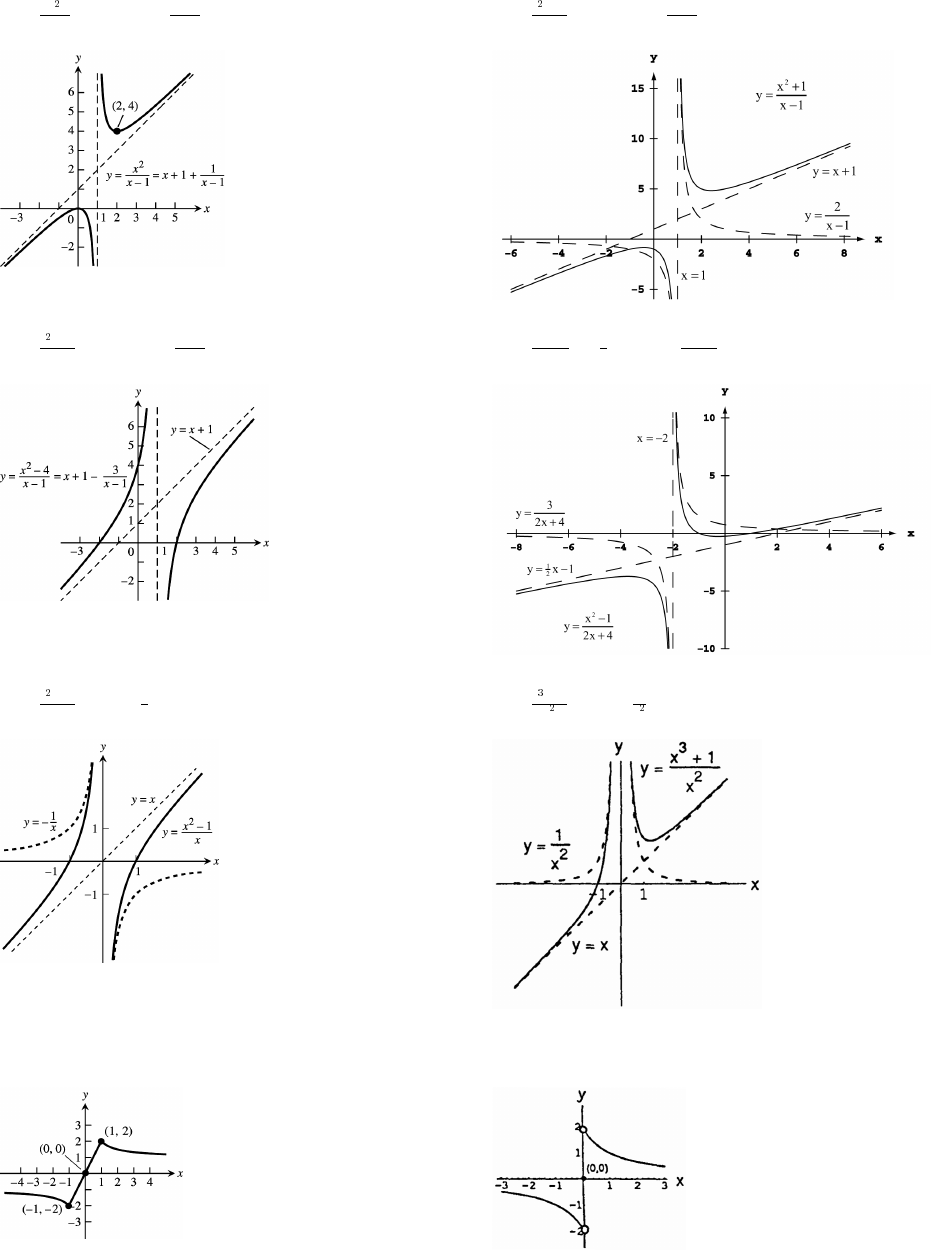
Section 2.5 Infinite Limits and Vertical Asymptotes 95
33. y x 1 34. y xœœ œ œ"
x x
x x x1 x1
" "
""#
35. y x 36. y xœœ" œœ"
x x
xx x x
% $ " " $
" " # % # # %
2
37. y x 38. y xœœ œœ
x1 x1
xx x x
" "
39. Here is one possibility. 40. Here is one possibility.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
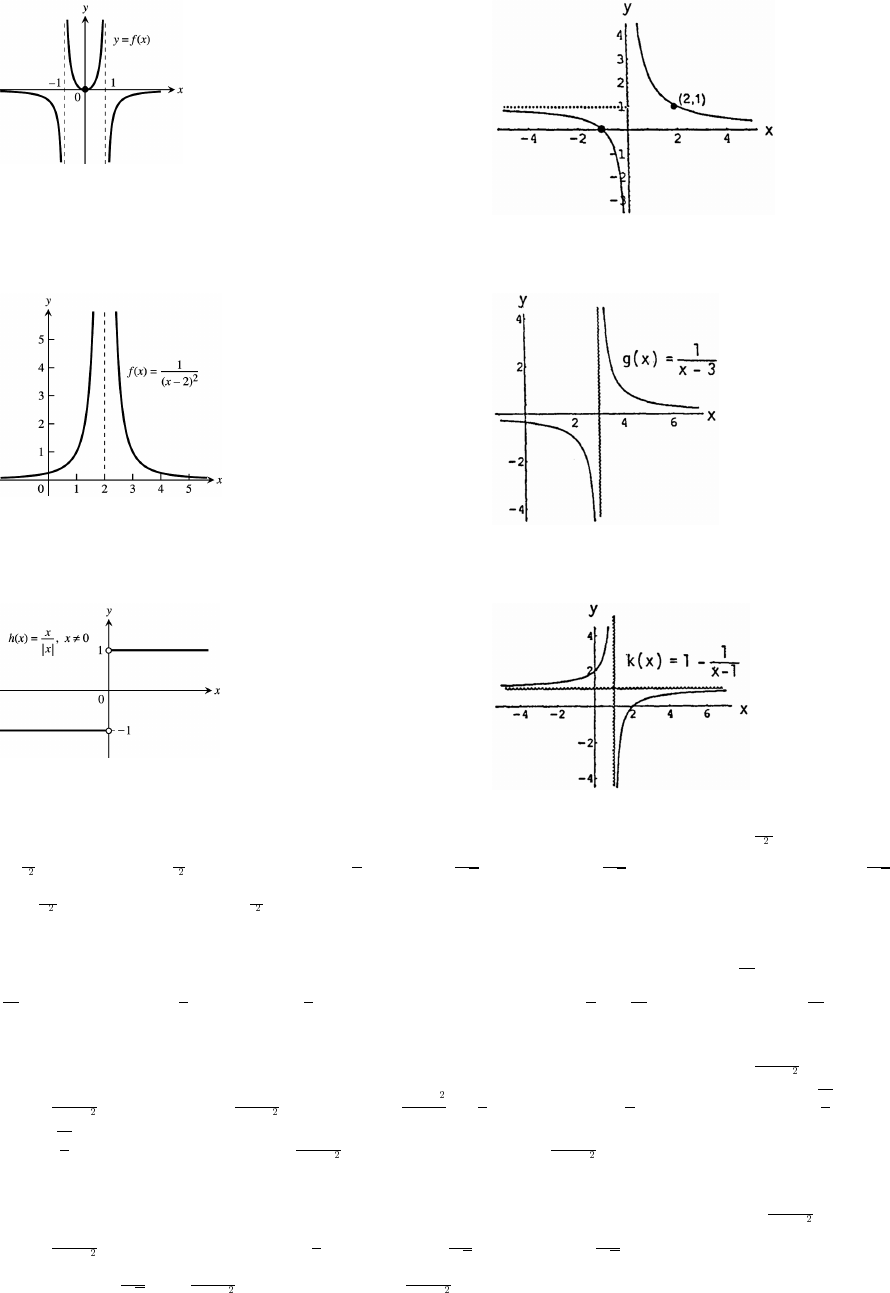
96 Chapter 2 Limits and Continuity
41. Here is one possibility. 42. Here is one possibility.
43. Here is one possibility. 44. Here is one possibility.
45. Here is one possibility. 46. Here is one possibility.
47. For every real number B 0, we must find a 0 such that for all x, 0 x 0 B. Now, Ê $$kk "
x
B B 0 x x . Choose , then 0 x x!Í Í Í œ Ê
"" """ "
#
xx B
BB B
kk kk kk
ÈÈ È
$$
B so that lim .Ê œ_
" "
xx
xÄ!
48. For every real number B 0, we must find a 0 such that for all x, x 0 B. Now, !Ê $$kk "
llx
B x . Choose . Then x 0 x B so that lim .
""" "" "
ll ll llxBB Bx x
!Íl l œ ! Êl l Ê œ_$$kk xÄ!
49. For every real number B 0, we must find a 0 such that for all x, 0 x 3 B. Ê $$kk
2
(x 3)
Now, B B 0 (x 3) . Choose
"
#
22 2 2
(x 3) (x 3) 2 B B B
(x 3)
! Í Í Í Í ! B$ kk
É
, then 0 x 3 B 0 so that lim .$$œ Ê œ_
Ékk
222
B (x3) (x3)
xÄ$
50. For every real number B 0, we must find a 0 such that for all x, 0 x ( 5) B. Ê$$kk 1
(x 5)
Now, B (x 5) x 5 . Choose . Then 0 x ( 5)
1
(x 5) B BB
#"" "
!Í Í œ kk k k
ÈÈ
$$
x 5 B so that lim .Ê Ê œ_kk
"" "
ÈB(x 5) (x 5)
xÄ&
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 2.5 Infinite Limits and Vertical Asymptotes 97
51. (a) We say that f(x) approaches infinity as x approaches x from the left, and write lim f(x) , if
!xxĜ_
for every positive number B, there exists a corresponding number 0 such that for all x,$
x x x f(x) B.
!!
Ê $
(b) We say that f(x) approaches minus infinity as x approaches x from the right, and write lim f(x) ,
!xxĜ_
if for every positive number B (or negative number B) there exists a corresponding number 0 such$
that for all x, x x x f(x) B.
!!
Ê $
(c) We say that f(x) approaches minus infinity as x approaches x from the left, and write lim f(x) ,
!xxĜ_
if for every positive number B (or negative number B) there exists a corresponding number 0 such$
that for all x, x x x f(x) B.
!!
Ê $
52. For B 0, B 0 x . Choose . Then x 0 x B so that lim .Í œ !ÊÊ œ_
""" "" "
xBB Bx x
$$
xÄ!
53. For B 0, B 0 B 0 x x. Choose . Then x Í Í Í œ !
"" "" "
xx BBB
$$
x B so that lim .Ê Ê œ_
"" "
Bx x
xÄ!
54. For B , B B (x 2) x 2 x 2 . Choose . Then! Í Í Í Í œ
"" """"
# #xx BBBB
$
2 x 2 x 2 x 2 0 B 0 so that lim . Ê!Ê Ê œ_$$ "" "
# #Bx x
xÄ#
55. For B 0, B x 2 . Choose . Then x x x 2 Í! œ ## Ê!# Ê!
""" "
#xBB B
$$$
B so that lim .Ê ! œ_
""
# #xx
xÄ#
56. For B 0 and x 1, B 1 x ( x)( x) . Now 1 since x 1. Choose! ÍÍ""
"" "
#
#
1x B B
1x
. Then x x 1 0 x ( x)( x)$$$ $ " "Ê Ê" Ê " "
""""
###BBBB
1x
ˆ‰
B for x 1 and x near 1 lim .Ê! Ê œ_
""
"1x x
xÄ"
57. y sec x 58. y sec xœ œ
" "
x x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
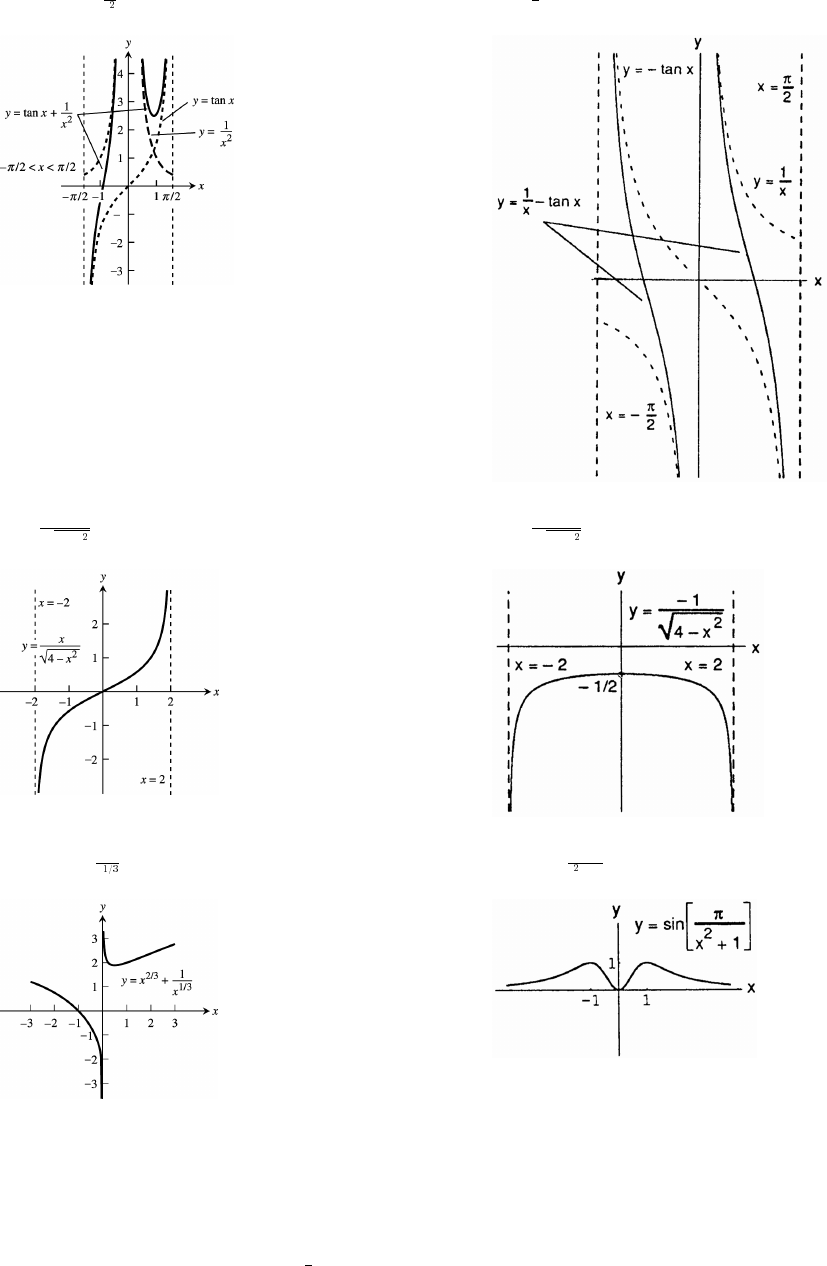
98 Chapter 2 Limits and Continuity
59. y tan x 60. y tan xœ œ
""
xx
61. y 62. yœœ
x
4x 4x
È È
"
63. y x 64. y sinœ œ
#Î$ "
xx1
ˆ‰
1
2.6 CONTINUITY
1. No, discontinuous at x 2, not defined at x 2œœ
2. No, discontinuous at x 3, lim g(x) g(3) 1.5œ"œ Á œ
xÄ$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
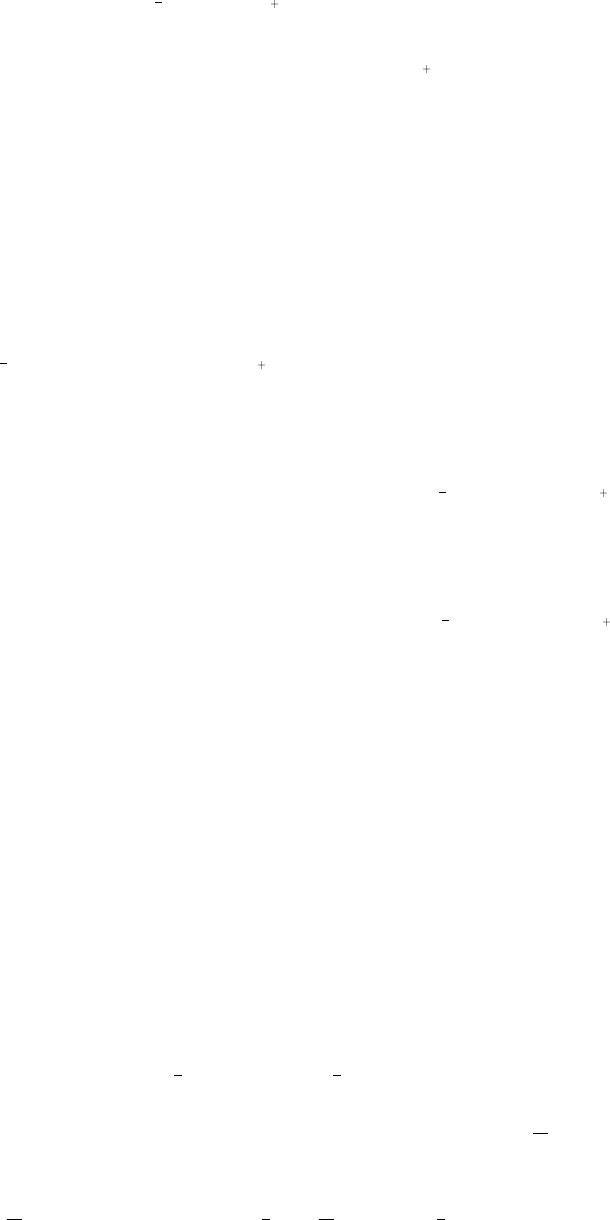
Section 2.6 Continuity 99
3. Continuous on [ 1 3]ß
4. No, discontinuous at x 1, 1.5 lim k(x) lim k(x)œœÁœ!
xx
Ä" Ä"
5. (a) Yes (b) Yes, lim f(x) 0
xÄ" œ
(c) Yes (d) Yes
6. (a) Yes, f(1) 1 (b) Yes, lim f(x) 2œœ
x1Ä
(c) No (d) No
7. (a) No (b) No
8. [ )()()()"ß! !ß" "ß# #ß$
9. f(2) 0, since lim f(x) 2(2) 4 0 lim f(x)œœœœ
xx
Ä# Ä#
10. f(1) should be changed to 2 lim f(x)œx1Ä
11. Nonremovable discontinuity at x 1 because lim f(x) fails to exist ( lim f(x) 1 and lim f(x) 0).œœœ
x1 xx
ÄÄ" Ä"
Removable discontinuity at x 0 by assigning the number lim f(x) 0 to be the value of f(0) rather thanœœ
xÄ!
f(0) 1.œ
12. Nonremovable discontinuity at x 1 because lim f(x) fails to exist ( lim f(x) 2 and lim f(x) 1).œœœ
x1 xx
ÄÄ" Ä"
Removable discontinuity at x 2 by assigning the number lim f(x) 1 to be the value of f(2) rather thanœœ
xÄ#
f(2) 2.œ
13. Discontinuous only when x 2 0 x 2 14. Discontinuous only when (x 2) 0 x 2œÊœ œÊœ
#
15. Discontinuous only when x x (x 3)(x 1) 0 x 3 or x 1
#% $œ! Ê œ Ê œ œ
16. Discontinuous only when x 3x 10 0 (x 5)(x 2) 0 x 5 or x 2
# œÊ œÊœ œ
17. Continuous everywhere. ( x 1 sin x defined for all x; limits exist and are equal to function values.)kk
18. Continuous everywhere. ( x 0 for all x; limits exist and are equal to function values.)kk"Á
19. Discontinuous only at x 0œ
20. Discontinuous at odd integer multiples of , i.e., x = (2n ) , n an integer, but continuous at all other x.
11
##
"
21. Discontinuous when 2x is an integer multiple of , i.e., 2x n , n an integer x , n an integer, but11œÊœ
n1
#
continuous at all other x.
22. Discontinuous when is an odd integer multiple of , i.e., (2n 1) , n an integer x 2n 1, n an
1111xx
####
œ Êœ
integer (i.e., x is an odd integer). Continuous everywhere else.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

100 Chapter 2 Limits and Continuity
23. Discontinuous at odd integer multiples of , i.e., x = (2n 1) , n an integer, but continuous at all other x.
11
##
24. Continuous everywhere since x 1 1 and sin x 1 0 sin x 1 1 sin x 1; limits exist
%##
"Ÿ Ÿ Ê Ÿ Ÿ Ê
and are equal to the function values.
25. Discontinuous when 2x 3 0 or x continuous on the interval . Ê ß_
33
##
‰
26. Discontinuous when 3x 1 0 or x continuous on the interval . Ê ß_
""
33
‰
27. Continuous everywhere: (2x 1) is defined for all x; limits exist and are equal to function values."Î$
28. Continuous everywhere: (2 x) is defined for all x; limits exist and are equal to function values."Î&
29. lim sin (x sin x) sin ( sin ) sin ( 0) sin 0, and function continuous at x .
xÄ1œœœœ œ11 1 1 1
30. lim sin cos (tan t) sin cos (tan (0)) sin cos (0) sin 1, and function continuous at t .
tÄ! ˆ‰ˆ ‰ˆ‰ˆ‰
11 11
## ##
œœœœ œ!
31. lim sec y sec y tan y 1 lim sec y sec y sec y lim sec (y 1) sec y sec ( ) sec 1
y1 y1 y1ÄÄÄ
a ba babab
## ## # #
œ œ œ""
sec 0 1, , and function continuous at y .œœ œ"
32. lim tan cos sin x tan cos (sin(0)) tan cos (0) tan 1, and function continuous at x .
xÄ! ‘‘ˆ‰ˆ‰ˆ‰
1111
4444
"Î$ œœœœ œ!
33. lim cos cos cos cos , and function continuous at t .
tÄ! ’“’“
1111
ÈÈÈ
È
19 3 sec 2t 19 3 sec 0 16 4
2
#
œœœœ œ!
34. lim csc x 5 3 tan x csc 5 3 tan 4 5 3 9 3, and function continuous at
xÄÉÈÈÈÈ
Ɉ‰ ˆ‰ ÊŠ‹
## "
œ œ œœ
11
66 3
È
x.œ1
'
35. g(x) x 3, x 3 g(3) lim (x 3) 6œœ œÁÊœ œ
x9
x3 (x3)
(x 3)(x 3)
xÄ$
36. h(t) t 5, t h(2) lim (t 5) 7œœ œÁ#Êœœ
t3t10
tt
(t 5)(t 2)
# #
tÄ#
37. f(s) , s 1 f(1) lim œœ œ ÁÊœ œ
sss ss13
s 1 (s 1)(s 1) s 1 s 1
ss1(s1)
" "
#
ab
s1ÄŠ‹
38. g(x) , x 4 g(4) lim œœ œÁÊœ œ
x16 x4 x4 8
x 3x4 (x4)(x1) x1 x1 5
(x 4)(x 4)
xÄ%ˆ‰
39. As defined, lim f(x) (3) 1 8 and lim (2a)(3) 6a. For f(x) to be continuous we must have
xx
Ä$ Ä$
œœ œ
#
6a 8 a .œÊœ
4
3
40. As defined, lim g(x) 2 and lim g(x) b( 2) 4b. For g(x) to be continuous we must have
xx
Ä# Ä#
œ œ œ
#
4b 2 b .œ Ê œ"
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
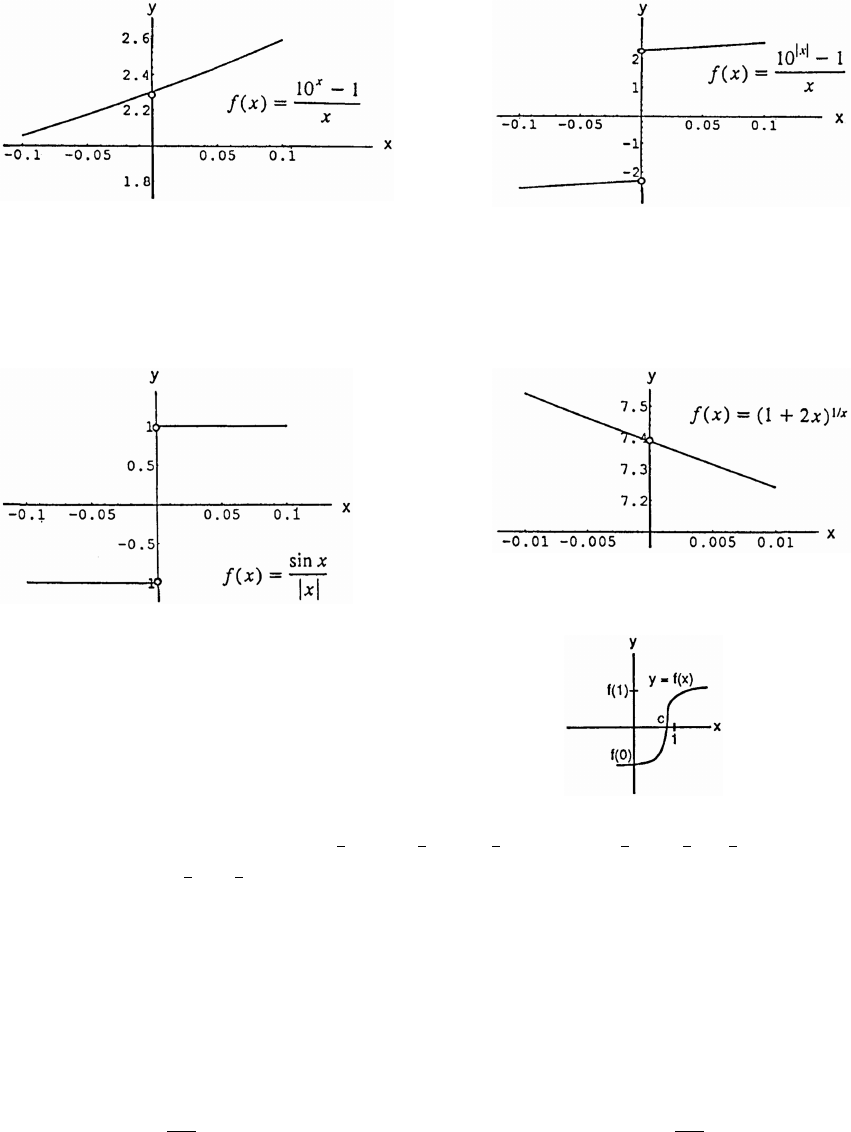
Section 2.6 Continuity 101
41. The function can be extended: f(0) 2.3. 42. The function cannot be extended to be continuous at¸
x 0. If f(0) 2.3, it will be continuous from theœ¸
right. Or if f(0) 2.3, it will be continuous from the¸
left.
43. The function cannot be extended to be continuous 44. The function can be extended: f(0) 7.39.¸
at x 0. If f(0) 1, it will be continuous fromœœ
the right. Or if f(0) 1, it will be continuousœ
from the left.
45. f(x) is continuous on [ ] and f(0) 0, f(1) 0!ß "
by the Intermediate Value Theorem f(x) takesÊ
on every value between f(0) and f(1) theÊ
equation f(x) 0 has at least one solution betweenœ
x 0 and x 1.œœ
46. cos x x (cos x) x 0. If x , cos 0. If x , cos 0. Thus cos x x 0œÊ œ œ œ œ
111 111
### ###
ˆ‰ˆ‰ ˆ‰
for some x between and according to the Intermediate Value Theorem.11
##
47. Let f(x) x 15x 1 which is continuous on [ 4 4]. Then f( 4) 3, f( 1) 15, f(1) 13, and f(4) 5.œ ß œ œ œ œ
$
By the Intermediate Value Theorem, f(x) 0 for some x in each of the intervals x 1, x 1, andœ%"
x 4. That is, x 15x 1 0 has three solutions in [ 4]. Since a polynomial of degree 3 can have at most 3" œ %ß
$
solutions, these are the only solutions.
48. Without loss of generality, assume that a b. Then F(x) (x a) (x b) x is continuous for all values ofœ
##
x, so it is continuous on the interval [a b]. Moreover F(a) a and F(b) b. By the Intermediate Valueßœœ
Theorem, since a b, there is a number c between a and b such that F(x) . œ
ab ab
# #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

102 Chapter 2 Limits and Continuity
49. Answers may vary. Note that f is continuous for every value of x.
(a) f(0) 10, f(1) 1 8(1) 10 3. Since 10, by the Intermediate Value Theorem, there exists a cœœœ $
$1
so that c 1 and f(c) .! œ1
(b) f(0) 10, f( 4) ( 4) 8( 4) 10 22. Since 22 3 10, by the Intermediate Valueœ œ œ
$È
Theorem, there exists a c so that 4 c 0 and f(c) 3. œ
È
(c) f(0) 10, f(1000) (1000) 8(1000) 10 999,992,010. Since 10 5,000,000 999,992,010, by theœœœ
$
Intermediate Value Theorem, there exists a c so that c 1000 and f(c) 5,000,000.! œ
50. All five statements ask for the same information because of the intermediate value property of continuous
functions.
(a) A root of f(x) x 3x 1 is a point c where f(c) 0.œ œ
$
(b) The points where y x crosses y 3x 1 have the same y-coordinate, or y x 3x 1œœ œœ
$ $
f(x) x 3x 1 0.Êœœ
$
(c) x 3x 1 x 3x 1 0. The solutions to the equation are the roots of f(x) x 3x 1.
$$ $
œÊ œ œ
(d) The points where y x 3x crosses y 1 have common y-coordinates, or y x 3x 1œ œ œœ
$ $
f(x) x 3x 1 .Êœœ!
$
(e) The solutions of x 3x 1 0 are those points where f(x) x 3x 1 has value 0.
$$
œ œ
51. Answers may vary. For example, f(x) is discontinuous at x 2 because it is not defined there.œœ
sin (x 2)
x2
However, the discontinuity can be removed because f has a limit (namely 1) as x 2.Ä
52. Answers may vary. For example, g(x) has a discontinuity at x 1 because lim g(x) does not exist.œœ
"
x1 xÄ"
lim g(x) and lim g(x) .
Š‹
xx
Ä" Ä"
œ_ œ_
53. (a) Suppose x is rational f(x ) 1. Choose . For any 0 there is an irrational number x (actually
!! "
#
Êœ œ %$
infinitely many) in the interval (x x ) f(x) 0. Then 0 x x but f(x) f(x )
!! ! !
ß Ê œ $$ $kk k k
1 , so lim f(x) fails to exist f is discontinuous at x rational.œœ Ê
"
#!
%xxÄ
On the other hand, x irrational f(x ) 0 and there is a rational number x in (x x ) f(x)
!! !!
Êœ ßÊ$$
1. Again lim f(x) fails to exist f is discontinuous at x irrational. That is, f is discontinuous atœÊ
xxÄ!
every point.
(b) f is neither right-continuous nor left-continuous at any point x because in every interval (x x ) or
!!!
ß$
(x x ) there exist both rational and irrational real numbers. Thus neither limits lim f(x) and
!!
ß$xxÄ
lim f(x) exist by the same arguments used in part (a).
xxÄ
54. Yes. Both f(x) x and g(x) x are continuous on [ ]. However is undefined at x sinceœœ !ß" œ
" "
# #
f(x)
g(x)
g 0 is discontinuous at x .
ˆ‰
""
##
œÊ œ
f(x)
g(x)
55. No. For instance, if f(x) 0, g(x) x , then h(x) 0 x 0 is continuous at x 0 and g(x) is not.œœÜÝ œÜÝœ œab
56. Let f(x) and g(x) x 1. Both functions are continuous at x 0. The composition f g f(g(x))œœ œ ‰œ
"
x1
is discontinuous at x 0, since it is not defined there. Theorem 10 requires that f(x) beœœ œ
""
(x 1) 1 x
continuous at g(0), which is not the case here since g(0) 1 and f is undefined at 1.œ
57. Yes, because of the Intermediate Value Theorem. If f(a) and f(b) did have different signs then f would have to
equal zero at some point between a and b since f is continuous on [a b].ß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
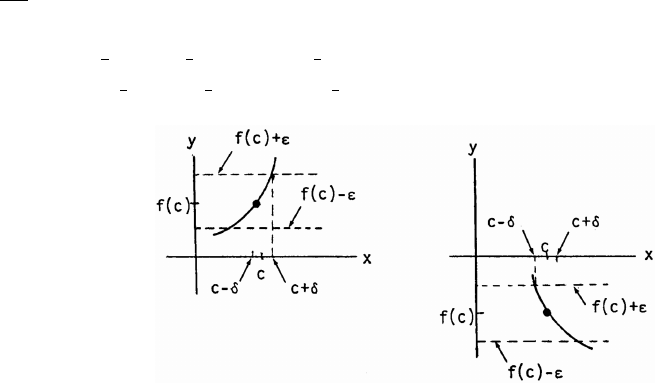
Section 2.7 Tangents and Derivatives 103
58. Let f(x) be the new position of point x and let d(x) f(x) x. The displacement function d is negative if x isœ
the left-hand point of the rubber band and positive if x is the right-hand point of the rubber band. By the
Intermediate Value Theorem, d(x) 0 for some point in between. That is, f(x) x for some point x, which isœœ
then in its original position.
59. If f(0) 0 or f(1) 1, we are done (i.e., c 0 or c 1 in those cases). Then let f(0) a 0 and f(1) b 1œœ œœ œ œ
because 0 f(x) 1. Define g(x) f(x) x g is continuous on [0 1]. Moreover, g(0) f(0) 0 a 0 andŸŸ œÊ ß œœ
g(1) f(1) 1 b 1 0 by the Intermediate Value Theorem there is a number c in ( ) such thatœ œ Ê !ß"
g(c) 0 f(c) c 0 or f(c) c.œÊ œ œ
60. Let 0. Since f is continuous at x c there is a 0 such that x c f(x) f(c)%$$%œ œ Ê
kkf(c)
#kk k k
f(c) f(x) f(c) .Ê%%
If f(c) 0, then f(c) f(c) f(x) f(c) f(x) 0 on the interval (c c ).œÊÊ ß%$$
""
## #
3
If f(c) 0, then f(c) f(c) f(x) f(c) f(x) 0 on the interval (c c ).œÊÊ ß%$$
""
## #
3
61. By Exercises 52 in Section 2.3, we have lim f x L lim f c h L.
xc h0
ÄÄ
ab a bœÍ œ
Thus, f x is continuous at x c lim f x f c lim f c h f c .ab ab ab a b abœÍ œ Í œ
xc h0
ÄÄ
62. By Exercise 61, it suffices to show that lim sin c h sin c and lim cos c h cos c.
h0 h0ÄÄ
ab abœ œ
Now lim sin c h lim sin c cos h cos c sin h sin c lim cos h cos c lim sin h
h0 h0 h0 h0ÄÄ Ä Ä
a b ababababab ab
‘
Š‹Š‹
œ œ
By Example 6 Section 2.2, lim cos h and lim sin h . So lim sin c h sin c and thus f x sin x is
h0 h0 h0ÄÄÄ
œ" œ! œ œab ab
continuous at x c. Similarly,œ
lim cos c h lim cos c cos h sin c sin h cos c lim cos h sin c lim sin h cos c.
h0 h0 h0 h0ÄÄ Ä Ä
ab ababababab ab
‘
Š‹Š‹
œ œ œ
Thus, g x cos x is continuous at x c.abœœ
63. x 1.8794, 1.5321, 0.3473 64. x 1.4516, 0.8547, 0.4030¸ ¸
65. x 1.7549 66. x 1.5596¸¸
67. x 3.5156 68. x 3.9058, 3.8392, 0.0667¸¸
69. x 0.7391 70. x 1.8955, 0, 1.8955¸¸
2.7 TANGENTS AND DERIVATIVES
1. P : m 1, P : m 5 2. P : m 2, P : m 0
"" ## "" ##
œœ œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
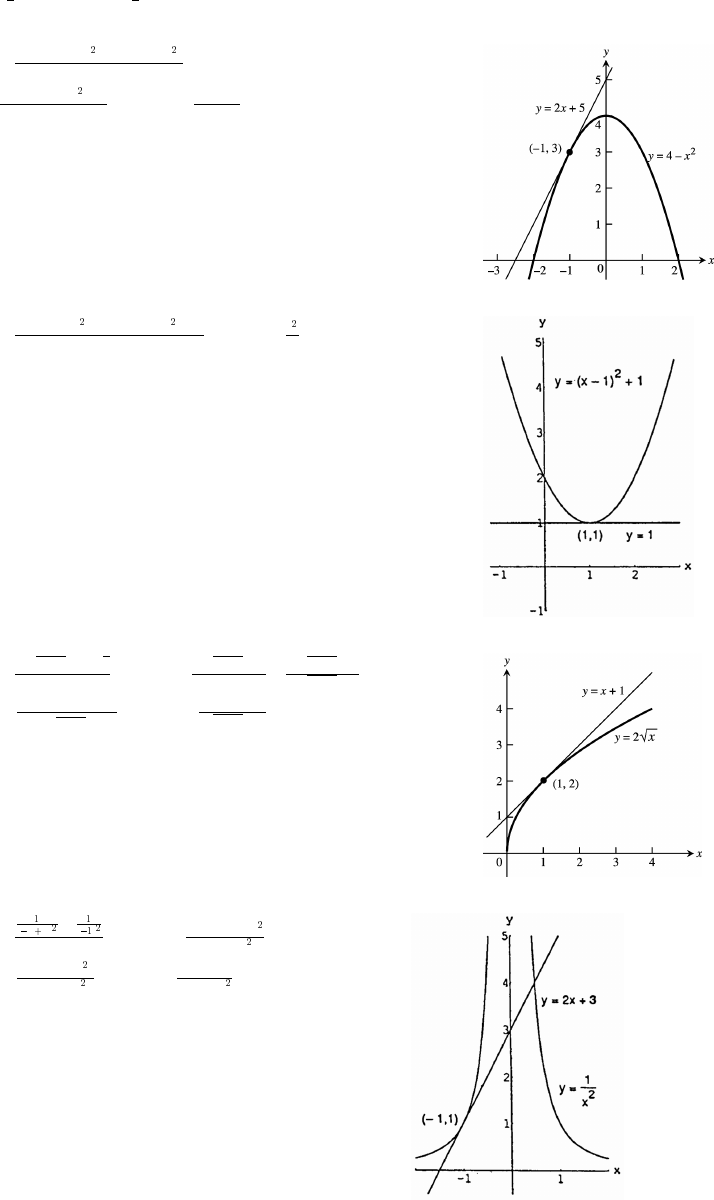
104 Chapter 2 Limits and Continuity
3. P : m , P : m 4. P : m 3, P : m 3
"" ## "" ##
##
"
œœ œœ
5
5. m lim œhÄ!
cdab4( h) 4(1)
h
"
lim lim 2;œœœ
hhÄ! Ä!
#
ab12hh 1
hh
h( h)
at ( ): y (x ( 1)) y 2x 5,"ß $ œ $ # Ê œ
tangent line
6. m lim lim œœ
hhÄ! Ä!
cdcd(1h1) 1 ( ) 1
hh
h
""
lim h 0; at ( ): y 1 0(x 1) y 1,œœ"ß"œÊœ
hÄ!
tangent line
7. m lim lim œœ
hhÄ! Ä!
21h21 21h2 21h2
hh
21h
ÈÈÈ
ÈÈ
#
†
lim lim 1;œœœ
hhÄ! Ä!
4(1 h) 4
2h 1h1
2
1h1
Š‹
ÈÈ
at ( ): y 2 1(x 1) y x 1, tangent line"ß # œ Ê œ
8. m lim lim œœ
hhÄ! Ä!
(1 h) ( )
hh(1h)
1(1h)
lim lim 2;œœœ
hhÄ! Ä!
ab2h h
h(1h) (1h)
2h
at ( ): y 1 2(x ( 1)) y 2x 3,"ß " œ Ê œ
tangent line
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
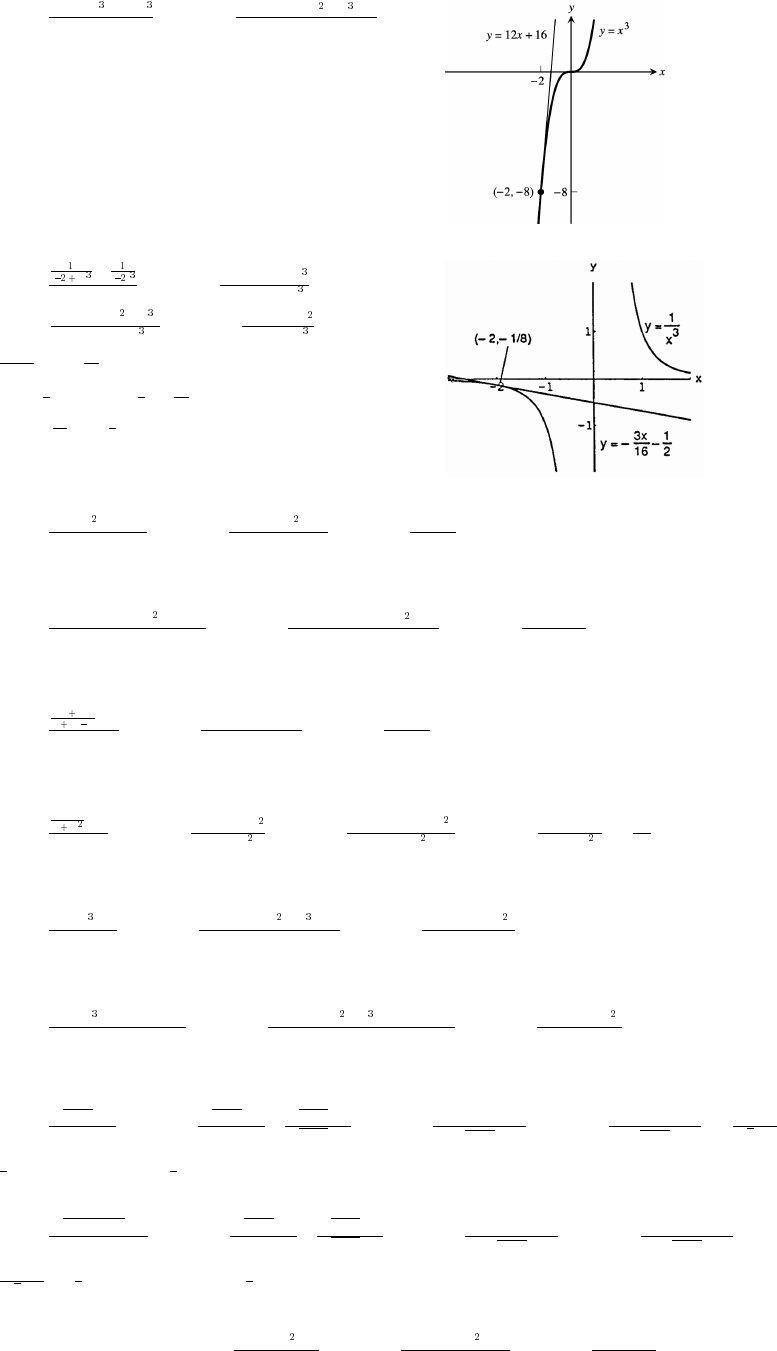
Section 2.7 Tangents and Derivatives 105
9. m lim lim œœ
hhÄ! Ä!
(2 h) (2)
hh
8 12h 6h h 8
lim 12 6h h 12;œœ
hÄ! ab
#
at ( 2 8): y 8 12(x ( 2)) y 12x 16,ß œ Ê œ
tangent line
10. m lim lim œœ
hhÄ! Ä!
(h)()
#
#h 8h( h)
8( h)
lim lim œœ
hhÄ! Ä!
#
ab12h 6h h
8h( h) 8( 2 h)
12 6h h
;œœ
"
23
8( 8) 16
at : y (x ( 2))
ˆ‰
#ß œ
""
8816
3
y x , tangent lineʜ
3
16
"
#
11. m lim lim lim ;œœœœ%
hhhÄ! Ä! Ä!
cd ab
(2 h) 1 5
hhh
54hh 5 h(4 h)
at (2 5): y 5 4(x 2), tangent lineߜ
12. m lim lim lim 3;œœœœ
hhhÄ! Ä! Ä!
cd ab
(h)2(1h) (1)
hhh
1h24h2h 1 h( 3 2h)
"
at ( ): y 1 3(x 1), tangent line"ß " œ
13. m lim lim lim 2;œœ œœ
hh hÄ! Ä! Ä!
3h
(3 h) 2
3
h h(h 1) h(h 1)
(3 h) 3(h 1) 2h
at ( ): y 3 2(x 3), tangent line$ß $ œ
14. m lim lim lim lim 2;œœ œ œ œœ
hh h hÄ! Ä! Ä! Ä!
8
(2 h)
2
h h(2 h) h(2 h) h(2 h) 4
8 2(2 h) 2h(4 h)
8244hh 8
ab
at (2 2): y 2 2(x 2)ߜ
15. m lim lim lim 12;œœ œ œ
hh hÄ! Ä! Ä!
(2 h) 8
hh h
8 12h 6h h 8 h 12 6h h
ab ab
at (2 ): y 8 12(t 2), tangent lineß) œ
16. m lim lim lim 6;œœ œœ
hh hÄ! Ä! Ä!
cdabab
(1 h) 3(1 h) 4
hhh
13h3h h 33h 4 h63hh
at ( ): y 4 6(t 1), tangent line"ß % œ
17. m lim lim lim lim œœ œœœ
hh h hÄ! Ä! Ä! Ä!
ÈÈÈ
ÈÈ
Š‹ Š‹
ÈÈ
4h2 4h2 4h2
hh
4h2
(4 h) 4
h4h h4h
h
4
# #
"
#
†
; at ( ): y 2 (x 4), tangent lineœ%ß#œ
""
44
18. m lim lim lim lim œœ œœ
hh hhÄ! Ä! Ä! Ä!
ÈÈÈ
ÈŠ‹ Š‹
ÈÈ
(8 h) 1 3
hh
9h3 9h3
9h3
(9 h) 9
h 9h3 h 9h3
h
†
; at (8 3): y 3 (x 8), tangent lineœœ ßœ
"" "
È93 66
19. At x 1, y 5 m lim lim lim 10, slopeœ œ Ê œ œ œ œ
hh hÄ! Ä! Ä!
5( h) 5 5h( 2 h)
hhh
51 2h h 5
"
ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

106 Chapter 2 Limits and Continuity
20. At x 2, y 3 m lim lim lim 4, slopeœœÊœ œ œ œ
hhhÄ! Ä! Ä!
cd ab
1(2h) (3)
hhh
144h h 3 h(4 h)
21. At x 3, y m lim lim lim , slopeœœÊœ œ œ œ
""
#
hhhÄ! Ä! Ä!
(3 h) 1
h 2h(2 h) 2h(2 h) 4
2(2h) h
22. At x 0, y 1 m lim lim lim 2, slopeœœÊœ œ œ œ
hh hÄ! Ä! Ä!
h1
h1
"
(1)
h h(h 1) h(h 1)
(h 1) (h ) 2h
23. At a horizontal tangent the slope m 0 0 m lim œÊœœ
hÄ!
cdab(x h) 4(x h) 1 x 4x 1
h
lim lim lim (2x h 4) 2x 4;œœœœ
hhhÄ! Ä! Ä!
abababx2xhh4x4h1 x4x1 2xhh4h
hh
2x 4 0 x 2. Then f( 2) 4 8 1 5 ( 2 5) is the point on the graph where there is aœ Ê œ œœÊß
horizontal tangent.
24. 0 m lim lim œœ œ
hhÄ! Ä!
cdab
abab
(x h) 3(x h) x 3x
hh
x3xh3xhh3x3h x3x
lim lim 3x 3xh h 3 3x 3; 3x 3 0 x 1 or x 1. ThenœœœœÊœœ
hhÄ! Ä!
3x h 3xh h 3h
h
####
ab
f( 1) 2 and f(1) 2 ( 2) and ( 2) are the points on the graph where a horizontal tangent exists. œ œ Ê "ß "ß
25. 1 m lim lim lim œ œ œ œ œ
hh hÄ! Ä! Ä!
(x h) 1 x 1
"
h h(x 1)(x h 1) h(x 1)(x h 1) (x 1)
(x 1) (x h 1) h
(x 1) 1 x 2x 0 x(x 2) 0 x 0 or x 2. If x 0, then y 1 and m 1Ê œÊ œÊ œÊœ œ œ œ œ
##
y 1 (x 0) (x 1). If x 2, then y 1 and m 1 y 1 (x 2) (x 3).Êœœ œ œ œÊœœ
26. m lim lim lim
"
4hh
xh x xh x xh x
xh x
(x h) x
hxh x
œœ œ œ
hh hÄ! Ä! Ä!
ÈÈÈ
ÈÈÈ
ÈÈŠ‹
ÈÈ
†
lim . Thus, x 2 x 4 y 2. The tangent line isœ œ œ Ê œÊœÊœ
hÄ!
h
hxh x xx
4
Š‹
ÈÈÈÈ
"""
##
È
y 2 (x 4) 1.œ œ
"
44
x
27. lim lim lim
hh hÄ! Ä! Ä!
f(2 h) f(2)
hh h
100 4.9( h) 100 4.9(2) 4.9 4 4h h 4.9(4)
#
œœ
abab ab
lim ( 19.6 4.9h) 19.6. The minus sign indicates the object is falling at a speed ofœœ
hÄ! downward
19.6 m/sec.
28. lim lim lim 60 ft/sec.
hh hÄ! Ä! Ä!
f(10 h) f(10) 3(10 h) 3(10)
hhh
3 20h h
œœœ
ab
29. lim lim lim lim (6 h) 6
hh h hÄ! Ä! Ä! Ä!
f(3h)f(3) (3h) (3)
hh h
96hh 9
œœ œœ
11 1cd
11
30. lim lim lim lim 12 6h h 16
hh h hÄ! Ä! Ä! Ä!
f(2 h) f(2)
hh h3
(2 h) (2) 12h 6h h 4
#
œœœœ
44 4
33 3
cd 1cd1
31. Slope at origin lim lim lim h sin 0 yes, f(x) does have a tangent atœœœœÊ
hhhÄ! Ä! Ä!
f(0 h) f(0)
hh h
h sin
"
ˆ‰
hˆ‰
the origin with slope 0.
32. lim lim lim sin . Since lim sin does not exist, f(x) has no tangent at
hhhhÄ! Ä! Ä! Ä!
g(0 h) g(0)
hhhh
h sin
""
œœ
ˆ‰
h
the origin.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
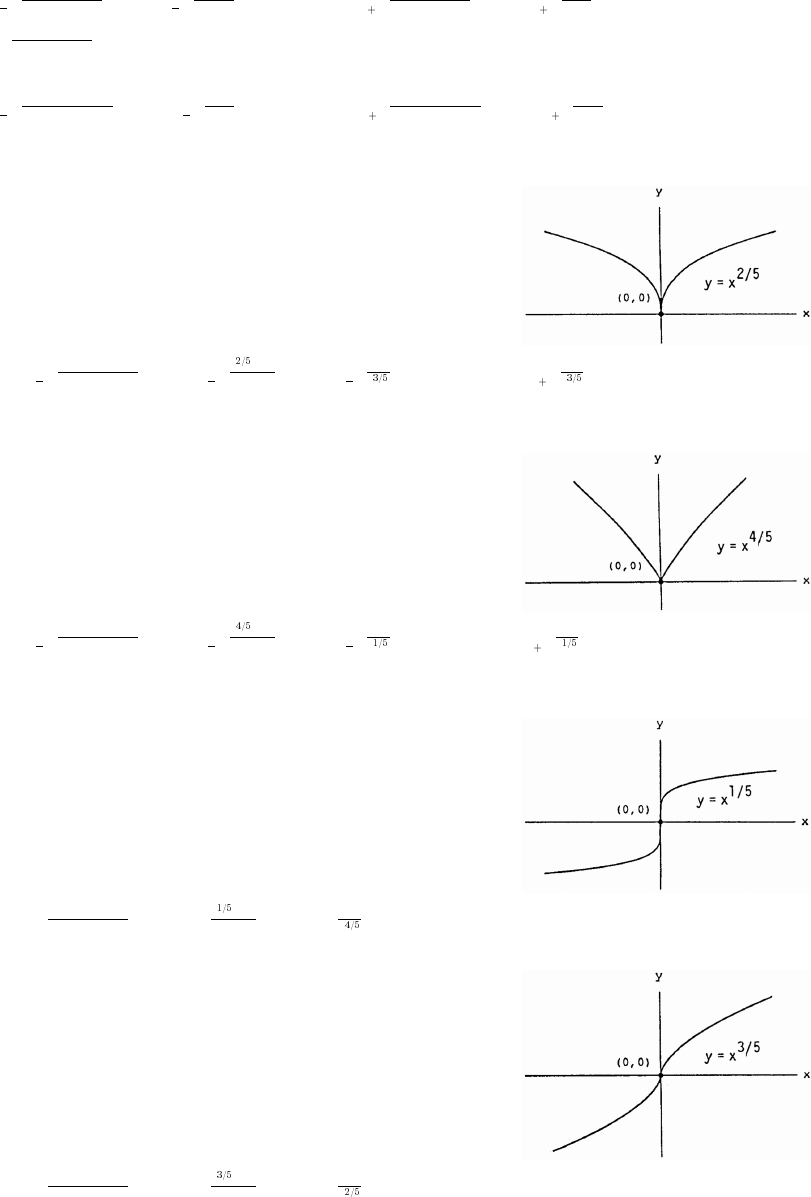
Section 2.7 Tangents and Derivatives 107
33. lim lim , and lim lim . Therefore,
hh hh
Ä! Ä! Ä! Ä!
f(0 h) f(0) f(0 h) f(0)
hh hh
10 10
œœ_ œœ_
lim yes, the graph of f has a vertical tangent at the origin.
hÄ!
f(0 h) f(0)
h
œ_ Ê
34. lim lim , and lim lim 0 no, the graph of f
hh hh
Ä! Ä! Ä! Ä!
U(0 h) U(0) U(0 h) U(0)
hh hh
01 11
œœ_ œœÊ
does not have a vertical tangent at ( ) because the limit does not exist.!ß "
35. (a) The graph appears to have a cusp at x 0.œ
(b) lim lim lim and lim limit does not exist
hhh h
Ä! Ä! Ä! Ä!
f(0 h) f(0)
hh
h0
hh
" "
œœœ_ œ_Ê
the graph of y x does not have a vertical tangent at x 0.Êœ œ
#Î&
36. (a) The graph appears to have a cusp at x 0.œ
(b) lim lim lim and lim limit does not exist
hhh h
Ä! Ä! Ä! Ä!
f(0 h) f(0)
hh
h0
hh
" "
œœœ_ œ_Ê
y x does not have a vertical tangent at x 0.Êœ œ
%Î&
37. (a) The graph appears to have a vertical tangent at x .œ!
(b) lim lim lim y x has a vertical tangent at x 0.
hhhÄ! Ä! Ä!
f(0 h) f(0)
hh
h0
h
" "Î&
œœœ_Êœ œ
38. (a) The graph appears to have a vertical tangent at x 0.œ
(b) lim lim lim the graph of y x has a vertical tangent
hhhÄ! Ä! Ä!
f(0 h) f(0)
hh
h0
h
" $Î&
œœœ_Ê œ
at x 0.œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
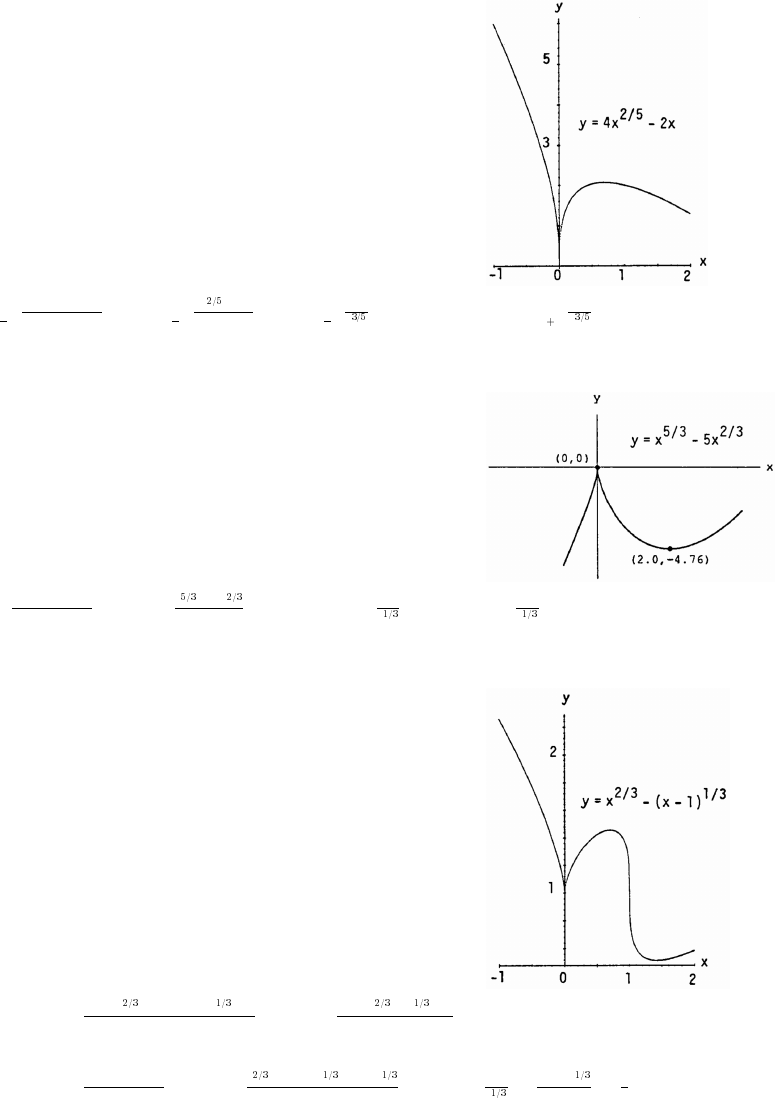
108 Chapter 2 Limits and Continuity
39. (a) The graph appears to have a cusp at x 0.œ
(b) lim lim lim 2 and lim
hhh h
Ä! Ä! Ä! Ä!
f(0 h) f(0)
hh
4h 2h 4 4
hh
œœœ_#œ_
limit does not exist the graph of y 4x 2x does not have a vertical tangent at x 0.ÊÊœ œ
#Î&
40. (a) The graph appears to have a cusp at x 0.œ
(b) lim lim lim h 0 lim does not exist the graph of
hhh hÄ! Ä! Ä! Ä!
f(0 h) f(0)
hh
h5h 5 5
hh
#Î$
œœœ Ê
y x 5x does not have a vertical tangent at x .œ œ!
&Î$ #Î$
41. (a) The graph appears to have a vertical tangent at x 1œ
and a cusp at x 0.œ
(b) x 1: lim lim œœœ_
hhÄ! Ä!
(1h) (1h1) (1h) h
hh
" "
y x (x 1) has a vertical tangent at x 1;Êœ œ
#Î$ "Î$
x 0: lim lim lim œœ œ
hh hÄ! Ä! Ä!
f(0 h) f(0) h (h 1) ( 1) (h )
hh hh
h
"
""
’“
does not exist y x (x 1) does not have a vertical tangent at x 0.Êœ œ
#Î$ "Î$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
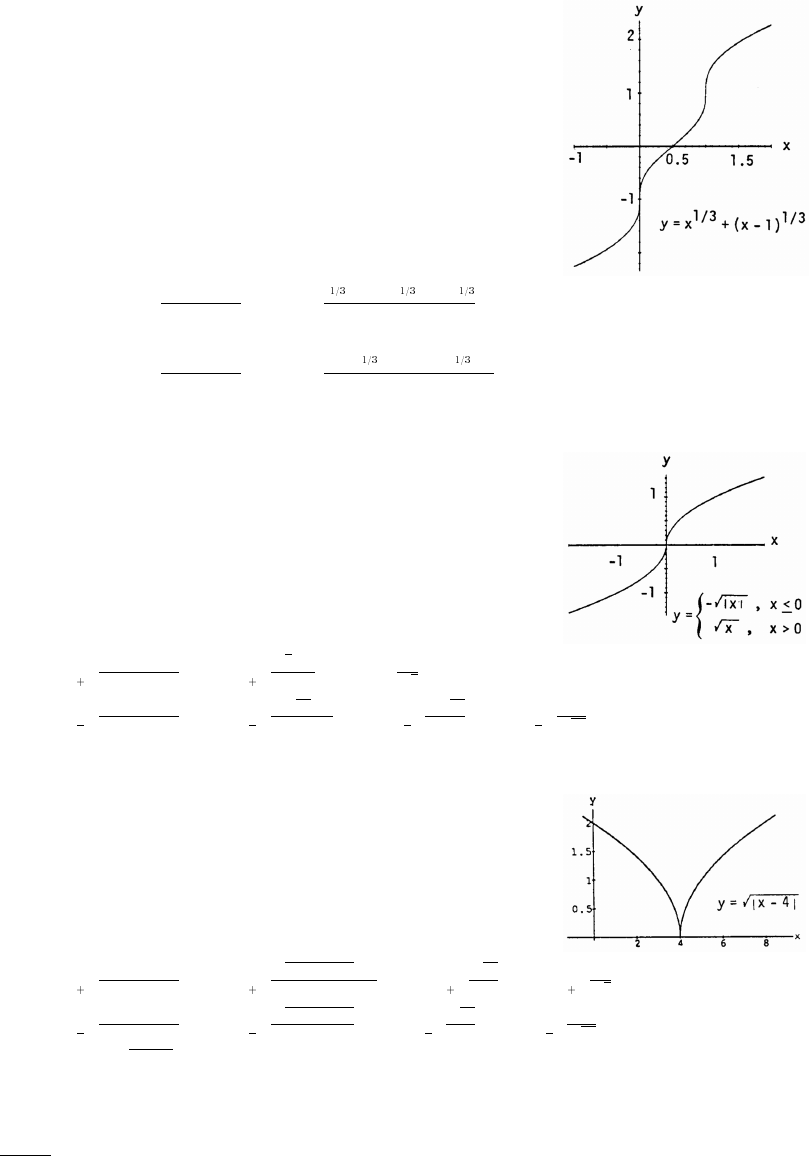
Section 2.7 Tangents and Derivatives 109
42. (a) The graph appears to have vertical tangents at x 0 andœ
x1.œ
(b) x 0: lim lim y x (x 1) has aœœ œ_Êœ
hhÄ! Ä!
f(0 h) f(0) h (h 1) ( )
hh
" "Î$ "Î$
vertical tangent at x 0;œ
x 1: lim lim y x (x 1) has aœœ œ_Êœ
hhÄ! Ä!
f(1h)f(1) (1h) ( h1) 1
hh
" "Î$ "Î$
vertical tangent at x .œ"
43. (a) The graph appears to have a vertical tangent at x 0.œ
(b) lim lim lim ;
hx
h
Ä! Ä! Ä!
f(0 h) f(0)
hh
h0
h
"
œœœ_
ÈÈ
lim lim lim lim
hhhhÄ! Ä! Ä! Ä!
f(0 h) f(0)
hhh
h0 h
h
"
œœœœ_
ÈÈ
kk kk
kk Èkk
y has a vertical tangent at x 0.ʜ
44. (a) The graph appears to have a cusp at x 4.œ
(b) lim lim lim lim ;
hh hhÄ! Ä! Ä! Ä!
f(4 h) f(4)
hhh
4(4h) 0 h
h
"
œœœœ_
ÈÈ
kk kk È
lim lim lim lim
hh hhÄ! Ä! Ä! Ä!
f(4 h) f(4)
hhh
4(4h) h
h
l l
"
œ œœœ_
ÈÈ
kk kk Èkk
y x does not have a vertical tangent at x 4.Êœ% œ
È
45-48. Example CAS commands:
:Maple
f := x -> x^3 + 2*x;x0 := 0;
plot( f(x), x=x0-1/2..x0+3, color=black, # part (a)
title="Section 2.7, #45(a)" );
q := unapply( (f(x0+h)-f(x0))/h, h ); # part (b)
L := limit( q(h), h=0 ); # part (c)
sec_lines := seq( f(x0)+q(h)*(x-x0), h=1..3 ); # part (d)
tan_line := f(x0) + L*(x-x0);
plot( [f(x),tan_line,sec_lines], x=x0-1/2..x0+3, color=black,
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
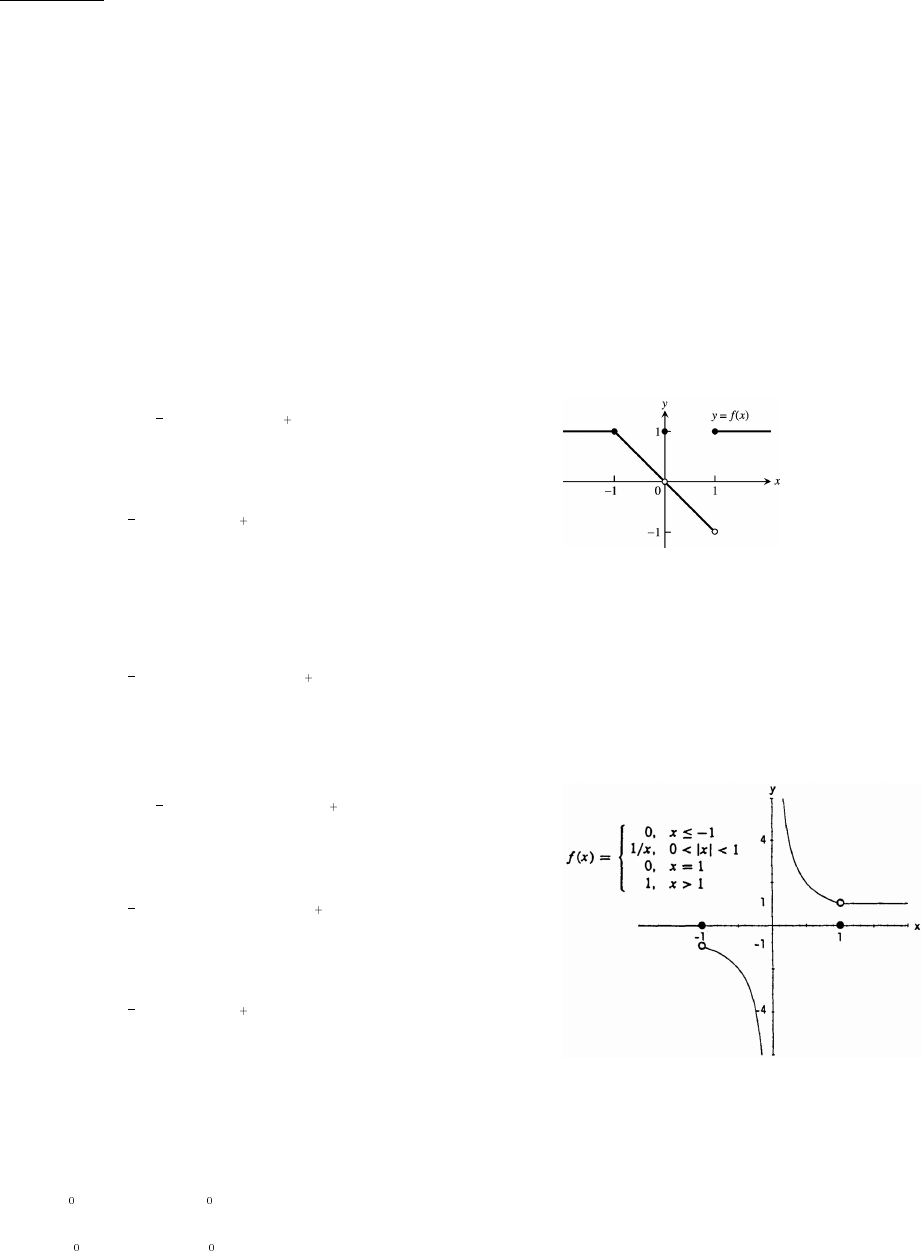
110 Chapter 2 Limits and Continuity
linestyle=[1,2,5,6,7], title="Section 2.7, #45(d)",
legend=["y=f(x)","Tangent line at x=0","Secant line (h=1)",
"Secant line (h=2)","Secant line (h=3)"] );
: (function and value for x0 may change)Mathematica
Clear[f,m,x,h]
x0 p;œ
f[x_]: Cos[x] 4Sin[2x]œ
Plot[f[x], {x, x0 1, x0 3}]
dq[h_]: (f[x0+h] f[x0])/hœ
m Limit[dq[h], h 0]π
ytan: f[x0] m(x x0)œ
y1: f[x0] dq[1](x x0)œ
y2: f[x0] dq[2](x x0)œ
y3: f[x0] dq[3](x x0)œ
Plot[{f[x], ytan, y1, y2, y3}, {x, x0 1, x0 3}]
CHAPTER 2 PRACTICE EXERCISES
1. At x 1: lim f(x) lim f(x) 1œ œ œ
xx
Ä" Ä"
lim f(x) 1 f( 1)Êœœ
x1Ä
f is continuous at x 1.ʜ
At x 0: lim f(x) lim f(x) 0 lim f(x) 0.œœœÊœ
xx
x
Ä! Ä!
Ä!
But f(0) 1 lim f(x)œÁ
xÄ!
f is discontinuous at x 0.ʜ
If we define f , then the discontinuity at x isab!œ! œ!
removable.
At x 1: lim f(x) 1 and lim f(x) 1œœ œ
xx
Ä" Ä"
lim f(x) does not existÊx1Ä
f is discontinuous at x 1.ʜ
2. At x 1: lim f(x) 0 and lim f(x) 1œ œ œ
xx
Ä" Ä"
lim f(x) does not existÊ"
xÄ
f is discontinuous at x 1.ʜ
At x 0: lim f(x) and lim f(x)œœ_ œ_
xx
Ä! Ä!
lim f(x) does not existÊxÄ!
f is discontinuous at x 0.ʜ
At x 1: lim f(x) lim f(x) 1 lim f(x) 1.œœœÊœ
xxx1
Ä" Ä" Ä
But f(1) 0 lim f(x)œÁ
x1Ä
f is discontinuous at x 1.ʜ
If we define f , then the discontinuity at x isab"œ" œ"
removable.
3. (a) lim 3f t 3 lim f t 3( 7) 21
tt ttÄÄ
ab abab œ œœ
(b) lim f t lim f t 49
tt ttÄÄ
ab ab abab Š‹
##
#
œœ(œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 2 Practice Exercises 111
(c) lim f t g t lim f t lim g t ( 7)(0) 0
tt tt ttÄÄÄ
a b ab abab ab††œœœ
(d) lim 1
ttÄ
ft
g(t) 7 lim g t 7 lim g t lim7 0 7
lim f t lim f t 7
ab ab ab
ab abab
œœ œœ
tt tt
tt tt tt
(e) lim cos g t cos lim g t cos 1
tt ttÄÄ
ab abab Š‹
œœ!œ
(f) lim f t lim f t 7 7
tt ttÄÄ
kk ab kkab ¹¹
œœœ
(g) lim f t g t lim f t lim g t 7 0 7
tt tt ttÄÄÄ
a b ab abab abœ œœ
(h) lim
ttÄŠ‹
"""
ft lim ft 7 7
1
ab ab
œœœ
tt
4. (a) lim g(x) lim g(x) 2
xxÄ! Ä!
œ œ
È
(b) lim g(x) f(x) lim g(x) lim f(x) 2
xxxÄ! Ä! Ä!
ab Š‹
Ȉ‰
††œœœ
"
##
È2
(c) lim f(x) g(x) lim f(x) lim g(x) 2
xxxÄ! Ä! Ä!
ab È
œ œ
"
#
(d) lim 2
xÄ!
"""
f(x) lim f(x)
œœœ
x
(e) lim x f(x) lim x lim f(x) 0
xxxÄ! Ä! Ä!
abœ œœ
""
##
(f) lim
xÄ!
f(x) cos x
x 1 lim x lim 1 0 1
lim f(x) lim cos x (1)
††
#
"
œœœ
xx
xx
ˆ‰
5. Since lim x 0 we must have that lim (4 g(x)) 0. Otherwise, if lim ( g(x)) is a finite positive
xx xÄ! Ä! Ä!
œœ%
number, we would have lim and lim so the limit could not equal 1 as
xx
Ä! Ä!
’“ ’“
4 g(x) 4 g(x)
xx
œ_ œ_
x 0. Similar reasoning holds if lim (4 g(x)) is a finite negative number. We conclude that lim g(x) 4.Ä œ
xxÄ! Ä!
6. 2 lim x lim g(x) lim x lim lim g(x) 4 lim lim g(x) 4 lim g(x)œ œ œ œ
xxx x
xxxx
Ä% Ä% Ä% Ä%
Ä! Ä! Ä! Ä!
’ “ ’“ ’“
†
(since lim g(x) is a constant) lim g(x) .
xxÄ! Ä!
Êœœ
2
% #
"
7. (a) lim f x lim x c f c for every real number c f is continuous on .
xc xcÄÄ
ab ab a bœœœ Ê _ß_
"Î$ "Î$
(b) lim g x lim x c g c for every nonnegative real number c g is continuous on .
xc xcÄÄ
ab abœœœ Ê Ò!ß_Ñ
$Î% $Î%
(c) lim h x lim x h c for every nonzero real number c h is continuous on and .
xc xcÄÄ
ab ab a b a bœ œ œ Ê _ß ! _ß _
#Î$ "
c
(d) lim k x lim x k c for every positive real number c k is continuous on
xc xcÄÄ
ab ab a bœ œ œ Ê !ß _
"Î' "
c
8. (a) n n , where I the set of all integers.
nI
-
−ß œ
ˆ‰ˆ‰ˆ‰
""
##
11
(b) n n 1 , where I the set of all integers.
nI
-
−ß œabab11
(c) abab_ß ß _11
(d) abab_ß! !ß_
9. (a) lim lim lim , x 2; the limit does not exist because
xxxÄ! Ä! Ä!
x 4x4 x2
x 5x 14x x(x 7)(x 2) x(x 7)
(x 2)(x 2)
œœÁ
lim and lim
xx
Ä! Ä!
x2 x2
x(x 7) x(x 7)
œ_ œ_
(b) lim lim lim , x 2, and lim 0
xxx xÄ# Ä# Ä# Ä#
x 4x4 x2 x2 0
x 5x 14x x(x 7)(x ) x(x 7) x(x 7) 2(9)
(x 2)(x 2)
#
œœÁ œœ
10. (a) lim lim lim lim , x 0 and x 1.
xx x x0
Ä! Ä! Ä! Ä
xx x1
x2xx
x(x 1)
x x 2x 1 x (x 1)(x 1) x (x 1)
"
œœœÁÁ
ab
Now lim and lim lim .
xx
x
Ä! Ä!
Ä!
11xx
x(x 1) x(x 1) x2xx
œ_ œ_ Ê œ_
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

112 Chapter 2 Limits and Continuity
(b) lim lim lim , x 0 and x 1. The limit does not
xx xÄ" Ä" Ä"
xx 1
x2xx
x(x 1)
x x 2x 1 x (x 1)
œœÁÁ
ab
exist because lim and lim .
xx
Ä" Ä"
""
x(x 1) x(x 1)
œ_ œ_
11. lim lim lim
x1 x1 x1ÄÄ Ä
1x x
1x 1x1x 1x
"
#
""
ÈÈ
ˆ‰ˆ‰
ÈÈ È
œœœ
12. lim lim lim
xa xa xaÄÄ Ä
xa
xa
xa
xaxa xa a
""
#
œœœ
ab
abab
13. lim lim lim (2x h) 2x
hh hÄ! Ä! Ä!
(x h) x
hh
x 2hx h x
œœœ
ab
14. lim lim lim (2x h) h
xx xÄ! Ä! Ä!
(x h) x
hh
x 2hx h x
œœœ
ab
15. lim lim lim
xx xÄ! Ä! Ä!
x
# #
" "
x 2x( x) 4 x 4
2(2x)
œœœ
16. lim lim lim x 6x 12 12
xx xÄ! Ä! Ä!
(x)8
xx
x6x12x88
# #
œœœ
ab
ab
17. lim [4 g(x)] 2 lim 4 g(x) 2 lim 4 g(x) 8, since 2 8. Then lim g(x) 2.
xxx xÄ! Ä! Ä! Ä!
"Î$ $
"Î$
œÊ œÊ œ œ œ
’“
18. lim 2 lim (x g(x)) 5 lim g(x) lim g(x) 5
xx x5 x5
Ä& Ä& ÄÄ
ÈÈ ÈÈ
""""
###xg(x)
œÊ œÊ œÊ œ
ÈÈ
19. lim lim g(x) 0 since lim 3x 1 4
x1 x1 x1ÄÄÄ
3x 1
g(x)
#
œ_ Ê œ œab
20. lim 0 lim g(x) since lim 5 x 1
xx xÄ# Ä# Ä#
5x
g(x)
#
ÈœÊ œ_ œab
21. lim lim . lim lim
xx x xÄ_ Ä_ Ä_ Ä_
# $ #! # # $ #! #
& ( &! & & ( &! &
#
& &
#
x x
x x
œœœ ## œ œœ
x x
xx
23. lim lim
xxÄ_ Ä_
xx
xxxx
% ) " % )
$$$$
œ œ!!!œ!
ˆ‰
24. lim lim
xxÄ_ Ä_
"!
( " "!!
"
xx œœœ!
x
xx
25. lim lim . lim lim
xx x xÄ_ Ä_ Ä_ Ä_
xx x xx x
x1 x
( ( "
"# "#)
" "#
œ œ _ #' œ œ _
xx
27. lim lim since int x as x lim .
xx xÄ_ Ä_ Ä_
ll ll
"
sin x sin x
xx xgh gh gh
Ÿ œ! Ä_ Ä_Ê œ!
28. lim lim lim .
)))Ä_ Ä_ Ä_
l "l l#l l "lcos cos ))
)) )
Ÿœ!Ê œ!
29. lim lim
xxÄ_ Ä_
xsin x x
xsin x
#
"!
"
"
"!!
Èœœœ"
sin x
xx
sin x
x
30. lim lim
xxÄ_ Ä_
xx x
xcosx
" "!
" "!
œœœ"
Œ
cos x
x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
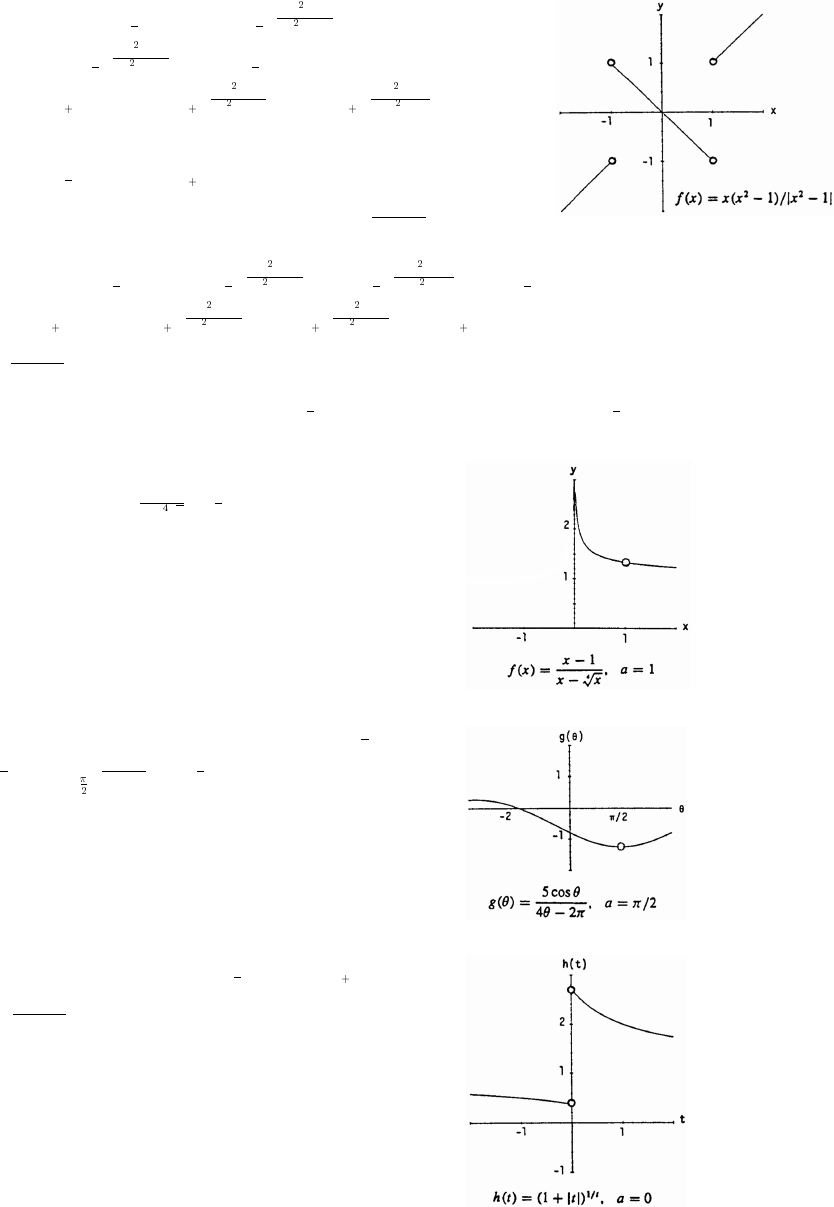
Chapter 2 Practice Exercises 113
31. At x 1: lim f(x) lim œ œ
xxÄ" Ä"
xx 1
x1
ab
kk
lim lim x 1, andœœœ
xxÄ" Ä"
xx 1
x1
ab
lim f(x) lim lim
xx xÄ" Ä" Ä"
œœ
xx 1 xx 1
x1 x
ab ab
kk ab
"
lim ( x) ( 1) 1. Sinceœœœ
x1Ä
lim f(x) lim f(x)
xx
Ä" Ä"
Á
lim f(x) does not exist, the function f beÊx1Ä cannot
extended to a continuous function at x 1.œ
At x 1: lim f(x) lim lim lim ( x) 1, andœœœ œœ
xx x xÄ" Ä" Ä" Ä"
xx 1 xx 1
x1 x1
ab ab
kk ab
lim f(x) lim lim lim x 1. Again lim f(x) does not exist so f
xx x x1 x1
Ä" Ä" Ä" Ä Ä
œœœœ
xx 1 xx 1
x1 x
ab ab
kk
"
be extended to a continuous function at x 1 either.cannot œ
32. The discontinuity at x 0 of f(x) sin is nonremovable because lim sin does not exist.œœ
ˆ‰
""
xx
xÄ!
33. Yes, f does have a continuous extension to a 1:œ
define f(1) lim .œœ
x1Ä
x4
xx3
"
È
34. Yes, g does have a continuous extension to a :œ1
#
g lim .
ˆ‰
1)
)1##
œœ
)Ä
5 cos 5
44
35. From the graph we see that lim h(t) lim h(t)
tt
Ä! Ä!
Á
so h be extended to a continuous functioncannot
at a 0.œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
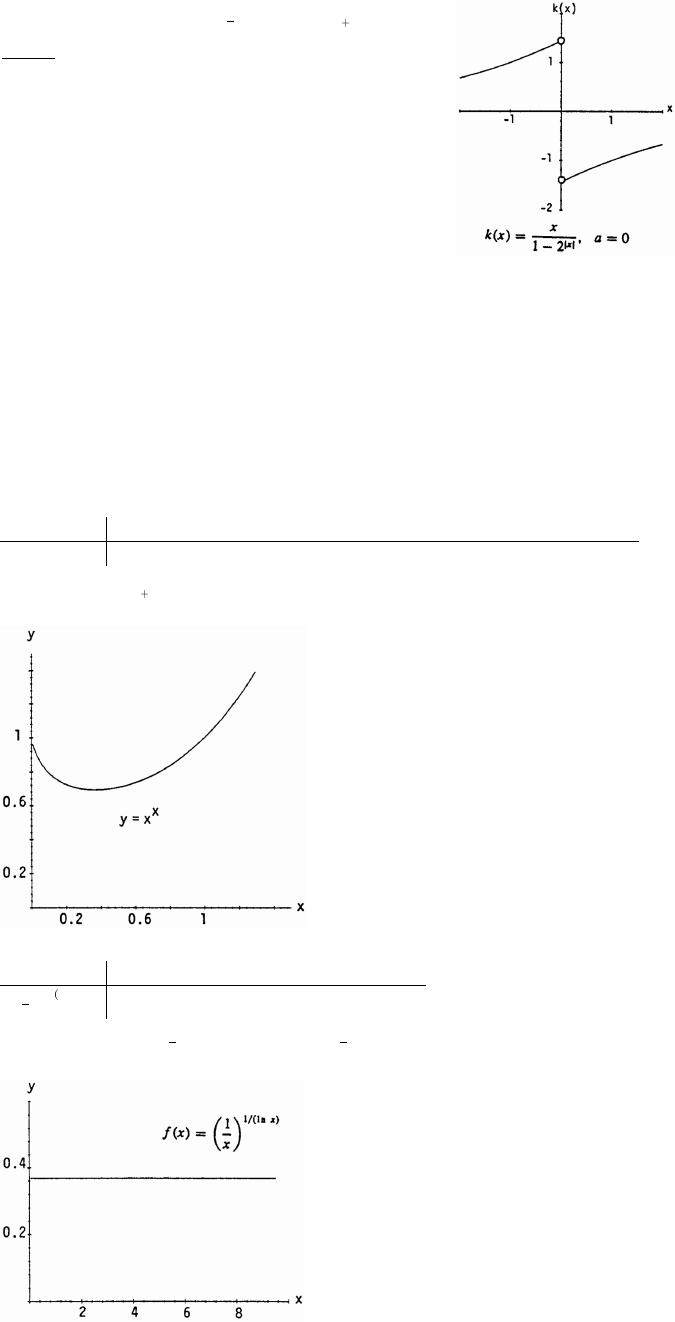
114 Chapter 2 Limits and Continuity
36. From the graph we see that lim k(x) lim k(x)
xx
Ä! Ä!
Á
so k be extended to a continuous functioncannot
at a 0.œ
37. (a) f( 1) 1 and f(2) 5 f has a root between 1 and 2 by the Intermediate Value Theorem.œ œ Ê
(b), (c) root is 1.32471795724
38. (a) f( 2) 2 and f(0) 2 f has a root between 2 and 0 by the Intermediate Value Theorem.œ œ Ê
(b), (c) root is 1.76929235424
CHAPTER 2 ADDITIONAL AND ADVANCED EXERCISES
1. (a) x 0.1 0.01 0.001 0.0001 0.00001
x 0.7943 0.9550 0.9931 0.9991 0.9999
x
Apparently, lim x 1
xÄ!
xœ
(b)
2. (a) x 10 100 1000
0.3679 0.3679 0.3679
ˆ‰
""Î Ñ
x
ln x
Apparently, lim 0.3678
xÄ_ ˆ‰
""
"ÎÐ Ñ
xe
ln x œœ
(b)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 2 Additional and Advanced Exercises 115
3. lim L lim L L 1 L 1 0
vc vcÄÄ
œ"œœœ
!! !
ÉÉ
É
vc
ccc
lim v
vc
The left-hand limit was needed because the function L is undefined if v c (the rocket cannot move faster
than the speed of light).
4. 1 0.2 0.2 1 0.2 0.8 1.2 1.6 x 2.4 2.56 x 5.76.
¹¹ È
ÈÈÈ
xxx
###
ÊÊÊÊ
1 0.1 0.1 1 0.1 0.9 1.1 1.8 x 2.2 3.24 x 4.84.
¹¹ È
ÈÈÈ
xxx
###
ÊÊÊÊ
5. 10 (t 70) 10 10 0.0005 (t 70) 10 0.0005 0.0005 (t 70) 10 0.0005kkkk‚Ê‚Ê‚
% % %
5 t 70 5 65° t 75° Within 5° F.Ê Ê Ê
6. We want to know in what interval to hold values of h to make V satisfy the inequality
V h . To find out, we solve the inequality:l "!!!l œ l$' "!!!l Ÿ "!1
hhhhl$' "!!!l Ÿ "! Ê "! Ÿ $' "!!! Ÿ "! Ê **! Ÿ $' Ÿ "!"! Ê Ÿ Ÿ111
**! "!"!
$' $'11
h . where 8.8 was rounded up, to be safe, and 8.9 was rounded down, to be safe.Ê )Þ) Ÿ Ÿ )Þ*
The interval in which we should hold h is about cm wide (1 mm). With stripes 1 mm wide, we can expect)Þ* )Þ) œ !Þ"
to measure a liter of water with an accuracy of 1%, which is more than enough accuracy for cooking.
7. Show lim f(x) lim x 7 f(1).
x1 x1ÄÄ
œœ'œab
#
Step 1: x76 x1 1 x 1 1 x 1.kkab ÈÈ
###
ÊÊ Ê %% % % % % %
Step 2: x1 x1 x .kk Ê Ê " "$$ $$ $
Then 1 or 1 . Choose min 1 1 1 1 , then "œ "œ œ ß $%$%$ %%
ÈÈ
ÈÈ
š›
0 x 1 x 6 and lim f(x) 6. By the continuity test, f(x) is continuous at x 1.Ê ( œ œkk k kab$%
#
x1Ä
8. Show lim g(x) lim 2 g .
xxÄÄ
œœœ
""
2x 4
ˆ‰
Step 1: 2 x .
¸¸
"" """
## ###xx x44
Ê # Ê# # Ê %% % % % %%
Step 2: x x .
¸¸
B Ê Ê
""""
4444
$$ $$ $
Then , or .œÊœœ œÊœœ$$ $$
"" "" "" ""
# # # # 44 44 4(2) 44 4 44(2)%%%%%%
%%
Choose , the smaller of the two values. Then 0 x 2 and lim 2.$$%œÊœ
%
%4( ) 4 x x# ##
"" "
¸¸ ¸ ¸ xÄ
By the continuity test, g(x) is continuous at x .œ"
4
9. Show lim h(x) lim 2x 3 h(2).
xxÄ# Ä#
œœ"œ
È
Step 1: 2x 3 1 2x 3 2x 3 x .
¹¹
ÈÈ È
Ê " Ê" " Ê %% % % %
(1 ) ( ) 3$ "
##
%%
Step 2: x 2 x 2 or x .kk Ê ##$$ $$ $
Then , or #œ Ê œ# œ œ #œ$$ %$
() () (1) ()" $ " $ " " $
#####
%%% %
%
. Choose , the smaller of the two values . Then,Êœ #œ œ œ$%$%
((" Ñ $ " Ñ "
### #
%%
%%
x 2 2x 3 , so lim 2x 3 1. By the continuity test, h(x) is continuous at x 2.!Ê " œ œkk ¹¹
ÈÈ
$%
xÄ#
10. Show lim F(x) lim 9 x F(5).
xxÄ& Ä&
œœ#œ
È
Step 1: 9x2 9x 9(2 ) x ( ).
¹¹
ÈÈ
Ê # Ê *#%% % % %
##
Step 2: 0x5 x x. Ê & Ê & &kk$$ $$ $
Then () () , or () () . &œ* # Ê œ # %œ # &œ* # Ê œ% # œ #$%$%%%$%$%%%
### # ##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

116 Chapter 2 Limits and Continuity
Choose , the smaller of the two values. Then, x 5 9 x , so$% % $ %œ# !Ê #
#kk ¹¹
È
lim 9 x . By the continuity test, F(x) is continuous at x 5.
xÄ&Èœ# œ
11. Suppose L and L are two different limits. Without loss of generality assume L L . Let (L L ).
"# #" #"
"
œ%3
Since lim f(x) L there is a 0 such that 0 x x f(x) L f(x) L
xxÄœÊÊ
"" !" " "
$$%%%kk k k
(L L ) L f(x) (L L ) L 4L L 3f(x) 2L L . Likewise, lim f(x) LÊ Ê œ
""
#" " #" " "# "# #
33 xxÄ
so there is a such that 0 x x f(x) L f(x) L$$%%%
#!## #
Ê Ê kk k k
(L L ) L f(x) (L L ) L 2L L 3f(x) 4L LÊ Ê
""
#" # #" # #" #"
33
L 4L 3f(x) 2L L . If min both inequalities must hold for 0 x x :Ê œ ß
"# #" "# !
$$$ $ef k k
5(L L ) 0 L L . That is, L L 0 L L 0,
4L L 3f(x) 2L L
LL 3f(x)2LL
"# "#
"# #" "# "# "# "#
% Ê and
a contradiction.
12. Suppose lim f(x) L. If k , then lim kf(x) lim 0 lim f(x) and we are done.
xc xc xc xcÄÄÄÄ
œ œ! œ œ!œ!†
If k 0, then given any , there is a so that x c f x L k f x LÁ ! ! !l l Êl l Êl ll l%$ $ %ab ab
%
l5l
k f x L | kf x kL . Thus, lim kf(x) kL k lim f(x) .Êl Êl l œ œab ababab ab Š‹
%%
xc xcÄÄ
13. (a) Since x 0 , 0 x x 1 x x 0 lim f x x lim f(y) B where y x x.ÄÊÄÊ œ œ œ
$ $ $ $
ab ab
xy
Ä! Ä!
(b) Since x 0 , 1 x x 0 x x 0 lim f x x lim f(y) A where y x x.ÄÊÄÊ œ œ œ
$$ $ $
ab ab
xy
Ä! Ä!
(c) Since x 0 , 0 x x 1 x x 0 lim f x x lim f(y) A where y x x .Ä Ê Ä Ê œ œ œ
% # #% #% #%
ab ab
xyÄ! Ä!
(d) Since x 0 , 1 x 0 x x 1 x x 0 lim f x x A as in part (c).Ä Ê!Ê Ä Ê œ
%##%#%
ab ab
xÄ!
14. (a) True, because if lim (f(x) g(x)) exists then lim (f(x) g(x)) lim f(x) lim [(f(x) g(x)) f(x)]
xa xa xa xaÄÄÄÄ
œ
lim g(x) exists, contrary to assumption.œxaÄ
(b) False; for example take f(x) and g(x) . Then neither lim f(x) nor lim g(x) exists, butœœ
""
xxxxÄ! Ä!
lim (f(x) g(x)) lim lim 0 0 exists.
xxxÄ! Ä! Ä!
œ œ œ
ˆ‰
""
xx
(c) True, because g(x) x is continuous g(f(x)) f(x) is continuous (it is the composite of continuousœÊœkk k k
functions).
(d) False; for example let f(x) f(x) is discontinuous at x 0. However f(x) 1 is
1, x 0
1, x 0
œÊ œ œ
Ÿ
œkk
continuous at x 0.œ
15. Show lim f(x) lim lim , x 1.
x1 x1 x1Ä Ä Ä
œœ œ#Á
x
x1 (x1)
(x 1)(x )
"
"
Define the continuous extension of f(x) as F(x) . We now prove the limit of f(x) as x 1
, x
2 , x 1
π
Á"
œ
œx1
x1
exists and has the correct value.
Step 1: ( ) (x 1) , x x .
¹¹
x
x1 (x1)
(x 1)(x )
"
"
# Ê # Ê # Á"Ê " "%% %% % % %
Step 2: x ( 1) x 1 x .kk Ê Ê " "$$ $$ $
Then , or . Choose . Then x ( 1) "œ " Ê œ "œ " Ê œ œ ! $ % $% $ % $% $% $kk
lim F(x) 2. Since the conditions of the continuity test are met by F(x), then f(x) has aÊ#Ê œ
¹¹
ab
x
x1
"
%x1Ä
continuous extension to F(x) at x 1.œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 2 Additional and Advanced Exercises 117
16. Show lim g(x) lim lim , x 3.
xx xÄ$ Ä$ Ä$
œœ œ#Á
x2x3
2x 6 2(x 3)
(x 3)(x )
"
Define the continuous extension of g(x) as G(x) . We now prove the limit of g(x) as
, x 3
2 , x 3
œÁ
œ
œx2x3
2x 6
x 3 exists and has the correct value.Ä
Step 1: 2 , x x .
¹¹
x2x3 x
x6 2(x3)
(x 3)(x )
"
# #
"
Ê # Ê # Á$Ê$# $#%% %% % % %
Step 2: x3 x3 x .kk Ê Ê$ $$$ $ $ $
Then, , or . Choose . Then x 3$ œ$# Ê œ# $œ$# Ê œ# œ# ! $ % $%$ % $% $% $kk
2 lim 2. Since the conditions of the continuity test hold for G(x),ÊÊ œ
¹¹
x2x3
2x 6 (x 3)
(x 3)(x )
#
"
%xÄ$
g(x) can be continuously extended to G(x) at 3.Bœ
17. (a) Let be given. If x is rational, then f(x) x f(x) 0 x 0 x 0 ; i.e., choose%%%! œÊ œÍ k kkk kk
. Then x 0 f(x) 0 for x rational. If x is irrational, then f(x) 0 f(x) 0$% $ % %œ Ê œÊ kk kk kk
which is true no matter how close irrational x is to 0, so again we can choose . In either case,Í! œ%$%
given there is a such that x 0 f(x) 0 . Therefore, f is continuous at%$% $ %! œ! !Ê kk k k
x0.œ
(b) Choose x c . Then within any interval (c c ) there are both rational and irrational numbers.œ! ß$$
If c is rational, pick . No matter how small we choose there is an irrational number x in%$œ!
c
#
(c c ) f(x) f(c) 0 c c . That is, f is not continuous at any rational c 0. Onß Ê œ œ œ $$ %kkkk
c
#
the other hand, suppose c is irrational f(c) 0. Again pick . No matter how small we choose Êœ œ !%$
c
#
there is a rational number x in (c c ) with x c x . Then f(x) f(c) x 0ß œ Í œ $$ %kk k kkk
cc3c
###
x f is not continuous at any irrational c 0.œœÊ kk c
#%
If x c 0, repeat the argument picking . Therefore f fails to be continuous at anyœ œ œ%kkcc
##
nonzero value x c.œ
18. (a) Let c be a rational number in [0 1] reduced to lowest terms f(c) . Pick . No matter howœßÊœœ
m
nnn
""
#
%
small is taken, there is an irrational number x in the interval (c c ) f(x) f(c) 0$$$! ß Ê œ kk
¸¸
"
n
. Therefore f is discontinuous at x c, a rational number.œ œ œ
""
#nn
%
(b) Now suppose c is an irrational number f(c) 0. Let 0 be given. Notice that is the only rationalʜ %"
#
number reduced to lowest terms with denominator 2 and belonging to [0 1]; and the only rationals withß"
33
2
denominator 3 belonging to [0 1]; and with denominator 4 in [0 1]; , , and with denominator 5 inßß
""
4 4 555 5
3234
[0 1]; etc. In general, choose N so that there exist only finitely many rationals in [ ] havingßÊ !ß"
"
N%
denominator N, say r , r , , r . Let min c r : i 1 p . Then the interval (c c )Ÿáœœßáß ß
"# pi
$$$efkk
contains no rational numbers with denominator N. Thus, 0 x c f(x) f(c) f(x) 0ŸÊœkk k kk k$
f(x) f is continuous at x c irrational.œŸÊ œkk"
N%
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
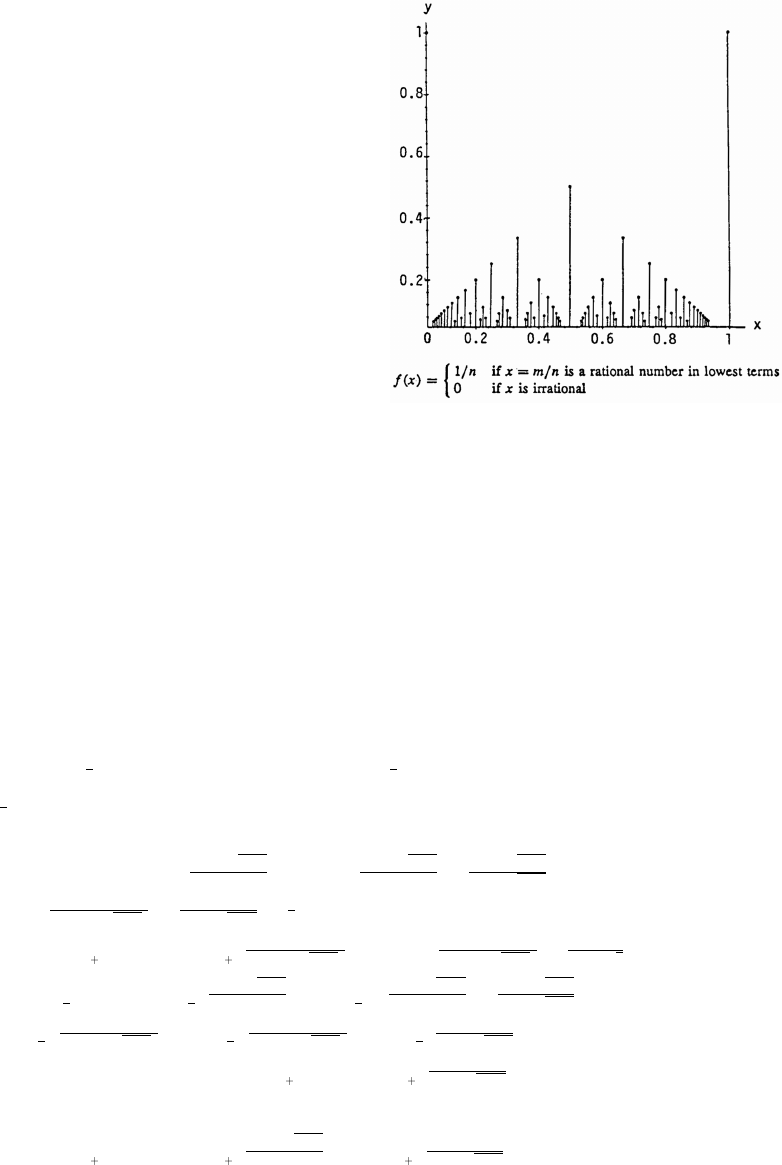
118 Chapter 2 Limits and Continuity
(c) The graph looks like the markings on a typical ruler
when the points (x f(x)) on the graph of f(x) areß
connected to the x-axis with vertical lines.
19. Yes. Let R be the radius of the equator (earth) and suppose at a fixed instant of time we label noon as the
zero point, 0, on the equator 0 R represents the midnight point (at the same exact time). Suppose xÊ1"
is a point on the equator “just after" noon x R is simultaneously “just after" midnight. It seemsÊ
"1
reasonable that the temperature T at a point just after noon is hotter than it would be at the diametrically
opposite point just after midnight: That is, T(x ) T(x R) 0. At exactly the same moment in time
""
1
pick x to be a point just before midnight x R is just before noon. Then T(x ) T(x R) 0.
####
Ê 11
Assuming the temperature function T is continuous along the equator (which is reasonable), the Intermediate
Value Theorem says there is a point c between 0 (noon) and R (simultaneously midnight) such that1
T(c) T(c R) 0; i.e., there is always a pair of antipodal points on the earth's equator where the œ1
temperatures are the same.
20. lim f(x)g(x) lim f(x) g(x) f(x) g(x) lim f(x) g(x) lim f(x) g(x)
xc xc xc xcÄÄ Ä Ä
œœ
""
%%
## ##
’“’ “
abab ab ab
Š‹Š‹
.œ$" œ#
"
%
##
ˆ‰
ab
21. (a) At x 0: lim r (a) lim lim œœ œ
aa aÄ! Ä! Ä!
" " "
"
ÈÈÈ
È
1a 1a 1a
aa
1a
Š‹Š‹
lim œœœ
aÄ!
1( a)
a1a 10
1
"
" "
"
#
ˆ‰
ÈÈ
At x 1: lim r (a) lim lim 1œ œ œ œ œ
aa a1
Ä" Ä" Ä
"
"
"
1(1a)
a1 1a a 1a
a
0
ˆ‰ ˆ‰
ÈÈÈ
(b) At x 0: lim r (a) lim lim œœ œ
aa aÄ! Ä! Ä!
" " "
"
ÈÈÈ
È
1a 1a 1a
aa
1a
Š‹Š‹
lim lim lim (because theœœœœ_
aaaÄ! Ä! Ä!
1( a)
a1a a11a 1a
a
"
" "
"
ˆ‰ ˆ‰
ÈÈÈ
denominator is always negative); lim r (a) lim (because the denominator
aaÄ! Ä!
"
"
œœ_
È1a
is always positive). Therefore, lim r (a) does not exist.
aÄ!
At x 1: lim r (a) lim lim 1œœœœ
aa a1Ä" Ä" Ä
"
"
11a
a1a
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
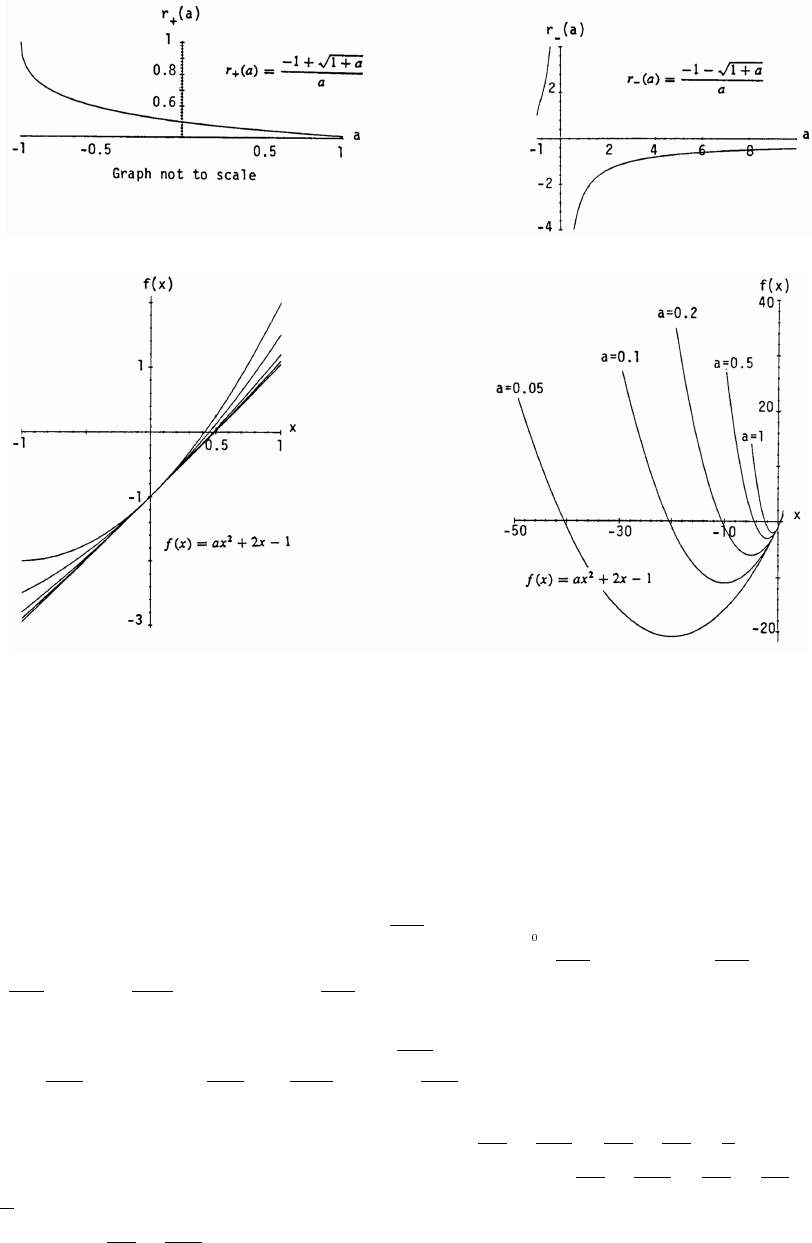
Chapter 2 Additional and Advanced Exercises 119
(c)
(d)
22. f(x) x 2 cos x f(0) 0 2 cos 0 2 0 and f( ) 2 cos ( ) 0. Since f(x) isœ Ê œ œ œ œ #11 11
continuous on [ ], by the Intermediate Value Theorem, f(x) must take on every value between [ ].ß! #ß#1 1
Thus there is some number c in [ ] such that f(c) 0; i.e., c is a solution to x 2 cos x 0.ß! œ œ1
23. (a) The function f is bounded on D if f(x) M and f(x) N for all x in D. This means M f(x) N for all xŸ ŸŸ
in D. Choose B to be max M N . Then f(x) B. On the other hand, if f(x) B, thene f kk kkkkkkߟ Ÿ
B f(x) B f(x) B and f(x) B f(x) is bounded on D with N B an upper bound andŸ ŸÊ ŸÊ œ
M B a lower bound.œ
(b) Assume f(x) N for all x and that L N. Let . Since lim f(x) L there is a such thatŸœ œ!%$
LN
#xxÄ
0 x x f(x) L L f(x) L L f(x) L Ê Í Í kk k k
!
##
$%%%
LN LN
f(x) . But L N N N f(x) contrary to the boundedness assumptionÍ ÊÊ
LN 3LN LN
## #
f(x) N. This contradiction proves L N.ŸŸ
(c) Assume M f(x) for all x and that L M. Let . As in part (b), 0 x xŸœ%$
ML
#!
kk
L f(x) L f(x) M, a contradiction.Ê Í
ML ML 3LM ML
####
24. (a) If a b, then a b 0 a b a b max (a b) a. Ê œÊ ßœ œ œ œkk ab ab ab 2a
ab
## ###
kk
If a b, then a b 0 a b (a b) b a max (a b)Ÿ Ÿ Ê œ œ Ê ß œ œ kk ab ab ba
ab
## ##
kk
b.œœ
2b
#
(b) Let min (a b) .ߜ
ab ab
##
kk
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

120 Chapter 2 Limits and Continuity
25. lim lim lim lim
x0 x0 x0 x0ÄÄ ÄÄ
œœ ††œ †
sin cos x sin cos x sin cos x
x cos x x cos x cos x x co
cos x cos x cos x
ab ab ab ab
" " "
" " " "
" " "
s x x cos x
sin x
œ"† lim
x0Äab"
lim .œ†œ"†œ!
x0Ä
sin x sin x
xcos x" #
!
ˆ‰
26. lim lim lim lim x .
x0 x0 x0 x0ÄÄ ÄÄ
sin x sin x x
sin x sin x x
x
ÈÈÈ
È
Š‹
œ † † œ"† † œ"†!†!œ!
B
"
sin x
xÈ
27. lim lim lim lim .
x0 x0 x0 x0ÄÄ ÄÄ
sin sin x sin sin x sin sin x
xsin xxsin xx
sin x sin x
ab ab ab
œ†œ†œ"†"œ"
28. lim lim x lim lim x
x0 x0 x0 x0ÄÄ ÄÄ
sin x x sin x x sin x x
xxx xx
ab ab ab
œ † " œ † " œ"†"œ"ab ab
29. lim lim x 2 lim lim x 2
x2 x2 x2 x2ÄÄ ÄÄ
sin x sin x sin x
x2 x x
ab ab ab% % %
% %
œ † œ † œ"†%œ%ab ab
30. lim lim lim lim
x9 x9 x9 x9ÄÄ ÄÄ
sin x sin x sin x
x9 xx x x
ˆ‰ ˆ‰ ˆ‰
ÈÈ È
ÈÈ È È
$ $ $
''
$ $ $ $
""""
œ†œ†œ"†œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

CHAPTER 3 DIFFERENTIATION
3.1 THE DERIVATIVE OF A FUNCTION
1. Step 1: f(x) 4 x and f(x h) 4 (x h)œ œ
##
Step 2:
f(x h) f(x) h( 2x h)
hh h hh
4(xh) 4x 4 x 2xh h 4 x 2xh h
œœ œœ
cdab
ab
2x hœ
Step 3: f (x) lim ( 2x h) 2x; f ( ) 6, f (0) 0, f (1) 2
wwww
œœ$œœœ
hÄ!
2. F(x) (x 1) 1 and F(x h) (x h 1) F (x) lim œ œ "Ê œ
##w
hÄ!
cdcd(xh1) 1 (x1) 1
h
lim lim lim (2x h 2)œœœ
hhhÄ! Ä! Ä!
ababx 2xhh 2x2h11 x 2x11
hh
2xh h 2h
2(x 1); F ( 1) 4, F (0) 2, F (2) 2œœœœ
www
3. Step 1: g(t) and g(t h)œœ
""
t(th)
Step 2:
g(t h) g(t)
h h h (th)th (th)th
tt2thh 2th h
œœ œ œ
(t h) t
t(th)
(t h) t
Œab
††
œœ
h( 2t h)
(t h) t h (t h) t
2t h
Step 3: g (t) lim ; g ( 1) 2, g (2) , g 3
wwww
"
œœœœœœ
hÄ!
2t h 2t 2 2
(t h) t t t t 4 33
†Š‹
ÈÈ
4. k(z) and k(z h) k (z) lim œœÊœ
1z
z2(zh) h
1(zh)
#
w
hÄ!
Š‹
(z h)
(z h) z
z
lim lim lim lim œœ œœ
hh hhÄ! Ä! Ä! Ä!
(1 z h)z ( z)(z h)
(z h)zh 2(z h)zh 2(z h)zh (z h)z
zz zhzhz zh h
"
# #
"
; k ( ) , k (1) , k 2œ"œ œ œ
" " " "
www
##2z 4
Š‹
È
5. Step 1: p( ) 3 and p( h) 3( h)))) )œœ
ÈÈ
Step 2:
p( h) p( ) (3 3h) 3
hh h
3( h) 3 33h 3 33h 3
33h 3 h 33h 3
)) ))
))
))))
)) ))
œœ œ
ÈÈŠ‹Š‹
ÈÈ
ÈÈ
Š‹Š‹
ÈÈ
ÈÈ
†
œœ
3h 3
h33h 3 33h 3
Š‹
ÈÈÈÈ
))
))
Step 3: p ( ) lim ; p (1) , p (3) , p
wwww
"
##
)œœœœœœ
hÄ!
3333 23
33h 3 3 3 23 23 32
ÈÈÈÈ È È È
))))) ˆ‰
6. r(s) 2s 1 and r(s h) 2(s h) 1 r (s) lim œ œ Êœ
ÈÈw
hÄ!
ÈÈ
2s 2h 1 2s 1
h
lim lim œœ
hhÄ! Ä!
Š‹Š ‹
ÈÈ
ÈÈ
Š‹Š‹
ÈÈ
ÈÈ
2s h 1 2s 1 2s 2h 1 2s 1
h2s 2h 1 2s 1 h 2s 2h 1 2s 1
(2s 2h 1) (2s 1)
†
lim lim œœœœ
hhÄ! Ä!
2h 2 2 2
h2s2h1 2s1 2s 2h 1 2s 1 2s1 2s1 22s1
Š‹
ÈÈÈÈÈÈ
È
; r (0) 1, r (1) , rœœœœ
""""
ww w
#
ÈÈÈ
2s 1 32
ˆ‰
7. y f(x) 2x and f(x h) 2(x h) lim lim œœ œÊœ œ
$$
dy 2(x h) 2x
dx h h
2 x 3x h 3xh h 2x
hhÄ! Ä!
ab
lim lim lim 6x 6xh 2h 6xœœ œœ
hh hÄ! Ä! Ä!
6x h 6xh 2h
hh
h 6x 6xh 2h
###
ab
ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

122 Chapter 3 Differentiation
8. r 1 lim lim œÊ œ œ
sdr
ds h h
11 (s h) 2 s 2
##
"
hhÄ! Ä!
”•
’“ cdcd
(s h) s
lim lim lim 3s 3sh h sœœœœ
" " "
####
###
hhhÄ! Ä! Ä!
s3sh3shh2s2 3
hh
h3s 3sh h
cd ab
9. s r(t) and r(t h) lim œœ œ Êœ
tthds
2t 1 2(t h) 1 dt h
hÄ!
Š‹
ˆ‰
th t
2(t h) 1 2t 1
lim lim œœ
hhÄ! Ä!
Š‹
(t h)(2t 1) t(2t 2h 1)
(2t 2h 1)(2t 1)
h (2t 2h 1)(2t 1)h
(t h)(2t 1) t(2t 2h 1)
lim lim lim œœœ
hhhÄ! Ä! Ä!
2t t 2ht h 2t 2ht t h
(2t 2h 1)(2t 1)h (2t 2h 1)(2t 1)h (2t 2h 1)(2t 1)
"
œœ
""
(2t 1)(2t 1) (2t 1)
10. lim lim lim
dv
dt h h h
(t h) t h
œœœ
hhhÄ! Ä! Ä!
’“ Š ‹
ˆ‰
th (th)t
th
h(th)tt(th)
tt
lim lim 1œœœœ
hhÄ! Ä!
ht h t h t ht 1 t 1
h(t h)t (t h)t t t
"
11. p f(q) and f(q h) lim œœ œ Êœ
""
ÈÈ Š‹Š‹
q1 (q h) 1
dp
dq h
hÄ!
(q h) 1 q1
lim lim œœ
hhÄ! Ä!
Œ
ÈÈ
ÈÈ
q1 qh1
qh1q1
h
q1 qh1
hqh1q1
lim lim œœ
hhÄ! Ä!
ˆ‰ˆ‰
ÈÈ
ÈÈ
ÈÈÈÈ
ÈÈ ÈÈ
ˆ‰ ˆ‰
q1 qh1 q1 qh1
hqh1q1 q1 qh1 hqh1q1 q1 qh1
(q 1) (q h 1)
†
lim lim œœ
hhÄ! Ä!
"
h
hqh1q1 q1 qh1 qh1q1 q1 qh1
ÈÈÈÈ
ÈÈ ÈÈ
ˆ‰ ˆ‰
œœ
" "
ÈÈ È È È
ˆ‰
q1q1 q1 q1 2(q1)q1
12. lim lim
dz
dw h
3w 2 3w 3h 2
h3w3h 2 3w 2
œœ
hhÄ! Ä!
Š‹
ÈÈ
ÈÈ
3(w h) 2 3w 2
lim œhÄ!
Š‹Š‹
ÈÈ
ÈÈ
ÈÈŠ‹
ÈÈ
3w 2 3w 3h 2 3w 2 3w 3h 2
h3w3h 2 3w 2 3w 2 3w 3h 2
†
lim œhÄ!
(3w 2) (3w 3h 2)
h 3w 3h 2 3w 2 3w 2 3w 3h 2
ÈÈ
ÈÈ
Š‹
lim œœ
hÄ!
33
3w 3h 2 3w 2 3w 2 3w 3h 2 3w 2 3w 2 3w 2 3w 2
ÈÈ
ÈÈ ÈÈÈ È
Š‹Š‹
œ
3
2(3w 2) 3w 2
È
13. f(x) x and f(x h) (x h) œ œ Ê œ
99
x(xh)hh
f(x h) f(x) (x h) x
’“’“
99
(x h) x
œœ œ
x(x h) 9x x (x h) 9(x h)
x(x h)h x(x h)h x(x h)h
x 2xhxh 9xx xh9x9h xhxh 9h
; f (x) lim 1 ; m f ( 3) 0œœ œ œœœœ
h(x xh 9)
x(x h)h x(x h) x(x h) x x
xxh9 xxh9 x9 9
ww
hÄ!
14. k(x) and k(x h) k (x) lim lim œœÊœ œ
""
#
w
x2(xh) h h
k(x h) k(x)
hhÄ! Ä!
Š‹
xh x
lim lim lim ;œœœœ
hhhÄ! Ä! Ä!
( x)(2xh)
h(2x)(2xh) h(2x)(2xh) (2x)( xh) (2x)
h
#
#
""
k(2)
w"
œ16
15. lim lim
ds
dt h h
(t h) (t h) t t t3th3thh t2thh tt
œœ
hhÄ! Ä!
cdab
abab
lim lim lim 3t 3th h 2t hœœœ
hhhÄ! Ä! Ä!
3th3thh2thh
hh
h3t 3th h 2t h
##
ab
ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.1 The Derivative of a Function 123
3t 2t; m 5œ œ œ
#
œ"
¸
ds
dt t
16. lim lim
dy (xh1) (x1) (x1) 3(x )h3(x1)h h (x1)
dx h h
œœ
hhÄ! Ä!
"
lim 3(x 1) 3(x 1)h h 3(x 1) ; m 3œ œ œ œ
hÄ!cd
¹
###
dy
dx x=
17. f(x) and f(x h) œœÊœ
88
x2 (x h) 2
f(x h) f(x)
hh
ÈÈ
88
(x h) 2 x2
œœ
8 x2 xh2 x2 xh2
hxh2x2 x2 xh2 hxh2x2 x2 xh2
8[(x 2) (x h 2)]
Š‹Š‹
ÈÈ
ÈÈ
ÈÈŠ‹ Š‹
ÈÈÈ
ÈÈ È
†
f (x) lim œÊœ
w
8h 8
hxh2x2 x2 xh2 xh2x2 x2 xh2
ÈÈ ÈÈ
ÈÈ ÈÈ
Š‹ Š‹
hÄ!
; m f (6) the equation of the tangentœœœœœÊ
"
w
#
844
x2x2 x2 x2 (x 2) x 2 4 4
ÈÈ È È
Š‹
ÈÈ
line at (6 4) is y 4 (x 6) y x y x .ß œ Ê œ $%Ê œ (
"" "
## #
18. g (z) lim lim
w
œœ
hhÄ! Ä!
ˆ‰
ÈŠ‹Š‹Š‹
ÈÈÈ
ÈÈ
Š‹
ÈÈ
14(zh)14z 4zh4z 4zh4z
hh
4zh 4z
†
lim lim lim ;œœœœ
hhhÄ! Ä! Ä!
(4 z h) (4 z)
h 4zh 4z h 4zh 4z 4zh 4z
h
24z
""
Š‹Š‹Š‹
ÈÈÈ
ÈÈÈ
È
m g (3) the equation of the tangent line at ( ) is w 2 (z 3)œœ œÊ $ß#œ
w" " "
# #
243
È
wz wz.ʜ#ʜ
"$ "(
## ##
19. s f(t) 1 3t and f(t h) 1 3(t h) 1 3t 6th 3h lim œœ œœ Êœ
####
ds
dt h
f(t h) f(t)
hÄ!
lim lim ( 6t 3h) 6t 6œœœÊœ
hhÄ! Ä!
abab13t 6th3h 13t
hdt
ds
¸t=
20. y f(x) and f(x h) 1 lim lim œœ" œ Êœ œ
""
xxhdxh h
dy f(x h) f(x) 11
hhÄ! Ä!
Š‹Š‹
xh x
lim lim lim œœœœÊœ
hhhÄ! Ä! Ä!
xxh
"" "
h x(x h)h x(x h) x dx 3
hdy ¹x= 3
21. r f( ) and f( h) lim lim œœ œ Êœ œ))
22dr
44( h) dh h
f( h) f( )
ÈÈ
)))
))
hhÄ! Ä!
22
4h4
lim lim œœ
hhÄ! Ä!
24 24 h 24 h
h4 4 h h4 4 h
224h
24 4 h
ÈÈ ÈÈ
ÈÈ ÈÈ Š‹
ÈÈ
Š‹
ÈÈ
# %
%
#
)) ))
)) ))
))
))
†
lim lim œœ
hhÄ! Ä!
4( ) 4( h)
2h44h4 4h 44h4 h
2
% %
%
))
)) ) ) )) ) )
ÈÈ È È ÈÈ È È
Š‹ Š‹
œœÊœ
2dr
(4 ) 2 4 (4 ) 4 d8
""
œ!
)) )) ))
Š‹
Èȸ
22. w f(z) z z and f(z h) (z h) z h lim œ œ œ Ê œ
ÈÈdw
dz h
f(z h) f(z)
hÄ!
lim lim lim 1œœœ
hhhÄ! Ä! Ä!
Š‹ Š‹
È È
ˆ‰
È È
ÈÈ
ÈÈ
Š‹
ÈÈ
zh zh z z zh z
hhh
hzhz zhz
zh z
–—
†
1 lim 1 lim œ œ œ" Ê œ
hhÄ! Ä!
(z h) z
hzh z zh z 2z
dw 5
dz 4
""
Š‹
ÈÈÈÈ
ȸz4
23. f x lim lim lim lim lim
w##
# # # # #
"
abœœœœœ
zx zx zx zx zxÄÄÄÄÄ
fz fx x z
z x zxzxzxzxzxz
xz
ab ab a b a b
ababab ababab abab
zx
x#
œ"
#abx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

124 Chapter 3 Differentiation
24. f x lim lim lim lim
w""
""
Ò""ÓÒ"
abœœ œ œ
zx zx zx zxÄÄ Ä Ä
fz fx x z
zx z x zxz x
xzxz
ab ab a b a b
ababab abababab
zx " Ó
""abababzxz x
lim limœœœœœ
zx zxÄÄ
abab ababab
ababab abab ab
ab ab
xzxz2 xz2 x x
zxzx zx x
xx
" " # # # "
"" "" "
" "
#
25. g x lim lim lim lim lim
w""
" " " "
"
abœœœœœ
zx zx zx zx zxÄÄÄÄÄ
gz gx zx xz
z x z x z x z x z x z x
zx
ab ab a b a b
ababab ababab
zx
zx ababzx" "
œ"
"abx
26. g x lim lim lim lim
w
" "
abœœ œ†œ
zx zx zx zxÄÄ Ä Ä
gz gx
z x z x z x
zx zx zx
zx z xzx
z x
ab ab ˆ ‰ˆ ‰ ÈÈ ÈÈ
ÈÈ ÈÈ ÈÈ
ab
ˆ‰
limœœ
zxÄ
""
#
ÈÈ È
zx x
27. Note that as x increases, the slope of the tangent line to the curve is first negative, then zero (when x 0),œ
then positive the slope is always increasing which matches (b).Ê
28. Note that the slope of the tangent line is never negative. For x negative, f (x) is positive but decreasing as x
w
#
increases. When x 0, the slope of the tangent line to x is 0. For x 0, f (x) is positive and increasing. Thisœ
w
#
graph matches (a).
29. f (x) is an oscillating function like the cosine. Everywhere that the graph of f has a horizontal tangent we
$ $
expect f to be zero, and (d) matches this condition.
w
$
30. The graph matches with (c).
31. (a) f is not defined at x 0, 1, 4. At these points, the left-hand and right-hand derivatives do not agree.
wœ
For example, lim slope of line joining ( 0) and ( ) but lim slope of
xx
Ä! Ä!
f(x) f(0) f(x) f(0)
x0 x0
#
"
œ %ß !ß # œ œ
line joining (0 2) and ( 2) 4. Since these values are not equal, f (0) lim does not exist.ß"ßœ œ
w
xÄ!
f(x) f(0)
x0
(b)
32. (a) (b) Shift the graph in (a) down 3 units
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
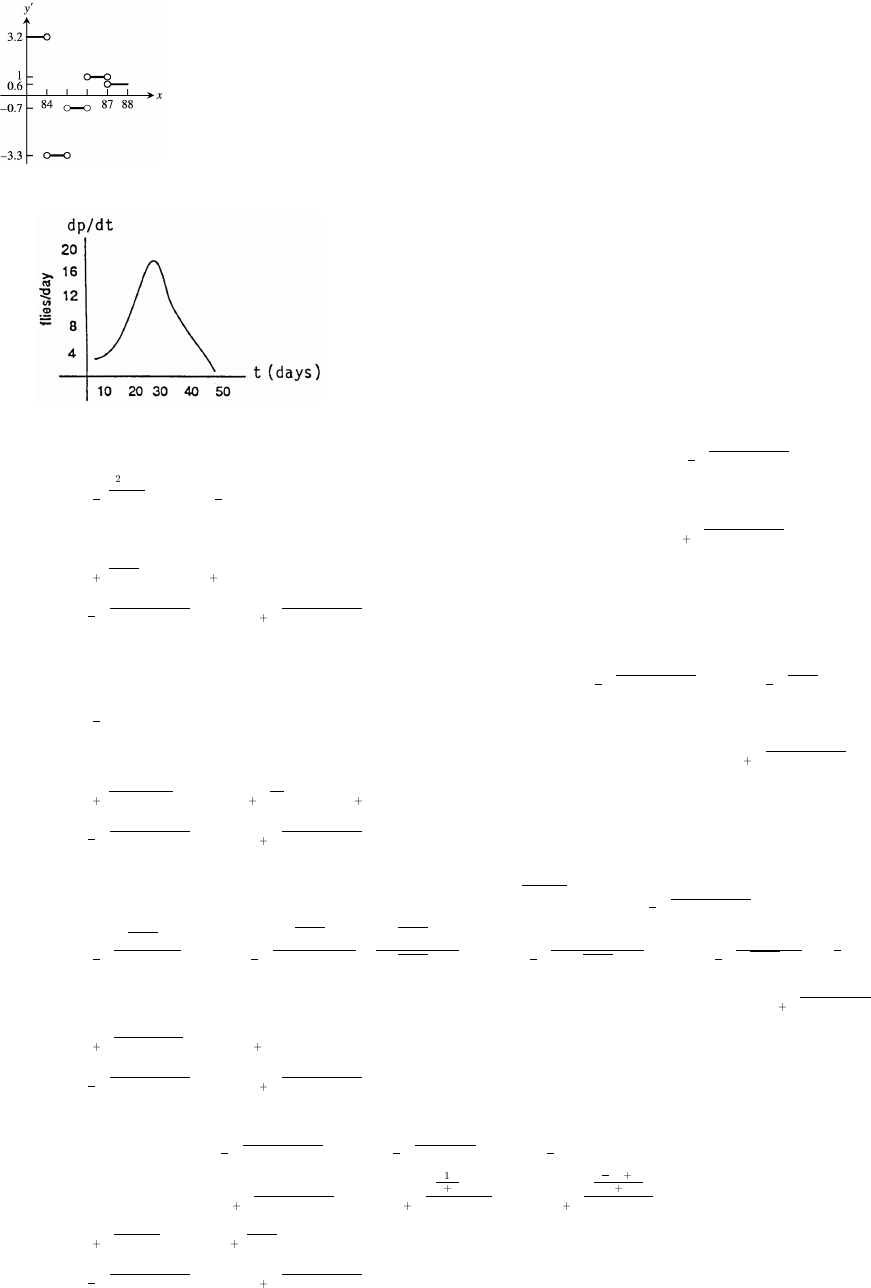
Section 3.1 The Derivative of a Function 125
33.
34. (a) (b) The fastest is between the 20 and 30 days;
th th
slowest is between the 40 and 50 days.
th th
35. Left-hand derivative: For h 0, f(0 h) f(h) h (using y x curve) lim œœ œ Ê
##
hÄ!
f(0 h) f(0)
h
lim lim h 0;œœœ
hhÄ! Ä!
h0
h
Right-hand derivative: For h 0, f(0 h) f(h) h (using y x curve) lim œœ œ Ê
hÄ!
f(0 h) f(0)
h
lim lim 1 1;œœœ
hhÄ! Ä!
h0
h
Then lim lim the derivative f (0) does not exist.
hh
Ä! Ä!
f(0 h) f(0) f(0 h) f(0)
hh
w
ÁÊ
36. Left-hand derivative: When h , 1 h 1 f(1 h) 2 lim lim ! Ê œ Ê œ
hhÄ! Ä!
f(1 h) f(1)
hh
22
lim 0 0;œœ
hÄ!
Right-hand derivative: When h , 1 h 1 f(1 h) 2(1 h) 2 2h lim ! Ê œ œ Ê
hÄ!
f(1 h) f(1)
h
lim lim lim 2 2;œœœœ
hhhÄ! Ä! Ä!
(2 2h) 2
hh
2h
Then lim lim the derivative f (1) does not exist.
hh
Ä! Ä!
f(1 h) f(1) f(1 h) f(1)
hh
w
ÁÊ
37. Left-hand derivative: When h 0, 1 h 1 f(1 h) 1 h lim ÊœÊ
ÈhÄ!
f( h) f(1)
h
"
lim lim lim lim ;œœ œ œœ
hh h hÄ! Ä! Ä! Ä!
ÈŠ‹Š‹
ÈÈ
Š‹ Š‹
ÈÈ
È
1h
hh
1h 1h
1h1 h 1h
(1 h)
1h1
" " "
"
" ""
#
†
Right-hand derivative: When h 0, 1 h 1 f(1 h) 2(1 h) 1 2h 1 lim ÊœœÊ
hÄ!
f( h) f(1)
h
"
lim lim 2 2;œœœ
hhÄ! Ä!
(2h 1)
h
"
Then lim lim the derivative f (1) does not exist.
hh
Ä! Ä!
f(1 h) f(1) f(1 h) f(1)
hh
w
ÁÊ
38. Left-hand derivative: lim lim lim 1 1;
hhhÄ! Ä! Ä!
f(1 h) f( ) (1 h)
hh
" "
œœœ
Right-hand derivative: lim lim lim
hhhÄ! Ä! Ä!
f(1 h) f( )
hhh
" "
œœ
Š‹ Š‹
1h 1h
1(1h)
lim lim 1;œœœ
hhÄ! Ä!
"
h
h(1 h) 1 h
Then lim lim the derivative f (1) does not exist.
hh
Ä! Ä!
f(1 h) f(1) f(1 h) f(1)
hh
w
ÁÊ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
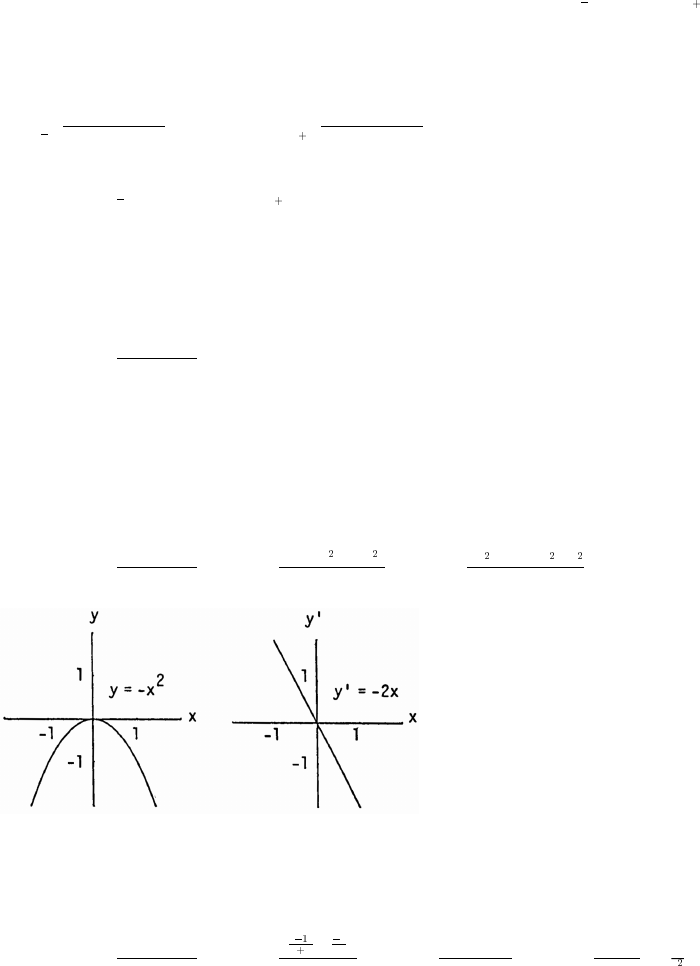
126 Chapter 3 Differentiation
39. (a) The function is differentiable on its domain x 2 (it is smooth)$ Ÿ Ÿ
(b) none
(c) none
40. (a) The function is differentiable on its domain x 3 (it is smooth)# Ÿ Ÿ
(b) none
(c) none
41. (a) The function is differentiable on x 0 and x 3$ Ÿ ! Ÿ
(b) none
(c) The function is neither continuous nor differentiable at x 0 since lim f(x) lim f(x)œÁ
xx
Ä! Ä!
42. (a) f is differentiable on x 1, x 0, 0 x 2, and 2 x 3# Ÿ " Ÿ
(b) f is continuous but not differentiable at x 1: lim f(x) 0 exists but there is a corner at x 1 sinceœ œ œ
x1Ä
lim 3 and lim 3 f ( 1) does not exist
hh
Ä! Ä!
f( 1 h) f( ) f( h) f( 1)
hh
" " w
œ œ Ê
(c) f is neither continuous nor differentiable at x 0 and x 2:œœ
at x 0, lim f(x) 3 but lim f(x) 0 lim f(x) does not exist;œœ œÊ
xxx0
Ä! Ä! Ä
at x 2, lim f(x) exists but lim f(x) f(2)œÁ
xxÄ# Ä#
43. (a) f is differentiable on x 0 and 0 x 2"Ÿ Ÿ
(b) f is continuous but not differentiable at x 0: lim f(x) 0 exists but there is a cusp at x 0, soœœ œ
xÄ!
f (0) lim does not exist
w
œhÄ!
f(0 h) f(0)
h
(c) none
44. (a) f is differentiable on x 2, 2 x 2, and 2 x 3$Ÿ Ÿ
(b) f is continuous but not differentiable at x 2 and x 2: there are corners at those pointsœ œ
(c) none
45. (a) f (x) lim lim lim lim ( 2x h) 2x
w
œœ œ œœ
hh h hÄ! Ä! Ä! Ä!
f(x h) f(x)
hh h
(x h) x x 2xh h x
ab
(b)
(c) y 2x is positive for x 0, y is zero when x 0, y is negative when x 0
www
œ œ
(d) y x is increasing for x 0 and decreasing for x ; the function is increasing on intervalsœ _ ! _
#
where y 0 and decreasing on intervals where y 0
ww
46. (a) f (x) lim lim lim lim
w
""
œœœœœ
hhhhÄ! Ä! Ä! Ä!
f(x h) f(x) x (x h)
h h x(x h)h x(x h) x
Š‹
xh x
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
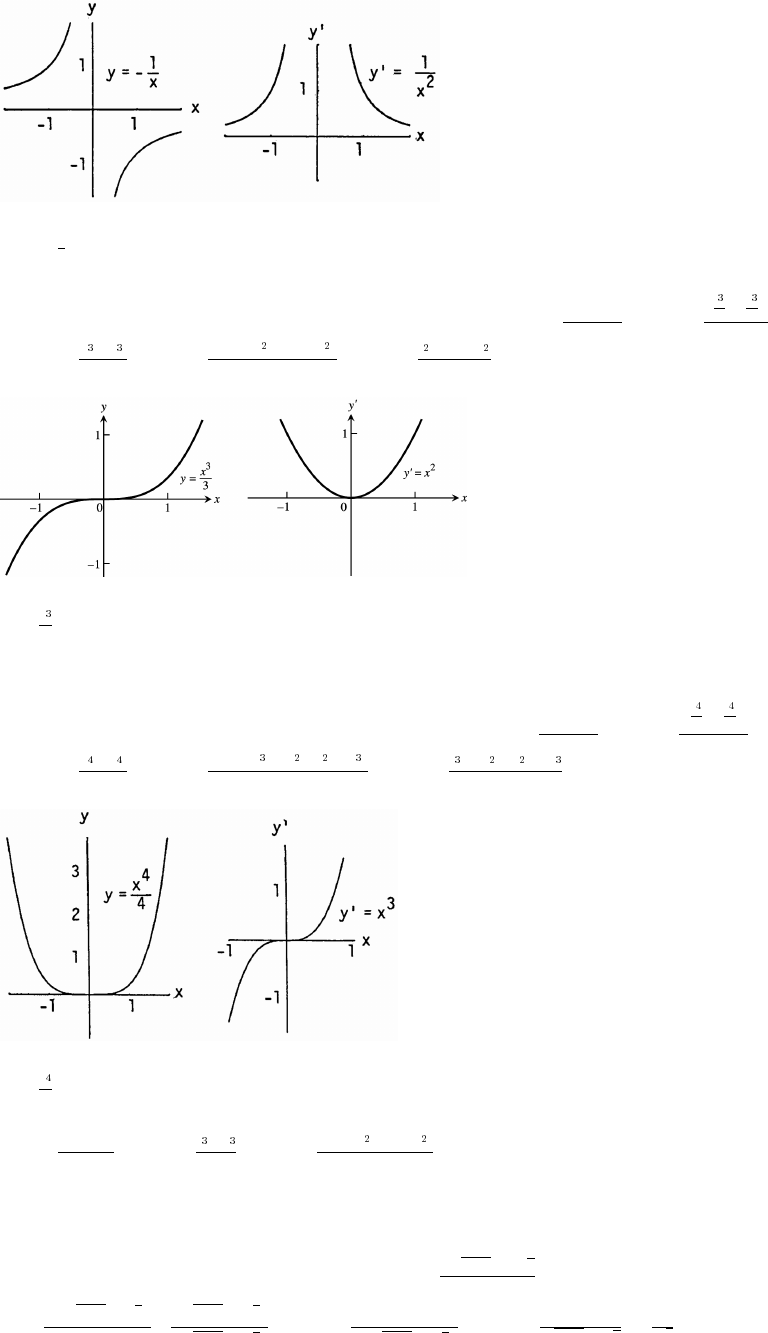
Section 3.1 The Derivative of a Function 127
(b)
(c) y is positive for all x 0, y is never 0, y is never negative
www
Á
(d) y is increasing for x 0 and xœ _ ! _
"
x
47. (a) Using the alternate formula for calculating derivatives: f (x) lim lim
w
œœ
zx zxÄÄ
f(z) f(x)
z x z x
Š‹
zx
33
lim lim lim x f (x) xœœ œ œÊœ
zx zx zxÄÄ Ä
z x z zx x
3(z x) 3(z x) 3
(z x) z zx x
#w #
ab
(b)
(c) y is positive for all x 0, and y 0 when x 0; y is never negative
www
Áœ œ
(d) y is increasing for all x 0 (the graph is horizontal at x 0) because y is increasing where y 0; y isœÁ œ
x
3w
never decreasing
48. (a) Using the alternate form for calculating derivatives: f (x) lim lim
w
œœ
zx zxÄÄ
f(z) f(x)
z x z x
Œ
zx
44
lim lim lim x f (x) xœœ œ œÊœ
zx zx zxÄÄ Ä
z x z xz x z x
4(z x) 4(z x) 4
(z x) z xz x z x
$w $
ab
(b)
(c) y is positive for x 0, y is zero for x 0, y is negative for x 0
www
œ
(d) y is increasing on 0 x and decreasing on x 0œ__
x
4
49. y lim lim lim lim x xc c 3c .
w###
œœœ œœ
xc xc xc xcÄÄÄ Ä
f(x) f(c)
xc xc xc
xc (x c) x xc c
ab ab
The slope of the curve y x at x c is y 3c . Notice that 3c 0 for all c y x never has a negativeœœœ Êœ
$w# # $
slope.
50. Horizontal tangents occur where y 0. Thus, y lim
ww
œœ
hÄ!
2xh2x
h
ÈÈ
lim lim lim .œœœœ
hhhÄ! Ä! Ä!
2xh x xh x
hxh x h xh x
2((x h) x)) 2
xh x x
Š‹Š‹
ÈÈ
ÈÈ
Š‹ Š‹
ÈÈ
ÈÈ
ÈÈ
È
"
†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
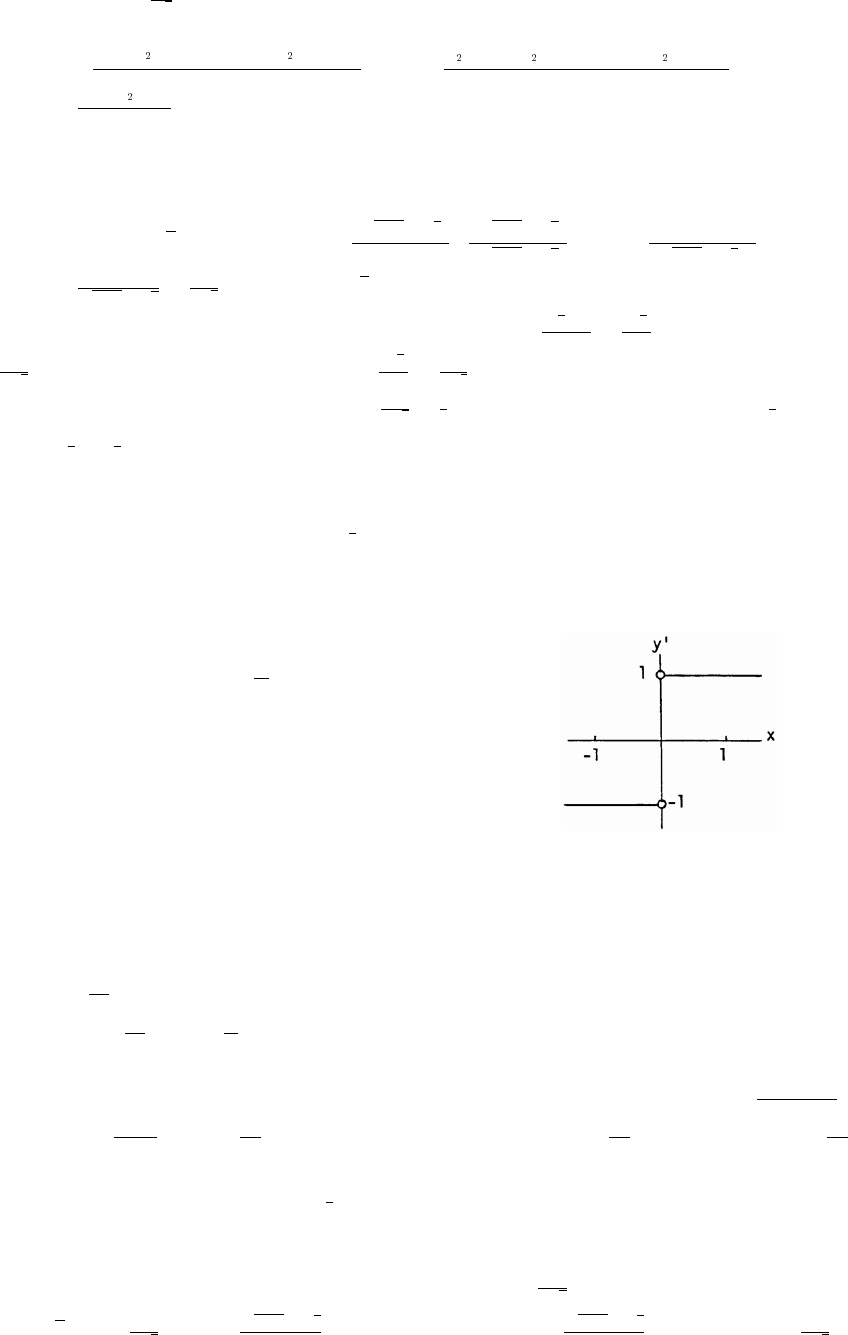
128 Chapter 3 Differentiation
Then y 0 when 0 which is never true the curve has no horizontal tangents.
w"
œœ Ê
Èx
51. y lim lim
w
œœ
hhÄ! Ä!
abab2(x h) 13(x h) 5 2x 13x 5
hh
2x 4xh 2h 13x 13h 5 2x 13x 5
lim lim (4x 2h 13) 4x 13, slope at x. The slope is 1 when 4x 13œœœ œ"
hhÄ! Ä!
4xh 2h 13h
h
4x 12 x 3 y 2 3 13 3 5 16. Thus the tangent line is y 16 ( 1)(x 3)Ê œ ʜʜ œ œ ††
#
y x and the point of tangency is (3 16).Êœ"$ ß
52. For the curve y x, we have y lim lim œœ œ
Èw
hhÄ! Ä!
Š‹Š‹
ÈÈ
ÈÈ
Š‹Š‹
ÈÈ
ÈÈ
xh x xh x
hxh x xh xh
(x h) x
†
lim . Suppose a is the point of tangency of such a line and ( ) is the pointœœ+ß "ß!
hÄ!
""
#
ÈÈ
È
xh x xˆ‰
È
on the line where it crosses the x-axis. Then the slope of the line is which must also equal
ÈÈ
a0 a
a(1) a1
œ
; using the derivative formula at x a 2a a 1 a 1. Thus such a line does
""
#2a a
a
a1
ÈÈ
È
œÊ œ Ê œÊœ
exist: its point of tangency is ( ), its slope is ; and an equation of the line is y 1 (x 1)"ß " œ œ
"" "
###
Èa
yx.ʜ
""
##
53. No. Derivatives of functions have the intermediate value property. The function f(x) x satisfies f(0) 0œÚ Û œ
and f(1) 1 but does not take on the value anywhere in [ ] f does not have the intermediate valueœ!ß"Ê
"
#
property. Thus f cannot be the derivative of any function on [ ] f cannot be the derivative of any function!ß " Ê
on ( )._ß _
54. The graphs are the same. So we know that
for f(x) x , we have f (x) .œœkk wkkx
x
55. Yes; the derivative of f is f so that f (x ) exists f (x ) exists as well. Ê
ww w
!!
56. Yes; the derivative of 3g is 3g so that g (7) exists 3g (7) exists as well.
ww w
Ê
57. Yes, lim can exist but it need not equal zero. For example, let g(t) mt and h(t) t. Then g(0) h(0)
tÄ!
g(t)
h(t) œœ œ
0, but lim lim lim m m, which need not be zero.œœœœ
tttÄ! Ä! Ä!
g(t)
h(t) t
mt
58. (a) Suppose f(x) x for x 1. Then f(0) 0 f(0) 0. Then f (0) lim kk kkŸ"ŸŸ ŸÊœ œ
##w
hÄ!
f(0 h) f(0)
h
lim lim . For h 1, h f(h) h h h f (0) lim 0œœ ŸŸŸÊŸŸÊœœ
hh hÄ! Ä! Ä!
f(h) 0 f(h) f(h) f(h)
hh h h
## w
kk
by the Sandwich Theorem for limits.
(b) Note that for x 0, f(x) x sin x sin x x 1 x (since sin x 1). By part (a),Áœ œ Ÿœ "ŸŸk k kkk k kk
¸¸
## ##
"
x†
f is differentiable at x 0 and f (0) 0.œœ
w
59. The graphs are shown below for h 1, 0.5, 0.1. The function y is the derivative of the functionœœ
"
2x
È
y x so that lim . The graphs reveal that y gets closer to yœœ œ œ
È" "
# #
È È
ÈÈ
ÈÈ
x x
xh x xh x
hh
hÄ!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
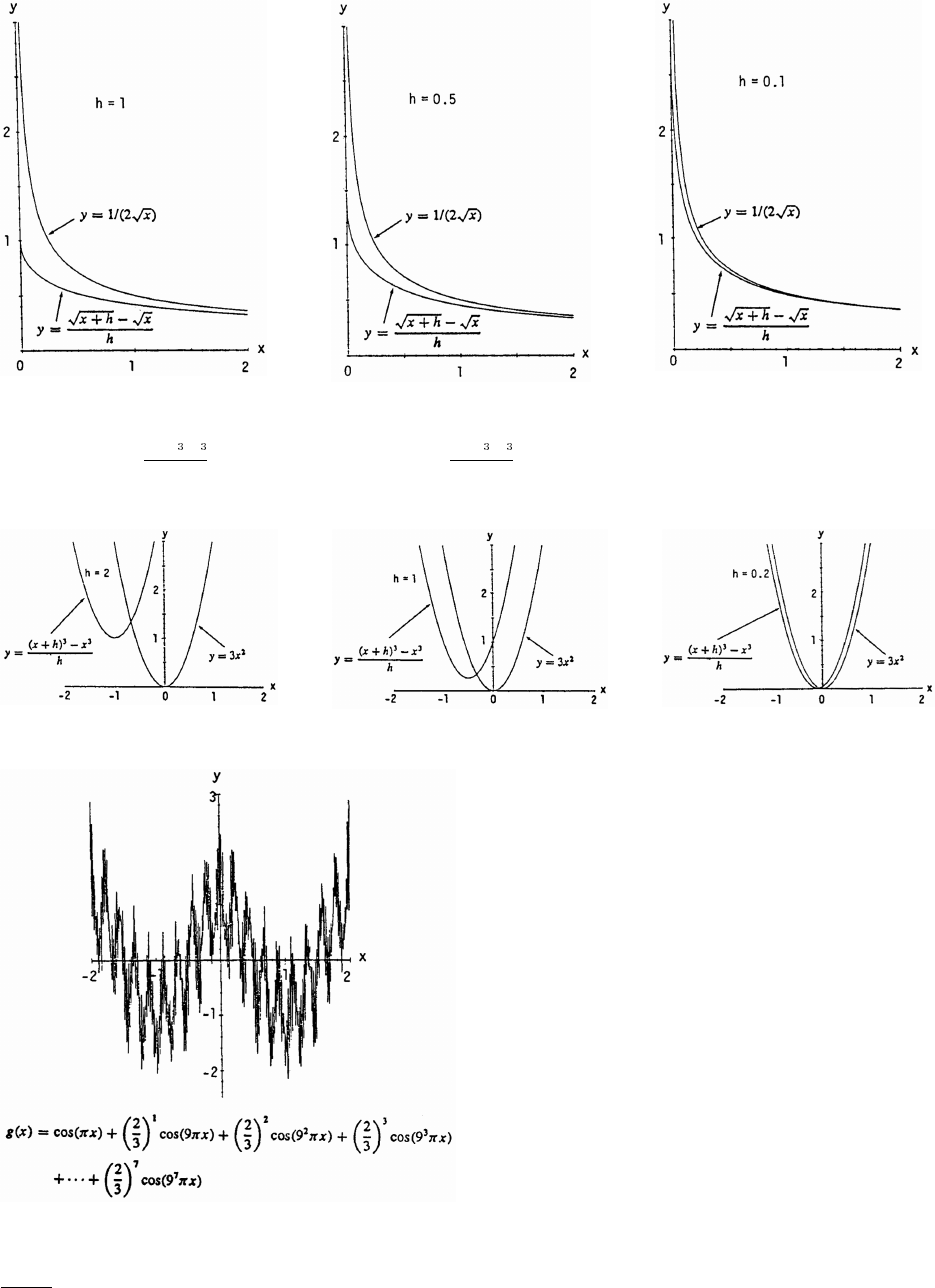
Section 3.1 The Derivative of a Function 129
as h gets smaller and smaller.
60. The graphs are shown below for h 2, 1, 0.5. The function y 3x is the derivative of the function y x soœœ œ
#$
that 3x lim . The graphs reveal that y gets closer to y 3x as h
# #
œœœ
hÄ!
(x h) x (x h) x
hh
gets smaller and smaller.
61. Weierstrass's nowhere differentiable continuous function.
62-67. Example CAS commands:
:Maple
f := x -> x^3 + x^2 - x;
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

130 Chapter 3 Differentiation
x0 := 1;
plot( f(x), x=x0-5..x0+2, color=black,
title="Section 3_1, #62(a)" );
q := unapply( (f(x+h)-f(x))/h, (x,h) ); # (b)
L := limit( q(x,h), h=0 ); # (c)
m := eval( L, x=x0 );
tan_line := f(x0) + m*(x-x0);
plot( [f(x),tan_line], x=x0-2..x0+3, color=black,
linestyle=[1,7], title="Section 3.1 #62(d)",
legend=["y=f(x)","Tangent line at x=1"] );
Xvals := sort( [ x0+2^(-k) $ k=0..5, x0-2^(-k) $ k=0..5 ] ): # (e)
Yvals := map( f, Xvals ):
evalf[4](< convert(Xvals,Matrix) , convert(Yvals,Matrix) >);
plot( L, x=x0-5..x0+3, color=black, title="Section 3.1 #62(f)" );
: (functions and x0 may vary) (see section 2.5 re. RealOnly ):Mathematica
<<Miscellaneous`RealOnly`
Clear[f, m, x, y, h]
x0= /4;1
f[x_]:=x Cos[x]
2
Plot[f[x], {x, x0 3, x0 3}]
q[x_, h_]:=(f[x h] f[x])/h
m[x_]:=Limit[q[x, h], h 0]Ä
ytan:=f[x0] m[x0] (x x0)
Plot[{f[x], ytan},{x, x0 3, x0 3}]
m[x0 1]//N
m[x0 1]//N
Plot[{f[x], m[x]},{x, x0 3, x0 3}]
3.2 DIFFERENTIATION RULES
1. y x 3 x (3) 2x 0 2œ Ê œ œ œ#B Ê œ
##
dy d y
dx dx dx dx
dd
ab
2. y x x 8 2x 1 0 2x 1 œ Ê œ œ Ê œ#
#dy d y
dx dx
3. s 5t 3t 5t 3t 15t 15t 15t 15t 30t 60tœÊœœÊœ œ
$& $ & # % # % $
ds d d d s d d
dt dt dt dt dt dt
ab ab ab ab
4. w 3z 7z 21z 21z 21z 42z 126z 42z 42œ Êœ Ê œ
($ # ' # &
dw d w
dz dz
5. y x x 4x 1 8xœÊœÊœ
4
3dx dx
dy d y
$#
6. y x x 2x 1 0 2x 1œÊ œÊ œ œ
xxx
34dx 4dx
dy d y
#
#"
7. w 3z z 6z z 18z 2zœÊœœÊœ œ
# " $ # % $
"dw 6 d w 18 2
dz z z dz z
z
8. s 2t 4t 2t 8t 4t 24tœ Ê œ œ Ê œ œ
" # # $ $ % ds 2 8 d s 4 24
dt t t dt t t
9. y 6x 10x 5x 12x 10 10x 12x 10 12 0 30x 12œ Ê œ œ Ê œ œ
## $ %
dy d y
dx x dx
10 30
x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.2 Differentiation Rules 131
10. y 4 2x x 3x 0 12xœ Ê œ# œ# Ê œ œ
$ % &
dy d y
dx dx x
312
x
11. r s s s s 2s 5sœ Êœ œÊœœ
"
# " $ # % $
##3 ds 3 3s 2s ds s
5dr2525dr 25
s
12. r 12 4 12 12 4 24 48 20œÊœœÊœ))) ) )) ) ) )
" $ % # % & $ & '
dr 12 12 4 d r
dd))))
)
œ
24 48 20
)))
13. (a) y 3 x x x 1 y 3 x x x 1 x x 1 3 xœ Ê œ abababababab
#$ w # $ $ #
††
dd
dx dx
3 x 3x 1 x x 1 ( 2x) 5x 12x 2x 3œ œ aba ba b
## $ % #
(b) y x 4x x 3x 3 y 5x 12x 2x 3œ Êœ
&$# w % #
14. (a) y (x 1) x x 1 y (x 1)(2x 1) x x 1 ( ) 3xœ Ê œ "œab ab
#w # #
(b) y (x 1) x x 1 x 1 y 3xœ œÊ œab
#$w#
15. (a) y x 1 x 5 y x 1 x 5 x 5 x 1œ Ê œ ab ab ab
ˆ‰ ˆ‰ˆ‰
#w# #
"""
xdxxxdx
dd
††
x 1 1 x x 5 x (2x) x 1 1 x 2x 10x 2 3x 10x 2œ œ œ aba ba b a ba b
## "# ## # "
x
(b) y x 5x 2x 5 y 3x 10x 2œ Ê œ
$# w #
""
xx
16. y x x 1œ
ˆ‰ˆ ‰
""
xx
(a) y x x 1 x x x 1 1 x 2x 1
w"# " # "
œ œ ababa bab†xx
2
(b) y x x y 2x 1œ Ê œ
#w
"" "
xx x x
2
17. y ; use the quotient rule: u 2x 5 and v 3x 2 u 2 and v 3 yœœœÊœœÊœ
2x 5 vu uv
3x 2 v
ww w
œœœ
(3x 2)(2) (2x 5)(3)
(3x 2) (3x ) (3x 2)
6x46x15 19
#
18. z œÊœ œ œ œ
2x 1 dz 2x 2 4x 2x 2x 2x 2
x1 dx
x 1 (2) (2x 1)(2x) 2 x x 1
x1 x1 x1 x1
ab a b
ab ab ab ab
19. g(x) ; use the quotient rule: u x 4 and v x 0.5 u 2x and v 1 g (x)œœœÊœœÊœ
x4 vu uv
x0.5 v
#www
œœœ
(x 0.5)(2x) x 4 ( )
(x 0.5) (x 0.5) (x 0.5)
2x xx 4 x x4
"
ab
20. f(t) , t f (t)œœ œÁ"Êœ œ œ
tt tt
tt2 t t t2
tt t t
t2 t2 t2
" " # " "
# "
" " # " " "
w
abab abababab
abab ab ab ab
222
21. v (1 t) 1 t œ œ Ê œ œ œab
#" " "
"
1 t dv t 2t 2t t 2t
1t dt
1 t ( ) (1 t)(2t)
1t 1t 1t
ab
ab ab ab
22. w wœÊœ œ œ
x5 2x72x10 17
2x 7 (2x 7) (2x 7) (2x 7)
(2x 7)(1) (x 5)(2)
w
23. f(s) f (s)œÊœ œ œ
Ȉ‰ˆ‰
Ȉ‰ ˆ‰
ÈÈ
Š‹ Š‹
ˆ‰ ˆ‰ ˆ‰
ÈÈÈÈÈ
ÈÈ
s
s1
ss1
s1 2 s s 1 s s 1
ss1
"
w"
" "
ss
NOTE: s from Example 2 in Section 2.1
d
ds s
ˆ‰
Ȝ"
#È
24. u œÊœ œ
5x du 5x 1
xdx 4x
2 x (5) (5x 1)
4x
"
#
Ȉ‰
ÈŠ‹
x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

132 Chapter 3 Differentiation
25. v vœÊœ œ
1x4x 2x
xxx
x1 1x4x
"
w
ÈÈ
Š‹
ˆ‰
È
2
x
26. r 2 r 2œÊœ œ
Š‹
È
"""
w
ÈÈŠ‹
)
)
)))
)(0) 1 "
#È)
27. y ; use the quotient rule: u 1 and v x 1 x x 1 u 0 andœœœÊœ
"
## w
aba bx1xx1 aba b
v x1(2x1)xx1(2x)2xx2x12x2x2x4x3x1
w# # $# $# $#
œ œœab a b
Êœ œ œ
dy
dx v
vu uv 4x 3x 1
0 1 4x 3x 1
x1xx1 x1xx1
ab
aba baba b
28. y yœœÊœ œ
(x 1)(x 2)
(x1)(x ) x 3x2 (x1)(x2) (x1)(x2)
x 3x 2 6x 12
x 3x 2 (2x 3) x 3x 2 (2x 3)
#
w
abab
œ
6x 2
(x 1) (x 2)
ab
29. y x x x y 2x 3x 1 y 6x 3 y 12x y 12 y 0 for all n 5œ Ê œ Ê œ Ê œ Ê œ Ê œ
"
##
% # w $ ww # www Ð%Ñ Ð Ñ
3n
30. y x y x y x y x y x y 1 y 0 for all n 6œ Êœ ʜʜʜʜʜ
""""
## #
&w %ww$www#Ð%Ñ Ð&Ñ ÐÑ
10 4 6
n
31. y x 7x 2x 7x x 2 14xœ œ Ê œ œ# Ê œ œ#
x7
xdx xdx x
dy d y
("%
#" # $
32. s 1 1 5t t 0 5t 2t 5t 2t œ œ œ Ê œ œ œ
t5t1 5 ds
ttt dt tt
" & #
" # # $ # $
10t 6tÊœ œ
ds
dt t t
$ % "! '
33. r 1 0 12œœœ"œÊœ$œ$œÊœœ
() 1 dr d r
dd
)))
))) ) ) )
)
)
" " " $ "#
$ % % &
ab ))) )
34. u 1 1 xœ œ œ œ œ œ
aba b a b abxxxx1 x(x1)xx xx1
xxxxx
xx x
" $
0 3x 3x 12xÊœ œ œÊ œ œ
du d u
dx dx x
x
% % &
$ "#
35. w (3 z) z 1 (3 z) z 3 z z z z 0 1 z 1œ œ œ œ Ê œœ
ˆ‰ ˆ ‰
13z 8dw
3z 3 3 3 dz
" "
" " " # #
2z 0 2zœ"Ê œ œ œ
" #
$ $
zdz z
dw
36. w (z 1)(z 1) z 1 z 1 z 1 z 1 4z 0 4z 12zœ œ œÊ œ œ Ê œababab
###% $$ #
dw d w
dz dz
37. p q q q q q q qœœœÊœœ
Š‹Š‹
q3 q1 qq3q3 dp
12q q 1 1 4 4 dq 6 6 6 6q q
12q
"" "" "" """
##
## % $&
q5qÊœ œ
dp
dq 6 6 q
q
"" " " &
#
% '
#6
38. p qœœ œœœœ
q3 q3 q3 q3
(q 1) (q 1) q 3q 3q 1 q 3q 3q 1 2q 6q 2q q 3 q
# #
""
"
abab ab
q qÊœ œÊ œ œ
dp d p
dq q dq q
"" "
##
# $
39. u(0) 5, u (0) 3, v(0) 1, v (0) 2œœœœ
ww
(a) (uv) uv vu (uv) u(0)v (0) v(0)u (0) 5 2 ( 1)( 3) 13
dd
dx dx
œ Ê œ œ œ
ww w w
¸x=0
†
(b) 7
d u vu uv d u
dx v v dx v (v(0)) ( 1)
v(0)u (0) u(0)v (0) ( )( 3) (5)(2)
ˆ‰ ¸ˆ‰
œÊ œ œ œ
"
x=0
(c)
d v uv vu d v 7
dx u u dx u (u(0)) (5) 25
u(0)v (0) v(0)u (0) (5)(2) ( 1)( 3)
ˆ‰ ¸ˆ‰
œÊ œ œ œ
x=0
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.2 Differentiation Rules 133
(d) (7v 2u) 7v 2u (7v 2u) 7v (0) 2u (0) 7 2 2( 3) 20
dd
dx dx
œ Ê œ œ œ
ww w w
¸x=0
†
40. u(1) 2, u (1) 0, v(1) 5, v (1) 1œœœœ
ww
(a) (uv) u(1)v (1) v(1)u (1) 2 ( 1) 5 0 2
¸
d
dx x=1 œœœ
ww
††
(b) ¸ˆ‰
du 2
dx v (v(1)) (5) 25
v(1)u ( ) u(1)v (1) 5 0 2 ( 1)
x=1 œœœ
" ††
(c) ¸ˆ‰
dv 1
dx u (u(1)) (2) 2
u(1)v ( ) v(1)u (1) 2 ( 1) 5 0
x=1 œœœ
" ††
(d) (7v 2u) 7v (1) 2u (1) 7 ( 1) 2 0 7
¸
d
dx œœœ
x=1
ww
††
41. y x 4x 1. Note that ( ) is on the curve: 1 2 4(2) 1œ #ß" œ
$$
(a) Slope of the tangent at (x y) is y 3x 4 slope of the tangent at ( ) is y (2) 3(2) 4 8. ThusßœÊ #ß" œœ
w# w #
the slope of the line perpendicular to the tangent at ( ) is the equation of the line perpendicular to#ß " Ê
"
8
to the tangent line at ( ) is y 1 (x 2) or y .#ß " œ œ
"
884
x5
(b) The slope of the curve at x is m 3x 4 and the smallest value for m is 4 when x 0 and y 1.œ œ œ
#
(c) We want the slope of the curve to be 8 y 8 3x 4 8 3x 12 x 4 x 2. WhenÊ œÊ œÊ œ Ê œÊœ„
w# ##
x 2, y 1 and the tangent line has equation y 1 8(x 2) or y 8x 15; when x 2,œœ œ œ œ
y ( 2) 4( 2) 1 1, and the tangent line has equation y 1 8(x 2) or y 8x 17.œ œ œ œ
$
42. (a) y x 3x 2 y 3x 3. For the tangent to be horizontal, we need m y 0 0 3x 3œÊ œ œœÊœ
$w# w #
3x 3 x 1. When x 1, y 0 the tangent line has equation y 0. The lineʜʜ„ œœÊ œ
#
perpendicular to this line at ( ) is x 1. When x 1, y 4 the tangent line has equation"ß ! œ œ œ Ê
y 4. The line perpendicular to this line at ( ) is x 1.œ "ß % œ
(b) The smallest value of y is 3, and this occurs when x 0 and y 2. The tangent to the curve at ( 2)
w œ œ !ß
has slope 3 the line perpendicular to the tangent at ( 2) has slope y 2 (x 0) or Ê !ß Ê œ
""
33
y x 2 is an equation of the perpendicular line.œ
"
3
43. y . When x 0, y 0 and yœÊœ œ œ œœ œ
4x 4x 4 8x
x1 dx 1
dy 4(0 1)
x 1 (4) (4x)(2x) 4 x
x1 x1 x1
"
w
ab a b
ab ab ab
, so the tangent to the curve at ( ) is the line y 4x. When x 1, y 2 y 0, so the tangent to theœ% !ß! œ œ œ Ê œ
w
curve at ( 2) is the line y 2."ß œ
44. y y . When x 2, y 1 and y , so the tangentœÊœ œ œœ œ œ
8 16x
x4
x 4 (0) 8(2x)
x4 x4 24
16(2)
#
w w
"
ab
ab ab ab
line to the curve at (2 ) has the equation y 1 (x 2), or y 2.ß" œ œ
"
##
x
45. y ax bx c passes through ( ) 0 a(0) b(0) c c 0; y ax bx passes through ( )œ !ß!Êœ Êœ œ "ß#
# #
2 a b; y 2ax b and since the curve is tangent to y x at the origin, its slope is 1 at x 0Êœ œ œ œ
w
y 1 when x 0 1 2a(0) b b 1. Then a b 2 a 1. In summary a b 1 and c 0 soÊœ œÊœ Êœ œÊœ œœ œ
w
the curve is y x x.œ
#
46. y cx x passes through ( ) 0 c(1) 1 c 1 the curve is y x x . For this curve,œ "ß ! Ê œ Ê œ Ê œ
# #
y 1 2x and x 1 y 1. Since y x x and y x ax b have common tangents at x 0,
ww##
œ œ Ê œ œ œ œ
y x ax b must also have slope 1 at x 1. Thus y 2x a 1 2 1 a a 3œ œ œ Êœ Êœ
#w
†
y x 3x b. Since this last curve passes through ( ), we have 0 1 3 b b 2. In summary,Êœ "ß! œÊœ
#
a 3, b 2 and c 1 so the curves are y x 3x 2 and y x x .œœœ œœ
##
47. (a) y x x y 3x 1. When x 1, y 0 and y 2 the tangent line to the curve at ( ) isœÊ œ œ œ œÊ "ß!
$w# w
y 2(x 1) or y 2x 2.œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
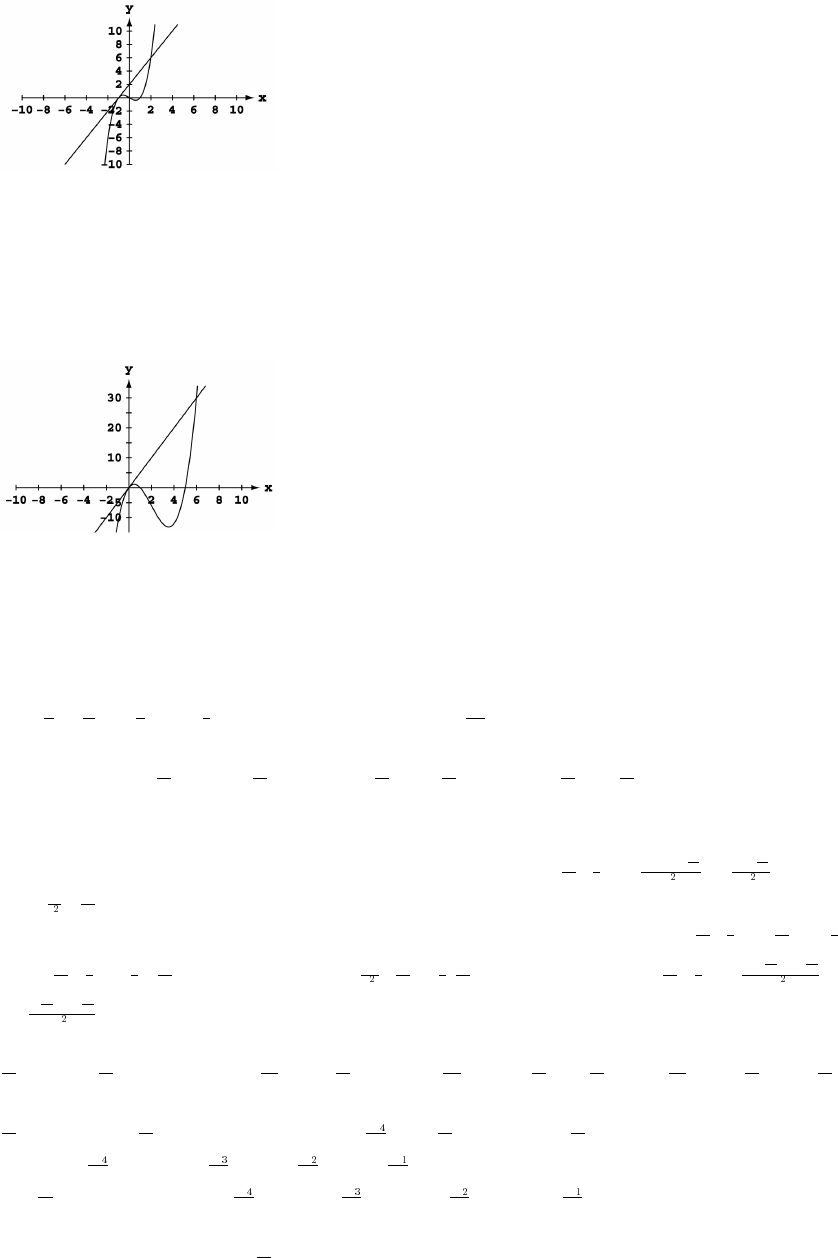
134 Chapter 3 Differentiation
(b)
(c) x x 2x 2 x 3x 2 (x 2)(x 1) 0 x 2 or x 1. Since
yx x
y2x2
œ
œ ʜʜ œÊœ œ
$$$ #
y 2 2 2 6; the other intersection point is (2 6)œœ ßab
48. (a) y x 6x 5x y 3x 12x 5. When x 0, y 0 and y 5 the tangent line to the curve atœ Ê œ œ œ œÊ
$# w # w
(0 0) is y 5x.ߜ
(b)
(c) x 6x 5x 5x x 6x 0 x (x 6) 0 x 0 or x 6.
y x 6x 5x
y 5x
œ
œÊ œ Ê œÊ œÊœ œ
$# $# $# #
Since y 5 6 , the other intersection point is (6 30).œ œ $! ßab
49. P x a x a x a x a x a P x na x n a x a x aab ab a bœ â Ê œ " â#
nn n n
nn n n
" # " ! " # "
" # w " #
50. R M M M , where C is a constant CM Mœœ Êœ
##$ #
##
"
ˆ‰
CM C dR
33 dM
51. Let c be a constant 0 (u c) u c u 0 c c . Thus when one of theÊœÊ œ œ œ
dc d dc du du du
dx dx dx dx dx dx
††† †
functions is a constant, the Product Rule is just the Constant Multiple Rule the Constant Multiple Rule isÊ
a special case of the Product Rule.
52. (a) We use the Quotient rule to derive the Reciprocal Rule (with u 1): œœœ
d
dx v v v
v0 1
ˆ‰
""†† †
dv dv
dx dx
.œ "
vdx
dv
†
(b) Now, using the Reciprocal Rule and the Product Rule, we'll derive the Quotient Rule: u
du d
dx v dx v
ˆ‰ ˆ ‰
Ϡ"
u (Product Rule) u (Reciprocal Rule) œ œ Êœ†† †
d du 1 dv du d u
dx v v dx v dx v dx dx v v
u v
ˆ‰ ˆ ‰ ˆ‰
"" "
dv du
dx dx
, the Quotient Rule.œv u
v
du dv
dx dx
53. (a) (uvw) ((uv) w) (uv) w (uv) uv w u v uv wu wv
dd dwd dwdvdudwdvdu
dx dx dx dx dx dx dx dx dx dx
œœœœ†† ˆ‰
uvw uv w u vwœ
ww w
(b) uuuu uuu u uuu u uuu uuuu
dd dd
dx dx dx dx dx
du
a ba bab ab a bab
"#$% "#$ % "#$ % "#$ "#$%
œœÊ
uuu u uu uu uu (using (a) above)œ
"#$%"#$"$#
du du du du
dx dx dx dx
ˆ‰
uuuu uuu uuu uuu uuu ʜ
d
dx dx dx dx dx
du du du du
ab
"#$% "#$ "#% "$% #$%
uuuu uuuu uuuu uuuuœ
"#$ "# % " $% #$%
wwww
%$#"
(c) Generalizing (a) and (b) above, u u u u u u u u u u u u u u
d
dx ab
" "#" "## #
www
" "
✠â â á â
nn nn n
nn
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.3 The Derivative as a Rate of Change 135
54. In this problem we don't know the Power Rule works with fractional powers so we can't use it. Remember
x (from Example 2 in Section 2.1)
d
dx x
ˆ‰
Ȝ"
#È
(a) x x x x x x (x) x x 1 x x
dd d d 3
dx dx dx dx x
x3x
ˆ‰ ˆ ‰ ˆ‰
ÈÈ È È
$Î# "Î# "Î#
"
####
œœœœœœ†† † †
ÈÈÈ
(b) x x x x x x x x x 2x x 2x x
dd d d 5
dx dx dx dx x
ˆ‰ ˆ ‰ ˆ‰
ÈÈ È
ab Š‹
&Î# # "Î# # # # $Î# $Î# $Î#
""
###
œœœœœ†††
È
(c) x x x x x x x x x 3x x 3x x
dd d d 7
dx dx dx dx x
ˆ‰ ˆ ‰ ˆ‰
ÈÈ È
ab Š‹
(Î# $ "Î# $ $ $ # &Î# &Î# &Î#
""
###
œœœœœ†††
È
(d) We have x x , x x , x x so it appears that x x
d3d5d7 dn
dx dx dx dx
ˆ‰ ˆ‰ ˆ‰ ab
$Î# "Î# &Î# $Î# (Î# &Î# Ð Î#Ñ"
### #
œœœ œ
nn
whenever n is an odd positive integer 3.
55. p . We are holding T constant, and a, b, n, R are also constant so their derivatives are zeroœ
nRT an
Vnb V
Êœ œ
dP nRT 2an
dV (V nb) (V nb) V
(V nb) 0 (nRT)(1) V(0) an (2V)
V
†ab
ab
56. A q cm km q cm q km q km qab ab ab ab
ˆ‰ ˆ‰
œ œ Ê œ œ Ê œ# œ
km h dA h km h d A km
qdqqdtq
hq
## ##
" # $ #
3.3 THE DERIVATIVE AS A RATE OF CHANGE
1. s t t , 0 tœ$#ŸŸ#
#
(a) displacement s s( ) s(0) m m m, v m/secœ œ # œ! # œ# œ œ œ"?av
?
?
s
t
#
#
(b) v t v(0) m/sec and v( ) 1 m/sec;œ œ# $ Ê œl$lœ$ # œ
ds
dt kk kk
a a(0) m/sec and a( ) m/secœœ#Ê œ# #œ#
ds
dt ##
(c) v 0 t 0 t . v is negative in the interval t and v is positive when t the bodyœ Ê# $œ Ê œ ! #Ê
$$$
###
changes direction at t .œ$
#
2. s t t , tœ' !Ÿ Ÿ'
#
(a) displacement s s( ) s(0) m, v m/secœ œ ' œ! œ œ œ!?av
?
?
s
t
!
'
(b) v v(0) m/sec and v( ) m/sec;œ œ'#> Ê œl'lœ' ' œl'lœ'
ds
dt kk kk
a a(0) m/sec and a( ) m/secœ œ # Ê œ # ' œ #
ds
dt ##
(c) v 0 t 0 t . v is positive in the interval t and v is negative when t the bodyœ Ê'#œ Êœ$ !$ $'Ê
changes direction at t .œ$
3. s t 3t 3t, 0 t 3œ Ÿ Ÿ
$#
(a) displacement s s(3) s(0) 9 m, v 3 m/secœœœ œœœ?av
?
?
s9
t3
(b) v 3t 6t 3 v(0) 3 3 m/sec and v(3) 12 12 m/sec; a 6t 6œœÊ œœ œ œ œ œ
ds ds
dt dt
#kkkk kkkk
a(0) 6 m/sec and a(3) 12 m/secÊœ œ
##
(c) v 0 3t 6t 3 0 t 2t 1 0 (t 1) 0 t 1. For all other values of t in theœ Ê œ Ê œ Ê œ Êœ
## #
interval the velocity v is negative (the graph of v 3t 6t 3 is a parabola with vertex at t 1 whichœ œ
#
opens downward the body never changes direction).Ê
4. s t t , 0 tœ ŸŸ$
t
4$#
(a) s s( ) s(0) m, v m/sec?œ$ œ œ œ œ
*$
%$%
av
?
?
s
t
(b) v t 3t 2t v(0) 0 m/sec and v( ) m/sec; a 3t 6t 2 a(0) 2 m/sec andœ Ê œ $œ' œ Ê œ
$# ##
kk kk
a( ) m/sec$œ"" #
(c) v 0 t 3t 2t 0 t(t 2)(t 1) 0 t 0, 1, 2 v t(t 2)(t 1) is positive in theœÊ œÊ œÊœ Êœ
$#
interval for 0 t 1 and v is negative for 1 t 2 and v is positive for t the body changes direction at #$Ê
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

136 Chapter 3 Differentiation
t 1 and at t .œœ#
5. s , 1 t 5œ ŸŸ
25 5
tt
(a) s s(5) s(1) 20 m, v 5 m/sec?œœ œœ
av 20
4
(b) v v(1) 45 m/sec and v(5) m/sec; a a(1) 140 m/sec andœÊ œ œ œÊ œ
"#
50 5 150 10
tt 5 t
t
kk kk
a(5) m/secœ4
25 #
(c) v 0 0 50 5t 0 t 10 the body does not change direction in the intervalœÊ œÊœÊœ Ê
50 5t
t
6. s , t 0œ%ŸŸ
25
t5
(a) s s(0) s( 4) 20 m, v 5 m/sec?œœ œœ
av 20
4
(b) v v( 4) 25 m/sec and v(0) m/sec; a a( 4) 50 m/sec andœÊœ œ" œÊœ
#
25 50
(t 5) (t 5)
kk kk
a(0) m/secœ2
5#
(c) v 0 0 v is never 0 the body never changes directionœÊ œÊ Ê
25
(t 5)
7. s t 6t 9t and let the positive direction be to the right on the s-axis.œ
$#
(a) v 3t 12t 9 so that v 0 t 4t 3 (t 3)(t 1) 0 t 1 or 3; a 6t 12 a(1)œ œÊœ œÊœ œÊ
##
6 m/sec and a(3) 6 m/sec . Thus the body is motionless but being accelerated left when t 1, andœ œ œ
##
motionless but being accelerated right when t 3.œ
(b) a 0 6t 12 0 t 2 with speed v(2) 12 24 9 3 m/secœÊ œÊœ œ œkkk k
(c) The body moves to the right or forward on 0 t 1, and to the left or backward on 1 t 2. TheŸ
positions are s(0) 0, s(1) 4 and s(2) 2 total distance s(1) s(0) s(2) s(1) 4 2œ œ œÊ œœkkkkkkkk
6 m.œ
8. v t 4t 3 a 2t 4œÊœ
#
(a) v 0 t 4t 3 0 t 1 or 3 a(1) 2 m/sec and a(3) 2 m/secœÊ œÊœ Ê œ œ
###
(b) v 0 (t 3)(t 1) 0 0 t 1 or t 3 and the body is moving forward; v 0 (t 3)(t 1) 0Ê ÊŸ Ê
t 3 and the body is moving backwardÊ"
(c) velocity increasing a 0 2t 4 0 t 2; velocity decreasing a 0 2t 4 0 t 2ÊÊ Ê ÊÊ Ê!Ÿ
9. s 1.86t v 3.72t and solving 3.72t 27.8 t 7.5 sec on Mars; s 11.44t v 22.88t and
mm jj
œÊœ œÊ¸ œ Êœ
# #
solving 22.88t 27.8 t 1.2 sec on Jupiter.œÊ¸
10. (a) v(t) s (t) 24 1.6t m/sec, and a(t) v (t) s (t) 1.6 m/secœœ œœ œ
www#
w
(b) Solve v(t) 0 24 1.6t 0 t 15 secœÊ œÊœ
(c) s(15) 24(15) .8(15) 180 mœ œ
#
(d) Solve s(t) 90 24t .8t 90 t 4.39 sec going up and 25.6 sec going downœÊ œÊœ ¸
#„
#
30 15 2
È
(e) Twice the time it took to reach its highest point or 30 sec
11. s 15t g t v 15 g t so that v 0 15 g t 0 g . Therefore g 0.75 m/secœ Êœ œÊœÊœ œœœ
"
#
# #
ss ss s
15 15 3
t204
12. Solving s 832t 2.6t 0 t(832 2.6t) 0 t 0 or 320 320 sec on the moon; solving
mœ œÊ œÊœ Ê
#
s 832t 16t 0 t(832 16t) 0 t 0 or 52 52 sec on the earth. Also, v 832 5.2t 0
e m
œœÊ œÊœ Ê œœ
#
t 160 and s (160) 66,560 ft, the height it reaches above the moon's surface; v 832 32t 0Êœ œ œ œ
m e
t 26 and s (26) 10,816 ft, the height it reaches above the earth's surface.Êœ œ
e
13. (a) s 179 16t v 32t speed v 32t ft/sec and a 32 ft/secœ ÊœÊ œœ œ
# #
kk
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
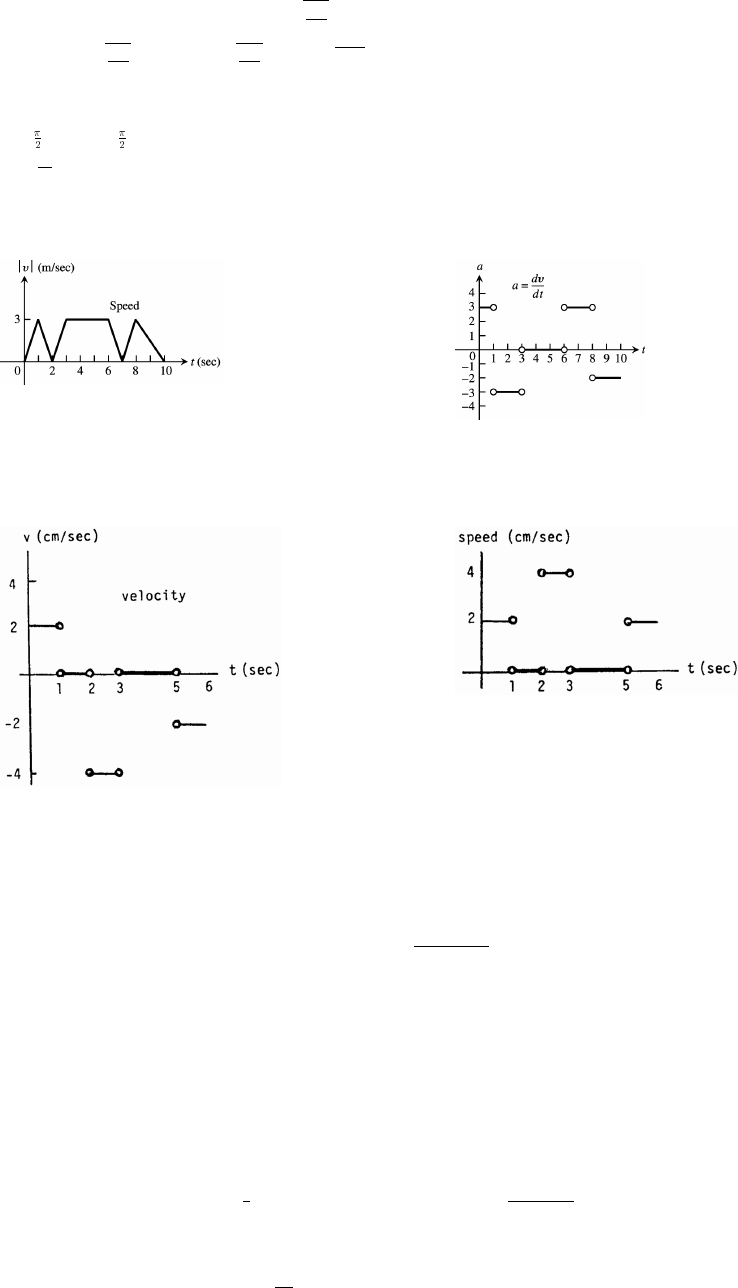
Section 3.3 The Derivative as a Rate of Change 137
(b) s 0 179 16t 0 t 3.3 secœÊ œÊœ ¸
#É179
16
(c) When t , v 32 8 179 107.0 ft/secœœœ¸
ÉÉ
È
179 179
16 16
14. (a) lim v lim 9.8(sin )t 9.8t so we expect v 9.8t m/sec in free fall
))ÄÄ
œœ œ)
(b) a 9.8 m/secœœ
dv
dt #
15. (a) at 2 and 7 seconds (b) between 3 and 6 seconds: t 6$Ÿ Ÿ
(c) (d)
16. (a) P is moving to the left when 2 t 3 or 5 t 6; P is moving to the right when 0 t 1; P is standing
still when 1 t 2 or 3 t 5
(b)
17. (a) 190 ft/sec (b) 2 sec
(c) at 8 sec, 0 ft/sec (d) 10.8 sec, 90 ft/sec
(e) From t 8 until t 10.8 sec, a total of 2.8 secœœ
(f) Greatest acceleration happens 2 sec after launch
(g) From t 2 to t 10.8 sec; during this period, a 32 ft/secœœ œ ¸
v(10.8) v(2)
10.8 2
#
18. (a) Forward: 0 t 1 and 5 t 7; Backward: 1 t 5; Speeds up: 1 t 2 and 5 t 6;Ÿ
Slows down: 0 t 1, 3 t 5, and 6 t 7Ÿ
(b) Positive: 3 t 6; negative: 0 t 2 and 6 t 7; zero: 2 t 3 and 7 t 9 Ÿ
(c) t 0 and 2 t 3œŸŸ
(d) 7 t 9ŸŸ
19. s 490t v 980t a 980œÊœÊœ
#
(a) Solving 160 490t t sec. The average velocity was 280 cm/sec.œÊœ œ
#
4
74/7
s(4/7) s(0)
(b) At the 160 cm mark the balls are falling at v(4/7) 560 cm/sec. The acceleration at the 160 cm markœ
was 980 cm/sec .
#
(c) The light was flashing at a rate of 29.75 flashes per second.
17
4/7 œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
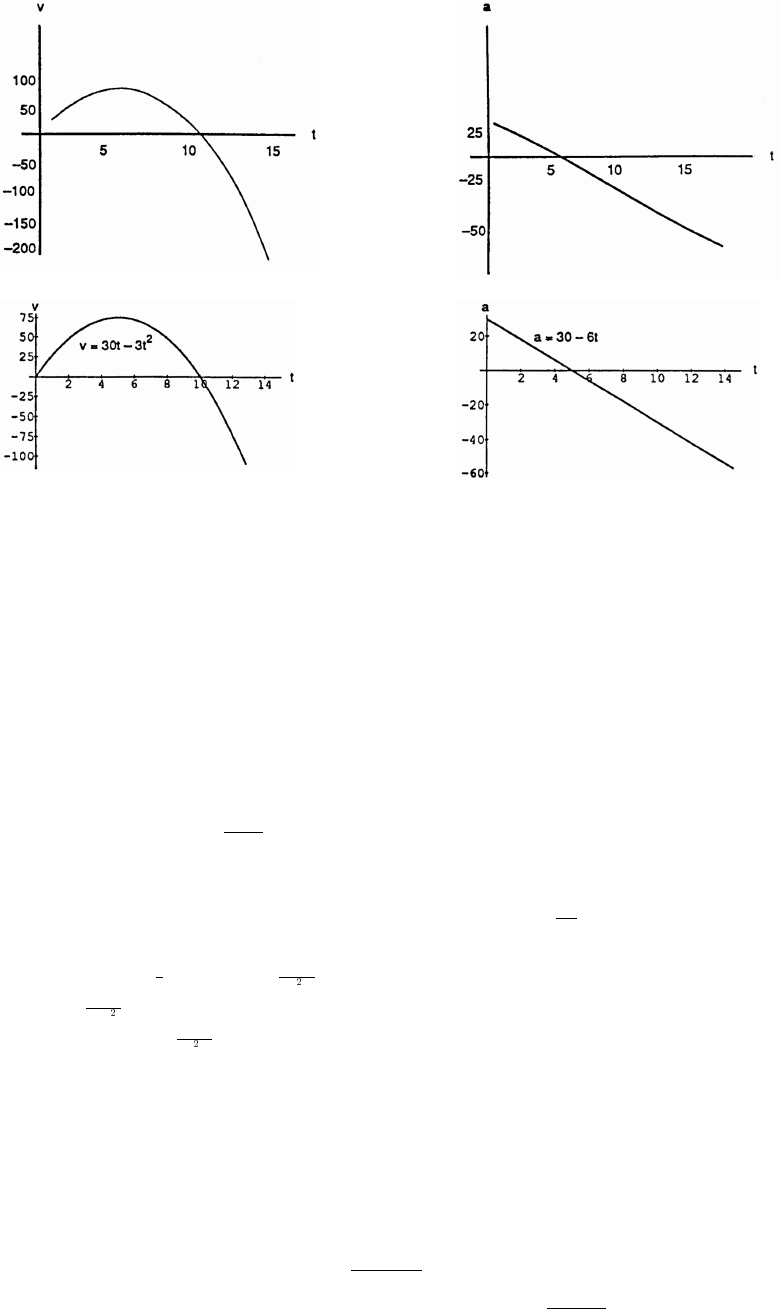
138 Chapter 3 Differentiation
20. (a)
(b)
21. C position, A velocity, and B acceleration. Neither A nor C can be the derivative of B because B'sœœ œ
derivative is constant. Graph C cannot be the derivative of A either, because A has some negative slopes while
C has only positive values. So, C (being the derivative of neither A nor B) must be the graph of position.
Curve C has both positive and negative slopes, so its derivative, the velocity, must be A and not B. That
leaves B for acceleration.
22. C position, B velocity, and A acceleration. Curve C cannot be the derivative of either A or B becauseœœ œ
C has only negative values while both A and B have some positive slopes. So, C represents position. Curve C
has no positive slopes, so its derivative, the velocity, must be B. That leaves A for acceleration. Indeed, A is
negative where B has negative slopes and positive where B has positive slopes.
23. (a) c(100) 11,000 c $110œÊœœ
av 11,000
100
(b) c(x) 2000 100x .1x c (x) 100 .2x. Marginal cost c (x) the marginal cost of producing 100œÊ œ œÊ
#w w
machines is c (100) $80
wœ
(c) The cost of producing the 101 machine is c(101) c(100) 100 $79.90
st œœ
201
10
24. (a) r(x) 20000 1 r (x) , which is marginal revenue.œÊœ
ˆ‰
"w
xx
20000
(b) r $
wab"!! œ œ #Þ
20000
100
(c) lim r (x) lim 0. The increase in revenue as the number of items increases without bound
xxÄ_ Ä_
wœœ
20000
x
will approach zero.
25. b(t) 10 10 t 10 t b (t) 10 (2) 10 t 10 (10 2t)œ Ê œ œ
'% $# w % $ $
ab
(a) b (0) 10 bacteria/hr (b) b (5) 0 bacteria/hr
w% w
œœ
(c) b (10) 10 bacteria/hr
w%
œ
26. Q(t) 200(30 t) 200 900 60t t Q (t) 200( 60 2t) Q (10) 8,000 gallons/min is the rateœœ ʜʜ
##w w
ab
the water is running at the end of 10 min. Then 10,000 gallons/min is the average rate the
Q(10) Q(0)
10
œ
water flows during the first 10 min. The negative signs indicate water is the tank.leaving
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
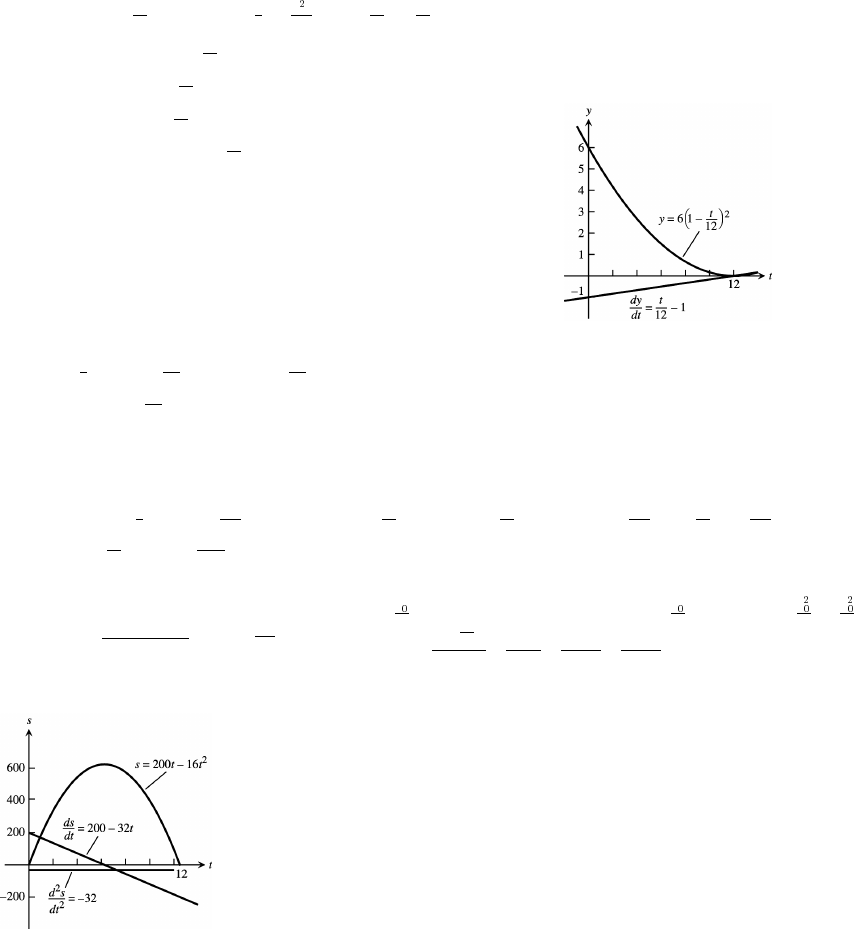
Section 3.3 The Derivative as a Rate of Change 139
27. (a) y 6 1 6 1 1œ œ Êœ
ˆ‰Š‹
ttt t
1 6 144 dt 12
dy
#
#
(b) The largest value of is 0 m/h when t 12 and the fluid level is falling the slowest at that time. The
dy
dt œ
smallest value of is 1 m/h, when t 0, and the fluid level is falling the fastest at that time.
dy
dt œ
(c) In this situation, 0 the graph of y is
dy
dt ŸÊ
always decreasing. As increases in value,
dy
dt
the slope of the graph of y increases from 1
to 0 over the interval 0 t 12.ŸŸ
28. (a) V r 4 r 4 (2) 16 ft /ftœÊœÊ œ œ
4dV dV
3dr dr
11 11
$# #$
¸r=2
(b) When r 2, 16 so that when r changes by 1 unit, we expect V to change by approximately 16 .œœ
dV
dr 11
Therefore when r changes by 0.2 units V changes by approximately (16 )(0.2) 3.2 10.05 ft . Note11œ¸ $
that V(2.2) V(2) 11.09 ft .¸ $
29. 200 km/hr 55 m/sec m/sec, and D t V t. Thus V t t 25 sec. Whenœœ œÊœ œÊœÊœ
5 500 10 20 500 20 500
99 9 9 999
#
t 25, D (25) mœœ œ
10 6250
99
#
30. s v t 16t v v 32t; v 0 t ; 1900 v t 16t so that t 1900œ Êœ œÊœ œ œÊ œ
!! !
# #
#
vv
32 32 3 64
vv
v (64)(1900) 80 19 ft/sec and, finally, 238 mph.Êœ œ ¸
!ÈÈ80 19 ft
sec 1 min 1 hr 5280 ft
60 sec 60 min 1 mi
Ȇ† †
31.
(a) v 0 when t 6.25 secœœ
(b) v 0 when 0 t 6.25 body moves up; v 0 when 6.25 t 12.5 body moves down ŸÊ ŸÊ
(c) body changes direction at t 6.25 secœ
(d) body speeds up on (6.25 12.5] and slows down on [0 6.25)ßß
(e) The body is moving fastest at the endpoints t 0 and t 12.5 when it is traveling 200 ft/sec. It'sœœ
moving slowest at t 6.25 when the speed is 0.œ
(f) When t 6.25 the body is s 625 m from the origin and farthest away.œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
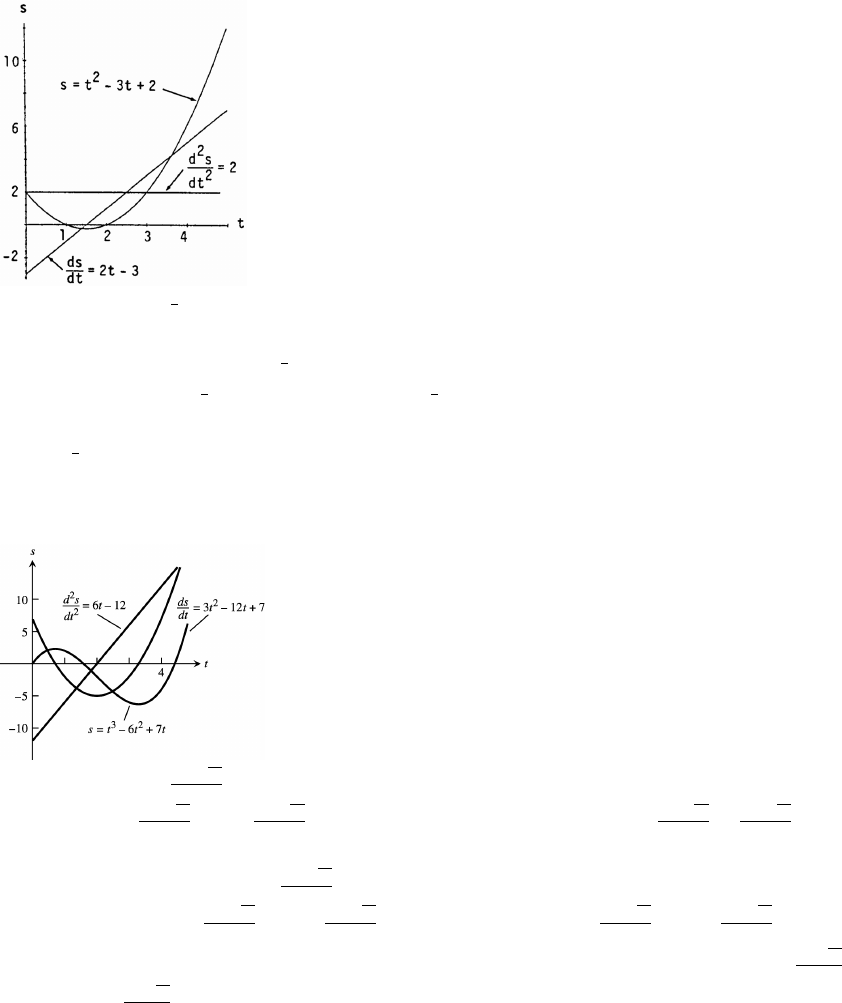
140 Chapter 3 Differentiation
32.
(a) v 0 when t secœœ
3
#
(b) v 0 when 0 t 1.5 body moves down; v 0 when 1.5 t 5 body moves upŸÊ ŸÊ
(c) body changes direction at t secœ3
#
(d) body speeds up on and slows down on
‘‰ˆ
33
##
ß& !ß
(e) body is moving fastest at t 5 when the speed v(5) 7 units/sec; it is moving slowest atœœœkk
t when the speed is 0œ3
#
(f) When t 5 the body is s 12 units from the origin and farthest away.œœ
33.
(a) v 0 when t secœœ
615
3
„È
(b) v 0 when t body moves left; v 0 when 0 t or t 4Ê Ÿ Ÿ
615 615 615 615
33 33
ÈÈ ÈÈ
body moves rightÊ
(c) body changes direction at t secœ615
3
„È
(d) body speeds up on and slows down on 0 .
Š‹ “ ‹Š‹Š’
615 615 615 615
33 33
ÈÈ ÈÈ
ß# ß% ß #ß
(e) The body is moving fastest at t 0 and t 4 when it is moving 7 units/sec and slowest at t secœœ œ
615
3
„È
(f) When t the body is at position s 6.303 units and farthest from the origin.œ¸
615
3
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.4 Derivatives of Trigonometric Functions 141
34.
(a) v 0 when tœœ
615
3
„È
(b) v 0 when 0 t or t 4 body is moving left; v 0 whenŸ ŸÊ
615 615
33
ÈÈ
t body is moving right
615 615
33
ÈÈ
Ê
(c) body changes direction at t secœ615
3
„È
(d) body speeds up on and slows down on
Š‹ “ ‹Š‹Š’
615 615 615 615
33 33
ÈÈ ÈÈ
ß# ß% !ß #ß
(e) The body is moving fastest at 7 units/sec when t 0 and t 4; it is moving slowest and stationary atœœ
tœ615
3
„È
(f) When t the position is s 10.303 units and the body is farthest from the origin.œ¸
615
3
È
35. (a) It takes 135 seconds.
(b) Average speed furlongs/sec.œ œ œ ¸ !Þ!')
?
?
F
t
&! &
($! ($
(c) Using a symmetric difference quotient, the horse's speed is approximately furlongs/sec.
?
?
F
tœ œ ¸ !Þ!((
%# #
&*$$ #'
(d) The horse is running the fastest during the last furlong (between the 9th and 10th furlong markers). This furlong takes
only 11 seconds to run, which is the least amount of time for a furlong.
(e) The horse accelerates the fastest during the first furlong (between markers 0 and 1).
3.4 DERIVATIVES OF TRIGONOMETRIC FUNCTIONS
1. y 10x 3 cos x 10 3 (cos x) 10 3 sin xœ Ê œ œ
dy
dx dx
d
2. y 5 sin x 5 (sin x) 5 cos xœ Ê œ œ
33d3
xdxxdxx
dy
3. y csc x 4 x 7 csc x cot x 0 csc x cot xœ Ê œ œ
Èdy
dx
42
xx#ÈÈ
4. y x cot x x (cot x) cot x x x csc x (cot x)(2x)œÊœ œ
## ###
"
xdx dx dx x x
dy dd2 2
†ab
x csc x 2x cot xœ
## 2
x
5. y (sec x tan x)(sec x tan x) (sec x tan x) (sec x tan x) (sec x tan x) (sec x tan x)œ Êœ
dy
dx dx dx
dd
(sec x tan x) sec x tan x sec x (sec x tan x) sec x tan x sec xœ abab
##
sec x tan x sec x tan x sec x sec x tan x sec x tan x sec x tan x sec x tan x sec x 0.œœabab
# #$# # #$ #
Note also that y sec x tan x tan x 1 tan x 1 0.
Š‹
abœœ œÊœ
## # # dy
dx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

142 Chapter 3 Differentiation
6. y (sin x cos x) sec x (sin x cos x) (sec x) sec x (sin x cos x)œ Êœ
dy
dx dx dx
dd
(sin x cos x)(sec x tan x) (sec x)(cos x sin x)œ œ
(sin x cos x) sin x
cos x cos x
cos x sin x
sec xœœœ
sin x cos x sin x cos x cos x sin x
cos x cos x
" #
Note also that y sin x sec x cos x sec x tan x 1 sec x.
Š‹
œ œÊœ
dy
dx #
7. y œÊœ œ
cot x
1 cot x dx (1 cot x) (1 cot x)
dy (1 cot x) (cot x) (cot x) (1 cot x) (1 cot x) csc x (cot x) csc x
dd
dx dx ab ab
œœ
csc x csc x cot x csc x cot x csc x
(1 cot x) (1 cot x)
8. y œÊœ œ
cos x
1 sin x dx (1 sin x) (1 sin x)
dy (1 sin x) (cos x) (cos x) (1 sin x) (1 sin x) sin x (cos x) cos x
dd
dx dx ab ab
œœœœ
"
sin xsinxcosx sin x1
(1 sin x) (1 sin x) (1 sin x) 1 sin x
(1 sin x)
9. y 4 sec x cot x 4 sec x tan x csc xœœ Êœ
4
cos x tan x dx
dy
"#
10. y œÊœœ
cos x x x sin x cos x cos x x sin x
x cos x dx x cos x x cos x
dy x( sin x) (cos x)(1) (cos x)(1) x( sin x)
11. y x sin x 2x cos x 2 sin x x cos x (sin x)(2x) (2x)( sin x) (cos x)(2) 2 cos xœ Êœ
##
dy
dx aba b
x cos x 2x sin x 2x sin x 2 cos x 2 cos x x cos xœ œ
##
12. y x cos x 2x sin x 2 cos x x ( sin x) (cos x)(2x) 2x cos x (sin x)(2) 2( sin x)œÊœ
##
dy
dx abab
x sin x 2x cos x 2x cos x 2 sin x 2 sin x x sin xœœ
##
13. s tan t t (tan t) 1 sec t 1 tan tœ Ê œ œ œ
ds d
dt dt ##
14. s t sec t 1 2t (sec t) 2t sec t tan tœ Ê œ œ
#ds d
dt dt
15. s œÊœ
1csc t ds
1csc t dt (1csc t)
(1 csc t)( csc t cot t) ( csc t)(csc t cot t)
"
œœ
csc t cot t csc t cot t csc t cot t csc t cot t 2 csc t cot t
(1 csc t) (1 csc t)
16. s œÊœ œ œ œ
sin t ds cos t cos t sin t cos t
1 cos t dt (1 cos t) (1 cos t) (1 cos t) 1 cos t
(1 cos t)(cos t) (sin t)(sin t)
" "
œ"
cos t 1
17. r 4 sin (sin ) (sin )(2 ) cos 2 sin ( cos sin )œ Ê œ œ œ #)) ) ) )) ) ))) ))) )
## #
dr d
dd))
ˆ‰
ab
18. r sin cos ( cos (sin )(1)) sin cos œÊœ œ)) ) ) ) ) )) )
dr
d)
19. r sec csc (sec )( csc cot ) (csc )(sec tan )œÊœ)) ) )) ) ))
dr
d)
sec cscœœœ
ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰
" " " " " " ##
cos sin sin sin cos cos sin cos
cos sin
))) ))) ) )
)) ))
20. r (1 sec ) sin ( sec ) cos (sin )(sec tan ) (cos ) tan cos secœ Ê œ" œ " œ )) ) ) ) )) ) ) ) )
dr
d)
##
21. p 5 tan q sec qœ& œ Ê œ
"#
cot q dq
dp
22. p (1 csc q) cos q (1 csc q)( sin q) (cos q)( csc q cot q) ( sin q 1) cot q sin q csc qœ Ê œ œ œ
dp
dq ##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
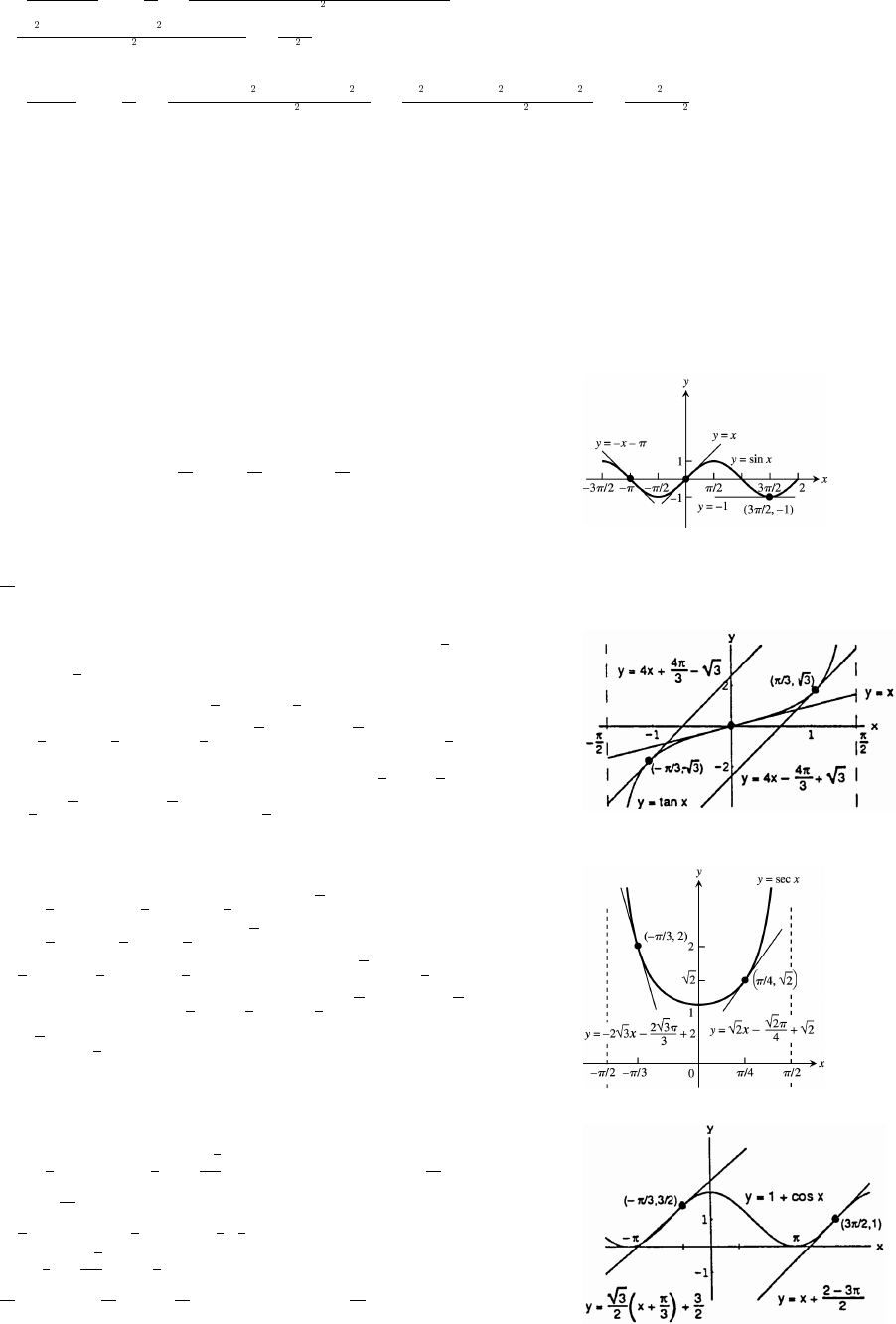
Section 3.4 Derivatives of Trigonometric Functions 143
23. p œÊœ
sin q cos q dp (cos q)(cos q sin q) (sin q cos q)( sin q)
cos q dq cos q
sec qœœœ
cos q cos q sin q sin q cos q sin q
cos q cos q
"#
24. p œÊœ œ œ
tan q dp sec q tan q sec q tan q sec q sec q
1 tan q dq (1 tan q) (1 tan q) (1 tan q)
(1 tan q) sec q (tan q) sec q
ab ab
25. (a) y csc x y csc x cot x y (csc x) csc x (cot x)( csc x cot x) csc x csc x cot xœÊœ Êœ œ
www# $#
abab
(csc x) csc x cot x (csc x) csc x csc x 1 2 csc x csc xœœœaba b
## ## $
(b) y sec x y sec x tan x y (sec x) sec x (tan x)(sec x tan x) sec x sec x tan xœÊœ Êœ œ
www# $#
ab
(sec x) sec x tan x (sec x) sec x sec x 1 2 sec x sec xœœœaba b
## ## $
26. (a) y 2 sin x y 2 cos x y 2( sin x) 2 sin x y 2 cos x y 2 sin xœ Ê œ Ê œ œ Ê œ Ê œ
w ww www Ð%Ñ
(b) y 9 cos x y 9 sin x y 9 cos x y 9( sin x) 9 sin x y 9 cos xœ Ê œ Ê œ Ê œ œ Ê œ
w ww www Ð%Ñ
27. y sin x y cos x slope of tangent atœÊœ Ê
w
x is y ( ) cos ( ) ; slope ofœ œ œ"11 1
w
tangent at x 0 is y (0) cos (0) 1; andœœœ
w
slope of tangent at x is y cos œœ
33 311 1
## #
wˆ‰
0. The tangent at ( ) is y 0 1(x ),œß!œ11
or y x ; the tangent at (0 0) isœ ß1
y 0 1(x 0), or y x; and the tangent atœ œ
1 is y 1.
ˆ‰
31
#ß œ
28. y tan x y sec x slope of tangent at xœÊœ Ê œ
w# 1
3
is sec 4; slope of tangent at x 0 is sec (0) 1;
##
ˆ‰
œ œ œ
1
3
and slope of tangent at x is sec 4. The tangentœœ
11
33
#ˆ‰
at tan 3 is y 3 4 x ;
ˆ‰ ˆ‰ˆ‰Š‹
ÈÈ
ß œß œ
11 1 1
33 3 3
the tangent at (0 0) is y x; and the tangent at tanßœ ß
ˆ‰ˆ‰
11
33
3 is y 3 4x .œß œ
Š‹
ÈÈ
ˆ‰
11
33
29. y sec x y sec x tan x slope of tangent atœÊœ Ê
w
x is sec tan 2 3 ; slope of tangentœ œ
111
333
ˆ‰ˆ‰ È
at x is sec tan 2 . The tangent at the pointœœ
111
444
ˆ‰ ˆ‰ È
sec is y 2 3 x ;
ˆ‰ˆ‰ ˆ‰ˆ‰ È
ß œß# œ#
11 1 1
33 3 3
the tangent at the point sec 2 is y 2
ˆ‰ˆ‰ Š‹
ÈÈ
11 1
44 4
ßœß
2x .œ
Ȉ‰
1
4
30. y 1 cos x y sin x slope of tangent atœ Ê œ Ê
w
x is sin ; slope of tangent at xœ œ œ
11 1
33
33
ˆ‰È
##
is sin 1. The tangent at the pointœ
ˆ‰
31
#
cos
ˆ‰ˆ‰ˆ‰
ß" œß
111
333
3
#
is y x ; the tangent at the pointœ
33
3##
Ȉ‰
1
cos 1 is y 1 x
ˆ‰ˆ‰ˆ‰
333 3111 1
### #
ß" œ ß œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
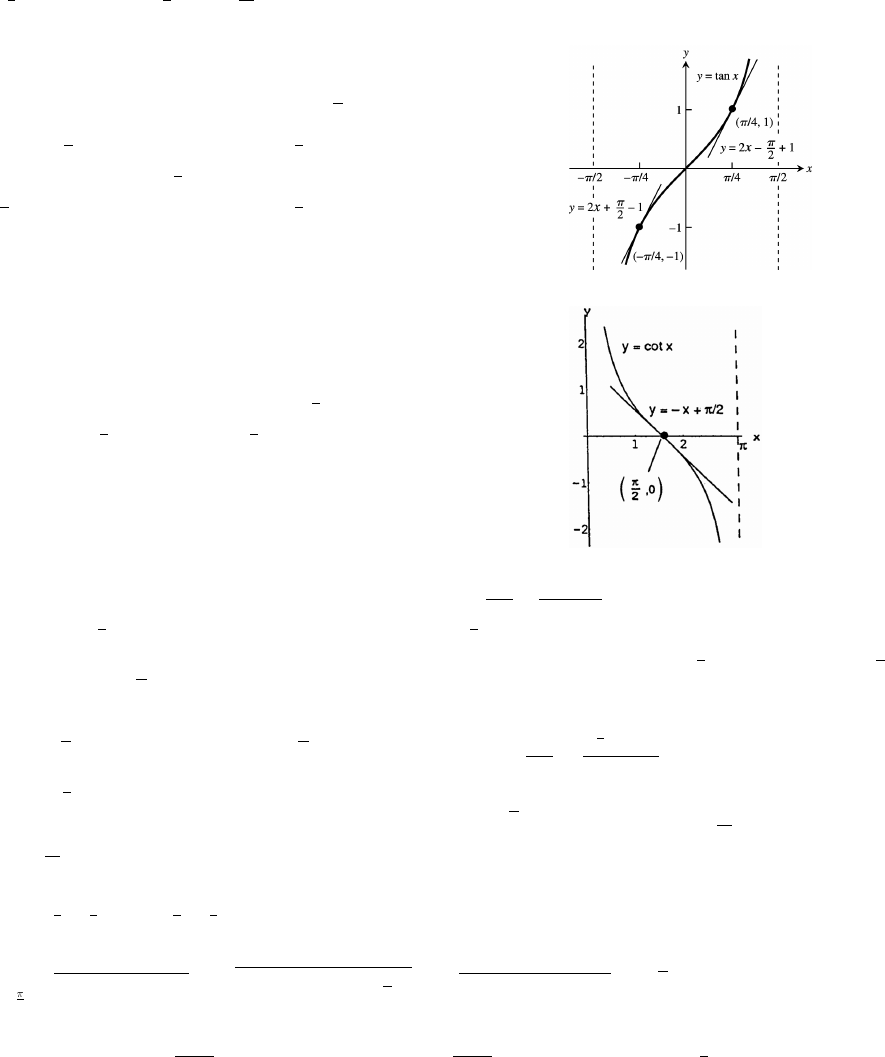
144 Chapter 3 Differentiation
31. Yes, y x sin x y cos x; horizontal tangent occurs where 1 cos x 0 cos x 1œ Ê œ" œ Ê œ
w
xʜ1
32. No, y 2x sin x y 2 cos x; horizontal tangent occurs where 2 cos x 0 cos x . But thereœ Êœ œÊ œ#
w
are no x-values for which cos x .œ#
33. No, y x cot x y 1 csc x; horizontal tangent occurs where 1 csc x 0 csc x 1. But thereœ Ê œ œ Ê œ
w# # #
are no x-values for which csc x 1.
#œ
34. Yes, y x 2 cos x y 1 2 sin x; horizontal tangent occurs where 1 2 sin x 0 1 2 sin xœ Ê œ œ Ê œ
w
sin x x or xÊœ Êœ œ
"
#
11
66
5
35. We want all points on the curve where the tangent
line has slope 2. Thus, y tan x y sec x soœÊœ
w#
that y 2 sec x 2 sec x 2
w#
œÊ œÊ œ„
È
x . Then the tangent line at hasÊœ„ ß"
11
44
ˆ‰
equation y 1 2 x ; the tangent line atœ
ˆ‰
1
4
has equation y 1 2 x .
ˆ‰ ˆ‰
ß" œ
11
44
36. We want all points on the curve y cot x whereœ
the tangent line has slope 1. Thus y cot xœ
y csc x so that y 1 csc x 1Êœ œÊ œ
w# w #
csc x 1 csc x 1 x . Theʜʜ„Êœ
#
#
1
tangent line at is y x .
ˆ‰
11
#ß! œ 2
37. y 4 cot x 2 csc x y csc x 2 csc x cot xœ Ê œ œ
w# "
ˆ‰ˆ ‰
sin x sin x
12 cos x
(a) When x , then y 1; the tangent line is y x 2.œœ œ
11
##
w
(b) To find the location of the horizontal tangent set y 0 1 2 cos x 0 x radians. When x ,
wœÊ œÊœ œ
11
33
then y 3 is the horizontal tangent.œ%È
38. y 1 2 csc x cot x y 2 csc x cot x csc xœ Ê œ œ
ÈȈ‰
Š‹
w#
"
sin x sin x
2 cos x 1
È
(a) If x , then y 4; the tangent line is y 4x 4.œœ œ
1
4w1
(b) To find the location of the horizontal tangent set y 0 2 cos x 1 0 x radians. When
wœÊ œÊœ
È3
4
1
x , then y 2 is the horizontal tangent.œœ
3
4
1
39. lim sin sin sin 0 0
x2Ĉ‰ˆ‰
"" ""
###xœ œ œ
40. lim 1 cos ( csc x) 1 cos csc 1 cos 2 2
xÄ
6ÈɈ‰ˆ‰ Èab
È
œœ œ11 1
1
6†ab
41. lim sec cos x tan 1 sec cos 0 tan 1 sec 1 tan 1 sec 1
xÄ! ‘‘‘ˆ‰ ˆ‰ ˆ‰
œœœœ1111
111
4 sec x 4 sec 0 4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.4 Derivatives of Trigonometric Functions 145
42. lim sin sin sin 1
xÄ! ˆ‰ˆ‰ˆ‰
11 1
#
tan x tan 0
tan x 2 sec x tan 0 2 sec 0
œœœ
43. lim tan 1 tan 1 lim tan (1 1) 0
ttÄ! Ä!
ˆ‰
Š‹
œ œ œ
sin t sin t
tt
44. lim cos cos lim cos cos 1
))Ä! Ä!
ˆ‰ ˆ ‰
Š‹
Œ
1) )
))sin sin 1
lim
œœœœ111††
""
sin
45. s sin t v 2 cos t a 2 sin t j 2 cos t. Therefore, velocity vœ## Ê œ œ Ê œ œ Ê œ œ œ
ds dv da
dt dt dt 4
ˆ‰
1
2 m/sec; speed v 2 m/sec; acceleration a 2 m/sec ; jerk j 2 m/sec .œ œ œ œ œ œ œ
ÈÈ ÈÈ
¸ ¸ ˆ‰ ˆ‰ˆ‰
111
444
#$
46. s sin t cos t v cos t sin t a sin t cos t j cos t sin t. Thereforeœ Êœœ Êœœ Êœœ
ds dv da
dt dt dt
velocity v 0 m/sec; speed v 0 m/sec; acceleration a 2 m/sec ;œœ œ œ œœ
ˆ‰ ¸ ¸ ˆ‰ˆ‰ È
11 1
44 4
#
jerk j 0 m/sec .œœ
ˆ‰
1
4$
47. lim f(x) lim lim 9 9 so that f is continuous at x 0 lim f(x) f(0)
xx x xÄ! Ä! Ä! Ä!
œœ œ œÊœ
sin 3x sin 3x sin 3x
x3x3x
ˆ‰ˆ‰
9c.ʜ
48. lim g(x) lim (x b) b and lim g(x) lim cos x 1 so that g is continuous at x 0 lim g(x)
xx x
xx
Ä! Ä! Ä!
Ä! Ä!
œœ œ œ œÊ
lim g(x) b 1. Now g is not differentiable at x 0: At x 0, the left-hand derivative isœÊœ œœ
xÄ!
(x b) 1, but the right-hand derivative is (cos x) sin 0 0. The left- and right-hand
¸¸
dd
dx dx
œ œœ
x=0 x=0
derivatives can never agree at x 0, so g is not differentiable at x 0 for any value of b (including b 1).œœ œ
49. (cos x) sin x because (cos x) cos x the derivative of cos x any number of times that is a
dd
dx dx
œœÊ
multiple of 4 is cos x. Thus, dividing 999 by 4 gives 999 249 4 3 (cos x)œÊ†d
dx
(cos x) (cos x) sin x.œœœ
dd d
dx dx
dx
’“
50. (a) y sec x sec x tan xœœÊœ œœ œ
""
cos x dx (cos x) cos x cos x cos x
dy (cos x)(0) (1)( sin x) sin x sin x
ˆ‰ˆ‰
(sec x) sec x tan xʜ
d
dx
(b) y csc x csc x cot xœœÊœ œ œ œ
""
sin x dx (sin x) sin x sin x sin x
dy (sin x)(0) (1)(cos x) cos x cos x
ˆ‰ˆ‰
(csc x) csc x cot xʜ
d
dx
(c) y cot x csc xœœÊœ œ œœ
cos x sin x cos x
sin x dx (sin x) sin x sin x
dy (sin x)( sin x) (cos x)(cos x) " #
(cot x) csc xʜ
d
dx #
51.
As h takes on the values of 1, 0.5, 0.3 and 0.1 the corresponding dashed curves of y getœsin (x h) sin x
h
closer and closer to the black curve y cos x because (sin x) lim cos x. The sameœœœ
d
dx h
sin (x h) sin x
hÄ!
is true as h takes on the values of 1, 0.5, 0.3 and 0.1.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
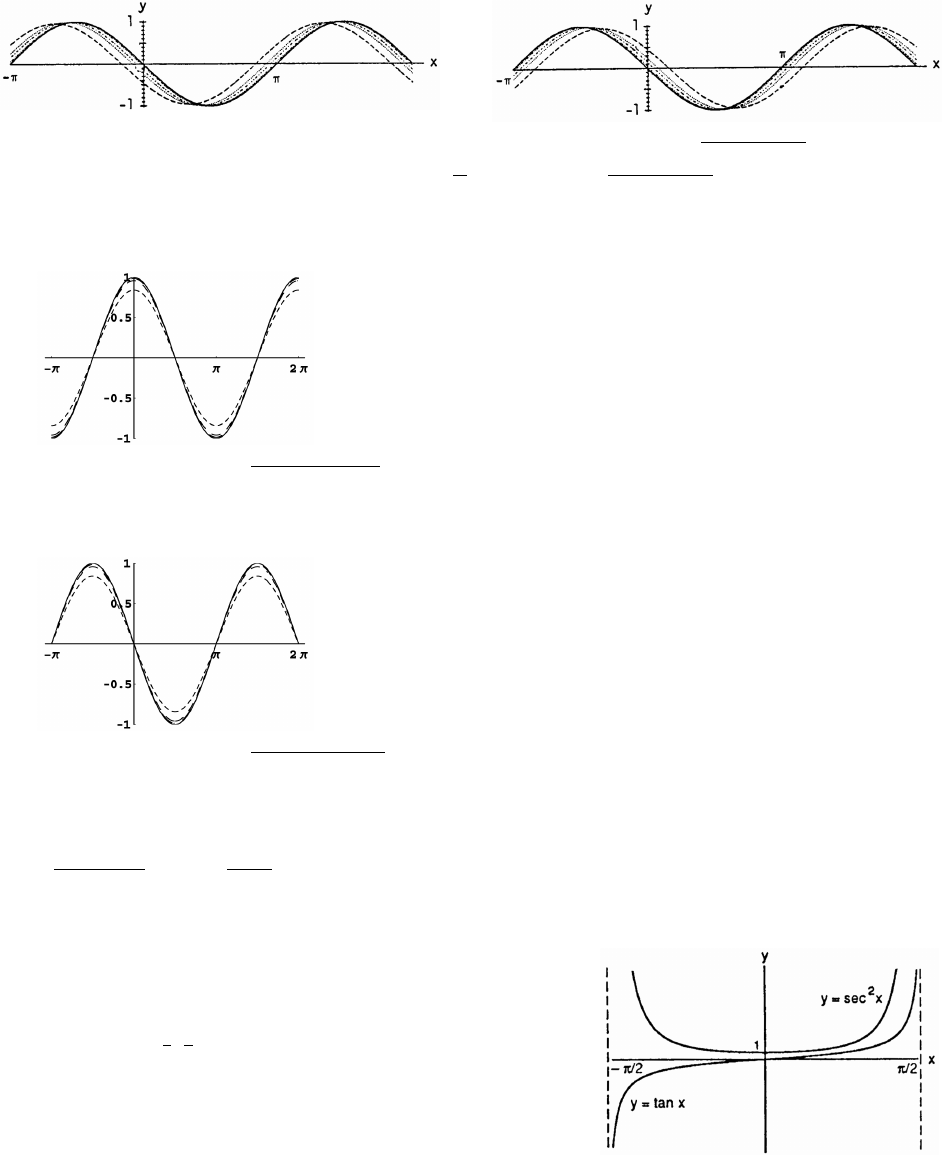
146 Chapter 3 Differentiation
52.
As h takes on the values of 1, 0.5, 0.3, and 0.1 the corresponding dashed curves of y getœcos (x h) cos x
h
closer and closer to the black curve y sin x because (cos x) lim sin x. Theœ œ œ
d
dx h
cos (x h) cos x
hÄ!
same is true as h takes on the values of 1, 0.5, 0.3, and 0.1.
53. (a)
The dashed curves of y are closer to the black curve y cos x than the corresponding dashedœœ
sin x h sin x h
h
abab
#
curves in Exercise 51 illustrating that the centered difference quotient is a better approximation of the derivative of
this function.
(b)
The dashed curves of y are closer to the black curve y sin x than the corresponding dashedœœ
cos x h cos x h
h
ab ab
#
curves in Exercise 52 illustrating that the centered difference quotient is a better approximation of the derivative of
this function.
54. lim lim lim 0 0 the limits of the centered difference quotient exists even
hh
x
Ä! Ä!
Ä!
kkkk kkkk0h 0h h h
2h 2h
œœœÊ
though the derivative of f(x) x does not exist at x 0.œœkk
55. y tan x y sec x, so the smallest valueœÊœ
w#
y sec x takes on is y 1 when x 0;
w# w
œœœ
y has no maximum value since sec x has no
w#
largest value on ; y is never negative
ˆ‰
ß
11
##
w
since sec x 1.
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
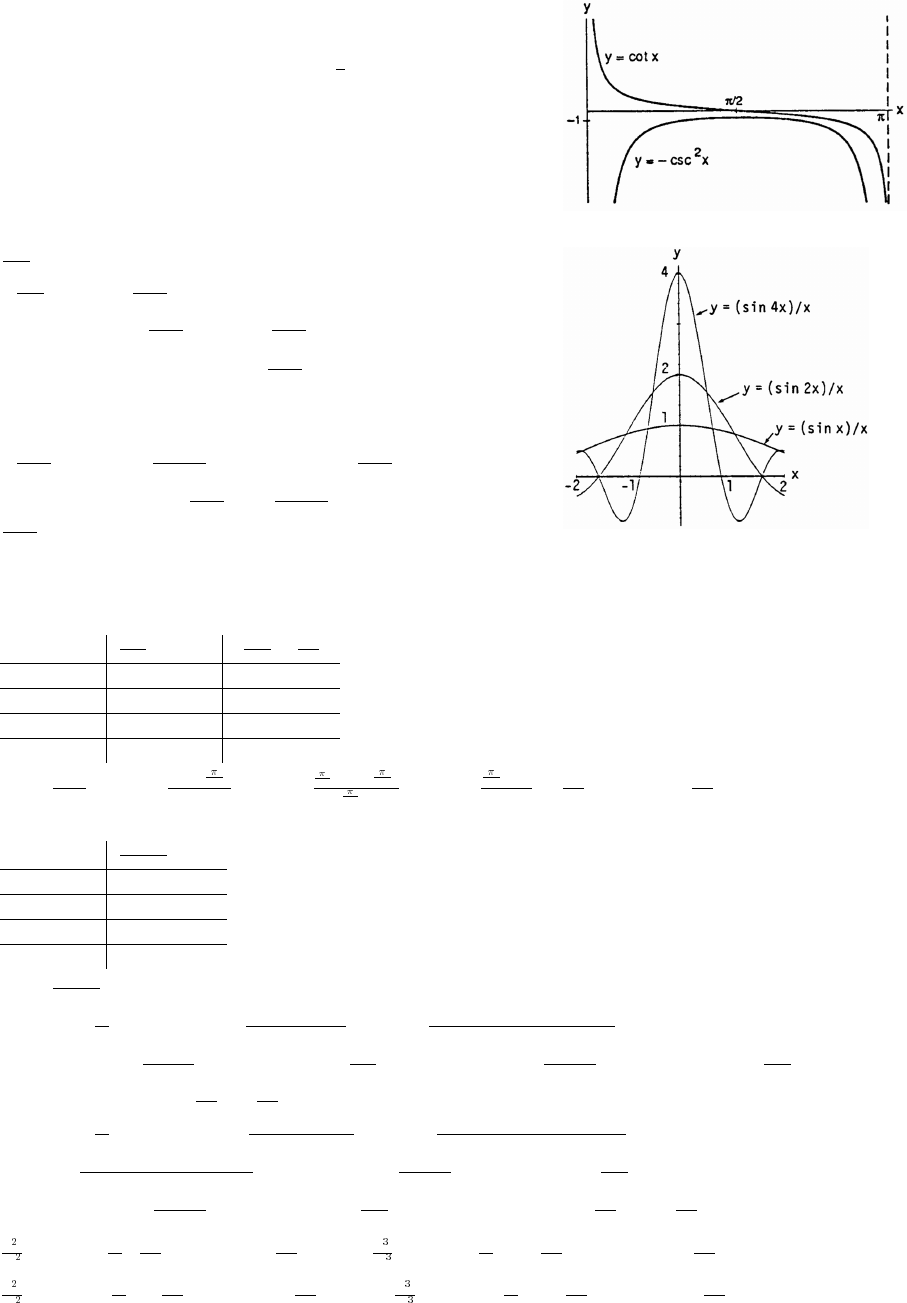
Section 3.4 Derivatives of Trigonometric Functions 147
56. y cot x y csc x so y has no smallestœÊœ
w#w
value since csc x has no minimum value on#
( ); the largest value of y is 1, when x ;!ß œ1w
#
1
the slope is never positive since the largest
value y csc x takes on is 1.
wœ
2
57. y appears to cross the y-axis at y 1, sinceœœ
sin x
x
lim 1; y appears to cross the y-axis
xÄ!
sin x sin 2x
xx
œœ
at y 2, since lim 2; y appears to
x
œœœ
Ä!
sin 2x sin 4x
xx
cross the y-axis at y 4, since lim 4.œœ
xÄ!
sin 4x
x
However, none of these graphs actually cross the y-axis
since x 0 is not in the domain of the functions. Also,œ
lim 5, lim 3, and lim
xx xÄ! Ä! Ä!
sin 5x sin kx
xx x
sin ( 3x)
œœ
k the graphs of y , y , andœÊ œ œ
sin 5x
xx
sin ( 3x)
y approach 5, 3, and k, respectively, asœ
sin kx
x
x 0. However, the graphs do not actually cross theÄ
y-axis.
58. (a) h
1 .017452406 .99994923
0.01 .017453292 1
0.001 .017453292 1
0.0001 .017453292 1
sin h sin h 180
hh
ˆ‰ˆ‰
1
lim lim lim lim ( h )
hh
x
Ä! Ä!
Ä! Ä!
sin h°
h h h 180 180
sin h sin h sin
œœ œœœ
ˆ‰ ˆ‰
††
†
180 180 180
180
180 )
)
)
11
)†
(converting to radians)
(b) h
1 0.0001523
0.01 0.0000015
0.001 0.0000001
0.0001 0
cos h 1
h
lim 0, whether h is measured in degrees or radians.
hÄ!
cos h 1
h
œ
(c) In degrees, (sin x) lim lim
d
dx h h
sin (x h) sin x (sin x cos h cos x sin h) sin x
œœ
hhÄ! Ä!
lim sin x lim cos x (sin x) lim (cos x) lim œœ
hh h hÄ! Ä! Ä! Ä!
ˆ‰ˆ‰ ˆ‰ ˆ‰
††† †
cos h 1 sin h cos h 1 sin h
hh h h
(sin x)(0) (cos x) cos xœ œ
ˆ‰
11
180 180
(d) In degrees, (cos x) lim lim
d
dx h h
cos (x h) cos x (cos x cos h sin x sin h) cos x
œœ
hhÄ! Ä!
lim lim cos x lim sin xœœ
hhhÄ! Ä! Ä!
(cos x)(cos h 1) sin x sin h
hhh
cos h 1 sin h
ˆ‰ˆ‰
††
(cos x) lim (sin x) lim (cos x)(0) (sin x) sin xœœœ
hhÄ! Ä!
ˆ‰ ˆ‰ ˆ‰
cos h 1 sin h
h h 180 180
11
(e) (sin x) cos x sin x; (sin x) sin x cos x;
dd dd
dx dx 180 180 dx dx 180 180
œœ œœ
ˆ ‰ ˆ‰ ˆ‰ ˆ‰
Š‹
11 1 1
##$
(cos x) sin x cos x; (cos x) cos x sin x
dd dd
dx dx 180 180 dx dx 180 180
œ œ œ œ
ˆ ‰ ˆ‰ ˆ‰ ˆ‰
Š‹
11 1 1
##$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

148 Chapter 3 Differentiation
3.5 THE CHAIN RULE AND PARAMETRIC EQUATIONS
1. f(u) 6u 9 f (u) 6 f (g(x)) 6; g(x) x g (x) 2x ; therefore f (g(x))g (x)œÊ œÊ œ œ Ê œ œ
ww %w$ ww
"
#
dy
dx
6 2x 12xœœ†$$
2. f(u) 2u f (u) 6u f (g(x)) 6(8x 1) ; g(x) 8x 1 g (x) 8; therefore f (g(x))g (x)œÊ œÊ œ œÊ œ œ
$w #w # w w w
dy
dx
6(8x 1) 8 48(8x 1)œ œ
##
†
3. f(u) sin u f (u) cos u f (g(x)) cos (3x 1); g(x) 3x 1 g (x) 3; therefore f (g(x))g (x)œÊœ Ê œ œÊœ œ
ww w ww
dy
dx
(cos (3x 1))(3) 3 cos (3x 1)œœ
4. f(u) cos u f (u) sin u f (g(x)) sin ; g(x) g (x) ; therefore f (g(x))g (x)œÊœÊ œ œÊœ œ
ww w ww
"
ˆ‰
xx
33 3dx
dy
sin sinœ œ
ˆ‰ˆ‰ ˆ‰
""xx
333 3
†
5. f(u) cos u f (u) sin u f (g(x)) sin (sin x); g(x) sin x g (x) cos x; thereforeœÊœÊ œ œÊœ
ww w
f (g(x))g (x) (sin (sin x)) cos x
dy
dx œœ
ww
6. f(u) sin u f (u) cos u f (g(x)) cos (x cos x); g(x) x cos x g (x) 1 sin x; thereforeœÊœ Ê œ œ Êœ
ww w
f (g(x))g (x) (cos (x cos x))(1 sin x)
dy
dx œœ
ww
7. f(u) tan u f (u) sec u f (g(x)) sec (10x 5); g(x) 10x 5 g (x) 10; thereforeœÊœ Ê œ œÊœ
w#w # w
f (g(x))g (x) sec (10x 5) (10) 10 sec (10x 5)
dy
dx œœœ
ww # #
ab
8. f(u) sec u f (u) sec u tan u f (g(x)) sec x 7x tan x 7x ; g(x) x 7xœ Ê œ Ê œ œ
ww###
abab
g (x) 2x 7; therefore f (g(x))g (x) (2x 7) sec x 7x tan x 7xÊœ œ œ
www##
dy
dx abab
9. With u (2x 1), y u : 5u 2 10(2x 1)œ œ œ œ œ
&%%
dy dy
dx du dx
du †
10. With u (4 3x), y u : 9u ( 3) 27(4 3x)œ œ œ œ œ
*) )
dy dy
dx du dx
du †
11. With u 1 , y : 7uœ œ? œ œ œ"
ˆ‰ ˆ‰ˆ‰
xdu x
7dxdudx 77
dy dy
( ) ")
†
12. With u 1 , y : 10u 5 1œ œ? œ œ œ
ˆ‰ ˆ‰ ˆ‰
xdux
dy dy
dx du dx###
"! "" """
†
13. With u x , y : 4u 1 4 x 1œ œ? œ œ œ
Š‹ Š‹
ˆ‰ ˆ‰
xduxxx
8 x dx du dx 4 x 8 x 4 x
dy dy
""""
%$ $
†
14. With u , y : 5u 1œ œ? œ œ œ
ˆ‰ ˆ‰ˆ‰ˆ‰
xdu1x
55x dx dudx 55x 55x x
dy dy
""""
&% %
†
15. With u tan x, y sec u: (sec u tan u) sec x (sec (tan x) tan (tan x)) sec xœœ œœ œ
dy dy
dx du dx
du ab
##
16. With u , y cot u: csc u cscœ œ œ œ œ 11
""""
##
xdxdudx xxx
dy dy du ab
ˆ‰ ˆ ‰
17. With u sin x, y u : 3u cos x 3 sin x (cos x)œœœœ œ
$##
dy dy
dx du dx
du ab
18. With u cos x, y 5u : 20u ( sin x) 20 cos x (sin x)œœ œœœ
% & &
dy dy
dx du dx
du ab ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.5 The Chain Rule and Parametric Equations 149
19. p 3 t (3 t) (3 t) (3 t) (3 t)œœ Êœ œ œ
È"Î# "Î# "Î#
"""
##
dp
dt dt
d
23t
†È
20. q 2r r 2r r 2r r 2r r 2r r (2 2r)œœ Êœ œ œ
Èab ab abab
#####
"Î# "Î# "Î#
"""
##
dq
dr dr
dr
2r r
†È
21. s sin 3t cos 5t cos 3t (3t) ( sin 5t) (5t) cos 3t sin 5tœ Êœ œ
44 ds4d4 d44
3 5 dt 3 dt 5 dt11 1 1 11
††
(cos 3t sin 5t)œ
4
1
22. s sin cos cos sin cos sinœ Êœ œ
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
3t 3t ds 3t d 3t 3t d 3t 3 3t 3 3t
dt dt dt 2 2
1 1 11 111111
# # ## ## # #
††
cos sin œ
33t3t
2
11 1
ˆ‰
##
23. r (csc cot ) (csc cot ) (csc cot )œ Êœ œ œ)) )) ))
" #
dr d csc cot csc
d d (csc cot ) (csc cot )
csc (cot csc )
))))))
)) ) )) )
œcsc
csc cot
)
))
24. r (sec tan ) (sec tan ) (sec tan )œ Ê œ œ œ)) )) ))
" #
dr d sec tan sec
d d (sec tan ) (sec tan )
sec (tan sec )
)) ))))
)) ) )) )
œsec
sec tan
)
))
25. y x sin x x cos x x sin x sin x x x cos x cos x (x)œ Êœ
# % # # % % # # #
dy
dx dx dx dx dx
ddd d
ab ab a b††
x 4 sin x (sin x) 2x sin x x 2 cos x (cos x) cos xœ
#$ % $ #
ˆ‰ˆ ‰
dd
dx dx
†
x 4 sin x cos x 2x sin x x 2 cos x ( sin x) cos xœ
#$ % $ #
ab a bab
4x sin x cos x 2x sin x 2x sin x cos x cos xœ
#$%$#
26. y sin x cos x y sin x sin x cos x cos xœÊœ
"""
& $ w & & $ $
x 3 xdx dx x 3dx dx 3
xd dxd dx
ab ab
ˆ‰ ˆ‰
††
5 sin x cos x sin x 3 cos x ( sin x) cos xœ
"" "
' & # $
xx33
x
ababa bab
ˆ‰ ˆ‰
ab
sin x cos x sin x x cos x sin x cos xœ
5
xx 3
' & # $
""
27. y (3x 2) 4 (3x 2) (3x 2) ( 1) 4 4œ Êœ
"" ""
('
###
" #
21 x dx 21 dx x dx x
dy 7d d
ˆ‰ ˆ‰ˆ‰
††
(3x 2) 3 ( 1) 4 (3x 2)œ œ
7
21 x x x4
''
"" "
#
#
†ˆ‰ˆ‰ Š‹
x
28. y (5 2x) 1 3(5 2x) ( 2) 1 6(5 2x) 1œ Ê œ œ
$ % %
" "
%$$
8x dx 8x x x x
24222
dy
ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ‰
œ
6
(5 2x)
1
x
Š‹
2
x
29. y (4x 3) (x 1) (4x 3) ( 3)(x 1) (x 1) (x 1) (4)(4x 3) (4x 3)œ Êœ
% $ % % $ $
dy
dx dx dx
dd
††
(4x 3) ( 3)(x 1) (1) (x 1) (4)(4x 3) (4) 3(4x 3) (x 1) 16(4x 3) (x 1)œ œ
%% $$ %% $$
3(4x 3) 16(x 1)œœ
(4x 3) (4x 3) (4x 7)
(x 1) (x 1)
cd
30. y (2x 5) x 5x (2x 5) (6) x 5x (2x 5) x 5x ( 1)(2x 5) (2)œ Êœ
" # " # # #
'&'
ab ab ab
dy
dx
6x 5xœab
#&
2x 5x
(2x 5)
ab
31. h(x) x tan 2 x 7 h (x) x tan 2x tan 2x (x) 0œÊœ
ˆ‰ ˆ ‰ ˆ‰
Ȉ‰
w "Î# "Î#
dd
dx dx
†
x sec 2x 2x tan 2x x sec 2 x tan 2 x x sec 2 x tan 2 xœœœ
# "Î# "Î# "Î# # #
"
ˆ‰ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
ÈÈÈÈÈ
††
d
dx x
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

150 Chapter 3 Differentiation
32. k(x) x sec k (x) x sec sec x x sec tan 2x secœÊœ œ
#w# ##
"""""""
ˆ‰ ˆ ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
ab
x dx x xdx x xdxx x
dd d
††
x sec tan 2x sec 2x sec sec tanœ œ
#"" " " " ""
ˆ‰ ˆ‰ˆ ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
xxx x x xx
†
33. f( ) f ( ) 2))œÊœ œ
ˆ‰ ˆ‰ˆ‰
sin sin d sin 2 sin
1cos 1cos d 1cos 1cos (1cos )
(1 cos )(cos ) (sin )( sin )
))))
))))))
)) ) )
#w
††
œœœ
(2 sin ) cos cos sin
(1cos ) (1cos ) (1cos )
(2 sin ) (cos 1) 2 sin
)) ) )
)))
)) )
ab
34. g(t) g (t)œ Ê œ œ
ˆ‰ ˆ‰ˆ‰
1cos t 1cos t d 1cos t sint
sin t sin t dt sin t (1 cos t) (sin t)
(sin t)( sin t) ( cos t)(cos t)
" #
w
"
††
œœ
"
absin t cos t cos t
(1 cos t) 1 cos t
35. r sin cos (2 ) sin ( sin 2 ) (2 ) cos (2 ) cosœÊœab ab a b abab)) ) )) )))
## ##
dr d d
dd d)) )
†
sin ( sin 2 )(2) (cos 2 ) cos (2 ) 2 sin sin ( ) 2 cos (2 ) cosœ œ #ab a b ab abab)) ))) )))))
####
36. r sec tan sec sec tan sec tan œÊœ
Š‹ Š‹ Š ‹Š‹
ÈÈ ÈÈ
ˆ‰ ˆ ‰ˆ ‰ ˆ‰
)) ))
"""""
#
#
)) )) ) )
dr
dÈ
sec sec tan sec tan sec œ œ
""""
#
#
)))
)
ÈÈÈÈ
ˆ‰ ˆ‰ Š‹
”•
))))
Ètan tan sec
Ȉ‰ ˆ‰
È
)
))
#
37. q sin cos cosœÊœ œ
Š‹ Š‹Š‹ Š‹
ttdtt
t1 t1 t1 t1
dq
dt dt
t1(1)t t1
t1
ÈÈÈÈ
ÈÈ
ˆ‰
ˆ‰
È
††
†d
dt
cos cos cosœœœ
Š‹ Š‹Š ‹Š ‹Š‹
ttt2t
t1 t1 t1
t1
t1
2(t 1) t
2(t 1) 2(t 1)
ÈÈ È
È
†
t
2t1
38. q cot csc cscœÊœ œ
ˆ‰ ˆ‰ ˆ‰ˆ ‰ˆ ‰ˆ‰
sin t sin t d sin t sin t t cos t sin t
tdt tdtt t t
dq ##
†
39. y sin ( t 2) 2 sin ( t 2) sin ( t 2) 2 sin ( t 2) cos ( t 2) ( t 2)œÊœ œ
#111111
dy
dt dt dt
dd
†††
2 sin(t2) cos(t2)œ11 1
40. y sec t (2 sec t) (sec t) (2 sec t)(sec t tan t) ( t) 2 sec t tan tœÊœ œ œ
# #
1 1 1 1 11 1 1 11
dy
dt dt dt
dd
††
41. y (1 cos 2t) 4(1 cos 2t) (1 cos 2t) 4(1 cos 2t) ( sin 2t) (2t)œ Ê œ œ œ
% & &
dy
dt dt dt (1 cos 2t)
d d 8 sin 2t
††
42. y 1 cot 2 1 cot 1 cot 2 1 cot cscœ Êœ œ
ˆ‰ ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
ttdtttdt
dy
dt dt dt######
# $ $ #
†††
œcsc
cot
ˆ‰
ˆ‰
t
t
ˆ‰
1
43. y sin cos (2t 5) cos (cos (2t 5)) cos (2t 5) cos (cos (2t 5)) ( sin (2t 5)) (2t 5)œÊœ œ ab
dy
dt dt dt
dd
†††
2 cos (cos (2t 5))(sin (2t 5))œ
44. y cos 5 sin sin 5 sin 5 sin sin 5 sin 5 cosœ Ê œ œ
ˆ‰ ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
ttdtttdt
3dt 3dt 3 3 3dt3
dy
††
sin 5 sin cosœ5tt
333
ˆ‰ˆ‰ˆ‰ ˆ‰
45. y 1 tan 3 1 tan 1 tan 3 1 tan 4 tan tanœ Ê œ œ
‘‘‘‘ ‘ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
%%%%$
######
$# #
ttdtttdt
1dt 1dt 1 1 1dt1
dy
††
12 1 tan tan sec 1 tan tan secœ œ
‘ ‘‘ ‘ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
%$# %$#
#### ###
##
"ttt ttt
1111 111
†
46. y 1 cos (7t) 1 cos (7t) 2 cos (7t)( sin (7t))(7) 7 1 cos (7t) (cos (7t) sin (7t))œ Êœ œ
"## #
$# #
6dt6
dy 3
cd cd cd†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.5 The Chain Rule and Parametric Equations 151
47. y 1 cos t 1 cos t 1 cos t 1 cos t sin t tœ Ê œ œ ab abababababab ab ab ab ˆ‰
######
"Î# "Î# "Î#
""
##
dy
dt dt dt
dd
††
1 cos t sin t 2tœ œ
"
#
##
"Î#
ababab ab†
t sin t
1cost
ab
Èab
48. y 4 sin 1 t 4 cos 1 t 1 t 4 cos 1 t 1 tœÊœ œ
Œ ŒŒŒ
ÉÉÉÉ
ÈÈÈÈÈ
ˆ‰
dy
dt dt dt
dd
1t
†††
"
#
ÉÈ
œœ
2 cos 1 t cos 1 t
1t2t tt
ŒŒ
ÉÉ
ÈÈ
ÉÉ
ÈÈ È
†
49. y 1 y 3 1 1 y 1 1œ Êœ œ Ê œ
ˆ‰ ˆ‰ˆ‰ ˆ‰ ˆ‰ˆ‰ˆ‰ˆ‰
"""" ""
$# # ##
www
x x x x x x dx x x dx x
33dd3
††
21 11111œ œœ
ˆ‰ˆ ‰ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ ‰ˆ‰ˆ‰
36666
x xx x x xxxxxx x
x
"" """"""
##
11œ
62
xx x
ˆ‰ˆ‰
"
50. y 1 x y 1 x x 1 x xœ Êœ œ
ˆ‰ ˆ‰ˆ ‰ˆ‰
ÈÈ È
" # #
w "Î# "Î#
""
##
y 1 x x x ( 2) 1 x xʜ
ww $Î# "Î# "Î#
"" "
## #
# $
’“
ˆ‰ˆ ‰ ˆ‰ˆ ‰
ÈÈ
x1x x1x x1x x1x1œœ
"" " "
## # #
$Î# " " "Î#
# $ $
’“
ˆ‰ ˆ‰ ˆ‰ ‘
ÈÈ È È
ˆ‰
1x 1 1xœ œ
"""" "
####
$ $
##
xx
xx
3
ˆ‰ ˆ‰
ÈÈ
Š‹ Š‹
ÈÈ
51. y cot (3x 1) y csc (3x 1)(3) csc (3x 1) y (csc (3x 1) csc (3x 1))œÊœ œ Êœ
"""
w# # ww
993 3dx
2d
ˆ‰ †
csc (3x 1)( csc (3x 1) cot (3x 1) (3x 1)) 2 csc (3x 1) cot (3x 1)œ œ
2d
3dx
†#
52. y 9 tan y 9 sec 3 sec y 3 2 sec sec tan 2 sec tanœÊœ œ Êœ œ
ˆ‰ ˆ ‰ˆ‰ ˆ‰ ˆ‰ˆ ‰ˆ‰ ˆ‰ ˆ‰ˆ‰ ˆ‰ ˆ‰
x x x x xx xx
3333 333333
w# # ww #
" "
†
53. g(x) x g (x) g(1) 1 and g (1) ; f(u) u 1 f (u) 5u f (g(1)) f (1) 5;œÊ œ Ê œ œ œÊ œÊ œœ
Èww&w%ww
""
##
Èx
therefore, (f g) (1) f (g(1)) g (1) 5‰œ œœ
ww w "
##
††
5
54. g(x) (1 x) g (x) (1 x) ( 1) g( 1) and g ( 1) ; f(u) 1œ Ê œ œ Êœ œ œ
" w # w
""""
#(1 x) 4 u
f (u) f (g( 1)) f 4; therefore, (f g) ( 1) f (g( 1))g ( 1) 4 1ʜʜ œ ‰œœœ
www www
"" "
#u 4
ˆ‰ †
55. g(x) 5 x g (x) g(1) 5 and g (1) ; f(u) cot f (u) cscœÊœÊœ œ œ Êœ
Ȉ‰ ˆ‰ˆ‰
ww w#
##
55uu
x10 10 10
È111
csc f (g(1)) f (5) csc ; therefore, (f g) (1) f (g(1))g (1)œÊœœœ ‰œœ
#ww # www
# #
11 1 1 1 1
10 10 10 10 10
u 5
ˆ‰ ˆ‰ †
= 1
4
56. g(x) x g (x) g and g ; f(u) u sec u f (u) 1 2 sec u sec u tan uœÊ œÊ œ œ œ Ê œ11 1
ww#w
""
ˆ‰ ˆ‰
44 4
1
†
1 2 sec u tan u f g f 1 2 sec tan 5; therefore, (f g) f g g 5œ Ê œ œ œ ‰ œ œ
#ww # www
""""
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰
44 44 4 44
111 1
57. g(x) 10x x 1 g (x) 20x 1 g(0) 1 and g (0) 1; f(u) f (u)œÊ œÊœ œ œ Ê œ
#w w w
2u
u1
u 1 (2) (2u)(2u)
u1
ab
ab
f (g(0)) f (1) 0; therefore, (f g) (0) f (g(0))g (0) 0 1 0œÊ œœ ‰œ œœ
ww www
2u 2
u1
ab †
58. g(x) 1 g (x) g( 1) 0 and g ( 1) 2; f(u) f (u) 2 œ Ê œ Ê œ œ œ Ê œ
"
www
#
x x u1 u1 du u1
2u1u1du1
ˆ‰ ˆ‰ˆ‰
2 f (g( 1)) f (0) 4; therefore,œœœÊœœ
ˆ‰
u1
u 1 (u 1) (u 1) (u 1)
(u 1)(1) (u 1)(1) 2(u 1)(2) 4(u 1)
ww
†
(f g) ( 1) f (g( 1))g ( 1) ( 4)(2) 8‰œ œ œ
www
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

152 Chapter 3 Differentiation
59. (a) y 2f(x) 2f (x) 2f (2) 2œÊœ Ê œœœ
dy dy
dx dx 3 3
2
ww
"
¹ˆ‰
x=2
(b) y f(x) g(x) f (x) g (x) f (3) g (3) 2 5œ Êœ Ê œ œ
dy dy
dx dx
ww ww
¹x=3
1
(c) y f(x) g(x) f(x)g (x) g(x)f (x) f(3)g (3) g(3)f (3) 3 5 ( 4)(2 ) 15 8œÊœÊœœœ††
dy dy
dx dx
ww ww
¹x=3
11
(d) y œÊœ Ê œ œ œ
f(x) dy g(x)f (x) f(x)g (x) dy g(2)f (2) f(2)g (2)
g(x) dx [g(x)] dx [g(2)] 6
(2) (8)( 3) 37
#
¹x=2
ˆ‰
3
(e) y f(g(x)) f (g(x))g (x) f (g(2))g (2) f (2)( 3) ( 3) 1œ Ê œ Ê œ œ œ œ
dy dy
dx dx 3
ww ww w "
¹x=2
(f) y (f(x)) (f(x)) f (x) œ Êœ œ Ê œ œœœ œ
"Î# "Î# w
"""
###
##
dy f (x) dy f (2) 2
dx dx 24
f(x) f(2) 86812
†ÈÈÈÈÈ
ˆ‰ È
¹x=2
3
(g) y (g(x)) 2(g(x)) g (x) 2(g(3)) g (3) 2( 4) 5œÊœ Êœ œœ
# $ w $ w $
#
dy dy
dx dx 3
5
††
¹x=3
(h) y (f(x)) (g(x)) (f(x)) (g(x)) 2f(x) f (x) 2g(x) g (x)œ Êœ ababa b
## ## w w
"Î# "Î#
"
#
dy
dx ††
(f(2)) (g(2)) 2f(2)f (2) 2g(2)g (2) 8 2 2 8 2 2 ( 3)Êœ œ
¹aba bab
ˆ‰
dy
dx 3
x=2
"""
##
## w w ##
"Î# "Î#
†† ††
œ 5
317
È
60. (a) y 5f(x) g(x) 5f (x) g (x) 5f (1) g (1) 5 1œÊœ Ê œ œœ
dy dy
dx dx 3 3
8
ww ww "
¹ˆ‰ˆ‰
x=1
(b) y f(x)(g(x)) f(x) 3(g(x)) g (x) (g(x)) f (x) f(0)(g(0)) g (0) (g(0)) f (0)œÊœ Êœ$
$#w$w #w$w
dy dy
dx dx
ab ¹x=0
3(1)(1) (1) (5) 6œœ
#$
"
ˆ‰
3
(c) y œÊœ Êœ
f(x) dy (g(x) 1)f (x) f(x) g (x) dy (g(1) 1)f (1) f(1)g (1)
g(x) 1 dx (g(x) 1) dx (g(1) 1)
¹x=1
1œœ
(4 ) (3)
(41)
"
ˆ‰ ˆ‰
33
8
(d) y f(g(x)) f (g(x))g (x) f (g(0))g (0) f (1)œÊœ Êœ œ œœ
dy dy
dx dx 3 3 3 9
ww ww w
""""
¹ˆ‰ ˆ ‰ˆ‰
x=0
(e) y g(f(x)) g (f(x))f (x) g (f(0))f (0) g (1)(5) (5)œÊœ Êœ œ œœ
dy dy
dx dx 3 3
840
ww ww w
¹ˆ‰
x=0
(f) y x f(x) 2 x f(x) 11x f (x) 2(1 f(1)) 11 f (1)œ Êœ Ê œ ab aba b ab
¹
"" "" "! w $ w
# $
dy dy
dx dx x=1
2(1 3) 11œ œ œ
$ ""
ˆ‰ˆ‰ˆ‰
3433
232
(g) y f(x g(x)) f (x g(x)) 1 g (x) f (0 g(0)) 1 g (0) f (1) 1œÊœÊœœ
dy dy
dx dx 3
ww www
"
ab ab
¹ˆ‰
x=0
œ œ
ˆ‰ˆ‰
"
33 9
44
61. : s cos sin sin 1 so that 1 5 5
ds ds d ds ds 3 ds ds d
dt d dt d d dt d dt
œœÊœÊœœ œœœ
))) )
)1)
†††))
¸ˆ‰
=3
2#
62. : y x 7x 5 2x 7 9 so that 9 3
dy dy dy dy dy dy
dt dx dt dx dx dt dx dt 3
dx dx
œœÊœÊœ œœœ†††
#"
¹x=1
63. With y x, we should get 1 for both (a) and (b):œœ
dy
dx
(a) y 7 ; u 5x 35 5; therefore, 5 1, as expectedœÊœ œÊœ œ œ œ
ududu
5 du 5 dx dx du dx 5
dy dy dy
""
††
(b) y 1 ; u (x 1) (x 1) (1) ; therefore œ Ê œ œ Ê œ œ œ
"" "
" #
u du u dx (x 1) dx du dx
dy dy dy
du du
†
(x 1) 1, again as expectedœœ œœ
" " " " "
#
u (x1) (x1) (x1)
(x 1)
†††
ab
64. With y x , we should get x for both (a) and (b):œœ
$Î# "Î#
#
dy
dx
3
(a) y u 3u ; u x ; therefore, 3u 3 x x,œÊœ œ Êœ œ œ œ œ
$# #
"""
###
#
#
dy dy dy
du dx dx du dx
du du 3
xxx
ÈÈÈ
ˆ‰
ÈÈÈ
†† †
as expected.
(b) y u ; u x 3x ; therefore, 3x 3x x ,œÊœ œÊœ œ œ œ œ
Èdy dy dy
du dx dx du dx
uu
du du 3
x
"""
##
$ # # # "Î#
##
ÈÈÈ
†† †
again as expected.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
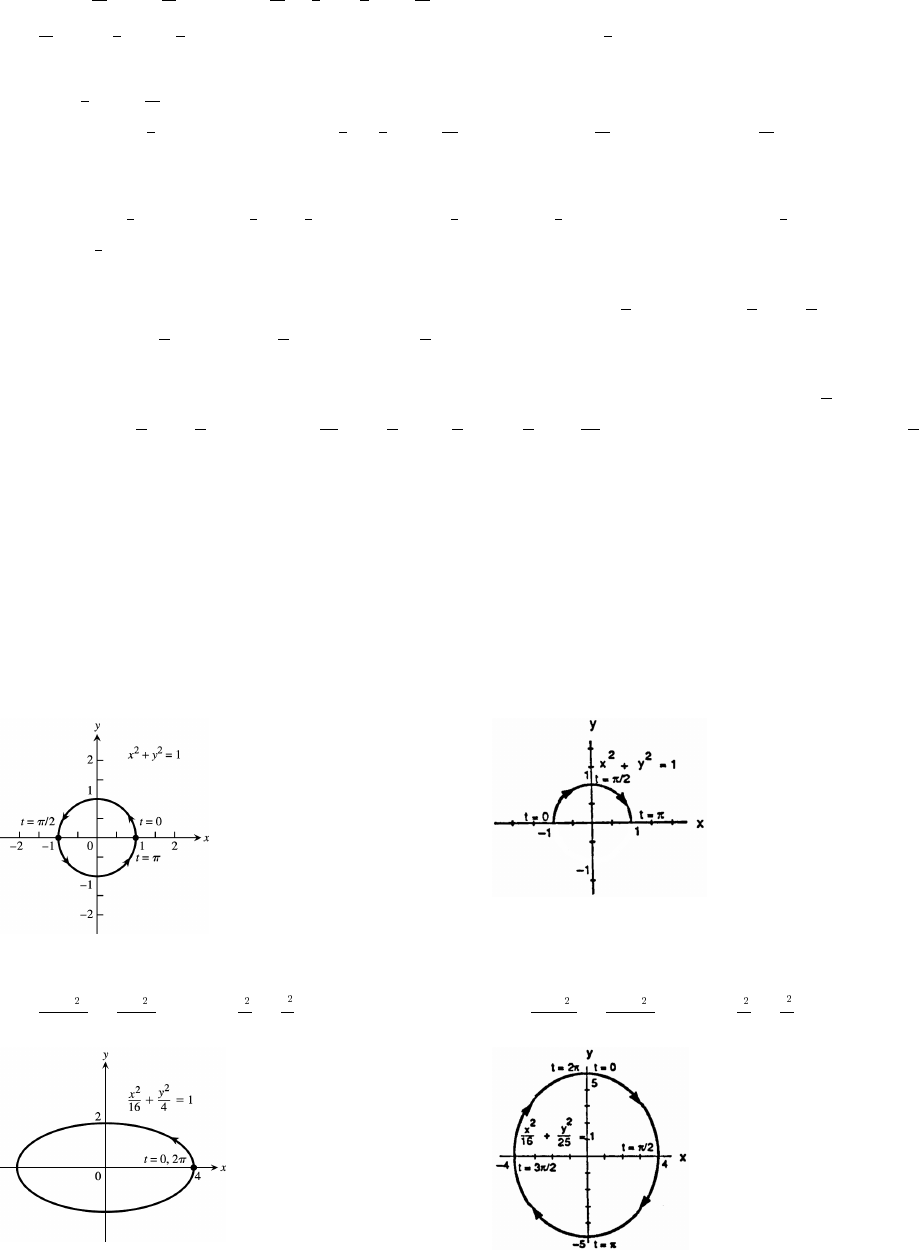
Section 3.5 The Chain Rule and Parametric Equations 153
65. y 2 tan 2 sec secœÊœ œ
ˆ‰ ˆ ‰ˆ‰
11111xxx
4dx 44 4
dy ##
#
(a) sec slope of tangent is 2; thus, y(1) 2 tan 2 and y (1) tangent line is
¹ˆ‰ ˆ‰
dy
dx 4 4
x=1
œœÊ œœœÊ
11 1
#
# w
11
given by y 2 (x 1) y x 2œ Êœ111
(b) y sec and the smallest value the secant function can have in x 2 is 1 the minimum
w#
#
œ#Ê
11
ˆ‰
x
4
value of y is and that occurs when sec 1 sec 1 sec x 0.
w##
###
111111
œÊœÊ„œÊœ
ˆ‰ ˆ‰ ˆ‰
xx x
44 4
66. (a) y sin 2x y 2 cos 2x y (0) 2 cos (0) 2 tangent to y sin 2x at the origin is y 2x;œÊœ Êœ œÊ œ œ
ww
y sin y cos y (0) cos 0 tangent to y sin at the origin isœ Ê œ Ê œ œ Ê œ
ˆ‰ ˆ‰ ˆ‰
xx x
### ## #
ww
"""
y x. The tangents are perpendicular to each other at the origin since the product of their slopes isœ"
#
1.
(b) y sin (mx) y m cos (mx) y (0) m cos 0 m; y sin y cosœÊœ ÊœœœÊœ
ww w
"
ˆ‰ ˆ‰
xx
mmm
y (0) cos (0) . Since m 1, the tangent lines are perpendicular at the origin.Êœ œ œ
w"" "
mm m
†ˆ‰
(c) y sin (mx) y m cos (mx). The largest value cos (mx) can attain is 1 at x 0 the largest valueœÊœ œÊ
w
y can attain is m because y m cos (mx) m cos mx m 1 m . Also, y sin
ww
kk kk k k kkk k kk kk ˆ‰
œœŸœ œ†x
m
y cos y cos cos the largest value y can attain is .Êœ Ê œ Ÿ Ÿ Ê
ww w
"""" "
mm m m m m m m
xxx
ˆ‰ ¸ ¸ ¸¸¸ ¸ ¸¸
kk ˆ‰ ˆ‰ kk
(d) y sin (mx) y m cos (mx) y (0) m slope of curve at the origin is m. Also, sin (mx) completesœÊœ ÊœÊ
ww
m periods on [0 2 ]. Therefore the slope of the curve y sin (mx) at the origin is the same as the numberߜ1
of periods it completes on [0 2 ]. In particular, for large m, we can think of “compressing" the graph ofß1
y sin x horizontally which gives more periods completed on [0 2 ], but also increases the slope of theϧ1
graph at the origin.
67. x cos 2t, y sin 2t, 0 t 68. x cos ( t), y sin ( t), 0 tœ œ ŸŸ œ œ ŸŸ1111
cos 2t sin 2t 1 x y 1 cos ( t) sin ( t) 1ʜʜ Ê œ
## ## # #
11
x y 1, yʜ !
##
69. x 4 cos t, y 2 sin t, 0 t 2 70. x 4 sin t, y 5 cos t, 0 t 2œ œ ŸŸ œ œ ŸŸ11
1 1 1 1Ê œÊ œ Ê œÊ œ
16 cos t 4 sin t x 16 sin t 25 cos t x
16 4 16 4 16 25 16 5
y y
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
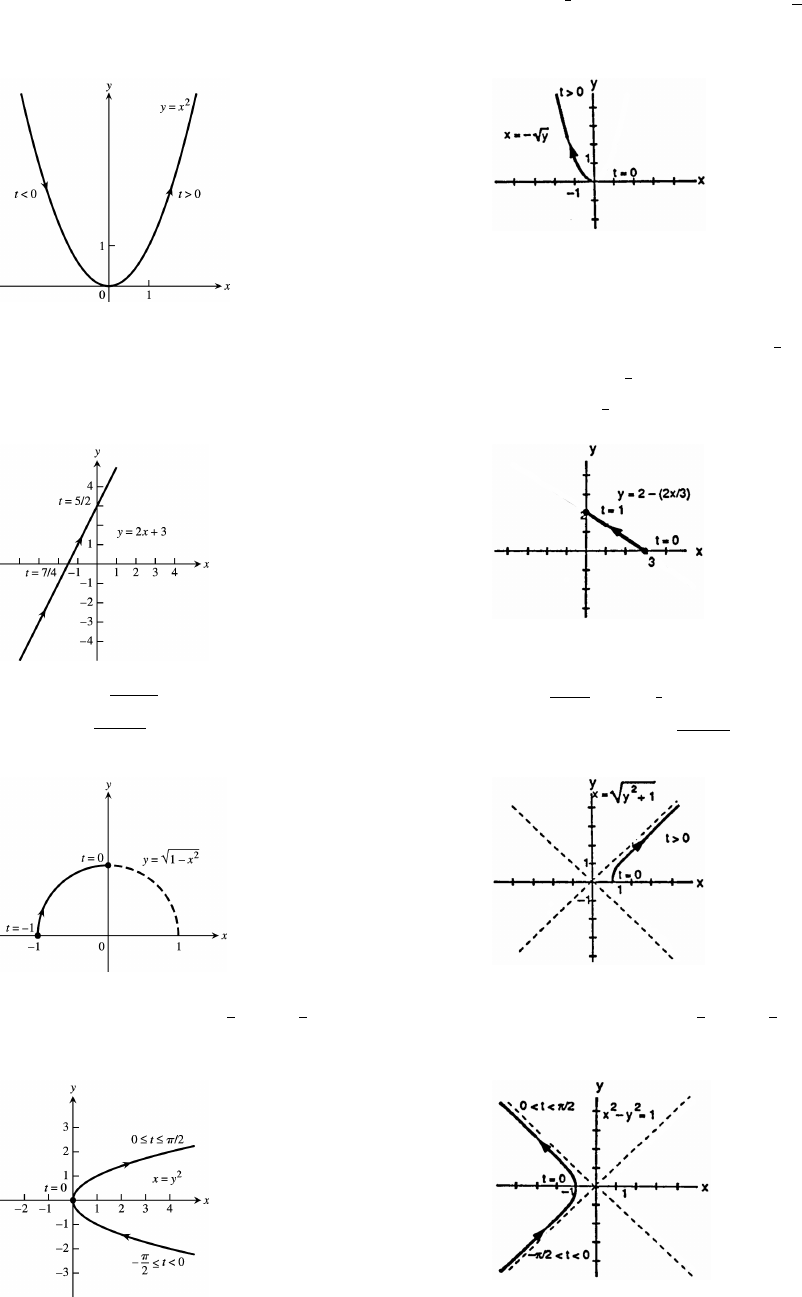
154 Chapter 3 Differentiation
71. x 3t, y 9t , t y x 72. x t , y t, t 0 x yœœ__Êœ œ œÊœ
##
ÈÈ
or y x , x 0œŸ
#
73. x 2t 5, y 4t 7, t 74. x 3 3t, y 2t, 0 t 1 tœ œ__ œ œ ŸŸÊ œ
y
#
x 5 2t 2(x 5) 4t x 3 3 2x 6 3yÊœ Ê œ Êœ Ê œ
ˆ‰
y
#
y 2(x 5) 7 y 2x 3 y 2 x, xÊœ Êœ Êœ !ŸŸ$
2
3
75. x t, y 1 t , 1 t 0 76. x t 1, y t, t 0œœ ŸŸ œ œ
ÈÈÈ
#
y 1 x y t x y 1, y 0Êœ Ê œÊœ
ÈÈ
# #
#
77. x sec t 1, y tan t, t 78. x sec t, y tan t, tœœ œ œ
#
## ##
11 11
sec t 1 tan t x y sec t tan t 1 x y 1ʜʜ ʜʜ
## # ## ##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.5 The Chain Rule and Parametric Equations 155
79. (a) x a cos t, y a sin t, 0 t 2 80. (a) x a sin t, y b cos t, tœœŸŸ œœ ŸŸ111
##
5
(b) x a cos t, y a sin t, 0 t 2 (b) x a cos t, y b sin t, 0 t 2œœŸŸ œœŸŸ11
(c) x a cos t, y a sin t, 0 t 4 (c) x a sin t, y b cos t, tœœŸŸ œœ ŸŸ111
##
9
(d) x a cos t, y a sin t, 0 t 4 (d) x a cos t, y b sin t, 0 t 4œœŸŸ œœŸŸ11
81. Using we create the parametric equations x at and y bt, representing a line which goesab"ß $ œ " œ $
through at t . We determine a and b so that the line goes through when t .ab ab"ß$ œ! %ß" œ"
Since a a . Since b b . Therefore, one possible parameterization is x t,%œ" Ê œ& "œ$ Ê œ% œ"&
y t, 0 t .œ$% Ÿ Ÿ"
82. Using we create the parametric equations x at and y bt, representing a line which goes throughab"ß$ œ" œ$
at t . We determine a and b so that the line goes through when t . Since a a .ab ab"ß $ œ ! $ß # œ " $ œ " Ê œ %
Since b b . Therefore, one possible parameterization is x t, y t, 0 t .#œ$ Ê œ& œ"% œ$& Ÿ Ÿ"
83. The lower half of the parabola is given by x y for y . Substituting t for y, we obtain one possibleœ" Ÿ!
#
parameterization x t , y t, t 0œ"œ ŸÞ
#
84. The vertex of the parabola is at , so the left half of the parabola is given by y x x for x . Substitutingab"ß " œ # Ÿ "
#
t for x, we obtain one possible parametrization: x t, y t t, t .œœ#Ÿ"
#
85. For simplicity, we assume that x and y are linear functions of t and that the point x, y starts at for t and passesab ab#ß $ œ !
through at t . Then x f t , where f and f .a b ab ab ab"ß " œ " œ ! œ # " œ "
Since slope , x f t t t. Also, y g t , where g and g .œ œ œ$ œ œ$ #œ#$ œ ! œ$ " œ"
?
?
x
t
"#
"! ab ab ab ab
Since slope 4. y g t t t.œ œ œ œ œ% $œ$%
?
?
y
t
3"
"! ab
One possible parameterization is: x t, y t, t .œ#$ œ$% !
86. For simplicity, we assume that x and y are linear functions of t and that the point x, y starts at for t andab a b"ß # œ !
passes through at t . Then x f t , where f and f .a b ab ab ab!ß! œ" œ !œ" "œ!
Since slope , x f t t t. Also, y g t , where g and g .œ œ œ" œ œ" " œ" œ ! œ# " œ!
?
?
x
t
! "
"!
ab ab a b ab ab ab
Since slope . y g t t t.œ œ œ# œ œ# #œ##
?
?
y
t
!#
"! ab
One possible parameterization is: x t, y t, t .œ" œ## !
87. t x 2 cos 2, y 2 sin 2; 2 sin t, 2 cos t cot tœ Ê œ œ œ œ œ œ Ê œ œ œ
11 1
4 4 4 dt dt dx dx/dt 2 sin t
dx 2 cos t
dy dy dy/dt
ÈÈ
cot 1; tangent line is y 2 1 x 2 or y x 2 2 ; csc tÊœœ œ œ œ
¹Š‹
ÈÈ È
dy dy
dx 4 dt
t4
1#
2Êœ œ œ Ê œ
dy dy/dt dy
dx dx/dt 2 sin t 2 sin t dx
csc t
"¹È
t4
88. t x cos , y 3 cos ; sin t, 3 sin t 3œ Ê œ œ œ œ œ œ Ê œ œ
22 2dx
33 3dtdt dxsin t
33 sin t
dy dy
11 1"
##
ÈÈÈ
ÈÈ
3 ; tangent line is y 3 x or y 3 x; 0 0Êœ œ œ œÊœœ
¹Š‹
ÈÈÈ
‘ˆ‰
dy dy d y
dx dt dx sin t
30
t2
3
È
##
"
0ʜ
¹
dy
dx t2
3
89. t x , y ; 1, 1; tangent line isœÊœ œ œ œ Ê œ œ Ê œ œ
11dx 1
4 4 dt dt dx dx/dt dx
dy dy dy/dt dy
t2t
"" "
###
ÈÈ
É
¹t1
44
y 1x or yx ; t t 2œœœÊœœÊ œ
"" "" "
#
$Î# $Î#
†ˆ‰ ¹
4 4 dt 4 dx dx/dt 4 dx
dy d y dy /dt d y
t1
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

156 Chapter 3 Differentiation
90. t 3 x 3 1 2, y 3(3) 3; (t 1) , (3t) œÊœ œ œ œ œ œ Ê œ
ÈÈdx 3
dt dt dx
dy dy (3t)
(t 1)
"
##
"Î# "Î#
ˆ‰
ˆ‰
3
2; tangent line is y 3 2[x ( 2)] or y 2x 1;œ œ œ œ œ œ
3t1 331
3t
dy
dx 3(3)
ÈÈ
ÈÈ
¹t3
dy d y
dt 3t dx
3t (t 1) 3 t 1 (3t) 33
2t 3t t 1 t 3t
œœÊœœ
È‘‘
ÈÈÈ
È
33 Š‹
Š‹
3
2t 3t t 1
1
2t1
ʜ
¹
dy
dx 3
t3
"
91. t 1 x 5, y 1; 4t, 4t t ( 1) 1; tangent line isœ Ê œ œ œ œ Ê œ œ œ Ê œ œ
dx 4t
dt dt dx dx/dt 4t dx
dy dy dy/dt dy
$##
¹t1
y 1 1 (x 5) or y x 4; 2t œ œ œ Ê œ œ œ Ê œ†
dy d y dy /dt d y
dt dx dx/dt 4t dx
2t ""
##
¹t1
92. t x sin , y 1 cos 1 ; 1 cos t, sin t œ Ê œ œ œ œœ œ œ Ê œ
1111 1
3 3 3 3 3 dt dt dx dx/dt
3dx dy dy dy/dt
È
###
""
3 ; tangent line is y 3 xœÊœ œœ œ
sin t
1cos t dx 3
dy sin
1cos
3
##
"
¹Š‹
ÈÈ
t3
ˆ‰
ˆ‰ Š‹
ˆ‰ È
3
3
3
1
y3x 2; Êœ œ œ Ê œ œ
È1Ȉ‰
3
3 dt (1 cos t) 1 cos t dx dx/dt 1 cos t
dy (1 cos t)(cos t) (sin t)(sin t) d y dy /dt
1
1
1 cos t
4œÊœ
1
(1 cos t) dx
dy
¹t3
93. t x cos 0, y 1 sin 2; sin t, cos t cot tœÊœ œ œ œ œ œ Ê œ œ
11 1
22 2dtdtdxsin t
dx cos t
dy dy
cot 0; tangent line is y 2; csc t csc t 1Êœœ œœÊœœÊ œ
¹ ¹
dy dy d y d y
dx dt dx sin t dx
csc t
t t
2 2
1
#
#$
94. t x sec 1 1, y tan 1; 2 sec t tan t, sec tœ Ê œ œ œ œ œ œ
11 1
44 4dtdt
dx dy
###
ˆ‰ ˆ‰
cot t cot ; tangent line isÊœ œ œ Ê œ œ
dy dy
dx 2 sec t tan t 2 tan t dx 4
sec t "" " "
###
¹ˆ‰
t4
1
y ( 1) (x 1) or y x ; csc t cot t œ œ œ Ê œ œ
"""" "
####
#$
dy d y
dt dx 2 sec t tan t 4
csc t
ʜ
¹
dy
dx 4
t4
"
95. s A cos (2 bt) v A sin (2 bt)(2 b) 2 bA sin (2 bt). If we replace b with 2b to double theœÊœœ œ11111
ds
dt
frequency, the velocity formula gives v 4 bA sin (4 bt) doubling the frequency causes the velocity toœ Ê11
double. Also v bA sin (2 bt) a 4 b A cos (2 bt). If we replace b with 2b in theœ# Ê œ œ11 1 1
dv
dt ##
acceleration formula, we get a 16 b A cos (4 bt) doubling the frequency causes the acceleration toœ Ê11
##
quadruple. Finally, a 4 b A cos (2 bt) j 8 b A sin (2 bt). If we replace b with 2b in the jerkœ Ê œ œ11 11
## $$
da
dt
formula, we get j 64 b A sin (4 bt) doubling the frequency multiplies the jerk by a factor of 8.œÊ11
$$
96. (a) y 37 sin (x 101) 25 y 37 cos (x 101) cos (x 101) .œÊœ œ
‘ ‘ˆ‰‘
222742
365 365 365 365 365
11111
w
The temperature is increasing the fastest when y is as large as possible. The largest value of
w
cos (x 101) is 1 and occurs when (x 101) 0 x 101 on day 101 of the year
‘
22
365 365
11
œÊœÊ
( April 11), the temperature is increasing the fastest.µ
(b) y (101) cos (101 101) cos (0) 0.64 °F/day
wœœœ¸
74 2 74 74
365 365 365 365
11 1 1
‘
97. s ( 4t) v (1 4t) (4) 2(1 4t) v(6) 2( 6) m/sec;œ" Ê œ œ œ Ê œ "% œ
"Î# "Î# "Î# "Î#
"
#
ds 2
dt 5
†
v 2( 4t) a 2(1 4t) (4) 4(1 4t) a(6) 4(1 4 6) m/secœ"Êœœ œÊœ œ
"Î# $Î# $Î# $Î# #
"
# #
dv 4
dt 15
††
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
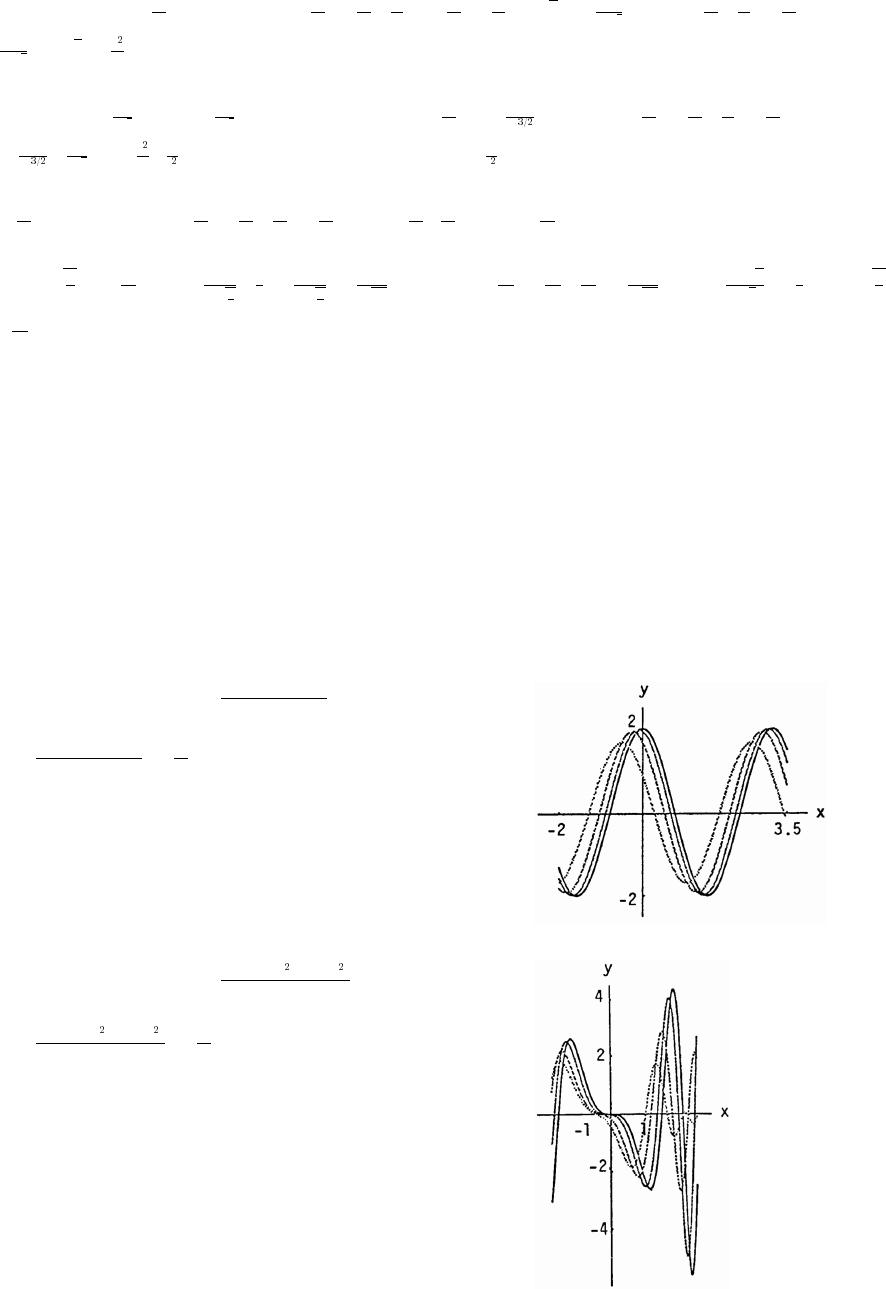
Section 3.5 The Chain Rule and Parametric Equations 157
98. We need to show a is constant: a and k s a vœœœœœÊœœ
dv dv dv ds dv d k dv ds dv
dt dt ds dt ds ds ds dt ds
2s
†††
ˆ‰
ÈÈ
k s which is a constant.œœ
kk
2s
ȆÈ#
99. v proportional to v for some constant k . Thus, a v
"
ÈÈ
ss
k dv k dv dv ds dv
ds dt ds dt ds
2s
Êœ Ê œ œ œ œ††
acceleration is a constant times so a is inversely proportional to s .œ œ Ê
kk k
2s sss
†È#
""
#
ˆ‰
100. Let f(x). Then, a f(x) f(x) (f(x)) f(x) f (x)f(x), as required.
dx dv dv dx dv d dx d
dt dt dx dt dx dx dt dx
œœœœœœ œ†† † †
ˆ‰ w
101. T 2 2 . Therefore, kL 2 kœÊœ œœ œœ œœ11 1
É É
LdT dTdTdL L
g dL g du dL du g
ggL gL
kL
g
†† † † †
"" "
##
ÉÉ
ÈÈÈ
È
LL
gg
11 1 1
, as required.œkT
2
102. No. The chain rule says that when g is differentiable at 0 and f is differentiable at g(0), then f g is‰
differentiable at 0. But the chain rule says nothing about what happens when g is not differentiable at 0 so
there is no contradiction.
103. The graph of y (f g)(x) has a horizontal tangent at x 1 provided that (f g) (1) 0 f (g(1))g (1) 0œ‰ œ ‰ œ Ê œ
www
either f (g(1)) 0 or g (1) 0 (or both) either the graph of f has a horizontal tangent at u g(1), or theÊœœÊ œ
ww
graph of g has a horizontal tangent at x 1 (or both).œ
104. (f g) ( 5) 0 f (g( 5)) g ( 5) 0 f (g( 5)) and g ( 5) are both nonzero and have opposite signs.‰ Ê Ê
wwwww
†
That is, either f (g( 5)) 0 and g ( 5) 0 or f (g( 5)) 0 and g ( 5) 0 .cdcd
wwww
105. As h 0, the graph of yĜ
sin 2(x h) sin 2x
h
approaches the graph of y 2 cos 2x becauseœ
lim (sin 2x) 2 cos 2x.
hÄ!
sin 2(x h) sin 2x
hdx
d
œœ
106. As h 0, the graph of yĜ
cos (x h) cos x
h
cdab
approaches the graph of y 2x sin x becauseœ ab
#
lim cos x 2x sin x .
hÄ!
cos (x h) cos x
hdx
d
cdab ##
œœcd abab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

158 Chapter 3 Differentiation
107. cos t and 2 cos 2t ; then 0 0
dx 2 cos 2t
dt dt dx dx/dt cos t cos t dx cos t
dy dy dy/dt dy
2 2 cos t 1 2 2 cos t 1
œœÊœœœ œÊœ
ab ab
2 cos t 1 0 cos t t , , , . In the 1st quadrant: t x sin andʜʜ„Êœ œÊœœ
#"
#
ÈÈ
24444 4 4
357 2
1111 1 1
y sin 2 1 1 is the point where the tangent line is horizontal. At the origin: x 0 and y 0œœÊß œœ
ˆ‰ Š‹
1
4
2
È
#
sin t 0 t 0 or t and sin 2t 0 t 0, , , ; thus t 0 and t give the tangent lines atÊ œ Êœ œ œ Êœ œ œ111
11
##
3
the origin. Tangents at origin: 2 y 2x and 2 y 2x
¹¹
dy dy
dx dx
t0 t
œÊœ œÊœ
108. 2 cos 2t and 3 cos 3t
dx 3 cos 3t
dt dt dx dx/dt 2 cos 2t 2 2 cos t 1
dy dy dy/dt 3(cos 2t cos t sin 2t sin t)
œœÊœœœ
ab
œœœ
3 2 cos t 1 (cos t) 2 sin t cos t sin t
22 cost 1 22 cost 1 22 cost
(3 cos t) 2 cos t 1 2 sin t (3 cos t) 4 cos t 3
cdab
ab ab ab
abab
1; then
0 0 3 cos t 0 or 4 cos t 3 0: 3 cos t 0 t , and
dy
dx 2 2 cos t 1
(3 cos t) 4 cos t 3 3
œÊ œÊ œ œ œÊœ
ab
ab
##
#11
4 cos t 3 0 cos t t , , , . In the 1st quadrant: t x sin 2
#
# #
œ Ê œ„ Êœ œ Ê œ œ
È È
3 3
66 6 6 6 6
5711111 1 1 1
ˆ‰
and y sin 3 1 1 is the point where the graph has a horizontal tangent. At the origin: x 0œœÊß œ
ˆ‰ Š‹
1
6
3
È
#
and y 0 sin 2t 0 and sin 3t 0 t 0, , , and t 0, , , , , t 0 and t giveœÊ œ œÊœ œ Êœ œ
1 1 11 11
##
11 1
3245
33 3 3
the tangent lines at the origin. Tangents at the origin: y x, and
¹¹
dy dy
dx 2 cos 0 dx
3 cos 0 3 3
t0 t
œœÊœ
##
yxœœÊœ
3 cos (3 )
2 cos (2 )
33
1
1##
109. From the power rule, with y x , we get x . From the chain rule, y xœœ œ
"Î% $Î%
"
dy
dx 4 ÉÈ
x x , in agreement.Êœ œ œ
dy
dx dx 4
xx
d
x
""""
##
#
$Î%
ÉÉ
ÈÈ
È
††
ˆ‰
È
110. From the power rule, with y x , we get x . From the chain rule, y x xœœ œ
$Î% "Î%
dy
dx 4
3ÉÈ
xx x x xÊœ Êœ œ œ
dy dy
dx dx dx
xx xx xx 4xx
d 3
x
3x
""""
###
##
ÉÉÉÉ
ÈÈÈÈ
ÈÈ
††††
ˆ‰ ˆ‰
ÈÈÈ
Š‹
x , in agreement.œœ
3x
4x x
3
4
È
ÈÈ
É"Î%
111. (a)
(b) 1.27324 sin 2t 0.42444 sin 6t 0.2546 sin 10t 0.18186 sin 14t
df
dt œ
(c) The curve of y approximates yœœ
df
dt dt
dg
the best when t is not , , 0, , nor .11
11
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
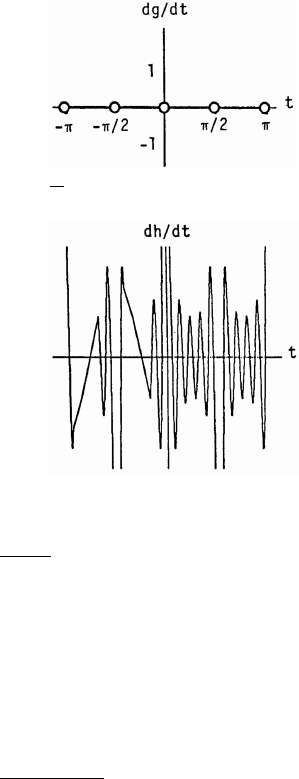
Section 3.5 The Chain Rule and Parametric Equations 159
112. (a)
(b) 2.5464 cos (2t) 2.5464 cos (6t) 2.5465 cos (10t) 2.54646 cos (14t) 2.54646 cos (18t)
dh
dt œ
(c)
111-116. Example CAS commands:
:Maple
f := t -> 0.78540 - 0.63662*cos(2*t) - 0.07074*cos(6*t)
- 0.02546*cos(10*t) - 0.01299*cos(14*t);
g := t -> piecewise( t<-Pi/2, t+Pi, t<0, -t, t<Pi/2, t, Pi-t );
plot( [f(t),g(t)], t=-Pi..Pi );
Df := D(f);
Dg := D(g);
plot( [Df(t),Dg(t)], t=-Pi..Pi );
: (functions, domains, and value for t0 may change):Mathematica
To see the relationship between f[t] and f'[t] in 111 and h[t] in 112
Clear[t, f]
f[t_] = 0.78540 0.63662 Cos[2t] 0.07074 Cos[6t] 0.02546 Cos[10t] 0.01299 Cos[14t]
f'[t]
Plot[{f[t], f'[t]},{t, , }]11
For the parametric equations in 113 - 116, do the following. Do NOT use the colon when defining tanline.
Clear[x, y, t]
t0 = p/4;
x[t_]:=1 Cos[t]
y[t_]:=1 Sin[t]
p1=ParametricPlot[{x[t], y[t]},{t, , }]11
yp[t_]:=y'[t]/x'[t]
ypp[t_]:=yp'[t]/x'[t]
yp[t0]//N
ypp[t0]//N
tanline[x_]=y[t0] yp[t0] (x x[t0])
p2=Plot[tanline[x], {x, 0, 1}]
Show[p1, p2]
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

160 Chapter 3 Differentiation
3.6 IMPLICIT DIFFERENTIATION
1. y x x 2. y x xœÊœ œ Êœ
*Î% &Î% $Î& )Î&
dy dy
dx 4 dx 5
9 3
3. y 2x (2x) (2x) 2 4. y 5x (5x) (5x) 5œœ Êœ œ œœ Êœ œ
ÈÈ
34
"Î$ #Î$ "Î% $Î%
" "
dy dy
dx 3 dx 4
2 5
3x 4x
††
5. y 7 x 6 7(x 6) (x 6)œœ Êœ œ
È"Î# "Î#
#
dy
dx
77
2x6
È
6. y 2 x 1 2(x 1) 1(x 1)œ œ Ê œ œ
È"Î# "Î# "
dy
dx x1
È
7. y (2x 5) (2x 5) 2 (2x 5)œ Êœ œ
"Î# $Î# $Î#
"
#
dy
dx †
8. y ( 6x) (1 6x) ( 6) 4(1 6x)œ" Ê œ œ
#Î$ "Î$ "Î$
dy
dx 3
2
9. y x x 1 y x x 1 x x 1 x 1 x xœ Êœ† #†"œ "œab ababab aba b
#w# # ###
"Î# "Î# "Î# "Î#
"
#
2x 1
x1
È
10. y x x 1 y x x 1 x x 1 x 1 x xœ Ê œ † # †"œ " œab ababab aba b
ˆ‰
#w# # ###
"Î# $Î# "Î# $Î#
" "
#abx1
11. s t t t 12. r œœÊœ œ œ Êœ
ÈÈ
74
#$
#Î( &Î( $Î% (Î%
ds 2 dr 3
dt 7 d4
)) )
)
13. y sin (2t 5) cos (2t 5) (2t 5) 2 (2t 5) cos (2t 5)œ Êœ œ
ˆ‰ ˆ‰ˆ‰ ˆ‰
#Î$ #Î$ &Î$ &Î$ #Î$
dy
dt 3 3
24
††
14. z cos ( 6t) sin ( 6t) (1 6t) ( ) 4(1 6t) sin (1 6t)œ" Êœ" 'œ
ˆ‰ ˆ‰ ˆ‰
#Î$ #Î$ "Î$ "Î$ #Î$
dz 2
dt 3
†
15. f(x) 1 x 1 x f (x) 1 x xœœ Ê œ œ œ
ÉȈ‰ ˆ‰ˆ ‰
"Î# w "Î# "Î#
"Î# "Î#
" " " "
##
41 xx 4x1 x
Š‹
ÉÉ
ÈÈ ˆ‰
È
16. g(x) 2 2x 1 g (x) 2x 1 ( 1)x 2x 1 xœÊœœ
ˆ‰ ˆ‰ ˆ‰
"Î# w "Î# $Î# "Î# $Î#
"Î$ %Î$ %Î$
22
33
†
17. h( ) 1 cos (2 ) (1 cos 2 ) h ( ) (1 cos 2 ) ( sin 2 ) 2 (sin 2 )(1 cos 2 ))))))) ))œ œ Ê œ œ
È
3"Î$ w #Î$ #Î$
"
33
2
††
18. k( ) (sin ( 5)) k ( ) (sin ( 5)) cos ( 5) cos ( 5)(sin ( 5)))) ) ) ) ) )œÊœ œ
&Î% w "Î% "Î%
55
44
†
19. x y xy 6:
##
œ
Step 1: x y 2x x 2y y 1 0
Š‹Š ‹
##
dy dy
dx dx
œ†† †
Step 2: x 2xy 2xy y
##
dy dy
dx dx
œ
Step 3: x 2xy 2xy y
dy
dx ab
##
œ
Step 4:
dy 2xy y
dx x 2xy
œ
20. x y 18xy 3x 3y 18y 18x 3y 18x 18y 3x
$$ # # # #
œ Ê œ Ê œ Êœ
dy dy dy dy 6y x
dx dx dx dx y 6x
ab
21. 2xy y x y:œ
#
Step 1: 2x 2y 2y 1
Š‹
dy dy dy
dx dx dx
œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.6 Implicit Differentiation 161
Step 2: 2x 2y 1 2y
dy dy dy
dx dx dx
œ
Step 3: (2x2y1) 2y
dy
dx œ"
Step 4:
dy 1 2y
dx 2x 2y 1
œ
22. x xy y 1 3x y x 3y 0 3y x y 3x
$$ # # # #
œÊ œÊ œ Ê œ
dy dy dy dy y 3x
dx dx dx dx 3y x
ab
23. x (x y) x y :
####
œ
Step 1: x 2(x y) 1 (x y) (2x) 2x 2y
##
’“Š‹
œ
dy dy
dx dx
Step 2: 2x (x y) 2y 2x 2x (x y) 2x(x y) œ
###
dy dy
dx dx
Step 3: 2x (x y) 2y 2x 1 x(x y) (x y)
dy
dx cdc d œ
##
Step 4:
dy
dx 2x (x y) 2y y x (x y) x y x y
2x 1 x(x y) (x y) x 1 x(x y) (x y) x 1 x xy x 2xy y
œœœ
cdcd
ab
œx2x 3xyxy
xy x y
24. (3xy 7) 6y 2(3xy 7) 3x 3y 6 2(3xy 7)(3x) 6 6y(3xy 7)œÊ œÊ œ
#†Š‹
dy dy dy dy
dx dx dx dx
[6x(3xy 7) 6] 6y(3xy 7) ʜʜœ
dy dy y(3xy 7) 3xy 7y
dx dx x(3xy 7) 1 1 3x y 7x
25. y 2y
#" "
œÊ œ œ Êœ
x2
x 1 dx (x 1) (x 1) dx y(x 1)
dy (x 1) (x 1) dy
26. x x x y x y 3x 2xy x y 1 y x 1 y 1 3x 2xy y
#$# ##ww#w#w
œ Ê œ Ê œ Ê œ Ê œ
xy 1 3x 2xy
xy x1
ab
27. x tan y 1 sec y cos yœÊœ Êœœab
##
"
dy dy
dx dx sec y
28. xy cot xy x y csc (xy) x y x x csc (xy) y csc (xy) yœÊœ Ê œ ab Š‹
dy dy dy dy
dx dx dx dx
###
x x csc (xy) y csc (xy)Ê œ " Ê œ œ
dy dy y
dx dx x
y csc (xy)
x csc (xy)
‘‘
## "
"
‘
‘
29. x tan (xy) 1 sec (xy) y x 0 x sec (xy) 1 y sec (xy) œ!Ê œÊ œ Êœcd
Š‹
###
" dy dy dy y sec (xy)
dx dx dx x sec (xy)
œœœ
1
x sec (xy) x x x x
y cos (xy) y cos (xy) y
30. x sin y xy 1 (cos y) y x (cos y x) y 1 œ Ê œ Ê œ Ê œ
dy dy dy dy y 1
dx dx dx dx cos y x
31. y sin 1 xy y cos ( 1) sin x y
Š‹ ’ “ Š‹Š‹
""""
y y y dx y dx dx
dy dy dy
œ Ê œ ʆ† †
cos sin x y
dy dy y y
dx y y y dx cos sin x y sin cos xy
’“Š‹ Š‹
œÊœ œ
"" "
yy y y y
Š‹ Š‹ Š‹ Š‹
32. y cos 2x 2y y sin ( 1) cos 2y 2 2
##
""""
Š‹ ’ “ Š‹Š‹
y y y dx y dx dx
dy dy dy
œ Ê œ ʆ† †
sin 2y cos 2 2
dy dy
dx y y dx
2
sin 2y cos
’“Š‹ Š‹
""
#
œÊœ
Š‹ Š‹
yy
33. r 1 r 0 ))
"Î# "Î# "Î# "Î#
"" ""
## ##
œ Ê œ Ê œ Ê œ œ†dr dr dr
dd d
r
2r r
2
)) )
)))
’“
ÈÈ ÈÈ
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

162 Chapter 3 Differentiation
34. r 2 œ Êœ Êœ
È)) ) ) )) )))
3 4 dr dr
3d d#
#Î$ $Î% "Î# "Î$ "Î% "Î# "Î$ "Î%
))
35. sin (r ) [cos (r )] r 0 [ cos (r )] r cos (r ) ,))) )))œÊ œÊ œ Ê œ œ
"
#
ˆ‰
dr dr dr r
dd d cos(r)
r cos (r )
)) ))))
)
cos (r ) 0)Á
36. cos r cot r ( sin r) csc r [ sin r ] r csc œÊ œÊœ Êœ)) ) ) ) )
dr dr dr dr r csc
ddd dsin r))) ))
)
##
37. x y 1 2x 2yy 0 2yy 2x y ; now to find , y
## w w w w
œÊ œÊ œÊœœ œ
dy d y
dx y dx dx dx y
xddx
ab Š‹
y since y yÊœ œ œÊ œœ œ œ
ww w ww
" "
y( 1) xy d y y x
yy ydx yyy
yx xyy
Š‹ ab
x
y
38. x y 1 x y 0 y x y ;
#Î$ #Î$ "Î$ "Î$ "Î$ "Î$ w "Î$
œ Ê œ Ê œ Ê œ œ œ
22 2 2 x
3 3 dx dx 3 3 dx x
dy dy dy y
y
‘ ˆ‰
Differentiating again, yww
œœ
xyyyx
xx
xy yx
†
†
ˆ‰ˆ‰ˆ‰ ˆ‰
Œ
33 33
y
x
xy yxÊœ œ
dy y
dx 3 3 3x 3y x
"" "
#Î$ "Î$ "Î$ %Î$
39. y x 2x 2yy 2x 2 y ; then y
## w w ww
œ Ê œÊ œ œ œ œ
2x 2 x 1
2y y y y
y(x1)y y(x1)
Š‹
x1
y
yÊœœ
dy y (x 1)
dx y
ww
40. y 2x 1 2y 2y y 2 2y y (2y 2) 2 y (y 1) ; then y (y 1) y
#wwww"ww#w
"
œ Ê œ Ê œÊ œ œ œ† †
y1
(y 1) (y 1) yœ Ê œ œ
# " ww "
dy
dx (y 1)
41. 2 y x y y y 1 y y y 1 1 y ; we can
Ȉ‰
œ Ê œ Ê œ Ê œ œ œ
"Î# w w w "Î# w "
dy
dx y 1
y1
y
È
È
differentiate the equation y y 1 1 again to find y : y y y y 1 y 0
w "Î# ww w $Î# w "Î# ww
"
#
ˆ‰ ˆ ‰ˆ‰
œ œ
y1yyy yÊœ Êœœ œ œ
ˆ‰
cd
"Î# ww w $Î# ww
"""
#
#
#
dy
dx
y
y1 2y y 1 1y
Œ
ab ab
ˆ‰
È
y1
42. xy y 1 xy y 2yy 0 xy 2yy y y (x 2y) y y ; yœÊ œÊ œÊ œÊœ œ
#wwww w w ww
ydy
(x 2y) dx
œœ œ
(x 2y)y y(1 2y )
(x 2y) (x 2y) (x 2y)
(x 2y) y 1 2 y(x 2y) y(x 2y) 2y
’“’ “Š‹ cd
yy
(x 2y) (x 2y) (x 2y)
œœœ
2y(x 2y) 2y 2y 2xy 2y(x y)
(x 2y) (x 2y) (x 2y)
43. x y 16 3x 3y y 0 3y y 3x y ; we differentiate y y x to find y :
$$ # #w #w # w #w # ww
œ Ê œÊ œ Ê œ œ
x
y
y y y 2y y 2x y y 2x 2y y y
#ww w w #ww w ww
#
œÊœÊœ œcd cd†
2x 2y 2x
yy
Š‹
x2x
yy
2œÊœœ
2xy 2x d y
ydx 32
32 32
¹(2 2)
44. xy y 1 xy y 2yy 0 y (x 2y) y y y ;œÊ œÊ œÊ œ Ê œ
#www w ww
y
(x 2y) (x 2y)
(x 2y) y ( y) 1 2yab a b
since y we obtain ykk
www
""
#
(0 1) (0 1)
œ œ œ
( 2) (1)(0)
44
ˆ‰
45. y x y 2x at ( ) and ( 1) 2y 2x 4y 2 2y 4y 2 2x
## % $ $
œ #ß " #ß Ê œ Ê œ
dy dy dy dy
dx dx dx dx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.6 Implicit Differentiation 163
2y 4y 2 2x 1 and 1Ê œ Ê œ Ê œ œ
dy dy dy dy
dx dx y y dx dx
x
ab ¹¹
$"
# (21) (2 1)
46. x y (x y) at( ) and ( 1) 2 x y 2x 2y 2(x y) 1ab ab
Š‹ Š‹
## # ##
#
œ "ß ! "ß Ê œ
dy dy
dx dx
2y x y (x y) 2x x y (x y) 1Ê œ Ê œ Ê œ
dy dy dy
dx dx 2y x y (x y) dx
2x x y (x y)
cdabab ¹
## ##
ab
ab (1 0)
and 1
¹
dy
dx (1 1) œ
47. x xy y 1 2x y xy 2yy 0 (x 2y)y 2x y y ;
## ww w w
œÊ œÊ œÊœ
2x y
2y x
(a) the slope of the tangent line m y the tangent line is y 3 (x 2) y xœœÊ œÊœk
w"
#
(2 3)
777
444
(b) the normal line is y 3 (x 2) y xœ Ê œ
4429
777
48. x y 25 2x 2yy 0 y ;
## w w
œ Ê œÊ œ
x
y
(a) the slope of the tangent line m y the tangent line is y 4 (x 3)œœœÊ œk¹
w
(3 4) (3 4)
x3 3
y4 4
yxʜ
325
44
(b) the normal line is y 4 (x 3) y xœ Ê œ
44
33
49. x y 9 2xy 2x yy 0 x yy xy y ;
## # # w # w # w
œÊ œÊ œ Ê œ
y
x
(a) the slope of the tangent line m y 3 the tangent line is y 3 3(x 1)œœœÊ œk¸
w
(13) (13)
y
x
y3x6ʜ
(b) the normal line is y 3 (x 1) y xœ Ê œ
""
333
8
50. y 2x 4y 2yy 2 4y 0 2(y 2)y 2 y ;
#wwww
"
#
"œ!Ê œÊ œÊœ
y
(a) the slope of the tangent line m y 1 the tangent line is y 1 1(x 2) y x 1œœÊ œÊœk
w
(21)
(b) the normal line is y 1 1(x 2) y x 3œ Ê œ
51. 6x 3xy 2y 17y 6 0 12x 3y 3xy 4yy 17y 0 y (3x 4y 17) 12x 3y
# # www w
œÊ œÊ œ
y;ʜ
w
12x 3y
3x 4y 17
(a) the slope of the tangent line m y the tangent line is y 0 (x 1)œœ œÊ œk¹
w"
(10) (10)
2x 3y
3x 4y 17 7 7
66
yxʜ
66
77
(b) the normal line is y 0 (x 1) y xœ Ê œ
777
666
52. x 3xy 2y 5 2x 3xy 3y 4yy 0 y 4y 3x 3y 2x y ;
## www w
œÊ œÊ œÊœ
ÈÈÈ ÈÈ
Š‹ ÈÈ
3y 2x
4y 3x
(a) the slope of the tangent line m y 0 the tangent line is y 2œœ œÊ œk¹
w
32 32
ÈÈ
3y 2x
4y 3x
(b) the normal line is x 3œÈ
53. 2xy sin y 2 2xy 2y (cos y)y 0 y (2x cos y) 2y y ;œÊ œÊ œÊœ11 1 1
www w
2y
2x cos y1
(a) the slope of the tangent line m y the tangent line isœœ œÊk¹
w
#
11
22
2y
2x cos y1
1
y(x1) yxœ Ê œ
11 1
## #
1
(b) the normal line is y (x 1) y xœ Ê œ
11
111##
222
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
164 Chapter 3 Differentiation
54. x sin 2y y cos 2x x(cos 2y)2y sin 2y 2y sin 2x y cos 2x y (2x cos 2y cos 2x)œÊ œ Ê
www
sin 2y 2y sin 2x y ;œ Ê œ
w
sin 2y 2y sin 2x
cos 2x 2x cos 2y
(a) the slope of the tangent line m y 2 the tangent line isœœ œœÊk¹
w
42 42
sin 2y 2y sin 2x
cos 2x 2x cos 2y
1
y2x y2xœ Ê œ
11
#ˆ‰
4
(b) the normal line is y x y xœ Ê œ
11 1
## #
""
ˆ‰
48
5
55. y 2 sin ( x y) y 2 [cos ( x y)] y y [1 2 cos ( x y)] 2 cos ( x y)œÊœ Êœ 111 111
www
†ab
y;ʜ
w
#
2 cos(x y)
1 cos(xy)
11
1
(a) the slope of the tangent line m y 2 the tangent line isœœ œÊk¹
w
(1 0) (1 0)
2 cos(x y)
12 cos(xy)
11
11
y02(x1) y 2x2œ Ê œ 111
(b) the normal line is y 0 (x 1) yœ Ê œ
""
##111
x
2
56. x cos y sin y 0 x (2 cos y)( sin y)y 2x cos y y cos y 0 y 2x cos y sin y cos y
## # w # w w #
œÊ œÊ cd
2x cos y y ;œ Ê œ
#w
2x cos y
2x cos y sin y cos y
(a) the slope of the tangent line m y 0 the tangent line is yœœ œÊ œk¹
w
(0 ) (0 )
2x cos y
2x cos y sin y cos y 1
(b) the normal line is x 0œ
57. Solving x xy y 7 and y 0 x 7 x 7 7 and 7 are the points where the
## #
œ œÊ œÊœ„ Êß! ß!
ÈÈ È
Š‹Š‹
curve crosses the x-axis. Now x xy y 7 2x y xy 2yy 0 (x 2y)y 2x y
## ww w
œÊ œÊ œ
y m the slope at 7 is m 2 and the slope at 7 isÊ œ Ê œ Ê ß! œ œ ß!
w
2x y 2x y
x2y x2y
27
7
Š‹ Š‹
ÈÈ
È
È
m 2. Since the slope is 2 in each case, the corresponding tangents must be parallel.œ œ
27
7
È
È
58. x xy y 7 2x y x 2y 0 (x 2y) 2x y and ;
##
œÊ œÊ œÊ œ œ
dy dy dy dy 2x y x 2y
dx dx dx dx x 2y dy 2x y
dx
(a) Solving 0 2x y 0 y 2x and substitution into the original equation gives
dy
dx œÊœÊœ
x x( 2x) ( 2x) 7 3x 7 x and y 2 when the tangents are parallel to the
###
œÊ œÊœ„ œ…
ÉÉ
77
33
x-axis.
(b) Solving 0 x 2y 0 y and substitution gives x x 7 7
dx x x x 3x
dy 4
œÊ œÊœ œÊ œ
###
##
ˆ‰ˆ‰
x 2 and y when the tangents are parallel to the y-axis.Êœ„ œ…
ÉÉ
77
33
59. y y x 4y y 2yy 2x 2 2y y y 2x y ; the slope of the tangent line at
%## $w w $ w w
œ Ê œ Ê œ Ê œab x
y2y
is 1; the slope of the tangent line at
Š‹ ¹ Š‹
ÈÈ È
33 3
4y2y 3 4
x
ßœœœœ ß
# # #
""
33
42
3
44
363
8
3
4
is 3
¹È
x
y2y 4 2
23
3
42
1œœœ
3
42
8
È
60. y (2 x) x 2yy (2 x) y ( 1) 3x y ; the slope of the tangent line is
#$w##w
œ Ê œ Ê œ
y3x
2y(2 x)
m 2 the tangent line is y 1 2(x 1) y 2x 1; the normal line isœœœÊ œÊœ
¹
y3x
2y(2 x)
4
#
(1 1)
y 1 (x 1) y xœ Ê œ
""
###
3
61. y 4y x 9x 4y y 8yy 4x 18x y 4y 8y 4x 18x y
%#%# $w w $ w$ $ w
œÊ œÊ œÊœ œab 4x 18x 2x 9x
4y 8y 2y 4y
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.6 Implicit Differentiation 165
m; ( 3 2): m ; ( ): m ; (3 ): m ; (3 ): mœ œß œ œ$ß#œ ß#œ ß#œ
x2x 9
y2y 4 2(8 4) 8 8 8 8
( 3)(18 9) 27 27 27 27
ab
ab
62. x y 9xy 0 3x 3y y 9xy 9y 0 y 3y 9x 9y 3x y
$$ # #w w w# # w
œÊ œÊ œ Êœ œab 9y 3x 3y x
3y 9x y 3x
(a) y and y ;kk
ww
(4 2) (2 4)
œœ
54
45
(b) y 0 0 3y x 0 y x 9x 0 x 54x 0
w#$'$
$
œÊ œÊ œÊœ Ê œÊ œ
3y x
y3x 3 3 3
xxx
Š‹ Š‹
x x 54 0 x 0 or x 54 3 2 there is a horizontal tangent at x 3 2 . To find theʜʜœœ Ê œ
$$ $$ $
ab ÈÈÈ
corresponding y-value, we will use part (c).
(c) 0 0 y 3x 0 y 3x ; y 3x x 3x 9x 3x 0
dx
dy 3y x
y3x
œÊ œÊ œÊœ„ œ Ê œ
#$
$
ÈÈ È È
Š‹
x 6 3 x 0 x x 6 3 0 x 0 or x 6 3 x 0 or x 108 3 4 .Ê œÊ œÊ œ œ Êœ œ œ
$ $Î# $Î# $Î# $Î# $Î# $$
ÈÈ ÈÈ
Š‹ È
Since the equation x y 9xy 0 is symmetric in x and y, the graph is symmetric about the line y x.
$$
œ œ
That is, if (a b) is a point on the folium, then so is (b a). Moreover, if y m, then y .ßßœœkk
ww
"
(a b) (b a) m
Thus, if the folium has a horizontal tangent at (a b), it has a vertical tangent at (b a) so one might expectßß
that with a horizontal tangent at x 54 and a vertical tangent at x 3 4, the points of tangency areœœ
$$
ÈÈ
54 3 4 and 3 4 54 , respectively. One can check that these points do satisfy the equation
Š‹Š‹
ÈÈ
ÈÈ
$$ $$
ßß
x y 9xy 0.
$$
œ
63. x 2tx 2t 4 2x 2x 2t 4t 0 (2x 2t) 2x 4t ;
##
œÊ œÊ œÊœ œ
dx dx dx dx 2x 4t x 2t
dt dt dt dt 2x 2t x t
2y 3t 4 6y 6t 0 ; thus ; t 2
$# #
œÊ œÊœœ œ œ œ œ
dy dy dy dy/dt t(x t)
dt dt 6y y dx dx/dt y (x 2t)
6t t Š‹
ˆ‰
t
y
x2t
xt
x 2(2)x 2(2) 4 x 4x 4 0 (x 2) 0 x 2; t 2 2y 3(2) 4Ê œÊœÊœÊœ œÊ œ
### # $#
2y 16 y 8 y 2; therefore 0ʜʜʜ œ œ
$$
¹
dy 2(2 2)
dx (2) (2 2(2))
t2
64. x 5 t 5 t t ; y(t 1) t y (t 1) tœÊœ œ œÊ œ
ÉÈÈ È
ˆ‰ˆ ‰
dx
dt dt
4t 5 t
dy
""" "
## #
"Î# "Î# "Î#
ÈÈ
É
t 1 y ; thus Ê œ Ê œ œ œ œ œ †ab
dy dy dy
dt dt t 1 dx
ttt2t
yyt
"
##
"#
ÈÈÈ
ab È
ttt2t
yt
4t 5 t
dy
dt
dx
dt
"#
#"
"
yt
tt
4t 5 t
È
ÈabÈÈ
É
; t 4 x 5 4 3; t 4 y(3) 4 2œœÊœœœÊœœ
#"# &
"
ˆ‰
ÈÈ
É
yt t
tÉÈÈ
È
therefore, ¹
dy
dx 3
14
t4
œœ
2224 4
4
Š‹
ab
ÈÈ
É
" &
"
65. x 2x t t 3x 2t 1 1 3x 2t 1 ; y t 1 2t y 4 œÊ œÊ œÊ œ œ
$Î# # "Î# "Î#
dx dx dx dx 2t 1
dt dt dt dt 13x
ˆ‰ ÈÈ
t1y (t1) 2y2t y 0 t1 2y 0Ê œÊ œ
dy dy dy y dy
dt dt dt y dt
2t1
t
ÈÈ
ˆ‰ ˆ ‰
ÈÈ
Š‹
""
##
"Î# "Î#
ÈÈ
t 1 2 y ; thusÊ œ Êœ œ
Š‹
ÈÈ
t
ydt dt
dy y dy
2t1
ÈÈ
Š‹
È
Š‹
ÈÈÈ
ÈÈ
y
2t1
t
y
2y
t1
yy4yt1
2 y (t 1) 2t t 1
; t 0 x 2x 0 x 1 2x 0 x 0; t 0
dy dy/dt
dx dx/dt
œ œ œÊ œÊ œÊœ œ
Œ
Š‹
yy4yt 1
2 y (t 1) 2t t 1
2t 1
13x
$Î# "Î#
ˆ‰
y 0 1 2(0) y 4 y 4; therefore 6Ê œÊœ œ œ
Èȹ
dy
dx t0
Œ
Œ
444(4)01
2 4(0 1) 2(0) 0 1
2(0) 1
13(0)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
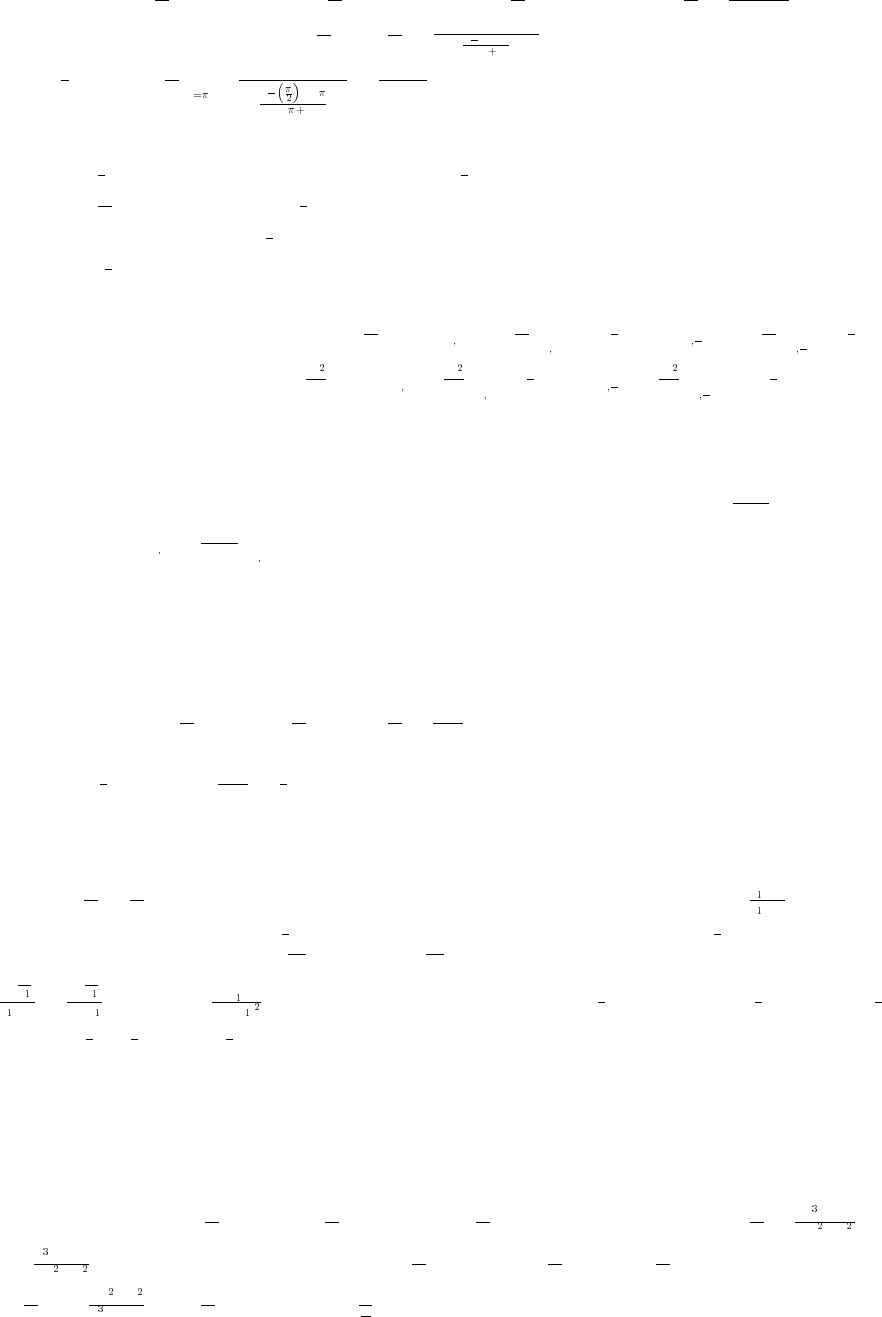
166 Chapter 3 Differentiation
66. x sin t 2x t sin t x cos t 2 1 (sin t 2) 1 x cos t ;œÊ œÊ œ Ê œ
dx dx dx dx 1 x cos t
dt dt dt dt sin t 2
t sin t 2t y sin t t cos t 2 ; thus ; t x sin 2xœÊ œ œ œ Ê œ
dy dy
dt dx
sin t t cos t 2
ˆ‰
1x cos t
sin t 2
111
x ; therefore 4Êœ œ œ œ
11111
1#
¹
dy
dx 2
sin cos 2 4 8
t–—
1cos
sin 2
67. (a) if f(x) x 3, then f (x) x and f (x) x so the claim f (x) x is falseœ œ œ œ
3
3#
#Î$ w "Î$ ww %Î$ ww "Î$
"
(b) if f(x) x 7, then f (x) x and f (x) x is trueœ œ œ
93
10 &Î$ w #Î$ ww "Î$
#
(c) f (x) x f (x) x is true
ww "Î$ www %Î$
"
œÊœ
3
(d) if f (x) x 6, then f (x) x is true
w #Î$ ww "Î$
#
œ œ
3
68. 2x 3y 5 4x 6yy 0 y y and y ;
## w w w w
œÊ œÊœÊ œ œ œ œ
2x 2x 2 2x 2
3y 3y 3 3y 3
kk
¹¹
(1 1) (1 1)
(1 1) (1 1)
also, y x 2yy 3x y y and y . Therefore
#$ w # w w w
##
œÊ œ Êœ Ê œ œ œ œ
3x 3x 3 3x 3
2y 2y 2y
kk
¹¹
(1 1) (1 1)
(1 1) (1 1)
the tangents to the curves are perpendicular at (1 1) and (1 1) (i.e., the curves are orthogonal at these twoßß
points of intersection).
69. x 2xy 3y 0 2x 2xy 2y 6yy 0 y (2x 6y) 2x 2y y the slope of the
## www w
œÊ œÊ œÊœ Ê
xy
3y x
tangent line m y 1 the equation of the normal line at (1 1) is y 1 1(x 1)œœ œÊ ßœk¹
w
(1 1) (1 1)
xy
3y x
y x 2. To find where the normal line intersects the curve we substitute into its equation:ʜ
x 2x(2 x) 3(2 x) 0 x 4x 2x 3 4 4x x 0 4x 16x 12 0
######
œÊœÊœab
x 4x 3 0 (x 3)(x 1) 0 x 3 and y x 2 1. Therefore, the normal to the curveÊ œÊ œ Ê œ œœ
#
at (1 1) intersects the curve at the point (3 1). Note that it also intersects the curve at (1 1).ßß ß
70. xy 2x y 0 x y 2 0 ; the slope of the line 2x y 0 is 2. In order to be œÊ œÊ œ œ
dy dy dy y 2
dx dx dx 1 x
parallel, the normal lines must also have slope of 2. Since a normal is perpendicular to a tangent, the slope of
the tangent is . Therefore, 2y 4 1 x x 3 2y. Substituting in the original equation,
""
##
y2
1x
œ Ê œ Ê œ
y( 3 2y) 2( 3 2y) y 0 y 4y 3 0 y 3 or y 1. If y 3, then x 3 and œ Ê œ Ê œ œ œ œ
#
y 3 2(x 3) y 2x 3. If y 1, then x 1 and y 1 2(x 1) y 2x 3. œ Ê œ œ œ œ Ê œ
71. y x . If a normal is drawn from (a 0) to (x y ) on the curve its slope satisfies 2y
#"
#
"" "
œÊ œ ß ß œ
dy y0
dx y xa
y 2y (x a) or a x . Since x 0 on the curve, we must have that a . By symmetry, theÊœ œ
""" " "
""
##
two points on the parabola are x x and x x . For the normal to be perpendicular,
ˆ‰ˆ ‰
ÈÈ
"" " "
ßß
1 1 x (a x ) x x x x and y .
Š‹Š‹ ˆ‰
ÈÈ
xx
xa ax (ax) 4
x
# #
"""""" "
#"""
#
œ Ê œ Ê œ Ê œ Ê œ œ „
Therefore, and a .
ˆ‰
""
#44
3
ß„ œ
72. Ex. 6b.) y x has no derivative at x 0 because the slope of the graph becomes vertical at x 0.œœ œ
"Î#
Ex. 7a.) y 1 x has a derivative only on ( ) because the function is defined only on [ ] andœ "ß " "ß "ab
#"Î%
the slope of the tangent becomes vertical at both x 1 and x 1.œ œ
73. xy x y 6 x 3y y x 2xy 0 3xy x y 2xy
$# # $# ## $
œÊ œÊ œ Êœ
Š‹ ab
dy dy dy dy y 2xy
dx dx dx dx 3xy x
; also, xy x y 6 x 3y y x y 2x 0 y 2xy 3xy xœ œ Ê œ Ê œ
y 2xy
3xy x dy dy dy
dx dx dx
$# # $ # $ ##
ab a b
Š‹
; thus appears to equal . The two different treatments view the graphs as functionsʜ
dx dx
dy y 2xy dy
3xy x
"
dy
dx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
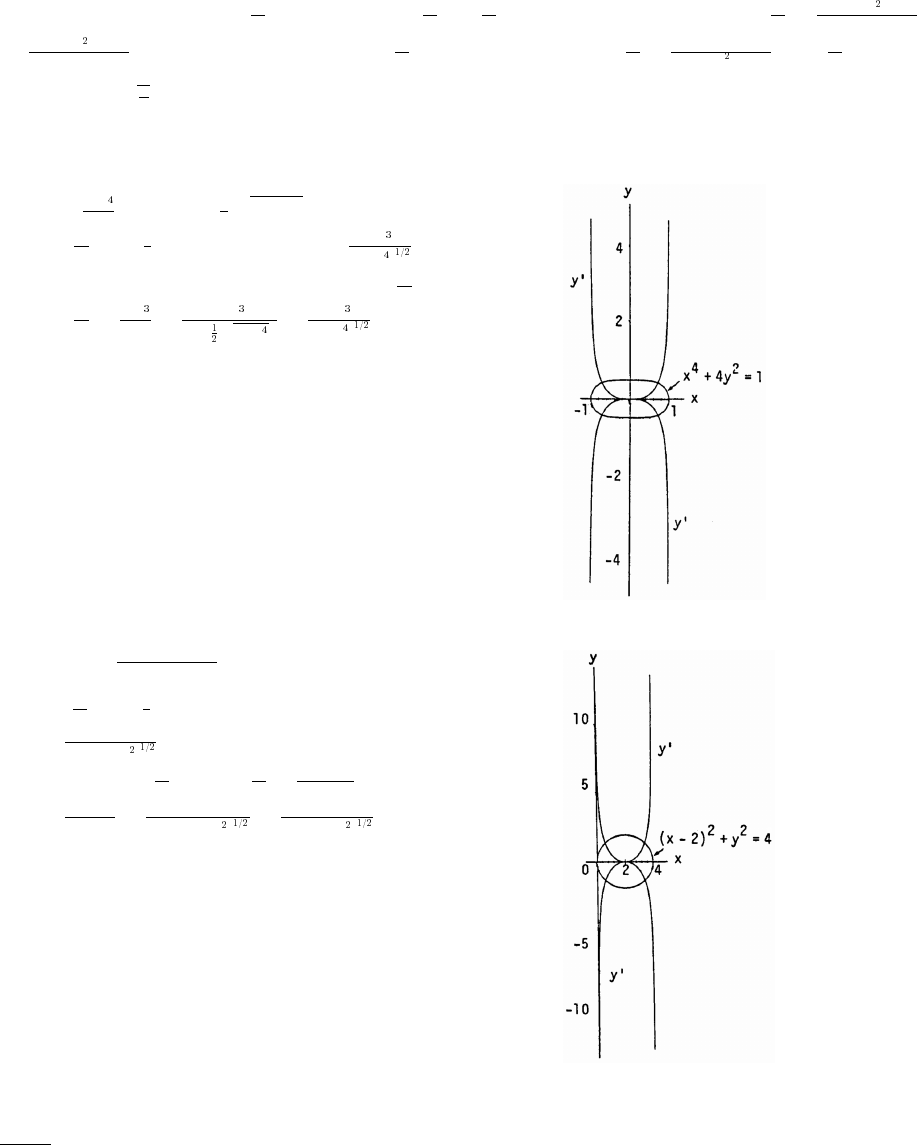
Section 3.6 Implicit Differentiation 167
symmetric across the line y x, so their slopes are reciprocals of one another at the corresponding pointsœ
(a b) and (b a).ßß
74. x y sin y 3x 2y (2 sin y)(cos y) (2y 2 sin y cos y) 3x
$# # # #
œ Ê œ Ê œ Ê œ
dy dy dy dy
dx dx dx dx 2y 2 sin y cos y
3x
; also, x y sin y 3x 2y 2 sin y cos y ; thus œœÊœÊœ
3x dx dx dx
2 sin y cos y 2y dy dy 3x dy
2 sin y cos y 2y
$# # #
appears to equal . The two different treatments view the graphs as functions symmetric across the line
"
dy
dx
y x so their slopes are reciprocals of one another at the corresponding points (a b) and (b a).œßß
75. x 4y 1:
%#
œ
(a) y y 1 x
#"
#%
œÊœ„
1x
4È
1 x 4x ;Êœ„ œ
dy
dx 4
x
1x
"„
%$
"Î#
abab
ab
differentiating implicitly, we find, 4x 8y 0
$œ
dy
dx
.Êœ œ œ
dy
dx 8y
4x 4x x
81x 1x
„
„
Š‹
Èab
(b)
76. (x 2) y 4:œ
##
(a) y 4 (x 2)œ„
È#
4(x2) (2(x2))Êœ„
dy
dx
"
#
#"Î#
ab
; differentiating implicitly,œ„
(x 2)
4(x2)cd
2(x 2) 2y 0 œÊ œ
dy dy 2(x 2)
dx dx 2y
.œœ œ
„
„ #
(x 2) (x 2) (x 2)
y4(x2) 4(x )cdcd
(b)
77-84. Example CAS commands:
:Maple
q1 := x^3-x*y+y^3 = 7;
pt := [x=2,y=1];
p1 := implicitplot( q1, x=-3..3, y=-3..3 ):
p1;
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

168 Chapter 3 Differentiation
eval( q1, pt );
q2 := implicitdiff( q1, y, x );
m := eval( q2, pt );
tan_line := y = 1 + m*(x-2);
p2 := implicitplot( tan_line, x=-5..5, y=-5..5, color=green ):
p3 := pointplot( eval([x,y],pt), color=blue ):
display( [p1,p2,p3], ="Section 3.6 #77(c)" );
: (functions and x0 may vary):Mathematica
Note use of double equal sign (logic statement) in definition of eqn and tanline.
<<Graphics`ImplicitPlot`
Clear[x, y]
{x0, y0}={1, /4};1
eqn=x + Tan[y/x]==2;
ImplicitPlot[eqn,{ x, x0 3, x0 3},{y, y0 3, y0 3}]
eqn/.{x x0, y y0}ÄÄ
eqn/.{ y y[x]}Ä
D[%, x]
Solve[%, y'[x]]
slope=y'[x]/.First[%]
m=slope/.{x x0, y[x] y0}ÄÄ
tanline=y==y0 m (x x0)
ImplicitPlot[{eqn, tanline}, {x, x0 3, x0 3},{y, y0 3, y0 + 3}]
3.7 RELATED RATES
1. A r 2 r œÊœ11
#dA dr
dt dt
2. S 4 r 8 r œÊœ11
#dS dr
dt dt
3. (a) V r h r (b) V r h 2 rh œÊœ œÊœ11 1 1
## #
dV dh dV dr
dt dt dt dt
(c) V r h r 2 rh œÊœ 111
##
dV dh dr
dt dt dt
4. (a) V r h r (b) V r h rh œÊœ œÊœ
"" "
## #
3dt3dt 3dt3dt
dV dh dV 2 dr
11 11
(c) r rh
dV dh 2 dr
dt 3 dt 3 dt
œ
"#
11
5. (a) 1 volt/sec (b) amp/sec
dV dI
dt dt 3
œœ
"
(c) R I R
dV dI dR dR dV dI dR dV V dI
dt dt dt dt I dt dt dt I dt I dt
œ ʜʜ
ˆ‰ ˆ‰ ˆ ‰ ˆ ‰
""
(d) 1 (3) ohms/sec, R is increasing
dR 12 3
dt 3
œœ œ
"""
## # #
‘ˆ‰ˆ‰
6. (a) P RI I 2RI œÊœ
##
dP dR dI
dt dt dt
(b) P RI 0 I 2RI œ Ê œ œ Ê œ œ œ
##
dP dR dI dR 2RI dI dI 2P dI
dt dt dt dt I dt I dt I dt
2ˆ‰
P
I
7. (a) s x y x y œœ Êœ
Èab
## ##
"Î#
ds x dx
dt dt
xy
È
(b) s x y x y œœ Êœ
Èab
## ##
"Î#
ds x dx
dt dt dt
xy xy
ydy
ÈÈ
(c) s x y s x y 2s 2x 2y 2s 0 2x 2y œÊœÊ œ Ê œ Êœ
È## ### ds dx dx dx
dt dt dt dt dt dt x dt
dy dy y dy
†
8. (a) s x y z s x y z 2s 2x 2y 2z œ ÊœÊ œ
È### #### ds dx dz
dt dt dt dt
dy
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.7 Related Rates 169
ʜ
ds x dx z dz
dt dt dt dt
xyz xyz xyz
ydy
ÈÈÈ
(b) From part (a) with 0
dx ds z dz
dt dt dt dt
ydy
xyz xyz
œÊ œ
ÈÈ
(c) From part (a) with 0 0 2x 2y 2z 0
ds dx dz dx z dz
dt dt dt dt dt x dt x dt
dy y dy
œÊœ Ê œ
9. (a) A ab sin ab cos (b) A ab sin ab cos b sin œÊœ œÊœ
"" """
## ###
)) )))
dA d dA d da
dt dt dt dt dt
) )
(c) A ab sin ab cos b sin a sin œÊœ
""""
####
))))
dA d da db
dt dt dt dt
)
10. Given A r , 0.01 cm/sec, and r 50 cm. Since 2 r , then 2 (50)œœ œ œ œ111
#"dr dA dr dA
dt dt dt dt 100
¸ˆ‰
r=50
cm /min.œ1#
11. Given 2 cm/sec, 2 cm/sec, 12 cm and w 5 cm.
ddw
dt dt
jœ œ jœ œ
(a) A w w 12(2) 5( 2) 14 cm /sec, increasingœjÊœj Êœ œ
dA dw d dA
dt dt dt dt
j#
(b) P 2 2w 2 2 2( 2) 2(2) 0 cm/sec, constantœj Ê œ œ œ
dP d dw
dt dt dt
j
(c) D w w w 2w 2 œ j œ j Ê œ j j Ê œ
Èab ab
ˆ‰
## ## ##
"Î# "Î# j
"j
#j
dD dw d dD
dt dt dt dt
w
w
dw d
dt dt
È
cm/sec, decreasingœœ
(5)(2) (12)( 2)
25 144
14
13
È
12. (a) V xyz yz xz xy (3)(2)(1) (4)(2)( 2) (4)(3)(1) 2 m /secœÊœ Ê œ œ
dV dx dz dV
dt dt dt dt dt
dy ¸(432)
$
(b) S 2xy 2xz 2yz (2y 2z) (2x 2z) (2x 2y) œ Êœ
dS dx dz
dt dt dt dt
dy
(10)(1) (12)( 2) (14)(1) 0 m /secÊœœ
¸
dS
dt (432)
#
(c) xyz xyz jœ œ Ê œ
Èab
### ###
"Î# j
dxdx zdz
dt dt dt dt
xyz xyz xyz
ydy
ÈÈÈ
(1) ( 2) (1) 0 m/secÊœ œ
¸Š‹ Š‹ Š‹
d43 2
dt 29 29 29
j
(432) ÈÈ È
13. Given: 5 ft/sec, the ladder is 13 ft long, and x 12, y 5 at the instant of time
dx
dt œœœ
(a) Since x y 169 (5) 12 ft/sec, the ladder is sliding down the wall
##
œ Ê œ œ œ
dy
dt y dt 5
xdx 12
ˆ‰
(b) The area of the triangle formed by the ladder and walls is A xy x y . The areaœÊœ
""
##
dA dx
dt dt dt
dy
ˆ‰
Š‹
is changing at [12( 12) 5(5)] 59.5 ft /sec.
"
##
#
œ œ
119
(c) cos sin (5) 1 rad/sec))œÊ œ Êœ œ œ
xddxd dx
13 dt 13 dt dt 13 sin dt 5
))
)
"""
††
ˆ‰
14. s y x 2s 2x 2y x y [5( 442) 12( 481)]
### ""
œ Ê œ Ê œ Ê œ
ds dx ds dx ds
dt dt dt dt s dt dt dt
dy dy
169
Š‹È
614 knotsœ
15. Let s represent the distance between the girl and the kite and x represents the horizontal distance between the
girl and kite s (300) x 20 ft/sec.Êœ Êœ œ œ
###
ds x dx
dt s dt 500
400(25)
16. When the diameter is 3.8 in., the radius is 1.9 in. and in/min. Also V 6 r 12 r
dr dV dr
dt 3000 dt dt
œœÊœ
"#
11
12 (1.9) 0.0076 . The volume is changing at about 0.0239 in /min.Êœ œ
dV
dt 3000
11
ˆ‰
"$
17. V r h, h (2r) r V h œœœÊœÊœ œÊœ
""
##
3 8 4 3 3 3 27 dt 9 dt
3 3r 4h 4h 16 h dV 16 h dh
11
ˆ‰ 11
(a) (10) 0.1119 m/sec 11.19 cm/sec
¸ˆ‰
dh 9 90
dt 16 4 256
h=4 œœ¸ œ
11
(b) r 0.1492 m/sec 14.92 cm/secœÊœ œ œ ¸ œ
4h dr 4 dh 4 90 15
3 dt 3 dt 3 256 32
ˆ‰
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

170 Chapter 3 Differentiation
18. (a) V r h and r V h œœÊœœÊœÊœœ
""
#
##
#
3 3 4 dt 4 dt dt 225 (5) 225
15h 15h 75 h dV 225 h dh dh 8
4( 50)
11
ˆ‰ ¸
11
11
h=5
0.0113 m/min 1.13 cm/min¸ œ
(b) r 0.0849 m/sec 8.49 cm/secœ Ê œ Ê œ œ ¸ œ
15h dr 15 dh dr 15 8 4
dt dt dt 225 15## #
¸ˆ‰ˆ‰
h=5 11
19. (a) V y (3R y) 2y(3R y) y ( 1) 6Ry 3y at R 13 andœÊœ Êœ Êœ
11 1
3 dt 3 dt dt 3 dt
dV dV
dy dy
###
"
cdab
‘
y 8 we have ( 6) m/minœœœ
dy
dt 144 24
""
11
(b) The hemisphere is on the circle r (13 y) 169 r 26y y m
## #
œ Êœ
È
(c) r 26y y 26y y (26 2y) œ Êœ Êœ Ê œab ab ¸ˆ‰
##
"Î# "Î#
""
# #
dr dr dr 13 8
dt dt dt dt dt 4
dy 13 y dy
26y y 26 8 64
ÈÈ
y=8 †1
m/minœ5
2881
20. If V r , S 4 r , and kS 4k r , then 4 r 4k r 4 r k, a constant.œœ œœ œÊœÊœ
4dV dVdrdrdr
3dt dtdtdtdt
11 1 1 11
$# # # ##
Therefore, the radius is increasing at a constant rate.
21. If V r , r 5, and 100 ft /min, then 4 r 1 ft/min. Then S 4 r œœ œ œ Êœ œÊ
4dV dVdrdr dS
3dt dtdtdt dt
111 1
$$# #
8 r 8 (5)(1) 40 ft /min, the rate at which the surface area is increasing.œœ œ11 1
dr
dt #
22. Let s represent the length of the rope and x the horizontal distance of the boat from the dock.
(a) We have s x 36 . Therefore, the boat is approaching the dock at
##
œ Ê œ œ
dx s ds s ds
dt x dt dt
s36
È
( 2) 2.5 ft/sec.
¸
dx 10
dt 10 36
s=10 œœ
È
(b) cos sin . Thus, r 10, x 8, and sin )) )œÊ œ Ê œ œ œ œ
6d6drd6dr 8
r dt r dt dt r sin dt 10
))
)
( 2) rad/secÊœ œ
d6 3
dt 20
10
)ˆ‰
8
10
†
23. Let s represent the distance between the bicycle and balloon, h the height of the balloon and x the horizontal
distance between the balloon and the bicycle. The relationship between the variables is s h x
###
œ
h x [68(1) 51(17)] 11 ft/sec.Êœ Êœ œ
ds dh dx ds
dt s dt dt dt 85
""
ˆ‰
24. (a) Let h be the height of the coffee in the pot. Since the radius of the pot is 3, the volume of the coffee is
V 9 h 9 the rate the coffee is rising is in/min.œÊœ Ê œ œ11
dV dh dh dV 10
dt dt dt 9 dt 9
"
11
(b) Let h be the height of the coffee in the pot. From the figure, the radius of the filter r V r hœÊ œ
h
3#
"#
1
, the volume of the filter. The rate the coffee is falling is ( 10) in/min.œœœœ
1
11 1
hdh 4 dV 4 8
1dt h dt 5 5
# #
25. y QD D QD (0) ( 2) L/min increasing about 0.2772 L/minœÊœ œœ Ê
" " # "
dy
dt dt dt 41 (41) 1681
dQ dD 233 466
26. (a) 3x 12x 15 3(2) 12(2) 15 (0.1) 0.3, 9 9(0.1) 0.9, 0.9 0.3 0.6
dc dx dr dx
dt dt dt dt dt
dp
œ œ œ œ œ œ œœaba b
##
(b) 3x 12x 45x 3(1.5) 12(1.5) 45(1.5) (0.05) = 1.5625, 70 70(0.05) 3.5,
dc dx dr dx
dt dt dt dt
œ œ œ œ œaba b
## # #
3.5 ( 1.5625) 5.0625
dp
dt œ œ
27. Let P(x y) represent a point on the curve y x and the angle of inclination of a line containing P and theߜ
#)
origin. Consequently, tan tan x sec cos . Since 10 m/sec)) ) )œÊ œœÊ œ Ê œ œ
y
x x dt dt dt dt dt
xddxddxdx
##
))
and cos , we have 1 rad/sec.k¸
#
"
)x=3 x=3
œœœ œ
x3 d
yx 93 10 dt
)
28. y ( x) and tan tan sec œ œ Ê œ Ê œ
"Î# #
)) )
y(x)
xxdtxdt
ddx
( x) ( 1)x ( x) (1)
)ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
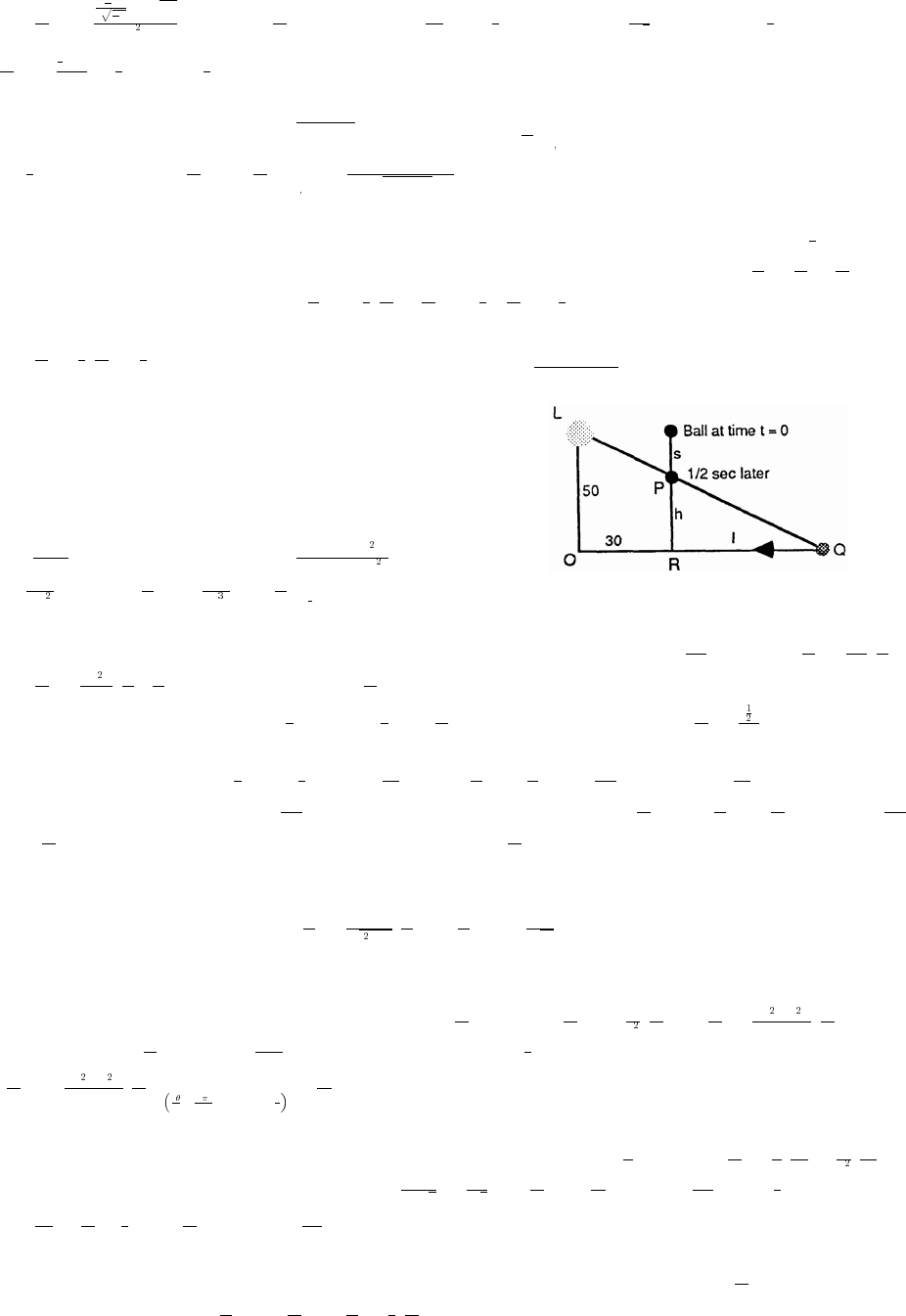
Section 3.7 Related Rates 171
cos . Now, tan cos cos . ThenÊœ œœÊ œ Ê œ
ddx224
dt x dt 4 5
x
5
)Œ
ab
ˆ‰
x
2x
# #
#
"
ÈÈ
)) ) )
( 8) rad/sec.
d42
dt 16 5 5
2
)œœ
Š‹
ˆ‰
4
4
29. The distance from the origin is s x y and we wish to find œ
ȸ
## ds
dt (5 12)
x y 2x 2y 5 m/secœ œ œ
"
#
##
"Î#
ab ¹Š‹
dx
dt dt
dy (5)( 1) (12)( 5)
25 144
(5 12) È
30. When s represents the length of the shadow and x the distance of the man from the streetlight, then s x.œ3
5
(a) If I represents the distance of the tip of the shadow from the streetlight, then I s x œ Ê œ
dI ds dx
dt dt dt
(which is velocity not speed) 5 8 ft/sec, the speed the tip of theÊœ œ œœ
¸¸ ¸ ¸ ¸¸¸¸ kk
dI 3 dx dx 8 dx 8
dt 5 dt dt 5 dt 5
shadow is moving along the ground.
(b) ( 5) 3 ft/sec, so the length of the shadow is at a rate of 3 ft/sec.
ds 3 dx 3
dt 5 dt 5
œœœ decreasing
31. Let s 16t represent the distance the ball has fallen,œ#
h the distance between the ball and the ground, and I
the distance between the shadow and the point directly
beneath the ball. Accordingly, s h 50 and sinceœ
the triangle LOQ and triangle PRQ are similar we have
I h 50 16t and IœÊœ œ
30h
50 h 50 50 16t
30 50 16t
#ab
ab
30 1500 ft/sec.œÊœ Ê œ
1500 dI 1500 dI
16t dt 8t dt ¸t=1
2
32. Let s distance of car from foot of perpendicular in the textbook diagram tan sec œÊœÊœ))
sdds
13 dt 13 dt##
#")
; 264 and 0 2 rad/sec. A half second later the car has traveled 132 ftÊ œ œ œ Ê œ
d cos ds ds d
dt 132 dt dt dt
)) )
)
right of the perpendicular , cos , and 264 (since s increases) (264) 1 rad/sec.Êœ œ œ Êœ œkk))
1)
4 dt dt 132
ds d
#"
#ˆ‰
33. The volume of the ice is V r 4 4 r in./min when 10 in /min, theœ Êœ Ê œ œ
4 4 dV dr dr 5 dV
3 3 dt dt dt 72 dt
11 1
$$ # $
¸r=6 1
thickness of the ice is decreasing at in/min. The surface area is S 4 r 8 r 48
5dSdrdS5
72 dt dt dt 721 1
œÊœ Ê œ11 1
#
¸ˆ‰
r=6
in /min, the outer surface area of the ice is decreasing at in /min.œ
10 10
3 3
# #
34. Let s represent the horizontal distance between the car and plane while r is the line-of-sight distance between
the car and plane 9 s r ( 160) 200 mphÊœ Ê œ Ê œ œ
##
ds r dr ds 5
dt dt dt
r9 16
ÈÈ
¸r=5
speed of plane speed of car 200 mph the speed of the car is 80 mph.ÊœÊ
35. When x represents the length of the shadow, then tan sec .))œÊ œ Êœ
80 d 80 dx dx x sec d
x dt x dt dt 80 dt
#)))
We are given that 0.27° rad/min. At x 60, cos
d3 3
dt 000 5
)1
œœ œ œÊ
#)
ft/min 0.589 ft/min 7.1 in./min.
¸¸ ¹¹¹
dx x sec d 3
dt 80 dt 16
œœ¸¸
)) 1
d3 5
dt 2000 3
= and sec =)
36. Let A represent the side opposite and B represent the side adjacent . tan sec ))))œÊ œ
AddAAdB
BdtBdtBdt
#")
t at A 10 m and B 20 m we have cos and ( 2) (1)Êœ œ œœ œ )20 2 d 10 4
10 5 5 dt 0 400 5
ÈÈ )‘ˆ‰ˆ‰ ˆ ‰
"
#
rad/sec /sec 6°/secœ œ œ ¸
ˆ‰ˆ‰
" " "
10 40 5 10
4 18°
1
37. Let x represent distance of the player from second base and s the distance to third base. Then 16 ft/sec
dx
dt œ
(a) s x 8100 2s 2x . When the player is 30 ft from first base, x 60
##
œ Ê œ Ê œ œ
ds dx ds x dx
dt dt dt s dt
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

172 Chapter 3 Differentiation
s 30 13 and ( 16) 8.875 ft/secÊœ œ œ ¸
Èds 60 32
dt 30 13 13
ÈÈ
(b) cos sin . Therefore, x 60 and s 30 13))
""
œÊ œ Ê œ œ œ œ
90 90 ds 90 ds 90 ds
s dt s dt dt s sin dt sx dt
dd))
)
††† È
rad/sec; sin cos Êœ œ œÊ œ Êœ
ddd
dt 65 s dt s dt dt s cos dt
90 32 8 90 90 ds 90 ds
30 13 (60) 13
)))
)
Š‹
ÈÈ
†††
Š‹
##
))
. Therefore, x 60 and s 30 13 rad/sec.œœœÊœ
90 ds 8
sx dt dt 65
d
†È)
(c) lim
d d
dt s sin dt s dt s dt x 8100 dt dt
90 ds 90 x dx 90 dx 90 dx
s
) )
)
œœ œœ ʆ††
ˆ‰
†x
sˆ‰ˆ‰ ˆ‰ˆ‰ ˆ ‰
xÄ!
lim ( 15) rad/sec; œœœœœ
xÄ!ˆ ‰ ˆ‰ˆ‰ ˆ ‰ˆ‰
Š‹
90 90 ds 90 x dx 90 dx
x 8100 6 dt s cos dt s s dt s dt
d
"
)
)
†
†x
s
lim rad/secœÊœ
ˆ‰
"
90 dx
x 8100 dt dt 6
d
xÄ!
)
38. Let a represent the distance between point O and ship A, b the distance between point O and ship B, and
D the distance between the ships. By the Law of Cosines, D a b 2ab cos 120°
###
œ
2a 2b a b . When a 5, 14, b 3, and 21, then Êœ œ œ œ œ œ
dD da db db da da db dD 413
dt D dt dt dt dt dt dt dt 2D
"
#‘
where D 7. The ships are moving 29.5 knots apart.œœ
dD
dt
3.8 LINEARIZATION AND DIFFERENTIALS
1. f(x) x 2x 3 f (x) 3x 2 L(x) f (2)(x 2) f(2) 10(x 2) 7 L(x) 10x 13 at x 2œ Ê œ Ê œ œ Ê œ œ
$w# w
2. f(x) x 9 x 9 f (x) x 9 (2x) L(x) f ( 4)(x 4) f( 4)œœ Ê œ œ Ê œ
Èab ab
ˆ‰
##w# w
"Î# "Î#
"
#
x
x9
È
(x 4) 5 L(x) x at x 4œ Ê œ œ
449
555
3. f(x) x f (x) 1 x L(x) f(1) f (1)(x 1) (x 1)œ Ê œ Ê œ œ#! œ#
"w# w
x
4. f(x) x f (x) L(x) f ( 8) x 8 f 8 (x 8) 2 L(x) xœÊ œ Ê œœÊ œ
"Î$ w w
"""
$##
x113
4
ababab
5. f(x) x 2x f (x) 2x 2 L(x) f (0)(x 0) f(0) 2(x 0) 0 L(x) 2x at x 0œ Ê œÊ œ œ Ê œ œ
#w w
6. f(x) x f (x) x L(x) f (1)(x 1) f(1) ( 1)(x 1) 1 L(x) x 2 at x 1œ Ê œ Ê œ œ Ê œ œ
" w # w
7. f(x) 2x 4x 3 f (x) 4x 4 L(x) f ( 1)(x 1) f( 1) 0(x 1) ( 5) L(x) 5 at x 1œÊœÊœœÊœœ
#w w
8. f(x) 1 x f (x) 1 L(x) f (8)(x 8) f(8) 1(x 8) 9 L(x) x 1 at x 8œ Ê œ Ê œ œ Ê œ œ
ww
9. f(x) x x f (x) x L(x) f (8)(x 8) f(8) (x 8) 2 L(x) x at x 8œœÊ œ Ê œ œÊ œ œ
$"Î$ w #Î$ w
"""
##
Ȉ‰
3113
4
10. f(x) f (x) L(x) f (1)(x 1) f(1) (x 1)œÊœ œ Êœ œ
x
x 1 (x 1) (x 1) 4
(1)(x 1) ( )(x)
#
ww
" """
L(x) x at x 1Êœ œ
""
44
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
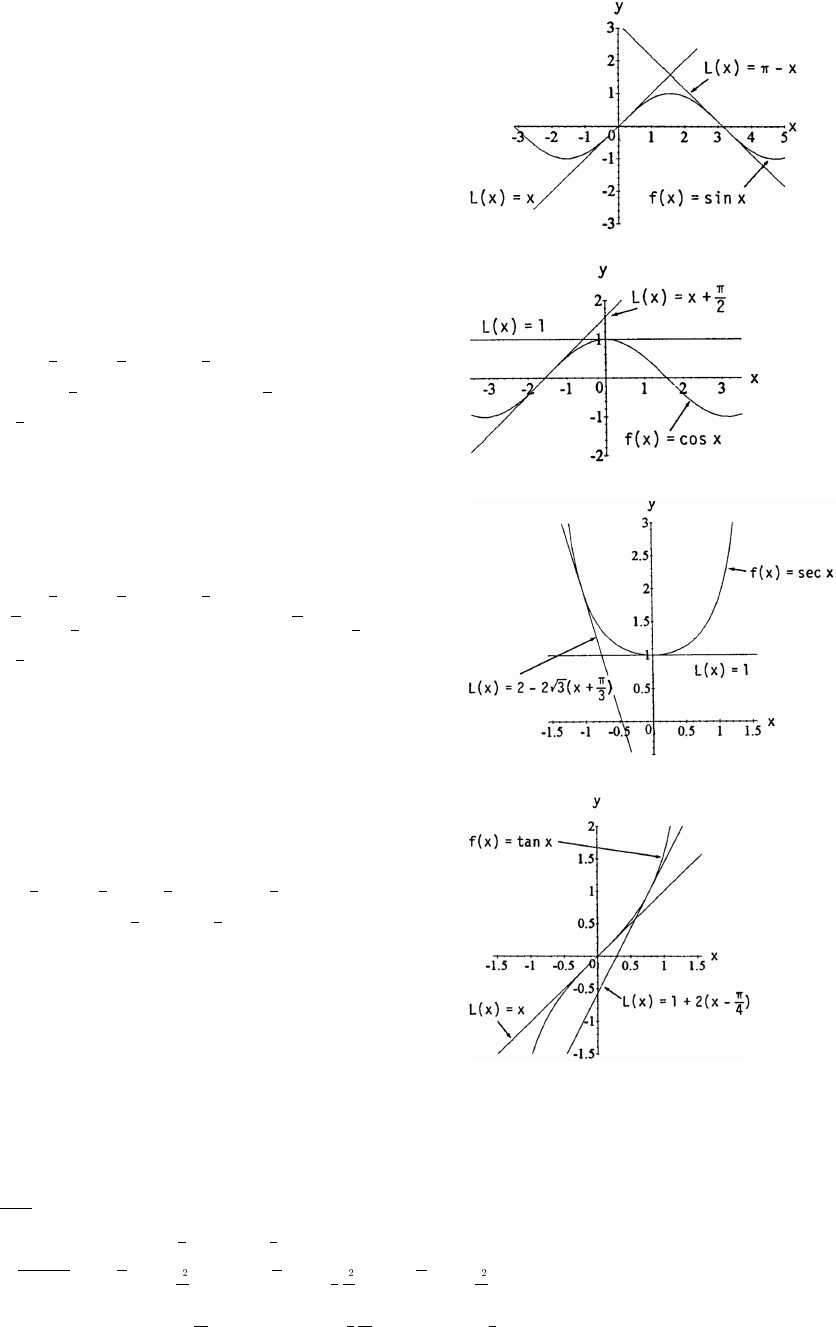
Section 3.8 Linearization and Differentials 173
11. f(x) sin x f (x) cos xœÊœ
w
(a) L(x) f (0)(x 0) f(0) 1(x 0) 0œœ
w
L(x) x at x 0Êœ œ
(b) L(x) f ( )(x ) f( ) ( 1)(x ) 0œœ
w111 1
L(x) x at xÊœ œ11
12. f(x) cos x f (x) sin xœÊœ
w
(a) L(x) f (0)(x 0) f(0) 0(x 0) 1œœ
w
L(x) 1 at x 0Êœ œ
(b) L(x) f x fœ
w
## #
ˆ‰ˆ ‰ˆ‰
11 1
( 1) x 0 L(x) xœ Ê œ
ˆ‰
11
#2
at x œ1
#
13. f(x) sec x f (x) sec x tan xœÊœ
w
(a) L(x) f (0)(x 0) f(0) 0(x 0) 1œœ
w
L(x) 1 at x 0Êœ œ
(b) L(x) f x fœ
wˆ‰ˆ ‰ˆ‰
11 1
33 3
2 3 x 2 L(x) 2 2 3 xœ Ê œ
ÈÈ
ˆ‰ ˆ‰
11
33
at x œ1
3
14. f(x) tan x f (x) sec xœÊœ
w#
(a) L(x) f (0)(x 0) f(0) 1(x 0) 0 xœœœ
w
L(x) x at x 0Êœ œ
(b) L(x) f x f 2 x 1œœ
wˆ‰ˆ ‰ ˆ‰ ˆ ‰
111 1
444 4
L(x) 1 2 x at xÊœ œ
ˆ‰
11
44
15. f x k x . We have f and f k. L x f f x k x kx
www
"
ab a b ab ab ab ab aba b a bœ " ! œ" ! œ œ ! ! ! œ" ! œ"
k
16. (a) f x x x x xaba b ab ab
‘
œ " œ " ¸"' œ"'
''
(b) f x x x xab ab abab
‘ ‘
œ œ# " ¸# " " œ##
#
"
"
x
(c) f x x xab a b ˆ‰
œ " ¸" œ"
"Î# "
##
x
(d) f x xab ÈÈÈÈ
Š‹ Š ‹Š‹
œ " œ #" ¸ #" œ #"
####%
"Î# "xxx
(e) f x xab a b ˆ‰ ˆ ‰ˆ‰
œ %$ œ% " ¸% " œ% "
"Î$ "Î$ "Î$ "Î$
$"$
%$%%
"Î$
xxx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

174 Chapter 3 Differentiation
(f) f xab ˆ ‰ ˆ‰ ˆ‰
’“
œ " œ " ¸" œ"
""#"#
# # $ # '$
Î$ Î$
xx xx
22
17. (a) (1.0002) (1 0.0002) 1 50(0.0002) 1 .01 1.01
&! &!
œ ¸ œ œ
(b) 1.009 (1 0.009) 1 (0.009) 1 0.003 1.003
$"Î$ "
Ȉ‰
œ ¸ œ œ
3
18. f(x) x 1 sin x (x 1) sin x f (x) (x 1) cos x L (x) f (0)(x 0) f(0)œ œ Ê œ Ê œ
Ȉ‰
"Î# w "Î# w
"
#f
(x 0) 1 L (x) x 1, the linearization of f(x); g(x) x 1 (x 1) g (x)œÊ œ œœ Ê
33
##
"Î# w
fÈ
(x 1) L (x) g (0)(x 0) g(0) (x 0) 1 L (x) x 1, the linearization of g(x);œ Êœ œÊœ
ˆ‰
"""
###
"Î# w
g g
h(x) sin x h (x) cos x L (x) h (0)(x 0) h(0) (1)(x 0) 0 L (x) x, the linearization ofœÊœ Ê œ œÊ œ
ww
h h
h(x). L (x) L (x) L (x) implies that the linearization of a sum is equal to the sum of the linearizations.
fgh
œ
19. y x 3 x x 3x dy 3x x dx dy 3x dxœ œ Ê œ Ê œ
$ $ "Î# # "Î# #
#
Ȉ‰Š‹
33
2x
È
20. y x 1 x x 1 x dy (1) 1 x (x) 1 x ( 2x) dxœœ Êœ
Èab ab ab
’“
ˆ‰
####
"Î# "Î# "Î#
"
#
1 x 1 x x dx dxœ œabc dab
###
"Î#
ab
È
12x
1x
21. y dy dx dxœÊœ œ
2x 2 2x
1x
(2) 1 x (2x)(2x)
1x 1x
Š‹
ab
ab ab
22. y dy dx dxœœ Êœ œ
2x
31 x
2x 3x 3 3
31 x
x31x 2x x
91 x 91 x
È
ˆ‰
Èab ˆ‰ˆ‰ˆ‰
ab ab
Š‹
3
dy dxʜ "
3x1 x
ÈÈ
ˆ‰
23. 2y xy x 0 3y dy y dx x dy dx 0 3y x dy (1 y) dx dy dx
$Î# "Î# "Î#
œÊ œÊ œ Ê œ
ˆ‰ 1y
3yx
È
24. xy 4x y 0 y dx 2xy dy 6x dx dy 0 (2xy 1) dy 6x y dx
# $Î# # "Î# "Î# #
œÊ œÊœ
ˆ‰
dy dxʜ
6xy
2xy 1
È
25. y sin 5 x sin 5x dy cos 5x x dx dy dxœ œ Êœ Êœ
ˆ‰ ˆ‰ ˆ ‰ˆ ‰
Ȉ‰
"Î# "Î# "Î#
#
55 cos 5 x
2x
ˆ‰
È
È
26. y cos x dy sin x (2x) dx 2x sin x dxœÊœ œab c d abab
## #
27. y 4 tan dy 4 sec x dx dy 4x sec dxœÊœ Êœ
Š‹ Š ‹ Š‹Š‹ab
xx x
33 3
## ##
28. y sec x 1 dy sec x 1 tan x 1 (2x) dx 2x sec x 1 tan x 1 dxœÊœ œ abcdcdabab abab
### ##
29. y 3 csc 1 2 x 3 csc 1 2x dy 3 csc 1 2x cot 1 2x x dxœœÊœ
ˆ‰ˆ‰ ˆ ‰ˆ‰ˆ‰
Ȉ‰
"Î# "Î# "Î# "Î#
dy csc 1 2 x cot 1 2 x dxʜ
3
x
Ȉ‰ˆ‰
ÈÈ
30. y 2 cot 2 cot x dy 2 csc x x dx dy csc dxœ œ Êœ Êœ
Š‹ Š‹
ˆ‰ ˆ‰ˆ‰ˆ‰
""""
"Î# # "Î# $Î# #
#
ÈÈÈ
x x
x
31. f(x) x 2x, x 1, dx 0.1 f (x) 2x 2œ œ œ Ê œ
#w
!
(a) f f(x dx) f(x ) f(1.1) f(1) 3.41 3 0.41?œ œ œ œ
!!
(b) df f (x ) dx [2(1) 2](0.1) 0.4œœœ
w!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.8 Linearization and Differentials 175
(c) f df 0.41 0.4 0.01kkk k?œ œ
32. f(x) 2x 4x 3, x 1, dx 0.1 f (x) 4x 4œ œ œ Ê œ
#w
!
(a) f f(x dx) f(x ) f( .9) f( 1) .02?œ œœ
!!
(b) df f (x ) dx [4( 1) 4](.1) 0œœœ
w!
(c) f df .02 0 .02kkkk?œ œ
33. f(x) x x, x 1, dx 0.1 f (x) 3x 1œ œ œ Ê œ
$w#
!
(a) f f(x dx) f(x ) f(1.1) f(1) .231?œ œ œ
!!
(b) df f (x ) dx [3(1) 1](.1) .2œœœ
w#
!
(c) f df .231 .2 .031kkk k?œ œ
34. f(x) x , x 1, dx 0.1 f (x) 4xœœœÊœ
%w$
!
(a) f f(x dx) f(x ) f(1.1) f(1) .4641?œ œ œ
!!
(b) df f (x ) dx 4(1) (.1) .4œœœ
w$
!
(c) f df .4641 .4 .0641kkk k?œ œ
35. f(x) x , x 0.5, dx 0.1 f (x) xœœœÊœ
" w #
!
(a) f f(x dx) f(x ) f(.6) f(.5)?œ œœ
!! "
3
(b) df f (x ) dx ( 4)œœœ
w!"
ˆ‰
10 5
2
(c) f dfkk
¸¸
?œœ
""
35 15
2
36. f(x) x 2x 3, x 2, dx 0.1 f (x) 3x 2œ œ œ Ê œ
$w#
!
(a) f f(x dx) f(x ) f(2.1) f(2) 1.061?œ œ œ
!!
(b) df f (x ) dx (10)(0.10) 1œœ œ
w!
(c) f df 1.061 1 .061kkk k?œ œ
37. V r dV 4 r dr 38. V x dV 3x dxœÊœ œÊœ
4
311
$# $#
! !
39. S 6x dS 12x dxœÊœ
#!
40. S r r h r r h , h constant r h r r r hœœ Êœ 11 1 1
Èab ab ab
## ## ## ##
"Î# "Î# "Î#
dS
dr †
dS dr, h constantʜ ʜ
dS
dr
rh r
rh
2r h
rh
11 1
ab
Èab
É
41. V r h, height constant dV 2 r h dr 42. S 2 rh dS 2 r dhœÊœ œÊœ1111
#!
43. Given r 2 m, dr .02 mœœ
(a) A r dA 2 r dr 2 (2)(.02) .08 mœÊœ œ œ1111
##
(b) (100%) 2%
ˆ‰
.08
4
1
1œ
44. C 2 r and dC 2 in. dC 2 dr dr the diameter grew about in.; A r dA 2 r drœœÊœÊœÊ œÊœ11 11
"#
11
2
2 (5) 10 in.œœ1ˆ‰
"#
1
45. The volume of a cylinder is V r h. When h is held fixed, we have rh, and so dV rh dr. For h in.,œœ#œ#œ$!111
#dV
dr
r in., and dr in., the volume of the material in the shell is approximately dV rh drœ' œ!Þ& œ# œ# ' $! !Þ&11aba ba b
in .œ ")! ¸ &'&Þ&1$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
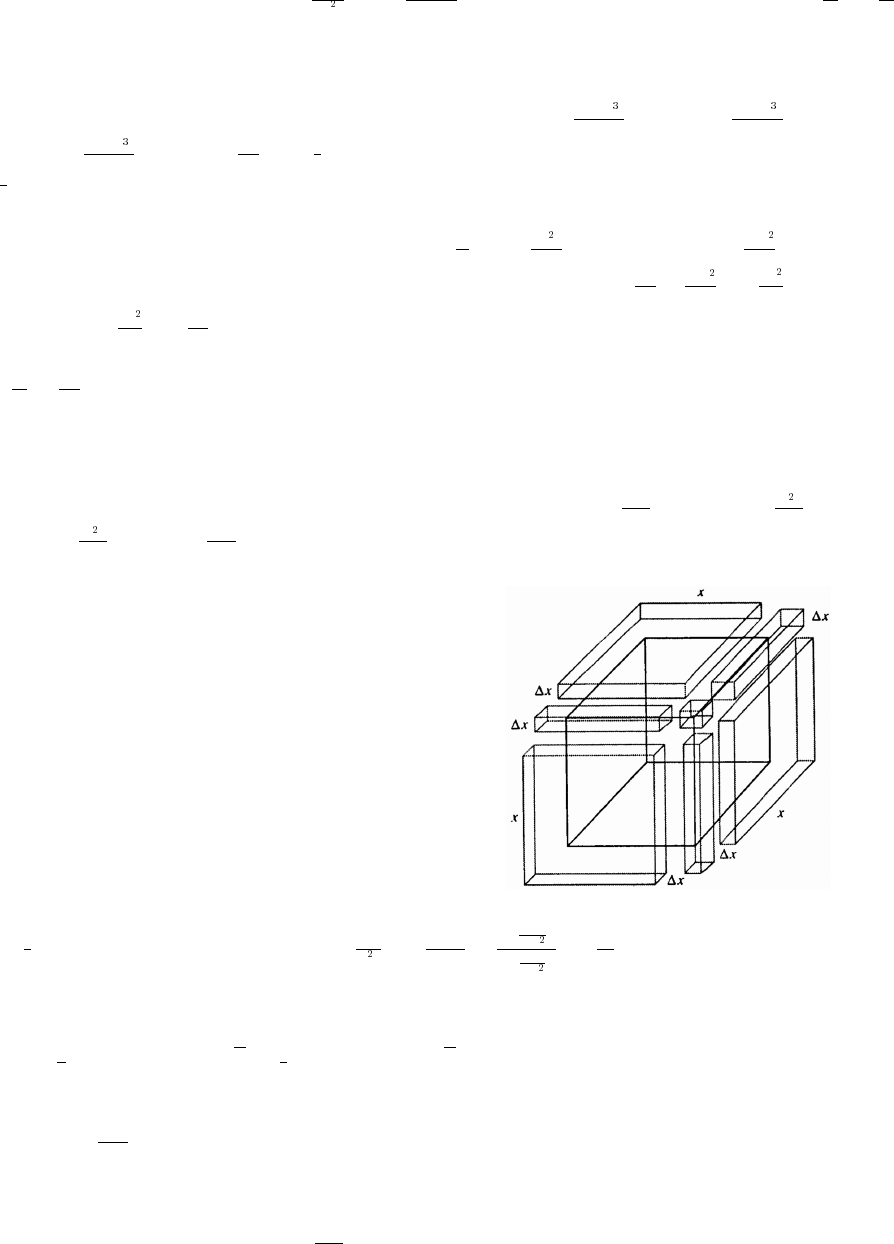
176 Chapter 3 Differentiation
46. Let angle of elevation and h height of building. Then h tan , so dh sec d . We want dh h,))))œ œ œ$! œ$! l l!Þ!%
#
which gives: sec d tan d d sin cos d sin cos l$! l!Þ!%l$! lÊ l l Êl l!Þ!% Êl l!Þ!%
#"!Þ!% &&
"# "#
)) ) ) ) ) ) )
cos cos
sin
))
)11
radian. The angle should be measured with an error of less than radian (or approximatley degrees),œ !Þ!" !Þ!" !Þ&(
which is a percentage error of approximately %.!Þ('
47. V h dV 3 h dh; recall that V dV. Then V (1%)(V) dVœÊœ ¸ Ÿ œ Ê Ÿ11 ? ?
$# kk kk
(1) h (1) h
100 100
ab ab11
3 h dh dh h % h. Therefore the greatest tolerated error in the measurementÊŸÊŸœkk kk ˆ‰
1#""
(1) h
100 300 3
ab1
of h is %.
"
3
48. (a) Let D represent the inside diameter. Then V r h h and h 10 V
iœœ œ œÊœ Ê11
#
##
#
ˆ‰
DDh 5 D
4
ii i
11
dV 5 D dD . Recall that V dV. We want V (1%)(V) dVœ¸ŸÊŸœ1? ?
ii kk kkˆ‰
Š‹
"
#100 40
5D D
11
ii
5 D dD 200. The inside diameter must be measured to within 0.5%.ÊŸÊŸ1ii
1D
40 D
dD
ii
i
(b) Let D represent the exterior diameter, h the height and S the area of the painted surface. S D h dS hdD
eee
œÊœ11
. Thus for small changes in exterior diameter, the approximate percentage change in the exterior diameterʜ
dS
SD
dDe
e
is equal to the approximate percentage change in the area painted, and to estimate the amount of paint required to
within 5%, the tanks's exterior diameter must be measured to within 5%.
49. V r h, h is constant dV 2 rh dr; recall that V dV. We want V V dVœÊœ ¸ ŸÊŸ11??
#"
kk kk
1000 1000
rh1
2 rh dr dr (.05%)r a .05% variation in the radius can be tolerated.ÊŸÊŸœÊkk kk11rh r
1000 000
#
50. Volume (x x) x 3x ( x) 3x( x) ( x)œœ????
$$ # # $
51. W a a bg dW bg dg 37.87, so a change ofœ œ Ê œ œ Ê œ œ œ
b32
g g dW 5.2
b dg dW
" # #
moon
earth
Š‹
Š‹
b dg
(5.2)
b dg
(32) ˆ‰
gravity on the moon has about 38 times the effect that a change of the same magnitude has on Earth.
52. (a) T 2 dT 2 L g dg L g dgœÊœœ11 1
Š‹ ÈÈ
ˆ‰
L
g
"Î# "
#
$Î# $Î#
(b) If g increases, then dg 0 dT 0. The period T decreases and the clock ticks more frequently. BothÊ
the pendulum speed and clock speed increase.
(c) 0.001 100 980 dg dg 0.977 cm/sec the new g 979 cm/secœ Ê ¸ Ê ¸1Ȉ‰
$Î# # #
53. The error in measurement dx (1%)(10) 0.1 cm; V x dV 3x dx 3(10) (0.1) 30 cm theœœ œÊœœ œÊ
$## $
percentage error in the volume calculation is (100%) 3%
ˆ‰
30
1000 œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 3.8 Linearization and Differentials 177
54. A s dA 2s ds; recall that A dA. Then A (2%)A dA 2s dsœÊ œ ¸ Ÿ œœÊ ŸÊ Ÿ
#??kk kk k k
2s s s s
100 50 50 50
ds (1%) s the error must be no more than 1% of the true value.ÊŸ œœ Êkk ss
(2s)(50) 100
55. Given D 100 cm, dD 1 cm, V dV D dD (100) (1) . Then (100%)œœœœÊœœœ
4D D 10 dV
36 V
1ˆ‰
####
$##
111 1
10 % % 3%œœœ
”• ”•
ab
10 10
10 10
66
#
56. V r dV dD; recall that V dV. Then V (3%)Vœœ œÊœ ¸ Ÿ œ
44DD D 3D
33 6 100 6
11 ? ?
$
##
$
ˆ‰ ˆ ‰
kk Š‹
11 1
dV dD dD (1%) D the allowable percentage error inœÊ ŸÊ ŸÊ Ÿœ Ê
1111DDDDD
200 200 00 100
kk kk
¹¹
##
measuring the diameter is 1%.
57. A 5% error in measuring t dt (5%)t . Then s 16t ds 32t dt 32t sÊœ œ œ Êœ œ œœœ
t t 32t 16t
20 20 20 10 10
#"
ˆ‰ ˆ‰
(10%)s a 10% error in the calculation of s.œÊ
58. From Example 8 we have 4 . An increase of 12.5% in r will give a 50% increase in V.
dV dr
Vr
œ
59. lim 1 60. lim lim (1)(1) 1
x0 x0 x0ÄÄÄ
ÈÈ
1x 10
1xxcos x
1
tan x sin x
"
x0
œœ œ œœ
ˆ‰ˆ‰
61. E(x) f(x) g(x) E(x) f(x) m(x a) c. Then E(a) 0 f(a) m(a a) c 0 c f(a). Nextœ Ê œ œÊ œÊœ
we calculate m: lim 0 lim 0 lim m 0 (since c f(a))
xa xa xaÄÄ Ä
E(x) f(x) m(x a) c f(x) f(a)
xa xa xa
œÊ œÊ œ œ
’“
f (a) m 0 m f (a). Therefore, g(x) m(x a) c f (a)(x a) f(a) is the linear approximation,ʜʜ œœ
ww w
as claimed.
62. (a) i. Q a f a implies that b f a .ab ab abœœ
!
ii. Since Q x b b x a , Q a f a implies that b f a .
wwww
"# "
ab a b ab ab abœ# œ œ
iii. Since Q x b , Q a f a implies that b .
ww ww ww
##
ab ab abœ# œ œ
2fa
ab
In summary, b f a , b f a , and b .
!"
w
#
œœ œab ab 2fa
ab
(b) f x xab a bœ" "
fx x x
w# #
ab abababœ"" " œ "
fx x x
ww $ $
ab abababœ#" " œ#"
Since f , f , and f , the coefficients are b , b , b . The quadraticab ab ab!œ" !œ" !œ# œ" œ" œ œ"
www !"#
#
#
approximation is Q x x x .abœ" #
(c) As one zooms in, the two graphs quickly become
indistinguishable. They appear to be identical.
(d) g x xabœ"
gx x
w#
abœ"
gx x
ww $
abœ#
Since g , g , and g , the coefficients are b , b , b . The quadraticab ab ab" œ" " œ" " œ# œ" œ" œ œ"
www !" #
#
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
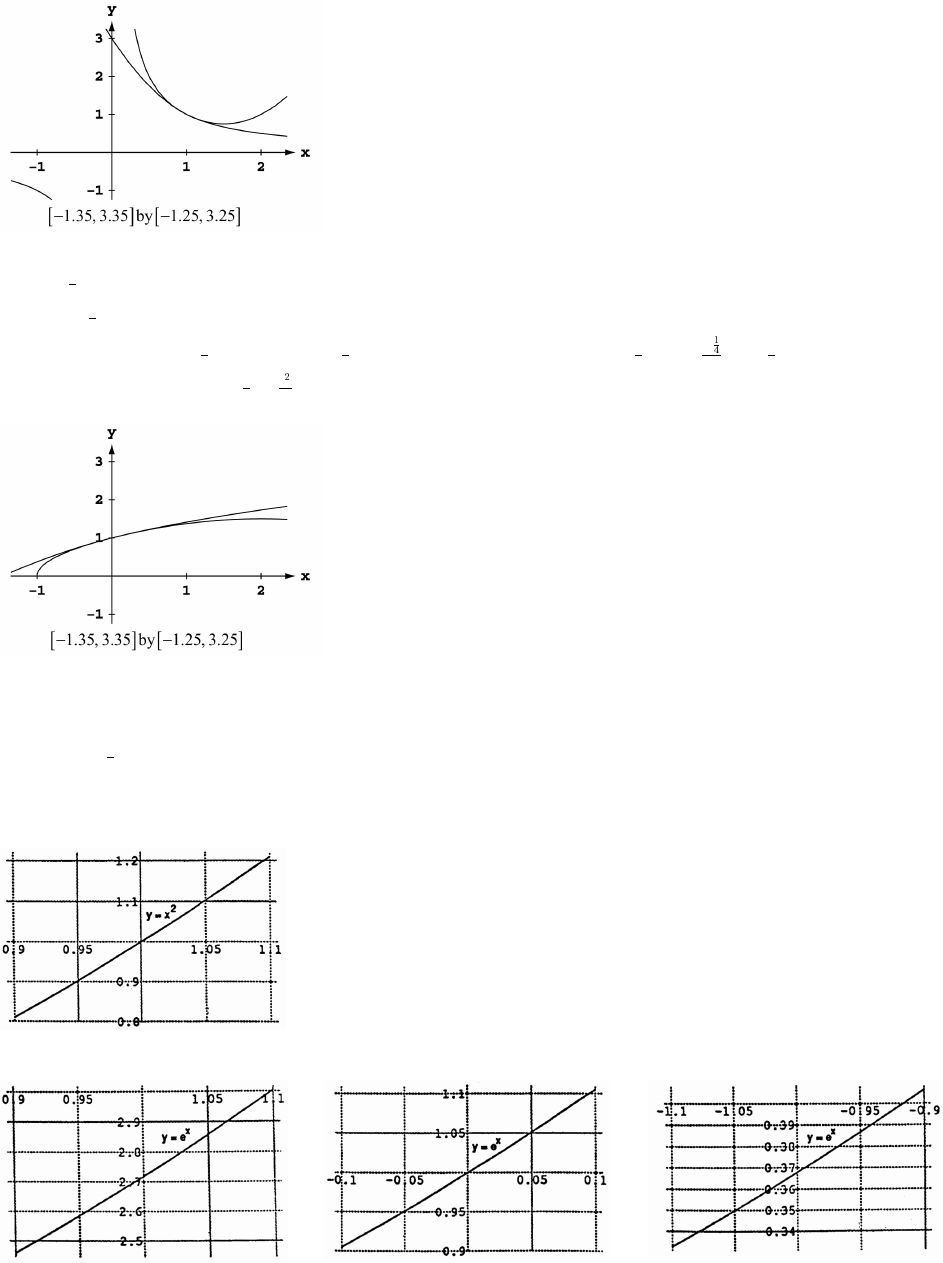
178 Chapter 3 Differentiation
approximation is Q x x x .ab ababœ" " "#
As one zooms in, the two graphs quickly become
indistinguishable. They appear to be identical.
(e) h x xab a bœ" "Î#
hx x
w"
#
"Î#
ab a bœ"
hx x
ww "
%
$Î#
ab a bœ "
Since h , h , and h , the coefficients are b , b , b . The quadraticab ab ab! œ" ! œ ! œ œ" œ œ œ
www
"" ""
#% #
!" #
28
approximation is Q x .abœ"
xx
8#
As one zooms in, the two graphs quickly become
indistinguishable. They appear to be identical.
(f) The linearization of any differentiable function u x at x a is L x u a u a x a b b x a , whereab ab ab aba b a bœœœ
w!"
b and b are the coefficients of the constant and linear terms of the quadratic approximation. Thus, the linearization
!"
for f x at x is x; the linearization for g x at x is x or x; and the linearization for h x atab ab a b abœ! " œ" " " #
x is .œ! "x
#
63. (a) x 1 œ
(b) x 1; m 2.5, e 2.7 x 0; m 1, e 1 x 1; m 0.3, e 0.4œœ ¸ œœœ œœ ¸
10 1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
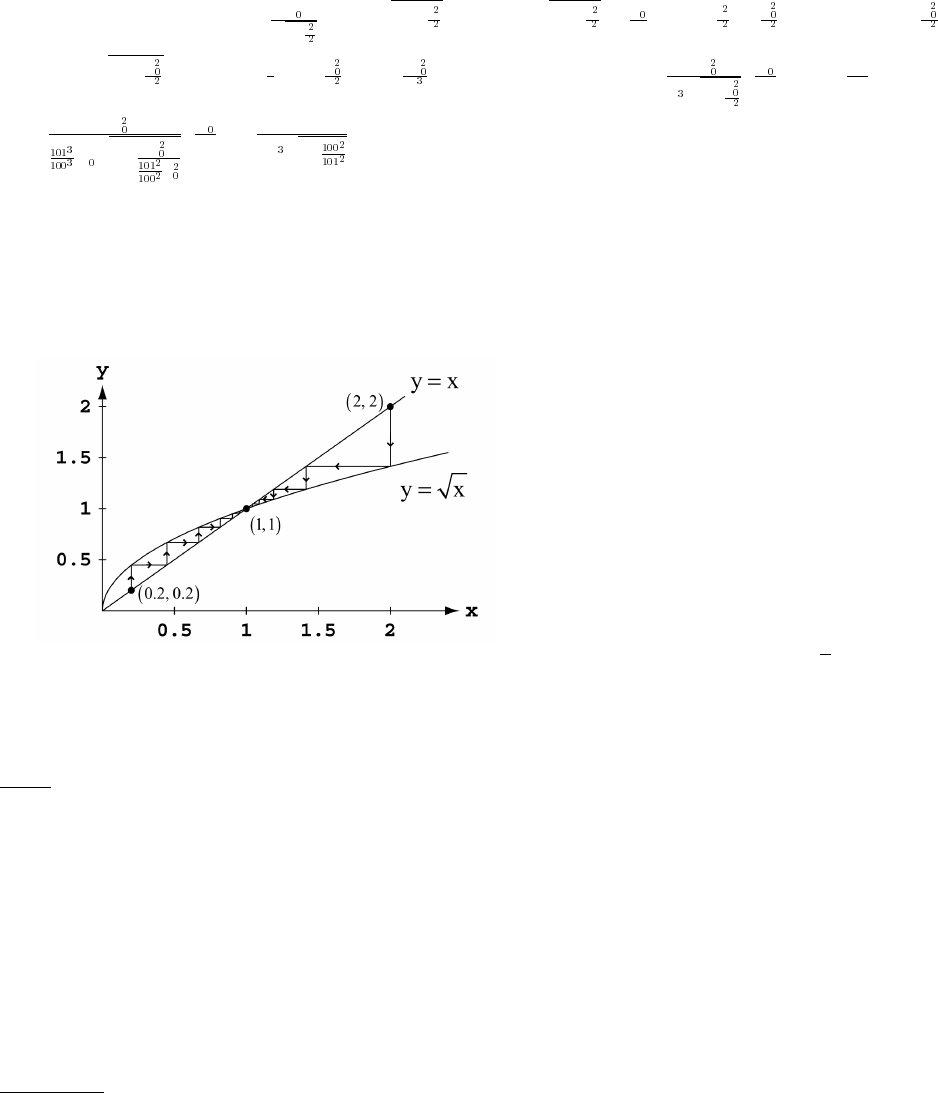
Section 3.8 Linearization and Differentials 179
64. If f has a horizontal tangent at x a, then f (a) 0 and the linearization of f at x a isœœ œ
w
L(x) f(a) f (a)(x a) f(a) 0 (x a) f(a). The linearization is a constant.œ œ œ
w†
65. Find v when m m . m m m v cll œ"Þ!" œ Ê "œ Ê "œ Ê"œ Êœ "
!!
"
##
mm
vvv
ccmcmm
mm
Év
cÉÉ Š‹
v c dv c dm, dm m dv . m m ,Ê l l œ " Ê œ † " œ !Þ!" Ê œ œ
ÉŠ‹Š‹ ˆ‰
m
mmm
mm c m
m
m
""!"
#"!! "!!
"Î# #!!
"
Êm
m
dv 0.69c. Body at rest v and v v dvœœ¸Êœ!œ
cm m1
†
"
"!!
!!!
"!" "
!!
m3m
m
Í
Í
Í
ÌÊ
ˆ‰
v 0.69c.ʜ
66. (a) The successive square roots of 2 appear to converge to the number 1. For tenth roots the convergence is more rapid.
(b) Successive square roots of 0.5 also converge to 1. In fact, successive square roots of any positive number converge
to 1.
A graph indicates what is going on:
Starting on the line y x, the successive square roots are found by moving to the graph of y x and then across toœœ
È
the line y x again. From any positive starting value x, the iterates converge to 1.œ
67-70. Example CAS commands:
:Maple
with(plots):
a:= 1: f:=x -> x 3 x 2 2*x;••
plot(f(x), x= 1..2);
diff(f(x),x);
fp := unapply ( ,x);
ww
L:=x -> f(a) fp(a)*(x a);
plot({f(x), L(x)}, x= 1..2);
err:=x -> abs(f(x) L(x));
plot(err(x), x= 1..2, title = absolute error function );##
err( 1);
: (function, x1, x2, and a may vary):Mathematica
Clear[f, x]
{x1, x2} = { 1, 2}; a = 1;
f[x_]:=x x 2x
32
Plot[f[x], {x, x1, x2}]
lin[x_]=f[a] f'[a](x a)
Plot[{f[x], lin[x]}, {x, x1, x2}]
err[x_]=Abs[f[x] lin[x]]
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

180 Chapter 3 Differentiation
Plot[err[x], {x, x1,x 2}]
err//N
After reviewing the error function, plot the error function and epsilon for differing values of epsilon (eps) and delta (del)
eps = 0.5; del = 0.4
Plot[{err[x], eps},{x, a del, a del}]
CHAPTER 3 PRACTICE EXERCISES
1. y x 0.125x 0.25x 5x 0.25x 0.25œ Ê œ
&# %
dy
dx
2. y 3 0.7x 0.3x 2.1x 2.1xœ Ê œ
$( #'
dy
dx
3. y x 3 x 3x 3(2x 0) 3x 6x 3x(x 2)œ Ê œ œ œ
$## # #
ab1dy
dx
4. y x 7x 7x 7œ Ê œ
('
"
ÈÈ
11dx
dy
5. y (x 1) x 2x (x 1) (2x 2) x 2x (2(x 1)) 2(x 1) (x 1) x(x 2)œ Ê œ œ
## # # #
ab ab c d
dy
dx
2(x1)2x 4x1œ ab
#
6. y (2x 5)(4 x) (2x 5)( 1)(4 x) ( 1) (4 x) (2) (4 x) (2x 5) 2(4 x)œ Êœ œ
" # " #
dy
dx cd
3(4 x)œ
#
7. y sec 1 3 sec 1 (2 sec tan )œ Êœ abab)) )) )))
##
$#
dy
d)
8. y 1 2 1 1 (csc cot )œ Ê œ œ
Š‹Š‹ Š‹
ˆ‰
csc csc csc cot csc
4d 4 4
dy
)) )) ))) ))
)#####
#)))
9. s œÊœ œ œ
Ȉ‰
Ȉ‰
ÈÈ
Š‹
ˆ‰ ˆ‰ ˆ‰
ÈÈÈÈÈ
ÈÈ
t
1t
ds
dt
1t t
1t 2t1t t1t
1t t
#
"
†
tt
10. s œÊœ œ
""
Ȉ‰
ÈŠ‹
ˆ‰ ˆ‰
ÈÈÈ
t1
ds
dt
t1(0)1
t1 2t t1
t
11. y 2 tan x sec x (4 tan x) sec x (2 sec x)(sec x tan x) 2 sec x tan xœÊœ œ
## # #
dy
dx ab
12. y csc x 2 csc x (2 csc x)( csc x cot x) 2( csc x cot x) (2 csc x cot x)(1 csc x)œœ Êœ œ
"#
sin x sin x dx
2dy
13. s cos (1 2t) 4 cos (1 2t)( sin (1 2t))( 2) 8 cos (1 2t) sin (1 2t)œ Êœ œ
%$ $
ds
dt
14. s cot 3 cot csc cot cscœÊœ œ
$####
ˆ‰ ˆ‰ˆ ‰ˆ ‰ ˆ‰ ˆ‰ˆ‰
2ds 2 2262 2
tdt t ttt t t
15. s (sec t tan t) 5(sec t tan t) sec t tan t sec t 5(sec t)(sec t tan t)œ Êœ œ
&%# &
ds
dt ab
16. s csc 1 t 3t 5 csc 1 t 3t csc 1 t 3t cot 1 t 3t ( 1 6t)œ Ê œ
&# %# # #
ab aba babab
ds
dt
5(6t 1) csc 1 t 3t cot 1 t 3tœ
&# #
abab
17. r 2 sin (2 sin ) (2 sin ) ( cos 2 sin )œœ Êœ #œ
È)) )) )) ) ) )
"Î# "Î#
"
#
dr cos sin
d2 sin
)
)) )
))
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 3 Practice Exercises 181
18. r 2 cos 2 (cos ) 2 (cos ) ( sin ) 2(cos ) 2 cos œœ Êœ œ)))) ) ) ) ) )
È È
ˆ‰
"Î# "Î# "Î#
"
#
dr sin
dcos
)
))
)
È
œ2 cos sin
cos
)) )
)
È
19. r sin 2 sin (2 ) cos (2 ) (2 ) (2)œœ Êœ œ
Ȉ‰
)) ) )
"Î# "Î# "Î#
"
#
dr
d
cos 2
2
)
)
)
È
È
20. r sin 1 cos 1 1 cos 1œÊœ œ
Š‹ Š‹Š‹ Š‹
ÈÈ È
)) )) ))
dr
d21
21
)))
)
"
#"
"
ÈÈ
È
21. y x csc x csc cot csc 2x csc cot x csc œÊœ œ
"""
## #
##
22222222
xdx xxx x xx x
dy ˆ‰ˆ‰ˆ‰ˆ‰
†
22. y 2 x sin x 2 x cos x sin x cos xœÊœ œ
ÈÈ È È È È
ˆ‰ ˆ‰
Š‹ Š‹
dy
dx 2x 2x x
2sin x
"
ÈÈÈ
È
23. y x sec (2x) x sec (2x) tan (2x) (2(2x) 2) sec (2x) xœÊœ
"Î# # "Î# # # # $Î#
"
#
dy
dx †ˆ‰
8x sec (2x) tan (2x) x sec (2x) x sec (2x) 16 tan (2x) x or sec x 16x tan 2xœœ #"
"Î# # # $Î# # "Î# # # # #
"" "
## #
#
c d ab ab
‘
x
2
24. y x csc (x 1) x csc (x 1)œœ
È$ "Î# $
x csc (x 1) cot (x 1) 3(x 1) csc (x 1) xʜ
dy
dx "Î# $ $ # $ "Î#
"
#
abab
ˆ‰
3 x (x 1) csc (x 1) cot (x 1) x csc (x 1) 6(x 1) cot (x 1)œ œ
ÈÈ
‘
#$$ $ #$
""
#
csc (x 1)
2x x
È
or csc(x 1) 1 6x(x 1) cot (x 1)
"
#
$#$
Èx cd
25. y 5 cot x 5 csc x (2x) 10x csc xœÊœ œ
#####
dy
dx ab ab
26. y x cot 5x x csc 5x (5) (cot 5x)(2x) 5x csc 5x 2x cot 5xœÊœ œ
### ##
dy
dx ab
27. y x sin 2x x 2 sin 2x cos 2x (4x) sin 2x (2x) 8x sin 2x cos 2x 2x sin 2xœÊœ œ
## # # # # # # $ # # # #
ab a ba b ab abab abab ab
dy
dx
28. y x sin x x 2 sin x cos x 3x sin x 2x 6 sin x cos x 2x sin xœÊœ œ
# # $ # $ $ # # $ $ $ $ $ # $
ab a ba ba b aba b ab ab abab ab
dy
dx
29. s 2 2œ Ê œ œ œ
ˆ‰ ˆ‰ ˆ‰
Š‹
4t ds 4t 4t 4
t 1 dt t 1 (t 1) t 1 (t 1) 8t
(t 1)(4) (4t)(1) (t 1)
# $ $
30. s (15t 1) ( 3)(15t 1) (15)œœÊœœ
" " "
$ %
15(15t 1) 15 dt 15
ds 3
(15t 1)
31. y 2œÊœ œœ
Š‹ Š‹
ÈÈ
Š‹
ˆ‰
È
xx
x 1 dx x 1 (x 1) (x 1) (x 1)
dy (x 1) 2x
(x 1) x (1) 1x
#
†
x
32. y 2 œÊœ œœ
Š‹ Š‹
2x 2x
2x1 2x 1
dy
dx
2x1 2x 4x
2x1 2x 1 2x1
4
ÈÈ
ÈÈ
ˆ‰ˆ‰
ÈÈ È
Š‹ Š‹ Š‹
ˆ‰ ˆ‰ˆ‰
ÈÈÈ
#
xx x
33. y 1 1œœÊœœ
Ɉ‰ ˆ‰ˆ‰
xx
xxdxxx
dy
x1
" """ "
"Î# "Î#
##
Éx
34. y 4x x x 4x x x 4x x x 1 x x x (4)œœ Êœ
ÉȈ‰ ˆ‰ˆ‰ˆ ‰ˆ‰
"Î# "Î# "Î# "Î#
"Î# "Î# "Î#
""
##
dy
dx
xx 2x1 4xx xx 2xx4x4xœ œ œ
ˆ‰ ˆ‰ˆ‰ˆ ‰
ÈÈÈÈÈ
’“Š‹
"Î# "Î#
"
#
ÈÈ
ÉÈ
x
6x 5 x
xx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

182 Chapter 3 Differentiation
35. r 2œÊœ
ˆ‰ ˆ‰
’“
sin dr sin
cos 1 d cos 1 (cos 1)
(cos 1)(cos ) (sin )( sin )
))
))) )
))))
#
2œœœ
ˆ‰
Š‹
sin cos cos sin 2 sin
cos (cos ) (cos 1) (cos )
(2 sin ) (1 cos )
)))) )
)) ) )
))
" " "
36. r 2œÊœ
ˆ‰ ˆ‰
’“
sin 1 dr sin 1
1 cos d 1 cos (1 cos )
(1 cos )(cos ) (sin )(sin )
))
)) ) )
)) ) )
#"
cos cos sin sin œœ
2(sin ) 2(sin 1)(cos sin 1)
(1 cos ) (1 c os )
))))
))
"
##
ab))))
37. y (2x 1) 2x 1 (2x 1) (2x 1) (2) 3 2x 1œ œ Êœ œ
ÈÈ
$Î# "Î#
#
dy
dx
3
38. y 20(3x 4) (3x 4) 20(3x 4) 20 (3x 4) (3)œ œ Êœ œ
"Î% "Î& "Î#! "*Î#!
"
dy
dx 20
3
(3x 4)
ˆ‰
39. y 3 5x sin 2x 3 5x sin 2x [10x (cos 2x)(2)]œ Êœ œab ab
ˆ‰
##
$Î# &Î#
#
dy 9(5x cos 2x)
dx
3
5x sin 2xab
40. y 3 cos 3x 3 cos 3x 3 cos 3x ( sin 3x)(3)œ Ê œ œab abab
$$#
"Î$ %Î$
"
dy
dx 3
3 cos 3x sin 3x
3 cos 3x
ab
41. xy 2x 3y 1 xy y 2 3y 0 xy 3y 2 y y (x 3) 2 y yœÊ œÊ œÊ œÊœab
wwww w w
y2
x3
42. x xy y 5x 2 2x x y 2y x 2y 5 2x y (x 2y)
##
œÊ &œ!Ê œÊ
Š‹
dy dy dy dy dy
dx dx dx dx dx
52xy œ Ê œ
dy 52xy
dx x 2y
43. x 4xy 3y 2x 3x 4x 4y 4y 2 4x 4y 2 3x 4y
$ %Î$ # "Î$ "Î$ #
œÊ œÊ œ
Š‹
dy dy dy dy
dx dx dx dx
4x 4y 2 3x 4y ʜʜ
dy dy 2 3x 4y
dx dx 4x 4y
ˆ‰
"Î$ #
44. 5x 10y 15 4x 12y 0 12y 4x x y
%Î& 'Î& "Î& "Î& "Î& "Î& "Î& "Î&
""
œÊ œÊ œÊœ œ
dy dy dy
dx dx dx 3 3(xy)
45. (xy) 1 (xy) x y 0 x y x y x y
"Î# "Î# "Î# "Î# "Î# "Î# "
"
#
œÊ œÊ œ Ê œ Ê œ
Š‹
dy dy dy dy y
dx dx dx dx x
46. x y 1 x 2y y (2x) 0 2x y 2xy
## # # # #
œÊ œÊ œ Ê œ
Š‹
dy dy dy y
dx dx dx x
47. y 2y
#
#
"
œÊ œ Êœ
x
x 1 dx (x 1) dx y(x 1)
dy (x 1)(1) (x)(1) dy
48. y y 4y
#%$
" "
"
"Î# Ð"
œÊœÊœ Êœ
ˆ‰
1x x
1x 1x dx ( x) dx 2y(1x)
dy dy
(1 x)(1) (1 x) )
49. p 4pq 3q 2 3p 4 p q 6q 0 3p 4q 6q 4p 3p 4q 6q 4p
$## # #
œÊ œÊ œ Ê œ
dp dp dp dp dp
dq dq dq dq dq
Š‹ ab
ʜ
dp 6q 4p
dq 3p 4q
50. q 5p 2p 1 5p 2p 10p 2 5p 2p (10p 2)œ Êœ Êœ ab ab ab
Š‹
## #
$Î# &Î# &Î#
#
32
dp dp dp
dq dq 3 dq
ʜ
dp
dq 3(5p 1)
5p 2pab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 3 Practice Exercises 183
51. r cos 2s sin s r( sin 2s)(2) (cos 2s) 2 sin s cos s 0 (cos 2s) 2r sin 2s 2 sin s cos sœÊ œÊ œ
#1ˆ‰
dr dr
ds ds
(2r 1)(tan 2s)Êœ œ œ
dr 2r sin 2s sin 2s
ds cos 2s cos 2s
(2r 1)(sin 2s)
52. 2rs r s s 3 2 r s 1 2s 0 (2s 1) 1 2s 2r œ Ê œ Ê œ Ê œ
#"
ˆ‰
dr dr dr dr 2s 2r
ds ds ds ds 2s 1
53. (a) x y 1 3x 3y 0
$$ # #
œÊ œÊ œ Ê œ
dy dy d y
dx dx y dx
xy ( 2x) x 2y
y
ab
Š‹
dy
dx
Êœ œ œ
d y 2xy 2x
dx y
2xy 2yx
yy
2xy
ab
Š‹
x
yy
2x
(b) y 1 2y yx yx y(2x) x
####
"" #
œÊ œÊœ Êœ Ê œ
22
x dx x dx yx dx dx dx
dy dy dy d y dy
ab ab’“
Êœ œ
d y 2xy 1
dx
2xy x
yx yx
Š‹
yx
54. (a) x y 1 2x 2y 0 2y 2x
##
œÊ œÊ œ Ê œ
dy dy dy
dx dx dx y
x
(b) (since y x 1)
dy d y y x
dx y dx y y y y
xy(1) x yx
œÊ œ œ œ œ œ
" ##
dy
dx
x
y
Š‹
55. (a) Let h(x) 6f(x) g(x) h (x) 6f (x) g (x) h (1) 6f (1) g (1) 6œÊ œ Ê œ œ %œ(
www www "
#
ˆ‰ ab
(b) Let h(x) f(x)g (x) h (x) f(x) g(x) g (x) g (x)f (x) h (0) f(0)g(0)g (0) g (0)f (0)œÊœ# Êœ#
# w w#w w w#w
ab
(1)(1) (1) ( )œ# $ œ#
ˆ‰
"
#
#
(c) Let h(x) h (x) h (1)œÊœ Êœ
f(x) (g(x) 1)f (x) f(x)g (x) (g(1) )f (1) f(1)g (1)
g(x) 1 (g(x) 1) (g(1) 1)
ww
"
œœ
(1) 3
(1)
& %
& "#
&
ˆ‰ ab
(d) Let h(x) f(g(x)) h (x) f (g(x))g (x) h (0) f (g(0))g (0) f (1)œÊœ Êœ œ œ œ
www wwww
""""
###%
ˆ‰ ˆ‰ˆ‰
(e) Let h(x) g(f(x)) h (x) g (f(x))f (x) h (0) g (f(0))f (0) g (1)f (0) ( )œÊœ Êœ œ œ%$œ"#
www wwwww
ab
(f) Let h(x) (x f(x)) h (x) (x f(x)) 1 f (x) h (1) (1 f(1)) 1 f (1)œ Êœ Êœ
$Î# w "Î# w w "Î# w
##
33
ab ab
(1 3) 1œ œ
3
###
"Î# "*
ˆ‰
(g) Let h(x) f(x g(x)) h (x) f (x g(x)) 1 g (x) h (0) f (g(0)) 1 g (0)œÊœ Êœ
ww w ww w
ab ab
f (1) 1œœ œ
w""$$
###%
ˆ ‰ ˆ‰ˆ‰
56. (a) Let h(x) x f(x) h (x) x f (x) f(x) h (1) 1 f (1) f(1) ( 3)œÊœ Êœ œœ
ÈÈ Èˆ‰
ww ww
""""
###
††
ÈÈ
x1510
13
(b) Let h(x) (f(x)) h (x) (f(x)) f (x) h (0) (f(0)) f (0) (9) ( 2)œÊœ Êœ œœ
"Î# w "Î# w w "Î# w "Î#
""""
###
ab 3
(c) Let h(x) f x h (x) f x h (1) f 1œÊœ Êœ œœ
ˆ‰ ˆ‰
ÈÈ Š‹
È
ww ww
"""""
###
†††
ÈÈ
x1510
(d) Let h(x) f(1 5 tan x) h (x) f (1 5 tan x) 5 sec x h (0) f (1 5 tan 0) 5 sec 0œ Êœ Êœ
ww # ww #
ab ab
f (1)( 5) ( 5) 1œœœ
w"
5
(e) Let h(x) h (x) h (0)œÊœ Êœ œœ
f(x) (2 cos x)f (x) f(x)( sin x) (2 1)f (0) f(0)(0) 3( 2)
2 cos x (2 cos x) (2 1) 9 3
2
ww
(f) Let h(x) 10 sin f (x) h (x) 10 sin 2f(x)f (x) f (x) 10 cosœÊœ
ˆ‰ ˆ‰ ˆ ‰ˆ‰
ab ˆ‰
11 11xx x
## ##
#w w#
h (1) 10 sin 2f(1)f (1) f (1) 10 cos 20( 3) 12Êœ œ!œ
ww#
###
"
ˆ‰ ˆ ‰ˆ‰ ˆ‰
ab ˆ‰
111
5
57. x t 2t; y 3 sin 2x 3(cos 2x)(2) 6 cos 2x 6 cos 2t 2 6 cos 2t ; thus,œ Ê œ œ Ê œ œ œ œ
###
11
dx
dt dx
dy abab
6 cos 2t 2t 6 cos (0) 0 0
dy dy dy
dt dx dt dt
dx
œœ Êœ œ†† †ab ¹
#
t=0
58. t u 2u u 2u (2u 2) u 2u (u 1); s t 5t 2t 5œ Êœ œ œÊœab ab ab
## ##
"Î$ #Î$ #Î$
"dt 2 ds
du 3 3 dt
2 u 2u 5; thus 2 u 2u 5 u 2u (u 1)œ œ œ ab ab ab
’“
ˆ‰
###
"Î$ "Î$ #Î$
ds ds dt 2
du dt du 3
†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

184 Chapter 3 Differentiation
2 2 2(2) 5 2 2(2) (2 1) 2 2 8 5 8 2(2 2 5)Êœ œ œœ
¸ˆ‰ˆ‰ˆ‰ˆ‰
’“
ab ab
ds 2 9
du 3 4
u=2
# # "Î$ #Î$
"Î$ #Î$ "
#
††
59. r 8 sin s 8 cos s ; w sin r 2 cos r 2œÊœ œ Êœ
ˆ‰ ˆ‰ ˆ ‰ ˆ ‰
ÈÈ
Š‹
11
6ds 6 dr
dr dw
r
"
#È
; thus, 8 cos sœœœ
cos 8 sin s 2
2 8 sin s 8 sin s
cos 8 sin s 2
ÉŠ‹
ˆ‰
ÉÉ
ˆ‰ ˆ‰
Ɉ‰
#
6
66
6
dw dw dr
ds dr ds 6
††
‘ˆ‰
1
3Êœ œ œ
¸È
dw
ds s=0
cos 8 sin 2 8 cos (cos 0)(8)
28 sin 24
Š‹ Š‹
Ɉ‰ ˆ‰
Ɉ‰ È
66
6
3
†
60. t 1 t 2 0 (2 t 1) ; r 7)) ) ) ) ) )
## # #
"Î$
œ Ê œ Ê œ Ê œ œ
ˆ‰ˆ‰ ab
dd d d
dt dt dt dt 2 t 1
)) ) ))
)
7 (2 ) 7 ; now t 0 and t 1 1 so that 1Êœ œ œ œÊœ œœ
dr 2 d1
d3 3 dt 1)
)"
## #
#Î$ #Î$
ab ab ¸
)))) ))) t=0, =1
and (1 7) ( 1)
¸¸¸¸ˆ‰
dr 2 dr dr d
d3 6dtddt6 6))
)
=1 t=0 t=0 t=0
œ œÊ œ œ œ
#Î$ """
†
61. y y 2 cos x 3y 2 sin x 3y 1 2 sin x
$# #
œ Ê œ Ê œ Ê œ Ê
dy dy dy dy dy
dx dx dx dx 3y 1 dx
2 sin x
ab ¹(0 1)
0; œœœ
2 sin (0) d y
31 dx
3y 1 ( 2 cos x) ( 2 sin x) 6y
3y 1
ab Š‹
ab
dy
dx
Êœ œ
¹
d y (3 1)( 2 cos 0) ( 2 sin 0)(6 0)
dx (3 1)
(0 1)
#
"
†
62. x y 4 x y 0 1;
"Î$ "Î$ #Î$ #Î$
""
œÊ œÊœÊ œ œ
3 3 dx dx dx dx
dy dy y dy dy y
xx
¹(8 8)
Êœ Ê œ
dy dy
dx dx
xy yx
x
88(1)88
8
ˆ‰ ˆ ‰ˆ ‰
Š‹
ab ˆ‰ ‘ˆ‰ˆ ‰
22
3dx 3
dy 22
33
¹(8 8)
†† †
œœœ
33 3
2
"
846
63. f(t) and f(t h) œœÊœœ
""
#
2t 1 (t h) 1 h h (2t 2h 1)(2t 1)h
f(th)f(t) 2t1(2t2h1)
(t h) 1 t 1
f (t) lim lim œœÊœœ
#
w
2h 2 2
(2t 2h 1)(2t 1)h (2t 2h 1)(2t 1) h (2t 2h 1)( t 1)
f(t h) f(t)
hhÄ! Ä!
œ#
(2t 1)
64. g(x) 2x 1 and g(x h) 2(x h) 1 2x 4xh 2h 1 œ œœÊ
####
g(x h) g(x)
h
4x 2h g (x) lim lim (4x 2h)œœœÊœœ
abab2x 4xh 2h 1 2x 1
hh h
4xh 2h g(x h) g(x)
w
hhÄ! Ä!
4xœ
65. (a)
(b) lim f(x) lim x 0 and lim f(x) lim x 0 lim f(x) 0. Since lim f(x) 0 f(0) it
xx x x
xx
Ä! Ä! Ä! Ä!
Ä! Ä!
œœ œœÊ œ œœ
##
follows that f is continuous at x 0.œ
(c) lim f (x) lim (2x) 0 and lim f (x) lim ( 2x) 0 lim f (x) 0. Since this limit exists, it
xx x
xx
Ä! Ä! Ä!
Ä! Ä!
ww w
œœ œœÊœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 3 Practice Exercises 185
follows that f is differentiable at x 0.œ
66. (a)
(b) lim f(x) lim x 0 and lim f(x) lim tan x 0 lim f(x) 0. Since lim f(x) 0 f(0), it
xx x x
xx
Ä! Ä! Ä! Ä!
Ä! Ä!
œœ œ œÊ œ œœ
follows that f is continuous at x 0.œ
(c) lim f (x) lim 1 1 and lim f (x) lim sec x 1 lim f (x) 1. Since this limit exists it
xx x
xx
Ä! Ä! Ä!
Ä! Ä!
ww#w
œœ œ œÊ œ
follows that f is differentiable at x 0.œ
67. (a)
(b) lim f(x) lim x 1 and lim f(x) lim (2 x) 1 lim f(x) 1. Since lim f(x) 1 f(1), it
xx x x
xx
Ä" Ä" Ä" Ä"
Ä" Ä"
œœ œ œÊ œ œœ
follows that f is continuous at x 1.œ
(c) lim f (x) lim 1 1 and lim f (x) lim 1 1 lim f (x) lim f (x), so lim f (x) does
xx x
xx x x1
Ä" Ä" Ä"
Ä" Ä" Ä" Ä
ww www
œœ œœÊ Á
not exist f is not differentiable at x 1.ʜ
68. (a) lim f(x) lim sin 2x 0 and lim f(x) lim mx 0 lim f(x) 0, independent of m; since
xx x
xx
Ä! Ä! Ä!
Ä! Ä!
œœ œœÊœ
f(0) 0 lim f(x) it follows that f is continuous at x 0 for all values of m.œœ œ
xÄ!
(b) lim f (x) lim (sin 2x) lim 2 cos 2x 2 and lim f (x) lim (mx) lim m m f is
xx x xx x
Ä! Ä! Ä! Ä! Ä! Ä!
ww ww
œœœ œœœÊ
differentiable at x 0 provided that lim f (x) lim f (x) m 2.œœÊœ
xx
Ä! Ä!
ww
69. y x (2x 4) 2(2x 4) ; the slope of the tangent is œ œ Ê œ Ê
x33
x4 dx
dy
## # # # #
"" "
" #
2(2x 4) 2 2(2x 4) 1 (2x 4) 1 4x 16x 16 1œ Êœ Ê œ Ê œ Ê œ
""
#
# # # #
(2x 4)
4x 16x 15 0 (2x 5)(2x 3) 0 x or x and are points on theÊœÊ œÊœ œÊß ß
#
### #
"53593
44
ˆ‰ˆ ‰
curve where the slope is .3
#
70. y x 1 1 ; the slope of the tangent is 3 3 1 2 xœ Ê œ œ Ê œ Ê œ Ê œ
"" """
###
#
2x dx (2x) x x x 4
dy 2
x and are points on the curve where the slope is 3.Êœ„ Ê ß ß
""" ""
### ##
ˆ‰ˆ‰
71. y 2x 3x 12x 20 6x 6x 12; the tangent is parallel to the x-axis when 0œÊœ œ
$# #
dy dy
dx dx
6x 6x 12 0 x x 2 0 (x 2)(x 1) 0 x 2 or x 1 ( ) and ( 7) areÊ œ Ê œ Ê œ Ê œ œ Ê #ß! "ß#
##
points on the curve where the tangent is parallel to the x-axis.
72. y x 3x 12; an equation of the tangent line at ( ) is y 8 12(x 2)œ Ê œ Ê œ #ß ) œ
$#
dy dy
dx dx ¹(2 8)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
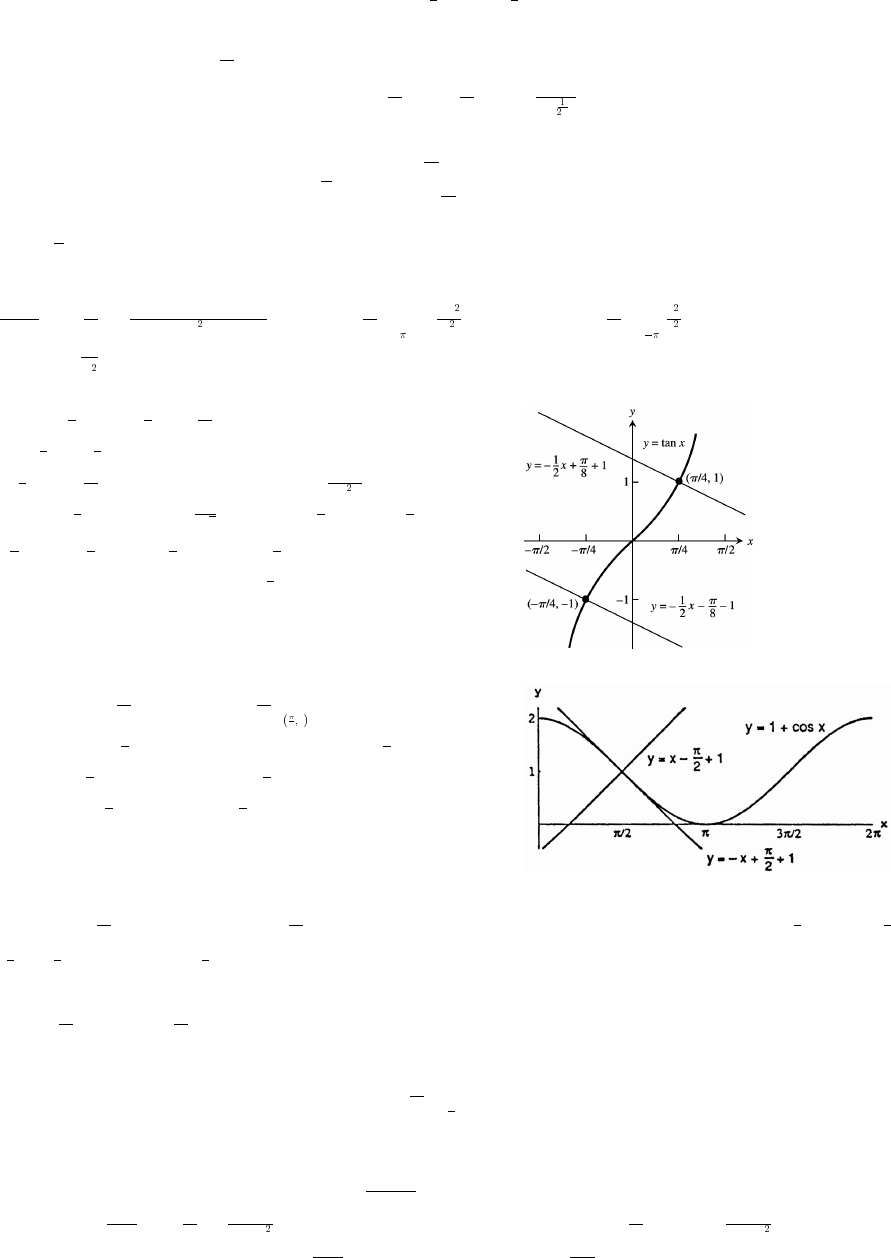
186 Chapter 3 Differentiation
y 12x 16; x-intercept: 0 12x 16 x ; y-intercept: y 12(0) 16 16 (0 16)Êœ œ ÊœÊß! œ œ Êß
44
33
ˆ‰
73. y 2x 3x 12x 20 6x 6x 12œÊœ
$# #
dy
dx
(a) The tangent is perpendicular to the line y 1 when 24; 6x 6x 12 24œ œ œ œ
x
24 dx
dy Š‹
"
#
ˆ‰
4
x x 2 4 x x 6 0 (x 3)(x 2) 0 x 2 or x 3 ( 16) and ( 11) areÊœÊœÊ œÊœ œÊ#ß $ß
##
points where the tangent is perpendicular to y 1 .œ
x
24
(b) The tangent is parallel to the line y 2 12x when 12 6x 6x 12 12 x x 0œ œÊ œÊœ
Èdy
dx ##
x(x 1) 0 x 0 or x 1 ( 20) and ( ) are points where the tangent is parallel toʜʜ œÊ!ß "ß(
y 2 12x.œ
È
74. y m 1 and m 1.œÊœ Êœœœ œ œ
111
11
11
sin x
x dx x dx dx
dy x( cos x) ( sin x)(1) dy dy
"#
¹¹
x= x=
Since m the tangents intersect at right angles.
""
œm
75. y tan x, x sec x; now the slopeœÊœ
11
##
#
dy
dx
of y is the normal line is parallel toœ Ê
x
##
"
y when 2. Thus, sec x 2 2œ œ œ Ê œ
xdy
dx cos x#
#"
cos x cos x x and xʜʜʜ œ
#"„"
#È244
11
for x 1 and are points Êß ß"
11 1 1
##
ˆ‰ˆ‰
44
where the normal is parallel to y .œx
#
76. y 1 cos x sin x 1œ Ê œ Ê œ
dy dy
dx dx ¹21
the tangent at 1 is the line y 1 xÊßœ
ˆ‰ ˆ ‰
11
##
y x 1; the normal at 1 isÊœ ß
11
##
ˆ‰
y1(1)x yx 1œ Ê œ
ˆ‰
11
##
77. y x C 2x and y x 1; the parabola is tangent to y x when 2x 1 x y ;œÊ œ œÊ œ œ œÊœÊœ
#""
##
dy dy
dx dx
thus, C C
"" "
##
#
œÊœ
ˆ‰ 4
78. y x 3x 3a the tangent line at a a is y a 3a (x a). The tangent lineœÊœ Ê œ Ê ß œ
$# # $$#
dy dy
dx dx ¹ab
x=a
intersects y x when x a 3a (x a) (x a) x xa a 3a (x a) (x a) x xa 2a 0œ œÊœÊœ
$$$# # ## # #
ab a b
(x a) (x 2a) 0 x a or x 2a. Now 3( 2a) 12a 4 3a , so the slope atÊ œÊœ œ œ œ œ
### #
¹ab
dy
dx x= 2a
x 2a is 4 times as large as the slope at a a where x a.œ ß œab
$
79. The line through ( ) and (5 2) has slope m 1 the line through ( ) and ( 2) is!ß $ ß œ œ Ê !ß $ &ß
3(2)
05
y x 3; y , so the curve is tangent to y x 3 1œ œ Ê œ œ Ê œ œ
cc c
x 1 dx (x 1) dx (x 1)
dy dy
(x 1) c, x 1. Moreover, y intersects y x 3 x 3, x 1Ê œ Á œ œ Ê œ Á
#
cc
x1 x1
c (x 1)( x 3), x 1. Thus c c (x 1) (x 1)( x 3) (x 1)[x 1 ( x 3)]Êœ Á œÊ œÊ
#
, x 1 (x 1)(2x 2) 0 x 1 (since x 1) c 4.œ! Á Ê œ Ê œ Á Ê œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Chapter 3 Practice Exercises 187
80. Let b a b be a point on the circle x y a . Then x y a 2x 2y 0
Š‹
È
ß„ œ œ Ê œ Ê œ
## ### ### dy dy
dx dx y
x
normal line through b a b has slope normal line isÊœ Ê ß„ Ê
¹Š‹
È
dy
dx b
b
ab
ab
x=b
„
## „
ÈÈ
yab (xb) yab xab y x„ œ Ê … œ … Ê œ„
Š‹
ÈÈÈ
## ## ##
„ „
ÈÈÈ
ab ab ab
bbb
which passes through the origin.
81. x 2y 9 2x 4y 0 the tangent line is y 2 (x 1)
## ""
œÊ œÊœÊ œÊ œ
dy dy dy
dx dx 2y dx 4 4
x¹(1 2)
x and the normal line is y 2 4(x 1) 4x 2.œ œ œ
"
44
9
82. x y 2 3x 2y 0 the tangent line is y 1 (x 1)
$# #
##
œÊ œÊœÊ œÊ œ
dy dy dy
dx dx 2y dx
3x 3 3
¹(1 1)
x and the normal line is y 1 (x 1) x .œ œ œ
35 2 2
333##
"
83. xy 2x 5y 2 x y 2 5 0 (x 5) y 2 2œÊ œÊ œÊ œ Ê œ
Š‹ ¹
dy dy dy dy y 2 dy
dx dx dx dx x 5 dx
(3 2)
the tangent line is y 2 2(x 3) 2x 4 and the normal line is y 2 (x 3) x .Êœœ œœ
"
###
17
84. (y x) 2x 4 2(y x) 1 2 (y x) 1 (y x) œÊ œÊ œÊœ Ê œ
#
Š‹ ¹
dy dy dy 1 y x dy
dx dx dx y x dx 4
3
(6 2)
the tangent line is y 2 (x 6) x and the normal line is y 2 (x 6) x 10.Êœœ œœ
335 4 4
44 3 3#
85. x xy 6 1 x y 0 x y 2 xy œÊ œÊœ Êœ Ê œ
ÈÈ
Š‹ ¹
"
#
ÈÈ
xy dx dx dx x dx 4
dy dy dy dy
2xyy 5
(4 1)
the tangent line is y 1 (x 4) = x 6 and the normal line is y (x 4) x .Ê œ œ"œ
55 4411
44 555
86. x 2y 17 x 3y 0 the tangent line is
$Î# $Î# "Î# "Î# "
œÊ œÊœÊ œÊ
3x
2dxdxdx4
dy dy dy
2y ¹(1 4)
y 4 (x 1) x and the normal line is y 4 4(x 1) 4x.œ œ œ œ
""
444
17
87. x y y x y x 3y y 3x 2y 1 3x y 2y 3x y
$$ # $ # $ # $# #$
œÊ œ Ê œ"
’“Š‹ab
dy dy dy dy dy dy
dx dx dx dx dx dx
3x y 2y 1 1 3x y , but is undefined.ʜʜ ʜ
dy dy 1 3x y dy dy
dx dx 3x y 2y 1 dx 4 dx
2
ab ¹¹
$# #$
(1 1) (1 1)
Therefore, the curve has slope at ( ) but the slope is undefined at ( 1). "ß " "ß
"
#
88. y sin (x sin x) [cos (x sin x)](1 cos x); y 0 sin (x sin x) 0 x sin x k ,œ Êœ œÊ œÊœ
dy
dx 1
k 2, 1, 0, 1, 2 (for our interval) cos (x sin x) cos (k ) 1. Therefore, 0 and y 0 whenœ Ê œ œ „ œ œ1dy
dx
1 cos x 0 and x k . For x 2 , these equations hold when k 2, 0, and 2 (sinceœ œ #ŸŸ œ111
cos ( ) cos 1). Thus the curve has horizontal tangents at the x-axis for the x-values 2 , 0, and 2œ œ 11 11
(which are even integer multiples of ) the curve has an infinite number of horizontal tangents.1Ê
89. x tan t, y sec t sin t sin ; tœœÊœœœœÊœœœ
""
## #
dy dy/dt dy
dx dx/dt sec t dx 3 3
sec t tan t
sec t
tan t 3
¹t3
11
È
x tan and y sec 1 y x ; 2 cos t Êœ œ œ œÊœ œ œ œ Ê
"" "
### #
$
11
3 3 4 dx dx/dt dx
33
dy dy/dt dy
cos t
sec t
ÈÈ ¸t3
2 cosœœ
$"
ˆ‰
1
34
90. x , y t (2) 3; t 2 x 1 andœ" œ" Ê œ œ œ Ê œ œ œ Ê œ œ
" "
##t t dx dx/dt 2 dx 4
333 5
dy dy/dt dy
Š‹
Š‹
3
t
2
t¹t2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
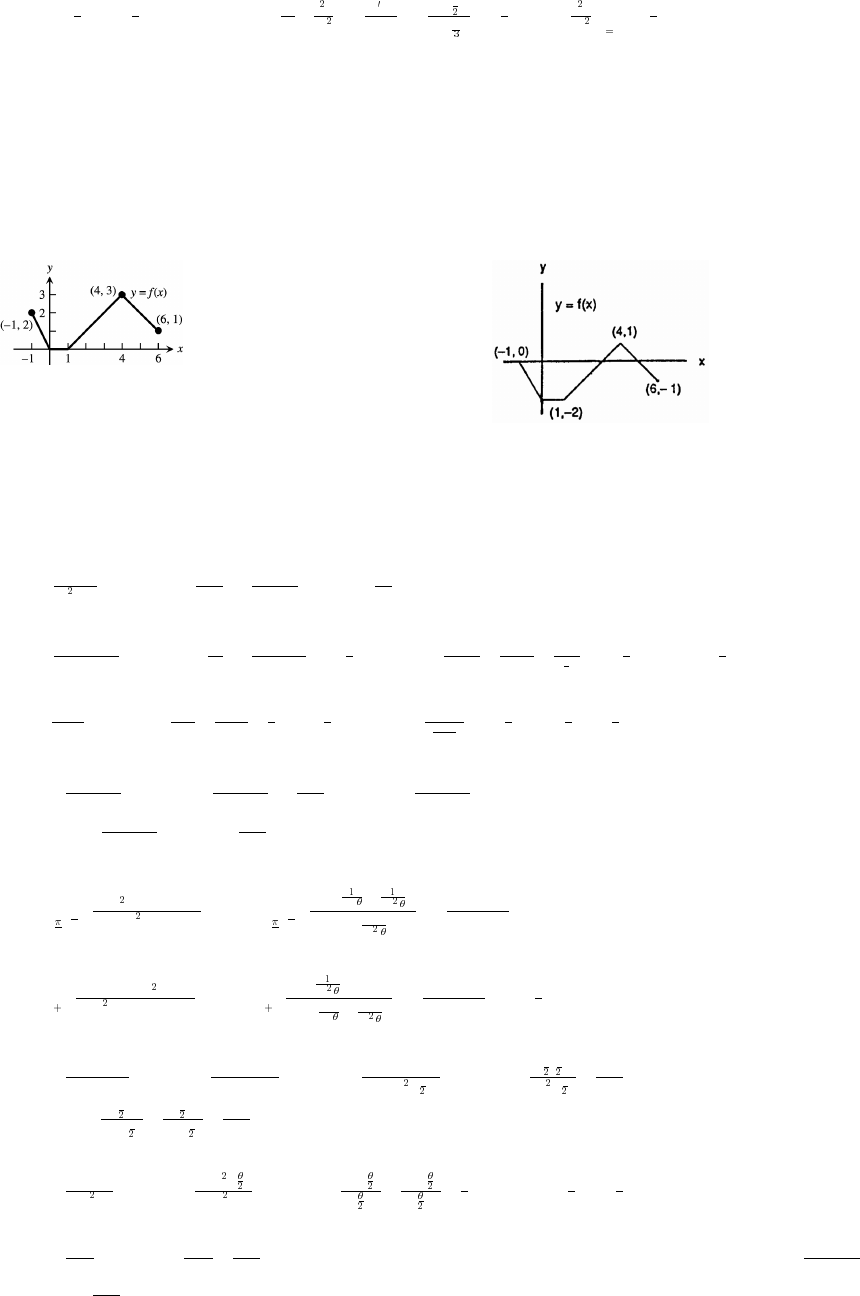
188 Chapter 3 Differentiation
y1 y 3x ; t (2) 6œœ Ê œ œ œ œ Ê œ œ
3333
4 dx dx/dt 4 dx 4
dy dy/dt dy
##
""
$$
ˆ‰
Š‹
3
2
t¹t2
91. B graph of f, A graph of f . Curve B cannot be the derivative of A because A has only negative slopesœœ
w
while some of B's values are positive.
92. A graph of f, B graph of f . Curve A cannot be the derivative of B because B has only negative slopesœœ
w
while A has positive values for x 0.
93. 94.
95. (a) 0, 0 (b) largest 1700, smallest about 1400
96. rabbits/day and foxes/day
97. lim lim (1) 1
xxÄ! Ä!
sin x sin x
2x x x ( x 1) 1
#
""
œœœ
’“
ˆ‰ ˆ‰
†
98. lim lim lim 1 1 2
xx xÄ! Ä! Ä!
3x tan 7x 3x sin 7x 3 sin 7x 3 7
x 2x 2x cos 7x cos 7x 7x 2
""
## #
œ œ œ œ
ˆ‰ ˆ‰
Š‹
†† ††
ˆ‰
2
7
99. lim lim (1) lim (1)
rr rÄ! Ä! Ä!
sin r sin r 2r cos 2r
tan 2r r tan 2r 1
œœœœ
ˆ ‰ ˆ‰ ˆ‰ ˆ‰
††
"" " ""
## # #
ˆ‰
sin 2r
2r
100. lim lim lim . Let x sin . Then x 0 as 0
)) )Ä! Ä! Ä!
sin (sin ) sin (sin ) sin (sin )
sin sin
sin
)) )
))))
)
œœœÄÄ
Š‹
ˆ‰ ))
lim lim 1Êœœ
)Ä! Ä!
sin (sin )
sin x
sin x
)
)x
101. lim lim 4
))ÄÄ
ˆ‰ ˆ‰
22
4 tan tan 1
tan (1 0)
4(400)
))
)
&
"
œœœ
Š‹
Š‹
tan tan
5
tan
102. lim lim
))Ä! Ä!
12 cot 2
5 cot 7 cot 8 (5 0 0) 5
2
5
(0 2)
)
))
œœœ
Š‹
Š‹
cot
78
cot cot
103. lim lim lim lim
xx x xÄ! Ä! Ä! Ä!
x sin x x sin x x sin x sin x
2 2 cos x 2(1 cos x) x
22 sin sin
œœ œ
ˆ‰ ˆ‰ˆ‰
xx
xx
’“
†
†
lim (1)(1)(1) 1œœœ
xÄ! ’“
ˆ‰ ˆ‰
ˆ‰ ˆ‰
xx
xx
sin sin
sin x
x
††
104. lim lim lim (1)(1)
)) )Ä! Ä! Ä!
1cos 2 sin sin sin
"""
###
)
))
œœ œœ
ˆ‰ ˆ‰ ˆ‰
ˆ‰ ˆ‰
’“
ˆ‰
††
105. lim lim 1; let tan x 0 as x 0 lim g(x) lim
xx xxÄ! Ä! Ä! Ä!
tan x sin x
xcos xx tan x
tan (tan x)
œœœÊÄÄÊœ
ˆ‰
"†))
lim 1. Therefore, to make g continuous at the origin, define g(0) 1.œœ œ
)Ä!
tan )
)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 3 Practice Exercises 189
106. lim f(x) lim lim 1 lim (us
xx x xÄ! Ä! Ä! Ä!
œœ œ
tan (tan x) tan (tan x)
sin (sin x) tan x sin (sin x) cos x sin (sin x)
sin x sin x
’“
†† †
"ing the result of
#105); let sin x 0 as x 0 lim lim 1. Therefore, to make f))œÊÄ ÄÊ œ œ
xÄ! Ä!
sin x
sin (sin x) sin
)
)
)
continuous at the origin, define f(0) 1.œ
107. (a) S 2 r 2 rh and h constant 4 r 2 h (4 r 2 h) œ Êœ œ11 1 1 11
#dS dr dr dr
dt dt dt dt
(b) S 2 r 2 rh and r constant 2 r œ Êœ11 1
#dS dh
dt dt
(c) S 2 r 2 rh 4 r r h (4 r 2 h) 2 r œ Êœ # œ 11 1 1 11 1
#dS dr dh dr dr dh
dt dt dt dt dt dt
ˆ‰
(d) S constant 0 0 (4 r 2 h) 2 r (2r h) r ʜʜ Ê œ Êœ
dS dr dh dr dh dr r dh
dt dt dt dt dt dt 2r h dt
11 1
108. S r r h r r h ;œÊœ 111
ÈÈ
## ##
dS dr
dt dt
r h
rh
†ˆ‰
È
dr dh
dt dt
(a) h constant 0 r h r h ʜʜ œ
dh dS dr r dr
dt dt dt dt
r
rh rh
11
dr
dt
ÈÈ
## ##
11
ÈÈ
’“
(b) r constant 0 ÊœÊ œ
dr dS rh dh
dt dt dt
rh
1
È
(c) In general, r h
dS r dr rh dh
dt dt dt
rh rh
œ
’“
È
1##
11
ÈÈ
109. A r 2 r ; so r 10 and m/sec (2 )(10) 40 m /secœÊœ œ œ Êœ œ11 1
# #
dA dr dr 2 dA 2
dt dt dt dt11
ˆ‰
110. V s 3s ; so s 20 and 1200 cm /min (1200) 1 cm/minœÊ œ Êœ œ œ Êœ œ
$# $
""dV ds ds dV dV ds
dt dt dt 3s dt dt dt 3(20)
†
111. 1 ohm/sec, 0.5 ohm/sec; and . Also,
dR dR dR dR
dt dt R R R R dt dt dt
dR
RR
œ œ œ Ê œ
""" " " "
R 75 ohms and R 50 ohms R 30 ohms. Therefore, from the derivative equation,
"#
"""
œœÊœÊœ
R7550
( 1) (0.5) ( 900)
" " " " " "
(30) dt (75) (50) 5625 5000 dt 5625 5000 50(5625) 50
dR dR 5000 5625 9(625)
œ œ Êœ œ œ
ˆ‰ ˆ‰
†
0.02 ohm/sec.œ
112. 3 ohms/sec and 2 ohms/sec; Z R X so that R 10 ohms and
dR dX dZ
dt dt dt
R X
RX
œœœÊœ œ
È##
dR dX
dt dt
È
X 20 ohms 0.45 ohm/sec.œÊœ œ¸
dZ
dt
(10)(3) (20)( 2)
10 20 5
"
ÈÈ
113. Given 10 m/sec and 5 m/sec, let D be the distance from the origin D x y 2D
dx dD
dt dt dt
dy
œœ ÊœÊ
###
2x 2y D x y . When (x y) ( ), D andœ Ê œ ßœ$ß%œ$%œ&
dx dD dx
dt dt dt dt dt
dy dy Éab
##
(5)(10) (12)(5) 22. Therefore, the particle is moving the origin at 22 m/sec&œ Ê œ œ
dD dD 110
dt dt 5 away from
(because the distance D is increasing).
114. Let D be the distance from the origin. We are given that 11 units/sec. Then D x y
dD
dt œœ
###
x x x x 2D 2x 3x x(2 3x) ; x 3 D 3 3 6œ œ Ê œ œ œÊ œ œ
# $Î# # $ #
##$
ˆ‰ È
dD dx dx dx
dt dt dt dt
and substitution in the derivative equation gives (2)(6)(11) (3)(2 9) 4 units/sec.œ Êœ
dx dx
dt dt
115. (a) From the diagram we have r h.
10 4 2
hr 5
œÊœ
(b) V r h h h , so 5 and h 6 ft/min.œœ œÊœ œœÊœ
""
##
3 3 5 75 dt 25 dt dt dt 144
2 4 h dV 4 h dh dV dh 125
11
ˆ‰ 11
1
116. From the sketch in the text, s r r . Also r 1.2 is constant 0œÊœ œ Êœ))
ds d dr dr
dt dt dt dt
)
r (1.2) . Therefore, 6 ft/sec and r 1.2 ft 5 rad/secÊœ œ œ œ Êœ
ds d d ds d
dt dt dt dt dt
)) )
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
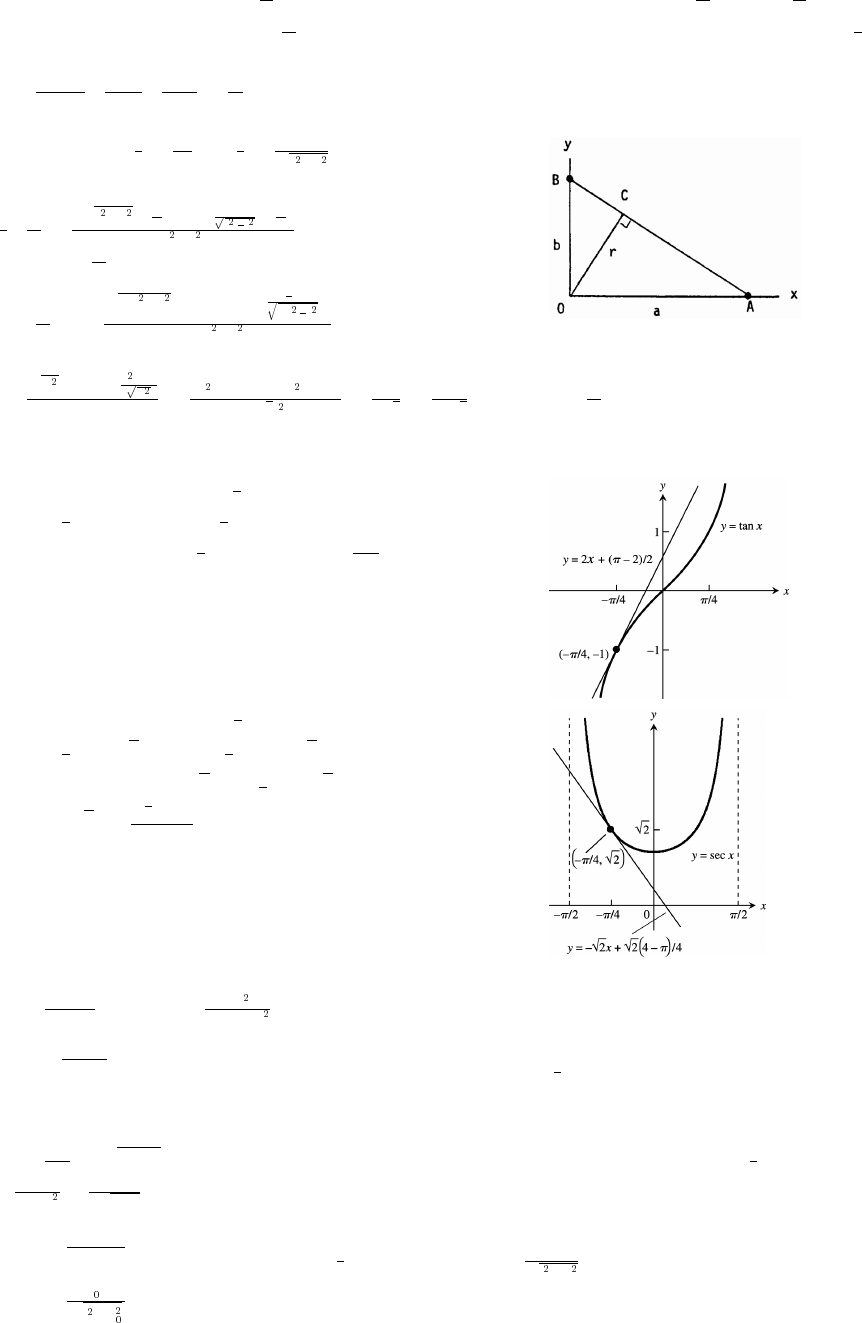
190 Chapter 3 Differentiation
117. (a) From the sketch in the text, 0.6 rad/sec and x tan . Also x tan sec ; at
ddxd
dt dt dt
) )
œ œ œ Ê œ)))
#
point A, x 0 0 sec 0 ( 0.6) 0.6. Therefore the speed of the light is 0.6 km/secœÊœÊ œ œ œ)dx 3
dt 5
ab
#
when it reaches point A.
(b) revs/min
(3/5) rad
sec 2 rad min
1 rev 60 sec 18
††
11
œ
118. From the figure, . We are given
ab a b
rBC r br
œÊœ
È
that r is constant. Differentiation gives,
. Then,
"
rdt br
da br (b)
†œŠ‹ Š‹
Ȉ‰ ˆ‰
db b db
dt dt
br
b 2r and 0.3rœœ
db
dt
rʜ
da
dt (2r) r
(2r) r ( 0.3r) (2r)
Ô×
ÖÙ
ÕØ
È
2r( 0.3r)
(2r) r
m/sec. Since is positive,œœ œœ
Èab ab
ÈÈÈ
3r ( 0.3r)
3r dt
3r ( 0.3r) 4r (0.3r)
33r 33 103
0.3r r da
4r (0.3r)
3r
the distance OA is increasing when OB 2r, and B is moving toward O at the rate of 0.3r m/sec.œ
119. (a) If f(x) tan x and x , then f (x) sec x,œœ œ
1
4w#
f 1 and f 2. The linearization of
ˆ‰ ˆ‰
œ œ
11
44
w
f(x) is L(x) 2 x ( 1) 2x .œœ
ˆ‰
11
4
2
#
(b) If f(x) sec x and x , then f (x) sec x tan x,œœ œ
1
4w
f 2 and f 2. The linearization
ˆ‰ ˆ‰
ÈÈ
œ œ
11
44
w
of f(x) is L(x) 2 x 2œ
ÈÈ
ˆ‰
1
4
2x .œ
ÈÈ2( )
4
%1
120. f(x) f (x) . The linearization at x 0 is L(x) f (0)(x 0) f(0) 1 x.œÊœ œ œœ
"
ww
1tan x (1tan x)
sec x
121. f(x) x 1 sin x 0.5 (x 1) sin x 0.5 f (x) (x 1) cos xœœÊ œ
Ȉ‰
"Î# w "Î#
"
#
L(x) f (0)(x 0) f(0) 1.5(x 0) 0.5 L(x) 1.5x 0.5, the linearization of f(x).Êœ œÊœ
w
122. f(x) 1 x 3.1 2(1 x) (1 x) 3.1 f (x) 2(1 x) ( 1) (1 x)œœ Ê œ
2
1x #
" "Î# w # "Î#
"
È
L(x) f (0)(x 0) f(0) 2.5x 0.1, the linearization of f(x).œ Êœ œ
2
(1 x) 21 x
"
w
È
123. S r r h , r constant dS r r h h dh dh. Height changes from h to h dhœ Êœ†#œ 11
Èab
## "
#
##
"Î#
!!
1 r h
rh
È
dSʜ
1 r h dh
rh
ab
É
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 3 Additional and Advanced Exercises 191
124. (a) S 6r dS 12r dr. We want dS (2%) S 12r dr dr . The measurement of theœÊœ Ÿ Ê Ÿ Ê Ÿ
#kk k k kk
12r r
100 100
edge r must have an error less than 1%.
(b) When V r , then dV 3r dr. The accuracy of the volume is (100%) (100%)œœ œ
$# ˆ‰ Š‹
dV 3r dr
Vr
(dr)(100%) (100%) 3%œœ œ
ˆ‰ ˆ‰ˆ ‰
33r
r r 100
125. C 2 r r , S 4 r , and V r . It also follows that dr dC, dS dC andœÊœ œ œ œ œ œ œ11 1
CC4C 2C
23611 1 11
#$ "
#
dV dC. Recall that C 10 cm and dC 0.4 cm.œœœ
C
21
(a) dr cm (100%) (100%) (.04)(100%) 4%œœ Ê œ œ œ
0.4 0.2 dr 0.2 2
2r 1011 1
1
ˆ‰ ˆ‰ˆ‰
(b) dS (0.4) cm (100%) (100%) 8%œœÊ œ œ
20 8 dS 8
S 10011 1
1
ˆ‰ ˆ‰ˆ‰
(c) dV (0.4) cm (100%) (100%) 12%œœÊ œ œ
10 20 dV 20 6
2 V 1000
11 1
1
ˆ‰ ˆ‰
Š‹
126. Similar triangles yield h 14 ft. The same triangles imply that h 120a 6
35 15 20 a a
h6 h 6
œÊœ œÊœ
"
dh 120a da da .0444 ft 0.53 inches.Êœ œ œ „œ „œ„¸„ œ„
# " "#! "
#"&"#
120 120 2
aa1 45
ˆ‰ˆ‰ˆ‰ˆ‰
CHAPTER 3 ADDITIONAL AND ADVANCED EXERCISES
1. (a) sin 2 2 sin cos (sin 2 ) (2 sin cos ) 2 cos 2 2[(sin )( sin ) (cos )(cos )]))) ) )) ) ))))œÊœ Êœ
dd
dd))
cos 2 cos sinʜ)))
##
(b) cos 2 cos sin (cos 2 ) cos sin 2 sin 2 (2 cos )( sin ) (2 sin )(cos )))) ) )) ) )) ))œÊ œ Ê œ
## ##
dd
dd))
ab
sin 2 cos sin sin cos sin 2 2 sin cos ʜ ʜ))))) ) ))
2. The derivative of sin (x a) sin x cos a cos x sin a with respect to x isœ
cos (x a) cos x cos a sin x sin a, which is also an identity. This principle does not apply to theœ
equation x 2x 8 0, since x 2x 8 0 is not an identity: it holds for 2 values of x ( 2 and 4), but not
##
œ œ
for all x.
3. (a) f(x) cos x f (x) sin x f (x) cos x, and g(x) a bx cx g (x) b 2cx g (x) 2c;œÊœÊœ œÊœÊœ
www #w ww
also, f(0) g(0) cos (0) a a 1; f (0) g (0) sin (0) b b 0; f (0) g (0)œÊ œÊœ œ Ê œÊœ œ
w w ww ww
cos (0) 2c c . Therefore, g(x) 1 x .Ê œ Ê œ œ
""
##
#
(b) f(x) sin (x a) f (x) cos (x a), and g(x) b sin x c cos x g (x) b cos x c sin x; also,œÊœ œ Êœ
ww
f(0) g(0) sin (a) b sin (0) c cos (0) c sin a; f (0) g (0) cos (a) b cos (0) c sin (0)œÊ œ Êœ œ Ê œ
ww
b cos a. Therefore, g(x) sin x cos a cos x sin a.Êœ œ
(c) When f(x) cos x, f (x) sin x and f (x) cos x; when g(x) 1 x , g (x) 0 and g (x) 0.œœ œ œœ œ
www Ð%Ñ # www Ð%Ñ
"
#
Thus f (0) 0 g (0) so the third derivatives agree at x 0. However, the fourth derivatives do not
www www
œœ œ
agree since f (0) 1 but g (0) 0. In case (b), when f(x) sin (x a) and g(x)
Ð%Ñ Ð%Ñ
œœ œ
sin x cos a cos x sin a, notice that f(x) g(x) for all x, not just x 0. Since this is an identity, weœ œ œ
have f (x) g (x) for any x and any positive integer n.
ÐÑ ÐÑnn
œ
4. (a) y sin x y cos x y sin x y y sin x sin x 0; y cos x y sin xœ Ê œ Ê œ Ê œ œ œ Ê œ
www ww w
y cos x y y cos x cos x 0; y a cos x b sin x y a sin x b cos xÊœ Êœ œ œ Êœ
ww ww w
y a cos x b sin x y y ( a cos x b sin x) (a cos x b sin x) 0Êœ Êœ œ
ww ww
(b) y sin (2x) y 2 cos (2x) y 4 sin (2x) y 4y 4 sin (2x) 4 sin (2x) 0. Similarly,œ Ê œ Ê œ Ê œ œ
www ww
y cos (2x) and y a cos (2x) b sin (2x) satisfy the differential equation y 4y 0. In general,œœ œ
ww
y cos (mx), y sin (mx) and y a cos (mx) b sin (mx) satisfy the differential equation y m y 0.œœ œ œ
ww #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
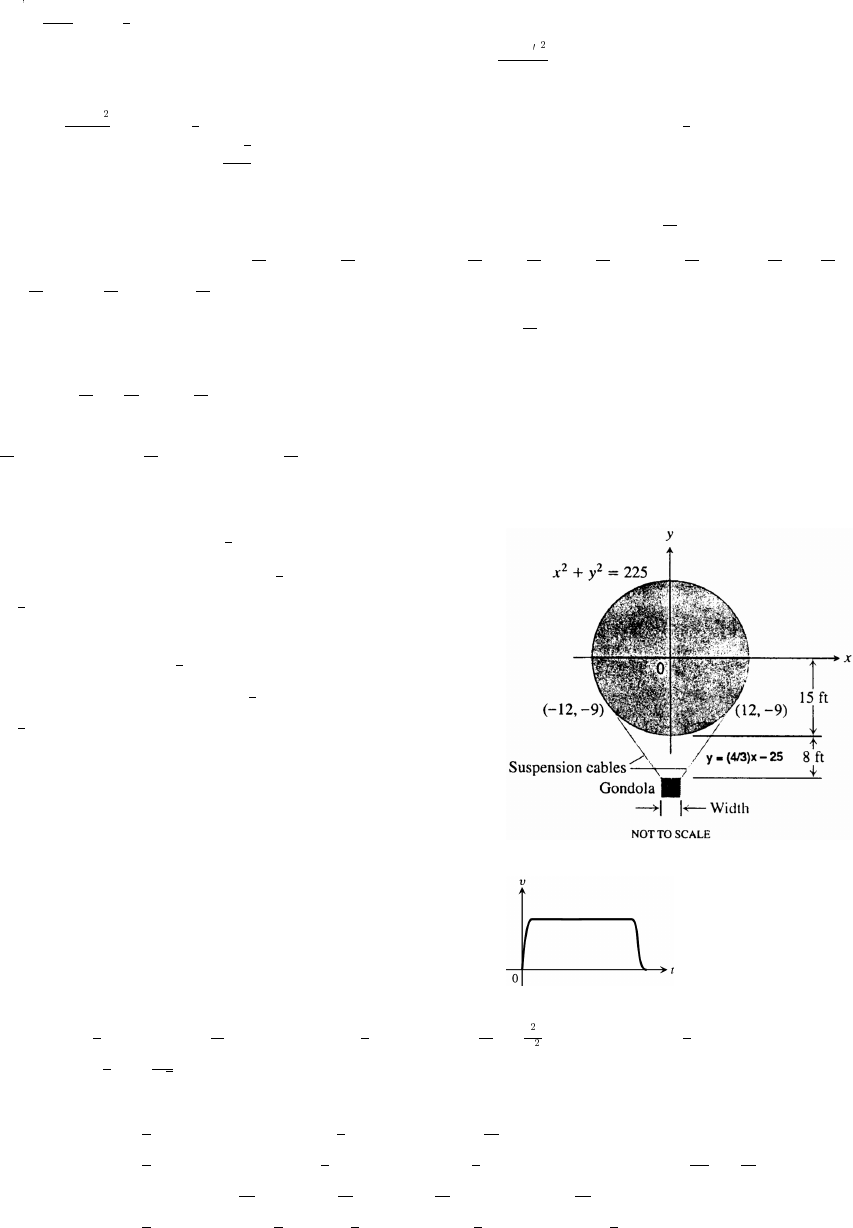
192 Chapter 3 Differentiation
5. If the circle (x h) (y k) a and y x 1 are tangent at ( ), then the slope of this tangent is œ œ "ß #
### #
m 2x 2 and the tangent line is y 2x. The line containing (h k) and ( ) is perpendicular tokœ œ œ ß "ß #
(1 2)
y 2x h 5 2k the location of the center is (5 2k k). Also, (x h) (y k) aœÊ œÊœÊ ß œ
k2
h1
"
#
###
x h (y k)y 0 1 y (y k)y 0 y . At the point ( ) we knowÊ œ Ê œ Ê œ "ß #
wwwww
#w
ab 1y
ky
ab
y 2 from the tangent line and that y 2 from the parabola. Since the second derivatives are equal at ( )
www
œ œ "ß #
we obtain 2 k . Then h 5 2k 4 the circle is (x 4) y a . Since ( )œ Ê œ œ œ Ê œ "ß #
1(2)
k
9 9
# # #
##
#
ˆ‰
lies on the circle we have that a .œ55
2
È
6. The total revenue is the number of people times the price of the fare: r(x) xp x 3 , whereœœ
ˆ‰
x
40
#
0 x 60. The marginal revenue is 3 2x 3 3 3ŸŸ œ Ê œ
dr x x dr x x 2x
dx 40 40 40 dx 40 40 40
ˆ‰ˆ‰ˆ‰ ˆ‰ ‘ˆ‰
#"
3 3 1 . Then 0 x 40 (since x 120 does not belong to the domain). When 40 peopleœ œÊœ œ
ˆ‰ˆ‰
xx dr
40 40 dx
are on the bus the marginal revenue is zero and the fare is p(40) 3 $4.00.œ œ
¹
ˆ‰
x
40
#
x=40
7. (a) y uv v u (0.04u)v u(0.05v) 0.09uv 0.09y the rate of growth of the total production isœÊœœœœÊ
dy
dt dt dt
du dv
9% per year.
(b) If 0.02u and 0.03v, then ( 0.02u)v (0.03v)u 0.01uv 0.01y, increasing at 1% per
du dv
dt dt dt
dy
œ œ œ œœ
year.
8. When x y 225, then y . The tangent
## w
œ œ
x
y
line to the balloon at (12 9) is y 9 (x 12)ß œ
4
3
y x 25. The top of the gondola is 15 8ʜ
4
3
23 ft below the center of the balloon. The inter-œ
section of y 23 and y x 25 is at the farœ œ
4
3
right edge of the gondola 23 x 25Ê œ
4
3
x . Thus the gondola is 2x 3 ft wide.Êœ œ
3
#
9. Answers will vary. Here is one possibility.
10. s(t) 10 cos t v(t) 10 sin t a(t) 10 cos tœ Ê œ œ Ê œ œ œ
ˆ‰ ˆ‰ ˆ‰
11 1
4 dt 4 dt dt 4
ds dv d s
(a) s(0) 10 cosœœ
ˆ‰
1
4
10
2
È
(b) Left: 10, Right: 10
(c) Solving 10 cos t 10 cos t 1 t when the particle is farthest to the left.
ˆ‰ ˆ‰
œÊ œÊœ
111
444
3
Solving 10 cos t 10 cos t 1 t , but t 0 t 2 when the particle
ˆ‰ ˆ‰
œ Ê œÊœ Êœ œ
111 11
444 44
7
1
is farthest to the right. Thus, v 0, v 0, a 10, and a 10.
ˆ‰ ˆ‰ ˆ‰ ˆ‰
373 7
444 4
111 1
œœœ œ
(d) Solving 10 cos t 0 t v 10, v 10 and a .
ˆ ‰ ˆ‰ ¸ ¸ ˆ‰ˆ‰
œÊœÊ œ œ œ!
1111 1
4444 4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 3 Additional and Advanced Exercises 193
11. (a) s(t) 64t 16t v(t) 64 32t 32(2 t). The maximum height is reached when v(t) 0œ Ê œœœ œ
#ds
dt
t 2 sec. The velocity when it leaves the hand is v(0) 64 ft/sec.Êœ œ
(b) s(t) 64t 2.6t v(t) 64 5.2t. The maximum height is reached when v(t) 0 t 12.31 sec.œ Ê œœ œÊ¸
#ds
dt
The maximum height is about s(12.31) 393.85 ft.œ
12. s 3t 12t 18t 5 and s t 9t 12t v 9t 24t 18 and v 3t 18t 12; v v
"#"#"#
$# $# # #
œ œ Êœ œ œ
9t 24t 18 3t 18t 12 2t 7t 5 0 (t 1)(2t 5) 0 t 1 sec and t 2.5 sec.Ê œ Ê œÊ œÊœ œ
###
13. m v v k x x m 2v k 2x m k m kx . Thenababˆ‰ˆ ‰ ˆ‰ ˆ‰
## ##
!! "
œ Ê œ Ê œ Ê œ
dv dx dv 2x dx dv dx
dt dt dt 2v dt dt v dt
substituting v m kx, as claimed.
dx dv
dt dt
œÊ œ
14. (a) x At Bt C on t t v 2At B v 2A B A t t B is theœ ßÊœœÊ œ œ
#"# "#
##
cd a b
ˆ‰ ˆ‰
dx
dt
tt tt
instantaneous velocity at the midpoint. The average velocity over the time interval is vav œ?
?
x
t
At t B.œœœ
abab
abc dab
AtBtC AtBtC
tt tt
ttAtt B
#"
ab
(b) On the graph of the parabola x At Bt C, the slope of the curve at the midpoint of the intervalœ
#
t t is the same as the average slope of the curve over the interval.cd
"#
ß
15. (a) To be continuous at x requires that lim sin x lim (mx b) 0 m b m ;œœÊœÊœ11
xx
ÄÄ
11
b
1
(b) If y is differentiable at x , then lim cos x m m 1 and b .
cos x, x
m, x
wœœœÊœœ
œ1
111
xÄ1
16. f x is continuous at because lim f . f (0) lim lim ab ab!œ!œ!œœ
xxxÄ! Ä! Ä!
" w
cos x
xx0x
f(x) f(0) 0
1 cos x
x
lim lim . Therefore f (0) exists with value .œœœ
xxÄ! Ä!
ˆ‰ˆ‰ ˆ‰ˆ‰
1cos x 1cos x sin x
x1cos x x1cos x
"" "
# #
#w
17. (a) For all a, b and for all x 2, f is differentiable at x. Next, f differentiable at x 2 f continuous at x 2ÁœÊœ
lim f(x) f(2) 2a 4a 2b 3 2a 2b 3 0. Also, f differentiable at x 2Ê œ Ê œÊ œ Á
x2Ä
f (x) . In order that f (2) exist we must have a 2a(2) b a 4a b 3a b.
a, x 2
2ax b, x 2
Êœ œÊœÊœ
ww
œ
Then 2a 2b 3 0 and 3a b a and b .œ œÊœ œ
39
44
(b) For x , the graph of f is a straight line having a slope of and passing through the origin; for x , the graph of f# #
$
%
is a parabola. At x , the value of the y-coordinate on the parabola is which matches the y-coordinate of the pointœ# $
#
on the straight line at x . In addition, the slope of the parabola at the match up point is which is equal to theœ# $
%
slope of the straight line. Therefore, since the graph is differentiable at the match up point, the graph is smooth there.
18. (a) For any a, b and for any x 1, g is differentiable at x. Next, g differentiable at x 1 g continuous atÁ œ Ê
x 1 lim g(x) g( 1) a 1 2b a b b 1. Also, g differentiable at x 1œ Ê œ Ê œ Ê œ Á
xÄ"
g (x) . In order that g ( 1) exist we must have a 3a( 1) 1 a 3a 1
a, x 1
3ax 1, x 1
Êœ œÊœ
ww#
#
œ
a.ʜ
"
#
(b) For x , the graph of f is a straight line having a slope of and a y-intercept of . For x , the graph of f isŸ" " "
"
#
a parabola. At x , the value of the y-coordinate on the parabola is which matches the y-coordinate of the pointœ" $
#
on the straight line at x . In addition, the slope of the parabola at the match up point is which is equal to theœ"
"
#
slope of the straight line. Therefore, since the graph is differentiable at the match up point, the graph is smooth there.
19. f odd f( x) f(x) (f( x)) ( f(x)) f ( x)( 1) f (x) f ( x) f (x) f is even.Êœ Ê œ Ê œ Ê œ Ê
dd
dx dx wwwww
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

194 Chapter 3 Differentiation
20. f even f( x) f(x) (f( x)) (f(x)) f ( x)( 1) f (x) f ( x) f (x) f is odd.Êœ Ê œ Êœ Êœ Ê
dd
dx dx wwwww
21. Let h(x) (fg)(x) f(x) g(x) h (x) lim lim œœ Êœ œ
w
xx xxÄÄ
h(x) h(x ) f(x) g(x) f(x ) g(x )
xx xx
lim lim f(x) lim g(x )œœ
xx xx xxÄÄÄ
f(x) g(x) f(x) g(x ) f(x) g(x ) f(x ) g(x ) g(x) g(x ) f(x) f(x )
xx xx xx
!
’“’“’“ ’“
f(x) lim g(x)f(x) 0 lim g(x)f(x) g(x)f(x), if g isœœœ
!!! !!!!
www
xx xxÄÄ
’“ ’“
g(x) g(x ) g(x) g(x )
xx xx
†
continuous at x . Therefore (fg)(x) is differentiable at x if f(x ) 0, and (fg) (x ) g(x ) f (x ).
!!!!!!
ww
œœ
22. From Exercise 21 we have that fg is differentiable at 0 if f is differentiable at 0, f(0) 0 and g is continuousœ
at 0.
(a) If f(x) sin x and g(x) x , then x sin x is differentiable because f (0) cos (0) 1, f(0) sin (0) 0œ œ œ œœœkk kk w
and g(x) x is continuous at x 0.œœkk
(b) If f(x) sin x and g(x) x , then x sin x is differentiable because f (0) cos (0) 1, f(0) sin (0) 0œ œ œ œœœ
#Î$ #Î$ w
and g(x) x is continuous at x 0.œœ
#Î$
(c) If f(x) 1 cos x and g(x) x, then x (1 cos x) is differentiable because f (0) sin (0) 0,œ œ œ œ
$$ w
ÈÈ
f(0) 1 cos (0) 0 and g(x) x is continuous at x 0.œ œ œ œ
"Î$
(d) If f(x) x and g(x) x sin , then x sin is differentiable because f (0) 1, f(0) 0 andœœ œœ
ˆ‰ ˆ‰
""
#w
xx
lim x sin lim lim 0 (so g is continuous at x 0).
xx
t
Ä! Ä! Ä_
ˆ‰
"
xt
sin sin t
œœœ œ
ˆ‰
x
x
23. If f(x) x and g(x) x sin , then x sin is differentiable at x 0 because f (0) 1, f(0) 0 andœœ œ œœ
ˆ‰ ˆ‰
""
#w
xx
lim x sin lim lim 0 (so g is continuous at x 0). In fact, from Exercise 21,
xx
t
Ä! Ä! Ä_
ˆ‰
"
xt
sin sin t
œœœ œ
ˆ‰
x
x
h (0) g(0) f (0) 0. However, for x 0, h (x) x cos 2x sin . But
ww w#
"" "
œœ Áœ
‘ˆ‰ˆ‰ˆ‰
xx x
lim h (x) lim cos 2x sin does not exist because cos has no limit as x 0. Therefore,
xxÄ! Ä!
w"" "
œ Ä
‘ ˆ‰ˆ‰ ˆ‰
xx x
the derivative is not continuous at x 0 because it has no limit there.œ
24. From the given conditions we have f(x h) f(x) f(h), f(h) 1 hg(h) and lim g(h) 1. Therefore,œ œ œ
hÄ!
f (x) lim lim lim f(x) f(x) lim g(h) f(x) 1 f(x)
w
œœ œ œœœ
hh h hÄ! Ä! Ä! Ä!
f(x h) f(x) f(x) f(h) f(x) f(h) 1
hh h
’“ ’ “ †
f (x) f(x) and f x exists at every value of x.ʜ
ww
ab
25. Step 1: The formula holds for n 2 (a single product) since y u u u u .œœÊœ
"# # "
dy
dx dx dx
du du
Step 2: Assume the formula holds for n k:œ
yuuu uuu u uu uuu .œ â Ê œ â âá â
"# #$ " $ "#kkkk-1
dy
dx dx dx dx
du du duk
If yuuuu uuuu, then u uuu œâ œ â œ â
"# "# "#
â
k k1 k k1 k1 k
ab dy d(u u u )
dx dx dx
du
kk1
uu u u u u uu u u uu u œ â âââ â
ˆ‰
du du
dx dx dx dx
du du
#$ " $ "# "#k k k1 k1 k
kk1
uu u u u u uu u u uu u .œ â âââ â
du du
dx dx dx dx
du du
#$ " $ "# "#k1 k1 k1 k1 k
kk1
Thus the original formula holds for n (k 1) whenever it holds for n k.œ œ
26. Recall . Then m and
ˆ‰ ˆ‰ ˆ‰ ˆ ‰
mm mm
k k! (m k)! 1 1! (m 1)! k k 1 k! (m k)! (k 1)! (m k 1)!
m! m! m! m!
œœœœ
. Now, we proveœœœ œ
m! (k 1) m! (m k) m! (m 1) (m 1)!
(k 1)! (m k)! (k 1)! (m k)! (k 1)! ((m 1) (k 1))! k 1
m1
ˆ‰
Leibniz's rule by mathematical induction.
Step 1: If n 1, then u v . Assume that the statement is true for n k, that is:œœ œ
d(uv)
dx dx dx
dv du
v k u .
d (uv)
dx dx dx dx 2 dx dx k 1 dv dx dx
du dudv dudv dudv dv
kk
k
kk k k k k
kk k kk
œ á
ˆ‰ ˆ ‰
Step 2: If n k 1, then v k k œ œ œ
d (uv) d (uv)
dx dx dx dx dx dx dx dx dx dx
d dududv dudvdudv
kk
kkkkkk
kk k k
Š‹ ’ “
‘
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 3 Additional and Advanced Exercises 195
vá
’“’ “
ˆ‰ ˆ‰ ˆ ‰ ˆ ‰
kk k k
2 dx dx 2 dx dx k 1 dx dx k 1 dx dx
d u dv d u dv du d v du du
kk k k
kk k k
u v(k1) œ á
‘ ‘ˆ‰ ˆ‰
dudv du du dudv dudv
dx dx dx dx dx dx 1 2 dx dx
kk
kk k k k
kk k k k
u v(k1) œ á
‘ ˆ‰ˆ‰ˆ‰
kk k1
k 1 k dx dx dx dx dx dx 2 dx dx
du dv d v d u du dv d u dv
kkk k k
kkk k k
u .
ˆ‰
k1
kdxdx dx
du d v d v
kk
kk
Therefore the formula (c) holds for n (k 1) whenever it holds for n k.œ œ
27. (a) T L L L 0.8156 ft
#œÊœÊœ ʸ
4L
g4 4
Tg 1 sec 32.2 ft/sec
1
11
aba b
(b) T T L; dT dL dL; dT ft 0.00613 sec.
###"
#!Þ)"&'
œÊœ œ† œ œ !Þ!"¸
4L
ggg
LLg ft 32.2 ft/sec
11 1 1 1
ÈÈÈÈÈ
aba b
Èab
(c) Since there are 86,400 sec in a day, we have 0.00613 sec 86,400 sec/day 529.6 sec/day, or 8.83 min/day; theaba b¸
clock will lose about 8.83 min/day.
28. v s s k s k. If s the initial length of the cube's side, then s s kœ Ê œ$ œ ' Ê œ# œ œ #
$## !"!
dv ds ds
dt dt dt
ab
k s s . Let t the time it will take the ice cube to melt. Now, tÊ# œ œ œ œ œ
!" #
ss
kss
v
vv
ab
ab ˆ‰
hr.œ¸""
"
"ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
196 Chapter 3 Differentiation
NOTES:
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
CHAPTER 4 APPLICATIONS OF DERIVATIVES
4.1 EXTREME VALUES OF FUNCTIONS
1. An absolute minimum at x c , an absolute maximum at x b. Theorem 1 guarantees the existence of suchœœ
#
extreme values because h is continuous on [a b].ß
2. An absolute minimum at x b, an absolute maximum at x c. Theorem 1 guarantees the existence of suchœœ
extreme values because f is continuous on [a b].ß
3. No absolute minimum. An absolute maximum at x c. Since the function's domain is an open interval, theœ
function does not satisfy the hypotheses of Theorem 1 and need not have absolute extreme values.
4. No absolute extrema. The function is neither continuous nor defined on a closed interval, so it need not fulfill
the conclusions of Theorem 1.
5. An absolute minimum at x a and an absolute maximum at x c. Note that y g(x) is not continuous butœœœ
still has extrema. When the hypothesis of Theorem 1 is satisfied then extrema are guaranteed, but when the
hypothesis is not satisfied, absolute extrema may or may not occur.
6. Absolute minimum at x c and an absolute maximum at x a. Note that y g(x) is not continuous but stillœœœ
has absolute extrema. When the hypothesis of Theorem 1 is satisfied then extrema are guaranteed, but when
the hypothesis is not satisfied, absolute extrema may or may not occur.
7. Local minimum at , local maximum at ab ab"ß ! "ß !
8. Minima at and , maximum at a b ab ab#ß! #ß! !ß#
9. Maximum at . Note that there is no minimum since the endpoint is excluded from the graph.ab ab!ß & #ß !
10. Local maximum at , local minimum at , maximum at , minimum at a b ab ab a b$ß! #ß! "ß# !ß"
11. Graph (c), since this the only graph that has positive slope at c.
12. Graph (b), since this is the only graph that represents a differentiable function at a and b and has negative slope at c.
13. Graph (d), since this is the only graph representing a funtion that is differentiable at b but not at a.
14. Graph (a), since this is the only graph that represents a function that is not differentiable at a or b.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
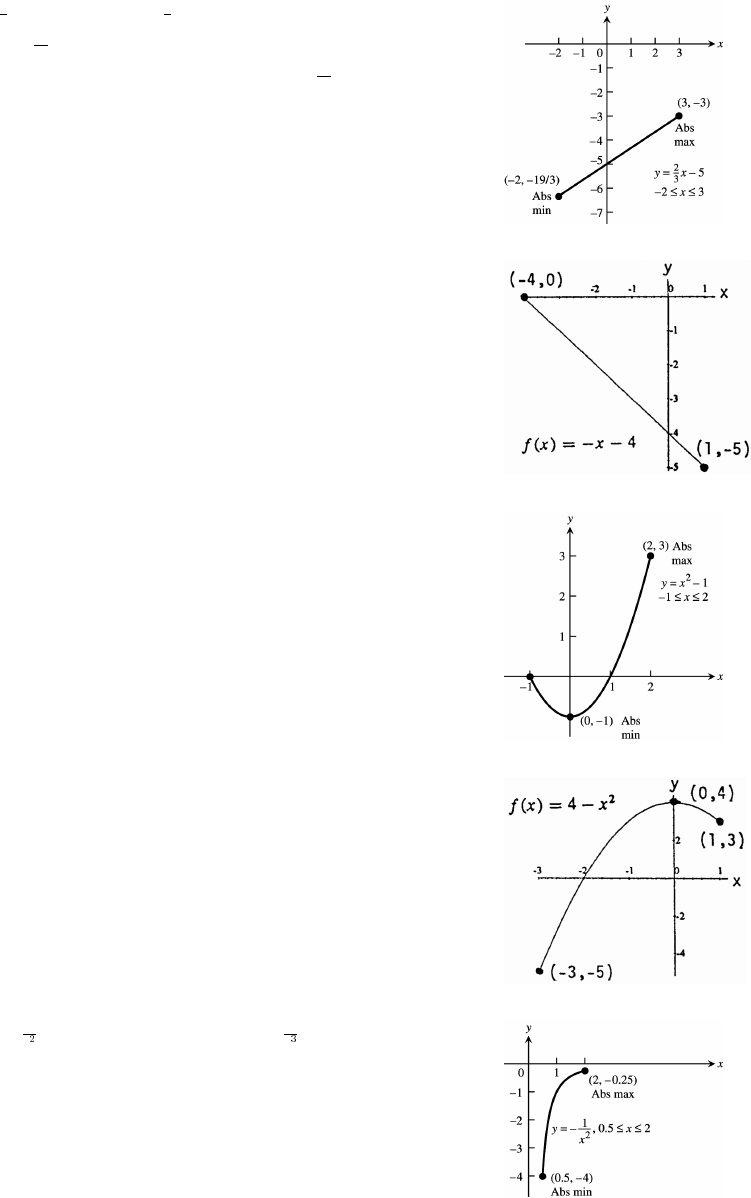
198 Chapter 4 Applications of Derivatives
15. f(x) x 5 f (x) no critical points;œÊ œÊ
22
33
w
f( 2) , f(3) 3 the absolute maximumœ œÊ
19
3
is 3 at x 3 and the absolute minimum is atœ
19
3
x2œ
16. f(x) x 4 f (x) 1 no critical points;œ Ê œ Ê
w
f( 4) 0, f(1) 5 the absolute maximum is 0œ œÊ
at x 4 and the absolute minimum is 5 at xœ œ"
17. f(x) x 1 f (x) 2x a critical point atœÊ œ Ê
#w
x 0; f( 1) 0, f(0) 1, f(2) 3 the absoluteœœ œ œÊ
maximum is 3 at x 2 and the absolute minimum is 1œ
at x 0œ
18. f(x) x f (x) 2x a critical point atœ% Ê œ Ê
#w
x 0; f( 3) 5, f(0) 4, f(1) 3 the absoluteœœ œ œÊ
maximum is 4 at x 0 and the absolute minimum is 5œ
at x 3œ
19. F(x) x F (x) 2x , howeverœ œ Ê œ œ
"# w $
xx
2
x 0 is not a critical point since 0 is not in the domain;œ
F(0.5) 4, F(2) 0.25 the absolute maximum isœ œ Ê
0.25 at x 2 and the absolute minimum is 4 atœ
x 0.5œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
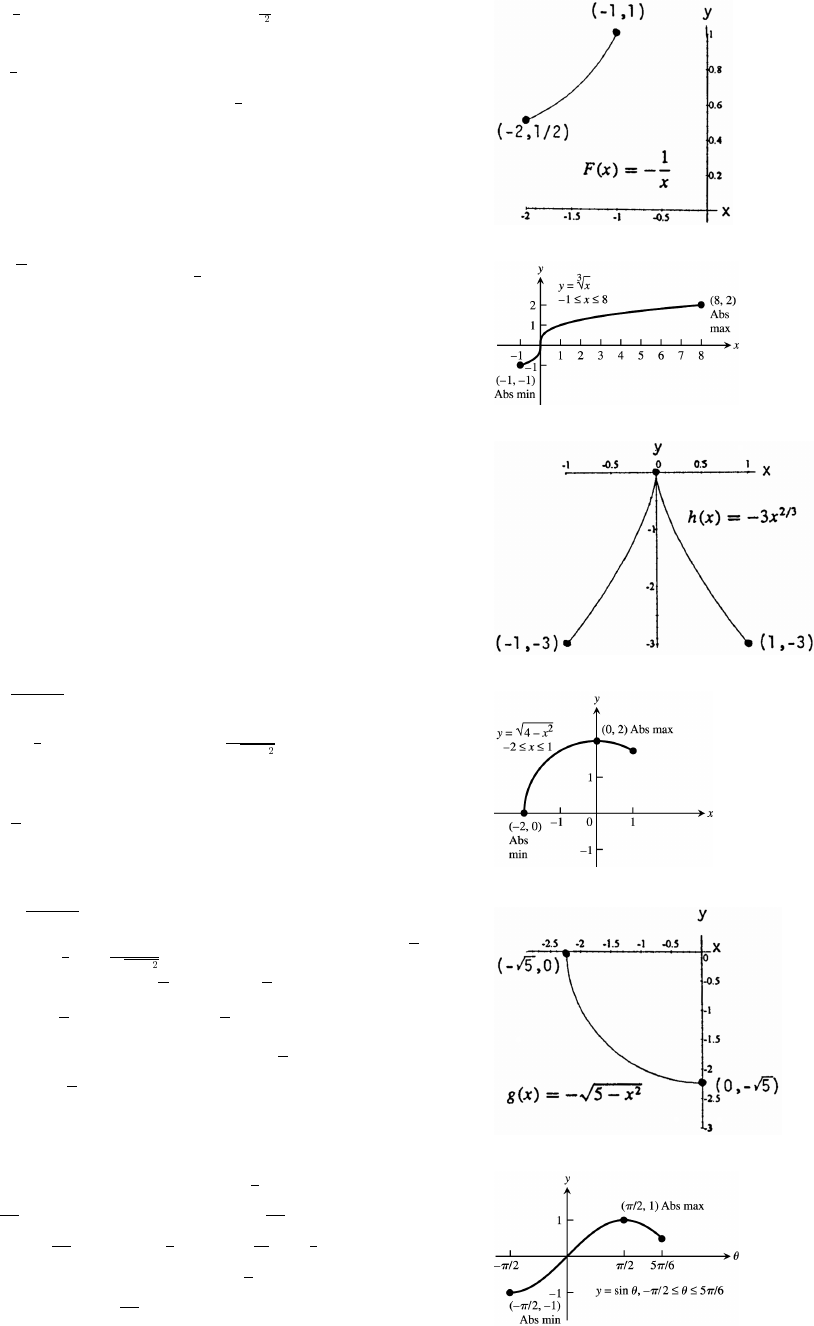
Section 4.1 Extreme Values of Functions 199
20. F(x) x F (x) x , howeverœ œ Ê œ œ
""
" w #
xx
x 0 is not a critical point since 0 is not in the domain;œ
F( 2) , F( 1) 1 the absolute maximum is 1 atœ œ Ê
"
#
x 1 and the absolute minimum is at x 2œ œ
"
#
21. h(x) x x h (x) x a critical pointœœÊ œ Ê
$"Î$ w #Î$
"
È3
at x 0; h( 1) 1, h(0) 0, h(8) 2 the absoluteœœ œ œÊ
maximum is 2 at x 8 and the absolute minimum is 1œ
at x 1œ
22. h(x) 3x h (x) x a critical point atœ Ê œ# Ê
#Î$ w "Î$
x 0; h( 1) 3, h(0) 0, h(1) 3 the absoluteœœ œ œÊ
maximum is 0 at x 0 and the absolute minimum is 3œ
at x 1 and at x 1œœ
23. g(x) 4 x 4 xœœ
Èab
##"Î#
g (x) 4 x ( 2x)Êœ œ
w#
"
#
"Î#
ab x
4x
È
critical points at x 2 and x 0, but not at x 2Êœœœ
because 2 is not in the domain; g( 2) 0, g(0) 2,œ œ
g(1) 3 the absolute maximum is 2 at x 0 and theœÊ œ
È
absolute minimum is 0 at x 2œ
24. g(x) 5 x x 5 x ( 2x)œ œ &
Èabab
###
"Î# "Î#
g (x) critical points at x 5Êœœ Ê œ
w"
#&
ˆ‰ È
x
x
È
and x 0, but not at x 5 because 5 is not in theœœ
ÈÈ
domain; f 5 0, f(0) 5
Š‹
ÈÈ
œ œ
the absolute maximum is 0 at x 5 and the absoluteʜ
È
minimum is 5 at x 0œ
È
25. f( ) sin f ( ) cos is a critical point,))) ))œÊœ Êœ
w
#
1
but is not a critical point because is not interior to)œ
##
11
the domain; f 1, f 1, f
ˆ‰ ˆ‰ ˆ‰
"
## #
111
œ œ œ
5
6
the absolute maximum is 1 at and the absoluteʜ)1
#
minimum is 1 at œ)
#
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
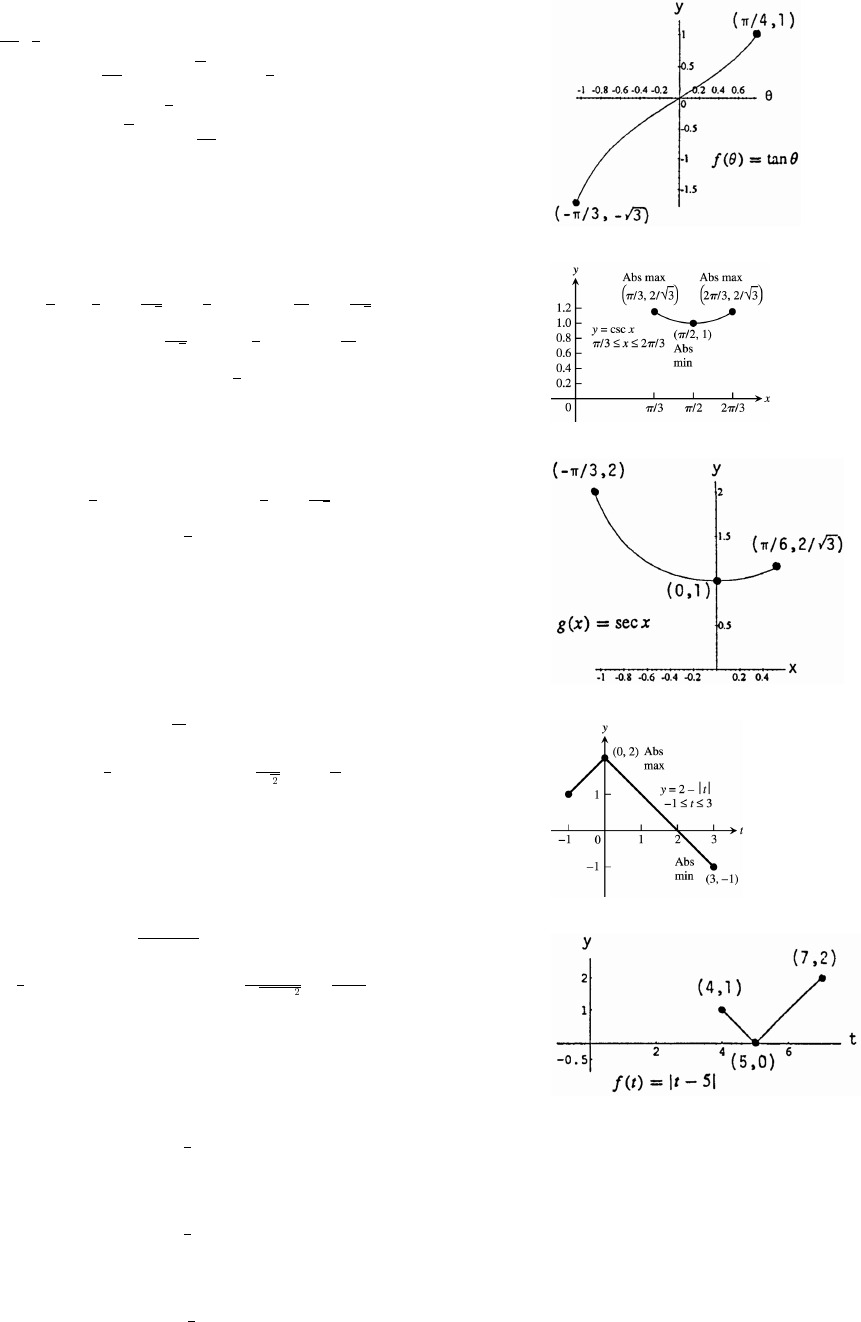
200 Chapter 4 Applications of Derivatives
26. f( ) tan f ( ) sec f has no critical points in))) )œÊœ Ê
w#
. The extreme values therefore occur at the
ˆ‰
11
34
ß
endpoints: f 3 and f 1 the absolute
ˆ‰ ˆ‰
È
11
34
œ œ Ê
maximum is 1 at and the absolute)œ1
4
minimum is 3 at œ
È)1
3
27. g(x) csc x g (x) (csc x)(cot x) a critical pointœÊœ Ê
w
at x ; g , g 1, g theœœ œ œÊ
11 1 1
##
ˆ‰ ˆ‰ ˆ ‰
33
222
33
ÈÈ
absolute maximum is at x and x , and the
22
333
Èœœ
11
absolute minimum is 1 at x œ1
#
28. g(x) sec x g (x) (sec x)(tan x) a critical point atœÊœ Ê
w
x 0; g 2, g(0) 1, g the absoluteœœ œ œÊ
ˆ‰ ˆ‰
11
36
2
3
È
maximum is 2 at x and the absolute minimum is 1œ1
3
at x 0œ
29. f(t) 2 t t tœ œ# œ#kk a b
È##"Î#
f (t) t (2t)Êœ œœ
w#
"
#
"Î#
ab tt
tt
Èkk
a critical point at t 0; f( 1) 1,Êœœ
f(0) 2, f(3) 1 the absolute maximum is 2 at t 0œœÊ œ
and the absolute minimum is 1 at t 3œ
30. f(t) t 5 (t 5) (t 5) f (t)œ œ œ Êkk a b
È##w
"Î#
(t 5) (2(t 5))œ œ œ
"
#
#"Î#
ab t5 t5
(t 5) t5
Èkk
a critical point at t 5; f(4) 1, f(5) 0, f(7) 2Ê œœœœ
the absolute maximum is 2 at t 7 and the absoluteʜ
minimum is 0 at t 5œ
31. f(x) x f (x) x a critical point at x 0; f( 1) 1, f(0) 0, f(8) 16 the absoluteœÊœ Ê œœœœÊ
%Î$ w "Î$
4
3
maximum is 16 at x 8 and the absolute minimum is 0 at x 0œœ
32. f(x) x f (x) x a critical point at x 0; f( 1) 1, f(0) 0, f(8) 32 the absoluteœÊ œ Ê œœ œ œÊ
&Î$ w #Î$
5
3
maximum is 32 at x 8 and the absolute minimum is 1 at x 1œœ
33. g( ) g ( ) a critical point at 0; g( 32) 8, g(0) 0, g(1) 1 the absolute)) ) ) )œÊ œ Ê œœ œ œÊ
$Î& w #Î&
3
5
maximum is 1 at 1 and the absolute minimum is 8 at 32))œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
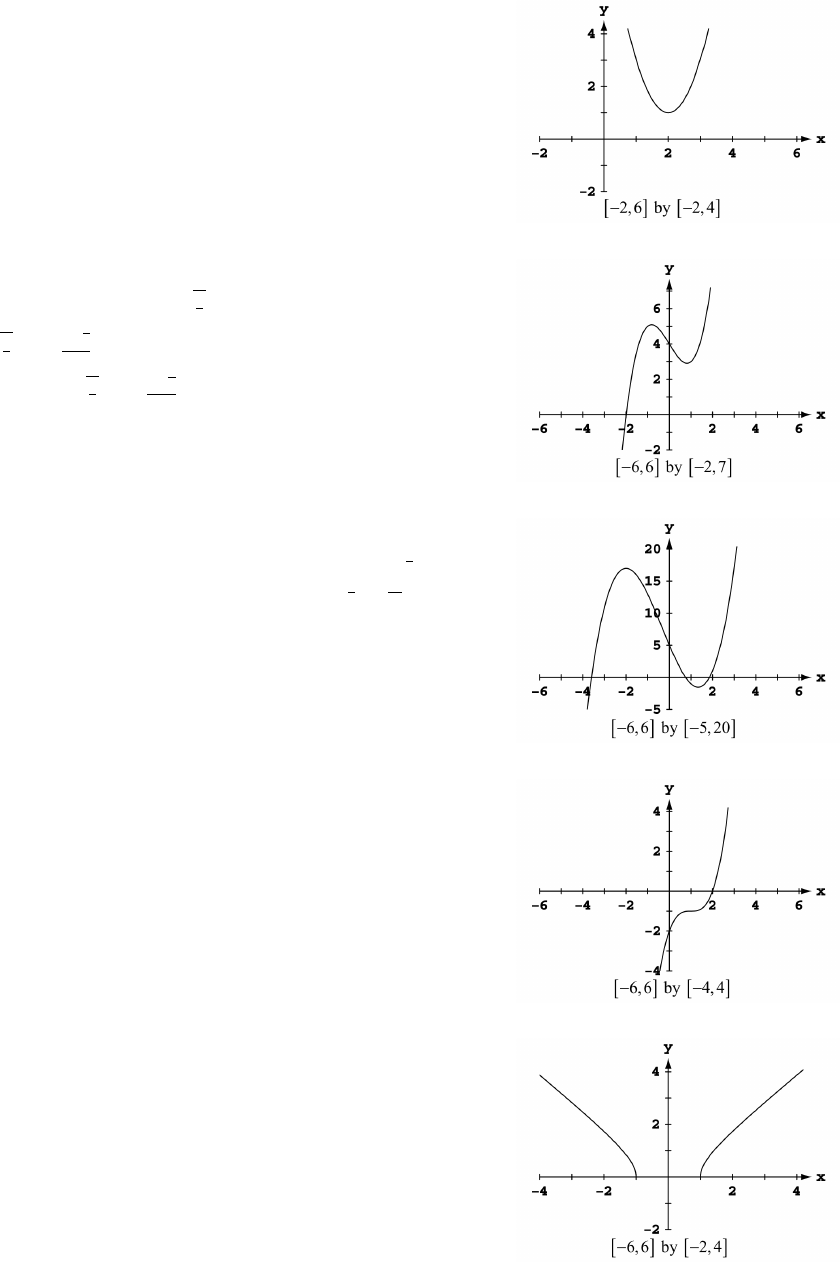
Section 4.1 Extreme Values of Functions 201
34. h( ) 3 h ( ) 2 a critical point at 0; h( 27) 27, h(0) 0, h(8) 12 the absolute)) )) )œÊœ Ê œœ œ œÊ
#Î$ w "Î$
maximum is 27 at 27 and the absolute minimum is 0 at 0))œ œ
35. Minimum value is 1 at x .œ#
36. To find the exact values, note that y x ,
w#
œ$ #
which is zero when x . Local maximum atœ„
É#
$
; local
Š‹
Éab ß % ¸ !Þ)"'ß &Þ!)*
#
$*
%'
È
minimum at
Š‹
Éab
#
$*
%'
ß % ¸ !Þ)"'ß #Þ*""
È
37. To find the exact values, note that that y x x
w#
œ$ # )
x x , which is zero when x or x .œ $ % # œ# œabab %
$
Local maximum at ; local minimum at ab ˆ‰
#ß "( ß
%%"
$#(
38. Note that y x x x , which is zero at
w# #
œ$ ' $œ$ "ab
x . The graph shows that the function assumes lowerœ"
values to the left and higher values to the right of this point,
so the function has no local or global extreme values.
39. Minimum value is 0 when x or x .œ" œ"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
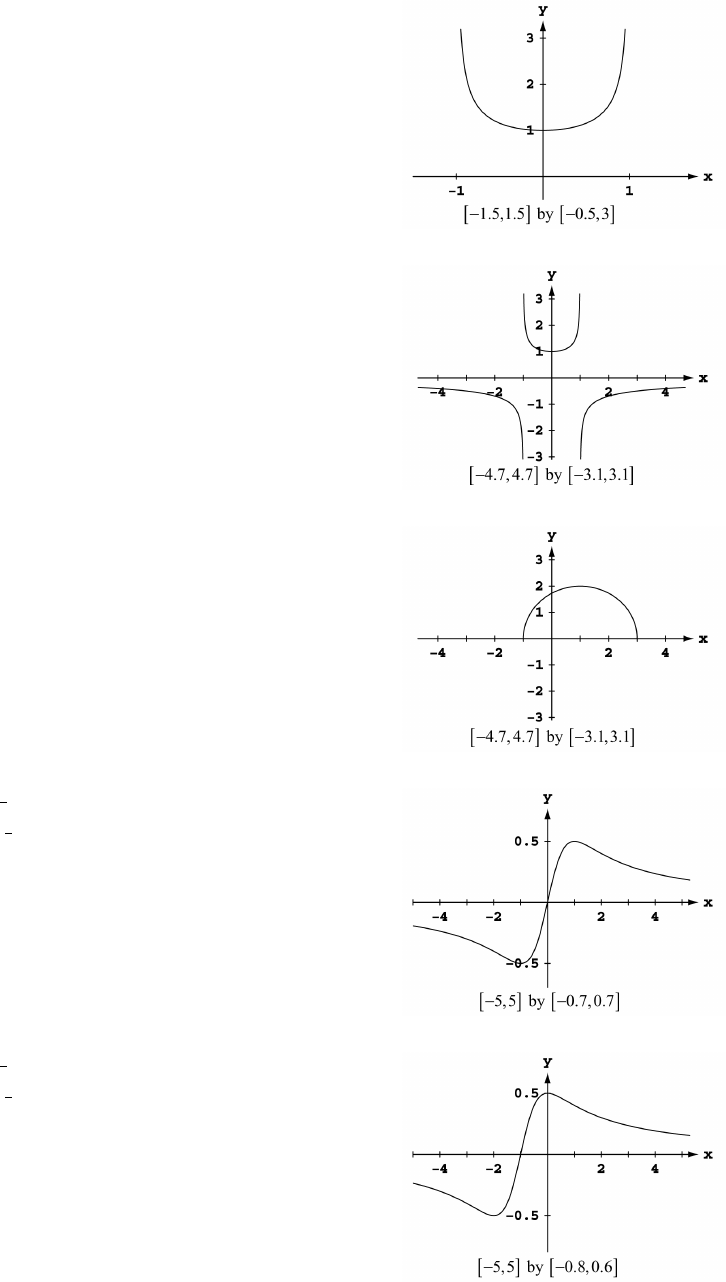
202 Chapter 4 Applications of Derivatives
40. The minimum value is 1 at x .œ!
41. The actual graph of the function has asymptotes at x ,œ„"
so there are no extrema near these values. (This is an
example of grapher failure.) There is a local minimum at
.ab!ß "
42. Maximum value is 2 at x ;œ"
minimum value is 0 at x and x .œ" œ$
43. Maximum value is at x
"
#œ"à
minimum value is as x .œ"
"
#
44. Maximum value is at x 0
"
#ψ
minimum value is as x 2.œ
"
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
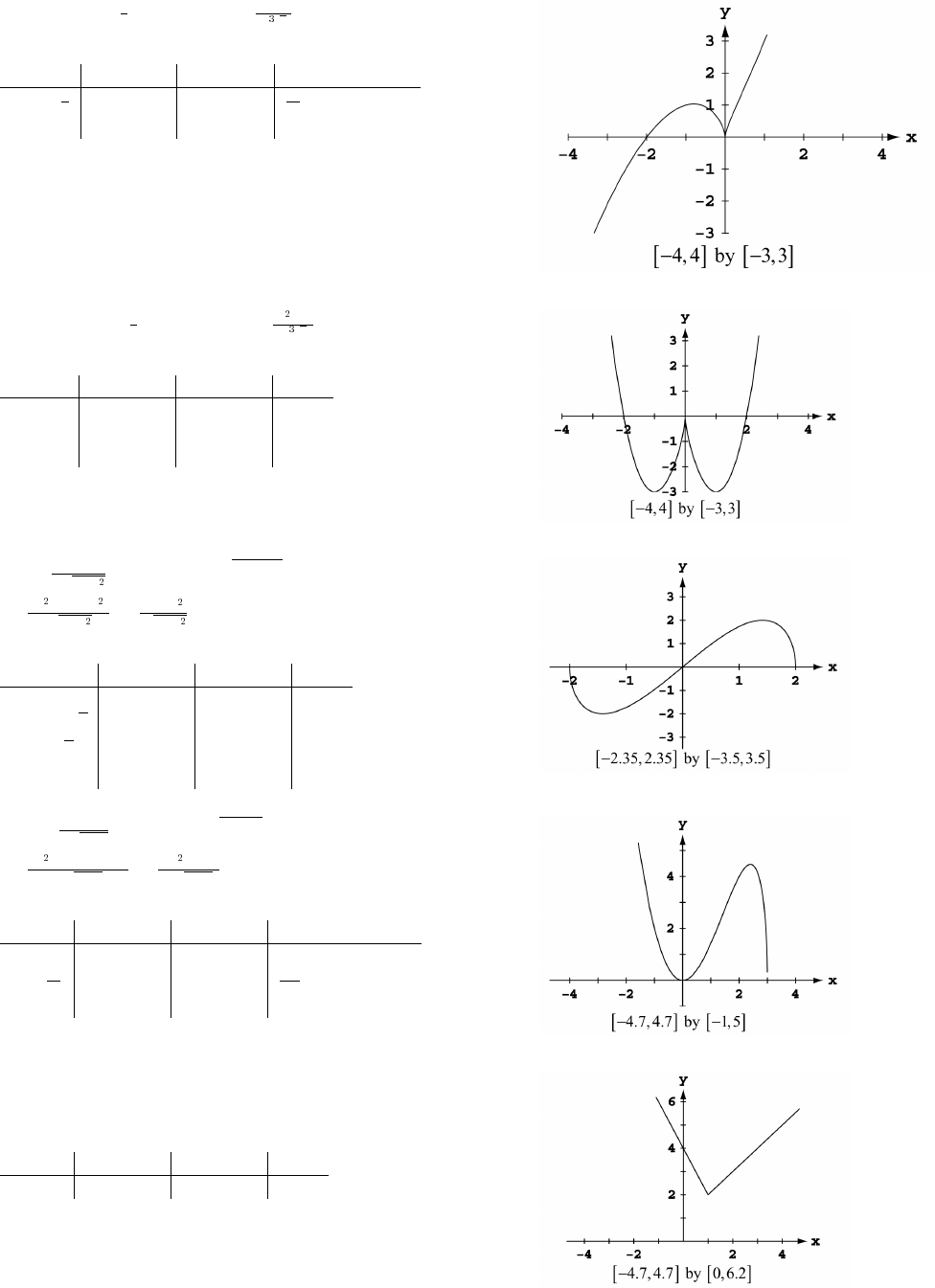
Section 4.1 Extreme Values of Functions 203
45. y x x x
w #Î$ "Î$
#&%
$$
œ" #œab a b x
x
È
crit. pt. derivative extremum value
x local max
x undefined local min 0
œ ! "! œ "Þ!$%
œ!
%"#
&#&
"Î$
46. y x x x x
w #Î$ "Î$ #
#))
$$
œ# %œab a b x
x
È
crit. pt. derivative extremum value
x minimum
x undefined local max 0
x minimum
œ" ! $
œ!
œ" ! $
47. y x x x
w"
#%
#
œ#"%
Èxabab
È
œœ
%
% %
%#
xx
xx
x
ab
ÈÈ
crit. pt. derivative extremum value
x undefined local max
x minimum
xmaximum
x undefined local min
œ# !
œ # ! #
œ# ! #
œ# !
È
È
48. y x 1 x x
w#
"
#$
œ#$
Èxab È
œœ
% $
#$ #$
"#
xxx
xx
_5x x
aba b
ÈÈ
crit. pt. derivative extremum value
x 0 minimum
x local max
x undefined minimum
œ! !
œ ! "& ¸ %Þ%'#
œ$ !
"# "%%
& "#&
"Î#
49. y ,x
,x
wœ# "
""
œ
crit. pt. derivative extremum value
x undefined minimumœ" #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
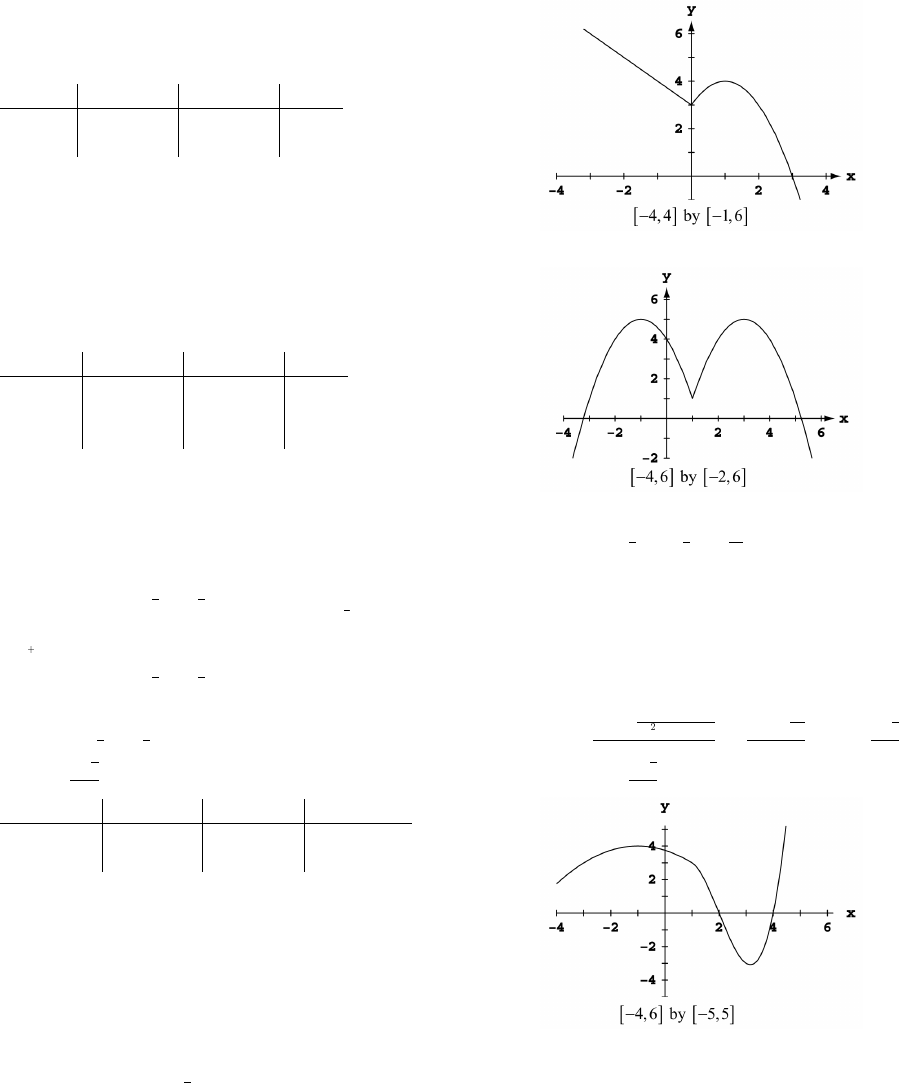
204 Chapter 4 Applications of Derivatives
50. y ,x
x, x
wœ" !
## !
œ
crit. pt. derivative extremum value
x undefined local min
x local max
œ! $
œ" ! %
51. y 2x 2, x 1
2x 6, x 1
wœ
œ
crit. pt. derivative extremum value
x 1 maximum 5
x 1 undefined local min 1
x 3 maximum 5
œ !
œ
œ!
52. We begin by determining whether f x is defined at x , where f x xx,x
xxx,x
w"""&
%#%
#
$#
ab ab œ
œ" œ Ÿ"
' ) "
Clearly, f x x if x , and f h . Also, f x x x if x , and
www#
""
## Ä!
ab a b abœ " " œ" œ$ "# ) "lim
h
f h . Since f is continuous at x , we have that f . Thus,lim
hÄ!
w w
ab ab" œ" œ" " œ"
fx x , x
xx ,x
w""
##
#
ab œ
œ Ÿ"
$"#) "
Note that x when x , and x x when x . œ! œ" $ "# )œ! œ œ œ#„
""
## #$ ' $
#"# „ "# % $ ) "# „ %) # $
ÈÈÈ
abab
ab
But , so the critical points occur at x and x .# ¸!Þ)%&" œ" œ# ¸$Þ"&&
#$ #$
$ $
È È
crit. pt. derivative extremum value
x local max 4
x local min
œ" !
¸ $Þ"&& ! ¸ $Þ!(*
53. (a) No, since f x x , which is undefined at x .
w#
$
"Î$
ab a bœ# œ#
(b) The derivative is defined and nonzero for all x . Also, f and f x for all x .Á# # œ! ! Á#ab ab
(c) No, f x need not have a global maximum because its domain is all real numbers. Any restriction of f to a closedab
interval of the form a, b would have both a maximum value and minimum value on the interval.ÒÓ
(d) The answers are the same as (a) and (b) with 2 replaced by a.
54. Note that f x . Therefore, f x .
x x, x or x x , x or x
x x, x or x x , x or x
ab ab
œœ
œœ
* Ÿ $ ! Ÿ $ $ * $ ! $
* $ ! $ $ * $ ! $
$ $
$ $
w
(a) No, since the left- and right-hand derivatives at x , are and , respectively.œ! * *
(b) No, since the left- and right-hand derivatives at x , are and , respectively.œ$ ") ")
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
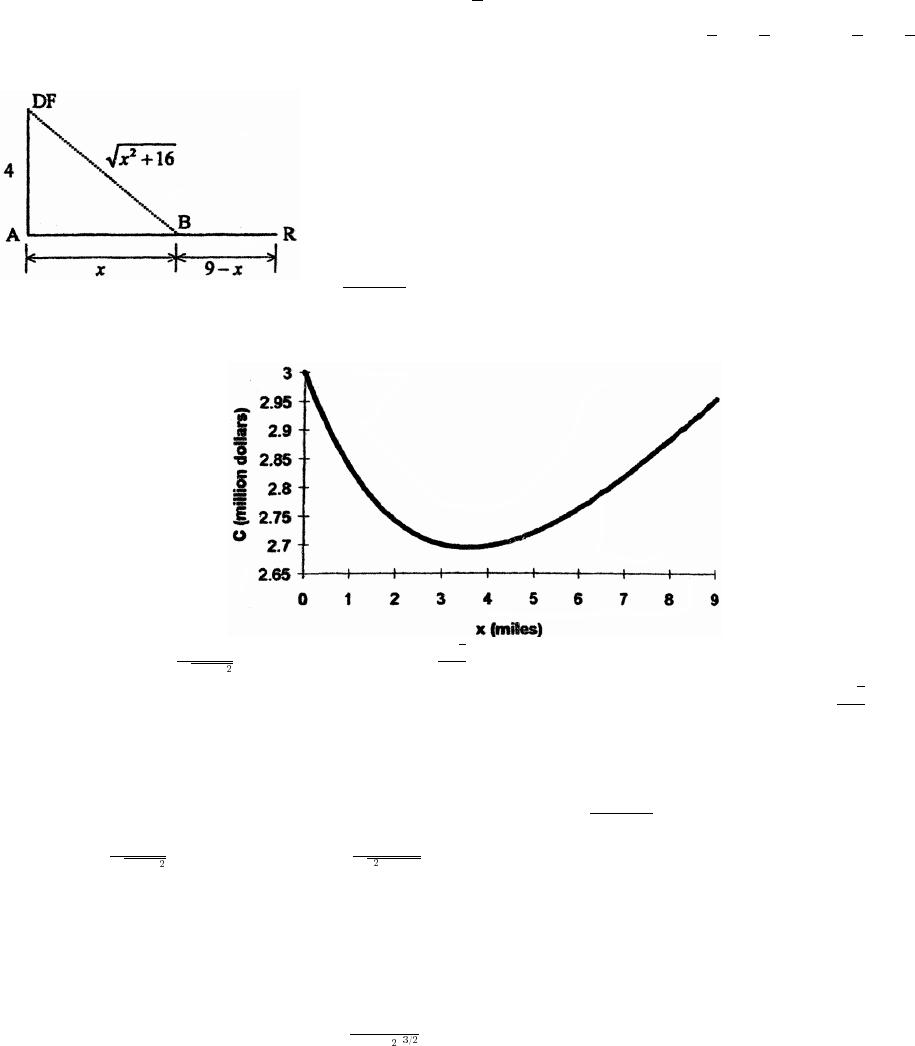
Section 4.1 Extreme Values of Functions 205
(c) No, since the left- and right-hand derivatives at x , are and , respectively.œ$ ") ")
(d) The critical points occur when f x (at x ) and when f x is undefined (at x and x ). The
ww
ab ab
È
œ! œ „ $ œ! œ „$
minimum value is at x , at x , and at x ; local maxima occur at and .! œ$ œ! œ$ $ß' $ $ß' $
Š‹Š‹
ÈÈ ÈÈ
55.
(a) The construction cost is C x x x million dollars, where x miles. The following isab a b
È
œ !Þ$ "' !Þ# * ! Ÿ Ÿ *
#
a graph of C x .ab
Solving C x gives x miles, but only x miles is a critical point is
w!Þ$
"'
)&
&
abœ !Þ# œ ! œ „ ¸ „ $Þ&) œ $Þ&)
x
x
ÈÈ
the specified domain. Evaluating the costs at the critical and endpoints gives C $3 million, C $2.694ab Š‹
!œ ¸
)&
&
È
million, and C $2.955 million. Therefore, to minimize the cost of construction, the pipeline should be placedab*¸
from the docking facility to point B, 3.58 miles along the shore from point A, and then along the shore from B to the
refinery.
(b) If the per mile cost of underwater construction is p, then C x p x x andab a b
È
œ "' !Þ# *
#
C x gives x , which minimizes the construction cost provided x . The value
w!Þ$ !Þ)
"' !Þ!%
abœ!Þ#œ! œ Ÿ*
x
xc c
p
ÈÈ
of p that gives x miles is . Consequently, if the underwater construction costs $218,864 per mile or less,
cœ * !Þ#"))'%
then running the pipeline along a straight line directly from the docking facility to the refinery will minimize the cost
of construction.
In theory, p would have to be infinite to justify running the pipe directly from the docking facility to point A (i.e., for
x to be zero). For all values of p there is always an x that will give a minimum value for C.
c c
!Þ#"))'% − Ð!ß *Ñ
This is proved by looking at C x which is always positive for p .
ww "'
"'
ab
cp
x
œ!
ab
c
56. There are two options to consider. The first is to build a new road straight from Village A to Village B. The second is to
build a new highway segment from Village A to the Old Road, reconstruct a segment of Old Road, and build a new
highway segment from Old Road to Village B, as shown in the figure. The cost of the first option is C million
"œ !Þ& "&!ab
dollars 75 million dollars.œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
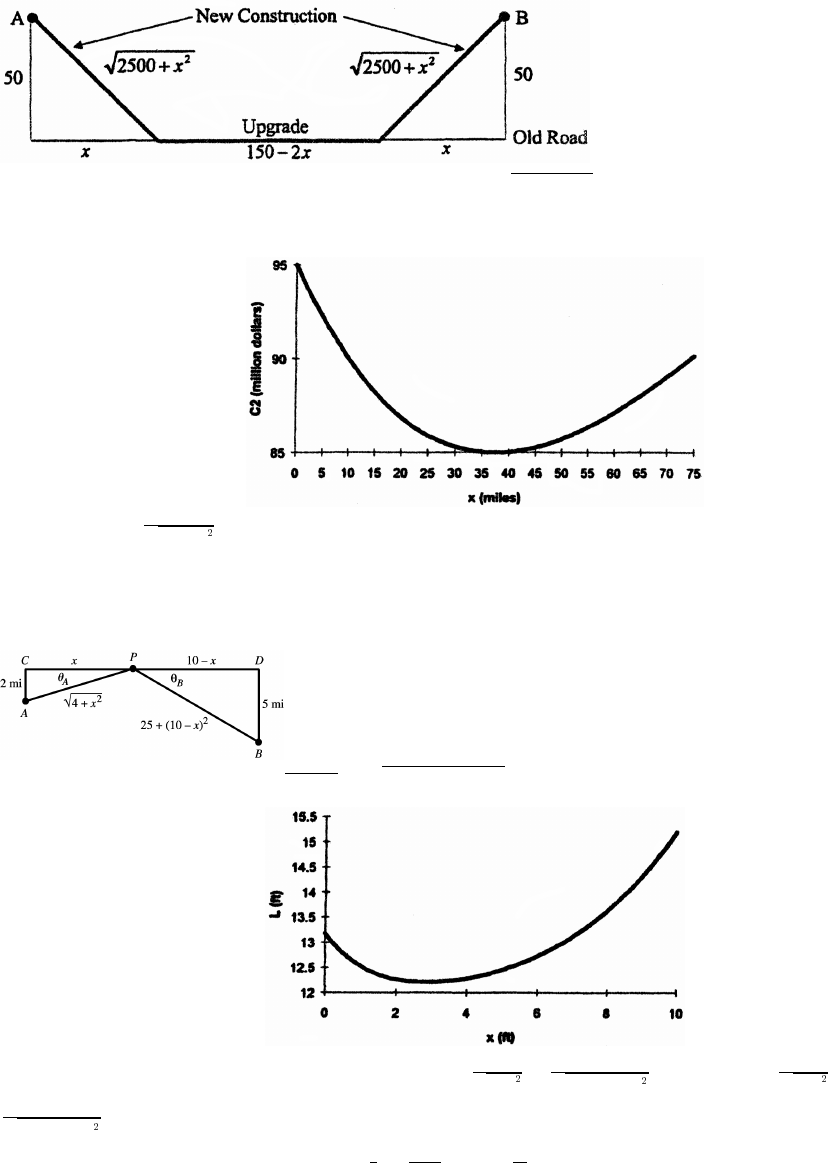
206 Chapter 4 Applications of Derivatives
The construction cost for the second option is C x x x million dollars for
##
ab a b
Š‹
È
œ !Þ& # #&!! !Þ$ "&! #
x miles. The following is a graph of C x .!Ÿ Ÿ(& #ab
Solving C x give x miles, but only x miles is in the specified domain. In
w
##&!!
abœ !Þ' œ ! œ „ $(Þ& œ $(Þ&
x
x
È
summary, C $75 million, C $95 million, C $85 million, and C $90.139 million. Consequently,
"# # #
œ ! œ $(Þ& œ (& œab a b a b
a new road straight from village A to village B is the least expensive option.
57.
The length of pipeline is L x x x for x . The following is a graph of L x .ab a b ab
ÈÉ
œ % #& "! ! Ÿ Ÿ "!
##
Setting the derivative of L x equal to zero gives L x . Note that cos andab ab
w
% %
"!
#& "!
œ œ! œ
xx
xx
x
xA
ÈÈ
ab
Éab )
cos , therefore, L x when cos cos , or and ACP is similar to BDP. Use
"!
#& "!
w
x
xBABAB
Éab
œœ!œœ˜˜)))))ab
simple proportions to determine x as follows: x miles along the coast from town A to town B.
xx
2œ Ê œ ¸ #Þ)&(
"! #!
&(
If the two towns were on opposite sides of the river, the obvious solution would be to place the pump station on a straight
line (the shortest distance) between two towns, again forcing . The shortest length of pipe is the same regardless of))
AB
œ
whether the towns are on thee same or opposite sides of the river.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
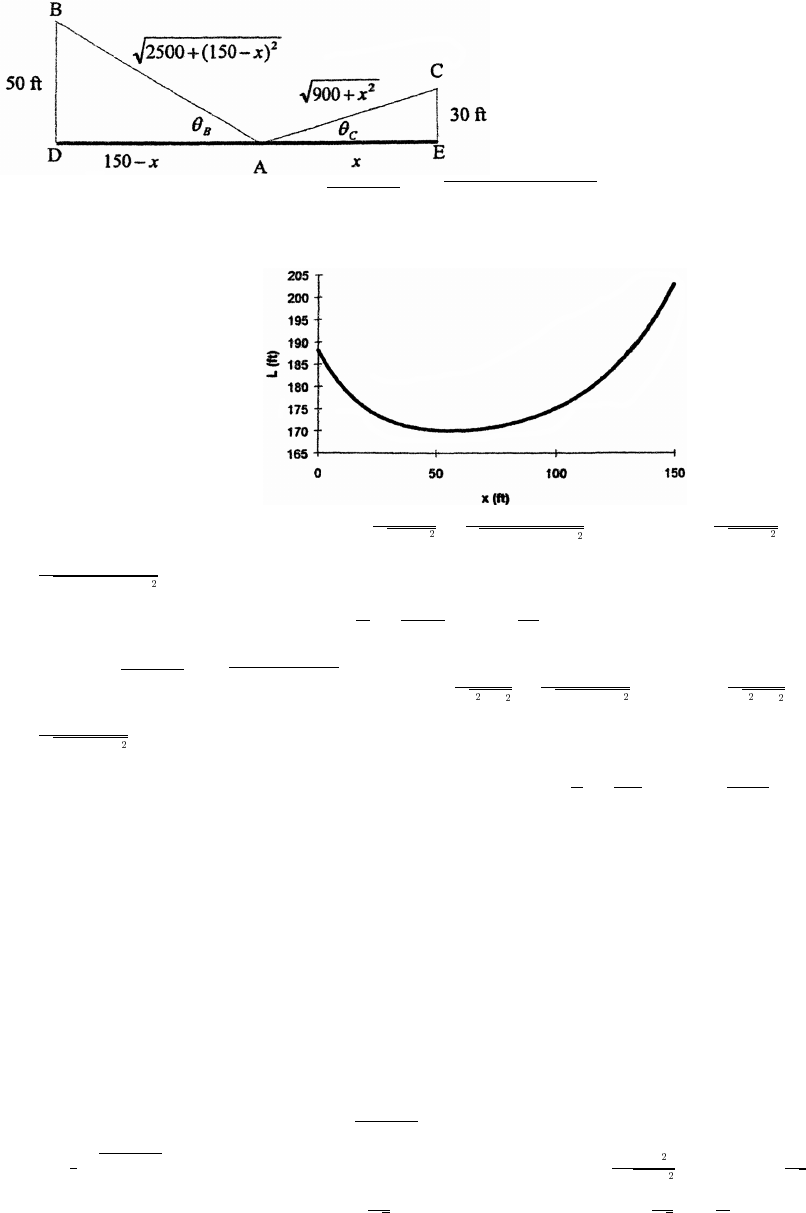
Section 4.1 Extreme Values of Functions 207
58.
(a) The length of guy wire is L x x x for x . The following is a graph ofab a b
ÈÉ
œ *!! #&!! "&! ! Ÿ Ÿ "&!
##
Lx.ab
Setting L x equal to zero gives L x . Note that cos and
ww
*!! *!!
"&!
#&!! "&!
ab abœ œ! œ
xx
xx
x
xA
ÈÈ
ab
Éab )
cos . Therefore, L x when cos cos , or and ACE is similar to ABD.
ab
Éab
"&!
#&!! "&!
w
x
xBABAB
œœ!œœ˜˜)))))ab
Use simple proportions to determine x: x feet.
xx
$! &! %
"&! ##&
œ Ê œ œ &'Þ#&
(b) If the heights of the towers are h and h , and the horizontal distance between them is s, then
BC
L x h x h s x and L x . However, cos andab a b ab
ÉÉ
œ œ œ
CBxx
hx hx
sx
hsx
##
##
w
G
ÉÉ É
ab
ab
CC
B
)
cos . Therefore, L x when cos cos , or and ACE is similar to ABD.
ab
Éab
sx
hsx BCBCB
w
B
œœ!œœ˜˜)))))ab
Simple proportions can again be used to determine the optimum x: x s.
xsx
hh hh
h
cB Bc
c
œÊœ
Š‹
59. (a) V x x x xabœ "'! &# %
#$
Vx x x x x
w#
ab a ba bœ "'! "!% "# œ % # $ #!
The only critical point in the interval is at x . The maximum value of V x is 144 at x .ab ab!ß & œ # œ #
(b) The largest possible volume of the box is 144 cubic units, and it occurs when x units.œ#
60. (a) P x x
w#
abœ # #!!
The only critical point in the interval is at x . The minimum value of P x is at x .ab ab!ß _ œ "! %! œ "!
(b) The smallest possible perimeter of the rectangel is 40 units and it occurs at x units which makes the rectangle aœ"!
10 by 10 square.
61. Let x represent the length of the base and x the height of the triangle. The area of the triangle is represented by
È#& #
A x x where x . Consequently, solving A x x . Sinceab ab
È
œ #& !Ÿ Ÿ& œ!Ê œ!Ê œ
x x
x
##w#&# &
##& #
ÈÈ
A A , A x is maximized at x . The largest possible area is A cm .ab ab ab Š‹
!œ &œ! œ œ
&&#&
##
%
#
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

208 Chapter 4 Applications of Derivatives
62. (a) From the diagram the perimeter P x rœ# # œ%!!1
x r. The area A is 2rxÊ œ #!! 1
A r r r where r .Ê œ %!! # ! Ÿ Ÿab 1##!!
1
(b) A r r so the only critical point is r .
w"!!
abœ %!! % œ1
1
Since A r if r and x r , theabœ! œ! œ#!! œ!1
values r 31.83 m and x m theœ ¸ œ "!!
"!!
1maximize
area over the interval r .!Ÿ Ÿ#!!
1
63. s gt v t s gt v t . Now s t s t v 0 t 0 or t .œ Ê œ œ!Ê œ œ Í œ Í œ œ
"
#
#!! !
ds
dt g 2 g
v2v
00
gt
ab ˆ‰ 0
Thus s g v s s s is the height over the interval 0 t .
Š‹ Š‹ Š‹
vvv 2v
ggg2g g
2
00 00
v
œ œ Ÿ Ÿ
"
#
20
maximum
64. sin t cos t, solving tan t t n where n is a nonnegative integer (in this exercise t is
dI dI
dt dt
œ# # œ!Ê œ"Ê œ
1
%1
never negative) the peak current is amps.Ê##
È
65. Yes, since f(x) x x x f (x) x (2x) is not defined at x 0. Thus itœœ œ Ê œ œ œ œkk ab ab
È##w #
"Î# "Î#
"
#
xx
xx
ab kk
is not required that f be zero at a local extreme point since f may be undefined there.
ww
66. If f(c) is a local maximum value of f, then f(x) f(c) for all x in some open interval (a b) containing c. SinceŸß
f is even, f( x) f(x) f(c) f( c) for all x in the open interval ( b a) containing c. That is, f assumesœ Ÿ œ ß
a local maximum at the point c. This is also clear from the graph of f because the graph of an even function
is symmetric about the y-axis.
67. If g(c) is a local minimum value of g, then g(x) g(c) for all x in some open interval (a b) containing c. Sinceß
g is odd, g( x) g(x) g(c) g( c) for all x in the open interval ( b a) containing c. That is, gœ Ÿ œ ß
assumes a local maximum at the point c. This is also clear from the graph of g because the graph of an odd
function is symmetric about the origin.
68. If there are no boundary points or critical points the function will have no extreme values in its domain. Such
functions do indeed exist, for example f(x) x for x . (Any other linear function f(x) mx bœ__ œ
with m 0 will do as well.)Á
69. (a) f x ax bx c is a quadratic, so it can have 0, 1, or 2 zeros, which would be the critical points of f. The
w#
abœ$ #
function f x x x has two critical points at x and x . The function f x x has one critical pointab abœ$ œ" œ" œ"
$ $
at x The function f x x x has no critical points.œ!Þ œ ab $
(b) The function can have either two local extreme values or no extreme values. (If there is only one critical point, the
cubic function has no extreme values.)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
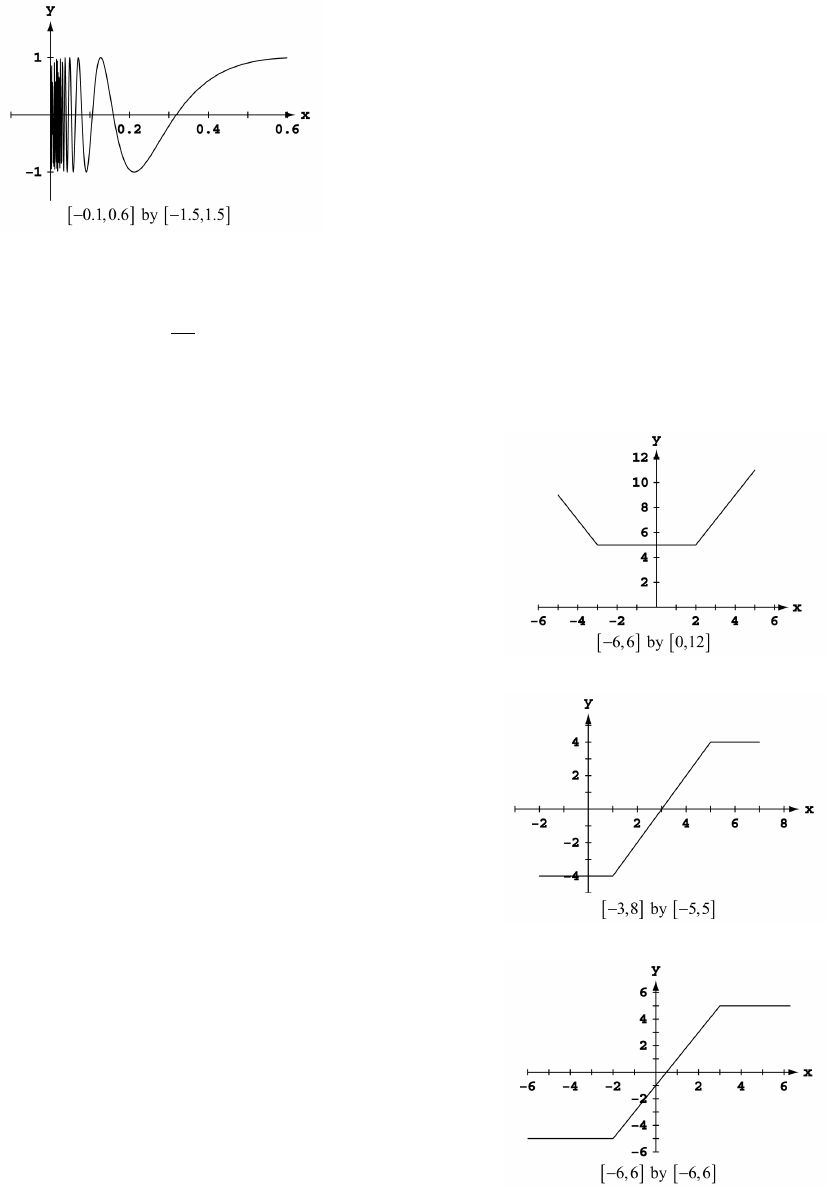
Section 4.1 Extreme Values of Functions 209
70. (a)
f is not a local extreme value because in any open interval containing x , there are infinitely many pointsab!œ! œ!
where f x and where f x .ab abœ" œ"
(b) One possible answer, on the interval :Ò!ß "Ó
fx xcos , x
, x
ab œab
œ" !Ÿ "
!œ"
"
"x
This function has no local extreme value at x . Note that it is continuous on .œ" Ò!ß"Ó
71. Maximum value is 11 at x ;œ&
minimum value is 5 on the interval ;Ò$ß #Ó
local maximum at ab&ß *
72. Maximum value is 4 on the interval ;Ò&ß (Ó
minimum value is on the interval .% Ò#ß "Ó
73. Maximum value is on the interval ;& Ò$ß _Ñ
minimum value is on the interval .& Ð_ß #Ó
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

210 Chapter 4 Applications of Derivatives
74. Minimum value is 4 on the interval Ò"ß $Ó
75-80. Example CAS commands:
:Maple
with(student):
f := x -> x^4 - 8*x^2 + 4*x + 2;
domain := x=-20/25..64/25;
plot( f(x), domain, color=black, title="Section 4.1 #75(a)" );
Df := D(f);
plot( Df(x), domain, color=black, title="Section 4.1 # 75(b)" )
StatPt := fsolve( Df(x)=0, domain )
SingPt := NULL;
EndPt := op(rhs(domain));
Pts :=evalf([EndPt,StatPt,SingPt]);
Values := [seq( f(x), x=Pts )];
Maximum value is 2.7608 and occurs at x=2.56 (right endpoint).
Minimum value is -6.2680 and occurs at x=1.86081 (singular point).
$%
: (functions may vary) (see section 2.5 re. RealsOnly ):Mathematica
<<Miscellaneous `RealOnly`
Clear[f,x]
a = 1; b = 10/3;
f[x_] =2 2x 3 x2/3
f'[x]
Plot[{f[x], f'[x]}, {x, a, b}]
NSolve[f'[x]==0, x]
{f[a], f[0], f[x]/.%, f[b]//N
In more complicated expressions, NSolve may not yield results. In this case, an approximate solution (say 1.1 here)
is observed from the graph and the following command is used:
FindRoot[f'[x]==0,{x, 1.1}]
4.2 THE MEAN VALUE THEOREM
1. When f(x) x 2x 1 for 0 x 1, then f (c) 3 2c 2 c .œ ŸŸ œ ʜʜ
#w
#
"
f(1) f(0)
10
2. When f(x) x for 0 x 1, then f (c) 1 c c .œŸŸ œÊœ Êœ
#Î$ w "Î$
#
f(1) f(0)
10 3 7
28
ˆ‰
3. When f(x) x for x 2, then f (c) 0 c 1.œ ŸŸ œ Ê œ" Ê œ
"" "
#
w
x21/2 c
f(2) f(1/2)
4. When f(x) x 1 for 1 x 3, then f (c) c .œ ŸŸ œ Êœ Êœ
Èf(3) f(1) 2
31 c1
3
# #
w"
#
ÈÈ
5. Does not; f(x) is not differentiable at x 0 in ( 8).œ"ß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 4.2 The Mean Value Theorem 211
6. Does; f(x) is continuous for every point of [0 1] and differentiable for every point in (0 1).ßß
7. Does; f(x) is continuous for every point of [0 1] and differentiable for every point in (0 1).ßß
8. Does not; f(x) is not continuous at x 0 because lim f(x) 1 0 f(0).œ œÁœ
xÄ!
9. Since f(x) is not continuous on 0 x 1, Rolle's Theorem does not apply: lim f(x) lim x 1ŸŸ œ œ
x1 x1ÄÄ
0 f(1).Áœ
10. Since f(x) must be continuous at x 0 and x 1 we have lim f(x) a f(0) a 3 andœœ œœÊœ
xÄ!
lim f(x) lim f(x) 1 3 a m b 5 m b. Since f(x) must also be differentiable at
x1 x1
ÄÄ
œ Êœ Ê œ
x 1 we have lim f (x) lim f (x) 2x 3 m 1 m. Therefore, a 3, m 1 and b 4.œœÊœÊœœœœ
x1 x1
ÄÄ
ww kkx=1 x=1
11. (a) i
ii
iii
iv
(b) Let r and r be zeros of the polynomial P(x) x a x a x a , then P(r ) P(r ) 0.
"# "! " #
œ á œ œ
nn-1
n-1
Since polynomials are everywhere continuous and differentiable, by Rolle's Theorem P (r) 0 for some r
wœ
between r and r , where P (x) nx (n 1) a x a .
"# "
wœ á
n-1 n-2
n-1
12. With f both differentiable and continuous on [a b] and f(r ) f(r ) f(r ) 0 where r , r and r are in [a b],ß œœœ ß
"#$ "#$
then by Rolle's Theorem there exists a c between r and r such that f (c ) 0 and a c between r and r
""# " ##$
wœ
such that f (c ) 0. Since f is both differentiable and continuous on [a b], Rolle's Theorem again applies and
ww
#ϧ
we have a c between c and c such that f (c ) 0. To generalize, if f has n 1 zeros in [a b] and f is
$"# $
wÐÑ
wϧ
n
continuous on [a b], then f has at least one zero between a and b.ßÐÑn
13. Since f exists throughout [a b] the derivative function f is continuous there. If f has more than one zero in
ww w w
ß
[a b], say f (r ) f (r ) 0 for r r , then by Rolle's Theorem there is a c between r and r such thatßœœÁ
ww
"# "# "#
f (c) 0, contrary to f 0 throughout [a b]. Therefore f has at most one zero in [a b]. The same argument
ww ww w
œß ß
holds if f 0 throughout [a b].
ww ß
14. If f(x) is a cubic polynomial with four or more zeros, then by Rolle's Theorem f (x) has three or more zeros,
w
f (x) has 2 or more zeros and f (x) has at least one zero. This is a contradiction since f (x) is a non-zero
ww www www
constant when f(x) is a cubic polynomial.
15. With f( 2) 11 0 and f( 1) 1 0 we conclude from the Intermediate Value Theorem thatœ œ
f(x) x 3x 1 has at least one zero between 2 and 1. Then 2 x 1 x 1œ Ê)
% $
32 4x 4 29 4x 3 1 f (x) 0 for 2 x 1 f(x) is decreasing on [ 1]Ê Ê Ê Ê #ß
$$w
f(x) 0 has exactly one solution in the interval ( 1).Êœ #ß
16. f(x) x 7 f (x) 3x 0 on ( 0) f(x) is increasing on ( 0). Also, f(x) 0 ifœ Ê œ _ß Ê _ß
$w#
48
xx
x 2 and f(x) 0 if 2 x 0 f(x) has exactly one zero in ( ). Ê _ß !
17. g(t) t t 1 4 g (t) 0 g(t) is increasing for t in ( ); g(3) 3 2 0œÊ œ Ê !ß_ œ
ÈÈÈ
w""
#
ÈÈ
t2t1
and g(15) 15 0 g(t) has exactly one zero in ( )œÊ !ß_Þ
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

212 Chapter 4 Applications of Derivatives
18. g(t) 1 t 3.1 g (t) 0 g(t) is increasing for t in ( 1 1);œ Ê œ Ê ß
"""
" "
w
t(t)
21t
ÈÈ
g( 0.99) 2.5 and g(0.99) 98.3 g(t) has exactly one zero in ( 1 1).œ œ Ê ß
19. r( ) sin 8 r ( ) 1 sin cos 1 sin 0 on ( ) r( ) is)) ) )œ Ê œ œ _ß_Ê
#w "
ˆ‰ ˆ‰ ˆ‰ ˆ ‰
))))
333333
22
increasing on ( ); r(0) 8 and r(8) sin 0 r( ) has exactly one zero in ( )._ß _ œ œ Ê _ß _
#ˆ‰
8
3)
20. r( ) 2 cos 2 r ( ) 2 2 sin cos 2 sin 2 0 on ( ) r( ) is increasing on)) ) ) )) ) )œ Ê œ œ _ß_Ê
#w
È
( ); r( ) 4 cos ( ) 2 4 1 2 0 and r(2 ) 4 1 2 0 r( ) has_ß _ # œ # œ œ Ê11 1 1 11 )
ÈÈ È
exactly one zero in ( )._ß _
21. r( ) sec 5 r ( ) (sec )(tan ) 0 on r( ) is increasing on ;)) ) )) )œÊœ !ßÊ !ß
"w
##))
11
3ˆ‰ ˆ‰
r(0.1) 994 and r(1.57) 1260.5 r( ) has exactly one zero in .¸ ¸ Ê !ß)ˆ‰
1
#
22. r( ) tan cot r ( ) sec csc 1 sec cot 0 on r( ) is increasing))))) )) )) )œ Ê œ œ !ß Ê
w## ##
#
ˆ‰
1
on 0 ; r 0 and r(1.57) 1254.2 r( ) has exactly one zero in .
ˆ‰ˆ‰ ˆ‰
ßœ ¸Ê !ß
11 1 1
# #44 )
23. By Corollary 1, f (x) 0 for all x f(x) C, where C is a constant. Since f( 1) 3 we have C 3
wœÊœ œ œ
f(x) 3 for all x.ʜ
24. g(x) 2x 5 g (x) 2 f (x) for all x. By Corollary 2, f(x) g(x) C for some constant C. ThenœÊ œœ œ
ww
f(0) g(0) C 5 5 C C 0 f(x) g(x) 2x 5 for all x.œÊœÊœÊ œœ
25. g(x) x g (x) 2x f (x) for all x. By Corollary 2, f(x) g(x) C.œÊ œœ œ
#w w
(a) f(0) 0 0 g(0) C 0 C C 0 f(x) x f(2) 4œÊœœÊœÊœÊœ
#
(b) f(1) 0 0 g(1) C 1 C C 1 f(x) x 1 f(2) 3œÊœ œÊ œÊ œÊ œ
#
(c) f( 2) 3 3 g( 2) C 3 4 C C 1 f(x) x 1 f(2) 3œÊœÊœ Ê œÊ œÊ œ
#
26. g(x) mx g (x) m, a constant. If f (x) m, then by Corollary 2, f(x) g(x) b mx b whereœÊ œ œ œœ
ww
b is a constant. Therefore all functions whose derivatives are constant can be graphed as straight lines
ymxb.œ
27. (a) y C (b) y C (c) y Cœ œ œ
xxx
34
#
28. (a) y x C (b) y x x C (c) y x x x Cœ œ œ
##$#
29. (a) y x y C (b) y x C (c) y 5x C
w# "" "
œ Ê œ œ œ
xx x
30. (a) y x y x C y x C (b) y 2 x C
w "Î# "Î#
"
#
œÊœÊœ œ
ÈÈ
(c) y 2x 2 x Cœ
#È
31. (a) y cos 2t C (b) y 2 sin Cœ œ
"
# #
t
(c) y cos 2t 2 sin Cœ
"
##
t
32. (a) y tan C (b) y y C (c) y tan Cœ œÊœ œ)))))
w "Î# $Î# $Î#
22
33
33. f(x) x x C; 0 f(0) 0 0 C C 0 f(x) x xœ œ œÊœÊ œ
## #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 4.2 The Mean Value Theorem 213
34. g(x) x C; 1 g( 1) ( 1) C C 1 g(x) x 1œ œ œ Ê œ Ê œ
"" "
## #
x1 x
35. r( ) 8 cot C; 0 r 8 cot C 0 2 1 C C 2 1)) ) 1 1œ œ œ Êœ Êœ
ˆ‰ ˆ‰ ˆ‰
11 1
44 4
r( ) 8 cot 2 1ʜ)) )1
36. r(t) sec t t C; 0 r(0) sec (0) 0 C C 1 r(t) sec t t 1œœœ ʜʜ
37. v t s t t C; at s and t we have C s t tœ œ*Þ) &Ê œ%Þ* & œ"! œ! œ"!Ê œ%Þ* & "!
ds
dt # #
38. v t s t t C; at s and t we have C s t tœ œ $# # Ê œ "' # œ % œ œ " Ê œ ' # "
ds
dt ##
"
#
39. v sin t s cos t C; at s and t we have C sœ œ Ê œ œ! œ! œ Ê œ
ds
dt
cos t
ab ab11
""
"
111
1ab
40. v cos s sin C; at s and t we have C s sinœ œ Êœ œ" œ œ"Êœ "
ds 2 t t t
dt 11 1 1
ˆ‰ ˆ‰ ˆ‰
## #
#
1
41. a v t C ; at v and t we have C v t s t t C ; at s andœ$#Ê œ$# œ#! œ! œ#!Ê œ$# #!Ê œ"' #! œ&
"" #
#
t we have C s t tœ! œ&Ê œ"' #! &
##
42. a 9.8 v 9.8t C ; at v and t we have C v t s t t C ; at s andœ Ê œ œ$ œ! œ$Ê œ*Þ) $Ê œ%Þ* $ œ!
"" #
#
t we have C s t tœ! œ!Ê œ%Þ* $
##
43. a sin t v cos t C ; at v and t we have C v cos t s sin t C ; at sœ% # Ê œ# # œ# œ! œ!Ê œ# # Ê œ # œ$ab ab ab ab
"" #
and t we have C s sin tœ! œ$Ê œ # $
#ab
44. a cos v sin C ; at v and t we have C v sin s cos C ; atœ Ê œ œ! œ! œ!Ê œ Ê œ
* $ $$ $$ $
"" #
1 1 11 11 1
ˆ‰ ˆ‰ ˆ‰ ˆ‰
tt tt
s and t we have C s cosœ" œ! œ!Ê œ
#$
ˆ‰
t
1
45. If T(t) is the temperature of the thermometer at time t, then T(0) 19° C and T(14) 100° C. From theœ œ
Mean Value Theorem there exists a 0 t 14 such that 8.5° C/sec T (t ), the rate at which œ œ
!!
w
T(14) T(0)
14 0
the temperature was changing at t t as measured by the rising mercury on the thermometer.œ!
46. Because the trucker's average speed was 79.5 mph, by the Mean Value Theorem, the trucker must have been going that
speed at least once during the trip.
47. Because its average speed was approximately 7.667 knots, and by the Mean Value Theorem, it must have been going that
speed at least once during the trip.
48. The runner's average speed for the marathon was approximately 11.909 mph. Therefore, by the Mean Value Theorem, the
runner must have been going that speed at least once during the marathon. Since the initial speed and final speed are both 0
mph and the runner's speed is continuous, by the Intermediate Value Theorem, the runner's speed must have been 11 mph
at least twice.
49. Let d(t) represent the distance the automobile traveled in time t. The average speed over 0 t 2 isŸŸ
. The Mean Value Theorem says that for some 0 t 2, d (t ) . The value d (t ) is
d(2) d(0) d(2) d(0)
0 0
# #
!! !
ww
œ
the speed of the automobile at time t (which is read on the speedometer).
!
50. a t v t v t t C; at we have C v t t. When t , then v m/sec.ab ab ab a b ab a bœ œ "Þ' Ê œ "Þ' !ß ! œ ! Ê œ "Þ' œ $! $! œ %)
w
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
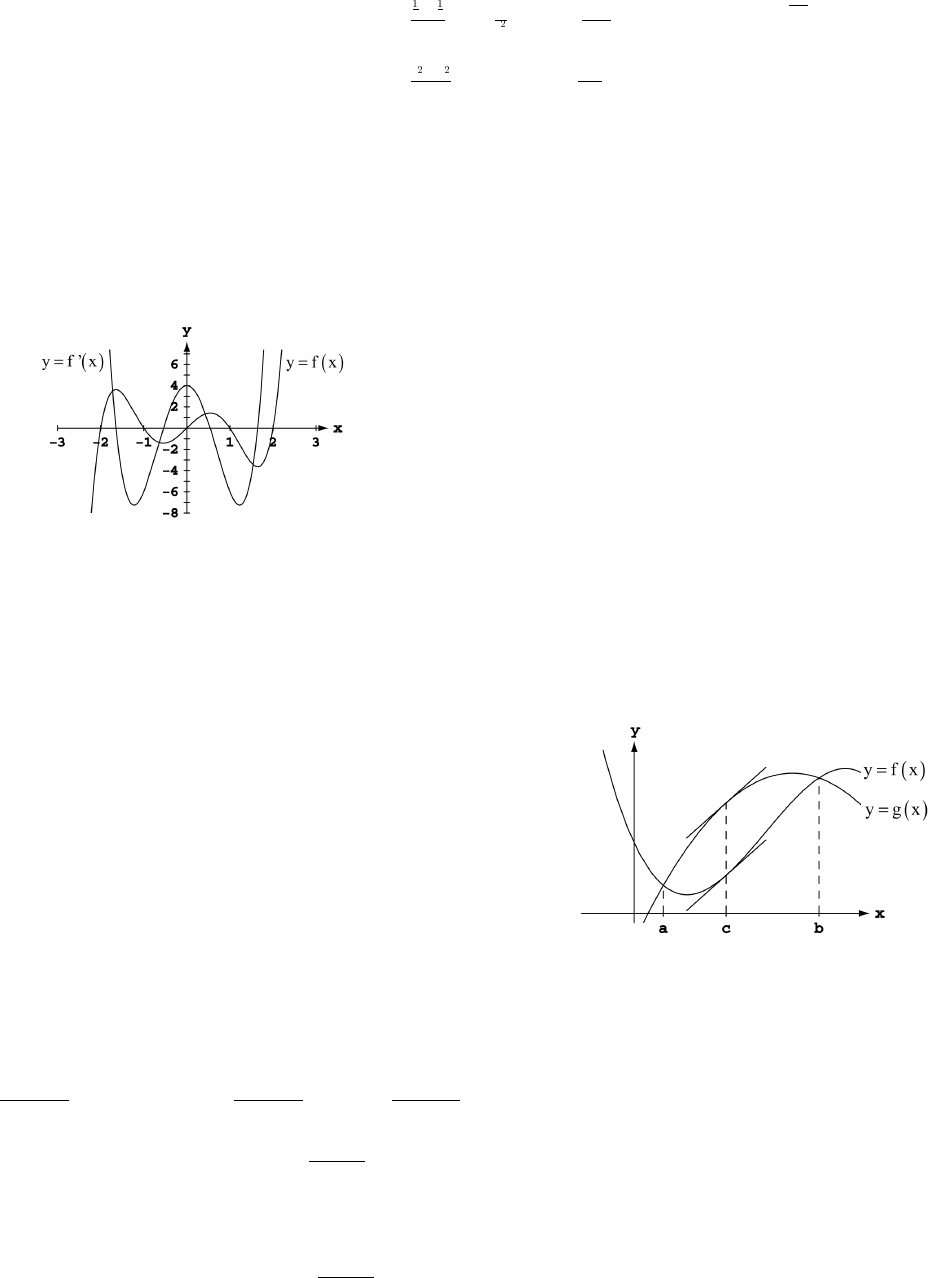
214 Chapter 4 Applications of Derivatives
51. The conclusion of the Mean Value Theorem yields c a b c ab.
ba
"
#
ba c ab
ab
œ Ê œ Ê œ
ˆ‰ È
52. The conclusion of the Mean Value Theorem yields 2c c .
ba ab
ba
#
œÊœ
53. f (x) [cos x sin (x 2) sin x cos (x 2)] 2 sin (x 1) cos (x 1) sin (x x 2) sin 2(x 1)
wœœ
sin (2x 2) sin (2x 2) 0. Therefore, the function has the constant value f(0) sin 1 0.7081œœ œ¸
#
which explains why the graph is a horizontal line.
54. (a) f x x x x x x x x x is one possibility.abababababœ#" "#œ&%
&$
(b) Graphing f x x x x and f x x x on by we see that each x-intercept ofab abœ & % œ & "& % Ò$ß $Ó Ò(ß (Ó
&$ w % #
f x lies between a pair of x-intercepts of f x , as expected by Rolle's Theorem.
wab ab
(c) Yes, since sin is continuous and differentiable on .ab_ß _
55. f x must be zero at least once between a and b by the Intermediate Value Theorem. Now suppose that f x is zero twiceab ab
between a and b. Then by the Mean Value Theorem, f x would have to be zero at least once between the two zeros of
wab
f x , but this can't be true since we are given that f x on this interval. Therefore, f x is zero once and only onceab ab ab
wÁ!
between a and b.
56. Consider the function k x f x g x . k x is continuousab ab ab abœ
and differentiable on a, b , and since k a f a g a andÒÓ œ ab ab ab
k b f b g b , by the Mean Value Theorem, there mustab ab abœ
be a point c in a, b where k c . But sinceab ab
wœ!
k c f c g c , this means that f c g c , and c is a
www ww
ab ab ab ab abœ œ
point where the graphs of f and g have tangent lines with the
same slope, so these lines are either parallel or are the same
line.
57. Yes. By Corollary 2 we have f(x) g(x) c since f (x) g (x). If the graphs start at the same point x a,œ œ œ
ww
then f(a) g(a) c 0 f(x) g(x).œÊœÊœ
58. Let f(x) sin x for a x b. From the Mean Value Theorem there exists a c between a and b such thatœŸŸ
cos c 1 1 1 sin b sin a b a .
sin b sin a sin b sin a sin b sin a
ba ba ba
œ ÊŸ ŸÊ ŸÊ Ÿ
¸¸kkkk
59. By the Mean Value Theorem we have f (c) for some point c between a and b. Since b a 0 and f(b) f(a),
f(b) f(a)
ba
w
œ
we have f(b) f(a) 0 f (c) 0.Ê
w
60. The condition is that f should be continuous over [a b]. The Mean Value Theorem then guarantees the
wß
existence of a point c in (a b) such that f (c). If f is continuous, then it has a minimum andߜ
f(b) f(a)
ba
ww
maximum value on [a b], and min f f (c) max f , as required.ߟŸ
ww w
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 4.3 Monotonic Functions and the First Derivative Test 215
61. f (x) 1 x cos x f (x) 1 x cos x 4x cos x x sin x
w% ww % $%
" #
œ Ê œ ab aba b
x 1 x cos x (4 cos x x sin x) 0 for 0 x 0.1 f (x) is decreasing when 0 x 0.1œ Ÿ Ÿ Ê Ÿ Ÿ
$% w
#
ab
min f 0.9999 and max f 1. Now we have 0.9999 1 0.09999 f(0.1) 1 0.1ʸ œ Ÿ ŸÊ ŸŸ
ww "f(0.1)
0.1
1.09999 f(0.1) 1.1.ÊŸŸ
62. f (x) 1 x f (x) 1 x 4x 0 for 0 x 0.1 f (x) is increasing when
w%ww %$ w
" #
œ Ê œ œ Ÿ Êab abab
4x
1x
ab
0 x 0.1 min f 1 and max f 1.0001. Now we have 1 1.0001ŸŸ Ê œ œ Ÿ Ÿ
ww f(0.1) 2
0.1
0.1 f(0.1) 2 0.10001 2.1 f(0.1) 2.10001.ÊŸ Ÿ ÊŸ Ÿ
63. (a) Suppose x 1, then by the Mean Value Theorem 0 f(x) f(1). Suppose x 1, then by theÊ
f(x) f(1)
x1
Mean Value Theorem 0 f(x) f(1). Therefore f(x) 1 for all x since f(1) 1.
f(x) f(1)
x1
Ê œ
(b) Yes. From part (a), lim 0 and lim 0. Since f (1) exists, these two one-sided
x1 x1
ÄÄ
f(x) f(1) f(x) f(1)
x1 x1
w
Ÿ
limits are equal and have the value f (1) f (1) 0 and f (1) 0 f (1) 0.
ww w w
ʟ ʜ
64. From the Mean Value Theorem we have f (c) where c is between a and b. But f (c) 2pc q 0
f(b) f(a)
ba
ww
œœœ
has only one solution c . (Note: p 0 since f is a quadratic function.)œ Á
q
p#
4.3 MONOTONIC FUNCTIONS AND THE FIRST DERIVATIVE TEST
1. (a) f (x) x(x 1) critical points at 0 and 1
wœÊ
(b) f increasing on ( ) and ( ), decreasing on ( )
wœ ± ± Ê _ß ! "ß _ !ß "
!"
(c) Local maximum at x 0 and a local minimum at x 1œœ
2. (a) f (x) (x 1)(x 2) critical points at 2 and 1
wœ Ê
(b) f increasing on ( ) and ( ), decreasing on ( 2 )
wœ ± ± Ê _ß # "ß _ ß "
# "
(c) Local maximum at x 2 and a local minimum at x 1œ œ
3. (a) f (x) (x 1) (x 2) critical points at 2 and 1
w#
œ Ê
(b) f increasing on ( 2 1) and ( ), decreasing on ( 2)
wœ ± ± Ê ß "ß _ _ß
# "
(c) No local maximum and a local minimum at x 2œ
4. (a) f (x) (x 1) (x 2) critical points at 2 and 1
w##
œ Ê
(b) f increasing on ( 2) ( ) ( ), never decreasing
wœ ± ± Ê _ß #ß " "ß _
# "
(c) No local extrema
5. (a) f (x) (x 1)(x 2)(x 3) critical points at 2, 1 and 3
wœÊ
(b) f increasing on ( 2 1) and ( ), decreasing on ( 2) and ( )
wœ ± ± ± Ê ß $ß _ _ß "ß $
# " $
(c) Local maximum at x 1, local minima at x 2 and x 3œœœ
6. (a) f (x) (x 7)(x 1)(x 5) critical points at 5, 1 and 7
wœÊ
(b) f increasing on ( 5 1) and (7 ), decreasing on ( 5) and ( 7)
wœ ± ± ± Ê ß ß _ _ß "ß
& " (
(c) Local maximum at x 1, local minima at x 5 and x 7œ œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
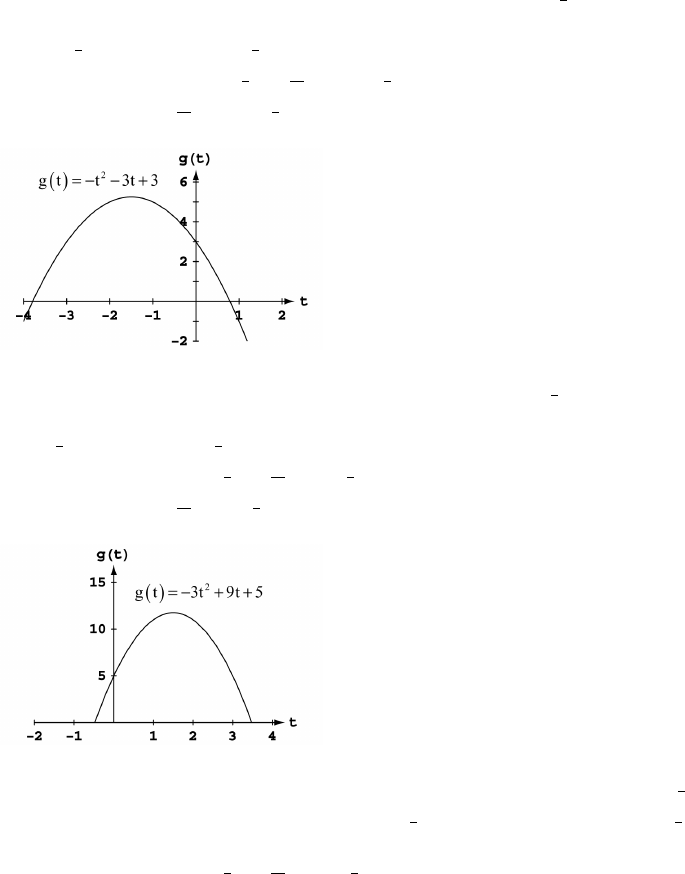
216 Chapter 4 Applications of Derivatives
7. (a) f (x) x (x 2) critical points at 2 and 0
w "Î$
œÊ
(b) f )( increasing on ( 2) and (0 ), decreasing on ( 2 0)
wœ ± Ê _ß ß _ ß
# !
(c) Local maximum at x 2, local minimum at x 0œ œ
8. (a) f (x) x (x 3) critical points at 0 and 3
w "Î#
œÊ
(b) f ( increasing on ( ), decreasing on (0 3)
wœ ± Ê $ß _ ß
!$
(c) No local maximum and a local minimum at x 3œ
9. (a) g(t) t 3t 3 g (t) 2t 3 a critical point at t ; g , increasing onœ Ê œ Ê œ œ ±
$Î#
#w w
#
3
, decreasing on
ˆ‰ ˆ‰
_ß ß _
33
##
(b) local maximum value of g at t
ˆ‰
œ œ
321 3
4##
(c) absolute maximum is at t
21 3
4œ#
(d)
10. (a) g(t) 3t 9t 5 g (t) 6t 9 a critical point at t ; g , increasing onœ Ê œ Ê œ œ ±
$Î#
#w w
#
3
, decreasing on
ˆ‰ ˆ‰
_ß ß _
33
2#
(b) local maximum value of g at t
ˆ‰
347 3
4##
œœ
(c) absolute maximum is at t
47 3
4œ#
(d)
11. (a) h(x) x 2x h (x) 3x 4x x(4 3x) critical points at x 0, œ Ê œ œ Ê œ
$# w # 4
3
h , increasing on 0 , decreasing on ( ) and Ê œ ± ± ß _ß ! ß _
!%Î$
wˆ‰ ˆ ‰
44
33
(b) local maximum value of h at x ; local minimum value of h(0) 0 at x 0
ˆ‰
432 4
327 3
œœ œœ
(c) no absolute extrema
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
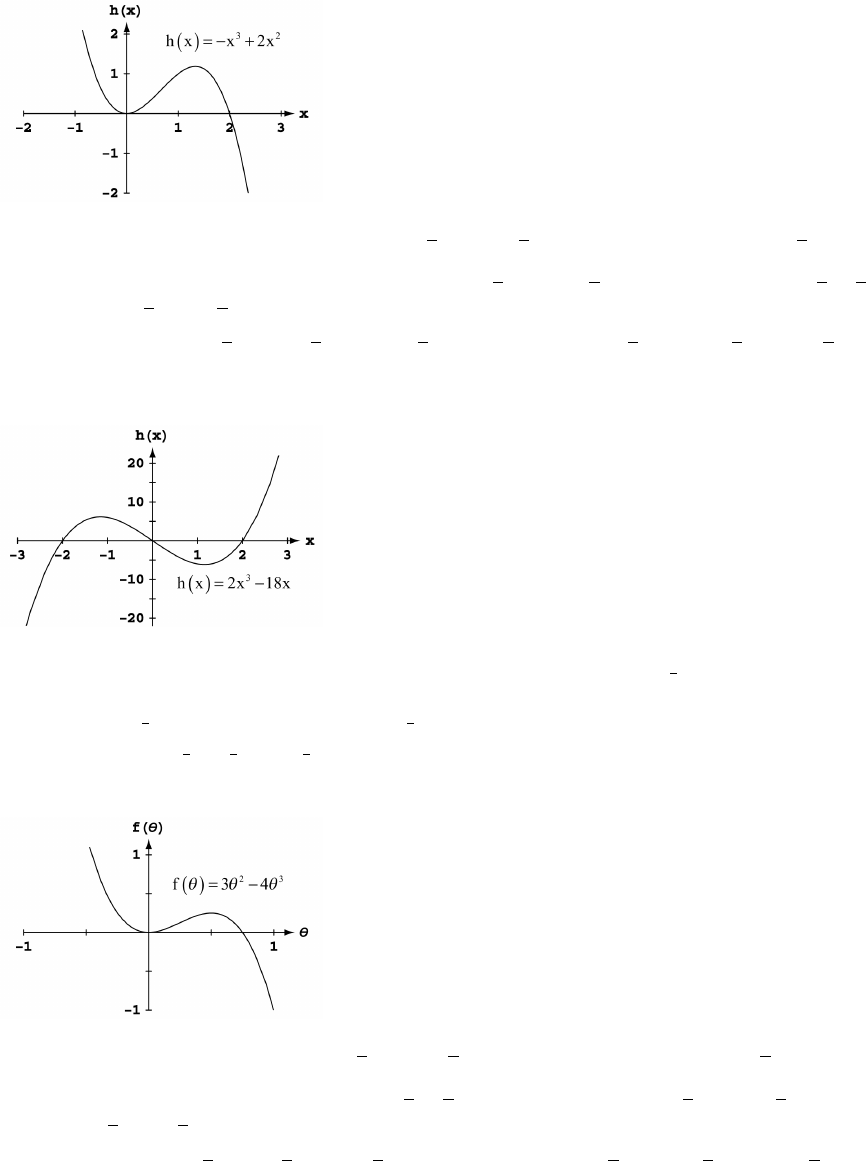
Section 4.3 Monotonic Functions and the First Derivative Test 217
(d)
12. (a) h(x) 2x 18x h (x) 6x 18 6 x 3 x 3 critical points at x 3œ Ê œœ Ê œ„
$w#
Š‹Š‹
ÈÈ È
h | | , increasing on 3 and , decreasing on 3Ê œ _ß $ß _ $ß
$ $
w
ÈÈ Š‹Š‹ Š‹
ÈÈ
ÈÈ
(b) a local maximum is h 3 12 3 at x 3; local minimum is h 3 12 3 at x 3
Š‹ Š‹
ÈÈ È È ÈÈ
œ œ œ œ
(c) no absolute extrema
(d)
13. (a) f( ) 3 4 f ( ) 6 12 6 (1 2 ) critical points at 0, f ,))) )))) ) )œ Ê œ œ Ê œ Ê œ ± ±
!"Î#
#$ w # w
"
#
increasing on 0 , decreasing on ( ) and
ˆ‰ ˆ ‰
ß _ß ! ß _
""
##
(b) a local maximum is f at , a local minimum is f(0) 0 at 0
ˆ‰
"" "
##
œœ œœ
4))
(c) no absolute extrema
(d)
14. (a) f( ) 6 f ( ) 6 3 3 2 2 critical points at 2 ))) ) ) ) ) )œ Ê œ œ Ê œ„ Ê
$w #
Š‹Š‹
ÈÈ È
f , increasing on 2 2 , decreasing on 2 and 2
wœ ± ± ß _ß ß _
# #
ÈÈ Š‹ Š ‹Š‹
ÈÈ È È
(b) a local maximum is f 2 4 2 at 2, a local minimum is f 2 2 at 2
Š‹ Š ‹
ÈÈ È È È È
œœ œ%œ))
(c) no absolute extrema
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
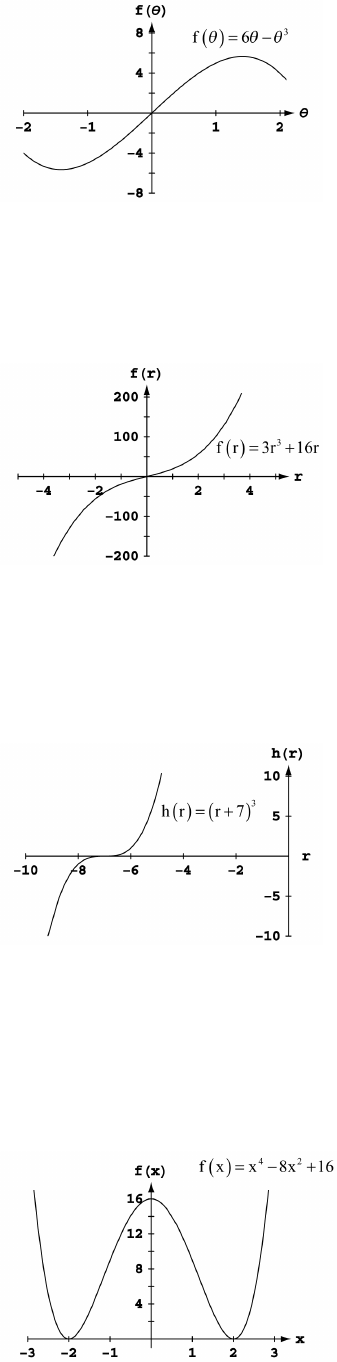
218 Chapter 4 Applications of Derivatives
(d)
15. (a) f(r) 3r 16r f (r) 9r 16 no critical points f , increasing on ( ), neverœ Ê œ Ê Ê œ _ß _
$w# w
decreasing
(b) no local extrema
(c) no absolute extrema
(d)
16. (a) h(r) (r 7) h (r) 3(r 7) a critical point at r 7 h , increasing onœ Ê œ Ê œ Ê œ ±
(
$w # w
( 7) ( ), never decreasing_ß (ß _
(b) no local extrema
(c) no absolute extrema
(d)
17. (a) f(x) x 8x 16 f (x) 4x 16x 4x(x 2)(x 2) critical points at x 0 and x 2œ Ê œ œ Ê œ œ„
%# w $
f , increasing on ( ) and ( ), decreasing on ( 2) and ( )Ê œ ± ± ± #ß ! #ß _ _ß !ß #
# ! #
w
(b) a local maximum is f(0) 16 at x 0, local minima are f 2 0 at x 2œœ „œœ„ab
(c) no absolute maximum; absolute minimum is 0 at x 2œ„
(d)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
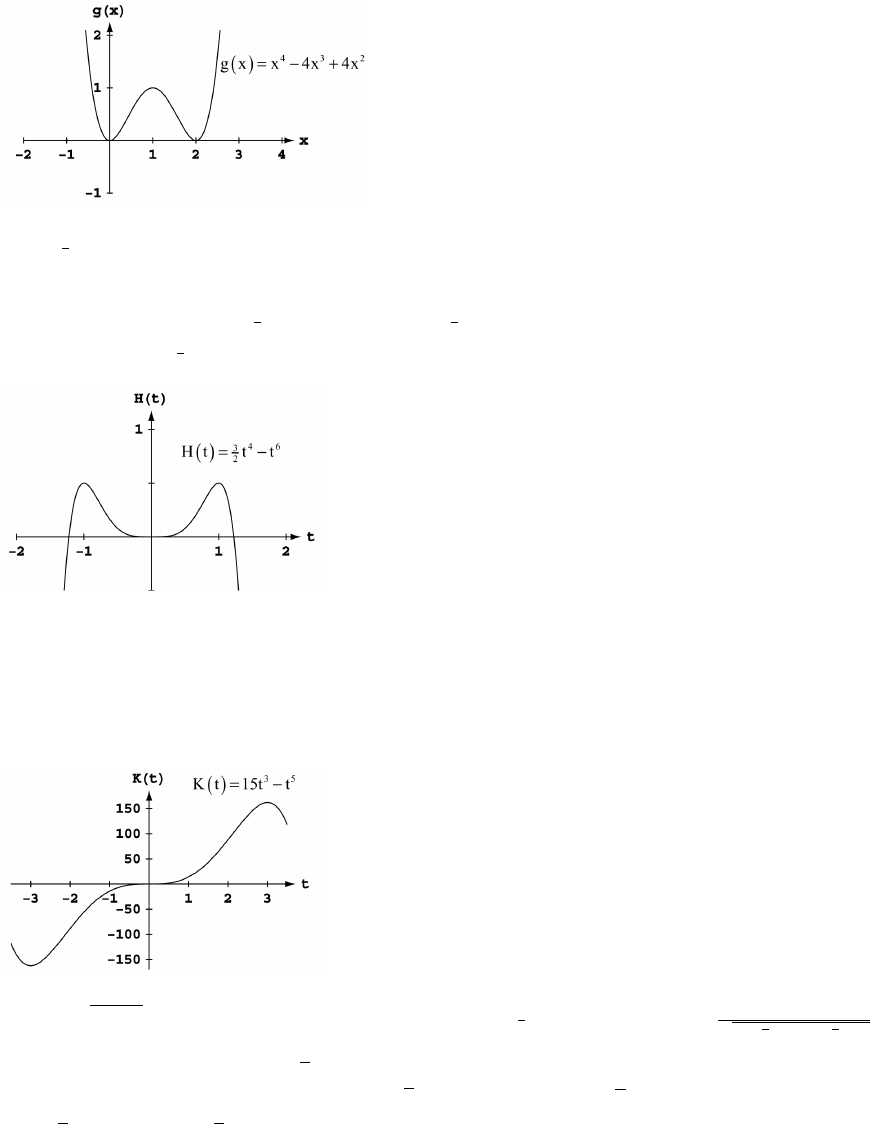
Section 4.3 Monotonic Functions and the First Derivative Test 219
18. (a) g(x) x 4x 4x g (x) 4x 12x x 4x(x 2)(x 1) critical points at x 0, 1, 2œ Ê œ )œ Ê œ
%$# w $ #
g , increasing on (0 1) and ( ), decreasing on ( 0) and (1 )Ê œ ± ± ± ß #ß _ _ß ß #
!"#
w
(b) a local maximum is g(1) 1 at x 1, local minima are g(0) 0 at x 0 and g(2) 0 at x 2œœ œœ œœ
(c) no absolute maximum; absolute minimum is 0 at x 0, 2œ
(d)
19. (a) H(t) t t H (t) 6t 6t 6t (1 t)( t) critical points at t 0, 1œ Ê œœ "Ê œ„
3
#
%' w $ & $
H , increasing on ( 1) and (0 1), decreasing on ( 0) and ( )Ê œ ± ± ± _ß ß "ß "ß _
" ! "
w
(b) the local maxima are H( 1) at t 1 and H(1) at t 1, the local minimum is H(0) 0 at t 0œ œ œ œ œ œ
""
##
(c) absolute maximum is at t 1; no absolute minimum
"
#œ„
(d)
20. (a) K(t) 15t t K (t) 45t 5t 5t (3 t)(3 t) critical points at t 0, 3œÊ œœ Ê œ„
$& w # % #
K , increasing on ( 3 0) (0 3), decreasing on ( 3) and (3 )Ê œ ± ± ± ß ß _ß ß _
$ ! $
w
(b) a local maximum is K(3) 162 at t 3, a local minimum is K( 3) 162 at t 3œœ œœ
(c) no absolute extrema
(d)
21. (a) g(x) x 8 x x 8 x g (x) 8 x x x ( 2x)œœ Ê œ ) œ
Èab ab ab
ˆ‰
##w # #
"Î# "Î# "Î#
"
#
2(2 x)(2 x)
22x 22 x
ÊŠ‹Š‹
ÈÈ
critical points at x 2, 2 2 g ( , increasing on ( ), decreasing onÊ œ „ „ Ê œ ± ± Ñ #ß #
# # # # ##
ÈÈÈ
w
2 and 2
Š‹Š‹
ÈÈ
# ß# #ß#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
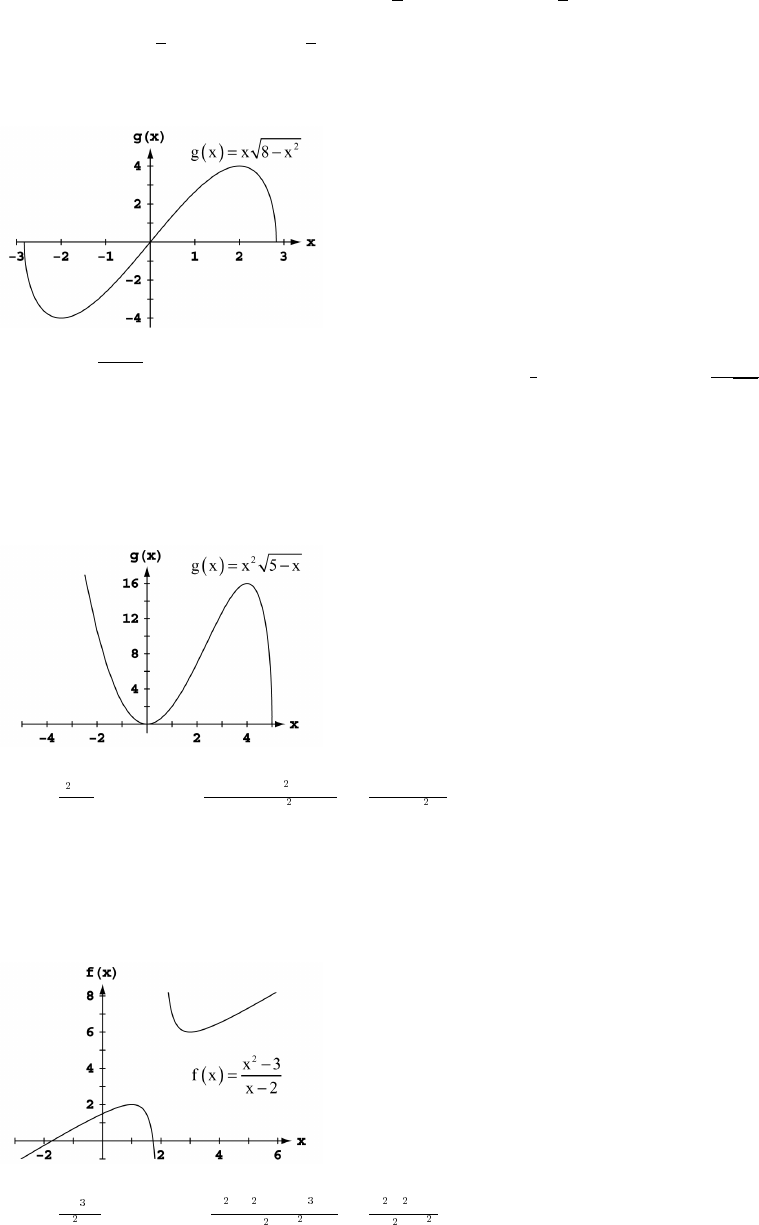
220 Chapter 4 Applications of Derivatives
(b) local maxima are g(2) 4 at x 2 and g 2 2 0 at x 2 2, local minima are g( 2) 4 atœœ œœ œ
Š‹
ÈÈ
x 2 and g 2 2 0 at x 2 2œ œ œ
Š‹
ÈÈ
(c) absolute maximum is 4 at x 2; absolute minimum is 4 at x 2œœ
(d)
22. (a) g(x) x 5 x x (5 x) g (x) 2x(5 x) x (5 x) ( 1)œœÊœ œ
# # "Î# w "Î# # "Î#
"
#
Ȉ‰ 5x(4 x)
25x
È
critical points at x 0, 4 and 5 g , increasing on (0 4), decreasing on ( )Ê œ Ê œ ± ± Ñ ß _ß !
!%&
w
and ( )%ß &
(b) a local maximum is g(4) 16 at x 4, a local minimum is 0 at x 0 and x 5œœ œ œ
(c) no absolute maximum; absolute minimum is 0 at x 0, 5œ
(d)
23. (a) f(x) f (x) critical points at x 1, 3œÊœ œ Ê œ
x3
x(x2)(x)
2x(x 2) x 3 (1) (x 3)(x )
# #
w "
ab
f )( , increasing on ( 1) and ( ), decreasing on ( ) and ( ),Ê œ ± ± _ß $ß _ "ß # #ß $
"$
#
w
discontinuous at x 2œ
(b) a local maximum is f(1) 2 at x 1, a local minimum is f(3) 6 at x 3œœ œœ
(c) no absolute extrema
(d)
24. (a) f(x) f (x) a critical point at x 0œÊœ œ Ê œ
x
3x 1
3x 3x 1 x (6x) 3x x 1
3x 1 3x 1
w
ab ab
ab ab
f , increasing on ( ) ( ), and never decreasingÊ œ ± _ß ! !ß _
!
w
(b) no local extrema
(c) no absolute extrema
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
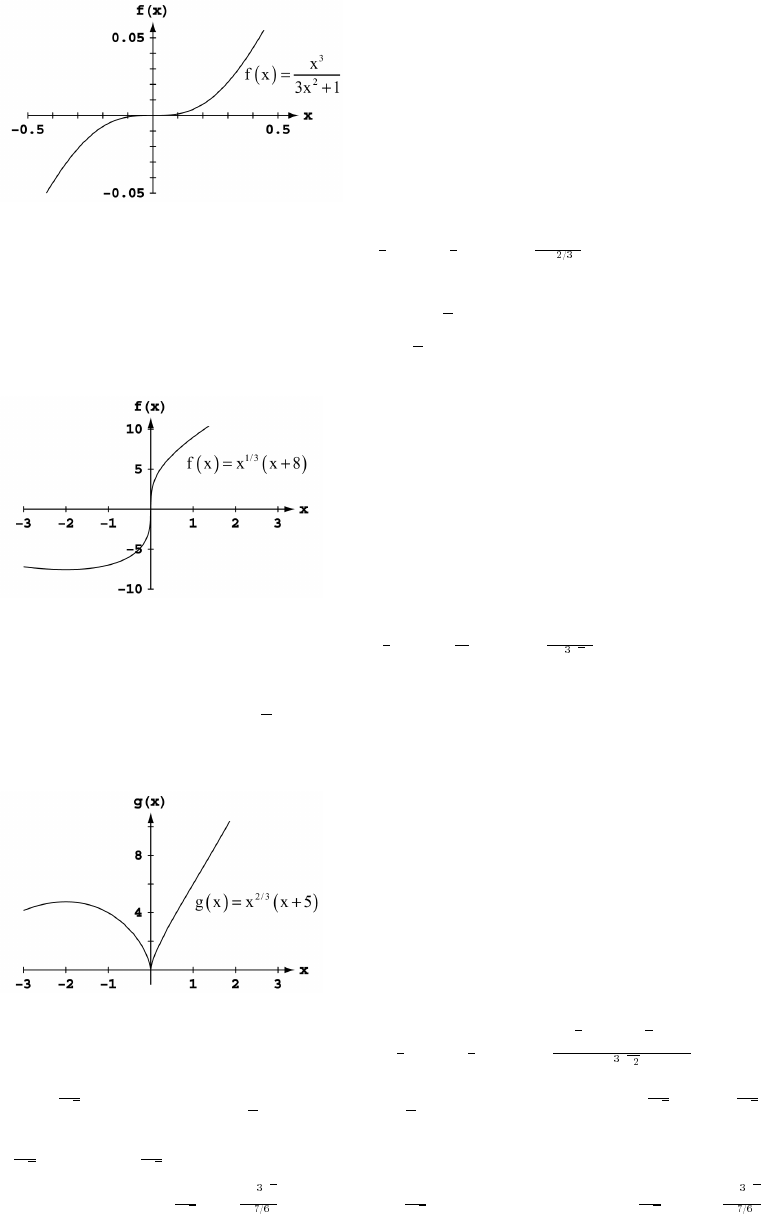
Section 4.3 Monotonic Functions and the First Derivative Test 221
(d)
25. (a) f(x) x (x 8) x 8x f (x) x x critical points at x 0, 2œœÊœ œ Ê œ
"Î$ %Î$ "Î$ w "Î$ #Î$
48
33
4(x 2)
3x
f )( , increasing on ( ) ( ), decreasing on ( 2)Ê œ ± #ß ! !ß _ _ß
# !
w
(b) no local maximum, a local minimum is f( 2) 6 2 7.56 at x 2œ ¸ œ
$
È
(c) no absolute maximum; absolute minimum is 6 2 at x 2œ
$
È
(d)
26. (a) g(x) x (x 5) x 5x g (x) x x critical points at x 2 andœœÊœ œ Ê œ
#Î$ &Î$ #Î$ w #Î$ "Î$
510
33
5(x 2)
3x
È
x 0 g )( , increasing on ( 2) and ( ), decreasing on ( 2 )œ Ê œ ± _ß !ß _ ß !
# !
w
(b) local maximum is g( 2) 3 4 4.762 at x 2, a local minimum is g(0) 0 at x 0œ ¸ œ œ œ
$
È
(c) no absolute extrema
(d)
27. (a) h(x) x x 4 x 4x h (x) x x critical points atœœÊœœ Ê
"Î$ # (Î$ "Î$ w %Î$ #Î$ #
ab 74
33
7x 2 7x
3x
Š‹Š‹
ÈÈ
È
x 0, h )( , increasing on and , decreasing onœ Ê œ ± ± _ß ß _
#Î ( #Î (
!
„
w
222
777
ÈÈÈ
ÈÈ Š‹Š‹
and
Š‹Š‹
22
77
ÈÈ
ß! !ß
(b) local maximum is h 3.12 at x , the local minimum is h 3.12
Š‹ Š‹
222
77 7
24 2 24 2
7 7
ÈÈ È
È È
œ¸ œ œ¸
(c) no absolute extrema
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
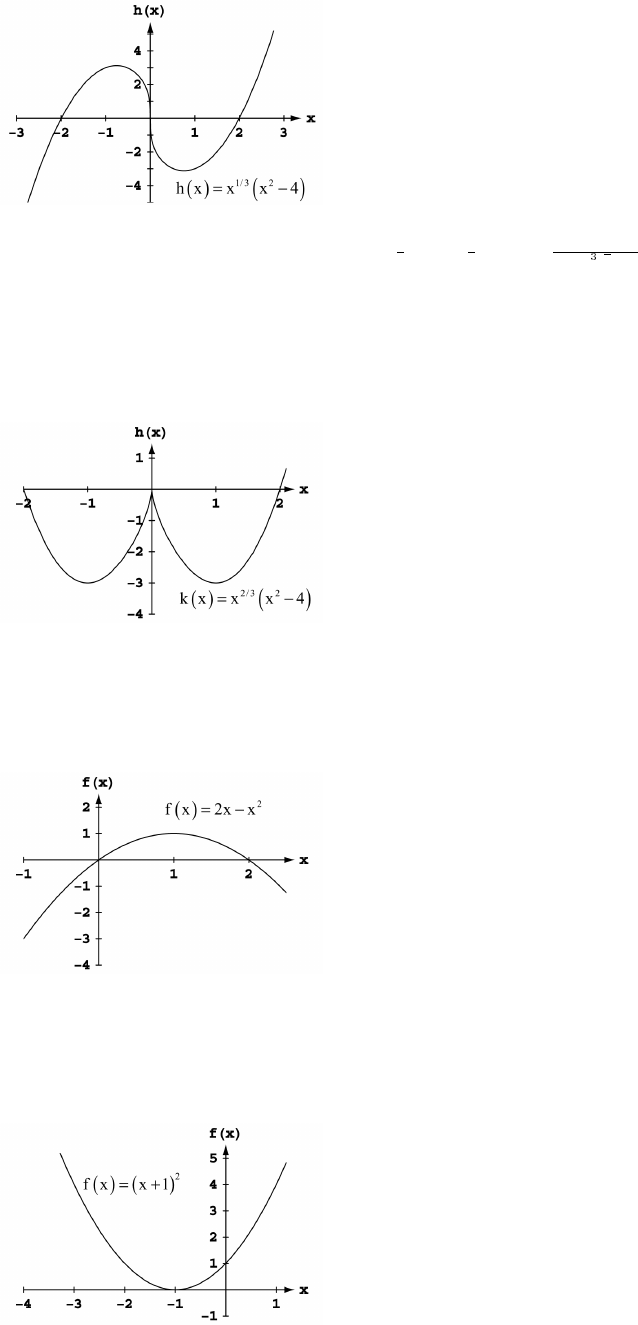
222 Chapter 4 Applications of Derivatives
(d)
28. (a) k(x) x x 4 x 4x k (x) x x critical points atœœÊœœ Ê
#Î$ # )Î$ #Î$ w &Î$ "Î$
ab 88
33
8(x 1)(x 1)
3x
È
x 0, 1 k )( , increasing on ( ) and ( ), decreasing on ( 1)œ „ Ê œ ± ± "ß ! "ß _ _ß
" "
!
w
and ( 1)!ß
(b) local maximum is k(0) 0 at x 0, local minima are k 1 3 at x 1œœ „œœ„ab
(c) no absolute maximum; absolute minimum is 3 at x 1œ„
(d)
29. (a) f(x) 2x x f (x) 2 2x 2(1 x) a critical point at x 1 f ] and f(1) 1,œ Ê œ œ Ê œ Ê œ ± œ
"#
#w w
f(2) 0 a local maximum is 1 at x 1, a local minimum is 0 at x 2œÊ œ œ
(b) absolute maximum is 1 at x 1; no absolute minimumœ
(c)
30. (a) f(x) (x 1) f (x) 2(x 1) a critical point at x 1 f ] and f( 1) 0, f(0) 1œ Ê œ Ê œ Ê œ ± œ œ
" !
#w w
a local maximum is 1 at x 0, a local minimum is 0 at x 1Êœ œ
(b) no absolute maximum; absolute minimum is 0 at x 1œ
(c)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
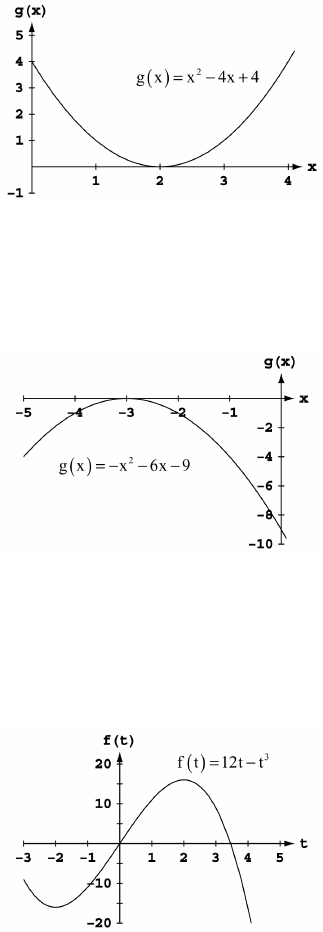
Section 4.3 Monotonic Functions and the First Derivative Test 223
31. (a) g(x) x 4x 4 g (x) 2x 4 2(x 2) a critical point at x 2 g [ andœ Ê œ œ Ê œ Ê œ ±
"#
#w w
g(1) 1, g(2) 0 a local maximum is 1 at x 1, a local minimum is g(2) 0 at x 2œœÊ œ œœ
(b) no absolute maximum; absolute minimum is 0 at x 2œ
(c)
32. (a) g(x) x 6x 9 g (x) 2x 6 2(x 3) a critical point at x 3 g [ andœ Ê œ œ Ê œ Ê œ ±
% $
#w w
g( 4) 1, g( 3) 0 a local maximum is 0 at x 3, a local minimum is 1 at x 4œ œ Ê œ œ
(b) absolute maximum is 0 at x 3; no absolute minimumœ
(c)
33. (a) f(t) 12t t f (t) 12 3t 3(2 t)(2 t) critical points at t 2 f [œ Ê œ œ Ê œ „ Ê œ ± ±
$ # #
$w # w
and f( 3) 9, f( 2) 16, f(2) 16 local maxima are 9 at t 3 and 16 at t 2, a localœ œ œ Ê œ œ
minimum is 16 at t 2œ
(b) absolute maximum is 16 at t 2; no absolute minimumœ
(c)
34. (a) f(t) t 3t f (t) 3t 6t 3t(t 2) critical points at t 0 and t 2œ Ê œ œ Ê œ œ
$# w #
f ] and f(0) 0, f(2) 4, f(3) 0 a local maximum is 0 at t 0 and t 3, aÊ œ ± ± œ œ œ Ê œ œ
!#$
w
local minimum is 4 at t 2œ
(b) absolute maximum is 0 at t 0, 3; no absolute minimumœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
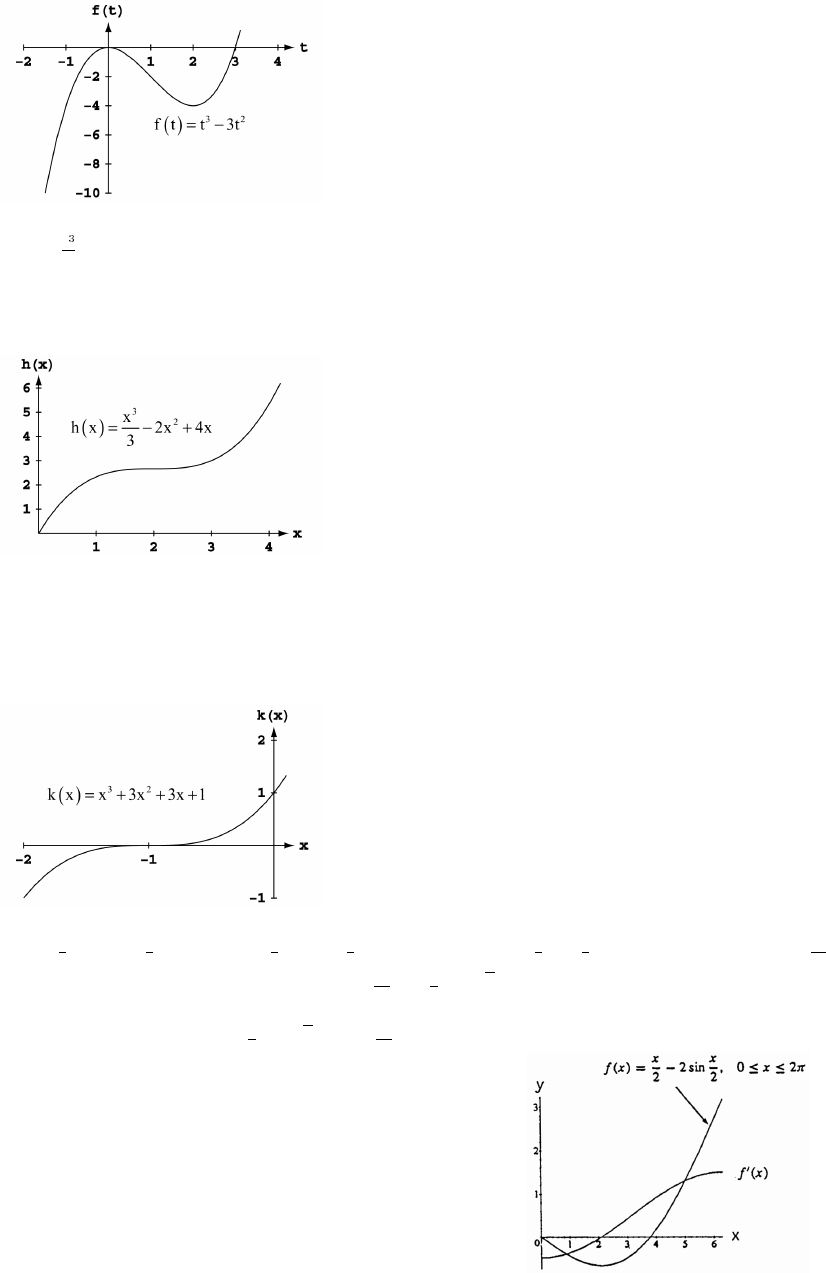
224 Chapter 4 Applications of Derivatives
(c)
35. (a) h(x) 2x 4x h (x) x 4x 4 (x 2) a critical point at x 2 h [ andœ Ê œ œ Ê œ Ê œ ±
!#
x
3#w# # w
h(0) 0 no local maximum, a local minimum is 0 at x 0œÊ œ
(b) no absolute maximum; absolute minimum is 0 at x 0œ
(c)
36. (a) k(x) x 3x 3x 1 k (x) 3x 6x 3 3(x 1) a critical point at x 1œ Ê œ œ Ê œ
$# w # #
k ] and k( 1) 0, k(0) 1 a local maximum is 1 at x 0, no local minimumÊ œ ± œ œ Ê œ
" !
w
(b) absolute maximum is 1 at x 0; no absolute minimumœ
(c)
37. (a) f(x) 2 sin f (x) cos , f (x) 0 cos a critical point at xœ Ê œ œ Ê œ Ê œ
xx x x 2
3## ## ##
ww
""
ˆ‰ ˆ‰ ˆ‰ 1
f [ ] and f(0) 0, f 3, f(2 ) local maxima are 0 at x 0 and Ê œ ± œ œ œ Ê œ
!#
#Î$
w
11
11 1
ˆ‰ È
2
33
11
at x 2 , a local minimum is 3 at xœœ111
33
2
È
(b) The graph of f rises when f 0, falls when f 0,
ww
and has a local minimum value at the point where fw
changes from negative to positive.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
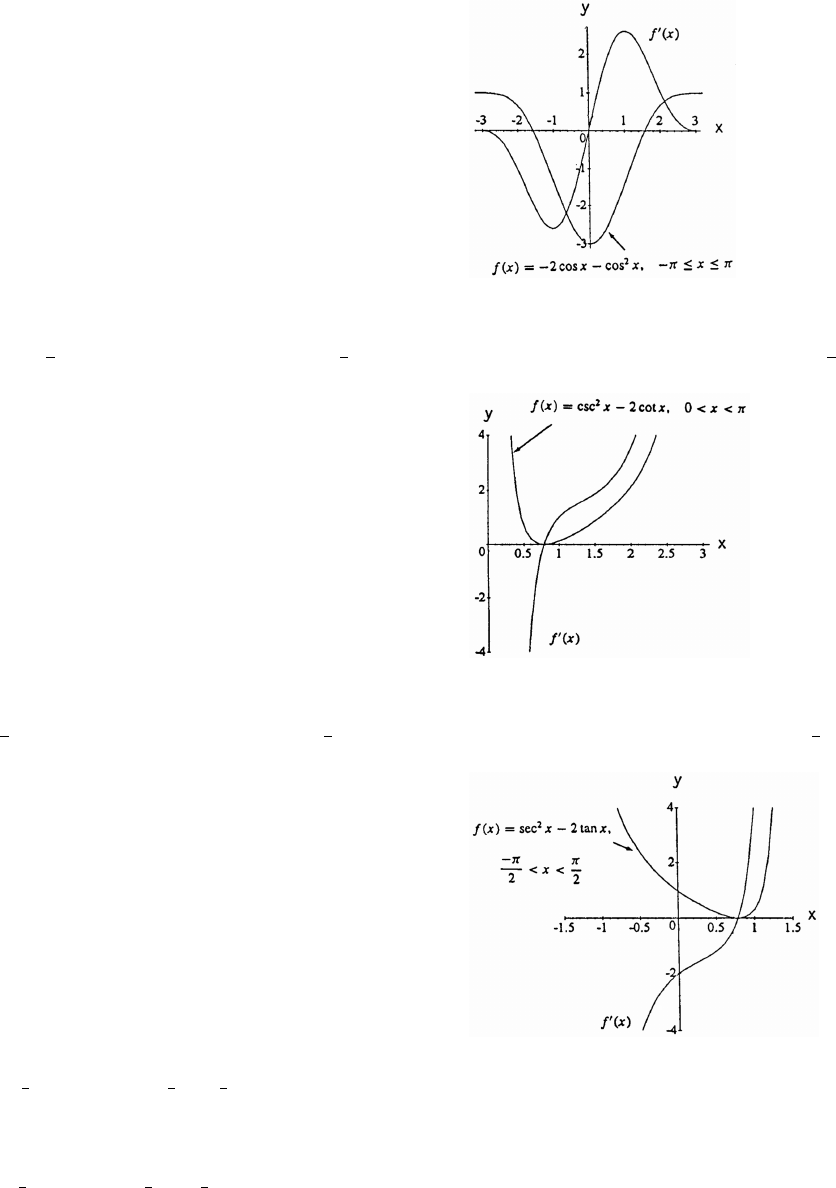
Section 4.3 Monotonic Functions and the First Derivative Test 225
38. (a) f(x) 2 cos x cos x f (x) 2 sin x 2 cos x sin x 2(sin x)(1 cos x) critical points atœ Ê œ œ Ê
#w
x , 0, f [ ] and f( ) 1, f(0) 3, f( ) 1 a local maximum is 1 atœ Ê œ ± œ œ œ Ê
!
11 1 1
11
w
x , a local minimum is 3 at x 0œ„ œ1
(b) The graph of f rises when f 0, falls when f 0,
ww
and has local extreme values where f 0. The
wœ
function f has a local minimum value at x 0, whereœ
the values of f change from negative to positive.
w
39. (a) f(x) csc x 2 cot x f (x) 2(csc x)( csc x)(cot x) 2 csc x 2 csc x (cot x 1) a criticalœ Êœ œ Ê
#w ##
abab
point at x f ( ) and f 0 no local maximum, a local minimum is 0 at xœ Ê œ ± œ Ê œ
!Î%
11 1
44 4
w
11ˆ‰
(b) The graph of f rises when f 0, falls when f 0,
ww
and has a local minimum value at the point where
f 0 and the values of f change from negative to
ww
œ
positive. The graph of f steepens as f (x) .
wĄ_
40. (a) f(x) sec x 2 tan x f (x) 2(sec x)(sec x)(tan x) 2 sec x 2 sec x (tan x 1) a critical pointœ Êœ œ Ê
#w ##
ab
at x f ( ) and f 0 no local maximum, a local minimum is 0 at xœ Ê œ ± œ Ê œ
Î# Î#
Î%
11 1
44 4
w
11
1ˆ‰
(b) The graph of f rises when f 0, falls when f 0,
ww
and has a local minimum value where f 0 and the
wœ
values of f change from negative to positive.
w
41. h( ) 3 cos h ( ) sin h [ ] , ( ) and ( 3) a local maximum is 3 at 0,)) 1 )
1
œ Ê œ Ê œ !ß $ # ß Ê œ
!#
ˆ‰ ˆ‰
))
###
ww
3
a local minimum is 3 at 2œ)1
42. h( ) 5 sin h ( ) cos h [ ] , ( 0) and ( 5) a local maximum is 5 at , a local)) 1 )1
1
œ Ê œ Ê œ !ß ß Ê œ
!
ˆ‰ ˆ‰
))
###
ww
5
minimum is 0 at 0)œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
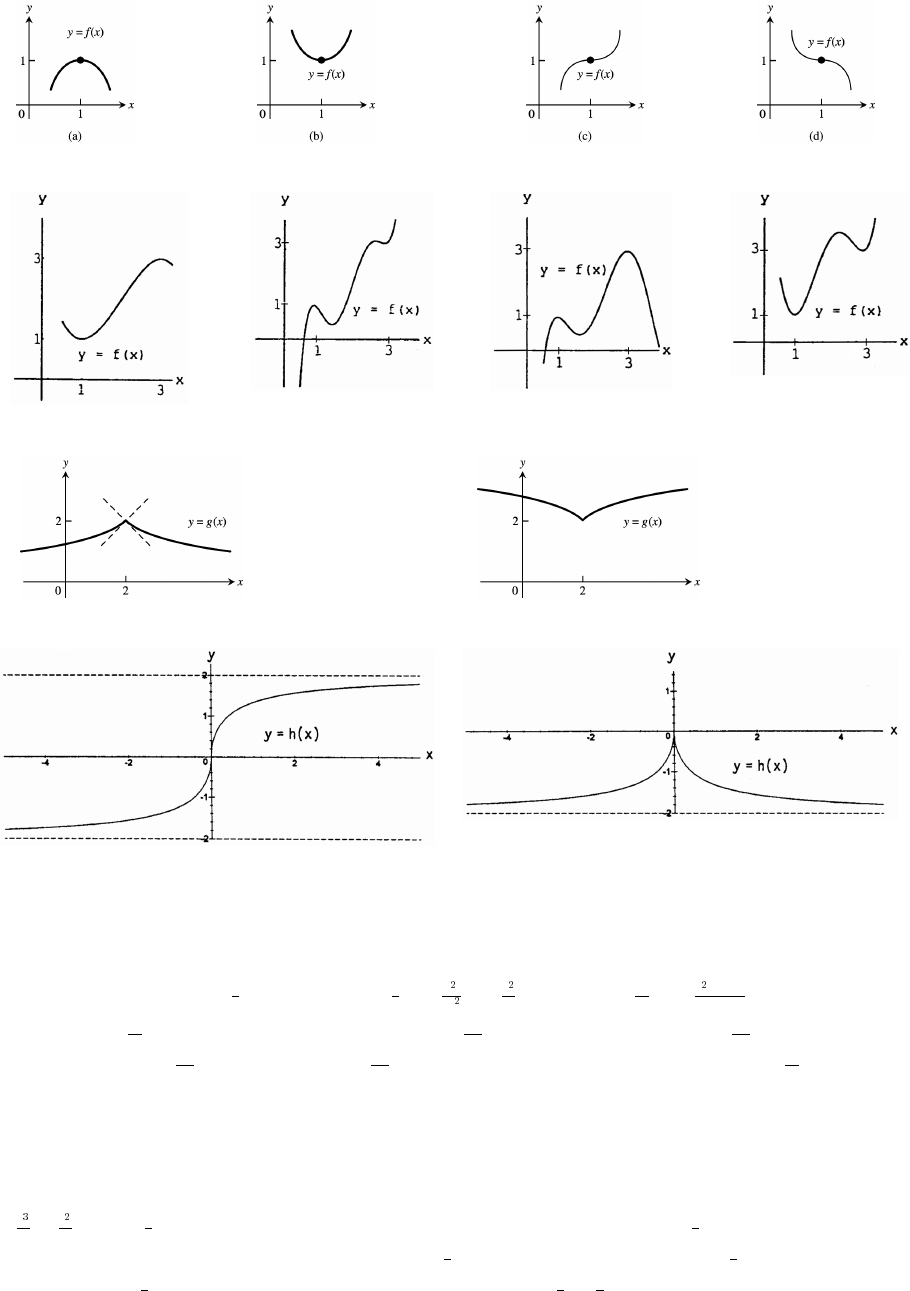
226 Chapter 4 Applications of Derivatives
43. (a) (b) (c) (d)
44. (a) (b) (c) (d)
45. (a) (b)
46. (a) (b)
47. f(x) x 3x 2 f (x) 3x 3 3(x 1)(x 1) f rising for x c sinceœ Ê œ œ Ê œ ± ± Ê œ œ #
" "
$w# w
f (x) 0 for x c 2.
wœœ
48. f(x) ax bx c a x x c a x x c a x , a parabola whoseœ œ œ œ
## # #
ˆ‰ ˆ‰
Š‹
bbbbbb 4ac
a a 4a 4a 2a 4a
vertex is at x . Thus when a 0, f is increasing on and decreasing on ; when a 0,œ ß _ _ß
bbb
2a 2a a
ˆ‰ ˆ ‰
#
f is increasing on and decreasing on . Also note that f (x) 2ax b 2a x for
ˆ‰ ˆ‰ ˆ‰
_ß ß _ œ œ Ê
## #
w
bb b
aa a
a 0, f | ; for a 0, f . œ œ ±
ww
b2a b2a
ÎÎ
4.4 CONCAVITY AND CURVE SKETCHING
1. y 2x y x x 2 (x 2)(x 1) y 2x 1 2 x . The graph is rising onœÊ œœ Ê œ œ
xx
33
# #
" "
w# ww ˆ‰
( 1) and ( ), falling on ( ), concave up on and concave down on . Consequently,_ß #ß _ "ß # ß _ _ß
ˆ‰ ˆ ‰
""
##
a local maximum is at x 1, a local minimum is 3 at x 2, and is a point of inflection.
3 3
4##
"
œ œ ß
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 4.4 Concavity and Curve Sketching 227
2. y 2x 4 y x 4x x x 4 x(x 2)(x 2) y 3x 4 3x 2 3x 2 . Theœ Ê œ œ œ Ê œ œ
x
4#w$ # ww#
ab Š‹Š‹
ÈÈ
graph is rising on ( 2 0) and ( ), falling on ( ) and ( ), concave up on and ß #ß _ _ß # !ß # _ß ß _
Š‹Š‹
22
33
ÈÈ
and concave down on . Consequently, a local maximum is 4 at x 0, local minima are 0 at
Š‹
ß œ
22
33
ÈÈ
x 2, and and are points of inflection.œ„ ß ß
Š‹Š‹
216 216
33
99
ÈÈ
3. y x 1 y x 1 (2x) x x 1 , y ) ( )(œ Ê œ œ œ ±
" "
!
332
443
ab ab ab
ˆ‰ˆ‰
#w# #w
#Î$ "Î$ "Î$
the graph is rising on ( ) and ( ), falling on ( ) and ( ) a local maximum is at x 0, localÊ "ß! "ß_ _ß" !ß" Ê œ
3
4
minima are 0 at x 1; y x 1 (x) x 1 (2x) ,œ„ œ œ
ww # #
"Î$ %Î$
"
ab ab
ˆ‰
3
x3
3 x 1
Éab
y ) ( )( the graph is concave up on 3 and 3 , concave
ww œ ± ± Ê _ß ß _
$ $
" "
ÈÈ Š‹Š‹
ÈÈ
down on 3 3 points of inflection at 3
Š‹ Š ‹
ÈÈ È
ß Ê „ ß
$%
%
È
4. y x x 7 y x x 7 x (2x) x x 1 , y )(œ Ê œ œ œ ± ±
" "
!
9393
14 14 14
"Î$ # w #Î$ # "Î$ #Î$ # w
#
ab ab ab
the graph is rising on ( 1) and ( ), falling on ( 1 ) a local maximum is at x 1, a localÊ_ß"ß_ß"Ê œ
27
7
minimum is at x 1; y x x 1 3x 2x x x 2x 1 , œœ œœ
27
7ww &Î$ # "Î$ "Î$ &Î$ &Î$ #
ab a b
y )( the graph is concave up on ( ), concave down on ( ) a point of inflection at
ww œ Ê !ß _ _ß ! Ê
!
()!ß !
5. y x sin 2x y 1 2 cos 2x, y [ ] the graph is rising on , fallingœ Ê œ œ ± ± Ê ß
# Î$ # Î$
Î$ Î$
ww
11
11 ˆ‰
11
33
on and local maxima are at x and at x , local minima are
ˆ‰ˆ‰
ß ß Ê œ œ
#
##
11 11 1 1 1 1
33 33 3 3 3 3
222
33
ÈÈ
at x and at x ; y 4 sin 2x, y [ ] the œ œ œ œ ± ± ± Ê
# Î$ # Î$
Î# Î#
!
1111
3333
33
22
ÈÈ
##
ww ww
11
11
graph is concave up on and , concave down on and points of inflection at
ˆ‰ˆ‰ ˆ ‰ˆ‰
ß! ß ß !ß Ê
111 111
## ##
22
33
, ( ), and
ˆ‰ ˆ‰
ß !ß! ß
11 11
## ##
6. y tan x 4x y sec x 4, y ( ) the graph is rising on andœ Ê œ œ ± ± Ê ß
Î# Î#
Î$ Î$
w# w
11
11 ˆ‰
11
23
, falling on a local maximum is 3 at x , a local minimum is 3 at x ;
ˆ‰ ˆ ‰ ÈÈ
11 11 1 1 1 1
333 33 33
44
ßßÊ œ œ
#
y 2(sec x)(sec x)(tan x) 2 sec x (tan x), y ( ) the graph is concave up on 0 ,
ww # ww
#
œ œ œ ± Ê ß
Î# Î#
!
ab ˆ‰
11
1
concave down on 0 a point of inflection at (0 )
ˆ‰
ß Ê ß!
1
2
7. If x 0, sin x sin x and if x 0, sin x sin ( x)œ œkk kk
sin x. From the sketch the graph is rising onœ
, and , falling on 2 ,
ˆ‰ˆ‰ˆ‰ ˆ ‰
ß !ß ß# ß
33 311 1 1 1
## # # #
11
and ; local minima are 1 at x
ˆ‰ˆ‰
ß! ß œ„
111 1
### #
33
and 0 at x ; local maxima are 1 at x andœ! œ „ 1
#
0 at x ; concave up on ( ) and ( ), andœ„# #ß ß#11111
concavedown on ( 0) and ( ) points of inflection ß !ß Ê11
are ( ) and ( )ß! ß!11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
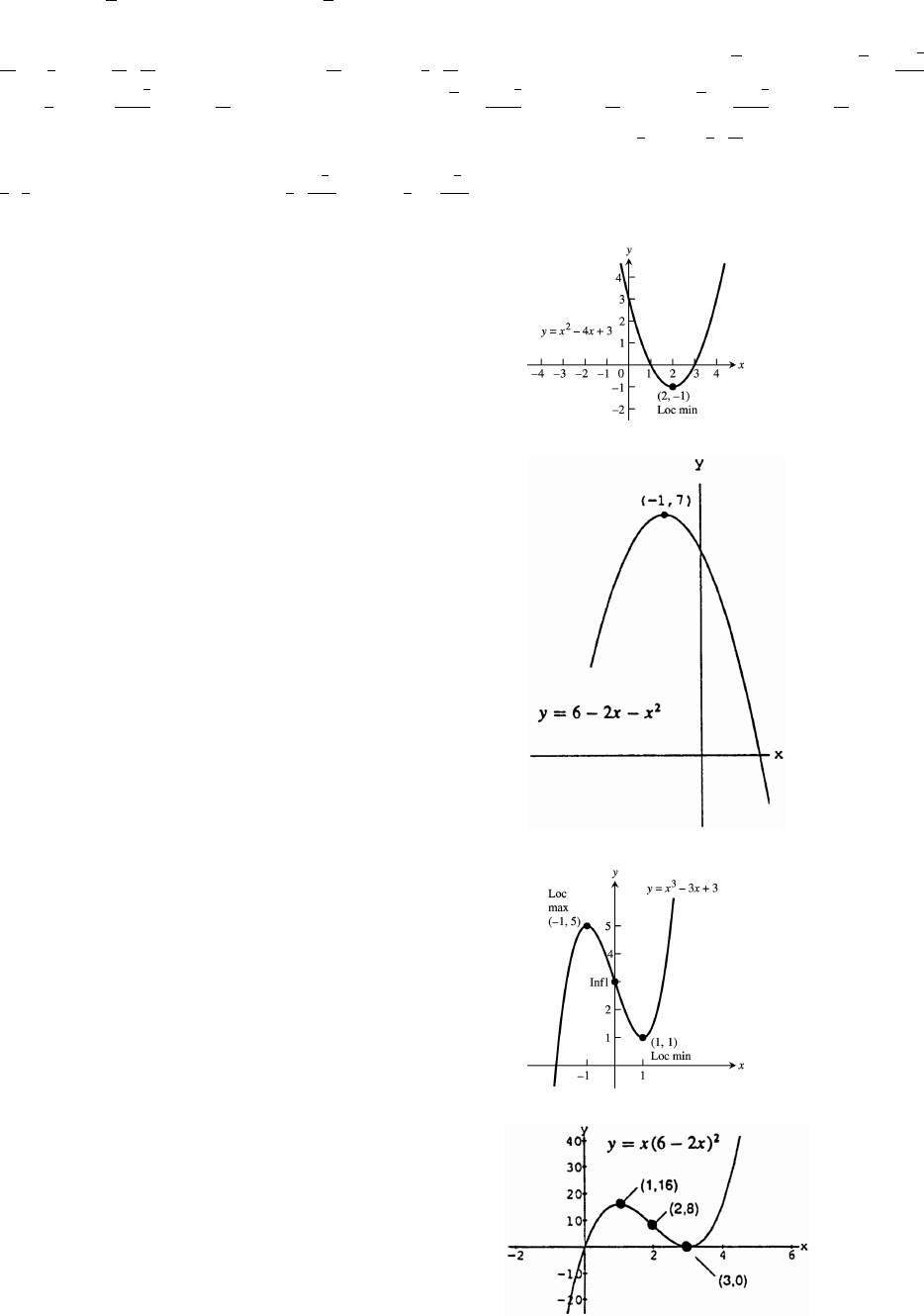
228 Chapter 4 Applications of Derivatives
8. y 2 cos x 2 x y 2 sin x 2, y [ ] rising onœ Ê œ œ ± ± ± Ê
$ Î% Î% & Î% $Î#
ÈÈ
ww
1111
1
and , falling on and local maxima are 2 2 at x , 2
ˆ‰ˆ‰ ˆ‰ˆ‰ ÈÈ
ß ß ß ß Ê œ
353 3 5
44 4 4 44 4
2
11 11 1 11 1
#111
È
at x and at x , and local minima are 2 at x and 2 at x ;œ œ œ œ
11 1 1
111
444 44
32 32 52
335
ÈÈÈ
## ÈÈ
y 2 cos x, y [ ] concave up on and , concave down on
ww ww
###
œ œ ± ± Ê ß ß
Î# Î# $Î#
1111
1
ˆ‰ˆ‰
1113
points of inflection at and
ˆ‰ Š‹Š‹
ß Ê ß ß
11 1 1
11
## # # # #
ÈÈ
22
9. When y x 4x 3, then y 2x 4 2(x 2) andœ œœ
#w
y 2. The curve rises on ( ) and falls on ( ).
ww œ #ß_ _ß#
At x 2 there is a minimum. Since y 0, the curve isœ
ww
concave up for all x.
10. When y 2x x , then y 2x 2( x) andœ' œ# œ "
#w
y 2. The curve rises on ( 1) and falls on
ww œ _ß
( 1 ). At x 1 there is a maximum. Since y 0, theß_ œ
ww
curve is concave down for all x.
11. When y x 3x 3, then y 3x 3 3(x 1)(x 1)œ œ œ
$w#
and y 6x. The curve rises on ( 1) ( ) and
ww œ _ß "ß _
falls on ( 1 1). At x 1 there is a local maximum and atß œ
x 1 a local minimum. The curve is concave down onœ
( 0) and concave up on ( ). There is a point of_ß !ß _
inflection at x 0.œ
12. When y x(6 2x) , then y 4x(6 2x) ( 2x)œ œ '
#w #
12(3 x)( x) and y 12(3 x) 12( x)œ " œ "
ww
24(x 2). The curve rises on ( ) ( ) andœ _ß" $ß_
falls on ( ). The curve is concave down on ( ) and"ß $ _ß #
concave up on ( ). At x 2 there is a point of#ß _ œ
inflection.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
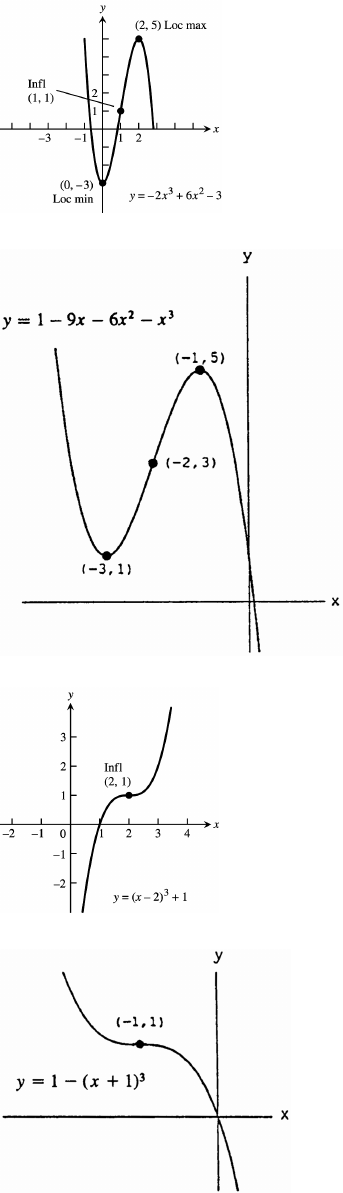
Section 4.4 Concavity and Curve Sketching 229
13. When y 2x 6x 3, then y 6x 12xœ œ
$# w #
6x(x 2) and y 12x 12 12(x 1). Theœ œ œ
ww
curve rises on ( ) and falls on ( 0) and ( ).!ß # _ß #ß _
At x 0 there is a local minimum and at x 2 a localœœ
maximum. The curve is concave up on ( ) and_ß "
concave down on ( ). At x 1 there is a point of"ß _ œ
inflection.
14. When y 1 9x 6x x , then y 9 12x 3xœ œ
#$ w #
(x 3)( 1) and y 12 6x 6(x 2).œ$ B œ œ
ww
The curve rises on ( ) and falls on ( 3) and$ß " _ß
( ). At x 1 there is a local maximum and at"ß _ œ
x 3 a local minimum. The curve is concave up onœ
( 2) and concave down on ( ). At x 2_ß #ß _ œ
there is a point of inflection.
15. When y (x 2) 1, then y 3(x 2) andœ œ
$w#
y 6(x 2). The curve never falls and there are no
ww œ
local extrema. The curve is concave down on ( )_ß #
and concave up on ( ). At x 2 there is a point#ß _ œ
of inflection.
16. When y 1 (x 1) , then y 3(x 1) andœ œ
$w #
y 6(x 1). The curve never rises and there are
ww œ
no local extrema. The curve is concave up on ( 1)_ß
and concave down on ( ). At x 1 there is a"ß _ œ
point of inflection.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
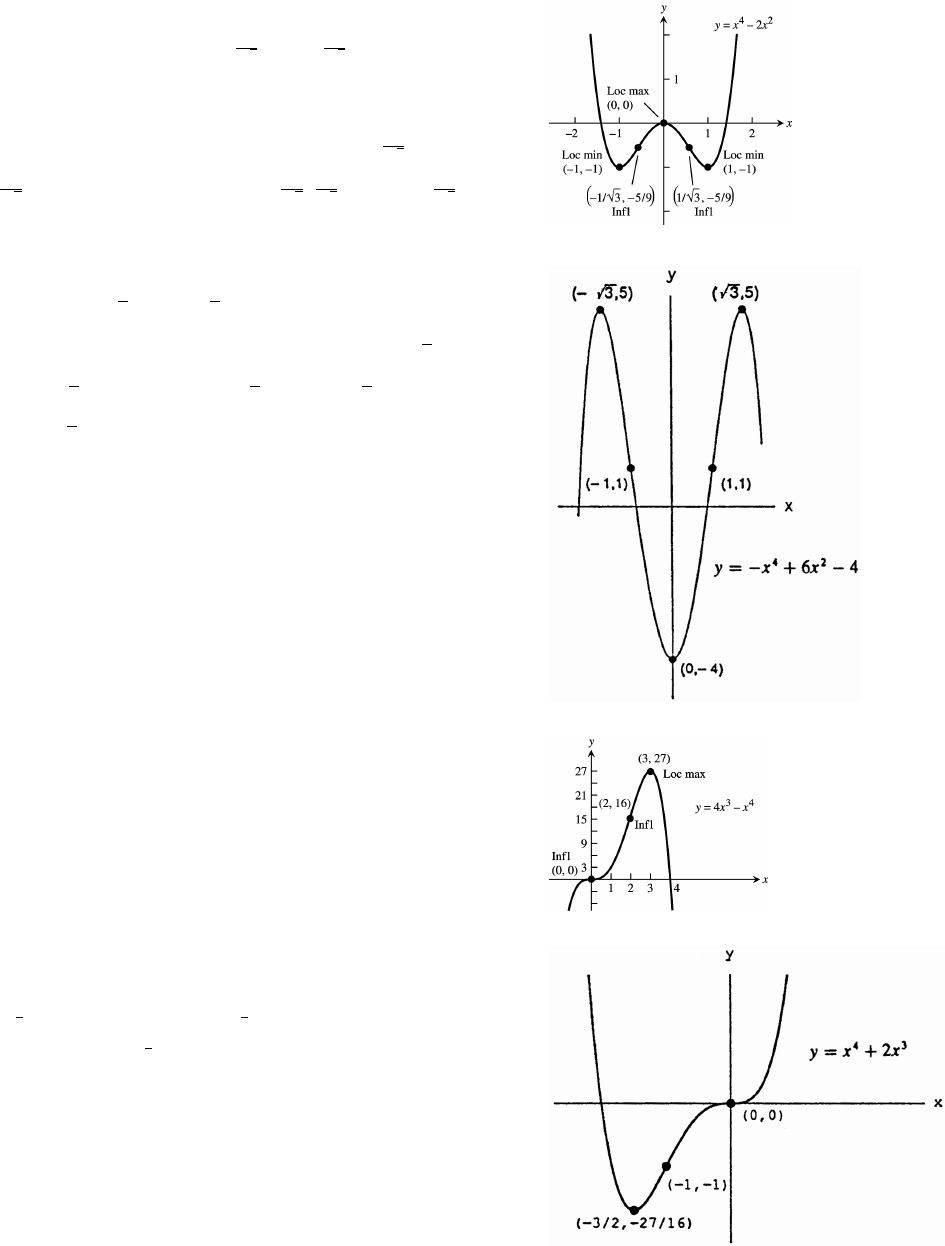
230 Chapter 4 Applications of Derivatives
17. When y x 2x , then y 4x 4x 4x(x 1)(x 1)œ œ œ
%# w $
and y 12x 4 12 x x . The curve
ww # ""
œœ
Š‹Š‹
ÈÈ
33
rises on ( ) and ( ) and falls on ( 1) and ( )."ß ! "ß _ _ß !ß "
At x 1 there are local minima and at x 0 a localœ„ œ
maximum. The curve is concave up on and
Š‹
_ß "
È3
and concave down on . At x
Š‹ Š ‹
"""„"
ÈÈÈÈ
3333
ß_ ß œ
there are points of inflection.
18. When y x 6x 4, then y 4x 12xœ œ
%# w $
4x x 3 x 3 and y 12x 12œ œ
Š‹Š‹
ÈÈww #
12(x 1)(x 1). The curve rises on 3œ _ß
Š‹
È
and 3 , and falls on 3 and 3 . At
Š‹ Š ‹Š ‹
ÈÈÈ
!ß ß ! ß _
x 3there are local maxima and at x 0 a localœ„ œ
È
minimum. The curve is concave up on ( ) and concave"ß "
down on ( 1) and ( ). At x 1 there are points_ß "ß _ œ „
of inflection.
19. When y 4x x , then y 12x 4x 4x ( x) andœ œ œ$
$% w # $ #
y 24x 12x 12x(2 x). The curve rises on
ww #
œ œ _ß$ab
and falls on . At x 3 there is a local maximum, butab$ß _ œ
there is no local minimum. The graph is concave up on
and concave down on and . There areab a b a b!ß # _ß ! #ß _
inflection points at x 0 and x 2.œœ
20. When y x 2x , then y 4x 6x 2x (2x 3) andœ œœ
%$ w $# #
y 12x 12x 12x(x 1). The curve rises on
ww #
œœ
and falls on . There is a local
ˆ‰ ˆ ‰
ß _ _ß
33
2#
minimum at x , but no local maximum. The curve isœ3
#
concave up on ( 1) and ( ), and concave down on_ß !ß _
( 1 0). At x 1 and x 0 there are points of inflection.ß œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
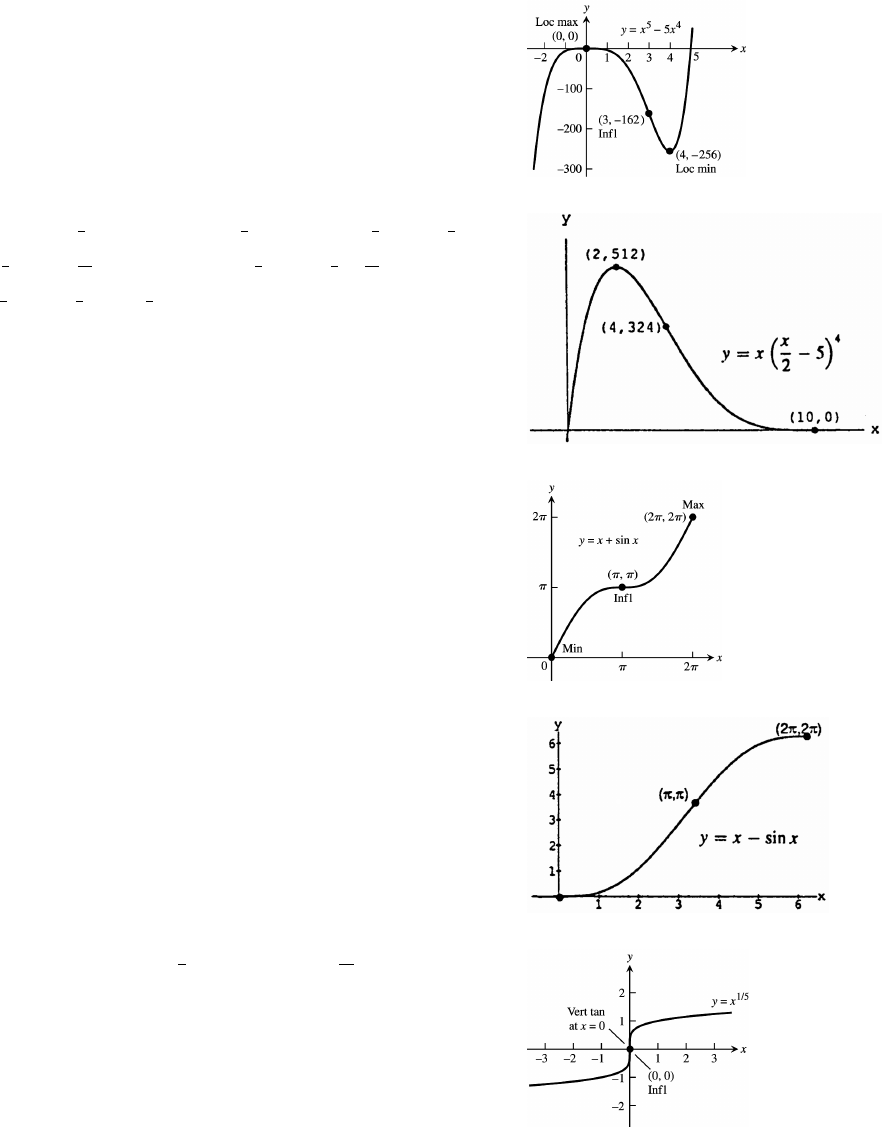
Section 4.4 Concavity and Curve Sketching 231
21. When y x 5x , then y 5x 20x 5x (x 4) andœ œ œ
&% w % $ $
y 20x 60x 20x (x 3). The curve rises on
ww $ # #
œœ
( ) and ( ), and falls on ( ). There is a local_ß! %ß_ !ß%
maximum at x 0, and a local minimum at x 4. Theœœ
curve is concave down on ( 3) and concave up on_ß
(3 ). At x 3 there is a point of inflection.ß_ œ
22. When y x 5 , then y 5 x(4) 5œ œ
ˆ‰ ˆ‰ ˆ‰ˆ‰
xxx
####
%%$
w"
5 5 , and y 3 5 5œ œ
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
x5x x 5x
## ###
$#
ww "
5 5 5 (x 4). The curve is rising œ
ˆ‰ˆ‰ˆ‰
x5x
###
$#
on ( ) and (10 ), and falling on ( 10). There is a_ß# ß_ #ß
local maximum at x 2 and a local minimum at x 10.œœ
The curve is concave down on ( ) and concave up on_ß %
( ). At x 4 there is a point of inflection.%ß _ œ
23. When y x sin x, then y cos x and y sin x.œ œ" œ
www
The curve rises on ( 2 ). At x 0 there is a local and!ß œ1
absolute minimum and at x 2 there is a local and absoluteœ1
maximum. The curve is concave down on ( ) and concave!ß 1
up on ( ). At x there is a point of inflection.11 1ß# œ
24. When y x sin x, then y cos x and y sin x.œ œ" œ
www
The curve rises on ( 2 ). At x 0 there is a local and!ß œ1
absolute minimum and at x 2 there is a local and absoluteœ1
maximum. The curve is concave up on ( ) and concave!ß 1
down on ( ). At x there is a point of inflection.11 1ß# œ
25. When y x , then y x and y x .œœ œ
"Î& w %Î& ww *Î&
"
525
4
The curve rises on ( ) and there are no extrema._ß _
The curve is concave up on ( ) and concave down_ß !
on ( ). At x 0 there is a point of inflection.!ß _ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
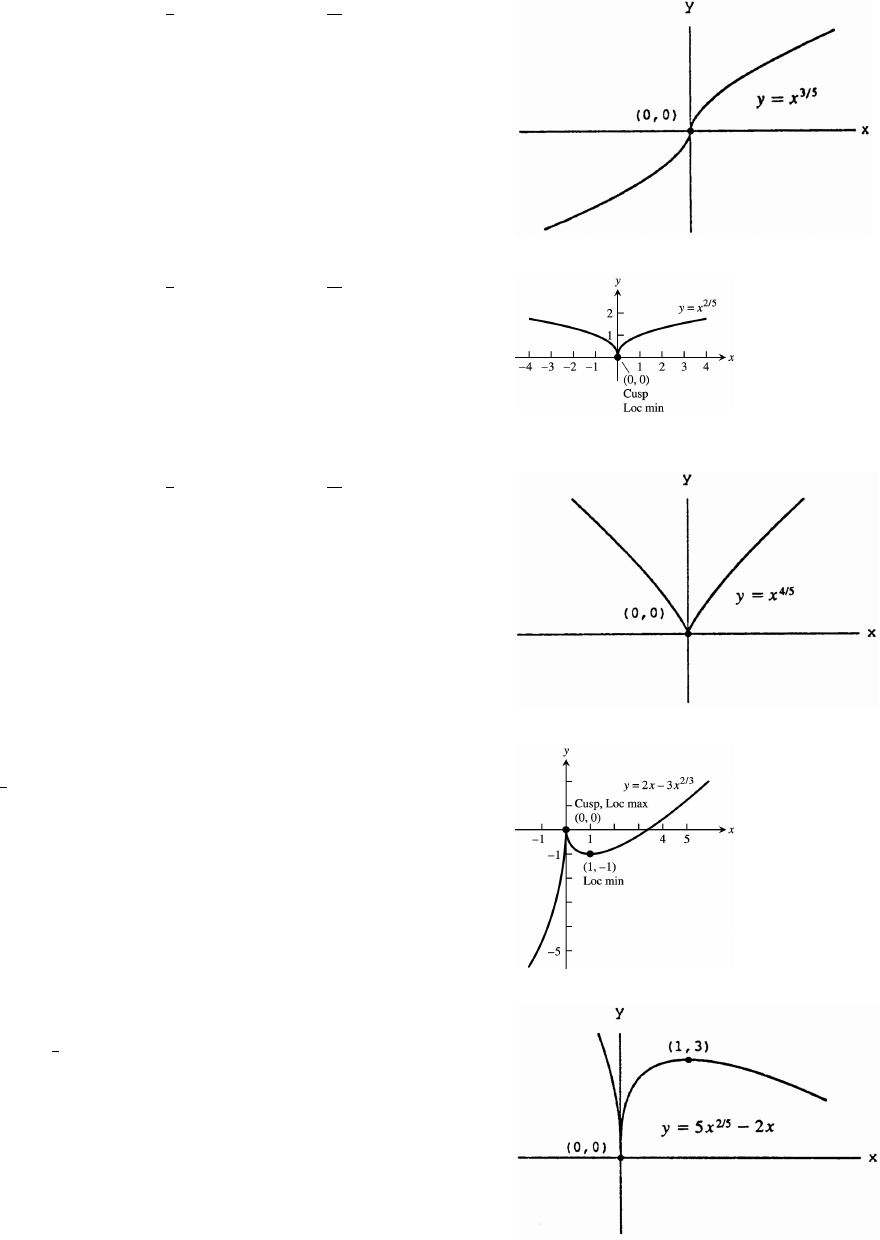
232 Chapter 4 Applications of Derivatives
26. When y x , then y x and y x .œœ œ
$Î& w #Î& ww (Î&
36
525
The curve rises on ( ) and there are no extrema._ß _
The curve is concave up on ( ) and concave down_ß !
on ( ). At x 0 there is a point of inflection.!ß _ œ
27. When y x , then y x and y x .œœ œ
#Î& w $Î& ww )Î&
26
525
The curve is rising on (0 ) and falling on ( ). Atß_ _ß!
x 0 there is a local and absolute minimum. There isœ
no local or absolute maximum. The curve is concave
down on ( ) and ( ). There are no points of_ß ! !ß _
inflection, but a cusp exists at x 0.œ
28. When y x , then y x and y x .œœ œ
%Î& w "Î& ww 'Î&
44
525
The curve is rising on (0 ) and falling on ( ). Atß_ _ß!
x 0 there is a local and absolute minimum. There isœ
no local or absolute maximum. The curve is concave
down on ( ) and ( ). There are no points of_ß ! !ß _
inflection, but a cusp exists at x 0.œ
29. When y 2x 3x , then y 2 2x andœ œ
#Î$ w "Î$
y x . The curve is rising on ( ) and
ww %Î$
œ _ß !
2
3
( ), and falling on ( ). There is a local maximum"ß _ !ß "
at x 0 and a local minimum at x 1. The curve isœœ
concave up on ( ) and ( ). There are no_ß ! !ß _
points of inflection, but a cusp exists at x 0.œ
30. When y 5x 2x, then y 2x 2 2 x 1œ œ œ
#Î& w $Î& $Î&
ˆ‰
and y x . The curve is rising on (0 1) and
ww )Î&
œ ß
6
5
falling on ( 0) and ( ). There is a local minimum_ß "ß _
at x 0 and a local maximum at x 1. The curve isœœ
concave down on ( ) and ( ). There are no_ß ! !ß _
points of inflection, but a cusp exists at x 0.œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
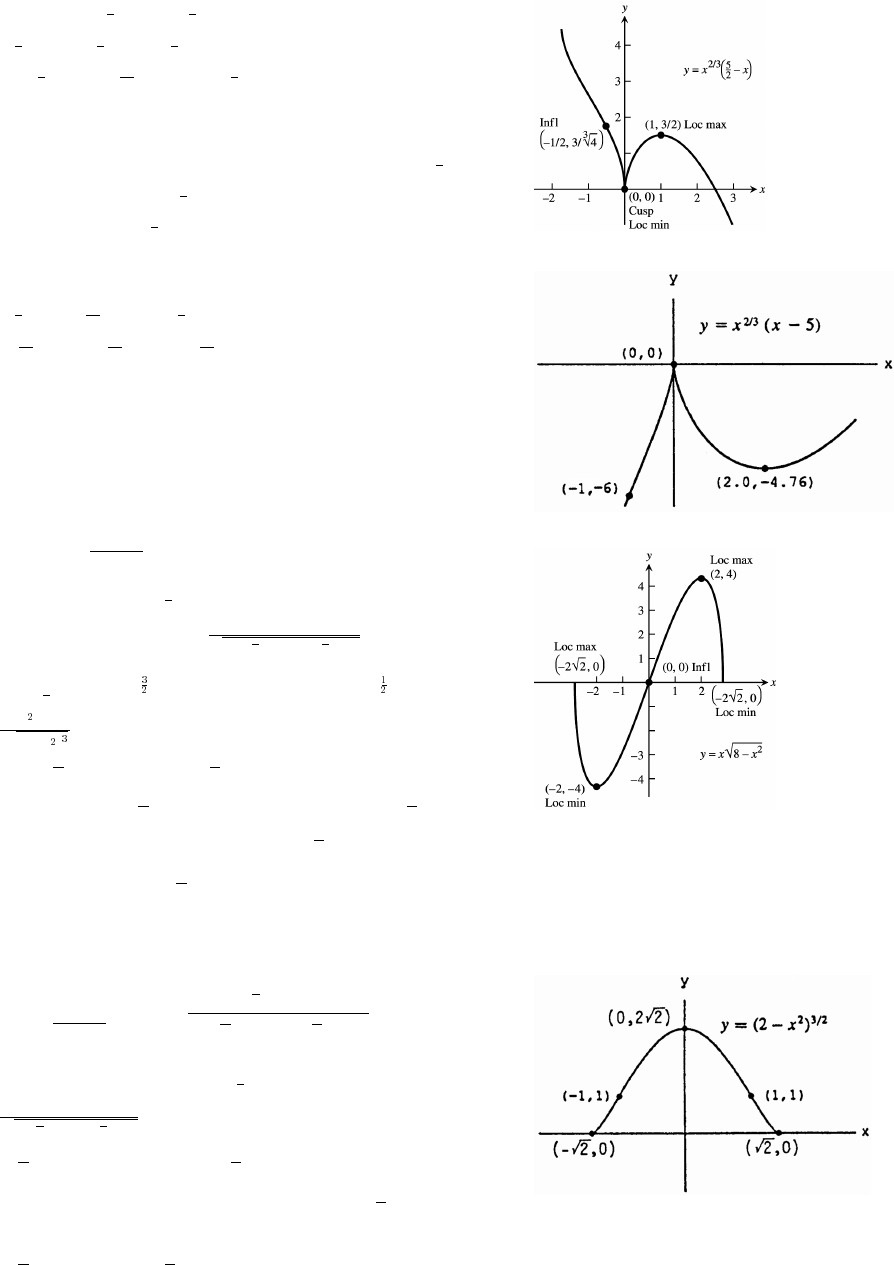
Section 4.4 Concavity and Curve Sketching 233
31. When y x x x x , thenœœ
#Î$ #Î$ &Î$
##
ˆ‰
55
y x x x (1 x) and
w "Î$ #Î$ "Î$
œœ
555
333
y x x x (1 2x).
ww %Î$ "Î$ %Î$
œ œ
510 5
99 9
The curve is rising on ( ) and falling on ( ) and!ß " _ß !
( ). There is a local minimum at x 0 and a local"ß _ œ
maximum at x 1. The curve is concave up on œ _ß
ˆ‰
"
#
and concave down on and (0 ). There is a point
ˆ‰
ß! ß_
"
#
of inflection at x and a cusp at x 0.œ œ
"
#
32. When y x (x 5) x 5x , thenœœ
#Î$ &Î$ #Î$
y x x x (x 2) and
w #Î$ "Î$ "Î$
œ œ
510 5
33 3
y x x x (x 1). The curve
ww "Î$ %Î$ %Î$
œœ
10 10 10
99 9
is rising on ( ) and ( ), and falling on ( )._ß! #ß_ !ß#
There is a local minimum at x 2 and a local maximumœ
at x 0. The curve is concave up on ( 0) and ( ),œ "ß !ß _
and concave down on ( 1). There is a point of_ß
inflection at x 1 and a cusp at x 0.œ œ
33. When y x 8 x x 8 x , thenœœ
Èab
##"Î#
y 8 x (x) 8 x ( x)
w# #
"Î# "Î#
"
#
œ #ab ab
ˆ‰
8x 82x andœ œaba b
##
"Î#
2(2 x)(2 x)
22x 22 x
ÊŠ‹Š‹
ÈÈ
y 8 x ( 2x) 8 2x 8 x ( 4x)
ww # # #
"
#
œ
ˆ‰
ab a bab
. The curve is rising on ( ), and fallingœ #ß #
2x x 12
8x
ab
Éab
on 2 2 2 and 2 2 . There are local minima
Š‹Š‹
ÈÈ
ß #ß
x 2 and x 2 2, and local maxima at x 2 2 andœ œ œ
ÈÈ
x 2. The curve is concave up on 2 2 andϧ!
Š‹
È
concave down on 2 . There is a point of inflection
Š‹
È
!ß #
at x 0.œ
34. When y 2 x , then y 2 x ( 2x)œ œ ab ab
ˆ‰
#w #
$Î# "Î#
#
3
3x2x 3x 2x 2x andœ œ
ÈÊŠ‹Š‹
ÈÈ
#
y ( 3) 2 x ( 3x) 2 x ( 2x)
ww # #
"Î# "Î#
"
#
œ ab ab
ˆ‰
. The curve is rising onœ"
6( x)(1 x)
2x 2x
ÊŠ‹Š‹
ÈÈ
2 and falling on 2 . There is a local
Š‹ Š‹
ÈÈ
ß! !ß
maximum at x 0, and local minima at x 2. Theœœ„
È
curve is concave down on ( ) and concave up on"ß "
2 and 2 . There are points of inflection at
Š‹Š‹
ÈÈ
ß" "ß
x1.œ„
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
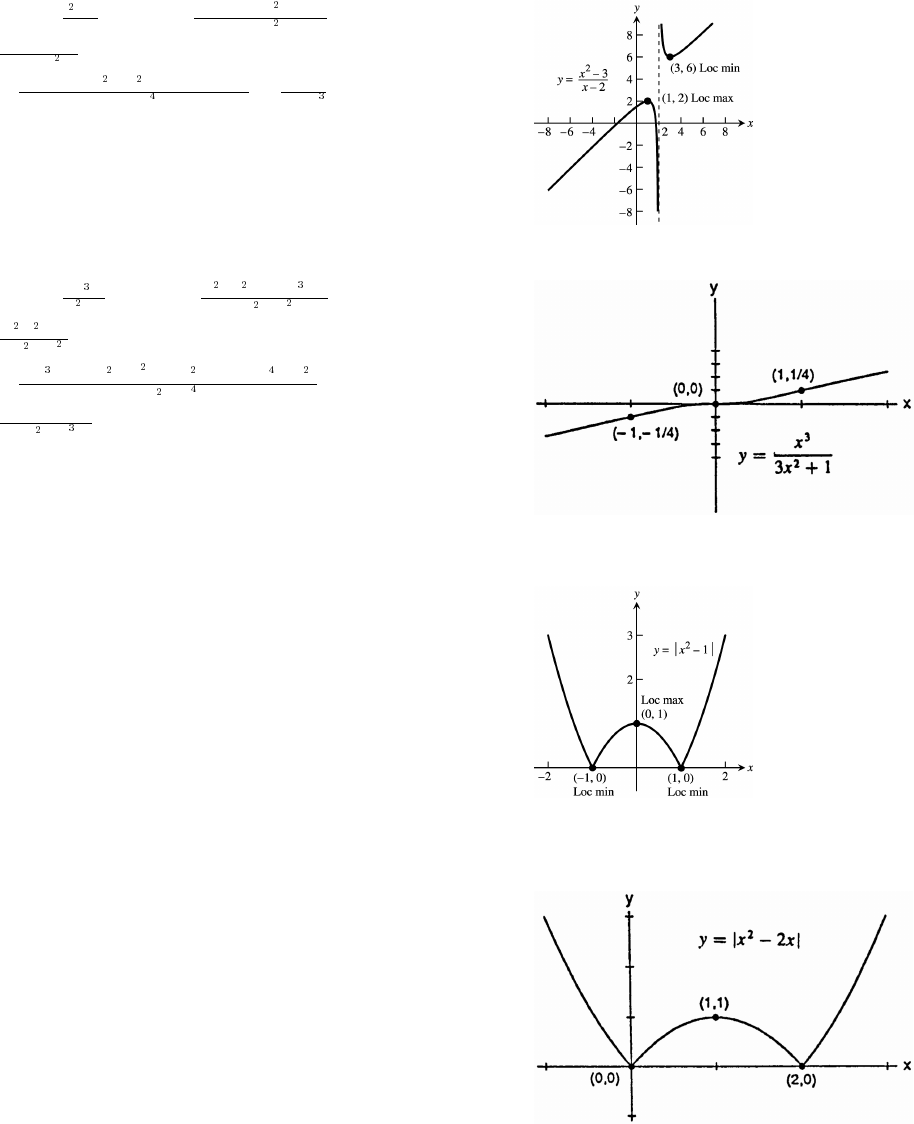
234 Chapter 4 Applications of Derivatives
35. When y , then yœœ
x3
x(x2)
2x(x 2) x 3 ( )
#
w "ab
andœ(x 3)(x 1)
(x 2)
y.
ww #
œœ
(2x 4)(x 2) x 4x 3 (x 2)
(x 2)
2
(x 2)
ab
The curve is rising on ( ) and ( ), and falling on_ß " $ß _
( ) and ( ). There is a local maximum at x 1 and a"ß # #ß $ œ
local minimum at x 3. The curve is concave down onœ
( ) and concave up on ( ). There are no points_ß # #ß _
of inflection because x 2 is not in the domain.œ
36. When y , then yœœ
x
3x 1
3x 3x 1 x (6x)
3x 1
w
ab
ab
andœ3x x 1
3x 1
ab
ab
y
ww ""
œa babab
ˆ‰
ab
12x 6x 3x 2 3x (6x) 3x 3x
3x 1
. The curve is rising on ( ) soœ _ß _
6x(1 x)( x)
3x 1
"
ab
there are no local extrema. The curve is concave up on
( ) and ( ), and concave down on ( ) and_ß" !ß" "ß!
( ). There are points of inflection at x , x 0,"ß _ œ " œ
and x 1.œ
37. When y x 1 , then
x 1, x 1
1x, x 1
œœ
kk
œkk
kk
##
#
y and y . The
2x, x 1 2, x
2x, x , x
www
œœ
"
" #"
œœ
kk kk
kk kk
curve rises on ( ) and ( ) and falls on ( 1)"ß ! "ß _ _ß
and (0 1). There is a local maximum at x 0 and localߜ
minima at x 1. The curve is concave up on ( 1)œ„ _ß
and ( ), and concave down on ( ). There are no"ß _ "ß "
points of inflection because y is not differentiable at x 1œ„
(so there is no tangent line at those points).
38. When y x 2x , then
x 2x, x 0
2x x , 0 x 2
x 2x, x 2
œœ
ŸŸ
kk
Ú
Û
Ü
#
#
#
#
y , and y .
2x 2, x 0 2, x 0
2 2x, 0 x 2 2, 0 x 2
2x 2, x 2 2, x 2
www
œœ
ÚÚ
ÛÛ
ÜÜ
The curve is rising on ( 1) and ( ), and falling on!ß #ß _
( ) and ( ). There is a local maximum at x 1 and_ß ! "ß # œ
local minima at x 0 and x 2. The curve is concave upœœ
on ( ) and ( ), and concave down on ( )._ß! #ß_ !ß#
There are no points of inflection because y is not
differentiable at x 0 and x 2 (so there is no tangentœœ
at those points).
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
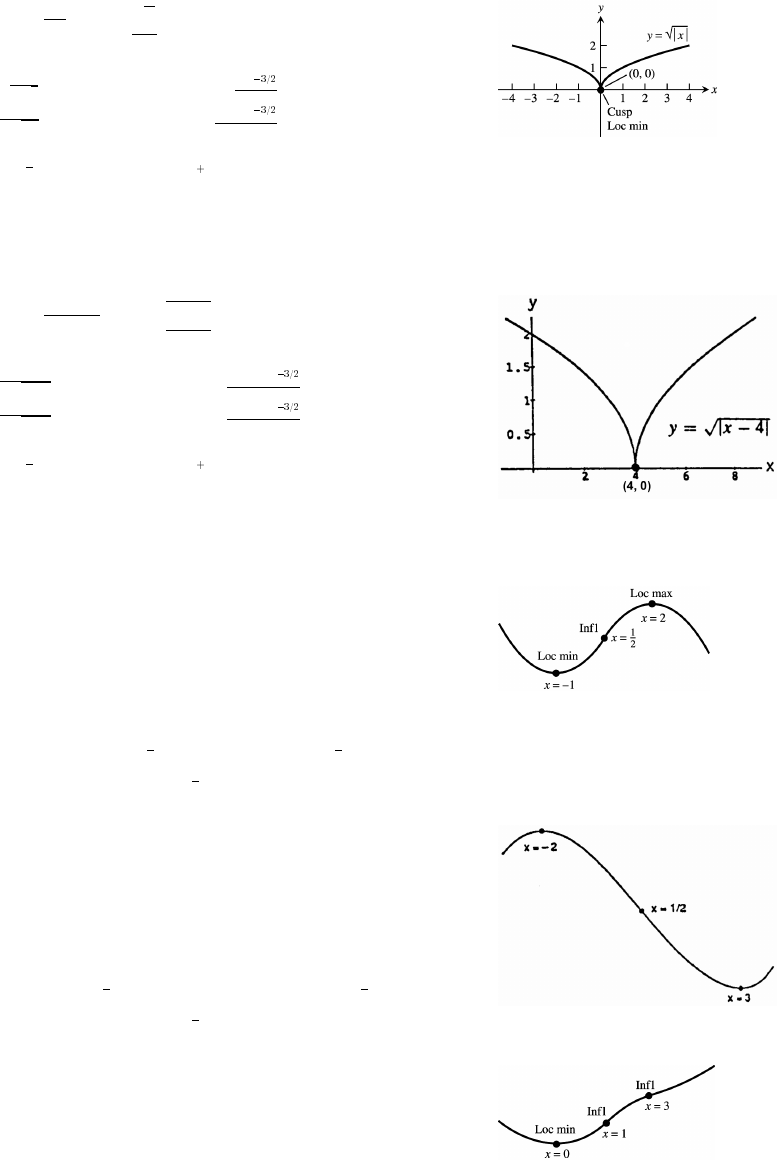
Section 4.4 Concavity and Curve Sketching 235
39. When y x , then
x , x 0
x, x 0
œœ
Èkk È
È
y and y .
, x 0
, x 0
, x 0
, x 0
www
"
#
"
œœ
Ú
Û
Ü
È
È
x
2x
x
4
(x)
4
Since lim y and lim y there is a
xx
Ä! Ä!
ww
œ_ œ_
cusp at x 0. There is a local minimum at x 0, but noœœ
local maximum. The curve is concave down on ( )_ß !
and ( ). There are no points of inflection.!ß _
40. When y x 4 , then
x 4 , x 4
4 x , x 4
œœ
Èkk
È
È
y and y .
, x 4
, x 4
, x 4
, x 4
www
"
"
#
œœ
Ú
Û
Ü
2x4
4x
(x 4)
4
(4 x)
4
È
È
Since lim y and lim y there is a cusp
x4 x4
ÄÄ
ww
œ_ œ_
at x 4. There is a local minimum at x 4, but no localœœ
maximum. The curve is concave down on ( )_ß %
and ( ). There are no points of inflection.%ß _
41. y 2 x x (1 x)( x), y
w# w
œ œ # œ ± ±
" #
rising on ( ), falling on ( 1) and ( )Ê "ß # _ß #ß _
there is a local maximum at x 2 and a local minimumʜ
at x 1; y 1 2x, yœ œ œ ±
"Î#
ww ww
concave up on , concave down on Ê_ß ß_
ˆ‰ ˆ‰
""
##
a point of inflection at xʜ
"
#
42. y x x 6 (x 3)(x 2), y
w# w
œ œ œ ± ±
# $
rising on ( ) and (3 ), falling on ( 2 3)Ê_ß#ß_ ß
there is a local maximum at x 2 and a localʜ
minimum at x 3; y 2x 1, yœ œ œ ±
"Î#
ww ww
concave up on , concave down on Êß_ _ß
ˆ‰ ˆ ‰
""
##
a point of inflection at xʜ
"
#
43. y x(x 3) , y rising on
w#w
œ œ ± ± Ê
!$
( ), falling on ( ) no local maximum, but there!ß _ _ß ! Ê
is a local minimum at x 0; y (x 3) x(2)(x 3)œœ
ww #
3(x 3)(x 1), y concaveœ œ ± ± Ê
"$
ww
up on ( ) and ( ), concave down on ( ) _ß" $ß_ "ß$ Ê
points of inflection at x 1 and x 3œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
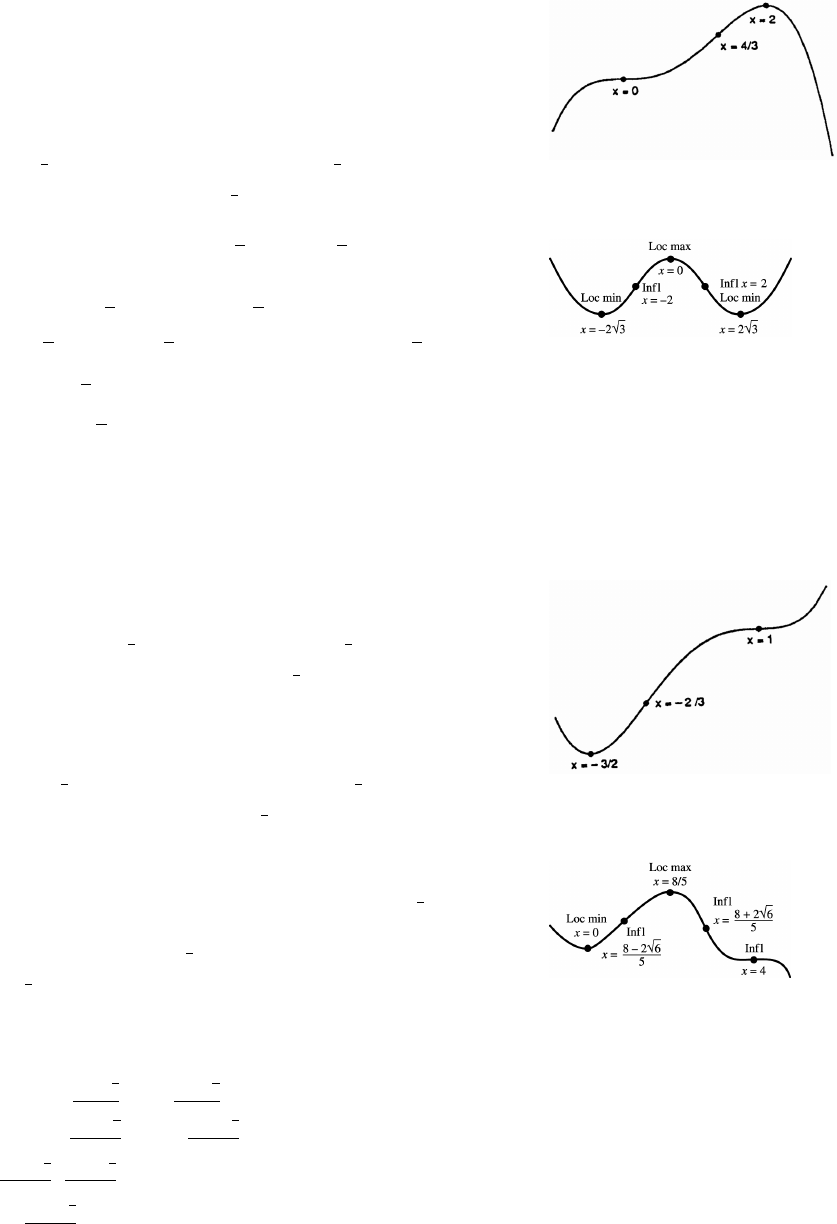
236 Chapter 4 Applications of Derivatives
44. y x (2 x), y rising on
w# w
œ œ ± ± Ê
!#
( ), falling on (2 ) there is a local maximum at_ß# ß_ Ê
x 2, but no local minimum; y 2x(2 x) x ( 1)œœ
ww #
x(4 3x), y concave upœ œ ± ± Ê
!%Î$
ww
on , concave down on ( ) and points
ˆ‰ ˆ ‰
!ß _ß! ß_ Ê
44
33
of inflection at x 0 and xœœ
4
3
45. y x x 12 x x 2 3 x 2 3 ,
w#
œœ ab
Š‹Š‹
ÈÈ
y rising on
wœ ± ± ± Ê
# $ # $
!
ÈÈ
2 3 and 3 , falling on 3
Š‹Š‹ Š ‹
ÈÈ È
ß! # ß_ _ß#
and 3 a local maximum at x 0, local minima
Š‹
È
!ß # Ê œ
at x 3 ; y (1) x 12 (x)(2x)œ„# œ
Èab
ww #
3(x 2)(x 2), yœ œ ± ±
# #
ww
concave up on ( ) and ( ), concave down onÊ _ß # #ß _
( ) points of inflection at x 2#ß # Ê œ „
46. y (x 1) (2x 3), y
w# w
œ œ ± ±
$Î# "
rising on , falling on no localÊ ß_ _ß Ê
ˆ‰ ˆ ‰
33
##
maximum, a local minimum at x ;œ3
#
y 2(x 1)(2x 3) (x 1) (2) 2(x 1)(3x 2),
ww #
œ œ
y concave up on
ww œ ± ± Ê
#Î$ "
and ( ), concave down on
ˆ‰ ˆ‰
_ß "ß_ ß"
22
33
points of inflection at x and x 1Êœœ
2
3
47. y 8x 5x (4 x) x(8 5x)( x) ,
w## #
œ œ%ab
y rising on ,
wœ ± ± ± Ê !ß
!)Î& %ˆ‰
8
5
falling on ( ) and a local maximum at_ß! ß_ Ê
ˆ‰
8
5
x , a local minimum at x 0;œœ
8
5
y (8 10x)(4 x) 8x 5x (2)( x)( 1)
ww # #
œ %ab
4(4 x) 5x 16x 8 ,œ ab
#
y concave up
ww
)# ' )# '
&&
œ ± ± ± Ê
%
ÈÈ
on and , concave down on
Š‹Š‹
_ß ß %
826 826
55
ÈÈ
and (4 ) points of inflection at
Š‹
826826
55
ÈÈ
ßß_Ê
x and x 4œœ
826
5
„È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
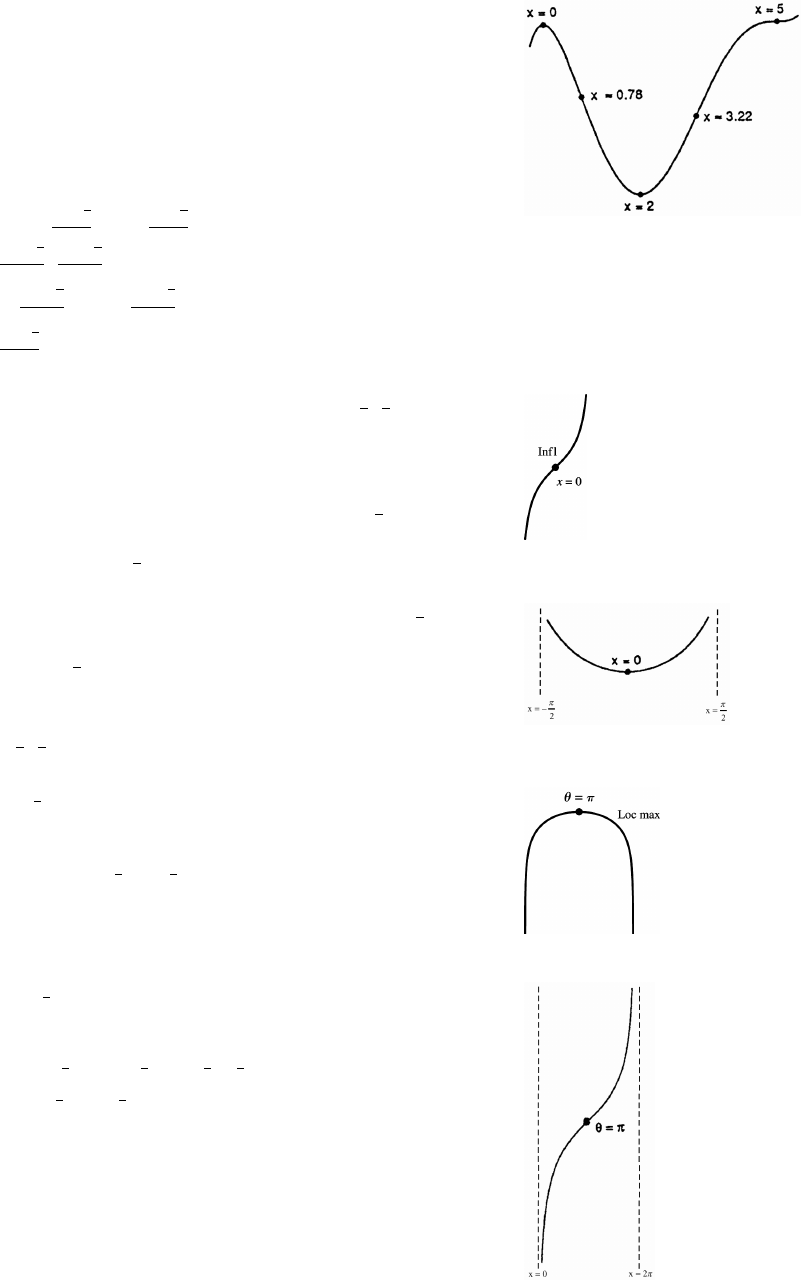
Section 4.4 Concavity and Curve Sketching 237
48. y x 2x (x 5) x(x 2)(x 5) ,
w# # #
œ œ ab
y rising on ( )
wœ ± ± ± Ê _ß !
!#&
and ( ), falling on ( ) a local maximum at x 0,#ß _ !ß # Ê œ
a local minimum at x 2;œ
y (2x 2)(x 5) x 2x (2)(x 5)
ww # #
œ ab
2(x5)2x 8x5,œ ab
#
y concave up
ww
% ' % '
##
œ ± ± ± Ê
&
ÈÈ
on and (5 ), concave down on
Š‹
4646
2
#
ÈÈ
ßß_
and points of inflection at
Š‹Š‹
_ß ß & Ê
%
#
ÈÈ
646
2
x and x 5œœ
46
2
„È
49. y sec x, y ( ) rising on ,
w#w
##
œ œ Ê ß
Î# Î#11 ˆ‰
11
never falling no local extrema;Ê
y 2(sec x)(sec x)(tan x) 2 sec x (tan x),
ww #
œœab
y ( ) concave up on , ,
ww
#
œ ± Ê !
Î# Î#
!
11 ˆ‰
1
concave down on , is a opoint of inflection.
ˆ‰
ß! !
1
#
50. y tan x, y ( ) rising on 0 ,
ww
#
œ œ ± Ê ß
Î# Î#
!
11 ˆ‰
1
falling on no local maximum, a local minimum
ˆ‰
ß! Ê
1
#
at x 0; y sec x, y ( ) concave upœ œ œ Ê
Î# Î#
ww # ww
11
on no points of inflection
ˆ‰
ß Ê
11
##
51. y cot , y ( ) rising on ( ),
ww
#
œ œ ± Ê !ß
!#
)
11
1
falling on ( ) a local maximum at , no local11 ) 1ß# Ê œ
minimum; y csc , y ( ) never
ww # ww
"
##
œ œ Ê
!#
)
1
concave up, concave down on ( ) no points of!ß # Ê1
inflection
52. y csc , y ( ) rising on ( 2 ), never
w#w
#
œ œ Ê !ß
!#
)
1
1
falling no local extrema;Ê
y 2 csc csc cot
ww
####
"
œ
ˆ‰ˆ ‰ˆ‰ˆ‰
)))
csc cot , y ( )œ œ ±
!#
ˆ‰ˆ‰
#ww
##
))
11
concave up on ( ), concave down on ( )Êß# !ß11 1
a point of inflection at ʜ)1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
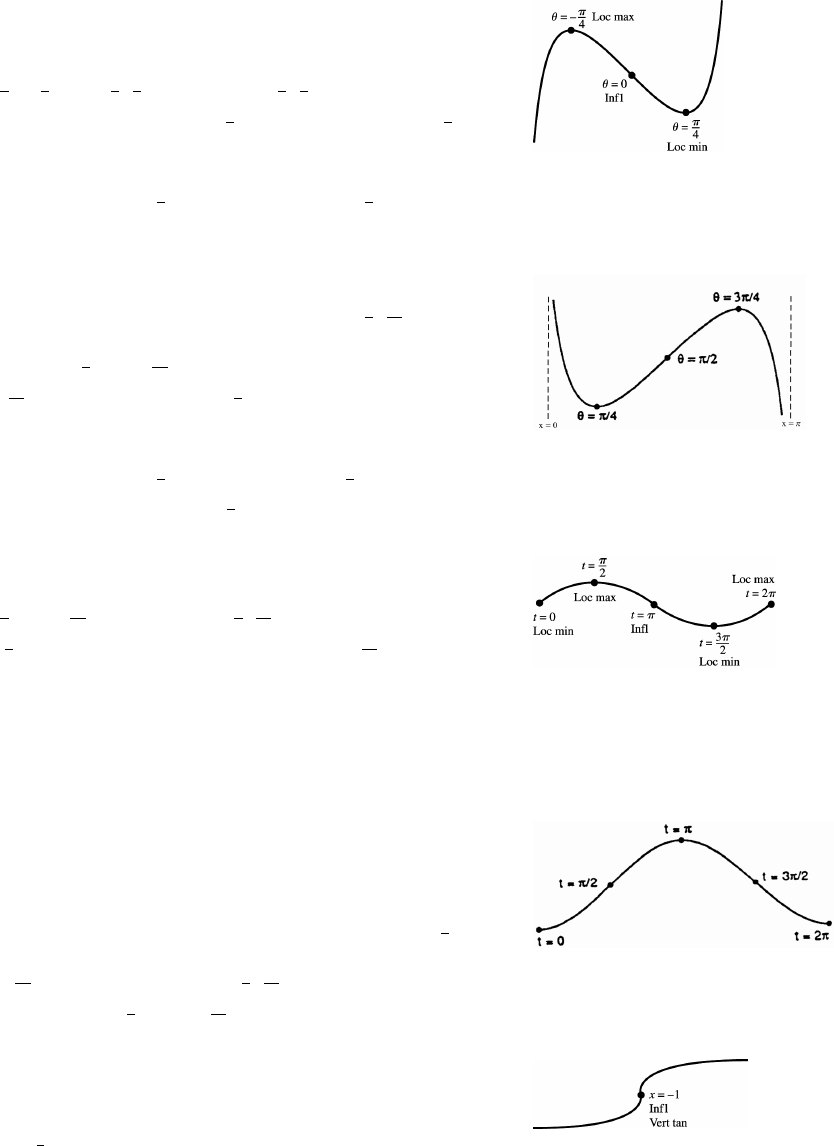
238 Chapter 4 Applications of Derivatives
53. y tan 1 (tan 1)(tan 1),
w#
œœ )))
y ( | ) rising on
wœ ± Ê
Î# Î% Î#
Î%
11 1
1
and , falling on
ˆ‰ˆ‰ ˆ‰
ß ß ß
1 1 11 11
##44 44
a local maximum at , a local minimum at ;Êœ œ))
11
44
y 2 tan sec , y ( )
ww # ww
œ œ ±
Î# Î#
!
))
11
concave up on , concave down on Ê!ß ß!
ˆ‰ ˆ ‰
11
##
a point of inflection at 0ʜ)
54. y 1 cot ( cot )(1 cot ),
w#
œ œ" )))
y ( | ) rising on ,
wœ ± Ê ß
!Î% $Î%
111ˆ‰
11
44
3
falling on 0 and a local maximum at
ˆ‰ˆ ‰
ßßÊ
11
44
31
, a local minimum at ;))œœ
3
44
11
y 2(cot ) csc , y ( )
ww # ww
œ œ ±
!Î#
))
11
ab
concave up on , concave down on Ê!ß ß
ˆ‰ ˆ‰
11
##
1
a point of inflection at ʜ)1
#
55. y cos t, y [ ] rising on
ww
œ œ ± ± Ê
!#
Î# $ Î#11 1
and 2 , falling on local maxima at
ˆ‰ˆ ‰ ˆ ‰
!ß ß ß Ê
11 11
## ##
33
1
t and t 2 , local minima at t 0 and t ;œœ œœ
11
##
13
y sin t, y [ ]
ww ww
œ œ ±
!#
11
concave up on ( ), concave downÊß#11
on ( ) a point of inflection at t!ß Ê œ11
56. y sin t, y [ ] rising on ( ),
ww
œ œ ± Ê !ß
!#
11
1
falling on ( 2 ) a local maximum at t , local11 1ßÊ œ
minima at t 0 and t 2 ; y cos t,œœœ1ww
y [ ] concave up on
ww
#
œ ± ± Ê !ß
!#
Î# $ Î#11 1ˆ‰
1
and , concave down on points
ˆ‰ ˆ‰
33111
###
ß# ß Ê1
of inflection at t and tœœ
11
##
3
57. y (x 1) , y ) ( rising on
w #Î$ w
œ œ Ê
"
( ), never falling no local extrema;_ß _ Ê
y(x1), y )(
ww &Î$ ww
œ œ
"
2
3
concave up on ( 1), concave down on ( )Ê _ß "ß _
a point of inflection and vertical tangent at x 1ʜ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
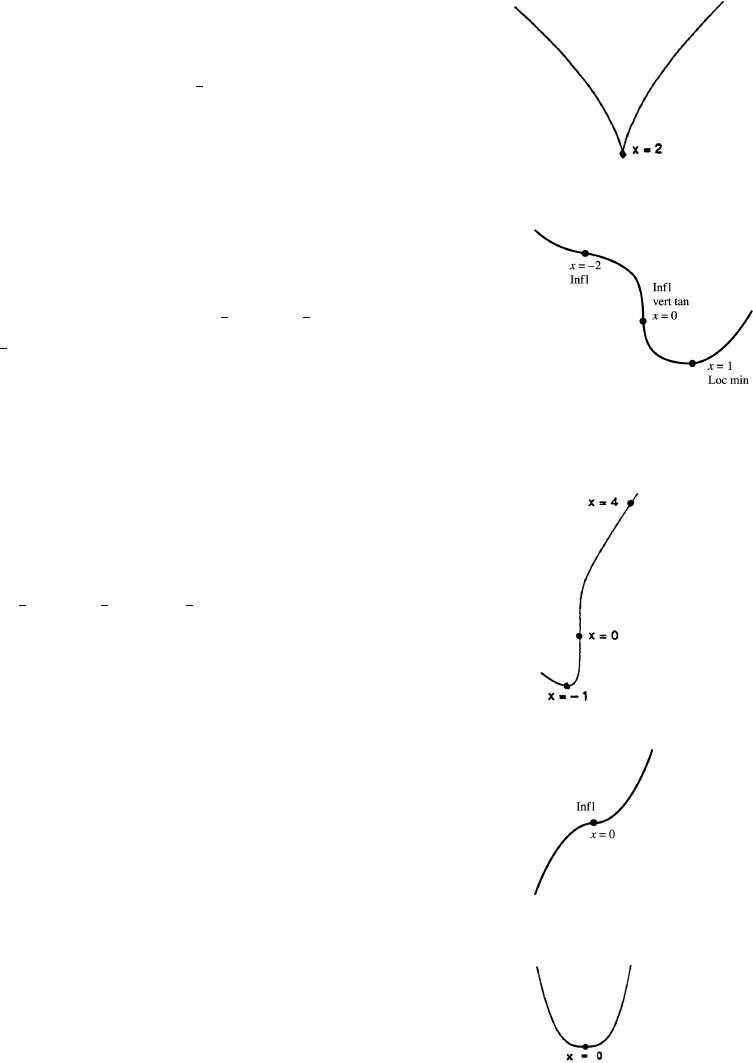
Section 4.4 Concavity and Curve Sketching 239
58. y (x 2) , y )( rising on (2 ),
w "Î$ w
œ œ Ê ß_
#
falling on ( ) no local maximum, but a local_ß# Ê
minimum at x 2; y (x 2) ,œœ
ww %Î$
1
3
y )( concave down on ( 2) and
ww œ Ê _ß
#
( ) no points of inflection, but there is a cusp at#ß_ Ê
x2œ
59. y x (x 1), y )( rising on
w #Î$ w
œ œ ± Ê
!"
( ), falling on ( ) no local maximum, but a"ß_ _ß" Ê
local minimum at x 1; y x xœœ
ww #Î$ &Î$
"
33
2
x(x2), y )(œ œ ±
# !
"&Î$ ww
3
concave up on ( 2) and ( ), concave down onÊ_ß!ß_
( ) points of inflection at x 2 and x 0, and a#ß! Ê œ œ
vertical tangent at x 0œ
60. y x (x 1), y )( rising on
w %Î& w
œ œ ± Ê
" !
( 0) and ( ), falling on ( ) no local"ß !ß_ _ß" Ê
maximum, but a local minimum at x 1;œ
y x x x (x 4),
ww %Î& *Î& *Î&
""
œœ
55 5
4
y )( concave up on ( 0) and
ww œ ± Ê _ß
!%
(4 ), concave down on (0 4) points of inflection atß_ ß Ê
x 0 and x 4, and a vertical tangent at x 0œœ œ
61. y , y rising on
x, x 0
2x, x 0
ww
œ œ ± Ê
# Ÿ
!
œ
( ) no local extrema; y ,
2, x 0
2, x 0
_ß_ Ê œ
ww œ
y )( concave up on ( ), concave
ww œ Ê !ß_
!
down on ( ) a point of inflection at x 0_ß! Ê œ
62. y , y rising on
x, x 0
x , x 0
ww
#
#
œ œ ± Ê
Ÿ
!
œ
( ), falling on ( ) no local maximum, but a!ß_ _ß! Ê
local minimum at x 0; y ,
2x, x 0
2x, x 0
œœ
Ÿ
ww œ
y concave up on ( )
ww œ ± Ê _ß_
!
no point of inflectionÊ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
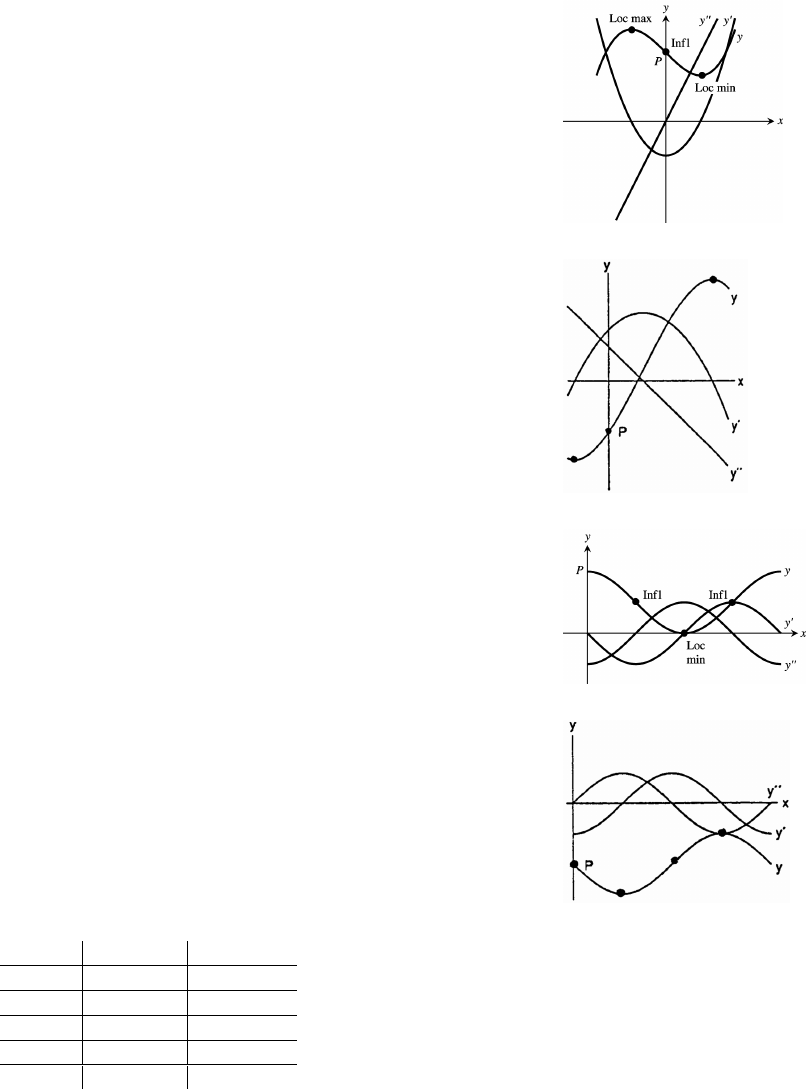
240 Chapter 4 Applications of Derivatives
63. The graph of y f (x) the graph of y f(x) is concaveœÊ œ
ww
up on ( ), concave down on ( ) a point of!ß_ _ß! Ê
inflection at x 0; the graph of y f (x)œœ
w
y the graph y f(x) hasÊ œ ± ± Ê œ
w
both a local maximum and a local minimum
64. The graph of y f (x) y theœ Ê œ ± Ê
ww ww
graph of y f(x) has a point of inflection, the graph ofœ
y f (x) y the graph ofœ Ê œ ± ± Ê
ww
y f(x) has both a local maximum and a local minimumœ
65. The graph of y f (x) yœ Ê œ ± ±
ww ww
the graph of y f(x) has two points of inflection, theʜ
graph of y f (x) y the graph ofœ Ê œ ± Ê
ww
y f(x) has a local minimumœ
66. The graph of y f (x) y theœ Ê œ ± Ê
ww ww
graph of y f(x) has a point of inflection; the graph ofœ
y f (x) y the graph ofœ Ê œ ± ± Ê
ww
y f(x) has both a local maximum and a local minimumœ
67. Point y y
P
Q
R
S
T
www
!
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
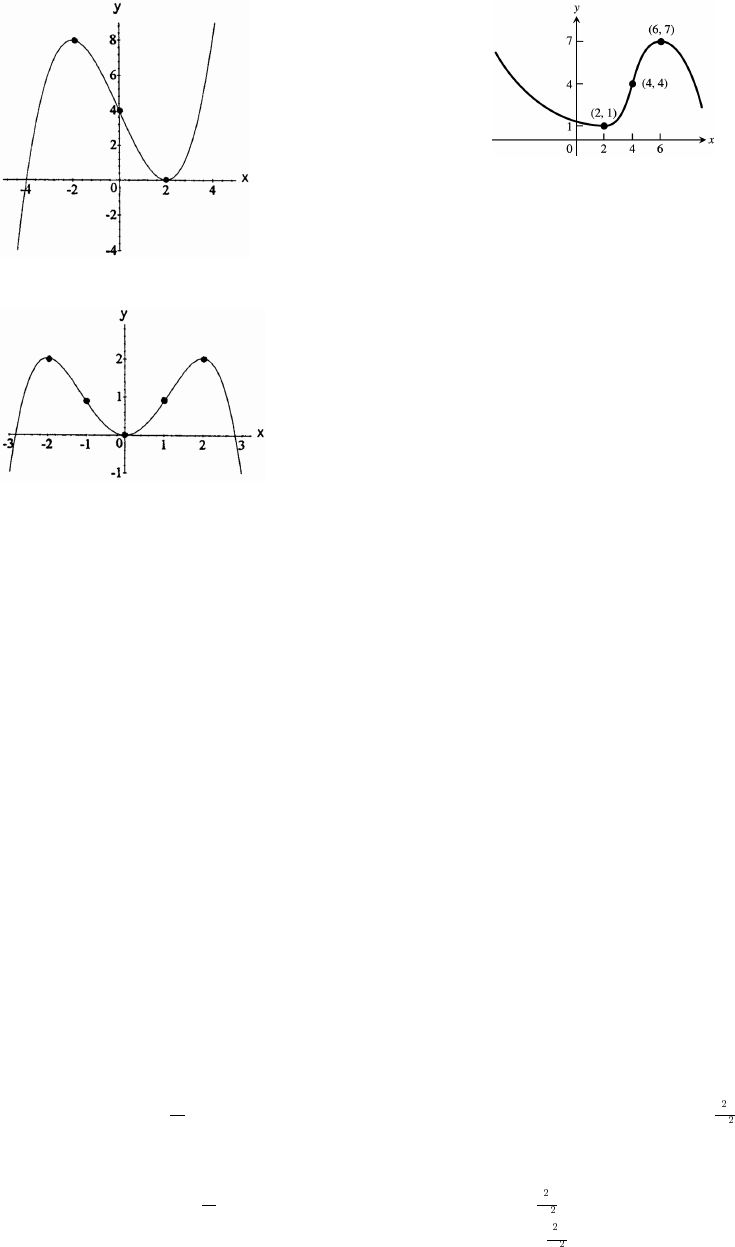
Section 4.4 Concavity and Curve Sketching 241
68. 69.
70.
71. Graphs printed in color can shift during a press run, so your values may differ somewhat from those given here.
(a) The body is moving away from the origin when displacement is increasing as t increases, 0 t 2 andkk
6 t 9.5; the body is moving toward the origin when displacement is decreasing as t increases, 2 t 6 kk
and 9.5 t 15
(b) The velocity will be zero when the slope of the tangent line for y s(t) is horizontal. The velocity is zeroœ
when t is approximately 2, 6, or 9.5 sec.
(c) The acceleration will be zero at those values of t where the curve y s(t) has points of inflection. Theœ
acceleration is zero when t is approximately 4, 7.5, or 12.5 sec.
(d) The acceleration is positive when the concavity is up, 4 t 7.5 and 12.5 t 15; the acceleration is
negative when the concavity is down, 0 t 4 and 7.5 t 12.5
72. (a) The body is moving away from the origin when displacement is increasing as t increases, 1.5 t 4,kk
10 t 12 and 13.5 t 16; the body is moving toward the origin when displacement is decreasing as t kk
increases, 0 t 1.5, 4 t 10 and 12 t 13.5
(b) The velocity will be zero when the slope of the tangent line for y s(t) is horizontal. The velocity is zeroœ
when t is approximately 0, 4, 12 or 16 sec.
(c) The acceleration will be zero at those values of t where the curve y s(t) has points of inflection. Theœ
acceleration is zero when t is approximately 1.5, 6, 8, 10.5, or 13.5 sec.
(d) The acceleration is positive when the concavity is up, 0 t 1.5, 6 t 8 and 10 t 13.5, the
acceleration is negative when the concavity is down, 1.5 t 6, 8 t 10 and 13.5 t 16.
73. The marginal cost is which changes from decreasing to increasing when its derivative is zero. This is a
dc dc
dx dx
point of inflection of the cost curve and occurs when the production level x is approximately 60 thousand units.
74. The marginal revenue is and it is increasing when its derivative is positive the curve is concave up
dy d y
dx dx Ê
t 2 and 5 t 9; marginal revenue is decreasing when 0 the curve is concave downÊ! Ê
dy
dx
2 t 5 and 9 t 12.Ê
75. When y (x 1) (x 2), then y 2(x 1)(x 2) (x 1) . The curve falls on ( 2) and rises on
w# ww #
œ œ _ß
( ). At x 2 there is a local minimum. There is no local maximum. The curve is concave upward on ( ) and#ß_ œ _ß"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

242 Chapter 4 Applications of Derivatives
, and concave downward on . At x 1 or x there are inflection points.
ˆ‰ ˆ‰
555
333
ß_ "ß œ œ
76. When y (x 1) (x 2)(x 4), then y 2(x 1)(x 2)(x 4) (x 1) (x 4) (x 1) (x 2)
w# ww # #
œ œ
(x 1) 2 x 6x 8 x 5x 4 x 3x 2 2(x 1) 2x 10x 11 . The curve rises onœ œ cdabababab
### #
( 2) and ( ) and falls on ( ). At x 2 there is a local maximum and at x 4 a local minimum. The_ß %ß_ #ß% œ œ
curve is concave downward on ( ) and and concave upward on 1 and_ß" ß ß
Š‹ Š‹
5353 53
2
##
ÈÈ È
. At x 1, and there are inflection points.
Š‹
53 53 53
###
ÈÈÈ
ß_ œ
77. The graph must be concave down for x 0 because
f (x) 0.
ww "
œ
x
78. The second derivative, being continuous and never zero, cannot change sign. Therefore the graph will always
be concave up or concave down so it will have no inflection points and no cusps or corners.
79. The curve will have a point of inflection at x 1 if 1 is a solution of y 0; y x bx cx dœœœ
ww $ #
y 3x 2bx c y 6x 2b and 6(1) 2b 0 b 3.Êœ Ê œ œÊœ
w# w
w
80. (a) True. If f(x) is a polynomial of even degree then f is of odd degree. Every polynomial of odd degree has
w
at least one real root f (x) 0 for some x r f has a horizontal tangent at x r.Êœ œÊ œ
w
(b) False. For example, f(x) x 1 is a polynomial of odd degree but f (x) 1 is never 0. As anotherœ œ
w
example, y x x x is a polynomial of odd degree, but y x 2x 1 (x 1) 0 for all x.œ œœ
"$# w # #
3
81. (a) f(x) ax bx c a x x c a x c a x a parabolaœœ œ B œ
## #
#
#
ˆ‰ ˆ‰
Š‹
bbbbbb4ac
a a 4a 4a a 4a
whose vertex is at x the coordinates of the vertex are œ Ê ß
bbb4ac
2a 2a 4a
Š‹
(b) The second derivative, f (x) 2a, describes concavity when a 0 the parabola is concave up and
ww œÊ
when a 0 the parabola is concave down.
82. No, f (x) could be decreasing to zero at x c and then increase again so it would be concave up on every
ww œ
interval even though f (x) 0. For example f(x) x is always concave up even though f (0) 0.
ww % ww
œœ œ
83. A quadratic curve never has an inflection point. If y ax bx c where a 0, then y 2ax b andœ Á œ
#w
y 2a. Since 2a is a constant, it is not possible for y to change signs.
ww ww
œ
84. A cubic curve always has exactly one inflection point. If y ax bx cx d where a 0, thenœ Á
$#
y 3ax 2bx c and y 6ax 2b. Since is a solution of y 0, we have that y changes its sign
w # ww ww ww
œ œ œ
b
3a
at x and y exists everywhere (so there is a tangent at x ). Thus the curve has an inflectionœ œ
b b
3a 3a
w
point at x . There are no other inflection points because y changes sign only at this zero.œb
3a ww
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
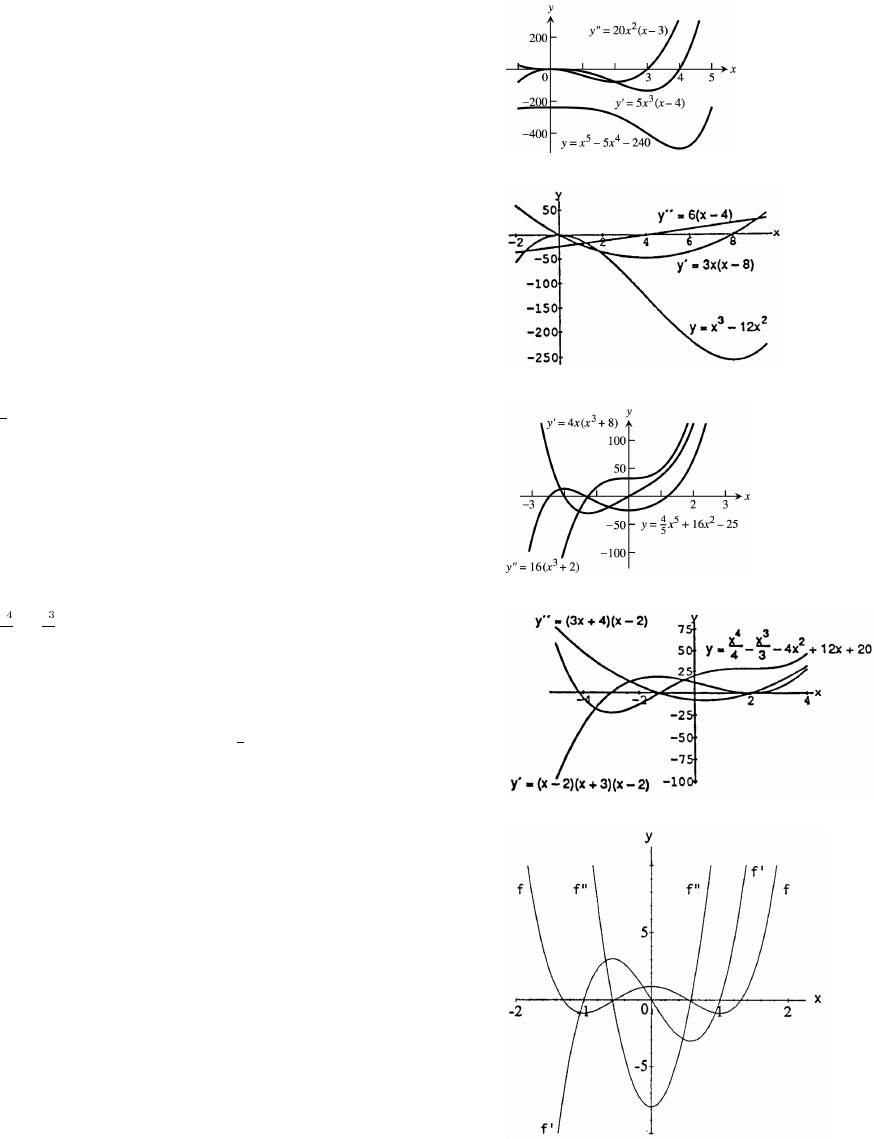
Section 4.4 Concavity and Curve Sketching 243
85. If y x 5x 240, then y 5x (x 4) andœ œ
&% w $
y 20x (x 3). The zeros of y are extrema, and
ww # w
œ
there is a point of inflection at x œ$Þ
86. If y x 12x , then y 3x(x 8) andœ œ
$# w
y 6(x 4). The zeros of y and y are
ww w ww
œ
extrema and points of inflection, respectively.
87. If y x 16x 25, then y 4x x 8 andœ œ
4
5&# w $
ab
y 16 x 2 . The zeros of y and y are
ww $ w ww
œab
extrema and points of inflection, respectively.
88. If y 4x 12x 20, thenœ
xx
43 #
y x x x (x 3)(x 2)
w$# #
œ ) "#œ Þ
So y has a local minimum at x as its only extremeœ$
value. Also y x x (3x 4)(x 2) and there
ww #
œ$ # )œ
are inflection points at both zeros, and 2, of y .%
$
ww
89. The graph of f falls where f 0, rises where f 0,
ww
and has horizontal tangents where f 0. It has local
wœ
minima at points where f changes from negative to
w
positive and local maxima where f changes from
w
positive to negative. The graph of f is concave down
where f 0 and concave up where f 0. It has an
ww ww
inflection point each time f changes sign, provided a tangent
ww
line exists there.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
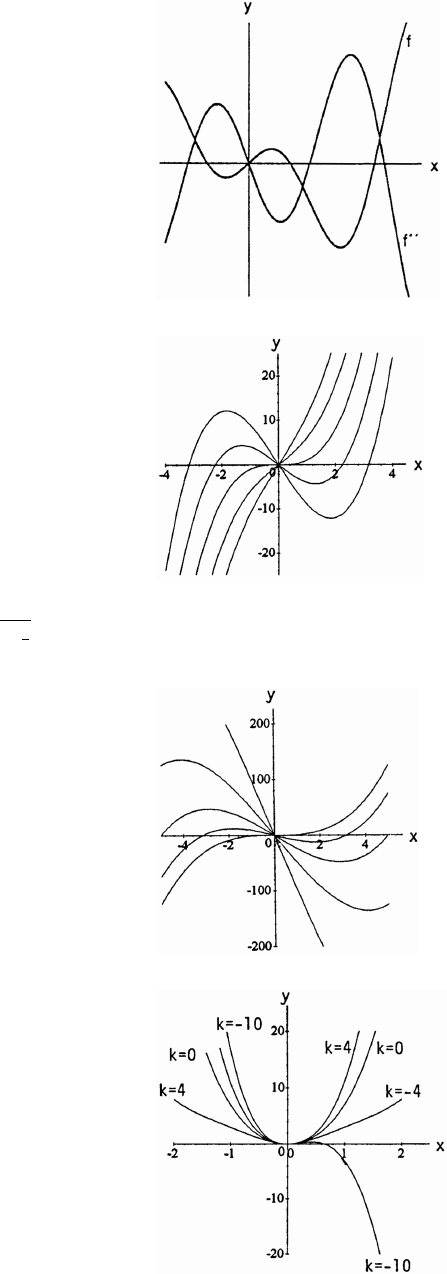
244 Chapter 4 Applications of Derivatives
90. The graph f is concave down where f 0, and concave
ww
up where f 0. It has an inflection point each time
ww
f changes sign, provided a tangent line exists there.
ww
91. (a) It appears to control the number and magnitude of the
local extrema. If k 0, there is a local maximum to the
left of the origin and a local minimum to the right. The
larger the magnitude of k (k 0), the greater the
magnitude of the extrema. If k 0, the graph has only
positive slopes and lies entirely in the first and third
quadrants with no local extrema. The graph becomes
increasingly steep and straight as k .Ä_
(b) f (x) 3x k the discriminant 0 4(3)(k) 12k is positive for k 0, zero for k 0, and
w# #
œÊ œ œ
negative for k 0; f has two zeros x when k 0, one zero x 0 when k 0 and no real zerosœ„œœ
wÉk
3
when k 0; the sign of k controls the number of local extrema.
(c) As k , f (x) and the graph becomesÄ_ Ä_
w
increasingly steep and straight. As k , theÄ_
crest of the graph (local maximum) in the second
quadrant becomes increasingly high and the trough
(local minimum) in the fourth quadrant becomes
increasingly deep.
92. (a) It appears to control the concavity and the number of
local extrema.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
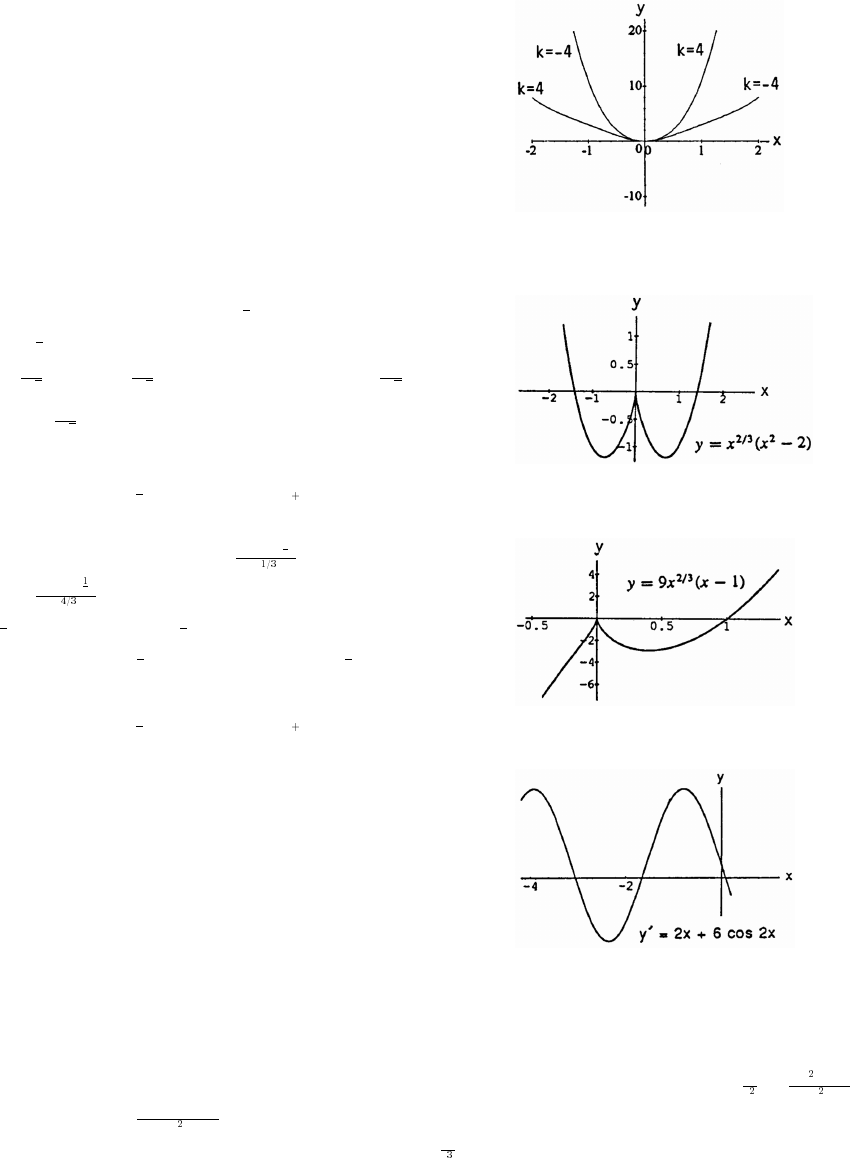
Section 4.5 Applied Optimization Problems 245
(b) f(x) x kx 6x f (x) 4x 3kx 12xœ Ê œ
%$# w $ #
f (x) 12x 6kx 12 the discriminant isÊœÊ
ww #
36k 4(12)(12) 36(k 4)(k 4), so the sign line
#œ
of the discriminant is the ± ± Ê
% %
discriminant is positive when k 4, zero whenkk
k 4, and negative when k 4; f (x) 0 hasœ„ œkk ww
two zeros when k 4, one zero when k 4, andkkœ„
no real zeros for k 4; the value of k controls thekk
number of possible points of inflection.
93. (a) If y x x 2 , then y x 2x 1 andœ œ
#Î$ # w "Î$ #
ab a b
4
3
y x 10x 1 . The curve rises on
ww %Î$ #
œ
4
9ab
0 and and falls on
Š‹Š‹ Š ‹
ß ß_ _ß
"" "
ÈÈ È
22 2
and . The curve is concave up on ( )
Š‹
!ß _ß!
"
È2
and ( ).!ß_
(b) A cusp since lim y and lim y .
xx
Ä! Ä!
ww
œ_ œ_
94. (a) If y 9x (x 1), then y andœ œ
#Î$ w 15 x
x
ˆ‰
2
5
y . The curve rises on ( ) and
ww
œ _ß!
10 x
x
ˆ‰
5
and falls on . The curve is concave
ˆ‰ ˆ‰
22
55
ß_ !ß
down on and concave up on and
ˆ‰ ˆ‰
_ß ß!
""
55
().!ß_
(b) A cusp since lim y and lim y .
xx
Ä! Ä!
ww
œ_ œ_
95. Yes: y x 3 sin 2x y 2x 6 cos 2x. The graphœ Êœ
#w
of y is zero near 3 and this indicates a horizontal tangent
w
near x 3.œ
4.5 APPLIED OPTIMIZATION PROBLEMS
1. Let and w represent the length and width of the rectangle, respectively. With an area of 16 in. , we havej#
that ( )(w) 16 w 16 the perimeter is P 2 2w 2 32 and P ( ) 2 .jœÊœjÊ œjœjj jœœ
" " w
jj
j
32 216
ab
Solving P ( ) 0 0 4, 4. Since 0 for the length of a rectangle, must be 4 and
wj j
j
jœ Ê œ Êjœ j j
2( 4)( 4)
w 4 the perimeter is 16 in., a minimum since P ( ) 0.œÊ jœ
ww
j
16
2. Let x represent the length of the rectangle in meters ( x ) Then the width is x and the area is! % %
A x x x x x . Since A x x, the critical point occurs at x . Since, A x for x andab a b ab abœ % œ% œ%# œ# ! ! #
#w w
A x for x , this critical point corresponds to the maximum area. The rectangle with the largest area measures
wab! # %
m by m, so it is a square.#%#œ#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
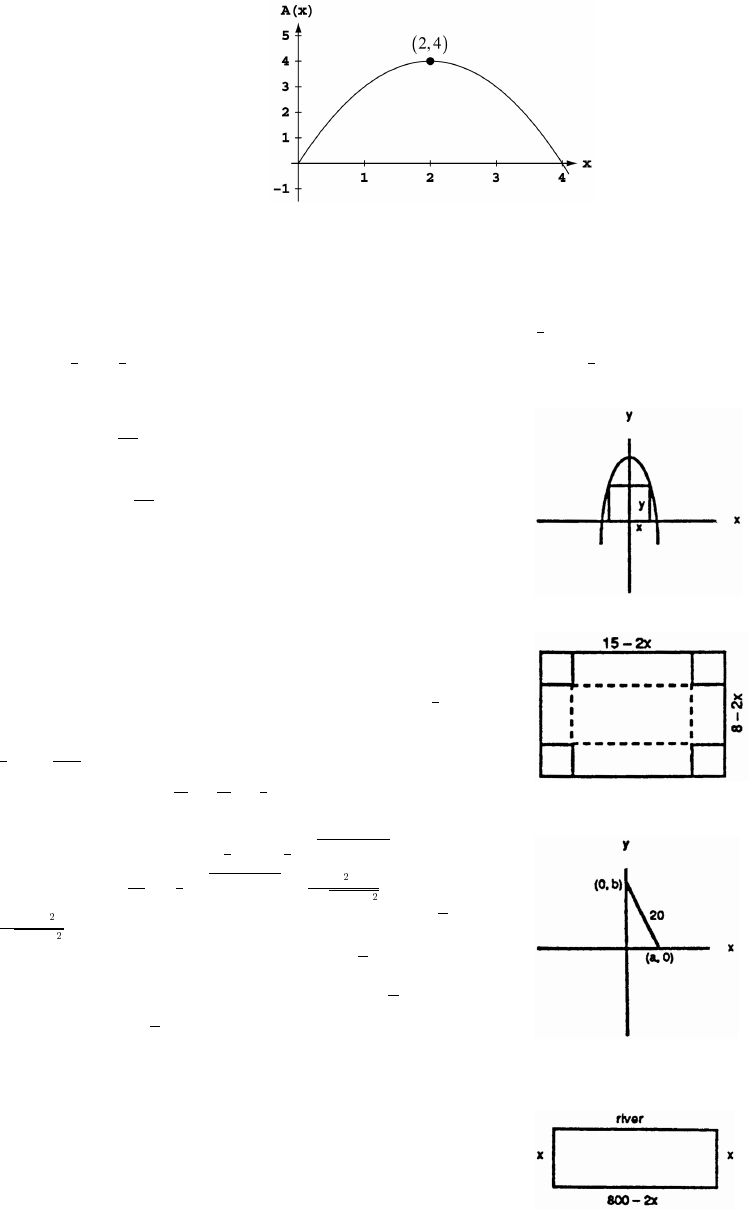
246 Chapter 4 Applications of Derivatives
Graphical Support:
3. (a) The line containing point P also contains the points ( ) and ( ) the line containing P is y 1 x!ß" "ß! Ê œ
a general point on that line is (x 1 x).Êß
(b) The area A(x) 2x(1 x), where 0 x 1.œ ŸŸ
(c) When A(x) 2x 2x , then A (x) 0 2 4x 0 x . Since A(0) 0 and A(1) 0, we concludeœ œÊœÊœ œ œ
#w "
#
that A sq units is the largest area. The dimensions are unit by unit.
ˆ‰
"" "
## #
œ"
4. The area of the rectangle is A 2xy 2x 12 x ,œœ ab
#
where 0 x 12 . Solving A (x) 0 24 6x 0ŸŸ œ Ê œ
Èw#
x 2 or 2. Now 2 is not in the domain, and sinceʜ
A(0) 0 and A 12 0, we conclude that A(2) 32œœ œ
Š‹
È
square units is the maximum area. The dimensions are 4 units
by 8 units.
5. The volume of the box is V(x) x(15 2x)(8 2x)œ
120x 46x 4x , where 0 x 4. Solving V (x) 0œ ŸŸ œ
#$ w
120 92x 12x 4(6 x)(5 3x) 0 xÊœœÊœ
#5
3
or 6, but 6 is not in the domain. Since V(0) V(4) 0,œœ
V in must be the maximum volume of
ˆ‰
5
3œ¸*"
#%&!
#(
$
the box with dimensions inches.
14 35 5
333
‚‚
6. The area of the triangle is A ba 400 b , whereœœ
"
## #
bÈ
0 b 20. Then 400 bŸŸ œ
dA b
db 2 400 b
"
##
ÈÈ
0 the interior critical point is b 10 2.œœÊ œ
200 b
400 b
ÈÈ
When b 0 or 20, the area is zero A 10 2 is theœÊ
Š‹
È
maximum area. When a b 400 and b 10 2, the
##
œ œÈ
value of a is also 10 2 the maximum area occurs when
ÈÊ
ab.œ
7. The area is A(x) x(800 2x), where 0 x 400.œ ŸŸ
Solving A (x) 800 4x 0 x 200. With
wœœÊœ
A(0) A(400) 0, the maximum area isœœ
A(200) 80,000 m . The dimensions are 200 m by 400 m.œ#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
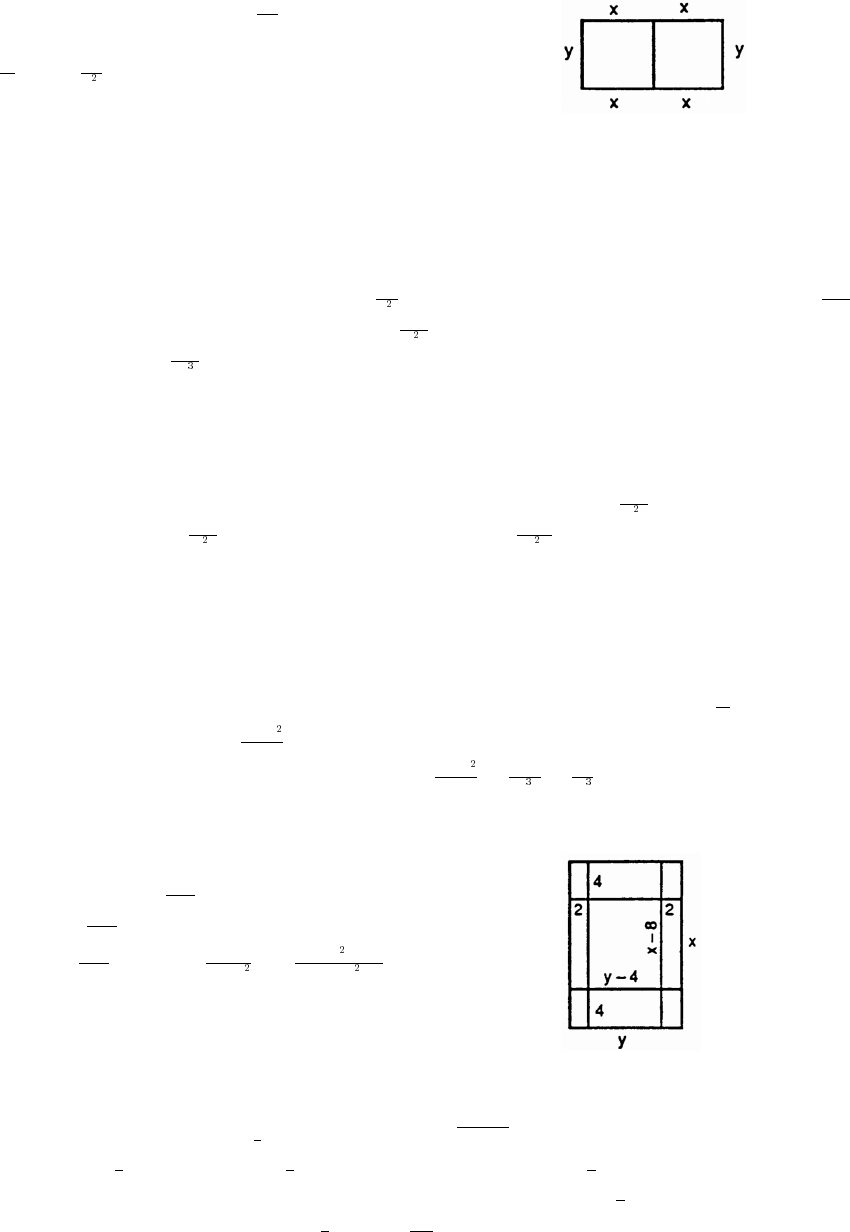
Section 4.5 Applied Optimization Problems 247
8. The area is 2xy 216 y . The amount of fenceœÊœ
108
x
needed is P 4x 3y 4x 324x , where x;œ œ !
"
4 0 x 81 0 the critical points are
dP 324
dx x
œ œ Ê œÊ
#
0 and 9, but 0 and 9 are not in the domain. Then„
P (9) 0 at x 9 there is a minimum the
ww Ê œ Ê
dimensions of the outer rectangle are 18 m by 12 m
72 meters of fence will be needed.Ê
9. (a) We minimize the weight tS where S is the surface area, and t is the thickness of the steel walls of the tank. Theœ
surace area is S x xy where x is the length of a side of the square base of the tank, and y is its depth. Theœ%
#
volume of the tank must be ft y . Therefore, the weight of the tank is w x t x . Treating the&!! Ê œ œ
$ #
&!! #!!!
xx
ab ˆ‰
thickness as a constant gives w x t x for x . The critical value is at x . Since
w#!!!
ab ˆ‰
œ# Þ! œ"!
x
w t , there is a minimum at x . Therefore, the optimum dimensions of the tank are ft on
ww %!!!
"!
ab ˆ‰
"! œ # ! œ "! "!
the base edges and ft deep.&
(b) Minimizing the surface area of the tank minimizes its weight for a given wall thickness. The thickness of the steel
walls would likely be determined by other considerations such as structural requirements.
10. (a) The volume of the tank being ft , we have that yx y . The cost of building the tank is""#& œ ""#& Ê œ
$#""#&
x
c x x x , where x. Then c x x the critical points are and , but is notab ab
ˆ‰
œ& $! ! œ"! œ!Ê ! "& !
#w
""#& $$(&!
xx
in the domain. Thus, c at x we have a minimum. The values of x ft and y ft will
wwab"& ! Ê œ "& œ "& œ &
minimize the cost.
(b) The cost function c x xy xy, can be separated into two items: (1) the cost of the materials and labor toœ& % "!ab
#
fabricate the tank, and (2) the cost for the excavation. Since the area of the sides and bottom of the tanks is x xy ,ab
#%
it can be deduced that the unit cost to fabricate the tanks is $ /ft . Normally, excavation costs are per unit volume of&#
excavated material. Consequently, the total excavation cost can be taken as xy x y . This suggests that the"! œ ˆ‰
ab
"! #
x
unit cost of excavation is where x is the length of a side of the square base of the tank in feet. For the least
$ft
x
"!Î
expensive tank, the unit cost for the excavation is . The total cost of the least expensive tank is
$ft
ft ft yd
$$
"!Î
"&
!Þ'( ")
œœ
$ , which is the sum of $ for fabrication and $ for the excavation.$$(& #'#& (&!
11. The area of the printing is (y 4)(x 8) 50.œ
Consequently, y 4. The area of the paper isœ
ˆ‰
50
x8
A(x) x 4 , where 8 x. Thenœ
ˆ‰
50
x8
A (x) 4 x 0
w
œ œ œ
ˆ‰
Š‹
50 50
x 8 (x 8) (x 8)
4(x 8) 400
the critical points are 2 and 18, but 2 is not in theÊ
domain. Thus A (18) 0 at x 18 we have
ww Ê œ
a minimum. Therefore the dimensions 18 by 9 inches
minimize the amount of paper.
12. The volume of the cone is V r h, where r x 9 y and h y 3 (from the figure in the text).œœœœ
"##
31È
Thus, V(y) 9 y (y 3) 27 9y 3y y V (y) 9 6y 3y (1 y)(3 y).œ œ Ê œœ
11 1
33 3
ab a b a b
##$w#
1
The critical points are 3 and 1, but 3 is not in the domain. Thus V (1) ( 6(1)) 0 at y 1 œ'Êœ
ww 1
3
we have a maximum volume of V(1) (8)(4) cubic units.œœ
11
33
32
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
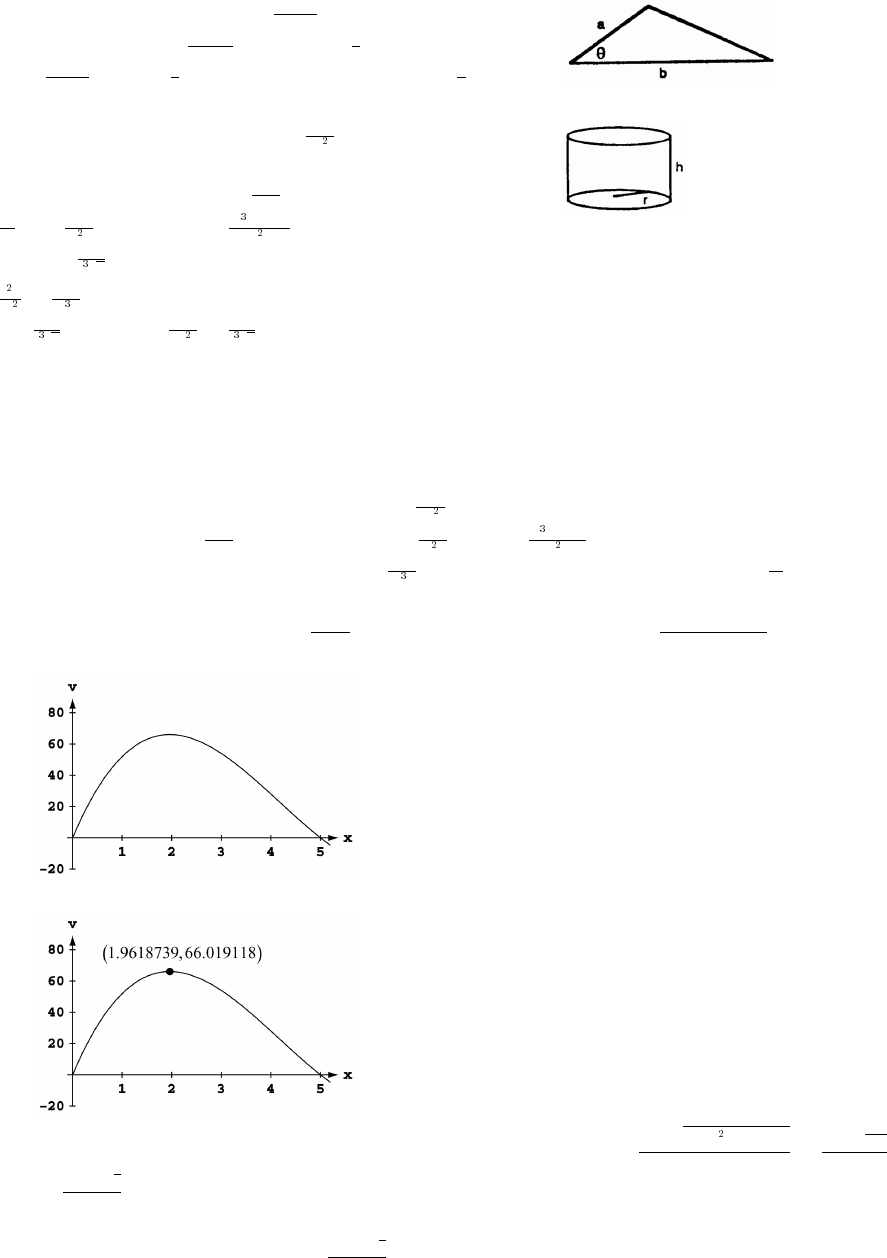
248 Chapter 4 Applications of Derivatives
13. The area of the triangle is A( ) , where 0 .))1œ
ab sin )
#
Solving A ( ) 0 0 . Since A ( )
www
##
)))œÊ œÊœ
ab cos )1
A 0, there is a maximum at .œ Ê œ
ab sin )1 1
## #
ww ˆ‰ )
14. A volume V r h 1000 h . The amount ofœœ Êœ1#1000
r1
material is the surface area given by the sides and bottom of
the can S 2 rh r r , 0 r. ThenÊœ œ 11 1
##
2000
r
2 r 0. The critical points
dS 2000 r 1000
dr r r
œ œ! Ê œ11
are 0 and , but 0 is not in the domain. Since
10
È1
0, we have a minimum surface area when
d S 4000
dr r
œ#1
r cm and h cm. Comparing this result toœœœ
10 1000 10
r
ÈÈ
11
1
the result found in Example 2, if we include both ends of the
can, then we have a minimum surface area when the can is
shorter-specifically, when the height of the can is the same as
its diameter.
15. With a volume of 1000 cm and V r h, then h . The amount of aluminum used per can isœœ1#1000
r1
A 8r 2 rh 8r . Then A (r) 16r 0 0 the critical points are 0 and 5,œ œ œ œÊ œÊ
## w
12000 2000 8r 1000
rrr
but r 0 results in no can. Since A (r) 16 0 we have a minimum at r 5 h and h:r 8: .œœœÊœœ
ww 1000 40
r11
16. (a) The base measures x in. by in., so the volume formula is V x x x x."! # œ œ # #& (&
"&#
##
"!# "&# $#
xxx x
ab abab
(b) We require x , x , and x . Combining these requirements, the domain is the interval . ! # "! # "& !ß &ab
(c) The maximum volume is approximately 66.02 in. when x in.
$¸"Þ*'
(d) V x x x . The critical point occurs when V x , at x
w# w &! „ &! % ' (&
#' "#
&! „ (!!
ab abœ' &! (& œ! œ œ
Éab abab
ab È
, that is, x or x . We discard the larger value because it is not in the domain. Sinceœ ¸ "Þ*' ¸ 'Þ$(
#&„& (
'
È
V x x , which is negative when x , the critical point corresponds to the maximum volume. The
wwabœ"# &! ¸"Þ*'
maximum volume occurs when x , which comfimrs the result in (c).œ ¸ "Þ*'
#&& (
'
È
17. (a) The" sides" of the suitcase will measure x in. by x in. and will be x in. apart, so the volume formula is#% # ") # #
Vxxx xxxx.abababœ # #% # ") # œ ) "') )'#
$#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
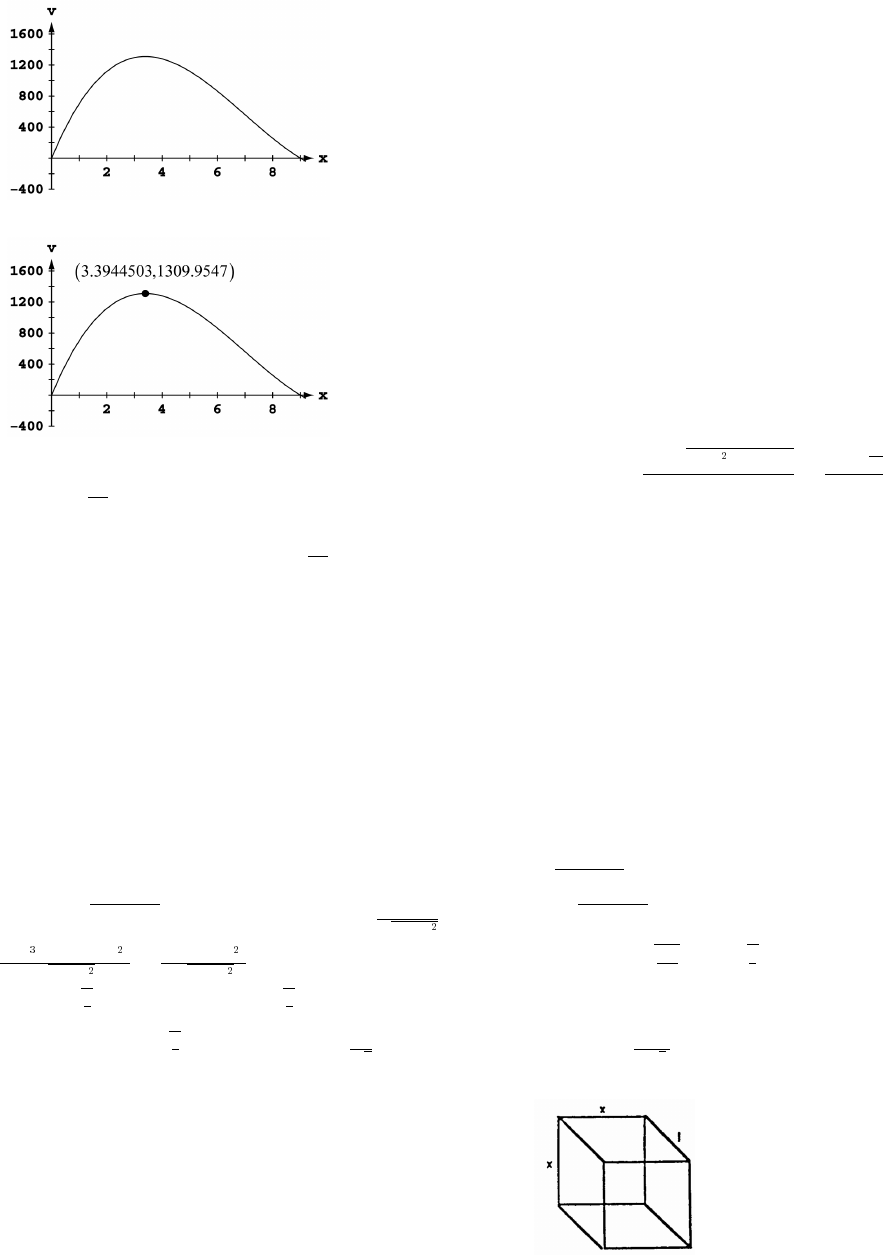
Section 4.5 Applied Optimization Problems 249
(b) We require x , x , and x . Combining these requirements, the domain is the interval . ! # ") # #% !ß *ab
(c) The maximum volume is approximately 1309.95 in. when x 3 3 in.
$¸Þ*
(d) V x x x x x . The critical point is at x
w# # "% „ "% % " $'
#" #
"% „ &#
ab a bœ #% $$' )'% œ #% "% $' œ œ
Éababab
ab È
, that is, x or x . We discard the larger value because it is not in the domain. Sinceœ ( „ "$ ¸ $Þ$* ¸ "!Þ'"
È
V x x which is negative when x , the critical point corresponds to the maximum volume. The
wwab a bœ #% # "% ¸ $Þ$*
maximum value occurs at x , which confirms the results in (c).œ ( "$ ¸ $Þ$*
È
(e) x x x 8 x x x x x x . Since is not in) "') )'# œ ""#! Ê #" "!) "%! œ ! Ê ) # & "% œ ! "%
$# $#
a b ababa b
the fomain, the possible values of x are x in. or x in.œ# œ&
(f) The dimensions of the resulting box are x in., x in., and x . Each of these measurements must be# #%# ")#abab
positive, so that gives the domain of .ab!ß *
18. If the upper right vertex of the rectangle is located at x cos x for x , then the rectangle has width x andabß % !Þ& ! #1
height cos x, so the area is A x x cos x. Solving A x graphically for x , we find that%!Þ& œ) !Þ& œ! !ab ab
w1
x . Evaluating x and cos x for x , the dimensions of the rectangle are approximately (width) by¸ #Þ#"% # % !Þ& ¸ #Þ#"% %Þ%$
(height), and the maximum area is approximately ."Þ(* (Þ*#$
19. Let the radius of the cylinder be r cm, r . Then the height is r and the volume is! "! # "!!
È#
V r r r cm . Then, V r r r r rab ab a b a b
ÈÈ
Š‹Š ‹
œ # "!! œ # # # "!! #111
#$w#
# #
"
"!!
Èr
. The critical point for r occurs at r . Since V r forœ œ ! "! œ œ"! !
# % "!! # #!! $
"!! "!!
#!! #
$$
w
11 1rr r r r
rr
ab a b
ÈÈ ÉÉ ab
r and V r for r , the critical point corresponds to the maximum volume. The! "! ! "! "!
ÉÉ
ab
##
$$
w
dimensions are r cm and h cm, and the volume is cm .œ "! ¸ )Þ"' œ ¸ ""Þ&& ¸ #%")Þ%!
É# #! %!!!
$$$$
$
ÈÈ
1
20. (a) From the diagram we have 4x 108 and V x .jœ œ j
#
The volume of the box is V(x) x (108 4x), whereœ
#
0 x 27. ThenŸ
V (x) 216x 12x 12x(18 x) 0
w#
œœ œ
the critical points are 0 and 18, but x 0 results inʜ
no box. Since V (x) 216 24x 0 at x 18 we
ww œ œ
have a maximum. The dimensions of the box are
18 18 36 in.‚‚
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
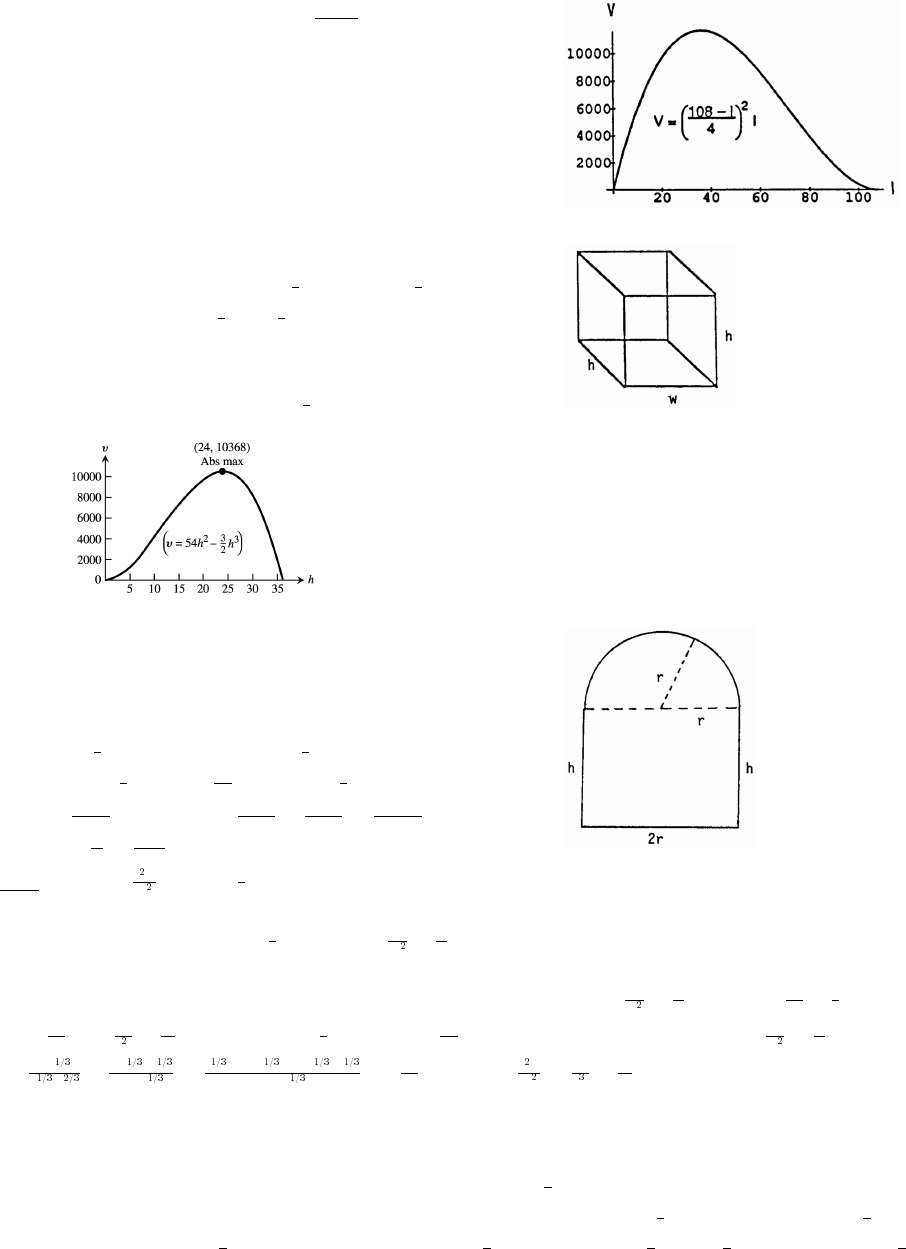
250 Chapter 4 Applications of Derivatives
(b) In terms of length, V( ) x . The graphjœ jœ j
#j #
ˆ‰
108
4
indicates that the maximum volume occurs near 36,jœ
which is consistent with the result of part (a).
21. (a) From the diagram we have 3h 2w 108 andœ
V h w V(h) h 54 h 54h h .œÊ œ œ
## #$
##
ˆ‰
33
Then V (h) 108h h h(24 h) 0
w#
##
œœ œ
99
h 0 or h 24, but h 0 results in no box. SinceÊœ œ œ
V (h) 108 9h 0 at h 24, we have a maximum
ww œ œ
volume at h 24 and w 54 h 18.œœœ
3
#
(b)
22. From the diagram the perimeter is P 2r 2h r,œ1
where r is the radius of the semicircle and h is the
height of the rectangle. The amount of light transmitted
proportional to
A 2rh r r(P 2r r) rœ œ
""
##
44
111
rP 2r r . Then P 4r r 0œ œ œ
##
#
3dA 3
4dr
11
r 2h P .Êœ Ê œ œ
2P 4P 2 P
83 83 83 83
(4 )P
1111
11
Therefore, gives the proportions that admit the
2r 8
h4
œ1
light since 4 0.most dA 3
dr œ
#1
23. The fixed volume is V r h r h , where h is the height of the cylinder and r is the radiusœ Êœ11
#$
2V2r
3r31
of the hemisphere. To minimize the cost we must minimize surface area of the cylinder added to twice the
surface area of the hemisphere. Thus, we minimize C 2 rh 4 r 2 r 4 r r .œœ œ111 1 1
###
ˆ‰
V2r 2V8
r3 r31
Then r 0 V r r . From the volume equation, h
dC 2V 16 8 3V V 2r
dr r 3 3 8 r 3
œ œ Ê œ Ê œ œ 11
$"Î$
ˆ‰
11
. Since 0, theseœ œ œ œ
4V 23 V 3 24V 23 V 3V dC 4V 16
33 3 dr r 3
11 1 1
††† ††
†† ††† ††
##
"Î$
ˆ‰ 1
dimensions do minimize the cost.
24. The volume of the trough is maximized when the area of the cross section is maximized. From the diagram
the area of the cross section is A( ) cos sin cos , 0 . Then A ( ) sin cos sin))))) ) )))œ œ
1
#
w##
2 sin sin 1 (2 sin 1)(sin 1) so A ( ) 0 sin or sin 1 becauseœ œ œ Ê œ œ Ê œab
#w
"
#
)) ) ) ) ) ) )
1
6
sin 1 when 0 . Also, A ( ) 0 for 0 and A ( ) 0 for . Therefore, at )))))) )Á œ
11111
# #
ww
66 6
there is a maximum.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
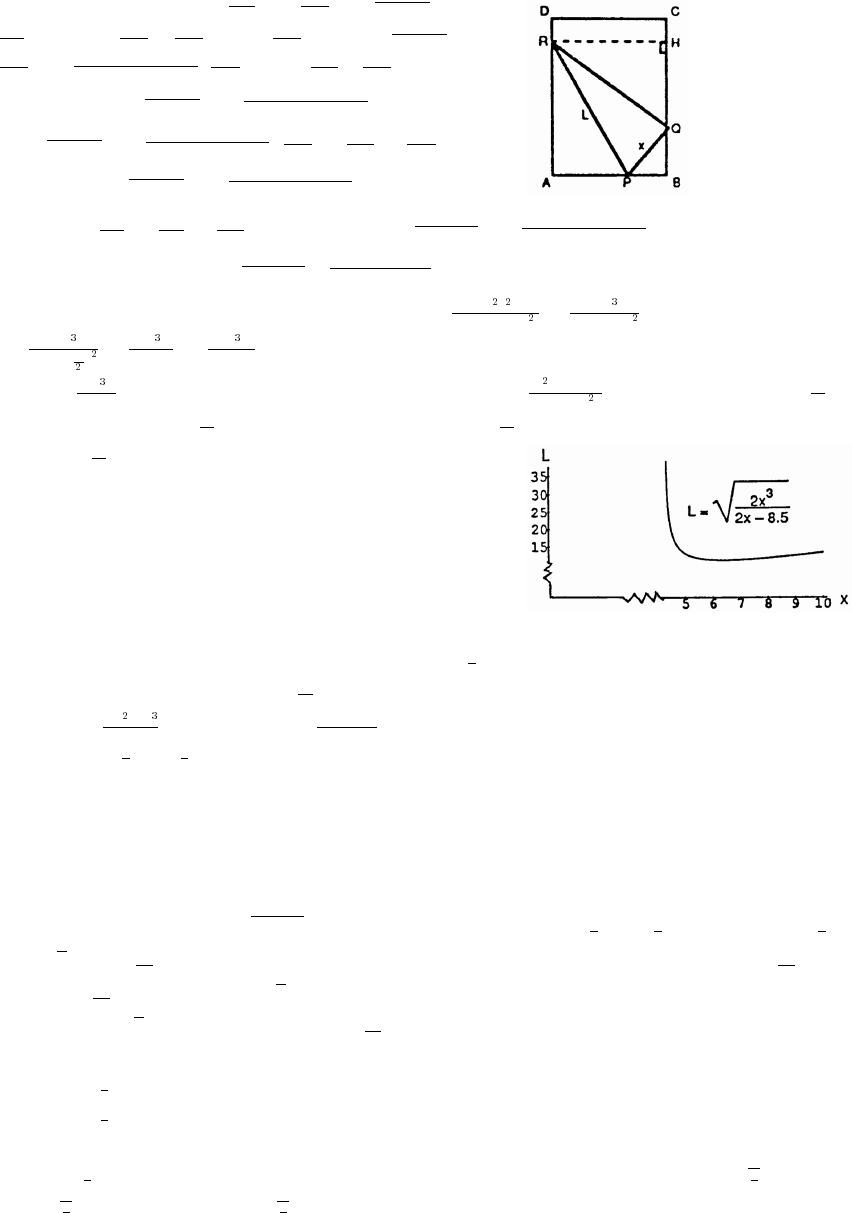
Section 4.5 Applied Optimization Problems 251
25. (a) From the diagram we have: AP x, RA L x ,œœ
È#
PB 8.5 x, CH DR 11 RA 11 L x ,œ œ œ œ
È#
QB x (8.5 x) , HQ 11 CH QBœ œ
È##
11 11 L x x (8.5 x)œ
’“
ÈÈ
## #
L x x (8.5 x) , RQ RH HQœ œ
ÈÈ
## #
##
#
(8.5) L x x (8.5 x) . Itœ
### #
#
Š‹
ÈÈ
follows that RP PQ RQ L x L x x (x 8.5) (8.5)
##### #
## # #
#
œ Êœ
Š‹
ÈÈ
L x L x 2 L x 17x (8.5) 17x (8.5) (8.5)ʜ
#### # #
## #
ÈÈ
17 x 4 L x 17x (8.5) L xÊœ Êœ œ
## # # # # #
aba b 17 x 17x
4 17x (8.5) 17x (8.5)
cd
.œœœ
17x 4x 2x
17x 4x 17 2x 8.5
ˆ‰
17
(b) If f(x) is minimized, then L is minimized. Now f (x) f (x) 0 when xœœÊ
4x 51
4x 17 (4x 17) 8
4x (8x 51)
#ww
and f (x) 0 when x . Thus L is minimized when x .
w#
œ
51 51
88
(c) When x , then L 11.0 in.œ¸
51
8
26. (a) From the figure in the text we have P 2x 2y y x. If P 36, then y 18 x. When theœ Êœ œ œ
P
#
cylinder is formed, x 2 r r and h y h 18 x. The volume of the cylinder is V r hœÊœ œÊœ œ11
x
#
#
1
V(x) . Solving V (x) 0 x 0 or 12; but when x 0, there is no cylinder.Êœ œ œÊœ œ
18x x
44
3x(12 x)
w
11
Then V (x) 3 V (12) 0 there is a maximum at x 12. The values of x 12 cm and
ww ww
#
œÊ Ê œ œ
3x
1ˆ‰
y 6 cm give the largest volume.œ
(b) In this case V(x) x (18 x). Solving V (x) 3 x(12 x) 0 x 0 or 12; but x 0 would result inœ œœÊœ œ11
#w
no cylinder. Then V (x) 6 (6 x) V (12) 0 there is a maximum at x 12. The values of
ww ww
œÊ Ê œ1
x 12 cm and y 6 cm give the largest volume.œœ
27. Note that h r and so r h . Then the volume is given by V r h h h h h for
## ## $
#$$ $
œ$ œ $ œ œ $ œ
Èab
11 1
1
h , and so r r . The critical point (for h ) occurs at h . Since for! $ œ œ " ! œ" !
Èab
dV dV
dh dh
11 1
##
h , and for h , the critical point corresponds to the maximum volume. The cone of greatest! " ! " $
dV
dh È
volume has radius m, height m, and volume m .
È#" #
$
$
1
28. (a) f(x) x f (x) x 2x a , so that f (x) 0 when x 2 implies a 16œÊ œ œ œ œ
#w#$ w
a
xab
(b) f(x) x f (x) 2x x a , so that f (x) 0 when x 1 implies a 1œÊ œ œ œ œ
#ww$$ ww
a
xab
29. If f(x) x , then f (x) 2x ax and f (x) 2 2ax . The critical points are 0 and , but x 0.œ œ œ Á
# w # ww $ $
#
a a
xÈ
Now f 6 0 at x there is a local minimum. However, no local maximum exists for any a.
ww $$
##
ˆ‰
ÈÈ
aa
œ Ê œ
30. If f(x) x ax bx, then f (x) 3x 2ax b and f (x) 6x 2a.œ œ œ
$# w # ww
(a) A local maximum at x 1 and local minimum at x 3 f ( 1) 0 and f (3) 0 3 2a b 0 andœ œÊ œ œÊœ
ww
27 6a b 0 a 3 and b 9. œ Ê œ œ
(b) A local minimum at x 4 and a point of inflection at x 1 f (4) 0 and f (1) 0 48 8a b 0œœÊœœÊœ
www
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
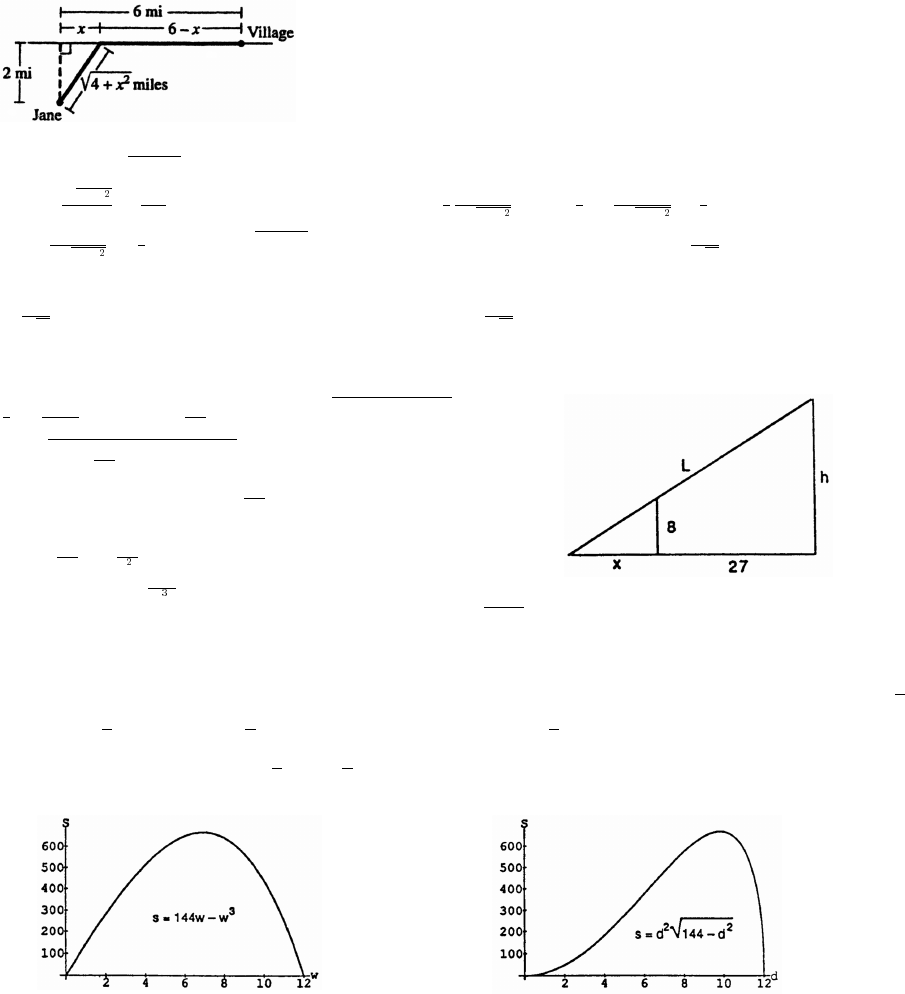
252 Chapter 4 Applications of Derivatives
and 6 2a 0 a 3 and b 24.œÊœ œ
31. (a) s t t t v t s t t . At t , the velocity is v ft/sec.ab ab ab abœ "' *' ""# Ê œ œ $# *' œ ! ! œ *'
#w
(b) The maximum height ocurs when v t , when t . The maximum height is s ft and it occurs at tab abœ! œ$ $ œ#&' œ$
sec.
(c) Note that s t t t t t , so s at t or t . Choosing the positive valueab ababœ"' *' ""#œ"' " ( œ! œ" œ(
#
of t, the velocity when s is v ft/sec.œ ! ( œ "#)ab
32.
Let x be the distance from the point on the shoreline nearest Jane's boat to the point where she lands her boat. Then she
needs to row x mi at 2 mph and walk x mi at 5 mph. The total amount of time to reach the village is
È% '
#
f x hours ( x ). Then f x x . Solving f x , weab ab a b abœ !ŸŸ' œ #œ œ!
ÈÈÈ
%
#& # & &
' " " " "
ww
#% #%
xx x
xx
have: x x x x x x . We discard the negative
x
x#%
" %
&####
#"
È È
œ Ê & œ # % Ê #& œ % % Ê #" œ "' Ê œ „
Èab
value of x because it is not in the domain. Checking the endpoints and critical point, we have f ,ab! œ #Þ#
f , and f . Jane should land her boat miles donw the shoreline from the point
Š‹ ab
% %
#" #"
È È
¸#Þ"# ' ¸$Þ"' ¸!Þ)(
nearest her boat.
33. h and L x h x
) #"'
#( ##
xx x
h
œÊœ) œ#(ab a b
É
x when x . Note that L x isœ) #( !
Ɉ‰
ab ab
#"' ##
x
minimized when f x x isab a b
ˆ‰
œ) #(
#"' ##
x
minimized. If f x , then
wabœ!
x# ) # #( œ!
ˆ‰ˆ‰
ab
#"' #"'
xx
x x (not acceptableÊ #( " œ ! Ê œ #(ab
ˆ‰
"(#)
x
since distance is never negative or x . Then L ftœ "# "# œ #"*( ¸ %'Þ)( ÞabÈ
34. (a) From the diagram we have d 4r w . The strength of the beam is S kwd kw 4r w . When
### # ##
œ œ œ ab
r 6, then S 144kw kw . Also, S (w) 144k 3kw 3k 48 w so S (w) 0 w 4 3 ;œœ œœ œÊœ„
$w # #w
ab È
S 4 3 0 and 4 3 is not acceptable. Therefore S 4 3 is the maximum strength. The dimensions
ww Š‹ Š‹
ÈÈ È
of the strongest beam are 4 3 by 4 6 inches.
ÈÈ
(b) (c)
Both graphs indicate the same maximum value and are consistent with each other. Changing k does not
change the dimensions that give the strongest beam (i.e., do not change the values of w and d that produce
the strongest beam).
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
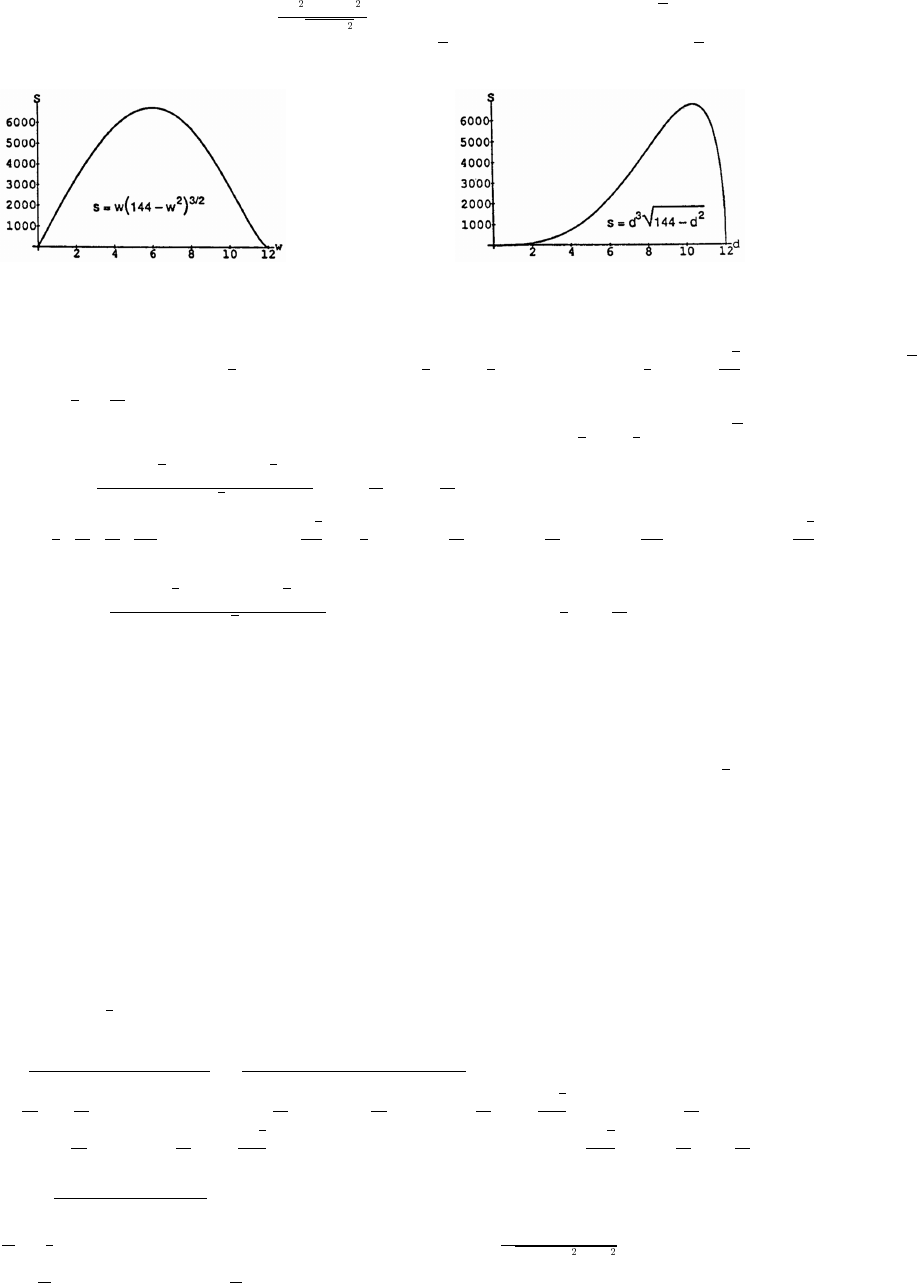
Section 4.5 Applied Optimization Problems 253
35. (a) From the situation we have w 144 d . The stiffness of the beam is S kwd kd 144 d ,
## $$#
"Î#
œ œ œ ab
where 0 d 12. Also, S (d) critical points at 0, 12, and 6 3. Both d 0 andŸŸ œ Ê œ
w
4kd 108 d
144 d
ab
ÈÈ
d 12 cause S 0. The maximum occurs at d 6 3. The dimensions are 6 by 6 3 inches.œœ œ
ÈÈ
(b) (c)
Both graphs indicate the same maximum value and are consistent with each other. The changing of k has
no effect.
36. (a) s s sin t sin t sin t sin t cos sin cos t sin t sin t cos t tan t 3
"# "
##
œÊ œ Ê œ Ê œ Ê œ
ˆ‰ È
111
333
3
È
t or ʜ
11
33
4
(b) The distance between the particles is s(t) s s sin t sin t sin t 3 cos tœœ œ kk
¸¸ˆ‰¹¹
È
"# "
#
1
3
s (t) since x critical times and endpointsÊœ œÊ
w
Š‹Š‹
ÈÈ
¹¹
Èkk
sin t 3 cos t cos t 3 sin t
2 sin t 3 cos t
dx
dx x
kk
are 0, , , , , 2 ; then s(0) , s 0, s 1, s 0, s 1, s(2 ) the
111 1 1 1 1 1
36 3 6 3 6 3 6
5411 5 4 11
3 3
11œ œœœ œœÊ
È È
# #
ˆ‰ ˆ‰ ˆ‰ ˆ‰
greatest distance between the particles is 1.
(c) Since s (t) we can conclude that at t and , s (t) has cusps and
w w
œœ
Š‹Š‹
ÈÈ
¹¹
È
sin t 3 cos t cos t 3 sin t
2 sin t 3 cos t 33
411
the distance between the particles is changing the fastest near these points.
37. (a) s 10 cos ( t) v 10 sin ( t) speed 10 sin ( t) 10 sin ( t) the maximum speed isœÊœ Êœ œ Ê111 1111kkkk
10 31.42 cm/sec since the maximum value of sin ( t) is 1; the cart is moving the fastest at t 0.5 sec,11¸ œkk
1.5 sec, 2.5 sec and 3.5 sec when sin ( t) is 1. At these times the distance is s 10 cos 0 cm andkk ˆ‰
1œœ
1
#
a 10 cos ( t) a 10 cos ( t) a 0 cm/secœ Êœ Êœ11 1 1
## #
kk k k kk
(b) a 10 cos ( t) is greatest at t 0.0 sec, 1.0 sec, 2.0 sec, 3.0 sec and 4.0 sec, and at these times thekk k kœœ11
#
magnitude of the cart's position is s 10 cm from the rest position and the speed is 0 cm/sec.kkœ
38. (a) 2 sin t sin 2t 2 sin t 2 sin t cos t 0 (2 sin t)(1 cos t) 0 t k where k is a positiveœÊ œÊ œÊœ1
integer
(b) The vertical distance between the masses is s(t) s s s s (sin 2t 2 sin t)œœ œ kkab a b
ˆ‰
"# "#
#"Î# #"Î#
s (t) (sin 2t 2 sin t) (2)(sin 2t 2 sin t)(2 cos 2t 2 cos t)ʜ
w#
"
#
"Î#
ˆ‰
ab
critical times atœœ Ê
2(cos 2t cos t)(sin 2t 2 sin t) 4(2 cos t 1)(cos t )(sin t)(cos t 1)
sin 2t 2 sin t sin 2t 2 sin t
"
kk kk
0, , , , 2 ; then s(0) 0, s sin 2 sin , s( ) 0, s
24 2 4 2 4
33 3 3 3 3
33
11 1 1 1 1
11 1œœ œ œ
ˆ‰¸ ¸ ˆ‰ˆ‰ ˆ‰ È
#
sin 2 sin , s(2 ) 0 the greatest distance is at t and œ œ œÊ œ
¸¸ˆ‰ ˆ‰
84 24
332 33
33 33
11 11
ÈÈ
1#
39. (a) s (12 12t) (8t) (12 12t) 64tœœ
Èab
## ##
"Î#
(b) (12 12t) 64t [2(12 12t)( 12) 128t]
ds 208t 144
dt (12 12t) 64t
œ œ
"
#
##
"Î#
ab È
12 knots and 8 knotsÊœ œ
¸¸
ds ds
dt dt
t=0 t=1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
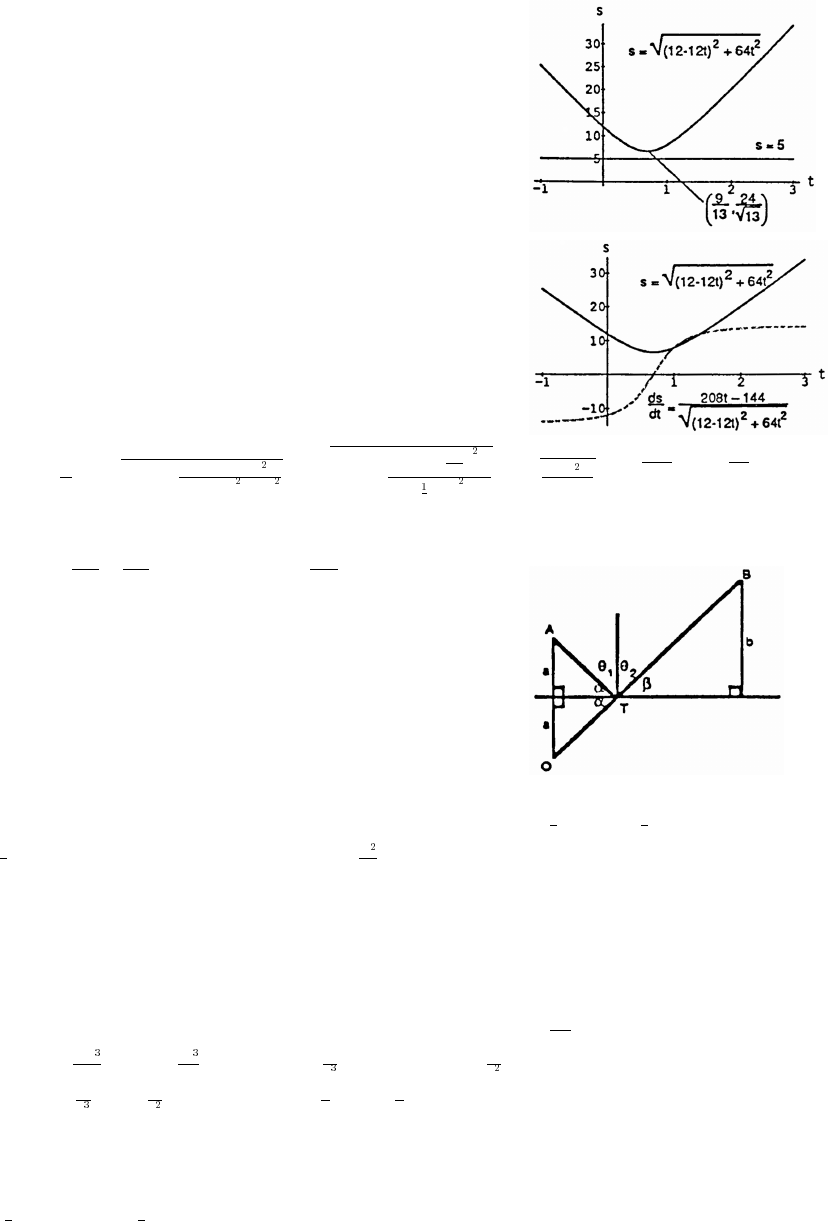
254 Chapter 4 Applications of Derivatives
(c) The graph indicates that the ships did not see
each other because s(t) 5 for all values of t.
(d) The graph supports the conclusions in parts (b)
and (c).
(e) lim lim lim 208 4 13
tt tÄ_ Ä_ Ä_
ds 208
dt 144( t) 64t 144 64
(208t 144) 208
144 1 64
œœœœœ
ÉËÉÈÈ
"
Š‹
Š‹
144
t
t
which equals the square root of the sums of the squares of the individual speeds.
40. The distance OT TB is minimized when OB is
a straight line. Hence .nœn Ê œ!"))
"#
41. If v kax kx , then v ka 2kx and v 2k, so v 0 x . At x there is a maximum sinceœ œ œ œÊœ œ
#w ww w
##
aa
v 2k 0. The maximum value of v is .
ww
#
ˆ‰
aka
4
œ
42. (a) According to the graph, y .
wab!œ!
(b) According to the graph, y L .
wabœ!
(c) y , so d . Now y x ax bx c, so y implies that c . There fore, y x ax bx andab ab ab ab!œ! œ! œ$ # !œ! œ! œ
w# w $#
y x ax bx. Then y L aL bL H and y L aL bL , so we have two linear
w# $# w #
ab ab abœ$ # œ œ œ$ # œ!
equations in two unknowns a and b. The second equation gives b . Substituting into the first equation, we haveœ$
#
aL
aL H, or H, so a . Therefore, b and the equation for y is œ œ œ# œ$
$$
##
aL aL H H
LL
y x x x , or y x H .ab ab ’“
ˆ‰ ˆ‰
œ# $ œ # $
HH x x
LL L L
$# $#
43. The profit is p nx nc n(x c) a(x c) b(100 x) (x c) a b(100 x)(x c)œœœœcd
"
a (bc 100b)x 100bc bx . Then p (x) bc 100b 2bx and p (x) 2b. Solving p (x) 0 œ œ œ œ Ê
#w ww w
x 50. At x 50 there is a maximum profit since p (x) 2b 0 for all x.œ œ œ
cc
##
ww
44. Let x represent the number of people over 50. The profit is p(x) (50 x)(200 2x) 32(50 x) 6000œ
2x 68x 2400. Then p (x) 4x 68 and p 4. Solving p (x) 0 x 17. At x 17 there is aœ œ œ œ Ê œ œ
#wwww
maximum since p (17) 0. It would take 67 people to maximize the profit.
ww
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
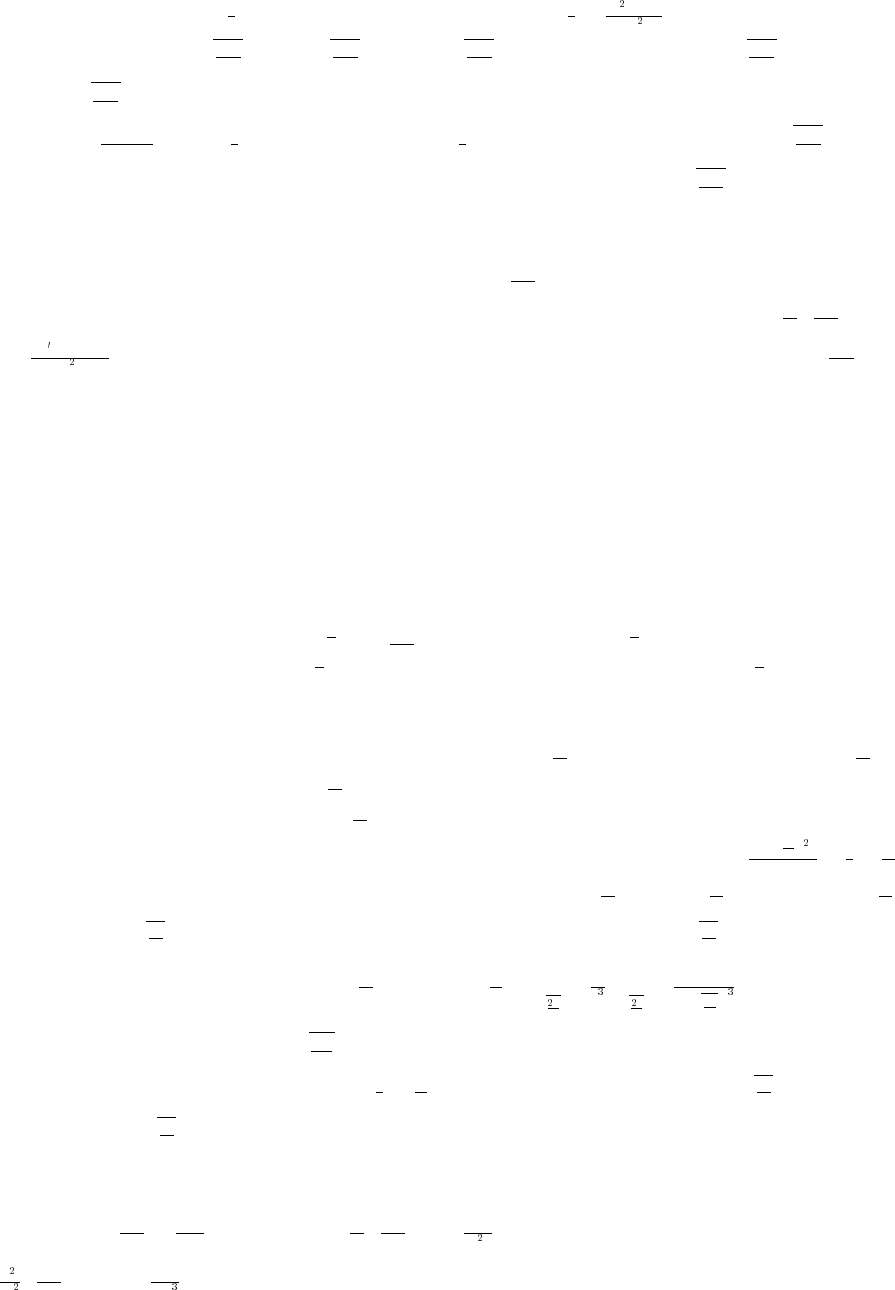
Section 4.5 Applied Optimization Problems 255
45. (a) A(q) kmq cm q, where q 0 A (q) kmq and A (q) 2kmq . Theœ Êœœ œ
" w # ww $
##
hh
hq 2km
2q
critical points are , 0, and , but only is in the domain. Then A 0 atÊ
ÉÉ É É
Š‹
2km 2km 2km 2km
hh h h
ww
q there is a minimum average weekly cost.σ2km
h
(b) A(q) cm q kmq bm cm q, where q 0 A (q) 0 at q as in (a).œœ Êœœ
(k bq)m
q h
h h 2km
##
" w É
Also A (q) 2kmq 0 so the most economical quantity to order is still q which minimizes
ww $
œ œ
É2km
h
the average weekly cost.
46. We start with c x the cost of producing x items, x , and the average cost of producing x items, assumedabœ!œ
cx
x
ab
to be differentiable. If the average cost can be minimized, it will be at a production level at which d
dx x
cx
Š‹
ab œ!
(by the quotient rule) x c x c x (multiply both sides by x ) c x whereʜ! ʜ! ʜ
x c x c x cx
x x
ab ab abw#w
ab ab ab
c x is the marginal cost. This concludes the proof. (Note: The theorem does not assure a production level that will give a
wab
minimum cost, but rather, it indicates where to look to see if there is one. Find the production levels where the average cost
equals the marginal cost, then check to see if any of them give a mimimum.)
47. The profit p(x) r(x) c(x) 6x x 6x 15x x 6x 9x, where x 0. Thenœ œ œ ab
$# $#
p (x) 3x 12x 9 3(x 3)(x 1) and p (x) 6x 12. The critical points are 1 and 3. Thus
w# w
w
œ œ œ
p (1) 6 0 at x 1 there is a local minimum, and p (3) 0 at x 3 there is a local maximum.
ww ww
œÊœ œ'Êœ
But p(3) 0 the best you can do is break even.œÊ
48. The average cost of producing x items is c x x x c x x x , theab abœ œ #! #!ß !!! Ê œ # #! œ ! Ê œ "!
cx
x
ab #w
only critical value. The average cost is c $ per item is a minimum cost because c .ab ab"! œ "*ß *!! "! œ # !
ww
49. (a) The artisan should order px units of material in order to have enough until the next delivery.
(b) The average number of units in storage until the next delivery is and so the cost of storing then is s per
px px
##
ˆ‰
day, and the total cost for x days is sx. When added to the delivery cost, the total cost for delivery and storage
ˆ‰
px
#
for each cycle is: cost per cycle d sx.œ
px
#
(c) The average cost per day for storage and delivery of materials is: average cost per day x.œ
ˆ‰
dxps
#
xx
dps
#
To minimize the average cost per day, set the derivative equal to zero. d x x d x
d
dx
ps ps
Š‹
ab ab
" #
##
œ œ!
x . Only the positive root makes sense in this context so that x . To verify that x gives aÊœ„ œ
ÉÉ
# #
‡‡
d d
ps ps
minimum, check the second derivative d x a minimum.
’“
ˆ‰
ab ºº
ddd
dx x
ps
œ œ !Ê
#
#
##
ÉÉ
dd
ps ps Œ
É#d
ps
The amount to deliver is px .
‡#
σpd
s
(d) The line and the hyperbola intersect when x. Solving for x gives x . For x ,
dd
xps
ps intersection
œœ„!
#
#
É
x x . From this result, the average cost per day is minimized when the average daily cost of
intersection d
ps
œœ
É#‡
delivery is equal to the average daily cost of storage.
50. Average Cost: x x x . Check for a minimum:
cx cx
xx dxx x
d
ab ab
œ *' % Ê œ # œ ! Ê œ "!!
#!!! #!!!
"Î# "Î#
Š‹
a minimum at x . At a production level of units,
d
dx x
cx
x
Š‹
º
ab
œ"!!
%!!!
"!!
$Î#
œ "!! œ !Þ!!$ ! Ê œ "!! "!!ß !!!
the average cost will be minimized at $ per unit."&'
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
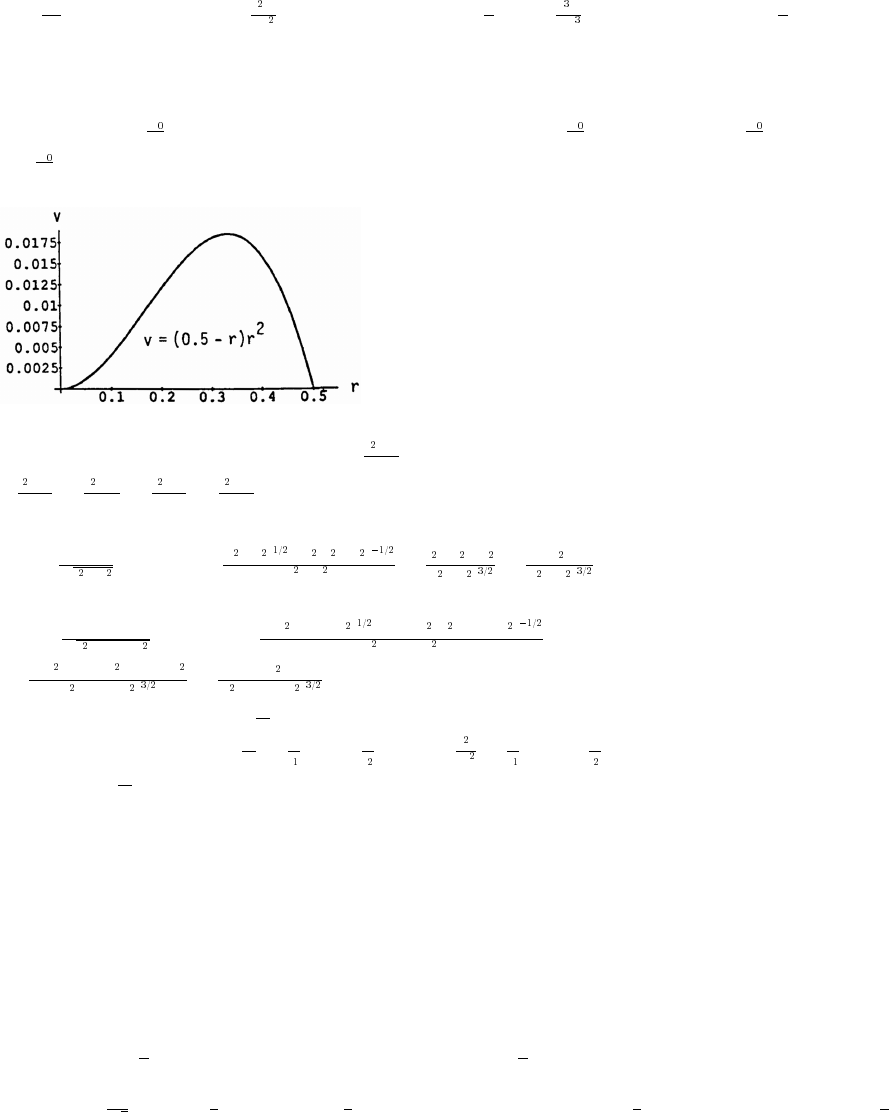
256 Chapter 4 Applications of Derivatives
51. We have CM M . Solving C M M . Also, at M there is a
dR d R C d R C
dM dM dM
œ œ#œ!Êœ œ#!Ê œ
#
##
maximum.
52. (a) If v cr r cr , then v 2cr r 3cr cr 2r 3r and v 2cr 6cr 2c r 3r . The solution ofœ œœ œœ
!!!!!
#$ w # ww
ab ab
v 0 is r 0 or , but 0 is not in the domain. Also, v 0 for r and v 0 for r at
www
œœ Ê
2r 2r 2r
333
r there is a maximum.œ2r
3
(b) The graph confirms the findings in (a).
53. If x 0, then (x 1) 0 x 1 2x 2. In particular if a, b, c and d are positive integers,ÊÊ
## x1
x
then 16.
Š‹Š‹Š‹Š‹
a1 b1 c1 d
abcd
"
54. (a) f(x) f (x) 0œÊœ œ œ
xaxxa
ax
ax xax
ax ax ax
Èab ab
ab ab ab
w
f(x) is an increasing function of xÊ
(b) g(x) g (x)œÊœ
dx
b(dx)
b (dx) (dx)b (dx)
b(dx)
w
Èab ab
0 g(x) is a decreasing function of xœœÊ
ab
aba b
b (dx) (dx)
b(dx) b (dx)
b
(c) Since c , c 0, the derivative is an increasing function of x (from part (a)) minus a decreasing
"#
dt
dx
function of x (from part (b)): f(x) g(x) f (x) g (x) 0 since f (x) 0 and
dt d t
dx c c dx c c
œ Êœ
"" " "
ww w
g (x) 0 is an increasing function of x.
wÊ
dt
dx
55. At x c, the tangents to the curves are parallel. Justification: The vertical distance between the curves isœ
D(x) f(x) g(x), so D (x) f (x) g (x). The maximum value of D will occur at a point c where D 0. Atœ œ œ
www w
such a point, f (c) g (c) 0, or f (c) g (c).
ww w w
œ œ
56. (a) f(x) 3 4 cos x cos 2x is a periodic function with period 2œ 1
(b) No, f(x) 3 4 cos x cos 2x 3 4 cos x 2 cos x 1 2 1 2 cos x cos x 2(1 cos x) 0œœ œœaba b
###
f(x) is never negativeÊ
57. (a) If y cot x 2 csc x where 0 x , then y (csc x) 2 cot x csc x . Solving y 0œ œ œ
ÈÈ
Š‹
1ww
cos x x . For 0 x we have y 0, and y 0 when x . Therefore, at xÊ œ Ê œ œ
"ww
È244 4 4
11 1 1
1
there is a maximum value of y 1.œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
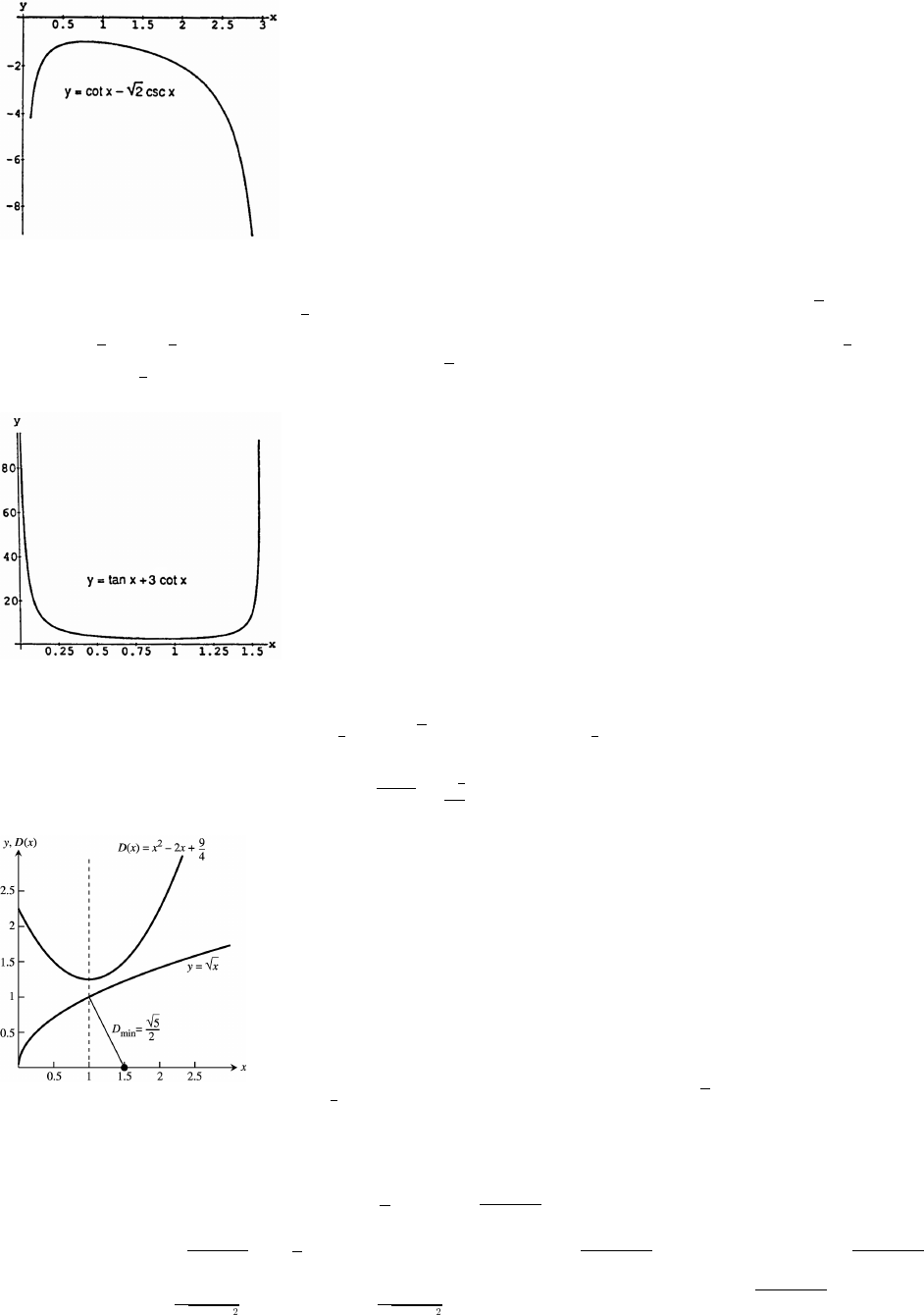
Section 4.5 Applied Optimization Problems 257
(b)
The graph confirms the findings in (a).
58. (a) If y tan x 3 cot x where 0 x , then y sec x 3 csc x. Solving y 0 tan x 3œ œ œÊ œ„
1
#
w# # w È
x , but is not in the domain. Also, y 2 sec x tan x 3 csc x cot x 0 for all 0 x .Êœ„ œ
11 1
33 2
ww # #
Therefore at x there is a minimum value of y 2 3.œœ
1
3È
(b)
The graph confirms the findings in (a).
59. (a) The square of the distance is D x x x x x , so D x x and the criticalab ab
ˆ‰ˆ ‰
È
œ !œ# œ##
$*
#%
###w
point occurs at x . Since D x for x and D x for x , the critical point corresponds to theœ" ! " ! "
ww
ab ab
minimum distance. The minimum distance is D .
Èab"œ
È&
#
(b)
The minimum distance is from the point to the point on the graph of y x, and this occurs at the
ˆ‰ ab È
$
#ß! "ß" œ
value x where D x , the distance squared, has its minimum value.œ" ab
60. (a) Calculus Method:
The square of the distance from the point to x x is given by
Š‹Š ‹
ÈÈ
"ß $ ß "' #
Dx x x x x x x x x.ab a b Š‹
ÈÈÈ
È
œ " "' $ œ # ""' # %)$ $œ # #!# %)$
####
###
Then D x x . Solving D x we have: x x
w w
#'
%)$ %)$
#
ab a b ab È
œ # ' œ # œ! ' œ# %)$
ÈÈ
x x
x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
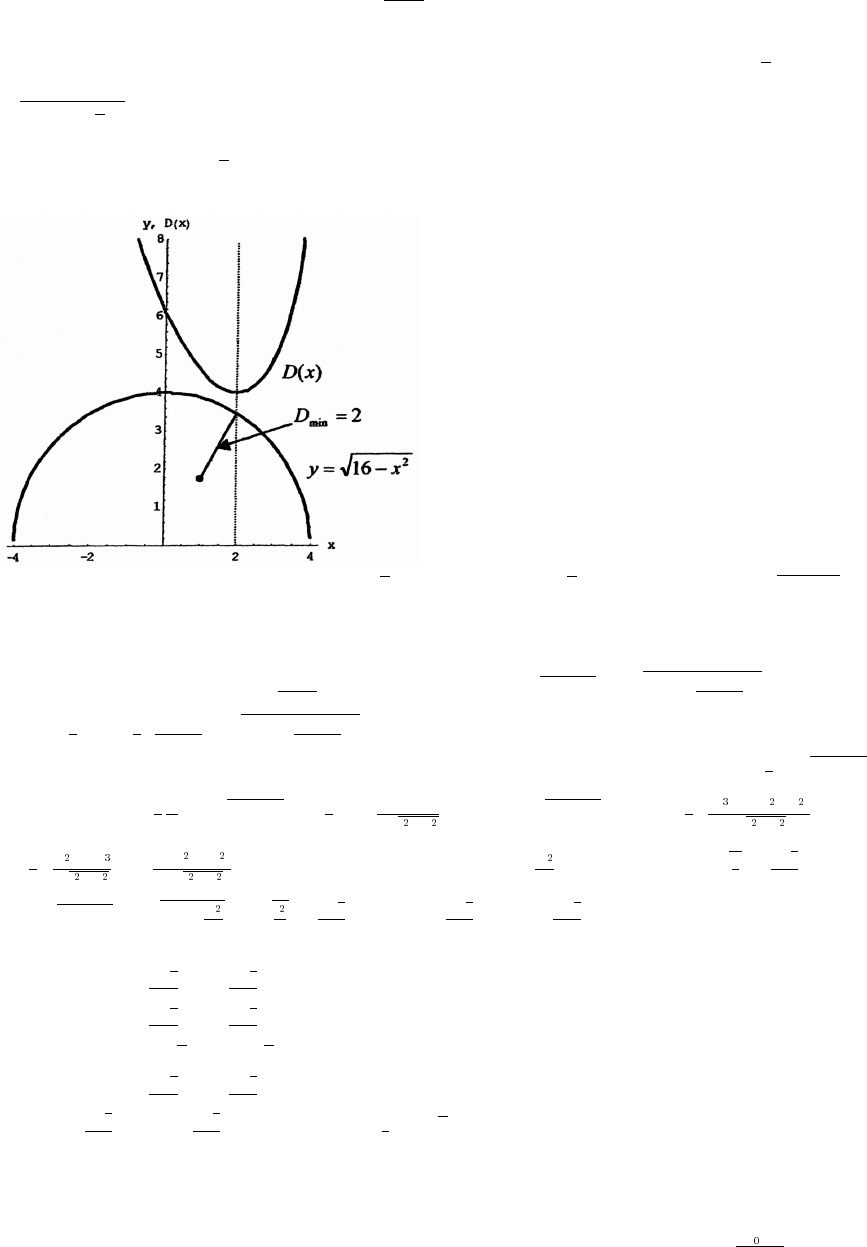
258 Chapter 4 Applications of Derivatives
x x x x x x . We discard x as an extraneous solution,Ê$'œ%%)$ Ê*œ%)$Ê"#œ%)Êœ„# œ#
#####
ab
leaving x . Since D x for x and D x for x , the critical point corresponds to theœ# ! % # ! # %
ww
ab ab
minimum distance. The minimum distance is D .
Èab#œ#
Geometry Method:
The semicircle is centered at the origin and has radius . The distance from the origin to is%"ß$
Š‹
È
. The shortest distance from the point to the semicircle is the distance along the radius
ÊŠ‹
È
" $ œ#
##
containing the point . That distance is .
Š‹
È
"ß $ % # œ #
(b)
The minimum distance is from the point to the point on the graph of y x , and this
Š‹ Š ‹
ÈÈ È
"ß $ #ß # $ œ "' #
occurs at the value x where D x , the distance squared, has its minimum value.œ# ab
61. (a) The base radius of the cone is r and so the height is h a r a . Therefore,œœœ
# #
##
## # #
11
11
ax a x
ÈɈ‰
Vx rh a .ab ˆ‰ ˆ‰
É
œœ
111 1
11$$# #
## #
##
#
a x a x
(b) To simplify the calculations, we shall consider the volume as a function of r: volume f r r a r , whereœœ ab È
1
$
###
ra. fr ra r r r a r r! œ œ † # # œ
w# #
$$ $
## ##
"
#
#
ab a b a b
Š‹ Š‹
ÈÈ
”•”•
11 1d
dr a r a r
r ra r
ÈÈ
ab
. The critical point occurs when r , which gives r a . Thenœœ œ œœ
11
$$$$
#$ # #
$
#$ #'
”• É
ar r a
a r a r
ra r a
ÈÈ
ab È
h a r a . Using r and h , we may now find the values of r and hœœœœ œ œ
ÈÉÉ
## #
#
$$$ $ $
$$
'
aa
aa
a
ÈÈÈ
for the given values of a.
When a : r , hœ% œ œ à
%'
$$
%$
ÈÈ
When a : r , hœ& œ œ à
&'
$$
&$
ÈÈ
When a : r , hœ' œ# ' œ# $à
ÈÈ
When a : r , hœ) œ œ à
)'
$$
)$
ÈÈ
(c) Since r and h , the relationship is .œœ œ#
aar
h
ÈÈ
'
$$
$È
62. (a) Let x represent the fixed value of x at the point P, so that P has the coordinates x a , and let m f x be the
!!!
w
ab abߜ
slope of the line RT. Then the equation of the line RT is y m x x a. The y-intercept of this line isœab
!
m x a a mx , and the x-intercept is the solution of m x x a , or x . Let O designateab ab! œ œ! œ
!! ! mx a
m
the origin. Then
(Area of triangle RST)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
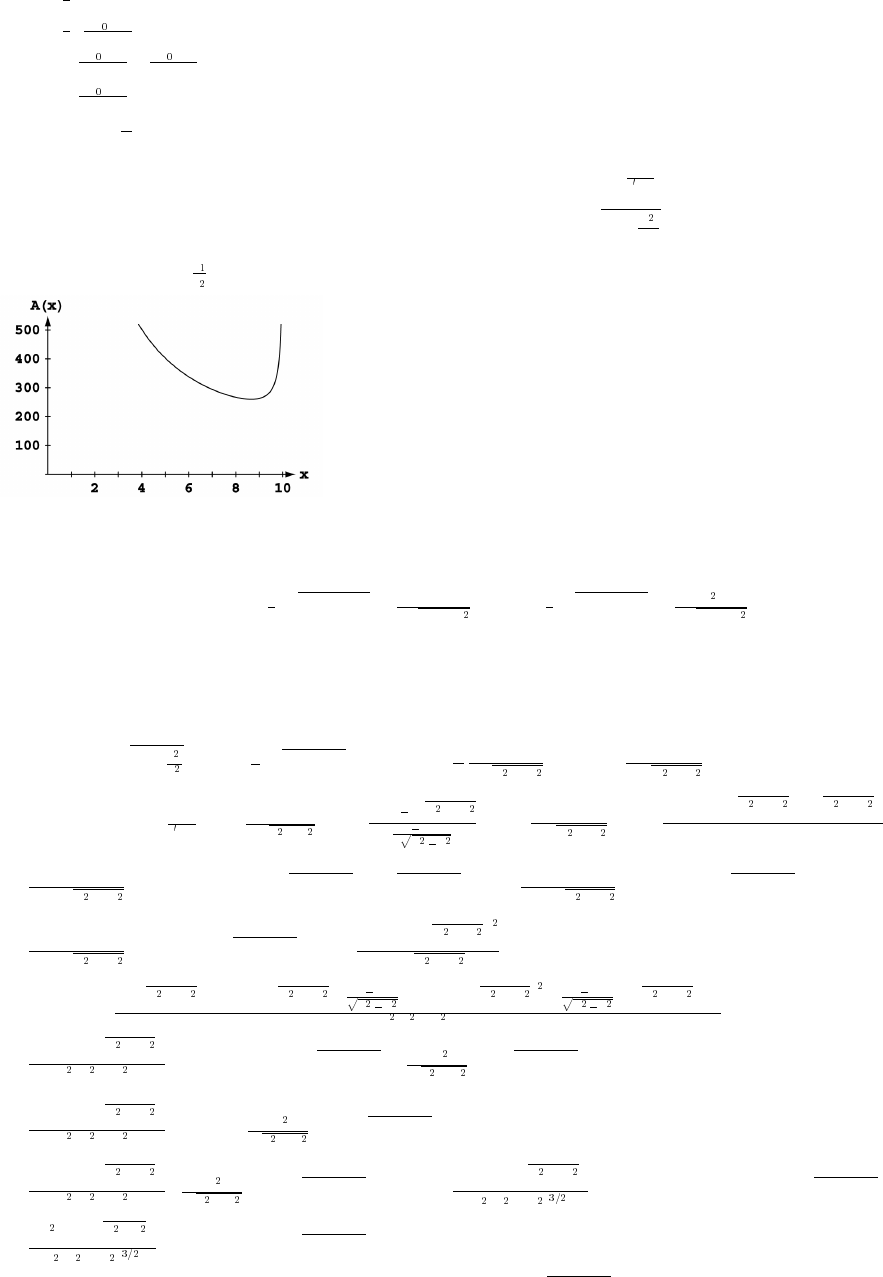
Section 4.5 Applied Optimization Problems 259
(Area of triangle ORT)œ#
(x-intercept of line RT)(y-intercept of line RT)œ#†"
#
amxœ#†
"
#
!
ˆ‰
ab
mx a
m
mœ ˆ‰ˆ‰
mx a mx a
mm
mœ ˆ‰
mx a
m
#
mxœ
ˆ‰
!
#
a
m
Substituting x for x , f x for m, and f x for a, we have A x f x x .
!ww
#
ab ab ab ab
”•
œ fx
fx
ab
ab
(b) The domain is the open interval . To graph, let y f x , y f x NDER y , anda b ab ab a b
É
!ß "! œ œ & & " œ œ
"#"
"!!
w
x
y A x y x . The graph of the area function y A x is shown below.
$# $
#
œœ œab ab
Š‹
y
y
The vertical asymptotes at x and x correspond to horizontal or vertical tangent lines, which do not formœ! œ"!
triangles.
(c) Using our expression for the y-intercept of the tangent line, the height of the triangle is
amx fx fxx x x x œ † œ & "!! œ & "!! ab ab ÈÈ
w""
##
##
"!! "!!
xx
2 x 2 x
ÈÈ
We may use graphing methods or the analytic method in part (d) to find that the minimum value of A x occurs atab
x . Substituting this value into the expression above, the height of the triangle is 15. This is 3 times the¸)Þ''
y-coordinate of the center of the ellipse.
(d) Part (a) remains unchanged. Assuming C B, the domain is C . To graph, note that!ßab
f x B B B C x and f x x . Therefore we haveab ab a b
ÉÈ
œ " œ œ #œ
xB
CC
## wBBx
CC x C C x
"
#
ÈÈ
Ax f x x x xab ab
”• Œ
œ œ œ
w
#
##
fx
fx
Bx
CC x
ab
ab ÈB C x Bx
CC x
BC B C x C x
Bx
B
CBx
CC x
ÈÈŠ‹Š‹
ÈÈ
Bx BC B C x C x Bx BC C x B C xœœ
""
BCx C x BCx C x
ÈÈ
”•”•
Š‹Š‹
ÈÈ È ab
####
## ## ##
##
BC C C xœœ
"
BCx C x x C x
BC C C x
ÈÈ
Š‹
È
”•
Š‹
È##
#
Ax BC
w
abϠ
Š‹Š‹Š‹Š‹Š ‹
ab ab
x C x C C x C C x x C x
ÈÈ È È
ab# "
xx
C x C x
xC x
x C Cx Cxœ #
BC C C x
xC x
Š‹
È
ab
–—
Š‹Š ‹
ÈÈ
### ##
x
C x
È
xCCxxCxœ#
BC C C x
xC x
Š‹
È
ab
”•
Èab
####
##
Cx
C x
È
CC x C Cx CC x C C xœœ
BC C C x BC C C x
xC x xC x
Š‹ Š‹
ÈÈ
ab ab
Š‹
ÈÈ
’“
ab
Cx
C x
È
## ##
#####
xCCCxœ#
BC C C x
xC x
Š‹
È
ab
Š‹
È
## ##
To find the critical points for x C, we solve: x C C C x x C x C C C x! #œ Ê%% œ
## % ##% %##
##
È
x C x x x C . The minimum value of A x for x C occurs at the critical pointÊ% $ œ!Ê % $ œ! !
%## ###
ab ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

260 Chapter 4 Applications of Derivatives
x , or x . The corresponding triangle height isœœ
CC
È$
#%
#$
amx fx fxxœ †ab ab
w
BCxœ
B
CÈ## Bx
CC
ÉC
BCxœ
B
CÈ## B
CC
Š‹
É
C
C
Bœ
BC
Cˆ‰
#
BC
C
Bœ
BB
##
$
Bœ$
This shows that the traingle has minimum arrea when its height is B.$
4.6 INDETERMINATE FORMS AND L'HOPITAL'S RULE
^
1. l'Hopital: lim or lim lim lim
^x2 x2 x2 x2ÄÄÄÄ
x2 x2 x2
x4 x 4 x4 x x x 4
x
" " ""
# ## #
œ#
œœ œ œ œ
¹abab
2. l'Hopital: lim 5 or lim 5 lim 5 1 5
5
^x0 x0 x0
ÄÄ
Ä
sin 5x 5 cos 5x sin 5x sin 5x
x1 x 5x
x
œ œ œ œ†œ
¹œ!
3. l'Hopital: lim lim lim or lim lim
^xxx xxÄ_ Ä_ Ä_ Ä_ Ä_
5x 3x 0x 3 10 5 5x 3x 5
7x 1 14x 14 7 7x 1 7
5
7
"
œœœ œœ
3
x
x
4. l'Hopital: lim lim or lim lim
^x1 x1 x1 x1ÄÄ ÄÄ
x1 3x 3 x1
4x x 3 12x 1 11 4x x 3 x 4x + 4x + 3
xxx
"
" "
œœ œ
aba b
aba b
2
lim œœ
x1Äab
ab
xx
4x + 4x + 3 11
3
"
2
5. l'Hopital: lim lim lim or lim lim
^xxx xxÄ! Ä! Ä! Ä! Ä!
1 cos x sin x cos x 1 cos x cos x
x2x2 x xco
cos x
""
#"
"
œœœ œ
”ˆ‰
ab
2s x •
lim lim œœ œ
xxÄ! Ä!
sin x sin x sin x
x cos x x x cos x
2ab" " #
""
”•
ˆ‰ˆ‰ˆ ‰
6. l'Hopital: lim lim lim or lim lim
^xxxxxÄ_ Ä_ Ä_ Ä_ Ä_
#$ % % # !
$ " ' "
"
xx x3 x3x
xx1 x x xx1
œ œ œ! œ œ œ!
x
3
x
xx
7. lim lim 0
t0 t0ÄÄ
sin t 2t cos t
t1
œœ
8. lim lim 2
xÄÎ ÄÎ1)122
2x 2 2
cos x sin x
"
1œœœ
9. lim lim
)1 )1ÄÄ
sin cos ))
1)""
"
œœœ"
10. lim lim lim
xx
x2 2 2ÄÎ ÄÎ ÄÎ111
1 sin x cos x sin x
1 cos 2x 2 sin 2x 4 cos 2x 4( 1) 4
""
œœœœ
11. lim lim
xxÄÎ% ÄÎ%11
sin x cos x cos x sin x
x
"##
##
œ œœ#
ÈÈÈ
12. lim lim
xxÄÎ$ ÄÎ$11
cos x
x
sin x
"#
$
œœ
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 4.6 Indeterminate Forms and L'Hopital's Rule 261
^
13. lim x tan x lim lim
x2 x2 x2ÄÎ ÄÎ ÄÎ111
œ œ œ œ"
ˆ‰
1
#"
" "
ˆ‰ ˆ‰ abx sin x x cos x sin x
cos x sin x
14. lim lim lim
xxxÄ! Ä! Ä!
## %†!
( (
"
%
#†!(
x
xx 2x
x
ÈÈ
È
œœœœ!
x
15. lim lim lim
xxx1
Ä" Ä" Ä
#$" #
" " "
#$ # %
xx x
xx
xx x xx
ab
Èœœœ"
x
16. lim lim lim
xx xÄ# Ä# Ä#
Èabab È
x5
x2x
x5 2x
2x 5
$
% '
""
œœœ
17. lim lim , where a 0.
x0 x0ÄÄ
Èab ÈÈ
aa x a
x
aa
aax a
# #
"
#
œœœ
18. lim lim lim lim
t0 t0 t0 t0ÄÄ ÄÄ
10(sin t t) 10(cos t )
ttt
sin t cos t 10
"
$'''$
"! "! †" &
œœœœœ
ab
19. lim lim lim lim lim
x0 x0 x0 x0 x0ÄÄ Ä Ä Ä
x(cos x )
sin x x cos x sin x sin x
xsin x cos x xcos x sin x xcos x sin x xs
"
"
" # #
œœœœ
in x cos x
cos x
$ $
"
œœ$
20. lim lim
h0 h0ÄÄ
sin a h sin a cos a h cos a
h
ab ab
"
œœ!
21. lim lim an lim r an, where n is a positive integer.
rr1 r1
Ä" ÄÄ
ar anr
r1
n
ab ab
nn
" †
"
"
œœœ
22. lim lim lim x
xx xÄ! Ä! Ä!
Š‹ Š‹Š ‹ ˆ‰
È
"" "
x x does not apply x
x
xl'Hopital's rule 1
œ œ œ "†œ_
ÈÈ
23. lim x x x lim x x x lim lim
xx xxÄ_ Ä_ Ä_ Ä_
Š‹Š‹Š‹
ÈÈ
œ œ œ
##
xxx
xxx xxx
xxx
È
ÈÈ
ab x
x
xxx
xx
lim œœ
xÄ_
" "
" " #
ÉxŠ‹
l'Hopital's rule
is unnecessary
24. lim x tan lim lim lim sec sec
xxx xÄ_ Ä_ Ä_ Ä_
ˆ‰ ˆ‰
""
##
xx
tan
œœ œ œ!œ"
Š‹
x
x
xx
x
sec ˆ‰
25. lim lim
xxĄ_ Ą_
$&
# # "
x3
xx 4x
œœ!
26. lim lim
x0 x0ÄÄ
sin x
tan x sec x
cos x
((†"(
"" "" "" ""†" ""
((
œœœ
ab
ab
27. lim lim lim 9 3
xxxÄ_ Ä_ Ä_
È
È9x 1
x1
9x 1 9
x1 1
œœœœ
ÉÉ
È
28. lim 1
xÄ!
È
Èx
sin x lim 1
œœœ
ÊÉ
""
x
sin x
x
29. lim lim lim 1
x2 x2 x2ÄÎ ÄÎ ÄÎ11 1
sec x cos x
tan x cos x sin x sin x
œœœ
ˆ‰ˆ‰
""
30. lim lim lim cos x 1
xx xÄ! Ä! Ä!
cot x
csc x œœœ
ˆ‰
Š‹
cos x
sin x
sin x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
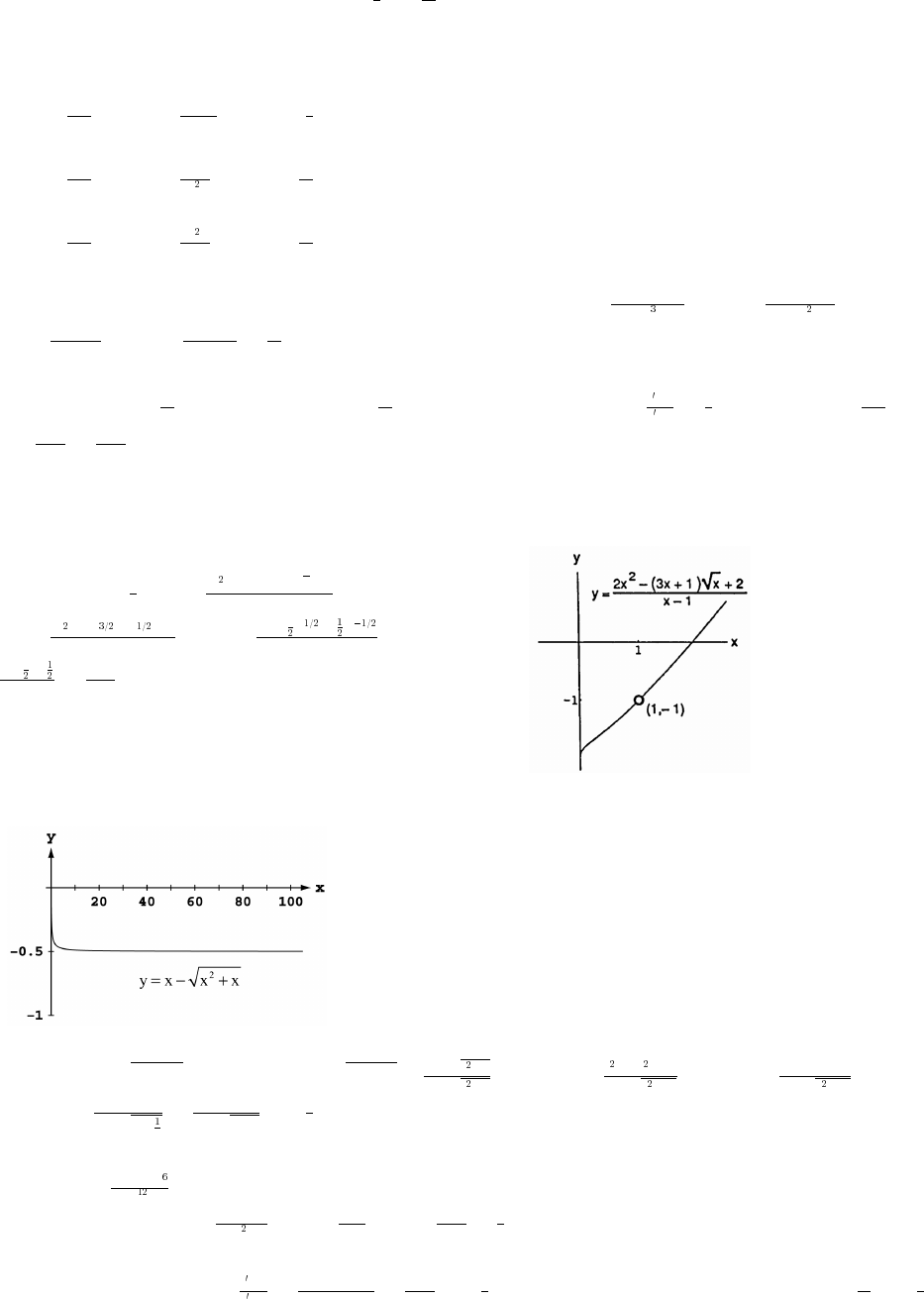
262 Chapter 4 Applications of Derivatives
31. Part (b) is correct because part (a) is neither in the nor form and so l'Hopital's rule may not be used.
^
0
0
_
_
32. Answers may vary.
(a) f x x ;g x xab abœ$ " œ
lim lim lim
xx xÄ_ Ä_ Ä_
f(x)
g(x) x
x
œœœ$
$" $
"
(b) f x x ;g x xab abœ" œ
#
lim lim lim
xx xÄ_ Ä_ Ä_
f(x)
g(x) x x
x
œœœ!
" "
#
(c) f x x ;g x xab abœœ"
#
lim lim lim
xx xÄ_ Ä_ Ä_
f(x)
g(x) x
xx
œœœ_
" "
#
33. If f(x) is to be continuous at x 0, then lim f(x) f(0) c f(0) lim lim œœÊœœœ
x0 x0 x0ÄÄÄ
9x 3 sin 3x 9 9 cos 3x
5x 15x
lim lim .œœœ
x0 x0ÄÄ
27 sin 3x 81 cos 3x 27
30x 30 10
34. (a) For x 0, f (x) (x 2) 1 and g (x) (x 1) 1. Therefore, lim 1, while lim Áœœ œœ œœ
ww
dd 1
dx dx g (x) 1 g(x)
f (x) f(x)
x0 x0ÄÄ
2.œœœ
x2 02
x1 01
(b) This does not contradict l'Hopital's rule because neither f nor g is differentiable at x 0
^œ
(as evidenced by the fact that neither is continuous at x 0), so l'Hopital's rule does not apply.
^
œ
35. The graph indicates a limit near 1. The limit leads to the
indeterminate form : lim
0
0x1
2x (3x 1) x 2
x1Ä
È
lim lim œœ
x1 x1ÄÄ
2x 3x x 2
x1 1
4x x x
9
1œœœ
4
11
45
9
36. (a)
(b) The limit leads to the indeterminate form :__
lim x x x lim x x x lim lim
xx xxÄ_ Ä_ Ä_ Ä_
Š‹Š‹Š‹Š‹
ÈÈ
œ œ œ
##
xxx
xxx xxx xxx
xxx x
È
ÈÈÈ
ab
lim œœœ
xÄ_
" " "
" " " "! #
ÉÈ
x
37. Graphing f x on th window by it appears that lim f x . However, we see that if we letab abœ Ò"ß "Ó Ò!Þ&ß "Ó œ !
"cos x
xx0Ä
u x , then lim f x lim lim lim .œœœœœ
'" "
###
x0 u0 u0 u0ÄÄ ÄÄ
ab cos u sin u cos u
uu
38. (a) We seek c in so that . Since f c and g c c we have that a b ab ab#ß! œ œ œ œ" œ# œ
fc f f
gc g g c
ab ab a b
ab ab a b
! #
! # !% # # #
!# " " "
ww
c.ʜ"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
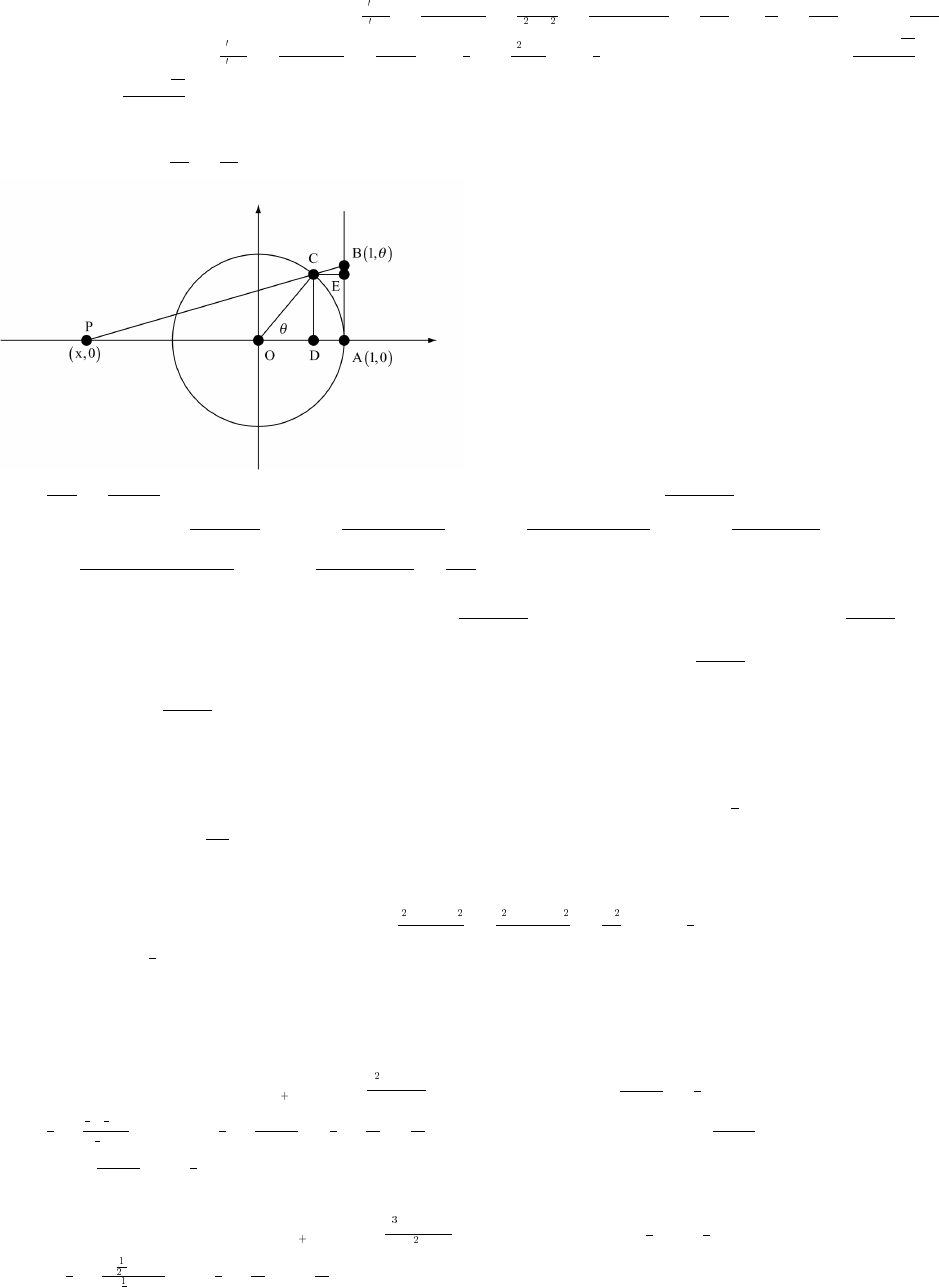
Section 4.7 Newton's Method 263
(b) We seek c in any open interval a b so that cabß œ œ œ œÊœÊœ
fc fb fa
gc gb ga b a baba ba c ba
ba ba ba
ab ab ab
ab ab ab a ba b
# #
"""
(c) We seek c in so that c c c .ab!ß$ œ œ œ Ê œ Ê$ # "#œ!Ê œ
fc f f
gc g g c
c
ab ab ab
ab ab ab È
$ !
$ ! *! $ # $ $
$! " % " #" $(
(Note that c is not in the given interval .)œ!ß$
" $(
$Èab
39. (a) By similar triangles, where E is the point on AB such that CE AB :
PA CE
AB EB
œ¼
←→ ←→ ←→
Thus , since the coordinates of C are cos sin . Hence, x .
" "
"
xcos
sin sin
cos
))) ))
)))
œß"œab)) ab
(b) lim x lim lim lim lim
)) ) ) )ÄÄ Ä Ä Ä00 0 0 0
ab" œ œ œ œ
))
)) ) )
)) ) )))) ))
ab"
"
" #
cos
sin cos sin
sin cos cos sin sin cos sin
sin
)
)
lim lim œœœœ$
))ÄÄ00
)) ) )
))
)) )
ab# $ !$
"
sin cos cos
cos cos
sin cos
(c) We have that lim x cos lim cos lim cos
)) )Ä_ Ä_ Ä_
‘
abab ab ab
”•”•
" " œ " œ " ")))
))
)) ))
)
ab"
cos
sin sin
As cos oscillates between and , and so it is bounded. Since lim ,))Ä" !# "œ""œ!_Ä_
, ab ˆ‰
)
)
))sin
lim cos . Geometrically, this means that as , the distance between points P and D
)Ä_ ab
”•
" " œ! Ä_))
)
))sin
approaches 0.
40. Throughout this problem note that r y , r y and that both r and y as
##
#
œ " Ä_ Ä_ Ä Þ)1
(a) lim r y lim
)1 )1ÄÎ ÄÎ22
œ œ!
"
ry
(b) lim r y lim
)1 )1ÄÎ ÄÎ22
##
œ "œ"
(c) We have that r y r y r ry y y .
$$ # # † $
œ œ œ œ$†aba b
r ryy y yyy y y
ry r r r
Since lim y lim sin y we have that lim r y .
)1 )1 )1ÄÎ ÄÎ ÄÎ22 2
$† œ $ † œ_ œ_
y
r)$$
4 7 NEWTON'S METHODÞ
1. y x x 1 y 2x 1 x x ; x 1 x 1œÊ œÊ œ œÊ œ œ
#w !"
#
n1 n
xx1
x1
nn
n
#
111 2
13
x x .61905; x 1 x 1 2Ê œ Ê œ œ œ ¸ œÊ œ œ
## !"
"
# #
2 2 469 2 13 111
331293121 1
1
1
42
93
4
3
x 2 1.66667Ê œ œ ¸
#"
42 5
41 3
2. y x 3x 1 y 3x 3 x x ; x 0 x 0œÊ œ Ê œ œÊ œœ
$w# !"
""
n1 n
x3x1
3x 3
nn
n
33
x 0.32222Êœ œœ¸
#"""
3 3 90 90
11
3
29
7
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
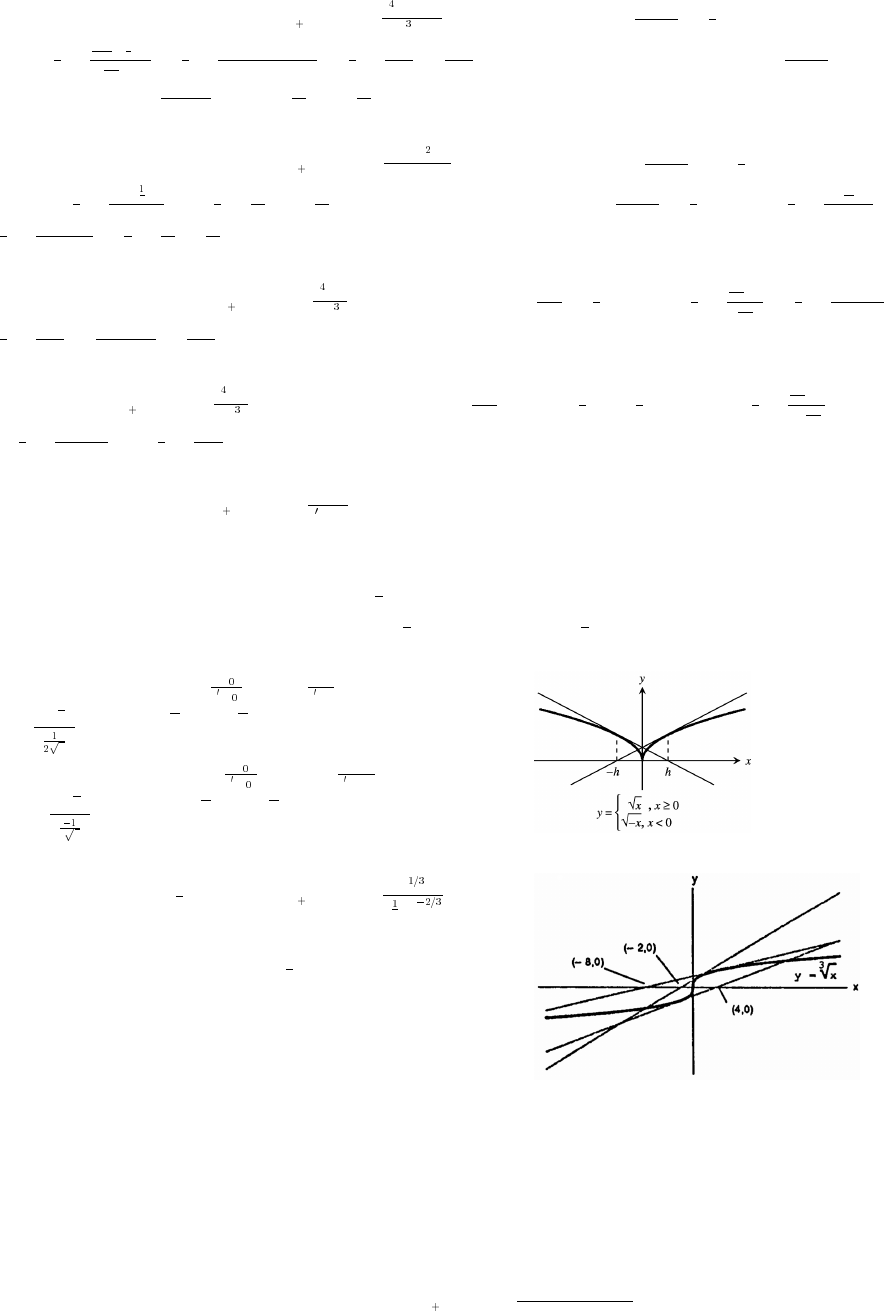
264 Chapter 4 Applications of Derivatives
3. y x x 3 y 4x 1 x x ; x 1 x 1œÊ œ Ê œ œÊ œ œ
%w$ !"
n1 n
xx3
4x 1
nn
n
113 6
41 5
x 1.16542; x 1 x 1Êœ œ œ œ ¸ œÊœ
#!"
"
6 6 1296 750 1875 6 171 5763 1 3
5 5 4320 625 5 4945 4945 4 1
3
1
1296 6
625 5
864
125
2 x 2 1.64516œ Ê œ# œ œ ¸
#
#
16 2 3 11 51
3 1 31 31
4. y 2x x 1 y 2 2x x x ; x 0 x 0œÊœ Ê œ œÊ œ œ
#w !"
" "
# #
n1 n
2xx1
22x
nn
n
00
0
x .41667; x 2 x 2 xÊœ œœ¸ œÊœ œÊœ
#!"#
""" "
# # # # # # # # #
" 151
111 4 5
54455
4 4
25
2.41667œ œ œ ¸
5 20254 5 29
1112## ##
"
5. y x 2 y 4x x x ; x 1 x 1 xœÊœ Ê œ œÊœ œÊœ œ
%w$ !" #
"
n1 n
x2
4x
n
n
2 5 5 5 625 512
4 4 4 4 2000
2
625
256
125
16
1.1935œ œ œ ¸
5 113 2500 113 2387
4 2000 2000 000
#
6. From Exercise 5, x x ; x 1 x 1 1 x
n1 n
œ œ Ê œ œ œ Ê œ
x2
4x
n
n
!" #
" "
255
444 4
2
625
256125
16
1.1935œ œ ¸
5 625 512 5 113
4 2000 4 2000
7. f(x ) 0 and f (x ) x x gives x x x x x x for all n 0. That is, all of
! ! "! #! !
w
œ Á!Ê œ œÊœÊœ
n1 n n
fx
fx
ab
ab
n
n
the approximations in Newton's method will be the root of f(x) 0.œ
8. It does matter. If you start too far away from x , the calculated values may approach some other root.œ1
#
Starting with x 0.5, for instance, leads to x as the root, not x .
!##
œ œ œ
11
9. If x h 0 x x h
!"!
œ Ê œ œ
f(x ) f(h)
f(x) f(h)
hhh2hh;œ œ œ
È
Š‹
h
hŠ‹Š ‹
ÈÈ
if x h 0 x x h
!"!
œ Ê œ œ
f(x ) f( h)
f(x) f( h)
hhh2hh.œ œ œ
È
Š‹
h
2h Š‹Š ‹
ÈÈ
10. f(x) x f (x) x x xœÊ œ Êœ
"Î$ w #Î$
"
ˆ‰
3n1 n x
x
n
3n
ˆ‰
2x ; x 1 x 2, x 4, x 8, andœ œ Ê œ œ œ
n!"#$
x 16 and so forth. Since x 2 x we may conclude
%œœllkk
nn1
that n x .Ä_Ê Ä_kk
n
11. i) is equivalent to solving x x .
$$ "œ!
ii) is equivalent to solving x x .
$$ "œ!
iii) is equivalent to solving x x .
$$ "œ!
iv) is equivalent to solving x x .
$$ "œ!
All four equations are equivalent.
12. f(x) x 1 0.5 sin x f (x) 1 0.5 cos x x x ; if x 1.5, thenœ Ê œ Ê œ œ
w!
n1 n
x 1 0.5 sin x
1 0.5 cos x
nn
n
x 1.49870
"œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
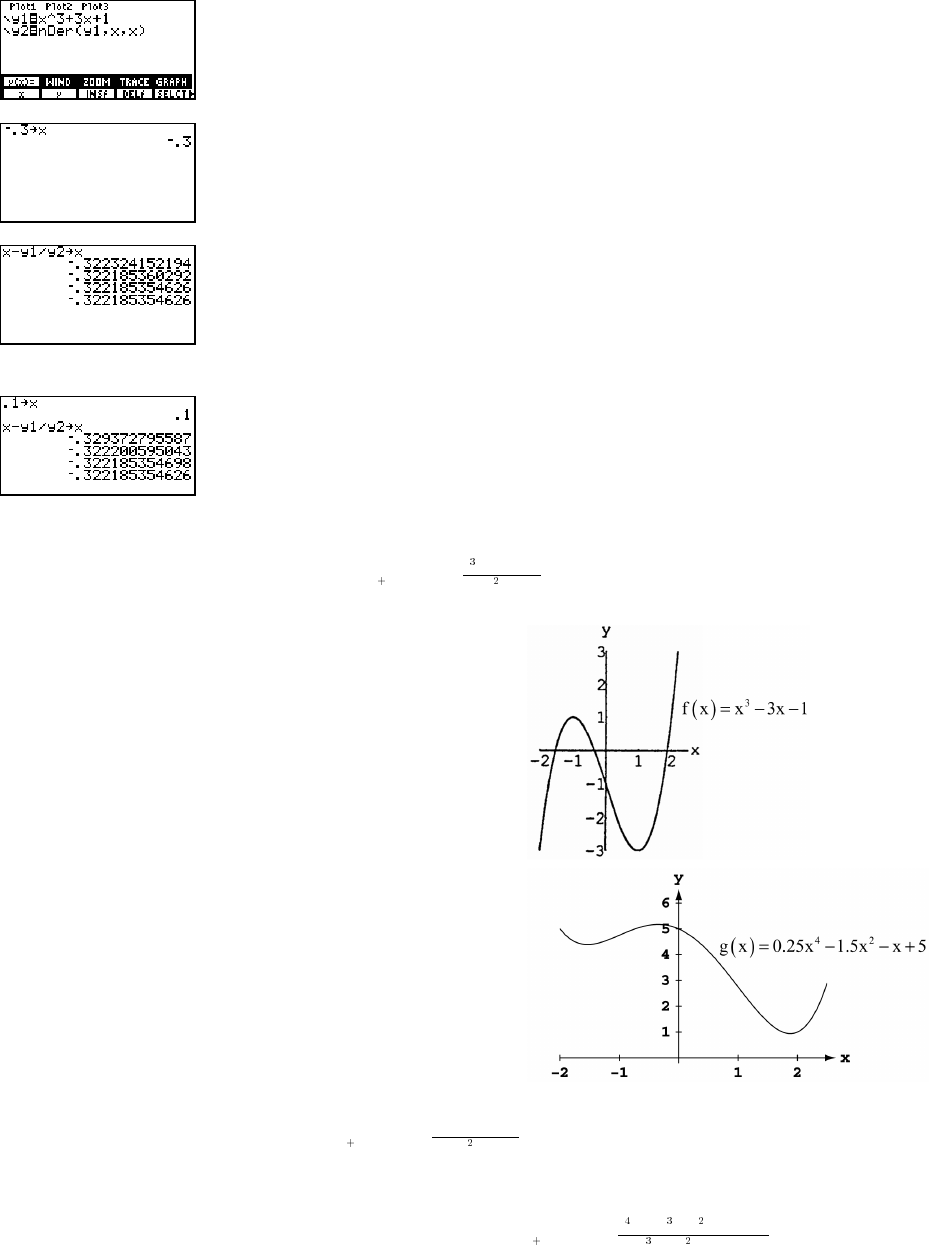
Section 4.7 Newton's Method 265
13. For x , the procedure converges to the root
!œ !Þ$ !Þ$##")&$&ÞÞÞÞ
(a)
(b)
(c)
(d) Values for x will vary. One possible choice is x 1.
!œ!Þ
(e) Values for x will vary.
14. (a) f(x) x 3x 1 f (x) 3x 3 x x the two negative zeros are 1.53209œÊ œ Ê œ Ê
$w#
n1 n
x3x1
3x 3
nn
n
and 0.34730
(b) The estimated solutions of x 3x 1 0 are
$œ
1.53209, 0.34730, 1.87939.
(c) The estimated x-values where
g(x) 0.25x 1.5x x 5 has horizontal tangentsœ
%#
are the roots of g (x) x 3x 1, and these are
w$
œ
1.53209, 0.34730, 1.87939.
15. f(x) tan x 2x f (x) sec x 2 x x ; x 1 x 12920445œÊ œ Êœ œÊœ
w# !"
n1 n
tan x 2x
sec x
ab
ab
nn
n
x 1.155327774 x x 1.165561185Êœ Ê œœ
#16 17
16. f(x) x 2x x 2x 2 f (x) 4x 6x 2x 2 x x ;œ Ê œ Ê œ
%$# w $# n1 n
x 2xx2x2
4x 6x 2x 2
nnn
n
nnn
if x 0.5, then x 0.630115396; if x 2.5, then x 2.57327196
!% !%
œœ œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
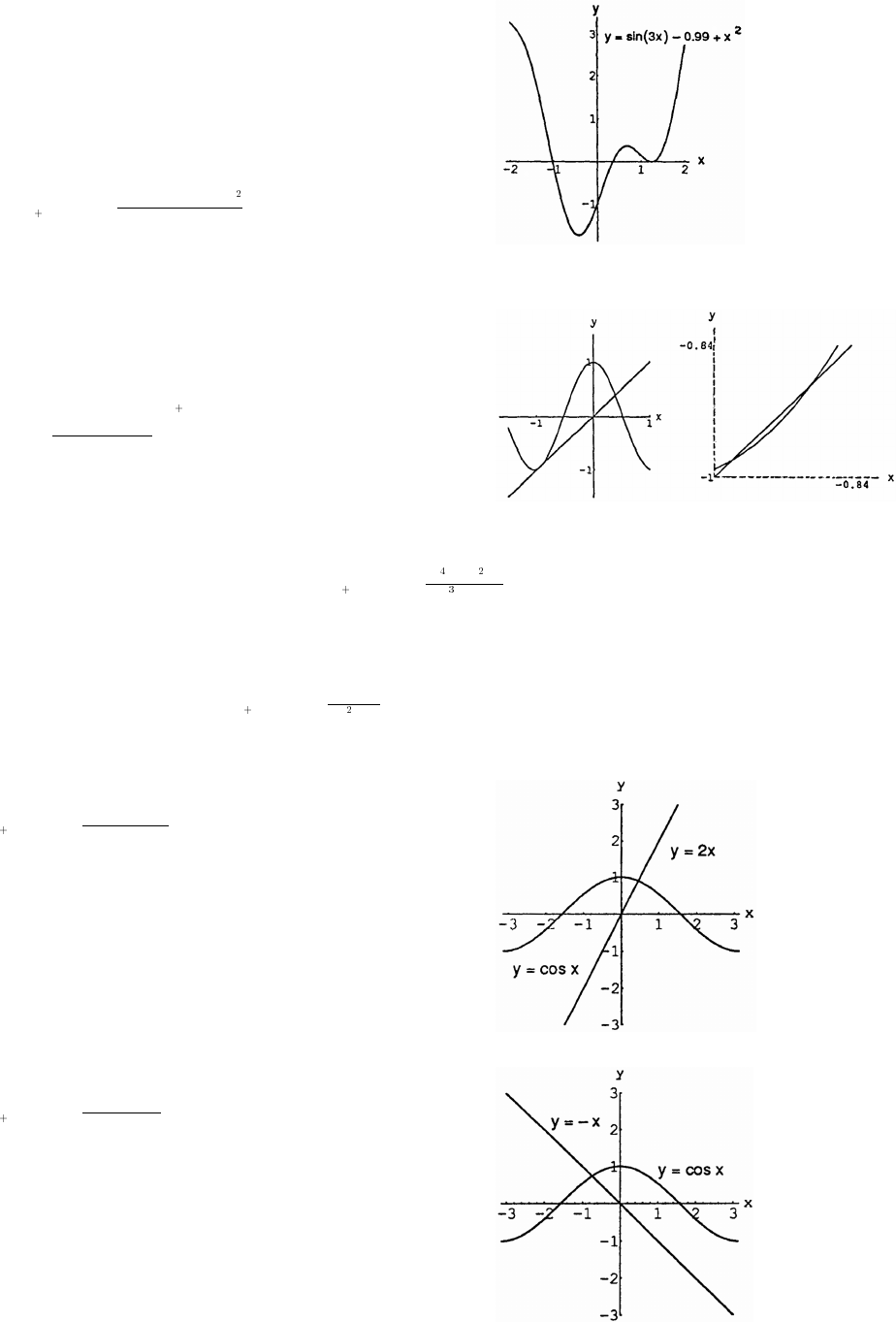
266 Chapter 4 Applications of Derivatives
17. (a) The graph of f(x) sin 3x 0.99 x in the windowœ
#
2 x 2, 2 y 3 suggests three roots.Ÿ Ÿ Ÿ Ÿ
However, when you zoom in on the x-axis near x 1.2,œ
you can see that the graph lies above the axis there.
There are only two roots, one near x 1, the otherœ
near x 0.4.œ
(b) f(x) sin 3x 0.99 x f (x) 3 cos 3x 2xœÊœ
#w
x x and the solutionsʜ
n1 n
sin (3x ) 0.99 x
3 cos (3x ) 2x
nn
nn
are approximately 0.35003501505249 and
1.0261731615301
18. (a) Yes, three times as indicted by the
graphs
(b) f(x) cos 3x x f (x)œÊ
w
3 sin 3x 1 xœ Ê n1
x; atœ
n
cos 3x x
3 sin 3x 1
ab
ab
nn
n
approximately 0.979367,
0.887726, and 0.39004 we have
cos 3x xœ
19. f(x) 2x 4x 1 f (x) 8x 8x x x ; if x 2, then x 1.30656296; ifœÊ œÊ œ œ œ
%# w $ !'
n1 n
2x 4x 1
8x 8x
nn
nn
x 0.5, then x 0.5411961; the roots are approximately 0.5411961 and 1.30656296 because f(x) is
!$
œ œ „ „
an even function.
20. f(x) tan x f (x) sec x x x ; x 3 x 3.13971 x 3.14159 and weœÊœ Êœ œÊœ Êœ
w# !" #
n1 n
tan x
sec x
ab
ab
n
n
approximate to be 3.14159.1
21. From the graph we let x 0.5 and f(x) cos x 2x
!œœ
x x x .45063ʜ ʜ
n1 n
cos x 2x
sin x 2
ab
ab
nn
n
"
x .45018 at x 0.45 we have cos x 2x.Êœ Ê ¸ œ
#
22. From the graph we let x 0.7 and f(x) cos x x
!œ œ
x x x .73944ʜ ʜ
n1 n
x cos x
1sinx
nn
n
ab
ab "
x .73908 at x 0.74 we have cos x x.Ê œ Ê ¸ œ
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 4.7 Newton's Method 267
23. If f(x) x 2x 4, then f(1) 1 0 and f(2) 8 0 by the Intermediate Value Theorem the equationœ œ œÊ
$
x 2x 4 0 has a solution between 1 and 2. Consequently, f (x) 3x 2 and x x .
$w#
œ œ œ
n1 n
x2x4
3x 2
nn
n
Then x 1 x 1.2 x 1.17975 x 1.179509 x 1.1795090 the root is approximately
!" # $ %
œÊ œ Ê œ Ê œ Ê œ Ê
1.17951.
24. We wish to solve 8x 14x 9x 11x 1 0. Let f(x) 8x 14x 9x 11x 1, then
%$# %$#
œ œ
f (x) 32x 42x 18x 11 x x .
w$#
œÊœ
n1 n
8x 14x 9x 11x 1
3 x 42x 18x 11
nnnn
nnn
#
x approximation of corresponding root
1.0 0.976823589
0.1 0.100363332
0.6 0.642746671
2.0 1.983713587
!
25. f(x) 4x 4x f (x) 16x 8x x x x . Iterations are performed using theœ Ê œ Ê œ œ
%# w $ i1i i
fx
fx
xx
x
ab
ab
i
i
ii
i
%#
procedure in problem 13 in this section.
(a) For x or x , x as i gets large.
!!
œ# œ!Þ) Ä"
i
(b) For x or x , x as i gets large.
!!
œ !Þ& œ !Þ#& Ä !
i
(c) For x or x , x as i gets large.
!!
œ!Þ) œ# Ä"
i
(d) (If your calculator has a CAS, put it in exact mode, otherwise approximate the radicals with a decimal value.)
For x or x , Newton's method does not converge. The values of x alternate between
!!
œ œ
ÈÈ
21 21
77 i
x or x as i increases.
!!
œ œ
ÈÈ
21 21
77
26. (a) The distance can be represented by
D(x) (x 2) x , where x 0. Theœ
Ɉ‰
##
"
#
#
distance D(x) is minimized when
f(x) (x 2) x is minimized. Ifœ
##
"
#
#
ˆ‰
f(x) (x 2) x , thenœ
##
"
#
#
ˆ‰
f (x) 4 x x 1 and f (x) 4 3x 1 0.
w$ w #
w
œ œ ab ab
Now f (x) 0 x x 1 0 x x 1 1
w$ #
œÊ œÊ œab
x.ʜ
"
x1
(b) Let g(x) x x 1 x g (x) x 1 (2x) 1 1œœÊ œ œ
"
#w#
" #
x1
2x
x1
ab ab ab
x x ; x 1 x 0.68233 to five decimal places.Êœ œÊœ
n1 n
Œ
ÎÑ
ÏÒ
x1
nn
2xn
x1 1
n
x
!%
27. f(x) (x 1) f (x) 40(x 1) x x . With x 2, our computerœ Ê œ Ê œ œ œ
%! w $* !
n1 n
ab
ab
x1
40 x 1
39x
40
n
n
n
"
gave x x x x 1.11051, coming within 0.11051 of the root x 1.
)( )) )* #!!
œ œ œâœ œ œ
28. f(x) 4x 4x f (x) 16x 8x 8x 2x 1 x x ; if x .65, thenœ Ê œ œ Ê œ œ
%# w $ # !
ab
n1 n
xx
22x 1
nn
n
ab
ab
"
x .000004, if x .7, then x 1.000004; if x .8, then x 1.000000. NOTE: .654654
"# ! "# ! '
¸ œ œ œ œ ¸
È21
7
29. f(x) x 3.6x 36.4 f (x) 3x 7.2x x x ; x 2 x 2.5303œ Ê œ Ê œ œÊ œ
$# w # !"
n1 n
x 3.6x 36.4
3x 7.2x
nn
nn
x 2.45418225 x 2.45238021 x 2.45237921 which is 2.45 to two decimal places. Recall thatʜ ʜ ʜ
#$%
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

268 Chapter 4 Applications of Derivatives
x 10 H O H O (x) 10 (2.45) 10 0.000245œÊœœ œ
% % %
$$
cdcdab ab
30. Newton's method yields the following:
the initial value 2 i 3 i
the approached value 1 5.55931i 29.5815 17.0789i
È
4.8 ANTIDERIVATIVES
1. (a) x (b) (c) x x
# #
xx
33
2. (a) 3x (b) (c) 3x 8x
# #
xx
88
3. (a) x (b) (c) x 3x
$ #
xx
33
4. (a) x (b) (c) x
#
#
xx xx
43 2
5. (a) (b) (c) 2x
"
xx x
55
6. (a) (b) (c)
"" "
#x4x4x
x
7. (a) x (b) x (c) x 2 x
È È
ÈÈ
$ $
2
3
8. (a) x (b) x (c) x x
%Î$ #Î$ %Î$ #Î$
"
##
33
4
9. (a) x (b) x (c) x
#Î$ "Î$ "Î$
10. (a) x (b) x (c) x
"Î# "Î# $Î#
11. (a) cos ( x) (b) 3 cos x (c) cos (3x)1
cos ( x)1
1
12. (a) sin ( x) (b) sin (c) sin sin x1 1
ˆ‰ ˆ‰ ˆ‰
11
1
x2x
##
13. (a) tan x (b) 2 tan (c) tan
ˆ‰ ˆ ‰
x23x
33
#
14. (a) cot x (b) cot (c) x 4 cot (2x)
ˆ‰
3x
#
15. (a) csc x (b) csc (5x) (c) 2 csc"
#5
x
ˆ‰
1
16. (a) sec x (b) sec (3x) (c) sec
42x
31
1
ˆ‰
#
17. (x 1) dx x C 18. (5 6x) dx 5x 3x C
''
œ œ
x
#
#
19. 3t dt t C 20. 4t dt t C
''
ˆ‰ Š‹
#$ $ %
##
œ œ
tt t t
4 6
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 4.8 Antiderivatives 269
21. 2x 5x 7 dx x x 7x C 22. 1 x 3x dx x x x C
''
ab ab
$%# #&$'
"""
## #
œ œ
5
3
23. x dx x x dx x C C
''
ˆ‰ˆ ‰
"" " " "
###
x 3 3 133 x33
xx xx
œ œ œ
24. 2x dx 2x 2x dx x C x C
'ˆ‰ˆ ‰
'Š‹
""" "
$ #
# #5x 5 5 xx
22x2x5
œ œ œ
25. x dx C x C 26. x dx C C
''
"Î$ #Î$ &Î%
#
œœ œ œ
x3 x 4
x
2
34È
27. x x dx x x dx C x x C
''
ˆ‰ˆ‰
ÈÈ
œœœ
$"Î# "Î$ $Î# %Î$
xx 2 3
34
34
3
28. dx x 2x dx 2 C x 4x C
''
Š ‹ Š‹ Š‹
ˆ‰
ÈÈ
x2xx
x3## #
"" "
"Î# "Î# $Î# "Î#
œ œ œ
3
29. 8y dy 8y 2y dy 2 C 4y y C
''
Š‹ Š‹
ˆ‰
œ œœ
2 8
y
8y y
3
"Î% # $Î%
#3
4
30. dy y dy y C C
''
Š‹ Š‹
ˆ‰
"""
&Î%
777 7
1 4
y y
yy
œ œœ
1
4
31. 2x 1 x dx 2x 2x dx 2 C x C
''
ab a b Š‹
œ œœ
$ # #
#
2x x 2
1x
32. x (x 1) dx x x dx C C
''
$ # $
# #
""
œ œ œab Š‹
xx
1xx
33. dt dt t t dt C 2 t C
'' '
tt t
ttt
tt t t 2
t
ÈÈ È
"Î# $Î#
œœ œœ
Š‹ Š‹
ˆ‰ È
34. dt dt 4t t dt 4 C C
'' '
4t
ttt t
4t t t 2 2
3t
$ &Î#
#
Èœ œ œ œ
Š‹ Š‹Š‹
ˆ‰ 3
35. 2 cos t dt 2 sin t C 36. 5 sin t dt 5 cos t C
''
œ œ
37. 7 sin d 21 cos C 38. 3 cos 5 d sin 5 C
''
))
33 5
3
))))œ œ
39. 3 csc x dx 3 cot x C 40. dx C
''
œ œ
#sec x tan x
33
41. d csc C 42. sec tan d sec C
''
csc cot 2 2
55
))
##
"
)) ))))œ œ
43. 4 sec x tan x 2 sec x dx 4 sec x 2 tan x C
'abœ
#
44. csc x csc x cot x dx cot x csc x C
'"""
#
##2abœ
45. sin 2x csc x dx cos 2x cot x C 46. (2 cos 2x 3 sin 3x) dx sin 2x cos 3x C
''
abœ œ
#"
#
47. dt cos 4t dt t C C
''
1 cos 4t sin 4t t sin 4t
428
""""
### ##
œ œ œ
ˆ‰ ˆ‰
48. dt cos 6t dt t C C
''
1 cos 6t sin 6t t sin 6t
6212
""""
### ##
œ œ œ
ˆ‰ ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

270 Chapter 4 Applications of Derivatives
49. 1 tan d sec d tan C
''
abœ œ
##
)) )) )
50. 2 tan d 1 1 tan d 1 sec d tan C
'' '
aba babœœœ
###
)) )) )) ) )
51. cot x dx csc x 1 dx cot x x C
''
##
œœab
52. 1 cot x dx 1 csc x 1 dx 2 csc x dx 2x cot x C
'' '
aba bababœœœ
## #
53. cos (tan sec ) d (sin 1) d cos C
')) )) ) ) ))œœ
'
54. d d d d sec d tan C
''
csc csc sin
csc sin csc sin sin 1 sin cos
)))
)) )) ) ) )
""#
)))))))œœœœœ
ˆ‰ˆ‰
'''
55. C (7x 2)
d
dx 28 28
(7x 2) 4(7x 2) (7)
Š‹
$
œ œ
56. C (3x 5)
d
dx 3 3
(3 x 5) (3x 5) (3)
Š‹Š‹
œ œ
#
57. tan (5x 1) C sec (5x 1) (5) sec (5x 1)
d
dx 5 5
ˆ‰
ab
""
##
œ œ
58. 3 cot C 3 csc csc
dx x x
dx 3 3 3 3
ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰
œ œ
" " " "
##
59. C ( 1)( 1)(x 1) 60. C
ddx
dx x 1 (x 1) dx x 1 (x 1) (x 1)
(x 1)( ) x(1)
ˆ‰ ˆ‰
" " "
# "
œ œ œ œ
61. (a) Wrong: sin x C sin x cos x x sin x cos x x sin x
dx 2x x x
dx Š‹
### #
œœÁ
(b) Wrong: ( x cos x C) cos x x sin x x sin x
d
dx œÁ
(c) Right: ( x cos x sin x C) cos x x sin x cos x x sin x
d
dx œœ
62. (a) Wrong: C (sec tan ) sec tan tan sec
dsec 3 sec
d3 3)
))
Š‹
œ œ Á)) )) ) )
$#
(b) Right: tan C (2 tan ) sec tan sec
d
d)ˆ‰
""
##
###
)))))œ œ
(c) Right: sec C (2 sec ) sec tan tan sec
d
d)ˆ‰
""
##
##
))))))œ œ
63. (a) Wrong: C 2(2x 1) (2x 1)
d
dx 3 3
(2x 1) 3(2x 1) (2)
Š‹
##
œ œ Á
(b) Wrong: (2x 1) C 3(2x 1) (2) 6(2x 1) 3(2x 1)
d
dx abœ œÁ
$###
(c) Right: (2x 1) C 6(2x 1)
d
dx abœ
$#
64. (a) Wrong: x x C x x C (2x 1) 2x 1
d2x1
dx 2x xC
abab È
##
"Î# "Î#
"
#
œ œ Á
È
(b) Wrong: x x C x x (2x 1) 2x 1
d2x1
dx 2x x
Š‹
ab ab È
##
"Î# "Î#
"
#
œ œ Á
È
(c) Right: 2x 1 C (2x 1) C (2x 1) (2) 2x 1
dd3
dx 3 dx 3 6
Œ
Š‹
ÈÈ
ˆ‰
""
$$Î# "Î#
œ œ œ
65. Graph (b), because 2 y x C. Then y(1) 4 C 3.
dy
dx œBÊ œ œ Ê œ
#
66. Graph (b), because y x C. Then y( 1) 1 C .
dy
dx
3
œB Ê œ œ Ê œ
"
##
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 4.8 Antiderivatives 271
67. 2x 7 y x 7x C; at x 2 and y 0 we have 0 2 7(2) C C 10 y x 7x 10
dy
dx œÊœ œ œ œ Êœ Êœ
###
68. 10 x y 10x C; at x 0 and y 1 we have 1 10(0) C C 1
dy
dx
x0
œÊœ œ œ œ Êœ
##
y 10x 1ʜ
x
#
69. x x x y x C; at x 2 and y 1 we have 1 2 C C
dy
dx x
x2
œœ Êœ œ œ œÊœ
" "
# " "
###
y x or yÊœ œ
"
## ##
"""xx
x
70. 9x 4x 5 y 3x 2x 5x C; at x 1 and y 0 we have 0 3( 1) 2( 1) 5( 1) C
dy
dx œÊœ œ œ œ
#$# $#
C 10 y 3x 2x 5x 10ʜ ʜ
$#
71. x y C ; at x 9x C; at x and y we have ( ) C C
dy
dx
x
œ$ Ê œ œ* œ œ" œ& &œ*" Ê œ%
#Î$ "Î$ "Î$
$
y9xʜ %
"Î$
72. x y x C; at x 4 and y 0 we have 0 4 C C 2 y x 2
dy
dx x
œ œ Êœ œ œ œ Ê œÊœ
""
##
"Î# "Î# "Î# "Î#
È
73. 1 cos t s t sin t C; at t 0 and s 4 we have 4 0 sin 0 C C 4 s t sin t 4
ds
dt œ Ê œ œ œ œ Ê œ Ê œ
74. cos t sin t s sin t cos t C; at t and s 1 we have 1 sin cos C C 0
ds
dt œÊœ œ œ œ Êœ111
s sin t cos tʜ
75. sin r cos ( ) C; at r 0 and 0 we have 0 cos ( 0) C C r cos ( ) 1
dr
d)œ Ê œ œ œ œ Ê œ" Ê œ 11) 1) ) 1 1)
76. cos r sin( ) C; at r 1 and 0 we have 1 sin ( 0) C C r sin ( ) 1
dr
d)1 1 1
œÊœœœ œÊœ"Êœ1) 1) ) 1 1)
"""
77. sec t tan t v sec t C; at v 1 and t 0 we have 1 sec (0) C C v sec t
dv
dt œÊœœœœÊœÊœ
"" " """
## # ###
78. 8t csc t v 4t cot t C; at v 7 and t we have 7 4 cot C C 7
dv
dt œ Ê œ œ œ œ Ê œ
## #
###
#
111
ˆ‰ ˆ‰ 1
v 4t cot t 7ʜ
##
1
79. 2 6x 2x 3x C ; at 4 and x 0 we have 4 2(0) 3(0) C C 4
d y dy dy
dx dx dx
œ Ê œ œ œ œ Ê œ
##
"""
2x 3x 4 y x x 4x C ; at y 1 and x 0 we have 1 0 0 4(0) C C 1Ê œ Êœ œ œ œ Ê œ
dy
dx ##$ #$
###
yxx4x1ʜ
#$
80. 0 C ; at 2 and x 0 we have C 2 2 y 2x C ; at y 0 and x 0 we
d y dy dy dy
dx dx dx dx
œÊ œ œ œ œÊ œÊœ œ œ
"" #
have 0 2(0) C C 0 y 2xœÊœÊœ
##
81. 2t t C ; at 1 and t 1 we have 1 (1) C C 2 t 2
dr 2 dr dr dr
dt t dt dt dt
œ œ Ê œ œ œ œ Ê œ Ê œ
$ # # #
"""
r t 2t C ; at r 1 and t 1 we have 1 1 2(1) C C 2 r t 2t 2 orÊœ œ œ œ Ê œÊœ
" " "
###
r2t2œ
"
t
82. C ; at 3 and t 4 we have 3 C C 0 s C ; at
d s 3t ds 3t ds ds 3t t
dt 8 dt16 dt 16 dt16 16
3(4)
œÊœ œ œ œ Ê œÊœ Êœ
"""#
s 4 and t 4 we have 4 C C 0 sœœ œÊœÊœ
4t
16 16
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

272 Chapter 4 Applications of Derivatives
83. 6 6x C ; at 8 and x 0 we have 8 6(0) C C 8 6x 8
dy dy dy dy
dx dx dx dx
œÊ œ œ œ œ Ê œÊ œ
"""
3x 8x C ; at 0 and x 0 we have 0 3(0) 8(0) C C 0 3x 8xÊœ œ œ œ ʜʜ
dy dy dy
dx dx dx
###
###
y x 4x C ; at y 5 and x 0 we have 5 0 4(0) C C 5 y x 4x 5Êœ œ œ œ Ê œÊœ
$# $ # $#
$$$
84. 0 C ; at 2 and t 0 we have 2 2t C ; at and t 0 we
ddd d d d
dt dt dt dt dt dt
))) ) ) )
œ Ê œ œ œ œ Ê œ œ œ
" # "
#
have 2(0) C C 2t t t C ; at 2 and t 0 we have œ Ê œ Ê œ Ê œ œ œ
""""
####
## $
#
d
dt
)))
È
20 (0)C C 2 t t 2
ÈÈÈ
œ Ê œ Ê œ
##
""
##
$$ )
85. y sin t cos t y cos t sin t C ; at y 7 and t 0 we have 7 cos (0) sin (0) C
Ð%Ñ www www
" "
œ Ê œ œ œ œ
C 6 y cos t sin t 6 y sin t cos t 6t C ; at y 1 and t 0 we haveʜʜ Êœ œ œ
" #
www ww ww
1 sin (0) cos (0) 6(0) C C 0 y sin t cos t 6t y cos t sin t 3t C ;œ Ê œ Ê œ Ê œ
## $
ww w #
at y 1 and t 0 we have 1 cos (0) sin (0) 3(0) C C 0 y cos t sin t 3t
w#w#
$$
œ œ œ Ê œ Ê œ
y sin t cos t t C ; at y 0 and t 0 we have 0 sin (0) cos (0) 0 C C 1Ê œ œ œ œ Ê œ
$ $
%%%
y sin t cos t t 1ʜ
$
86. y cos x 8 sin (2x) y sin x 4 cos (2x) C ; at y 0 and x 0 we have
Ð%Ñ www www
"
œ Ê œ œ œ
0 sin (0) cos (2(0)) C C 4 y sin x 4 cos (2x) 4 y cos x 2 sin (2x) 4x C ;œ % Ê œ Ê œ Ê œ
"" #
www ww
at y 1 and x 0 we have 1 cos (0) 2 sin (2(0)) 4(0) C C 0 y cos x 2 sin (2x) 4x
ww ww
##
œœ œ ʜʜ
y sin x cos (2x) 2x C ; at y 1 and x 0 we have 1 sin (0) cos (2(0)) 2(0) C C 0Êœ œ œ œ Ê œ
w#w #
$$$
y sin x cos (2x) 2x y cos x sin (2x) x C ; at y 3 and x 0 we haveÊœ Êœ œ œ
w# $
"
#%
2
3
3 cos (0) sin (2(0)) (0) C C 4 y cos x sin (2x) x 4œ Ê œ Ê œ
" "
# #
$$
%%
22
33
87. m y 3 x 3x y 2x C; at ( 4) we have 4 2(9) C C 50 y 2x 50œœœ Êœ *ß œ ʜʜ
w "Î# $Î# $Î# $Î#
È
88. (a) 6x 3x C ; at y 0 and x 0 we have 0 3(0) C C 0 3x
dy dy dy
dx dx dx
œÊœ œ œ œ ʜʜ
#w # #
"""
y x C ; at y 1 and x 0 we have C 1 y x 1Êœ œ œ œÊœ
$$
##
(b) One, because any other possible function would differ from x 1 by a constant that must be zero because
$
of the initial conditions
89. 1 x y 1 x dx x x C; at (1 0.5) on the curve we have 0.5 1 1 C
dy
dx 3 3
44
œ Êœ œ ß œ
"Î$ "Î$ %Î$ %Î$
'ˆ‰
C 0.5 y x xʜ ʜ
%Î$ "
#
90. x 1 y (x 1) dx x C; at ( 1 1) on the curve we have 1 ( 1) C
dy ()
dx
x
œ Ê œ œ ß œ
'##
"
C y xʜʜ
""
###
x
91. sin x cos x y (sin x cos x) dx cos x sin x C; at ( 1) on the curve we have
dy
dx œ Êœ œ ß
'1
cos ( ) sin ( ) C C 2 y cos x sin x 2"œ Ê œÊ œ 11
92. sin x x sin x y x sin x dx x cos x C; at (1 ) on the
dy
dx x
œ œ Êœ œ ß#
"" "
###
"Î# "Î# "Î#
È11 11 1 1
'ˆ‰
curve we have 2 1 cos (1) C C 0 y x cos xœ ʜʜ
"Î# 11
È
93. (a) 9.8t 3 s 4.9t 3t C; (i) at s 5 and t 0 we have C 5 s 4.9t 3t 5;
ds
dt œÊœ œ œ œÊœ
# #
displacement s(3) s(1) ((4.9)(9) 9 5) (4.9 3 5) 33.2 units; (ii) at s 2 and t 0 we haveœœ œ œ œ
C 2 s 4.9t 3t 2; displacement s(3) s(1) ((4.9)(9) 9 2) (4.9 3 2) 33.2 units;œÊœ œœ œ
#
(iii) at s s and t 0 we have C s s 4.9t 3t s ; displacement s(3) s(1)œœ œÊœ œ
!!!
#
((4.9)(9) 9 s ) (4.9 3 s ) 33.2 unitsœœ
!!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
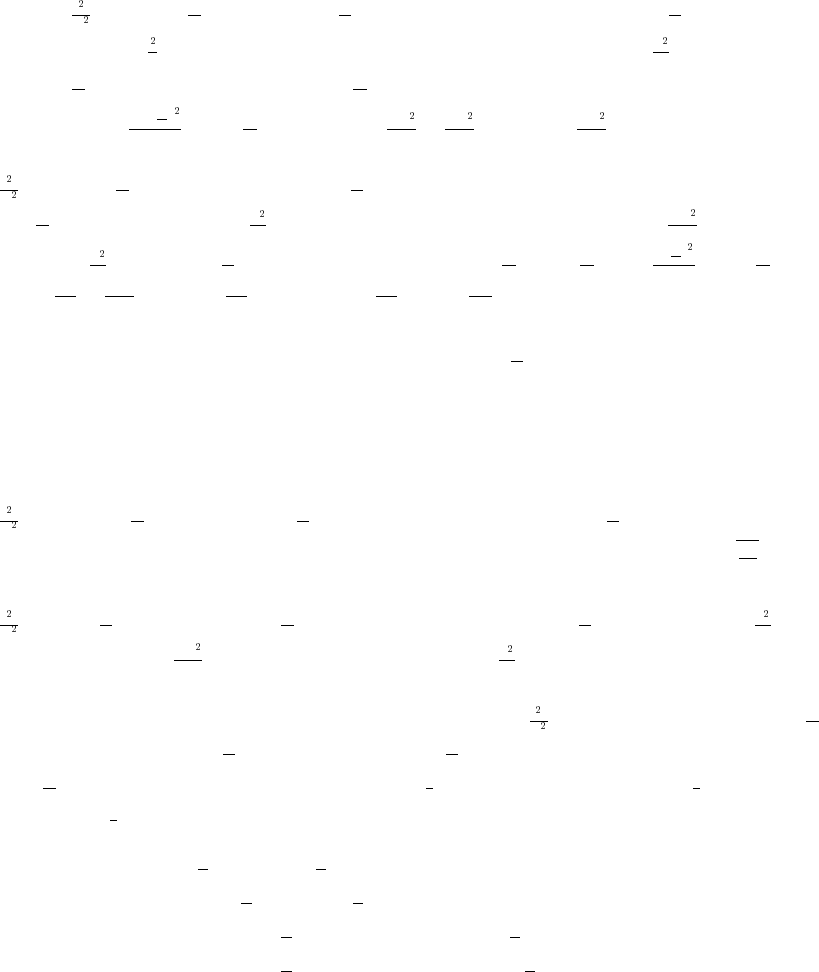
Section 4.8 Antiderivatives 273
(b) True. Given an antiderivative f(t) of the velocity function, we know that the body's position function is
s f(t) C for some constant C. Therefore, the displacement from t a to t b is (f(b) C) (f(a) C)œ œ œ
f(b) f(a). Thus we can find the displacement from any antiderivative f as the numerical differenceœ
f(b) f(a) without knowing the exact values of C and s.
94. a(t) v (t) 20 v(t) 20t C; at (0 ) we have C 0 v(t) 20t. When t 60, then v(60) 20(60)œœÊœ ß! œÊœ œ œ
w
1200 m/sec.œ
95. Step 1: k kt C ; at 88 and t 0 we have C 88 kt 88
d s ds ds ds
dt dt dt dt
œ Ê œ œ œ œ Ê œ Ê
""
s k 88t C ; at s 0 and t 0 we have C 0 s 88tœ œ œ œ Ê œ
Š‹
tkt
# #
##
Step 2: 0 0 kt 88 t
ds 88
dt k
œÊœ Êœ
Step 3: 242 88 242 242 k 16œ Êœ Êœ Êœ
#
k88
k2kk2k
(88) (88) (88)
ˆ‰
88
kˆ‰
96. k k dt kt C; at 44 when t 0 we have 44 k(0) C C 44
d s ds ds
dt dt dt
œ Ê œ œ œ œ œ Ê œ
'
kt 44 s 44t C ; at s 0 when t 0 we have 0 44(0) C C 0ʜʜ œ œ œ Ê œ
ds kt
dt
k(0)
##
"""
s 44t. Then 0 kt 44 0 t and s 44 45Êœ œÊ œÊœ œ œ
kt ds 44 44 44
dt k k k
k
# #
ˆ‰ ˆ‰
ˆ‰
44
k
45 45 k 21.5 .Ê œ Ê œ Ê œ ¸
968 1936 968 968 ft
kk k 45 sec
2
97. (a) v a dt 15t 3t dt 10t 6t C; (1) 4 4 10(1) 6(1) C C 0œœ œ œÊœ Êœ
''ˆ‰
"Î# "Î# $Î# "Î# $Î# "Î#
ds
dt
v 10t 6tʜ
$Î# "Î#
(b) s v dt 10t 6t dt 4t 4t C; s(1) 0 0 4(1) 4(1) C C 0œœ œ œÊœ Êœ
''ˆ‰
$Î# "Î# &Î# $Î# &Î# $Î#
s4t 4tʜ
&Î# $Î#
98. 5.2 5.2t C ; at 0 and t 0 we have C 0 5.2t s 2.6t C ; at s 4
d s ds ds ds
dt dt dt dt
œ Ê œ œ œ œ Ê œ Ê œ œ
"" #
#
and t 0 we have C 4 s 2.6t 4. Then s 0 0 2.6t 4 t 1.24 sec, since t 0œœÊœœÊœÊœ¸
###
É4
2.6
99. a a dt at C; v when t 0 C v at v s v t C ; s s
d s ds ds ds at
dt dt dt dt
œÊ œ œ œ œÊ œ Ê œ Êœ œ
'!!!!"!
#
when t 0 s v (0) C C s s v t sœÊ œ Ê œ Êœ
!!""! !!
##
a(0) at
100. The appropriate initial value problem is: Differential Equation: g with Initial Conditions: v and
ds ds
dt dt
œ œ !
s s when t 0. Thus, g dt gt C ; (0) v v ( g)(0) C C vœœ œœœÊœÊœ
!"!!""!
ds ds
dt dt
'
gt v . Thus s gt v dt gt v t C ; s(0) s (g)(0) v (0) C C sÊœ œ œ œ œ Ê œ
ds
dt !!!#!!##!
""
##
##
'ab
Thus s gt v t sœ
"
#
#!!.
101. (a) f(x) dx 1 x C x C (b) g(x) dx x 2 C x C
''
œ œ œ œ
ÈÈ
""
(c) f(x) dx 1 x C x C (d) g(x) dx (x 2) C x C
''
œ œ œ œ
ˆ‰
ÈÈ
""
(e) [f(x) g(x)] dx 1 x (x 2) C x x C
' œ œ
ˆ‰
ÈÈ
"
(f) [f(x) g(x)] dx 1 x (x 2) C x x C
' œ œ
ˆ‰
ÈÈ
"
102. Yes. If F(x) and G(x) both solve the initial value problem on an interval I then they both have the same first
derivative. Therefore, by Corollary 2 of the Mean Value Theorem there is a constant C such that
F(x) G(x) C for all x. In particular, F(x ) G(x ) C, so C F(x ) G(x ) 0. Hence F(x) G(x)œ œ œ œ œ
!! !!
for all x.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

274 Chapter 4 Applications of Derivatives
103 106 Example CAS commands:
:Maple
with(student):
f := x -> cos(x)^2 + sin(x);
ic := [x=Pi,y=1];
F := unapply( int( f(x), x ) + C, x );
eq := eval( y=F(x), ic );
solnC := solve( eq, {C} );
Y := unapply( eval( F(x), solnC ), x );
DEplot( diff(y(x),x) = f(x), y(x), x=0..2*Pi, [[y(Pi)=1]],
color=black, linecolor=black, stepsize=0.05, title="Section 4.8 #103" );
: (functions and values may vary)Mathematica
The following commands use the definite integral and the Fundamental Theorem of calculus to construct the solution
of the initial value problems for exercises 103 - 105.
Clear[x, y, yprime]
yprime[x_] = Cos[x] Sin[x];
2
initxvalue = ; inityvalue = 1;1
y[x_] = Integrate[yprime[t], {t, initxvalue, x}] inityvalue
If the solution satisfies the differential equation and initial condition, the following yield True
yprime[x]==D[y[x], x] //Simplify
y[initxvalue]==inityvalue
Since exercise 106 is a second order differential equation, two integrations will be required.
Clear[x, y, yprime]
y2prime[x_] = 3 Exp[x/2] 1;
initxval = 0; inityval = 4; inityprimeval = 1;
yprime[x_] = Integrate[y2prime[t],{t, initxval, x}] inityprimeval
y[x_] = Integrate[yprime[t], {t, initxval, x}] inityval
Verify that y[x] solves the differential equation and initial condition and plot the solution (red) and its derivative (blue).
y2prime[x]==D[y[x], {x, 2}]//Simplify
y[initxval]==inityval
yprime[initxval]==inityprimeval
Plot[{y[x], yprime[x]}, {x, initxval 3, initxval 3}, PlotStyle {RGBColor[1,0,0], RGBColor[0,0,1]}] Ä
CHAPTER 4 PRACTICE EXERCISES
1. No, since f(x) x 2x tan x f (x) 3x 2 sec x 0 f(x) is always increasing on its domainœ Ê œ Ê
$w##
2. No, since g(x) csc x 2 cot x g (x) csc x cot x 2 csc x (cos x 2) 0œ Ê œ œœ
w#"cos x 2
sin x sin x sin x
g(x) is always decreasing on its domainÊ
3. No absolute minimum because lim (7 x)(11 3x) . Next f (x)
xÄ_ œ_ œ
"Î$ w
(11 3x) (7 x)(11 3x) x 1 and x are critical points. œ œ Êœ œ
"Î$ #Î$
(11 3x) (7 x) 4(1 x)
(11 3x) (11 3x)
11
3
Since f 0 if x 1 and f 0 if x 1, f(1) 16 is the absolute maximum.
ww
œ
4. f(x) f (x) ; f (3) 0 ( a b a) a b .œ Ê œ œ œ Ê * ' œ!Ê& $ œ!
ax b
x1
a x 1 2x(ax b) ax 2bx a
x1 x1
"
'%
ww
ab a b
ab ab
We require also that f(3) 1. Thus 3a b . Solving both equations yields a 6 and b 10. Now,œ"œÊœ) œœ
3a b
8
f (x) so that f . Thus f changes sign at x from
113
1/3
ww w
# $ " $
œ œ ± ± ± ± œ $
abab
ab
xx
x1
positive to negative so there is a local maximum at x which has a value f(3) 1.œ$ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
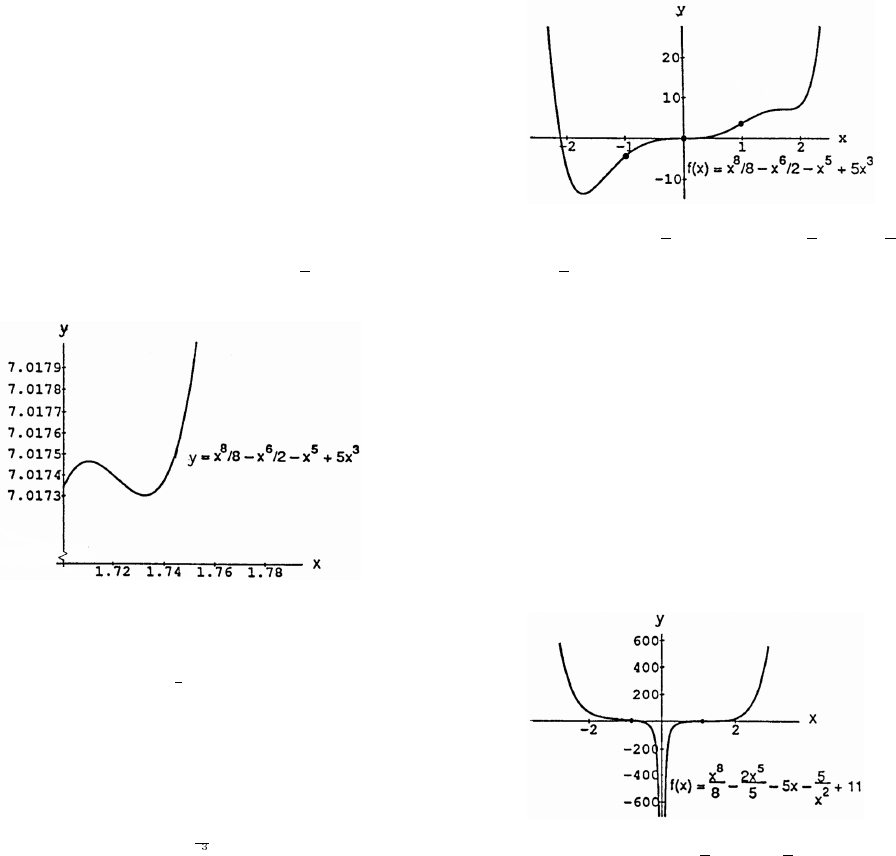
Chapter 4 Practice Exercises 275
5. Yes, because at each point of [ except x 0, the function's value is a local minimum value as well as a!ß "Ñ œ
local maximum value. At x 0 the function's value, 0, is not a local minimum value because each openœ
interval around x 0 on the x-axis contains points to the left of 0 where f equals 1.œ
6. (a) The first derivative of the function f(x) x is zero at x 0 even though f has no local extreme value atœœ
$
x0.œ
(b) Theorem 2 says only that if f is differentiable and f has a local extreme at x c then f (c) 0. It does notœœ
w
assert the (false) reverse implication f (c) 0 f has a local extreme at x c.
wœÊ œ
7. No, because the interval 0 x 1 fails to be closed. The Extreme Value Theorem says that if the function is
continuous throughout a finite closed interval a x b then the existence of absolute extrema is guaranteed onŸŸ
that interval.
8. The absolute maximum is 1 1 and the absolute minimum is 0 0. This is not inconsistent with the Extreme Valuekk kkœ œ
Theorem for continuous functions, which says a continuous function on a closed interval attains its extreme values on that
interval. The theorem says nothing about the behavior of a continuous function on an interval which is half open and half
closed, such as , so there is nothing to contradict.Ò"ß "Ñ
9. (a) There appear to be local minima at x 1.75œ
and 1.8. Points of inflection are indicated at
approximately x 0 and x 1.œœ„
(b) f (x) x 3x 5x 15x x x 3 x 5 . The pattern y
w (&% ### $ w
$
œ œ œ ± ± ± ±
$ & $
!
abab ÈÈÈ
indicates a local maximum at x 5 and local minima at x 3 .œœ„
$
ÈÈ
(c)
10. (a) The graph does not indicate any local
extremum. Points of inflection are indicated at
approximately x and x .œ œ"
$
%
(b) f (x) x 2x 5 x x 2 x 5 . The pattern f )( indicates
w(% $$ ( w
($
œ œ œ ± ±
!&#
10
xabab ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

276 Chapter 4 Applications of Derivatives
a local maximum at x 5 and a local minimum at x 2 .œœ
($
ÈÈ
(c)
11. (a) g(t) sin t 3t g (t) 2 sin t cos t 3 sin (2t) 3 g 0 g(t) is always falling and hence mustœÊœ œ ÊÊ
#w w
decrease on every interval in its domain.
(b) One, since sin t 3t 5 0 and sin t 3t 5 have the same solutions: f(t) sin t 3t 5 has the same
## #
œ œ œ
derivative as g(t) in part (a) and is always decreasing with f( 3) 0 and f(0) 0. The Intermediate Value
Theorem guarantees the continuous function f has a root in [ 0].$ß
12. (a) y tan sec 0 y tan is always rising on its domain y tan increases on everyœ Ê œ Êœ Êœ)) ) )
dy
d)
#
interval in its domain
(b) The interval is not in the tangent's domain because tan is undefined at . Thus the tangent
‘
1 1
4ߜ1))
#
need not increase on this interval.
13. (a) f(x) x 2x 2 f (x) 4x 4x. Since f(0) 2 0, f(1) 1 0 and f (x) 0 for 0 x 1, weœ Ê œ œ œ ŸŸ
%# w $ w
may conclude from the Intermediate Value Theorem that f(x) has exactly one solution when 0 x 1.ŸŸ
(b) x 0 x 3 1 and x 0 x .7320508076 .8555996772
##
„
#
œÊœÊ¸ ¸
248
ÈÈÈ
14. (a) y y 0, for all x in the domain of y is increasing in every interval inœÊœ Êœ
xxx
x1 (x1) x1 x1
w"
its domain
(b) y x 2x y 3x 2 0 for all x the graph of y x 2x is always increasing and can neverœ Ê œ Ê œ
$w# $
have a local maximum or minimum
15. Let V(t) represent the volume of the water in the reservoir at time t, in minutes, let V(0) a be the initialœ!
amount and V(1440) a (1400)(43,560)(7.48) gallons be the amount of water contained in the reservoirœ
!
after the rain, where 24 hr 1440 min. Assume that V(t) is continuous on [ 1440] and differentiable onœ!ß
( 1440). The Mean Value Theorem says that for some t in ( 1440) we have V (t )!ß !ß œ
!!
w
V(1440) V(0)
1440 0
316,778 gal/min. Therefore at t the reservoir's volumeœœœ
a (1400)(43,560)(7.48) a 456,160,320 gal
1440 1440 min
!
was increasing at a rate in excess of 225,000 gal/min.
16. Yes, all differentiable functions g(x) having 3 as a derivative differ by only a constant. Consequently, the
difference 3x g(x) is a constant K because g (x) 3 (3x). Thus g(x) 3x K, the same form as F(x).œœœ
wd
dx
17. No, 1 differs from by the constant 1. Both functions have the same derivative
x1x 1
x1 x1 x1 x1
œ Ê
.
dx d
dx x 1 (x 1) (x 1) dx x 1
(x 1) x(1)
ˆ‰ ˆ‰
""
œœœ
18. f (x) g (x) f(x) g(x) C for some constant C the graphs differ by a vertical shift.
ww
œœ Êœ Ê
2x
x1ab
19. The global minimum value of occurs at x .
"
#œ#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
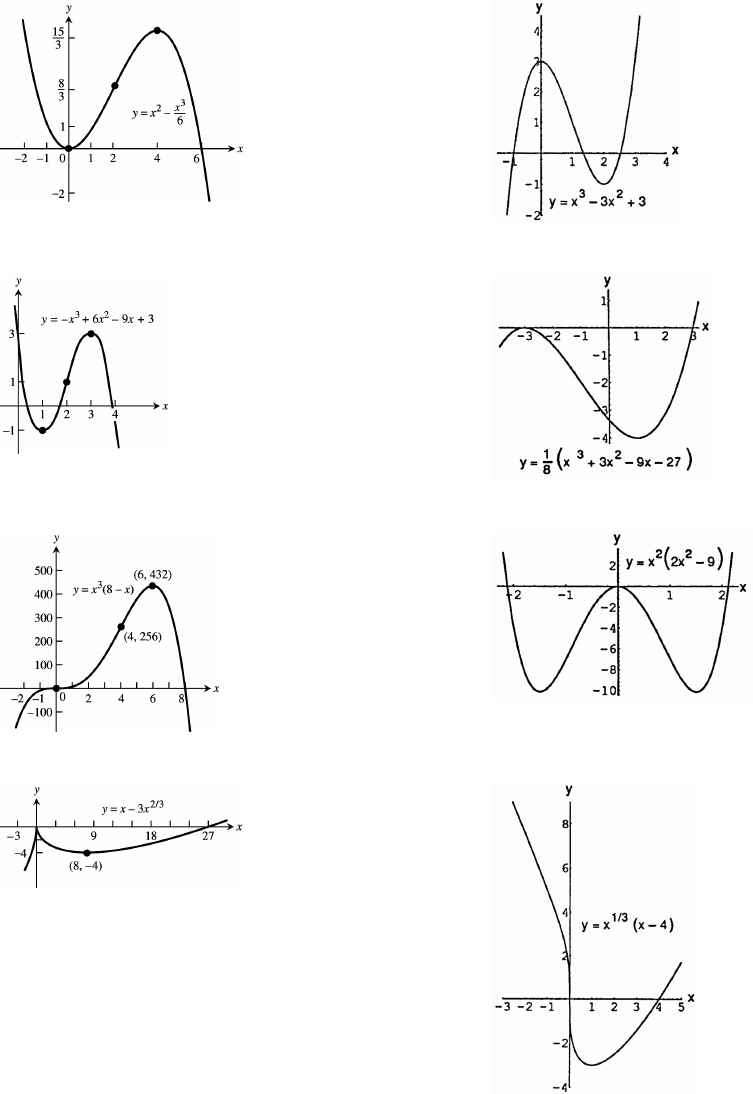
Chapter 4 Practice Exercises 277
20. (a) The function is increasing on the intervals and .Ò$ß #Ó Ò"ß #Ó
(b) The function is decreasing on the intervals and .Ò#ß !Ñ Ð!ß "Ó
(c) The local maximum values occur only at x , and at x ; local minimum values occur at x and at xœ# œ# œ$ œ"
provided f is continuous at x .œ!
21. (a) t 0, 6, 12 (b) t 3, 9 (c) 6 t 12 (d) 0 t 6, 12 t 14œ œ
22. (a) t 4 (b) at no time (c) 0 t 4 (d) 4 t 8œ
23. 24.
25. 26.
27. 28.
29. 30.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
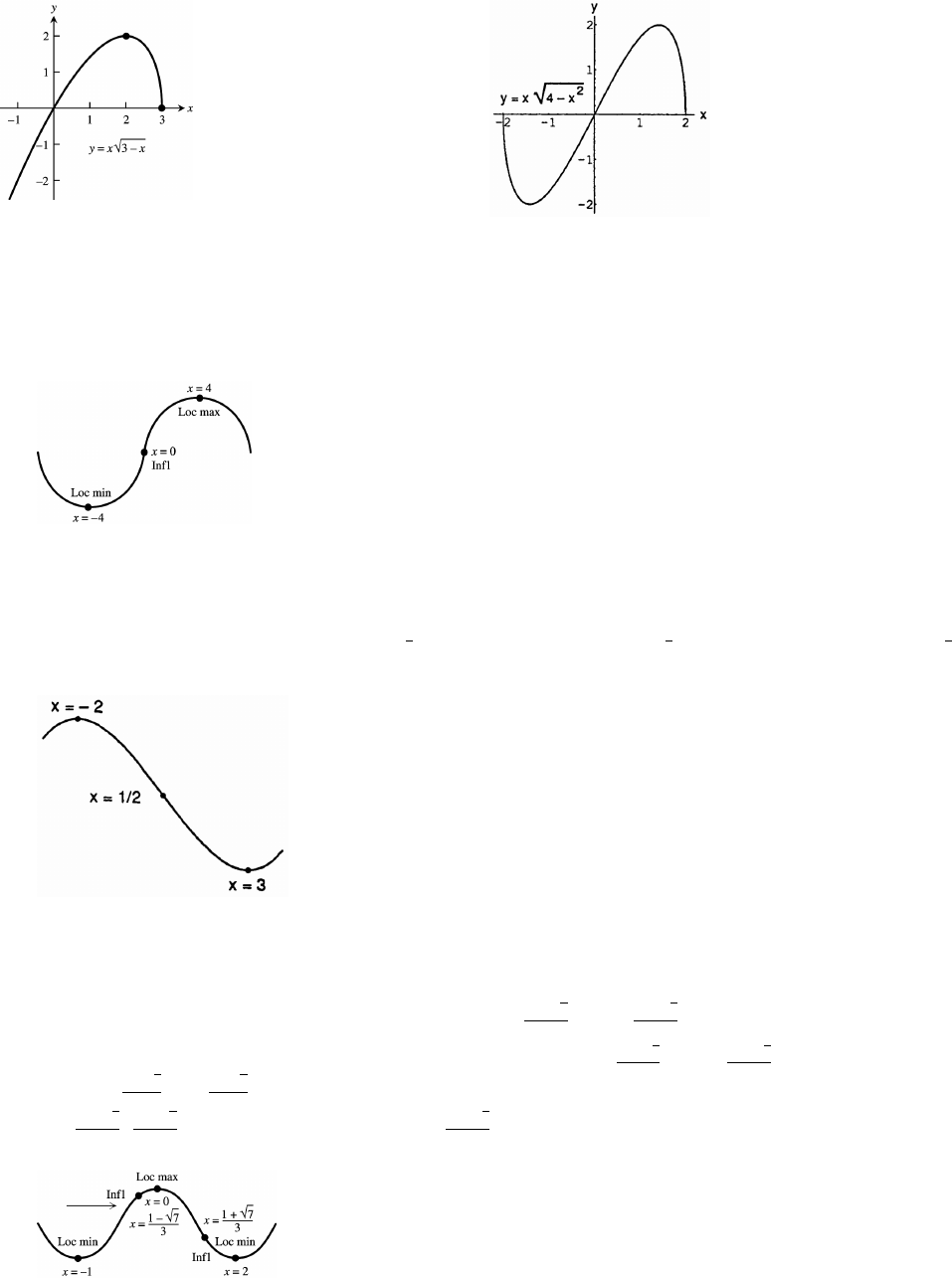
278 Chapter 4 Applications of Derivatives
31. 32.
33. (a) y 16 x y the curve is rising on ( ), falling on ( 4) and ( )
w#w
œ Ê œ ± ± Ê %ß % _ß %ß _
% %
a local maximum at x 4 and a local minimum at x 4; y 2x y the curveÊ œ œ œ Ê œ± Ê
!
ww ww
is concave up on ( ), concave down on ( ) a point of inflection at x 0_ß ! !ß _ Ê œ
(b)
34. (a) y x x 6 (x )(x 2) y the curve is rising on ( 2) and ( ),
w# w
œ œ $ Ê œ ± ± Ê _ß $ß _
# $
falling on ( ) local maximum at x 2 and a local minimum at x 3; y 2x 1#ß $ Ê œ œ œ
ww
y concave up on , concave down on a point of inflection at xÊ œ ± Ê ß _ _ß Ê œ
"Î#
ww "" "
## #
ˆ‰ ˆ ‰
(b)
35. (a) y 6x(x 1)(x 2) 6x 6x 12x y the graph is rising on ( )
w$#w
œ œ Ê œ ± ± ± Ê "ß !
" ! #
and ( ), falling on ( 1) and ( ) a local maximum at x 0, local minima at x 1 and#ß _ _ß !ß # Ê œ œ
x 2; y 18x 12x 12 6 3x 2x 2 6 x x œœœ œ Ê
ww # #
ab
Š‹Š‹
17 17
33
ÈÈ
y the curve is concave up on and , concave down
ww
" ( " (
$$
œ ± ± Ê _ß ß _
ÈÈ ÈÈ
Š‹Š‹
17 17
33
on points of inflection at x
Š‹
1717 17
33 3
„
ÈÈ È
ßÊ œ
(b)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 4 Practice Exercises 279
36. (a) y x (6 4x) 6x 4x y the curve is rising on , falling on
w# # $ w
##
œ œ Ê œ ± ± Ê _ß ß _
!$Î# ˆ‰ ˆ‰
33
a local maximum at x ; y 12x 12x 12x( x) y concave up onÊ œ œ œ " Ê œ ± ± Ê
!"
3
#
ww # ww
( ), concave down on ( ) and ( ) points of inflection at x 0 and x 1!ß " _ß ! "ß _ Ê œ œ
(b)
37. (a) y x 2x x x 2 y the curve is rising on 2 and
w% ### w
œ œ Ê œ ± ± ± Ê _ß
# #
!
ab ÈÈ Š‹
È
2 , falling on 2 2 a local maximum at x 2 and a local minimum at x 2 ;
Š‹ Š ‹
ÈÈÈ È È
ß_ ß Ê œ œ
y 4x 4x 4x(x 1)(x 1) y concave up on ( 0) and ( ),
ww $ ww
œ œ Ê œ ± ± ± Ê "ß "ß _
" ! "
concave down on ( 1) and (0 1) points of inflection at x 0 and x 1_ß ß Ê œ œ „
(b)
38. (a) y 4x x x 4 x y the curve is rising on ( 2 0) and (0 2),
w#%# # w
œ œ Ê œ ± ± ± Ê ß ß
# ! #
ab
falling on ( 2) and ( ) a local maximum at x 2, a local minimum at x 2; y 8x 4x_ß #ß _ Ê œ œ œ
ww $
4x 2 x y concave up on 2 and 0 2 , concaveœ Ê œ ± ± ± Ê _ß ß
# #
!
ab ÈÈ Š‹Š‹
ÈÈ
#ww
down on 2 0 and 2 points of inflection at x 0 and x 2
Š‹Š‹
ÈÈ È
ß ß_Ê œ œ„
(b)
39. The values of the first derivative indicate that the curve is rising on ( ) and falling on ( 0). The slope!ß _ _ß
of the curve approaches as x , and approaches as x 0 and x 1. The curve should therefore_ Ä ! _ Ä Ä
have a cusp and local minimum at x 0, and a vertical tangent at x 1.œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
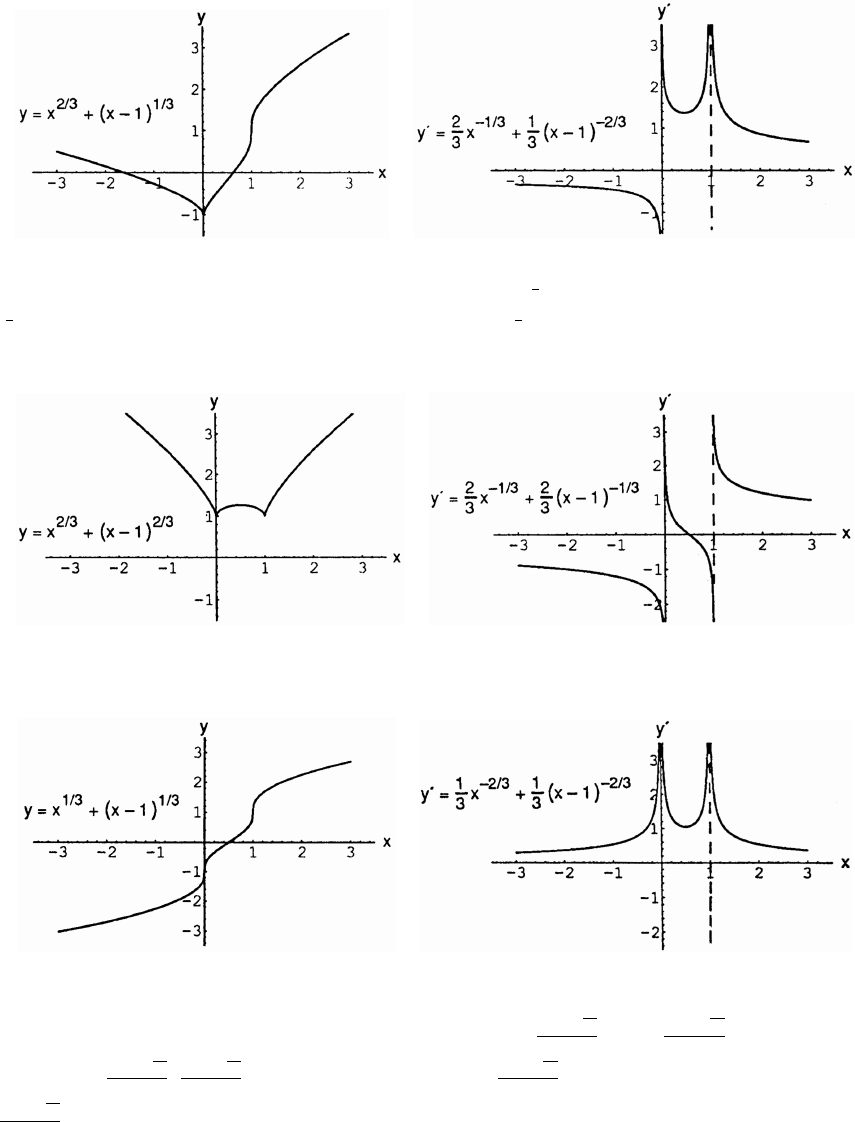
280 Chapter 4 Applications of Derivatives
40. The values of the first derivative indicate that the curve is rising on and ( ), and falling on ( )
ˆ‰
!ß "ß _ _ß !
"
#
and . The derivative changes from positive to negative at x , indicating a local maximum there. The
ˆ‰
" "
# #
ß" œ
slope of the curve approaches as x 0 and x 1 , and approaches as x 0 and as x 1 ,_ Ä Ä _ Ä Ä
indicating cusps and local minima at both x 0 and x 1.œœ
41. The values of the first derivative indicate that the curve is always rising. The slope of the curve approaches _
as x 0 and as x 1, indicating vertical tangents at both x 0 and x 1.ÄÄ œœ
42. The graph of the first derivative indicates that the curve is rising on and , falling
Š‹Š ‹
!ß ß _
17 33 17 33
16 16
ÈÈ
on ( ) and a local maximum at x , a local minimum at_ß ! ß Ê œ
Š‹
17 33 17 33 17 33
16 16 16
ÈÈ È
x . The derivative approaches as x 0 and x 1, and approaches as x 0 ,œ_ÄÄ_Ä
17 33
16
È
indicating a cusp and local minimum at x 0 and a vertical tangent at x 1.œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
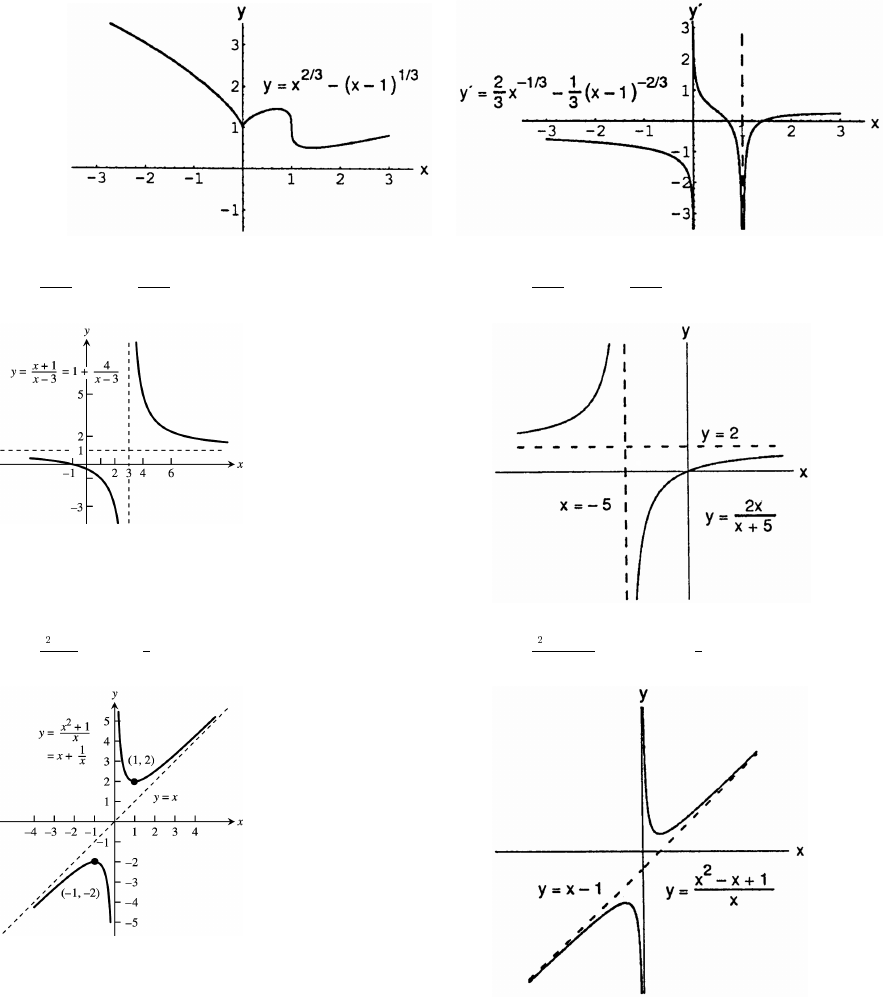
Chapter 4 Practice Exercises 281
43. y 1 44. y 2œœ œœ
x 1 4 2x 10
x 3x 3 x 5x 5
45. y x 46. y x 1œœ œ œ
x 1 x x 1
xx x x
" "
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
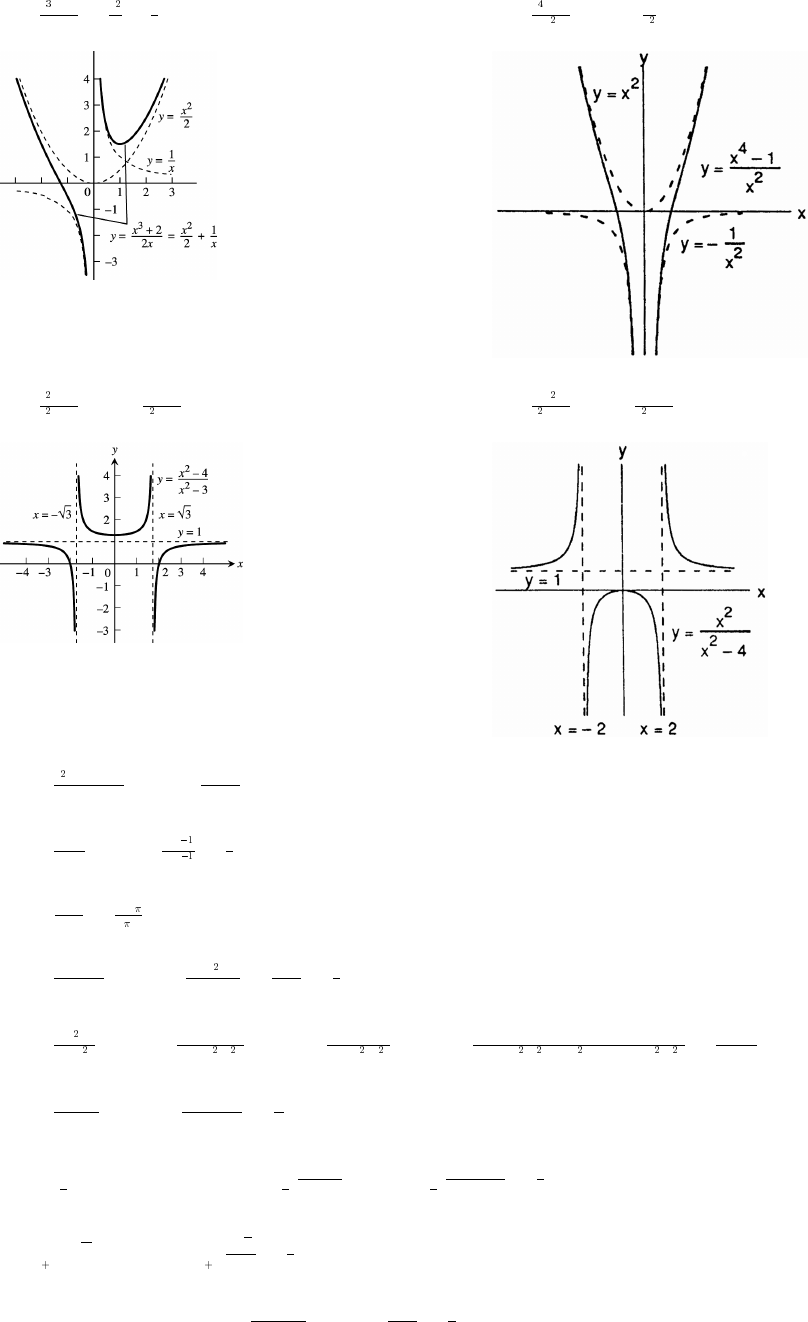
282 Chapter 4 Applications of Derivatives
47. y 48. y xœœ œœ
x 2 x x 1
xx x x
" "
##
#
49. y 1 50. y 1œœ œœ
x 4 x4
x 3x 3 x 4x 4
"
51. lim lim
xxÄ" Ä"
x x x
x
$ % # $
" "
œœ&
52. lim lim
xxÄ" Ä"
xaxa
xbx
b
aa
bb
"
" œœ
53. lim
xÄ1
tan x tan
xœœ!
54. lim lim
xxÄ! Ä!
tan x sec x
xsin x cos x " "" #
""
œœœ
55. lim lim lim lim
xx x xÄ! Ä! Ä! Ä!
sin x sin x cos x
tan x x sec x x sec x x sec x tan x x
sin x cos x
ab ab ab a b
ab ab
ab ab
œœœ
#†
####†#
###
sec x#!#†"
#
ab
œœ"
56. lim lim
xxÄ! Ä!
sin mx m cos mx
sin nx n cos nx n
m
ab ab
ab ab
œœ
57. lim sec x cos x lim lim
xxxÄÎ# ÄÎ# ÄÎ#111
ab ab($œ œ œ
cos x sin x
cos x sin x
ab ab
ab ab
$$$
((((
$
58. lim x sec x lim
xxÄ! Ä!
Èœœœ!
Èx
cos x
!
"
59. lim csc x cot x lim lim
xxxÄ! Ä! Ä!
abœ œ œœ!
" !
"
cos x sin x
sin x cos x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Chapter 4 Practice Exercises 283
60. lim lim lim x lim x lim
xxx xxÄ! Ä! Ä! Ä! Ä!
ˆ‰ Š‹ ab ab
"" " " "
##
xx x x
x
x
œ œ"†œ"œ œ"†_œ_
61. lim x x x x lim x x x x
xxÄÄ__
" œ " †
Š‹Š‹
ÈÈ
ÈÈ
## ##
"
"
ÈÈ
ÈÈ
x x x x
x x x x
lim œ_
xÄ
#"
"
x
x x x x
ÈÈ
Notice that x x for x so this is equivalent toœ!
È#
lim lim œœ œœ"
__
xxÄÄ
x
xx
x x x x
xx xx
x
ÉÉ É
É
#
" "
#
" "
ÈÈ
62. lim lim lim lim lim
xx xxxÄÄ ÄÄÄ__ ___
œ œ œ œ
Š‹
xx x x
x x x x x
xx xx
x
" " " " %
" " #'"#
"
abab
abab x
x"#
lim lim œœœ!
__
xxÄÄ
"# "
#% #xx
63. (a) Maximize f(x) x 36 x x (36 x) where 0 x 36œ œ ŸŸ
ÈÈ"Î# "Î#
f (x) x (36 x) ( 1) derivative fails to exist at 0 and 36; f(0) 6,Êœ œ Ê œ
w "Î# "Î#
""
##
#
ÈÈ
ÈÈ
36 x x
x 36 x
and f(36) 6 the numbers are 0 and 36œÊ
(b) Maximize g(x) x 36 x x (36 x) where 0 x 36œ œ ŸŸ
ÈÈ"Î# "Î#
g (x) x (36 x) ( 1) critical points at 0, 18 and 36; g(0) 6,Êœ œ Ê œ
w "Î# "Î#
""
##
#
ÈÈ
ÈÈ
36 x x
x 36 x
g(18) 2 18 6 2 and g(36) 6 the numbers are 18 and 18œœ œÊ
ÈÈ
64. (a) Maximize f(x) x (20 x) 20x x where 0 x 20 f (x) 10x xœœ ŸŸÊœ
È"Î# $Î# w "Î# "Î#
#
3
0 x 0 and x are critical points; f(0) f(20) 0 and f 20œœÊœ œ œœ œ
20 3x 20 20 20 20
x3333
#Ȉ‰ ˆ ‰
É
the numbers are and .œÊ
40 20
33
20 40
33
È
È
(b) Maximize g(x) x 20 x x (20 x) where 0 x 20 g (x) 0œ œ ŸŸ Ê œ œ
È"Î# w
#
2 20 x 1
20 x
ÈÈ
20 x x . The critical points are x and x 20. Since g and g(20) 20,ʜʜ œ œ œ œ
Ȉ‰
"
#
79 79 79 81
4444
the numbers must be and .
79
44
"
65. A(x) (2x) 27 x for 0 x 27œŸŸ
"
#
#
ab È
A (x) 3(3 x)(3 x) and A (x) 6x.Êœ œ
ww
w
The critical points are 3 and 3, but 3 is not in the
domain. Since A (3) 18 0 and A 27 0,
wwœ œ
Š‹
È
the maximum occurs at x 3 the largest area isœÊ
A(3) 54 sq units.œ
66. The volume is V x h 32 h . TheœœÊœ
#32
x
surface area is S(x) x 4x x ,œ œ
##
ˆ‰
32 128
xx
where x 0 S (x)Ê œ
w2(x 4) x 4x 16
x
ab
the critical points are 0 and 4, but 0 is not in theÊ
domain. Now S (4) 2 0 at x 4 there
wwœ Ê œ
256
4
is a minimum. The dimensions 4 ft by 4 ft by 2 ft
minimize the surface area.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
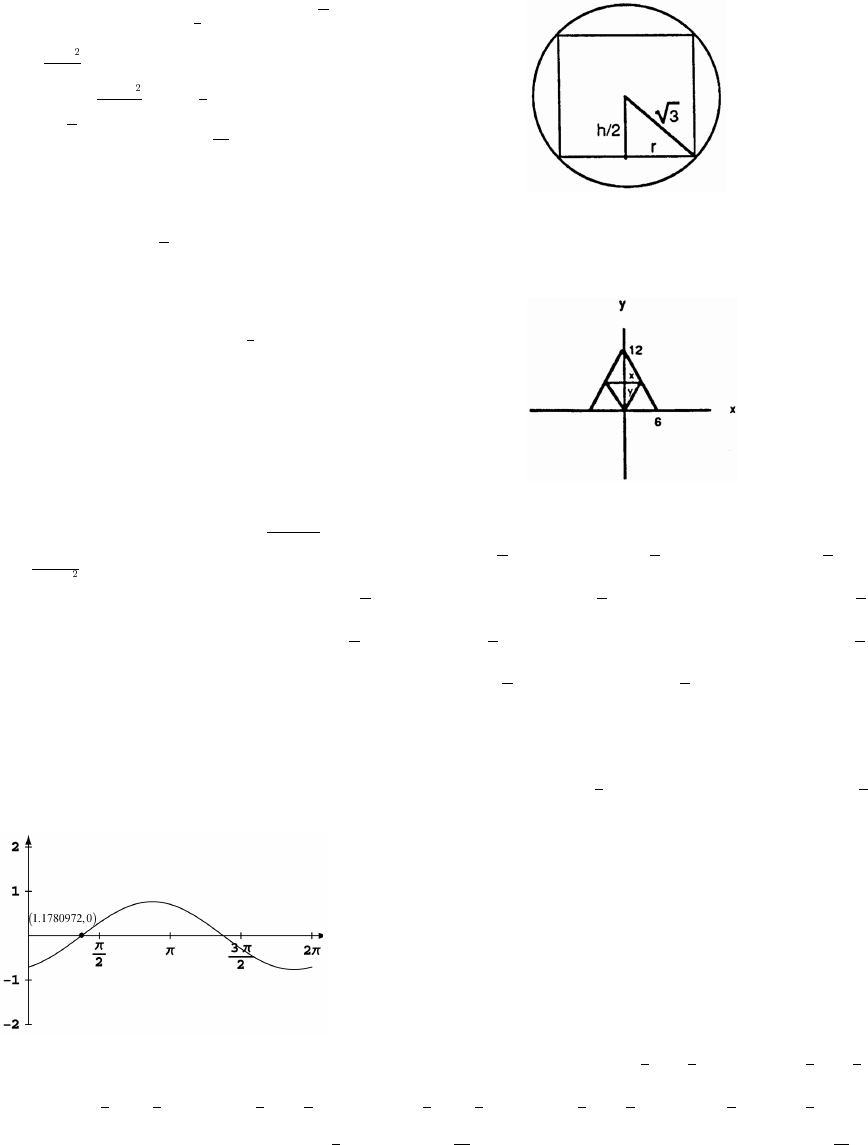
284 Chapter 4 Applications of Derivatives
67. From the diagram we have r 3
ˆ‰ Š‹
È
h
#
###
œ
r . The volume of the cylinder isʜ
#12 h
4
V r h h 12h h , whereœœ œ 11
#$
Š‹ ab
12 h
44
1
0 h 2 3 . Then V (h) (2 h)(2 h)ŸŸ œ
Èw3
4
1
the critical points are 2 and 2, but 2 is not inÊ
the domain. At h 2 there is a maximum sinceœ
V (2) 3 0. The dimensions of the largest
wwœ 1
cylinder are radius 2 and height 2.œœ
È
68. From the diagram we have x radius andœ
y height 12 2x and V(x) x (12 2x), whereœœ œ
"#
31
0 x 6 V (x) 2 x(4 x) and V (4) 8 . TheŸŸ Ê œ œ
ww
w
11
critical points are 0 and 4; V(0) V(6) 0 x 4œœÊœ
gives the maximum. Thus the values of r 4 andœ
h 4 yield the largest volume for the smaller cone.œ
69. The profit P 2px py 2px p , where p is the profit on grade B tires and 0 x 4. Thusœœ ŸŸ
ˆ‰
40 10x
5 x
P (x) x 10x 20 the critical points are 5 5 , 5, and 5 5 , but only 5 5 is in
w#
œÊ
2p
(5 x) ab Š‹Š‹ Š‹
ÈÈ È
the domain. Now P (x) 0 for 0 x 5 5 and P (x) 0 for 5 5 x 4 at x 5 5 there
ww
ʜ
Š‹ Š‹ Š‹
ÈÈ È
is a local maximum. Also P(0) 8p, P 5 5 4p 5 5 11p, and P(4) 8p at x 5 5 thereœœ¸ œÊœ
Š‹Š‹ Š‹
ÈÈ È
is an absolute maximum. The maximum occurs when x 5 5 and y 2 5 5 , the units areœ œ
Š‹ Š‹
ÈÈ
hundreds of tires, i.e., x 276 tires and y 553 tires.¸¸
70. (a) The distance between the particles is f t where f t cos t cos t . Then, f t sin t sin t .ll œ œ ab ab ab
ˆ‰ ˆ‰
11
%%
w
Solving f t graphically, we obtain t , t , and so on.
wabœ! ¸"Þ"() ¸%Þ$#!
Alternatively, f t may be solved analytically as follows. f t sin t sin t
ww
)) ))
ab ab ’“’“
ˆ‰ ˆ‰
œ! œ
11 11
sin t cos cos t sin sin t cos cos t sin sin cos tœ œ#
’“’“
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
11 11 11 11 1 1
)) )) )) )) ) )
so the critical points occur when cos t , or t k . At each of these values, f t cos
ˆ‰ abœ! œ œ„
11 1
)) )
$$
1
units, so the maximum distance between the particles is units.¸ „ !Þ('& !Þ('&
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
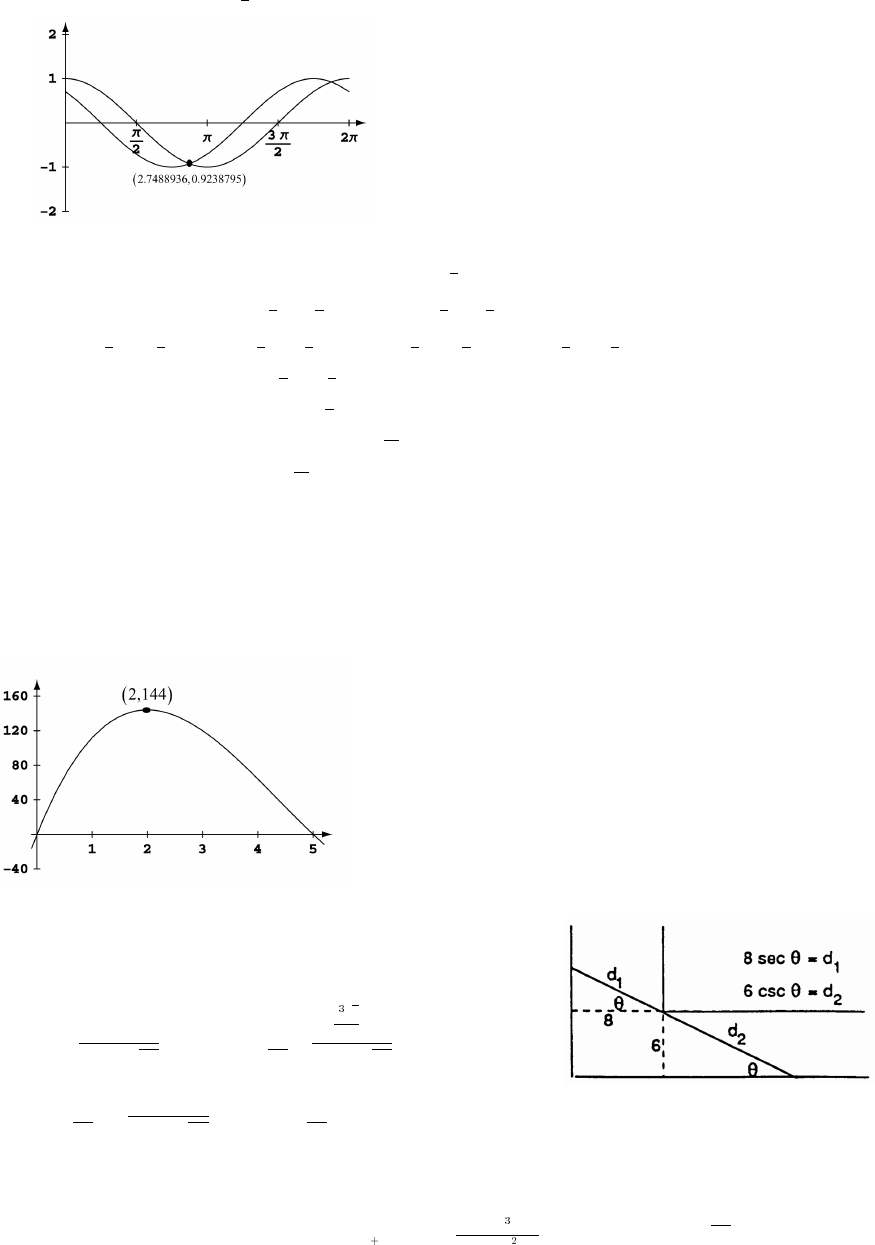
Chapter 4 Practice Exercises 285
(b) Solving cos t cos t graphically, we obtain t , t , and so on.œ ¸ #Þ(%* ¸ &Þ)*!
ˆ‰
1
%
Alternatively, this problem can be solved analytically as follows.
cos t cos tœ
ˆ‰
1
%
cos t cos t
’“’“
ˆ‰ ˆ‰
œ
11 11
)) ))
cos t cos sin t sin cos t cos sin t sin
ˆ‰ ˆ‰ ˆ‰ ˆ‰
œ
11 11 11 11
)) )) )) ))
sin t sin# œ!
ˆ‰
11
))
sin t
ˆ‰
œ!
1
)
tkœ
(
)
11
The particles collide when t . (plus multiples of if they keep going.)œ ¸ #Þ(%*
(
)
11
71. The dimensions will be x in. by x in. by x in., so V x x x x x x x for"! # "' # œ "! # "' # œ % &# "'!ababab
$#
x . Then V x x x x x , so the critical point in the correct domain is x .! & œ "# "!% "'! œ % # $ #! œ #
w#
ab a ba b
This critical point corresponds to the maximum possible volume because V x for x and V x for
ww
ab ab! ! # !
2 x . The box of largest volume has a height of 2 in. and a base measuring 6 in. by 12 in., and its volume is 144 in.& $
Graphical support:
72. The length of the ladder is d d 8 sec 6 csc . We
"#
œ ))
wish to maximize I( ) 8 sec 6 csc I ( )))))œ Ê
w
8 sec tan 6 csc cot . Then I ( ) 0œ œ)) )) )
w
8 sin 6 cos 0 tan ʜʜÊ
$$
#
)) )
È6
d 4 4 36 and d 36 4 36
"#
$$$
œ œ
ÉÉ
ÈÈÈ
the length of the ladder is aboutÊ
436436436 ft.
Š‹ Š‹
ÈÈÈ
É
œ ¸ "*Þ(
$$ $
$Î#
73. g(x) 3x x 4 g(2) 2 0 and g(3) 14 0 g(x) 0 in the interval [ 3] by the IntermediateœÊ œ œÊ œ #ß
$
Value Theorem. Then g (x) 3 3x x x ; x 2 x 2.22 x 2.196215, and
w# !" #
œ Ê œ œÊœ Êœ
n1 n
3x x 4
33x
nn
n
so forth to x 2.195823345.
&œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
286 Chapter 4 Applications of Derivatives
74. g(x) x x 75 g(3) 21 0 and g(4) 117 0 g(x) 0 in the interval [ ] by the Intermediateœ Ê œ œ Ê œ $ß%
%$
Value Theorem. Then g (x) 4x 3x x x ; x 3 x 3.259259
w$# !"
œ Ê œ œÊœ
n1 n
x x 75
4x 3x
nn
nn
x 3.229050, and so forth to x 3.22857729.Êœ œ
#&
75. x 5x 7 dx 7x C
'ab
$
#
œ
x5x
4
76. 8t t dt C 2t C
'Š‹
$%
###
œ œ
t 8ttt tt
46 6
77. 3 t dt 3t 4t dt C 2t C
''
ˆ‰ˆ ‰
Èœ œœ
43t4t4
t1t
"Î# # $Î#
Š‹
3
78. dt t 3t dt C t C
''
Š‹ˆ‰
Œ È
"" " "
###
"Î# %
Èt
3t3t
t(3) t
œ œ œ
79. Let u r 5 du drœ Ê œ
u du C u C C
''
dr du u
r 5 u1 r 5
ab ab
# "
"
œœ œœœ
'
80. Let u r 2 du drœ Ê œ
È
6 6 6 u du 6 C 3u C C
'''
6 dr dr du u 3
r 2 r 2 r2
u
Š‹ Š‹ Š‹
ÈÈ È
$ #
#
œœœœœœ
'Š‹
81. Let u 1 du 2 d du dœÊ œ Ê œ)))))
#"
#
3 1 d u du u du C u C 1 C
''
)) ) )
ÈȈ‰ Œ ab
### #
"Î# $Î# # $Î#
œ œ œ œ œ
33 3u
'3
82. Let u 7 du 2 d du dœ Ê œ Ê œ)))))
2"
#
d du u du C u C 7 C
''
)
)
ÈÈ
7 u
u2
"" " "
## #
"Î# "Î#
2))œœœœœ
ˆ‰ Œ È
'
83. Let u 1 x du 4x dx du x dxœ Ê œ Ê œ
%$ $
"
4
x 1 x dx u du u du C u C 1 x C
'$ % "Î% "Î% $Î% %
"Î% $Î%
"" " " "
ab ab
ˆ‰ Œ
œ œ œ œ œ
''
44 4 3 3
u3
4
84. Let u 2 x du dx du dxœ Ê œ Ê œ
(2 x) dx u ( du) u du C u C (2 x) C
'œœ œœœ
$Î& $Î& $Î& )Î& )Î&
''
u5 5
88
Š‹
8
5
85. Let u du ds 10 du dsœÊœ Ê œ
s
10 10
"
sec ds sec u (10 du) 10 sec u du 10 tan u C 10 tan C
'## #
s s
10 10
œœœœ
''
ab
86. Let u s du ds du dsœÊœ Ê œ11
"
1
csc s ds csc u du csc u du cot u C cot s C
'## #
"" " "
11œœœœ
''
ab
ˆ‰
11 1 1
87. Let u 2 du 2 d du dœÊœ Ê œ
ÈÈ
)))
"
È2
csc 2 cot 2 d (csc u cot u) du ( csc u) C csc 2 C
''
ÈÈ È
Š‹
))) )œœœ
"" "
ÈÈ È
22 2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 4 Additional and Advanced Exercises 287
88. Let u du d 3 du dœÊ œ Ê œ
)
33
"))
sec tan d (sec u tan u)(3 du) 3 sec u C 3 sec C
')) )
33 3
)œœœ
'
89. Let u du dx 4 du dxœÊ œ Ê œ
x
44
"
sin dx sin u (4 du) 4 du 2 (1 cos 2u) du 2 u C
'' '
##
##
x 1 cos 2u sin 2u
4œœ œœab ˆ‰ ˆ ‰
'
2u sin 2u C 2 sin 2 C sin Cœ œ œ
ˆ‰ ˆ‰
xxxx
44##
90. Let u du dx 2 du dxœÊ œ Ê œ
x
##
"
cos dx cos u (2 du) 2 du (1 cos 2u) du u C
'' '
##
## #
x 1 cos 2u sin 2u
œœ œœab ˆ‰
'
sin x Cœ
x
##
"
91. y dx 1 x dx x x C x C; y 1 when x 1 1 C 1œœœœœœÊœ
''
x 1
xx1
" "
# "
ab
C 1 y x 1ʜʜ
"
x
92. y x dx x 2 dx x 2 x dx 2x x C 2x C;œ œ œ œ œ
'' '
ˆ‰ ˆ ‰ ab
"" "
## # # "
xx 33x
xx
y 1 when x 1 2 C 1 C y 2xœœÊœÊœÊœ
""""
31 3 3 x3
1x
93. 15 t dt 15t 3t dt 10t 6t C; 8 when t 1
dr 3 dr
dt dt
t
œœœœœ
''
Š‹
Ȉ‰
È"Î# "Î# $Î# "Î#
10(1) 6(1) C 8 C 8. Thus 10t 6t 8 r 10t 6t 8 dtÊ œÊœ œ Êœ
$Î# "Î# $Î# "Î# $Î# "Î#
dr
dt 'ˆ‰
4t 4t 8t C; r 0 when t 1 4(1) 4(1) 8(1) C 0 C 0. Therefore,œœ œÊ œÊœ
&Î# $Î# &Î# $Î# ""
r4t4t8tœ
&Î# $Î#
94. cos t dt sin t C; r 0 when t 0 sin 0 C 0 C 0. Thus, sin t
dr dr
dt dt
œ œ œ œÊ œÊ œ œ
'ww
sin t dt cos t C ; r 0 when t 0 1 C 0 C 1. Then cos t 1Êœ œ œ œÊœÊ œ œ
dr dr
dt dt
'"""
w
r (cos t 1) dt sin t t C ; r 1 when t 0 0 0 C 1 C 1. Therefore,Ê œ œ œ œ Ê œ Ê œ
'###
rsin tt1œ
CHAPTER 4 ADDITIONAL AND ADVANCED EXERCISES
1. If M and m are the maximum and minimum values, respectively, then m f(x) M for all x I. If m MŸŸ − œ
then f is constant on I.
2. No, the function f(x) has an absolute minimum value of 0 at x 2 and an absolute
3x 6, 2 x 0
9 x , 0 x 2
œœ
Ÿ
ŸŸ
œ#
maximum value of 9 at x 0, but it is discontinuous at x 0.œœ
3. On an open interval the extreme values of a continuous function (if any) must occur at an interior critical
point. On a half-open interval the extreme values of a continuous function may be at a critical point or at the
closed endpoint. Extreme values occur only where f 0, f does not exist, or at the endpoints of the interval.
ww
œ
Thus the extreme points will not be at the ends of an open interval.
4. The pattern f indicates a local maximum at x 1 and a local
wœ ± ± ± ± œ
"#$%
minimum at x 3.œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

288 Chapter 4 Applications of Derivatives
5. (a) If y 6(x 1)(x 2) , then y 0 for x 1 and y 0 for x 1. The sign pattern is
w#w w
œ
f f has a local minimum at x 1. Also y 6(x 2) 12(x 1)(x 2)
www #
œ ± ± Ê œ œ
" #
6(x 2)(3x) y 0 for x 0 or x 2, while y 0 for 0 x 2. Therefore f has points of inflectionœ Ê
www
w
at x 0 and x 2. There is no local maximum.œœ
(b) If y 6x(x 1)(x 2), then y 0 for x 1 and 0 x 2; y 0 for x 0 and x 2. The sign
ww w
œ "
sign pattern is y . Therefore f has a local maximum at x 0 and
wœ ± ± ± œ
" ! #
local minima at x 1 and x 2. Also, y x x , so y 0 forœ œ œ ")
ww ww
$$
’“’“Š‹ Š‹
17 17
ÈÈ
x and y 0 for all other x f has points of inflection at x .
17 17 17 „
$$ $
ww
ÈÈ È
Ê œ
6. The Mean Value Theorem indicates that f (c) 2 for some c in (0 6). Then f(6) f(0) 12
f(6) f(0)
60
w
œŸ ß Ÿ
indicates the most that f can increase is 12.
7. If f is continuous on [a c) and f (x) 0 on [a c), then by the Mean Value Theorem for all x [a c) we haveßŸß −ß
w
0 f(c) f(x) 0 f(x) f(c). Also if f is continuous on (c b] and f (x) 0 on (c b], then for
f(c) f(x)
cx
w
ŸÊ ŸÊ ß ß
all x (c b] we have 0 f(x) f(c) 0 f(x) f(c). Therefore f(x) f(c) for all x [a b].−ß Ê Ê −ß
f(x) f(c)
xc
8. (a) For all x, (x 1) 0 (x 1) 1 x 2x 1 x . ŸŸ Ê Ÿ Ÿ ÊŸ Ÿ
### #
""
# #
ab ab x
1x
(b) There exists c (a b) such that , from part (a)−ß œ Ê œ Ÿ
cc
1c ba ba 1c
f(b) f(a) f(b) f(a)
#
"
¹¹
¸¸
f(b) f(a) b a .ÊŸkkkk
"
#
9. No. Corollary 1 requires that f (x) 0 for x in some interval I, not f (x) 0 at a single point in I.
ww
œœall
10. (a) h(x) f(x)g(x) h (x) f (x)g(x) f(x)g (x) which changes signs at x a since f (x), g (x) 0 whenœÊœ œ
ww w ww
x a, f (x), g (x) 0 when x a and f(x), g(x) 0 for all x. Therefore h(x) does have a local maximum
ww
at x a.œ
(b) No, let f(x) g(x) x which have points of inflection at x 0, but h(x) x has no point of inflectionœœ œ œ
$'
(it has a local minimum at x 0).œ
11. From (ii), f( 1) 0 a 1; from (iii), either 1 lim f(x) or 1 lim f(x). In either case,œ œ Ê œ œ œ
"
#
a
bc xxÄ_ Ä_
lim f(x) lim lim b 0 and c . For if b , then
xx xĄ_ Ą_ Ą_
œ œ œ"Ê œ œ" œ"
x
bx cx
"
#
1
bx c
x2
x
lim and if c 0, then lim lim . Thus a 1, b 0, and c 1.
xxxĄ_ Ą_ Ą_
111
xc bx
xxx
222
xxx
œ! œ œ œ „_ œ œ œ
12. 3x 2kx 3 0 x x has only one value when 4k 36 0 k 9 or
dy
dx 6
2k 4k 36
œœÊœ Ê œÊœ
###
„
È
k3.œ„
13. The area of the ABC is A(x) (2) 1 x 1 x ,?œœ
"
###"Î#
Èab
where 0 x 1. Thus A (x) 0 and 1 areŸŸ œ Ê „
w
x
1x
È
critical points. Also A 1 0 so A(0) 1 is theab„œ œ
maximum. When x 0 the ABC is isosceles sinceœ?
AC BC 2 .œœ
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
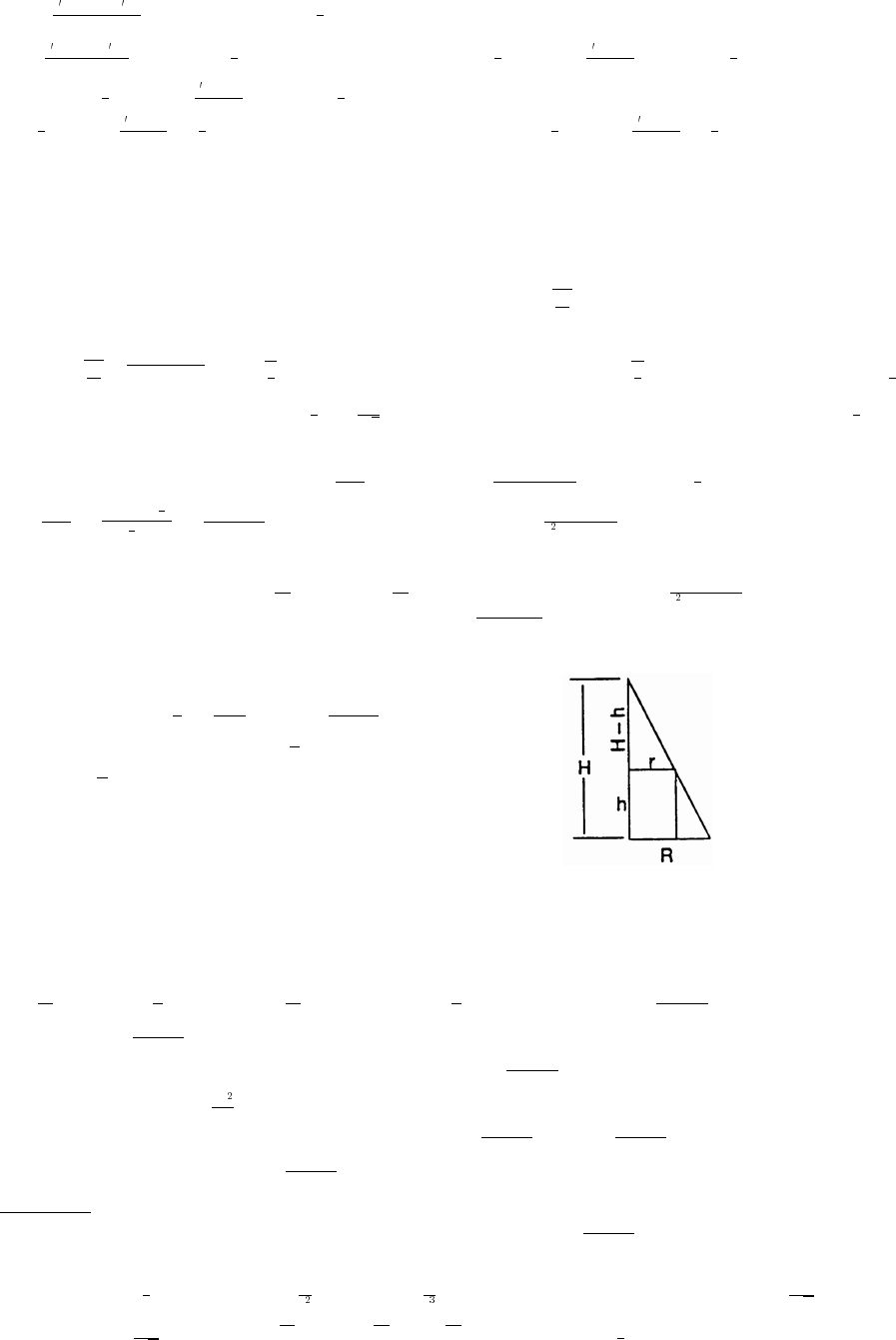
Chapter 4 Additional and Advanced Exercises 289
14. lim f (c) for f (c) 0 there exists a 0 such that 0 h
h0Ä
f(c h) f(c)
h
ww ww
"
#
œÊœ %$$kk kk
f (c) f (c) . Then f (c) 0 f (c) f (c) f (c)Ê œÊ
¹¹
kk kk kk
f(c h) f(c) f(c h)
h h
ww ww w ww ww ww
"""
###
f (c) f (c) f (c) f (c) . If f (c) 0, then f (c) f (c)Ê œ
ww ww ww ww ww ww ww
""
##
kk kk kk
f(c h)
h
f (c) f (c) 0; likewise if f (c) 0, then 0 f (c) f (c).Ê
3 3
f(c h) f(c h)
h h## ##
ww ww ww ww ww
""
(a) If f (c) 0, then h 0 f (c h) 0 and 0 h f (c h) 0. Therefore, f(c) is a local
ww w w
Ê Ê$$
maximum.
(b) If f (c) 0, then h 0 f (c h) 0 and 0 h f (c h) 0. Therefore, f(c) is a local
ww w w
Ê Ê$$
minimum.
15. The time it would take the water to hit the ground from height y is , where g is the acceleration of
É2y
g
gravity. The product of time and exit velocity (rate) yields the distance the water travels:
D(y) 64(h y) 8 hy y , 0 y h D (y) 4 hy y (h 2y) 0, and hœœŸŸÊœÊ
ÉÈÉÉ
ab ab
2y
gg g
22h
#w#
"Î# "Î#
#
are critical points. Now D(0) 0, D and D(h) 0 the best place to drill the hole is at y .œœ œÊ œ
ˆ‰
h8h h
g
# #
È
16. From the figure in the text, tan ( ) ; tan ( ) ; and tan . These equations") ") )œ œ œ
ba a
h 1 tan tan h
tan tan
")
")
give . Solving for tan gives tan or
ba bh
h h a tan h a(b a)
h tan a
œœ œ
tan
1 tan
"
"
a
h
a
h
"
"""
h a(b a) tan bh. Differentiating both sides with respect to h givesab
# œ"
2h tan h a(b a) sec b. Then 0 2h tan b 2h b"" " œ œÊ œÊ œab Š‹
##
dd
dh dh h a(b a)
bh
""
2bh bh ab(b a) h a(b a) h a(a b) .ʜʜʜ
## # È
17. The surface area of the cylinder is S 2 r 2 rh. Fromœ11
#
the diagram we have h and
rHh RHrH
RH R
œÊœ
S(r) 2 r(r h) 2 r r H rœœ 11
ˆ‰
H
R
2 1 r 2 Hr, where 0 r R.œ ŸŸ11
ˆ‰
H
R#
Case 1: H R S(r) is a quadratic equation containingÊ
the origin and concave upward S(r) is maximum atÊ
rR.œ
Case 2: H R S(r) is a linear equation containing theœÊ
origin with a positive slope S(r) is maximum atÊ
rR.œ
Case 3: H R S(r) is a quadratic equation containing the origin and concave downward. ThenÊ
4 1 r 2 H and 0 4 1 r 2 H 0 r . For simplification
dS H dS H RH
dr R dr R 2(H R)
œ œÊ œÊœ11 11
ˆ‰ ˆ‰
we let r .
‡
œRH
2(H R)
(a) If R H 2R, then 0 H 2R H 2(H R) R which is impossible. Ê Ê
RH
2(H R)
(b) If H 2R, then r R S(r) is maximum at r R.œœœÊ œ
‡2R
2R
(c) If H 2R, then 2R H 2H H 2(H R) 1 R r R. Therefore, ÊÊÊÊ
HRH
2(H R) 2(H R)
‡
S(r) is a maximum at r r .œœ
‡
RH
2(H R)
: If H (0 R] or H 2R, then the maximum surface area is at r R. If H (R 2R), then r RConclusion −ß œ œ − ß
which is not possible. If H (2R ), then the maximum is at r r .−ß_ œœ
‡
RH
2(H R)
18. f(x) mx 1 f (x) m and f (x) 0 when x 0. Then f (x) 0 x yields aœÊ œ œ œÊœ
"" "
ww w
w
xxx
2
m
È
minimum. If f 0, then m 1 m 2 m 1 0 m . Thus the smallest acceptable value
Š‹ ÈÈÈ
" "
Èm4
œÊ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

290 Chapter 4 Applications of Derivatives
for m is .
"
4
19. (a) lim lim lim
xxxÄ! Ä! Ä!
#& #& &
$$&$$
&
"! "! "!
sin x sin x sin x
xx
x
ab ab ab
ab ab
œœ œ†"œ
(b) lim sin x cot x lim lim
xxxÄ! Ä! Ä!
abab&$œ œ œ
sin x cos x sin x sin x cos x cos x
sin x cos x
ab ab abab ab ab
ab ab
&$ $&$&&$
$$$$
&
(c) lim x csc x lim lim lim lim
xxxxxÄ! Ä! Ä! Ä! Ä!
#
#
#
##
È#œ œ œ œ
x
sin x
x
sin x
ÈÈ
Š‹
È
"
##
sin x cos x
x
x
x
cos x
Š‹
È
lim œœ
xÄ!
""
##†# #
cos x
Š‹
È
(d) lim sec x tan x lim lim
x/2 x/2 x/2ÄÄÄ111
abœ œ œ!Þ
"
sin x cos x
cos x sin x
(e) lim lim lim lim lim li
xxxxxÄ! Ä! Ä! Ä! Ä!
x sin x cos x cos x cos x sin x
x tan x sec x tan x tan x tan x sec x
" " "
" #
œœœœ œm
xÄ! sin x
sin x
cos x
œ
lim œœ
xÄ!
cos x
# #
"
(f) lim lim lim
xx xÄ! Ä! Ä!
sin x x cos x x sin x cos x
xsin x xcos x sin x xsin x cos x
ab ab a b ab ab
œœ œœ"
###
##
#
(g) lim lim lim
xx xÄ! Ä! Ä!
sec x sec x tan x sec x tan x sec x
xx
" "! "
####
œœ œœ
(h) lim lim lim
xx xÄ# Ä# Ä#
xxx
xxx x
xxx
) # % %%%
% # # # %
# # %
œœœœ$
aba b
abab
20. (a) lim lim lim
xxxÄ_ Ä_ Ä_
È
Èx
x
&
&
"
"
œœ œœ"
x
x
x
x
x
x
É"
"
(b) lim lim lim
xxxÄ_ Ä_ Ä_
##
( "!
x
xx
Èœœ œœ#
x
x
xx
xx
#
"(
É
21. (a) The profit function is P x c ex x a bx ex c b x a. P x ex c bab a b a b a b abœ œ œ#œ!
#w
x . P x e if e so that the profit function is maximized at x .Êœ œ#! ! œ
cb cb
e e
# #
wwab
(b) The price therefore that corresponds to a production level yeilding a maximum profit is
p c e dollars.
¹ˆ‰
x
cb cb
e
œ
##
cb
e
œ œ
(c) The weekly profit at this production level is P x e c b a a.ab a b
ˆ‰ ˆ‰
œ œ
cb cb
eee
cb
##%
#ab
(d) The tax increases cost to the new profit function is F x c ex x a bx tx ex c b t x a.ab a b a b a bœ œ
#
Now F x ex c b t when x . Since F x e if e , F is maximized
www
# #
ab abœ# œ! œ œ œ# ! !
tbc cbt
ee
when x units per week. Thus the price per unit is p c e dollars. Thus, such a taxœœœ
cbt cbt cbt
e e
###
ˆ‰
increases the cost per unit by dollars if units are priced to maximize profit.
cbt cb t
###
œ
22. (a)
The x-intercept occurs when x .
"" "
$xx
$œ!Ê œ$Ê œ
(b) By Newton's method, x x . Here f x x . So x x x x
nn n nn n
fx
fx x
nn
" "
w# #
"
œ œ œ œ œ $
ab
ab
n
n n
ab Š‹
" $
xn
xn
xn
xx x x xx x.œ $ œ# $ œ #$
nn n n n
nn
##
ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 4 Additional and Advanced Exercises 291
23. x x x x so that x is a weighted average of x
"! ! ! "
" "
œ œ œ œ œ
fx
fx q q
q
ab
ab xa qxxa xq a
qx qx qx x
a
qqqq
qq q q
"ab Š‹ Š‹ !
and with weights m and m .
a
xq!"
" "
œœ
q
qq
In the case where x we have x a and x .
!"
!
" "
""
œœœœœ
a
x
qqq
qq qq
q
aaa a
xxx x
qqq q
Š‹ Š‹ Š ‹
24. We have that x h y h r and so x h y h and y h hold.abab abab ab œ # # œ! ## # œ!
##
#dy dy d y
dx dx dx
Thus x y h h , by the former. Solving for h, we obtain h . Substituting this into the second## œ## œ
dy dy
dx dx
xy
"
dy
dx
dy
dx
equation yields y . Dividing by 2 results in y .## # # œ! " œ!
dy d y dy d y
dx dx dx dx
Œ Œ
xy xy
" "
dy dy
dx dx
dy dy
dx dx
25. (a) a t s t k k s t kt C , where s C s t kt . Soab ab a b ab ab abœ œ ! Ê œ ! œ))Ê œ))Ê œ ))
ww w w w
""
s t t C where s C so s t t. Now s t whenab ab ab abœ )) ! œ ! Ê œ ! œ )) œ "!!
##
##
kt kt
t . Solving for t we obtain t . At such t we want s t , thus
#
)) „ )) #!! w
kt k
k
)) œ "!! œ œ !
Èab
k or k . In either case we obtain k )) œ ! )) œ ! )) #!! œ !
Š‹ Š‹
)) )) #!! )) )) #!! #
ÈÈ
kk
kk
so that k ft/sec .œ ¸ $)Þ(#
))
#!!
#
(b) The initial condition that s ft/sec implies that s t kt and s t t where k is as above.
ww
#
ab ab ab! œ%% œ %% œ %%
kt
The car is stopped at a time t such that s t kt t . At this time the car has traveled a distance
w%%
abœ %%œ!Ê œ k
s feet. Thus halving the initial velocity quarters
ˆ‰ ˆ‰ ˆ‰ ˆ ‰
%% %% %% %% *') #!!
##))
#
kk kkk
k
œ %% œ œ œ *') œ #&
stopping distance.
26. h x f x g x h x f x f x g x g x f x f x g x g x f x g x g x f xab ab ab ab abab abab abab abab abab aba b
‘ ‘
abœÊœ# # œ# œ#
## w w w w w
. Thus h x c, a constant. Since h , h x for all x in the domain of h. Thus h .œ#†!œ! œ ! œ& œ& "! œ&ab ab ab a b
27. Yes. The curve y x satisfies all three conditions since everywhere, when x , y , and everywhere.œœ"œ!œ!œ!
dy d y
dx dx
28. y x for all x y x x C where C C y x x .
w# $ $ $
œ$ # Ê œ # "œ" #†" Ê œ%Ê œ # %
29. s t a t v s t C. We seek v s C. We know that s t b for some t and s is at a
ww # w w ‡ ‡
$!
ab ab ab a bœœÊœ œ œ !œ œ
t
maximum for this t . Since s t Ct k and s we have that s t Ct and also s t so that
‡w‡
ab ab ab a bœ ! œ! œ œ!
tt
12 12
t C . So C C b C C b C b C
‡"Î$ %Î$
"Î$ "Î$ "Î$ "Î$
$ $$ %
"# % $
œ$ $ œÊ$ œÊ$ œÊ$ œab ab ab ab
ˆ‰ ˆ‰
‘
abC
12
CC b
C . Thus v s b .Êœ œ!œ œ
ab ab È
%%
$$$
!w $Î%
##
bb
ab
30. (a) s t t t v t s t t t k where v k v t t t
ww "Î# "Î# w $Î# "Î# $Î# "Î#
#%#%
$$$$
ab ab ab ab abœÊœœ# !œœÊœ#Þ
(b) s t t t t k where s k . Thus s t t t t .ab ab abœ !œœ œ
%%% % %%%%
"&$$ "& "&$$"&
&Î# $Î# &Î# $Î#
##
31. The graph of f x ax bx c with a is a parabola opening upwards. Thus f x for all x if f x for at mostab ab abœ ! ! œ!
#
one real value of x. The solutions to f x are, by the quadratic equation . Thus we requireabœ! # „ # %
#
bbac
a
Éab
bac bac.ab#%Ÿ!ÊŸ!
##
32. (a) Clearly f x a x b a x b for all x. Expanding we seeabab abœ ÞÞÞ !
""
##
nn
fx ax abx b ax abx babababœ #ÞÞÞ#
## # ## #
""
"" nn
nn
a a a x ab ab ab x b b b .œ ÞÞÞ # ÞÞÞ ÞÞÞ !aba ba b
## ## ## #
" "
# #
"" ##
n n
nn
Thus a b a b a b a a a b b b by Exercise 31.ababab
"" ## ### ### #
""
##
ÞÞÞ ÞÞÞ ÞÞÞ Ÿ!
nn nn
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
292 Chapter 4 Applications of Derivatives
Thus ab ab ab a a a b b b .ababab
"" ## ### ### #
""
##
ÞÞÞ Ÿ ÞÞÞ ÞÞÞ
nn nn
(b) Referring to Exercise 31: It is clear that f x for some real x b ac , by quadratic formula.abœ! Í % œ!
#
Now notice that this implies that
fx ax b ax babab abœ ÞÞÞ
""
##
nn
a a a x ab ab ab x b b bœ ÞÞÞ # ÞÞÞ ÞÞÞ œ!aba ba b
## ## ## #
" "
# #
"" ##
n n
nn
ab ab ab a a a b b bÍ ÞÞÞ ÞÞÞ ÞÞÞ œ !ababab
"" ## ### ### #
""
##
nn nn
ab ab ab a a a b b bÍ ÞÞÞ œ ÞÞÞ ÞÞÞababab
"" ## ### ### #
""
##
nn nn
But now f x a x b for all i n a x b for all i n.abœ!Í œ! œ"ß#ßÞÞÞß Í œ œ! œ"ß#ßÞÞÞß
ii i i
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
CHAPTER 5 INTEGRATION
5.1 ESTIMATING WITH FINITE SUMS
1. f x xabœ#
Since f is increasing on , we use left endpoints to obtainÒ!ß "Ó
lower sums and right endpoints to obtain upper sums.
(a) x and x i x a lower sum is ˜œ œ œ˜œ Ê † œ ! œ
"! " " " " "
## # ### # )
œ!
"###
iii
i
!ˆ‰ ˆ‰
Š‹
(b) x and x i x a lower sum is ˜œ œ œ˜œ Ê † œ ! œ † œ
"! " " " " " $ " ( (
%% % # %)$#
œ!
$#####
iii
i444 4 4
!ˆ‰ ˆ‰ ˆ‰ ˆ‰
Š‹
(c) x and x i x an upper sum is +1˜œ œ œ˜œ Ê † œ œ
"! " " " " &
## # #### )
œ
###
iii
i1
2
!ˆ‰ ˆ‰
Š‹
(d) x and x i x an upper sum is +1˜œ œ œ˜œ Ê † œ œ † œ
"! " " " " " $ " $! "&
%% % # %"'$#
œ"
%####
#
iii
i4444 4
!ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ ‰
Š‹
2. f x xabœ$
Since f is increasing on , we use left endpoints to obtainÒ!ß "Ó
lower sums and right endpoints to obtain upper sums.
(a) x and x i x a lower sum is ˜œ œ œ˜œ Ê † œ ! œ
"! " " " " "
## # ### # "'
œ!
"$$$
iii
i
!ˆ‰ ˆ‰
Š‹
(b) x and x i x a lower sum is ˜œ œ œ˜œ Ê † œ ! œ œ
"! " " " " " $ $' *
% % % # #&' '%
œ!
$$$$$$
iii
i444 4 4
!ˆ‰ ˆ‰ ˆ‰ ˆ‰
Š‹
(c) x and x i x an upper sum is +1˜œ œ œ˜œ Ê † œ œ † œ
"! " " " " " * *
# # # # ### #)"'
œ
$$$
iii
i1
2
!ˆ‰ ˆ‰
Š‹
(d) x and x i x an upper sum is +1˜œ œ œ˜œ Ê † œ œœ œ
" ! " " " " " $ "!! #&
% % % # #&' '%
œ"
%$$$$
$
iii
i4444 4
!ˆ‰ ˆ‰ ˆ‰ ˆ‰
Š‹
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
294 Chapter 5 Integration
3. f xabœ"
x
Since f is decreasing on , we use left endpoints to obtainÒ!ß "Ó
upper sums and right endpoints to obtain lower sums.
(a) x and x i x i a lower sum is ˜ œ œ# œ" ˜ œ"# Ê †#œ# œ
&" " " " "'
#$& "&
œ"
#
i
ix
!ˆ‰
i
(b) x 1 and x i x i a lower sum is ˜œ œ œ"˜œ"Ê †"œ" œ
&" " """" ((
%#$%& '!
œ"
%
i
ix
!ˆ‰
i
(c) x and x i x i an upper sum is ˜ œ œ# œ" ˜ œ"# Ê †#œ# " œ
&" "")
#$$
œ!
"
i
ix
!ˆ‰
i
(d) x 1 and x i x i an upper sum is ˜œ œ œ"˜œ"Ê †"œ"" œ
&" " " " " #&
%#$% "#
œ!
$
i
ix
!ˆ‰
i
4. f x xabœ% #
Since f is increasing on and decreasing on , we useÒ#ß !Ó Ò!ß #Ó
left endpoints on and right endpoints on to obtainÒ#ß !Ó Ò!ß #Ó
lower sums and use right endpoints on and left endpointsÒ#ß !Ó
on to obtain upper sums.Ò!ß #Ó
(a) x and x i x i a lower sum is ˜ œ œ# œ# ˜ œ## Ê #† % # #† %# œ!
# # #
#
#
ab iˆ‰
ab a b
(b) x and x i x i a lower sum is x x˜œ œ" œ#˜œ#Ê % †" % †"
# # ##
%œ! œ$
"%
ab iii
ii
!!
ˆ‰ˆ‰
ab ab
œ" % # % " %" %# œ'
ˆ‰ˆ‰ˆ‰
ab ab a ba b
##
##
(c) x and x i x i a upper sum is ˜ œ œ# œ# ˜ œ## Ê #† % ! #† %! œ"'
# # #
#
#
ab iˆ‰
ab a b
(d) x and x i x i a upper sum is x x˜œ œ" œ#˜œ#Ê % †" % †"
# # ##
%œ" œ#
#$
ab iii
ii
!!
ˆ‰ˆ‰
ab ab
œ" %" %! %! %" œ"%
ˆ‰ˆ‰
abababab
####
5. f x xabœ#
Using 2 rectangles x f fʘ œ œ Ê
"! " " " $
###% %
ˆ‰ˆ‰ ˆ‰
œœœ
"" $ "! &
#% % $# "'
##
Š‹
ˆ‰ ˆ‰
Using 4 rectangles xʘ œ œ
"! "
%%
Ê
""$&(
%))))
ˆ‰ˆ‰ ˆ‰ ˆ‰ ˆ‰
ffff
œ œ
""$&( #"
%)))) '%
####
Š‹
ˆ‰ ˆ‰ ˆ‰ ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
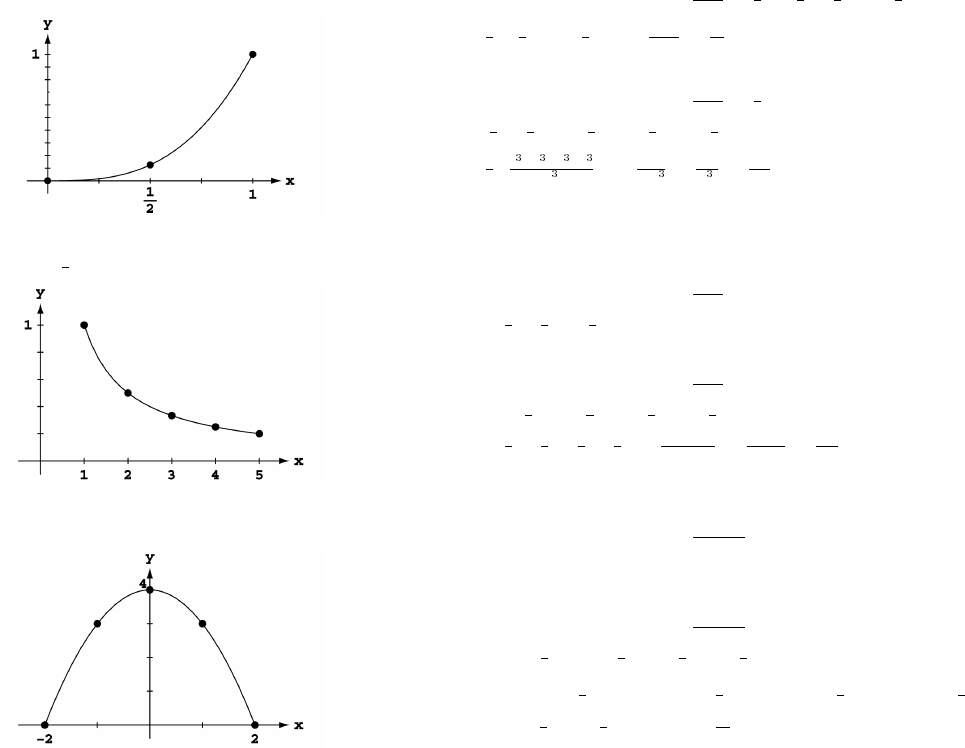
Section 5.1 Estimating with Finite Sums 295
6. f x xabœ$
Using 2 rectangles x f fʘ œ œ Ê
"! " " " $
###% %
ˆ‰ˆ‰ ˆ‰
œœœ
"" $ #) (
#% % #†'% $#
$$
Š‹
ˆ‰ ˆ‰
Using 4 rectangles xʘ œ œ
"! "
%%
Ê
""$&(
%))))
ˆ‰ˆ‰ ˆ‰ ˆ‰ ˆ‰
ffff
œœœœ
" " $ & ( %*' "#% $"
% ) % † ) ) "#)
Š‹
7. f xabœ"
x
Using 2 rectangles x f fʘ œ œ#Ê# # %
&"
#abab ab
œ# œ
ˆ‰
"" $
#% #
Using 4 rectangles xʘ œ œ"
&"
%
Ê"
ˆ‰ˆ‰ ˆ‰ ˆ‰ ˆ‰
ffff
$&(*
####
œ" œ œ œ
ˆ‰
#### "%)) %*' %*'
$&(* $†&†(†* &†(†* $"&
8. f x xabœ% #
Using 2 rectangles x f fʘ œ œ#Ê# " "
# #
#
ab ababab
œ#$$ œ"#ab
Using 4 rectangles xʘ œ œ"
# #
%
ab
Ê"
ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰
ffff
$ ""$
# ###
œ" % % % %
Š‹Š‹Š‹Š‹Š‹
ˆ‰ ˆ‰ ˆ‰ ˆ‰
$ ""$
# ###
# ###
œ "' † # † # œ "' œ ""
ˆ‰
*" "!
%% #
9. (a) D (0)(1) (12)(1) (22)(1) (10)(1) (5)(1) (13)(1) (11)(1) (6)(1) (2)(1) (6)(1) 87 inches¸œ
(b) D (12)(1) (22)(1) (10)(1) (5)(1) (13)(1) (11)(1) (6)(1) (2)(1) (6)(1) (0)(1) 87 inches¸ œ
10. (a) D (1)(300) (1.2)(300) (1.7)(300) (2.0)(300) (1.8)(300) (1.6)(300) (1.4)(300) (1.2)(300)¸
(1.0)(300) (1.8)(300) (1.5)(300) (1.2)(300) 5220 meters (NOTE: 5 minutes 300 seconds)œ œ
(b) D (1.2)(300) (1.7)(300) (2.0)(300) (1.8)(300) (1.6)(300) (1.4)(300) (1.2)(300) (1.0)(300)¸
(1.8)(300) (1.5)(300) (1.2)(300) (0)(300) 4920 meters (NOTE: 5 minutes 300 seconds)œ œ
11. (a) D (0)(10) (44)(10) (15)(10) (35)(10) (30)(10) (44)(10) (35)(10) (15)(10) (22)(10)¸
(35)(10) (44)(10) (30)(10) 3490 feet 0.66 milesœ ¸
(b) D (44)(10) (15)(10) (35)(10) (30)(10) (44)(10) (35)(10) (15)(10) (22)(10) (35)(10)¸
(44)(10) (30)(10) (35)(10) 3840 feet 0.73 milesœ ¸
12. (a) The distance traveled will be the area under the curve. We will use the approximate velocities at the
midpoints of each time interval to approximate this area using rectangles. Thus,
D (20)(0.001) (50)(0.001) (72)(0.001) (90)(0.001) (102)(0.001) (112)(0.001) (120)(0.001)¸
(128)(0.001) (134)(0.001) (139)(0.001) 0.967 miles¸
(b) Roughly, after 0.0063 hours, the car would have gone 0.484 miles, where 0.0060 hours 22.7 sec. At 22.7œ
sec, the velocity was approximately 120 mi/hr.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

296 Chapter 5 Integration
13. (a) Because the acceleration is decreasing, an upper estimate is obtained using left end-points in summing
acceleration t. Thus, t 1 and speed [32.00 19.41 11.77 7.14 4.33](1) 74.65 ft/sec†??œ ¸ œ
(b) Using right end-points we obtain a lower estimate: speed [19.41 11.77 7.14 4.33 2.63](1)¸
45.28 ft/secœ
(c) Upper estimates for the speed at each second are:
t0 12345
v 0 32.00 51.41 63.18 70.32 74.65
Thus, the distance fallen when t 3 seconds is s [32.00 51.41 63.18](1) 146.59 ft.œ¸œ
14. (a) The speed is a decreasing function of time right end-points give an lower estimate for the height (distance)Ê
attained. Also
t012345
v 400 368 336 304 272 240
gives the time-velocity table by subtracting the constant g 32 from the speed at each time incrementœ
t 1 sec. Thus, the speed 240 ft/sec after 5 seconds.?œ¸
(b) A lower estimate for height attained is h [368 336 304 272 240](1) 1520 ft.¸ œ
15. Partition [ ] into the four subintervals [0 0.5], [0.5 1], [1 1.5], and [1.5 2]. The midpoints of these!ß # ß ß ß ß
subintervals are m 0.25, m 0.75, m 1.25, and m 1.75. The heights of the four approximating
"#$ %
œœœ œ
rectangles are f(m ) (0.25) , f(m ) (0.75) , f(m ) (1.25) , and f(m ) (1.75)
"#$ %
$$$ $
œœ œœ œœ œœ
1 27 125 343
64 64 64 64
Notice that the average value is approximated by """"""$"
#####"'
$$$
$
’“
ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ‰
4444
357
œ
. We use this observation in solving the next several exercises.
approximate area under
curve f(x) x
œœ
"
!ß# $
length of [ ] †”•
16. Partition [1 9] into the four subintervals [ ], [3 ], [ ], and [ ]. The midpoints of these subintervals areß "ß$ ß& &ß( (ß*
m 2, m 4, m 6, and m 8. The heights of the four approximating rectangles are f(m ) ,
"#$ % ""
#
œœœ œ œ
f(m ) , f(m ) , and f(m ) . The width of each rectangle is x 2. Thus,
#$ %
"" "
œœ œ œ
46 8 ?
Area2222 average value .¸œÊ ¸ œœ
ˆ‰ ˆ‰ ˆ‰ ˆ‰
""""
##"ß*4 6 8 1 length of [ ] 8 96
25 area 25
ˆ‰
25
12
17. Partition [0 2] into the four subintervals [0 0.5], [0.5 1], [1 1.5], and [1.5 2]. The midpoints of the subintervalsßßßßß
are m 0.25, m 0.75, m 1.25, and m 1.75. The heights of the four approximating rectangles are
"#$ %
œœœ œ
f(m ) sin 1, f(m ) sin 1, f(m ) sin
"# $
""" " "" " ""
######
## #
#
œ œœ œ œœ œ œ
111
424 24
35
2
Š‹
È
1, and f(m ) sin 1. The width of each rectangle is x . Thus,œœ œ œ œ œ
"" " " " "
## # #
%##
24
7
2
1Š‹
È?
Area (1111) 2 average value 1.¸ œ Ê ¸ œ œ
ˆ‰
"
#ß#
area 2
length of [0 2]
18. Partition [0 4] into the four subintervals [0 1], [1 2 ], [2 3], and [3 4]. The midpoints of the subintervalsßßßßßß
are m , m , m , and m . The heights of the four approximating rectangles are
"#$ %
"
### #
œœœ œ
35 7
f(m ) 1 cos 1 cos 0.27145 (to 5 decimal places),
"
%%
œ œ œ
Š‹Š‹ ˆ‰ˆ‰
11
ˆ‰
48
f(m ) 1 cos 1 cos 0.97855, f(m ) 1 cos 1 cos
#
%%%%
œ œ œ œ œ
Š‹ Š‹Š‹ Š‹
ˆ‰ ˆ‰ˆ‰ ˆ‰
1 1
1 1
ˆ‰ ˆ‰
3 5
48 48
3 5
3
0.97855, and f(m ) 1 cos 1 cos 0.27145. The width of each rectangle isœœœœ
%
%%
Š‹Š‹ ˆ‰ˆ‰
11
ˆ‰
7
48
7
x . Thus, Area (0.27145)(1) (0.97855)(1) (0.97855)(1) (0.27145)(1) 2.5 average?œ"¸œÊ
value .¸œœ
area 2.5 5
length of [0 4] 4 8ß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 5.1 Estimating with Finite Sums 297
19. Since the leakage is increasing, an upper estimate uses right endpoints and a lower estimate uses left
endpoints:
(a) upper estimate (70)(1) (97)(1) (136)(1) (190)(1) (265)(1) 758 gal,œœ
lower estimate (50)(1) (70)(1) (97)(1) (136)(1) (190)(1) 543 gal.œ œ
(b) upper estimate (70 97 136 190 265 369 516 720) 2363 gal,œ œ
lower estimate (50 70 97 136 190 265 369 516) 1693 gal.œ œ
(c) worst case: 2363 720t 25,000 t 31.4 hrs;œ ʸ
best case: 1693 720t 25,000 t 32.4 hrsœ ʸ
20. Since the pollutant release increases over time, an upper estimate uses right endpoints and a lower estimate
uses left endpoints:
(a) upper estimate (0.2)(30) (0.25)(30) (0.27)(30) (0.34)(30) (0.45)(30) (0.52)(30) 60.9 tonsœœ
lower estimate (0.05)(30) (0.2)(30) (0.25)(30) (0.27)(30) (0.34)(30) (0.45)(30) 46.8 tonsœœ
(b) Using the lower (best case) estimate: 46.8 (0.52)(30) (0.63)(30) (0.70)(30) (0.81)(30) 126.6 tons,œ
so near the end of September 125 tons of pollutants will have been released.
21. (a) The diagonal of the square has length 2, so the side length is . Area
ÈÈ
Š‹
#œ#œ#
#
(b) Think of the octagon as a collection of 16 right triangles with a hypotenuse of length 1 and an acute angle measuring
.
#
"' )
11
œ
Area sin cos sin œ"' œ% œ# #¸#Þ)#)
ˆ‰ˆ ‰ˆ ‰ È
"
#) ) %
11 1
(c) Think of the 16-gon as a collection of 32 right triangles with a hypotenuse of length 1 and an acute angle measuring
.
#
$# "'
11
œ
Area sin cos sin œ$# œ) œ# #¸$Þ!'"
ˆ‰ˆ ‰ˆ ‰ È
"
#"' "' )
11 1
(d) Each area is less than the area of the circle, . As n increases, the area approaches .11
22. (a) Each of the isosceles triangles is made up of two right triangles having hypotenuse 1 and an acute angle measuring
. The area of each isosceles triangle is A sin cos sin .
#""#
###
11 1 1 1
nn n n n
T
œœ#œ
ˆ‰ˆ ‰ˆ ‰
(b) The area of the polygon is A nA sin , so sin
PT
nn
nn
nn
sin
œœ œ † œ
##
##
Ä_ Ä_
11
lim lim 11
n
n
ˆ‰
(c) Multiply each area by r .
#
Arsin
Tn
œ"#
#
#1
Arsin
Pn
n
œ#
##1
Arlim
nP
Ä_
#
œ1
23-26. Example CAS commands:
:Maple
with( Student[Calculus1] );
f := x -> sin(x);
a := 0;
b := Pi;
plot( f(x), x=a..b, title="#23(a) (Section 5.1)" );
N := [ 100, 200, 1000 ]; # (b)
for n in N do
Xlist := [ a+1.*(b-a)/n*i $ i=0..n ];
Ylist := map( f, Xlist );
end do:
for n in N do # (c)
Avg[n] := evalf(add(y,y=Ylist)/nops(Ylist));
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
298 Chapter 5 Integration
end do;
avg := FunctionAverage( f(x), x=a..b, output=value );
evalf( avg );
FunctionAverage(f(x),x=a..b,output=plot); # (d)
fsolve( f(x)=avg, x=0.5 );
fsolve( f(x)=avg, x=2.5 );
fsolve( f(x)=Avg[1000], x=0.5 );
fsolve( f(x)=Avg[1000], x=2.5 );
: (assigned function and values for a and b may vary):Mathematica
Symbols for , , powers, roots, fractions, etc. are available in Palettes (under File).1Ä
Never insert a space between the name of a function and its argument.
Clear[x]
f[x_]:=x Sin[1/x]
{a,b}={ /4, }11
Plot[f[x],{x, a, b}]
The following code computes the value of the function for each interval midpoint and then finds the average. Each
sequence of commands for a different value of n (number of subdivisions) should be placed in a separate cell.
n =100; dx = (b a) /n;
values = Table[N[f[x]], {x, a dx/2, b, dx}]
average=Sum[values[[i]],{i, 1, Length[values]}] / n
n =200; dx = (b a) /n;
values = Table[N[f[x]],{x, a + dx/2, b, dx}]
average=Sum[values[[i]],{i, 1, Length[values]}] / n
n =1000; dx = (b a) /n;
values = Table[N[f[x]],{x, a dx/2, b, dx}]
average=Sum[values[[i]],{i, 1, Length[values]}] / n
FindRoot[f[x] == average,{x, a}]
5.2 SIGMA NOTATION AND LIMITS OF FINITE SUMS
1. 7
!
2
k1
6k 6 12
k1 11 21 2 3
6(1) 6(2)
œœœ
2. 0
!
3
k1
k1 11 21 31 1 2 7
k 123 236
œœœ
3. cos k cos(1)cos(2)cos(3)cos(4) 1111 0
!
4
k1
11111œœœ
4. sin k sin(1)sin(2)sin(3)sin(4)sin(5)00000 0
!
5
k1
111111œœœ
5. ( 1) sin ( 1) sin ( 1) sin ( ) sin 0 1
!
3
k1
k1
œ"œœ
1 111
k1 3
332
"" #" $"
###
ÈÈ
6. ( 1) cos k ( 1) cos (1 ) ( 1) cos (2 ) ( 1) cos (3 ) ( 1) cos (4 )
!
4
k1
k
œ11111
"#$%
(1) 1 (1) 1 4œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 5.2 Sigma Notation and Limits of Finite Sums 299
7. (a) 222222212481632
!
6
k1
k1
œœ
"" #" $" %" &" '"
(b) 2222222 12481632
!
5
k0
kœœ
!"#$%&
(c) 22 2222212481632
!
4
k
k1
œ œ
"" !" "" #" $" %"
All of them represent 12481632
8. (a) (2) (2) (2) (2) (2) (2) (2) 12481632
!
6
k1
k1
œ œ
"" #" $" %" &" '"
(b) (1)2 (1)2 )2 (1)2 (1)2 (1)2 (1)2 12481632
!
5
k0
kk
œ Ð" œ
!! "" ## $$ %% &&
(c) ( 1) 2 ) 2 ( ) 2 ( ) 2 ( 1) 2 ( ) 2
!
3
k2
k1 k2
œÐ" " " "
#" ## "" "# !" !# "" "# #" ##
(1)2 12481632; œ
$" $#
(a) and (b) represent 12481632; (c) is not equivalent to the other two
9. (a) 1
!
4
k2
()(1)()()
k1 21 31 41 3
" " "
#
""
kœœ
(b) 1
!
2
k0
()(1)()()
k1 01 11 21 3
" " "
#
""
kœœ
(c) 1
!
1
k
() (1) () ()
k2 12 02 12 3
" " "
#
""
kœœ
(a) and (c) are equivalent; (b) is not equivalent to the other two.
10. (a) (k 1) (1 1) (2 1) (3 1) (4 1) 0149
!
4
k1
œœ
# ####
(b) (k1) (11) (01) (11) (21) (31) 014916
!
3
k1
œ œ
# #####
(c) k ( 3) ( 2) ( 1) 9 4 1
!
k3
# ###
œ œ
(a) and (c) are equivalent to each other; (b) is not equivalent to the other two.
11. k 12. k 13.
!!!
644
k1 k1 k1
#"
#k
14. 2k 15. ( 1) 16. ( 1)
!!!
555
k1 k1 k1
k1 k
"
k5
k
17. (a) 3a 3 a 3( 5) 15
!!
nn
k1 k1
kk
œ œœ
(b) b (6) 1
!!
nn
k1 k1
k
b
66 6
kœœœ
""
(c) (a b ) a b 5 6 1
!!!
nnn
k1 k1 k1
kk k k
œ œœ
(d) (a b ) a b 5 6 11
!!!
nnn
k1 k1 k1
kk k k
œ œœ
(e) (b 2a ) b 2 a 6 2( 5) 16
!!!
nnn
k1 k1 k1
kk k k
œ œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

300 Chapter 5 Integration
18. (a) 8a 8 a 8(0) 0 (b) 250b 250 b 250(1) 250
!! ! !
nn n n
k1 k1 k1 k1
kk kk
œœœ œ œœ
(c) (a 1) a 1 0 n n (d) (b 1) b 1 n
!!! !!!
nnn n nn
k1 k1 k1 k1 k1 k1
kk kk
œ œœ œ œ"
19. (a) k 55 (b) k 385
!!
10 10
k1 k1
œœ œ œ
10(10 1) 10(10 1)(2(10) 1)
6
#
#
(c) k 55 3025
!’“
10
k1
$#
#
#
œœœ
10(10 1)
20. (a) k 91 (b) k 819
!!
13 13
k1 k1
œœ œ œ
13(13 1) 13(13 1)(2(13) 1)
6
#
#
(c) k 91 8281
!’“
13
k1
$#
#
#
œœœ
13(13 1)
21. 2k 2 k 2 56 22. k
!! !!
Š‹ Š‹
77 55
k1 k1 k1 k1
œ œ œ œ œ œ
7(7 ) 5(5 1)
k
15 15 15
"
# #
11 1 1
23. 3 k 3 k 3(6) 73
!!!
ab
666
k1 k1 k1
œ œ œ
##
" 6(6 )(2(6) 1)
6
24. k 5 k 5 5(6) 61
!!!
ab
666
k1 k1 k1
## "
œ œ œ
6(6 )(2(6) 1)
6
25. k(3k 5) 3k 5k 3 k 5 k 3 5 240
!! !!
ab Š‹Š‹
55 55
k1 k1 k1 k1
œ œ œ œ
##
#
5(5 1)(2(5) 1) 5(5 1)
6
26. k(2k 1) 2k k 2 k k 2 308
!! !!
ab Š‹
77 77
k1 k1 k1 k1
œ œ œ œ
##
#
7(7 1)(2(7) 1) 7(7 1)
6
27. k k k 3376
!! !!
Œ Œ Š‹Š‹
55 55
k1 k1 k1 k1
k
225 2 5 25
5(5 1) 5(5 1)
œœ œ
$$
""
####
$
#$
28. k k k 588
Œ Œ
!! ! !
Š‹Š‹
77 7 7
k1 k1 k1 k1
##
""
$
##
##
œ œ œ
k
44 4
7(7 1) 7(7 1)
29. (a) (b) (c)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
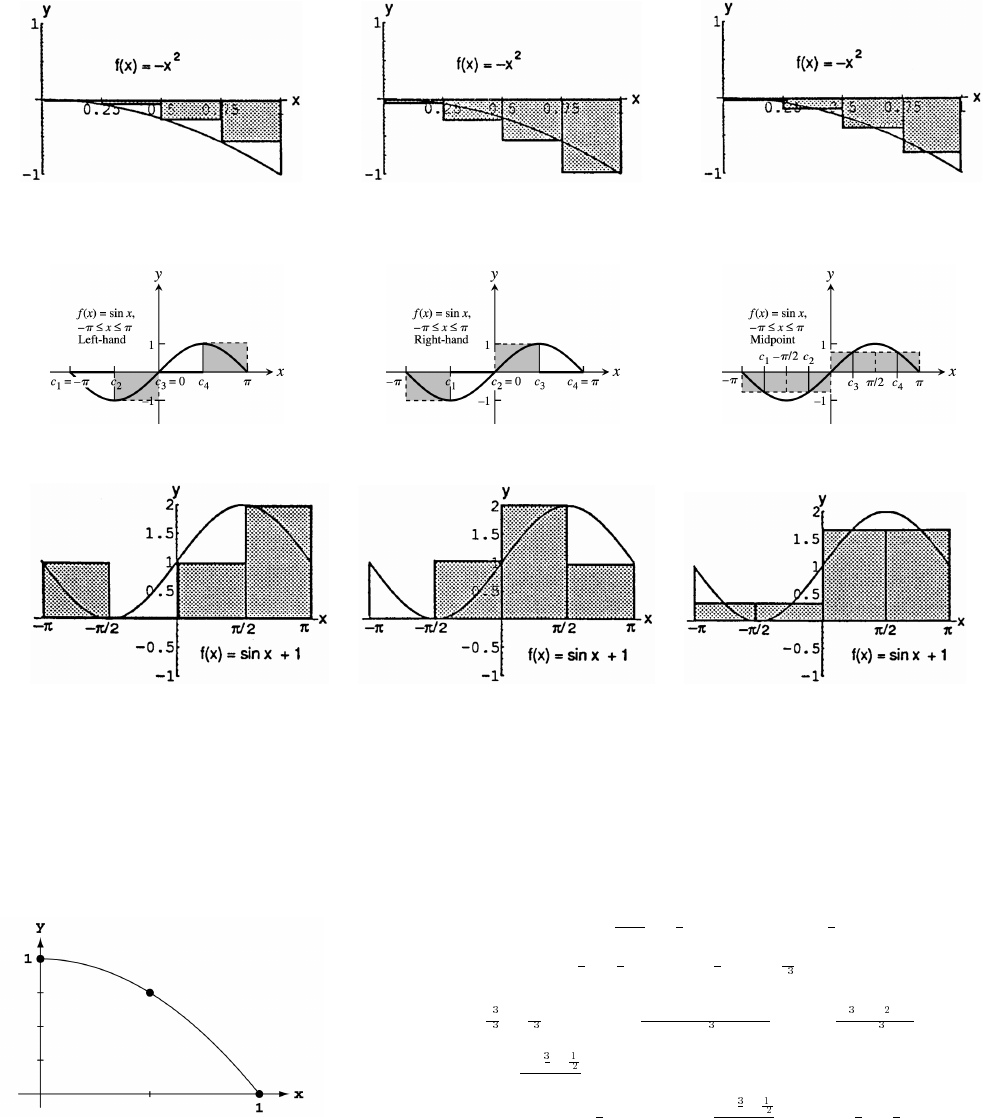
Section 5.2 Sigma Notation and Limits of Finite Sums 301
30. (a) (b) (c)
31. (a) (b) (c)
32. (a) (b) (c)
33. x x 1.2 0 1.2, x x 1.5 1.2 0.3, x x 2.3 1.5 0.8, x x 2.6 2.3 0.3,kkkkkkk kkkk kkkk k
"! #" $# %$
œœ œœ œœ œœ
and x x 3 2.6 0.4; the largest is P 1.2.kkkk ll
&%
œ œ œ
34. x x 1.6 ( 2) 0.4, x x 0.5 ( 1.6) 1.1, x x 0 ( 0.5) 0.5,kkk kkkk kkkk k
"! #" $#
œœ œ œ œ œ
x x 0.8 0 0.8, and x x 1 0.8 0.2; the largest is P 1.1.kkkk kkkk ll
%$ &%
œ œ œ œ œ
35. f x xabœ" #
Since f is decreasing on , 1 we use left endpoints to obtainÒ! Ó
upper sums. x and x i x . So an upper sum˜œ œ œ˜œ
"! "
nn n
ii
is x n i
!! !
ab ab
Š‹
ˆ‰
ii i
nn n
inn n n
i
œ! œ! œ!
" " "
###
"" "
#
" œ " œ
œ œ" œ"
nnnn
nn n n
i
nnnn
"#$
œ!
#" # " "
''
!iaba bab
œ"#
'
nn. Thus,
xlim lim
nn
i
n
in
Ä_ Ä_
œ!
" #""#
#
'$$
!ab Œ
" œ " œ" œ
nn
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
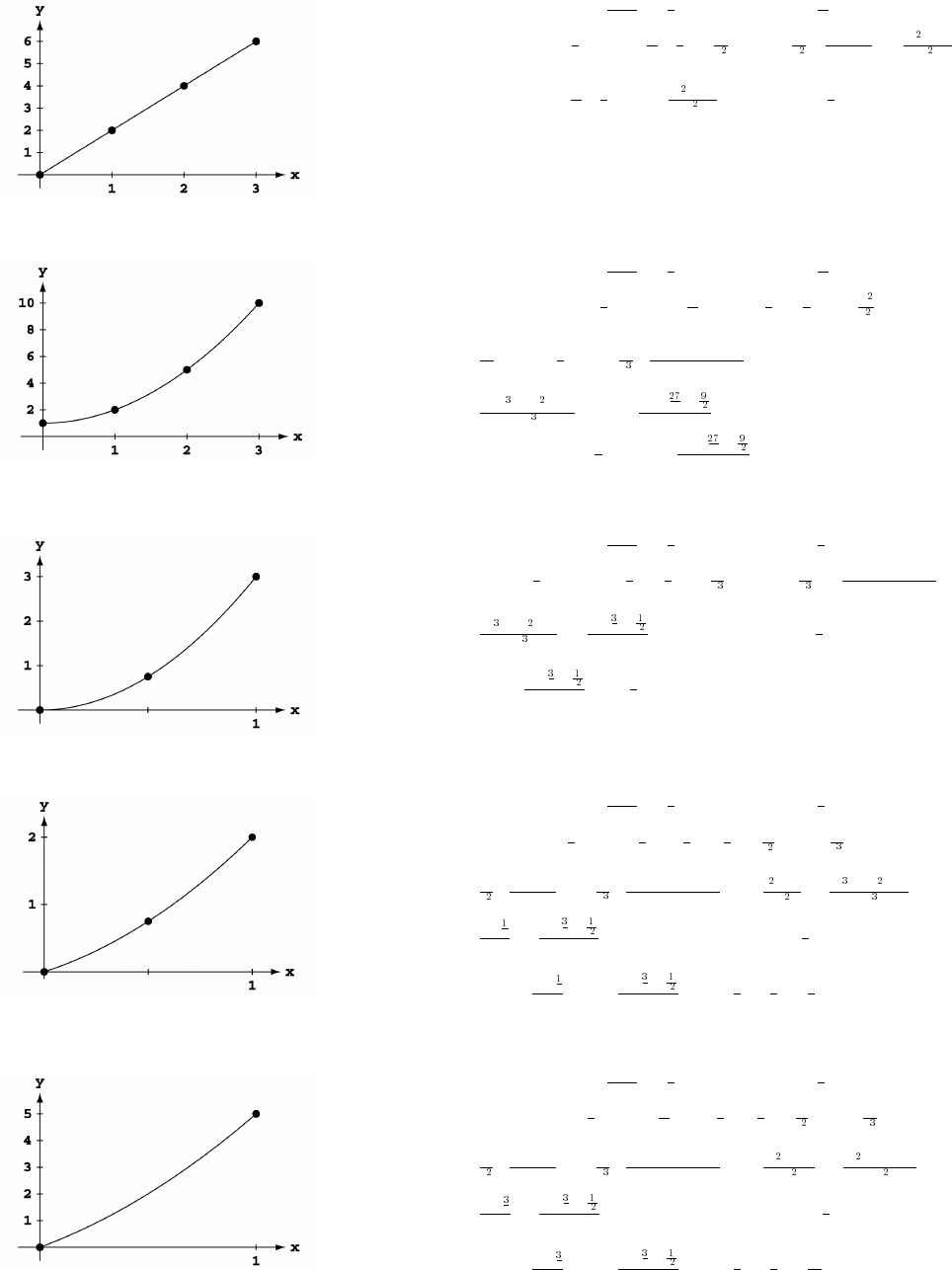
302 Chapter 5 Integration
36. f x xabœ#
Since f is increasing on , we use right endpoints to obtainÒ! $Ó
upper sums. x and x i x . So an upper˜œ œ œ˜œ
$! $ $
nn n
ii
sum is x i
!!!
ˆ‰
ii i
nn n
innnn n n
inn
nn
œ" œ" œ"
$'$")") **
"
#
#œ †œ œ† œ
ab
Thus, .lim lim lim
nnn
i
ninn
nn n n
Ä_ Ä_ Ä_
œ"
'$ ** *
!ˆ‰
†œ œ * œ*
37. f x xabœ"
#
Since f is increasing on , we use right endpoints to obtainÒ! $Ó
upper sums. x and x i x . So an upper˜œ œ œ˜œ
$! $ $
nn n
ii
sum is x
!! !
ab Š‹Š‹
ˆ‰
ii i
nn n
innnnn
ii
œ" œ" œ"
#$$$$*
#
" œ " œ "
œ†œ $
#( $ #(
œ"
#" # "
'nnn
i
nnn n
!Š‹
in aba b
œ$œ$Þ
*# $
##
")
abnnn
n
nn Thus,
x .lim lim
nn
i
n
in
Ä_ Ä_
œ"
#$")
#
!ab Œ
" œ $ œ*$œ"#
nn
38. f x xabœ$ #
Since f is increasing on , we use right endpoints to obtainÒ! "Ó
upper sums. x and x i x . So an upper sum˜œ œ œ˜œ
"! "
nn n
ii
is x i
!! !
ˆ‰ ˆ‰ˆ‰ Š‹
ii i
nn n
innnnn
inn n
œ" œ" œ"
##
""$$
#" # "
'
$œ$ œ œ†
aba b
œœ $
#$ "
##
#
Ä_ œ"
#
nnn
nn
ni
n
i
nn. Thus, xlim !ˆ‰
œœœ"lim
nÄ_
#
##
#
Œ
nn.
39. f x x x x xab a bœ œ "
#
Since f is increasing on , we use right endpoints to obtainÒ! "Ó
upper sums. x and x i x . So an upper sum˜œ œ œ˜œ
"! "
nn n
ii
is x x i i
!! !!
abŠ‹
ˆ‰
ii ii
nn nn
iinnnnn
ii
n
œ" œ" œ" œ"
##
""""
#
œ œ
œ œ
"" #$
" " # "
#'#'nnn
nn nn n
n
nn n nn
Š‹Š ‹
ab aba b
œ
"
#'
#
Ä_ œ"
#"
nn
n. Thus, x xlim
ni
n
iin
!ab
œ œœlim
nÄ_
"
#'#''
# "# &
”•
Š‹
Œ
nn
n.
40. f x x xabœ$ # #
Since f is increasing on , we use right endpoints to obtainÒ! "Ó
upper sums. x and x i x . So an upper sum˜œ œ œ˜œ
"! "
nn n
ii
is x x i i
!! !!
ab
Š‹
ˆ‰
ii ii
nn nn
iinnnnn
ii
n
œ" œ" œ" œ"
##
"$ "$#
#
$# œ # œ
œ œ
$# $$#$"
" " # "
#'#$nnn
nn nn n
n
nn nn
Š‹Š ‹
ab aba b
œ $#
$
#$
#
Ä_ œ"
#"
nn
n. Thus, x xlim
ni
n
iin
!ab
œ œœlim
nÄ_
$
#$#$'
# $# "$
”•
Š‹
Œ
nn
n.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 5.3 The Definite Integral 303
5.3 THE DEFINITE INTEGRAL
1. x dx 2. 2x dx 3. x 3x dx
'''
0
2#$#
" (
!&
ab
4. dx 5. dx 6. 4 x dx
'''
"#
%$"
""
#
x1x
0È
7. (sec x) dx 8. (tan x) dx
''
!
0
9. (a) g(x) dx 0 (b) g(x) dx g(x) dx 8
'''
#&"
"&2
œœœ
(c) 3f(x) dx 3 f(x) dx 3( 4) 12 (d) f(x) dx f(x) dx f(x) dx 6 ( 4) 10
'' '''
"" #""
&&22 2
œ œœ œ œœ
(e) [f(x) g(x)] dx f(x) dx g(x) dx 6 8 2
'''
"""
&&&
œ œœ
(f) [4f(x) g(x)] dx 4 f(x) dx g(x) dx 4(6) 8 16
'''
"""
&&&
œ œœ
10. (a) 2f(x) dx 2 f(x) dx 2( 1) 2
''
""
**
œ œœ
(b) [f(x) h(x)] dx f(x) dx h(x) dx 5 4 9
'''
(((
***
œ œœ
(c) [2f(x) 3h(x)] dx 2 f(x) dx 3 h(x) dx 2(5) 3(4) 2
'''
(((
***
œ œœ
(d) f(x) dx f(x) dx ( 1) 1
''
*"
"*
œ œ œ
(e) f(x) dx f(x) dx f(x) dx 1 5 6
'''
"" (
(* *
œœœ
(f) [h(x) f(x)] dx [f(x) h(x)] dx f(x) dx h(x) dx 5 4 1
'' ''
*( ((
(* **
œ œ œœ
11. (a) f(u) du f(x) dx 5 (b) 3 f(z) dz 3 f(z) dz 5 3
'' ' '
"" " "
22 2 2
œœ œ œ
ÈÈ È
(c) f(t) dt f(t) dt 5 (d) [ f(x)] dx f(x) dx 5
'' ' '
#" " "
"
œ œ œ œ
222
12. (a) g(t) dt g(t) dt 2 (b) g(u) du g(t) dt 2
'' ''
!$ $$
$ ! ! !
œ œ œ œ
ÈÈ
(c) [ g(x)] dx g(x) dx 2 (d) dr g(t) dt 2 1
'' ''
$ $ $ $
!! !!
""
œ œ œ œ œ
ÈÈ
Š‹Š‹
g(r)
22 2
ÈÈ È
13. (a) f(z) dz f(z) dz f(z) dz 7 3 4
'''
$!!
%%$
œ œœ
(b) f(t) dt f(t) dt 4
''
%$
$%
œ œ
14. (a) h(r) dr h(r) dr h(r) dr 6 0 6
'''
"""
$$ "
œ œœ
(b) h(u) du h(u) du h(u) du 6œ œ œ
'''
$""
"$$
Œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
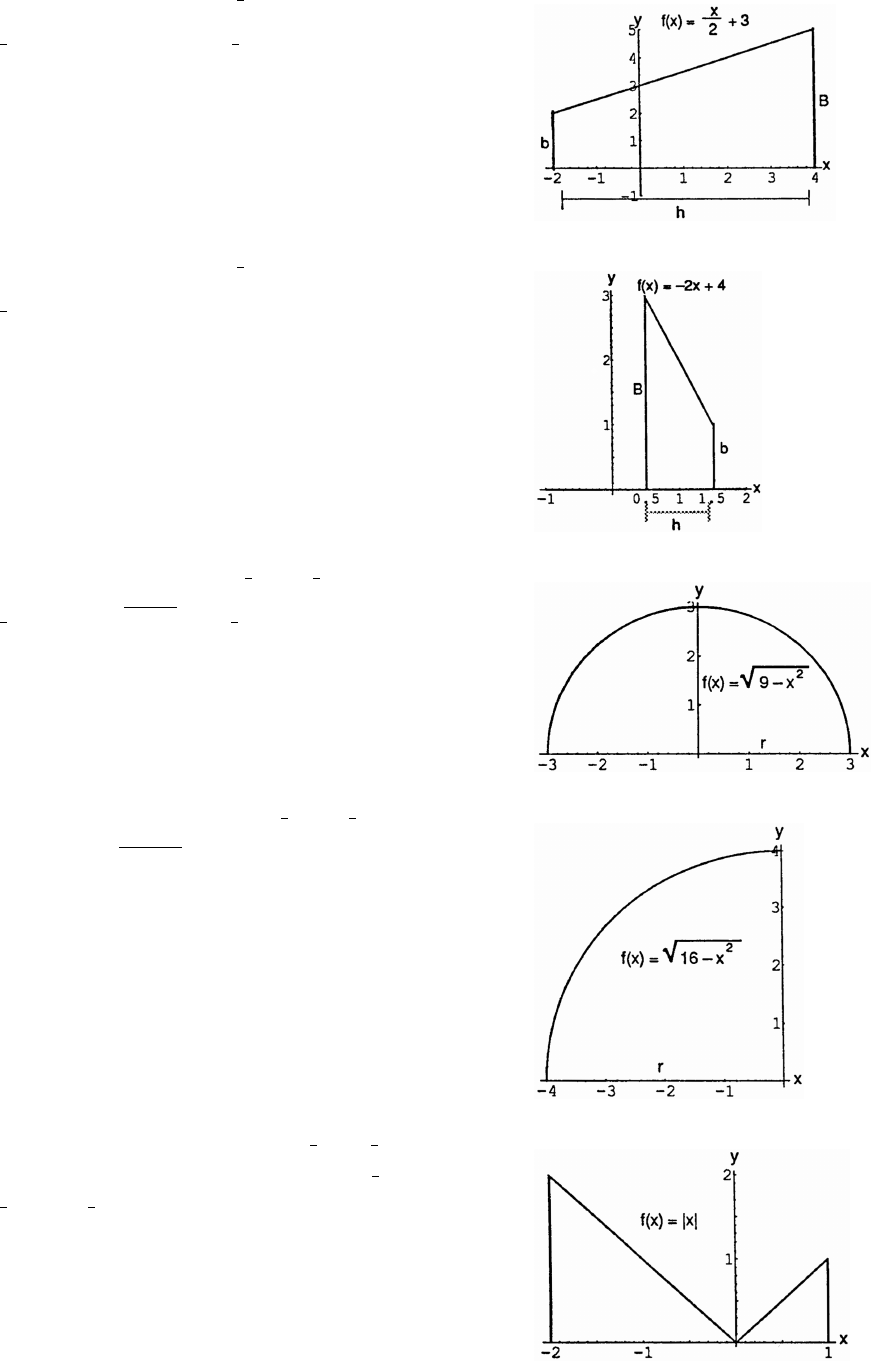
304 Chapter 5 Integration
15. The area of the trapezoid is A (B b)hœ
"
#
(5 2)(6) 21 3 dxœ œÊ
"
##
#
%
'ˆ‰
x
21 square unitsœ
16. The area of the trapezoid is A (B b)hœ
"
#
(3 1)(1) 2 ( 2x 4) dxœ œÊ
"
#"Î#
$Î#
'
2 square unitsœ
17. The area of the semicircle is A r (3)œœ
""
##
##
11
9 x dx square unitsœÊ œ
99
##
$
$
#
11
'È
18. The graph of the quarter circle is A r (4)œœ
""
##
44
11
4 16 x dx 4 square unitsœÊ œ11
'%
!
#
È
19. The area of the triangle on the left is A bh (2)(2)œœ
""
##
2. The area of the triangle on the right is A bhœœ
"
#
(1)(1) . Then, the total area is 2.5œœ
""
##
x dx 2.5 square unitsʜ
'#
"kk
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
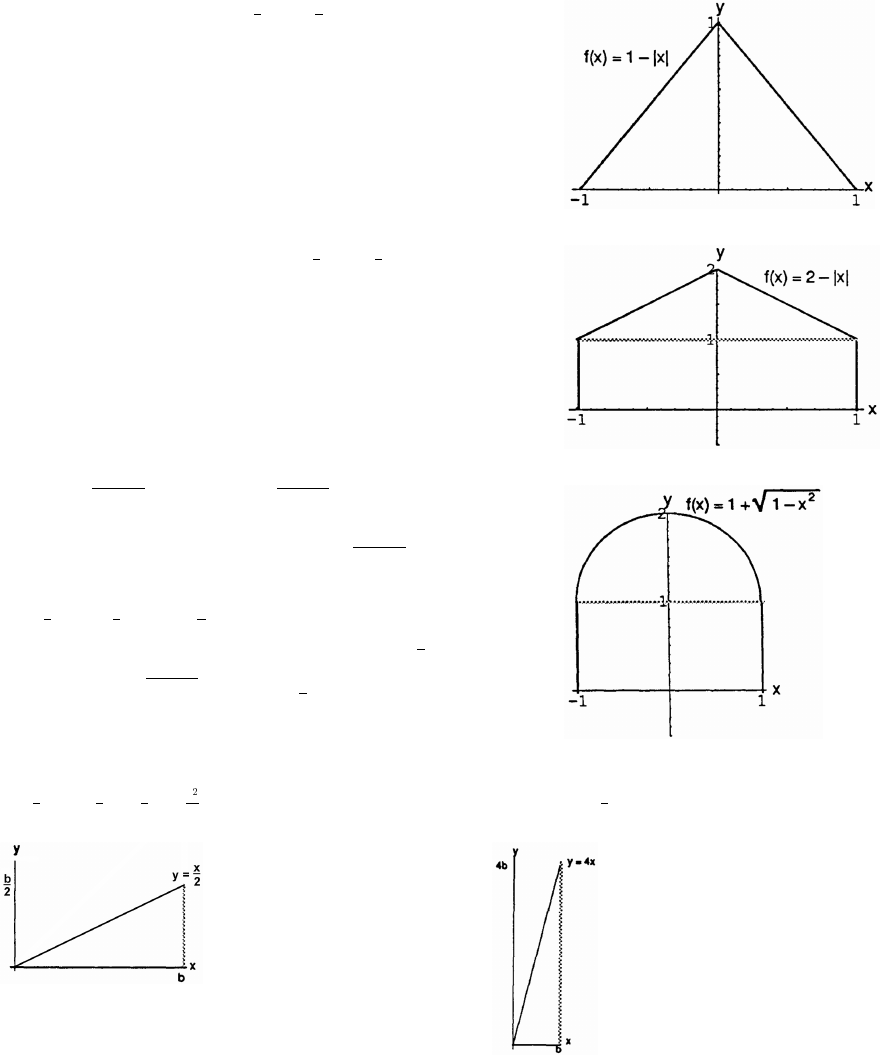
Section 5.3 The Definite Integral 305
20. The area of the triangle is A bh (2)(1) 1œœ œ
""
##
1 x dx 1 square unitʜ
'"
"abkk
21. The area of the triangular peak is A bh (2)(1) 1.œœ œ
""
##
The area of the rectangular base is S w (2)(1) 2.œj œ œ
Then the total area is 3 2 x dx 3 square unitsʜ
'"
"abkk
22. y 1 1 x y 1 1 xœ Ê œ
ÈÈ
##
(y 1) 1 x x (y 1) 1, a circle withÊ œÊ œ
### #
center ( ) and radius of 1 y 1 1 x is the!ß " Ê œ
È#
upper semicircle. The area of this semicircle is
A r (1) . The area of the rectangular baseœœ œ
""
## #
##
11 1
is A w (2)(1) 2. Then the total area is 2œj œ œ 1
#
1 1 x dx 2 square unitsʜ
'"
"
##
Š‹
È1
23. dx (b)( ) 24. 4x dx b(4b) 2b
''
! !
" "
# #
#
b b
xbb
224
œœ œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
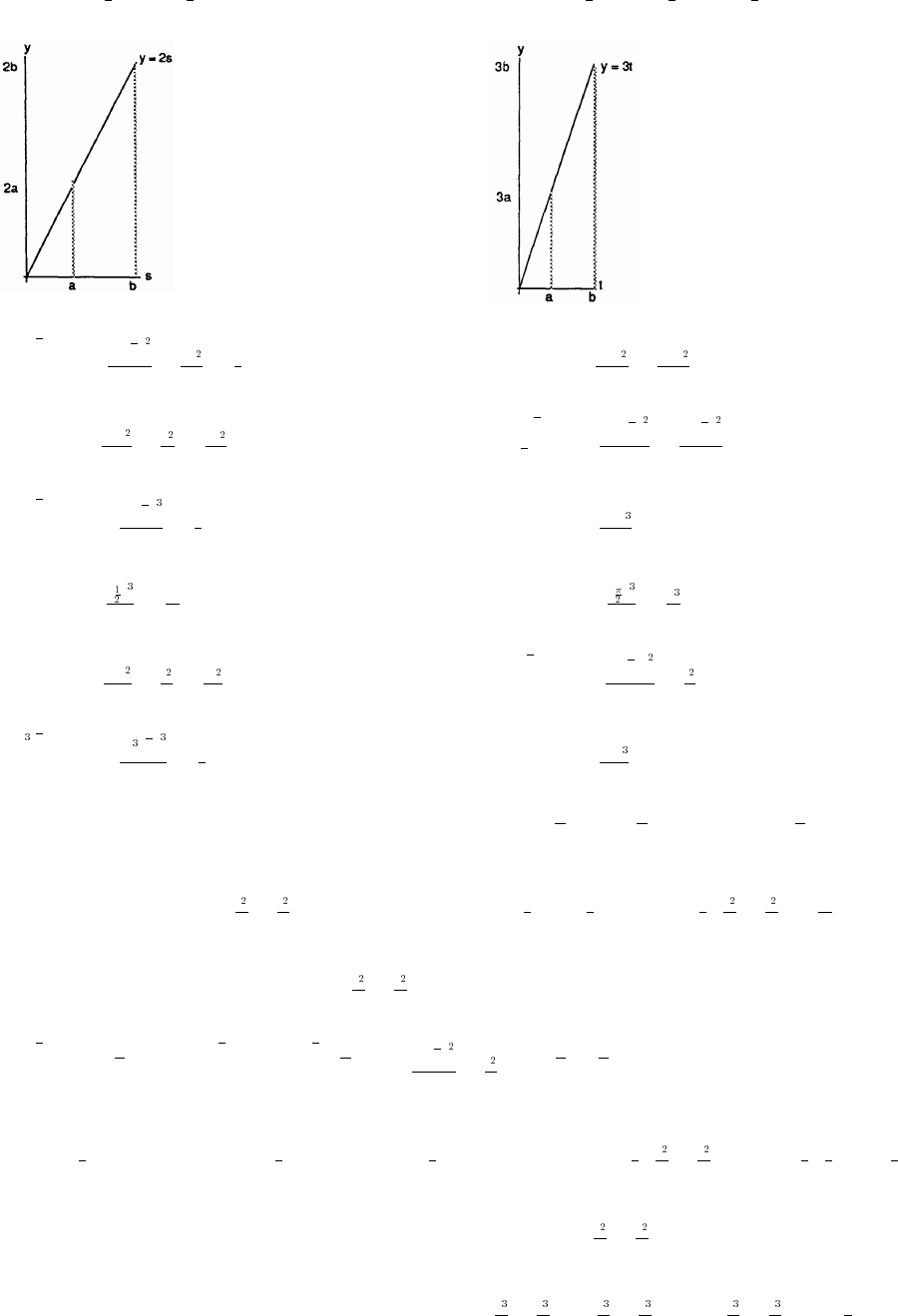
306 Chapter 5 Integration
25. 2s ds b(2b) a(2a) b a 26. 3t dt b(3b) a(3a) b a
''
a a
b b 3
œœ œœ
"" ""
## ###
## ##
ab
27. x dx 28. x dx 3
''
"!Þ&
##Þ&
### ##
"
ÈŠ‹
È
œ œ œœ
2(1) (2.5) (0.5)
29. d 30. r dr 24
''
1
1
111
#&#
### # #
#
))œœ œ œ
(2 ) 352 2
È
ÈŠ‹ Š‹
ÈÈ
31. x dx 32. s ds 0.009
''
0
77
33 3
7(0.3)
ÈŠ‹
È
33
# #
!
!Þ$
œœ œœ
33. t dt 34. d
''
! !
"Î# Î#
# #
"
#
œœ œœ
ˆ‰ ˆ‰
324 3 4
1
1
))
35. x dx 36. x dx a
''
a a
a a
(2a) a3a a
3a
# $
### # #
#
œœ œ œ
ÈŠ‹
È
37. x dx 38. x dx 9b
''
! !
##$
$
ÈŠ‹
È
b b
b
33 3
b(3b)
œœ œœ
39. 7 dx 7(1 3) 14 40. 2 dx 2 ( ) 2 2
''
$ !
"
œœ œ #!œ
2ÈÈ È
41. 5x dx 5 x dx 5 10 42. dx x dx 1
'' ''
!! $$
## ##
&&
""
22
20 x 53 16
88 8 16
œ œ œ œ œ œœ
’“ ’“
43. (2t 3) dt 2 t dt 3 dt 2 3(2 0) 4 6 2
'''
!"!
"
##
22
20
œ œ œœ
’“
44. t 2 dt t dt 2 dt 2 2 0 1 2 1
'''
!!!
##
ÈÈÈ
Š‹
È
222
20
Š‹ ’“
ÈÈÈÈ
–—
œ œ œœ
45. 1 dz 1 dz dz 1 dz z dz 1[1 2]
'''''
####"
""""#
### #####
"""
ˆ‰ ˆ‰
’“
œ œ œœ"œ
zz 2137
4
46. (2z 3) dz 2z dz 3 dz 2 z dz 3 dz 2 3[0 3] 9 9 0
'''''
$$$!$
!!!$!
##
œ œ œœœ
’“
30
47. 3u du 3 u du 3 u du u du 3 3 3 7
''''
""!!
###"
## ## "
œ œ œ œ œ œ
”•
Š‹’“’“’“ ˆ‰
20 0 21 7
33 33 33 3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
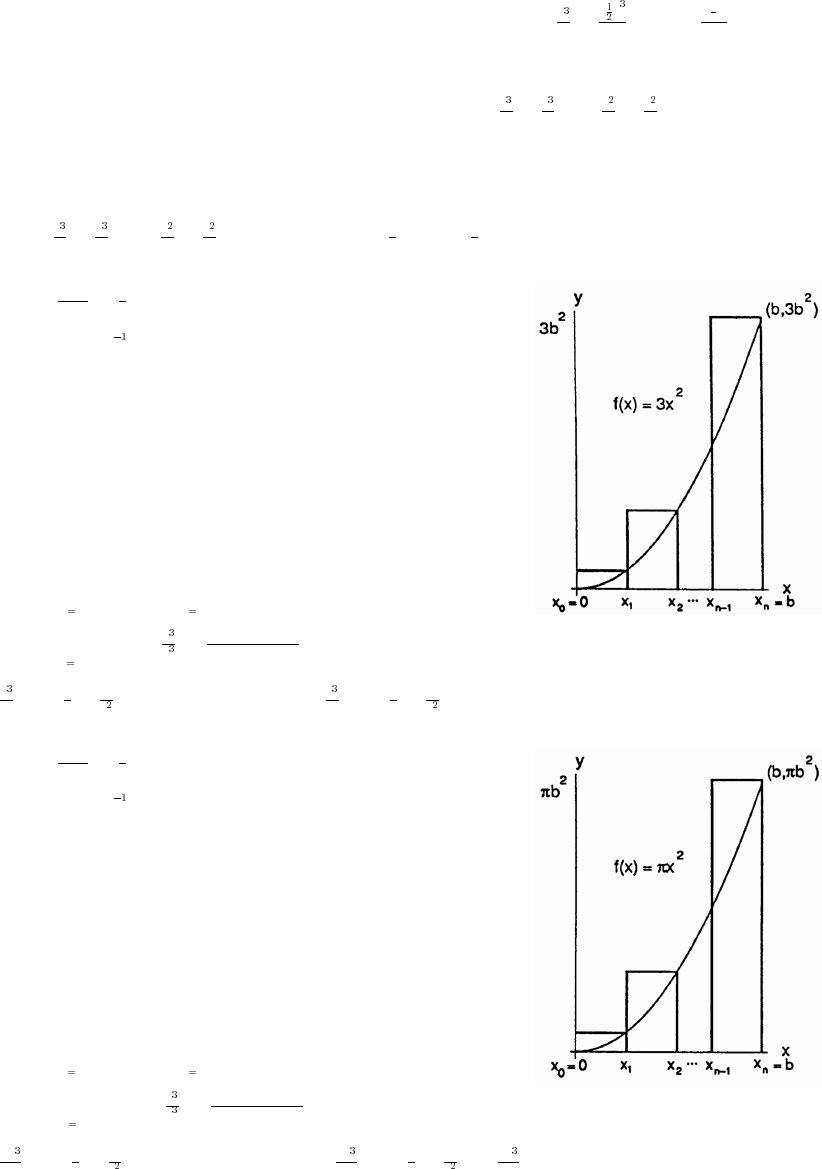
Section 5.3 The Definite Integral 307
48. 24u du 24 u du 24 u du u du 24 24 7
''''
"Î# "Î# ! !
" " " "Î#
## ##
œœœœœ
–—
”•
’“
1
33 3
ˆ‰ ˆ‰
7
8
49. 3x x 5 dx 3 x dx x dx 5 dx 3 5[2 0] (8 2) 10 0
''''
!!!!
####
##
##
ab ’“’“
œ œ œœ
20 20
33
50. 3x x 5 dx 3x x 5 dx 3 x dx x dx 5 dx
'' '''
"! !!!
!" """
###
ab ab
”•
œ œ
3 5(1 0) 5œ œœ
’“Š‹Š‹ ˆ‰
10 10 3 7
33 ## # #
51. Let x and let x 0, x x,??œœ œ œ
b0 b
nn
!"
x 2 x x (n 1) x, x n x b.
#œßáßœ œ œ???
nn
Let the c 's be the right end-points of the subintervals
k
c x , c x , and so on. The rectanglesÊœ œ
""##
defined have areas:
f(c ) x f( x) x 3( x) x 3( x)
"#$
??????œœ œ
f(c)xf(2x)x3(2x)x3(2)(x)
###$
??? ?? ?œœ œ
f(c)xf(3x)x3(3x)x3(3)(x)
$##$
??? ?? ?œœ œ
ã
f(c)xf(nx)x3(nx)x3(n)(x)
n??? ?? ?œœ œ
##$
Then S f(c ) x 3k ( x)
nk
nn
k1 k1
œœ
!!
??
#$
3( x) k 3œœ?$#
!Š‹Š ‹
n
k1
b
n6
n(n1)(2n1)
2 3x dx lim 2 b .œ Ê œ œ
b3 b3
nn nn
b
##
""
!
#$
ˆ‰ ˆ‰
'nÄ_
52. Let x and let x 0, x x,??œœ œ œ
b0 b
nn
!"
x 2 x x (n 1) x, x n x b.
#œßáßœ œ œ???
nn
Let the c 's be the right end-points of the subintervals
k
c x , c x , and so on. The rectanglesÊœ œ
""##
defined have areas:
f(c) x f(x) x (x) x (x)
"#$
???1??1?œœ œ
f(c ) x f(2 x) x (2 x) x (2) ( x)
###$
???1??1?œœ œ
f(c ) x f(3 x) x (3 x) x (3) ( x)
$##$
???1??1?œœ œ
ã
f(c ) x f(n x) x (n x) x (n) ( x)
n???1??1?œœ œ
##$
Then S f(c ) x k ( x)
nk
nn
k1 k1
œœ
!!
?1?
#$
(x) kœœ1? 1
$#
!Š‹Š ‹
n
k1
b
n6
n(n1)(2n1)
2 x dx lim 2 .œ Ê œ œ
111b3 b3 b
6nn 6nn3
b
ˆ‰ ˆ‰
""
!
#
'1nÄ_
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
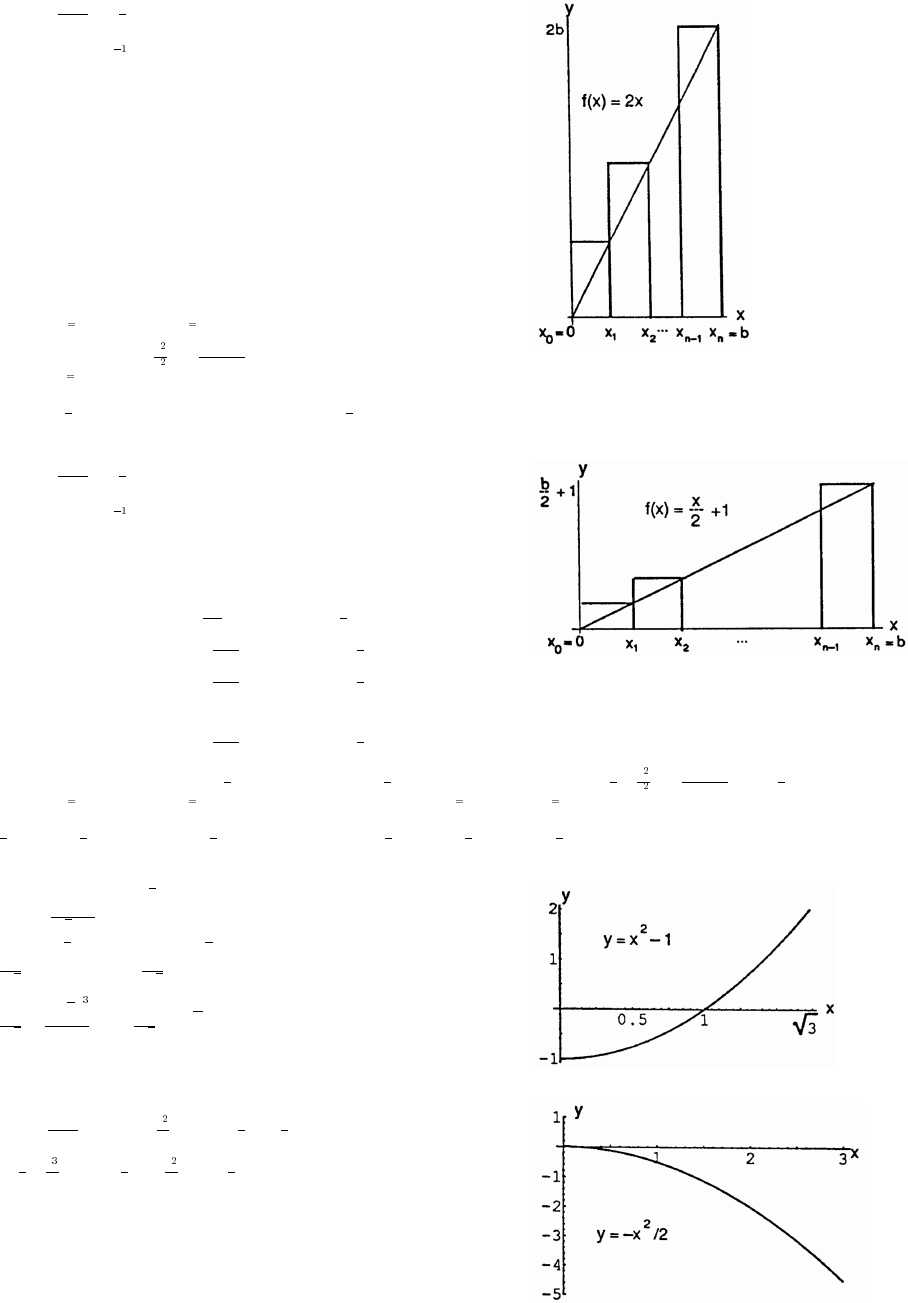
308 Chapter 5 Integration
53. Let x and let x 0, x x,??œœ œ œ
b0 b
nn
!"
x 2 x x (n 1) x, x n x b.
#œßáßœ œ œ???
nn
Let the c 's be the right end-points of the subintervals
k
c x , c x , and so on. The rectanglesÊœ œ
""##
defined have areas:
f(c) x f(x) x 2(x)(x) 2(x)
"#
??? ?? ?œœ œ
f(c ) x f(2 x) x 2(2 x)( x) 2(2)( x)
##
??? ?? ?œœ œ
f(c ) x f(3 x) x 2(3 x)( x) 2(3)( x)
$#
??? ?? ?œœ œ
ã
f(c ) x f(n x) x 2(n x)( x) 2(n)( x)
n??? ?? ?œœ œ
#
Then S f(c ) x 2k( x)
nk
nn
k1 k1
œœ
!!
??
#
2( x) k 2œœ?#
!Š‹Š ‹
n
k1
b
n2
n(n 1)
b 1 2x dx lim b 1 b .œÊ œ œ
###
""
!
ˆ‰ ˆ‰
nn
b
'nÄ_
54. Let x and let x 0, x x,??œœ œ œ
b0 b
nn
!"
x 2 x x (n 1) x, x n x b.
#œßáßœ œ œ???
nn
Let the c 's be the right end-points of the subintervals
k
c x , c x , and so on. The rectanglesÊœ œ
""##
defined have areas:
f(c) x f(x) x 1(x) (x) x
"##
"#
??? ? ??œœœ
ˆ‰
?x
f(c ) x f(2 x) x 1 ( x) (2)( x) x
###
"#
??? ? ??œœœ
ˆ‰
2x?
f(c ) x f(3 x) x 1 ( x) (3)( x) x
$##
"#
??? ? ??œœœ
ˆ‰
3x?
ã
f(c ) x f(n x) x 1 ( x) (n)( x) x
nnx
??? ? ??œœœ
ˆ‰
?
##
"#
Then S f(c ) x k( x) x ( x) k x 1 (n)
nk
nn nn
k1 k1 k1 k1
œœ œ œ
!! !!
ˆ‰ ˆ‰
Š‹Š ‹
?????
"" "
## #
##
bb
n2 n
n(n 1)
b 1 b 1 dx lim b 1 b b b.œÊœ œ
""""
###
!#4n 4n 4
1x
b
ˆ‰ ˆ‰ ˆ ‰ˆ‰
'nÄ_
55. av(f) x 1 dxœ
Š‹ab
"
!
$#
È
È
30 '
x dx 1 dxœ
""
!!
$$
#
ÈÈ
ÈÈ
33
''
30 11 0.œ œœ
""
ÈÈ
Š‹
È
33
3
3
Š‹
È
56. av(f) dx x dxœœ
ˆ‰ ˆ‰
Š‹
"""
# #
!!
$$
#
30 3
x
''
; .œ œ œ
"
## #63
33x3
Š‹
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
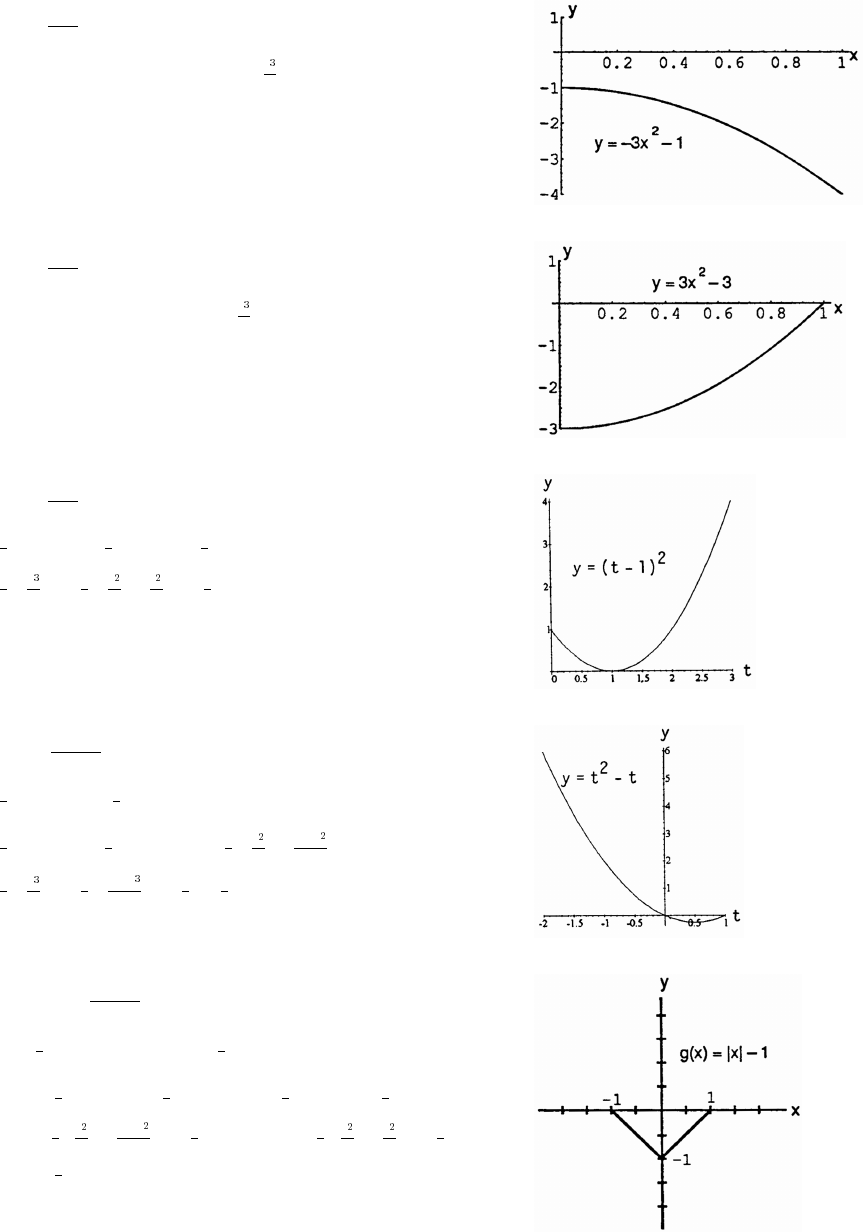
Section 5.3 The Definite Integral 309
57. av(f) 3x 1 dxœœ
ˆ‰ab
"
!
"#
10'
3 x dx 1 dx 3 (1 0)œ œ
''
!!
""
#Š‹
1
3
.œ#
58. av(f) 3x 3 dxœœ
ˆ‰ ab
"
!
"#
10'
3 x dx 3 dx 3 3(1 0)œœ
''
!!
""
#Š‹
1
3
.œ#
59. av(f) (t 1) dtœ
ˆ‰
"
!
$#
30'
t dt t dt 1 dtœ
""
!!!
$$$
#
333
2
'''
(3 0) 1.œœ
""
##33 3 3
3230
Š‹ Š ‹
60. av(f) t t dtœ
Š‹ab
1
1(2) #
"#
'
t dt t dtœ
""
# #
""
#
33
''
t dt t dtœ
"" "
!!
"#
##
##
33 3
1(2)
'' Š‹
.œ œ
"" "
##33 3 3
13
(2)
Š‹ Š ‹
61. (a) av(g) x 1 dxœ
Š‹
abkk
"
"
"
1(1) '
( x 1) dx (x 1) dxœ
""
##
" !
!"
''
x dx 1 dx x dx 1 dxœ
"" ""
## ##
" " ! !
!!""
''''
(0 ( 1)) (1 0)œ
""""
## # # ## # #
Š‹ Š‹
010
(1)
.œ"
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
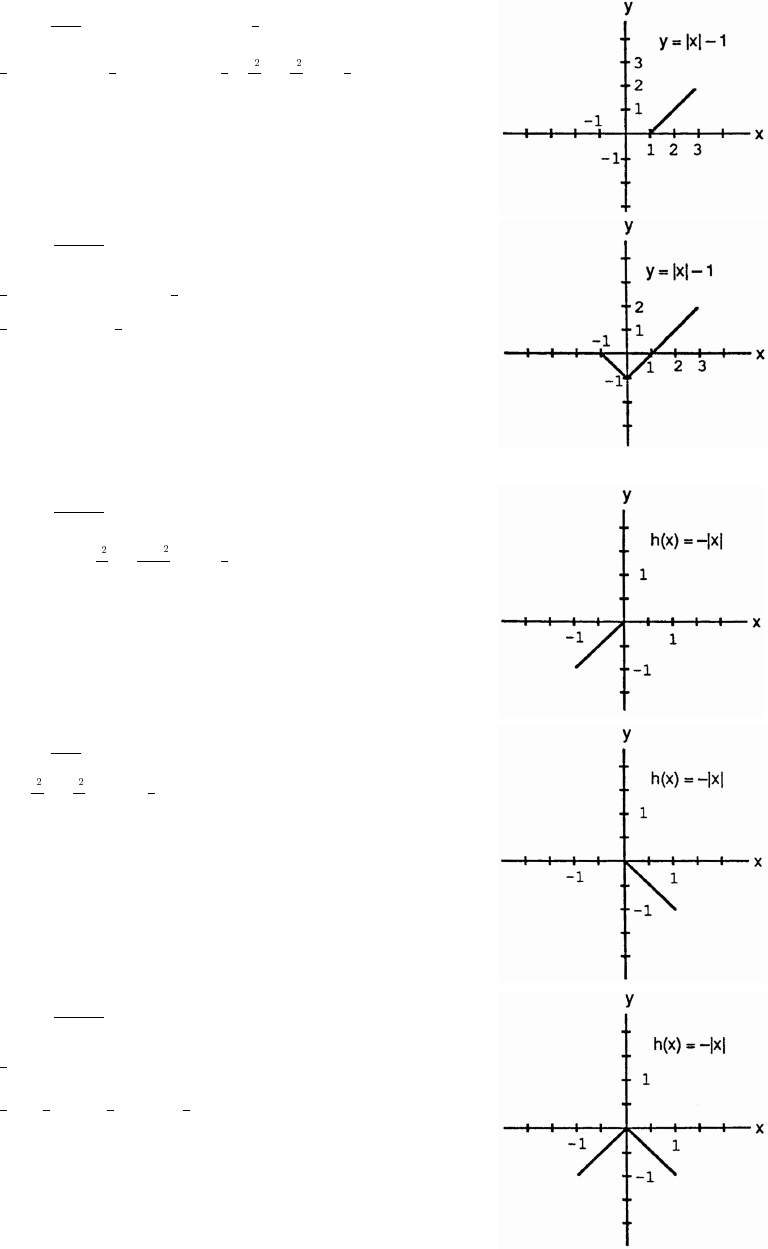
310 Chapter 5 Integration
(b) av(g) x 1 dx (x 1) dxœœ
ˆ‰abkk
""
#
""
$$
31''
x dx 1 dx (3 1)œ œ
"" " "
## ####
""
$$
''Š‹
31
1.œ
(c) av(g) x 1 dxœ
Š‹
abkk
"
"
$
3(1) '
x 1 dx x 1 dxœ
""
" "
"$
44
''
ab abkk kk
( 1 2) (see parts (a) and (b) above).œœ
""
44
62. (a) av(h) x dx ( x) dxœœ
Š‹kk
"
" "
0(1)
00
''
x dx .œœœ
'" ## #
"
00(1)
(b) av(h) x dx x dxœœ
ˆ‰ kk
"
""
10 00
''
.œ œ
Š‹
""
## #
0
(c) av(h) x dxœ
Š‹ kk
"
"
"
1(1) '
x dx x dxœ
"
#"
"
Œ
kk kk
''
0
0
(see parts (a) and (b)œ œ
"" " "
## # #
ˆ‰ˆ‰
above).
63. To find where x x 0, let x x 0 x(1 x) 0 x 0 or x 1. If 0 x 1, then 0 x x a 0 œÊ œÊœ œ Êœ
## #
and b 1 maximize the integral.œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 5.3 The Definite Integral 311
64. To find where x 2x 0, let x 2x 0 x x 2 0 x 0 or x 2. By the sign graph,
%# %# ##
Ÿ œÊ œÊœ œ„ab È
0 0 0 , we can see that x 2x 0 on 2 2 a 2 and b 2 Ÿ ß Ê œ œ
# #
!
ÈÈ ’“
ÈÈ È È
%#
minimize the integral.
65. f(x) is decreasing on [0 1] maximum value of f occurs at 0 max f f(0) 1; minimum value of fœßÊ Êœœ
"
1x
occurs at 1 min f f(1) . Therefore, (1 0) min f dx (1 0) max fÊœœœ Ÿ Ÿ
"" "
#
"
11 1x
0
'
dx 1. That is, an upper bound 1 and a lower bound .ÊŸ Ÿ œ œ
"" "
# #
"
'01x
66. See Exercise 65 above. On [0 0.5], max f 1, min f 0.8. Thereforeßœœœœ
""
10 1(0.5)
(0.5 0) min f f(x) dx (0.5 0) max f dx . On [0.5 1], max f 0.8 andŸ Ÿ ÊŸ Ÿ ß œœ
''
00
0.5 0.5
2
51x 1(0.5)
"" "
#
min f 0.5. Therefore (1 0.5) min f dx (1 0.5) max f dx .œœ Ÿ Ÿ ÊŸ Ÿ
"""
""
11 1x 4 1x 5
0.5 0.5
12
''
Then dx dx dx .
"" "" "
#
""
4 5 1x 1x 5 20 1x 10
22139
00.5 0
0.5
Ÿ Ÿ Ê Ÿ Ÿ
'' '
67. 1 sin x 1 for all x (1 0)( 1) sin x dx (1 0)(1) or sin x dx 1 sin x dx cannotŸ Ÿ Ê Ÿ Ÿ Ÿ Êab ab
####
"""
'''
000
equal 2.
68. f(x) x 8 is increasing on [ ] max f f(1) 1 8 3 and min f f(0) 0 8 2 2 .œ !ß"Ê œœœ œœœ
ÈÈÈ
È
Therefore, (1 0) min f x 8 dx (1 0) max f 2 2 x 8 dx 3.ŸŸ ÊŸŸ
''
00
""
ÈÈ
È
69. If f(x) 0 on [a b], then min f 0 and max f 0 on [a b]. Now, (b a) min f f(x) dx (b a) max f.ß ß Ÿ Ÿ
'a
b
Then b a b a 0 (b a) min f 0 f(x) dx 0.ÊÊ Ê
'a
b
70. If f(x) 0 on [a b], then min f 0 and max f 0. Now, (b a) min f f(x) dx (b a) max f. ThenŸß Ÿ Ÿ Ÿ Ÿ
'a
b
b a b a 0 (b a) max f 0 f(x) dx 0.ÊÊ ŸÊ Ÿ
'a
b
71. sin x x for x 0 sin x x 0 for x 0 (sin x x) dx 0 (see Exercise 70) sin x dx x dxŸÊŸÊ Ÿ Ê
'''
000
"""
0 sin x dx x dx sin x dx sin x dx . Thus an upper bound is .ŸÊ Ÿ Ê Ÿ Ê Ÿ
''' '
000 0
10
""" "
## # #
""
Š‹
72. sec x 1 on sec x 1 0 on sec x 1 dx 0 (see ß Ê ß Ê
xx x
0
### # ## #
"
ˆ‰ ˆ‰
Š‹ ’ “Š‹
11 11 '
Exercise 69) since [0 1] is contained in sec x dx 1 dx 0 sec x dxßßÊÊ
ˆ‰ Š‹
11
## #
"" "
'' '
00 0
x
1 dx sec x dx 1 dx x dx sec x dx (1 0) sec x dx . Ê Ê Ê
''''' '
00000 0
x17
36
""""" "
## #
""
#
Š‹ Š‹
Thus a lower bound is .
7
6
73. Yes, for the following reasons: av(f) f(x) dx is a constant K. Thus av(f) dx K dxœœ
"
ba aaa
bbb
'''
K(b a) av(f) dx (b a)K (b a) f(x) dx f(x) dx.œÊ œœ œ
'''
aaa
bbb
ba
†"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
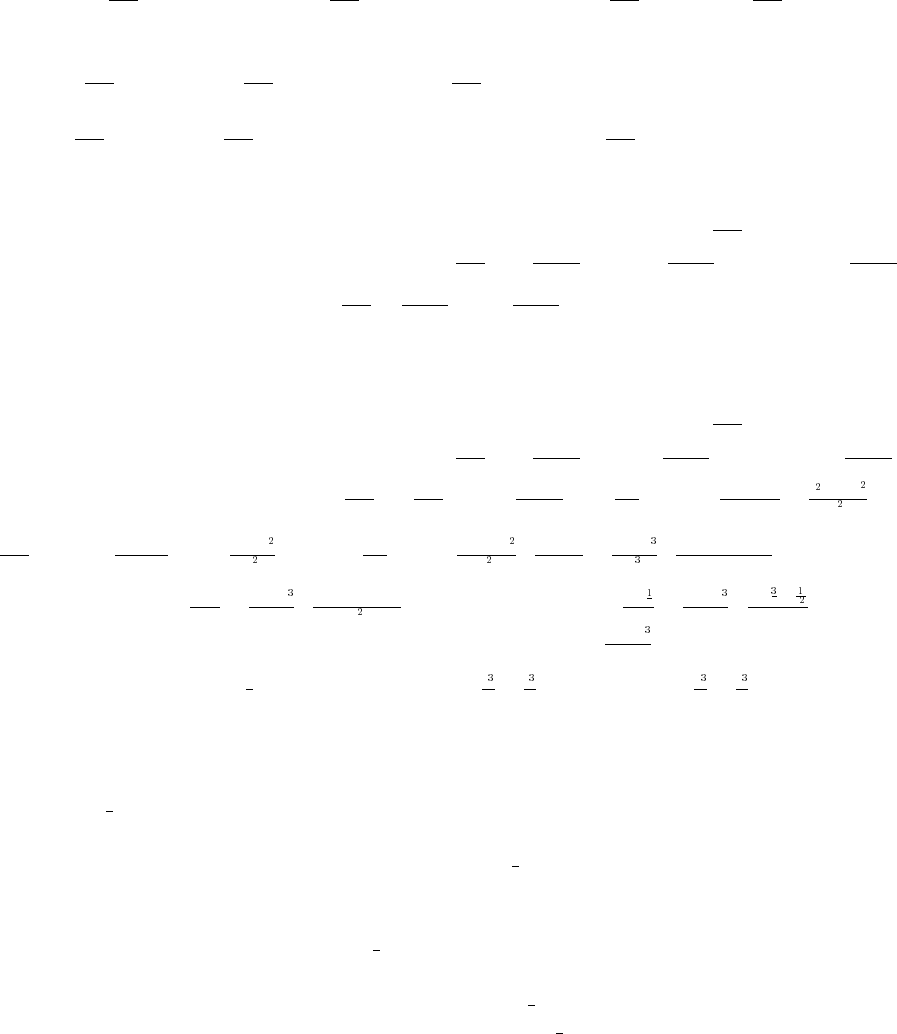
312 Chapter 5 Integration
74. All three rules hold. The reasons: On any interval [a b] on which f and g are integrable, we have:ß
(a) av(f g) [f(x) g(x)] dx f(x) dx g(x) dx f(x) dx g(x) dxœ œ œ
"" ""
ba ba ba ba
aaaaa
bbbbb
'''''
”•
av(f) av(g)œ
(b) av(kf) kf(x) dx k f(x) dx k f(x) dx k av(f)œœœœ
"" "
ba ba ba
aaa
bbb
'''
”•” •
(c) av(f) f(x) dx g(x) dx since f(x) g(x) on [a b], and g(x) dx av(g).œŸ Ÿß œ
"" "
ba ba ba
aa a
bb b
'' '
Therefore, av(f) av(g).Ÿ
75. Consider the partition P that subdivides the interval a, b into n subintervals of width x and let c be the rightÒÓ ˜œ
ba
nk
endpoint of each subinterval. So the partition is P a, a , a , . . . , a and c a .œÖ × œ
ba
nn n n
ba nba kba
k
# ab ab ab
We get the Riemann sum f c x c n c b a . As n and P
!! !
ab a b
kk k
nn n
kba
nn n
cb a cb a
œ" œ" œ"
˜ œ † œ "œ † œ Ä_ m mÄ!
ab ab
this expression remains c b a . Thus, c dx c b a .ab abœ
'a
b
76. Consider the partition P that subdivides the interval a, b into n subintervals of width x and let c be the rightÒÓ ˜œ
ba
nk
endpoint of each subinterval. So the partition is P a, a , a , . . ., a and c a .œÖ × œ
ba
nn n n
ba nba kba
k
# ab ab ab
We get the Riemann sum f c x c a a
!! ! !
ab ˆ‰ Š‹Š ‹
kk k k
nn n n
kkba ba ba
nn n n n n
kb a akb a k b a
œ" œ" œ" œ"
##
#
#
˜œ œ œ
ab ab ab
akknaœ œ†††
ba ba
nnnnn n
kkk
nnn
aba ba aba nn ba nn n
œ" œ" œ"
###
# # " "#"
#'
Œ
!!!
ab ab ab abab aba b
baa aba baa abaœ † † œ † †abab abab
##
#"#" #
"
'"'"
" #
n
nn
ba n n baababa b ab
nn
n
As n and P this expression has value b a a a b aÄ_ m mÄ! †" †#abab
##
'
abba
ba a ab a b a b b a ba a . Thus, x dx .œ # $$ œ œ
#$##$ $# #$ #
"
$$$$$
ab
ba ba
a
b
'
77. (a) U max x max x max x where max f(x ), max f(x ), , max f(x ) since f isœá œ œáœ
" # ""##
?? ?
nnn
increasing on [a b]; L min x min x min x where min f(x ), min f(x ), ,ßœ á œ œ á
" # "!#"
?? ?
n
min f(x ) since f is increasing on [a b]. Therefore
nn1
ϧ
U L (max min ) x (max min ) x (max min ) xχ
"" ##
?? ?
nn
(f(x ) f(x )) x (f(x ) f(x )) x (f(x ) f(x )) x (f(x ) f(x )) x (f(b) f(a)) x.œ á œ œ
"! #" !
?? ? ??
nn1 n
(b) U max x max x max x where max f(x ), max f(x ), , max f(x ) since fœá œ œáœ
"" ## " " # #
?? ?
nn nn
is increasing on[a b]; L min x min x min x whereßœ á
"" ##
?? ?
nn
min f(x ), min f(x ), , min f(x ) since f is increasing on [a b]. Therefore
"!#"
œœáœ ß
nn1
U L (max min ) x (max min ) x (max min ) xχ
""" ###
?? ?
nnn
(f(x ) f(x )) x (f(x ) f(x )) x (f(x ) f(x )) xœ á
"!"#"#
?? ?
nn1n
(f(x ) f(x )) x (f(x ) f(x )) x (f(x ) f(x )) x . ThenŸ á
"! #"
?? ?
max max n n 1 max
U L (f(x ) f(x )) x (f(b) f(a)) x f(b) f(a) x since f(b) f(a). ThusŸ œ œ
n max max max!???kk
lim (U L) lim (f(b) f(a)) x 0, since x P .
ll llP0 P0ÄÄ
œ œ œ??
max max ll
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
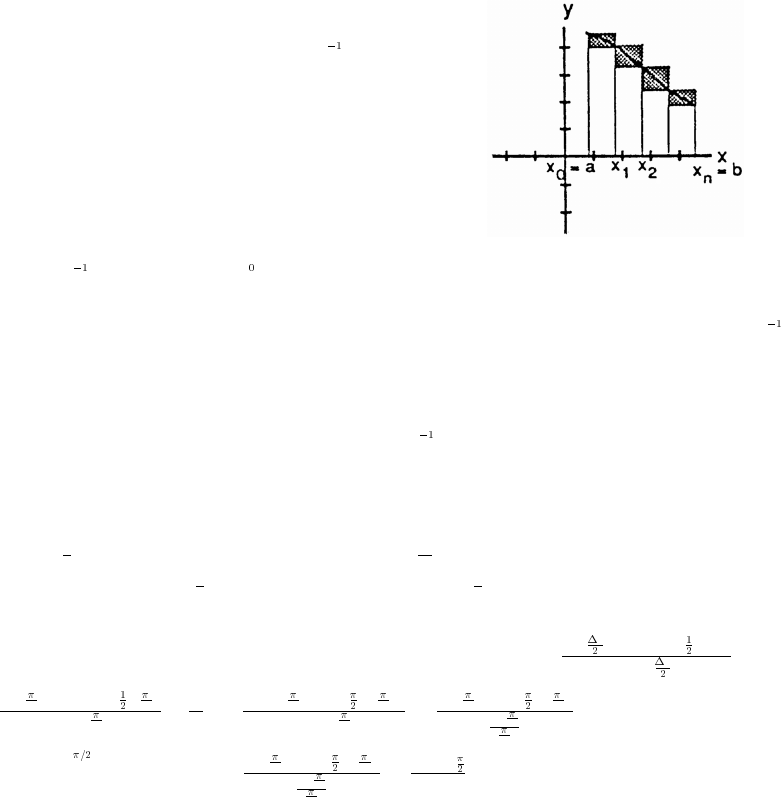
Section 5.3 The Definite Integral 313
78. (a) U max x max x max x whereχ
"#
?? ?
n
max f(x ), max f(x ), , max f(x )
"!#"
œœáœ
nn
since f is decreasing on [a b];ß
L min x min x min x whereχ
"#
?? ?
n
min f(x ), min f(x ) , min f(x )
""##
œœßáœ
nn
since f is decreasing on [a b]. Thereforeß
U L (max min ) x (max min ) xœ
"" ##
??
(max min ) xá
nn
?
(f(x ) f(x )) x (f(x ) f(x )) xœ
!" "#
??
(f(x ) f(x )) x (f(x ) f(x )) xá œ
nn n
??
(f(a) f(b)) x.œ?
(b) U max x max x max x where max f(x ), max f(x ), , max f(x ) sinceœá œ œáœ
"" ## " ! # "
?? ?
nn nn
f is decreasing on[a b]; L min x min x min x whereßœ á
"" ##
?? ?
nn
min f(x ), min f(x ), , min f(x ) since f is decreasing on [a b]. Therefore
""##
œœáœ ß
nn
U L (max min ) x (max min ) x (max min ) xχ
""" ###
?? ?
nnn
(f(x ) f(x )) x (f(x ) f(x )) x (f(x ) f(x )) xœ á
!"""##
?? ?
nnn
(f(x ) f(x )) x (f(a) f(b) x f(b) f(a) x since f(b) f(a). ThusŸ œ œ Ÿ
!n max max max
?? ?kk
lim (U L) lim f(b) f(a) x 0, since x P .
ll llP0 P0ÄÄ
œ œ œkk ll??
max max
79. (a) Partition 0 into n subintervals, each of length x with points x 0, x x,
‘
ßœœœ
11
##
!"
??
n
x 2 x, , x n x . Since sin x is increasing on 0 , the upper sum U is the sum of the areas
###
œáœœ ß??
n
11
‘
of the circumscribed rectangles of areas f(x ) x (sin x) x, f(x ) x (sin 2 x) x, , f(x ) x
"#
???? ?? ?œœá
n
(sin n x) x. Then U (sin x sin 2 x sin n x) x xœœáœ?? ? ? ?? ?
”•
cos cos n x
sin
x
x
#
ˆ‰ˆ‰
?
œœœ
”•
ˆ‰
cos cos n cos cos cos cos
sin 4n sin
4n 2n 4n 4n 4n 4n
4n 4n sin 4n
4n
#
ˆ‰ ˆ ‰ ˆ‰ˆ‰ ˆ ‰
Š‹
1
#n
1
(b) The area is sin x dx lim 1.
'!
œœœ
nÄ_
cos cos
4n 4n
sin 4n
4n
ˆ‰
Š‹
1cos
1
80. (a) The area of the shaded region is x m which is equal to L.
!
i
n
ii
œ"
˜†
(b) The area of the shaded region is x M which is equal to U.
!
i
n
ii
œ"
˜†
(c) The area of the shaded region is the difference in the areas of the shaded regions shown in the second part of the figure
and the first part of the figure. Thus this area is U L.
81. By Exercise 80, U L x M x m where M max f x on the ith subinterval andœ ˜† ˜† œ Ö ×
!! ab
ii
nn
ii ii i
œ" œ"
m min f x on the ith subinterval . Thus U L M m x x provided x for each
iiii i i
ii
nn
œ Ö × œ ˜ †˜ ˜ab a b
!!
œ" œ"
%$
i , n. Since x x b a the result, U L b a follows.œ "ßÞÞÞ †˜ œ ˜ œ
!!
ab ab
ii
nn
ii
œ" œ"
%% % %
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

314 Chapter 5 Integration
82. The car drove the first 150 miles in 5 hours and the
second 150 miles in 3 hours, which means it drove 300
miles in 8 hours, for an average of mi/hr
300
8
37.5 mi/hr. In terms of average values of functions,œ
the function whose average value we seek is
v(t) , and the average value is
30, 0 t 5
50, 5 1 8
œŸŸ
Ÿ
œ
37.5.
(30)(5) (50)(3)
8
œ
83-88. Example CAS commands:
:Maple
with( plots );
with( Student[Calculus1] );
f := x -> 1-x;
a := 0;
b := 1;
N :=[ 4, 10, 20, 50 ];
P := [seq( RiemannSum( f(x), x=a..b, partition=n, method=random, output=plot ), n=N )]:
display( P, insequence=true );
89-92. Example CAS commands:
:Maple
with( Student[Calculus1] );
f := x -> sin(x);
a := 0;
b := Pi;
plot( f(x), x=a..b, title="#23(a) (Section 5.1)" );
N := [ 100, 200, 1000 ]; # (b)
for n in N do
Xlist := [ a+1.*(b-a)/n*i $ i=0..n ];
Ylist := map( f, Xlist );
end do:
for n in N do # (c)
Avg[n] := evalf(add(y,y=Ylist)/nops(Ylist));
end do;
avg := FunctionAverage( f(x), x=a..b, output=value );
evalf( avg );
FunctionAverage(f(x),x=a..b,output=plot); # (d)
fsolve( f(x)=avg, x=0.5 );
fsolve( f(x)=avg, x=2.5 );
fsolve( f(x)=Avg[1000], x=0.5 );
fsolve( f(x)=Avg[1000], x=2.5 );
83-92. Example CAS commands:
: (assigned function and values for a, b, and n may vary)Mathematica
Sums of rectangles evaluated at left-hand endpoints can be represented and evaluated by this set of commands
Clear[x, f, a, b, n]
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
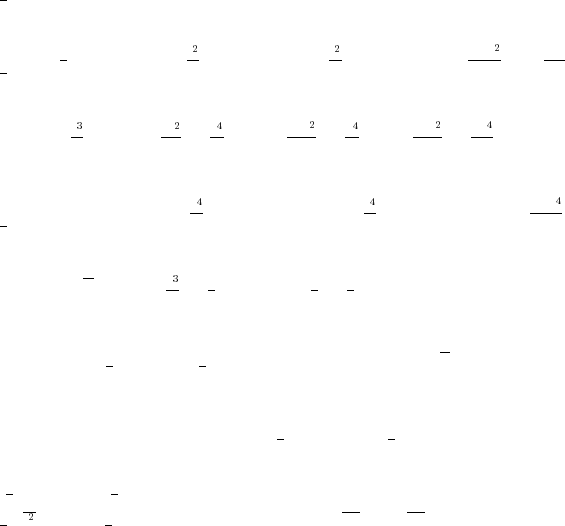
Section 5.4 The Fundamental Theorem of Calculus 315
{a, b}={0, }; n =10; dx = (b a)/n;1
f = Sin[x] ;
2
xvals =Table[N[x], {x, a, b dx, dx}];
yvals = f /.x xvals;Ä
boxes = MapThread[Line[{{#1,0},{#1, #3},{#2, #3},{#2, 0}]&,{xvals, xvals dx, yvals}];
Plot[f, {x, a, b}, Epilog boxes];Ä
Sum[yvals[[i]] dx, {i, 1, Length[yvals]}]//N
Sums of rectangles evaluated at right-hand endpoints can be represented and evaluated by this set of commands.
Clear[x, f, a, b, n]
{a, b}={0, }; n =10; dx = (b a)/n;1
f = Sin[x] ;
2
xvals =Table[N[x], {x, a dx, b, dx}];
yvals = f /.x xvals;Ä
boxes = MapThread[Line[{{#1,0},{#1, #3},{#2, #3},{#2, 0}]&,{xvals dx,xvals, yvals}];
Plot[f, {x, a, b}, Epilog boxes];Ä
Sum[yvals[[i]] dx, {i, 1,Length[yvals]}]//N
Sums of rectangles evaluated at midpoints can be represented and evaluated by this set of commands.
Clear[x, f, a, b, n]
{a, b}={0, }; n =10; dx = (b a)/n;1
f = Sin[x] ;
2
xvals =Table[N[x], {x, a dx/2, b dx/2, dx}];
yvals = f /.x xvals;Ä
boxes = MapThread[Line[{{#1,0},{#1, #3},{#2, #3},{#2, 0}]&,{xvals dx/2, xvals dx/2, yvals}];
Plot[f, {x, a, b},Epilog boxes];Ä
Sum[yvals[[i]] dx, {i, 1, Length[yvals]}]//N
5.4 THE FUNDAMENTAL THEOREM OF CALCULUS
1. (2x 5) dx x 5x 0 5(0) ( 2) 5( 2) 6
'2
0
œ œœcda ba b
## #
!
#
2. 5 dx 5x 5(4) 5( 3)
'3
4ˆ‰’“Š ‹Š ‹
œœ œ
x x 4 133
44 44
(3)
#
%
$
3. 3x dx 8
'0
4Š‹’“Š ‹Š ‹
œœœ
x3xx 4
4161616
3(4) 3(0) (0)
###
%
!
4. x 2x 3 dx x 3x 2 3(2) ( 2) 3( 2) 12
'2
2ab
’“Š ‹Š ‹
$## #
#
#
œ œ œ
x2
44 4
(2)
5. x x dx x 0 1
'0
1ˆ‰ ˆ‰
È’“
# $Î# "
!
"
œ œœ
x2 2
33 33
6. x dx x (5) 0 2(5) 10 5
'0
5
$Î# &Î# &Î# $Î#
&
!
œœœœ
‘ È
22
55
7. x dx 5x ( 5)
'1
32
'Î& "Î& $#
"##
œ œ œ
‘ˆ‰
55
8. dx 2x dx 2x 1
''
22
11
222
x1
œ œ œœ
# " "
#
#
cdˆ‰ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

316 Chapter 5 Integration
9. sin x dx [ cos x] ( cos ) ( cos 0) ( 1) ( 1) 2
'0œ œ œ œ
1
!1
10. (1 cos x) dx [x sin x] ( sin ) (0 sin 0)
'0œœœ
1
!11 1
11. 2 sec x dx [2 tan x] 2 tan (2 tan 0) 2 3 0 2 3
'0
3
#Î$
!
œœœœ
11
ˆ‰ˆ‰ ÈÈ
3
12. csc x dx [ cot x] cot cot 3 3 2 3
'6
56
#&Î'
Î'
œ œ œ œ
1
1
11
ˆ‰ˆ‰ˆ‰ ˆ‰ Š‹Š‹
ÈÈÈ
5
66
13. csc cot d [ csc ] csc csc 2 2 0
'4
34
))) )œ œ œ œ
$Î%
Î%
1
1
11
ˆ‰ˆ‰ˆ‰ ˆ‰ ÈÈ
Š‹
3
44
14. 4 sec u tan u du [4 sec u] 4 sec 4 sec 0 4(2) 4(1) 4
'0
3
œ œ œœ
11
Î$
!ˆ‰
3
15. dt cos 2t dt t sin 2t (0) sin 2(0) sin 2
''
22
00
" " " " " " " " "
### # # ###
!
Î#
cos 2t
444
œ œ œ
ˆ‰‘ˆ ‰ˆ ‰ˆ‰ ˆ‰
1
11
œ1
4
16. dt cos 2t dt t sin 2t
''
33
33
" " " " "
####
Î$
Î$
cos 2t
4
œ œ
ˆ‰‘
1
1
sin 2 sin 2 sin sinœ œ œ
ˆ‰ˆ ‰ ˆ‰ˆ‰ ˆ‰ ˆ ‰ ˆ ‰
"" " " " "
##
111 111111
34 3 34 3 64 364 3 34
22
3
È
17. 8y sin y dy cos y cos cos
'ab
’“
ŒŒ
ˆ‰
#Î#
Î# ##
œ œœ
8y
333 3
88 2
1
1
111
ˆ‰ ˆ ‰
18. 4 sec t dt 4 sec t t dt 4 tan t
''
33
###
Î%
Î$
ˆ‰ ‘
abœ œ
11
1
1
tt
1
4 tan 4 tan (4( 1) 4) 4 3 3 4 3 3œ œœ
Š‹Š‹Š‹
ˆ‰ ˆ‰ Š‹
ÈÈ
11 11
43
ˆ‰ ˆ‰
43
19. (r 1) dr r 2r 1 dr r r ( 1) ( 1) 1 1
''
""
" "
## # # #
"
"
œ œ œ œab
’“Š ‹Š ‹
r18
33 33
(1)
20. (t 1) t 4 dt t t 4t 4 dt 2t 4t
''
#$# #
$
$
33
33
œ œab a b’“
tt
43
È
È
2343 2343 103œ œ
Š‹ Š‹Š‹
ÈÈ È È È
Š‹ Š‹ Š ‹ Š ‹
ÈÈ È È
33 3 3
43 4 3
##
21. du u du
''
22
""
##
""""
& "
#
Š‹ Š ‹’ “Š ‹
uuu1 3
u1616164
4u 4(1)
2
42
œ œœ œ
ÈŠ‹
È
Š‹
È
22. dv v v dv
''
12 12
""
"" " " " " "
$ % "
"Î#
ˆ‰ ‘
ab Š‹
Œ
v 2v 3v 2(1) 3(1) 6
v
15
23
œ œ œ œ
ˆ‰ ˆ‰
23. ds 1 s ds s 2 1 2 2 1
''
11
22
ss
s
222
s21
$Î# $Î%
#
"
ÈÈÈ
È
ÉÈ
œ œœœ
ˆ‰
’“ Š‹
ÈÈ
281œ
ÈÈ
%
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 5.4 The Fundamental Theorem of Calculus 317
24. du u 1 du 2 u u 2 4 4 2 9 9 3
''
99
44
1u
u
"Î# %
*
È
Èœœœœ
ˆ‰‘
ÈŠ‹Š‹
ÈÈ
25. x dx x dx x dx x dx x dx
''' ''
44 4
kk kk kk ’“ ’“Š ‹Š ‹
œœœœ
xx 0 40
(4)
## ####
!%
% !
16œ
26. cos x cos x dx (cos x cos x) dx (cos x cos x) dx cos x dx [sin x]
''''
"""
###
Î#
!
abkkœ œ œ
1
sin sin 0 1œœ
1
#
27. (a) cos t dt [sin t] sin x sin 0 sin x cos t dt sin x cos x x
''
x x
x
œœœÊ œ œ
È
!"
#
"Î#
ÈÈ ÈÈ
Œ
ˆ‰ ˆ‰
dd
dx dx
œcos x
2x
È
È
(b) cos t dt cos x x cos x x
dd
dx dx
cos x
2x
Œ
ˆ‰ˆ ‰ˆ‰ˆ‰
ÈÈ È
ˆ‰
'x
œœœ
"
#
"Î# È
È
28. (a) 3t dt t sin x 1 3t dt sin x 1 3 sin x cos x
''
11
sin x sin x
sin x
#$ $ # $ #
"
œœÊ œ œcd a b
Œ
dd
dx dx
(b) 3t dt 3 sin x (sin x) 3 sin x cos x
dd
dx dx
Œ
ab
ˆ‰
'1
sin x
## #
œœ
29. (a) u du u du u t 0 t u du t 4t
'' '
tt t
t
ÈÈ
‘ ˆ‰
ab Œ
œœœœÊ œœ
"Î# $Î# % ' ' &
!
$Î#
22 2d d2
33 3dt dt3
(b) u du t t t 4t 4t
dd
dt dt
Œ
ÈȈ‰
ab a b
't
œœœ
%%#$&
30. (a) sec y dy [tan y] tan (tan ) 0 tan (tan ) sec y dy (tan (tan ))
''
tan tan
tan
# #
œœ œ Ê œ)) )
dd
dd))
Œ
sec (tan ) secœab
##
))
(b) sec y dy sec (tan ) (tan ) sec (tan ) sec
dd
dd))
Œ
ab ab
ˆ‰
'tan
## ##
œœ)) ))
31. y 1 t dt 1 x 32. y dt , x 0œ Êœ œ Êœ
''
x x
1
ÈÈ
## ""
dy dy
dx t dx x
33. y sin t dt sin t dt sin x x (sin x) xœ œ Ê œ œ œ
''
x
x
## "Î#
#"
#
dy
dx dx
dsin x
2x
Š‹
ˆ‰ˆ ‰ ˆ ‰
ÈÈ
ˆ‰ È
34. y cos t dt cos x x 2x cos xœÊœ œ
'xÈŠ‹
Ȉ‰
ab kk
dy
dx dx
d
##
35. y , x (sin x) (cos x) 1 since xœÊœ œœœœ
'sin x dt d cos x cos x
1t 1sinx cosx
dy
dx dx cos x cos x
ÈÈÈ
kk
# #
""
kk kk
ˆ‰
1 1
36. y (tan x) sec x 1œÊœ œ œ
'tan x dt d
1t dx 1tanx dx secx
dy
""
#
ˆ‰ˆ ‰ˆ‰
ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
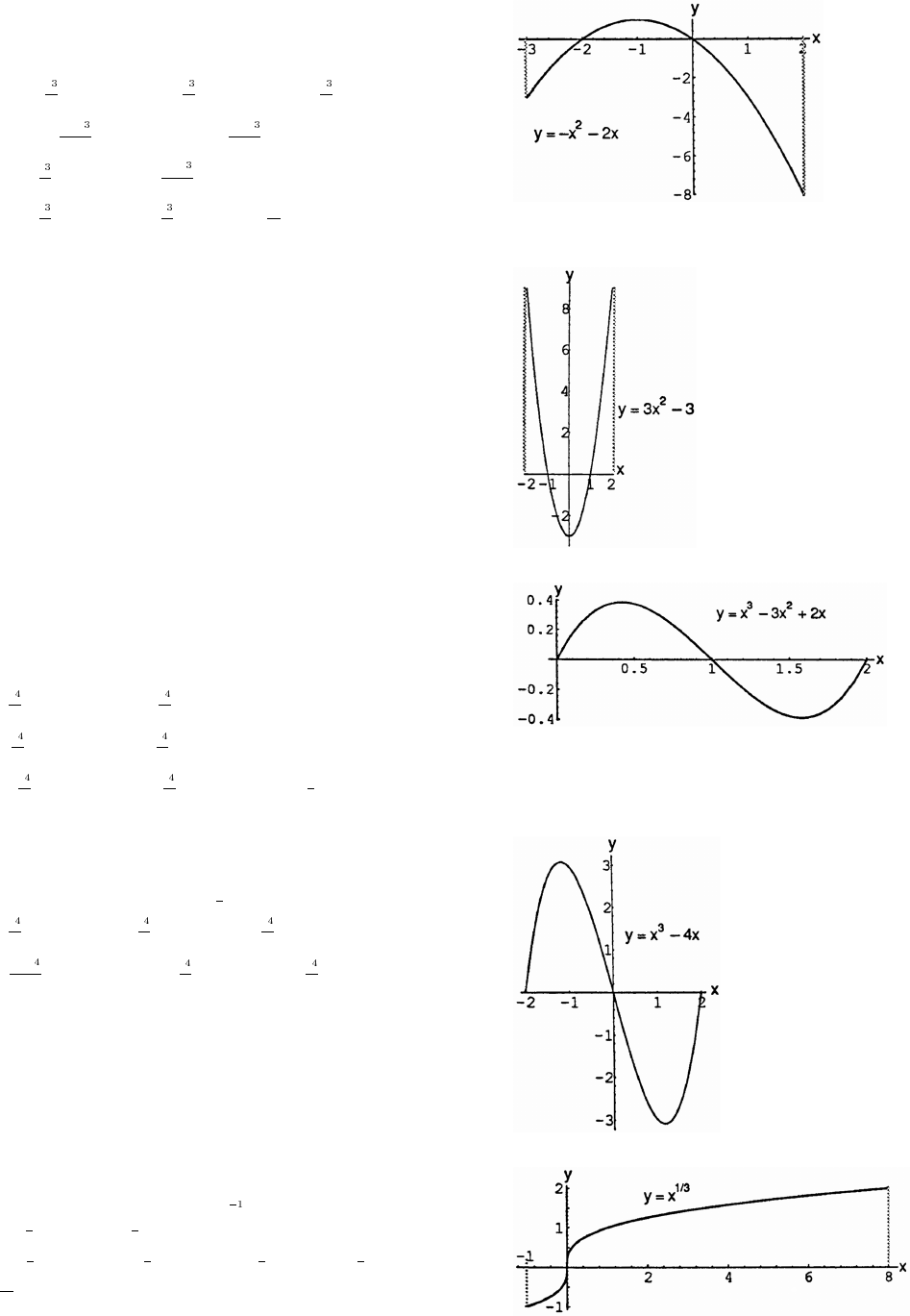
318 Chapter 5 Integration
37. x 2x 0 x(x 2) 0 x 0 or x 2; Area œÊ œÊœ œ
#
x 2x dx x 2x dx x 2x dxœ
'''
$ # !
# ! #
###
ababab
xxxœ
’“’“’“
xxx
333
###
# ! #
$ # !
(2) (3)œ
Š‹Š‹Š‹
(2) (3)
33
##
0(2)
Š‹Š‹Š ‹
0
33
(2)
##
20 œ
Š‹Š‹Š‹
2028
333
##
38. 3x 3 0 x 1 x 1; because of symmetry about
##
œ Ê œ Ê œ„
the y-axis, Area 2 3x 3 dx 3x 3 dxœ
Œ
ab ab
''
!"
"#
##
2 x 3x x 3x 2 1 3(1) 0 3(0)
Š‹
cdcdca babab œ
$$ $ $
"#
!"
2 3(2) 1 3(1) 2(6) 12 œœdaa b a b
$$
39. x 3x 2x 0 x x 3x 2 0
$# #
œÊ œab
x(x 2)(x 1) 0 x 0, 1, or 2;ʜʜ
Area x 3x 2x dx x 3x 2x dxœ
''
!"
"#
$# $#
abab
xx xxœ
’“’“
xx
44
$# $#
"#
!"
11 00œ
Š‹Š‹
10
44
$# $#
22 11œ
’“Š‹Š‹
21
44
$# $# "
#
40. x 4x 0 x x 4 0 x(x 2)(x 2) 0
$#
œÊ œÊ œab
x 0, 2, or 2. Area x 4x dx x 4x dxÊœ œ
''
2
!#
$$
!
ab ab
2x 2x 2(0)œ œ
’“’“Š ‹
xx0
444
## #
!#
# !
2( 2) 2(2) 2(0) 8 œ
Š‹’ “Š‹Š‹
(2)
444
20
###
41. x 0 x 0; Area x dx x dx
"Î$ "Î$ "Î$
!)
!
œÊœ œ
''
xxœ
‘‘
33
44
%Î$ %Î$
!)
" !
(0) ( 1) (8) (0)œ
ˆ ‰ˆ ‰ˆ‰ˆ‰
3333
4444
%Î$ %Î$ %Î$ %Î$
œ51
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 5.4 The Fundamental Theorem of Calculus 319
42. x x 0 x 1 x 0 x 0 or
"Î$ "Î$ #Î$ "Î$
œ Ê œ Ê œ
ˆ‰
1 x 0 x 0 or 1 x x 0 orœÊœ œ Êœ
#Î$ #Î$
1 x x 0 or 1;œÊœ „
#
Area xxdx xxdx xxdxœ
'''
!" )
"Î$ "Î$ "Î$
!"
ˆ‰ ˆ‰ˆ‰
xxxœ
’“’“’“
3x 3x3x
444
%Î$ %Î$ %Î$
###
!")
"!"
(0) ( 1)œ
’“Š‹Š ‹
303
44
(1)
%Î$ %Î$
##
(1) (0)
’“Š‹Š‹
3130
44
%Î$ %Î$
##
(8) (1)
’“Š‹Š‹
3831
44
%Î$ %Î$
##
2œ! œ
"" $"
#44 4 4
83
ˆ‰
43. The area of the rectangle bounded by the lines y 2, y 0, x , and x 0 is 2 . The area under the curveœœœ œ11
y 1 cos x on [0 ] is (1 cos x) dx [x sin x] ( sin ) (0 sin 0) . Therefore the area ofœ ß œ œ œ1111
'!!
1
the shaded region is 2 .11 1œ
44. The area of the rectangle bounded by the lines x , x , y sin sin , and y 0 isœœ œ œœ œ
11 1 1
66 6 6
55"
#
. The area under the curve y sin x on is sin x dx [ cos x]
"
#
&Î'
Î'
ˆ‰ ‘
5 5
66 3 66
11 1 11 1
1
œ œ ß œ
'6
56
cos cos 3. Therefore the area of the shaded region is 3 .œ œ œ
ˆ‰ˆ‰
Š‹ ÈÈ
5
66 3
33
11 1
ÈÈ
##
45. On 0 : The area of the rectangle bounded by the lines y 2, y 0, 0, and is 2
‘ ˆ‰
ÈÈ
ß œ œ œ œ
111
444
))
. The area between the curve y sec tan and y 0 is sec tan d [ sec ]œœœœ
1
1
È2
4)) ))) )
'4
!
Î%
( sec 0) sec 2 1. Therefore the area of the shaded region on is 2 1 .œ œ ß!
ˆ‰ ‘ˆ‰ÈÈ
Š‹
1 1 1
444
2
È
On 0 : The area of the rectangle bounded by , 0, y 2, and y 0 is 2 . The area
‘ ˆ‰
ÈÈ
ßœœœœœ
111
1
4444
2
)) È
under the curve y sec tan is sec tan d [sec ] sec sec 0 2 1. Therefore the areaœœœœ)) ))) )
'411
Î%
!4È
of the shaded region on is 2 1 . Thus, the area of the total shaded region is
‘ Š‹
È
!ß
11
44
2
È
21 21 .
Š‹Š‹
ÈÈ
111
ÈÈÈ
222
44
œ
#
46. The area of the rectangle bounded by the lines y 2, y 0, t , and t 1 is 2 1 2 . Theœœœ œ œ
111
44
ˆ‰ˆ‰ #
area under the curve y sec t on is sec t dt [tan t] tan 0 tan 1. The areaœß! œ œœ
##!
Î%
‘ ˆ‰
11
1
44
'4
under the curve y 1 t on [ ] is 1 t dt t 1 0 . Thus, the totalœ !ß " œ œ œ
##
!
"
!
'ab’“Š‹Š‹
t102
3333
area under the curves on is 1 . Therefore the area of the shaded region is 2 .
‘ ˆ‰
ß" œ œ
111
433 33
25 5
##
"
47. y dt 3 and y( ) dt 3 0 3 3 (d) is a solution to this problem.œ Ê œ œ œœÊ
''
x"""
tdxx t
dy 1
48. y sec t dt 4 sec x and y( 1) sec t dt 4 0 4 4 (c) is a solution to this problem.œ Ê œ œ œœ Ê
''
1 1
x 1
dy
dx
49. y sec t dt 4 sec x and y(0) sec t dt 4 0 4 4 (b) is a solution to this problem.œ Ê œ œ œœ Ê
''
xdy
dx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
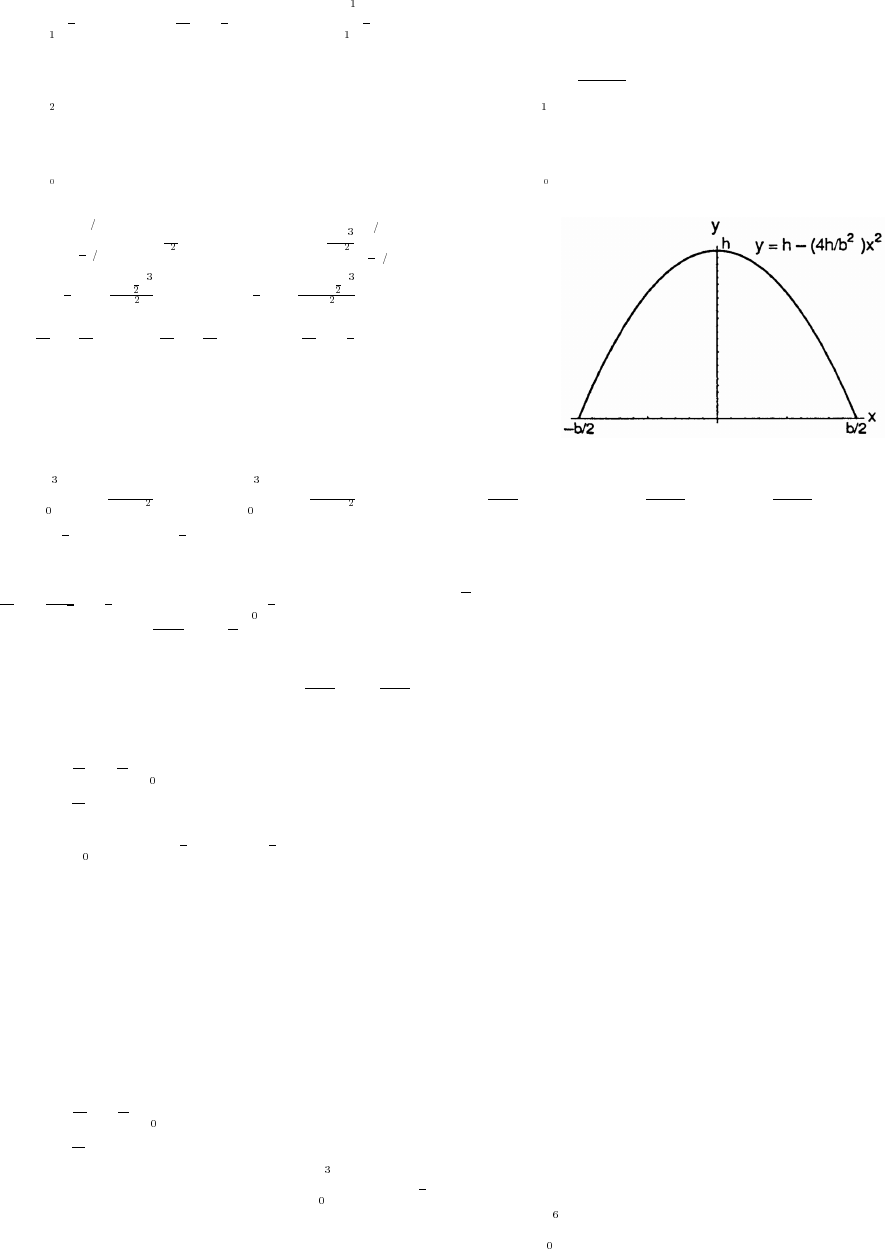
320 Chapter 5 Integration
50. y dt 3 and y(1) dt 3 0 3 3 (a) is a solution to this problem.œ Ê œ œ œœÊ
''
x"""
tdxx t
dy
51. y sec t dt 3 52. y 1 t dt 2œ œ
''
x x È#
53. s f(x) dx s 54. v g(x) dx vœ œ
''
t t
t t
! !
55. Area h x dx hxœ œ
'b2
b2 b2
b2
ˆ‰ˆ‰ ’“
4h 4hx
b3b
#
hhœ
ŒŒ
ˆ‰ ˆ ‰
bb
4h 4h
3b 3b##
ˆ‰ ˆ ‰
bb
bh bhœœœ
ˆ‰ˆ ‰
bh bh bh bh bh 2
6633##
56. r 2 dx 2 1 dx 2 x 2 3 0œ œ œ œ
''
Š‹ Š‹ ’ “
‘ˆ‰ Š‹Š‹
21
(x 1) (x 1) x 1 (3 1) (0 1)
"""
$
!
2 3 1 2 2 4.5 or $4500œœ œ
‘ˆ‰
""
44
57. x c t dt t x
dc
dx x
œœ Êœ œ œ
"" "
###
"Î# "Î# "Î#
È'xx
0
‘ È
c(100) c(1) 100 1 $9.00œ œ
ÈÈ
58. By Exercise 57, c(400) c(100) 400 100 20 10 $10.00 œ œœ
ÈÈ
59. (a) v f(x) dx f(t) v(5) f(5) 2 m/secœœ œ Ê œ œ
ds d
dt dt 't
(b) a is negative since the slope of the tangent line at t 5 is negativeœœ
df
dt
(c) s f(x) dx (3)(3) m since the integral is the area of the triangle formed by y f(x), the x-axis,œœœ œ
'3"
##
9
and x 3œ
(d) t 6 since from t 6 to t 9, the region lies below the x-axisœœœ
(e) At t 4 and t 7, since there are horizontal tangents thereœœ
(f) Toward the origin between t 6 and t 9 since the velocity is negative on this interval. Away from theœœ
origin between t 0 and t 6 since the velocity is positive there.œœ
(g) Right or positive side, because the integral of f from 0 to 9 is positive, there being more area above the
x-axis than below it.
60. (a) v g(x) dx g(t) v(3) g(3) 0 m/sec.œœ œ Ê œ œ
dg
dt dt
d't
(b) a is positive, since the slope of the tangent line at t 3 is positiveœœ
df
dt
(c) At t 3, the particle's position is g(x) dx (3)( 6) 9œœœ
'"
#
(d) The particle passes through the origin at t 6 because s(6) g(x) dx 0œœœ
'
(e) At t 7, since there is a horizontal tangent thereœ
(f) The particle starts at the origin and moves away to the left for 0 t 3. It moves back toward the origin
for 3 t 6, passes through the origin at t 6, and moves away to the right for t 6. œ
(g) Right side, since its position at t 9 is positive, there being more area above the x-axis than below it at t .œœ*
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 5.4 The Fundamental Theorem of Calculus 321
61. k 0 one arch of y sin kx will occur over the interval 0 the area sin kx dx cos kxÊ œ ß Ê œ œ
‘ ‘
11
kk
'kk
"Î
!
cos k cos (0)œ œ
""
kk k k
2
ˆ‰ˆ ‰ˆ‰
1
62. dt .lim lim lim lim
xxxx
xx
t
tx
Ä! Ä! Ä! Ä!
""
" $ "
'x
œœœœ_
'xt
t
x
x
dt
x$ab
63. f(t) dt x 2x 1 f(x) f(t) dt x 2x 1 2x 2
''
11
xx
œÊ œ œ œ
##
dd
dx dx ab
64. f(t) dt x cos x f(x) f(t) dt cos x x sin x f(4) cos (4) (4) sin (4) 1
''
xx
œÊœ œ Êœ œ1111111
d
dx
65. f(x) 2 dt f (x) f (1) 3; f(1) 2 dt 2 0 2;œ Ê œ œ Ê œ œ œœ
''
x999 9
1t 1(x1) x2 1t
ww
L(x) 3(x 1) f(1) 3(x 1) 2 3x 5œ œ œ
66. g(x) 3 sec (t 1) dt g (x) sec x 1 (2x) 2x sec x 1 g ( 1) 2( 1) sec ( 1) 1œ Ê œ œ Ê œ
'1
x
w# #w #
ab ab abab
2; g( 1) 3 sec (t 1) dt 3 sec (t 1) dt 3 0 3; L(x) 2(x ( 1)) g( 1)œ œ œ œœ œ
''
11
ab" "
2(x 1) 3 2x 1œ œ
67. (a) True: since f is continuous, g is differentiable by Part 1 of the Fundamental Theorem of Calculus.
(b) True: g is continuous because it is differentiable.
(c) True, since g (1) f(1) 0.
wœœ
(d) False, since g (1) f (1) 0.
ww w
œ
(e) True, since g (1) 0 and g (1) f (1) 0.
wwww
œœ
(f) False: g (x) f (x) 0, so g never changes sign.
ww w ww
œ
(g) True, since g (1) f(1) 0 and g (x) f(x) is an increasing function of x (because f (x) 0).
ww w
œœ œ
68. (a) True: by Part 1 of the Fundamental Theorem of Calculus, h (x) f(x). Since f is differentiable for all x,
wœ
h has a second derivative for all x.
(b) True: they are continuous because they are differentiable.
(c) True, since h (1) f(1) 0.
wœœ
(d) True, since h (1) 0 and h (1) f (1) 0.
wwww
œœ
(e) False, since h (1) f (1) 0.
ww w
œ
(f) False, since h (x) f (x) 0 never changes sign.
ww w
œ
(g) True, since h (1) f(1) 0 and h (x) f(x) is a decreasing function of x (because f (x) 0).
ww w
œœ œ
69. 70. The limit is 3x#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

322 Chapter 5 Integration
71-74. Example CAS commands:
:Maple
with( plots );
f := x -> x^3-4*x^2+3*x;
a := 0;
b := 4;
F := unapply( int(f(t),t=a..x), x ); # (a)
p1 := plot( [f(x),F(x)], x=a..b, legend=["y = f(x)","y = F(x)"], title="#71(a) (Section 5.4)" ):
p1;
dF := D(F); # (b)
q1 := solve( dF(x)=0, x );
pts1 := [ seq( [x,f(x)], x=remove(has,evalf([q1]),I) ) ];
p2 := plot( pts1, style=point, color=blue, symbolsize=18, symbol=diamond, legend="(x,f(x)) where F '(x)=0" ):
display( [p1,p2], title="71(b) (Section 5.4)" );
incr := solve( dF(x)>0, x ); # (c)
decr := solve( dF(x)<0, x );
df := D(f); # (d)
p3 := plot( [df(x),F(x)], x=a..b, legend=["y = f '(x)","y = F(x)"], title="#71(d) (Section 5.4)" ):
p3;
q2 := solve( df(x)=0, x );
pts2 := [ seq( [x,F(x)], x=remove(has,evalf([q2]),I) ) ];
p4 := plot( pts2, style=point, color=blue, symbolsize=18, symbol=diamond, legend="(x,f(x)) where f '(x)=0" ):
display( [p3,p4], title="71(d) (Section 5.4)" );
75-78. Example CAS commands:
:Maple
a := 1;
u := x -> x^2;
f := x -> sqrt(1-x^2);
F := unapply( int( f(t), t=a..u(x) ), x );
dF := D(F); # (b)
cp := solve( dF(x)=0, x );
solve( dF(x)>0, x );
solve( dF(x)<0, x );
d2F := D(dF); # (c)
solve( d2F(x)=0, x );
plot( F(x), x=-1..1, title="#75(d) (Section 5.4)" );
79. Example CAS commands:
:Maple
f := `f`;
q1 := Diff( Int( f(t), t=a..u(x) ), x );
d1 := value( q1 );
80. Example CAS commands:
:Maple
f := `f`;
q2 := Diff( Int( f(t), t=a..u(x) ), x,x );
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 5.5 Indefinite Integrals and the Substitution Rule 323
value( q2 );
71-80. Example CAS commands:
: (assigned function and values for a, and b may vary)Mathematica
For transcendental functions the FindRoot is needed instead of the Solve command.
The Map command executes FindRoot over a set of initial guesses
Initial guesses will vary as the functions vary.
Clear[x, f, F]
{a, b}= {0, 2 }; f[x_] = Sin[2x] Cos[x/3]1
F[x_] = Integrate[f[t], {t, a, x}]
Plot[{f[x], F[x]},{x, a, b}]
x/.Map[FindRoot[F'[x]==0, {x, #}] &,{2, 3, 5, 6}]
x/.Map[FindRoot[f'[x]==0, {x, #}] &,{1, 2, 4, 5, 6}]
Slightly alter above commands for 75 - 80.
Clear[x, f, F, u]
a=0; f[x_] = x 2x 3
2
u[x_] = 1 x2
F[x_] = Integrate[f[t], {t, a, u(x)}]
x/.Map[FindRoot[F'[x]==0,{x, #}] &,{1, 2, 3, 4}]
x/.Map[FindRoot[F''[x]==0,{x,#}] &,{1, 2, 3, 4}]
After determining an appropriate value for b, the following can be entered
b = 4;
Plot[{F[x], {x, a, b}]
5.5 INDEFINTE INTEGRALS AND THE SUBSTITUTION RULE
1. Let u 3x du 3 dx du dxœÊœ Ê œ
"
3
sin 3x dx sin u du cos u C cos 3x C
''
œœœ
"" "
33 3
2. Let u 2x du 4x dx du x dxœÊœ Ê œ
#"
4
x sin 2x dx sin u du cos u C cos 2x C
''
ab
##
"" "
œœœ
44 4
3. Let u 2t du 2 dt du dtœÊ œ Ê œ
"
#
sec 2t tan 2t dt sec u tan u du sec u C sec 2t C
''
œœœ
"""
###
4. Let u 1 cos du sin dt 2 du sin dtœ Ê œ Ê œ
tt t
22
"
##
1 cos sin dt 2u du u C 1 cos C
''
ˆ‰ˆ‰ ˆ‰
œœœ
tt 2 2 t
33## #
#$
#$
5. Let u 7x 2 du 7 dx du dxœÊ œ Ê œ
"
7
28(7x 2) dx (28)u du 4u du u C (7x 2) C
'''
œ œ œœ
& & & % %
"
7
6. Let u x du 4x dx du x dxœ"Ê œ Ê œ
%$$
"
4
x x 1 dx u du C x 1 C
''
$% # %
#$
""
##
ab abœ œœ
411
u
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

324 Chapter 5 Integration
7. Let u 1 r du 3r dr 3 du 9r drœ Ê œ Ê œ
$# #
3u du 3(2)u C 6 1 r C
'9r dr
1r
È
"Î# "Î# $ "Î#
œ œ œ
'ab
8. Let u y 4y 1 du 4y 8y dy 3 du 12 y 2y dyœ Ê œ Ê œ
%# $ $
ab ab
12y4y1y2y dy 3u duuCy4y1 C
''
abab ab
%# $ # $ %#
#$
œ œœ
9. Let u x 1 du x dx du x dxœÊœ Ê œ
$Î# "Î#
#
32
3È
x sin x 1 dx sin u du sin 2u C x 1 sin 2x 2 C
''
Ȉ‰ ˆ ‰ ˆ‰ˆ ‰
# $Î# # $Î# $Î#
#
"""
œ œ œ
22u
334 3 6
10. Let u du dxœ Ê œ
""
xx
cos dx cos u du cos u du sin 2u C sin C
'''
"" " ""
## #
#xx 4 2x4x
u2
ˆ‰ ˆ ‰ ˆ ‰
ab abœœ œ œ
sin Cœ
""
2x 4 x
2
ˆ‰
11. (a) Let u cot 2 du 2 csc 2 d du csc 2 dœÊœ Êœ))) ))
##
"
#
csc 2 cot 2 d u du C C cot 2 C
''
# #
"" "
###
))) )œ œ œ œ
Š‹
uu
44
(b) Let u csc 2 du 2 csc 2 cot 2 d du csc 2 cot 2 dœÊœ Êœ)))) )))
"
#
csc 2 cot 2 d u du C C csc 2 C
''
# #
"" "
###
))) )œ œ œ œ
Š‹
uu
44
12. (a) Let u 5x 8 du 5 dx du dxœÊ œ Ê œ
"
5
du u du 2u C u C 5x 8 C
'' '
dx 22
5x 8 55 5 55
u
ÈÈ
"" " "
"Î# "Î# "Î#
œœœœœ
Š‹ ˆ‰ È
(b) Let u 5x 8 du (5x 8) (5) dx duœÊœ Ê œ
È"
#
"Î#
2dx
55x 8
È
du uC 5x8C
''
dx 2 2 2
5x 8 55 5
Èœœœ
È
13. Let u 3 2s du 2 ds du dsœ Ê œ Ê œ
"
#
3 2s ds u du u du u C (3 2s) C
'' '
ÈȈ‰ ˆ‰ˆ‰
œ œ œ œ
"" " "
## #
"Î# $Î# $Î#
2
33
14. Let u 2x 1 du 2 dx du dxœÊ œ Ê œ
"
#
(2x 1) dx u du u du C (2x 1) C
'''
œ œ œ œ
$$ $ %
"" " "
## #
ˆ‰ ˆ‰
Š‹
u
48
15. Let u 5s 4 du 5 ds du dsœÊ œ Ê œ
"
5
ds du u du 2u C 5s 4 C
'' '
"""" "
"Î# "Î#
ÈÈ
5s 4 u55 5 5
2
œœœœ
ˆ‰ ˆ‰ˆ‰ È
16. Let u 2 x du dx du dxœ Ê œ Ê œ
dx 3 u du 3 C C
'''
3u3
(2 x) u 1 2 x
3( du)
#
œœ œœ
Š‹
17. Let u 1 du 2 d du dœ Ê œ Ê œ))) ))
#"
#
1 d u du u du u C 1 C
'' '
))) )
ÈȈ‰ ˆ‰ˆ‰ abœ œ œ œ
#%"" "
## #
"Î% &Î% # &Î%
42
55
18. Let u 1 du 2 d 4 du 8 dœÊ œ Ê œ)))))
#
8 1 d u (4 du) 4 u du 4 u C 3 1 C
'''
)) ) )
ÈȈ‰ ab
#$"Î$ %Î$ # %Î$
œ œ œ œ
3
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 5.5 Indefinite Integrals and the Substitution Rule 325
19. Let u 7 3y du 6y dy du 3y dyœ Ê œ Ê œ
#"
#
3y 7 3y dy u du u du u C 7 3y C
'' '
ÈȈ‰ ˆ‰ˆ‰ abœ œ œ œ
#"" " "
## #
"Î# $Î# # $Î#
2
33
20. Let u 2y 1 du 4y dyœÊœ
#
du u du 2u C 2 2y 1 C
'4y dy
2y 1 u
ÈÈ
""Î# "Î# #
œœ œœ
'' È
21. Let u 1 x du dx 2 du dxœ Ê œ Ê œ
È""
2x x
ÈÈ
dx C C
'"
"
ÈÈ
ˆ‰ È
xx
2 du 2 2
uu 1x
œœœ
'
22. Let u 1 x du dx 2 du dxœ Ê œ Ê œ
È""
2x x
ÈÈ
dx u (2 du) 2 u C 1 x C
'ˆ‰
È
È
1x
x4
$%
""
#
%
œœœ
'ˆ‰ ˆ ‰
È
23. Let u 3z 4 du 3 dz du dzœÊ œ Ê œ
"
3
cos (3z 4) dz (cos u) du cos u du sin u C sin (3z 4) C
'' '
œ œ œ œ
ˆ‰
"" " "
33 3 3
24. Let u 8z 5 du 8 dz du dzœÊ œ Ê œ
"
8
sin (8z 5) dz (sin u) du sin u du ( cos u) C cos (8z 5) C
'' '
œ œ œœ
ˆ‰
"" " "
88 8 8
25. Let u 3x 2 du 3 dx du dxœÊ œ Ê œ
"
3
sec (3x 2) dx sec u du sec u du tan u C tan (3x 2) C
'' '
###
"" " "
œ œ œ œ ab
ˆ‰
33 3 3
26. Let u tan x du sec x dxœÊœ
#
tan x sec x dx u du u C tan x C
''
## # $ $
""
œœœ
33
27. Let u sin du cos dx 3 du cos dxœÊœ Êœ
ˆ‰ ˆ‰ ˆ‰
xx x
333 3
"
sin cos dx u (3 du) 3 u C sin C
''
&&''
""
#
ˆ‰ ˆ‰ ˆ ‰ ˆ‰
xx x
33 6 3
œœœ
28. Let u tan du sec dx 2 du sec dxœÊœ Êœ
ˆ‰ ˆ‰ ˆ‰
xx x
### #
"##
tan sec dx u (2 du) 2 u C tan C
''
(# ( ) )
## #
""
ˆ‰ ˆ‰ ˆ ‰ ˆ‰
xx x
84
œœœ
29. Let u 1 du dr 6 du r drœÊ œ Ê œ
rr
18 6 #
r 1 dr u (6 du) 6 u du 6 C 1 C
'''
#&&
& '
Š‹ Š‹ Š‹
rur
18 6 18
œ œ œ œ
30. Let u 7 du r dr 2 du r drœ Ê œ Ê œ
r
10
"
#
%%
r 7 dr u ( 2 du) 2 u du 2 C 7 C
'''
%$$
$ %
"
#
Š‹ Š‹ Š‹
œœ œœ
rur
10 4 10
31. Let u x 1 du x dx du x dxœÊœ Ê œ
$Î# "Î# "Î#
#
32
3
x sin x 1 dx (sin u) du sin u du ( cos u) C cos x 1 C
'''
"Î# $Î# $Î#
ˆ‰ ˆ‰ ˆ‰
œ œ œœ
22 2 2
33 3 3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

326 Chapter 5 Integration
32. Let u x 8 du x dx du x dxœÊœ Ê œ
%Î$ "Î$ "Î$
43
34
x sin x 8 dx (sin u) du sin u du ( cos u) C cos x 8 C
'''
"Î$ %Î$ %Î$
ˆ‰ ˆ‰ ˆ‰
œ œ œœ
33 3 3
44 4 4
33. Let u sec v du sec v tan v dvœÊœ
ˆ‰ ˆ‰ˆ‰
111
###
sec v tan v dv du u C sec v C
''
ˆ‰ˆ‰ ˆ‰
œœœ
11 1
## #
34. Let u csc du csc cot dv 2 du csc cot dvœÊœ Êœ
ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ‰
vvv vv "
# ### ##
111 11
csc cot dv 2 du 2u C 2 csc C
''
ˆ‰ˆ‰ ˆ‰
vv v
## #
11 1
œ œœ
35. Let u cos (2t 1) du 2 sin (2t 1) dt du sin (2t 1) dtœÊœ Êœ
"
#
dt C C
''
sin (2t 1)
cos (2t 1) u u cos (2t 1)
du
###
"" "
œ œœ
36. Let u 2 sin t du cos t dtœ Ê œ
dt du 6 u du 6 C 3(2 sin t) C
'''
6 cos t 6 u
(2 sin t) u#
$ #
œœ œœ
Š‹
37. Let u cot y du csc y dy du csc y dyœÊœ Êœ
##
cot y csc y dy u ( du) u du u C (cot y) C cot y C
'''
ÈÈab
# "Î# $Î# $Î# $ "Î#
œ œ œ œ œ
22 2
33 3
38. Let u sec z du sec z tan z dzœÊœ
dz du u du 2u C 2 sec z C
'''
sec z tan z
sec z u
ÈÈ
œœ œœ
""Î# "Î# È
39. Let u 1 t 1 du t dt du dtœœ Ê œ Ê œ
""
" #
tt
cos 1 dt (cos u)( du) cos u du sin u C sin 1 C
'''
"" "
tt t
ˆ‰ ˆ‰
œ œ œœ
40. Let u t 3 t 3 du t dt 2 du dtœœÊœ Ê œ
È"Î# "Î#
""
#Èt
cos t 3 dt (cos u)(2 du) 2 cos u du 2 sin u C 2 sin t 3 C
'''
"
Ètˆ‰ ˆ‰
ÈÈ
œ œ œ œ
41. Let u sin du cos d du cos dœÊœ Êœ
""" ""
))) ))
ˆ‰ˆ‰
))
sin cos d u du u C sin C
''
""" " " "
##
##
))) )
)œ œ œ
42. Let u csc du csc cot d 2 du cot csc dœÊœ Êœ
ÈÈÈ ÈÈ
Š‹Š‹
)))) )))
""
#ÈÈ
))
d cot csc d 2 du 2u C 2 csc C C
'' '
cos
sin sin
2
È
ÈÈ È È
)
)) ) )
)))) )œœœœœ
"ÈÈ È
43. Let u s 2s 5s 5 du 3s 4s 5 dsœ Ê œ
$# #
ab
s 2s 5s 5 3s 4s 5 ds u du C C
''
abab
$# #
##
œ œœ
us2s5s5
ab
44. Let u 2 8 2 du 4 4 8 d du 2 dœ Ê œ Ê œ ))) )) ) )) )
%# $ $
"
ab ab
4
2 8 2 2 d u du u du C C
'''
abab
ˆ‰ Š‹
))) )) )
%# $ "" "
#
œ œ œ œ
44 4 8
u282
ˆ‰
)))
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 5.5 Indefinite Integrals and the Substitution Rule 327
45. Let u 1 t du 4t dt du t dtœ Ê œ Ê œ
%$ $
"
4
t 1 t dt u du u C 1 t C
''
$% $ % %
$%
""" "
ab ab
ˆ‰ˆ‰
œ œ œ
444 16
46. Let u 1 du dxœ Ê œ
""
xx
dx dx 1 dx u du u du u C 1 C
'' ' ''
ÉÉÉȈ‰
x1 x1 2 2
xxxxx 3 3x
""" "
"Î# $Î# $Î#
œœœœœœ
47. Let u x . Then du xdx and du xdx and x u . Thus x x dx u u duœ" œ# œ œ" "œ "
##$
" "
# #
#
''
Èab
È
uudu u u Cu uCx x Cœœœœ""
" "## "" " "
# #&$ &$ & $
$Î# "Î# &Î# $Î# &Î# $Î# # #
&Î# $Î#
'ab
’“ abab
48. Let u x du x dx and x u . So x dx u u du u u duœ"Ê œ$ œ" $B "œ " œ
$ # $ & $Î# "Î#
$
'''
ab
Èab
È
uuCx x Cœœ""
## # #
&$ & $
&Î# $Î# $ $
&Î# $Î#
abab
49. (a) Let u tan x du sec x dx; v u dv 3u du 6 dv 18u du; w 2 v dw dvœÊœ œÊœ Êœ œÊœ
#$ # #
dx du 6 w dw 6w C C
'''''
18 tan x sec x 18u 6 dv 6 dw 6
2tanx 2u (2 v) w v
ab ab
#
# "
œœœœœœ
CCœ œ
66
2u 2tanx
(b) Let u tan x du 3 tan x sec x dx 6 du 18 tan x sec x dx; v 2 u dv duœÊœ Êœ œÊœ
$## ##
dx C C C
'''
18 tan x sec x 6 du 6 dv 6 6 6
2tanx (2 u) v v 2 u tan x
ab#
œ œ œ œ œ
(c) Let u 2 tan x du 3 tan x sec x dx 6 du 18 tan x sec x dxœ Ê œ Ê œ
$## ##
dx C C
''
18 tan x sec x 6 du 6 6
2tanx uu 2tanx
ab
œœœ
50. (a) Let u x 1 du dx; v sin u dv cos u du; w 1 v dw 2v dv dw v dvœ Ê œ œ Ê œ œ Ê œ Ê œ
#"
#
1 sin (x 1) sin (x 1) cos (x 1) dx 1 sin u sin u cos u du v 1 v dv
''
ÈÈÈ
'
œ œ
###
w dwwC1v C1sinu C1sin(x1) Cœ œ œ œ œ
'"" " " "
#
$Î# # # #
$Î# $Î# $Î#
Èab a b a b
33 3 3
(b) Let u sin (x 1) du cos (x 1) dx; v 1 u dv 2u du dv u duœÊœ œÊœ Êœ
#"
#
1 sin (x 1) sin (x 1) cos (x 1) dx u 1 u du v dv v dv
''''
ÈÈÈ
œ œ œ
##
""
##
"Î#
v C v C 1u C 1sin(x1) Cœœœœ
ˆ‰ˆ‰ ab a b
""" "
#
$Î# $Î# # #
$Î# $Î#
2
333 3
(c) Let u 1 sin (x 1) du 2 sin (x 1) cos (x 1) dx du sin (x 1) cos (x 1) dxœ Ê œ Ê œ
#"
#
1 sin (x 1) sin (x 1) cos (x 1) dx u du u du u C
'''
ÈȈ‰
œ œ œ
#"""
###
"Î# $Î#
2
3
1 sin (x 1) Cœ
"#$Î#
3ab
51. Let u 3(2r 1) 6 du 6(2r 1)(2) dr du (2r 1) dr; v u dv du dvœÊœ Ê œ œ Êœ Ê
#"""
##
16
u
ÈÈ
duœ"
#1u
È
dr du (cos v) dv sin v C sin u C
'(2r 1) cos 3(2r 1) 6
3(2r 1) 6
cos u
u1666
""""
#
ÈÈ
ÈÈ
œœœœ
''
Š‹
ˆ‰ ˆ‰ È
sin 3(2r 1) 6 Cœ
"#
6È
52. Let u cos du sin d 2 du dœÊœ Êœ
ÈÈ
Š‹Š‹
))) )
"
#ÈÈ
È
))
)sin
d d 2 u du 2 2u C C
''
sin sin
cos cos
2 du 4
uu
ÈÈ
ÉÉ
ÈÈÈ È
))
)) ) )
))œ œ œ œ œ
''
$Î# "Î#
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
328 Chapter 5 Integration
Cœ
4
cos
ÉÈ)
53. Let u 3t 1 du 6t dt 2 du 12t dtœÊ œ Ê œ
#
s 12t 3t 1 dt u (2 du) 2 u C u C 3t 1 C;œ œ œ œ œ
''
ab ab
ˆ‰
#$%%#
$ %
"""
##4
s 3 when t 1 3 (3 1) C 3 8 C C 5 s 3t 1 5œ œÊœ Êœ Ê œÊœ
""
##
%#
%
ab
54. Let u x 8 du 2x dx 2 du 4x dxœÊ œ Ê œ
#
y 4x x 8 dx u (2 du) 2 u C 3u C 3 x 8 C;œ œ œ œ œ
''
ab ab
ˆ‰
# "Î$ #Î$ #Î$ #
"Î$ #Î$
#
3
y 0 when x 0 0 3(8) C C 12 y 3 x 8 12œ œÊœ Ê œ Êœ
#Î$ # #Î$
ab
55. Let u t du dtœ Ê œ
1
1#
s 8 sin t dt 8 sin u du 8 sin 2u C 4 t 2 sin 2t C;œœ œœ
''
##
## #
"
ˆ‰ ˆ ‰ ˆ‰ ˆ‰
111
1416
u
s 8 when t 0 8 4 2 sin C C 8 1 9œ œ Ê œ Ê œœ
ˆ‰ ˆ‰
11 1 1
16 3 3#
s 4 t 2 sin 2t 9 4t 2 sin 2t 9Êœ œ
ˆ‰ ˆ‰ ˆ‰
111 1
163 6#
56. Let u du dœÊ œ
1
4))
r 3 cos d 3 cos u du 3 sin 2u C sin 2 C;œ œ œ œ
''
##
###
"
ˆ‰ ˆ ‰ ˆ‰ ˆ ‰
111
4444
u33
)) ) )
r when 0 sin C C r sin 2œœÊœÊœÊœ
11111 111
8884 444 4
33 3 3 3 3
)))
## # ##
ˆ‰ ˆ ‰
r sin2 r cos 2ʜ ʜ
33 3 33 3
4842484##
)) ))
ˆ‰
11 1
57. Let u 2t du 2 dt 2 du 4 dtœ Ê œ Ê œ
1
#
4 sin 2t dt (sin u)( 2 du) 2 cos u C 2 cos 2t C ;
ds
dt œ œ œ œ
''
ˆ‰ ˆ‰
1 1
# #
""
at t 0 and 100 we have 100 2 cos C C 100 2 cos 2t 100œœ œÊœÊœ
ds ds
dt dt
ˆ‰ ˆ ‰
11
##
""
s 2 cos 2t 100 dt (cos u 50) du sin u 50u C sin 2t 50 2t C ;Êœ œ œ œ
''
ˆ ‰ ˆ‰ˆ‰ˆ‰
111
###
##
at t 0 and s 0 we have 0 sin 50 C C 1 25œœ œÊœ
ˆ‰ ˆ‰
11
##
## 1
s sin 2t 100t 25 (1 25 ) s sin 2t 100t 1ʜ ʜ
ˆ‰ ˆ‰
11
##
11
58. Let u tan 2x du 2 sec 2x dx 2 du 4 sec 2x dx; v 2x dv 2 dx dv dxœÊœ Êœ œÊœÊœ
## "
#
4 sec 2x tan 2x dx u(2 du) u C tan 2x C ;
dy
dx œœœœ
''
###
""
at x 0 and 4 we have 4 0 C C 4 tan 2x 4 sec 2x 1 4 sec 2x 3œ œ œ Ê œ Ê œ œ œ
dy dy
dx dx
"" ## #
ab
y sec 2x 3 dx sec v 3 dv tan v v C tan 2x 3x C ;Êœ œ œ œ
''
abab
ˆ‰
##
"" "
## # #
##
3
at x 0 and y 1 we have 1 (0) 0 C C 1 y tan 2x 3x 1œœ œÊœÊœ
""
##
##
59. Let u 2t du 2 dt 3 du 6 dtœÊ œ Ê œ
s 6 sin 2t dt (sin u)(3 du) 3 cos u C 3 cos 2t C;œœ œœ
''
at t 0 and s 0 we have 0 3 cos 0 C C 3 s 3 3 cos 2t s 3 3 cos ( ) 6 mœœ œÊœÊœ Êœ œ
ˆ‰
1
#1
60. Let u t du dt du dtœÊ œ Ê œ1111
#
v cos t dt (cos u)( du) sin u C sin ( t) C ;œœ œœ
''
11 1 1 11
#""
at t 0 and v 8 we have 8 (0) C C 8 v sin ( t) 8 s ( sin ( t) 8) dtœœ œÊœÊœœ Êœ 11111
"" ds
dt '
sin u du 8t C cos ( t) 8t C ; at t 0 and s 0 we have 0 1 C C 1œœœœ œÊœ
'## ##
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 5.6 Substitution and Area Between Curves 329
s 8t cos ( t) 1 s(1) 8 cos 1 10 mÊœ Ê œ œ11
61. All three integrations are correct. In each case, the derivative of the function on the right is the integrand on
the left, and each formula has an arbitrary constant for generating the remaining antiderivatives. Moreover,
sinxC1cosxC C1C; also cosxC C CC C .
## #
""#" # #$#"
## # #
"""
œ Ê œ œ Ê œœ
cos 2x
62. Both integrations are correct. In each case, the derivative of the function on the right is the integrand on the
left, and each formula has an arbitrary constant for generating the remaining antiderivatives. Moreover,
CCC
tan x sec x 1 sec x
####
"
œ œ
ðñò
ˆ‰
a constant
63. (a) V sin 120 t dt 60 V cos (120 t) [cos 2 cos 0]
Š‹ ‘ˆ‰
""
"Î'!
!#
60 0120
V
'0
160
max max
111œ œ
11
max
[1 1] 0œ œ
Vmax
#1
(b) V 2 V 2 (240) 339 volts
max rms
œœ ¸
ÈÈ
(c) V sin 120 t dt V dt (1 cos 240 t) dt
'''
000
160 160 160
max max
ab ab ˆ‰
##
#
##
11œœ
1 cos 240 t V
1ab
max
t sin 240 t sin (4 ) 0 sin (0)œ œ œ
ab ab abVV V
240 60 240 40 1 0
max max max
## ##
""""
"Î'!
!
‘ ‘ˆ‰ ˆ ‰ˆ ‰ˆ‰ ˆ‰
111
11
5.6 SUBSTITUTION AND AREA BETWEEN CURVES
1. (a) Let u y 1 du dy; y 0 u 1, y 3 u 4œ Ê œ œ Ê œ œ Ê œ
y 1 dy u du u (4) (1) (8) (1)
''
01
34
È ‘ ˆ‰ ˆ‰ ˆ‰ ˆ‰
œ œ œ œœ
"Î# $Î# $Î# $Î#
%
"
222 2214
333 333
(b) Use the same substitution for u as in part (a); y 1 u 0, y 0 u 1œ Ê œ œ Ê œ
y 1 dy u du u (1) 0
''
10
01
È‘ˆ‰
œ œ œ œ
"Î# $Î# $Î#
"
!
22 2
33 3
2. (a) Let u 1 r du 2r dr du r dr; r 0 u 1, r 1 u 0œ Ê œ Ê œ œ Ê œ œ Ê œ
#"
#
r 1 r dr u du u 0 (1)
''
01
10
ÈÈ‘ˆ‰
œ œ œ œ
#"" ""
#
$Î# $Î#
!
"
333
(b) Use the same substitution for u as in part (a); r 1 u 0, r 1 u 0œ Ê œ œ Ê œ
r 1 r dr u du 0
''
10
10
ÈÈ
œ œ
#"
#
3. (a) Let u tan x du sec x dx; x 0 u 0, x u 1œÊœ œÊœœÊœ
#1
4
tan x sec x dx u du 0
''
00
41
#
## #
"
!
"
œœœœ
’“
u1
(b) Use the same substitution as in part (a); x u 1, x 0 u 0œÊœ œÊœ
1
4
tan x sec x dx u du 0
''
41
00
#
###
!
"
""
œœœœ
’“
u
4. (a) Let u cos x du sin x dx du sin x dx; x 0 u 1, x u 1œ Ê œ Ê œ œ Ê œ œ Ê œ1
3 cos x sin x dx 3u du u ( 1) (1) 2
''
01
1
##$$$
"
"
œ œ œœcd a b
(b) Use the same substitution as in part (a); x 2 u 1, x 3 u 1œÊœ œÊœ11
3 cos x sin x dx 3u du 2
''
21
31
##
œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

330 Chapter 5 Integration
5. (a) u 1 t du 4t dt du t dt; t 0 u 1, t 1 u 2œ Ê œ Ê œ œ Ê œ œ Ê œ
%$ $
"
4
t 1 t dt u du
''
01
12
$% $
$"#
"
ab ’“
œ œ œœ
416161616
u2115
(b) Use the same substitution as in part (a); t 1 u 2, t 1 u 2œ Ê œ œ Ê œ
t 1 t dt u du 0
''
12
12
$% $
$"
abœ œ
4
6. (a) Let u t 1 du 2t dt du t dt; t 0 u 1, t 7 u 8œÊ œ Ê œ œ Ê œ œ Ê œ
#"
#È
t t 1 dt u du u (8) (1)
''
01
78
ab ‘ ˆ‰ ˆ‰ˆ‰ˆ‰
# "Î$ %Î$ %Î$ %Î$
"Î$ ""
##
)
"
œ œ œœ
33345
4888
(b) Use the same substitution as in part (a); t 7 u 8, t 0 u 1œ Ê œ œ Ê œ
È
t t 1 dt u du u du
'''
781
018
ab
# "Î$ "Î$
"Î$ ""
##
œ œ œ45
8
7. (a) Let u 4 r du 2r dr du r dr; r 1 u 5, r 1 u 5œ Ê œ Ê œ œÊ œ œ Ê œ
#"
#
dr 5 u du 0
''
"
#
#
15
15
5r
4rabœœ
(b) Use the same substitution as in part (a); r 0 u 4, r 1 u 5œÊœ œÊœ
dr 5 u du 5 u 5 (5) 5 (4)
''
04
15
5r
4r 8
ab
"""""
####
# " " "
&
%
œœœœ
‘ˆ‰ˆ‰
8. (a) Let u 1 v du v dv du 10 v dv; v 0 u 1, v 1 u 2œ Ê œ Ê œ œ Ê œ œ Ê œ
$Î# "Î#
#
320
3È
dv du u du
'' '
01 1
12 2
10 v
1v u3 3 3u 3 1 3
20 20 20 20 1 10
È
ab
"""
# #
"#
œ œ œ œ œ
ˆ‰ ‘ ‘
(b) Use the same substitution as in part (a); v 1 u 2, v 4 u 1 4 9œÊœ œÊœ œ
$Î#
dv du
''
12
49
10 v
1v u3 3u 39 2 3 18 7
20 20 20 1 20 7 70
È
ab
"""
*
##
œœœœœ
ˆ‰ ‘ ˆ‰ ˆ‰
9. (a) Let u x 1 du 2x dx 2 du 4x dx; x 0 u 1, x 3 u 4œÊ œ Ê œ œÊœ œ Êœ
#È
dx du 2u du 4u 4(4) 4(1) 4
'''
011
344
4x 2
x1 u
ÈÈ
"Î# "Î# "Î# "Î#
%
"
œ œ œ œœ
‘
(b) Use the same substitution as in part (a); x 3 u 4, x 3 u 4œ Ê œ œ Ê œ
ÈÈ
dx du 0
''
34
34
4x 2
x1 u
ÈÈ
œœ
10. (a) Let u x 9 du 4x dx du x dx; x 0 u 9, x 1 u 10œÊ œ Ê œ œÊœ œÊœ
%$$
"
4
dx u du (2)u (10) (9)
''
09
110
x
x9 44
10 3
ÈÈ
"" ""
"Î# "Î# "Î# "Î#
"!
*## #
œœœœ
‘
(b) Use the same substitution as in part (a); x 1 u 10, x 0 u 9œ Ê œ œ Ê œ
dx u du u du
'' '
110 9
09 10
x
x9 44
310
ÈÈ
""
"Î# "Î#
#
œœœ
11. (a) Let u 1 cos 3t du 3 sin 3t dt du sin 3t dt; t 0 u 0, t u 1 cos 1œ Ê œ Ê œ œ Ê œ œ Ê œ œ
"
#36
11
(1 cos 3t) sin 3t dt u du (1) (0)
''
00
61
œœœœ
"" """
#
"
!
##
33 666
u
’“Š‹
(b) Use the same substitution as in part (a); t u 1, t u 1 cos 2œÊœ œÊœ œ
11
63 1
(1 cos 3t) sin 3t dt u du (2) (1)
''
61
32
œœœœ
"" """
#
#
"
##
33 662
u
’“Š‹
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 5.6 Substitution and Area Between Curves 331
12. (a) Let u 2 tan du sec dt 2 du sec dt; t u 2 tan 1, t 0 u 2œ Ê œ Ê œ œ Ê œ œ œ Ê œ
tt t
4### ##
"
##
11
ˆ‰
2 tan sec dt u (2 du) u 2 1 3
''
21
02
ˆ‰ cd œ œ œœ
tt
##
####
#
"
(b) Use the same substitution as in part (a); t u 1, t u 3œÊœœÊœ
##
11
2 tan sec dt 2 u du u 3 1 8
''
21
23
ˆ‰ cd œ œ œœ
tt
##
####
$
"
13. (a) Let u 4 3 sin z du 3 cos z dz du cos z dz; z 0 u 4, z 2 u 4œ Ê œ Ê œ œ Ê œ œ Ê œ
"
31
dz du 0
''
04
24
cos z
43 sin z u3
ÈÈ
""
œœ
ˆ‰
(b) Use the same substitution as in part (a); z u 4 3 sin ( ) 4, z u 4œÊœ œ œÊœ111
dz du 0
''
cos z
43 sin z u3
ÈÈ
""
œœ
4
4ˆ‰
14. (a) Let u 3 2 cos w du 2 sin w dw du sin w dw; w u 3, w 0 u 5œ Ê œ Ê œ œ Ê œ œ Ê œ
"
##
1
dw u du u
''
23
05
sin w
(3 2 cos w) 5 3 15###
# "
"" """"
&
$
œœœœ
ˆ‰ ˆ‰
cd
(b) Use the same substitution as in part (a); w 0 u 5, w u 3œÊœ œ Êœ
1
#
dw u du u du
''
23
5
5
3
sin w
(3 2 cos w) 15##
# #
"" "
œœ œ
ˆ‰
'
15. Let u t 2t du 5t 2 dt; t 0 u 0, t 1 u 3œ Ê œ œ Ê œ œ Ê œ
&%
ab
t 2t 5t 2 dt u du u (3) (0) 2 3
''
00
13
Èab ‘ È
&% "Î# $Î# $Î# $Î#
$
!
œ œ œœ
222
333
16. Let u 1 y du ; y 1 u 2, y 4 u 3œ Ê œ œ Ê œ œ Ê œ
Èdy
2y
È
du u du u
'''
122
433
dy
2y1 y u326
11
ÈÈ
ˆ‰
""
# " $
#
œœ œœœcdˆ‰ˆ‰
17. Let u cos 2 du 2 sin 2 d du sin 2 d ; 0 u 1, u cos 2œÊœ Êœ œÊœœÊœ œ))) ))))
" "
# #
11
66
ˆ‰
cos 2 sin 2 d u du u du
'''
61212
11
$ $ $
"" " ""
## #
"Î#
"
)))œœ œ œœ
ˆ‰ ’“Š‹
24(1)4
u3
4ˆ‰
1
18. Let u tan du sec d 6 du sec d ; u tan , œÊœ Êœ œÊœœœÊ
ˆ‰ ˆ‰ ˆ‰ ˆ‰
)) ) 11
666 6 6
3
3" "
##
#
)))1 )
È
utan 1œœ
1
4
cot sec d u (6 du) 6 12
''
32 1
13
&# &
"
"Î $
"
"Î $ #
ˆ‰ ˆ‰ ‘
’“Š‹
))
66 4
u333
2u 2(1)
)œœœœœ
ÈÈŠ‹
3
19. Let u 5 4 cos t du 4 sin t dt du sin t dt; t 0 u 5 4 cos 0 1, t œ Ê œ Ê œ œ Ê œ œ œ Ê
"
41
u 5 4 cos 9œ œ1
5 (5 4 cos t) sin t dt 5u du u du u 9 1
'''
œœœœœ$"
"Î% "Î% "Î% &Î% &Î% &Î#
"*
"
11
99
ˆ‰ ‘ˆ‰
44 45
554
20. Let u 1 sin 2t du 2 cos 2t dt du cos 2t dt; t 0 u 1, t u 0œ Ê œ Ê œ œ Ê œ œ Ê œ
"
#
1
4
(1 sin 2t) cos 2t dt u du u (0) (1)
''
40
1
œœœœ
$Î# $Î# &Î# &Î# &Î#
"" "
#
!
"
‘ˆ‰ˆ‰ˆ‰
25 5 5 5
211
21. Let u 4y y 4y 1 du 4 2y 12y dy; y 0 u 1, y 1 u 4(1) (1) 4(1) 1 8œ Ê œ œÊœ œÊœ œ
#$ # # $
ab
4y y 4y 1 12y 2y 4 dy u du 3u 3(8) 3(1) 3
''
1 8
1
abab ‘
œ œ œœ
# $ # #Î$ "Î$ "Î$ "Î$
#Î$ )
"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

332 Chapter 5 Integration
22. Let u y 6y 12y 9 du 3y 12y 12 dy du y 4y 4 dy; y 0 u 9, y 1œÊœ Ê œ œÊœœ
$# # #
"
abab
3
u4ʜ
y 6y 12y 9 y 4y 4 dy u du 2u (4) (9) (2 3)
''
1 4
9
abab ‘ˆ‰
$ # # "Î# "Î# "Î# "Î#
"Î# ""
%
*
œ œ œœ
33 333
22 2
œ2
3
23. Let u du d du d ; 0 u 0, uœÊœ Ê œ œÊœœ Êœ)))))) )11
$Î# "Î#
#
$#
32
3ÈÈ
cos d cos u du sin 2u sin 2 (0)
''
Ȉ‰ ˆ‰ ‘ ˆ ‰ˆ‰
))) 1
# $Î# #
##
""
!
œœœœ
22u 2 2
334 34 33
111
24. Let u 1 du t dt; t 1 u 0, t u 1œ Ê œ œÊ œ œ Ê œ
""
#
#t
t sin 1 dt sin u du sin 2u sin ( 2) sin 0
''
1
12 1
# # #
"""""
"
!##
ˆ‰ ‘ ˆ ‰ˆ ‰ˆ‰
’“
œ œ œ
t2444
u0
sin 2œ
""
#4
25. Let u 4 x du 2x dx du x dx; x 2 u 0, x 0 u 4, x 2 u 0œ Ê œ Ê œ œÊœ œÊœ œÊœ
#"
#
A x 4 x dx x 4 x dx u du u du 2 u du u duœ œ œ œ
'' ''''
2 4
02 4044
ÈÈ
##
"""
###
"Î# "Î# "Î# "Î#
u (4) (0)œ œœ
‘
22216
3333
$Î# $Î# $Î#
%
!
26. Let u 1 cos x du sin x dx; x 0 u 0, x u 2œ Ê œ œ Ê œ œ Ê œ1
(1 cos x) sin x dx u du 2
''
œ œ œœ
2’“
u20
2
#
!##
27. Let u 1 cos x du sin x dx du sin x dx; x u 1 cos ( ) 0, x 0œ Ê œ Ê œ œ Ê œ œ œ11
u1cos 02Êœ œ
A 3 (sin x) 1 cos x dx 3u ( du) 3 u du 2u 2(2) 2(0) 2œ œ œ œ œœ
'''
022
È‘
"Î# "Î# $Î# $Î# $Î# &Î#
#
!
28. Let u sin x du cos x dx du cos x dx; x u sin 0, x 0 uœ Ê œ Ê œ œÊœ œ œÊœ11 1 11 1
"
##1
11
ˆ‰
Because of symmetry about x , A 2 (cos x) (sin ( sin x)) dx 2 (sin u) duœ œ œ
11 1
1## #
"
''
2
0
11 ˆ‰
sin u du [ cos u] ( cos ) ( cos 0) 2œœœœ
'1
!1
29. For the sketch given, a 0, b ; f(x) g(x) 1 cos x sin x ;œœ œ œ œ1##
#
1 cos 2x
A dx (1 cos 2x) dx x [( 0) (0 0)]œ œ œ œ œ
''
( cos 2x) sin 2x
"
## ### #
"""
!
‘
11
1
30. For the sketch given, a , b ; f(t) g(t) sec t 4 sin t sec t 4 sin t;œ œ œ œ
11
33
""
##
####
ab
A sec t 4 sin t dt sec t dt 4 sin t dt sec t dt 4 dtœœœ
'''''
33333
33333
ˆ‰
"" "
## # #
## # # # "( cos 2t)
sec t dt 2 (1 cos 2t) dt [tan t] 2[t ] 3 4 3œ œ œ œ
""
###
#Î$
Î$
Î$
Î$
''
33
33 1
1
1
1
11sin 2t 4
33
ÈÈ
†
31. For the sketch given, a 2, b 2; f(x) g(x) 2x x 2x 4x x ;œ œ œ œ
#% # #%
ab
A 4x x dxœ œ œ œœ œ
'2
2ab
’“
ˆ‰ ‘ˆ‰
#% #
#
4x x 32 32 32 32 64 64 320 192 128
3 5 35 3 5 35 15 15
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 5.6 Substitution and Area Between Curves 333
32. For the sketch given, c 0, d 1; f(y) g(y) y y ;œœ œ
#$
A y y dy y dy y dyœ œ œ œ œœ
'''
111
ab ’“ ’“
#$ # $ ""
!!
" " "" "
#
yy(0)(0)
34 34341
33. For the sketch given, c 0, d 1; f(y) g(y) 12y 12y 2y 2y 10y 12y 2y;œœ œ œ abab
#$ # #$
A 10y 12y 2y dy 10y dy 12y dy 2y dy y y yœœ œ
' '''
1 111
ab ‘‘‘
#$ # $ $ % #
"""
!!
!#
10 12 2
34
0 (30)(10)œ œ
ˆ‰
10 4
33
34. For the sketch given, a 1, b 1; f(x) g(x) x 2x x 2x ;œ œ œ œ
# %#%
ab
A x 2x dxœ œ œ œœ œ
'1
1ab
’“
ˆ‰ ‘ˆ‰
#% "
"
"" x 2x 2 2 24101222
3 5 35 3 5 35 15 15
35. We want the area between the line y 1, 0 x 2, and the curve y , the area of a triangleœ Ÿ Ÿ œ 738?=
x
4
(formed by y x and y 1) with base 1 and height 1. Thus, A 1 dx (1)(1) xœœ œœ
'2Š‹ ’“
xx
41
""
###
#
!
22œ œœ
ˆ‰
825
136## #
""
36. We want the area between the x-axis and the curve y x , 0 x 1 the area of a triangle (formed by x 1,œŸŸ:6?= œ
#
x y 2, and the x-axis) with base 1 and height 1. Thus, A x dx (1)(1)œ œ œ œœ
'1
#""""
###
"
!
’“
x5
336
37. AREA A1 A2œ
A1: For the sketch given, a 3 and we find b by solving the equations y x 4 and y x 2xœ œ œ
##
simultaneously for x: x 4 x 2x 2x 2x 4 0 2(x 2)(x 1) x 2 or x 1 so
## #
œ Ê œ Ê Ê œ œ
b 2: f(x) g(x) x 4 x 2x 2x 2x 4 A1 2x 2x 4 dxœ œ œ Ê œ aba b a b
### #
'3
2
4x 4 8 ( 18 9 12) 9 ;œ œœœ
’“
ˆ‰
2x 2x 16 16 11
33 33
#
#
$
A2: For the sketch given, a 2 and b 1: f(x) g(x) x 2x x 4 2x 2x 4œ œ œ œ abab
## #
A2 2x 2x 4 dx x 4x 1 4 4 8Êœ œ œ
'2
1ab
’“
ˆ‰ˆ ‰
##
"
#
2x 2 16
333
14 489;œ œ
216
33
Therefore, AREA A1 A2 9œœœ
11 38
33
38. AREA A1 A2œ
A1: For the sketch given, a 2 and b 0: f(x) g(x) 2x x 5x x 3x 2x 8xœ œ œ œ abab
$# # $
A1 2x 8x dx 0 (8 16) 8;Êœ œ œœ
'2
0ab
’“
$
#
!
#
2x 8x
4
A2: For the sketch given, a 0 and b 2: f(x) g(x) x 3x 2x x 5x 8x 2xœœœœaba b
#$# $
A2 8x 2x dx (16 8) 8;Êœ œ œœ
'0
2ab
’“
$#
!
8x 2x
24
Therefore, AREA A1 A2 16œœ
39. AREA A1 A2 A3œ
A1: For the sketch given, a 2 and b 1: f(x) g(x) ( x 2) 4 x x x 2œ œ œ œ ab
##
A1 x x 2 dx 2x 2 4 ;Ê œ œ œ œ œ œ
'2
1ab
’“
ˆ‰ˆ‰
#
## #
"
#
"" " "xx 84 7 1431
3332366
A2: For the sketch given, a 1 and b 2: f(x) g(x) 4 x ( x 2) x x 2œ œ œ œ ab a b
##
A2 x x 2 dx 2x 4 2 3 8 ;Êœ œ œœœ
'1
2ab
’“
ˆ‰ˆ ‰
#
## ##
#
"
"x x 84 11 9
3332
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
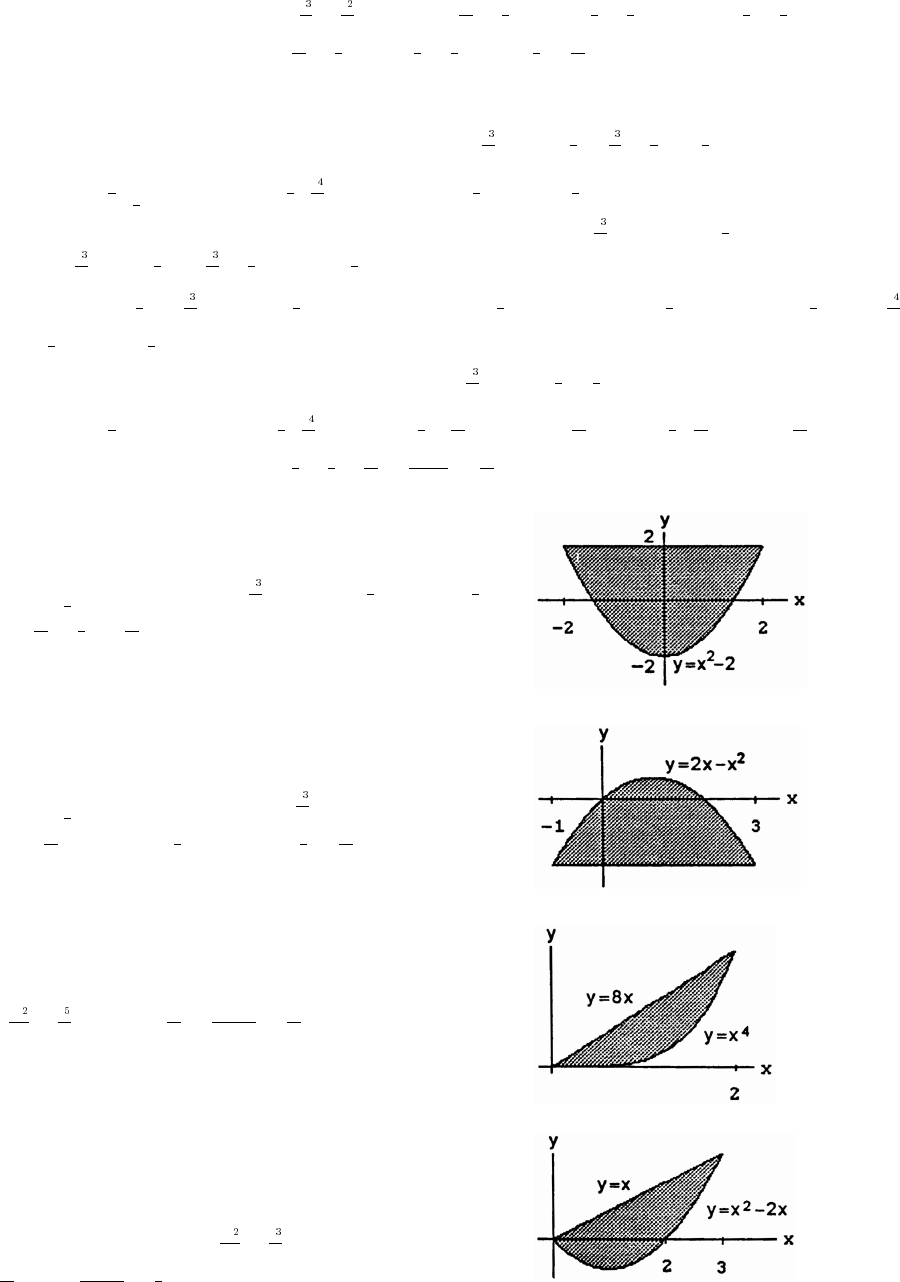
334 Chapter 5 Integration
A3: For the sketch given, a 2 and b 3: f(x) g(x) ( x 2) 4 x x x 2œœœœab
##
A3 x x 2 dx 2x 6 4 9 ;Ê œ œ œ œ
'2
3ab
’“
ˆ‰ˆ‰
#
## #
$
#
xx 279 84 98
33323
Therefore, AREA A1 A2 A3 9 9œœœœ
11 9 9 8 5 49
6366##
ˆ‰
40. AREA A1 A2 A3œ
A1: For the sketch given, a 2 and b 0: f(x) g(x) x x x 4xœ œ œ œ œ
Š‹ ab
xxx4
33333
"$
A1 x 4x dx 2x 0 (4 8) ;Êœ œ œœ
"" "
$#
!
#
33433
x4
'2
0ab’“
A2: For the sketch given, a 0 and we find b by solving the equations y x and y simultaneouslyœœœ
xx
33
for x: x x 0 (x 2)(x 2) 0 x 2, x 0, or x 2 so b 2:
xxx4 x
3333 3
œÊ œÊ œÊœ œ œ œ
f(x) g(x) x x 4x A2 x 4x dx 4x x 2x œ œ Ê œ œ œ
xx x
33 3 3 3 3 4
Š‹ ’ “
ab ab ab
""""
$$$#
#
!
''
00
22
(8 4) ;œœ
"
33
4
A3: For the sketch given, a 2 and b 3: f(x) g(x) x x 4xœœœœ
Š‹ ab
xx
333
"$
A3 x 4x dx 2x 2 9 8 14 ;Êœ œ œ œ œ
""" "
$#
$
#
3343443412
x81168125
'2
3ab’“
‘ˆ‰ˆ‰ˆ‰
†
Therefore, AREA A1 A2 A3œœœ œ
4425322519
3312 1 4
#
41. a 2, b 2;œ œ
f(x) g(x) 2 x 2 4 xœœab
##
A4xdx4x 8 8Êœ œ œ
'2
2ab’“
ˆ‰ˆ ‰
##
#
x88
333
2œœ†ˆ‰
24 8 32
33 3
42. a 1, b 3;œ œ
f(x) g(x) 2x x ( 3) 2x x 3œœab
##
A 2x x 3 dx x 3xÊœ œ
'1
3ab
’“
##
$
"
x
3
991311œœœ
ˆ‰ˆ‰
27 1 32
3333
"
43. a 0, b 2;œœ
f(x) g(x) 8x x A 8x x dxœÊœ
%%
'0
2ab
16œ œœ œ
’“
8x x 32803248
25 555
#
!
44. Limits of integration: x 2x x x 3x
##
œÊ œ
x(x 3) 0 a 0 and b 3;ʜʜ œ
f(x) g(x) x x 2x 3x xœœab
##
A 3x x dxÊœ œ
'0
3ab
’“
#$
!
3x x
23
9œœ œ
27 27 18 9
###
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
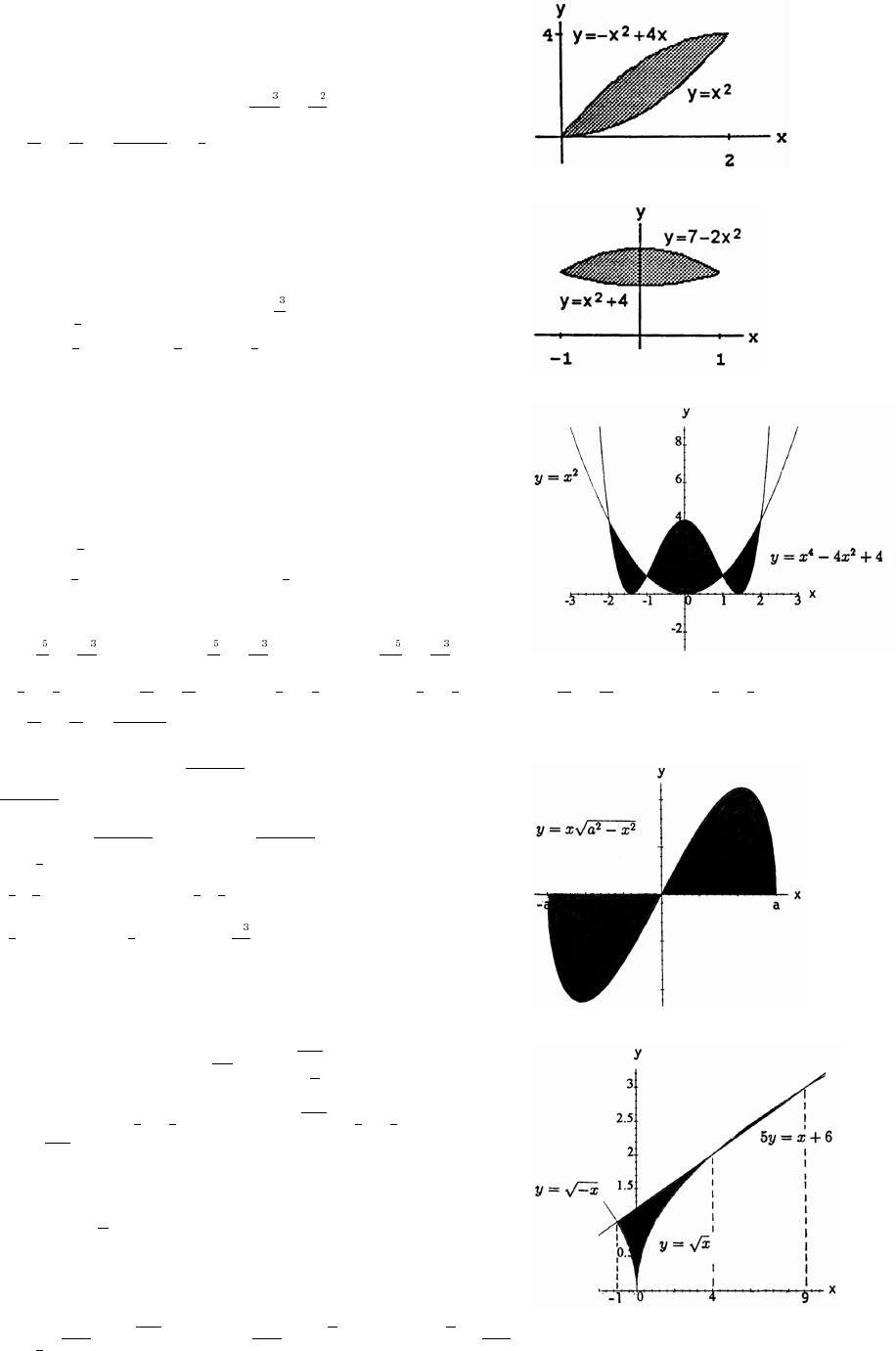
Section 5.6 Substitution and Area Between Curves 335
45. Limits of integration: x x 4x 2x 4x 0
## #
œ Ê œ
2x(x 2) 0 a 0 and b 2;ʜʜ œ
f(x) g(x) x 4x x 2x 4xœœab
###
A 2x 4x dxÊœ œ
'0
2ab
’“
##
!
2x 4x
32
œ œ œ
16 16 32 48 8
363#
46. Limits of integration: 7 2x x 4 3x 3 0œÊ œ
## #
3(x 1)(x 1) 0 a 1 and b 1;ʜʜ œ
f(x) g(x) 7 2x x 4 3 3xœœabab
## #
A 3 3x dx 3 xÊœ œ
'1
1ab’“
#"
"
x
3
31 1 6 4œœ œ
‘ˆ‰ˆ‰ˆ ‰
""
333
2
47. Limits of integration: x 4x 4 x
%# #
œ
x5x40 x4x10Ê œÊ œ
%# # #
abab
(x 2)(x 2)(x 1)(x 1) x 2, 1, 1, 2;ʜ!ʜ
f(x) g(x) x 4x 4 x x 5x 4 and œ œ ab
%# #%#
g(x) f(x) x x 4x 4 x 5x 4œœ
#% # % #
ab
A x 5x 4 dx x 5x 4 dxʜ
''
21
11
abab
%# %#
x5x4dx
'1
2ab
%#
4x 4x 4xœ
’“’“’“
x5x x5x x5x
53 53 5 3
" " #
# " "
4844 84œ
ˆ‰ˆ ‰ˆ‰ˆ ‰ˆ ‰ˆ ‰
""" "
53 5 3 53 53 5 3 53
5 3240 5 5 3240 5
8œ œ œ
60 60 300 180
53 15
48. Limits of integration: x a x 0 x 0 or
È##
œÊœ
a x 0 x 0 or a x 0 x a, 0, a;
È## ##
œÊœ œÊœ
A x a x dx x a x dxœ
''
a0
0a
ÈÈ
## ##
ax axœ
""
##
## ##
$Î# $Î#
!
!
’“’“
ab ab
22
33
a
a
aaœ œ
""
##
$Î# $Î#
333
2a
ab ab
’“
49. Limits of integration: y x and
x, x 0
x, x 0
œœ
Ÿ
Èkk ÈÈ
5y x 6 or y ; for x 0: xœ œ Ÿ œ
x6 x6
55 55
È
5 x x 6 25( x) x 12x 36ʜʜ
È#
x 37x 36 0 (x 1)(x 36) 0Ê œÊ œ
#
x 1, 36 (but x 36 is not a solution);Êœ œ
for x 0: 5 x x 6 25x x 12x 36œÊœ
È#
x 13x 36 0 (x 4)(x 9) 0Ê œÊ œ
#
x 4, 9; there are three intersection points andʜ
A x dx x dx x dxœ
'''
104
049
ˆ ‰ˆ‰ˆ‰
ÈÈÈ
x6 x6 x6
55 5
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
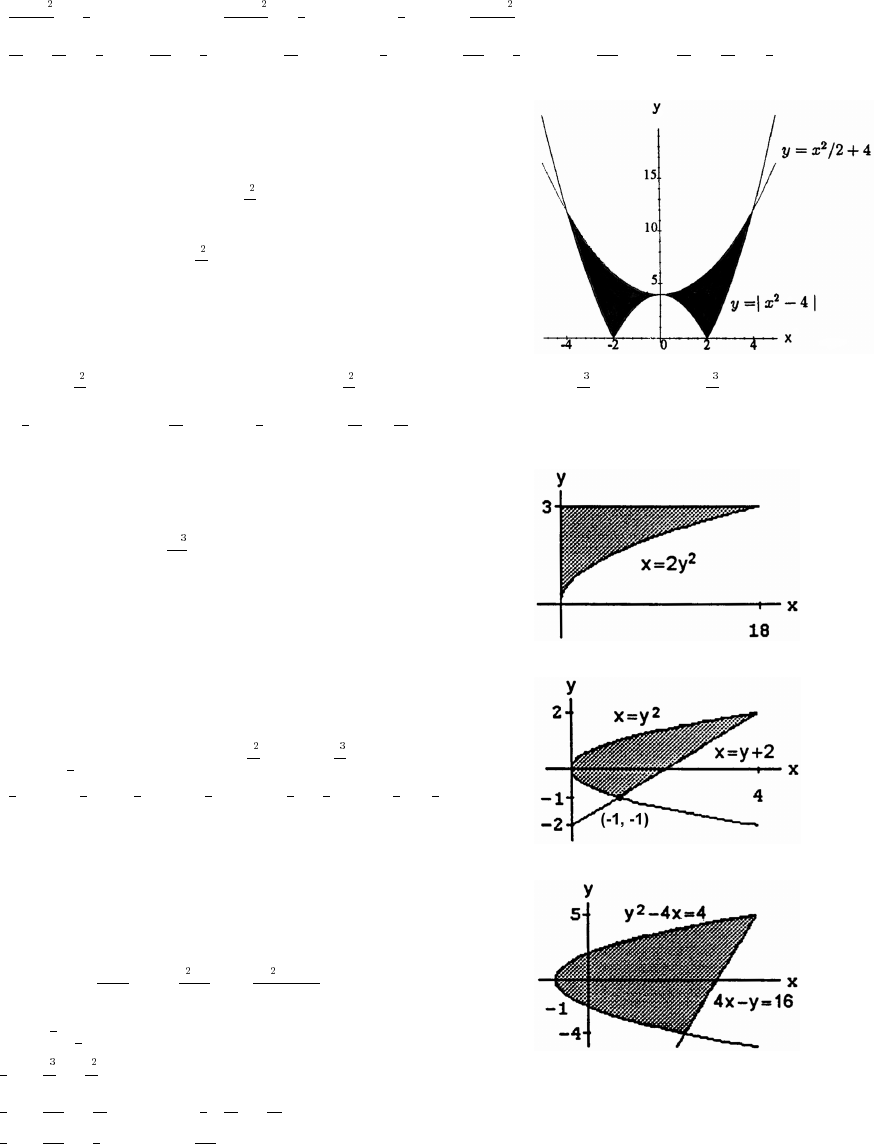
336 Chapter 5 Integration
(x) x xœ
’ “’“’“
(x 6) (x 6) (x 6)
10 3 10 3 3 10
222
$Î# $Î# $Î#
!%*
"!%
409 4œ œœ
ˆ‰ˆ ‰ˆ ‰
36 25 2 100 2 36 2 225 2 100 50 20 5
10 10 3 10 3 10 3 10 3 10 10 3 3
†††
$Î# $Î# $Î#
50. Limits of integration:
yx4 x 4, x 2 or x 2
4 x , 2 x 2
œœ Ÿ
ŸŸ
kk
œ
##
#
for x 2 and x 2: x 4 4Ÿ œ
#x
2
2x 8 x 8 x 16 x 4;ʜʜʜ„
## #
for 2 x 2: 4 x 4 8 2x x 8Ÿ Ÿ œ Ê œ
###
#
x
x 0 x 0; by symmetry of the graph,ʜʜ
#
A2 44xdx2 4x4dx2 28xœœ
''
02
24
’“’“’“’“Š‹ Š‹
ab ab
xxxx
2226
##
#%
!#
20232 16 40œ œœ
ˆ‰ˆ ‰
8 64 8 56 64
66 33#
51. Limits of integration: c 0 and d 3;œœ
f(y) g(y) 2y 0 2yœœ
##
A 2y dy 2 9 18Êœ œ œ œ
'0
3
#$
!
’“
2y
3†
52. Limits of integration: y y 2 (y 1)(y 2) 0
#œ Ê œ
c 1 and d 2; f(y) g(y) (y 2) yÊœ œ œ
#
A y 2 y dy 2yÊœ œ
'1
2ab
’“
#
#
#
"
yy
3
4262œœœ
ˆ‰ˆ‰
48 8 9
3333## ##
"" ""
53. Limits of integration: 4x y 4 and 4x 16 yœ œ
#
y 4 16 y y y 20 0 ʜʜÊ
##
(y 5)(y 4) 0 c 4 and d 5;œÊœ œ
f(y) g(y)œ œ
ˆ‰
Š‹
16 y y 4 y y 20
44 4
A y y 20 dyʜ
"#
4'4
5ab
20yœ
"
#
&
%
43
yy
’“
100 80œ
""
#432 43
125 25 64 16
ˆ‰ˆ‰
180œ œ
"
432 8
189 9 243
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
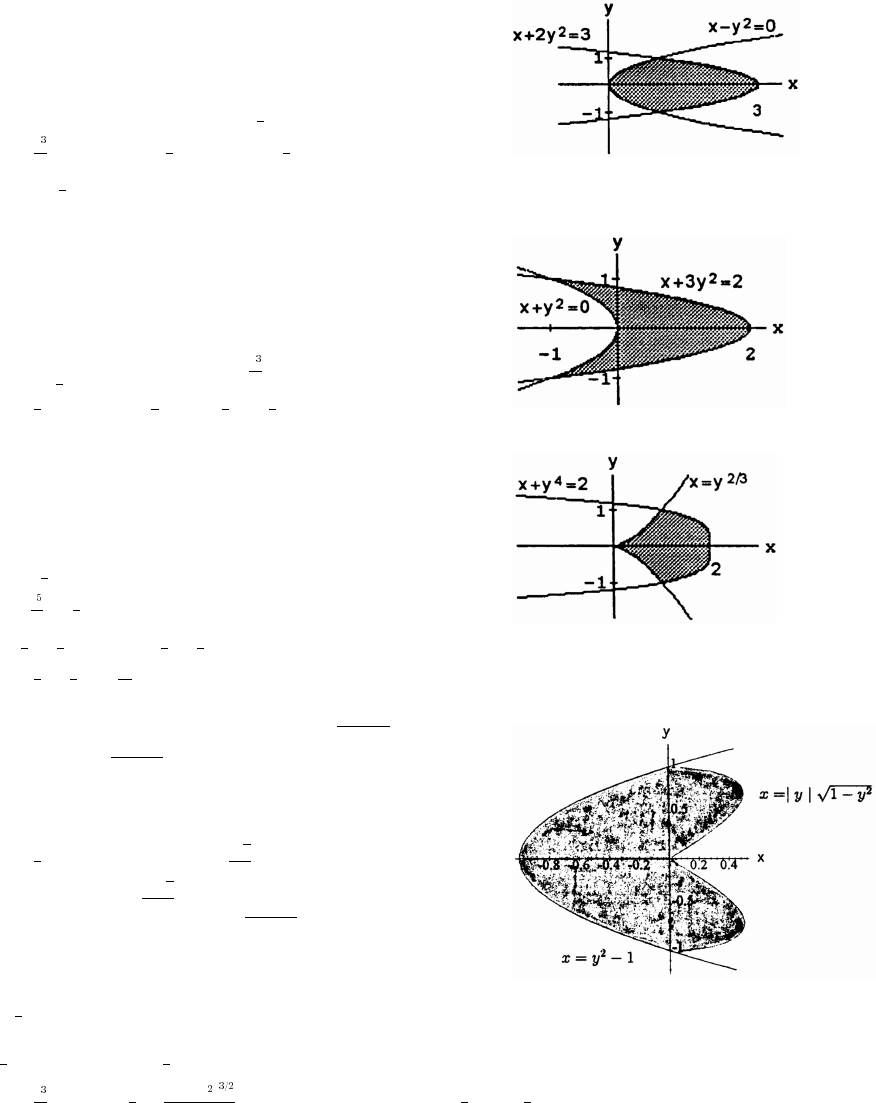
Section 5.6 Substitution and Area Between Curves 337
54. Limits of integration: x y and x 3 2yœœ
##
y 3 2y 3y 3 3(y 1)(y 1) 0Êœ Ê œÊ œ
###
c 1 and d 1; f(y) g(y) 3 2y yÊœ œ œ ab
##
33y 31y A 3 1y dyœ œ Ê œ
## #
ab ab
'1
1
3y 31 3 1œ œ
’“ ˆ‰ˆ ‰
y
333
"
"
""
321 4œœ†ˆ‰
"
3
55. Limits of integration: x y and x 2 3yœ œ
##
y 2 3y 2y 2 0Ê œ Ê œ
###
2(y 1)(y 1) 0 c 1 and d 1;ʜʜ œ
f(y) g(y) 2 3y y 2 2y 2 1 yœœœabab ab
## # #
A 2 1 y dy 2 yÊœ œ
'1
1ab ’“
#"
"
y
3
21 2 1 4œœ œ
ˆ‰ˆ ‰ˆ‰
""
3333
28
56. Limits of integration: x y and x 2 yœœ
#Î$ %
y 2 y c 1 and d 1;ʜʜ œ
#Î$ %
f(y) g(y) 2 y yœab
% #Î$
A 2 y y dyʜ
'1
1ˆ‰
% #Î$
2y yœ
’“
y
55
3&Î$ "
"
22œ
ˆ‰ˆ ‰
""
55 55
33
22œœ
ˆ‰
"
55 5
312
57. Limits of integration: x y 1 and x y 1 yœ œ
##
kkÈ
y1y1y y2y1y1yÊœ Ê œ
#%###
#
kk a b
È
y2y1yy 2y3y10Ê œÊ œ
%# #% %#
2y 1 y 1 0 2y 1 0 or y 1 0Ê œÊœ œabab
## # #
y or y 1 y or y 1.Ê œ œ Ê œ„ œ„
##
"
##
È2
Substitution shows that are not solutions y 1;
„
#
È2Êœ„
for 1 y 0, f(x) g(x) y 1 y y 1Ÿ Ÿ œ
Èab
##
1 y y 1 y , and by symmetry of the graph,œ
##
"Î#
ab
A2 1y y1y dyœ
'1
0’“
ab
##
"Î#
2 1 y dy 2 y 1 y dyœ
''
11
00
ab ab
##
"Î#
2y 2 2( 0) 1 0 2œ œ!œ
’“ˆ‰ ‘ ˆ ‰
”• ˆ‰
y
33 33
21 y 2
!
"
""
#
!
"
ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
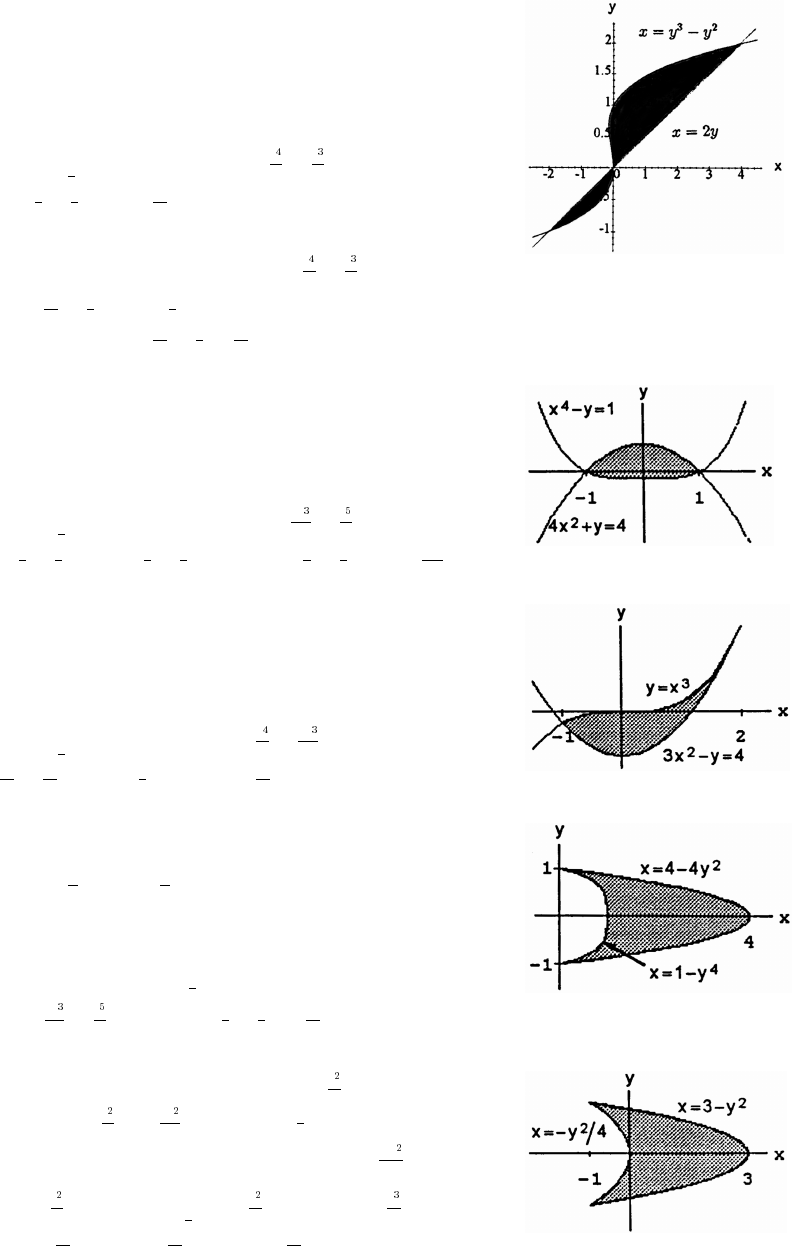
338 Chapter 5 Integration
58. AREA A1 A2œ
Limits of integration: x 2y and x y y œœÊ
$#
y y 2y y y y 2 y(y 1)(y 2) 0
$# #
œ Ê œ œab
y 1, 0, 2:ʜ
for 1 y 0, f(y) g(y) y y 2yŸ Ÿ œ
$#
A1 y y 2y dy yÊœ œ
'1
0ab
’“
$# #
!
"
yy
43
01;œ œ
ˆ‰
""
43 12
5
for 0 y 2, f(y) g(y) 2y y yŸŸ œ
$#
A2 2y y y dy yÊœ œ
'!
$# # #
!
2ab
’“
yy
43
40;ʜ
ˆ‰
16 8 8
43 3
Therefore, A1 A2œœ
5837
12 3 12
59. Limits of integration: y 4x 4 and y x 1œ œ
#%
x 1 4x 4 x 4x 5 0ÊœÊ œ
%#%#
x 5 (x 1)(x 1) 0 a 1 and b 1;Ê œÊœ œab
#
f(x) g(x) 4x 4 x 1 4x x 5 œ œ
#% #%
A 4x x 5 dx 5xÊœ œ
'1
1ab
’“
#% "
"
4x x
35
5525œœœ
ˆ‰ˆ‰ˆ‰
4 4 4 104
35 35 35 15
"" "
60. Limits of integration: y x and y 3x 4œœ
$#
x3x40 xx2(x2)0Ê œÊ œ
$# #
ab
(x 1)(x 2) 0 a 1 and b 2;Ê œÊœ œ
#
f(x) g(x) x 3x 4 x 3x 4œœ
$# $#
ab
A x 3x 4 dx 4xÊœ œ
'1
2ab
’“
$# #
"
x3x
43
84œ"œ
ˆ‰ˆ‰
16 24 1 27
43 4 4
61. Limits of integration: x 4 4y and x 1 yœ œ
#%
44y 1y y4y30Ê œ Ê œ
#%%#
y 3 y 3 (y 1)(y 1) 0 c 1Ê œÊœ
Š‹Š‹
ÈÈ
and d 1 since x 0; f(y) g(y) 4 4y 1 yœœabab
#%
3 4y y A 3 4y y dyœ Ê œ
#% #%
'1
1ab
3y 2 3œ œœ
’“
ˆ‰
4y y
35 35 15
456
"
"
"
62. Limits of integration: x 3 y and xœ œ
#y
4
3 y 3 0 (y 2)(y 2) 0Ê œ Ê œÊ œ
#y3y
44 4
3
c 2 and d 2; f(y) g(y) 3 yÊœ œ œ ab
Š‹
#y
4
3 1 A 3 1 dy 3 yœÊœ œ
Š‹ Š‹ ’“
yyy
441
'2
2
#
#
#
32 2 34 12 4 8œœœœ
‘ˆ‰ˆ‰ˆ ‰
88 16
12 12 12
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
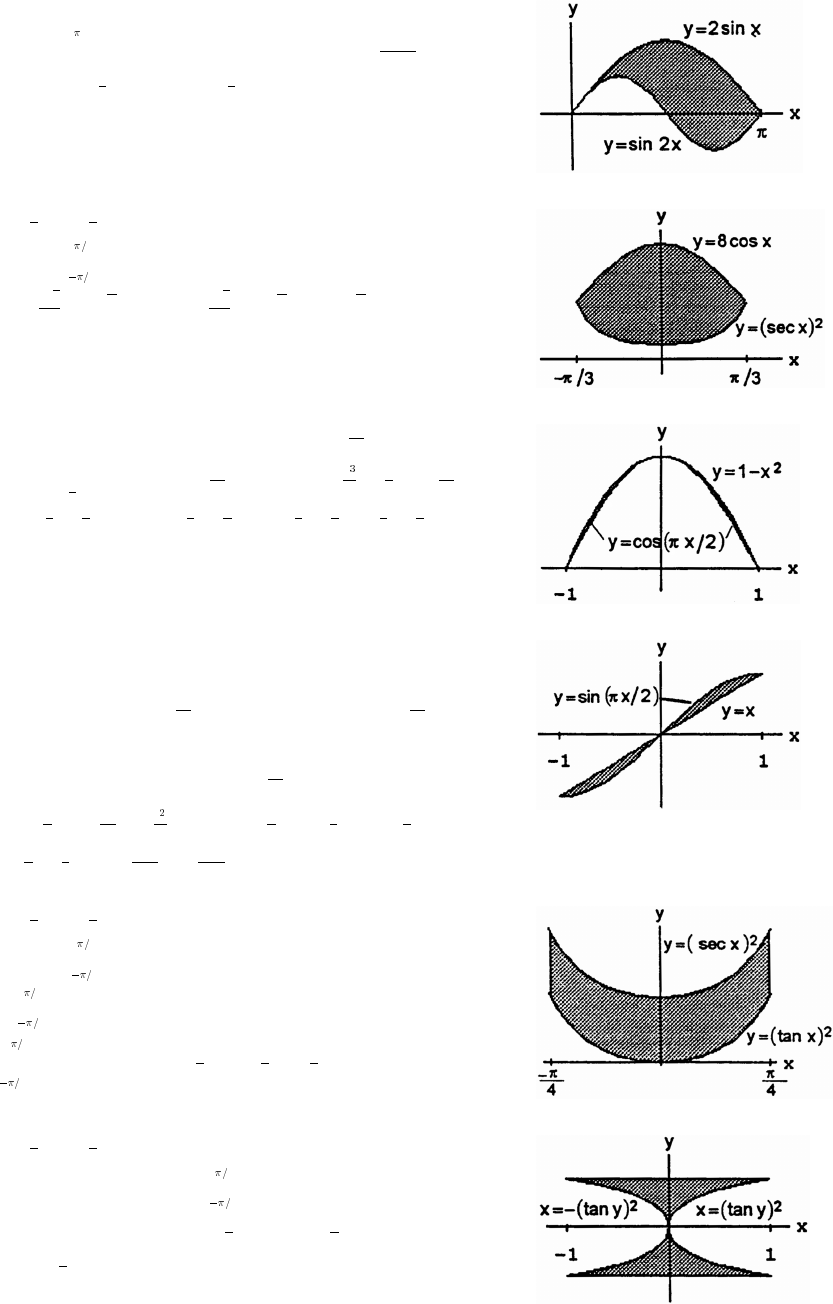
Section 5.6 Substitution and Area Between Curves 339
63. a 0, b ; f(x) g(x) 2 sin x sin 2xœœ œ 1
A (2 sin x sin 2x) dx 2 cos xÊœ œ
'0‘
cos 2x
2
1
!
2( 1) 2 1 4œ œ
‘ˆ‰
""
##
†
64. a , b ; f(x) g(x) 8 cos x sec xœ œ œ
11
33 #
A 8 cos x sec x dx [8 sin x tan x]Êœ œ
'3
3ab
#Î$
Î$
1
1
838363œœ
Š‹Š ‹
ÈÈÈ
††
ÈÈ
33
##
65. a 1, b 1; f(x) g(x) 1 x cosœ œ œ abˆ‰
#
#
1x
A 1 x cos dx x sinÊœ œ
'1
1‘ ˆ‰ˆ‰ ’“
#
##
"
"
11
1
xx2x
3
112œœ œ
ˆ‰ˆ ‰ˆ‰
""
3333
222244
1111
66. A A1 A2œ
a 1, b 0 and a 0, b 1;
"" ##
œ œ œ œ
f (x) g (x) x sin and f (x) g (x) sin x
"" ##
##
œ œ
ˆ‰ ˆ‰
11xx
by symmetry about the origin,Ê
A A 2A A 2 sin x dx
"# " #
œ Êœ
'0
1‘ˆ‰
1x
2 cos 2 0 10œ œ
’“
ˆ‰ ‘ˆ‰ˆ‰
2xx 2 2
111
1
## #
"
!
"
††
22œœ œ
ˆ‰ˆ‰
244
2111
11"
#
67. a , b ; f(x) g(x) sec x tan xœ œ œ
11
44 ##
A sec x tan x dxʜ
'4
4ab
##
sec x sec x 1 dxœ
'4
4cdab
##
1dx [x]œœœœ
'ˆ‰
4
4
†
1
1
111
Î%
Î% #44
68. c , d ; f(y) g(y) tan y tan y 2 tan yœ œ œ œ
11
44 ###
ab
2 sec y 1 A 2 sec y 1 dyœÊœ ab ab
##
'4
4
2[tan y y] 2 1 1œœ
1
1
11
Î%
Î% ‘ˆ‰ˆ ‰
44
41 4œœ
ˆ‰
1
41
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
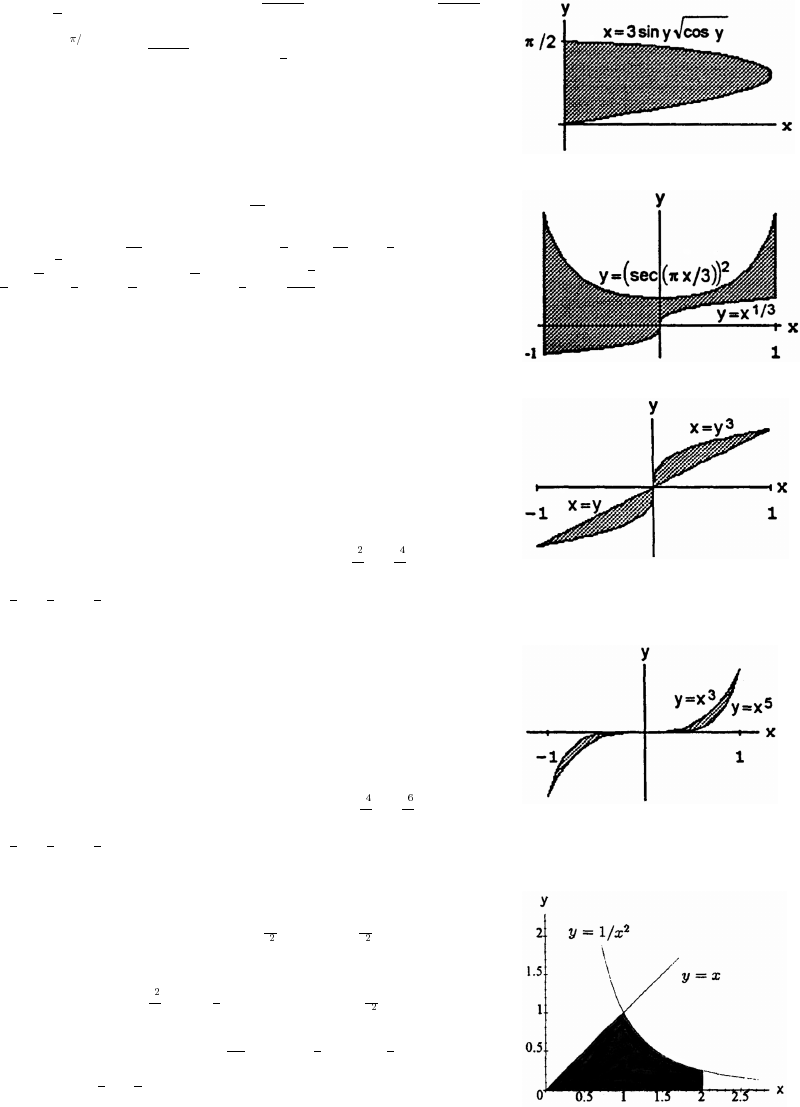
340 Chapter 5 Integration
69. c 0, d ; f(y) g(y) 3 sin y cos y 0 3 sin y cos yœœ œ œ
1
#ÈÈ
A 3 sin y cos y dy 3 (cos y)Êœ œ
'0
2È‘
2
3$Î# Î#
!
1
2(0 1) 2œ œ
70. a 1, b 1; f(x) g(x) sec xœ œ œ
# "Î$
ˆ‰
1x
3
A sec x dx tan xÊœ œ
'1
1‘ ‘ˆ‰ ˆ‰
# "Î$ %Î$ "
"
11
1
x3x3
334
33œœ
Š‹’ “
ÈÈ
Š‹
333 3
44
63
11 1
È
71. A A Aœ
"#
Limits of integration: x y and x y y yœœÊœ
$$
y y 0 y(y 1)(y 1) 0 c 1, d 0Ê œÊ œÊ œ œ
$""
and c 0, d 1; f (y) g (y) y y and
##"" $
œœ œ
f (y) g (y) y y by symmetry about the origin,
## $
œÊ
A A 2A A 2 y y dy 2
"# # $
#
"
!
œ Êœ œ
'0
1ab ’“
yy
4
2œœ
ˆ‰
"" "
##4
72. A A Aœ
"#
Limits of integration: y x and y x x xœœÊœ
$&$&
x x 0 x (x 1)(x 1) 0 a 1, b 0Ê œÊ œÊ œ œ
&$ $ ""
and a 0, b 1; f (x) g (x) x x and
##"" $&
œœ œ
f (x) g (x) x x by symmetry about the origin,
## &$
œÊ
A A 2A A 2 x x dx 2
"# # $& "
!
œ Êœ œ
'0
1ab’“
xx
46
2œœ
ˆ‰
"" "
46 6
73. A A Aœ
"#
Limits of integration: y x and y x , x 0œœÊœÁ
""
xx
x 1 x 1 , f (x) g (x) x 0 xÊ œ Ê œ œœ
$""
A x dx ; f (x) g (x) 0Êœ œ œ œ
"##
"
!
""
#
'0
1’“
x
2x
x A x dx 1 ;œÊœ œ œœ
# #
#" " "
#
"##
'1
2‘
x
AA A 1œ œœ
"#
""
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
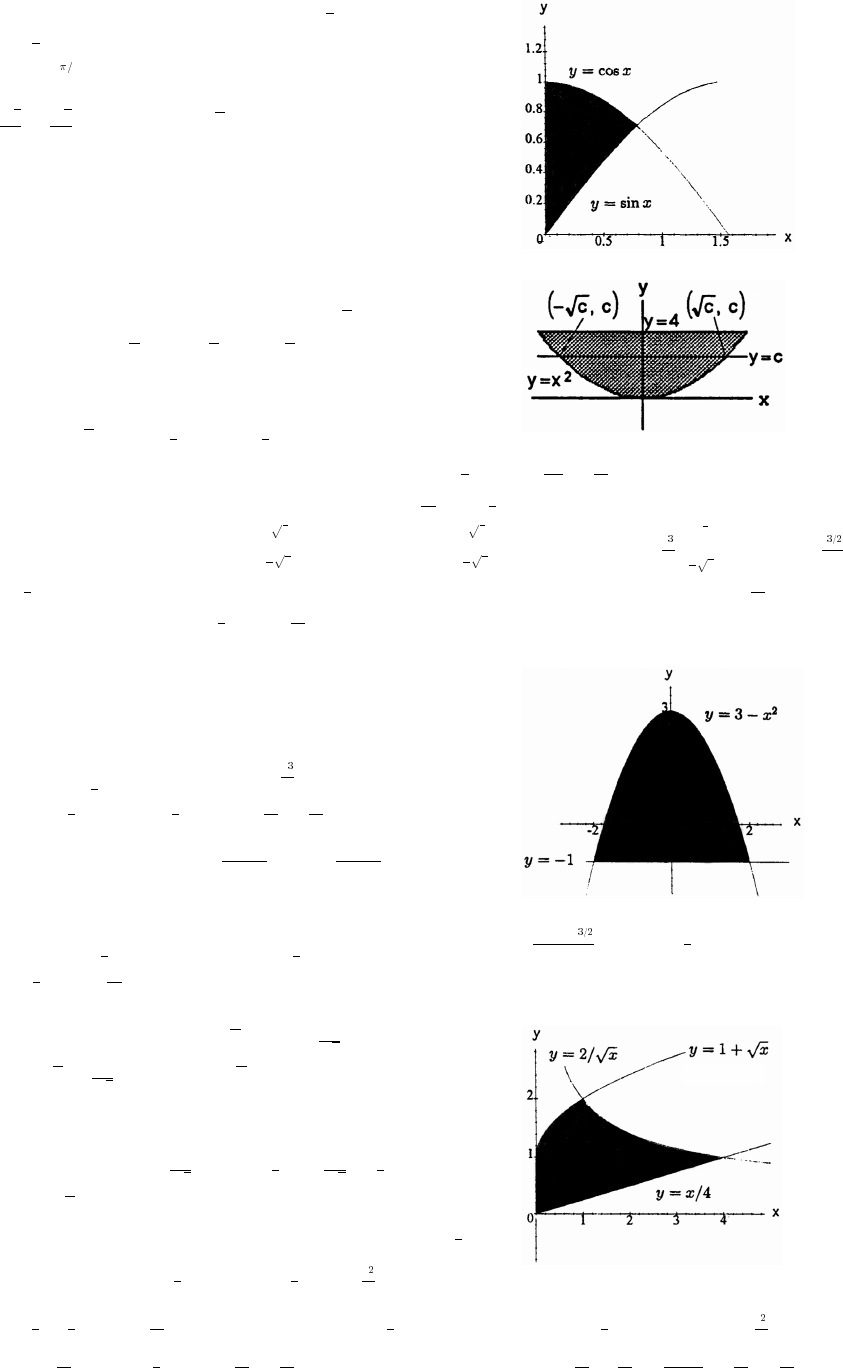
Section 5.6 Substitution and Area Between Curves 341
74. Limits of integration: sin x cos x x a 0œÊœÊœ
1
4
and b ; f(x) g(x) cos x sin xœœ
1
4
A (cos x sin x) dx [sin x cos x]Êœ œ
'0
41Î%
!
(0 1) 2 1œœ
Š‹ È
ÈÈ
22
##
75. (a) The coordinates of the points of intersection of the
line and parabola are c x x c and y cœÊœ„ œ
#È
(b) f(y) g(y) y y 2 y the area of theœœ Ê
ÈÈÈ
ˆ‰
lower section is, A [f(y) g(y)] dy
L0
c
œ
'
2 y dy 2 y c . The area of theœœœ
'0
cc
È‘
24
33
$Î# $Î#
!
entire shaded region can be found by setting c 4: A 4 . Since we want c to divide the regionœœ œœ
ˆ‰
44832
333
$Î# †
into subsections of equal area we have A 2A 2 c c 4œÊœ Êœ
L32 4
33
ˆ‰
$Î# #Î$
(c) f(x) g(x) c x A [f(x) g(x)] dx c x dx cx 2 cœÊœ œ œ œ
# # $Î#
Lcc
cc c
c
''
ab’“ ’ “
xc
33
È
c . Again, the area of the whole shaded region can be found by setting c 4 A . From theœœÊœ
432
3 3
$Î#
condition A 2A , we get c c 4 as in part (b).œœÊœ
L432
33
$Î# #Î$
76. (a) Limits of integration: y 3 x and y 1œ œ
#
3 x 1 x 4 a 2 and b 2;Ê œÊ œÊœ œ
##
f(x) g(x) 3 x ( 1) 4 xœœab
##
A 4 x dx 4xÊœ œ
'1
2ab’“
##
#
x
3
8816œœœ
ˆ‰ˆ ‰
8 8 16 32
3333
(b) Limits of integration: let x 0 in y 3 xœœ
#
y 3; f(y) g(y) 3 y 3 yÊœ œ
ÈÈ
ˆ‰
2(3 y)œ
"Î#
A 2 (3 y) dy 2 (3 y) ( 1) dy ( 2) 0 (3 1)Êœ œ œ œ
''
11
33
"Î# "Î# $Î#
$
"
’“
ˆ‰ ‘
2(3 y)
33
4
(8)œœ
ˆ‰
432
33
77. Limits of integration: y 1 x and yœ œ
È2
x
È
1 x , x 0 x x 2 x (2 x)Ê œ ÁÊ œÊœ
ÈÈ
2
x
È#
x 4 4x x x 5x 4 0Êœ Ê œ
##
(x 4)(x 1) 0 x 1, 4 (but x 4 does notÊ œÊœ œ
satisfy the equation); y and y œœÊœ
2x2x
xx
44
ÈÈ
8 x x 64 x x 4.Êœ Ê œ Êœ
È$
Therefore, AREA A A : f (x) g (x) 1 xœ œ
"#" " "Î#
ˆ‰
x
4
A 1 x dx x xÊœ œ
""Î# $Î# "
!
'0
1ˆ‰
’“
x2x
438
1 0 ; f (x) g (x) 2x A 2x dx 4xœœ œ Ê œ œ
ˆ‰ ˆ‰
’“
237 x x x
38 24 4 4 8
"## #
"Î# "Î# "Î# %
"
'1
4
4 2 4 4 ; Therefore, AREA A Aœ œœ œ œœ œœ
ˆ‰ˆ‰
†16 15 17 37 17 37 51 88 11
8888 24824243
"
"#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

342 Chapter 5 Integration
78. Limits of integration: (y 1) 3 y y 2y 1œÊ
##
3 y y y 2 0 (y 2)(y 1) 0œ Ê œ Ê œ
#
y 2 since y 0; also, 2 y 3 yÊœ œ
È
4y 9 6y y y 10y 9 0ÊœÊ œ
##
(y 9)(y 1) 0 y 1 since y 9 does notÊ œÊœ œ
satisfy the equation;
AREA A Aœ
"#
f (y) g (y) 2 y 0 2y
"" "Î#
œœ
È
A 2 y dy 2 ; f (y) g (y) (3 y) (y 1)Ê œ œ œ œ
"##
"Î# #
"
!
'0
1’“
2y
33
4
A 3y(y1) dy 3y y (y1) 62 3 0 1 ;Ê œ œ œ œ œ
###$
"" " " ""
###
#
"
'1
2cd
‘ˆ‰ˆ‰
3336
7
Therefore, A A
"#
œœ œ
47 15 5
3662
79. Area between parabola and y a : A 2 a x dx 2 a x x 2 a 0 ;œœ œ œœ
####$$
"
!
'0
aa
ab‘
Š‹
333
a4a
Area of triangle AOC: (2a) a a ; limit of ratio lim which is independent of a.
"
#
#$
abœœœ
aÄ!
a
Š‹
4a
3
3
4
80. A 2f(x) dx f(x) dx 2 f(x) dx f(x) dx f(x) dx 4œœœœ
'''''
aa aaa
bb bbb
81. Neither one; they are both zero. Neither integral takes into account the changes in the formulas for the
region's upper and lower bounding curves at x 0. The area of the shaded region is actuallyœ
A [ x (x)] dx [x ( x)] dx 2x dx 2x dx .œ œ œ#
''''
10 10
01 01
82. It is sometimes true. It is true if f(x) g(x) for all x between a and b. Otherwise it is false. If the graph of f
lies below the graph of g for a portion of the interval of integration, the integral over that portion will be
negative and the integral over [a b] will be less than the area between the curves (see Exercise 53).ß
83. Let u 2x du 2 dx du dx; x 1 u 2, x 3 u 6œÊœ Ê œ œÊœ œÊœ
"
#
dx du du F(u) F(6) F(2)
'' '
12 2
36 6
sin 2x sin u sin u
xu
œœœœ
ˆ‰
uˆ‰ cd
"
#
'
#
84. Let u 1 x du dx du dx; x 0 u 1, x 1 u 0œ Ê œ Ê œ œ Ê œ œ Ê œ
f(1 x) dx f(u) ( du) f(u) du f(u) du f(x) dx
' ' '''
0 1 100
1 0 011
œ œ œ œ
85. (a) Let u x du dx; x 1 u 1, x 0 u 0œ Ê œ œ Ê œ œ Ê œ
f odd f( x) f(x). Then f(x) dx f( u) ( du) f(u) ( du) f(u) du f(u) duÊœ œ œ œ œ
'' ' ' '
11 1 1 0
00 0 0 1
3œ
(b) Let u x du dx; x 1 u 1, x 0 u 0œ Ê œ œ Ê œ œ Ê œ
f even f( x) f(x). Then f(x) dx f( u) ( du) f(u) du f(u) du 3Êœ œ œ œ œ
'' ''
11 1 0
00 01
86. (a) Consider f(x) dx when f is odd. Let u x du dx du dx and x a u a and x
'a
0
œ Ê œ Ê œ œ Ê œ œ!
u . Thus f(x) dx f( u) du f(u) du f(u) du f(x) dx.Êœ! œ œ œ œ
'' ' ' '
aa a 0 0
00 0 a a
Thus f(x) dx f(x) dx f(x) dx f(x) dx f(x) dx .
''' ''
aa0 00
a0a aa
œœœ!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
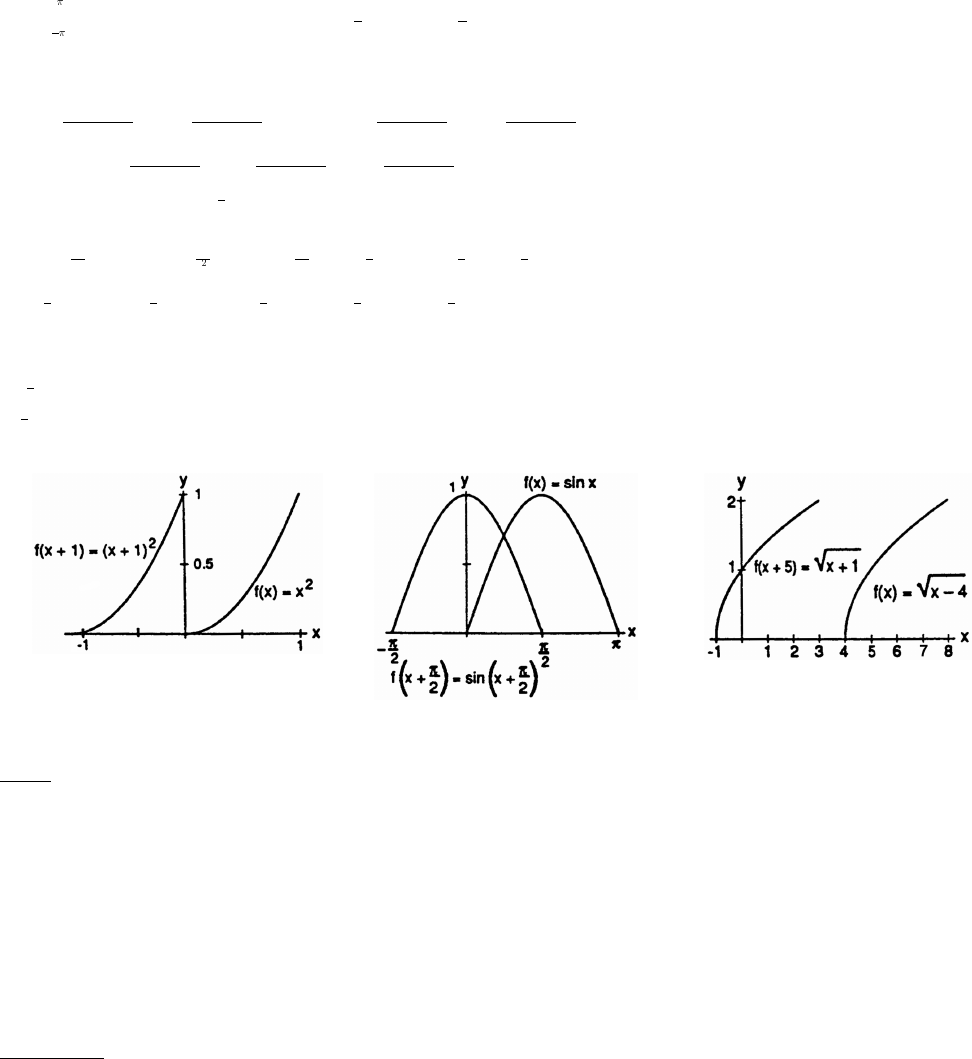
Section 5.6 Substitution and Area Between Curves 343
(b) sin x dx [ cos x] cos cos .
'/2
/2
œ œ œ!!œ!
1
1
11
Î#
Î# ##
ˆ‰ ˆ ‰
87. Let u a x du dx; x 0 u a, x a u 0œ Ê œ œ Ê œ œ Ê œ
I ( du)œœ œœ
'' ''
0a 00
a0 aa
f(x) dx f(a u) f(a u) du f(a x) dx
f(x) f(a x) f(a u) f(u) f(u) f(a u) f(x) f(a x)
I I dx dx [x] a 0 a.Êœœ œœœœ
''' '
00 0 0
aa a a
a
f(x) dx f(a x) dx f(x) f(a x)
f(x) f(a x) f(x) f(a x) f(x) f(a x)
!
Therefore, 2I a I .œÊœ
a
#
88. Let u du dt du dt du dt; t x u y, t xy u 1. Therefore,œÊœ Ê œ Ê œ œÊœœÊœ
xy xy
ttxytut
t"""
dt du du du dt
'' '''
xy y11
xy 1 1 y y
" " """
tu uut
œ œ œ œ
89. Let u x c du dx; x a c u a, x b c u bœ Ê œ œ Ê œ œ Ê œ
f(x c) dx f(u) du f(x) dx
'''
ac a a
bc b b
œ œ
90. (a) (b) (c)
91-94. Example CAS commands:
:Maple
f := x -> x^3/3-x^2/2-2*x+1/3;
g := x -> x-1;
plot( [f(x),g(x)], x=-5..5, legend=["y = f(x)","y = g(x)"], title="#91(a) (Section 5.6)" );
q1 := [ -5, -2, 1, 4 ]; # (b)
q2 := [seq( fsolve( f(x)=g(x), x=q1[i]..q1[i+1] ), i=1..nops(q1)-1 )];
for i from 1 to nops(q2)-1 do # (c)
area[i] := int( abs(f(x)-g(x)),x=q2[i]..q2[i+1] );
end do;
add( area[i], i=1..nops(q2)-1 ); # (d)
: (assigned functions may vary)Mathematica
Clear[x, f, g]
f[x_] = x Cos[x]
2
g[x_] = x x
3
Plot[{f[x], g[x]}, {x, 2, 2}]
After examining the plots, the initial guesses for FindRoot can be determined.
pts = x/.Map[FindRoot[f[x]==g[x],{x, #}]&, { 1, 0, 1}]
i1=NIntegrate[f[x] g[x], {x, pts[[1]], pts[[2]]}]
i2=NIntegrate[f[x] g[x], {x, pts[[2]], pts[[3]]}]
i1 i2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
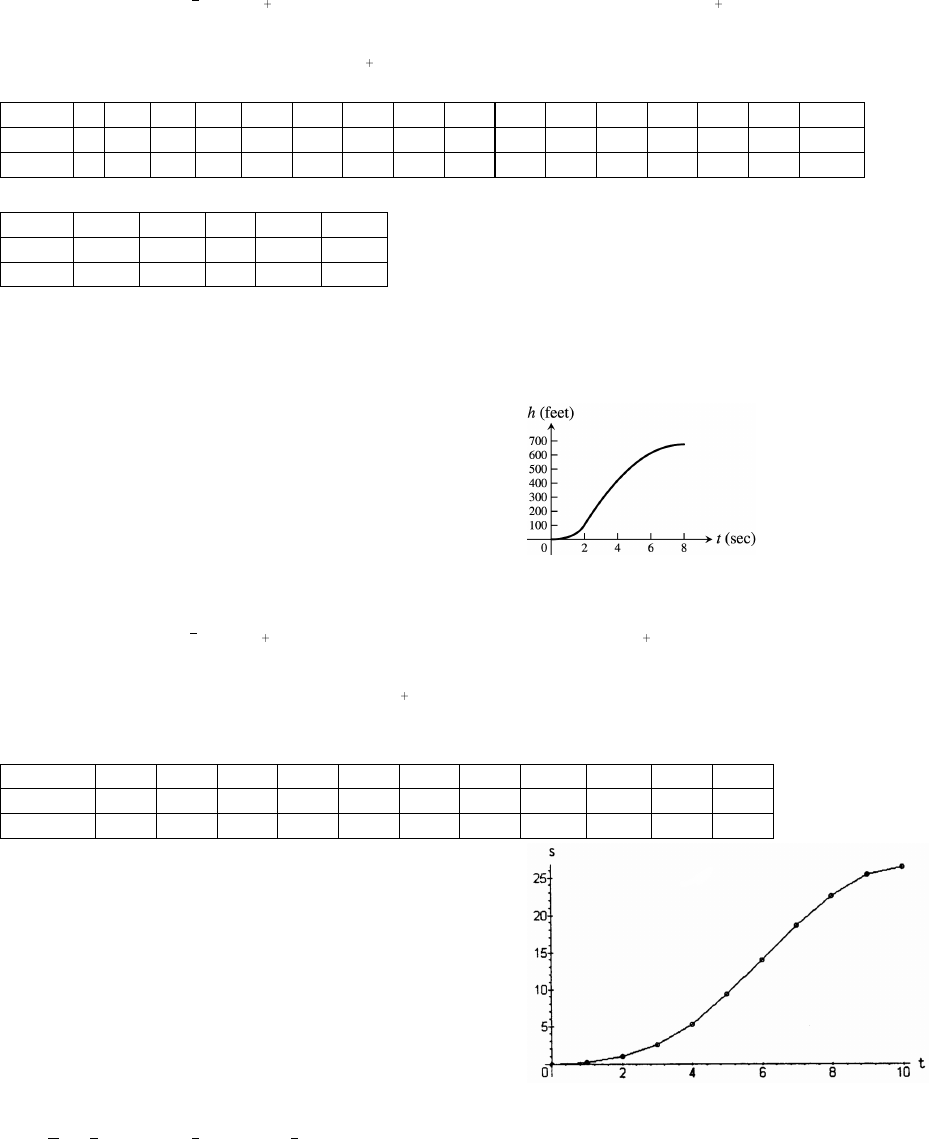
344 Chapter 5 Integration
CHAPTER 5 PRACTICE EXERCISES
1. (a) Each time subinterval is of length t 0.4 sec. The distance traveled over each subinterval, using the?œ
midpoint rule, is h v v t, where v is the velocity at the left endpoint and v the velocity at??œ
"
#ab
ii1 i i1
the right endpoint of the subinterval. We then add h to the height attained so far at the left endpoint v to?i
arrive at the height associated with velocity v at the right endpoint. Using this methodology we build
i1
the following table based on the figure in the text:
t (sec) 0 0.4 0.8 1.2 1.6 2.0 2.4 2.8 3.2 3.6 4.0 4.4 4.8 5.2 5.6 6.0
v (fps) 0 10 25 55 100 190 180 165 150 140 130 115 105 90 76 65
h (ft) 0 2 9 25 56 114 188 257 320 378 432 481 525 564 592 620.2
t (sec) 6.4 6.8 7.2 7.6 8.0
v (fps) 50 37 25 12 0
h (ft) 643.2 660.6 672 679.4 681.8
NOTE: Your table values may vary slightly from ours depending on the v-values you read from the graph.
Remember that some shifting of the graph occurs in the printing process.
The total height attained is about 680 ft.
(b) The graph is based on the table in part (a).
2. (a) Each time subinterval is of length t 1 sec. The distance traveled over each subinterval, using the?œ
midpoint rule, is s v v t, where v is the velocity at the left, and v the velocity at the??œ
"
#ab
ii1 i i1
right, endpoint of the subinterval. We then add s to the distance attained so far at the left endpoint v?i
to arrive at the distance associated with velocity v at the right endpoint. Using this methodology we
i1
build the table given below based on the figure in the text, obtaining approximately 26 m for the total
distance traveled:
t (sec) 0 1 2 3 4 5 6 7 8 9 10
v (m/sec) 0 0.5 1.2 2 3.4 4.5 4.8 4.5 3.5 2 0
s (m) 0 0.25 1.1 2.7 5.4 9.35 14 18.65 22.65 25.4 26.4
(b) The graph shows the distance traveled by the
moving body as a function of time for
0 t 10.ŸŸ
3. (a) a ( 2) (b) (b 3a ) b 3 a 25 3( 2) 31
!! ! !!
10 10 10 10 10
k1 k1 k1 k1 k1œœ œ œœ
a
44 4
kœ œ œ œ œ œ
"""
#
kkkkk
(c) (a b 1) a b 2 25 (1)(10) 13
!!!!
10 10 10 10
k1 k1 k1 k1œœœœ
kk k k
œ"œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 5 Practice Exercises 345
(d) b b (10) 25 0
!!!
ˆ‰
10 10 10
k1 k1 k1œœœ
555
###
œ œ œ
kk
4. (a) 3a 3 a 3(0) 0 (b) (a b ) a b 0 7 7
!! ! !!
20 20 20 20 20
k1 k1 k1 k1 k1œœ œ œœ
kk kkkk
œ œ œ œ œœ
(c) b (20) (7) 8
!!!
ˆ‰
20 20 20
k1 k1 k1œœœ
"""
###
œ œ œ
2b
77 7
22
kk
(d) a 2 a 2 0 2(20) 40
!!!
ab
20 20 20
k1 k1 k1œœœ
kk
œ œ œ
5. Let u 2x 1 du 2 dx du dx; x 1 u 1, x 5 u 9œÊ œ Ê œ œÊœ œÊœ
"
#
(2x 1) dx u du u 3 1 2
''
11
59
œ œ œœ
"Î# "Î# "Î#
"
#
*
"
ˆ‰‘
6. Let u x 1 du 2x dx du x dx; x 1 u 0, x 3 u 8œÊ œ Ê œ œÊœ œÊœ
#"
#
x x 1 dx u du u (16 0) 6
''
10
38
ab ˆ‰ ‘
# "Î$ %Î$
"Î$ "
#
)
!
œ œ œœ
33
88
7. Let u 2 du dx; x u , x 0 u 0œÊ œ œÊœ œÊœ
x
211
#
cos dx (cos u)(2 du) [2 sin u] 2 sin 0 2 sin 2(0 ( 1)) 2
''
00
2
ˆ‰ ˆ ‰
x
# #
!
Î#
œœœœœ
1
1
8. Let u sin x du cos x dx; x 0 u 0, x u 1œÊœ œÊœœÊœ
1
#
(sin x)(cos x) dx u du
''
00
21
œœœ
’“
u
2
"
!
"
#
9. (a) f(x) dx 3 f(x) dx (12) 4 (b) f(x) dx f(x) dx f(x) dx 6 4 2
'' '''
22 222
22 552
œ œ œ œ œœ
""
33
(c) g(x) dx g(x) dx 2 (d) ( g(x)) dx g(x) dx (2) 2
'' ' '
52 2 2
25 5 5
œ œ œ œ œ11 11
(e) dx f(x) dx g(x) dx (6) (2)
'''
222
555
Š‹
f(x) g(x)
55 5 555
8
"" ""
œ œœ
10. (a) g(x) dx 7 g(x) dx (7) 1 (b) g(x) dx g(x) dx g(x) dx 1 2 1
'' '''
00 100
22 221
œ œ œ œ œœ
""
77
(c) f(x) dx f(x) dx (d) 2 f(x) dx 2 f(x) dx 2 ( ) 2
'' ' '
20 0 0
02 2 2
œ œ œ œ œ111
ÈÈ ÈÈ
(e) [g(x) 3 f(x)] dx g(x) dx 3 f(x) dx 1 3
'''
000
222
œ œ1
11. x 4x 3 0 (x 3)(x 1) 0 x 3 or x 1;
# œÊ œÊœ œ
Area x 4x 3 dx x 4x 3 dxœ
''
01
13
abab
##
2x 3x 2x 3xœ
’“’“
xx
33
##
"$
!"
2(1) 3(1) 0œ
’“Š‹
"#
3
2(3) 3(3) 2(1) 3(1)
’“Š‹Š‹
31
33
##
10 1œ œ
ˆ‰ ‘ˆ‰
""
333
8
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
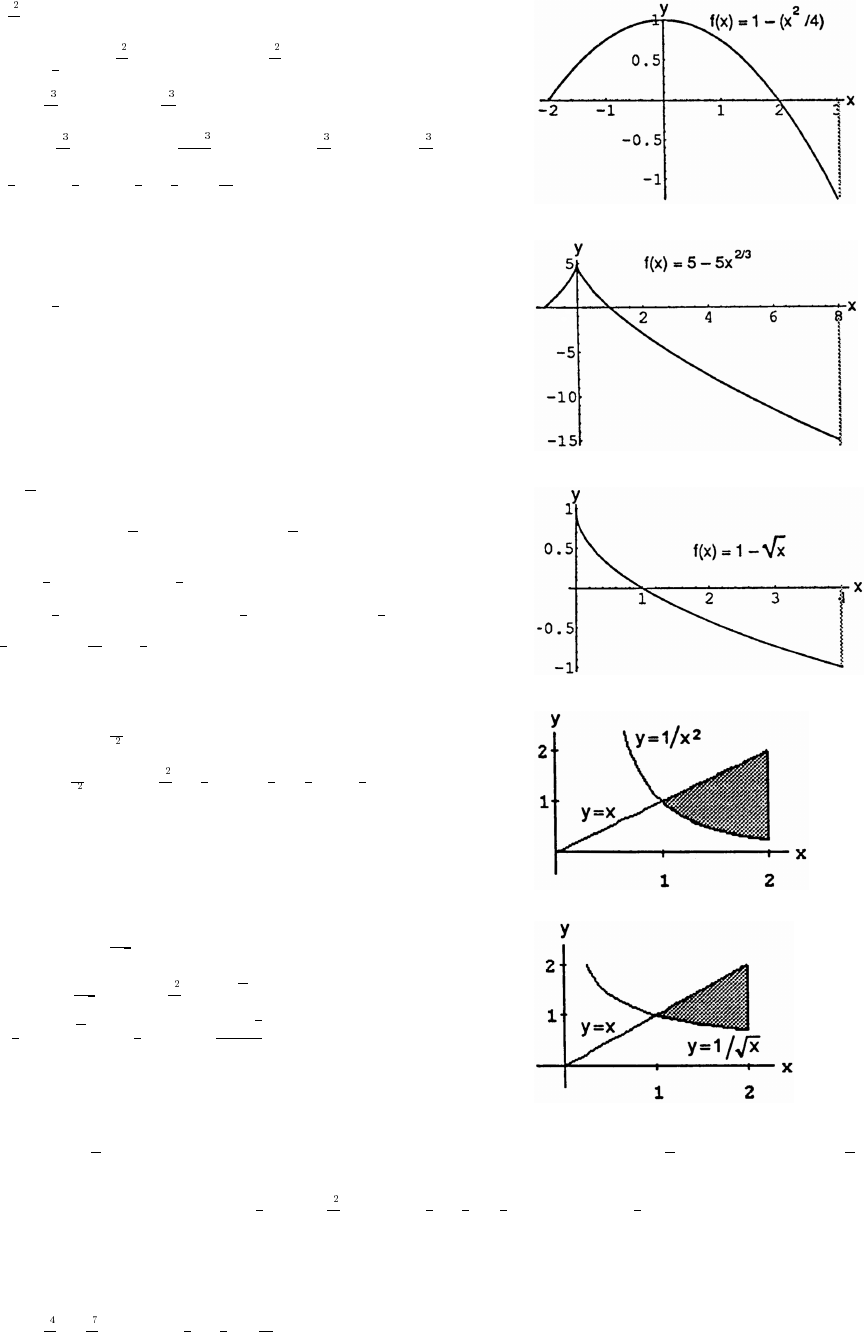
346 Chapter 5 Integration
12. 1 0 4 x 0 x 2;œÊÊœ„
x
4#
Area 1 dx 1 dxœ
''
22
23
Š‹ Š‹
xx
44
xxœ
’“’“
xx
12 12
#$
# #
22 32œ
’“’“Š‹Š ‹Š‹Š‹
232
12 12 12 12
(2)
œ œ
‘ˆ‰ˆ‰
443413
33434
13. 5 5x 0 1 x 0 x 1;œÊœÊœ„
#Î$ #Î$
Area 55x dx 55x dxœ
''
11
18
ˆ‰ˆ‰
#Î$ #Î$
5x 3x 5x 3xœ
‘‘
&Î$ &Î$
")
" "
5(1) 3(1) 5( 1) 3( 1)œ
‘ˆ‰ˆ ‰
&Î$ &Î$
5(8) 3(8) 5(1) 3(1)
‘ˆ‰ˆ‰
&Î$ &Î$
[2 ( 2)] [(40 96) 2] 62œ œ
14. 1 x 0 x 1;œÊœ
È
Area 1 x dx 1 x dxœ
''
01
14
ˆ‰ ˆ‰
ÈÈ
xx xxœ
‘‘
22
33
$Î# $Î#
"%
!"
1 (1) 0 4 (4) 1 (1)œ
‘ ‘ˆ‰ˆ‰ˆ‰
222
333
$Î# $Î# $Î#
42œ œ
""
333
16
‘ˆ‰
15. f(x) x, g(x) , a 1, b 2 A [f(x) g(x)] dxœœœœÊœ
"
x'a
b
x dx 11œ œ œœ
'1
2ˆ‰ ˆ‰ˆ‰
’“
""""
####
#
"
xx
x4
16. f(x) x, g(x) , a 1, b 2 A [f(x) g(x)] dxœœœœÊœ
"
Èx'a
b
xdx 2xœ œ
'1
2Š‹’ “
È
"
#
#
"
Èx
x
22 2œ œ
Š‹
Ȉ‰
4
2
74 2
"
##
È
17. f(x) 1 x , g(x) 0, a 0, b 1 A [f(x) g(x)] dx 1 x dx 1 2 x x dxœ œœœÊœ œ œ
ˆ‰ ˆ‰ ˆ ‰
ÈÈÈ
# #
'''
a00
b11
12x x dx x x 1 (683)œœœœœ
'0
1ˆ‰
’“
"Î# $Î#
##
"
!
"" "4x 4
3366
18. f(x) 1 x , g(x) 0, a 0, b 1 A [f(x) g(x)] dx 1 x dx 1 2x x dxœ œ œ œÊ œ œ œ ab ab a b
$$$'
# #
'''
a00
b11
x1œ œœ
’“
xx 9
7714
##
"
!
""
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
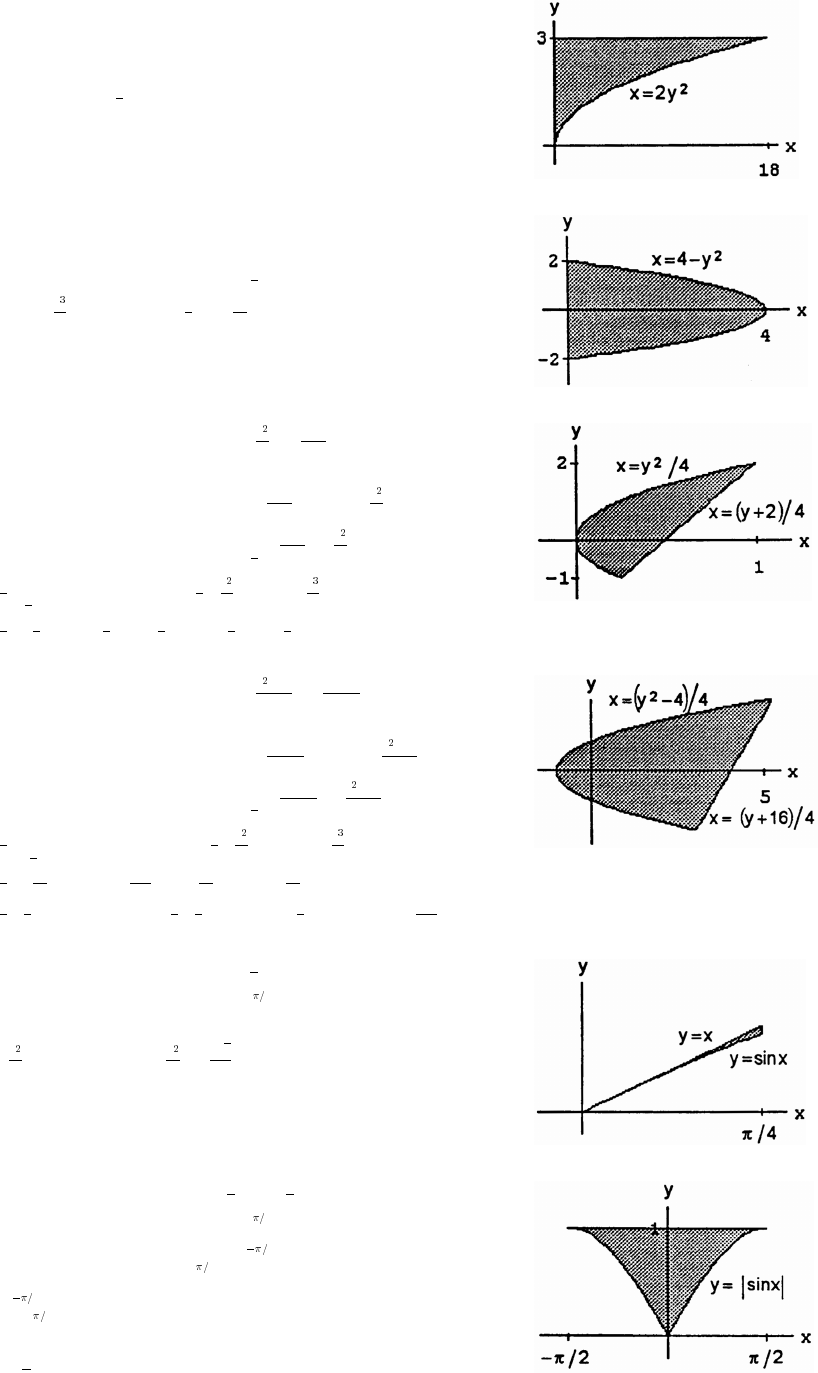
Chapter 5 Practice Exercises 347
19. f(y) 2y , g(y) 0, c 0, d 3œœœœ
#
A [f(y) g(y)] dy 2y 0 dyÊœ œ
''
c0
d3
ab
#
2 y dy y 18œœœ
'0
3
#$
$
!
2
3cd
20. f(y) 4 y , g(y) 0, c 2, d 2œ œ œ œ
#
A [f(y) g(y)] dy 4 y dyÊœ œ
''
c2
d2
ab
#
4y 2 8œ œ œ
’“ˆ‰
y
333
832
#
#
21. Let us find the intersection points: yy2
44
œ
y y 2 0 (y 2)(y 1) 0 y 1ÊœÊ œÊœ
#
or y 2 c 1, d 2; f(y) , g(y)œÊœ œ œ œ
y2 y
44
A [f(y) g(y)] dy dyÊœ œ
''
c1
d2
Š‹
y2 y
44
y 2 y dy 2yœœ
""
#
#
#
"
443
yy
'1
2ab
’“
42œ œ
"""
##43 38
48 9
‘ˆ‰ˆ‰
22. Let us find the intersection points: y4 y16
44
œ
y y 20 0 (y 5)(y 4) 0 y 4ÊœÊ œÊœ
#
or y 5 c 4, d 5; f(y) , g(y)œÊœ œ œ œ
y16 y 4
44
A [f(y) g(y)] dy dyÊœ œ
''
c4
d5
Š‹
y16 y 4
44
y 20 y dy 20yœœ
""
#
#
&
%
443
yy
'4
5ab
’“
100 80œ
""
##43 3
25 125 6 64
‘ˆ‰ˆ‰
180 63 117 (9 234)œœ œœ
"""
##4488
9 9 243
ˆ‰ˆ‰
23. f(x) x, g(x) sin x, a 0, bœœ œœ
1
4
A [f(x) g(x)] dx (x sin x) dxÊœ œ
''
a0
b4
cos x 1œ œ
’“Š‹
x
3
2
###
Î%
!
11È
24. f(x) 1, g(x) sin x , a , bœœ œœkk 11
#2
A [f(x) g(x)] dx 1 sin x dxÊœ œ
''
a2
b2
abkk
(1 sin x) dx (1 sin x) dxœ
''
20
02
2 (1 sin x) dx 2[x cos x]œœ
'0
21Î#
!
21 2œœ
ˆ‰
1
#1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
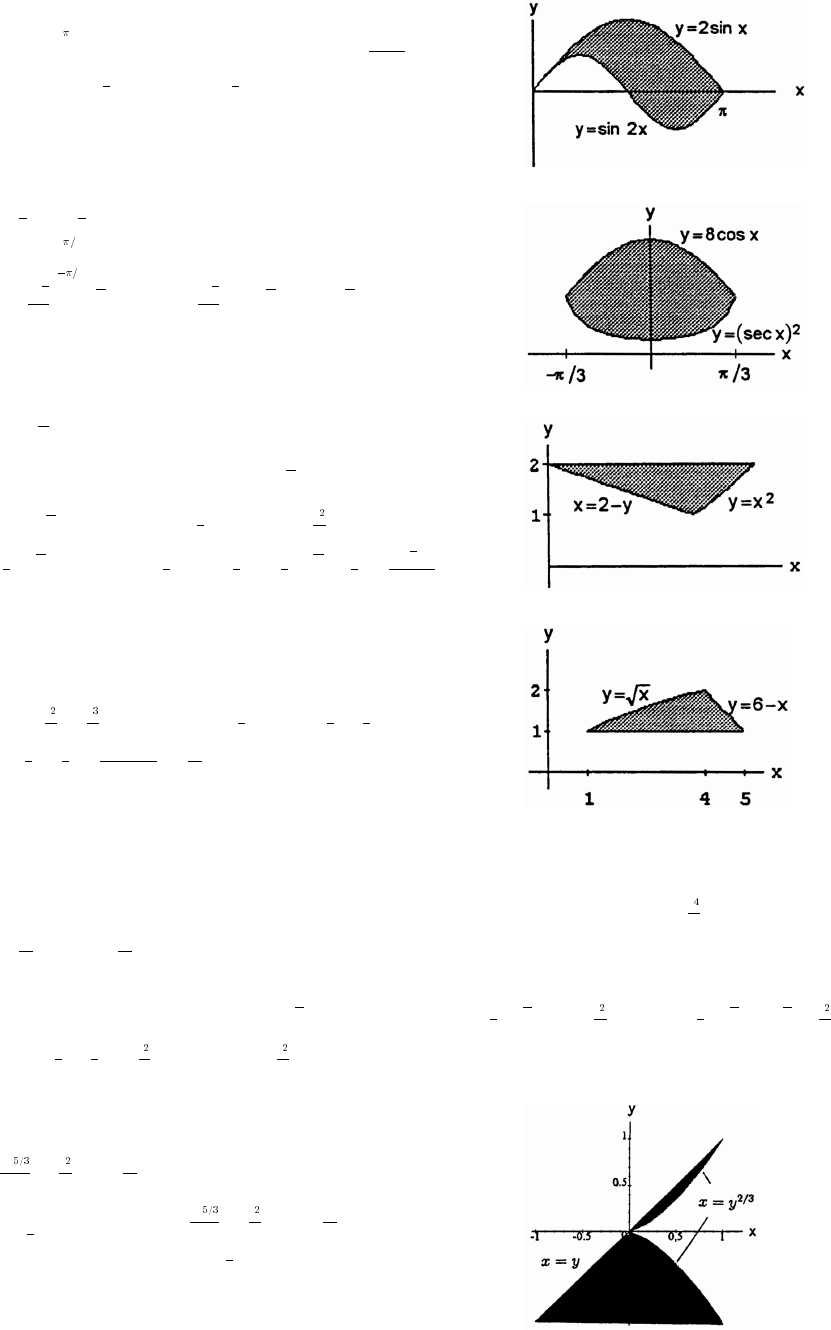
348 Chapter 5 Integration
25. a 0, b , f(x) g(x) 2 sin x sin 2xœœ œ 1
A (2 sin x sin 2x) dx 2 cos xÊœ œ
'0‘
cos 2x
#!
1
2(1) 21 4œ œ
‘ˆ‰
††
""
##
26. a , b , f(x) g(x) 8 cos x sec xœ œ œ
11
33 #
A 8 cos x sec x dx [8 sin x tan x]Êœ œ
'3
3ab
#Î$
Î$
1
1
838363œœ
Š‹Š ‹
ÈÈÈ
††
ÈÈ
33
##
27. f(y) y, g(y) 2 y, c 1, d 2œœœœ
È
A [f(y) g(y)] dy y (2 y) dyÊœ œ
''
c1
d2
‘
È
y 2 y dy y 2yœœ
'1
2ˆ‰
È’“
2
3
y
$Î#
#
#
"
242 2 2œœœ
Š‹
ÈÈ
ˆ‰
4247
33366
827
"
#
È
28. f(y) 6 y, g(y) y , c 1, d 2œ œ œ œ
#
A [f(y) g(y)] dy 6 y y dyÊœ œ
''
c1
d2
ab
#
6y 12 2 6œ œ
’“
ˆ‰ˆ‰
yy
333
8
##
#
"
""
4œœ œ
7 24143 13
366
"
#
29. f(x) x 3x x (x 3) f (x) 3x 6x 3x(x 2) fœ œ Ê œ œ Ê œ ± ±
!#
$## w # w
f(0) 0 is a maximum and f(2) 4 is a minimum. A x 3x dx xÊ œ œ œ œ
'0
3ab’“
$# $
$
!
x
4
27œ œ
ˆ‰
81 27
44
30. A a x dx a 2 a x x dx ax a x a a a aœ œ œ œ
''
00
aa a
0
ˆ‰ˆ ‰
ÈÈÈÈ
’“
"Î# "Î# "Î# $Î# #
#
##
4x4 a
33
†
a1 (683)œœœ
#"
#
ˆ‰
4a a
36 6
31. The area above the x-axis is A y y dy
"#Î$
œ
'0
1ˆ‰
; the area below the x-axis isœœ
’“
3y y
510
#
"
!
"
Ayy dy
##Î$
#
!
"
œœœ
'1
0ˆ‰
’“
3y y
510
11
the total area is A Aʜ
"#
6
5
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 5 Practice Exercises 349
32. A (cos x sin x) dx (sin x cos x) dxœ
''
04
454
(cos x sin x) dx [sin x cos x]œ
'54
32 1Î%
!
[ cos x sin x] [sin x cos x]
&Î% $Î#
Î% & Î%
11
11
(0 1)œ
’“’ “Š‹ Š‹Š ‹
ÈÈ ÈÈ ÈÈ
22 22 22
## ## ##
(1 0) 2 4 2 2 œ œ
’“Š‹ È
ÈÈ È
22 82
## #
33. y x dt 2x 2 ; y(1) 1 dt 1 and y (1) 2 1 3œ Ê œ Ê œ œ œ œœ
# w
""""
''
1 1
x 1
tdx xdx x t
dy d y
34. y 1 2 sec t dt 1 2 sec x 2 (sec x) (sec x tan x) sec x (tan x);œ Êœ Êœ œ
'0
xˆ‰ ˆ‰
ÈÈÈ
dy d y
dx dx
"
#
"Î#
x 0 y 1 2 sec t dt 0 and x 0 1 2 sec 0 3œÊœ œ œÊ œ œ
'0
0ˆ‰
ÈÈ
dy
dx
35. y dt 3 ; x 5 y dt 3 3œÊœœÊœœ
''
5 5
x 5
sin t sin x sin t
tdxx t
dy
36. y 2 sin t dt 2 so that 2 sin x; x 1 y 2 sin t dt 2 2œ œ œÊœ œ
''
1 1
x 1
ÈÈ È
## #
dy
dx
37. Let u cos x du sin x dx du sin x dxœÊœ Êœ
2(cos x) sin x dx 2u ( du) 2 u du 2 C 4u C
'''
"Î# "Î# "Î# "Î#
œ œ œ œ
Š‹
u
4(cos x) Cœ
"Î#
38. Let u tan x du sec x dxœÊœ
#
(tan x) sec x dx u du C 2u C C
''
$Î# # $Î# "Î#
œœœœ
u2
(tan x)
ˆ‰
39. Let u 2 1 du 2 d du dœÊ œ Ê œ)))
"
#
[2 1 2 cos (2 1)] d (u 2 cos u) du sin u C sin (2 1) C
''
))) ) œ œ œ
ˆ‰
"
#""
u
44
(2 1)
)
sin (2 1) C, where C C is still an arbitrary constantœ œ )) )
#""
4
40. Let u 2 du 2 d du dœÊ œ Ê œ)1 ) )
"
#
2 sec ( ) d 2 sec u du u 2 sec u du
'Š‹Š‹
ˆ‰ ˆ ‰
""""
# # "Î# #
##
ÈÈ
2u
)1
# œ œ )1 ) ''
(2 tan u) C u tan u C (2 ) tan (2 ) Cœ œœ
""
##
"Î# "Î#
Š‹
u)1 )1
41. t t dt t dt t 4t dt 4 C C
'''
ˆ‰ˆ‰ ˆ ‰ ab Š‹
œœ œ œ
22 4 t t t4
tt t 3 1 3t
###
42. dt dt dt t 2t dt 2 C C
''' '
(t 1) 1
tt
t2t 2 t t
tt (1) tt
" ""
# $
#
œœœœœ
ˆ‰ ab Š‹
43. Let u t du t dt du t dtœ# Ê œ$ Ê œ
$Î# "
$
ÈÈ
t sin t dt sin u du cos u C cos t C
''
Ȉ‰ ˆ‰
#œ œœ#
$Î# $Î#
"""
$$$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

350 Chapter 5 Integration
44. Let u sec du sec tan d sec tan sec d u du u Cœ" Ê œ Ê " œ œ ))))))))
''
È"Î# $Î#
#
$
sec Cœ"
#
$
$Î#
ab)
45. 3x 4x 7 dx x 2x 7x 1 2(1) 7(1) ( 1) 2( 1) 7( 1) 6 ( 10) 16
'1
1abc dc dc d
#$#$#$#
"
"
œ œ œ œ
46. 8s 12s 5 ds 2s 4s 5s 2(1) 4(1) 5(1) 0 3
'0
1abcdc d
$# %$ % $
"
!
œœ œ
47. dv 4v dv 4v 2
''
11
22
444
v1
œ œ œœ
# " #
"
#
cd
ˆ‰ˆ‰
48. x dx 3x 3(27) 3(1) 3 3(1) 2
'1
27
%Î$ "Î$ "Î$ "Î$
#(
"
"
œ œ œ œ
‘ ˆ ‰ˆ‰
3
49. t dt 2t 1
'''
11 1
44 4
dt dt 2
tt t41
(2)
ÈÈÈ
œœ œ œœ
$Î# "Î# %
"
‘
50. Let x 1 u dx u du 2 dx ; u 1 x 2, u 4 x 3œ Ê œ Ê œ œ Ê œ œ Ê œ
È"
#
"Î# du
u
È
du x (2 dx) 2 x 3 2 4 3 2 3 3 2 2
'1
4
2
3
ˆ‰
È
È
1u
u
244 84
333 33
"Î# $Î# $Î# $Î#
$
#
œ œ œœœ
' ‘ ˆ‰ ˆ‰ˆ‰ ÈÈ
ÈÈ
Š‹
51. Let u 2x 1 du 2 dx 18 du 36 dx; x 0 u 1, x 1 u 3œÊ œ Ê œ œÊœ œÊœ
18u du 8
''
01
13
36 dx 8u 9 9 9
(2x 1) 2 u 3 1
$ "
$
"
$
"
œ œ œ œœ
’“‘ ˆ‰ˆ‰
52. Let u 7 5r du 5 dr du dr; r 0 u 7, r 1 u 2œ Ê œ Ê œ œ Ê œ œ Ê œ
"
5
(7 5r) dr u du 3u 7 2
'' '
00 7
11 2
dr 3
(7 5r) 55 5
È
#Î$ #Î$ "Î$
""
#
(
$$
œ œ œ œ
ˆ‰‘Š‹
ÈÈ
53. Let u 1 x du x dx du x dx; x u 1 ,œ Ê œ Ê œ œ Ê œ œ
#Î$ "Î$ "Î$
#
""
#Î$
23 3
3884
ˆ‰
x1 u11 0œÊœ œ
#Î$
x 1 x dx u du u (0)
''
18 34
10
"Î$ #Î$ $Î# &Î# &Î#
$Î# !
#
!
$Î% $Î%
&Î#
ˆ ‰ ˆ ‰ˆ‰ ‘ ˆ‰ˆ‰
’“Š‹
œœ œœ
33u 3 3 33
25554
5
œ27 3
160
È
54. Let u 1 9x du 36x dx du x dx; x 0 u 1, x u 1 9œ Ê œ Ê œ œ Ê œ œ Ê œ œ
%$ $
"""
##
%
36 16
25
ˆ‰
x 1 9x dx u du u
''
01
1 2 25 16
$ % $Î# "Î#
$Î# "" "
#&Î"'
"
#&Î"'
"
ab ˆ‰ ‘
’“Š‹
œ œ œ
36 36 18
u
(1)œ œ
"""
"Î# "Î#
18 16 18 90
25
ˆ‰ ˆ ‰
55. Let u 5r du 5 dr du dr; r 0 u 0, r u 5œÊ œ Ê œ œÊœ œÊœ
"
511
sin 5r dr sin u du 0
''
00
5
##
"" &
!## #
œœœœab
ˆ‰ ‘ ˆ ‰ˆ ‰
5524 0 20
u sin 2u sin 10 sin 0
111 1
56. Let u 4t du 4 dt du dt; t 0 u , t uœ Ê œ Ê œ œÊœ œ Êœ
1111
44 444
3"
cos 4t dt cos u du
''
04
34
##
"" " "
$Î%
Î%
ˆ‰ ˆ‰ ‘
ab Š‹Š ‹
œ œ œ
111
1
1
44424484484
usin 2u 3 sin sin
ˆ‰ ˆ ‰
3
œ œ
11
81616 8
""
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 5 Practice Exercises 351
57. sec d [tan ] tan tan 0 3
'0
#Î$
!
)) )œœœ
11
3È
58. csc x dx [ cot x] cot cot 2
'4
34
#$Î%
Î%
œ œ œ
1
1
11
ˆ‰ˆ‰
3
44
59. Let u du dx 6 du dx; x u , x 3 uœÊ œ Ê œ œÊœ œ Êœ
x
66 6
"
#
11
11
cot dx 6 cot u du 6 csc u 1 du [6( cot u u)] 6 cot 6 cot
'' '
32 2
66
### Î#
Î' ##
x
666
œœœœab ˆ‰ˆ‰
1
1
11 11
63 2œ
È1
60. Let u du d 3 du d ; 0 u 0, uœÊ œ Ê œ œÊœ œÊœ
) 1
33 3
"))) )1
tan d sec 1 d 3 sec u 1 du [3 tan u 3u]
'' '
00 0
3
## # Î$
!
)) 1
33
))œœ œ
ˆ‰ ab
3 tan 3 (3 tan 0 0) 3 3œœ
‘ˆ‰ È
11
33 1
61. sec x tan x dx [sec x] sec 0 sec 1 2 1
'3
0
œ œ œœ
!
Î$1
1
ˆ‰
3
62. csc z cot z dz [ csc z] csc csc 2 2 0
'4
34
œ œ œ œ
$Î%
Î%
1
1
11
ˆ‰ˆ‰
ÈÈ
3
44
63. Let u sin x du cos x dx; x 0 u 0, x u 1œÊœ œÊœœÊœ
1
#
5(sin x) cos x dx 5u du 5 u 2u 2(1) 2(0) 2
'0
2
0
1
$Î# $Î# &Î# &Î# &Î# &Î#
""
!!
œ œ œ œœ
'‘‘ˆ‰
2
5
64. Let u 1 x du 2x dx du 2x dx; x 1 u 0, x 1 u 0œ Ê œ Ê œ œÊ œ œ Ê œ
#
2x sin 1 x dx sin u du 0
''
10
10
abœ œ
#
65. Let u sin 3x du 3 cos 3x dx du cos 3x dx; x u sin 1, x u sinœÊœ Êœ œÊœœœÊœ
"
####3
331111
ˆ‰ ˆ‰
1œ
15 sin 3x cos 3x dx 15u du 5u du u ( 1) (1) 2
'''
211
211
%%%&&&
""
"
œœœœœ
ˆ‰ cd
3
66. Let u cos du sin dx 2 du sin dx; x 0 u cos 1, x u cosœ Ê œ Ê œ œÊœ œ œ Êœ
ˆ‰ ˆ‰ ˆ‰ ˆ‰ Š‹
xx x 02
3### # # #
"12
3
œ"
#
cos sin dx u ( 2 du) 2 (1) (8 1)
''
01
23 12
% % $
## #
"Î#
"
"$
ˆ‰ ˆ‰ ˆ‰
’“Š‹
xx u 2 2 2 14
33 33 3
œœ œœœ
67. Let u 1 3 sin x du 6 sin x cos x dx du 3 sin x cos x dx; x 0 u 1, xœ Ê œ Ê œ œ Ê œ œ
#"
##
1
u 1 3 sin 4Êœ œ
#
#
1
dx du u du u 4 1 1
'''
011
244
3 sin x cos x u
13 sinx u2
ÈÈ
"" " "
##
"Î# "Î# "Î# "Î#
%
"
%
"
œ œ œ œ œœ
ˆ‰ ‘
’“Š‹
68. Let u 1 7 tan x du 7 sec x dx du sec x dx; x 0 u 1 7 tan 0 1,œ Ê œ Ê œ œ Ê œ œ
##
"
7
x u 1 7 tan 8œÊœ œ
11
44
dx du u du u (8) (1)
'''
011
488
sec x u 3 3 3 3
(1 7 tan x) u 77 7 7777
"
"" " "
#Î$ "Î$ "Î$ "Î$
)
"
)
œ œ œ œ œœ
ˆ‰ ‘
’“Š‹
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

352 Chapter 5 Integration
69. Let u sec du sec tan d ; 0 u sec 0 1, u sec 2œ Ê œ œÊœ œ œ Êœ œ))))) )
11
33
d d d du u du
'' ' ' '
00 0 1 1
33 3 2 2
tan sec tan sec tan
2 sec sec 2 sec 2 (sec ) 2 u 2
)))))
))) )
ÈÈÈÈÈ
)))œœœœ
""
$Î#
21œœœœ
"
##
""
ÈÈÈÈ
ˆ‰
2
u222
2u 2(2) 2(1)
’“’ “ Š ‹
È
70. Let u sin t du cos t t dt dt 2 du dt; t u sin ,œÊœ œ Êœ œÊœœ
ÈÈ
ˆ‰ˆ‰
" "
# #
"Î# cos t cos t
2t t 36 6
ÈÈ
ÈÈ
11
t usin 1œÊœ œ
11
4#
dt (2 du) 2 u du 4 u 4 1 4 2 2 2
'''
36 12 12
41 1
cos t
t sin t u
È
ÉÈÈ
œœœœœ
""
"Î# "
"Î# #
‘
ÈÈÈ
ÉŠ‹
71. (a) av(f) (mx b) dx bx b(1) b( 1) (2b) bœœœœœ
""" "
# # # #
"
"
1(1) 2 2
mx m(1) m( 1)
'1
1’“’ “Š‹Š ‹
(b) av(f) (mx b) dx bx b(k) b( k)œœœ
"""
# # #
k(k) k 2 k 2
mx m(k) m( k)
'k
kk
k
’“’ “Š‹Š ‹
(2bk) bœœ
"
#k
72. (a) y 3x dx 3 x dx x (3) (0) 2 3 2
av 00
33
œœ œœœœ
""
"Î# $Î# $Î# $Î#
$
!
30 3 3 3 3 3 3 3
33 3
222
''
ÈÈ È
‘ ‘ Š‹
ÈÈ È
(b) y ax dx a x dx x (a) (0) a a a
av 00
aa a
œœœœœœ
""
"Î# $Î# $Î# $Î#
!
a0 a a 3 a 3 3 a 3 3
aa a
222 22
''
ÈÈ È
‘ ˆ ‰ ˆ‰
ÈÈ È
73. f axf (x) dx [f(x)] [f(b) f(a)] so the average value of f over [a b] is the
ww w
"""
av a
a
b
b
œœœœ ß
b a ba ba b a
f(b) f(a)
'È
slope of the secant line joining the points (a f(a)) and (b f(b)), which is the average rate of change of f over [a b].ßß ß
74. Yes, because the average value of f on [a b] is f(x) dx. If the length of the interval is 2, then b a 2ߜ
"
ba
'a
b
and the average value of the function is f(x) dx.
"
#'a
b
75. We want to evaluate
f(x) dx sin x dx sin x dx dx
""# $(# #&
$'& ! $'& $'& $'& $'& $'&
'' ' '
œ $( "!" #& œ "!"
Œ
”• ”•
ab ab
11
Notice that the period of y sin x is and that we are integrating this function over an iterval ofœ "!" œ $'&
”•
ab
##
$'&
11
length 365. Thus the value of sin x dx dx is .
$( # #& $( #&
$'& $'& $'& $'& $'&
''
”•
ab
1 "!" † ! † $'& œ #&
76. T T dT T
" " #' "Þ)(
'(&#! '&& #†"! $†"!
#
& #
#!
'(&
'abab
”•
)Þ#( "! #' "Þ)( œ )Þ#(
TT
œ )Þ#( '(& )Þ#( #! ¸ $(#%Þ%% "'&Þ%!
" "
'&& #†"! $†"! #†"! $†"! '&&
#' '(& "Þ)( '(& #' #! "Þ)( #!
Œ
”•”•
ab ab a b
ab ab ab ab
the average value of C on [20, 675]. To find the temperature T at which C , solveœ&Þ%$œ œ&Þ%$
vv
T T for T. We obtain T T&Þ%$ œ )Þ#( "! #' "Þ)( "Þ)( #' #)%!!! œ !
& # #
ab
T . So T or T . Only T lies in theÊ œ œ œ $)#Þ)# œ $*'Þ(# œ $*'Þ(#
#' „ #' % "Þ)( #)%!!!
# "Þ)( $Þ(%
#' „ #"#%**'
Éab a ba b
ab È
interval [20, 675], so T C.œ $*'Þ(#‰
77. cos x
dy
dx œ#
È$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 5 Practice Exercises 353
78. cos x x x cos x
dy
dx dx
d
œ#(†(œ"%#(
ÈÈ
abab ab
$# $#
#
79. dt
dy
dx dx
dx
tx
œ œ
Œ
'1
''
$ $
80. dt dt sec x
dy
dx dx t dx t sec x dx sec x
d d d sec x tan x
sec x
sec x
œœœœ
ŒŒ ab
''
#"""
" " " "
#
81. Yes. The function f, being differentiable on [a b], is then continuous on [a b]. The Fundamental Theorem ofßß
Calculus says that every continuous function on [a b] is the derivative of a function on [a b].ßß
82. The second part of the Fundamental Theorem of Calculus states that if F(x) is an antiderivative of f(x) on
[a b], then f(x) dx F(b) F(a). In particular, if F(x) is an antiderivaitve of 1 x on [0 1], thenßœ ß
'a
bÈ%
1 x dx F(1) F(0).
'0
1Ȝ
%
83. y 1 t dt 1 t dt 1 t dt 1 t dt 1 xœ œ Ê œ œ œ
'' ' '
11 1 1
xx x x
dy
dx dx dx
dd
ÈÈ È ÈÈ
”•”•
## # ##
84. y dt dt dt dtœœ Êœ œ
'' ' '
cos x 0 0 0
0 cos x cos x cos x
"" " "
1t 1t dx dx 1t dx 1t
dy dd
”•”•
(cos x) ( sin x) csc xœ œ œ œ
ˆ‰ˆ ‰ˆ‰
"""
1 cos x dx sin x sin x
d
85. We estimate the area A using midpoints of the vertical intervals, and we will estimate the width of the parking lot on each
interval by averaging the widths at top and bottom. This gives the estimate
A¸"&†
ˆ‰
!$' $'&% &%&" &"%*Þ& %*Þ&&% &%'%Þ% '%Þ%'(Þ& '(Þ&%#
########
A ft . The cost is Area ($2.10/ft ) 5961 ft $2.10/ft $12,518.10 the job cannot be done for $11,000.¸ &*'" ¸ œ Ê
####
†aba b
86. (a) Before the chute opens for A, a 32 ft/sec . Since the helicopter is hovering, v 0 ft/secœ œ
#!
v 32 dt 32t v 32t. Then s 6400 ft s 32t dt 16t s 16t 6400.Ê œ œ œ œ Ê œ œ œ
''
!! !
##
At t 4 sec, s 16(4) 6400 6144 ft when A's chute opens;œœœ
#
(b) For B, s 7000 ft, v 0, a 32 ft/sec v 32 dt 32t v 32t s 32t dt
!! !
#
œ œ œ Ê œ œ œ Ê œ
''
16t s 16t 7000. At t 13 sec, s 16(13) 7000 4296 ft when B's chute opens;œ œ œ œ œ
## #
!
(c) After the chutes open, v 16 ft/sec s 16 dt 16t s . For A, s 6144 ft and for B,œ Ê œ œ œ
'!!
s 4296 ft. Therefore, for A, s 16t 6144 and for B, s 16t 4296. When they hit the ground,
!œœœ
s 0 for A, 0 16t 6144 t 384 seconds, and for B, 0 16t 4296 tœ Ê œ Ê œ œ œ Ê œ
6144 4296
16 16
268.5 seconds to hit the ground after the chutes open. Since B's chute opens 58 seconds after A's opensœ
B hits the ground first.Ê
87. av(I) (1200 40t) dt 1200t 20t (1200(30) 20(30) 1200(0) 20(0)œœœ
"""
###
$!
!
30 30 30
'0
30 cdc dabab
(18,000) 600; Average Daily Holding Cost (600)($0.03) $18œœ œ œ
"
30
88. av(I) (600 600t) dt 600t 300t 600(14) 300(14) 0 4800; Average Dailyœœœœ
"""
##
"%
!
14 14 14
'0
14 cdc d
Holding Cost (4800)($0.04) $192œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

354 Chapter 5 Integration
89. av(I) 450 dt 450t 450(30) 0 300; Average Daily Holding Costœœœœ
"""
#
$!
!
30 30 6 30 6
tt 30
'0
30Š‹’“’ “
(300)($0.02) $6œœ
90. av(I) 600 20 15t dt 600 20 15 t dt 600t 20 15 tœœ œ
"" "
"Î# $Î# '!
!
60 60 60 3
2
''
00
60 60
Š‹Š ‹’ “
ÈÈÈ
ˆ‰
600(60) (60) 0 36,000 15 200; Average Daily Holding Costœ œœ
""
$Î# #
60 3 60 3
40 15 320
’“
ˆ‰ˆ‰
È
(200)($0.005) $1.00œœ
CHAPTER 5 ADDITIONAL AND ADVANCED EXERCISES
1. (a) Yes, because f(x) dx 7f(x) dx (7) 1
''
00
11
œœœ
""
77
(b) No. For example, 8x dx 4x 4, but 8x dx 2 2 1 0
''
00
11
œœ œ œ cd È’“
ÈŠ‹ ˆ‰
# $Î# $Î#
"
!
"
!
x42
3
3È
4œÁ
42
3
ÈÈ
2. (a) True: f(x) dx f(x) dx 3
''
52
25
œ œ
(b) True: [f(x) g(x)] dx f(x) dx g(x) dx f(x) dx f(x) dx g(x) dx
''''''
222222
555255
œ œ
4329œœ
(c) False: f(x) dx 4 3 7 2 g(x) dx [f(x) g(x)] dx 0 [g(x) f(x)] dx 0.
''''
2222
5555
œœœ Ê Ê
On the other hand, f(x) g(x) [g(x) f(x)] 0 [g(x) f(x)] dx 0 which is a contradiction.ŸÊ Ê
'2
5
3. y f(t) sin a(x t) dt f(t) sin ax cos at dt f(t) cos ax sin at dtœœ
"" "
aa a
'' '
00 0
xx x
f(t) cos at dt f(t) sin at dt cos ax f(t) cos at dtœ Êœ
sin ax cos ax
aadx
dy
'' '
00 0
xx x
Œ
f(t) cos at dt sin ax f(t) sin at dt f(t) sin at dt
sin ax d cos ax d
adx adx
Œ Œ
'' '
00 0
xx x
cos ax f(t) cos at dt (f(x) cos ax) sin ax f(t) sin at dt (f(x) sin ax)œ
''
0 0
x x
sin ax cos ax
aa
cos ax f(t) cos at dt sin ax f(t) sin at dt. Next,ʜ
dy
dx ''
00
xx
a sin ax f(t) cos at dt (cos ax) f(t) cos at dt a cos ax f(t) sin at dt
dy
dx dx
d
œ
'''
000
xxx
Œ
(sin ax) f(t) sin at dt a sin ax f(t) cos at dt (cos ax)f(x) cos axœ
Œ
d
dx ''
00
xx
a cos ax f(t) sin at dt (sin ax)f(x) sin ax a sin ax f(t) cos at dt a cos ax f(t) sin at dt f(x).œ
'''
000
xxx
Therefore, y a y a cos ax f(t) sin at dt a sin ax f(t) cos at dt f(x)
ww #
œ
''
00
xx
a f(t) cos at dt f(t) sin at dt f(x). Note also that y (0) y(0) 0.œœœ
# w
Œ
sin ax cos ax
aa
''
00
xx
4. x dt (x) dt dt from the chain ruleœÊœ œ
'''
000
yyy
"""
ÈÈÈ
14t 14t 14t
dd d
dx dx dy dx
dy
”•
Š‹
1 1 4y . Then 1 4y 1 4yÊœ Ê œ œ œ
"
###
È14y
dy dy d y dy
dx dx dx dx dy dx
dd
Š‹ Š‹
ÈÈÈ
ˆ‰ˆ‰
1 4y (8y) 4y. Thus 4y, and the constant ofœ œ œ œ œ
"
#
#"Î#
ab Š‹
dy d y
dx dx
4y
14y 14y
4y 1 4y
Š‹
ÈÈ
ˆ‰
È
dy
dx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
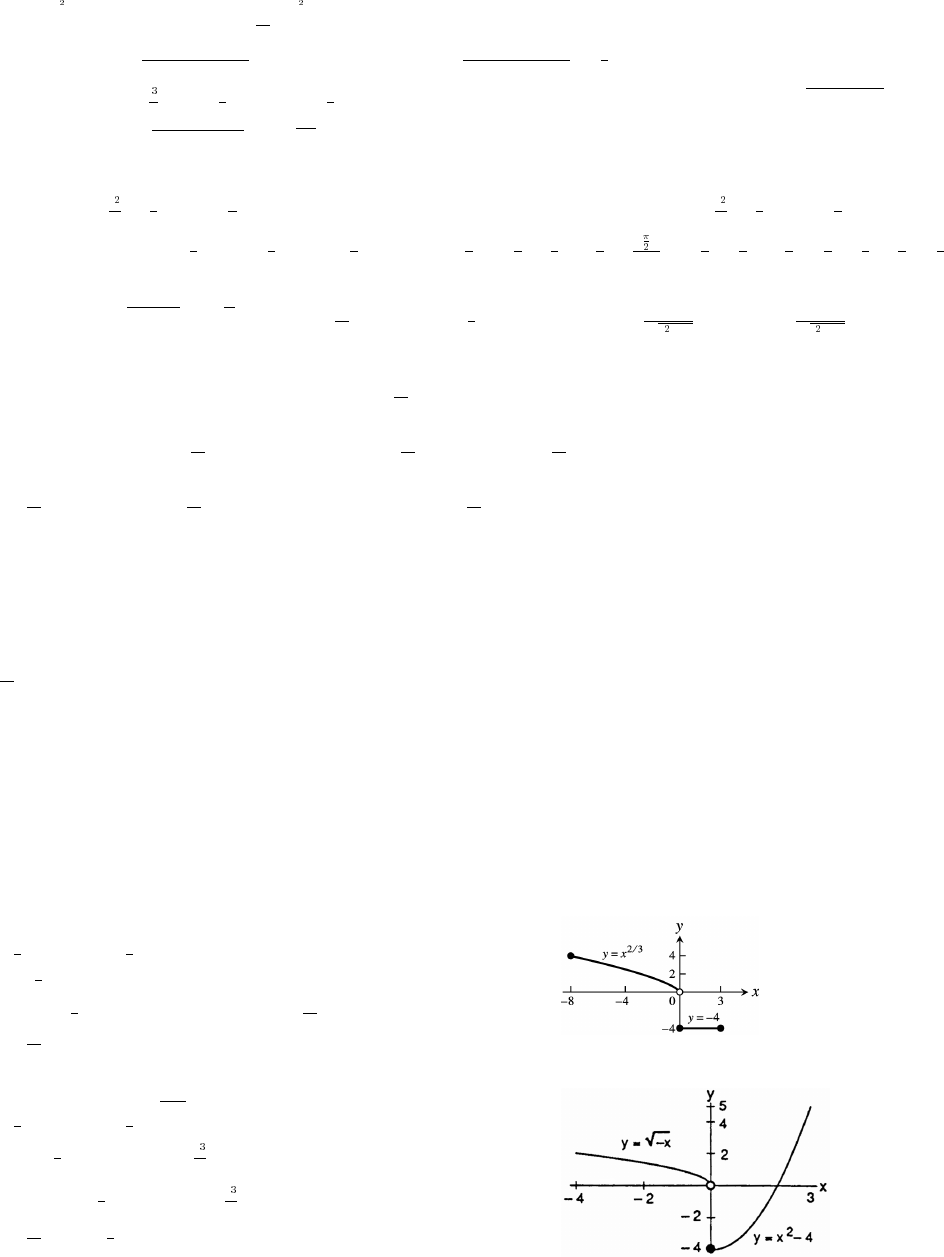
Chapter 5 Additional and Advanced Exercises 355
proportionality is 4.
5. (a) f(t) dt x cos x f(t) dt cos x x sin x f x (2x) cos x x sin x
''
00
xx
œÊ œ Ê œ1111111
d
dx ab
#
f x . Thus, x 2 f(4)Êœ œÊœ œab
#"cos x x sin x cos 2 2 sin 2
2x 4 4
11 1 11 1
(b) t dt (f(x)) (f(x)) x cos x (f(x)) 3x cos x f(x) 3x cos x
'0
f(x) f(x)
#$$$
!
"" $
œœ Ê œ Ê œ Êœ
’“ È
t
33 3 11 1
f(4) 3(4) cos 4 12Êœ œ
$$
ÈÈ
1
6. f(x) dx sin a cos a. Let F(a) f(t) dt f(a) F (a). Now F(a) sin a cos a
''
0 0
a a
œ œ Ê œ œ
aa aa
## # ## #
w
1 1
f(a) F (a) a sin a cos a sin a f sin cos sin Êœ œ Ê œ œœ
w""""
# # # # ## # # ## # ### #
a111111111
ˆ‰ ˆ‰
7. f(x) dx b 1 2 f(b) f(x) dx b 1 (2b) f(x)
''
11
bb
œÊœ œ œ Êœ
ÈÈ ab
#"
#
#"Î#
dbx
db b1 x1
ÈÈ
8. The derivative of the left side of the equation is: f(t) dt du f(t) dt; the derivative of the right
d
dx ”•”•
'' '
00 0
xu x
œ
side of the equation is: f(u)(x u) du f(u) x du u f(u) du
ddd
dx dx dx
”•
'''
000
xxx
œ
x f(u) du u f(u) du f(u) du x f(u) du xf(x) f(u) du xf(x) xf(x)œœ œ
dd d
dx dx dx
”• ” •
''' ' '
000 0 0
xxx x x
f(u) du. Since each side has the same derivative, they differ by a constant, and since both sides equal 0œ'0
x
when x 0, the constant must be 0. Therefore, f(t) dt du f(u)(x u) du.œœ
'' '
00 0
xu x
”•
9. 3x 2 y 3x 2 dx x 2x C. Then (1 1) on the curve 1 2(1) C 1 C 4
dy
dx œÊœ œ ß Ê œÊœ
##$ $
'ab
y x 2x 4ʜ
$
10. The acceleration due to gravity downward is 32 ft/sec v 32 dt 32t v , where v is the initialÊœœ
#!!
'
velocity v 32t 32 s ( 32t 32) dt 16t 32t C. If the release point, at t , is s 0, thenÊœ Êœ œ œ! œ
'#
C 0 s 16t 32t. Then s 17 17 16t 32t 16t 32t 17 0. The discriminant of thisœÊ œ œ Ê œ Ê œ
###
quadratic equation is 64 which says there is no real time when s 17 ft. You had better duck.œ
11. f(x) dx x dx 4 dx
'''
880
303
œ
#Î$
x [ 4x]œ
‘
3
5&Î$ $
!
) !
0 ( 8) ( 4(3) 0) 12œ œ
ˆ‰
396
55
&Î$
œ36
5
12. f(x) dx x dx x 4 dx
'' '
44 0
30 3
œ
Èab
#
(x) 4xœ
‘
’“
2x
33
$Î# !
%
$
!
0 (4) 4(3) 0œ
‘ˆ‰
’“Š‹
23
33
$Î#
3œœ
16 7
33
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
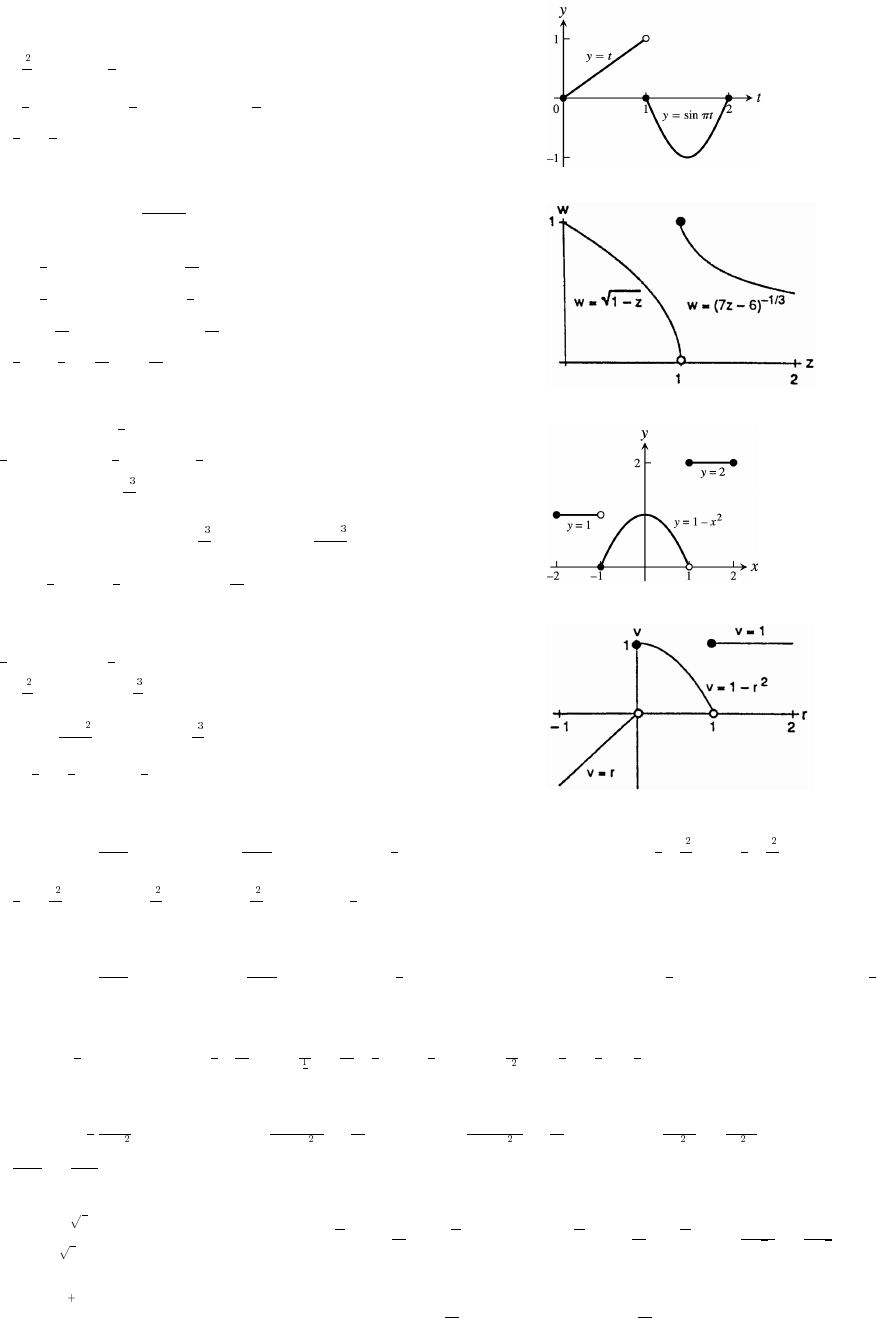
356 Chapter 5 Integration
13. g(t) dt t dt sin t dt
'''
001
212
œ1
cos tœ
’“ ‘
t
2
"
!
"#
"
11
0 cos 2 cos œ
ˆ‰ ‘ˆ‰
"" "
#11
11
œ
"
#
2
1
14. h(z) dz 1 z dz (7z 6) dz
'' '
00 1
21 2
œ
È"Î$
(1 z) (7z 6)œ
‘‘
23
314
$Î# #Î$
"#
!"
(1 1) (1 0)œ
‘ˆ‰
22
33
$Î# $Î#
(7(2) 6) (7(1) 6)
‘
33
14 14
#Î$ #Î$
œ œ
263 55
3 7 14 42
ˆ‰
15. f(x) dx dx 1 x dx 2 dx
''' '
221 1
211 2
œab
#
[x] x [2x]œ
" #
#
"
" "
’“
x
3
1 ( 2) 1 1 2(2) 2(1)œ ab
”•
Š‹Š ‹
’“
1
33
(1)
1 42œ œ
22 13
33 3
ˆ‰
16. h(r) dr r dr 1 r dr dr
''' '
110 1
201 2
œab
#
r [r]œ
’“ ’ “
rr
23
!"
" !
#
"
01021œ
Š‹Š ‹Š‹ ab
(1) 1
3
#
1œ œ
"
#
27
36
17. Ave. value f(x) dx f(x) dx x dx (x 1) dx xœœ œœ
""" ""
# # ##
"#
!"
ba 0 2 2
xx
''''
a001
b212
”•
’“ ’ “
021œ œ
""
#####
’“Š‹Š‹Š‹
121
18. Ave. value f(x) dx f(x) dx dx 0 dx dx [10032]œ œ œ œ œ
""" "
ba 30 3 3 3
2
'''''
a0012
b3123
”•
19. f(x) dt f (x) xœ Ê œ œ œœ
'1/x
x""""""""
w
t x dx dx x x x x x x
dx d 2
ˆ‰ ˆ ‰ ˆ ‰
Š‹ ˆ‰
x
20. f(x) dt f (x) (sin x) (cos x)œÊœ œ
'cos x
sin x "" " "
w
t 1 t 1 sin x dx 1 cos x dx cos x sin x
ddcos xsin x
ˆ‰ˆ ‰ˆ‰ˆ ‰
œ
""
cos x sin x
21. g(y) sin t dt g (y) sin 2 y 2 y sin y yœÊœ œ
'y
2y
#w ##
Š‹Š‹Š‹Š‹
ˆ‰ ˆ‰ ˆ‰ ˆ‰
ÈÈ ÈÈ
dd
dy dy y 2 y
sin 4y sin y
ÈÈ
22. f(x) t(5 t) dt f (x) (x 3)( (x 3)) (x 3) x(5 x) (x 3)(2 x) x(5 x)œÊœ& œ
'x
x3
wˆ‰ ˆ‰
ddx
dx dx
6 x x 5x x 6 6x. Thus f (x) 0 6 6x 0 x 1. Also, f (x) 6 x 1 gives aœ œ œ Ê œ Ê œ œ!Ê œ
## w ww
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 5 Additional and Advanced Exercises 357
maximum.
23. Let f(x) x on [0 1]. Partition [0 1] into n subintervals with x . Then , , , are theœß ß œœ á
&" "
?10 2 n
nn nn n
right-hand endpoints of the subintervals. Since f is increasing on [0 1], U is the upper sum forߜ
!Š‹ˆ‰
j1
j
nn
&"
f(x) x on [0 1] lim lim lim œßÊ œ áœ
&&" " " á
&&&
nn nÄ_ Ä_ Ä_
!Š‹ ’ “ ’ “
ˆ‰ ˆ‰ ˆ‰ ˆ‰
j1
j
nn nn n n n
2n 12n
x dxœœœ
'0
1
&"
!
"
’“
x
66
24. Let f(x) x on [0 1]. Partition [0 1] into n subintervals with x . Then , , , are theœß ß œœ á
$" "
?10 2 n
nn nn n
right-hand endpoints of the subintervals. Since f is increasing on [0 1], U is the upper sum forߜ
!Š‹ˆ‰
j1
j
nn
$"
f(x) x on [0 1] lim lim lim œßÊ œ áœ
$$" " " á
$$$
nn nÄ_ Ä_ Ä_
!Š‹ ’ “ ’ “
ˆ‰ ˆ‰ ˆ‰ ˆ‰
j1
j
nn nn n n
2n 12n
n
x dxœœœ
'0
1
$"
!
"
’“
x
44
25. Let y f(x) on [0 1]. Partition [0 1] into n subintervals with x . Then , , , are theœß ß œœ á?10 2 n
nn nn n
" "
right-hand endpoints of the subintervals. Since f is continuous on [ 1], f is a Riemann sum of!ß !Š‹
ˆ‰
j1
j
nn
"
y f(x) on [0 1] lim f lim f f f f(x) dxœßÊ œ áœ
nnÄ_ Ä_
!Š‹
ˆ‰ ‘ˆ‰ ˆ‰ ˆ‰
j1 0
1
j
nn n n n n
2n""" '
26. (a) lim [2 4 6 2n] lim 2x dx x 1, where f(x) 2x
nnÄ_ Ä_
"" #"
!
n nnnn n
246 2n
á œ á œ œ œ œ
‘
cd
'0
1
on [0 1] (see Exercise 25)ß
(b) lim 1 2 n lim x dx , where
nnÄ_ Ä_
"" "
"& "& "& "&
"& "& "& "
!
nnnnn1616
12 n x
cd
’“’“
ˆ‰ ˆ‰ ˆ‰
á œ á œ œ œ
'0
1
f(x) x on [0 1] (see Exercise 25)ϧ
"&
(c) lim sin sin sin sin n dx cos x cos cos 0
nÄ_
""""
"
!
nn n n
2n
‘‘ˆ‰
11 1
111
á œ œ œ
'0
1
111
, where f(x) sin x on [0 1] (see Exercise 25)œœß
2
11
(d) lim 1 2 n lim lim 1 2 n lim x dx
nnn nÄ_ Ä_ Ä_ Ä_
""" "
"& "& "& "& "& "& "&
nnn n
cd cd
Š‹Š ‹Š‹
á œ á œ '0
1
0 0 (see part (b) above)œœ
ˆ‰
"
16
(e) lim 1 2 n lim 1 2 n
nnÄ_ Ä_
""& "& "& "& "& "&
nn
n
cdcdá œ á
lim n lim 1 2 n lim n x dx (see part (b) above)œáœœ_
Š‹Š ‹Š‹
cd
nn nÄ_ Ä_ Ä_
""& "& "& "&
n'0
1
27. (a) Let the polygon be inscribed in a circle of radius r. If we draw a radius from the center of the circle (and
the polygon) to each vertex of the polygon, we have n isosceles triangles formed (the equal sides are equal
to r, the radius of the circle) and a vertex angle of where . The area of each triangle is))
nn
œ2
n
1
A r sin the area of the polygon is A nA sin sin .
nn nn
œÊ œœœ
"
###
#))
nr nr 2
n
1
(b) lim A lim sin lim sin lim r r lim r
nn n n 2n 0
Ä_ Ä_ Ä_ Ä_ ÎÄ
œœ œ œ œ
nr 2 n r 2
n2n
sin sin
#
## #
111
1ab ab11 1
ˆ‰ ˆ‰
ˆ‰ ˆ‰
22
nn
22
nn
1
28. y sin x cos 2t dt sin x cos 2t dt y cos x cos 2x ; when x we haveœ "œ "Ê œ œ
''
x
xwab 1
y cos cos 2 . And y sin x 2sin 2x ; when x , y sin cos 2t dt
www
œ œ""œ# œ œ œ "11 1 1ab ab 'x
1
.œ!!"œ"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
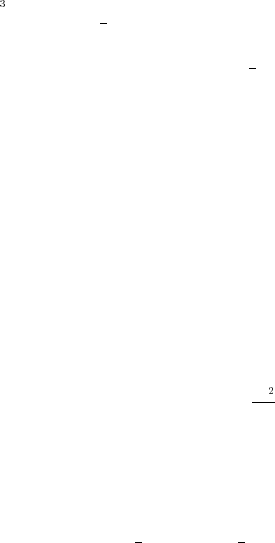
358 Chapter 5 Integration
29. (a) g f t dtab ab"œ œ!
'1
1
(b) g f t dtab ab abab$ œ œ # " œ"
'1
"
#
(c) g f t dt f t dta b ab ab a b" œ œ œ # œ
''
11
11
"
%
#
11
(d) g x f x x , , and the sign chart for g x f x is . So g has a
31 3
ww
ab ab ab abœ œ ! Ê œ $ " $ œ ± ± ±
relative maximum at x .œ"
(e) g f is the slope and g f t dt , by (c). Thus the equation is y x
w
ab ab ab ab a b"œ "œ# "œ œ œ# "
'1
1
11
yx .œ# #1
(f) g x f x at x and g x f x is negative on and positive on so there is an
ww w ww w
ab ab ab ab a b a bœ œ ! œ " œ $ß " "ß "
inflection point for g at x . We notice that g x f x for x on and g x f x for x onœ" œ ! "ß# œ !
ww w ww w
ab ab a b ab ab
, even though g does not exist, g has a tangent line at x , so there is an inflection point at x .ab ab#ß% # œ# œ#
ww
(g) g is continuous on and so it attains its absolute maximum and minimum values on this interval. We saw in (d)Ò$ß %Ó
that g x x , , . We have that
wabœ!Ê œ$"$
g f t dt f t dta b ab ab$ œ œ œ œ #
''
1
$ "
$
#
#
11
gft dtab ab"œ œ!
'1
1
gft dtab ab$œ œ"
'1
$
gft dtab ab% œ œ" †"†"œ
'1
%""
##
Thus, the absolute minimum is and the absolute maximum is . Thus, the range is .# ! Ò# ß !Ó11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Chapter 5 Additional and Advanced Exercises 359
NOTES:
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
360 Chapter 5 Integration
NOTES:
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

CHAPTER 6 APPLICATIONS OF DEFINITE INTEGRALS
6.1 VOLUMES BY SLICING AND ROTATION ABOUT AN AXIS
1. (a) A (radius) and radius 1 x A(x) 1 xœœÊœ11
##
#
Èab
(b) A width height, width height 2 1 x A(x) 4 1 xœœœÊœ†Èab
##
(c) A (side) and diagonal 2(side) A ; diagonal 2 1 x A(x) 2 1 xœœÊœœÊœ
# #
##
ÈÈab
(diagonal)
(d) A (side) and side 2 1 x A(x) 3 1 xœœÊœ
È3
4##
#
ÈÈab
2. (a) A (radius) and radius x A(x) xœœÊœ11
#È
(b) A width height, width height 2 x A(x) 4xœœœÊœ†È
(c) A (side) and diagonal 2(side) A ; diagonal 2 x A(x) 2xœœÊœœÊœ
#
#
ÈÈ
(diagonal)
(d) A (side) and side 2 x A(x) 3xœœÊœ
È3
4#ÈÈ
3. A(x) 2x (see Exercise 1c); a 0, b 4;œœ œ œœ
(diagonal) xx
##
ˆ‰
ÈÈ
ˆ‰
V A(x) dx 2x dx x 16œœœœ
''
a0
b4
cd
#%
!
4. A(x) 1 2x x ; a 1, b 1;œœ œ œœœ
111
(diameter)
44 4
2x x 21x
cdcdab ab #%
1ab
V A(x) dx 1 2x x dx x x 2 1œœœœœ
''
a1
b1
11 1ab
’“
ˆ‰
#% $ "
"
"2x 2 16
35 3515
1
5. A(x) (edge) 1 x 1 x 2 1 x 4 1 x ; a 1, b 1;œœœœœœ
# #
## #
##
’“Š‹
ÈÈ È
Š‹ ab
V A(x) dx 4 1 x dx 4 x 8 1œœœœœ
''
a1
b1
ab ’“ ˆ‰
#"
"
"x16
333
6. A(x) 2 1 x (see Exercise 1c); a 1, b 1;œœ œ œ œœ
(diagonal) 1x 1x 21x
## #
#
’“Š‹
ÈÈ È
Š‹ ab
V A(x) dx 2 1 x dx 2 x 4 1œœœœœ
''
a1
b1
ab ’“ ˆ‰
#"
"
"x8
333
7. (a) STEP 1) A(x) (side) (side) sin 2 sin x 2 sin x sin 3 sin xœœ œ
""
##
†† † †
ˆ‰ ˆ‰
Š‹Š‹
ÈÈ È
11
33
STEP 2) a 0, bœœ1
STEP 3) V A(x) dx 3 sin x dx 3 cos x 3(1 1) 2 3œœ œ œœ
''
a0
bÈÈÈÈ
’“
1
!
(b) STEP 1) A(x) (side) 2 sin x 2 sin x 4 sin xœœ œ
#Š‹Š‹
ÈÈ
STEP 2) a 0, bœœ1
STEP 3) V A(x) dx 4 sin x dx 4 cos x 8œœ œœ
''
a0
bcd
1
!
8. (a) STEP 1) A(x) (sec x tan x) sec x tan x 2 sec x tan xœœœ
111
(diameter)
44 4
###
ab
sec x sec x 1 2 œ
1
4cosx
sin x
‘
ab
##
STEP 2) a , bœ œ
11
33
STEP 3) V A(x) dx 2 sec x 1 dx 2 tan x x 2œœ œ
''
a3
b3
11
1
1
4cosx4 cos x
2 sin x
ˆ‰ ‘ˆ‰
#"Î$
Î$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
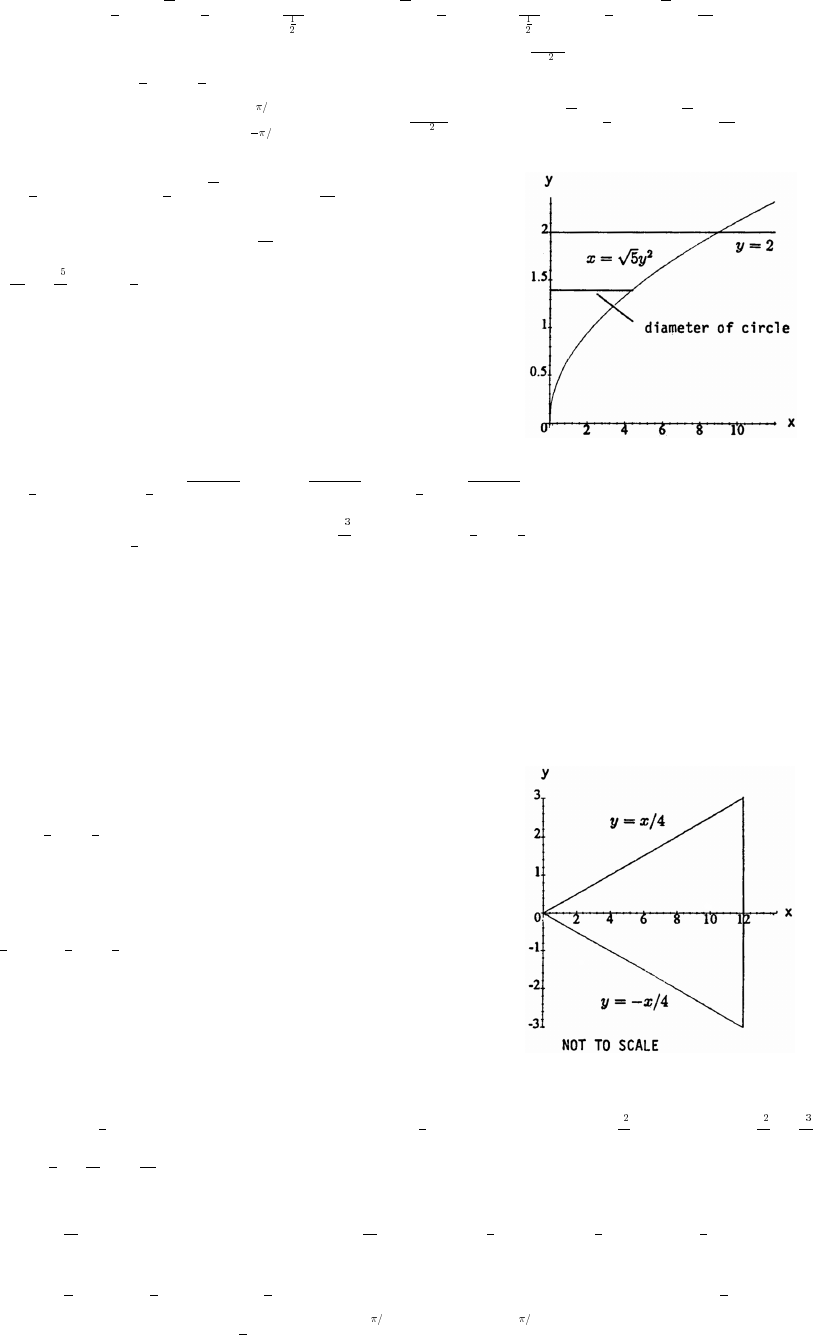
362 Chapter 6 Applications of Definite Integrals
23 2 23 2 43œœ
11 1 1 1
43 3 4 3
2
’“Š‹
ÈÈ È
Š‹Š ‹Š‹
""
ˆ‰ ˆ‰
(b) STEP 1) A(x) (edge) (sec x tan x) 2 sec x 1 2 œœœ
###
ˆ‰
sin x
cos x
STEP 2) a , bœ œ
11
33
STEP 3) V A(x) dx 2 sec x 1 dx 2 2 3 4 3œœ œœ
''
a3
b3
ˆ‰
Š‹
ÈÈ
#2 sin x 2
cos x 3 3
11
9. A(y) (diameter) 5y 0 y ;œœœ
11 1
44 4
5
## %
#
Š‹
È
c 0, d 2; V A(y) dy y dyœœ œ œ
''
c0
d2
5
4
1%
208œœœ
’“
ˆ‰
Š‹ ab
5
45 4
y
11
#
!
&1
10. A(y) (leg)(leg) 1 y 1 y 2 1 y 2 1 y ; c 1, d 1;œœœœœœ
"" "
## #
## #
##
#
‘ˆ‰
ÈÈ È
ˆ‰ ab
V A(y) dy 2 1 y dy 2 y 4 1œœœœœ
''
c1
d1
ab ’“ ˆ‰
#"
"
"
y
333
8
11. (a) It follows from Cavalieri's Principle that the volume of a column is the same as the volume of a right
prism with a square base of side length s and altitude h. Thus, STEP 1) A(x) (side length) s ;œœ
##
STEP 2) a 0, b h; STEP 3) V A(x) dx s dx s hœœ œ œ œ
''
a0
bh
##
(b) From Cavalieri's Principle we conclude that the volume of the column is the same as the volume of the
prism described above, regardless of the number of turns V s hʜ
#
12. 1) The solid and the cone have the same altitude of 12.
2) The cross sections of the solid are disks of diameter
x . If we place the vertex of the cone at theœ
ˆ‰
xx
##
origin of the coordinate system and make its axis of
symmetry coincide with the x-axis then the cone's cross
sections will be circular disks of diameter
(see accompanying figure).
xxx
44
œ
ˆ‰#
3) The solid and the cone have equal altitudes and identical
parallel cross sections. From Cavalieri's Principle we
conclude that the solid and the cone have the same
volume.
13. R(x) y 1 V [R(x)] dx 1 dx 1 x dx xœœ Ê œ œ œ œ
xxxxx
412## #
###
!
'''
00 0
22 2
11 1 1
ˆ‰ Š‹’ “
2œœ1ˆ‰
48 2
212 3
1
14. R(y) x V [R(y)] dy dy y dy y 8 6œœ Ê œ œ œ œ œ œ
3y 3y 933
444##
##$
##
!
'''
000
222
11 1111
ˆ‰ ‘ ††
15. R(x) tan y ; u y du dy 4 du dy; y 0 u 0, y 1 u ;œœÊœÊœœÊœœÊœ
ˆ‰
11 1 1
44 4 4
1
V [R(y)] dy tan y dy 4 tan u du 4 1 sec u du 4[ u tan u]œœ œœœ
'' ''
00 00
11 44
11
###
#Î%
!
‘ˆ‰ ab
11
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
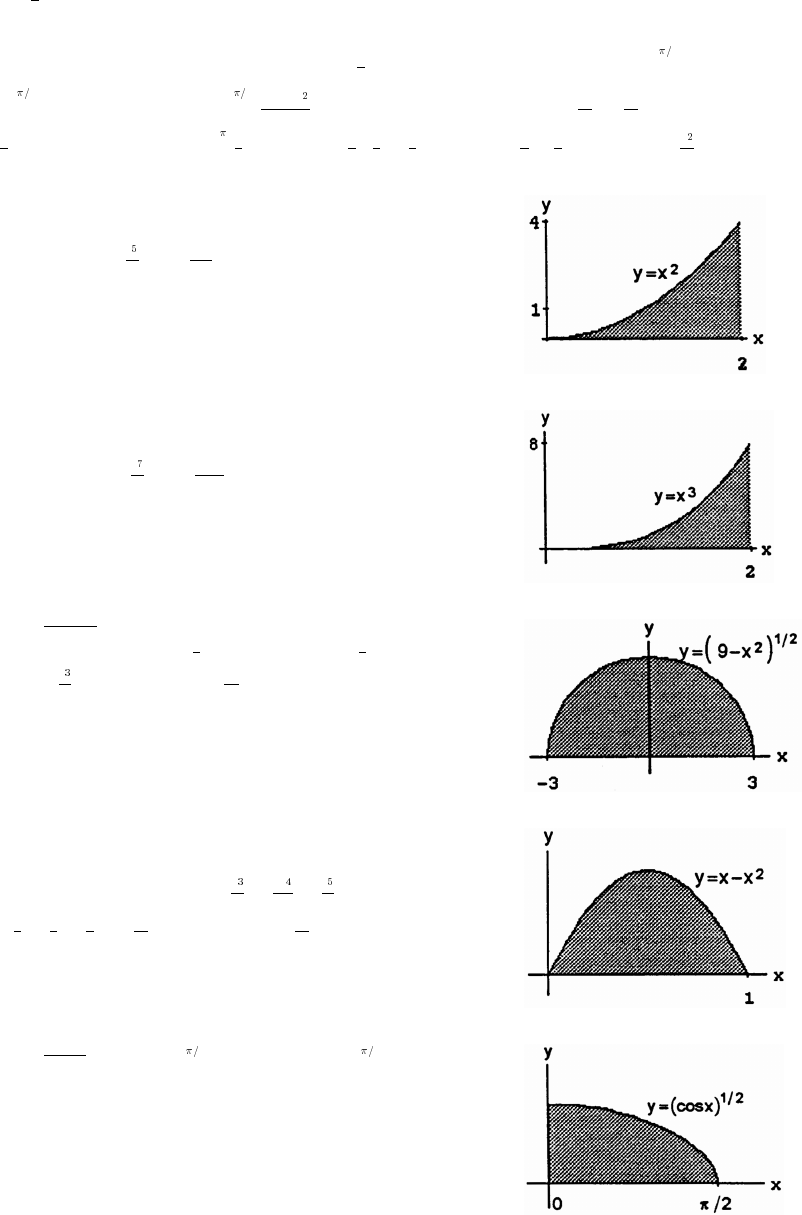
Section 6.1 Volumes by Slicing and Rotation About an Axis 363
4104œœ
ˆ‰
1
41
16. R(x) sin x cos x; R(x) 0 a 0 and b are the limits of integration; V [R(x)] dxœœÊœœ œ
1
#
#
'0
2
1
(sin x cos x) dx dx; u 2x du 2 dx ; x 0 u 0,œœœÊœÊœœÊœ11
''
00
22
#(sin 2x)
484
du dx
x u V sin u du sin 2u 0 0
‘‘‘ˆ‰
œÊœ Äœ œ œ œ
11111
1
###
""
#
!
11
'08848 16
u
17. R(x) x V [R(x)] dx x dxœÊœ œ
###
#
''
00
22
11ab
x dxœœœ11
'0
2%#
!
’“
x32
55
1
18. R(x) x V [R(x)] dx x dxœÊœ œ
$#$
#
''
00
22
11ab
x dxœœœ11
'0
2'#
!
’“
x 128
77
1
19. R(x) 9 x V [R(x)] dx 9 x dxœÊœ œ
Èab
###
''
33
33
11
9x 2 9(3) 2 18 36œ œ œ œ11 11
’“ ‘
x27
33
$
$
††
20. R(x) x x V [R(x)] dx x x dxœ Ê œ œ
###
#
''
00
11
11ab
x2xx dxœœ11
'0
1ab
’“
#$% "
!
x2xx
345
(10156)œœ œ1ˆ‰
1
3 5 30 30
""
#
11
21. R(x) cos x V [R(x)] dx cos x dxœÊœ œ
È''
00
22
11
#
sin x (1 0)œœœ111cd
1Î#
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
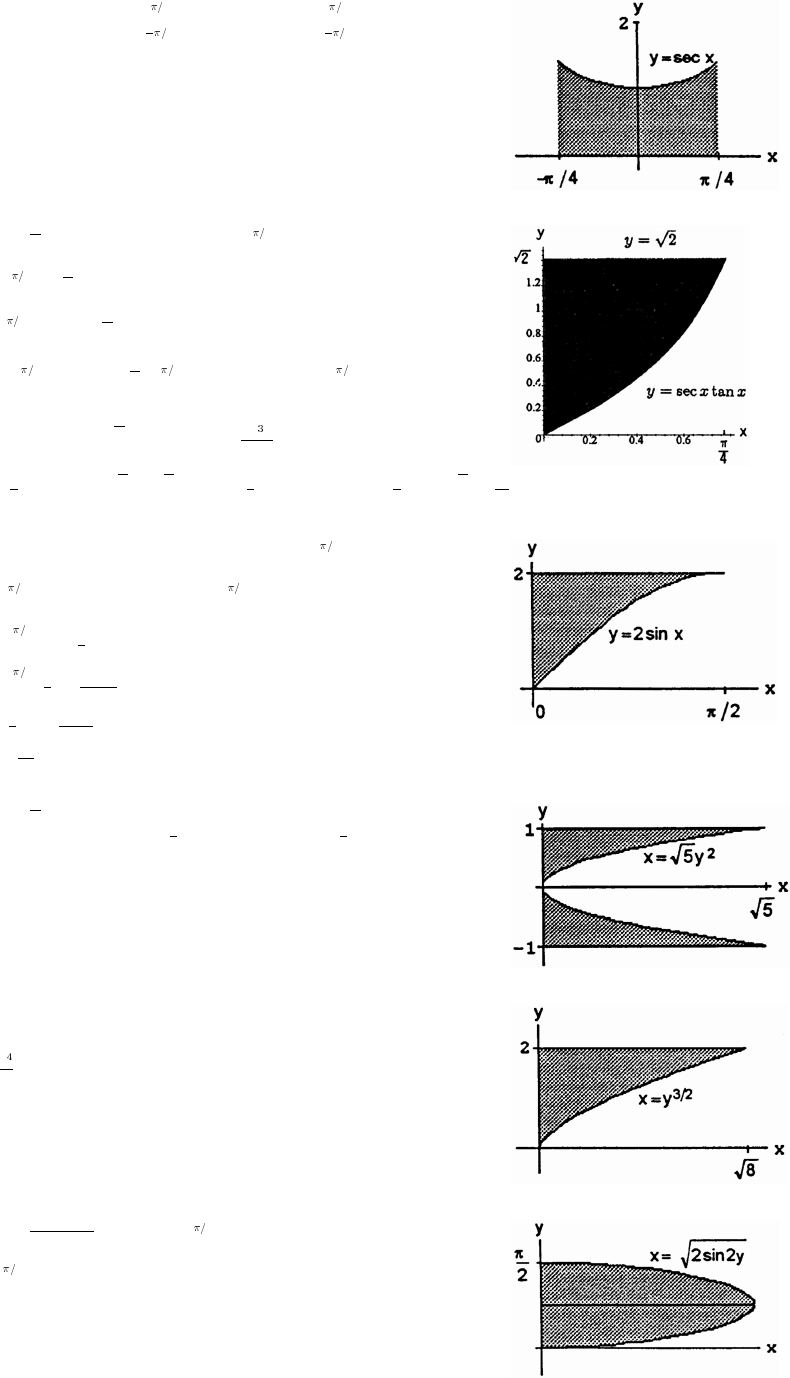
364 Chapter 6 Applications of Definite Integrals
22. R(x) sec x V [R(x)] dx sec x dxœÊœ œ
''
44
44
11
##
tan x [1 ( 1)] 2œœœ11 1cd
1
1
Î%
Î%
23. R(x) 2 sec x tan x V [R(x)] dxœ Êœ
È'0
4
1#
2 sec x tan x dxœ1'0
4Š‹
È#
2 2 2 sec x tan x sec x tan x dxœ 1'0
4Š‹
È##
2 dx 2 2 sec x tan x dx (tan x) sec x dxœ 1Œ
È
'' '
00 0
44 4
##
[2x] 2 2 [sec x]œ 1Œ
È’“
11
1
Î% Î%
!!
Î%
!
tan x
3
02221 10 22œ œ11
’“Š‹
ˆ‰
ÈÈ È
Š‹
ab
11
##
"$
33
11
24. R(x) 2 2 sin x 2(1 sin x) V [R(x)] dxœ œ Ê œ
'0
2
1#
4(1 sin x) dx 4 1 sin x 2 sin x dxœœ11
''
00
22
##
ab
4 1 (1 cos 2x) 2 sin x dxœ1'0
2‘
"
#
4 2 sin xœ1'0
2ˆ‰
3 cos 2x
2#
4 x 2 cos xœ1‘
3sin 2x
4#
Î#
!
1
4 00 (002) (3 8)œœ111
‘ˆ‰
3
4
1
25. R(y) 5 y V [R(y)] dy 5y dyœÊœ œ
Ȇ##%
''
11
11
11
y[1(1)]2œœœ11 1cd
&"
"
26. R(y) y V [R(y)] dy y dyœÊœ œ
$Î# # $
''
00
22
11
4œœ11
’“
y
4
#
!
27. R(y) 2 sin 2y V [R(y)] dyœÊœ
È'0
2
1#
2 sin 2y dy cos 2yœœ11
'0
2cd
1Î#
!
[1 ( 1)] 2œœ11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
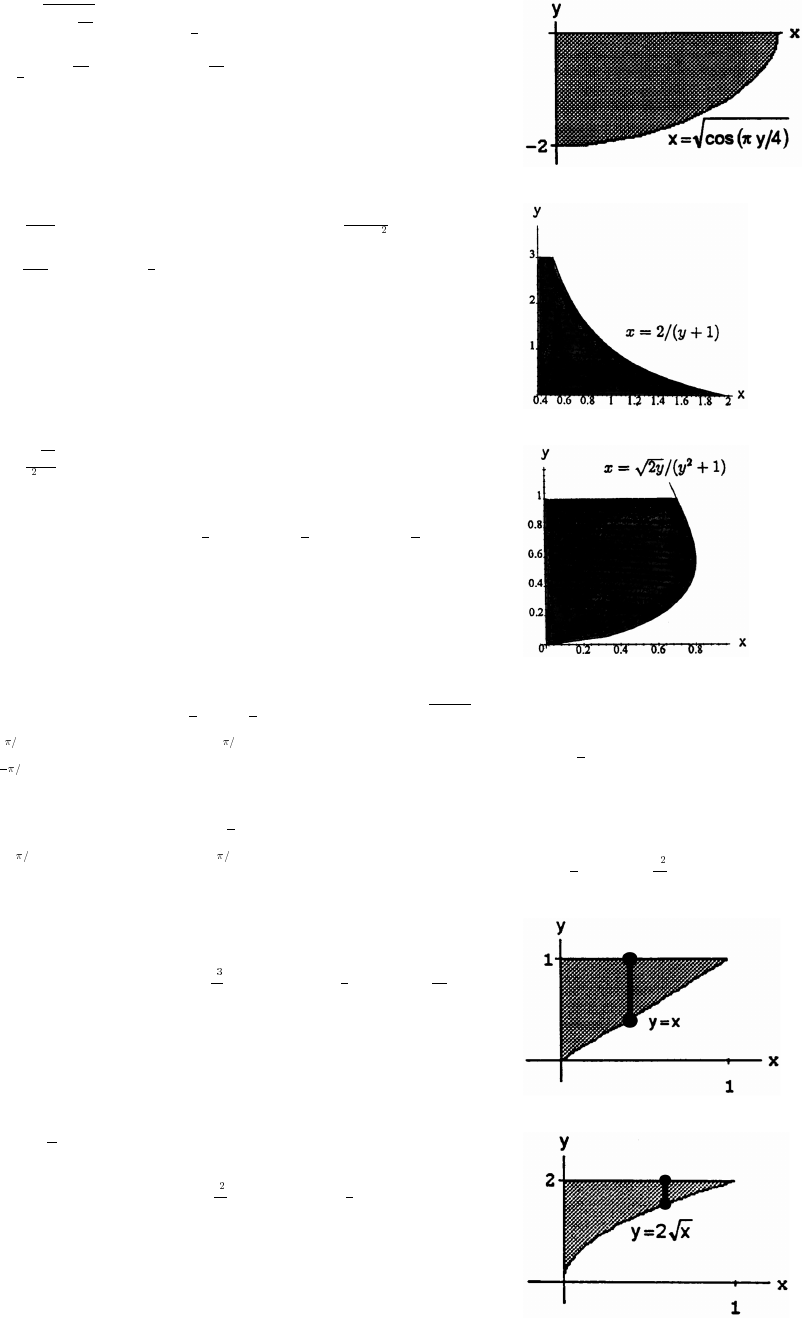
Section 6.1 Volumes by Slicing and Rotation About an Axis 365
28. R(y) cos V [R(y)] dyœÊœ
É1y
4'2
0
1#
cos dy 4 sin 4[0 ( 1)] 4œœœœ1'2
0ˆ‰ ‘
11yy
44
!
#
29. R(y) V [R(y)] dy 4 dyœÊœ œ
2
y1 (y1)
#"
''
00
33
11
44(1)3œœœ11 1
’“ ‘
" "
$
!
y1 4
30. R(y) V [R(y)] dy 2y y 1 dy;œÊœ œ
È2y
y1
##
#
''
00
11
11ab
u y 1 du 2y dy; y 0 u 1, y 1 u 2cdœÊ œ œÊœ œÊœ
#
V u du ( 1)Äœ œ œœ111
'1
2# ""
#
"##
‘ ‘
u
1
31. For the sketch given, a , b ; R(x) 1, r(x) cos x; V [R(x)] [r(x)] dxœ œ œ œ œ
11
##
##
Èab
'a
b
1
(1 cos x) dx 2 (1 cos x) dx 2 [x sin x] 2 1 2œœ œœœ
''
20
22
11 1111
11
Î#
!#
#
ˆ‰
32. For the sketch given, c 0, d ; R(y) 1, r(y) tan y; V [R(y)] [r(y)] dyœœ œ œ œ
1
4'c
d
1ab
##
1 tan y dy 2 sec y dy [2y tan y] 1œ œ œ œœ11 111
''
00
44
ab ab ˆ‰
##
Î%
!##
111
33. r(x) x and R(x) 1 V [R(x)] [r(x)] dxœœÊœ
'0
1
1ab
##
1 x dx x 1 0œœœœ
'0
1
111ab ’“‘ˆ‰
#"
!
"x2
333
1
34. r(x) 2 x and R(x) 2 V [R(x)] [r(x)] dxœœÊœ
Èab
'0
1
1##
(4 4x) dx 4 x 4 1 2œœœœ1111
'0
1’“ ˆ‰
x
##
"
!
"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
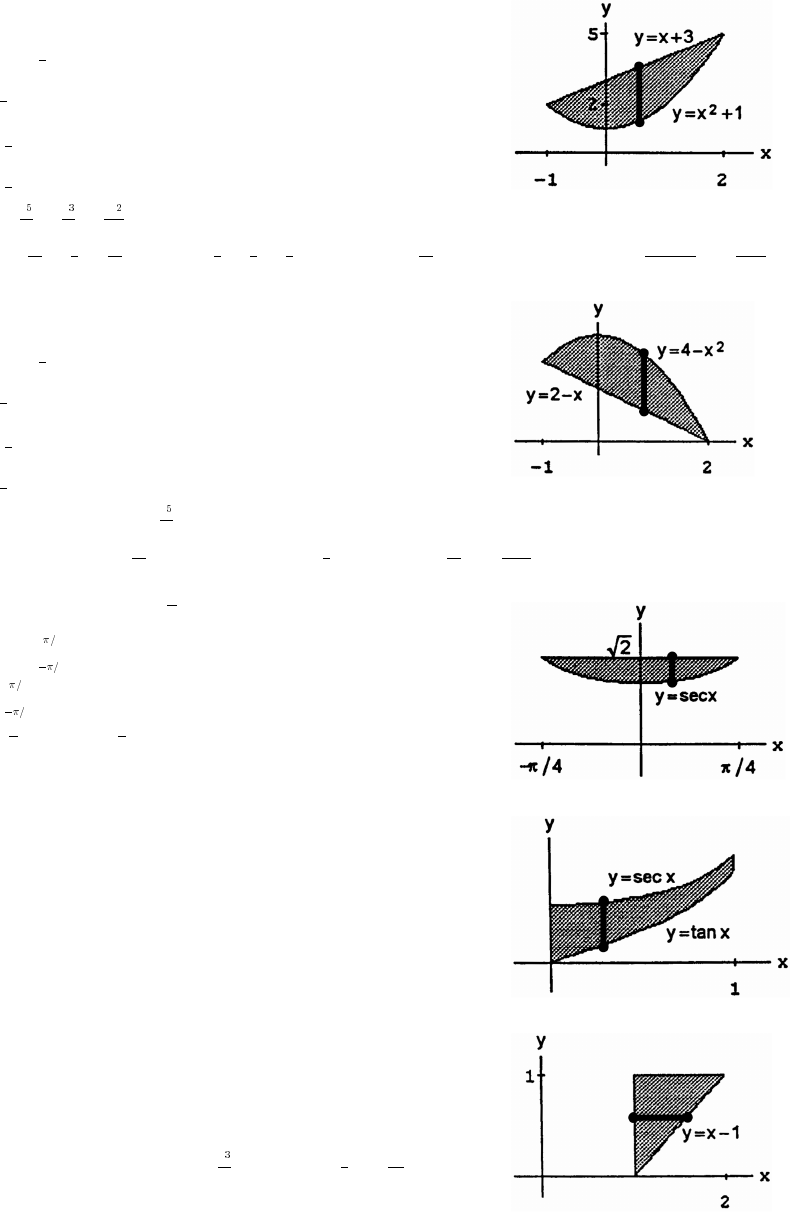
366 Chapter 6 Applications of Definite Integrals
35. r(x) x 1 and R(x) x 3œ œ
#
V [R(x)] [r(x)] dxʜ
'1
2
1ab
##
(x 3) x 1 dxœ1'1
2’“
ab
###
x6x9 x2x1 dxœ1'1
2cdaba b
#%#
xx6x8 dxœ1'1
2ab
%#
8xœ 1’“
xx6x
53 #
#
"
16 8 3 28 3 8œ œ œ œ111
‘ˆ‰ˆ‰ˆ‰ˆ‰
32 8 24 6 33 5 30 33 117
53 53 5 5 5##
"" †1
36. r(x) 2 x and R(x) 4 xœ œ
#
V [R(x)] [r(x)] dxʜ
'1
2
1ab
##
4 x (2 x) dxœ1'1
2’“
ab
##
#
16 8x x 4 4x x dxœ1'1
2cdabab
#% #
12 4x 9x x dxœ1'1
2ab
#%
12x 2x 3xœ 1’“
#$ #
"
x
5
24824 1223 15œ œ œ11
‘ˆ‰ˆ‰ˆ‰
32 33 108
5555
"1
37. r(x) sec x and R(x) 2œœ
È
V [R(x)] [r(x)] dxʜ
'4
4
1ab
##
2 sec x dx [2x tan x]œ œ11
'4
4ab
#Î%
Î%
1
1
11(2)œœ111
‘ˆ‰ˆ ‰
11
##
38. R(x) sec x and r(x) tan xœœ
V [R(x)] [r(x)] dxʜ
'0
1
1ab
##
sec x tan x dx 1 dx [x]œœœœ1111
''
00
11
ab
## "
!
39. r(y) 1 and R(y) 1 yœœ
V [R(y)] [r(y)] dyʜ
'0
1
1ab
##
(1 y) 1 dy 1 2y y 1 dyœœ11
''
00
11
cda b
##
2y y dy y 1œœœœ111
'0
1ab’“
ˆ‰
##
"
!
"
y
333
41
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
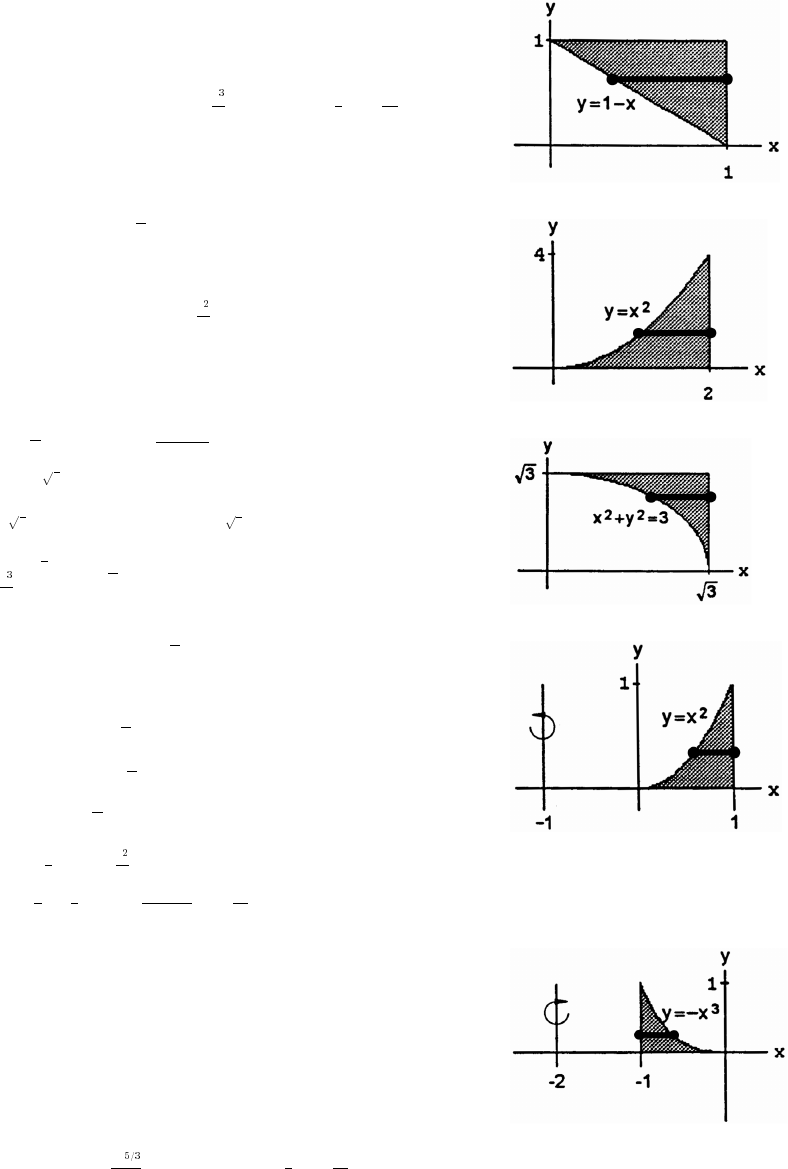
Section 6.1 Volumes by Slicing and Rotation About an Axis 367
40. R(y) 1 and r(y) 1 y V [R(y)] [r(y)] dyœœÊœ
'0
1
1ab
##
1 (1 y) dy 1 1 2y y dyœœ11
''
00
11
cdc dab
##
2y y dy y 1œœœœ111
'0
1ab’“
ˆ‰
##
"
!
"
y
333
21
41. R(y) 2 and r(y) yœœ
È
V [R(y)] [r(y)] dyʜ
'0
4
1ab
##
(4 y) dy 4y (16 8) 8œœœœ1111
'0
4’“
y
2
%
!
42. R(y) 3 and r(y) 3 yœœ
ÈÈ#
V [R(y)] [r(y)] dyʜ
'0
3
1ab
##
3 3 y dy y dyœœ11
''
00
33
cdab
##
3œœ11
’“ È
y
3
È$
!
43. R(y) 2 and r(y) 1 yœœ
È
V [R(y)] [r(y)] dyʜ
'0
1
1ab
##
41 y dyœ1'0
1’“
ˆ‰
È#
412yy dyœ1'0
1ˆ‰
È
32yy dyœ1'0
1ˆ‰
È
3y yœ1’“
4
3
y
$Î#
#
"
!
3œœ œ11
ˆ‰ˆ‰
418837
366
"
#
1
44. R(y) 2 y and r(y) 1œ œ
"Î$
V [R(y)] [r(y)] dyʜ
'0
1
1ab
##
2y 1 dyœ1'0
1’“
ˆ‰
"Î$ #
44yy1 dyœ1'0
1ˆ‰
"Î$ #Î$
3 4y y dyœ1'0
1ˆ‰
"Î$ #Î$
3y 3y 3 3œ œœ11
’“
ˆ‰
%Î$ "
!
3y
555
33
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
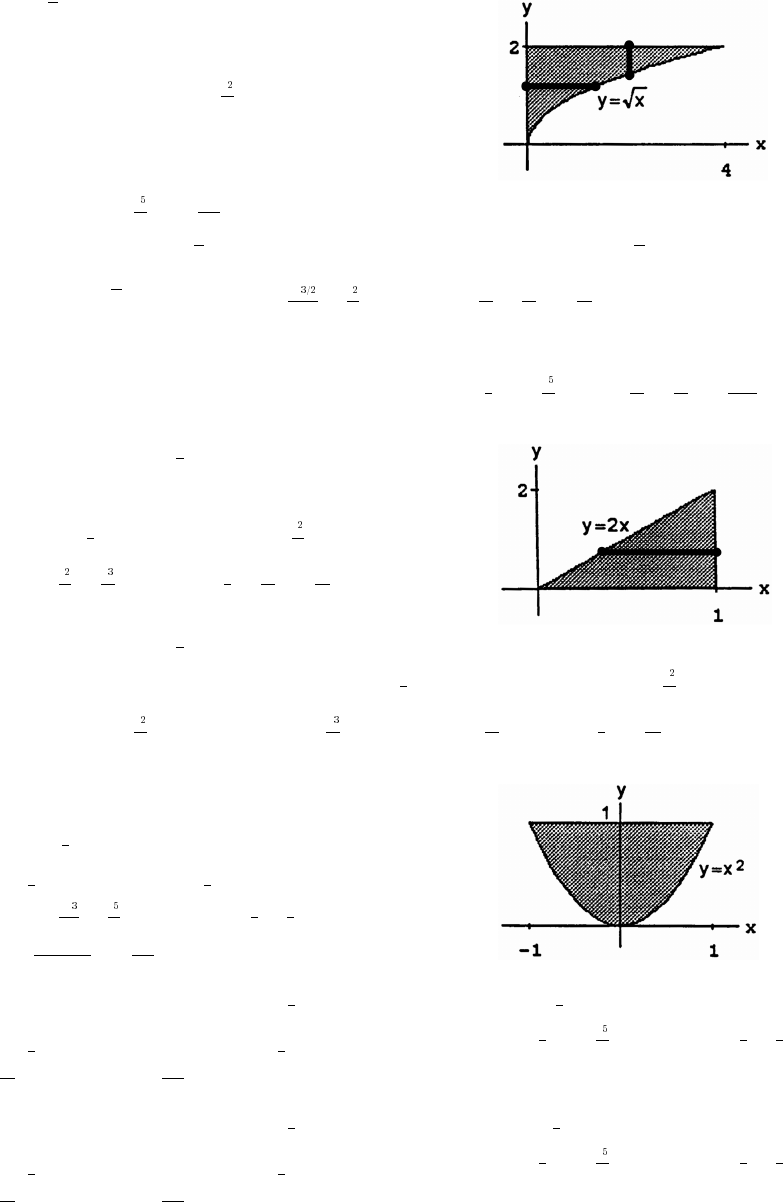
368 Chapter 6 Applications of Definite Integrals
45. (a) r(x) x and R(x) 2œœ
È
V [R(x)] [r(x)] dxʜ
'0
4
1ab
##
(4 x) dx 4x (16 8) 8œœœœ1111
'0
4’“
x
#
%
!
(b) r(y) 0 and R(y) yœœ
#
V [R(y)] [r(y)] dyʜ
'0
2
1ab
##
y dyœœœ11
'0
2%#
!
’“
y
55
321
(c) r(x) 0 and R(x) 2 x V [R(x)] [r(x)] dx 2 x dxœœÊœ œ
ÈÈ
ab
ˆ‰
''
00
44
11
## #
4 4 x x dx 4x 16œ œœœ111
'0
4ˆ‰ ˆ‰
È’“
8x x 64 16 8
333
##
%
!
1
(d) r(y) 4 y and R(y) 4 V [R(y)] [r(y)] dy 16 4 y dyœ œ Ê œ œ
####
#
''
00
22
11ab ab
’“
16 16 8y y dy 8y y dy yœœ œœœ1111
''
00
22
abab
’“
ˆ‰
#% #% $ #
!
8 64 32 224
35 3515
y1
46. (a) r(y) 0 and R(y) 1œœ
y
#
V [R(y)] [r(y)] dyʜ
'0
2
1ab
##
1 dy 1 y dyœœ 11
''
00
22
ˆ‰ Š‹
yy
4#
#
yœ œ#œ11
’“
ˆ‰
yy
12 2 12 3
48 2
#
#
!
1
(b) r(y) 1 and R(y) 2œœ
y
#
V [R(y)] [r(y)] dy 2 1 dy 4 2y 1 dyÊœ œ œ
'''
000
222
11 1ab
’“Š ‹
ˆ‰
##
#
#
yy
4
3 2y dy 3y y 6 4 2œœœœœ1111
'0
2Š‹’ “
ˆ‰ˆ‰
yy
4121233
828
##
!
1
47. (a) r(x) 0 and R(x) 1 xœœ
#
V [R(x)] [r(x)] dxʜ
'1
1
1ab
##
1 x dx 1 2x x dxœœ11
''
11
11
ab a b
##%
#
x21œ œ 11
’“
ˆ‰
2x x 2 1
35 35
"
"
2œœ1ˆ‰
15 10 3 16
15 15
1
(b) r(x) 1 and R(x) 2 x V [R(x)] [r(x)] dx 2 x 1 dxœœÊœ œ
####
#
''
11
11
11abab
’“
4 4x x 1 dx 3 4x x dx 3x x 2 3œœœœ1111
''
11
11
abab
’“
ˆ‰
#% #% $ "
"
4x 41
35 35
(45203)œœ
256
15 15
11
(c) r(x) 1 x and R(x) 2 V [R(x)] [r(x)] dx 4 1 x dxœ œ Ê œ œ
####
#
''
11
11
11ab ab
’“
4 1 2x x dx 3 2x x dx 3x x 2 3œœœœ1111
''
11
11
abab
’“
ˆ‰
#% #% $ "
"
2x 21
35 35
(45103)œœ
264
15 15
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
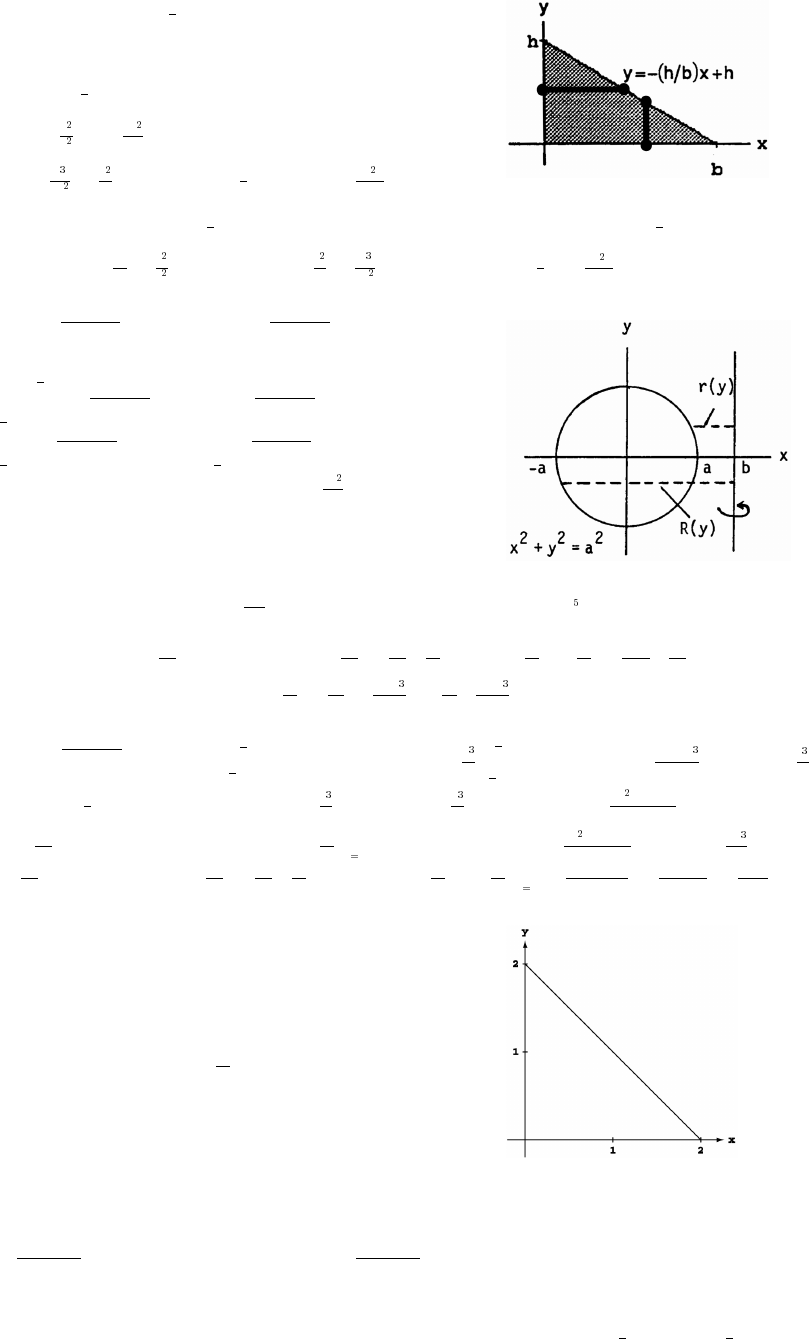
Section 6.1 Volumes by Slicing and Rotation About an Axis 369
48. (a) r(x) 0 and R(x) x hœœ
h
b
V [R(x)] [r(x)] dxʜ
'0
b
1ab
##
x h dxœ1'0
bˆ‰
h
b
#
xxh dxœ1'0
bŠ‹
h2h
bb
##
hxhbbœœœ11
##
!
’“
ˆ‰
xx b hb
3b b 3 3
b
1
(b) r(y) 0 and R(y) b 1 V [R(y)] [r(y)] dy b 1 dyœœÊœ œ
ˆ‰ ˆ‰
ab
yy
hh
''
00
hh
11
## # #
b 1 dy b y b h hœœœœ111
###
!
'0
hh
Š‹’ “
ˆ‰
2y y y y
hh h3h 3 3
hbh
1
49. R(y) b a y and r(y) b a yœ œ
ÈÈ
## ##
V [R(y)] [r(y)] dyʜ
'a
a
1ab
##
b a y b a y dyœ1'a
a’“
ˆ‰ˆ‰
ÈÈ
## ##
##
4b a y dy 4b a y dyœœ11
''
aa
aa
ÈÈ
## ##
4b area of semicircle of radius a 4b 2a bœœœ111††
1a
#
##
50. (a) A cross section has radius r y and area r y. The volume is ydy y .œ # œ# # œ œ#&
Ècd11 1 1 1
##
&
!
'0
(b) V h A h dh, so A h . Therefore A h , so .ab ab ab abœœ œ†œ†œ†
'dV dV dV dh dh dh dV
dh dt dh dt dt dt A h dt
"
ab
For h , the area is , so .œ% # % œ) œ †$ œ †11ab dh units units
dt sec sec
"$
))11
51. (a) R(y) a y V a y dy a y a h a aœÊœ œ œ
Èab ’“’ “Š‹
## ## # # $ $
111
'a
ha ha
a
y(ha)
333
a
a h h 3h a 3ha a a h h a haœ œ œ11
’“Š‹
ab
#$##$ # ##
"
3333
ah h (3a h)
1
(b) Given 0.2 m /sec and a 5 m, find . From part (a), V(h) 5 h
dV dh h
dt dt 3 3
h (15 h)
œœ œœ
$ #
¸h4
11
1
10 h h h(10 h) m/sec.Êœ Êœ œ Ê œ œ œ
dV dV dV dh dh dh 0.2
dh dt dh dt dt dt 4 (10 4) (20 )(6) 1 0
11 1
#
#
""
†¸h4 111
52. Suppose the solid is produced by revolving y 2 x aboutœ
the y-axis. Cast a shadow of the solid on a plane parallel to
the xy-plane.
Use an approximation such as the Trapezoid Rule, to
estimate R y dy y.
'a
b
11cdab !Œ
#
œ"
#
¸˜
k
ndk
^
#
53. The cross section of a solid right circular cylinder with a cone removed is a disk with radius R from which a disk of radius
h has been removed. Thus its area is A R h R h . The cross section of the hemisphere is a disk of
"## ##
œœ 111ab
radius R h . Therefore its area is A R h R h . We can see that A A . The altitudes of
ÈÈ
Š‹
ab
## ##
#"#
###
œœœ11
both solids are R. Applying Cavalieri's Principle we find
Volume of Hemisphere (Volume of Cylinder) (Volume of Cone) R R R R R .œœœab ab11 1
##$
"
33
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
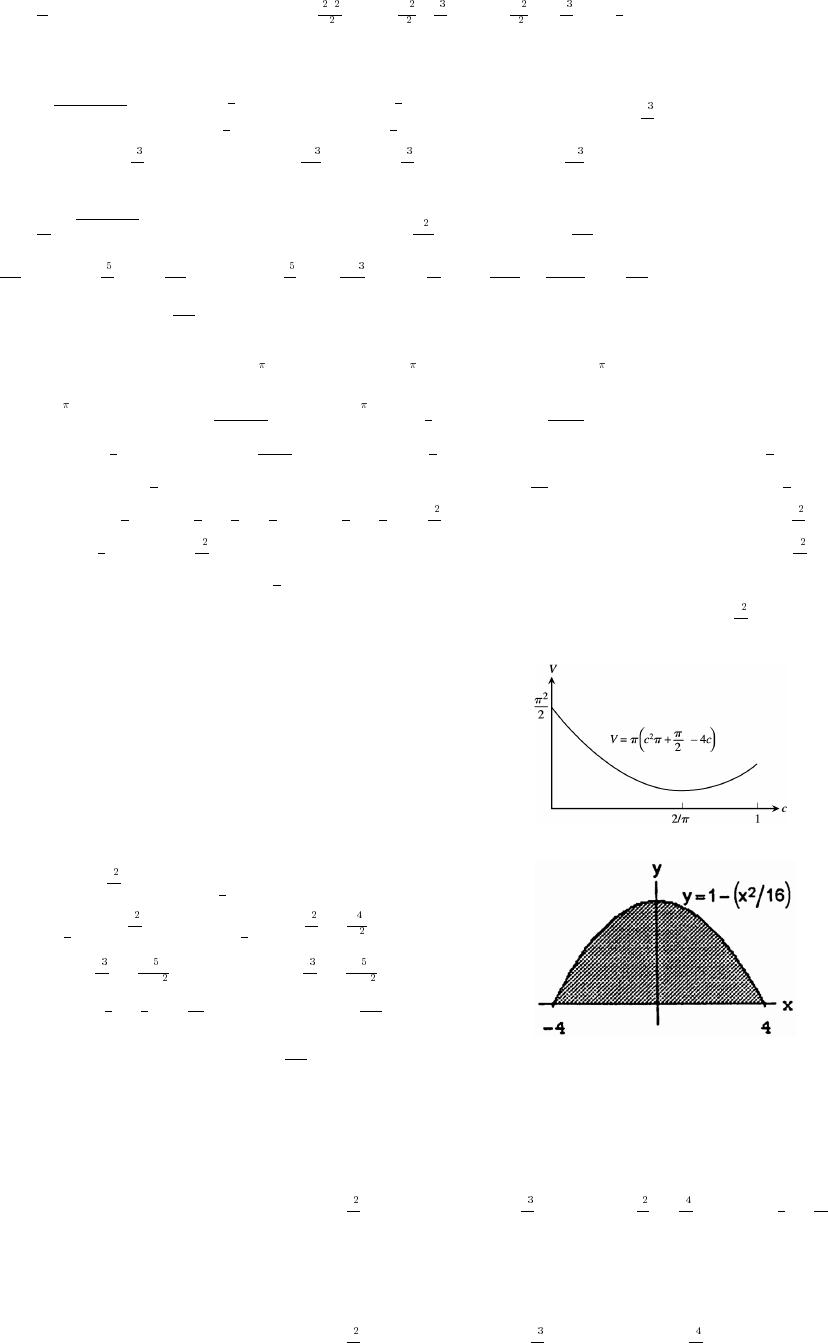
370 Chapter 6 Applications of Definite Integrals
54. R(x) V [R(x)] dx dx r h, the volume ofœÊœ œ œ œ œ
rx r x r x r h
hhh3h33
''
00
hh
h
11 1
##
!
"
11
’“ Š‹Š‹
a cone of radius r and height h.
55. R(y) 256 y V [R(y)] dy 256 y dy 256yœÊœ œ œ
Èab’“
### (
"'
''
16 16
77
11 1
y
3
(256)( 7) (256)( 16) 256(16 7) 1053 cm 3308 cmœœœ ¸111
’“Š‹Š‹
716716
3333
$$
56. R(x) 36 x V [R(x)] dx 36 x dx 36x x dxœÊœ œ œ
xx
1 144 144#####%
Èab a b
'' '
00 0
66 6
11 1
12x 12 6 12 cm . The plumb bob willœœ œœ œ
11 1 11
144 5 144 5 144 5 144 5 5
x 6 6 36 196 60 36 36
’“Š ‹
ˆ‰ˆ‰ˆ‰
$$ $
'
!
†
†
weigh about W (8.5) 192 gm, to the nearest gram.œ¸
ˆ‰
36
5
1
57. (a) R(x) c sin x , so V [R(x)] dx (c sin x) dx c 2c sin x sin x dxœ œ œ œ kk a b11 1
'' '
00 0
####
c 2c sin x dx c 2c sin x dxœ œ11
''
00
ˆ‰ˆ ‰
##
"
###
1 cos 2x cos 2x
c x 2c cos x c 2c 0 (0 2c 0) c 4c . Letœ œ œ 11111
‘ ‘ˆ‰ˆ‰ ˆ ‰
## #
"
## #
!
sin 2x
4
111
V(c) c 4c . We find the extreme values of V(c): (2c 4) 0 c is a criticalœ œœÊœ11 11
ˆ‰
#
#
1
1
dV 2
dc
point, and V 4; Evaluate V at the endpoints: V(0) and
ˆ‰ ˆ ‰ ˆ ‰
248 4
11 1 1
111 1
œ œ œ œ11
### #
V(1) 4 (4 ) . Now we see that the function's absolute minimum value is 4,œœ 11 11
ˆ‰
3
## #
1 1
taken on at the critical point c . (See also the accompanying graph.)œ2
1
(b) From the discussion in part (a) we conclude that the function's absolute maximum value is , taken on at
1
#
the endpoint c 0.œ
(c) The graph of the solid's volume as a function of c for
0 c 1 is given at the right. As c moves away fromŸŸ
[ ] the volume of the solid increases without bound.!ß "
If we approximate the solid as a set of solid disks, we
can see that the radius of a typical disk increases without
bounds as c moves away from [0 1].ß
58. (a) R(x) 1 V [R(x)] dxœ Ê œ
x
16 '4
4
1#
1 dx 1 dxœœ11
''
44
44
Š‹ Š ‹
xxx
16 8 16
#
x24œ œ 11
’“Š‹
xx 44
24 5 16 24 5 16
††
%
%
2 4 (60 40 12) ftœœ œ1ˆ‰
84 2 64
3 5 15 15
11
$
(b) The helicopter will be able to fly (7.481)(2) 201 additional miles.
ˆ‰
64
15
1¸
6.2 VOLUME BY CYLINDRICAL SHELLS
1. For the sketch given, a 0, b 2;œœ
V 2 dx 2 x 1 dx 2 x dx 2 2œ œ œ œœ
'''
a00
b22
11111
ˆ‰ ˆ‰
Š‹ Š‹ Š‹ ’ “
shell shell
radius height 4 4 16 16
xxxx416
##
#
!
236œœ11†
2. For the sketch given, a 0, b 2;œœ
V 2 dx 2 x 2 dx 2 2x dx 2 x 2 (4 1) 6œ œ œ œœœ
'''
a00
b22
111111
ˆ‰
Š‹ Š ‹ Š ‹ ’ “
shell shell
radius height 4 4 16
xxx
##
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
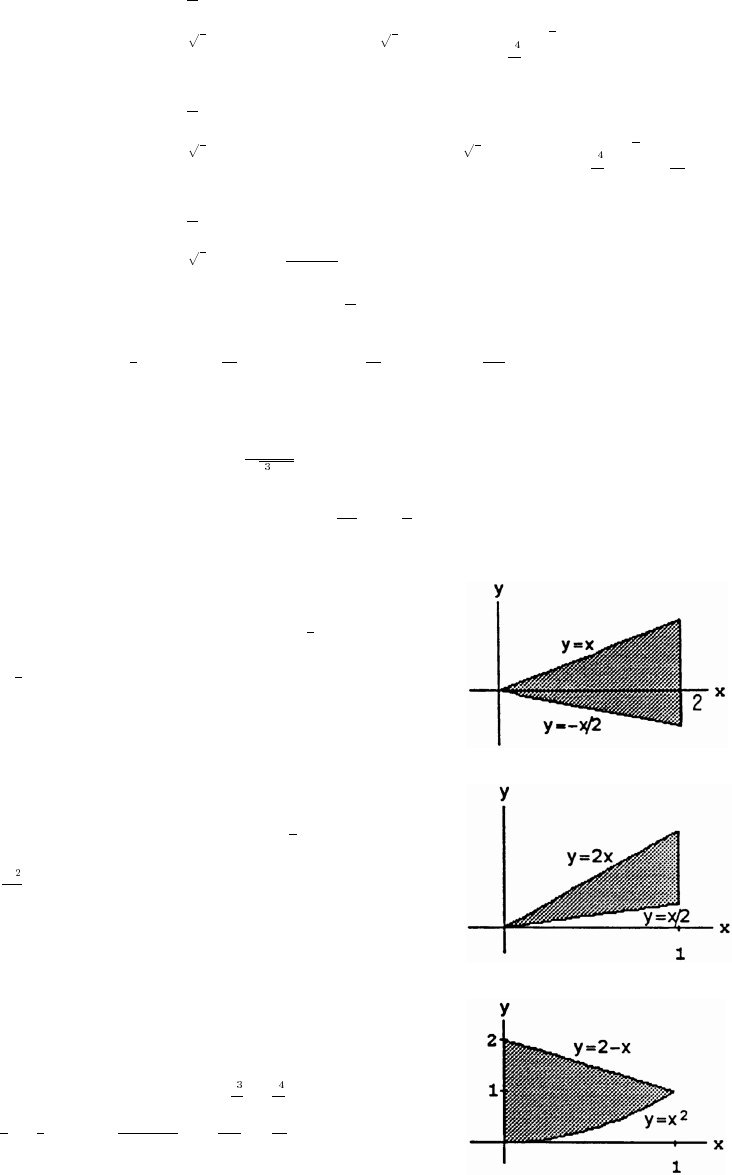
Section 6.2 Volume by Cylindrical Shells 371
3. For the sketch given, c 0, d 2;œœ
È
V 2 dy 2 y y dy 2 y dy 2 2œœœœœ
'''
c00
d22
11111
ˆ‰
Š‹ ’“
ab
shell shell
radius height 4
y
†#$#
!
È
4. For the sketch given, c 0, d 3;œœ
È
V 2 dy 2 y 3 3 y dy 2 y dy 2œœœœœ
'' '
c0 0
d3 3
1111
ˆ‰
Š‹ ’“
cdab
shell shell
radius height 4
y39
†#$
!#
È1
5. For the sketch given, a 0, b 3;œœ
È
V 2 dx 2 x x 1 dx;œœ
''
a0
b3
11
ˆ‰
Š‹ Š ‹
È
shell shell
radius height †#
u x 1 du 2x dx; x 0 u 1, x 3 u 4
’“
È
œÊ œ œÊœ œ Êœ
#
V u du u 4 1 (8 1)Äœ œ œ œ œ11
'1
4"Î# $Î# $Î#
%
"
‘ ˆ ‰ˆ‰
22 2 14
33 3 3
111
6. For the sketch given, a 0, b 3;œœ
V 2 dx 2 x dx;œœ
''
a0
b3
11
ˆ‰
Š‹ Š ‹
shell shell
radius height
9x
x9
È
u x 9 du 3x dx 3 du 9x dx; x 0 u 9, x 3 u 36c dœÊ œ Ê œ œÊœ œÊœ
$# #
V 2 3u du 6 2u 12 36 9 36Äœ œ œ œ111 1
'9
36 "Î# "Î# $'
*
‘ Š‹
ÈÈ
7. a 0, b 2;œœ
V 2 dx 2 x x dxœœ
''
a0
b2
11
ˆ‰ ‘
Š‹ ˆ‰
shell shell
radius height 2
x
2 x dx 3x dx x 8œœœœ
''
00
22
11 11
##$
#
#
!
†3cd
8. a 0, b 1;œœ
V 2 dx 2 x 2x dxœœ
''
a0
b1
11
ˆ‰ ˆ ‰
Š‹
shell shell
radius height 2
x
2 dx 3x dx xœœœœ1111
'0
11
0
Š‹ 'cd
3x
#
#$
"
!
9. a 0, b 1;œœ
V 2 dx 2 x (2 x) x dxœœ
''
a0
b1
11
ˆ‰
Š‹ cd
shell shell
radius height #
2 2xx x dx 2xœœ11
'0
1ab
’“
#$ # "
!
xx
34
21 2œœ œœ11
ˆ‰ˆ‰
""
3 4 12 12 6
1243 10 511
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
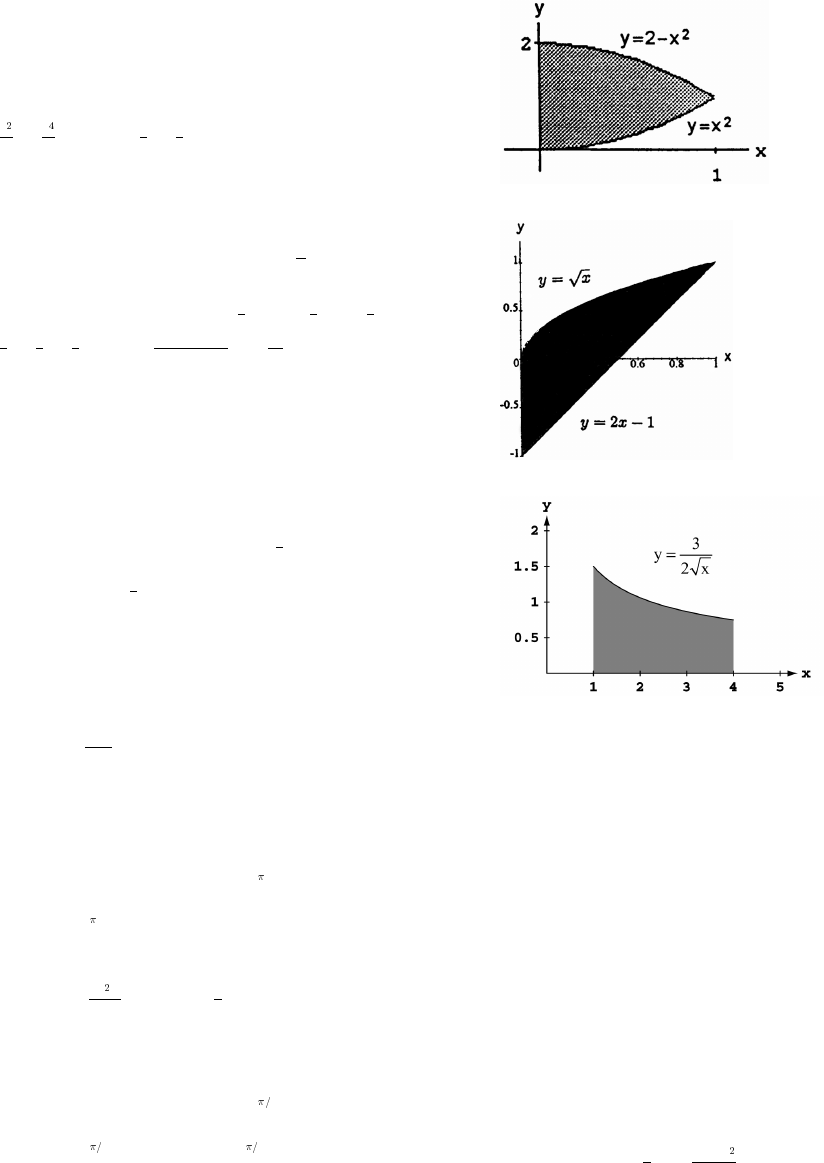
372 Chapter 6 Applications of Definite Integrals
10. a 0, b 1;œœ
V 2 dx 2 x 2 x x dxœœ
''
a0
b1
11
ˆ‰
Š‹ cdab
shell shell
radius height ##
2 x2 2x dx 4 x x dxœœ11
''
00
11
ab ab
#$
44œœœ111
’“ˆ‰
xx
424
#
"
!
""
11. a 0, b 1;œœ
V 2 dx 2 x x (2x 1) dxœœ
''
a0
b1
11
ˆ‰ ‘
Š‹ È
shell shell
radius height
2 x 2x x dx 2 x x xœœ11
'0
1ˆ‰ ‘
$Î# # &Î# $ #
"
#
"
!
22
53
22œœ œ11
ˆ‰ˆ‰
2 2 12 20 15 7
5 3 30 15
"
#
1
12. a , b 4;œ" œ
V 2 dx 2 x x dxœœ
''
a1
b4
11
ˆ‰ ˆ ‰
Š‹
shell shell
radius height 2
3"Î#
3 x dx 3 x 2 4œœœ"111
'1
4"Î# $Î# $Î#
%
"
‘ ˆ ‰
2
3
2(8 1) 14œœ11
13. (a) xf(x) xf(x) ; since sin 0 0 we have
x, 0x
x, x 0
sin x, 0 x
0, x 0
œÊœ œ
Ÿ
œ
Ÿ
œ
œœ
†sin x
x11
xf(x) xf(x) sin x, 0 x
sin x, 0 x
sin x, x 0
œÊœŸŸ
Ÿ
œ
œ1
1
(b) V 2 dx 2 x f(x) dx and x f(x) sin x, 0 x by part (a)œœ œŸŸ
''
a0
b
11 1
ˆ‰
Š‹
shell shell
radius height ††
V 2 sin x dx 2 [ cos x] 2 ( cos cos 0) 4Êœ œ œ œ11111
'0
1
!
14. (a) xg(x) xg(x) ; since tan 0 0 we have
x, 0x
x 0, x 0
tan x, 0 x /4
0, x 0
œÊœ œ
Ÿ
œ
Ÿ
œ
œœ
†
†
tan x
x4
1#1
xg(x) xg(x) tan x, 0 x /4
tan x, 0 x /4
tan x, x 0
œÊœŸŸ
Ÿ
œ
œ#
##
1
1
(b) V 2 dx 2 x g(x) dx and x g(x) tan x, 0 x /4 by part (a)œœ œŸŸ
''
a0
b4
11 1
ˆ‰
Š‹
shell shell
radius height ††
#
V 2 tan x dx 2 sec x 1 dx 2 [tan x x] 2 1Êœ œ œ œ œ11 1 1
''
00
44
## Î%
!
#
ab ˆ‰
1111
4
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
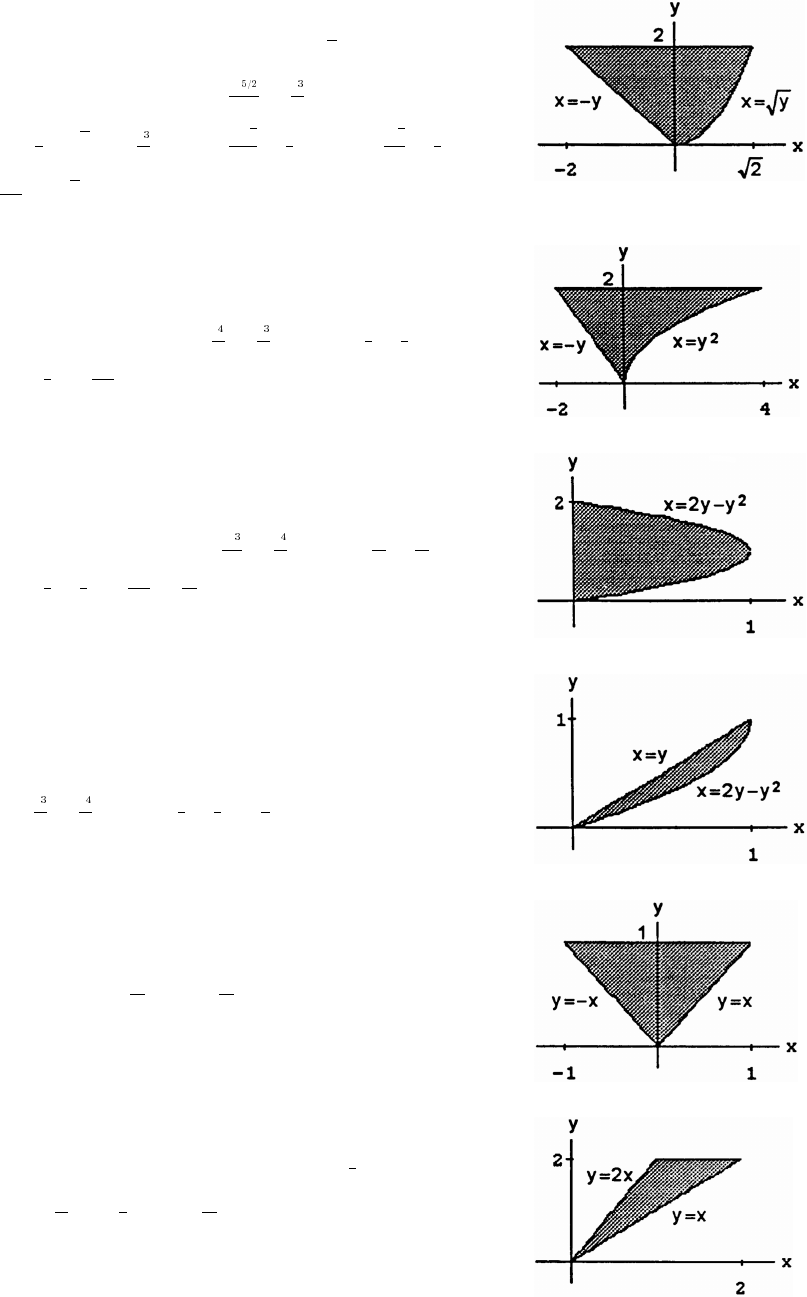
Section 6.2 Volume by Cylindrical Shells 373
15. c 0, d 2;œœ
V 2 dy 2 y y ( y) dyœœ
''
c0
d2
11
ˆ‰ ‘
Š‹ È
shell shell
radius height
2 y y dy 2œœ11
'0
2ˆ‰’“
$Î# # #
!
2y y
53
22 2 16œœœ111
”•
Š‹ Š ‹ Š ‹
È
22 8
535353
82 2
&"
ÈÈ
32 5œ
16
15
1Š‹
È
16. c 0, d 2;œœ
V 2 dy 2 y y ( y) dyœœ
''
c0
d2
11
ˆ‰
Š‹ cd
shell shell
radius height #
2 y y dy 2 16œœœ111
'0
2ab ’“ ˆ‰
$# #
!
"
yy
43 43
2
16œœ1ˆ‰
540
63
1
17. c 0, d 2;œœ
V 2 dy 2 y 2y y dyœœ
''
c0
d2
11
ˆ‰
Š‹ ab
shell shell
radius height #
2 2y y dy 2 2œœœ111
'0
2ab’“
ˆ‰
#$ #
!
"
2y y
34 34
16 6
32œœœ1ˆ‰
""
34 12 3
32 811
18. c 0, d 1;œœ
V 2 dy 2 y 2y y y dyœœ
''
c0
d1
11
ˆ‰
Š‹ ab
shell shell
radius height #
2 y y y dy 2 y y dyœœ11
''
00
11
ab a b
##$
22œœœ11
’“ˆ‰
yy
34 34 6
1
"
!
"1
19. c 0, d 1;œœ
V 2 dy 2 y[y ( y)]dyœœ
''
c0
d1
11
ˆ‰
Š‹
shell shell
radius height
2 2y dy yœœœ1'0
1#$
"
!
44
33
11
cd
20. c 0, d 2;œœ
V 2 dy 2 y y dyœœ
''
c0
d2
11
ˆ‰ ˆ‰
Š‹
shell shell
radius height 2
y
2 dy yœœœ1'0
2y
23 3
318
211
cd
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
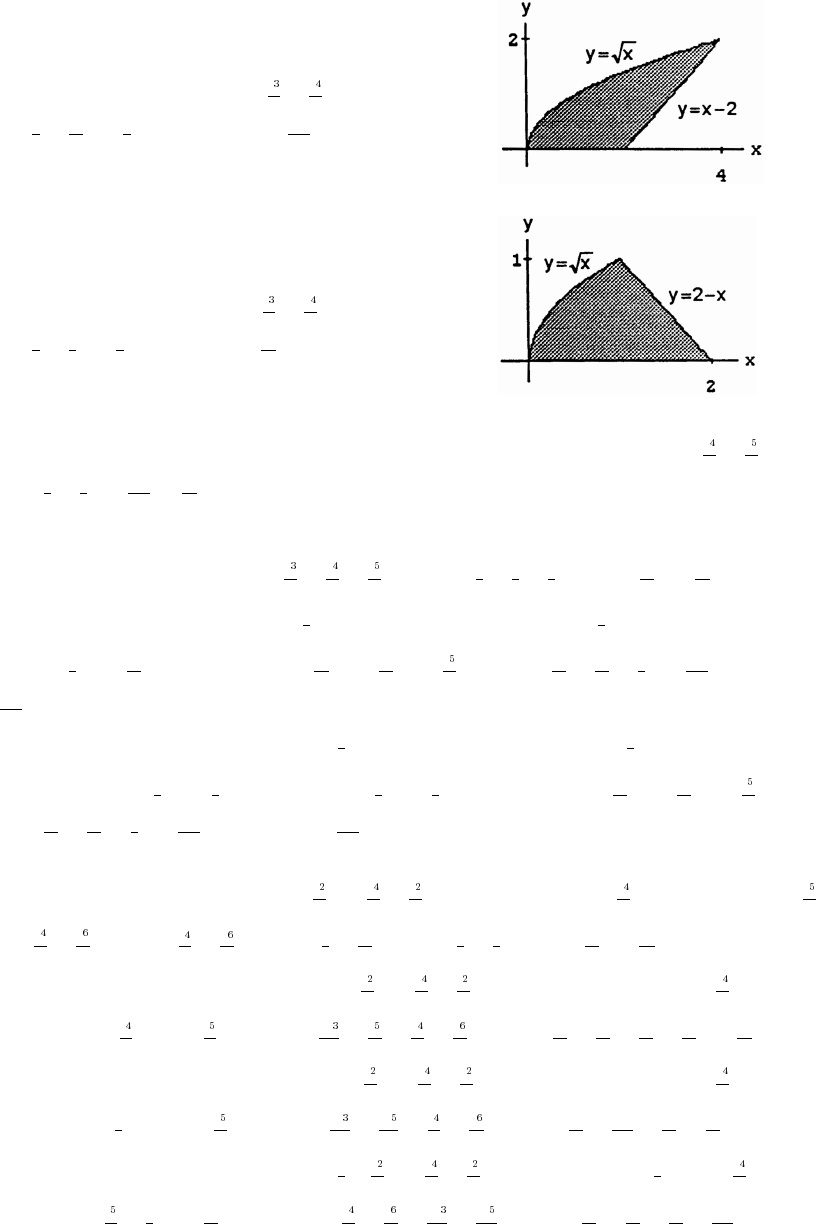
374 Chapter 6 Applications of Definite Integrals
21. c 0, d 2;œœ
V 2 dy 2 y (2 y) y dyœœ
''
c0
d2
11
ˆ‰
Š‹ cd
shell shell
radius height #
2 2y y y dy 2 yœœ11
'0
2ab
’“
#$ # #
!
yy
34
24 (483248)œœœ1ˆ‰
816 16
34 6 3
11
22. c 0, d 1;œœ
V 2 dy 2 y (2 y) y dyœœ
''
c0
d1
11
ˆ‰
Š‹ cd
shell shell
radius height #
2 2yy y dy 2yœœ11
'0
1ab
’“
#$ # "
!
yy
34
21 (1243)œœœ1ˆ‰
11 5
34 6 6
11
23. (a) V 2 dy 2 y 12 y y dy 24 y y dy 24œ œ œ œ
'' '
c0 0
d1 1
1111
ˆ‰
Š‹ ’ “
ab ab
shell shell
radius height 45
yy
†#$ $% "
!
24œœœ1ˆ‰
11 24 6
45 20 5
11
(b) V 2 dy 2 (1 y) 12 y y dy 24 (1 y) y y dyœœœ
'' '
c0 0
d1 1
11 1
ˆ‰
Š‹ cd abab
shell shell
radius height #$ #$
24 y 2y y dy 24 24 24œœœœœ1111
'0
1ab
’“
ˆ‰ˆ‰
#$% "
!
""
yyy
325 325 30 5
11 4
1
(c) V 2 dy 2 y 12 y y dy 24 y y y dyœœœ
'' '
c0 0
d1 1
11 1
ˆ‰ ˆ‰ ˆ‰
Š‹ cd abab
shell shell
radius height 5 5
88
#$ #$
24 y y y dy 24 y y 24 (32 39 12)œœœœ111
'0
1ˆ‰ ˆ‰
’“
8 13 8 13 8 13 1 24
5 5 15 20 5 15 20 5 60
y
#$% $%
"
!
1
2œœ
24
12
11
(d) V 2 dy 2 y 12 y y dy 24 y y y dyœœœ
'' '
c0 0
d1 1
11 1
ˆ‰ ˆ‰ ˆ‰
Š‹ cd abab
shell shell
radius height 5 5
22
#$ #$
24 y y y y dy 24 y y y dy 24 y yœœ œ111
''
00
11
ˆ‰ˆ‰
’“
$%#$ #$% $ % "
!
22 23 2 3
55 55 1520 5
y
24 (8 9 12) 2œœœœ11
ˆ‰
231 24 24
15 20 5 60 12
11
24. (a) V 2 dy 2 y dy 2 y y dy 2 y dyœœœœ
'' ''
c0 00
d2 22
11 11
ˆ‰
Š‹ ’ “ Š‹ Š‹Š‹
shell shell
radius height 4 4 4
yyy y y
##
#$
2 2 32 32 32œœœœœ œ11 111
’“Š‹ˆ‰ˆ‰ˆ‰
yy
424 424 42446243
22 4 2 8
#
!
""" 1
(b) V 2 dy 2 (2 y) dy 2 (2 y) y dyœœœ
'' '
c0 0
d2 2
11 1
ˆ‰
Š‹ ’ “ Š ‹Š‹
shell shell
radius height 4 4
yyy y
##
#
2 2y y dy 2 2œ œ œ œ111
'0
2Š‹’“
ˆ‰
#$
#
#
!
y y 2yyyy
2 4 3 104 4 310424 5
16 32 16 64 81
(c) V 2 dy 2 (5 y) dy 2 (5 y) y dyœœœ
'' '
c0 0
d2 2
11 1
ˆ‰
Š‹ ’ “ Š ‹Š‹
shell shell
radius height 4 4
yyy y
##
#
2 5y y y dy 2 2 8œœœœ1111
'0
2Š‹’“
ˆ‰
#%$
#
#
!
540 160 16 64
44 32044320424
y 5y5yyy
(d) V 2 dy 2 y dy 2 y y dyœœœ
'' '
c0 0
d2 2
11 1
ˆ‰ ˆ‰ ˆ‰
Š‹ ’ “ Š ‹Š‹
shell shell
radius height 8 4 8 4
55
yyy y
##
#
2 y y y dy 2 2 4œœœœ1111
'0
2Š‹’“
ˆ‰
$#%
##
#
!
y yy5y5y
4 8 32 4 4 4 160 4 24 24 160
5 5 16 64 40 160
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
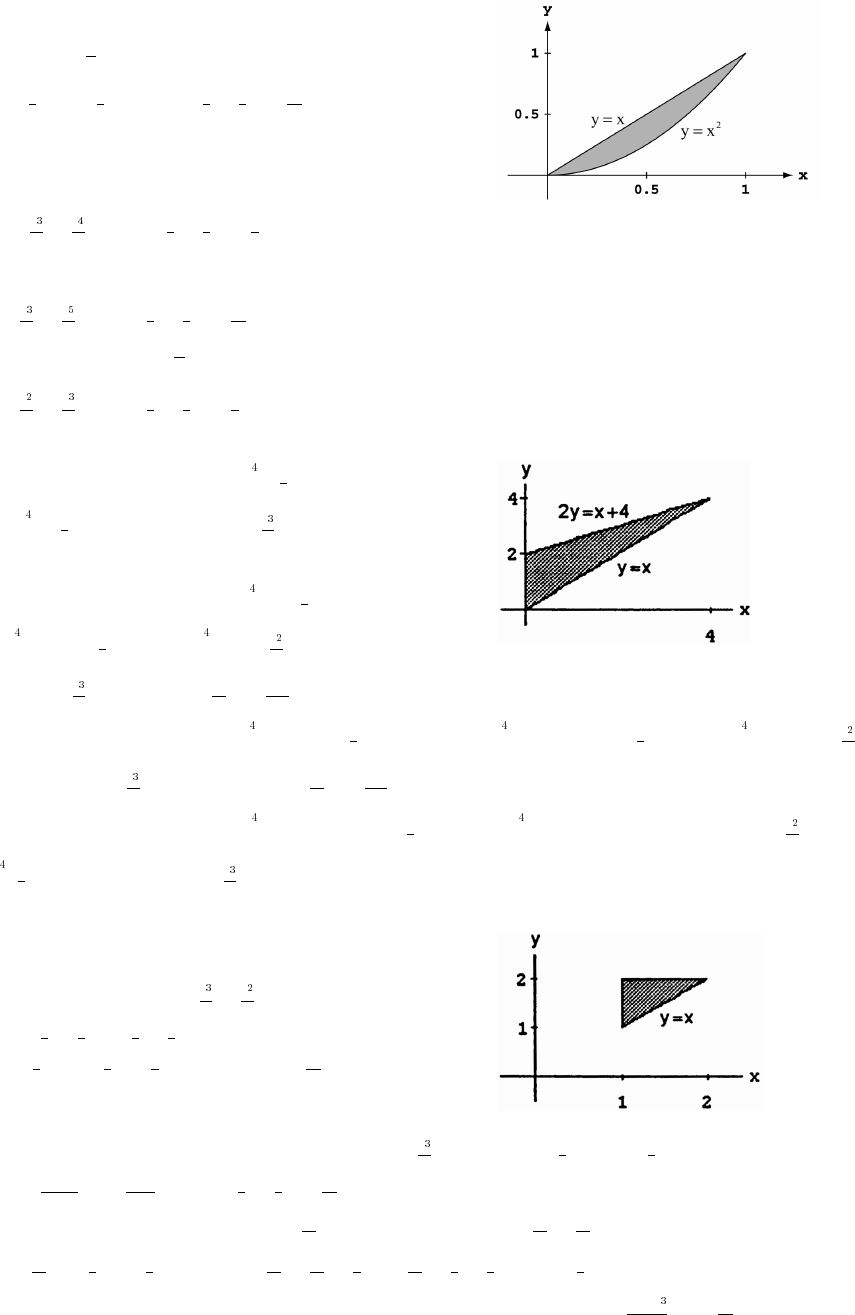
Section 6.2 Volume by Cylindrical Shells 375
25. (a) About x-axis: V 2 dyœ'c
d
1ˆ‰
Š‹
shell shell
radius height
2 y y y dy 2 y y dyœœ
''
00
11
11
ˆ‰ ˆ ‰
È$Î# #
2y y 2œœœ11
‘ˆ‰
#" #"#
&$ &$"&
&Î# $ "
!
1
About y-axis: V 2 dxœ'a
b
1ˆ‰
Š‹
shell shell
radius height
2 x x x dx 2 x x dxœœ
''
00
11
11ab a b
#23
22œœœ11
’“ˆ‰
xx
$% $% '
"
!
"" 1
(b) About x-axis: R x x and r x x V R x r x dx x x dxab ab ab ab c d
‘
œœÊœ œ
##%
##
''
a0
b1
11
œœœ11
’“
ˆ‰
xx
$& $& "&
"
!
"" #1
About y-axis: R y y and r y y V R y r y dy y y dyab ab ab ab c d
È‘
œœÊœœ
''
c0
d1
11
## 2
œœœ11
’“
ˆ‰
yy
#$ #$ '
"
!
"" 1
26. (a) V R x r x dx x dxœœ#
''
a0
b
11
‘ˆ‰
ab ab ’“
##
#
##
x
xxdx xxœ # % œ %11
'0ˆ‰
’“
$
%%
##
%
!
x
œ "' "' "' œ "'11ab
(b) V 2 dx x x dxœœ##
''
a0
b
11
ˆ‰ ˆ ‰
Š‹
shell shell
radius height
x
#
xdx xdxœ## œ# #
''
00
11
ˆ‰ Š‹
xx
##
xœ# œ# "' œ11
’“ˆ‰
#
''$
%
!
'% $#x1
(c) V 2 dx x x dx x dx x dxœ œ # % # œ # % # œ# )%
'' ' '
a0 0 0
b
11 11
ˆ‰ ˆ ‰ ˆ ‰
Š‹ Š ‹
ab ab
shell shell
radius height
xxx
###
xxœ# ) # œ# $#$# œ11
’“
ˆ‰
#
''$
%
!
'% '%x1
(d) V R x r x dx x dx x x x dxœ œ ) ' œ '% "' $' '
'' '
a0 0
b
11 1
‘ ˆ‰
ab ab a b a b
’“’ “Š‹
## #
#%
##
xx
xxdx xx111 11
'0ˆ‰
’“
‘
aba b aba b aba b
$
%%
##
%
!
"! #) œ & #) œ "' & "' ( "' œ $ "' œ %)
x
27. (a) V 2 dy 2 y(y 1) dyœœ
''
c1
d2
11
ˆ‰
Š‹
shell shell
radius height
2 y y dy 2œœ11
'1
2ab ’“
#
#
#
"
yy
3
2œ 1‘ˆ‰ˆ‰
84
32 3
""
#
2 2 (14123)œœœ1ˆ‰
75
33 3
"
#
11
(b) V 2 dxœ'a
b
1ˆ‰
Š‹
shell shell
radius height
2 x(2 x) dx 2 2x x dx 2 x 2 4 1œ œ œœ
''
11
22
11 11ab ’“‘ˆ‰ˆ‰
##
#
"
"x8
333
22œœœ11
‘ˆ‰ˆ‰ˆ‰
12 8 3 4 2 4
33 333
" 1
(c) V 2 dx 2 x (2 x) dx 2 x x dxœœœ
'' '
a1 1
b2 2
111
ˆ‰ ˆ ‰ ˆ ‰
Š‹
shell shell
radius height 3 3 3
10 20 16 #
2xxx 2 2 2œœœœ11 11
‘ ‘ˆ‰ˆ‰ˆ‰
20 8 40328 208 3
3 3 3 3 33 333 3
#$
""
#
"
(d) V 2 dy 2 (y 1)(y 1) dy 2 (y 1) 2œœœœœ
'' '
c1 1
d2 2
1111
ˆ‰
Š‹ ’“
shell shell
radius height 33
(y 1) 2
##
"
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
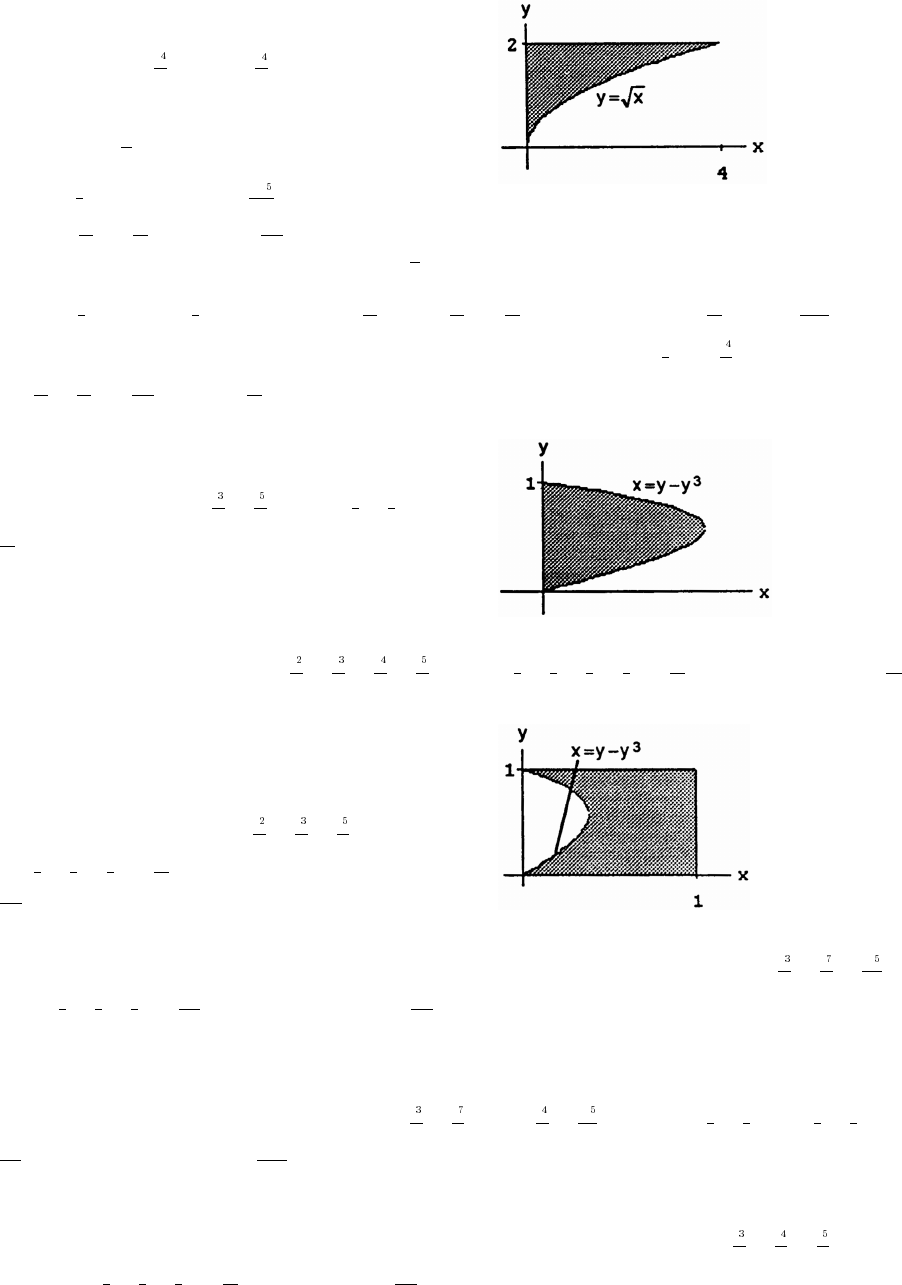
376 Chapter 6 Applications of Definite Integrals
28. (a) V 2 dy 2 y y 0 dyœœ
''
c0
d2
11
ˆ‰
Š‹ ab
shell shell
radius height #
2 y dy 2 2 8œœœœ1111
'0
2$#
!
’“ Š‹
y
44
2
(b) V 2 dxœ'a
b
1ˆ‰
Š‹
shell shell
radius height
2 x 2 x dx 2 2x x dxœœ
''
00
44
11
ˆ‰ ˆ ‰
È$Î#
2x x 2 16œ œ 11
‘
Š‹
# &Î# %
!
222
55
†
2 16 (80 64)œœœ1ˆ‰
64 2 32
55 5
11
(c) V 2 dx 2 (4 x) 2 x dx 2 8 4x 2x x dxœœœ
'' '
a0 0
b4 4
111
ˆ‰ ˆ ‰ ˆ ‰
Š‹ È
shell shell
radius height "Î# $Î#
2 8x x x x 2 32 16 (240 320 192) (112)œ œœ œ œ11
‘ˆ‰
8 2 64 64 2 2 224
3 5 3 5 15 15 15
$Î# # &Î# %
!
111
(d) V 2 dy 2 (2 y) y dy 2 2y y dy 2 yœœœœ
'''
c00
d22
1111
ˆ‰
Š‹ ’ “
ab a b
shell shell
radius height 34
2y
##$$
#
!
2(43)œœœ1ˆ‰
16 16 32 8
34 12 3
11
29. (a) V 2 dy 2 y y y dyœœ
''
c0
d1
11
ˆ‰
Š‹ ab
shell shell
radius height $
2y y dy 2 2œœœ
'0
1
111ab ’“ˆ‰
#% "
!
""
yy
35 35
œ4
15
1
(b) V 2 dyœ'c
d
1ˆ‰
Š‹
shell shell
radius height
2(1 y)y y dyœ
'0
1
1ab
$
2 yy y y dy2 2 (30201512)œ œ œ œ œ111
'0
1ab
’“
ˆ‰
#$%
##
"
!
""""
yyyy
3 4 5 3 4 5 60 30
27
11
30. (a) V 2 dyœ'c
d
1ˆ‰
Š‹
shell shell
radius height
2y1 y y dyœ
'0
1
1cdab
$
2 y y y dy 2œœ11
'0
1ab
’“
#%
#
"
!
yyy
35
2 (15 10 6)œœ 1ˆ‰
"""
#35 30
21
œ11
15
1
(b) Use the washer method:
V R (y) r (y) dy 1 y y dy 1 y y 2y dy yœ œ œ œ
'' '
c0 0
d1 1
111 1cd aba b
’“ ’ “
## # $ #'%
#"
!
yy2y
37 5
1 (105 35 15 42)œ œ œ1ˆ‰
""
3 7 5 105 105
29711
(c) Use the washer method:
V R (y) r (y) dy 1 y y 0 dy 1 2 y y y y dyœœœ
'' '
c0 0
d1 1
11 1c d c d abab
’“’ “
ab
## $ $ $
##
1yy2y2y2y dy y y 1 1œ œ œ 111
'0
1ab
’“
ˆ‰
#' $ % #
##
"
!
"" "
yy y2y
37 5 37 5
2
(70 30 105 2 42)œœ
11
210 210
121
†
(d) V 2 dy 2 (1 y) 1 y y dy 2 (1 y) 1 y y dyœœœ
'' '
c0 0
d1 1
11 1
ˆ‰
Š‹ cd abab
shell shell
radius height $$
2 1yy yy y dy2 12yy y y dy2yyœ œ œ 111
''
00
11
abab
’“
$ #% #$% # "
!
yyy
345
2 1 1 (20 15 12)œ œ œ1ˆ‰
"""
3 4 5 60 30
22311
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
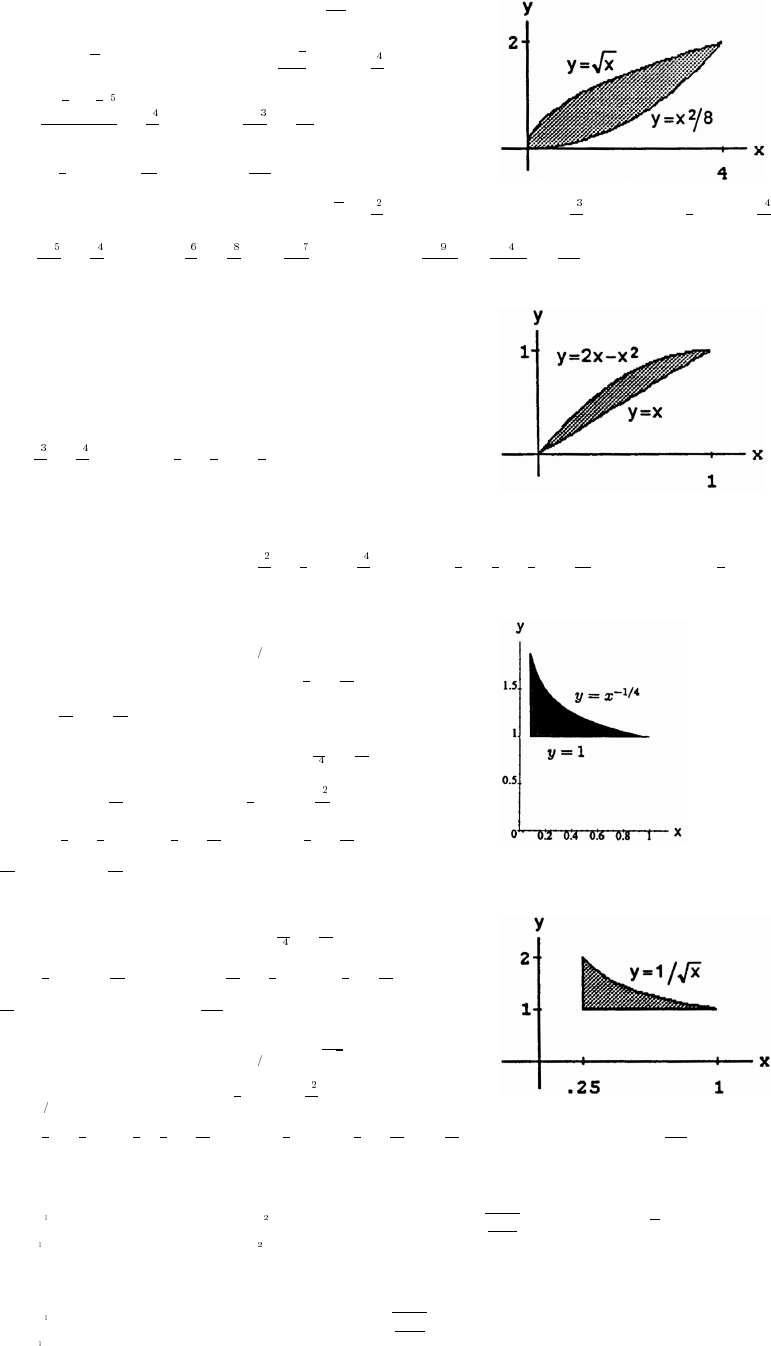
Section 6.2 Volume by Cylindrical Shells 377
31. (a) V 2 dy 2 y 8y y dyœœ
''
c0
d2
11
ˆ‰ ˆ ‰
Š‹ È
shell shell
radius height #
222yy dy2 yœœ11
'0
2Š‹’“
È$Î# $ &Î# #
!
42 y
54
È
22œœ11
Š‹
42 2
54 54
24244
ÈÈ
Š‹
†
†
†
24 1 (85)œœœ1†ˆ‰
88 24
55 5
11
(b) V 2 dx 2 x x dx 2 x dx 2 xœ œ œ œ
'' '
a0 0
b4 4
1111
ˆ‰
Š‹ Š ‹ Š ‹ ’ “
È
shell shell
radius height 8 8 5 32
xx2x
$Î# &Î# %
!
2 2 (32 20)œ œ œ œœœ11
Š‹Š‹
22 4 2 2 2 23 23 48
5 3 5 32 160 160 5 5
† † †† ††
#
1111
32. (a) V 2 dxœ'a
b
1ˆ‰
Š‹
shell shell
radius height
2 x 2x x x dxœ
'0
1
1cdab
#
2 xx x dx 2 x x dxœœ11
''
00
11
ab a b
##$
22œœœ11
’“ˆ‰
xx
34 34 6
"
!
"" 1
(b) V 2 dx 2 (1 x) 2x x x dx 2 (1 x) x x dxœœœ
'' '
a0 0
b1 1
11 1
ˆ‰
Š‹ cd abab
shell shell
radius height ##
2 x2x x dx 2 x 2 (683)œœœœœ111
'0
1ab
’“
ˆ‰
#$ $ "
!
"
#
x2 x 12 2
2 3 4 234 1 6
11
33. (a) V R (x) r (x) dx x 1 dxœœ
''
a116
b1
11cdˆ‰
# # "Î#
2x x (2 1) 2œœ11
‘ ‘ˆ‰
"Î# "
"Î"'
""
†416
1œœ1ˆ‰
79
16 16
1
(b) V 2 dy 2 y dyœœ
''
a1
b2
11
ˆ‰
Š‹ Š ‹
shell shell
radius height 16
y
""
2 y dy 2 yœœ11
'1
2ˆ‰ ’“
$ # #
"
yy
16 2 32
1
22œœ 11
‘ˆ‰ˆ‰ˆ‰
"" "" ""
##88 3 432
(8 1)œœ
29
32 16
11
34. (a) V R (y) r (y) dy dyœœ
''
c1
d2
11cd
Š‹
## ""
y16
yœ œ 11
‘ ‘ˆ‰ˆ‰
"""""
$ #
"
3 16 248 316
y
(26163)œœ
11
48 48
11
(b) V 2 dx 2 x dxœœ"
''
a14
b1
11
ˆ‰
Š‹ Š ‹
shell shell
radius height x
"
È
2 x x dx 2 xœœ11
'14
1ˆ‰ ’“
"Î# $Î# "
"Î%
2x
32
2 1 (4 16 48 8 3)œœœ œ11
‘ˆ‰ˆ‰ˆ ‰
22 4 11
3 3 8 3 3 6 16 48 48
""" ""
##
††
11
35. (a) k: V V VH3= œ
"#
V [R (x)] dx and V [R (x)] with R (x) and R (x) x,
"" ## " #
##
œœ œœ
''
aa
bb
11
ÉÈ
x2
3
a 2, b 1; a 0, b 1 two integrals are required
""##
œ œ œ œ Ê
(b) : V V V[+=2/< œ
"#
V [R (x)] [r (x)] dx with R (x) and r (x) 0; a 2 and b 0;
""" " "" "
##
œ œ œœœ
'a
b
1ab
Éx2
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

378 Chapter 6 Applications of Definite Integrals
V [R (x)] [r (x)] dx with R (x) and r (x) x; a 0 and b 1
### # ###
##
œ œ œœœ
'a
b
1ab
ÉÈ
x2
3
two integrals are requiredÊ
(c) : V 2 dy 2 y dy where shell height y 3y 2 2 2y ;W2/66 œ œ œ œ
''
cc
dd
11
ˆ‰
Š‹ Š‹ ab
shell shell shell
radius height height ## #
c 0 and d 1. Only integral is required. It is, therefore preferable to use the method.œœ 98/ =2/66
However, whichever method you use, you will get V .œ1
36. (a) k: V V V VH3= œ
"#$
V [R (y)] dy, i 1, 2, 3 with R (y) 1 and c 1, d 1; R (y) y and c 0 and d 1;
ii
c
d
œœœœœœœœ
'i
i
1#"""# ##
È
R (y) ( y) and c 1, d 0 three integrals are required
$$$
"Î%
œ œ œ Ê
(b) : V V V[+=2/< œ
"#
V [R (y)] [r (y)] dy, i 1, 2 with R (y) 1, r (y) y, c 0 and d 1;
iii
c
d
œœ œœœœ
'i
i
1ab È
## "" " "
R (y) 1, r (y) ( y) , c 1 and d 0 two integrals are required
## # #
"Î%
œœœ œÊ
(c) : V 2 dx 2 x dx, where shell height x x x x ,W2/66 œ œ œ œ
''
aa
bb
11
ˆ‰
Š‹ Š‹ ab
shell shell shell
radius height height #%#%
a 0 and b 1 only one integral is required. It is, therefore preferable to use the method.œœÊ =2/66
However, whichever method you use, you will get V .œ5
6
1
6.3 LENGTHS OF PLANE CURVES
1. 1 and 3 ( 1) (3) 10
dx dx
dt dt dt dt
dy dy
œ œ Ê œ œ
ʈ‰ Š‹ ÈÈ
####
Length 10 dt 10 t 10 10Êœ œ œœ
'
2/3
11
2/3 2
33
510
ÈÈ È È
cd Š‹
È
2. sin t and 1 cos t ( sin t) (1 cos t) 2 2 cos t
dx dx
dt dt dt dt
dy dy
œ œ Ê œ œ
ʈ‰ Š‹ ÈÈ
####
Length 2 2 cos t dt 2 (1 cos t) dt 2 dtÊœ œ œ
'' '
ÈÈÈ
Ɉ‰ É
1cos t sint
1cos t 1cos t
2 dt (since sin t 0 on [0 ]); [u 1 cos t du sin t dt; t 0 u 0,œßœÊœœÊœ
È'sin t
1cos t
È1
t u 2] 2 u du 2 2u 4œÊœ Ä œ œ1ÈÈ
‘
'2"Î# "Î# #
!
3. 3t and 3t 3t (3t) 9t 9t 3t t 1 since t 0 on 0 3
dx dx
dt dt dt dt
dy dy
œœÊœœœß
#####%##
#
ʈ‰ Š‹ Š ‹
Éab ÈÈ’“
È
Length 3t t 1 dt; u t 1 du 3t dt; t 0 u 1, t 3 u 4Êœ œÊœœÊœœÊœ
'3È’“
È
##
#
3
u du u (81) 7Ä œ œœ
'1
43
#
"Î# $Î# %
"
‘
4. t and (2t 1) t (2t 1) (t 1) t 1 t 1 since 0 t 4
dx dx
dt dt dt dt
dy dy
œœÊ œœœœ ŸŸ
"Î# ####
ʈ‰ Š‹ ÈÈ
kk
Length (t 1) dt t (8 4) 12Ê œ œ œœ
'0
4’“
t
2
%
!
5. (2t 3) and 1 t (2t 3) (1 t) t 4t 4 t 2 t 2
dx dx
dt dt dt dt
dy dy
œ œÊ œ œ œœ
"Î# ####
ʈ‰ Š‹ ÈÈkk
since 0 t 3 Length (t 2) dt 2tŸŸ Ê œ œ œ
'0’“
t21
2
$
!#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
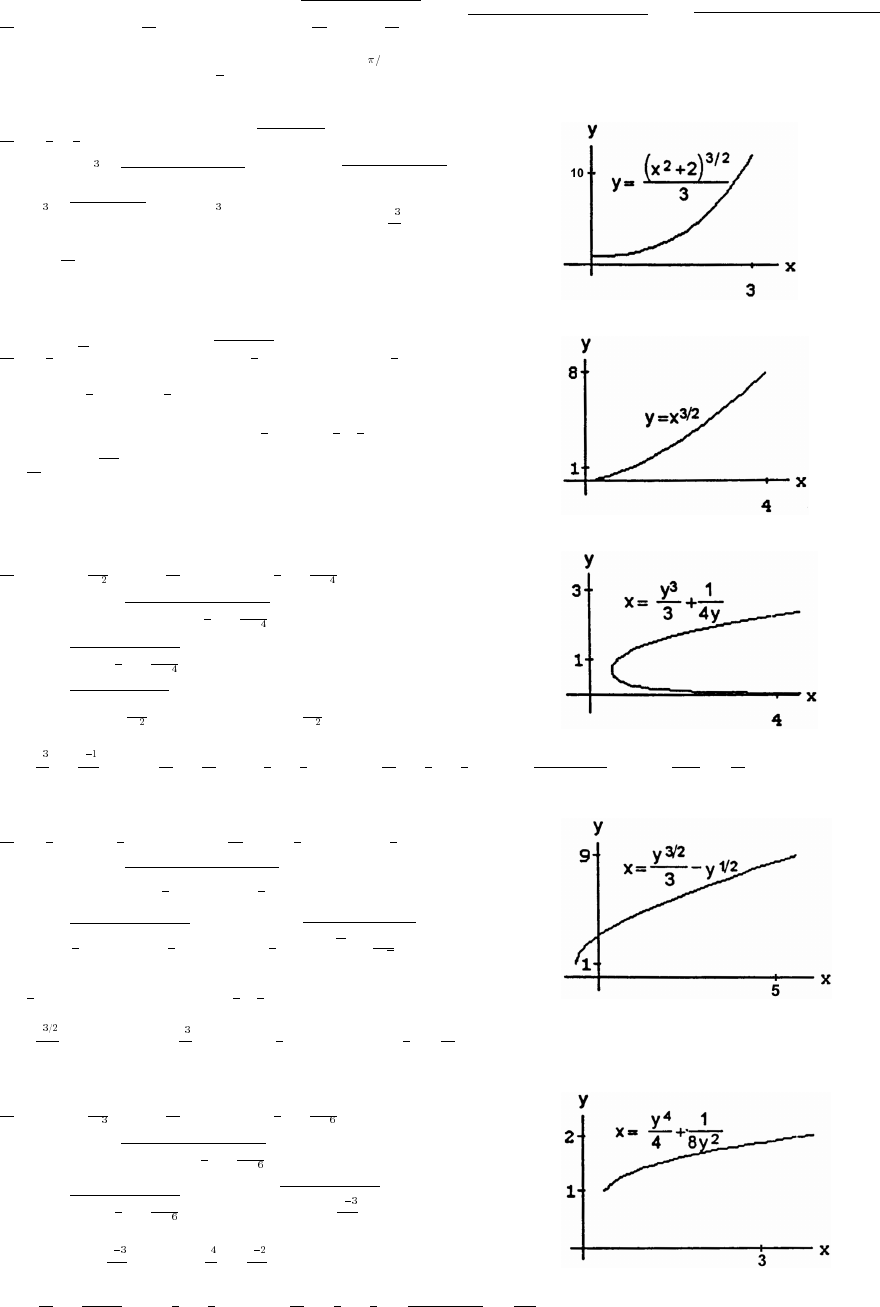
Section 6.3 Lengths of Plane Curves 379
6. 8t cos t and 8t sin t (8t cos t) (8t sin t) 64t cos t 64t sin t
dx dx
dt dt dt dt
dy dy
œœÊœœ
ʈ‰ Š‹ ÈÈ
########
8t 8t since 0 t Length 8t dt 4tœœ ŸŸÊ œ œ œkk c d
11
#
##
Î#
!
'0
2
1
7. x 2 2x x 2 x
dy
dx 3
3
œ œ
"
#
#"Î# #
†† †ab ab
È
L 1 x 2 x dx 1 2x x dxÊœ œ
''
00
3
Èab È
## #%
1 x dx 1 x dx xœœœ
''
00
Éab ab’“
###$
!
x
3
312œ œ
27
3
8. x L 1 x dx; u 1 x
dy
dx 4 4
399
œÊœ œ
#ÈÉ
'0
4
du dx du dx; x 0 u 1; x 4Êœ Ê œ œÊœ œ
94
49
u 10 L u du udˆ‰ ‘
Êœ Ä œ œ
'1
10 "Î# $Î# "!
"
442
993
10 10 1œ
8
27 Š‹
È
9. y y
dx dx
dy 4y dy 16y
œ Ê œ
#%
"""
#
#
Š‹
L 1 y dyʜ
'1
3É%""
#16y
y dyœ
'1
3É%""
#16y
y dy y dyœœ
''
11
33
ÊŠ‹ Š‹
#""
##
4y 4y
999œ œ œ œ œ œ
’“
ˆ‰ˆ‰
yy (143) (2)
34 31 34 134 1 1 6
27 53
$
"
""" """
####
10. y y y 2
dx dx
dy dy 4 y
œ Ê œ
"" " "
##
"Î# "Î# #
Š‹ Š ‹
L 1 y 2 dyʜ
'1
9ÊŠ‹
""
4y
y 2 dy y dyœœ
''
11
99
ÊŠ‹ Š‹
ÊÈ
"" " "
#
#
4y y
È
yy dy y2yœœ
""
##
"Î# "Î# $Î# "Î# *
"
'1
9ˆ‰ ‘
2
3
y3111œ œœœ
’“Š‹
ˆ‰
y
33333
332
"Î# *
"
""
11. y y
dx dx
dy 4y dy 16y
œ Ê œ
$'
"""
#
#
Š‹
L 1 y dyʜ
'1
2É'""
2 16y
y dy y dyœœ
''
11
22
ÉÊŠ‹
'$
"" #
2 16y 4
y
y dyœ œ
'1
2Š‹’“
$#
"
yyy
448
4œ œœ œ
Š‹
ˆ‰
16 128 1 8 4 123
4 (16)(2) 4 8 32 4 8 32 32
" " " " " "
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
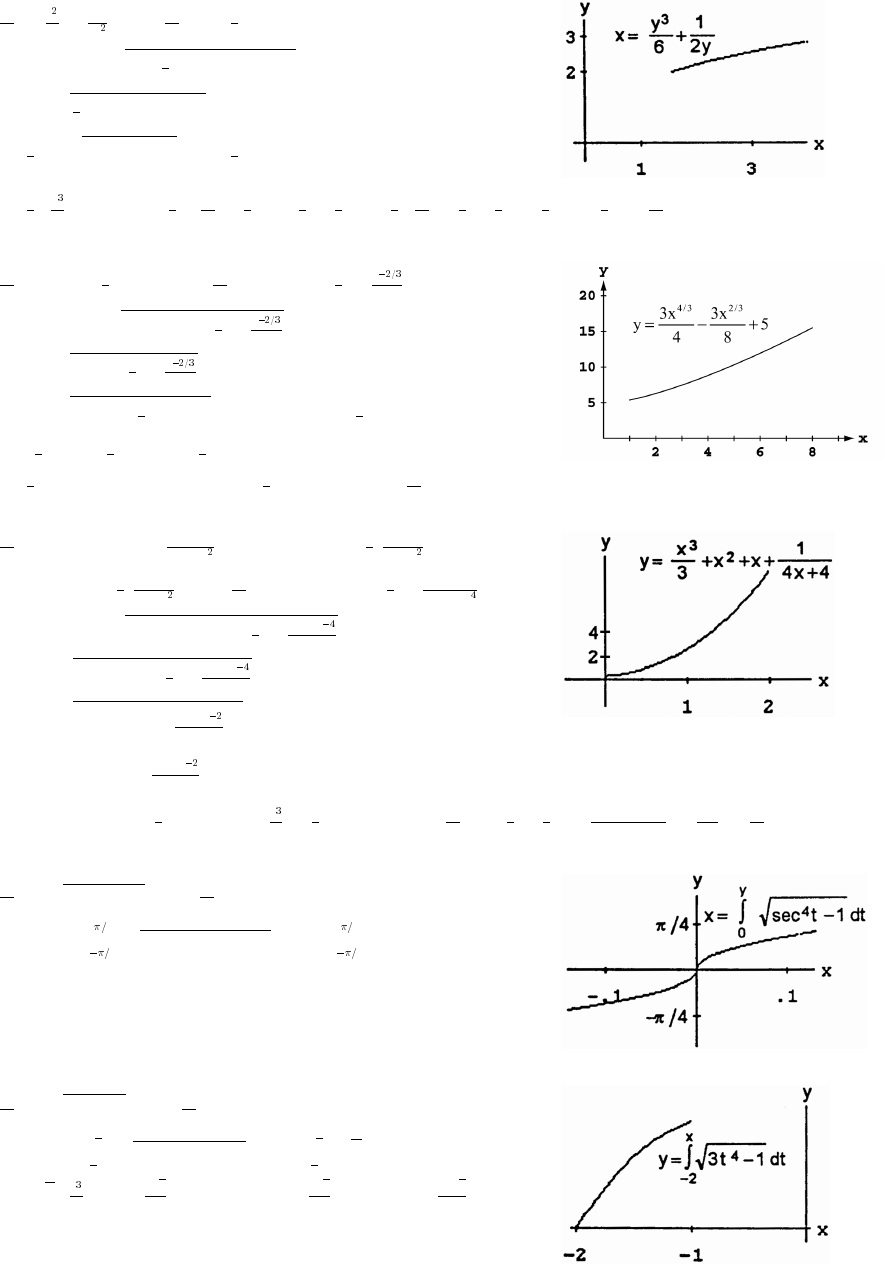
380 Chapter 6 Applications of Definite Integrals
12. y 2 y
dx dx
dy y dy 4
y
œ Ê œ
##
""
#%%
Š‹ ab
L 1 y 2 y dyʜ
'2
3Éab
"%%
4
y2y dyœ
'2
3Éab
"%%
4
y y dy y y dyœœ
""
##
##
###
''
22
33
Éab ab
y6œ œ œ œ œ
""""""""
## #####
" $
#
’“
‘ˆ‰ˆ‰ˆ‰ˆ‰
y
333333 4
27 8 26 8 13
13. x x x
dy dy
dx 4 dx 16
x
œ Ê œ
"Î$ "Î$ #Î$
""
#
#
Š‹
L 1 x dxʜ
'1
8É#Î$ "
#
x
16
x dxœ
'1
8É#Î$ "
#
x
16
x x dx x x dxœ œ
''
11
88
Ɉ‰ˆ‰
"Î$ "Î$
""
#"Î$ "Î$
44
x x 2x xœ œ
‘‘
33 3
48 8
%Î$ #Î$ %Î$ #Î$
))
""
22 2 (21) (3243)œœœ
3399
888
cdab†%#
14. x 2x 1 x 2x 1
dy
dx (4x 4) 4 (1 x)
4
œ œ
##
""
(1 x) (1 x)œ Ê œ
#%
"" " "
#
#
4(1x) dx
dy
16(1 x)
Š‹
L 1 (1 x) dxʜ
'0
2É%"
#
(1 x)
16
(1 x) dxœ
'0
2É%"
#
(1 x)
16
(1 x) dxœ
'0
2Ê’“
##
(1 x)
4
(1 x) dx; u 1 x du dx; x 0 u 1, x 2 u 3œ œÊœœÊœœÊœ
'0
2’“
cd
#(1 x)
4
L u u du u 9Äœ œ œ œ œ œ
'1
3ˆ‰ ˆ‰ˆ‰
’“
## "
" " " " "
$
"#4 3 4 1 3 4 12 12 6
u 108 1 4 3 106 53
15. sec y 1 sec y 1
dx dx
dy dy
œÊœ
ÈŠ‹
%#%
L 1 sec y 1 dy sec y dyÊœ œ
''
44
44
Èab
%#
tan y 1 ( 1) 2œœœcd
1
1
Î%
Î%
16. 3x 1 3x 1
dy dy
dx dx
œÊ œ
ÈŠ‹
%#%
L 1 3x 1 dx 3 x dxÊœ œ
''
22
11
Èab È
%#
31(2)(8)œœœ"œ
È’“ cd
x
33 3 3
3373
"
#
$
ÈÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
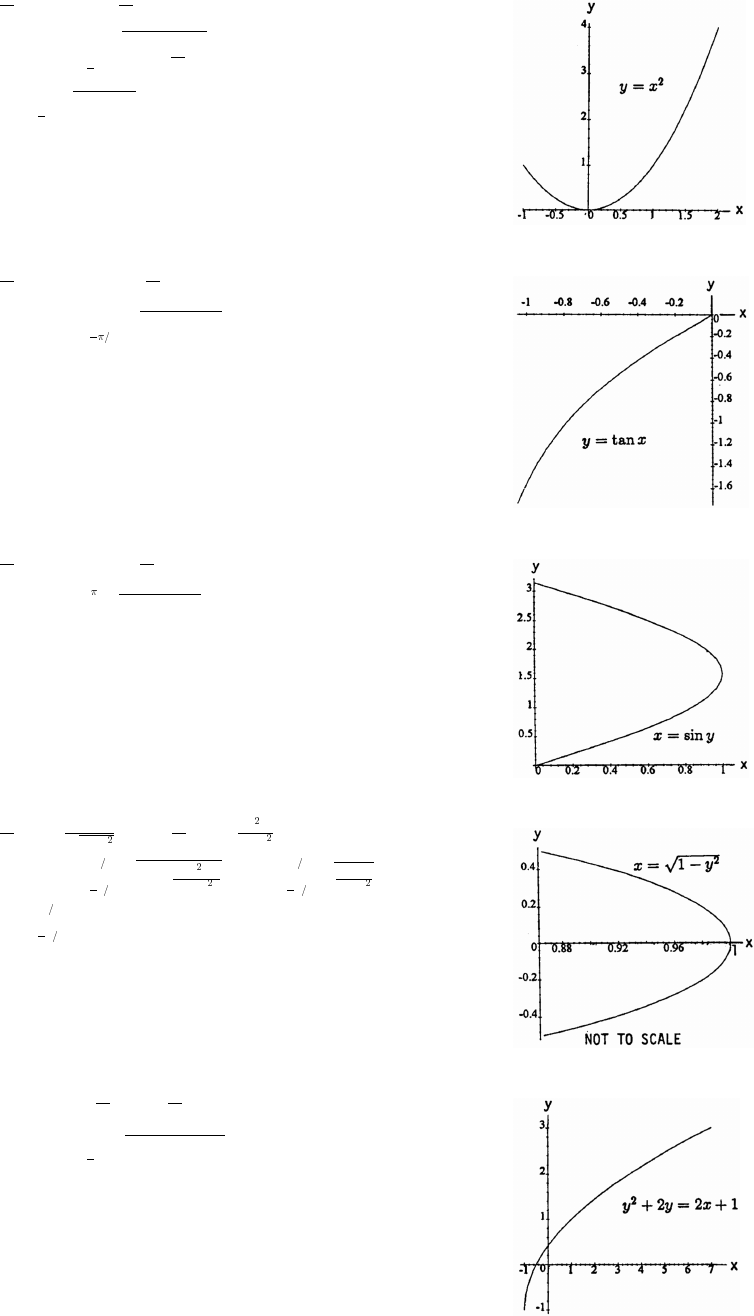
Section 6.3 Lengths of Plane Curves 381
17. (a) 2x 4x
dy dy
dx dx
œÊ œ
Š‹
##
L 1 dxʜ
'1
2ÊŠ‹
dy
dx
#
14x dxœ
'1
2È#
(c) L 6.13¸
(b)
18. (a) sec x sec x
dy dy
dx dx
œÊ œ
#%
#
Š‹
L 1 sec x dxʜ
'3
0È%
(c) L 2.06¸
(b)
19. (a) cos y cos y
dx dx
dy dy
œÊ œ
Š‹
##
L 1 cos y dyʜ
'0È#
(c) L 3.82¸
(b)
20. (a)
dx dx
dy dy 1 y
yy
1y
œ Ê œ
È
#
Š‹
L 1 dy dyÊœ œ
''
12 12
12 12
ÉÉ
y
1y 1y
ab
"
1 y dyœ
'12
12ab
#"Î#
(c) L 1.05¸
(b)
21. (a) 2y 2 2 (y 1)œ Ê œ
dx dx
dy dy
Š‹
##
L 1 (y 1) dyʜ
'1
3È#
(c) L 9.29¸
(b)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
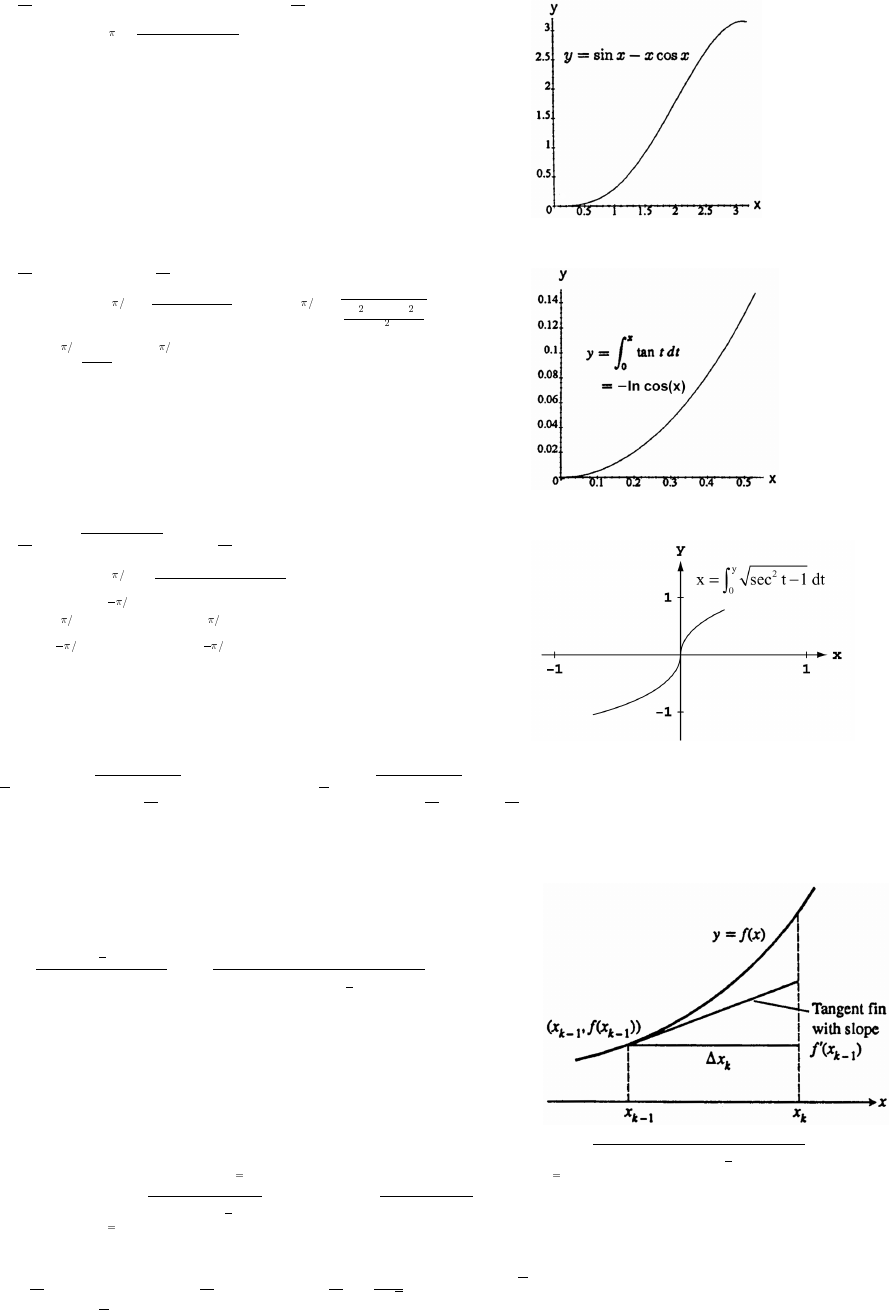
382 Chapter 6 Applications of Definite Integrals
22. (a) cos x - cos x + x sin x x sin x
dy dy
dx dx
œÊœ
Š‹
###
L 1 x sin x dxʜ
'0È##
(c) L 4.70¸
(b)
23. (a) tan x tan x
dy dy
dx dx
œÊ œ
Š‹
##
L 1 tan x dx dxÊœ œ
''
00
66
ÈÉ
#sin x cos x
cos x
sec x dxœœ
''
00
66
dx
cos x
(c) L 0.55¸
(b)
24. (a) sec y 1 sec y 1
dx dx
dy dy
œÊœ
ÈŠ‹
###
L 1 sec y 1 dyʜ
'3
4Èab
#
sec y dy sec y dyœœ
''
33
44
kk
(c) L 2.20¸
(b)
25. 2 x 1 dt, x 0 2 1 1 y f(x) x C where C is any
ÈÈ
ÊÊ
Š‹ Š‹
œ ʜʜ„Êœœ„
'0
xdy dy dy
dt dx dx
##
real number.
26. (a) From the accompanying figure and definition of the
differential (change along the tangent line) we see that
dy f (x ) x length of kth tangent fin isœ˜Ê
wk1 k
(x) (dy) (x) [f(x)x].
ÈÈ
˜ œ˜ ˜
kkk1k
## #w #
(b) Length of curve lim (length of kth tangent fin) lim ( x ) [f (x ) x ]œœ˜˜
nnÄ_ Ä_
!!
È
nn
k1 k1
kk1k
#w #
lim 1 [f (x )] x 1 [f (x)] dxœ˜œ
nÄ_ !ÈÈ
n
k1
k1 k a
b
w# w#
'
27. (a) correspondes to here, so take as . Then y x C and since ( ) lies on the curve, C 0.
Š‹ È
dy dy
dx 4x dx x
#""
#Èœ "ß" œ
So y x from ( ) to (4 2).œ"ß"ß
È
(b) Only one. We know the derivative of the function and the value of the function at one value of x.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 6.3 Lengths of Plane Curves 383
28. (a) correspondes to here, so take as . Then x C and, since ( ) lies on the curve, C 1
Š‹
dx
dy dx y y
y
dy
#"""
œ !ß" œ
So y .œ"
"x
(b) Only one. We know the derivative of the function and the value of the function at one value of x.
29. (a) 2 sin 2t and 2 cos 2t ( 2 sin 2t) (2 cos 2t) 2
dx dx
dt dt dt dt
dy dy
œ œ Ê œ œ
ʈ‰ Š‹ È
####
Length 2 dt 2tÊœ œœ
'0
2cd
1Î#
!1
(b) cos t and sin t ( cos t) ( sin t)
dx dx
dt dt dt dt
dy dy
œœœœœ11 11 11 11 1
ʈ‰ Š‹ È
####
Length dt tÊœ œ œ
'12
12
11 1cd
"Î#
"Î#
30. x a( sin ) a(1 cos ) a 1 2 cos cos and y a(1 cos )œ Êœ Ê œ œ)) ) ) ) )
dx dx
dd))
ˆ‰ ab
###
a sin a sin Length d 2a (1 cos ) dÊœ Ê œ Ê œ œ
dy dy dy
dd dd
dx
)) ))
)) ) ))
Š‹ Š‹
ʈ‰ È
##
## ##
''
00
22
a 2 2 d 2a sin d 2a sin d 4a cos 8aœœœœœ
ÈÈ
ɸ¸ ‘
'''
000
222
1cos
2
###
#
!
))))
1
)))
31-36. Example CAS commands:
:Maple
with( plots );
with( Student[Calculus1] );
with( student );
f := x -> sqrt(1-x^2);a := -1;
b := 1;
N := [2, 4, 8 ];
for n in N do
xx := [seq( a+i*(b-a)/n, i=0..n )];
pts := [seq([x,f(x)],x=xx)];
L := simplify(add( distance(pts[i+1],pts[i]), i=1..n )); # (b)
T := sprintf("#31(a) (Section 6.3)\nn=%3d L=%8.5f\n", n, L );
P[n] := plot( [f(x),pts], x=a..b, title=T ): # (a)
end do:
display( [seq(P[n],n=N)], insequence=true, scaling=constrained );
L := ArcLength( f(x), x=a..b, output=integral ):
L = evalf( L ); # (c)
37-40. Example CAS commands:
:Maple
with( plots );
with( student );
x := t -> t^3/3;
y := t -> t^2/2;
a := 0;
b := 1;
N := [2, 4, 8 ];
for n in N do
tt := [seq( a+i*(b-a)/n, i=0..n )];
pts := [seq([x(t),y(t)],t=tt)];
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

384 Chapter 6 Applications of Definite Integrals
L := simplify(add( student[distance](pts[i+1],pts[i]), i=1..n )); # (b)
T := sprintf("#37(a) (Section 6.3)\nn=%3d L=%8.5f\n", n, L );
P[n] := plot( [[x(t),y(t),t=a..b],pts], title=T ): # (a)
end do:
display( [seq(P[n],n=N)], insequence=true );
ds := t ->sqrt( simplify(D(x)(t)^2 + D(y)(t)^2) ): # (c)
L := Int( ds(t), t=a..b ):
L = evalf(L);
31-40. Example CAS commands:
: (assigned function and values for a, b, and n may vary)Mathematica
Clear[x, f]
{a, b} = { 1, 1}; f[x_] = Sqrt[1 x ]
2
p1 = Plot[f[x], {x, a, b}]
n = 8;
pts = Table[{xn, f[xn]}, {xn, a, b, (b a)/n}]/ / N
Show[{p1,Graphics[{Line[pts]}]}]
Sum[ Sqrt[ (pts[[i 1, 1]] pts[[i, 1]]) (pts[[i 1, 2]] pts[[i, 2]]) ], {i, 1, n}]
22
NIntegrate[ Sqrt[ 1 f'[x] ],{x, a, b}]2
6.4 MOMENTS AND CENTERS OF MASS
1. Because the children are balanced, the moment of the system about the origin must be equal to zero:
5 80 x 100 x 4 ft, the distance of the 100-lb child from the fulcrum.††œÊœ
2. Suppose the log has length 2a. Align the log along the x-axis so the 100-lb end is placed at x a and theœ
200-lb end at x a. Then the center of mass x satisfies x x . That is, x is locatedœœÊœ
100( a) 200(a)
300 3
a
at a distance a (2a) which is of the length of the log from the 200-lb (heavier) end (see figure)œ œ
a2a
333 3
""
or of the way from the lighter end toward the heavier end.
2
3
(2a)
"
3
èëëéëëê
100 lbs. 200 lbsñïïïïïïïïïïïïïïñïïïïñïïïïïïñ
!
axa/3 a
œ
3. The center of mass of each rod is in its center (see Example 1). The rod system is equivalent to two point
masses located at the centers of the rods at coordinates and 0 . Therefore x
ˆ‰ ˆ‰
LL
##
ß! ß œ m
m
y
and y is the center ofœœœœœœœÊß
xm xm
mm mm m mm mm
m0 mym ym 0m
L
x2
L
††
LLLL
4444
ˆ‰
mass location.
4. Let the rods have lengths x L and y 2L. The center of mass of each rod is in its center (see Example 1).œœ
The rod system is equivalent to two point masses located at the centers of the rods at coordinates and
ˆ‰
L
#ß!
( L). Therefore x and y is the center of mass location.!ß œ œ œ œ Ê ß
L††
††
m02m
m2m m2m
mL2m
!
L2LL2L
6363
ˆ‰
5. M x 4 dx 4 4 8; M 4 dx [4x] 4 2 8 x 1
!##
#
!
#
!
œœœœœœœœÊœœ
''
00
22
†† †
’“
x4 M
M
6. M x 4 dx 4 (9 1) 16; M 4 dx [4x] 12 4 8 x 2
!##
$
"
$
"
œœœœœœœœÊœœœ
''
1 1
3 3
†’“
x4 16
M
M8
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
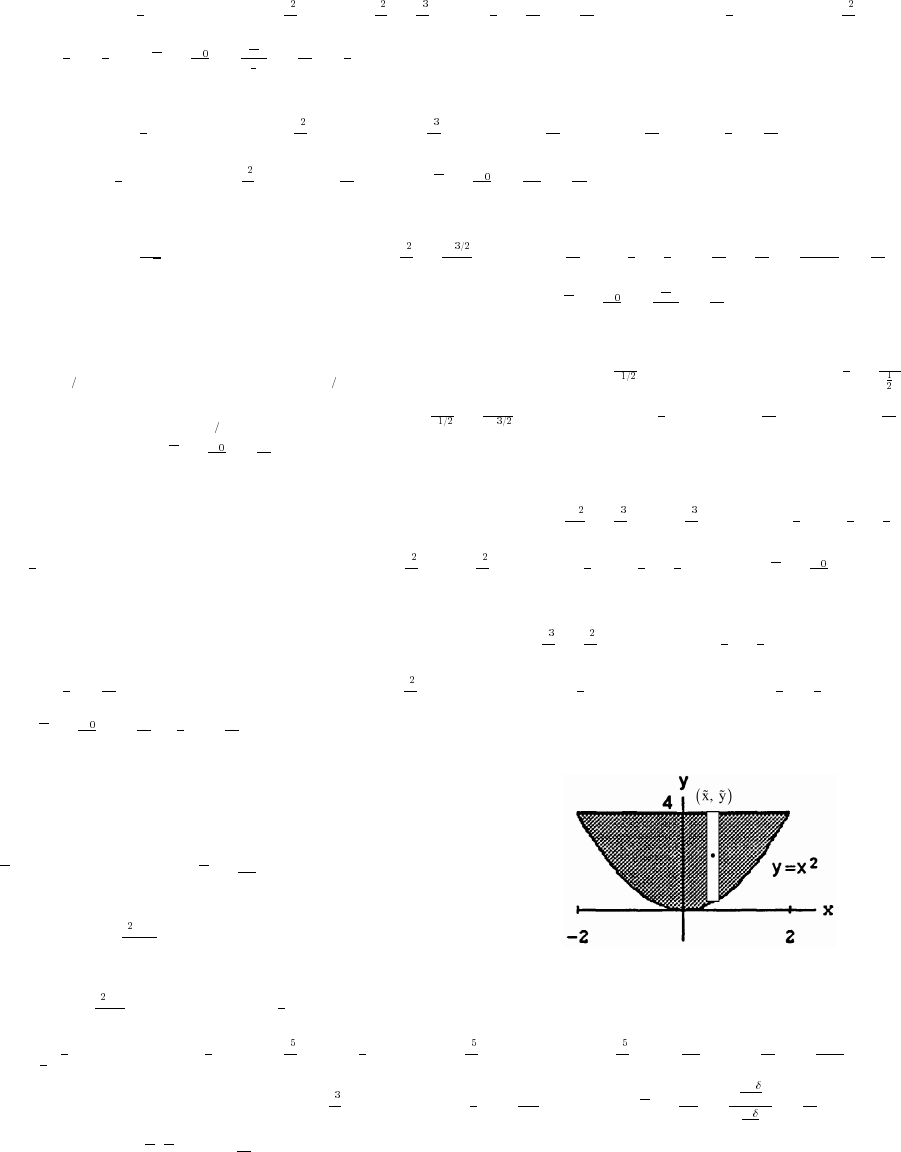
Section 6.4 Moments and Centers of Mass 385
7. M x 1 dx x dx ; M 1 dx x
!##
$$
!!
œœœœœœœ
'' '
00 0
33 3
ˆ‰ ˆ ‰ ˆ‰
Š‹’ “ ’“
xxxx92715xx
33929 36
3 xœœ Ê œ œ œ œ
99 155
6M93
M
#
ˆ‰
ˆ‰
15
2
9
2
8. M x 2 dx 2x dx x 16 16 16 ;
!#%
!
œœœœœœœ
''
00
44
ˆ‰ ˆ ‰
Š‹’“
xxx6416232
4 4 12 12 3 3 3
†
M 2 dx 2x 8 6 xœœœœÊœœœ
'0
4ˆ‰’“
x x 16 32 16
488 M369
M
%
!†
9. M x 1 dx x x dx 8 ;
!""
"Î#
###
%
"
œ œ œ œ œœ œ
''
11
44
Š‹ ’ “
ˆ‰ ˆ‰ˆ‰
Èx
x 2x 16 2 15 14 45 28 73
3 3 3 366
M 1x dx x2x (44)(12)5 xœ œ œœÊœ œ œ
'1
4ˆ‰‘
"Î# "Î# %
"
M
M530
73
ˆ‰
73
6
10. M x 3 x x dx 3 x x dx 3 2x 3 (2 2) 2
!$Î# &Î# "Î# $Î# "Î# "
"Î%
"
#
œœœœ
''
14 14
11
† †
ˆ‰ˆ‰‘
’“Š‹
22
xˆ‰
3(4 1) 9; M 3 x x dx 3 3 2 4 3 2œœ œ œ œ œ
'14
1ˆ‰‘ ‘ˆ‰ˆ‰ˆ ‰
$Î# &Î# "
"Î%
22 2 16 14
x3x 33 3
6 14 20 xœ œ Ê œ œ
M
M20
9
11. M x(2 x) dx x x dx 2x x dx x dx 1
!##
#
"#
!"
""
œ œ œ œ
''' '
010 1
121 2
†ab ’“’“
ˆ‰ˆ‰
2x x x 8
33 333
3; M (2 x) dx x dx 2x 2 3 x 1œœ œ œ œœÊœ œ
9xx4
3 M
M
''
01
12
’“’“
ˆ‰ˆ‰
## ###
"#
!"
""
12. M x(x 1) dx 2x dx x x dx 2x dx x (4 1)
!##
"
!
#
"""
œ œ œœ
''''
0101
1212
ab cd
’“ ˆ‰
xx
32 32
3 ; M (x 1) dx 2 dx x 2x 1 (4 ) 2œœ œ œ œ #œœ
523 x 37
66 ''
01
12
’“
cd ˆ‰
## ##
"
!
#
""
xÊœ œ œ
M
M6721
23 2 23
ˆ‰ˆ‰
13. Since the plate is symmetric about the y-axis and its density is
constant, the distribution of mass is symmetric about the y-axis
and the center of mass lies on the y-axis. This means that
x 0. It remains to find y . We model the distribution ofœœ
M
M
x
mass with strips. The typical strip has center of mass:@/<>3-+6
( x y ) x , length: 4 x , width: dx, area:
µµ
ßœß
Š‹
x4
#
#
dA 4 x dx, mass: dm dA 4 x dx. The moment of the strip about the x-axis isœ œ œ ab ab
##
$$
dm 4 x dx 16 x dx. The moment of the plate about the x-axis is M dmCœ œ œC
µ µ
Š‹
ab a b
x4
##
#%
$$
x'
16 x dx 16x 16 2 16 2 32 . The mass of theœœœ œœ
'2
2$$ $ $ $
## # #
%#
#
ab’“’ “Š‹Š ‹
ˆ‰
x 2 2 2 32 128
55555
††
†
plate is M 4 x dx 4x 2 8 . Therefore y . The plate's center ofœœœœ œœœ
'$$ $ab ’“ ˆ‰
##
#
x 8 32 Mx 12
333 M5
$Š‹
Š‹
128
5
32
3
mass is the point (x y) .ßœ!ß
ˆ‰
12
5
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
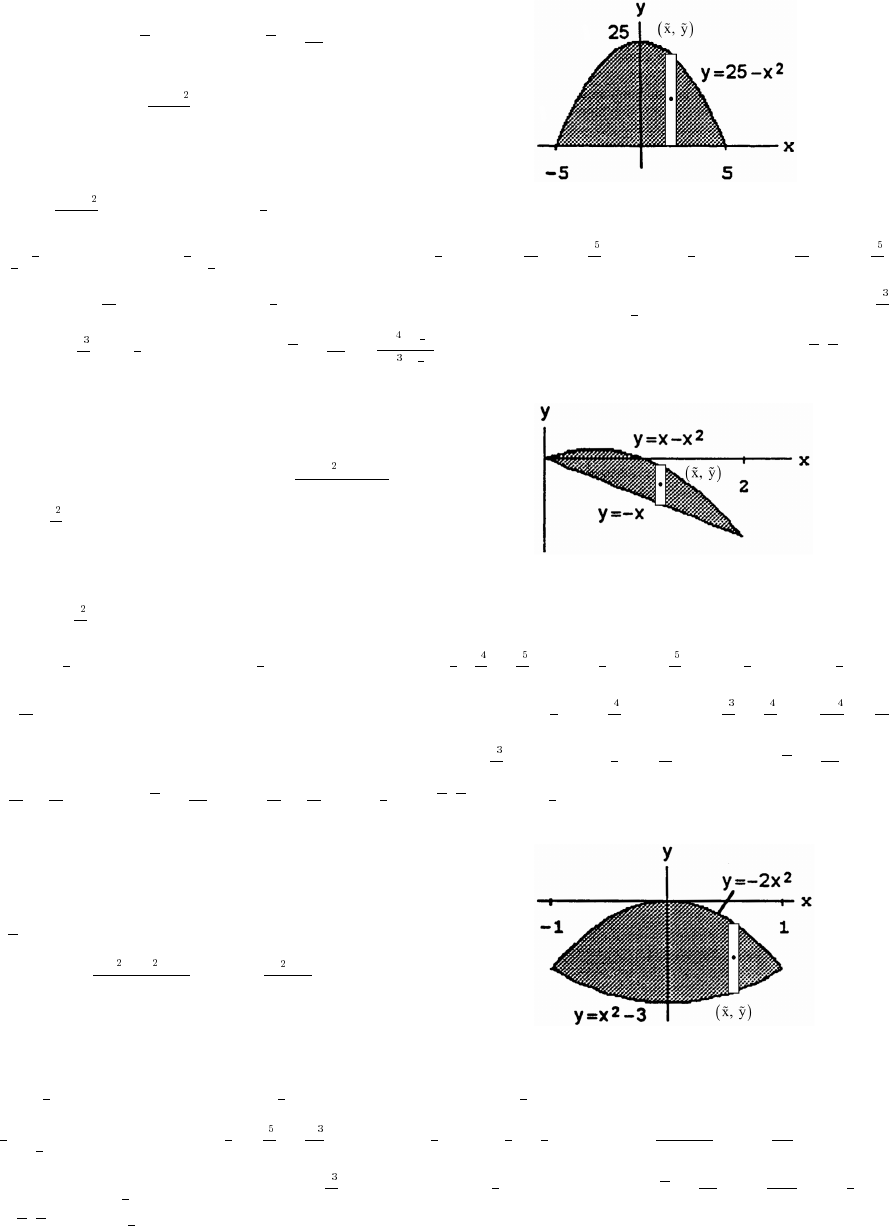
386 Chapter 6 Applications of Definite Integrals
14. Applying the symmetry argument analogous to the one in
Exercise 13, we find x 0. To find y , we use theœœ
M
M
x
strips technique. The typical strip has center of@/<>3-+6
mass: ( x y ) x , length: 25 x , width: dx,
µµ
ßœß
Š‹
25 x
#
#
area: dA 25 x dx, mass: dm dA 25 x dx.œ œ œ ab ab
##
$$
The moment of the strip about the x-axis is
y dm 25 x dx 25 x dx. The moment of the plate about the x-axis is M y dm
µ µ
œœ œ
Š‹
abab
25 x
##
##
#
$$
x'
25 x dx 625 50x x dx 625x x 2 625 5 5œœ œœ
''
55
55
$$ $ $
## # #
##%$ $
#&
&
ab a b’“Š ‹
50 x 50 5
35 3 5
†††
625 5 1 625 . The mass of the plate is M dm 25 x dx 25xœœ œœœ$$ $$†††
ˆ‰ ˆ‰ ab’“
10 8 x
33 3
''5
5#&
&
2 5 5 . Therefore y 10. The plate's center of mass is the point (x y) ( 10).œœ œœ œ ßœ!ß$$
Š‹
$$
54
33 M
M
†x$
$
††
††
5
5
ˆ‰
ˆ‰
8
3
4
3
15. Intersection points: x x x 2x x 0œÊ œ
##
x(2 x) 0 x 0 or x 2. The typical Ê œ Ê œ œ @/<>3-+6
strip has center of mass: ( x y ) x
µµ
ßœß
Š‹
abx x ( x)
#
x , length: x x ( x) 2x x , width: dx,œß œ
Š‹ ab
x
#
##
area: dA 2x x dx, mass: dm dA 2x x dx.œ œ œ ab ab
##
$$
The moment of the strip about the x-axis is
y dm 2x x dx; about the y-axis it is x dm x 2x x dx. Thus, M y dm
µµµ
œ œ œ
Š‹
ab ab
x
#
##
$$†x'
x 2x x dx 2x x dx 2 2 1œ œ œ œ œ
''
00
22
ˆ‰ ˆ‰
ab a b ’“ Š‹
$$$$$
######
## $% $ $
#
!
xx 2 4
55 5
†
; M x dm x 2x x dx 2x x x 2 ;œ œ œ œ œ œ œ œ
µ
42x 22 24
534 3413
$$$
y00
22
'''
††$$ $$ab a b
’“Š ‹
##$$
#
!#
†
M dm 2x x dx 2x x dx x 4 . Therefore, xœœ œ œœœ œ
'''
00
22
$$ $$ab ab’“
ˆ‰
###
#
!
x84
333 M
M
$y
1 and y (x y) 1 is the center of mass.œœœœœÊßœß
ˆ‰ˆ‰ ˆ ‰ˆ‰ ˆ ‰
43 43 3 3
34 M 54 5 5
M
$$
$$
x
16. Intersection points: x 3 2x 3x 3 0
###
œ Ê œ
3(x 1)(x 1) 0 x 1 or x 1. Applying theʜʜ œ
symmetry argument analogous to the one in Exercise 13, we
find x 0. The typical strip has center of mass:œ @/<>3-+6
(x y ) x x ,
µµ
ßœß œß
Š‹Š‹
##
2x x 3 x 3
ab
length: 2x x 3 3 1 x , width: dx, œ
## #
abab
area: dA 3 1 x dx, mass: dm dA 3 1 x dx.œ œ œ ab ab
##
$$
The moment of the strip about the x-axis is
y dm x 3 1 x dx x 3x x 3 dx x 2x 3 dx; M y dm
µ µ
œ œ œ œ
33 3
## #
## %## %#
$$ $abab a b a b
x'
x 2x 3 dx 3x 2 3 3 ;œœœ œ œ
3 3 x 2x 3 2 3 10 45 32
53 53 15 5###
%# "
"
"
$$$$
'1
1ab
’“ˆ‰ˆ‰
††
$
M dm 3 1 x dx 3 x 3 2 1 4 . Therefore, yœœ œœ œ œœœ
'$$$$
'1
1ab ’“ ˆ‰
#"
"
"x32 8
33 M545
M
†x$
$
†
††
(x y) 0 is the center of mass.Êßœß
ˆ‰
8
5
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
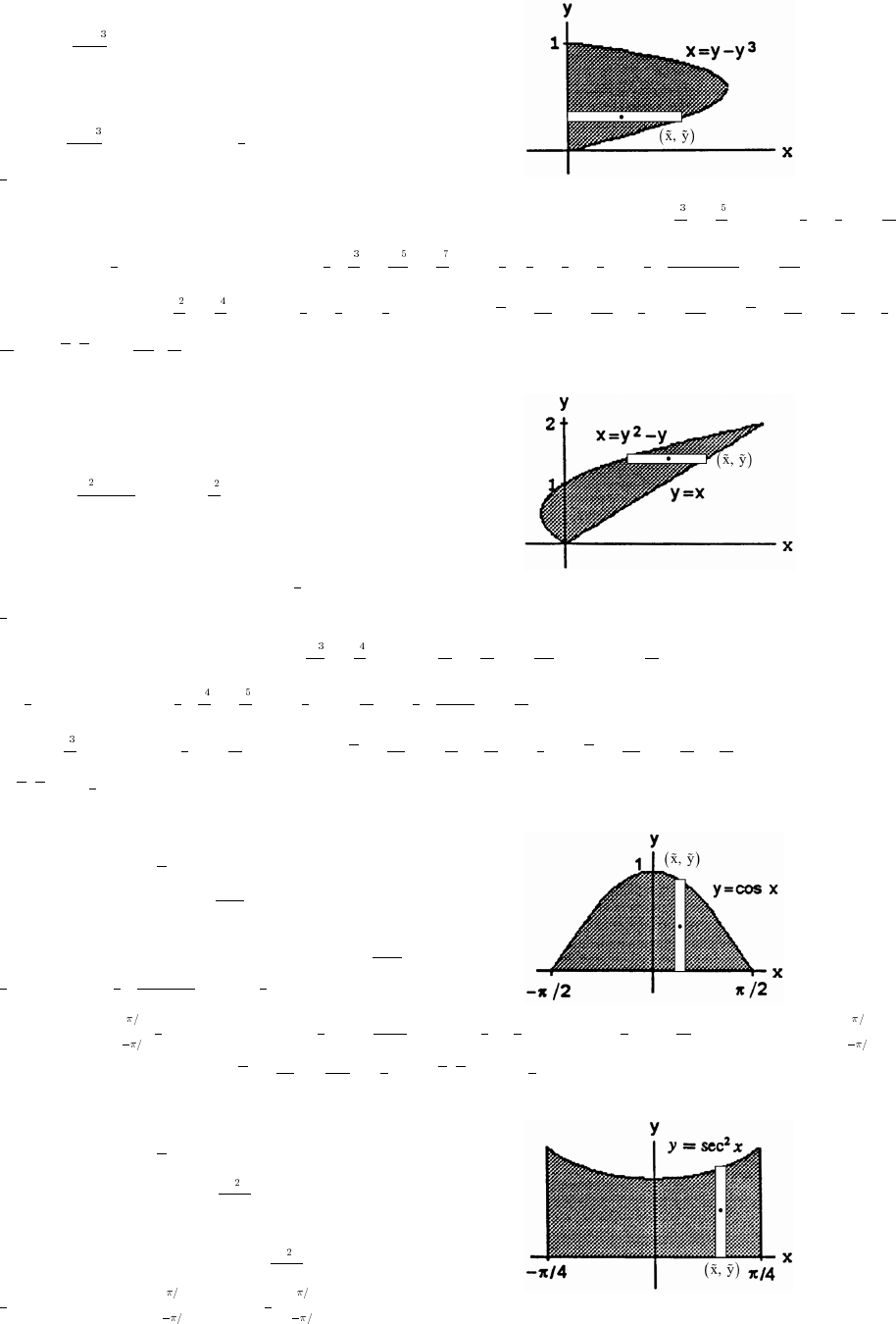
Section 6.4 Moments and Centers of Mass 387
17. The typical strip has center of mass:29<3D98>+6
( x y ) y , length: y y , width: dy,
µµ
ßœ ß
Š‹
yy
#
$
area: dA y y dy, mass: dm dA y y dy.œ œ œ ab ab
$$
$$
The moment of the strip about the y-axis is
x dm y y dy y y dy
µœœ$Š‹
ab ab
yy
##
$$
#
$
y 2y y dy; the moment about the x-axis isœ
$
#
#%'
ab
y dm y y y dy y y dy. Thus, M y dm y y dy ;
µµ
œ œ œ œ œœœ$$ $ $$abab ab’“
ˆ‰
$#% #% "
!
""
x0
1
''yy
35 35 15
2$
M x dm y 2y y dy ; M dm
y0
1
œœœœœ œœ
µ
' '
$$$$$
####
#%' "
!
""
'ab
’“
ˆ‰ˆ‰
y2yy
357 357 357 105
2 354215 4
††
y y dy . Therefore, x and yœœœœ œœ œ œœ$$$
'0
1ab ’“
ˆ ‰ ˆ ‰ˆ‰ ˆ ‰ˆ‰
$
##
"
!
""
yy
4 4 4 M 105 105 M 15
M44 16 24
M
$$ $
$$
yx
(x y) is the center of mass.œÊßœ ß
8168
15 105 15
ˆ‰
18. Intersection points: y y y y 2y 0œÊ œ
##
y(y 2) 0 y 0 or y 2. The typicalʜʜ œ
strip has center of mass:29<3D98>+6
(x y ) y y ,
µµ
ßœ ßœß
Š‹Š‹
abyyy
2
y
#
length: y y y 2y y , width: dy,œab
##
area: dA 2y y dy, mass: dm dA 2y y dy.œ œ œ ab ab
##
$$
The moment about the y-axis is x dm y 2y y dy
µœ
$
#
##
†ab
2y y dy; the moment about the x-axis is y dm y 2y y dy 2y y dy. Thus,œ œœ
µ
$
#
$% ##$
ab abab$$
M y dm 2y y dy (4 3) ; M x dm
x y
0
2
œœ œœœœœ
µ µ
''
'$$$ab’“
ˆ‰
#$ #
!#
2y y
34 34 1 3
16 16 16 4
$$
2y y dy 8 ; M dm 2y y dyœœœœ œœœ
''
0 0
2 2
$$$$$
####
$% #
#
!
ab ab
’“
ˆ‰ˆ‰
yy
25 5 5 5
32 40 32 4 '$
y 4 . Therefore, x and y 1œœœ œœ œ œœ œ$$
’“
ˆ ‰ ˆ‰ˆ‰ ˆ‰ˆ‰
##
!
y
3 3 3 M 54 5 M 34
84 43 3 43
MM
$$ $
$$
yx
(x y) is the center of mass.Êßœß"
ˆ‰
3
5
19. Applying the symmetry argument analogous to the one used
in Exercise 13, we find x 0. The typical strip hasœ @/<>3-+6
center of mass: ( x y ) x , length: cos x, width: dx,
µµ
ßœß
ˆ‰
cos x
#
area: dA cos x dx, mass: dm dA cos x dx. Theœœœ$$
moment of the strip about the x-axis is y dm cos x dx
µœ$††
cos x
#
cos x dx dx (1 cos 2x) dx; thus,œœ œ
$$ $
###
#
ˆ‰
1 cos 2x
4
M y dm (1 cos 2x) dx x 0 ; M dm cos x dx
x2 2
2 2
œœ œ œœœœ
µ
''
''
$$ $11$1
1
1
44 4 4
sin 2x
‘ ‘ˆ‰ˆ‰
###
Î#
Î# $
[sin x] 2 . Therefore, y (x y) is the center of mass.œœ œœœÊßœ!ß$$
1
1
$1 1 1
$
Î#
Î# #
M
M4 8 8
x
†ˆ‰
20. Applying the symmetry argument analogous to the one used
in Exercise 13, we find x 0. The typical vertical strip hasœ
center of mass: ( x y ) x , length: sec x, width: dx,
µµ
ßœß
Š‹
sec x
#
#
area: dA sec x dx, mass: dm dA sec x dx. Theœœœ
##
$$
moment about the x-axis is y dm sec x dx
µœŠ‹
ab
sec x
#
#
$
sec x dx. M y dm sec x dxœœœ
µ
$$
##
%%
x44
44
''
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
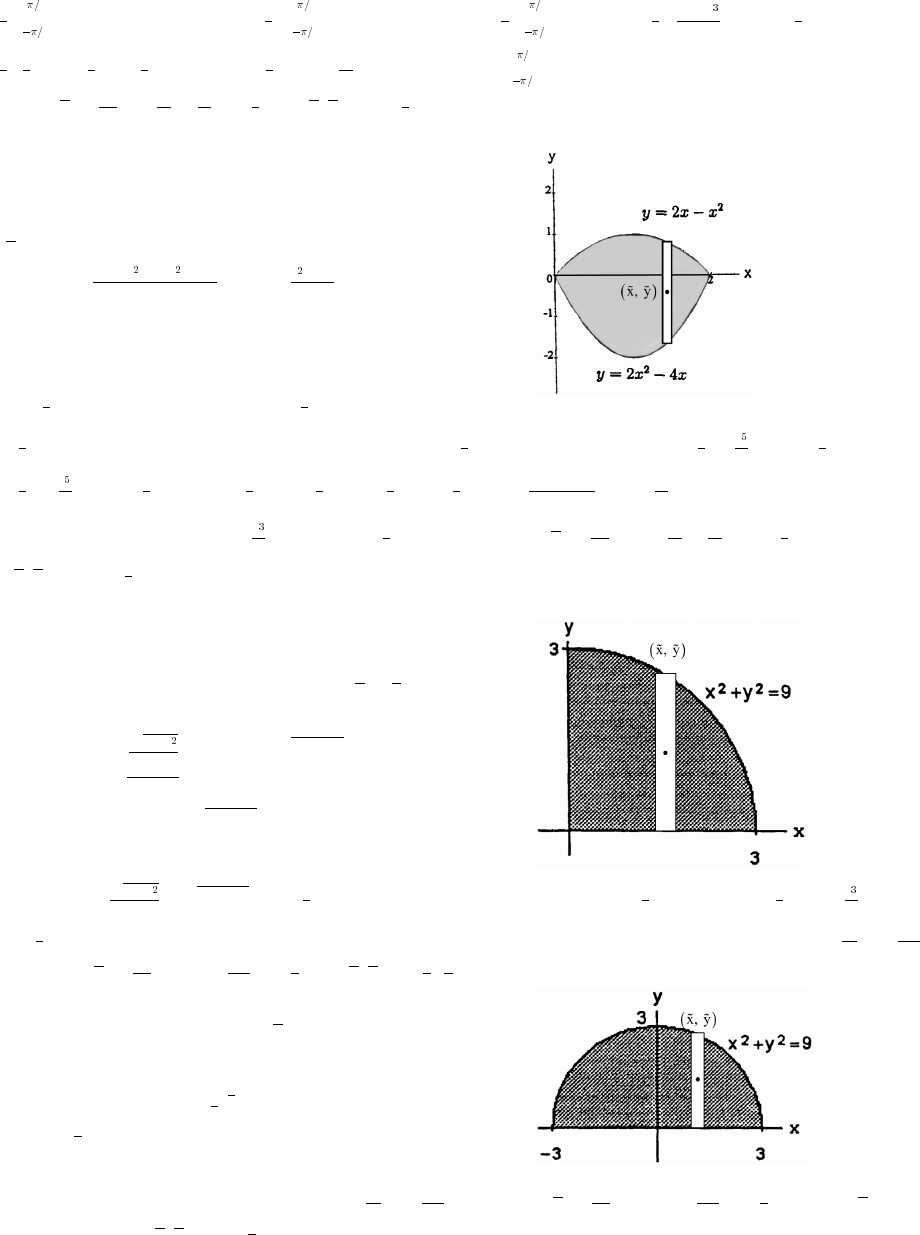
388 Chapter 6 Applications of Definite Integrals
tan x 1 sec x dx (tan x) sec x dx sec x dx [tan x]œ œ œ
$$$$$
1
1
1
1
### #
## ## # Î
Î
Î%
Î%
'''
444
444
a bab ab ’“
23
(tan x) 4
4
[1 ( 1)] ; M dm sec x dx [tan x] [1 ( 1)] 2 .œœœ œ œ œ œœ
$$$$ 1
1
23 3 3 3
44
4
‘ˆ‰
""
#
#Î
Î
$$$$$
''4
4
Therefore, y (x y) is the center of mass.œœ œÊßœ!ß
M
M323 3
42 2
xˆ‰ˆ‰ ˆ ‰
$
$
"
21. Since the plate is symmetric about the line x 1 and itsœ
density is constant, the distribution of mass is symmetric
about this line and the center of mass lies on it. This means
that x 1. The typical strip has center of mass:œ @/<>3-+6
(x y ) x x ,
µµ
ßœß œß
Š‹Š‹
aba b2x x 2x 4x x2x
##
length: 2x x 2x 4x 3x 6x 3 2x x ,aba b ab œœ
## # #
width: dx, area: dA 3 2x x dx, mass: dm dAœ œab
#$
3 2x x dx. The moment about the x-axis isœ$ab
#
y dm x 2x 2x x dx x 2x dx
µœ œ
33
##
## #
#
$$abab ab
x 4x 4x dx. Thus, M y dm x 4x 4x dx x xœ œ œ œ
µ
333x4
2253#
%$# %$# % $
#
!
$$$ab ab
’“
x0
2
''
22 21 2 ; Mdmœ œ œ œ œ
3 2 4 3 2 2 3 6 15 10 8
25 3 5 3 15 5
$$$
Š‹
ˆ‰ ˆ‰
%$ % %
##
†† †
$'
3 2x x dx 3 x 3 4 4 . Therefore, yœœœœ œœœ
'0
2
$$$$ab ’“ˆ‰ ˆ‰ˆ‰
##
#
!
"x8 82
33 M545
Mx$
$
(x y) 1 is the center of mass.Êßœß
ˆ‰
2
5
22. (a) Since the plate is symmetric about the line x y andœ
its density is constant, the distribution of mass is
symmetric about this line. This means that x y. Theœ
typical strip has center of mass:@/<>3-+6
( x y ) x , length: 9 x , width: dx,
µµ
ßœß
Š‹È
È9x
##
area: dA 9 x dx,œ
È#
mass: dm dA 9 x dx.œœ$$
È#
The moment about the x-axis is
y dm 9 x dx 9 x dx. Thus, M y dm 9 x dx 9x
µµ
œœ œœœ$Š‹ ’ “
Èab ab
È9x x
3
## ##
###
$
!
$$$
x0
3
''
(27 9) 9 ; M dm dA dA (Area of a quarter of a circle of radius 3) .œœœœœœ œœ
$11$
#$$$$ $
'' ' ˆ‰
99
44
Therefore, y (9 ) (x y) is the center of mass.œœ œÊßœß
M
M9
44 44
x$ˆ‰ ˆ ‰
1$ 1 1 1
(b) Applying the symmetry argument analogous to the one
used in Exercise 13, we find that x 0. The typicalœ
vertical strip has the same parameters as in part (a).
Thus, M y dm 9 x dx
x3
3
œœ
µ
''$
#
#
ab
9 x dx 2(9 ) 18 ;œ# œ œ
'0
3$
#
#
ab $$
M dm dA dAœœ œ
'' '
$$
(Area of a semi-circle of radius 3) . Therefore, y (18 ) , the same yœœœœœœ$$ $
ˆ‰ ˆ ‰
99 24
22 M 9
M
11$
1$ 1
x
as in part (a) (x y) 0 is the center of mass.Êßœß
ˆ‰
4
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
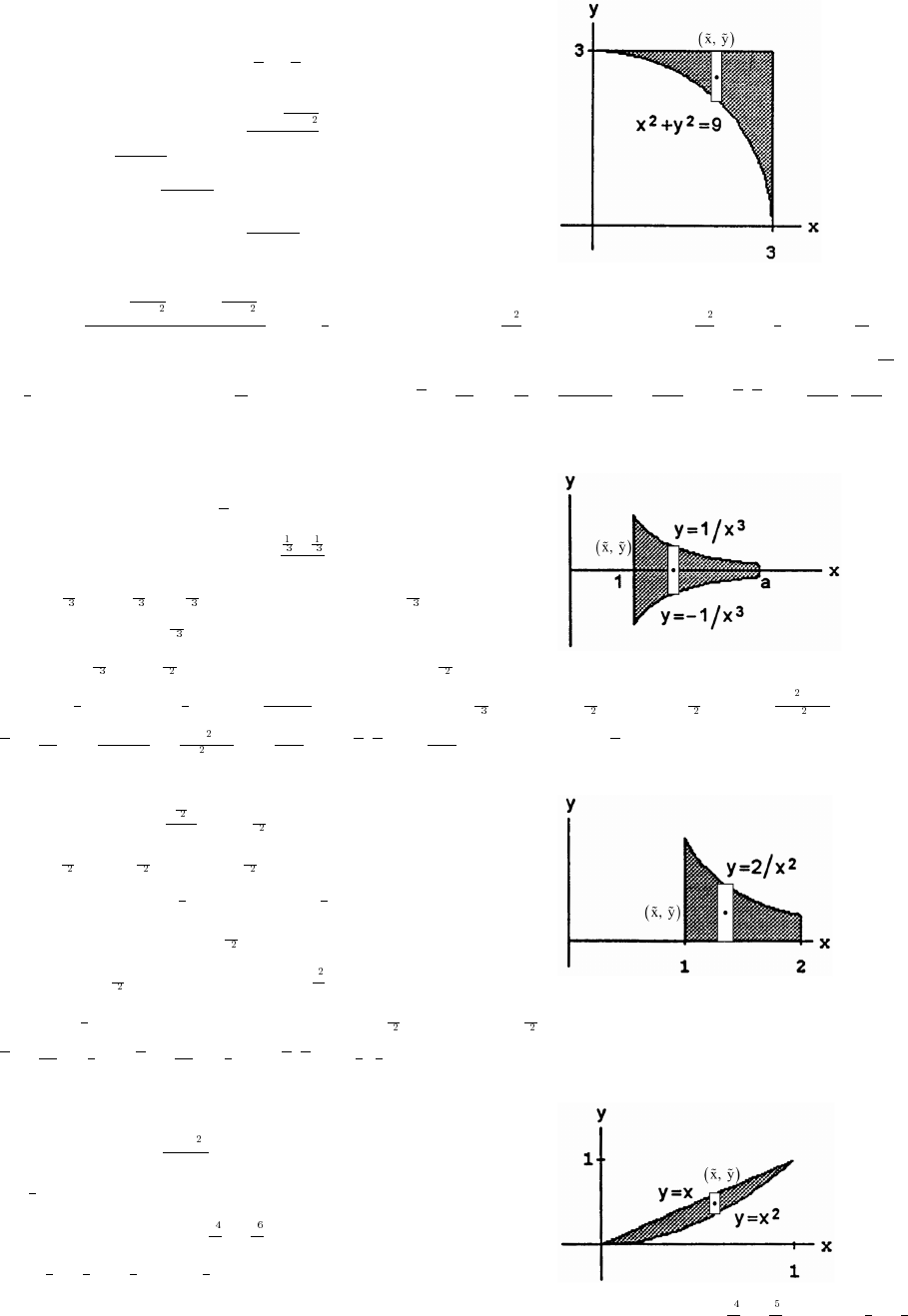
Section 6.4 Moments and Centers of Mass 389
23. Since the plate is symmetric about the line x y and itsœ
density is constant, the distribution of mass is symmetric
about this line. This means that x y. The typical œ @/<>3-+6
strip has
center of mass: ( x y ) x ,
µµ
ßœß
Š‹
39x
#
È
length: 3 9 x , width: dx,
È#
area: dA 3 9 x dx,œ
Š‹
È#
mass: dm dA 3 9 x dx.œœ$$
Š‹
È#
The moment about the x-axis is
y dm dx 9 9 x dx dx. Thus, M dx x . The area
µœœœœœœ$Š‹Š‹
ÈÈ
39x39x xx9
6
## # # #
#$
$
!
$$ $$$
cd cdab x0
3
'
equals the area of a square with side length 3 minus one quarter the area of a disk with radius 3 A 3ʜ
#19
4
(4 ) M A (4 ). Therefore, y (x y) is theœÊœœ œœ œ Êßœ ß
99 94222
44 M9(4)444
M
1$ 1
$$
$1 1 1 1
xˆ‰ ˆ ‰
’“
#
center of mass.
24. Applying the symmetry argument analogous to the one used
in Exercise 13, we find that y 0. The typical stripœ @/<>3-+6
has center of mass: ( x y ) x (x 0),
µµ
ßœß œß
Œ
xx
#
length: , width: dx, area: dA dx,
""
xxx x
22
œ œ
ˆ‰
mass: dm dA dx. The moment about the y-axis isœœ$2
x
$
x dm x dx dx. Thus, M x dm dx
µµ
œœ œœ†22 2
xx x
$$ $
y1
a
''
2 2 1 ; M dm dx 1 . Therefore,œ œ œ œ œ œ œœ$$ $$
‘ ˆ ‰ ‘ ˆ ‰
"" ""
" "
xaa xxaa
2(a 1) 2a1
a a
1
a
$$$
''ab
x (x y) 0 . Also, lim x 2.œœ œ Êßœ ß œ
M
M a a 1 a1 a1
2(a 1) a2a 2a
y’“’“ ˆ‰
$
$
ab aÄ_
25. M y dm dx
x1
2
œœ †
µ
''Š‹
2
x
#$†ˆ‰
2
x
x dx dx 2 x dxœœœ
'''
111
222
ˆ‰ ˆ‰
ab
"##
xx x
22
2 x 2 ( 1) 2 1;œ œ œ œcd ‘ˆ‰ˆ‰
" #
"""
##
M x dm x dx
y1
2
œœ
µ
''††$ˆ‰
2
x
x x dx 2 x dx 2œœœ
''
11
22
ab
ˆ‰ ’“
#
#
#
"
2x
x
2 2 4 1 3; M dm dx x dx 2 dx 2[x] 2(2 1) 2. Soœ œœ œ œ œ œ œ œ œ
ˆ ‰ ˆ‰ ˆ‰
"
#
##
"
''' '
11 1
22 2
$22
xx
x and y (x y) is the center of mass.œœ œœÊßœß
M
MM
33
M
yx
####
""
ˆ‰
26. We use the strip approach:@/<>3-+6
M y dm x x dx
x0
1
œœ
µ
''abxx
#
#
ab†$
x x 12x dxœ
"
#
#%
'0
1ab†
6 x x dx 6œœ
'0
1ab’“
$& "
!
xx
46
61;œœœ
ˆ‰
"" "
#46 4
6
M x dm x x x dx x x 12x dx 12 x x dx 12 12
y00 0
11 1
œœ œ œ œœ
µ
''' '
ab ab ab ’“ˆ‰
##$ $% "
!
""
††$xx
45 45
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
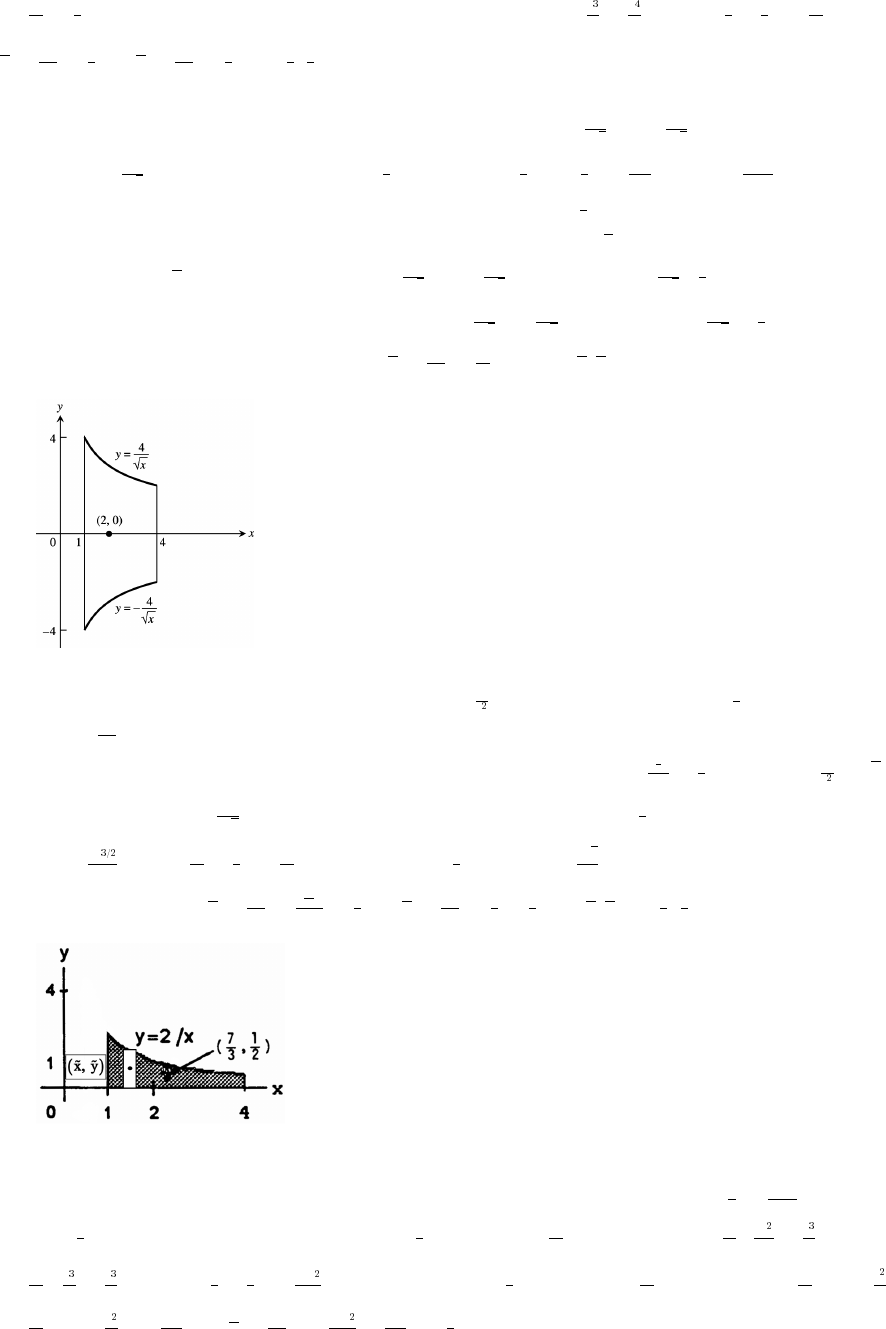
390 Chapter 6 Applications of Definite Integrals
; M dm x x dx 12 x x dx 12 12 1. Soœœ œ œ œ œ œ œœ
12 3 xx 12
05 34 34 12#
##$ "
!
""
''ab a b ’“ˆ‰
1
00
1
†$'
x and y is the center of mass.œœ œœÊß
M
M5 M 5
33
M
yx""
##
ˆ‰
27. (a) We use the shell method: V 2 dx 2 x dxœœ
''
a1
b4
11
ˆ‰
Š‹ ’ “Š‹
shell shell
radius height
44
xx
ÈÈ
16 dx 16 x dx 16 x 16 8 (8 1)œœ œœœœ11 11
''
11
44
x 2 2 2 32 224
x33333
È"Î# $Î# %
"
‘ ˆ ‰
†
11
(b) Since the plate is symmetric about the x-axis and its density (x) is a function of x alone, the$œ"
x
distribution of its mass is symmetric about the x-axis. This means that y 0. We use the vertical stripœ
approach to find x: M x dm x dx x dx 8 x dx
y111
444
œœ œ œ
µ
''''
††††
’“Š‹
44 8
xx x
x
ÈÈ È
$""Î#
8 2x 8(2 2 2) 16; M dm dx 8 dx 8 x dxœœœœœ œ œ
‘ ˆ‰
’“ Š‹Š‹
"Î# $Î#
%
"
""
††
''''
111
444
44
xx x
x
ÈÈ È
$
8 2x 8[ 1 ( 2)] 8. So x 2 (x y) (2 0) is the center of mass.œ œ œ œ œ œ Ê ß œß
‘
"Î# %
"
M
M8
16
y
(c)
28. (a) We use the disk method: V R (x) dx dx 4 x dx 4œœœœ
'' '
a1 1
b4 4
1111
##
"%
"
ˆ‰ ‘
4
xx
4 ( 1) [ 1 4] 3œœœ111
‘
"
4
(b) We model the distribution of mass with vertical strips: M y dm dx x dx
x11
44
œœ œ
µ
'''
ˆ‰
2
x
2x x
22
†† †
ˆ‰ È
$
2 x dx 2 2[ 1 ( 2)] 2; M x dm x dx 2 x dxœœœœœœ œ
µ
'''
111
444
y
$Î# "Î#
%
"
’“
22
xx
È'††$
2 2 ; M dm dx 2 dx 2 x dx 2 2xœœœœœ œ œ œ
’“ ‘ ‘
2x 16 2 28 2
3333 x x
x
%
"
"Î# "Î# %
"
''''
111
444
†$È
2(4 2) 4. So x and y (x y) is the center of mass.œœ œœ œ œœœÊßœß
M
M43 M4 3
72 7
M
y28
3x
ˆ‰ ""
##
ˆ‰
(c)
29. The mass of a horizontal strip is dm dA L dy, where L is the width of the triangle at a distance of y aboveœœ$$
its base on the x-axis as shown in the figure in the text. Also, by similar triangles we have L
bh
hy
œ
L (h y). Thus, M y dm y (h y) dy hy y dyÊœ œ œ œ œ
µ
bbbb
hhhh3
hy y
x00
hh h
'''
$ˆ‰ ab ’“
$$
#
#!
bh ; M dm (h y) dy h y dy hyœœ œ œœ œ œ
$$ $$bh h bh b b b
h3 36 h h h2
y
Š‹ ’“
ˆ‰ ˆ‰ ab
##
#""
!
$$
'''
00
hh h
h . So y the center of mass lies above the base of theœœ œœ œÊ
$$ $
$
b h bh bh 2 h
h22 M6bh3
M
Š‹ Š‹
ˆ‰
#x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
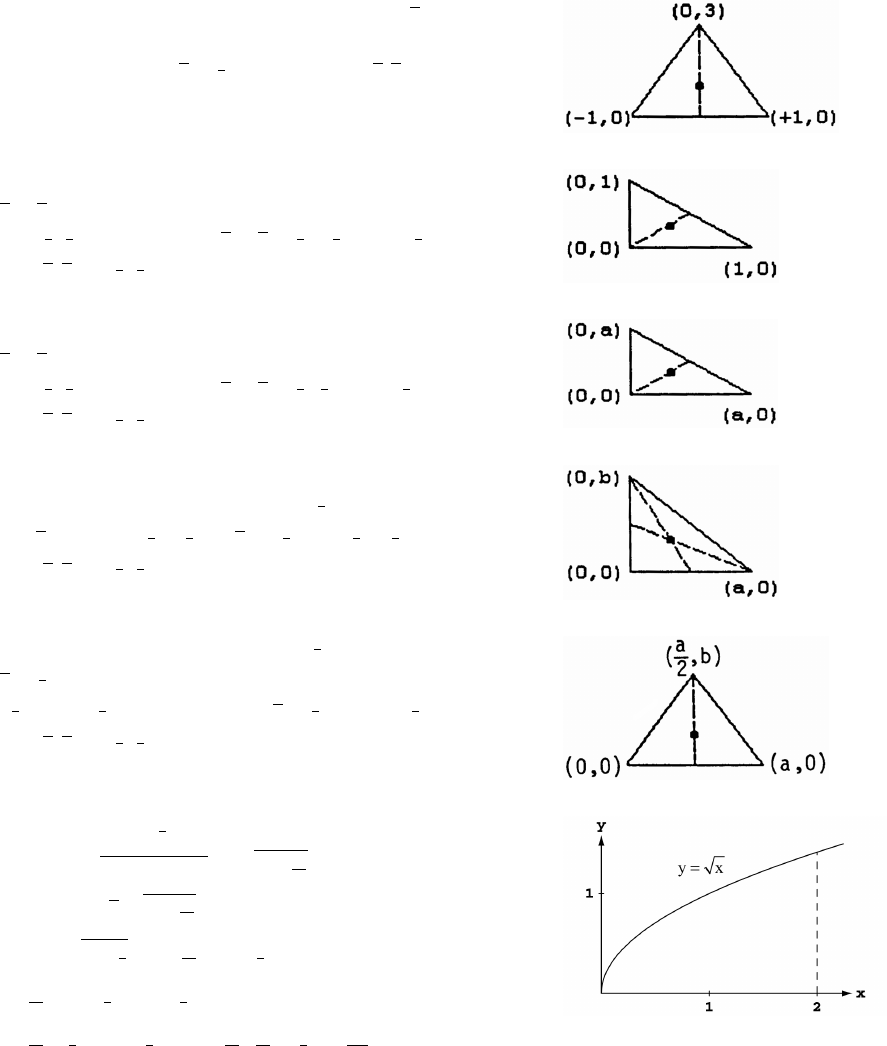
Section 6.4 Moments and Centers of Mass 391
triangle one-third of the way toward the opposite vertex. Similarly the other two sides of the triangle can be
placed on the x-axis and the same results will occur. Therefore the centroid does lie at the intersection of the
medians, as claimed.
30. From the symmetry about the y-axis it follows that x 0.œ
It also follows that the line through the points ( ) and!ß !
( ) is a median y (3 0) 1 (x y) ( ).!ß $ Ê œ œ Ê ß œ !ß "
"
3
31. From the symmetry about the line x y it follows thatœ
x y. It also follows that the line through the points ( )œ!ß!
and is a median y x 0
ˆ‰ ˆ ‰
"" " "
## #
ßÊœœœ
2
33
†
(x y) .Êßœß
ˆ‰
""
33
32. From the symmetry about the line x y it follows thatœ
x y. It also follows that the line through the point ( )œ!ß!
and is a median y x 0 a
ˆ‰ ˆ ‰
aa 2 a
33## #
"
ßÊœœœ
(x y) .Êßœß
ˆ‰
aa
33
33. The point of intersection of the median from the vertex (0 b)ß
to the opposite side has coordinates ˆ‰
!ß a
#
y (b 0) and xÊœ œ œ ! œ††
"
#33 33
ba2a
ˆ‰
(x y) .Êßœß
ˆ‰
ab
33
34. From the symmetry about the line x it follows thatœa
#
x . It also follows that the line through the pointsœa
#
and b is a median y (b 0)
ˆ‰ ˆ‰
aa b
33##
"
ß! ß Ê œ œ
(x y) .Êßœß
ˆ‰
ab
3#
35. y x dy x dxœÊœ
"Î# "Î#
"
#
ds (dx) (dy) 1 dx ;Êœ œ
ÈÉ
## "
4x
Mx1 dx
x0
2
œ$'ÈÉ"
4x
x dx xœœ$'0
2É’“
ˆ‰
""
$Î# #
!
43 4
2$
2œ
2
34 4
$’“
ˆ‰ˆ‰
""
$Î# $Î#
œœœ
29 227 13
34 4 38 8 6
$$$
’“
ˆ‰ ˆ‰ ˆ ‰
$Î# ""
$Î#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
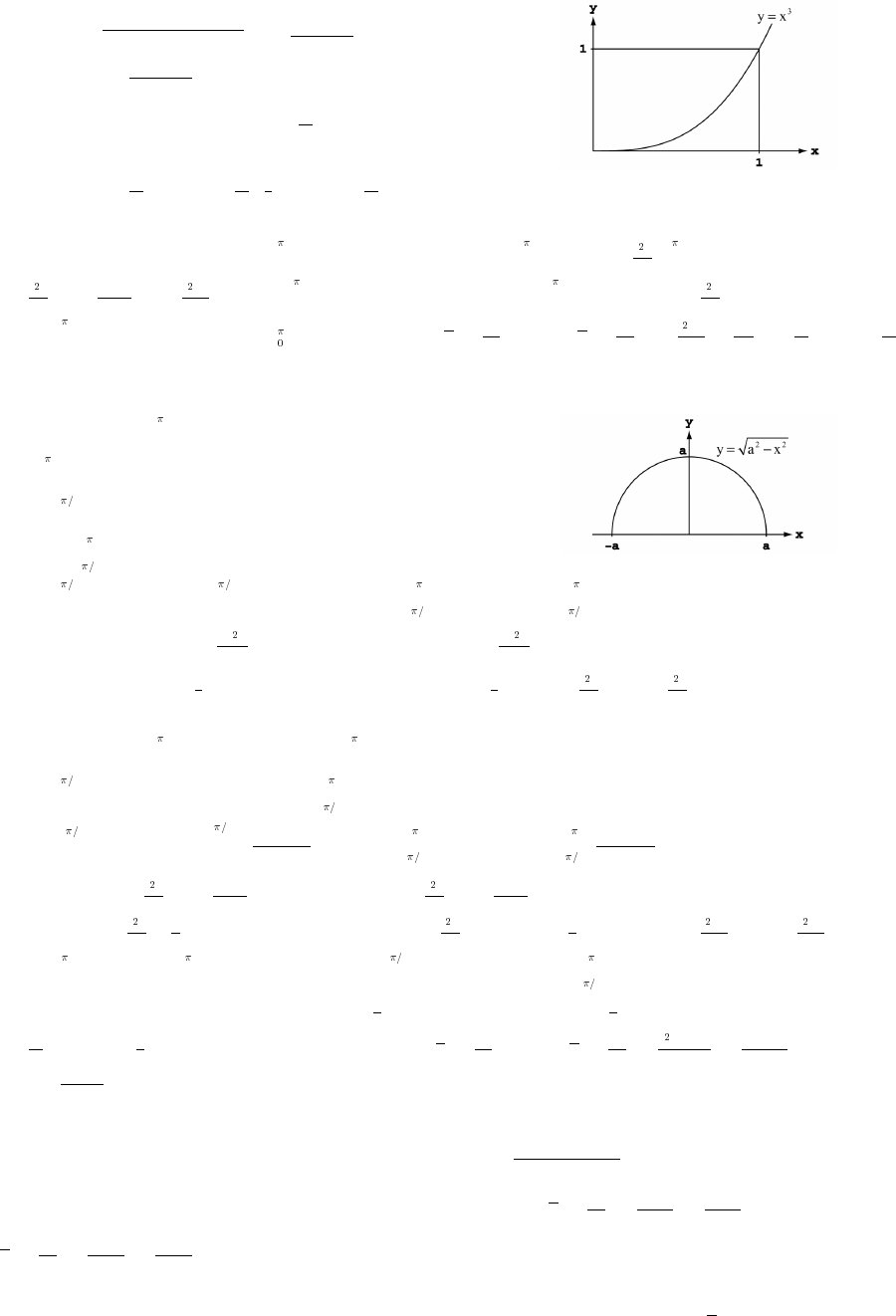
392 Chapter 6 Applications of Definite Integrals
36. y x dy 3x dxœÊœ
$#
dx (dx) 3x dx 1 9x dx;Êœ œ
Éab
È
## %
#
M x 1 9x dx;
x0
1
œ$'$%
È
[u 1 9x du 36x dx du x dx;œ Ê œ Ê œ
%$ $
"
36
x 0 u 1, x 1 u 10]œÊœ œÊœ
M u du u 10 1Äœ œ œ
x1
10
$'""Î# $Î# $Î#
"!
"
36 36 3 54
2$$
‘ ˆ ‰
37. From Example 6 we have M a(a sin )(k sin ) d a k sin d (1 cos 2 ) d
x000
œœœ
'''
))) )) ))
##
#
ak
; M a(a cos )(k sin ) d a k sin cos d sin 0;œ œ œ œ œ œ
ak sin 2 ak ak
## # #
!
##
!
‘ cd))))))))
)1
11
y00
''
M ak sin d ak[ cos ] 2ak. Therefore, x 0 and y œœœ œœœœœÊ!ß
'0
)) ) M
MM22ak44
Mak a a
yxŠ‹
ˆ‰ ˆ ‰
111"
is the center of mass.
38. M y dm (a sin ) a d
x0
œœ
µ
'')$ )††
a sin 1 k cos dœ
'0aba bkk
#)))
a (sin )(1 k cos ) dœ
#'0
2
)))
a (sin )(1 k cos ) d
#'2
)))
a sin d a k sin cos d a sin d a k sin cos dœ
## ##
'' ''
00 22
22
)) ) )) )) ) ))
a [ cos ] ak a[ cos ] akœ
####
Î#
!##
Î#
!Î#
Î#
))
1))
11
1
11
’“ ’“
sin sin
a[0(1)]ak 0 a[(1)0]ak0 a aœ œ
### ###
""
####
ˆ‰ ˆ‰ ak ak
2a ak a(2 k);œœ
## #
M x dm (a cos ) a d a cos 1 k cos d
y00
œœ œ
µ
'''
)$ ) ) ) )†† aba bkk
#
a (cos )(1 k cos ) d a (cos )(1 k cos ) dœ
##
''
02
2
))) )))
a cos dak da cos dak dœ
## ##
##
'''
022
22
0
)) ) )) )
'ˆ‰ ˆ‰
1cos 2 1cos 2))
a [sin ] a [sin ]œ
##
Î#
!## ##
Î#
!Î#
Î#
)) ))
1))
11
1
11
ak sin 2 ak sin 2
‘ ‘
a (1 0) 0 ( 0) a (0 1) ( 0) 0 a a 0;œ ! œ œ
## ##
## # #
ak ak ak ak
44
‘‘ˆ‰ ˆ‰
1111
1
M a d a (1 k cos ) d a (1 k cos ) d a (1 k cos ) dœœ œ
'' ' '
00 0 2
2
$ ) ) ) )) ))†kk
a[ k sin ] a[ k sin ] a k 0 a ( 0) kœ œ )) )) 1
11
1
11
Î#
!Î# ##
‘ ‘ˆ‰ ˆ‰
ak a k a 2ak a( 2k). So x 0 and yœ œ œ œ œ œ œ œ
aM
MMa(k)k
Ma(2 k) a(2 k)
11
11## # #
ˆ‰
11 yx
0 is the center of mass.Êß
ˆ‰
2a ka
k
#1
39. Consider the curve as an infinite number of line segments joined together. From the derivation of arc
length we have that the length of a particular segment is ds (dx) (dy) . This implies thatœ
È##
M y ds, M x ds and M ds. If is constant, then x and
xy
œœ œ œœœ
'' '
$$ $$ M
M length
x ds x ds
ds
y''
'
y.œœ œ
M
M length
y ds y ds
ds
x''
'
40. Applying the symmetry argument analogous to the one used in Exercise 13, we find that x 0. The typicalœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
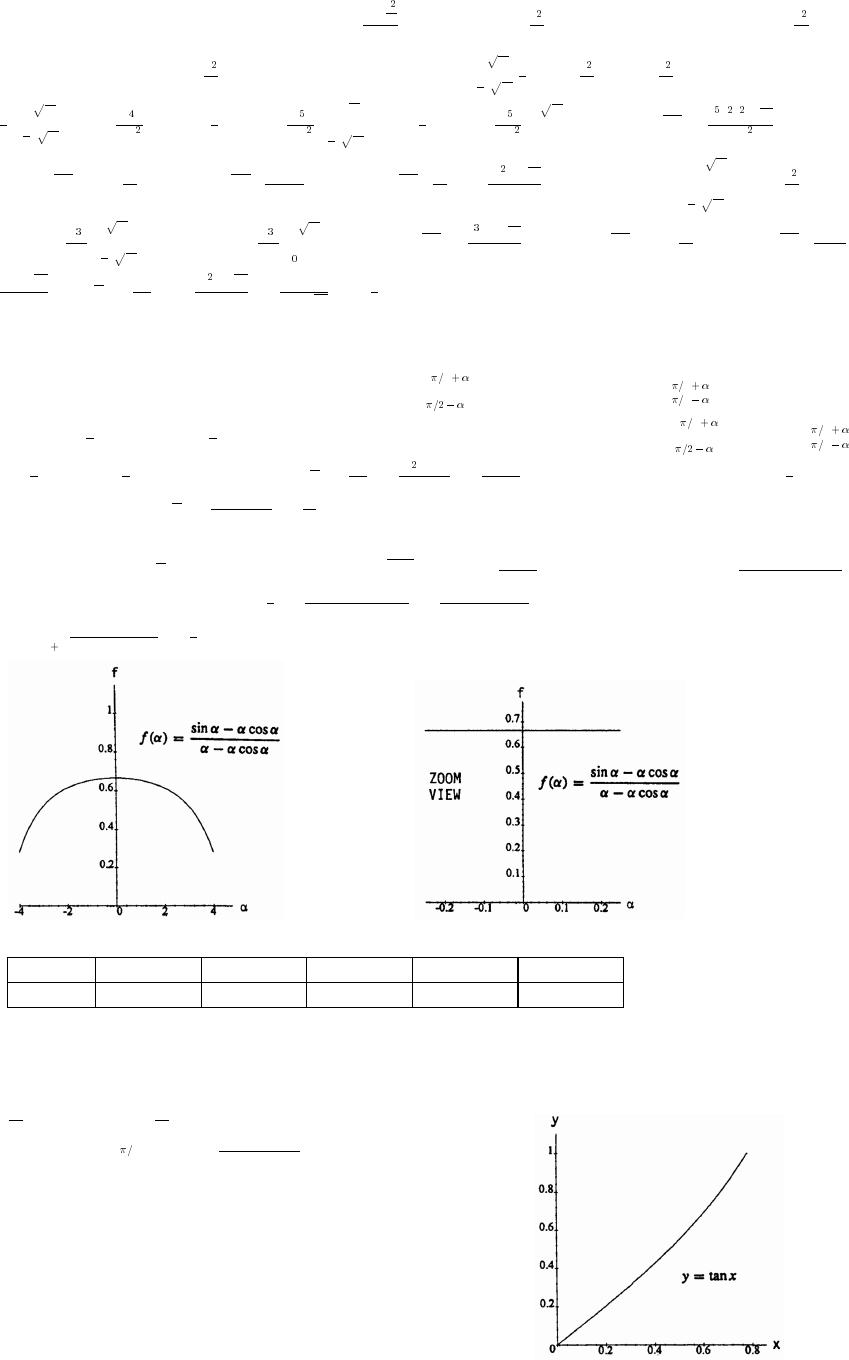
Section 6.5 Areas of Surfaces of Revolution and the Theorems of Pappus 393
vertical strip has center of mass: ( x y ) x , length: a , width: dx, area: dA a dx,
µµ
ßœß œ
Œ Š‹
a
24p 4p
xx
x
4p
mass: dm dA a dx. Thus, M y dm a a dxœœ œ œ
µ
$$ $
Š‹ Š‹Š‹
xxx
4p 4p 4p
x2pa
2pa
''"
#
a dx a x 2 a x 2a paœœœœ
$$$
###
## # #
#
'2pa
2pa pa 2 pa
2pa 0
Š‹’“ ’“Š ‹
È
xx x
16p 80p 80p 80p
2pa pa
ÈÈ
†$
2a pa 1 2a pa 2a pa ; M dm a dxœœ œ œœœ
###
"
$$$ $
ÈÈÈ
ˆ‰ ˆ‰ ˆ‰ 'Š‹
16 80 6 64 x
80 80 80 5 4p
8a pa
$È'
2pa
2pa
ax 2 ax 2 2a pa 4a pa 1 4a paœ œ œ œ œ$$$ $$
’“ ’“ Š ‹
ÈÈÈ
ˆ‰ ˆ‰
xx 4124
12p 12p 12p 12 1
2pa pa
2pa
2pa
2pa
†È
#
. So y a, as claimed.œœœ œ
8a pa 8a pa
3M5 5
M33
8a pa
$$
$
ÈÈ
È
xŠ‹Š‹
41. Since the density is constant, its value will not affect our answers, so we can set .$œ"
A generalization of Example 6 yields M y dm a sin d a [ cos ]
x
22
2
œœ œ
µ
''##
)) )
a cos cos a (sin sin ) 2a sin ; M dm a d a[ ]œ œ œ œ œ œ
###
##
‘ˆ‰ˆ‰
11
!!!!! ))
''22
2
a 2a . Thus, y . Now s a(2 ) and a sin œœ œœ œ œ œ
‘ˆ‰ˆ‰
11 !!
!!## #
!!! ! !
M
M2a
2a sin a sin c
x
c 2a sin . Then y , as claimed.Êœ œ œ!a(2a sin )
2a s
ac
!
!
42. (a) First, we note that y (distance from origin to AB) d a cos d d .œÊœÊœ
a sin a(sin cos )
!
!!
!! !
!
Moreover, h a a cos . The graphs below suggest thatœ Ê œ œ!dsin cos
h a( cos ) cos
a(sin cos )!! !
!! ! !! !
!! !
lim .
!Ä!
sin cos 2
cos 3
!! !
!! !
¸
(b) 0.2 0.4 0.6 0.8 1.0
f( ) 0.666222 0.664879 0.662615 0.659389 0.655145
!
!
6.5 AREAS OF SURFACES OF REVOLUTION AND THE THEOREMS OF PAPPUS
1. (a) sec x sec x
dy dy
dx dx
œÊ œ
#%
#
Š‹
S 2 (tan x) 1 sec x dxʜ 1'0
4È%
(c) S 3.84¸
(b)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
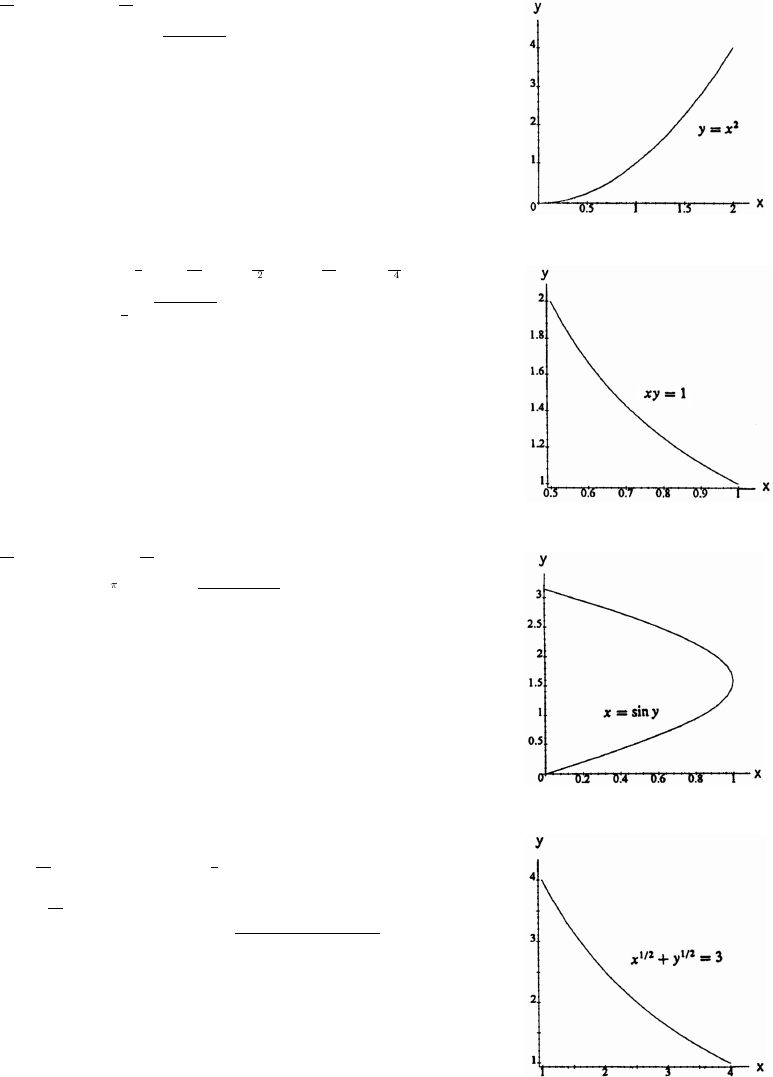
394 Chapter 6 Applications of Definite Integrals
2. (a) 2x 4x
dy dy
dx dx
2
œÊ œ
Š‹
#
S 2 x 1 4x dxʜ 1'0
2##
È
(c) S 53.23¸
(b)
3. (a) xy 1 x œÊœÊ œ Ê œ
"" "
#
ydy y dy
dx dx
y
Š‹
S 2 1 y dyʜ 1'1
2"%
yÈ
(c) S 5.02¸
(b)
4. (a) cos y cos y
dx dx
dy dy
œÊ œ
Š‹
##
S 2 (sin y) 1 cos y dyÊœ 1'0È#
(c) S 14.42¸
(b)
5. (a) x y 3 y 3 x
"Î# "Î# "Î# #
œÊœ
ˆ‰
23 x xʜ
dy
dx ˆ‰ˆ ‰
"Î# "Î#
"
#
13xʜ
Š‹ ˆ‰
dy
dx
#"Î# #
S 2 3 x 1 1 3x dxʜ 1'1
4ˆ‰
Éab
"Î# #"Î# #
(c) S 63.37¸
(b)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
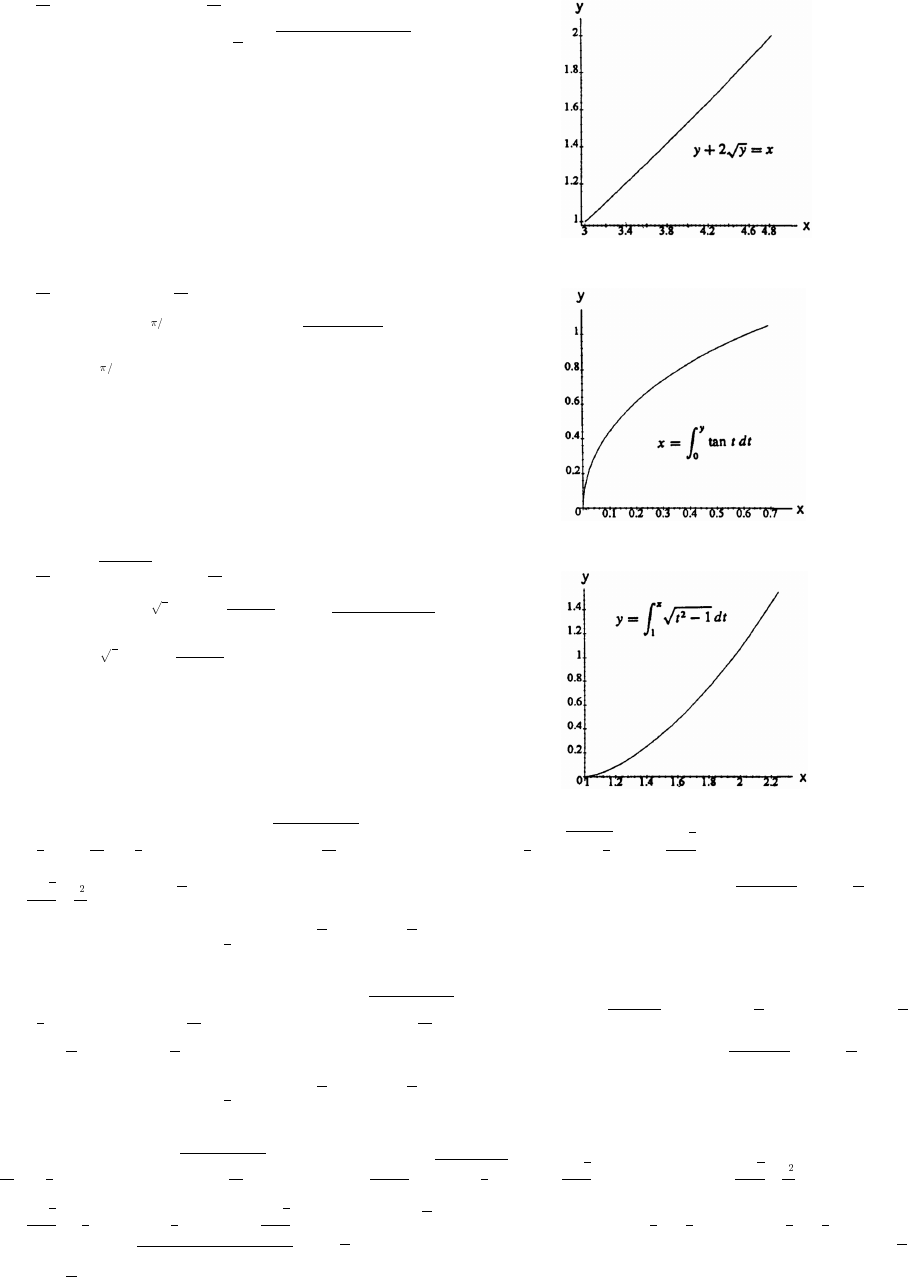
Section 6.5 Areas of Surfaces of Revolution and the Theorems of Pappus 395
6. (a) 1 y 1 y
dx dx
dy dy
œ Ê œ
"Î# "Î#
##
Š‹ ˆ‰
S 2 y2y 1 1y dxʜ 1'1
2ˆ‰
ÈÉab
"Î# #
(c) S 51.33¸
(b)
7. (a) tan y tan y
dx dx
dy dy
œÊ œ
Š‹
##
S 2 tan t dt 1 tan y dyʜ 1''
00
3y
Š‹
È#
2 tan t dt sec y dyœ1''
00
3y
Š‹
(c) S 2.08¸
(b)
8. (a) x 1 x 1
dy dy
dx dx
œÊ œ
ÈŠ‹
###
S 2 t 1 dt 1 x 1 dxʜ 1''
11
5x
Š‹
ÈÈab
##
2 t 1 dt x dxœ1''
11
5x
Š‹
È#
(c) S 8.55¸
(b)
9. y ; S 2 y 1 dx S 2 1 dx x dxœÊ œ œ Êœ œ
x x
dy dy
dx dx 4
5
## # #
" "
#
'''
a00
b44
11
ÊŠ‹ ˆ‰
É1È
4 5; Geometry formula: base circumference 2 (2), slant height 4 2 2 5œœ œ œœ
1È5x
##
%
!
##
’“ È È
È
11
Lateral surface area (4 ) 2 5 4 5 in agreement with the integral valueÊœœ
"
#11
Š‹
ÈÈ
10. y x 2y 2; S 2 x 1 dy 2 2y 1 2 dy 4 5 y dy 2 5 yœÊœ Ê œ œ œ œ œ
xdx dx
dy dy#
####
!
'' '
c0 0
d2 2
1111
ÊŠ‹ ÈÈÈ
cd†
2 5 4 8 5; Geometry formula: base circumference 2 (4), slant height 4 2 2 5œœ œ œœ11 1
ÈÈ È
È
†##
Lateral surface area (8 ) 2 5 8 5 in agreement with the integral valueÊœœ
"
#11
Š‹
ÈÈ
11. ; S 2 y 1 dx 2 1 dx (x 1) dx x
dy dy (x 1)
dx dx
55
x
œœ œ œ œ
""
######
# $
#
"
'' '
a1 1
b3 3
11
ÊŠ‹ ’ “
Ɉ‰ 11
ÈÈ
3 1 (4 2) 3 5; Geometry formula: r 1, r 2,œ œ œ œœ œœ
11
ÈÈ
55
9 3
# # # # ## ##
""" "
"#
‘ˆ‰ˆ‰ È
1
slant height (2 1) (3 1) 5 Frustum surface area (r r ) slant height (1 2) 5œœÊ œ‚ œ
ÈÈÈ
## "#
11
3 5 in agreement with the integral valueœ1È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
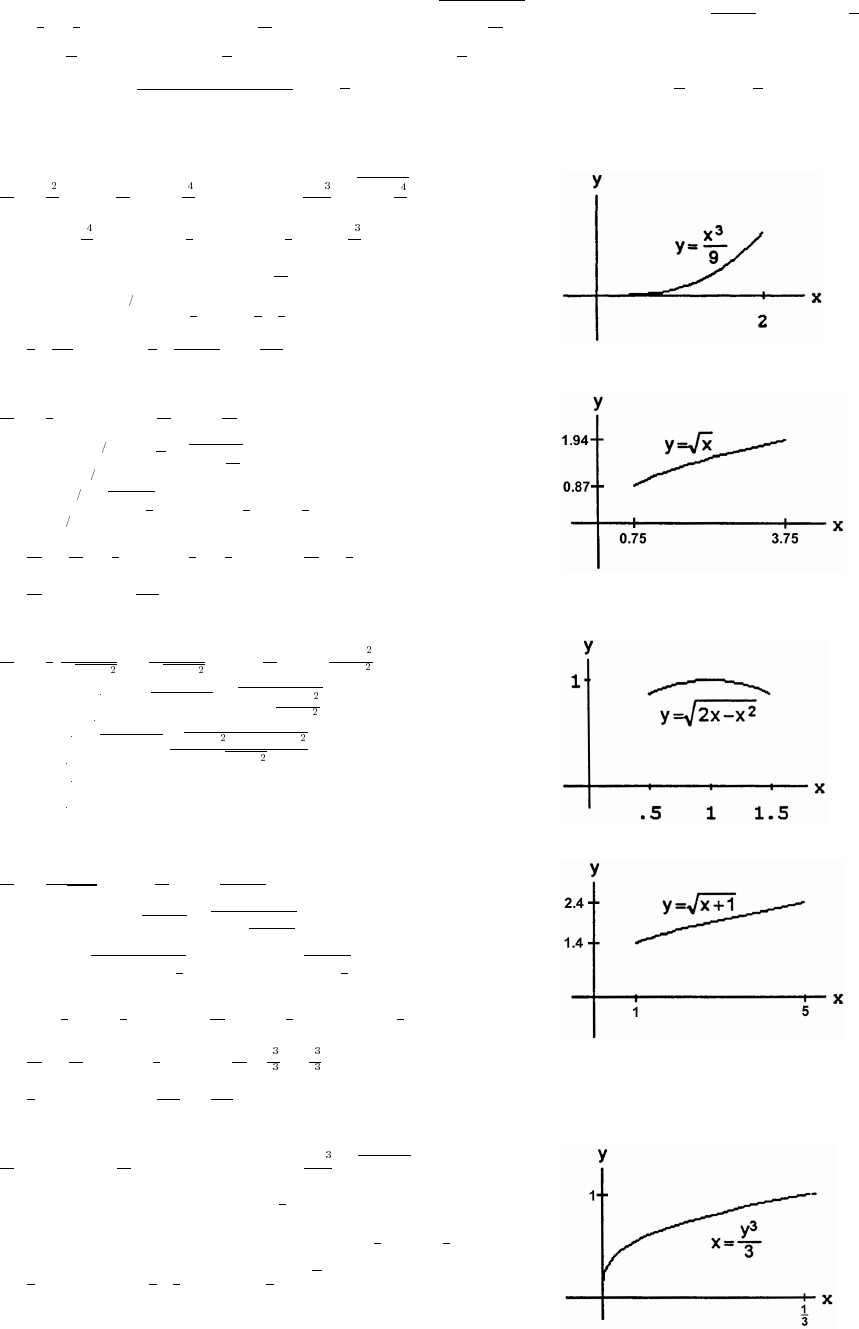
396 Chapter 6 Applications of Definite Integrals
12. y x 2y 1 2; S 2 x 1 dy 2 (2y 1) 1 4 dy 2 5 (2y 1) dyœ Ê œ Ê œ œ œ œ
xdx dx
dy dy##
"#
'' '
c1 1
d2 2
111
ÊŠ‹ ÈÈ
2 5 y y 2 5 [(4 2) (1 1)] 4 5; Geometry formula: r 1, r 3,œ œ œ œ œ11 1
ÈÈ È
cd
##
""#
slant height (2 1) (3 1) 5 Frustum surface area (1 3) 5 4 5 in agreement withœœÊ œ œ
ÈÈÈÈ
## 11
the integral value
13. S 1 dx;
dy dy
dx 3 dx 9 9 9
xx2xx
œÊ œÊœ
Š‹ É
#'0
21
u 1 du x dx du dx;
’œ Ê œ Ê œ
x4 x
9949
$"
x 0 u 1, x 2 u ‘
œÊœ œÊ œ
25
9
S 2 u du uÄœ œ1'1
25 9 "Î# $Î#
"
#
#&Î*
"
†43
21‘
1œœ œ
11 1
3 27 3 27 81
125 125 27 98
ˆ‰ˆ‰
14. x
dy dy
dx dx 4x
œÊœ
""
#
"Î# #
Š‹
S 2 x 1 dxʜ
'34
15 4
1ÈÉ"
4x
2 x dx 2 xœœ11
'34
15 4É’“
ˆ‰
""
$Î# "&Î%
$Î%
434
2
1œœ
415 3 44
344 44 32
11
’“’“
ˆ‰ˆ‰ ˆ‰
""
$Î# $Î# $
(8 1)œœ
428
33
11
15.
dy (2 2x) dy (1 x)
dx dx 2x x
2x x 2x x
1x
œœÊœ
"
#
#
ÈÈ Š‹
S 2 2x x 1 dxʜ
'05
15
1ÈÉ
#
(1 x)
2x x
2 2x x dxœ1'05
15
È#
ÈÈ
2x x 1 2x x
2x x
2dx2[x]2œœœ111
'05
15 "Þ&
!Þ&
16.
dy dy
dx dx 4(x 1)
2x1
œÊœ
""
#
ÈŠ‹
S 2 x 1 1 dxʜ
'1
5
1ÈÉ"
4(x 1)
2 (x 1) dx 2 x dxœœ11
''
11
55
ÉÉ
"
44
5
2x 5 1œœ1’“’ “
ˆ‰ ˆ‰ˆ‰
25 4 5 5
34 3 4 4
$Î# $Î# $Î#
&
"
1
œœ
425 9 453
34 4 322
11
’“Š‹
ˆ‰ ˆ‰
$Î# $Î#
(125 27)œœœ
111
663
98 49
17. y y S 1 y dy;
dx dx
dy dy 3
2y
œÊ œÊœ
#%
#%
Š‹ È
'0
11
u 1 y du 4y dy du y dy; y 0
œ Ê œ Ê œ œ
%$ $
"
4
u 1, y 1 u 2 S 2 u dudˆ‰ ˆ ‰
Êœ œÊœ Äœ
'1
2
1""
"Î#
34
u du u 8 1œœœ
111
6639
2
'1
2"Î# $Î# #
"
‘Š‹
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 6.5 Areas of Surfaces of Revolution and the Theorems of Pappus 397
18. x y y 0, when 1 y 3. To get positiveœŸ ŸŸ
ˆ‰
"$Î# "Î#
3
area, we take x y yœ
ˆ‰
"$Î# "Î#
3
y y y2yÊœ Ê œ
dx dx
dy dy 4
""
#
"Î# "Î# "
#
ˆ‰
Š‹ ab
S 2 y y 1 y 2 y dyʜ
'1
3
1ˆ‰
Éab
""
$Î# "Î# "
34
2 y y y2y dyœ 1'1
3ˆ‰
Éab
""
$Î# "Î# "
34
2 y y dy y y 1 y dy y 1 (y 1) dyœ œ œ 111
'''
111
333
ˆ ‰ ˆ‰ ˆ‰
Š‹
""""
$Î# "Î# "Î# "Î#
#333
yy
y
Éab
y y 1 dy y 3 1 3 1œ œ œ œ 111 1
'1
3ˆ‰ ‘ˆ ‰
’“
ˆ‰ˆ‰
""" ""
#$
"
3 3 9 3 9 3 93 93
2279
yy
(1813)œ œ
11
99
16
19. S 2 2 4 y 1 dy 4 (4 y) 1 dy
dx dx
dy dy 4 y 4 y
4y
œÊ œÊœ œ
" " "
#
ÈŠ‹ ÈÉÈ
''
00
15 4 15 4
11†
4 5y dy 4 (5y) 5 5 5œœœœ11
'0
15 4 È‘ ˆ‰ ˆ‰
’“’“
281585
33434
$Î# $Î# $Î#
"&Î%
!
$Î# $Î#
11
55œœ œ
88
38383
55 40555 35 5
11
1
Š‹Š‹
ÈÈÈÈÈ
20. S 2 2y 1 1 dy 2 (2y 1) 1 dy
dx dx
dy dy 2y 1 2y 1
2y 1
œÊœÊœ œ
"" "
#
ÈŠ‹ ÈÉÈ
''
58 58
11
11
2 2 y dy 2 2 y 1 1œœœœ11
'58
1ÈÈ
‘ ˆ‰
’“Š‹
"Î# $Î# $Î#
"
&Î)
$Î#
25
3383
42 42 55
88
11
ÈÈÈ
È
16 2 5 5œœ
42
312
82 2 5 5
82 2
11
ÈÈ
ÈÈ
Š‹Š ‹
ÈÈ
†
†
21. ds dx dy y 1 dy y 1 dy y dyœ œ œ œ
ÈÊŠ‹Š‹Š‹
ÊÊ
## $ ' '
"""""
#
##4y 16y 16y
y dy y dy; S 2 y ds 2 y y dy 2 y y dyœ œ œ œ œ
ÊŠ‹Š‹ Š‹ ˆ‰
$"" " "
#$$%#
4y 4y 4y 4
'' '
11 1
22 2
11 1
2 y 2 2 (8 31 5)œ œ œ œ œ11 1
’“
‘ˆ‰ˆ‰ˆ‰
y
54 58 54 58 40 20
32 31 2 253
"""""
" #
"
11
†
22. y x 2 dy x x 2 dx ds 1 2x x dx S 2 x 1 2x x dxœ Êœ Êœ Êœ
"#$Î# ##% #%
3ab a b
ÈÈÈ
1'0
2
2 x x 1 dx 2 x x 1 dx 2 x x dx 2 2 4œœœœœœ111111
'''
000
222
Éab ab ab ’“ ˆ‰
###$
#
#
!
xx 42
442
È
23. y a x a x ( 2x) œÊœ œ Ê œ
Èab Š‹
## "
#
##
"Î#
#
dy dy
dx dx a x
xx
ax
Èab
S 2 a x 1 dx 2 a x x dx 2 a dx 2 a[x]Êœ œ œ œ1111
'''
aaa
aaa
a
a
ÈÉÈab
## ## #
x
ax
ab
2 a[a ( a)] (2 a)(2a) 4 aœœ œ111
#
24. y x S 2 x 1 dx 2 x dxœÊœÊ œÊœ œ
rr r rr rhr
hdxhdxh h h hh
dy dy
Š‹ ÉÉ
#
11
''
00
hh
x dx h r h r r h rœœœœ
2r h r 2r x 2r h
hh h h
111
ÉÈÈÈ
’“ Š‹
## ## ##
##
'0
hh
0
1
25. y cos x sin x sin x S 2 (cos x) 1 sin x dxœÊœÊ œ Êœ
dy dy
dx dx
Š‹ È
###
1'2
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

398 Chapter 6 Applications of Definite Integrals
26. y 1 x 1 x x 1œ Ê œ œ Ê œ œ
ˆ‰ ˆ‰ˆ ‰ Š‹
#Î$ #Î$ "Î$
$Î# "Î#
#
#"
dy dy
dx 3 dx
32 1x
1x
xxx
ˆ‰
S 2 2 1 x 1 1 dx 4 1 x x dxÊœ œ
''
0 0
1 1
11
ˆ‰ ˆ‰ ˆ‰
ÉÈ
#Î$ #Î$
$Î# $Î#
"#Î$
x
4 1 x x dx; u 1 x du x dx du x dx; œ œÊœ Êœ1'0
1ˆ‰
#Î$ "Î$ #Î$ "Î$ "Î$
$Î# 23
32
x 0 u 1, x 1 u 0 S 4 u du 6 u 6 0dˆ‰ ‘ ˆ‰
œÊœ œÊœ Äœ œ œ œ111
'1
0$Î# &Î#
#
!
"
32 212
555
1
27. The area of the surface of one wok is S 2 x 1 dy. Now, x y 16 x 16 yœ œÊœ
'c
d
1ÊŠ‹ È
dx
dy
### # ##
; S 2 16 y 1 dy 2 16 y y dyÊœ Ê œ œ œ
dx dx
dy dy 16 y 16 y
yy y
16 y
#
## ## #
ÈŠ‹ ÈÉÈab
''
16 16
77
11
2 16 dy 32 9 288 904.78 cm . The enamel needed to cover one surface of one wok isœœœ¸111
'16
7
†#
V S 0.5 mm S 0.05 cm (904.78)(0.05) cm 45.24 cm . For 5000 woks, we needœœ œ œ†† $$
5000 V 5000 45.24 cm (5)(45.24)L 226.2L 226.2 liters of each color are needed.††œœœÊ
$
28. y r x ; S 2 r x 1 dxœÊœ œ Ê œ œ
ÈÈ
Š‹ É
## ##
"
#
#
dy
dx dy r x r x
2x x dx x x
rx rx
ÈÈ 1'a
ah
2 r x x dx 2 r dx 2 rh, which is independent of a.œœœ111
''
aa
ah ah
Èab
## #
29. y R x ; S 2 R x 1 dxœÊœ œ Ê œ œ
ÈÈ
Š‹ É
## ##
"
#
#
dy
dx dy R x R x
2x x dx x x
Rx Rx
ÈÈ 1'a
ah
2 R x x dx 2 R dx 2 Rhœœœ111
''
aa
ah ah
Èab
## #
30. (a) x y 45 x 45 y ;
## # ##
#
œ Êœ Ê œ Ê œ
ÈŠ‹
dx dx
dy dy 45 y
yy
45 y
È
S 2 45 y 1 dy 2 45 y y dy 2 45 dyœœ œ
'''
22 5 22 5 22 5
45 45 45
111
ÈÉÈab
## ## #
y
45 y †
(2 )(45)(67.5) 6075 square feetœœ11
(b) 19,085 square feet
31. y x 1 1 S 2 x 1 1 dx 2 ( x) 2 dx 2 x 2 dxœÊ œÊ œÊœ œ
Š‹ Š‹ kkÈÈÈ
dy dy
dx dx
#111
'''
110
202
22 22 22 0 22(2 0) 52œ œ œ
ÈÈÈÈÈ
’“ ’“ ˆ‰
11111
xx
## #
!#
" !
"
32. by symmetry of the graph that S 2 2 1 dx; u 1
dy dy
dx 3 dx 9 99 9
xx xx x
œÊ œÊ œ œ
Š‹ Š ‹ ’
É
#'3
0
1
du x dx du dx; x 3 u 2, x 0 u 1 S 4 u du
“
Ȉ‰
Ê œ Ê œ œ Ê œ œ Ê œ Ä œ
4x
949 4
$"Î#
" "
1'2
1
u du u 8 8 1 . If the absolute value bars are dropped theœ œ œ œ 111
'2
1"Î# $Î# "
#
‘ Š‹Š‹
ÈÈ
2222
3333
1
integral for S 2 f(x) ds will equal zero since 2 1 dx is the integral of an odd functionœ
''
33
33
11
Š‹
É
xx
99
over the symmetric interval 3 x 3.ŸŸ
ÈÈ
33. sin t and cos t ( sin t) (cos t) 1 S 2 y ds
dx dx
dt dt dt dt
dy dy
œ œ Ê œ œ Ê œ
ʈ‰ Š‹ È
#### '1
2 (2 sin t)(1) dt 2 2t cos t 2 [(4 1) (0 1)] 8œ œ œ œ
'0
2
1111 1cd
#
!#
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 6.5 Areas of Surfaces of Revolution and the Theorems of Pappus 399
34. t and t t t S 2 x ds
dx dx t 1
dt dt dt dt t
dy dy
œœÊœœÊœ
"Î# "Î# ##"
ʈ‰ Š‹ ÈÉ'1
2 t dt t t 1 dt; u t 1 du 2t dt; t 0 u 1,œœœÊœœÊœ
''
00
33
1ˆ‰
ÉÈc
2t 4
3t3
$Î# #
" #
1
t 3 u 4 u du u
’“
ÈÈ‘
œÊœÄ œ œ
'1
42428
399
111
$Î# %
"
Note: 2 t dt is an improper integral but lim f(t) exists and is equal to 0, where
'0
3
1ˆ‰
É
2t1
3t
$Î#
tÄ!
f(t) 2 t . Thus the discontinuity is removable: define F(t) f(t) for t 0 and F(0) 0œœœ1ˆ‰
É
2t
3t
$Î# "
F(t) dt .ʜ
'0
328
9
1
35. 1 and t 2 1 t 2 t 2 2 t 3 S 2 x ds
dx dx
dt dt dt dt
dy dy
œœÊœœÊœ
ÈÈÈ
ÊÊ
ˆ‰ Š‹ Š ‹ É
###
## '1
2 t 2 t 2 2 t 3 dt; u t 2 2 t 3 du 2t 2 2 dt; t 2 u 1,œœÊœœÊœ
'2
2
1Š‹ Š ‹
ÈÈ È È È
É’
##
t 2 u 9 u du u (27 1)œÊœÄ œ œ œ
È“È‘
'1
9
11
22 52
33 3
$Î# *
"
11
36. a 1 cos t and a sin t a sin t
a1 cos t
dx dx
dt dt dt dt
dy dy
œ œ Ê œ
ab c dab
ʈ‰ Š‹ Éab
####
a 2 a cos t a cos t a sin t 2a 2a cos t a 2 1 cos t S 2 y dsœ œ œ Êœ
ÈÈÈÈ
22 2222 22 '1
2 a 1 cos t a 2 1 cos t dt 2 2 a 1 cos t dtœ†œ
''
0 0
2 2
11ab ab
ÈÈ
È23/2
37. 2 and 1 2 1 5 S 2 y ds 2 (t 1) 5 dt
dx dx
dt dt dt dt
dy dy
œœÊœœÊœ œ
ʈ‰ Š‹ ÈÈÈ
#### '11
'0
1
2 5 t 3 5. Check: slant height is 5 Area is (1 2) 5 3 5 .œœ Ê œ11 11
ÈÈ È ÈÈ
’“
t
2
"
!
38. h and r h r S 2 y ds 2 rt h r dt
dx dx
dt dt dt dt
dy dy
œœÊœÊœ œ
ʈ‰ Š‹ ÈÈ
#### ##
'11
'0
1
2 r h r t dt 2 r h r r h r . Check: slant height is h r Area isœ œœ Ê111
ÈÈÈ È
’“
## ## ## ##
"
!
'0
1t
2
rh r.1È##
39. (a) An equation of the tangent line segment is
(see figure) y f(m ) f (m )(x m ).œ
kkk
w
When x x we haveœk1
r f(m ) f (m )(x m )
"w
œ
kk1k
f(m) f(m) f(m) f(m) ;œ œ
kk kk
ww
##
ˆ‰
??xx
kk
when x x we haveœk
r f(m ) f (m )(x m )
#w
œ
kk k
f(m) f(m) ;œ
kk
w
#
?xk
(b) L ( x ) (r r )
k
## #
#"
œ?k
( x ) f (m ) f (m ) œ ?kk k
#w w
##
#
‘ˆ‰
??xx
kk
( x ) [f (m ) x ] L ( x ) [f (m ) x ] , as claimedœ Êœ ?? ??
kkk kkk
#w # #w #
kÈ
(c) From geometry it is a fact that the lateral surface area of the frustum obtained by revolving the tangent
line segment about the x-axis is given by S (r r )L [2f(m )] x [f (m ) x ]?1 1 ? ?
kkkkk
œ œ
"# #w#
kÉab
using parts (a) and (b) above. Thus, S 2 f(m ) 1 [f (m )] x .?1 ?
kk kk
œ
Èw#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
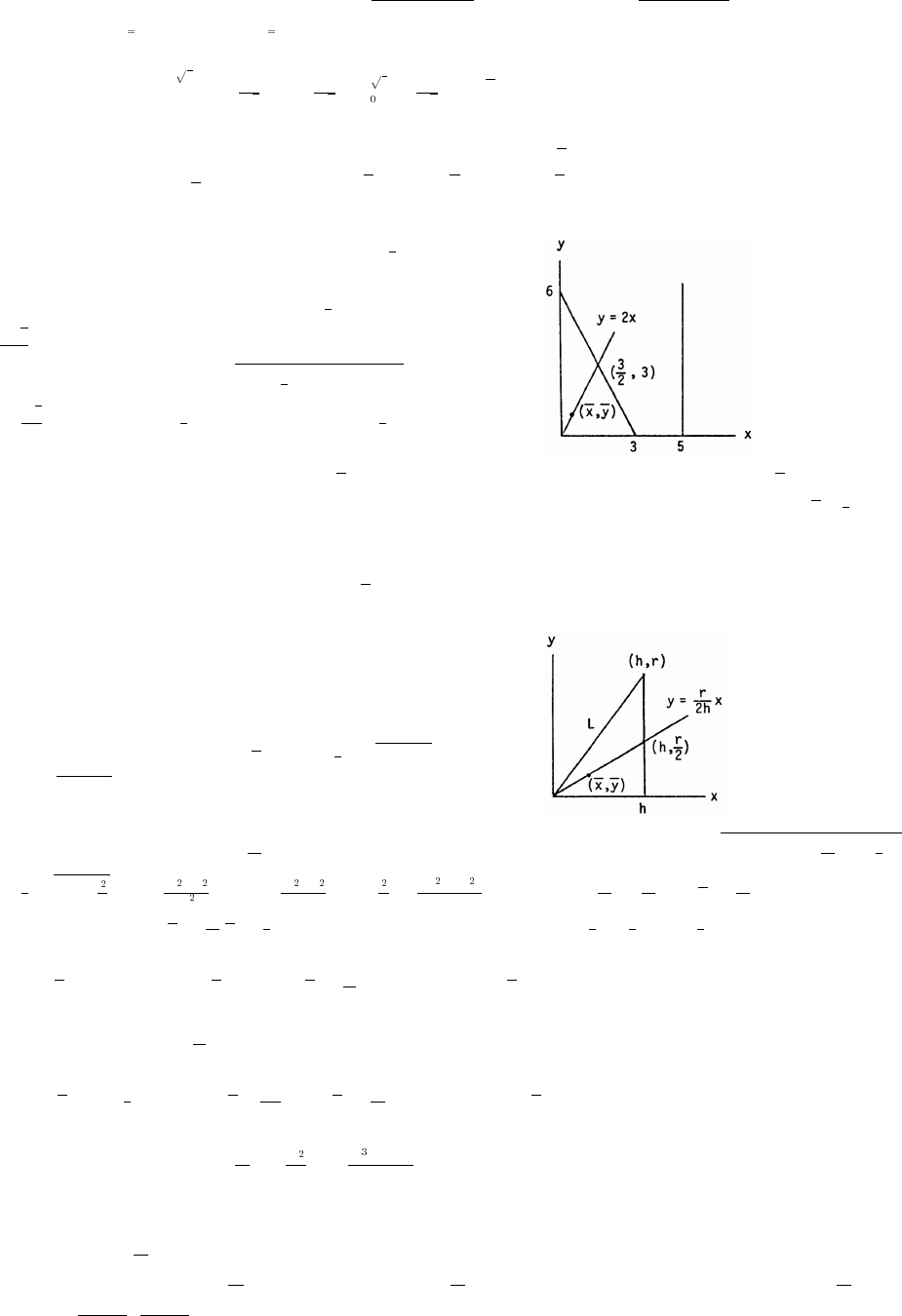
400 Chapter 6 Applications of Definite Integrals
(d) S lim S lim 2 f(m ) 1 [f (m )] x 2 f(x) 1 [f (x)] dxœœ œ
nnÄ_ Ä_
!!
ÈÈ
nn
k1 k1
kkkk
a
b
?1 ?1
w# w#
'
40. S 2 f(x) dx 2 dx x 3œœ œœœ
''
a0
b3 3
11 1†x3
33 3
ÈÈ È
11
cd È
#
41. The centroid of the square is located at ( ). The volume is V (2 ) y (A) (2 )(2)(8) 32 and the#ß # œ œ œ111ab
surface area is S (2 ) y (L) (2 )(2) 4 8 32 2 (where 8 is the length of a side).œœ œ11 1ab Š‹
ÈÈ
È
42. The midpoint of the hypotenuse of the triangle is 3
ˆ‰
3
#ß
y 2x is an equation of the median the lineÊœ Ê
y 2x contains the centroid. The point isϧ$
ˆ‰
3
#
units from the origin the x-coordinate of the
35
È
#Ê
centroid solves the equation x (2x 3)
Ɉ‰
3
#
##
x 3x 4x 12x 9œÊ œ
È595
44#
##
ˆ‰
ab
5x 15x 9 1ʜ
#
x 3x 2 (x 2)(x 1) 0 x 1 since the centroid must lie inside the triangle y 2. By theÊœ œÊœ Êœ
#
Theorem of Pappus, the volume is V (distance traveled by the centroid)(area of the region) 2 5 x (3)(6)œœ1ab
‘
"
#
(2 )(4)(9) 72œœ11
43. The centroid is located at ( ) V (2 ) x (A) (2 )(2)( ) 4#ß ! Ê œ œ œ1111ab #
44. We create the cone by revolving the triangle with vertices
(0 0), (h r) and (h 0) about the x-axis (see the accompanyingßß ß
figure). Thus, the cone has height h and base radius r. By
Theorem of Pappus, the lateral surface area swept out by the
hypotenuse L is given by S 2 yL 2 h rœœ 11
ˆ‰
È
r
###
r r h . To calculate the volume we need the positionœ1È##
of the centroid of the triangle. From the diagram we see that
the centroid lies on the line y x. The x-coordinate of the centroid solves the equation (x h) xœ
rrr
2h 2h
Ɉ‰
##
#
h x x 0 x or x , since the centroid must lieœÊ œÊœ Êœ
"
##
344h 2h49 33 3
r 4h r 4h r r 2h 4h 2h
2r 4h
ÉŠ‹Š‹ ab
inside the triangle y x . By the Theorem of Pappus, V 2 hr r h.Êœ œ œ œ
rr r
2h 3 3 3
‘ˆ‰ˆ‰
11
""
#
#
45. S 2 y L 4 a 2 y ( a) y , and by symmetry x 0œÊœ Êœ œ1111
#ab 2a
1
46. S 2 L 2 a ( a) 2 a ( 2)œÊ œ 13 1 1 1 1
‘ˆ‰
2a
1
#
47. V 2 yA ab 2 y y and by symmetry x 0œÊ œ Êœ œ111
4ab4b
33
#
#
ab
ˆ‰
1
1
48. V 2 A V 2 aœÊœ œ13 1
‘ˆ‰
Š‹
4a a
33
a(3 4)
1
111
#
49. V 2 A (2 )(area of the region) (distance from the centroid to the line y x a). We must find theœœ œ13 1 †
distance from 0 to y x a. The line containing the centroid and perpendicular to y x a has slope
ˆ‰
ßœ œ
4a
31
1 and contains the point . This line is y x . The intersection of y x a and y x is!ßœ œœ
ˆ‰
4a 4a 4a
33 311 1
the point . Thus, the distance from the centroid to the line y x a is
ˆ‰
4a 3a 4a 3a
66
11
11
ߜ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
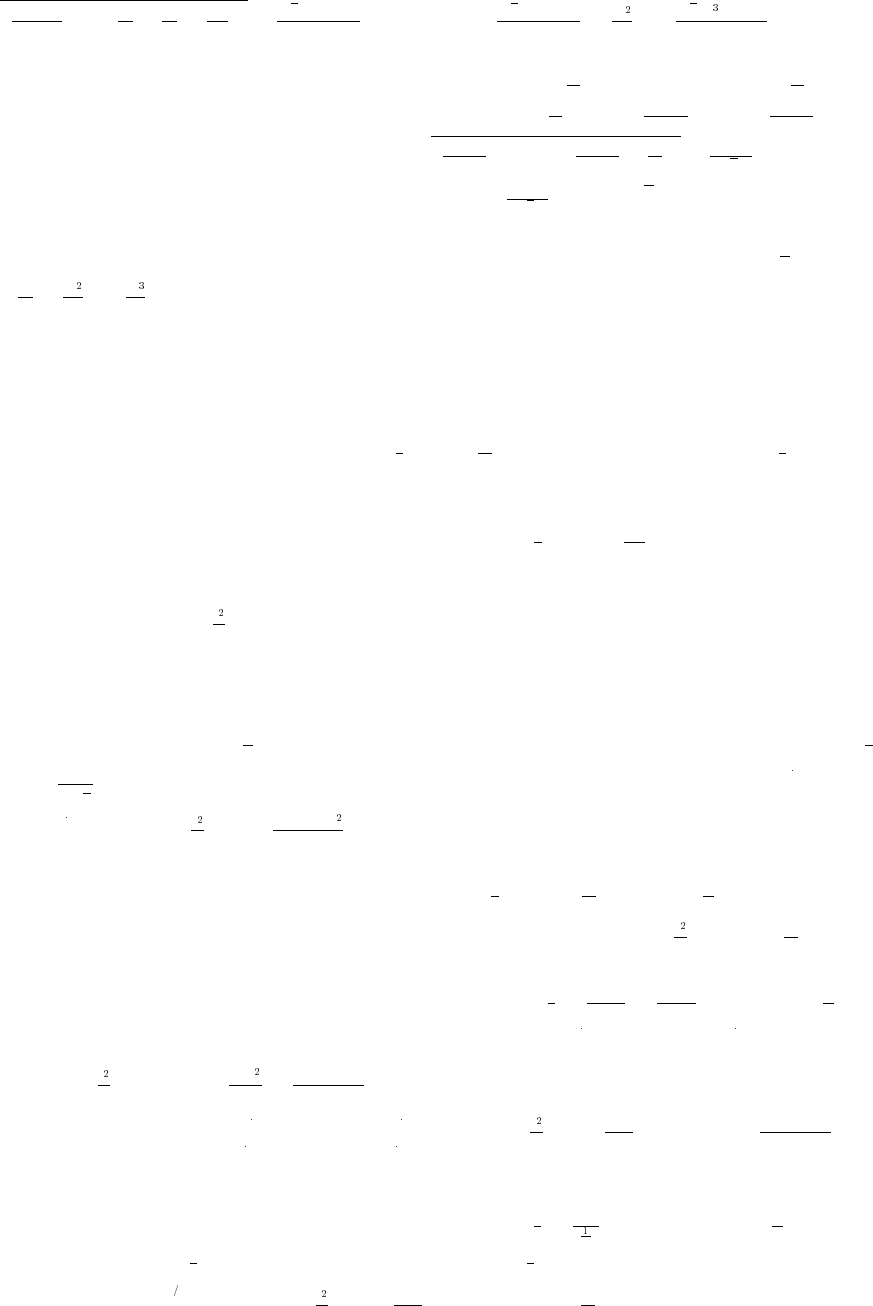
Section 6.6 Work 401
V(2)
Ɉ‰ˆ ‰ Š‹Š‹
4a 3a 4a 4a 3a a
6366 6 6 6
2 (4a 3a ) 2 (4a 3a ) 2 a (4 3 )
##
#
11 1
1111 1 1
1111
œ Êœ œ
ÈÈÈ
1
50. The line perpendicular to y x a and passing through the centroid has equation y x . Theœ !ß œ
ˆ‰
2a 2a
11
intersection of the two perpendicular lines occurs when x a x x y . Thusœ Êœ Êœ
2a 2a a 2a a
2211 1
11
the distance from the centroid to the line y x a is 0 .œ œ
Ɉ‰ˆ ‰
2a a 2a a 2a
22
a(2 )
2
##
#
111
1
È
Therefore, by the Theorem of Pappus the surface area is S 2 ( a) 2 a (2 ).œœ1111
’“ È
a(2 )
2
#
1
1
È
51. From Example 4 and Pappus's Theorem for Volumes we have the moment about the x-axis is M y M
xœ
.œœ
ˆ‰
Š‹
4a a 2a
331
1
#
6.6 WORK
1. The force required to stretch the spring from its natural length of 2 m to a length of 5 m is F(x) kx. Theœ
work done by F is W F(x) dx k x dx x . This work is equal to 1800 J k 1800œœœœ Êœ
''
00
33
k9k 9
## #
#$
!
cd
k 400 N/mʜ
2. (a) We find the force constant from Hooke's Law: F kx k k 200 lb/in.œÊœÊœœ
F 800
x4
(b) The work done to stretch the spring 2 inches beyond its natural length is W kx dxœ'0
2
200 x dx 200 200(2 0) 400 in lb 33.3 ft lbœœœœœ
'0
2’“
x
#
#
!
††
(c) We substitute F 1600 into the equation F 200x to find 1600 200x x 8 in.œœœÊœ
3. We find the force constant from Hooke's law: F kx. A force of 2 N stretches the spring to 0.02 mœ
2 k (0.02) k 100 . The force of 4 N will stretch the rubber band y m, where F ky yÊœ Êœ œ Êœ†N F
m k
y y 0.04 m 4 cm. The work done to stretch the rubber band 0.04 m is W kx dxÊœ Êœ œ œ
4N
100 N
m'0
004
100 x dx 100 0.08 Jœœœœ
'0
004 ’“
x(100)(0.04)
##
!Þ!%
!
4. We find the force constant from Hooke's law: F kx k k k 90 . The work done toœÊœÊœÊœ
F90 N
x1 m
stretch the spring 5 m beyond its natural length is W kx dx 90 x dx 90 (90) 1125 Jœœ œœœ
''
00
55
’“ ˆ‰
x25
##
&
!
5. (a) We find the spring's constant from Hooke's law: F kx k k 7238 œÊœœ œ Êœ
Flb
x85 3 in
21,714 21,714
(b) The work done to compress the assembly the first half inch is W kx dx 7238 x dxœœ
''
00
05 05
7238 (7238) 905 in lb. The work done to compress the assembly theœœœ¸
’“
x(0.5) (7238)(0.25)
###
!Þ&
!
†
second half inch is: W kx dx 7238 x dx 7238 1 (0.5)œœ œ œœ
''
05 05
10 10 ’“ cd
x 7238 (7238)(0.75)
## #
"Þ!
!Þ&
#
2714 in lb¸†
6. First, we find the force constant from Hooke's law: F kx k 16 150 2,400 . If someoneœÊœœ œ œ
F 150 lb
xin
ˆ‰
16
†
compresses the scale x in, he/she must weigh F kx 2,400 300 lb. The work done to compress theœœœœ
""
88
ˆ‰
scale this far is W kx dx 2400 18.75 lb in. ft lbœœ œœ œ
'0
18 ’“
x 2400 25
264 16
#
"Î)
!†
††
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

402 Chapter 6 Applications of Definite Integrals
7. The force required to haul up the rope is equal to the rope's weight, which varies steadily and is proportional to
x, the length of the rope still hanging: F(x) 0.624x. The work done is: W F(x) dx 0.624x dxœœœ
''
00
50 50
0.624 780 Jœœ
’“
x
#
&!
!
8. The weight of sand decreases steadily by 72 lb over the 18 ft, at 4 lb/ft. So the weight of sand when the bag is x ft off the
ground is F x x. The work done is: W F(x) dx x dx 144x 2x 1944 ft lbab a b c dœ "%% % œ œ "%% % œ œ
''
a0
b18 #")
!†
9. The force required to lift the cable is equal to the weight of the cable paid out: F(x) (4.5)(180 x) where xœ
is the position of the car off the first floor. The work done is: W F(x) dx 4.5 (180 x) dxœœ
''
00
180 180
4.5 180x 4.5 180 72,900 ft lbœœœœ
’“Š ‹
x 180 4.5 180
###
")!
!
#†
†
10. Since the force is acting the origin, it acts opposite to the positive x-direction. Thus F(x) . Thetoward œ k
x
work done is W dx k dx k kœ œ œ œ œ
''
aa
bb b
a
k
xxxbaab
k(a b)
""""
‘ ˆ ‰
11. The force against the piston is F pA. If V Ax, where x is the height of the cylinder, then dV A dxœœ œ
Work F dx pA dx p dV.Êœ œ œ
'' 'pV
pV
12. pV c, a constant p cV . If V 243 in and p 50 lb/in , then c (50)(243) 109,350 lb.
"Þ% "Þ% $ $ "Þ%
""
œÊœ œ œ œœ
Thus W 109,350V dVœœœœ
'243
32 "Þ% $#
#%$
"" ""
##
‘ ˆ ‰ ˆ‰
109,350 109,350 109,350
0.4V 3 43
0.4 0.4 4 9
37,968.75 in lb. Note that when a system is compressed, the work done by the system is negative.œ œ
(109,350)(5)
(0.4)(36) †
13. Let r the constant rate of leakage. Since the bucket is leaking at a constant rate and the bucket is rising at a constant raœte,
the amount of water in the bucket is proportional to x , the distance the bucket is being raised. The leakage rate ofab#!
the water is 0.8 lb/ft raised and the weight of the water in the bucket is F 0.8 x . So:œ#!ab
W 0.8 x dx 0.8 20x 160 ft lb.œ#!œ œ†
'0
20 ab ’“
x
#
#!
!
14. Let r the constant rate of leakage. Since the bucket is leaking at a constant rate and the bucket is rising at a constant raœte,
the amount of water in the bucket is proportional to x , the distance the bucket is being raised. The leakage rate ofab#!
the water is 2 lb/ft raised and the weight of the water in the bucket is F 2 x . So:œ#!ab
W 2 x dx 2 20x 400 ft lb.œ#!œ œ †
'0
20 ab ’“
x
#
#!
!
Note that since the force in Exercise 14 is 2.5 times the force in Exercise 13 at each elevation, the total work is also 2.5
times as great.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
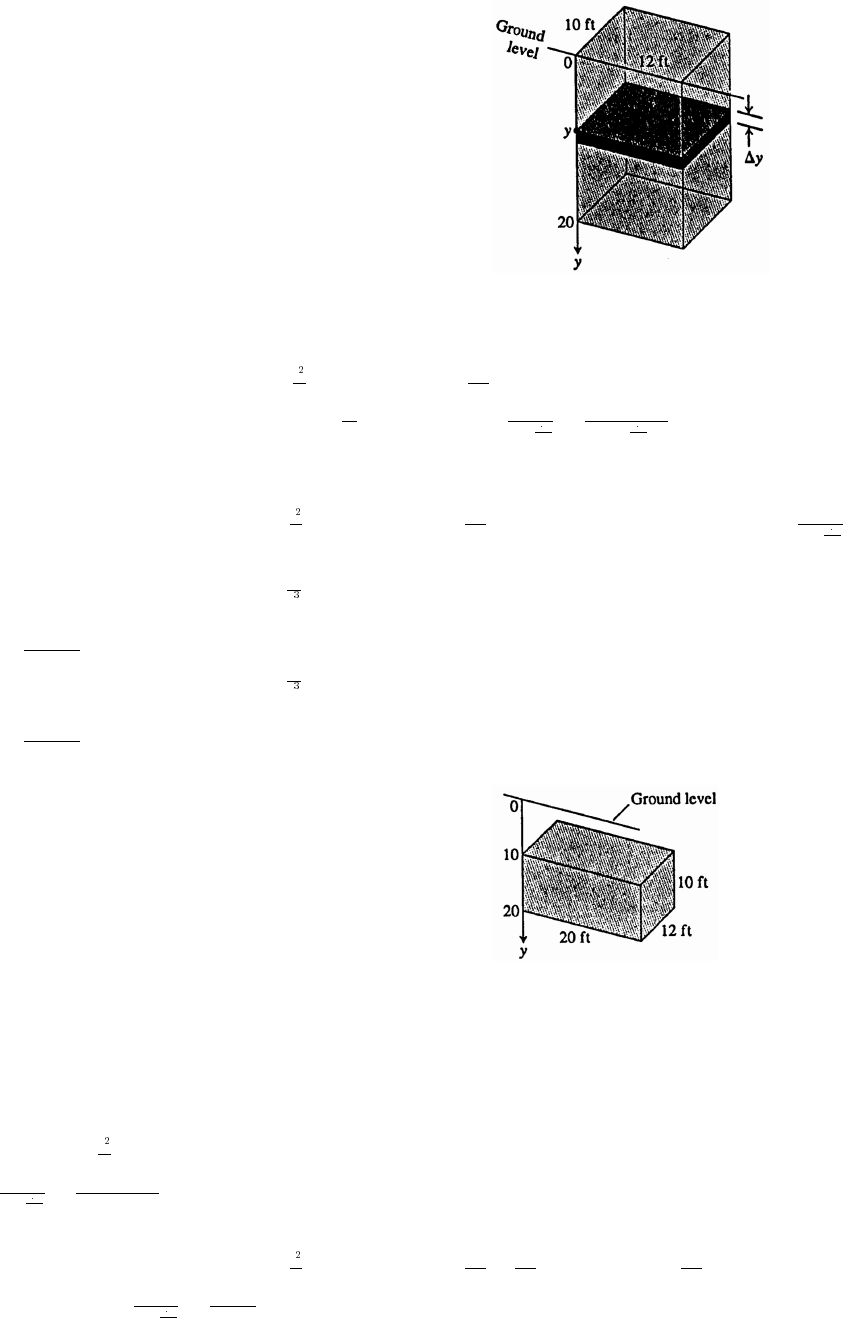
Section 6.6 Work 403
15. We will use the coordinate system given.
(a) The typical slab between the planes at y and y y has?
a volume of V (10)(12) y 120 y ft . The force???œœ
$
F required to lift the slab is equal to its weight:
F 62.4 V 62.4 120 y lb. The distance throughœœ??†
which F must act is about y ft, so the work done lifting
the slab is about W force distance?œ‚
62.4 120 y y ft lb. The work it takes to lift allœ††† †?
the water is approximately W W¸!
20
0
?
62.4 120y y ft lb. This is a Riemann sum forœ!
20
0
†† †?
the function 62.4 120y over the interval 0 y 20. The work of pumping the tank empty is the limit of these sums:†ŸŸ
W 62.4 120y dy (62.4)(120) (62.4)(120) (62.4)(120)(200) 1,497,600 ft lbœœœœœ
'0
20
† †
’“ ˆ‰
y400
##
#!
!
(b) The time t it takes to empty the full tank with –hp motor is t 5990.4 sec
ˆ‰
5W
11 250 250
1,497,600 ft lb
œœ œ
ft lb ft lb
sec sec
†
1.664 hr t 1 hr and 40 minœÊ¸
(c) Following all the steps of part (a), we find that the work it takes to lower the water level 10 ft is
W 62.4 120y dy (62.4)(120) (62.4)(120) 374,400 ft lb and the time is tœœ œœ œ
'0
10
††
’“ ˆ‰
y100 W
250
##
"!
!ft lb
sec
1497.6 sec 0.416 hr 25 minœœ¸
(d) In a location where water weighs 62.26 :
lb
ft
a) W (62.26)(24,000) 1,494,240 ft lb.œœ†
b) t 5976.96 sec 1.660 hr t 1 hr and 40 minœœ ¸ ʸ
1,494,240
250
In a location where water weighs 62.59 lb
ft
a) W (62.59)(24,000) 1,502,160 ft lbœœ†
b) t 6008.64 sec 1.669 hr t 1 hr and 40.1 minœœ ¸ ʸ
1,502,160
250
16. We will use the coordinate system given.
(a) The typical slab between the planes at y and y y has?
a volume of V (20)(12) y 240 y ft . The force???œœ
$
F required to lift the slab is equal to its weight:
F 62.4 V 62.4 240 y lb. The distance throughœœ??†
which F must act is about y ft, so the work done lifting
the slab is about W force distance?œ‚
62.4 240 y y ft lb. The work it takes to lift all the water is approximately W Wœ ¸††† †??
!
20
10
62.4 240y y ft lb. This is a Riemann sum for the function 62.4 240y over the intervalœ!
20
10
†† † †?
10 y 20. The work it takes to empty the cistern is the limit of these sums: W 62.4 240y dyŸŸ œ
'10
20
†
(62.4)(240) (62.4)(240)(200 50) (62.4)(240)(150) 2,246,400 ft lbœœœœ
’“
y
#
#!
"!
†
(b) t 8168.73 sec 2.27 hours 2 hr and 16.1 minœœ ¸ ¸ ¸
W
275
2,246,400 ft lb
275
ft lb
sec
†
(c) Following all the steps of part (a), we find that the work it takes to empty the tank halfway is
W 62.4 240y dy (62.4)(240) (62.4)(240) (62.4)(240) 936,000 ft.œœ œœœ
'10
15
†’“ ˆ‰ ˆ‰
y225 100 125
####
"&
"!
Then the time is t 3403.64 sec 56.7 minœœ¸ ¸
W
275
936,000
75
ft lb
sec #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
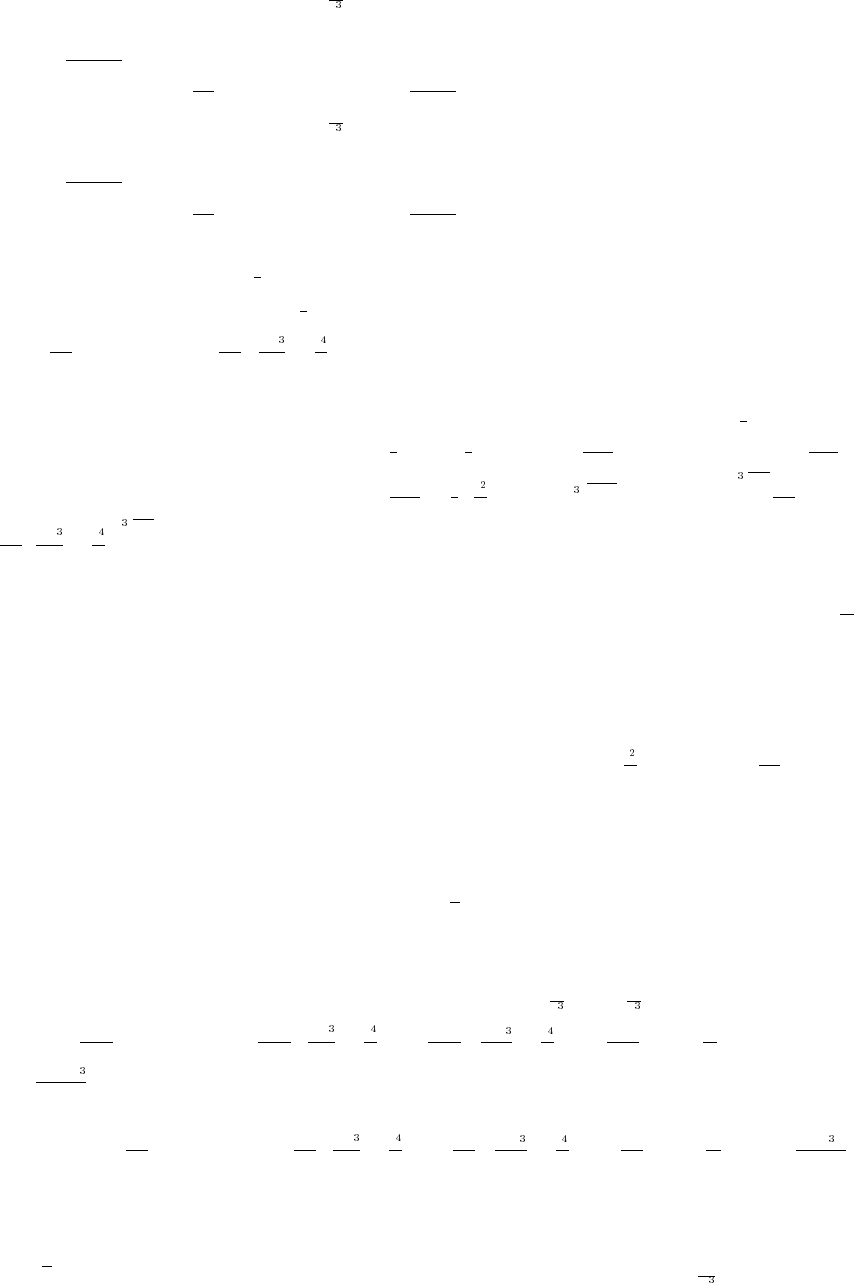
404 Chapter 6 Applications of Definite Integrals
(d) In a location where water weighs 62.26 :
lb
ft
a) W (62.26)(240)(150) 2,241,360 ft lb.œœ†
b) t 8150.40 sec 2.264 hours 2 hr and 15.8 minœœ œ ¸
2,241,360
275
c) W (62.26)(240) 933,900 ft lb; t 3396 sec 0.94 hours 56.6 minœœœœ¸¸
ˆ‰
125 933,900
75##
†
In a location where water weighs 62.59 lb
ft
a) W (62.59)(240)(150) 2,253,240 ft lb.œœ†
b) t 8193.60 sec 2.276 hours 2 hr and 16.56 minœœ œ ¸
2,253,240
275
c) W (62.59)(240) 938,850 ft lb; t 3414 sec 0.95 hours 56.9 minœœœ¸¸¸
ˆ‰
125 938,850
275#
†
17. The slab is a disk of area x , thickness y, and height below the top of the tank y . So the work to pump11
#
#
#
œ ˜ "!
ˆ‰ ab
y
the oil in this slab, W, is 57 y . The work to pump all the oil to the top of the tank is˜"!ab
ˆ‰
1y
#
#
W y y dy 11,875 ft lb 37,306 ft lb.œ"!œ œ †¸ †
'0
10 57 57
44
yy
11
ab’“
#$ "!
$%
"!
!1
18. Each slab of oil is to be pumped to a height of 14 ft. So the work to pump a slab is y and since the tank isabab
ˆ‰
"% 1y
#
#
half full and the volume of the original cone is V r h ft , half the volume ft , andœœ&"!œ œ
" " #&! #&!
$$ $ '
##
11abab 11
33
with half the volume the cone is filled to a height y, y y ft. So W y y dy
#&! "
'$%
&!! #$
11
œ Ê œ &!! œ "% 1y57
4
Èab
'0
È
60,042 ft lb.œ¸ †
57
4
yy
1’“
"%
$%
&!!
!
È
19. The typical slab between the planes at y and and y y has a volume of V (radius) (thickness) yœœ??1 1?
#
#
#
ˆ‰
20
100 y ft . The force F required to lift the slab is equal to its weight: F 51.2 V 51.2 100 y lbœœœ1? ? 1?† †
$
F 5120 y lb. The distance through which F must act is about (30 y) ft. The work it takes to lift all theʜ 1?
kerosene is approximately W W 5120 (30 y) y ft lb which is a Riemann sum. The work to pump the¸œ
!!
30 30
00
?1?†
tank dry is the limit of these sums: W 5120 (30 y) dy 5120 30y 5120 (5120)(450 )œœœœ
'0
30
11 1 1
’“ ˆ‰
y900
##
$!
!
7,238,229.48 ft lb¸†
20. (Alternate Solution) Each method must pump all of the water the 15 ft to the base of the tank. Pumping to the rim requires
all the water to be pumped an additional 6 feet. Pumping into the bottom requires that the water be pumped an average of 3
additional feet. Thus pumping through the valve requires ft 6 ft lb/ft 14,115 ft lb less work and thus
Èab a b$ % '#Þ% ¸133 †
less time.
21. (a) Follow all the steps of Example 5 but make the substitution of 64.5 for 57 . Then,
lb lb
ft ft
W (10 y)y dy 8 2œœœœ
'0
864.5 64.5 64.5 10 8 8 64.5 10
443443443
10y y
1111
# $
)
!
’“Š‹
ˆ‰ˆ ‰
ab
†
21.5 8 34,582.65 ft lbœœ ¸
64.5 8
3
1†1††
$
(b) Exactly as done in Example 5 but change the distance through which F acts to distance (13 y) ft.¸
Then W (13 y)y dy 8 2œœœœ œ
'0
857 57 57 13 8 8 57 13 57 8 7
44344344334
13y y
1111 1
#$
)
!
’“Š‹
ˆ‰ ˆ ‰
ab
†††
†
(19 ) 8 (7)(2) 53.482.5 ft lbœ¸1ab
#†
22. The typical slab between the planes of y and y y has a volume of about V (radius) (thickness)œ??1
#
y y xy y m . The force F(y) is equal to the slab's weight: F(y) 10,000 Vœœ œ1?? ?
ˆ‰
È#$N
m†
10,000y y N. The height of the tank is 4 16 m. The distance through which F(y) must act to liftœœ1? #
the slab to the level of the top of the tank is about (16 y) m, so the work done lifting the slab is about
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
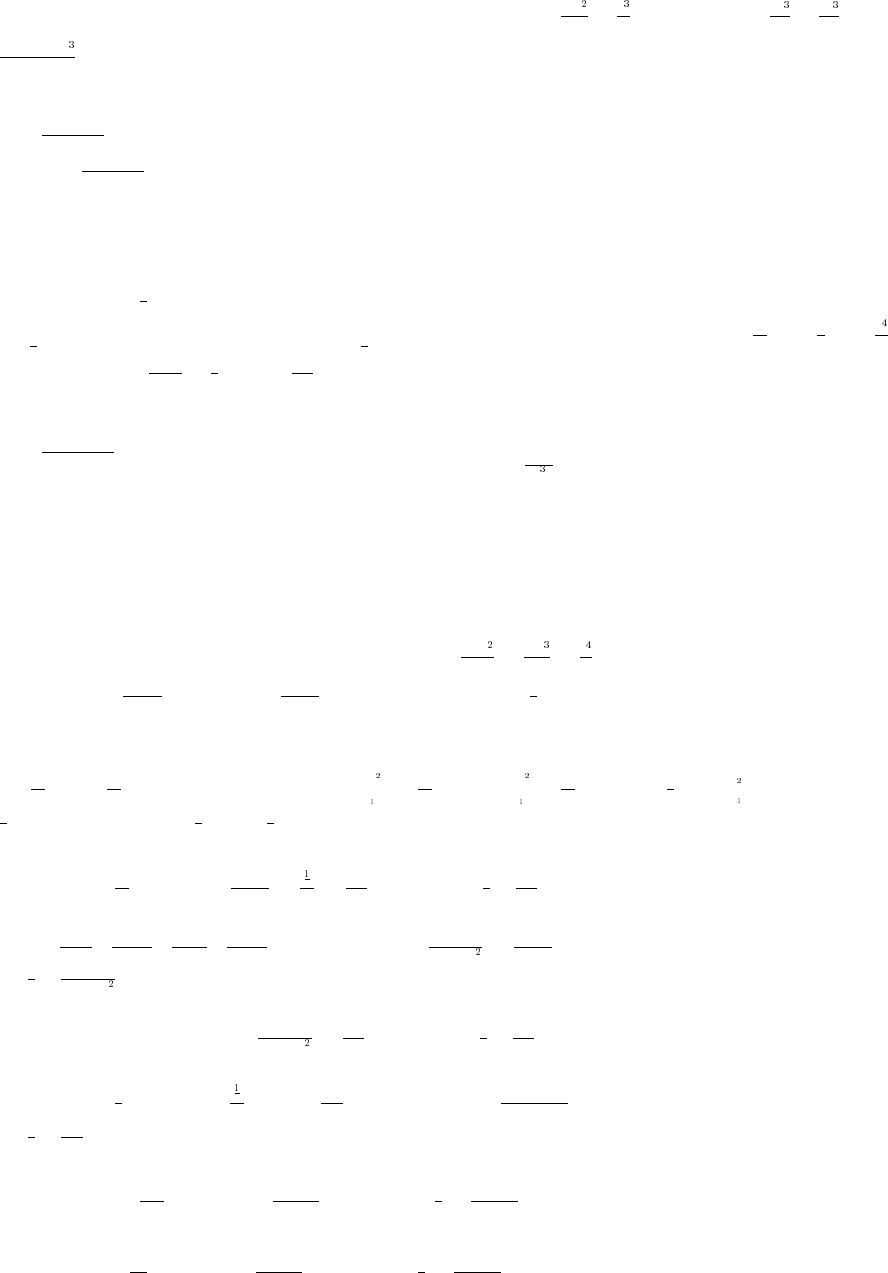
Section 6.6 Work 405
W 10,000 y(16 y) y N m. The work done lifting all the slabs from y 0 to y 16 to the top is?1?œ œœ†
approximately W 10,000 y(16 y) y. Taking the limit of these Riemann sums, we get¸
!
16
0
1?
W 10,000 y(16 y) dy 10,000 16y y dy 10,000 10,000œœœœ
''
00
16 16
11 1 1ab ’“ Š‹
#
##
"'
!
16y y
33
16 16
21,446,605.9 Jœ¸
10,000 16
6
††1
23. The typical slab between the planes at y and y y has a volume of about V (radius) (thickness)œ??1
#
25 y y m . The force F(y) required to lift this slab is equal to its weight: F(y) 9800 Vœ œ1? ?
ˆ‰
È##$†
9800 25 y y 9800 25 y y N. The distance through which F(y) must act to lift theœœ1?1?
ˆ‰
Èab
###
slab to the level of 4 m above the top of the reservoir is about (4 y) m, so the work done is approximately
W 9800 25 y (4 y) y N m. The work done lifting all the slabs from y 5 m to y 0 m is?1 ?¸ œœab
#†
approximately W 9800 25 y (4 y) y N m. Taking the limit of these Riemann sums, we get¸
!ab
0
5
1?
#†
W 9800 25 y (4 y) dy 9800 100 25y 4y y dy 9800 100 y yœœ œC
''
55
00
11 1ab a b ’“
##$#$
#
!
&
25 4
34
y
9800 500 125 15,073,099.75 Jœ ¸1ˆ‰
25 25 4 625
34
†
#
†
24. The typical slab between the planes at y and y y has a volume of about V (radius) (thickness)œ??1
#
100 y y 100 y y ft . The force is F(y) V 56 100 y y lb. Theœœ œ œ1?1? ?1?
ˆ‰
Èab ab
###$ #
56 lb
ft †
distance through which F(y) must act to lift the slab to the level of 2 ft above the top of the tank is about
(12 y) ft, so the work done is W 56 100 y (12 y) y lb ft. The work done lifting all the slabs¸?1 ?ab
#†
from y 0 ft to y 10 ft is approximately W 56 100 y (12 y) y lb ft. Taking the limit of theseœœ ¸
!ab
10
0
1?
#†
Riemann sums, we get W 56 100 y (12 y) dy 56 100 y (12 y) dyœœ
''
00
10 10
11ab ab
##
56 1200 100y 12y y dy 56 1200œœC11
'0
10 ab
’“
#$
#
"!
!
100y 12y y
34
56 12,000 4 1000 (56 ) 12 5 4 (1000) 967,611 ft lb.œ œ ¸11
ˆ‰ˆ‰
10,000 10,000
4
5
##
††
It would cost (0.5)(967,611) 483,805¢ $4838.05. Yes, you can afford to hire the firm.œœ
25. F m mv by the chain rule W mv dx m v dx m v (x)œœ Êœ œ œ
dv dv dv dv
dt dx dx dx
''
xx
xx x
x
ˆ‰ ‘
"
#
#
m v (x ) v (x ) mv mv , as claimed.œœ
"""
###
## ##
#" #"
cd
26. weight 2 oz lb; mass slugs; W slugs (160 ft/sec) 50 ft lbœœ œ œœ œ ¸
2
16 32 3 56 56
weight 8
## ##
""" #
ˆ‰ˆ ‰ †
27. 90 mph 132 ft/sec; m slugs;œœœœ
90 mi 1 hr 1 min 5280 ft 0.3125 lb 0.3125
1 hr 60 min 60 sec 1 mi 32 ft/sec 32
†††
W (132 ft/sec) 85.1 ft lbœ¸
ˆ‰ˆ ‰
"
#
#
0.3125 lb
32 ft/sec †
28. weight 1.6 oz 0.1 lb m slugs; W slugs (280 ft/sec) 122.5 ft lbœœÊœ œ œ œ
0.1 lb
32 ft/sec 30 30
"""
###
#
ˆ‰ˆ ‰ †
29. weight 2 oz lb m slugs slugs; 124 mph 181.87 ft/sec;œœ Êœ œ œ ¸
""
#8 32 56 (60)(60)
(124)(5280)
8
W slugs (181.87 ft/sec) 64.6 ft lbœ¸
ˆ‰ˆ ‰
""
#
#
256 †
30. weight 14.5 oz lb m slugs; W slugs (88 ft/sec) 109.7 ft lbœœÊœ œ ¸
14.5 14.5 4.5
16 (16)(32) (16)(32)
ˆ‰
Š‹
""
#
#†
31. weight 6.5 oz lb m slugs; W slugs (132 ft/sec) 110.6 ft lbœœÊœ œ ¸
6.5 6.5 6.5
16 (16)(32) (16)(32)
ˆ‰
Š‹
"
#
#†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
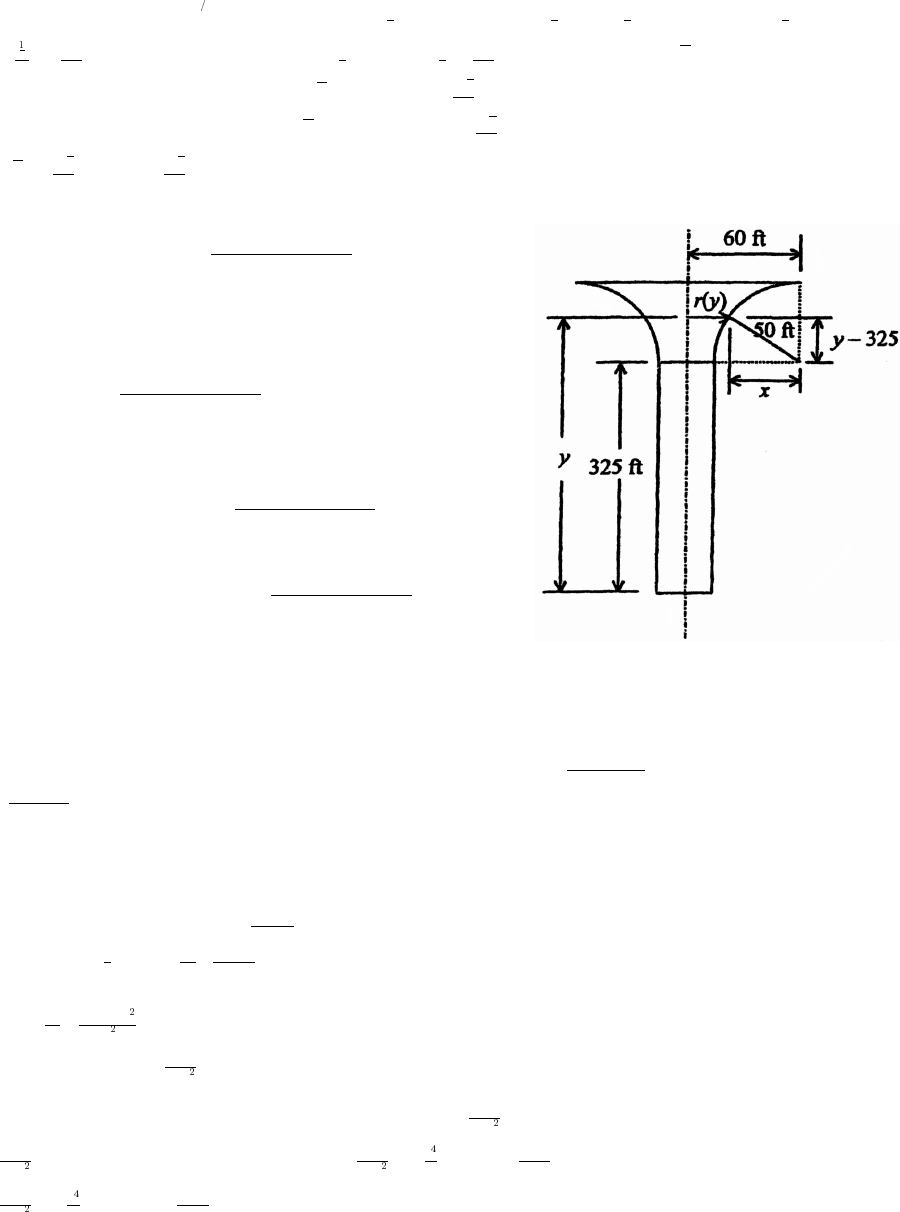
406 Chapter 6 Applications of Definite Integrals
32. F (18 lb/ft)x W 18x dx 9x ft lb. Now W mv mv , where W ft lb,œÊœ œœ œ œ
'0
16 cd
###
"Î
!""
##
"
611
44
††
m slugs and v 0 ft/sec. Thus, ft lb. slugs v v 8 2 ft/sec. With v 0œœ œ œ Êœ œ
8
32 56 4 56
1"""
###
"#
†ˆ‰ˆ ‰ È
at the top of the bearing's path and v 8 2 32t t sec when the bearing is at the top of its path.œÊœ
ÈÈ2
4
The height the bearing reaches is s 8 2 t 16t at t the bearing reaches a height ofœÊœ
È#È2
4
8 2 (16) 2 ft
Š ‹Š‹ Š‹
ÈÈÈ
22
44
œ
#
33. (a) From the diagram,
r y x y 325ab a b
É
œ'! œ'! &!
##
for 325 y 375 ft.ŸŸ
(b) The volume of a horizontal slice of the funnel
is V r y y˜¸ ˜1‘
ab#
y 325 yœ '! &! ˜1”•
Éab
###
(c) The work required to lift the single slice of
water is W 62.4 V y˜ ¸ ˜ $(& ab
62.4 y y 325 y.œ $(& '! &! ˜ab ab
”•
É
1###
The total work to pump our the funnel is W
62.4 375 y 50 y 325 dyœ '!
'325
375 ab ab
”•
É
1###
6.3358 10 ft lb.¸††
(
34. (a) From the result in Example 6, the work to pump out the throat is 1,353,869,354 ft lb. Therefor, the total work†
required to pump out the throat and the funnel is 1,353,869,354 63,358,000 1,417227,354 ft lb.œ †
(b) In horsepower-hours, the work required to pump out the glory hole is 715.8. Therefore, it would take
1,417227,354
1.98 10†6œ
0.7158 hours 43 minutes.
715.8 hp h
1000 hp
†œ¸
35. We imagine the milkshake divided into thin slabs by planes perpendicular to the y-axis at the points of a
partition of the interval [ ]. The typical slab between the planes at y and y y has a volume of about!ß ( ?
V (radius) (thickness) y in . The force F(y) required to lift this slab is equal to its?1 1 ?œœ
#$
#
ˆ‰
y 17.5
14
weight: F(y) V y oz. The distance through which F(y) must act to lift this slab toœœ
44
9914
y 17.5
??
1ˆ‰
#
the level of 1 inch above the top is about (8 y) in. The work done lifting the slab is about
W (8 y) y in oz. The work done lifting all the slabs from y 0 to y 7 is??œ œœ
ˆ‰
4
914
(y 17.5)
1†
approximately W (y 17.5) (8 y) y in oz which is a Riemann sum. The work is the limit ofœ
!
7
0
4
914
1
†
#?†
these sums as the norm of the partition goes to zero: W (y 17.5) (8 y) dyœ
'0
74
914
1
†
#
2450 26.25y 27y y dy 9y y 2450yœœ
4 4 26.25
914 914 4
y
11
††
'0
7ab
’“
#$ $ #
#
(
!
9 7 7 2450 7 91.32 in ozœ ¸
4 7 26.25
914 4
1
†’“
†† † †
$#
#
36. We fill the pipe and the tank. To find the work required to fill the tank follow Example 6 with radius 10 ft. Thenœ
V 100 y ft . The force required will be F 62.4 V 62.4 100 y 6240 y lb. The distance through? 1 ? ? 1? 1?œœœœ†††
$
which F must act is y so the work done lifting the slab is about W 6240 y y lb ft. The work it takes to?1?
"œ†† †
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 6.7 Fluid Pressures and Forces 407
lift all the water into the tank is: W W 6240 y y lb ft. Taking the limit we end up with
""
¸œ
!!
385 385
360 360
?1?†† †
W 6240 y dy 6240 385 360 182,557,949 ft lb
"##
$)&
$'!
##
œœœ¸
'360
385
11
’“ cd
y62401†
To find the work required to fill the pipe, do as above, but take the radius to be in ft.
4
6#
"
œ
Then V y ft and F 62.4 V y. Also take different limits of summation and?1? ? ?œœœ††
"$
36 36
62.41
integration: W W W y dy 352,864 ft lb.
### ##
$'!
!
¸Êœ œ œ ¸
!’“ Š ‹
ˆ‰
360
00
360
?1
'62.4 62.4 62.4 360
36 36 36
y
11 †
The total work is W W W 182,557,949 352,864 182,910,813 ft lb. The time it takes to fill theœ¸ ¸
"# †
tank and the pipe is Time 110,855 sec 31 hrœ¸ ¸ ¸
W
1650 1650
182,910,813
37. Work dr 1000 MG 1000 MGœœ œ
''
6 370 000 6 370 000
35 780 000 35 780 000
1000 MG dr
rrr
‘
"$&ß()!ß!!!
'ß$(!ß!!!
(1000) 5.975 10 6.672 10 5.144 10 Jœ¸‚aba b
Š‹
††
#% "" "!
""
6,370,000 35,780,000
38. (a) Let be the x-coordinate of the second electron. Then r ( 1) W F( ) d3333
##
œ Ê œ
'1
0
d 23 10 1 11.5 10œœœ‚œ‚
'1
0ab23 10
(1)
23 10
‚
" #
‚"
!
"
#* #*
33
3’“
ab
ˆ‰
(b) W W W where W is the work done against the field of the first electron and W is the work doneœ
"# " #
against the field of the second electron. Let be the x-coordinate of the third electron. Then r ( 1)33
##
"œ
and r ( 1) W d d 23 10
## #*
#"‚‚ "
" "
&
$
œÊœœœ‚333
''
33
55
23 10 23 10
r()
33
’“
23 10 10 , and W d dœ ‚ œ ‚ œ œab
ˆ‰
#* #*
"" ‚ ‚
#"
#
44 ()
23 23 10 23 10
r
''
33
55
33
3
23 10 23 10 (3 2) 10 . Thereforeœ ‚ œ ‚ œ œ ‚
#* #* #*
"""‚
"
&
$
’“ab
ˆ‰
36 4 12 12
23 10 23
W W W 10 10 10 7.67 10 Jœœ‚ ‚ œ‚ ¸ ‚
"# #* #* #* #*
ˆ‰ˆ‰
23 23 23
4123
6.7 FLUID PRESSURES AND FORCES
1. To find the width of the plate at a typical depth y, we first find an equation for the line of the plate's
right-hand edge: y x 5. If we let x denote the width of the right-hand half of the triangle at depth y, thenœ
x 5 y and the total width is L(y) 2x 2(5 y). The depth of the strip is ( y). The force exerted by theœ œ œ
water against one side of the plate is therefore F w( y) L(y) dy 62.4 ( y) 2(5 y) dyœ œ
''
55
22
†††
124.8 5y y dy 124.8 y y 124.8 4 8 25 125œœœ
'5
2ab ‘ ‘ˆ‰ˆ ‰
##$
###
"""
#
&
555
333
†† † †
(124.8) (124.8) 1684.8 lbœœ œ
ˆ‰ ˆ‰
105 117 315 234
36#
2. An equation for the line of the plate's right-hand edge is y x 3 x y 3. Thus the total width isœ Ê œ
L(y) 2x 2(y 3). The depth of the strip is (2 y). The force exerted by the water isœœ
F w(2 y)L(y) dy 62.4 (2 y) 2(3 y) dy 124.8 6 y y dy 124.8 6yœ œ œ œ
'' '
33 3
00 0
†† ab ’“
#
#
!
$
yy
3
( 124.8) 18 9 ( 124.8) 1684.8 lbœ œ œ
ˆ‰ˆ‰
927
##
3. Using the coordinate system of Exercise 4, we find the equation for the line of the plate's right-hand edge is
y x 3 x y 3. Thus the total width is L(y) 2x 2(y 3). The depth of the strip changes to (4 y)œ Ê œ œ œ
F w(4 y)L(y) dy 62.4 (4 y) 2(y 3) dy 124.8 12 y y dyÊœ œ œ
'' '
33 3
00 0
†† ab
#
124.8 12y ( 124.8) 36 9 ( 124.8) 2808 lbœœœœ
’“ ˆ‰ˆ‰
yy
3
945
###
!
$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
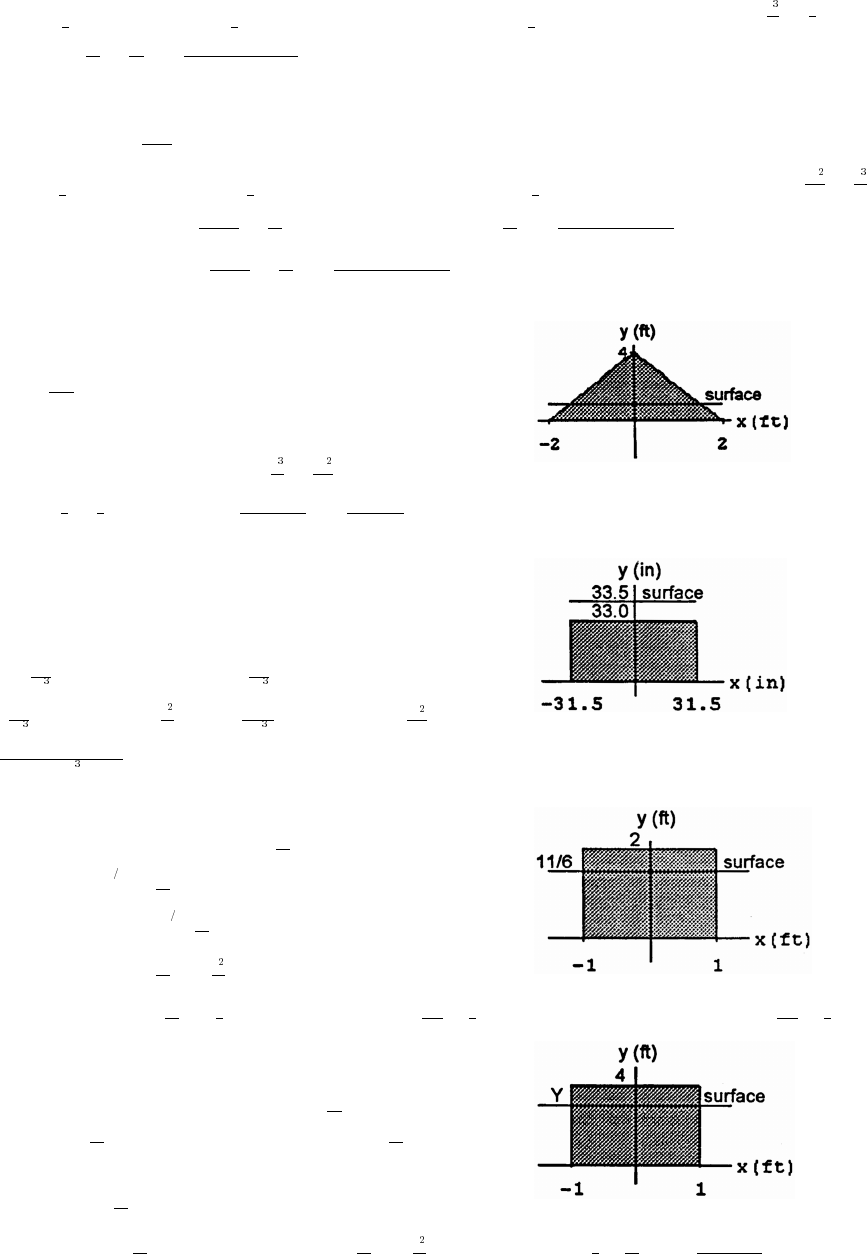
408 Chapter 6 Applications of Definite Integrals
4. Using the coordinate system of Exercise 4, we see that the equation for the line of the plate's right-hand edge
remains the same: y x 3 x 3 y and L(y) 2x 2(y 3). The depth of the strip changes to ( y)œ Ê œ œ œ
F w( y)L(y) dy 62.4 ( y) 2(y 3) dy 124.8 y 3y dy 124.8 yÊœ œ œ œ
'' '
33 3
00 0
†† ab ’“
##
#
!
$
y
3
3
( 124.8) 561.6 lbœ œ œ
ˆ‰
27 27
36
( 124.8)(27)(2 3)
#
5. Using the coordinate system of Exercise 4, we find the equation for the line of the plate's right-hand edge to be
y 2x 4 x and L(y) 2x y 4. The depth of the strip is (1 y).œÊœ œœ
y4
#
(a) F w(1 y)L(y) dy 62.4 (1 y)(y 4) dy 62.4 4 3y y dy 62.4 4yœ œ œ œ
'' '
44 4
00 0
†ab
’“
#
#
!
%
3y y
3
( 62.4) ( 4)(4) ( 62.4) 16 24 1164.8 lbœ œ œ œ
’“
ˆ‰
(3)(16) ( 62.4)( 120 64)
64 64
333#
(b) F ( 64.0) ( 4)(4) 1194.7 lbœ œ ¸
’“
(3)(16) ( 64.0)( 120 64)
64
33#
6. Using the coordinate system given, we find an equation for
the line of the plate's right-hand edge to be y 2x 4œ
x and L(y) 2x 4 y. The depth of theÊœ œ œ
4y
#
strip is (1 y) F w(1 y)(4 y) dyʜ
'0
1
62.4 y 5y 4 dy 62.4 4yœœ
'0
1ab
’“
#
#
"
!
y5y
3
(62.4) 4 (62.4) 114.4 lbœœ œœ
ˆ‰ˆ‰
"
#366
5 2 15 24 (62.4)(11)
7. Using the coordinate system given in the accompanying
figure, we see that the total width is L(y) 63 and the depthœ
of the strip is (33.5 y) F w(33.5 y)L(y) dyʜ
'0
33
(33.5 y) 63 dy (63) (33.5 y) dyœœ
''
00
33 33
64 64
112#
††
ˆ‰
(63) 33.5y (33.5)(33)œœ
ˆ‰ ˆ ‰
’“ ’ “
64 64 63 33
12 1
y
## #
$$
!
†
1309 lbœœ
(64)(63)(33)(67 33)
()12
#ab
8. (a) Use the coordinate system given in the accompanying
figure. The depth of the strip is y ft
ˆ‰
11
6
F w y (width) dyʜ
'0
11 6 ˆ‰
11
6
(62.4)(width) y dyœ
'0
11 6ˆ‰
11
6
(62.4)(width) yœ
’“
11
6
y
#
""Î'
!
(62.4)(width) F (62.4)(2) 209.73 lb and F (62.4)(4) 419.47 lbœ Êœ¸œ¸
’“
ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ‰
11 121 121
636 36
end side
#"" "
## #
†
(b) Use the coordinate system given in the accompanying
figure. Find Y from the condition that the entire volume
of the water is conserved (no spilling): 2 4 2 2 Y
11
6†† ††œ
Y ft. The depth of a typical strip is y ftʜ
11 11
33
ˆ‰
and the total width is L(y) 2 ft. Thus,œ
F w y L(y) dyœ
'0
113 ˆ‰
11
3
(62.4) y 2 dy (62.4)(2) y (62.4)(2) 838.93 lb the fluidœœœ œ¸Ê
'0
113 ˆ‰ ˆ‰ˆ‰
’“ ’“
11 11 11
33 39
y (62.4)(12 )
†
##
""Î$
!
"#"
force doubles.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
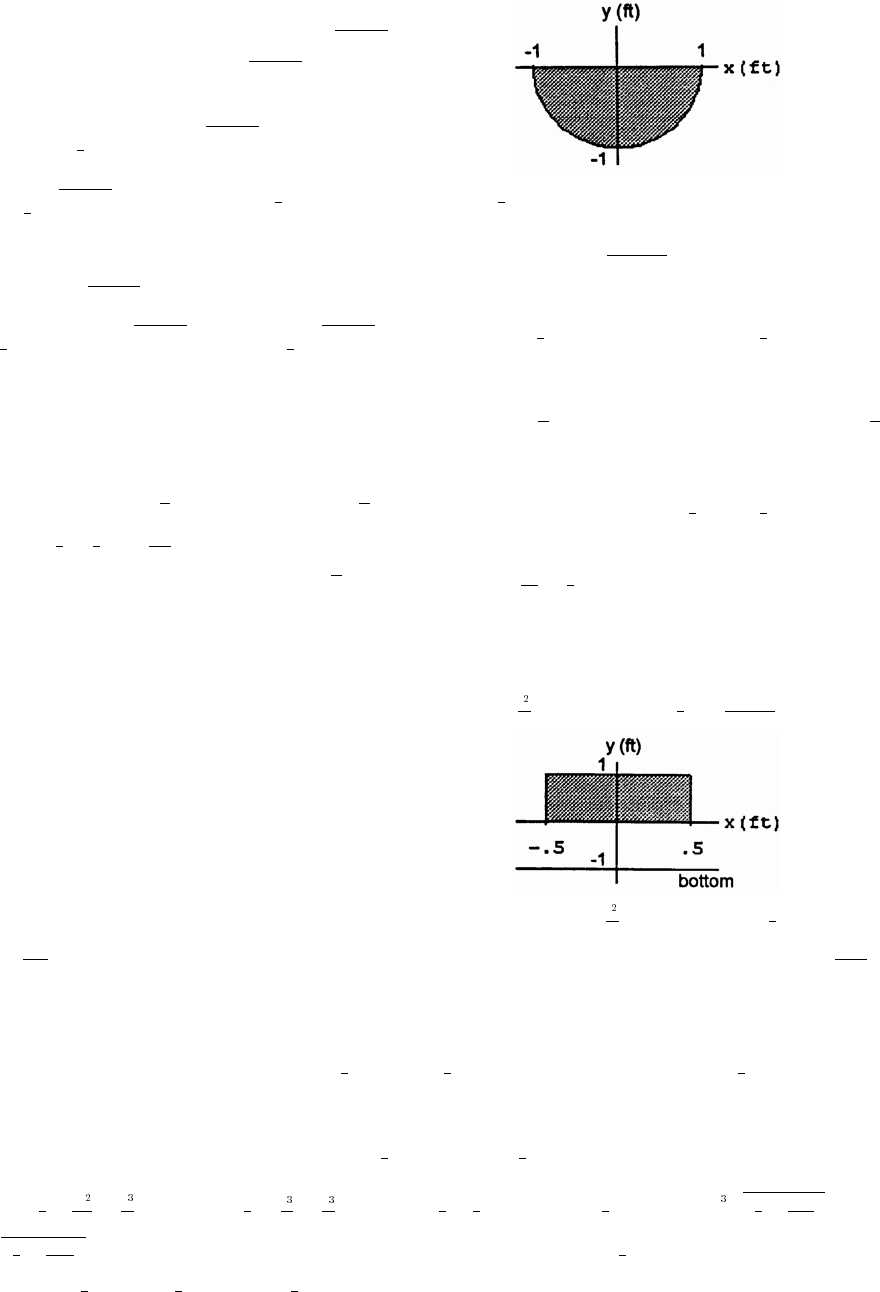
Section 6.7 Fluid Pressures and Forces 409
9. Using the coordinate system given in the accompanying
figure, we see that the right-hand edge is x 1 yœ
È#
so the total width is L(y) 2x 2 1 y and the depthœœ
È#
of the strip is ( y). The force exerted by the water is
therefore F w ( y) 2 1 y dyœ
'1
0
††
È#
62.4 1 y d 1 y 62.4 1 y (62.4) (1 0) 416 lbœœœ œ
'1
0Èab ab
’“ˆ‰
###
$Î# !
"
22
33
10. Using the same coordinate system as in Exercise 15, the right-hand edge is x 3 y and the total width isœ
È##
L(y) 2x 2 9 y . The depth of the strip is ( y). The force exerted by the milk is thereforeœœ
È#
F w ( y) 2 9 y dy 64.5 9 y d 9 y 64.5 9 y (64.5) (27 0)œœ œ œ
''
33
00
††
ÈÈ
ab ab
’“ˆ‰
##
##
$Î# !
$
22
33
(64.5)(18) 1161 lbœœ
11. The coordinate system is given in the text. The right-hand edge is x y and the total width is L(y) 2x 2 y.œœœ
ÈÈ
(a) The depth of the strip is (2 y) so the force exerted by the liquid on the gate is F w(2 y)L(y) dyœ
'0
1
50(2 y) 2 y dy 100 (2 y) y dy 100 2y y dy 100 y yœ œ œ œ
'''
000
111
†ÈÈ
ˆ‰ ‘
"Î# $Î# $Î# &Î# "
!
42
35
100 (20 6) 93.33 lbœœ œ
ˆ‰ˆ‰
4 2 100
35 15
(b) We need to solve 160 w(H y) 2 y dy for h. 160 100 H 3 ftœ œ ÊœÞ
'0
1
†Èˆ‰
2H 2
35
12. Use the coordinate system given in the accompanying figure. The total width is L(y) 1.œ
(a) The depth of the strip is (3 1) y (2 y) ft. The force exerted by the fluid in the window isœ
F w(2 y)L(y) dy 62.4 (2 y) 1 dy (62.4) 2y (62.4) 2 93.6 lbœ œ œ œ œœ
''
00
11
†’“ ˆ‰
y (62.4)(3)
###
"
!
"
(b) Suppose that H is the maximum height to which the
tank can be filled without exceeding its design
limitation. This means that the depth of a typical
strip is (H 1) y and the force is
F w[(H 1) y]L(y) dy F , whereœ œ
'0
1
max
F 312 lb. Thus, F w [(H 1) y] 1 dy (62.4) (H 1)y (62.4) H
max max 0
1
œœœœ
'†’“
ˆ‰
y3
##
"
!
(2H 3) 93.6 62.4H. Then F 93.6 62.4H 312 93.6 62.4H Hœ œ œ Ê œ Êœ
ˆ‰
62.4 405.6
62.4#max
6.5 ftœ
13. Suppose that h is the maximum height. Using the coordinate system given in the text, we find an equation for
the line of the end plate's right-hand edge is y x x y. The total width is L(y) 2x y and theœÊœ œœ
52 4
55#
depth of the typical horizontal strip at level y is (h y). Then the force is F w(h y)L(y) dy F ,œœ
'0
h
max
where F 6667 lb. Hence, F w (h y) y dy (62.4) hy y dy
max 0
hh
0
œœœ
max 44
55
'†ˆ‰
'ab
#
(62.4) (62.4) (62.4) h (10.4) h hœœœ œÊœ
ˆ‰ ˆ‰ ˆ‰ˆ‰ ˆ‰ ˆ‰ˆ ‰
’“ Š‹ É
44hh445
5 3 5 3 5 6 5 4 10.4
hy y F
##
"$$
h
0
max
9.288 ft. The volume of water which the tank can hold is V (Base)(Height) 30, whereœ¸ œ
$"
#
Ɉ‰ˆ ‰
5 6667
4 10.4 †
Height h and (Base) h V h (30) 12h 12(9.288) 1035 ft .œœÊœœ¸¸
"
#
## #$
22
55
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
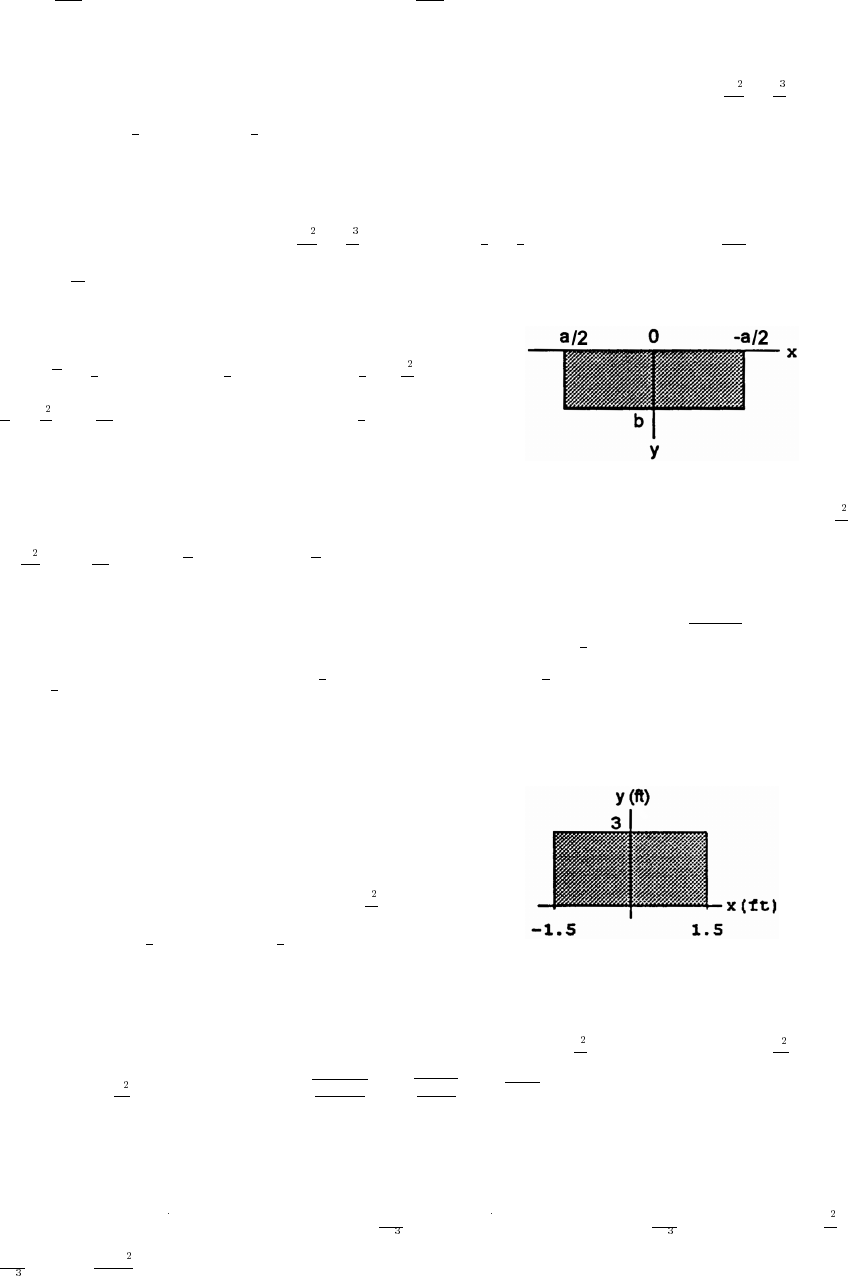
410 Chapter 6 Applications of Definite Integrals
14. (a) After 9 hours of filling there are V 1000 9 9000 cubic feet of water in the pool. The level of the waterœœ†
is h , where Area 50 30 1500 h 6 ft. The depth of the typical horizontal strip atœœœÊœœ
V 9000
Area 1500
†
level y is then (6 y) for the coordinate system given in the text. An equation for the drain plate's
right-hand edge is y x total width is L(y) 2x 2y. Thus the force against the drain plate isœÊ œ œ
F w(6 y)L(y) dy 62.4 (6 y) 2y dy (62.4)(2) 6y y (62.4)(2)œ œ œ œ
'' '
00 0
11 1
†ab ’“
#
#
"
!
6y y
3
(124.8) 3 (124.8) 332.8 lbœœ œ
ˆ‰ ˆ‰
"
33
8
(b) Suppose that h is the maximum height. Then, the depth of a typical strip is (h y) and the force
F w(h y)L(y) dy F , where F 520 lb. Hence, F (62.4) (h y) 2y dyœ œ œ œ
''
0 0
1 1
max max max †
124.8 hy y dy (124.8) (124.8) (20.8)(3h 2) 3h 2œœœœÊœ
'0
1ab ’“ ˆ‰
#
##
"
!
"
hy y
3 3 20.8
h 520
h9 ftÊœ œ
27
3
15. The pressure at level y is p(y) w y the averageœÊ†
pressure is p p(y) dy w y dy wœœœ
"""
#bbb
y
''
00
bb b
0
†’“
. This is the pressure at level , whichœœ
ˆ‰
Š‹
wb wb b
b## #
is the pressure at the middle of the plate.
16. The force exerted by the fluid is F w(depth)(length) dy w y a dy (w a) y dy (w a)œœœœ
'''
000
bbb
b
0
†† † † ’“
y
#
w (ab) p Area, where p is the average value of the pressure (see Exercise 21).œœ œ
Š‹ˆ‰
ab wb
##
†
17. When the water reaches the top of the tank the force on the movable side is (62.4) 2 4 y ( y) dy
'2
0ˆ‰
È
#
(62.4) 4 y ( 2y) dy (62.4) 4 y (62.4) 4 332.8 ft lb. The forceœœœ œ
'2
0ab ab
’“ˆ‰ˆ ‰
# # $Î#
"Î# $Î# !
#
22
33
†
compressing the spring is F 100x, so when the tank is full we have 332.8 100x x 3.33 ft. ThereforeœœÊ¸
the movable end does not reach the required 5 ft to allow drainage the tank will overflow.Ê
18. (a) Using the given coordinate system we see that the total
width is L(y) 3 and the depth of the strip is (3 y).œ
Thus, F w(3 y)L(y) dy (62.4)(3 y) 3 dyœ œ
''
00
33
†
(62.4)(3) (3 y) dy (62.4)(3) 3yœœ
'0
3’“
y
#
$
!
(62.4)(3) 9 (62.4)(3) 842.4 lbœœ œ
ˆ‰ ˆ‰
99
##
(b) Find a new water level Y such that F (0.75)(842.4 lb) 631.8 lb. The new depth of the strip is
Yœœ
(Y y) and Y is the new upper limit of integration. Thus, F w(Y y)L(y) dyœ
Y0
Y
'
62.4 (Y y) 3 dy (62.4)(3) (Y y) dy (62.4)(3) Yy (62.4)(3) Yœœ œ œ
''
00
YY Y
0
†’“ Š‹
yY
##
#
(62.4)(3) . Therefore, Y 6.75 2.598 ft. So, Y 3 Yœœœœ¸œ
Š‹ ÉÉÈ
Y 1263.6
2F
(62.4)(3) 187.2
#
Y?
3 2.598 0.402 ft 4.8 in¸ ¸ ¸
19. Use a coordinate system with y 0 at the bottom of the carton and with L(y) 3.75 and the depth of a typical strip beingœœ
(7.75 y). Then F w(7.75 y)L(y) dy (3.75) (7.75 y) dy (3.75) 7.75yœ œ œ
''
00
775 775
ˆ‰ ˆ‰ ’“
64.5 64.5
12 12
y
#
(Þ(&
!
(3.75) 4.2 lbœ¸
ˆ‰
64.5
12
(7.75)
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 6 Practice Exercises 411
20. The force against the base is F pA whA w h (length)(width) (10)(5.75)(3.5) 6.64 lb.
base œœ œ œ ¸†† ˆ‰
57
12
To find the fluid force against each side, use a coordinate system with y 0 at the bottom of the can, so that the depth of aœ
typical strip is (10 y): F w(10 y) dy 10yœ œ
'0
10 ˆ‰ˆ‰ˆ‰
’“
width of width of
the side 12 the side
57 y
#
"!
!
F (50)(3.5) 5.773 lb and F (50)(5.75) 9.484 lbœÊœ¸œ¸
ˆ‰ˆ ‰ˆ‰ ˆ‰ ˆ‰
57 100 57 57
12 the side 12 12
width of
#end side
21. (a) An equation of the right-hand edge is y x x y and L(y) 2x . The depth of the stripœÊœ œœ
32
33
4y
#
is (3 y) F w(3 y)L(y) dy (62.4)(3 y) y dy (62.4) 3y y dyÊœ œ œ
'' '
00 0
33 3
ˆ‰ ˆ‰ab
44
33
†#
(62.4) y (62.4) (62.4) 374.4 lbœœœœ
ˆ‰ ˆ‰ ‘ ˆ‰ˆ ‰
’“
43 427 27 427
33 33 36
y
##
#$
!
(b) We want to find a new water level Y such that F (374.4) 187.2 lb. The new depth of the strip is
Yœœ
"
#
(Y y), and Y is the new upper limit of integration. Thus, F w(Y y)L(y) dyœ
Y'0
Y
62.4 (Y y) y dy (62.4) Yy y dy (62.4) Y (62.4)œ œ œ œ
''
00
YY Y
ˆ ‰ ˆ‰ ˆ‰ ˆ‰
ab ’“ Š‹
44 4 4YY
33 33323
yy
#
#
†
(62.4) Y . Therefore Y Y 13.5 2.3811 ft. So,œœœÊœœ¸
ˆ‰ ÉÈ
2
9 2 (62.4) 124.8 124.8
9F (9)(187.2) (9)(187.2)
$$ $
Y
†
Y 3 Y 3 2.3811 0.6189 ft 7.5 in. to the nearest half inch.?œ ¸ ¸ ¸
(c) No, it does not matter how long the trough is. The fluid pressure and the resulting force depend only on depth of the
water.
22. The area of a strip of the face of height y and parallel to the base is 100 y, where the factor of accounts for??
ˆ‰
26 26
24 24
† the
inclination of the face of the dam. With the origin at the bottom of the dam, the force on the face is then:
F w(24 y) 100 dy y 1,946,880 lb.œ œ '('! #% œ '('! #% œ
'0
24 ab
ˆ‰ ’“ Š‹
26
24
y
##
##%
CHAPTER 6 PRACTICE EXERCISES
1. A(x) (diameter) x xœœ
11
44
##
#
ˆ‰
È
x 2 x x x ; a 0, b 1œ œœ
1
4ˆ‰
Ȇ#%
V A(x) dx x 2x x dxÊœ œ
''
a0
b1
1
4ˆ‰
&Î# %
xœ œ
11
47 5475
x4 x 4
’“
ˆ‰
##
(Î# "
!
""
(354014)œœ
11
4 70 280
9
†
2. A(x) (side) sin 2 x xœœ
"
#
##
ˆ‰ ˆ ‰
È
1
34
3
È
4x 4x x x ; a 0, b 4œœœ
È3
4ˆ‰
È#
V A(x) dx 4x 4x x dxÊœ œ
''
a0
b4
È3
4ˆ‰
$Î# #
2x x 32œœ
ÈÈ
33
453453
8x 83264
’“
ˆ‰
# &Î# %
!
†
1 (15 24 10)œœœ
32 3 8 3 8 3
45315 15
82
ÈÈ È
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
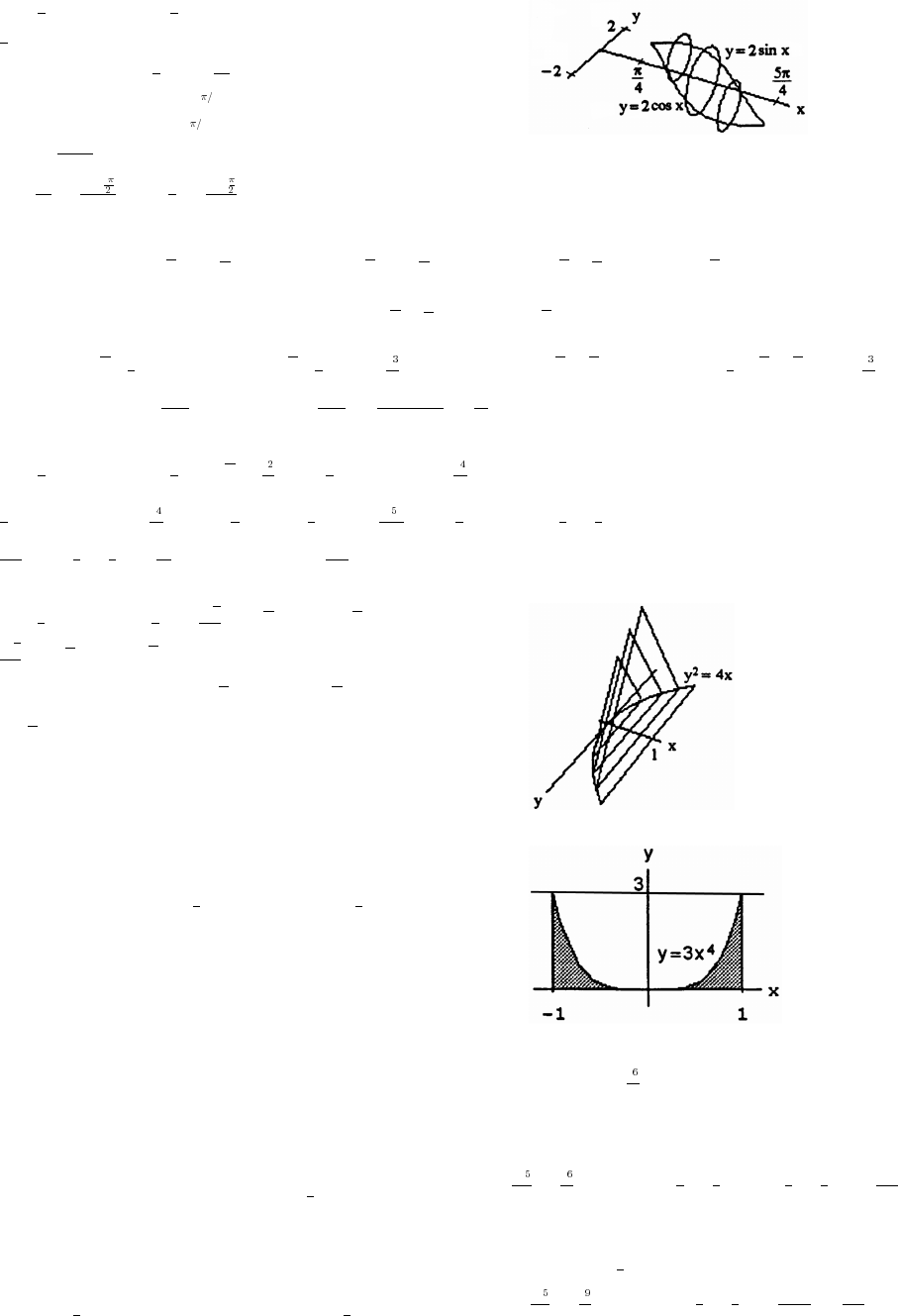
412 Chapter 6 Applications of Definite Integrals
3. A(x) (diameter) (2 sin x 2 cos x)œœ
11
44
##
4 sin x 2 sin x cos x cos xœ
1
4†ab
##
(1 sin 2x); a , bœ œ œ111
44
5
V A(x) dx (1 sin 2x) dxÊœ œ
''
a4
b54
1
xœ1‘
cos 2x
#
&Î%
Î%
1
1
œœ11
’“Š‹Š‹
5
44
cos cos
11
5
##
#
4. A(x) (edge) 6 x 0 6 x 36 24 6 x 36x 4 6 x x ;œœœœ
#$Î# #
#%
#
Œ
Š‹ Š‹
ÈÈÈÈ
ÈÈÈ
a 0, b 6 V A(x) dx 36 24 6 x 36x 4 6 x x dxœœÊœ œ
''
a0
b6
Š‹
ÈÈ
È$Î# #
36x 24 6 x 18x 4 6 x 216 16 6 6 6 18 6 6 6 6œ œ
’“
È È ÈÈ ÈÈ
†† ††††
22x 86
353 53
$Î# # &Î# # #
'
!
216 576 648 72 360œ œ œ œ
1728 1728 1800 1728 72
5555
5. A(x) (diameter) 2 x 4x x ; a 0, b 4 V A(x) dxœœœœœÊœ
11 1
444416
xx
# &Î#
#
Š‹Š ‹
È'a
b
4x x dx 2x x 32 32 32œœœ
111
41647516475
x2x 82
'0
4Š‹’ “
ˆ‰
&Î# # (Î# %
!
†
††
1 (35 40 14)œœœ
32 8 2 8 72
47535 35
11 1
ˆ‰
6. A(x) (edge) sin 2 x 2 xœœ
"
#
##
ˆ‰ ‘
ÈÈ
ˆ‰
1
34
3
È
4 x 4 3 x; a 0, b 1œœœœ
È3
4ˆ‰
ÈÈ
#
V A(x) dx 4 3 x dx 2 3 xÊœ œ œ
''
a0
b1
ÈÈ
’“
#"
!
23œÈ
7. (a) :.3=5 7/>29.
V R (x) dx 3x dx 9x dxœœ œ
'' '
a1 1
b1 1
111
#%)
#
ab
x2œœ11cd
*"
"
(b) :=2/66 7/>29.
V 2 dx 2 x 3x dx 2 3 x dx 2 3œœœœœ
'''
a00
b11
11111
ˆ‰
Š‹ ’“
ab
shell shell
radius height 6
x
%&"
!
††
Note: The lower limit of integration is 0 rather than 1.
(c) :=2/66 7/>29.
V 2 dx 2 (1 x) 3x dx 2 2œœœœœ
''
a1
b1
11 11
ˆ‰ ‘
Š‹ ’ “
ab ˆ‰ˆ ‰
shell shell
radius height 5 2 5 5 5
3x x 3 3 12
%"
"
""
##
1
(d) :A+=2/< 7/>29.
R(x) 3, r(x) 3 3x 3 1 x V R (x) r (x) dx 9 9 1 x dxœœœÊœ œ
%% ## %
#
ab c d ab
’“
''
a1
b1
11
9 1 1 2x x dx 9 2x x dx 9 18œœ œœœœ1111
''
11
11
cdabab ’“ ‘
%) %) "
"
"2x x 2 2 13 26
59 59 5 5
11†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
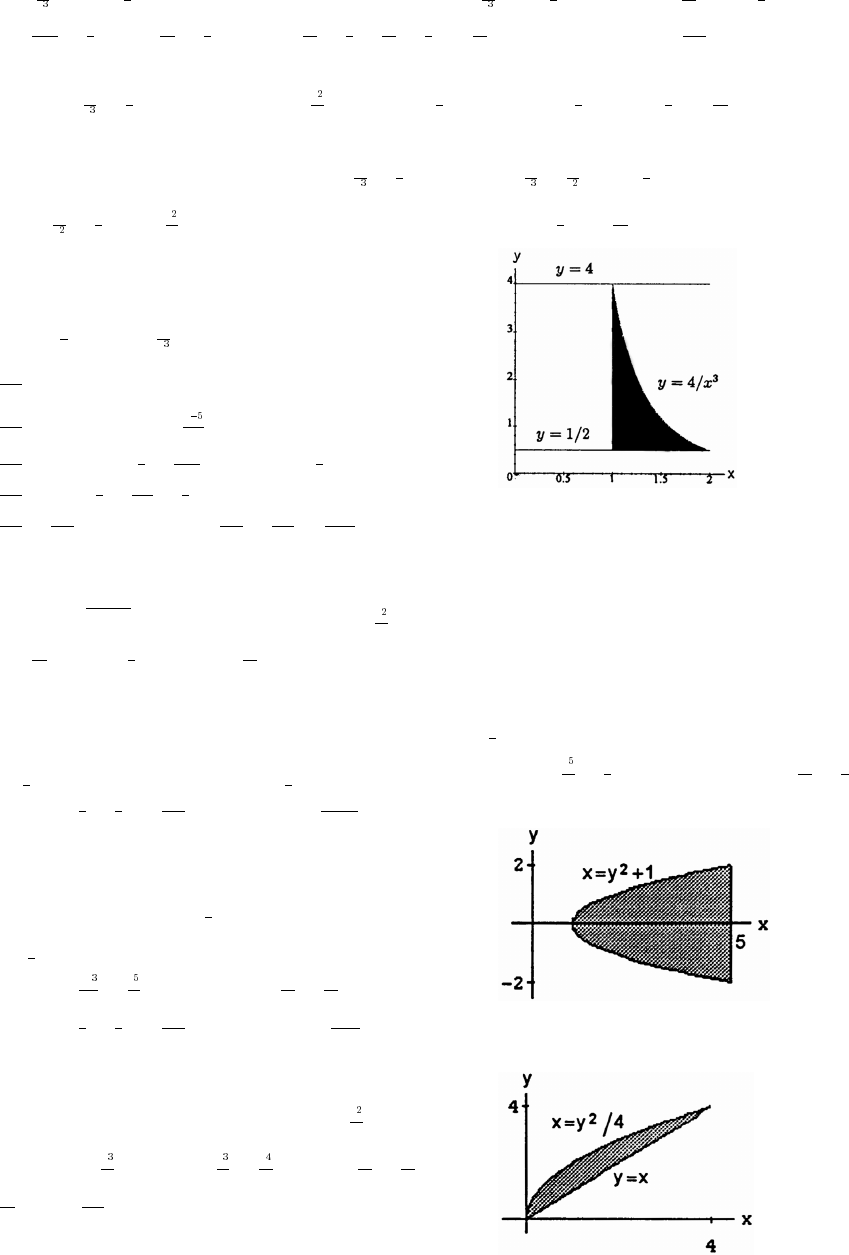
Chapter 6 Practice Exercises 413
8. (a) :A+=2/< 7/>29.
R(x) , r(x) V R (x) r (x) dx dx xœœÊœ œ œ
4416x
xx54
""
##
## &
##
#
"
''
a1
b2
111cd
’“
ˆ‰ ˆ‰ ‘
( 2 10 64 5)œ œ œ œ11
‘ˆ‰ˆ‰ˆ ‰
" " "" "
## #
16 16 16 57
532 5 4 10 5 4 20 0†
11
(b) :=2/66 7/>29.
V 2 x dx 2 4x 2 1 4 2œœœœœ111 1
'1
2ˆ‰ ‘ˆ‰
’“
ˆ‰ˆ‰
4x4 55
x4 44
""
###
" #
"
1
(c) :=2/66 7/>29.
V 2 dx 2 (2 x) dx 2 1 dxœœœ11 1
'' '
a1 1
b2 2
ˆ‰ ˆ ‰ ˆ ‰
Š‹
shell shell
radius height x x x
484x
"
##
2 x 2(1221) 441œ œ œ11
’“
‘ˆ‰
44 x 3
xx 4 4
#
"
"
#
1
(d) :A+=2/< 7/>29.
V R (x) r (x) dxœ
'a
b
1cd
##
4 dxœ1'1
2’“
ˆ‰ ˆ ‰
74
x#
##
16 1 2x x dxœ
49
4
11'1
2ab
$ '
16xxœ
49 x
45
11’“
# #
"
16 2 1 1œ
49
44535
11‘ˆ‰ˆ‰
"" "
#†
16œ
49
4 4 160 5
11ˆ‰
"""
(40 1 32)œ œœ
49 16 49 71 103
4 160 4 10 20
11 11 1
9. (a) :.3=5 7/>29.
V x 1 dx (x 1) dx xœœœ111
''
11
55
Š‹ ’“
È#&
#"
x
51 48œœœ111
‘ˆ‰ˆ‰ˆ‰
25 24
## #
"
(b) :A+=2/< 7/>29.
R(y) 5, r(y) y 1 V R (y) r (y) dy 25 y 1 dyœœÊœ œ
### #
#
''
c2
d2
11cd ab
’“
25 y 2y 1 dy 24 y 2y dy 24y y 2 24 2 8œœ œœ 1111
''
22
22
abab
’“
ˆ‰
%# %# $
#
#
y
53 53
2322
††
32 3 (45 6 5)œœ œ1ˆ‰
2 32 1088
5 3 15 15
"11
(c) :.3=5 7/>29.
R(y) 5 y 1 4 yœ œab
##
V R (y) dy 4 y dyÊœ œ
''
c2
d2
11
##
#
ab
16 8y y dyœ1'2
2ab
#%
16y 2 32œœ11
’“
ˆ‰
8y y
35 35
64 32
#
#
64 1 (15 10 3)œœ œ1ˆ‰
2 64 512
3 5 15 15
"11
10. (a) :=2/66 7/>29.
V 2 dy 2 y y dyœœ
''
c0
d4
11
ˆ‰
Š‹ Š ‹
shell shell
radius height 4
y
2 y dy 2 2œœœ111
'0
4Š‹ ’“ˆ‰
#%
!
yyy
431634
64 64
64œœ
232
13
11
#
†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

414 Chapter 6 Applications of Definite Integrals
(b) :=2/66 7/>29.
V 2 dx 2 x 2 x x dx 2 2x x dx 2 xœœœœ
'''
a00
b44
1111
ˆ‰ ˆ ‰ ˆ ‰
Š‹ ’ “
È
shell shell
radius height 53
4x
$Î# # &Î# %
!
232œœ1ˆ‰
4 64 128
5315
†
1
(c) :=2/66 7/>29.
V 2 dx 2 (4 x) 2 x x dx 2 8x 4x 2x x dxœœœ
'' '
a0 0
b4 4
111
ˆ‰ ˆ ‰ ˆ ‰
Š‹ È
shell shell
radius height "Î# $Î# #
2 x 2x x 2 8 32 32 64 1œœœ111
’“
ˆ‰ˆ‰
16 4 x 16 4 64 4 4 2
353353353
$Î# # &Î# %
!
††
64 1œœ1ˆ‰
464
55
1
(d) :=2/66 7/>29.
V 2 dy 2 (4 y) y dy 2 4y y y dyœ œ œ
'' '
c0 0
d4 4
111
ˆ‰
Š‹ Š ‹ Š ‹
shell shell
radius height 4 4
yy
##
2 4y2y dy22y y 232 6416 322 1œœœœœ1111
'0
4Š‹’ “
ˆ‰ˆ‰
##$
%
!
yy
43163 33
22 832
†
1
11. :.3=5 7/>29.
R(x) tan x, a 0, b V tan x dx sec x 1 dx [tan x x]œœœÊœ œ œœ
1111
3 3
33
11 1
''
00
33
## Î$
!
ab Š‹
È
12. :.3=5 7/>29.
V (2 sin x) dx 4 4 sin x sin x dx 4 4 sin x dxœ œ œ11 1
'' '
00 0
##
#
ab
ˆ‰
1 cos 2x
4x4 cos x 4 4 0 (0400) 8 (9 16)œ œ œ œ 111 11
‘ ‘ˆ‰ˆ‰
xsin 2x 9
4## ##
!
1111
13. (a) :.3=5 7/>29.
V x 2x dx x 4x 4x dx x x 16œœœœ11 1 1
''
00
22
ab a b’“
ˆ‰
# %$# % $
##
!
x 4 32 32
53 5 3
(6 15 10)œœ
16 16
15 15
11
(b) :A+=2/< 7/>29.
V 1 x 2x dx dx x dxœ"œ"œ# œ#†œ
'''
000
222
1111111
’“ ’“
ab ab
## #%"
&&&
#
!
#)
abx1
(c) :=2/66 7/>29.
V 2 dx 2 (2 x) x 2x dx 2 (2 x) 2x x dxœœœ
'' '
a0 0
b2 2
11 1
ˆ‰
Š‹ cd abab
shell shell
radius height ##
2 4x 2x 2x x dx 2 x 4x 4x dx 2 x 2x 2 4 8œ œ œ œ 1111
''
00
22
abab
’“
ˆ‰
##$ $# $#
#
!
x4 32
43 3
(36 32)œœ
28
33
11
(d) :A+=2/< 7/>29.
V 2 x 2x dx 2 dx 4 4 x 2x x 2x dx 8œ œ 111 1
'''
000
222
c d ababab ’“
####
##
4 4x 8x x 4x 4x dx 8 x 4x 8x 4 dx 8œ œ 1111
''
0 0
2 2
abab
# %$# %$
x 4x 4x 8 16 16 8 8 (32 40) 8œ œ œ œ œ11111
’“
ˆ‰
x32 724032
555555
%# #
!
1111
14. :.3=5 7/>29.
V 2 4 tan x dx 8 sec x 1 dx 8 [tan x x] 2 (4 )œœœœ11 111
''
00
44
## Î%
!
ab 1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 6 Practice Exercises 415
15. The material removed from the sphere consists of a cylinder
and two "caps." From the diagram, the height of the cylinder
is 2h, where h , i.e. h . Thus
##
#
$ œ# œ"
Š‹
È
V h ft . To get the volume of a cap,
cyl œ# $ œ'ab
Š‹
È
11
#$
use the disk method and x y : V x dy
## # #
"
œ# œ
cap '2
1
ydy yœ% œ%
'"
##
"
2
11ab ’“
y
3
3
8 ft . Therefore,œ%œ1‘ˆ‰ˆ‰
8
333
"&
$
1
VVV ft.
removed cyl cap 33
œ#œ'œ1"! #) $
11
16. We rotate the region enclosed by the curve y 12 1 and the x-axis around the x-axis. To find theœ
Ɉ‰
4x
121
volume we use the method: V R (x) dx 12 1 dx 12 1 dx.3=5 œ œ œ
'' '
a112 112
b112 112
11 1
##
Š‹ Š‹
Ɉ‰
4x 4x
121 121
12 1 dx 12 x 24 132 1œœœ œ111 1
'11 2
11 2 Š‹ ’“ ’ “ ’ “
ˆ‰ˆ‰ ˆ‰
Š‹
4x 4x 11 4 11 4 11
121 363 2 363 363 4
""Î#
""Î# #
$
132 1 88 276 inœœœ¸11
ˆ‰
"$
33
2641
17. y x x x 2 x L 1 2 x dxœÊœ Ê œ Êœ
"Î# "Î# "Î#
" " "" ""
##
#
x
3dx dx4x 4x
dy dy
Š‹ ˆ‰ ˆ‰
É
'1
4
L 2 x dx x x dx x x dx 2x xÊœ œ œ œ
'' '
11 1
44 4
Ɉ‰ ˆ ‰ ‘
Éab
"" " " "
"Î# "Î# #
##
"Î# "Î# "Î# $Î# %
"
4x 4 3
2
482 2œ œœ
""
##
‘ˆ‰ˆ‰ˆ‰
2 2 14 10
33 33
†
18. x y x L 1 dy 1 dyœÊœ Ê œ Êœ œ
#Î$ "Î$ ##
dx 2 dx 4x dx 4
dy 3 dy 9 dy 9x
Š‹ Š‹
ÊÉ
''
11
88
dx 9x 4 x dx; u 9x 4 du 6y dy; x 1 u 13,œœ œÊœœÊœ
''
11
88
È9x 4
3x 3
"#Î$ "Î$ #Î$ "Î$
Ȉ‰
x 8 u 40 L u du u 40 13 7.634d‘ ‘
œÊœ Äœ œ œ ¸
"""
"Î# $Î# $Î# $Î#
%!
"$ #18 18 3 7
2
'13
40
19. y x x x x x 2 xœÊœ Ê œ
55
12 8 dx dx 4
dy dy
'Î& %Î& "Î& "Î& #Î& #Î&
"" "
##
#
Š‹ ˆ‰
L 1 x 2 x dx L x 2 x dx x x dxÊœ Êœ œ
''
11
32 32 32
1
ÉÉ
ab abab
'É
"""
#Î& #Î& #Î& #Î& "Î& "Î& #
444
x x dx x x 2 2œœœœ
'1
32 "" " "
## # #
"Î& "Î& 'Î& %Î& ' %
$#
"
ˆ‰ ‘ ‘ˆ‰ˆ‰ˆ‰
5 5 5 5 5 5 315 75
64 64 64 64
††
(1260 450)œœœ
"
48 48 8
1710 285
20. x y y y L 1 y dyœÊœÊ œÊœ
"" "" """ """
###
$# %
#%
1 y dy 4 y dy 16 16
dx dx
yy
Š‹ Š ‹
Ê
'1
2
y dy y dy y dy yœœ œœ
'''
111
222
ÉÊŠ‹ Š‹’“
""" "" "" ""
%#
# #
##
#$
"
16 4y 4y 1 y
y
1œœœ
ˆ‰ˆ‰
8713
12 1 1 12
"" "
## ##
21. 5 sin t 5 sin 5t and 5 cos t 5 cos 5t
dx dx
dt dt dt dt
dy dy
œ œ Ê
ʈ‰ Š‹
##
5 sin t 5 sin 5t 5 cos t 5 cos 5tœ
Éabab
##
5 sin 5t sin t sin 5t sin t cos t cos t cos 5t cos 5t sin t sin 5t cos t cos 5 tœ##œ&##
ÈÈab
####
5 cos t 5 cos t sin t sin t sin t (since t )œ # " % œ % " % œ "! # œ "!l # l œ "! # ! Ÿ Ÿ
Èab ab
Ɉ‰ È
"
# #
#1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
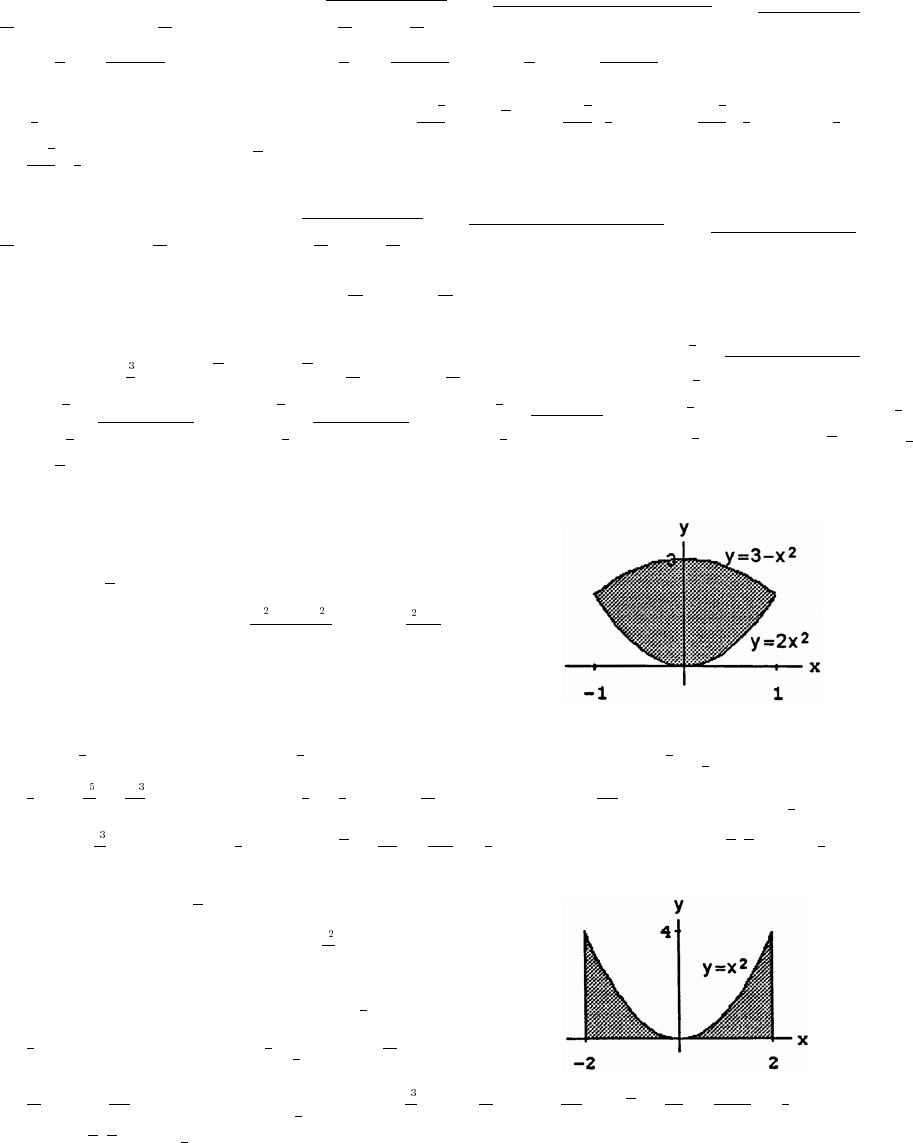
416 Chapter 6 Applications of Definite Integrals
Length sin t dt 5 cos tÊ œ "! # œ # œ&"&"œ"!
'!
ÎÎ#
!
11
2c d abababab
22. 3t 12t and 3t 12t 3t 12t 3t 12t 288t 8t
dx dx
dt dt dt dt
22
dy dy 22 4
œ œÊ œ œ "
ʈ‰ Š‹ Éabab
È
####
#
3 2 t 16 t Length 3 2 t 16 t dt 3 2 t 16 t dt; u 16 t du 2t dtœÊœ œ œÊœ
ÈÈÈ
kk kk
ÈÈÈ
’
222
2
''
!!
""
du t dt; t 0 u 16; t 1 u 17 ; u du u 17 16Êœ œÊœ œÊœ œ œ
"
#
"
“È‘ Š‹
ab ab
32 32 32
223233
16
7222
3/2 17
16
3/2 3/2
ÈÈÈ
'
17 64 2 17 64 8.617.œ† œ ¸
32
23
23/2 3/2
ÈŠ‹Š‹
ab ab
È
23. sin and cos sin cos sin cos
dx dx
dd dd
dy dy
)) ))
œ$ œ$ Ê œ $ $ œ $ œ$)) ))))
ʈ‰ Š‹ Éababa b
È
####
##
Length d dÊœ$œ$ œ$!œ
''
!!
$Î $Î $*
##
11
11
22
))
ˆ‰
24. x t and y t, 3 t 3 2t and t Length 2t t dtœœŸŸÊœ œ"Êœ "
# #
##
#
tdx
3dtdt
dy
3
3
ÈÈ Éab a b
'È
È
t t dt t 2t dt t dt t dt tœ#"œ"œ "œ"œ
'''
%# %# # #
#
ÈÈ È
ÈÈ È
È
ÈÈ
È
33 3
33 3
3
3t
3
3
3
ÈÈÉab ab’“
'3
43œÈ
25. Intersection points: 3 x 2x 3x 3 0œ Ê œ
## #
3(x 1)(x 1) 0 x 1 or x 1. Symmetryʜʜ œ
suggests that x 0. The typical strip hasœ @/<>3-+6
center of mass: ( x y ) x x ,
µµ
ßœß œß
Š‹Š‹
2x 3 x x3
##
ab
length: 3 x 2x 3 1 x , width: dx,ab ab œ
## #
area: dA 3 1 x dx, and mass: dm dAœ œab
#$†
3 1 x dx the moment about the x-axis isœ Ê$ab
#
y dm x 3 1 x dx x 2x 3 dx M y dm x 2x 3 dx
µµ
œ œ Ê œ œ
33 3
## #
# # %# %#
"
$$ $abab a b a b
x1
''
3x 3 3 ( 3 10 45) ; M dm 3 1 x dxœ œœœ œ œ
3 x 2x 2 3 32
53 53 15 5#
"
"
""#
$$ $
’“
ˆ‰ ab
$$
''1
3 x 6 1 4 y . Therefore, the centroid is (x y) .œ œœÊœœœ ßœ!ß$$$
’“ ˆ‰ ˆ‰
x3288
33 M545 5
M
"
"
"x$
$†
26. Symmetry suggests that x 0. The typical œ @/<>3-+6
strip has center of mass: ( x y ) x , length: x ,
µµ
ßœß
Š‹
x
#
#
width: dx, area: dA x dx, mass: dm dA x dxœœœ
##
$$†
the moment about the x-axis is y dm x x dxʜ
µ$
#
##
†
x dx M y dm x dx xœÊœœ œ
µ
$$$
##
%%&
#
#
x2
2
''10 cd
2 ; M dm x dx 2 y . Therefore, theœœœœ œ œœÊœœœ
232 x216 3236
10 5 3 3 3 M 5 16 5
M
$$ $$ $
$
ab ab
’“
&#$
#
#
'$$
'2
2
x††
††
centroid is(x y) .ßœ!ß
ˆ‰
6
5
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
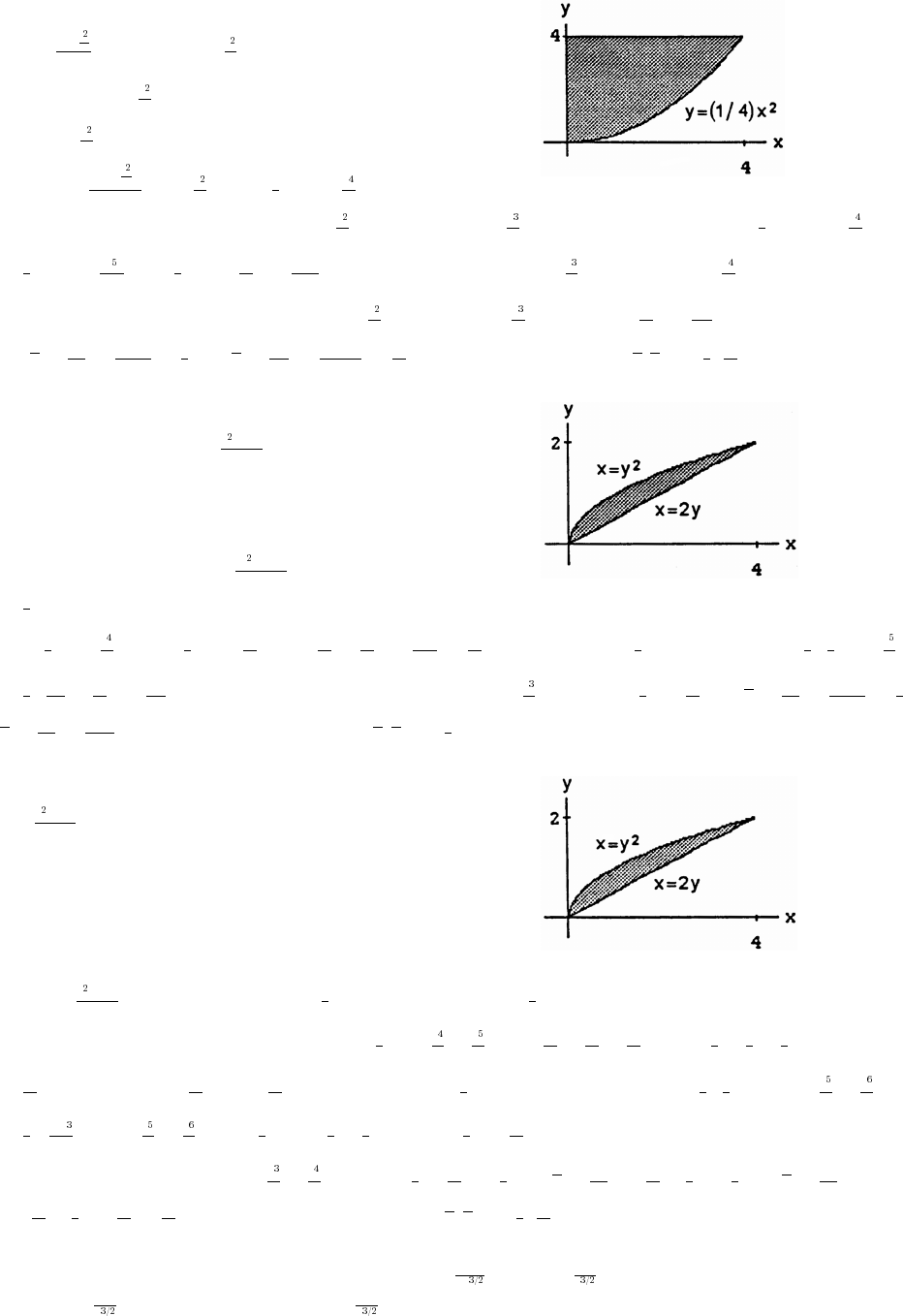
Chapter 6 Practice Exercises 417
27. The typical strip has: center of mass: ( x y )@/<>3-+6 ß
µµ
x , length: 4 , width: dx,ϧ
Œ
4x
4
#
x
4
area: dA 4 dx, mass: dm dAœ œ
Š‹
x
4$†
4 dx the moment about the x-axis isœ Ê$Š‹
x
4
y dm 4 dx 16 dx; the
µœœ$†
Š‹
4xx
416
##
x
4Š‹ Š ‹
$
moment about the y-axis is x dm 4 x dx 4x dx. Thus, M y dm 16 dx
µµ
œ œ œ œ $$
Š‹ Š ‹ Š ‹
xx x
44 16
†x0
4
'$
#'
16x 64 ; M x dm 4x dx 2xœœœ œ œ œ
µ
$$$
2516 55 4 16
x 64 128 x x
’“ Š‹’“
‘
†
% %
! !
#
#
y0
4
'$$
'
(32 16) 16 ; M dm 4 dx 4x 16œœ œ œ œ œ œ$$$ $$
''0
4Š‹ ’ “ˆ‰
x x 64 32
41213
%
!#
$
x and y . Therefore, the centroid is (x y) .Êœ œ œ œ œ œ ßœß
M
M32 2 532 5 5
16 3 3 128 3 12 3 12
y†† †
†††
$$
$$
M
M
x†
#
ˆ‰
28. A typical strip has:29<3D98>+6
center of mass: ( x y ) y , length: 2y y ,
µµ
ßœ ß
Š‹
y2y
#
#
width: dy, area: dA 2y y dy, mass: dm dAœ œab
#$†
2y y dy; the moment about the x-axis isœ$ab
#
y dm y 2y y dy 2y y ; the moment
µœœ$$††aba b
##$
about the y-axis is x dm 2y y dy
µœ$††
aby2y
#
#
ab
4y y dy M y dm 2y y dyœ Êœ œ
µ
$
#
#% #$
ab ab
x0
2
'$'
y 8 ; M x dm 4y y dy yœœ œœœœ œ œ
µ
$$$
’“ ’“
ˆ‰ˆ‰ ab
2 2 16 16 16 16 4 4
34 3 4 34123 35
y y
$#% $
# #
! !
##
†
$$ $ $†
y0
2
''
; M dm 2y y dy y 4 x andœœ œœ œœœÊœœœ
$$ $$
$#
##
#
!
ˆ‰ ˆ‰
ab ’“
4 8 32 32 84 3238
3 5 15 3 3 3 M 15 4 5
yM
†††
††
'$$$
'0
2y
y 1. Therefore, the centroid is (x y) 1 .œœ œ ßœß
M
M34 5
43 8
x††
††
$
$ˆ‰
29. A typical horizontal strip has: center of mass: ( x y )
µµ
ß
y , length: 2y y , width: dy,ϧ
Š‹
y2y
#
#
area: dA 2y y dy, mass: dm dAœ œab
#$†
(1 y) 2y y dy the moment about theœ Êab
#
x-axis is y dm y(1 y) 2y y dy
µœ ab
#
2y 2y y y dyœab
# $$%
2y y y dy; the moment about the y-axis isœab
#$%
x dm (1 y) 2y y dy 4y y (1 y) dy 4y 4y y y dy
µœœœ
Š‹ aba b a b
y2y
###
# #% # $%&
""
M y dm 2y y y dy y 16Ê œ œ œ œœ
µ
x0
2
''ab
’“
ˆ‰ˆ‰
#$% $ #
!
""2 161632 2
3 45 345 345
yy
(20 15 24) (11) ; M x dm 4y 4y y y dy y yœœ œ œ œ œ
µ
16 4 44 4
60 15 15 356
yy
y0
2
''""
##
# $%& $% #
!
ab
’“
2 4 2 42 ; M dm (1y)2yy dyœœœœœœ
"
#
% #
Š‹
ˆ‰ˆ‰ ab
42 2 2 4 4 8 4 24
356356 55
†''0
2
2y y y dy y 4 x and yœœœœÊœœ œ œ
'0
2ab
’“
ˆ‰ ˆ‰ˆ‰
#$ # #
!
yy
34 34 3 M 58 5 M
8168 2439
MM
yx
. Therefore, the center of mass is (x y) .œœœ ßœß
ˆ‰ˆ‰ ˆ ‰
44 3 44 11 9 11
15 8 40 10 5 10
30. A typical vertical strip has: center of mass: ( x y ) x , length: , width: dx,
µµ
ßœß
ˆ‰
33
2x x
area: dA dx, mass: dm dA dx the moment about the x-axis isœœœÊ
33
xx
$$††
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

418 Chapter 6 Applications of Definite Integrals
y dm dx dx; the moment about the y-axis is x dm x dx dx.
µµ
œœ œœ
33 9 3 3
xx xx
2x
#
††$$
$ $
(a) M dx ; M x dx 3 2x 12 ;
xy
11
99
œœœœ œœ$$$$
''
"
###
*
"
"Î# *
"
ˆ‰ ˆ ‰ ‘
’“
99x20 3
x9
x
$$
M dx 6 x 4 x 3 and yœœœÊœœœœœœ$$$
'1
93125
x
M
M4 M 4 9
M
‘
"Î# *
"
yx
$
$$
ˆ‰
20
9
(b) M dx 4; M x dx 2x 52; M x dx
xy
11 1
99 9
œœœœ œœœ
'' '
x9 9 3 3
xx xx
##
"*
"
# $Î# *
"
ˆ‰ ‘ ˆ‰ ‘ ˆ‰
6 x 12 x and yœœÊœœœœ
‘
"Î# *
"
"
M
M3 M3
13 M
yx
31. S 2 y 1 dx; S 2 2x 1 1 dxœ œÊœÊœ
''
a 0
b 3
11
ÊŠ‹ Š‹ ÈÉ
dy dy dy
dx dx dx x 1 x 1
2x 1
##
"" "
# #
È
2 2x 1 dx 2 2 x 1 dx 2 2 (x 1) 2 2 (8 1)œ œ œ œ œ1111
''
00
33
ÈÈ
ÉÈÈ È
‘
2x 2 2 2
2x 1 3 3 3
28 2
$Î# $
!
†
1È
32. S 2 y 1 dx; x x S 2 1 x dx 1 x 4x dxœ œÊ œÊœ œ
'''
a00
b11
11
ÊŠ‹ Š‹ ÈÈ
ab
dy dy dy
dx dx dx 3 6
x
##
#% $
%%
†
1
1x d1x 1x 221œœœ
111
6639
2
'0
1Èab ab
’“’“
È
%%%
$Î# "
!
33. S 2 x 1 dy; 1œ œœÊœ œ
'c
d
1ÊŠ‹ Š‹
dx dx dx 4
dy dy dy 4y y 4y y
(4 2y)
4y y 4y y
2 y 4y y 4 4y y
##
ˆ‰
ÈÈ
S 2 4y y dy 4 dx 4Êœ œ œ
''
11
22
111
ÈÉ
#
4
4y y
34. S 2 x 1 dy; 1 1 S 2 y dyœ œÊœœÊœ
''
c 2
d 6
11
ÊŠ‹ Š‹ È
dx dx 1 dx
dy dy 2 y dy 4y 4y
4y 1 4y 1
4y
##
"
È È
È
†
4y 1 dy (4y 1) (125 27) (98)œœœœœ1'2
6È‘
1111
43 6 6 3
249
$Î# '
#
35. x and y 2t, 0 t 5 t and 2 Surface Area 2 (2t) t 4 dt 2 u duœœŸŸÊœœÊ œ œ
tdx
dt dt
dy
##"Î#
ÈÈ
''
04
59
11
2 u , where u t 4 du 2t dt; t 0 u 4, t 5 u 9œœ œÊœœÊœœÊœ1‘ È
276
33
$Î# #
*
%
1
36. x t and y 4 t , t 1 2t and œ œ ŸŸ Ê œ œ
#"" "
2t dt 2t dt
2
dx 2
dy
t
ÈÈÈ
Surface Area 2 t 2t dt 2 t 2t dtÊœœ
''
12 12
1 1
11
ˆ‰ˆ ‰ ˆ‰ˆ ‰
ÊŠ‹ É
##
"" ""
###
##
#
t2t t t
2
t
È
2 t 2t dt 2 2t t dt 2 t t tœœ œ111
''
12 12
11
ˆ‰ˆ ‰ ˆ ‰ ‘
#$$%#
"" " " "
##
"
"Î #
2t 2t 4 2 8
33
È
22œ1Š‹
32
4
È
37. The equipment alone: the force required to lift the equipment is equal to its weight F (x) 100 N.ʜ
"
The work done is W F (x) dx 100 dx [100x] 4000 J; the rope alone: the force required
"" %!
!
œœœœ
''
a0
b40
to lift the rope is equal to the weight of the rope paid out at elevation x F (x) 0.8(40 x). The workʜ
#
done is W F (x) dx 0.8(40 x) dx 0.8 40x 0.8 40 640 J;
## ###
%!
!
#
œœœœœœ
''
a0
b40 ’“Š‹
x40
(0.8)(1600)
the total work is W W W 4000 640 4640 Jœœ œ
"#
38. The force required to lift the water is equal to the water's weight, which varies steadily from 8 800 lb to†
8 400 lb over the 4750 ft elevation. When the truck is x ft off the base of Mt. Washington, the water weight is†
F(x) 8 800 (6400) 1 lb. The work done is W F(x) dxœœ œ††
ˆ‰ ˆ‰
2 4750 x x
2 4750 9500
†
†
'a
b
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
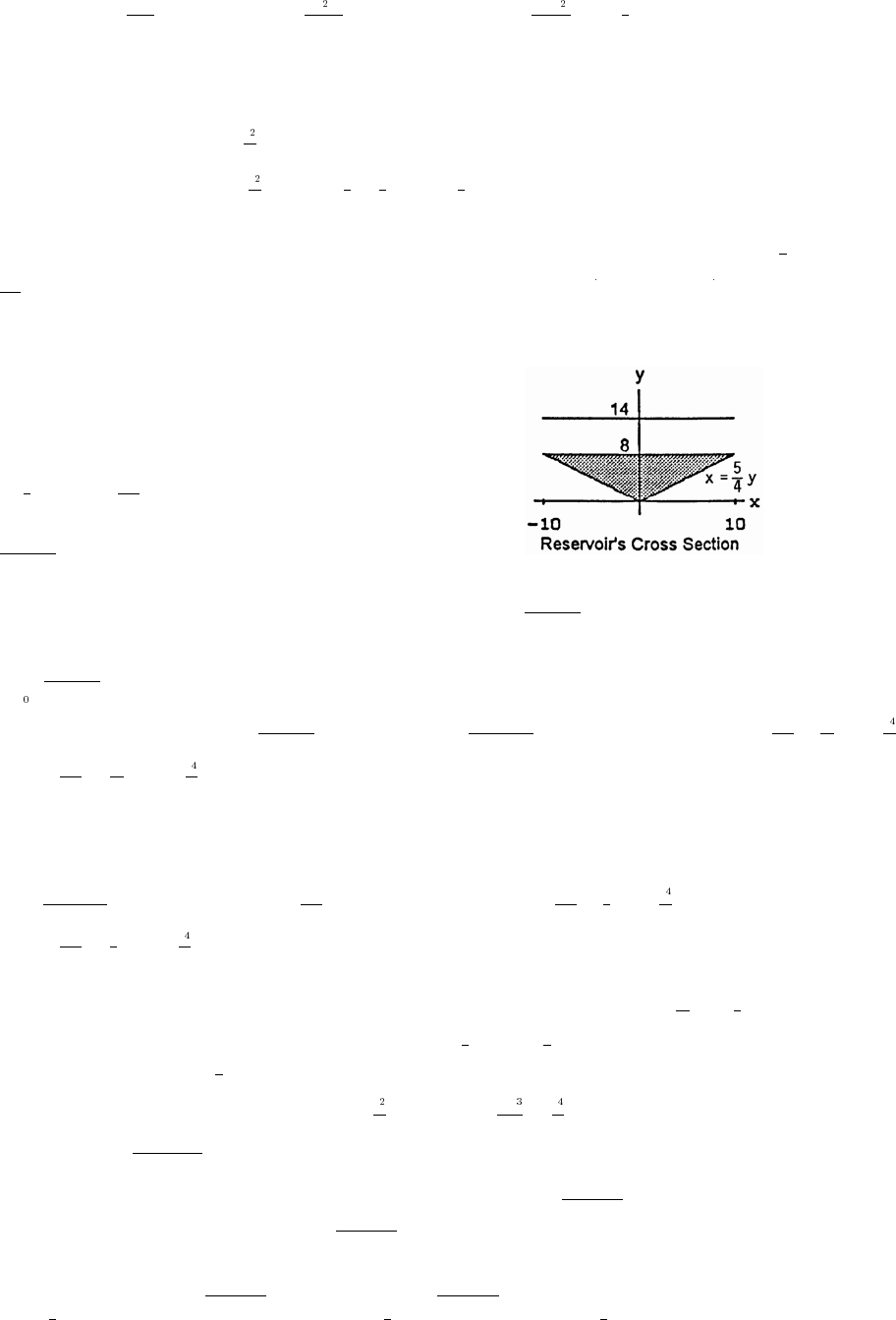
Chapter 6 Practice Exercises 419
6400 1 dx 6400 x 6400 4750 (6400)(4750)œœœœ
'0
4750 ˆ‰ ˆ‰
’“ Š ‹
x x 4750 3
9500 2 9500 4 4750 4
††
%(&!
!
22,800,000 ft lbϠ
39. Force constant: F kx 20 k 1 k 20 lb/ft; the work to stretch the spring 1 ft isœÊœ Êœ†
W kx dx k x dx 20 10 ft lb; the work to stretch the spring an additional foot isœœœœ
''
00
11
’“
x
#
"
!
†
W kx dx k x dx 20 20 20 30 ft lbœœœœœœ
''
11
22
’“ ˆ‰ˆ‰
x4 3
####
#
"
"†
40. Force constant: F kx 200 k(0.8) k 250 N/m; the 300 N force stretches the spring xœÊ œ Êœ œ
F
k
1.2 m; the work required to stretch the spring that far is then W F(x) dx 250x dxœœ œ œ
300
250 ''
00
12 12
[125x ] 125(1.2) 180 Jœœœ
#"Þ# #
!
41. We imagine the water divided into thin slabs by planes
perpendicular to the y-axis at the points of a partition of the
interval [0 8]. The typical slab between the planes at y andß
y y has a volume of about V (radius) (thickness)œ??1
#
y y y y ft . The force F(y) required toœœ1? ?
ˆ‰
525
416
##$
1
lift this slab is equal to its weight: F(y) 62.4 Vœ?
y y lb. The distance through which F(y)œ(62.4)(25)
16 1?
#
must act to lift this slab to the level 6 ft above the top is
about (6 8 y) ft, so the work done lifting the slab is about W y (14 y) y ft lb. The work done œ ?1?
(62.4)(25)
16 #†
lifting all the slabs from y 0 to y 8 to the level 6 ft above the top is approximatelyœœ
W y (14 y) y ft lb so the work to pump the water is the limit of these Riemann sums as the norm of¸
!
8(62.4)(25)
16 1?
#†
the partition goes to zero: W y (14 y) dy 14y y dy (62.4) yœœœ
''
00
88
(62.4)(25) (62.4)(25) y
(16) 16 16 3 4
25 14
1##$$
)
!
11
ab ˆ‰
’“
(62.4) 8 418,208.81 ft lbœ¸
ˆ‰
Š‹
25 14 8
16 3 4
1
††
$
42. The same as in Exercise 41, but change the distance through which F(y) must act to (8 y) rather than
(6 8 y). Also change the upper limit of integration from 8 to 5. The integral is:
W y (8 y) dy (62.4) 8y y dy (62.4) yœœ œ
''
00
55
(62.4)(25) y
16 16 16 3 4
25 25 8
111
##$$
&
!
ˆ‰ ˆ‰
ab ’“
(62.4) 5 54,241.56 ft lbœ¸
ˆ‰
Š‹
25 8 5
16 3 4
1
††
$
43. The tank's cross section looks like the figure in Exercise 41 with right edge given by x y . A typicalœœ
5
10
y
#
horizontal slab has volume V (radius) (thickness) y y y. The force required to lift this?1 1? ?œœœ
##
#
#
ˆ‰
y
4
1
slab is its weight: F(y) 60 y y. The distance through which F(y) must act is (2 10 y) ft, so theϠ
1
4#?
work to pump the liquid is W 60 (12 y) dy 15 22,500 ft lb; the time neededœœœ
'0
10
11 1
Š‹ ’ “
y 12y y
434
"!
!
†
to empty the tank is 257 sec
22,500 ft lb
275 ft lb/sec
†
†¸
44. A typical horizontal slab has volume about V (20)(2x) y (20) 2 16 y y and the force required to?? ?œœ
ˆ‰
È#
lift this slab is its weight F(y) (57)(20) 2 16 y y. The distance through which F(y) must act isœ
ˆ‰
È#?
(6 4 y) ft, so the work to pump the olive oil from the half-full tank is
W 57 (10 y)(20) 2 16 y dy 2880 10 16 y dy 1140 16 y ( 2y) dyœ œ
'''
444
000
ˆ‰
ÈÈ
ab
##
#"Î#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
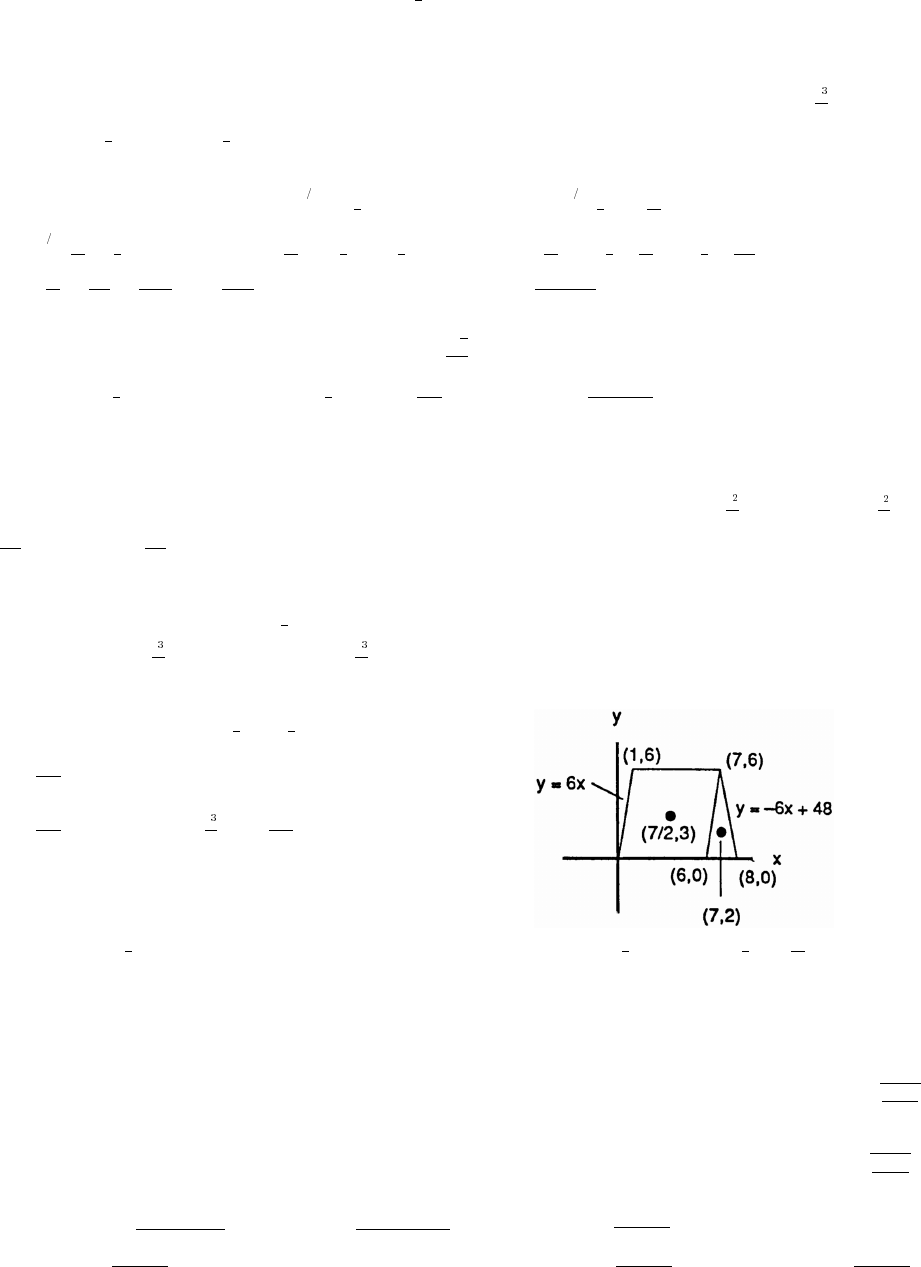
420 Chapter 6 Applications of Definite Integrals
22,800 (area of a quarter circle having radius 4) (1140) 16 y (22,800)(4 ) 48,640œœ†2
3’“
ab
#$Î# !
%
1
335,153.25 ft lbϠ
45. F W L(y) dy F 2 (62.4)(2 y)(2y) dy 249.6 2y y dy 249.6 yœÊœœœ
'''
a00
b22
††
Š‹ ’ “
ab
strip
depth 3
y
##
#
!
(249.6) 4 (249.6) 332.8 lbœœ œ
ˆ‰ ˆ‰
84
33
46. F W L(y) dy F 75 y (2y 4) dy 75 y 2y 4y dyœÊœœ
'''
a00
b5656
††
Š‹ ˆ‰ ˆ ‰
strip
depth 6 3 3
5510
#
75 y 2y dy 75 y y y (75)œœœ
'0
56
ˆ‰ ‘ ‘ˆ‰ˆ‰ˆ‰ˆ‰ˆ ‰
10 7 10 7 2 50 7 25 2 125
3 3 3 6 3 18 6 36 3 216
##$
&Î'
!
(75) (25 216 175 9 250 3) 118.63 lb.œœ œ¸
ˆ‰ˆ‰
25 175 250 75
9 216 3 16 9 16 9 16
(75)(3075)
†† †## #
†††
47. F W L(y) dy F 62.4 (9 y) 2 dy 62.4 9y 3y dyœÊœœ
'''
a00
b44
†† †
Š‹ Š ‹ ˆ‰
strip
depth 2
y
È"Î# $Î#
62.4 6y y (62.4) 6 8 32 (48 5 64) 2196.48 lbœœ†œ œœ
‘ˆ‰ˆ‰
$Î# &Î# %
!
2 2 62.4
5555
(62.4)(176)
††
48. Place the origin at the bottom of the tank. Then F W L(y) dy, h the height of the mercury column,œœ
'0
h
††
Š‹
strip
depth
strip depth h y, L(y) 1 F 849(h y) dy (849) (h y) dy 849 hy 849 hœ œÊ œ " œ œ œ
''
00
hh h
’“ Š‹
yh
##
!
#
h . Now solve h 40000 to get h 9.707 ft. The volume of the mercury is s h 1 9.707 9.707 ftœœ¸ œ†œÞ
849 849
22
22## $
49. F w (8 y)(2)(6 y) dy w (8 y)(2)(y 6) dy 2w 48 14y y dy 2w 48 2y y dyœ œ
"# "#
##
'' ''
060 6
60 6 0
abab
2w 48y 7y 2w 48y y 216w 360wœœ
"# "#
##
'!
!'
’“’“
yy
33
50. (a) F 62.4 (10 y) 8 dyœ
'0
6‘ˆ‰ˆ‰
yy
66
240 34y y dyœ
62.4
3'ab
6
0
#
240y 17y (1440 612 72)œœ
62.4 62.4
333
y
’“
#'
!
18,720 lb.œ
(b) The centroid 3 of the parallelogram is located at the intersection of y x and y x . The centroid of
ˆ‰
76636
2755
ßœœ
the triangle is located at (7 2). Therefore, F (62.4)(7)(36) (62.4)(8)(6) (300)(62.4) 18,720 lbßœœœ
CHAPTER 6 ADDITIONAL AND ADVANCED EXERCISES
1. V f(x) dx b ab f(t) dt x ax for all x a [f(x)] 2x a f(x)œœÊœÊœÊœ„11 1
''
aa
bx
cd cd É
##
## # 2x a
1
2. V [f(x)] dx a a [f(t)] dt x x for all x a [f(x)] 2x 1 f(x)œœÊœÊœÊœ„11 1
''
00
ax
## ## #
É2x 1
1
3. s(x) Cx 1 [f (t)] dt Cx 1 [f (x)] C f (x) C 1 for C 1œÊ œÊ œÊ œ
'0
xÈÈ È
w# w # #
w
f(x) C 1 dt k. Then f(0) a a 0 k f(x) C 1 dt a f(x) x C 1 a,Êœ œÊœÊœ Êœ
''
0 0
x x
ÈÈÈ
###
where C 1.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
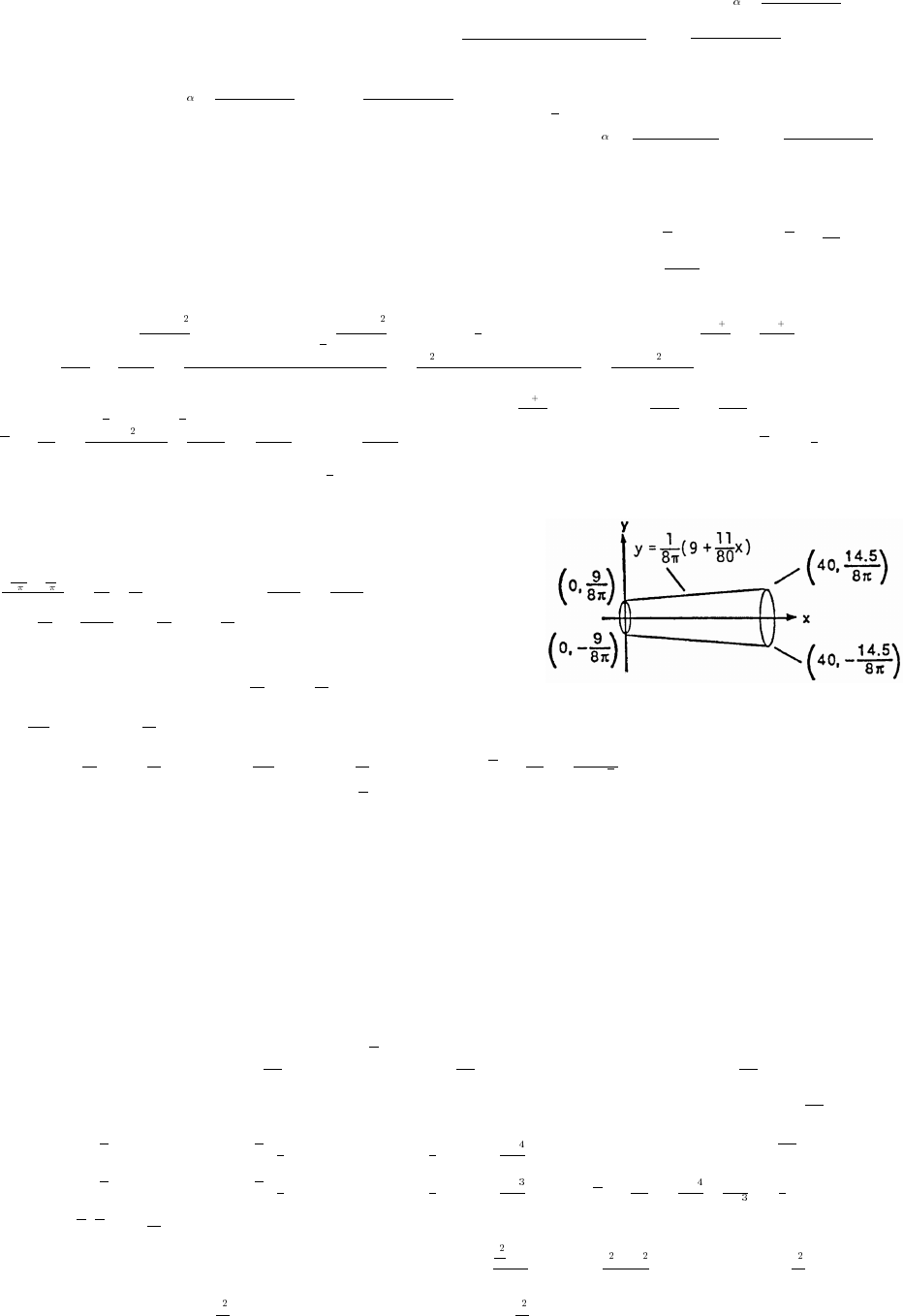
Chapter 6 Additional and Advanced Exercises 421
4. (a) The graph of f(x) sin x traces out a path from ( ) to ( sin ) whose length is L 1 cos d .œ!ß!ßœ!! ))
'0È#
The line segment from (0 0) to ( sin ) has length ( 0) (sin 0) sin . Since theßß œ!! ! ! ! !
ÈÈ
####
shortest distance between two points is the length of the straight line segment joining them, we have
immediately that 1 cos d sin if 0 .
'0ÈÈ
Ÿ
### #
)) ! ! ! 1
(b) In general, if y f(x) is continuously differentiable and f(0) 0, then 1 [f (t)] dt f ( )œœ
'0ÈÈ
w# # #
!!
for 0.!
5. From the symmetry of y 1 x , n even, about the y-axis for 1 x 1, we have x 0. To find y , weœ ŸŸ œ œ
nM
M
x
use the vertical strips technique. The typical strip has center of mass: ( x y ) x , length: 1 x ,
µµ
ßœß
ˆ‰
1x
2
nn
width: dx, area: dA 1 x dx, mass: dm 1 dA 1 x dx. The moment of the strip about theœ œ œab ab
nn
†
x-axis is y dm dx M dx 2 1 2x x dx x
µœÊœ œœ
ab ab1x 1x 2x x
n1 n1
### #
""
!
nn
x10
11
n2n
''
ab
‘
n1 2n1
1 .œ œ œ œ
2 2n 3n14n2n1 2n
n 1 n 1 (n 1)( n 1) (n 1)( n 1) (n 1)( n 1)
(n 1)(2n 1) 2(2n ) (n 1)
# # # #
"
"
Also, M dA 1 x dx 2 1 x dx 2 x 2 1 . Therefore,œ œœ œ œœ
'' '
11 0
11 1
nn
ab ab ‘ˆ‰
x2n
n1 n1 n1
n1
"
!
"
y is the location of the centroid. As n , y soœ œ œ Ê !ß Ä _ Ä
M
M (n1)(2n1) 2n 2n1 n1
2n n n
(n 1)
x
# #
"
†ˆ‰
the limiting position of the centroid is .
ˆ‰
!ß "
#
6. Align the telephone pole along the x-axis as shown in the
accompanying figure. The slope of the top length of pole is
(14.5 9) . Thus,
ˆ‰
14.5 9
88
""
40 8 40 8 40 8 80
5.5 11
œœœ
111
††
††
y x 9 x is an equation of theœ œ
911 11
8880 8 8011 1†
"ˆ‰
line representing the top of the pole. Then,
M x y dx x 9 x dx
yœœ
''
a0
b40
†11
#"#
‘ˆ‰
880
11
1
x 9 x dx; M y dxœ œ
"##
64 80
11
1''
0a
40 b
ˆ‰ 1
9 x dx 9 x dx. Thus, x 23.06 (using a calculator to computeœœ œ¸¸1''
00
40 40
‘ ˆ‰ˆ‰
""
##
880 64 80 M
11 11 M129,700
5623.3
11
y
the integrals). By symmetry about the x-axis, y 0 so the center of mass is about 23 ft from the top of the pole.œ
7. (a) Consider a single vertical strip with center of mass ( x y ). If the plate lies to the right of the line, then
µµ
ß
the moment of this strip about the line x b is (x b) dm (x b) dA the plate's first momentœœ Ê
µµ
$
about x b is the integral (x b) dA x dA b dA M b A.œœœ
''
$$$ $
'y
(b) If the plate lies to the left of the line, the moment of a vertical strip about the line x b isœ
b x dm b x dA the plate's first moment about x b is (b x) dA b dA x dAababœ Ê œ œ
µµ
$$$$
'''
bA M.œ$y
8. (a) By symmetry of the plate about the x-axis, y 0. A typical vertical strip has center of mass:œ
( x y ) (x 0), length: 4 ax, width: dx, area: 4 ax dx, mass: dm dA kx 4 ax dx, for some
µµ
ßœß œ œ
ÈÈ È
$†
proportionality constant k. The moment of the strip about the y-axis is M x dm 4kx ax dx
y0
a
œœ
µ
''#È
4k a x dx 4k a x 4ka a . Also, M dm 4kx ax dxœœœœœœ
ÈÈ È
‘
''
0 0
a a
a
0
&Î# (Î# "Î# (Î#
2 2 8ka
777
†'
4k a x dx 4k a x 4ka a . Thus, x aœœœœœœœ
ÈÈ
‘
'0
aa
0
$Î# &Î# "Î# &Î#
2 2 8ka 8ka 5 5
5 5 5 M 7 8ka 7
M
††
y
(x y) 0 is the center of mass.Êßœ ß
ˆ‰
5a
7
(b) A typical horizontal strip has center of mass: ( x y ) y y , length: a ,
µµ
ßœ ßœ ß
Œ
Š‹
y
4a
#
ay4a y
8a 4a
width: dy, area: a dy, mass: dm dA y a dy. Thus, M y dm
Š‹ Š‹
kkœœœ
µ
yy
4a 4a
$x'
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

422 Chapter 6 Applications of Definite Integrals
y y a dy y a dy y a dyœœ
'''
2a 2a 0
2a 0 2a
kkŠ‹ Š‹ Š‹
yyy
4a 4a 4a
##
ay dy ay dy y yœ œ
''
2a 0
02a
a
a
Š‹Š‹’ “’“
##$$
##
!#
# !
yyyy
4a 4a 3 0a 3 0a
aa
0; M x dm y a dyœ œ œ œ
µ
8a 32a 8a 32a
3 20a 3 0a 8a 4a
y 4a y
#
y2a
2a
''Š‹Š‹
kk
y y 4a dy y 16a y dyœ œ
""
## %%
8a 4a 32a
4a y
'2a
2a 2a
2a
kka b kka b
Š‹ '
16a y y dy 16a y y dy 8a y 8a yœ œ
"""
###
%& %& %# %#
!#
# !
3a 32a 3a 6 3a 6
yy
1
''
2a 0
02a
a
a
ab ab
’“’“
8a 4a 8a 4a 32a 32a a ;œœœœ
"" ""
%# %# ' ' %
32a 6 32a 6 16a 3 16a 3 3
64a 64a 32a 2 4
’“’“Š‹
ab†† †
M dm y dy y 4a y dyœœ œ
'' '
2a 2a
2a 2a
kk kka b
Š‹
4a y
4a 4a
"##
4a y y dy 4a y y dy 2a y 2a yœ œ
""""
#$ #$ ## ##
!#
# !
4a 4a 4a 4 4a 4
yy
''
2a 0
02a
a
a
ab ab
’“’“
2 2a 4a 8a 4a 2a . Therefore, x a andœœœ œœœ††
"" "
## % % $ %
#4a 4 a M 3 2a 3
16a 4 2a
M
Š‹
ab ˆ‰ˆ‰
y
y 0 is the center of mass.œœ
M
M
x
9. (a) On [0 a] a typical strip has center of mass: ( x y ) x, ,ß @/<>3-+6 ß œ
µµ Š‹
ÈÈ
bx ax
#
length: b x a x , width: dx, area: dA b x a x dx, mass: dm dA
ÈÈ ÈÈ
Š‹
## ## ## ##
œ œ$
b x a x dx. On [a b] a typical strip has center of mass:œ ß @/<>3-+6$Š‹
ÈÈ
## ##
( x y ) x , length: b x , width: dx, area: dA b x dx,
µµ
ßœß œ
Š‹ÈÈ
Èbx
### ##
mass: dm dA b x dx. Thus, M y dmœœ œ
µ
$$
È'
## x
bx ax bx ax dx bx bx dxœ
''
0 a
a b
" "
# #
## ## ## ## ## ##
Š‹Š‹
ÈÈ ÈÈ ÈÈ
$$
b x a x dx b x dx b a dx b x dxœœ
$$$$
####
## ## ## ## ##
''''
0a0a
abab
c d ab ab ababab
bax bx baa b baœ œ
$$$$
####
## # ## $ #
!
cd cdab ab
’“ ’ “Š‹Š ‹
ab
xba
333
a
ab a b ab ; M x dmœ œœ œ
µ
$$ $$
##
#$ $ #
ab
Š‹ Š‹
'
2abab a
33333
$y
x b x a x dx x b x dxœ
''
0a
ab
$$
Š‹
ÈÈ È
## ## ##
xb x dx xa x dx xb x dxœ $$ $
'''
00a
aab
ab ab ab
## ## ##
"Î# "Î# "Î#
œ
###
!
$$$
”•”•”•
2b x 2a x 2b x
333
ab ab ab
aa b
0a
ba b 0a 0ba M;œ œœ œ
$$$$$
$
333333
ba ba
’“’“’“
abab ab ab
## # # ##
$Î# $Î# $Î# $Î#
ab x
We calculate the mass geometrically: M A b a . Thus, xœœ œ œ$$ $
Š‹ Š‹ ab
11$1ba
444 M
M
## y
; likewiseœœœœ
$
$1 1 1 1
ab abab
ab
ba (ba)aabb 4aabb
3 b a 3 b a 3 (b a)(b a) 3 (a b)
44ba4
†Š‹
y.œœ
M
M3(ab)
4a ab b
xab
1
(b) lim (x y) is the limiting
baÄ
4 aabb 4 aaa 4 3a 2a 2a2a
3ab 3 aa 32a11 1111
Š‹Š‹Š‹
ˆ‰ ˆ‰ ˆ ‰
œœœÊßœß
position of the centroid as b a. This is the centroid of a circle of radius a (and we note the two circlesÄ
coincide when b a).œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
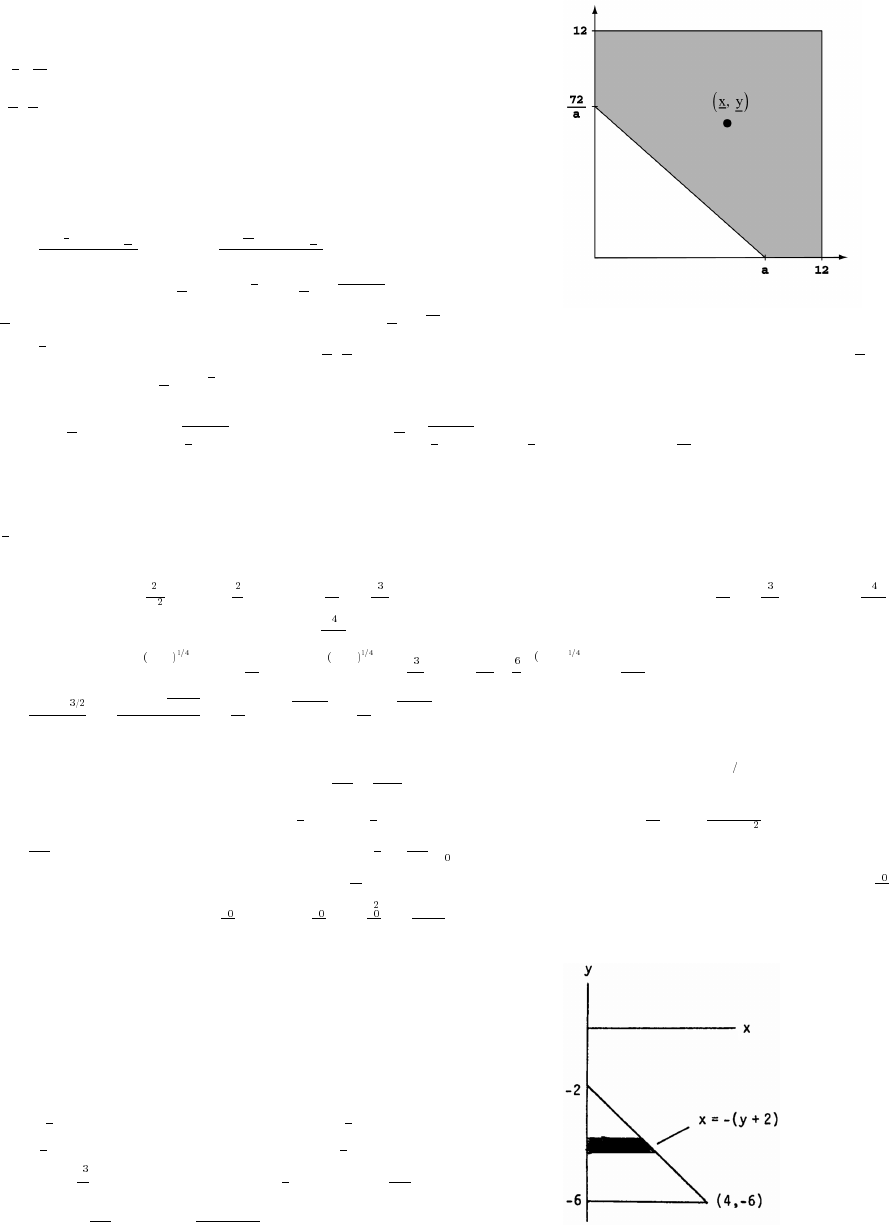
Chapter 6 Additional and Advanced Exercises 423
10. Since the area of the traingle is 36, the diagram may be
labeled as shown at the right. The centroid of the triangle is
, . The shaded portion is 144 36 108. Write
ˆ‰
a24
3a œ
, for the centroid of the remaining region. The centroidabxy
of the whole square is obviously 6, 6 . Think of the squareab
as a sheet of uniform density, so that the centroid of the
square is the average of the centroids of the two regions,
weighted by area:
and 'œ 'œ
$' "!) $' "!)
"%% "%%
ˆ‰ ˆ ‰
ab ab
a24
3a
x y
which we solve to get and . Setx yœ) œ
aa
a*
)"ab
7 in. (Given). It follows that a , whence x yœœ*œ
'%
*
7 in. The distances of the centroid , from the other sides are easily computed. (Note that if we set 7 in.œ œ
"
*abx y y
above, we will find 7 .)xœ"
*
11. y 2 x ds 1 dx A 2 x 1 dx (1 x)œÊœÊœ œ œ
ÈÈ
ÉÉ
‘
""
$Î# $
!
xx33
428
'0
3
12. This surface is a triangle having a base of 2 a and a height of 2 ak. Therefore the surface area is11
(2 a)(2 ak) 2 a k.
"
#
##
11 1œ
13. F ma t a v C; v 0 when t 0 C 0 x C ;œ œ Ê œœ Êœ œ œ œÊ œÊ œ Êœ
#"
dx t dx t dx t t
dt m dt 3m dt 3m 12m
x 0 when t 0 C 0 x . Then x h t (12mh) . The work done isœœÊœÊœ œÊœ
""Î%
t
12m
W F dx F(t) dt t dt (12mh)œœ œ œ œ
'’“ ˆ‰
''
00
12mh 12mh 12mh)
0
††
dx t t
dt 3m 3m 6 18m
# 'Î%
""
2 3mh 3mhœœ œ œ
(12mh)
18m 18m 3 3
12mh 12mh 2h 4h
†È†ÈÈ
14. Converting to pounds and feet, 2 lb/in 24 lb/ft. Thus, F 24x W 24x dxœœ œÊœ
2 lb 12 in
1 in 1 ft
†'0
12
12x 3 ft lb. Since W mv mv , where W 3 ft lb, m lbœœ œ œ œcd ˆ‰ˆ ‰
###
"Î#
!"" " "
## #
!"
††
10 3 ft/sec
slugs, and v 0 ft/sec, we have 3 v v 3 640. For the projectile height,œœ œÊœ
"""
"##
##
!
320 3 0
ˆ‰ˆ ‰ †
s 16t v t (since s 0 at t 0) v 32t v . At the top of the ball's path, v 0 tœ œ œ Ê œ œ œ Ê œ
#!!
#
ds
dt 3
v
and the height is s 16 v 30 ft.œ œ œ œ
ˆ‰ ˆ‰
vv
3 3 64 64
v3 640
##
#
!
†
15. The submerged triangular plate is depicted in the figure
at the right. The hypotenuse of the triangle has slope 1
y ( 2) (x 0) x (y 2) is an equationÊ œ Ê œ
of the hypotenuse. Using a typical horizontal strip, the fluid
pressure is F (62.4) dyœ'††
Š‹Š‹
strip strip
depth length
(62.4)( y)[ (y 2)] dy 62.4 y 2y dyœœ
''
66
22
ab
#
62.4 y (62.4) 4 36œœ
’“ ‘ˆ‰ˆ ‰
y
333
8 216
##
'
(62.4) 32 2329.6 lbœœ¸
ˆ‰
208
33
(62.4)(112)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
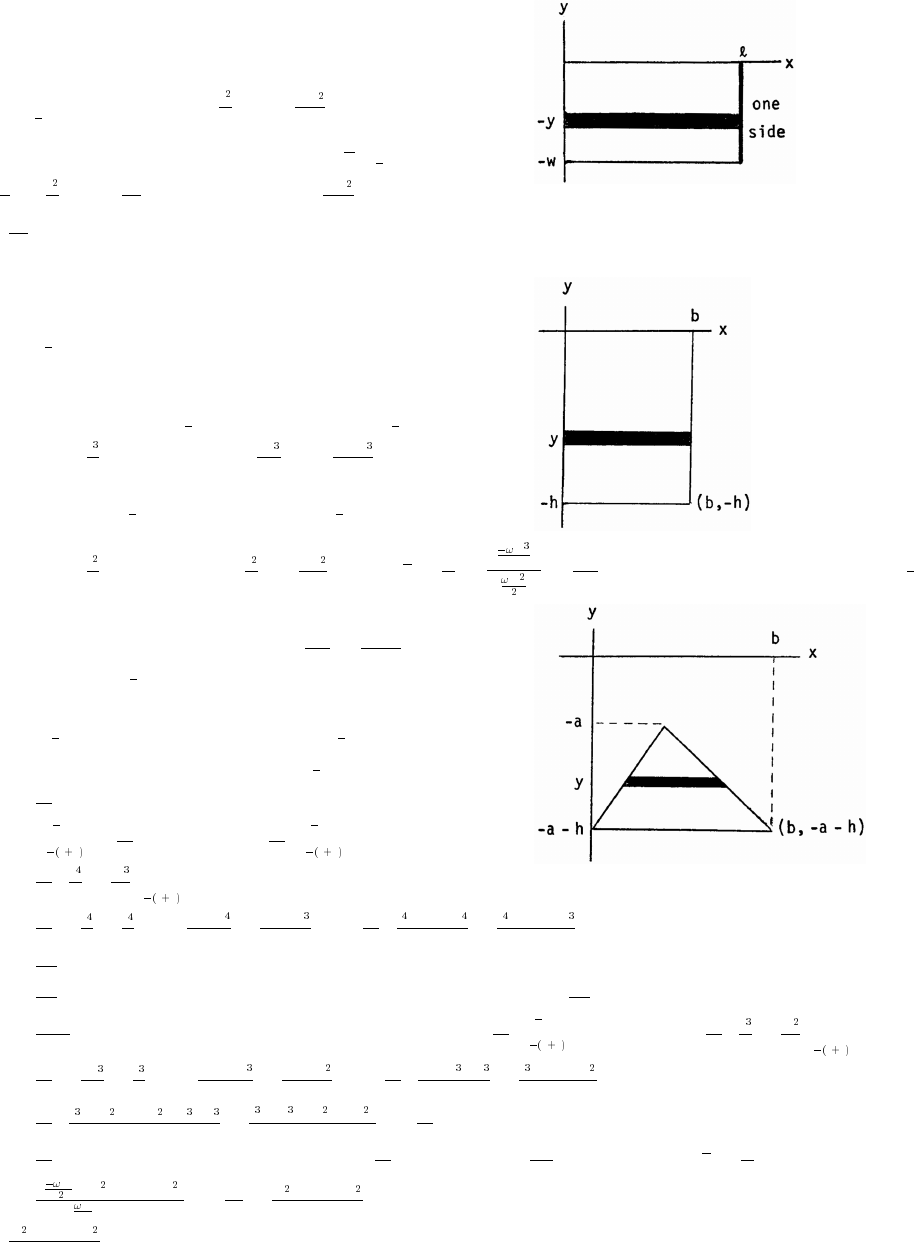
424 Chapter 6 Applications of Definite Integrals
16. Consider a rectangular plate of length and width w.j
The length is parallel with the surface of the fluid of
weight density . The force on one side of the plate is=
F ( y)( ) dy . Theœjœj œ==
'w
0
w
’“
yw
##
!
j=
average force on one side of the plate is F ( y)dy
av w
0
œ
=
w'
. Therefore the force œ œ
== =
w
yww
’“
## #
!
j
w
( w) (the average pressure up and down) (the area of the plate).œjœ
ˆ‰
=w
#
†
17. (a) We establish a coordinate system as shown. A typical
horizontal strip has: center of pressure: ( x y )
µµ
ß
y , length: L(y) b, width: dy, area: dAœß œ
ˆ‰
b
#
b dy, pressure: dp y dA b y dyœœœ==kk kk
F y dp y b y dy b y dyÊœ œ œ
µ
xhh
00
'''
†==kk #
bb0 ;œ œ œ==
’“ ’ “Š‹
y
333
hbh
!
h
=
F dp y L(y) dy b y dyœœ œ
'''
hh
00
==kk
b b 0 . Thus, y the distance below the surface is h.œ œ œ œ œ œ Ê==
’“ ’ “
yhbh 2h 2
F
F3 3
###
!
h
=xŠ‹
Š‹
bh
3
bh
(b) A typical horizontal strip has length L(y). By similar
triangles from the figure at the right, L(y) y a
bh
œ
L(y) (y a). Thus, a typical strip has centerʜ
b
h
of pressure: ( x y ) ( x y), length: L(y)
µµ µ
ßœß
(y a), width: dy, area: dA (y a) dy,œ œ
bb
hh
pressure: dp y dA ( y) (y a) dyœœ==kk ˆ‰
b
h
y ay dy F y dpœÊœ
µ
=b
hab
#x'
y y ay dy y ay dyœœ
''
ah ah
aa
†
==bb
hh
ab a b
#$#
œ
=b
h4 3
yay
’“
a
ah
œ œ
==ba a b
h43 4 3 h 4 3
(a h) a(a h) a (a h) a a(a h)
’“’“Š‹Š ‹
3a a4ah6ah4ahh 4aaa3ah3ahhœ
=b
12h c dabababab
%%$##$% %$# #$
12a h 12a h 4ah 12a h 18a h 12ah 3h 6a h 8ah 3hœ œ
= =b b
12h 12h
abab
$ ## $ $ ## $ % ## $ %
6a 8ah 3h ; F dp y L(y) dy y ay dyœœœ œ œ
## #
===bh b b
12 h h 3 2
yay
ab kk ab
’“
''
='ah
aa
ah
œ œ
==baa b
h3 3 h 3 2
(ah) a(ah) (ah) a a a(ah)
’“’“Š‹Š ‹
##
23ah 3ah h 32ah ahœœ
==ba3ah3ahha b
h3 6h
aa2ahah
’“
cdabab
#
##$ ##
ab
6a h 6ah 2h 6a h 3ah 3ah 2h (3a 2h). Thus, yœœœ œ
===bbbh
6h 6h 6 F
F
abab
##$## #$ x
the distance below the surface isœœ Ê
ˆ‰
ˆ‰
bh
1bh
6
ab6a 8ah 3h
(3a 2h)
6a 8ah 3h
3a 2h
"
#
ˆ‰
Š‹
.
6a 8ah 3h
6a 4h
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
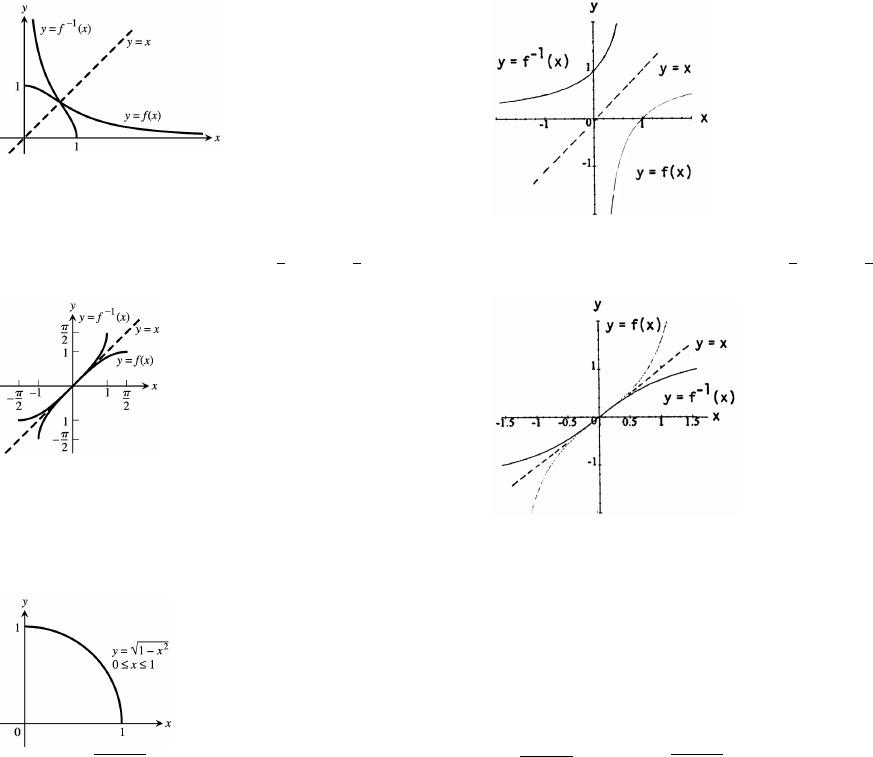
CHAPTER 7 TRANSCENDENTAL FUNCTIONS
7.1 INVERSE FUNCTIONS AND THEIR DERIVATIVES
1. Yes one-to-one, the graph passes the horizontal test.
2. Not one-to-one, the graph fails the horizontal test.
3. Not one-to-one since (for example) the horizontal line y intersects the graph twice.œ#
4. Not one-to-one, the graph fails the horizontal test.
5. Yes one-to-one, the graph passes the horizontal test
6. Yes one-to-one, the graph passes the horizontal test
7. Domain: 0 x 1, Range: 0 y 8. Domain: x 1, Range: y 0Ÿ Ÿ
9. Domain: 1 x 1, Range: y 10. Domain: x , Range: yŸŸ ŸŸ __ Ÿ
11 11
## ##
11. The graph is symmetric about y x.œ
(b) y 1 x y 1 x x 1 y x 1 y y 1 x f (x)œ ʜʜʜ Êœ œ
ÈÈ
È
###
#### "
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

426 Chapter 7 Transcendental Functions
12. The graph is symmetric about y x.œ
y x y f(x)œÊœÊœœ
"""
"
xyx
13. Step 1: y x 1 x y 1 x y 1œÊ œÊœ
## È
Step 2: y x 1 f (x)œœ
È"
14. Step 1: y x x y, since x .œ Ê œ Ÿ!
#È
Step 2: y x f (x)œ œ
È"
15. Step 1: y x 1 x y 1 x (y 1)œÊ œÊœ
$ $ "Î$
Step 2: y x 1 f (x)œœ
$"
È
16. Step 1: y x 2x 1 y (x 1) y x 1, since x 1 x 1 yœÊœ Ê œ Êœ
##
ÈÈ
Step 2: y1 xf(x)œ œ
È"
17. Step 1: y (x 1) y x 1, since x 1 x y 1œ Ê œ Êœ
#ÈÈ
Step 2: y x 1 f (x)œœ
È"
18. Step 1: y x x yœÊœ
#Î$ $Î#
Step 2: y x f (x)œœ
$Î# "
19. Step 1: y x x yœÊœ
& "Î&
Step 2: y x f (x);œœ
&"
È
Domain and Range of f : all reals;
"
f f (x) x x and f (f(x)) x xab ab
ˆ‰
" "Î& " &
&"Î&
œœ œœ
20. Step 1: y x x yœÊœ
% "Î%
Step 2: y x f (x);œœ
%"
È
Domain of f : x 0, Range of f : y 0;
" "
f f (x) x x and f (f(x)) x xab ab
ˆ‰
" "Î% " %
%"Î%
œœ œœ
21. Step 1: y x 1 x y 1 x (y 1)œÊ œÊœ
$ $ "Î$
Step 2: y x 1 f (x);œœ
$"
È
Domain and Range of f : all reals;
"
f f (x) (x 1) 1 (x 1) 1 x and f (f(x)) x 1 1 x xab a bab
ˆ‰ ab
" "Î$ " $ $
$"Î$ "Î$
œ œœ œ œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
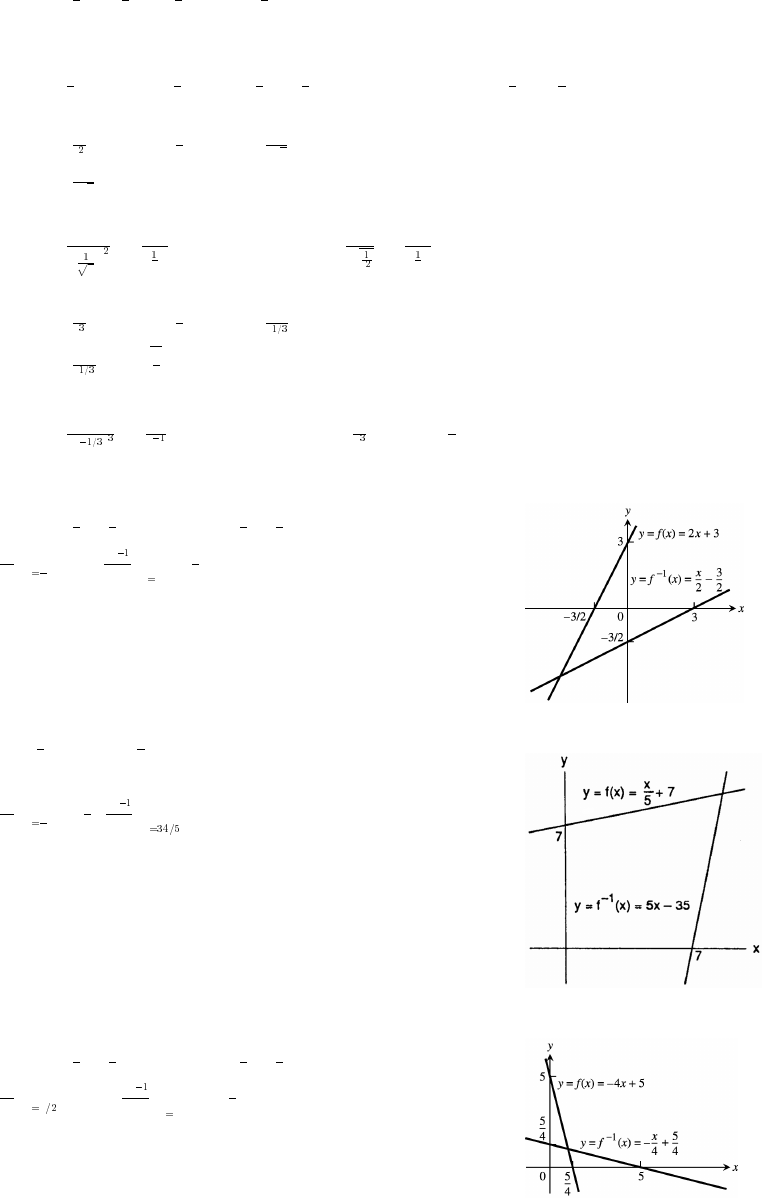
Section 7.1 Inverse Functions and Their Derivatives 427
22. Step 1: y x x y x 2y 7œÊ œÊœ
""
## # #
77
Step 2: y 2x 7 f (x);œœ
"
Domain and Range of f : all reals;
"
f f (x) (2x 7) x x and f (f(x)) 2 x 7 (x 7) 7 xab ˆ‰ ˆ ‰
" "
""
#### ##
œ œœ œ œœ
777 7
23. Step 1: y x xœÊœÊœ
"""
#
xyy
È
Step 2: y f (x)œœ
""
Èx
Domain of f : x 0, Range of f : y 0;
" "
f f (x) x and f (f(x)) x since x 0ab
" "
"" ""
œœœ œœœ
Š‹ Š‹ Š‹
É
xxx
x
24. Step 1: y x xœÊœÊœ
"""
$
xy
y
Step 2: y f (x);œœ œ
""
$"
xx
É
Domain of f : x 0, Range of f : y 0;
" "
ÁÁ
f f (x) x and f (f(x)) xab ˆ‰ ˆ‰
" "
"" " "
"Î$ "
œœœ œ œœ
abxxxx
25. (a) y 2x 3 2x y 3œÊ œ
x f (x)ÊœÊ œ
y3x3
## ##
"
(c) 2,
¸¹
df df
dx dx
x1 x1
œœ
"
#
(b)
26. (a) y x 7 x y 7œÊ œ
""
55
x 5y 35 f (x) 5x 35Êœ Ê œ
"
(c) , 5
¸¹
df df
dx 5 dx
x1 x
œœ
"
(b)
27. (a) y 5 4x 4x 5 yœ Ê œ
x f (x)ÊœÊ œ
55x
44 44
y"
(c) 4,
¸¹
df df
dx dx 4
x1 x3
œ œ"
(b)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

428 Chapter 7 Transcendental Functions
28. (a) y 2x x yœÊœ
##
"
#
x y f (x)Êœ Ê œ
""
#
È2
x
ÈÈ
(c) 4x 20,
¸k
df
dx xx5
œœ
x
¹¹
df
dx 0
2
x0 x50
œœ
""
#
"Î#
#
È
(b)
29. (a) f(g(x)) x x, g(f(x)) x xœœ œœ
ˆ‰
ÈÈ
$$$
(c) f (x) 3x f (1) 3, f ( 1) 3;
w#w w
œÊ œœ
g (x) x g (1) , g ( 1)
w #Î$ w w
"""
œÊœœ
333
(d) The line y 0 is tangent to f(x) x at ( );œ œ !ß !
$
the line x 0 is tangent to g(x) x at (0 0)œœß
$
È
(b)
30. (a) h(k(x)) (4x) x,œœ
""Î$ $
4ˆ‰
k(h(x)) 4 xœœ
Š‹
†x
4
"Î$
(c) h (x) h (2) 3, h ( 2) 3;
www
œÊ œ œ
3x
4
k (x) (4x) k (2) , k ( 2)
w #Î$ w w
""
œÊœœ
4
333
(d) The line y 0 is tangent to h(x) at ( );œ œ !ß !
x
4
the line x 0 is tangent to k(x) (4x) atœœ
"Î$
()!ß !
(b)
31. 3x 6x 32. 2x 4
df df df df
dx dx 9 dx dx 6
œÊ œ œ œÊ œ œ
#" "
¹¹
ºº
xf(3) xf(5)
x3 x5
""
df df
dx dx
33. 3 34.
¹¹ ¹¹
ºº
df df
dx dx dx dx 2
dg dg
x4 xf(2) x0 xf(0)
x2 x0
œœœœ œœœ
""
df dg
dx dx
" "
ˆ‰
3
35. (a) y mx x y f (x) xœÊœ Ê œ
""
"
mm
(b) The graph of y f (x) is a line through the origin with slope .œ" "
m
36. y mx b x f (x) x ; the graph of f (x) is a line with slope and y-intercept .œÊœÊ œ
y
mm m m m m
bb b
" "
""
37. (a) y x 1 x y 1 f (x) x 1œ Ê œ Ê œ
"
(b) y x b x y b f (x) x bœ Ê œ Ê œ
"
(c) Their graphs will be parallel to one another and lie on
opposite sides of the line y x equidistant from thatœ
line.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
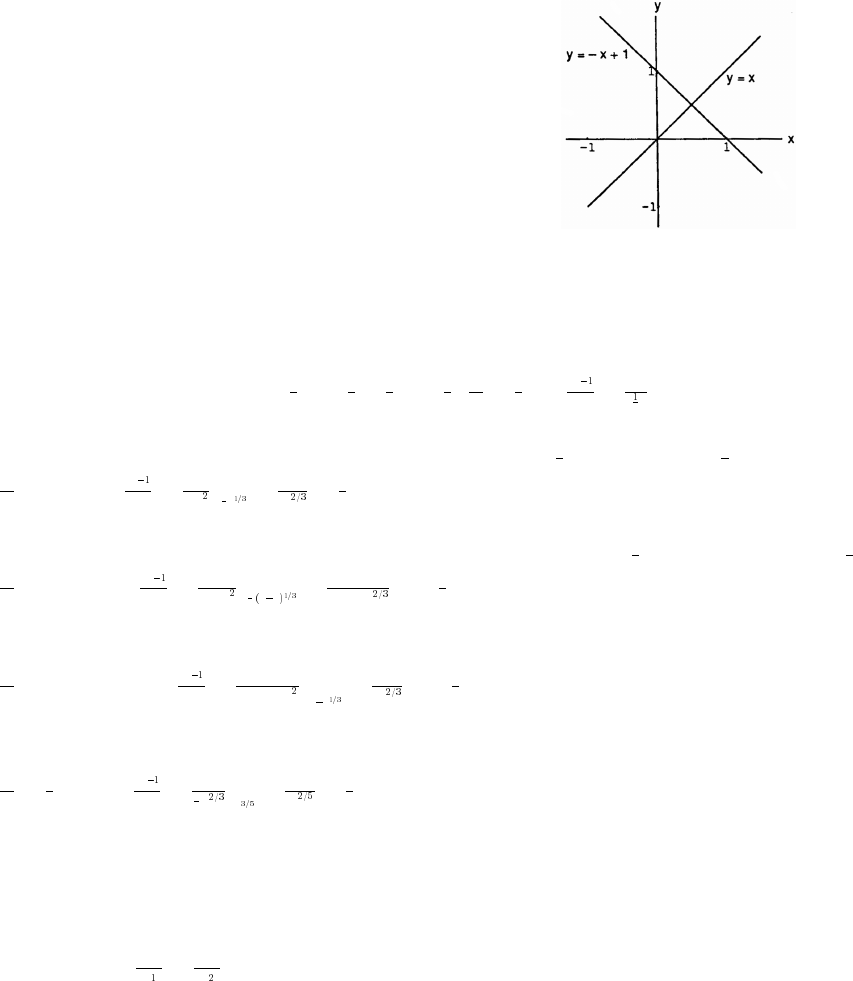
Section 7.1 Inverse Functions and Their Derivatives 429
38. (a) y x 1 x y 1 f (x) 1 x;œÊ œÊ œ
"
the lines intersect at a right angle
(b) y x b x y b f (x) b x;œ Ê œ Ê œ
"
the lines intersect at a right angle
(c) Such a function is its own inverse.
39. Let x x be two numbers in the domain of an increasing function f. Then, either x x or
"# "#
Á
x x which implies f(x ) f(x ) or f(x ) f(x ), since f(x) is increasing. In either case,
"# "#"#
f(x ) f(x ) and f is one-to-one. Similar arguments hold if f is decreasing.
"#
Á
40. f(x) is increasing since x x x x ; 3
#" # "
"" " "
Ê œÊ œ œ
3636dx3dx
5 5 df df ˆ‰
3
41. f(x) is increasing since x x 27x 27x ; y 27x x y f (x) x ;
#" $ $ $ "Î$ " "Î$
#"""
Ê œ Êœ Ê œ
33
81x x
df df
dx dx 81x 9
9x
œÊœ œœ
# #Î$
"""
¸1
3x
42. f(x) is decreasing since x x 1 8x 1 8x ; y 1 8x x (1 y) f (x) (1 x) ;
#" $ $ $ "Î$ " "Î$
#"""
##
Ê œ Êœ Ê œ
24x (1 x)
df df
dx dx 24x 6
6( x)
œ Ê œ œ œ
# #Î$
"""
"
¸1
21x
43. f(x) is decreasing since x x (1 x ) (1 x ) ; y (1 x) x 1 y f (x) 1 x ;
#" # "
$ $ $ "Î$ " "Î$
Ê œ Êœ Ê œ
3(1 x) x
df df
dx dx 3(1 x) 3
3x
œ Ê œ œ œ
# #Î$
"""
¹1x
44. f(x) is increasing since x x x x ; y x x y f (x) x ;
#" &Î$ &Î$
#"&Î$ $Î& " $Î&
Ê œ Êœ Ê œ
x x
df 5 df 3 3
dx 3 dx 5
x5x
œÊœ œœ
#Î$ #Î&
"¹
5
3x
45. The function g(x) is also one-to-one. The reasoning: f(x) is one-to-one means that if x x then
"#
Á
f(x ) f(x ), so f(x ) f(x ) and therefore g(x ) g(x ). Therefore g(x) is one-to-one as well.
"# " # " #
ÁÁ Á
46. The function h(x) is also one-to-one. The reasoning: f(x) is one-to-one means that if x x then
"#
Á
f(x ) f(x ), so , and therefore h(x ) h(x ).
"# " #
""
ÁÁ Á
f(x ) f(x )
47. The composite is one-to-one also. The reasoning: If x x then g(x ) g(x ) because g is one-to-one. Since
"# " #
ÁÁ
g(x ) g(x ), we also have f(g(x )) f(g(x )) because f is one-to-one. Thus, f g is one-to-one because
"# " #
ÁÁ ‰
x x f(g(x )) f(g(x )).
"# " #
ÁÊ Á
48. Yes, g must be one-to-one. If g were not one-to-one, there would exist numbers x x in the domain of g
"#
Á
with g(x ) g(x ). For these numbers we would also have f(g(x )) f(g(x )), contradicting the assumption
"# " #
œœ
that f g is one-to-one.‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

430 Chapter 7 Transcendental Functions
49. The first integral is the area between f(x) and the x-axis
over a x b. The second integral is the area betweenŸŸ
f(x) and the y-axis for f(a) y f(b). The sum of theŸŸ
integrals is the area of the larger rectangle with corners
at (0 0), (b 0), (b f(b)) and (0 f(b)) minus the area of theßßß ß
smaller rectangle with vertices at (0 0), (a 0), (a f(a)) andßßß
(0 f(a)). That is, the sum of the integrals is bf(b) af(a).ß
50. f x . Thus if ad bc , f x is either always positive or always negative. Hence f x i
w w
ab ab abœœ Á!
abab
ab ab
cx d a ax b c
cx d cx d
ad bc s
either always increasing or always decreasing. If follows that f x is one-to-one if ad bc .ab Á!
51. (g f)(x) x g(f(x)) x g (f(x))f (x) 1‰œÊ œÊ œ
ww
52. W(a) f (y) a dy 0 2 x[f(a) f(x)] dx S(a); W (t) f (f(t)) a f (t)œœœœœ
''
f(a) a
f(a) a
11 1
’“ ’ “
ab a b
" # w " # w
# #
t a f (t); also S(t) 2 f(t) x dx 2 xf(x) dx f(t)t f(t)a 2 xf(x) dxœ œ œ 111111ab c d
##w ##
'' '
aa a
tt t
S (t) t f (t) 2 tf(t) a f (t) 2 tf(t) t a f (t) W (t) S (t). Therefore, W(t) S(t)Êœ œ Ê œ œ
w#w #w ##w ww
111 11ab
for all t [a b].−ß
53-60. Example CAS commands:
:Maple
with( plots );#53
f := x -> sqrt(3*x-2);
domain := 2/3 .. 4;
x0 := 3;
Df := D(f); # (a)
plot( [f(x),Df(x)], x=domain, color=[red,blue], linestyle=[1,3], legend=["y=f(x)","y=f '(x)"],
title="#53(a) (Section 7.1)" );
q1 := solve( y=f(x), x ); # (b)
g := unapply( q1, y );
m1 := Df(x0); # (c)
t1 := f(x0)+m1*(x-x0);
y=t1;
m2 := 1/Df(x0); # (d)
t2 := g(f(x0)) + m2*(x-f(x0));
y=t2;
domaing := map(f,domain); # (e)
p1 := plot( [f(x),x], x=domain, color=[pink,green], linestyle=[1,9], thickness=[3,0] ):
p2 := plot( g(x), x=domaing, color=cyan, linestyle=3, thickness=4 ):
p3 := plot( t1, x=x0-1..x0+1, color=red, linestyle=4, thickness=0 ):
p4 := plot( t2, x=f(x0)-1..f(x0)+1, color=blue, linestyle=7, thickness=1 ):
p5 := plot( [ [x0,f(x0)], [f(x0),x0] ], color=green ):
display( [p1,p2,p3,p4,p5], scaling=constrained, title="#53(e) (Section 7.1)" );
(assigned function and values for a, b, and x0 may vary)Mathematica:
If a function requires the odd root of a negative number, begin by loading the RealOnly package that allows Mathematica
to do this. See section 2.5 for details.
<<Miscellaneous `RealOnly`
Clear[x, y]
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.1 Inverse Functions and Their Derivatives 431
{a,b} = { 2, 1}; x0 = 1/2 ;
f[x_] = (3x 2) / (2x 11)
Plot[{f[x], f'[x]}, {x, a, b}]
solx = Solve[y == f[x], x]
g[y_] = x /. solx[[1]]
y0 = f[x0]
ftan[x_] = y0 f'[x0] (x-x0)
gtan[y_] = x0 1/ f'[x0] (y y0)
Plot[{f[x], ftan[x], g[x], gtan[x], Identity[x]},{x, a, b},
Epilog Line[{{x0, y0},{y0, x0}}], PlotRange {{a,b},{a,b}}, AspectRatio Automatic]ÄÄÄ
61-62. Example CAS commands:
:Maple
with( plots );
eq := cos(y) = x^(1/5);
domain := 0 .. 1;
x0 := 1/2;
f := unapply( solve( eq, y ), x ); # (a)
Df := D(f);
plot( [f(x),Df(x)], x=domain, color=[red,blue], linestyle=[1,3], legend=["y=f(x)","y=f '(x)"],
title="#62(a) (Section 7.1)" );
q1 := solve( eq, x ); # (b)
g := unapply( q1, y );
m1 := Df(x0); # (c)
t1 := f(x0)+m1*(x-x0);
y=t1;
m2 := 1/Df(x0); # (d)
t2 := g(f(x0)) + m2*(x-f(x0));
y=t2;
domaing := map(f,domain); # (e)
p1 := plot( [f(x),x], x=domain, color=[pink,green], linestyle=[1,9], thickness=[3,0] ):
p2 := plot( g(x), x=domaing, color=cyan, linestyle=3, thickness=4 ):
p3 := plot( t1, x=x0-1..x0+1, color=red, linestyle=4, thickness=0 ):
p4 := plot( t2, x=f(x0)-1..f(x0)+1, color=blue, linestyle=7, thickness=1 ):
p5 := plot( [ [x0,f(x0)], [f(x0),x0] ], color=green ):
display( [p1,p2,p3,p4,p5], scaling=constrained, title="#62(e) (Section 7.1)" );
(assigned function and values for a, b, and x0 may vary)Mathematica:
For problems 61 and 62, the code is just slightly altered. At times, different "parts" of solutions need to be used, as in the
definitions of f[x] and g[y]
Clear[x, y]
{a,b} = {0, 1}; x0 = 1/2 ;
eqn = Cos[y] == x1/5
soly = Solve[eqn, y]
f[x_] = y /. soly[[2]]
Plot[{f[x], f'[x]}, {x, a, b}]
solx = Solve[eqn, x]
g[y_] = x /. solx[[1]]
y0 = f[x0]
ftan[x_] = y0 f'[x0] (x x0)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
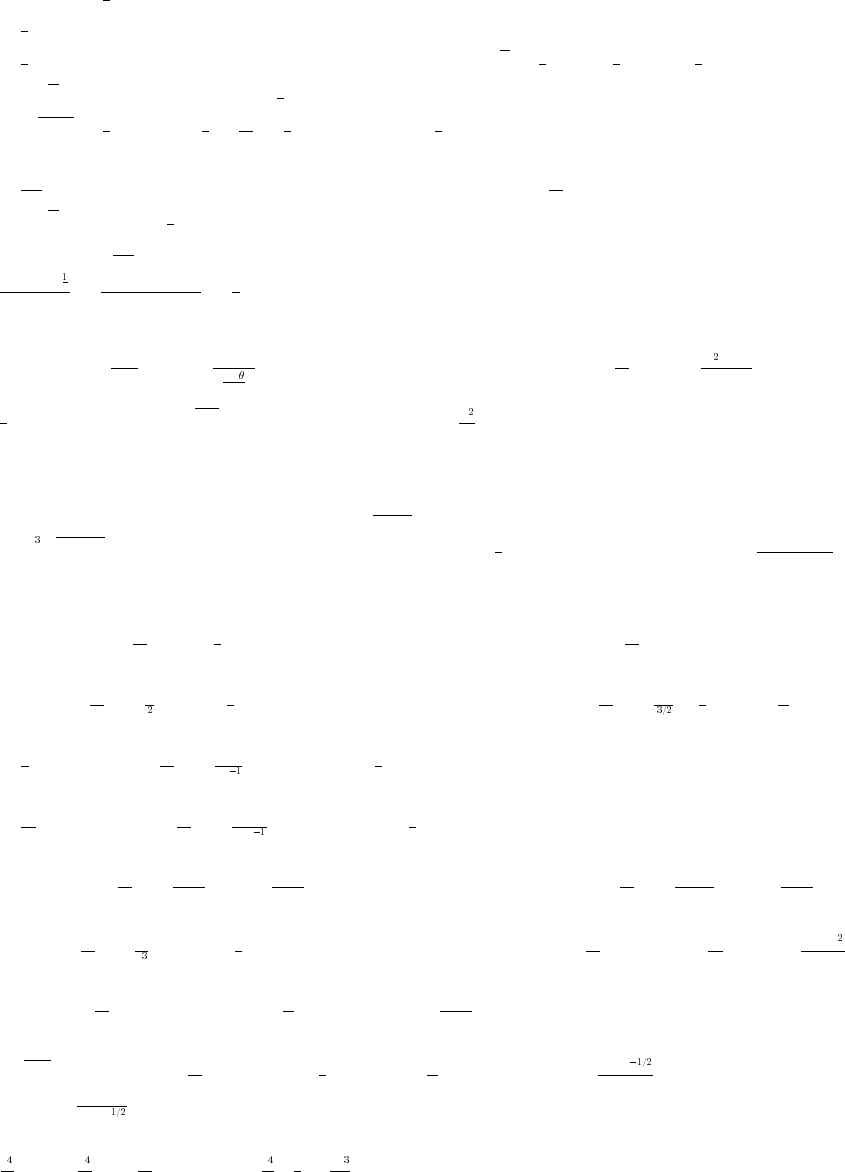
432 Chapter 7 Transcendental Functions
gtan[y_] = x0 1/ f'[x0] (y y0)
Plot[{f[x], ftan[x], g[x], gtan[x], Identity[x]},{x, a, b},
Epilog Line[{{x0, y0},{y0, x0}}], PlotRange {{a, b}, {a, b}}, AspectRatio Automatic]ÄÄÄ
7.2 NATURAL LOGARITHMS
1. (a) ln 0.75 ln ln 3 ln 4 ln 3 ln 2 ln 3 2 ln 2œ œœ œ
3
4#
(b) ln ln 4 ln 9 ln 2 ln 3 2 ln 2 2 ln 3
4
9œœœ
##
(c) ln ln 1 ln 2 ln 2 (d) ln 9 ln 9 ln 3 ln 3
"""
#
$#
œœ œ œ œ
È33 3
2
(e) ln 3 2 ln 3 ln 2 ln 3 ln 2
Èœ œ
"Î# "
#
(f) ln 13.5 ln 13.5 ln ln 3 ln 2 (3 ln 3 ln 2)
Èabœœœœ
""" "
#### #
$
27
2. (a) ln ln 1 3 ln 5 3 ln 5 (b) ln 9.8 ln ln 7 ln 5 2 ln 7 ln 5
"#
125 5
49
œ œ œ œ œ
(c) ln 7 7 ln 7 ln 7 (d) ln 1225 ln 35 2 ln 35 2 ln 5 2 ln 7
Èœœ œœ œ
$Î# #
#
3
(e) ln 0.056 ln ln 7 ln 5 ln 7 3 ln 5œœœ
7
125 $
(f)
ln 35 ln
ln 25 ln 5
ln 5 ln 7 ln 7
"
##
7œœ
3. (a) ln sin ln ln ln 5 (b) ln 3x 9x ln ln ln (x 3))œ œ œ œ
ˆ‰ ˆ‰
ab Š‹
sin sin 3x 9x
53x 3x
))
Š‹
sin
5
#"
(c) ln 4t ln 2 ln 4t ln 2 ln 2t ln 2 ln ln t
"
# #
%##
%
ab ab
ÈŠ‹
œ œ œ œ
2t
4. (a) ln sec ln cos ln [(sec )(cos )] ln 1 0)) ))œ œœ
(b) ln (8x 4) ln 2 ln (8x 4) ln 4 ln ln (2x 1)œœ œ
#
ˆ‰
8x 4
4
(c) 3 ln t 1 ln (t 1) 3 ln t 1 ln (t 1) 3 ln t 1 ln (t 1) ln
Èab ab
ˆ‰ Š‹
###
"Î$ ""
œ œ œ
3(t 1)
(t 1)(t )
ln (t 1)œ
5. y ln 3x y (3) 6. y ln kx y (k) xœÊœ œ œÊœ œ
w w
""
ˆ‰ ˆ‰
1
3x x kx
7. y ln t (2t) 8. y ln t tœÊœ œ œ Êœ œab ˆ‰ ˆ ‰ ˆ ‰ˆ ‰
#$Î# "Î#
" "
#
dy dy
dt t t dt 2t
233
t
9. y ln ln 3x 3xœœ Êœ œ
3
xdx3x x
dy
" #
""
ˆ‰
ab
10. y ln ln 10x 10xœœ Êœ œ
10
x dx 10x x
dy
" #
""
ˆ‰
ab
11. y ln ( 1) (1) 12. y ln (2 2) (2)œÊœ œ œ Êœ œ))
dy dy
d 1 1 d 2 1)) ) ) ) )
ˆ‰ ˆ‰
"" " "
#
13. y ln x 3x 14. y (ln x) 3(ln x) (ln x)œÊœ œ œ Êœ œ
$# $#
"
dy dy 3(ln x)
dx x x dx dx x
3 d
ˆ‰
ab †
15. y t(ln t) (ln t) 2t(ln t) (ln t) (ln t) (ln t) 2 ln tœ Êœ œœ
## # #
dy
dt dt t
d 2t ln t
†
16. y t ln t t(ln t) (ln t) t(ln t) (ln t) (ln t)œœ Êœ œ
È"Î# "Î# "Î# "Î#
"
##
dy t(ln t)
dt dt t
d
†
(ln t)œ
"Î# "
#(ln t)
17. y ln x x ln x x ln xœÊœœ
xx x4x
416dx 4x16
dy $$
"
†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.2 Natural Logarithms 433
18. y ln x x ln x x ln xœÊœœ
xx x3x
39dx 3x9
dy ##
"
†
19. y œÊœ œ
ln t
tdt
dy t (ln t)(1)
tt
1 ln t
ˆ‰
t
20. y œÊœ œ œ
" " ln t 1 ln t ln t
tdt t t
dy t ( ln t)(1)
t
ˆ‰
t"
21. y yœÊœ œ œ
ln x
1 ln x x(1 ln x)
(1 ln x) (ln x)
(1 ln x) (1 ln x)
w
"
ˆ‰ ˆ‰
xxxxx
ln x ln x
22. y y 1œÊœ œ œ
x ln x ln x
1 ln x (1 ln x) (1 ln x)
(1 ln x) (x ln x)
(1 ln x)
( ln x) ln x
w
"
ˆ‰ˆ‰
ln x x†xx
23. y ln (ln x) yœÊœ œ
w"" "
ˆ‰ˆ‰
ln x x x ln x
24. y ln (ln (ln x)) y (ln (ln x)) (ln x)œÊœ œ œ
w""""
ln (ln x) dx ln (ln x) ln x dx x (ln x) ln (ln x)
dd
†††
25. y [sin (ln ) cos (ln )] [sin (ln ) cos (ln )] cos (ln ) sin (ln )œÊœ )) ) ) )) ) )
dy
d)))
‘
††
""
sin (ln ) cos (ln ) cos (ln ) sin (ln ) 2 cos (ln )œœ)))) )
26. y ln (sec tan ) sec œÊœ œ œ)) )
dy sec (tan sec )
d sec tan tan sec
sec tan sec
))) ))
)) ) )) )
27. y ln ln x ln (x 1) yœœÊœœœ
"" """
##
w
xx1 x x 1 2x(x 1) 2x(x 1)
2(x 1) x 3x 2
Ȉ‰
28. y ln ln (1 x) ln (1 x) y ( 1)œœÊœœ œ
" " " " " " "
## # #"
w
1x 1x1x
1x 1x 1x (1x)( x) 1x
cd
‘ˆ‰ ’“
29. y œÊœ œ œ
1ln t 2
1 ln t dt (1 ln t) (1 ln t) t(1 ln t)
dy
(1 ln t) (1 ln t)
ˆ‰ ˆ ‰
t t tttt
ln t ln t
30. y ln t ln t ln t ln t ln t tœœ Êœ œ
ÉȈ‰ ˆ‰ ˆ‰ˆ‰ ˆ‰
"Î# "Î# "Î# "Î# "Î#
"Î# "Î# "Î#
"""
##
dy
dt dt dt
dd
t
†††
ln t tœœ
""""
##
"Î# "Î#
"Î#
ˆ‰
††
t4t ln t
ÉÈ
31. y ln (sec (ln )) (sec (ln )) (ln )œÊœ œ œ)))
dy sec (ln ) tan (ln ) tan (ln )
dsec(ln )d sec(ln ) d
dd
))) )) )
)) )
"††
32. y ln (ln sin ln cos ) ln (1 2 ln ) œœÊœ
Èsin cos
1 2 ln d sin cos 1 ln
dy cos sin
))
)))))
))
# # #
""
)) ) ˆ‰
2
cot tan œ
"
#
’“
)) 4
(1 2 ln )))
33. y ln 5 ln x 1 ln (1 x) y ( 1)œœÊœœ
Š‹ab ˆ‰
ab
È
x1
1x
5 2x 10x
x1 1x x1 (1x)
#w
""""
###
†
34. y ln [5 ln (x 1) 20 ln (x 2)] yœœÊœœ
Ɉ‰
’“
(x 1) (x 2) 4(x 1)
(x 2) x 1 x (x 1)(x 2)
5205
# ###
""
w
œ53x2
(x 1)(x )##
’“
35. y ln t dt ln x x ln 2x ln x x ln œÊœ œ
'x2
xÈŠ‹ Š‹Š‹
Èab kk
É
dy
dx dx dx
dxdx x
2
##
##
†† kk
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

434 Chapter 7 Transcendental Functions
36. y ln t dt ln x x ln x x ln x x ln x xœÊœ œ
'x
xdy
dx dx dx 3
dd
ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰
ÈÈÈÈ È È
$$ $
""
#Î$ "Î#
#
††
œ
ln x
3 x
ln x
2x
È
ÈÈ
È
37. dx ln x ln 2 ln 3 ln 38. dx ln 3x 2 ln 2 ln 5 ln
''
3 1
2 0
"# !
$ "
#x33x 5
23 2
œ œœ œ œœcd c dkk k k
39. dy ln y 25 C 40. dr ln 4r 5 C
''
2y
y25 4r 5
8r
# #
œ œ kk kk
41. dt ln 2 cos t ln 3 ln 1 ln 3; or let u 2 cos t du sin t dt with t 0
'0
sin t
2cos t!
œ œœ œ Êœ œcdkk
1
u 1 and t u 3 dt du ln u ln 3 ln 1 ln 3Êœ œÊœÊ œ œ œœ1''
01
3
sin t
2cos t u
"$
"
cdkk
42. d ln 1 4 cos ln 1 2 ln 3 ln ; or let u 1 4 cos du 4 sin d
'0
34 sin
14 cos 3
)
)
1
Î$
!"
)) )))œ œœœ œ Êœcdkkkk
with 0 u 3 and u 1 d du ln u ln 3 ln )) )œ Ê œ œ Ê œ Ê œ œ œ œ
1)
)314 cos u 3
4 sin
''
03
31
""
"
$
cdkk
43. Let u ln x du dx; x 1 u 0 and x 2 u ln 2;œÊœ œÊœ œÊœ
"
x
dx 2u du u (ln 2)
''
10
2ln 2ln 2
0
2 ln x
xœœœcd
##
44. Let u ln x du dx; x 2 u ln 2 and x 4 u ln 4;œÊœ œÊœ œÊœ
"
x
du ln u ln (ln 4) ln (ln 2) ln ln ln ln 2
''
2ln 2
4ln 4 ln 4
ln 2
dx ln 4 ln 2 2 ln 2
x ln x u ln 2 ln 2 ln 2
œ œœœœ œ œ
"cd ˆ‰ ˆ ‰
Š‹
45. Let u ln x du dx; x 2 u ln 2 and x 4 u ln 4;œÊœ œÊœ œÊœ
"
x
u du
''
2ln 2
4ln 4 ln 4
ln 2
dx
x(ln x) u ln 4 ln ln ln 2 2 ln ln ln 2 ln 4
œœœœœœœ
# """""""""
## ###
‘
46. Let u ln x du dx; x 2 u ln 2 and x 16 u ln 16;œÊœ œÊœ œÊœ
"
x
u du u ln 16 ln 2 4 ln 2 ln 2 2 ln 2 ln 2 ln 2
''
2ln 2
16 ln 16 ln 16
ln 2
dx
2x ln x
Èœ œ œœ œœ
"
#
"Î# "Î#
‘ ÈÈÈ È ÈÈÈ
47. Let u 6 3 tan t du 3 sec t dt;œ Ê œ #
dt ln u C ln 6 3 tan t C
''
3 sec t du
63 tan t u
œœ œ kk k k
48. Let u 2 sec y du sec y tan y dy;œ Ê œ
dy ln u C ln 2 sec y C
''
sec y tan y
sec y u
du
# œœ œ kk k k
49. Let u cos du sin dx 2 du sin dx; x 0 u 1 and x u ;œÊœ Êœ œÊœ œÊœ
xx x
2
### # #
" "1È
tan dx dx 2 2 ln u 2 ln 2 ln 2 ln 2
'' '
00 1
22 12 12
1
xdu
sin
cos u 2
#
"
œœœœœœ
x
xcdkk È
È
50. Let u sin t du cos t dt; t u and t u 1;œÊœ œÊœ œÊœ
11
42
"
#
È
cot t dt dt ln u ln ln 2
'''
4412
221
œœœœœ
cos t du
sin t u 2
cdkk È
"
"Î #
"
ÈÈ
51. Let u sin du cos d 6 du 2 cos d ; u and u ;œÊœ Êœ œÊœ œÊœ
)) )1
333 3
3
""
## #
))))1
È
2 cot d d 6 6 ln u 6 ln ln 6 ln 3 ln 27
'' '
2212
32 32
12
)
3u
2 cos
sin
du 3
))œœœœœœ
3
3cdkk Š‹
È
È
##
"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.2 Natural Logarithms 435
52. Let u cos 3x du 3 sin 3x dx 2 du 6 sin 3x dx; x 0 u 1 and x u ;œÊœ Êœ œÊœœÊœ
1
12
#
"
È
6 tan 3x dx dx 2 2 ln u 2 ln ln 1 2 ln 2 ln 2
'' '
00 1
12 12 1 2 12
1
œœœœœœ
6 sin 3x du
cos 3x u 2
cdkk È
"
È
53. ; let u 1 x du dx; ln u C
'' '
dx dx dx du
2x2x 2x1 x x 2x1 x u
ÈÈÈ ÈÈÈ
ˆ‰ ˆ‰
#
"
œœÊœ œœ
Èkk
'
ln 1 x C ln 1 x Cœœ
¸¸ ˆ‰
ÈÈ
54. Let u sec x tan x du sec x tan x sec x dx (sec x)(tan x sec x) dx sec x dx ;œ Êœ œ Ê œab
#du
u
(ln u) du 2(ln u) C 2 ln (sec x tan x) C
'sec x dx du
ln (sec x tan x) uln u u
ÈÈ
"Î# "Î#
"
œœ œ œ
''È
†
55. y x(x 1) (x(x 1)) ln y ln (x(x 1)) 2 ln y ln (x) ln (x 1) œœ Êœ Ê œÊœ
È"Î# """
#
2y
yxx1
y x(x 1)Êœ œ œ
w""" "
#
ˆ‰ ˆ ‰
Èx x 1 2x(x 1)
x(x 1) (2x 1) 2x
2x(x1)
ÈÈ
56. y x 1 (x 1) ln y ln x 1 2 ln (x 1) œÊœ Êœ
Èab c dab ˆ‰
##
""
##
#y
yx1x1
2x 2
y x +1 (x 1) x 1 (x 1)Êœ œ œ
w## # #
"
ÈÈ
ab a b
ˆ‰ ’“
xxxx1
x1 x1 x1(x1)
2x x1 x1
x1(x1)
ab abkk
È
57. y ln y [ln t ln (t 1)] œœ ʜʜ
Ɉ‰ ˆ ‰
tt
t1 t1 ydt t t1
dy
# #
"Î# """""
Êœ œ œ
dy
dt t 1 t t 1 t 1 t(t 1)
tt
2t(t1)
"""" " "
# #
ÉÉ
ˆ‰ ’“
È
58. y [t(t 1)] ln y [ln t ln (t 1)] œœÊœÊœ
Ɉ‰
1
t(t 1) y dt t t 1
dy
# #
"Î# """""
Êœ œ
dy
dt t(t 1) t(t 1)
12t 2t1
2t t
""
#
É’“ ab
59. y 3 (sin ) ( 3) sin ln y ln ( 3) ln (sin ) œ œ Ê œ Ê œ
È))) ) ) )
"Î# """
##yd ( 3) sin
dy cos
)) )
)
3 (sin ) cot ʜ
dy
d2(3)))
È’“
)) )
"
60. y (tan ) 2 1 (tan )(2 1) ln y ln (tan ) ln (2 1) œœÊœÊœ)) )) ) )
Ȉ‰ˆ ‰
"Î# """
###yd tan 1
dy sec 2
)) )
)
(tan ) 2 1 sec 2 1Êœ œ
dy
dtan 1
sec tan
21
)))
))
)
)) ))
ÈÈ
Š‹
ab
"
#
#
È
61. y t(t 1)(t 2) ln y ln t ln (t 1) ln (t 2) œ Ê œ Ê œ
""""
#ydt t t1 t
dy
t(t 1)(t+2) t(t 1)(t 2) 3t 6t 2Êœ œ œ
dy (t 1)(t 2) t(t 2) t(t 1)
dt t t 1 t t(t 1)(t 2)
ˆ‰ ’“
"" "
#
#
62. y ln y ln 1 ln t ln (t 1) ln (t 2) œ Ê œÊ œ
"""""
#t(t1)(t2) ydt t t1 t
dy
Êœ œ
dy (t 1)(t 2) t(t 2) t(t 1)
dt t(t 1)(t 2) t t 1 t t(t 1)(t ) t(t 1)(t 2)
"""" "
# #
‘
’“
œ 3t 6t 2
t3t2t
ab
63. y ln y ln ( 5) ln ln (cos ) œÊœ Êœ
) )
)) ) ) ) )
"""
5sin
cos y d 5 cos
dy
)))
tan ʜ
dy
d cos 5
5
)))) )
)
ˆ‰ˆ ‰
""
)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

436 Chapter 7 Transcendental Functions
64. y ln y ln ln (sin ) ln (sec ) œÊœ Êœ
)) )
))) ) )
))
sin cos
sec y d sin 2 sec
dy (sec )(tan )
È)) )
"""
#’“
cot tan ʜ
dy
d
sin
sec
))
))
)
Ȉ‰
""
#
))
65. y ln y ln x ln x 1 ln (x 1) œÊœÊœ
xx 1 y
(x 1)
2x2
3 y xx13(x1)
È
""
#
#
ab
yʜ
w
"
xx 1
(x 1) xx13(x1)
x2
È’“
66. y ln y [10 ln (x 1) 5 ln (2x 1)] œÊœÊœ
É(x 1) y
(2x1) y x1 2x1
55
#
"
yʜ
w
Ɉ‰
(x 1)
(2x1) x1 2x1
55
67. y ln y ln x ln (x 2) ln x 1 œÊœÊœ
Écdab ˆ‰
x(x 2) y
x1 3 y 3x x x1
2x
#
""""
#
y ʜ
w"""
#3x1xx x1
x(x 2) 2x
Ɉ‰
68. y ln y ln x ln (x 1) ln (x 2) ln x 1 ln (2x 3)œ Ê œ
Écdab
x(x 1)(x 2)
x1(2x3) 3
"#
ab
y ʜ
w""""
# 3 x 1 (2x 3) x x 1 x x 1 2x 3
x(x 1)(x 2) 2x 2
Ɉ‰
ab
69. (a) f(x) ln (cos x) f (x) tan x 0 x 0; f (x) 0 for x 0 and f (x) 0 forœ Ê œ œ œ Ê œ Ÿ
www
sin x
cos x 4
1
0 x there is a relative maximum at x 0 with f(0) ln (cos 0) ln 1 0; f ln cosŸ Ê œ œ œ œ œ
111
344
ˆ‰ ˆ ‰ˆ‰
ln ln 2 and f ln cos ln ln 2. Therefore, the absolute minimum occurs atœœ œ œœ
Š‹ ˆ‰ ˆ ‰ˆ‰
"" "
##
È233
11
x with f ln 2 and the absolute maximum occurs at x 0 with f(0) 0.œœ œœ
11
33
ˆ‰
(b) f(x) cos (ln x) f (x) 0 x 1; f (x) 0 for x 1 and f (x) 0 for 1 x 2œÊœœÊœŸ Ÿ
www
"
#
sin (ln x)
x
there is a relative maximum at x 1 with f(1) cos (ln 1) cos 0 1; f cos lnÊœœœœœ
ˆ‰ ˆ ‰ˆ‰
""
##
cos ( ln 2) cos (ln 2) and f(2) cos (ln 2). Therefore, the absolute minimum occurs at x andœ œ œ œ
"
#
x 2 with f f(2) cos (ln 2), and the absolute maximum occurs at x 1 with f(1) 1.œœœ œœ
ˆ‰
"
#
70. (a) f(x) x ln x f (x) 1 ; if x 1, then f (x) 0 which means that f(x) is increasingœ Ê œ
ww
"
x
(b) f(1) 1 ln 1 1 f(x) x ln x 0, if x 1 by part (a) x ln x if x 1œ œ Ê œ Ê
71. (ln 2x ln x) dx ( ln x ln 2 ln x) dx (ln 2) dx (ln 2)(5 1) ln 2 ln 16
'' '
11 1
55 5
œœ œœœ
%
72. A tan x dx tan x dx dx dx ln cos x ln cos xœ œ œ
''''
40 40
0303
!
Î%
Î$
!
sin x sin x
cos x cos x cdcdkk kk
1
1
ln 1 ln ln ln 1 ln 2 ln 2 ln 2œ œ œ
Š‹
ˆ‰
È
""
##
È2
3
73. V dy 4 dy 4 ln y 1 4 (ln 4 ln 1) 4 ln 4œœœœœ11111
''
00
33
Š‹ cdkk
2
y1 y1
È
#"
$
!
74. V cot x dx dx ln (sin x) ln 1 ln ln 2œœœ œœ111 1 1
''
66
22
cos x
sin x cdˆ‰
1
1
Î#
Î'
"
#
75. V 2 x dx 2 dx 2 ln x 2 ln 2 ln 2 (2 ln 2) ln 2 ln 16œœœœœœœ1111111
''
12 12
22
ˆ‰ ˆ ‰
cdkk
"" "
#
"Î# #
%
xx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
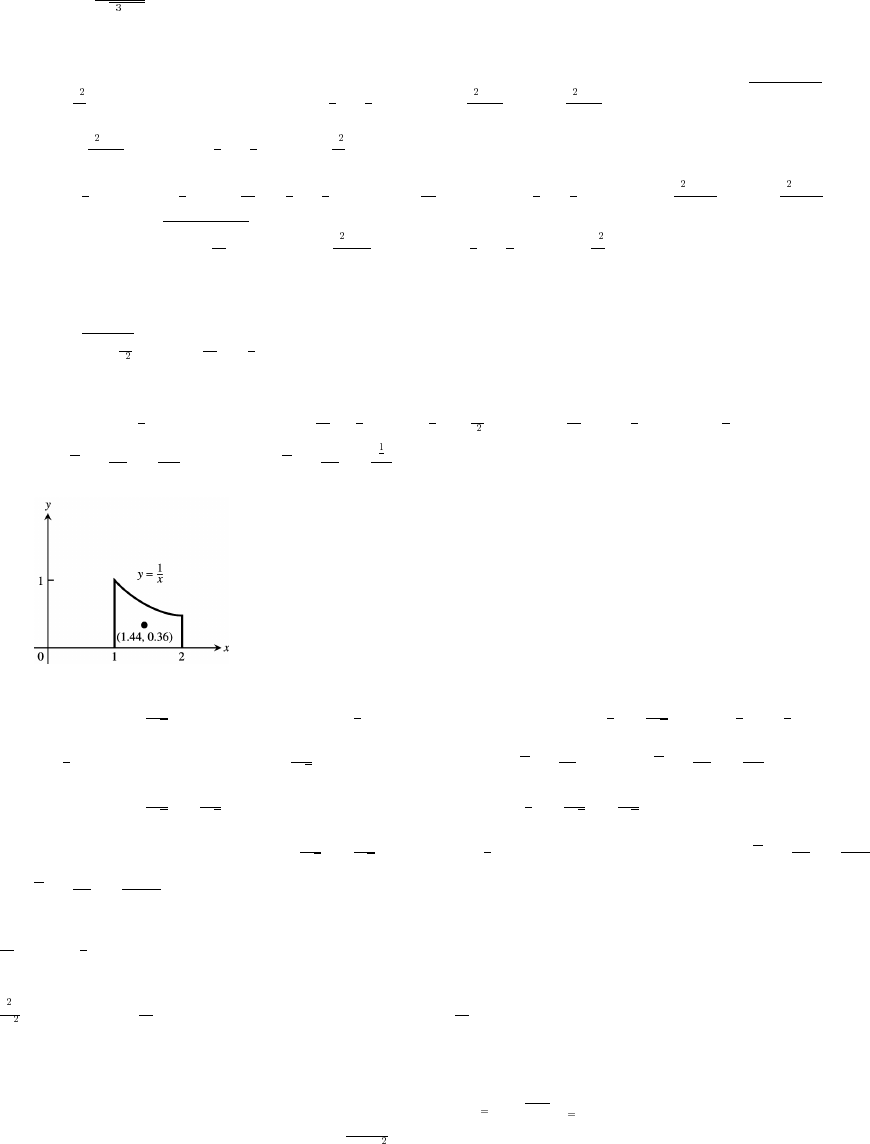
Section 7.2 Natural Logarithms 437
76. V dx 27 dx 27 ln x 9 27 (ln 36 ln 9)œœœœ1111
''
00
33
Š‹ cdab
9x
x9
È
#$$
!
27 (ln 4 ln 9 ln 9) 27 ln 4 54 ln 2œœœ111
77. (a) y ln x 1 y 1 1 L 1 y dxœ Ê œ œ œ Êœ
x x x4 x4
84x4x4x
ab ab
ˆ‰ Š‹Š‹ É
w#"
### w#
'4
8
dx dx ln x (8 ln 8) (2 ln 4) 6 ln 2œœœœœ
''
44
88
x4 x x
4x 4 x 8
" )
%
ˆ‰’“
kk
(b) x 2 ln 1 1 1œ ÊœÊ œœ œ
ˆ‰ ˆ‰ Š‹ Š‹ Š‹Š‹
yy y y y16y16
4 4 dy 8 y dy 8 y 8y 8y
dx 2 dx 2
#####
L 1 dy dy dy 2 ln y (9 2 ln 12) (1 2 ln 4)Êœ œ œ œ œ
'''
444
12 12 12
ÊŠ‹ Š ‹ ’ “
dx 2
dy 8y 8 y 16
y16 y y
#"#
%
8 2 ln 3 8 ln 9œ œ
78. L 1 dx y ln x C ln x C since x 0 0 ln 1 C C 0 y ln xœ Ê œÊœ œ Êœ Ê œÊœ
'1
2Ékk
""
xdxx
dy
79. (a) M x dx 1, M dx dx , M dx ln x ln 2
yx
111 1
222 2
œœœ œœœœœœ
''' '
ˆ‰ ˆ‰ˆ‰ ‘ cdkk
""""""""
#
#
"
#
"
x2xxx2x4x
x 1.44 and y 0.36Êœ œ ¸ œ œ ¸
M
Mln 2 Mln 2
M
yx4
"ˆ‰
(b)
80. (a) M x dx x dx x 42; M dx dx
y x
11 1 1
16 16 16 16
œœœœœ œ
'' ' '
Š‹ Š‹Š‹
‘
""""
"Î# $Î# "'
"
"
##
È È
È
x x
2
3xx
ln x ln 4, M dx 2x 6 x 7 and yœœœœœÊœœœœ
""
#
"'
""Î# "'
"
cdkk ‘
'1
16
Èx
M
MM6
Mln 4
yx
(b) M x dx 4 dx 60, M dx x dx
y x
111 1
16 16 16 16
œœœœ œ#
''' '
Š‹Š‹ Š‹Š‹Š‹
""
"
#
$Î#
ÈÈ ÈÈ
È
xx xx
44
x
4 x 3, M dx 4 dx 4 ln x 4 ln 16 x andœ œ œ œ œ œ Ê œ œ
‘ Š‹Š‹ cdkk
"Î# "'
"
""
"'
"
''
11
16 16
ÈÈ
xx
415
xMln 16
My
yœœ
M
M4 ln 16
3
x
81. 1 at ( 3) y x ln x C; y 3 at x 1 C 2 y x ln x 2
dy
dx x
œ "ß Êœ œ œÊ œÊœ
"kk kk
82. sec x tan x C and 1 tan 0 C tan x 1 y (tan x 1) dx
d y dy dy
dx dx dx
œ Êœ œÊœÊœ
#'
ln sec x x C and 0 ln sec 0 0 C C 0 y ln sec x xœœÊœÊœkk kk kk
"""
83. (a) L(x) f(0) f (0) x, and f(x) ln (1 x) f (x) 1 L(x) ln 1 1 x L(x) xœ œ Ê œ œÊ œ Ê œ
ww
"
††k¸
x0 x0
1x
(b) Let f x ln x . Since f x on , the graph of f is concave down on this interval and theab a b abœ " œ ! Ò!ß !Þ"Ó
ww "
"abx
largest error in the linear approximation will occur when x . This error is ln to fiveœ !Þ" !Þ" "Þ" ¸ !Þ!!%'*ab
decimal places.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
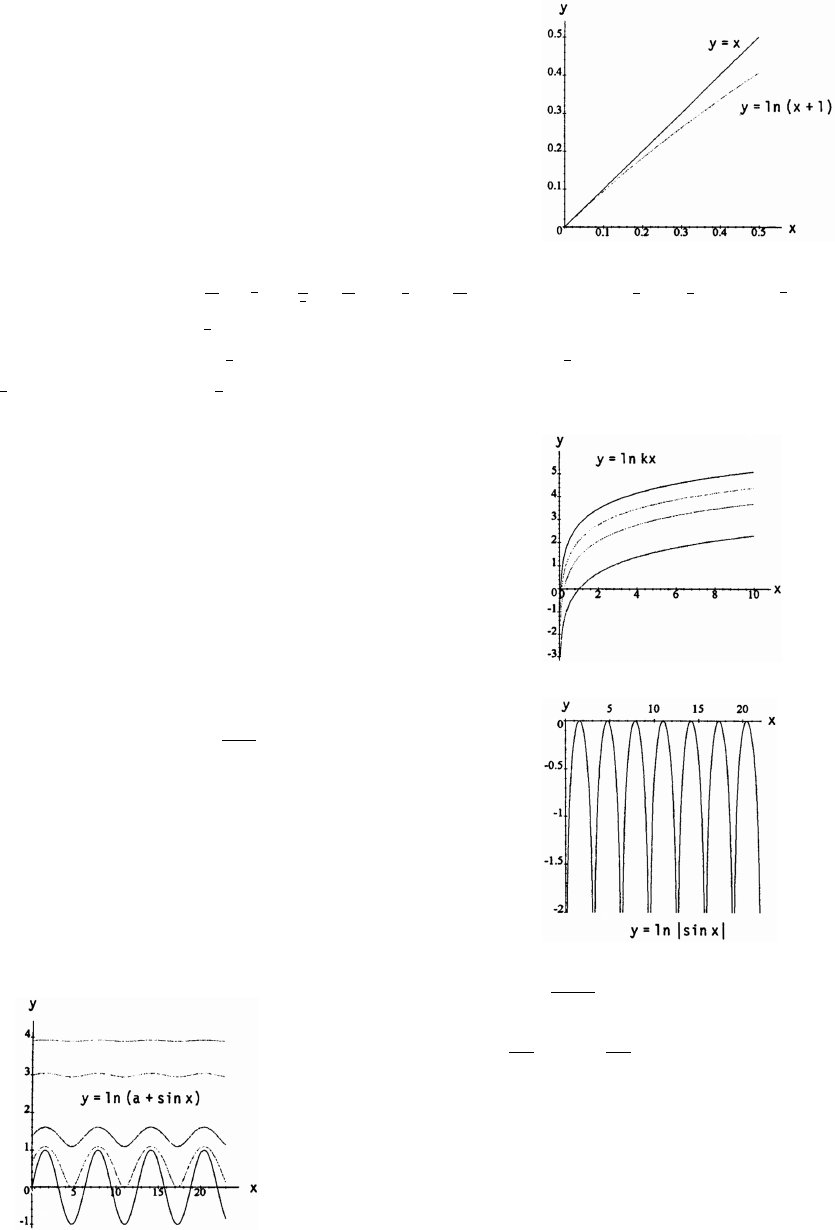
438 Chapter 7 Transcendental Functions
(c) The approximation y x for ln (1 x) is best for smallerœ
positive values of x; in particular for 0 x 0.1 in theŸŸ
graph. As x increases, so does the error x ln (1 x).
From the graph an upper bound for the error is
0.5 ln (1 0.5) 0.095; i.e., E(x) 0.095 for¸ Ÿkk
0 x 0.5. Note from the graph that 0.1 ln (1 0.1)ŸŸ
0.00469 estimates the error in replacing ln (1 x) by¸
x over 0 x 0.1. This is consistent with the estimateŸŸ
given in part (b) above.
84. For all positive values of x, and 0 . Since and have
ln ln
ln a ln x ln a ln x
d1a1d 11
dx x x dx x x
a a
x x
cd c dœ†œ œœ
a
x2
the same derivative, then ln ln a ln x C for some constant C. Since this equation holds for all positve values of x,
a
xœ
it must be true for x 1 ln ln 1 ln x C 0 ln x C ln ln x C. By part 3 we know thatœÊ œ œ Ê œ
11
xx
ln ln x C 0 ln ln a ln x.
1a
xx
œ Ê œ Ê œ
85. y ln kx y ln x ln k; thus the graph ofœÊœ
y ln kx is the graph of y ln x shifted verticallyœœ
by ln k, k 0.
86. To turn the arches upside down we would use the
formula y ln sin x ln .œ œkk "
kksin x
87. (a) (b) y . Since sin x and cos x are less than
w
œllll
cos x
asin x
or equal to 1, we have for a "
y for all x.
" "
" "
w
aa
ŸŸ
Thus, y for all x the graph of y lookslim
aÄ_
wœ! Ê
more and more horizontal as a .Ä_
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.3 The Exponential Function 439
88. (a) The graph of y x ln x to be concaveœ
Èappears
upward for all x 0.
(b) y x ln x y y 1 0 x 4 x 16.œ Ê œ Ê œ œ œÊ œÊœ
ÈÈ
Š‹
www
"" " ""
#ÈÈ
xxxx4
4x
x
Thus, y 0 if 0 x 16 and y 0 if x 16 so a point of inflection exists at x 16. The graph of
ww ww
œ
y x ln x closely resembles a straight line for x 10 and it is impossible to discuss the point ofœ
È
inflection visually from the graph.
7.3 THE EXPONENTIAL FUNCTION
1. (a) e 7.2 (b) e (c) e e
ln 7.2 ln x ln x ln y ln x y
exy
x
œœœœœ
ÐÎÑ
""
ln x
2. (a) e x y (b) e (c) e e
ln x y ln 0 3 ln x ln 2 ln x 2
e0.3
x
ab
## Þ ÐÎÑ
""
#
œ œ œ œ œ
ln 0 3
11
1
3. (a) 2 ln e 2 ln e (2) ln e 1 (b) ln ln e ln (e ln e) ln e 1
Ȉ‰ abœœ œ œ œœ
"Î# "
#
e
(c) ln e x y ln e x y
ab ## ##xyœ œ ab
4. (a) ln e (sec )(ln e) sec (b) ln e e (ln e) e
ˆ‰ ab
sec e x x)œœ œœ)) ab
x
(c) ln e ln e ln x 2 ln x
ˆ‰Š‹
2lnx lnx
œœœ
#
5. ln y 2t 4 e e y e 6. ln y t 5 e e y eœÊ œ Êœ œÊ œ Êœ
lny 2t4 2t4 lny t5 t5
7. ln (y 40) 5t e e y 40 e y e 40œÊ œÊœÊœ
ln y 40) 5t 5t 5tÐ
8. ln (1 2y) t e e 1 2y e 2y e 1 yœÊ œÊœÊœÊœ
ln 1 2y) t t t e
Ð "
#
Š‹
t
9. ln (y 1) ln 2 x ln x ln (y 1) ln 2 ln x x ln x e e e œ Ê œÊ œÊ œ Ê œ
ˆ‰
y1 y1
2x x
ln x x
#
ˆ‰
y1
2x
y 1 2xe y 2xe 1ʜ ʜ
xx
10. ln y 1 ln (y 1) ln (sin x) ln ln (sin x) ln (y 1) ln (sin x) e eab Š‹
#ÐÑ Ð Ñ
"
œ Ê œ Ê œ Ê œ
y
y1
ln y 1 ln sin x
y 1 sin x y sin x 1ʜ ʜ
11. (a) e 4 ln e ln 4 2k ln e ln 2 2k 2 ln 2 k ln 2
2k 2k
œÊ œ Ê œ Ê œ Êœ
#
(b) 100e 200 e 2 ln e ln 2 10k ln e ln 2 10k ln 2 k
10k 10k 10k ln 2
10
œÊœÊ œÊ œÊœÊœ
(c) e a ln e ln a ln e ln a ln a k 1000 ln a
k 1000 k 1000 kk
1000 1000
ÎÎ
œÊ œÊ œÊ œÊœ
12. (a) e ln e ln 4 5k ln e ln 4 5k ln 4 k
5k 5k
4 5
ln 4
œ Ê œ Ê œ Ê œ Ê œ
""
(b) 80e 1 e 80 ln e ln 80 k ln e ln 80 k ln 80
kk k
œÊ œ Ê œ Ê œ Êœ
" "
(c) e 0.8 e 0.8 (0.8) 0.8 k 1
ÐÞÑ Þln 0 8 k ln 0 8 k
k
œÊ œÊ œÊœ
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
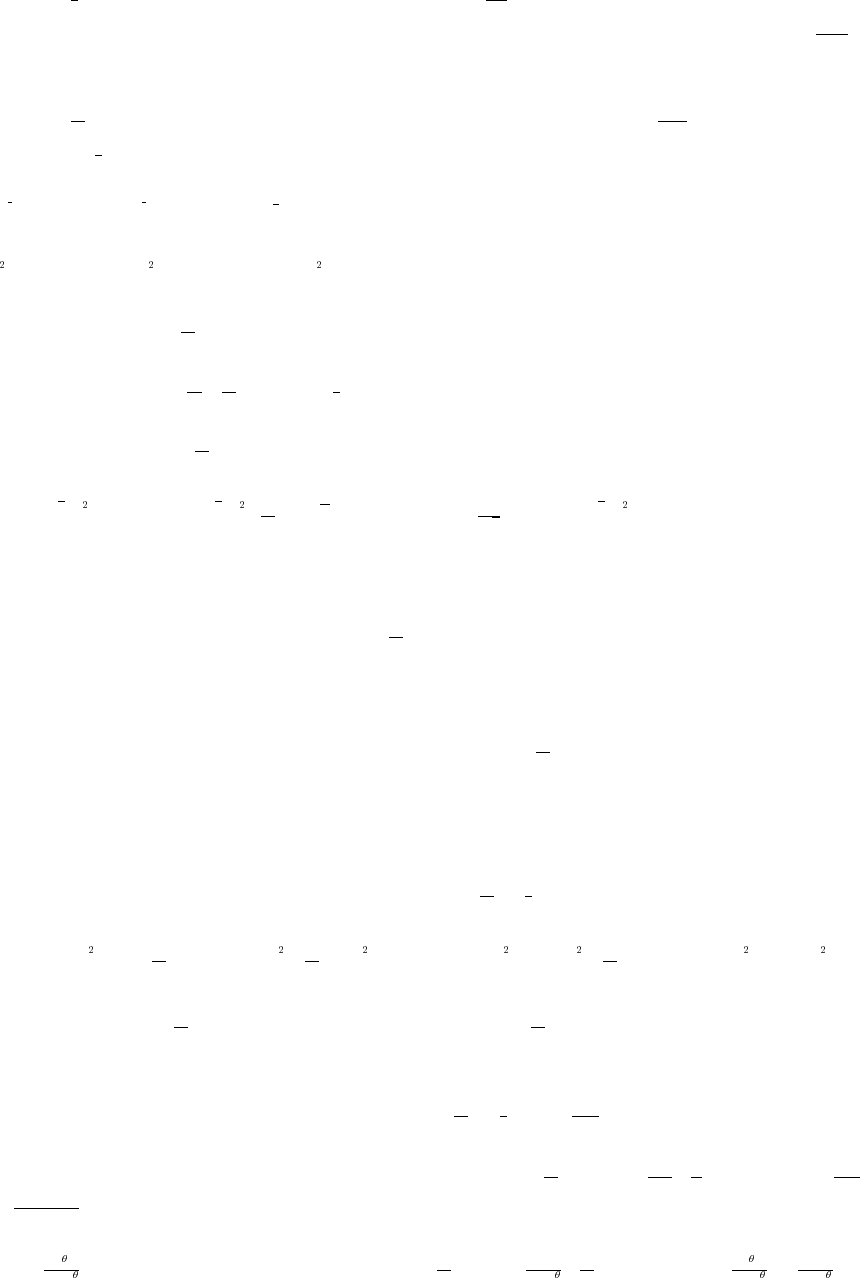
440 Chapter 7 Transcendental Functions
13. (a) e 27 ln e ln 3 ( 0.3t) ln e 3 ln 3 0.3t 3 ln 3 t 10 ln 3
Þ Þ $03t 03t
œÊ œ Ê œ Êœ Êœ
(b) e ln e ln 2 kt ln e ln 2 t
kt kt ln 2
k
œÊ œ œ œ Êœ
"
#
"
(c) e 0.4 e 0.4 0.2 0.4 ln 0.2 ln 0.4 t ln 0.2 ln 0.4 t
ÐÞÑ Þln 0 2 t ln 0 2 t t
tln 0.4
ln 0.2
œÊ œÊ œÊ œ Ê œ Êœ
ˆ‰
14. (a) e 1000 ln e ln 1000 ( 0.01t) ln e ln 1000 0.01t ln 1000 t 100 ln 1000
Þ Þ0 01t 0 01t
œÊ œÊ œÊœÊœ
(b) e ln e ln 10 kt ln e ln 10 kt ln 10 t
kt kt
10 k
ln 10
œ Ê œ œ œ Ê œ Ê œ
""
(c) e e 2 2 2 t 1
Ð Ñ " "
"
#
ln 2 t ln 2 t
t
œÊ œÊœÊœ
ˆ‰
15. e x ln e ln x t 2 ln x t 4(ln x)
ÈÈ
tt
œÊ œ Ê œ Êœ
## #
È
16. e e e e e ln e ln e t x 2x 1
x 2x1 t x 2x1 t x 2x1 t #
œÊ œÊ œ Êœ
17. y e y e ( 5x) y 5e œÊœ Êœ
w w5x 5x 5x
d
dx
18. y e y e y eœÊœ Êœ
2x 3 2x 3 2x 3
d2x 2
dx 3 3
ÎwÎ w Î
ˆ‰
19. y e y e (5 7x) y 7eœÊœ Êœ
57x 57x 57x
d
dx
w w
20. y e y e 4 x x y 2x eœÊœ Êœ
ˆ‰ ˆ‰ ˆ‰
ÈÈ È
È
4xx 4xx 4xx
d2
dx x
w #w
ˆ‰
ÈŠ‹
21. y xe e y e xe e xe œÊœ œ
xx x x x xwab
22. y (1 2x) e y 2e (1 2x)e ( 2x) y 2e 2(1 2x) e 4xeœ Ê œ Ê œ œ
w w 2x 2x 2x 2x 2x 2x
d
dx
23. y x 2x 2 e y (2x 2)e x 2x 2 e x eœ Êœ œab ab
#w##xxxx
24. y 9x 6x 2 e y (18x 6)e 9x 6x 2 e (3x) y (18x 6)e 3 9x 6x 2 eœ Êœ Êœ ab ab ab
#w # w #3x 3x 3x 3x 3x
d
dx
27x eœ#3x
25. y e (sin cos ) y e (sin cos ) e (cos sin ) 2e cos œÊœ œ
))))
)) )) )) )
w
26. y ln 3 e ln 3 ln ln e ln 3 ln 1œœœÊœ
ˆ‰
)) ))
"
))
))
dy
d
27. y cos e sin e e sin e e 2 e sin eœÊœ œ œ
Š‹ Š‹Š‹Š ‹Š‹ Š‹Š‹ ab
#)))))))
)) )
dy
dd d
dd
))
28. y e cos 5 3 e cos 5 cos 5 e ( 2 ) 5(sin 5 ) eœÊœ )) ) ))) )))
$ # # # $ # $ #))) )
))
dy
dd
d
ab a b
ˆ‰ ˆ‰
e (3 cos 5 2 cos 5 5 sin 5 )œ))))))
# #)
29. y ln 3te ln 3 ln t ln e ln 3 ln t t 1œœœÊœœab
"
ttdy
dt t t
1t
30. y ln 2e sin t ln 2 ln e ln sin t ln 2 t ln sin t 1 (sin t) 1œœœÊœ œab ˆ‰
"
tt dy
dt sin t dt sin t
dcos t
œcos t sin t
sin t
31. y ln ln e ln 1 e ln 1+e 1 1 e 1œœœ Êœ œœ
ede
1e 1e 1e 1e
dy
dd
""
)) ) )
))
ˆ‰ ˆ‰ ˆ‰ˆ‰
)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.3 The Exponential Function 441
32. y ln ln ln 1 1œœÊœ
ÈÈÈÈ
)
)))
)) )
1 1
dy
dd d
dd
""
ÈÈ È È
Š‹ Š‹Š‹Š‹Š‹
)) ) )
œ œœœ
Š‹Š‹Š ‹Š‹
"" " " " "
##
#
#
ÈÈ ÈÈ Š‹
ÈÈ
Š‹ Š‹
ÈÈ
ab
)) ))
))
)) ))))
1
1
21 1 1
33. y e e e te e te (cos t) (1 t sin t) eœœœÊœ œ
ÐÑcos t ln t cos t ln t cos t cos t cos t cos t
dy
dt dt
d
34. y e ln t 1 e (cos t) ln t 1 e e ln t 1 (cos t)œÊœ œ
sin t sin t sin t sin t
dy
dt t t
22
ab ab ab
‘
###
35. sin e dt y sin e (ln x)
'0
ln x tlnx
dsin x
dx x
Êœ œ
wˆ‰
†
36. y ln t dt y ln e e ln e e (2x) 2e 4 x e 4 xœÊœ œ
'e
e2x 2x 4 x 4 x 2x 4 x
dd d
dx dx dx
4x
2x
wabab ab
Š ‹Š‹ Š‹
ˆ‰ ˆ‰
ÈÈ
†† †
ÈÈ È
4xe 4 x e 4xe 8eœ œ
2x 4 x 2x 4 x
2
x
ÈŠ‹
ÈÈ
È
37. ln y e sin x y y e (sin x) e cos x y e sin x e cos xœÊœ Ê œ
yyyyy
yy
Š‹ Š ‹
ab
""
ww w
y e cos x yʜʜ
ww
Š‹
1 ye sin x ye cos x
y 1 ye sin x
y
yy
y
38. ln xy e ln x ln y e y 1 y e y e eœÊœÊ œ Ê œ
xy xy xy xy xy
xy y x
www
"" " "
Š‹ Š ‹
ab
y yʜʜ
ww
" "
Š‹
1ye
yx x1ye
xe yxe
xy xy xy
xy
ab
ab
39. e sin (x 3y) 2e 1 3y cos (x 3y) 1 3y 3y 1
2x 2x 2e 2e
cos (x 3y) cos (x 3y)
œÊœ Êœ Êœ ab
www
2x 2x
yʜ
w
2e cos (x 3y)
3 cos (x 3y)
2x
40. tan y e ln x sec y y e yœ Ê œÊ œ
xx
xx
xe cos y
ab
#w w
""ab
x
41. e 5e dx 5e C 42. 2e 3e dx 2e e C
''
ab a b
3x x x x 2x x 2x
e 3
3
œ œ
#
3x
43. e dx e e e 3 2 1 44. e dx e e e 1 2 1
''
ln 2 ln 2
ln 3 ln 3
x x ln 3 ln 2 x x ln 2
ln 3 0
ln 2 ln 2
œ œœœ œ œœœcd c d
!
45. 8e dx 8e C 46. 2e dx e C
''
ÐÑ ÐÑ Ð Ñ Ð Ñx1 x1 2x1 2x1
œ œ
47. e dx 2e 2 e e 2 e e 2(3 2) 2
'ln 4
ln 9 x 2 x 2 ln 9 2 ln 4) 2 ln 3 ln 2
ln 9
ln 4
ÎÎ ÐÑÎÐÎ
œœœœœ
‘ ‘ˆ ‰
48. e dx 4e 4 e e 4 e 1 4(2 1) 4
'0
ln 16 x4 x4 ln16 4 0 ln2
ln 16
0
ÎÎ ÐÑÎ
œœœœœ
‘ ˆ ‰ˆ ‰
49. Let u r du r dr 2 du r dr;œÊœ Ê œ
"Î# "Î# "Î#
"
#
dr e r dr 2 e du 2e C 2e C 2e C
''
e
r
ruurr
r
ÈÈ
œœœœœ
'†"Î#
50. Let u r du r dr 2 du r dr;œ Ê œ Ê œ
"Î# "Î# "Î#
"
#
dr e r dr 2 e du 2e C 2e C
'' '
e
r
rurr
r
ÈÈ
œœœœ
"Î#
†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

442 Chapter 7 Transcendental Functions
51. Let u t du 2t dt du 2t dt;œ Ê œ Ê œ
#
2te dt e du e C e C
''
tuu t
œ œ œ
52. Let u t du 4t dt du t dt;œÊ œ Ê œ
%$ $
"
4
t e dt e du e C
''
$""
tut
44
œœ
53. Let u du dx du dx;œÊ œ Êœ
"" "
xx x
dx e du e C e C
''
e
x
uu 1x
1x œ œœ
Î
54. Let u x du 2x dx du x dx;œ Ê œ Ê œ
# $ $
"
#
dx e x dx e du e C e C e C
'' '
e
x
xuux1x
1x œœœœœ
$ Î
""" "
### #
†
55. Let u tan du sec d ; 0 u 0, u 1;œÊœ œÊœœÊœ)))) )
#1
4
1 e sec d sec d e du tan e tan tan (0) e e
'''
000
441
tan u u
4
04
11
)11
ÎÎ
## "!
Î"
!
ˆ‰ ‘
cd cd a b
ˆ‰
œœœ)) )) )
(1 0) (e 1) eœœ
56. Let u cot du csc d ; u 1, u 0;œÊœ œÊœœÊœ)))))
#11
42
1 e csc d csc d e du cot e cot cot e e
'''
11
11
)1
1
11
ÎÎ
ÎÎ
## !"
Î
Î
!
"
441
220
cot u u
2
424
ˆ‰ ‘
cdcd ab
ˆ‰ ˆ‰
œœœ)) )) )
(0 1) (1 e) eœœ
57. Let u sec t du sec t tan t dt sec t tan t dt;œÊœ Êœ1 111 11
du
1
e sec ( t) tan ( t) dt e du C C
''
sec t u ee
ÐÑ "
1
111
11œœœ
usect
58. Let u csc ( t) du csc ( t) cot ( t) dt;œÊœ 111
e csc ( t) cot ( t) dt e du e C e C
''
csc t u u csc tÐÑ ÐÑ1 1
11 œ œ œ
59. Let u e du e dv 2 du 2e dv; v ln u , v ln u ;œÊ œ Ê œ œ Êœ œ Êœ
vv v
66
1111
##
2e cos e dv 2 cos u du 2 sin u 2 sin sin 2 1 1
''
ln 6 6
ln 2 2
vv 2
66
ÐÎÑ Î
ÐÎÑ Î Î
Î##
"
11
11
1
1
11
œœœœœcd ‘ˆ‰ˆ‰ ˆ‰
60. Let u e du 2xe dx; x 0 u 1, x ln u e ;œÊœ œÊœœ Êœ œ
xx ln
È11
1
2xe cos e dx cos u du sin u sin ( ) sin (1) sin (1) 0.84147
''
01
ln xx
È11
1
Š‹ cdœ œ œ œ ¸
"1
61. Let u 1 e du e dr;œ Ê œ
rr
dr du ln u C ln 1 e C
''
e
1e u
r
r
r
"
œœœkk a b
62. dx dx;
''
"
1e e 1
e
xx
x
œ
let u e 1 du e dx du e dx;œÊœ Êœ
xxx
dx du ln u C ln e 1 C
''
e
e1 u
x
x
x
"
œ œ œ kk a b
63. e sin e 2 y e sin e 2 dt;
dy
dt
tt tt
œÊœ ab ab
'
let u e 2 du e dt y sin u du cos u C cos e 2 C; y(ln 2) 0œÊ œ Ê œ œ œ œ
tt t
'ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.3 The Exponential Function 443
cos e 2 C 0 cos (2 2) C 0 C cos 0 1; thus, y 1 cos e 2Ê œ Ê œ Ê œ œ œ
ˆ‰ ab
ln 2 t
64. e sec e y e sec e dt;
dy
dt
tt tt
œÊœ
# #
ab ab11
'
let u e du e dt du e dt y sec u du tan u Cœ Ê œ Ê œ Ê œ œ 11
#
"""
tt t
111
'
tan e C; y(ln 4) tan e C tan Cœ œ Ê œ Ê œ
""""
111111
ab ˆ‰ ˆ‰
111
tln4
222
4
†
(1) C C ; thus, y tan eÊ œ Ê œ œ
""
11111
23 3 t
ab1
65. 2e 2e C; x 0 and 0 0 2e C C 2; thus 2e 2
d y dy dy dy
dx dx dx dx
xx x
œ Ê œ œ œ Ê œ Ê œ œ
!
y2e 2xC; x0 and y1 12e C C 1 y2e 2x12e x 1Êœ œ œÊœ Ê œÊœ œ
!
"""
xxx
ab
66. 1 e t e C; t 1 and 0 0 1 e C C e 1; thus
d y dy dy
dt dt dt
2t 2t
œ Ê œ œ œ Ê œ Ê œ
"""
###
##
t e e 1 y t e e 1 t C ; t 1 and y 1 e e 1 C
dy
dt 4 4
2t 2t
œ Êœ œ œÊ"œ
"" "" " """
## # # # #
### ##
""
ˆ‰
C e y t e e 1 t eʜ ʜ
""" " " " ""
####
## # #
44 4
2t ˆ‰ˆ‰
67. f(x) e 2x f (x) e 2; f (x) 0 e 2 x ln 2; f(0) 1, the absolute maximum;œ Ê œ œÊ œÊœ œ
xx xww
f(ln 2) 2 2 ln 2 0.613706, the absolute minimum; f(1) e 2 0.71828, a relative or local maximumœ ¸ œ¸
since f (x) e is always positive.
ww œx
68. The function f(x) 2e has a maximum whenever sin 1 and a minimum whenever sin 1.œœœ
sin x 2 xx
ÐÎÑ
##
Therefore the maximums occur at x 2k(2 ) and the minimums occur at x 3 2k(2 ), where k is anyœ œ 11 11
integer. The maximum is 2e 5.43656 and the minimum is 0.73576.¸¸
2
e
69. f(x) x ln f (x) 2x ln x x 2x ln x x(2 ln x 1); f (x) 0 x 0 orœÊœ œœ œÊœ
#w ## w
""""
xx x
Š‹
ab
x
ln x . Since x 0 is not in the domain of f, x e . Also, f (x) 0 for 0 x andœ œ œ œ
"""
#
"Î# w
ÈÈ
ee
f (x) 0 for x . Therefore, f ln e ln e ln e is the absolute maximum value
w"Î#
""""""
##
œ œ œœ
ÈÈ
ee
ee ee
Š‹ È
of f assumed at x .œ"
Èe
70. f(x) (x 3) e f (x) 2(x 3) e (x 3) eœ Ê œ
#w #xxx
(x 3) e (2 x 3) (x 1)(x 3) e ; thusœ œ
xx
f (x) 0 for x 1 or x 3, and f (x) 0 for
ww
1 x 3 f(1) 4e 10.87 is a local maximum and Ê œ ¸
f(3) 0 is a local minimum. Since f(x) 0 for all x,œ
f(3) 0 is also an absolute minimum.œ
71. e e dx e e e 3 1 2 2
'0
ln 3ab
’“Š ‹Š‹
ˆ‰ˆ‰
2x x x ln 3
eee9 8
ln 3
0
œœœœœ
2x 2ln3
######
!"
72. e e dx 2e 2e 2e 2e 2e 2e (4 1) (2 2) 5 4 1
'0
2 ln 2ˆ‰ ‘ˆ ‰
ab
x2 x2 x2 x2 ln2 ln2
2ln2
0
ÎÎ Î Î ! !
œ œ œœœ
73. L 1 dx y e C; y(0) 0 0 e C C 1 y e 1œ Ê œ Êœ œÊœ Ê œÊœ
'0
1x2
Éee
4dx
dy x2 0
xx2
#
Î
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
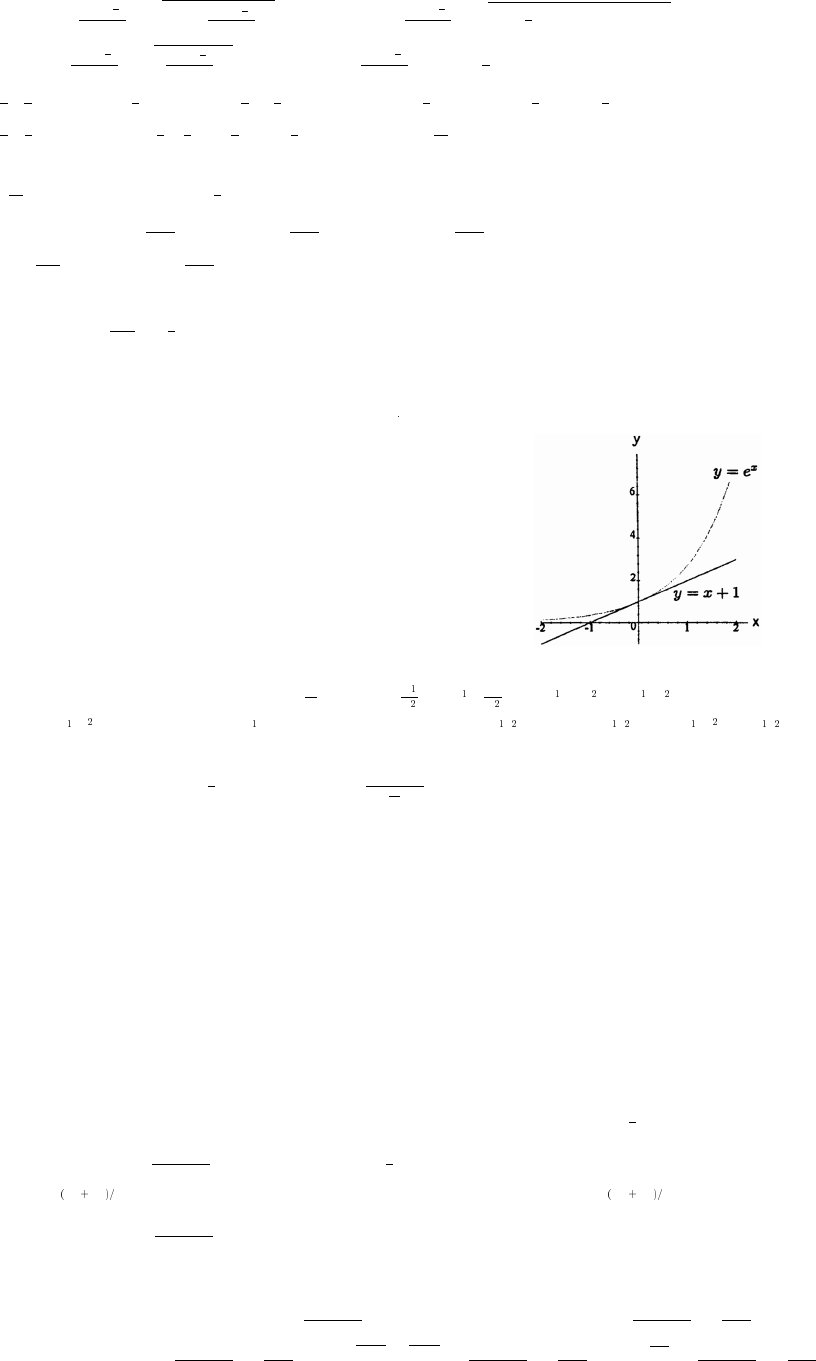
444 Chapter 7 Transcendental Functions
74. S 2 1 dy 2 1 e 2 e dyœœ 11
''
00
ln 2 ln 2
ˆ‰ ˆ‰ ˆ‰
ÉÉab
ee ee ee
42y 2y
yy yy
yy
"
## #
#
2 dy 2 dy e 2 e dyœœœ11
''
0 0
ln 2 ln 2
ˆ‰ˆ‰ ˆ‰
É'ab
ee ee ee
0
ln 2 2y 2y
yy yy
yy
## # #
##
1
e2ye e 2 ln 2e 0œ œ
11
## # # # # # #
"" " """
‘ ‘ˆ‰ˆ‰
2y 2y 2ln2 2ln2
ln 2
0
4 2 ln 2 2 2 ln 2 ln 2œœœ
11
## # #
""""
ˆ‰ˆ‰ˆ‰
††
48 16
15
1
75. (a) (x ln x x C) x ln x 1 0 ln x
d
dx x
œ œ†"
(b) average value ln x dx x ln x x [(e ln e e) (1 ln 1 1)]œœœ
"" "
e1 e1 e1
e
1
'1
ecd
(ee1)œœ
""
e1 e 1
76. average value dx ln x ln 2 ln 1 ln 2œ œ œœ
""
#
"
21 x
'1
2cdkk
77. (a) f(x) e f (x) e ; L(x) f(0) f (0)(x 0) L(x) 1 xœÊ œ œ Ê œ
xxww
(b) f(0) 1 and L(0) 1 error 0; f(0.2) e 1.22140 and L(0.2) 1.2 error 0.02140œœÊœœ¸ œÊ¸
02
(c) Since y e 0, the tangent line
ww œ
x
approximation always lies below the curve y e .œx
Thus L(x) x 1 never overestimates e .œ x
78. (a) e e e e 1 e for all x; e e e e
xx xx x x x x xx
eee
e
ÐÑ!
""
œœœÊœ œ œ œ
x
x
xx
ˆ‰
(b) y e ln y x ln e x x x x e e y e e eœÊœ œœÊœÊœÊœab ab
xx ln yxxxxxxx
x x
##""#
79. f(x) ln(x) 1 f (x) x x x x 2 ln (x ) . Then x 2œÊ œÊ œ Ê œ œ
w" "
xn1 n n1 n n
ln (x ) 1
n
1
xn
ˆ‰ cd
x 2.61370564, x 2.71624393 and x 2.71828183, where we have used Newton's method.Êœ œ œ
#$ &
80. e x and ln e x for all x 0
ln x x
œœab
81. Note that y ln x and e x are the same curve; ln x dx area under the curve between 1 and a;œœ œ
y
1
a
'
e dy area to the left of the curve between 0 and ln a. The sum of these areas is equal to the area of the rectangle
'0
ln a yœ
ln x dx e dy a ln a.ʜ
''
10
aln a
y
82. (a) y e y e 0 for all x the graph of y e is always concave upwardœÊ œ Ê œ
xx xww
(b) area of the trapezoid ABCD e dx area of the trapezoid AEFD (AB CD)(ln b ln a) Ê
'ln a
ln b x"
#
e dx (ln b ln a). Now (AB CD) is the height of the midpoint
'ln a
ln b xŠ‹
ee
ln a ln b
"
##
M e since the curve containing the points B and C is linear e (ln b ln a)œÊ
ln a ln b 2 ln a ln b 2
e dx (ln b ln a)
'ln a
ln b xŠ‹
ee
ln a ln b
#
(c) e dx e e e b a, so part (b) implies that
'ln a
ln b xxlnblna
ln b
ln a
œœœcd
e (ln b ln a) b a (ln b ln a) e
ÐÑÎ ÐÑÎ
##
lna lnb 2 lna lnb 2
ee ba ab
ln b ln a
Ê
Š‹
ln a ln b
ee ee abÊÊÊ
ln a 2 ln b 2 ba ab ba ab ba ab
ln b ln a ln b ln a ln b ln a
ln a ln b
ÎÎ
# # #
†ÈÈ È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.4 a and log x 445
xa
7.4 a and log x
x
a
1. (a) 5 7 (b) 8 2 (c) 1.3 75
log 7 log 2 log 75
5 8 13
œœ œ
È
(d) log 16 log 4 2 log 4 2 1 2 (e) log 3 log 3 log 3 1 0.5
44 4 3 3 3
œœ œœ œ œ œœœ
#"Î# """
###
††
È
(f) log log 4 1 log 4 1 1 1
44 4
ˆ‰
""
4œœœœ†
2. (a) 2 3 (b) 10 (c) 7
log 3 log 1 2 log 7
210
œœœ
"
#1
(d) log 121 log 11 2 log 11 2 1 2
11 11 11
œœ œœ
#†
(e) log 11 log 121 log 121 1
121 121 121
œœ œœ
"Î# """
###
ˆ‰ ˆ‰†
(f) log log 3 2 log 3 2 1 2
33 3
ˆ‰
"#
9œœœœ†
3. (a) Let z log x 4 x 2 x 2 x 2 xœ Ê œÊ œÊ œÊ œ
4z2z z z
ab È
#
(b) Let z log x 3 x 3 x 3 x 9 xœ ÊœÊ œÊ œÊœ
3zz 2zz
ab
####
(c) log e log 2 sin x
22
ln 2 sin x sin x
abœœ
4. (a) Let z log 3x 5 3x 25 9xœÊœÊœ
5zz
ab
## %
(b) log e x
ex
abœ
(c) log 2 log 4
44
ee
ˆ‰
xx
x
sin x sin x e sin x
œœ
Î#
#
5. (a) (b)
log x log x
log x ln ln 3 ln ln x ln 2 log x ln ln 8 ln ln x ln
ln x ln x ln x ln 3 ln 3 ln x ln x ln x ln 8 3 ln 2
2 2
3 8
œƒœ œ œƒœ œ
## ##
††
2œ3
(c) 2
log a
log a ln x ln x ln x ln a ln x
ln a ln a ln a ln x 2 ln x
x
xœƒ œ œ œ†
6. (a)
log x
log x ln 9 ln 3 2 ln 3 ln x 2
ln x ln x ln x ln 3 1
9
3œƒœ œ†
(b)
log x
log x ln x ln 10
ln x ln x ln x ln 2
ln 10 ln 2 ln 10
ln 2
10
2œƒœ œ
ÈÈ
ˆ‰ ˆ‰
†
(c)
log b
log a ln a ln b ln a ln a ln a
ln b ln a ln b ln b ln b
a
bœƒœ œ†ˆ‰
#
7. 3 2 5 7 5 x x 12
log 7 log 5 log x
32 5
ÐÑ ÐÑ ÐÑ
œÊœÊœ
8. 8 e x 7 3 5 x 3x 0 x 3x 2 (x 1)(x 2) x 1 or x 2
log 3 ln 5 log 3x
87
ÐÑ # Ð Ñ # #
œ Ê œ Ê œ œ Ê œ œ
9. 3 5e 3 10 x 5x 6 x 5x 6 0 (x 2)(x 3) 0 x 2 or x 3
log x ln x log 2
310
ab
œ Ê œ Ê œÊ œÊœ œ†ÐÑ # #
10. ln e 4 log 100 1 4 log 10 1 x (2) 1 0 œ Ê œ Ê œ Êœ
ÐÑ # #
""""
2 log x log x
xxxxx
10 10 2
44
ab ˆ‰
x 2x 1 0 (x 1) 0 x 1ʜʜʜ
##
11. y 2 y 2 ln 2 12. y 3 y 3 (ln 3)( 1) 3 ln 3œÊœ œ Êœ œ
xx xx xw w
13. y 5 5 (ln 5) s 5œÊœ œ
ss s
dy
ds
ln 5
2s
ˆ‰
Š‹
"
#
"Î# È
14. y 2 2 (ln 2)2s ln 2 s2 (ln 4)s2œÊœ œ œ
ss s s
dy
ds ab
Š‹
#
15. y x y x 16. y t (1 e) tœÊœ œ Êœ
w111ee
dy
dt
17. y (cos ) 2 (cos ) (sin )œÊœ)))
221
dy
d)È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

446 Chapter 7 Transcendental Functions
18. y (ln ) (ln )œÊœ œ)1)
dy (ln )
d)))
1)
1ˆ‰
"1
19. y 7 ln 7 7 ln 7 (ln 7)(sec tan ) 7 (ln 7) (sec tan )œÊœ œ
sec sec sec
dy
d)ab )) ))
#
20. y 3 ln 3 3 ln 3 (ln 3) sec 3 (ln 3) secœÊœ œ
tan tan tan
dy
d)ab###
))
21. y 2 2 ln 2 (cos 3t)(3) (3 cos 3t) 2 (ln 2)œÊœ œ
sin 3t sin 3t sin 3t
dy
dt ab ab
22. y 5 5 ln 5 (sin 2t)(2) (2 sin 2t) 5 (ln 5)œÊœ œ
cos 2t cos 2t cos 2t
dy
dt ab ab
23. y log 5 (5)œœÊœ œ
2)ln 5
ln d ln 5 ln
dy
)
)))## #
"" "
ˆ‰ˆ‰
24. y log (1 ln 3) (ln 3)œœ Êœ œ
3)ln (1 ln 3) dy
ln 3 d ln 3 1 ln 3 1 ln 3
"" "
)
)) )
ˆ‰ˆ ‰
25. y 2 3 yœ œ œ Êœ
ln x ln x ln x ln x ln x 3
ln 4 ln 4 ln 4 ln 4 ln 4 x ln 4
w
26. y (x ln x) y 1œœœ Êœ œ
x ln e ln x x ln x x 1
ln 5 2 ln 5 ln 5 2 ln 5 ln 5 ln 5 x 2x ln 5## # #
"""
w
ˆ‰ ˆ‰ˆ ‰
27. y log r log r (2 ln r)œœœÊœ œ
24
†ˆ‰ˆ‰ ˆ‰
’“
ln r ln r ln r 2 ln r
ln ln 4 (ln 2)(ln 4) dr (ln 2)(ln 4) r r(ln 2)(ln 4)
dy
#
""
28. y log r log r (2 ln r)œœœÊœ œ
39
†ˆ‰ˆ‰ ˆ‰
’“
ln r ln r ln r 2 ln r
ln 3 ln 9 (ln 3)(ln 9) dr (ln 3)(ln 9) r r(ln 3)(ln 9)
dy ""
29. y log ln ln (x 1) ln (x 1)œœœœœ
3
ln 3
Š‹
ˆ‰ ˆ‰
x1 x1
x1 ln 3 ln 3 x1
(ln 3) ln
ln ˆ‰
x1
x1
ln 3 x1
x1
Š‹
Êœœ
dy
dx x 1 x 1 (x 1)(x 1)
2""
30. y log log lnœœœœœ
55
ln 5 ln 5 2
Ɉ‰ ˆ‰ ˆ‰ ˆ‰
”•
7x 7x ln 5 7x
3x 2 3x 2 ln 5 ln 5 3x # ##
"
ln ln
ˆ‰ ˆ‰
7x 7x
3x 2 3x 2
ln 5 2
ln 7x ln (3x 2) œ Êœ œ œ
"" "
##
dy (3x 2) 3x
dx 2 7x 2 (3x 2) 2x(3x 2) x(3x 2)
73
††
31. y sin (log ) sin sin cos sin (log ) cos (log )œœÊœ œ))) ) ) )
777
ˆ‰ ˆ‰ ‘ˆ ‰ˆ‰
ln ln ln
ln 7 d ln 7 ln 7 ln 7 ln 7
dy
)))
))
""
32. y log œœ œ
7ˆ‰
sin cos
e
ln (sin ) ln (cos ) ln e ln 2 ln (sin ) ln (cos ) ln 2
ln 7 ln 7
)) )) ))))
#
(cot tan 1 ln 2)Êœ œ
dy
d (sin )(ln 7) (cos )(ln 7) ln 7 ln 7 ln 7
cos sin ln 2
)) )
))""
ˆ‰ ))
33. y log e yœœœÊœ
5xln e x
ln 5 ln 5 ln 5
xw"
34. y log œœ œ
2Š‹
xe
2x1
ln x ln e ln 2 ln x 1
ln 2 ln 2
2 ln x 2 ln 2 ln (x 1)
ÈÈ
yÊœ œ œ
w"
# #
23x4
x ln 2 (ln 2)(x 1) 2x(x 1)(ln 2) 2x(x 1) ln
4(x 1) x
35. y 3 3 3 (ln 3) log 3 3œœ Êœ œ
log t ln t ln 2 ln t ln 2 log t
2
2 2
dy
dt t ln 2 t
cdab
ˆ‰
""
36. y 3 log (log t) œœœÊœ œ
82
3 ln (log t) dy
ln 8 ln 8 dt ln 8 (ln t)/(ln 2) t ln t(ln t)(ln 8)
3 ln 33
2ln t
ln 2
ˆ‰ ˆ‰ ˆ‰
’“
""
#
œ"
#t(ln t)(ln )
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.4 a and log x 447
xa
37. y log 8t 3 ln t œœœ œÊœ
2ln 2
abln 8 ln t
ln ln dt t
3 ln 2 (ln 2)(ln t) dy
##
"
ˆ‰
ln 2
38. y t sin t sin t t cos tœœœœÊœ
t ln e
ln 3 ln 3 ln 3 dt
t ln 3 t(sin t)(ln 3) dy
Š‹
ˆ‰ ˆ‰
ln 3 sin t sin t
39. y (x 1) ln y ln (x 1) x ln (x 1) ln (x 1) x y (x 1) ln (x 1)œ Ê œ œ Ê œ Ê œ
xx x
y
y(x1) x1
x
†"
w‘
40. y x ln y ln x (x 1) ln x ln x (x 1) ln x 1œÊœ œ Êœ œ
xx y
yxx
ˆ‰
""
y x 1 ln xʜ
w"
x1ˆ‰
x
41. y t t t ln y ln t ln t (ln t)œœœÊœœ Êœ œ
ˆ ‰ ˆ ‰ ˆ‰ ˆ‰ ˆ‰ˆ‰
Ètttt
"Î# Î#
#####
"" " "
ttln t
ydt t
dy
tʜ
dy
dt
ln t
ˆ‰ˆ ‰
Èt
##
"
42. y t t ln y ln t t (ln t) t (ln t) tœœ Ê œ œ Ê œ œ
tt t ˆ‰ ˆ ‰ ˆ‰
"Î# "Î# "Î#
"" "
#ydt t
dy ln t 2
2t
È
tʜ
dy
dt
ln t 2
2t
Š‹
Èt
43. y (sin x) ln y ln (sin x) x ln (sin x) ln (sin x) x y (sin x) ln (sin x) x cot xœÊœ œ Êœ Êœ
xx x
y
ysin x
cos x
ˆ‰ cd
w
44. y x ln y ln x (sin x)(ln x) (cos x)(ln x) (sin x)œÊœ œ Êœ œ
sin x sin x y sin x x (ln x)(cos x)
yxx
ˆ‰
"
yxʜ
w
sin x ’“
sin x x(ln x)(cos x)
x
45. y x , x 0 ln y (ln x) 2(ln x) y xœÊœ Êœ Êœ
ln x ln x#w
"
y
yx x
ln x
ˆ‰ ab
Š‹
46. y (ln x) ln y (ln x) ln (ln x) ln (ln x) (ln x) (ln x)œÊœ Êœ œ
ln x yln(ln x)
yx ln xdx x x
d
ˆ‰ ˆ ‰
"" "
y (ln x)ʜ
w"
Š‹
ln (ln x)
x
ln x
47. 5 dx C 48. (1.3) dx C
''
x x
œ œ
5
ln 5 ln (1.3)
(1.3)
xx
49. 2 d d
''
00
11
))œ œ œœœ œ
ˆ‰ –—
""""
##
"
!
)Š‹
Š‹ Š‹ Š‹ Š‹
ln ln ln ln 2(ln 1 ln 2) ln 2
50. 5 d d (1 25)
''
22
00
))œœœœœœ
"""
!
#
ˆ‰ –—
5ln 1 ln 5 ln 5
ln ln ln ln
24 24
)Š‹ Š‹
Š‹ Š‹ Š‹ Š‹
55
5555
51. Let u x du 2x dx du x dx; x 1 u 1, x 2 u 2;œÊœ Ê œ œÊœ œ Êœ
#"
#È
x2 dx 2 du 2 2
''
11
22
u
abx2
ln 2 ln 2 ln
œœœœ
ˆ‰ ‘ ˆ ‰
ab
"" " "
### #
#
"
#"
u
52. Let u x du x dx 2 du ; x 1 u 1, x 4 u 2;œÊœ Ê œ œÊœœÊœ
"Î# "Î#
"
#
dx
x
È
dx 2 x dx 2 2 du 2 2
'' '
11 1
44 2
xu
224
xln ln ln
x
Èœœœœœ†"Î# $ #
## #
#
"
"
’“ˆ‰
ab
u1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

448 Chapter 7 Transcendental Functions
53. Let u cos t du sin t dt du sin t dt; t 0 u 1, t u 0;œÊœ Êœ œÊœœÊœ
1
#
7 sin t dt 7 du 7 7
''
01
20
cos t u
œ œ œ œ
‘ˆ‰
ab
76
ln 7 ln 7 ln 7
u!
"
" !
54. Let u tan t du sec t dt; t 0 u 0, t u 1;œÊœ œÊœœÊœ
#1
4
sec t dt du
''
00
41
tan t u
ˆ‰ ˆ‰ ˆ ‰ˆ‰ ˆ‰
–— ’“
"" """
#
"
!
!
3 3 ln 3 3 3 3 ln 3
ln
2
œœœœ
Š‹
Š‹
3
3
u
55. Let u x ln u 2x ln x 2 ln x (2x) 2u(ln x 1) du x (1 ln x) dx;œÊ œ Ê œ Êœ Ê œ
2x 2x
"" "
#udx x dx
du du
ˆ‰
x 2 u 2 16, x 4 u 4 65,536;œÊœ œ œÊœ œ
%)
x (1 ln x) dx du u (65,536 16) 32,760
''
216
4 65 536
2x 65 536
16
œ œ œ œœ
"""
### #
cd 65,520
56. Let u ln x du dx; x 1 u 0, x 2 u ln 2;œÊœ œÊœœÊœ
"
x
dx 2 du 2 2
''
10
2ln 2
uln2
ln 2
0
22 2
x ln ln ln
ln x ln 2
œœœœ
‘ ˆ‰
ab
u
## #
""
!
57. 3x dx C 58. x dx C
''
321
œ œ
3x x
31 2
31 2
È È
59. 2 1 x dx x 3 60. x dx
''
0 1
3 e
2ln 2 1
22 e
1
Š‹ ’“
È‘
œ œ œœœœ
$
!##
"xe121
ln ln 2 ln 2 ln
ln 2 ln 2 ln 2
61. dx dx; u ln x du dx
'log x
x ln 10 x x
ln x
10 œœÊœ
'ˆ‰ˆ‰ ‘
""
dx u du u C CÄœœœ
''
ˆ‰ˆ‰ ˆ‰ˆ‰
ln x
ln 10 x ln 10 ln 10 2 ln 10
(ln x)
"" ""
#
#
62. dx dx; u ln x du dx; x 1 u 0, x 4 u ln 4
''
11
44
log x
xln x x
ln x
2œœÊœœÊœœÊœ
ˆ‰ˆ‰ ‘
#
""
dx u du u (ln 4) ln 4Ä œ œ œ œœœ
''
10
4ln 4 ln 4
0
ˆ‰ˆ‰ ˆ‰ ˆ‰‘ ˆ‰ ‘
ln x
ln x ln ln ln 2 ln ln 4
(ln 4) (ln 4)
# # ## ## #
" " "" ""
##
63. dx dx dx (ln x) (ln 4) (ln 1) (ln 4)
'' '
11 1
44 4
ln 2 log x
xxln x
ln 2 ln x ln x
2œœœœœ
ˆ‰ˆ‰ ‘ cd
####
"" "
####
%
"
(2 ln 2) 2(ln 2)œœ
"
#
##
64. dx dx (ln x) (ln e) (ln 1) 1
''
11
ee e
1
2 ln 10 (log x) (ln 10)(2 ln x)
x (ln 10) x
10 œœœœ
ˆ‰ cd
"###
65. dx ln (x 2) dx
''
00
22
log (x 2) (ln (x 2)) (ln 4) (ln 2)
x ln x ln ln
2
# # # # # # # #
""" "
#
!
œ œ œcd
ˆ ‰ ˆ‰ ˆ‰
’“ ’ “
ln 2œœ
ˆ‰
’“
"
## # #ln
4(ln 2) (ln 2) 3
66. dx ln (10x) dx
''
110 110
10 10
log (10x) (ln (10x)) (ln 100) (ln 1)
x ln 10 10x ln 10 0 ln 10 0
000
10 œœœ
""" "
###
"!
"Î"!
cd
ˆ‰ ˆ‰ ˆ‰
’“ ’ “
ln 10œœ#
ˆ‰
’“
"
#
0
ln 10 0
4(ln 10)
67. dx ln (x 1) dx
''
00
99
2 log (x 1) (ln (x 1)) (ln 10) (ln )
x 1 ln 10 x 1 ln 10 ln 10 2
222
10 "
##
"*
!
œœ œ
ˆ‰ ˆ‰ ˆ‰
’“ ’ “
ln 10œ
68. dx ln (x 1) dx ln 2
''
22
33
2 log (x 1) (ln (x 1)) (ln 2) (ln )
x 1 ln 2 x 1 ln 2 ln 2 2
222
2"
##
"$
#
œœ œ œ
ˆ‰ ˆ‰ ˆ‰
’“ ’ “
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
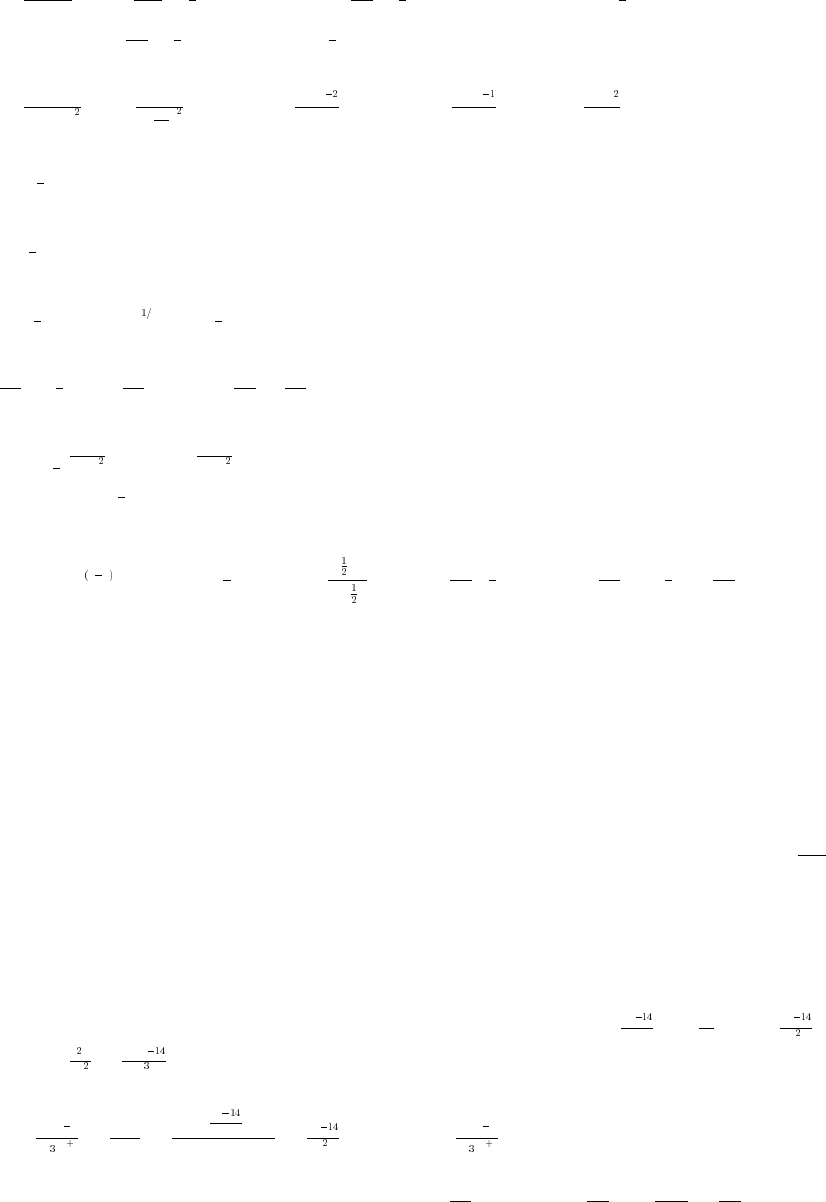
Section 7.4 a and log x 449
xa
69. dx (ln 10) dx; u ln x du dx
'' '
dx ln 10
x log x ln x x ln x x x
10 œœ œÊœ
ˆ ‰ˆ‰ ˆ ‰ˆ‰ ‘
""" "
(ln 10) dx (ln 10) du (ln 10) ln u C (ln 10) ln ln x CÄœœœ
''
ˆ‰ˆ‰ kk k k
"" "
ln x x u
70. (ln 8) dx (ln 8) C C
'' '
dx dx
x (log x) x 1 ln x
x
(ln x) (ln x) (ln 8)
8œœ œ œ
ˆ‰
ln x
ln 8
##
71. dt ln t ln ln x ln 1 ln (ln x), x 1
'1
ln x "
t
ln x
1
œœœ cd kkkk
72. dt ln t ln e ln 1 x ln e x
'1
eex
xx
"
t1
œœœœcdkk
73. dt ln t ln ln 1 ln 1 ln x ln 1 ln x, x 0
'1
1/x x
1
""
tx
œœœœcd a bkk kk
¸¸
74. dt ln t log x, x 0
"" "
ln a t ln a ln a ln a
ln x ln 1
'1
xx
1a
œ œœ
‘
kk
75. A dx 2 dx; u 1 x du 2x dx; x 0 u 1, x 2 u 5œœ œÊœœÊœœÊœ
''
20
22
2x 2x
1x 1x
#
cd
A 2 du 2 ln u 2(ln 5 ln 1) 2 ln 5Äœ œ œ œ
'1
5"&
"
ucdkk
76. A 2 dx 2 dx 2 2œœ œœœœ
''
""
######
"
"
11
11
1x x
ˆ‰ ˆ ‰ ˆ ‰ˆ ‰
–—
Š‹
Š‹
x
ln
2233
ln ln ln
77. Let H O x and solve the equations 7.37 log x and 7.44 log x. The solutions of these equationscd
$œœœ
10 10
are 10 and 10 . Consequently, the bounds for H O are 10 10 .
(Þ$( (Þ%% (Þ%% (Þ$(
$
cdc dß
78. pH log 4.8 10 (log 4.8) 8 7.32œ ‚ œ œ
10 10
ab
)
79. Let O original sound level 10 log I 10 db from Equation (6) in the text. Solvingœœ‚
10 ab
"#
O 10 10 log kI 10 for k 10 log I 10 10 10 log kI 10 log I 10 1œ ‚ Ê ‚ œ ‚ Ê ‚
10 10 10 10
ab ab ab ab
"# "# "# "#
log kI 10 log I 10 1 log k log I 10 1 log k 1œ ‚ Ê ‚ œ ‚ Êœ Êœ
10 10 10 10 10
a b ab ab
"# "# "# ln k
ln 10
ln k ln 10 k 10ʜ ʜ
80. Sound level with 10I 10 log 10I 10 10 log 10 log I 10 10 10 log I 10œ‚œ‚œ‚
10 10 10 10
abc d abab
"# "# "#
original sound level 10 an increase of 10 dbœÊ
81. (a) If x H O and S x OH , then x(S x) 10 S x 1œœ œÊœÊœcd cd
$ "% 10 dS 10
xdx x
and 0 a minimum exists at x 10
dS 210
dx x
œÊ œ
†(
(b) pH log 10 7œ œ
10 ab
(
(c) the ratio equals 1 at x 10
cd cd
cd cd
OH OH
HO x x HO
Sx 10
œœ œ Ê œ
(
Š‹
xx
x
10
x
82. Yes, it's true for all positive values of a and b: log b and log a log b
ab a
œœÊœœ
ln b ln a ln b
ln a ln b log a ln a
"
b
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
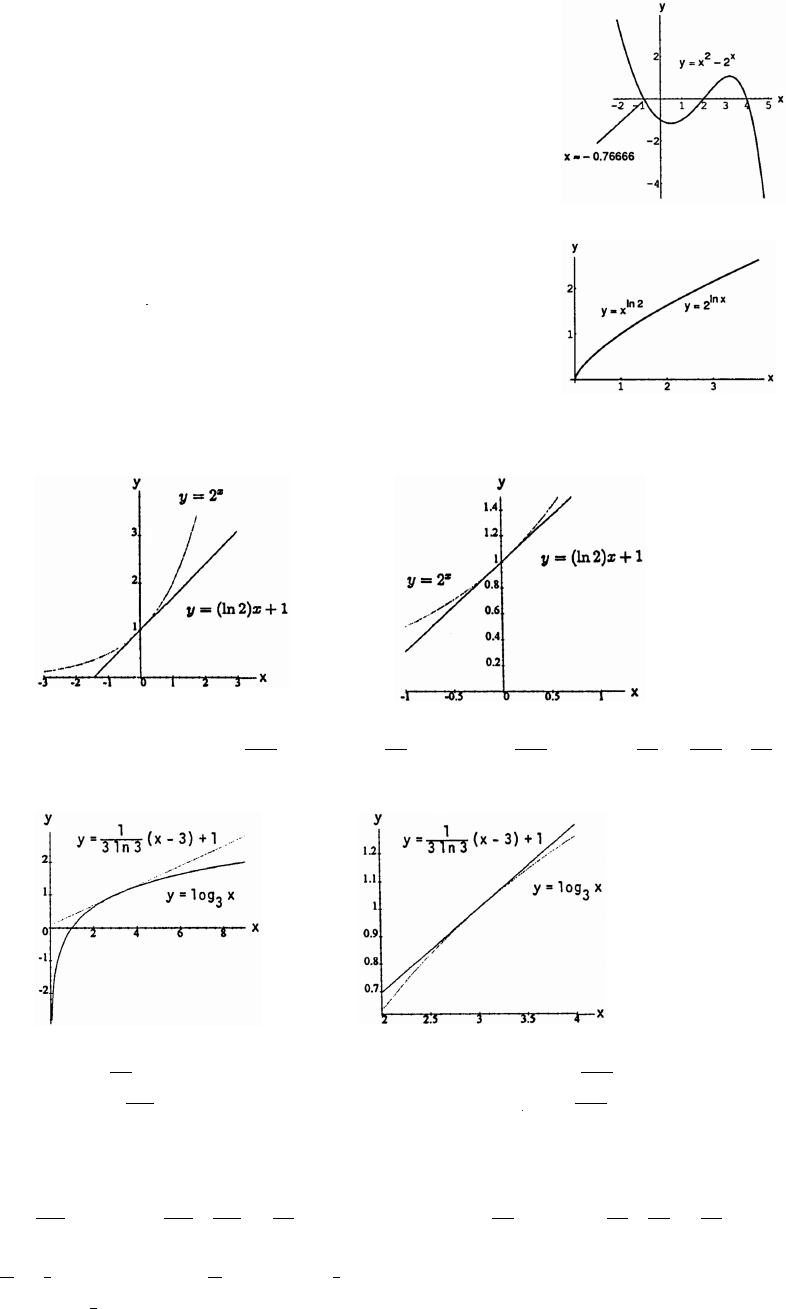
450 Chapter 7 Transcendental Functions
83. From zooming in on the graph at the right, we estimate
the third root to be x 0.76666¸
84. The functions f(x) x and g(x) 2 appear toœœ
ln 2 ln x
have identical graphs for x 0. This is no accident,
because x e e 2 .
ln 2 ln 2 ln x ln 2 ln x
ln x
œœ œab
85. (a) f(x) 2 f (x) 2 ln 2; L(x) 2 ln 2 x 2 x ln 2 1 0.69x 1œÊ œ œ œ ¸
xxw!!
ab
(b)
86. (a) f(x) log x f (x) , and f(3) L(x) (x 3) 1œÊœ œÊœ œ
3w"""
x ln 3 ln 3 3 ln 3 ln 3 3 ln 3 ln 3
ln 3 ln 3 x
0.30x 0.09¸
(b)
87. (a) log 8 1.89279 (b) log 0.5 0.35621
3 7
œ¸ œ ¸
ln 8 ln 0.5
ln 3 ln 7
(c) log 17 0.94575 (d) log 7 2.80735
20 05
œ¸ œ ¸
ln 17 ln 7
ln 0 ln 0.5#
(e) ln x (log x)(ln 10) 2.3 ln 10 5.29595 (f) ln x (log x)(ln 2) 1.4 ln 2 0.97041œœ¸ œœ¸
10 2
(g) ln x (log x)(ln 2) 1.5 ln 2 1.03972 (h) ln x (log x)(ln 10) 0.7 ln 10 1.61181œ œ ¸ œ œ ¸
210
88. (a) log x log x (b) log x log x
ln 10 ln 10 ln x ln x ln a ln a ln x ln x
ln ln ln 10 ln ln b ln b ln a ln b###
†† ††
10 2 a b
œœœ œœœ
89. x k x and ln x c .
dd
dx dx x
ˆ‰ abœ œ
""
#
#
Since x for any x , these two curves will have perpendicular tangent lines.† œ" Á!
"
x
90. e x for x and ln e x for all x
ln x x
œ! œab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.5 Exponential Growth and Decay 451
91. Using Newton's Method: f x ln x f x x x x x ln x .ab ab ab a b
’“
œ"ʜʜ Êœ#
w"" "
xnn nn n
ln xab
n
x
"
Then, x 2, x 2.61370564, x 2.71624393, and x 2.71828183. Many other methods may be used. For example,
12 3
œœ œ œ
&
graph y ln x and determine the zero of y.œ"
92. (a) The point of tangency is p ln p and m since . The tangent line passes through theab abßœœ !ß!Ê
tangent pdxx
dy
""
equation of the tangent line is y x. The tangent line also passes through p ln p ln p p p e, andœßÊœœ"Êœ
" "
p p
ab
the tangent line equation is y x.œ"
e
(b) for x y ln x is concave downward over its domain. Therefore, y ln x lies below the graph of
dy
dx x
œ Á!Ê œ œ
"
y x for all x , x e, and ln x for x , x e.œ !Á !Á
"
ee
x
(c) Multiplying by e, e ln x x or ln x x.
e
(d) Exponentiating both sides of ln x x, we have e e , or x e for all positive x e.
eln xxex
Á
e
(e) Let x to see that e . Therefore, e is bigger.œ11
e11
7.5 EXPONENTIAL GROWTH AND DECAY
1. (a) y y e 0.99y y e k 0.00001œÊ œ Êœ¸
!!!
kt 1000k ln 0.99
1000
(b) 0.9 e ( 0.00001)t ln (0.9) t 10,536 yearsœÊœÊœ¸
0 00001)t ln (0.9)
0.00001
(c) y y e y e y (0.82) 82%œ¸œÊ
!!!
20 000 k 0 2
2. (a) kp p p e where p 1013; 90 1013e k 0.121
dp ln (90) ln (1013)
dh 20
œÊœ œ œ Êœ ¸
!!
kh 20k
(b) p 1013e 2.389 millibarsœ¸
605
(c) 900 1013e 0.121h ln h 0.977 kmœÊœÊœ ¸
0121h ˆ‰
900
1013 0.121
ln (1013) ln (900)
3. 0.6y y y e ; y 100 y 100e y 100e 54.88 grams when t 1 hr
dy
dt œ Ê œ œ Ê œ Ê œ ¸ œ
!!
06t 06t 06
4. A A e 800 1000e k A 1000e , where A represents the amount ofœÊœ Êœ Êœ
!kt 10k ln (0 8 10 t
ln (0.8)
10
sugar that remains after time t. Thus after another 14 hrs, A 1000e 585.35 kgœ¸
ln 0 8 10 24
5. L(x) L e L e ln 18k k 0.0385 L(x) L e ; when the intensityœÊœ ʜʜ¸ Êœ
!! !
##
"
kx 18k 0 0385x
Lln 2
18
is one-tenth of the surface value, L e ln 10 0.0385x x 59.8 ft
L
10 œÊœÊ¸
!0 0385x
6. V(t) V e 0.1V V e when the voltage is 10% of its original value t 40 ln (0.1)œÊœ Êœ
!!!
t40 t40
92.1 sec¸
7. y y e and y 1 y e at y 2 and t 0.5 we have 2 e ln 2 0.5k k ln 4.œ œÊœ Ê œ œ œ Ê œ Êœ œ
!!
kt kt 0 5k ln 2
0.5
Therefore, y e y e 4 2.81474978 10 at the end of 24 hrsœÊœœœ ‚
ln 4 t 24 ln 4 24 14
8. y y e and y(3) 10,000 10,000 y e ; also y(5) 40,000 y e . Therefore y e 4y eœœÊœ œœ œ
!!!!!
kt 3k 5k 5k 3k
e 4e e 4 k ln 2. Thus, y y e 10,000 y e y e 10,000 8yÊœ ʜʜ œ Ê œ œ Ê œ
5k 3k 2k ln 2 t 3 ln 2 ln 8
!!!!
y 1250Êœ œ
!10,000
8
9. (a) 10,000e 7500 e 0.75 k ln 0.75 and y 10,000e . Now 1000 10,000e
k 1 k ln0 75 t ln0 75 t
œÊœÊœ œ œ
ln 0.1 (ln 0.75)t t 8.00 years (to the nearest hundredth of a year)Êœ Êœ¸
ln 0.1
ln 0.75
(b) 1 10,000e ln 0.0001 (ln 0.75)t t 32.02 years (to the nearest hundredth of aœÊœÊœ¸
ln 0 75 t ln 0.0001
ln 0.75
year)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
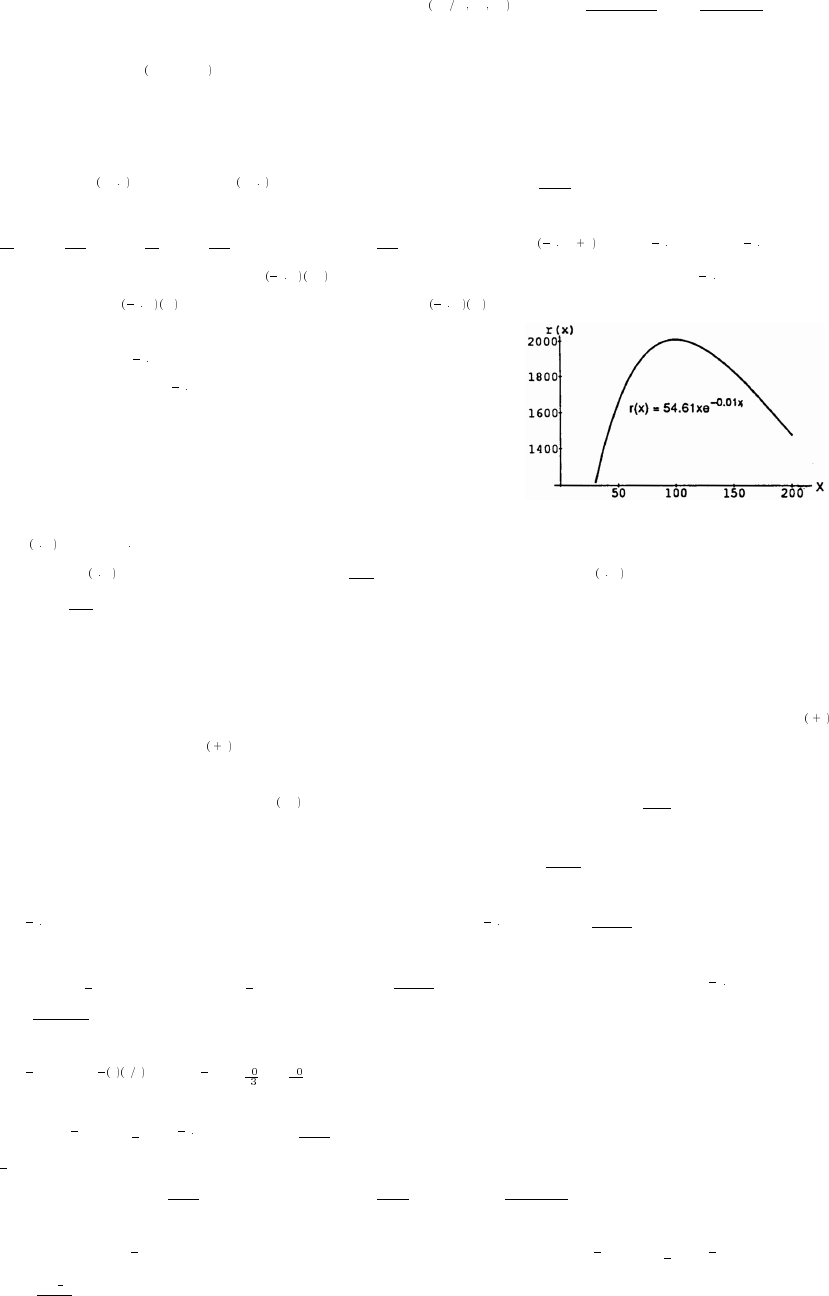
452 Chapter 7 Transcendental Functions
10. (a) There are (60)(60)(24)(365) 31,536,000 seconds in a year. Thus, assuming exponential growth,œ
P 257,313,431e and 257,313,432 257,313,431e lnœœÊœ
kt 14k 31 536 000 Š‹
257,313,432
257,313,431 31,536,000
14k
k 0.0087542ʸ
(b) P 257,313,431e 293,420,847 (to the nearest integer). Answers will vary considerablyœ¸
0.0087542 ab"&
with the number of decimal places retained.
11. 0.9P P e k ln 0.9; when the well's output falls to one-fifth of its present value P 0.2P
!! !
œÊœ œ
k
0.2P P e 0.2 e ln (0.2) (ln 0.9)t t 15.28 yrÊœ Êœ Ê œ Êœ¸
!!
ln 0 9 t ln 0 9 t ln 0.2
ln 0.9
12. (a) p dx ln p x C p e e e C e ;
dp dp
dx 100 p 100 100
œ Ê œ Ê œ Ê œ œ œ
"" " "
001x C C 001x 001x
p(100) 20.09 20.09 C e C 20.09e 54.61 p(x) 54.61e (in dollars)œÊœ Êœ ¸Êœ
""
001 100 001x
(b) p(10) 54.61e $49.41, and p(90) 54.61e $22.20œœ œœ
0 01 10 0 01 90
(c) r(x) xp(x) r (x) p(x) xp (x);œÊœ
ww
p (x) .5461e r (x)
ww
œ Ê
001x
(54.61 .5461x)e . Thus, r (x) 0œ œ
001x w
54.61 .5461x x 100. Since r 0ʜ ʜ
w
for any x 100 and r 0 for x 100, then
w
r(x) must be a maximum at x 100.œ
13. (a) A e A e
!!
004 5 02
œ
(b) 2A A e ln 2 (0.04)t t 17.33 years; 3A A e ln 3 (0.04)t
!! !!
œÊœÊœ¸ œÊœ
004 t 004t
ln 2
0.04
t 27.47 yearsÊœ ¸
ln 3
0.04
14. (a) The amount of money invested A after t years is A(t) A e
!!
œt
(b) If A(t) 3A , then 3A A e ln 3 t or t 1.099 yearsœœÊœ¸
!!!
t
(c) At the beginning of a year the account balance is A e , while at the end of the year the balance is A e .
!!
tt1
The amount earned is A e A e A e (e 1) 1.7 times the beginning amount.
!!!
t1 t t
œ ¸
15. A(100) 90,000 90,000 1000e 90 e ln 90 100r r 0.0450 or 4.50%œÊœ ʜʜʜ¸
r 100 100r ln 90
100
16. A(100) 131,000 131,000 1000e ln 131 100r r 0.04875 or 4.875%œÊœ ʜʜ¸
100r ln 131
100
17. y y e represents the decay equation; solving (0.9)y y e t 0.585 daysœœÊœ¸
!!!
0 18t 018t ln (0.9)
0.18
18. A A e and A A e e k 0.00499; then 0.05A A eœœÊœÊœ¸ œ
!!! !!
""
##
kt 139k 139k 0 00499t
ln (0.5)
139
t 600 daysÊœ ¸
ln 0.05
0.00499
19. y y e y e y e (0.05)(y ) after three mean lifetimes less than 5% remainsœœ œœœ Ê
!! ! !
kt k 3 k 3 yy
e20
20. (a) A A e e k 0.262œÊœÊœ¸
!"
##
kt 2 645k ln 2
.645
(b) 3.816 years
"
k¸
(c) (0.05)A A exp t ln 20 t t 11.431 yearsœ Êœ Êœ ¸
ˆ‰ ˆ‰
ln 2 ln 2 2.645 ln 20
2.645 2.645 ln #
21. T T (T T ) e , T 90°C, T 20°C, T 60°C 60 20 70e eœ œ œ œ Ê œ Êœ
ss s
kt 10k 10k
!! 4
7
k 0.05596Êœ ¸
ln
10
ˆ‰
7
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.6 Relative Rates of Growth 453
(a) 35 20 70e t 27.5 min is the total time it will take 27.5 10 17.5 minutes longer to reachœ ʸ Ê œ
0 05596t
35°C
(b) T T (T T ) e , T 90°C, T 15°C 35 15 105e t 13.26 minœ œ œ Ê œ ʸ
ss s
kt 0 05596t
!!
22. T 65° (T 65°) e 35° 65° (T 65°) e and 50° 65° (T 65°) e . Solvingœ Ê œ œ
!! !
kt 10k 20k
30° (T 65°) e and 15° (T 65°) e simultaneously (T 65°) e 2(T 65°) eœ œ Ê œ
!! !!
10k 20k 10k 20k
e 2 k and 30° 30° e 65° 60° 5°Ê œÊœ œ Ê œœ
10k 10 ln 2
ln 2
10 e
T 65°
10k
ln 2
10
‘
œ Ê œ T 65° T 65° 30° e
ˆ‰
23. T T (T T ) e 39 T (46 T ) e and 33 T (46 T ) e e andœ Ê œ œ Ê œ
ss ss ss
kt 10k 20k 10k
!
39 T
46 T
s
s
e e (33 T )(46 T ) (39 T ) 1518 79T T
33 T 33 T 39 T
46 T 46 T 46 T
####
ss
ss
œœ Ê œ Ê œÊ
20k 10k ss s s
s
ab Š‹
s
s
1521 78T T T 3 T 3°CœÊœÊœ
sss
s
#
24. Let x represent how far above room temperature the silver will be 15 min from now, y how far above room
temperature the silver will be 120 min from now, and t the time the silver will be 10°C above room
!
temperature. We then have the following time-temperature table:
time in min. 0 20 (Now) 35 140 t
temperature T 70° T 60° T x T y T 10°
!
s s sss
T T (T T ) e (60 T ) T (70 T ) T e 60 70e k lnœ Ê œ Ê œ Êœ
s s ss ss
kt 20k 20k
!"
cd ˆ‰ˆ‰
20 7
6
0.00771¸
(a) T T (T T ) e (T x) T (70 T ) T e x 70e 53.44°Cœ Ê œ Êœ ¸
ss ss ss
0 00771t 0 00771 35 0 26985
!cd
(b) T T (T T ) e (T y) T (70 T ) T e y 70e 23.79°Cœ Ê œ Êœ ¸
ss ss ss
0 00771t 0 00771 140 1 0794
!cd
(c) T T (T T ) e (T 10) T (70 T ) T e 10 70eœ Ê œ Ê œ
ss ss ss
0 00771t 0 00771 t 0 00771t
!cd
ln 0.00771t t ln 252.39 252.39 20 232 minutes from now theÊœ Êœ œ Ê ¸
ˆ‰ ˆ ‰ ˆ‰
"""
!!
7 0.00771 7
silver will be 10°C above room temperature
25. From Example 5, the half-life of carbon-14 is 5700 yr c c e k 0.0001216Êœ Êœ¸
"
#!!
k 5700 ln 2
5700
c c e (0.445)c c e t 6659 yearsÊœ Ê œ Êœ ¸
!!!
0 0001216t 0 0001216t ln (0.445)
0.0001216
26. From Exercise 25, k 0.0001216 for carbon-14.¸
(a) c c e (0.17)c c e t 14,571.44 years 12,571 BCœÊœÊ¸ Ê
!!!
0 0001216t 0 0001216t
(b) (0.18)c c e t 14,101.41 years 12,101 BC
!!
œÊ¸ Ê
0 0001216t
(c) (0.16)c c e t 15,069.98 years 13,070 BC
!!
œÊ¸ Ê
0 0001216t
27. From Exercise 25, k 0.0001216 for carbon-14. Thus, c c e (0.995)c c e¸œÊœ
!!!
0 0001216t 0 0001216t
t 41 years oldÊœ ¸
ln (0.995)
0.0001216
7.6 RELATIVE RATES OF GROWTH
1. (a) slower, lim lim 0
xxÄ_ Ä_
œœ
x3
ee
"
xx
(b) slower, lim lim lim lim 0 by the
xx x xÄ_ Ä_ Ä_ Ä_
œœœœ
x sin x 3x 2 sin x cos x 6x 2 cos 2x 6 4 sin 2x
ee ee
xx xx
Sandwich Theorem because for all reals and lim 0 lim
xx
2 6 4 sin 2x 10 2 0
eee e e
xxx x x
ŸŸ œœ
Ä_ Ä_
"
(c) slower, lim lim lim lim 0
xxx xÄ_ Ä_ Ä_ Ä_
œœ œ œ
ÈŠ‹ È
x
ee e
xx
xe
xx x x
"
#
(d) faster, lim lim since 1
xxÄ_ Ä_
œœ_
444
eee
x
x
xˆ‰
(e) slower, lim lim 0 since 1
xxÄ_ Ä_
œœ
Š‹
3x
x
e2e2e
33
x
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

454 Chapter 7 Transcendental Functions
(f) slower, lim lim 0
xxÄ_ Ä_
œœ
e
ee
x2
xx2
"
(g) same, lim lim
xxÄ_ Ä_
œœ
Š‹
ex
ex""
##
(h) slower, lim lim lim lim 0
xxxxÄ_ Ä_ Ä_ Ä_
œœœ œ
log x
e (ln 10) e (ln 10) e (ln 10)xe
ln x
10
xxxx
x"
2. (a) slower, lim lim lim lim lim 0
xxxxxÄ_ Ä_ Ä_ Ä_ Ä_
œœœœœ
10x 30x 1 40x 30 20x 240x 240
eeeee
"
xxxxx
(b) slower, lim lim lim lim lim
xx x x xÄ_ Ä_ Ä_ Ä_ Ä_
œœ œ œ
x ln x x ln x 1 1 ln x
ee e ee
x (ln x 1) ln x1x
xx x xx
Š‹
x
lim lim 0
xx
œœœ
Ä_ Ä_
Š‹
x
exe
xx
"
(c) slower, lim lim lim lim lim lim
x x xx xxÄ_ Ä_ Ä_ Ä_ Ä_ Ä_
œœœœœ
È1x
e e 2e 4e 8e 16e
1 x 4x 12x 24x 24
x2x2x2x2x2x
ÉÉÉÉÉ
00œœ
È
(d) slower, lim lim 0 since 1
xxÄ_ Ä_
œœ
Š‹
5x
x
ee2e
55
x
ˆ‰
#
(e) slower, lim lim 0
xxÄ_ Ä_
œœ
e
ee
x
x2x
"
(f) faster, lim lim x
xxÄ_ Ä_
œœ_
xe
e
x
x
(g) slower, since for all reals we have 1 cos x 1 e e e and alsoŸ Ÿ Ê Ÿ Ÿ Ê Ÿ Ÿ
" "cos x ee e
eee
xxx
cos x
lim 0 lim , so by the Sandwich Theorem we conclude that lim 0
xx xÄ_ Ä_ Ä_
œœ œ
ee e
ee e
xx x
cos x
(h) same, lim lim lim
xx xÄ_ Ä_ Ä_
œœœ
e
eee
e
x1
xxx1
"""
3. (a) same, lim lim lim 1
xxxÄ_ Ä_ Ä_
œœœ
x4x 2x4 2
x2x
#
(b) faster, lim lim x 1
xxÄ_ Ä_
œœ_
xx
x
$
ab
(c) same, lim lim lim 1 1 1
xxxÄ_ Ä_ Ä_
œœœœ
Èxx
xx
xx
x
"
ÉɈ‰
È
(d) same, lim lim lim 1
xxxÄ_ Ä_ Ä_
œœœ
(x 3) 2(x 3)
xx
2
##
(e) slower, lim lim lim 0
xxxÄ_ Ä_ Ä_
œœ œ
x ln x ln x
xx1
Š‹
x
(f) faster, lim lim lim
xx xÄ_ Ä_ Ä_
œœ œ_
2
x2x
(ln 2) 2 (ln 2) 2
xxx
#
(g) slower, lim lim lim 0
xxxÄ_ Ä_ Ä_
œœœ
xe x
xee
x
xx
"
(h) same, lim lim 8 8
xxÄ_ Ä_
œœ
8x
x
4. (a) same, lim lim 1 1
xxÄ_ Ä_
œœ
xx
xx
"
Ȉ‰
(b) same, lim lim 10 10
xxÄ_ Ä_
œœ
"0x
x
(c) slower, lim lim 0
xxÄ_ Ä_
œœ
xe
xe
x
x
"
(d) slower, lim lim lim lim lim 0
xx x x xÄ_ Ä_ Ä_ Ä_ Ä_
œœ œ œ œ
log x
x x ln 10 x ln 10 2x ln 10 x
2 ln x 2
10 Š‹ Š‹
ln x
ln 10 x
"""
(e) faster, lim lim (x 1)
xxÄ_ Ä_
œœ_
xx
x
(f) slower, lim lim 0
xxÄ_ Ä_
œœ
Š‹
10
x
x
x10x
"
(g) faster, lim lim lim
xx xÄ_ Ä_ Ä_
œœ œ_
(1.1) (ln 1.1)(1.1) (ln 1.1) (1.1)
xx
xx x
##
(h) same, lim lim 1 1
xxÄ_ Ä_
œœ
x 100x 100
xx
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.6 Relative Rates of Growth 455
5. (a) same, lim lim lim
xx xÄ_ Ä_ Ä_
œœœ
log x
ln x ln x ln 3 ln 3
3Š‹
ln x
ln 3 ""
(b) same, lim lim 1
xxÄ_ Ä_
œœ
ln 2x
ln x
ˆ‰
ˆ‰
2
x
x
(c) same, lim lim lim
xx xÄ_ Ä_ Ä_
œœœ
ln x
ln x ln x
ln x
ÈŠ‹ ""
##
(d) faster, lim lim lim lim lim
xxx x xÄ_ Ä_ Ä_ Ä_ Ä_
œœ œ œœ_
È È
Š‹
Š‹ È
x x
ln x ln x
xx
x
x
x##
(e) faster, lim lim lim x
xx xÄ_ Ä_ Ä_
œœœ_
x
ln x
"
Š‹
x
(f) same, lim lim 5 5
xxÄ_ Ä_
œœ
5 ln x
ln x
(g) slower, lim lim 0
xxÄ_ Ä_
œœ
Š‹
x
ln x x ln x
"
(h) faster, lim lim lim xe
xxxÄ_ Ä_ Ä_
œœœ_
ee
ln x
x
xx
x
ˆ‰
6. (a) same, lim lim lim lim lim 2
xx x x xÄ_ Ä_ Ä_ Ä_ Ä_
œœ œ œœ
log x
ln x ln x ln ln x ln ln x ln
ln x 2 ln x 2
2Š‹
ln x
ln 2 "" "
## #ln #
(b) same, lim lim lim lim lim
xx x x xÄ_ Ä_ Ä_ Ä_
œœ œ œ
log 10x
ln x ln x ln 10 ln x ln 10 ln 10
ln 10x
10 Š‹ Š‹
Š‹
ln 10x 0
ln 10 10x
x
"""
Ä_ œ 1 "
ln 10
(c) slower, lim lim 0
xxÄ_ Ä_
œœ
Š‹ ˆ‰
È
x
ln x x(ln x)
"
(d) slower, lim lim 0
xxÄ_ Ä_
œœ
Š‹
x
ln x x ln x
"
(e) faster, lim lim 2 lim 2 lim 2 lim x 2
xx x x xÄ_ Ä_ Ä_ Ä_ Ä_
œœ œ œœ_
x2 ln x x x
ln x ln x ln x
"
ˆ‰
Š‹ Š‹
Š‹
x
(f) slower, lim lim 0
xxÄ_ Ä_
œœ
e
ln x e ln x
x
x"
(g) slower, lim lim lim 0
xxxÄ_ Ä_ Ä_
œœœ
ln (ln x)
ln x ln x
Š‹
Š‹
/x
ln x
x
"
(h) same, lim lim lim lim lim 1 1
xxxxxÄ_ Ä_ Ä_ Ä_ Ä_
œœœœœ
ln (2x 5)
ln x 2x 5
2x 2
#
Š‹
Š‹
2
2x 5
x
7. lim lim e e grows faster than e ; since for x e we have ln x e and lim
xx xÄ_ Ä_ Ä_
œœ_Ê
e
e
x2 x x2 e (ln x)
e
x
x2
x
x
ÎÎ
lim (ln x) grows faster than e ; since x ln x for all x 0 and lim lim
xxx
œœ_Ê œ
Ä_ Ä_ Ä_
ˆ‰ ˆ‰
ln x xx
e(ln x) ln x
xxx x
x
x
x grows faster than (ln x) . Therefore, slowest to fastest are: e , e , (ln x) , x so the order is d, a, c, bœ_ Ê xx x2xxxÎ
8. lim lim lim lim (ln 2) 0
xx x xÄ_ Ä_ Ä_ Ä_
œœ œ œ
(ln 2) (ln (ln 2))(ln 2) (ln (ln 2)) (ln 2) (ln (ln 2))
xx
x
xx x
###
(ln 2) grows slower than x ; lim lim lim 0 x grows slower than 2 ;
xx x
ÊœœœÊ
Ä_ Ä_ Ä_
x x
x2x 2
2 (ln )2 (ln 2)
# #
##
xx x
lim lim 0 2 grows slower than e . Therefore, the slowest to the fastest is: (ln 2) , x , 2
xxÄ_ Ä_
œœÊ
22
ee
xxx xx
x
xˆ‰ #
and e so the order is c, b, a, d
x
9. (a) false; lim 1
xÄ_ œ
x
x
(b) false; lim 1
xÄ_ œœ
x
x5 1
"
(c) true; x x 5 1 if x 1 (or sufficiently large) Ê
x
x5
(d) true; x 2x 1 if x 1 (or sufficiently large)Ê
x
2x
(e) true; lim lim 0
xx0
Ä_ œœ
Ä
e
ee
x
2x x
"
(f) true; 1 1 1 2 if x 1 (or sufficiently large)
x ln x ln x
xxx
x
x
"
œ œ
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

456 Chapter 7 Transcendental Functions
(g) false; lim lim lim 1 1
xx xÄ_ Ä_ Ä_
œœœ
ln x
ln 2x Š‹
Š‹
x
2
x
(h) true; 1 6 if x 1 (or sufficiently large)
ÈÈ
x5
xxxx
(x 5) x5 5
œ
10. (a) true; 1 if x 1 (or sufficiently large)
Š‹
Š‹
x3
x
œ
x
x3
(b) true; 1 2 if x 1 (or sufficiently large)
Š‹
Š‹
xx
x
œ
"
x
(c) false; lim lim 1 1
xxÄ_ Ä_
œœ
Š‹
Š‹
xx
x
ˆ‰
"
x
(d) true; 2 cos x 3 if x is sufficiently largeŸÊ Ÿ
2cos x 3
##
(e) true; 1 and 0 as x 1 2 if x is sufficiently large
ex x x x
eee e
x
xxx x
œ Ä Ä_Ê
(f) true; lim lim lim 0
xxxÄ_ Ä_ Ä_
œœ œ
x ln x ln x
xx1
Š‹
x
(g) true; 1 if x is sufficiently large
ln (ln x)
ln x ln x
ln x
œ
(h) false; lim lim lim lim
xxxxÄ_ Ä_ Ä_ Ä_
œœœœ
ln x x
ln x 1 x xab Š‹
Š‹
####
" " " "
x
2x
x1 ˆ‰
11. If f(x) and g(x) grow at the same rate, then lim L 0 lim 0. Then
xxÄ_ Ä_
œÁ Ê œÁ
f(x) g(x)
g(x) f(x) L
"
L 1 if x is sufficiently large L 1 L 1 L 1 if x is sufficiently large
¹¹ kk
f(x) f(x) f(x)
g(x) g(x) g(x)
Ê Ê Ÿ
f O(g). Similarly, 1 g O(f).Êœ Ÿ Ê œ
g(x)
f(x) L
¸¸
"
12. When the degree of f is less than the degree of g since in that case lim 0.
xÄ_ œ
f(x)
g(x)
13. When the degree of f is less than or equal to the degree of g since lim 0 when the degree of f is smaller
xÄ_ œ
f(x)
g(x)
than the degree of g, and lim (the ratio of the leading coefficients) when the degrees are the same.
xÄ_ œ
f(x)
g(x) b
a
14. Polynomials of a greater degree grow at a greater rate than polynomials of a lesser degree. Polynomials of the
same degree grow at the same rate.
15. lim lim lim lim 1 and lim lim
xxxx x xÄ_ Ä_ Ä_ Ä_ Ä_ Ä_
œœœœ œ
ln (x ) ln (x 999)
ln x x 1 1 ln x
x
"
"
Š‹ Š‹
Š‹ Š‹
x1 x999
x x
lim 1
x
œœ
Ä_
x
x 999
16. lim lim lim lim 1. Therefore, the relative rates are the same.
xxxxÄ_ Ä_ Ä_ Ä_
œœœœ
ln (x a)
ln x x a 1
x
"
Š‹
Š‹
xa
x
17. lim lim 10 and lim lim 1 1. Since the growth rate
xx xxÄ_ Ä_ Ä_ Ä_
œœ œœœ
ÈÈ
ÈÈ
10x 1 x 1
xx
0x 1 x 1
xx
"
ÉÉ
ÈÈ
is transitive, we conclude that 10x 1 and x 1 have the same growth rate that of x .
ÈÈ ˆ‰
È
18. lim lim 1 and lim lim 1. Since the growth rate is
xx x xÄ_ Ä_ Ä_ Ä_
œœ œ œ
ÈÈ
xx
xx
xx xx
xx
xx
ÉÉ
transitive, we conclude that x x and x x have the same growth rate that of x .
ÈÈab
%%$ #
19. lim lim lim 0 x o e for any non-negative integer n
xx xÄ_ Ä_ Ä_
œœáœœÊœ
xnx n!
ee e
nx
nn1
xx x ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
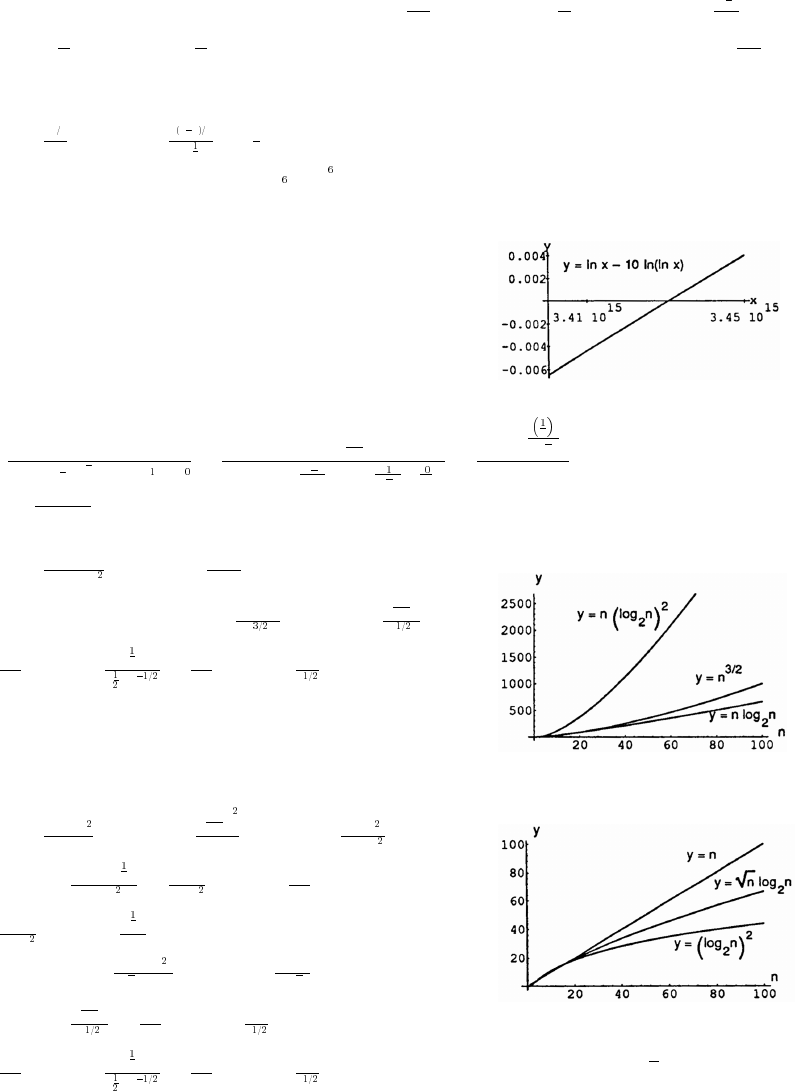
Section 7.6 Relative Rates of Growth 457
20. If p(x) a x a x a x a , then lim a lim a lim
xx x
œ á œ á
Ä_ Ä_ Ä_
nn1 n n1
nn1 p(x)
ee e
xx
"!
xx x
nn1
a lim a lim where each limit is zero (from Exercise 19). Therefore, lim 0
xx x
œ
Ä_ Ä_ Ä_
"!
"x
ee e
p(x)
xx x
e grows faster than any polynomial.Êx
21. (a) lim lim lim x ln x o x for any positive integer n
xx xÄ_ Ä_ Ä_
œœ œ_Êœ
xx
ln x n
n
1n 1n
1n 1 n n
x
ˆ‰ ˆ‰ ˆ ‰
"ÎÎ
(b) ln e 17,000,000 e e 24,154,952.75ab Š‹
17 000 000 110
ß ß "(‚"! "(
Î
œ œ¸
(c) x 3.430631121 10¸‚
"&
(d) In the interval 3.41 10 3.45 10 we havecd‚ß ‚
"& "&
ln x 10 ln (ln x). The graphs cross at aboutœ
3.4306311 10 .‚"&
22. lim
xÄ_ œœ
ln x
ax a x ax a a
lim
x
lim a
x
lim
x
nn1 n
nn1
n
á
Ä_
Ä_ á
Ä_
Š‹
Š‹
–—
ln x
xn
aa
n1
xx
a
xn1 n
x
nxn1
lim 0 ln x grows slower than any non-constant polynomial (n 1)
x
œœÊ
Ä_
"
aba banx
nn
23. (a) lim lim 0 n log n grows
nnÄ_ Ä_
œœÊ
n log n
nlog n log n 2
2
22
ab "
slower than n (log n) ; lim lim
nn
2n log n
nn
#
Ä_ Ä_
œ
2Š‹
ln n
ln 2
lim lim 0
nn
œœœ
Ä_ Ä_
""
##ln ln
n
2
n
Š‹
ˆ‰
n
n log n grows slower than n . Therefore, n log nÊ22
$Î#
grows at the slowest rate the algorithm that takesÊ
O(n log n) steps is the most efficient in the long run.
2
(b)
24. (a) lim lim lim
nnnÄ_ Ä_ Ä_
œœ
(log n) (ln n)
n n n(ln 2)
2Š‹
ln n
ln 2
lim lim
nn
œœ
Ä_ Ä_
2(ln n)
(ln 2) (ln 2) n
2ln n
Š‹
n
lim 0 (log n) grows slower
n
œœÊ
Ä_
2
(ln 2) 1 2
Š‹
n#
than n; lim lim
nnÄ_ Ä_
œ
(log n) log n
n log n n
22
2
ÈÈ
lim lim
nn
œœ
Ä_ Ä_
Š‹
ln n
ln 2
nn
ln
ln n
"
#
(b)
lim lim 0 (log n) grows slower than n log n. Therefore (log n) grows
xn
œœœÊ
Ä_ Ä_
""
##
##
ln ln
n
2
n222
Š‹
ˆ‰
nÈ
at the slowest rate the algorithm that takes O (log n) steps is the most efficient in the long run.Êab
2#
25. It could take one million steps for a sequential search, but at most 20 steps for a binary search because
2 524,288 1,000,000 1,048,576 2 .
"* #!
œœ
26. It could take 450,000 steps for a sequential search, but at most 19 steps for a binary search because
2 262,144 450,000 524,288 2 .
") "*
œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

458 Chapter 7 Transcendental Functions
7.7 INVERSE TRIGONOMETRIC FUNCTIONS
1. (a) (b) (c) 2. (a) (b) (c)
111 111
436 436
3. (a) (b) (c) 4. (a) (b) (c)
11 1 1 11
64 3 6 43
5. (a) (b) (c) 6. (a) (b) (c)
111 111
346 346
325
7. (a) (b) (c) 8. (a) (b) (c)
32 5
46 3 4 63
11 1 1 11
9. (a) (b) (c) 10. (a) (b) (c)
111 111
436 436
11. (a) (b) (c) 12. (a) (b) (c)
32 5
46 3 4 63
11 1 1 11
13. sin cos , tan , sec , csc , and cot ! !!!! !œ Êœœœœ œ
" ˆ‰
5 12 5 13 13 12
13 13 12 12 5 5
14. tan sin , cos , sec , csc , and cot ! !!!! !œ Êœœœœ œ
" ˆ‰
4 4355 3
3 5534 4
15. sec 5 sin , cos , tan 2, csc , and cot !!!!!!œ Ê œ œ œ œ œ
" Š‹
È21 1
55
5
22
ÈÈ È
16. sec sin , cos , tan , csc , and cot !!!!!!œ Ê œ œ œ œ œ
"
##
Š‹
È È
ÈÈ
13 13
323 2
13 13 33
17. sin cos sin 18. sec cos sec 2
Š‹
ˆ‰ ˆ ‰ ˆ‰
" "
# #
""
ÈÈ
2
4 3
2
œœ œœ
1 1
19. tan sin tan 20. cot sin cot
ˆ ‰ ˆ‰ ˆ‰ˆ‰ Š‹Š‹
" "
"" "
# #
œ œ œ œ
1 1
6 3
3 3
3
È È
È
21. csc sec 2 cos tan 3 csc cos cos csc cosabŠ‹Š‹
Ȉ ‰ ˆ‰ ˆ‰ ˆ‰ˆ‰
" " " ""
##
œ œœœ
11 1
33 3
2
323
43
ÈÈ
È
22. tan sec 1 sin csc 2 tan cos sin sin tan (0) sin 0aba bab ˆ‰ˆ ‰ ˆ‰ˆ‰ˆ‰
" " " "
"""
##
œ œœœ
12 6
11
23. sin sin cos sin sin 1
ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰
" "
""
## #
œ œ œ
11 1
63
2
24. cot sin sec 2 cot cos cot cot 0
ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰
" " "
""
###
œ œœœ
1111
663
25. sec tan 1 csc 1 sec sin sec sec 2ab
ˆ‰ˆ‰ˆ‰
È
" " "
#
œ œœ œ
1111
41 4 4
13
26. sec cot 3 csc ( 1) sec sin ( ) sec sec 2
Š‹
Ȉ‰ˆ‰ˆ‰
" " " "
#
œ œœœ
1 111 1
61 32 3
27. sec sec sec cos
" " "
#
ˆ‰ˆ‰ Š‹ Š‹
œ œ œ
11
66
2
3
3
ÈÈ
28. cot cot cot ( 1)
" "
ˆ‰ˆ‰
œ œ
11
44
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
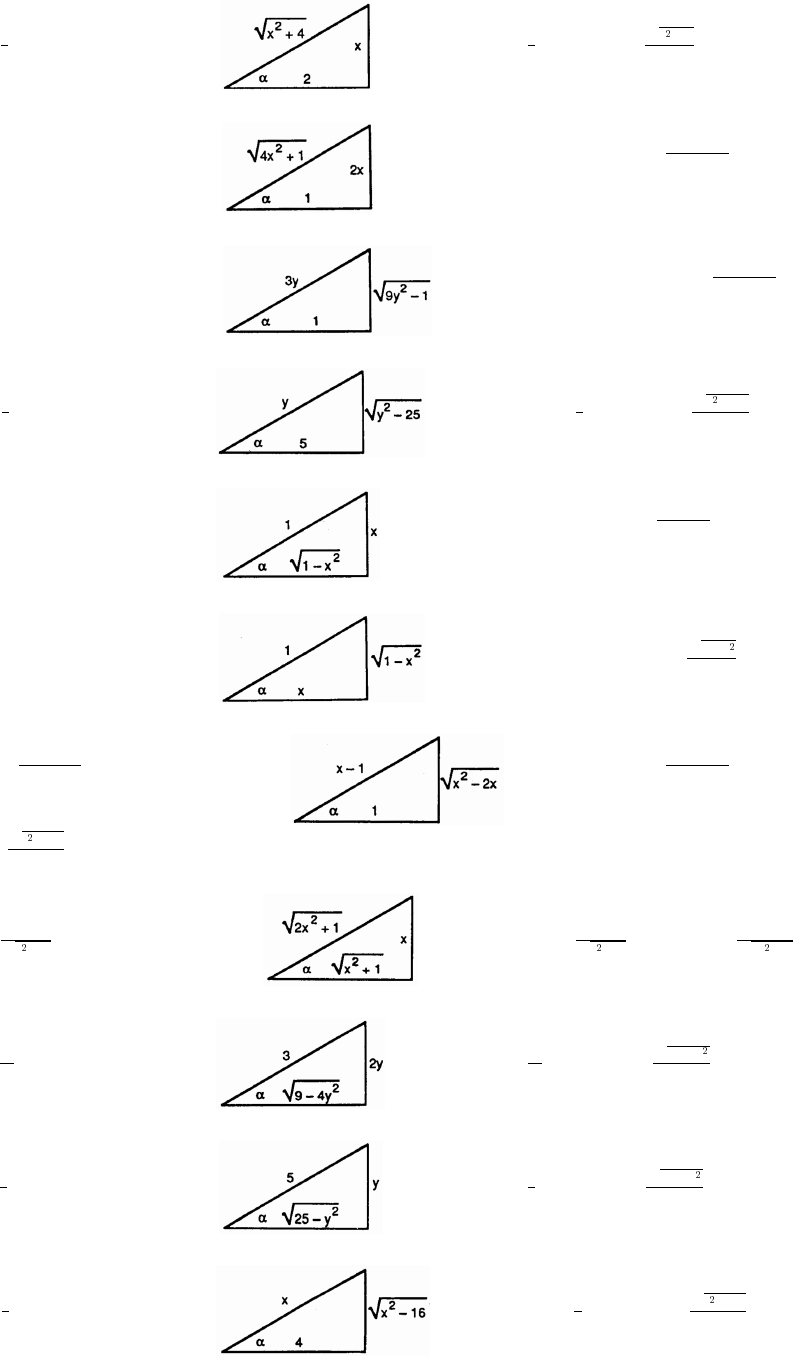
Section 7.7 Inverse Trigonometric Functions 459
29. tan indicates the diagram sec tan sec ! !œÊœœ
" "
###
x x x4
ˆ‰ È
30. tan 2x indicates the diagram sec tan 2x sec 4x 1! !œÊœœ
" " #
ab È
31. sec 3y indicates the diagram tan sec 3y tan 9y 1! !œÊœœ
" " #
ab È
32. sec indicates the diagram tan sec tan ! !œÊœœ
" "
y y
555
y25
ˆ‰ È
33. sin x indicates the diagram cos sin x cos 1 x! !œÊœœ
" " #
ab È
34. cos x indicates the diagram tan cos x tan ! !œÊœœ
" "
ab È1x
x
35. tan x 2x indicates the diagram sin tan x 2x!œ Ê
" "
# #
ÈÈ
Š‹
sin œœ!Èx2x
x1
36. tan indicates the diagram sin tan sin ! !œÊœœ
" "
xxx
x1 x1 2x1
ÈÈÈ
Š‹
37. sin indicates the diagram cos sin cos ! !œÊœœ
" "
2y 2y
333
94y
ˆ‰ È
38. sin indicates the diagram cos sin cos ! !œÊœœ
" "
y y
555
25 y
ˆ‰ È
39. sec indicates the diagram sin sec sin ! !œÊœœ
" "
x x
44x
x16
ˆ‰ È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

460 Chapter 7 Transcendental Functions
40. sec indicates the diagram sin sec sin ! !œÊœœ
" "
È È È
x4 x4
x x
2
x4
Š‹
41. lim sin x 42. lim cos x
x1 x1
ÄÄ
" "
#
œœ
11
43. lim tan x 44. lim tan x
xxÄ_ Ä_
" "
# #
œœ
1 1
45. lim sec x 46. lim sec x lim cos
xxxÄ_ Ä_ Ä_
" " "
# #
"
œœœ
1 1
ˆ‰
x
47. lim csc x lim sin 0 48. lim csc x lim sin 0
xx x xÄ_ Ä_ Ä_ Ä_
" " " "
" "
œœ œ œ
ˆ‰ ˆ‰
x x
49. y cos x 50. y cos sec x œÊœœ œœÊœ
" # " "
""
ab ˆ‰
dy dy
dx x dx
2x 2x
1x 1x x x 1
Éab È È
kk
51. y sin 2t 52. y sin (1 t) œÊœ œ œÊœœ
" "
" "
Èdy 2 2 dy
dt dt
12t 12t 2t t
1(1t)
ÈÈ
ÊŠ‹
ÈÈÈÈ
53. y sec (2s 1) œÊœ œ œ
"
"
dy
ds
22
2s 1 (2s 1) 1 2s 1 4s 4s 2s 1 s s
kk
ÈÈÈ
kk kk
54. y sec 5s œÊœ œ
"
"
dy
ds
5
5s (5s) 1 s 25s 1
kk
ÈÈ
kk
55. y csc x 1 œÊœ œ
" #
ab
dy
dx
2x 2x
x1 x1 1 x1 x2x
kkab
Éab
È
56. y csc œÊœ œœ
"
#
"
ˆ‰
x2
dy
dx 1
x x x 4
Š‹
ÉÉ
ˆ‰ kk kkÈ
¸¸
xx x4
4
57. y sec cos t œœÊœ
" "
""
ˆ‰
tdt
dy
1t
È
58. y sin csc œœ Êœ œœ
" "
ˆ‰ Š‹
3t 2t6
t3dt
dy
1
t tt 9
ˆ‰
¹¹ Š‹
2t
3
tt
33
t9
9
ÊÉÈ
59. y cot t cot t œœ Êœœ
" " "Î#
"
#
Èdy
dt
t
1t t(1 t)
Š‹
ab È
60. y cot t 1 cot (t 1) œœÊœ œ œ
" " "Î#
" "
Èdy
dt
(t 1)
1(t1) 2 t 1 (1 t 1) 2t t 1
Š‹
cd
ÈÈ
61. y ln tan x œÊœœab
" "
dy
dx tan x tan x 1 x
Š‹abab
1x
62. y tan (ln x) œÊœœ
"
"
dy
dx 1 (ln x) x 1 (ln x)
ˆ‰
xcd
63. y csc e œÊœ œ
"
"
ab
tdy
dt
e
e e 1 e1
t
tt 2t
kk ab
ÉÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.7 Inverse Trigonometric Functions 461
64. y cos e œÊœœ
"
ab
tdy
dt
ee
1e 1e
tt
t2t
Éab È
65. y s 1 s cos s s 1 s cos s 1 s s 1 s ( 2s)œ œ Êœ
Èab ab ab
ˆ‰
#" # " # #
"Î# "Î# "Î#
""
#
dy
ds 1s
È
1s 1sœ œ œ œ
ÈÈ
##
" s s1 1ss1 2s
1s 1s 1s 1s 1s
ÈÈ È È È
66. y s 1 sec s s 1 sec s s 1 (2s)œ œ Êœ œ
Èab ab
ˆ‰
#" # " #
"Î# "Î#
"""
#
dy
dx s s1 s1 s s1
s
kk kk
ÈÈ È
œs s 1
s s 1
kk
kkÈ
67. y tan x 1 csc x tan x 1 csc x œœÊœ
" " " # "
#"Î#
"
Èab dy
dx
x 1 (2x)
1x1 x x 1
Š‹
ab
’“
ab kkÈ
0, for x 1œ œ
""
xx 1 x x 1
ÈÈ
kk
68. y cot tan x tan x tan x 0 0œ œ Êœ œœ
" " " " "
""""
#
ˆ‰ ab
xdx1xx11x
dy x
1x
1ab
69. y x sin x 1 x x sin x 1 x sin x x 1 x ( 2x)œœÊœ
" " # " #
#"Î# "Î#
""
#
Èab ab
Š‹
ˆ‰
dy
dx 1x
È
sin x sin xœœ
" "
xx
1x 1x
ÈÈ
70. y ln x 4 x tan tan x tanœ Êœ œ ab ˆ‰ ˆ‰ ˆ‰
–—
#" " "
## #
x2xx 2xx2x
dy
dx x4 x4 4x
1
Š‹
ˆ‰
x
tanœ "
#
ˆ‰
x
71. dx sin C
'"
"
È9x
x
3
œ
ˆ‰
72. dx dx , where u 2x and du 2 dx
'' '
"" "
##
ÈÈ È
14x 1u
2du
1 (2x)
œœ œœ
sin u C sin (2x) Cœœ
""
##
" "
73. dx dx tan C
''
"""
"
17 x 17 x 17 17
x
œœ
Š‹
ÈÈÈ
74. dx dx tan C tan C
''
""" "
" "
93x 3 9
3x 33 3 3
xx
3
œœœ
Š‹
ÈÈÈ È
È
Š‹ Š‹
75. , where u 5x and du 5 dx
''
dx du
x 25x 2 u u 2
ÈÈ
œœœ
sec C sec Cœœ
""
" "
ÈÈ ÈÈ
22 22
u5x
¹¹ ¹¹
76. , where u 5x and du 5 dx
''
dx du
x5x 4 uu 4
ÈÈ
œœœ
ÈÈ
sec C sec Cœœ
""
## # #
" "
¸¸ ¹¹
u5x
È
77. 4 sin 4 sin sin 0 4 0
'0
14 ds s 2
4s 63
È
" " "
##
"
!
"
œœœœ
‘ˆ ‰ˆ‰
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

462 Chapter 7 Transcendental Functions
78. , where u 2s and du 2 ds; s 0 u 0, s u
''
00
324 324
ds du
94s 9u
32 32
4
ÈÈ ÈÈ
"
# #
œœœœÊœœÊœ
sin sin sin 0 0œœœœ
‘ ˆ‰
Š‹
"" "
####
" " "
u
348
2
322
0È11
79. , where u 2t and du 2 dt; t 0 u 0, t 2 u 2 2
''
00
222
dt du
82t 8u
2
"
œœœœÊœœÊœ
ÈÈÈ È
tan tan tan 0 tan 1 tan 0 0œœœœœ
’“Š ‹
ab
ˆ‰
"" " " "
" " " " "
##
!
ÈÈ È È
ÈÈ
288 8
u
444416
22
†11
80. , where u 3t and du 3 dt; t 2 u 2 3, t 2 u 2 3
''
223
223
dt du
43t 4u
3
"
œœœœÊœœÊœ
ÈÈÈ È È
tan tan 3 tan 3œœœœ
’“’ “
ÈÈ
Š‹ ‘ˆ‰
"" " "
##
" " "
#$
# $ ##
ÈÈ ÈÈ
ÈÈ
33 333
u
33
†111
81. , where u 2y and du 2 dy; y 1 u 2, y u 2
''
12
22 2
dy 2
y4y 1
du
uu 1
ÈÈ È
#
œ œ œ œ Ê œ œ Ê œ
È
sec u sec 2 sec 2œ œ œœcd kkkk ¹¹
È
" " "
#
# #
È11 1
43 1
82. , where u 3y and du 3 dy; y u 2, y u 2
''
23 2
23 2
dy 2
y9y 1
du 2
uu 1 33
ÈÈ È
œ œ œ œ Ê œ œ Ê œ
È
sec u sec 2 sec 2œ œ œœcd kkkk ¹¹
È
" " "
#
# #
È11 1
43 1
83. , where u 2(r 1) and du 2 dr
''
3 dr 3 du
14(r1) 1u
ÈÈ
#
œœœ
sin u C sin 2(r 1) Cœœ
33
##
" "
84. 6 , where u r 1 and du dr
''
6 dr du
4(r1) 4u
ÈÈ
œœœ
6 sin C 6 sin Cœœ
" "
##
ur1
ˆ‰
85. , where u x 1 and du dx
''
dx du
2(x1) 2u
œœœ
tan C tan Cœœ
""
" "
ÈÈ È È
22 2 2
ux1
Š‹
86. , where u 3x 1 and du 3 dx
''
dx du
1 (3x 1) 3 1 u
"
œœœ
tan u C tan (3x 1) Cœœ
""
" "
33
87. , where u 2x 1 and du 2 dx
''
dx du
(2x 1) (2x 1) 4 uu 4
"
#
ÈÈ
œœœ
sec C sec Cœœ
"" "
## # #
" "
†¸¸ ¸ ¸
u2x1
4
88. , where u x 3 and du dx
''
dx du
(x 3) (x 3) 25 uu 25
ÈÈ
œœœ
sec C sec Cœœ
""
" "
55 5 5
ux3
¸¸ ¸ ¸
89. 2 , where u sin and du cos d ; u , u
''
21
21
2 cos d du
1(sin ) 1u
)) 11
) # #
œœœœÊœ"œÊœ")))) )
2 tan u 2 tan 1 tan ( 1) 2œœœœcda b
‘ˆ‰
" " "
"
" 11
44
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.7 Inverse Trigonometric Functions 463
90. , where u cot x and du csc x dx; x u 3 , x u 1
''
63
41
csc x dx du
1(cot x) 1u 6 4
#
œ œ œ œ Ê œ œ Ê œ
11
È
tan u tan 1 tan 3œ œ œ œcd È
" " "
"
$#
È11 1
431
91. , where u e and du e dx; x 0 u 1, x ln 3 u 3
''
01
ln 3 3 xx
e dx du
1e 1u
x
2x
œœœœÊœœÊœ
ÈÈ
tan u tan 3 tan 1œ œ œœcd È
" " "
$
"#
È11 1
341
92. 4 , where u ln t and du dt; t 1 u 0, t e u
''
10
e4 4
4 dt du
t1 lnt 1 u t 4ab
"
œœœœÊœœÊœ
1
4 tan u 4 tan tan 0 4 tan œœœcdˆ‰
" " " "
Î%
!
111
44
93. , where u y and du 2y dy
''
y dy
1y
du
1u
ÈÈ
"
#
#
œœœ
sin u C sin y Cœœ
""
##
" " #
94. , where u tan y and du sec y dy
''
sec y dy
1tany
du
1u
ÈÈ
#
œœœ
sin u C sin (tan y) Cœœ
" "
95. sin (x 2) C
'' '
dx dx dx
x4x3 1x4x4 1(x2)
ÈÈ È
ab
"
œœœ
96. sin (x 1) C
'' '
dx dx dx
2x x 1x2x1 1(x1)
ÈÈ È
ab
"
œœœ
97. 6 6 6 sin
'' '
"
#
!
"
11 1
00 0
6 dt dt dt t 1
32tt 4t2t1 2(t1)
ÈÈ È
ab
œœœ
‘ˆ‰
6sin sin 0 6 0œœœ
‘ˆ‰ˆ‰
" "
"
#1
61
98. 3 3 3 sin
'' '
12 12 12
11 1
6 dt 2 dt 2 dt 2t 1
34t4t 44t4t1 2 (2t 1)
ÈÈ È
ab
"
#
"
"Î#
œœœ
‘ˆ‰
3sin sin 0 3 0œœœ
‘ˆ‰ˆ‰
" "
"
##
11
6
99. tan C
'' '
dy dy dy y 1
y 2y5 4y 2y1 (y1)
# # #
""
œœœ
ˆ‰
100. tan (y 3) C
'' '
dy dy dy
y 6y10 1 y 6y9 1(y3)
"
œœœ
ab
101. 8 8 8 tan (x 1)
'' '
11 1
22 2
8 dx dx dx
x 2x 2 1 x 2x 1 1 (x 1)
" #
"
œœœ
ab cd
8 tan 1 tan 0 8 0 2œœœab
ˆ‰
" " 1
41
102. 2 2 2 tan (x 3)
'' '
22 2
44 4
2 dx dx dx
x 6x10 1 x 6x9 1(x3)
" %
#
œœœ
ab cd
2 tan 1 tan ( 1) 2œœœcd
‘ˆ‰
" " 11
44
1
103.
'' '
dx dx dx
(x1)x 2x (x1)x 2x11 (x 1) (x 1) 1
ÈÈ È
œœ
, where u x 1 and du dxœœœ
'du
uu 1
È
sec u C sec x 1 Cœœ
" "
kk k k
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

464 Chapter 7 Transcendental Functions
104. '' '
dx dx dx
(x2)x 4x3 (x2)x 4x41 (x 2) (x 2) 1
ÈÈ È
œœ
du, where u x 2 and du dxœœœ
'"
uu 1
È
sec u C sec x 2 Cœœ
" "
kk k k
105. dx e du, where u sin x and du
''
edx
1x 1x
sin x
ÈÈ
"
œœœ
u
eCe Cœœ
usin x
106. dx e du, where u cos x and du
''
edx
1x 1x
cos x
ÈÈ
"
œ œ œ
u
eC e Cœ œ
ucos x
107. dx u du, where u sin x and du
''
ab
ÈÈ
sin x
1x 1x
dx
#"
œœœ
CCœœ
u
33
sin x
ab
108. dx u du, where u tan x and du
''
Ètan x
1x 1x
dx
"Î# "
œœœ
uC tanx C tanxCœœ œ
22 2
33 3
$Î# " $Î# " $
ab ab
É
109. dy dy du, where u tan y and du
''
""
"
abab Š‹
tan y 1 y tan y u 1 y
dy
œœ œ œ
'1y
ln u C ln tan y Cœœ kk k k
"
110. dy dy du, where u sin y and du
''
""
"
ab
È È
sin y 1 y 1y
sin y u
dy
œœ œœ
'1y
ln u C ln sin y Cœœ kk k k
"
111. dx sec u du, where u sec x and du ; x 2 u , x 2 u
''
24
23
sec sec x
xx 1 xx 1
dx
43
ab
È È
#"
œœœœÊœœÊœ
È11
tan u tan tan 3 1œ œœcd È
1
111
Î$
Î434
112. dx cos u du, where u sec x and du ; x u , x 2 u
''
2
cos sec x
xx 1 xx 1
dx 2
363
36
23
ab
ÈÈÈ
"
œœœœÊœœÊœ
11
sin u sin sin œ œœcd
1
111
Î$
Î'
"
#36
3
È
113. lim lim 5
x0 x0ÄÄ
sin 5x
x1
œœ
Š‹
5
1 25x
114. lim lim lim lim x x 1
x1 x1 x1 x1ÄÄ Ä Ä
Èab Š‹
ab
Œ
x1
sec x sec x
x1 x 1 (2x)
œœ œœ
x x 1 kk
115. lim x tan lim lim lim 2
xxxxÄ_ Ä_ Ä_ Ä_
"
ˆ‰
22
xx x14x
tan 2x
œœœœ
ab Š‹
2x
14x
116. lim lim lim
x0 x0 x0ÄÄÄ
2 tan 3x 6 6
7x 14x 7
71 9x
œœ œ
Š‹ ab
12x
19x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.7 Inverse Trigonometric Functions 465
117. If y ln x ln 1 x C, then dy dxœ œ
""
#
#
ab –—
tan x x
xx1xx
tan x
Š‹
x
1x
dx dx dx,œ œ œ
Š‹
""
x 1x x1x x x1x x
x tan x tan x
x1 x x x tan x 1 x
ab ab
ab abab
which verifies the formula
118. If y cos 5x dx, then dy x cos 5x dxœ œ
x5x x55x
44 4 4
1 25x 1 25x 1 25x
" $ "
'ÈÈÈ
’“Š‹Š‹Š‹
x cos 5x dx, which verifies the formulaœab
$"
119. If y x sin x 2x 2 1 x sin x C, thenœab È
" "
##
dy sin x 2 sin x 2 1 x dx sin x dx, which verifiesœ œ
’“
ab ab
ÈŠ‹
" " "
# #
"
#
2x sin x
1x 1x 1x
2x
ab
ÈÈ È
the formula
120. If y x ln a x 2x 2a tan C, then dy ln a x 2 dxœ œab ab
ˆ‰ –—
## " ##
x2x2
aax
1Š‹
x
a
ln a x 2 2 dx ln a x dx, which verifies the formulaœ œ
’“
ab ab
Š‹
## ##
ax
ax
121. dy y sin x C; x 0 and y 0 0 sin 0 C C 0 y sin x
dy
dx 1x 1x
dx
œÊœÊœœœÊœÊœÊœ
"
" " "
ÈÈ
122. 1 dy 1 dx y tan (x) x C; x 0 and y 1 1 tan 0 0 C
dy
dx x 1 1 x
œÊœ Êœ œ œÊœ
""
" "
ˆ‰
C 1 y tan (x) x 1ʜʜ
"
123. dy y sec x C; x 2 and y sec 2 C C sec 2
dy
dx xx 1 xx 1
dx
œÊœÊœ œœÊœÊœ
"
" " "
ÈÈ kk 11 1
ysec(x) , x1œœ Ê œ 111 1
33 3
22
"
124. dy dx y tan x 2 sin x C; x 0 and y 2
dy
dx 1x 1x
22
1x 1x
œ Êœ Êœ œ œ
""
" "
ÈÈ
Š‹
2 tan 0 2 sin 0 C C 2 y tan x 2 sin x 2Êœ Ê œÊœ
" " " "
125. The angle is the large angle between the wall and the right end of the blackboard minus the small angle!
between the left end of the blackboard and the wall cot cot .ʜ !" "
ˆ‰ ˆ‰
xx
15 3
126. V 2 (sec y) dy 4y tan y 3œ œœ111
'0
3cdcd
Š‹
È
## Î$
!
114
3
127. V r h (3 sin ) (3 cos ) 9 cos cos , where 0 9 (sin ) 1 3 cosœœ œ ŸŸÊœ
ˆ‰ ˆ‰ ab ab
""
## $ #
#33 d
dV
11))1)) ) 1) )
1)
sin 0 or cos the critical points are: 0, cos , and cos ; butœ! Ê œ œ „ Ê ))
"""
" "
ÈÈÈ
333
Š‹ Š ‹
cos is not in the domain. When 0, we have a minimum and when cos 54.7°, we
" "
" "
Š‹ Š‹
œœ¸
È È
3 3
))
have a maximum volume.
128. 65° (90° ) (90° ) 180° 65° 65° tan 65° 22.78° 42.22° œ Êœœ ¸ ¸"! !" " ˆ‰
21
50
129. Take each square as a unit square. From the diagram we have the following: the smallest angle has a!
tangent of 1 tan 1; the middle angle has a tangent of 2 tan 2; and the largest angle ʜ ʜ!"" #
" "
has a tangent of 3 tan 3. The sum of these three angles is ʜ ʜ#1!"#1
"
tan 1 tan 2 tan 3 .ʜ
" " " 1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
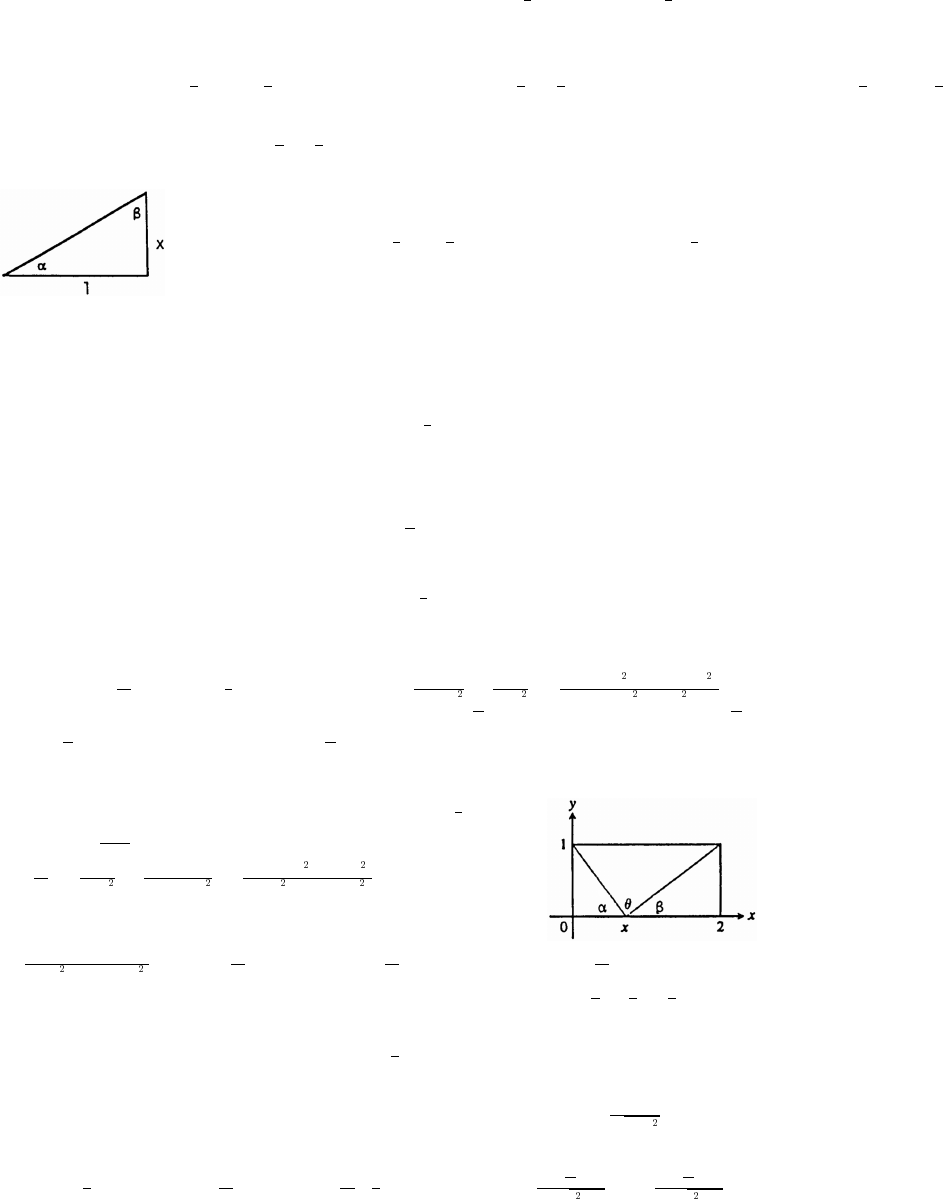
466 Chapter 7 Transcendental Functions
130. (a) From the symmetry of the diagram, we see that sec x is the vertical distance from the graph of1"
y sec x to the line y and this distance is the same as the height of y sec x above the x-axis atœœ œ
" "
1
x; i.e., sec x sec ( x).œ1" "
(b) cos ( x) cos x, where 1 x 1 cos cos , where x 1 or x 1
" " " "
""
œ ŸŸ Ê œ Ÿ11
ˆ‰ ˆ‰
xx
sec ( x) sec xʜ
" "
1
131. sin (1) cos (1) 0 ; sin (0) cos (0) 0 ; and sin ( 1) cos ( 1) .
" " " " " "
## ## # #
œœ œœ œœ
11 11 11
1
If x ( 0) and x a, then sin (x) cos (x) sin ( a) cos ( a) sin a cos a− "ß œ œ œ
" " " " " "
ab1
sin a cos a from Equations (3) and (4) in the text.œ œœ11ab
" "
##
11
132. tan x and tan tan x tan .Êœ œÊœœ !" !"
""
#
" "
xx
1
133. (a) Defined; there is an angle whose tangent is 2.
(b) Not defined; there is no angle whose cosine is 2.
134. (a) Not defined; there is no angle whose cosecant is .
"
#
(b) Defined; there is an angle whose cosecant is 2.
135. (a) Not defined; there is no angle whose secant is 0.
(b) Not defined; there is no angle whose sine is 2.
È
136. (a) Defined; there is an angle whose cotangent is ."
#
(b) Not defined; there is no angle whose cosine is 5.
137. (x) cot cot , x 0 (x) ; solving!!œ Êœœ
" " w
ˆ‰ ˆ‰
xx 153
15 3 225 x 9 x 225 x 9 x
15 9 x 3 225 x
aba b
abab
(x) 0 135 15x 675 3x 0 x 3 5 ; (x) 0 when 0 x 3 5 and (x) 0 for!!!
w##w w
œÊ œÊœ
ÈÈ
x 3 5 there is a maximum at 3 5 ft from the front of the roomÊ
ÈÈ
138. From the accompanying figure, , cot !") 1 !œ œ
x
1
and cot cot x cot (2 x)")1œÊœ
2x
1
" "
Êœ œ
d
dx 1x 1(2x) 1x1(2x)
1(2x) 1x
)""
ab
abc d
; solving 0 x 1; 0 for x 1 and 0 for x 1œœÊœ!
44x d d d
1x1(2x) dx dx dx
abc d )) )
at x 1 there is a maximum cot 1 cot (2 1)Ê œ œ œœ)1 1
" "
#
111
44
139. Yes, sin x and cos x differ by the constant
" "
#
1
140. Yes, the derivatives of y cos x C and y cos ( x) C are both œ œ
" " "
È1x
141. csc u sec u csc u sec u 0 , u 1
" " " "
##
œ Ê œ œ œ
11dd
dx dx u u 1 u u 1
ab kk
ˆ‰du du
dx dx
kk kk
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.7 Inverse Trigonometric Functions 467
142. y tan x tan y x (tan y) (x)œÊœÊ œ
" dd
dx dx
sec y 1 ʜʜœab
#""
dy dy
dx dx sec y 1x
Š‹
È
, as indicated by the triangleœ"
1x
143. f(x) sec x f (x) sec x tan x .œÊœ Ê œ œ œ
w
œ
"" "
„"
df
dx sec sec b tan sec b
xb bb
¹df
dx xf b
¹Š‹
abab È
Since the slope of sec x is always positive, we the right sign by writing sec x .
" " "
ll "
d
dx xx
œÈ
144. cot u tan u cot u tan u 0
" " " "
##
œ Ê œ œ œ
11dd
dx dx 1 u 1 u
ab
ˆ‰
du du
dx dx
145. The functions f and g have the same derivative (for x 0), namely . The functions therefore differ"
Èx(x 1)
by a constant. To identify the constant we can set x equal to 0 in the equation f(x) g(x) C, obtainingœ
sin ( 1) 2 tan (0) C 0 C C . For x 0, we have sin 2 tan x .
" " " "
## #
œ ʜʜ œ
11 1
ˆ‰ È
x1
x1
146. The functions f and g have the same derivative for x 0, namely . The functions therefore differ by a"
1x
constant for x 0. To identify the constant we can set x equal to 1 in the equation f(x) g(x) C, obtainingœ
sin tan 1 C C C 0. For x 0, we have sin tan .
" " " "
"""
Š‹
È È
2x1
44 x
œÊœÊœ œ
11
147. V dx dx tan x tan 3 tanœœœœ1111
''
33 33
33 3
33
Š‹ ’ “
cd ÈŠ‹
""
#
" " "
ÈÈ
1x 1x 3
3
œœ1‘ˆ‰
111
36
#
148. y 1 x 1 x y 1 x ( 2x) 1 y ; L 1 y dxœœ Êœ Ê œ œ
Èab ab ab ab
ˆ‰ É
# w
#w # w
"Î# "Î#
""
#
##
1x '12
12
2 dx 2 sin x 2 0œœœœ
'0
12 12
0
"
"
È1x 63
cdˆ‰
11
149. (a) A(x) (diameter) V A(x) dx œœœÊœœ
11 1 1
4 4 1x 1x
1x 1x
dx
#""
#
’“Š‹
ÈÈ ''
a1
b1
tan x ( )(2)œœœ11cd ˆ‰
" "
" #
11
4
(b) A(x) (edge) V A(x) dxœœ œÊœ œ
#""
#
’“Š‹
ÈÈ
1x 1x
44 dx
1x 1x
''
a1
b1
4 tan x 4 tan (1) tan ( 1) 4 2œœœœcdc d
‘ˆ‰
" " "
"
" 11
441
150. (a) A(x) (diameter) 0 V A(x) dxœœœœÊœ
11 1 1
44 4
24
1x 1x 1x
#
#
Š‹Š‹
ÈÈÈ 'a
b
dx sin x sin sinœœœœœ
'22
22 22
22
1111
ÈÈÈ
1x
22
44
" " "
## #
11 1cd ’“Š‹ Š ‹ ‘ˆ‰
(b) A(x) 0 V A(x) dx dxœœ œÊœ œ
(diagonal)
22
12 2 2
1x 1x 1x
Š‹
ÈÈÈ
#
''
a22
b22
2sin x 2 2œœœcd ˆ‰
" 22
22 1
4†1
151. (a) sec 1.5 cos 0.84107 (b) csc ( 1.5) sin 0.72973
" " " "
" "
œ¸ œ¸
1.5 1.5
ˆ‰
(c) cot 2 tan 2 0.46365
" "
#
œ ¸
1
152. (a) sec ( 3) cos 1.91063 (b) csc 1.7 sin 0.62887
" " " "
""
œ ¸ œ ¸
ˆ‰ ˆ‰
31.7
(c) cot ( 2) tan ( 2) 2.67795
" "
#
œ ¸
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
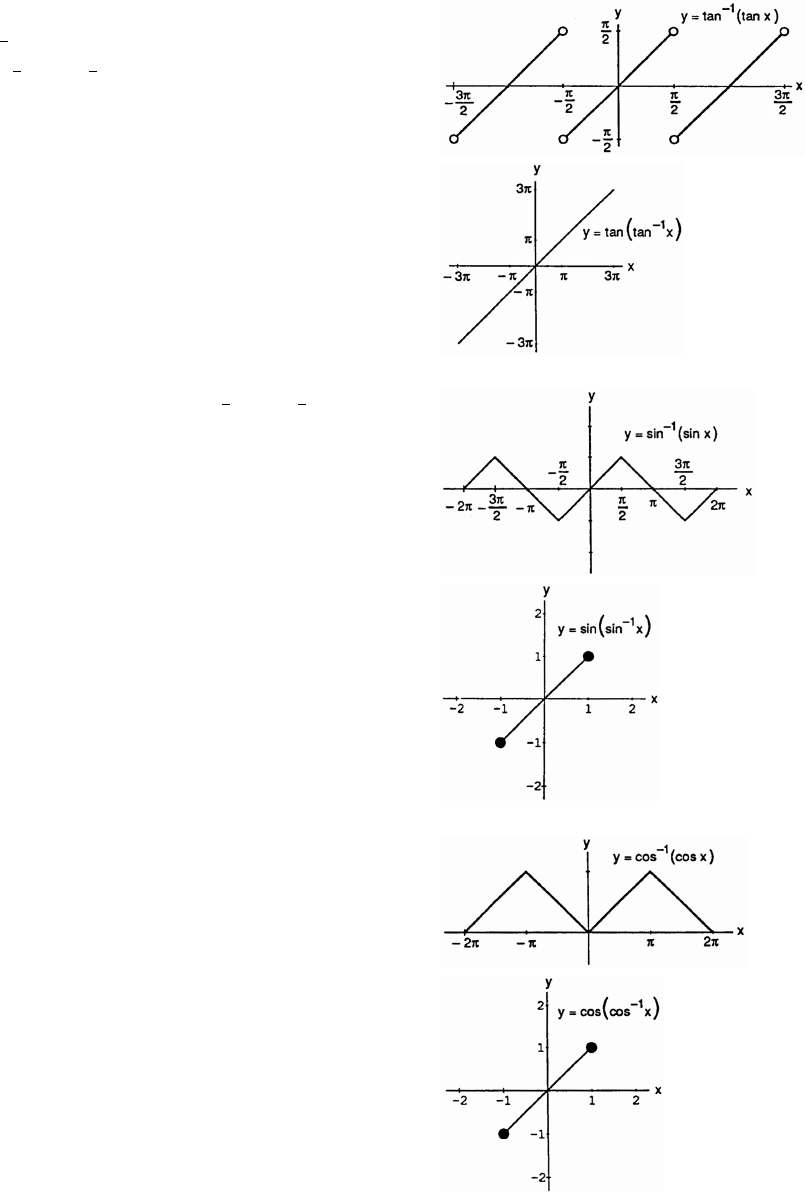
468 Chapter 7 Transcendental Functions
153. (a) Domain: all real numbers except those having
the form k where k is an integer.
1
#1
Range: y
11
##
(b) Domain: x ; Range: y_ _ _ _
The graph of y tan (tan x) is periodic, theœ"
graph of y tan tan x x for x .œœ_Ÿ_ab
"
154. (a) Domain: x ; Range: y__ ŸŸ
11
##
(b) Domain: x 1; Range: y 1" Ÿ Ÿ " Ÿ Ÿ
The graph of y sin (sin x) is periodic; theœ"
graph of y sin sin x x for x 1.œœ"ŸŸab
"
155. (a) Domain: x ; Range: 0 y_ _ Ÿ Ÿ 1
(b) Domain: 1 x 1; Range: y 1Ÿ Ÿ "Ÿ Ÿ
The graph of y cos (cos x) is periodic; theœ"
graph of y cos cos x x for x 1.œœ"ŸŸab
"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
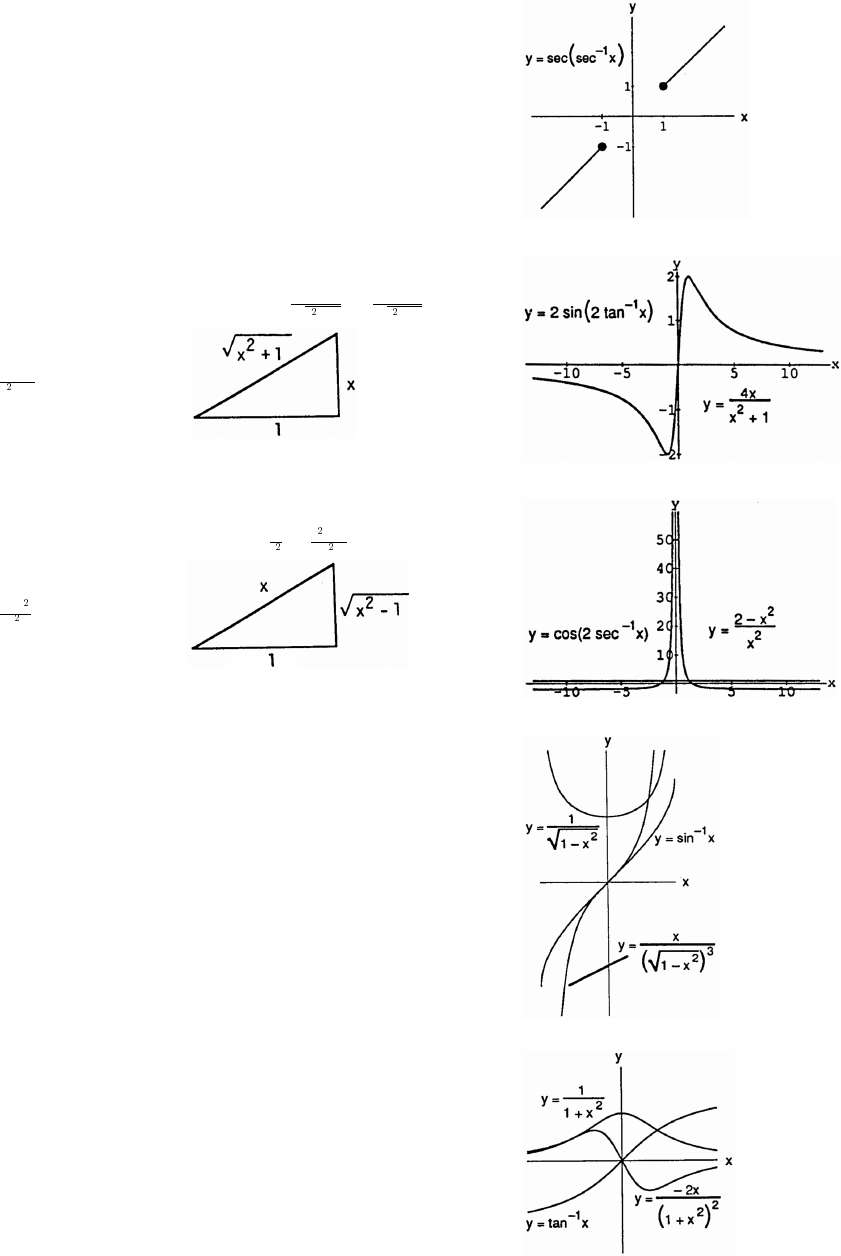
Section 7.7 Inverse Trigonometric Functions 469
156. Since the domain of sec x is ( 1] [ ), we
" _ß "ß_
have sec sec x x for x 1. The graph ofab kk
" œ
y sec sec x is the line y x with the openœœab
"
line segment from ( ) to ( ) removed."ß" "ß"
157. The graphs are identical for y 2 sin 2 tan xœab
"
4 sin tan x cos tan x 4œœcdcdabab
Š‹Š‹
" "
"x
x1 x1
ÈÈ
from the triangle œ4x
x1
158. The graphs are identical for y cos 2 sec xœab
"
cos sec x sin sec xœœ
#" #" "
abab
xx
x1
from the triangle œ2x
x
159. The values of f increase over the interval [ 1] because"ß
f 0, and the graph of f steepens as the values of f
ww
increase towards the ends of the interval. The graph of f
is concave down to the left of the origin where f 0,
ww
and concave up to the right of the origin where f 0.
ww
There is an inflection point at x 0 where f 0 andœœ
ww
f has a local minimum value.
w
160. The values of f increase throughout the interval ( )_ß _
because f 0, and they increase most rapidly near the
w
origin where the values of f are relatively large. The
w
graph of f is concave up to the left of the origin where
f 0, and concave down to the right of the origin
ww
where f 0. There is an inflection point at x 0
ww œ
where f 0 and f has a local maximum value.
ww w
œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

470 Chapter 7 Transcendental Functions
7.8 HYPERBOLIC FUNCTIONS
1. sinh x cosh x 1 sinh x 1 1 , tanh x ,œ Ê œ œ œ œ œ œ œ œ
3 3 9 25 5 sinh x 3
4 4 16 16 4 cosh x 5
ÈɈ‰ÉÉ
##
ˆ‰
ˆ‰
3
4
5
4
coth x , sech x , and csch xœœ œœ œœ
"" "
tanh x 3 cosh x 5 sin x 3
54 4
2. sinh x cosh x 1 sinh x 1 , tanh x , coth x ,œÊ œ œ œ œ œ œ œ œ œ
4 16 25 5 sinh x 4 5
3 9 9 3 cosh x 5 tanh x 4
ÈÉÉ
#"
ˆ‰
ˆ‰
4
3
5
3
sech x , and csch xœœ œœ
""
cosh x 5 sinh x 4
33
3. cosh x , x 0 sinh x cosh x 1 1 1 , tanh xœ Ê œ œ œ œ œ œ œ
17 17 289 64 8 sinh x
15 15 225 225 15 cosh x
ÈɈ‰ ÉÉ
##ˆ‰
ˆ‰
8
15
17
15
, coth x , sech x , and csch xœœœœœ œœ
81715 15
17 tanh x 8 cosh x 17 sinh x 8
"" "
4. cosh x , x 0 sinh x cosh x 1 1 , tanh x ,œ Ê œ œ œ œ œ œ œ
13 169 144 12 sinh x 12
525255cosh x13
ÈÉÉ
#ˆ‰
ˆ‰
12
5
13
5
coth x , sech x , and csch xœœ œœ œœ
"" "
tanh x 12 cosh x 13 sinh x 12
13 5 5
5. 2 cosh (ln x) 2 e xœœœ
Š‹
ee ln x
ex
ln x ln x
ln x
""
#
6. sinh (2 ln x) œœœœ
ee ee x
x
x
2lnx 2lnx lnx lnx x
"
####
Š‹
7. cosh 5x sinh 5x eœœ
ee ee 5x
5x 5x 5x 5x
##
8. cosh 3x sinh 3x eœœ
ee ee 3x
3x 3x 3x 3x
##
9. (sinh x cosh x) e eœ œœ
%
##
%%
ˆ‰
ab
ee ee x4x
xx xx
10. ln (cosh x sinh x) ln (cosh x sinh x) ln cosh x sinh x ln 1 0 œ œœab
##
11. (a) sinh 2x sinh (x x) sinh x cosh x cosh x sinh x 2 sinh x cosh xœœœ
(b) cosh 2x cosh (x x) cosh x cosh x sinh x sin x cosh x sinh xœœ œ
##
12. cosh x sinh x e e e e e e e e
##
"
##
##
œœ
ˆ‰ˆ‰cdcdabababab
ee ee
4
xx xxxx xx
xx xx
2e 2e 4e (4) 1œœœœ
"""
!
444
xx
aba b ab
13. y 6 sinh 6 cosh 2 cosh œÊœ œ
xxx
3dx 33 3
dy ˆ‰ˆ‰
"
14. y sinh (2x 1) [cosh (2x 1)](2) cosh (2x 1)œÊœ œ
""
##
dy
dx
15. y 2 t tanh t 2t tanh t sech t t 2t tanh t tœœ Êœ
ÈÈ ‘ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰
"Î# "Î# # "Î# "Î# "Î# "Î# "Î#
"
#
dy
dt
sech tœ
#Ètanh t
t
È
È
16. y t tanh t tanh t sech t t t (2t) tanh t sech 2t tanh œœ Êœ œ
# # " # " # # " #
"""
tdt tt
dy cdabababab
17. y ln (sinh z) coth z 18. y ln (cosh z) tanh zœÊœœ œ Êœœ
dy dy
dz sinh z dz cosh z
cosh z sinh z
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.8 Hyperbolic Functions 471
19. y (sech )(1 ln sech ) (sech ) ( sech tanh )(1 ln sech )œ Êœ )) ))))
dy
dsech
sech tanh
))
))
ˆ‰
sech tanh (sech tanh )(1 ln sech ) (sech tanh )[1 (1 ln sech )]œ œ )) )) ) )) )
(sech tanh )(ln sech )œ)) )
20. y (csch )(1 ln csch ) (csch ) (1 ln csch )( csch coth )œÊœ )) ) )))
dy
dcsch
csch coth
))
))
ˆ‰
csch coth (1 ln csch )(csch coth ) (csch coth )(1 1 ln csch ) (csch coth )(ln csch )œ œ œ)) ) )) )) ) )) )
21. y ln cosh v tanh v (2 tanh v) sech v tanh v (tanh v) sech vœ Êœ œ
""
##
###
dy
dv cosh v
sinh v ˆ‰ ab ab
(tanh v) 1 sech v (tanh v) tanh v tanh vœœ œabab
##$
22. y ln sinh v coth v (2 coth v) csch v coth v (coth v) csch vœ Êœ œ
""
##
###
dy
dv sinh v
cosh v ˆ‰ ab ab
(coth v) 1 csch v (coth v) coth v coth vœœ œabab
##$
23. y x 1 sech (ln x) x 1 x 1 x 1 2x 2œ œ œ œ œÊœab ab ab ab
ˆ‰ ˆ‰ ˆ‰
## ##
222x
ee xx x1 dx
dy
ln x ln x
24. y 4x 1 csch (ln 2x) 4x 1 4x 1 4x 1œ œ œ œab ab ab ab
ˆ‰ ˆ‰
Š‹
## ##
224x
ee 2x (2x) 4x 1
ln 2x ln 2x
4x 4œÊœ
dy
dx
25. y sinh x sinh x œœ Êœœœ
" " "Î#
""
#
#
Ȉ‰ dy
dx
x
1x x1x x(1 x)
Š‹
Éab ÈÈÈ
26. y cosh 2 x 1 cosh 2(x 1) œœÊœ œ œ
" " "Î#
""
Ȉ‰
dy
dx
(2) (x 1)
2(x 1) 1 x14x3 4x 7x 3
Š‹
ÉcdÈÈ È
27. y (1 ) tanh (1 ) ( 1) tanh tanhœ Ê œ œ )) ) ) )
" " "
""
dy
d1 1)) )
ˆ‰
28. y 2 tanh ( 1) 2 (2 2) tanh ( 1)œ Êœ ab ab
’“
)) ) )) ) )
#" # "
"
dy
d1(1)))
(2 2) tanh ( 1) (2 2) tanh ( 1) 1œ œ
))
))
" "
2
2))))
29. y (1 t) coth t (1 t) coth t (1 t) ( 1) coth t coth tœ œ Ê œ œ
" " "Î# " "Î# "
"
#
È È
ˆ‰ ˆ‰
–—
dy
dt
t
1t t
Š‹
ab È
30. y 1 t coth t 1 t ( 2t) coth t 1 2t coth tœ Ê œ œab ab
ˆ‰
# " # " "
"
dy
dt 1 t
31. y cos x x sech x x (1) sech x sech xœ Êœ œ
" " " "
" " " "
dy
dx 1x x1x 1x 1x
ÈÈ ÈÈ
’“Š‹
sech xœ "
32. y ln x 1 x sech x ln x 1 x sech x œ œ Ê
Èab
#" # "
"Î# dy
dx
1 x 1 x ( 2x) sech x sech x sech xœ œ œ
""" ""
# # " " "
"Î# "Î#
#xxx
x1x 1x 1x
xx
ab ab
Š‹
ˆ‰
ÈÈÈ
33. y csch œ Ê œ œ œ
" "
#
ˆ‰
))
dy ln (1) ln (2)
d
ln
111
ln 2
’“Š‹Š‹
Š‹ Š‹
Ë”• ÊÊ
Š‹ Š‹
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

472 Chapter 7 Transcendental Functions
34. y csch 2 œÊœ œ
"
))
dy (ln 2) 2
d212
ln 2
12
Éab È
35. y sinh (tan x) sec xœÊœœœœœ
"
dy
dx sec x sec x
sec x sec x sec x
1 (tan x) sec x
sec x sec x
ÈÈ
kk kk
kkkkkk
36. y cosh (sec x) sec x, 0 xœ Êœœœœ
"
#
dy (sec x)(tan x) (sec x)(tan x) (sec x)(tan x)
dx tan x
sec x 1 tan x
ÈÈ
kk 1
37. (a) If y tan (sinh x) C, then sech x, which verifies the formulaœœœœ
"
dy
dx 1 sinh x cosh x
cosh x cosh x
(b) If y sin (tanh x) C, then sech x, which verifies the formulaœœœœ
"
dy
dx sech x
sech x sech x
1tanhx
È
38. If y sech x 1 x C, then x sech x x sech x,œœ œ
xx2x
dy
dx x1x 41 x
## #
" " "
""
#
ÈŠ‹
ÈÈ
which verifies the formula
39. If y coth x C, then x coth x x coth x, which verifiesœœ œ
xx x
dy
dx 1 x
" " " "
## ##
" " "
Š‹
ˆ‰
the formula
40. If y x tanh x ln 1 x C, then tanh x x tanh x, which verifiesœœœ
" # " "
"""
##
ab ˆ‰ˆ‰
dy
dx 1x 1x
2x
the formula
41. sinh 2x dx sinh u du, where u 2x and du 2 dx
''
œœœ
"
#
CCœœ
cosh u cosh 2x
##
42. sinh dx 5 sinh u du, where u and du dx
''
xx
555
œœœ
"
5 cosh u C 5 cosh Cœœ
x
5
43. 6 cosh ln 3 dx 12 cosh u du, where u ln 3 and du dx
''
ˆ‰
xx
###
"
œ œ œ
12 sinh u C 12 sinh ln 3 Cœœ
ˆ‰
x
#
44. 4 cosh (3x ln 2) dx cosh u du, where u 3x ln 2 and du 3 dx
''
œ œ œ
4
3
sinh u C sinh (3x ln 2) Cœœ
44
33
45. tanh dx 7 du, where u and du dx
''
x sinh u x
7 cosh u 7 7
œœœ
"
7 ln cosh u C 7 ln cosh C 7 ln C 7 ln e e 7 ln 2 Cœœ œ œkk ¸¸ ¸ ¸
¹¹
"" " "
#
ÎÎ
xee
7
x7 x7
x7 x7
7 ln e e Cœkk
x7 x7
46. coth d 3 du, where u and du
''
)))
ÈÈÈ
333
cosh u d
sinh u
)œœœ
È
3 ln sinh u C 3 ln sinh C 3 ln Cœœ œ
ÈÈ È
kk ¹¹ ¹ ¹
"" "
#
)
È3
ee
3 ln e e 3 ln 2 C 3 ln e e Cœœ
ÈÈÈ
¹¹ ¹¹
)) ))Î $ Î $ Î Î
"
ÈÈ ÈÈ
33
47. sech x dx sech u du, where u x and du dx
''
##
""
##
ˆ‰ ˆ‰
œ œ œ
tanh u C tanh x Cœœ
ˆ‰
"
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.8 Hyperbolic Functions 473
48. csch (5 x) dx csch u du, where u (5 x) and du dx
''
##
œ œ œ
( coth u) C coth u C coth (5 x) Cœ œ œ
49. dt 2 sech u tanh u du, where u t t and du
''
sech t tanh t
t2t
dt
ÈÈ
È È
œœœœ
È"Î#
2( sech u) C 2 sech t Cœ œ
È
50. dt csch u coth u du, where u ln t and du
''
csch (ln t) coth (ln t)
t t
dt
œœœ
csch u C csch (ln t) Cœ œ
51. coth x dx dx du ln u ln ln ln ln ,
'''
ln 2 ln 2 3 4
ln 4 ln 4 15 8
œœœœœœ
cosh x 15 3 15 4 5
sinh x u 8 4 8 3
""&Î)
$Î% #
cdkk ¸¸ ¸¸ ¸ ¸
†
where u sinh x, du cosh x dx, the lower limit is sinh (ln 2) and the upperœœ œœœ
ee 3
2
4
ln 2 ln 2
##
Š‹
limit is sinh (ln 4) œœœ
ee 15
4
8
ln 4 ln 4
##
Š‹
4
52. tanh 2x dx dx du ln u ln ln 1 ln , where
'' '
00 1
ln 2 ln 2 17 8
œœœœœ
sinh 2x 17 17
cosh 2x u 8 8
""" " "
### #
"(Î)
"
cdkk ‘ˆ‰
u cosh 2x, du 2 sinh (2x) dx, the lower limit is cosh 0 1 and the upper limit is cosh (2 ln 2) cosh (ln 4)œœ œ œ
œœœ
ee 17
4
8
ln 4 ln 4
##
Š‹
4
53. 2e cosh d 2e d e 1 d
'' '
ln 4 ln 4 ln 4
ln 2 ln 2 ln 2 2ln 2
ln 4
))
)) ) ) )œœœ
Š‹ ab‘
ee
#
e2
#
ln 2 ln 4 ln 2 ln 4 ln 2 2 ln 2 ln 2œœœœ
Š‹Š‹
ˆ‰ˆ‰
ee 3 3
83232 3
2ln2 2ln4
## #
""
54. 4e sinh d 4e d 2 1 e d 2
'' '
00 0
ln 2 ln 2 ln 2 2ln 2
0
)) ) ) )œœœ
Š‹ ’ “
ab
ee e
##
2 ln 2 0 2 ln 2 2 ln 2 1 ln 4œœœœ
’“Š‹Š‹
ˆ‰
ee 3
844
2ln2 0
## #
"" "
55. cosh (tan ) sec d cosh u du sinh u sinh (1) sinh ( 1)
''
41
41
)))
#"
"
##
œœœœcd Š‹Š‹
ee e e
e e , where u tan , du sec d , the lower limit is tan 1 and the upperœœœœ œ
eeee
4
#
" #
))) ˆ‰
1
limit is tan 1
ˆ‰
1
4œ
56. 2 sinh (sin ) cos d 2 sinh u du 2 cosh u 2(cosh 1 cosh 0) 2 1
''
00
21
)))œœœœcd Š‹
"
!
#
ee
e e 2, where u sin , du cos d , the lower limit is sin 0 0 and the upper limit is sin 1œ œ œ œ œ
"
#
))) ˆ‰
1
57. dt cosh u du sinh u sinh (ln 2) sinh (0) 0 , where
''
10
2ln 2 ln 2
0
cosh (ln t)
t 4
ee 3
2
œœœœœœcd ln 2 ln 2
##
u ln t, du dt, the lower limit is ln 1 0 and the upper limit is ln 2œœ œ
"
t
58. dx 16 cosh u du 16 sinh u 16(sinh 2 sinh 1) 16
''
11
42
8 cosh x
x
ee ee
È
Èœœœœcd ’“Š‹Š‹
#
"
##
8 e e e e , where u x x , du x dx , the lower limit is 1 1 and the upperœ œœ œ œ œab
ÈÈ
# # " "Î# "Î#
"
#
dx
2x
È
limit is 4 2
Ȝ
59. cosh dx dx (cosh x 1) dx sinh x x
'''
ln 2 ln 2 ln 2
000 0
ln 2
#
### #
" " "
ˆ‰ cd
x cosh x
œœœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

474 Chapter 7 Transcendental Functions
[(sinh 0 0) (sinh ( ln 2) ln 2)] (0 0) ln 2 ln 2œœ œ
"""
#####
’“Š‹
–—
ee 2
ln 2 ln 2 Š‹
1 ln 2 ln 2 ln 2œ œ œ
"" "
##
ˆ‰ È
48 8
33
60. 4 sinh dx 4 dx 2 (cosh x 1) dx 2 sinh x x
'' '
00 0
ln 10 ln 10 ln 10 ln 10
0
#
##
ˆ‰ ˆ ‰ cd
x cosh x 1
œœœ
2[(sinh (ln 10) ln 10) (sinh 0 0)] e e 2 ln 10 10 2 ln 10 9.9 2 ln 10œœœœ
ln 10 ln 10 "
10
61. sinh ln 1 ln 62. cosh ln 1 ln 3
" "
#
ˆ ‰ ˆ‰ ˆ‰
Š‹ Š‹
ÉÉ
5525 2 5525
1 12 144 3 3 3 9
œ œ œ œ
63. tanh ln 64. coth ln ln 9 ln 3
" "
"" ""
## # # #
ˆ‰ ˆ‰
Š‹ Š‹
œ œ œ œ œ
1 (1/2) (9/4)
1 (1/2) 4 (1/4)
ln 3 5
65. sech ln ln 3 66. csch ln 3 ln 3 2
" "
"
ˆ‰ Š‹ Š‹ Š‹
ÈÈ
3
5 (3/5)
1 1 (9/25)
3
4/3
1/ 3
œœ œœ
È È
ÈŠ‹
È
67. (a) sinh sinh 3 sinh 0 sinh 3
'0
23 23
0
dx x
4x
È
" " "
#
œœœ
‘ ÈÈ
(b) sinh 3 ln 3 3 1 ln 3 2
" ÈÈ È
Š‹Š‹
È
œœ
68. (a) 2 , where u 3x, du 3 dx, a 1
''
00
13 1
6 dx dx
19x a u
ÈÈ
œœœœ
2 sinh u 2 sinh 1 sinh 0 2 sinh 1œœœcda b
" " " "
"
!
(b) 2 sinh 1 2 ln 1 1 1 2 ln 1 2
" #
œœ
Š‹Š‹
ÈÈ
69. (a) dx coth x coth 2 coth
'54
2"
" " "
#
&Î%
1x 4
5
œœcd
(b) coth 2 coth ln 3 ln ln
" " """
##
œœ
59/4
41/43
‘ˆ‰
70. (a) dx tanh x tanh tanh 0 tanh
'0
12 """
##
" " " "
"Î#
!
1x œœœcd
(b) tanh ln ln 3
" "" "
## #
œœ
Š‹
1 (1/2)
1 (1/2)
71. (a) , where u 4x, du 4 dx, a 1
''
15 45
313 1213
dx du
x116x ua u
ÈÈ
œœœœ
sech u sech sech œ œ cd
" " "
12 13
45
12 4
13 5
(b) sech sech ln lnœ
" "
12 4
13 5 (12/13) (4/5)
1 1 (12/13) 1 1 (4/5)
Š‹Š‹
ÈÈ
ln ln ln ln ln 2 ln œ œ œ
Š‹Š‹
ˆ‰ ˆ‰
13 169 144 5 25 16
14412
53 135 3
# #
ÈÈ
ln 2 ln œœ
ˆ‰
†24
33
72. (a) csch csch 1 csch csch csch 1
'1
2dx x
x4x
È
"" """
### ###
" " " " "
#
"
œ œ œ
‘ˆ‰ˆ‰¸¸
(b) csch csch 1 ln 2 ln 1 2 ln
"" " "
## # #
" "
ˆ‰
’“Š‹Š‹Š‹
È
œœ
ÈÈ
È
5/4
(1/2)
25
12
73. (a) dx du sinh u sinh 0 sinh 0 0, where u sin x, du cos x dx
''
00
0
cos x
1sinx 1u
ÈÈ
"" " "
!
!
œ œ œœ œ œcd
(b) sinh 0 sinh 0 ln 0 0 1 ln 0 0 1 0
" "
œœ
Š‹Š‹
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 7.8 Hyperbolic Functions 475
74. (a) , where u ln x, du dx, a 1
''
10
e1
dx du
x 1 (ln x) au x
ÈÈ
"
œœœœ
sinh u sinh 1 sinh 0 sinh 1œ œœcd
" " " "
"
!
(b) sinh 1 sinh 0 ln 1 1 1 ln 0 0 1 ln 1 2
" " ##
œœ
Š‹Š‹Š‹
ÈÈÈ
75. (a) Let E(x) and O(x) . Then E(x) O(x)œœ œ
f(x) f( x) f(x) f( x) f(x) f( x) f(x) f( x)
## ##
f(x). Also, E( x) E(x) E(x) is even, andœœ œ œ œ Ê
2f(x) f( x) f( ( x)) f(x) f( x)
###
O( x) O(x) O(x) is odd. Consequently, f(x) can be written as œ œ œ Ê
f( x) f( ( x)) f(x) f( x)
##
a sum of an even and an odd function.
(b) f(x) because 0 if f is even and f(x) because 0 if f is odd.œœœœ
f(x) f( x) f(x) f( x) f(x) f( x) f(x) f( x)
## ##
Thus, if f is even f(x) 0 and if f is odd, f(x) 0œ œ
2f(x) 2f(x)
##
76. y sinh x x sinh y x 2x e 2xe e 1 e 2xe 1 0œÊœÊœÊœÊœÊœ
" "
#
ee y
e
yy
yy2y 2y y
e e x x 1 sinh x y ln x x 1 . Since e 0, we cannotÊœ Êœ Ê œœ
yy y
2x 4x 4„
###
"
ÈÈÈ
Š‹
choose e x x 1 because x x 1 0.
yœ
ÈÈ
##
77. (a) v tanh t sech t g sech t .œÊœ œ
ÉÉ
Œ ŒŒ Œ
ÉÉÉÉ
”•
mg gk mg gk gk gk
kmdtk mm m
dv ##
Thus m mg sech t mg tanh t mg kv . Also, since tanh x when x , v
dv
dt m m
gk gk
œ œ " œ œ! œ! œ!
###
ŒŒ
ÉÉ
Œ
when t .œ!
(b) lim v lim tanh t lim tanh t (1)
tt tÄ_ Ä_ Ä_
œœœœ
ÉÉ ÉÉ
Œ Œ
ÉÉ
mg kg mg kg mg mg
kmk mkk
(c) 80 5 178.89 ft/sec
ÉÉÈ
160 400
0.005 5
160,000
5
œœœ¸
È
78. (a) s(t) a cos kt b sin kt ak sin kt bk cos kt ak cos kt bk sin ktœ Êœ Êœ
ds d s
dt dt ##
k (a cos kt b sin kt) k s(t) acceleration is proportional to s. The negative constant kœ œ Ê
## #
implies that the acceleration is directed toward the origin.
(b) s(t) a cosh kt b sinh kt ak sinh kt bk cosh kt ak cosh kt bk sinh ktœ Êœ Êœ
ds d s
dt dt ##
k (a cosh kt b sinh kt) k s(t) acceleration is proportional to s. The positive constant k impliesœœÊ
## #
that the acceleration is directed away from the origin.
79. y dx dx y sech (x) 1 x C; x 1 and
dy
dx x1x 1x x1x 1x
xx
œÊœ Êœ œ
" "
" #
ÈÈ È È
'' È
y0 C0 ysech(x) 1xœÊ œÊœ
" #
È
80. To find the length of the curve: y cosh ax y sinh ax L 1 (sinh ax) dxœÊœÊœ
"w#
a'0
bÈ
L cosh ax dx sinh ax sinh ab. Then the area under the curve is A cosh ax dxÊœ œ œ œ
''
0 0
b b
b
0
‘
"" "
aa a
sinh ax sinh ab sinh ab which is the area of the rectangle of height and length Lœœœ
‘ ˆ‰ˆ‰
"""" "
aaaa a
b
0
as claimed.
81. V cosh x sinh x dx 1 dx 2 œœœ111
''
00
22
ab
##
82. V 2 sech x dx 2 tanh x 2œœœœ1111
'0
ln 3 ln 3
0
#
cd –—
ÈÈ
Š‹
ÈÈ
Š‹
31/3
31/3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
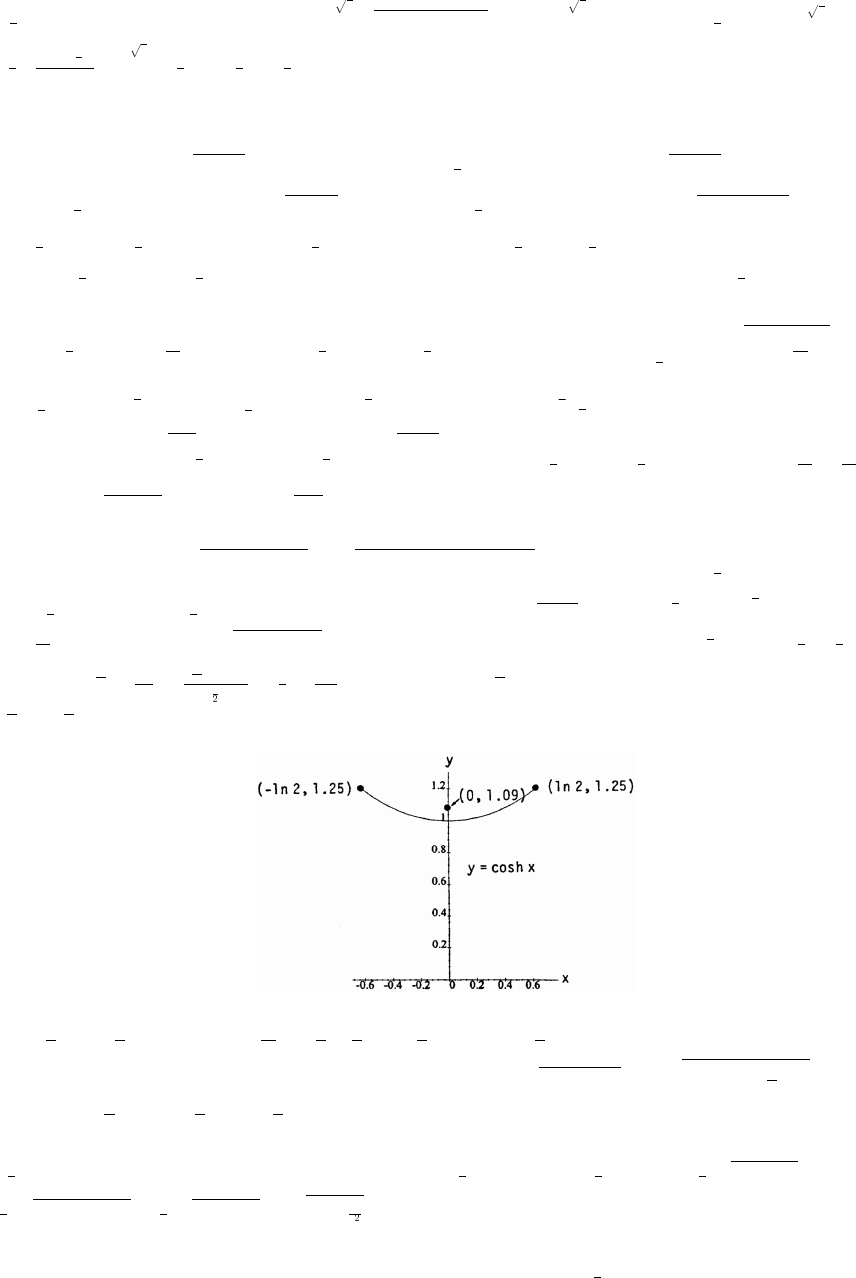
476 Chapter 7 Transcendental Functions
83. y cosh 2x y sinh 2x L 1 (sinh 2x) dx cosh 2x dx sinh 2xœÊœÊœ œ œ
" "
# #
w#
''
00
ln 5 ln 5 ln 5
0
È‘
5œœœ
’“Š‹ ˆ‰
" " "
##
ee 6
455
2x 2x ln 5
0
84. (a) Let the point located at (cosh u 0) be called T. Then A(u) area of the triangle OTP minus the areaߜ?
under the curve y x 1 from A to T A(u) cosh u sinh u x 1 dx.œ Ê œ
ÈÈ
# #
"
#'1
cosh u
(b) A(u) cosh u sinh u x 1 dx A (u) cosh u sinh u cosh u 1 (sinh u)œÊœ
""
##
##
w##
'1
cosh uÈab
Š‹
È
cosh u sinh u sinh u cosh u sinh u (1)œœ œœ
"" " ""
## # ##
### ##
ab
ˆ‰
(c) A (u) A(u) C, and from part (a) we have A(0) 0 C 0 A(u) u 2A
w"
## #
œÊ œ œÊ œÊ œÊœ
u u
85. y 4 cosh 1 1 sinh cosh ; the surface area is S 2 y 1 dxœÊœœ œ
xxx
4dx 4 4 dx
dy dy
Š‹ Š‹
ˆ‰ ˆ‰ Ê
# #
## 'ln 16
ln 81
1
8 cosh dx 4 1 cosh dx 4 x 2 sinh œœœ11 1
''
ln 16 ln 16
ln 81 ln 81 ln 81
ln 16
#
##
ˆ‰ ˆ ‰ ‘
xxx
4
4 ln 81 2 sinh ln 16 2 sinh 4 ln (81 16) 2 sinh (ln 9) 2 sinh (ln 4)œ œ 11
‘ˆ‰ˆ ‰ˆ‰ ˆ ‰ cd
ln 81 ln 16
##
†
4 ln (9 4) e e e e 4 2 ln 36 9 4 4 4 ln 6œ œ œ 111cdabab
‘ˆ‰ˆ‰ˆ‰
†#""
ln 9 ln 9 ln 4 ln 4
94 94
80 15
4 4 ln 6 16 ln 6œœ11
ˆ‰
320 135 455
36 9
1
86. (a) y cosh x ds (dx) (dy) (dx) sinh x (dx) cosh x dx; M y dsœÊœœ œ œ
ÈÈab
## # ## xln 2
ln 2
'
cosh x ds cosh x dx (cosh 2x 1) dx x e e ln 2œœ œœœ
'' '
ln 2 ln 2 0
ln 2 ln 2 ln 2 ln 2
0
ln 4 ln 4
#
#
"
‘
ab
sinh 2x
4
ln 2; M 2 1 sinh x dx 2 cosh x dx 2 sinh x e e 2 .œ œ œ œ œ œœ
15 3
16 ''
00
ln 2 ln 2 ln 2
0
ln 2 ln 2
Ècd
#"
##
Therefore, y , and by symmetry x 0.œœ œ œ
M
M83
ln 2 5ln 4
x
15
16 3
ˆ‰
ˆ‰
(b) x 0, y 1.09œ¸
87. (a) y cosh x tan sinh x sinh xœÊœœ œ
Hw Hww w
wH dxwHH H
dy
ˆ‰ ˆ‰ ‘ ˆ‰ˆ‰
9
(b) The tension at P is given by T cos H T H sec H 1 tan H 1 sinh x999œÊœ œ œ
ÈɈ‰
##
w
H
H cosh x w cosh x wyœœ œ
ˆ‰ ˆ‰ ˆ‰
wHw
HwH
88. s sinh ax sinh ax as ax sinh as x sinh as; y cosh ax cosh axœÊœÊœÊœ œœ
""""
" " #
aaaa
È
sinh ax 1 a s 1 sœœœ
"" "
####
aa a
ÈÈ
É
89. (a) Since the cable is 32 ft long, s 16 and x 15. From Exercise 88, x sinh as 15a sinh 16aœœ œ Êœ
"" "
a
sinh 15a 16a.ʜ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
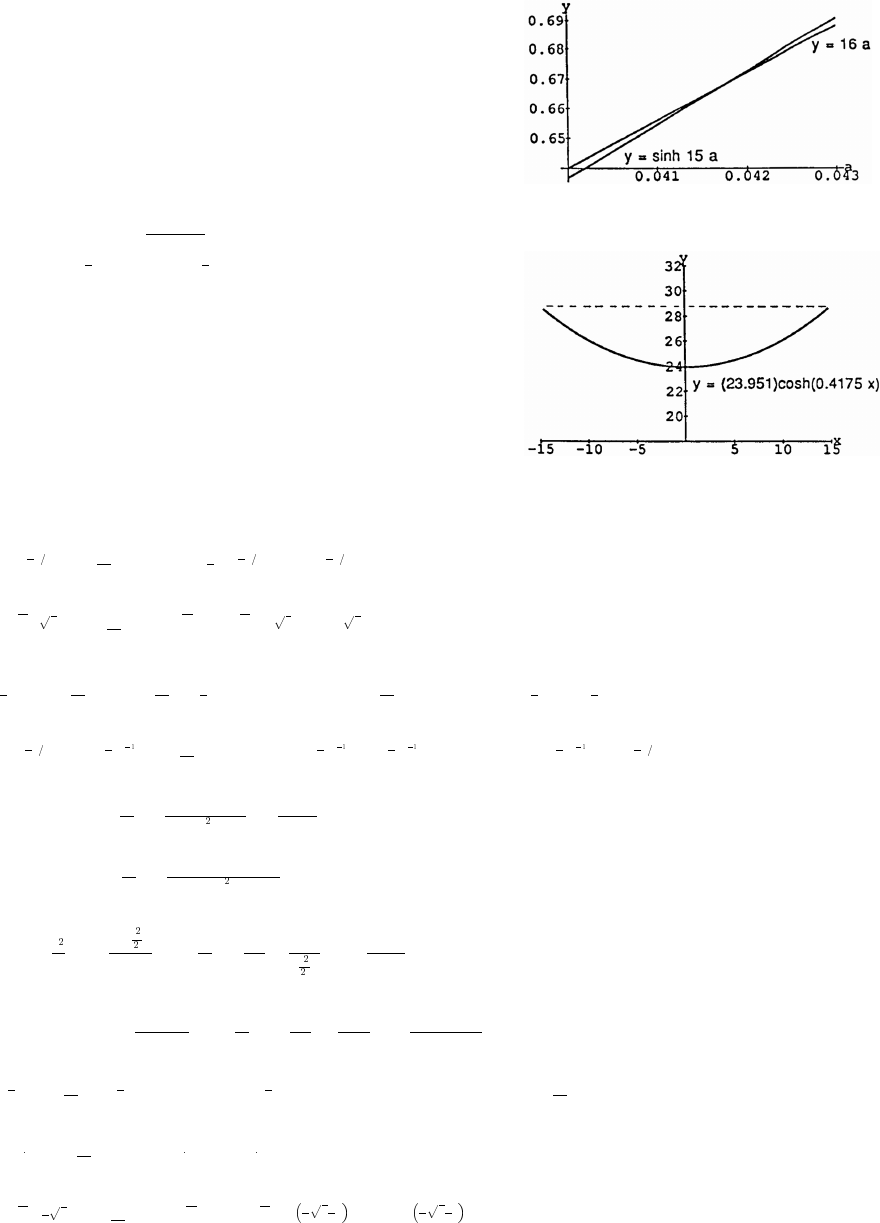
Chapter 7 Practice Exercises 477
(b) The intersection is near (0.042 0.672).ß
(c) Newton's method indicates that at a 0.0417525 the curves y 16a and y sinh 15a intersect.¸œœ
(d) T wy (2 lb) 47.90 lbœ¸ ¸
ˆ‰
"
0.0417525
(e) The sag is cosh a 4.85 ft.
""
aa
ab"& ¸
CHAPTER 7 PRACTICE EXERCISES
1. y 10e (10) e 2eœÊœœ
x5 x5 x5
dy
dx 5
ˆ‰
"
2. y 2 e 2 2 e 2eœÊœ œ
ÈÈÈ
Š‹Š‹
2x 2x 2x
dy
dx
3. y xe e x 4e e (1) 4e xe e e xeœ Êœ œœ
"" " " ""
416 dx4 16 44
dy
4x 4x 4x 4x 4x 4x 4x 4x 4x
cdabab
4. y x e x e x 2x e e (2x) (2 2x)e 2e (1 x)œœ Êœ œ œ
## ##2 x 2x 2x 2x 2x 2 x
dy
dx cdab
5. y ln sin 2 cot œÊœ œœab
#))
dy 2(sin )(cos )
dsin sin
2 cos
)))
)) )
6. y ln sec 2 tan œÊœ œab
#))
dy 2(sec )(sec tan )
dsec))
)))
7. y log œœÊœ œ
2Š‹
xx2
ln
ln dx ln (ln 2)x
dy
## #
"
Š‹ Š‹
x
x
8. y log (3x 7) œœÊœ œ
5
ln (3x 7) dy
ln 5 dx ln 5 3x 7 (ln 5)(3x 7)
33
"
ˆ‰ˆ ‰
9. y 8 8 (ln 8)( 1) 8 (ln 8) 10. y 9 9 (ln 9)(2) 9 (2 ln 9)œÊœ œ œÊœ œ
tt t 2t2t2t
dy dy
dt dt
11. y 5x 5(3.6)x 18xœÊœ œ
36 26 26
dy
dx
12. y 2 x 2 2 x 2xœÊœ œ
ÈÈÈ
Š‹Š ‹
221 21
dy
dx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

478 Chapter 7 Transcendental Functions
13. y (x 2) ln y ln (x 2) (x 2) ln (x 2) (x 2) (1) ln (x 2)œ Ê œ œ Ê œ
x2 x2 y
yx
ˆ‰
"
#
(x 2) ln (x 2) 1ʜ
dy
dx
x2
cd
14. y 2(ln x) ln y ln 2(ln x) ln (2) ln (ln x) 0 (ln (ln x))œÊœ œ Êœ
x2 x2
cd ˆ‰ ˆ‰ ˆ‰
’“
xx
y
yln x###
"
ˆ‰
x
y ln (ln x) 2 (ln x) (ln x) ln (ln x)Êœ œ
w"" "
##
‘ ‘ˆ‰
ln x ln x
x2 x2
15. y sin 1 u sin 1 u œœÊœ œ œ
" " #
#"Î#
Èab dy
du
1 u ( 2u)
11u
uu
1u 1 1u u 1u
ab
Ê’ “
ab ÈÈ
Èabkk
12
, 0u1œœ
"
u
u1u 1 u
ÈÈ
16. y sin sin v œœÊœœœœ
" " "Î#
"""
Š‹
ÈÈÈ
ÉÉ
ab È
v
dy
dv
v
1v 2v 1 v 2v
v
2v v 1
v1
v
œ"
2v v 1
È
17. y ln cos x yœÊœœab
" w "
Š‹
È
1x
cos x 1x cosx
18. y z cos z 1 z z cos z 1 z cos z 1 z ( 2z)œœÊœ
" " # " #
#"Î# "Î#
"
#
Èab ab
ˆ‰
dy
dz
z
1z
È
cos z cos zœœ
" "
zz
1z 1z
ÈÈ
19. y t tan t ln t tan t t tan tœ Êœœ
" " "
"""""
##
ˆ‰ ˆ ‰ ˆ‰ˆ‰
dy
dt 1 t t 1 t 2t
t
20. y 1 t cot 2t 2t cot 2t 1 tœ Ê œ ab ab
ˆ‰
#" " #
dy
dt 1 4t
2
21. y z sec z z 1 z sec z z 1 z sec z (1) z 1 (2z)œœÊœ
" " # " #
#"Î# "Î#
""
#
Èab ab ab
Š‹
dy
dz zz1kkÈ
sec z sec z, z 1œœ
zz 1z
zz1 z1 z1kkÈÈ È
" "
22. y 2 x 1 sec x 2(x 1) sec xœ œ
ÈȈ‰
" "Î# " "Î#
2 (x 1) sec x (x 1) 2Êœ œ œ
dy
dx xx
x
xx1 2x1 x1
sec x sec x
–—
ˆ‰ ˆ ‰
Š‹
"""
# #
"Î# " "Î# "Î#
Š‹
ÈÈÈÈ
ÈÈ
23. y csc (sec ) 1, 0œÊœ œœ
"
#
))
dy
dtan
sec tan tan
sec sec 1
))
)) ) 1
))kk
Èkk
24. y 1 x e y 2xe 1 x 2xe eœ Ê œ œ ab ab
Š‹
#w #
tan x tan x tan x tan x
e
1x
tan x
25. y ln y ln ln (2) ln x 1 ln (cos 2x) 0œÊœ œ Êœ
2x 1 2x 1
cos 2x cos 2x
y ( 2 sin 2x)
y x 1 cos 2x
2x
ab ab
ÈÈ
#""
##
Š‹ ab ˆ‰
y tan 2x y tan 2xÊœ œ
w
ˆ‰ˆ‰
2x 2x
x1 x1
2x 1
cos 2x
ab
È
26. y ln y ln ln (3x 4) ln (2x 4) œÊœ œ Êœ
ÉÉ
cd
ˆ‰
3x 4 3x 4 3 2
2x 4 2x 4 10 y 10 3x 4 2x 4
y
" "
yyÊœ œ
w"" " "
10 3x 4 x 2 2x 4 10 3x 4 x 2
33x43
ˆ‰ˆ‰ˆ‰
É
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
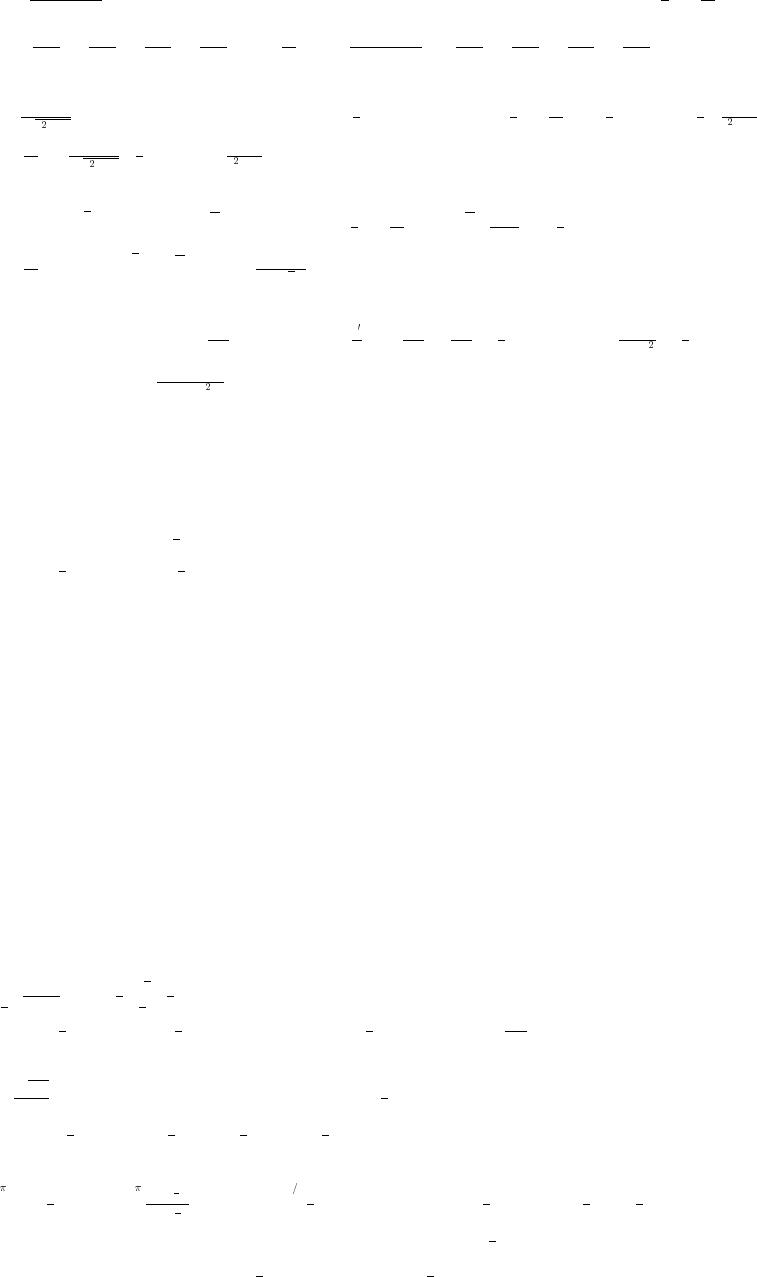
Chapter 7 Practice Exercises 479
27. y ln y 5 ln (t 1) ln (t 1) ln (t 2) ln (t 3) œ Ê œ Ê
’“ Š‹Š‹
cd
(t 1)(t 1) dy
(t 2)(t 3) ydt
&"
5 5œ Êœ
ˆ‰ ˆ‰
’“
"""" """"
# #
&
t1 t1 t t3 dt (t2)(t3) t1 t1 t t3
dy (t 1)(t 1)
28. y ln y ln 2 ln u u ln 2 ln u 1 ln 2œÊœÊ œ
2u2 2u
u1 ydu u u1
dy
u
È
""""
##
#
ab
Š‹Š‹ ˆ‰
ln 2ʜ
dy
du u u 1
2u2 u
u1
u
È
"
ˆ‰
29. y (sin ) ln y ln (sin ) ln (sin )œÊœ Ê œ ))) )))
È)
))
)
ÈÈ
Š‹Š‹ ˆ‰
""
#
"Î#
yd sin
dy cos
(sin ) cot ʜ
dy ln (sin )
d2
)
))
)
)))
ÈÈ
Š‹
È
30. y (ln x) ln y ln (ln x) ln (ln x)œÊœ Êœ
1lnx
ln x y ln x ln x x (ln x) x
y
Î""""""
ˆ‰ ˆ‰ˆ‰ˆ‰ ˆ‰
’“
y (ln x)ʜ
wÎ
1lnx 1ln(ln x)
x(ln x)
’“
31. e sin e dx sin u du, where u e and du e dx
''
xx x x
ab œœœ
cos u C cos e Cœ œ ab
x
32. e cos 3e 2 dt cos u du, where u 3e 2 and du 3e dt
''
tt t t
3
abœ œ œ
"
sin u C sin 3e 2 Cœœ
""
33
t
ab
33. e sec e 7 dx sec u du, where u e 7 and du e dx
''
xx x x##
abœ œ œ
tan u C tan e 7 Cœœ ab
x
34. e csc e 1 cot e 1 dy csc u cot u du, where u e 1 and du e dy
''
yy y y y
ababœ œœ
csc u C csc e 1 Cœ œ ab
y
35. sec x e dx e du, where u tan x and du sec x dx
''
ab
##tan x u
œœœ
eCe Cœœ
utan x
36. csc x e dx e du, where u cot x and du csc x dx
''
ab
# #cot x œ œ œ
u
eC e Cœ œ
ucotx
37. dx du, where u 3x 4, du 3 dx; x 1 u 7, x 1 u 1
''
17
11
"""
3x 4 3 u
œ œ œ œÊœ œÊœ
ln u ln 1 ln 7 [0 ln 7]œœœœ
"" "
"
(
33 3 3
ln 7
cd c dkk kk kk
38. dx u du, where u ln x, du dx; x 1 u 0, x e u 1
''
10
e1
Èln x
xx
œœœœÊœœÊœ
"Î# "
u10œ œœ
‘ ‘
2222
3333
$Î# $Î# $Î#
"
!
39. tan dx dx 3 du, where u cos , du sin dx; x 0 u 1, x
'' '
00 1
12
ˆ‰ ˆ‰ ˆ‰
xxx
3u333
sin
cos
œœ œœ œÊœœ
ˆ‰
ˆ‰
x
3
x
3
"" 1
uʜ
"
#
3 ln u 3 ln ln 1 3 ln ln 2 ln 8œ œ œ œ œcd kkkk ‘¸¸
"Î#
"""
##
$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

480 Chapter 7 Transcendental Functions
40. 2 cot x dx 2 dx du, where u sin x, du cos x dx; x u , x
'''
16 16 12
14 14 1 2
1111œœ œœœÊœœ
cos x 2
sin x u 6 4
1
11
""""
#
uʜ
"
È2
ln u ln ln ln 1 ln 2 ln 1 ln 2 ln 2œœœœœ
22 2 2ln 2
2
11 1 11
cdkk ’“¹¹ ¸¸ ‘ ‘
12
12
"" " "
## #
È
41. dt du, where u t 25, du 2t dt; t 0 u 25, t 4 u 9
''
025
49
2t
t25 u
"#
œ œ œ œÊœ œÊœ
ln u ln 9 ln 25 ln 9 ln 25 ln œœœœcd kkkkkk*
#&
9
25
42. dt du, where u 1 sin t, du cos t dt; t u 2, t u
''
22
612
cos t
1sin t u 6##
" "
œ œ œ œ Ê œ œ Ê œ
11
ln u ln ln 2 ln 1 ln 2 ln 2 2 ln 2 ln 4œ œ œ œ œcd kkkk ‘¸¸
"Î#
#"
#
43. dv tan u du du, where u ln v and du dv
'tan (ln v)
vcos u v
sin u
œœ œ œ
''"
ln cos u C ln cos (ln v) Cœ œ kk k k
44. dv du, where u ln v and du dv
'"" "
v ln v u v
œœœ
'
ln u C ln ln v Cœœ kk k k
45. dx u du, where u ln x and du dx
'(ln x)
xx
œœœ
'$ "
C (ln x) Cœœ
u
# #
"#
46. dx u du, where u ln (x 5) and du dx
'ln (x 5)
x5 x5
"
œœœ
'
CCœœ
uln (x 5)
2
#
cd
47. csc (1 ln r) dr csc u du, where u 1 ln r and du dr
'" "
##
r r
œ œ œ
'
cot u C cot (1 ln r) Cœ œ
48. dv cos u du, where u 1 ln v and du dv
'cos (1 ln v)
v v
"
œ œ œ
'
sin u C sin (1 ln v) Cœ œ
49. x3 dx 3 du, where u x and du 2x dx
''
xu
œœœ
"
#
#
3C 3 Cœœ
""
## ln 3 ln 3
ux
ab Š‹
50. 2 sec x dx 2 du, where u tan x and du sec x dx
''
tan x u##
œœœ
2C Cœœ
"
##ln ln
u2
ab tan x
51. dx 3 dx 3 ln x 3 ln 7 ln 1 3 ln 7
''
11
77
3
xx
œœœœ
"(
"
cd a bkk
52. dx dx ln x ln 32 ln 1 ln 32 ln 32 ln 2
''
11
32 32
"""" " "
$#
"
5x 5 x 5 5 5
œœœœœœcd a bkk Š‹
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 7 Practice Exercises 481
53. dx x dx x ln x ln 4 ln 1 ln 4
''
11
44
ˆ‰ ˆ‰ ‘ ‘
kk ˆ‰ˆ‰
x16 15
8x 4 x 8 8 8 16
œ œ œœ
"""""" " " "
## # # #
#%
"
ln 4 ln 2œ œ
15 15
16 16
È
54. dx 12x dx ln x 12x ln 8 (ln 1 12)
''
11
88
ˆ‰ ˆ ‰ ‘
cdkk ˆ‰
28 2 2 2 12
3x x 3 x 3 3 8
œ œ œ
"# " )
"
ln 8 12 ln 8 (ln 8) 7 ln 8 7 ln 4 7œ œ œ œ œ
23 2212
333
ˆ‰ˆ‰ ˆ‰
##
#Î$
55. e dx e du, where u (x 1), du dx; x 2 u 1, x 1 u 0
''
21
10
u
Ð Ñx1 œ œ œ œ Ê œ œ Ê œ
eeee1œ œ œ cd a b
u!
"!"
56. e dw e du, where u 2w, du 2 dw; w ln 2 u ln , w 0 u 0
''
ln 2 n 1 4
00
2w u
œœœœÊœœÊœ
" "
#l4
eee1œœœœ
"" ""
## #
!
cd c d ˆ‰
uln14
0
ln 1 4 48
3
57. e 3e 1 dr u du, where u 3e 1, du 3e dr; r 0 u 4, r ln 5 u 16
''
14
ln 5 16
rr r r
abœ œœœÊœœÊœ
$Î# "$Î#
3
u164œ œ œ œ œ
22 2 2
33 34346
‘ ˆ ‰ˆ‰ˆ ‰ˆ‰ˆ‰
"Î# "Î# "Î#
"'
%
"" " "
#
58. e e 1 d u du, where u e 1, du e d ; 0 u 0, ln 9 u 8
''
00
ln 9 8
abœ œœœÊœœÊœ
"Î# "Î#
))))
u8020œœœœœ
22 2 2
33 3 33
32 2
‘ ˆ ‰ ˆ ‰
$Î# $Î# $Î# *Î#
)
!È
59. (1 7 ln x) dx u du, where u 1 7 ln x, du dx, x 1 u 1, x e u 8
''
11
e8
""
"Î$ "Î$
x7 x
7
œ œœœÊœœÊœ
u81(41)œœœœ
33 3 9
14 14 14 14
‘ ˆ ‰ˆ‰
#Î$ #Î$ #Î$
)
"
60. dx (ln x) dx u du, where u ln x, du dx; x e u 1, x e u 2
'' '
ee 1
ee 2
"" "
"Î# "Î# #
xln x xx
Èœœ œœœÊœœÊœ
2u 2 2 1 2 2 2œœœ
‘ Š‹
ÈÈ
"Î# #
"
61. dv [ln (v 1)] dv u du, where u ln (v 1), du dv;
'' '
11 ln2
33 ln4
[ln (v 1)]
v1 v1 v1
##
""
œ œ œœ
v 1 u ln 2, v 3 u ln 4;œÊœ œÊœ
u (ln 4) (ln 2) (2 ln 2) (ln 2) (8 1) (ln 2)œ œ œ œ œ
"" "
$$$$$ $
33 3 3 3
(ln 2) 7
cd c d c d
ln 4
ln 2
62. (1 ln t)(t ln t) dt (t ln t)(1 ln t) dt u du, where u t ln t, du (t) (ln t)(1) dt
'''
222 ln2
444 ln4
œœ œœ
ˆ‰ˆ‰
"
t
(1 ln t) dt; t 2 u 2 ln 2, t 4œ œÊœ œ
u 4 ln 4ʜ
u (4 ln 4) (2 ln 2) (8 ln 2) (2 ln 2) (16 1) 30 (ln 2)œœ œ œ œ
"" "
## # #
##### #
cdcdcd
4ln4
2ln2
(2 ln 2)
63. d (ln ) d u du, where u ln , du d , 1 u 0, 8 u ln 8
'' '
11 0
88 ln8
log
ln 4 ln 4
4)
)) )
))) ))) )œœ œœœÊœœÊœ
""" "
ˆ‰
u (ln 8) 0œœ œœ
""
#
###
ln 4 ln 16 4 ln 2 4
(3 ln 2) 9 ln 2
cd c d
ln 8
64. d d 8 (ln ) d 8 u du, where u ln , du d ;
''''
1110
eee1
8(ln 3)(log ) 8(ln 3)(ln )
(ln 3)
3))
)) ) )
)))) ))œœ œ œœ
ˆ‰
""
1 u 0, e u 1))œÊœ œÊœ
4u 41 0 4œœœcd a b
###
"
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

482 Chapter 7 Transcendental Functions
65. dx 3 dx 3 du, where u 2x, du 2 dx;
'' '
34 34 32
34 34 32
62
94x 3 u
3 (2x)
ÈÈ È
"
œœ œœ
x u , x uœÊœ œÊœ
3333
44##
3sin 3sin sin 3 3œœœœœ
‘ ‘ ‘ˆ‰ˆ‰ ˆ‰ ˆ ‰ ˆ ‰
" " "
$Î#
$Î#
""
##
u
3663
11 1
1
66. dx dx du, where u 5x, du 5 dx;
'' '
15 15 1
15 15 1
66 5 6
4 25x 2 u
55
2 (5x)
ÈÈÈ
"
œœ œœ
x u 1, x u 1œÊœ œÊœ
11
55
sin sin sinœœœœœ
6u6 6 62
525 566535
‘ ‘ ‘ˆ‰ˆ‰ ˆ‰ ˆ ‰ ˆ ‰
" " "
"
"
""
##
11 11
67. dt 3 dt 3 du, where u 3t, du 3 dt;
'' '
22 23
22 23
3
43t 2 u
3
23t
"
œœ œœ
ÈÈ ÈÈ
È
Š‹
È
t 2 u 2 3, t 2 u 2 3œÊœ œÊœ
ÈÈ
3 tan tan 3 tan 3œœœœ
ÈÈÈ
‘ ‘ˆ‰ ˆ ‰
’“Š‹ Š ‹
"
## #
" " "
u
233
33
3
23
23 ÈÈ
È
111
68. dt dt tan tan 3 tan 1
''
33
33 3
3
""" " "
" " "
3t 34 36
3t 33 3 3
t3
œœ œœœ
Š‹
ÈÈÈÈ È È
’“Š ‹Š‹ Ȉ‰
11 1
69. dy dy du, where u 2y and du 2 dy
'' '
""
y 4y 1 (2y) (2y) 1
2
uu 1
ÈÈÈ
œœ œœ
sec u C sec 2y Cœœ
" "
kk k k
70. dy 24 dy 24 sec C 6 sec C
''
24
yy 16 yy 4 44 4
yy
ÈÈ
""
" "
œœœ
ˆ‰ ¸¸¸¸
71. dy dy du, where u 3y, du 3 dy;
'' '
23 23 2
23 23 2
""
kk k k
ÈÈÈ
kk
y 9y 1 3y (3y) 1
3
uu1
œœ œœ
y u 2, y u 2œÊœ œÊœ
È2
33
2
È
sec u sec 2 sec 2œ œ œœcd
’“
È
" " "
2
2
11 1
3412
72. dy dy du,
'' '
2/ 5 2/ 5 2
65 65 6
" "
kkÈÈ
ÈÈ È È
ÊŠ ‹ Š ‹ Ê Š ‹
y 5y 3
5
5y 5y 3 u u 3
œœ
where u 5y, du 5 dy; y u 2, y u 6œ œ œ Ê œ œ Ê œ
ÈÈ È
2
55
6
ÈÈ
È
sec sec 2 sec œ œ œ œ œ œ
’“’ “¹¹ Ȉ‰ ‘
" " "
" " "
#
ÈÈ È ÈÈ È È
È
33 3 33 3 123
u1 2 32
46 121 36
3
6
2
11 1 1 1 1
73. dx dx dx du, where u x 1 and
'' ' '
"" ""
ÈÈ È È
ab
2x x 1 u
1x2x1 1(x1)
œœœ œ
du dxœ
sin u C sin (x 1) Cœœ
" "
74. dx dx dx du
'' ' '
"" " "
ÈÈ
ab ÊŠ ‹ ÊŠ ‹
ÈÈ
x4x1 3x4x4 3(x2) 3u
œœ œ
where u x 2 and du dxœ œ
sin C sin Cœœ
" "
Š‹ Š ‹
ux2
33
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 7 Practice Exercises 483
75. dv 2 dv 2 dv 2 du,
'' ''
22 20
11 11
2
v 4v 5 1 v 4v 4 1 (v 2) 1 u
"""
œœœ
ab
where u v 2, du dv; v 2 u 0, v 1 u 1œ œ œÊ œ œÊ œ
2 tan u 2 tan 1 tan 0 2 0œœœœcda b
ˆ‰
" " "
"
!#
11
4
76. dv dv dv du
'' ' '
11 1 12
11 1 32
33 3 3
4v 4v 4 4 4 4
vv vu
"""
œœ œ
3
44 33
Š‹ Œ Œ
Š‹
where u v , du dv; v 1 u , v 1 uœ œ œÊ œ œ Ê œ
""
###
3
tan tan 3 tanœœœœœ
32 2u 2
436 66
33 3
3333
’“’ “Š‹ Š ‹
È‘ˆ‰ˆ‰
ÈÈ È
ÈÈÈÈ
" " "
$Î#
"Î# #####
"11 11 1
†
œÈ3
4
1
77. dt dt dt du
'' ' '
"" ""
(t 1) t 2t 8 (t 1) t 2t 1 9 (t 1) (t 1) 3 uu 3
ÈÈ ÈÈ
ab
œœœ
where u t 1 and du dtœ œ
sec C sec Cœœ
""
" "
33 3 3
ut1
¸¸ ¸ ¸
78. dt dt dt du
'' ' '
"" """
(3t 1) 9t 6t (3t1) 9t 6t1 1 (3t 1) (3t 1) 1 3uu 1
ÈÈ È È
ab
œœœ
where u 3t 1 and du 3 dtœ œ
sec u C sec 3t 1 Cœœ
""
" "
33
kk k k
79. 3 2 ln 3 ln 2 y(ln 3) (y 1) ln 2 (ln 3 ln 2)y ln 2 ln y ln 2 y
yy1 y y1 3ln 2
ln
œ Ê œ Ê œ Ê œÊ œÊœ
#
ˆ‰ Š‹
3
80. 4 3 ln 4 ln 3 y ln 4 (y 2) ln 3 2 ln 3 (ln 3 ln 4)y (ln 12)y 2 ln 3
yy2 y y2
œÊ œ Êœ Êœ Ê œ
yʜ
ln 9
ln 12
81. 9e x e ln e ln 2y(ln e) ln y ln ln ln ln x ln 3
2y 2y 2y
xx xxxx
99 9993
œÊœÊœÊ œÊœ œœœ
#"
#
Š‹ Š‹ Š‹ ɸ¸ kk
82. 3 3 ln x ln 3 ln (3 ln x) y ln 3 ln (3 ln x) y
yy ln (3 ln x) ln 3 ln (ln x)
ln 3 ln 3
œÊœÊœÊœœ
83. ln (y 1) x ln y e e e e y 1 ye y ye 1 y 1 e 1œ Ê œ œ Êœ Ê œÊ œ
ln y 1 x lny x lny x x xÐÑ Ð Ñ ab
yʜ
"
1e
x
84. ln (10 ln y) ln 5x e e 10 ln y 5x ln y e e y eœÊ œÊ œÊœÊœÊœ
ln 10 ln y ln 5x ln y x 2 x 2
x
ÐÑ Î Î
#
85. The limit leads to the indeterminate form : lim lim ln 10
x0
0101
0x 1
(ln 10)10
x0Ä
xx
œœ
Ä
86. The limit leads to the indeterminate form : lim lim ln 3
031
01
(ln 3)3
))ÄÄ00
)œœ
87. The limit leads to the indeterminate form : lim lim ln 2
x0
021
0e1 e
2 (ln 2)(cos x)
x0Ä
sin x
xx
sin x
œœ
Ä
88. The limit leads to the indeterminate form : lim lim ln 2
02
0e1 e
2 (ln 2)( cos x)
x0Ä
sin x
xx
sin x
"
œœ
x0Ä
89. The limit leads to the indeterminate form : lim lim lim 5
x0
0 5 5 cos x 5 sin x 5 cos x
0ex1 e1 e
x0Ä
xxx
œœ œ
Ä
x0Ä
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

484 Chapter 7 Transcendental Functions
90. The limit leads to the indeterminate form : lim lim 4
x0
0 4 4e 4e
0xe exe
x0Ä
xx
xxx
œœ
Ä
91. The limit leads to the indeterminate form : lim
0
0t
tln(12t)
2t
t lim
t
Ä! Ä!
œœ_
Š‹
12
12t
92. The limit leads to the indeterminate form : lim lim
x4
0
0e3x e1
sin ( x) 2 (sin x)(cos x)
x4Ä
1111
x4 x4
π
lim lim 2
x4 x4
œœ œ
ÄÄ
11 1 1 sin(2x) 2 cos(2x)
e1 e
x4 x4
#
1
93. The limit leads to the indeterminate form : lim lim lim 1
0e e e
0tt t 1
tttÄ! Ä! Ä!
Š‹ Š‹
ttt
œ œ œ
""
94. The limit leads to the indeterminate form : lim e ln y lim lim
_
_
Î
yyyÄ! Ä! Ä!
1y ln y y
ee
œœ
yyy
lim 0œ œ
yÄ!
y
ey
95. Let f(x) 1 ln f(x) lim ln f(x) lim ; the limit leads to theœ Ê œ Ê œ
ˆ‰
3
xx x
ln 1 3x ln 1 3x
xab ab
xxÄ_ Ä_
indeterminate form : lim lim 3 lim 1 lim e e
033
0x x
1
xx xxÄ_ Ä_ Ä_ Ä_
Š‹
3x
13x
3
x
$
œœÊœœ
ˆ‰
xln f x
96. Let f(x) 1 ln f(x) x ln 1 lim ln f(x) lim ; the limit leads to theœ Ê œ Ê œ
ˆ‰ ˆ‰
33
xx x
ln 1 3x
x
xxÄ! Ä!
ab
indeterminate form : lim lim 0 lim 1 lim e e 1
_
_
!
xx xxÄ! Ä! Ä! Ä!
Š‹
3x
13x
xx3 x
3x 3
œœÊœœœ
ˆ‰
xln f x
97. (a) lim lim lim same rate
xx xÄ_ Ä_ Ä_
log x
log x ln 2 ln
ln 3 ln 3
2
3œœœÊ
Š‹
Š‹
ln x
ln 2
ln x
ln 3 #
(b) lim lim lim lim 1 same rate
xxxxÄ_ Ä_ Ä_ Ä_
xx2x
xx1 x
#
Š‹
x
œœœ"œÊ
(c) lim lim lim faster
xxxÄ_ Ä_ Ä_
ˆ‰
x
100
xe 100x 100
xe e
x
xx
œœœ_Ê
(d) lim faster
xÄ_
x
tan x œ_ Ê
(e) lim lim lim lim 1 same rate
xx x xÄ_ Ä_ Ä_ Ä_
csc x sin x
xx
1
Š‹ ab ÊŠ‹
x
x
1x
x
œœ œ œÊ
"
(f) lim lim lim same rate
xÄ_
sinh x e
ee
ee
xx
xx 2x
œœœÊ
xxÄ_ Ä_
ab
###
" "
98. (a) lim lim 0 slower
xxÄ_ Ä_
32
23
x
xœœÊ
ˆ‰
x
(b) lim lim lim same rate
xx xÄ_ Ä_ Ä_
ln 2x ln 2 ln x ln 2
ln x 2 (ln x) ln x
œœœÊ
""
###
ˆ‰
(c) lim lim lim lim 0 slower
xxxxÄ_ Ä_ Ä_ Ä_
10x 2x 30x 4x 60x 4 60
eeee
xxx
œœœœÊ
x
(d) lim lim lim lim 1 same rate
xx xxÄ_ Ä_ Ä_ Ä_
tan tan x
xx
1
Š‹ Š ‹
Š‹ ab
x
x
x
1x
x
œœœœÊ
"
(e) lim lim lim lim faster
xx x xÄ_ Ä_ Ä_ Ä_
sin sin x
x2x
x
21
Š‹
Š‹ ab É
x
x
œœ œœ_Ê
x
1x
x
(f) lim lim lim lim 2 same rate
xx x xÄ_ Ä_ Ä_ Ä_
sech x 2 2
eeeee1e
xxxxx 2x
œœ œœÊ
Š‹ ab
2
ee
xx
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 7 Practice Exercises 485
99. (a) 1 2 for x sufficiently large true
Š‹
Š‹
xx
x
"
œ Ÿ Ê
x
(b) x 1 M for any positive integer M whenever x M false
Š‹
Š‹
xx
x
#
œ Ê
È
(c) lim lim 1 the same growth rate false
xxÄ_ Ä_
x
xln x 1
"
œœÊ Ê
x
(d) lim lim lim 0 grows slower true
xxxÄ_ Ä_ Ä_
ln (ln x)
ln x ln x
œœœÊ Ê
–—
ˆ‰
x
ln x
x
"
(e) for all x true
tan x
1ŸÊ
1
#
(f) 1 e (1 1) 1 if x 0 true
cosh x
exœ Ÿœ Ê
""
##
ab
2x
100. (a) 1 if x 0 true
Š‹
Š‹
x
xx
"
œŸ Ê
x1
(b) lim lim 0 true
xxÄ_ Ä_
Š‹
Š‹
x
xx
"
œœÊ
ˆ‰
x1
(c) lim lim 0 true
xxÄ_ Ä_
ln x
x1 1œœÊ
Š‹
x
(d) 1112 if x2 true
ln 2x ln 2
ln x ln x
œ Ÿœ Ê
(e) if x 1 true
sec x
111
cos
œŸœÊ
Š‹ ˆ‰
x1
#
(f) 1 e if x 0 true
sinh x
exœ Ÿ Ê
""
##
ab
2x
101. e 1
df df df
dx dx dx e 1 1 3
œÊœÊœœœ
xŠ‹ Š‹
xfln2 xfln2œÐ Ñ œÐ Ñ
""""
#
Š‹ ab
df
dx xln2
xln2
x
102. y f(x) y 1 y 1 x f (x) ; f (f(x)) x andœÊœÊœÊœÊ œ œ œœ
"" " " " "
" "
xx y1 x1 11
Š‹ Š‹
xx
ff(x) 1 1(x1)x; x;ab ¹¹
" #
"""
œ œ œ œ œ œ
Š‹ ’“Š‹
x1 x
df
dx (x 1) 11
fx fx
f (x)
w""
œ Ê œ
xdx f(x)
df ¹fx
103. y x ln 2x x y x ln (2x) 1 ln 2x;œÊœœ
wˆ‰
2
2x
solving y 0 x ; y 0 for x and y 0 for
ww w
""
##
œÊœ
x relative minimum of at x ; fÊ œ œ
"""""
####
ˆ‰
ee
and f 0 absolute minimum is at x and
ˆ‰
e
###
""
œÊ œ
the absolute maximum is 0 at x œe
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

486 Chapter 7 Transcendental Functions
104. y 10x(2 ln x) y 10(2 ln x) 10xœÊœ
w"
ˆ‰
x
20 10 ln x 10 10(1 ln x); solving y 0œ œ œ
w
x e; y 0 for x e and y 0 for x eʜ
ww
relative maximum at x e of 10e; y on e andÊœ!Ð!ßÓ
#
y e 10e (2 2 ln e) 0 absolute minimum is 0ab
##
œœÊ
at x e and the absolute maximum is 10e at x eœœ
#
105. A dx 2u du u 1, whereœœœœ
''
10
e1
2 ln x
xcd
#"
!
u ln x and du dx; x 1 u 0, x e u 1œœœÊœœÊœ
"
x
106. (a) A dx ln x ln 20 ln 10 ln ln 2, and A dx ln x ln 2 ln 1 ln 2
" #
" "
#! #
"! "
œ œ œœœ œ œ œœ
''
10 1
20 2
x10x
20
cd cdkk kk
(b) A dx ln x ln kb ln ka ln ln ln b ln a, and A dx ln x
" #
" "
œ œ œœœœ œ œ
''
ka a
kb b
kb b
ka a
xkaax
kb b
cd cdkk kk
ln b ln aœ
107. y ln x ; x m/secœÊœ œ Êœ œÊ œ
dy dy dy dy dy
dx x dt dx dt dt x dt e
dx
x
""""
ˆ‰È¹
Èe
108. y 9e 3e ; ; x 9 y 9eœÊœ œÊœ œÊœ
x3 x3
dy (dy/dt)
dx dt (dy/dx) dt 3e
dx dx 9y
Š‹
È
$
4
x3
e e 1 5 ft/secÊœ œ ¸
¸ÈÈ
dx
dt 4
9
x9
Š‹
É
Š‹
"$$
4
9
e
3
e
109. A xy xe e (x)( 2x) e e 1 2x . Solving 0 1 2x 0œœ Ê œ œ œÊ œ
xx xx
dA dA
dx dx
ab
##
x ; 0 for x and 0 for 0 x absolute maximum of e atÊœ Ê œ
"" " ""
"Î#
ÈÈ È ÈÈ
22 2 2
dA dA
dx dx 2e
x units long by y e units high.œœœ
""
"Î#
ÈÈ
2e
110. A xy x . Solving 0 1 ln x 0 x e;œœ œ Ê œ œ œÊ œÊœ
ˆ‰
ln x ln x dA ln x 1 ln x dA
xxdxxxx dx
"
0 for x e and 0 for x e absolute maximum of at x e units long and y units
dA dA ln e
dx dx e e e
Ê œœ œ
""
high.
111. K ln (5x) ln (3x) ln 5 ln x ln 3 ln x ln 5 ln 3 ln œ œœœ
5
3
112. (a) No, there are two intersections: one at x 2œ
and the other at x 4œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
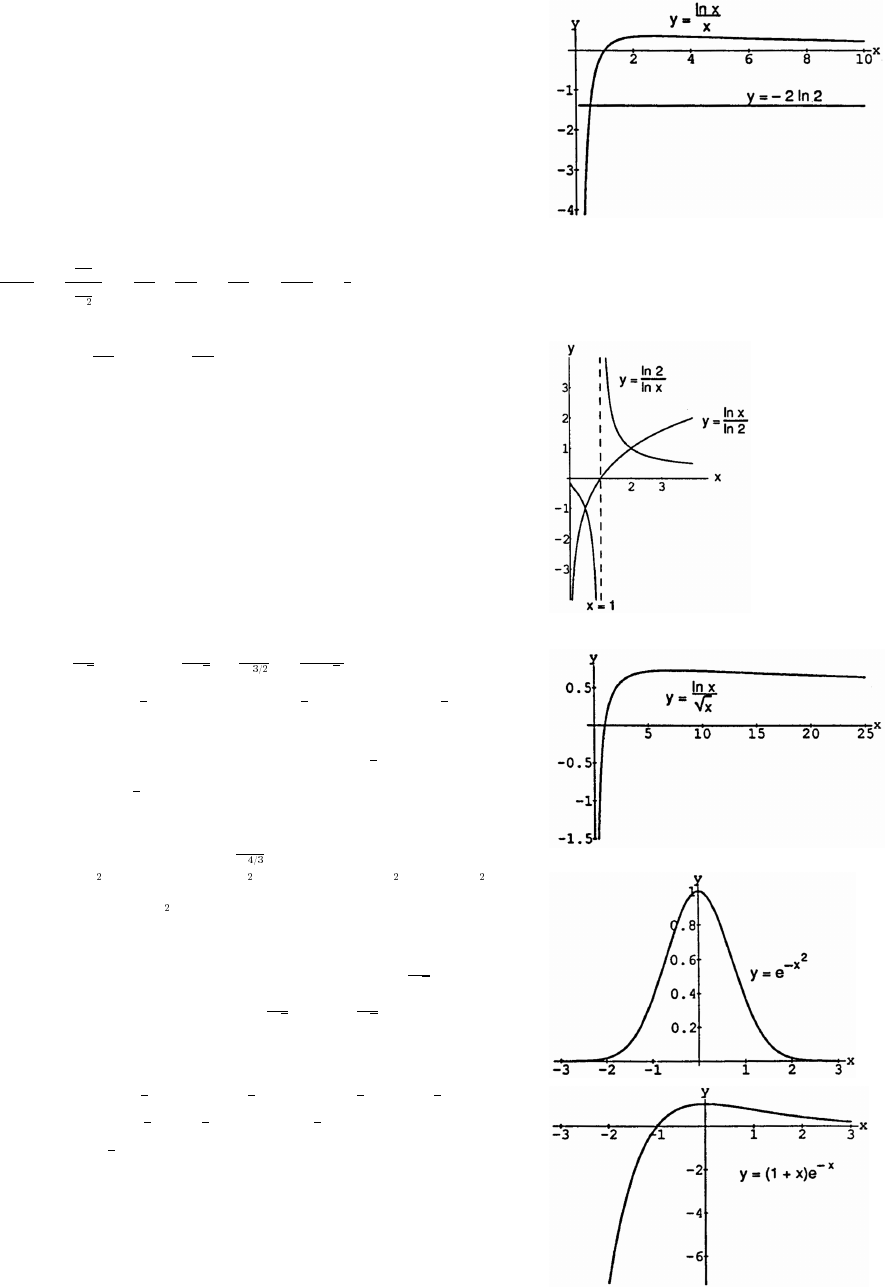
Chapter 7 Practice Exercises 487
(b) Yes, because there is only one intersection
113. log x
log x ln 4 ln x ln 4 2 ln 2
ln x ln 2 ln 2 ln 2
4
2œœ œœœ
Š‹
Š‹
ln x
ln 4
ln x
ln
†"
#
114. (a) f(x) , g(x)œœ
ln 2 ln x
ln x ln #
(b) f is negative when g is negative, positive when g is
positive, and undefined when g 0; the values of fœ
decrease as those of g increase
115. (a) y yœÊœœ
ln x ln x 2 ln x
xxx 2xx
2x
ÈÈ È
w"
y x (2 ln x) x x ln x 2 ;Êœ œ
ww &Î# &Î# &Î#
"
#
33
44
ˆ‰
solving y 0 ln x 2 x e ; y 0 for x e and
w#w#
œÊ œÊœ
and y 0 for x e a maximum of ; y 0
w# ww
Ê œ
2
e
ln x x e ; the curve is concave down onʜʜ
8
3)Î$
0 e and concave up on e ; so there is an
ˆ‰ ˆ ‰
ßß_
)Î$ )Î$
inflection point at e .
ˆ‰
)Î$ )
$
ße
(b) y e y 2xe y 2e 4x eœÊœ Êœ
w ww#xxxx
4x 2 e ; solving y 0 x 0; y 0 forœ œÊœab
# w wx
x 0 and y 0 for x 0 a maximum at x 0 ofÊ œ
w
e 1; there are points of inflection at x ; the
!"
œœ„
È2
curve is concave down for x and concave
""
ÈÈ
22
up otherwise.
(c) y (1 x) e y e (1 x) e xeœ Ê œ œ
xx xxw
y e xe (x 1) e ; solving y 0Êœ œ œ
ww wxx x
xe 0 x 0; y 0 for x 0 and y 0Ê œ Ê œ
xww
for x 0 a maximum at x 0 of (1 0) e 1;Ê œ œ
!
there is a point of inflection at x 1 and the curve isœ
concave up for x 1 and concave down for x 1.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

488 Chapter 7 Transcendental Functions
116. y x ln x y ln x x ln x 1; solving y 0œ Êœ œ œ
ww
"
ˆ‰
x
ln x 1 0 ln x 1 x e ; y 0 forʜʜʜ
" w
x e and y 0 for x e a minimum of e ln eÊ
" w " " "
at x e . This minimum is an absolute minimumœ œ
""
e
since y is positive for all x .
ww "
œ!
x
117. Since the half life is 5700 years and A(t) A e we have A e e ln (0.5) 5700kœœÊœÊœ
!!
##
"
kt 5700k 5700k
A
k . With 10% of the original carbon-14 remaining we have 0.1A A e 0.1 eÊœ œ Ê œ
ln (0.5)
5700 !!
ln 0 5 ln 0 5
5700 5700
tt
ln (0.1) t t 18,935 years (rounded to the nearest year).ʜʜ ¸
ln (0.5) (5700) ln (0.1)
5700 ln (0.5)
118. T T (T T ) e 180 40 (220 40) e , time in hours, k 4 ln 4 ln 70 40œ Ê œ Êœ œ Ê
sos
kt k 4 ˆ‰ ˆ‰
79
97
(220 40) e t 1.78 hr 107 min, the total time the time it took to cool fromœ Êœ ¸ ¸ Ê
4ln 9 7 t ln 6
4 ln ˆ‰
9
7
180° F to 70° F was 107 15 92 minœ
119. cot cot , 0 x 50 )1œ Ê œ
" "
ˆ‰ ˆ ‰
x5x d
60 3 30 dx 11
)Š‹ Š ‹
ˆ‰ Š‹
1
60 30
x
60 50 x
30
30 ; solving 0 x 200x 3200 0 x 100 20 17, butœ œÊ œÊœ „
’“ È
2d
60 x 30 (50 x) dx
"#
)
100 20 17 is not in the domain; 0 for x 20 5 17 and 0 for 20 5 17 x 50
ÈÈÈ
Š‹ Š‹
dd
dx dx
))
x 20 5 17 17.54 m maximizes Êœ ¸
Š‹
È)
120. v x ln x (ln 1 ln x) x ln x 2x ln x x x(2 ln x 1); solving 0œœœÊœœ œ
## # #
" "
ˆ‰ ˆ‰
xdxxdx
dv dv
2 ln x 1 0 ln x x e ; 0 for x e and 0 for x e a relativeʜʜʜ Ê
"
#
12 12 12
dv dv
dx dx
maximum at x e ; x and r 1 h e e 1.65 cmœœœÊœœ¸
12 12
r
hÈ
CHAPTER 7 ADDITIONAL AND ADVANCED EXERCISES
1. lim dx lim sin x lim sin b sin 0 lim sin b 0 lim sin b
b1 b1 b1 b1 b1ÄÄÄ Ä Ä
'0
bb
0
"
" " " " "
#
È1x œœœœœcd a b a b 1
2. lim tan t dt lim form
xxÄ_ Ä_
"_
"
_xx
tan t dt
'0
xœ'0
xˆ‰
lim œœ
xÄ_
tan x
1
1
#
3. y cos x ln y ln cos x and lim lim lim œÊœ œ œ
ˆ‰ ˆ‰
ÈÈ
1x ""
#xx
ln cos x sin x tan x
2x cos x x
xx xÄ! Ä! Ä!
ˆ‰ È È
ÈÈÈ È
lim lim cos x eœ œ Ê œ œ
"" "
##
xxÄ! Ä!
x secx
xe
ÈÈ
ˆ‰
È1x 12
4. y x e ln y lim ln y lim lim lim 2œ Ê œ Ê œ œ œ œab
x2x 2 ln x e 2 1 e
xxe1ee
2e 2e
ab ab
xx
xxx
xx
xx x xÄ_ Ä_ Ä_ Ä_
lim x e lim e eÊœœ
xxÄ_ Ä_
ab
xy
2x #
5. lim lim
xxÄ_ Ä_
ˆ ‰ ˆ‰ ˆ‰ ˆ‰
–—–— –—
"" " " " "
# #
n1 n n n n n
11 1
112 1n
ᜠá
Š‹ Š‹ Š‹
nn n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
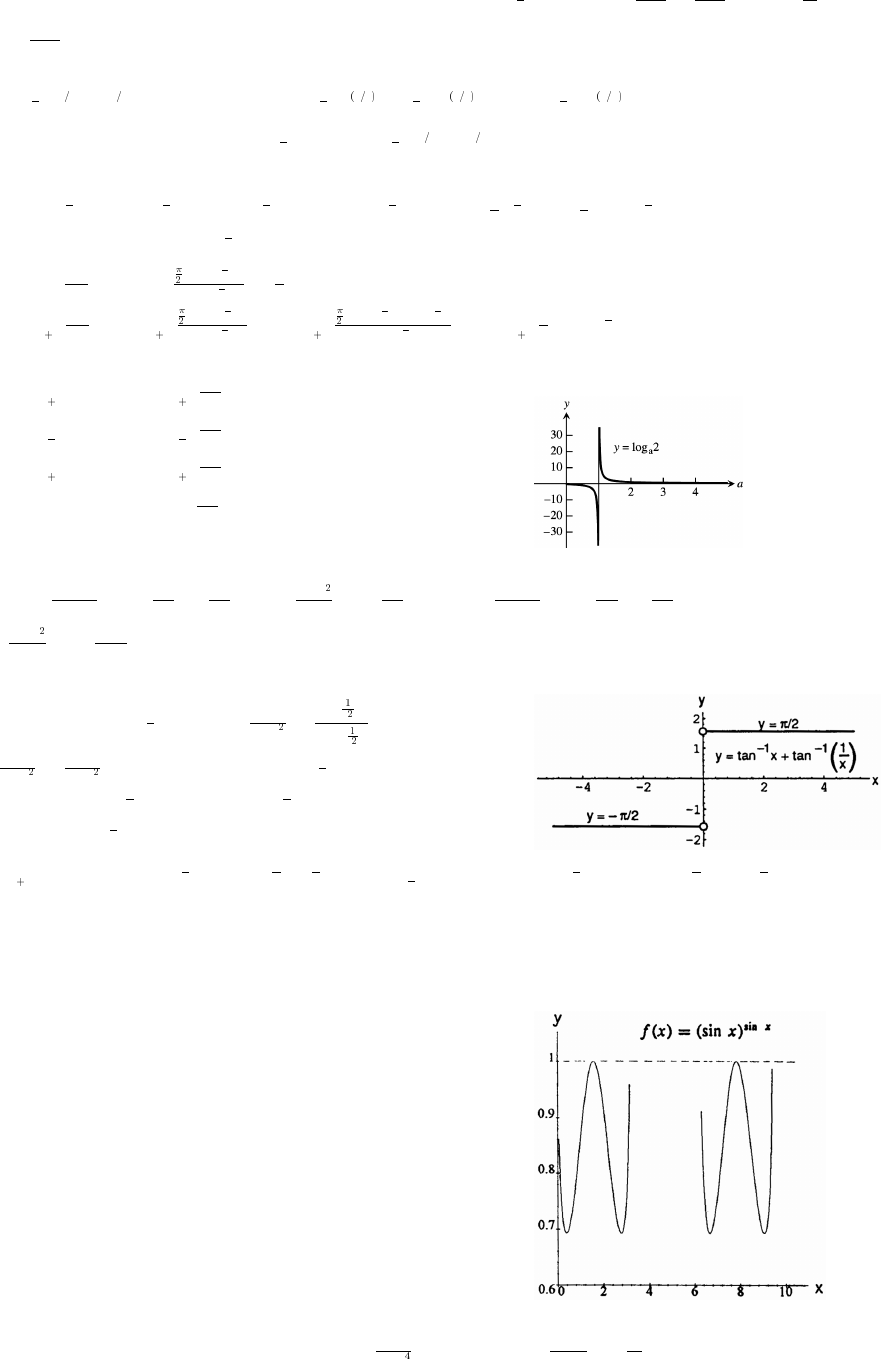
Chapter 7 Additional and Advanced Exercises 489
which can be interpreted as a Riemann sum with partitioning x lim ?œÊ á
""""
# #nn1nn
xÄ_ ˆ‰
dx ln (1 x) ln 2œœœ
'0
1"
"
!
1x cd
6. lim e e e lim e e e which can be interpreted as a
xxÄ_ Ä_
""""
nnnn
cd
‘ˆ‰ ˆ‰ ˆ‰
1n 2n 1n 21n n1n
ᜠá
Riemann sum with partitioning x lim e e e e dx e e 1?œÊ ᜠœ œ
"" "
!
nn
xÄ_ cdcd
1n 2n x x
0
1
'
7. A(t) e dx e 1 e , V(t) e dx e 1 eœœœœ œœ
''
00
tt
xx t 2x 2x 2t
t
0
t
0
cd a b
‘
111
##
(a) lim A(t) lim 1 e 1
ttÄ_ Ä_
œœab
t
(b) lim lim
ttÄ_ Ä_
V(t)
A(t) 1 e
1e
œœ
ˆ‰
#
2t
t
1
(c) lim lim lim lim 1 e
tt t tÄ! Ä! Ä! Ä!
V(t)
A(t) 1e 1e
1e 1e 1e
œœ œœ
ˆ‰ abab
ab
#
2t t t
tt
1ab
t1
8. (a) lim log 2 lim 0;
aaÄ! Ä!
aœœ
ln 2
ln a
lim log 2 lim ;
a1 a1ÄÄ
aœœ_
ln 2
ln a
lim log 2 lim ;
a1 a1ÄÄ
aœœ_
ln 2
ln 1
lim log 2 lim 0
aaÄ_ Ä_
aœœ
ln 2
ln a
(b)
9. A dx dx ; A dx dx
"#
"
#
œœ œœœœ
'' ''
11 11
ee ee
e
1
2 log x (ln x) 2 log x
x ln 2 x ln 2 ln 4 ln 4 x
2ln x 2ln x
2 4
’“
A:A 2:1œœÊœ
’“
(ln x)
2 ln ln 2
##
""#
e
1
10. y tan x tan yœ Êœ
" " w
""
ˆ‰
x1x
1
Š‹
Š‹
x
x
0 tan x tan is a constantœœÊ
"" "
" "
1x 1x x
ˆ‰
and the constant is for x 0; it is for x 0 since
11
##
tan x tan is odd. Next the
" " "
ˆ‰
x
lim tan x tan and lim tan x tan 0
xx
Ä! Ä!
‘ ˆ‰ˆ‰ˆ‰ ˆ‰
" " " "
""
## # #
œ!œ œœ
xx
11 1 1
11. ln x x ln x and ln x x ln x x ln x; then, x ln x x ln x x x ln x x x or ln x
abxx x x x x x
x
xœ œ œ œ Ê œ!Ê œ œ!Þab a b
####
ln x x ; x x x ln x 2 ln x x 2. Therefore, x x when x 2 or x .œ!Ê œ" œ Ê œ Ê œ œ œ œ"
xxx
x
#ab
xab
12. In the interval x 2 the function sin x 011
(sin x) is not defined for all values in thatÊsin x
interval or its translation by 2 .1
13. f(x) e f (x) e g (x), where g (x) f (2) eœÊ œ œ Êœ œ
gx gx x22
1x 116 17
ÐÑ w ÐÑ w w w !
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

490 Chapter 7 Transcendental Functions
14. (a) e 2x
df 2 ln e
dx e
x
œœ
x
x†
(b) f(0) dt 0œœ
'1
12 ln t
t
(c) 2x f(x) x C; f(0) 0 C 0 f(x) x the graph of f(x) is a parabola
df
dx œ Ê œ œÊ œÊ œ Ê
##
15. Triangle ABD is an isosceles right triangle with its right angle at B and an angle of measure at A. We
1
4
therefore have DAB DAE CAB tan tan .
1
43
œn œn n œ
" "
""
#
16. (a) The figure shows that ln e e ln ln e ln e
ln e ln
e
ee
Ê Ê Ê
1
1
11
11 11
(b) y y ; solving y 0 ln x 1 x e; y 0 for x e andœÊœ Ê œÊ œÊœ
ln x ln x 1 ln x
xxxxx
www
""
ˆ‰ˆ‰
y 0 for 0 x e an absolute maximum occurs at x e
wÊ œ
17. The area of the shaded region is sin x dx sin y dy, which is the same as the area of the region to
''
00
11
" "
œ
the left of the curve y sin x (and part of the rectangle formed by the coordinate axes and dashed lines y 1,œ œ
x ) . The area of the rectangle is sin y dy sin x dx, so we haveœœ
11
##
"
''
00
12
sin x dx sin x dx sin x dx sin x dx.
11
##
" "
œÊœ
'' ' '
00 0 0
122 1
18. (a) slope of L slope of L slope of L
$#"
""
Ê
bbaa
ln b ln a
(b) area of small (shaded) rectangle area under curve area of large rectangle
(b a) dx (b a) Ê Ê
"""""
bxabbaa
ln b ln a
'a
b
19. (a) g(x) h(x) 0 g(x) h(x); also g(x) h(x) 0 g( x) h( x) 0 g(x) h(x) 0 œÊ œ œÊœÊ œ
g(x) h(x); therefore h(x) h(x) h(x) 0 g(x) 0Êœ œÊœÊœ
(b) f (x);
f(x) f( x) f (x) f (x) f (x) f (x)
f (x) f ( x) f ( x)
## #
œœœ
cd
EO O
EEOEO
(x) f
E
f(x)
f(x) f( x) f (x) f (x) f (x) f (x)
f (x) f (x) f ( x) f ( x)
## #
œœœ
cdc d
EO E O EOEO O
(c) Part b such a decomposition is unique.Ê
20. (a) g(0 0) 1 g (0) g(0) 2g(0) g(0) g (0) 2g(0) g (0) g(0) 0œ Ê œ Ê œ Ê œ
g(0) g(0)
1 g(0) g(0)
#$$
cd
g(0) g (0) 1 0 g(0) 0ʜʜcd
#
(b) g (x) lim lim lim
w
œœ œ
h0 h0 h0ÄÄ Ä
g(x h) g(x) g(x) g(h) g(x) g (x) g(h)
h h h 1 g(x) g(h)
g(x)
’“ cd
g(x) g(h)
1 g(x) g(h)
lim 1 1 g (x) 1 g (x) 1 [g(x)]œœœœ
h0Ä’“’ “ cd
g(h) 1 g (x)
h 1 g(x) g(h)
## #
†
(c) 1 y dx tan y x C tan (g(x)) x C; g(0) 0 tan 0 0 C
dy dy
dx 1 y
œ Ê œ Ê œ Ê œ œ Ê œ
#"" "
C 0 tan (g(x)) x g(x) tan xÊœÊ œÊ œ
"
21. M dx 2 tan x and M dx ln 1 x ln 2 xœœœœœœÊœ
''
00
11
y
22x
1x 1x M
M
#
" #
"
!!
"
cd c dab
1y
; y 0 by symmetryœœ œ
ln 2 ln 4
ˆ‰ 1
22. (a) V dx dx ln x ln 4 ln ln 16 ln 2 ln 2œœœœœœœ1 1
''
14 14
44
Š‹ cd abkk ˆ‰
"" "
#
#%
"Î% %
Èx4x 4 4 44 4
11 1 11
(b) M x dx x dx x ;
y14 14
44
œœœœœœ
''
Š‹ ‘ˆ ‰
"""
#
"Î# $Î# %
"Î% #
Èx
1864163
23324424
M dx dx ln x ln 16 ln 2;
x14 14
44
œœœœœ
''
"" " " " " "
# #
#
%
"Î%
Š‹Š‹ ‘
kk
ÈÈ
x2x
1
8x 8 8
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
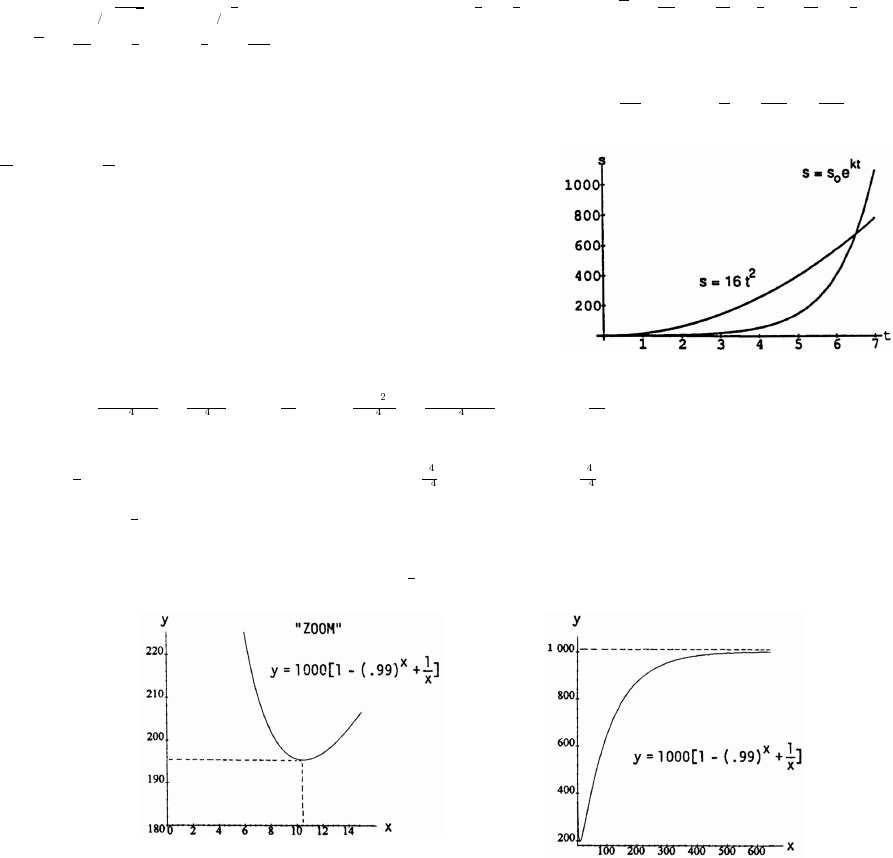
Chapter 7 Additional and Advanced Exercises 491
M dx x dx x 2 ; therefore, x andœœ œœœ œœœœ
''
14 14
44
"" "
#
"Î# "Î# %
"Î% ## #
Èx2M24314
3632217
M
‘ ˆ‰ˆ‰
y
y ln 2œœ œ
M
M33
2ln 2
xˆ‰ˆ‰
"
#
23. A(t) A e ; A(t) 2A 2A A e e 2 rt ln 2 t tœ œ Ê œ Ê œ Ê œ Êœ ʸ œ œ
!!!!
rt rt rt ln 2 .7 70 70
r r 100r (r%)
24. ks k dt ln s kt C s s e
ds ds
dt s
œÊœ Ê œÊœ
!kt
the 14th century model of free fall was exponential;Ê
note that the motion starts too slowly at first and then
becomes too fast after about 7 seconds
25. (a) L k k ; solving 0œÊœ œ
ˆ‰
Š‹
a b cot b csc dL b csc b csc cot dL
Rr R r
dd
)) )))
))
r b csc bR csc cot 0 (b csc ) r csc R cot 0; but b csc 0 sinceÊ œÊ œ Á
%# % % %
))) ))) )ab
r csc R cot 0 cos cos , the critical value of ))))) )ÁÊ œÊ œ Êœ
1
#
%% "
rr
RR
Š‹
(b) cos cos (0.48225) 61°)œ¸ ¸
" "
%
ˆ‰
5
6
26. Two views of the graph of y 1000 1 (.99) are shown below.œ
‘
x"
x
(a) At about x 11 there is a minimumœ
(b) There is no maximum; however, the curve is asymptotic to y 1000. The curve is near 1000 whenœ
x 643.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
492 Chapter 7 Transcendental Functions
NOTES:
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
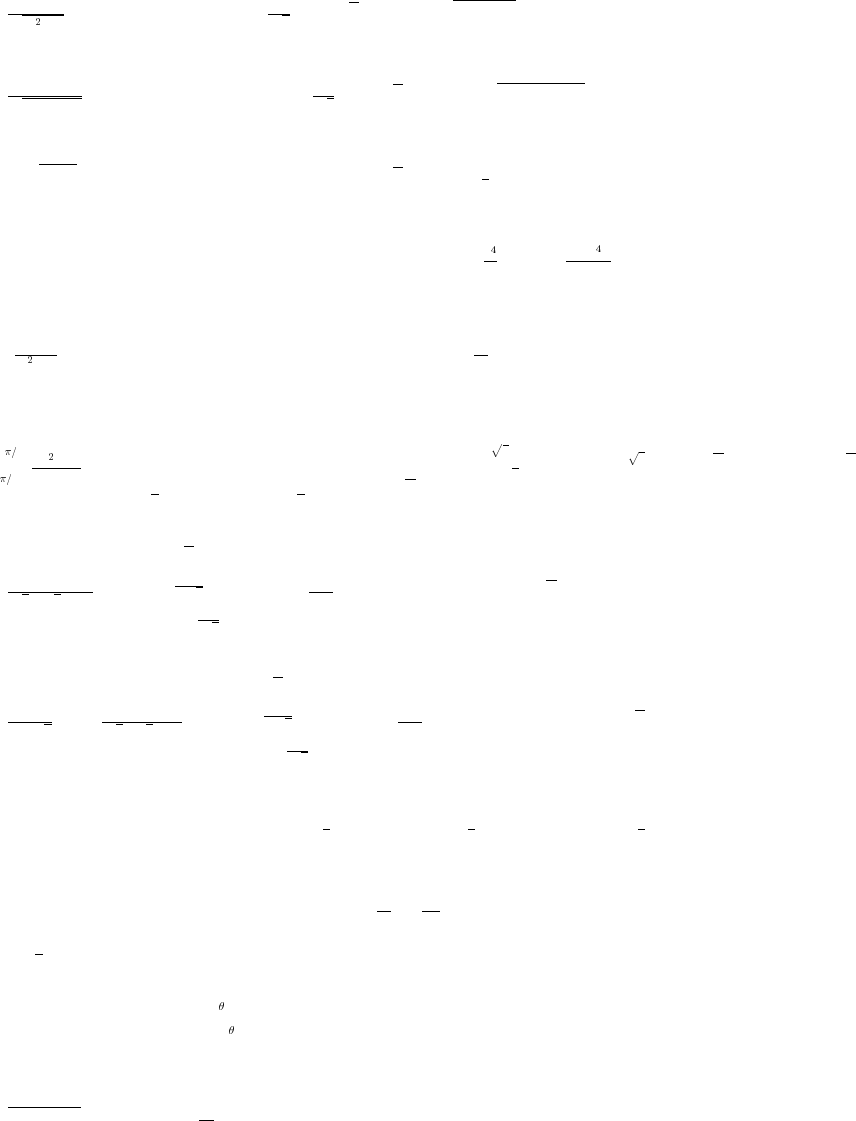
CHAPTER 8 TECHNIQUES OF INTEGRATION
8.1 BASIC INTEGRATION FORMULAS
1. ; 2 u C 2 8x 1 C
u8x 1
du 16x dx
''
16x dx du
8x 1 u
ÈÈ
##
”• ÈÈ
œ
œÄœœ
2. ; 2 u C 2 1 3 sin x C
u 1 3 sin x
du 3 cos x dx
''
3 cos x dx du
13 sin x u
ÈÈ
”•
ÈÈ
œ
œÄœœ
3. 3 sin v cos v dv; 3 u du 3 u C 2(sin v) C
usin v
du cos v dv
''
È”•
È
œ
œÄœœ†2
3$Î# $Î#
4. cot y csc y dy; u ( du) C C
u cot y
du csc y dy
''
$# $
#
”•
œ
œ Äœœ
u
44
cot y
5. ; ln u ln 10 ln 2 ln 5
u8x 2
du 16x dx
x 0 u 2, x 1 u 10
''
0 2
110
16x dx du
8x 2 u
#
"!
#
Ô×
ÕØ
cdkk
œ
œ
œÊœ œÊœ
Äœ œœ
6. ; du ln u ln 3 ln 1 ln 3
utan z
du sec z dz
z u 1, z u 3
''
4 1
3 3 3
1
sec z dz
tan z u
43
Ô×
ÖÙ
ÕØ
Ècdkk ÈÈ
œ
œ
œÊœ œÊœ
Äœœœ
#"
11
7. ; 2 ln u C 2 ln x 1 C
ux
du dx
2 du
''
dx 2 du
xx1 x
dx
x
u
ÈÈ
ˆ‰ È
È
"
#
Ô×
ÖÙ
ÖÙ
ÕØ
Èkk ˆ‰
È
œ"
œ
œ
Äœ œ
8. ; 2 ln u C 2 ln x 1 C
ux1
du dx
2 du
'' '
dx dx 2 du
xx xx1 x
dx
x
u
"
#
ÈÈÈ
ˆ‰ È
È
œÄœœ
œ
œ
œ
Ô×
ÖÙ
ÖÙ
ÕØ
Èkk ¸¸
È
9. cot (3 7x) dx; cot u du ln sin u C ln sin (3 7x) C
u37x
du 7 dx
''
Äœœ
œ
œ
”• kk k k
"" "
77 7
10. csc ( x 1) dx; csc u ln csc u cot u C
ux1
du dx
''
11
1
Ĝ
œ
œ
”• kk†du
11
"
ln csc ( x 1) cot ( x 1) Cœ
"
1kk11
11. e csc e 1 d ; csc u du ln csc u cot u C ln csc e 1 cot e 1 C
ue 1
du e d
''
)) ))
ˆ‰ ¸ ¸
”• kk ˆ‰ˆ‰
Ä œ œ
œ
œ
))
12. dx; cot u du ln sin u C ln sin (3 ln x) C
u3ln x
du
''
cot (3 ln x)
xdx
x
”• kk k k
œ
œÄœœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

494 Chapter 8 Techniques of Integration
13. sec dt; 3 sec u du 3 ln sec u tan u C 3 ln sec tan C
u
du
''
t3 tt
333
t
dt
3
–— kk¸¸
œ
œÄœœ
14. x sec x 5 dx; sec u du ln sec u tan u C
ux 5
du 2x dx
''
ab k k
”•
##""
##
Ĝ
œ
œ
ln sec x 5 tan x 5 Cœ
"
#
##
kkabab
15. csc (s ) ds; csc u du ln csc u cot u C ln csc (s ) cot (s ) C
us
du ds
''
Ä œ œ
œ
œ
111
1
”• kkk k
16. csc d ; csc u du ln csc u cot u C ln csc cot C
u
du
''
"" ""
"
)) ))
)
)
)
)–— kk
¸¸
œ
œÄ œ œ
d
17. 2xe dx; e du e e e 2 1 1
ux
du 2x dx
x 0 u 0, x ln 2 u ln 2
''
0 0
ln 2 ln 2 uuln2
ln 2
0
xÔ×
ÕØ
Ècd
œ
œ
œÊœ œ Êœ
Ä œ œ œœ
#
!
18. sin (y) e dy; e du e du e 1 e
u cos y
du sin y dy
y u 0, y u 1
'''
201
10
u
cos y uu e
e
Ô×
ÕØ
cd
œ
œ
œÊœ œÊœ
Ä œ œ œœ
1
#
!
" " "
1
19. e sec v dv; e du e C e C
utan v
du sec v dv
''
tan v u u tan v##
”•
œ
œÄœœ
20. ; 2e du 2e C 2e C
ut
du
''
e dt
tdt
2t
uu t
t
ÈÈÈ
–—
È
œ
œÄœœ
21. 3 dx; 3 du 3 C C
ux1
du dx
''
x1 u u
ln 3 ln 3
3
"
”• ˆ‰
œ
œÄœœ
x1
22. dx; 2 du C C
u ln x
du
''
222
xln ln
dx
x
u
ln x u ln x
”•
œ
œÄœœ
##
23. ; 2 du C C
uw
du
''
2 dw 2 2
wdw
wln ln
wuw
####
ÈÈ
–—
È
œ
œÄœœ
u
24. 10 d ; 10 du C C
u2
du 2 d
''
2u
10 10
ln 10 ln 10
)))
)
”• Š‹
œ
œÄœœ
""
## #
u2
25. ; 3 tan x C 3 tan 3u C
x3u
dx 3 du
''
9 du 3 dx
19u 1x
" "
”•
œ
œÄœ œ
26. ; 2 tan u C 2 tan (2x 1) C
u2x1
du 2 dx
''
4 dx 2 du
1 (2x 1) 1 u
" "
”•
œ
œÄœ œ
27. ; sin u 0
u3x
du 3 dx
x 0 u 0, x u
''
0 0
16 12
dx du
19x 1u
6
33 3618
È È
""
#
"" "
" "Î#
!
Ô×
ÕØ
‘ˆ‰
œ
œ
œÊœ œÊœ
Äœ œœ
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.1 Basic Integration Formulas 495
28. sin sin 0
'0
1dt t
4t 6
È
" "
##
"
!
"
œœœ
‘ ˆ‰1
29. ; sin u C sin s C
us
du 2s ds
''
2s ds du
1s 1u
ÈÈ
#
" " #
”•
œ
œÄœœ
30. ; sin u C sin (2 ln x) C
u 2 ln x
du
''
2 dx du
x14 lnx 1u
2 dx
x
ÈÈ
" "
”•
œ
œÄœœ
31. 5 sec 5x C 6 sec 5x C
''
6 dx 6 dx 6
x 25x 1 5x x 5
ÈÉ
" "
œœ œ
5
†kk kk
32. sec C
'dr r
rr 9 33
È
""
œ
¸¸
33. ; tan u C tan e C
ue
du e dx
'' '
dx e dx du
ee e 1 u1
xx 2x
x
" "
œÄœœ
œ
œ
”•
x
x
x
34. ; sec u C sec e C
ue
du e dy
'' '
dy e dy
e1 uu1
ee 1
du
ÈÈ
Éab
2y
y
yy
" "
œÄœœ
œ
œ
”• kk
y
y
y
35. ; sec u du ln sec u tan u
u ln x
du
x 1 u 0, x e u
'''
1
dx du
x cos (ln x) cos u
dx
x
3
e33
300
3Ô×
ÕØ
cdkk
œ
œ
œÊœ œ Êœ
Äœ œ
1
1Î$
!
ln sec tan ln sec 0 tan 0 ln 2 3 ln (1) ln 2 3œœœ
¸¸
kk
Š‹ Š‹
ÈÈ
11
33
36. ; ln 1 4u C ln 1 4 ln x C
ulnx
du ln x dx
'' '
ln x dx ln x dx du
x 4x ln x x 1 4 ln x 1 4u 8 8
2
x
#
#"" " #
œÄœœ
œ
œ
ab
”• kk a b
37. 8 ; 8 8 tan u
ux1
du dx
x 1 u 0, x 2 u
'' '
11
8 dx dx du
x 2x2 1(x1) 1u
22 1
0
" "
!
œÄœ
œ
œ
œÊœ œÊœ"
Ô×
ÕØ
cd
8 tan 1 tan 0 8 0 2œœœab
ˆ‰
" " 1
41
38. 2 ; 2 2 tan u
ux3
du dx
x2 u 1, x4 u1
'' '
22 1
44 1
2 dx dx du
x 6x10 (x3) 1 u 1
" "
"
œÄœ
œ
œ
œÊœ œÊœ
Ô×
ÕØ
cd
2 tan 1 tan ( 1) 2œœœcd
‘ˆ‰
" " 11
44
1
39. ; sin u C sin (t 2) C
ut2
du dt
'' '
dt dt du
t4t3 1(t2) 1u
ÈÈ È
" "
œÄœœ
œ
œ
”•
40. ; sin u C sin ( 1) C
u1
du d
'' '
dd du
21u
1( 1)
))
)) )
ÈÈ È
" "
œÄœœ
œ
œ
”•
)
))
41. ; sec u C sec x 1 C,
ux1
du dx
'' '
dx dx du
(x 1) x 2x (x 1) (x 1) 1 uu 1
" "
ÈÈ È
œÄœœ
œ
œ
”• kk k k
ux11kk k kœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

496 Chapter 8 Techniques of Integration
42. ; sec u C
ux2
du dx
'' '
dx dx du
(x 2) x 4x 3 (x 2) (x 2) 1 uu 1
"
ÈÈ È
œÄœ
œ
œ
”• kk
sec x 2 C, u x 2 1œ œ
" kkkkkk
43. (sec x cot x) dx sec x 2 sec x cot x cot x dx sec x dx 2 csc x dx csc x 1 dx
'' '
œ œ
## # # #
ab ab
''
tan x 2 ln csc x cot x cot x x Cœ kk
44. (csc x tan x) dx csc x 2 csc x tan x tan x dx csc x dx 2 sec x dx sec x 1 dx
'' '''
œ œ
## # # #
ab ab
cot x 2 ln sec x tan x tan x x Cœ kk
45. csc x sin 3x dx (csc x)(sin 2x cos x sin x cos 2x) dx (csc x) 2 sin x cos x sin x cos 2x dx
'' '
œœ ab
#
2 cos x cos 2x dx [(1 cos 2x) cos 2x] dx (1 2 cos 2x) dx x sin 2x Cœœœ œ
'' '
ab
#
46. (sin 3x cos 2x cos 3x sin 2x) dx sin (3x 2x) dx sin x dx cos x C
'''
œœœ
47. dx 1 dx x ln x 1 C
''
x
x1 x1
"
œ œ
ˆ‰ kk
48. dx 1 dx x tan x C
''
x
x1 x1
""
œ œ
ˆ‰
49. dx 2x dx x ln x 1 (9 ln 8) (2 ln 1) 7 ln 8
''
22
33 3
2
2x 2x
x1 x1
##
œ œœœ
ˆ‰
cdkk
50. dx (2x 3) dx x 3x ln 2x 3 (9 9 ln 9) (1 3 ln 1) ln 9 4
''
11
33
4x 7 2
2x 3 2x 3
#$
"
œ œœœ
‘
cdkk
51. dt (4t 1) dt 2t t 2 tan C
''
4t t 16t 4 t
t4 t4
#
#"
œ œ
‘ ˆ‰
52. d 1 d ln 2 5 C
''
277 5 5
25 25 3
))) ) )
))
##
#
))) ) ) )œ œ
‘
ab kk
53. dx sin x 1 x C
'''
1 x dx x dx
1x 1x 1x
" #
ÈÈÈ
œœ
È
54. dx (x 1) ln x C
'''
x2x1
2x x 1 2 x 1
dx dx
x
"Î#
È
ÈÈ
œœkk
55. dx sec x sec x tan x dx tan x sec x 1 2 ( 1) 2
''
00
44
1sin x
cos x
#Î%
!
œ œœ!œabcd
Š‹
ÈÈ
1
56. dx dx tan (2x) ln 1 4x
''
00
12 12
28x 2 8x
14x 14x 14x
" # "Î#
!
œœ
ˆ‰
cdkk
tan 1 ln 2 tan 0 ln 1 ln 2œœabab
" " 1
4
57. dx dx sec x sec x tan x dx tan x sec x C
'' ' '
dx
1sin x 1sinx cosx
(1 sin x) (1 sin x)
#
œœœ œ
ab ab
58. 1 cos x 1 cos 2 2 cos sec dx tan Cœ œ Ê œ œ œ
ˆ‰ ˆ‰
†x x dx dx x x
1cos x 2 cos
## ###
##
"
'' '
ˆ‰
x
59. d d ; ln u C ln 1 sin C
u1sin
du cos d
'' '
"
sec tan u
du
))
)) )
)
))
œÄœœ
œ
œ
”•kk k k
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.1 Basic Integration Formulas 497
60. d d ; ln u C ln 1 cos C
u1cos
du sin d
'' '
"
csc cot 1 cos u
sin du
)) )
)
)) )
)
))
œÄœœ
œ
œ
”• kk k k
61. dx dx 1 dx 1 dx 1 csc x dx
'''''
""
#
1sec x cos x1 cos x1 sinx sinx
cos x 1 cos x cos x
œ œœœ
ˆ‰ˆ‰ˆ ‰
1cscxcsc x cot x dx xcot xcsc xCœ œ
'ab
#
62. dx dx 1 dx 1 dx
''' '
""
1csc x sin x1 sin x1 (sin x1)(sin x1)
sin x sin x 1
œœœ
ˆ‰
Š‹
1 dx 1 sec x dx 1 sec x sec x tan x dx x tan x sec x Cœ œ œ œ
'' '
ˆ‰ˆ ‰
ab
1 sin x sin x
cos x cos x
##
63. dx sin dx; sin dx 2 cos 2(cos cos 0)
sin 0
for 0 2
'' '
00 0
22 2
ɸ¸ ˆ‰ ‘
”•
1cos x x x x
x
x
## ##
#
#
#
!
œÄœœ
ŸŸ11
1
( 2)( 2) 4œ œ
64. 1 cos 2x dx 2 sin x dx; 2 sin x dx 2 cos x
sin x 0
for 0 x
'' '
00 0
ÈÈÈÈ
kk”• ’“
œ Ä œ
ŸŸ1
1
!
2 (cos cos 0) 2 2œ œ
ÈÈ
1
65. 1 cos 2t dt 2 cos t dt; 2 cos t dt 2 sin t
cos t 0
for t
'' '
22 2
ÈÈÈÈ
kk”• ’“
œ Ä œ
Ÿ
ŸŸ
1
1
1
#Î#
1
2 sin sin 2œ œ
ÈÈ
ˆ‰
11
#
66. 1 cos t dt 2 cos dt; 2 cos dt 2 2 sin
cos 0
for t 0
'' '
00 0
ÈÈÈÈ
¸¸
”• ’“
œ Ä œ
ŸŸ
ttt
t
###
#!
11
22sin 0 sin 22œœ
ÈÈ
‘ˆ‰
1
#
67. 1 cos d sin d ; sin d cos cos 0 cos ( )
sin 0
for 0
'' '
00 0
Èkk cd
”•
œ Äœ œ
Ÿ
Ÿ Ÿ
#!
)) ) ) )) ) 1
)
1) 1
1 ( 1) 2œ œ
68. 1 sin d cos d ; cos d sin sin sin 1
cos 0
for
'' '
22 2
Èkk c d
”•
œ Äœœœ
Ÿ
ŸŸ
#
#Î# #
)) ) ) )) ) 1
)
)1
1
1
1
1
69. tan y 1 dy sec y dy; sec y dy ln sec y tan y
sec y 0
for y
'' '
44 4
44 4
Èkk c d
”• kk
#Î%
Î%
œ Ä œ
ŸŸ
11
1
1
44
ln 2 1 ln 2 1œ
¹¹¹¹
ÈÈ
70. sec y 1 dy tan y dy; tan y dy ln cos y ln
tan y 0
for y 0
'' '
44 4
00 0
Èkk c d
”• kk Š‹
#!
Î% "
œ Ä œ œ
Ÿ
ŸŸ
11
42
È
ln 2œÈ
71. (csc x cot x) dx csc x 2 csc x cot x cot x dx 2 csc x 1 2 csc x cot x dx
'' '
44 4
34 34 34
œ œ
## # #
abab
2 cot x x 2 csc x 2 cot 2 csc 2 cot 2 csc œ œ cd
ˆ‰ˆ‰
$Î%
Î%
1
1
11 1 11 133 3
44 4 44 4
2( 1) 2 2 2(1) 2 2 4œ œ
’“’“Š‹ Š‹
ÈÈ
3
44
111
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

498 Chapter 8 Techniques of Integration
72. (sec x 4 cos x) dx sec x 8 16 dx tan x 16x 4 sin 2x
''
00
44
œ œ
##
#
Î%
!
‘ˆ‰cd
1 cos 2x 1
tan 4 4 sin (tan 0 0 4 sin 0) 5 4œ œ
ˆ‰
11
411
#
73. cos csc (sin ) d ; csc u du ln csc u cot u C
usin
du cos d
''
))) )
))
”• kk
œ
œÄœ
ln csc (sin ) cot (sin ) Cœ kk))
74. 1 cot (x ln x) dx; cot u du ln sin u C ln sin (x ln x) C
uxln x
du 1 dx
''
ˆ‰ ”•
ˆ‰ kk k k Ä œœ
œ
œ
""
xx
75. (csc x sec x)(sin x cos x) dx (1 cot x tan x 1) dx cot x dx tan x dx
''''
œ œ
ln sin x ln cos x Cœkkkk
76. 3 sinh ln 5 dx sinh u du 6 cosh u C 6 cosh ln 5 C
uln5
2 du dx
'ˆ‰ ˆ‰
”•
x x
2
x
2
œ œ' œ œ
œ
œ'#
77. ; 12 tan u C 12 tan y C
uy
du dy
''
6 dy
y(1 y) 1 u
2y
12 du
ÈÈ
"" "
–—
ÈÈ
œ
œÄœ œ
78. ; sec u C sec 2x C
u2x
du 2 dx
'' '
dx 2 dx du
x4x 1 uu 1
2x (2x) 1
ÈÈ È
" "
œÄœœ
œ
œ
”• kk k k
79. ; 7 sec C
ux1
du dx
'' '
7 dx 7 dx 7 du u
(x1)x2x48 uu49
(x 1) (x 1) 49 77
""
ÈÈ È
œÄœ
œ
œ
”• ¸¸
†
sec Cœ
" "
¸¸
x
7
80. ; sec u C
u2x1
du 2 dx
'' '
dx dx du
(2x 1) 4x 4x (2x 1) (2x 1) 1 2u u 1
"
#
"
ÈÈ È
œÄœ
œ
œ
”• kk
sec 2x 1 Cœ
"
#
" kk
81. sec t tan (tan t) dt; tan u du ln cos u C ln sec u C ln sec (tan t) C
utan t
du sec t dt
''
##
”• kk kk k k
œ
œÄœœœ
82. csch C
'dx x
xx
ÈÈ
$
"
$
"
$
œ
¹¹
83. (a) cos d (cos ) 1 sin d ; 1 u du u C sin sin C
usin
du cos d
'' '
$# # $
"
)) ) ) ) ) )
)
))
œ Äœœ
œ
œ
ab ab
”• u
33
(b) cos d (cos ) 1 sin d 1 u du 1 2u u du u u C
'' '
&###%$
##
)) ) ) )œœœœababa b
'2u
35
sin sin sin Cœ)))
2
35
$&
"
(c) cos d cos (cos ) d 1 sin (cos ) d
'' '
*) #
%
)) ) ) ) ) ) )œœab a b
84. (a) sin d 1 cos (sin ) d ; 1 u ( du) u C
u cos
du sin d
'' '
$# #
)) ) ) ) )
))
œ Äœ
œ
œ
ab ab
”• u
3
cos cos Cœ ))
"$
3
(b) sin d 1 cos (sin ) d 1 u ( du) 1 2u u du
'' ' '
&# # #%
##
)) ) ) )œ œœab ab a b
cos cos cos Cœ)))
2
35
$&
"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
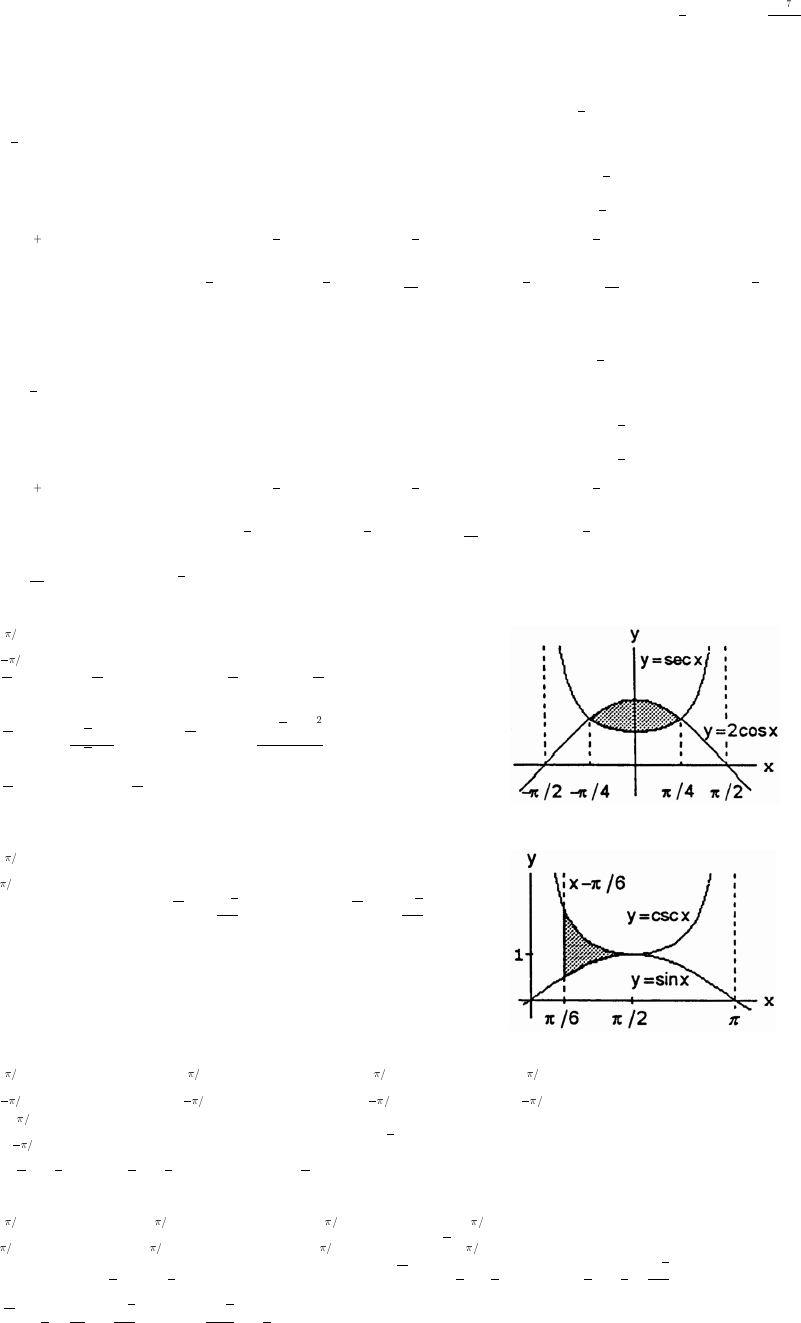
Section 8.1 Basic Integration Formulas 499
(c) sin d 1 u ( du) 1 3u 3u u du cos cos cos C
'' '
(# #%' $&
$
)) ) ) )œ œ œ ab a b 3cos
57
)
(d) sin d sin (sin ) d 1 cos (sin ) d
'' '
"$ "# # '
)) ) ) ) ) ) )œœab a b
85. (a) tan d sec 1 (tan ) d sec tan d tan d tan tan d
'' ' '
$# # #
"
#
)) ) ) ) ) )) )) ) ))œ œ œab '
tan ln cos Cœ
"
#
#))kk
(b) tan d sec 1 tan d tan sec d tan d tan tan d
'' ' ' '
&#$$#$%$
"
)) ) ) ) ) )) )) ) ))œ œ œabab 4
(c) tan d sec 1 tan d tan sec d tan d tan tan d
'' ' ' '
(#&&#&'&
"
)) ) ) ) ) )) )) ) ))œ œ œabab 6
(d) tan d sec 1 tan d tan sec d tan d ;
'' ' '
2k1 2k1 2k1 2k1
)) ) ) ) ) )) ))œ œ abab
##
u du tan d u tan d tan tan d
utan
du sec d
”•
œ
œÄ œ œ
)
)) )) )) ) ))
#""
#
'' ' '
2k 1 2k 1 2k 2k 1 2k 2k 1
2k k
86. (a) cot d csc 1 (cot ) d cot csc d cot d cot cot d
'' ' ' '
$# # #
"
#
)) ) ) ) ) )) )) ) ))œ œ œab
cot ln sin Cœ
"
#
#))kk
(b) cot d csc 1 cot d cot csc d cot d cot cot d
'' ' ' '
&#$$#$ %$
"
)) ) ) ) ) )) )) ) ))œ œ œabab 4
(c) cot d csc 1 cot d cot csc d cot d cot cot d
'' ' ' '
(#&&#& '&
"
)) ) ) ) ) )) )) ) ))œ œ œabab 6
(d) cot d csc 1 cot d cot csc d cot d ;
'' ' '
2k1 2k1 2k1 2k1
)) ) ) ) ) )) ))œ œ abab
##
u du cot d u cot d
u cot
du csc d
”•
œ
œ Ä œ
)
)) )) ))
#"
#
'' '
2k 1 2k 1 2k 2k 1
k
cot cot dœ
"
2k
2k 2k 1
)))
'
87. A (2 cos x sec x) dx 2 sin x ln sec x tan xœœ
'4
4cdkk
1
1
Î%
Î%
2 ln 21 2ln 21œ
’“’ “
ÈÈ ÈÈ
Š‹ Š‹
22 ln 22 lnœ œ
ÈÈ
Š‹
È
ÈŠ‹
È
2
21
21
21
"
22 ln3 22œ
ÈÈ
Š‹
88. A (csc x sin x) dx ln csc x cot x cos xœœ
'6
2cdkk
1
1
Î#
Î'
ln 1 0 ln 2 3 ln 2 3œ œ kk¹¹ Š‹
ÈÈ
ÈÈ
33
##
89. V (2 cos x) dx sec x dx 4 cos x dx sec x dxœœ
''''
44 44
44 44
1111
## # #
2 (1 cos 2x) dx tan x 2 x sin 2x [1 ( 1)]œ œ 1111
'4
4cd ‘
1
1
1
1
Î%
Î%
"
#
Î%
Î%
22212œœœ11111
‘ˆ‰ˆ‰ˆ ‰
11 1
44
""
## #
#
90. V csc x dx sin x dx csc x dx (1 cos 2x) dxœœ
'' ''
66 66
22 22
111
###
#
1
cot x x sin 2x 0 3 0œ œ 11cd ‘ ˆ‰
’“’ “Š‹ Š ‹
È
1
1
1111
1
1
Î#
Î' ## ## ##
""
Î#
Î' 6
3
†È
3œ œ 11
ÈŠ‹Š‹
11 1
#
2
64 86
373
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
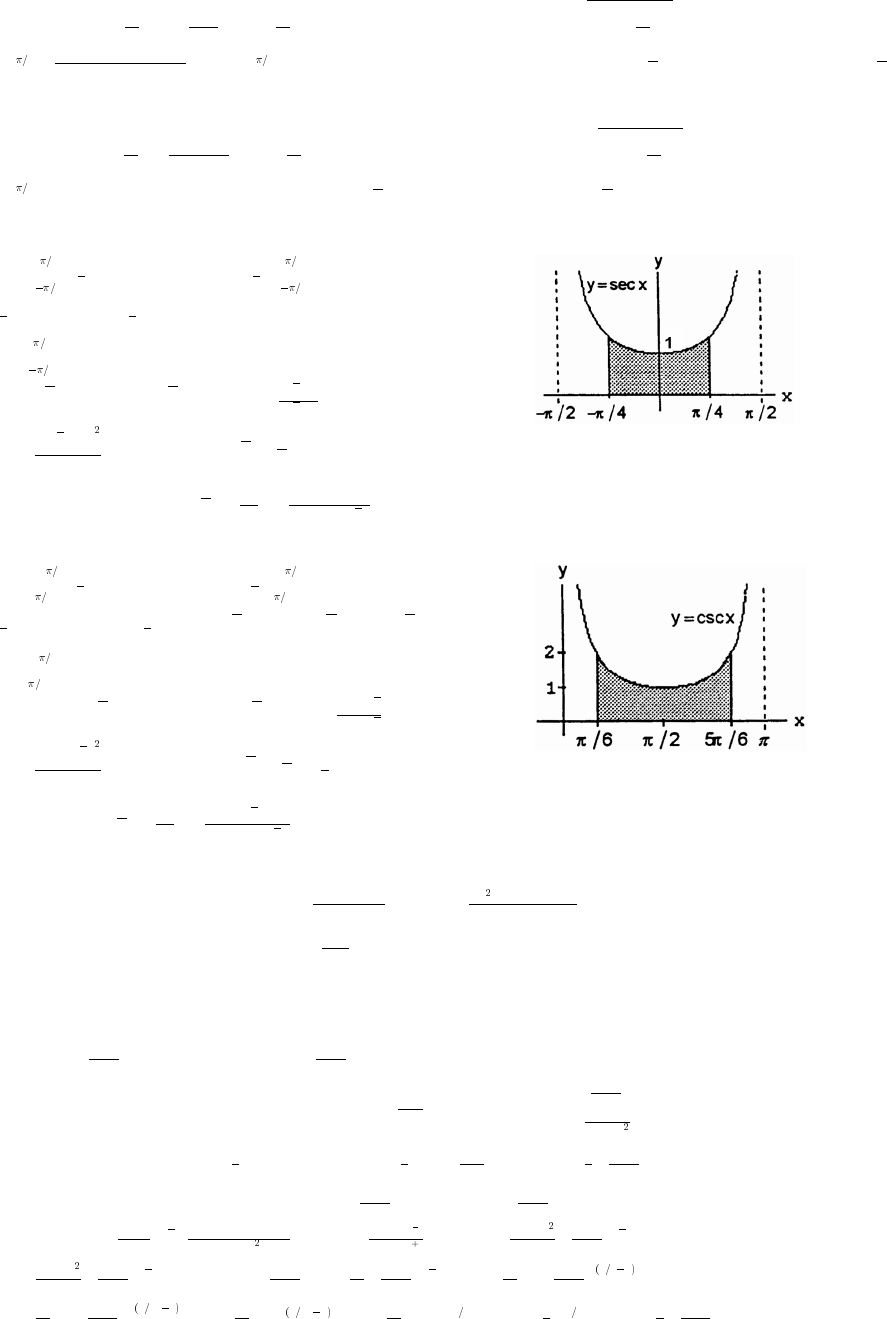
500 Chapter 8 Techniques of Integration
91. y ln (cos x) tan x sec x 1; L 1 dxœÊœÊœœœ
dy dy dy
dx cos x dx dx
sin x Š‹ Š‹
Ê
##
## 'a
b
1 sec x 1 dx sec x dx ln sec x tan x ln 2 3 ln 1 0 ln 2 3œœ œ œœ
''
00
33
Èab c d kkkk
¹¹ Š‹
ÈÈ
#Î$
!
1
92. y ln (sec x) tan x sec x 1; L 1 dxœÊœÊœœœ
dy dy dy
dx sec x dx dx
sec x tan x Š‹ Š‹
Ê
##
## 'a
b
sec x dx ln sec x tan x ln 2 1 ln 1 0 ln 2 1œ œ œ œ
'0
4cd kkkk
¹¹ Š‹
ÈÈ
1Î%
!
93. M sec x (sec x) dx sec x dx
x44
44
œœ
''
ˆ‰
""
##
#
tan x 1 ( 1) 1;œœœ
""
##
Î%
Î%
cd c d
1
1
M sec x dx ln sec x tan xœœ
'4
4cdkk
1
1
Î%
Î%
ln 2 1 ln 2 1 lnœœ
¹¹¹¹Š‹
ÈÈ È
È2
21
"
ln ln 3 2 2 ; x 0 byœœœ
Š‹
È
Š‹
È2
1
"
#
symmetry of the region, and y œœ
M
Mln 3 2 2
x"
Š‹
È
94. M csc x (csc x) dx csc x dx
x66
56 56
œœ
''
ˆ‰
""
##
#
cot x 3 3 3;œ œ œ
""
##
&Î'
Î'
cd ’“Š‹Š‹
ÈÈÈ
1
1
M csc x dx ln csc x cot xœœ
'6
56 cdkk
&Î'
Î'
1
1
ln 2 3 ln 2 3 ln œ œ
¹¹Š ‹¹¹
ÈÈ
¹¹23
23
È
È
ln 2 ln 2 3 ; x by symmetryœœœ
Š‹
È
Š‹
È
23
43
#
1
of the region, and y œœ
M
M
3
2 ln 2 3
xÈ
Š‹
È
95. csc x dx (csc x)(1) dx (csc x) dx dx;
'''
œœ œ
'ˆ‰
csc x cot x csc x csc x cot x
csc x cot x csc x cot x
ln u C ln csc x cot x C
u csc x cot x
du csc x cot x csc x dx
”•
ab kk k k
œ
œ Äœœ
#
'du
u
96. x 1 (x 1) (x 1)(x 1) (x 1) (x 1) (x 1) (x 1) (x 1)cdcdab ‘
# # #Î$ %Î$ # #Î$ #Î$
#Î$ #Î$
œœœ
(x 1) (x 1) 1œ œ
# #
#Î$ #Î$
ˆ‰ ˆ ‰
x1 2
x1 x1
(a) x 1 (x 1) dx (x 1) 1 dx; u
du dx
''
cdab ˆ‰–—
##
#Î$
#Î$ "
"
œ œ
œ
2
x1
x1
(x 1)
(1 2u) du (1 2u) C 1 C CÄ œ œ œ
'#Î$ "Î$
###
"Î$ "Î$
3323x1
x1 x 1
ˆ‰ ˆ‰
(b) x 1 (x 1) dx (x 1) dx; u
''
cdab ˆ‰ ˆ‰
##
#Î$
#Î$
œ œ
x1 x1
x1 x1
k
du k dx 2k dx; dx duÊœ œ œ
ˆ‰ ˆ‰
x1 x1
x 1 (x 1) (x 1) k x 1
(x 1) (x 1) (x 1) (x 1)
#
k1 k1
cd k1
k1
du; then, du duœœ
(x 1)
2k x1 x1 kx1 k x1
x1 x1 x1 x1
""
##
#Î$
ˆ‰ ˆ‰ ˆ‰ ˆ‰
1k 1k 13k
''
du u du (3k) u C u C Cœœœœœ
" " "
# # # # #
"Î$
kx1 k k x1
x1 3 3x1
'ˆ‰ ˆ‰
k13k 1 13k 1 13k 13k
'
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.2 Integration by Parts 501
(c) x 1 (x 1) dx (x 1) dx;
''
cdab ˆ‰
##
#Î$
#Î$
œ x1
x1
du;
utanx
xtan u
dx
Ô×
ÕØ ˆ‰ˆ‰ ˆ ‰
œ
œ
œ
Ĝ
"
" "
#Î$ #Î$
du
cos u
(tan u1) tan u1 cosu (sin ucos u) sin ucos u
tan u 1 du sin u cos u
''
sin u cos u sin u sin u 2 sin cos u
sin u cos u sin u sin u 2 cos sin u
–—
ˆ‰ ˆ‰
ˆ‰ ˆ‰ ’“
œ œ
œ œ Ä
111
111
#
#
"
44
44 2 cos u cos
sin u
'ˆ‰ ˆ‰
ˆ‰
4
4
u
#Î$
4
du
tan u sec u du tan u C Cœœœ
"
###
#Î$ # "Î$ "Î$
'ˆ‰ˆ‰ ˆ‰ ’“
11 1
4 4 4 1 tan u tan
33
tan u tan 4
4
Cœ
3x1
x1#
"Î$
ˆ‰
(d) u tan x tan u x tan u x dx 2 tan u du du ;œÊœÊœÊœ œœ
" # "
ÈÈ ˆ‰
cos u cos u cos u
2 sin u 2d(cos u)
x1tanu1 ; x1tanu1 ;œ œ œ œ œ œ
##
"sin u cos u 1 2 cos u cos u sin u
cos u cos u cos u cos u
(x 1) (x 1) dx
''
œ
#Î$ %Î$ "
ab
ab ab
12 cosu
cos u cos u
2d(cos u)
cos u
††
1 2 cos u ( 2) cos u d(cos u) 1 2 cos u d 1 2 cos uœ œ
'ab abab
###
#Î$ #Î$
"
#
†† † †
'
12 cosu C C Cœ œ œ
333x1
x1###
#"Î$
"Î$
"Î$
ab–— ˆ‰
Š‹
Š‹
12 cosu
cos u
cos u
(e) u tan tan u x 1 2(tan u 1) dx 2d(tan u);œÊœÊœÊœœ
"
##
ˆ‰
x1 x1 2 du
cos u
(x 1) (x 1) dx (tan u) (tan u 1) 2 2 d(tan u)
''
œ
#Î$ %Î$ #Î$ %Î$ #
†††
1d1 1 C1Cœ œ œ
"" " "
# # #
#Î$ "Î$ "Î$
'ˆ‰ˆ‰ˆ‰ ˆ‰
tan u1 tan u1 tan u1 x1
332
Cœ
3x1
x1#
"Î$
ˆ‰
(f)
u cos x
x cos u
dx sin u du
Ô×
ÕØ
œ
œ
œ
Ä œ
"
''
sin u du sin u du
cos u 1 (cos u 1) sin u 2 cos
Éab ab
ˆ‰
u
œ œ œ
'''
du du du
(sin u) 2 cos 2 sin cos
cos
sin cos
ˆ‰ ˆ‰ˆ‰ ˆ‰
uuu
u
uu
"
#
"Î$
Š‹
tan d tan tan C tan C Cœ œ œ œ
'"Î$ #Î$ #
##### # #
"Î$ "Î$
ˆ‰ˆ ‰ ˆ ‰ ˆ ‰
uu3u3 u 3cos u1
cos u 1
Cœ
3x
x1#
" "Î$
ˆ‰
(g) x 1 (x 1) dx;
ucoshx
x cosh u
dx sinh u
''
cdab Ô×
ÕØ
##Î$
"
Ä
œ
œ
œ
sinh u du
cosh u 1 (cosh u 1)
Éab
œœœ
'' '
sinh u du du du
sinh u (cosh u 1) (sinh u) 4 cosh sinh cosh
Èab ÉÉ
ˆ ‰ ˆ‰ ˆ‰
"
#
uuu
tanh d tanh tanh C C Cœ œ œ œ
'ˆ‰ˆ‰ˆ‰ ˆ ‰ ˆ‰
u u 3 u 3 cosh u 1 3 x 1
coshu1 x1##### #
"Î$ #Î$
"Î$ "Î$
8.2 INTEGRATION BY PARTS
1. u x, du dx; dv sin dx, v 2 cos ;œœ œ œ
xx
##
x sin dx 2x cos 2 cos dx 2x cos 4 sin C
''
xxx xx
### ##
œ œ
ˆ ‰ ˆ‰ ˆ‰
2. u , du d ; dv cos d , v sin ;œœ œ œ)) 1)) 1)
"
1
cos d sin sin d sin cos C
''
) 1) ) 1) 1) ) 1) 1)œ œ
))
11 11
""
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
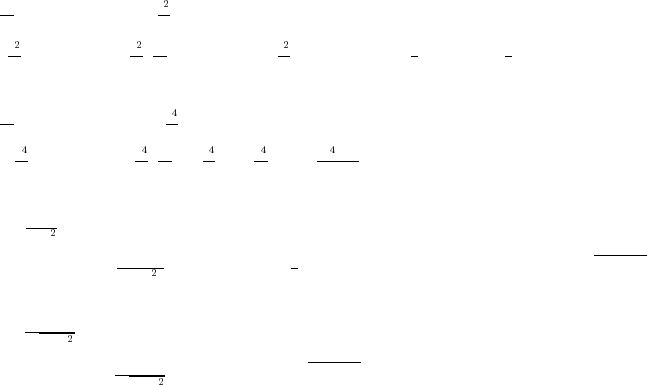
502 Chapter 8 Techniques of Integration
3. cos t
tsin t
#ïïïïî
ÐÑ
2t cos tïïïïî
ÐÑ
2 sin tïïïïî
ÐÑ
0 t cos t dt t sin t 2t cos t 2 sin t C
'##
œ
4. sin x
x cos x
#ïïïïî
ÐÑ
2x in xsïïïïî
ÐÑ
2 cos xïïïïî
ÐÑ
0 x sin x dx x cos x 2x sin x 2 cos x C
'##
œ
5. u ln x, du ; dv x dx, v ;œœœœ
dx x
x#
x ln x dx ln x 2 ln 2 2 ln 2 ln 4
''
11
22
œ œœœ
’“ ’“
xxdxx 33
x4 44
##
##
""
6. u ln x, du ; dv x dx, v ;œœœ œ
dx x
x4
$
x ln x dx ln x
''
11
ee
ee
11
$
œœœ
’“ ’“
x x dx e x 3e 1
4 4 x 4 16 16
7. u tan y, du ; dv dy, v y;œœœœ
"
dy
1y
tan y dy y tan y y tan y ln 1 y C y tan y ln 1 y C
''
" " " # "
#
"#
œœœ
y dy
1yab ab È
8. u sin y, du ; dv dy, v y;œœ œœ
"
dy
1y
È
sin y dy y sin y y sin y 1 y C
''
" " "
#
œœ
y dy
1y
ÈÈ
9. u x, du dx; dv sec x dx, v tan x;œœ œ œ
#
x sec x dx x tan x tan x dx x tan x ln cos x C
''
#œ œ kk
10. 4x sec 2x dx; [y 2x] y sec y dy y tan y tan y dy y tan y ln sec y C
'''
##
œÄ œ œ kk
2x tan 2x ln sec 2x Cœ kk
11. ex
x e
$ïïïïî
ÐÑ x
3x e
#ïïïïî
ÐÑ x
6x eïïïïî
ÐÑ x
6 eïïïïî
ÐÑ x
0 x e dx x e 3x e 6xe 6e C x 3x 6x 6 e C
'$$# $#xxxxx x
œ œab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.2 Integration by Parts 503
12. e p
p e
%ïïïïî
ÐÑ p
4p
e
$ïïïïî
ÐÑ p
12p e
#ïïïïî
ÐÑ p
24p eïïïïî
ÐÑ p
24 eïïïïî
ÐÑ p
0 p e dp p e 4p e 12p e 24pe 24e C
'%%$#pppppp
œ
p 4p 12p 24p 24 e Cœ ab
%$ # p
13. ex
x 5x e
# ïïïïî
ÐÑ x
2x 5 e ïïïïî
ÐÑ x
2 eïïïïî
ÐÑ x
0 x 5x e dx x 5x e (2x 5)e 2e C x e 7xe 7e C
'ab ab
## #
œœ
xxxxxxx
x7x7eCœ ab
#x
14. er
r r 1 e
# ïïïïî
ÐÑ r
2r 1 e ïïïïî
ÐÑ r
2 eïïïïî
ÐÑ r
0 r r 1 e dr r r 1 e (2r 1) e 2e C
'abab
##
œ
rrrr
r r 1 (2r 1) 2 e C r r 2 e Cœ œ cdabab
##rr
15. ex
x e
&ïïïïî
ÐÑ x
5x e
%ïïïïî
ÐÑ x
20x e
$ïïïïî
ÐÑ x
60x e
#ïïïïî
ÐÑ x
120x eïïïïî
ÐÑ x
120 ee ïïïïî
ÐÑ x
0 x e dx x e 5x e 20x e 60x e 120xe 120e C
'& &%$#x xxxx xx
œ
x 5x 20x 60x 120x 120 e Cœ ab
&%$# x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

504 Chapter 8 Techniques of Integration
16. e4t
t e
#"
ïïïïî
ÐÑ
4
4t
2t eïïïïî
ÐÑ "
16
4t
2 eïïïïî
ÐÑ "
64
4t
0 t e dt e e e C e e e C
'#"
#
4t 4t 4t 4t 4t 4t 4t
œœ
t2t2 tt
41664 483
eCœ
Š‹
tt
483
"
#
4t
17. sin 2)
cos 2))
#"
ïïïïî
ÐÑ
2
2 sin 2))ïïïïî
ÐÑ "
4
2 cos 2ïïïïî
ÐÑ "
8)
0 sin 2 d cos 2 sin 2 cos 2
'0
2
))) ) ) )
#
##
"Î#
!
œ
’“
)) 1
4
(1) 0 (1) 0 0 1œ œ œ
’“
‘
11 11
844 488
4
††† †
"""
#
18. cos 2x
x sin 2x
$"
ïïïïî
ÐÑ
2
3x cos 2x
#"
ïïïïî
ÐÑ
4
6x sin 2xïïïïî
ÐÑ "
8
6 os 2x cïïïïî
ÐÑ "
16
0 x cos 2x dx sin 2x cos 2x sin 2x cos 2x
'0
2$
#
Î#
!
œ
’“
x3x 3x3
448
1
0 ( 1) 0 ( 1) 0 0 0 1œ œ œ
’“
‘
11 1 1 1
16 16 8 8 8 16 4 16
333 333
34
†† †† † ab
19. u sec t, du ; dv t dt, v ;œœœœ
"
#
dt t
tt 1
È
t sec t dt sec t 2
'''
23 23 23
222
" "
##
#
#Î $
œ œ
’“ Š‹ ˆ‰
t t dt 2 t dt
tt 1 2t 1
336
ÈÈÈ
††
11
t1 3 1 3œœœœœ
55455
99393939
33533
11 11
1
’“ Š ‹Š‹
ÈÈÈ
É
"" "
## #
##
#Î $
ÈÈÈÈ
20. u sin x , du ; dv 2x dx, v x ;œœœœ
" # #
ab 2x dx
1x
È
2x sin x dx x sin x x
'''
000
12 12 12
" # # " # #
"Î #
!
"
#
ab c dab ˆ‰ˆ‰
œœ
ÈÈÈ
ˆ‰
†2x dx
1x 21x
6
d1 x
1
1x 1œ œ œ
11
1
1141
36312
###
%"Î #
!
’“
ÈÉ
ÈÈ
21. I e sin d ; u sin , du cos d ; dv e d , v e I e sin e cos d ;œœœœœÊœ
''
)) ) )) ) ) ))cd
u cos , du sin d ; dv e d , v e I e sin e cos e sin dcd
Š‹
œœ œœÊœ)))) ))))
'
e sin e cos I C 2I e sin e cos C I e sin e cos C, where C isœÊœÊœ œ)) )) ))
ww
"
##
ababC
another arbitrary constant
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
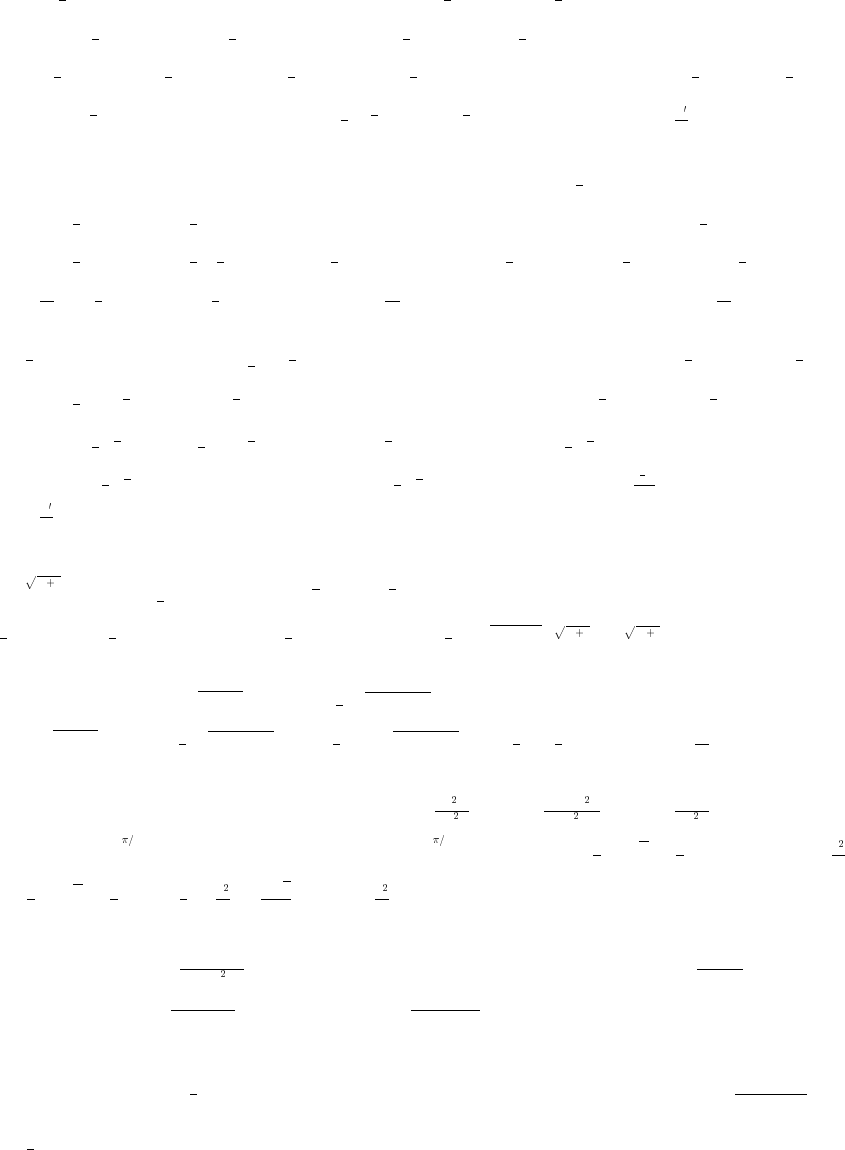
Section 8.2 Integration by Parts 505
22. I e cos y dy; u cos y, du sin y dy; dv e dy, v eœœœœœ
'yyy
cd
I e cos y e ( sin y) dy e cos y e sin y dy; u sin y, du cos y dy;Êœ œ œ œ
yy yy
''
ab c
dv e dy, v e I e cos y e sin y e cos y dy e cos y e sin y I Cdab
Š‹
œ œ Ê œ œ
yy y y y yy
'w
2I e (sin y cos y) C I e sin y e cos y C, where C is another arbitrary constantÊœ Êœ œ
yyyw"
##
ab
C
23. I e cos 3x dx; u cos 3x; du 3 sin 3x dx, dv e dx; v eœœœœœ
'2x 2x 2x
‘
"
#
I e cos 3x e sin 3x dx; u sin 3x, du 3 cos 3x, dv e dx; v eÊœ œ œ œ œ
" "
## #
2x 2x 2x 2x
3'‘
I e cos 3x e sin 3x e cos 3x dx e cos 3x e sin 3x I CÊœ œ
"" "
#### #
w
2x 2x 2x 2x 2x
33 39
44
Š‹
'
I e cos 3x e sin 3x C (3 sin 3x 2 cos 3x) C, where C CÊœ Ê œ
13 3 e 4
4 4 13 13
"
#
ww
2x 2x 2x
24. e sin 2x dx; [y 2x] e sin y dy I; u sin y, du cos y dy; dv e dy, v e
''
2x y yy
œÄ œœ œ œ œ
"
#cd
I e sin y e cos y dy u cos y, du sin y; dv e dy, v eÊœ œ œ œ œ
"
#Š‹
cd
yy yy
'
I e sin y e cos y e ( sin y) dy e (sin y cos y) I CÊœ œ
"" "
## #
w
yy y y
Š‹
ab
'
2I e (sin y cos y) C I e (sin y cos y) C (sin 2x cos 2x) C, whereÊ œ Ê œ œ
""
#
w
yy
44
e2x
CœC
#
25. e ds; e x dx xe dx; u x, du dx; dv e dx, v e ;
3s 9 x
ds x dx
'''
3s 9 x x x x
”• cd
œ
œÄœ œœœœ
#
2
3
22
33
†
xe dx xe e dx xe e C 3s 9 e e C
22 2 2
33 3 3
'Š‹ Š ‹
ab È
xxx xx 3s93s9
œ œœ
'
26. u x, du dx; dv 1 x dx, v (1 x) ;œœ œ œ
ÈÈ
2
3$
x 1 x dx (1 x) x (1 x) dx (1 x)
''
00
11
È‘ ‘
ÈÈ
œ œ œ
22 224
33 3515
$$
"
!!
&Î# "
27. u x, du dx; dv tan x dx, v tan x dx dx dx dxœœ œ œ œ œ œ
## "
''' ''
sin x cos x dx
cos x cos x cos x
tan x x; x tan x dx x(tan x x) (tan x x) dx 3 ln cos xœ œ œ
''
00
33
#Î$
!#
Î$
!
cd kk
Š‹’ “
È
111 1
33
x
3 ln ln 2œœ
11 1 1
1
33 183 18
3
Š‹
È"
#È
28. u ln x x , du ; dv dx, v x; ln x x dx x ln x x x dxœ œ œ œ œ ab ab ab
'
###
"
(2x 1) dx
xx x(x 1)
2x
'†
x ln x x x ln x x dx x ln x x 2x ln x 1 Cœ œ œab ab ab kk
## #
"
''
(2x 1) dx 2(x 1)
x1 x1
29. sin (ln x) dx; du dx (sin u) e du. From Exercise 21, (sin u) e du e C
u ln x
dx e du
'''
Ô×
ÕØ ˆ‰
œ
œÄ œ
œ
"
#x
sin u cos u
u
uuu
x cos (ln x) x sin (ln x) Cœ
"
#cd
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

506 Chapter 8 Techniques of Integration
30. z(ln z) dz; du dz e u e du e u du;
u ln z
dz e du
'''
###
"
Ô×
ÕØ
œ
œÄ œ
œ
z
uu 2u
u
†† †
e
2u
u e
#"
ïïïïî
ÐÑ
2
2u
2u
eïïïïî
ÐÑ "
4
2u
2 eïïïïî
ÐÑ "
8
2u
0 u e du e e e C 2u 2u 1 C
'##
##
"
2u 2u 2u 2u
œ œ
uu e
44
2u cd
2(ln z) 2 ln z 1 Cœ
z
4cd
#
31. (a) u x, du dx; dv sin x dx, v cos x;œœ œ œ
S x sin x dx [ x cos x] cos x dx [sin x]
"!!
œœœœ
''
00
11
11
(b) S x sin x dx [ x cos x] cos x dx 3 [sin x] 3
###
œ œ œ œ
''
22
”•
cd
11
11
11
(c) S x sin x dx [ x cos x] cos x dx 5 [sin x] 5
$$$
##
œœœœ
''
22
33
11
11
11
(d) S ( 1) x sin x dx ( 1) [ x cos x] [sin x]
8" œ œ
n1 n1 n1 n1
n
n1
nn
'cd
( 1) (n 1) ( 1) n ( 1) 0 (2n 1)œ œ
n1 n n1
cd11 1
32. (a) u x, du dx; dv cos x dx, v sin x;œœ œ œ
S x cos x dx [x sin x] sin x dx [cos x] 2
"##
œ œ œ œ
''
22
32 32
32 32
2 2
”•
ˆ‰
311 1
(b) S x cos x dx [x sin x] sin x dx [cos x] 4
###
œœœœ
''
32 32
52 52
2 2
2 2
‘ˆ‰
5311 1
(c) S x cos x dx [x sin x] sin x dx [cos x] 6
$##
œ œ œ œ
''
52 52
72 72
2 2
2 2
”•
ˆ‰
7511 1
(d) S ( 1) x cos x dx ( 1) [x sin x] sin x dx
nnnn
2n12 2n12
2n 1 2 2n 1 2
n1 2
2n 1 2
œ œ
''
”•
( 1) ( 1) ( 1) [cos x] (2n 2n ) 2nœ œ œ
nn n1
n1 2
2n 1 2
’“
(2n 1) (2n 1)
## #
"
11 11 11 1
33. V 2 (ln 2 x) e dx 2 ln 2 e dx 2 xe dxœœ
'''
000
ln 2 ln 2 ln 2
xxx
111
(2 ln 2) e 2 xe e dxœ11cd c d
Œ
xxx
ln 2 ln 2
00
0
ln 2
'
2 ln 2 2 2 ln 2 e 2 ln 2 2 2 (1 ln 2)œ œœ11 111
ˆ‰
cd
xln 2
0
34. (a) V 2 xe dx 2 xe e dxœœ
''
00
11
xxx
11
Œ
cd
"
!
2e2 1œ œ11
Š‹
cd ˆ‰
"""
"
!
eee
x
2œ14
e
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
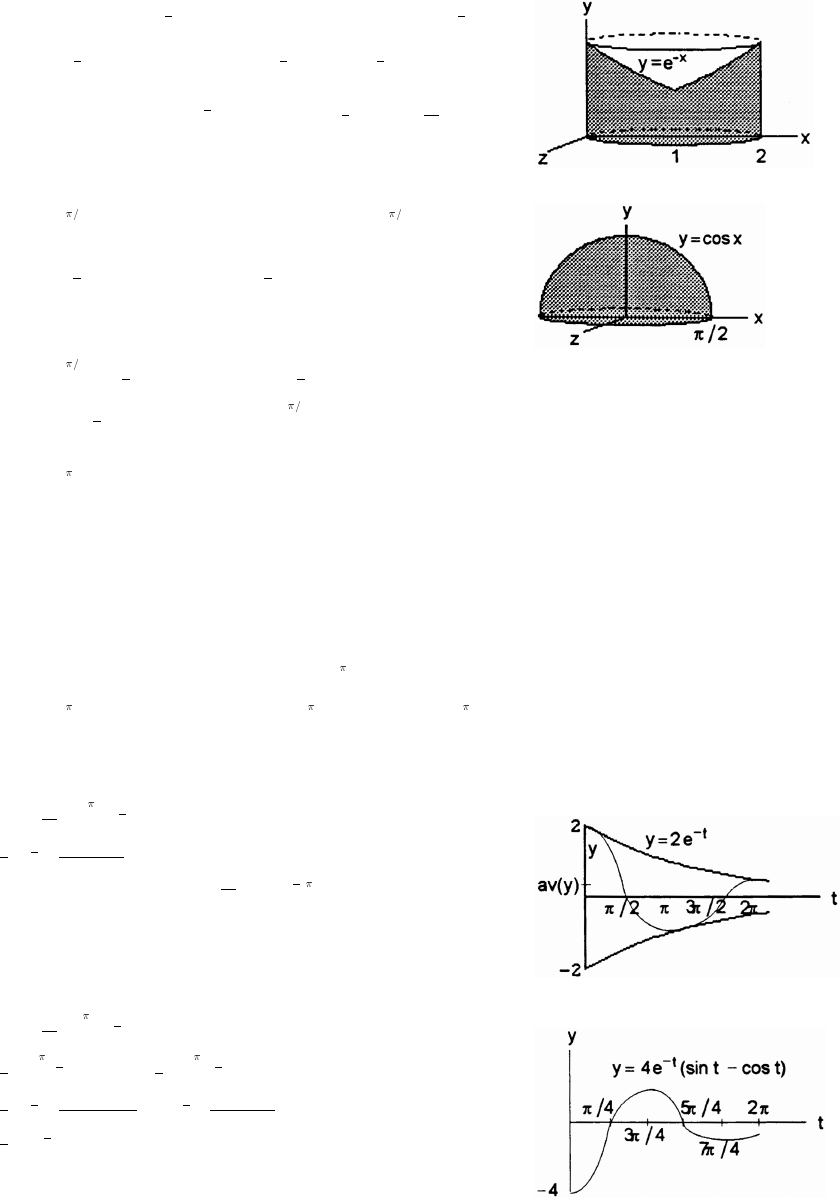
Section 8.2 Integration by Parts 507
(b) V 2 (1 x)e dx; u 1 x, du dx; dv e dx,œ œœœ
'0
1xx
1
v e ; V 2 (1 x) e e dxœ œ
xxx
0
1
1”•
cdab
"
!'
2[01(1)] e 21 1œ œœ11
’“
cd ˆ‰
x"
!"
ee
21
35. (a) V 2 x cos x dx 2 [x sin x] sin x dxœœ
''
00
22
11
Œ
1Î#
!
2 [cos x] 2 0 1 ( 2)œ œœ1111
Š‹
ˆ‰
11
1
##
Î#
!
(b) V 2 x cos x dx; u x, du dx; dv cos x dx, v sin x;œ œœœ œ
'0
2
1ˆ‰
11
##
V 2 x sin x 2 sin x dx 0 2 [ cos x] 2 (0 1) 2œ œ œœ11111
‘ˆ‰
111
#
Î#
!
Î#
!
'0
2
36. (a) V 2 x(x sin x) dx;œ'0
1
sin x
x cos x
#ïïïïî
ÐÑ
2x in xsïïïïî
ÐÑ
2 cos xïïïïî
ÐÑ
0 V 2 x sin x dx 2 x cos x 2x sin x 2 cos x 2 4Êœ œ œ 11 11
'0
## #
!
cdab
1
(b) V 2 ( x)x sin x dx 2 x sin x dx 2 x sin x dx 2 [ x cos x sin x] 2 8œ œ œ
'''
000
11 1 1 1 1 1
### $
!
1ab
8œ1
37. av(y) 2e cos t dtœ"
#1'0
2t
eœ"
#
#
!
1
1
‘ˆ‰
tsin t cos t
(see Exercise 22) av(y) 1 eʜ
"
#1ab
2
38. av(y) 4e (sin t cos t) dtœ
"
#1'0
2t
e sin t dt e cos t dtœ
22
11
''
00
22
tt
eeœ
2 sin t cos t sin t cos t
1
1
‘ˆ‰ˆ‰
tt
##
#
!
e sin t 0œ œ
2
1
1
cd
t#
!
39. I x cos x dx; u x , du nx dx; dv cos x dx, v sin xœœœœœ
'nnn
cd
"
I x sin x nx sin x dxʜ
nn
'"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

508 Chapter 8 Techniques of Integration
40. I x sin x dx; u x , du nx dx; dv sin x dx, v cos xœœœœœ
'nnn
cd
"
I x cos x nx cos x dxʜ
nn
'"
41. I x e dx; u x , du nx dx; dv e dx, v eœœœœœ
'nax n n ax ax
a
‘
" "
I e x e dx, aÊœ Á!
xe n
aa
ax n ax
nax '"
42. I ln x dx; u ln x , du dx; dv dx, v xœœœœ"œ
'ab ab
’“
nnnln x
x
ab
n
I x ln x n ln x dxʜ ab ab
nn
'"
43. sin x dx x sin x sin y dy x sin x cos y C x sin x cos sin x C
''
" " " " "
œ œœ ab
44. tan x dx x tan x tan y dy x tan x ln cos y C x tan x ln cos tan x C
''
" " " " "
œ œœ kk k kab
45. sec x dx x sec x sec y dy x sec x ln sec y tan y C
''
" " "
œ œkk
x sec x ln sec sec x tan sec x C x sec x ln x x 1 Cœ œ
" " " " #
kkabab ¹¹
È
46. log x dx x log x 2 dy x log x C x log x C
''
22 2 2
y
œœœ
2x
ln ln
y
##
47. Yes, cos x is the angle whose cosine is x which implies sin cos x 1 x .
" " #
ab
È
œ
48. Yes, tan x is the angle whose tangent is x which implies sec tan x 1 x .
" " #
ab
È
œ
49. (a) sinh x dx x sinh x sinh y dy x sinh x cosh y C x sinh x cosh sinh x C;
''
" " " " "
œ œœ ab
check: d x sinh x cosh sinh x C sinh x sinh sinh x dxcdabab’“
" " " "
"
œ
x
1x 1x
ÈÈ
sinh x dxœ"
(b) sinh x dx x sinh x x dx x sinh x 1 x 2x dx
'' '
" " " #
""
#
"Î#
œ œ
Š‹ ab
È1x
x sinh x 1 x Cœ
" # "Î#
ab
check: d x sinh x 1 x C sinh x dx sinh x dx
’“’“
ab
" # " "
"Î#
œ œ
xx
1x 1x
ÈÈ
50. (a) tanh x dx x tanh x tanh y dy x tanh x ln cosh y C
''
" " "
œ œkk
x tanh x ln cosh tanh x C;œ
" "
kkab
check: d x tanh x ln cosh tanh x C tanh x dxcdkkab ’“
" " "
"
œ
x
1x coshtanhx1x
sinh tanh x
ab
ab
tanh x dx tanh x dxœœ
‘
" "
xx
1x 1x
(b) tanh x dx x tanh x dx x tanh x dx x tanh x ln 1 x C
'''
" " " " #
##
""
œœ œ
x2x
1x 1x kk
check: d x tanh x ln 1 x C tanh x dx tanh x dx
‘‘
kk
" # " "
"
#
œ œ
xx
1x 1x
8.3 INTEGRATION OF RATIONAL FUNCTIONS BY PARTIAL FRACTIONS
1. 5x 13 A(x 2) B(x 3) (A B)x (2A 3B)
5x 13 A B
(x 3)(x 2) x 3 x 2
œ Êœœ
B (10 13) B 3 A 2; thus,
AB5
2A 3B 13
Êʜʜʜ œ
œ
œ
5x 13 2 3
(x 3)(x 2) x 3 x
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.3 Integration of Rational Functions by Partial Fractions 509
2. 5x 7 A(x 1) B(x 2) (A B)x (A 2B)
5x 7 5x 7 A B
x 3x 2 (x 2)(x 1) x 2 x 1
œœÊœœ
B 2 A 3; thus,
AB5
A2B7
Êʜʜ œ
œ
œ
5x 7 3 2
x 3x 2 x 2 x 1
3. x 4 A(x 1) B Ax (A B) A 1 and B 3;
A1
AB4
x 4 A B
(x 1) x 1 (x 1)
œ ÊœœÊ Êœ œ
œ
œ
thus,
x 4 1 3
(x 1) x 1 (x 1)
œ
4. 2x 2 A(x 1) B Ax ( A B) A2
AB2
2x 2 2x 2 A B
x 2x 1 (x 1) x 1 (x 1)
œœ ÊœœÊ
œ
œ
A 2 and B 4; thus, Êœ œ œ
2x 2 2 4
x 2x 1 x 1 (x 1)
5. z 1 Az(z 1) B(z 1) Cz z 1 (A C)z ( A B)z B
z 1 A B C
z (z 1) z z z 1
##
œ Êœ Êœ
B 1 A 2 C 2; thus,
AC0
AB1
B1
Êʜʜʜœ
œ
œ
œ
Þ
ß
àz 2 2
z (z 1) z z z 1
" "
6. 1 A(z 2) B(z 3) (A B)z (2A 3B)
zAB
z z 6z z z 6 (z 3)(z 2) z 3 z
#
""
œœ œÊœœ
5B 1 B A ; thus,
AB0
2A 3B 1
Êʜʜʜ œ
œ
œ
""
5 5 z z 6z z 3 z 2
z55
7. 1 (after long division);
t 8 5t 2 5t 2 5t 2 A B
t 5t 6 t 5t 6 t 5t 6 (t 3)(t 2) t 3 t 2
œ œ œ
5t 2 A(t 2) B(t 3) (A B)t ( 2A 3B) B (10 2) 12
AB5
2A 3B 2
Êœœ Ê Êœœ
œ
œ
B 12 A 17; thus, 1ʜʜ œ
t 8 17 12
t 5t 6 t 3 t 2
8. 1 1 (after long division);
t 9 9t 9 9t 9 9t 9 A B Ct D
t 9t t 9t t t 9 t t 9 t t t 9
œ œ œ
ab ab
9t 9 At t 9 B t 9 (Ct D)t (A C)t (B D)t 9At 9BÊœ œ
### #$#
abab
A 0 C 0; B 1 D 10; thus, 1
AC0
BD 9
9A 0
9B 9
ÊʜʜœÊœœ
œ
œ
œ
œ
Þ
á
á
ß
á
á
àt 9 10
t 9t tt 9
"
9. 1 A(1 x) B(1 x); x 1 A ; x 1 B ;
"""
# #1 x 1 x 1 x
AB
œ ÊœœÊœœÊœ
ln 1 x ln 1 x C
'''
dx dx dx
1 x 1 x 1 x###
"" "
œœcdkkkk
10. 1 A(x 2) Bx; x 0 A ; x 2 B ;
"""
# #x 2x x x 2
AB
œ Êœ œÊ œ œÊ œ
ln x ln x 2 C
'''
dx dx dx
x 2x x x 2
# ##
"" "
œ œ cdkk k k
11. x 4 A(x 1) B(x 6); x 1 B ; x 6 A ;
x 4 A B 5 2 2
x 5x 6 x 6 x 1 7 7 7
œ ÊœœÊœœÊœœ
dx ln x 6 ln x 1 C ln (x 6) (x 1) C
'''
x 4 2 dx 5 dx 2 5
x 5x 6 7 x 6 7 x 1 7 7 7
"
#&
œœœkk kk k k
12. 2x 1 A(x 3) B(x 4); x 3 B 7 ; x 4 A 9;
2x 1 A B 79
x 7x 12 x 4 x 3 1 1
œ ÊœœÊœœœÊœœ
dx 9 7 9 ln x 4 7 ln x 3 C ln C
'''
2x 1 dx dx
x 7x 12 x 4 x 3
(x 4)
(x 3)
œœœ kk kk ¹¹
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

510 Chapter 8 Techniques of Integration
13. y A(y 1) B(y 3); y 1 B ; y 3 A ;
y
y 2y 3 y 3 y 1 4 4 4
AB 1 3
"
œ ÊœœÊœœœÊœ
ln y 3 ln y 1 ln 5 ln 9 ln 1 ln 5
'''
444
888
y dy dy dy
y 2y 3 4 y 3 4 y 1 4 4 4 4 4 4
33 33
""""
)
%
œœœ
‘ˆ‰ˆ‰
kk kk
ln 5 ln 3œœ
""
## #
ln 15
14. y 4 A(y 1) By; y 0 A 4; y 1 B 3 ;
y 4
y y y y 1 1
AB 3
œ Ê œ œ Ê œ œ Ê œ œ
dy 4 3 4 ln y 3 ln y 1 (4 ln 1 3 ln 2) 4 ln 3 ln
'''
12 12 12
111
y 4 dy dy
y y y y 1
3
##
"
"Î# "
œ œœcdkk k k ˆ‰
ln ln ln ln 16 ln œ œ œ
"" "
816 8 88 4
27 27 27
ˆ‰
††
15. 1 A(t 2)(t 1) Bt(t 1) Ct(t 2); t 0 A ; t 2
" "
#t t 2t t t2 t1
AB C
œ Êœ œÊ œ œ
B; t1 C; Êœ œÊœ œ
1dtdtdtdt
6 3 tt2t t 6 t2 3 t1
""""
#
''''
ln t ln t 2 ln t 1 Cœ
"" "
#kk kk kk
63
16. (x 3) A(x 2)(x 2) Bx(x 2) Cx(x 2); x 0 A ; x 2
x 3 A B C 3
2x 8x x x 2 x 8
"
##
œ ÊœœÊœ œ
B ; x 2 C ; dxÊœ œÊœ œ
""
16 16 2x 8x 8 x 16 x 2 16 x 2
5 x 3 3 dx dx 5 dx
''''
ln x ln x 2 ln x 2 C ln Cœœ
35
816 16 16x
(x 2) (x 2)
kk kk kk ¹¹
""
17. (x 2) (after long division); 3x 2 A(x 1) B
x 3x 2 3x 2 A B
x 2x 1 (x 1) (x 1) x 1 (x 1)
œ œ Ê œ
Ax (A B) A 3, A B 2 A 3, B 1; œÊœœÊœœ
'0
1x dx
x 2x 1
(x 2) dx 3 2x 3 ln x 1œ œ
'''
000
111
dx dx x
x 1 (x 1) x 1#
""
!
’“
kk
2 3 ln 2 (1) 3 ln 2 2œ œ
ˆ‰
""
##
18. (x 2) (after long division); 3x 2 A(x 1) B
x 3x 2 3x 2 A B
x 2x 1 (x 1) (x 1) x 1 (x 1)
œ œ Ê œ
Ax ( A B) A 3, A B 2 A 3, B 1; œ Ê œ œÊ œ œ '1
0x dx
x 2x 1
(x 2) dx 3 2x 3 ln x 1œ œ
'''
111
000
dx dx x
x 1 (x 1) x 1#
"!
"
’“
kk
0 0 3 ln 1 2 3 ln 2 2 3 ln 2œœ
Š‹Š‹
"" "
# #(1) ( )
19. 1 A(x 1)(x 1) B(x 1)(x 1) C(x 1) D(x 1) ;
"
####
abx 1
AB C D
x 1 x 1 (x 1) (x 1)
œ Êœ
x 1 C ; x 1 D ; coefficient of x A B A B 0; constant A B C DœÊ œ œ Ê œ œ Ê œ œ
""
$
44
A B C D 1 A B ; thus, A B ; Ê œ Ê œ œ Ê œ
"""
#
44
dx
x 1
'ab
ln Cœ œ
""" " "
4 x 1 4 x 1 4 (x 1) 4 (x 1) 4 x 1 2 x 1
dx dx dx dx x 1 x
''' ' ¸¸ab
20. x A(x 1) B(x 1)(x 1) C(x 1); x 1
xABC
(x 1) x 2x 1 x 1 x 1 (x 1)
##
ab
œ Êœœ
C ; x 1 A ; coefficient of x A B A B 1 B ; Êœ œÊœ œÊœÊœ
""
#
2 4 4 (x 1) x 2x 1
3x dx
'ab
ln x 1 ln x 1 Cœ œ
""" "
#4 x 1 4 x 1 2 (x 1) 4 4 (x 1)
dx 3 dx dx 3
''' kk kk
Cœ
ln (x 1)(x 1)
42(x 1)
kk "
21. 1 A x 1 (Bx C)(x 1); x 1 A ; coefficient of x
1ABx C
(x 1) x 1 x 1 x 1 #
"
# #
ab
œ Êœ œÊœab
A B A B 0 B ; constant A C A C 1 C ; œ Ê œÊ œ œ Ê œÊ œ
1dx
2 (x 1) x 1
"
#
'0
1ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.3 Integration of Rational Functions by Partial Fractions 511
dx ln x 1 ln x 1 tan xœ œ
"" " " "
# # #
#"
"
!
2x 1 x 1 4
dx (x 1)
''
00
11 ‘
kk a b
ln 2 ln 2 tan 1 ln 1 ln 1 tan 0 ln 2œ œœ
ˆ‰ˆ‰ˆ‰
""" """ ""
#### #
" "
44448
( 2 ln 2)
11
22. 3t t 4 A t 1 (Bt C)t; t 0 A 4; coefficient of t
3t t 4 A Bt C
t t t t 1
## #
œ Ê œ œÊ œab
A B A B 3 B 1; coefficient of t C C 1; dtœ Ê œÊ œ œ Ê œ'1
33t t 4
t 1
4 dt 4 ln t ln t 1 tan tœ œ
''
11
33
dt
tt 1 2
(t 1)
"#"
$
"
‘
kk a b È
4 ln 3 ln 4 tan 3 4 ln 1 ln 2 tan 1 2 ln 3 ln 2 ln 2œ œ
Š‹
ÈÈ
ˆ‰
"" "
## #
" " 11
34
2 ln 3 ln 2 lnœœ
"
## #
11
11
9
2
Š‹
È
23. y 2y 1 (Ay B) y 1 Cy D
y 2y 1 Ay B Cy D
y 1 y 1
y 1
##
ab ab
œ Êœab
Ay By (A C)y (B D) A 0, B 1; A C 2 C 2; B D 1 D 0;œ Ê œ œ œÊ œ œÊ œ
$#
dy dy 2 dy tan y C
'''
y 2y 1 y
y 1 y 1
y 1 y 1
""
"
ab ab
œ œ
24. 8x 8x 2 (Ax B) 4x 1 Cx D
8x 8x 2 Ax B Cx D
4x 1 4x 1
4x 1
##
ab ab
œ Êœ ab
4Ax 4Bx (A C)x (B D); A 0, B 2; A C 8 C 8; B D 2 D 0;œ œœœÊœœÊœ
$#
dx 2 8 tan 2x C
'''
8x 8x 2 dx x dx
4x 1 4x 1
4x 1 4x 1
"
"
ab ab
œ œ
25. 2s 2
2s 2 As B C D E
s 1 (s 1) s 1 s 1 (s 1) (s 1)
ab œ Ê
(As B)(s 1) C s 1 (s 1) D s 1 (s 1) E s 1œ
$# ## #
ab ab ab
As ( 3A B)s (3A 3B)s ( A 3B)s B C s 2s 2s 2s 1 D s s s 1œ cdabab
% $ # %$# $#
Es 1ab
#
(AC)s (3AB2CD)s (3A3B2CDE)s (A3B2CD)s(BCDE)œ
%$ #
summing all eq
A C 0
3A B 2C D 0
3A 3B 2C D E 0
A3B2CD 2
B C D E 2
Ê
œ
œ
œ
œ
œ
Þ
á
á
á
á
ß
á
á
á
á
à
uations 2E 4 E 2;ʜʜ
summing eqs (2) and (3) 2B 2 0 B 1; summing eqs (3) and (4) 2A 2 2 A 0; C 0Ê œ Ê œ Ê œ Ê œ œ
from eq (1); then 1 0 D 2 2 from eq (5) D 1; œ Ê œ
ds 2 (s1) (s1) tansC
''''
2s 2 ds ds ds
s 1 (s 1) s 1 (s 1) (s 1)
# " "
ab œ œ
26. s 81 A s 9 (Bs C)s s 9 (Ds E)s
s 81 A Bs C Ds E
ss 9 s 9
ss 9
%# #
#
ab ab
œ Ê œ ab ab
A s 18s 81 Bs Cs 9Bs 9Cs Ds Esœaba b
%# %$ # #
(A B)s Cs (18A 9B D)s (9C E)s 81A 81A 81 or A 1; A B 1 B 0;œ Ê œ œ œÊœ
%$ #
C 0; 9C E 0 E 0; 18A 9B D 0 D 18; ds 18œœÊœ œÊœ œ
'''
s81 ds s ds
ss 9 s 9
s
ab ab
ln s Cœ kk 9
s 9ab
27. 2 5 8 4 (A B) 2 2 C D
2 5 8 4 A B C D
2 2 2 2
2
))) ) )
)) ))
))
#
$# #
ab ab
œ Ê œ ))) ) )) )ab
A (2A B) (2A 2B C) (2B D) A 2; 2A B 5 B 1; 2A 2B C 8 C 2;œ Êœ œÊœ œÊœ)) )
$#
2B D 4 D 2; d d dœÊ œ œ
'''
2 5 8 4 2 1 2 2
2 2 2 2
2 2
))) ) )
)) ))
))
ab ab
ab
)) )
dœ œ
'''''
2 2 d d
2 2 2 2 ( 1) 1 2
d 2 2 d 2 2
2 2
)) )
)) )) )) ) ))
)) ))
))
"
# # #
)abab
ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

512 Chapter 8 Techniques of Integration
ln 2 2 tan ( 1) Cœ
"
#
#"
))
2 ab)) )
28. 4 2 3 1
)))) ) ) )
)))
)
4 2 3 1 A B C D E F
1 1 1
1
%$#
ab abab
œ Ê))))
(A B) 1 (C D) 1 E F (A B) 2 1 C D C D E Fœ œ )) )) ) ))) ))) )ab ab a ba b
## %#$#
#
A B 2A 2B A B C D C D E Fœabab)) ) )) ))) )
&% $ # $#
A B (2A C) (2B D) (A C E) (B D F) A 0; B 1; 2A C 4œ Êœ œ œ)))) )
&%$#
C 4; 2B D 2 D 0; A C E 3 E 1; B D F 1 F 0;Êœ œÊœ œÊœ œÊœ
d4 tan211C
''''
)))) ) )) ))
)))
)
4 2 3 1 d d d
1 1 1
1 4
"
" # #
" #
ab ab ab
))))œ œabab
29. 2x 2x ; 1 A(x 1) Bx; x 0 A 1;
2x 2x 1 A B
x x x x x(x 1) x(x 1) x x 1
" " "
œ œ œ Êœ œÊœ
x 1 B 1; 2x dx x ln x ln x 1 C x ln CœÊ œ œ œ œ
''''
2x 2x 1 dx dx x 1
x x x x 1 x
##
kk k k ¸¸
30. x 1 x 1 ; 1 A(x 1) B(x 1);
xAB
x 1 x 1 (x 1)(x 1) (x 1)(x 1) x 1 x 1
##
"""
œ œ œ Êœ ab ab
x 1 A ; x 1 B ; dx x 1 dxœ Ê œ œ Ê œ œ
"" ""
## ##
#
'' ''
xdxdx
x 1 x 1 x 1
ab
x x ln x 1 ln x 1 C x ln Cœœ
"" " "
$
## #33x 1
xx 1
kk kk ¸¸
31. 9 (after long division);
9x 3x 1 9x 3x 9x 3x 1 A B C
x x x (x 1) x (x 1) x x x 1
"
œ œ
9x 3x 1 Ax(x 1) B(x 1) Cx ; x 1 C 7; x 0 B 1; A C 9 A 2;Ê œ œÊ œ œÊ œ œÊ œ
##
dx 9 dx 2 7 9x 2 ln x 7 ln x 1 C
'''''
9x 3x 1 dx dx dx
x x x x x 1 x
"
œ œkk k k
32. (4x 4) ; 12x 4 A(2x 1) B
16x 12x 4 12x 4 A B
4x 4x 1 4x 4x 1 (2x 1) 2x 1 (2x 1)
œ œ Ê œ
A 6; A B 4 B 2; dx 4 (x 1) dx 6 2ÊœœÊœ œ
''''
16x dx dx
4x 4x 1 2x 1 (2x 1)
2(x 1) 3 ln 2x 1 C 2x 4x 3 ln 2x 1 (2x 1) C, where C 2 Cœœ œ
##"
"
" "
kk kk
2x 1
33. y ; 1 A y 1 (By C)y (A B)y Cy A
y y 1 By C
y y y y 1 y y 1 y y 1
A
"" ##
œ œ Ê œ œ
abab ab
A 1; A B 0 B 1; C 0; dy y dyÊœ œÊœ œ œ
''''
y y 1 dy y dy
y y y y 1
ln y ln 1 y Cœ
y
##
"#
kk a b
34. 2y 2 ;
2y By C
y y y 1 y y y 1 y y y 1 y 1 (y 1) y 1 y 1
22 2A
œ œ œ
ab
2 A y 1 (By C)(y 1) Ay A By Cy By C (A B)y ( B C)y (A C)Êœ œ œ ab a ba b
####
A B 0, B C 0 or C B, A C A B 2 A 1, B 1, C 1;Êœœ œ œœÊœ œ œ
dy 2 (y 1) dy dy
'''''
2y dy y dy
y y y 1 y 1 y 1 y 1
œ
(y 1) ln y 1 ln y 1 tan y C y 2y ln y 1 ln y 1 tan y C,œ œ
# # " # # "
""
##
"
kk a b kk a b
where C C 1œ
"
35. e y ln C ln C
''''
e dt e 1
e 3e 2 y 3y 2 y 1 y 2 y 2 e
dy dy dy y 1
t t
2t t t
#
œœ œœ œ cd ¹¹ Š‹
t
36. dt e dt; dy y dy
ye
dy e dt
'' '' '
e 2e e e 2e 1
e 1 e 1 y 1 y 1 2 y 1
y 2y 1 y 1 y y
4t 2t t 3t t
2t 2t
32
œÄœœ
œ
œ
t
t
t
”• Š‹ dy 'dy
y 1
ln y 1 tan y C e ln e 1 tan e Cœ œ
y
22
2t 2t t
2"""
##
#" "
ab ab ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.3 Integration of Rational Functions by Partial Fractions 513
37. ; [sin y t, cos y dy dt] dt ln C
'''
cos y dy dy
sin y sin y 6 t t 6 5 t 2 t 3 5 t 3
t 2
"" " "
œœÄœœ
ˆ‰¸¸
ln Cœ
"
5sin y 3
sin y 2
¹¹
38. ; cos y ln C ln
''''
sin d cos 2
cos cos 2 y y 2 3 y 2 3 y 1 3 y 1 3 cos 1
dy dy dy y 2
)) )
)) )
"" " "
cd ¹¹ ¸¸
)œÄ œœ œ C
ln C ln Cœœ
" "
31 cos 3cos 2
2 cos cos 1
¸¸ ¸¸
))
))
39. dx dx 3 dx
'''
(x 2) tan (2x) 12x 3x tan (2x)
4x 1 (x 2) 4x 1 (x 2)
x
ab œ
tan (2x) d tan (2x) 3 6 3 ln x 2 Cœœ
"
#
" "
'''
ab kk
dx dx 6
x 2 (x 2) 4 x 2
tan 2x
ab
40. dx dx dx
'''
(x 1) tan (3x) 9x x tan (3x)
9x 1 (x 1) 9x 1 (x 1)
x
ab œ
tan (3x) d tan (3x) ln x 1 Cœœ
"" "
3 x 1 (x 1) 6 x 1
dx dx 1
tan 3x
'''
ab kk
ab
41. t 3t 2 1; x ln C; Ce ; t 3 and x 0ab ¸¸
#
œœ œœ œœ œ
dx dt dt dt t 2 t 2
dt t 3t 2 t 2 t 1 t 1 t 1
x
'''
C e x ln 2 ln t 2 ln t 1 ln 2ÊœÊ œ Êœ œ
""
##
t 2 t 2
t 1 t 1
x¸¸ˆ‰ kkkk
42. 3t 4t 1 2 3; x 2 3 3 3ab
ÈÈ È È
%#
œ œ œ
dx dt dt dt
dt t 1
3t 4t 1 t
'''
3
3 tan 3t 3 tan t C; t 1 and x C CœœœÊœÊœ
" "
Š‹
ÈÈ 11
ÈÈ È
33 3
444
11 1
x 3 tan 3t 3 tan tʜ
" "
Š‹
ÈÈ 1
43. t 2t 2x 2; ln x 1 ln x 1 ln C;a b kk kk
'' ¸¸
#""""
# # # # #
œ œ Ê œ Êœ
dx dx dt dt dt t
dt x 1 t 2t t t 2 t
''
t 1 and x 1 ln 2 ln C C ln 2 ln 3 ln 6 ln x 1 ln 6 x 1œ œÊ œÊœœ Ê œ Êœ
"
#3t 2 t
t6t
kk ¸¸
x 1, t 0ʜ
6t
t #
44. (t 1) x 1 tan x ln t 1 C; t 0 and x tan ln 1 CœÊ œ Ê œœ œÊ œ
dx dx dt
dt x 1 t 1 4 4
#" "
'' kk kk
11
C tan 1 tan x ln t 1 1 x tan (ln (t 1) 1), t 1Êœ œÊ œ Êœ
" "
1
4kk
45. V y dx dx 3 dx 3 ln 3 ln 25œœ œœ œ11 1 1 1
'' '
05 05 05
25 25 25
#
"" #Þ&
!Þ&
9x
3x x x 3 x x 3
Œ
ˆ‰‘¸¸
46. V 2 xy dx 2 dx 4 dxœœ œ11 1
'' '
00 0
11 1
2x 2
(x 1)(2 x) 3 x 1 3 2 x
"" "
ˆ‰ˆ‰ˆ‰
ln x 1 2 ln 2 x (ln 2)œ œ
‘
abkk kk
44
33
11
"
!
47. A tan x dx x tan x dxœœ
''
00
33
3
0
" "
cd x
1 x
ln x 1 ln 2;œ œ
11
ÈÈ
33
33
‘
ab
"
#
#3
0
x x tan x dxœ""
A'0
3
x tan x dxœ
"" "
##
#"
A1 x
x
Œ
‘
3
00
3
'
xtanxœ
""
##
"
A’“
‘
ab
13
0
1.10œœ œ
µ
""
## #A6A3
33
2
Š‹Š‹
111
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
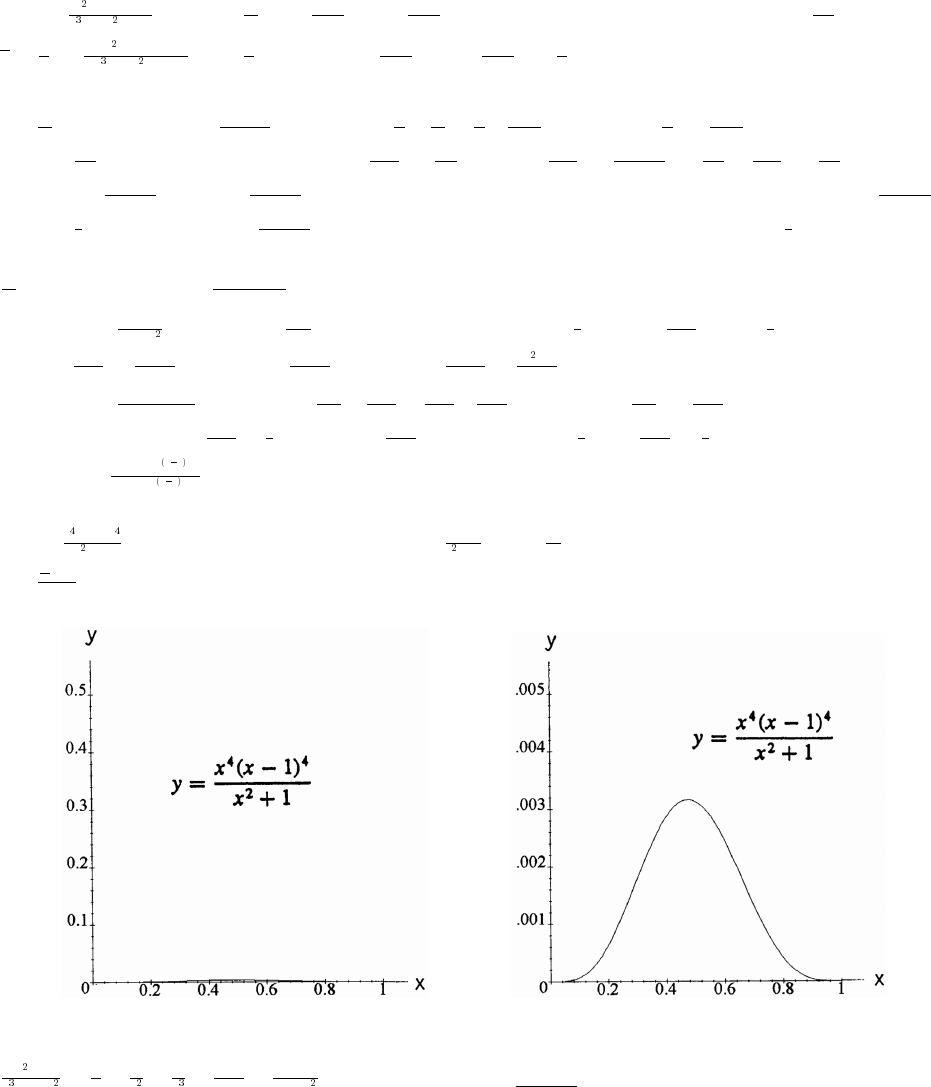
514 Chapter 8 Techniques of Integration
48. A dx 3 2 3 ln x ln x 3 2 ln x 1 ln ;œœœœ
''''
3333
5555
4x 13x 9 dx dx dx 125
x 2x 3x x x 3 x 1 9
&
$
cdkkkk kk
x dx 4x 3 2 (8 11 ln 2 3 ln 6) 3.90œœœœ
µ
"" "
&
$
A x 2x 3x A x 3 x 1 A
x 4x 13x 9 dx dx
'''
333
555
ab
Š‹
cd
49. (a) kx(N x) k dt k dt ln kt C;
dx dx dx dx x
dt x(N x) N x N N x N N x
œÊ œ Ê œ Ê œ
'' '''
"" "
¸¸
k , N 1000, t 0 and x 2 ln C ln lnœœ œ œÊ œÊ œ
"""""
250 1000 998 1000 1000 x 250 1000 499
2xt
¸¸ ¸ ¸ ˆ‰
ln 4t e 499x e (1000 x) 499 e x 1000e xʜʜʜʜʜ
¸¸ ab
499x 499x 1000e
1000 x 1000 x 499 e
4t 4t 4t 4t
4t
4t
(b) x N 500 500 500 499 500e 1000e e 499 t ln 499 1.55 daysœœ Ê œ Ê œ Êœ Êœ ¸
" "
#
1000e
499 e 4
4t 4t 4t
4t
4t †
50. k(a x)(b x) k dt
dx dx
dt (a x)(b x)
œ Ê œ
(a) a b: k dt kt C; t 0 and x 0 C ktœœÊœœœÊœÊœ
''
dx
(a x) a x a a x a
""""
ax x aÊœ Êœ Êœ œ
""
a x a akt 1 akt 1 akt 1
akt a a a kt
(b) a b: k dt k dt ln kt C;ÁœÊœÊœ
'''''
dx dx dx b x
(a x)(b x) b a a x b a b x b a a x
"" "
¸¸
t 0 and x 0 ln C ln (b a)kt ln eœœÊ œÊ œÊœ
"
ÐÑ
ba a ax a ax a
bbx bbxb
bakt
¸¸ ˆ‰
xʜ
ab 1 e
abe
‘
bakt
bakt
51. (a) dx x 4x 5x 4x 4 dx
''
00
11
x(x 1)
x1 x1 7
422
'&%#
œ œ
ˆ‰
1
(b) 100% 0.04%
22
71
1
†œ
µ
(c) The area is less than 0.003
52. P(x) ax bx c, P(0) c 1 and P (0) 0 b 0 P(x) ax 1. Next,œ œœ œÊœÊ œ
#w #
; for the integral to be a function, we must have A 0 and
ax 1 A B C D E
x(x1) x x x x1 (x1)
œ œrational
D 0. Thus, ax 1 Bx(x 1) C(x 1) Ex (B E)x (C 2B)x (B 2C)x Cœœœ
###$$#
E B; x 1 a 1 E; therefore, 1 2B a 1 2E a 1 2(a 1) a
BE0
C2Ba
C
ÊÊœœÊœœÊœÊœ
œ
œ
œ"
Þ
ß
à
a3ʜ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.4 Trigonometric Integrals 515
8.4 TRIGONOMETRIC INTEGRALS
1. sin x dx sin x sin x dx cos x sin x dx 2cos x cos x sin x dx
'' ' '
00 0 0
11 1 1/2 /2 /2 /2
5 4
œœ"œ"ab a b a b
## #
##
sin x dx 2cos x sin x dx cos x sin x dx cos xœ œ#
'' '
00 0 0
11 1 1
/2 /2 /2 4cos x cos x
35
/2
#’“
35
œ!" œab ˆ‰
#" )
$& "&
2. sin dx (using Exercise 1) sin dx 2cos sin dx cos sin dx
''''
0000
1111
5 4
x x xx xx
2 2 22 22
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
œ
#
cos cos cosœ# œ!# œ
‘ˆ‰ˆ‰ ˆ‰ ˆ‰ ab
xxx
23 25 2
35
%# %#"'
$& "&
1
0
3. cos x dx cos x cos x dx sin x cos x dx cos x dx sin x cos x dx
'' ' ''
## #
11 1 11
11 1 11
/2 /2 /2 /2 /2
/2 /2 /2 /2 /2
3œœ"œab a b
sin xœ œ""œ
’“
ˆ‰ˆ ‰
sin x
3
31
1
Î#
Î#
""%
$$$
4. 3cos 3x dx cos 3x cos 3x 3dx sin 3x cos 3x 3dx sin 3x sin 3x cos 3x 3dx
'' ' '
00 0 0
/6 /6 /6 /6
5
11 1 1
œ †œ" †œ"# †ab a b a b
## #%
##
cos 3x 3dx sin 3x cos 3x 3dx sin 3x cos 3x 3dx sin 3xœ † # † † œ #
'' '
00 0
/6 /6 /6 sin 3x sin 3x
35
6
11 1 1
#% Î
’“
35
0
œ" !œ
ˆ‰
ab
2
$& "&
")
5. sin y dy sin y sin y dy cos y sin y dy sin y dy cos y sin y dy
'' ' ' '
00 0 0 0
/2 /2 /2 /2 /2
76 2 2
11 1 1 1
œœ"œ$ab
$
cos y sin y dy cos y sin y dy cos y$ œ $$ œ!""œ
''
00
/2 /2
46 cos y cos y cos y
35
11 1
’“
ab ˆ‰
3
(&($&
Î# $" "'
0
6. 7cos t dt (using Exercise 5) 7 cos t dt sin t cos t dt sin t cos t dt sin t cos t dt
'''''
00000
/2 /2 /2 /2 /2
7246
11111
œ$$
”•
7sin t 7 7œ $$ œ""!œ
’“
ˆ‰
ab
sin t sin t sin t
35
3
(&(&
Î# $" "'
1
0
7. sin x dx dx cos x cos x dx dx cos x dx dx
'' ' '' '
00 0 00 0
11 1 11 1
) œ) œ# "# # # œ# # # †# #
4cos x cos 4x
ˆ‰ ab
" # "
# #
##
x sin x dx cos 4x dx x sin 4xœ## # œ# œ# œ$cd ‘
111 1
000 0
'' 1111
"
#
8. cos 2 x dx dx cos 4 x cos 4 x dx dx cos 4 x dx dx
'' ' '''
00 0 000
11 1 111
)œ) œ#"# œ#% #
4cos 4 x cos x
1111
ˆ‰ ab
" " )
# #
##
1 1
x sin 4 x dx cos x dx x sin xœ# ) œ# ) œ#"œ$
‘ ‘
""
""
)11
11 1
000
11
0
''
9. 16 sin x cos x dx 16 dx cos x dx dx dx
'' '''
## #
" # " # "
## #
11 111
11 111
/4 /4 /4 /4 /4
/4 /4 /4 /4 /4
cos x cos x cos 4x
œœ%"#œ%%
ˆ‰ˆ‰ ˆ‰
ab
4x dx cos 4x dx 2x =2œ## œ œcd ‘ ˆ‰ˆ‰
1
111
11 1
1
11
/4
/4 /4 /4
/4 /4 sin 4x
2
/4
/4
##
'' 11 1 1
10. 8 sin y cos y dy 8 dy dy cos y dy cos y dy cos y dy
'' ''''
00 0000
11 1111
4cos y cos y
##$
" # " #
##
#
œ œ###
ˆ‰ˆ‰
y sin 2y dy sin y cos y dy dy cos 4y dy cos y dyœ " # # œ #
‘ˆ‰
ab
"""
"
###
#
2
cos 4y
111 111
000 000
'' '''
1
sin y cos y dy y sin 4y sin 2y##œ† œœ
'00
1111
#""""
#)## ##
11
’“
sin 2y
3
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

516 Chapter 8 Techniques of Integration
11. 35 sin x cos x dx 35 sin x sin x cos x dx 35 sin x cos x dx 35 sin x cos x dx
'' ''
00 00
11 11/2 /2 /2 /2
43 4 4 6
œ"œ ab
#
35 35 7 5œ œ!œ#
’“
abab
sin x sin x
57
/2
57
1
0
12. cos 2x sin 2x dx
'00
11
2cos 2x
3
œ œ œ!
’“
"""
#''
3
13. 8cos 2 sin 2 d 8 cos 2
'000
1)11
/4 34
cos 2
4
/4 /4
))) )œ œ œ!"œ"
’“
ˆ‰ cdabab
"
#
4
14. sin 2 cos 2 d sin 2 sin 2 cos 2 d sin 2 cos 2 d sin 2 cos 2 d
'' ''
00 00
11 11/2 /2 /2 /2
23 2 2 2 4
)))))))))))))œ" œ ab
œ† † œ!
’“
""
##
sin 2 sin 2
35
/2
35
))
1
0
15. dx sin dx sin dx cos
'''
000 0
222
cos xxxx
2
111 1
ɹ¹ ‘
"
####
œœœ#œ##œ%
16. cos 2x dx sin 2x dx sin 2x dx cos 2x
'''
000 0
111 1
ÈÈÈÈÈÈÈ
’“
" œ#llœ# œ# œ##œ##
17. sin t dt cos t dt cos t dt cos t dt sin t sin t
''''
000 0
1111
1
11
1
Ècd cd" œ l l œ œ œ"!!"œ#
#/2
/2
/2
/2
18. cos d sin d sin d cos
'''
000
0
111
1
Ècd" œ l l œ œ œ""œ#
#)) ) ) )) )
19. tan x dx sec x dx sec x dx ln sec x tan x ln ln
'''
#
111
111 1
1
/4 /4 /4
/4 /4 /4 /4
/4
Ècd
Š‹Š‹
ÈÈ
" œ l l œ œ l l œ #" #"
ln lnœœ#"#
Š‹Š ‹
È
È
È#"
#"
20. sec x dx tan x dx tan x dx tan x dx ln sec x ln sec x
''''
!
#!!
!
111
11 1 1
/4 /4 /4
/4 /4 /4 /4
Ècdcd"œllœ œllll
/4
ln ln ln ln ln lnœ " # # " œ# #œ #ab ab
ÈÈ È
21. cos 2 d sin d sin d cos sin
'' '
00 0 0
11 1 1
/2 /2 /2 /2
)))))) ))))))
ÈÈÈ È ÈÈ
cdab" œ #l l œ# œ# œ#"œ#
22. cos t dt sin t dt sin t dt sin t dt sin t dt cos t sin t dt
''''''
!
## $$$ #
$Î# $Î# !!
1111 1
111 1
ab ab ab
¸¸
" œ œ œ œ "
cos t sin t dt sin t dt cos t sin t dt sin t dt cos t sin t dt cos t" œ œ
'''''
!!!
###
!! !
111
11 1
ab ’“
cos t
3
3
cos t œ " " " " œ
’“
ˆ‰ˆ‰
cos t
3
31
!
"" "")
$$ $$$
23. 2 sec x dx; u sec x, du sec x tan x dx, dv sec x dx, v tan x;
'
!$#
1/3 œœ œ œ
2 sec x dx 2 sec x tan x sec x tan x dx sec x sec x dx
'' '
!! !
$!
Î$
11 1
1
/3 /3 /3
22
œ # œ#†"†!#†#† $# "cd ab
È
sec x dx sec x dx; 2 2 sec x dx ln sec x + tan xœ% $# # œ% $ # l l
ÈÈ
cd
'''
!!!
$$
!
Î$
111 1
/3 /3 /3
2 2 sec x dx ln + ln ln
'
!$
1/3 œ% $# l" !l# l# $lœ% $# # $
ÈÈÈÈ
Š‹
2 sec x dx ln
'
!$
1/3 œ# $ # $
ÈÈ
Š‹
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.4 Trigonometric Integrals 517
24. e sec e dx; u sec e , du sec e tan e e dx, dv sec e e dx, v tan e .
'x x x x xx xx x$ #
ab ab ab ab ab abœœ œ œ
e sec e dx sec e tan e sec e tan e e dx
''
xx xx x xx$#
ab ab ab ab abœ
sec e tan e sec e sec e e dxœ "ab ab aba bab
xx x x x
'#
sec e tan e sec e e dx sec e e dxœ ab ab ab ab
x x xx xx
''
$
e sec e dx sec e tan e ln sec e tan e C#œ
'xx xx x x$ab ab ab ab ab
¸¸
e sec e dx sec e tan e ln sec e tan e C
'xx xx x x$"
#
ab ab ab ab ab
ˆ‰
¸¸
œ
25. sec d tan sec d sec d tan sec d tan
'' ''
!! ! !
Î
!
11 1 1 )1
/4 /4 /4 /4
422222
tan
3
4
)) ) )) )) ) )) )œ" œ œab ’“
3
œ" !œ
ˆ‰
ab
"%
$$
26. 3sec 3x dx tan 3x sec 3x 3dx sec 3x 3dx tan 3x sec 3x 3dx
'' ''
!! !!
11 11/12 /12 / /12
422222
ab a b ab ab ab ababœ" œ
tan 3xœ œ"!œ
’“
ab ab
ˆ‰
tan 3x
3
12
3ab1Î
!
"%
$$
27. csc d cot csc d csc d cot csc d cot
'' ''
11 11
11 11 )1
1
/4 /4 /4 /4
/2 /2 /2 /2
4cot
3
2
/4
)) ) )) )) ) )) )œ" œ œab ’“
## # ## Î
œ!" œab ˆ‰
"%
$$
28. csc d cot csc d csc d cot csc d cot
'' ''
11 11
11 11
)))))))
1
1
/2 /2 /2 /2
4cot
32
$œ$" œ$ $ œ''
#######
## # ##
Î
))))
ˆ‰ ’“
œ '†!#†! '†"#†" œ)abab
29. 4 tan x dx 4 sec x tan x dx 4 sec x tan x dx 4 tan x dx ln sec x
'' ' '
00 0 0
/4 /4 /4 /4
3tan x 4
11 1 1 1
œ"œ œ%%llab ’“
##
#
Î
!
2ln ln lnœ " % ##†!% "œ## #ab È
30. 6 tan x dx 6 sec x tan x dx 6 sec x tan x dx 6 tan x dx
'' ' '
##
11 1 1
11 1 1
/4 /4 /4 /4
/4 /4 /4 /4
4222
œ"œ ab
6 sec x tan x dx 6 sec x 1 dx 6 sec x dx 6 dxœœ'
'' ''
$
Î
Î
#
11 11
11 11
1
1
/4 /4 /4 /4
/4 /4 /4 /4
22 2 tan x 4
4
ab
’“
tan x xœ#" " ' ' œ%'" " œ$ )abcdcd abab ab
11
11
11
ÎÎ
Î Î
$$
##
44
44 1
31. cot x dx csc x cot x dx csc x cot x dx cot x dx ln csc x
'' ' '
11 1 1
11 1 1 1
1
/6 /6 /6 /6
/3 /3 /3 /3
32 2 cot x 3
6
œ"œ œllab ’“
#
Î
Î
ln ln lnœ $ # œ $
"" # %
#$ $
$
ˆ‰
Š‹
È
È
32. 8 cot t dt 8 csc t cot t dt 8 csc t cot t dt 8 cot t dt
'' ' '
11 1 1
11 1 1
/4 /4 /4 /4
/2 /2 /2 /2
422222
œ"œ ab
8 8 csc t dt cot t tœ " œ !" ) ) œ ) !" % # œ#
’“ a b abcdcd ab
cot t
33
2
4/4
/2 222
44
31
11
111
11
Î
Î
))"'
ÎÎ
ÎÎ
$$
'11 1
33. sin 3x cos 2x dx sin x sin 5x dx cos x cos 5x
''
!!
""""""'
##&#&&&
!
11 1
œœœ""œab
‘ˆ‰
34. sin 2x cos 3x dx sin x sin 5x dx cos x cos 5x
''
!!
ÎÎ
""""""#
##&##&&
Î
!
11 1
22 2
œœ œ!"œabab abab ‘ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

518 Chapter 8 Techniques of Integration
35. sin 3x sin 3x dx cos cos 6x dx dx cos 6x dx x sin 6x
'' ''
"""""
####"###
11 11
11 11 1
1
11
œ!œ œ œ!œab ‘ 1
36. sin x cos x dx sin sin 2x dx sin 2x dx cos 2x
'' '
!! !
ÎÎ Î
"""""
##%%#
Î#
!
11 1 1
22 2
œ ! œ œ œ "" œab cdab
37. cos 3x cos 4x dx cos x cos 7x dx sin x sin 7x 0 0
''
!!
""""
#(
!
11 1
œ œœœabababab ‘
22
38. cos 7x cos x dx cos 6x cos 8x dx sin 6x sin 8x 0
''
Î Î
ÎÎ
""""
#
Î
Î
11
11 1
1
22
22
26 8
2
2
œœœab
‘
39. x t t x ; y y ; t x 2 ;œ Ê œ œ Ê œ !Ÿ Ÿ#Ê!Ÿ Ÿ
#Î$ # $ #Î$
##
tx
A x dx; u du u
ux
du 9x dx
œ# " Ä "œ†"
œ
œ
''
!!
#% $
*#
%%
%
$
*Ð Ñ $Î# *Ð Ñ
!
22
x9
99
2
1Š‹ ’ “
É”•Èab
11
2œ "* "
#
#(
#Î$ $Î#
1’“
ˆ‰ˆ‰
40. y ln cos x ; y tan x; y tan x; tan x dx sec x dx ln sec x tan xœœœœ "œllœllab ab c d
È
ww#
#
!!
ÎÎ
#!
sin x
cos x
33 /3
''
11 1
ln 2 ln ln 2œ$"!œ$
Š‹ Š‹
ÈÈ
ab
41. y ln sec x ; y tan x; y tan x; tan x dx sec x dx ln sec x tan xœœœœ "œllœllab ab c d
È
ww#
#
!!
ÎÎ
#!
sec x tan x
sec x
44 /4
''
11 1
ln ln lnœ #" !" œ #"
Š‹ Š‹
ÈÈ
ab
42. M sec x dx ln sec x tan x ln ln lnœœllœ#"l#"lœ
'Î
Î
Î
#"
#"
1
11
1
4
4/4
4
cd
Š‹
ÈÈÈ
È
y dx tan xœœœ""œ
""""
Î
Î
#
Î
Î
ln ln ln ln
'1
11
1
4
4sec x 4
4
##
cd a bab
x, y lnÊœ!ßabŒ
Š‹
È
È#"
#"
"
43. V sin x dx dx dx cos 2x dx x sin 2xœœ œ œœ!!!œ11 1
'' ''
!! !!
#"
## # # #
!!
11 11
11 11 1 1 1
11
cos 2x
244
cd c d a b a b
44. A cos 4x dx cos 2x dx cos 2x dx cos 2x dx cos 2x dxœ" œ#llœ# # #
'' '''
!! !Î%$Î%
Î% $ Î%11 111
11
ÈÈÈ È È
sin 2x sin 2x sin 2xœ œ "! "" !" œ # #œ# #
ÈÈ È ÈÈÈ
## # ###
## # ###
Î% $ Î%
!Î% $Î%
cd cd cd aba bab
ÈÈ È
11
1
1
1
45. (a) m n m n and m n sin mx sin nx dx cos m n x cos m n x dx
## # #
"
#
ÁÊÁ! Á!Ê œ
''
kk
kk11
cdab ab
sinm nx sinm nxœ
"" "
#
#
‘
ab ab
mn mn
k1
k
sin m n k sin m n k sin m n k sin m n kœ # #
"" " "" "
# #
ˆ‰ˆ‰
abababababa b aba b ab ab
mn mn mn mn
11
sin m n k sin m n k sin m n k sin m n kœœ!
""""
# # # #ab ab ab abmn mn mn mn
ab ab ab abab ab ab ab
sin mx and sin nx are orthogonal.Ê
(b) Same as part since cos dx . m n m n and m n cos mx cos nx dx
"
#
# #
##
''
k k
k k1 1
!œ ÁÊÁ! Á!Ê1
cosm nx cosm nxdx sinm nx sinm nxœœ
""""
##
# #
'k
k
mn mn
k
11
c d ab abab ab ‘
k
sin m n k sin m n k sin m n k sin m n kœ##
""""
# # # #ab ab ab abmn mn mn mn
abababababa b aba b ab ab11
sin m n k sin m n k sin m n k sin m n kœœ!
""""
# # # #ab ab ab abmn mn mn mn
ab ab ab abab ab ab ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.5 Trigonometric Substitutions 519
cos mx and cos nx are orthogonal.Ê
(c) Let m n sin mx cos nx sin sin m n x and sin dx and sin m n x dx 0œÊ œ ! ! œ! œ
"""
###
# #
ab abab abab ''
kk
kk11
sin mx and cos nx are orthogonal if m n.ʜ
Let m n.Á
sin mx cos nx dx sinm nx sinm nxdx cosm nx cosm nx
''
kk
kk
mn mn
k
# #
""""
##
#
11 1
œœc d ab abab ab ‘
k
cos m n k cos m n k cos m n k cos m n kœ # #
""""
# # # #ab ab ab abmn mn mn mn
abababababa b aba b ab ab11
cos m n k cos m n k cos m n k cos m n kœ œ!
""" "
# # # #ab ab ab abmn mn mn mn
ab ab ab abab ab ab ab
sin mx and cos nx are orthogonal.Ê
46. f x sin mx dx sin nx sin mx dx. Since sin nx sin mx dx ,
for m n
1 for m n
" "
œ"
11 1
11 1
11 1
'' '
ab !œ
œœ
!Á
œ
n
Nan
the sum on the right has only one nonzero term, namely sin mx sin mx dx a .
am
m
11
1
'œ
8.5 TRIGONOMETRIC SUBSTITUTIONS
1. y 3 tan , , dy , 9 y 9 1 tan œœœœÊœœ)) )
11 ) )
))
)
##
## "
3 d 9 cos
cos cos 3 3
9y
cos
ab Èkk
because cos 0 when ;
ˆ‰
))
11
##
3 ln sec tan C ln C ln 9 y y C
'''
dy y
9y
cos d d
3 cos cos 3 3
9y
ÈÈ
ww
#
œœœœœ
)) )
))
kk
¹¹¸¸
È
))
2. ; 3y x ; x tan t, t , dx , 1 x ;
''
3 dy
19y
dx dt
1x cos t cos t
ÈÈ
## #"
cd È
œÄ œ œ œ
11
ln sec t tan t C ln x 1 x C ln 1 9y 3y C
''
dx dt
1x cos t
ÈŠ‹
##
œœœœ
cos t kk
¹¹
ȸ¸
È
3. tan tan 1 tan ( 1)
'# # # # # #
""" ""
" " "
#
#
2
2dx x
4x 444
œœœœ
‘ ˆ‰ˆ‰ ˆ‰ˆ ‰
111
4. tan tan 1 tan 0 0
''
00
22
dx dx x
82x 4x 416### ### # ##
""" """ ""
" " "
#
!
œœ œ œ œ
‘ ˆ ‰ ˆ‰ˆ‰ˆ‰
11
5. sin sin sin 0 0
'0
2
3dx x
9x 366
Î
" " "
$Î#
!
"
#
Èœœœœ
‘ 11
6. ; t 2x sin t sin sin 0 0
''
00
12 2 12 2 12
0
2 dx dt
14x 1t 244
ÈÈ È
" " "
"
cd cdœÄ œ œ œœ
11
7. t 5 sin , , dt 5 cos d , 25 t 5 cos ;œœ œ)) )) )
11
## #
È
25 t dt (5 cos )(5 cos ) d 25 cos d 25 d 25 C
'' ''
Ȉ‰
œ œ œ œ
##
##
))) )) )
1cos 2 sin 2
4
)))
sin cos C sin C sin Cœ œ œ
25 25 t t 25 t
55 5 5
25 t t 25 t
## ##
" "
ab
’“
ˆ‰ ˆ‰ ˆ‰
Š‹
))) ÈÈ
8. t sin , , dt cos d , 1 9t cos ;œœ œ
""
## #
33
)) )) )
11 È
1 9t dt (cos )(cos ) d cos d sin cos C sin (3t) 3t 1 9t C
'' '
È È
ab
’“
œ œ œ œ
# #
""" "
#"
336 6
))) )) ) ))
9. x sec , 0 , dx sec tan d , 4x 49 49 sec 49 7 tan ;œ œ œ œ
77
### ##
)) ))) ) )
1ÈÈ
sec d ln sec tan C ln C
''
dx 2x
4x 49
sec tan d
7 tan 77
4x 49
Ȉ‰ È
"" "
## #
œœœœ
7)))
)')) ) )kk¹¹
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

520 Chapter 8 Techniques of Integration
10. x sec , 0 , dx sec tan d , 25x 9 9 sec 9 3 tan ;œ œ œ œ
33
55
)) ))) ) )
1
###
ÈÈ
sec d ln sec tan C ln C
''
5 dx 5x
25x 9
5 sec tan d
3 tan 3 3
25x 9
Ȉ‰ È
œœœœ
3
5)))
)')) ) )kk
¹¹
11. y 7 sec , 0 , dy 7 sec tan d , y 49 7 tan ;œœ œ)) ))) )
1
##
È
dy 7 tan d 7 sec 1 d 7(tan ) C
''
Èy49
y 7 sec
(7 tan )(7 sec tan ) d
##
œœœœ
))))
)''
)) ) ) ) )ab
7secCœ
’“
ˆ‰
Èy49
77
y
"
12. y 5 sec , 0 , dy 5 sec tan d , y 25 5 tan ;œœ œ)) ))) )
1
##
È
dy tan cos d sin d (1 cos 2 ) d
'' ' ' '
Èy25
y 125 sec 5 5 10
(5 tan )(5 sec tan ) d
"""
## #
œœœœ
))))
)))) )) ))
sin cos C sec C Cœ œ œ
""
"
#10 10 5 y y 10 y
yy25 y25
5sec
ab
’“’“
ˆ‰ Š‹Š‹
))) ÈÈ
ˆ‰
y
5
13. x sec , 0 , dx sec tan d , x 1 tan ;œœ œ)) ))) )
1
##
È
sin C C
'' '
dx sec tan d d
xx1 sec tan sec x
x1
ÈÈ
œœœœ
))) )
)) ) )
14. x sec , 0 , dx sec tan d , x 1 tan ;œœ œ)) ))) )
1
##
È
2 cos d 2 d sin cos C
'' ' '
2 dx 2 tan sec d 1 cos 2
xx1 sec tan
È
#
#
œœœ œ
))) )
)) )) ) ) ) )
ˆ‰
tan cos C sec x x 1 C sec x Cœ œ œ )))
#" "
#"#
Ȉ‰
xx
x1
È
15. x 2 tan , , dx , x 4 ;œœ œ))
11 )
))## #
2 d 2
cos cos
È
88 ;
'' ' '
x dx sin d
x4
8 tan (cos ) d cos 1 ( sin ) d
cos cos cos
Èab a b
œœœ
))) ) ))
)
))
))
t cos 8 dt 8 dt 8 C 8 sec Ccd ˆ‰ ˆ ‰ Š‹
œÄ œœœ))
''
t1 sec
tt
tt3t 3
"" "" )
8Cx44x4Cœ œ
Œ
abÈ
Èab
x4 x4
83 3
#
"#$Î# #
†
16. x tan , , dx sec d , x 1 sec ;œœ œ)) )) )
11
##
##
È
CC
'''
dx sec d cos d
xx1 tan sec sin sin x
x1
ÈÈ
"
œœœœ
)) ))
)) ) )
17. w 2 sin , , dw 2 cos d , 4 w 2 cos ;œœ œ)) )) )
11
## #
È
22 cot C C
'' '
8 dw 8 2 cos d d
w4w 4 sin 2 cos sin w
24w
ÈÈ
œœœœ
†
†
)) )
)) ) )
18. w 3 sin , , dw 3 cos d , 9 w 3 cos ;œœ œ)) )) )
11
## #
È
dw cot d d csc 1 d
'' '' '
È9w
w9 sin sin
3 cos 3 cos d 1 sin
##
œœœœ
))) )
))
†)) ) ) )
Š‹ ab
cot C sin Cœ œ )) È9w
w3
w
" ˆ‰
19. x sin , 0 , dx cos d , 1 x cos ;œŸŸœ œ)) )) )
1
3ab
#$
$Î#
4 d 4 sec 1 d
'' ' '
00 0 0
32 3 3 3
4x dx 4 sin cos d 1 cos
1x cos cos
ab
#
œœ œ
))) )
))
Š‹ ab)))
4tan 4 3œœcd
È
))
11
Î$
!4
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.5 Trigonometric Substitutions 521
20. x 2 sin , 0 , dx 2 cos d , 4 x 8 cos ;œŸŸœ œ)) )) )
1
6ab
#$
$Î#
tan
'' '
00 0
16 6
dx 2 cos d d
4x 8 cos 4 cos 4 12
3
43
ab ÈÈ
"" "
Î'
!
œœœœœ
)) )
))
1
cd)
21. x sec , 0 , dx sec tan d , x 1 tan ;œœ œ)) ))) )
1
2ab
#$
$Î#
CC
'' '
dx sec tan d cos d x
x1 tan sin sin x1
ab È
"
œœœœ
))) ))
)))
22. x sec , 0 , dx sec tan d , x 1 tan ;œœ œ)) ))) )
1
2ab
#&
&Î#
dC C
'' '
x dx sec sec tan d cos x
x1 3x 1
tan 3 sin
sin
ab ab
"
œœœœ
)))) )
))
)
†)
23. x sin , , dx cos d , 1 x cos ;œ œ œ)) )) )
11
##
#$
$Î#
ab
cot csc d C C
'' '
ab È
1x dx
xsin 55x
cos cos d cot 1x
%# "&
œœ œœ
))) )
)
†))) Š‹
24. x sin , , dx cos d , 1 x cos ;œ œ œ)) )) )
11
##
#"Î#
ab
cot csc d C C
'''
ab È
1x dx
xsin
cos cos d cot
33x
1x
## "$
œœ œœ
))) )
)
†))) Š‹
25. x tan , , dx sec d , 4x 1 sec ;œœ œ
""
####
## %
#
)) )) )
11 ab
4 cos d 2( sin cos ) C 2 tan 2x C
'' '
8 dx 4x
4x 1
8 sec d
sec 4x 1
ab ˆ‰ ab
#"
œœœœ
))
))) ) ) )
26. t tan , , dt sec d , 9t 1 sec ;œœ œ
""
##
## #
33
)) )) )
11
2 cos d sin cos C tan 3t C
'' '
6 dt 3t
9t 1
6 sec d
sec 9t 1
ab ˆ‰ ab
#"
œœœœ
3))
))) ) ) )
27. v sin , , dv cos d , 1 v cos ;œœ œ)) )) )
11
##
#&
&Î#
ab
tan sec d C C
'' '
v dv sin cos d tan v
1v cos 3 3 1v
ab È
## "
$
œœ œœ
))) )
)))) Š‹
28. r sin , ;œ))
11
##
cot csc d C C
'' '
ab È
1r dr
rsin 77r
cos cos d cot 1r
'# "(
œœ œœ
))) )
)
†))) ’“
29. Let e 3 tan , t ln (3 tan ), tan tan , dt d , e 9 9 tan 9 3 sec ;
t2t
œœ ŸŸ œ œ œ)) ) ) ))
" "
"%
$$ #
ˆ‰ ˆ‰ ÈÈ
sec
tan
)
)
sec d ln sec tan
'' '
0tan13 tan13
ln 4 tan 4 3 tan 4 3 tan 4
e dt 3 tan sec d
e9 tan 3 sec
t
2t
Èœœœ
)))
))
†
†
)) ) )cdkk
3
tan 1 3
ln ln ln 9 ln 1 10œ œ
ˆ‰Š‹ Š‹
È
54
33 3 3
10
È"
30. Let e tan , t ln (tan ), tan tan , dt d , 1 e 1 tan sec ;
t2t
œœ ŸŸ œ œœ)) ) ) ))
" " # #
ˆ‰ ˆ‰
34sec
43tan
)
)
cos d sin
'' '
ln 3 4 tan 3 4 tan 3 4
ln 4 3 tan 4 3 tan 4 3 tan 4
e dt
1e
(tan ) d
sec
t
2t
ab Š‹
œœœ
))
)
sec
tan )) )cd3
tan œœ
43
55 5
"
31. ; u 2 t, du dt ; u tan , , du sec d , 1 u sec ;
''
112 1 3
14 1
2 dt 2 du
t4tt t 1u 6 4
ÈÈ È
"
###
’“
È
œœÄ œŸŸœ œ
)) )) )
11
2 2
''
13 6
14
2 du 2 sec d
1u sec 4 6 6
Î%
Î'
œœœœ
)) 1 1 1
)
1
1
cd ˆ‰
)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

522 Chapter 8 Techniques of Integration
32. y e , 0 , dy e sec d , 1 (ln y) 1 tan sec ;œŸŸœ œœ
tan tan
4
))
1
))) ))
###
ÈÈ
d sec d ln sec tan ln 1 2
'' '
1
e4 4
dy
y 1 (ln y) 00
esec
e sec
È
Î%
!
œœœœ
tan
tan
)
)
1
)))))cdkk
Š‹
È
33. x sec , 0 , dx sec tan d , x 1 sec 1 tan ;œ œ œ œ)) ))) ) )
1
###
ÈÈ
Csec xC
''
dx sec tan d
xx 1 sec tan
È
"
œœœ
)))
)) )
34. x tan , dx sec d , 1 x sec ;œœ œ))) )
###
CtanxC
''
dx sec d
x1 sec
"
œœœ
))
))
35. x sec , dx sec tan d , x 1 sec 1 tan ;œ œ œ œ)))) ) )
ÈÈ
##
sec d tan C x 1 C
'' '
x dx sec sec tan d
x1 tan
È
##
œœœœ
))))
)
†)) ) È
36. x sin , dx cos d , ;œœ ))))
11
##
CsinxC
''
dx cos d
1x cos
È
"
œœœ
))
))
37. x x 4; dy x 4 ; y dx;
x 2 sec , 0
dx 2 sec tan d
x 4 2 tan
dy
dx x x
dx x4
œœ œ
œ
œ
œ
ÈÈ Ô×
ÖÙ
ÕØ
È
## #
#
'È))
)))
)
1
y 2tan d2sec 1 d2(tan )CÄœ œ œ œ
'''
(2 tan )(2 sec tan ) d
2 sec
))))
)
##
)) ) ) ) )ab
2 sec C; x 2 and y 0 0 0 C C 0 y 2 sec œ œœÊœÊœÊœ
’“ ’“
ˆ‰
È È
x4 x4
x x
## ##
" "
38. x 9 1, dy ; y ; y
x 3 sec , 0
dx 3 sec tan d
x 9 3 tan
ÈÔ×
ÖÙ
ÕØ
È
#
#
#
œ œ œ Äœ
œ
œ
œ
dy
dx 3 tan
dx dx 3 sec tan d
x9 x9
ÈÈ
''
))
)))
)
1
)))
)
sec d ln sec tan C ln C; x 5 and y ln 3 ln 3 ln 3 C C 0œœœœœÊœÊœ
')) ) )kk
¹¹
x
33
x9
È
y ln ʜ
¹¹
x
33
x9
È
39. x 4 3, dy ; y 3 tan C; x 2 and y 0 0 tan 1 Cab
#""
## #
œœ œ œ œ œÊœ
dy
dx x 4 x 4
3 dx dx 3 x 3
'
C y tanʜ ʜ
33x3
88
11
##
" ˆ‰
40. x 1 x 1, dy ; x tan , dx sec d , x 1 sec ;ab ab
È
### $
#$Î#
#
œœ œ œ œ
dy
dx
dx
x1ab ))) )
y cos d sin C tan cos C C C; x 0 and y 1œœ œœ œœœœ
''
sec d tan x
sec sec x1
)) )
))
)) ) ) ) È
10C y 1ʜʜ
x
x1
È
41. A dx; x 3 sin , 0 , dx 3 cos d , 9 x 9 9 sin 3 cos ;œœŸŸœœœ
'0
3È9x
3
###
)) )) ) )
1ÈÈ
A 3 cos d sin cos œœœœ
''
00
22
3 cos 3 cos d 3 3
34
))) 1
1
†#
#
Î#
!
)) ) ) )cd
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
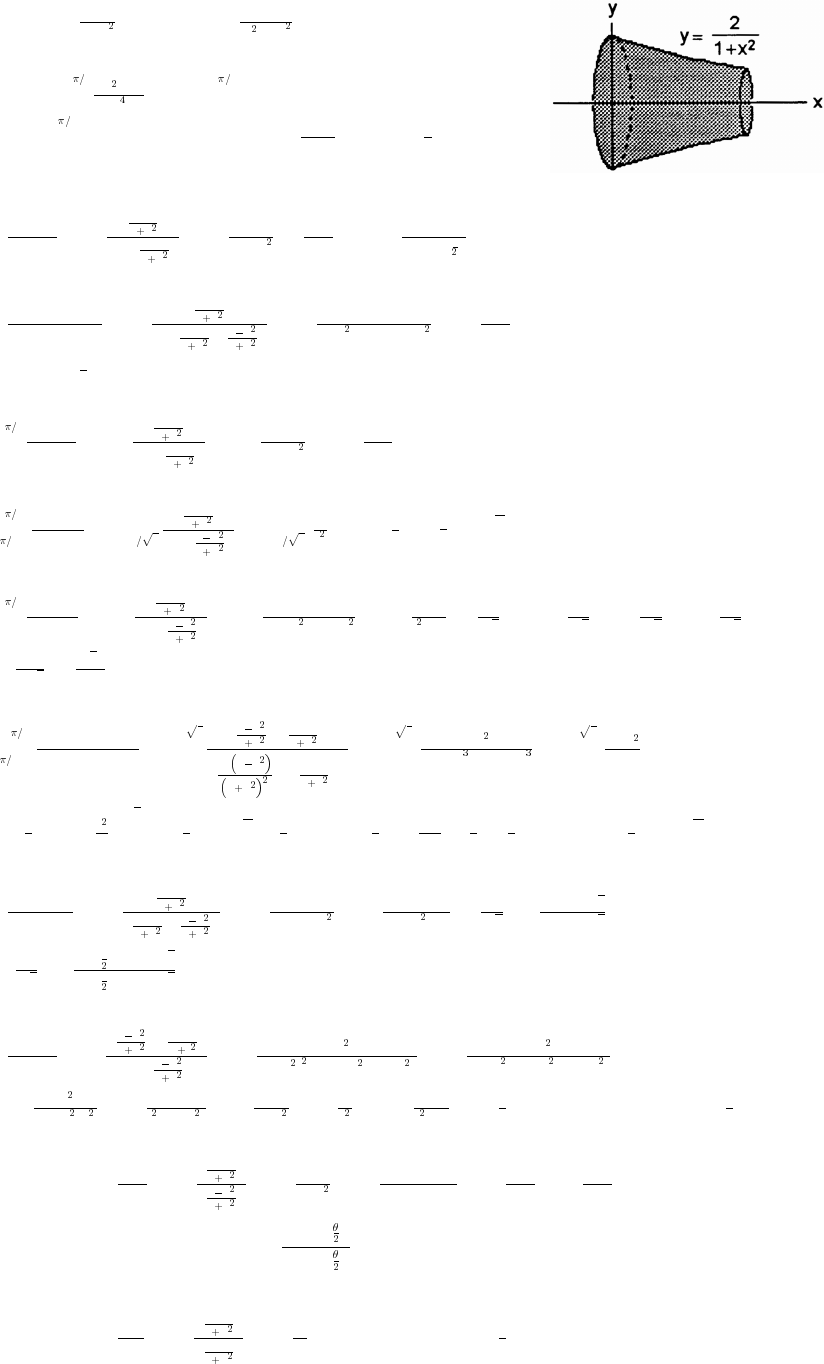
Section 8.5 Trigonometric Substitutions 523
42. V dx 4 ;œœ
''
00
11
11
ˆ‰
2dx
1x x1
#
ab
x tan , dx sec d , x 1 sec ;œœ œ))) )
## #
V4 4 cos dœœ11))
''
00
44
sec d
sec
))
)
#
2 (1 cos 2) d 2 1œœœ1))1)1
'0
4‘ˆ‰
sin 2)1
1
##
Î%
!
43. C C
'' '
dx 2 dz 2 2
1sin x (1z) 1z
11tan
œœœœ
Š‹
Š‹ ˆ‰
2 dz
1z
2z
1z
x
44. ln 1 z C
'' ' '
dx 2 dz dz
1sin xcos x 1z 2z1z 1z
1
œœœœ
Š‹
Š‹
2 dz
1z
2z 1 z
1z 1z kk
ln tan 1 Cœ
¸¸ˆ‰
x
#
45. (1 2) 1
'' '
00 0
21 1
dx 2 dz 2
1sin x (1z) 1z
1
"
!
œ œ œ œ œ
Š‹
Š‹
2 dz
1z
2z
1z ‘
46. 3 1
'' '
313 13
21 1
dx dz 1
1cos x z z
1
"
"Î $
œœœœ
Š‹
Š‹ È
2 dz
1z
1z
1z ‘ È
47. tan tan
'' ' '
00 0 0
21 1 1
d 2 dz 2 dz 2 z 2
2cos 22z 1z z 3
23333
)
)
" "
"
!
"
œœ œœ œ
Š‹
Š‹ ÈÈÈÈ
2 dz
1z
1z
1z ’“
œœ
11
33
3
9
ÈÈ
48.
'' ''
21 1 1
23 3 3 3
cos d 1
sin cos sin 2z 2z 2z 2z
21 z dz
))
)) )
œœœ
Š‹Š‹
Ô×
ÕØ
Š‹
ab
1 z 2 dz
1z 1z
2z 1 z
1z
2z
1z
z
2z dz
ln z ln 3 0 (ln 3 2) ln 3 1œœ œœœ
’“Š ‹ Š‹
ÈÈ
ˆ‰
"" """"
## ##
$
"
z3ln 3
44444
È
49. ln C
'' ''
dt 2 dz 2 dz
sin t cos t 2z 1 z (z 1) 2 2z12
z1 2
"
œœœœ
Š‹
Š‹ ÈÈ
È
2 dz
1z
2z 1 z
1z 1z ¹¹
ln Cœ
"
ÈÈ
ˆ‰ È
ˆ‰
2tan 12
tan 1 2
ºº
t
t
50. '' ' '
cos t dt
1cos t 1z 1z 1z
1
21 z dz 21 z dz
1z 1z 1z
œœ œ
Š‹Š‹
Š‹ ab ab
ababab aba b
1 z 2 dz
1z 1z
1z
1z
2 2 tan z C cot t Cœœœœœ
'''''
ab
ab ab
1z dz
1zz z1z 1z z z 1 z
dz dz dz dz t
#
"" ˆ‰
51. sec d
''''' ''
))œœ œ œ œ
d 2 dz 2 dz dz dz
cos 1z (1z)(1z) 1z 1z
)
)
Š‹
Š‹
2 dz
1z
1z
1z
ln 1 z ln 1 z C ln Cœ œ kkkk »»
1tan
1tan
Š‹
Š‹
52. csc d ln z C ln tan C
''''
))œœ œœœ
ddz
sin z
))
)
Š‹
Š‹
2 dz
1z
2z
1z kk ¸¸
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

524 Chapter 8 Techniques of Integration
8.6 INTEGRAL TABLES AND COMPUTER ALGEBRA SYSTEMS
1. tan C
'dx 2 x 3
xx3 3 3
ÈÈ
"
œ
É
(We used FORMULA 13(a) with a 1, b 3)œœ
2. ln C ln C
'dx
xx4 x42
4x44
x4 4 x42
ÈÈ È È
ÈÈ
È
È
""
#
œœ
¹¹ ¹¹
(We used FORMULA 13(b) with a 1, b 4)œœ
3. 2 x 2 dx 2 x 2 dx
'' '' '
x dx dx
x2 x2 x2
(x 2) dx
ÈÈ È
""
œœ
Š‹ Š‹
ÈÈ
2 x2 4Cœ œ
ˆ‰ ˆ‰ È’“
22
13 11 3
x2 x2 2(x 2)
Š‹ Š‹
ÈÈ
(We used FORMULA 11 with a 1, b 2, n 1 and a 1, b 2, n 1)œœœ œœœ
4. '''''
x dx 3 dx dx 3 dx
(2x 3) (2x 3) (2x 3)
(2x 3) dx
2x 3 2x 3
""
####
œœ
Ȉ‰
È
2x 3 dx 2x 3 dx Cœœ
""
# # ## ##
" $
''
Š‹ Š‹
ÈÈ
ˆ‰ˆ‰ ˆ‰ˆ‰
3232
2x 3 2x 3
1(1)
ˆ‰ ˆ‰
ÈÈ
(2x33)C Cœœ
"
#
ÈÈ
2x 3 2x 3
(x 3)
(We used FORMULA 11 with a 2, b 3, n 1 and a 2, b 3, n 3)œœœ œœœ
5. x 2x 3 dx (2x 3) 2x 3 dx 2x 3 dx 2x 3 dx 2x 3 dx
'' '' '
ÈÈÈÈÈ
Š‹ Š‹
œ œ
""
####
$"
33
C1CCœœœ
ˆ‰ˆ‰ ˆ‰ˆ‰ ‘
"
## ## #
232 2x3
2x 3 2x 3
53 5 5
(2x 3) (2x 3) (x 1)
Š‹ Š‹
ÈÈ
(We used FORMULA 11 with a 2, b 3, n 3 and a 2, b 3, n 1)œœœ œœœ
6. x(7x 5) dx (7x 5)(7x 5) dx (7x 5) dx 7x 5 dx 7x 5 dx
'' '''
œœ
$Î# $Î# $Î#
""
&$
7777
55
ˆ‰ ˆ‰
ÈÈ
C2Cœœ
ˆ‰ˆ‰ ˆ‰ˆ‰ ’“’ “
"
77 7 77 5 49 7
252
7x 5 7x 5 (7x 5) 2(7x 5)
ˆ‰ ˆ‰
ÈÈ
Cœ
’“
ˆ‰
(7x 5)
49 7
14x 4
(We used FORMULA 11 with a 7, b 5, n 5 and a 7, b 5, n 3)œœœ œœœ
7. dx C
''
ÈÈ È
94x 94x
xx
(4) dx
x94x
#
œ
(We used FORMULA 14 with a 4, b 9)œ œ
2 ln Cœ
ÈÈÈ
ÈÈÈ
94x 94x 9
x994x9
"
Š‹¹ ¹
(We used FORMULA 13(b) with a 4, b 9)œ œ
ln Cœ
ÈÈ
È
94x 94x3
x3
2
94x3
¹¹
8. C
''
dx 4 dx
x 4x9 x4x9
4x 9
(9)x 18
ÈÈ
È
œ
(We used FORMULA 15 with a 4, b 9)œœ
tan Cœ
ÈÈ
4x 9
9x 9 9
22 4x9
9
"
ˆ‰
Š‹ É
(We used FORMULA 13(a) with a 4, b 9)œœ
tan Cœ
È4x 9
9x 27 9
44x9
"
É
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.6 Integral Tables and Computer Algebra Systems 525
9. x 4x x dx x 2 2x x dx sin C
''
ÈÈ ˆ‰
œ œ
##
##
"
†
(x 2)(2x 3 2) 2 2 x x
6
2x2
†††
È
4 sin C 4 sin Cœœ
(x 2)(2x 6) 4x x (x 2)(x 3) 4x x
63
x2 x2
" "
##
ÈÈ
ˆ‰ ˆ‰
(We used FORMULA 51 with a 2)œ
10. dx dx 2 x x sin C x x sin (2x 1) C
''
ÈÉ
xx
xx
2xx x
"" "
## #
##
" "
œ œ œ
†ÉŠ‹ È
†
We used FORMULA 52 with a
ˆ‰
œ"
#
11. ln C ln C
''
dx dx
x7x x7x 77
77x
xx
77x
ÈÈ È
ÊŠ ‹
È
ÈÈ
ÊŠ ‹ ÈÈ
""
œœ œ
ââ
ââ
ââ
ââ
ââ
ââ¹¹
We used FORMULA 26 with a 7
Š‹
È
œ
12. ln C ln C
''
dx dx
x7x x7x 77
77x
xx
77x
ÈÈ È
ÊŠ ‹
È
ÈÈ
ÊŠ ‹ ÈÈ
""
œœ œ
ââ
ââ
ââ
ââ
ââ
ââ¹¹
We used FORMULA 34 with a 7
Š‹
È
œ
13. dx dx 2 x 2 ln C 4 x 2 ln C
''
ÈÈ È È
4x 2 x 2 2 x 2 4x
xx x x
## #
œ œ œ
ÈÈ
¹¹ ¹¹
(We used FORMULA 31 with a )œ#
14. dx dx x 2 2 sec C x 4 2 sec C
''
ÈÈ
x4 x2
xx
xx
## #
" "
##
œœœ
ÈÈ
¸¸ ¸¸
(We used FORMULA 42 with a )œ#
15. 25 p dp 5 p dp 5 p sin C 25 p sin C
''
ÈÈÈ È
œ œ œ
##### #
## # #
" "
ppp p
525
55
(We used FORMULA 29 with a 5)œ
16. q 25 q dq q 5 q dq sin q 5 q 5 2q C
''
## " ##
### ##
"
ÈÈ È
ˆ‰ abœ œ
5
858
q
sin q 25 q 25 2q Cœ
625
858
q
" #
"#
ˆ‰ Èab
(We used FORMULA 30 with a 5)œ
17. dr dr sin r 2 r C 2 sin r 4 r C
''
rr2r r
4r 2 r
ÈÈ
### ##
" "
""
## #
œœœ
ˆ‰ ˆ‰
ÈÈ
(We used FORMULA 33 with a 2)œ
18. cosh C ln s s 2 C ln s s 2 C
''
ds ds s
s2 s2 2
ÈÈ
ÊŠ‹
È
" ##
#
œ œ œ œ
»»
ÊŠ‹ ¹ ¹
ÈÈ
We used FORMULA 36 with a 2
Š‹
È
œ
19. tan tan C tan tan C
'd2 542
54 sin 2 54 4 3 3 4
22516
)1)1
)#
""
" "
œœ
È’“
Ɉ‰ ‘ˆ‰
)
(We used FORMULA 70 with b 5, c 4, a 2)œœœ
20. ln C ln C
'd 1 5 4 sin 2 3 cos 2
4 5 sin 2 4 5 sin 2 6 4 5 sin 2
22516
5 4 sin 2 25 16 cos 2
)))
)) )
))
"
œœ
ÈÈ
¹¹
¸¸
(We used FORMULA 71 with a 2, b 4, c 5)œœœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

526 Chapter 8 Techniques of Integration
21. e cos 3t dt (2 cos 3t 3 sin 3t) C (2 cos 3t 3 sin 3t) C
'2t œœ
ee
23 13
2t 2t
(We used FORMULA 108 with a 2, b 3)œœ
22. e sin 4t dt ( 3 sin 4t 4 cos 4t) C ( sin 4t 4 cos 4t) C
'3t œœ$
ee
(3) 4 25
3t 3t
(We used FORMULA 107 with a 3, b 4)œ œ
23. x cos x dx x cos x dx cos x cos x
'' ' '
" " " " "
##
""
œœœ
x x dx x x dx
11 11 1x 1x
11 11
ÈÈ
(We used FORMULA 100 with a 1, n 1)œœ
cos x sin x x 1 x C cos x sin x x 1 x Cœ œ
xx
44
### ## #
" " " "
"" " " " "
##
ˆ‰
Š‹
ÈÈ
(We used FORMULA 33 with a 1)œ
24. x tan x dx x tan x dx tan x tan x
'' ' '
" " " " "
##
""
"
œ"œ" œab ab
x x dx x x dx
11 11 1x
1x
11 11
ab
(We used FORMULA 101 with a 1, n 1)œœ
tan x dx (after long division)œ"
x
1x
##
" ""
'ˆ‰
tan x dx dx tan x x tan x C x tan x x Cœ œœ"
x x
1x
###### #
" " " # "
""" "" "
'' abab
25. ln C
''
ds ds s s 3
9s 3 s 23 3 s 43 s 3
ab a b ab
"
œœ
†† †
3¸¸
(We used FORMULA 19 with a 3)œ
ln Cœ
ss3
18 9 s 108 s 3ab
"
¸¸
26. ln C
''
dd
2222 2 42
2
2
)) )
)))
)
)
ab ”•
Š‹
ÈŠ‹Š‹
ÈÈ
”•
Š‹
ÈÈ
È
"
œœ
3¹¹
We used FORMULA 19 with a 2
Š‹
È
œ
ln Cœ
)
)
)
)
42 82 2
2
abÈÈ
È
"
¹¹
27. dx
''
ÈÈ
È
4x 9 4x 9
xx2
4dx
x4x9
œ
(We used FORMULA 14 with a 4, b 9)œœ
2 ln C ln Cœ œ
ÈÈ ÈÈ
ÈÈ È
È
È
4x9 4x9 9 4x9 4x93
xx3
94x99
2
4x93
"
Š‹ ¹¹¹¹
(We used FORMULA 13(b) with a 4, b 9)œœ
28. dx C
''
ÈÈ
È
9x 4 9x 4
xx2
9dx
x9x4
œ
(We used FORMULA 14 with a 9, b 4)œœ
tan C tan Cœ œ
ÈÈÈ
È
9x 4 9x 4 9x 4
x4x
92 9x4 9
4
###
" "
Š‹
É
(We used FORMULA 13(a) with a 9, b 4)œœ
29. dt 2 3t 4 ( 4)
''
ÈÈ
3t 4
t
dt
t3t4
œ
È
(We used FORMULA 12 with a 3, b 4)œœ
2 3t 4 4 tan C 2 3t 4 4 tan Cœ œ
ÈÈ
Š‹
É
23t4
44
3t 4
ÈÈ
" "
#
(We used FORMULA 13(a) with a 3, b 4)œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.6 Integral Tables and Computer Algebra Systems 527
30. dt 2 3t 9 9
''
ÈÈ
3t 9
t
dt
t3t9
œ
È
(We used FORMULA 12 with a 3, b 9)œœ
2 3t 9 9 ln C 2 3t 9 3 ln Cœ œ
ÈÈ
Š‹ ¹¹¹¹
1
93t99
3t 9 9 3t 9 3
3t 9 3
ÈÈ È
ÈÈ
È
È
(We used FORMULA 13(b) with a 3, b 9)œœ
31. x tan x dx tan x dx tan x dx
'''
#" " "
""
œ œ
xxxx
2 1 2 1 1 x 3 3 1 x
21 21
(We used FORMULA 101 with a 1, n 2);œœ
dx x dx ln 1 x C x tan x dx
''' '
xx dxx
1 x 1 x
##
"##"
œ œÊab
tan x ln 1 x Cœ
xx
366
" #
"ab
32. dx x tan x dx tan x dx tan x dx
'' ' '
tan x x x x x
x ( 2 1) ( 2 1) 1 x ( 1) 1 x
œœ œ
# " " "
"
21 21 ab
(We used FORMULA 101 with a 1, n 2);œœ
ln x ln 1 x C
'' ''
x dx dx dx x dx
1x x1 x x 1x
#
"#
œœœ
ab kk a b
dx tan x ln x ln 1 x Cʜ
'tan x
xx
""
" #
#
kk a b
33. sin 3x cos 2x dx C
'œ
cos 5x cos x
10 #
(We used FORMULA 62(a) with a 3, b 2)œœ
34. sin 2x cos 3x dx C
'œ
cos 5x cos x
10 #
(We used FORMULA 62(a) with a 2, b 3)œœ
35. 8 sin 4t sin dx sin sin C 8 C
't87t89t
79 79
sin sin
###
œœ
ˆ‰ ˆ‰ –—
Š‹ Š‹
7t 9t
(We used FORMULA 62(b) with a 4, b )œœ
"
#
36. sin sin dt 3 sin sin C
'tt t t
36 6
œ
ˆ‰ ˆ‰
#
(We used FORMULA 62(b) with a , b )œœ
""
36
37. cos cos d 6 sin sin C
')) ) )
34 127 1
67
)œ
ˆ‰ ˆ‰
#
(We used FORMULA 62(c) with a , b )œœ
""
34
38. cos cos 7 d sin sin C C
')))
2 13 2 15 13 15
13 1 15 sin sin
))œœ
"
#
ˆ‰ ˆ‰ Š‹ Š‹
13 15
(We used FORMULA 62(c) with a , b 7)œœ
"
2
39. dx
'''''
x x 1 x dx dx dx
x 1 x 1 x 1
x 1 x 1
dx 1
"
#
ab ab ab
ab
œ œ
ln x 1 tan x Cœ
""
##
#"
abx
21 xab
(For the second integral we used FORMULA 17 with a 1)œ
40. dx 3 3
''''' ''
x 6x dx 6x dx 3 dx dx dx
x 3 x 3 x 3 x 3
x 3 x 3
dx 3
x 3
ab ab ab ab
Š‹
Èab ”•
Š‹
È
œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

528 Chapter 8 Techniques of Integration
tan 3 tan Cœ
" "
" "
ÈÈ È
ab Š‹Š‹
ÈÈ
Œ
Š‹
È
33 3
x3 x x
x 3 23 3 x 23
Š‹ Š‹
ÎÑ
ÏÒ
For the first integral we used FORMULA 16 with a 3; for the third integral we used FORMULA 17
ŠÈ
œ
with a 3‹
È
œ
tan Cœ
""
23 3
x3 x
x 3 2 x 3
ÈÈ ab
Š‹
41. sin x dx; 2 u sin u du 2 sin u du
ux
xu
dx 2u du
'' '
" " " "
#
"
ÈÔ×
ÕØ
ÈŠ‹
œ
œ
œ
Ĝ
uu
11 11 1 u
11 11
È
u sin uœ
#"
'u du
1 u
È
(We used FORMULA 99 with a 1, n 1)œœ
u sin u sin u u 1 u C u sin u u 1 u Cœ œ
#" " # "
"" " "
## # #
##
Š‹
ÈÈ
ˆ‰
(We used FORMULA 33 with a 1)œ
x sinx xxCœ
ˆ‰ÈÈ
""
##
" #
42. dx; 2u du 2 cos u du 2 u cos u 1 u C
ux
xu
dx 2u du
'''
cos x
x
cos u
u1
È
ÈÔ×
ÕØ
ÈŠ‹
È
œ
œ
œ
Äœœ
#" " "#
†
(We used FORMULA 97 with a 1)œ
2x cos x 1xCœ
Š‹
ÈÈ
È
"
43. dx; du 2 du 2 sin u u 1 u C
ux
xu
dx 2u du
'''
È
ÈÈÈ
x
1 x
u2u u
1 u 1 u
#
""
##
" #
Ô×
ÕØ
ÈŠ‹
È
œ
œ
œ
Äœ œ
†
sin u u 1 u Cœ
" #
È
(We used FORMULA 33 with a 1)œ
sin x x1xCsin x xx Cœœ
" " #
ÈÈ È
ÈÈ
44. dx; 2u du 2 2 u du
ux
xu
dx 2u du
'''
ÈÈ
È
2 x
x
2 u
u
###
Ô×
ÕØ
ÈÊŠ‹
È
œ
œ
œ
Ĝ
†
2 2 u sin C u 2 u 2 sin Cœ œ
–—
ÊŠ‹ Š‹ Š‹
ÈÈ
uu u
2
22
##
###
" "
Š‹
ÈÈÈ
We used FORMULA 29 with a 2
Š‹
È
œ
2x x 2 sin Cœ
ÈÈ
#"
#
x
45. (cot t) 1 sin t dt ;
usin t
du cos t dt
'' '
È”•
œ Ä
œ
œ
#
ÈÈ
1 sin t (cos t) dt
sin t u
1 u du
1u ln Cœ
ȹ¹
#1 1 u
u
È
(We used FORMULA 31 with a 1)œ
1 sin t ln Cœ
ȹ¹
#1 1 sin t
sin t
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.6 Integral Tables and Computer Algebra Systems 529
46. ; ln C
usin t
du cos t dt
'' '
dt cos t dt du
(tan t) 4 sin t (sin t) 4 sin t u 4 u
2 4 u
u
ÈÈ È È
"
#
œÄœ
œ
œ
”• ¹¹
(We used FORMULA 34 with a 2)œ
ln Cœ
"
#
¹¹
2 4 sin t
sin t
È
47. ; ln u 3 u C
u ln y
ye
dy e du
'''
dy
y 3 (ln y)
e du du
e3 u 3 u
ÈÈÈ
#
Ô×
ÕØ ¹¹
È
œ
œ
œ
Äœœ
u
u
u
u
ln ln y 3 (ln y) Cœ
¸¸
È#
We used FORMULA 20 with a 3
Š‹
È
œ
48. ; ln u 5 u C ln sin 5 sin C
usin
du cos d
''
cos d du
5 sin 5 u
))
)
ÈÈ
##
”• ¹¹¹ ¹
ÈÈ
œ
œÄ œ œ
)
)) ))
We used FORMULA 20 with a 5
Š‹
È
œ
49. ; ln u u 1 C ln 3r 9r 1 C
u3r
du 3 dr
''
3 dr du
9r 1 u 1
ÈÈ
##
”• ¹¹¹ ¹
ÈÈ
œ
œÄ œœ
(We used FORMULA 36 with a 1)œ
50. ; ln u 1 u C ln 3y 1 9y C
u3y
du 3 dy
''
3 dy
1 9y
du
1 u
ÈÈ
##
”• ¹¹
ȸ¸
È
œ
œÄ œ œ
(We used FORMULA 20 with a 1)œ
51. cos x dx; 2 t cos t dt 2 cos t dt t cos t dt
tx
xt
dx 2t dt
''''
" " " # "
###
"
ÈÔ×
ÕØ
ÈŠ‹
œ
œ
œ
Äœœ
tt t
1 t 1 t
ÈÈ
(We used FORMULA 100 with a 1, n 1)œœ
t cos t sin t t 1 t Cœ
#" "
""
##
#
È
(We used FORMULA 33 with a 1)œ
x cos x sin x x 1 x C x cos x sin x x x Cœœ
" " " "
"" ""
## ##
#
ÈÈÈ ÈÈ
ÈÈ
52. tan y dy; 2 t tan t dt 2 tan t dt t tan t dt
ty
yt
dy 2t dt
''''
" " " # "
###
"
ÈÔ×
ÕØ
È’“
œ
œ
œ
Äœœ
tt t
1 t 1 t
(We used FORMULA 101 with n 1, a 1)œœ
t tan t dt t tan t t tan t C y tan y tan y y Cœ œœ
# " # " " " "
''
t 1 dt
t 1 1 t ÈÈÈ
53. sin 2x dx sin 2x dx sin 2x dx
'' '
&$
##
œ œ
sin 2x cos 2x 5 1 sin 2x cos 2x 4 sin 2x cos 2x 3 1
55 10533
††
’“
(We used FORMULA 60 with a 2, n 5 and a 2, n 3)œœ œœ
sin 2x cos 2x cos 2x C Cœ œ
sin 2x cos 2x 2 8 sin 2x cos 2x 2 sin 2x cos 2x 4 cos 2x
10 15 15 10 15 15
#"
#
ˆ‰
54. sin d sin d sin cos sin d
'' '
&$%
#####
)))))
)) )œ œ
sin cos sin cos
53
5 1 2 4 3 1
5553
† †
’“
We used FORMULA 60 with a , n 5 and a , n 3
ˆ‰
œœ œœ
""
##
sin cos sin cos 2 cos C sin cos sin cos cos Cœ œ
28 8 2816
5 15 15 5 15 15
%# %#
## ## # ## ## #
)) )) ) )) )) )
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

530 Chapter 8 Techniques of Integration
55. 8 cos 2 t dt 8 cos 2 t dt
''
%#
11œ
Š‹
cos 2 t sin 2 t 4 1
42 4
11
1†
(We used FORMULA 61 with a 2 , n 4)œœ1
6Cœ
cos 2 t sin 2 t t sin (2 2 t)
42
11
11
1
’“
#
††
†
(We used FORMULA 59 with a 2 )œ1
3t C 3t Cœœ
cos 2 t sin 2 t 3 sin 4 t cos 2 t sin 2 t 3 cos 2 t sin 2 t
42
11 1 11 11
1111
56. 3 cos 3y dy 3 cos 3y dy
''
&$
œ
Š‹
cos 3y sin 3y
53 5
5 1
†
cos 3y dyœ
cos 3y sin 3y cos 3y sin 3y
5533 3
12 3 1
Š‹
†
'
(We used FORMULA 61 with a 3, n 5 and a 3, n 3)œœ œœ
cos 3y sin 3y cos 3y sin 3y sin 3y Cœ
"%#
515 15
48
57. sin 2 cos 2 d sin 2 cos 2 d
''
#$ #
# #
))) )))œ
sin 2 cos 2 3 1
(2 3) 3
))
(We used FORMULA 69 with a 2, m 3, n 2)œœœ
sin 2 cos 2 d sin 2 d(sin 2 ) Cœ œ œ
sin 2 cos 2 2 sin 2 cos 2 2 sin 2 cos 2 sin 2
10 5 10 5 10 15
)) )) )) )
''
##
"
#
))) ) )
’“
58. 9 sin cos d 9 sin cos d
''
$ $Î# $Î#
))) )))œ
’“
sin cos 3 1
3 3
))
ˆ‰ ˆ‰
33
2 sin cos 4 cos sin dœ
# &Î# $Î#
)) )))
'
We used FORMULA 68 with a 1, n 3, m
ˆ‰
œœ œ
3
#
2 sin cos 4 cos d(cos ) 2 sin cos 4 cos Cœ œ
# &Î# $Î# # &Î# &Î#
)) )) )) )
'ˆ‰
2
5
2 cos sin Cœ
ˆ‰ˆ‰
&Î# #
))
4
5
59. 2 sin t sec t dt 2 sin t cos t dt 2 cos t dt
'' '
#% #% %
œœ
Š‹
sin t cos t 2 1
2 4 2 4
(We used FORMULA 68 with a 1, n 2, m 4)œœ œ
sin t cos t cos t dt sin t cos t sec t dt sin t cos t sec t dtœ œœ
$ % $ % $ #
'' '
Š‹
sec t tan t 4 2
4 1 4 1
(We used FORMULA 92 with a 1, n 4)œœ
sin t cos t tan t C sec t tan t tan t C tan t sec t 1 Cœœ œ
$ # #
Š‹ ab
sec t tan t 2 2 2 2
33 3 3 3
tan t Cœ
2
3$
An easy way to find the integral using substitution:
2 sin t cos t dt 2 tan t sec t dt 2 tan t d(tan t) tan t C
'''
#%### $
œœœ
2
3
60. csc y cos y dy sin y cos y dy sin y cos y dy
'' '
#& #& #$
#
œœ
Š‹
sin y cos y
52 5
5 1
sin y cos y dyœ
Š‹ Š‹
sin y sin y
cos y cos y
333 23
43 1
#
#
'
(We used FORMULA 69 with n 2, m 5, a 1 and n 2, m 3, a 1)œ œ œ œ œ œ
cos y sin y d(sin y) Cœ œ
Š‹
sin y cos y
3 3 sin y 3 3 sin y 3 sin y 3 sin y
48 8
cos y 4 cos y
Š‹
"##
'
61. 4 tan 2x dx 4 tan 2x dx tan 2x 4 tan 2x dx
'''
$#
#
œ œ
Š‹
tan 2x
2†
(We used FORMULA 86 with n 3, a 2)œœ
tan 2x ln sec 2x C tan 2x 2 ln sec 2x Cœ œ
##
#
4kk kk
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.6 Integral Tables and Computer Algebra Systems 531
62. tan dx tan dx tan tan dx
'' '
%#$#
####
ˆ‰ ˆ‰ ˆ‰ ˆ‰
xx2xx
tan
(4 1) 3
œ œ
ˆ‰
x
(We used FORMULA 86 with n 4, a )œœ
"
#
tan 2 tan x Cœ
2x x
3$
##
(We used FORMULA 84 with a )œ"
#
63. 8 cot t dt 8 cot t dt
''
%#
œ
Š‹
cot t
3
(We used FORMULA 87 with a 1, n 4)œœ
8 cot t cot t t Cœ
ˆ‰
"$
3
(We used FORMULA 85 with a 1)œ
64. 4 cot 2t dt 4 cot 2t dt cot 2t 4 cot 2t dt
'''
$#
œ œ
’“
cot 2t
2(3 1)
(We used FORMULA 87 with a 2, n 3)œœ
cot 2t ln sin 2t C cot 2t 2 ln sin 2t Cœ œ
##
#
4kk kk
(We used FORMULA 83 with a 2)œ
65. 2 sec x dx 2 sec x dx
''
$
11œ
’“
sec x tan x 3 2
(3 1) 3 1
11
1
(We used FORMULA 92 with n 3, a )œœ1
sec x tan x ln sec x tan x Cœ
""
11
11 1 1kk
(We used FORMULA 88 with a )œ1
66. csc dx csc dx
''
""
## # #
$
x3 2x
(3 1) 3 1
œ
Š‹
csc cot
xx
We used FORMULA 93 with a , n 3
ˆ‰
œœ
"
#
csc cot ln csc cot C csc cot ln csc cot Cœ œ
"""
### ## #### ##
‘¸¸¸¸
xx x x xx x x
We used FORMULA 89 with a
ˆ‰
œ"
#
67. 3 sec 3x dx 3 sec 3x dx
''
%#
œ
’“
sec 3x tan 3x 4 2
3(4 1) 4 1
(We used FORMULA 92 with n 4, a 3)œœ
tan 3x Cœ
sec 3x tan 3x 2
33
(We used FORMULA 90 with a 3)œ
68. csc d csc d
''
%#
))
34 13
(4 1)
4 2
))œ
csc cot
33
3
We used FORMULA 93 with n 4, a
ˆ‰
œœ
"
3
csc cot 3 cot C csc cot 2 cot Cœ œ
##
)) ) )) )
333 3 33 3
2†
We used FORMULA 91 with a
ˆ‰
œ"
3
69. csc x dx csc x dx csc x dx
'' '
&$
œ œ
csc x cot x 5 2 csc x cot x 3 csc x cot x 3 2
5 1 5 1 4 4 3 1 3 1
Š‹
(We used FORMULA 93 with n 5, a 1 and n 3, a 1)œœ œœ
csc x cot x csc x cot x ln csc x cot x Cœ
"$
488
33
kk
(We used FORMULA 89 with a 1)œ
70. sec x dx sec x dx sec x dx
'' '
&$
œ œ
sec x tan x 5 2 sec x tan x 3 sec x tan x 3 2
5 1 5 1 4 4 3 1 3 1
Š‹
(We used FORMULA 92 with a 1, n 5 and a 1, n 3)œœ œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

532 Chapter 8 Techniques of Integration
sec x tan x sec x tan x ln sec x tan x Cœ
"$
488
33
kk
(We used FORMULA 88 with a 1)œ
71. 16x (ln x) dx 16 x ln x dx 16 x dx
'' '
$# $ $
""
#
œ œ
’“’ “’“
x(ln x) x(ln x) x(ln x)
44 4 44
2
(We used FORMULA 110 with a 1, n 3, m 2 and a 1, n 3, m 1)œœ œ œœ œ
16 C 4x (ln x) 2x ln x Cœœ
Š‹
x(ln x) x(ln x)
483
xx
##
%#%
72. (ln x) dx (ln x) dx x(ln x) 3 ln x dx x(ln x) 3x(ln x) dx
'' ' '
$#$ $#
"
"
œ œ œ '
x(ln x) x(ln x)
11 11 1
32 x ln x
’“ Š‹
x(ln x) 3x(ln x) 6x ln x 6x Cœ
$#
(We used FORMULA 110 with n 0, a 1 and m 3, 2, 1)œœ œ
73. xe dx (3x 1) C (3x 1) C
'3x ee
39
œœ
3x 3x
(We used FORMULA 104 with a 3)œ
74. xe dx ( 2x 1) C (2x 1) C
'2x œ œ
ee
(2) 4
2x 2x
(We used FORMULA 104 with a 2)œ
75. x e dx 2x e 3 2 x e dx 2x e 6 2x e 2 2 xe dx
'' '
$$ #$#x2 x2 x2 x2 x2 x2
œ œ ††
Š‹
2x e 12x e 24 4e 1 C 2x e 12x e 96e 1 Cœ œ
$# $#
##
x2 x2 x2 x2 x2 x2
†ˆ‰ ˆ‰
xx
We used FORMULA 105 with a twice and FORMULA 104 with a
ˆ‰
œœ
""
##
76. x e dx x e xe dx
''
##
"
111
11
xxx
2
œ
(We used FORMULA 105 with n 2, a )œœ1
xe e ( x 1) C xe ( x 1) Cœ œ
""
##
111 1 1
11 1xx x
22e
†
†11
ˆ‰
x
(We used FORMULA 104 with a )œ1
77. x 2 dx x2 dx 2 dx C
'' '
#
####
"
xœ œ œ
x2 2 x2 2 x2 x2 2 x2 2
ln 2 ln 2 ln ln 2 ln 2 ln 2 ln ln ln (ln 2)
xx
xxxxxx
Š‹’“
(We used FORMULA 106 with a 1, b 2, n 2, n 1)œœœœ
78. x 2 dx x2 dx 2 dx
'' '
#
#
"
xx
œ œ
x2 2 x2 2 x2
ln 2 ln 2 ln ln 2 ln 2 ln 2
x
xxx
Š‹
Cœ
x2 2 x2 2
ln ln ln (ln 2)
xxx
###
’“
(We used FORMULA 106 with a 1, b 2, n 2, n 1)œœœœ
79. x dx dx C C
''
11
xx
xx x
ln ln ln ln ln ln (ln )
œ œ œ
11111
11 111 1 1
xxxxx
""
ˆ‰
(We used FORMULA 106 with n 1, b , a 1)œœœ1
80. x2 dx 2 dx C
''
ÈÈ
ÈÈ È
2x 2x
x2 x2 2
2 ln 2 2 ln 2 2 ln 2 (ln 2)
œ œ
2x x2 x2
"
#
(We used FORMULA 106 with a 2, b 2, n 1)œœœ
È
81. e sec e dt; sec x dx sec x dx
xe
dx e dt
'''
tt t
tsec x tan x 3 2
31 31
$$
ab
”•
" Ä œ
œ"
œ
(We used FORMULA 92 with a 1, n 3)œœ
ln sec x tan x C sec e 1 tan e 1 ln sec e 1 tan e 1 Cœ œ
sec x tan x tt t t
## #
""
kkc dababk kabab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.6 Integral Tables and Computer Algebra Systems 533
82. d ; 2 csc t dt 2 csc t dt
t
t
d2t dt
'''
csc csc t cot t 3 2
31 31
È
È)
))
)
)
)
Ô×
ÕØ
È’“
œ
œ
œ
Ĝ
#$
(We used FORMULA 93 with a 1, n 3)œœ
2 ln csc t cot t C csc cot ln csc cot Cœ œ
‘
kk ÈÈ È È
¹¹
csc t cot t
##
")) ) )
83. 2 x 1 dx; x tan t 2 sec t sec t dt 2 sec t dt 2 sec t dt
''' '
000 0
144 4
Ècd ”•
‘
##$
Î%
!
œÄ œ œ †sec t tan t 3 2
31 31
†1
(We used FORMULA 92 with n 3, a 1)œœ
sec t tan t ln sec t tan t 2 ln 2 1œœcdkk
ÈÈ
Š‹
†
1Î%
!
84. ; y sin x sec x dx sec x dx
''' '
000 0
32 3 3 3
dy
1y
cos x dx sec x tan x 4 2
cosx 41 41
ab
%#
Î$
!
cd ’“
œÄ œ œ
1
(We used FORMULA 92 with a 1, n 4)œœ
tan x 3 3 2 3œ œœ
’“
ˆ‰ ˆ‰
ÈÈÈ
sec x tan x 2 4 2
33 3 3
1Î$
!
85. dr; r sec (sec tan ) d tan d tan d
''''
1000
2333
abr1
r sec 4 1
tan tan
%#
Î$
!
cd ’“
œÄ œ œ ) ) ) ) )) ))
))
)
1
tan 3œœœ
’“
È
tan
3333
33
)11
1
))
Î$
!
È
(We used FORMULA 86 with a 1, n 4 and FORMULA 84 with a 1)œœ œ
86. ; t tan cos d cos d
''' '
000 0
13 6 6 6
dt sec d cos sin 5 1
t1 sec 55
ab
&$
Î'
!
cd ’“
ˆ‰
œÄ œ œ ))) ))
)) ) )
)
1
cos dœ
’“’“
”•
ˆ‰
cos sin 4 cos sin 3 1
553 3
)) ))
11Î' Î'
!!
'0
6
))
cos sin sin œ
’“
cos sin 4 8
515 15
)) 1
#Î'
!
)) )
(We used FORMULA 61 with a 1, n 5 and a 1, n 3)œœ œœ
œ œœ œ
Š‹
ˆ‰ È
3
5 15 15 160 10 15 480 480
4 8 9 4 3 9 48 32 4 203
3
ˆ‰ ˆ‰ˆ‰ˆ‰
Š‹
## #
#"" " ††
87. sinh 3x dx sinh 3x dx
''
""
&$
88535
sinh 3x cosh 3x 5 1
œ
Š‹
†
sinh 3x dxœ
sinh 3x cosh 3x sinh 3x cosh 3x 3 1
120 10 3 3 3
"
Š‹
†'
(We used FORMULA 117 with a 3, n 5 and a 3, n 3)œœ œœ
cosh 3x Cœ
sinh 3x cosh 3x sinh 3x cosh 3x 2
1 0 90 30 3
#
"
ˆ‰
sinh 3x cosh 3x sinh 3x cosh 3x cosh 3x Cœ
""
#
%
1 0 90 45
1
88. dx; 2 cosh u du 2 cosh u du
ux
du
'' '
cosh x
xdx
2x
cosh u sinh u 4 1
44
È
ÈÈ
–—
ÈŠ‹
œ
œÄœ
%#
Cœ
cosh u sinh u 3 sinh 2u u
4
## #
ˆ‰
(We used FORMULA 118 with a 1, n 4 and FORMULA 116 with a 1)œœ œ
cosh x sinh x sinh 2 x x Cœ
"
#
$ÈÈ ÈÈ
33
84
89. x cosh 3x dx sinh 3x x sinh 3x dx sinh 3x cosh 3x cosh 3x dx
'' '
#"
œ œ
x2 x2x
33 3333
Š‹
(We used FORMULA 122 with a 3, n 2 and FORMULA 121 with a 3, n 1)œœ œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

534 Chapter 8 Techniques of Integration
sinh 3x cosh 3x sinh 3x Cœ
x2x2
3927
90. x sinh 5x dx cosh 5x sinh 5x C
'œ
x
525
"
(We used FORMULA 119 with a 5)œ
91. sech x tanh x dx C
'(œ
sech x
7
(We used FORMULA 135 with a 1, n 7)œœ
92. csch 2x coth 2x dx C C
'$
#
œ œ
csch 2x csch 2x
36
†
(We used FORMULA 136 with a 2, n 3)œœ
93. u ax b x dx ;œÊœ Ê œ
ub du
aa
du ln u C ln ax b C
'' '
x dx du b b b
(ax b) au a a u u a u a ax b
(u b)
"" " "
œœœœ
ˆ‰ ‘ ‘
kk k k
94. x a tan a x a sec 2x dx 2a sec tan dx a sec d ;œÊœ Êœ Êœ))))))
# # ## ## #
d (1 cos 2 ) d sin 2 C
'' ''
dx a sec d
ax a sec a sec 2a 2a
ab a b
"" ""
#
œœœœ
))
))
)))))
ˆ‰
sin cos C cos C Cœ œ œ
"" "
#
#
a 2a cos 2a 1 tan
sin tan
ab
‘ˆ‰ˆ‰
))) ) ) )
))
))
tan C tan Cœœ
""
" "
2a a 2a a x 2a a
xx x x
a1
–—
Š‹ ab
x
a
95. x a sin a x a cos 2x dx 2a cos sin d dx a cos d ;œÊœ Êœ Êœ)) )))))
#### #
a x dx a cos (a cos ) d a cos d (1 cos 2 ) d C
'' ''
Ȉ‰
## ##
###
œ œ œ œ ))) )) )) )
aasin 2)
cos sin C 1 sin sin C sin Cœ œ œ
aa axx
aaa
ax
## #
#"
ab
Š‹Š‹
È
))) ) ))††
È
sin a x Cœ
axx
a
##
" ##
È
96. x a sec x a a tan 2x dx 2a tan sec d dx a sec tan d ;œÊœ Êœ Êœ))))))))
## ## # #
cos d sin C 1 cos C
'' ''
dx a tan sec d d
xxa a sec a tan a sec a a a
Èab
"""
#
œœœœœ
))) )
)) ) )) ) )
È
CCCCœœ œœ
ˆ‰ ˆ‰ ˆ‰
"" "
"
a a sec a a x
1sec 1 x a
ÉÉ
ˆ‰ ÈÈ
ˆ‰
cos
cos
x
ax
a
)
)
97. x sin ax dx x d(cos ax) (cos ax) x cos ax nx dx
'' '
nœ œ
nnn1
aaa
ˆ‰ ˆ ‰
"""
†
cos ax x cos ax dxœ
xn
aa
n1
n'
We used integration by parts u dv uv v du with u x , v cos ax
Š ‹
''
œ œ œ
n"
a
98. x (ln ax) dx (ln ax) d m(ln ax) dx
'' '
nm m m1
xx
n1 n1 n1 x
x(ln ax)
œœ
Š‹ Š‹ ˆ‰
n1 n1
n1 m
"
x (ln ax) dx, nœ Á"
x(ln ax)
n1 n1
mnm1
n1 m
'
We used integration by parts u dv uv v du with u (ln ax) , v
Š ‹
''
œ œ œ
mx
n1
n1
99. x sin ax dx sin ax d sin ax dx
'' '
n" " "
œœ
Š‹ Š‹
xx x a
n1 n1 n1 1(ax)
n1 n1 n1 È
sin ax , n 1œ Á
xax dx
n1 n1 1ax
n1 n1
"
'È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
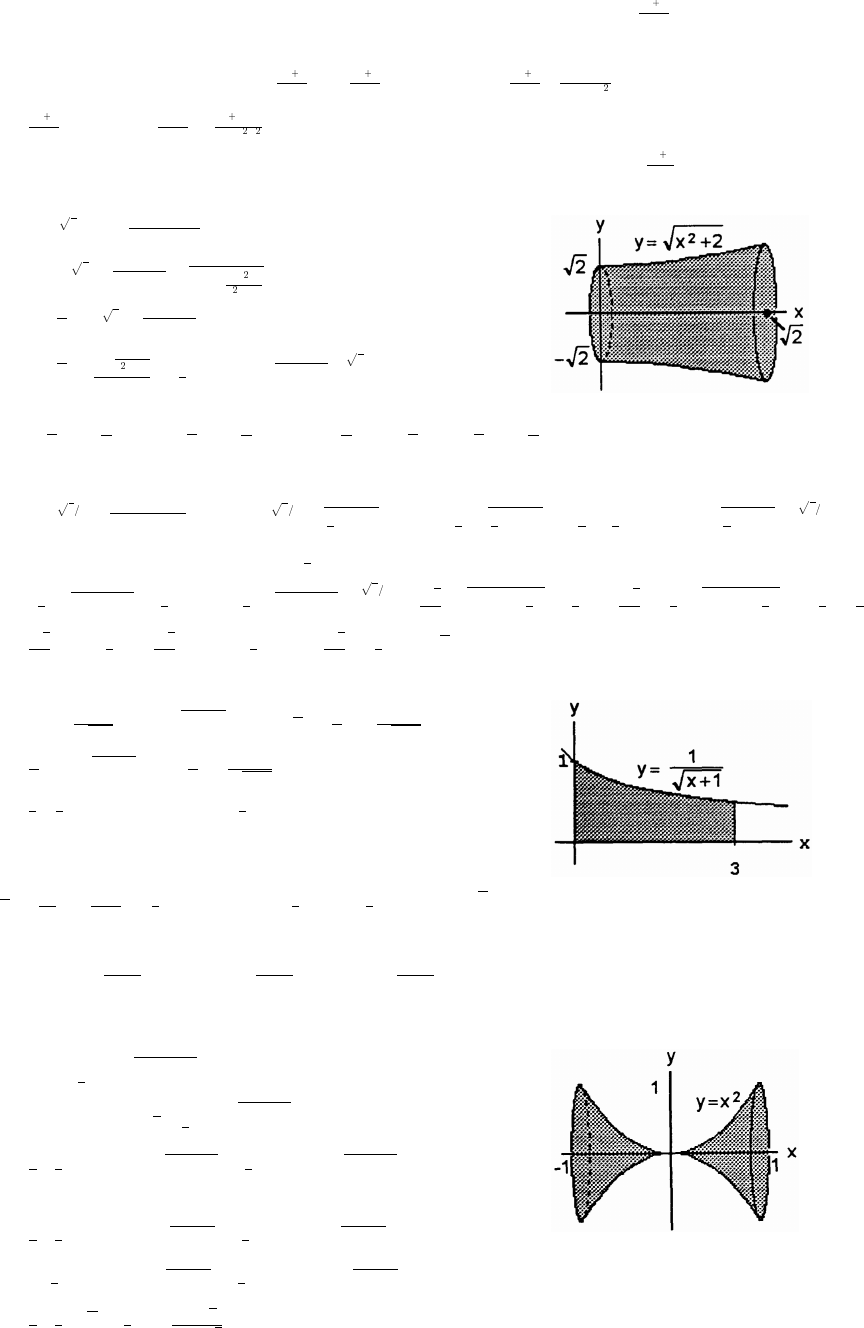
Section 8.6 Integral Tables and Computer Algebra Systems 535
We used integration by parts u dv uv v du with u sin ax, v
Š ‹
''
œ œ œ
"
x
n1
n1
100. x tan ax dx tan ax d tan ax dx
'' '
n" " "
œœ
Š‹ Š‹
xx xa
n1 n1 n1 1(ax)
n1 n1 n1
tan ax , n 1œ Á
xax dx
n1 n1 1ax
n1 n1
" '
We used integration by parts u dv uv v du with u tan ax, v
Š ‹
''
œ œ œ
"
x
n1
n1
101. S 2 y 1 (y ) dxœ
'0
2
1Èw#
2 x 2 1 dxœ1'0
2ÈÉ
#
x
x2
2 2 x 1 dxœ
ÈÈ
1'0
2#
22 ln x x 1œ
ÈÈ
’“¹¹
1xx 1
È
##
"# 2
0
(We used FORMULA 21 with a 1)œ
26ln23 23 2 ln23œœ
ÈÈ ÈÈ
’“Š‹
ÈÈÈ È
Š‹
111
102. L 1 (2x) dx 2 x dx 2 x ln x xœœ œ
''
00
32 32 32
0
ÈÉÉ É
’“
ˆ‰ˆ‰ Š‹
### #
"""""
##4444
x
We used FORMULA 2 with a
ˆ‰
œ"
#
14x lnx 14x 14 ln 14 ln œ œ
’“Š‹
ÈÈ
Š‹
ÉÉ
ˆ‰ ˆ‰
x33
444444
33
## ###
##
"" " " ""
32
0
ÈÈ
(2) ln 1 ln 2 ln 3 2œ œ
ÈÈ È
33 3
44 4 4
"""
##
Š‹ Š‹
È
103. A 2 x 1 2; x œœœœ
''
00
33
dx x dx
x1 x 1
A
ÈÈ
$
!
"
’“
È
x 1 dxœ
""
AA
dx
x1
''
00
33
ÈÈ
(x 1) 1 ;œœ
"
#
$Î# $
!
†24
33
‘
(We used FORMULA 11 with a 1, b 1, n 1 andœœœ
a 1, b 1, n 1)œœœ
y ln (x 1) ln 4 ln 2 ln 2œ œ œœœ
"" ""
# #
$
!
Ax14 4
dx
'0
3cd È
104. M x dx 18 dx 54 18x 27 ln 2x 3
y000
333
œœœ
'''
ˆ‰ cdkk
36 2x 3 dx
2x 3 2x 3 2x 3
$
!
18 3 27 ln 9 ( 27 ln 3) 54 27 2 ln 3 27 ln 3 54 27 ln 3œ œ œ††
105. S 2 x 1 4x dx;œ1'1
1##
È
u1u du
u2x
du 2 dx
”• È
œ
π
1
4'2
2##
12u 1u lnu 1uœ
1
48 8
u
’“
ab
ÈÈ
Š‹
###
"#
#
(We used FORMULA 22 with a 1)œ
(1 2 4) 1 4 ln 2 1 4œ
1
48 8
2
’Š‹
ÈÈ
†"
(1 2 4) 1 4 ln 2 1 4 “
ÈÈ
Š‹
2
88
†"
5 ln 7.62œ ¸
1
48
925
25
’“
ÈŠ‹
#
"
È
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

536 Chapter 8 Techniques of Integration
106. (a) The volume of the filled part equals the length of the
tank times the area of the shaded region shown in the
accompanying figure. Consider a layer of gasoline
of thickness dy located at height y where
r y r d. The width of this layer is
2 r y . Therefore, A 2 r y dy
ÈÈ
## ##
œ
'r
rd
and V L A 2L r y dyœœ †'r
rd
È##
(b) 2L r y dy 2L sin
'r
rd rd
r
È’“
##
##
"
œ
yr y ry
r
È
(We used FORMULA 29 with a r)œ
2L 2rd d sin 2L 2rd d sinœœ
’“’“
ÈÈ
ˆ‰ ˆ‰ ˆ‰ ˆ ‰
Š‹ ˆ‰
(d r) rdrr d-r r dr
rr
##### # #
##
" "
11
107. The integrand f(x) x x is nonnegative, so the integral is maximized by integrating over the function'sœ
È#
entire domain, which runs from x 0 to x 1œœ
x x dx 2 x x dx 2 x x sinÊœ œ
''
00
11
ÈÉÉ
”•
Š‹
## #
""
####
"
"
!
††
ˆ‰ ˆ‰
xx
We used FORMULA 48 with a
ˆ‰
œ"
#
x x sin (2x 1)œœœ
’“
Ȉ‰
ˆ‰
x
8888
###
#"""
" "
!
†
111
108. The integrand is maximized by integrating g(x) x 2x x over the largest domain on which g isœ
È#
nonnegative, namely [ 2]!ß
x 2x x dx sin (x 1)ʜ
'0
2È’“
# "
#
" #
!
(x 1)(2x 3) 2x x
6È
(We used FORMULA 51 with a )œ"
œœ
""
## # # #
†
111
ˆ‰
CAS EXPLORATIONS
109. Example CAS commands:
:Maple
q1 := Int( x*ln(x), x ); # (a)
q1 = value( q1 );
q2 := Int( x^2*ln(x), x ); # (b)
q2 = value( q2 );
q3 := Int( x^3*ln(x), x ); # (c)
q3 = value( q3 );
q4 := Int( x^4*ln(x), x ); # (d)
q4 = value( q4 );
q5 := Int( x^n*ln(x), x ); # (e)
q6 := value( q5 );
q7 := simplify(q6) assuming n::integer;
q5 = collect( factor(q7), ln(x) );
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.6 Integral Tables and Computer Algebra Systems 537
110. Example CAS commands:
:Maple
q1 := Int( ln(x)/x, x ); # (a)
q1 = value( q1 );
q2 := Int( ln(x)/x^2, x ); # (b)
q2 = value( q2 );
q3 := Int( ln(x)/x^3, x ); # (c)
q3 = value( q3 );
q4 := Int( ln(x)/x^4, x ); # (d)
q4 = value( q4 );
q5 := Int( ln(x)/x^n, x ); # (e)
q6 := value( q5 );
q7 := simplify(q6) assuming n::integer;
q5 = collect( factor(q7), ln(x) );
111. Example CAS commands:
:Maple
q := Int( sin(x)^n/(sin(x)^n+cos(x)^n), x=0..Pi/2 ); # (a)
q = value( q );
q1 := eval( q, n=1 ): # (b)
q1 = value( q1 );
for N in [1,2,3,5,7] do
q1 := eval( q, n=N );
print( q1 = evalf(q1) );
end do:
qq1 := PDEtools[dchange]( x=Pi/2-u, q, [u] ); # (c)
qq2 := subs( u=x, qq1 );
qq3 := q + q = q + qq2;
qq4 := combine( qq3 );
qq5 := value( qq4 );
simplify( qq5/2 );
109-111. Example CAS commands:
: (functions may vary)Mathematica
In Mathematica, the natural log is denoted by Log rather than Ln, Log base 10 is Log[x,10]
Mathematica does not include an arbitrary constant when computing an indefinite integral,
Clear[x, f, n]
f[x_]:=Log[x] / xn
Integrate[f[x], x]
For exercise 111, Mathematica cannot evaluate the integral with arbitrary n. It does evaluate the integral (value is /4 in1
each case) for small values of n, but for large values of n, it identifies this integral as Indeterminate
109. (e) x ln x dx x dx, n 1
''
nn
x ln x
n1 n1
œ Á
n1
"
(We used FORMULA 110 with a 1, m 1)œœ
Cln x Cœœ
x ln x x x
n1 (n1) n1 n1
n1 n1 n1
"
ˆ‰
110. (e) x ln x dx x dx, n 1
''
"
nn
x ln x
n 1 (n)1
œ Á
n1
(We used FORMULA 110 with a 1, m 1, n n)œœœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
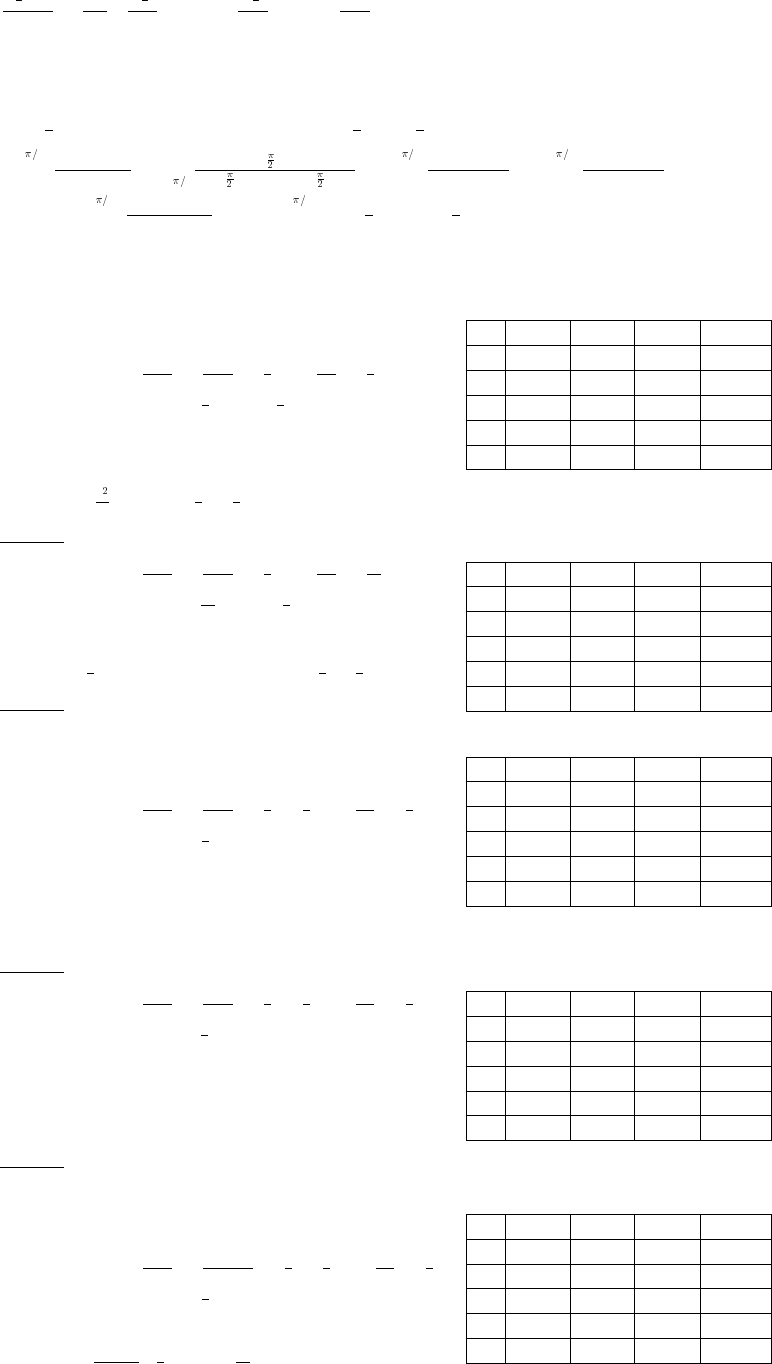
538 Chapter 8 Techniques of Integration
Cln x Cœ œ
x ln x x x
1n 1n 1n 1n 1n
1n 1n 1n
""
Š‹ ˆ‰
111. (a) Neither MAPLE nor MATHEMATICA can find this integral for arbitrary n.
(b) MAPLE and MATHEMATICA get stuck at about n 5.œ
(c) Let x u dx du; x 0 u , x u 0;œÊ œ œ Ê œ œ Ê œ
111
###
I œœ œœ
'' ''
02 00
20 2 2
sin x dx cos u du cos x dx
sinx cosx cosu sinu cosx sinx
sin u du
sin u cos u
nnn
nn nn nn
n
nn
ˆ‰
ˆ‰ ˆ‰
I I dx dx IÊœ œ œ Êœ
''
00
22
ˆ‰
sin x cos x
sin x cos x 4
nn
nn
#
11
8.7 NUMERICAL INTEGRATION
1. x dx
'1
2
I. (a) For n 4, x ;œœœœÊœ?ba 21 x
n44 8
" "
#
?
mf(x ) 12 T (12) ;
!iœÊœ œ
"
#8
3
f(x) x f (x) 1 f 0 M 0œÊ œÊ œÊ œ
www
E0Êœkk
T
x f(x ) m mf(x )
x1 1 1 1
x 5/4 5/4 2 5/2
x 3/2 3/2 2 3
x 7/4 7/4 2 7/2
x2 2 1 2
ii i
!
"
#
$
%
(b) x dx 2 E x dx T 0
''
11
22
T
œœœÊœ œ
’“ kk
x3
2
#
"
"
##
(c) 100 0%
kkE
True Value
T‚œ
II. (a) For n 4, x ;œœœœÊœ?ba 21 x
n44312
" "?
mf(x ) 18 S (18) ;
!iœÊœ œ
"
#12
3
f (x) 0 M 0 E 0
Ð%Ñ œÊ œÊ œkk
S
(b) x dx E x dx S 0
''
11
22
S
œ Ê œ œœ
333
###
kk
(c) 100 0%
kkE
True Value
S‚œ
x f(x ) m mf(x )
x1 1 1 1
x 5/4 5/4 4 5
x 3/2 3/2 2 3
x 7/4 7/4 4 7
x2 2 1 2
ii i
!
"
#
$
%
2. (2x 1) dx
'1
3
I. (a) For n 4, x ;œœœœœÊœ?ba 31 2 x
n442 4
" "
#
?
mf(x ) 24 T (24) 6 ;
!iœÊœ œ
"
4
f(x) 2x 1 f (x) 2 f 0 M 0œÊ œÊ œÊ œ
www
E0Êœkk
T
x f(x ) m mf(x )
x1 1 1 1
x3/2 2 2 4
x2 3 2 6
x5/2 4 2 8
x3 5 1 5
ii i
!
"
#
$
%
(b) (2x 1) dx x x (9 3) (1 1) 6 E (2x 1) dx T 6 6 0
''
1 1
3 3
T
œ œœÊ œ œœcd kk
#$
"
(c) 100 0%
kkE
True Value
T‚œ
II. (a) For n 4, x ;œœœœœÊœ?ba 31 2 x
n44236
" "?
mf(x ) 36 S (36) 6 ;
!iœÊœ œ
"
6
f (x) 0 M 0 E 0
Ð%Ñ œÊ œÊ œkk
S
(b) (2x 1) dx 6 E (2x 1) dx S
''
11
33
S
œÊœ kk
660œœ
(c) 100 0%
kkE
True Value
S‚œ
x f(x ) m mf(x )
x1 1 1 1
x3/2 2 4 8
x2 3 2 6
x5/2 4 4 16
x3 5 1 5
ii i
!
"
#
$
%
3. x 1 dx
'
#
1
1ab
I. (a) For n 4, x œœœ œœÊœà?ba 2 x
n44 4
1(1)
""
##
?
mf(x ) 11 T (11) 2.75
!iœÊœ œ à
"
4
f(x) x 1 f (x) 2x f (x) 2 M 2œÊ œ Ê œÊ œ
#w ww
E (2) or 0.08333ÊŸ œkk ˆ‰
T
1(1)
11
## #
""
#
x f(x ) m mf(x )
x121 2
x 1/2 5/4 2 5/2
x0 1 2 2
x 1/2 5/4 2 5/2
x1 2 1 2
ii i
!
"
#
$
%
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.7 Numerical Integration 539
(b) x 1 dx x 1 1 E x 1 dx T
''
# #
"
"
"
#
1 1
1 1
T
ab ab
’“ˆ‰ˆ ‰
œœœÊœ œœ
x118 811
3333 341
E 0.08333Êœ¸kk¸¸
T"
#1
(c) 100 100 3%
kkE
True Value
T‚œ ‚¸
Š‹
1
8
3
II. (a) For n 4, x œœœ œœÊœà?ba 2 x
n44 36
1(1)
""
#
?
mf(x ) 16 S (16) 2.66667 ;
!iœÊœ œœ
"
63
8
f (x) 0 f (x) 0 M 0 E 0
Ð$Ñ Ð%Ñ
œÊ œÊ œÊ œkk
S
(b) x 1 dx x
'
#"
"
1
1ab’“
œœ
x8
33
Ex1 dxS 0Ê œ œœkk a b
S1
1
'
#88
33
(c) 100 0%
kkE
True Value
S‚œ
x f(x ) m mf(x )
x121 2
x 1/2 5/4 4 5
x0 1 2 2
x 1/2 5/4 4 5
x1 2 1 2
ii i
!
"
#
$
%
4. x 1 dx
'
#
2
0ab
I. (a) For n 4, x œœœ œœÊœ?ba 2 x
n44 4
0(2)
""
##
?
mf(x ) 3 T (3) ;
!iœÊœ œ
"
44
3
f(x) x 1 f (x) 2x f (x) 2œÊ œ Ê œ
#w ww
M 2 E (2) 0.08333ÊœÊ Ÿ œœkk ˆ‰
T
0(2)
11
## #
""
#
x f(x ) m mf(x )
x231 3
x 3/2 5/4 2 5/2
x102 0
x 1/2 3/4 2 3/2
x0 11 1
ii i
!
"
#
$
%
(b) x 1 dx - x 0 2 E x 1 dx T
''
# #
!
#
"
2 2
0 0
T
ab ab
’“ ˆ‰
œ œ œ Ê œ œœ
x82 23
333 3412
EÊœkk
T"
12
(c) 100 100 13%
kkE
True Value
T‚œ ‚¸
Š‹
12
2
3
II. (a) For n 4, xœœœ œœ?ba 2
n44
0(2)
"
#
; mf(x ) 4 S (4) ;Êœ œÊœ œ
?x2
36 6 3
""
!i
f (x) 0 f (x) 0 M 0 E 0
Ð$Ñ Ð%Ñ
œÊ œÊ œÊ œkk
S
(b) x 1 dx E x 1 dx S
''
##
22
00
S
ab kkabœÊœ
2
3
0œœ
22
33
(c) 100 0%
kkE
True Value
S‚œ
x f(x ) m mf(x )
x231 3
x 3/2 5/4 4 5
x102 0
x 1/2 3/4 4 3
x0 11 1
ii i
!
"
#
$
%
5. t t dt
'0
2ab
$
I. (a) For n 4, xœœœœœ?ba 20 2
n442
"
; mf(t ) 25 T (25) ;Êœ œÊœ œ
?x25
444#
""
!i
f(t) t t f (t) 3t 1 f (t) 6tœÊ œ Ê œ
$w# ww
M 12 f (2) E (12)Êœœ Ê Ÿ œ
ww " "
##
#
kk ˆ‰
T20
12
t f(t ) m mf(t )
t0 0 1 0
t 1/2 5/8 2 5/4
t1 2 2 4
t 3/2 39/8 2 39/4
t 2 10 1 10
ii i
!
"
#
$
%
(b) t t dt 0 6 E t t dt T 6 E
''
0 0
2 2
T T
a b kk a b kk
’“Š‹
$ $
##
#
!
""
œœœÊ œ œœÊ œ
tt 22 25
44 444
(c) 100 100 4%
kk ¸¸
E
True Value 6
T‚œ ‚¸
4
II. (a) For n 4, x ;œ œ œ œœÊ œ?ba 20 2 x
n44236
" "?
mf(t ) 36 S (36) 6 ;
!iœÊœ œ
"
6
f (t) 6 f (t) 0 M 0 E 0
Ð$Ñ Ð%Ñ
œÊ œÊ œÊ œkk
S
(b) t t dt 6 E t t dt S
''
00
22
S
ab kk ab
$$
œÊ œ
660œœ
(c) 100 0%
kkE
True Value
S‚œ
t f(t ) m mf(t )
t0 0 1 0
t 1/2 5/8 4 5/2
t1 2 2 4
t 3/2 39/8 4 39/2
t 2 10 1 10
ii i
!
"
#
$
%
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
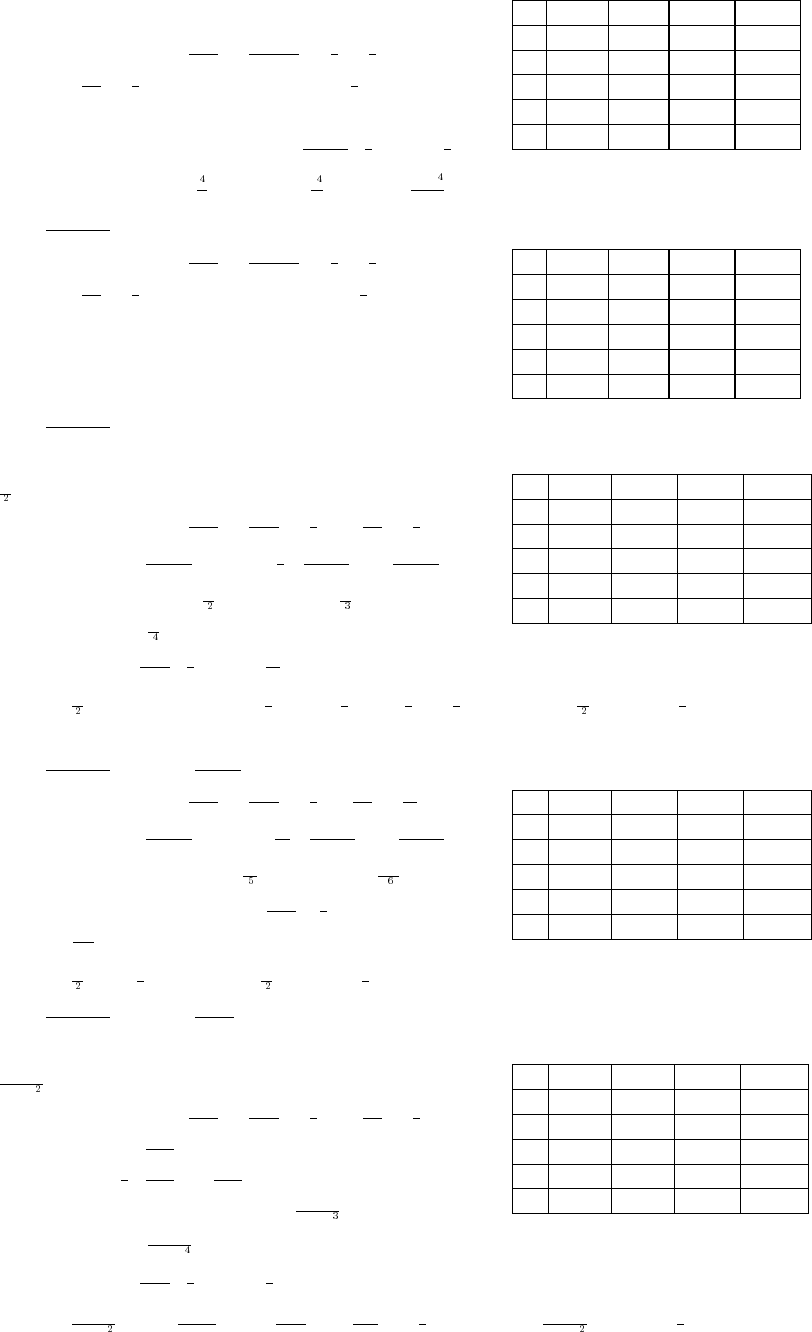
540 Chapter 8 Techniques of Integration
6. t 1 dt
'
$
1
1ab
I. (a) For n 4, xœœœ œœ?ba 2
n44
1(1)
"
#
; mf(t ) 8 T (8) 2 ;Êœ œÊœ œ
?x
44#
""
!i
f(t) t 1 f (t) 3t f (t) 6tœÊ œ Ê œ
$w#ww
M 6 f (1) E (6)Êœœ Ê Ÿ œ
ww
##
""
#
kk ˆ‰
T
1(1)
14
t f(t ) m mf(t )
t101 0
t 1/2 7/8 2 7/4
t0 1 2 2
t 1/2 9/8 2 9/4
t1 2 1 2
ii i
!
"
#
$
%
(b) t 1 dt t 1 ( 1) 2 E t 1 dt T 2 2 0
''
$ $
"
"
1 1
1 1
T
ab kk ab
’“Š ‹Š ‹
œ œ œ Ê œ œœ
t1
444
(1)
(c) 100 0%
kkE
True Value
T‚œ
II. (a) For n 4, xœœœ œœ?ba 2
n44
1(1)
"
#
; mf(t ) 12 S (12) 2 ;Êœ œÊœ œ
?x
36 6
""
!i
f (t) 6 f (t) 0 M 0 E 0
Ð$Ñ Ð%Ñ
œÊ œÊ œÊ œkk
S
(b) t 1 dt 2 E t 1 dt S
''
$$
11
11
S
ab kk abœÊœ
220œœ
(c) 100 0%
kkE
True Value
S‚œ
t f(t ) m mf(t )
t101 0
t 1/2 7/8 4 7/2
t0 1 2 2
t 1/2 9/8 4 9/2
t1 2 1 2
ii i
!
"
#
$
%
7. ds
'1
2"
s
I. (a) For n 4, x ;œœœœÊœ?ba 21 x
n44 8
" "
#
?
mf(s ) T
!Š‹
iœÊœ œ
179,573 179,573 179,573
44,100 8 44,100 352,800
"
0.50899; f(s) f (s)¸œÊœ
"w
ss
2
f(s) M 6 f(1)ʜʜœ
ww ww
6
s
E (6) 0.03125ÊŸ œœkk ˆ‰
T2
14 3
" " "
##
#
s f(s ) m mf(s )
s1 1 1 1
s 5/4 16/25 2 32/25
s 3/2 4/9 2 8/9
s 7/4 16/49 2 32/49
s 2 1/4 1 1/4
ii i
!
"
#
$
%
(b) ds s ds E ds T 0.50899 0.00899
'' '
11 1
22 2
T
"""""
# #
"## #ss1s
11
œœœœÊœœœ
‘ ˆ‰
E 0.00899Êœkk
T
(c) 100 100 2%
kkE
True Value 0.5
0.00899
T‚œ ‚¸
II. (a) For n 4, x ;œœœœÊœ?ba 21 x
n44312
" "?
mf(s ) S
!Š‹
iœÊœ œ
264,821 264,821 264,821
44,100 12 44,100 529,200
"
0.50042; f (s) f (s)¸œÊœ
Ð$Ñ Ð%Ñ
24 120
ss
M 120 E (120)Êœ Ê Ÿkk¸¸ˆ‰
S2
180 4
" " %
0.00260œ¸
"
384
s f(s ) m mf(s )
s1 1 1 1
s 5/4 16/25 4 64/25
s 3/2 4/9 2 8/9
s 7/4 16/49 4 64/49
s 2 1/4 1 1/4
ii i
!
"
#
$
%
(b) ds E ds S 0.50042 0.00042 E 0.00042
''
11
22
S S
"""
##ss
1
œÊ œ œ œ Ê œkk
(c) 100 100 0.08%
kkE
True Value 0.5
0.0004
S‚œ ‚¸
8. ds
'2
4"
(s 1)
I. (a) For n 4, x ;œœœœÊœ?ba 42 x
n42 4
" "
#
?
mf(s )
!iœ1269
450
T 0.70500;Êœ œ œ
"
4 450 1800
1269 1269
ˆ‰
f(s) (s 1) f (s)œ Ê œ
# w
2
(s 1)
f(s) M 6ʜ ʜ
ww
6
(s 1)
E (6) 0.25ÊŸ œœkk ˆ‰
T42
14
" "
##
#
s f(s ) m mf(s )
s2 1 1 1
s 5/2 4/9 2 8/9
s 3 1/4 2 1/2
s 7/2 4/25 2 8/25
s 4 1/9 1 1/9
ii i
!
"
#
$
%
(b) ds E ds T 0.705 0.03833
''
2 2
4 4
T
"""" "
#
%
#
(s 1) (s 1) 4 1 1 3 (s 1) 3
22
œœœÊœ œ¸
’“ˆ‰ˆ‰
E 0.03833ʸkk
T
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
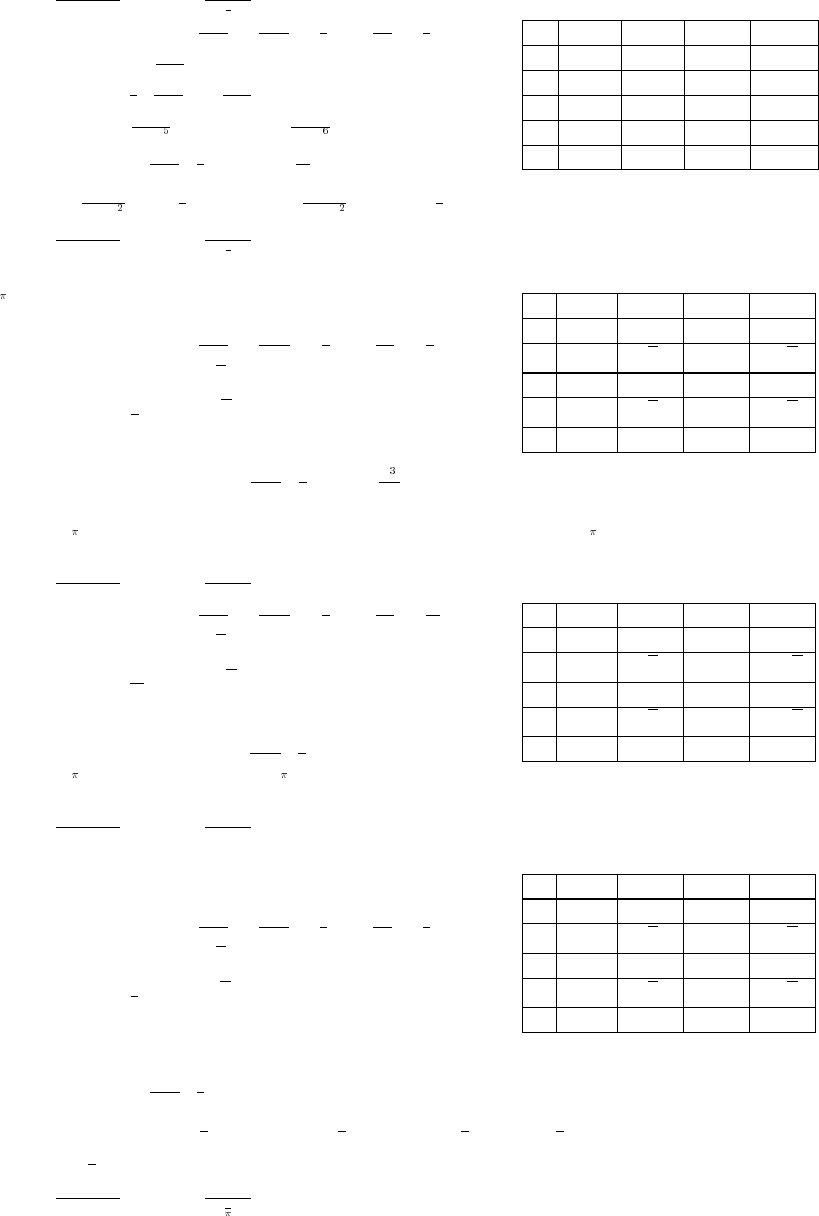
Section 8.7 Numerical Integration 541
(c) 100 100 6%
kk ˆ‰
E
True Value
0.03833
T‚œ ‚¸
2
3
II. (a) For n 4, x ;œœœœÊœ?ba 42 x
n4236
" "?
mf(s )
!iœ1813
450
S 0.67148;Êœ œ ¸
"
6 450 2700
1813 1813
ˆ‰
f (s) f (s) M 120
Ð$Ñ Ð%Ñ
œÊ œÊœ
24 120
(s 1) (s 1)
E (120) 0.08333ÊŸ œ¸kk ˆ‰
S42
180 12
" "
#
%
s f(s ) m mf(s )
s2 1 1 1
s 5/2 4/9 4 16/9
s 3 1/4 2 1/2
s 7/2 4/25 4 16/25
s 4 1/9 1 1/9
ii i
!
"
#
$
%
(b) ds E ds S 0.67148 0.00481 E 0.00481
''
22
44
S S
""
(s 1) 3 (s 1) 3
22
œÊ œ ¸ œ Ê ¸kk
(c) 100 100 1%
kk ˆ‰
E
True Value
0.00481
S‚œ ‚¸
2
3
9. sin t dt
'0
I. (a) For n 4, x ;œœœœÊœ?ba 0 x
n44 8
#
11?1
mf(t ) 2 2 2 4.8284
!È
iœ ¸
T 2 2 2 1.89612;Êœ ¸
1
8Š‹
È
f(t) sin t f (t) cos t f (t) sin tœÊœ Ê œ
www
M 1 E (1)ÊœÊ Ÿ œkk ˆ‰
T
11 1
##
#
0
14 19
0.16149¸
t f(t ) m mf(t )
t0 0 1 0
t/42/22 2
t/21 2 2
t 3 /4 2/2 2 2
t010
ii i
!
"
#
$
%
1
1
1
1
ÈÈ
ÈÈ
(b) sin t dt [ cos t] ( cos ) ( cos 0) 2 E sin t dt T 2 1.89612 0.10388
''
0 0
T
œ œ œ Ê œ ¸ œ
1
!1kk
(c) 100 100 5%
kkE
True Value 2
0.10388
T‚œ ‚¸
II. (a) For n 4, x ;œœœœÊœ?ba 0 x
n44312
11?1
mf(t ) 2 4 2 7.6569
!È
iœ ¸
S 2 4 2 2.00456;Êœ ¸
1
12 Š‹
È
f (t) cos t f (t) sin t
Ð$Ñ Ð%Ñ
œ Ê œ
M 1 E (1) 0.00664ÊœÊ Ÿ ¸kk ˆ‰
S
11%
0
180 4
t f(t ) m mf(t )
t0 0 1 0
t/42/2422
t/21 2 2
t3/4 2/2 4 22
t010
ii i
!
"
#
$
%
1
1
1
1
ÈÈ
ÈÈ
(b) sin t dt 2 E sin t dt S 2 2.00456 0.00456 E 0.00456
''
00
S S
œÊ œ ¸ œ Ê ¸kk
(c) 100 100 0%
kkE
True Value 2
0.00456
S‚œ ‚¸
10. sin t dt
'0
1
1
I. (a) For n 4, x ;œœœœÊœ?ba 10 1 x 1
n44 8
#
?
mf(t ) 2 2 2 4.828
!È
iœ ¸
T 2 2 2 0.60355; f(t) sin tÊœ ¸ œ
1
8Š‹
È1
f (t) cos tʜ
w11
f (t) sin t Mʜ ʜ
ww # #
11 1
E 0.05140ÊŸ ¸kk ab
ˆ‰
T101
14
#
##
1
t f(t ) m mf(t )
t0 0 1 0
t 1/4 2/2 2 2
t1/2 1 2 2
t 3/4 2/2 2 2
t1 0 1 0
ii i
!
"
#
$
%
ÈÈ
ÈÈ
(b) sin t dt [ cos t] cos cos 0 0.63662 E sin t dt T
''
0 0
1 1
T
111 1œ œ œ ¸ Ê œ
"""
"
!
1111
ˆ‰ˆ‰ kk
2
0.60355 0.03307¸ œ
2
1
(c) 100 100 5%
kk ˆ‰
E
True Value
0.03307
T‚œ ‚¸
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
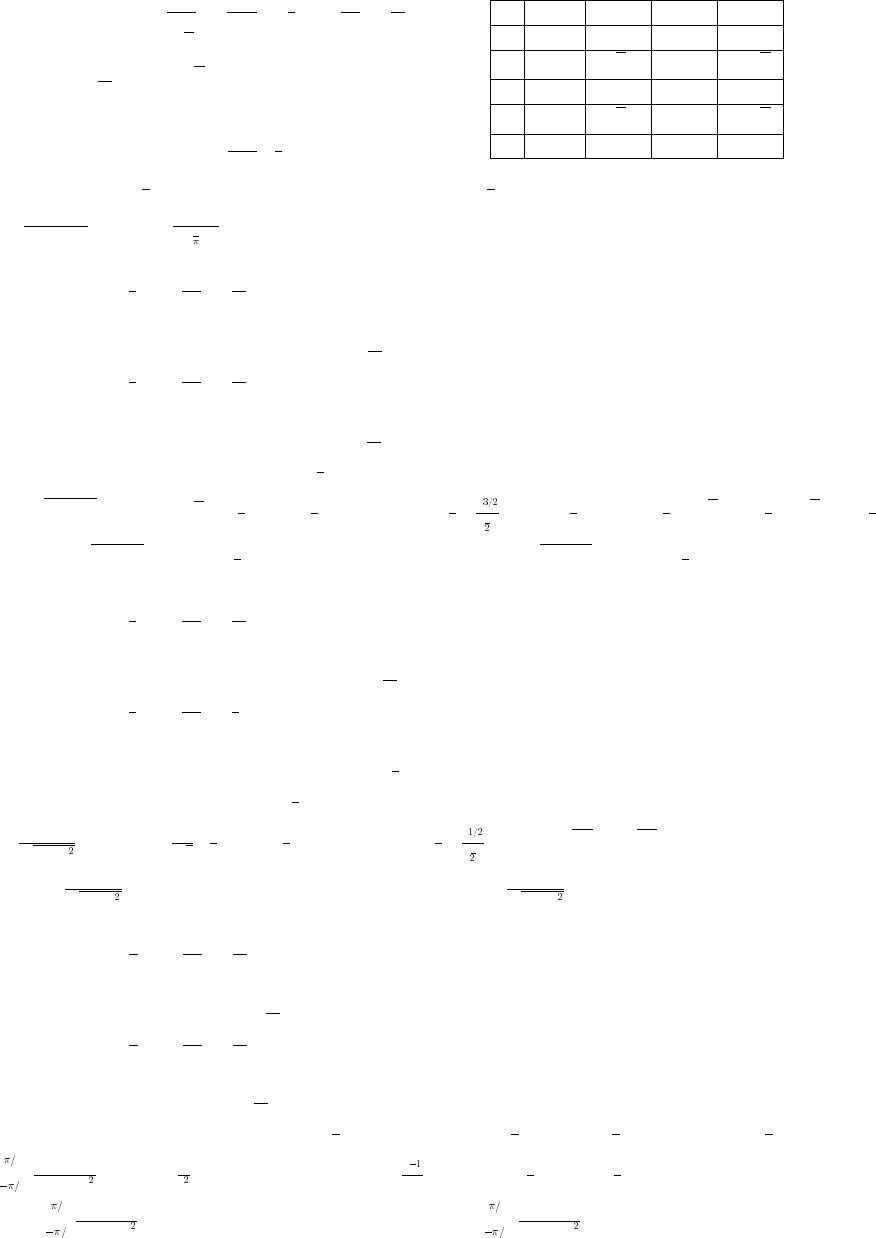
542 Chapter 8 Techniques of Integration
II. (a) For n 4, x ;œœœœÊœ?ba 10 1 x 1
n44312
?
mf(t ) 2 4 2 7.65685
!È
iœ ¸
S 2 4 2 0.63807;Êœ ¸
1
12 Š‹
È
f (t) cos t f (t) sin t
Ð$Ñ $ Ð%Ñ %
œ Ê œ11 11
M E 0.00211ÊœÊ Ÿ ¸11
%%
%
kk ab
ˆ‰
S101
180 4
t f(t ) m mf(t )
t0 0 1 0
t1/4 2/2 4 22
t1/2 1 2 2
t3/4 2/2 4 22
t1 0 1 0
ii i
!
"
#
$
%
ÈÈ
ÈÈ
(b) sin t dt 0.63662 E sin t dt S 0.63807 0.00145 E 0.00145
''
00
11
S S
11œ¸ Ê œ ¸ œ Ê ¸
22
11
kk
(c) 100 100 0%
kk ˆ‰
E
True Value
0.00145
S‚œ ‚¸
2
11. (a) n 8 x ;œÊ œÊ œ?""
#816
x?
mf(x ) 1(0.0) 2(0.12402) 2(0.24206) 2(0.34763) 2(0.43301) 2(0.48789) 2(0.49608)
!iœ
2(0.42361) 1(0) 5.1086 T (5.1086) 0.31929œÊœ œ
"
16
(b) n 8 x ;œÊ œÊ œ?""
8324
x?
mf(x ) 1(0.0) 4(0.12402) 2(0.24206) 4(0.34763) 2(0.43301) 4(0.48789) 2(0.49608)
!iœ
4(0.42361) 1(0) 7.8749 S (7.8749) 0.32812œÊœ œ
"
24
(c) Let u 1 x du 2x dx du x dx; x 0 u 1, x 1 u 0œ Ê œ Ê œ œ Ê œ œ Ê œ
#"
#
x 1 x dx u du u du u 1 0 ;
'' '
01 0
10 1
ÈȈ‰ ‘
’ “ Š‹ Š‹Š‹ ÈÈ
œœ œ œœœ
#"" " " " " "
##
"Î# $Î#
"$$
!
"
!
23333
u3
E x 1 x dx T 0.31929 0.01404; E x 1 x dx S 0.32812 0.00521
T S
0 0
1 1
œ¸œ œ¸œ
''
ÈÈ
##
""
33
12. (a) n 8 x ;œÊ œÊ œ?3x3
816
?
#
mf( ) 1(0) 2(0.09334) 2(0.18429) 2(0.27075) 2(0.35112) 2(0.42443) 2(0.49026)
!)iœ
2(0.58466) 1(0.6) 5.3977 T (5.3977) 1.01207œÊœ œ
3
16
(b) n 8 x ;œÊ œÊ œ?3x
838
?"
mf( ) 1(0) 4(0.09334) 2(0.18429) 4(0.27075) 2(0.35112) 4(0.42443) 2(0.49026)
!)iœ
4(0.58466) 1(0.6) 8.14406 S (8.14406) 1.01801œÊœ œ
"
8
(c) Let u 16 du 2 d du d ; 0 u 16, 3 u 16 3 25œ Ê œ Ê œ œÊœ œÊœœ)))))) )
# #
"
#
d du u du 25 16 1;
'' '
016 16
325 25
)
)
ÈÈ
16 u2
u
"" " "
##
"Î# #&
"'
)œ œ œ œœ
ˆ‰ ’“Š‹ ÈÈ
1
E d T 1 1.01207 0.01207; E d S 1 1.01801 0.01801
T S
0 0
3 3
œ¸œœ¸œ
''
))
))
ÈÈ
16 16
))
13. (a) n 8 x ;œÊ œ Ê œ?1?1
816
x
#
mf(t ) 1(0.0) 2(0.99138) 2(1.26906) 2(1.05961) 2(0.75) 2(0.48821) 2(0.28946) 2(0.13429)
!iœ
1(0) 9.96402 T (9.96402) 1.95643œ Êœ ¸
1
16
(b) n 8 x ;œÊ œ Ê œ?1?1
8324
x
mf(t ) 1(0.0) 4(0.99138) 2(1.26906) 4(1.05961) 2(0.75) 4(0.48821) 2(0.28946) 4(0.13429)
!iœ
1(0) 15.311 S (15.311) 2.00421œ ʸ ¸
1
24
(c) Let u 2 sin t du cos t dt; t u 2 sin 1, t u 2 sin 3œ Ê œ œÊœ œ œ Êœ œ
1111
####
ˆ‰
dt du 3 u du 3 3 3 2;
'''
211
233
3 cos t 3 u 1
(2 sin t) u 1 3 1
# $
"
"
œœ œ œœ
’“Š‹ ˆ‰ˆ‰
E dt T 2 1.95643 0.04357; E dt S
T S
2 2
2 2
œ¸œœ
''
3 cos t 3 cos t
(2 sin t) (2 sin t)
2 2.00421 0.00421¸ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.7 Numerical Integration 543
14. (a) n 8 x ;œÊ œ Ê œ?1?1
32 64
x
#
mf(y ) 1(2.0) 2(1.51606) 2(1.18237) 2(0.93998) 2(0.75402) 2(0.60145) 2(0.46364)
!iœ
2(0.31688) 1(0) 13.5488 T (13.5488) 0.66508œÊ¸ œ
1
64
(b) n 8 x ;œÊ œ Ê œ?1?1
32 3 96
x
mf(y ) 1(2.0) 4(1.51606) 2(1.18237) 4(0.93988) 2(0.75402) 4(0.60145) 2(0.46364)
!iœ
4(0.31688) 1(0) 20.29734 S (20.29734) 0.66423œÊ¸ œ
1
96
(c) Let u cot y du csc y dy; y u 1, y u 0œÊœ œÊœœÊœ
#
#
11
4
csc y cot y dy u ( du) u du 1 0 ;
'''
410
201
ab
ÈÈ’“ Š‹ Š‹
ÈÈ
# "Î# "$$
!
œœ œœœ
u2 2 2
33 3
3
2
E csc y cot y dy T 0.66508 0.00159; E csc y cot y dy S
T S
4 4
2 2
œ¸œœ
''
ab ab
ÈÈ
# #
2
3
0.66423 0.00244¸ œ
2
3
15. (a) M 0 (see Exercise 1): Then n 1 x 1 E (1) (0) 0 10œœÊœÊœœ?kk
T"
#
#%
1
(b) M 0 (see Exercise 1): Then n 2 (n must be even) x E (0) 0 10œœÊœÊœœ?"""
##
%%
kk ˆ‰
S180
16. (a) M 0 (see Exercise 2): Then n 1 x 2 E (2) (0) 0 10œœÊœÊœœ?kk
T2
1#
#%
(b) M 0 (see Exercise 2): Then n 2 (n must be even) x E (1) (0) 0 10œœÊœ"Êœœ?kk
S2
180 %%
17. (a) M 2 (see Exercise 3): Then x E (2) 10 n 10 n 10œœÊŸœÊÊ?2224 4 4
n12n3n 3 3
kk ab ab
ˆ‰ É
T
#% # % %
n 115.4, so let n 116Ê œ
(b) M 0 (see Exercise 3): Then n 2 (n must be even) x E (1) (0) 0 10œœÊœ"Êœœ?kk
S2
180 %%
18. (a) M 2 (see Exercise 4): Then x E (2) 10 n 10 n 10œœÊŸœÊÊ?2224 4 4
n12n3n 3 3
kk ab ab
ˆ‰ É
T
#% # % %
n 115.4, so let n 116Ê œ
(b) M 0 (see Exercise 4): Then n 2 (n must be even) x E (1) (0) 0 10œœÊœ"Êœœ?kk
S2
180 %%
19. (a) M 12 (see Exercise 5): Then x E (12) 10 n 8 10 n 8 10œœÊŸœÊÊ?2228
n12nn
kk ab ab
ˆ‰ È
T
#% # % %
n 282.8, so let n 283Ê œ
(b) M 0 (see Exercise 5): Then n 2 (n must be even) x E (1) (0) 0 10œœÊœ"Êœœ?kk
S2
180 %%
20. (a) M 6 (see Exercise 6): Then x E (6) 10 n 4 10 n 4 10œœÊŸœÊÊ?2224
n12nn
kk ab ab
ˆ‰ È
T
#% # % %
200, so let n 201œœ
(b) M 0 (see Exercise 6): Then n 2 (n must be even) x E (1) (0) 0 10œœÊœ"Êœœ?kk
S2
180 %%
21. (a) M 6 (see Exercise 7): Then x E (6) 10 n 10 n 10œœÊŸœÊÊ?1111
n12n2n
kk ab ab
ˆ‰ É
T
#% # %
""
##
%
n 70.7, so let n 71Ê œ
(b) M 120 (see Exercise 7): Then x E (120) 10 n 10œœÊœœÊ?""
%% % %
n 180 n 3
12 2
3n
kk a b
ˆ‰
S
n 10 n 9.04, so let n 10 (n must be even)Ê Ê œ
%%
Éab
2
3
22. (a) M 6 (see Exercise 8): Then x E (6) 10 n 4 10 n 4 10œœÊŸœÊÊ?2224
n12nn
kk ab ab
ˆ‰ È
T
#% # % %
n 200, so let n 201Ê œ
(b) M 120 (see Exercise 8): Then x E (120) 10 n 10œœÊŸœÊ?22264 64
n 180 n 3
3n
kk a b
ˆ‰
S
%% % %
n 10 n 21.5, so let n 22 (n must be even)Ê Ê œ
%%
Éab
64
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

544 Chapter 8 Techniques of Integration
23. (a) f(x) x 1 f (x) (x 1) f (x) (x 1) M .œÊ œ Ê œ œ Êœ œ
Èw "Î# ww $Î#
"""""
#
44
4x1 41
ˆ‰
ÈŠ‹
È
Then x E 10 n 10 n 10 n 75,?œÊ Ÿ œ Ê Ê Ê
3339 9 9
n 12 n 4 16n 16 16
kk ab ab
ˆ‰ˆ‰ É
T
#"% # % %
so let n 76œ
(b) f (x) (x 1) f (x) (x 1) M . Then x
Ð$Ñ &Î# Ð%Ñ (Î#
œ Ê œ œ Êœ œ œ
3151515153
816 16n
16 x 1 16 1
ˆ‰
ÈŠ‹
È?
E 10 n n n 10.6, so letÊ Ÿ œ Ê Ê Êkk ˆ‰ˆ‰ É
S33 15
180 n 16 16(180) 16(180)
3 (15)
16(180)n
3 (15) 10 3 (15) 10
%% % ˆ‰ ab
n 12 (n must be even)œ
24. (a) f(x) f (x) (x 1) f (x) (x 1) M .œÊœ Êœœ Êœ œ
""
w $Î# w &Î#
#
w
Ȉ‰
ÈŠ‹
È
x1
3333
44
4x1 41
Then x E 10 n n n 129.9, so let?œÊ Ÿ œ Ê Ê Ê
33333
n 12 n 4 48n 48 48
310 310
kk ˆ‰ˆ‰ É
T
#% # ˆ‰ ab
n 130œ
(b) f (x) (x 1) f (x) (x 1) M . Then x
Ð$Ñ (Î# Ð%Ñ *Î#
œ Ê œ œ Ê œ œ œ
15 105 105 105 105 3
816 16n
16 x 1 16 1
ˆ‰
ÈŠ‹
È?
E 10 n n n 17.25, soÊ Ÿ œ Ê Ê Êkk ˆ‰ˆ ‰ É
S3 3 105
180 n 16 16(180) 16(180)
3 (105)
16(180)n
3 (105) 10 3 (105) 10
%% % ˆ‰ ab
let n 18 (n must be even)œ
25. (a) f(x) sin (x 1) f (x) cos (x 1) f (x) sin (x 1) M 1. Then x E (1)œ Ê œ Ê œ Ê œ œÊ Ÿ
www #
?222
n12n
kk ˆ‰
T
10 n n n 81.6, so let n 82œ Ê Ê Ê œ
8
12n 12 1
810 810
% #
#
ˆ‰ ab
É
(b) f (x) cos (x 1) f (x) sin (x 1) M 1. Then x E (1) 10
Ð$Ñ Ð%Ñ %
%
œ Ê œ Ê œ œ Ê Ÿ œ ?22232
n 180 n 180n
kk ˆ‰
S
n n n 6.49, so let n 8 (n must be even)Ê Ê Ê œ
%32 10
180 180
32 10
ˆ‰ ab
É
26. (a) f(x) cos (x ) f (x) sin (x ) f (x) cos (x ) M 1. Then xœÊœÊœÊœ œ11 1?
www 2
n
E (1) 10 n n n 81.6, so let n 82Ê Ÿ œ Ê Ê Ê œkk ˆ‰ É
T22 8
12 n 12n 12 1
810 810
#% #
#
ˆ‰ ab
(b) f (x) sin (x ) f (x) cos (x ) M 1. Then x E (1) 10
Ð$Ñ Ð%Ñ %
%
œÊ œ Êœ œÊŸ œ11?
22232
n 180 n 180n
kk ˆ‰
S
n n n 6.49, so let n 8 (n must be even)Ê Ê Ê œ
%32 10
180 180
32 10
ˆ‰ ab
É
27. 6.0 2 8.2 2 9.1 2 12.7 13.0 30 15,990 ft .
5
2
3
ababab ab a b ÞÞÞ œ
28. (a) Using Trapezoid Rule, x 200 100;?œÊœœ
?x 200
22
mf(x ) 13,180 Area 100 (13,180)
!iœÊ¸
1,318,000 ft . Since the average depth 20 ftœœ
#
we obtain Volume 20 (Area) 26,360,000 ft . ¸¸ $
(b) Now, Number of fish 26,360 (to the nearestœœ
Volume
1000
fish) Maximum to be caught 75% of 26,360ʜ
19,770 Number of licenses 988œÊ œœ
19,770
0#
x f(x ) m mf(x )
x 0 0 1 0
x 200 520 2 1040
x 400 800 2 1600
x 600 1000 2 2000
x 800 1140 2 2280
x 1000 1160 2 2320
x
ii i
!
"
#
$
%
'
5
1200 1110 2 2220
x 1400 860 2 1720
x 1600 0 1 0
(
)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
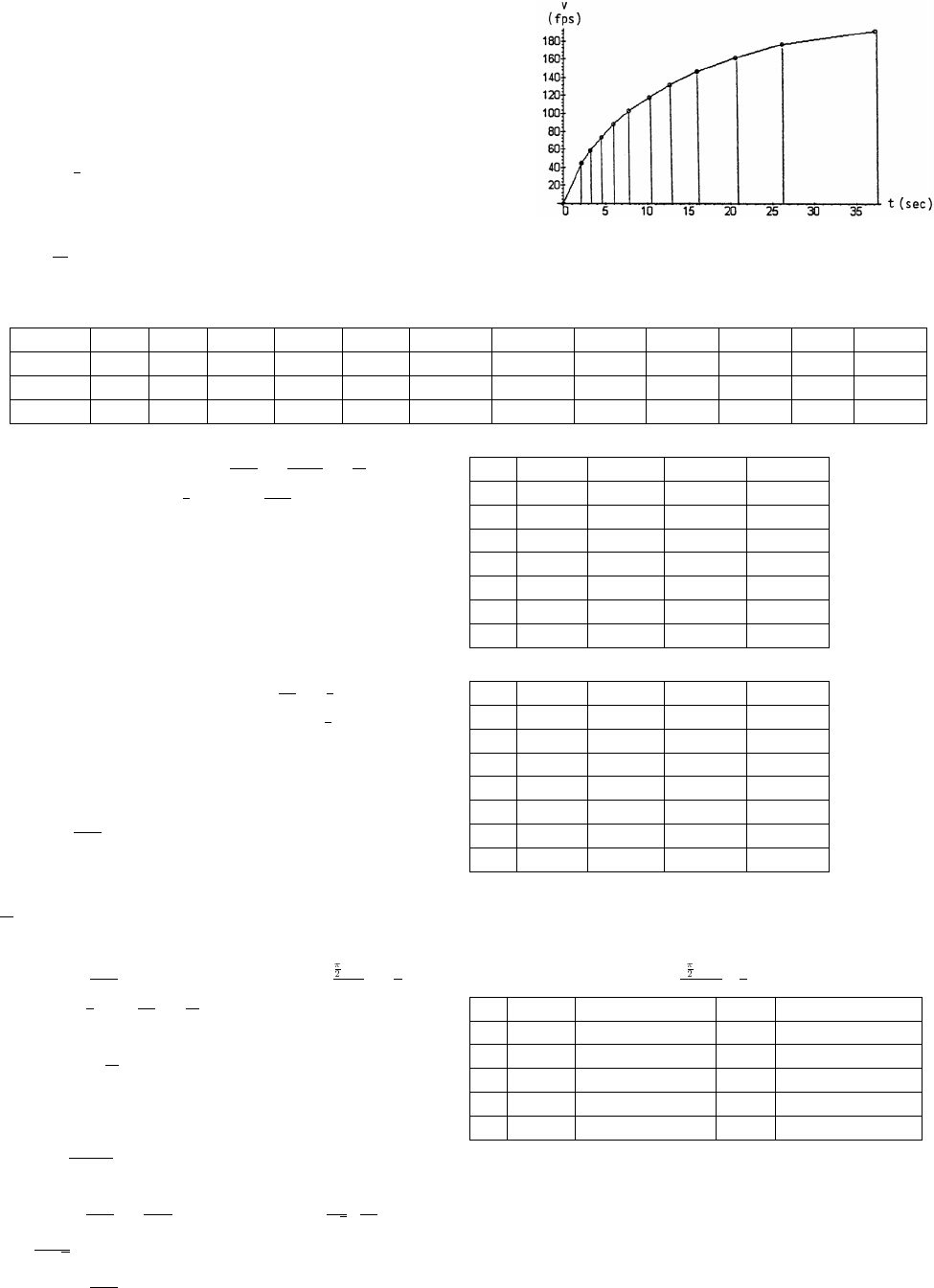
Section 8.7 Numerical Integration 545
29. Use the conversion 30 mph 44 fps (ft perœ
sec) since time is measured in seconds. The
distance traveled as the car accelerates from,
say, 40 mph 58.67 fps to 50 mph 73.33 fpsœœ
in (4.5 3.2) 1.3 sec is the area of theœ
trapezoid (see figure) associated with that time
interval: (58.67 73.33)(1.3) 85.8 ft. The
"
#œ
total distance traveled by the Ford Mustang
Cobra is the sum of all these eleven trapezoids
(using and the table below):
?t
#
s (44)(1.1) (102.67)(0.5) (132)(0.65) (161.33)(0.7) (190.67)(0.95) (220)(1.2) (249.33)(1.25)œ
(278.67)(1.65) (308)(2.3) (337.33)(2.8) (366.67)(5.45) 5166.346 ft 0.9785 miœ¸
v (mph) 0 30 40 50 60 70 80 90 100 110 120 130
v (fps) 0 44 58.67 73.33 88 102.67 117.33 132 146.67 161.33 176 190.67
t (sec) 0 2.2 3.2 4.5 5.9 7.8 10.2 12.7 16 20.6 26.2 37.1
t/2 0 1.1 0.5 0.65 0.7 0.95 1.2 1.25 1.65 2.3 2.8 5.45?
30. Using Simpson's Rule, x 4;?œœ œœ
ba 240 24
n66
my 350 S (350) 466.7 in.
!iœÊœ œ¸
4 1400
33 #
x y m my
x 0 0 1 0
x 4 18.75 4 75
x 8 24 2 48
x 12 26 4 104
x 16 24 2 48
x 20 18.75 4 75
x24 0 1 0
ii i
5
!
"
#
$
%
'
31. Using Simpson's Rule, x 1 ;?œÊ œ
?x
33
"
my 33.6 Cross Section Area (33.6)
!iœÊ ¸
"
3
11.2 ft . Let x be the length of the tank. Then theœ#
Volume V (Cross Sectional Area) x 11.2x.œœ
Now 5000 lb of gasoline at 42 lb/ft$
V 119.05 ftÊœ œ
5000
42 $
119.05 11.2x x 10.63 ftʜʸ
x y m my
x 0 1.5 1 1.5
x 1 1.6 4 6.4
x 2 1.8 2 3.6
x 3 1.9 4 7.6
x 4 2.0 2 4.0
x 5 2.1 4 8.4
x 6 2.1 1 2.1
ii i
5
!
"
#
$
%
'
32. 4.2 L
0.019 2 0.020 2 0.021 2 0.031 0.035
24
2cd
abab abÞÞÞ
œ
33. (a) E x M; n 4 x ; f 1 M 1 E (1) 0.00021kk a b kk
¸¸ ˆ‰
S S
ŸœÊœœŸÊœÊŸ¸
ba
180 4 8 180 8
00
%Ð%Ñ
%
??
11
ˆ‰
(b) x ;?œÊ œ
1?1
834
x
#
mf(x ) 10.47208705
!iœ
S (10.47208705) 1.37079Êœ ¸
1
#4
x f(x ) m mf(x )
x0 1 1 1
x /8 0.974495358 4 3.897981432
x /4 0.900316316 2 1.800632632
x 3 /8 0.784213303 4 3.136853212
x /2 0.636619772 1 0.63
ii i1
!
"
#
$
%
1
1
1
16619772
(c) 100 0.015%¸‚¸
ˆ‰
0.00021
1.37079
34. (a) x 0.1 erf 1 y 4y 2y 4y 4y y?œ œ œÊ œ ÞÞÞ
ba 10 2 0.1
n10 3
30123 910
ab a b
ˆ‰
È
e 4e 2e 4e 4e e 0.843
2
30
0 0.01 0.04 0.09 0.81 1
È1abÞÞÞ¸
(b) E 0.1 12 6.7 10kk abab
SŸ¸‚
10
180
46
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
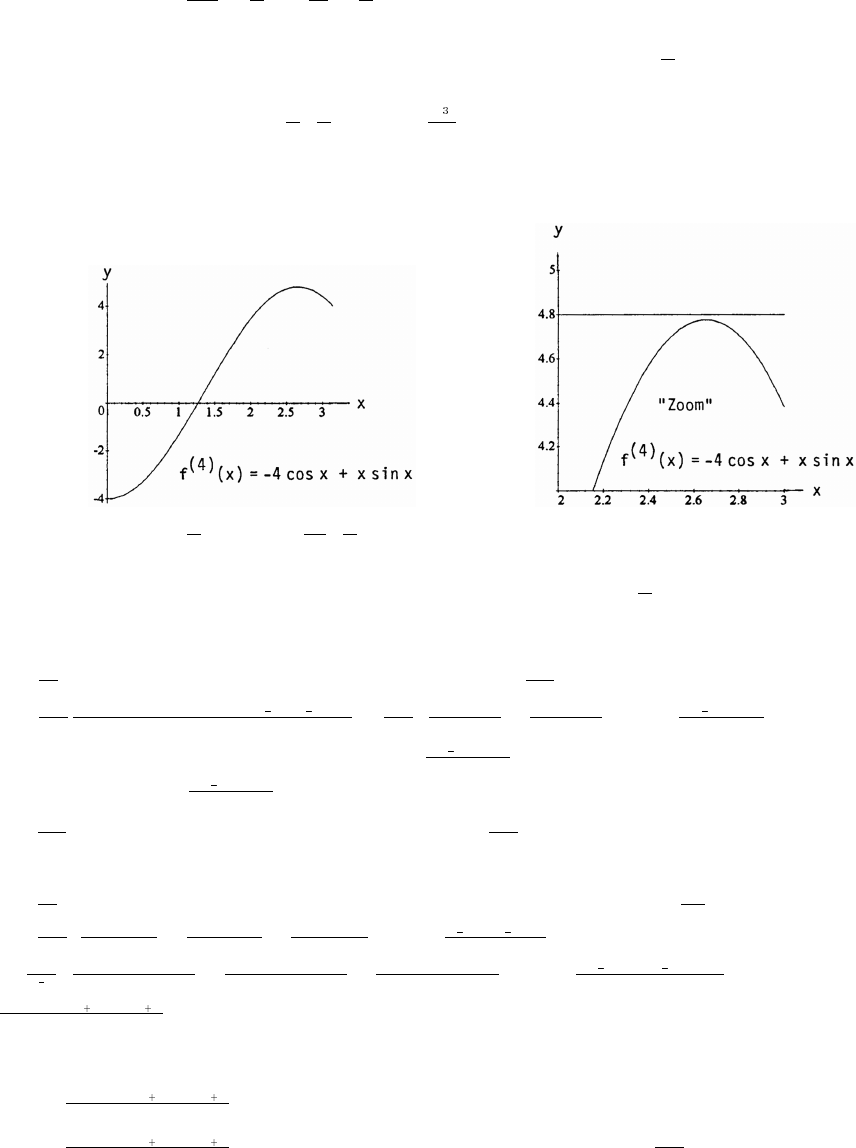
546 Chapter 8 Techniques of Integration
35. (a) n 10 x ;œÊ œ œÊ œ?11?1
##
0x
10 10 0
mf(x ) 1(0) 2(0.09708) 2(0.36932) 2(0.76248) 2(1.19513) 2(1.57080) 2(1.79270)
!iœ
2(1.77912) 2(1.47727) 2(0.87372) 1(0) 19.83524 T (19.83524) 3.11571œÊœ œ
1
#0
(b) 3.11571 0.025881¸
(c) With M 3.11, we get E (3.11) (3.11) 0.08036œŸœkk ˆ‰
T
11 1
1 10 1200#
#
36. (a) f (x) 2 cos x x sin x f (x) 3 sin x x cos x f (x) 4 cos x x sin x. From the graphs
ww Ð$Ñ Ð%Ñ
œÊœ Êœ
shown below, 4 cos x x sin x 4.8 for 0 x .kk ŸŸ1
(b) n 10 x E (4.8) 0.00082œÊ œÊ Ÿ ¸?111
10 180 10
kk ˆ‰
S
%
(c) mf(x ) 1(0) 4(0.09708) 2(0.36932) 4(0.76248) 2(1.19513) 4(1.57080) 2(1.79270)
!iœ
4(1.77912) 2(1.47727) 4(0.87372) 1(0) 30.0016 S (30.0016) 3.14176œÊœ œ
1
30
(d) 3.14176 0.00017kk1¸
37. T y 2y 2y 2y 2y y where x and f is continuous on [a, b]. Soœ ÞÞÞ œ
?xba
2 n
0123 n1n
ab
?
T .œ œ ÞÞÞ
ba ba
n2 n222
yyyyy y y y fx fx fx fx fx fx
ÞÞÞ a b ab ab ab ab a b ab
01122 n1n1n 0 1 1 2 n1 n
Š‹
Since f is continuous on each interval [x , x ], and is always between f x and f x , there is a point c
k1 k k1 k k
fx fx
#
abab
k1 k ab ab in
[x , x ] with f c ; this is a consequence of the Intermediate Value Theorem. Thus our sum is
k1 k k fx fx
#
abœabab
k1 k
f c which has the form x f c with x for all k. This is a Riemann Sum for f on [a, b].
!!
ˆ‰
ab ab
k1 k1
nn
ba ba
nn
kkkk
œœ
??œ
38. S y 4y 2y 4y 2y 4y y where n is even, x and f is continuous on [a, b]. Soœ ÞÞÞ œ
?xba
3 n
0123 n2n1n
ab
?
Sœ ÞÞÞ
ba
n333 3
y4yy y4yy y4yy y 4y y
ˆ‰
012 234 456 n2n1n
œ ÞÞÞ
bafx 4fx fx fx 4fx fx fx 4fx fx fx 4fx fx
666 6
n
2
012 234 456 n2n1n
Š ‹
ab ab ab ab ab ab ab ab ab a b a b ab
is the average of the six values of the continuous function on the interval [x , x ], so it is b
fx 4fx fx
62k 2k 2
ababab
2k 2k 1 2k 2
etween
the minimum and maximum of f on this interval. By the Extreme Value Theorem for continuous functions, f takes on its
maximum and minimum in this interval, so there are x and x with x x , x x and
a b 2k a b 2k 2
ŸŸ
f x f x . By the Intermediate Value Theorem, there is c in [x , x ] withab ab
ab k2k2k2
fx 4fx fx
6
ŸŸ
ababab
2k 2k 1 2k 2
f c . So our sum has the form x f c with x a Riemann sum for f on [a, b].ab ab
!
kkk k
fx 4fx fx
6n/2
k1
n/2 ba
œœß
ababab ab
2k 2k 1 2k 2
œ
??
Exercises 39-42 were done using a graphing calculator with n 50œ
39. 1.08943 40. 1.37076 41. 0.82812 42. 51.05400
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
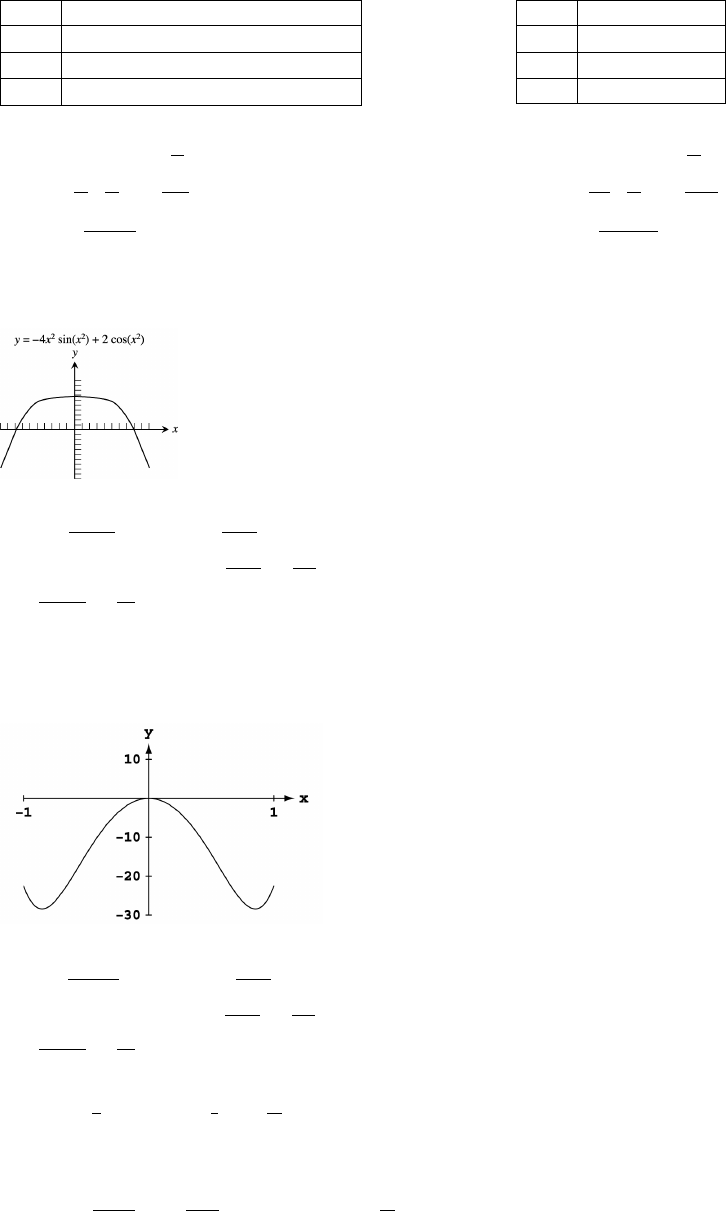
Section 8.7 Numerical Integration 547
43. (a) T 1.983523538 44. (a) S 2.000109517
10 10
¸¸
T 1.999835504 S 2.000000011
100 100
¸¸
T 1.999998355 S 2.000000000
1000 1000
¸¸
(b) n 2 T (b) n 2 S
EE
10 0.016476462 1.6476462 10 10 1.09517 10
100 1.64496 10 100 1.1 10
1000 1.646 10 1000 0
kk kk
TS
nn
24
48
6
œ œ
œ‚ ‚
‚‚
‚
(c) 10 (c) 10
EE EE
kk kk kk kk
TT SS
2 4
10n n 10n n
¸¸
(d) b a , x , M 1 (d) b a , x , M 1œ œ œ œ œ œ1? 1?ab ab
2 4
n n
1 1
2 4
2 4
EE
kk kk
Š‹ Š‹
T S
12 n 12n 180 n 180n
n n
23 45
22 44
Ÿœ Ÿ œ
11 1 1 1 1
10 10
EE E E
kk kk kk kk
TT S S
12 10n 180 10n
2 4
10n n 10n n
3 5
2 4
ŸŸ Ÿ Ÿ
1 1
ab ab
45. (a) f x 2x cos x , f x 2x 2x sin x 2cos x 4x sin x 2cos x
www
ab ab ab a bab ab ab abœœ†œ
222222
(b)
(c) The graph shows that 3 f x 2 so f x 3 for 1 x 1.ŸŸ ŸŸŸ
ww ww
ab k kab
(d) x 3
E
kk abab
T11 2 x
12
Ÿœ
#
ab ab
??2
(e) For 0 x 0.1, 0.005 0.01
E
Ÿ Ÿœ ?kk
Tx0.1
2
ab?22
#
(f) n 20œ
11
x0.1
2
ab
?
46. (a) f x 4x 2x cos x 8x sin x 4x sin x 8x cos x 12x sin x
''' 2 2 2 2 3 2 2
ab ab ab ab ab abœ † œ
f x 8x 2x sin x 24x cos x 12x 2x cos x 12 sin x 16x 12 sin x 48 x cos x
ab43222 2 24222
ab ab ab ab ab a bab abœ † † œ
(b)
(c) The graph shows that 30 f x 0 so f x 30 for 1 x 1.Ÿ Ÿ Ÿ ŸŸ
ab ab44
ab ab
¸¸
(d) x 30
E
kk abab
S11 4 x
180 3
Ÿœ
ab ab
??4
(e) For 0 x 0.4, 0.00853 0.01
E
Ÿ Ÿ¸ ?kk
Sx
33
0.4
ab?42
(f) n 5œ
11
x0.4
2
ab
?
47. (a) Using d , and A yields the following areas (in square inches, rounded to the nearest tenth):œœœ
CdC
24
2
11
1ˆ‰ 2
2.3, 1.6, 1.5, 2.1, 3.2, 4.8, 7.0, 9.3, 10.7, 10.7, 9.3, 6.4, 3.2
(b) If C y is the circumference as a function of y, then the area of a cross section isab
A y , and the volume is C y dy.ab ab
Š‹
œœ1Cy
24 4
2Cy 12
ab ab
Î1
11
2'0
6
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

548 Chapter 8 Techniques of Integration
(c) A y dy C y dy
''
00
66
ab abœ1
4
2
1
5.4 2 4.5 4.4 5.1 6.3 7.8 9.4 10.8 11.6 11.6 10.8 9.0 6.3
¸
160
424
2222222222222
1ˆ‰
c d
a b
34.7 in¸3
(d) V C y dy 5.4 4 4.5 2 4.4 4 5.1 2 6.3 4 7.8 2 9.4 10.8œ ¸ %
1160
4436
2 2222222 2
11
'0
6ab ababababababa b
ˆ‰
’
2 11.6 11.6 2 10.8 9.0 6.3 34.792 in%%œabababab “
22222 3
by Simpson's Rule. The Simpson's Rule estimate should be more accurate than the trapezoid estimate. The error in the
Simpson's estimate is proportional to y 0.0625 whereas the error in the trapezoid estimate is proportional toab?4œ
y 0.25, a larger number when y 0.5 in.ab??
2œœ
48. (a) Displacement Volume V y 4y 2y 4y 2y 4y y , x 0, x 10 x,¸ ÞÞÞ œ œ
?x
30123 n2n1n0 n
ab
?
x 2.54, n 10 A x dx 0 4 1.07 2 3.84 4 7.82 2 12.20 4 15.18 2 16.14?œœÊ ¸
'x
x2.54
3
0
nab abababa ba ba b
’
4 14.00 2 9.21 4 3.24 0 248.02 209.99 210 ft . œ œ¸a babab a b
“2.54
3
3
(b) The weigth of water displaced is approximately 64 120 13,440 lb.†œ
(c) The volume of a prism 2.54 16.14 409.96 410 ft . Thus, the prismatic coefficient is 0.51.œœ¸ ¸aba b 3210 ft
410 ft
3
3
49. (a) a 1, e Length 4 1 cos t dtœœÊ œ
""
##
'0
2É4
2 4 cos t dt f(t) dt; use theœœ
''
00
22
È#
Trapezoid Rule with n 10 tœÊ œ œ?ba
n10
0
ˆ‰
. 4 cos t dt mf(x ) 37.3686183œ¸œ
1
##
0'0
210
n0
n
È!
T (37.3686183) (37.3686183)Êœ œ
?1t
40#
2.934924419 Length 2(2.934924419)œÊœ
5.870¸
(b) f (t) 1 M 1kk
ww Ê œ
E t M 1 0.0032ÊŸ Ÿ Ÿkk a b ˆ‰
Tba
110
0
###
##
?ˆ‰ 1
x f(x ) m mf(x )
x 0 1.732050808 1 1.732050808
x /20 1.739100843 2 3.478201686
x /10 1.759400893 2 3.
ii i
!
"
#
1
1518801786
x 3 /20 1.790560631 2 3.581121262
x /5 1.82906848 1 3.658136959
x /4 1.870828693 1 3.741657387
x 3 /10 1.911676881 2 3.823353762
$
%
'
1
1
1
1
5
x 7 /20 1.947791731 2 3.895583461
x 2 /5 1.975982919 2 3.951965839
x 9 /20 1.993872679 2 3.987745357
x/2 2 1 2
(
)
*
"!
1
1
1
1
50. x ; mf(x ) 29.184807792?œœÊœ œ
11?10x
88324
!i
S 29.18480779 3.82028Êœ ¸
1
24 ab x f(x ) m mf(x )
x 0 1.414213562 1 1.414213562
x /8 1.361452677 4 5.445810706
x /4 1.224744871 2 2.44948974
ii i
!
"
#
1
13
x 3 /8 1.070722471 4 4.282889883
x/2 1 2 2
x 5 /8 1.070722471 4 4.282889883
x 3 /4 1.224744871 2 2.449489743
x 7 /8 1.361452677 4 5.4458107
$
%
'
(
1
1
1
1
1
5
06
x 1.414213562 1 1.414213562
)1
51. The length of the curve y sin x from 0 to 20 is: L 1 dx; cos x œœœÊ
ˆ‰ ˆ‰
ÊŠ‹ Š‹
333
0dxdx00dx
dy dy dy
111
###
##
'0
20
cos x L 1 cos x dx. Using numerical integration we find L 21.07 inœÊœ ¸
93 93
400 0 400 0
11 11
#
##
#
ˆ‰ ˆ‰
É
'0
20
52. First, we'll find the length of the cosine curve: L 1 dx; sinœ œ
'25
25 ÊŠ‹ ˆ‰
dy dy
dx dx 50 50
25 x
#11
sin L 1 sin dx. Using a numerical integrator we findʜ ʜ
Š‹ ˆ‰ ˆ‰
É
dy
dx 4 50 4 50
xx
###
11 11
'25
25
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.8 Improper Integrals 549
L 73.1848 ft. Surface area is: A length width (73.1848)(300) 21,955.44 ft.¸œ¸œ†
Cost 1.75A (1.75)(21,955.44) $38,422.02. Answers may vary slightly, depending on the numericalœœ œ
integration used.
53. y sin x cos x cos x S 2 (sin x) 1 cos x dx; a numerical integration givesœÊœ Ê œ Êœ
dy dy
dx dx
Š‹ È
###
'0
1
S 14.4¸
54. y S 2 1 dx; a numerical integration gives S 5.28œÊœÊ œÊœ ¸
xx x xx
4dx dx 4 4 4
dy dy
#
#
Š‹ Š‹
É
'0
2
1
55. y x sin 2x 1 2 cos 2x (1 2 cos 2x) ; by symmetry of the graph we have thatœ Ê œ Ê œ
dy dy
dx dx
Š‹
##
S 2 2 (x sin 2x) 1 (1 2 cos 2x) dx; a numerical integration gives S 54.9œ ¸
'0
23
1È#
56. y 36 x œÊœ œ œ
xxx
1dx1212 12 1
dy ( 2x)
36 x 36 x
36 x 12 36 x 36 x
36 x x
###
#
""
ÈÈÈ
ÈÈÈ
ab
†
S 36 x 1 dxœœÊœÊœ
"
#
##
1 dx 36 36 x 12 36 36 x
36 2x 18 x 18 x 18 x
36 x 6 36 x
dy 2x
abab ab ab
ÈÈ ab ab
Š‹ ÈÉ
'0
61†
36 x dx; using numerical integration we get S 41.8œ ¸
'0
61x18x
66
Éab
ˆ‰
##
57. A calculator or computer numerical integrator yields sin 0.6 0.643501109.
" ¸
58. A calculator or computer numerical integrator yields 3.1415929.1¸
8.8 IMPROPER INTEGRALS
1. lim lim tan x lim tan b tan 0 0
''
00
bb
0
dx dx
x 1 x 1
##
" " "
œœ œœœ
bb bÄ_ Ä_ Ä_
cd a b
11
2. lim lim 1000x lim 1000 1000
''
11
b0001 b
dx dx 1000
xx b
1 001 1 001 0 001
œœœœ
bb bÄ_ Ä_ Ä_
cd
ˆ‰
3. lim x dx lim 2x lim 2 2 b 2 0 2
''
0b
11 12
b
dx
x
Èœ œ œ œœ
bb0b0Ä! Ä Ä
"Î# cd Š‹
È
4. lim 4 x dx lim 2 4 b 2 4 0 4 4
''
00
4b
dx
4 x
È
"Î#
œ œ œœ
b4 b4ÄÄ
ab ’“
ÈŠ‹
È
5. lim 3x lim 3x
'''
110
101 b
1c
dx dx dx
xxx
œœ
bc
Ä! Ä!
‘ ‘
"Î$ "Î$ "
lim 3b 3( 1) lim 3(1) 3c (0 3) (3 0) 6œ œœ
bc
Ä! Ä!
‘‘
"Î$ "Î$ "Î$ "Î$
6. lim x lim x
'''
880
101 b
c
dx dx dx 3 3
xxx
œœ
bc
Ä! Ä!
‘ ‘
##
#Î$ #Î$ "
lim b ( 8) lim (1) c 0 (4) 0œ œœ
bc
Ä! Ä!
‘‘‘ˆ‰
33 3 3 3 3 9
## # # # # #
#Î$ #Î$ #Î$ #Î$
7. lim sin x lim sin b sin 0 0
'0
1b
0
dx
1 x
È
" " "
##
œœœœ
b1 b1ÄÄ
cd a b
11
8. lim 1000r lim 1000 1000b 1000 0 1000
'0
10001 0001
1
b
dr
r0 999 œœœœ
bbÄ! Ä!
cd a b
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

550 Chapter 8 Techniques of Integration
9. lim ln x 1 lim ln x 1 lim ln
'''
222 22
bb b
2 dx dx dx x 1
x 1 x 1 x 1 x 1
œœ œ
bb bÄ_ Ä_ Ä_
cd cdkk kk ‘¸¸
lim ln ln ln 3 ln lim ln 3 ln 1 ln 3œ œ œœ
bbÄ_ Ä_
ˆ‰¸¸ ¸ ¸ Š‹
"
3b 1 b
1b 1 b 1
10. lim tan lim tan 1 tan
'22
b
2 dx x b 3
x 4 2 4 4
# #
" " "
œœœœ
bbÄ_ Ä_
‘ ˆ ‰ˆ‰
111
11. lim 2 ln lim 2 ln 2 ln 2 ln (1) 2 ln 0 2 ln 2 ln 4
'2
b
2 dv v b 2
v v v b
##
" " " "
œœœœœ
bbÄ_ Ä_
‘ˆ ‰ ˆ‰¸¸ ¸¸ ¸¸
12. lim ln lim ln ln ln (1) ln 0 ln 3 ln 3
'2
b
2 dt t b 2
t 1 t 1 b 1 1 3
#
" " " "
œœœœœ
bbÄ_ Ä_
‘ ˆ ‰ ˆ‰¸¸ ¸¸ ¸¸
13. ; lim lim
ux 1
du 2x dx
''' ''
2x dx 2x dx 2x dx du du
x 1 x 1 x 1 uu u u
ab ab ab
#""
œ Äœ
œ
œ
0 1
01
1c
b1
”• ‘ ‘
bc
Ä_ Ä_
lim 1 lim ( 1) ( 1 0) (0 1) 0œ œœ
bc
Ä_ Ä_
ˆ‰ ‘
""
bc
14. ;
ux 4
du 2x dx
''' ''
x dx x dx x dx du du
x 4 x 4 x 4 2u 2u
ab ab ab
#
œ Ä
œ
œ
0 4
04
”•
lim lim lim lim 0 0 0œ œ œ œ
bb
cc
Ä_ Ä_
Ä_ Ä_
’“ ’“ Š ‹ Š ‹
ˆ‰ˆ‰
""""""""
####
ÈÈ ÈÈ
uu c
b
b
c
15. d ; lim lim u lim 3 b
u2
du 2( ) d
'''
00b
133
3
b
)
))
du du
2 2u 2u
"
#
ÈÈÈ
)))
))
”• ‘
ÈŠ‹
ÈÈ
œ
œ" Äœ œ œ
bbbÄ! Ä! Ä!
30 3œœ
ÈÈ
16. ds ; lim
u4s
du 2s ds
''' ''
000 40
222 0c
s 2s ds ds du ds
4 s 4 s 4 s 4 s
u
" " "
##
#
ÈÈÈ ÈÈ
œ Ä
œ
œ
”• c2Ä
lim lim lim u lim sin œ œ
bb
c2 c2
Ä! Ä!
ÄÄ
''
b0
4c 4
b
c
du ds s
2u 4 s
ÈÈ
"
#!
‘ ‘
È
lim 2 b lim sin sin 0 (2 0) 0œ œœ
bc2
Ä! Ä
Š‹
Ȉ‰ˆ‰
" "
###
c4 11
17. ; lim lim 2 tan u
ux
du
'''
000
bb
0
dx 2 du 2 du
(1 x) x dx
2x u 1 u 1
"
ÈÈ
–—
Ècd
œ
œÄœ œ
bbÄ_ Ä_
lim 2 tan b 2 tan 0 2 2(0)œœœ
bÄ_ ab
ˆ‰
" "
#
11
18. lim lim
''' ' '
112 b 2
22c
dx dx dx dx dx
x x 1 x x 1 x x 1 x x 1 x x 1
ÈÈ È È È
œ œ
b1 c
ÄÄ_
lim sec x lim sec x lim sec 2 sec b lim sec c sec 2œœ
b1 b1
cc
ÄÄ
Ä_ Ä_
cd cd a b a bkk kk
" " " " " "
2c
b2
0œœ
ˆ‰ˆ‰
1111
33##
19. lim ln 1 tan v lim ln 1 tan b ln 1 tan 0
'0
b
0
dv
1 v 1 tan vaba b
" " "
œœ
bbÄ_ Ä_
cdcdkkkk kk
ln 1 ln (1 0) ln 1œœ
ˆ‰ ˆ‰
11
##
20. dx lim 8 tan x lim 8 tan b 8 tan 0 8 8(0) 2
'0
b
0
16 tan x
1 x
#
" " " #
###
#
œœœœ
bbÄ_ Ä_
’“’“
ab abab
ˆ‰
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.8 Improper Integrals 551
21. e d lim e e 0 e e lim be e 1 lim
'00
b
bb
)) )
)))
œœœ
bbbÄ_ Ä_ Ä_
‘ ˆ‰
ab cd†!! "b
eb
1 lim (l'Hopital's rule for form)
^
œ bÄ_ ˆ‰
"_
_
eb
10 1œ œ
22. 2e sin d lim 2e sin d
''
00
b
))
)) ))œbÄ_
lim 2 ( sin cos ) (FORMULA 107 with a 1, b 1)œ œœ
bÄ_ ’“
e
1 1
))
b
0
lim 0 1œœœ
bÄ_
2(sin b cos b) 2(sin 0 cos 0) 2(0 1)
2e 2e 2
b
23. e dx e dx lim e lim 1 e (1 0) 1
''
00
xx x b
b
œ œ œ œœ
bbÄ_ Ä_
cd a b
!
24. 2xe dx 2xe dx 2xe dx lim e lim e
'''
xxx x x
0
0
0c
b0
œœ
bc
Ä_ Ä_
cd cd
lim 1 e lim e ( 1) ( 1 0) (0 1) 0œ œœ
bc
Ä_ Ä_
cdcdab
bc
25. x ln x dx lim ln x ln 1 lim ln b lim 0
'0
11
b
œœœ
bbbÄ! Ä! Ä!
’“ Š‹
ˆ‰
xx bb ln b
44 44
## #
"" " Š‹
2
b
lim lim 0œ œ œ œ
""""
44444
b
bbÄ! Ä!
Š‹
Š‹
b
4
bŠ‹
26. ( ln x) dx lim x x ln x 1 1 ln 1 lim b b ln b 1 0 lim 1 lim
'0
1
b
œ œ œ œ
bbbbÄ! Ä! Ä! Ä!
cdcdcd
"
ln b
Š‹ Š ‹
Š‹
b
b
b
1 lim b101œ œœ
bÄ!
27. lim sin lim sin sin 0 0
'0
2b
0
ds s b
4 s
È
" " "
####
œœœœ
b2 b2ÄÄ
‘ ˆ‰ 11
28. lim 2 sin r lim 2 sin b 2 sin 0 2 0
'0
1b
0
4r dr
1 r
È
" # " # "
#
œœœœ
b1 b1ÄÄ
cdcdab ab †
11
29. lim sec s sec 2 lim sec b 0
'1
2
b
ds
ss 1 33
È
" " "
œœœœ
b1 b1ÄÄ
cd 11
30. lim sec lim sec sec 0
'2
4
b
dt t 4 b
tt 4 36
È
"""""
## ### ## #
" " "
œœœœ
b2 b2ÄÄ
‘ ‘ˆ‰ˆ‰ ˆ‰
11
†
31. lim lim lim 2 x lim 2 x
'''
11c
4b4 b4
1c
dx dx dx
xxx
ÈÈÈ
kkœœ
bb
cc
Ä! Ä!
Ä! Ä!
‘ ‘
ÈÈ
lim 2 b 2 ( 1) 2 4 lim 2 c 0 2 2 2 0 6œ œ œ
bc
Ä! Ä!
Š‹
Ȉ‰
ÈÈȆ
32. lim 2 1 x lim 2 x 1
'''
001
212 b
c
dx dx dx
x 1 1 x x 1
ÈÈÈ
kk
œœ
b1 c1
ÄÄ
’“ ’“
ÈÈ
lim 21b 210 221 lim 2c1 0220 4œ œœ
b1 c1
ÄÄ
Š‹Š ‹ Š‹
ÈÈÈ
È
33. lim ln lim ln ln 0 ln ln 2
'1
b
1
d 2 b 2 2
5 6 3 b 3 1 3
))
)) )
#
""
œœœœ
bbÄ_ Ä_
‘ ‘¸¸ ˆ‰¸¸ ¸¸
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

552 Chapter 8 Techniques of Integration
34. lim ln x 1 ln x 1 tan x lim ln tan x
'0
b
0
b
0
dx x 1
(x 1) x 1 4 x 1
# # # #
"" " ""
#" "
ab È
œœ
bbÄ_ Ä_
‘
kk a b ’“Š‹
lim ln tan b ln tan 0 ln 1 ln 1 0œœœ
bÄ_ ’“’“Š‹
""" """ " "" "
#########
" "
b
b 1 1 4
ÈȆ†
11
35. tan d lim ln cos lim ln cos b ln 1 lim ln cos b ,
'0
2
22 2
b
0
)) )œ œ œ œ_
bb bÄÄ Ä
cdcd cdkk kk kk
the integral diverges
36. cot d lim ln sin ln 1 lim ln sin b lim ln sin b ,
'0
2
b
)) )œœœœ_
b0 b0 b0ÄÄÄ
cd cd cdkk kk kk
the integral diverges
37. ; x . Since 0 for all 0 x and
''' '
00 0
0
sin d sin x dx sin x dx sin x dx
xx xx x
))
1)
ÈÈÈÈÈÈ
"
cd1) 1œ Ä œ Ÿ Ÿ ŸŸ
converges, then dx converges by the Direct Comparison Test.
'0
sin x
x
È
38. ; . Since 0
x2
d
'''
220
202
cos d
(2) 2x x 2x 2
x
dx
cos dx sin dx sin
))
1)
1
#
##
#
"
Ô×
ÕØ
œ
œ
œ
Äœ ŸŸ
1)
)
)
ˆ‰ ˆ‰
cxx x
x for all
0 x 2 and converges, then converges by the Direct Comparison Test.ŸŸ1''
00
22
dx
2x x
sin dx
x
#
39. x e dx; y e dy lim e lim e e
'''
01ln2
ln 2 1 ln 2
1x y y b 1ln2
b
1ln2
# "
‘ cd cdc d
xy
ye dy
œÄ œ œ œ
y
bbÄ_ Ä_
0 e e , so the integral converges.œ œ
1ln2 1ln2
40. dx; y x 2 e dy 2 , so the integral converges.
''
00
11
y
e2
xe
x
È‘
È
œÄ œ
41. . Since for 0 t , 0 and converges, then the original integral
''
0 0
dt dt
tsin t tsin t t t
ÈÈÈÈ
""
ŸŸ Ÿ Ÿ1
converges as well by the Direct Comparison Test.
42. ; let f(t) and g(t) , then lim lim lim lim
'0
1dt t3t6t
t sin t t sin t t g(t) t sin t 1 cos t sin t
f(t)
""
œœ œœœ
t0 t0 t0 t0ÄÄ Ä Ä
lim 6. Now, lim lim , which diverges œ œ œ œ œ_ Ê
t0 bb
ÄÄ! Ä!
6dt dt
cos t t t b t sin t
''
0 0
1 1
1
b
‘ ‘
"" "
## #
diverges by the Limit Comparison Test.
43. and lim ln lim ln 0 , which
''' '
001 0
212 1 b
0
dx dx dx dx 1 x b
1x 1x 1x 1x 1x 1b # #
" ""
œ œ œ œ_
b1 b1ÄÄ
‘ ‘¸¸ ¸¸
diverges diverges as well.Ê'0
2dx
1x
44. and lim ln (1 x) lim ln (1 b) 0 , which
''' '
001 0
212 1 b
0
dx dx dx dx
1x 1x 1x 1x
œ œœœ_
b1 b1ÄÄ
cdcd
diverges diverges as well.Ê'0
2dx
1x
45. ln x dx ln ( x) dx ln x dx; ln x dx lim x ln x x [1 0 1] lim [b ln b b]
'' ''
11 00
10 11 1
b
kk c dœ œ œ
bbÄ! Ä!
†
1 0 1; ln ( x) dx 1 ln x dx 2 converges.œ œ œ Ê œ
''
11
01
kk
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.8 Improper Integrals 553
46. x ln x dx x ln ( x) dx ( x ln x) dx lim ln x lim ln x
'' '
110
10 1 11
bc
abc dkk ’“’“
œœ
bcÄ! Ä!
xx xx
44
##
ln 1 lim ln b ln 1 - lim ln c 0 0 0 the integralœ œœÊ
‘ ‘
’“ ’“
"" "" ""
### #444 444
bb cc
bcÄ! Ä!
converges (see Exercise 25 for the limit calculations).
47. ; 0 for 1 x and converges converges by the Direct
'''
111
dx dx dx
1x x 1 x x 1x
""
ŸŸ Ÿ_ Ê
Comparison Test.
48. ; lim lim lim 1 and lim 2 x ,
''
4 4
b
4
dx dx
x1 x1 x
x
110
ÈÈ È
Š‹
Š‹ È
""
xxx b
Ä_ Ä_ Ä_ Ä_
1
x1
xx
œœœœœ œ_
‘
È
which diverges diverges by the Limit Comparison Test.Ê'4
dx
x1
È
49. ; lim lim lim 1 and lim 2 v ,
''
2 2
b
dv dv
v1 v1 10
v
1v
ÈÈÈÈ
Š‹
Š‹ ÈÉ
""
vvv b
Ä_ Ä_ Ä_ Ä_
1
v1
v
œœœœ œ œ_
v‘
È
which diverges diverges by the Limit Comparison Test.Ê'2
dv
v1
È
50. ; 0 for 0 and lim e lim e 1 1
''
00
b
0
b
dd
1e 1e e e
))
""
ŸŸ Ÿ_ œ œ œ)bbÄ_ Ä_
cd a b
converges converges by the Direct Comparison Test.ÊÊ
''
00
dd
e1e
))
51. and lim
''''''
001011
11 b
1
dx dx dx dx dx dx
x1 x1 x1 x1 xx 2x
ÈÈÈÈ
"
œ œ
bÄ_ ‘
lim converges by the Direct Comparison Test.œœÊ
bÄ_ ˆ‰
"" "
###
b
dx
x1
'0È
52. ; lim lim lim 1; dx lim ln b ,
''
2 2
b
2
dx x
x1 x1 1x
ÈÈ
Š‹
Š‹ É
""
xxx b
Ä_ Ä_ Ä_ Ä_
x1
xx
œœ œœœ_cd
which diverges diverges by the Limit Comparison Test.Ê'2
dx
x1
È
53. dx; lim lim lim 1; dx
'''
111
ÈÈÈ
Œ
Œ ÈÉ
x1
x x
xx
x1 1
dx
x
"
xxxÄ_ Ä_ Ä_
x
x
x1
xx
œœ œœ
lim 2x lim 2 2 dx converges by the Limit Comparison Test.œ œ œÊ
bbÄ_ Ä_
‘ Š‹
"Î#
b
11
2
b
x1
x
ÈÈ
'
54. ; lim lim lim 1; lim ln x ,
'''
222
b
2
x dx x dx dx
x1 x1 x
x
1x
ÈÈÈ
Š‹
Š‹ ÈÉ
"
xxx b
Ä_ Ä_ Ä_ Ä_
x
x1
x
xx
œœ œœœœ_cd
which diverges diverges by the Limit Comparison Test.Ê'2
x dx
x1
È
55. dx; 0 for x and lim ln x , which diverges
''
2cos x 2cos x dx
xxx x
"
Ÿ œ œ_1bÄ_ cd
b
dx diverges by the Direct Comparison Test.Ê'2cos x
x
56. dx; 0 for x and dx lim lim
''
1 sin x sin x 2 2 2 2 2 2
xxx x x b
"
ŸŸ œ œ œ1bbÄ_ Ä_
‘ ˆ ‰
b
11
converges dx converges by the Direct Comparison Test.ÊÊ
''
2 dx 1 sin x
xx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

554 Chapter 8 Techniques of Integration
57. ; lim 1 and lim 4t lim 2 2 converges
'' '
44 4
b
4
2 dt t 2 dt 4 2 dt
t1 t1 t t
b
"Î#
tbb
Ä_ Ä_ Ä_
œ œœ œÊ
‘ Š‹
È
converges by the Limit Comparison Test.Ê'4
2 dt
t1
58. ; 0 for x 2 and diverges diverges by the Direct Comparison Test.
'''
222
dx dx dx
ln x x ln x x ln x
Ê
""
59. dx; 0 for x 1 and diverges diverges by the Direct Comparison Test.
'''
111
e e dx e dx
xxx x x
xx x
Ê
"
60. ln (ln x) dx; x e (ln y) e dy; 0 ln y (ln y) e for y e and ln y dy lim y ln y y
'' '
ee e
yy y b
e
ecd c dœÄ œ
bÄ_
, which diverges ln e dy diverges ln (ln x) dx diverges by the Direct Comparison Test.œ_ Ê Ê
''
ee
y
e
61. ; lim lim lim 1; e dx
'''
111
x2
dx dx
ex ex
e
110
ÈÈÈÈ
Š‹
Š‹ ÈÉ
xx
x
""
xxxÄ_ Ä_ Ä_
ex
e
x
e
x
xxx
œœ œœœ
e
lim 2e 2e 2e e dx converges convergesœ œÊ Ê
b lim
b
Ä_
œ
Ä_
cd a b
x2 b2 12 x2
b
11
2dx
eex
ÈÈ
''
x
by the Limit Comparison Test.
62. ; lim lim lim 1 and lim e
''
1 1
xb
1
dx e dx
e2 e2 10 e
1
x x
xx
""
xxx b
Ä_ Ä_ Ä_ Ä_
ˆ‰
ˆ‰
e2
e2
e
xx
xœœ œœœ
x
xx Š‹ cd
lim e e converges converges by the Limit Comparison Test.œœÊ Ê
bÄ_ ab
b
11
" "
ee e2
dx dx
''
xxx
63. 2 ; and
' ''''''
dx dx dx dx dx dx dx
x1 x1 x1 x1 x1 x1 x
È ÈÈÈÈÈ
œœ
00 01 01
11
lim lim 1 1 converges by the Direct Comparison Test.
''
1
b
1
dx dx
xx b x1
œœœÊ
bbÄ_ Ä_
‘ ˆ ‰
""
È
64. 2 ; 0 for x 0; converges 2 converges by the
'' ' '
dx dx dx dx
ee ee ee e e ee
xxx x x
xxx x
""
œ Ê
000
x
Direct Comparison Test.
65. (a) ; t ln x lim t lim (ln 2)
''
10
2ln2
1p 1p
ln 2
b
dx dt b
x(ln x) t p 1 p 1 1 p
pp
1p
cd ’“
œÄ œ œ
bbÄ! Ä!
""
the integral converges for p 1 and diverges for p 1Ê
(b) ; t ln x and this integral is essentially the same as in Exercise 65(a): it converges
''
2ln2
dx dt
x(ln x) t
pp
cdπ
for p 1 and diverges for p 1Ÿ
66. lim ln x 1 lim ln b 1 0 lim ln b 1 the integral dx
''
0
b
0
2x dx 2x
x1 x1
## #
œœœœ_Ê
bb bÄ_ Ä_ Ä_
cdcd abab ab
diverges. But lim lim ln x 1 lim ln b 1 ln b 1 lim ln
bb b bÄ_ Ä_ Ä_ Ä_
'bb
b
2x dx b
x1 b1
###
"
œœœcd c dab abab Š‹
lim (ln 1) 0œœ
bÄ_
67. A e dx lim e lim e eœœœ
'0
xxb0
b
0
bbÄ_ Ä_
cd abab
011œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.8 Improper Integrals 555
68. x xe dx lim xe e lim be e 0 e e 0 1 1;œ œ œ œœ
"
A'0
xxxbb00
b
0
bbÄ_ Ä_
cdaba b†
y e dx e dx lim e lim e e 0œœœœœœ
" " "" "" "" ""
#
#######2A 44
''
00
x2x 2x 2b20
b
0
ab ‘ ˆ‰ˆ‰
bbÄ_ Ä_
69. V 2 xe dx 2 xe dx 2 lim xe e 2 lim be e 1 2œœœœœ
''
00
x x xx bb
b
0
11 1 1 1
bbÄ_ Ä_
cd ab
’“
70. V e dx e dx lim e lim eœœœœœ
''
00
x2x 2x 2b
b
0
11 1 1ab ‘ ˆ ‰
#"""
####
bbÄ_ Ä_
1
71. A (sec x tan x) dx lim ln sec x tan x ln sec x lim ln 1 ln 1 0œœ œ
'0
2
22
b
0
bbÄÄ
cd kkkkkkˆ‰¸¸
tan b
sec b
lim ln 1 sin b ln 2œœ
bÄ2kk
72. (a) V sec x dx tan x dx sec x tan x dx sec x sec x 1 dxœœœ
'' ' '
00 0 0
22 2 2
111 1
## ## ##
abc dab
dxœœ1'0
2
1
#
(b) S 2 sec x 1 sec x tan x dx 2 sec x(sec x tan x) dx lim tan x
outer 00
22
2
b
0
œ œ
''
111
Ècd
## #
bÄ
lim tan b 0 lim tan b S diverges; S 2 tan x 1 sec x dxœœœ_Ê œ11 1
”•
cd ab È
bbÄÄ
22
outer inner 0
2
## %
'
2 tan x sec x dx lim tan x lim tan b 0 lim tan bœœœœ_
'0
2
22 2
b
0
11 1 1
### #
bb bÄÄ Ä
cd cd ab
”•
S divergesÊinner
73. (a) e dx lim e lim e e 0 e e
'3
3x 3x 3b 3 3 9 9
b
3
œœœœ
bbÄ_ Ä_
‘ ˆ‰ˆ‰
"""""
33333
†
0.0000411 0.000042. Since e e for x 3, then e dx 0.000042 and therefore¸ Ÿ
x3x x
3
'
e dx can be replaced by e dx without introducing an error greater than 0.000042.
''
00
3
ccxx
(b) e dx = 0.88621
'0
3
cxµ
74. (a) V dx lim lim (0 1)œœœœœ
'1
b
1
11 1 11
ˆ‰ ‘ ˆ‰ˆ‰
’“
""""
#
xxb1
bbÄ_ Ä_
(b) When you take the limit to , you are no longer modeling the real world which is finite. The comparison_
step in the modeling process discussed in Section 4.2 relating the mathematical world to the real world
fails to hold.
75. (a)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
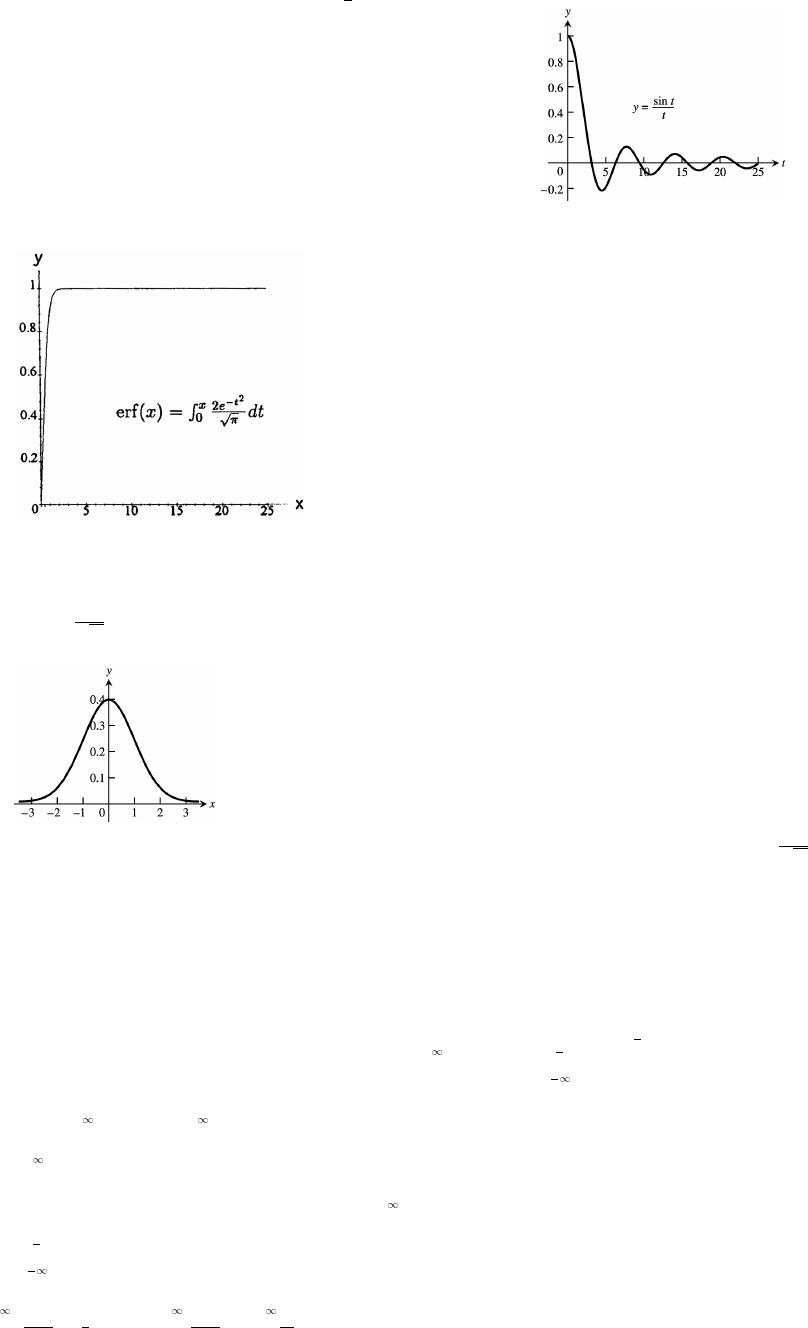
556 Chapter 8 Techniques of Integration
(b) > int((sin(t))/t, t=0..infinity); answer is
ˆ‰
1
#
76. (a)
(b) > f:= 2*exp( t^2)/sqrt(Pi);
> int(f, t=0..infinity); (answer is 1)
77. (a) f x eabœ1
2
x/2
È1
2
f is increasing on ( , 0]. f is decreasing on [0, ). f has a local maximum at 0, f 0_ _ œ !ßabab Š‹
1
2
È1
(b) Maple commands:
>f: exp( x^2/2)(sqrt(2*pi);œ
>int(f, x 1..1); 0.683œ ¸
>int(f, x 2..2); 0.954œ ¸
>int(f, x 3..3); 0.997œ ¸
(c) Part (b) suggests that as n increases, the integral approaches 1. We can take f(x) dx as close to 1 as we want by
'n
n
choosing n 1 large enough. Also, we can make f(x) dx and f(x) dx as small as we want by choosing n large''
n
n
enough. This is because 0 f x e for x 1. (Likewise, 0 f x e for x 1.) ab ab
x/2 x/2
Thus, f(x) dx e dx.
''
nn
x/2
e dx e dx 2e
2e 2e 2e
''
nn
Ä_ Ä_ Ä_
x/2 x/2 n/2
cc c
cx/2 c/2 n/2
c
n
œœœ œ
lim lim limcdc d
As n , 2e 0, for large enough n, f(x) dx is as small as we want. Likewise for large enough n,Ä_ Ä
n/2 'n
f(x) dx is as small as we want.
'n
78. dx , since the left hand integral converges but both of the right hand
'''
333
ˆ‰
""
# #xx x x
dx dx
Á
integrals diverge.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 8.8 Improper Integrals 557
79. (a) The statement is true since f(x) dx f(x) dx f(x) dx, f(x) dx f(x) dx f(x) dx
''''''
bab b
ab a a
œ œ
and f(x) dx exists since f(x) is integrable on every interval [a b].
'a
bß
(b) f(x) dx f(x) dx f(x) dx f(x) dx f(x) dx f(x) dx
''' '''
aabb
a aaa
œ
f(x) dx f(x) dx f(x) dx f(x) dx f(x) dxœœ
'''''
ba b
ba b
80. (a) f(x) dx f(x) dx f(x) dx f( u) du f(x) dx
''' ' '
œœ
00
00
f( u) du f(x) dx 2 f(x) dx, where u xœ œ œ
'' '
00 0
(b) f(x) dx f(x) dx f(x) dx f( u) du f(x) dx
''' ' '
œœ
00
00
f(u) du f(x) dx f(x) dx f(x) dx 0, where u xœ œ œ œ
''''
00 00
81. ; diverges because lim
''''
dx dx dx dx
x1 x1 x1 x1
ÈÈÈÈ Š‹
Š‹
œ
1
11 xÄ_
x
x1
lim lim 1 1 and diverges; therefore, divergesœœœ
xxÄ_ Ä_
ÈÈ
x1
xxx
dx dx
x1
"
É''
1
82. dx converges, since dx 2 dx which was shown to converge in
'''
"""
ÈÈÈ
1x 1x 1x
œ0
Exercise 51
83. ; and lim e lim e 1 1
'' '
dx e dx e dx
ee e1e1 ee e e
x x 2x 2x x x x x
xx
""
œœœœœ
0
xc
c
0
ccÄ_ Ä_
cd a b
2 convergesʜ
''
e dx dx
e1 ee
x
2x x x
0
84. ; , where u x, and since (u 1) and
'''''
e dx e dx e dx e dx e du e
x1 x1 x1 x1 1u 1u u
xxxxu u
"
œ œ œ
11
11
diverges, the integral diverges diverges
'''
11
du e du e dx
u1ux1
ux
Ê
85. e dx 2 e dx 2 lim e dx 2 lim e 2, so the integral converges.
'' '
xx x x
00
bb
0
œœ œ œ
bbÄ_ Ä_ cd
86. ;
'' '''
dx dx dx dx dx
(x 1) (x 1) (x 1) (x 1) (x 1)
œ
12
12
lim lim , which diverges diverges
b1 b1Ä Ä
''
bb
dx dx
(x 1) x 1 (x 1)
"
œ œ_ Ê
‘
87. dx 2 dx 2 dx 2 lim dx
''' '
kkkk kkkk
kk
sin x cos x sin x cos x
x 1 x1 x1 x1
sin x cos x dx
œœ
00 0
b
bÄ_
2 lim ln x 1 , which diverges dx divergesœœ_ Ê
bÄ_ cdkk
b
0'kkkk
kk
sin x cos x
x1
88. dx 0 by Exercise 80(b) because the integrand is odd and the integral
'x
x1x2abab
œ
converges
''
00
x dx dx
x1x2 xabab
Ÿ
89. Example CAS commands:
:Maple
f := (x,p) -> x^p*ln(x);
domain := 0..exp(1);
fn_list := [seq( f(x,p), p=-2..2 )];
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

558 Chapter 8 Techniques of Integration
plot( fn_list, x=domain, y=-50..10, color=[red,blue,green,cyan,pink], linestyle=[1,3,4,7,9], thickness=[3,4,1,2,0],
legend=["p= -2","p = -1","p = 0","p = 1","p = 2"], title="#89 (Section 8.8)" );
q1 := Int( f(x,p), x=domain );
q2 := value( q1 );
q3 := simplify( q2 ) assuming p>-1;
q4 := simplify( q2 ) assuming p<-1;
q5 := value( eval( q1, p=-1 ) );
i1 := q1 = piecewise( p<-1, q4, p=-1, q5, p>-1, q3 );
90. Example CAS commands:
:Maple
f := (x,p) -> x^p*ln(x);
domain := exp(1)..infinity;
fn_list := [seq( f(x,p), p=-2..2 )];
plot( fn_list, x=exp(1)..10, y=0..100, color=[red,blue,green,cyan,pink], linestyle=[1,3,4,7,9], thickness=[3,4,1,2,0],
legend=["p = -2","p = -1","p = 0","p = 1","p = 2"], title="#90 (Section 8.8)" );
q6 := Int( f(x,p), x=domain );
q7 := value( q6 );
q8 := simplify( q7 ) assuming p>-1;
q9 := simplify( q7 ) assuming p<-1;
q10 := value( eval( q6, p=-1 ) );
i2 := q6 = piecewise( p<-1, q9, p=-1, q10, p>-1, q8 );
91. Example CAS commands:
:Maple
f := (x,p) -> x^p*ln(x);
domain := 0..infinity;
fn_list := [seq( f(x,p), p=-2..2 )];
plot( fn_list, x=0..10, y=-50..50, color=[red,blue,green,cyan,pink], linestyle=[1,3,4,7,9], thickness=[3,4,1,2,0],
legend=["p = -2","p = -1","p = 0","p = 1","p = 2"], title="#91 (Section 8.8)" );
q11 := Int( f(x,p), x=domain ):
q11 = lhs(i1+i2);
`` = rhs(i1+i2);
`` = piecewise( p<-1, q4+q9, p=-1, q5+q10, p>-1, q3+q8 );
`` = piecewise( p<-1, -infinity, p=-1, undefined, p>-1, infinity );
92. Example CAS commands:
:Maple
f := (x,p) -> x^p*ln(abs(x));
domain := -infinity..infinity;
fn_list := [seq( f(x,p), p=-2..2 )];
plot( fn_list, x=-4..4, y=-20..10, color=[red,blue,green,cyan,pink], linestyle=[1,3,4,7,9],
legend=["p = -2","p = -1","p = 0","p = 1","p = 2"], title="#92 (Section 8.8)" );
q12 := Int( f(x,p), x=domain );
q12p := Int( f(x,p), x=0..infinity );
q12n := Int( f(x,p), x=-infinity..0 );
q12 = q12p + q12n;
`` = simplify( q12p+q12n );
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 8 Practice Exercises 559
89-92. Example CAS commands:
: (functions and domains may vary)Mathematica
Clear[x, f, p]
f[x_]:= x Log[Abs[x]]
p
int = Integrate[f[x], {x, e, 100)]
int /. p 2.5Ä
In order to plot the function, a value for p must be selected.
p = 3;
Plot[f[x], {x, 2.72, 10}]
CHAPTER 8 PRACTICE EXERCISES
1. x 4x 9 dx; u du u C 4x 9 C
u4x 9
du 8x dx
''
È”•
Èab
##"" "
$Î# #
#
$Î#
Äœœ
œ
œ8831
2
†
2. 6x 3x 5 dx; u du u C 3x 5 C
u3x 5
du 6x dx
''
È”•
Èab
##$Î# # $Î#
Äœœ
œ
œ
22
33
3. x(2x 1) dx; u du u du u du u u C
u2x1
du 2 dx
''''
Äœœ
œ
œ
"Î# $Î# "Î# &Î# $Î#
" " "
##
”•
ˆ‰ ˆ ‰
ÈŠ‹
u 1 2 2
4453
Cœ
(2x 1) (2x 1)
10 6
4. dx; du u du u 2u C
u1x
du dx
'''
x 2
1 x
(1 u)
uu
3
ÈÈÈ
"$Î# "Î#
”• Š‹
È
œ
œ Ä œ œ
(1 x) 2(1 x) Cœ
2
3$Î# "Î#
5. ; 2u C C
u8x 1
du 16x dx
''
x dx du
8x 1 16 16 8
u
8x 1
ÈÈ
È
#""
"Î#
”•
œ
œÄœ œ†
6. ; 2u C C
u94x
du 8x dx
''
x dx du
9 4x 88 4
u
9 4x
ÈÈ
È
#""
"Î#
”•
œ
œ Ä œ œ †
7. ; ln u C ln 25 y C
u25y
du 2y dy
''
y dy
25 y u
du
###
#"" " #
”• kk a b
œ
œÄœœ
8. ; ln u C ln 4 y C
u4y
du 4y dy
''
y dy
4y 4u 4 4
du
%
$
"" " %
”• kk a b
œ
œÄœœ
9. ; 2u C C
u94t
du 16t dt
''
t dt du
94t 16 16 8
u
94t
ÈÈ
È
%
$
""
"Î#
”•
œ
œ Ä œ œ †
10. ; tan u C tan t C
ut
du 2t dt
''
2t dt du
t1 u1
#
" " #
”•
œ
œÄœœ
11. z z 1 dz; u du u C z 1 C
uz
du z dz
''
#Î$ &Î$ #Î$ &Î$ &Î$
#Î$ &Î$
&Î$
#Î$ #
ˆ‰ ˆ‰
”•
Äœœ
œ"
œ5
3
3339
5555
†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

560 Chapter 8 Techniques of Integration
12. z 1 z dz; u du 2 u C 1 z C
u1z
du z dz
''
"Î& %Î& "Î# %Î&
"Î# "Î#
%Î&
"Î& #
ˆ‰ ˆ‰
”• È
Äœœ
œ
œ4
5
55 5
44
†
13. ; C C
u1cos 2
du sin 2 d
''
sin 2 d du
(1 cos 2) u 2u (1 cos 2)
))
) )##
"" "
”•
œ
œ# Äœœ
)
))
14. ; 2u C 2 1 sin C
u1sin
du cos d
''
cos d du
(1 sin ) u
))
)
"Î#
”• È
œ
œÄœœ
)
)) )
15. ; ln u C ln 3 4 cos t C
u 3 4 cos t
du 4 sin t dt
''
sin t dt du
34 cos t 4 u 4 4
"" "
”• kk k k
œ
œ Ä œ œ
16. ; ln u C ln 1 sin 2t C
u 1 sin 2t
du 2 cos 2t dt
''
cos 2t dt du
1sin 2t 2 u 2 2
"" "
”• kk k k
œ
œÄœœ
17. (sin 2x) e dx; e du e C e C
u cos 2x
du 2 sin 2x dx
''
cos 2x u u cos 2x
”•
œ
œ Ä œ œ
"""
###
18. (sec x tan x) e dx; e du e C e C
u sec x
du sec x tan x dx
''
sec x u u sec x
”•
œ
œÄœœ
19. e sin e cos e d ; u du u C cos e C
u cos e
du sin e e d
''
ab ab ab
”•
ˆ‰
ˆ‰
##$$
""
))
œ
œ Ä œ œ
)
)
†33
20. e sec e d ; sec u du tan u C tan e C
ue
du e d
''
##
ab ab
”•
))
œ
œÄœœ
21. 2 dx C 22. 5 dx C
''
x1 œ œ
2 5
ln 2 ln 5
2
x1 x2
x2
È"
ÈŠ‹
23. ; ln u C ln ln v C
u ln v
du dv
''
dv du
v ln v u
v
”• kk k k
œ
œÄœœ
"
24. ; ln u C ln 2 ln v C
u2ln v
du dv
''
dv du
v(2 ln v) u
v
"
”• kk k k
œ
œÄœœ
25. ; ln u C ln 2 tan x C
u2tanx
du
''
dx du
x12tanx u
dx
x1
aba b
"
"
”•
kk k k
œ
œÄœœ
26. ; u du u C sin x C
usinx
du
''
sin x dx
1x dx
1x
ÈÈ
"
""
##
#"
#
–— ab
œ
œÄœœ
27. ; sin u C sin (2x) C
u2x
du 2 dx
''
2 dx du
14x 1u
ÈÈ
" "
”•
œ
œÄœœ
28. ; sin u C sin C
u
du dx
'' '
dx dx du x
49 x 1 u
7 7
1
x
7
7
ÈÈ
Ɉ‰
"
"" "
œÄœœ
œ
œ
x
7”• ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 8 Practice Exercises 561
29. ; sin u C sin C
ut
du dt
'' '
dt dt du 3t
16 9t 1 u
43334
1
3
4
3
4
ÈÈ
ÊŠ‹
""""
" "
œÄœœ
œ
œ
3t
4–— ˆ‰
30. ; sin u C sin C
ut
du dt
'' '
dt dt du 2t
94t 1u
32223
1
2
3
2
3
ÈÈ
ÊŠ‹
""""
" "
œÄœœ
œ
œ
2t
3–— ˆ‰
31. ; tan u C tan C
ut
du dt
'' '
dt dt du t
9t 9 3 1u 3 3 3
1
3
3
""""
"
"" "
œÄœœ
œ
œ
ˆ‰
t
3–— ˆ‰
32. ; tan u C tan (5t) C
u5t
du 5 dt
''
dt du
1 25t 5 1 u 5 5
"" "
" "
”•
œ
œÄœœ
33. sec C
''
4 dx 4 dx 5x
5x 25x 16 25 5 4
xx
ÈÉ
""
œœ
16
25 ¸¸
34. 3 2 sec C
''
6 dx dx 2x
x4x 9 xx 3
ÈÉ
"
œœ
9
4¸¸
35. sin C
''
dx x 2
4x x
d(x 2)
4(x2)
ÈÈ
"
#
œœ
ˆ‰
36. sin (x 2) C
''
dx
4x x 3
d(x 2)
1(x2)
ÈÈ
"
œœ
37. tan C
''
dy d(y 2) y 2
y4y8 (y2)4
# #
""
œœ
ˆ‰
38. tan (t 2) C
''
dt
t4t5 (t2)1
d(t 2)
"
œœ
39. sec x 1 C
''
dx
(x 1) x 2x
d(x 1)
(x 1) (x 1) 1
"
ÈÈ
œœkk
40. sec v 1 C
''
dv
(v 1) v 2v
d(v 1)
(v 1) (v 1) 1
"
ÈÈ
œœkk
41. sin x dx dx C
''
#
##
œœ
1 cos 2x x sin 2x
4
42. cos 3x dx dx C
''
#"
##
œœ
cos 6x x sin 6x
12
43. sin d 1 cos sin d ; 2 1 u du 2u C
u cos
du sin d
'' '
$# #
###
#
"
##
)))
)
)
))
)
œ Ä œ
œ
œ
ˆ‰ˆ‰
–—
ab2u
3
cos 2 cos Cœ
2
3$
##
))
44. sin cos d 1 cos (sin ) cos d ; 1 u u du u u du
u cos
du sin d
'' ''
$# # # ## %#
))) ) ) )) )
))
œ Ä œ
œ
œ
abab ab ab
”•
CCœœ
uu cos cos
53 5 3
))
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

562 Chapter 8 Techniques of Integration
45. tan 2t dt (tan 2t) sec 2t 1 dt tan 2t sec 2t dt tan 2t dt; u2t
du 2 dt
'' ' '
$# #
œœ
œ
œ
ab ”•
tan u sec u du tan u du tan u ln cos u C tan 2t ln cos 2t CÄœœ
""""""
## # #
## #
''
44
kk kk
tan 2t ln sec 2t Cœ
""
#
#4kk
46. 6 sec t dt 6 tan t 1 sec t dt; 6 u 1 du 2u 6u C
utan t
du sec t dt
'' '
%## #$
#
œ Äœ
œ
œ
abab ab
”•
2 tan t 6 tan t Cœ
$
47. csc 2x dx ln csc 2x cot 2x C
'''
dx dx
2 sin x cos x sin 2x
œœ œ
"
#kk
48. ; sec u du ln sec u tan u C
u2x
du 2 dx
'' ''
2 dx 2 dx du
cos x sin x cos 2x cos u
œÄœœ
œ
œ
”• kk
ln sec 2x tan 2x Cœkk
49. csc y 1 dy cot y dy ln sin y ln 1 ln ln 2
''
44
22 2
4
Ècdkk È
#"
œ œ œ œ
È2
50. cot t 1 dt csc t dt ln csc t cot t ln csc cot ln csc cot
''
44
34 34 34
4
Ècdkk¸¸¸¸
#œ œ œ
33
44 44
11 11
ln 2 1 ln 2 1 ln ln ln 3 2 2œ œ œ œ
¹¹¹¹¹¹ Š ‹
ÈÈ È
»»
È
ÈŠ‹Š‹
ÈÈ
2
21
221
1
"
"
#
51. 1 cos 2x dx sin 2x dx sin 2x dx sin 2x dx
''''
0002
22
02
Èkk ‘‘
œ œ œ
###
cos 2x cos 2x
2œ œ
ˆ‰ ‘ˆ‰
"" " "
## # #
52. 1 sin dx cos dx cos dx cos dx 2 sin 2 sin
''''
000
22 2
0
ȸ¸ ‘‘
œ œ œ
## #####
x xxxxx
(2 0) (0 2) 4œœ
53. 1 cos 2t dt 2 sin t dt 2 2 sin t dt 2 2 cos t 2 2 [0 ( 1)] 2 2
'''
220
222
2
0
ÈÈÈ ÈÈÈ
kk ’“
œ œ œ œœ
54. 1 cos 2t dt 2 cos t dt 2 cos t dt 2 cos t dt
''''
22322
32
ÈÈÈÈ
kkœ œ
2 sin t 2 sin t 2 ( 1 0) 2 [0 ( 1)] 2 2œ œ œ
ÈÈ ÈÈ È
cd cd
2#
$Î#
1
1
55. x x 2 tan C
''
x dx 4 dx x
x4 x4
#
"
œ œ
ˆ‰
56. dx x dx ln 9 x C
'' '
x dx 9x x 9
9x x9 x9
xx 9 9x
##
#
œœœ
’“
ˆ‰ ab
ab
57. dx (2x 1) dx x x 2 ln 2x 1 C
''
4x 3 4
2x 1 x 1
#
#
œ œ
‘ kk
58. 2 dx 2x 8 ln x 4 C
''
2x dx 8
x4 x4
œ œ
ˆ‰ kk
59. dy ln y 4 tan C
'''
2y 1 2y dy dy y
y4 y4 y4
##
#"
"
œœ ab ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 8 Practice Exercises 563
60. dy 4 ln y 1 4 tan y C
'''
y 4 y dy dy
y1 y1 y1
#
"#"
œ œ ab
61. dt 2 4 t 2 sin C
'''
t 2 t dt dt t
4t 4t 4t
#"
#
ÈÈÈ
œ œ
Ȉ‰
62. dt 2 1 t ln t C
'''
2t 1 t
t1t 1 t
2t dt dt
t
#
È
ÈÈ
œœ
Èkk
63. dx dx
''' '
tan x dx sin x dx sin x 1 cos x
tan xsec x sin x1 1sinx cosx
(sin x)(1 sin x)
œœ œ
dx tan xxC xtan xsec xCœ œ œ
'''
d(cos x)
cos x cos x cos x
dx "
64. dx dx
''' '
cot x dx cos x dx cos x 1 sin x
cot xcsc x cos x1 1cosx sinx
(cos x)(1 cos x)
œœ œ
dx cot xxCxcot xcsc xCœœœ
'''
d(sin x)
sin x sin x sin x
dx "
65. sec (5 3x) dx; sec y sec y dy ln sec y tan y C
y53x
dy 3 dx
'''
Äœœ
œ
œ
”• Š‹ kk†
dy
33 3
""
ln sec (5 3x) tan (5 3x) Cœ
"
3kk
66. x csc x 3 dx csc x 3 d x 3 ln csc x 3 cot x 3 C
''
ab abab k kabab
### ##
""
##
œ œ
67. cot dx 4 cot d 4 ln sin C
''
ˆ‰ ˆ‰ˆ‰ ¸ ¸ˆ‰
xxxx
4444
œœ
68. tan (2x 7) dx tan (2x 7) d(2x 7) ln cos (2x 7) C ln sec (2x 7) C
''
œ œ œ
"""
###
kkkk
69. x 1 x dx; (1 u) u du u u du u u C
u1x
du dx
'''
È”• Ȉ‰
Äœœ
œ
œ
$Î# "Î# &Î# $Î#
22
53
(1 x) (1 x) C 2 Cœ œ
22
53 35
1x 1x
&Î# $Î#
–—
Š‹Š‹
ÈÈ
70. 3x 2x 1 dx; 3 u du u u du u u C
u2x1
du 2 dx
'''
È”•
ˆ‰ ˆ ‰
È
Ä œœ
œ
œ
u1 3 3 2 3 2
44543
"
##
$Î# "Î# &Î# $Î#
†††
(2x 1) (2x 1) C Cœœ
3
10 10
32x1 2x1
&Î# $Î#
"
##
ˆ‰ˆ‰
ÈÈ
71. z 1 dz; tan 1 sec d sec d
ztan
dz sec d
'''
ÈÈ
”•
##
##$
Ĝ
œ
œ
)
)) )))))†
sec d (FORMULA 92)œ
sec tan 3 2
31 31
))
'))
ln sec tan C ln z 1 z Cœ œ
sin
2 cos
zz 1
)
)
""
###
#
kk ¹¹
È
)) È
72. 16 z dz; cos d sin C C
z 4 tan
dz 4 sec d
'''
ab”•
Äœœœ
œ
œ
#$Î#
#""
)
)) )) )
4 sec d z
64 sec d 16 16 16 16 z
))
)) È
Cœ
z
16 16 zab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

564 Chapter 8 Techniques of Integration
73. , u ; sec d
utan
du sec d
''' ''
dy dy y
25 y 55
1
du sec d
1u 1tan
ÈÈ È
Ɉ‰
"
#
œœ œ Äœ
œ
œ
y
5‘
”•
)
)) ))
))
)
ln sec tan C ln 1 u u C ln 1 C ln Cœ œ œ œ kk
¹¹ ¹¹
鼼
Ɉ‰
))
"" ""
##
yy
55 5
25 y y
È
ln y 25 y Cœ
¸¸
È#
74. ln 1 u u C from Exercise 73
'' '
dy dy
25 9y 533
1
du
1u
ÈÈ
ÊŠ‹
"""
#"
œœœ
3y
5¹¹
È
ln 25 9y 3y CÄ
"#
3¸¸
È
75. ; csc d cot C C
xsin
dx cos d
'''
dx cos d
x1x sin cos x
1x
ÈÈ
#
”•
œ
œÄœœœ
)
)) )) )
))
))
76. ; sin d 1 cos (sin ) d ;
xsin
dx cos d
''''
x dx sin cos d
1x cos
È
$#
”• ab
œ
œÄœœ
)
)) )) ) ) )
)))
)
u cos 1 u du u C cos cos 1 x 1 x Ccdab ab
'È
œ Ä œ œ œ )))
#$#
""
#$Î#
u
33 3
: Ans 1 x C by another methodNote ´
#
x1x
33
2
ÈÈ
77. ; sin d d sin 2 C
xsin
dx cos d
''''
x dx sin cos d 1 cos 2
1x cos 4
È
#""
##
”•
œ
œÄœœœ
)
)) )) ) ) )
))) )
)
sin cos Cœ œ
""
## # #
)))
sin x x1x
È
78. 4 x dx; 2 cos 2 cos d 2 (1 cos 2 ) d 2 sin 2 C
x 2 sin
dx 2 cos d
'''
È”• ˆ‰
Äœœ
œ
œ
#"
#
)
)) ))) ))) )†
2 2 sin cos C 2 sin x 1 C 2 sin Cœ œ œ ))) " "
## #
#
ˆ‰ ˆ‰ ˆ‰
É
xx x
x4x
2
È
79. ; sec d
x 3 sec
dx 3 sec tan d
' '''
dx 3 sec tan d 3 sec tan d
x9 9 sec 9 3 tan
ÈÈ
”•
œ
œÄœœ
)
))) ))
))) )))
))
ln sec tan C ln 1 C ln C ln x x 9 Cœ œ œ œ kk
ºº
Ɉ‰ ¹¹ ¹ ¹
È
))
"""
# #
xx
33 3
xx9
È
80. ; ;
xsec usin
dx sec tan d du cos d
''''
12 dx 12 sec tan d 12 cos d 12 du
x1 tan sin u
ab
”• ”•
œœ
œœ
Äœ Ä
))
))) ))
))) ))
))
CC Cœ œ œ
12 12 12 x
usin x1
)È
81. dw; sec tan d tan d sec 1 d
w sec
dw sec tan d
''''
Èw1
wsec
tan
##
”•
ˆ‰ ab
œ
œÄœœ
)
))) ))) )) ) )
)
)
†
tan C w 1 sec w Cœœ )) È#"
82. dz; 4 tan d 4(tan ) C
z 4 sec
dz 4 sec tan d
'''
Èz16
z 4sec
4 tan 4 sec tan d
#
”•
œ
œÄœœ
)
))) )) ) )
))))
)
†
z164 sec Cœ
Ȉ‰
#" z
4
83. u ln (x 1), du ; dv dx, v x;œ œ œ œ
dx
x1
ln (x 1) dx x ln (x 1) dx x ln (x 1) dx x ln (x 1) x ln (x 1) C
''''
œ œ œ
xdx
x1 x1 "
(x 1) ln (x 1) x C (x 1) ln (x 1) (x 1) C, where C C 1œ œ œ
""
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 8 Practice Exercises 565
84. u ln x, du ; dv x dx, v x ;œœœ œ
dx
x3
#$
"
x ln x dx x ln x x dx ln x C
''
#$$
"""
œ œ
33x39
xx
ˆ‰
85. u tan 3x, du ; dv dx, v x;œœœœ
"
3 dx
19x
tan 3x dx x tan 3x ; x tan 3x
y19x
dy 18x dx
'' '
" " "
#"
œ Ä
œ
œ
3x dx
19x 6 y
dy
”•
x tan (3x) ln 1 9x Cœ
" #
"
6ab
86. u cos , du ; dv dx, v x;œœœœ
"
#
ˆ‰
xdx
4x
È
cos dx x cos ; x cos
y4x
dy 2x dx
'' '
" " "
## ##
#"
ˆ‰ ˆ‰ ˆ‰
”•
x x x dx x
4x
dy
y
œ Ä
œ
œ
ÈÈ
x cos 4 x C x cos 2 1 Cœœ
" "
###
##
ˆ‰ ˆ‰ ˆ‰
ÈÉ
xxx
87. ex
(x 1) e ïïïïî
ÐÑ
#x
2(x 1) e ïïïïî
ÐÑ x
2 eïïïïî
ÐÑ x
0 (x 1) e dx (x 1) 2(x 1) 2 e CÊ œ
'##xx
cd
88. sin (1 x)
x cos (1 x)
#ïïïïî
ÐÑ
2x sin (1 x)ïïïïî
ÐÑ
2 cos(1x)ïïïïî
ÐÑ
0 x sin (1 x) dx x cos (1 x) 2x sin (1 x) 2 cos (1 x) Cʜ
'##
89. u cos 2x, du 2 sin 2x dx; dv e dx, v e ;œœ œœ
xx
I e cos 2x dx e cos 2x 2 e sin 2x dx;œœ
''
xx x
u sin 2x, du 2 cos 2x dx; dv e dx, v e ;œœ œœ
xx
I e cos 2x 2 e sin 2x 2 e cos 2x dx e cos 2x 2e sin 2x 4I I Cœ œ Êœ
xx x xx
’“
'e cos 2x 2e sin 2x
55
xx
90. u sin 3x, du 3 cos 3x dx; dv e dx, v e ;œœ œœ
2x 2x
"
#
I e sin 3x dx e sin 3x e cos 3x dx;œœ
''
2x 2x 2x
"
#
3
2
u cos 3x, du 3 sin 3x dx; dv e dx, v e ;œœ œœ
2x 2x
"
#
I e sin 3x e cos 3x e sin 3x dx e sin 3x e cos 3x Iœ œ
"" "
### # #
2x 2x 2x 2x 2x
33 39
44
’“
'
I e sin 3x e cos 3x C e sin 3x e cos 3x CÊœ œ
43 23
13 4 13 13
ˆ‰
"
#
2x 2x 2x 2x
91. 2 ln x 2 ln x 1 C
'''
x dx 2 dx dx
x 3x2 x2 x1
œ œ kkkk
92. ln x 3 ln x 1 C
'''
x dx 3 dx dx 3
x 4x3 x3 x1
# # # #
""
œ œkk kk
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

566 Chapter 8 Techniques of Integration
93. dx ln x ln x 1 C
''
dx 1 1
x(x1) x x1 (x1) x1
" "
œ œ
Š‹
kk k k
94. dx dx 2 ln C 2 ln x 2 ln x 1 C
''
x1 2 2 x
x(x1) x1xx x x x
""""
œ œ œ
ˆ‰¸¸ kk k k
95. ; cos y ln C
''''
sin d
cos cos 2 y y2 3 y1 3 y 3 y1
dy dy dy y 2
))
))
#
"""
cd ¹¹
)œÄ œ œ
ln C ln Cœœ
" "
3cos 1 3cos 2
cos 2 cos 1
¸¸ ¸¸
))
))
96. ; sin x ln C
''''
cos d dx dx dx sin 2
sin sin 6 x x6 5 x2 5 x3 5 sin 3
)) )
)) )
"" "
cd ¸¸
)œÄ œœ
97. dx dx dx 4 ln x ln x 1 4 tan x C
'''
3x 4x 4 4 x 4
xx x x1
"
#
#"
œ œ kk a b
98. 2 tan C
''
4x dx 4 dx x
x4x x4
#
"
œœ
ˆ‰
99. dv ln v ln v 2 ln v 2 C
''
(v 3) dv
2v 8v 4v 8(v 2) 8(v ) 8 16 16
35 3 5
# #
"" "
œ œ
Š‹
kk kk kk
ln Cœ
"
16 v
(v 2) (v 2)
¹¹
100. ln C
''''
(3v 7) dv ( 2) dv (v 2)(v 3)
(v 1)(v 2)(v 3) v 1 v 2 v 3 (v 1)
dv dv
œœ
¹¹
101. tan t tan C tan t tan C
'''
dt dt dt t t
t4t3 t1 t3 6
33 3
3
"" " " "
# # # #
" " " "
#
œ œ œ
ÈÈ È
È
Š‹
102. ln t 2 ln t 1 C
'''
t dt t dt t dt
tt2 3t2 3t1 6 6
"" " "
##
œœkk ab
103. dx x dx x dx
'' '''
x x 2x 2 dx 4 dx
x x2 x x2 3 x1 3 x2
œ œ
ˆ‰
ln x 2 ln x 1 Cœ
x4 2
33
#kk kk
104. dx 1 dx 1 dx dx x ln x 1 ln x C
'' ' '''
x1 x dx dx
xx xx x(x1) x1 x
" "
œ œ œ œ
ˆ‰’“ kkkk
105. dx x dx x dx
'' '''
x4x 3x 3 dx 9 dx
x 4x3 x 4x3 x1 x3
# #
œ œ
ˆ‰
ln x 3 ln x 1 Cœ
x9 3
## #
kk kk
106. dx (2x 3) dx (2x 3) dx
'' '''
2x x 21x 24 x dx 2 dx
x2x8 x2x8 3 x 3 x4
"
#
œ œ
‘
x 3x ln x 4 ln x 2 Cœ
#"2
33
kk kk
107. ; ln u 1 ln u 1 C
ux1
du
dx 2u du
''''
dx 2 u du du du
x3 x 1
dx
2x1 3u1u3u13u13 3
ˆ‰
ÈÈab
"" " "
Ô×
ÖÙ
ÕØ
Èkk kk
œ
œ
œ
Ä œ œ
ln Cœ
""
3
x1
x11
¹¹
È
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 8 Practice Exercises 567
108. ; 3 3 ln C 3 ln C
ux
du
dx 3u du
'''
dx 3u du du u
x1 x 1x
dx
3x u (1 u) u(1 u) u 1
x
ˆ‰
È È
È
#
Ô×
ÖÙ
ÕØ
ȸ¸ ¹¹
œ
œ
œ
Äœ œ œ
109. ; ln C ln C ln 1 e C
ue 1
du e ds
ds
''''
ds du du du u e
e 1 u(u 1) u 1 u u 1 e
s
s
du
u 1
s s
s
"
Ô×
ÕØ ¸¸ ¸¸ kk
œ
œ
œ
Äœœœœ
s
110. ; 2 ln
ue1
du
ds
'''''
ds 2u du du du du u
e 1
s
e ds
2e1
2u du
u 1
u u 1 (u 1)(u 1) u 1 u 1 u
ÈÈab
s
s
"
Ô×
ÖÙ
ÕØ
ȸ¸
œ
œ
œ
Ä œ œœ
s1C
ln Cœ
¹¹
È
Èe 1
e 1 1
s
s
"
111. (a) 16 y C
''
y dy
16 y 16 y
d 16 y
ÈÈ
ab
"
#
#
œ œ
È
(b) ; y 4 sin x 4 4 cos x C C 16 y C
''
y dy
16 y
sin x cos x dx
cos x 4
4 16 y
ÈÈ
#
cd È
œ Ä œ œ œ
112. (a) 4 x C
''
x dx
4 x 4 x
d4 x
ÈÈ
ab
"
#
#
œœ
È
(b) ; x 2 tan y 2 sec y tan y dy 2 sec y C 4 x C
''
x dx
4 x
2 tan y 2 sec y dy
2 sec y
È
#
cd 'È
œÄ œ œœ
†
113. (a) ln 4 x C
''
x dx
4 x 4 x
d4 x
# #
""
#
œ œ
ab kk
(b) ; x 2 sin tan d ln cos C ln C
''
x dx 2 sin 2 cos d
4 x 4 cos 2
4 x
cd kk
'Š‹
œÄ œ œ œ ))))
)))
)
†È
ln 4 x Cœ
"
#
#
kk
114. (a) 4t 1 C
''
t dt
4t 1 4t 1
84
d4t 1
ÈÈ
ab
""
#
œœ
È
(b) ; t sec sec d C C
'''
t dt tan
4t 1
sec tan sec d
tan 4 4 4
4t 1
ÈÈ
""
#
#
‘
œÄ œ œœ)))
)) ))
)
)
†
115. ; ln u C ln C ln C
u9x
du 2x dx
''
x dx du
9 x u u9 x
##
#"" " "
”• kk
œ
œ Ä œ œ œ
ÈÈ
116. ln x ln 3 x ln 3 x C
''''
dx dx dx dx
x9 x 9 x 183 x 183 x 9 18 18ab
"" " " " "
œ œkk kk kk
ln x ln 9 x Cœ
"" #
918
kk k k
117. ln 3 x ln 3 x C ln C
'''
dx dx dx x 3
9 x 6 3 x 6 3 x 6 6 6 x 3
"" " " "
œ œ œ kk kk ¸¸
118. ; d d C sin C
x 3 sin
dx 3 cos d
''
dx 3 cos x
9 x 3 cos 3
È
"
”• '
œ
œÄœœœ
)
)) )))
)
)
119. sin x cos x dx cos x 1 cos x sin x dx cos x sin x dx cos x sin x dx C
'' ''
34 4 2 4 6 cos x cos x
57
œœœab 57
120. cos x sin x dx sin x cos x cos x dx sin x 1 sin x cos x dx
'' '
55 5 4 5 2
2
œœab
sin x cos x dx 2 sin x cos x dx sin x cos x dx Cœ œ
'''
579
sin x 2sin x sin x
6810
6810
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

568 Chapter 8 Techniques of Integration
121. tan x sec x dx C
'42 tan x
5
œ
5
122. tan x sec x dx sec x 1 sec x sec x tan x dx sec x sec x tan x dx sec x sec x tan x dx
'' ' '
33 2 2 4 2
œ †† œ †† ††ab
Cœ
sec x sec x
53
53
123. sin 5 cos 6 d sin sin 11 d sin d sin 11 d cos cos 11 C
'' ''
) )) ) ) ) )) )) ) )œ œ œ
"""""
######
a b ab ab abab ab
cos cos 11 Cœ
""
###
))
124. cos 3 cos 3 d cos 0 cos 6 d d cos 6 d sin 6 C
'' ''
))) )) ) ))) )œ œ œ
""""
####
ab 1
12
125. 1 cos dt 2 dt 4 2 C
cos sin
''
Ɉ‰ ¸ ¸ ¸ ¸
ÈÈ
œ œ
ttt
244
126. e tan e 1 dt e dt ln C
sec e sec e tan e
''
tt
2t ttt
Èkk k kœ œ
127. E ( x) M where x ; f(x) x f (x) x f (x) 2x f'''(x) 6xkk
sŸ˜ ˜œœ œœÊœÊ œ Ê œ
3 3 2
180 n n x
" " "
% " w # ww $ %
f (x) 24x which is decreasing on [1 3] maximum of f (x) on [1 3] is f (1) 24 M 24. ThenÊœ ßÊ ß œÊœ
Ð%Ñ & Ð%Ñ Ð%Ñ
E 0.0001 (24) 0.0001 0.0001 (0.0001) n 10,000kk ˆ ‰ˆ‰ ˆ‰ˆ‰ ˆ‰ ˆ‰
sŸÊ ŸÊ ŸÊŸ Ê
3 2 768 180 768
180 n 180 768 180
nn
" " "
%%
n 14.37 n 16 (n must be even)Ê Ê
128. E ( x) M where x ; 0 f (x) 8 M 8. Then E 10 (8) 10kk kk ˆ‰
T T
Ÿ˜ ˜œœŸŸÊœ Ÿ Ê Ÿ
1 0 1 0
12 n n 12 n
" ""
#ww $$
#
10 1000 n n 25.82 n 26ÊŸ Ê Ê Ê Ê
2 3n 2000
3n 3
$ #
#
129. x ;˜œ œ œ Ê œ
b a 0 x
n66 1
˜
##
11 1
mf(x ) 12 T (12) ;
!ˆ‰
i0
6
iœÊœ œ
1
12 1
x f(x ) m mf(x )
x0 0 1 0
x/61/221
x/33/223
x/2224
x 2 /3 3/2 2 3
x 5 /6 1/2 2 1
x010
ii i
!
"
#
$
%
&
'
1
1
1
1
1
1
mf(x ) 18 and
!
i0
6
iœœÊ
˜x
318
1
S (18) .œœ
ˆ‰
1
18 1
x f(x ) m mf(x )
x0 0 1 0
x/61/242
x/33/223
x/2248
x 2 /3 3/2 2 3
x 5 /6 1/2 4 2
x010
ii i
!
"
#
$
%
&
'
1
1
1
1
1
1
130. f (x) 3 M 3; x . Hence E 10 (3) 10 10 n
¸¸ ˆ‰ˆ‰
kk
Ð%Ñ & & & %
" " " " "
%
ŸÊœ˜œœ ŸÊ ŸÊŸÊ
22 10
n n 180 n 60
60n
s
n 6.38 n 8 (n must be even)Ê Ê
131. y 37 sin (x 101) 25 dx 37 cos (x 101) 25x
av 0
365
œœ
""
$'&
!
365 0 365 365 2 365
2 365 2
'‘ ‘ˆ‰ ˆ ‰ˆ‰
11
1
37 cos (365 101) 25(365) 37 cos (0 101) 25(0)œ
"
365 2 365 2 365
365 2 365 2
‘ˆ‰ˆ‰ˆ‰ ‘ ˆ‰ ‘
11
11
cos (264) 25 cos ( 101) cos (264) cos ( 101) 25œ œ
37 2 37 2 37 2 2
2 365 2 365 2 365 365111
1111
ˆ‰ ˆ ‰ˆ ‰ˆ‰ˆ ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 8 Practice Exercises 569
(0.16705 0.16705) 25 25° F¸ œ
37
#1
132. av(C ) 8.27 10 26T 1.87T dT 8.27T T T
v20
675
œœ
"""
& # # $ '(&
#!
675 20 655 10 10
3 0.62333
'cdab
‘
[(5582.25 59.23125 1917.03194) (165.4 0.052 0.04987)] 5.434;¸¸
"
655
8.27 10 26T 1.87T 5.434 1.87T 26T 283,600 0 TœÊœÊ¸
& # #
#
ab 26 676 4(1.87)(283,600)
(1.87)
È
396.45° C¸
133. (a) Each interval is 5 min hour.œ1
12
2.42 gal
2.5 2 2.4 2 2.3 2 2.4 2.3
129
24 12
cd
ab ab abÞÞÞ
œ¸
(b) 60 mph hours/gal 24.83 mi/galab
ˆ‰
12
29 ¸
134. Using the Simpson's rule, x 15 5;˜œ Ê œ
˜x
3
mf(x ) 1211.8 Area 1211.8 5 6059 ft ;
!abab
iœÊ¸ œ
2
The cost is Area $2.10/ft 6059 ft $2.10/ft†¸ababab
222
$12,723.90 the job cannot be done for $11,000.œÊ
x f(x ) m mf(x )
x 0 0 1 0
x 15 36 4 144
x 30 54 2 108
x 45 51 4 204
x 60 49.5 2 99
x 75 54 4 216
x 90 64.4 2 128.8
x
ii i
!
"
#
$
%
'
(
5
105 67.5 4 270
x 120 42 1 42
)
135. lim lim sin lim sin sin 0
''
00
3b b
0
dx dx x b 0
9x 9x 333
ÈÈ
" " "
##
œœ œœœ
b3 b3 b3ÄÄ Ä
‘ ˆ‰ ˆ‰ˆ‰ 11
136. ln x dx lim x ln x x (1 ln 1 1) lim b ln b b 1 lim 1 lim
'0
11
b
œœœœ
bbbbÄ! Ä! Ä! Ä!
cd cd†ln b
Š‹ Š ‹
Š‹
b
b
b
10 1œ œ
137. 2 2 3 lim y 6 1 lim b 6
''' '
110 0
101 1 1
b
dy dy dy dy
yyy y
œœ œ œ œ†
bbÄ! Ä!
‘ Š‹
"Î$ "Î$
138. converges if each integral converges, but
''''
2212
12
dddd
(1) (1) (1) (1)
))))
))))
œ
lim 1 and diverges diverges
)Ä_
)) )
)) )
(1) ( 1)
dd
œÊ
''
22
139. lim ln lim ln ln 0 ln ln 3
'''
333
b
3
2 du du du u 2 b 2 3 2
u2u u2 u u b 3 3
"
œœ œ œœ
bbÄ_ Ä_
‘ ‘¸¸ ˆ‰¸¸ ¸¸
140. dv dv lim ln v ln (4v 1)
''
11
b
1
3v 1 4
4v v v v 4v 1 v
"" "
œ œ
ˆ‰ ‘
bÄ_
lim ln (ln 1 1 ln 3) ln 1 ln 3 1 ln œœœ
bÄ_ ‘ˆ‰
b 3
4b 1 b 4 4
""
141. x e dx lim x e 2xe 2e lim b e 2be 2e ( 2) 0 2 2
'0
xxxxbbb
b
0
## #
œ œ œœ
bbÄ_ Ä_
cdab
142. xe dx lim e e lim e e 0
'03x 3x 3x 3b 3b
0
b
œ œ œ œ
bbÄ_ Ä_
‘ ˆ‰
xb
39 9 39 9 9
"" """
143. 2 lim tan lim tan tan (0)
'''
dx dx dx 2 2x 2 2b
4x9 4x9 33 333
x
## #
"" " "
" " "
œœœ œ
00
b
0
9
4bbÄ_ Ä_
‘ ‘ˆ‰ ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

570 Chapter 8 Techniques of Integration
0œœ
"
##
ˆ‰
2
36
†
11
144. 2 2 lim tan 2 lim tan tan (0) 2 0
''
4 dx 4 dx x b
x16 x16 4 4
#
" " "
œœ œ œœ
0
b
0
bbÄ_ Ä_
‘ ‘ ˆ‰ˆ‰ ˆ‰
Š‹
11
145. lim 1 and diverges diverges
)Ä_
)) )
))
)
ÈÈ
11
dd
œÊ
''
66
146. I e cos u du lim e cos u e sin u du 1 lim e sin u e cos u duœœœ
'' '
00 0
uuu uu
bb
00
bbÄ_ Ä_
cd cdab
I 1 0 I 2I 1 I convergesÊœÊ œ Êœ
"
#
147. dz dz dz lim 0 lim
'''
11e
eeb
1e
ln z ln z ln z 1
zz z2 2 2
(ln z) (ln z) (ln b)
œ œ œ
’“ ’“Š ‹ ’ “
bbÄ_ Ä_
##
"
divergesœ_ Ê
148. 0 e for t 1 and e dt converges dt convergesŸ Ê
ee
tt
t t
ÈÈ
tt
11
''
149. 2 converges converges
''' '
2 dx 2 dx 4 dx 2 dx
ee ee e ee
xxx x
xx x
œ Ê
00
150. ;
'''''
dx dx dx dx dx
x1 e x1 e x1 e x1 e x1 e
ab ab ab ab ab
xxxxx
œ
101
10 1
lim lim lim 1 e 2 and diverges diverges
x0 x0 x0ÄÄÄ
Š‹
’“ ab ab
x
x
x1e
œœœ Ê
x1 e
x xx1e
dx dx
x
x
ab
x
00
11
''
divergesÊ'dx
x1 e
abx
151. ; 2u 2u 2 du u u 2u 2 ln 1 u C
ux
du
'''
x dx u 2u du 2 2
1x dx
x1u 1u 3
#
#$#
ÈÈ
–—
Ȉ‰ kk
œ
œÄœœ
†
x2x2 ln1 x Cœ
2x
3ÈÈ
ˆ‰
152. dx x dx x dx ln x 2 ln x 2 C
'' '''
x 2 4x 2 3 dx 5 dx x 3 5
4x x 4 x2 x2
#####
œ œ œ
ˆ‰ kk kk
153. ; d(sin )
xtan
dx sec d
''''
dx sec d cos d 1 sin
xx 1 tan sec sin sin
ab
#
”• Š‹
œ
œÄœœ
)
)) )
)) )) )
)) ))
ln sin sin C ln Cœœ kk ¹¹Š‹
))
""
##
#
#
xx
x1 x1
ÈÈ
154. dx; 2 cos u du 2 sin u C 2 sin x C
ux
du
'''
cos x
xdx
x
cos u 2u du
u
È
ÈÈ
–—
ÈÈ
œ
œÄœœœ
#
†
155. sin (x 1) C
''
dx
2x x
d(x 1)
1(x1)
ÈÈ
"
œœ
156. ' u C t 2t C
ut 2t
du (2t 2) dt 2(t 1) dt
''
(t 1) dt
t2t
du
u
#"
##
ÈÈ
”•
ÈÈ
œ
œ œ Äœœ
157. ; u tan ln sec tan C ln 1 u u C
''
du sec d
1u sec
È
#
cd k k ¹¹
È
œÄ œ œ )))
))
)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 8 Practice Exercises 571
158. e cos e dt sin e C
'tt t
œ
159. dx 2 csc x dx csc x dx 2 cot x ln csc x cot x C
''''
2 cos x sin x cos x dx
sin x sin x sin x
"
#
œœkk
2 cot x csc x ln csc x cot x Cœ kk
160. d d sec d d tan C
'' ' '
sin 1 cos
cos cos
))
))
)))))))œœœ
#
161. ln tan C
''''
9 dv dv dv dv 3 v v
81 v v9 12 3v 1 3v 12 3v 6 3
"""""
# #
"
œœ
¸¸
162. tan (sin x) C
''
cos x dx
1sinx 1sinx
d(sin x)
"
œœ
163. cos (2 1))
sin (2 1)))ïïïïî
ÐÑ "
#
1 cos(2 1)
ïïïïî
ÐÑ "
4)
0 cos(21) d sin(21) cos(21)Cʜ
')) ) ) )
)
#
"
4
164. lim lim ( 1) 0 1 1
'2
b
2
dx
(x1) 1x 1b
""
œ œ œœ
bbÄ_ Ä_
‘ ‘
165. x 2 dx (x 2) dx 3
'' ' ''
x dx 3x 2 dx dx
x 2x1 x 2x1 x1 (x1)
œ œ
ˆ‰
2x 3 ln x 1 Cœ
x
x1
#
"
kk
166. ; 2 x dx 2 x 4x C
x1
dx
d 2(x 1) dx
''''
ddx 4
1
d
2
2(x 1) dx
xx
3
)
)
)
)
ÉÈÈÈÈ
$Î# "Î#
Ô×
ÖÙ
ÕØ
ÈÈ
œ
œ
œ
Äœœ
)
)
141C4 1Cœ œ
4
33
1
Š‹Š‹
ÈÈ È
Ô×
ÕØ
É
)) )
$Î# "Î#
Œ
ÉÈ)
167. ; 2 sin 2y dy cos (2y) C cos 2 x C
yx
dy
'''
2 sin x dx
x sec x dx
2x
2 sin y 2y dy
y sec y
È
ÈÈ È
–—
Ȉ‰
È
œ
œÄœ œœ
†
168. x dx dx ln C
'' '
x dx 16x x 2x 2x x x 4
x16 x16 x4 x4 x4
# #
œ œ œ
ˆ‰ ˆ ‰ ¹¹
169. 2 csc (2y) dy ln csc (2y) cot (2y) C
'''
dy 2 dy
sin y cos y sin 2y
œœ œ kk
170. tan C
''
dd
24 (1)3 3
3
3
)) )
)) )
" "
œœ
ÈÈ
Š‹
171. dx tan x sec x dx tan x d(tan x) tan x C
''
tan x
cos x œœœ
##
"
#
'†
172. sec r 1 C
''
dr
(r 1) r 2r
d(r 1)
(r 1) (r 1) 1
"
ÈÈ
œœkk
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

572 Chapter 8 Techniques of Integration
173. ; u C 4 (r 2) C
u(r2)
du 2(r 2) dr
'' '
(r 2) dr (r 2) dr
r4r 4(r2)
du
2u
##
ÈÈ È
œÄœœ
œ%
œ
”•ÈÈ
174. tan C
''
y dy y
4y
dy
4y 4
""
##
"
œœ
ab
ab Š‹
175. C sec C
''
sin 2 d
(1 cos 2 ) (1 cos 2 ) (1 cos 2 ) 4
d(1 cos 2 )
))
)))
)
##
"""
#
œ œ œ )
176. ln C (FORMULA 19)
''
dx dx x x
x1 1x 21 x 4 x 1
ab ab ab
""
œœ
¸¸
177. 1 cos 4x dx 2 cos 2x dx sin 2x
''
44
22
2
4
ÈÈ’“
œ œ œ
ÈÈ
22
##
178. (15) dx (15) d(2x 1) C
'2x 1 2x 1
œœ
""
##
'Š‹
15
ln 15
2x 1
179. ; y 4y C (2 x) 4(2 x) C
y2x
dy dx
''
x dx 2 2
2x
(2 y) dy
y3 3
ÈÈ
$Î# "Î# $Î# "Î#
”•
œ
œ Ä œ œ
222xCœ
–—
È
Š‹
È2x
3
180. dv; v sin csc d d cot C
'''''
Èab
1v
vsinsin
cos cos d 1sin d
#
cdœÄ œ œ œ))))))
)))
))
))
†
sin v Cœ
"
È1v
v
181. tan (y 1) C
''
dy d(y 1)
y2y2 (y1)1
"
œœ
182. ln x 1 dx; ln y 2y dy; u ln y, du ; dv 2y dy, v y
yx1
dy
''
È–—
È
Äœœœœ
œ
œdx
2x1
dy
y
È
#
†
2y ln y dy y ln y y dy y ln y y C (x 1) ln x 1 (x 1) CÊœœœ
''
###
""
##
"
È
(x1) ln x1 x C x ln x1 xln x1 Cœ œ
"""
###
"
cdc dkk kk kk
ˆ‰
183. tan d tan d ln sec C
''
))) )) )
#$ $$ $
""
ab abab k kœœ
33
184. sin C
''
x dx x 1
82x x
dx 1
9x1 3
Èab
Éab
""
##
"
œœ
Š‹
185. dz dz ln z ln z 4 tan C
''
z1 z1 z
zz 4 4 z z z 4 4 4z 8 8
"""""" "
#
#"
abœ œ
ˆ‰
kk a b
186. x e dx x e d x x e e C C
''
$###
""
## #
xx xx
œœœab ˆ‰
abx1e
x
187. 9 4t C
''
t dt
94t 94t
84
d9 4t
ÈÈ
ab
""
#
œ œ
È
188. 1 cos 5 d 2 cos d sin sin 0
''
00
10 10
ÈȈ‰ ‘ ˆ ‰ˆ‰
œ œ œ œ)) )
55 2
22 22
5545
)) 1
1
##
Î"!
!
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 8 Practice Exercises 573
189. ;
xsin
dx cos d
'' '''
cot d cos d dx dx x dx
1 sin (sin ) 1 sin x 1 x x x 1
)) ))
)))
œÄœ
œ
œ
ab ab
”•
)
))
ln sin ln 1 sin Cœkk a b))
"
#
#
190. u tan x, du ; dv , v ;œœœœ
"
"dx dx
1x x x
tan x tan x
''''
tan x dx dx dx x dx
xx x1xx x1x
œ œ
""
" "
ab
tan x ln x ln 1 x C ln x ln 1 x Cœ œ
""
" #
##
xx
tan x
kk a b kk È
191. ; y x ln sec x C ln sec y C
''
tan y dy
2y 2x
tan x 2x dx
È
È‘ ¸¸
ÈÈ
kkœÄ œ œ
†
192. ; e x ln x 1 ln x 2 C
''''
edt dx dx dx
e 3e 2 (x 1)(x 2) x 1 x
t
2t t
#
cd kkkk
tœÄ œ œ
ln C ln Cœœ
¸¸ ˆ‰
xe
xe
" "
# #
t
t
193. 1 d d ln 2 ln 2 C
'' '''
)) ) )
)) ))
d4 dd
44 # #
œ œ œ
ˆ‰ kkkk)) )) )
ln Cœ )¸¸
)
)
2
2
194. dx tan x dx sec x 1 dx tan x x C
'''
1 cos 2x
1 cos 2x
##
œœœab
195. ; cos u du sin u C sin sin x C x C
usinx
du
''
cos sin x dx
1x dx
1x
ab
ÈÈ
"
"
–— ab
œ
œÄ œ œ œ
196. 2 csc 2x dx
'' ' ''
cos x dx cos x dx cos x dx 2 dx
sin x sin x (sin x) 1 sin x (sin x) cos x sin 2x
œ œ œ œ
ab ab
ln csc (2x) cot (2x) Cœkk
197. sin cos dx sin dx sin x dx cos x C
'' '
xx xx
## # ## # #
"""
œœ œ
ˆ‰
198. dx tan x 2 C
'''
xx2 dx x dx x
x2 x2
x2 22
" "
#
" # "
ab abÈÈ
œ œ
Š‹ ab
tan Cœ
""
"
#
ÈÈ
ab
22
x
x2
Š‹
199. ln 1 e C
'e dt
1e
t
t
œab
t
200. tan t dt (tan t) sec t 1 dt tan t dt ln sec t C
'' '
$#
##
œ œ œ ab kk
tan t tan t
201. ; dx xe dx lim e e
x ln y
dx
dy e dx
'''
100
x
2x 2x 2x b
0
ln y dy
ye 4
dy
y
xe x
Ô×
ÖÙ
ÕØ ‘
œ
œ
œ
Äœœ
†x
3x bÄ_ #
"
lim 0œœ
bÄ_ ˆ‰ˆ‰
" ""b
2e 4e 4 4
2b 2b
202. dx 3 cot x dx cos x dx 3 ln sin x ln tan x sin x C
''''
3secxsin x secx dx
tan x tan x
œœkkkk
203. ; ln u C ln ln (sin v) C
u ln (sin v)
du
'' '
cot v dv cos v dv du
ln (sin v) (sin v) ln (sin v) u
cos v dv
sin v
œÄœœ
œ
œ
”• kk k k
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

574 Chapter 8 Techniques of Integration
204. ;
u2x1
du 2 dx
'' ' '
dx 2 dx 2 dx du
(2x 1) x x (2x 1) 4x 4x u u 1
(2x 1) (2x 1) 1
ÈÈ È È
œœ Ä
œ
œ
”•
sec u C sec 2x 1 Cœœ
" "
kk k k
205. e dx x dx x C
''
ln x
Èœœ
È2
3$Î#
206. e 3 4e d ; 3 u du (3 u) C 3 4e C
u4e
du 4e d
''
) )
)
)
)
È”•
ÈabÄœœ
œ
œ
))
"" "
$Î# $Î#
443 6
2
†
207. ; tan u C tan (cos 5t) C
u cos 5t
du 5 sin 5t dt
''
sin 5t dt du
1(cos 5t) 5 1u 5 5
"" "
" "
”•
œ
œ Ä œ œ
208. ; sec x C sec e C
xe
dx e dv
''
dv dx
e1 xx 1
ÈÈ
2v
" "
”• ab
œ
œÄœœ
v
v
v
209. (27) d (27) d(3 1) (27) C C
'31 31 3)) ) "
))œœœ
"""
3 3 ln 27 3 ln 27
27
'Š‹
31
210. sin x
x cos x
&ïïïïî
ÐÑ
5x n x si
%ïïïïî
ÐÑ
20x cos x
$ïïïïî
ÐÑ
60x sin x
#ïïïïî
ÐÑ
120x cos xïïïïî
ÐÑ
120 sin xïïïïî
ÐÑ
0 x sin x dx x cos x 5x sin x 20x cos x 60x sin x 120x cos xʜ
'&&%$#
120 sin x C
211. ; 2 du 2u 2 ln 1 u C 2 r 2 ln 1 r C
ur
du
'''
dr 2u du 2
1r dr
2r 1u 1u
ÈÈ
–—
Ȉ‰ ˆ‰
kk ÈÈ
œ
œÄœ œœ
212. dx ln x 10x 9 C
''
4x 20x
x 10x 9 x 10x 9
d x 10x 9
%#
œœ
ˆ‰
kk
213. ln C
' ''''
8 dy dy 2 dy 4 dy dy y
y(y2) y y y (y2) y2 y y
22
œ œ
¹¹
214. ; 3u C t 2t C
ut 2t
du 2(t 1) dt
''
(t 1) dt
t2t
du 3
u
#""
## #
"Î$ # "Î$
ab”• ab
œ
œ Äœœ†
215. 4 sec C
''
8 dm 8 dm 7m
m 49m 4 7mm
ÈɈ‰
"
#
œœ
2
7¸¸
216. ;
u ln t
du
'''
dt du du
t(1 ln t) (ln t)(2 ln t) (1 u) u(2 u)
dt
t(u 1) (u 1) 1
ÈÈÈ
”•
œ
œÄœ
sec u 1 C sec ln t 1 Cœœ
" "
kk k k
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 8 Practice Exercises 575
217. If u 1 (t 1) dt and dv 3(x 1) dx, then du 1 (x 1) dx, and v (x 1) so integrationœ œ œ œ
'0
xÈÈ
%%
#$
by parts 3(x 1) 1 (t 1) dt dx (x 1) 1 (t 1) dtÊ œ
'' '
00 0
1x x
#$
%%
"
!
’“’ “
ÈÈ
(x1) 1(x1) dx 1(x1) œ œ
'0
1$%
%"$Î# "
!
"
È’“
ab
66
8
È
218. 4v v 1
4v v1 A B C DvE
v(v 1) v 1 v v v 1 v 1
$
ab
œ Ê
Av(v1)v1B(v1)v1Cvv1(DvE)v(v1)œ ab abab ab
#### #
v0: 1 B B1;œœÊœ
v1: 42C C2;œœÊœ
coefficient of v : 0 A C D A D 2;
%œ Ê œ
coefficient of v : 4 A B E D
$œ
coefficient of v : 0 A B C E C D 4 D 2 (summing with previous equation);
#œ Ê œ Ê œ
coefficient of v: 1 A B A 0;œ Ê œ
in summary: A 0, B 1, C 2, D 2 and E 1œœœœ œ
dv lim v dvʜ
''
22
b
4v v 1 2 2v
v(v 1) v 1 v 1 1 v 1 v
"
#
ab bÄ_ ˆ‰
lim ln (v 1) tan v ln 1 vœ
bÄ_ ‘
ab
#" #
"
v
b
2
lim ln tan b ln 1 tan 2 ln 5 0 0 0 tan 2 ln 5œœ
bÄ_ ’“Š‹ ˆ‰ˆ‰ˆ‰
(b 1)
1b b
# ##
"" "
" " "
1
ln (5) tan 2œ
1
##
""
219. u f(x), du f (x) dx; dv dx, v x;œœ œœ
w
f(x) dx x f(x) xf (x) dx f f cos x dx
'' '
22 2
32 32 32
32
2
œ œcd ‘ˆ‰ ˆ‰
w
## ##
3311 11
sin x 3b a ( 1) 1 3b a 2œ œ œ
ˆ‰
cd abc dab
3b a11 1 1
## # #
32
2
220. tan x tan a; lim tan x lim tan b tan a tan a;
''
0a
aab
0a
dx dx
1x 1x #
" " " " " "
œœ œ œ œcd cd a b
bbÄ_ Ä_
1
therefore, tan a tan a tan a a 1 since a 0.
" " "
#
œ Ê œ Êœ
11
4
CHAPTER 8 ADDITIONAL AND ADVANCED EXERCISES
1. u sin x , du ; dv dx, v x;œœœœab
" #
2 sin x dx
1x
È
sin x dx x sin x ;
''
ab ab
" "
##
œ
2x sin x dx
1x
È
u sin x, du ; dv , v 2 1 x ;œœ œœ
"
#
dx 2x dx
1x 1x
ÈÈ
È
2 sin x 1 x 2 dx 2 sin x 1 x 2x C; thereforeœ œ
''
2x sin x dx
1x
È
" "
##
ab ab
ÈÈ
sin x dx x sin x 2 sin x 1 x 2x C
'ab abab
È
" " "
## #
œ
2. ,
""
xx
œ
,
"""
x(x1) x x1
œ
,
""""
#x(x 1)(x 2) 2x x 1 (x 2)
œ
,
" """"
# # x(x 1)(x 2)(x 3) 6x (x 1) (x 2) 6(x 3)
œ
the following pattern:
" """" "
# # x(x 1)(x 2)(x 3)(x 4) 4x 6(x 1) 4(x ) 6(x 3) 24(x 4)
œ Ê
; therefore
"
â â
"
x(x 1)(x 2) (x m) (k!)(m k)!(x k) x(x 1)(x 2) (x m)
() dx
œ!
m
k0
k'
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

576 Chapter 8 Techniques of Integration
ln x k Cœ
!’“
kk
m
k0
()
(k!)(m k)!
"
k
3. u sin x, du ; dv x dx, v ;œœ œœ
"
#
dx x
1x
È
x sin x dx sin x ; x sin x dx sin x
xsin
dx cos d
'' ''
" " " "
# #
œ Ä œ
œ
œ
x x dx x sin cos d
21x 2 cos
È”•
)
))
)))
)
sin x sin d sin x C sin x Cœ œœ
x x sin 2 x sin cos
44
## ### #
" # " "
""
')) ˆ‰
)) )))
sin x Cœ
xx1x sin x
4
#
"
È
4. sin y dy; 2z sin z dz; from Exercise 3, z sin z dz
zy
dz
'''
" " "
È–—
È
œ
π
dy
2y
È
C sin y dy y sin y Cœ Ê œ
z sin z z1z sinz
4
y1ysin y
# #
" "
ÈÈÈ
È
'ÈÈ
y sin y Cœ
"
##
ÈÈÈ
yy sin y
5. d d (sec 2 1) d C
'' ' '
d cos 1 cos 2
1 tan cos sin 2 cos 4
ln sec 2 tan 2 2
)) )
))) )
)))
##
"
œœœœ ))))
kk
6. u ln x 1 x , du ; dv dx, v x;œœ œ œœ
Š‹Š‹Š‹
ÈÈdx dx
x 1x 21x 2x1x
x
ÈÈ
ÈÈÈ È
""
#
ln x 1 x dx x ln x 1 x ; ;
'''
Š‹Š‹
ÈÈ
ÈÈ
œ
""
##
x dx x dx
x1x x
ÈÈɈ‰
4
sec sec d
x sec
dx sec tan d
–— ab
œ
œÄœ
""
##
"
#
""
#
#
)
))) )))
4
(sec 1) sec tan d
tan
''
))))
)
†
ˆ‰
CCœœ
tan ln sec tan 2x xln 2x12x x
)))
##
kk ÈÈ
¹¹
ln x 1 x dx x ln x 1 x Cʜ
'Š‹Š‹
ÈÈ
ÈÈ
2x xln 2x12x x
4
ÈÈ
¹¹
7. ; ;
tsin
dt cos d
utan
du sec d
d
''''
dt cos d d du
t1t sin cos tan 1 (u 1) u 1
du
u1
#
Èab
”• Ô×
ÕØ
œ
œÄœ Ä
œ
œ
œ
)
))
)
))
)
)) )
)) )
ln tan u C ln Cœ œ œ
"" " "" """
# # # # # # #
"
'''
du du u du u 1 tan
u1 u1 u1 sec
u1
¹¹ ¸¸
È)
))
ln t 1 t sin t Cœ
""
##
#"
Š‹
È
8. ; ;
ue
du e dx
'''
ab
ÈÈÈ
É
2e e dx
3e 6e 1
(2u 1) du (2u 1) du
3u 6u 1 3(u 1)
2x x
2x x
"
”•
œ
œÄœ
x
x4
3
sec 1 (sec ) d sec d sec d
u 1 sec
du sec tan d
Ô×
ÕØ
Š‹
œ
œÄœ
2
3
2
3
33 3
44
3
È
ÈÈÈ È
)
))) ))) )) ))
""
#
'''
tan ln sec tan C (u 1) 1 ln (u 1) (u 1) 1 Cœ œ
443 3
334 4
33
3
)))
""
" "
##
#
ÈÈ
È
kkÉÉ
¹¹
†
3u 6u 1 ln u 1 (u 1) C ln œ
24
33
33
3
ȹ¹Š‹
É
##
""
"#
ÈÈ
È
2e 2e ln e 1 e 2e Cœ
"" "
È333
’“
ÉÉ
¹¹
2x x 2x x
x
9. dx dx dx
'' '
"" "
x4 x2 4x x2x2x2x2
œœ
ab abab
dxœ
"
# 16 x 2x 2 (x 1) 1 x 2x (x 1) 1
2x222x22
'’“
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 8 Additional and Advanced Exercises 577
ln tan (x 1) tan (x 1) Cœ
""
#
" "
16 x 2x 8
x2x2
¹¹
cd
10. dx dx
''
""""
x1 6 x1x1xx1xx1
x2 x2
œ
ˆ‰
ln dxœ
" " "
#
6x11 xx1 xx1
x1 2x 3 2x1 3
xx
¸¸ ”•
'ˆ‰ ˆ‰
33
44
ln ln 2 3 tan 2 3 tan Cœ
""" "
#
" "
6x11 xx1
xxx 2x1 2x1
33
¸¸ ’“¹ ¹ Š‹ Š‹
ÈÈ
ÈÈ
11. lim sin t dt lim cos t lim cos x cos ( x) lim cos x cos x lim 0 0
xxx x xÄ_ Ä_ Ä_ Ä_ Ä_
'x
xx
x
œœœœ œcd c d a b
12. lim dt; lim lim 1 lim dt diverges since diverges
xtt xÄ! Ä! Ä! Ä!
'''
xx0
111
cos t cos t dt
tcos ttt
Š‹
Š‹
t
cos t
t
œœÊ
"; thus
lim x dt is an indeterminate 0 form and we apply l'Hopital's rule:
^
xÄ! 'x
1cos t
t†_
lim x dt lim lim lim cos x 1
xxxxÄ! Ä! Ä! Ä!
'x
1cos t
t
dt
œœœœ
'1
xcos t
t
x
cos x
x
x
Š‹
Š‹
13. lim ln 1 lim ln 1 k ln (1 x) dx; u 1 x, du dx
x0 u1, x1 u2
nnÄ_ Ä_
!!
Ɉ‰ˆ‰ˆ‰ ”•
nn
k1 k1 0
1
nœ œ œ œ
œÊœ œÊœ
k
nnn
"" '
ln u du u ln u u (2 ln 2 2) (ln 1 1) 2 ln 2 1 ln 4 1Äœœœœ
'1
2cd
#
"
14. lim lim lim
nn nÄ_ Ä_ Ä_
!! !
Š‹
ˆ‰ ˆ‰
ÎÑ
ÏÒ
n1 n1 n1
k0 k0 k0
""""
ÈÈ Ê’ “Š‹
nk nk
n
nn
1k
œœ
n
dx sin xœœœ
'0
1"
" "
!#
È1x cd
1
15. cos 2x 1 1 cos 2x 2 cos x; L 1 cos 2t dt 2 cos t dt
dy dy
dx dx
œÊœœ œ œ
ÈÈ
Š‹ Š ‹
ÊÈÈ
##
##
''
00
44
2sin t 1œœ
Ècd
1Î%
!
16. 1 ; L 1 dx
dy dy dy
dx 1 x dx 1 x dx
2x 12x x 1x
1x 4x
1x 1x
œÊ œ œ œ œ
###
Š‹ Š ‹ Š‹
Ê
ab
ab ab '0
12
dx 1 dx 1 dx x ln œœœœ
'' '
00 0
12 12 12
Š‹ ˆ‰ˆ ‰ ‘¸¸
" " "
"Î#
!
x2 1x
1x 1x 1x 1x 1x
ln 3 (0 ln 1) ln 3œ œ
ˆ‰
""
##
17. V 2 dx 2 xy dxœœ
''
a0
b1
11
ˆ‰
Š‹
shell shell
radius height
6 x 1 x dx;
u1x
du dx
x(1u)
œ
œ
œ
œ
1'0
1#
##
ÈÔ×
ÕØ
6 (1 u) u duÄ 1'1
0#È
6 u2uu duœ 1'1
0ˆ‰
"Î# $Î# &Î#
6uuu 6œ œ 11
‘ˆ‰
242 242
357 357
$Î# &Î# (Î# !
"
66œœœ11
ˆ‰ˆ‰
70 84 30 16 32
105 105 35
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
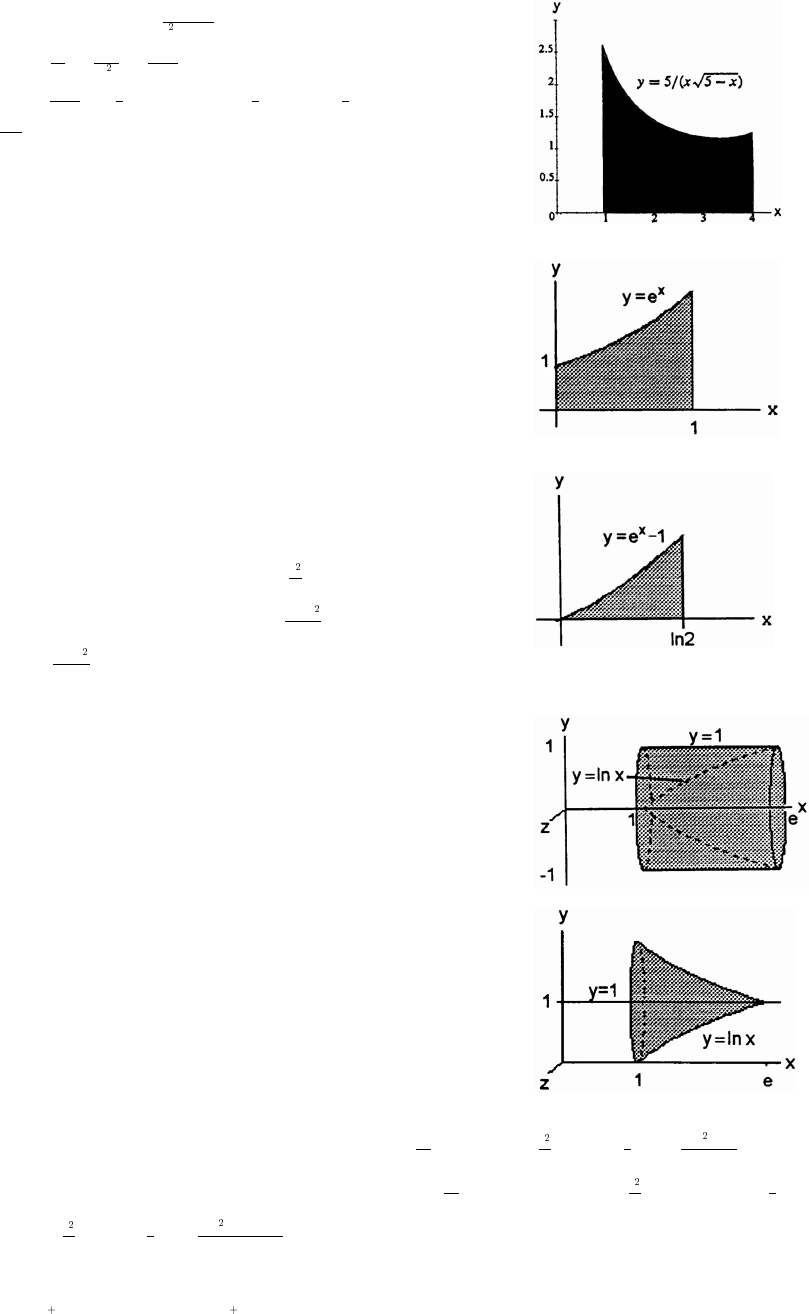
578 Chapter 8 Techniques of Integration
18. V y dx œœ
''
a1
b4
11
#
25 dx
x(5 x)
œ1'1
4ˆ‰
dx 5 dx dx
xx 5x
ln ln 4 ln 5œœ111
‘ˆ‰ˆ‰¸¸
x5 5
5x x 4 4
%
"
"
2 ln 4œ
15
4
11
19. V 2 dx 2 xe dxœœ
''
a0
b1
x
11
ˆ‰
Š‹
shell shell
radius height
2xe e 2œœ11cd
xx
"
!
20. V 2 (ln 2 x) e 1 dxœ
'0
ln 2 x
1ab
2 (ln 2) e ln 2 xe x dxœ1'0
ln 2 xx
cd
2 (ln 2) e (ln 2)x xe eœ1’“
xxx
ln 2
0
x
#
2 2 ln 2 (ln 2) 2 ln 2 2 2 (ln 2 1)œ11
’“
#
#
(ln 2)
2ln 21œ 1’“
(ln 2)
#
21. (a) V 1 (ln x) dxœ
'1
e
1cd
#
x x(ln x) 2 ln x dx œ 11cd
#e
11
e
'
(FORMULA 110)
x x(ln x) 2(x ln x x)œ 1cd
#e
1
x x(ln x) 2x ln xœ 1cd
#e
1
ee2e(1)œœ11cd
(b) V (1 ln x) dx 1 2 ln x (ln x) dxœ œ
''
11
ee
11
##
cd
x 2(x ln x x) x(ln x) 2 ln x dxœ 11cd
#e
11
e
'
x 2(x ln x x) x(ln x) 2(x ln x x)œ 1cd
#e
1
5x 4x ln x x(ln x)œ 1cd
#e
1
(5e4ee)(5) (2e5)œœ11cd
22. (a) V e 1 dy e 1 dy y 1œœœœœ1111
''
00
11
y2y
‘ ‘ ˆ‰
ab a b ’“
#
####
"
!
"ee e3
2y 1ab
(b) V e 1 dy e 2e 1 dy 2e y 2e 1 2œœ œœ11 1 1
''
00
11
y2yy y
ab a b ‘ ˆ‰
’“Š‹
#
###
"
!
"ee
2y
2eœœ1Š‹
e5
e4e5
## #
1ab
23. (a) lim x ln x 0 lim f(x) 0 f(0) f is continuous
xxÄ! Ä!
œÊ œœ Ê
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
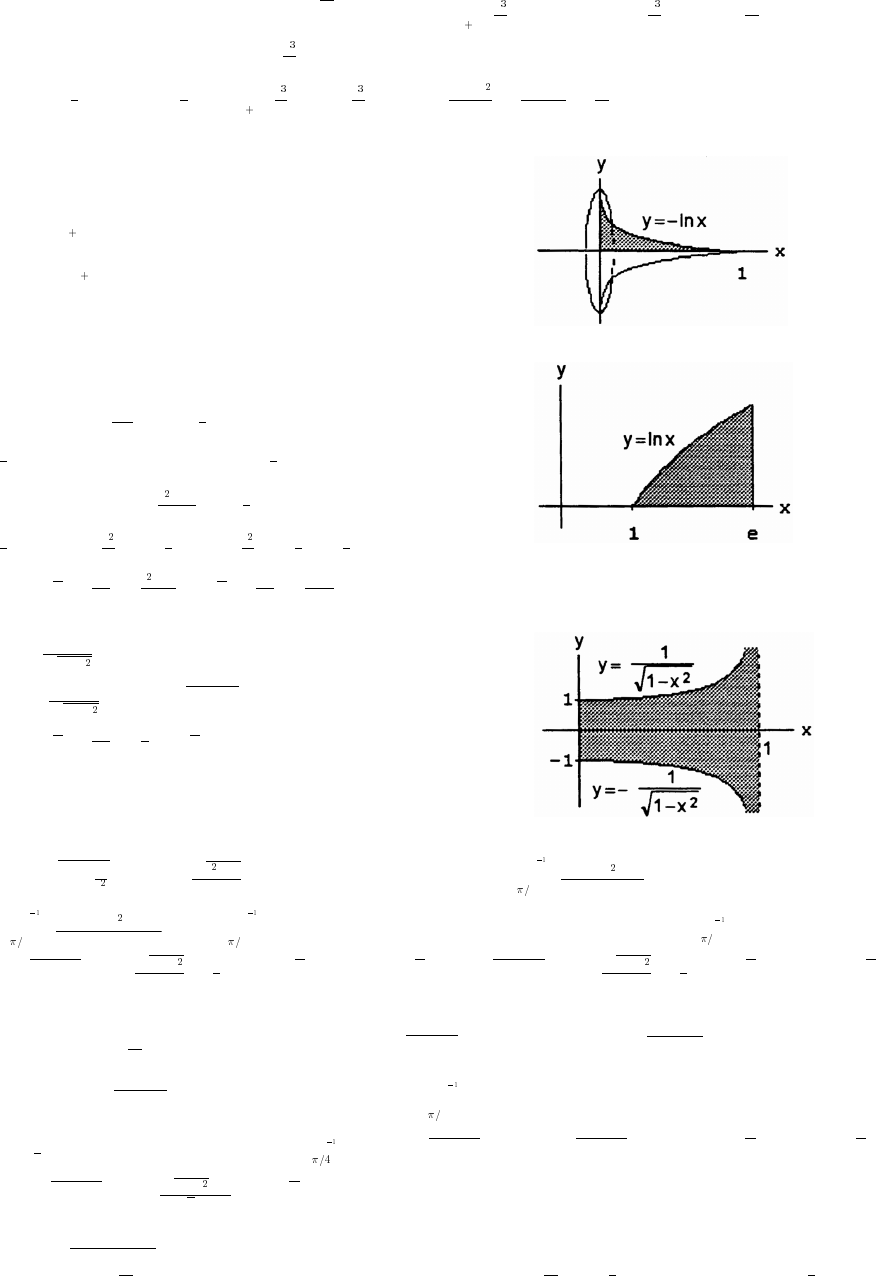
Chapter 8 Additional and Advanced Exercises 579
(b) V x (ln x) dx; lim (ln x) (2 ln x)
u (ln x)
du (2 ln x)
dv x dx
v
π
œ
œ
œ
œ
''
0 0
2 2
b
11
## #
#
#
#
Ô×
ÖÙ
ÖÙ
ÖÙ
ÕØ
Œ
’“Š‹
dx
x
x
3
xxdx
33x
bÄ!
(ln 2) lim ln xœ œ11
”•
ˆ‰ ˆ‰ ’“’ “
82xx 16
3339 3927
8(ln 2) 16(ln 2)
#
bÄ!
2
b
24. V ( ln x) dxœ
'0
1
1#
lim x(ln x) 2 ln x dxœ1Œ
cd
bÄ!
#1
b0
1
'
2 lim x ln x x 2œ œ11
bÄ! cd
1
b
25. M ln x dx x ln x x (e e) (0 1) 1;œœœœ
'1
ee
1
cd
M (ln x) dx (ln x) dx
x11
ee
œœ
''
ˆ‰
ln x
##
"#
x(ln x) 2 ln x dx (e 2);œœ
""
##
#
Š‹
cd
e
11
e
'
M x ln x dx x dx
y11
ee
e
1
œœ
''
’“
x ln x
##
"
x ln x e e 1 ;œœœ
""""
#####
###
’“’ “Š‹ ab
xe
4
e
1
therefore, x and yœœ œœ
M
M4 M
e1 e2
M
yx
#
26. M 2 sin x ;œœ œ
'0
12 dx
1x
È
" "
!
cd1
M21x2;
y0
1
œœœ
'2x dx
1x
È
#"
!
’“
È
therefore, x and y 0 by symmetryœœ œ
M
M
2
y
1
27. L 1 dx dx; L
xtan
dx sec d
œœ Äœ
œ
œ
'' '
11 4
ee tane
É”•
"
#
xx tan
x1 sec sec d
È)
))
)))
)
†
d (tan sec csc ) d sec ln csc cot œœœ
''
44
tan e tan e tan e
4
(sec ) tan 1
tan
))
)
ab))))))))cdkk
1e ln 2ln1 2 1e ln 2ln1 2œ œ
Š‹’“Š‹Š‹
ÈÈÈÈÈÈ
¹¹ Š‹
# #
" "
È È
1e 1e
ee ee
28. y ln x 1 1 x S 2 x 1 x dy S 2 e 1 e dy; ue
du e dy
œÊ œÊœ Êœ œ
œ
Š‹ ÈÈ”•
dx
dy
###
11
''
c0
d1
y2y
y
y
S 2 1 u du; 2 sec sec d
utan
du sec d
Äœ Ä
œ
œ
11)))
)
))
''
14
etane
È”•
###
†
2 sec tan ln sec tan 1 e e ln 1 e e 2 1 ln 2 1œœ1)) ))1 1
ˆ‰
cdkk
’“’“Š‹¹ ¹ Š‹
ÈÈ ÈÈ
"
###
tan e
†
e1 e ln 2œ 1’“
ÈÈ
Š‹
#
ÈÈ
1e e
21
29. L 4 1 dx; x y 1 y 1 x 1 x xœ œÊœÊœ
'0
1ÊŠ‹ ˆ‰ ˆ‰ˆ‰ˆ‰
dy dy
dx dx 3
32
##Î$ #Î$ #Î$ #Î$ "Î$
$Î# "Î#
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
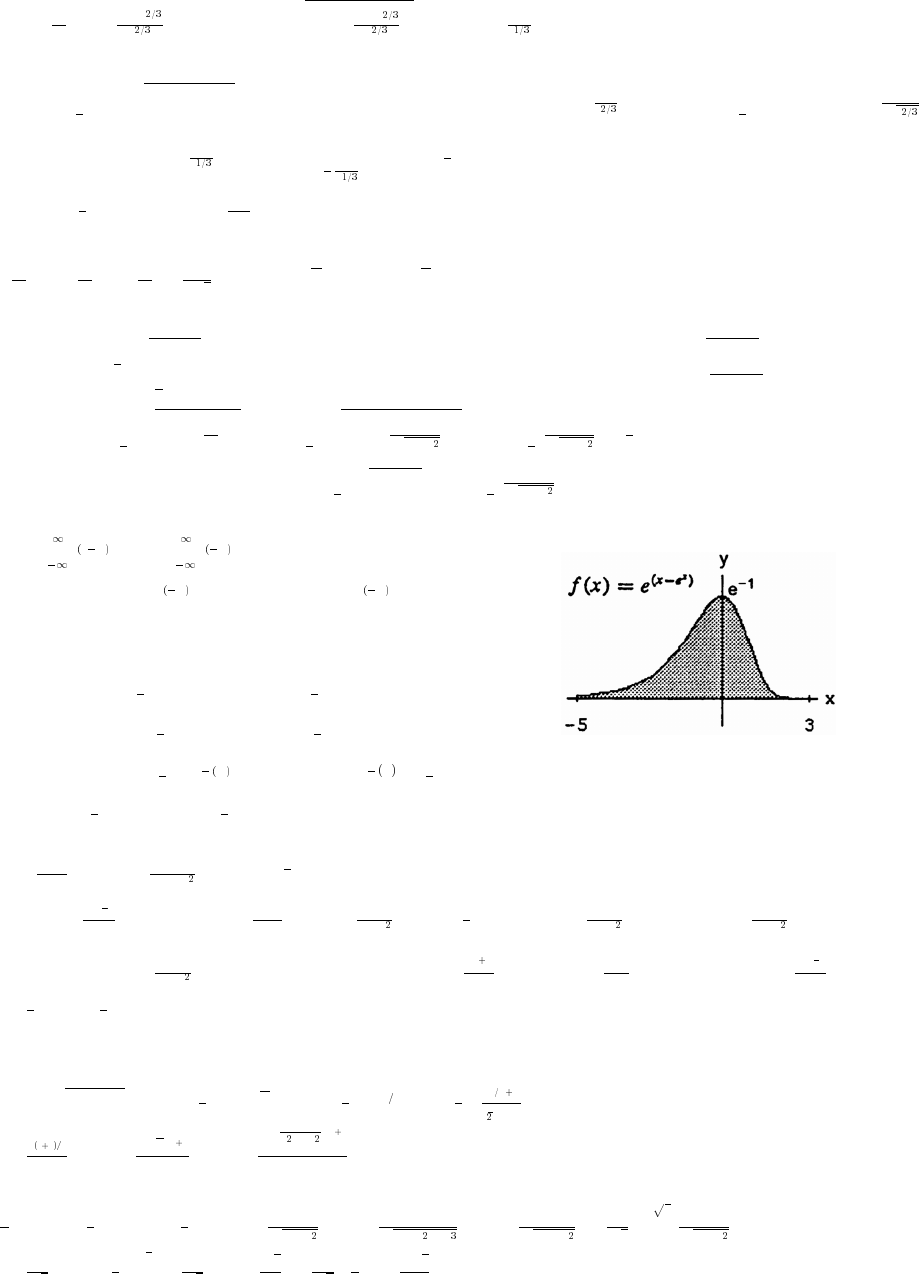
580 Chapter 8 Techniques of Integration
L 4 1 dx 4 6 x 6ʜʜ œ œ œ
Š‹ Š ‹
Ê‘
dy
dx
1x 1x dx
xxx
#
#Î$ "
!
''
00
11
30. S 2 f(x) 1 f (x) dx; f(x) 1 x f (x) 1 S 2 1 xœ œÊœÊœ1 1
''
1 1
1 1
Écd cd
ˆ‰ ˆ‰
w##Î$ w #Î$
$Î# $Î#
#"
x
dx
x
†È
4 1 x dx; 4 (1 u) du 6 (1 u) d(1 u)
ux
du
œ Ä œ
œ
œ
111
'''
000
111
ˆ‰ˆ‰
–—
#Î$ $Î# $Î#
$Î# "#Î$
#
x2dx
3x
3
†
6(1u)œ œ1†212
55
‘
&Î# "
!
1
31. y x or y x, 0 x 4
Š‹ ÈÈ
dy dy
dx 4x dx x
#"„"
#
œÊœ Êœ œ ŸŸ
È
32. The integral 1 x dx is the area enclosed by the x-axis and the semicircle y 1 x . This area is half
'1
1ÈÈ
œ
# #
the circle's area, or and multiplying by 2 gives . The length of the circular arc y 1 x from x 1 to
1
##
1œ œ
È
x 1 is L 1 dx 1 dx (2 ) since L is half theœœ œ œ œ œ
'' '
11 1
11 1
ÊŠ‹ Š ‹
Ê
dy
dx
xdx
1x 1x
##
"
#
ÈÈ
11
circle's circumference. In conclusion, 2 1 x dx .
''
11
11
Ȝ
#
dx
1x
È
33. (b) e dx e e dx
''
xe e x
xx
œ
lim e e dx lim e e dx;œ
ab
Ä_ Ä_
''
a0
0b
ex ex
xx
ue
du e dx
”•
œ
π
x
x
lim e du lim e du
ab
Ä_ Ä_
''
e
1uu
a1
eb
lim e lim eœ
ab
Ä_ Ä_
cd cd
uu
1e
ea
b
1
lim e lim eœ
ab
Ä_ Ä_
‘‘
""
ee
eaeb
e0 1œ œ
ˆ‰ˆ‰
""
!
ee
(a)
34. u , du ; dv ny dy, v y ;œœ œ œ
"
1y (1y)
dy n1 n
lim dy lim dy lim dy. Now, 0 y
nn nÄ_ Ä_ Ä_
'''
000
111
ny y y y y
1y 1y 1y 1y 1y
n
n1 n n n n
#
"
!
"
œœ ŸŸ
Œ
’“
0 lim dy lim y dy lim lim 0 lim dyÊŸ Ÿ œ œ œÊ
nnnnnÄ_ Ä_ Ä_ Ä_ Ä_
'' '
00 0
11 1
n
yy ny
1y n1 n1 1y
nn1
"
!
"
’“
n1
0œœ
""
##
35. u x a du 2x dx;œ Ê œ
##
x x a dx u du u du C, n 2
'''
Š‹ Š‹
Ȉ‰
È
## """
###
œ œ œ Á
nnn2 u
1
n2 1
n
CC Cœœ œ
u
nn n
uxa
n2 2 n2
n2
# # #
ˆ‰
ÈŠ‹
È
36. sin sin
1
6
xdx dx dx du
4x 4x x 42x 4u
2
œœ œ œ
" "
" "
##
"
!
‘
'' ' '
00 0 0
11 1 2
ÈÈ ÈÈÈ
sin sin œœœœ
"""
" "
##
ÈÈÈ
ÈÈÈ
222
u22
48
‘ ˆ‰
2
0
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 8 Additional and Advanced Exercises 581
37. dx lim dx lim ln x 1 ln x lim ln
''
11
bb
1
b
1
ˆ‰ ˆ‰ ‘
ab ’“
ax ax a
x1 x x1 x x
x1
# # # # #
"" ""
#
œ œ œ
bb bÄ_ Ä_ Ä_
ab
a
lim ln ln 2 ; lim lim lim b if a the improperœ œœ_Ê
bbbbÄ_ Ä_ Ä_ Ä_
" "
# #
’“
ab abb1 b1
bbb
b
aa
2a
a2a
1
2
integral diverges if a ; for a : lim lim 1 1 lim ln ln 2œ œ œÊ
"" " "
## #
"Î#
bb bÄ_ Ä_ Ä_
Èab
b1
bb b
b1
É”•
ln 1 ln 2 ; if a : 0 lim lim lim (b 1) 0œœ Ÿ œ œ
"" "
## #
ˆ‰
ln 2
4bb1
b1 (b 1)
bbbÄ_ Ä_ Ä_
ab
a2a 2a 1
lim ln the improper integral diverges if a ; in summary, the improper integralÊœ_Ê
bÄ_
abb1
b
"
#
a
dx converges only when a and has the value
'1ˆ‰
ax ln 2
x1 x 4
# #
""
œ
38. G(x) lim e dt lim e lim if x 0 xG(x) xœœœœœÊœ
bb bÄ_ Ä_ Ä_
'0
bxt xt b
0
‘ ˆ‰
Š‹
"" "
xxxx x
1e 10
xb
1 if x 0œ
39. A converges if p 1 and diverges if p 1. Thus, p 1 for infinite area. The volume of the solid of revolutionœŸŸ
'1
dx
xp
about the x-axis is V dx which converges if 2p 1 and diverges if 2p 1. Thus we wantœœ Ÿ
''
11
11
ˆ‰
"#
xx
dx
p2p
p for finite volume. In conclusion, the curve y x gives infinite area and finite volume for values of p satisfyingœ
"
#
p
p1.
"
#Ÿ
40. The area is given by the integral A ;œ'0
1dx
xp
p 1: A lim ln x lim ln b , diverges;œ œ œ œ_
bbÄ! Ä!
cd
1
b
p 1: A lim x 1 lim b , diverges;œ œ œ_
bbÄ! Ä!
cd
1p 1p
1
b
p 1: A lim x lim b 1 0, converges; thus, p 1 for infinite area.œ œ" œ
bbÄ! Ä!
cd
1p 1p
1
b
The volume of the solid of revolution about the x-axis is V which converges if 2p 1 or
x0
1
œ1'dx
x2p
p , and diverges if p . Thus, V is infinite whenever the area is infinite (p 1).
""
##
x
The volume of the solid of revolution about the y-axis is V R(y) dy which
y11
œœ11
''
cd
#dy
y2p
converges if 1 p 2 (see Exercise 39). In conclusion, the curve y x gives infinite area and finite
2
pÍ œp
volume for values of p satisfying 1 p 2, as described above.Ÿ
41. e cos 3x
2xÐÑ
2e sin 3x
21
3
xÐÑ
4e cos 3x
21
9
xÐÑ
I sin 3x cos 3x I I (3 sin 3x 2 cos 3x) I (3 sin 3x 2 cos 3x) Cœ Êœ Êœ
e2e 413e e
39999 13
2x 2x 2x 2x
42. e sin 4x
3xÐÑ
3e cos 4x
3
4
xÐÑ "
9e sin 4x
3
16
xÐÑ "
I cos 4x sin 4x I I (3 sin 4x 4 cos 4x) I (3 sin 4x 4 cos 4x) Cœ Ê œ Ê œ
e3e925e e
416161616 25
3x 3x 3x 3x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
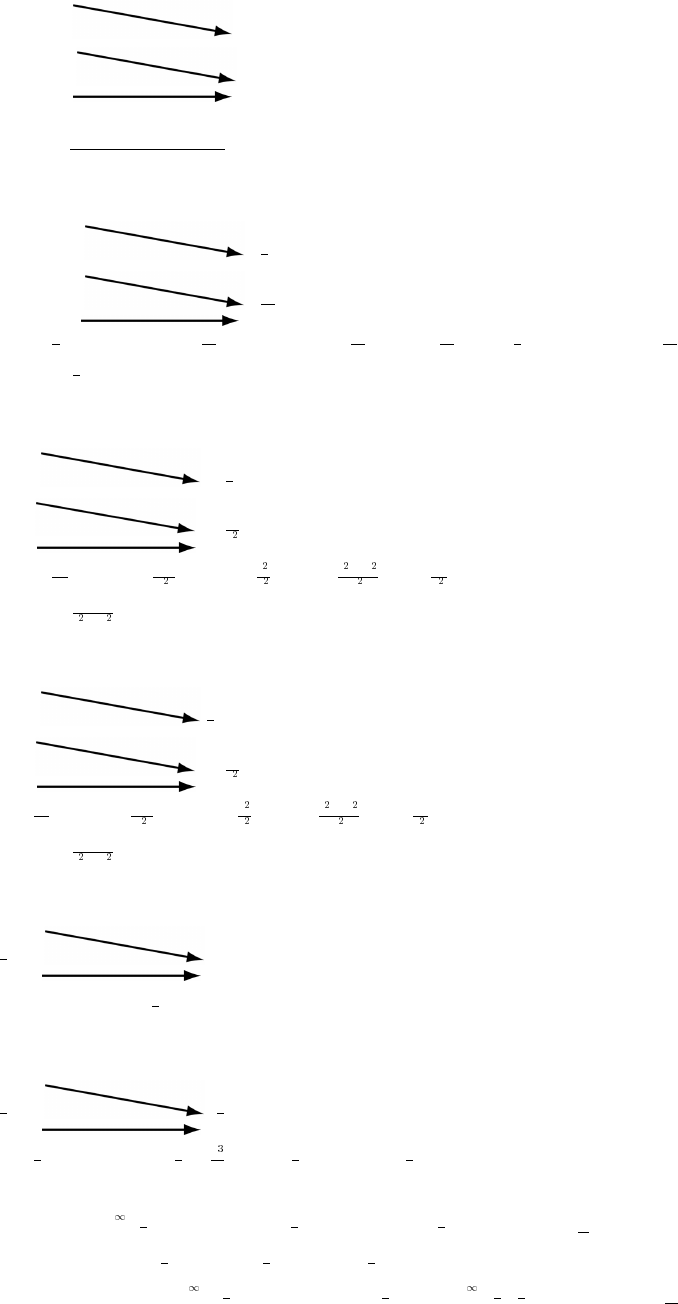
582 Chapter 8 Techniques of Integration
43. sin 3x sin xÐÑ
3 cos 3x cos xÐÑ
9 sin 3x sin x
ÐÑ
I sin 3x cos x 3 cos 3x sin x 9I 8I sin 3x cos x 3 cos 3x sin xœ Ê œ
ICʜ
sin 3x cos x 3 cos 3x sin x
8
44. cos 5x sin 4xÐÑ
sin 5x cos 4x ÐÑ "
4
25cos 5x sin 4
ÐÑ "
16
I cos 5x cos 4x sin 5x sin 4x I I cos 5x cos 4x sin 5x sin 4xœ Ê œ
" "
4161616416
5259 5
I (4 cos 5x cos 4x 5 sin 5x sin 4x) Cʜ
"
9
45. e sin bx
ax ÐÑ
ae cos bx
ax ÐÑ "
b
a e sin bx
#"
ax ÐÑ b
I cos bx sin bx I I (a sin bx b cos bx)œ Ê œ
eaeaabe
bbbbb
ax ax ax
Š‹
I (a sin bx b cos bx) Cʜ
e
ab
ax
46. e cos bx
ax ÐÑ
ae sin bx
ax ÐÑ "
b
a e cos bx
#"
ax ÐÑ b
I sin bx cos bx I I (a cos bx b sin bx)œ Ê œ
eae aabe
bb bbb
ax ax ax
Š‹
I (a cos bx b sin bx) Cʜ
e
ab
ax
47. ln (ax) 1ÐÑ
x
"
xÐÑ
I x ln (ax) x dx x ln (ax) x Cœ œ
'ˆ‰
"
x
48. ln (ax) xÐÑ #
x
""
$
x3
ÐÑ
I x ln (ax) dx x ln (ax) x Cœ œ
""""
$$$
3x339
x
'ˆ‰
Š‹
49. (a) (1) e dt lim e dt lim e lim ( 1) 0 1 1>œ œ œ œ œœ
''
00
ttt
bb
0
bbbÄ_ Ä_ Ä_
cd ‘
"
eb
(b) u t , du xt dt; dv e dt, v e ; x fixed positive realœœ œ œœ
xx1 t t
(x 1) t e dt lim t e x t e dt lim 0 e x (x) x (x)Êœ œ œ œ>>>
''
00
xt xt x1t
b
0
bbÄ_ Ä_
cd ˆ‰
b
e
x
x
b!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
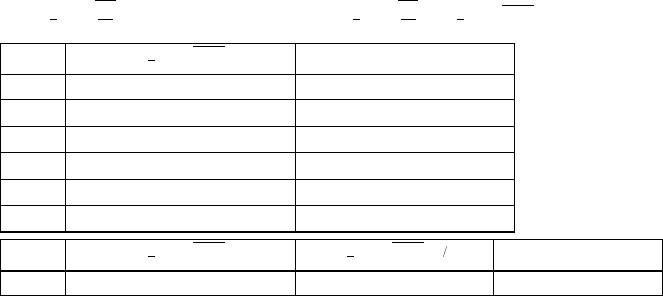
Chapter 8 Additional and Advanced Exercises 583
(c) (n 1) n (n) n!:>>œ œ
n 0: (0 1) (1) 0!;œœœ>>
n k: Assume (k 1) k! for some k 0;œœ >
n k 1: (k 1 1) (k 1) (k 1) from part (b)œ œ >>
(k 1)k! induction hypothesisœ
(k 1)! definition of factorialœ
Thus, (n 1) n (n) n! for every positive integer n.>>œ œ
50. (a) (x) and n (n) n! n! n 2n>> 1¸œÊ¸œ
ˆ‰ ˆ‰ ˆ‰
ÉÉ
È
x2 n2 n
ex ene
xnn
11
(b) n 2n calculator
10 3598695.619 3628800
20 2.4227868 10 2.432902 10
ˆ‰È
n
e
n1
‚‚
") ")
$# $#
%( %(
'% '%
)" )"
30 2.6451710 10 2.652528 10
40 8.1421726 10 8.1591528 10
50 3.0363446 10 3.0414093 10
60 8.3094383 10 8.3209871 10
‚‚
‚‚
‚‚
‚‚
(c) n 2n 2n e calculator
10 3598695.619 3628810.051 3628800
ˆ‰ ˆ‰
ÈÈ
nn
ee
nn
1 12n
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
584 Chapter 8 Techniques of Integration
NOTES:
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

CHAPTER 9 FURTHER APPLICATIONS OF INTEGRATION
9.1 SLOPE FIELDS AND SEPARABLE DIFFERENTIAL EQUATIONS
1. (a) y e y e 2y 3y 2 e 3e eœÊœÊœ œ
xx xxxww
ab
(b) y e e y e e 2y 3y 2 e e 3 e e eœ Êœ Ê œ œ
x 3x2 x 3x2 x 3x2 x 3x2 xww
##
33
ˆ‰
ab
(c) y e Ce y e Ce 2y 3y 2 e Ce 3 e Ce eœ Êœ Ê œ œ
x 3x2 x 3x2 x 3x2 x 3x2 xww
##
33
ˆ‰
ab
2. (a) y y yœ Ê œ œ œ
"""
w#
#
xxx
ˆ‰
(b) y y yœ Ê œ œ œ
"""
w#
#
x 3 (x 3) (x 3)
’“
(c) y y yœÊœ œ œ
"""
w#
#
xC (xC) xC
‘
3. y dt y dt x y dt e x dt e xy eœ Ê œ Ê œ œ œ
""" "
w#w
xt xt xx t xt
11 11
eeee e
'' ''
xx xx
xxx
ttxt t
ˆ‰ˆ‰ Š‹
x y xy eʜ
#w x
4. y 1 t dt y 1 t dt 1 xœÊœ
"" "
%%%
w
#
È È
Š‹
È
1x 1x
11
4x
1x
''
xx
ÈÈÈ
–— Š‹
y 1 t dt 1 y y 1 y y 1Êœ Êœ Ê œ
www
"
%
Š‹Š ‹ Š‹
È
2x 2x 2x
1x 1x 1x
1x 1
È'x
†
5. y e tan 2e y e tan 2e e 2e e tan 2eœÊœ œ
xx xxx xxx" w " "
"
ab ab ab ab
’“
12e
2
14e
ab
x2x
y y y y ; y( ln 2) e tan 2e 2 tan 1 2Êœ Êœ œ œ œ œ
w w " "
#
22
14e 14e 4
2x 2x ln 2 ln 2
ab ˆ‰
11
6. y (x 2) e y e 2xe (x 2) y e 2xy; y(2) (2 2) e 0œ Ê œ Ê œ œ œ
xxx x 2ww
ˆ‰
7. y y y y xy sin x yœ Ê œ Ê œ Ê œ Ê œ
cos x x sin x cos x sin x cos x sin x
xx xxxxx
y
ww ww
"
ˆ‰
xy y sin x; y 0Êœ œ œ
w
#
ˆ‰
11
1
cos ( /2)
(/2)
8. y y y x y x y xy y ; y(e) e.œÊœ Êœ Ê œ Ê œ œœ
xxx e
ln x (ln x) ln x (ln x) ln x (ln x) ln e
ln x x
w w #w #w #
""
Š‹
x
9. 2 xy 1 2x y dy dx 2y dy x dx 2y dy x dx 2 y
Ȉ‰
dy
dx 3
2
œÊ œ Ê œ Ê œ Ê
"Î# "Î# "Î# "Î# "Î# "Î# $Î#
''
2x C y x C, where C CœÊ œ œ
"Î# $Î# "Î#
""
"
#
2
3
10. x y dy x y dx y dy x dx y dy x dx 2y C
dy
dx 3
x
œÊœ Ê œÊ œ Êœ
# # "Î# "Î# # "Î# # "Î#
È''
2y x Cʜ
"Î# $
"
3
11. e dy e e dx e dy e dx e dy e dx e e C e e C
dy
dx œÊœ Ê œ Ê œ ʜʜ
xy x y y x y x y x y x
''
12. 3 e dy 3 e dx e dy 3 dx e dy 3 dx e C e C
dy
dx œÊœ ÊœÊ œ ʜʜxx x xxx
yyyyyy
33
''
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

586 Chapter 9 Further Applications of Integration
13. y cos y dy y cos y dx dy dx dy dx. In the integral on the left-hand
dy
dx y y
sec y sec y
œÊœ ʜʜ
ÈÈ ÈÈ
ˆ‰
##
ÈÈ
ÈÈ
''
side, substitute u y du dy 2 du dy, and we have sec u du dx 2 tan u x CœÊœ Ê œ œ Ê œ
È11
2y y
ÈÈ ''
#
x 2 tan y CÊ œ
È
14. 2xy 1 dy dx 2 ydy dx 2 y dy x dx 2 y dy x dx
ÈÈÈ È
È
dy
dx
11
2xy x
1/2 1/2 1/2 1/2
œÊ œ Ê œ Ê œ Ê œ
ÈÈ
''
2 dy C 2 y 3 x C 2 y 3 x C, where C CÊœÊœÊ œ œ
ÈÈÈ
ÈÈ
ˆ‰
È
yx3 3
11 1
3/2
22
3
3/2
3
2
1/2
15. x e dy dx e dy dx e dy dx In the integral on the
Èdy dy
dx dx
ee ee e e
xx x x
œÊœÊœ Ê œ Ê œ Þ
yxÈyyxx x x
ÈÈ È È
yy
''
right-hand side, substitute u x du dx 2 du dx, and we have e dy 2 e duœÊœ Ê œ œ
È""
#ÈÈ
xx ''
yu
e2eC e2eC, where CCÊ œ Ê œ œ
yu y x
11
16. sec x e e cos x dy e e cos x dx e dy e cos x dxab a b
dy dy
dx dx
œÊœ Êœ Êœ
y sin x y sin x y sin x y sin x
e dy e cos x dx e e C e e C, where C CÊœ ʜʜ œ
''
yyysin x sin x sin x
11
17. 2x 1 y dy 2x 1 y dx 2x dx 2x dx sin y x C since y
dy dy dy
dx 22
1y 1y
œÊœÊ œÊ œ Ê œ "
ÈÈ kk
ÈÈ
" #
22
''
ysinx Cʜ ab
2
18. dy dx dy dx dx e dy e dx e dy e dx e C
dy
dx e e e e e
ee eee e
2y x 2y x x 1
œÊœ Êœ œ Ê œ Ê œ Êœ
2x y 2x y 2x y x 2y
xy xy xy 2y '' #
e 2e C where C 2CÊ œ œ
2y x 1
19. y x y slope of 0 for the line y x.
wœÊ œ
For x, y 0, y x y slope 0 in Quadrant I. œÊ
w
For x, y 0, y x y slope 0 in Quadrant III. œÊ
w
For y x , y 0, x 0, y x y slope 0 inkk kk œÊ
w
Quadrant II above y x.œ
For y x , y 0, x 0, y x y slope 0 inkk kk œÊ
w
Quadrant II below y x.œ
For y x , x 0, y 0, y x y slope 0 inkk kk œÊ
w
Quadrant IV above y x.œ
For y x , x 0, y 0, y x y slope 0 inkk kk œÊ
w
Quadrant IV below y x.œ
All of the conditions are seen in slope field (d).
20. y y 1 slope is constant for a given value of y, slope
wœÊ
is 0 for y 1, slope is positive for y 1 and negative forœ
y 1. These characteristics are evident in slope field (c).
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
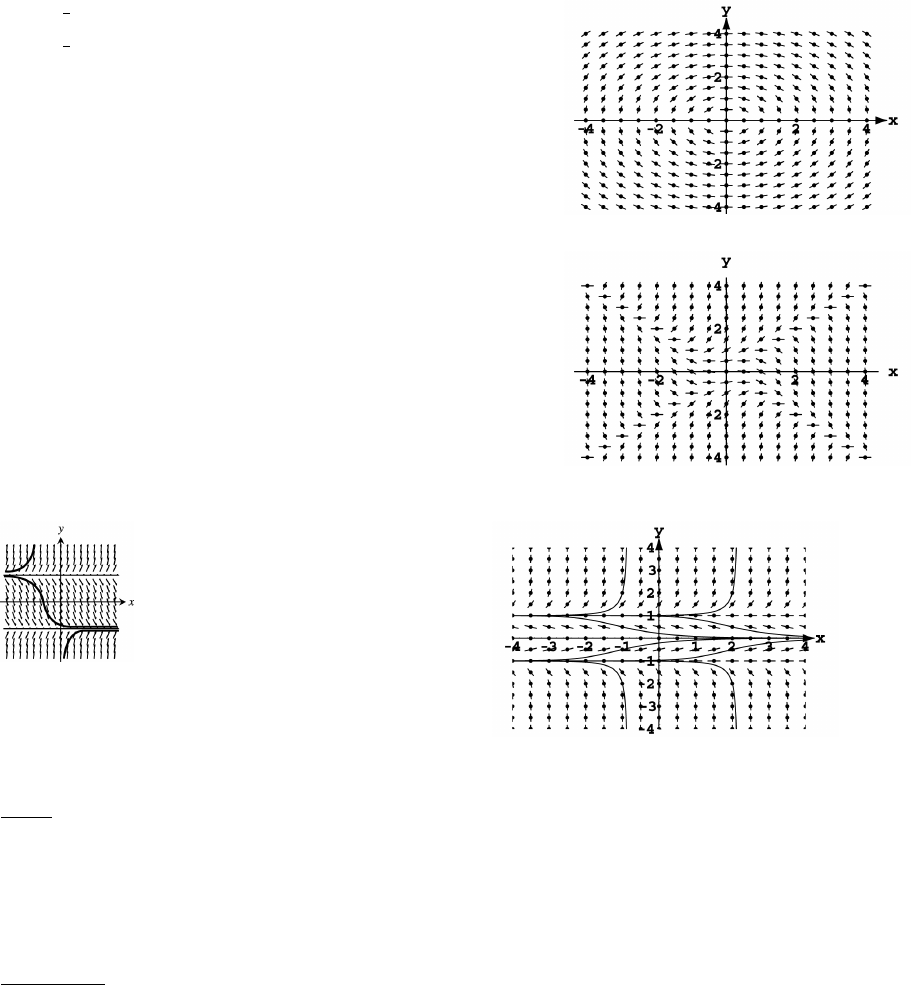
Section 9.1 Slope Fields and Separable Differential Equations 587
21. y slope 1 on y x and 1 on y x.
wœ Ê œ œ œ
x
y
y slope 0 on the y-axis, excluding 0, 0 ,
wœ Ê œ
x
yab
and is undefined on the x-axis. Slopes are positive for
x 0, y 0 and x 0, y 0 (Quadrants II and IV),
otherwise negative. Field (a) is consistent with these
conditions.
22. y y x slope is 0 for y x and for y x.
wœÊ œ œ
22
For y x slope is positive and for y x slope iskk kk kk kk
negative. Field (b) has these characteristics.
23. 24.
25-36. Example CAS commands:
:Maple
ode := diff( y(x), x ) = y(x);
icA := [0, 1];
icB := [0, 2];
icC := [0,-1];
DEplot( ode, y(x), x=0..2, [icA,icB,icC], arrows=slim, linecolor=blue, title="#25 (Section 9.1)" );
:Mathematica
To plot vector fields, you must begin by loading a graphics package.
<<Graphics`PlotField`
To control lengths and appearance of vectors, select the Help browser, type PlotVectorField and select Go.
Clear[x, y, f]
yprime = y (2 y);
pv = PlotVectorField[{1, yprime}, {x, 5, 5}, {y, 4, 6}, Axes True, AxesLabel {x, y}]; Ä Ä
To draw solution curves with Mathematica, you must first solve the differential equation. This will be done with
the DSolve command. The y[x] and x at the end of the command specify the dependent and independent variables.
The command will not work unless the y in the differential equation is referenced as y[x].
equation = y'[x] == y[x] (2 y[x]) ;
initcond = y[a] == b;
sols = DSolve[{equation, initcond}, y[x], x]
vals = {{0, 1/2}, {0, 3/2}, {0, 2}, {0, 3}}
f[{a_, b_}] = sols[[1, 1, 2]];
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
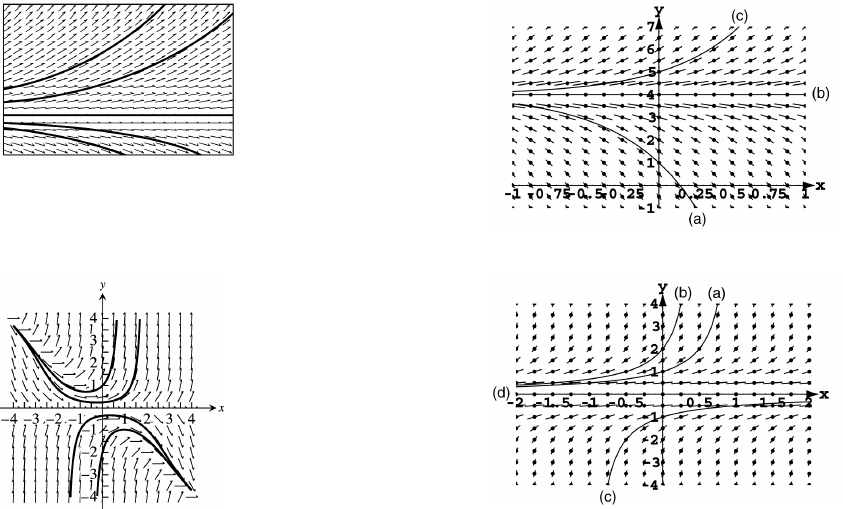
588 Chapter 9 Further Applications of Integration
solnset = Map[f, vals]
ps = Plot[Evaluate[solnset, {x, 5, 5}];
Show[pv, ps, PlotRange { 4, 6}];Ä
The code for problems such as 33 & 34 is similar for the direction field, but the analytical solutions involve
complicated inverse functions, so the numerical solver NDSolve is used. Note that a domain interval is
specified.
equation = y'[x] == Cos[2x y[x]] ;
initcond = y[0] == 2;
sol = NDSolve[{equation, initcond}, y[x], {x, 0, 5}]
ps = Plot[Evaluate[y[x]/.sol, {x, 0, 5}];
N[y[x] /. sol/.x 2]Ä
Show[pv, ps, PlotRange {0, 5}];Ä
Solutions for 35 can be found one at a time and plots named and shown together. No direction fields here.
For 36, the direction field code is similar, but the solution is found implicitly using integrations. The plot
requires loading another special graphics package.
<<Graphics`ImplicitPlot`
Clear[x,y]
solution[c_] = Integrate[2 (y 1), y] == Integrate[3x 4x 2, x] c
2
values = { 6, 4, 2, 0, 2, 4, 6};
solns = Map[solution, values];
ps = ImplicitPlot[solns, {x, 3, 3}, {y, 3, 3}]
Show[pv, ps]
25. 26.
27. 28.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 9.2 First-Order Linear Differential Equations 589
29. 30.
9.2 FIRST-ORDER LINEAR DIFFERENTIAL EQUATIONS
1. x y e y , P(x) , Q(x)
dy dy
dx dx x x x x
xee
œ Ê œ œ œ
ˆ‰
""
xx
P(x) dx dx ln x ln x, x 0 v(x) e e x
''
œœœÊœ œœ
"
xkk 'Px dxÐÑ ln x
y v(x) Q(x) dx x dx e C , x 0œœœœ
"""
v(x) x x x x
eeC
''ˆ‰ ab
xxx
2. e 2e y 1 2y e , P(x) 2, Q(x) e
xdy dy
dx dx
xxx
œÊœ œ œ
P(x) dx 2 dx 2x v(x) e e
''
œœÊœ œ
'Px dxÐÑ 2x
y e e dx e dx e C e Ceœ œ œ œ
"""
eee
2x 2x 2x
'2x x x x x 2x
†'ab
3. xy 3y , x 0 y , P(x) , Q(x)
wœ Ê œ œ œ
sin x 3 sin x 3 sin x
xdxxxxx
dy ˆ‰
dx 3 ln x ln x , x 0 v(x) e x
'3
xœœÊœœkk $$ln x
y x dx sin x dx ( cos x C) , x 0œœœœ
"""
$
xx x x x
sin x C cos x
'ˆ‰ '
4. y (tan x) y cos x, x (tan x) y cos x, P(x) tan x, Q(x) cos x
w# # #
##
œÊœ œ œ
11
dy
dx
tan x dx dx ln cos x ln (cos x) , x v(x) e (cos x)
''
œœœ Êœœ
sin x
cos x kk " "
##
11 ln cos xÐÑ
y (cos x) cos x dx (cos x) cos x dx (cos x)(sin x C) sin x cos x C cos xœœœœ
"" #
(cos x) ''
†
5. x 2y 1 , x 0 y , P(x) , Q(x)
dy dy
dx x dx x x x x x x
22
œ Ê œ œ œ
"""""
ˆ‰
dx 2 ln x ln x , x 0 v(x) e x
'2
xœœÊœœkk ##ln x
y x dx (x 1) dx x C , x 0œœœœ
""" " " ""
#
##xxx x x xx
xC
''
ˆ‰ Š‹
6. (1 x) y y x y , P(x) , Q(x)œÊ œ œ œ
w""
Ȉ‰
dy
dx 1x 1 x 1x 1x
xx
ÈÈ
dx ln (1 x), since x 0 v(x) e 1
'"
1x œ Êœ œ
ln 1 x
y (1 x) dx x dx x Cœ œ œ œ
"""
$Î#
1x 1x 1x 1x 3 3(1x) 1x
x22xC
''
Š‹ Ȉ‰ˆ ‰
È
7. y e P(x) , Q(x) e P(x) dx x v(x) e
dy
dx œ Ê œ œ Ê œ Ê œ
"" " " "
## # # #
x2 x2 x2
'
y e e dx e dx e x C xe CeÊœ œ œ œ
"" " " "
####ex2 ''
x2 x2 x2 x2 x2 x2
ˆ‰ ˆ ‰
8. 2y 2xe P(x) 2, Q(x) 2xe P(x) dx 2 dx 2x v(x) e
dy
dx œ Ê œ œ Ê œ œ Ê œ
2x 2x 2x
''
y e 2xe dx 2x dx e x C x e CeÊœ œ œ œ
""
##
ee
2x 2x
''
2x 2x 2x 2x 2x
ab ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

590 Chapter 9 Further Applications of Integration
9. y 2 ln x P(x) , Q(x) 2 ln x P(x) dx dx ln x, x 0
dy
dx x x x
œ Êœ œ Ê œ œ
ˆ‰
"" "
''
v(x) e y x (2 ln x) dx x (ln x) C x (ln x) CxÊœœÊœ œ œ
ln x "" ##
xx
'ˆ‰ cd
10. y , x 0 P(x) , Q(x) P(x) dx dx 2 ln x ln x , x 0
dy
dx x x x x x
2cos x 2 cos x 2
œ Êœ œÊ œ œ œ
ˆ‰ kk
'' #
v(x) e x y x dx cos x dx (sin x C)ÊœœÊœ œ œ œ
ln x ##
"""
xx x x x
cos x sin x C
''
ˆ‰
11. s P(t) , Q(t) P(t) dt dt 4 ln t 1 ln (t 1)
ds 4 t 1 4 t 1 4
dt t 1 (t 1) t 1 (t 1) t 1
œÊœ œÊ œ œœ
ˆ‰ kk
%
''
v(t) e (t 1) s (t 1) dt t 1 dtÊœ œÊœ œ
ln t 1Ð Ñ %%#
"""
(t 1) (t 1)
t
(t 1)
''
’“ ab
tCœœ
"
(t1) 3(t1) (t1) (t1)
tttC
3
Š‹
12. (t 1) 2s 3(t 1) s 3 P(t) , Q(t) 3 (t 1)œÊ œÊœ œ
ds ds 2 2
dt (t 1) dt t 1 (t 1) t 1
""
$
ˆ‰
P(t) dt dt 2 ln t 1 ln (t 1) v(t) e (t 1)ÊœœœÊœœ
''
2
t1
##
kk ln t 1Ð Ñ
s (t 1) 3 (t 1) dt 3(t 1) (t 1) dtÊœ œ
""
#$ #"
(t 1) (t 1)
''
cdc d
(t1) ln t1 C (t1)(t1) ln(t1) , t 1œœ
"
$#
(t 1) (t 1)
C
cdkk
13. (cot ) r sec P( ) cot , Q( ) sec P( ) d cot d ln sin v( ) e
dr
d)œÊœ œÊ œ œ Êœ)))))) )))) ))
'' kk ln sin
sin because 0 r (sin )(sec ) d tan d ln sec CœÊœ œœ)) ))))) )
1
)))#
"""
sin sin sin
''
abkk
(csc ) ln sec Cœ))abkk
14. tan r sin (cot ) r sin cos P( ) cot , Q( ) sin cos )) ))))))))
dr dr r sin dr
d d tan tan d)))))
)
œ Ê œ Ê œ Ê œ œ
#
P( ) d cot d ln sin ln (sin ) since 0 v( ) e sin Êœœœ Êœœ
''
)) )) ) ) ) ) )kk 1
#
ln sinÐÑ)
r (sin ) (sin cos ) d sin cos d CÊœ œ œ œ
"""
#
sin sin sin 3 3 sin
sin sin C
))))
))
''
)))) )))
ˆ‰
Š‹
15. 2y 3 P(t) 2, Q(t) 3 P(t) dt 2 dt 2t v(t) e y 3e dt
dy
dt e
œÊ œ œÊ œ œÊ œ Êœ
''
'2t 2t
"
2t
e C ; y(0) 1 C 1 C y eœ œÊœÊœÊœ
"""
#####e
33 3
2t ˆ‰
2t 2t
16. t P(t) , Q(t) t P(t) dt 2 ln t v(t) e t y t t dt
dy 2y
dt t t t
2
œÊ œ œÊ œ Ê œ œÊœ
## ###
"
''
kk abab
ln t
t dt C ; y(2) 1 1 C yœœœœÊœÊœÊœ
""
%
tt55t 54 555t
ttC 8C 12t12
'Š‹
17. y P( ) , Q( ) P( ) d ln v( ) e
dy
d
sin sin
)) ) ) )
))
œÊœ œÊ œ Êœœ
ˆ‰ kk kk
""
)) )))) )
'ln
y d d for 0 y sin d ( cos C)Êœ œ ÁÊœ œ
"" ""
kk)))) ) )
))
'' '
kkˆ‰ ˆ‰
))))) )) )
sin sin
cos ; y 1 C y cos œ œ Ê œ Ê œ
""
##)) ) )
11 1
))
C
2
ˆ‰
18. y sec tan P( ) , Q( ) sec tan P( ) d 2 ln v( ) e
dy
d
22
)) )
œ Êœ œ Ê œ Êœ
ˆ‰ kk))) ) )))) )) ) )
##
'2ln
y sec tan d sec tan d (sec C) sec C ;œÊœ œ œ œ ) )))))) )))) ) )))
# # # # # # #
"
)''
aba b
y 2 2 (2) C C 2 y sec 2
ˆ‰ ˆ ‰
Š‹ Š‹
111
11399
18 18
œÊœ Ê œ Êœ )) )
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 9.2 First-Order Linear Differential Equations 591
19. (x 1) 2 x x y 2 y 2xy P(x) 2x,œÊ œ Êœ Êœ
dy dy x(x 1) dy
dx x 1 dx x 1 (x 1) dx (x 1)
eee
ab ’“
#
xx
x
Q(x) P(x) dx 2x dx x v(x) e y e dxœÊ œœÊœÊœ
e e
(x 1) (x 1)
x
e
x x
#
"
'' '
x
x’“
e dx e C Ce ; y(0) 5 C 5 C 5œ œ œ œÊœÊ"œ
xx x
(x 1) 1 x 1 0 1
(x 1) e1
'"
’“
x
C 6 y 6eʜʜ
xe
x1
x
20. xy x P(x) x, Q(x) x P(x) dx x dx v(x) e y e x dx
dy
dx
xx2 x2
e
œÊ œ œÊ œ œ Ê œ Êœ
'' '
#
ÎÎ
"
x2
†
e C 1 ; y(0) 6 1 C 6 C 7 y 1œ œ œ Ê œ Ê œ Ê œ
"Î
ee e
x2 C 7
x2 x2 x2
Š‹
21. ky 0 P(t) k, Q(t) 0 P(t) dt k dt kt v(t) e
dy
dt
kt
œÊ œ œÊ œ œÊ œ
''
y e (0) dt e (0 C) Ce ; y(0) y C y y y eÊœ œ œ œ Ê œ Êœ
"!!!
e
kt kt kt kt
kt 'ˆ‰
22. (a) v 0 P(t) , Q(t) 0 P(t) dt dt t v(t) e
dv k k k k kt
dt m m m m m
œÊ œ œÊ œ œœÊ œ
'' kt m
y e 0 dt ; v(0) v v C v v v eÊœ œ œ Ê œ Ê œ Êœ
"ÎÐ Î Ñ
!!!!
eee
kt m kmt
CC
kt m kt m k 0 m
'†
(b) v dt ln v t C v e v e e . Let e C
dv k dv k k
dt m v m m
kmt C kmt C C 1
œ Ê œ Ê œ Ê œ Ê œ † œ Þ
Î ÐÎÑab
Then v C and v 0 v C C . So v v eœ† œœ †œ œ
11
ee
10110
kmt
kmt km 0
ab Ð Î Ñ
23. x dx x ln x C x ln x Cx (b) is correct
'"
xœœÊabkkkk
24. cos x dx (sin x C) tan x (b) is correct
""
cos x cos x cos x
C
'œœÊ
25. Let y(t) the amount of salt in the container and V(t) the total volume of liquid in the tank at time t.œœ
Then, the departure rate is (the outflow rate).
y(t)
V(t)
(a) Rate entering 10 lb/minœœ
2 lb
gal min
5 gal
†
(b) Volume V(t) 100 gal (5t gal 4t gal) (100 t) galœœ œ
(c) The volume at time t is (100 t) gal. The amount of salt in the tank at time t is y lbs. So the
concentration at any time t is lbs/gal. Then, the rate leaving (lbs/gal) 4 (gal/min)
yy
100 t 100 t
Ϡ
lbs/minœ4y
100 t
(d) 10 y 10 P(t) , Q(t) 10 P(t) dt dt
dy 4y dy
dt 100 t dt 100 t 100 t 100 t
44 4
œ Ê œ Ê œ œ Ê œ
ˆ‰ ''
4 ln (100 t) v(t) e (100 t) y (100 t) (10 dt)œÊœœÊœ
4ln 100 t %%
"
(100 t) '
C 2(100 t) ; y(0) 50 2(100 0) 50œœœÊœ
10 C C
(100 t) (100 t) (100 0)
(100 t)
5
Š‹
C (150)(100) y 2(100 t) y 2(100 t)ʜ ʜ ʜ
%
(150)(100)
(100 t)
150
1
ˆ‰
t
100
(e) y(25) 2(100 25) 188.56 lbs concentration 1.5 lb/galœ ¸ Ê œ¸¸
(150)(100) y(25)
(100 25) volume 125
188.6
26. (a) 5 3 2 V 100 2t
dV
dt œœÊœ ab
The tank is full when V 200 100 2t t 50 minœœÊœ
(b) Let y t be the amount of concentrate in the tank at time t.ab
53 y
dy gal y gal dy y dy
dt gal min 100 2t gal min dt 2 2 50 t dt 2 t 50 2
lb lb 5 3 3 5
œ ʜʜ
Š‹Š‹Š ‹Š‹ ˆ‰
"
# ab
Q(t) ; P(t) P(t) dt dt ln t 50 since t 50 0œœ Ê œ œ
531 313
2250t 2t502
ˆ‰ ab
''
vt e e t 50ab a bœœ œ
'P(t) dt ln t 50 3/2
3
2ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

592 Chapter 9 Further Applications of Integration
yt t50 dt t50 yt t50
t50 C
ab ab ab ab
‘
ab
œœ Êœ
15 C
t50 t50
2
3/2 3/2 5/2
ab ab
3/2 3/2
'
Apply the initial condition (i.e., distilled water in the tank at t 0):œ
y 0 0 50 C 50 y t t 50 . When the tank is full at t 50,ab abœœ Ê œ Ê œ œ
C50
50
5/2
t50
3/2 3/2
5/2
ab
y 50 100 83.22 pounds of concentrate.abœ ¸
50
100
5/2
3/2
27. Let y be the amount of fertilizer in the tank at time t. Then rate entering 1 1 1 and theœœ
lb lb
gal min min
gal
†
volume in the tank at time t is V(t) 100 (gal) [1 (gal/min) 3 (gal/min)]t min (100 2t) gal. Henceœ œ
rate out 3 lbs/min 1 lbs/min y 1œœ Êœ Êœ
ˆ‰ ˆ ‰ ˆ‰
y3y dy 3y dy
100 2t 100 2t dt 100 2t dt 100 2t
3
P(t) , Q(t) 1 P(t) dt dt v(t) eÊœ œÊ œ œ Êœ
33
100 2t 100 2t
3 ln (100 2t)
#
'' 3 ln 100 2t 2
(100 2t) y (100 2t) dt (100 2t) Cœ Êœ œ
$Î# $Î# $Î#
"
#
(100 2t)
2(100 2t)
'’“
(100 2t) C(100 2t) ; y(0) 0 [100 2(0)] C[100 2(0)] C(100) 100œ œÊ Ê œ
$Î# $Î# $Î#
C (100) y (100 2t) . Let 0 2Êœ œ Êœ œÊ œ
"Î# "
10 10 dt dt 10
(100 2t) dy dy (100 2t) ( 2)
ˆ‰
3
2 0 20 3 100 2t 400 9(100 2t) 400 900 18t 500 18tœ œ Ê œ Ê œ Ê œ Ê œ
3 100 2t
10
ÈÈ
t 27.8 min, the time to reach the maximum. The maximum amount is thenʸ
y(27.8) [100 2(27.8)] 14.8 lbœ ¸
[100 2(27.8)]
10
28. Let y y(t) be the amount of carbon monoxide (CO) in the room at time t. The amount of CO entering theœ
room is ft /min, and the amount of CO leaving the room is ft /min.
ˆ‰ ˆ‰ˆ‰
43 12 3
100 10 1000 4500 10 15,000
yy
‚œ œ
$ $
Thus, y P(t) , Q(t) v(t) e
dy y dy
dt 1000 15,000 dt 15,000 1000 15,000 1000
12 12 12
œ Ê œ Ê œ œ Ê œ
"" t 15 000Îß
y e dt y e e C e 180e C ;Êœ Êœ œ
"
e 1000 1000
12 12 15,000
t 15 000 't 15 000 t 15,000 t 15 000 t 15 000Îß Î Îß Îßt 15 000 ˆ‰
ab
†
y(0) 0 0 1(180 C) C 180 y 180 180e . When the concentration of CO is 0.01%œÊœ Ê œ Êœ t 15 000
in the room, the amount of CO satisfies y 0.45 ft . When the room contains this amount we
y
4500 100
.01
œÊœ $
have 0.45 180 180e e t 15,000 ln 37.55 min.œ Ê œ Êœ ¸
t15000 179.55 179.55
180 180
Î ßt 15 000 ˆ‰
29. Steady State and we want i 1 e 1 e eœœÊœÊœÊœ
VVVV
RRRR
"" " "
## # #
ˆ‰ ˆ‰ ab
Î Î ÎRt L Rt L Rt L
ln ln t t ln 2 secÊœÊ œÊœ
""
##
Rt L L
LR R
30. (a) i 0 di dt ln i C i e e Ce ; i(0) I I C
di R R Rt
dt L i L L
œÊ œ Ê œ Êœ œ œÊœ
""CRtL ÎRt L
iIe ampÊœÎRt L
(b) I I e e ln ln 2 t ln 2 sec
"""
###
œÊœÊœœÊœ
Î ÎRt L Rt L Rt L
LR
(c) t i I e I e ampœÊœ œ
L
R
Ð Î ÑÐ Î ÑRt L L R t
31. (a) t i 1 e 1 e 0.9502 amp, or about 95% of the steady state valueœÊœ œ¸
3L V V V
RR R R
abab
Ð ÑÐ Î ÑR/L 3L R 3
(b) t i 1 e 1 e 0.8647 amp, or about 86% of the steady state valueœÊœ œ¸
2L V V V
RR R R
abab
Ð ÑÐ Î ÑR/L 2L R 2
32. (a) i P(t) , Q(t) P(t) dt dt v(t) e
di R V R V R Rt
dt L L L L L L
œÊ œ œÊ œ œÊ œ
'' Rt L
i e dt e C CeÊœ œ œ
""
eLeRLR
VLVV
Rt L Rt L
'Rt L Rt L R L t
ˆ‰ ‘ˆ‰
(b) i(0) 0 C 0 C i eœÊ œÊ œ Êœ
VVVV
RRRR
Rt L
(c) i 0 i 0 i is a solution of Eq. (11); i CeœÊœÊœ œÊœ œ
Vdi diR RVV V
Rdt dtL LRL R
ˆ‰ˆ‰ RLt
33. y y y ; we have n 2, so let u y y . Then y u and 1y y
w
œ œ œ œ œ œ Ê œ
2121122
du du
dx dx dx dx
dy dy
u u u u 1. With e e as the integrating factor, we haveÊ œ Ê œ œ
212 dxx
du du
dx dx '
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
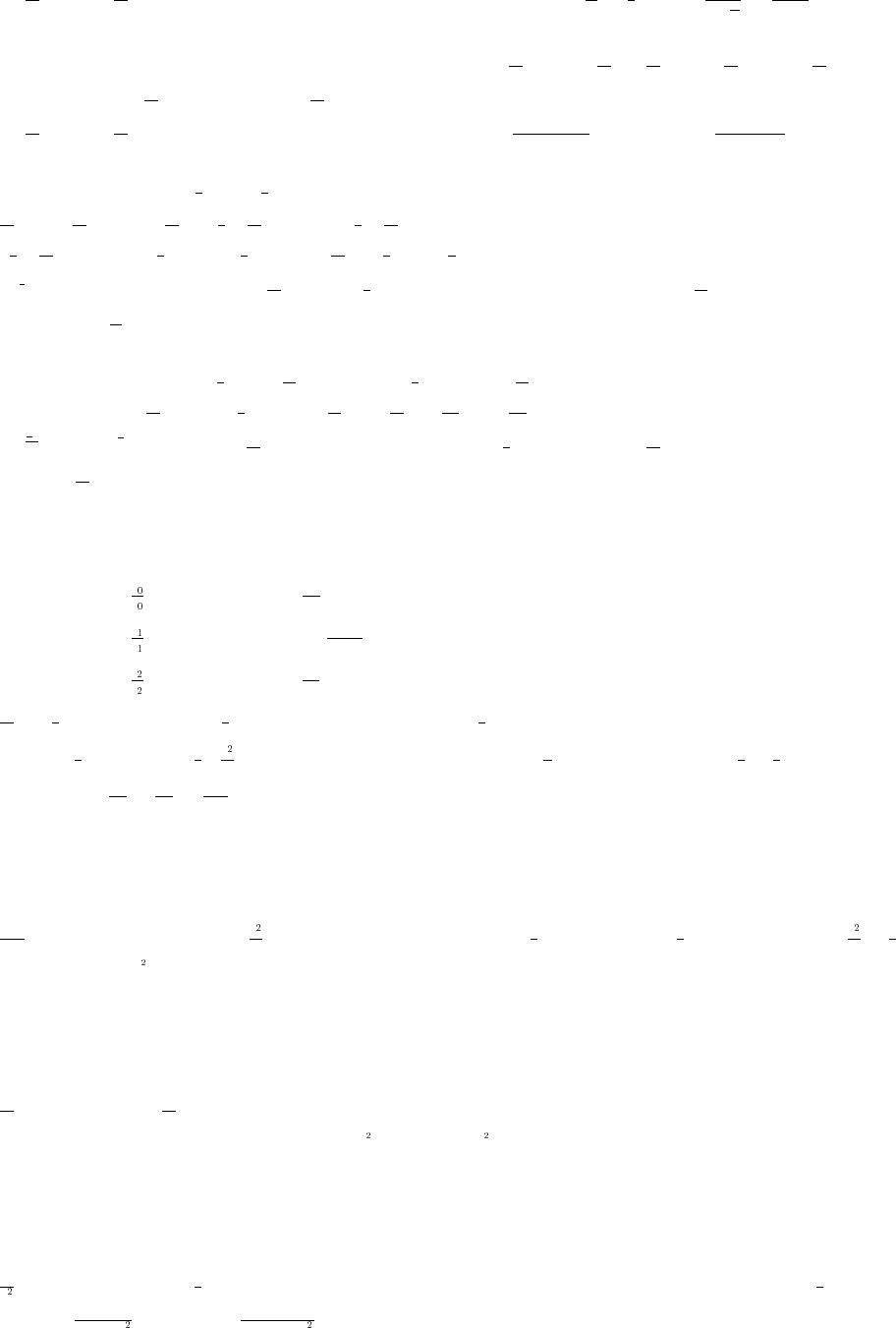
Section 9.3 Euler's Method 593
e u e u e . Integrating, we get e u e C u 1 y
xxx xx
du d C1 1 e
dx dx ey eC
1
ˆ‰
abœ œ œÊœœÊœ œ
xCx
ex
x
34. y y xy ; we have n 2, so let u y . Then y u and y y u .
w
œ œ œ œ œ Ê œ œ
211222
du du du
dx dx dx dx dx
dy dy
Substituting: u u xu u x. Using e e as an integrating factor:œÊœ œ
212 dxx
du du
dx dx '
e u eu x e eu e 1 x C u y u
xxxxx 1
du d e
dx dx e e xe C
e1 x C
ˆ‰
ab a b œ œ Ê œ Êœ Êœ œ
x
xxx
x
ab
35. xy y y y y y . Let u y y y u and y u .
ww
œ Ê œ œ œ Êœ œ
2 2 1 2 3 1/3 2 2/3
11
xx
ˆ‰ ˆ‰ ab
3y y y u . Thus we have
du 1 du 1 du
dx dx dx 3 dx 3 dx
222/3
dy dy
œÊœœ œ
w
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ ‰
ab
u u u u 1. The integrating factor, v x , is
ˆ‰ˆ‰ˆ ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ab
1du 1 1 du 3 3
3dx x x dx x x
2/3 1/3 2/3
œ Êœ
e e e x . Thus x u x 3x x u x C u 1 y
'3
x3
3
dx 3ln x ln x 3 3 3 2 3 3 3
d3 C
dx x x
œœœ œ œÊœÊœœabˆ‰
y1ʜ
ˆ‰
C
x
1/3
3
36. x y 2xy y y y y . P x , Q x , n 3. Let u y y .
23 3 132
21 2 1
xx x x
ww
œÊ œ œ œ œ œ œ
ˆ‰ ˆ‰ ˆ‰ ˆ‰
ab ab
22
Substituting gives 2 u 2 u . Let the integrating factor, v x , be
du 2 1 du 4 2
dx x x dx x x
œ Ê œab ab
ˆ‰ ˆ‰ ˆ ‰
22
e e x . Thus x u 2x x u x C u Cx y
'ab
4
x4
dx ln x 4 4 6 4 5 4 2
d22
dx 5 5x
œœ œÊœÊœœ
ab
yCxʜ
ˆ‰
2
5x
41/2
9.3 EULER'S METHOD
1. y y 1 dx 1 1 (.5) 0.25,
"!
#
œ œ œ
Š‹ ˆ‰
y
x
1
y y 1 dx 0.25 1 (.5) 0.3,
#"
œ œ œ
Š‹ ˆ‰
y
x2.5
0.25
y y 1 dx 0.3 1 (.5) 0.75;
$#
œ œ œ
Š‹ ˆ‰
y
x3
0.3
y 1 P(x) , Q(x) 1 P(x) dx dx ln x ln x, x 0 v(x) e x
dy
dx x x x
œÊœ œÊ œ œœ Êœœ
ˆ‰ kk
"" "
''ln x
y x 1 dx C ; x 2, y 1 1 1 C 4 yÊœ œ œ œÊœ Ê œÊœ
""
# #xx 2 x
xCx4
'†Š‹
y(3.5) 0.6071Ê œœ ¸
3.5 4 4.25
3.5 7#
2. y y x (1 y ) dx 0 1(1 0)(.2) .2,
"!! !
œ œ œ
y y x (1 y ) dx .2 1.2(1 .2)(.2) .392,
#"" "
œ œ œ
y y x (1 y ) dx .392 1.4(1 .392)(.2) .5622;
$## #
œ œ œ
x dx ln 1 y C; x 1, y 0 ln 1 C C ln 1 y
dy
1y
x x
# ####
"" "
œÊœœœÊœÊœÊœkk kk
y 1 e y(1.6) .5416Êœ Ê ¸
ab1x 2Î
3. y y (2x y 2y ) dx 3 [2(0)(3) 2(3)](.2) 4.2,
"! !! !
œ œ œ
y y (2x y 2y ) dx 4.2 [2(.2)(4.2) 2(4.2)](.2) 6.216,
#" "" "
œ œ œ
y y (2x y 2y ) dx 6.216 [2(.4)(6.216) 2(6.216)](.2) 9.6969;
$# ## #
œ œ œ
2y(x 1) 2(x 1) dx ln y (x 1) C; x 0, y 3 ln 3 1 C C ln 3 1
dy dy
dx y
œÊœ Ê œœœÊœÊœkk #
ln y (x 1) ln 3 1 y e e e 3e y(.6) 14.2765ʜʜ œ œ Ê ¸
#ÐÑ ÐÑx1 ln31 ln3x 2x xx2
4. y y y (1 2x ) dx 1 1 [1 2( 1)](.5) .5,
"! !
##
!
œ œ œ
y y y (1 2x ) dx .5 (.5) [1 2( .5)](.5) .5,
#" "
##
"
œ œ œ
y y y (1 2x ) dx .5 (.5) [1 2(0)](.5) .625;
$# #
##
#
œ œ œ
(1 2x) dx x x C; x 1, y 1 1 1 ( 1) C C 1 1 x x
dy
yy y
œ Ê œ œ œ Ê œ Ê œ Ê œ
" "
###
y y(.5) 4Êœ Ê œ œ
""
1xx 1.5(.5)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

594 Chapter 9 Further Applications of Integration
5. y y 2x e dx 2 2(0)(.1) 2,
"! !
œ œ œ
x
y y 2x e dx 2 2(.1) e (.1) 2.0202,
#" "
œ œ œ
x1Þ
y y 2x e dx 2.0202 2(.2) e (.1) 2.0618,
$# #
œ œ œ
x2
Þ
dy 2xe dx y e C; y(0) 2 2 1 C C 1 y e 1 y(.3) e 1 2.0942œÊœœÊœÊœÊœÊœ¸
xx x3Þ
6. y y y e 2 dx 2 2 e 2 (.5) 2.5,
"! ! !
œ œ œabab
x
y y y e 2 dx 2.5 2.5 e 2 (.5) 3.5744,
#" " Þ
œ œ œabab
x5
y y y e 2 dx 3.5744 3.5744 e 2 (.5) 5.7207;
$# # "
œ œ œab a b
x
y e 2 P(x) 1, Q(x) e 2 P(x) dx x v(x) e y e e 2 dx
dy
dx e
xx x
œ Ê œ œ Ê œÊ œ Ê œ
''
"xxx
ab
e x 2e C ; y(0) 2 2 2 C C 0 y xe 2 y(1.5) 1.5e 2 8.7225œ œÊœÊœÊœÊ œ ¸
x x
ab
x15
7. y 1 1(.2) 1.2,
"œ œ
y 1.2 (1.2)(.2) 1.44,
#œ œ
y 1.44 (1.44)(.2) 1.728,
$œ œ
y 1.728 (1.728)(.2) 2.0736,
%œ œ
y 2.0736 (2.0736)(.2) 2.48832;
&œ œ
dx ln y x C y Ce ; y(0) 1 1 Ce C 1 y e y(1) e 2.7183
dy
y
xx
œ Ê œ Êœ œÊœ Ê œÊœ Ê œ¸
"!
8. y 2 (.2) 2.4,
"œ œ
ˆ‰
2
1
y 2.4 (.2) 2.8,
#œ œ
ˆ‰
2.4
1.2
y 2.8 (.2) 3.2,
$œ œ
ˆ‰
2.8
1.4
y 3.2 (.2) 3.6,
%œ œ
ˆ‰
3.2
1.6
y 3.6 (.2) 4;
&œ œ
ˆ‰
3.6
1.8
ln y ln x C y kx; y(1) 2 2 k y 2x y(2) 4
dy
yx
dx
œ Ê œ Êœ œÊœÊœ Ê œ
9. y 1 (.5) .5,
"
œ œ
’“
(1)
1
È
y .5 (.5) .39794,
#
œ œ
’“
(.5)
1.5
È
y .39794 (.5) .34195,
$
œ œ
’“
( .39794)
2
È
y .34195 (.5) .30497,
%
œ œ
’“
( .34195)
2.5
È
y .27812, y .25745, y .24088, y .2272;
&'()
œ œ œ œ
2 x C; y(1) 1 1 2 C C 1 y y(5) .2880
dy
yy
dx
x1x 15
œ Êœ œÊ œ Ê œÊ œ Ê œ ¸
ÈÈÈ
"""
# #
È
10. y 1 1 e 1,
"!"
œ œab
ˆ‰
3
y 1 1 e 0.68408,
##Î$ "
œ œ
ˆ‰ˆ‰
3
y 0.68408 0.68408 e 0.35245,
$%Î$ "
œ œ
ˆ‰ˆ‰
3
y 0.35245 0.35245 e 2.93295,
%'Î$ "
œ œ
ˆ‰ˆ‰
3
y 2.93295 2.93295 e 8.70790,
&)Î$ "
œ œ
ˆ‰ˆ‰
3
y 8.7079 8.7079 e 20.95441;
'"!Î$ "
œ œ
ˆ‰ˆ‰
3
y y e P(x) 1, Q(x) e P(x) dx x v(x) e y e e dx
w
"
œ Ê œ œ Ê œ Ê œ Ê œ
2x 2x x x 2x
e
''
xab
e e C ; y(0) 1 1 1 C C 2 y e 2e y(2) e 2e 39.8200œ œÊœ Ê œÊœ Ê œ ¸
xx 2x x
ab %#
11. Let z y 2y x 1 dx and y y y x 1 z x 1 dx with x 0, y 3, and dx 0.2.
n n1 n1 n1 n n1 n1 n1 n n 0 0
œ œ œ œ œ
ab a babab
The exact solution is y 3e . Using a programmable calculator or a spreadsheet (I used a spreadsheet) gives theœxx 2ab
values in the following table.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 9.3 Euler's Method 595
x z y-approx y-exact Error
0 --- 3 3 0
0.2 4.2 4.608 4.658122 0.050122
0.4 6.81984 7.623475 7.835089 0.211614
0.6 11.89262 13.56369 14.27646 0.712777
12. Let z y x 1 y dx and y y dx with x 1, y 0, and dx 0.2.
nn1n1 n1 nn1 0 0
x1y x1z
2
œ œ œ œ œ
ab Š‹
n1 n1 n n
abab
The exact solution is y 1 e . Using a programmable calculator or a spreadsheet (I used a spreadsheet) gives theœ
ˆ‰
1x 2Î
2
values in the following table.
x z y-approx y-exact Error
1 --- 0 0 0
1.2 0.2 1.196 0.197481 0.001481
1.4 0.38896 0.378026 0.381217 0.003191
1.6 0.552178 0.536753 0.541594 0.004841
13. 2xe , y 0 2 y y 2x e dx y 2x e 0.1 y 0.2x e
dy
dx n1nn nn n n
œœÊœœ œ
xxxx
22 2
nn n
ab a b
2
On a TI-92 Plus calculator home screen, type the following commands:
2 STO > y: 0 STO > x: y (enter)
y 0.2*x*e^(x^2) STO > y: x 0.1 STO > x: y (enter, 10 times)
The last value displayed gives y 1 3.45835
Eulerab¸
The exact solution: dy 2xe dx y e C; y 0 2 e C C 1 y 1 eœ Êœ œœ Ê œÊœ
xx x
22 2
ab 0
y 1 1 e 3.71828Êœ¸
exactab
14. y e 2, y 0 2 y y y e 2 dx y 0.5 y e 2
dy
dx
xxx
n1 n n n n
œ œÊ œ œ ab ab ab
nn
On a TI-92 Plus calculator home screen, type the following commands:
2 STO > y: 0 STO > x: y (enter)
y 0.5*(y e 2) STO > y: x 0.5 STO > x: y (enter, 4 times)
x
The last value displayed gives y 2 9.82187
Eulerab¸
The exact solution: y e 2 P x 1, Q x e 2 P(x) dx x v x e
dy
dx
xx x
œ Ê œ œ Ê œÊ œab ab ab
'
y e e 2 dx e x 2e C ;y 0 2 2 2 C C 0Êœ œ œÊœ Ê œ
1
e
xx x x
x'
ab a bab
y xe 2 y 2 2e 2 16.7781Êœ Ê œ ¸
x2
exactab
15. , y 0 y 0 y y dx y 0.1 y 0.
dy
dx y y y y
xn1 n n n
xx x
œ ß œ"Ê œ œ œ"
ÈÈÈÈ
ab a b
nn n
nn n
On a TI-92 Plus calculator home screen, type the following commands:
1 STO > y: 0 STO > x: y (enter)
y 0.1*( x /y) STO > y: x 0.1 STO > x: y (enter, 10 times)
È
The last value displayed gives y 1 1.5000
Eulerab¸
The exact solution: dy dx y dy x dx x C; 0 C CœÊœ Êœ œœœ Êœ
Èabab
x
y2322232
y2112 1
3/2 y0 3/2
Èab
222
x y x 1 y 1 1 1.5275Êœ Êœ Ê "œ ¸
y
23 2 3 3
21 4 4
3/2 3/2 exact 3/2
2Éab ab
É
16. 1 y , y 0 0 y y 1 y dx y 1 y 0.1 y 0.1 1 y
dy
dx
2222
n1 n n n
nn n
œ œÊ œ œ œ ab ab abab ab
On a TI-92 Plus calculator home screen, type the following commands:
0 STO > y: 0 STO > x: y (enter)
y 0.1*(1 y ) STO > y: x 0.1 STO > x: y (enter, 10 times)
2
The last value displayed gives y 1 1.3964
Eulerab¸
The exact solution: dy 1 y dx dx tan y x C; tan y 0 tan 0 0 0 C C 0œ Ê œ Ê œ œ œœÊœab ab
2111
dy
1y
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
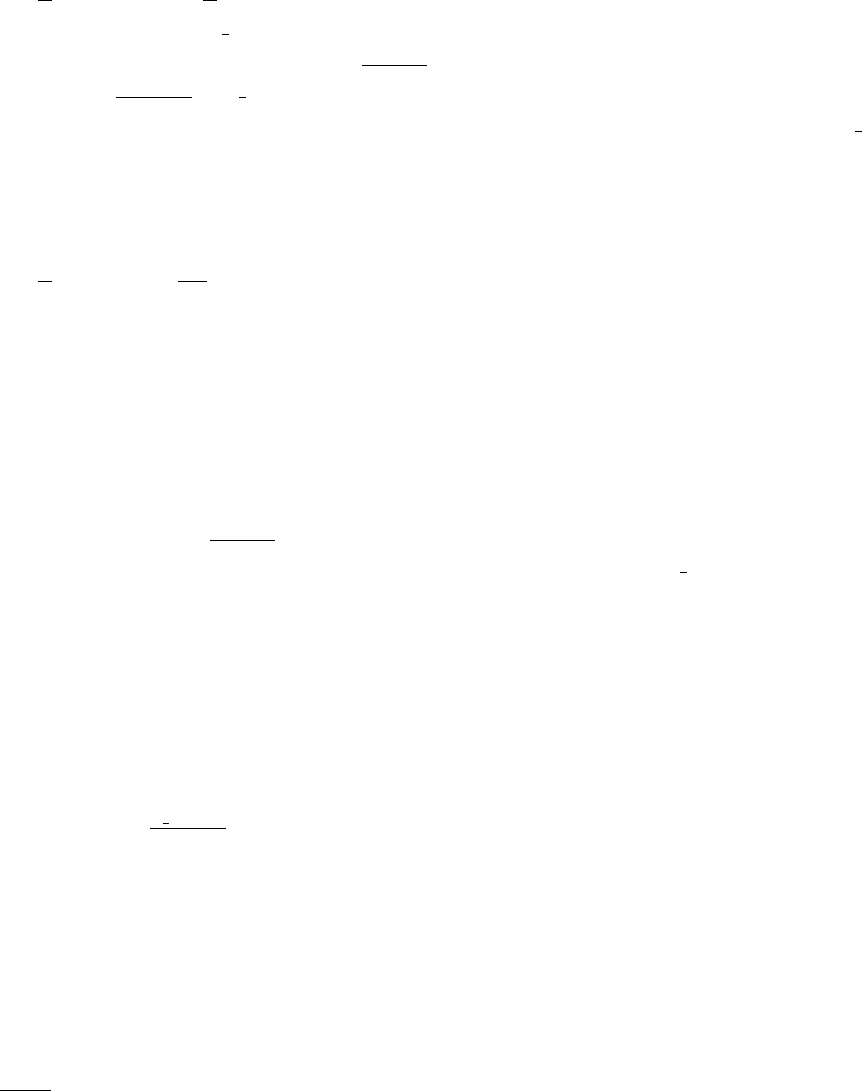
596 Chapter 9 Further Applications of Integration
tan y x y tan x y tan 1 1.5574ʜʜÊ"œ¸
1exactab
17. (a) 2y x 1 2 x 1 dx y dy 2x 2 dx y x 2x C
dy dy
dx y
222
œÊœÊ œÊœab ab a b
2''
"
Initial value: y 2 2 2 2 2 C C 2ab abœ Ê œ Ê œ
"
#
2
Solution: y x 2x 2 or yœ œ
"
21
x2x2
2
y 3 0.2abœ œ œ
11
3232 5
2ab
(b) To find the approximation, set y 2y x 1 and use EULERT with initial values x 2 and y and step size
12
œ œ œab "
#
0.2 for 5 Points. This gives y 3 0.1851; error 0.0149.ab¸ ¸
(c) Use step size 0.1 for 10 points. This gives y 3 0.1929; error 0.0071.ab¸ ¸
(d) Use step size 0.05 for 20 points. This gives y 3 0.1965; error 0.0035.ab¸ ¸
18. (a) y 1 dx ln y 1 x C y 1 e y 1 e e y Ae 1
dy dy
dx y 1
xC Cx x
œÊ œ Ê œÊœ Êœ„ Êœ
'
'kk kk
Initial value: y 0 3 3 Ae 1 A 2abœÊœ Ê œ
0
Solution: y 2e 1œ
x
y 1 2e 1 6.4366abœ¸
(b) To find the approximation, set y y 1 and use a graphing calculator or CAS with initial values x 0 and y 3
1œ œ œ
and step size 0.2 for 5 Points. This gives y 1 5.9766; error 0.4599ab¸¸
(c) Use step size 0.1 for 10 points. This gives y 1 6.1875; error 0.2491.ab¸¸
(d) Use step size 0.05 for 20 points. This gives y 1 6.3066; error 0.1300.ab¸¸
19. The exact solution is y , so y 3 0.2. To find the approximation, let z y 2y x 1 dx andœœ œ
1
x2x2 nn1 n1
2
n1
2ab a b
y y y x 1 z x 1 dx with initial values x 2 and y . Use a spreadsheet, graphing
nn1 n1 0 0
222
n1 nn
œ œ œ
"
#
ababab
calculator, or CAS as indicated in parts (a) through (d).
(a) Use dx 0.2 with 5 steps to obtain y 3 0.2024 error 0.0024.œ¸Ê¸ab
(b) Use dx 0.1 with 10 steps to obtain y 3 0.2005 error 0.0005.œ¸Ê¸ab
(c) Use dx 0.05 with 20 steps to obtain y 3 0.2001 error 0.0001.œ¸Ê¸ab
(d) Each time the step size is cut in half, the error is reduced to approximately one-fourth of what it was for the larger step
size.
20. The exact solution is y 2e 1, so y 1 2e 1 6.4366. To find the approximation, let z y y 1 dxœ œ¸ œ
xnn1 n1
ab a b
and y y dx with initial value y 3. Use a spreadsheet, graphing calculator, or CAS as indicated in
nn1 n
yz2
2
œ œ
ˆ‰
n1 n
parts (a) through (d).
(a) Use dx 0.2 with 5 steps to obtain y 1 6.4054 error 0.0311.œ¸Ê¸ab
(b) Use dx 0.1 with 10 steps to obtain y 1 6.4282 error 0.0084œ¸Ê¸ab
(c) Use dx 0.05 with 20 steps to obtain y 1 6.4344 error 0.0022œ¸Ê¸ab
(d) Each time the step size is cut in half, the error is reduced to approximately one-fourth of what it was for the larger step
size.
13-16. Example CAS commands:
:Maple
ode := diff( y(x), x ) = 2*x*exp(x^2);ic := y(0)=2;
xstar := 1;
dx := 0.1;
approx := dsolve( {ode,ic}, y(x), numeric, method=classical[foreuler], stepsize=dx ):
approx(xstar);
exact := dsolve( {ode,ic}, y(x) );
eval( exact, x=xstar );
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 9.3 Euler's Method 597
evalf( % );
17. Example CAS commands:
:Maple
ode := diff( y(x), x ) = 2*y(x)*(x-1);ic := y(2)=-1/2;
xstar := 3;
exact := dsolve( {ode,ic}, y(x) ); # (a)
eval( exact, x=xstar );
evalf( % );
approx1 := dsolve( {ode,ic}, y(x), # (b)
numeric, method=classical[foreuler], stepsize=0.2 ):
approx1(xstar);
approx2 := dsolve( {ode,ic}, y(x), # (c)
numeric, method=classical[foreuler], stepsize=0.1 ):
approx2(xstar);
approx3 := dsolve( {ode,ic}, y(x), # (d)
numeric, method=classical[foreuler], stepsize=0.05 ):
approx3(xstar);
19. Example CAS commands:
:Maple
ode := diff( y(x), x ) = 2*y(x)*(x-1);ic := y(2)=-1/2;
xstar := 3;
approx1 := dsolve( {ode,ic}, y(x), # (a)
numeric, method=classical[heunform], stepsize=0.2 ):
approx1(xstar);
approx2 := dsolve( {ode,ic}, y(x), # (b)
numeric, method=classical[heunform], stepsize=0.1 ):
approx2(xstar);
approx3 := dsolve( {ode,ic}, y(x), # (c)
numeric, method=classical[heunform], stepsize=0.05 ):
approx3(xstar);
21. Example CAS commands:
:Maple
ode := diff( y(x), x ) = x + y(x);ic := y(0)=-7/10;
x0 := -4;x1 := 4;y0 := -4; y1 := 4;
b := 1;
P1 := DEplot( ode, y(x), x=x0..x1, y=y0..y1, arrows=thin, title="#21(a) (Section 9.3)" ):
P1;
Ygen := unapply( rhs(dsolve( ode, y(x) )), x,_C1 ); # (b)
P2 := seq( plot( Ygen(x,c), x=x0..x1, y=y0..y1, color=blue ), c=-2..2 ): # (c)
display( [P1,P2], title="#21(c) (Section 9.3)" );
CC := solve( Ygen(0,C)=rhs(ic), C ); # (d)
Ypart := Ygen(x,CC);
P3 := plot( Ypart, x=0..b, title="#21(d) (Section 9.3)" ):
P3;
euler4 := dsolve( {ode,ic}, numeric, method=classical[foreuler], stepsize=(x1-x0)/4 ): # (e)
P4 := odeplot( euler4, [x,y(x)], x=0..b, numpoints=4, color=blue ):
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

598 Chapter 9 Further Applications of Integration
display( [P3,P4], title="#21(e) (Section 9.3)" );
euler8 := dsolve( {ode,ic}, numeric, method=classical[foreuler], stepsize=(x1-x0)/8 ): # (f)
P5 := odeplot( euler8, [x,y(x)], x=0..b, numpoints=8, color=green ):
euler16 := dsolve( {ode,ic}, numeric, method=classical[foreuler], stepsize=(x1-x0)/16 ):
P6 := odeplot( euler16, [x,y(x)], x=0..b, numpoints=16, color=pink ):
euler32 := dsolve( {ode,ic}, numeric, method=classical[foreuler], stepsize=(x1-x0)/32 ):
P7 := odeplot( euler32, [x,y(x)], x=0..b, numpoints=32, color=cyan ):
display( [P3,P4,P5,P6,P7], title="#21(f) (Section 9.3)" );
< < N | h | `percent error` >, # (g)
< 4 | (x1-x0)/ 4 | evalf[5]( abs(1-eval(y(x),euler4(b))/eval(Ypart,x=b))*100 ) >,
< 8 | (x1-x0)/ 8 | evalf[5]( abs(1-eval(y(x),euler8(b))/eval(Ypart,x=b))*100 ) >,
< 16 | (x1-x0)/16 | evalf[5]( abs(1-eval(y(x),euler16(b))/eval(Ypart,x=b))*100 ) >,
< 32 | (x1-x0)/32 | evalf[5]( abs(1-eval(y(x),euler32(b))/eval(Ypart,x=b))*100 ) > >;
13-24. Example CAS commands:
: (assigned functions, step sizes, and values for initial conditions may vary)Mathematica
For exercises 13 - 20, find the exact solution as follows. Set up two error lists.
Clear[x, y, f]
f[x_,y_]:= 2 y (x 1)
2
a = 2; b = 1/2;
xstar = 3;
desol=DSolve[{y'[x] == f[x, y[x]], y[a] == b}, y[x], x] //Simplify
actual[x_] = desol[[1, 1, 2]];
{xstar, actual[xstar]}
errorlisteuler = { };
errorlisteulerimp = { };
pa = Plot[actual[x], {x, a, xstar}]
Euler's method with error at x*. The command is used with a sequence of commands that are repeated n times.Do
a = 2; b = -1/2;
dx = 0.2;
xstar = 3; n = (xstar a) /dx;
solnslist = {{a,b}};
Do[ {new = b + f[a,b] dx, a = a + dx, b = new, AppendTo[solnslist, {a,b}]},{n}]
solnslist
error= actual[xstar] solnslist[[n, 2]]
relativeerror= error / actual[xstar]
AppendTo[errorlisteuler, error]
pe = ListPlot[solnslist, PlotStyle {Hue[.4], PointSize[0.02]}]Ä
Show[pa, pe]
Rerun with different values for dx, starting from largest to smallest. After doing this, observe what happens to the
error as the step size decreases by entering the input command: errorlisteuler
Improved Euler's method. with error at x*
a = 2; b = 1/2;
dx = 0.2;
xstar = 3; n = (xstar a) /dx;
solnslist = {{a,b}};
Do[{new1 = b f[a,b] dx, new2 = b + (f[a, b] f[a+dx, new1])/2 dx, a = a dx, b = new2,
AppendTo[solnslist, {a,b}]},{n}]
solnslist
error= actual[xstar] solnslist[[n, 2]
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
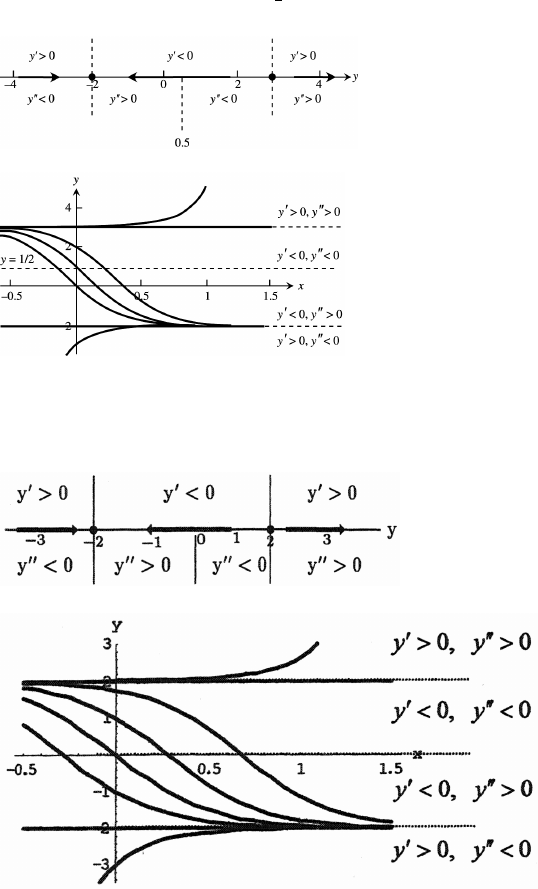
Section 9.4 Graphical Solutions of Autonomous Differential Equations 599
relativeerror= error / actual[xstar]
AppendTo[errorlisteulerimp, error]
peimp = ListPlot[solnslist, PlotStyle {Hue[.8], PointSize[0.02]}]Ä
Show[pa, peimp]
Rerun with different values for dx, starting from largest to smallest. After doing this, observe what happens to the
error as the step size decreases by entering the input command: errorlisteulerimp
You can also type Show[pa, pe, peimp]. This would be appropriate for a fixed value of dx with each method.
You can also make a list of relative errors.
Problems 21 - 24 involve use of code from section 9.1 together with the above code for Euler's method.
9.4 GRAPHICAL SOUTIONS OF AUTONOMOUS DIFFERENTIAL EQUATIONS
1. y y 2 y 3
wœ abab
(a) y 2 is a stable equilibrium value and y 3 is an unstable equilibrium.œ œ
(b) y 2y 1 y 2 y 2 y y 3
ww w
œ œ a b ab ab
ˆ‰
1
2
(c)
2. y y 2 y 2
wœ abab
(a) y 2 is a stable equilibrium value and y 2 is an unstable equilibrium.œ œ
(b) y 2yy 2y 2yy 2
ww w
œœ abab
(c)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
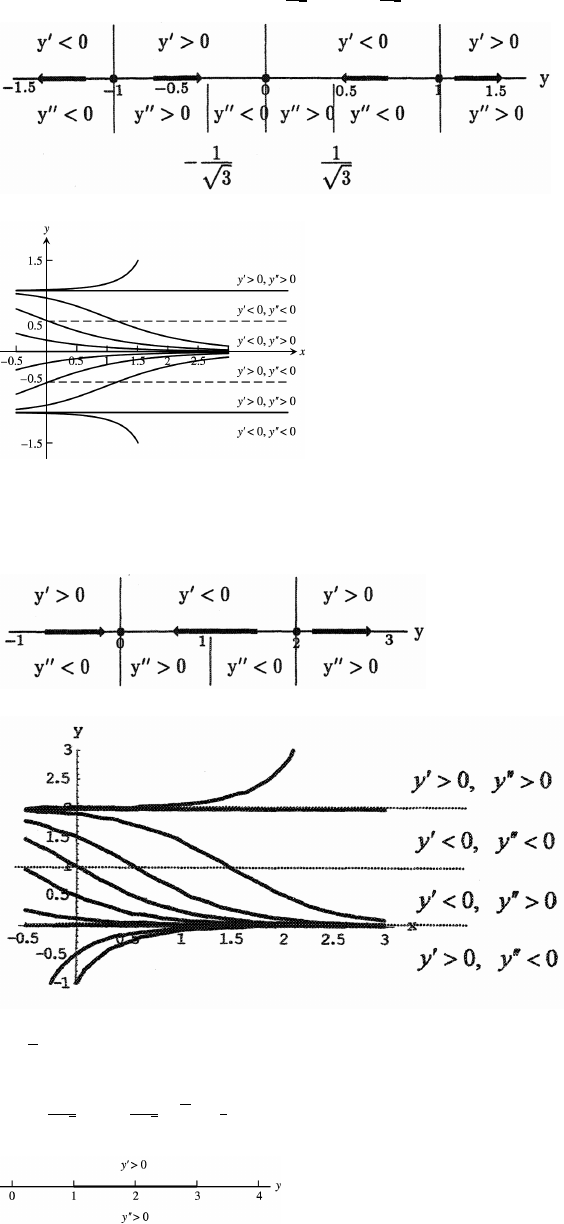
600 Chapter 9 Further Applications of Integration
3. y y y y 1 y y 1
wœœ
3abab
(a) y 1 and y 1 is an unstable equilibrium and y 0 is a stable equilibrium value.œ œ œ
(b) y 3y 1 y 3 y 1 y y y y 1
ww w
œœ a b ab ab
Š‹Š‹
211
33
ÈÈ
(c)
4. y y y 2
wœab
(a) y 0 is a stable equilibrium value and y 2 is an unstable equilibrium.œœ
(b) y 2y 2 y 2y y 1 y 2
ww w
œ œ a b abab
(c)
5. y y, y 0
wœ
È
(a) There are no equilibrium values.
(b) y y y
ww w "
#
œœ œ
11
2y 2y
ÈÈ
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 9.4 Graphical Solutions of Autonomous Differential Equations 601
(c)
6. y y y, y 0
wœ
È
(a) y 1 is an unstable equilibrium.œ
(b) y 1 y 1 y y y y 1
ww w "
#
œ œ œ
Š‹Š‹
ˆ‰ˆ‰ˆ‰
ÈÈ È
11
2y 2y
ÈÈ
(c)
7. y y 1 y 2 y 3
wœababab
(a) y 1 and y 3 is an unstable equilibrium and y 2 is a stable equilibrium value.œœ œ
(b) y 3y 12y11y1y2y3 3y1y y2y y3
ww
œœa babababab ab ab
Š‹Š‹
263 63
33
ÈÈ
(c)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
602 Chapter 9 Further Applications of Integration
8. y y y y y 1
wœœ
32 2
ab
(a) y 0 and y 1 is an unstable equilibrium.œœ
(b) y 3y 2y y y y 3y 2 y 1
ww œ œ abababab
2323
(c)
9. 1 2P has a stable equilibrium at P . 2 2 1 2P
dP d P dP
dt dt dt
œ œ œ œ
"
#
2
2ab
10. P 1 2P has an unstable equilibrium at P 0 and a stable equilibrium at P .
dP
dt œ œ œab "
#
14P P14P12P
dP dP
dt dt
2
2œ œ ababab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 9.4 Graphical Solutions of Autonomous Differential Equations 603
11. 2P P 3 has a stable equilibrium at P 0 and an unstable equilibrium at P 3.
dP
dt œ œ œab
2 2P 3 4P 2P 3 P 3
dP dP
dt dt
2
2œœ ab abab
12. 3P 1 P P has a stable equilibria at P 0 and P 1 an unstable equilibrium at P .
dP
dt œ œ œ œab
ˆ‰
" "
# #
6P 6P+1 P P P P P 1
dP 3 dP 3
dt dt 6 6
233 33
2
2œ œ
## #
"
ab ab
Š‹Š‹
ˆ‰
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
604 Chapter 9 Further Applications of Integration
13.
Before the catastrophe, the population exhibits logistic growth and P t M , the stable equilibrium. After theabÄ0
catastrophe, the population declines logistically and P t M , the new stable equilibrium.abÄ1
14. rP M P P m , r, M, m 0
dP
dt œ abab
The model has 3 equilibrium points. The rest point P 0, P M are asymptotically stable while P m is unstable. Forœœ œ
initial populations greater than m, the model predicts P approaches M for large t. For initial populations less than m, the
model predicts extinction. Points of inflection occur at P a and P b where a and
Mm M mMm
œœ œ
"
322
‘
È
b.
Mm M mMm
œ
"
322
‘
È
(a) The model is reasonable in the sense that if P m, then P 0 as t ; if m P M, then P M as t ; ifÄÄ_ ÄÄ_
P M, then P M as t .ÄÄ_
(b) It is different if the population falls below m, for then P 0 as t (extinction). If is probably a more realisticÄÄ_
model for that reason because we know some populations have become extinct after the population level became too
low.
(c) For P M we see that rP M P P m is negative. Thus the curve is everywhere decreasing. Moreover,œ
dP
dt abab
P M is a solution to the differential equation. Since the equation satisfies the existence and uniqueness conditions,´
solution trajectories cannot cross. Thus, P M as t .ÄÄ_
(d) See the initial discussion above.
(e) See the initial discussion above.
15. g v , g, k, m 0 and v t 0
dv k
dt m
2
œ ab
Equilibrium: g v 0 v
dv k
dt m k
2mg
œ œÊœ
É
Concavity: 2 v 2 v g v
dv k dv k k
dt m dt m m
2
2
2œ œ
ˆ‰ ˆ‰ˆ ‰
(a)
(b)
(c) v 178.9 122 mph
terminal 160 ft
0.005 s
œœ œ
É
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
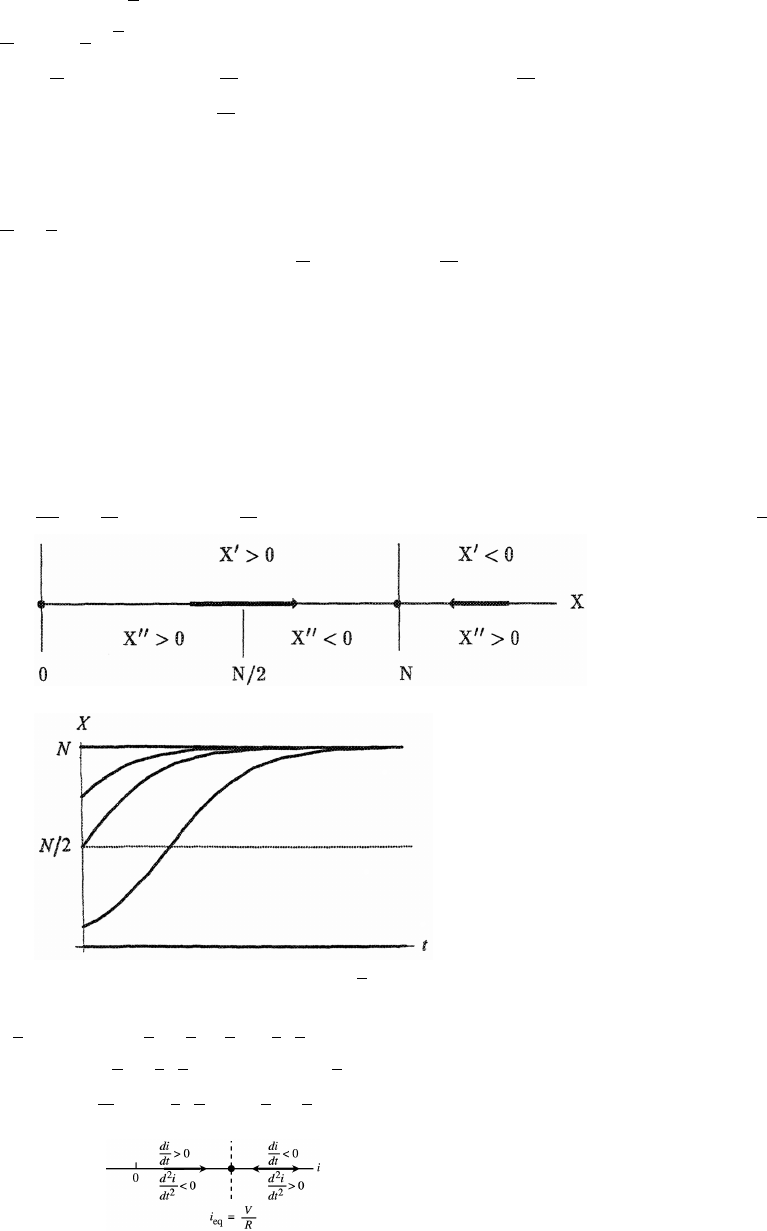
Section 9.4 Graphical Solutions of Autonomous Differential Equations 605
16. F F Fœ
pr
ma mg k vœ
È
g v, v 0 v
dv k
dt m 0
œ œ
Èab
Thus, 0 implies v , the terminal velocity. If v , the object will fall faster and faster, approaching the
dv
dt k k
mg mg
22
0
œœ
ˆ‰ ˆ‰
terminal velocity; if v , the object will slow down to the terminal velocity.
0mg
k
2
ˆ‰
17. F F Fœ
pr
ma 50 5 vœkk
50 5 v
dv 1
dt m
œabkk
The maximum velocity occurs when 0 or v 10 .
dv ft
dt sec
œœ
18. (a) The model seems reasonable because the rate of spread of a piece of information, an innovation, or a cultural fad is
proportional to the product of the number of individuals who have it (X) and those who do not (N X). When X is
small, there are only a few individuals to spread the item so the rate of spread is slow. On the other hand, when
(N X) is small the rate of spread will be slow because there are only a few indiciduals who can receive it during the
interval of time. The rate of spread will be fastest when both X and (N X) are large because then there are a lot of
individuals to spread the item and a lot of individuals to receive it.
(b) There is a stable equilibrium at X N and an unstable equilibrium at X 0.œœ
k N X kX k X N X N 2X inflection points at X 0, X , and X N.
d X dX dX N
dt dt dt 2
2
2
2œœÊ œœ œab aba b
(c)
(d) The spread rate is most rapid when x . Eventually all of the people will receive the item.œN
2
19. L Ri V i i , V, L, R 0
di di V R R V
dt dt L L L R
œÊœœ
ˆ‰
Equilibrium: i 0 i
di R V V
dt L R R
œœÊœ
ˆ‰
Concavity: i
di R di R V
dt L dt L R
2
2
2œ œ
ˆ‰ ˆ‰ˆ ‰
Phase Line:
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
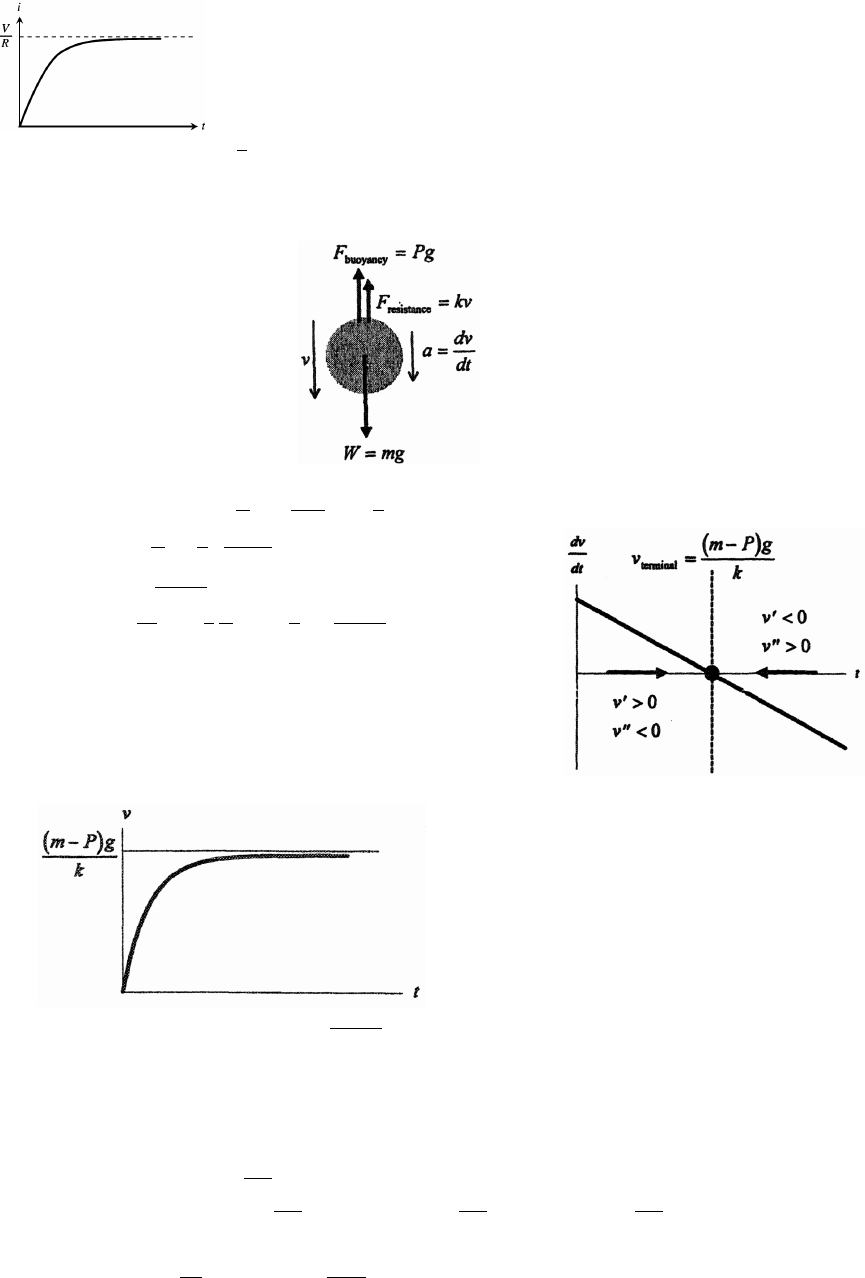
606 Chapter 9 Further Applications of Integration
If the switch is closed at t 0, then i 0 0, and the graph of the solution looks like this:œœab
As t , it i . (In the steady state condition, the self-inductance acts like a simple wire connector and, asÄ_ Ä œ
steady state V
R
a result, the current throught the resistor can be calculated using the familiar version of Ohm's Law.)
20. (a) Free body diagram of he pearl:
(b) Use Newton's Second Law, summing forces in the direction of the acceleration:
mg Pg kv ma g v.œ Êœ
dv m P k
dt m m
ˆ‰
(c) Equilibrium: v 0
dv k
dt m k
mPg
œœ
Š‹
ab
vʜ
terminal mPg
k
ab
Concavity: v
dv kdv k
dt m dt m k
2mPg
2
2œ œ
ˆ‰
Š‹
ab
(d)
(e) The terminal velocity of the pearl is .
abmPg
k
9.5 APPLICATIONS OF FIRST ORDER DIFFERENTIAL EQUATIONS
1. Note that the total mass is 66 7 73 kg, therefore, v v e v 9eœ œ Êœ
0kmt 3.9t73Î Îab
(a) s t 9e dt e Cabœœ
'Î Î3.9t 73 3.9t 73
2190
13
Since s 0 0 we have C and s t 1 e 168.5ab ab ˆ‰
œœ œœ¸
2190 2190 2190
13 13 13
tt
3.9t 73
lim lim
Ä_ Ä_
Î
The cyclist will coast about 168.5 meters.
(b) 1 9e ln 9 t 41.13 secœÊœÊœ¸
Î3.9t 73 3.9t 73 ln 9
73 3.9
It will take about 41.13 seconds.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
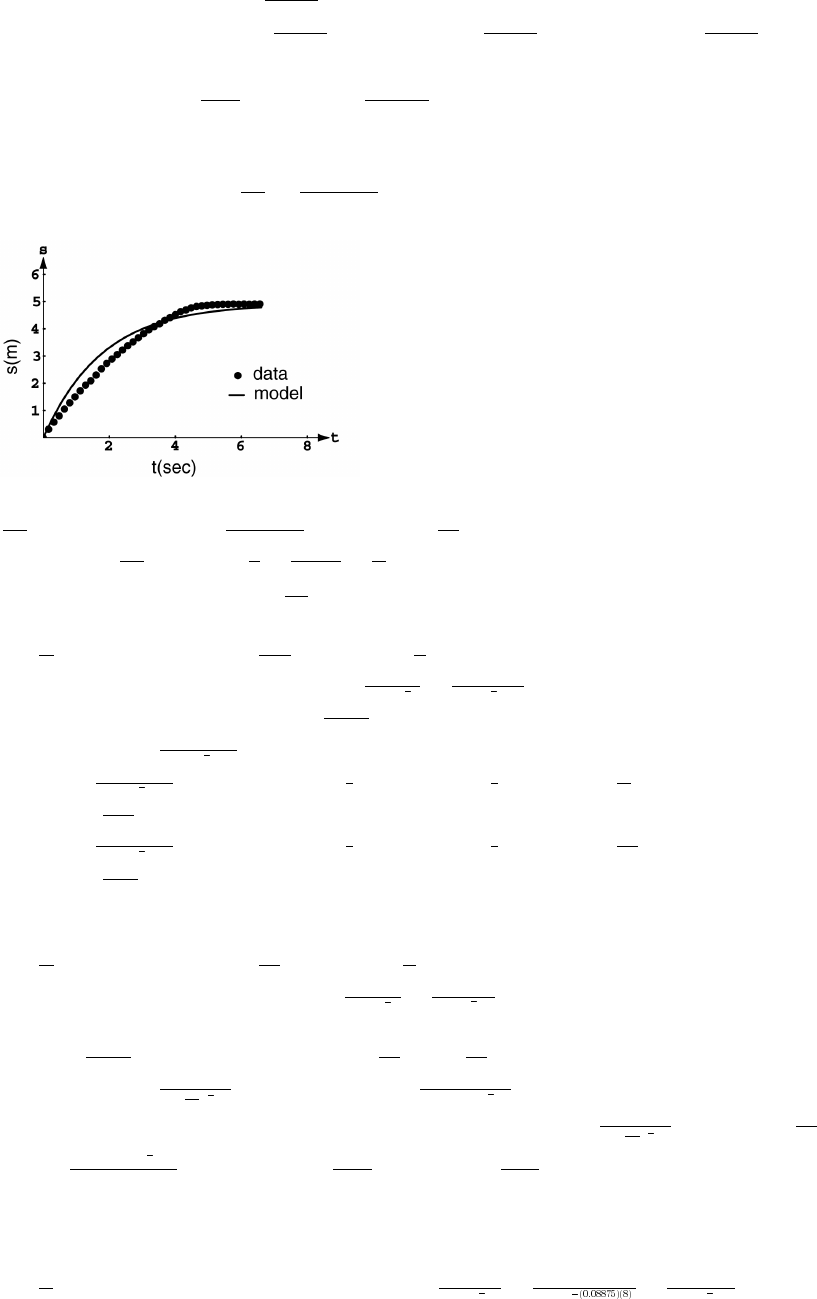
Section 9.5 Applications of First-Order Differential Equations 607
2. v v e v 9e v 9eœÊœ Êœ
0k m t 59,000 51,000,000 t 59t 51,000Î Î Îab a b
(a) s t 9e dt e Cabœœ
'Î Î59t 51,000 59t 51,000
459,0000
59
Since s 0 0 we have C and s t 1 e 7780 mab ab ˆ‰
œœ œ œ¸
459,0000 459,0000 459,0000
59 59 59
tt
59t 51,000
lim lim
Ä_ Ä_
Î
The ship will coast about 7780 m, or 7.78 km.
(b) 1 9e ln 9 t 1899.3 secœÊœÊœ¸
Î59t 51,000 59t
51,000 59
51,000 ln 9
It will take about 31.65 minutes.
3. The total distance traveled 4.91 k 22.36. Therefore, the distance traveled is given by theœÊ œ Êœ
vm
kk
2.75 39.92
0aba b
function s t 4.91 1 e . The graph shows s t and the data points.ab ab
ˆ‰
œ
ab22.36/39.92 t
4. coasting distance 1.32 k
vm
kk33
0.80 49.90 998
0œÊœÊœ
aba b
We know that 1.32 and .
vm
k m 33 49.9 33
k 998 20
0œœœ
ab
Using Equation 3, we have: s t 1 e 1.32 1 e 1.32 1 eab a b
ˆ‰ˆ‰
œ œ ¸
vm
k
k/m t 20t/33 0.606t
0ab
5. (a) 0.0015P 150 P P 150 P P M P
dP 0.255 k
dt 150 M
œœœab abab
Thus, k 0.255 and M 150, and Pœœœœ
M 150
1Ae 1Ae
kt 0.255t
Initial condition: P 0 6 6 1 A 25 A 24abœÊœ Ê œ Ê œ
150
1Ae0
Formula: P œ150
1 24e0.255t
(b) 100 1 24e 24e e 0.255t ln 48œÊœÊœÊœÊœ
150 3
1 24e 2 48
0.255t 0.255t 0.255t
#
""
0.255t
t 17.21 weeksÊœ ¸
ln 48
0.255
125 1 24e 24e e 0.255t ln 120œÊœÊœÊœÊœ
150 6
1 24e 5 5 120
0.255t 0.255t 0.255t
""
0.255t
t 21.28Êœ ¸
ln 120
0.255
It will take about 17.21 weeks to reach 100 guppies, and about 21.28 weeks to reach 125 guppies.
6. (a) 0.0004P 250 P P 150 P P M P
dP 0.1 k
dt 250 M
œœœababab
Thus, k 0.1 and M 250, and Pœœ œœ
M 250
1Ae 1Ae
kt 0.1t
Initial condition: P 0 28, where t 0 represents the year 1970abœœ
28 28 1 A 250 A 1 7.9286œÊœÊœœ¸
250 250 111
1Ae 28 140ab
Formula: P or approximately Pœœ
250 250
1e 1 7.9286e
111 0.1t
14 0.1t
(b) The population P t will round to 250 when P t 249.5 249.5 249.5 1 e 250ab ab ˆ‰
Êœ Ê œ
250 111
1e 14
0.1t
111
14 0.1t
0.5 e 0.1t ln t 10 ln 55,389 ln 14 82.8.ʜʜʜʜ¸
ab
ˆ‰
249.5 111e
14 55,389 55,389
0.1t 14 14
0.1t ab
It will take about 83 years.
7. (a) Using the general solution form Example 2, part (c),
0.08875 10 8 10 y y y t
dy
dt 1 Ae 1 Ae
77 M810810
1Ae
œ‚‚Êœœ œababab
‚‚
rMt 0.71t
77
t
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
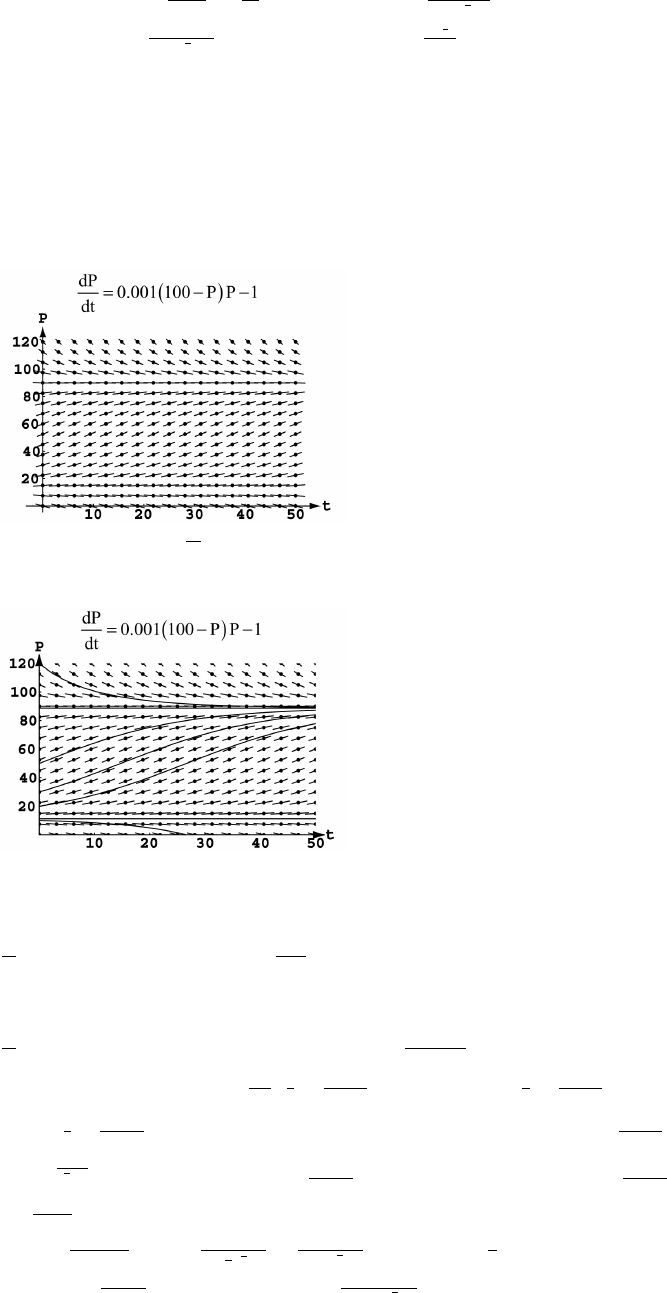
608 Chapter 9 Further Applications of Integration
Apply the initial condition:
y 0 1.6 10 1 4 y 1 2.69671 10 kg.ab abœ‚ œ ÊœÊ œ ¸ ‚
7 7
810 8 810
1 A 1.6 1 4e
‚‚
77
0.71
(b) y t 4 10 4e 1 t 1.95253 years.abœ‚ œ Ê œÊœ ¸
7 0.71t
810
14e 0.71
ln
‚
7
0.71t
1
4
ˆ‰
8. (a) If a part of the population leaves or is removed from the environment (e.g., a preserve or a region) each year, then c
would represent the rate of reduction of the population due to this removal and/or migration. When grizzly bears
become a nuisance (e.g., feeding on livestock) or threaten human safety, they are often relocated to other areas or even
eliminated, but only after relocation efforts fail. In addition, bears are killed, sometimes accidently and sometimes
maliciously. For an environment that has a capacity of about 100 bears, a realistic value for c would probably be
between 0 and 4.
(b)
Equilibrium solutions: 0 0.001 100 P P 1 P 100P 1000 0 P 11.27 (unstable) and
dP
dt
2eq
œœ ʜʸab
P 88.73 (stable)
eq ¸
(c)
For 0 P 0 11, the bear population will eventually disappear, for 12 P 0 88, the population will grow toŸ ŸŸab ab
about 89, the population will remain at about 89, and for P 0 89, the population will decrease to about 89 bears.ab
9. (a) 1 y dy 1 y dt dt ln 1 y t C e e 1 y e e
dy dy
dt 1 y 1ln 1 y t C t C
œÊ œ Ê œ Ê œ Ê œ Ê œab kk kk
kk 11
1 y C e y Ce 1, where C e and C C . Apply the initial condition: y 0 1 Ce 1œ„ Êœ œ œ„ œœ
222
tt C 0
1ab
C2 y2e 1.ʜʜ
t
(b) 0.5 400 y y dy 0.5 400 y y dt 0.5 dt. Using the partial fraction decomposition in
dy dy
dt 400 y y
œÊœÊ œab abab
Example 2, part (c), we obtain dy 0.5 dt dy 200 dt
11 1 1 1
400 y 400 y y 400 y
Š‹ Š‹
œÊœ
dy 200 dt ln y ln y 400 200t C ln 200t CÊ œ ÊœÊ œ
''
Š‹ ¹¹
kk k k
11
y 400 y y 400
11
y
e e e e C e (where C e ) C eÊœœÊœ œÊœ„
ln 200t C 200t C 200t C 200t
yy
y 400 y 400
22 2
¹¹
y
y 400 11 1
¹¹
Ce (where C C ) y Ce y 400 Ce 1 Ce y 400 CeÊœ œ„Êœ Ê œ
y
y 400
200t 200t 200t 200t 200t
2
ab
y y , where A . Apply the initial condition:Êœ Êœ œ œ
400 Ce 400 400 1
Ce 1 1 Ae C
1e
200t
200t 1 200t
C200t
y0 2 A 199 ytab abœœ Ê œ Ê œ
400 400
1 Ae 1 199e
0 200t
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 9.5 Applications of First-Order Differential Equations 609
10. r M P P dP r M P P dt r dt. Using the partial fraction decomposition in Example 6, part (c),
dP dP
dt M P P
œÊœ Ê œab ab ab
we obtain dP r dt dP rM dt dP rM dt
11 1 1 1 1 1
MP MP P MP P P M
ˆ‰ ˆ‰ ˆ‰
œÊœÊœ
''
ln P ln P M rM t C ln rM t C e e e eÊœ Ê œ Ê œ œkk k kab ab
¸¸
11
P
PM
ln rM t C rM t C
¸¸ ab ab
P
PM 11
C e (where C e ) C e Ce (where C C )Ê œ œ Ê œ„ Ê œ œ„
¸¸
PPP
P M PM PM
22 2 2
rM t C rM t rM t
ab ab ab
1
P Ce P MCe 1 Ce P MCe P PÊœ Ê œ Êœ Êœ
ab ab ab abrM t rM t rM t rM t MCe
Ce 1
M
1e
ˆ‰ rM t
rM t 1
CrM t
P , where A .Êœ œ
M1
1Ae C
rM t
11. (a) kP P dP k dt P kt C P
dP
dt kt C
22
œÊ œ ʜʜ
''
""
Initial condition: P 0 P P CabœÊœÊœ
00 11
CP
0
Solution: P œ œ
1
kt 1/P 1 kP t
P
ab
00
0
(b) There is a vertical asymptote at t œ1
kpO
12. (a) r M P P m r 1200 P P 100 r 1100 r
dP dP 1 dP 1100 dP
dt dt 1200 P P 100 dt 1200 P P 100 dt
œ Êœ Ê œÊ œabab a ba b
abab abab
1100 r 1100 r dP 1100 r dtʜʜʜ
aba b
abab
P 100 1200 P
1200 P P 100 dt 1200 P P 100 dt 1200 P P 100
dP 1 1 dP 1 1
ˆ‰ˆ‰
dP 1100 r dt ln 1200 P ln P 100 1100 r t Cʜ ʜ
''
ˆ‰ abab
11
1200 P P 100 1
ln 1100 r t C ln 1100 r t C e e Ceʜʜʜ„Êœ
¸¸ ¸¸
P 100 P 100 P 100 P 100
1200 P 1200 P 1200 P 1200 P
11
C 1100 r t 1100 r t
1
where C e P 100 1200Ce CPe P 1 Ce 1200Ce 100œ„ʜʜ
C 1100 r t 1100 r t 1100 r t 1100 r t
1ab
P P where A .Êœ œ Êœ œ
1200Ce 100 1200 100Ae 1
Ce 1 1 Ae C
1200 e
1e
1100 r t 1100 r t
1100 r t 1 1100 r t
100
C1100 r t
C1100 r t
(b) Apply the initial condition: 300 300 300A 1200 100A A Pœ ʜʜʜ Þ
1200 100A 9 2400 900Ae
1A 2 29e
1100 r t
1100 r t
(Note that P 1200 as t .)ÄÄ_
(c) r M P P m r r M m r M m
dP 1 dP M m dP dP
dt M P P m dt M P P m dt M P P m dt
Pm MP
œ Ê œÊ œÊ œabab ab ab
abab abab abab
abab
rM m dP rM mdtÊ œÊ œ
ˆ‰ ˆ‰
ab ab
11dP 11
MP Pmdt MP Pm
''
ln M P ln P m M m r t C ln M m r t C e eÊœÊ œÊœ„ababab ab
¸¸
11
Pm Pm
MP MP
CMm rt
1ab
Ce where C e P m MCe CPeÊœ œ„Êœ
Pm
MP
M m rt C M m rt M m rt
ab ab ab
1
P1 Ce MCe m P P PÊ œ Êœ Êœ Êœ
ˆ‰
ab abMm rt Mm rt MCe m M mAe
Ce 1 1 Ae
Me
1e
Mm rt Mm rt
Mm rt Mm rt
m
CMm rt
1
CMm rt
A.œ1
C
Apply the initial condition P 0 Pabœ0
PPPAMmAAP
000
MmA
1A P m
MP MP m mM P e
Pm MPe
œÊœÊœÊœ
0
0
00
Mm rt
00
Mm rt
abab
abab
(Note that P M as t provided P m.)ÄÄ_
0
13. y mx m 0 y . So forœÊœÊ œÊœ
yxyy y
xx x
w
2
orthogonals: y dy x dx C
dy y
dx y 2 2
xx
œ Ê œ Ê œ
22
xyCʜ
22 1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
610 Chapter 9 Further Applications of Integration
14. y cx c 0 x y 2xyœÊœÊ œÊ œ
22
y x y 2xy
xx
24
2w
y . So for the orthogonals: Êœ œ
w2y dy
xdx2y
x
2ydy xdx y C y C,ʜʜʜ„
2xx
22
22
É
C0
15. kx y 1 1 y kx k
22 2 21y
x
œÊœ Ê œ
2
2
0 2yx y 1 y 2xʜʜ
x2yy 1 y2x
x
22
22
ab ˆ‰
wabab
y . So for the orthogonals:Êœ œ
w
ˆ‰ ˆ‰
ab1y 2x 1y
2xy xy
22
2
dy x dx ln y C
dy xy y
dx 1 y y 2 2
1y x
œ Ê œ Ê œ
2
222
ˆ‰
16. 2x y c 4x 2yy 0 y . For
222 4x 2x
2y y
œÊ œÊœœ
ww
orthogonals: ln y ln x C
dy y dy
dx 2x y 2x
dx
œÊœÊ œ
"
#
ln y ln x ln C y C xʜ ʜ
1/2 11
1/2
kk
17. y ce cœÊœÊ œ!
xy
ex
ey ye 1
e
xx
x2
ccabab
ab
e y ye y y. So for the orthogonals:ʜʜ
w wxx
ydy dx x C
dy y
dx y 2
1
œÊ œ Ê œ
2
y 2xC y 2xCÊœ Êœ„
211
È
18. y e ln y kx k 0œÊ œÊ œÊ œ
kx ln y
x
xyln y
x
Š‹
1
y
2
c
y ln y 0 y . So for the orthogonals:ʜʜ
Š‹
x
yx
yln y
ww
y ln y dy x dx
dy
dx y ln y
x
œÊ œ
yln y y x Cʜ
""
##
222
1
4ab ˆ‰
y ln y x Cʜ
22
y
21
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 9.5 Applications of First-Order Differential Equations 611
19. 2x 3y 5 and y x intersect at 1, 1 . Also, 2x 3y 5 4x 6y y 0 y y 1, 1
22 23 22 4x 2
6y 3
œ œ œÊ œÊœÊ œab ab
ww w
y x 2y y 3x y y 1, 1 . Since y y 1, the curves are orthogonal.
1
23 2
1111 1
3x 3 2 3
2y 2 3 2
œÊ œ Êœ Ê œ †œ œ
www ww
2
1ab ˆ‰ˆ‰
20. (a) x dx y dy 0 C is the general equationœÊœ
x
22
y
22
of the family with slope y . For the orthogonals:
wœ
x
y
y ln y ln x C or y C x
wœÊ œ Ê œ œ
ydy
xyx
dx 1
(where C e is the general equation of the
1C
τ
orthogonals.
(b) x dy 2y dx 0 2y dx x dyœÊœÊœ
dy
2y x
dx
ln y ln x C y C x isʜʜʜ
""
##
Š‹
dy
yx
dx 12
the equation for the solution family.
ln y ln x C 0 y
""
##
w
œÊœÊœ
y2y
yx x
1
slope of orthogonals is ʜ
dy
dx 2y
x
2y dy x dx y C is the generalʜʜ
2x
2
2
equation of the orthogonals.
2 . y 4a 4ax and y 4b 4bx (at intersection) 4a 4ax 4b 4bx a b x a b"œ œÊ œ Êœ
22 22 2 2 22
ab
a b a b a b x x a b. Now, y 4a 4a a b 4a 4a 4ab 4ab y 2 ab.Ê œ Êœ œ œ œ Êœ„ababab ab È
22 22
Thus the intersections are at a b, 2 ab . So, y 4a 4ax y which are equal to and
Š‹
È
„ œ Êœ
22 14a 4a
2y 22 ab
w
Š‹
È
and at the intersections. Also, y 4b 4bx y which are equal to andœ œÊœ
4a a a 4b 4b
22ab 22 ab
bb 2y
22 2
Š‹ Š‹
È È
w
ÈÈ
and at the intersections. y y . Thus the curves are orthogonal.
4b b b
22ab aa 12
Š‹
È
ww
œ † œ"
ÉÉ abab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

612 Chapter 9 Further Applications of Integration
CHAPTER 9 PRACTICE EXERCISES
. y cos y dx 2tan y x C y tan"œ Ê œÊ œÊœ
dy dy
dx y cos y 2
2 1 xC 2
ÈÈ È ˆ‰ˆ‰
ÈÈ
2
2. y dy 3 x 1 dx y ln y x 1 C
w
œÊœÊœ
3yx1 y1 2 3
y1 y
ab ab
2ab ab
3. yy sec y sec x sec x dx tan x C sin y 2tan x C
wœÊœÊœÊœab ab
22 2 2
y dy
sec y 2
sin y 1
ab ˆ‰
2
2
4. y cos x dy sin x dx 0 y dy dx C y C
2sin x 1 2
cos x 2 cos x cos x
y1
ab É
œÊœÊœÊœ„
2
2
ab ab ab
5. y xe x 2 e dy x x 2 dx e C e C
w
œÊœÊœ Êœ
yy y y
2x 2 3x 4 2x 2 3x 4
15 15
ÈÈ aba b aba b
3/2 3/2
ylnCylnCÊ œ Ê œ
’“’“
2x 2 3x 4 2x 2 3x 4
15 15
aba b aba b
3/2 3/2
6. y xye e x dx ln y e C
w"
#
œÊœ Êœ
xx x
dy
y
22 2
7. sec x dy x cos y dx 0 tan y cos x x sin x CœÊœÊœ
2dy
cos y sec x
xdx
2
8. 2x dx 3 y csc x dy 0 3 y dy dx 2y 2 2 x cos x 4x sin x C
23/22
2x
csc x
œÊœÊœ
ÈÈ ab
2
y 2 x cos x 2x sin x Cʜ
3/2 2 1
ab
9. y ye dy y 1 e ln x C
w
œÊ œÊ œ
edx
xy x
yy
yab kk
10. y xe csc y y csc y dy x e dx sin y cos y x 1 e C
w w
œÊœÊœÊœ
xy x x
xe e e
ecsc y 2
xy y
yabab
11. x x 1 dy y dx 0 x x 1 dy y dx ln y ln x 1 ln x Cab ab ababœÊœÊœ Êœ
dy
yxx1
dx
ab
ln y lnx 1 lnx ln C ln y ln yÊœ Êœ Êœabab Š‹
1Cx 1 Cx 1
xx
11
ab ab
12. y y 1 x ln x C ln 2ln x ln C C x
w
œ Ê œÊ œ Ê œ Ê œabab Š‹
21 2
dy y1 y1
y1 x 2 y1 y1
dx 11
2
lnŠ‹
y1
y1
13. 2y y xe y y e .
ww
"
#
œ Ê œ
x/2 x/2
x
2
px , vx e e .ab abœ œ œ
"
#
'ˆ‰
c
"
#dx x/2
e y e y e e e y e y C y e C
w
"
#
x/2 x/2 x/2 x/2 x/2 x/2 x/2
xxd x x x
22dx 2 4 4
œ œÊ œÊ œ Êœ
ˆ‰ˆ‰ˆ‰ ˆ ‰ Š‹
22
14. y e sin x y 2y 2e sin x.
y
2
xx
œ Ê œ
w
px 2, vx e e .ab abœœœ
'2dx 2x
e y 2e y 2e e sin x 2e sin x e y 2e sin x e y e sin x cos x C
2x 2x 2x x x 2x x 2x x
d
dx
w
œ œÊ œÊœab a b
y e sin x cos x Ceʜ
x2x
ab
15. xy 2y 1 x y y .
ww
œ Ê œ
1211
xxx
ˆ‰ 2
vx e e e x.abœœœœ
22ln xln x2
'dx
x2
xy 2xy x 1 xy x 1 xy x C y
222
dx1C
dx 2 x x
w"
#
œÊ œÊ œ Êœab 2
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 9 Practice Exercises 613
16. xy y 2x ln x y y 2 ln x.
ww
œ Ê œ
ˆ‰
1
x
v x e e . y y ln xab ˆ‰ ˆ‰
œœœ œÊ
w
'dx
xln x 11 1 2
xx x x
2
y ln x y C y x Cx
ln x ln x
d1 2 1
dx x x x
22
ˆ‰ cd cd†œ ʆœ Êœ
17. 1 e dy ye e dx 0 1 e y e y e y y .aba b ab œÊœÊœ œ
xxx xxx ee
1e 1e
ww
xx
xx
ab
vx e e e 1.abœœ œ
'edx
x
1e
xx
ln e 1 xab
e1y e1 y e1 e e1ye C
e1y
abab abc d ab
ˆ‰ ab
xx x xxx
ee d
1e 1e dx
x
œ Ê œÊœ
w
xx
xx
ab
yÊœ œ
eC eC
e1 1e
xx
xx
18. x 4ye 0 x x 4ye . Let v y e e . Then e x xe 4ye xe 4ye
dx d
dy dy
y y dy y y y 2y y 2y
œÊ œ œ œ œ Ê œ
ww
ab a b
'
xe 2y 1 e C x 2y 1 e Ceʜ ʜ
y2y yy
ab ab
19. x 3y dy y dx 0 x dy y dx 3y dy xy 3y dy xy y Cab abœÊœÊœÊœ
2223
d
dx
20. y dx 3x y cos y dx 0 x x y cos y. Let v y e e e y . œÊ œ œ œ œ œab ab
Š‹
w2 3 3ln y ln y 3
3
y
'3dy
y3
Then y x 3y x cos y and y x cos y dy sin y C. So x y sin y C
32 3 3w
œ œ œ œ
'ab
21. e e dy e dx e e C. We have y 0 2, so e e C C 2e and
dy
dx
xy2 y x2 y x2 2 2 2
œÊœ Êœ œœÊœ
ab ab ab
e e 2e y ln e 2e
yx22 x22
œ Ê œ
ab ab
ˆ‰
22. ln ln y tan x C y e . We have y 0 e e e
dy y ln y dy
dx 1 x y ln y 1 x
dx 1e 22e
œÊœÊ œ Êœ œÊœ
22
tan x C tan 0 C
11
a b ab ab
e 2tan0Cln 20Cln 2Cln 2yeʜʜʜʜʜ
tan 0 C 1 e
1tan x ln 2
1
ab
ab
23. x 1 2y x y y . Let v x e e e x 1 .ab ab ab
ˆ‰
œÊ œ œ œ œ œ
dy
dx x1 x1
2x dx 2lnx 1 lnx 1 2
w
'2
x1
2
ab ab
So y x 1 x 1 y x 1 xx 1 yx 1 xx 1dx
yx 1
w
ab ab ab abab ab
‘
ab
œ Ê œ Ê œ
22 2 2
2xd
x1 x1 dx
2
ab ab '
y x 1 C y x 1 C . We have y 0 1 1 C. Soʜʜ œÊœab ab ab
Š‹
22
xx xx
32 32
32 32
yx1 1œ ab
Š‹
2xx
32
32
24. x 2y x 1 y y x . Let v x e e x . So x y 2xy x x
dy
dx x x
2ln x223
21 dx
œÊ œ œ œ œ œ
w w
ˆ‰ ab 'ˆ‰
2
x
2
x y x x x y C y . We have y 1 1 1 C C .Ê œÊ œÊœ œÊœÊœ
dxxxC 11
dx 4 2 4 x 4 4
23 2
ab ab
42 2
2
""
##
So y œ œ
x 1 x2x1
44x 4x
242
22
"
#
25. 3x y x . Let v x e e . So e y 3x e y x e e y x e e y e C.
dy
dx dx 3
2 2 3x dx x x 2 x 2 x x 2 x x x
d1
œ œ œ œ Ê œ Êœab Š‹
'233 3 3 3 33 3
w
We have y 0 1 e 1 e C 1 C C and e y e y eab a bœÊ œ ʜʜ œ Êœ
00 xx x
1141414
3333333
33 33 3
26. xdy y cos x dx 0 xy y cos x 0 y y . Let v x e e x. œÊ œÊ œ œ œ œab ab
ˆ‰
ww
1cos x
xx
dx ln x
'1
x
So xy x y cos x xy cos x xy cos x dx xy sin x C. We have y 0 0 1 C
w œ Ê œ Êœ Êœ œÊ œ
ˆ‰ ˆ‰ ˆ‰
ab
1d
xdx 22
'11
C 1. So xy 1 sin x yÊœ œ Êœ
1sin x
x
27. x dy y y dx 0 2ln y 1 ln x C. We have y 1 1 2 ln 1 1 ln 1 C œÊ œÊ œ œÊ œ
ˆ‰ ˆ‰
ÈÈ
ab Š‹
È
dy
yy
dx
x
ˆ‰
È
2 ln 2 C ln 2 ln 4. So 2 ln y 1 ln x ln 4 ln 4x ln y 1 ln 4x ln 4xÊ œœ œ œœ Ê œ œ
21/2
ˆ‰ ˆ‰
ÈÈ
ab ab ab
"
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

614 Chapter 9 Further Applications of Integration
e e y1 2x y 2x1ʜʜʜ
ln y 1 ln 4x 2
ˆ‰
Èab
1/2 ÈÈÈ
ˆ‰
28. y dx e e C. We have y 0 1 e e C C .
2xx00
dx e e 1 1
dy e 1 e y 3 3 3
dy y 1
œÊ œÊœ œÊœÊœ
x2x
2x x 2
33
ab ab
So ee y 3ee 1y3ee 1
y
33
xx 3 xx xx
11/3
3œ Êœ Êœ
ab c dab
29. xy x 2 y 3x e y y 3x e . Let v x e e . So
ww
œ Ê œ œ œ œab ab
ˆ‰
3x 2x dx x2ln x
x2 e
xx
'ˆ‰
x2
x
x
2
y y 3 y 3 y 3x C. We have y 1 0 0 3 1 C C 3
eex2 de e
xxx dxx x
xx x x
22 2 2
w
œÊ†œÊ†œ œÊœÊœ
ˆ‰ ˆ ‰ ab ab
y 3x3 y xe3x3ʆ œ Êœ
e
x
2x
x
2
ab
30. y dx 3x xy 2 dy 0 0 x 1 x . œÊ œÊœÊ œab Š‹
dx dx 3x 2 dx 3 2
dy y dy y y dy y y
3x xy 2
Py 1 Pydy 3ln y y vy e yeab ab abœÊ œ Ê œ œ
3
y
3ln y y 3 y
'
ye x ye 1 x 2ye ye x 2ye dy 2e y 2y 2 C
3y 3y 2y 3y 2y y2
3
y
w
œÊœ œ
Š‹ ab
'
y . We have y 2 1 1 C 4e andÊ œ œ Ê œ Ê œ
32y 2y 2 Ce
x2
2122 Ce
ˆ‰ ab
2y 1
ab
yʜ
32y 2y 2 4e
x
ˆ‰
2y1
31. To find the approximate values let y y y cos x 0.1 with x 0, y 0, and 20 steps. Use a
nn1 n1 n1 0 0
œ œ œ
abab
spreadsheet, graphing calculator, or CAS to obtain the values in the following table.
x y
0 0
0.1 0.1000
0.2 0.2095
0.3 0.3285
0.4 0.4568
0.5 0.5946
0.6 0.7418
0.7 0.8986
0.8 1.0649
0.9 1.2411
1.0 1.4273
x y
1.1 1.6241
1.2 1.8319
1.3 2.0513
1.4 2.2832
1.5 2.5285
1.6 2.7884
1.7 3.0643
1.8 3.3579
1.9 3.6709
2.0 4.0057
32. To find the approximate values let z y 2 y 2 x 3 0.1 and
nn1 n1 n1
œ
abababa b
y y 0.1 with initial values x 3, y 1, and 20 steps. Use a
nn1 00
2y 2 x 3 2z2 x 3
2
œ œœ
Š‹
ab
aba babab
n1 n1 n n
spreadsheet, graphing calculator, or CAS to obtain the values in the following table.
x y
3 1
2.9 0.6680
2.8 0.2599
2.7 0.2294
2.6 0.8011
2.5 1.4509
2.4 2.1687
2.3 2.9374
2.2 3.7333
2.1 4.
5268
2.0 5.2840
x y
1.9 5.9686
1.8 6.5456
1.7 6.9831
1.6 7.2562
1.5 7.3488
1.4 7.2553
1.3 6.9813
1.2 6.5430
1.1 5.9655
1.0 5.2805
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
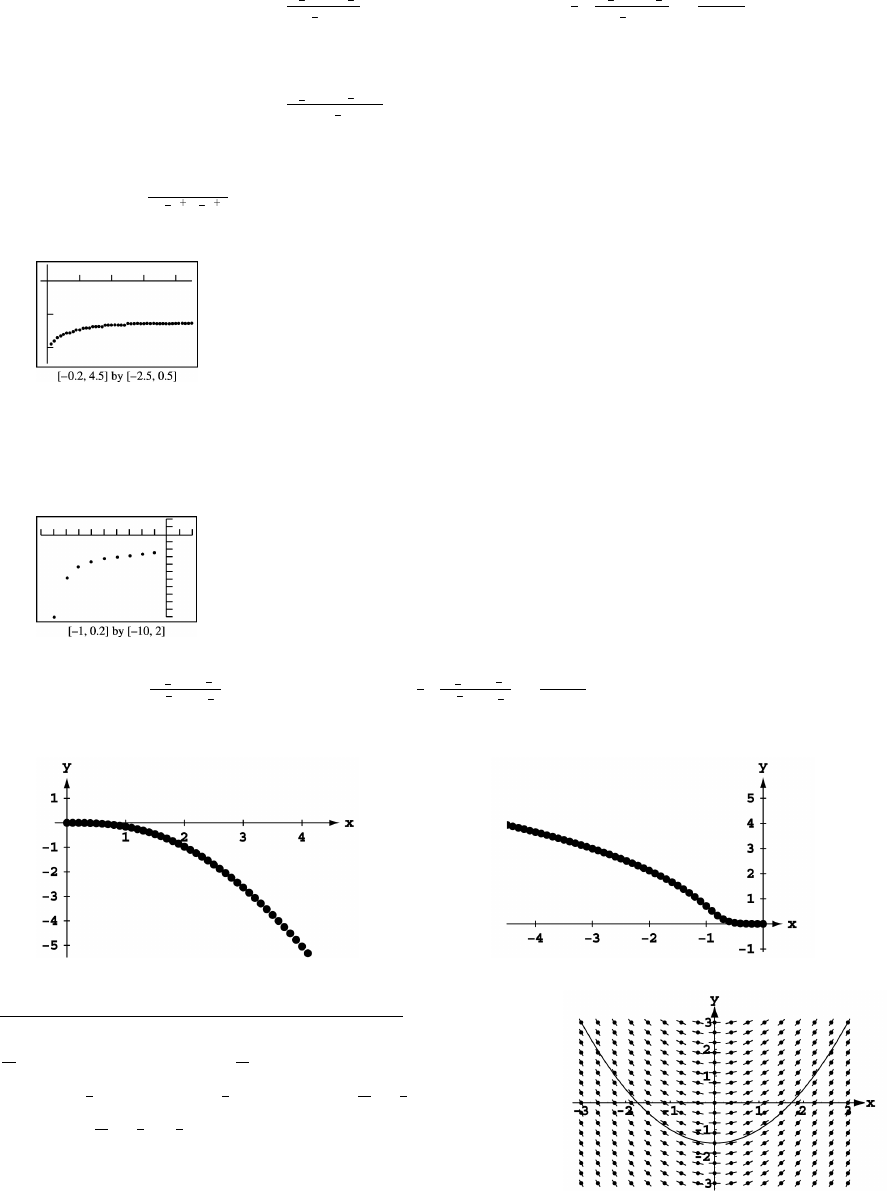
Chapter 9 Practice Exercises 615
33. To estimate y 3 , let z y 0.05 and y y 0.05 with initial valuesab ab ab
Š‹ Š ‹
nn1 nn1
x2y x2y
x1 x1 x1
x2z
œ œ
#
"
n1 n1 n1 n1
n1 n1 n
nn
x 0, y 1, and 60 steps. Use a spreadsheet, graphing calculator, or CAS to obtain y 3 0.9063.
00
œœ ¸ab
34. To estimate y 4 , let z y 0.05 with initial values x 1, y 1, and 60 steps. Use aab a b
Š‹
nn1 0 0
x2y1
x
œ œ œ
2
n1 n1
n1
spreadsheet, graphing calculator, or CAS to obtain y 4 4.4974.ab¸
35. Let y y dx with starting values x 0 and y 2, and steps of 0.1 and 0.1. Use a spreadsheet,
nn1 0 0
1
e
œ œ œ
ˆ‰
ab
xy2
n1 n1
programmable calculator, or CAS to generate the following graphs.
(a)
(b) Note that we choose a small interval of x-values because the y-values decrease very rapidly and our calculator cannot
handle the calculations for x 1. (This occurs because the analytic solution is y 2 ln 2 e , which has anŸ œ ab
x
asymptote at x ln 2 0.69. Obviously, the Euler approximations are misleading for x 0.7.)œ ¸ Ÿ
36. Let z y dx and y y dx with starting values x 0 and y
nn1 nn1 0
xy xy
ex ex ex
xz
œ œ œ
#
"
Š‹ Š ‹
ab ab
22
n1 n1 n
n1 n1
yy
n1 n1
n1 n1 n
2n
zn0œ0,
and steps of 0.1 and 0.1. Use a spreadsheet, programmable calculator, or CAS to generate the following graphs.
(a) (b)
37. x 1 1.2 1.4 1.6 1.8 2.0
y 1 0.8 0.56 0.28 0.04 0.4
x dy x dx y C; x 1 and y 1
dy
dx 2
x
œÊ œ Êœ œ œ
2
1 C C y exactÊ œ Ê œ Ê œ
"
#
3x3
222
ab
2
y 2 is the exact value.Êœœab 23
22
2"
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
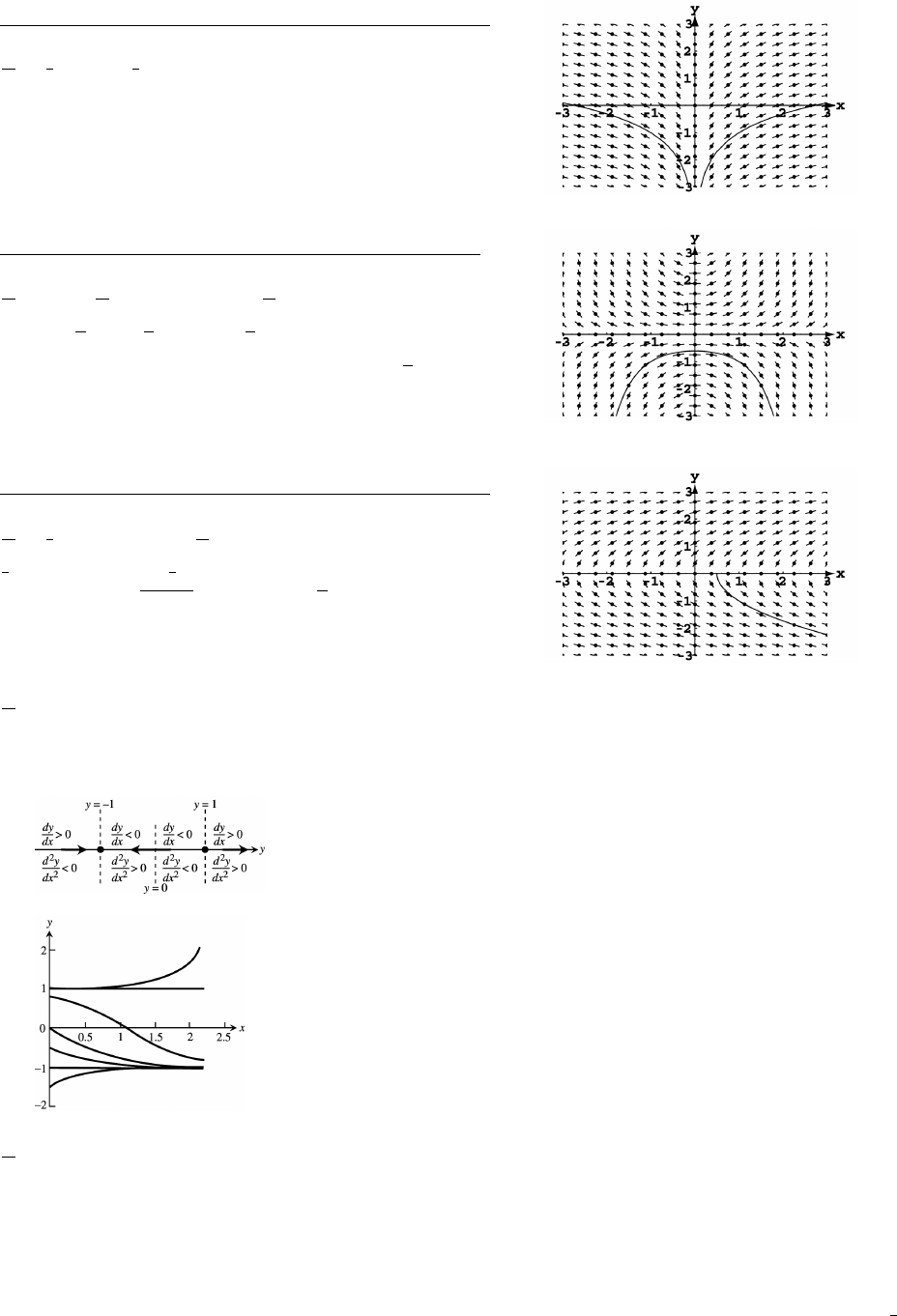
616 Chapter 9 Further Applications of Integration
38. x 1 1.2 1.4 1.6 1.8 2.0
y 1 0.8 0.6333 0.4904 0.3654 0.2544
dy dx y ln x C; x 1 and y 1
dy
dx x x
11
œÊ œ Êœ œ œkk
1 ln 1 C C 1 y exact ln x 1Ê œ Ê œ Ê œ abkk
y 2 ln 2 1 0.3069 is the exact value.Êœ¸ab
39. x 1 1.2 1.4 1.6 1.8 2.0
y 1 1.2 0.488 1.9046 2.5141 3.4192
xy x dx ln y C
dy dy
dx y 2
x
œÊœ Ê œkk 2
ye e e Ce; x1 and y 1Êœ œ † œ œ œ
xx x
22 2
22 2
CC
1
1 C e C e y exact e eÊ œ Ê œ œ †
11
1/2 1/2 1/2
ab x2
2
e y 2 e 4.4817 is theœ Ê œ ¸
ˆ‰
x1/2 3/2
2ab
exact value.
40. x 1 1.2 1.4 1.6 1.8 2.0
y 1 1.2 1.3667 1.5130 1.6452 1.7688
y dy dx x C; x 1 and y 1
dy y
dx y 2
1
œÊ œ Ê œ œ œ
2
1 C C y 2x 1
""
##
œ Ê œÊ œ
2
y exact 2x 1 y 2 3 1.7321 is theÊ œ Ê œ ¸ab ab
ÈÈ
exact value.
41. y 1 y y 1 y 1 . We have y 0 y 1 0, y 1 0 y 1, 1.
dy
dx
2
œÊœ œÊœ œÊœ
ww
abab abab
(a) Equilibrium points are 1 (stable) and 1 (unstable)
(b) y y 1 y 2yy y 2y y 1 2y y 1 y 1 . So y 0 y 0, y 1, y 1.
w ww w ww ww
œÊ œ Ê œ œ œÊœ œ œ
2 2
a babab
(c)
42. y y y y 1 y . We have y 0 y 1 y 0 y 0, 1 y 0 y 0, 1.
dy
dx
2
œ Ê œ œÊ œÊœ œÊ œ
ww
ab ab
(a) The equilibrium points are 0 and 1. So, 0 is unstable and 1 is stable.
(b) Let increasing, decreasing.ïî œ íï œ
y
yyy
01
qqíïïïïïqqñqqïïïïïîqqñqqíïïïïïqqp
! ! !
www
y y y y y 2yy y y y 2y y y y y 2y 2y y 2y 3y y
wwwwwww ww
œ Ê œ Ê œ œ Ê œ
2 2 2 223 32
abab
y 2y 3y 1 y y 2y 1 y 1 . So, y 0 y 0, 2y 1 0, y 1 0 y 0, y ,œ Ê œ œÊœ œ œÊœ œababab
2ww ww "
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
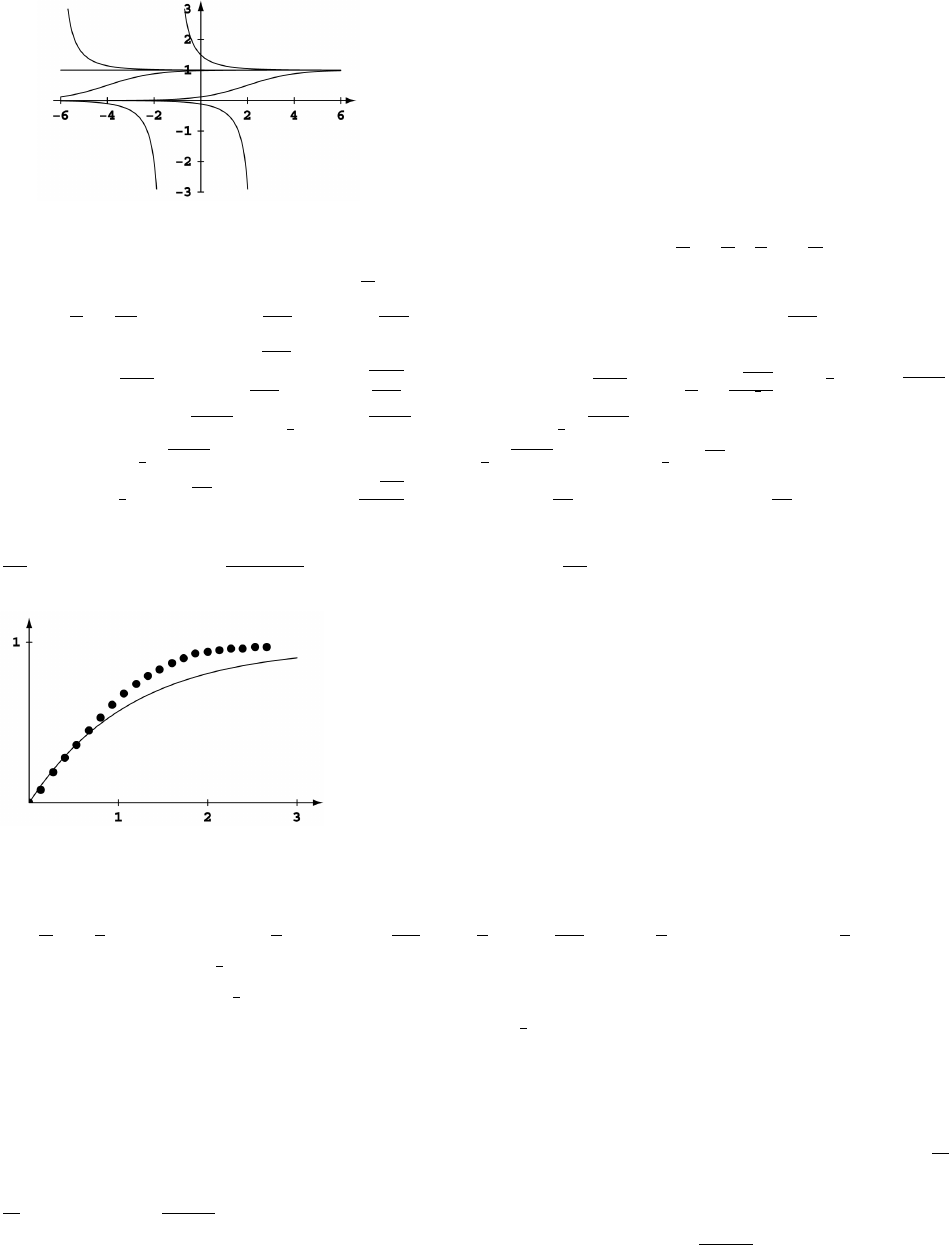
Chapter 9 Additional and Advanced Exercises 617
y1.œ
Let concave up, concave down.ïî œ íï œ
y
yyyy
01
1/2
qíïïïïïqqñqqïïïïïîqqñqqíïïïïïqqñqqïïïïïîqp
! ! ! !
ww ww ww ww
(c)
43. (a) Force Mass times Acceleration (Newton's Second Law) or F ma. Let a v . Thenœœœœ†œ
dv dv ds dv
dt ds dt ds
ma mgR s a gR s v gR s v dv gR s ds v dv gR s dsœ Ê œ Ê œ Ê œ Ê œ
22 22 22 22 22
dv
ds
''
C v 2C C. When t 0, v v and s R v Cʜʜœ œœ œÊœ
v
2s s s R
gR 2gR 2gR 2gR
11 0
2 2
0
2222 2
C v 2gR v v 2gRÊœ Ê œ
222
00
2gR
s
2
(b) If v 2gR, then v v , since v 0 if v 2gR. Then s ds 2gR dt
0 0
22gR 2gR
ss dt
ds 2gR
s
2
œœÊœ œÊœ
ÈÈ
ÉÈÈ
222
ÈÈ
s ds 2gR dt s 2gR t C s 2gR t C; t 0 and s RÊœ Êœ Êœ œœ
''
1/2 3/2 3/2
22 2
23
32
1
ÈÈ È
ˆ‰
R 2gR 0 C C R s 2gR t R R 2g t RÊœ ʜʜ œ
3/2 3/2 3/2 3/2 3/2
333
222
22
ˆ‰ ˆ‰ ˆ‰
ÈÈ
ab È
RRt1RsR
R2gt1 t1 1 t
œœœÊœ
3/2 3/2 3/2
3
2
1/2 3 2gR
2R
3v 3v
2R 2R
2/3
‘ ‘‘
ˆ‰
È’“Š‹ ˆ‰ ˆ‰
È00
44. coasting distance 0.97 k 27.343. s t 1 e s t 0.97 1 e
vm vm
kk k
0.86 30.84 k/m t 27.343/30.84 t
0 0
œÊœÊ¸œÊœ
aba b ab a b
ab ab
ˆ‰ ˆ ‰
s t 0.97 1 e . A graph of the model is shown superimposed on a graph of the data.ʜ ab a b
0.8866t
CHAPTER 9 ADDITIONAL AND ADVANCED EXERCISES
1. (a) k c y dy k y c dt k dt k dt ln y c k t C
dy dy dy
dt V V y c V y c V V
AA A A A
1
œ Ê œ Ê œ Ê œ Ê œ ab ab kk
''
y c e e . Apply the initial condition, y 0 y y c C C y cÊœ„ œ Ê œ Ê œ
Ckt 00 0
1A
V
ab
yc y ce .ʜ ab
0ktA
V
(b) Steady state solution: y y t c y c 0 c
cyce
_Ä_ Ä_
œœ œœ
lim lim
tt 0kt 0
ab a ba b
‘
ab
A
V
2. Measure the amounts of oxygen involved in mL. Then the inflow of oxygen is 1000 mL/min (Assumed: it will take 5
minutes to deliver the 5L 5000mL); the amount of oxygen at t 0 is 210 mL; letting A the amount of oxygen in theœœœ
flask, the concentration at time t is A mL/L; the outflow rate of oxygen is A mL/L (lb/sec). The rate of change in A, ,
dA
dt
equals the rate of gain (1000 mL/min) minus rate of loss (A mL/min). Thus:
1000 A dt ln A 1000 t C A 1000 Ce . At t 0, A 210, so C 790 and
dA dA
dt 1000 A
t
œÊ œÊ œÊœ œœ œ
ab
A 1000 790e . Thus, A 5 1000 790e 994.7 mL. The concentration is 99.47%.œ œ ¸ œ
t5 994.7 mL
1000 mL
ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
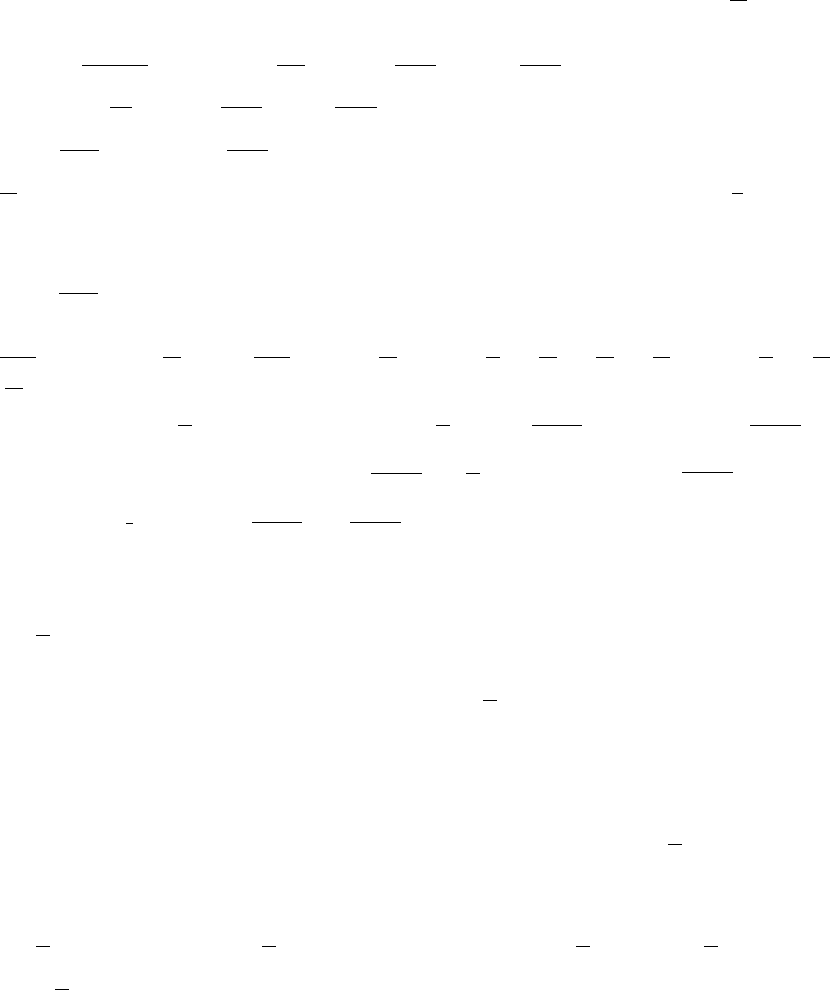
618 Chapter 9 Further Applications of Integration
3. The amount of CO in the room at time t is A t . The rate of change in the amount of CO , is the rate of internal
2 2 dA
dt
ab
production (R ) plus the inflow rate (R ) minus the outflow rate (R ).
12 3
R 20 30 students ft 0.04 1.39
1breaths/min 100
student 1728 ft min
3ft CO ft CO
œ¸
ˆ‰ ˆ‰
ab
Š‹
33
22
3
R 1000 0.0004 0.4
2ft
min min min
ft CO ft CO
œœ
Š‹Š ‹
333
22
R 1000 0.1A
3A
10,000 min
ft CO
œœ
Š‹ 32
1.39 0.4 0.1A 1.79 0.1A A 0.1A 1.79. Let v t e . We have Ae 1.79e
dA d
dt dt
0.1dt 0.1dt 0.1dt
œœÊœ œ œ
wab Š‹
'''
Ae 1.79e dt 17.9e C. At t 0, A 10,000 0.0004 4 ft CO C 13.9Êœ œ œœ œ Êœ
0.1t 0.1t 0.1t 3 2
'abab
A 17.9 13.9e . So A 60 17.9 13.9e 17.87 ft of CO in the 10,000 ft room. The percent ofÊœ œ ¸
0.1t 0.1 60 3 3
2
ab ab
CO is 100 0.18%
217.87
10,000 ‚œ
4. F v u F v u F m v v u F m u .
dmv dmv
dt dt dt dt dt dt dt dt dt dt
dm dm dv dm dm dm dv dm
ab ab
œÊœÊœÊœab ab
b m b t C. At t 0, m m , so C m and m m b t.
dm
dt 00 0
œ Ê œ œ œ œ œ kk kk
Thus, F m b t u b m b t g g v gt u ln Cœ œ Êœ Êœ abkkabkkkk kk Š‹
00 1
dv dv
dt dt m b t m
ub m btkk kk
kk
00
0
v 0 at t 0 C 0. So v gt u ln y dt and u c, y 0 at
gt u ln
œœÊœ œ œÊœ œœ
1mbt
mdt
dy mbt
m
Š‹ Š‹
0
0
0
0
kk kk
'’“
t0 y gt c
tln
œÊœ
"
#
2mbt mbt
bm
’“
Š‹Š‹
00
0
kk kk
kk
5. (a) Let y be any function such that v x y v x Q x dx C, v x e . Thenab ab ab abœœ
''Px dxab
vx y vx y y v x vxQx. We have vx e v x e Px vxPx.
d
dx
Px dx Px dx
a b ab ab ab ab ab ab ab ababab†œ †† œ œ Ê œœ œ
ww w
''
ab ab
Thus v x y y v x P x v x Q x y y P x Q x the given y is a solution.ab abab ab ab ab ab†† œ Ê œ Ê
ww
(b) If v and Q are continuous on and x a, b , then v t Q t dt v x Q x
a, b
c d a b ab ab ab ab
’“
−œ
d
dx x
x
'0
v t Q t dt v x Q x dx. So C y v x v x Q x dx. From part (a), v x y v x Q x dx C.Êœ œ œ
'x
x
00
0abab ab ab a b abab ab ab ab
'' '
Substituting for C: v x y v x Q x dx y v x v x Q x dx v x y y v x when x x .ab ab ab a b abab ab a bœÊœ œ
''
00 00 0
6. (a) y P x y 0, y x 0. Use v x e as an integrating factor. Then v x y 0 v x y C
wœ œ œ œÊœab a b ab a b abab
0Px dx d
dx
'ab
y Ce and y C e , y C e , y x y x 0, y y C C eÊœ œ œ œ œ œ
#
''' '
Px dx Px dx Px dx Px dx
11 2 10 20 12 12
ab ab ab ab
ab ab a b
C e and y y 0 0 0. So y y is a solution to y P x y 0 with y x 0.œ œœ œ œ
312 12 0
Px dx w
'ab ab a b
(b) v x e C C C .
yx yx eCC
dd dd
dx dx dx dx
12 Px dx Px dx 12 12 3
ab abababc d
ab ab Š‹
‘
ab
œœœœ!
''
ab ab
v x dx v x dx C
yx yx yx yx
''
d
dx 12 12
abababc d abc d
ab ab ab ab
œœ!œ
(c) y C e , y C e , y y y . So y x 0 C e C e
11 2 12 0 1
Px dx Px dx Px dx Px dx
œœœœÊœ!
# #
'' ''
ab ab ab ab
ab
CC 0C C yxyx for axb.ÊœÊœÊ œ
12 1 2 1 2
ab ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
CHAPTER 10 CONIC SECTIONS AND POLAR COORDINATES
10.1 CONIC SECTIONS AND QUADRATIC EQUATIONS
1. x 4p 8 p 2; focus is (2 0), directrix is x 2œÊ œÊœ ß œ
y
8
2. x 4p 4 p 1; focus is ( 1 0), directrix is x 1œ Ê œ Ê œ ß œ
y
4
3. y 4p 6 p ; focus is , directrix is yœ Ê œ Ê œ !ß œ
x333
6## #
ˆ‰
4. y 4p 2 p ; focus is , directrix is yœÊ œÊœ !ß œ
x111
2## #
ˆ‰
5. 1 c 4 9 13 foci are 13 ; vertices are 2 0 ; asymptotes are y x
x 3
49
y
œÊœ œ Ê „ ß! „ß œ„
ÈÈÈ
Š‹ ab #
6. 1 c 9 4 5 foci are 0 5 ; vertices are 0 3
x
49
y
œÊœ œ Ê ß„ ß„
ÈÈÈ
Š‹ ab
7. y 1 c 2 1 1 foci are 1 0 ; vertices are 2
x
2œÊœ œÊ „ß „ ß!
#ÈÈ
ab Š‹
8. x 1 c 4 1 5 foci are 0 5 ; vertices are 2 ; asymptotes are y 2x
y
4œÊœ œ Ê ß„ !ß„ œ„
#ÈÈÈ
Š‹ ab
9. y 12x x 4p 12 p 3; 10. x 6y y 4p 6 p ;
# #
# #
œ Êœ Ê œ Êœ œ Êœ Ê œÊœ
y
1 6
x3
focus is ( ), directrix is x 3 focus is , directrix is y$ß ! œ !ß œ
ˆ‰
33
##
11. x 8y y 4p 8 p 2; 12. y 2x x 4p 2 p ;
# #
# #
"
œ Êœ Ê œÊœ œ Êœ Ê œÊœ
x
8
y
focus is ( 2), directrix is y 2 focus is , directrix is x!ß œ ß ! œ
ˆ‰
""
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
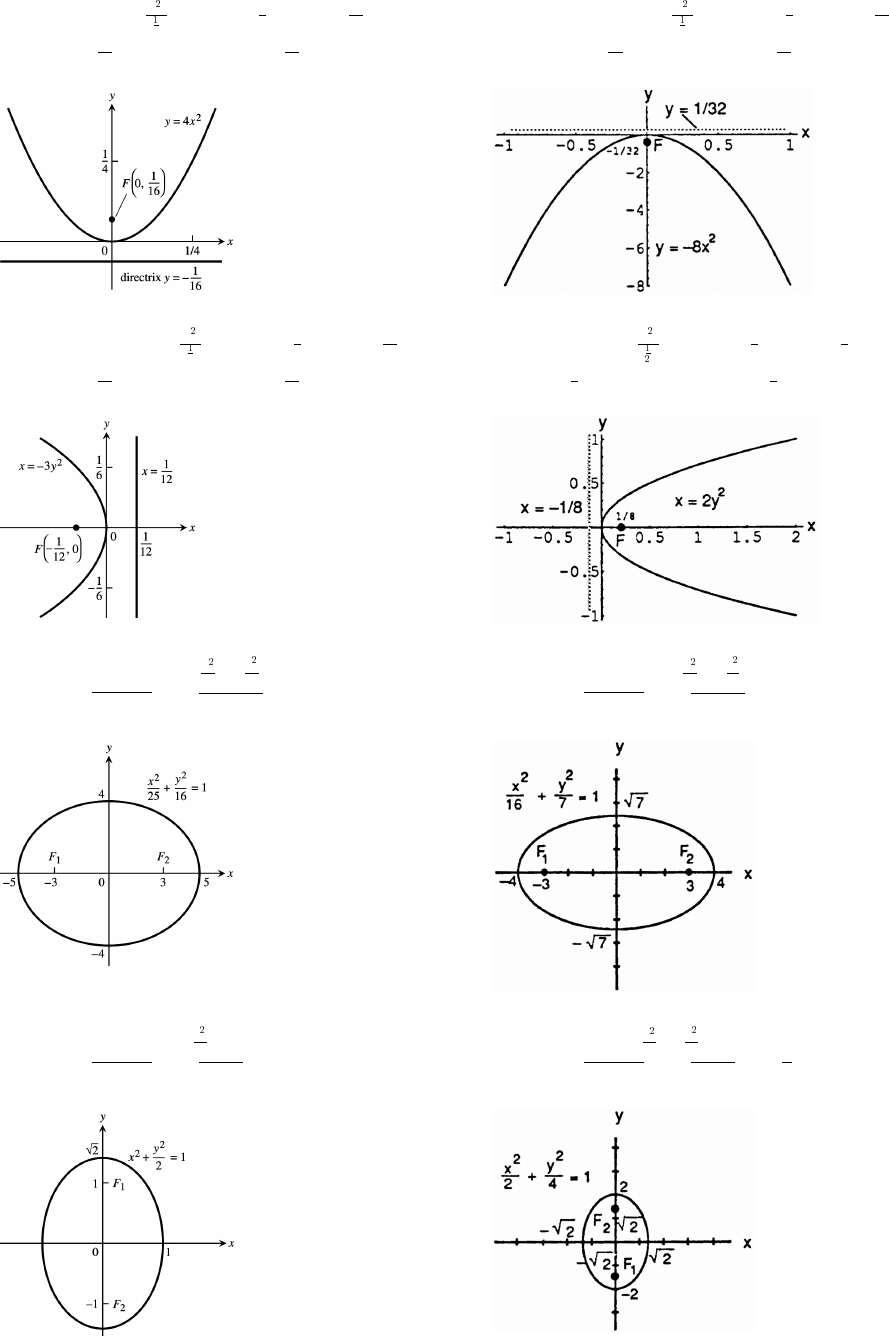
620 Chapter 10 Conic Sections and Polar Coordinates
13. y 4x y 4p p ; 14. y 8x y 4p p ;œÊœÊœÊœ œÊœÊœÊœ
# #
"" ""x x
416 832
ˆ‰ ˆ‰
4 8
focus is , directrix is y focus is , directrix is y
ˆ‰ ˆ ‰
!ß œ !ß œ
"" ""
#16 16 32 3
15. x 3y x 4p p ; 16. x 2y x 4p p ;œ Êœ Ê œ Êœ œ Êœ Ê œ Êœ
# #
"" ""
##
y y
31 8
ˆ‰ ˆ‰
3
focus is , directrix is x focus is , directrix is x
ˆ‰ ˆ‰
ß! œ ß! œ
"" " "
##11 8 8
17. 16x 25y 400 1 18. 7x 16y 112 1
## ##
#
œÊœ œÊœ
x x
516 16 7
y y
cab 25163 cab 1673Êœ œ œ Êœ œ œ
ÈÈ
ÈÈ
## ##
19. 2x y 2 x 1 20. 2x y 4 1
## # ##
##
œÊ œ œÊ œ
y y
x
4
cab 211 cab 422Êœ œ œ Êœ œ œ
ÈÈ
ÈÈÈ
## ##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
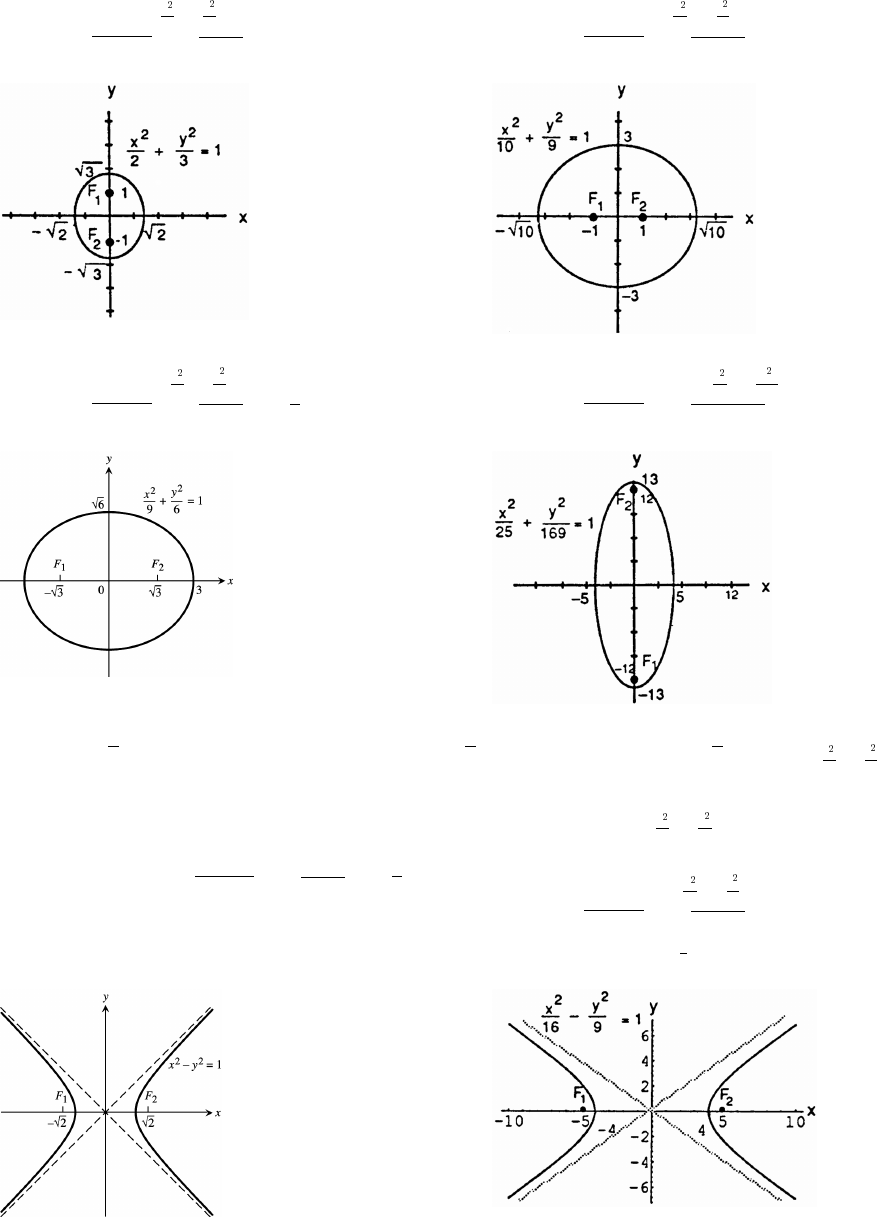
Section 10.1 Conic Sections and Quadratic Equations 621
21. 3x 2y 6 1 22. 9x 10y 90 1
## # #
#
œÊœ œÊœ
x x
y y
310 9
cab 321 cab 1091Êœ œ œ Êœ œ œ
ÈÈ
ÈÈ
## ##
23. 6x 9y 54 1 24. 169x 25y 4225 1
## ##
œÊœ œ Êœ
x x
96 25 169
y y
c a b 9 6 3 c a b 169 25 12Êœ œ œ Êœ œ œ
ÈÈ
ÈÈ È
## ##
25. Foci: 2 , Vertices: 2 0 a 2, c 2 b a c 4 2 2 1
Š‹ Š‹
ÈÈÈ
ab„ ß! „ß Êœ œ Ê œœ œÊ œ
###
#
#
x
4
y
26. Foci: 4 , Vertices: 0 5 a 5, c 4 b 25 16 9 1ab ab!ß„ ß„ Êœ œÊ œœÊ œ
#
#
x
95
y
27. x y 1 c a b 1 1 2 ; 28. 9x 16y 144 1
## ##
##
œÊœ œ œ œ Ê œ
ÈÈ
Èx
16 9
y
asymptotes are y x c a b 16 9 5;œ„ Ê œ œ œ
ÈÈ
##
asymptotes are y xœ„
3
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
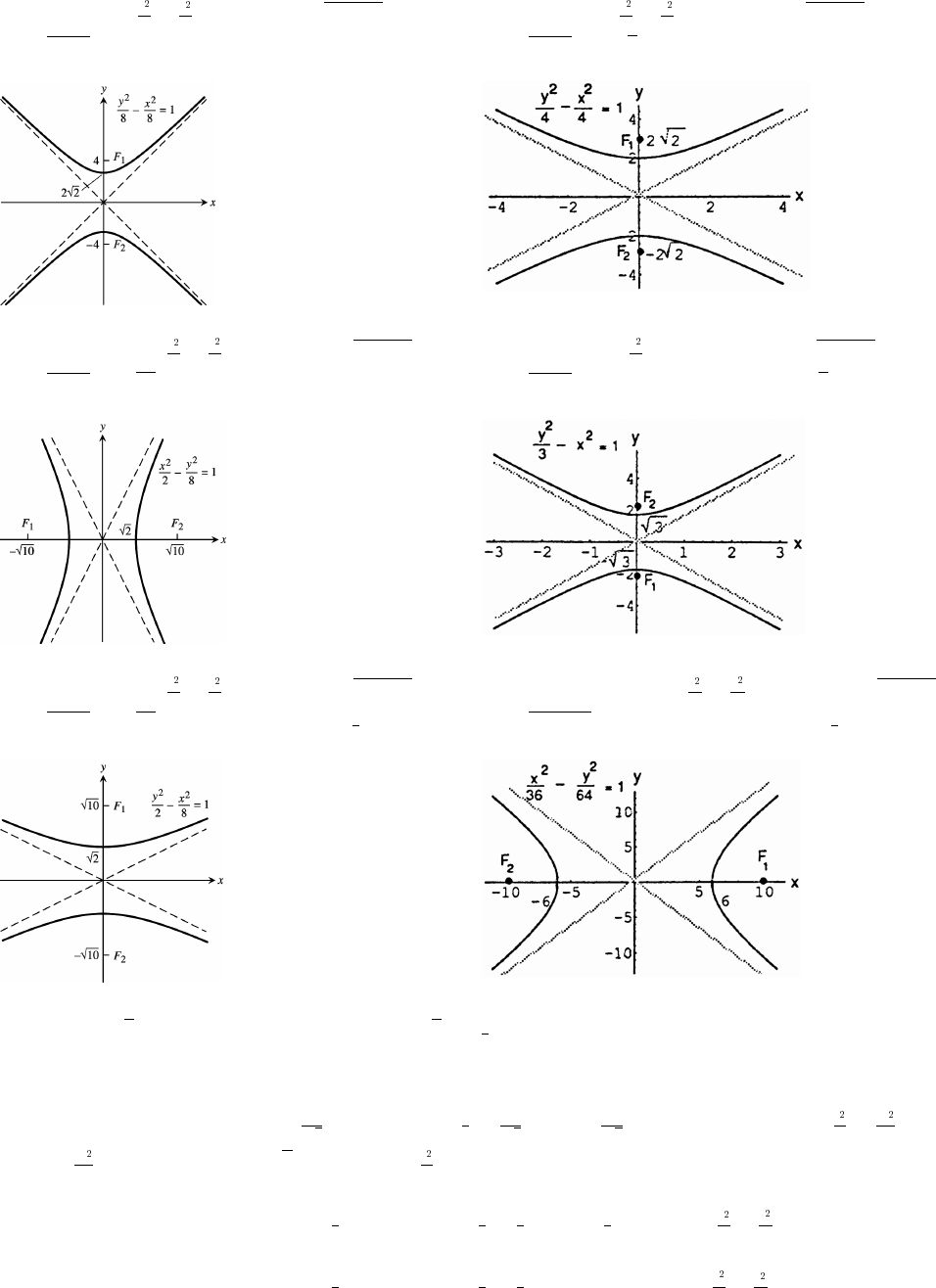
622 Chapter 10 Conic Sections and Polar Coordinates
29. y x 8 1 c a b 30. y x 4 1 c a b
## ##
## ##
œÊ œÊœ œÊ œÊœ
y y
88 44
x x
ÈÈ
8 8 4; asymptotes are y x 4 4 2 2; asymptotes are y xœœ œ„ œœ œ„
ÈÈ
È
31. 8x 2y 16 1 c a b 32. y 3x 3 x 1 c a b
## ## #
#
## ##
œÊœÊœ œÊœÊœ
xyy
83
ÈÈ
2 8 10 ; asymptotes are y 2x 3 1 2; asymptotes are y 3xœœ œ„ œœ œ„
ÈÈ
È È
33. 8y 2x 16 1 c a b 34. 64x 36y 2304 1 c a b
## # #
#
## ##
œ Ê œÊœ œ Ê œÊœ
y y
x x
836 64
ÈÈ
2 8 10 ; asymptotes are y 36 64 10; asymptotes are yœœ œ„ œ œ œ„
ÈÈ
Èx 4
3#
35. Foci: 2 , Asymptotes: y x c 2 and 1 a b c a b 2a 2 2a
Š‹
ÈÈ
!ß „ œ „ Ê œ œ Ê œ Ê œ œ Ê œ
a
b
### # #
a 1 b 1 y x 1ÊœÊœÊ œ
##
36. Foci: 2 , Asymptotes: y x c 2 and b c a b aab„ß! œ„ Ê œ œ Ê œ Ê œ œ œ
""
####
ÈÈÈ
333
ba a4a
a33
4 a 3 a 3 b 1 y 1Êœ Ê œÊœ ÊœÊ œ
4a x
33
##
È
37. Vertices: 3 0 , Asymptotes: y x a 3 and b (3) 4 1ab„ß œ„ Ê œ œ Ê œ œ Ê œ
4b44x
3a33916
y
38. Vertices: 2 , Asymptotes: y x a 2 and b 2(2) 4 1ab!ß „ œ „ Ê œ œ Ê œ œ Ê œ
1a1 x
2b2 416
y
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
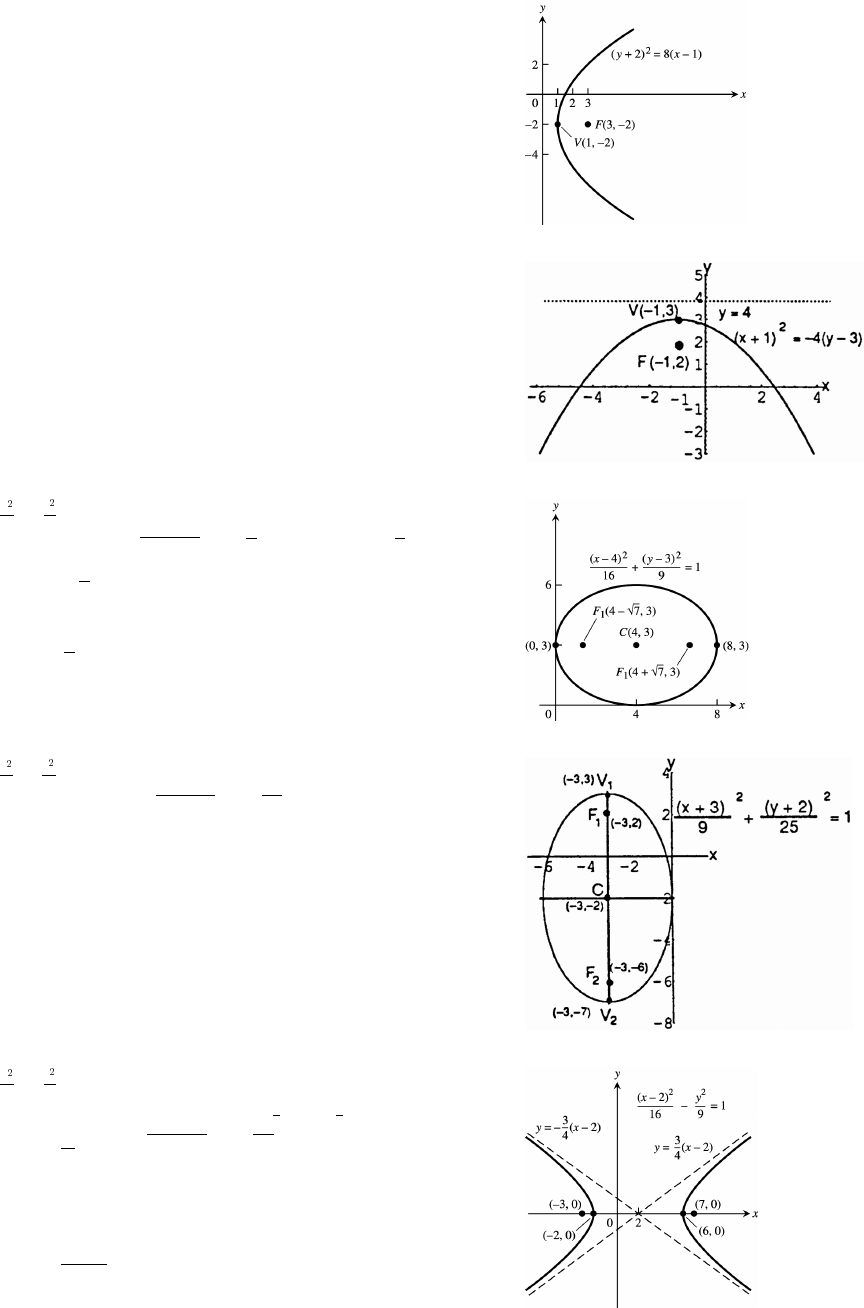
Section 10.1 Conic Sections and Quadratic Equations 623
39. (a) y 8x 4p 8 p 2 directrix is x 2,
#œ Ê œÊœÊ œ
focus is ( ), and vertex is ( 0); therefore the new#ß ! !ß
directrix is x 1, the new focus is (3 2), and theœ ß
new vertex is (1 2)ß
40. (a) x 4y 4p 4 p 1 directrix is y 1,
#œ Ê œ Ê œ Ê œ
focus is ( 1), and vertex is ( 0); therefore the new!ß !ß
directrix is y 4, the new focus is ( 1 2), and theϧ
new vertex is ( 1 3)ß
41. (a) 1 center is ( 0), vertices are ( 4 0)
x
16 9
y
œÊ !ß ß
and ( ); c a b 7 foci are 7 0%ß ! œ œ Ê ß
ÈÈÈ
Š‹
##
and 7 ; therefore the new center is ( ), the
Š‹
È
ß! %ß$
new vertices are ( 3) and (8 3), and the new foci are!ß ß
47
Š‹
È
„ß$
42. (a) 1 center is ( 0), vertices are (0 5)
x
925
y
œÊ !ß ß
and (0 5); c a b 16 4 foci areß œ œ œ Ê
ÈÈ
##
( 4) and ( 4) ; therefore the new center is ( 3 2),!ß !ß ß
the new vertices are ( 3 3) and ( 3 7), and the newß ß
foci are ( 3 2) and ( 3 6)ß ß
43. (a) 1 center is ( 0), vertices are ( 4 0)
x
16 9
y
œÊ !ß ß
and (4 0), and the asymptotes are orßœ„
x
43
y
y ; c a b 25 5 foci areœ„ œ œ œ Ê
3x
4ÈÈ
##
( 5 0) and (5 0) ; therefore the new center is (2 0), theß ß ß
new vertices are ( 2 0) and (6 0), the new fociß ß
are ( 3 0) and (7 0), and the new asymptotes areß ß
yœ„
3(x 2)
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

624 Chapter 10 Conic Sections and Polar Coordinates
44. (a) 1 center is ( 0), vertices are (0 2)
y
45
x
œÊ !ß ß
and (0 2), and the asymptotes are orßœ„
y
2
x
5
È
y ; c a b 9 3 foci areœ„ œ œ œ Ê
2x
5
ÈÈÈ
##
(0 3) and (0 3) ; therefore the new center is (0 2),ßß ß
the new vertices are (0 4) and (0 0), the new fociß ß
are (0 1) and (0 5), and the new asymptotes areßß
y2œ„
2x
5
È
45. y 4x 4p 4 p 1 focus is ( 0), directrix is x 1, and vertex is (0 0); therefore the new
#œ Ê œÊœÊ "ß œ ß
vertex is ( 2 3), the new focus is ( 1 3), and the new directrix is x 3; the new equation isß ß œ
(y 3) 4(x 2)œ
#
46. y 12x 4p 12 p 3 focus is ( 3 0), directrix is x 3, and vertex is (0 0); therefore the new
#œ Ê œ Ê œ Ê ß œ ß
vertex is (4 3), the new focus is (1 3), and the new directrix is x 7; the new equation is (y 3) 12(x 4)ßß œ œ
#
47. x 8y 4p 8 p 2 focus is (0 2), directrix is y 2, and vertex is (0 0); therefore the new
#œ Ê œÊœÊ ß œ ß
vertex is (1 7), the new focus is (1 5), and the new directrix is y 9; the new equation isß ß œ
(x 1) 8(y 7)œ
#
48. x 6y 4p 6 p focus is , directrix is y , and vertex is (0 0); therefore the new
#
## #
œ Ê œ Ê œ Ê !ß œ ß
33 3
ˆ‰
vertex is ( 3 2), the new focus is 3 , and the new directrix is y ; the new equation isß ß œ
ˆ‰
"
##
7
(x 3) 6(y 2)œ
#
49. 1 center is ( 0), vertices are (0 3) and ( 3); c a b 9 6 3 foci are 3
x
69
y
œ Ê !ß ß !ß œ œ œ Ê !ß
ÈÈÈ È
Š‹
##
and 3 ; therefore the new center is ( 1), the new vertices are ( 2 2) and ( 4), and the new foci
Š‹
È
!ß #ß ß #ß
are 1 3 ; the new equation is 1
Š‹
È
#ß „ œ
(x 2) (y 1)
69
50. y 1 center is ( 0), vertices are 2 and 2 ; c a b 2 1 1 foci are
x
2œÊ !ß ß! ß! œ œ œÊ
###
Š‹Š ‹
ÈÈ È
È
( 1 0) and ( ); therefore the new center is (3 4), the new vertices are 3 2 4 , and the new fociß "ß! ß „ ß
Š‹
È
are (2 4) and (4 4); the new equation is (y 4) 1ßß œ
(x 3)
#
#
51. 1 center is ( 0), vertices are 3 and 3 ; c a b 3 2 1 foci are
x
3
y
œÊ !ß ß! ß! œ œ œÊ
###
Š‹Š ‹
ÈÈ È
È
( 1 0) and ( ); therefore the new center is (2 3), the new vertices are 2 3 3 , and the new fociß "ß! ß „ ß
Š‹
È
are (1 3) and (3 3); the new equation is 1ßß œ
(x 2) (y 3)
3
#
52. 1 center is ( 0), vertices are ( ) and ( 5); c a b 25 16 3 foci are
x
16 5
y
œ Ê !ß !ß & !ß œ œ œ Ê
###
ÈÈ
(0 3) and (0 3); therefore the new center is ( 4 5), the new vertices are ( 4 0) and ( 4 10), and the newß ß ß ß ß
foci are ( 4 2) and ( 4 8); the new equation is 1ß ß œ
(x 4) (y 5)
16 5
#
53. 1 center is ( 0), vertices are (2 0) and ( 2 0); c a b 4 5 3 foci are ( ) and
x
45
y
œ Ê !ß ß ß œ œ œ Ê $ß !
ÈÈ
##
( 3 0); the asymptotes are y ; therefore the new center is (2 2), the new vertices areß „ œ Ê œ„ ß
xy
5
5x
##
ÈÈ
(4 2) and (0 2), and the new foci are (5 2) and ( 1 2); the new asymptotes are y 2 ; the newßß ßß œ„
È5(x 2)
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
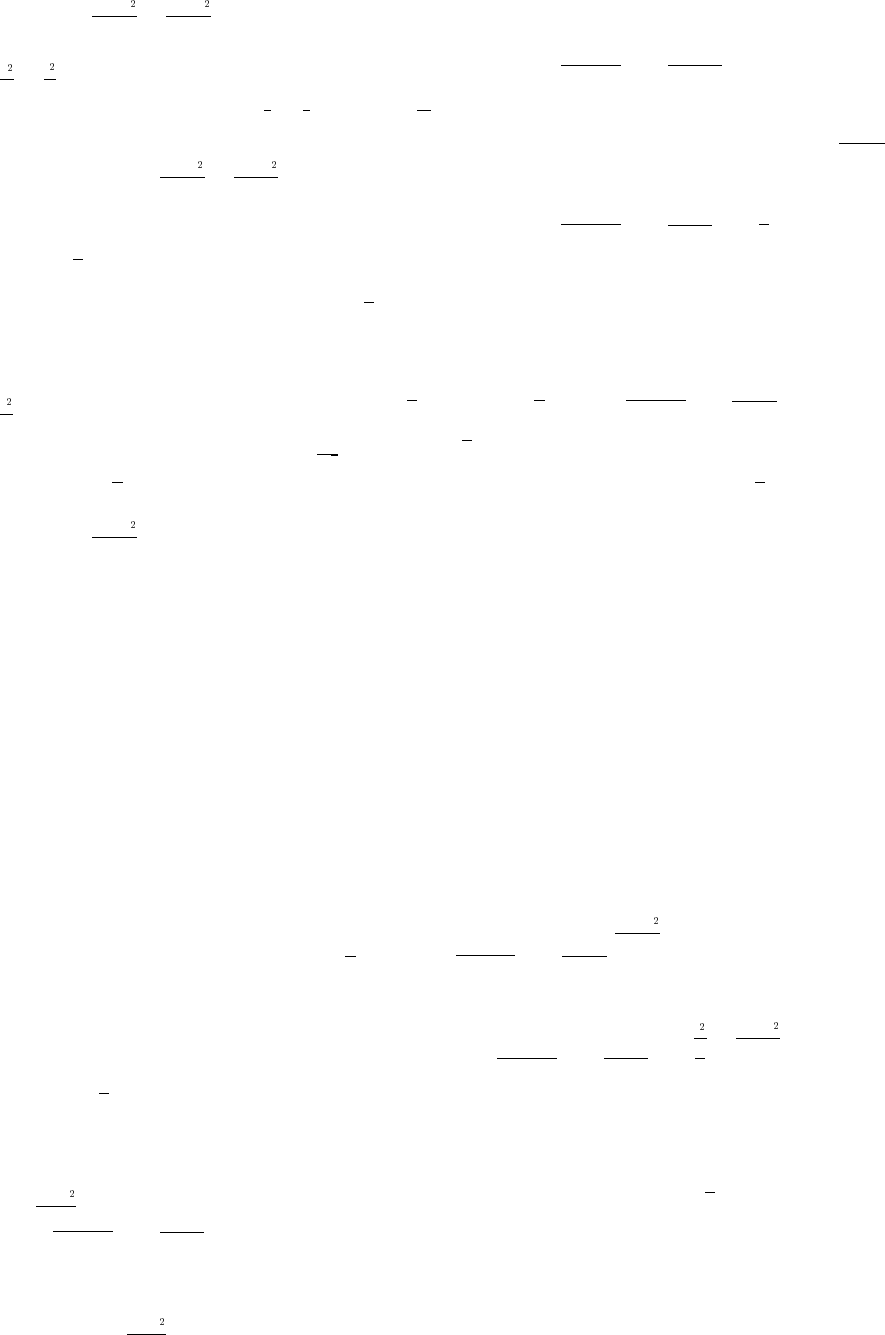
Section 10.1 Conic Sections and Quadratic Equations 625
equation is 1
(x 2) (y 2)
45
œ
54. 1 center is ( 0), vertices are (4 0) and ( 4 0); c a b 16 9 5 foci are ( 5 )
x
16 9
y
œ Ê !ß ß ß œ œ œ Ê ß!
ÈÈ
##
and (5 0); the asymptotes are y ; therefore the new center is ( 5 1), the new vertices areß „ œ Ê œ„ ß
x3x
43 4
y
( 1 1) and ( 9 1), and the new foci are ( 10 1) and (0 1); the new asymptotes are y 1 ;ß ß ß ß œ„
3(x 5)
4
the new equation is 1
(x 5) (y 1)
16 9
œ
55. y x 1 center is ( 0), vertices are (0 1) and (0 1); c a b 1 1 2 foci are
## ##
œÊ !ß ß ß œ œ œ Ê
ÈÈ
È
2 ; the asymptotes are y x; therefore the new center is ( 1 1), the new vertices are ( 1 0) and
Š‹
È
!ß „ œ „ ß ß
( 1 2), and the new foci are 1 1 2 ; the new asymptotes are y 1 (x 1); the new equation isß ß „ œ„
Š‹
È
(y 1) (x 1) 1œ
##
56. x 1 center is ( 0), vertices are 0 3 and 3 ; c a b 3 1 2 foci are ( )
y
3œÊ !ß ß !ß œ œ œÊ !ß#
###
Š‹Š ‹
ÈÈ
ÈÈ
and ( 2); the asymptotes are x y 3x; therefore the new center is (1 3), the new vertices!ß „ œ Ê œ „ ß
y
3
ÈÈ
are 3 , and the new foci are ( ) and (1 1); the new asymptotes are y 3 3 (x 1); the new
Š‹
ÈÈ
"ß $ „ "ß & ß œ „
equation is (x 1) 1
(y 3)
3
#
œ
57. x 4x y 12 x 4x 4 y 12 4 (x 2) y 16; this is a circle: center at
## # # ##
œ Ê œÊ œ
C( 2 0), a 4ß œ
58. 2x 2y 28x 12y 114 0 x 14x 49 y 6y 9 57 49 9 (x 7) (y 3) 1;
## # # # #
œÊœÊœ
this is a circle: center at C(7 3), a 1ß œ
59. x 2x 4y 3 0 x 2x 1 4y 3 1 (x 1) 4(y 1); this is a parabola:
## #
œÊ œÊ œ
V( 11), F( 10)ß ß
60. y 4y 8x 12 0 y 4y 4 8x 12 4 (y 2) 8(x 2); this is a parabola:
## #
œÊ œÊ œ
V( 2), F( )#ß !ß #
61. x 5y 4x 1 x 4x 4 5y 5 (x 2) 5y 5 y 1; this is an ellipse: the
## # # ## #
œÊœÊœÊ œ
(x 2)
5
center is ( 2 0), the vertices are 2 5 0 ; c a b 5 1 2 the foci are ( 4 0) and ( 0)ß „ ß œ œ œ Ê ß !ß
Š‹
ÈÈÈ
##
62. 9x 6y 36y 0 9x 6 y 6y 9 54 9x 6(y 3) 54 1; this is an ellipse:
## # # # #
œÊ œÊ œÊ œab x
69
(y 3)
the center is (0 3), the vertices are ( 0) and ( 6); c a b 9 6 3 the foci areß !ß !ß œ œ œ Ê
ÈÈÈ
##
03 3
Š‹
È
ß „
63. x 2y 2x 4y 1 x 2x 1 2 y 2y 1 2 (x 1) 2(y 1) 2
## # # # #
œÊ œÊœab
(y 1) 1; this is an ellipse: the center is (1 1), the vertices are 2 ;Ê œ ß "„ß"
(x 1)
2
#Š‹
È
c a b 2 1 1 the foci are (2 1) and (0 1)œœœÊ ß ß
ÈÈ
##
64. 4x y 8x 2y 1 4 x 2x 1 y 2y 1 4 4(x 1) (y 1) 4
## # # # #
œÊ œÊ œab
(x 1) 1; this is an ellipse: the center is ( 1 1), the vertices are ( 1 3) andÊ œ ß ß
#(y 1)
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
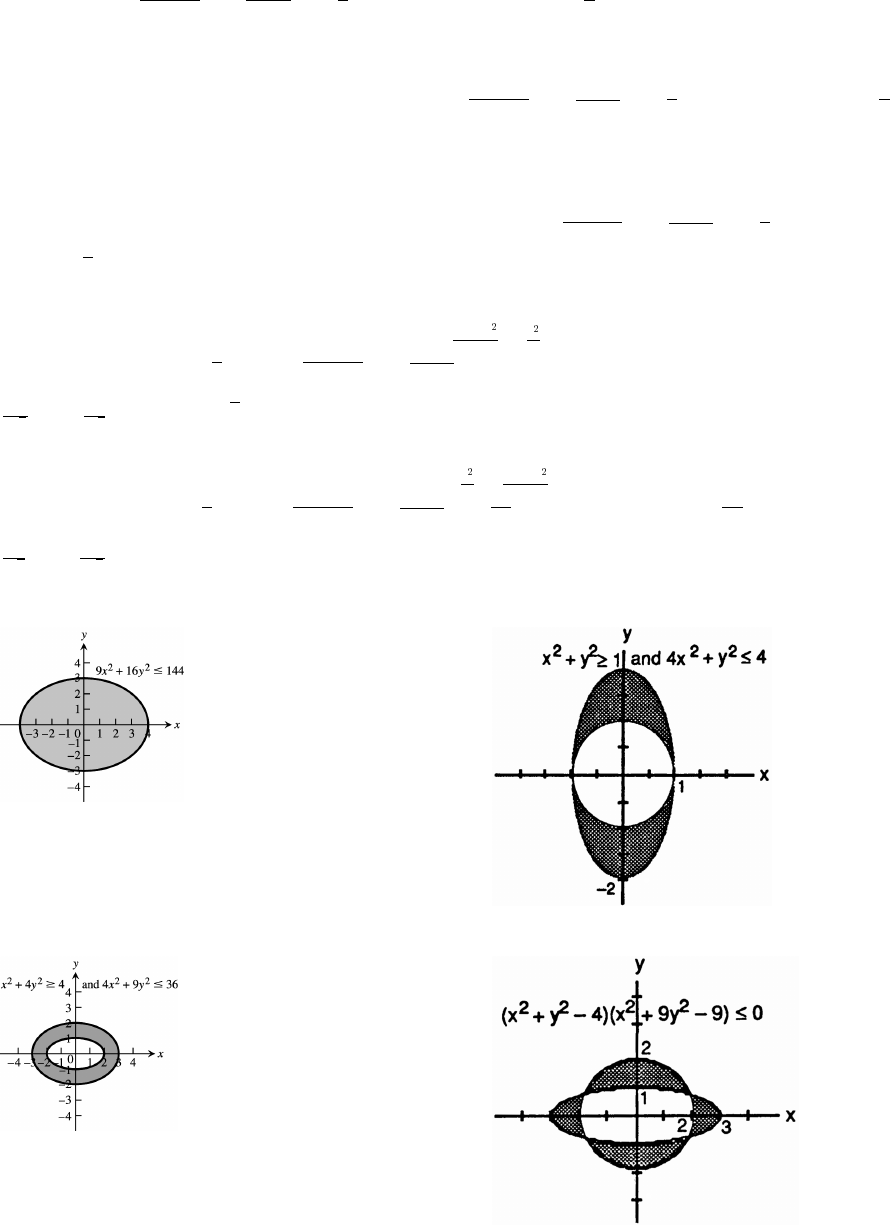
626 Chapter 10 Conic Sections and Polar Coordinates
( 1 1); c a b 4 1 3 the foci are 1 3ß œ œ œ Ê ß"„
ÈÈÈÈ
Š‹
##
65. x y 2x 4y 4 x 2x 1 y 4y 4 1 (x 1) (y 2) 1; this is a hyperbola:
## # # # #
œÊ œÊ œab
the center is (1 2), the vertices are (2 2) and ( 2); c a b 1 1 2 the foci are 1 2 ;ß ß !ß œ œ œ Ê „ ß #
ÈÈ È
ÈŠ‹
##
the asymptotes are y 2 (x 1)œ„
66. x y 4x 6y 6 x 4x 4 y 6y 9 1 (x 2) (y 3) 1; this is a hyperbola:
## # # # #
œÊ œÊ œab
the center is ( 2 3), the vertices are ( 1 3) and ( 3 3); c a b 1 1 2 the foci areß ß ß œ œ œ Ê
ÈÈ
È
##
2 2 3 ; the asymptotes are y 3 (x 2)
Š‹
È
„ ß œ„
67. 2x y 6y 3 2x y 6y 9 6 1; this is a hyperbola: the center is ( ),
## # #
œ Ê œ Ê œ !ß $ab(y 3)
63
x
the vertices are 3 6 ; c a b 6 3 3 the foci are (0 6) and ( 0); the asymptotes are
Š‹
ÈÈÈ
!ß „ œ œ œ Ê ß !ß
##
y2x3
y3
63
x
ÈÈ
œ„ Ê œ„
È
68. y 4x 16x 24 y 4 x 4x 4 8 1; this is a hyperbola: the center is (2 0),
## # #
œÊ œÊ œ ßab
y(x2)
82
the vertices are 2 8 ; c a b 8 2 10 the foci are 2 10 ; the asymptotes are
Š‹ Š ‹
ÈÈÈ
ÈÈ
ß„ œ œ œ Ê ß„
##
y 2(x 2)
y
8
x2
2
ÈÈ
œ„ Ê œ„
69. 70.
71. 72.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
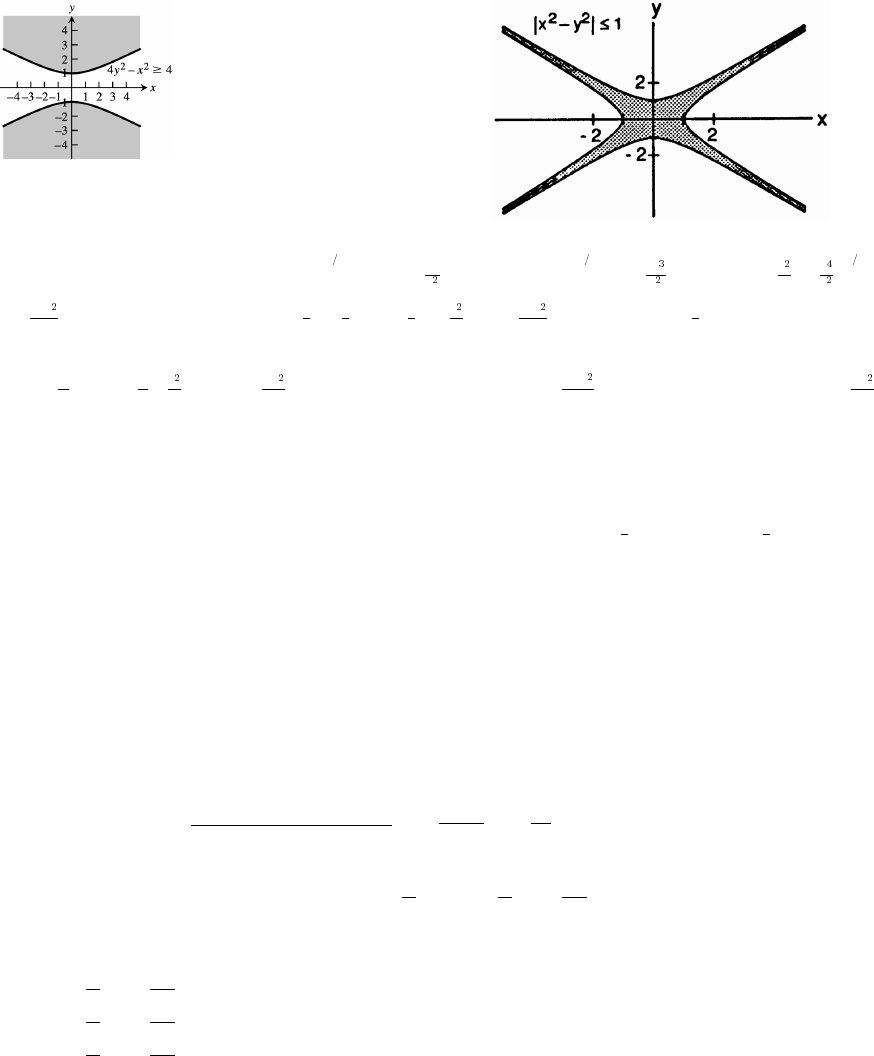
Section 10.1 Conic Sections and Quadratic Equations 627
73. 74. x y 1 1 x y 1 1 x y andkk
## ## ##
ŸÊŸŸÊŸ
x y 1 1 y x and x y 1
## ## ##
ŸÊ Ÿ
75. Volume of the Parabolic Solid: V 2 x h x dx 2 h x dx 2 h
"#
!
œœ œ
''
00
b2 b2 b2
11 1
ˆ‰ Š‹ ’“
4h 4x x x
bb2b
; Volume of the Cone: V h h ; therefore V Vœœœœœ
1 1hb b b hb 3
833412
#"#
""
##
#
11
ˆ‰ Š‹
76. y x dx C C; y 0 when x 0 0 C C 0; therefore y is theœœœœœÊœÊœ œ
'wwx wx wx
H H 2H 2H 2H
w(0)
Š‹
#
equation of the cable's curve
77. A general equation of the circle is x y ax by c 0, so we will substitute the three given points into
##
œ
this equation and solve the resulting system: c and a b ; therefore
a c 1
b c 1
2a 2b c 8
Þ
ß
à
œ
œ
œ
Êœ œœ
47
33
3x 3y 7x 7y 4 0 represents the circle
##
œ
78. A general equation of the circle is x y ax by c 0, so we will substitute each of the three given points
##
œ
into this equation and solve the resulting system: a 2, b 2, and c 23;
2a 3b c 13
3a 2b c 13
4a 3b c 25
Þ
ß
à
œ
œ
œ
Êœ œ œ
therefore x y 2x 2y 23 0 represents the circle
##
œ
79. r ( 2 1) (1 3) 13 (x 2) (y 1) 13 is an equation of the circle; the distance from the
### ##
œ œ Ê œ
center to (1.1 2.8) is ( 1.1) (1 2.8) 12.85 13 , the radius the point is inside the circleß#œ Ê
ÈÈÈ
##
80. (x 2) (y 1) 5 2(x 2) 2(y 1) 0 ; y 0 (x 2) (0 1) 5 œÊ œÊ œ œÊ œ
## ##
dy dy
dx dx y 1
x2
(x 2) 4 x 4 or x 0 the circle crosses the x-axis at (4 0) and ( 0); x 0Ê œ Ê œ œ Ê ß !ß œ
#
(0 2) (y 1) 5 (y 1) 1 y 2 or y 0 the circle crosses the y-axis at ( 2) and ( ).Ê œ Ê œ Ê œ œ Ê !ß !ß !
## #
At (4 0): 2 the tangent line is y 2(x 4) or y 2x 8ßœœÊ œ œ
dy
dx 0 1
42
At ( ): 2 the tangent line is y 2x!ß ! œ œ Ê œ
dy
dx 0 1
02
At ( ): 2 the tangent line is y 2 2x or y 2x 2!ß # œ œ Ê œ œ
dy
dx 2 1
02
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

628 Chapter 10 Conic Sections and Polar Coordinates
81. (a) y kx x ; the volume of the solid formed by
#œÊœ
y
k
revolving R about the y-axis is V dy
""
#
œ'0
kx
1Š‹
y
k
y dy ; the volume of the rightœœ
11
k5
xkx
'0
kx %È
circular cylinder formed by revolving PQ about the
y-axis is V x kx the volume of the solid
##
œÊ1È
formed by revolving R about the y-axis is
#
V V V . Therefore we can see the
$#"
œœ
4x kx
5
1È
ratio of V to V is 4:1.
$"
(b) The volume of the solid formed by revolving R about the x-axis is V kt dt k t dt
#"
#
œœ
''
00
xx
11
Š‹
È
. The volume of the right circular cylinder formed by revolving PS about the x-axis isœ1kx
#
V kx x kx the volume of the solid formed by revolving R about the x-axis is
# "
##
œœÊ11
Š‹
È
V V V kx . Therefore the ratio of V to V is 1:1.
$#" $"
#
##
œœ œ111kx kx
82. Let P ( p y ) be any point on x p, and let P(x y) be a point where a tangent intersects y 4px. Now
"" #
ß œ ß œ
y 4px 2y 4p ; then the slope of a tangent line from P is
#"
œÊ œÊœ œœ
dy dy 2p y y dy 2p
dx dx y x ( p) dx y
y yy 2px 2p . Since x , we have y yy 2p 2p y yy y 2pÊ œ œ œ Ê œ
## # ####
"""
"
#
yy
4p 4p
Š‹
y yy 2p 0 y y y 4p . Therefore the slopes of the twoʜʜ œ„
"
##
##
""
„ ##
2y 4y 16p
ÈÈ
tangents from P are m and m m m 1
"" # "#
œœÊœœ
2p 2p 4p
y y 4p y y 4p yy4p
ÈÈ ab
the lines are perpendicularÊ
83. Let y 1 on the interval 0 x 2. The area of the inscribed rectangle is given byœ ŸŸ
Éx
4
A(x) 2x 2 1 4x 1 (since the length is 2x and the height is 2y)œœ
Š‹
ÉÉ
xx
44
A (x) 4 1 . Thus A (x) 0 4 1 0 4 1 x 0 x 2Ê œ œÊ œÊ œÊ œ
ww ##
ÉÉ
Š‹
xx xx x
444
11
ÉÉ
x x
4 4
x 2 (only the positive square root lies in the interval). Since A(0) A(2) 0 we have that A 2 4Êœ œ œ œ
È È
Š‹
is the maximum area when the length is 2 2 and the height is 2.
ÈÈ
84. (a) Around the x-axis: 9x 4y 36 y 9 x y 9 x and we use the positive root
## # # #
œÊœ Êœ„
99
44
É
V 2 9 x dx 2 9 x dx 2 9x x 24Êœ œ œ œ
''
00
22
1111
Š‹
Ɉ‰ ‘
993
444
###$
#
!
(b) Around the y-axis: 9x 4y 36 x 4 y x 4 y and we use the positive root
## # # #
œÊœ Êœ„
44
99
É
V 2 4 y dy 2 4 y dy 2 4y y 16Êœ œ œ œ
''
00
33
1111
Š‹
Ɉ‰ ‘
444
9927
###$
$
!
85. 9x 4y 36 y y x 4 on the interval 2 x 4 V x 4 dx
## #
##
##
#
œÊœ Êœ„ ŸŸÊœ
9x 36 3 3
4ÈÈ
Š‹
'2
4
1
x 4 dx 4x 16 8 8 (56 24) 24œœœœœœ
9 9 x 9 64 8 9 56 3
443433434
111 11
'2
4ab ’“‘ˆ‰ˆ‰ˆ‰
#%
#1
86. x y 1 x 1 y on the interval 3 y 3 V 1 y dy 2 1 y dy
## ###
##
œÊœ„ ŸŸÊ œ œ
ÈÈÈ
ˆ‰ ˆ‰
''
30
33
11
2 1 y dy 2 y 24œœœ111
'0
3ab ’“
#$
!
y
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
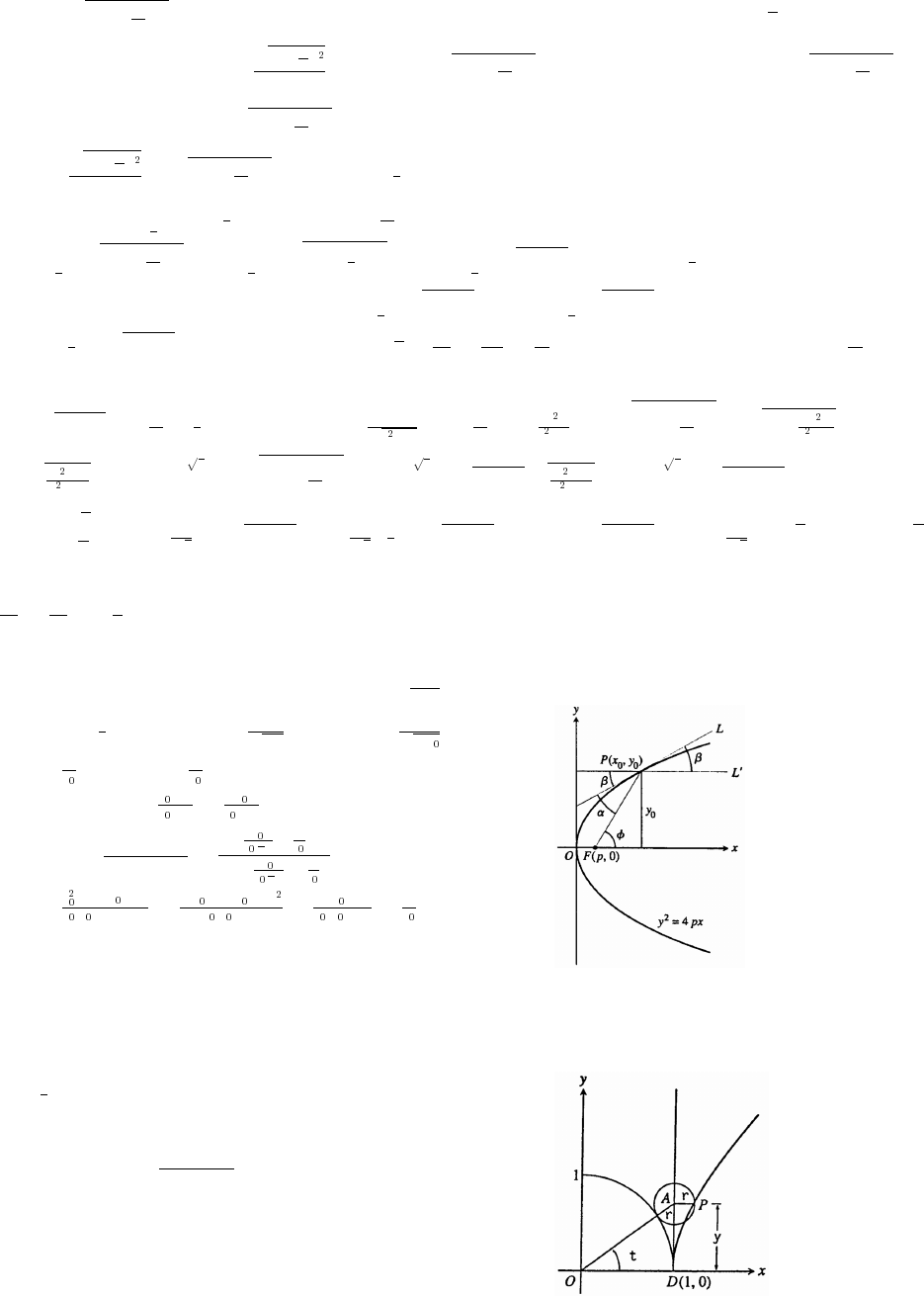
Section 10.1 Conic Sections and Quadratic Equations 629
87. Let y 16 x on the interval 3 x 3. Since the plate is symmetric about the y-axis, x 0. For aœ ŸŸ œ
É16
9#
vertical strip: x y x , length 16 x , width dx area dA 16 x dxab
ÉÉ
µµ
ßœß œ œÊ œœ
É16 x 16 16
99
###
16
9
mass dm dA 16 x dx. Moment of the strip about the x-axis:Êœœœ $$
É16
9#
y dm 16 x dx 8 x dx so the moment of the plate about the x-axis is
µœœ
É16 x 16 8
99
###
16
9Š‹
Ɉ‰
$$
M y dm 8 x dx 8x x 32 ; also the mass of the plate is
x3
3
œœ œ œ
µ
''$$ $
ˆ‰ ‘
88
927
#$
$
$
M 16 x dx 4 1 x dx 4 3 1 u du where u 3 du dx; x 3œœœ œÊœœ
'' '
33 1
33 1
$$$
ÉɈ‰ È
16 x
93 3
##
"#
u 1 and x 3 u 1. Hence, 4 3 1 u du 12 1 u duÊœ œÊœ œ $$
''
11
11
ÈÈ
##
12 u 1 u sin u 6 y . Therefore the center of mass is .œœÊœœœ !ß$1$
’“Š‹
Ȉ‰
"#" "
"
2M633
M32 16 16
x$
1$ 1 1
88. y x 1 x 1 (2x) 1 1œÊœ œ Ê œ Ê œ
Èab Š‹ Š‹
ÊÉ
#"
#
#"Î#
##
dy dy dy
dx dx x 1 dx x 1
xx x
x1
È
S 2 y 1 dx 2 x 1 dx 2 2x 1 dx ;œÊœ œ œ
ÉÉ
ÊŠ‹ ÈÈ
2x 1 2x 1
x1 dx x1
dy
###
'' '
00 0
22 2
11 1
u1 du uu1lnu u1 25ln2 5
u2x
du 2 dx
–—
È
ÈÈÈÈ
’“’“Š‹Š‹Š‹ÈÈ
œ
œÄ œ œ
22
22 2
2
11 1
ÈÈ È
'0
2###
"#
!
89. (r r ) 0 r r C, a constant the points P(t) lie on a hyperbola with foci at A
dr dr
dt dt dt
d
AB
œÊ œÊœ Ê
AB AB
and B
90. (a) tan m tan f (x ) where f(x) 4px ;""œÊ œ œ
Lw!È
f (x) (4px) (4p) f (x )
w "Î# w
"
#!
œœÊœ
2p 2p
4px 4px
ÈÈ
tan .œÊ œ
2p 2p
yy
"
(b) tan m9œœ œ
FP
y0 y
xp xp
(c) tan !œœ
tan tan
1tan tan
9"
9"
Š‹
Š‹Š‹
y
xp y
2p
y
xp y
2p
c
b1
œœ œœ
y 2p(x p)
y (x p 2p) y (x p) y (x p) y
4px 2px 2p 2p(x p) 2p
91. PF will always equal PB because the string has constant length AB FP PA AP PB.œœ
92. (a) In the labeling of the accompanying figure we have
tan t so the coordinates of A are (1 tan t). The
y
1ϧ
coordinates of P are therefore (1 r tan t). Sinceß
1 y (OA) , we have 1 tan t (1 r)
## # # # #
œ œ
1 r 1 tan t sec t r sec t 1.Êœ œ Êœ
È#
The coordinates of P are therefore (x y) (sec t tan t)ßœ ß
xy secttant1Êœ œ
## # #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
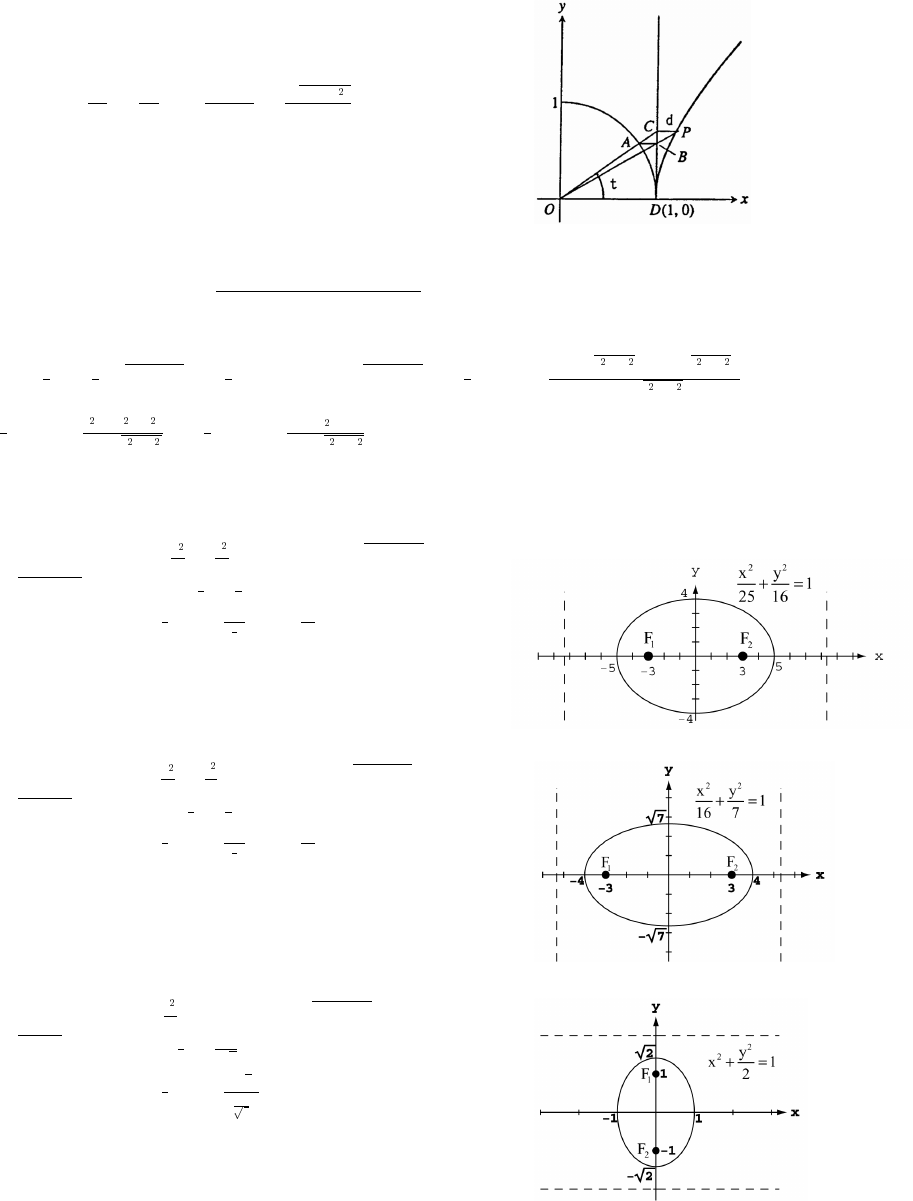
630 Chapter 10 Conic Sections and Polar Coordinates
(b) In the labeling of the accompany figure the coordinates
of A are (cos t sin t), the coordinates of C are (1 tan t),ßß
and the coordinates of P are (1 d tan t). By similarß
triangles,
dOC d
AB OA 1 cos t 1
1tant
œÊ œ
È
d (1 cos t)(sec t) sec t 1. The coordinatesÊœ œ
of P are therefore (sec t tan t) and P moves on theß
hyperbola x y 1 as in part (a).
##
œ
93. x 4py and y p x 4p x 2p. Therefore the line y p cuts the parabola at points ( 2p p) and
###
œœÊœÊœ„ œ ß
(2p p), and these points are [2p ( 2p)] (p p) 4p units apart.ߜ
È##
94. lim x x a lim x x a lim
xxxÄ_ Ä_ Ä_
Š‹Š‹
ÈÈ
–—
bb b b
aa a a
xxaxxa
xxa
œ œ
## ##
Š‹Š‹
ÈÈ
È
lim lim 0œœœ
bba
aa
xxa
xxa xxa
xxÄ_ Ä_
’“ ’“
ab
ÈÈ
10.2 CLASSIFYING CONIC SECTIONS BY ECCENTRICITY
1. 16x 25y 400 1 c a b
##
###
œÊœÊœ
x
516
yÈ
25 16 3 e ; F 3 0 ;œœÊœœ „ß
Èab
c3
a5
directrices are x 0œ „ œ„ œ„
a525
e3
ˆ‰
3
5
2. 7x 16y 112 1 c a b
## ##
œÊœÊœ
x
16 7
yÈ
16 7 3 e ; F 3 0 ;œœÊœœ „ß
Èab
c3
a4
directrices are x 0œ „ œ„ œ„
a416
e3
ˆ‰
3
4
3. 2x y 2 x 1 c a b
## # ##
œÊ œÊœ
y
2È
2 1 1 e ; F 0 1 ;œœÊœœ ß„
Èab
c1
a2
È
directrices are y 0 2œ „ œ„ œ„
a
e
2
È
Š‹
1
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
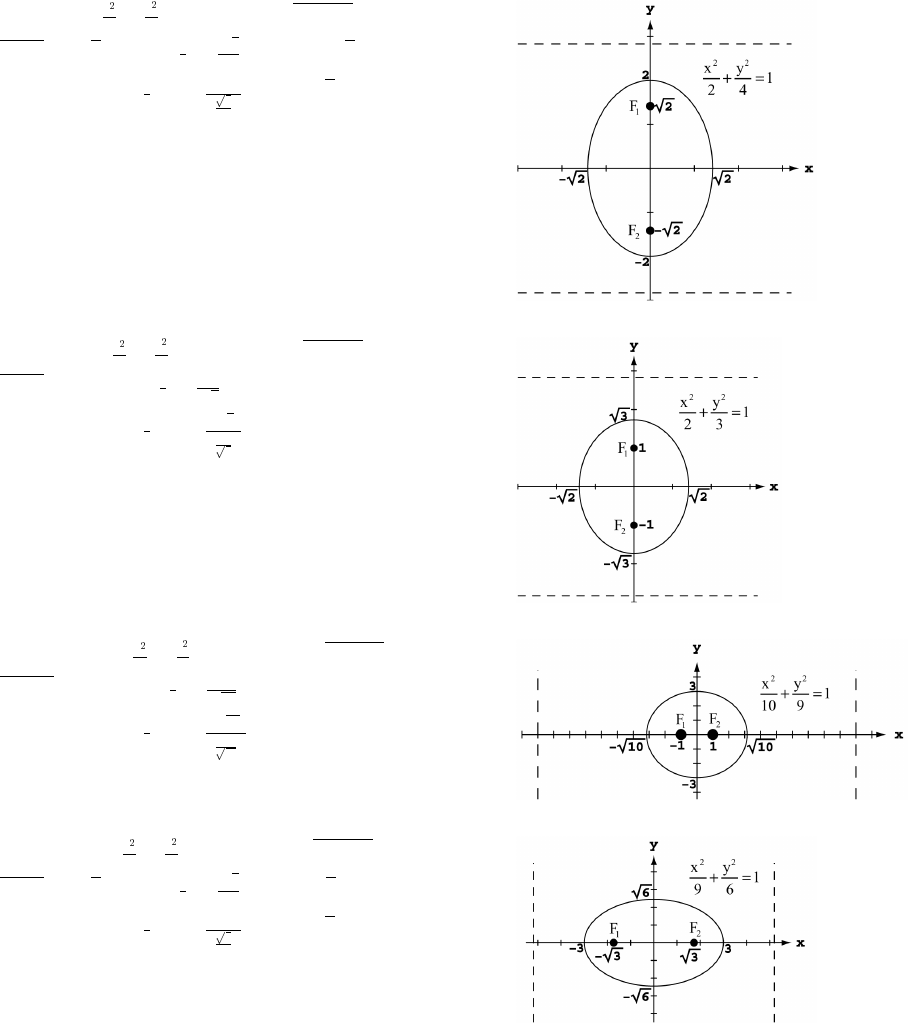
Section 10.2 Classifying Conic Sections by Eccentricity 631
4. 2x y 4 1 c a b
##
###
œÊ œÊœ
xy
4È
4 2 2 e ; F 0 2 ;œœ Êœœ ß„
ÈÈ È
Š‹
c
a2
2
È
directrices are y 0 2 2œ „ œ„ œ„
a2
eŠ‹
2
2È
5. 3x 2y 6 1 c a b
##
###
œÊœÊœ
xy
3È
3 2 1 e ; F 0 1 ;œœÊœœ ß„
Èab
c1
a3
È
directrices are y 0 3œ „ œ„ œ„
a
e
3
È
Š‹
1
3
6. 9x 10y 90 1 c a b
## ##
œÊœÊœ
x
10 9
yÈ
10 9 1 e ; F 1 0 ;œœÊœœ „ß
Èab
c1
a10
È
directrices are x 0 10œ „ œ„ œ„
a
e
10
È
Š‹
1
10
7. 6x 9y 54 1 c a b
## ##
œÊœÊœ
x
96
yÈ
9 6 3 e ; F 3 0 ;œœ Êœœ „ß
ÈÈ È
Š‹
c
a3
3
È
directrices are x 0 3 3œ „ œ„ œ„
a3
eŠ‹
3
3È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
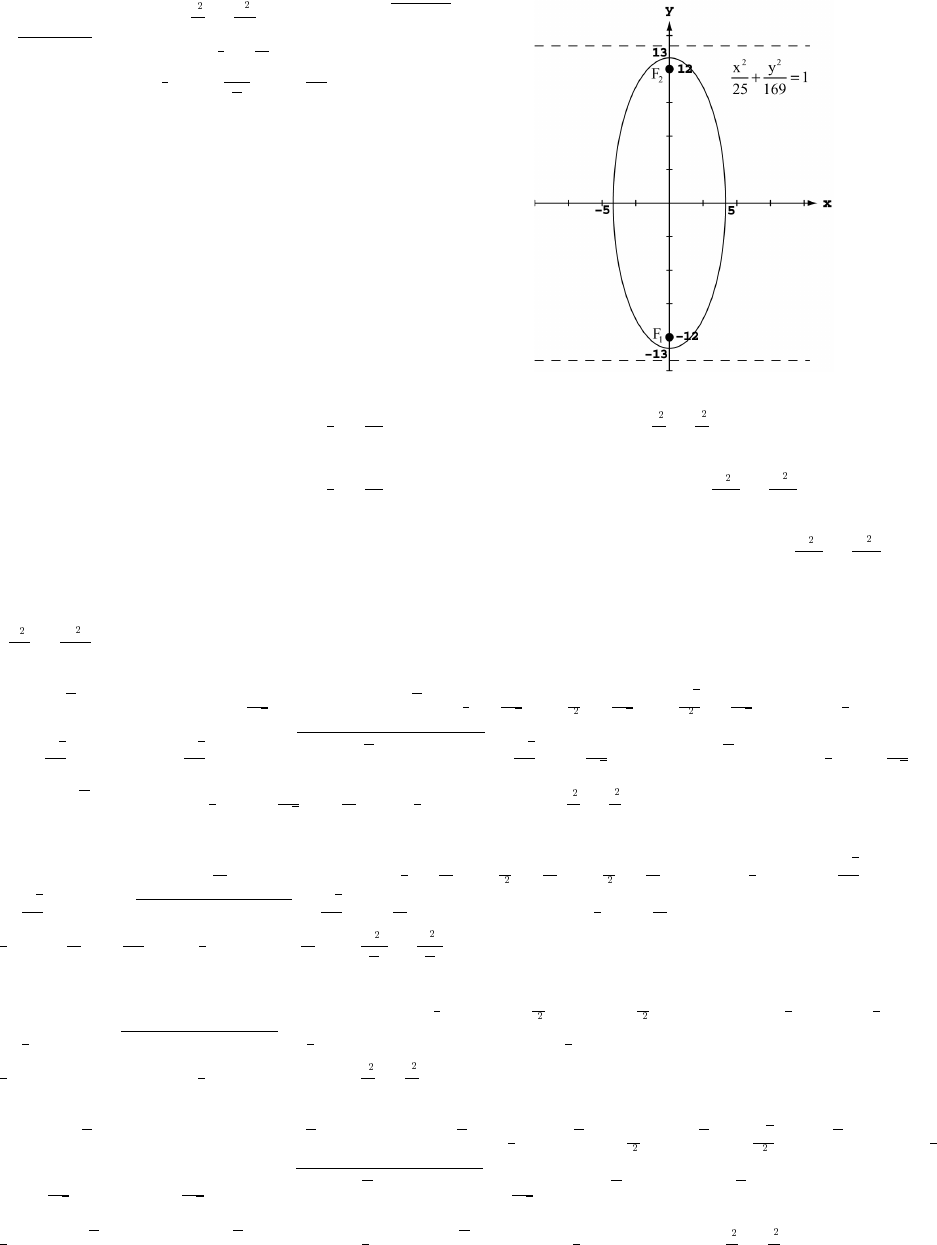
632 Chapter 10 Conic Sections and Polar Coordinates
8. 169x 25y 4225 1 c a b
## ##
œ ʜʜ
x
25 169
yÈ
169 25 12 e ; F 0 12 ;œœÊœœ ß„
Èab
c12
a13
directrices are y 0œ „ œ„ œ„
a 13 169
e12
ˆ‰
12
13
9. Foci: 0 3 , e 0.5 c 3 and a 6 b 36 9 27 1abß„ œ Ê œ œ œ œ Ê œ œ Ê œ
c3 x
e0.5 736
y
#
#
10. Foci: 8 0 , e 0.2 c 8 and a 40 b 1600 64 1536 1ab„ß œ Ê œ œ œ œ Ê œ œ Ê œ
c8 x
e 0. 1600 1536
y
#
#
11. Vertices: 0 70 , e 0.1 a 70 and c ae 70(0.1) 7 b 4900 49 4851 1abß„ œ Ê œ œ œ œ Ê œ œ Ê œ
#x
4851 4900
y
12. Vertices: 10 0 , e 0.24 a 10 and c ae 10(0.24) 2.4 b 100 5.76 94.24ab„ß œ Êœ œ œ œ Ê œ œ
#
1Ê œ
x
100 94.24
y
13. Focus: 5 , Directrix: x c ae 5 and e
Š‹
ÈÈ
ß! œÊœœ œÊœÊœÊœ
9a9ae995
5555
ee e 9
5
ÈÈÈÈ
È#
e . Then PF PD x 5 (y 0) x x 5 y xÊœ œ ʜʜ
ÈÈ È
ÈÈ
55 5
33 3 9
959
55
ÊŠ‹ ¹¹Š‹ Š‹
ÈÈ
###
##
x25x5y x x xy4 1Ê œ Ê œÊœ
### ##
ÈŠ‹
518814 x
959 94
5
y
È
14. Focus: ( 0), Directrix: x c ae 4 and e e . Then%ß œÊœœ œÊœÊœÊœÊœ
16 a16 ae16 4 16 3
3e3e3e34
3
#
#
È
PF PD (x 4) (y 0) x (x 4) y x x 8x 16 yœ Ê œ Êœ Ê
ÈÈ
33
16 3 16
343##
## ## # #
#
ȸ¸ ˆ‰
xx xy 1œÊœÊœ
3 32 256 16 x
4394 3
y
ˆ‰
###
"ˆ‰ ˆ‰
64 16
33
15. Focus: ( 0), Directrix: x 16 c ae 4 and 16 16 16 e e . Then%ß œÊœœ œÊœÊœÊœÊœ
aae 4 1
ee e 4
#"
#
PF PD (x 4) (y 0) x 16 (x 4) y (x 16) x 8x 16 yœ Ê œ Êœ Ê
111
4##
## ## # # #
Èkk
x 32x 256 x y 48 1œÊœÊœ
13x
4 4 64 48
y
ab
###
16. Focus: 2 , Directrix: x 2 2 c ae 2 and 2 2 2 2 2 2 e
Š‹
ÈÈÈÈÈÈ
ß! œÊœœ œÊœÊœÊœ
aae
ee e
2
È#"
#
e . Then PF PD x 2 (y 0) x 2 2 x 2 yÊœ œ Êœ Ê
11 1
22 2
ÈÈ È
ÊŠ‹ ¹ ¹Š‹
ÈÈÈ
##
##
x22 x22x2y x42x8 xy 2 1œ Ê œ ʜʜ
"""
####
#### ##
Š‹ Š ‹
ÈÈ È x
4
y
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
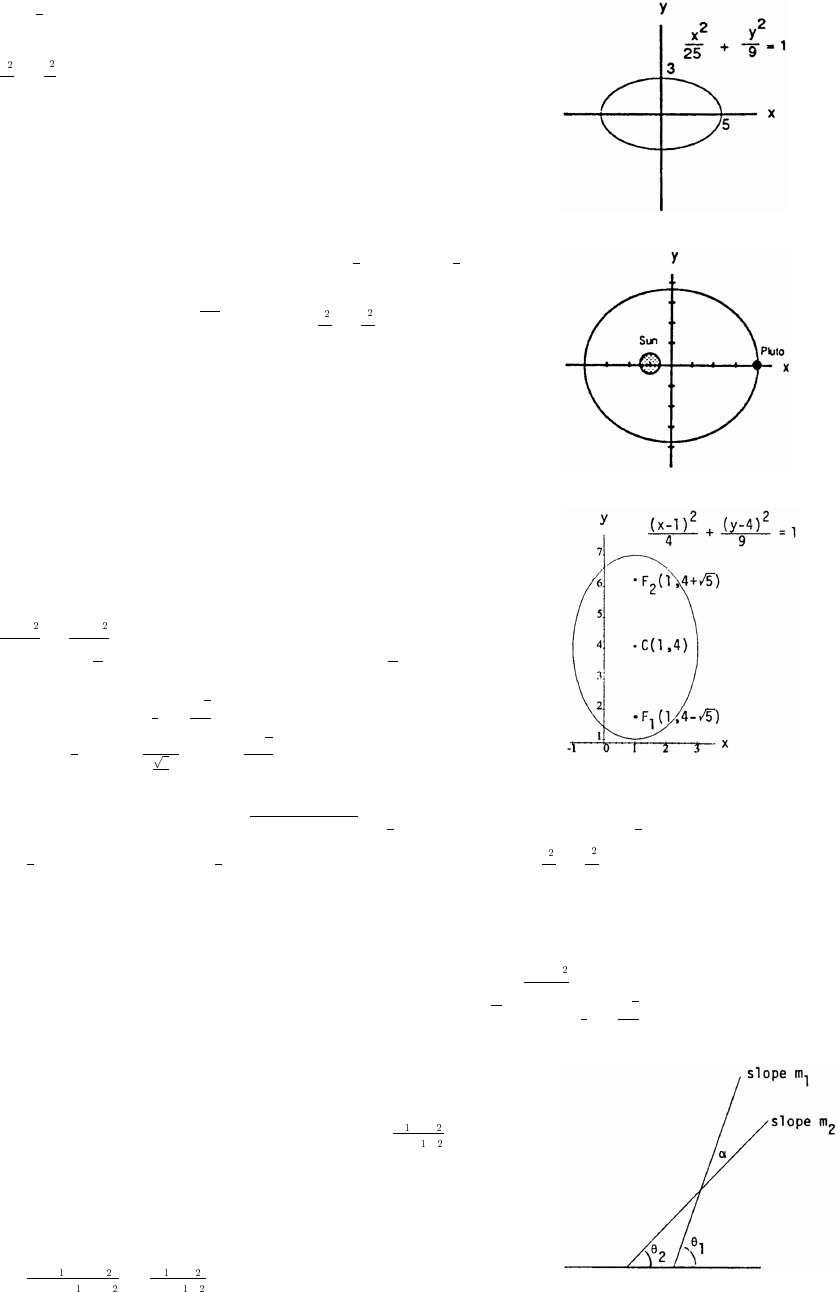
Section 10.2 Classifying Conic Sections by Eccentricity 633
17. e take c 4 and a 5; c a bœÊ œ œ œ
4
5
###
16 25 b b 9 b 3; thereforeʜʜʜ
##
1
x
59
y
#œ
18. The eccentricity e for Pluto is 0.25 e 0.25Êœœ œ
c
a4
"
take c 1 and a 4; c a b 1 16 bÊœ œœÊœ
### #
b 15 b 15 ; therefore, 1 is aʜʜ œ
#Èx
16 15
y
model of Pluto's orbit.
19. One axis is from A( ) to B( 7) and is 6 units long; the"ß " "ß
other axis is from C( ) to D( 1 4) and is 4 units long.$ß % ß
Therefore a 3, b 2 and the major axis is vertical. Theœœ
center is the point C( 4) and the ellipse is given by"ß
1; cab325
(x 1) (y 4)
49
#####
œ œœœ
c 5 ; therefore the foci are F 1 4 5 , theʜ ߄
ÈÈ
Š‹
eccentricity is e , and the directrices areœœ
c
a3
5
È
y4 4 4 .œ„œ„ œ„
a3
e5
95
Š‹ È
5
3
20. Using PF e PD, we have (x 4) y x 9 (x 4) y (x 9) x 8x 16 yœ œ Ê œ Ê †Èkk
## ## # # #
24
39
x 18x 81 x y 20 5x 9y 180 or 1.œÊœÊœ œ
45 x
9 9 36 20
y
ab
#####
21. The ellipse must pass through ( 0) c 0; the point ( 1 2) lies on the ellipse a 2b 8. The ellipse!ß Ê œ ß Ê œ
is tangent to the x-axis its center is on the y-axis, so a 0 and b 4 the equation is 4x y 4y 0.ÊœœÊœ
##
Next, 4x y 4y 4 4 4x (y 24) 4 x 1 a 2 and b 1 (now using the
## # # #
œÊ œÊ œÊœ œ
(y 2)
4
standard symbols) c a b 4 1 3 c 3 e .Ê œ œœÊœ Êœœ
###
#
Èc
a
3
È
22. We first prove a result which we will use: let m , and
"
m be two nonparallel, nonperpendicular lines. Let be
#!
the acute angle between the lines. Then tan .!œmm
1mm
To see this result, let be the angle of inclination of the)"
line with slope m , and be the angle of inclination of the
"#
)
line with slope m . Assume m m . Then and we
#"#"#
))
have . Then tan tan ( )!) ) ! ) )œ œ
"# "#
, since m tan and andœœ œ
tan tan m m
1tan tan 1mm
))
))
""
)
mtan .
##
œ)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
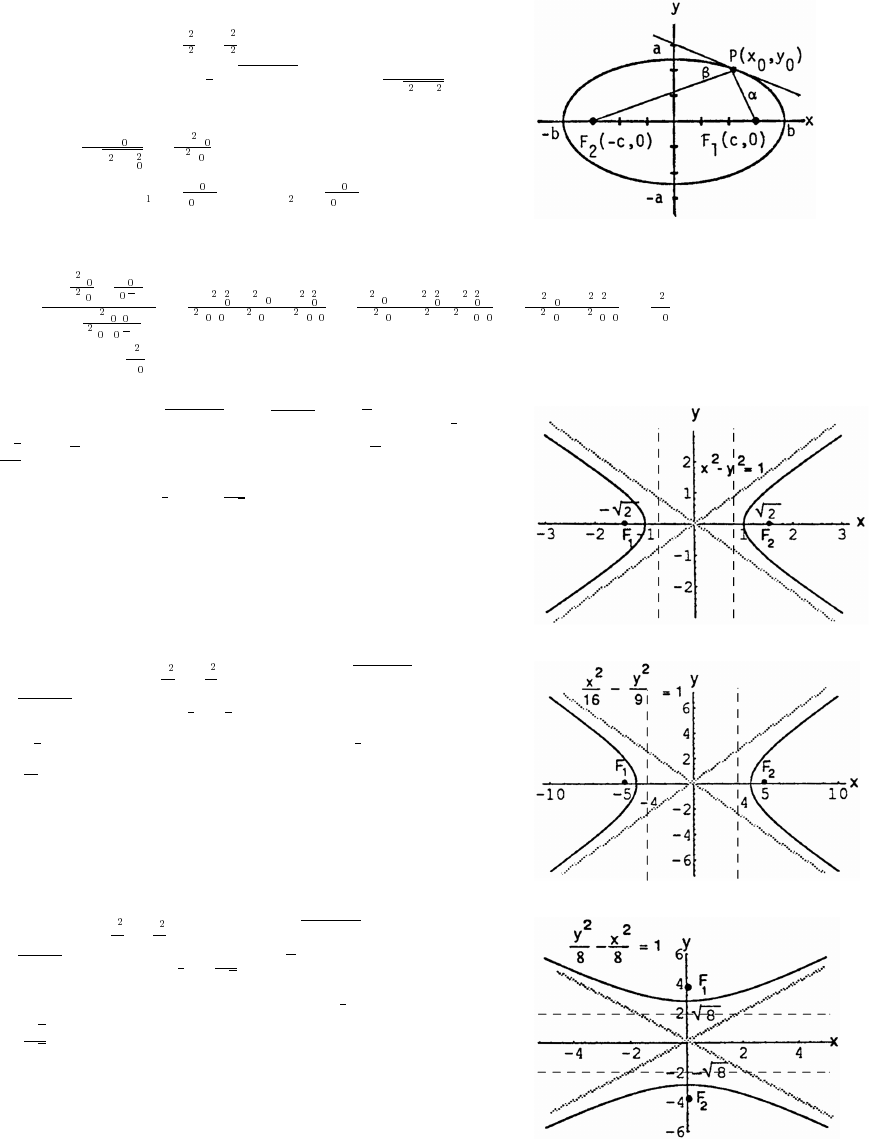
634 Chapter 10 Conic Sections and Polar Coordinates
Now we prove the reflective property of ellipses (see the
accompanying figure): If 1, then
x
ab
y
œ
b x a y a b and y a x y .
## ## ## w
##
œ œ Êœ
bbx
aaa x
ÈÈ
Let P(x y ) be any point on the ellipse
!!
ß
y (x ) . Let F (c 0) and F ( c 0)Êœ œ ß ß
w!"#
bx b x
aa x ay
É
be the foci. Then m and m . Let and
PF PF
yy
xc xc
œœ
!
be the angles between the tangent line and PF and PF ,""#
respectively. Then
tan !œœ œ œ
Œ
Š‹
cc
c
bx y
ay xc
bxy
ay(x c)
1
bx bxc ay bxc bx ay
ayx ayc bxy ayc a b xy
bxc
ab
ab ab
ayc cxy cy
b
œ.
Similarly, tan . Since tan tan , and and are both less than 90°, we have ."!"!" !"œœ œ
b
cy
23. x y 1 c a b 1 1 2 e
## ##
œÊœ œ œ Êœ
ÈÈ
Èc
a
2 ; asymptotes are y x; F 2 ;œœ œ„ „ß!
È2
1ÈÈ
Š‹
directrices are x 0œ„œ„
a
e2
"
È
24. 9x 16y 144 1 c a b
## ##
œÊœÊœ
x
16 9
yÈ
16 9 5 e ; asymptotes areœœÊœœ
Èc5
a4
y x; F 5 ; directrices are x 0œ„ „ ß! œ „
3a
4e
ab
œ„
"6
5
25. y x 8 1 c a b
## ##
œÊ œÊœ
y
88
xÈ
8 8 4 e 2 ; asymptotes areœœÊœœœ
ÈÈ
c4
a8
È
y x; F 0 4 ; directrices are y 0œ„ ß„ œ „ab a
e
2œ„ œ„
È
È8
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
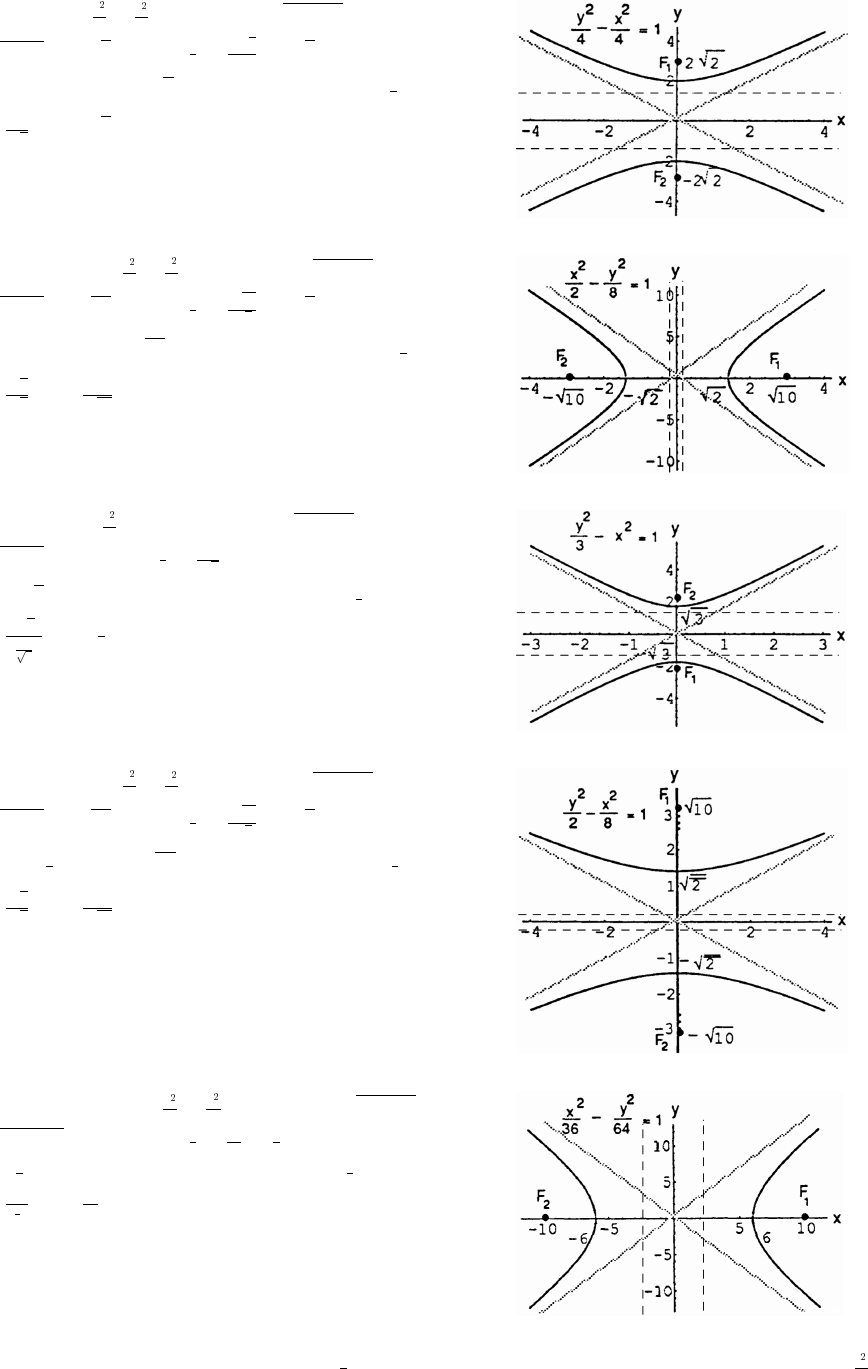
Section 10.2 Classifying Conic Sections by Eccentricity 635
26. y x 4 1 c a b
## ##
œÊ œÊœ
y
44
xÈ
4 4 2 2 e 2 ; asymptotesœœ Êœœ œ
ÈÈÈ
c
a2
22
È
are y x; F 0 2 2 ; directrices are y 0œ„ ß„ œ „
Š‹
Èa
e
2œ„ œ„
2
2
ÈÈ
27. 8x 2y 16 1 c a b
## ##
œÊœÊœ
x
28
yÈ
2 8 10 e 5 ; asymptotesœœ Êœœ œ
ÈÈÈ
c
a
10
2
È
È
are y 2x; F 10 ; directrices are x 0œ„ „ ß! œ „
Š‹
Èa
e
œ„ œ„
È
ÈÈ
2
510
2
28. y 3x 3 x 1 c a b
## # ##
œÊœÊœ
y
3È
3 1 2 e ; asymptotes areœœÊœœ
Èc2
a3
È
y 3 x; F 0 2 ; directrices are y 0œ„ ß„ œ „
Èab a
e
œ„ œ„
È
Š‹
33
2
3
#
29. 8y 2x 16 1 c a b
## ##
œÊœÊœ
y
28
xÈ
2 8 10 e 5 ; asymptotesœœ Êœœ œ
ÈÈÈ
c
a
10
2
È
È
are y ; F 0 10 ; directrices are y 0œ„ ß„ œ „
xa
e#Š‹
È
œ„ œ„
È
ÈÈ
2
510
2
30. 64x 36y 2304 1 c a b
## ##
œ ʜʜ
x
36 64
yÈ
36 64 10 e ; asymptotes areœœÊœœœ
Èc105
a63
y x; F 10 ; directrices are x 0œ„ „ ß! œ „
4a
3e
ab
œ„ œ„
618
5
ˆ‰
5
3
31. Vertices 1 and e 3 a 1 and e 3 c 3a 3 b c a 9 1 8 y 1ab!ß„ œÊœ œœÊœ œÊ œœœÊ œ
c x
a 8
### #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

636 Chapter 10 Conic Sections and Polar Coordinates
32. Vertices 2 and e 2 a 2 and e 2 c 2a 4 b c a 16 4 12 1ab„ß! œÊœ œœÊœ œÊ œœ œ Ê œ
c x
a41
y
###
#
33. Foci 3 and e 3 c 3 and e 3 c 3a a 1 b c a 9 1 8 x 1ab„ß! œÊœ œœÊœ ÊœÊ œ œœÊ œ
c
a 8
y
### #
34. Foci 5 and e 1.25 c 5 and e 1.25 c a 5 a a 4 b c aab!ß„ œ Êœ œœ œÊœÊœÊœÊœ
c55 5
a44 4
###
25 16 9 1œœÊ œ
y
16 9
x
35. Focus (4 0) and Directrix x 2 c ae 4 and 2 2 2 e e 2 . ThenߜʜœœÊœÊœÊœ#Êœ
aae 4
ee e
#È
PF 2 PD (x 4) (y 0) 2 x 2 (x 4) y 2(x 2) x 8x 16 yœ Ê œ Êœ Ê
ÈÈ
Èkk
## ## # # #
2 x 4x 4 x y 8 1œÊœÊœab
###
x
88
y
36. Focus 10 and Directrix x 2 c ae 10 and 2 2 2 e 5
Š‹
ÈÈ
ÈÈÈÈ
È
ß! œÊœœ œÊœÊ œÊœ
aae
ee e
10
È#
e 5. Then PF 5PD x10(y0) 5 x2 x10yÊœ œ ÊœÊ
%% %
##
##
ÈÈ È
ÊŠ‹ ¹¹Š‹
ÈÈ
È
5x 2 x 210x10y 5x 22x2 1 5x y 2510œÊ œ Ê œ
ÈÈÈÈ
Š‹ Š ‹Š‹
ÈÈ
È
#### ##
1 1ʜʜ
Š‹
È
ÈÈ ÈÈ
15x
510 2510 25 1025
yy
x
#
37. Focus ( 2 0) and Directrix x c ae 2 and e 4 e 2. Thenß œÊœ œ œ Ê œ Ê œ Ê œÊœ
""""
####
#
aae 2
ee e
PF 2PD (x 2) (y 0) 2 x (x 2) y 4 x x 4x 4 yœ Ê œ Êœ Ê
ȸ¸ ˆ‰
## ""
##
## # #
#
4 x x 3x y 3 x 1œÊœÊœ
ˆ‰
####
"
43
y
38. Focus ( 6 0) and Directrix x c ae 6 and e 3 e 3. Then ß œ# Ê œ œ œ# Ê œ# Ê œ# Ê œ Ê œ
aae 6
ee e
#È
PF 3 PD (x 6) (y 0) 3 x 2 (x 6) y 3(x 2) x 12x 36 yœ Ê œ Êœ Ê
ÈÈ
Èkk
## ## # # #
3 x 4x 4 2x y 24 1œÊœÊœab
###
#
x
124
y
39. (x 1) (y 3) y 2 x 2x 1 y 6y 9 y 4y 4 4x 5y 8x 60y 4 0
Èkk a b œ Ê œ Ê œ
##
#
## # ##
39
4
4 x 2x 1 5 y 12y 36 4 4 180 1ÊœÊ œaba b
## (y 6) (x 1)
36 45
40. c a b b c a ; e c ea c e a b e a a a e 1 ; thus,
### ### ### ######
œÊœ œÊœÊœ Êœ œ
c
aab
1; the asymptotes of this hyperbola are y e 1 x as e increases, the
xx
ab aae1
yy
œ"Ê œ œ„ Ê
ab
#
ab
absolute values of the slopes of the asymptotes increase and the hyperbola approaches a straight line.
41. To prove the reflective property for hyperbolas:
1 a y b x a b and .
xxb
a b dx ya
ydy
œÊ œ œ
## ## ##
Let P(x y ) be a point of tangency (see the accompanying
!!
ß
figure). The slope from P to F( c 0) is and fromß y
xc
P to F (c 0) it is . Let the tangent through P meet
#
ßy
xc
the x-axis in point A, and define the angles F PAnœ
"!
and F PA . We will show that tan tan . Fromnœ œ
#"!"
the preliminary result in Exercise 22,
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
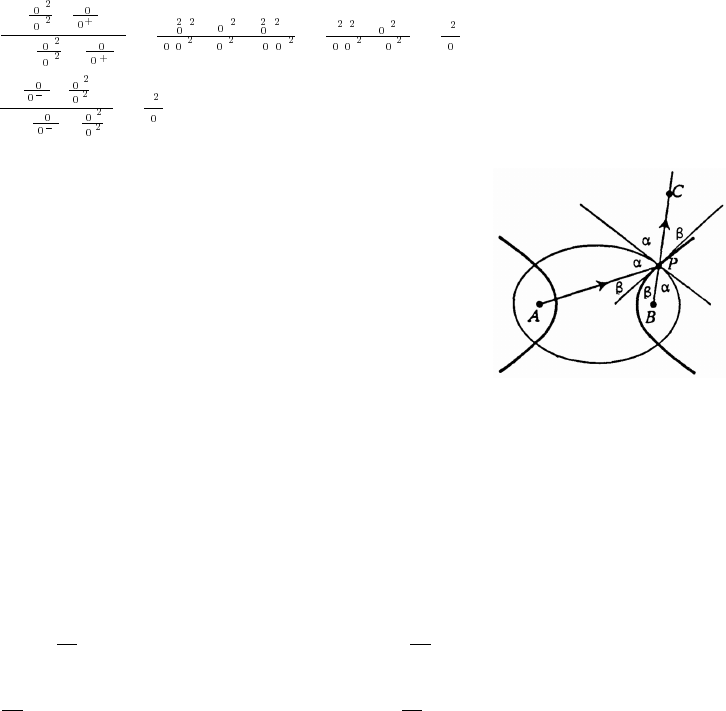
Section 10.3 Quadratic Equations and Rotations 637
tan . In a similar ma!œœ œœ
Œ
Š‹Š ‹
xb y
ya xc
xb y
ya xc
c
b1
xb xbc y a
xya yac xyb xyc yac yc
ab xbc b
nner,
tan . Since tan tan , and and are acute angles, we have ."!"!"!"œœ œ œ
Œ
Š‹Š‹
yxb
xc ya
yxb
xc ya
1
b
yc
42. From the accompanying figure, a ray of light emanating from
the focus A that met the parabola at P would be reflected
from the hyperbola as if it came directly from B
(Exercise 41). The same light ray would be reflected off the
ellipse to pass through B. Thus BPC is a straight line.
Let be the angle of incidence of the light ray on the"
hyperbola. Let be the angle of incidence of the light ray!
on the ellipse. Note that is the angle between the!"
tangent lines to the ellipse and hyperbola at P. Since BPC is
a straight line, 2 2 180°. Thus 90°.!" !"œ œ
10.3 QUADRATIC EQUATIONS AND ROTATIONS
1. x 3xy y x 0 B 4AC ( 3) 4(1)(1) 5 0 Hyperbola
## # #
œÊ œ œÊ
2. 3x 18xy 27y 5x 7y 4 B 4AC ( 18) 4(3)(27) 0 Parabola
## # #
œÊœ œÊ
3. 3x 7xy 17y 1 B 4AC ( 7) 4(3) 17 0.477 0 Ellipse
####
œÊ œ ¸ Ê
ÈÈ
4. 2x 15 xy 2y x y 0 B 4AC 15 4(2)(2) 1 0 Ellipse
## # #
œÊ œ œÊ
ÈÈ
Š‹
5. x 2xy y 2x y 2 0 B 4AC 2 4(1)(1) 0 Parabola
## # #
œÊ œ œÊ
6. 2x y 4xy 2x 3y 6 B 4AC 4 4(2)( 1) 24 0 Hyperbola
## # #
œÊ œ œ Ê
7. x 4xy 4y 3x 6 B 4AC 4 4(1)(4) 0 Parabola
## ##
œÊ œ œÊ
8. x y 3x 2y 10 B 4AC 0 4(1)(1) 4 0 Ellipse (circle)
## # #
œ Ê œ œÊ
9. xy y 3x 5 B 4AC 1 4(0)(1) 1 0 Hyperbola œÊ œ œÊ
###
10. 3x 6xy 3y 4x 5y 12 B 4AC 6 4(3)(3) 0 Parabola
## ##
œÊ œ œÊ
11. 3x 5xy 2y 7x 14y 1 B 4AC ( 5) 4(3)(2) 1 0 Hyperbola
## # #
œÊ œ œÊ
12. 2x 4.9xy 3y 4x 7 B 4AC ( 4.9) 4(2)(3) 0.01 0 Hyperbola
## # #
œÊœ œÊ
13. x 3xy 3y 6y 7 B 4AC ( 3) 4(1)(3) 3 0 Ellipse
## # #
œÊ œ œÊ
14. 25x 21xy 4y 350x 0 B 4AC 21 4(25)(4) 41 0 Hyperbola
## ##
œÊœ œÊ
15. 6x 3xy 2y 17y 2 0 B 4AC 3 4(6)(2) 39 0 Ellipse
## ##
œÊ œ œÊ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
638 Chapter 10 Conic Sections and Polar Coordinates
16. 3x 12xy 12y 435x 9y 72 0 B 4AC 12 4(3)(12) 0 Parabola
## ##
œÊœ œÊ
17. cot 2 0 2 ; therefore x x cos y sin ,!!! !!œœœÊœÊœ œ
AC 0
B1 4
#
ww
11
yx sin y cos xx y , yx yœ Êœ œ
w w ww ww
## ##
!! ÈÈ ÈÈ
22 22
x y x y 2 x y 2 x y 4 HyperbolaÊ œÊœÊœÊ
Š‹Š‹
ÈÈÈÈ
22 22
## ## ##
ww ww ww ww
""
## ##
18. cot 2 0 2 ; therefore x x cos y sin ,!!! !!œœœÊœÊœ œ
AC 11
B1 4
#
ww
11
yx sin y cos xx y , yx yœ Êœ œ
w w ww ww
## ##
!! ÈÈ ÈÈ
22 22
xy xy xy xy1Ê œ
Š‹Š‹Š‹Š‹
ÈÈ ÈÈÈÈ ÈÈ
22 22 22 22
## ## ## ##
ww ww ww ww
# #
xxyyxyxxyy1 xy1 3xy2 EllipseÊ œÊ œÊœÊ
" """" " "
# #### # ##
wwwwwwwwww ww ww
# #### # ## ##
3
19. cot 2 2 ; therefore x x cos y sin ,!!!!!œœœÊœÊœ œ
AC 31
B36
23 3
" ww
ÈÈ 11
y x sin y cos x x y , y x yœ Êœœ
ww wwww
## ##
"
!! ÈÈ
33
1
3xy23 xyxy xy8xyÊ
Š‹Š‹Š‹Š‹Š‹
È
ÈÈÈÈÈ
33333
1111
## #### ## ##
ww ww w w w w ww
# # "
8 3 x y 0 4x 16y 0 ParabolaœÊœÊ
ÈŠ‹
"
##
ww ww
#
È3
20. cot 2 2 ; therefore x x cos y sin ,!!!!!œœœÊœÊœ œ
AC 12
B36
33
"
ww
ÈÈ 11
y x sin y cos x x y , y x yœ Êœœ
ww wwww
## ##
"
!! ÈÈ
33
1
xy 3 xy x y2x y 1 x y1Ê œÊœ
Š‹Š‹Š‹Š‹
È
ÈÈÈÈ
3333
1111 5
## #### ## # #
ww ww w w w w w w
# # "##
x 5y 2 EllipseÊ œÊ
ww
##
21. cot 2 0 2 ; therefore x x cos y sin ,!!! !!œœœÊœÊœ œ
AC 11
B2 2 4
ww
11
y x sin y cos x x y , y x yœ Êœ œ
w w ww ww
## ##
!! ÈÈ ÈÈ
22 22
xy2xy xy xy2 y1Ê œÊœ
Š‹Š‹Š‹Š‹
ÈÈ ÈÈÈÈ ÈÈ
22 22 22 22
## ## ## ##
ww ww ww ww w
# # #
Parallel horizontal linesÊ
22. cot 2 2 ; therefore x x cos y sin ,!!!!!œœ œÊœÊœ œ
AC 31 2
B33
23 3
"
ww
ÈÈ 11
y x sin y cos x x y , y x yœ Êœ œ
ww ww ww
## ##
!! 11
33
ÈÈ
3 x y 2 3 x y x y x y 1 4y 1Ê œÊœ
Š‹Š‹Š‹Š‹
È
1111
3333
## ## ## ##
ww ww ww ww w
# # #
ÈÈÈÈ
Parallel horizontal linesÊ
23. cot 2 0 2 ; therefore x x cos y sin ,!!!!!œœ œÊœÊœ œ
AC
B24
22
22
ww
ÈÈ
È11
y x sin y cos x x y , y x yœ Êœ œ
w w ww ww
## ##
!! ÈÈ ÈÈ
22 22
2x y 22x y x y 2x yÊ
ÈÈ È
Š‹Š‹Š‹Š‹
ÈÈ ÈÈÈÈ ÈÈ
22 22 22 22
## ## ## ##
ww ww ww ww
# #
8 x y 8 x y 0 2 2x 8 2 y 0 ParabolaœÊœÊ
Š‹Š‹
ÈÈ
ÈÈ ÈÈ
22 22
## ##
ww ww w w
#
24. cot 2 0 2 ; therefore x x cos y sin ,!!! !!œœœÊœÊœ œ
AC 00
B1 2 4
ww
11
y x sin y cos x x y , y x yœ Êœ œ
w w ww ww
## ##
!! ÈÈ ÈÈ
22 22
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 10.3 Quadratic Equations and Rotations 639
xy xy xy xy10 xy22x2Ê œÊ
Š‹Š‹Š‹Š‹ È
ÈÈÈÈ ÈÈ ÈÈ
22 22 22 22
## ## ## ##
ww ww ww ww ww w
##
0 HyperbolaœÊ
25. cot 2 0 2 ; therefore x x cos y sin ,!!! !!œœœÊœÊœ œ
AC 33
B2 2 4
ww
11
y x sin y cos x x y , y x yœ Êœ œ
w w ww ww
## ##
!! ÈÈ ÈÈ
22 22
3 x y 2 x y x + y 3 x y 19 4x 2y 19Ê œÊœ
Š‹Š‹Š‹Š‹
ÈÈ ÈÈÈÈ ÈÈ
22 22 22 22
## ## ## ##
ww ww ww ww ww
# # ##
EllipseÊ
26. cot 2 2 ; therefore x x cos y sin ,!!!!!œœ œÊœÊœ œ
AC
B36
3(1)
43 3
"
ww
ÈÈ 11
y x sin y cos x x y , y x yœ Êœœ
ww wwww
## ##
!! ÈÈ
33
11
3 x y 4 3 x y x y x y 7 5x 3y 7Ê œÊœ
Š‹Š‹Š‹Š‹
È
ÈÈÈÈ
3333
1111
## #### ##
ww ww w w w w w w
# # ##
HyperbolaÊ
27. cot 2 cos 2 (if we choose 2 in Quadrant I); thus sin !!! !œœÊ œ œ œ œ
14 2 3 3 1 cos 2
16 4 5 2
1
5
"
#
ÉÉ
!ˆ‰ È
3
5
and cos (or sin and cos )!!!œœœ œ œ
ÉÉ
1cos 2 2 2
1
55 5
"
##
!ˆ‰ ÈÈÈ
3
5
28. cot 2 cos 2 (if we choose 2 in Quadrant II); thus sin !!!!œœœÊ œ œ
AC 4 3 3 1cos 2
B44 5 2
"
É!
and cos (or sin and cos )œœ œ œœ œ œ
ÉÉ
É
11
21cos 2 112
5555
###
ˆ‰ ˆ‰
ÈÈÈÈ
3 3
5 5
!!!
!
29. tan 2 2 26.57° 13.28° sin 0.23, cos 0.97; then A 0.9, B 0.0,!!!!!œœÊ¸ ʸ Ê ¸ ¸ ¸ ¸
" "
#
ww
13
C 3.1, D 0.7, E 1.2, and F 3 0.9 x 3.1 y 0.7x 1.2y 3 0, an ellipse
www w wwww
##
¸ ¸ ¸ œ Ê œ
30. tan 2 2 11.31° 5.65° sin 0.10, cos 1.00; then A 2.1, B 0.0,!!!!!œœÊ¸ ʸʸ ¸ ¸¸
""
ww
2(3) 5
C 3.1, D 3.0, E 0.3, and F 7 2.1 x 3.1 y 3.0x 0.3y 7 0, a hyperbola
www w wwww
##
¸ ¸ ¸ œÊ œ
31. tan 2 2 53.13° 26.5 ° sin 0.45, cos 0.89; then A 0.0, B 0.0,!!!!!œœÊ¸ ʸ(Ê ¸ ¸ ¸ ¸
ww
44
14 3
C 5.0, D 0, E 0, and F 5 5.0 y 5 0 or y 1.0, parallel lines
www w w w
#
¸¸¸ œÊœœ„
32. tan 2 2 36.87° 18.43° sin 0.32, cos 0.95; then A 0.0, B 0.0,!!!!!œœÊ¸ ʸ Ê ¸ ¸ ¸ ¸
ww
12 3
218 4
C 20.1, D 0, E 0, and F 49 20.1 y 49 0, parallel lines
www w w
#
¸¸¸ œÊœ
33. tan 2 5 2 78.69° 39.35° sin 0.63, cos 0.77; then A 5.0, B 0.0,!!! !!œœÊ¸ ʸ Ê ¸ ¸ ¸ ¸
5
32
ww
C 0.05, D 5.0, E 6.2, and F 1 5.0 x 0.05 y 5.0x 6.2y 1 0, a hyperbola
www w wwww
##
¸ ¸ ¸ œ Ê œ
34. tan 2 1 2 45.00° 22.5° sin 0.38, cos 0.92; then A 0.5, B 0.0,!!!!!œ œ Ê ¸ Ê ¸ Ê ¸ ¸ ¸ ¸
7
29
ww
C 10.4, D 18.4, E 7.6, and F 86 0.5 x 10.4 y 18.4x 7.6y 86 0, an ellipse
www w wwww
##
¸¸¸ œÊ œab
35. 90° x x cos 90° y sin 90° y and y x sin 90° y cos 90° x!œÊœ œ œ œ
ww www w
(a) 1 (b) 1 (c) x y a
xx
ba ab
yy
œ œ œ
ww#
##
(d) y mx y mx 0 D m and E 1; 90° D 1 and E m my x 0 y xœÊœÊœ œ œ Êœ œÊœÊœ!ww wwww
"
m
(e) y mx b y mx b 0 D m and E 1; 90° D 1, E m and F bœÊœÊœ œ œ Êœ œ œ!ww w
my x b 0 y xʜʜ
ww w w
"
mm
b
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
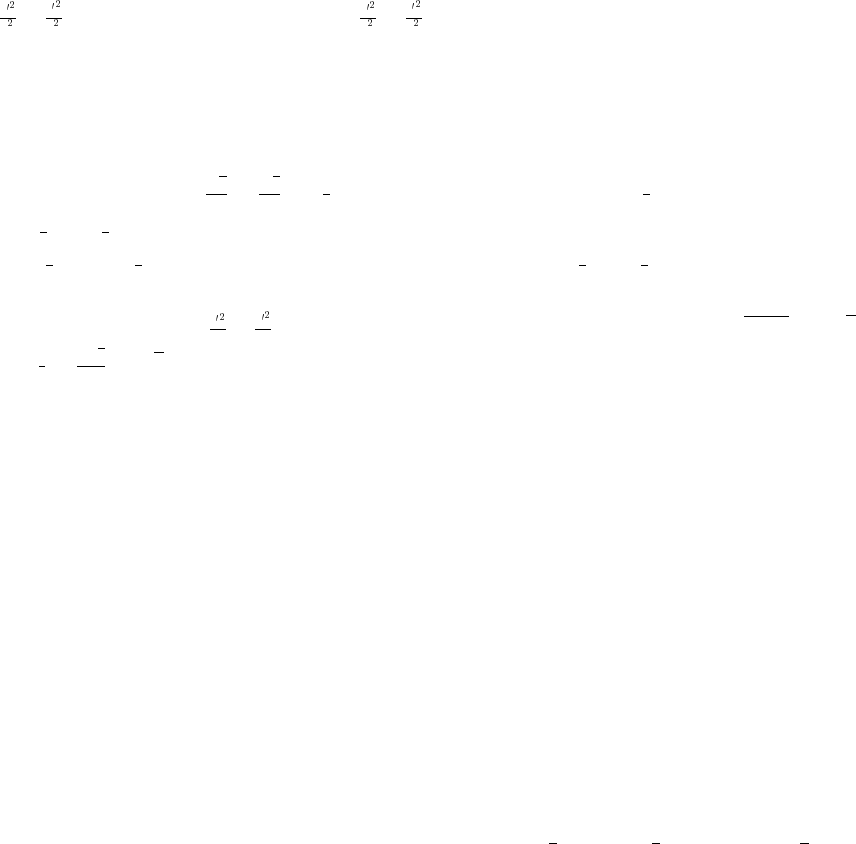
640 Chapter 10 Conic Sections and Polar Coordinates
36. 180° x x cos 180° y sin 180° x and y x sin 180° y cos 180° y!œ Ê œ œ œ œ
ww www w
(a) 1 (b) 1 (c) x y a
xx
ab ab
yy
œ œ œ
ww#
##
(d) y mx y mx 0 D m and E 1; 180° D m and E 1 y mx 0 œÊœÊœ œ œ Êœ œÊœÊ!ww ww
ymx
ww
œ
(e) y mx b y mx b 0 D m and E 1; 180° D m, E 1 and F bœÊœÊœ œ œ Êœ œ œ!ww w
ymxb0 ymxbÊ œ Ê œ
ww w w
37. (a) A cos 45° sin 45° , B 0, C cos 45° sin 45° , F 1
wwww
## # #
""
œ œ œ œ œ œ œ
Š‹Š‹
ÈÈ
22
x y 1 x y 2ʜʜ
""
##
ww ww
## ##
(b) A , C (see part (a) above), D E B 0, F a x y a x y 2a
ww wwww ww ww
"" ""
## ##
## ##
œœ œœœœÊœÊœ
38. xy 2 x y 4 1 (see Exercise 37(b)) a 2 and b 2 c 4 4 2 2œÊ œÊ œ Êœ œÊœ œ
ww
## x
44
yÈÈ
e2Êœœ œ
c
a
22
È
#È
39. Yes, the graph is a hyperbola: with AC 0 we have 4AC 0 and B 4AC 0.
#
40. The one curve that meets all three of the stated criteria is the ellipse x 4xy 5y 1 0. The reasoning:
##
œ
The symmetry about the origin means that ( x y) lies on the graph whenever (x y) does. Addingß ß
Ax Bxy Cy Dx Ey F 0 and A( x) B( x)( y) C( y) D( x) E( y) F 0 and dividing
## # #
œ œ
the result by 2 produces the equivalent equation Ax Bxy Cy F 0. Substituting x 1, y 0 (because
##
œ œœ
the point (1 0) lies on the curve) shows further that A F. Then Fx Bxy Cy F 0. By implicitßœœ
##
differentiation, 2Fx By Bxy 2Cyy 0, so substituting x 2, y 1, and y 0 (from Property 3) œ œœ œ
ww w
gives 4F B 0 B 4F the conic is Fx 4Fxy Cy F 0. Now substituting x 2 and y 1œ Ê œ Ê œ œ œ
##
again gives 4F 8F C F 0 C 5F the equation is now Fx 4Fxy 5Fy F 0. Finally, œÊ œ Ê œ
##
dividing through by F gives the equation x 4xy 5y 1 0.œ
##
41. Let be any angle. Then A cos sin 1, B 0, C sin cos 1, D E 0 and F a!!!!!
w# # w w# # ww w#
œœœœœœœ œ
xy a.ʜ
ww#
##
42. If A C, then B B cos 2 (C A) sin 2 B cos 2 . Then 2 B B cos 0 so theœœœ œÊœÊœœ
w w
##
!!!!!
11 1
4
xy-term is eliminated.
43. (a) B 4AC 4 4(1)(4) 0, so the discriminant indicates this conic is a parabola
##
œ œ
(b) The left-hand side of x 4xy 4y 6x 12y 9 0 factors as a perfect square: (x 2y 3) 0
## #
œ œ
x 2y 3 0 2y x 3; thus the curve is a degenerate parabola (i.e., a straight line).Ê œÊ œ
44. (a) B 4AC 6 4(9)(1) 0, so the discriminant indicates this conic is a parabola
##
œ œ
(b) The left-hand side of 9x 6xy y 12x 4y 4 0 factors as a perfect square: (3x y 2) 0
## #
œ œ
3x y 2 0 y 3x 2; thus the curve is a degenerate parabola (i.e., a straight line).ʜʜ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
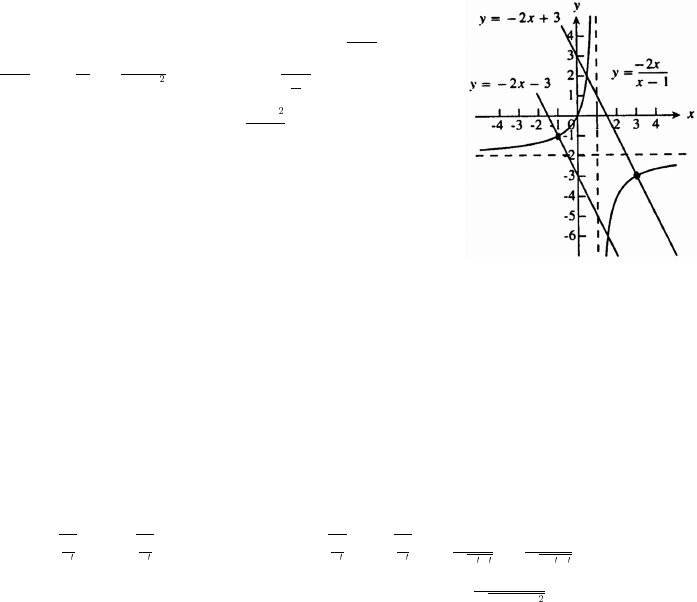
Section 10.3 Quadratic Equations and Rotations 641
45. (a) B 4AC 1 4(0)(0) 1 hyperbola
#œ œÊ
(b) xy 2x y 0 y(x 1) 2x yœÊ œÊœ
2x
x1
(c) y and we want 2,œÊœ œ
2x 2 1
x 1 dx (x 1)
dy Š‹
dy
dx
the slope of y 2x 2œ Ê œ(x 1)
#
(x 1) 4 x 3 or x 1; x 3Ê œÊœ œ œ
#
y 3 (3 3) is a point on the hyperbolaÊœÊß
where the line with slope m 2 is normalœ
the line is y 3 2(x 3) or y 2x 3;Êœœ
x 1 y 1 ( 1 1) is a point on theœ Ê œ Ê ß
hyperbola where the line with slope m 2 isœ
normal the line is y 1 2(x 1) orʜ
y2x3œ
46. (a) False: let A C 1, B 2 B 4AC 0 parabolaœœ œÊ œÊ
#
(b) False: see part (a) above
(c) True: AC 0 4AC 0 B 4AC 0 hyperbolaÊ Ê Ê
#
47. Assume the ellipse has been rotated to eliminate the xy-term the new equation is A x C y 1 theÊœÊ
ww ww
##
semi-axes are and the area is . Since B 4AC
ÉÉ
ÉÉ
Š‹Š‹
"" "" #
AC AC
AC 4AC
2
Êœœ111
ÈÈ
B 4A C 4A C (because B 0) we find that the area is as claimed.œ œ œ
www ww w
#
2
4AC B
1
È
48. (a) A C A cos B cos sin C sin A sin B cos sin C sin
ww####
œ abab!!! ! !!! !
A cos sin C sin cos A Cœœabab
## # #
!! ! !
(b) D E (D cos E sin ) ( D sin E cos ) D cos 2DE cos sin E sin
ww # ### ##
##
œ œ !! ! ! ! !! !
D sin 2DE sin cos E cos D cos sin E sin cos D E œ œ
## # # # # # # # # # #
!!!! !! !!abab
49. B 4A C
www
#
B cos 2 (C A) sin 2 4 A cos B cos sin C sin A sin B cos sin C cosœ ababab! ! !!! !!!! !
#### #
B cos 2 2B(C A) sin 2 cos 2 (C A) sin 2 4A cos sin 4AB cos sin œ
## ## ## # $
!!!!!!!!
4AC cos 4AB cos sin 4B cos sin 4BC cos sin 4AC sin 4BC cos sin
%$###$%$
!!!!! !! !!!
4C cos sin## #
!!
B cos 2 2BC sin 2 cos 2 2AB sin 2 cos 2 C sin 2 2AC sin 2 A sin 2œ
## ## # ##
!!!!!! !!
4A cos sin 4AB cos sin 4AC cos 4AB cos sin B sin 2 4BC cos sin
###$%$##$
! ! !! ! ! ! ! !!
4AC sin 4BC cos sin 4C cos sin
%$###
!!!!!
B 2BC(2 sin cos ) cos sin 2AB(2 sin cos ) cos sin C 4 sin cosœ
### #####
!! ! ! !! ! ! ! !ab abab
2AC 4 sin cos A 4 sin cos 4A cos sin 4AB cos sin 4AC cosabab
## ### ### $ %
!! !! !! !! !
4AB cos sin 4BC cos sin 4AC sin 4BC cos sin 4C cos sin!! !! ! !! !!
$$ % $###
B 8AC sin cos 4AC cos 4AC sinœ
### % %
!! ! !
B 4AC cos 2 sin cos sinœ
#%##%
ab!!!!
B4ACcos sinœ
###
#
ab!!
B4ACœ
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
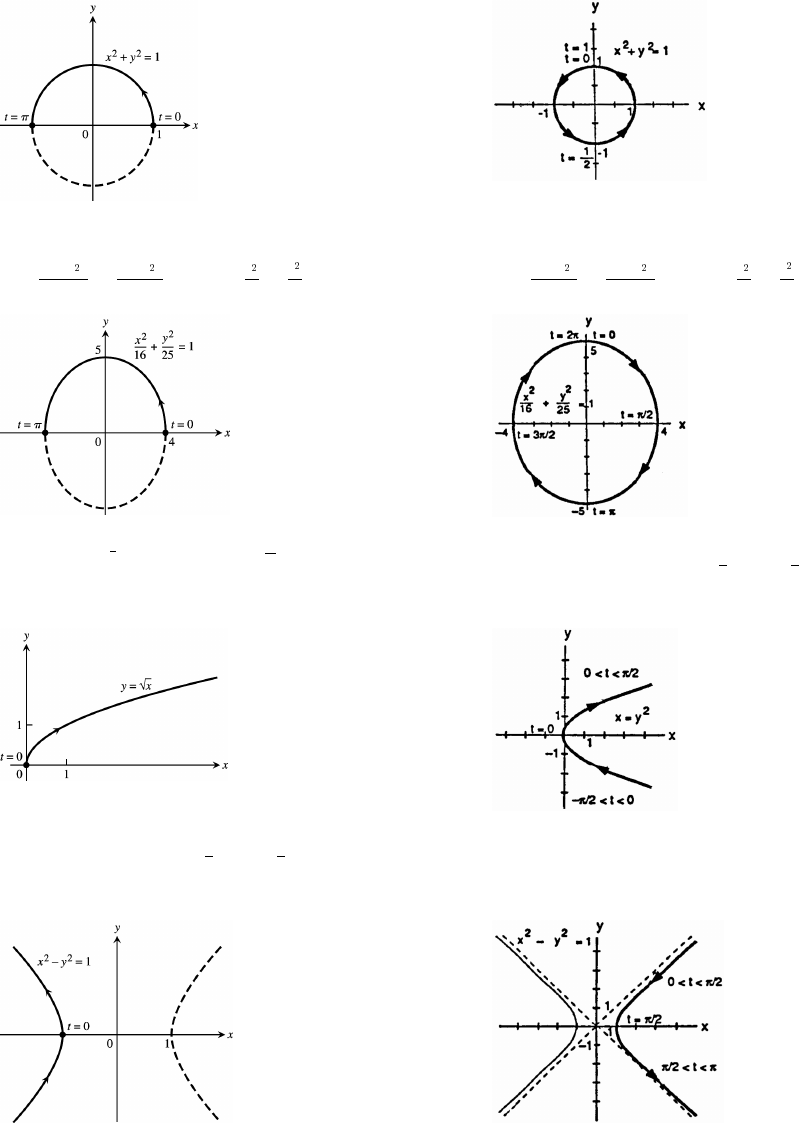
642 Chapter 10 Conic Sections and Polar Coordinates
10.4 CONICS AND PARAMETRIC EQUATIONS; THE CYCLOID
1. x cos t, y sin t, 0 t 2. x sin (2 (1 t)), y cos (2 (1 t)), 0 t 1œ œ ŸŸ œ œ ŸŸ111
cos t sin t 1 x y 1 sin (2 (1 t)) cos (2 (1 t)) 1ʜʜ Ê œ
## ## # #
11
xy 1ʜ
##
3. x 4 cos t, y 5 sin t, 0 t 4. x 4 sin t, y 5 cos t, 0 t 2œ œ ŸŸ œ œ ŸŸ11
1 1 1 1Ê œÊ œ Ê œÊ œ
16 cos t 25 sin t x 16 sin t 25 cos t x
16 25 16 25 16 25 16 5
y y
#
5. x t, y t, t 0 y x 6. x sec t 1, y tan t, tœœ Êœ œ œ
ÈÈ#
##
11
sect1tant xyʜʜ
## #
7. x sec t, y tan t, t 8. x csc t, y cot t, 0 tœ œ œ œ
11
## 1
sec t tan t 1 x y 1 1 cot t csc t 1 y x x y 1Ê œÊ œ Ê œ Êœ Ê œ
## ## # # ####
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
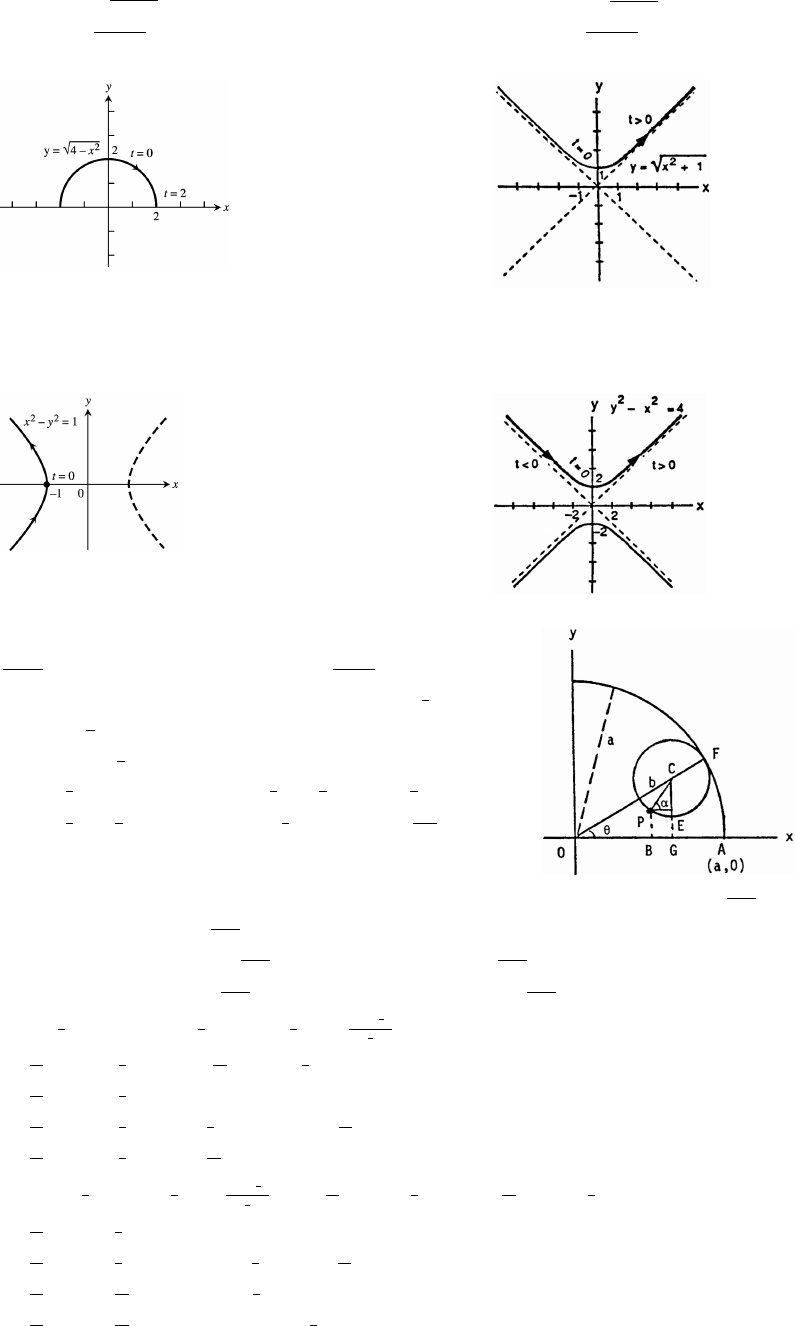
Section 10.4 Conics and Parametric Equations; The Cycloid 643
9. x t, y 4 t , 0 t 2 10. x t , y t 1, t 0œœ ŸŸ œ œ
ÈÈ
# %
#
y 4 x y x 1, x 0ʜ ʜ
ÈÈ
# #
11. x cosh t, y sinh t, 1 12. x 2 sinh t, y 2 cosh t, tœ œ _ _ œ œ _ _
cosh t sinh t 1 x y 1 4 cosh t 4 sinh t 4 y x 4Ê œÊ œ Ê œÊ œ
# # ## # # ##
13. Arc PF Arc AF since each is the distance rolled andœ
FCP Arc PF b( FCP);
Arc PF Arc AF
ba
œn Ê œ n œ)
Arc AF a a b( FCP) FCP ;ʜʜnÊnœ)) )
a
b
OCG ; OCG OCP PCEnœnœnn
1
#)
OCP . Now OCP FCPœn n œ n
ˆ‰
1
#!1
. Thus OCG œ n œ Ê 1) 1) ! )
aa
bb
11
##
.œ Ê œ œ1) !!1))1 )
aaab
bbb
1
#
ˆ‰
Then x OG BG OG PE (a b) cos b cos (a b) cos b cosœœœ œ )! ) 1)
ˆ‰
ab
b
(a b) cos b cos . Also y EG CG CE (a b) sin b sin œ œ œ œ )) )!
ˆ‰
ab
b
(a b) sin b sin (a b) sin b sin . Thereforeœ œ )1) ) )
ˆ‰ ˆ‰
ab ab
bb
x (a b) cos b cos and y (a b) sin b sin .œ œ )) ))
ˆ‰ ˆ‰
ab ab
bb
If b , then x a cos cosœœ
aaa
444
a
ˆ‰ Š‹
))
ˆ‰
ˆ‰
a
4
a
4
cos cos 3 cos (cos cos 2 sin sin 2 )œ œ
3a a 3a a
44 44
)))))))
cos (cos ) cos sin (sin )(2 sin cos )œ
3a a
44
)))))))abab
##
cos cos cos sin sin cos œ
3a a a 2a
44 4 4
)))) ))
$##
cos cos (cos ) 1 cos a cos ;œ œ
3a a 3a
44 4
)) ) ) )
$#$
ab
y a sin sin sin sin 3 sin (sin cos 2 cos sin 2 )œ œ œ
ˆ‰ Š‹
aa 3aa 3aa
4 4 44 44
a
)))))))))
ˆ‰
ˆ‰
a
4
a
4
sin (sin ) cos sin (cos )(2 sin cos )œ
3a a
44
)))))))abab
##
sin sin cos sin cos sin œ
3a a a 2a
44 4 4
)))) ))
#$ #
sin sin cos sinœ
3a 3a a
44 4
))))
#$
sin (sin ) 1 sin sin a sin .œ œ
3a 3a a
44 4
)) ) ))ab
#$$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
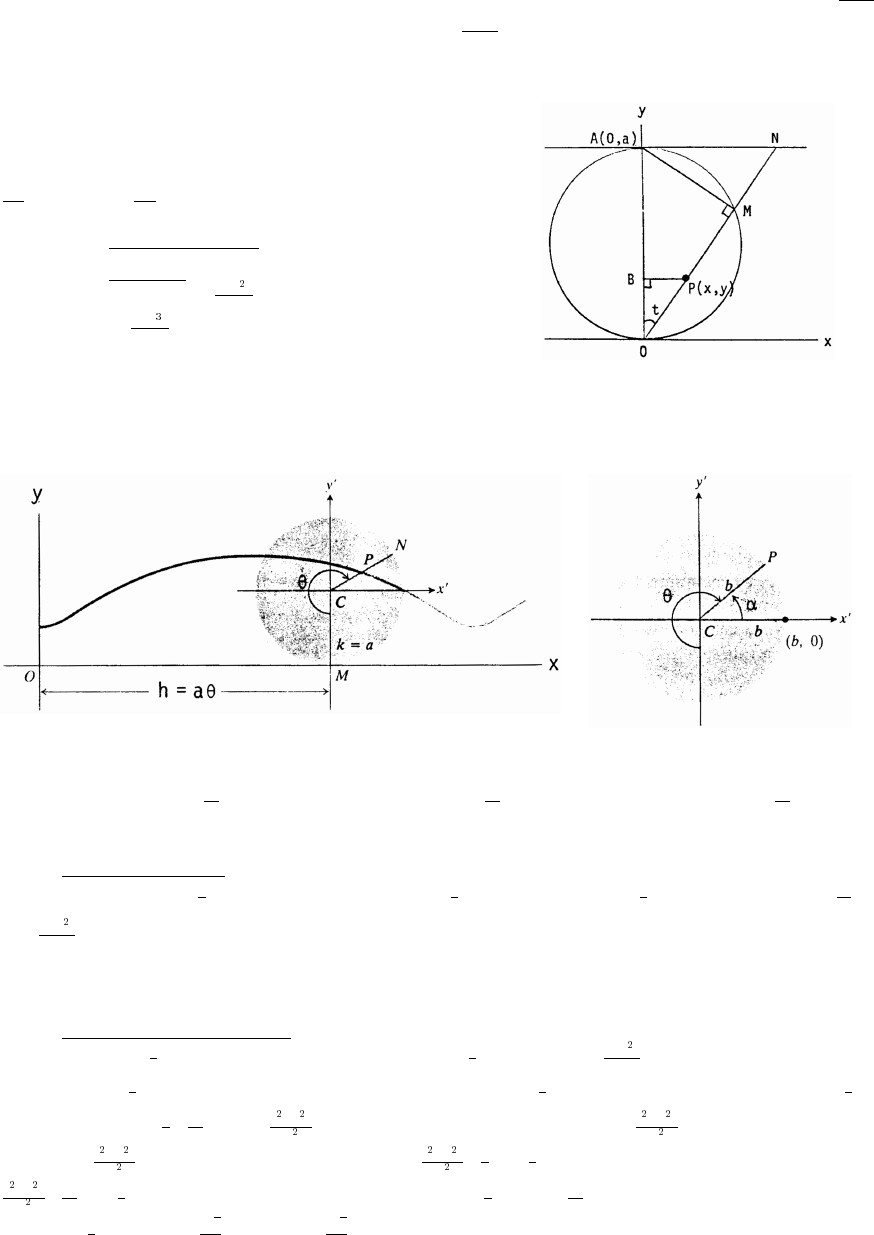
644 Chapter 10 Conic Sections and Polar Coordinates
14. P traces a hypocycloid where the larger radius is 2a and the smaller is a x (2a a) cos a cosʜ ))
ˆ‰
2a a
a
2a cos , 0 2 , and y (2a a) sin a sin a sin a sin 0. Therefore P traces theœ ŸŸ œ œœ))1 ) ) ) )
ˆ‰
2a a
a
diameter of the circle back and forth as goes from 0 to 2 .)1
15. Draw line AM in the figure and note that AMO is a rightn
angle since it is an inscribed angle which spans the diameter
of a circle. Then AN MN AM . Now, OA a,
###
œ œ
tan t, and sin t. Next MN OP
AN AM
aa
œœ œ
OP AN AM a tan t a sin tÊœœ
#######
OP a tan t a sin tʜ
È## ##
(a sin t) sec t 1 . In triangle BPO,œœ
È#a sin t
cos t
x OP sin t a sin t tan t andœœœ
a sin t
cos t
#
y OP cos t a sin t x a sin t tan t and y a sin t.œœÊœ œ
## #
16. Let the x-axis be the line the wheel rolls along with the y-axis through a low point of the trochoid
(see the accompanying figure).
Let denote the angle through which the wheel turns. Then h a and k a. Next introduce x y -axes))œœ ww
parallel to the xy-axes and having their origin at the center C of the wheel. Then x b cos and
wœ!
y b sin , where . It follows that x b cos b sin and y b sin
www
## #
œœ œœœ!! ) ) ) )
33 311 1
ˆ‰ ˆ‰
b cos x h x a b sin and y k y a b cos are parametric equations of the trochoid.œ Êœœ œœ))) )
ww
17. D (x 2) y D (x 2) y (t 2) t D t 4tœ Ê œ œ Ê œ
Ɉ‰ ˆ‰ ˆ‰
#"""
###
###
## ## #%
17
4
4t 4 0 t 1. The second derivative is always positive for t 0 t 1 gives a localÊœœÊœ ÁÊœ
dD
dt
ab $
minimum for D (and hence D) which is an absolute minimum since it is the only extremum the closest
#Ê
point on the parabola is (1 1).ß
18. D 2 cos t (sin t 0) D 2 cos t sin t œÊœÊ
Ɉ‰ ˆ‰
33
44dt
dD
##
###
ab
2 2 cos t ( 2 sin t) 2 sin t cos t ( 2 sin t) 3 cos t 0 2 sin t 0 or 3 cos t 0œ œ œÊœ œ
ˆ‰ ˆ‰
333
4##
t 0, or t , . Now 6 cos t 3 cos t 6 sin t so that (0) 3 relativeÊœ œ œ œÊ111
3 3 dt dt
5dD dD
ab ab
##
maximum, ( ) 9 relative maximum, relative minimum, and
dD dD
dt dt 3 2
9
ab ab
1œ Ê œ Ê
ˆ‰
1
relative minimum. Therefore both t and t give points on the ellipse closest to
dD
dt 3 3 3
59 5
ab
ˆ‰
111
œÊ œ œ
#
the point 1 and 1 are the desired points.
ˆ‰ Š‹Š ‹
3
4
33
ß! Ê ß ß
ÈÈ
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 10.4 Conics and Parametric Equations; The Cycloid 645
19. (a) (b) (c)
20. (a) (b) (c)
21.
22. (a) (b) (c)
23. (a) (b)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
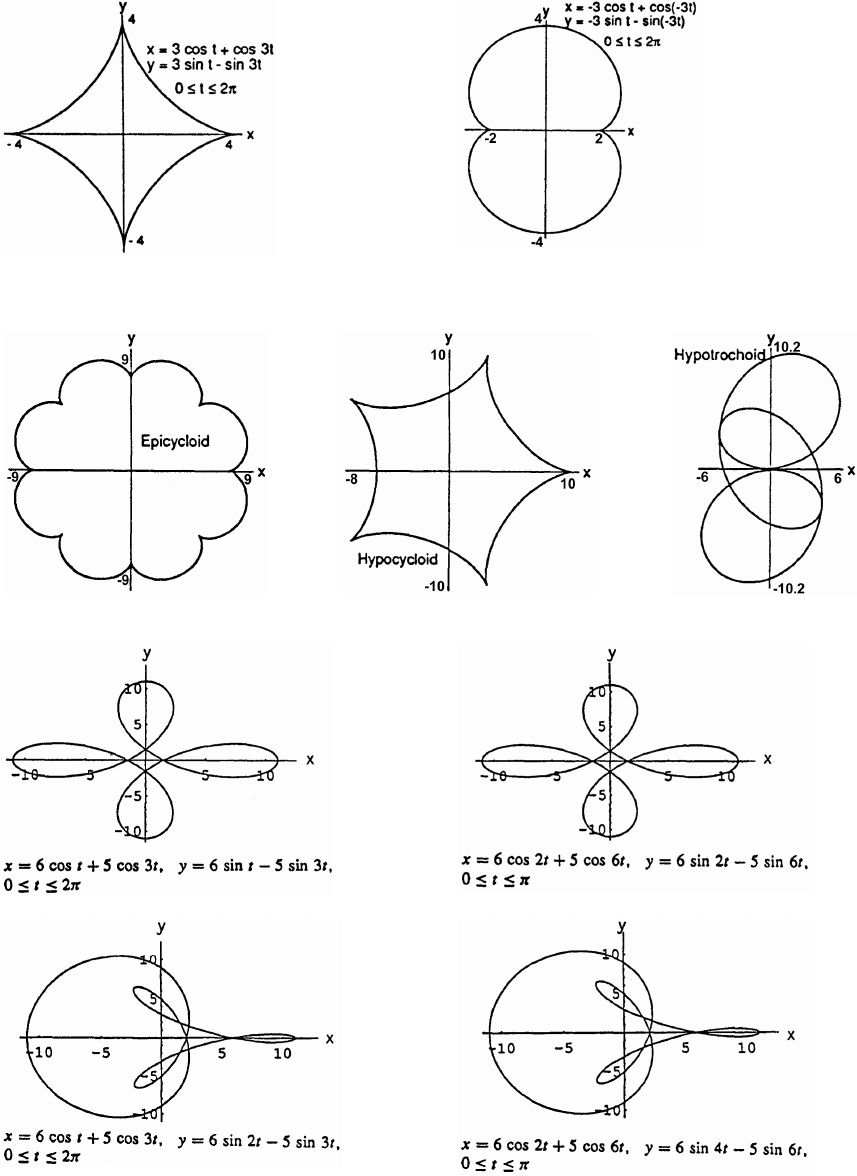
646 Chapter 10 Conic Sections and Polar Coordinates
24. (a) (b)
25. (a) (b) (c)
26. (a) (b)
(c) (d)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 10.5 Polar Coordinates 647
10.5 POLAR COORDINATES
1. a, e; b, g; c, h; d, f 2. a, f; b, h; c, g; d, e
3. (a) 2 2n and 2 (2n 1) , n an integer
ˆ‰ˆ ‰
ß ß
11
##
11
(b) ( 2n ) and ( (2n 1) ), n an integer#ß #ß 11
(c) 2 2n and 2 (2n 1) , n an integer
ˆ‰ˆ ‰
ß ß
3311
##
11
(d) ( (2n 1) ) and ( 2n ), n an integer#ß #ß11
4. (a) 3 2n and 3 2n , n an integer
ˆ‰ˆ ‰
ß ß
11
44
5
11
(b) 3 2n and 3 2n , n an integer
ˆ‰ˆ‰
ß ß
11
44
5
11
(c) 3 2n and 3 2n , n an integer
ˆ‰ˆ‰
ß ß
11
44
3
11
(d) 3 2n and 3 2n , n an integer
ˆ‰ˆ‰
ß ß
11
44
3
11
5. (a) x r cos 3 cos 0 3, y r sin 3 sin 0 0 Cartesian coordinates are ( 0)œœ œœœœÊ $ß))
(b) x r cos 3 cos 0 3, y r sin 3 sin 0 0 Cartesian coordinates are ( 0)œœœœœœÊ $ß))
(c) x r cos 2 cos 1, y r sin 2 sin 3 Cartesian coordinates are 1 3œœ œœœ œÊ ß))
22
33
11
ÈÈ
Š‹
(d) x r cos 2 cos 1, y r sin 2 sin 3 Cartesian coordinates are 1 3œœ œœœ œÊ ß))
77
33
11
ÈÈ
Š‹
(e) x r cos 3 cos 3, y r sin 3 sin 0 Cartesian coordinates are (3 0)œœœœœœÊ ß)1 )1
(f) x r cos 2 cos 1, y r sin 2 sin 3 Cartesian coordinates are 1 3œœ œœœ œÊ ß))
11
33
ÈÈ
Š‹
(g) x r cos 3 cos 2 3, y r sin 3 sin 2 0 Cartesian coordinates are ( 3 0)œœ œœœ œÊ ß)1 )1
(h) x r cos 2 cos 1, y r sin 2 sin 3 Cartesian coordinates are 1 3œœœœœœÊ ß))
ˆ‰ ˆ‰
ÈÈ
Š‹
11
33
6. (a) x 2 cos 1, y 2 sin 1 Cartesian coordinates are (1 1)œœœœÊ ß
ÈÈ
11
44
(b) x 1 cos 0 1, y 1 sin 0 0 Cartesian coordinates are (1 0)œœœœÊ ß
(c) x 0 cos 0, y 0 sin 0 Cartesian coordinates are ( 0)œœœœÊ !ß
11
##
(d) x 2 cos 1, y 2 sin 1 Cartesian coordinates are ( 1 1)œ œ œ œ Ê ß
ÈÈ
ˆ‰ ˆ‰
11
44
(e) x 3 cos , y 3 sin Cartesian coordinates are œ œ œ œ Ê ß
553 3
62 6
33 33
11
È È
###
Š‹
(f) x 5 cos tan 3, y 5 sin tan 4 Cartesian coordinates are ( 4)œœœœÊ $ß
ˆ‰ ˆ‰
" "
44
33
(g) x 1 cos 7 1, y 1 sin 7 0 Cartesian coordinates are (1 0)œ œ œ œ Ê ß11
(h) x 2 3 cos 3, y 2 3 sin 3 Cartesian coordinates are 3 3œœœœÊ ß
ÈÈÈ È
Š‹
22
33
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
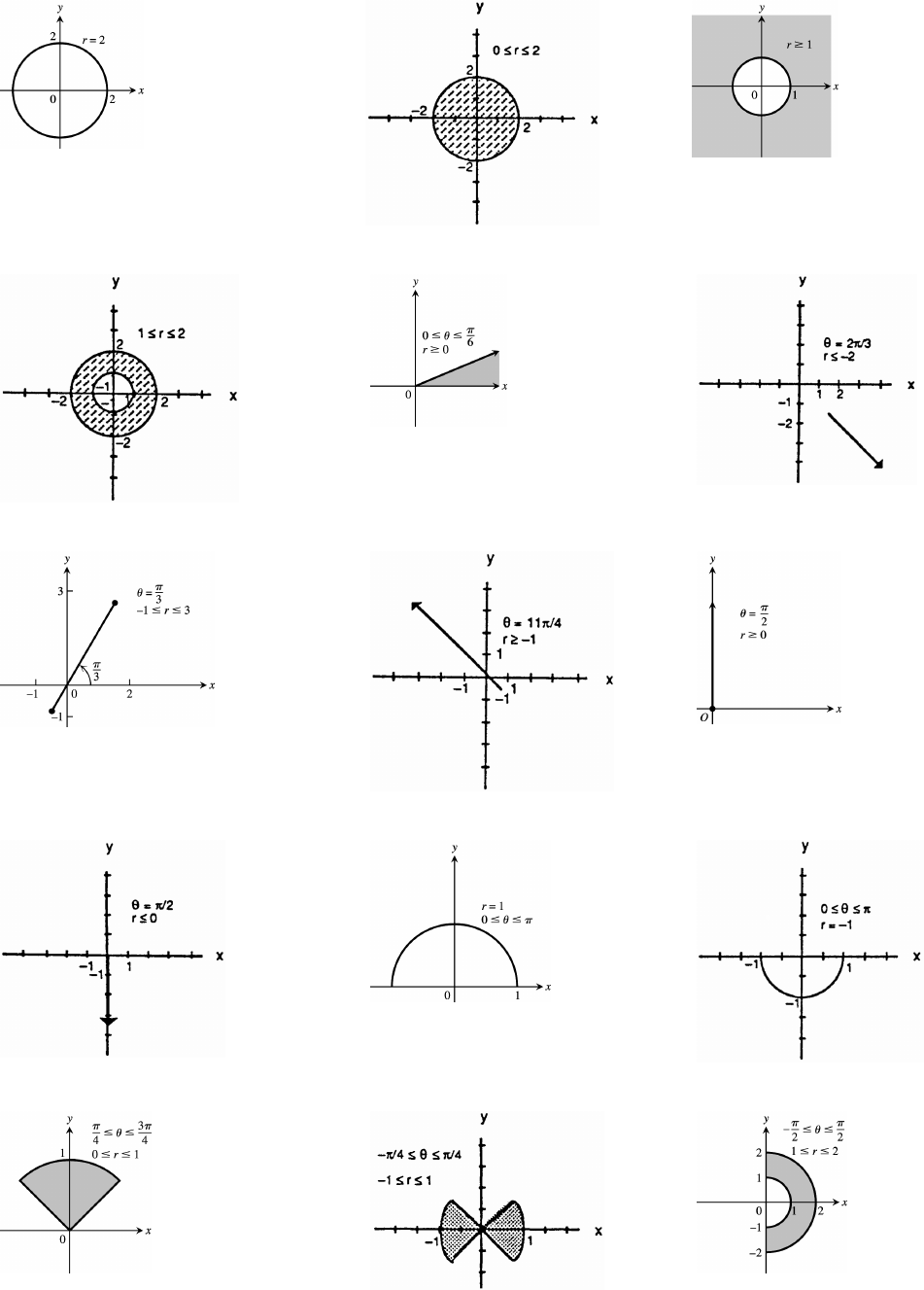
648 Chapter 10 Conic Sections and Polar Coordinates
7. 8. 9.
10. 11. 12.
13. 14. 15.
16. 17. 18.
19. 20. 21.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 10.5 Polar Coordinates 649
22.
23. r cos 2 x 2, vertical line through ( 0) 24. r sin 1 y 1, horizontal line through (0 1)))œÊœ #ß œÊœ ß
25. r sin 0 y 0, the x-axis 26. r cos 0 x 0, the y-axis))œÊœ œÊœ
27. r 4 csc r r sin 4 y 4, a horizontal line through (0 4)œÊœÊœÊœ ß))
4
sin )
28. r 3 sec r r cos 3 x 3, a vertical line through ( 3 0)œ Ê œ Ê œ Ê œ ß))
3
cos )
29. r cos r sin 1 x y 1, line with slope m 1 and intercept b 1))œÊœ œ œ
30. r sin r cos y x, line with slope m 1 and intercept b 0))œÊœ œ œ
31. r 1 x y 1, circle with center C ( 0) and radius 1
###
œÊ œ œ!ß
32. r 4r sin x y 4y x y 4y 4 4 x (y 2) 4, circle with center C (0 2) and radius 2
##### ##
œÊœÊœÊœ œß)
33. r r sin 2r cos 5 y 2x 5, line with slope m 2 and intercept b 5œÊœÊœ œ œ
5
sin 2 cos ))))
34. r sin 2 2 2r sin cos 2 (r sin )(r cos ) 1 xy 1, hyperbola with focal axis y x
##
)))))œÊ œÊ œÊ œ œ
35. r cot csc r sin cos r sin r cos y x, parabola with vertex (0 0)œœ ʜʜʜ ß)) ) ) ) )
ˆ‰ˆ‰
cos
sin sin
)
))
"### #
which opens to the right
36. r 4 tan sec r 4 r cos 4 sin r cos 4r sin x 4y, parabola withœÊœÊœÊœÊœ)) ) ) ) )
ˆ‰
sin
cos
)
)
### #
vertex ( 0) which opens upwardœ!ß
37. r (csc ) e r sin e y e , graph of the natural exponential functionœÊœÊœ))
r cos r cos x
38. r sin ln r ln cos ln (r cos ) y ln x, graph of the natural logarithm function)))œ œ Êœ
39. r 2r cos sin 1 x y 2xy 1 x 2xy y 1 (x y) 1 x y 1, two parallel
## ## # # #
œÊ œÊ œÊœÊœ„))
straight lines of slope 1 and y-intercepts b 1œ„
40. cos sin r cos r sin x y x y x y, two perpendicular
###### ##
)) ) )œÊ œ ʜʜʄœkk kk
lines through the origin with slopes 1 and 1, respectively.
41. r 4r cos x y 4x x 4x y 0 x 4x 4 y 4 (x 2) y 4, a circle with
#########
œ ʜʜʜʜ)
center C( 2 0) and radius 2ß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

650 Chapter 10 Conic Sections and Polar Coordinates
42. r 6r sin x y 6y x y 6y 0 x y 6y 9 9 x (y 3) 9, a circle with
####### ##
œ ʜʜʜʜ)
center C(0 3) and radius 3ß
43. r 8 sin r 8r sin x y 8y x y 8y 0 x y 8y 16 16œ Êœ Êœ ʜʜ))
#######
x (y 4) 16, a circle with center C(0 4) and radius 4Êœ ß
##
44. r 3 cos r 3r cos x y 3x x y 3x 0 x 3x yœ Êœ Êœ ʜʜ))
#######
99
44
x y , a circle with center C and radius Ê œ ß!
ˆ‰ ˆ‰
39 3 3
4###
##
45. r 2 cos 2 sin r 2r cos 2r sin x y 2x 2y x 2x y 2y 0œÊœ ʜʜ)) ) )
#####
(x 1) (y 1) 2, a circle with center C(1 1) and radius 2Ê œ ß
## È
46. r 2 cos sin r 2r cos r sin x y 2x y x 2x y y 0œÊœ ʜʜ)) ) )
#####
(x 1) y , a circle with center C 1 and radius Ê œ ß
#""
###
#
ˆ‰ ˆ‰
5
4
5
È
47. r sin 2 r sin cos cos sin 2 r sin r cos 2 y x 2
ˆ‰ ˆ ‰
))) ))œÊ œÊ œÊ œ
111
666
33
ÈÈ
## ##
""
3 y x 4, line with slope m and intercept bÊœ œ œ
È"
ÈÈ
33
4
48. r sin 5 r sin cos cos sin 5 r cos r sin 5 x y 5
ˆ‰ ˆ ‰
222
333
33
111
œÊ œÊ œÊ œ)))))
ÈÈ
## ##
""
3 x y 10, line with slope m 3 and intercept b 10Êœ œ œ
ÈÈ
49. x 7 r cos 7 50. y 1 r sin 1œÊ œ œÊ œ))
51. x y r cos r sin 52. x y 3 r cos r sin 3œÊ œ Êœ œÊ œ))) ))
1
4
53. x y 4 r 4 r 2 or r 2
## #
œÊ œÊœ œ
54. x y 1 r cos r sin 1 r cos sin 1 r cos 2 1
## ## ## # # # #
œÊ œÊ œÊ œ)) )) )ab
55. 1 4x 9y 36 4r cos 9r sin 36
x
94
y
œÊ œ Ê œ
## ## ##
))
56. xy 2 (r cos )(r sin ) 2 r cos sin 2 2r cos sin 4 r sin 2 4œÊ œÊ œÊ œÊ œ) ) )) )) )
###
57. y 4x r sin 4r cos r sin 4 cos
### #
œÊ œ Ê œ)) ))
58. x xy y 1 x y xy 1 r r sin cos 1 r (1 sin cos ) 1
## ## ## #
œÊ œÊ œÊ œ)) ))
59. x (y 2) 4 x y 4y 4 4 x y 4y r 4r sin r 4 sin
# # ## ## #
œÊ œÊ œ Ê œ Êœ))
60. (x 5) y 25 x 10x 25 y 25 x y 10x r 10r cos r 10 cos œ Ê œ Êœ Êœ Êœ
## # # ## # ))
61. (x 3) (y 1) 4 x 6x 9 y 2y 1 4 x y 6x 2y 6 r 6r cos 2r sin 6 œÊ œÊ œÊœ
## # # ## #
))
62. (x 2) (y 5) 16 x 4x 4 y 10y 25 16 x y 4x 10y 13 rœ Ê œ Êœ Ê
## # # ## #
4r cos 10r sin 13œ ))
63. ( ) where is any angle!ß ))
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
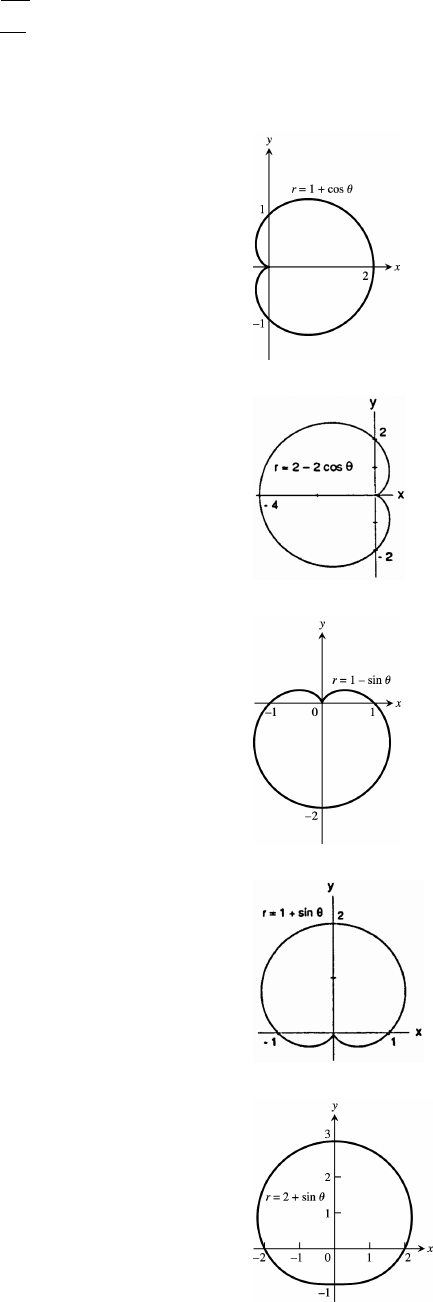
Section 10.6 Graphing in Polar Coordinates 651
64. (a) x a r cos a r r a sec œÊ œÊœ Êœ))
a
cos )
(b) y b r sin b r r b csc œÊ œÊœ Êœ))
b
sin )
10.6 GRAPHING IN POLAR COORDINATES
1. 1 cos ( ) 1 cos r symmetric about theœ œÊ))
x-axis; 1 cos ( ) r and 1 cos ( )Á )1)
1 cos r not symmetric about the y-axis;œ ÁÊ)
therefore not symmetric about the origin
2. 2 2 cos ( ) 2 2 cos r symmetric about theœ œÊ))
x-axis; 2 cos ( ) r and 2 2 cos ( )# Á )1)
2 2 cos r not symmetric about the y-axis;œ Á Ê)
therefore not symmetric about the origin
3. 1 sin ( ) 1 sin r and 1 sin ( )œ Á )) 1)
1 sin r not symmetric about the x-axis;œ ÁÊ)
1 sin ( ) 1 sin r symmetric aboutœœÊ1) )
the y-axis; therefore not symmetric about the origin
4. 1 sin ( ) 1 sin r and 1 sin ( )œ Á )) 1)
1 sin r not symmetric about the x-axis;œ ÁÊ)
1 sin ( ) 1 sin r symmetric about theœœÊ1) )
y-axis; therefore not symmetric about the origin
5. 2 sin ( ) 2 sin r and 2 sin ( )œ Á )) 1)
2 sin r not symmetric about the x-axis;œ ÁÊ)
2 sin ( ) 2 sin r symmetric about theœœÊ1) )
y-axis; therefore not symmetric about the origin
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
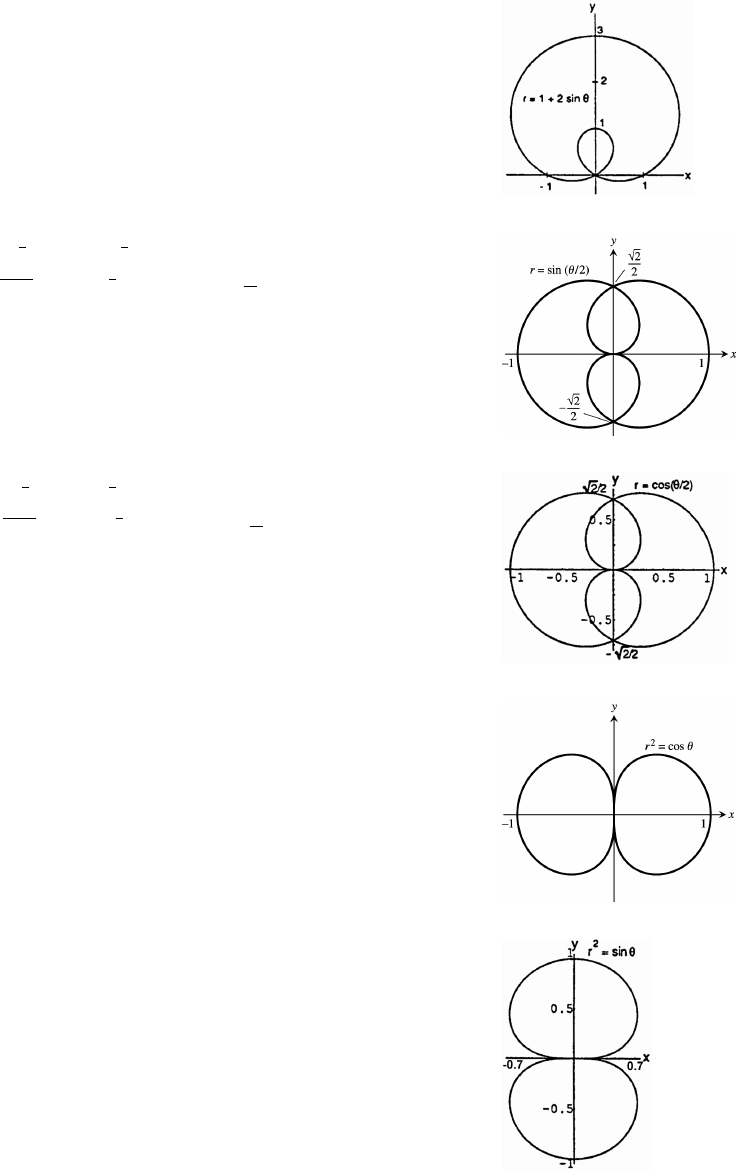
652 Chapter 10 Conic Sections and Polar Coordinates
6. 1 2 sin ( ) 1 2 sin r and 1 2 sin ( )œ Á )) 1)
1 2 sin r not symmetric about the x-axis;œ ÁÊ)
1 2 sin ( ) 1 2 sin r symmetric about theœœÊ1) )
y-axis; therefore not symmetric about the origin
7. sin sin r symmetric about the y-axis;
ˆ‰ ˆ‰
œ œÊ
))
##
sin sin , so the graph symmetric about the
ˆ‰ ˆ‰
2
2
1) )
#œis
x-axis, and hence the origin.
8. cos cos r symmetric about the x-axis;
ˆ‰ ˆ‰
œ œÊ
))
##
cos cos , so the graph symmetric about the
ˆ‰ ˆ‰
2
2
1) )
#œis
y-axis, and hence the origin.
9. cos ( ) cos r (r ) and ( r ) are on theœ œ Êß ß)) ) )
#
graph when (r ) is on the graph symmetric about theßÊ)
x-axis and the y-axis; therefore symmetric about the origin
10. sin ( ) sin r (r ) and ( r ) are on1) ) 1) 1)œ œ Êß ß
#
the graph when (r ) is on the graph symmetric aboutßÊ)
the y-axis and the x-axis; therefore symmetric about the
origin
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 10.6 Graphing in Polar Coordinates 653
11. sin ( ) sin r (r ) and ( r )œœÊß ß1) ) 1) 1)
#
are on the graph when (r ) is on the graph symmetricßÊ)
about the y-axis and the x-axis; therefore symmetric about
the origin
12. cos ( ) cos r (r ) and ( r ) are onœ œÊß ß)) ) )
#
the graph when (r ) is on the graph symmetric aboutßÊ)
the x-axis and the y-axis; therefore symmetric about the
origin
13. Since r are on the graph when (r ) is on the graphab„ß ß))
r 4 cos 2( ) r 4 cos 2 , the graph is
ˆ‰
ab„œ Êœ
##
))
symmetric about the x-axis and the y-axis the graph isÊ
symmetric about the origin
14. Since (r ) on the graph ( r ) is on the graphßÊß))
r 4 sin 2 r 4 sin 2 , the graph is
ˆ‰
ab„œ Êœ
##
))
symmetric about the origin. But 4 sin 2( ) 4 sin 2œ))
r and 4 sin 2( ) 4 sin (2 2 ) 4 sin ( 2 )Áœœ
#1) 1 ) )
4 sin 2 r the graph is not symmetric aboutœ Á Ê)#
the x-axis; therefore the graph is not symmetric about
the y-axis
15. Since (r ) on the graph ( r ) is on the graphßÊß))
r sin 2 r sin 2 , the graph is
ˆ‰
ab„œ Êœ
##
))
symmetric about the origin. But sin 2( ) ( sin 2 )œ))
sin 2 r and sin 2( ) sin (2 2 ))1)1)Á œ
#
sin ( 2 ) ( sin 2 ) sin 2 r the graphœ œ œ Á Ê)))
#
is not symmetric about the x-axis; therefore the graph is
not symmetric about the y-axis
16. Since r are on the graph when (r ) is on theab„ß ß))
graph r cos 2( ) r cos 2 , the
ˆ‰
ab„œ Êœ
##
))
graph is symmetric about the x-axis and the y-axis theÊ
graph is symmetric about the origin.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
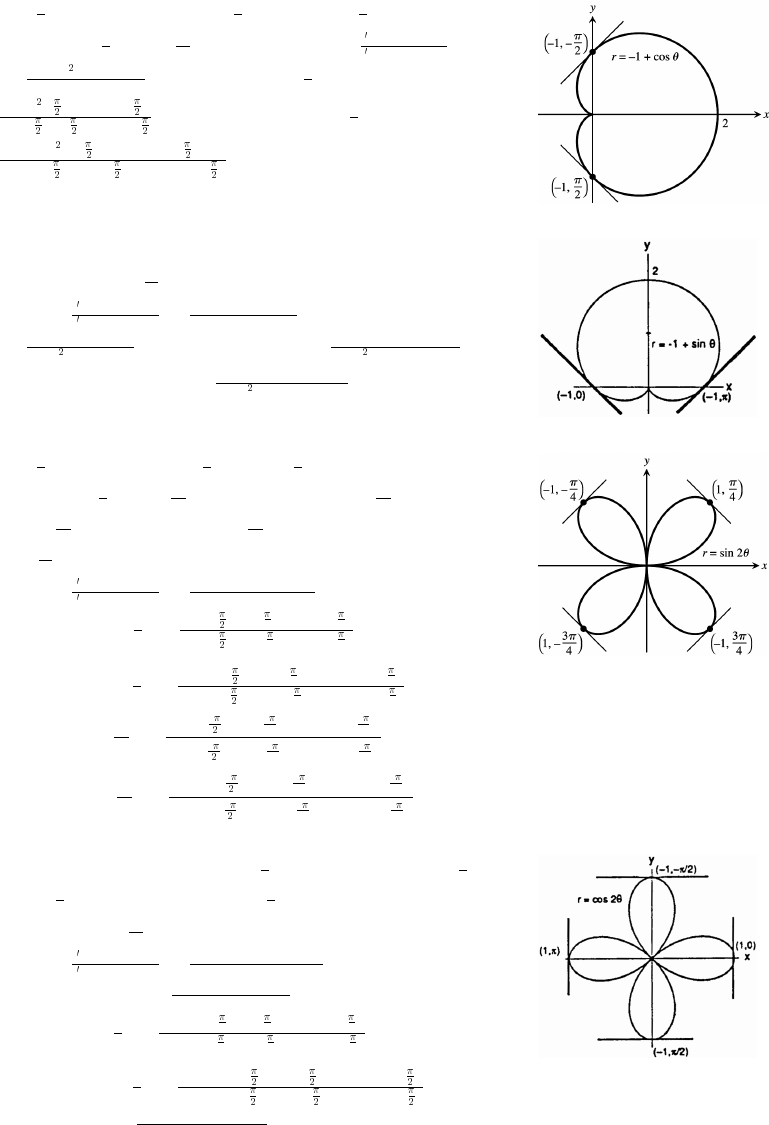
654 Chapter 10 Conic Sections and Polar Coordinates
17. r 1 1 , and r 1))œ Ê œ Ê ß œ Ê œ
111
###
ˆ‰
1 ; r sin ; SlopeÊß œ œ œ
ˆ‰
1))
)))#
wdr r sin r cos
d r cos r sin
)
Slope at 1 isœÊß
#
sin r cos
sin cos r sin
)) 1
)) ) ˆ‰
1; Slope at 1 is
#
sin ( 1) cos
sin cos ( 1) sin
ˆ‰ œ ß
ˆ‰
1
1
sin ( 1) cos
sin cos ( 1) sin
ˆ‰ ˆ‰
ˆ‰ˆ‰ ˆ‰
œ
18. 0 r 1 ( 0), and r 1))1œ Ê œ Ê "ß œ Ê œ
( ); r cos ;Ê"ß œ œ1)
wdr
d)
Slope œœ
r sin r cos cos sin r cos
r cos r sin cos cos r sin
)) )))
)) )))
Slope at ( 0) is œÊ"ß
cos sin r cos
cos r sin cos 0 ( 1) sin 0
cos 0 sin 0 ( 1) cos 0
)) )
))
1; Slope at ( ) is 1œ "ß œ1cos sin ( 1) cos
cos ( 1) sin
11 1
11
19. r 1 ; r 1))œ Ê œ Ê "ß œ Ê œ
111
444
ˆ‰
1; r1 ;Êß œ Ê œÊ"ß
ˆ‰ ˆ‰
11 1
44 4
33
)
r1 1 ;)œ Ê œ Ê ß
33
44
11
ˆ‰
r2 cos 2;
wœœ
dr
d))
Slope œœ
r sin r cos 2 cos 2 sin r cos
r cos r sin 2 cos 2 cos r sin
)) )))
)) )))
Slope at 1 is 1;Êß œ
ˆ‰
1
4
2 cos sin (1) cos
2 cos cos (1) sin
ˆ‰ ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰
44
44
Slope at 1 is 1;
ˆ‰
ß œ
1
4
2 cos sin ( 1) cos
2 cos cos ( 1) sin
ˆ‰ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰
44
44
Slope at 1 is 1;
ˆ‰
ß œ
3
4
2 cos sin ( 1) cos
2 cos cos ( 1) sin
1Š‹ Š‹ Š‹
Š‹ Š‹ Š‹
33 3
44
33 3
44
Slope at 1 is 1
ˆ‰
ß œ
3
4
2 cos sin (1) cos
2 cos cos (1) sin
1Š‹Š‹ Š‹
Š‹Š‹ Š‹
33 3
44
33 3
44
20. 0 r 1 (1 0); r 1 1 ;))œÊœÊß œ ÊœÊß
11
22
ˆ‰
r1 ; r1))1œ Ê œ Ê "ß œ Ê œ
11
#ˆ‰
2
(1 ); r 2 sin 2 ;Êß œ œ1)
wdr
d)
Slope œœ
r sin r cos 2 sin 2 sin r cos
r cos r sin 2 sin 2 cos r sin
)) )))
)) )))
Slope at (1 0) is , which is undefined;Êß
2 sin 0 sin 0 cos 0
2 sin 0 cos 0 sin 0
Slope at 1 is 0;
ˆ‰
ß œ
1
2
2 sin 2 sin ( 1) cos
2 sin 2 cos ( 1) sin
ˆ‰ ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰
22 2
22 2
Slope at 1 is 0;
ˆ‰
ß œ
1
2
2 sin 2 sin ( 1) cos
2 sin 2 cos ( 1) sin
ˆ‰ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰
Slope at ( ) is , which is undefined"ß 1
2 sin 2 sin cos
2 sin 2 cos sin
11 1
11 1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
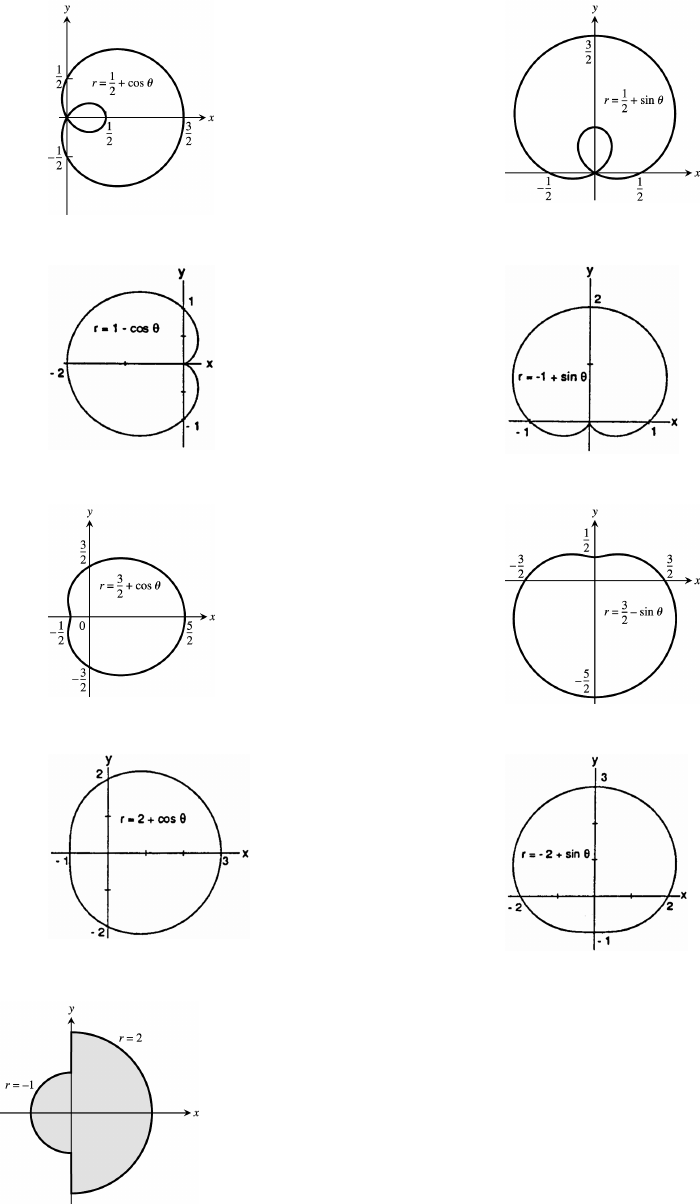
Section 10.6 Graphing in Polar Coordinates 655
21. (a) (b)
22. (a) (b)
23. (a) (b)
24. (a) (b)
25.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
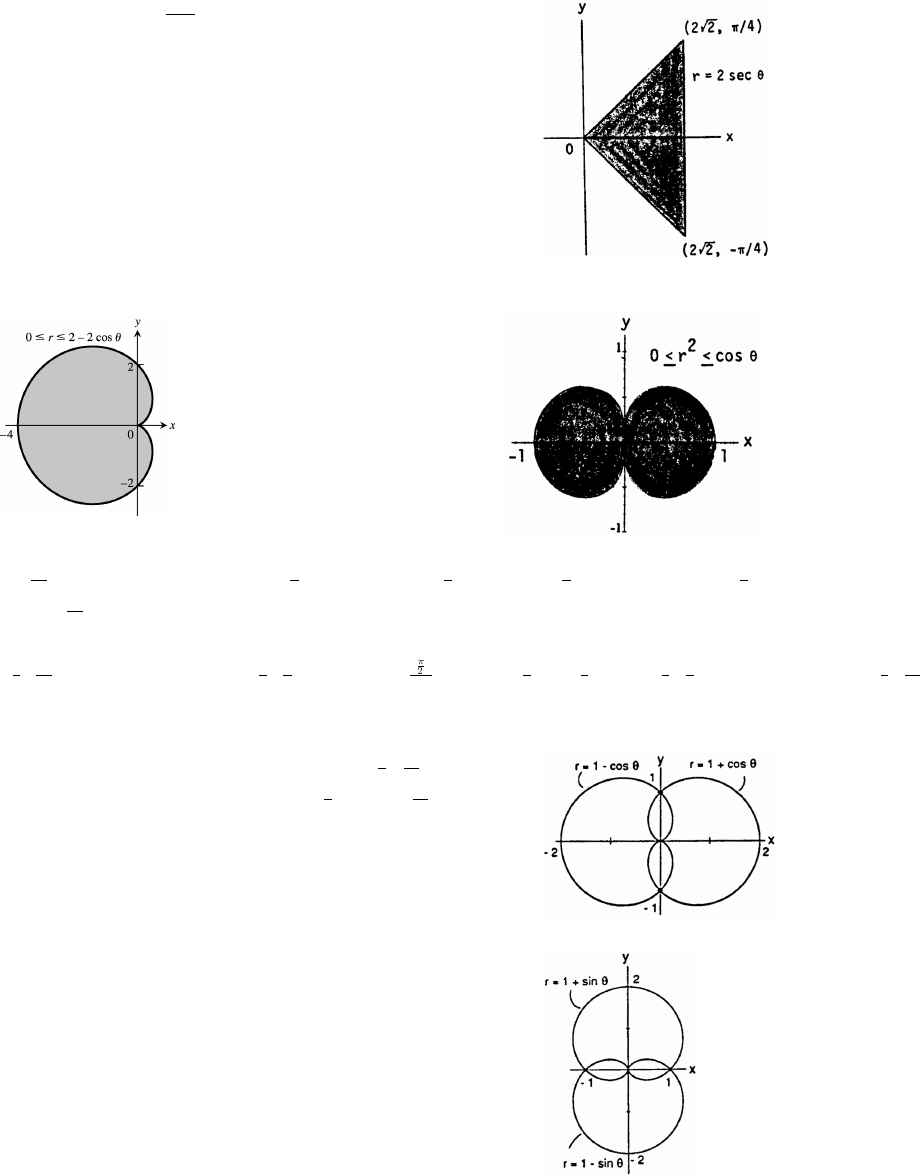
656 Chapter 10 Conic Sections and Polar Coordinates
26. r 2 sec r r cos 2 x 2œÊœÊœÊœ))
2
cos )
27. 28.
29. is the same point as 2 ; r 2 sin 2 2 sin 2 2 is on the graph
ˆ ‰ ˆ ‰ ˆ‰ ˆ‰ ˆ ‰
#ß ß œ œ œÊß
3
444 4
11111
#
is on the graphÊ#ß
ˆ‰
3
4
1
30. is the same point as ; r sin sin is on the graph
ˆ‰ ˆ‰ ˆ‰ ˆ‰
Š‹
"" """
## #####
ßßœœœÊßÊß
3 3
2236
11111
ˆ‰
is on the graph
31. 1 cos 1 cos cos 0 , œ Ê œÊœ))))
11
##
3
r 1; points of intersection are and .Ê œ "ß "ß
ˆ‰ˆ‰
11
##
3
The point of intersection ( 0) is found by graphing.!ß
32. 1 sin 1 sin sin 0 0, r 1;œ Ê œÊœÊœ))))1
points of intersection are (1 0) and (1 ). The point ofßß1
intersection ( 0) is found by graphing.!ß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
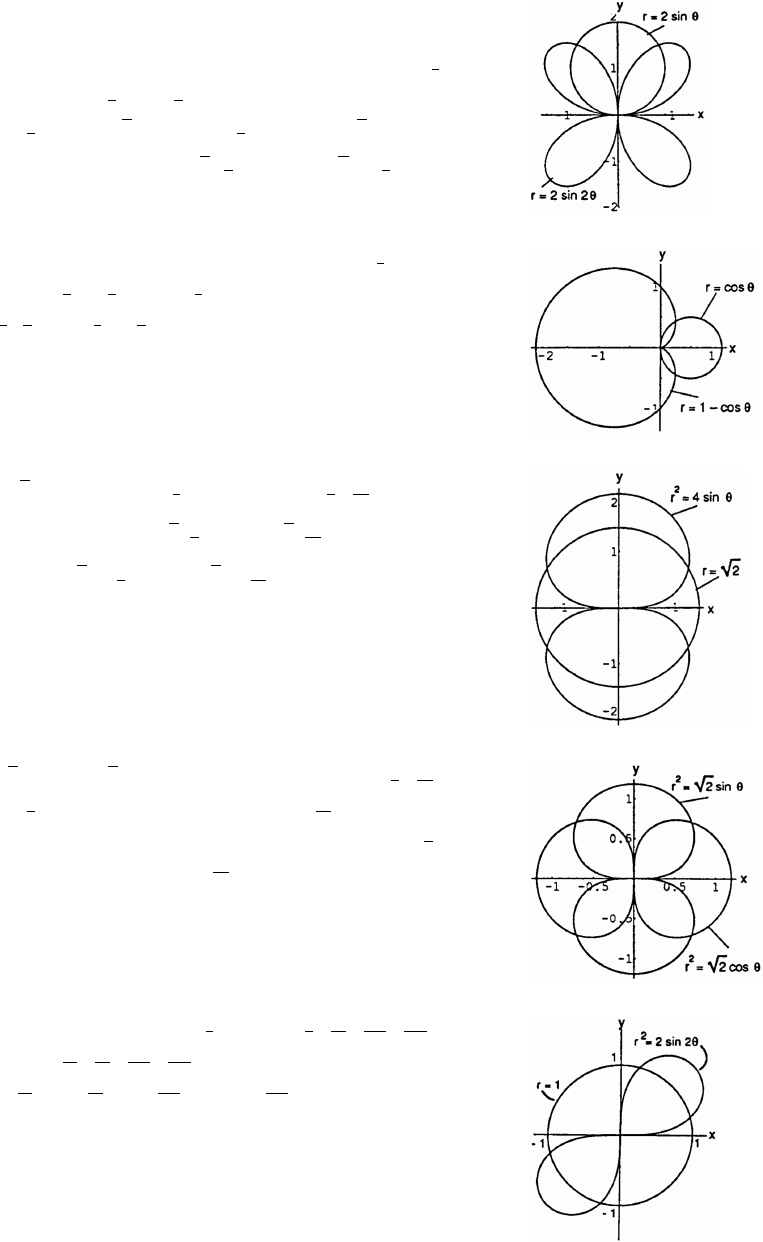
Section 10.6 Graphing in Polar Coordinates 657
33. 2 sin 2 sin 2 sin sin 2 sin )))))œÊœÊ
2 sin cos sin 2 sin cos 0œÊœ)) ) ))
(sin )(1 2 cos ) 0 sin 0 or cos ʜʜ œ)) ))
"
#
0, , , or ; 0 or r 0,Êœ œ Êœ)1 ) 1
11
33
r 3 , and r 3 ; points of))œÊœ œ Êœ
11
33
ÈÈ
intersection are ( 0), 3 , and 3!ß ß ß
Š‹Š ‹
ÈÈ
11
33
34. cos 1 cos 2 cos 1 cos ))) )œ Ê œ Ê œ
"
#
, r ; points of intersection areʜ ʜ)11
33
"
#
and , . The point (0 0) is found by
ˆ‰ˆ ‰
""
##
ß ß
11
33
graphing.
35. 2 4 sin sin , ; points
Š‹
È#
"
#
œÊœÊœ)))
11
66
5
of intersection are 2 and 2 . The
Š‹Š ‹
ÈÈ
ßß
11
66
5
points 2 and 2 are found by
Š‹Š ‹
ÈÈ
ß ß
11
66
5
graphing.
36. 2 sin 2 cos sin cos , ;
ÈÈ
)))))œÊœÊœ
11
44
5
r 1 r 1 and r 1))œÊ œÊœ„ œ Êœ
11
44
5
##
no solution for r; points of intersection are 1 .Ê„ß
ˆ‰
1
4
The points ( 0) and 1 are found by graphing.!ß „ ß
ˆ‰
3
4
1
37. 1 2 sin 2 sin 2 2 , , , œÊœÊœ)) )
"
#
1111
66 6 6
51317
, , , ; points of intersection areʜ)1111
12 12 12 12
51317
1 , 1 , 1 , and 1 . No other
ˆ‰ˆ‰ˆ‰ˆ‰
ßßß ß
11 1 1
12 12 1 1
513 17
##
points are found by graphing.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
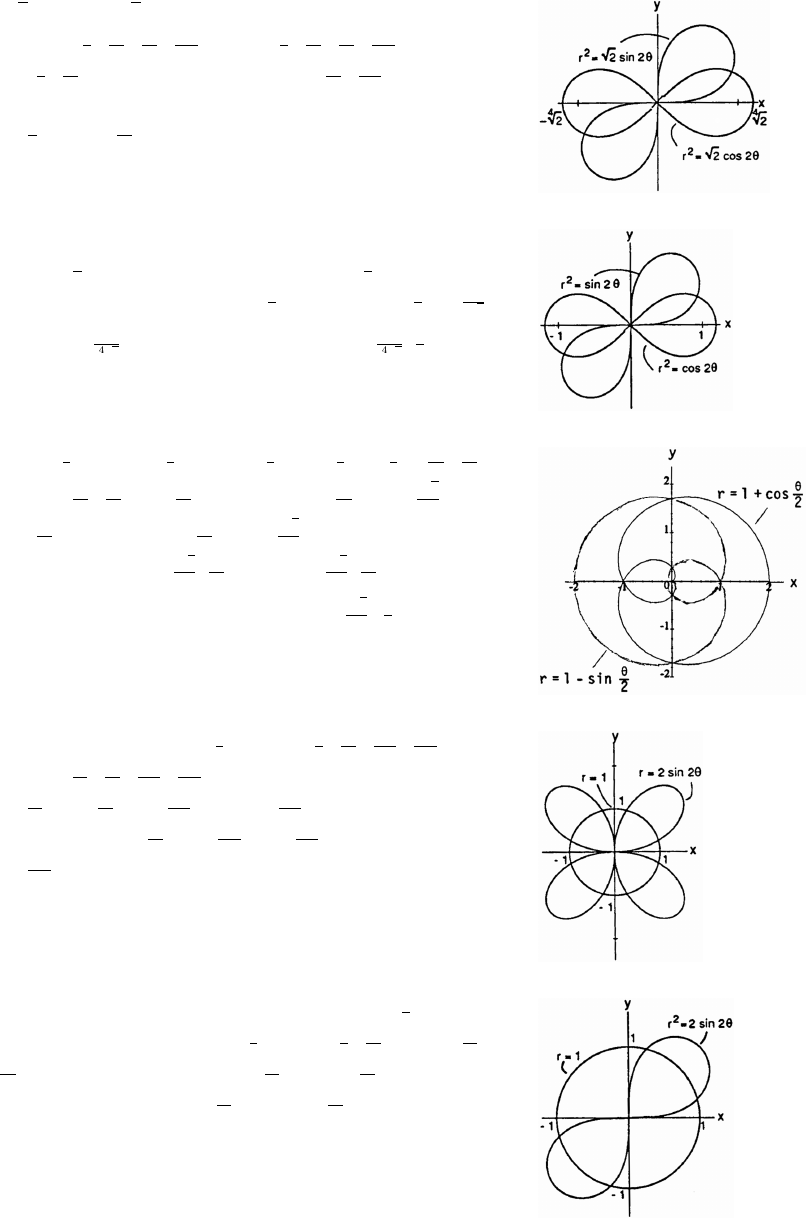
658 Chapter 10 Conic Sections and Polar Coordinates
38. 2 cos 2 2 sin 2 cos 2 sin 2
ÈÈ
))))œÊœ
2 , , , , , , ;ʜ ʜ))
111 1 111 1
44 4 4 88 8 8
5913 5913
, r 1 r 1; , ))œÊœÊœ„œ
11 1 1
88 8 8
9513
#
r 1 no solution for r; points of intersection areÊœÊ
#
1 and 1 . The point of intersection ( 0) is found
ˆ‰ˆ‰
ßß !ß
11
88
9
by graphing.
39. r sin 2 and r cos 2 are generated completely for
##
œœ))
0 . Then sin 2 cos 2 2 is the onlyŸŸ œ Ê œ))))
11
#4
solution on that interval r sin 2Êœ Ê œ œ)11
88
2
#"
ˆ‰ È
r ; points of intersection are .Êœ„ „ ß
""
ÈÈ
22
8
Š‹
1
The point of intersection ( 0) is found by graphing.!ß
40. 1 sin 1 cos sin cos , œ Êœ Êœ
)))))11
#####
37
44
, ; r 1 cos 1 ;Ê œ œ Ê œ œ))
37 3 3
4
2
11 1 1
## # #
È
r 1 cos 1 ; points of)œ Ê œ œ
77
4
2
11
##
È
intersection are and 1 . The
Š‹Š‹
" ß ß
ÈÈ
22
37
## ##
11
three points of intersection (0 0) and 1 areß„ß
Š‹
È2
##
1
found by graphing and symmetry.
41. 1 2 sin 2 sin 2 2 , , , œÊœÊœ)) )
"
#
1111
66 6 6
51317
, , , ; points of intersection areʜ)1111
11 1 1
51317
## # #
, , 1 , and . The points
ˆ‰ˆ‰ˆ‰ˆ‰
"ß "ß ß "ß
11 1 1
11 1 12
513 17
## #
of intersection 1 , , and
ˆ‰ˆ‰ˆ‰
ß"ß "ß
71119
11 1
111
## #
are found by graphing and symmetry.
ˆ‰
"ß 23
1
1
#
42. r 2 sin 2 is completely generated on 0 so
#
#
œŸŸ))
1
that 1 2 sin 2 sin 2 2 , ,œÊœÊœÊœ))) )
"
#
11 1
66 12
5
; points of intersection are 1 and . The
55
111
111
###
ˆ‰ˆ‰
ß"ß
points of intersection and 1 are found
ˆ‰ˆ‰
"ß ß
11
11
5
##
by graphing.
43. Note that (r ) and ( r ) describe the same point in the plane. Then r 1 cos 1 cos ( )ßß œÍ))1 ) )1
1 (cos cos sin sin ) 1 cos (1 cos ) r; therefore (r ) is on the graph ofœ œ œ œ ß)1 )1 ) ) )
r 1 cos ( r ) is on the graph of r 1 cos the answer is (a).œ Íß œ Ê))1 )
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
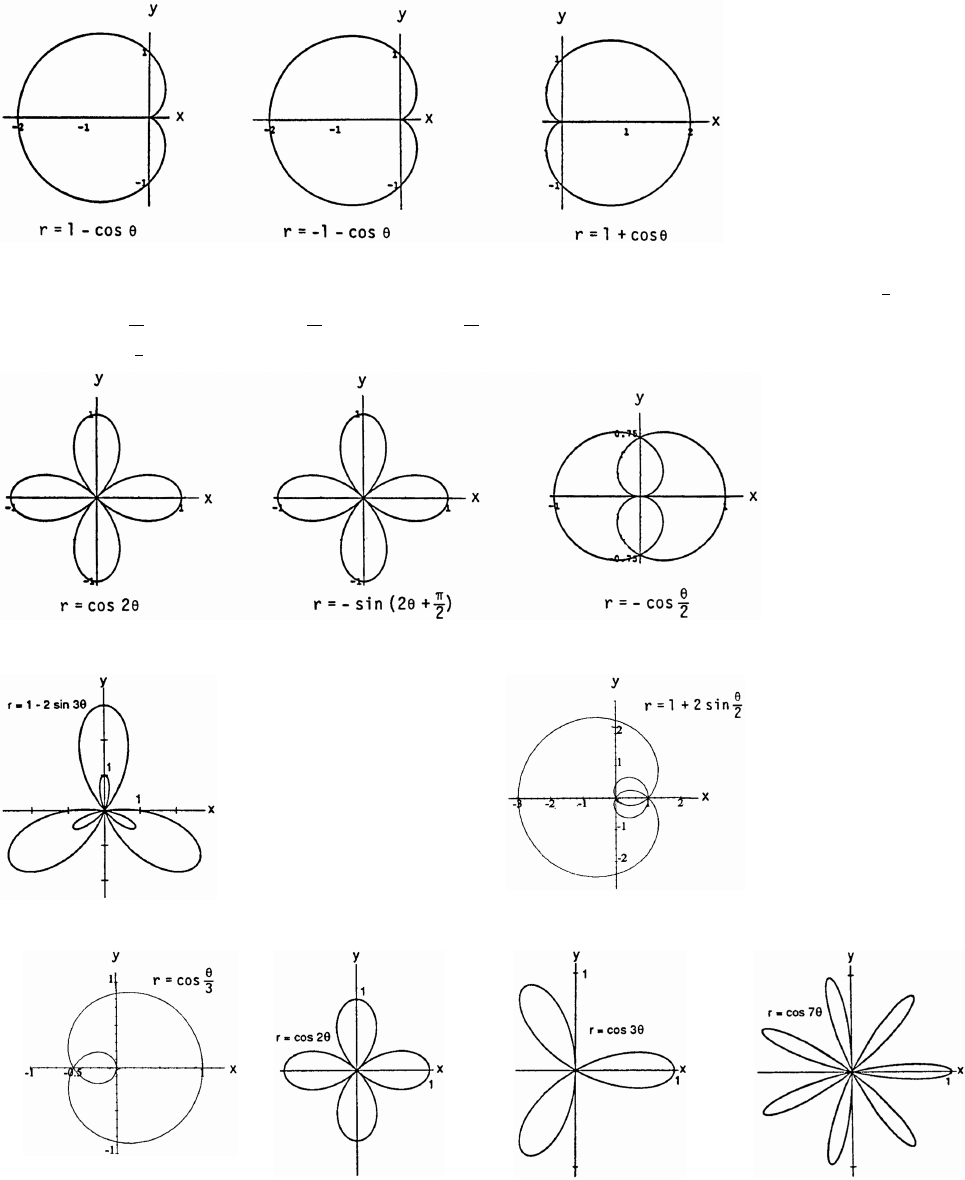
Section 10.6 Graphing in Polar Coordinates 659
44. Note that (r ) and ( r ) describe the same point in the plane. Then r cos 2 sin 2( ))ßß œ Í ))1 ) )1
ˆ‰
1
#
sin 2 sin (2 ) cos cos (2 ) sin cos 2 r; therefore (r ) is on the graph ofœ œ œ œ ß
ˆ ‰ ˆ‰ ˆ‰
)) ) ) )
555111
###
r sin 2 the answer is (a).œ Ê
ˆ‰
)1
#
45. 46.
47. (a) (b) (c) (d)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
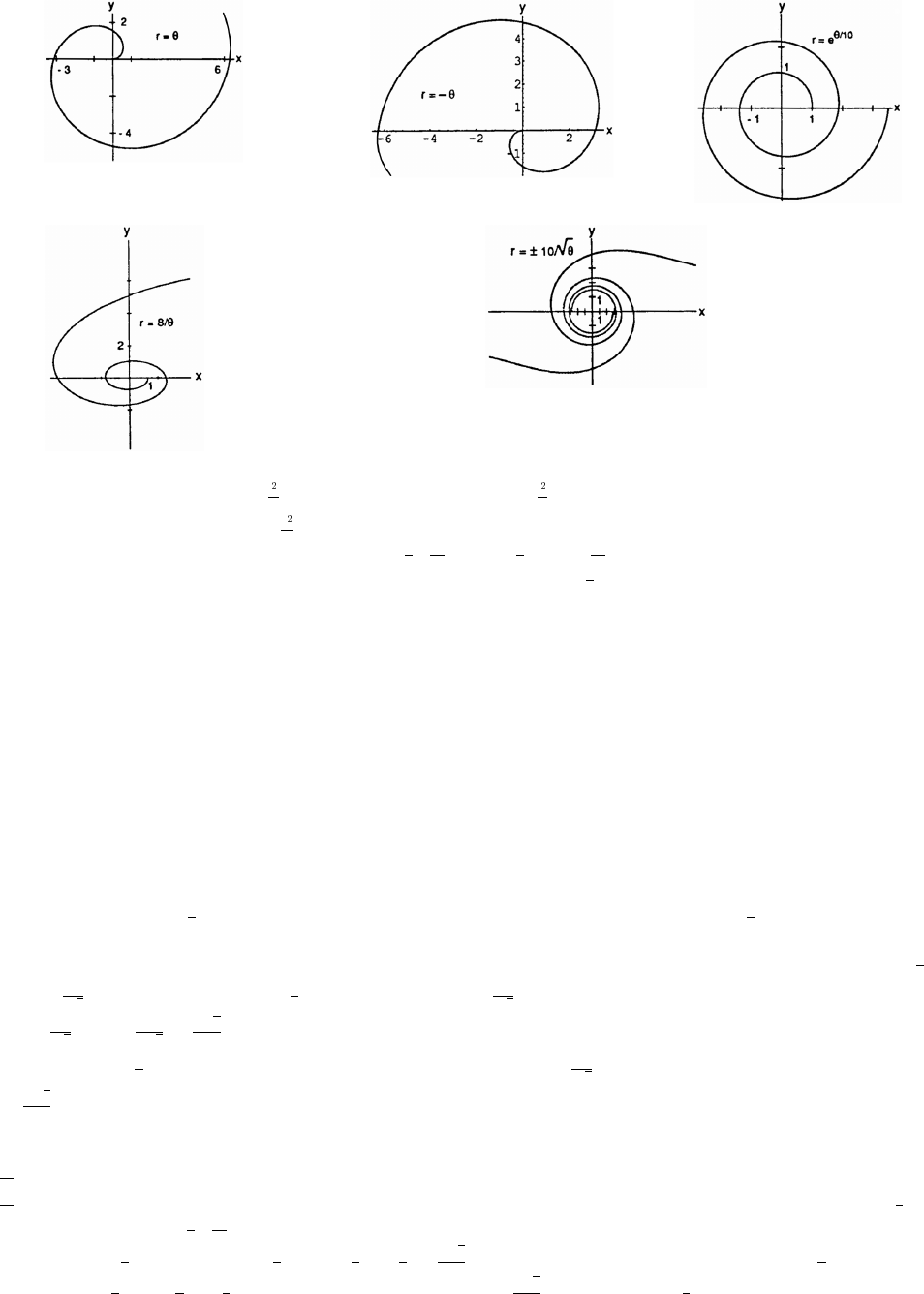
660 Chapter 10 Conic Sections and Polar Coordinates
48. (a) (b) (c)
(d) (e)
49. (a) r 4 cos cos ; r 1 cos r 1 0 r 4r 4 (r 2) 0
###
œ Ê œ œ Ê œ Ê œ Ê œ)) )
rr
44
Š‹
r 2; therefore cos 1 (2 ) is a point of intersectionÊ œ œ œ Ê œ Ê ß))11
2
4
(b) r 0 0 4 cos cos 0 , or is on the graph; r 0 0 1 cos œÊ œ Ê œÊœ Ê!ß !ß œÊœ
#
## # #
)) ) )
11 1 133
ˆ‰ˆ ‰
cos 1 0 (0 0) is on the graph. Since ( 0) for polar coordinates, the graphsÊ œ Ê œ Ê ß !ß œ !ß)) ˆ‰
1
#
intersect at the origin.
50. (a) Let r f( ) be symmetric about the x-axis and the y-axis. Then (r ) on the graph (r ) is on theœßÊß)))
graph because of symmetry about the x-axis. Then ( r ( )) ( r ) is on the graph because ofß œ ß))
symmetry about the y-axis. Therefore r f( ) is symmetric about the origin.œ)
(b) Let r f( ) be symmetric about the x-axis and the origin. Then (r ) on the graph (r ) is on theœßÊß)))
graph because of symmetry about the x-axis. Then ( r ) is on the graph because of symmetry aboutß)
the origin. Therefore r f( ) is symmetric about the y-axis.œ)
(c) Let r f( ) be symmetric about the y-axis and the origin. Then (r ) on the graph ( r ) is on theœßÊß)))
graph because of symmetry about the y-axis. Then ( ( r) ) (r ) is on the graph because of ß œ ß))
symmetry about the origin. Therefore r f( ) is symmetric about the x-axis.œ)
51. The maximum width of the petal of the rose which lies along the x-axis is twice the largest y value of the curve
on the interval 0 . So we wish to maximize 2y 2r sin 2 cos 2 sin on 0 . LetŸŸ œ œ ŸŸ)))))
1 1
4 4
f( ) 2 cos 2 sin 2 1 2 sin (sin ) 2 sin 4 sin f ( ) 2 cos 12 sin cos . Then))) ))))))))œœ œÊœab
#$w#
f ( ) 0 2 cos 12 sin cos 0 (cos ) 1 6 sin 0 cos 0 or 1 6 sin 0 or
w# # #
#
))))))) ))œÊ œÊ œÊ œ œÊœab 1
sin . Since we want 0 , we choose sin f( ) 2 sin 4 sin))))))œŸŸœÊœ
„"
" $
1
66
4
ÈÈ
1Š‹
2 4 . We can see from the graph of r cos 2 that a maximum does occur in theœœ œ
Š‹
""
ÈÈ
È
666
26
9
†)
interval 0 . Therefore the maximum width occurs at sin , and the maximum widthŸŸ œ))
1
46
" "
Š‹
È
is .
26
9
È
52. We wish to maximize y r sin 2(1 cos )(sin ) 2 sin 2 sin cos . Thenœœ œ ))))))
2 cos 2(sin )( sin ) 2 cos cos 2 cos 2 sin 2 cos 2 cos 4 cos 2; thus
dy
d)œ œ œ ))))))))))
## #
0 4 cos 2 cos 2 = 0 2 cos cos 1 0 (2 cos 1)(cos 1) 0 cos
dy
d)œÊ Ê œÊ œÊ œ
## "
#
)) )) ) ) )
or cos 1 , , . From the graph, we can see that the maximum occurs in the first quadrant so))1œ Ê œ 11
33
5
we choose . Then y 2 sin 2 sin cos . The x-coordinate of this point is x r cos )œœ œ œ
1111 1
3333 3
33
È
#
2 1 cos cos . Thus the maximum height is h occurring at x .œ œ œ œ
ˆ‰ˆ‰
11
33
3 3
33
###
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
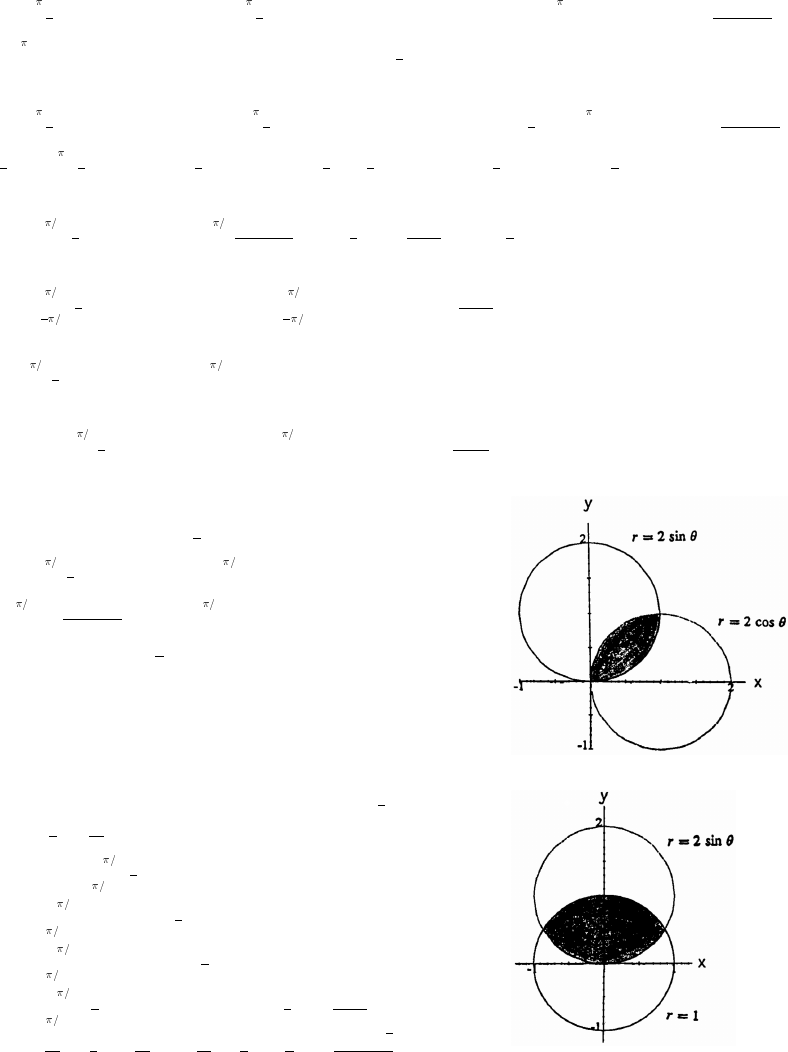
Section 10.7 Area and Lengths in Polar Coordinates 661
10.7 AREA AND LENGTHS IN POLAR COORDINATES
1. A (4 2 cos ) d 16 16 cos 4 cos d 8 8 cos 2 dœ œ œ
'' '
00 0
22 2
""
## #
##
)) ) )) ) )ab
‘ˆ‰
1cos 2)
(9 8 cos cos 2 ) d 9 8 sin sin 2 18œ œ œ
'0
2
))))) ) 1
‘
"#
!
2
1
2. A [a(1 cos )] d a 1 2 cos cos d a 1 2 cos dœ œ œ
'' '
00 0
22 2
"" "
## ##
## ##
)) ) )) ) )ab
ˆ‰
1cos 2)
a 2 cos cos 2 d a 2 sin sin 2 aœ œœ
""""
## # ## #
###
#
!
'0
2ˆ‰ ‘
333
4
))) )))1
1
3. A 2 cos 2 d dœœœœ
''
00
44
""
###
#Î%
!
)) ) )
1cos 4 sin 4
48
))1
1
‘
4. A 2 2a cos 2 d 2a cos 2 d 2a 2aœœœœ
''
44
44
"
#
## # #
Î%
Î%
ab ‘
)) )) sin 2
2
)1
1
5. A (4 sin 2 ) d 2 sin 2 d cos 2 2œœœœ
''
00
22
"
#
Î#
!
)) )) )cd
1
6. A (6)(2) (2 sin 3 ) d 12 sin 3 d 12 4œœœœ
''
00
66
"
#
Î'
!
)) )) ‘
cos 3
3
)1
7. r 2 cos and r 2 sin 2 cos 2 sin œœÊœ))))
cos sin ; thereforeʜʜ)))
1
4
A 2 (2 sin ) d 4 sin dœœ
''
00
44
"
#
##
)) ))
4 d (2 2 cos 2 ) dœœ
''
00
44
ˆ‰
1cos 2
#
))))
2sin 2 1œ œcd))
11
Î%
!#
8. r 1 and r 2 sin 2 sin 1 sin œœ Ê œÊœ)) )
"
#
or ; thereforeʜ)11
66
5
A (1) (2 sin ) 1 dœ 1))
###
"
#
'6
56 cd
2 sin dœ 1))
'6
56
ˆ‰
#"
#
1 cos 2 dœ 1))
'6
56
ˆ‰
"
#
cos 2 dœ œ 1))1)
'6
56
ˆ‰‘
""
##
&Î'
Î'
2
sin 2)1
1
sin sin œ œ1ˆ‰ˆ‰
55
131236
433
1111
1
## #
""
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
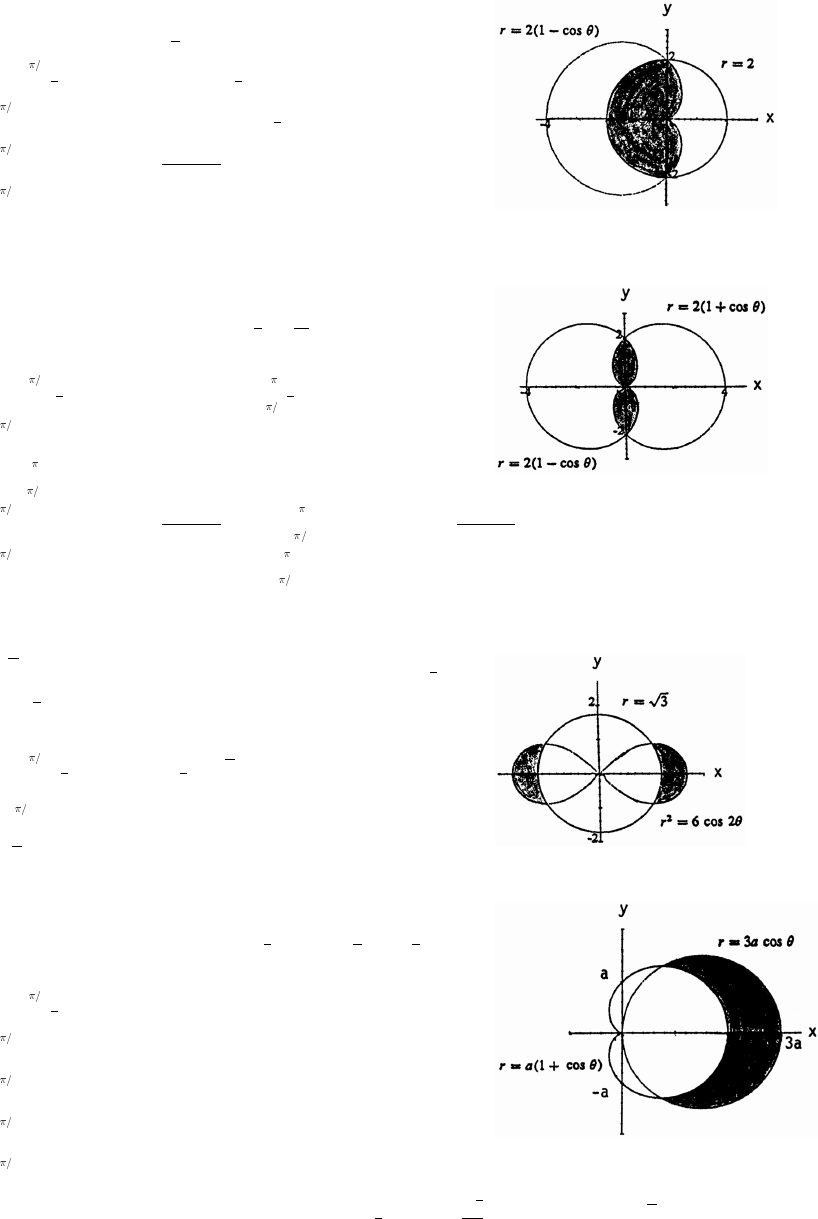
662 Chapter 10 Conic Sections and Polar Coordinates
9. r 2 and r 2(1 cos ) 2 2(1 cos )œœÊœ))
cos 0 ; thereforeʜʜ„))
1
#
A 2 [2(1 cos )] d area of the circleœ
'0
2""
##
#
))
4 1 2 cos cos d (2)œ
'0
2ab
ˆ‰
)))1
##
"
#
4 1 2 cos d 2œ
'0
2ˆ‰
))1
1cos 2
#
)
(4 8 cos 2 2 cos 2 ) d 2œ
'0
2
)))1
6 8 sin sin 2 2 5 8œ œcd)))11
1Î#
!
10. r 2(1 cos ) and r 2(1 cos ) 1 cos œ œ Ê)))
1 cos cos 0 or ; the graph alsoœ Ê œ Ê œ)) )
11
##
3
gives the point of intersection (0 0); thereforeß
A 2 [2(1 cos )] d 2 [2(1 cos )] dœ
''
02
2""
##
##
)) ))
4 1 2 cos cos dœ
'0
2ab)))
#
4 1 2 cos cos d
'2ab)))
#
4 1 2 cos d 4 1 2 cos dœ
''
02
2ˆ‰ˆ‰
)) ))
1cos 2 1cos 2
##
))
(6 8 cos 2 cos 2 ) d (6 8 cos 2 cos 2 ) dœ
''
02
2
))) )))
6 8 sin sin 2 6 8 sin sin 2 6 16œ œcdcd))) )))1
11
1
Î#
!Î#
11. r 3 and r 6 cos 2 3 6 cos 2 cos 2œœÊœÊœ
È#"
#
)))
(in the 1st quadrant); we use symmetry of theʜ)1
6
graph to find the area, so
A4 (6 cos 2) 3 dœ
'0
6”•
Š‹
È
""
##
#
))
2 (6 cos 2 3) d 2 3 sin 2 3œœ
'0
6
)) ))cd
1Î'
!
33œ
È1
12. r 3a cos and r a(1 cos ) 3a cos a(1 cos )œœÊœ))))
3 cos 1 cos cos or ;ʜʜʜ))))
"
#
11
33
the graph also gives the point of intersection (0 0); thereforeß
A 2 (3a cos ) a (1 cos ) dœ
'0
3"
#
## #
cd)))
9a cos a 2a cos a cos dœ
'0
3ab
## # # ##
))))
8a cos 2a cos a dœ
'0
3ab
## # #
)))
4a (1 cos 2 ) 2a cos a dœ
'0
3cd
###
)))
3a 4a cos 2 2a cos dœ
'0
3ab
## #
)))
3a 2a sin 2 2a sin a 2a 2a a 1 3œ œ œcd
ˆ‰ Š‹ Š ‹
È
## # ## # #
Î$
!"
##
)))1 1
1È3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
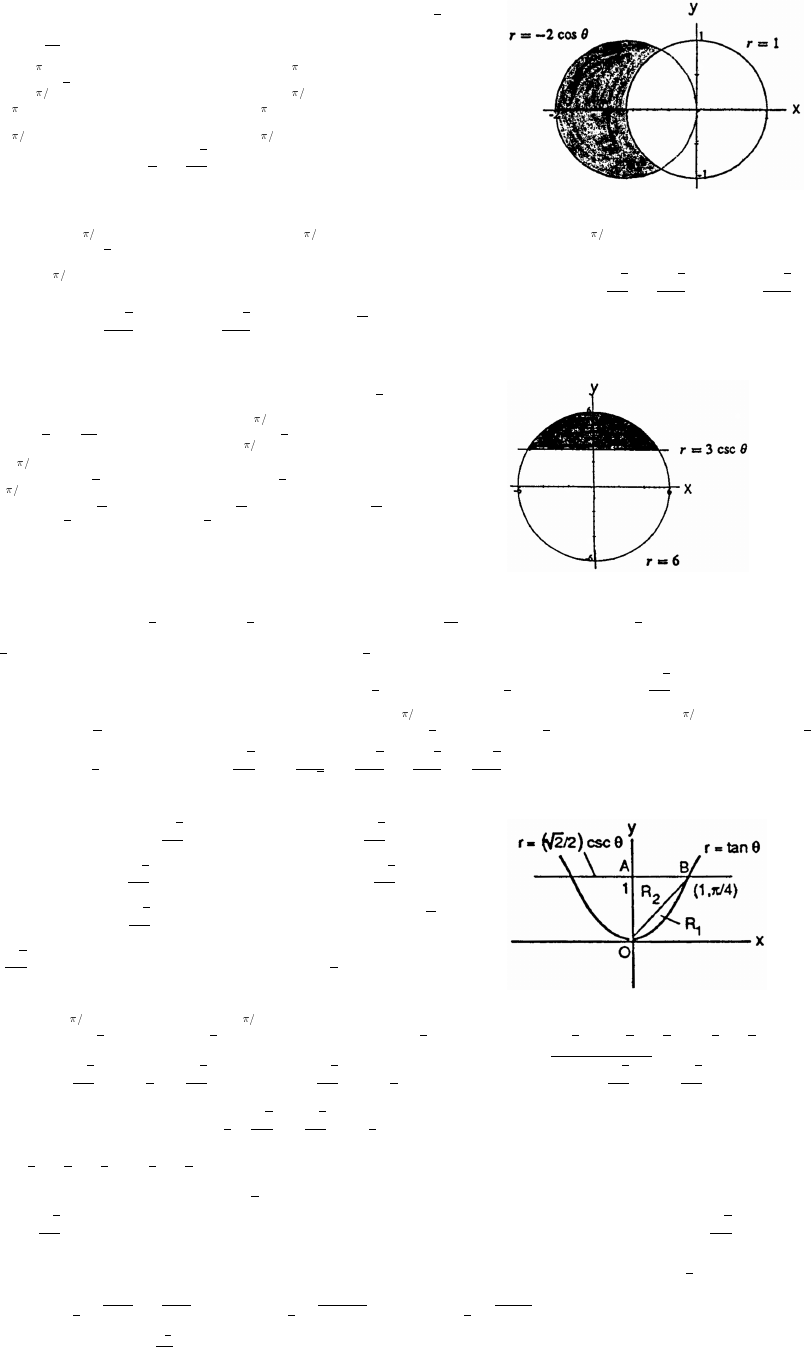
Section 10.7 Area and Lengths in Polar Coordinates 663
13. r 1 and r 2 cos 1 2 cos cos œœÊœÊœ)))
"
#
in quadrant II; thereforeʜ)2
3
1
A 2 ( 2 cos ) 1 d 4 cos 1 dœœ
''
23 23
"
#
## #
cdab)) ))
[2(1 cos 2 ) 1] d (1 2 cos 2 ) dœœ
''
23 23
)) ))
sin 2œ œcd))
1
1
1
#Î$ #3
3
È
14. (a) A 2 (2 cos 1) d 4 cos 4 cos 1 d [2(1 cos 2 ) 4 cos 1] dœœœ
'' '
00 0
23 23 23
"
#
##
)) ) )) ) ))ab
(3 2 cos 2 4 cos ) d 3 sin 2 4 sin 2 2œ œ œœ
'0
23
)))))) 1 1cd
#Î$
!## #
1ÈÈ È
343 33
(b) A 2 3 3 (from 14(a) above and Example 2 in the text)œ œ
Š‹Š‹
È
111
33 33
ÈÈ
##
15. r 6 and r 3 csc 6 sin 3 sin œœ Ê œÊœ)) )
"
#
or ; therefore A 6 9 csc dÊœ œ )))
11
66
5'6
56
"
#
##
ab
18 csc d 18 cot œ œ
'6
56
ˆ‰‘
99
##
#&Î'
Î'
)) ) )
1
1
15 3 3 3 12 9 3œ œ
Š‹Š‹
ÈÈÈ
111
99
##
16. r 6 cos 2 and r sec sec 6 cos 2 cos cos 2 cos 2 cos 1
#####
#
œœÊœÊœÊœ )))) )) ))
39 9 3
4248
aba b
2 cos cos 2 cos cos 0 16 cos 8 cos 3 0Êœ Ê œÊ œ
33
88
%# %# % #
)) )) ) )
4 cos 1 4 cos 3 0 cos or cos cos (the second equation has no realÊ œÊœ œÊœ„abab
## ##
"
#
)) )) )
3
44
3
È
roots) (in the first quadrant); thus A 2 6 cos 2 sec d 6 cos 2 sec dÊœ œ œ )))))))
1
644
99
''
00
66
"
#
##
ˆ‰ˆ‰
3 sin 2 tan 3œ œ œœ
‘
Š‹
))
99
444
3333333
43
1Î'
!##
ÈÈÈÈ
È
17. (a) r tan and r csc tan csc œœ Êœ))))
Š‹ Š‹
ÈÈ
22
##
sin cos 1 cos cos ʜ ʜ
##
##
))))
Š‹ Š‹
ÈÈ
22
cos cos 1 0 cos 2 orÊ œÊœ
#
#
)) )
Š‹ È
È2
(use the quadratic formula) (the solution
È2
4#ʜ)1
in the first quadrant); therefore the area of R is
"
A tan d sec 1 d tan tan ;
""" " " "
## # # #
## Î%
!
œœœœœ
''
00
44
)) ) ) ) )abcd
ˆ‰
111 1
44 8
AO csc and OB csc 1 AB 1œœœœÊœœ
Š‹ Š‹ Š‹
Ê
ÈÈ È ÈÈ
22 2 22
4### # # #
##
11
the area of R is A ; therefore the area of the region shaded in the text isÊœœ
##
""
## #
Š‹Š‹
ÈÈ
22
4
2 . Note: The area must be found this way since no common interval generates the region. For
ˆ‰
""
##
œ
11
84 4
3
example, the interval 0 generates the arc OB of r tan but does not generate the segment AB of the lineŸŸ œ))
1
4
r csc . Instead the interval generates the half-line from B to on the line r csc .œ_œ
È È
2 2
# #
) )
(b) lim tan and the line x 1 is r sec in polar coordinates; then lim (tan sec )
)1 )1ÄÎ ÄÎ2 2
)) ))œ_ œ œ
= lim lim lim 0 r tan approaches
)1 )1 )1ÄÎ ÄÎ ÄÎ222
ˆ‰ ˆ‰ ˆ‰
sin sin 1 cos
cos cos cos sin
)))
)) ) )
œ œ œÊœ
"
)
r sec as r sec (or x 1) is a vertical asymptote of r tan . Similarly, r sec œÄÊœ œ œ œ)) ) ) )
1
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

664 Chapter 10 Conic Sections and Polar Coordinates
(or x 1) is a vertical asymptote of r tan .œ œ )
18. It is not because the circle is generated twice from 0 to 2 . The area of the cardioid is)1œ
A 2 (cos 1) d cos 2 cos 1 d 2 cos 1 dœœœ
'' '
00 0
"
# #
##
)) ) )) ))ab
ˆ‰
1cos 2)
2 sin . The area of the circle is A the area requested is actuallyœ œ œ œÊ
‘ ˆ‰
3sin 2 3
24 4
)) 1 1
1
)1
!##
"#
35
44
11 1
#œ
19. r , 0 5 2 ; therefore Length (2 ) d 4 dœŸŸÊœ œ œ )) ) ) )) )))
### %#
#
ÈÉab È
dr
d)''
00
55
4 d (since 0) 4 d ; u 4 du d ; 0 u 4,œ œ œÊœœÊœ
''
00
55
kkÈÈ
)) ) ) )) ) ) )))
##
#"
#
5 u 9 u du u
“
ÈÈ‘
)œÊœÄ œ œ
'4
9""
##
$Î# *
%
219
33
20. r , 0 ; therefore Length d 2 dœŸŸÊœ œ œ
edre ee e
22 22
d
ÈÈ ÈÈ
)1 ) )
)''
00
ÊŠ‹ Š‹ Š‹
Ê
##
#
2
e d e e 1œœœ
'0
))1
1
)‘
!
21. r 1 cos sin ; therefore Length (1 cos ) ( sin ) dœ Ê œ œ )) )))
dr
d)'0
2È##
2 2 2 cos d 2 d 4 d 4 cos d 4 2 sin 8œ œ œ œ œ œ
''''
0000
ÈÉɈ‰ ‘
)) ) ) )
4(1 cos ) 1cos
2
###
!
))))
1
22. r a sin , 0 , a 0 a sin cos ; therefore Length a sin a sin cos dœŸŸÊœ œ
#
### ###
###
))) )))
)
)1 )
dr
d'0Ɉ ‰ ˆ ‰
a sin a sin cos d a sin sin cos d (since 0 ) a sin dœ œ œŸŸ
''
00 0
ÉÉ
¸¸ ˆ‰
'
#% ## # # #
### ### #
))) ))) )
)))1)
2a cos 2aœ œ
‘
)1
2!
23. r , 0 ; therefore Length dœŸŸÊœ œ
6 dr 6 sin 6 6 sin
1cos d (1cos ) 1cos (1cos )#
##
))) ))
1) )
) )
'0
2ʈ‰
Š‹
d6 1 dœœ
''
00
22
ɸ¸
É
36 36 sin sin
(1 cos ) 1 cos (1 cos )
1cos
"
)))
))
)
ab
))
since 0 on 0 6 dœŸŸ
ˆ‰ˆ‰
É
""
#1cos 1cos (1cos )
1 2 cos cos sin
)))
1)))
))
'0
2
6 d 6 2 6 2 3 sec dœœœœ
''''
0000
2222
ˆ‰ ¸¸
ÉÈÈ
"
#
$
1cos (1cos )
22 cos d d
(1 cos ) 2 cos
))
))))
)
))
ˆ‰
3 sec d 6 sec u du (use tables) 6 sec u duœœ œ
'' '
00 0
24 4
$$
# #
Î%
!
")1
)Œ
‘
sec u tan u
2
6 ln sec u tan u 3 2 ln 1 2œ œ
Š‹’“
‘
kk
ÈÈ
Š‹
"" Î%
!
È22
1
24. r , ; therefore Length dœŸŸÊœ œ
2 dr 2 sin 2 2 sin
1cos d (1cos ) 1cos (1cos )#
##
))) ))
1) )
)1 )
'2ʈ‰
Š‹
1 d dœœ
''
22
ÊŠ‹
¸¸
É
4sin 2
(1 cos ) 1 cos (1 cos )
1cos
(1 cos ) sin
)))
)
)
))
ab
))
since 1 cos 0 on 2 dœŸŸ
ˆ‰ˆ‰
É
))1 )
1)))
))#
"
'21cos (1cos )
1 2 cos cos sin
2 d 2 2 2 2 csc dœœœœ
''''
2222
ˆ‰ ¸¸
ÉÈÈ
"
#
$
1cos (1cos )
22 cos d d
(1 cos ) 2 sin
))
))))
)
))
ˆ‰
csc d since csc 0 on 2 csc u du (use tables)œœŸŸ œ
''
2 4
2
$$
###
ˆ‰ ˆ ‰
))1
))1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 10.7 Area and Lengths in Polar Coordinates 665
2 csc u du 2 ln csc u cot u 2 ln 2 1
Œ
‘ ‘
Š‹’“
kk Š‹
È
œœ
csc u cot u
22
22
1
1 1
1
Î#
Î% Î%
""" ""
# #
Î#
'4
2
ÈÈ
2ln1 2œ
ÈÈ
Š‹
25. r cos sin cos ; therefore Length cos sin cos dœÊœ œ
$# $#
##
))) )))
)3d 3 3 3 3 3
dr '0
4Ɉ ‰ ˆ ‰ )
cos sin cos d cos cos sin d cos dœ œ œ
'''
000
444
ÉÉ
ˆ‰ ˆ‰ ˆ‰ ˆ ‰ ˆ‰ ˆ‰ ˆ‰
'#% ##
##
))) ) )) )
333 3 33 3
)))
d sin œœœ
'0
41cos 32 3
23 88
##
"Î%
!
ˆ‰
2
3))
‘
)1
1
26. r 1 sin 2 , 0 2 (1 sin 2 ) (2 cos 2 ) (cos 2 )(1 sin 2 ) ; thereforeœ ŸŸ Êœ œ
ÈÈ
))1 ) ) ) )
dr
d)
"
#
"Î# "Î#
Length (1 sin 2 ) d dœ œ
''
00
22
ÉÉ
)) )
cos2 12 sin 2sin2cos2
(1 sin 2 ) 1 sin 2
))))
))
d 2 d 2 2œœœœ
''
00
22
ÉÈÈ
’“
22 sin 2
1sin 2
#
!
)
)
1
)))1
È
27. r 1 cos 2 (1 cos 2 ) ( 2 sin 2 ); therefore Length (1 cos 2 ) dœ Êœ œ
ÈÉ
))) ))
dr sin 2
d(1 cos 2 )) )
)"
#
"Î# '0
2
d d 2 d 2 2œœœœœ
'''
000
222
ÉÉÈÈ
’“
12 cos 2cos2sin2 22 cos 2
1cos 2 1cos 2
#
!
))) )
))
1
))))1
È
28. (a) r a 0; Length a 0 d a d a 2 aœÊ œ œ œ œ œ
dr
d)
1
''
00
22
Èkk c d
## #
!
)))1
(b) r a cos a sin ; Length (a cos ) ( a sin ) d a cos sin dœÊœ œ œ )) ))))))
dr
d)''
00
ÈÈab
#####
a d a aœœœ
'0kk c d)) 1
1
!
(c) r a sin a cos ; Length (a cos ) (a sin ) d a cos sin dœÊœ œ œ )) ))) )))
dr
d)''
00
ÈÈab
## ###
a d a aœœœ
'0kk c d)) 1
1
!
29. r cos 2 , 0 (cos 2 ) ( sin 2 )(2) ; therefore Surface AreaœŸŸÊœ œ
È)) ) )
1)
))
4d
dr sin 2
cos 2
"
#
"Î# È
(2 r cos ) cos 2 d 2 cos 2 (cos ) cos 2 dœœ
''
0 0
4 4
1) ) ) 1 ) ) ) )
ÊŠ‹Š‹ Š ‹
ÈÈ
É
##
sin 2 sin 2
cos 2 cos 2
))
))
È
2 cos 2 (cos ) d 2 cos d 2 sin 2œœœœ
''
00
44
Š‹
ÈÉcdÈ
1)) ) 1))1)1
"Î%
!
cos 2)
1
30. r 2e , 0 2 e e ; therefore Surface AreaœŸŸÊœ œ
ÈÈ
ˆ‰
222
)1
)###
"dr
d
2
È
2 2e (sin ) 2e e d 2 2e (sin ) 2e e dœœ
''
0 0
2 2
2 2
22
Š‹Š‹Š‹ Š‹
ÈÈ È
ÊÉ
1) )1) )
##
##
"
È2
2 2 e (sin ) e d 2 2 e (sin ) e d 2 5 e sin dœœ œ
'' '
00 0
22 2
222
Š‹ Š‹Š‹
ÈÈ
ÉÈ
1))1))1 ))
55
2
#
È
È
2 5 (sin cos ) 5 e 1 where we integrated by partsœœ1))1
ÈÈ
‘
ab
e
2
1Î#
!
2
31. r cos 2 r cos 2 ; use r cos 2 on 0 (cos 2 ) ( sin 2 )(2) ;
#"Î#
"
#
œÊœ„ œ ßÊœ œ))) ))
ÈÈ
‘
1)
))
4d
dr sin 2
cos 2
È
therefore Surface Area 2 2 cos 2 (sin ) cos 2 d 4 cos 2 (sin ) dœœ
''
0 0
4 4
Š‹
ÈÈ
ÉÉ
1)) ) )1 )) )
sin 2
cos 2 cos 2
)
))
"
4 sin d 4 cos 4 ( 1) 2 2 2œœœœ1))1)1 1
'0
4cd ’“Š‹
È
1Î%
!#
È2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

666 Chapter 10 Conic Sections and Polar Coordinates
32. r 2a cos 2a sin ; therefore Surface Area 2 (2a cos )(cos ) (2a cos ) ( 2a sin ) dœÊœ œ )) 1)))))
dr
d)'0È##
4a cos 4a cos sin d 8a cos a d 8a cos dœœœ1) )))1))1))
'''
000
ab a b abkk
È
####
## #
8a d 4a (1 cos 2 ) d 4a sin 2 4aœœœœ
## ###
"
#!
1)1))1))1
''
00
ˆ‰ ‘
1cos 2
2
)1
33. Let r f( ). Then x f( ) cos f ( ) cos f( ) sin f ( ) cos f( ) sin œœÊœÊœ) ) ) ) )) ) ) )))
dx dx
dd))
ww
##
ˆ‰ cd
f ( ) cos 2f ( ) f( ) sin cos [f( )] sin ; y f( ) sin f ( ) sin f( ) cos œ œÊœcd
w#w ## w
#
) ) )))) ) ) )) ))) )
dy
d)
f ( ) sin f( ) cos f ( ) sin 2f ( )f( ) sin cos [f( )] cos . ThereforeÊœ œ
Š‹ cdcd
dy
d)
#ww#w##
##
))) ) ) ) )))) ) )
f( ) cos sin [f( )] cos sin f( ) [f( )] r .
ˆ‰ ˆ‰
Š‹ cdababcd
dx dr
dd d
dy
)) )
# #
#w## ###w ##
##
œ œ œ))))))))
Thus, L d r d .œœ
''
ʈ‰ É ˆ‰
Š‹
dx dr
dd d
dy
)) )
##
##
))
34. (a) r a(1 cos ) d sin a
av 0
2
œœœ
"
#
!
20 2
a
11
1
')) ) )cd
(b) r a d a a
av 0
2
œœœ
""
#
#
!
2011
1
'))cd
(c) r a cos d a sin
av 2
2
œœœ
""
Î#
Î#
ˆ‰ˆ ‰')) )
11
1
1
cd 2a
35. r 2f( ), 2f ( ) r [2f( )] 2f ( ) Length 4[f( )] 4 f ( ) dœŸŸÊœÊœ Êœ )! ) " ) ) ) ) ) )
dr dr
dd))
w# #w
###w
#
ˆ‰ cd cd
É
'
2 [f( )] f ( ) d which is twice the length of the curve r f( ) for .œ œŸŸ
'Écd))) )!)"
#w
#
36. Again r 2f( ) r [2f( )] 2f ( ) Surface Area 2 [2f( ) sin ] 4[f( )] 4 f ( ) dœÊœ Ê œ ))) 1)))))
#w
###w
#
ˆ‰ cd cd
É
dr
d
2
)'
4 2 [f( ) sin ] [f( )] f ( ) d which is four times the area of the surface generated by revolvingœ
'1) ) ) ) )
Écd
#w
#
r f( ) about the x-axis for .œŸŸ)!)"
37. x œœ œ
22 2
33 3
'' '
''
00 0
22 2
00
22
r cos d [a(1 cos )] (cos ) d a 1 3 cos 3 cos cos (cos ) d
r d [a(1 cos )] d
)) ) ) ) ) ) ) ) )
)))
ab
a 1 2 cos cos d
'0
2ab)))
(After considerable algebra usingœœ
2 1 cos 2 1 cos 2
3
1 cos 2
a cos 3 3 1 sin (cos ) d
12 cos d
'
'
0
2
0
2
’“
ˆ‰ ˆ‰
ab
‘ˆ‰
))))
))
the identity cos A
‰
#
#
œ1 cos 2A a cos cos 2 2 cos sin cos 4 d
2 cos cos 2 d
'
'
0
2
0
2
ˆ‰
ˆ‰
15 8 4
12 3 3 12
3
)))) ))
)))
a;œœœ
a sin sin 2 sin sin 4
2 sin sin 2
a
36
5
‘
‘
ˆ‰
15 8 2 2
12 3 3 3 48
3
4
15
6
)) ) ) )
)) )
1
1
y ; u a(1 cos ) du sin d ; 0 u 2a;œœ œÊœœÊœ
22
33
r sin d [a(1 cos )] (sin ) d
r d 3a
''
'
00
22
0
2
)) ) ) )
)1
"
))))
2 u 2a 0. Therefore the centroid is y a 0dab
ˆ‰
)1œÊœ Ä œœ Bßœß
2
3a
u du
33 6
05
'2a
2a
11
38. r d a d a a ; x 0;
''
00
####
!
)))1œœœœ œ œ œœcd
1)
)) ))
)111
22
33 2
3
r cos d a cos d
r d aaa
asin 0
''
'
00
0
cd
y . Therefore the centroid is x y 0 .œœœœœ ßœß
22
33
24
33
r sin d a sin d
r d aaa3 3
acos a 4a 4a
''
'
00
0
)) ))
)1111 1
)cdˆ‰
abˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
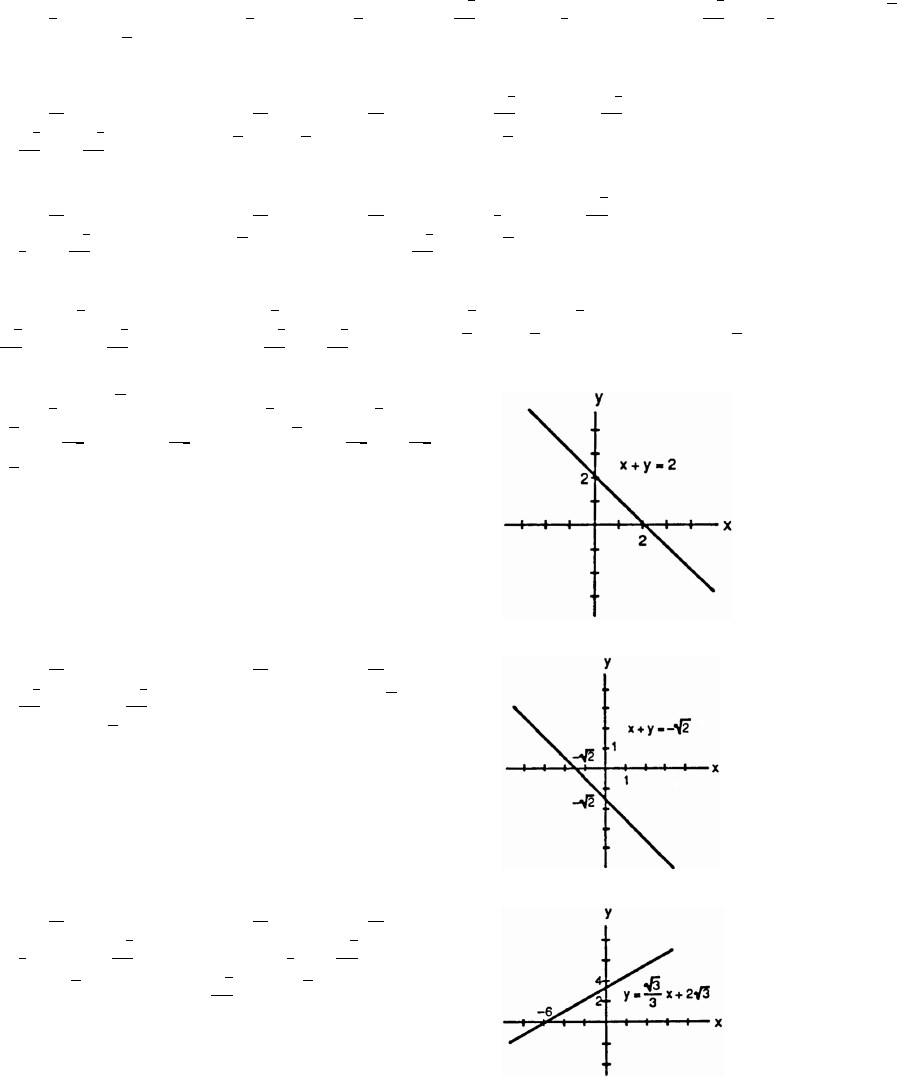
Section 10.8 Conic Sections in Polar Coordinates 667
10.8 CONIC SECTIONS IN POLAR COORDINATES
1. r cos 5 r cos cos sin sin 5 r cos r sin 5 x y 5 3 x y
ˆ‰ ˆ ‰ È
))) )) œÊ œÊ œÊ œÊ
111
666
33
ÈÈ
## ##
""
10 y 3 x 10œÊœ
È
2. r cos 2 r cos cos sin sin 2 r cos r sin 2
ˆ‰ ˆ ‰
))) ))œÊ œÊ œ
333
444
22
111
ÈÈ
##
x y 2 2 x 2 y 4 y x 2 2Ê œ Ê œ Ê œ
ÈÈ
22
## ÈÈ È
3. r cos 3 r cos cos sin sin 3 r cos r sin 3
ˆ‰ ˆ ‰
))) ))œÊ œÊ œ
4441
333
3
111
##
È
x y 3 x 3 y 6 y x 2 3Ê œ Ê œ Ê œ
133
3##
ÈÈ
ÈÈ
4. r cos 4 r cos 4 r cos cos sin sin 4
ˆ‰ ˆ‰ˆ ‰ˆ‰
)))) œ Ê œ Ê œ
11 11
44 44
r cos r sin 4 x y 4 2 x 2 y 8 y x 4 2Ê œÊ œÊ œÊœ
ÈÈ ÈÈ
22 22
## ##
)) ÈÈ È
5. r cos 2 r cos cos sin sin
ˆ‰ ˆ ‰
È
)))œ Ê
111
444
2 r cos r sin 2 x yœÊ œÊ
ÈÈ
"" ""
ÈÈ ÈÈ
22 22
))
2 x y 2 y 2 xœÊœÊœ
È
6. r cos 1 r cos cos sin sin 1
ˆ‰ ˆ ‰
)))œÊ œ
333
444
111
r cos r sin 1 x y 2Ê œ Ê œ
ÈÈ
22
22
)) È
yx 2ʜ
È
7. r cos 3 r cos cos sin sin 3
ˆ‰ ˆ ‰
)))œÊ œ
222
333
111
r cos r sin 3 x y 3Ê œ Ê œ
1
22
33
))
ÈÈ
"
##
x3y6 y x23Ê œ Ê œ
ÈÈ
È3
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
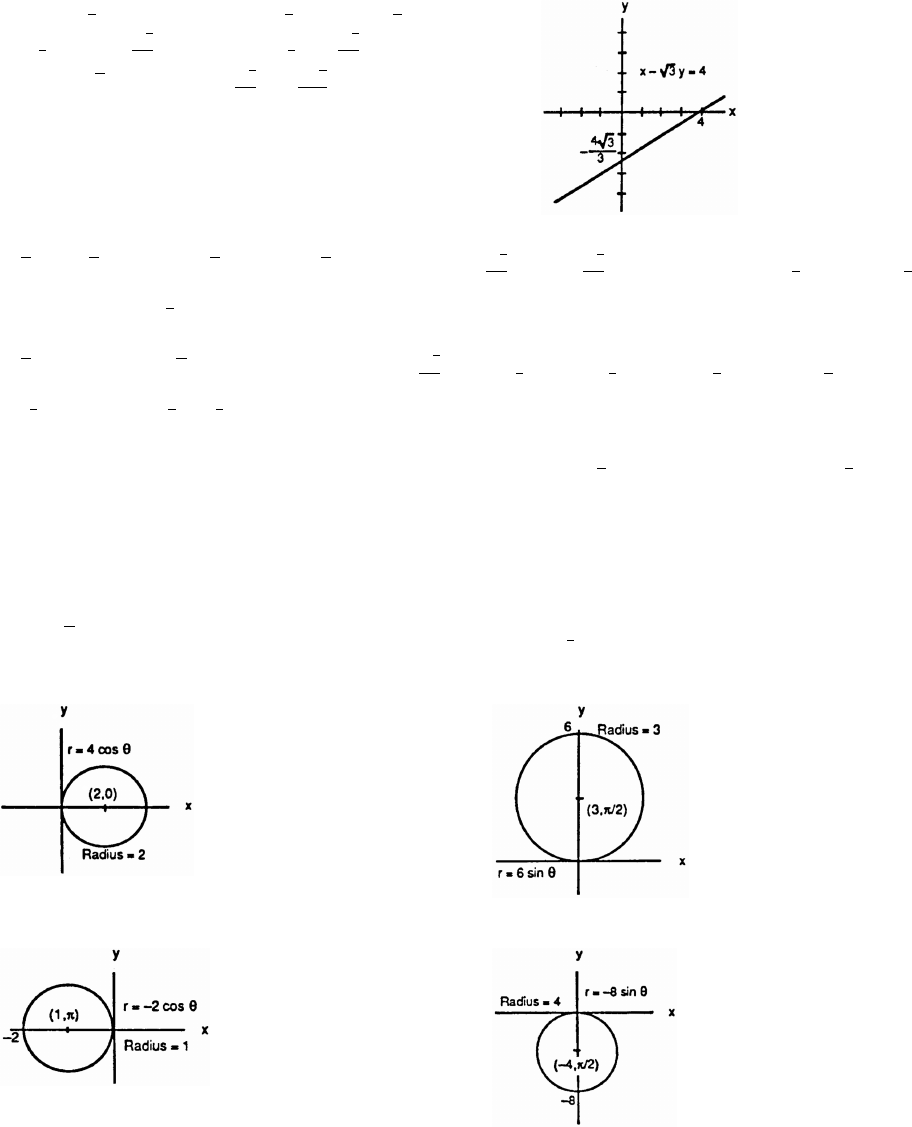
668 Chapter 10 Conic Sections and Polar Coordinates
8. r cos 2 r cos cos sin sin 2
ˆ‰ ˆ ‰
)))œÊ œ
111
333
r cos r sin 2 x y 2Ê œÊœ
1
22
33
))
ÈÈ
"
##
x3y4 y xÊ œÊœ
ÈÈÈ
343
33
9. 2 x 2 y 6 2 r cos 2 r sin 6 r cos sin 3 r cos cos sin sin
ÈÈ È È Š‹
ˆ‰
œÊ œÊ œÊ )) )) ))
ÈÈ
22
44##
11
3 r cos 3œÊ œ
ˆ‰
)1
4
10. 3 x y 1 3 r cos r sin 1 r cos sin r cos cos sin sin
ÈÈ Š‹
ˆ‰
œ Ê œ Ê œ Ê )) ) ) ) )
È31
66## #
"11
r cosœÊ œ
""
##
ˆ‰
)1
6
11. y 5 r sin 5 r sin 5 r sin ( ) 5 r cos ( ) 5 r cos 5œÊ œÊ œÊ œÊ œÊ œ))) ))
ˆ‰ ˆ‰
11
##
12. x 4 r cos 4 r cos 4 r cos ( ) 4œ Ê œ Ê œ Ê œ)))1
13. r 2(4) cos 8 cos 14. r 2(1) sin 2 sin œ œ œ œ)) ) )
15. r 2 2 sin 16. r 2 cos cos œœœ
Ȉ‰
)))
"
#
17. 18.
19. 20.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 10.8 Conic Sections in Polar Coordinates 669
21. (x 6) y 36 C (6 0), a 6 22. (x 2) y 4 C ( 2 0), a 2œ Êœß œ œÊœß œ
## ##
r 12 cos is the polar equation r 4 cos is the polar equationʜ ʜ))
23. x (y 5) 25 C ( 5), a 5 24. x (y 7) 49 C ( 7), a 7
## ##
œ Ê œ!ß œ œ Ê œ!ß œ
r 10 sin is the polar equation r 14 sin is the polar equationʜ ʜ))
25. x 2x y 0 (x 1) y 1 26. x 16x y 0 (x 8) y 64
# # ## # # ##
œÊ œ œÊ œ
C ( 1 0), a 1 r 2 cos is C (8 0), a 8 r 16 cos is theÊœß œÊœ Êœß œÊœ))
the polar equation polar equation
27. x y y 0 x y 28. x y y 0 x y
## # ## #
""
#
##
œÊ œ œÊ œ
ˆ‰ ˆ‰
4339
424
C , a r sin is the C 0 , a r sin is theÊ œ !ß œ Ê œ Ê œ ß œ Ê œ
ˆ‰ ˆ‰
""
## ))
22 4
33 3
polar equation polar equation
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
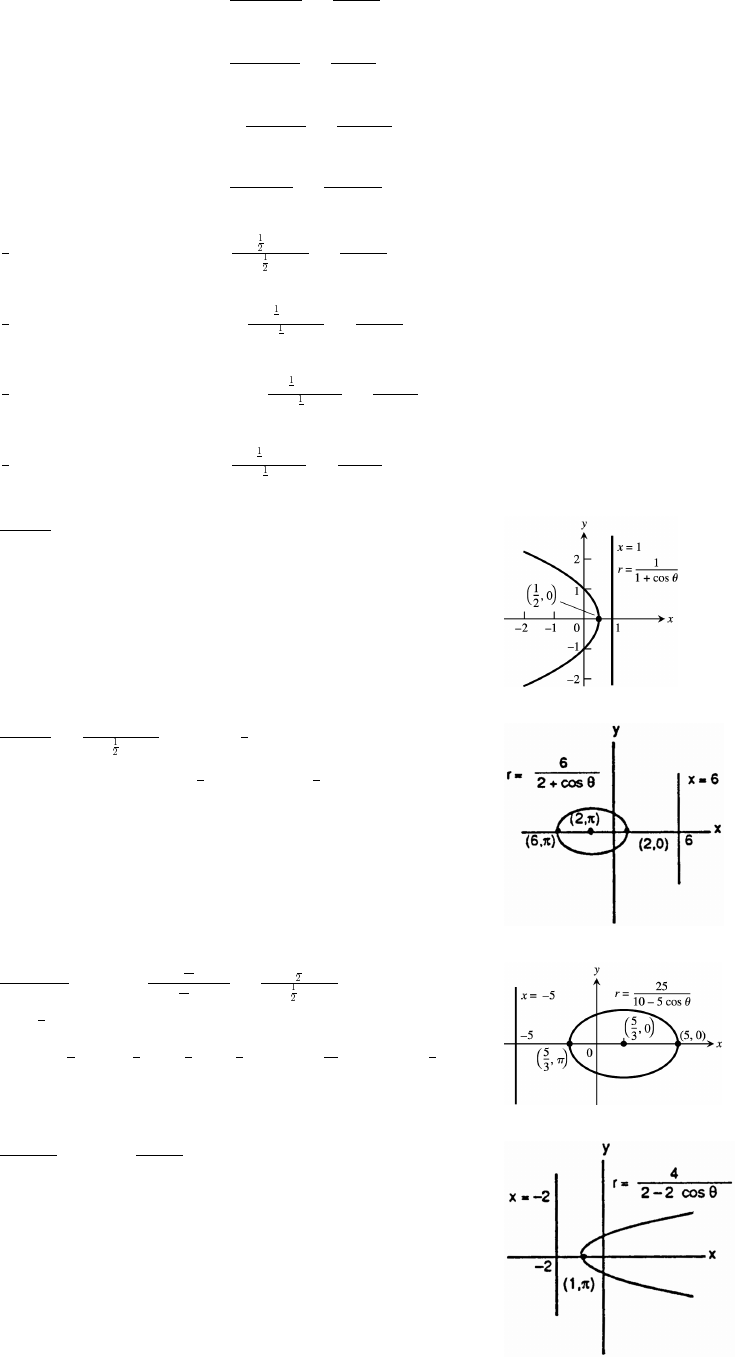
670 Chapter 10 Conic Sections and Polar Coordinates
29. e 1, x 2 k 2 rœœÊœÊœ œ
2(1)
1 (1) cos 1 cos
2
))
30. e 1, y 2 k 2 rœœÊœÊœ œ
2(1)
1 (1) sin 1 sin
2
))
31. e 5, y 6 k 6 rœœÊœÊœ œ
6(5)
1 5 sin 1 5 sin
30
))
32. e 2, x 4 k 4 rœœÊœÊœ œ
4(2)
1 2 cos 1 2 cos
8
))
33. e , x 1 k 1 rœœÊœÊœ œ
"
#
ˆ‰
ˆ‰
(1)
1 cos
1
2cos
))
34. e , x 2 k 2 rœœÊœÊœ œ
"
44cos
(2)
1 cos
2
ˆ‰
ˆ‰
4
4))
35. e , x 10 k 10 rœœÊœÊœ œ
"
55sin
(10)
1 sin
10
ˆ‰
ˆ‰
5
5))
36. e , y 6 k 6 rœœÊœÊœ œ
"
33sin
(6)
1 sin
6
ˆ‰
ˆ‰
3
3))
37. r e 1, k 1 x 1œÊœœÊœ
"
1cos )
38. r e , k 6 x 6;œœ ÊœœÊœ
63
2cos 1 cos
#
"
))
ˆ‰
a 1 e ke a 1 3 a 3ab ’“
ˆ‰
œÊ œÊ œ
#"
#
#3
4
a 4 ea 2ÊœÊ œ
39. r rœÊœ œ
25
10 5 cos 1 cos 1 cos
)))
ˆ‰ ˆ‰
ˆ‰ ˆ‰
25 5
10
5
10
e , k 5 x 5; a 1 e keÊœ œÊœ œ
"
#
#
ab
a 1 a a eaÊ œÊ œÊœ Ê œ
’“
ˆ‰
"
## #
#535 10 5
433
40. r r e 1, k 2 x 2œÊœÊœœÊœ
42
22 cos 1cos ))
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 10.8 Conic Sections in Polar Coordinates 671
41. r r rœÊœ Êœ
400 25
16 8 sin 1 sin 1 sin
)))
ˆ‰
ˆ‰ ˆ‰
400
16
8
16
e , k 50 y 50; a 1 e keœœÊœ œ
"
#
#
ab
a 1 25 a 25 aÊ œÊ œÊœ
’“
ˆ‰
"
#
#3 100
43
eaʜ
50
3
42. r r e 1, 43. r r e 1,œÊœÊœ œÊœÊœ
12 4 8 4
33 sin 1sin 22 sin 1sin )) ))
k4 y4 k4 y 4œÊœ œÊœ
44. r r e , k 4œÊœ Êœœ
42
2sin 1 sin
#
"
))
ˆ‰
y 4; a 1 e ke a 1 2Êœ œ Ê œab ’“
ˆ‰
#"
#
#
a2 a eaʜʜʜ
384
433
45. 46.
47. 48.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
672 Chapter 10 Conic Sections and Polar Coordinates
49. 50.
51. 52.
53. 54.
55. 56.
57. (a) Perihelion a ae a(1 e), Aphelion ea a a(1 e)œœ œœ
(b) Planet Perihelion Aphelion
Mercury 0.3075 AU 0.4667 AU
Venus 0.7184 AU 0.7282 AU
Earth 0.9833 AU 1.0167 AU
Mars 1.3817 AU 1.6663 AU
Jupiter 4.9512 AU 5.4548 AU
Saturn 9.0210 AU 10.0570 AU
Uranus 18.2977 AU 20.0623 AU
Neptune 29.8135 AU 30.3065 AU
Pluto 29.6549 AU 49.2251 AU
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 10.8 Conic Sections in Polar Coordinates 673
58. Mercury: r œœ
(0.3871) 1 0.2056
1 0.2056 cos 1 0.2056 cos
0.3707
ab
))
Venus: r œœ
(0.7233) 1 0.0068
1 0.0068 cos 1 0.0068 cos
0.7233
ab
))
Earth: r œœ
1 1 0.0167
1 0.0167 cos 1 0.0617 cos
0.9997
ab
))
Mars: r œœ
(1.524) 1 0.0934
1 0.0934 cos 1 0.0934 cos
1.511
ab
))
Jupiter: r œœ
(5.203) 1 0.0484
1 0.0484 cos 1 0.0484 cos
5.191
ab
))
Saturn: r œœ
(9.539) 1 0.0543
1 0.0543 cos 1 0.0543 cos
9.511
ab
))
Uranus: r œœ
(19.18) 1 0.0460
1 0.0460 cos 1 0.0460 cos
19.14
ab
))
Neptune: r œœ
(30.06) 1 0.0082
1 0.0082 cos 1 0.0082 cos
30.06
ab
))
59. (a) r 4 sin r 4r sin x y 4y;œÊœ Êœ))
###
r 3 sec r r cos 3œÊœÊœ
ÈÈ
))
È3
cos )
x3; x3 3y4yÊœ œ Ê œ
ÈÈÈ
Š‹
##
y 4y 3 0 (y 3)(y 1) 0 y 3ÊœÊ œÊœ
#
or y 1. Therefore in Cartesian coordinates, the pointsœ
of intersection are 3 3 and 3 1 . In polar
Š‹Š‹
ÈÈ
ßß
coordinates, 4 sin 3 sec 4 sin cos 3))))œÊ œ
ÈÈ
2 sin cos sin 2 2 orʜʜʜ)) ) )
ÈÈ
33
3##
1
or ; r 2, and
2
3636 3
1111 1
Êœ œ Êœ œ)) )
r 2 3 2 and 2 3 are the pointsÊœ Ê ß ß
ÈÈ
ˆ‰ Š‹
11
63
of intersection in polar coordinates.
(b)
60. (a) r 8 cos r 8r cos x y 8xœÊœ Êœ))
###
x 8x y 0 (x 4) y 16;Ê œÊ œ
## ##
r 2 sec r r cos 2œÊœÊœ))
2
cos )
x2; x2 2 8(2)y 0Êœ œÊ œ
##
y 12 y 2 3. Therefore 2 2 3ʜʜ„ ß„
#ÈÈ
Š‹
are the points of intersection in Cartesian coordinates.
In polar coordinates, 8 cos 2 sec 8 cos 2)) )œÊ œ
#
cos cos , , , orʜʜ„Êœ
#""
#
)))
4333
24111
; and r 4, and and
55 24
333 33
111 11
))œÊœœ
r 4 4 and 4 are the points ofÊœÊ ß ß
ˆ‰ˆ‰
11
33
5
(b)
intersection in polar coordinates. The points 4 and 4 are the same points.
ˆ‰ˆ‰
ß ß
24
33
11
61. r cos 4 x 4 k 4: parabola e 1 r)œÊœÊœ ʜʜ 4
1cos )
62. r cos 2 r cos cos sin sin 2 r sin 2 y 2 k 2: parabola e 1
ˆ‰ ˆ ‰
)))) œÊ œÊ œÊœÊœ Êœ
111
###
rʜ 2
1sin )
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
674 Chapter 10 Conic Sections and Polar Coordinates
63. (a) Let the ellipse be the orbit, with the Sun at one focus.
Then r a c and r a c
max min rr
rr
œ œ Êmax min
max min
eœœœœ
(a c) (a c)
(a c) (a c) 2a a
2c c
(b) Let F , F be the foci. Then PF PF 10 where
"# " #
œ
P is any point on the ellipse. If P is a vertex, then
PF a c and PF a c
"#
œ œ
(a c) (a c) 10Ê œ
2a 10 a 5. Since e we have 0.2ʜʜ œ œ
cc
a5
c 1.0 the pins should be 2 inches apart.Êœ Ê
64. e 0.97, Major axis 36.18 AU a 18.09, Minor axis 9.12 AU b 4.56 (1 AU 1.49 10 km)œœÊœ œÊœ¸‚
)
(a) r AUœœœ œ
ke 1.07
1e cos 1e cos 10.97 cos 10.97 cos
a1 e (18.09) 1 (0.97)
)) ) )
ab cd
(b) 0 r 0.5431 AU 8.09 10 km)œÊœ ¸ ¸ ‚
1.07
10.97
(
(c) r 35.7 AU 5.32 10 km)1œÊœ ¸ ¸ ‚
1.07
10.97
*
65. x y 2ay 0 (r cos ) (r sin ) 2ar sin 0
## # #
œÊ œ)) )
r cos r sin 2ar sin 0 r 2ar sin ʜʜ
## ## #
)) ) )
r 2a sin ʜ )
66. y 4ax 4a (r sin ) 4ar cos 4a r sin
## # ###
œ Ê œ Ê)) )
4ar cos 4a r 1 cos 4ar cos 4aœÊœ)))
## # #
ab
r r cos 4ar cos 4a rÊ œ Ê
### # #
))
r cos 4ar cos 4a r (r cos 2a)œ Êœ
## # # #
)) )
r (r cos 2a) r r cos 2a orÊœ„ Ê œ))
r r cos 2a r or r ;œÊœ œ)2a 2a
1cos 1cos
))
the equations have the same graph, which is a parabola
opening to the right
67. x cos y sin p r cos cos r sin sin p!! )!)!œÊ œ
r(cos cos sin sin ) p r cos ( ) pʜʜ)! )! )!
68. x y 2ax x y a y 0abab
## ## ##
#
œ
r 2a(r cos ) r a (r sin ) 0Ê œab ab
####
#))
r 2ar cos a r sin 0Ê œ
%$ ###
))
r r 2ar cos a 1 cos 0 (assume r 0)Ê œ Á
## # #
cdab))
r 2ar cos a a cos 0Ê œ
####
))
r 2ar cos a cos a 0Ê œab
####
))
(r a cos ) a r a cos aÊ œ Ê œ„))
##
r a(1 cos ) or r a(1 cos );Êœ œ ))
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 10 Practice Exercises 675
the equations have the same graph, which is a cardioid
69 - 70. Example CAS commands:
:Maple
with( plots );#69
f := (r,k,e) -> k*e/(1+e*cos(theta));
elist := [3/4,1,5/4]; # (a)
P1 := seq( plot( f(r,-2,e), theta=-Pi..Pi, coords=polar ), e=elist ):
display( [P1], insequence=true, view=[-20..20,-20..20], title="#69(a) (Section 10.8)\nk=-2" );
P2 := seq( plot( f(r,2,e), theta=-Pi..Pi, coords=polar ), e=elist ):
display( [P2], insequence=true, view=[-20..20,-20..20], title="#69(a) (Section 10.8)\nk=2" );
elist2 := [7/6,5/4,4/3,3/2,2,3,5,10,20]; # (b)
P3 := seq( plot( f(r,-1,e), theta=-Pi..Pi, coords=polar ), e=elist2 ):
display( [P3], insequence=true, view=[-20..20,-20..20], title="#69(b) (Section 10.8)\nk=-1, e>1" );
elist3 := [1/2,1/3,1/4,1/10,1/20];
P4 := seq( plot( f(r,-1,e), theta=-Pi..Pi, coords=polar ), e=elist3 ):
display( [P4], insequence=true, title="#69(b) (Section 10.8)\nk=-1, e<1" );
klist := -5..-1; # (c)
P5 := seq( plot( f(r,k,1/2), theta=-Pi..Pi, coords=polar ), k=klist ):
display( [P5], insequence=true, title="#69(c) (Section 10.8)\ne=1/2, k<0" );
P6 := seq( plot( f(r,k,1), theta=-Pi..Pi, coords=polar ), k=klist ):
display( [P6], insequence=true, view=[-4..50,-50..50], title="#69(c) (Section 10.8)\ne=1, k<0" );
P7 := seq( plot( f(r,k,2), theta=-Pi..Pi, coords=polar ), k=klist ):
display( [P5], insequence=true, title="#69(c) (Section 10.8)\ne=2, k<0" );
: (assigned function and values for parameters and bounds may vary):Mathematica
To do polar plots in Mathematica, it is necessary to first load a graphics package
In the command, it is assumed that the variable r is given as a function of the variable .PolarPlot )
<<Graphics`Graphics`
f[ _, k_,ec_]:= (k ec) / (1 ec Cos[ ])))
PolarPlot[{ f[ , 2, 3/4], f[ , 2, 1], f[ , 2, 5/4]}, { , 0, 2 }, PlotRange { 20, 20},))))1 Ä
PlotStyle {RGBColor[1, 0, 0], RGBColor[0, 1, 0], RGBColor[0, 0, 1]}];Ä
PolarPlot[{ f[ , 1, 1], f[ , 2, 1], f[ , 3, 1], f[ , 4, 1], f[ , 5, 1]}, { , 0, 2 }, PlotRange { 20, 20},))))) )1 Ä
PlotStyle Ä
{RGBColor[1, 0, 0], RGBColor[0, 1, 0], RGBColor[0, 0, 1, RGBColor[.5, .5, 0], RGBColor[0, .5, .5]}];ß
The limitation on the range is primarily needed when plotting hyperbolas.
Problem 70 can be done in a similar fashion.
CHAPTER PRACTICE EXERCISES"!
1. x 4y y 4p 4 p 1; 2. x 2y y 4p 2 p ;
# #
##
"
œ Êœ Ê œÊœ œ Ê œÊ œÊœ
xx
4
therefore Focus is (0 1), Directrix is y 1 therefore Focus is ; Directrix is yß œ !ß œ
ˆ‰
""
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
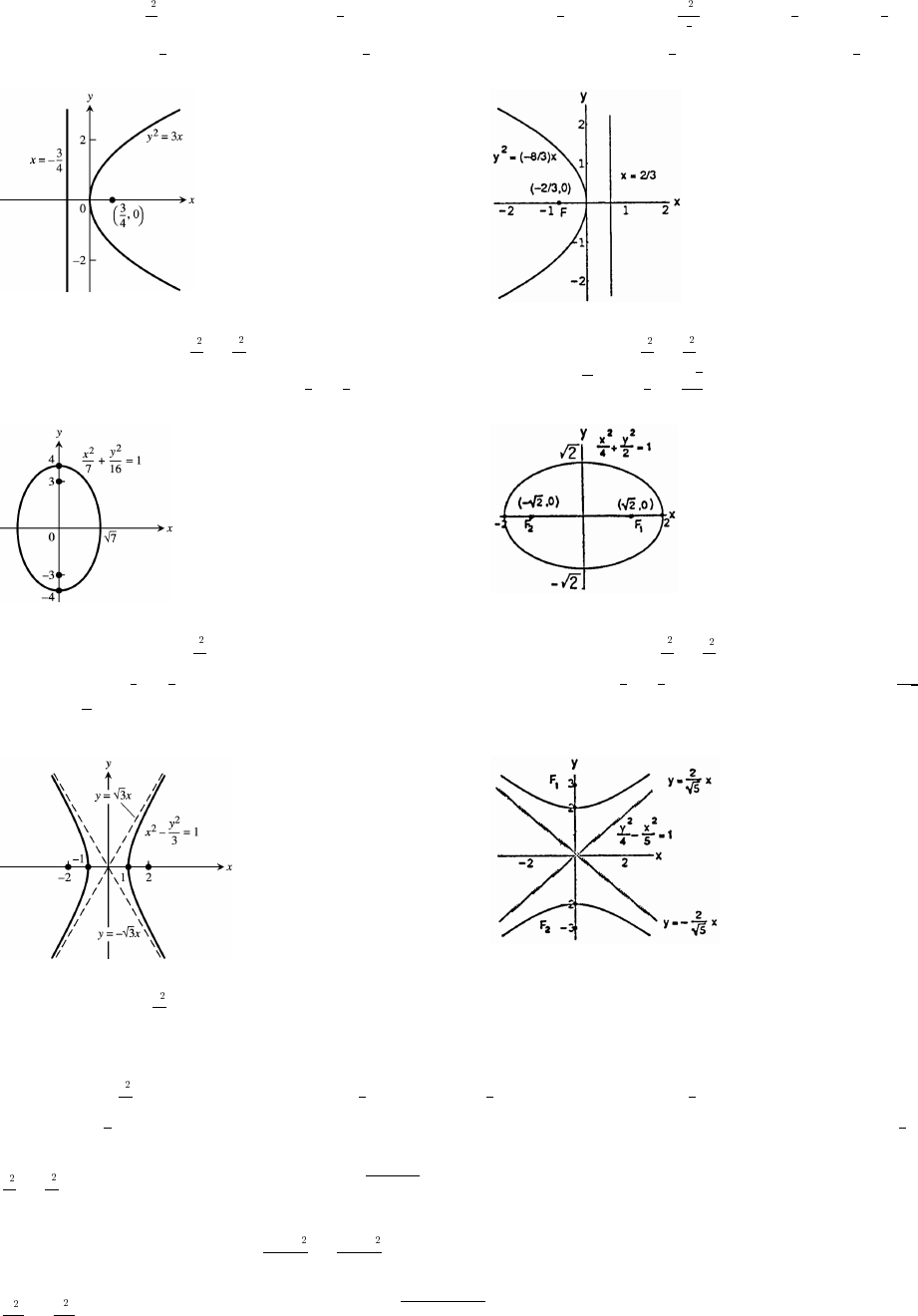
676 Chapter 10 Conic Sections and Polar Coordinates
3. y 3x x 4p 3 p ; 4. y x x 4p p ;
# #
œÊœÊœÊœ œ Êœ ʜʜ
y y
34 3 33
38 82
ˆ‰
8
3
therefore Focus is 0 , Directrix is x therefore Focus is , Directrix is x
ˆ‰ ˆ ‰
33 22
44 33
ßœ ß!œ
5. 16x 7y 112 1 6. x 2y 4 1 c 4 2 2
## ## #
#
œ Ê œ œ Ê œ Ê œœ
xx
716 4
yy
c 16 7 9 c 3; e c 2 ; eÊ œ œÊœ œœ Êœ œœ
#
#
c3 c
a4 a
2
ÈÈ
7. 3x y 3 x 1 c 1 3 4 8. 5y 4x 20 1 c 4 5 9
## # # # # #
œ Ê œ Ê œœ œ Ê œ Ê œœ
y y
345
x
c 2; e 2; the asymptotes are c 3, e ; the asymptotes are y xÊœ œœœ Êœ œœ œ„
c2 c3 2
a1 a5
#È
y3xœ„
È
9. x 12y y 4p 12 p 3 focus is ( 3), directrix is y 3, vertex is (0 0); therefore new
#
#
œ ÊœÊ œ ÊœÊ !ß œ ß
x
1
vertex is (2 3), new focus is (2 0), new directrix is y 6, and the new equation is (x 2) 12(y 3)ßß œ œ
#
10. y 10x x 4p 10 p focus is 0 , directrix is x , vertex is (0 0); therefore new
#
## #
œÊœÊœÊœÊ ß œ ß
y
10
55 5
ˆ‰
vertex is 1 , new focus is (2 1), new directrix is x 3, and the new equation is (y 1) 10 x
ˆ‰ ˆ‰
ß ß œ œ
" "
# #
#
11. 1 a 5 and b 3 c 25 9 4 foci are 4 , vertices are 5 , center is
x
95
y
œÊœ œÊœ œÊ !ß„ !ß„
#Èab ab
(0 0); therefore the new center is ( 5), new foci are ( 3 1) and ( 3 9), new vertices are ( 10) andß $ß ß ß $ß
( 0), and the new equation is 1$ß œ
(x 3) (y 5)
95
#
12. 1 a 13 and b 12 c 169 144 5 foci are 5 0 , vertices are 13 0 , center
x
169 144
y
œÊœ œÊœ œÊ „ß „ß
Èab a b
is (0 0); therefore the new center is (5 12), new foci are (10 12) and (0 12), new vertices are (18 12) andßßßßß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 10 Practice Exercises 677
( 8 12), and the new equation is 1ß œ
(x 5) (y 12)
169 144
13. 1 a 2 2 and b 2 c 8 2 10 foci are 0 10 , vertices are
y
82
x
œÊœ œ Êœ œ Ê ß„
ÈÈÈÈÈ
Š‹
0 2 2 , center is (0 0), and the asymptotes are y 2x; therefore the new center is 2 2 2 , new foci are
Š‹ Š‹
È È
ß„ ß œ „ ß
2 2 2 10 , new vertices are 2 4 2 and ( 0), the new asymptotes are y 2x 4 2 2 and
Š‹ Š‹
ÈÈ È
È
ß„ ß #ß œ
y 2x 4 2 2; the new equation is 1œ œ
ÈŠ‹
È
y22
8
(x 2)
#
14. 1 a 6 and b 8 c 36 64 10 foci are 10 0 , vertices are 6 0 , the center
x
36 64
y
œÊœ œÊœ œ Ê „ß „ß
Èab ab
is (0 0) and the asymptotes are or y x; therefore the new center is ( 10 3), the new foci areßœ„œ„ ß
y
86 3
x4
( 20 3) and (0 3), the new vertices are ( 16 3) and ( 4 3), the new asymptotes are y x andß ß ß ß œ
431
33
y x ; the new equation is 1œ œ
449
3 3 36 64
(x 10) (y 3)
15. x 4x 4y 0 x 4x 4 4y 4 (x 2) 4y 4 y 1, a hyperbola; a 2 and
### # ## #
œÊ œÊ œÊ œ œ
(x 2)
4
b 1 c 1 4 5 ; the center is (2 0), the vertices are ( 0) and (4 0); the foci are 2 5 0 andœ Ê œ œ ß !ß ß „ ß
ÈÈÈ
Š‹
the asymptotes are y œ„
x2
#
16. 4x y 4y 8 4x y 4y 4 4 4x (y 2) 4 x 1, a hyperbola; a 1 and
## ## # # #
œÊ œÊ œÊ œ œ
(y 2)
4
b 2 c 1 4 5 ; the center is ( 2), the vertices are (1 2) and ( 2), the foci are 5 2 andœÊœ œ !ß ß "ß „ ß
ÈÈÈ
Š‹
the asymptotes are y 2x 2œ„
17. y 2y 16x 49 y 2y 1 16x 48 (y 1) 16(x 3), a parabola; the vertex is ( 1);
## #
œ Ê œ Ê œ $ß
4p 16 p 4 the focus is ( 7 1) and the directrix is x 1œÊœÊ ß œ
18. x 2x 8y 17 x 2x 1 8y 16 (x 1) 8(y 2), a parabola; the vertex is (1 2);
## #
œ Ê œ Ê œ ß
4p 8 p 2 the focus is (1 4) and the directrix is y 0œÊœÊ ß œ
19. 9x 16y 54x 64y 1 9 x 6x 16 y 4y 1 9 x 6x 9 16 y 4y 4 144
## # # # #
œÊ œÊ œabab a ba b
9(x 3) 16(y 2) 144 1, an ellipse; the center is ( 3 2); a 4 and b 3Ê œ Ê œ ß œ œ
## (x 3) (y 2)
16 9
c 16 9 7 ; the foci are 7 2 ; the vertices are (1 2) and ( 7 2)Êœ œ $„ ß ß ß
ÈÈÈ
Š‹
20. 25x 9y 100x 54y 44 25 x 4x 9 y 6y 44 25 x 4x 4 9 y 6y 9 225
## # # # #
œÊ œÊ œabab a ba b
1, an ellipse; the center is (2 3); a 5 and b 3 c 25 9 4; the foci areÊœ ßœ œÊœœ
(x 2) (y 3)
925
È
(2 1) and (2 7); the vertices are (2 2) and (2 8)ßß ßß
21. x y 2x 2y 0 x 2x 1 y 2y 1 2 (x 1) (y 1) 2, a circle with center (1 1) and
## # # # #
œÊ œÊ œ ß
radius 2œÈ
22. x y 4x 2y 1 x 4x 4 y 2y 1 6 (x 2) (y 1) 6, a circle with center ( 2 1)
## # # # #
œÊ œÊ œ ß
and radius 6œÈ
23. B 4AC 1 4(1)(1) 3 0 ellipse 24. B 4AC 4 4(1)(4) 0 parabola
###
œ œÊ œ œÊ
25. B 4AC 3 4(1)(2) 1 0 hyperbola 26. B 4AC 2 4(1)( 2) 12 0 hyperbola
## ##
œ œÊ œœÊ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
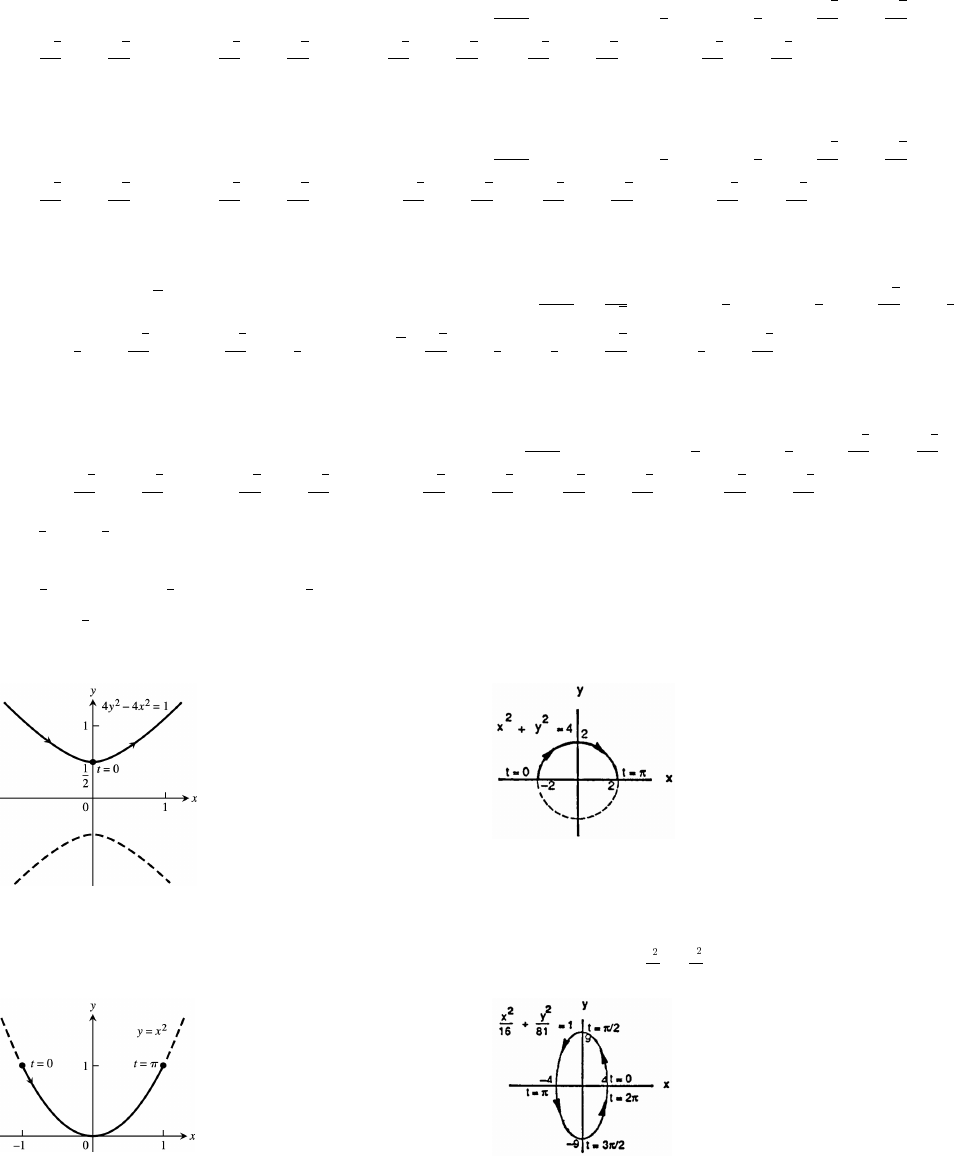
678 Chapter 10 Conic Sections and Polar Coordinates
27. x 2xy y 0 (x y) 0 x y 0 or y x, a straight line
## #
œÊœÊœ œ
28. B 4AC ( 3) 4(1)(4) 7 0 ellipse
##
œ œÊ
29. B 4AC 1 4(2)(2) 15 0 ellipse; cot 2 0 2 ; x x y and
## ww
###
œ œÊ œ œÊœÊœœ !!!
AC
B4
22
11
ÈÈ
y x y 2 x y x y x y 2 x y 15 0œÊ œ
ÈÈ ÈÈ ÈÈÈÈ ÈÈ
22 22 22 22 22
## ## ## ## ##
ww ww ww ww ww
# #
Š‹Š‹Š‹Š‹
5x 3y 30ʜ
ww
##
30. B 4AC 2 4(3)(3) 32 0 ellipse; cot 2 0 2 ; x x y and
## ww
###
œ œÊ œ œÊœÊœœ !!!
AC
B4
22
11
ÈÈ
yxy 3xy2 xy xy3xy19œ Ê œ
ÈÈ ÈÈ ÈÈÈÈ ÈÈ
22 22 22 22 22
## ## ## ## ##
ww ww ww ww ww
# #
Š‹Š‹Š‹Š‹
4x 2y 19ʜ
ww
##
31. B 4AC 2 3 4(1)( 1) 16 hyperbola; cot 2 2 ; x x y
#ww
#"
##
œ œÊ œ œÊœÊœœ
Š‹
È!!!
AC 1
B36
3
3
ÈÈ
11
and yx y xy 23 xy x y x y 4œ Ê œ
11111
33 3 3 3
## ## #### ##
ww ww wwww ww
# #
ÈÈ È È È
Š‹Š‹Š‹Š‹
È
2x 2y 4 y x 2ʜʜ
ww ww
## ##
32. B 4AC ( 3) 4(1)(1) 5 0 hyperbola; cot 2 0 2 ; x x y
## ww
###
œ œÊ œ œÊœÊœœ !!!
AC
B4
22
11
ÈÈ
and yxy xy3 xy xy xy5œÊ œ
ÈÈ ÈÈ ÈÈ ÈÈ ÈÈ
22 22 22 22 22
## ## ## ## ##
ww ww ww ww ww
# #
Š‹Š‹Š‹Š‹
y x 5 or 5y x 10Êœ œ
5
##
ww ww
## ##
"
33. x tan t and y sec t x tan t 34. x 2 cos t and y 2 sin t x 4 cos t andœœÊœ œœÊœ
"" "
##
## ##
4
and y sec t 4x tan t and y 4 sin t x y 4
#### ####
"
œÊœ œÊœ
4
4y sec t 4x 1 4y 4y 4x 1
## # # ##
œÊœÊœ
35. x cos t and y cos t y ( x) x 35. x 4 cos t and y 9 sin t x 16 cos t andœ œ Ê œ œ œ œ Ê œ
### ##
y 81 sin t 1
##
œÊœ
x
16 81
y
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
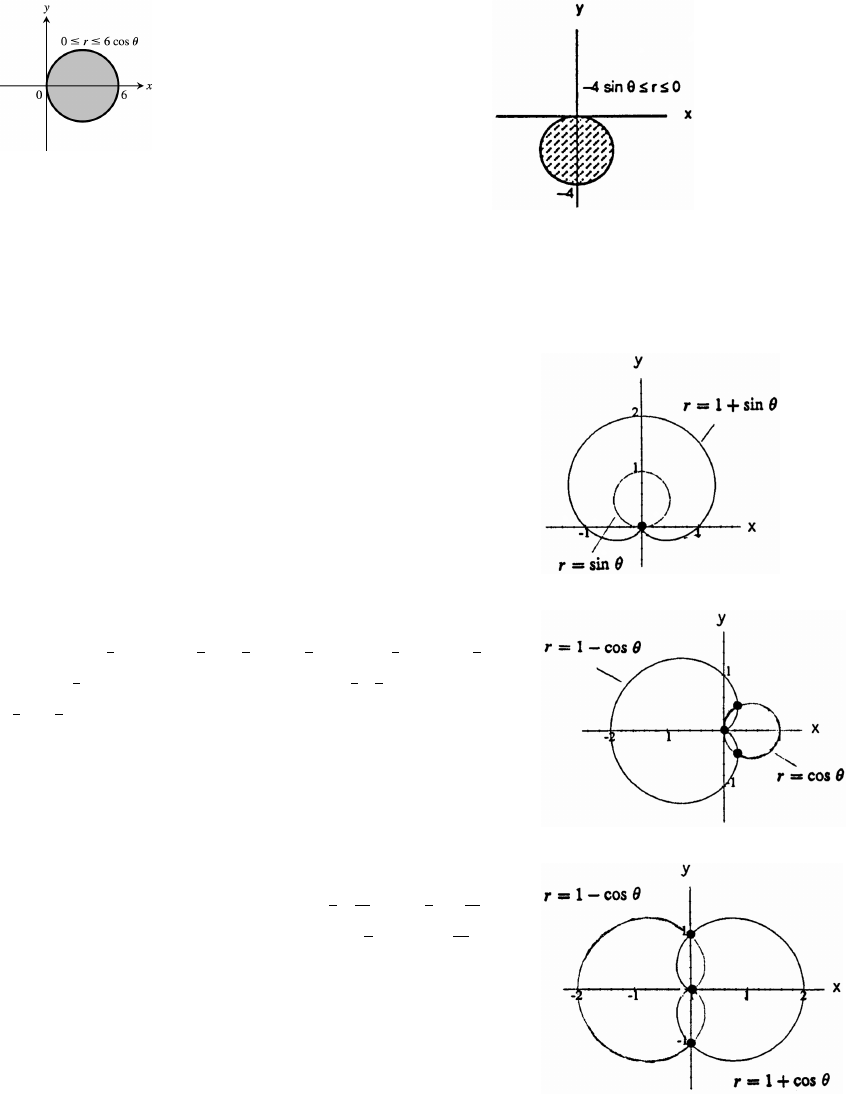
Chapter 10 Practice Exercises 679
37. 38.
39. d 40. e 41. l 42. f
43. k 44. h 45. i 46. j
47. r sin and r 1 sin sin 1 sin 0 1œœÊœÊœ))))
so no solutions exist. There are no points of intersection
found by solving the system. The point of intersection
(0 0) is found by graphing.ß
48. r cos and r 1 cos cos 1 cos œœÊœ))))
cos , ; r ; ʜʜœÊœœ)) ) )
""
##
11 1 1
33 3 3
r . The points of intersection are andÊœ ß
""
##
ˆ‰
1
3
. The point of intersection (0 0) is found
ˆ‰
"
#ß ß
1
3
by graphing.
49. r 1 cos and r 1 cos 1 cos 1 cos œ œ Ê œ))))
2 cos 0 cos 0 , ; or ʜʜʜ œ))))
11 1 1
## # #
33
r 1. The points of intersection are 1 and 1 .Êœ ß ß
ˆ‰ˆ‰
11
##
3
The point of intersection (0 0) is found by graphing.ß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
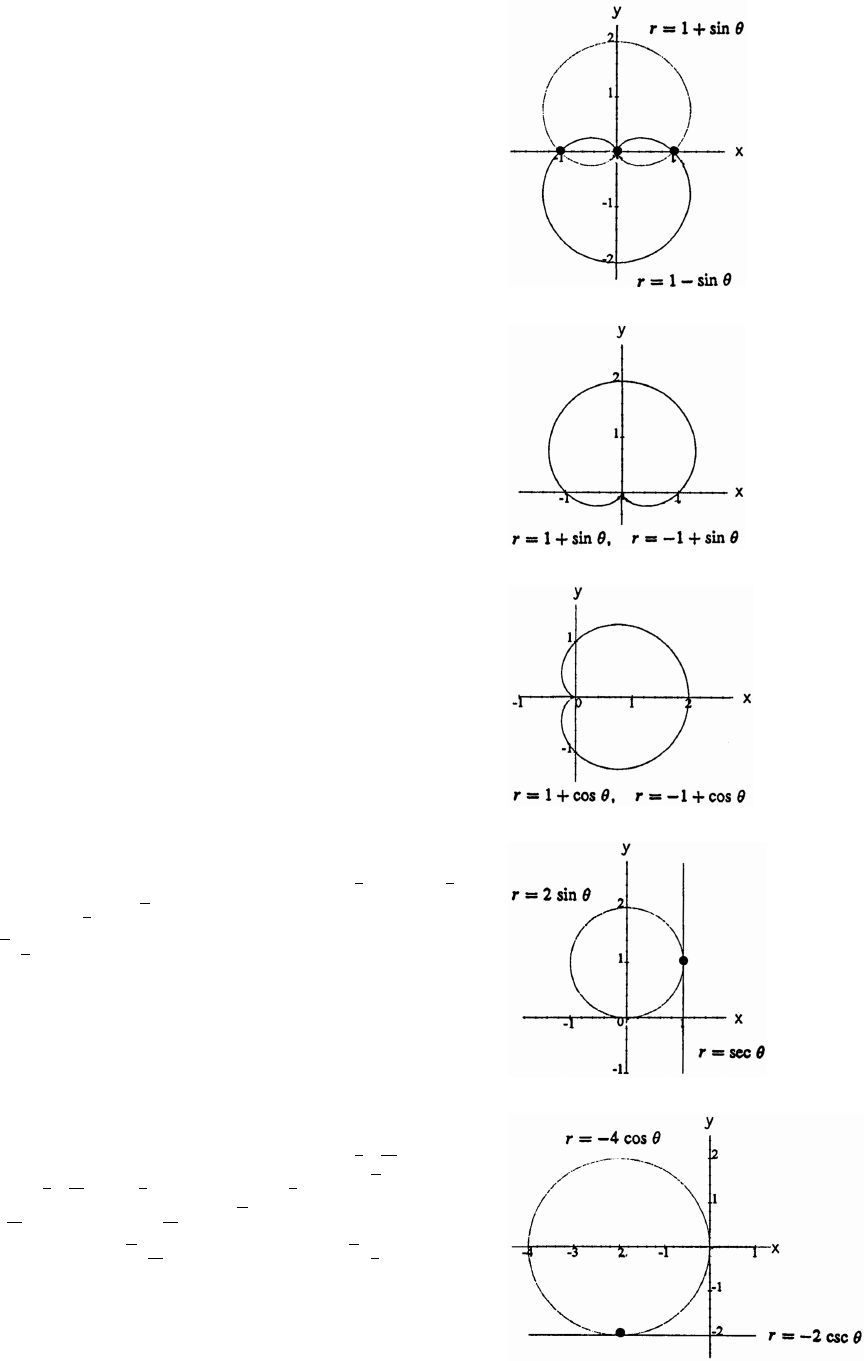
680 Chapter 10 Conic Sections and Polar Coordinates
50. r 1 sin and r 1 sin 1 sin 1 sin œ œ Ê œ))))
2 sin 0 sin 0 0, ; 0 or ʜʜʜœ)))1)1
r 1. The points of intersection are (1 0) and (1 ).Êœ ß ß1
The point of intersection ( 0) is found by graphing.!ß
51. r 1 sin and r 1 sin intersect at all points ofœ œ))
r 1 sin because the graphs coincide. This can beœ )
seen by graphing them.
52. r 1 cos and r 1 cos intersect at all points ofœ œ))
r 1 cos because the graphs coincide. This can beœ )
seen by graphing them.
53. r sec and r 2 sin sec 2 sin œœÊœ))))
1 2 sin cos 1 sin 2 2 Êœ Êœ Ê œ Êœ)) ) ) )
11
#4
r 2 sin 2 the point of intersection isÊœ œ Ê
1
4È
2 . No other points of intersection exist.
Š‹
Èß1
4
54. r 2 csc and r 4 cos 2 csc 4 cos œ œ Ê œ))))
1 2 sin cos 1 sin 2 2 , Êœ Êœ Ê œ)) ) )
11
##
5
, ; r 4 cos 2 2 ;Ê œ œ Ê œ œ))
11 1 1
44 4 4
5È
r 4 cos 2 2 . The point of)œÊœ œ
55
44
11
È
intersection is 2 2 and the point 2 2 is the
Š‹ Š ‹
ÈÈ
ßß
5
44
11
same point.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
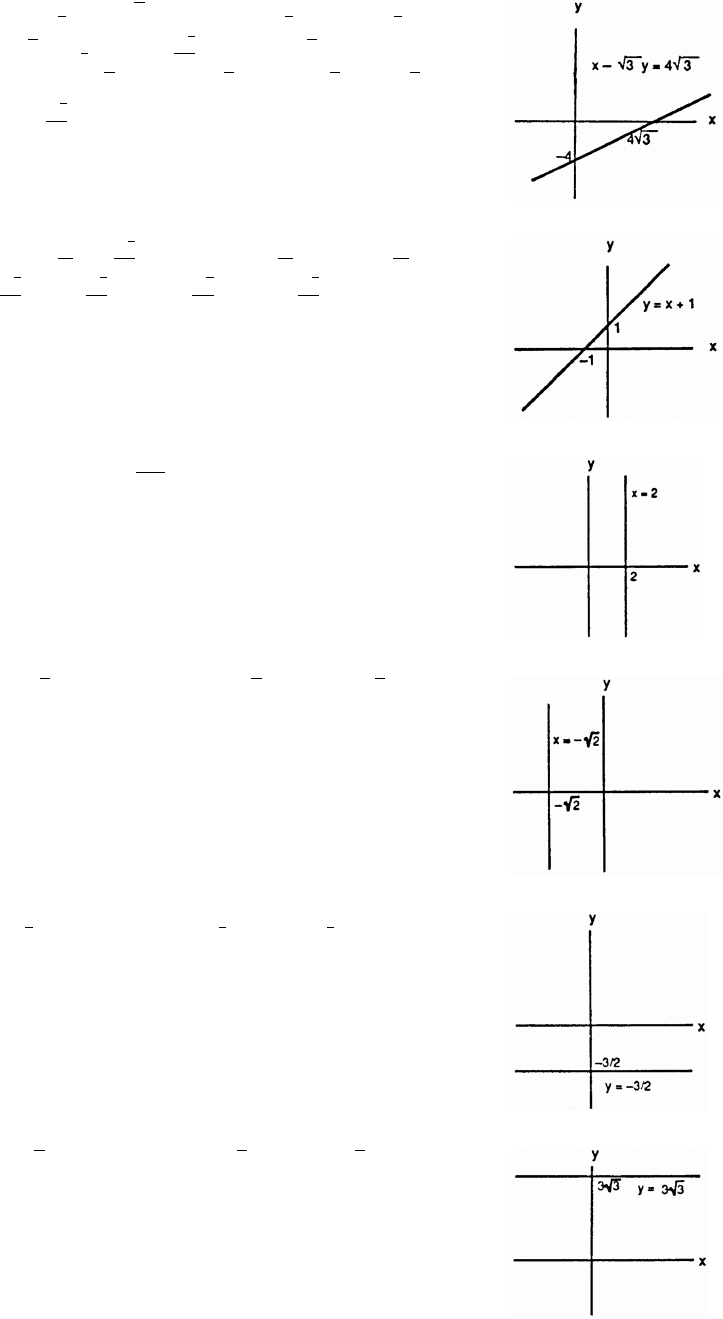
Chapter 10 Practice Exercises 681
55. r cos 2 3 r cos cos sin sin
ˆ‰ ˆ ‰
È
)))œ Ê
111
333
2 3 r cos r sin 2 3œÊ œ
ÈÈ
"
##
))
È3
r cos 3 r sin 4 3 x 3 y 4 3Ê œÊœ))
ÈÈÈÈ
yx4ʜ
È3
3
56. r cos r cos cos sin sin
ˆ‰ ˆ ‰
)))œ Ê
333
444
2
111
È
#
r cos r sin x y 1œÊ œÊœ
ÈÈ È È
22 2 2
## # #
))
yx1ʜ
57. r 2 sec r r cos 2 x 2œÊœÊœÊœ))
2
cos )
58. r 2 sec r cos 2 x 2œ Ê œ Ê œ
ÈÈÈ
))
59. r csc r sin yœ Ê œ Ê œ
333
###
))
60. r 3 3 csc r sin 3 3 y 3 3œÊœÊœ
ÈÈÈ
))
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
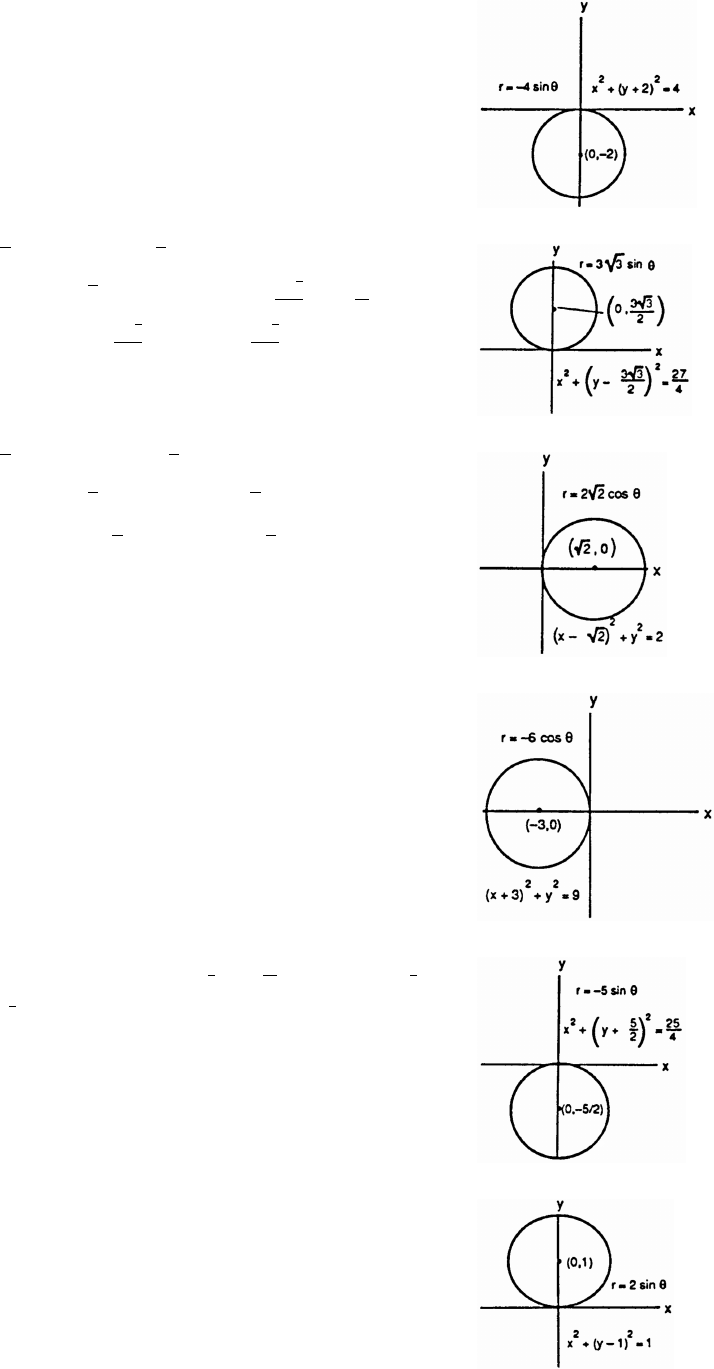
682 Chapter 10 Conic Sections and Polar Coordinates
61. r 4 sin r 4r sin x y 4y 0œ Ê œ Ê œ))
###
x (y 2) 4; circle with center ( 2) andÊ œ !ß
##
radius 2.
62. r 3 3 sin r 3 3 r sin œÊœ
ÈÈ
))
#
xy33y0 x y ;Ê œÊ œ
## #
#
#
ÈŠ‹
33 27
4
È
circle with center and radius
Š‹
!ß 33 33
ÈÈ
##
63. r 2 2 cos r 2 2 r cos œÊœ
ÈÈ
))
#
xy22x0 x 2 y 2;Ê œÊ œ
## #
#
ÈÈ
Š‹
circle with center 2 0 and radius 2
Š‹
ÈÈ
ß
64. r 6 cos r 6r cos x y 6x 0œ Ê œ Ê œ))
###
(x 3) y 9; circle with center ( 3 0) andÊœ ß
##
radius 3
65. x y 5y 0 x y C
## #
##
#
œÊ œ Ê œ!ß
ˆ‰ ˆ‰
525 5
4
and a ; r 5r sin 0 r 5 sin œ œÊœ
5
#
#))
66. x y 2y 0 x (y 1) 1 C ( 1) and
## # #
œÊ œÊ œ!ß
a 1; r 2r sin 0 r 2 sin œ œÊœ
#))
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
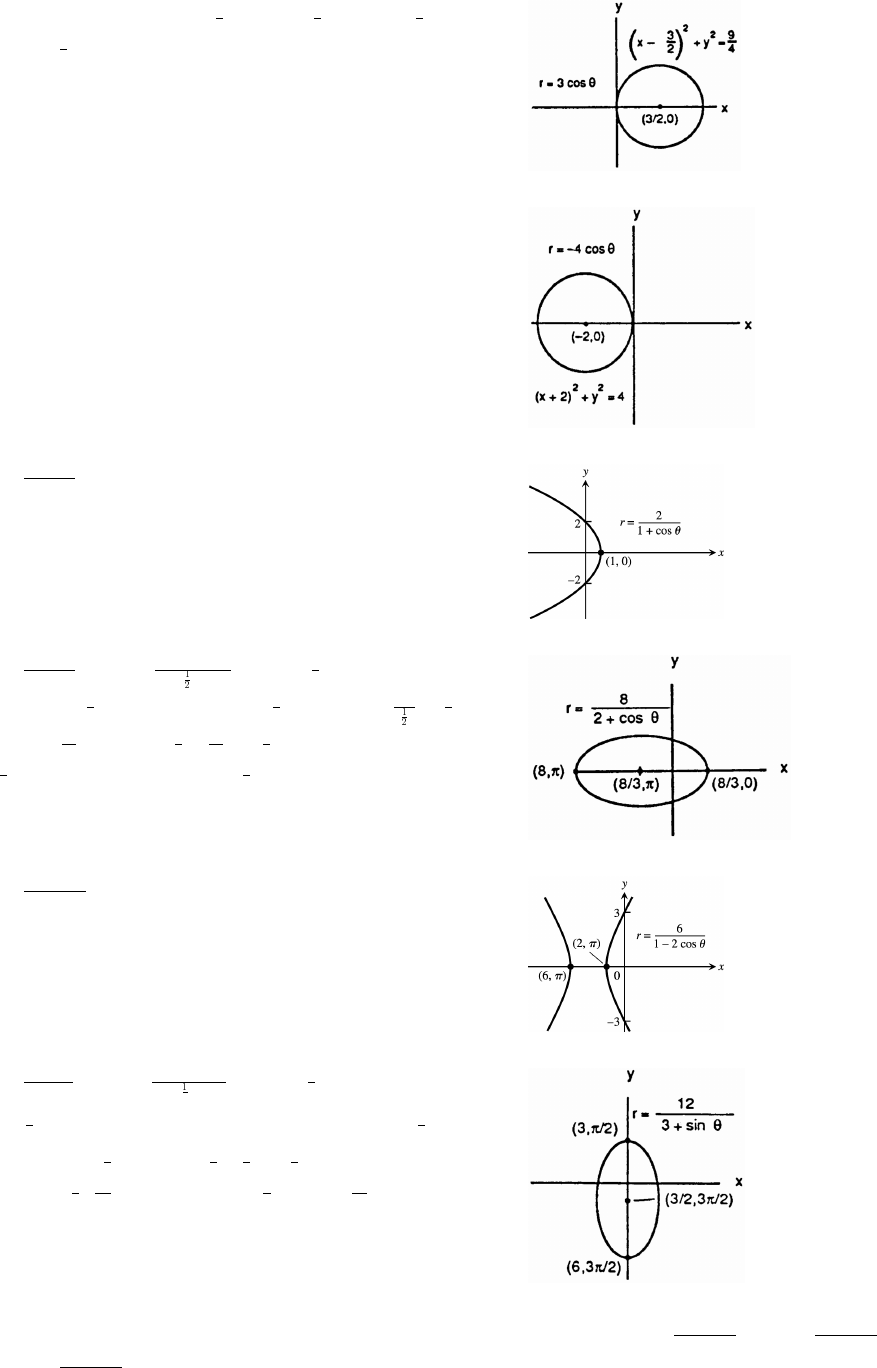
Chapter 10 Practice Exercises 683
67. x y 3x 0 x y C
## #
##
#
œÊ œÊ œß!
ˆ‰ ˆ‰
39 3
4
and a ; r 3r cos 0 r 3 cos œ œÊœ
3
#
#))
68. x y 4x 0 (x 2) y 4 C ( 2 0)
## ##
œÊ œÊ œß
and a 2; r 4r cos 0 r 4 cos œ œÊœ
#))
69. r e 1 parabola with vertex at (1 0)œÊœÊ ß
2
1cos )
70. r r e ellipse;œÊœ ÊœÊ
84
2cos 1 cos
#
"
))
ˆ‰
ke 4 k 4 k 8; k ea 8 aœÊ œÊœ œÊœ
""
##
aa
eˆ‰
a ea ; therefore the center isÊœ Ê œ œ
16 16 8
333
ˆ‰ˆ ‰
"
#
; vertices are ( ) and 0
ˆ‰ ˆ‰
88
33
ß)ßß11
71. r e 2 hyperbola; ke 6 2k 6œ ÊœÊ œÊ œ
6
12 cos )
k 3 vertices are (2 ) and (6 )ÊœÊ ß ß11
72. r r e ; ke 4œÊœ Êœœ
12 4
3sin 3
1 sin
"
))
ˆ‰
3
k 4 k 12; a 1 e 4 a 1ʜʜ œÊ
""
##
33
ab ’“
ˆ‰
4 a ea ; therefore theœÊœÊ œ œ
993
3###
"
ˆ‰ˆ‰
center is ; vertices are 3 and 6
ˆ ‰ ˆ‰ˆ‰
33 3
## # #
ßßß
111
73. e 2 and r cos 2 x 2 is directrix k 2; the conic is a hyperbola; r rœ œÊœ Êœ œ Êœ)ke
1 e cos 1 cos
(2)(2)
#))
rʜ 4
1 cos # )
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

684 Chapter 10 Conic Sections and Polar Coordinates
74. e 1 and r cos 4 x 4 is directrix k 4; the conic is a parabola; r rœœÊœÊœ œÊœ)ke
1e cos 1cos
(4)(1)
))
rʜ 4
1cos )
75. e and r sin 2 y 2 is directrix k 2; the conic is an ellipse; r rœ œÊœ Êœ œ Êœ
"
#
)ke
1e sin
(2)
1 sin
))
ˆ‰
ˆ‰
rʜ 2
2sin )
76. e and r sin 6 y 6 is directrix k 6; the conic is an ellipse; r rœœÊœÊœ œÊœ
"
31e sin
ke (6)
1 sin
)))
ˆ‰
ˆ‰
3
3
rʜ 6
3sin )
77. A 2 r d (2 cos ) d 4 4 cos cos d 4 4 cos dœœœœ
'' ' '
00 0 0
"
# #
## #
))) ))) ))ab
ˆ‰
1cos 2)
4 cos d 4 sin œ œ œ
'0ˆ‰ ‘
9 cos 2 9 sin 2 9
24## #
!
)))) 1
))
1
78. A sin 3 d d sin 6œœœœ
''
00
33
"""
##
#Î$
!
ab ˆ‰ ‘
)) ) ) )
1cos 6
46 12
)1
1
79. r 1 cos 2 and r 1 1 1 cos 2 0 cos 2 2 ; thereforeœ œ Ê œ Ê œ Ê œ Ê œ)))))
11
#4
A 4 (1 cos 2 ) 1 d 2 1 2 cos 2 cos 2 1 dœœ
''
00
44
"
#
## #
cda b)) )))
2 2 cos 2 d 2 sin 2 2 1 0 2œœœœ
'0
4ˆ‰‘ˆ‰
))))
""
##
Î%
!
cos 4 sin 4
28 8 4
))11
1
80. The circle lies interior to the cardioid (see the graphs in Exercises 61 and 63). Thus,
A 2 [2(1 sin )] d (the integral is the area of the cardioid minus the area of the circle)œ
'2
2"
#
#
))1
4 1 2 sin sin d (6 8 sin 2 cos 2 ) d 6 8 cos sin 2œ œ œ
''
22
22
ab c d) ))1 ) ))1 ) ) ) 1
#Î#
Î#
1
1
3(3) 5œœcd1 111
81. r 1 cos sin ; Length ( 1 cos ) ( sin ) d 2 2 cos dœ Ê œ œ œ )) ))) ))
dr
d)''
00
22
ÈÈ
##
d 2 sin d 4 cos ( 4)( 1) ( 4)(1) 8œœœœœ
''
00
22
É‘
4(1 cos )
2
##
#
!
)))
1
))
82. r 2 sin 2 cos , 0 2 cos 2 sin ; r (2 sin 2 cos ) (2 cos 2 sin )œ ŸŸÊœ œ ))) )) )) ))
1
))#
###
#
dr dr
dd
ˆ‰
8sin cos 8 L 8 d 2 2 2 2 2œœÊœ œ œ œab È’“
ÈÈÈ
ˆ‰
## Î#
!#
)) ) ) 1
'0
211
83. r 8 sin , 0 8 sin cos ; r 8 sin 8 sin cos œŸŸÊœ œ
$##$#
## #
ˆ‰ ˆ‰ ˆ‰ ˆ ‰ ‘ ‘ˆ‰ ˆ‰ ˆ‰
)1 )) ) ))
))34d33d 3 33
dr dr
)
64 sin L 64 sin d 8 sin d 8 dœÊœ œ œ
%#
%
#
ˆ‰ ˆ‰ ˆ‰
É’“
)))
333
1cos
'''
000
444
)) )
ˆ‰
2
3
4 4 cos d 4 6 sin 4 6 sin 0 3œ œ œ œ
'0
4 ‘ ‘ ˆ‰ ˆ‰ˆ‰ ˆ‰
22
3346
))11
1
)) 1
Î%
!
84. r 1 cos 2 (1 cos 2 ) ( 2 sin 2 ) œ Êœ œ Ê œ
Ȉ‰
)))
dr sin 2 dr sin 2
dd1cos 2
1cos 2
)))
))
)
"
#
"Î#
#
È
r1cos 2Ê œ œ œ
##
ˆ‰
dr sin 2 1 2 cos 2 cos 2 sin 2
d 1 cos 2 1 cos 2 1 cos 2
(1 cos 2 ) sin 2
))))
))))
))
)
2 L 2 d 2 2œœÊœ œœ
22 cos 2
1cos 2
##
)11
)'2
2ÈÈ È
‘ˆ‰
)1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 10 Practice Exercises 685
85. r cos 2 ; Surface Area 2 (r sin ) r dœÊœ œ
ÈɈ‰
)1))
dr sin 2 dr
dd
cos 2
))
)
)
##
È'0
4
2 cos 2 (sin ) cos 2 d 2 cos 2 (sin ) d 2 sin dœœ œ
'''
000
444
1)) ) ) 1)) ) 1))
ÈÈ
ÉÉ
sin 2
cos 2 cos 2
)
))
"
2( cos ) 2 1 2 2œ œ œcd
Š‹Š‹
È
1) 1 1
1Î%
!#
È2
86. r sin 2 2r 2 cos 2 r cos 2 ; Surface Area 2 2 (r cos ) r d
###
œÊœ Êœ œ ))) 1))
dr dr dr
dd d)) )
'0
2Ɉ‰
2 2 (cos ) r r d 2 2 (cos ) (sin 2 ) (cos 2 ) d 2 2 cos dœœ œ
'' '
00 0
22 2
1) ) 1) ) )) 1))
Ɉ‰ È
%##
#
dr
dt
2 2 sin 4œœcd1) 1
1Î#
!
87. (a) Around the x-axis: 9x 4y 36 y 9 x y 9 x and we use the positive root:
## # # #
œÊœ Êœ„
99
44
É
V 2 9 x dx 2 9 x dx 2 9x x 24œœœœ
''
00
22
1111
Š‹
Ɉ‰ ‘
993
444
###$
#
!
(b) Around the y-axis: 9x 4y 36 x 4 y x 4 y and we use the positive root:
## # # #
œÊœ Êœ„
44
99
É
V 2 4 y dy 2 4 y dy 2 4y y 16œœœœ
''
00
33
1111
Š‹
Ɉ‰ ‘
444
9927
###$
$
!
88. 9x 4y 36, x 4 y y x 4 ; V x 4 dx x 4 dx
## # #
##
##
#
œ œÊœ Êœ œ œ
9x 36 3 3 9
4 4
ÈÈ
Š‹ ab
''
22
44
11
4x 16 8 (32) 24œœ œœ œ
9x 9 64 8 956 24 3
43 4 3 3 43 3 4
11 11
’“‘ˆ‰ˆ‰ˆ‰
%
#1
89. Each portion of the wave front reflects to the other focus, and since the wave front travels at a constant speed
as it expands, the different portions of the wave arrive at the second focus simultaneously, from all directions,
causing a spurt at the second focus.
90. The velocity of the signals is v 980 ft/ms. Let t be theœ"
time it takes for the signal to go from A to S. Then
d 980t and d 980(t 1400)
""# "
œœ
d d 980(1400) 1.372 10 ft or 259.8 miles.Êœ œ ‚
#" '
The ship is 259.8 miles closer to A than to B.
The difference of the distances is always constant (259.8
miles) so the ship is traveling along a branch of a hyperbola
with foci at the two towers. The branch is the one having
tower A as its focus.
91. The time for the bullet to hit the target remains constant, say t t . Let the time it takes for sound toœ!
travel from the target to the listener be t . Since the listener hears the sounds simultaneously, t t t
#"!#
œ
where t is the time for the sound to travel from the rifle to the listener. If v is the velocity of sound, then
"
vt vt vt or vt vt vt . Now vt is the distance from the rifle to the listener and vt is the distance
"!#"#! " #
œ œ
from the target to the listener. Therefore the difference of the distances is constant since vt is constant so
!
the listener is on a branch of a hyperbola with foci at the rifle and the target. The branch is the one with the
target as focus.
92. Let (r ) be a point on the graph where r a . Let (r ) be on the graph where r a and
"" " " ## # #
ߜߜ))))
2 . Then r and r lie on the same ray on consecutive turns of the spiral and the distance between)) 1
#" " #
œ
the two points is r r a a a( ) 2 a, which is constant.
#" # " # "
œœ œ)) )) 1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
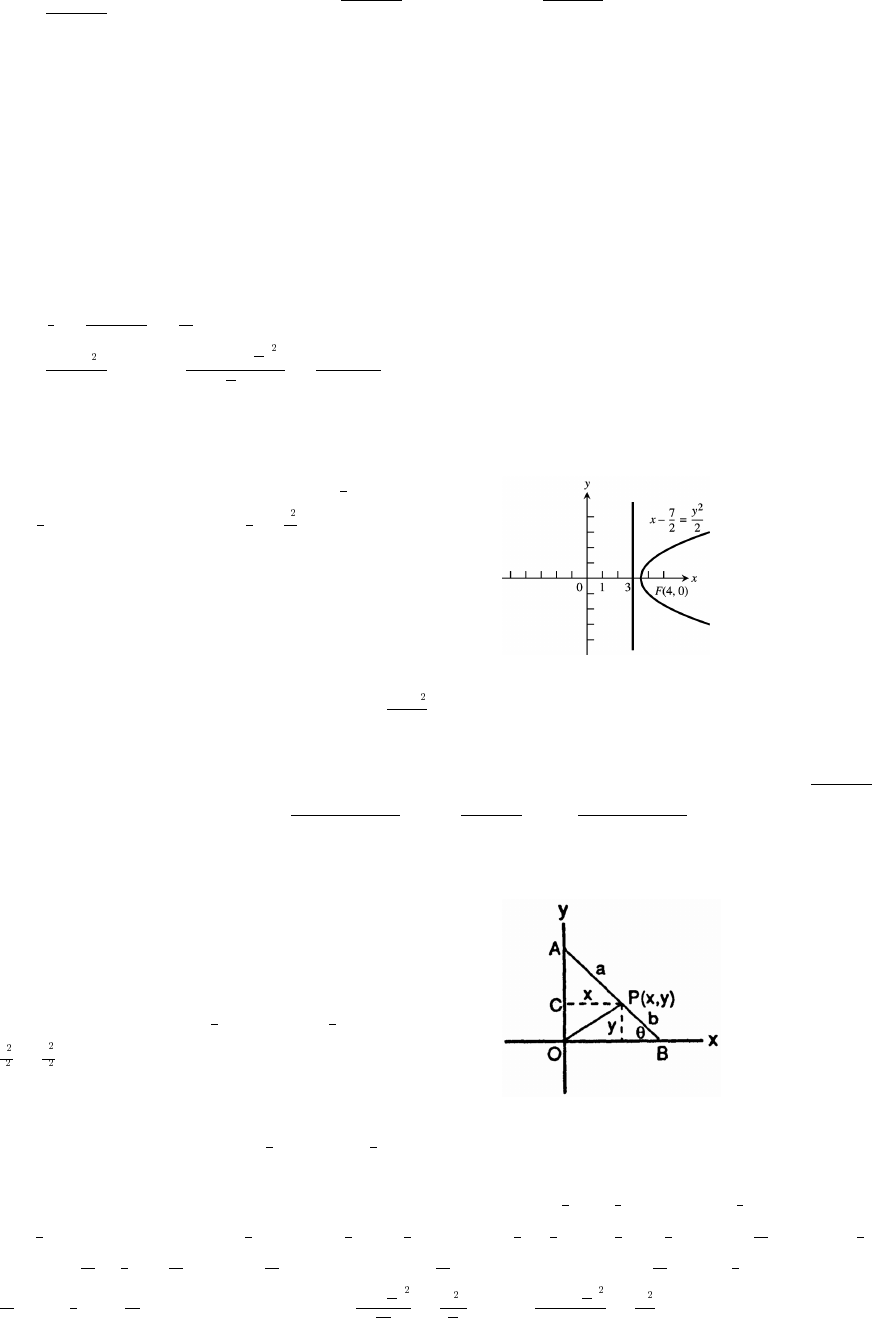
686 Chapter 10 Conic Sections and Polar Coordinates
93. (a) r r er cos k x y ex k x y k ex x yœ Ê œÊœÊœÊ
k
1e cos ## ## ##
))ÈÈ
k 2kex e x x e x y 2kex k 0 1 e x y 2kex k 0œ ÊœÊ œ
######## ####
ab
(b) e 0 x y k 0 x y k circle;œÊ œÊ œ Ê
### ## #
0 e 1 e 1 e 1 0 B 4AC 0 4 1 e (1) 4 e 1 0 ellipse;Ê Ê Ê œ œ Ê
## # # # #
ab ab
e 1 B 4AC 0 4(0)(1) 0 parabola;œÊ œ œÊ
##
e 1 e 1 B 4AC 0 4 1 e (1) 4e 4 0 hyperbolaÊ Ê œ œ Ê
## ###
ab
94. (a) The length of the major axis is 300 miles 8000 miles 1000 miles 2a a 4650 miles. If theœÊœ
center of the earth is one focus and the distance from the center of the earth to the satellite's low point is
4300 miles (half the diameter plus the distance above the North Pole), then the distance from the center
of the ellipse to the focus (center of the earth) is 4650 miles 4300 miles 350 miles c. Thereforeœœ
e.œœ œ
c 350 miles 7
a 4650 miles 93
(b) r r mileœÊœ œ
a1 e
1 e cos 93 7 cos
4650 1
1 cos
430,000
ab ’“
ˆ‰
ˆ‰
))
)
7
93
7
93
CHAPTER 10 ADDITIONAL AND ADVANCED EXERCISES
1. Directrix x 3 and focus (4 0) vertex is œßÊß!
ˆ‰
7
#
p the equation is xÊœÊ œ
"
###
7y
2. x 6x 12y 9 0 x 6x 9 12y y vertex is (3 0) and p 3 focus is (3 3) and the
##
œ Ê œ Ê œ Ê ß œ Ê ß
(x 3)
12
directrix is y 3œ
3. x 4y vertex is ( 0) and p 1 focus is ( 1); thus the distance from P(x y) to the vertex is x y
###
œ Ê !ß œ Ê !ß ß
È
and the distance from P to the focus is x (y 1) x y 2 x (y 1)
ÈÈÈ
######
Ê œ
x y 4 x (y 1) x y 4x 4y 8y 4 3x 3y 8y 4 0, which is a circleÊœ ÊœÊ œ
## # # ## # # # #
cd
4. Let the segment a b intersect the y-axis in point A and
intersect the x-axis in point B so that PB b and PA aœœ
(see figure). Draw the horizontal line through P and let it
intersect the y-axis in point C. Let PBOnœ)
APC . Then sin and cos Ên œ œ œ)) )
y
ba
x
cos sin 1.Êœ œ
x
ab
y##
))
5. Vertices are 2 a 2; e 0.5 c 1 foci are 0 1ab ab!ß „ Ê œ œ Ê œ Ê œ Ê ß „
cc
a#
6. Let the center of the ellipse be (x 0); directrix x 2, focus (4 0), and e c 2 2 cߜߜʜʜ
2a a
3e e
a (2 c). Also c ae a a 2 a a a a a ; x 2Êœ œ œ Êœ Êœ Ê œ Êœ œ
2222445412a
333339935e
ˆ‰
x 2 x the center is 0 ; x 4 c c 4 so that c a bÊœ œ Êœ Ê ß œÊœ œ œ
ˆ‰ˆ‰ ˆ ‰
12 3 18 28 28 28 8
55 5 5 55#
###
; therefore the equation is 1 or 1œœ œ œ
ˆ‰ ˆ‰
12 8 80
5 5 25 144 16
x25x
y5y
##
ˆ‰ ˆ‰
ˆ‰ ˆ‰
28 28
55
144 80
25 25
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
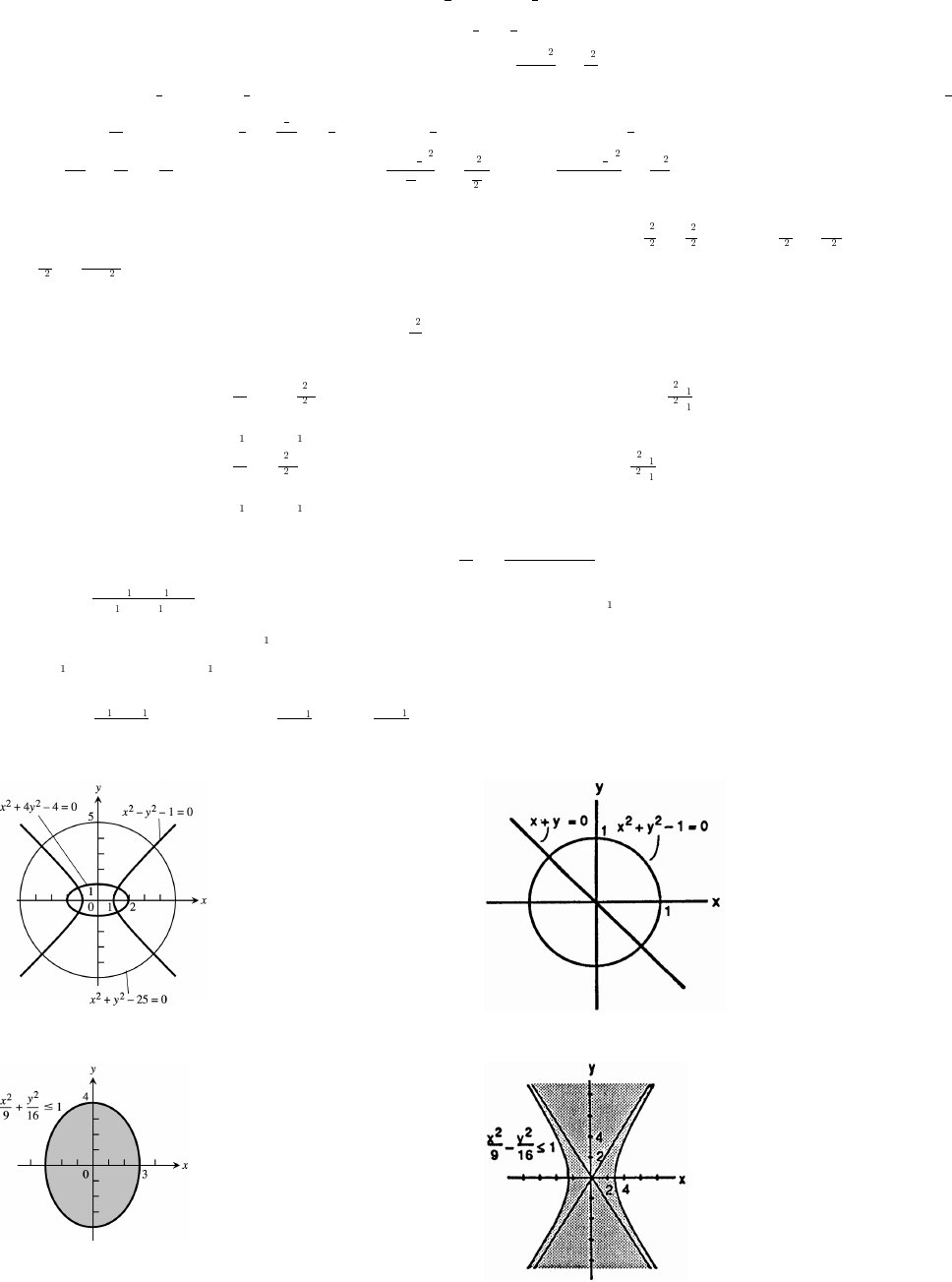
Chapter 10 Additional and Advanced Exercises 687
7. Let the center of the hyperbola be (0 y).ß
(a) Directrix y 1, focus (0 7) and e 2 c 6 c 6 a 2c 12. Also c ae 2aœ ß œÊœÊœÊœ œœ
aa
ee
a 2(2a) 12 a 4 c 8; y ( 1) 2 y 1 the center is (0 1); c a bÊœ ʜʜ œœœÊœÊ ß œ
a4
e#
###
b c a 64 16 48; therefore the equation is 1Ê œœœ œ
### (y 1)
16 48
x
(b) e 5 c 6 c 6 a 5c 30. Also, c ae 5a a 5(5a) 30 24a 30 aœÊœÊœÊœ œœÊœ Ê œ Êœ
aa 5
ee 4
c ; y ( 1) y the center is ; c a b b c aÊœ œœ œ ÊœÊ !ß œ Ê œ
25 a 3 3
4e544 4
ˆ‰
5
4"### ###
ˆ‰
; therefore the equation is 1 or 1œœ œ œ
625 25 75 x 2x
16 16 25 75
y16y
#
ˆ‰ ˆ‰
ˆ‰ ˆ‰
33
44
25
16
75
8. The center is (0 0) and c 2 4 a b b 4 a . The equation is 1 1ߜʜʜ œÊœ
## # # y
ab a b
x 49 144
1 49 4 a 144a a 4 a 196 49a 144a 4a a a 197a 196Ê œÊ œ Ê œ Ê
49 144
a4a
ab
# ### ###%%#
ab ab
0 a 196 a 1 0 a 14 or a 1; a 14 b 4 (14) 0 which is impossible; a 1œÊ œÊœ œ œ Ê œ œabab
## # #
b 4 1 3; therefore the equation is y 1Ê œœ œ
##
x
3
9. (a) b x a y a b ; at (x y ) the tangent line is y y (x x )
## ## ## "" " "
œ Êœ ß œ
dy
dx ay ay
bx bx
Š‹
ayy bxx bx ay ab bxx ayy ab 0ÊœœÊœ
# # ## ## ## # # ##
"" ""
(b) b x a y a b ; at (x y ) the tangent line is y y (x x )
## ## ## "" " "
œ Êœ ß œ
dy
dx ay ay
bx bx
Š‹
b xx a yy b x a y a b b xx a yy a b 0ÊœœÊœ
# # ## ## ## # # ##
"" ""
10. Ax Bxy Cy Dx Ey F 0 has the derivative ; at (x y ) the tangent line is
##
""
œ œ ß
dy 2Ax By D
dx Bx 2Cy E
yy (xx) Byx2CyyEyByx2CyEyœ Ê
"""""""
#
Š‹
2AxByD
Bx 2Cy E
2Axx Bxy Dx 2Ax Bx y Dx 2Axx B(yx xy ) 2Cyy Dx Dx Ey Eyœ Ê
"" """ " "" " " "
#
2Ax 2Bx y 2Cy . Now add 2Dx 2Ey to both sides of this last equation, divide the result byœ
##
"" " "
2, and represent the constant value on the right by F to get:
AxxB CyyD E F
""
###
œ
ˆ ‰ ˆ‰ˆ‰
yx xy y y
xx
11. 12.
13. 14.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
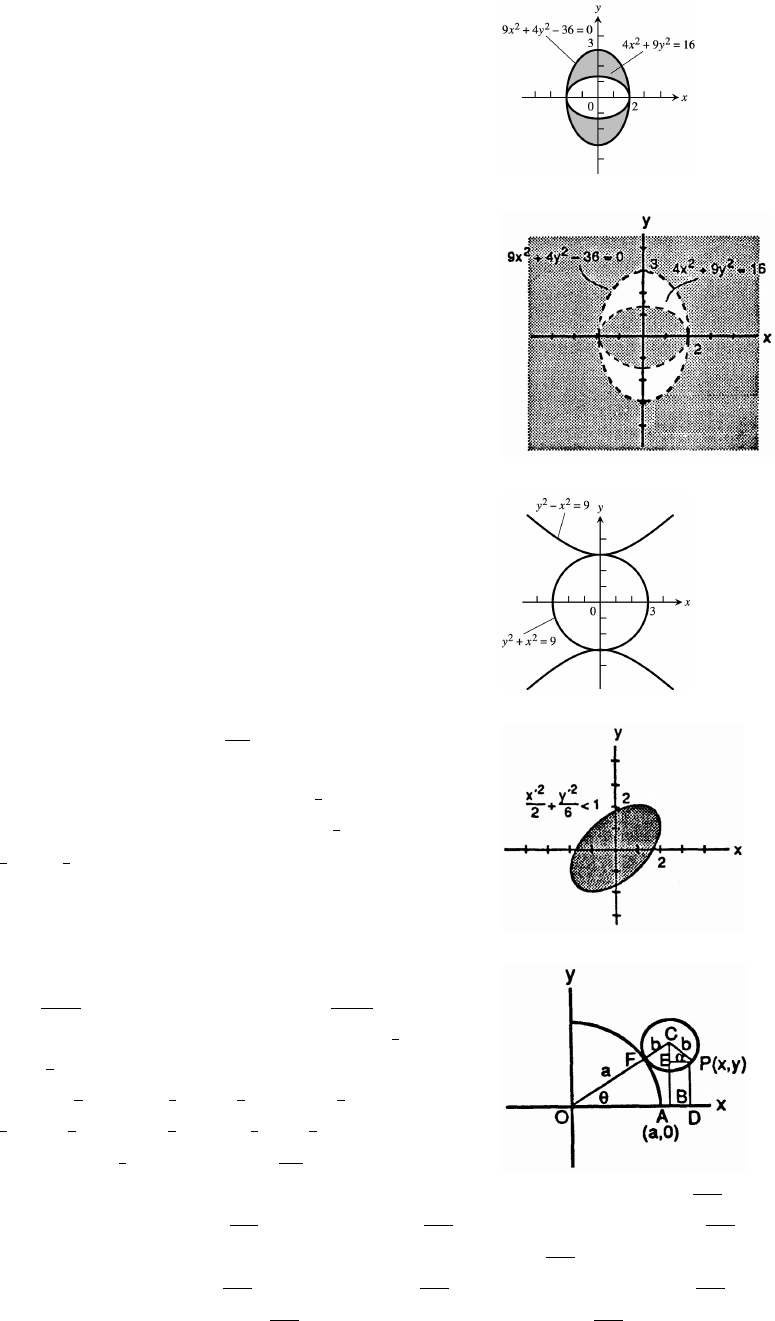
688 Chapter 10 Conic Sections and Polar Coordinates
15. 9x 4y 36 4x 9y 16 0abab
## ##
Ÿ
9x 4y 36 0 and 4x 9y 16 0ÊŸ
## ##
or 9x 4y 36 0 and 4x 9y 16 0
## ##
Ÿ
16. 9x 4y 36 4x 9y 16 0, which is theabab
## ##
complement of the set in Exercise 15
17. x y 9 0 x y 9 0 or
%# ##
#
œÊœab ab
x y 9 0 y x 9 or x y 9
# # ## ##
œÊ œ œab
18. x xy y 3 tan 2 which is undefined
## "
Ê œ!11
2 90° 45° AÊœ Êœ Ê!! w
cos 45° cos 45° sin 45° sin 45° , B 0,œ œœ
##w
#
3
C sin 45° sin 45° cos 45° cos 45°
w# # "
#
œ œ
x y 3 which is the interior of aÊ
3
##
ww
##
"
rotated ellipse
19. Arc PF Arc AF since each is the distance rolled;œ
PCF Arc PF b( PCF); nœ Ê œn œ
Arc PF Arc AF
ba
)
Arc AF a a b( PCF) PCF ;ʜʜnÊnœ)) )
ˆ‰
a
b
OCB and OCB PCF PCEnœ nœnn
1
#)
PCF œn œ Ê
ˆ‰ˆ‰ˆ‰
111
###
!)! )
a
b
œÊœ
ˆ‰ ˆ ‰ ˆ‰
aa
bb
)! ))!
11 1
## #
.ʜ ʜ!1) ) !1 )
ˆ‰ ˆ ‰
aab
bb
Now x OB BD OB EP (a b) cos b cos (a b) cos b cosœœœ œ )! ) 1 )
ˆ‰ˆ‰
ab
b
(a b) cos b cos cos b sin sin (a b) cos b cos andœ œ )1 ) 1 ) ) )
ˆ‰ ˆ‰ ˆ‰ˆ‰ ˆ‰ ˆ‰
ab ab ab
bb b
y PD CB CE (a b) sin b sin (a b) sin b sinœœœ œ )! ) )
ˆ‰ˆ‰
ab
b
(a b) sin b sin cos b cos sin (a b) sin b sin ;œ œ )1 ) 1 ) ) )
ˆ‰ ˆ‰ ˆ‰ˆ‰ ˆ‰ ˆ‰
ab ab ab
bb b
therefore x (a b) cos b cos and y (a b) sin b sinœ œ )) ))
ˆ‰ ˆ‰ˆ‰ ˆ‰
ab ab
bb
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 10 Additional and Advanced Exercises 689
20. (a) x a(t sin t) a(1 cos t) and let 1 dm dA y dx y dtœ Ê œ œÊ œ œ œ
dx dx
dt dt
$ˆ‰
a(1 cos t) a (1 cos t) dt a (1 cos t) dt; then A a (1 cos t) dtœ œ œ
## ##
'0
2
a 1 2 cos t cos t dt a 1 2 cos t cos 2t dt a t 2 sin tœœ œ
### #
""
##
#
!
''
00
22
ab
ˆ‰‘
3sin 2t
24
1
3 a ; x = x a(t sin t) and y = y a(1 cos t) M y dm y dAœœ œÊœœ
µµ µµ
1 $
#""
## x''
a(1 cos t) a (1 cos t) dt a (1 cos t) dt 1 3 cos t 3 cos t cos t dtœ œ œ
'''
000
222
""
###
##$ $ #$
aab
1 3 cos t 1 sin t (cos t) dt t 3 sin t sin tœ œ
a 3 3 cos 2t a 5 3 sin 2t sin t
243
### #
##
!
'0
2‘
ab ’“
1
. Therefore y a. Also, M x dm x dAœœœœœœ
µµ
5a 5
M
M3a 6 y
1
1
#
x
5a
Š‹ ''
$
a(t sin t) a (1 cos t) dt a t 2t cos t t cos t sin t 2 sin t cos t sin t cos t dtœ œ
''
00
22
##$ # #
ab
a 2 cos t 2t sin t t cos 2t sin 2t cos t sin t 3 a . Thusœ œ
$# ##$
"" #
!
’“
ttcost
2484 3
1
1
x a a a is the center of mass.œœ œ Ê ß
M
M3a 6
3a 5
y1
111
ˆ‰
(b) x t t and y 2t t ; let 1 dm dA y dx y dtœÊœ œÊœ œÊœœœ
2dx dx
3dt dt dt
dy
$Î# "Î# "Î# "Î# $ˆ‰
2t t dt 2t dt; x = x t and y = t M y dm t (2t dt)ÊœœœÊœœ
µµ µ
ˆ‰ˆ‰
"Î# "Î# $Î# "Î# "Î#
#
2
3
yx
3
''
0
È
2t dt t 3. Also, M x dm x dA t (2t dt)œœœ œœœ
µµ
'''
0
ÈÈÈ
3412 2
55 3
y0
3
$Î# &Î# $Î#
$
!
‘ È'
4
t dt t 27.œœœ
'0
ÈÈ
348 8
321 7
&Î# (Î# $
!
‘ È
4
21. (a) x e cos t and y e sin t x y e cos t e sin t e . Also tan tœœÊœœœœ
2t 2t 4t 4t 4t## # # y
xe cos t
e sin t
2t
2t
t tan x y e is the Cartesian equation. Since r x y andÊœ Ê œ œ
" # # # # #
ˆ‰
y
x
%Îtan y xab
tan , the polar equation is r e or r e for r 0)œœœ
" #
ˆ‰
y
x
42
(b) ds r d dr ; r e dr 2e d
### #
œœÊœ))
22))
ds r d 2e d e d 4e dÊœ œ
### # #
##
)) ))
ˆ‰ˆ‰
22 4)) )
5e d ds 5 e d L 5 e dœÊœ Êœ
42 2)) )
)) )
#ÈÈ
'0
2
e1œœ
’“ ab
ÈÈ
5e 5
2
4
2#
!#
11
22. r 2 sin dr 2 sin cos d ds r d dr 2 sin d 2 sin cos dœÊœ Êœœ
$# ####$##
##
ˆ‰ ˆ‰ ˆ‰ ‘ ‘ˆ‰ ˆ‰ ˆ‰
))) )))
333 333
)) ) )
4 sin d 4 sin cos d 4 sin sin cos d 4 sin dœ œ œ
'# % ## % # # # %#
ˆ‰ ˆ‰ ˆ‰ ‘ ‘ ˆ‰ˆ‰ ˆ‰ ˆ‰
))) ))) )
333 333 3
)) ))
ds 2 sin d . Then L 2 sin d 1 cos d sin 3Êœ œ œ œ œ
## $
!
ˆ‰ ˆ‰ ‘ ‘ˆ‰ ˆ‰
))))
1
33323
232
))))1
''
00
33
23. r 1 cos and S 2 ds, where y r sin ; ds r d drœ œ œœ œ )133))
'È## #
(1 cos ) d sin d 1 2 cos cos sin d 2 2 cos d 4 cos dœ œ œ
ÈÈÈɈ‰
) ) )) ) ) )) )) )
## # # # # #
#
)
2 cos d since 0 . Then S 2 (r sin ) 2 cos d 4 (1 cos ) sin cos dœŸŸœ œ
ˆ‰ ˆ‰ ˆ‰
)1 ) )
## # #
)) 1) )1)))
''
00
22
††
4 2 cos 2 sin cos cos d 16 cos sin dœœœ
''
0 0
2 2
1)1)
‘ ‘ ˆ‰ ˆ‰ˆ‰ ˆ‰ ˆ‰ ˆ‰ ’“
#%
## # ##
Î#
!
) ))) )) 11
25
32 cos ˆ‰
œœ
(32)
555
32 32 4 2
1111
Š‹ È
2ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
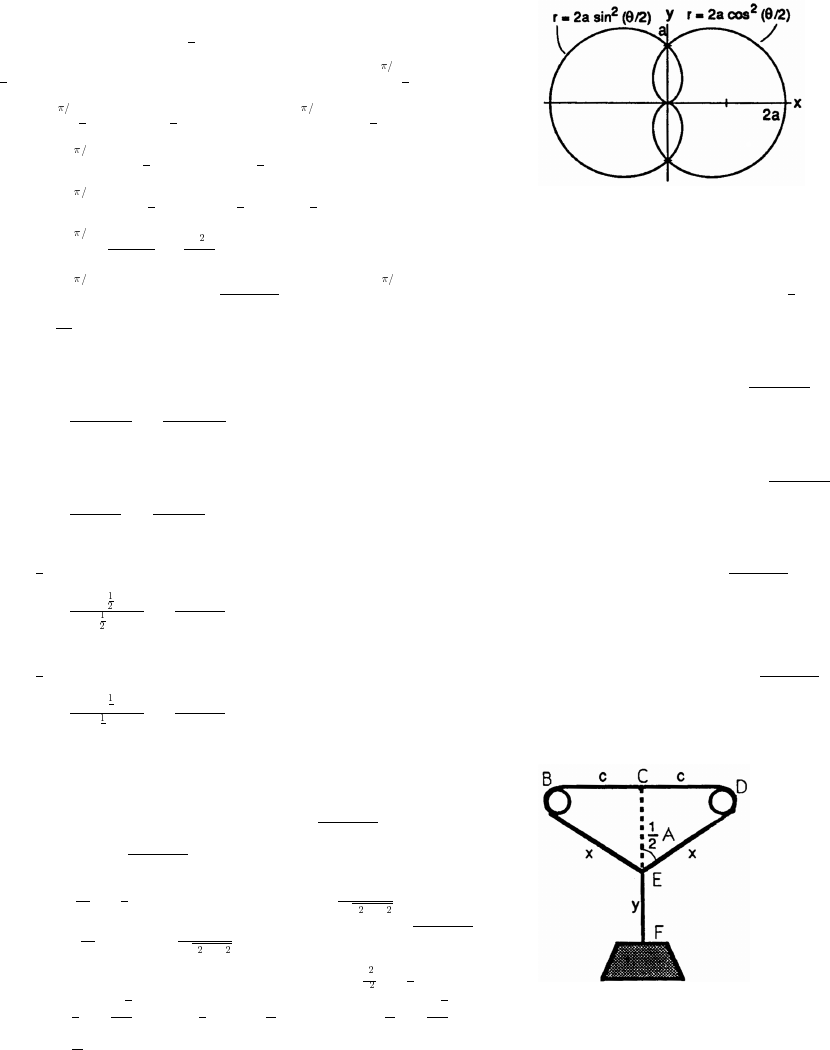
690 Chapter 10 Conic Sections and Polar Coordinates
24. The region in question is the figure eight in the middle.
The arc of r 2a sin in the first quadrant givesœ#
#
ˆ‰
)
of that region. Therefore the area is A 4 r d
""
#
#
4œ'0
2
)
4 2a sin d 8a sin dœœ
''
00
22
"
## #
##%
#
‘ ˆ‰ˆ‰
))
))
8a sin 1 cos dœ
## #
##
'0
2ˆ‰ ‘ˆ‰
))
)
8a sin sin cos dœ
## ##
###
'0
2‘ˆ‰ ˆ‰ ˆ‰
)))
)
8a dœ
#
#
'0
2Š‹
1cos sin
4
))
)
2a 2 2 cos d a (3 4 cos cos 2 ) d a 3 4 sin sin 2œ œœ
###
"
#
Î#
!
''
00
22
ˆ‰ ‘
)) ))))))
1cos 2
2
)1
a4œ
#
#
ˆ‰
31
25. e 2 and r cos 2 x 2 is the directrix k 2; the conic is a hyperbola with rœ œÊœ Êœ œ)ke
1e cos )
rÊœ œ
(2)(2)
12 cos 12 cos
4
))
26. e 1 and r cos 4 x 4 is the directrix k 4; the conic is a parabola with rœœÊœ Êœ œ)ke
1e cos )
rÊœ œ
(4)(1)
1cos 1cos
4
))
27. e and r sin 2 y 2 is the directrix k 2; the conic is an ellipse with rœ œÊœ Êœ œ
"
#
)ke
1e sin )
rÊœ œ
2
1 sin
2
2sin
ˆ‰
ˆ‰
))
28. e and r sin 6 y 6 is the directrix k 6; the conic is an ellipse with rœœÊœ Êœ œ
"
31e sin
ke
))
rÊœ œ
6
1 sin
6
3sin
ˆ‰
ˆ‰
3
3
))
29. The length of the rope is L 2x 2c y 8c.œ
(a) The angle A ( BED) occurs when the distancen
CF is maximized. Now x c yœj jœ
È##
xcL2x2cÊjœ
È##
x c (2x) 2 2.Êœ œ
dx
dx xc
j"
#
##
"Î#
ab È
Thus 0 2 0 x 2 x c
dx
dx xc
j
##
œÊ œÊœ
ÈÈ
x 4x 4c 3x 4c Êœ Ê œ Êœ
### ##
c3
x4
. Since sin we have sin Êœ œ œ
ccAA
xx
33
ÈÈ
####
60° A 120°Êœ Êœ
A
#
(b) If the ring is fixed at E (i.e., y is held constant) and E is moved to the right, for example, the rope will slip
around the pegs so that BE lengthens and DE becomes shorter BE ED is always 2x L y 2c,Ê œ
which is constant the point E lies on an ellipse with the pegs as foci.Ê
(c) Minimal potential energy occurs when the weight is at its lowest point E is at the intersection of theÊ
ellipse and its minor axis.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 10 Additional and Advanced Exercises 691
30. d d 30;
dd dd
cc c cc c
30 30
œ Ê œ œ
"#
d d 30. Therefore P and Q lie on an ellipse withʜ
$%
F and F as foci. Now 2a d d 30 a 15 and
"# "#
œœ Êœ
the focal distance is 10 b 15 10 125Êœœ
###
an equation of the ellipse is 1. Nextʜ
x
225 125
y
xxvtxv x10.
#"! "! "
œ œ œ
Š‹
10
v
If the plane is flying level, then P and Q must be symmetric to the y-axis x x x x 10ʜʜ
"###
x 5 1 y y since y must be positive. Therefore the position ofÊœÊ œÊœ Êœ
###
#
5 1000
225 125 9 3
y10 10
È
the plane is where the origin (0 0) is located midway between the two stations.
Š‹
&ß ß
10 10
3
È
31. If the vertex is ( 0), then the focus is (p 0). Let P(x y) be the present position of the comet. Then!ß ß ß
(x p) y 4 10 . Since y 4px we have (x p) 4px 4 10 (x p) 4px 16 10 .
ÈÈ
œ‚ œ œ‚ Ê œ‚
## #
(# ( # "%
Also, xp410 cos 60°210 xp210. Therefore 210 4pp210 1610œ‚ œ‚ Ê œ‚ ‚ ‚ œ ‚
(( ( ( ("%
#
aba b
4 10 4p 8p 10 16 10 4p 8p 10 12 10 0 p 2p 10 3 10 0Ê‚ ‚ œ‚ Ê ‚ ‚ œÊ ‚ ‚ œ
"% # ( "% # ( "% # ( "%
p 3 10 p 10 0 p 3 10 or p 10 . Since p is positive we obtain p 10 miles.Ê‚ œÊœ‚ œ œabab
(( ( ( (
32. x 2t and y t y ; let D (x 0) 3 x x 9 x 9œœÊœ œœœ
#####
#
##
"xxx3x
4 4 16 16
Ɉ‰
ÉÉ
x 8x 144 be the distance from any point on the parabola to (0 3). We want to minimize D. Thenœ ß
"%#
4È
x 8x 144 4x 16x 0 x 2x 0 x 4x 0 x 0 or
dD
dx 8
x2x
x8x144
œ œ œÊœÊœÊœ
" "
%# $ $ $
"Î#
#
abab
ˆ‰
È
x 2. Now x 0 y 0 and x 2 y 1. The distance from (0 0) to (0 3) is D 3. The distanceœ„ œ Ê œ œ„ Ê œ ß ß œ
from 2 1 to ( 3) is D 2 (1 3) 2 2 which is less than 3. Therefore the points closest toab ab
ÉÈ
„ ß !ß œ „ œ
##
(0 3) are 2 1 .ß„ßab
33. cot 2 0 45° is the angle of rotation A cos 45° cos 45° sin 45° sin 45° , B 0,!!œœÊœ Êœ œ œ
AC 3
B
w# # w
#
and C sin 45° sin 45° cos 45° cos 45° x y 1 b and a 2 c a b
w# # w w ###
""
## #
##
œ œÊœÊœ œÊœ
32
3
ÉÈ
2 c . Therefore the eccentricity is e 0.82.œœ Ê œ œ œ œ ¸
24 2 c 2
33 a 3
32
ÈÈ
Š‹
2
3É
34. The angle of rotation is A sin cos , B 0, and C sin cos 1!œÊ œ œ œ œ œÊ œ
111 11
444 44
xy
www
""
####
a 2 and b 2 c a b 4 c 2. Therefore the eccentricity is e 2 .Êœ œ Ê œ œÊœ œœ œ
ÈÈ È
### c2
a2
È
35. x y 1 x 2 xy y 1 2 xy 1 (x y) 4xy 1 2(x y) (x y)
ÈÈÈ È
œÊ œÊ œ Ê œ
#
4xy x 2xy y 2x 2y 1 x 2xy y 2x 2y 1 0 B 4AC ( 2) 4(1)(1) 0Ê œ Ê œÊ œ œ
## ## # #
the curve is part of a parabolaÊ
36. A 2 sin cos 1, B 0, C 2 sin cos 1, D 2 sin 1, E 2 cos !œÊœ œœœ œœ œœ
111 11 1 1
444 44 4 4
www ww
ÈÈ
1, F2 xyxy20 xx yy 2 xx yyœ œ Ê œ Ê œÊ
w wwww ww ww ww ww
## # # # #
""
Š‹Š‹ Š ‹Š ‹
44
2 1. The center is (x y ) x cos sin andœ Ê œ ß œ ß Ê œ œ
ˆ‰ˆ‰ È
yx
44
2
## ## # # #
ww "" " "
ˆ‰ ˆ‰
11
y sin cos 0 or the center is (x y) 0 . Next a 2 the vertices areœ œ ßœß œÊ
""
## #
11
44
2
Š‹ È
È
(x y ) 2 and 2 x cos 2 sin 1 and
ww """ " " "
### # # # #
ßœ ß ß Êœ œ
Š‹Š ‹ Š‹
ÈÈ È
11
44
2
È
y sin 2 cos 1 or (x y) 1 1 is one vertex, and x cos 2 sin œ œßœß œ
"" ""
## # # #
11 11
44 44
2
Š‹ Š ‹ Š ‹
È È
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

692 Chapter 10 Conic Sections and Polar Coordinates
1 and y sin 2 sin 1 or (x y) 1 1 is the other vertex. Alsoœ œ œ ßœ ß
È È
2 2
44## # #
""11
Š‹ Š ‹
È
c 2 2 4 c 2 the foci are (x y ) and x cos sin and
#ww
"" "
## # # # # #
œœ Ê œ Ê ß œ ß ß Ê œ œ
ˆ‰ˆ ‰
35 3
44
2
11
È
y sin cos 2 or (x y) 2 is one focus, and x cos sin andœ œ ßœß œ œ
" "
## # # # #
11 11
44 44
3 5
232
ÈÈ
Š‹
ÈÈ
y sin cos 2 or (x y) 2 is the other focus. The asymptotes areœ œ ßœß
"
## #
11
44
532
ÈÈ
Š‹
È
y x in the rotated system. Since x x y and y x y x y x
w w ww ww w
" " "" ""
##
œ„ œ œ Êœ
ˆ‰ ÈÈ ÈÈ È
22 22 2
2
x y x and x y y x y y ; the asymptotes areÊœ œ Êœ
ÈÈ ÈÈ
È
22 22
2
2
## ##
ww w
x y x y the asymptotes are 2 x 1 0 or x and 2 y 0 orœ„ Ê œ œ œ
ÈÈ ÈÈ È
22 22
2
### ###
"" "
Š‹ ÈÈ
y 0. Finally, the x -axis is the line through 0 with a slope of 1 recall that y x .œßœÊœ
w
# #
Š‹ ˆ‰
È È
2 2
4
!1
The y -axis is the line through 0 with a slope of 1 y x .
w
##
Š‹
ÈÈ
22
ßÊœ
37. (a) The equation of a parabola with focus ( 0) and vertex (a 0) is r and rotating this parabola!ß ß œ 2a
1cos )
through 45° gives r .!œœ
2a
1cos
ˆ‰
)4
(b) Foci at ( 0) and (2 0) the center is (1 0) a 3 and c 1 since one vertex is at (4 0). Then e!ß ßÊ ßÊœ œ ß œ
c
a
. For ellipses with one focus at the origin and major axis along the x-axis we have rœ œ
"
31e cos
a1 eab
)
.œœ
31
1 cos
8
3cos
ˆ‰
ˆ‰
9
3))
(c) Center at and focus at ( 0) c 2; center at 2 and vertex at a 1. Then e
ˆ‰ ˆ‰ ˆ‰
#ß !ß Ê œ ß "ß Ê œ œ
111
###
c
a
2. Also k ae (1)(2) . Therefore r .œœ œ œ œ œ œ œ
2a3ke3
1 e 1e sin 12 sin 12 sin
(2)
"
## )))
ˆ‰
3
38. Let (d ) and (d ) be the polar coordinates of P and P , respectively. Then , and we have
"" ## " # # "
ßß œ)) ))1
d and d . Therefore
"#
""
œœ œ
33
2cos 2cos( ) d d 3 3
2cos 2cos( )
))1
))1
.œœ
4 cos cos cos sin sin
33
4
))1)1
39. Arc PT Arc TO since each is the same distance rolled. Now Arc PT a( TAP) and Arc TO a( TBO)œœnœn
TAP TBO. Since AP a BO we have that ADP is congruent to BCO CO DP OP isÊn œn œ œ Ê œ Ê??
parallel to AB TBO TAP . Then OPDC is a square r CD AB AD CB AB 2CBÊn œn œ Êœœœ)
r 2a 2a cos 2a(1 cos ), which is the polar equation of a cardioid.Êœ œ ))
40. Note first that the point P traces out a circular arc as the door
closes until the second door panel PQ is tangent to the circle.
This happens when P is located at , since OPQ is
Š‹
""
ÈÈ
22
ßn
90° at that time. Thus the curve is the circle x y 1 for
##
œ
0 x . When x , the second door panel isŸŸ
""
ÈÈ
22
tangent to the curve at P. Now let t represent POQ so thatn
as t runs from to 0, the door closes. The coordinates of P
1
#
are given by (cos t sin t), and the coordinates of Q byß
(2 cos t 0) (since triangle POQ is isosceles). Therefore at a fixed instant of time t, the slope of the lineß
formed by the second panel PQ is m tan t the tangent line PQ isœœ œ Ê
?
?
y
xcos t2 cos t
sin t 0
y 0 ( tan t)(x 2 cos t) y ( tan t) x 2 sin t. Now, to find an equation of the curve forœ Ê œ
x 1, we want to find, for x, the largest value of y as t ranges over the interval 0 t . We
"
È24
ŸŸ ŸŸfixed 1
solve 0 sec t x 2 cos t 0 sec t x 2 cos t x 2 cos t. (Note that
dy
dt œÊ œÊ œ Êœab ab
## $
2 sec t tan t x 2 sin t 0 on 0 t , so a maximum occurs for y.) Now x 2 cos t the
dy
dt œ Ÿ Ÿ œ Êab
# $
#
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
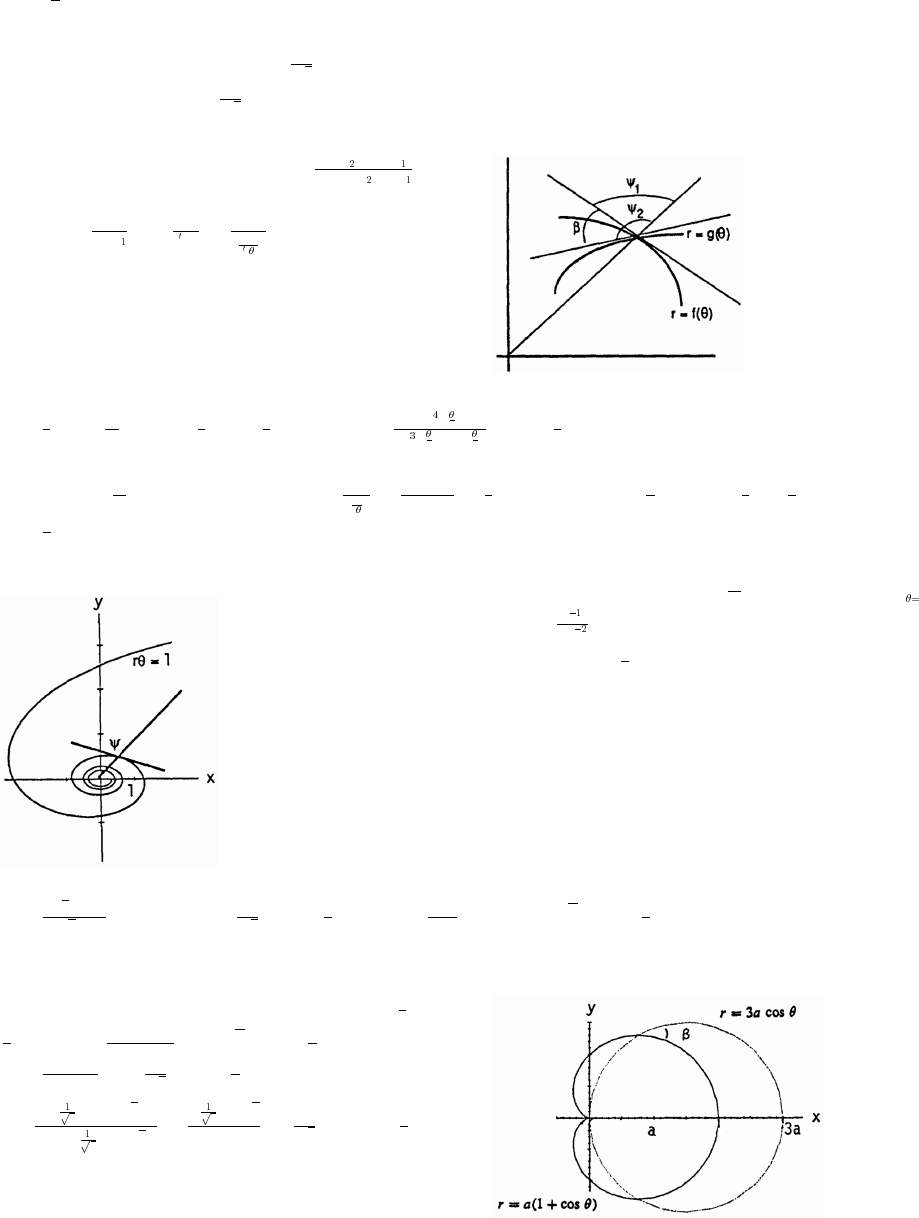
Chapter 10 Additional and Advanced Exercises 693
corresponding y value is y ( tan t) 2 cos t 2 sin t 2 sin t cos t 2 sin t (2 sin t) cos t 1œ œ œ ab a b
$# #
2 sin t. Therefore parametric equations for the path of the curve are given by x 2 cos t and y 2 sin tœœœ
$$$
for 0 t . In Cartesian coordinates, we have the curve x y 2 cos t 2 sin tŸŸ œ
1
4#Î$ #Î$ $ $
#Î$ #Î$
abab
2 cos t sin t 2 the curve traced out by the door is given byœœÊ
#Î$ # # #Î$
ab
x y 1 for 0 x
xy2 for x1
Þ
ß
à
## "
#Î$ #Î$ #Î$ "
œ ŸŸ
œ ŸŸ
È
È
2
2
41. tan tan ( ) ;"< < " < <œ Ê œ œ
#" #"
tan tan
1tan tan
<<
<<
the curves will be orthogonal when tan is undefined, or"
when tan <#" "
œÊœ
tan g ( )
r
<)
’“
r
f()
rf()g()ʜ
#ww
))
42. r sin sin cos tan tanœÊœ Êœ œ
%$
ˆ‰ ˆ‰ ˆ‰ ˆ‰
))) )
)4d 4 4 4
dr sin
sin cos
<ˆ‰
ˆ‰ ˆ‰
4
44
43. r 2a sin 3 6a cos 3 tan tan 3 ; when , tan tan œÊœ Êœœœ œœ))< ))<
dr r 2a sin 3
d 6a cos 3 3 6 3))
)11
ˆ‰
dr
d
""
#
ʜ<1
#
44. (a) (b) r 1 r tan )) )<œÊœ Ê œ Ê
" #
dr
d)k1
lim tan œœÊ œ_
)
)
)<
)Ä_
from the right as the spiral winds inÊÄ<1
#
around the origin.
45. tan cot is at ; tan tan is 3 at ; since the product of<))<))
"#
"
œœœ œœ œ
È
ÈÈ
3 cos
3 sin 3 3cos 3
sin
)
)
1) 1
)È
these slopes is 1, the tangents are perpendicular
46. a(1 cos ) 3a cos 1 2 cos cos orœ Êœ Êœ)) ))
"
#
; tan is 3 at ;)< )œœ œ
11
)
)3a sin 3
1a(1 cos )
È
tan is at . Then<)
23a cos
3a sin 3
3
œœ
)1
)
"
È
tan ""œœœÊœ
#
"
33
3
Š‹
ÈÈ
Š‹Š‹
ÈÈ
33
13 36
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
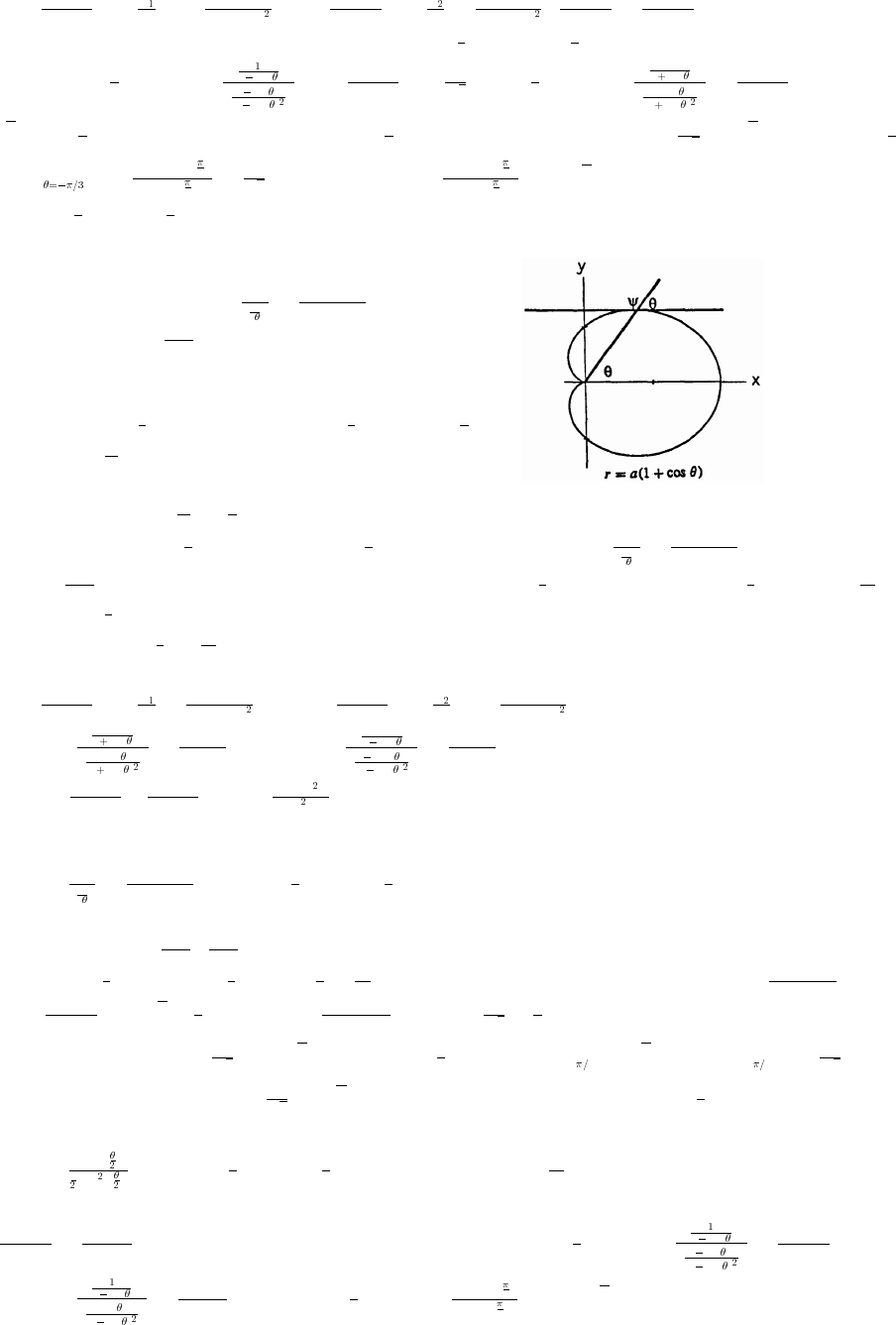
694 Chapter 10 Conic Sections and Polar Coordinates
47. r ; r ;
"#
" "
œÊœ œÊœ œ
1cos d (1cos ) 1cos d (1cos ) 1cos 1cos
dr dr
sin 3 3 sin 3
)) ) )) ) ) )
))
1 cos 3 3 cos 4 cos 2 cos r r 2 the curves intersect at theÊ œ Ê œÊ œÊœ„Ê œœÊ)))))
"
#"#
1
3
points ; tan is at ; tan
ˆ‰
#ß „ œ œ œ œ œ
1)1
)3sin 3
1cos 1cos
3
<)<
"#
"
ˆ‰
’“ ’“
ˆ‰
1cos
sin 3 sin
(1 cos ) (1 cos )
3
1cos
È)
)sin is
3 at ; therefore tan is undefined at since 1 tan tan 1 3 0 ;
È È
Š‹Š‹
)")<< "œœœœÊœ
11 1
333
"# "
#
È
tan and tan 3 tan is also undefinedkk
È
<< "
"#
"œ Î$
œ œ œ œ Ê
1 cos 1 cos
sin sin
3
ˆ‰ ˆ‰
ˆ‰ ˆ‰
È
33
33
)1
at )"œ Ê œ
11
3#
48. (a) We need , so that tan tan ( )<) 1 < 1)œ œ
tan . Now tan œ œ œ)<
ra(1 cos )
a sin
ˆ‰
dr
d
)
)
tan cos cos sinœ œ Ê œ))))
sin
cos
)
)
##
cos cos 1 cosʜ)) )
##
2 cos cos 1 0ʜ
#))
cos or cos 1; cos Êœ œ œÊœ„))))
""
##
1
3
r ; cos 1 r 0.Êœ œÊ œÊœ
3a
#))1
Therefore the points where the tangent line
is horizontal are and ( ).
ˆ‰
3a
3#ß„ !ß
11
(b) We need so that tan tan cot . Thus tan cot <) < ) ) < )œ œ œ œ œ œ
11 )
)##
ˆ‰ ra(1 cos )
a sin
ˆ‰
dr
d
sin sin cos sin cos cos or sin 0; cos œÊ œ Ê œ œ œÊœ„
cos 2
sin 3
) 1
)))) )) ) ) ) )
""
##
r ; sin 0 0 (not , see part (a)) r 2a. Therefore the points where the tangent lineÊœ œ Ê œ Êœ
a
#))1
is vertical are and (2a 0).
ˆ‰
a2
3#ß„ ß
1
49. r and r ; then
"#
œÊœ œÊœ
a a sin b b sin
1cos d (1cos ) 1cos d (1cos )
dr dr
)) ) )) )
))
tan and tan 1 tan tan << <<
"# "#
œœ œœÊ
ˆ‰
’“ ’“
ˆ‰
a
1cos
a sin b sin
(1 cos ) (1 cos )
b
1cos
1cos 1cos
sin sin
))
))
1 1 0 is undefined the parabolas are orthogonal at eachœ œ œ Ê Ê
ˆ‰ˆ‰
1cos 1cos 1cos
sin sin sin
)) )
)) ) "
point of intersection
50. tan is 1 at <)<œœ œÊœ
ra(1 cos )
a sin 4
ˆ‰
dr
d
#
)
)
11
51. r 3 sec r ; 4 4 cos 3 4 cos 4 cos (2 cos 3)(2 cos 1) 0œÊœ œÊœ Ê œ) ) ))))
33
cos cos ))
#
cos or cos or (the second equation has no solutions); tan Êœ œÊœ œ))) <
"
##
#
35
3 3 4 sin
4(1 cos )
11 )
)
is 3 at and tan cot is at . Then tan is undefined sinceœ œ œ
1 cos 3 sec
sin 3 3 sec tan 3
3
"
"
)1 ) 1
)))
È<) "
È
1 tan tan 1 3 0 . Also, tan 3 and tan œœÊœ œ œ<< " < <
"# # "
" "
#
Š‹Š ‹
ÈÈ
kk
È È
3 3
1
53 53
1 tan tan 1 3 0 tan is also undefined .Ê œ œÊ Ê œ<< " "
"# "
#
Š‹Š‹
È
È3
1
52. tan 1 at ; m tan ( ) tan 1<)<)<œœœÊœœœœ
a tan
sec 44
3
ˆ‰
ˆ‰
a
11 1
#tan
53. 1 cos 1 sin cos sin ; tan ;
""
"
1cos 1sin 4sin
1cos
)) )
1)
œÊœÊœÊœ œ œ)))))<
ˆ‰
’“
1cos
sin
(1 cos )
tan . Thus at , tan 1 2 and<)<
#"
œœ œœœ
ˆ‰
’“
1sin
cos
(1 sin )
1sin
cos 4
1cos
sin
)1
)
ˆ‰
ˆ‰
4
4È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
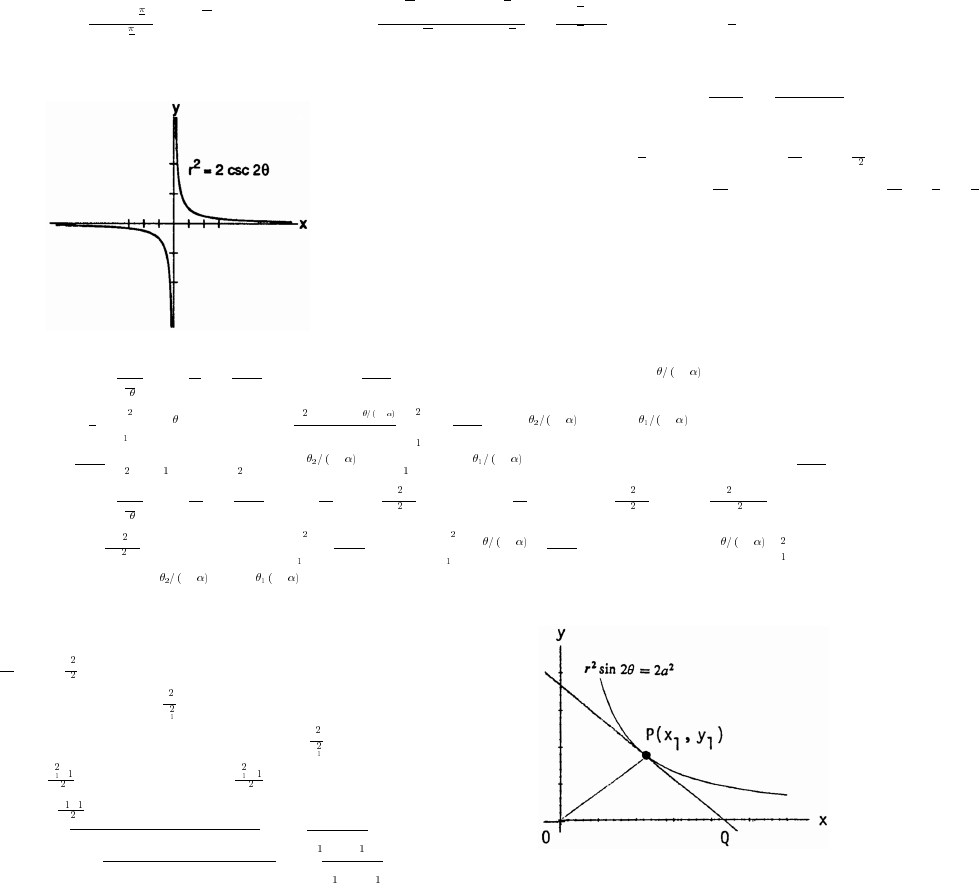
Chapter 10 Additional and Advanced Exercises 695
tan 2 1. Then tan 1 <" "
#
œœ œ œœÊœ
1sin
cos
21 1 2
12112
222
222 4
ˆ‰ È
ˆ‰ Š‹Š‹
ÈÈ
Š‹Š‹
ÈÈ
È
4
4È1
54. (a) (b) r 2 csc 2
#œœœ)22
sin 2 2 sin cos )))
r sin cos 1 xy 1, a hyperbolaʜʜ
#))
(c) At , x y 1 1)œ œ œ Ê œ œ
1
4dxx
dy "
m œÊœÊœœœ
tan 9<9)
33
444
1111
#
55. (a) tan ln r C (by integration) r Be for some constant B;!œÊœ Êœ Êœ
rdrd
rtan tan
ˆ‰
dr
d
))
!!
tan
A Be d Be Beœœœ
"
#
#Î # #
')
)
2 2 tan 2 tanabtan B(tan )e
44
tan
!!)
)
!
)’“
cd
2tan
r r since r B e and r B e ; constant of proportionality Kœ œ œ œ
tan tan
4 4
! !
ab
## ## ##2tan 2tan
(b) tan r r r!œÊœ Ê œ Ê œœ
rdrr dr r dr r tan1
d tan d tan d tan tan
ˆ‰
dr
d)! ) ! ) ! !
!
ˆ‰ ˆ‰ Š‹
##
###
r Length r d Be d B (sec ) eœÊœ œ œ
#Š‹ ˆ‰ cd
sec sec sec
tan tan tan
!!!
!!!
)
)
''
))
))
))!
tan tan
†
(sec ) Be Be K (r r ) where K sec is the constant of proportionalityœœœ!!cd
tan tan #"
56. r sin 2 2a r sin cos a xy a and
### ##
)))œÊ œÊœ
. If P(x y ) is a point on the curve, the tangent
dy
dx x
a
œ ß
""
line is y y (x x ), so the tangent line crossesœ
""
a
x
the x-axis when y 0 y (x x )œÊœ
""
a
x
x x x x x x 2xÊ œ Êœ œœ
xy x y
aa
"""""
since 1. Let Q be (2x 0). Then
xy
aϧ
"
PQ (2x x ) (0 y ) x y andœœ
ÈÈ
"" "
####
OP r (x 0) (y 0) x y OP PQ and the triangle is isosceles.œœ œ Ê œ
ÈÈ
""
####
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
696 Chapter 10 Conic Sections and Polar Coordinates
NOTES:
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

CHAPTER 11 INFINITE SEQUENCES AND SERIES
11.1 SEQUENCES
1. a 0, a , a , a
"#$%
""
#
œœ œœ œœ œœ
11 2 13 2 14 3
1 4 39 416
2. a 1, a , a , a
"#$%
""
#
œœ œœ œœ œœ
11111
1! ! 2 3! 6 4! 24
3. a 1, a , a , a
"# $ %
"
#
"" "
œœœœœœ œœ
(1) ( ) (1) (1)
1 413 615 817
4. a 2 ( 1) 1, a 2 ( 1) 3, a 2 ( 1) 1, a 2 ( 1) 3
"#$%
"#$%
œ œ œ œ œ œ œ œ
5. a , a , a , a
"#$%
#####
""""
#
œœ œœ œœ œœ
2222
22
6. a , a , a , a
"#$%
"""
##
œœœœœœœœ
2213217215
24 28 16
2
7. a 1, a 1 , a , a , a , a ,
"# $ % & '
"" " "
## ## # #
œ œœ œ œ œ œ œ œ œ
3 3 7 7 15 15 31 63
4 4 8 8 16 32
a, a, a, a
()*"!
œœœ œ
127 255 511 1023
64 128 256 512
8. a 1, a , a , a , a , a , a , a ,
"# $ % & ' ( )
"" " """"
####
œœœœœœœœœœ œ
ˆ‰ ˆ‰ ˆ‰
3 6 4 4 5 1 0 7 0 5040 40,320
64
a, a
*"!
""
œœ
362,880 3,628,800
9. a 2, a 1, a , a , a ,
"# $ % &
####
"""
œœ œœ œ œ œ œ œ
(1)(2) (1)(1)
248
(1) (1)
ˆ‰ ˆ‰
4
a , a , a , a , a
'( ) * "!
"""""
##
œœœœ œ
16 3 64 1 8 256
10. a 2, a 1, a , a , a , a ,
"#$%&'
##
""
œ œ œ œ œ œ œ œ œ œ
1( 2) 2( 1)
33 4 5 5 3
22
34
††
††
ˆ‰ ˆ‰
2
3
a, a, a, a
()*"!
""
œ œ œ œ
22
749 5
11. a 1, a 1, a 1 1 2, a 2 1 3, a 3 2 5, a 8, a 13, a 21, a 34, a 55
"#$%&'()*"!
œ œ œœ œœ œœ œ œ œ œ œ
12. a 2, a 1, a , a , a 1, a 2, a 2, a 1, a , a
"# $ % & ' () * "!
"" ""
## ##
œ œ œ œ œ œ œ œ œ œ œ œ
ˆ‰ ˆ‰
ˆ‰
1
13. a ( 1) , n 1, 2, 14. a ( 1) , n 1, 2,
n n
n1 n
œ œ á œ œ á
15. a ( 1) n , n 1, 2, 16. a , n 1, 2,
n n
n1 ()
n
œ œ á œ œ á
# " n1
17. a n 1, n 1, 2, 18. a n 4 , n 1, 2,
n n
œœá œœá
#
19. a 4n 3, n 1, 2, 20. a 4n 2 , n 1, 2,
n n
œ œ á œ œ á
21. a , n 1, 2, 22. a , n 1, 2,
n n
1(1) n(1) n
œœá œ œÚÛœá
###
n1 nˆ‰
23. lim 2 (0.1) 2 converges (Theorem 5, #4)
nÄ_ œÊ
n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
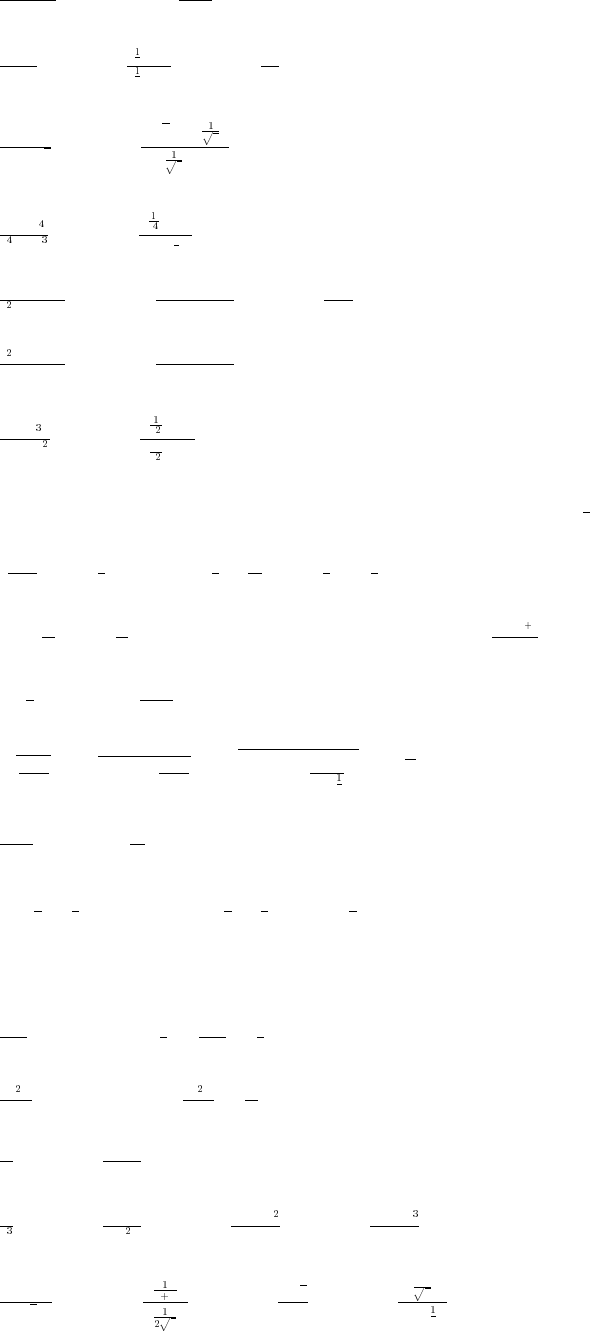
698 Chapter 11 Infinite Sequences and Series
24. lim lim 1 1 converges
nnÄ_ Ä_
n( ) (1)
nn
"
nn
œœÊ
25. lim lim lim 1 converges
nn nÄ_ Ä_ Ä_
"
# #
2n 2
1n
2
2
œœœÊ
ˆ‰
ˆ‰
n
n
26. lim lim diverges
nnÄ_ Ä_
2n
13n
2n
3
"
ÈÈŠ‹
Š‹
œœ_Ê
n
n
27. lim lim 5 converges
nnÄ_ Ä_
"
5n
n8n
5
1
œœÊ
Š‹
ˆ‰
n
8
n
28. lim lim lim 0 converges
nn nÄ_ Ä_ Ä_
n3 n3
n 5n 6 (n 3)(n 2) n
"
#
œœœÊ
29. lim lim lim (n 1) diverges
nn nÄ_ Ä_ Ä_
n2n1
n1 n1
(n 1)(n 1)
œœœ_Ê
30 lim lim diverges
nnÄ_ Ä_
"
n
70 4n
n
4
œœ_Ê
Š‹
Š‹
n
70
n
31. lim 1 ( 1) does not exist diverges 32. lim ( 1) 1 does not exist diverges
nnÄ_ Ä_
ab ˆ‰
Ê Ê
n n "
n
33. lim 1 lim 1 converges
nnÄ_ Ä_
ˆ‰ˆ‰ ˆ ‰ˆ‰
n
nn nn
" " " " " "
####
œ œÊ
34. lim 2 3 6 converges 35. lim 0 converges
nnÄ_ Ä_
ˆ‰ˆ‰
œÊ œÊ
""
## #
"
nn
n1
()
n1
36. lim lim 0 converges
nnÄ_ Ä_
ˆ‰
œ œÊ
"
##
"
n()
n
n
37. lim lim lim 2 converges
nnnÄ_ Ä_ Ä_
ÉÉÊŠ‹
È
2n 2n
n1 n1
œœ œÊ
2
1n
38. lim lim diverges
nnÄ_ Ä_
""
(0.9) 9
0
nœœ_Ê
ˆ‰
n
39. lim sin sin lim sin 1 converges
nnÄ_ Ä_
ˆ‰ ˆ‰
Š‹
111
###
""
œ œ œÊ
nn
40. lim n cos (n ) lim (n )( 1) does not exist diverges
nnÄ_ Ä_
11 1œ Ê
n
41. lim 0 because converges by the Sandwich Theorem for sequences
nÄ_
sin n sin n
nnnn
œŸŸÊ
""
42. lim 0 because 0 converges by the Sandwich Theorem for sequences
nÄ_
sin n sin n
###
"
nnn
œŸŸÊ
43. lim lim 0 converges (using l'Hopital's rule)
^
nnÄ_ Ä_
n
ln 2##
"
nn
œœÊ
44. lim lim lim lim diverges (using l'Hopital's rule)
^
nn n nÄ_ Ä_ Ä_ Ä_
33 ln 3
n3n 6n 6
3(ln 3) 3(ln 3)
nn nn
œœœœ_Ê
45. lim lim lim lim 0 converges
nnnnÄ_ Ä_ Ä_ Ä_
ln (n )
n
2n
n1 1
"
ÈÈŠ‹
Š‹
œœœ œÊ
ˆ‰
Š‹
n1
n
2
n
n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.1 Sequences 699
46. lim lim 1 converges
nnÄ_ Ä_
ln n
ln 2n œœÊ
ˆ‰
ˆ‰
n
2
2n
47. lim 8 1 converges (Theorem 5, #3)
nÄ_
1nœÊ
48. lim (0.03) 1 converges (Theorem 5, #3)
nÄ_
1nœÊ
49. lim 1 e converges (Theorem 5, #5)
nÄ_ ˆ‰
œÊ
7
n
n(
50. lim 1 lim 1 e converges (Theorem 5, #5)
nnÄ_ Ä_
ˆ‰ ’“
œ œ Ê
"" "
nn
()
nn
51. lim 10n lim 10 n 1 1 1 converges (Theorem 5, #3 and #2)
nnÄ_ Ä_
È
nœœœÊ
1n 1nÎÎ
††
52. lim n lim n 1 1 converges (Theorem 5, #2)
nnÄ_ Ä_
Ȉ‰
È
nn
###
œœœÊ
53. lim 1 converges (Theorem 5, #3 and #2)
nÄ_ ˆ‰
3
n1
1n lim 3
lim n
Î"
œœœÊ
n
n
1n
1n
54. lim (n 4) lim x 1 converges; (let x n 4, then use Theorem 5, #2)
nx
Ä_ Ä_
œ œÊ œ
1n4 1xÎÐ Ñ Î
55. lim diverges (Theorem 5, #2)
nÄ_
ln n
n lim n
lim ln n
1
1n 1n
œœœ_Ê
n
n
_
56. lim ln n ln (n 1) lim ln ln lim ln 1 0 converges
nnnÄ_ Ä_ Ä_
cd
ˆ‰ Š‹
œ œ œœÊ
nn
n1 n1
57. lim 4 n lim 4 n 4 1 4 converges (Theorem 5, #2)
nnÄ_ Ä_
ÈÈ
nn
nœœœÊ†
58. lim 3 lim 3 lim 3 3 9 1 9 converges (Theorem 5, #3)
nn nÄ_ Ä_ Ä_
È
n2n 1 21n 1n
Î # Î
œœœœÊ
ab ††
59. lim lim lim 0 and 0 lim 0 converges
nn n nÄ_ Ä_ Ä_ Ä_
n! n! n!
n nnn nn n n n
2 3 (n 1)(n)
nnn
œŸœÊœÊ
"â
â
"
††
†† † ˆ‰
60. lim 0 converges (Theorem 5, #6)
nÄ_
(4)
n!
nœÊ
61. lim lim diverges (Theorem 5, #6)
nnÄ_ Ä_
n!
106n (10 )n
n!
œœ_Ê
"
Š‹
62. lim lim diverges (Theorem 5, #6)
nnÄ_ Ä_
n!
23
nn 6n
n!
œœ_Ê
"
ˆ‰
63. lim lim exp ln lim exp e converges
nn nÄ_ Ä_ Ä_
ˆ‰ ˆ ‰ ˆ ‰ˆ‰
"""
ÎÐ Ñ "
nln nnln n
1lnn ln 1 ln n
œœœÊ
64. lim ln 1 ln lim 1 ln e 1 converges (Theorem 5, #5)
nnÄ_ Ä_
ˆ‰ ˆ‰
Š‹
œ œœÊ
""
nn
nn
65. lim lim exp n ln lim exp
nn nÄ_ Ä_ Ä_
ˆ‰ ˆ ‰ˆ‰ Š‹
3n 3n
3n 1 3n 1
nln (3n 1) ln (3n 1)
" "
œœ
n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

700 Chapter 11 Infinite Sequences and Series
lim exp lim exp exp e convergesœœœœÊ
nnÄ_ Ä_
Š‹
ˆ‰
33
3n 1 3n 1
n
Š‹ 6n 6
(3n 1)(3n 1) 9
#Î$
66. lim lim exp n ln lim exp lim exp
nn n nÄ_ Ä_ Ä_ Ä_
ˆ‰ ˆ ‰ˆ‰ Š‹
nn
n1 n1
nln nln(n1)
œœ œ
ˆ‰ Š‹
n
nn1
n
lim exp e convergesœœÊ
nÄ_ Š‹
n
n(n 1)
"
67. lim lim x x lim exp ln x lim exp
nn n nÄ_ Ä_ Ä_ Ä_
ˆ‰ ˆ‰ ˆ ‰ˆ‰ Š‹
x
2n 1 n 1 n n 1 n
1n 1n ln (2n 1)
n
# #
Î"""
Î
œœ œ
x lim exp xe x, x 0 convergesœœœÊ
nÄ_ ˆ‰
!
2
2n 1
68. lim 1 lim exp n ln 1 lim exp lim exp
nn n nÄ_ Ä_ Ä_ Ä_
ˆ‰ ˆ ‰ˆ‰ – —
œ œ œ
""
nn
nln 1 1
Š‹ ‚
ˆ‰ Š‹Š ‹
Š‹
n
n
2
nn
n
lim exp e 1 convergesœœœÊ
nÄ_ ˆ‰
!
2n
n1
69. lim lim 0 converges (Theorem 5, #6)
nnÄ_ Ä_
36 36
2n! n!
nn n
n
†
†œœÊ
70. lim lim lim 0 converg
nn nÄ_ Ä_ Ä_
ˆ‰ ˆ‰ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰
10 12 10 120
11 11 11 121
nnnn
9 11 12 9 12 11 108
10 12 11 10 11 12 110
n n nn nn n
œœœÊ
1es
(Theorem 5, #4)
71. lim tanh n lim lim lim lim 1 converges
nn nnnÄ_ Ä_ Ä_ Ä_ Ä_
œœœœ"œÊ
ee e 2e
ee e 1 2e
n n 2n 2n
n n 2n 2n
"
72. lim sinh (ln n) lim lim diverges
nnnÄ_ Ä_ Ä_
œœœ_Ê
ee
2
n
ln n ln n n
#
ˆ‰
73. lim lim lim lim converges
nn n nÄ_ Ä_ Ä_ Ä_
n sin
2n 1
ˆ‰
n
#
"
œœ œœÊ
sin cos
cos
ˆ‰ ˆ‰
Š‹ Š ‹
ˆ‰ˆ‰Š‹ ˆ‰
n n
222
nnnn
nn
2
n
#
74. lim n 1 cos lim lim lim sin 0 converges
nnnnÄ_ Ä_ Ä_ Ä_
ˆ‰ ˆ‰
œ œ œ œÊ
" "
n n
ˆ‰
ˆ‰ ‘ˆ‰Š‹
Š‹
"cos sin
n
n
nn
n
75. lim tan n converges 76. lim tan n 0 0 converges
nnÄ_ Ä_
" "
# #
"
œÊ œ œÊ
1 1
Èn
†
77. lim lim 0 converges (Theorem 5, #4)
nnÄ_ Ä_
ˆ‰ ˆ‰
Š‹Š‹
"" " "
33
nn
22
n
œ œÊ
ÈÈ
n
78. lim n n lim exp lim exp e 1 converges
nn nÄ_ Ä_ Ä_
È’“ ˆ‰
n#
!
œ œ œ œ Ê
ln n n
nnn
2n 1
ab
79. lim lim lim lim 0 converges
nn n nÄ_ Ä_ Ä_ Ä_
(ln n) 200 (ln n) 200 199 (ln n)
nn n n
200!
œœ œáœœÊ
†
80. lim lim lim lim lim 0 converges
nn n n nÄ_ Ä_ Ä_ Ä_ Ä_
(ln n) 10(ln n) 80(ln n)
nnnn
3840
ÈÈÈÈ
œ œœœáœœÊ
–—
Š‹
Š‹
5(ln n)
n
n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.1 Sequences 701
81. lim n n n lim n n n lim lim
nn nnÄ_ Ä_ Ä_ Ä_
Š‹Š‹Š‹
ÈÈ
œ œ œ
##
"
nnn
nnn nnn
n
11
È
ÈÈ
Én
convergesœÊ
"
#
82. lim lim lim
nn nÄ_ Ä_ Ä_
""
ÈÈÈ
ÈÈÈ
ÈÈ
ÈÈ
n1 nn n1 nn n1 nn
n1 nn n1 nn
1n
œœ
Š‹Š‹
lim 2 convergesœœÊ
nÄ_ ÉÉ
ˆ‰
11
1
nn
n
83. lim dx lim lim 0 converges (Theorem 5, #1)
nnnÄ_ Ä_ Ä_
"" "
nx n n
ln n
'1
nœœœÊ
84. lim dx lim lim 1 if p 1 converges
nn nÄ_ Ä_ Ä_
'1
nn
1
""""""
x1px1pnp1
pp1p1
œœœÊ
’“ ˆ‰
85. 1, 1, 2, 4, 8, 16, 32, 1, 2 , 2 , 2 , 2 , 2 , 2 , x 1 and x 2 for n 2ᜠá Ê œ œ
!"#$%& "nn2
86. (a) 1 2(1) 1, 3 2(2) 1; let f(a b) (a 2b) 2(a b) a 4ab 4b 2a 4ab 2b
## ## # ## ## #
œ œ ßœ œ
2b a ; a 2b 1 f(a b) 2b a 1; a 2b 1 f(a b) 2b a 1œ œÊßœœ œÊßœœ
### # ## # # ##
(b) r 2 2 r 2
# „" "
# #
nn
œ œ œ œ Ê œ „
ˆ‰ ÊŠ‹
a 2b a 4ab 4b 2a 4ab 2b
a b (a b) (a b) y y
a2b
ab
nn
In the first and second fractions, y n. Let represent the (n 1)th fraction where 1 and b n 1
n
aa
bb
for n a positive integer 3. Now the nth fraction is and a b 2b 2n 2 n y n. Thus,Ê
a2b
ab
n
lim r 2.
nÄ_ nœÈ
87. (a) f(x) x 2; the sequence converges to 1.414213562 2œ ¸
#È
(b) f(x) tan (x) 1; the sequence converges to 0.7853981635œ ¸
1
4
(c) f(x) e ; the sequence 1, 0, 1, 2, 3, 4, 5, divergesœ á
x
88. (a) lim nf lim lim f (0), where x
nxx
Ä_ Ä! Ä!
ˆ‰
" "
w
nx x n
f( x) f(0 x) f(0)
œœ œ œ
??
??
?? ?
(b) lim n tan f (0) 1, f(x) tan x
nÄ_
" w "
""
ˆ‰
n10
œœ œ œ
(c) lim n e 1 f (0) e 1, f(x) e 1
nÄ_ ab
1n x
œ œœ œ
w!
(d) lim n ln 1 f (0) 2, f(x) ln (1 2x)
nÄ_ ˆ‰
œ œ œ œ
22
n 1 2(0)
w
89. (a) If a 2n 1, then b 2n 2n 2n 2n, c 2n 2nœ œÚ ÛœÚ ÛœÚ Ûœ œÜ ÝœÜ Ý
a4n4n1 a
## # # #
" "
## #
2n 2n 1 and a b (2n 1) 2n 2n 4n 4n 1 4n 8n 4nœ œ œ
# ## # # # %$#
#
ab
4n 8n 8n 4n 1 2n 2n 1 c .œœ œ
%$# # #
#
ab
(b) lim lim 1 or lim lim sin lim sin 1
aa aa 2
Ä_ Ä_ Ä_ Ä_ ÄÎ
ÚÛ ÚÛ
ÜÝ ÜÝ
aa
aa
œœœœœ
2n 2n
2n 2n 1
))
)1
90. (a) lim (2n ) lim exp lim exp lim exp e 1;
nn n nÄ_ Ä_ Ä_ Ä_
112n ln 2n
2n n
Î !
##
"
ab Š‹
œœ œœœ
ˆ‰ ˆ‰
1
2
2n
n! 2n , Stirlings approximation n! (2n ) for large values of n¸Ê¸¸
ˆ‰ ˆ‰
ÈÈ
nnn
eee
12n
nn
11
Îab
(b) n n!
40 15.76852702 14.71517765
50 19.48325423 18.393
È
nn
e
97206
60 23.19189561 22.07276647
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

702 Chapter 11 Infinite Sequences and Series
91. (a) lim lim lim 0
nn nÄ_ Ä_ Ä_
ln n
ncn cn
cc1c
œœœ
ˆ‰
n"
(b) For all 0, there exists an N e such that n e ln n ln n ln%œÊÊ
Ð ÑÎ Ð ÑÎ "
ln c ln c c
ln
c
%%
%
%
ˆ‰
n 0 lim 0
n
ÊÊÊ Ê œ
Ä_
c
nn n
"" " "
%cc c
%%
¸¸
92. Let {a } and {b } be sequences both converging to L. Define {c } by c b and c a , where
nn n2nn2n1n
œœ
n 1, 2, 3, . For all 0 there exists N such that when n N then a L and there exists Nχ %%
"" #
kk
n
such that when n N then b L . If n 1 2max{N N }, then c L , so {c } converges to L.ß
#"#
kk kk
nnn
%%
93. lim n lim exp ln n lim exp e 1
nn nÄ_ Ä_ Ä_
1n
nn
Î!
""
œœœœ
ˆ‰ ˆ‰
94. lim x lim exp ln x e 1, because x remains fixed while n gets large
nnÄ_ Ä_
1n
n
Î!
"
œœœ
ˆ‰
95. Assume the hypotheses of the theorem and let be a positive number. For all there exists a N such that%%
"
when n N then a L a L L a , and there exists a N such that whenÊÊ
" #
kk
nn n
%% % %
n N then c L c L c L . If n max{N N }, thenÊÊß
#"#
kk
nnn
%% % %
L abcL bL lim bL. Ÿ Ÿ Ê Ê œ%%%
nnn n n
kk nÄ_
96. Let . We have f continuous at L there exists so that x L f(x) f(L) . Also, a L there%$$%! Ê Ê Ä Êkk k k n
exists N so that for n N a L . Thus for n N, f(a ) f(L) f(a ) f(L). Ê Äkk k k
nnn
$%
97. a a 3n 3n 4n 4 3n 6n n 2
n1 n 3(n 1) 1
(n 1) 1 n 1 n n 1
3n 1 3n 4 3n 1
#
##
Ê ÊÊ
4 2; the steps are reversible so the sequence is nondecreasing; 3 3n 1 3n 3Ê Ê
3n
n1
"
1 3; the steps are reversible so the sequence is bounded above by 3Ê
98. a a
n1 n (2(n 1) 3)! (2n 3)! (2n 5)! (2n 3)! (2n 5)! (n 2)!
((n 1) 1)! (n 1)! (n 2)! (n 1)! (2n 3)! (n 1)!
Ê ÊÊ
(2n 5)(2n 4) n 2; the steps are reversible so the sequence is nondecreasing; the sequence is notÊ
bounded since (2n 3)(2n 2) (n 2) can become as large as we please
(2n 3)!
(n 1)!
œ â
99. a a 2 3 n 1 which is true for n 5; the steps are
n1 n 23 23 23
(n 1)! n! 2 3 n!
(n 1)!
ŸÊ Ÿ Ê Ÿ Ê Ÿ
n1n1 nn n1n1
nn †
reversible so the sequence is decreasing after a , but it is not nondecreasing for all its terms; a 6, a 18,
&"#
œœ
a 36, a 54, a 64.8 the sequence is bounded from above by 64.8
$%&
œœœœÊ
324
5
100. a a 2 2 ; the steps are
n1 n 2222 2
n1 n n n1 n(n 1)
# # # # #
"" "" "
Ê Ê Ê
n1 n n1 n n1
reversible so the sequence is nondecreasing; 2 2 the sequence is bounded from above Ÿ Ê
2
n
"
#n
101. a 1 converges because 0 by Example 1; also it is a nondecreasing sequence bounded above by 1
nœ Ä
""
nn
102. a n diverges because n and 0 by Example 1, so the sequence is unbounded
nœ Ä_ Ä
""
nn
103. a 1 and 0 ; since 0 (by Example 1) 0, the sequence converges; also it is
n21
2nn
œœ Ä ÊÄ
n
nn n n
" """ "
## #
a nondecreasing sequence bounded above by 1
104. a ; the sequence converges to by Theorem 5, #4
n21 2
333
n
œœ !
n
nn
"
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
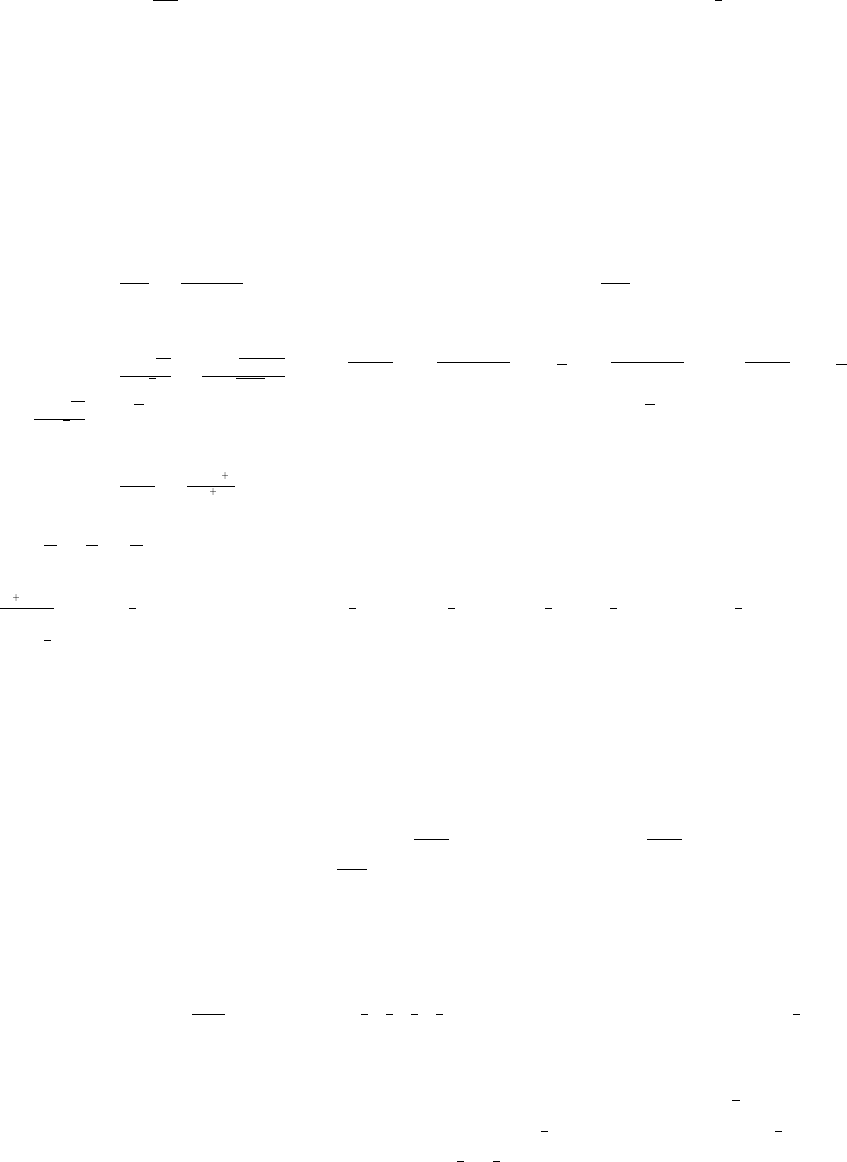
Section 11.1 Sequences 703
105. a ( 1) 1 diverges because a 0 for n odd, while for n even a 2 1 converges to 2; it
nnn
nn1
n n
œ œ œ ab
ˆ‰ ˆ ‰
"
diverges by definition of divergence
106. x max {cos 1 cos 2 cos 3 cos n} and x max {cos 1 cos 2 cos 3 cos (n 1)} x with x 1
nn1 nn
œ ßßßáß œ ßßßáß Ÿ
so the sequence is nondecreasing and bounded above by 1 the sequence converges.Ê
107. If {a } is nonincreasing with lower bound M, then { a } is a nondecreasing sequence with upper bound M.
nn
By Theorem 1, { a } converges and hence {a } converges. If {a } has no lower bound, then { a } has no
nnn n
upper bound and therefore diverges. Hence, {a } also diverges.
n
108. a a n 2n 1 n 2n 1 0 and 1; thus the sequence is
nn1 n1 n1
nn1 n
(n 1)
Í ÍÍ
"
##
nonincreasing and bounded below by 1 it convergesÊ
109. a a n 1 2n 2n n 2n 2n n 1 n
nn1 12n
n
2(n 1)
n1
Í Í Í
"
##
ÈÈ
ÈÈ ÈÈ
ÈÈ
ÈÈ
and 2 ; thus the sequence is nonincreasing and bounded below by 2 it converges
12n
n
È
ÈÊ
ÈÈ
110. a a 2 2 4 2 2 4 2 2 2 4 2 4
nn1 14 14
2
n1 n1n n nn1 n1 n n1n nn1
ÍÍÍ
#
nn1
nn1
2 1 2 4 4 1 4 (2 4) 1 ( 2) 4 ; thus the sequence is nonincreasing. However,Í Í Í††
nn1 n n
a 2 which is not bounded below so the sequence diverges
n4
2
n
œœ
""
##
nn n
n
111. 4 so a a 4 4 1 and
43 3 3 3 3 3 3
44 4444 4
nnnnn1
nn1
n1 n
n
"
œ Í Í Í
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
4 4; thus the sequence is nonincreasing and bounded below by 4 it converges Ê
ˆ‰
3
4
n
112. a 1, a 2 3, a 2(2 3) 3 2 2 3, a 2 2 2 3 3 2 2 1 3,
"# $ %
##$$
œ œ œ œ " œ " œ ab a b abab
22
††
a 2 2 2 1 3 3 2 2 1 3, , a 2 2 1 3 2 3 2 3
&$ $ % % " " "
œœáœ œ cdab abab nnn n n1
†
2(13)3 23; a a 23 2 3 2 2 12œ œ Í Í Í Ÿ
n1 n n n1 n n1
nn1
so the sequence is nonincreasing but not bounded below and therefore diverges
113. Let 0 M 1 and let N be an integer greater than . Then n N n n nM M Ê Ê
MM
1M 1M
n M nM n M(n 1) M.Ê Ê Ê
n
n1
114. Since M is a least upper bound and M is an upper bound, M M . Since M is a least upper bound and M
"#"##"
Ÿ
is an upper bound, M M . We conclude that M M so the least upper bound is unique.
#" "#
Ÿœ
115. The sequence a 1 is the sequence , , , , . This sequence is bounded above by ,
n() 33 3
œ á
"
# #### #
""
n
but it clearly does not converge, by definition of convergence.
116. Let L be the limit of the convergent sequence {a }. Then by definition of convergence, for there
n%
#
corresponds an N such that for all m and n, m N a L and n N a L . NowÊ Ê kk kk
mn
%%
##
a a a L L a a L L a whenever m N and n N.kkk kkkkk
mn m n m n
œ Ÿ œ
%%
##%
117. Given an 0, by definition of convergence there corresponds an N such that for all n N,%
La and La . Now LL LaaL La aL 2.kk kk kkk kkkkk
"# #"#"#"
œ Ÿ œ
nn nnnn
%% %%%
L L 2 says that the difference between two fixed values is smaller than any positive number 2 .kk
#"
% %
The only nonnegative number smaller than every positive number is 0, so L L 0 or L L .kk
"# " #
œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

704 Chapter 11 Infinite Sequences and Series
118. Let k(n) and i(n) be two order-preserving functions whose domains are the set of positive integers and whose
ranges are a subset of the positive integers. Consider the two subsequences a and a , where a L ,
kn in knÐÑ ÐÑ ÐÑ "
Ä
a L and L L . Thus a a L L 0. So there does not exist N such that for all m, n N
in kn inÐÑ ÐÑ ÐÑ
#"# "#
Ä Á Ä
¸¸
kk
a a . So by Exercise 116, the sequence a is not convergent and hence diverges.Ê Ö×kk
mn n
%
119. a L given an 0 there corresponds an N such that 2k N a L . Similarly,
2k 2k
ÄÍ Ê %%
""
cdkk
a L 2k 1 N a L . Let N max{N N }. Then n N a L whether
2k 1 2k 1 n# "#
ÄÍ Ê œ ß Ê cd kkkk%%
n is even or odd, and hence a L.
nÄ
120. Assume a 0. This implies that given an 0 there corresponds an N such that n N a 0
n n
Ä Ê%%kk
a a a 0 a 0. On the other hand, assume a 0. This implies thatÊÊ Ê Ê Ä Äkk k k k k kk kkkk kk
nn n n n
%% %
given an 0 there corresponds an N such that for n N, a 0 a a%%%%ÊÊkk kk kkkk kk
nnn
a 0 a 0.ÊÊÄkk
nn
%
121. 0.5 1 10 1 n n 692.8
¹¹
Ȉ‰ ˆ‰ ˆ‰
n
999
1000
Ê Ê Ê Ê
$ "" " "
##
Î
1000 1000 1000 1000
1n 999 1001
nn
ln
ln ˆ‰
ˆ‰
N 692; a and lim a 1Êœ œ œ
nn
1n
ˆ‰
"
#
Î
nÄ_
122. n 1 10 n 1 n n 9123 N 9123;
¸ ¸ ˆ‰ ˆ‰
È
n Ê Ê Ê Ê œ
$ Î
""
1000 1000 1000 1000
1n 999 1001
nn
a n n and lim a 1
nn
1n
œœ œ
È
nÎnÄ_
123. (0.9) 10 n ln (0.9) 3 ln 10 n 65.54 N 65; a and lim a 0
n3 ln 10 9
ln (0.9) 10
nn
n
Ê Ê ¸ Êœ œ œ
$ ˆ‰ nÄ_
124. 10 n! 2 10 and by calculator experimentation, n 14 N 14; a and lim a 0
2 2
n! n!
nnn
n n
Ê Êœ œ œ
( ( nÄ_
125. (a) f(x) x a f (x) 2x x x xœÊ œ Ê œ Ê œ œ œ
#w
##
n1 n n1
xa 2x xa xa
x2x2x
x
nnnnn
nnn
na
x
ab ˆ‰
(b) x 2, x 1.75, x 1.732142857, x 1.73205081, x 1.732050808; we are finding the positive
"# $ % &
œœ œ œ œ
number where x 3 0; that is, where x 3, x 0, or where x 3 .
##
œ œ œ
È
126. x 1.5, x 1.416666667, x 1.414215686, x 1.414213562, x 1.414213562; we are finding the
"#$%&
œœœœœ
positive number x 2 0; that is, where x 2, x 0, or where x 2 .
##
œ œ œ
È
127. x 1, x 1 cos (1) 1.540302306, x 1.540302306 cos (1 cos (1)) 1.570791601,
"# $
œœ œ œ œ
x 1.570791601 cos (1.570791601) 1.570796327 to 9 decimal places. After a few steps, the
%#
œ œœ
1
arc x and line segment cos x are nearly the same as the quarter circle.ab ab
n1 n1
128. (a) S 6.815, S 6.4061, S 6.021734, S 5.66042996, S 5.320804162, S 5.001555913,
"# $ % & '
œœ œ œ œ œ
S 4.701462558, S 4.419374804, S 4.154212316, S 3.904959577, S 3.670662003,
()*"!""
œœœœœ
S 3.450422282 so it will take Ford about 12 years to catch up
"# œ
(b) x 11.8¸
129-140. Example CAS Commands:
:Maple
with( Student[Calculus1] );
f := x -> sin(x);
a := 0;
b := Pi;
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.1 Sequences 705
plot( f(x), x=a..b, title="#23(a) (Section 5.1)" );
N := [ 100, 200, 1000 ]; # (b)
for n in N do
Xlist := [ a+1.*(b-a)/n*i $ i=0..n ];
Ylist := map( f, Xlist );
end do:
for n in N do # (c)
Avg[n] := evalf(add(y,y=Ylist)/nops(Ylist));
end do;
avg := FunctionAverage( f(x), x=a..b, output=value );
evalf( avg );
FunctionAverage(f(x),x=a..b,output=plot); # (d)
fsolve( f(x)=avg, x=0.5 );
fsolve( f(x)=avg, x=2.5 );
fsolve( f(x)=Avg[1000], x=0.5 );
fsolve( f(x)=Avg[1000], x=2.5 );
: (sequence functions may vary):Mathematica
Clear[a, n]
a[n_]; = n1 / n
first25= Table[N[a[n]],{n, 1, 25}]
Limit[a[n], n 8]Ä
The last command (Limit) will not always work in Mathematica. You could also explore the limit by enlarging your table
to more than the first 25 values.
If you know the limit (1 in the above example), to determine how far to go to have all further terms within 0.01 of the
limit, do the following.
Clear[minN, lim]
lim= 1
Do[{diff=Abs[a[n] lim], If[diff < .01, {minN= n, Abort[]}]}, {n, 2, 1000}]
minN
For sequences that are given recursively, the following code is suggested. The portion of the command a[n_]:=a[n] stores
the elements of the sequence and helps to streamline computation.
Clear[a, n]
a[1]= 1;
a[n_]; = a[n]= a[n 1] (1/5) (n 1)
first25= Table[N[a[n]], {n, 1, 25}]
The limit command does not work in this case, but the limit can be observed as 1.25.
Clear[minN, lim]
lim= 1.25
Do[{diff=Abs[a[n] lim], If[diff < .01, {minN= n, Abort[]}]}, {n, 2, 1000}]
minN
141. Example CAS Commands:
:Maple
with( Student[Calculus1] );
A := n->(1+r/m)*A(n-1) + b;
A(0) := A0;
A(0) := 1000; r := 0.02015; m := 12; b := 50; # (a)
pts1 := [seq( [n,A(n)], n=0..99 )]:
plot( pts1, style=point, title="#141(a) (Section 11.1)");
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

706 Chapter 11 Infinite Sequences and Series
A(60);
The sequence { A[n] } is not unbounded;
limit( A[n], n=infinity ) = infinity.
A(0) := 5000; r := 0.0589; m := 12; b := -50; # (b)
pts1 := [seq( [n,A(n)], n=0..99 )]:
plot( pts1, style=point, title="#141(b) (Section 11.1)");
A(60);
pts1 := [seq( [n,A(n)], n=0..199 )]:
plot( pts1, style=point, title="#141(b) (Section 11.1)");
# This sequence is not bounded, and diverges to -infinity:
limit( A[n], n=infinity ) = -infinity.
A(0) := 5000; r := 0.045; m := 4; b := 0; # (c)
for n from 1 while A(n)<20000 do end do; n;
It takes 31 years (124 quarters) for the investment to grow to $20,000 when the interest rate is 4.5%, compounded
quarterly.
r := 0.0625;
for n from 1 while A(n)<20000 do end do; n;
When the interest rate increases to 6.25% (compounded quarterly), it takes only 22.5 years for the balance to reach
$20,000.
B := k -> (1+r/m)^k * (A(0)+m*b/r) - m*b/r; # (d)
A(0) := 1000.; r := 0.02015; m := 12; b := 50;
for k from 0 to 49 do
printf( "%5d %9.2f %9.2f %9.2f\n", k, A(k), B(k), B(k)-A(k) );
end do;
A(0) := 'A(0)'; r := 'r'; m := 'm'; b := 'b'; n := 'n';
eval( AA(n+1) - ((1+r/m)*AA(n) + b), AA=B );
simplify( % );
142. Example CAS Commands:
:Maple
r := 3/4.; # (a)
for k in $1..9 do
A := k/10.;
L := [0,A];
for n from 1 to 99 do
A := r*A*(1-A);
L := L, [n,A];
end do;
pt[r,k/10] := [L];
end do:
plot( [seq( pt[r,a], a=[($1..9)/10] )], style=point, title="#142(a) (Section 11.1)" );
R1 := [1.1, 1.2, 1.5, 2.5, 2.8, 2.9]; # (b)
for r in R1 do
for k in $1..9 do
A := k/10.;
L := [0,A];
for n from 1 to 99 do
A := r*A*(1-A);
L := L, [n,A];
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 11.1 Sequences 707
end do;
pt[r,k/10] := [L];
end do:
t := sprintf("#142(b) (Section 11.1)\nr = %f", r);
P[r] := plot( [seq( pt[r,a], a=[($1..9)/10] )], style=point, title=t );
end do:
display( [seq(P[r], r=R1)], insequence=true );
R2 := [3.05, 3.1, 3.2, 3.3, 3.35, 3.4]; # (c)
for r in R2 do
for k in $1..9 do
A := k/10.;
L := [0,A];
for n from 1 to 99 do
A := r*A*(1-A);
L := L, [n,A];
end do;
pt[r,k/10] := [L];
end do:
t := sprintf("#142(c) (Section 11.1)\nr = %f", r);
P[r] := plot( [seq( pt[r,a], a=[($1..9)/10] )], style=point, title=t );
end do:
display( [seq(P[r], r=R2)], insequence=true );
R3 := [3.46, 3.47, 3.48, 3.49, 3.5, 3.51, 3.52, 3.53, 3.542, 3.544, 3.546, 3.548]; # (d)
for r in R3 do
for k in $1..9 do
A := k/10.;
L := [0,A];
for n from 1 to 199 do
A := r*A*(1-A);
L := L, [n,A];
end do;
pt[r,k/10] := [L];
end do:
t := sprintf("#142(d) (Section 11.1)\nr = %f", r);
P[r] := plot( [seq( pt[r,a], a=[($1..9)/10] )], style=point, title=t );
end do:
display( [seq(P[r], r=R3)], insequence=true );
R4 := [3.5695]; # (e)
for r in R4 do
for k in $1..9 do
A := k/10.;
L := [0,A];
for n from 1 to 299 do
A := r*A*(1-A);
L := L, [n,A];
end do;
pt[r,k/10] := [L];
end do:
t := sprintf("#142(e) (Section 11.1)\nr = %f", r);
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
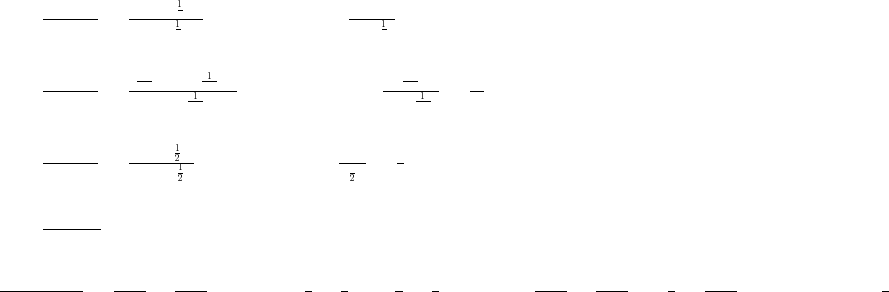
708 Chapter 11 Infinite Sequences and Series
P[r] := plot( [seq( pt[r,a], a=[($1..9)/10] )], style=point, title=t );
end do:
display( [seq(P[r], r=R4)], insequence=true );
R5 := [3.65]; # (f)
for r in R5 do
for k in $1..9 do
A := k/10.;
L := [0,A];
for n from 1 to 299 do
A := r*A*(1-A);
L := L, [n,A];
end do;
pt[r,k/10] := [L];
end do:
t := sprintf("#142(f) (Section 11.1)\nr = %f", r);
P[r] := plot( [seq( pt[r,a], a=[($1..9)/10] )], style=point, title=t );
end do:
display( [seq(P[r], r=R5)], insequence=true );
R6 := [3.65, 3.75]; # (g)
for r in R6 do
for a in [0.300, 0.301, 0.600, 0.601 ] do
A := a;
L := [0,a];
for n from 1 to 299 do
A := r*A*(1-A);
L := L, [n,A];
end do;
pt[r,a] := [L];
end do:
t := sprintf("#142(g) (Section 11.1)\nr = %f", r);
P[r] := plot( [seq( pt[r,a], a=[0.300, 0.301, 0.600, 0.601] )], style=point, title=t );
end do:
display( [seq(P[r], r=R6)], insequence=true );
11.2 INFINITE SERIES
1. s lim s 3
nn
a1 r
(1 r)
21
1 1
2
œœ Ê œœ
ab ˆ‰ˆ‰
ˆ‰ ˆ‰
n3
n
33
nÄ_
2. s lim s
nn
a1 r
(1 r) 11
1
1 1
œœ Ê œœ
abˆ‰ˆ ‰ ˆ‰ˆ‰
ˆ‰ ˆ‰
"
n99
100 100 100
n
100 100
nÄ_
3. s lim s
nn
a1 r
(1 r) 3
1
1
2
œœ Ê œœ
ab ˆ‰
ˆ‰ ˆ‰
"
nn
3
nÄ_
4. s , a geometric series where r 1 divergence
n1 ( 2)
1 ( 2)
œÊ
nkk
5. s lim s
""" """" """" "
# # # # # # #(n 1)(n ) n 1 n 3 3 4 n 1 n n
n n
œ Êœá œ Ê œ
ˆ‰ˆ‰ ˆ ‰ nÄ_
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.2 Infinite Series 709
6. s 5 5
5 5 5 5 55 55 5 5 5 5 5
n(n 1) nn 1 2 23 34 n 1n nn 1 n 1
n
œ Êœá œ
ˆ‰ˆ‰ˆ‰ˆ‰ˆ‰
lim s 5ʜ
nÄ_ n
7. 1 , the sum of this geometric series is á œ œ
"" " " "
41664 5
1 1
4
ˆ‰ ˆ‰
44
8. , the sum of this geometric series is
"" " "
#16 64 256 1
1
á œ
ˆ‰
ˆ‰
16
4
9. , the sum of this geometric series is
77 7 7
41664 3
1
á œ
ˆ‰
ˆ‰
7
4
4
10. 5 , the sum of this geometric series is 4á œ
55 5 5
41664 1
ˆ‰
4
11. (5 1) , is the sum of two geometric series; the sum is á
ˆ‰ˆ‰ˆ‰
555
34987##
"" "
10
5323
1 1
"
##
ˆ‰ ˆ‰
œœ
3
12. (5 1) , is the difference of two geometric series; the sum is á
ˆ‰ˆ‰ˆ‰
555
34987##
"" "
10
5317
1 1
"
##
ˆ‰ ˆ‰
œœ
3
13. (1 1) , is the sum of two geometric series; the sum is á
ˆ‰ˆ‰ˆ ‰
11 1
5425815##
"" "
2
1517
1 1 66
"
ˆ‰ ˆ‰
œœ
5
14. 2 2 1 ; the sum of this geometric series is 2 áœ á œ
48 16 24 8 10
525125 525125 3
1
ˆ‰ Š‹
"
ˆ‰
2
5
15. s 1
4
(4n 3)(4n 1) 4n 3 4n 1 5 5 9 9 13 4n 7 4n 3
n
" " """"" " "
œ Êœ á
ˆ‰ˆ‰ˆ ‰ ˆ ‰
1 lim s lim 1 1œÊ œ œ
ˆ‰ ˆ‰
"" " "
4n 3 4n 1 4n 1 4n 1
n
nnÄ_ Ä_
16. A(2n 1) B(2n 1) 6
6AB
(2n 1)(2n 1) 2n 1 2n 1 (2n 1)(2n 1)
A(2n 1) B(2n 1)
œœ Êœ
(2A 2B)n (A B) 6 2A 6 A 3 and B 3. Hence,
2A 2B 0 A B 0
A B6 AB6
Ê œÊ Ê Ê œÊœ œ
œ œ
œ œ
œœ
3 3
!!
ˆ‰
Š‹
kk
n1 n1œœ
6
(2n 1)(2n 1) n 1 n 1 133557 (k 1) 12k 1 k 1 # # # #
" " """""" " " "
œ œ á
3 1 the sum is lim 3 1 3œ Ê œ
ˆ‰ ˆ‰
""
# #k 1 k 1
kÄ_
17. 40n A B C D
(2n 1) (2n 1) (2n 1) (2n 1) (2n 1) (2n 1)
œ
œA(2n 1)(2n 1) B(2n 1) C(2n 1)(2n 1) D(2n 1)
(2n 1) (2n 1)
A(2n 1)(2n 1) B(2n 1) C(2n 1)(2n 1) D(2n 1) 40nÊ œ
## ##
A8n4n2n1B4n4n1C8n4n2n1D4n4n140nÊ œ œabababab
$##$# #
(8A 8C)n (4A 4B 4C 4D)n ( 2A 4B 2C 4D)n ( A B C D) 40nÊ œ
$#
8A 8C 0 8A 8C 0
4A 4B 4C 4D 0 A B C D 0
2A 4B 2C 4D 40 A 2
A B C D 0
ÊÊ
œ œ
œ œ
œ
œ
ÚÚ
ÝÝ
ÝÝ
ÛÛ
ÝÝ
ÝÝ
ÜÜ
BC2D20 2B2D 20
A BC D 0
4B 20 B 5
B D 0
œ œ
œ
Êʜʜ
œ
œ
and D 5 C 0 and A 0. Hence,
A C 0
A5C50
œ Ê Ê œ œ
œ
œ
œ!’“
k
n1œ
40n
( n 1) (2n 1)#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

710 Chapter 11 Infinite Sequences and Series
5 5œ œ á
!’“Š ‹
k
n1œ
" " """ " " " " "
# # # # # #( n 1) ( n 1) 1 9 9 5 5 (2(k 1) 1) ( k 1) ( k 1)
5 1 the sum is lim 5 1 5œ Ê œ
Š‹ Š‹
""
(2k 1) (2k 1)
nÄ_
18. s 1
2n 1
n (n 1) n (n 1) 4 4 9 9 16 (n 1) n n (n 1)
n
"" """"" "" ""
œ Êœ á
ˆ‰ˆ‰ˆ ‰ ’“’“
lim s lim 1 1Êœœ
nnÄ_ Ä_
n(n 1)
’“
"
19. s 1 1
n22 4 n 1
33 nn
n 1 n 1
œá œ
Š‹Š‹Š‹Š ‹Š ‹
""""" """" "
ÈÈÈÈÈ ÈÈÈÈ È
lim s lim 1 1Êœœ
nnÄ_ Ä_
nn 1
Š‹
"
È
20. s
nœá œ
ˆ‰ˆ‰ˆ‰ˆ ‰ˆ ‰
"" "" "" " " " " " "
# #
##### # ### #
1n1 1n 1n 1n1 1n1
lim sÊ œœ
nÄ_ n1
"" "
##
21. snln 3 ln ln 4 ln 3 ln 5 ln 4 ln (n 1) ln n ln (n 2) ln (n 1)
χ
ˆ‰ˆ‰ˆ‰Š‹Š ‹
"" "" "" " " " "
#
lim sœ Ê œ
"" "
# #ln ln (n 2) ln
n
nÄ_
22. s tan (1) tan (2) tan (2) tan (3) tan (n 1) tan (n)
nχcdcdc d
" " " " " "
tan (n) tan (n 1) tan (1) tan (n 1) lim s tan (1) œ Ê œ œœcd
" " " " "
##
nÄ_ n44
111 1
23. convergent geometric series with sum 2 2
"
1
2
21
Š‹ È
È
2
œœ
È
24. divergent geometric series with r 2 1 25. convergent geometric series with sum 1kk È
œ œ
Š‹
Š‹
3
1
26. lim ( 1) n 0 diverges 27. lim cos (n ) lim ( 1) 0 diverges
nnnÄ_ Ä_ Ä_
ÁÊ œ ÁÊ
n1 n1
28. cos (n ) ( 1) convergent geometric series with sum 1œ Ê œ
n
1
5
6
"
Š‹
5
29. convergent geometric series with sum "
1
e
e1
Š‹
e
œ
30. lim ln 0 diverges
nÄ_
"
nœ_Á Ê
31. convergent geometric series with sum 2
220182
1 999
Š‹
10
œœ
32. convergent geometric series with sum "
1
x
x 1
Š‹
x
œ
33. difference of two geometric series with sum 3
""
##
1 1
33
Š‹ Š‹
2
33
œœ
34. lim 1 lim 1 e 0 diverges
nnÄ_ Ä_
ˆ‰ ˆ ‰
œ œÁÊ
""
"
nn
nn
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.2 Infinite Series 711
35. lim 0 diverges 36. lim lim lim n diverges
nnnnÄ_ Ä_ Ä_ Ä_
n! nnnn
1000 n! 1 n
n
n
œ_Á Ê œ œ_ Ê
†
†
â
#â
37. ln ln (n) ln (n 1) s ln (1) ln (2) ln (2) ln (3) ln (3) ln (4)
!!
ˆ‰ c dcdcdcd
__
œœn1 n1
n
n 1œ Êœá
n
ln (n 1) ln (n) ln (n) ln (n 1) ln (1) ln (n 1) ln (n 1) lim s , diverges œ œ Ê œ_ Êcdcd nÄ_ n
38. lim a lim ln ln 0 diverges
nnÄ_ Ä_
nn
2n 1
œœÁÊ
ˆ‰ˆ‰
#
"
39. convergent geometric series with sum "
1 e
ˆ‰
eœ1
1
40. divergent geometric series with r 1kkœ¸
e 23.141
22.459
1e
41. ( 1) x ( x) ; a 1, r x; converges to for x 1
!! kk
__
œœn0 n0
œ œœ œ
nn n ""
1 ( x) 1 x
42. ( 1) x x ; a 1, r x ; converges to for x 1
!!
ab kk
__
œœn0 n0
œ œœ
n2n n
1 x
##
"
43. a 3, r ; converges to for 1 1 or 1 x 3œœ œ
x 1 3 6 x
1 3 x
"
##
Š‹
x
44. ; a , r ; converges to
!!
ˆ‰ ˆ‰
__
œœn0 n0
(1)
3 sin x 3 sin x 3 sin x
nn
1
# # #
"""""
nœœœ ˆ‰
Š‹
3 sin x
for all x since for all xœœ ŸŸ
3 sin x 3 sin x
2(4 sin x) 8 2 sin x 4 3 sin x
"""
#
ˆ‰
45. a 1, r 2x; converges to for 2x 1 or xœœ
""
#1 2x kk kk
46. a 1, r ; converges to for 1 or x 1.œœ œ
""
xx 1x
1
x1
Š‹
x¸¸ kk
47. a 1, r (x 1) ; converges to for x 1 1 or 2 x 0œ œ œ
n
1 (x 1) x
""
# kk
48. a 1, r ; converges to for 1 or 1 x 5œœ œ
3 x 2 3 x
1 x 1
"
##
Š‹
3 x ¸¸
49. a 1, r sin x; converges to for x (2k 1) , k an integerœœ Á
"
#1 sin x
1
50. a 1, r ln x; converges to for ln x 1 or e x eœœ
"
"
1 ln x kk
51. 0.23 52. 0.234 œœœ œ œœ
!!
ˆ‰ ˆ‰
_ _
œ œn0 n0
23 23 234 234
100 10 99 1000 10 999
n n
1 1
" "
Š‹ Š‹
ˆ‰ Š‹
23 234
100 1000
1000
100
53. 0.7 54. 0.d œœœ œœœ
!!
ˆ‰ ˆ‰
_ _
œ œn0 n0
77 dd
10 10 9 10 10 9
n n
1 1
" "
Š‹ Š‹
Š‹ Š‹
7 d
10 10
10 10
55. 0.06 œœœœ
!ˆ‰ˆ‰ˆ‰
_
œn0
16 6
10 10 10 90 15
n
1
""
Š‹
Š‹
6
100
10
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

712 Chapter 11 Infinite Sequences and Series
56. 1.414 1 1 1œ œ œ œ
!ˆ‰
_
œn0
414 414 413
1000 10 999 999
n
1
""
Š‹
Š‹
414
1000
1000
57. 1.24123 œ œ œ œ œ œ
124 123 124 124 123 124 123
100 10 10 100 100 10 10 100 99,900 99,900 33,300
n
1
123,999 41,333
!ˆ‰
_
œn0
"
Š‹
Š‹
123
10
10
58. 3.142857 3 3 3œ œ œ œ œ
!ˆ‰
_
œn0
142,857 142,857 3,142,854 116,402
10 10 10 1 999,999 37,037
n
1
"
Š‹
Š‹
142,857
10
10
59. (a) (b) (c)
!!!
___
œ œ œn 2 n0 n5
"" "
#(n 4)(n 5) (n 2)(n 3) (n 3)(n )
60. (a) (b) (c)
!!!
___
œ œ œn 1 n3 n20
55 5
(n 2)(n 3) (n 2)(n 1) (n 19)(n 18)
61. (a) one example is 1
""" "
#
ᜠœ
4816 1
Š‹
Š‹
(b) one example is 3 ᜠœ
333 3
4816 1
#
Š‹
Š‹
3
(c) one example is 1 ; the series k where k is any positive or á ᜠœ
""" "
##
4816 48
kkk
1
Š‹
Š‹
k
negative number.
62. The series k is a geometric series whose sum is k where k can be any positive or negative number.
!ˆ‰
_
œn0
1
2
n1
1
Š‹
Š‹
k
œ
63. Let a b . Then a b 1, while (1) diverges.
nn n n
nn
a
b
œœ œ œ œ œ
ˆ‰ ˆ‰
!!! ! !
Š‹
""
##
__ _ _ _
œœ œ œ œn1 n1 n1 n1 n1
n
n
64. Let a b . Then a b 1, while a b AB.
nn n n nn
nnn
43
œœ œ œ œ œ œÁ
ˆ‰ ˆ‰ ˆ‰
!!! ! !
ab
""""
##
__ _ _ _
œœ œ œ œn1 n1 n1 n1 n1
65. Let a and b . Then A a , B b 1 and 1 .
nn n n
43bB
nn n
aA
œœ œœœœ œœÁ
ˆ‰ ˆ‰ ˆ‰
!!!!
Š‹
"" " "
# #
____
œœœœn1 n1 n1 n1
n
n
66. Yes: diverges. The reasoning: a converges a 0 diverges by the
!! !
Š‹ Š‹
"""
aaa
nn
nnn
Ê Ä Ê Ä_Ê
nth-Term Test.
67. Since the sum of a finite number of terms is finite, adding or subtracting a finite number of terms from a series
that diverges does not change the divergence of the series.
68. Let A a a a and lim A A. Assume a b converges to S. Let
nnnnn
œá œ
"# nÄ_ !ab
S(ab)(ab) (ab) S (aa a)(bb b)
nnnnnn
œá Êœáá
"" ## "# "#
b b b S A lim b b b S A b converges. ThisÊáœ Ê á œÊ
"# "#nnn n n
nÄ_ ab
!
contradicts the assumption that b diverges; therefore, a b diverges.
!!
ab
nnn
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 11.3 The Integral Test 713
69. (a) 5 1 r r ; 2 2 2
22 333
1r 5 5 5 5
#
œÊœÊœ á
ˆ‰ ˆ‰
(b) 5 1 r r ;
Š‹
13
2
1 r 10 10 2 10 10 10
13 3 13 13 3 13 3 13 3
###
#$
œÊœÊœá
ˆ‰ ˆ‰ ˆ‰
70. 1 e e 9 1 e e b ln ᜠœÊ œ Ê œÊœ
b2b b b
1e 999
88""
bˆ‰
71. s 1 2r r 2r r 2r r 2r , n 0, 1,
n2n 2n 1
œ á œ á
#$%&
s 1rr r 2r2r2r 2r lim sÊ œ á á Ê œ
n n
2n 2n 1
1r 1r
2r
aba b
#% $ & "
nÄ_
, if r 1 or r 1œ
12r
1r
#
kk kk
72. L sœ œ
naar
1r 1r 1r
a1 r
ab
nn
73. distance 4 2 (4) (4) 4 2 28 mœ ᜠœ
’“
ˆ‰ ˆ‰
33 3
44 1
#
Š‹
3
4
74. time 2 2 2 2χχ
ÉÉ ÉÉ
ˆ ‰ˆ‰ ˆ ‰ˆ‰ ˆ ‰ˆ‰ ˆ‰
ÉÉÉ
”•
É
443 43 43 4433
4.9 4.9 4 4.9 4 4.9 4 4.9 4.9 4 4
#$ #
12.58 secœ œ œ œ ¸
24 24
4.9 4.9 4.9 4.9 2 3
1
3423
423 43
4.9 2 3 4.9 2 3
ÈÈ ÈÈ È
ÈÈ
Š‹
ÈÈ
ÈÈÈÈ
Š‹ Š‹
Š‹ Š‹Š ‹
–—
ÉÉ
3
4
3
4
75. area 2 2 (1) 4 2 1 8 mœ á œ á œ œ
## #
##
""
#
Š‹ Š‹
ÈÈ2
4
1
76. area 2 4 8œáœáœ œ
–—–—–—
ˆ‰
111 1
Š‹ Š‹ Š‹ Š‹
Š‹
### #
""
48 4
11
4816
1
1
77. (a) L 3, L 3 , L 3 , , L 3 lim L lim 3
"# $
#
œœ œ áœ Ê œ œ_
ˆ‰ ˆ‰ ˆ‰ ˆ‰
44 4 4
33 3 3
nn
n1 n1
nnÄ_ Ä_
(b) Using the fact that the area of an equilateral triangle of side length s is s , we see that A ,
ÈÈ
33
44
2"œ
AA3 , AA34 ,
#" $#
""
##
œ œ œ œ
Š‹ Š‹
ˆ‰ ˆ‰
ab
È ÈÈ È ÈÈÈ
3 33 3 333
43 4 1 43 4 12 7
22
2
A A 3 4 , A A 3 4 , . . . ,
%$ ""
œ œab ab
Š‹ Š‹
ˆ‰ ˆ‰
23
33
43 43
22
54
ÈÈ
34
A 34 334 33 .
n
nn n
k2 k2 k2
œ œ œ
ÈÈÈ È
333 3
4434 94
k2 k
k1 k1 4
9
!! !
ab ab
Š‹
ˆ‰ ˆ‰
ÈÈ
Œ
$
""
2
k
k1
lim A lim 3 3 3 3 3 3
nnÄ_ Ä_
n
n
k2
œ œ œ œ
ŒŒ
ÈÈÈ
Œ
!ˆ‰
ÈÈÈÈ
33323
444205
41
91
k
k1
1
36 4
9
78. Each term of the series represents the area of one of the squares shown in the figure, and all of the
!
_
œn1
"
n
squares lie inside the rectangle of width 1 and length 2. Since the squares do not fill the
!ˆ‰
n0
""
#
n
1
œœ
rectangle completely, and the area of the rectangle is 2, we have 2.
!
_
œn1
"
n
11.3 THE INTEGRAL TEST
1. converges; a geometric series with r 1 2. converges; a geometric series with r 1œ œ
" "
10 e
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
714 Chapter 11 Infinite Sequences and Series
3. diverges; by the nth-Term Test for Divergence, lim 1 0
nÄ_
n
n1œÁ
4. diverges by the Integral Test; dx 5 ln (n 1) 5 ln 2 dx
''
11
n55
x1 x1
œÊ Ä_
5. diverges; 3 , which is a divergent p-series (p )
!!
__
œœn1 n1
3
nn
ÈÈ
œœ
""
#
6. converges; 2 , which is a convergent p-series (p )
!!
__
œœn1 n1
"
#
23
nn n
Èœ œ
7. converges; a geometric series with r 1œ
"
8
8. diverges; 8 and since diverges, 8 diverges
!! ! !
__ _ _
œœ œ œn1 n1 n1 n1
"81 1
nn n n
œ
9. diverges by the Integral Test: dx ln n ln 2 dx
''
22
nln x ln x
xx
œÊ Ä_
"
#
#
ab
10. diverges by the Integral Test: dx; te dt lim 2te 4e
t ln x
dt
dx e dt
''
2ln2
ln x
x
dx
x
t
t2 t2 t2
ÈÔ×
ÕØ ‘
œ
œ
œ
Ĝ
ÎÎÎ
bÄ_
b
ln 2
lim 2e (b 2) 2e (ln 2 2)œœ_
bÄ_ ‘
b2 ln2 2ÎÐÑÎ
11. converges; a geometric series with r 1œ
2
3
12. diverges; lim lim lim 0
nn nÄ_ Ä_ Ä_
55 ln 5ln 55
43 4 ln 4 ln 4 4
n
nn
nn
œœ œ_Á
ˆ‰ˆ‰
13. diverges; 2 , which diverges by the Integral Test
!!
__
œœn0 n0
"
2
n1 n 1
œ
14. diverges by the Integral Test: ln (2n 1) as n
'1
ndx
2x 1#
"
œ Ä_ Ä_
15. diverges; lim a lim lim 0
nn nÄ_ Ä_ Ä_
n22 ln 2
n1 1
œœ œ_Á
nn
16. diverges by the Integral Test: ; ln n 1 ln 2
ux
du
''
12
nn1
dx du
xx1 dx
xu
ÈÈ
ˆ‰ È
–—
Ȉ‰
È
œ"
œÄœ
as n Ä_ Ä_
17. diverges; lim lim lim 0
nn nÄ_ Ä_ Ä_
ÈÈ
Š‹
Š‹
nn
ln n œœœ_Á
2n
n#
18. diverges; lim a lim 1 e 0
nnÄ_ Ä_
nn
n
œœÁ
ˆ‰
"
19. diverges; a geometric series with r 1.44 1œ¸
"
#ln
20. converges; a geometric series with r 0.91 1œ¸
"
ln 3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.3 The Integral Test 715
21. converges by the Integral Test: dx; du
u ln x
du dx
''
3ln3
Š‹
ÈÈ
x
(ln x) (ln x) 1 xuu 1
""
”•
œ
π
lim sec u lim sec b sec (ln 3) lim cos sec (ln 3)œœœ
bb bÄ_ Ä_ Ä_
cd c dkk ‘ˆ‰
" " " " "
"
b
ln 3 b
cos (0) sec (ln 3) sec (ln 3) 1.1439œ œ ¸
" " "
#
1
22. converges by the Integral Test: dx dx; du
u ln x
du dx
'' '
11 0
""
"
x 1 ln x 1 (ln x) 1 u
x
ab Š‹
π
œ
œ
x”•
lim tan u lim tan b tan 0 0œœœœ
bbÄ_ Ä_
cd a b
" " "
##
b
0
11
23. diverges by the nth-Term Test for divergence; lim n sin lim lim 1 0
nn
x0
Ä_ Ä_ Ä
ˆ‰
"
nx
sin x
œœœÁ
sin ˆ‰
ˆ‰
n
n
24. diverges by the nth-Term Test for divergence; lim n tan lim lim
nnnÄ_ Ä_ Ä_
ˆ‰
"
nœœ
tan sec
ˆ‰
ˆ‰ Š‹ˆ‰
Š‹
n
n
nn
n
lim sec sec 0 1 0œœœÁ
nÄ_
##
"
ˆ‰
n
25. converges by the Integral Test: dx; du lim tan u
ue
du e dx
''
1e
x
x
e
1e 1u
x
2x
""
”• cd
œ
œÄœ
nÄ_
b
e
lim tan b tan e tan e 0.35œœ¸
bÄ_ ab
" " "
#
1
26. converges by the Integral Test: dx; du du
ue
du e dx
dx du
'''
1ee
2222
1e u(1u) u u1
x
x
u
"
xÔ×
ÕØ ˆ‰
œ
œ
œ
Ĝ
lim 2 ln lim 2 ln 2 ln 2 ln 1 2 ln 2 ln 0.63œ œ œœ¸
bbÄ_ Ä_
‘ ˆ‰ ˆ‰ ˆ‰ ˆ‰
ube ee
u1 b1 e1 e1 e1
b
e
27. converges by the Integral Test: dx; 8u du 4u 4
utanx
du
''
14
22
4
8 tan x 3
1x 4 16 4
dx
1x
"
#
”• cd Š‹
œ
œÄœœœ
11 1
28. diverges by the Integral Test: dx; lim ln u
ux 1
du 2x dx
''
12
xdu
x1 4
##
#""
”• ‘
œ
œÄœ
bÄ_
b
2
lim (ln b ln 2)œœ_
bÄ_
"
#
29. converges by the Integral Test: sech x dx 2 lim dx 2 lim tan e
''
11
bb
1
œœ
bbÄ_ Ä_
e
1e
x
x
x
"
ab cd
2 lim tan e tan e 2 tan e 0.71œœ¸
bÄ_ ab
" " "b1
30. converges by the Integral Test: sech x dx lim sech x dx lim tanh x lim (tanh b tanh 1)
''
11
bb
1
##
œœœ
bbbÄ_ Ä_ Ä_
cd
1 tanh 1 0.76œ ¸
31. dx lim a ln x 2 ln x 4 lim ln ln ;
'1ˆ‰ ˆ‰
cdkkkk
a 3
x2 x4 b4 5
(b 2)
"
œ œ
bbÄ_ Ä_
b
1
aa
lim a lim (b 2) the series converges to ln if a 1 and diverges to if
, a 1
1, a 1
bbÄ_ Ä_
(b 2)
b4 3
a1 5
aœœ Ê œ _
_
œ
œˆ‰
a 1. If a 1, the terms of the series eventually become negative and the Integral Test does not apply. From
that point on, however, the series behaves like a negative multiple of the harmonic series, and so it diverges.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
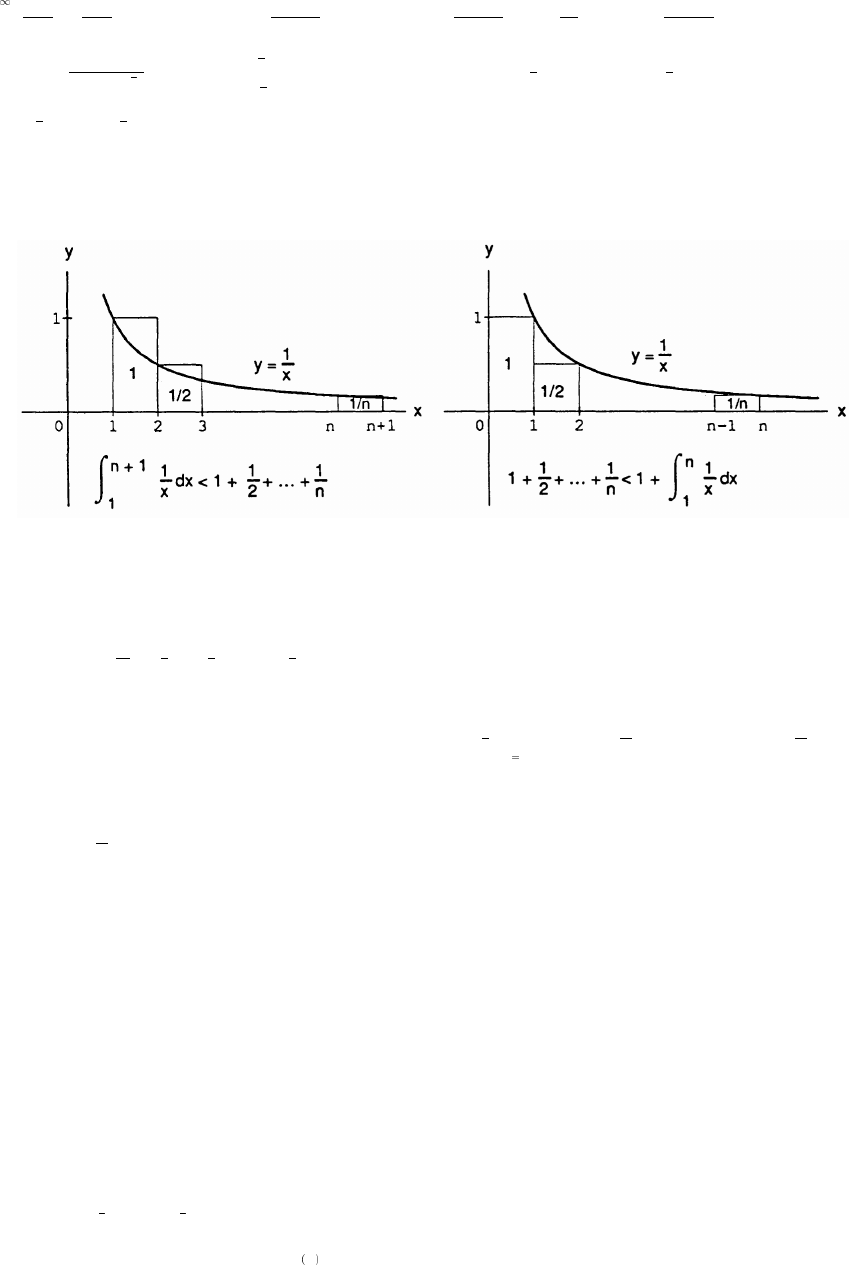
716 Chapter 11 Infinite Sequences and Series
32. dx lim ln lim ln ln ; lim
'3
b
3
ˆ‰ ˆ‰
’“¹¹
""
x1 x1 (x1) (b1) 4 (b1)
2a x1 b1 2 b
œ œ
bb bÄ_ Ä_ Ä_
2a 2a 2a 2a
lim the series converges to ln ln 2 if a and diverges to if
1, a
, a
œœÊ œœ_
œ
_
bÄ_
" "
# # #
"
#
"
#
a(b 1)
4
2a 1 ˆ‰
if a . If a , the terms of the series eventually become negative and the Integral Test does not apply.
""
##
From that point on, however, the series behaves like a negative multiple of the harmonic series, and so it
diverges.
33. (a)
(b) There are (13)(365)(24)(60)(60) 10 seconds in 13 billion years; by part (a) s 1 ln n whereab
*nŸ
n (13)(365)(24)(60)(60) 10 s 1 ln (13)(365)(24)(60)(60) 10œÊŸab a bab
**
n
1 ln (13) ln (365) ln (24) 2 ln (60) 9 ln (10) 41.55œ ¸
34. No, because and diverges
!!!
___
œœœn1 n1 n1
"" " "
nx x n n
œ
35. Yes. If a is a divergent series of positive numbers, then a also diverges and a .
!!!
ˆ‰ ˆ‰
_ _
œ œn1 n1
nnn
aa
"
## #
_
n1
œ
nn
There is no “smallest" divergent series of positive numbers: for any divergent series a of positive
!
_
œn1
n
numbers has smaller terms and still diverges.
!ˆ‰
_
œn1
an
#
36. No, if is a convergent series of positive numbers, then 2 a 2a also converges, and 2a a .
!!!
___
œœœn1 n1 n1
a
nnn nn
œ
There is no “largest" convergent series of positive numbers.
37. Let A and B 2 a , where {a } is a nonincreasing sequence of positive terms converging to
nkn k
k2
œœ
!!
nn
k1 k1œœ
a ab
k
0. Note that {A } and {B } are nondecreasing sequences of positive terms. Now,
nn
B2a4a8a 2a 2a 2a2a 2a2a2a2a
nn2
œá œ á
#%) # %% ))))
ab
naba b
2a 2a 2a 2a 2a 2a 2a 2a 2a 2a 2a á Ÿ á
ðóóóóóóóóóóóóóóñóóóóóóóóóóóóóóò
ˆ‰
aba b
ab ab ab22 2
nn n "# $% &'()
2 terms
n1
2a 2a 2a 2A 2 a . Therefore if a converges, ᜟ
ˆ‰
!!
ab a b ab ab
221 22 kk
n1 n1 nn
_
œk1
then {B } is bounded above 2 a converges. Conversely,
nÊ!k2k
Aa aa aaaa aa2a4a 2a aB a 2a.
nnn
nk
22
œ á á œ
" #$ %&'( " # % " "
aba b !
ab ab
nk
_
œk1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.4 Comparison Tests 717
Therefore, if 2 a converges, then {A } is bounded above and hence converges.
!
_
œk1
k2n
ab
k
38. (a) a 2 a 2 , which diverges
ab ab
ab
22
2 ln 2 2 n(ln 2) n(ln 2) ln n
nn
nn
nn n n
œœ Ê œ œ
"" """
##††
!! !
__ _
œœ œn2 n2 n2
diverges.Ê!
_
œn2
"
n ln n
(b) a 2 a 2 , a geometric series that
ab ab ab
22
nn
2
n
nn
np np p 1 p 1
n
œÊ œ œ œ
""""
###
!!!!
ˆ‰
____
œœœœn1 n1 n1 n1
†
converges if 1 or p 1, but diverges if p 1.
"
#p1 Ÿ
39. (a) ; u du lim lim b (ln 2)
u ln x
du
''
2ln2
pb
ln 2
dx u
x(ln x) p 1 1 p
dx
x
p1 p1
p
p1
”• ’“ Š‹
cd
œ
œÄœ œ
bbÄ_ Ä_
"
the improper integral converges if p 1 and diverges
(ln 2) , p 1
, p
œÊ
_"
œ"
p1
p1
if p 1. For p 1: lim ln (ln x) lim ln (ln b) ln (ln 2) , so the improperœ œ œ œ_
'2
b
2
dx
x ln x bbÄ_ Ä_
cd c d
integral diverges if p 1.œ
(b) Since the series and the integral converge or diverge together, converges if and only if p 1.
!
_
œn2
"
n(ln n)p
40. (a) p 1 the series divergesœÊ
(b) p 1.01 the series convergesœÊ
(c) ; p 1 the series diverges
!!
__
œœn2 n2
"" "
n ln n 3 n(ln n)ab
œœÊ
(d) p 3 the series convergesœÊ
41. (a) From Fig. 11.8 in the text with f(x) and a , we have dx 1œ œ Ÿá
"" " """
#xk x 3n
k'1
n1
1 f(x) dx ln (n 1) 1 1 ln n 0 ln (n 1) ln nŸ Ê ŸáŸ Ê Ÿ
'1
n"" "
#3n
1 ln n 1. Therefore the sequence 1 ln n is bounded aboveŸ á Ÿ á
ˆ‰ ˜ ™ˆ‰
"" " "" "
# #3n 3n
by 1 and below by 0.
(b) From the graph in Fig. 11.8(a) with f(x) , dx ln (n 1) ln nœ œ
"" "
xn1 x
'n
n1
0 ln (n 1) ln n 1 ln (n 1) 1 ln n .Ê œ á á
"""""""
##n1 3 n1 3 n
cd
ˆ‰ˆ‰
If we define a 1 ln n, then 0 a a a a {a } is a decreasing sequence of
nn1nn1nn
3n
œœ Ê Ê
"""
#
nonnegative terms.
42. e e for x 1, and e dx lim e lim e e e e dx converges by
xx x b1
Ÿ œœœÊ
''
1 1
x1x
bbÄ_ Ä_
cd ˆ‰
b
"
the Comparison Test for improper integrals e 1 e converges by the Integral Test.ʜ
!!
__
œœn0 n1
nn
11.4 COMPARISON TESTS
1. diverges by the Limit Comparison Test (part 1) when compared with , a divergent p-series:
!
_
œn1
"
Èn
lim lim lim
nnnÄ_ Ä_ Ä_
Œ
Š‹
nn
n
œœ œ
È
ÈÈ
n
2n n n
""
# #
ˆ‰
16
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

718 Chapter 11 Infinite Sequences and Series
2. diverges by the Direct Comparison Test since n n n n n 0 , which is the nth Ê
È3
nnn
"
È
term of the divergent series or use Limit Comparison Test with b
!
n1
""
nn
nœ
3. converges by the Direct Comparison Test; , which is the nth term of a convergent geometric series
sin n
2nn
Ÿ"
#
4. converges by the Direct Comparison Test; and the p-series converges
1cos n 2
nn n
"
Ÿ!
5. diverges since lim 0
nÄ_
2n 2
3n 1 3œÁ
6. converges by the Limit Comparison Test (part 1) with , the nth term of a convergent p-series:
"
n
lim lim 1
nnÄ_ Ä_
Š‹
Š‹
n
nn
n
œœ
ˆ‰
n
n
"
7. converges by the Direct Comparison Test; , the nth term of a convergent geometric
ˆ‰ˆ‰ˆ‰
nn
3n13n3
nn
n
"
œ
series
8. converges by the Limit Comparison Test (part 1) with , the nth term of a convergent p-series:
"
n
lim lim lim 1 1
nnnÄ_ Ä_ Ä_
Š‹
Š‹
n
n2
œœœ
ÉÉ
n2 2
nn
9. diverges by the Direct Comparison Test; n ln n ln n ln ln n and Ê Ê
"" " "
n ln n ln (ln n) n
!
_
œn3
diverges
10. diverges by the Limit Comparison Test (part 3) when compared with , a divergent p-series:
!
_
œn2
"
n
lim lim lim lim lim lim n
nnn nnnÄ_ Ä_ Ä_ Ä_ Ä_ Ä_
Š‹
ˆ‰
(ln n)
nnn
œœ œœ œœ_
nn
(ln n) ln n
(ln n)
"" " ""
### #
Š‹ Š‹
11. converges by the Limit Comparison Test (part 2) when compared with , a convergent p-series:
!
_
œn1
"
n
lim lim lim 2 lim 0
nnn nÄ_ Ä_ Ä_ Ä_
’“
Š‹
(ln n)
n
n
n
œœ œœ
(ln n)
n1 n
2(ln n) ln n
Š‹
12. converges by the Limit Comparison Test (part 2) when compared with , a convergent p-series:
!
_
œn1
"
n
lim lim lim 3 lim 3 lim 6 lim
nnn n n nÄ_ Ä_ Ä_ Ä_ Ä_ Ä_
’“
Š‹
(ln n)
n
n
nn
œœ œ œ œ
(ln n) (ln n)
n1 n 1 n
3(ln n) 2(ln n) ln n
Š‹ Š‹
60 0œœ†
13. diverges by the Limit Comparison Test (part 3) with , the nth term of the divergent harmonic series:
"
n
lim lim lim lim
nnnnÄ_ Ä_ Ä_ Ä_
’“ Š‹
ˆ‰ ˆ‰
1
n ln n 2 n
nn
œœ œœ_
ÈÈ
nn
ln n 2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.4 Comparison Tests 719
14. converges by the Limit Comparison Test (part 2) with , the nth term of a convergent p-series:
"
n
lim lim lim 8 lim 8 lim 32 l
nnn nnÄ_ Ä_ Ä_ Ä_ Ä_
’“
Š‹ Š‹ Š‹
ˆ‰ ˆ‰
(ln n)
n
n4n 4n
2 ln n
nn
œœ œœ œ
(ln n)
nn
ln n im 32 0 0
nÄ_
"
nœœ†
15. diverges by the Limit Comparison Test (part 3) with , the nth term of the divergent harmonic series:
"
n
lim lim lim lim n
nnnnÄ_ Ä_ Ä_ Ä_
ˆ‰
ˆ‰
1ln n
nn
œœœœ_
n
1ln n
"
Š‹
16. diverges by the Limit Comparison Test (part 3) with , the nth term of the divergent harmonic series:
"
n
lim lim lim lim lim lim
nnnnnnÄ_ Ä_ Ä_ Ä_ Ä_ Ä_
Š‹
ˆ‰ ’“
(1 ln n)
n2(1 ln n)
n
2
n
œœ œ œœœ_
nnn
(1 ln n) (1 ln n)##
"
"Š‹
17. diverges by the Integral Test: dx u du lim u lim b ln 3
''
2ln3
ln (x 1)
x1 2
#
""
###
œœ œ œ_
bbÄ_ Ä_
‘ ab
b
ln 3
18. diverges by the Limit Comparison Test (part 3) with , the nth term of the divergent harmonic series:
"
n
lim lim lim lim lim lim
nnnnnnÄ_ Ä_ Ä_ Ä_ Ä_ Ä_
Š‹
ˆ‰ ˆ‰
1lnn
n2 ln n
n2
n
œœœœœœ_
nnn
1lnn ln n##
"
"Š‹
19. converges by the Direct Comparison Test with , the nth term of a convergent p-series: n 1 n for
"#
n
n 2 n n 1 n n n 1 n or use Limit Comparison Test with .Ê Ê Ê
# # $ $Î#
#""
ab Ènnn 1
1
n
È
20. converges by the Direct Comparison Test with , the nth term of a convergent p-series: n 1 n
"##
n
n 1 nn n or use Limit Comparison Test with .Ê Ê Ê
# $Î# $Î#
" "
Èn1
n
n
n1 nn
ÈÈ
21. converges because which is the sum of two convergent series:
!!!
___
œœœn1 n1 n1
" " "
#
n
n2 n2
nnn
œ
converges by the Direct Comparison Test since , and is a convergent geometric
!!
_ _
œ œn1 n1
""""
##n2 n 2
nnn n
series
22. converges by the Direct Comparison Test: and , the sum of
!!
ˆ‰
__
œœn1 n1
n2
n2 n2 n n2 n n
""""""
#
n
nn nn
œ Ÿ
the nth terms of a convergent geometric series and a convergent p-series
23. converges by the Direct Comparison Test: , which is the nth term of a convergent geometric
""
313
n1 n1
series
24. diverges; lim lim 0
nnÄ_ Ä_
Š‹ ˆ‰
3
3333
n1
nn
" " " "
œœÁ
25. diverges by the Limit Comparison Test (part 1) with , the nth term of the divergent harmonic series:
"
n
lim lim 1
nx0
Ä_ Ä
ˆ‰
ˆ‰
sin n
n
œœ
sin x
x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

720 Chapter 11 Infinite Sequences and Series
26. diverges by the Limit Comparison Test (part 1) with , the nth term of the divergent harmonic series:
"
n
lim lim lim 1 1 1
nn x0
Ä_ Ä_ Ä
ˆ‰ ˆ‰
ˆ‰ ˆ‰
tan sin
cos
nn
nn
n
œœœœ
Š‹ ˆ‰ˆ‰
""
cos x x
sin x †
27. converges by the Limit Comparison Test (part 1) with , the nth term of a convergent p-series:
"
n
lim lim lim lim 10
nnnnÄ_ Ä_ Ä_ Ä_
Š‹
Š‹
10n
n(n 1)(n 2)
n
œœœœ
10n n 20n 1 20
n3n2 2n3 2
28. converges by the Limit Comparison Test (part 1) with , the nth term of a convergent p-series:
"
n
lim lim lim lim 5
nnnnÄ_ Ä_ Ä_ Ä_
Š‹
5n 3n
n(n 2) n 5
n
œœœœ
5n 3n 15n 3 30n
n2n5n10 3n4n5 6n4
29. converges by the Direct Comparison Test: and is the product of a
tan n
nn n n
11 11 11 11
œ
!!
__
œœn1 n1
1
#
"
convergent p-series and a nonzero constant
30. converges by the Direct Comparison Test: sec n and is the
"
##
"
Ê œ
11sec n
nn n n
13 13 13 13
ˆ‰ ˆ‰
!!
__
œœn1 n1
product of a convergent p-series and a nonzero constant
31. converges by the Limit Comparison Test (part 1) with : lim lim coth n lim
"
nee
ee
nnnÄ_ Ä_ Ä_
Š‹
Š‹
coth n
n
n
œœ
nn
nn
lim 1œœ
nÄ_
"
e
1e
2n
2n
32. converges by the Limit Comparison Test (part 1) with : lim lim tanh n lim
"
nee
ee
nnnÄ_ Ä_ Ä_
Š‹
Š‹
tanh n
n
n
œœ
nn
nn
lim 1œœ
nÄ_
"
e
1e
2n
2n
33. diverges by the Limit Comparison Test (part 1) with : lim lim 1.
11
nn
nnÄ_ Ä_
Š‹
ˆ‰
1
nn
n
1
n
œœ
È
n
34. converges by the Limit Comparison Test (part 1) with : lim lim n 1
"
nnnÄ_ Ä_
Š‹
Š‹
nn
n
n
n
œœ
È
35. . The series converges by the Limit Comparison Test (part 1) with :
" "
á 123 n n(n1) n
2
œœ
"
ˆ‰
n(n 1)
lim lim lim lim 2.
nnnnÄ_ Ä_ Ä_ Ä_
Š‹
Š‹
2
nn 1
n
œœœœ
2n 4n 4
nn 2n1 2
36. the series converges by the Direct
"
á 12 3 n n(n1)(2n1) n
66
œœ ŸÊ
"
n(n1)(2n1)
6
Comparison Test
37. (a) If lim 0, then there exists an integer N such that for all n N, 0 1 1 1
nÄ_
aaa
bbb
nnn
nnn
œÊ
¹¹
a b . Thus, if b converges, then a converges by the Direct Comparison Test.Ê
nn n n
!!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 11.4 Comparison Tests 721
(b) If lim , then there exists an integer N such that for all n N, 1 a b . Thus, if
nÄ_
a a
b b nn
n n
n n
œ_ Ê
b diverges, then a diverges by the Direct Comparison Test.
!!
nn
38. Yes, converges by the Direct Comparison Test because a
!
_
œn1
aa
nn
n
n n
39. lim there exists an integer N such that for all n N, 1 a b . If a converges,
nÄ_
a a
b b nn n
n n
n n
œ_ Ê Ê !
then b converges by the Direct Comparison Test
!n
40. a converges lim a 0 there exists an integer N such that for all n N, 0 a 1 a a
!nn nn
n
ÊœÊ ŸÊ
nÄ_
#
a converges by the Direct Comparison TestÊ!#
n
41. Example CAS commands:
:Maple
a := n -> 1./n^3/sin(n)^2;
s := k -> sum( a(n), n=1..k ); # (a)]
limit( s(k), k=infinity );
pts := [seq( [k,s(k)], k=1..100 )]: # (b)
plot( pts, style=point, title="#41(b) (Section 11.4)" );
pts := [seq( [k,s(k)], k=1..200 )]: # (c)
plot( pts, style=point, title="#41(c) (Section 11.4)" );
pts := [seq( [k,s(k)], k=1..400 )]: # (d)
plot( pts, style=point, title="#41(d) (Section 11.4)" );
evalf( 355/113 );
:Mathematica
Clear[a, n, s, k, p]
a[n_]:= 1 / ( n Sin[n] )
32
s[k_]= Sum[ a[n], {n, 1, k}]
points[p_]:= Table[{k, N[s[k]]}, {k, 1, p}]
points[100]
ListPlot[points[100]]
points[200]
ListPlot[points[200]
points[400]
ListPlot[points[400], PlotRange All]Ä
To investigate what is happening around k = 355, you could do the following.
N[355/113]
N[ 355/113]1
Sin[355]//N
a[355]//N
N[s[354]]
N[s[355]]
N[s[356]]
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

722 Chapter 11 Infinite Sequences and Series
11.5 THE RATIO AND ROOT TESTS
1. converges by the Ratio Test: lim lim lim
nn nÄ_ Ä_ Ä_
a
a
(n 1) 2
n
n1
n
2
n1
n
2
œœ
”•
”•
(n 1) 2
2n1
n2
n
#
†
lim 1 1œœ
nÄ_ ˆ‰ˆ‰
"""
##n
2
È
2. converges by the Ratio Test: lim lim lim 1 1
nn n lim
n
Ä_ Ä_ Ä_ œÄ_
a
aennee
(n 1) e
n1
n
2
n1 2
n
œœ œ
Š‹
Š‹
(n 1)2
en1
n
en
"" "
#
†ˆ‰ˆ‰
3. diverges by the Ratio Test: lim lim lim lim
nn n nÄ_ Ä_ Ä_ Ä_
a
aen!e
(n )! en
n1
nn1
n
œœ œœ_
Š‹
ˆ‰
(n 1)!
en1
n!
en
" "
†
4. diverges by the Ratio Test: lim lim lim lim
nn n nÄ_ Ä_ Ä_ Ä_
a
a10n!10
(n )! 10 n
n1
nn1
n
œœ œœ_
Š‹
ˆ‰
(n 1)!
10n1
n!
10n
" †
5. converges by the Ratio Test: lim lim lim lim 1
nn n nÄ_ Ä_ Ä_ Ä_
a
a10nn
(n ) 10
n1
nn1
n
œœ œ
Š‹
Š‹
(n 1)
10n1
n
10n
" ""!
†ˆ‰ˆ
‰
"
10
1œ
"
10
6. diverges; lim a lim lim 1 e 0
nn nÄ_ Ä_ Ä_
nn2 2
nn
nn
œœœÁ
ˆ‰ ˆ ‰
#
7. converges by the Direct Comparison Test: 2 ( 1) (3) which is the n term of a convergent
2(1)
(1.25) 5 5
44
nn
nth
n
nœŸ
ˆ‰ ˆ‰
cd
geometric series
8. converges; a geometric series with r 1kk ¸¸
œ
2
3
9. diverges; lim a lim 1 lim 1 e 0.05 0
nn nÄ_ Ä_ Ä_
n33
nn
nn
œœœ¸Á
ˆ‰ ˆ ‰
$
10. diverges; lim a lim 1 lim 1 e 0.72 0
nn nÄ_ Ä_ Ä_
n3n n
n
n
œœ œ¸Á
ˆ‰
""Î$
Š‹
3
11. converges by the Direct Comparison Test: for n 2, the n term of a convergent p-series.
ln n n
nnn
th
œ
"
12. converges by the nth-Root Test: lim a lim lim lim
nn n nÄ_ Ä_ Ä_ Ä_
ÈÉ
nnn
n
n1n
n1n
n(ln n)
nn
(ln n)
n
ln n
œœ œ
ab
ab
lim 0 1œœ
nÄ_ Š‹
n
1
13. diverges by the Direct Comparison Test: for n 2 or by the Limit Comparison Test (part 1)
"" ""
#nn n n
n1
œ
ˆ‰
with .
"
n
14. converges by the nth-Root Test: lim a lim lim
nn nÄ_ Ä_ Ä_
ÈɈ‰ ˆ ‰ˆ‰
nn
nnn nn
nn
1n
œœ
"" "" Î
lim 0 1œœ
nÄ_ ˆ‰
""
nn
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.5 The Ratio and Root Tests 723
15. diverges by the Direct Comparison Test: for n 3
ln n
nn
"
16. converges by the Ratio Test: lim lim 1
nnÄ_ Ä_
a
an ln(n)
(n 1) ln (n 1) 2
n1
nn1
n
œœ
##
"
†
17. converges by the Ratio Test: lim lim 0 1
nnÄ_ Ä_
a
a (n 1)! (n 1)(n 2)
(n 2)(n 3) n!
n1
nœœ
†
18. converges by the Ratio Test: lim lim 1
nnÄ_ Ä_
a
aene
(n 1) e
n1
nn1
n
œœ
"
†
19. converges by the Ratio Test: lim lim lim 1
nn nÄ_ Ä_ Ä_
a
a 3!(n1)!3 (n3)! 3(n1) 3
(n 4)! 3! n! 3 n 4
n1
nn1
n
œœœ
"
†
20. converges by the Ratio Test: lim lim
nnÄ_ Ä_
a
a 3 (n 1)! n2 (n 1)!
(n 1)2 (n 2)! 3n!
n1
n
n1
n1 n
n
œ
†
lim 1œœ
nÄ_ ˆ‰ˆ‰ˆ‰
n12n2 2
n3n1 3
21. converges by the Ratio Test: lim lim lim 0 1
nn nÄ_ Ä_ Ä_
a
a (2n 3)! n! (2n 3)(2n 2)
(n 1)! (2n 1)! n
n1
nœœœ
"
†
22. converges by the Ratio Test: lim lim lim lim
nn n nÄ_ Ä_ Ä_ Ä_
a
a(n1)n!n1
(n 1)! nn
n
n1
nn1
n
œœœ
"
†ˆ‰ ˆ‰
n
n
n
lim 1œœ
nÄ_
""
ˆ‰
1n
ne
23. converges by the Root Test: lim a lim lim lim 0 1
nn nnÄ_ Ä_ Ä_ Ä_
ÈÉ
nnn
n
nn
(ln n) ln n ln n
n
œ œœœ
È"
24. converges by the Root Test: lim a lim lim 0 1
nn nÄ_ Ä_ Ä_
ÈÉ
nnn2
nn
nn
(ln n)
n
ln n lim ln n
lim n
œœœœ
È
ÈÈ
È
n
n
lim n 1
Š‹
È
nÄ_
nœ
25. converges by the Direct Comparison Test: n! ln n ln n n
n(n 2)! n(n 1)(n 2) n(n 1)(n 2) (n 1)(n ) n#
""
œœ
which is the nth-term of a convergent p-series
26. diverges by the Ratio Test: lim lim lim 1
nn nÄ_ Ä_ Ä_
a
a (n1)2 3 (n1)
3n2 n33
n1
n
n1 n 3
n1 n 3
œœœ
##
†ˆ‰
27. converges by the Ratio Test: lim lim 0 1
nnÄ_ Ä_
a
aa
a
n1
nn
nn
œœ
ˆ‰
1sin n
28. converges by the Ratio Test: lim lim lim 0 since the numerator
nn nÄ_ Ä_ Ä_
a
aa n
atan n
n1
nn
n
œœœ
Š‹
1tan n
n"
approaches 1 while the denominator tends to _
1
#
29. diverges by the Ratio Test: lim lim lim 1
nn nÄ_ Ä_ Ä_
a
aa2n1
a3n 1 3
n 1 2n 1
nn
n
œœœ
ˆ‰
3n 1
#
30. diverges; a a a a a a
n1 n n1 n1 n1 n2
nnn1 nn1n2
n1 n1 n n1 n n1
œÊœ Êœ
ˆ‰ˆ ‰ ˆ‰ˆ‰ˆ ‰
a a a a , which is a constant times theÊœ â ʜʜ
n1 n1 n1
nn1n2 3
n1nn1 n1 n1
a
"
#
"
ˆ‰ˆ‰ˆ‰ˆ‰
general term of the diverging harmonic series
31. converges by the Ratio Test: lim lim lim 0 1
nn nÄ_ Ä_ Ä_
a
aan
a2
n1
nn
n
œœœ
Š‹
2
n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

724 Chapter 11 Infinite Sequences and Series
32. converges by the Ratio Test: lim lim lim 1
nn nÄ_ Ä_ Ä_
a
aa n
a
n1
nn
n
œœœ
Œ
nn
n
Èn"
#
33. converges by the Ratio Test: lim lim lim lim 0 1
nn n nÄ_ Ä_ Ä_ Ä_
a
aa nn
aln n
n1
nn
n
œœœœ
Š‹
1ln n
n" "
34. 0 and a a 0; ln n 10 for n e n ln n n 10 1
nln n nln n
n10 n10
n
"
#
""!
œÊÊÊ
a a a ; thus a a lim a 0, so the series diverges by the nth-Term TestÊœ Ê Á
n1 n n n1 n n
nln n
n10
"
#
nÄ_
35. diverges by the nth-Term Test: a , a , a , a , ,
"# $ %
" " "" ""
œœ œ œ œ œá
3 3 33 33
ÉÉÉ ÉÉ
ÊÊ
Ë
22 2
33
6!
a lim a 1 because is a subsequence of whose limit is 1 by Table 8.1
nn
œÊ œ
ÉÉÉ
š› š›
n! n! n
"""
333
nÄ_
36. converges by the Direct Comparison Test: a , a , a , a ,
"# $ %
"" "" ""
## ## ##
##''#%
$%
œœœœœœá
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
Š‹ Š‹
a which is the nth-term of a convergent geometric seriesʜ
n
n! n
ˆ‰ ˆ‰
""
##
37. converges by the Ratio Test: lim lim lim
nn nÄ_ Ä_ Ä_
a
a (2n 2)! 2 n! n! (2n
2 (n 1)! (n 1)! (2n)! 2(n 1)(n 1)
n1
n
n1
n
œœ
† )(2n 1)#
lim 1œœ
nÄ_
n
2n 1
" "
#
38. diverges by the Ratio Test: lim lim
nnÄ_ Ä_
a
a (n 1)! (n 2)! (n 3)! (3n)!
(3n 3)! n! (n 1)! (n 2)!
n1
nœ
†
lim lim 3 3 3 3 27 1œœœœ
nnÄ_ Ä_
(3n 3)(3 2)(3n 1)
(n 1)(n 2)(n 3) n n 3
3n 2 3n 1
#
ˆ‰ˆ‰††
39. diverges by the Root Test: lim a lim lim 1
nn nÄ_ Ä_ Ä_
ÈÉ
nnn
n
n(n!)
n
n!
n
´œœ_
ab
40. converges by the Root Test: lim lim lim lim
nnnnÄ_ Ä_ Ä_ Ä_
ÉɈ‰ˆ‰ˆ‰ ˆ ‰ˆ‰
nnn
n
n
nnn
(n!) (n!)
nn
n! 2 3 n 1 n
n nnn n n
œœœ â
ab "
lim 0 1Ÿœ
nÄ_
"
n
41. converges by the Root Test: lim a lim lim lim 0 1
nn nnÄ_ Ä_ Ä_ Ä_
ÈÉ
nnn
nnn
nnn
2 ln 2
œœœœ
##
"
42. diverges by the Root Test: lim a lim lim 1
nn nÄ_ Ä_ Ä_
ÈÉ
nnn
n
nnn
4
œœœ_
ab#
43. converges by the Ratio Test: lim lim
nnÄ_ Ä_
a
a 4 2 (n 1)! 1 3 (2n 1)
1 3 (2n 1)(2n 1) 42n!
n1
nn1n1
nn
œ†† †
†† †
â
â
†
lim 1œœ
nÄ_
2n
(4 )(n 1) 4
" "
#†
44. converges by the Ratio Test: an13 (2n 1) 1234 (2n 1)(2n) (2n)!
(2 4 n) 3 1 (2 4 2n) 3 1 2n! 3 1
œœ œ
† †††
††
â â
â# â
ab ababa b
nn
nn
lim lim ʜ
nnÄ_ Ä_
(2n 2)!
2 (n 1)! 3 1
2 n! 3 1 (2n )(2n 2) 3 1
(2n)! 2 (n 1) 3 1
"
cdab
abab ab
ab
n1 n1
nn n
n1
†
lim 1 1œœœ
nÄ_ Š‹
4n 6n 2
4n 8n 4 3 3 3 3
1 3
" "
ab
ab
n
n†
45. Ratio: lim lim lim 1 1 no conclusion
nn nÄ_ Ä_ Ä_
a
a (n 1) 1 n 1
nn
p
n1
np
p
œœœœÊ
"
†ˆ‰ p
Root: lim a lim lim 1 no conclusion
nnnÄ_ Ä_ Ä_
ÈÉ
nn
pp
np
nn(1)
n
œœ œœÊ
"""
ˆ‰
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.6 Alternating Series, Absolute and Conditional Convergence 725
46. Ratio: lim lim lim lim lim
nn n n nÄ_ Ä_ Ä_ Ä_ Ä_
a
a (ln (n 1)) 1 ln (n 1) n
(ln n) ln n n
pp
p
n1
np
p
œœœœ
""
†’“ Š‹
”•
ˆ‰
ˆ‰
n
n1
(1) 1 no conclusionœœÊ
p
Root: lim a lim ; let f(n) (ln n) , then ln f(n)
nnÄ_ Ä_
ÈÉ
nnpp
n(ln n) n
1n ln (ln n)
œœ œ œ
"" Î
Š‹
lim (ln n)
nÄ_
1n
lim ln f(n) lim lim lim 0 lim (ln n)ÊœœœœÊ
nnnn nÄ_ Ä_ Ä_ Ä_ Ä_
ln (ln n)
n1n ln n
1n
ˆ‰
n ln n "Î
lim e e 1; therefore lim a 1 no conclusionœœœ œ œœÊ
nnÄ_ Ä_
ln f n n (1)
ÐÑ ! ""
È
npp
Š‹
lim (ln n)
nÄ_
1n
47. a for every n and the series converges by the Ratio Test since lim 1
nnn 2
22n
(n )
Ÿœ
nn n1
n
!
n1 # #
" "
nÄ_
†
a converges by the Direct Comparison TestÊ!
n1
n
11.6 ALTERNATING SERIES, ABSOLUTE AND CONDITIONAL CONVERGENCE
1. converges absolutely converges by the Absolute Convergence Test since a which is aʜ
!!
kk
__
œœn1 n1
nn
"
convergent p-series
2. converges absolutely converges by the Absolute Convergence Test since a which is aʜ
!!
kk
__
œœn1 n1
nn
"
convergent p-series
3. diverges by the nth-Term Test since for n 10 1 lim 0 ( 1) diverges Ê Ê ÁÊ
nn n
10 10 10
nn
n1
nÄ_ ˆ‰ ˆ‰
!
_
œn1
4. diverges by the nth-Term Test since lim lim (after 10 applications of L'Hopital's
^
nnÄ_ Ä_
""
0
n 10!
0 (ln 10)
nn
œœ_
rule)
5. converges by the Alternating Series Test because f(x) ln x is an increasing function of x is decreasingœÊ
"
ln x
u u for n 1; also u 0 for n 1 and lim 0Ê œ
nn1 n ln n
"
nÄ_
6. converges by the Alternating Series Test since f(x) f (x) 0 when x e f(x) isœÊ œ Ê
ln x 1 ln x
xx
w
decreasing u u ; also u 0 for n 1 and lim u lim lim 0Ê œ œ œ
nn1 n n ln n
n1
nn nÄ_ Ä_ Ä_ Š‹
n
7. diverges by the nth-Term Test since lim lim lim 0
nn nÄ_ Ä_ Ä_
ln n ln n
ln n 2 ln n
œœœÁ
""
##
8. converges by the Alternating Series Test since f(x) ln 1 x f (x) 0 for x 0 f(x) isœ Ê œ Êab
" w "
x(x 1)
decreasing u u ; also u 0 for n 1 and lim u lim ln 1 ln lim 1 ln 1 0Ê œ œ œ œ
nn1 n n nn
""
nn nÄ_ Ä_ Ä_
ˆ‰ ˆ‰
Š‹
9. converges by the Alternating Series Test since f(x) f (x) 0 f(x) is decreasingœÊœ Ê
ÈÈ
È
x 1x2x
x1 2x(x1)
"
w
u u ; also u 0 for n 1 and lim u lim 0Ê œ œ
nn1 n nnÄ_ Ä_
nn
n1
È"
10. diverges by the nth-Term Test since lim lim 3 0
nnÄ_ Ä_
3n1
n1
31
1
È
ÈÉŠ‹
œœÁ
n
n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

726 Chapter 11 Infinite Sequences and Series
11. converges absolutely since a a convergent geometric series
!!
kk ˆ‰
n1 n1
n10
n
œ"
12. converges absolutely by the Direct Comparison Test since which is the nth
¹¹ ˆ‰
( 1) (0.1)
n (10) n 10
n
""
n1 n
n
œ
term of a convergent geometric series
13. converges conditionally since 0 and lim 0 convergence; but a
"" " "
ÈÈ È
nn
n1 nn
œÊ œ
nÄ_ !!
kk
__
œœn1 n1
is a divergent p-series
14. converges conditionally since 0 and lim 0 convergence; but
"" "
1n 1n
1n1
ÈÈ È
œÊ
nÄ_
a is a divergent series since and is a divergent p-series
!! !
kk
__ _
œœ œn1 n1 n1
n1n 1n n n
œ
""""
#
ÈÈÈ
15. converges absolutely since a and which is the nth-term of a converging p-series
!!
kk
__
œœn1 n1
nnn
n1 n1 n
œ
"
16. diverges by the nth-Term Test since lim
nÄ_
n!
#nœ_
17. converges conditionally since 0 and lim 0 convergence; but a
"" "
n3 (n1)3 n3 n
œÊ
nÄ_ !kk
_
œn1
diverges because and is a divergent seriesœ
!!
__
œœn1 n1
""""
n3 n3 4n n
18. converges absolutely because the series converges by the Direct Comparison Test since
!¸¸ ¸¸
_
œn1
sin n sin n
nnn
Ÿ"
19. diverges by the nth-Term Test since lim 1 0
nÄ_
3n
5n
œÁ
20. converges conditionally since f(x) ln x is an increasing function of x is decreasingœÊœ
""
3 ln x ln xab
0 for n 2 and lim 0 convergence; but a Ê œÊ œ
"" " "
3 ln n 3 ln (n 1) 3 ln n ln n
n
nÄ_ !!
kk
__
œœn2 n2 ab
diverges because and divergesœ
!!
__
œœn2 n2
""""
3 ln n 3 ln n 3n n
21. converges conditionally since f(x) f (x) 0 f(x) is decreasing and henceœÊ œ Ê
"" "
w
xx xx
2
ˆ‰
u u 0 for n 1 and lim 0 convergence; but a
nn1 n
œÊ œ
nÄ_ ˆ‰ !!
kk
""
nn n
1n
__
œœn1 n1
is the sum of a convergent and divergent series, and hence divergesœ
!!
__
œœn1 n1
""
nn
22. converges absolutely by the Direct Comparison Test since 2 which is the nth term
¹¹ ˆ‰
(2)
n5 n5 5
22
n
n1
nn
n1
œ
of a convergent geometric series
23. converges absolutely by the Ratio Test: lim lim 1
nnÄ_ Ä_
Š‹ ”•
u
u3
2
n1
nœœ
(n )
n
" ˆ‰
ˆ‰
2
3
n1
2
3
n
24. diverges by the nth-Term Test since lim a lim 10 1 0
nnÄ_ Ä_
n1n
œœÁ
Î
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.6 Alternating Series, Absolute and Conditional Convergence 727
25. converges absolutely by the Integral Test since tan x dx lim
'1
b
1
ab
ˆ‰ ’“
" "
#1x
tan x
œbÄ_ ab
lim tan b tan 1œœœ
bÄ_ ’“’“
abab ˆ‰ ˆ‰
" "
##
"
##
##
11 1
432
3
26. converges conditionally since f(x) f (x) 0 f(x) is decreasingœÊœ Ê
"w
x ln x (x ln x)
ln (x) 1cd
u u 0 for n 2 and lim 0 convergence; but by the Integral Test,Ê œÊ
nn1 nÄ_
"
n ln n
lim dx lim ln (ln x) lim ln (ln b) ln (ln 2)
''
22
bb
2
dx
x ln x ln x
œœœœ_
bbbÄ_ Ä_ Ä_
cd c d
Š‹
x
a divergesʜ
!!
kk
__
œœn1 n1
nn ln n
"
27. diverges by the nth-Term Test since lim 1 0
nÄ_
n
n1œÁ
28. converges conditionally since f(x) f (x)œÊœ
ln x
x ln x (x ln x)
(x ln x) (ln x) 1
w
Š‹ Š ‹
xx
0 u u 0 when n e and lim œœÊ
1ln x
(x ln x) (x ln x) n ln n
1 ln x ln n
nn1
Š‹ Š‹
ln x ln x
xx
nÄ_
lim 0 convergence; but n ln n n so thatœœÊ ÊÊ
nÄ_ Š‹
Š‹
n
n
1nln n n nln n n
ln n
"" "
a diverges by the Direct Comparison Test
!!
kk
_
œn1
nln n
nln n
œ
n1
29. converges absolutely by the Ratio Test: lim lim lim 0 1
nn nÄ_ Ä_ Ä_
Š‹
u
u (n 1)! (100) n 1
( 00) n! 00
n1
n
n1
n
œœœ
"
"
†
30. converges absolutely since a is a convergent geometric series
!!
kk ˆ‰
__
œœn1 n1
n5
n
œ"
31. converges absolutely by the Direct Comparison Test since a and
!!
kk
__
œœn1 n1
nn2n1
œ"
which is the nth-term of a convergent p-series
""
n2n1 n
32. converges absolutely since a is a convergent
!! ! !
kk ˆ‰ ˆ‰ ˆ‰
__ _ _
œœ œ œn1 n1 n1 n1
nln n ln n
ln n 2 ln n
œœ œ
nn
n
"
#
geometric series
33. converges absolutely since a is a convergent p-series
!! !
kk ¹¹
__ _
œœ œn1 n1 n1
n(1)
nn n
œœ
"
n
È
34. converges conditionally since is the convergent alternating harmonic series, but
!!
__
œœn1 n1
cos n
nn
(1)
1œn
a diverges
!!
kk
__
œœn1 n1
nn
œ"
35. converges absolutely by the Root Test: lim a lim lim 1
nn nÄ_ Ä_ Ä_
Èkk Š‹
nn
n
nœœœ
(n 1)
(2n) n
1n n
Î" "
##
36. converges absolutely by the Ratio Test: lim lim lim
nn nÄ_ Ä_ Ä_
¹¹
a
a ((2n 2)!) (n!) (2n 2)(2n 1)
(n 1)! (2n)! (n 1)
n1
nœœœ
ab
†"
41
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

728 Chapter 11 Infinite Sequences and Series
37. diverges by the nth-Term Test since lim a lim lim
nn nÄ_ Ä_ Ä_
kk
n(2n)! (n )(n 2) (2n)
2n!n 2n
œœ
n
" â
n
lim lim 0œœ_Á
nnÄ_ Ä_
(n 1)(n 2) (n (n 1)) n1
n1
â
##
n1 ˆ‰
38. converges absolutely by the Ratio Test: lim lim
nnÄ_ Ä_
¹¹
a
a (2n 3)! n! n! 3
(n 1)! (n 1)! 3 (2n 1)!
n1
n
n1
n
œ
†
lim 1œœ
nÄ_
(n 1) 3
(2n 2)(2n 3) 4
3
39. converges conditionally since and is a
ÈÈ
ÈÈ
ÈÈ È
ÈÈ È
n1 n n1 n
1n1 n n1 n n1 n
""
†œš›
decreasing sequence of positive terms which converges to 0 converges; butÊ!
_
œn1
()
n1 n
"
n
ÈÈ
a diverges by the Limit Comparison Test (part 1) with ; a divergent p-series:
!!
kk
__
œœn1 n1
nn1 n n
œ" "
È È
È
lim lim lim
nnnÄ_ Ä_ Ä_
n1 n
n1
n
œœœ
È
ÈÈÉ
n
n1 n
1
11
"
#
40. diverges by the nth-Term Test since lim n n n lim n n n
nnÄ_ Ä_
Š‹Š‹Š‹
ÈÈ
##
œ †È
Ènnn
nnn
lim lim 0œœœÁ
nnÄ_ Ä_
n
nnn 11
ÈÉ
""
#
n
41. diverges by the nth-Term Test since lim n n n lim n n n
nnÄ_ Ä_
Š‹Š‹
ÉÉ
ÈÈ ÈÈ
–—
œ ÉÈÈ
ÉÈÈ
nnn
nnn
lim lim 0œœœÁ
nnÄ_ Ä_
È
ÉÉ
ÈÈ
n
nnn 11
""
#
n
42. converges conditionally since is a decreasing sequence of positive terms converging to 0
š›
"
ÈÈ
nn1
converges; but lim lim lim Êœœœ
!
_
œn1
()
nn1 nn1
n
11
"
""
#
n
n
ÈÈ
ÈÈ
ÈÉ
nnnÄ_ Ä_ Ä_
Š‹
Š‹
nn1
n
so that diverges by the Limit Comparison Test with which is a divergent p-series
!!
_ _
œ œn1 n1
""
ÈÈÈ
nn1 n
43. converges absolutely by the Direct Comparison Test since sech (n) which is theœœœ
22e2e2
ee e 1 e e
n n 2n 2n n
nn
nth term of a convergent geometric series
44. converges absolutely by the Limit Comparison Test (part 1): a
!!
kk
__
œœn1 n1
n2
ee
œnn
Apply the Limit Comparison Test with , the n-th term of a convergent geometric series:
1
en
lim lim lim 2
nnnÄ_ Ä_ Ä_
Œ
2
ee
nn
1
enœœœ
2e 2
ee 1e
n
nn 2n
45. error ( 1) 0.2 46. error ( 1) 0.00001kk kk
¸¸ ¸ ¸ˆ‰ ˆ ‰
œ œ
' '
" "
510
47. error ( 1) 2 10 48. error ( 1) t t 1kk kkk k
¹¹
œ‚ œ
' "" % % %
(0.01)
5
49. (2n)! 200,000 n 5 1 0.54030
"""""
#(2n)! 10 5 !4!6!8!
510
Ê œ Êʸ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 11.6 Alternating Series, Absolute and Conditional Convergence 729
50. n! n 9 1 1 0.367881944
" """""""
#n! 10 5 ! 3! 4! 5! 6! 7! 8!
510
Ê Êʸ
51. (a) a a fails since
nn1 3
""
#
(b) Since a is the sum of two absolutely convergent
!! ! !
kk ‘ ˆ‰ ˆ‰ˆ‰ ˆ‰
__ _ _
œœ œ œn1 n1 n1 n1
n33
nn n n
œœ
"" " "
##
series, we can rearrange the terms of the original series to find its sum:
1
ˆ‰ˆ‰
"" " """ " "
###
3927 48 11
á ᜠœœ
ˆ‰ ˆ‰
ˆ‰ ˆ‰
3
3
52. s 1 0.6687714032 s 0.692580927
#! #!
""" " " ""
###
œá ¸ Ê ¸
3 4 19 20 1
†
53. The unused terms are ( 1) a ( 1) a a ( 1) a a
!abab
jn1
j1 n1 n3
j n1n2 n3n4
œ á
( 1) a a a a . Each grouped term is positive, so the remainderœ á
n1 n1 n2 n3 n4
cdabab
has the same sign as ( 1) , which is the sign of the first unused term.n1
54. s
n1 2 3 3 4 n(n 1) k(k 1) k k 1
œá œ œ
""" " " ""
#††† !!
ˆ‰
nn
k1 k1œœ
1 which are the first 2n termsχ
ˆ‰ˆ‰ˆ‰ˆ‰ ˆ ‰
""""""" ""
## 33445 nn1
of the first series, hence the two series are the same. Yes, for
s 1 1
nkk1 3 34 45 n1n nn1 n1
œ œá œ
!ˆ ‰ˆ‰ˆ‰ˆ‰ˆ‰ ˆ ‰ˆ ‰
n
k1œ
"" """"""" """" "
##
lim s lim 1 1 both series converge to 1. The sum of the first 2n 1 terms of the firstÊœœÊ
nnÄ_ Ä_
nn1
ˆ‰
"
series is 1 1. Their sum is lim s lim 1 1.
ˆ‰ ˆ‰
œ œ œ
"" "
n1 n1 n1
n
nnÄ_ Ä_
55. Theorem 16 states that a converges a converges. But this is equivalent to a diverges a
!! !!
kk kk
__ __
œœ œœn1 n1 n1 n1
nn nn
ÊÊ
diverges.
56. a a a a a a for all n; then a converges a converges and thesek k kk kk kk kk
!!
"# " #
á Ÿ á Ê
nnnn
__
œœn1 n1
imply that a a
ºº
!!
kk
__
œœn1 n1
nn
Ÿ
57. (a) a b converges by the Direct Comparison Test since a b a b and hence
!kk kkkkkk
_
œn1
nn nn n n
Ÿ
a b converges absolutely
!ab
_
œn1
nn
(b) b converges b converges absolutely; since a converges absolutely and
!! !
kk
__ _
œœ œn1 n1 n1
nn n
Ê
b converges absolutely, we have a ( b ) a b converges absolutely by part (a)
!!!
cdab
___
œœœn1 n1 n1
œ
nnnnn
(c) a converges k a ka converges ka converges absolutely
!!!!
kk kk kk k k
____
œœœœn1 n1 n1 n1
nnnn
Êœ Ê
58. If a b ( 1) , then ( 1) converges, but a b diverges
nn nn
nn
nn n
œœ œ
"" "
ÈÈ
!!!
___
œœœn1 n1 n1
59. s , s 1 ,
"#
"""
###
œ œ œ
s 1 0.5099,
$" """"""""""
####
œ¸
468101 141618 02
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
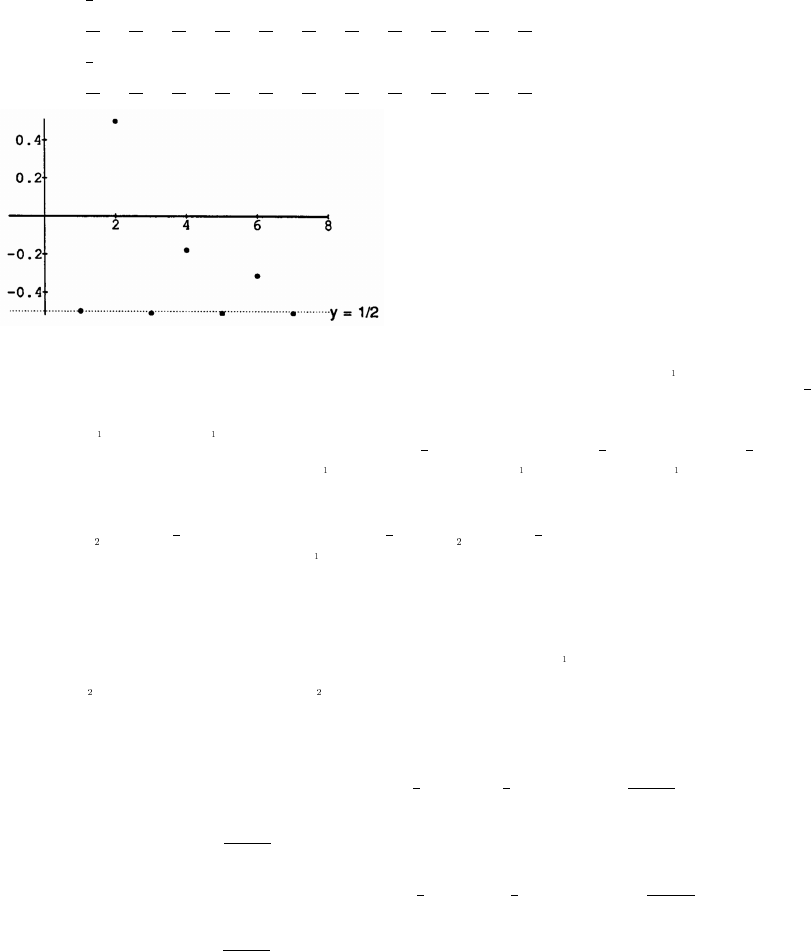
730 Chapter 11 Infinite Sequences and Series
s s 0.1766,
%$
"
œ¸
3
s s 0.512,
&%
"""""""""""
### #
œ¸
4 6 8303 343638404244
s s 0.312,
'&
"
œ¸
5
s s 0.51106
('
"""""""""""
œ¸
46 48 50 52 54 56 58 60 62 64 66
60. (a) Since a converges, say to M, for 0 there is an integer N such that a M
!!
kk kk
ºº
n n
%
"#
N1
n1
œ
%
a a a a a . Also, aÍ ÍÍ
»»»»
!!! ! ! !
kk kk kk kk kk
N1 N1
n1 n1 nN nN nN
œœœ œ œ
___
nnn n n n
%%%
###
converges to L for 0 there is an integer N (which we can choose greater than or equal to N ) suchÍ%#"
that s L . Therefore, a and s L .kk kk kk
!
NN
%%%
###
_
œnN
n
(b) The series a converges absolutely, say to M. Thus, there exists N such that a M
!!
kk kk
ºº
_
œ œn1 n1
k
n n"%
whenever k N . Now all of the terms in the sequence b appear in a . Sum together all of the"ef efkk kk
nn
terms in b , in order, until you include all of the terms a , and let N be the largest index in theef efkk kk
nn
N
n1
œ#
sum b so obtained. Then b M as well b converges to M.
!! !
kk kk kk
ºº
NN
n1 n1 n1
œœ œ
_
nn n
Ê%
61. (a) If a converges, then a converges and a a
!!!!!
kk kk
_____
œœœœœn1 n1 n1 n1 n1
nnnn
aa
""
## #
œ
nn
kk
converges where b .
a , if a 0
0, if a 0
naa nn
n
œœ
nn
#kk œ
(b) If a converges, then a converges and a a
!!!!!
kk kk
_____
œœœœœn1 n1 n1 n1 n1
nnnn
aa
""
## #
œ
nn
kk
converges where c .
0, if a 0
a , if a 0
naa n
nn
œœ
nn
#kk œ
62. The terms in this conditionally convergent series were not added in the order given.
63. Here is an example figure when N 5. Notice that u u u and u u u , but u u forœ
$#" $&% nn1
n5.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
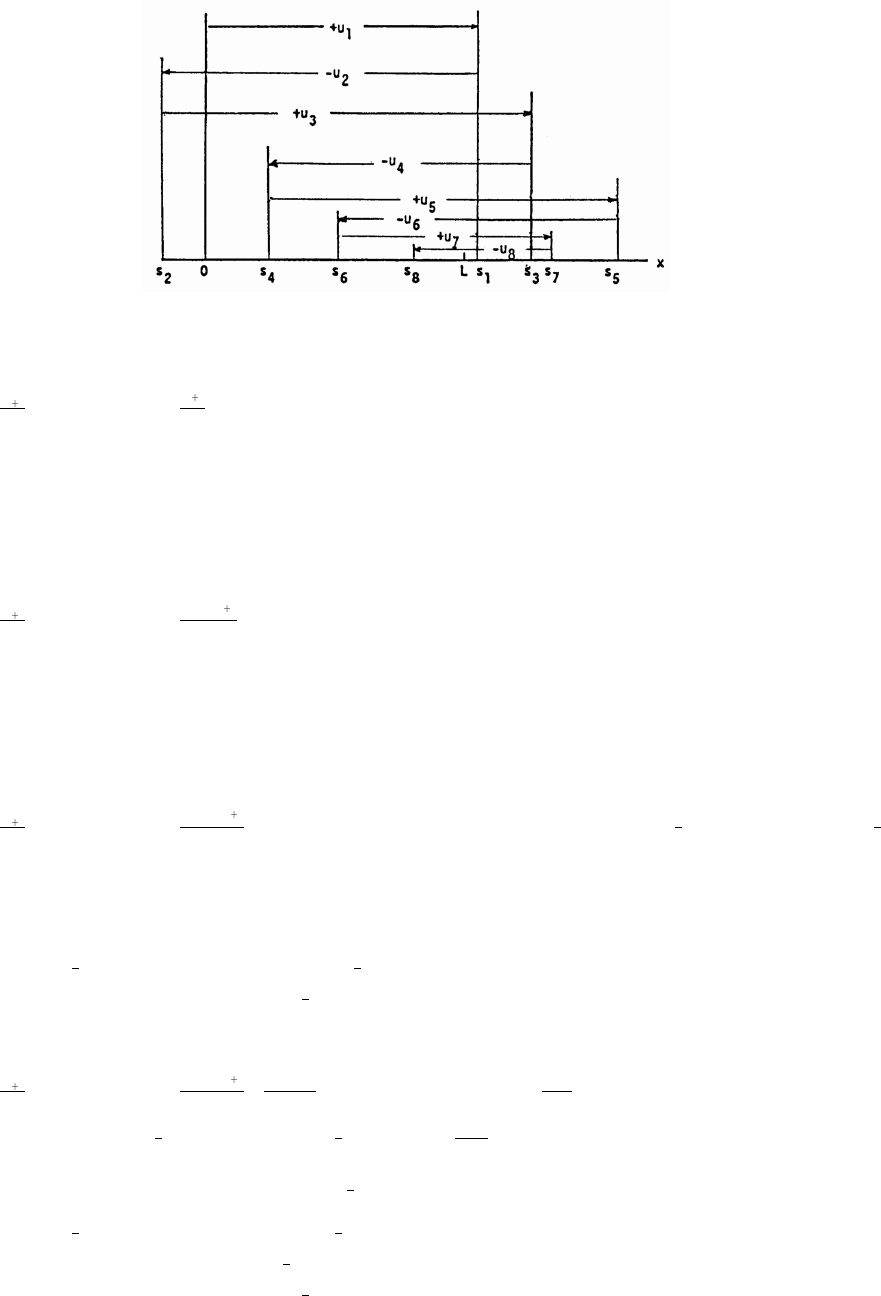
Section 11.7 Power Series 731
11.7 POWER SERIES
1. lim 1 lim 1 x 1 1 x 1; when x 1 we have ( 1) , a divergent
nnÄ_ Ä_
¹¹ ¹¹ kk !
u
ux
x
n1
n
n1
n
Ê Ê Ê œ
_
œn1
n
series; when x 1 we have 1, a divergent seriesœ!
_
œn1
(a) the radius is 1; the interval of convergence is 1 x 1
(b) the interval of absolute convergence is 1 x 1
(c) there are no values for which the series converges conditionally
2. lim 1 lim 1 x 5 1 6 x 4; when x 6 we have
nnÄ_ Ä_
¹¹ ¹ ¹ kk
u
u(x5)
(x 5)
n1
n
n1
n
Ê Ê Ê œ
( 1) , a divergent series; when x 4 we have 1, a divergent series
!!
_ _
œ œn1 n1
œ
n
(a) the radius is 1; the interval of convergence is 6 x 4
(b) the interval of absolute convergence is 6 x 4
(c) there are no values for which the series converges conditionally
3. lim 1 lim 1 4x 1 1 1 4x 1 1 x 0; when x we
nnÄ_ Ä_
¹¹ ¹ ¹ kk
u
u (4x 1)
(4x 1)
n1
n
n1
n
Ê Ê Ê Ê œ
##
""
have ( 1) ( 1) ( 1) 1 , a divergent series; when x 0 we have ( 1) (1)
!!! !
___ _
œœœ œn1 n1 n1 n1
œ œ œ
nn 2n n nn
( 1) , a divergent seriesœ
!
_
œn1
n
(a) the radius is ; the interval of convergence is x 0
""
#4
(b) the interval of absolute convergence is x 0
"
#
(c) there are no values for which the series converges conditionally
4. lim 1 lim 1 3x 2 lim 1 3x 2 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
ˆ‰
u
u n 1 (3x 2) n 1
(3x 2) nn
n1
n
n1
n
Ê Ê Ê
†
1 3x 2 1 x 1; when x we have which is the alternating harmonic series and isÊ Ê œ
""
"
33n
()
!
_
œn1
n
conditionally convergent; when x 1 we have , the divergent harmonic seriesœ!
_
œn1
"
n
(a) the radius is ; the interval of convergence is x 1
""
33
Ÿ
(b) the interval of absolute convergence is x 1
"
3
(c) the series converges conditionally at x œ"
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

732 Chapter 11 Infinite Sequences and Series
5. lim 1 lim 1 1 x 2 10 10 x 2 10
nnÄ_ Ä_
¹¹ ¹ ¹ kk
u
u10(x2)10
(x 2) 10 x2
n1
n
n1
n1 n
n
Ê Ê Ê Ê
†kk
8 x 12; when x 8 we have ( ) , a divergent series; when x 12 we have 1, a divergentÊ œ " œ
!!
_ _
œ œn1 n1
n
series
(a) the radius is 0; the interval of convergence is 8 x 12"
(b) the interval of absolute convergence is 8 x 12
(c) there are no values for which the series converges conditionally
6. lim 1 lim 1 lim 2x 1 2x 1 x ; when x we have
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
u
u (2x)
(2x)
n1
n
n1
n
Ê Ê Ê Ê œ
"" "
## #
( ) , a divergent series; when x we have 1, a divergent series
!!
__
œœn1 n1
" œ
n"
#
(a) the radius is ; the interval of convergence is x
"""
###
(b) the interval of absolute convergence is x
""
##
(c) there are no values for which the series converges conditionally
7. lim 1 lim 1 x lim 1 x 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
u
u (n3) nx (n3)(n)
(n 1)x (n 2) (n 1)(n 2)
n1
n
n1
n
Ê Ê Ê
†
1 x 1; when x 1 we have ( ) , a divergent series by the nth-term Test; when x weÊ œ " œ"
!
_
œn1
nn
n#
have , a divergent series
!
_
œn1
n
n#
(a) the radius is ; the interval of convergence is x"""
(b) the interval of absolute convergence is x" "
(c) there are no values for which the series converges conditionally
8. lim 1 lim 1 x 2 lim 1 x 2 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
ˆ‰
u
un1(x2) n1
(x 2) nn
n1
n
n1
n
Ê Ê Ê
†
1 x 2 1 3 x 1; when x 3 we have , a divergent series; when x we haveÊ Ê œ œ"
!
_
œn1
"
n
, a convergent series
!
_
œn1
(1)
n
n
(a) the radius is ; the interval of convergence is 3 x"Ÿ"
(b) the interval of absolute convergence is 3 x "
(c) the series converges conditionally at x 1œ
9. lim 1 lim 1 lim lim 1
nn nnÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹Š ‹
É
u
ux3n1n1
xnn
(n 1) n 1 3
nn3 x
n1
n
n1
n1
n
n
Ê Ê
ÈÈkk
†
(1)(1) 1 x 3 3 x 3; when x 3 we have , an absolutely convergent series;ÊÊÊ œ
kkx
3
()
n
kk !
_
œn1
" n
when x 3 we have , a convergent p-seriesœ!
_
œn1
1
n
(a) the radius is 3; the interval of convergence is 3 x 3Ÿ Ÿ
(b) the interval of absolute convergence is 3 x 3Ÿ Ÿ
(c) there are no values for which the series converges conditionally
10. lim 1 lim 1 x 1 lim 1 x 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
É
u
u(x1)n1
(x 1)
n1
nn
n1
n
n1
n
Ê Ê Ê
ÈÈ
†
1 x 1 1 0 x 2; when x 0 we have , a conditionally convergent series; when x 2Ê Ê œ œ
!
_
œn1
()
n
" n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.7 Power Series 733
we have , a divergent series
!
_
œn1
1
n
(a) the radius is 1; the interval of convergence is 0 x 2Ÿ
(b) the interval of absolute convergence is 0 x 2
(c) the series converges conditionally at x 0œ
11. lim 1 lim 1 x lim 1 for all x
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk ˆ‰
u
u(n1)!x n1
xn!
n1
n
n1
n
Ê Ê
"
†
(a) the radius is ; the series converges for all x_
(b) the series converges absolutely for all x
(c) there are no values for which the series converges conditionally
12. lim 1 lim 1 3 x lim 1 for all x
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk ˆ‰
u
u (n1)! 3x n1
3x n!
n1
n
n1 n1
nn
Ê Ê
"
†
(a) the radius is ; the series converges for all x_
(b) the series converges absolutely for all x
(c) there are no values for which the series converges conditionally
13. lim 1 lim 1 x lim 1 for all x
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰
u
u(n1)!x n1
xn!
n1
n
2n 3
2n 1
Ê Ê
#"
†
(a) the radius is ; the series converges for all x_
(b) the series converges absolutely for all x
(c) there are no values for which the series converges conditionally
14. lim 1 lim 1 (2x 3) lim 1 for all x
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰
u
u (n 1)! (2x 3) n 1
(2x 3) n!
n1
n
2n 3
2n 1
Ê Ê
#"
†
(a) the radius is ; the series converges for all x_
(b) the series converges absolutely for all x
(c) there are no values for which the series converges conditionally
15. lim 1 lim 1 x lim x 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
É
u
uxn2n4
xn3
(n 1) 3
n3
n1
n
n1
n
Ê Ê "Ê
ÈÈ
†
1 x 1; when x 1 we have , a conditionally convergent series; when x 1 we haveÊ œ œ
!
_
œn1
()
n3
"
n
È
, a divergent series
!
_
œn1
"
Èn3
(a) the radius is 1; the interval of convergence is 1 x 1Ÿ
(b) the interval of absolute convergence is 1 x 1
(c) the series converges conditionally at x 1œ
16. lim 1 lim 1 x lim x 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
É
u
uxn2n4
xn3
(n 1) 3
n3
n1
n
n1
n
Ê Ê "Ê
ÈÈ
†
1 x 1; when x 1 we have , a divergent series; when x 1 we have ,Ê œ œ
!!
_ _
œ œn1 n1
"
"
ÈÈ
n3 n3
()
n
a conditionally convergent series
(a) the radius is 1; the interval of convergence is 1 x 1 Ÿ
(b) the interval of absolute convergence is 1 x 1
(c) the series converges conditionally at x 1œ
17. lim 1 lim 1 lim 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰
u
u5n(x3)5n5
(n 1)(x 3) 5n
x3 x3
n1
n
n1
n1 n
n
Ê Ê Ê
"
†kk kk
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

734 Chapter 11 Infinite Sequences and Series
x 3 5 5 x 3 5 8 x 2; when x 8 we have ( 1) n, a divergentÊ Ê Ê œ œ kk !!
__
œœn1 n1
n( 5)
5
n
nn
series; when x 2 we have n, a divergent seriesœœ
!!
__
œœn1 n1
n5
5
n
n
(a) the radius is 5; the interval of convergence is 8 x 2
(b) the interval of absolute convergence is 8 x 2
(c) there are no values for which the series converges conditionally
18. lim 1 lim 1 lim 1 x 4
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ¹ ¹ kk
u
u 4 n2n2 nx 4 nn2n2
(n 1)x 4n 1 (n 1)n 1
x
n1
n
n1
n1 n
n
Ê Ê Ê
ab ab
ab ab
kk
†
4 x 4; when x 4 we have , a conditionally convergent series; when x 4 we haveÊ œ œ
!
_
œn1
n( 1)
n1
n
, a divergent series
!
_
œn1
n
n1
(a) the radius is 4; the interval of convergence is 4 x 4Ÿ
(b) the interval of absolute convergence is 4 x 4
(c) the series converges conditionally at x 4œ
19. lim 1 lim 1 lim 1 1 x 3
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ Ɉ‰ kk
u
u33n3
n1x x x
3n1
nx
n1
n
n1
n1
n
n
Ê Ê Ê Ê
ÈÈkk kk
†
3 x 3; when x 3 we have ( 1) n , a divergent series; when x 3 we haveÊ œ œ
!È
_
œn1
n
n, a divergent series
!È
_
œn1
(a) the radius is 3; the interval of convergence is 3 x 3
(b) the interval of absolute convergence is 3 x 3
(c) there are no values for which the series converges conditionally
20. lim 1 lim 1 2x 5 lim 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹
kk
u
u
n 1 (2x 5) n 1
n (2x 5) n
n1
n
n1 n1
n1
n n
n
Ê Ê
ÈÈ
ÈÈ
2x 5 1 2x 5 1 1 2x 5 1 3 x 2; when x 3 we haveÊ Ê Ê Ê œkk kk
Œ
lim t
lim n
t
n
È
È
t
n
( 1) n, a divergent series since lim n 1; when x 2 we have n, a divergent series
!!
ÈÈÈ
_ _
œ œn1 n1
œœ
n
nÄ_
nn
(a) the radius is ; the interval of convergence is 3 x 2
"
#
(b) the interval of absolute convergence is 3 x 2
(c) there are no values for which the series converges conditionally
21. lim 1 lim 1 x 1 x 1 x 1
nnÄ_ Ä_
¹¹ »»
kk kk kk
ˆ‰
u
u e
1 x lim 1
1 x lim 1
e
n1
nn
n1 t
n1
nn
Ê Ê Ê Ê
Š‹ Š‹
Š‹ Š‹
n1 t
nn
t
n
1 x 1; when x 1 we have ( 1) 1 , a divergent series by the nth-Term Test sinceÊ œ
!ˆ‰
_
œn1
n
n
n
"
lim 1 e 0; when x 1 we have 1 , a divergent series
nÄ_ ˆ‰ ˆ‰
!
œÁ œ
""
nn
nn
_
œn1
(a) the radius is ; the interval of convergence is 1 x 1"
(b) the interval of absolute convergence is 1 x 1
(c) there are no values for which the series converges conditionally
22. lim 1 lim 1 x lim 1 x lim 1 x 1
nn n nÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ kk kk kk
ºº ˆ‰
u
ux ln n n1
ln (n 1)x n
n1
n
n1
n
Ê Ê Ê Ê
ˆ‰
ˆ‰
n1
n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.7 Power Series 735
1 x 1; when x 1 we have ( 1) ln n, a divergent series by the nth-Term Test sinceÊ œ
!
_
œn1
n
lim ln n 0; when x 1 we have ln n, a divergent series
nÄ_ Áœ!
_
œn1
(a) the radius is 1; the interval of convergence is 1 x 1
(b) the interval of absolute convergence is 1 x 1
(c) there are no values for which the series converges conditionally
23. lim 1 lim 1 x lim 1 lim (n 1) 1
nn nnÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹Š ‹
kk ˆ‰
u
unx n
(n 1) x n
n1
n
n1n1
nn
Ê Ê
"
e x lim (n 1) 1 only x 0 satisfies this inequalityÊÊœkknÄ_
(a) the radius is 0; the series converges only for x 0œ
(b) the series converges absolutely only for x 0œ
(c) there are no values for which the series converges conditionally
24. lim 1 lim 1 x 4 lim (n 1) 1 only x 4 satisfies this
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk
u
un!(x4)
(n 1)! (x 4)
n1
n
n1
n
Ê Ê Ê œ
inequality
(a) the radius is 0; the series converges only for x 4œ
(b) the series converges absolutely only for x 4œ
(c) there are no values for which the series converges conditionally
25. lim 1 lim 1 lim 1 1 x 2 2
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰ kk
u
u (n1)2 (x2) n1
(x 2) n2 n
x2 x2
n1
n
n1
n1 n
n
Ê Ê Ê Ê
# #
†kk kk
2 x 2 2 4 x 0; when x 4 we have , a divergent series; when x 0 we haveÊ Ê œ œ
!
_
œn1
"
n
, the alternating harmonic series which converges conditionally
!
_
œn1
(1)
n
n1
(a) the radius is 2; the interval of convergence is 4 x 0 Ÿ
(b) the interval of absolute convergence is 4 x 0
(c) the series converges conditionally at x 0œ
26. lim 1 lim 1 2 x 1 lim 1 2 x 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
ˆ‰
u
u ( 2) (n 1)(x 1) n 1
( 2) (n 2)(x 1) n2
n1
n
n1 n1
nn
Ê Ê Ê
x 1 x 1 x ; when x we have (n 1) , a divergent series; when xÊ Ê Ê œ œkk !
"" "" "
## ## # # #
3 3
_
œn1
we have ( 1) (n 1), a divergent series
!
_
œn1
n
(a) the radius is ; the interval of convergence is x
""
###
3
(b) the interval of absolute convergence is x
"
##
3
(c) there are no values for which the series converges conditionally
27. lim 1 lim 1 x lim lim 1
nn nnÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹Š ‹
kk
u
uxn1ln(n1)
xnln n
(n 1) ln (n 1)
n(ln n)
n1
n
n1
n
Ê Ê
#
ab
†
x (1) lim 1 x lim 1 x 1 1 x 1; when x 1 we haveÊÊÊÊœkk kk kk
Œ Š‹
nnÄ_ Ä_
ˆ‰
ˆ‰
n
n1
#
#
n1
n
which converges absolutely; when x 1 we have which converges
!!
_ _
œ œn1 n1
(1)
n(ln n) n(ln n)
"
nœ
(a) the radius is ; the interval of convergence is 1 x 1"ŸŸ
(b) the interval of absolute convergence is 1 x 1Ÿ Ÿ
(c) there are no values for which the series converges conditionally
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

736 Chapter 11 Infinite Sequences and Series
28. lim 1 lim 1 x lim lim 1
nn nnÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹Š ‹
kk
u
u (n 1) ln (n 1) x n 1 ln (n 1)
xn
n ln (n) ln (n)
n1
n
n1
n
Ê Ê
†
x (1)(1) 1 x 1 1 x 1; when x 1 we have , a convergent alternating series;ÊÊÊ œkk kk !
_
œn2
(1)
n ln n
n
when x 1 we have which diverges by Exercise 38, Section 11.3œ!
_
œn2
"
n ln n
(a) the radius is ; the interval of convergence is 1 x 1"Ÿ
(b) the interval of absolute convergence is 1 x 1
(c) the series converges conditionally at x 1œ
29. lim 1 lim 1 (4x 5) lim 1 (4x 5) 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ Š ‹
u
u (4x 5) n 1
(4x 5)
(n 1)
nn
n1
n
2n 3
2n 1
Ê Ê Ê
##
$Î#
†
4x 5 1 1 4x 5 1 1 x ; when x 1 we have which isÊÊÊ œ œkk !!
3(1)
nn
#
"
__
œœn1 n1
2n 1
absolutely convergent; when x we have , a convergent p-seriesœ3()
n
#
"
!
_
œn1
2n 1
(a) the radius is ; the interval of convergence is 1 x
"
#4
3
ŸŸ
(b) the interval of absolute convergence is 1 xŸŸ
3
#
(c) there are no values for which the series converges conditionally
30. lim 1 lim 1 3x 1 lim 1 3x 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
ˆ‰
u
u 2n4 (3x1) 2n4
(3x 1) 2n 2 2n 2
n1
n
n2
n1
Ê Ê Ê
†
1 3x 1 1 x 0; when x we have , a conditionally convergent series;Ê Ê œ
22
332n1
(1)
!
_
œn1
n1
when x 0 we have , a divergent seriesœœ
!!
__
œœn1 n1
()
2n 1 n 1
"
#
"
n1
(a) the radius is ; the interval of convergence is x 0
"
33
2
Ÿ
(b) the interval of absolute convergence is x 0
2
3
(c) the series converges conditionally at x œ2
3
31. lim 1 lim 1 x lim 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ¹ ¹
kk É
u
u(x) n1
(x )
n1
nn
n1
n
n1
n
Ê Ê
1
1
ÈÈ
†1
x lim 1 x 1 1 x 1 1 x 1 ;Ê Ê ÊÊkk kk
Ɉ‰
11111
nÄ_
n
n1
when x 1 we have , a conditionally convergent series; when x 1 we haveœ œ œ 1 1
!!
__
œœn1 n1
(1) ( )
nn
"
nn
È
, a divergent p-series
!!
__
œœn1 n1
""
n
Ènn
œ
(a) the radius is ; the interval of convergence is ( 1 ) x (1 )"Ÿ11
(b) the interval of absolute convergence is 1 x 1 11
(c) the series converges conditionally at x 1œ 1
32. lim 1 lim 1 lim 1 1
nn nÄ_ Ä_ Ä_
¹¹ »» kk
u
u2
x2 x2
2
x2
n1
n
2n 3
n 1 2n 1
n
Ê Ê
Š‹ Š‹
ÈÈ
Š‹
È
#
†
1 x 2 2 x 2 2 2 x 2 2 0 x 2 2 ; whenÊÊÊÊÊ
Š‹
È
x2
#
#
Š‹ ¹¹
ÈÈÈÈÈÈÈ
x 0 we have 2 which diverges since lim a 0; when x 2 2œœœ Áœ
!!!
ÈÈ
___
œœœn1 n1 n1
Š‹
È
#
2
2
2n
2n 1
nn
n12
nÄ_
we have 2, a divergent series
!!!
È
___
œœœn1 n1 n1
Š‹
È2
22
2
2n 1
nn
n12
œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.7 Power Series 737
(a) the radius is 2; the interval of convergence is 0 x 2 2
ÈÈ
(b) the interval of absolute convergence is 0 x 2 2
È
(c) there are no values for which the series converges conditionally
33. lim 1 lim 1 lim 1 1 (x 1) 4 x 1 2
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk k k
u
u4(x1)4
(x 1) (x 1)
4
n1
n
2n 2
n1 2n
n
Ê Ê Ê Ê
#
†
2 x 1 2 1 x 3; at x 1 we have 1, which diverges; at x 3Ê Ê œ œ œ œ
!!!
___
œœœn0 n0 n0
(2)
44
4
2n
nn
n
we have 1, a divergent series; the interval of convergence is 1 x 3; the series
!!!
___
œœœn0 n0 n0
24
44
2n n
nn
œœ
is a convergent geometric series when 1 x 3 and the sum is
!!
Š‹
ˆ‰
__
œœn0 n0
(x )
4
x1 n
"
#
#
2n
nœ
""
1
44
4 x 2x 1 3 2x x
Š‹ ’“
x4(x )
4
œœ œ
34. lim 1 lim 1 lim 1 1 (x 1) 9 x 1 3
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk k k
u
u9(x1)9
(x 1) (x 1)
9
n1
n
2n 2
n1 2n
n
Ê Ê Ê Ê
#
†
3 x 1 3 4 x 2; when x 4 we have 1 which diverges; at x 2 we haveÊ Ê œ œ œ
!!
__
œœn0 n0
(3)
9
2n
n
which also diverges; the interval of convergence is 4 x 2; the series
!!
__
œœn0 n0
3
9
2n
nœ"
is a convergent geometric series when 4 x 2 and the sum is
!!
Š‹
ˆ‰
__
œœn0 n0
(x 1)
93
x1 n
#
2n
nœ
""
1
99
9 x 2x 1 8 2x x
Š‹ ’“
x1
3
9(x1)
9
œœ œ
35. lim 1 lim 1 x 2 2 2 x 2 2 0 x 4
nnÄ_ Ä_
¹¹ ºº
¸¸
ÈÈÈ
u
u2
x2 2
x2
n1
n
n1
n1
n
n
Ê Ê Ê Ê
ˆ‰
Ȉ‰
È
†
0 x 16; when x 0 we have ( 1) , a divergent series; when x 16 we have (1) , a divergentÊ œ œ
!!
_ _
œ œn0 n0
nn
series; the interval of convergence is 0 x 16; the series is a convergent geometric series when !Š‹
_
œn0
Èx2
#
n
0 x 16 and its sum is œ œ
""
1
2
4x
ŒŒ È
x2 2 x2
36. lim 1 lim 1 ln x 1 1 ln x 1 e x e; when x e or e we
nnÄ_ Ä_
¹¹ ¹ ¹ kk
u
u(ln x)
(ln x)
n1
n
n1
n
Ê Ê Ê Ê œ
" "
obtain the series 1 and ( 1) which both diverge; the interval of convergence is e x e;
!!
__
œœn0 n0
nn
"
(ln x) when e x e
!
_
œn0
nœ
"
"
1ln x
37. lim 1 lim 1 lim 1 1 1 x 2
nn nÄ_ Ä_ Ä_
¹¹ Š ‹
ºº
ˆ‰ kk
u
u3x13 3
x1 3 x
n1 nx1
n1
nÊ Ê Ê Ê
"
#
†ab
x 2 2 x 2 ; at x 2 we have (1) which diverges; the interval of convergence isÊ Ê œ„kk ÈÈÈ È !
_
œn0
n
2 x 2 ; the series is a convergent geometric series when 2 x 2 and its sum is
ÈÈ ÈÈ
!Š‹
_
œn0
x1
3
n
""
#
1
3
x
Š‹Š ‹
x1 3x1
33
œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

738 Chapter 11 Infinite Sequences and Series
38. lim 1 lim 1 x 1 2 3 x 3 ; when x 3 we
nnÄ_ Ä_
¹¹ ¹ ¹ kk ÈÈ È
u
u2
x1 2
x1
n1
n
n1
n1
n
n
Ê Ê Ê œ„
abab
#
†
have 1 , a divergent series; the interval of convergence is 3 x 3 ; the series is a
! !
ÈÈ Š‹
_ _
œ œn0 n0
n x1
2
n
convergent geometric series when 3 x 3 and its sum is œ œ
ÈÈ ""
1
2
3x
Š‹
x1
22x1
39. lim 1 x 3 2 1 x 5; when x 1 we have (1) which diverges;
nÄ_ ¹¹
kk !
(x 3) 2
(x 3)
n
#
n1
n1 n
n
†Ê Ê œ
n1
when x 5 we have ( 1) which also diverges; the interval of convergence is 1 x 5; the sum of thisœ
!
_
œn1
n
convergent geometric series is . If f(x) 1 (x 3) (x 3) (x 3)
""""
# #
#
1
2
x1 4
nn
Š‹
x3 œ œá á
ˆ‰
then f (x) (x 3) n(x 3) is convergent when 1 x 5, and divergesœœáá
2
x1
nn1
## #
w
"" "
ˆ‰
when x 1 or 5. The sum for f (x) is , the derivative of .œw
22
(x 1) x 1
40. If f(x) 1 (x 3) (x 3) (x 3) then f(x) dxœ á áœ
"" "
##
#
4x1
nn2
ˆ‰ '
x . At x 1 the series diverges; at x 5œá á œ œ
(x 3) (x 3) (x 3)
412 n1 n1
n2
"
#
ˆ‰ !
n1 _
œn1
the series converges. Therefore the interval of convergence is 1 x 5 and the sum is
!
_
œn1
(1)2
n1
nŸ
2 ln x 1 (3 ln 4), since dx 2 ln x 1 C, where C 3 ln 4 when x 3.kk kk œ œ œ
'2
x1
41. (a) Differentiate the series for sin x to get cos x 1œ á
3x 5x 7x 9x 11x
3! 5! 7! 9! 11!
1 . The series converges for all values of x sinceœ á
xxxxx
!4!6!8!10!
#
lim x lim 0 1 for all x.
nnÄ_ Ä_
¹¹Š‹
x
(2n 2)! x 2n 1 2n 2
n! 2
2n 2
#"
†ab abab
œœ
(b) sin 2x 2x 2xœ ᜠá
2 x 2 x 2 x 2 x 2 x 8x 32x 128x 512x 2048x
3! 5! 7! 9! 11! 3! 5! 7! 9! 11!
(c) 2 sin x cos x 2 (0 1) (0 0 1 1)x 0 1 0 0 1 x 0 0 1 0 0 1 xœ
ˆ‰ˆ‰
† †† † †† †† ††
" " "
##
#$
3!
0100001x00100 001x
ˆ‰ˆ ‰
††††† ††††††
""" """ "
##
%&
4! 3! 4! 3! 5!
010000001x 2x áœá
‘ˆ‰
’“
†††††††
"""""
#
'
6! 4! 3! 5! 3! 5!
4x 16x
2xœ á
2x 2x 2x 2x 2 x
3! 5! 7! 9! 11!
42. (a) e 1 1 x e ; thus the derivative of e is e itself
d 2x3x4x5x xxx
x 2!3!4!5! !3!4!
xxxx
abœáœáœ
#
(b) e dx e C x C, which is the general antiderivative of e
'xx xxxx
3! 4! 5!
œœá
#
x
(c) e 1 x ; e e 1 1 (1 1 1 1)x 1 1 1 1 x
#
###
""
xxxxx
!3!4!5! ! !
œá œ
xx
† ††† †††
ˆ‰
11 11x11 11x
ˆ‰ˆ ‰
†† †† †† † ††
"""" """"""
## ##
$%
3! ! ! 3! 4! 3! ! ! 3! 4!
1 1 1 1x 100000 áœá
ˆ‰
††††††
" " "" "" " "
##
&
5! 4! ! 3! 3! ! 4! 5!
43. (a) ln sec x C tan x dx x dxkk Š‹
œ œ á
''
x 2x 17x 62x
3 15 315 2835
C; x 0 C 0 ln sec x ,œ á œÊ œÊ œ á
x x x 17x 31x x x x 17x 31x
1 45 2520 14,175 12 45 2520 14,175
## #
kk
converges when x
11
##
(b) sec x x 1 x , converges
# #
œ œ áœá
d(tan x)
dx dx 3 15 315 2835 3 45 315
d x 2x 17x 62x 2x 17x 62x
Š‹
when x
11
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.8 Taylor and Maclaurin Series 739
(c) sec x (sec x)(sec x) 1 1
#
##
œœáá
Š‹Š‹
x5x61x x5x61x
24 720 24 720
1x x xœ á
ˆ‰ˆ ‰ˆ ‰
"" "
##
#% '
5 5 615561
24 4 24 720 48 48 720
1 x , xχ
#
##
2x 17x 62x
3 45 315
11
44. (a) ln sec x tan x C sec x dx 1 dxkk Š‹
œ œá
''
x5x61x
224720
x C; x 0 C 0 ln sec x tan xœ á œÊ œÊ
x x 61x 277x
6 24 5040 72,576 kk
x , converges when xœ á
x x 61x 277x
6 24 5040 72,576
11
##
(b) sec x tan x 1 x , convergesœœáœá
d(sec x)
dx dx 24 720 6 120 1008
d x 5x 61x 5x 61x 277x
Š‹
#
when x
11
##
(c) (sec x)(tan x) 1 xœ á á
Š‹Š‹
x5x61x x2x17x
24 720 3 15 315
#
xx x xx ,œ ᜠá
ˆ‰ˆ ‰ˆ ‰
"" " "
#
$& (
3 15 6 24 315 15 72 720 6 120 1008
2 5 17 5 61 5x 61x 277x
x
11
##
45. (a) If f(x) a x , then f (x) n(n 1)(n 2) (n (k 1)) a x and f (0) k!aœ œ â œ
!!
__
œœn0 nk
nnk
nk nkkÐÑ ÐÑ
a ; likewise if f(x) b x , then b a b for every nonnegative integer kÊœ œ œ Êœ
knkkk
f(0) f(0)
k! k!
n
k k
!
_
œn0
(b) If f(x) a x 0 for all x, then f (x) 0 for all x from part (a) that a 0 for everyœœ œ Ê œ
!
_
œn0
n k
nkÐÑ
nonnegative integer k
46. 1 x x x x x x 1 2x 3x 4x
""
#$% # $
1 x (1 x) (1 x)
x
œáÊ œ áÊ
’“
ab
x2x 3x 4x x x14x9x 16x œáÊ œ áÊ
#$% # $
’“
ab
1x xx
(1 x) (1 x)
x 4x 9x 16x 6œ á Ê œ á Ê œ
#$ % "
#
ˆ‰
4
ˆ‰
8
n
4916 n
4816 2
!
n1
47. The series converges conditionally at the left-hand endpoint of its interval of convergence [ 1 1 ; the
!
_
œn1
x
n
nß Ñ
series converges absolutely at the left-hand endpoint of its interval of convergence [ 1 1]
!
_
œn1
x
n
n
ab ß
48. Answers will vary. For instance:
(a) (b) (x 1) (c)
!!!
ˆ‰ ˆ‰
___
œœœn1 n1 n1
xx3
3
nnn
#
11.8 TAYLOR AND MACLAURIN SERIES
1. f(x) ln x, f (x) , f (x) , f (x) ; f(1) ln 1 0, f (1) 1, f (1) 1, f (1) 2 P (x) 0,œ œ œ œ œ œ œ œ œ Ê œ
w ww www w ww www
"" !
xxx
2
P (x) (x 1), P (x) (x 1) (x 1) , P (x) (x 1) (x 1) (x 1)
"# $
"""
##
##$
œ œ œ
3
2. f(x) ln (1 x), f (x) (1 x) , f (x) (1 x) , f (x) 2(1 x) ; f(0) ln 1 0,œ œ œ œ œ œœ
w "ww #www $
"
1x
f (0) 1, f (0) (1) 1, f (0) 2(1) 2 P (x) 0, P (x) x, P (x) x , P (x)
w ww # www $ !"# $
#
œ œ œ œ œ œ Ê œ œ œ
1 x
1
xœ
xx
3
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

740 Chapter 11 Infinite Sequences and Series
3. f(x) x , f (x) x , f (x) 2x , f (x) 6x ; f(2) , f (2) , f (2) , f (x)œ œ œ œ œ œ œ œ œ
""""
" w # ww $ www % w ww www
#x44 8
3
P (x) , P (x) (x 2), P (x) (x 2) (x 2) ,Ê œ œ œ
!" #
""" "" "
## #
#
448
P (x) (x 2) (x 2) (x 2)
$"" " "
#
#$
œ
48 16
4. f(x) (x 2) , f (x) (x 2) , f (x) 2(x 2) , f (x) 6(x 2) ; f(0) (2) , f (0) (2)œ œ œ œ œ œ œ
" w # ww $ www % " w #
"
#
, f (0) 2(2) , f (0) 6(2) P (x) , P (x) , P (x) ,œ œ œ œ œ Ê œ œ œ
"" """
ww $ www % !" #
## #44 8 448
3xxx
P(x)
$"
#
œ
xx x
4816
5. f(x) sin x, f (x) cos x, f (x) sin x, f (x) cos x; f sin , f cos ,œ œ œ œ œ œ œ œ
w ww www w
##
ˆ‰ ˆ‰
11 1 1
44 4 4
22
ÈÈ
f sin , f cos P , P (x) x ,
ww www
#####
!"
ˆ‰ ˆ‰ ˆ ‰
11 1 1 1
44 4 4 4
22222
œ œ œ œ Ê œ œ
ÈÈÈÈÈ
P (x) x x , P (x) x x x
#$
## ## #
##$
œ œ
ÈÈ È ÈÈ È È
22 2 22 2 2
44 4 44 4 1 4
ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰
11 11 1
6. f(x) cos x, f (x) sin x, f (x) cos x, f (x) sin x; f cos ,œœœ œœœ
w ww www "
ˆ‰
11
44
2
È
f sin , f cos , f sin P (x) ,
wwwwww
""""
!
ˆ‰ ˆ‰ ˆ‰
11 1 1 11
44 4 4 44
2222
œ œ œ œ œ œ Ê œ
ÈÈÈÈ
P (x) x , P (x) x x ,
"#
"" "" "
#
#
œ œ
ÈÈ ÈÈ È
22 22 2
444
ˆ‰ ˆ‰ ˆ‰
111
P (x) x x x
$"" " "
#
#$
œ
ÈÈ È È
22 2 62
44 4
ˆ‰ ˆ‰ ˆ‰
11 1
7. f(x) x x , f (x) x , f (x) x , f (x) x ; f(4) 4 2,œœ œ œ œ œœ
Ȉ‰ ˆ ‰ ˆ‰ È
"Î# w "Î# ww $Î# www &Î#
""
#48
3
f (4) 4 , f (4) 4 ,f (4) 4 P (x) 2, P (x) 2 (x 4),
w "Î# ww $Î# www &Î#
"" " " "
#!"
œœœœœœÊœœ
ˆ‰ ˆ ‰ ˆ‰
4 4 32 8 256 4
33
P(x)2 (x4) (x4), P(x)2 (x4) (x4) (x4)
#$
"" "" "
##$
#
œ œ
4 64 4 64 51
8. f(x) (x 4) , f (x) (x 4) , f (x) (x 4) , f (x) (x 4) ; f(0) (4) 2,œ œ œ œ œ œ
"Î# w "Î# ww $Î# www &Î# "Î#
""
#
ˆ‰ ˆ ‰ ˆ‰
48
3
f (0) (4) , f (0) (4) , f (0) (4) P (x) 2,
w "Î# ww $Î# www &Î#
"" " "
#!
œœœœœœÊœ
ˆ‰ ˆ ‰ ˆ‰
4 4 32 8 256
33
P (x) 2 x, P (x) 2 x x , P (x) 2 x x x
"# $
""" """
##$
œ œ œ
4 4 64 4 64 512
9. e e 1 x
xx
x xxx
n! n! ! 3! 4!
(x)
œ Ê œ œá
!!
__
œœn0 n0
nn
#
10. e e 1
xxxxxx
n! n! 4 2! 2 3! 24!
œ Êœ œá
!!
__
œœn0 n0
nn
x2 ˆ‰
x
2
#†††
11. f(x) (1 x) f (x) (1 x) , f (x) 2(1 x) , f (x) 3!(1 x) f (x)œ Ê œ œ œ Êá
" w # ww $ www % k
( 1) k!(1 x) ; f(0) 1, f (0) 1, f (0) 2, f (0) 3!, f (0) ( 1) k!œ œ œ œ œ áß œ
kk1 w ww www kk
1 x x x (x) (1)xÊ œáœ œ
"
#$
1x
nn
!!
__
œœn0 n0
n
12. f(x) (1 x) f (x) (1 x) , f (x) 2(1 x) , f (x) 3!(1 x) f (x)œ Ê œ œ œ Êá
" w # ww $ www % k
k!(1 x) ; f(0) 1, f (0) 1, f (0) 2, f (0) 3!, f (0) k!œ œ œ œ œáß œ
k1 kwwwwww
1xx x xÊ œáœ
"
#$
1x
n
!
_
œn0
13. sin x sin 3x 3xœ Ê œ œ œá
!!!
___
œœœn0 n0 n0
()x ()(3x) ()3 x
(n 1)! (n 1)! (n 1)! 3! 5!
3x 3x
" " "
# # #
n2n1 n 2n1 n2n12n1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.8 Taylor and Maclaurin Series 741
14. sin x sin œ Ê œ œ œá
!!!
___
œœœn0 n0 n0
()x ()x
( n 1)! ( n 1)! (2n 1)! 2 3! 2 5!
xxxx
()
" "
# # # # #
"
n2n1 n2n1
nx2n 1
2n 1
ˆ‰
††
15. 7 cos ( x) 7 cos x 7 7 , since the cosine is an even functionœ œ œá
!
_
œn0
()x
(2n)! ! 4! 6!
7x 7x 7x
"
#
n2n
16. cos x 5 cos x 5 5œ Ê œ œá
!!
__
œœn0 n0
(1)x (1)(x)
(2n)! ( n)! 2! 4! 6!
5x 5x 5x
#
n2n n 2n
11111
17. cosh x 1 x 1 x 1œ œ á á œá
ee xxx xxx xxx
!3!4! !3!4! !4!6!
xx
"
## # # #
#
’“Š‹Š‹
œ!
_
œn0
x
(2n)!
2n
18. sinh x 1 x 1 x xœ œ á á œá
ee xxx xxx xxx
! 3! 4! ! 3! 4! 3! 5! 6!
xx
"
## # #
’“Š‹Š‹
œ!
_
œn0
x
(2n 1)!
2n 1
19. f(x) x 2x 5x 4 f (x) 4x 6x 5, f (x) 12x 12x, f (x) 24x 12, f (x) 24œ Ê œ œ œ œ
% $ w $ # ww # www Ð Ñ4
f (x) 0 if n 5; f(0) 4, f (0) 5, f (0) 0, f (0) 12, f (0) 24, f (0) 0 if n 5Êœœœœ œ œ œ
ÐÑ w ww www ÐÑ ÐÑn4n
x 2x 5x 4 4 5x x x x 2x 5x 4 itselfÊ œ œ
%$ $ %%$
12 24
3! 4!
20. f(x) (x 1) f (x) 2(x 1); f (x) 2 f (x) 0 if n 3; f(0) 1, f (0) 2, f (0) 2, f (0) 0 ifœ Ê œ œÊ œ œ œ œ œ
#w ww ÐÑ wwwÐÑnn
n3 (x1) 12x x 12xxÊ œ œ
###
#
2
!
21. f(x) x 2x 4 f (x) 3x 2, f (x) 6x, f (x) 6 f (x) 0 if n 4; f(2) 8, f (2) 10,œÊ œ œ œÊ œ œ œ
$ w # ww www Ð Ñ wn
f (2) 12, f (2) 6, f (2) 0 if n 4 x 2x 4 8 10(x 2) (x 2) (x 2)
ww www Ð Ñ $ # $
œ œ œ Ê œ
n12 6
2! 3!
8 10(x 2) 6(x 2) (x 2)œ
#$
22. f(x) 2x x 3x 8 f (x) 6x 2x 3, f (x) 12x 2, f (x) 12 f (x) 0 if n 4; f(1) 2,œ Ê œ œ œ Ê œ œ
$ # w # ww www Ð Ñn
f (1) 11, f (1) 14, f (1) 12, f (1) 0 if n 4 2x x 3x 8
wwwwwwÐÑ $#
œœ œ œÊ
n
211(x1) (x1) (x1) 211(x1)7(x1) 2(x1)œ œ
14 12
2! 3!
#$ #$
23. f(x) x x 1 f (x) 4x 2x, f (x) 12x 2, f (x) 24x, f (x) 24, f (x) 0 if n 5;œÊ œ œ œ œ œ
% # w $ ww # www Ð Ñ Ð Ñ4n
f( 2) 21, f ( 2) 36, f ( 2) 50, f ( 2) 48, f ( 2) 24, f ( 2) 0 if n 5 x x 1œ œ œ œ œ œ Ê
w ww www ÐÑ ÐÑ % #4n
21 36(x 2) (x 2) (x 2) (x 2) 21 36(x 2) 25(x 2) 8(x 2) (x 2)œ œ
50 48 24
2! 3! 4!
#$% #$%
24. f(x) 3x x 2x x 2 f (x) 15x 4x 6x 2x, f (x) 60x 12x 12x 2,œÊ œ œ
&% $# w % $ # ww $ #
f (x) 180x 24x 12, f (x) 360x 24, f (x) 360, f (x) 0 if n 6; f( 1) 7,
www # Ð Ñ Ð Ñ Ð Ñ
œœœ œœ
45n
f ( 1) 23, f ( 1) 82, f ( 1) 216, f ( 1) 384, f ( 1) 360, f ( 1) 0 if n 6
w ww www ÐÑ ÐÑ ÐÑ
œ œ œ œ œ œ
45n
3x x 2x x 2 723(x1) (x1) (x1) (x1) (x1)Ê œ
&%$# #$%&
82 216 384 360
2! 3! 4! 5!
7 23(x 1) 41(x 1) 36(x 1) 16(x 1) 3(x 1)œ
#$%&
25. f(x) x f (x) 2x , f (x) 3! x , f (x) 4! x f (x) ( 1) (n 1)! x ;œÊ œ œ œ Ê œ
# w $ ww % www & Ð Ñ nnn2
f(1) 1, f (1) 2, f (1) 3!, f (1) 4!, f (1) ( 1) (n 1)! œœœ œ œÊ
w ww www Ð Ñ "
nn
x
1 2(x 1) 3(x 1) 4(x 1) ( 1) (n 1)(x 1)œáœ
#$
!
_
œn0
nn
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

742 Chapter 11 Infinite Sequences and Series
26. f(x) f (x) (1 x) , f (x) 2(1 x) , f (x) 3! (1 x) f (x) n! (1 x) ;œÊ œ œ œÊ œ
x
1x
nn1
w #ww $www % ÐÑ
f(0) 0, f (0) 1, f (0) 2, f (0) 3! x x x xœ œ œ œ Ê œáœ
wwwwww #$
x
1x
n1
!
_
œn0
27. f(x) e f (x) e , f (x) e f (x) e ; f(2) e , f (2) e , f (2) eœÊ œ œÊ œ œ œá œ
xxxnx nwww ÐÑ #w#ÐÑ#
e e e(x2) (x2) (x2) (x2)Êœáœ
x n
ee e
3! n!
## # $
#!
_
œn0
28. f(x) 2 f (x) 2 ln 2, f (x) 2 (ln 2) , f (x) 2 (ln 2) f (x) 2 (ln 2) ; f(1) 2, f (1) 2 ln 2,œÊ œ œ œ Ê œ œ œ
xx x xnxnw ww # www $ Ð Ñ w
f (1) 2(ln 2) , f (1) 2(ln 2) , , f (1) 2(ln 2)
ww # www $ Ð Ñ
œœáœ
nn
2 2 (2 ln 2)(x 1) (x 1) (x 1) Êœ áœ
x2(ln 2) 2(ln 2) 2(ln 2) (x 1)
3! n!
#
#$
!
_
œn0
nn
29. If e (x a) and f(x) e , we have f (a) e f or all n 0, 1, 2, 3,
xœ œ œ œá
!
_
œn0
f(a)
n!
nxna
nÐÑ
e e e 1 (x a) at x aÊœ áœáœ
xa a
(x a) (x a) (x a) (x a)
0! 1! 2! 2!
’“’“
30. f(x) e f (x) e for all n f (1) e for all n 0, 1, 2, œÊ œ Ê œ œ á
xn x nÐÑ ÐÑ
e ee(x1) (x1) (x1) e1(x1)ʜᜠá
xee
!3! 2!3!
(x 1) (x 1)
#
#$
’“
31. f(x) f(a) f (a)(x a) (x a) (x a) f (x)œ áÊ
w#$w
#
f (a) f (a)
3!
f (a) f (a)(x a) 3(x a) f (x) f (a) f (a)(x a) 4 3(x a)œ áÊ œ á
w ww # ww ww www #
f (a) f (a)
3! 4!
4
†
f (x) f (a) f (a)(x a) (x a)Êœ á
ÐÑ ÐÑ ÐÑ #
#
nnn1 f(a)
n2
f(a) f(a) 0, f (a) f (a) 0, , f (a) f (a) 0Êœ œá œ
w w ÐÑ ÐÑnn
32. E(x) f(x) b b (x a) b (x a) b (x a) b (x a)χ
!" # $
#$
nn
0 E(a) f(a) b b f(a); from condition (b),Êœ œ Ê œ
!!
lim 0
xaÄ
f(x) f(a) b (x a) b (x a) b (x a) b (x a)
(x a)
á
nn
nœ
lim 0ʜ
xaÄ
f(x) b 2b(x a) 3b(x a) nb(x a)
n(x a)
á
nn1
n1
b f (a) lim 0Êœ Ê œ
"w á "
xaÄ
f (x) 2b 3! b (x a) n(n )b (x a)
n(n 1)(x a)
nn2
n2
b f (a) lim 0Êœ Ê œ
#"
##
ww á
xaÄ
f (x) 3! b n(n 1)(n 2)b (x a)
n(n 1)(n )(x a)
nn3
n3
b f (a) lim 0 b f (a); therefore,œœ Ê œÊ œ
$""
www Ð Ñ
3! n! n!
f (x) n! b nn
xaÄ
nn
g(x) f(a) f (a)(x a) (x a) (x a) P (x)œ á œ
w#
f (a) f (a)
2! n!
nn
n
33. f(x) ln (cos x) f (x) tan x and f (x) sec x; f(0) 0, f (0) 0, f (0) 1œ Ê œ œ œ œ œ
www#www
L(x) 0 and Q(x)Êœ œ
x
2
34. f(x) e f (x) (cos x)e and f (x) ( sin x)e (cos x) e ; f(0) 1, f (0) 1,œÊœ œ œ œ
sin x sin x sin x sin xwww #w
f (0) 1 L(x) 1 x and Q(x) 1 x
ww
#
œ Ê œ œ
x
35. f(x) 1 x f (x) x 1 x and f (x) 1 x 3x 1 x ; f(0) 1,œ Ê œ œ œab ab ab ab
#w #ww ###
"Î# $Î# $Î# &Î#
f (0) 0, f (0) 1 L(x) 1 and Q(x) 1
www
#
œœÊœ œ
x
36. f(x) cosh x f (x) sinh x and f (x) cosh x; f(0) 1, f (0) 0, f (0) 1 L(x) 1 and Q(x) 1œÊœ œ œœ œÊœ œ
www www
#
x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.9 Convergence of Taylor Series; Error Estimates 743
37. f(x) sin x f (x) cos x and f (x) sin x; f(0) 0, f (0) 1, f (0) 0 L(x) x and Q(x) xœÊœ œ œ œ œÊœ œ
www www
38. f(x) tan x f (x) sec x and f (x) 2 sec x tan x; f(0) 0, f (0) 1, f 0 L(x) x and Q(x) xœÊœ œ œ œœÊœ œ
w # ww # w ww
11.9 CONVERGENCE OF TAYLOR SERIES; ERROR ESTIMATES
1. e 1 x e 1 ( 5x) 1 5x
x5x
x x 5x 5x
!n! ! !3! n!
( 5x) ( 1) 5 x
œ áœ Ê œ ᜠáœ
###
!!
_ _
œ œn0 n0
nnnn
2. e 1 x e 1 1
xx2
xx x xxx
!n! ! 2!23!
œ áœ Ê œ ᜠá
#####
Î
!ˆ‰
_
œn0
nx
ˆ‰
œ!
_
œn0
(1)x
2n!
nn
n
3. sin x x 5 sin ( x) 5 ( x)œáœ Ê œ á
xx
3! 5! ( n 1)! 3! 5!
(1)x (x) (x)
!’“
_
œn0
#
n2n1
œ!
_
œn0
5( 1) x
(n 1)!
#
n12n1
4. sin x x sin œáœ Ê œá
xx x x
3! 5! ( n 1)! 3! 5! 7!
(1)x
!
_
œn0
# # #
n2n1 xxx
11
ˆ‰ ˆ‰ ˆ‰
œ!
_
œn0
(1) x
2(n1)!
#
n2n12n1
2n 1
1
5. cos x cos x 1 1œÊœ œ œá
!!!
È
___
œœœn0 n0 n0
(1)x
(2n)! (2n)! (2n)! ! 4! 6!
(1) x1 (1)x1 x1 x1
x1
#
n2n n2n
nn
’“
ab ab ab ab
6. cos x cos cos œÊœ œ œ
!!!
Š‹ Š‹
Œ
__
œœn0 n0
(1)x (1)x
(2n)! ( n)! 2 (2n)!
xx
2
(1)
n0
##
"Î# _
œ
n2n n3n
nx
2n
n
Ȍ
Š‹
1χ
xx x
22! 2 4! 2 6!
†††
7. e xe x x x
xx
x x x xxx
n! n! n! ! 3! 4!
n0
œ Ê œ œ œá
!!!
Œ
__
œœn0 n0
nnn1
_
œ
#
#
8. sin x x sin x x xœ Ê œ œ œá
!!!
Œ
___
œœœn0 n0 n0
(1)x (1)x (1)x
(2n 1)! ( n 1)! (2n 1)! 3! 5! 7!
xxx
#
## $
n2n1 n2n1 n2n3
9. cos x 1 cos x 1 1 1œ Ê œ œ á
!!
__
œœn0 n0
(1)x (1)x
(2n)! ( n)! 2 4! 6! 8! 10!
x x x xxxxx
####
n2n n2n
œ áœ
xxxx
4! 6! 8! 10! ( n)!
(1)x
!
_
œn2
#
n2n
10. sin x sin x x xœÊœ
!!
Œ
__
œœn0 n0
(1)x (1)x
(2n 1)! 3! ( n 1)! 3!
xx
#
n2n1 n2n1
xx œ ᜠáœ
Š‹ !
xxxxx x xxxx
3! 5! 7! 9! 11! 3! 5! 7! 9! 11! (2n 1)!
(1)x
_
œn2
n2n1
11. cos x x cos x x xœÊœ œ œá
!!!
___
œœœn0 n0 n0
(1)x (1)(x) ( ) x
(2n)! ( n)! ( n)! 2! 4! 6!
xxx
"
##
n2n n 2n n2n2n1
111
111
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

744 Chapter 11 Infinite Sequences and Series
12. cos x x cos x x xœ Ê œ œ œá
!!!
ab
___
œœœn0 n0 n0
(1)x ( )x
(2n)! ( n)! ( n)! 2! 4! 6!
(1) x xx x
"
### #
##
n2n n4n2
n2n
ab
13. cos x 1
#""" ""
# # ## ##
œ œ œ á
cos 2x ( 1) (2x) (2x) (2x) (2x) (2x)
(2n)! 2!4!6!8!
!’“
_
œn0
n2n
11 1 œáœ œ
(2x) (2x) (2x) (2x) ( 1) (2x) ( 1) 2 x
2 2! 2 4! 2 6! 2 8! 2 (2n)! (2n)!
†††† †
!!
__
œœn1 n1
n 2n n 2n 1 2n
14. sin x cos 2x 1
#"" ""
### ###
œ œ œ áœá
ˆ‰ Š‹
1 cos 2x (2x) (2x) (2x) (2x) (2x) (2x)
!4!6! 22!24!26!
†††
œœ
!!
__
œœn1 n1
(1) (2x) (1) 2 x
(2n)! (2n)!
#
n1 2n n 2n1 2n
†
15. x x (2x) 2 x x 2x 2 x 2 x
x
12x 12x
nnn2
# # # $#%$&
"
œ œ œ œá
ˆ‰ !!
__
œœn0 n0
16. x ln (1 2x) x 2xœ œ œá
!!
__
œœn1 n1
(1) (2x) (1) 2x
nn 45
2x 2x 2x
#
#
n1 n n1nn1
17. x 1 x x x 1 2x 3x nx
"""
#$ #
1x dx 1x (1x)
nn1
d
œ œáÊ œ œ áœ
!!
ˆ‰
_ _
œ œn0 n1
(n 1)xœ
!
_
œn0
n
18. 1 2x 3x 2 6x 12x n(n 1)x
2d d d
1x dx 1 x dx (1 x) dx
n2
ab
""
##
œœ œáœáœ
ˆ‰ Š‹ab !
_
œn2
(n 2)(n 1)xœ
!
_
œn0
n
19. By the Alternating Series Estimation Theorem, the error is less than x 5! 5 10
kkx
5! Ê ‚kk aba b
&%
x 600 10 x 6 10 0.56968Ê‚ Ê‚ ¸kk kk È
&% #
20. If cos x 1 and x 0.5, then the error is less than 0.0026, by Alternating Series Estimation Theorem;œ œ
x(.5)
24
#kk ¹¹
since the next term in the series is positive, the approximation 1 is too small, by the Alternating Series Estimationx
#
Theorem
21. If sin x x and x 10 , then the error is less than 1.67 10 , by Alternating Series Estimation Theorem;œ ¸‚kk $
ab10
3!
10
The Alternating Series Estimation Theorem says R (x) has the same sign as . Moreover, x sin x
#
x
3!
0 sin x x R (x) x 0 10 x 0.Ê œ ÊÊ
#$
22. 1 x 1 . By the Alternating Series Estimation Theorem the error
Èkk
¹¹
œ á
xx x x
816 88
(0.01)
#
1.25 10œ‚
&
23. R (x) 1.87 10 , where c is between 0 and xkk
¹¹
#
œ ‚
ex
3! 3!
3 (0.1) 4
c01
24. R (x) 1.67 10 , where c is between 0 and xkk
¹¹
#%
œœ‚
ex
3! 3!
(0.1)
c
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
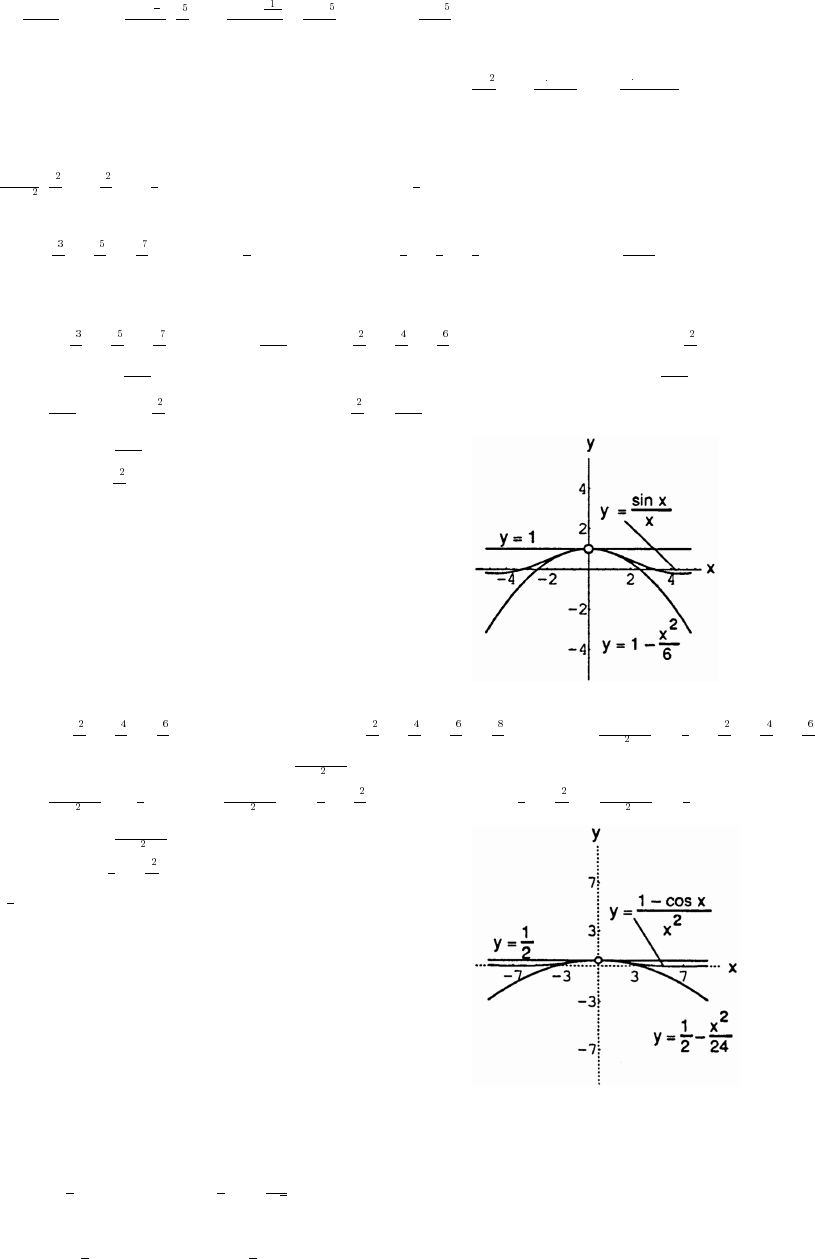
Section 11.9 Convergence of Taylor Series; Error Estimates 745
25. R (x) x (1.13) 0.000294kk
¸¸
¹¹
%&
##
œ œ ¸
cosh c e e x
5! 5! 5! 5!
1.65 (0.5) (0.5)
cc 1.65 †
26. If we approximate e with 1 h and 0 h 0.01, then error h
heh e hh e(0.0)
ŸŸ ŸŸkk
¹¹ Š ‹
c001 001
## #
"
†
0.00505h 0.006h (0.6%)h, where c is between 0 and h.œœ
27. R x .01 x (1%) x .01 0 x .02k k kk kk kk kk
¹¹¸¸ ¸¸
""
# # # #
œœœÊÊ
(1 c) !
xxx x
28. tan x x tan 1 1 ; error .01
" " """ "
#
œáÊ œ œá
xxx
357 4 357 n1
1kk
2n 1 100 n 49Ê Ê
29. (a) sin x x 1 , s 1 and s 1 ; if L is the sum of theœáÊ œá œ œ
xxx sin x xxx x
3! 5! 7! x 3! 5! 7! 6
"#
series representing , then by the Alternating Series Estimation Theorem, L s 1 0 and
sin x sin x
x x
œ
"
L s 1 0. Therefore 1 1œ
#sin x x x sin x
x6 6x
Š‹
(b) The graph of y , x 0, is bounded below by theœÁ
sin x
x
graph of y 1 and above by the graph of y 1 asœ œ
x
6
derived in part (a).
30. (a) cos x 1 1 cos x ;œáÊ œáÊ œá
xxx xxxx 1cos x xxx
!4!6! !4!6!8! x 4!6!8!
## #
"
if L is the sum of the series representing , then by the Alternating Series Estimation Theorem
1cos x
x
L s - 0 and 0. Therefore .œ
"" " " "
## ###
1 cos x 1 cos x x x 1 cos x
xx4! 4x
Š‹
(b) The graph of y is bounded below byœ1cos x
x
the graph of y and above by the graph ofœ
"
#
x
24
y as indicated in part (a).œ"
#
31. sin x when x 0.1; the sum is sin (0.1) 0.099833417œ¸
32. cos x when x ; the sum is cos 0.707106781œœ¸
11
44
2
ˆ‰ "
È
33. tan x when x ; the sum is tan 0.808448
" "
œ¸
11
33
ˆ‰
34. ln (1 x) when x ; the sum is ln (1 ) 1.421080œ ¸11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

746 Chapter 11 Infinite Sequences and Series
35. e sin x 0 x x x x x x
x
3! ! 3! 3! 5! ! 3! 4! 5! 3! 3! 5!
œ á
#$%& '
"" "" """" """"
##
ˆ‰ˆ‰ˆ ‰ˆ ‰
xxxxxχ
#$&'
"" "
33090
36. e cos x 1 x x x x x
x
! ! ! 3! 4! ! 2! 4! 4! 2! 3! 5!
œ á
#$% &
"" "" """" """"
## # #
ˆ‰ˆ‰ˆ ‰ˆ ‰
1x x x xœ á
"" "
$% &
3630
37. sin x cos 2x 1
#"" ""
### ## #
œ œ œ áœá
ˆ‰ Š‹
1 cos 2x 2x 2x 2x
(2x) (2x) (2x)
2! 4! 6! ! 4! 6!
sin x 2x 2 sin x cos xÊ œ ᜠáÊ
d d 2x 2x 2x
dx dx 2! 4! 6! 3! 5! 7!
(2x) (2x) (2x)
abŠ‹
#
2x sin 2x, which checksœáœ
(2x) (2x) (2x)
3! 5! 7!
38. cos x cos 2x sin x 1
##
##
œ œá á
Š‹Š‹
(2x) (2x) (2x) (2x)
!4!6!8! !4!6!8!
2x 2x 2x 2x
11xxxxœáœ á
2x 2x 2x 2
! 4! 6! 3 45 315
#
#% ' )
""
39. A special case of Taylor's Theorem is f(b) f(a) f (c)(b a), where c is between a and bœ Ê
w
f(b) f(a) f (c)(b a), the Mean Value Theorem.œ
w
40. If f(x) is twice differentiable and at x a there is a point of inflection, then f (a) 0. Therefore,œœ
ww
L(x) Q(x) f(a) f (a)(x a).œœ
w
41. (a) f 0, f (a) 0 and x a interior to the interval I f(x) f(a) (x a) 0 throughout I
ww w #
#
Ÿœ œ ÊœŸ
f(c)
f(x) f(a) throughout I f has a local maximum at x aÊŸ Ê œ
(b) similar reasoning gives f(x) f(a) (x a) 0 throughout I f(x) f(a) throughout I f has aœ Ê Ê
f(c)
#
#
local minimum at x aœ
42. f(x) (1 x) f (x) (1 x) f (x) 2(1 x) f (x) 6(1 x)œ Ê œ Ê œ Ê œ
"w #ww $ÐÑ %3
f (x) 24(1 x) ; therefore 1 x x x . x 0.1 Êœ ¸ÊÊ
ÐÑ & # $
"""
&
4
1x 11 1x 9 (1x) 9
10 10 10
kk ¹¹
ˆ‰
x the error e (0.1) 0.00016935 0.00017, since .Ê Ê Ÿ œ œ
¹¹ ¹ ¹ ¹¹¹¹
ˆ‰ ˆ‰
x10 10
(1 x) 9 4! 9 4! (1 x)
max f (x) x f (x)
%%
&&
$"
4 4
43. (a) f(x) (1 x) f (x) k(1 x) f (x) k(k 1)(1 x) ; f(0) 1, f (0) k, and f (0) k(k 1)œ Ê œ Ê œ œ œ œ
kk1 k2w ww w ww
Q(x) 1 kx xʜ
k(k )"
#
#
(b) R (x) x x 0 x or 0 x .21544kk kk
¸¸
#"" " "
$$
œÊÊ
32
3! 100 100 100
††
44. (a) Let P x x P .5 10 since P approximates accurate to n decimals. Then,œ Ê œ ‚11 1kk k k n
P sin P ( x) sin ( x) ( x) sin x (x sin x) (P sin P) œ œ œ Ê 111 1 1kk
sin x x 10 .5 10 P sin P gives an approximation to correct to 3nœŸ‚‚ Êkk
kkx
3! 3!
0.125 3n 3n
1
decimals.
45. If f(x) a x , then f (x) n(n 1)(n 2) (n k 1)a x and f (0) k! aœ œ â œ
!!
__
œœn0 nk
nnk
nk nkkÐÑ ÐÑ
a for k a nonnegative integer. Therefore, the coefficients of f(x) are identical with theʜ
kf(0)
k!
k
corresponding coefficients in the Maclaurin series of f(x) and the statement follows.
46. : f even f( x) f(x) f ( x) f (x) f ( x) f (x) f odd;Note Êœ Êœ Ê œ Ê
www ww
f odd f( x) f(x) f ( x) f (x) f ( x) f (x) f even;Êœ Êœ Ê œ Ê
wwwww
also, f odd f( 0) f(0) 2f(0) 0 f(0) 0Êœ Ê œÊ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
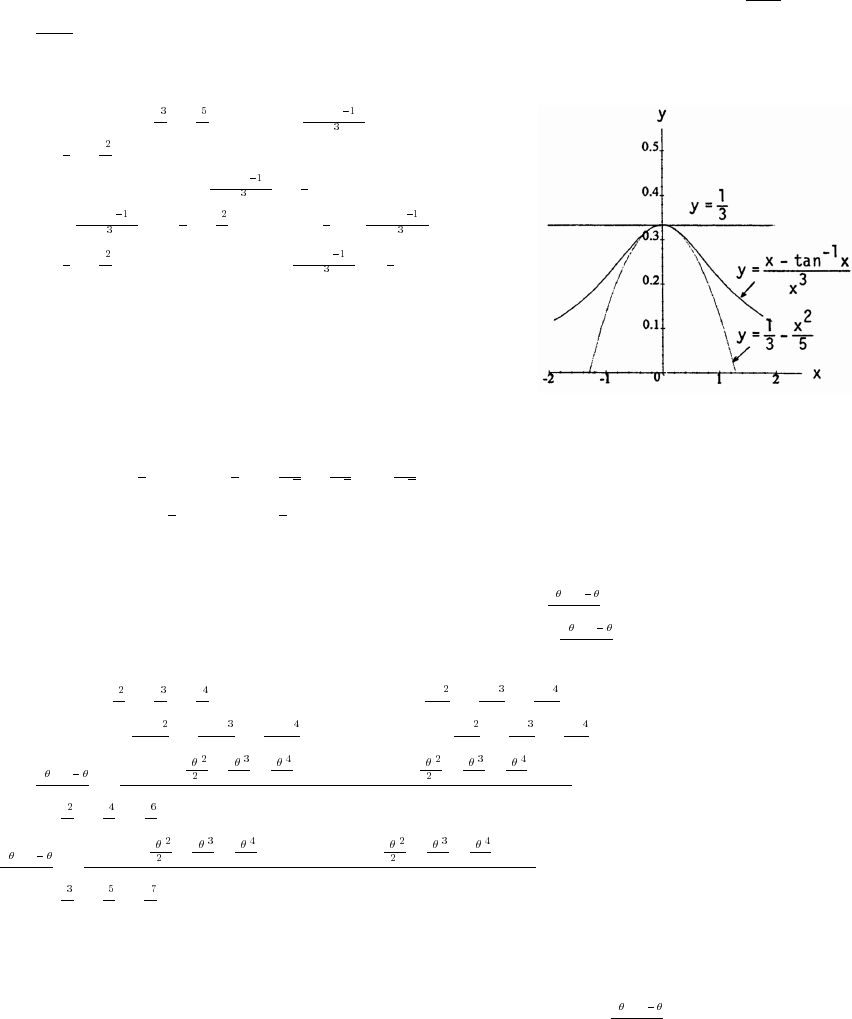
Section 11.9 Convergence of Taylor Series; Error Estimates 747
(a) If f(x) is even, then any odd-order derivative is odd and equal to 0 at x 0. Therefore,œ
a a a 0; that is, the Maclaurin series for f contains only even powers.
"$&
œœœáœ
(b) If f(x) is odd, then any even-order derivative is odd and equal to 0 at x 0. Therefore,œ
a a a 0; that is, the Maclaurin series for f contains only odd powers.
!#%
œœœáœ
47. (a) Suppose f(x) is a continuous periodic function with period p. Let x be an arbitrary real number. Then f
!
assumes a minimum m and a maximum m in the interval [x x p]; i.e., m f(x) m for all x in
"#!!"#
ß Ÿ Ÿ
[x x p]. Since f is periodic it has exactly the same values on all other intervals [x p x 2p],
!! !!
ß ß
[x 2p x 3p], , and [x p x ], [x 2p x p], , and so forth. That is, for all real numbers
!! !!!!
ß á ß ß á
x we have m f(x) m . Now choose M max m , m . Then_ _ Ÿ Ÿ œ
"# "#
efkkkk
M m m f(x) m m M f(x) M for all x.Ÿ Ÿ Ÿ Ÿ Ÿ Ÿ Ê Ÿkk kk kk
"" ##
(b) The dominate term in the nth order Taylor polynomial generated by cos x about x a is (x a) orœ
sin (a)
n!
n
(x a) . In both cases, as x increases the absolute value of these dominate terms tends to ,
cos (a)
n!
n
_kk
causing the graph of P (x) to move away from cos x.
n
48. (b) tan x x
"
œáÊ
xx xtanx
35 x
; from the Alternating Seriesœ á
"
35
x
Estimation Theorem, 0
xtanx
x3
"
0 ÊÊ
xtanx x xtanx
x35 3x
" "
Š‹
; therefore, the lim œ
""
35 x 3
xxtanx
x0Ä
49. (a) e cos ( ) i sin ( ) 1 i(0) 1
i1œ œœ11
(b) e cos i sin (1 i)
i4
44
22 2
i
111
Î""
œ œœ
ˆ‰ ˆ‰ Š‹
ÈÈ È
(c) e cos i sin 0 i( 1) i
Î
##
i2111
œ œœ
ˆ‰ ˆ‰
50. e cos i sin e e cos ( ) i sin ( ) cos i sin ;
iii())))
œ Êœœœ)) ) ) ))
e e cos i sin cos i sin 2 cos cos ;
ii ee
))
œ œ Ê œ
#
)))) ) )
ii
e e cos i sin (cos i sin ) 2i sin sin
ii ee
i
))
œ œ Ê œ
#
)))) ) )
ii
51. e 1 x e 1 i and
xi
xxx
!3!4! 2! 3! 4!
(i ) (i ) (i )
œáÊ œá
#
))))
)
e1i 1i
#
i( i) ( i) ( i) (i) (i) (i)
2! 3! 4! ! 3! 4!
)))) )))
œ áœá))
ʜ
ee
ii
##
Š‹Š‹
1i 1iáá))
(i ) (i ) (i ) (i ) (i ) (i )
!3!4! !3!4!
1 cos ;œáœ
)))
#!4!6! )
ee
ii
ii
##
œŠ‹Š‹
1i 1iáá))
(i ) (i ) (i ) (i ) (i ) (i )
!3!4! !3!4!
sin œáœ))
)))
3! 5! 7!
52. e cos i sin e e cos ( ) i sin ( ) cos i sin
iii)))
œ Êœœœ)) ) )))
ÐÑ
(a) e e (cos i sin ) (cos i sin ) 2 cos cos cosh i
ii ee
))
œ œ Ê œ œ
#
)) )) ) ) )
ii
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

748 Chapter 11 Infinite Sequences and Series
(b) e e (cos i sin ) (cos i sin ) 2i sin i sin sinh i
ii ee
2
))
œ œ Ê œ œ
)) )) ) ) )
ii
53. e sin x 1 x x
xxxx xxx
!3!4! 3!5!7!
œ á á
Š‹Š‹
#
(1)x (1)x x x x x x x x ;œ ᜠá
#$% &#$&
"" "" " " " " "
####
ˆ‰ˆ‰ˆ ‰
6661014 330
e e e e (cos x i sin x) e cos x i e sin x e sin x is the series of the imaginary part
xix 1ix x x x x
†œœ œ Ê
ÐÑ ab
of e which we calculate next; e 1 (x ix)
ÐÑ ÐÑ
#
1ix 1ix (x ix) (x ix) (x ix) (x ix)
n! !3!4!
œ œá
!
_
œn0
n
1 x ix 2ix 2ix 2x 4x 4x 4ix 8ix the imaginary partœ áÊ
"" " " "
#
#$$%&& '
!3! 4! 5! 6!
ab a b a b a b a b
of e is xxxxx xxxx x in agreement with our
ÐÑ #$&' #$ & '
#
"" "
1ix 2248
!3!5!6! 33090
ᜠá
product calculation. The series for e sin x converges for all values of x.
x
54. e e (cos bx i sin bx) ae (cos bx i sin bx) e ( b sin bx bi cos bx)
dd
dx dx
aib ax ax ax
ˆ‰cd
Ð Ñ œœ
ae (cos bx i sin bx) bie (cos bx i sin bx) ae ibe (a ib)eœ œœ
ax ax aibx aibx aibxÐ Ñ Ð Ñ Ð Ñ
55. (a) e e (cos i sin )(cos i sin ) (cos cos sin sin ) i(sin cos sin cos )
ii))
œ œ ) ) ) ) )) )) )) ))
" " # # "# "# "# #"
cos( ) i sin( ) eœ œ)) ))
"# "# ÐÑi))
(b) e cos( ) i sin( ) cos i sin (cos i sin )
""
icos i sin
cos i sin cos i sin e
)))
)) ))
œ œ œ œ œ) ) )) ))
ˆ‰ i
56. e C iC e (cos bx i sin bx) C iC
abi abi
ab ab
abix ax
Ð Ñ "# "#
œ
ˆ‰
(a cos bx ia sin bx ib cos bx b sin bx) C iCœ
e
ab
ax
"#
[(a cos bx b sin bx) (a sin bx b cos bx)i] C iCœ
e
ab
ax
"#
CiC;œ
e (a cos bx b sin bx) ie (a sin bx b cos bx)
ab ab
ax ax
"#
e e e e (cos bx i sin bx) e cos bx ie sin bx, so that given
Ð Ñabix axibx ax ax ax
œœ œ
e dx e C iC we conclude that e cos bx dx C
''
Ð Ñ Ð Ñ
"# "
abix abix ax
abi
ab ab
e (a cos bx b sin bx)
œ œ
ax
and e sin bx dx C
'ax e (a sin bx b cos bx)
ab
œ
ax
#
57-62. Example CAS commands:
:Maple
f := x -> 1/sqrt(1+x);
x0 := -3/4;
x1 := 3/4;
# Step 1:
plot( f(x), x=x0..x1, title="Step 1: #57 (Section 11.9)" );
# Step 2:
P1 := unapply( TaylorApproximation(f(x), x = 0, order=1), x );
P2 := unapply( TaylorApproximation(f(x), x = 0, order=2), x );
P3 := unapply( TaylorApproximation(f(x), x = 0, order=3), x );
# Step 3:
D2f := D(D(f));
D3f := D(D(D(f)));
D4f := D(D(D(D(f))));
plot( [D2f(x),D3f(x),D4f(x)], x=x0..x1, thickness=[0,2,4], color=[red,blue,green], title="Step 3: #57 (Section 11.9)" );
c1 := x0;
M1 := abs( D2f(c1) );
c2 := x0;
M2 := abs( D3f(c2) );
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.9 Convergence of Taylor Series; Error Estimates 749
c3 := x0;
M3 := abs( D4f(c3) );
# Step 4:
R1 := unapply( abs(M1/2!*(x-0)^2), x );
R2 := unapply( abs(M2/3!*(x-0)^3), x );
R3 := unapply( abs(M3/4!*(x-0)^4), x );
plot( [R1(x),R2(x),R3(x)], x=x0..x1, thickness=[0,2,4], color=[red,blue,green], title="Step 4: #57 (Section 11.9)" );
# Step 5:
E1 := unapply( abs(f(x)-P1(x)), x );
E2 := unapply( abs(f(x)-P2(x)), x );
E3 := unapply( abs(f(x)-P3(x)), x );
plot( [E1(x),E2(x),E3(x),R1(x),R2(x),R3(x)], x=x0..x1, thickness=[0,2,4], color=[red,blue,green],
linestyle=[1,1,1,3,3,3], title="Step 5: #57 (Section 11.9)" );
# Step 6:
TaylorApproximation( f(x), view=[x0..x1,DEFAULT], x=0, output=animation, order=1..3 );
L1 := fsolve( abs(f(x)-P1(x))=0.01, x=x0/2 ); # (a)
R1 := fsolve( abs(f(x)-P1(x))=0.01, x=x1/2 );
L2 := fsolve( abs(f(x)-P2(x))=0.01, x=x0/2 );
R2 := fsolve( abs(f(x)-P2(x))=0.01, x=x1/2 );
L3 := fsolve( abs(f(x)-P3(x))=0.01, x=x0/2 );
R3 := fsolve( abs(f(x)-P3(x))=0.01, x=x1/2 );
plot( [E1(x),E2(x),E3(x),0.01], x=min(L1,L2,L3)..max(R1,R2,R3), thickness=[0,2,4,0], linestyle=[0,0,0,2],
color=[red,blue,green,black], view=[DEFAULT,0..0.01], title="#57(a) (Section 11.9)" );
abs(`f(x)`-`P`[1](x) ) <= evalf( E1(x0) ); # (b)
abs(`f(x)`-`P`[2](x) ) <= evalf( E2(x0) );
abs(`f(x)`-`P`[3](x) ) <= evalf( E3(x0) );
: (assigned function and values for a, b, c, and n may vary)Mathematica
Clear[x, f, c]
f[x_]= (1 x)3/2
{a, b}= { 1/2, 2};
pf=Plot[ f[x], {x, a, b}];
poly1[x_]=Series[f[x], {x,0,1}]//Normal
poly2[x_]=Series[f[x], {x,0,2}]//Normal
poly3[x_]=Series[f[x], {x,0,3}]//Normal
Plot[{f[x], poly1[x], poly2[x], poly3[x]}, {x, a, b},
PlotStyle {RGBColor[1,0,0], RGBColor[0,1,0], RGBColor[0,0,1], RGBColor[0,.5,.5]}];Ä
The above defines the approximations. The following analyzes the derivatives to determine their maximum values.
f''[c]
Plot[f''[x], {x, a, b}];
f'''[c]
Plot[f'''[x], {x, a, b}];
f''''[c]
Plot[f''''[x], {x, a, b}];
Noting the upper bound for each of the above derivatives occurs at x = a, the upper bounds m1, m2, and m3 can be defined
and bounds for remainders viewed as functions of x.
m1=f''[a]
m2=-f'''[a]
m3=f''''[a]
r1[x_]=m1 x /2!
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
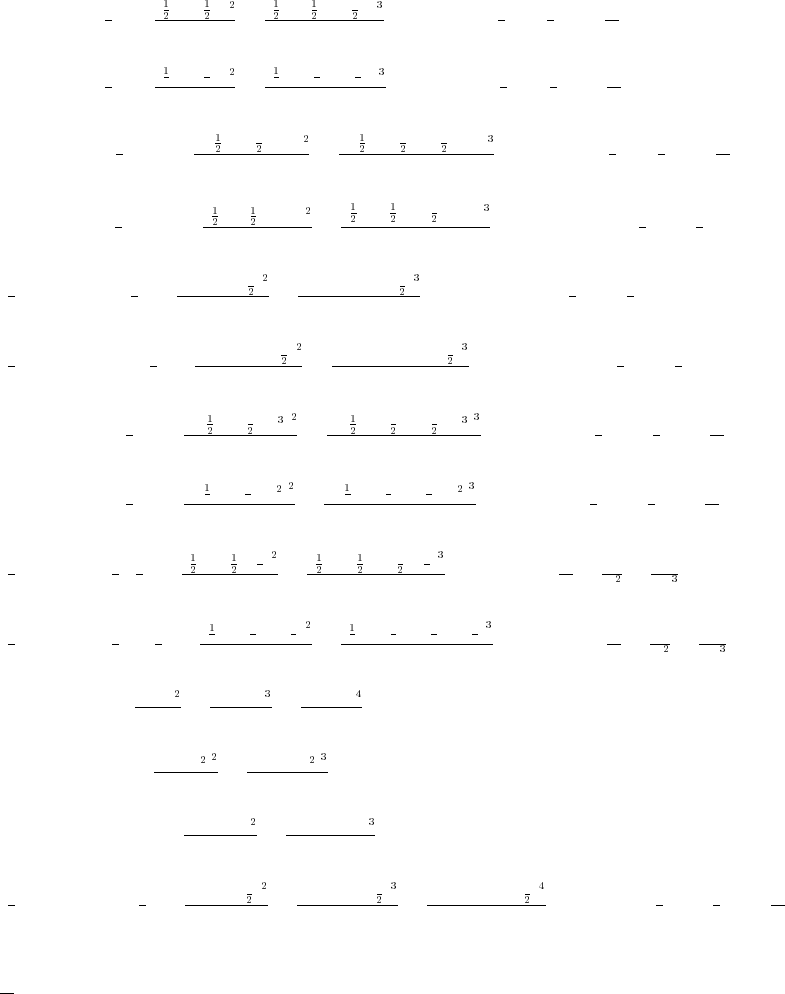
750 Chapter 11 Infinite Sequences and Series
Plot[r1[x], {x, a, b}];
r2[x_]=m2 x /3!
3
Plot[r2[x], {x, a, b}];
r3[x_]=m3 x /4!
4
Plot[r3[x], {x, a, b}];
A three dimensional look at the error functions, allowing both c and x to vary can also be viewed. Recall that c must be a
value between 0 and x, so some points on the surfaces where c is not in that interval are meaningless.
Plot3D[f''[c] x /2!, {x, a, b}, {c, a, b}, PlotRange All]
2Ä
Plot3D[f'''[c] x /3!, {x, a, b}, {c, a, b}, PlotRange All]
3Ä
Plot3D[f''''[c] x /4!, {x, a, b}, {c, a, b}, PlotRange All]
4Ä
11.10 APPLICATIONS OF POWER SERIES
1. (1 x) 1 x 1 x x x œ ᜠá
"Î# #$
""""
## #
ˆ‰ˆ ‰ ˆ‰ˆ ‰ˆ ‰
xx
!3! 816
3
2. (1 x) 1 x 1 x x x œ ᜠá
"Î$ #$
"""
#3 ! 3! 3 9 81
5
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
33 333
225
xx
3. (1 x) 1 ( x) 1 x x x œ á œ á
"Î# #$
" "
## #
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
335
(x) (x)
!3! 816
35
4. (1 2x) 1 ( 2x) 1 x x x œ áœá
"Î# #$
"
##
ˆ‰ˆ ‰
( 2x)
!3! 22
( 2x) 11
Š‹Š ‹Š ‹
3
5. 1 1 1 x x x
ˆ‰ ˆ‰
œ # á œ
xx 3
!3! 4### #
# #$
"
(2)(3) (2)(3)(4)
ˆ‰ ˆ‰
xx
6. 1 1 1 x x x
ˆ‰ ˆ‰
œ# áœá
xx 3
!3! 4### #
# #$
"
(2)(3) (2)(3)(4)
ˆ‰ ˆ‰
xx
7. 1 x 1 x 1 x x xab œ ᜠá
$$ $' *
"Î# " "
## #
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
ab ab
335
xx
!3! 816
35
8. 1 x 1 x 1 x x xab œ ᜠá
## #% '
"Î$ " "
#3 ! 3! 3 9 81
214
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
ab ab
33 333
447
xx
9. 1 1 1
ˆ‰ ˆ‰
œ áœá
11 1
x x ! 3! x 8x 16x
"Î# """
## #
ˆ‰ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰ˆ‰
131
xx
10. 1 1 1
ˆ‰ ˆ‰
œ ᜠá
22 24 40
x 3 x ! 3! 3x 9x 81x
"Î$ "
#
ˆ‰ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰ˆ‰
33x 333x
22 252
11. (1 x) 1 4x 1 4x 6x 4x xœ œ
%#$%
#
(4)(3)x (4)(3)(2)x (4)(3)(2)x
!3! 4!
12. 1 x 1 3x 1 3x 3x xab œ œ
## #%'
$
#
(3)(2) x (3)(2)(1) x
!3!
ab ab
13. (1 2x) 1 3( 2x) 1 6x 12x 8xœ œ
$#$
#
(3)(2)( 2x) (3)(2)(1)( 2x)
!3!
14. 1 1 4 1 2x x x x
ˆ‰ ˆ‰
œ œ
xx 3
!3! 4! 216### #
%#$ %
""
(4)(3) (4)(3)(2) (4)(3)(2)(1)
ˆ‰ ˆ‰ ˆ‰
xx x
15. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na xÊœ á á
dy
dx nn1
"#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.10 Applications of Power Series 751
y (a a ) (2a a )x (3a a )x (na a )xÊœ á áœ!
dy
dx nn1
n1
"! #" $#
#
a a 0, 2a a 0, 3a a 0 and in general na a 0. Since y 1 when x 0 we haveÊœœœ œ œ œ
"! #" $# nn1
a 1. Therefore a 1, a , a , , a
!"#$
""
##
œœœœœœáœœ
aa
21 3 3 n n!
na(1)
††
n1 n
y1x x x x eÊœ á ᜠœ
""
#
#$
"
3! n! n!
(1) ( )x
nx
nnn
!
_
œn0
16. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na xÊœ á á
dy
dx nn1
"#
2y (a 2a ) (2a 2a )x (3a 2a )x (na 2a )xÊœ á áœ!
dy
dx nn1
n1
"! #" $#
#
a 2a 0, 2a 2a 0, 3a 2a 0 and in general na 2a 0. Since y 1 when x 0 we haveÊœœœ œ œ œ
"! #" $# nn1
a 1. Therefore a 2a 2(1) 2, a a (2) , a a , ,
!"!#"$#
## # # #
œœœœœœœœœœá
22 2 2222
33 3
Š‹ †
a a a y 1 2x x x x
nn1 n2
222 2 22 2
n n n 1 n! 3! n!
n
œ œ œÊœáá
ˆ‰ ˆ‰
Š‹
#
#$
n1 n n
1 (2x) eœáᜠœ
(2x) (2x) (2x) (2x)
2! 3! n! n!
2x
nn
!
_
œn0
17. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na xÊœ á á
dy
dx nn1
"#
y (a a ) (2a a )x (3a a )x (na a )x 1Êœ á áœ
dy
dx nn1
n1
"! #" $#
#
a a 1, 2a a 0, 3a a 0 and in general na a 0. Since y 0 when x 0 we haveÊœœœ œ œ œ
"! #" $# nn1
a 0. Therefore a 1, a , a , a , , a
!"#$%
## # #
"" " "
œ œ œœ œœ œœ á œ œ
aa a
33 443 n n!
na
†††
n1
y 0 1x x x x xÊœ á á
"" " "
## #
#$ %
343 n!
n
†††
11x x x x x 1 1 e 1œ á ᜠœ
ˆ‰
!
"" " "
##
#$ %
3 4 3 2 n! n!
nx
x
†††
_
œn0
n
18. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na xÊœ á á
dy
dx nn1
"#
y (a a ) (2a a )x (3a a )x (na a )x 1Êœ á áœ
dy
dx nn1
n1
"! #" $#
#
a a 1, 2a a 0, 3a a 0 and in general na a 0. Since y 2 when x 0 we haveÊœœœ œ œ œ
"! #" $# nn1
a 2. Therefore a 1 a 1, a , a , , a
!"!#$
## #
""
"
œœœœœœœáœœ
aa
133 nn!
na()
††
n1 n
y2xx x x 11xx x xÊ œ á ᜠá á
"" ""
## ##
#$ #$
" "
3n! 3n!
() ()
nn
††
n n
Š‹
1 1eœ œ
!
_
œn0
(1)x
n!
x
nn
19. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na xÊœ á á
dy
dx nn1
"#
y (a a ) (2a a )x (3a a )x (na a )x xÊœ á áœ
dy
dx nn1
n1
"! #" $#
#
a a 0, 2a a 1, 3a a 0 and in general na a 0. Since y 0 when x 0 we haveÊœœœ œ œ œ
"! #" $# nn1
a 0. Therefore a 0, a , a , a , , a
!"#$%
## # #
"" " "
œœœœœœœœáœœ
1a a a
33 443 n n!
na
†††
n1
y 0 0x x x x xÊœ á á
"" " "
## #
#$ %
343 n!
n
†††
11x x x x x 1x 1x e x1œ á ᜠœ
ˆ‰
!
"" " "
## #
#$ %
343 n! n!
nx
x
†††
_
œn0
n
20. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na xÊœ á á
dy
dx nn1
"#
y (a a ) (2a a )x (3a a )x (na a )x 2xÊœ á áœ
dy
dx nn1
n1
"! #" $#
#
a a 0, 2a a 2, 3a a 0 and in general na a 0. Since y 1 when x 0 we haveÊœœœ œ œ œ
"! #" $# nn1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
752 Chapter 11 Infinite Sequences and Series
a 1. Therefore a 1, a , a , , a
!"#$
## #
""
"
œ œ œ œ œ œ á œ œ
2a a
33 nn!
na()
†
n1 n
y 1 1x x x xÊœ á á
""
##
#$ "
3n!
() n
†
n
11x x x x 22x 22x e 2x2œ á ᜠœ
Š‹
!
""
##
#$
"
3n! n!
() (1)x
nx
†
nnn
_
œn0
21. y xy a (2a a )x (3a a )x (na a )x 0 a 0, 2a a 0, 3a a 0,
w
"#!$" "#!$"
œá áœÊœ œ œ
nn2
n1
4a a 0 and in general na a 0. Since y 1 when x 0, we have a 1. Therefore a ,
%# ! #
##
"
œ œ œ œ œ œœ
nn2 a
a 0, a , a 0, , a and a 0
$% &
""
##â
œœ œœ œœá œ œ
aa a
3445 462n
2n 2n 1
†††
y 1 x x x x eÊœ á ᜠœ œ
"" " "
## # #â
#% ' Î
††† ††4 4 6 4 6 2n 2 n! n!
2n x 2
x
!!
__
œœn0 n0
2n
n
xn
Š‹
22. y x y a 2a x (3a a )x (4a a )x (na a )x 0 a 0, a 0,
w# # $
" # $! %" " #
œá áœÊœœ
nn3
n1
3a a 0, 4a a 0 and in general na a 0. Since y 1 when x 0, we have a 1. Therefore
$! %" !
œ œ œ œ œ œ
nn3
a , a 0, a 0, a , , a , a 0 and a 0
$ %&'
"""
â
œœ œœ œœ œœ á œ œ œ
a aaa
3 3 4 5 6 36 369 3n
3n 3n 1 3n 2
†††
y 1 x x x x eÊœ á ᜠœ œ
"" " "
$' * Î
â3 36 369 369 3n 3n! n!
3n x 3
x
††† †† !!
__
œœn0 n0
3n
n
x
3
n
Š‹
23. (1 x)y y (a a ) (2a a a )x (3a 2a a )x (4a 3a a )xœ á
w#$
"! #"" $ ## % $$
(na (n 1)a a )x 0 a a 0, 2a 2a 0, 3a 3a 0 and in áœÊœ œ œ
nn1n1
n1
"! #" $#
general (na na ) 0. Since y 2 when x 0, we have a 2. Therefore
nn1
œ œ œ œ
!
a 2, a 2, , a 2 y 2 2x 2x 2x
"# #
œœáœÊœáœ œ
nn2
1x
!
_
œn0
24. 1 x y 2xy a (2a 2a )x (3a 2a a )x (4a 2a 2a )x (na na )xabœ á á
#w # $
" #! $"" %## nn2
n1
0 a 0, 2a 2a 0, 3a 3a 0, 4a 4a 0 and in general na na 0. Since y 3 whenœÊœœœœ œ œ
"#!$"%# nn2
x 0, we have a 3. Therefore a 3, a 0, a 3, , a 0, a ( 1) 3œœ œœœáœœ
!#$%2n 1 2n n
y 3 3x 3x 3( 1) x 3 xʜᜠœ œ
#% #
!!
ab
__
œœn0 n0
n2n n3
1x
25. y a a x a x a x y 2a 3 2a x n(n 1)a x y yœ á á Ê œ á á Ê
!" # # $
#ww ww
nn
nn2
†
(2a a ) (3 2a a )x (4 3a a )x (n(n 1)a a )x 0 2a a 0,œá áœÊœ
#! $" %# #!
#
†† nn2
n2
3 2a a 0, 4 3a a 0 and in general n(n 1)a a 0. Since y 1 and y 0 when x 0,††
$" %# w
œ œ œ œ œ œ
nn2
we have a 0 and a 1. Therefore a 0, a , a 0, a , , a and
! " #$ %&
"" "
###
œ œ œœ œœ á œ
3 543 ( n 1)!
2n 1
† †††
a 0 y x x x sinh x
2n 3! 5! (2n 1)!
x
œÊœáœ œ
""
$&
!
_
œn0
2n 1
26. y a a x a x a x y 2a 3 2a x n(n 1)a x y yœ á á Ê œ á á Ê
!" # # $
#ww ww
nn
nn2
†
(2a a ) (3 2a a )x (4 3a a )x (n(n 1)a a )x 0 2a a 0,œá áœÊœ
#! $" %# #!
#
†† nn2
n2
3 2a a 0, 4 3a a 0 and in general n(n 1)a a 0. Since y 0 and y 1 when x 0,††
$" %# w
œ œ œ œ œ œ
nn2
we have a 1 and a 0. Therefore a , a 0, a , a 0, , a 0 and a
!" #$%&
""
## #
"
œœ œœœœáœ œ
43 ( n)!
2n 1 2n ()
††
n
y1 x x cos xÊœ ᜠœ
""
#%
2 4! (2n)!
(1)x
!
_
œn0
n2n
27. y a a x a x a x y 2a 3 2a x n(n 1)a x y yœ á á Ê œ á á Ê
!" # # $
#ww ww
nn
nn2
†
(2a a ) (3 2a a )x (4 3a a )x (n(n 1)a a )x x 2a a 0,œá áœÊœ
#! $" %# #!
#
†† nn2
n2
3 2a a 1, 4 3a a 0 and in general n(n 1)a a 0. Since y 1 and y 2 when x 0,††
$" %# w
œ œ œ œ œ œ
nn2
we have a 2 and a 1. Therefore a , a 0, a , a 0, , a 2 and
!" #$%&
"
#
œœ œ"œœœáœ
43 ( n)!
2n (1)
†
†
n1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
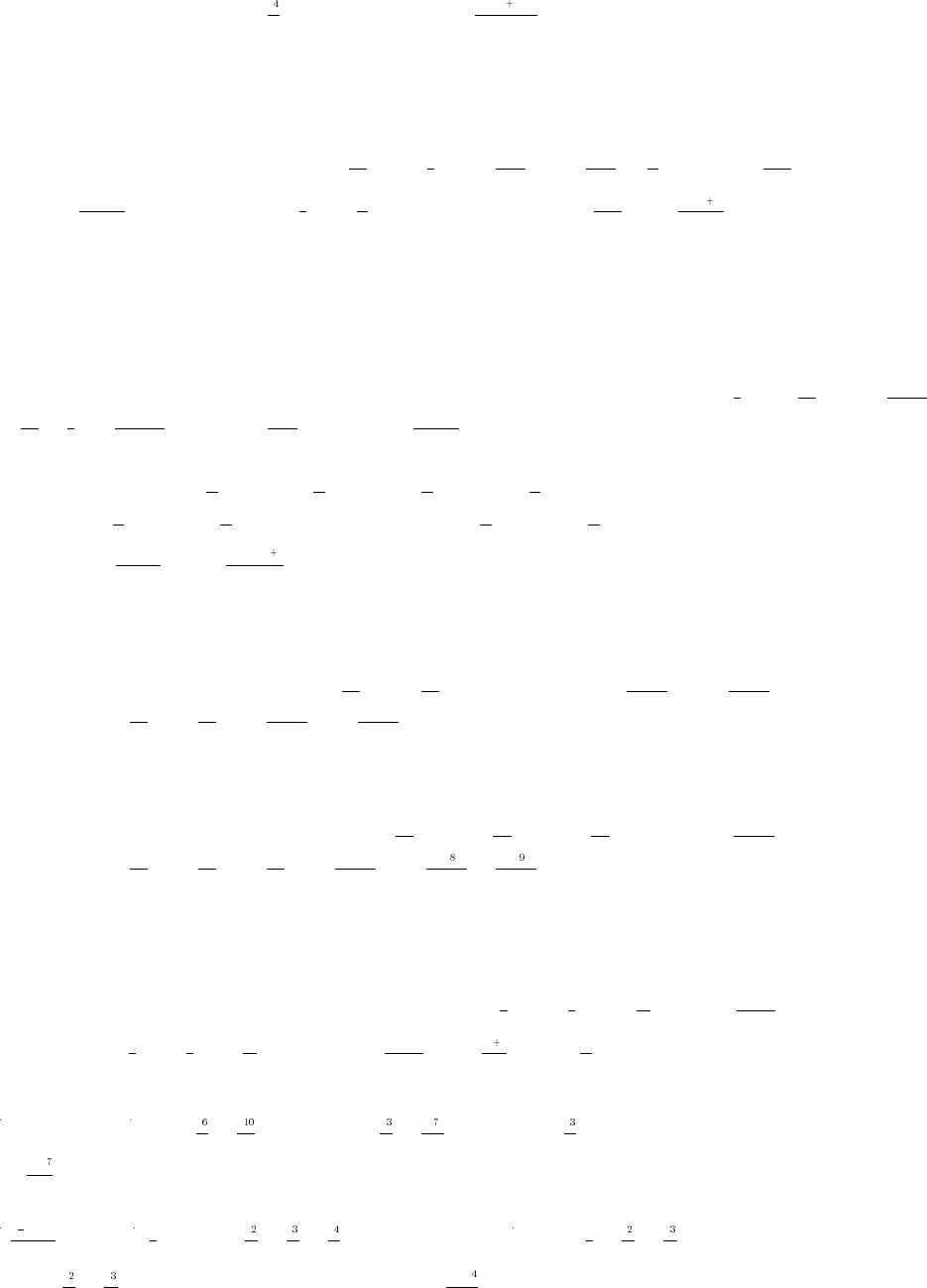
Section 11.10 Applications of Power Series 753
a 0 y2xx 2 2x2 xcos 2x
2n 1 x
4! (2n)!
(1) x
#
œ Ê œ ᜠœ†!
_
œn1
n12n
28. y a a x a x a x y 2a 3 2a x n(n 1)a x y yœ á á Ê œ á á Ê
!" # # $
#ww ww
nn
nn2
†
(2a a ) (3 2a a )x (4 3a a )x (n(n 1)a a )x x 2a a 0,œá áœÊœ
#! $" %# #!
#
†† nn2
n2
3 2a a 1, 4 3a a 0 and in general n(n 1)a a 0. Since y 2 and y 1 when x 0,††
$" %# w
œ œ œ œ œ œ
nn2
we have a 1 and a 2. Therefore a , a , a , a , , a
!" #$%&
" " " "
## # #
œ œ œ œ œ œ œ á œ
234 54 5! ( n)!
31
2n
†† ††
and a y 1 2x x x 1 2x
2n 1 33x3x
(2n 1)! 3! (2n)! (2n 1)!
#
"#$
œÊœáœ
!!
__
œœn1 n1
2n 2n 1
29. y a a x 2 a x 2 a x 2œ á á
!" # #
abab ab
nn
y 2a 32ax2 n(n1)ax2 y yÊœ á áÊ
ww ww
#$
†ab ab
nn2
(2a a ) (3 2a a )(x 2) (4 3a a )(x 2) (n(n 1)a a )(x 2) xœ á á œ
#! $" %#
#
†† nn2 n2
x 2 2 2a a 2, 3 2a a 1, and n(n 1)a a 0 for n 3. Since y 0 when x 2,œ Ê œ œ œ œ œab #! $"
†nn2
we have a 0, and since y 2 when x 2, we have a 2. Therefore a 1, a , a 1 ,
!"#$%
w"
# † †††
œ œ œ œ œ œ œ œ
12
43 4321
ab
a , . . . , a , and a . Since a 2, we have a x 2 2 x 2 and
&""
† # ††††
"
œœ œ œ œ œ
13 2 3
54 54321 2n! (2n 1)!
2n 2n 1
ˆ‰ ababab
ab
2x2 31x2 3x2 1x2 x23x2.ababa bababababab ab œ œ œ
yx23x2 x2 x2 x2 x2 . . .ʜ ababababab
2323
2! 3! 4! 5!
2345
y x 2 x 2 x 2 . . . 3 x 2 x x 2 x 2 . . .ʜ
22 33
2! 4! 3! 5!
24 35
abab ababab
y x2 3 ʜ
!!
__
œœn0 n0
(x 2) (x 2)
(2n)! (2n 1)!
2n 2n 1
30. y x y 2a 6a x (4 3a a )x (n(n 1)a a )x 0 2a 0, 6a 0,
ww # #
#$ %! # $
œ á áœÊ œ œ†nn4
n2
4 3a a 0, 5 4a a 0, and in general n(n 1)a a 0. Since y b and y a when x 0,††
%! &" w
œ œ œ œ œ œ
nn4
we have a a, a b, a 0, a 0, a , a , a 0, a 0, a , a
!"#$% & '() *
œœœœœ œ œœœ œ
ab a b
34 45 3478 4589† † ††† †††
y a bx x x x xÊœá
ab a b
34 45 3478 4589† † ††† †††
%&)*
31. y x y 2a 6a x (4 3a a )x (n(n 1)a a )x x 2a 0, 6a 1,
ww # #
#$ %! # $
œ á áœÊ œ œ†nn4
n2
4 3a a 0, 5 4a a 0, and in general n(n 1)a a 0. Since y b and y a when x 0,††
%! &" w
œ œ œ œ œ œ
nn4
we have a a and a b. Therefore a 0, a , a , a , a 0, a
!" #$%&'(
""
##
œ œ œ œ œ œ œ œ
††† †††33445 367
ab
y a bx x x x xÊœ á
1ab 1 axbx
23 34 45 2367 3478 4589† † † ††† ††† †††
$%& (
32. y 2y y (2a 2a a (2 3a 4a a )x (3 4a 2 3a a )x
ww w #
#"! $#" % $#
œ Ñ á†††
((n 1)na 2(n 1)a a )x 0 2a 2a a 0, 2 3a 4a a 0, áœÊ œ œ
nnn2
n2
" # " ! $ # "
†
3 4a 2 3a a 0 and in general (n 1)na 2(n 1)a a 0. Since y 1 and y 0 when††
%$# " w
œ œ œ œ
nnn2
when x 0, we have a 0 and a 1. Therefore a 1, a , a , a and aœ œ œ œœœœ œ
! " #$%&
""
#
11
624 (n1)!
n
y x x x x x x xeÊœ ᜠœ œ œ
#$% &
"" "
## 64 (n1)! n! n!
xx x
x
!!!
__ _
œœ œn1 n0 n0
nn1 n
33. sin x dx x dx 0.00267 with error
''
00
02 02
## !Þ# !Þ#
!!
œáœá¸¸
Š‹’“’“
xx x x x
3! 5! 3 7 3! 3
†
E 0.0000003kkŸ¸
(.2)
73!
†
34. dx 1 x 1 dx 1 dx
'' '
00 0
02 02 02
e xxx xxx
x x !3!4! 6 24
x" "
##
œ á œ á
Š‹Š‹
x 0.19044 with error E 0.00002œ á ¸ Ÿ ¸
’“ kk
xx
418 96
(0.2)
!Þ#
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

754 Chapter 11 Infinite Sequences and Series
35. dx 1 dx x [x] 0.1 with error
''
00
01 01
"
!Þ"
!
!Þ"
!
È1 x
x3x x
28 10
œáœá¸¸
Š‹’“
E 0.000001kkŸœ
(0.1)
10
36. 1 x dx 1 dx x x 0.25174 with error
''
00
025 025
$#!Þ#& !Þ#&
!!
ÈŠ‹’“’“
œ á œ á ¸ ¸
xx xx x
39 945 9
E 0.0000217kkŸ¸
(0.25)
45
37. dx 1 dx x x
''
00
01 01
sin x xxx xxx xx
x 3! 5! 7! 3 3! 5 5! 7 7! 3 3! 5 5!
œ á œ á ¸
Š‹’ “’“
††† ††
!Þ" !Þ"
!!
0.0999444611, E 2.8 10¸Ÿ¸‚kk (0.1)
77!
12
7
†
38. exp x dx 1 x dx x x
''
00
01 01
ab Š‹’“’“
œ á œ á ¸
## !Þ" !Þ"
!!
xxx xx x xx x
2! 3! 4! 3 10 42 3 10 42
0.0996676643, E 4.6 10¸Ÿ¸‚kk (0.1)
216
12
9
39. 1 x (1) (1) x (1) x (1) xa b ab ab abœ
% "Î# "Î# % $Î# % &Î# %
"Î# # $
#
Š‹
1! 3!
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
3
(1) x 1 ᜠá
ˆ‰ˆ‰ˆ‰ˆ‰
35
4! 8 16 128
xxx 5x
(Î# % %
#
ab
1 dx x 0.100001, E 1.39 10Ê á ¸ ¸ Ÿ ¸ ‚
'0
01
Š‹’“
kk
xxx 5x x
8 16 128 10 72
(0.1) 11
#
!Þ"
!
9
40. dx dx
''
00
11
ˆ‰ Š‹’“
1cos x xxx x xx x x x
x 4! 6! 8! 10! 3 4! 5 6! 7 8! 9 10!
"
##
"
!
œ á ¸
††††
0.4863853764, E 1.9 10¸Ÿ¸‚kk 1
11 12!
10
†
41. cos t dt 1 dt t error .00011
''
00
11
#
#
"
!
"
œ á œ á Ê ¸
Š‹’ “
kk
ttt t t t
4! 6! 10 9 4! 13 6! 13 6!
†† †
42. cos t dt 1 dt t
''
00
11
ÈŠ‹’ “
œ á œá
tttt t t t t
4! 6! 8! 4 3 4! 4 6! 5 8!#
"
!
†††
error 0.000004960ʸkk"
58!†
43. F(x) t dt œ á œ á ¸
'0
xx
Š‹’ “
#
!
tt t t t t t x x x
3! 5! 7! 3 7 3! 11 5! 15 7! 3 7 3! 11 5!
††† ††
error 0.000013ʸkk"
15 7!†
44. F(x) t t dtœ á œ á
'0
xx
Š‹’ “
#%
!
ttt t tt t t t t
2! 3! 4! 5! 3 5 7 2! 9 3! 11 4! 13 5!
††††
error 0.00064¸ Ê ¸
xx x x x
3 5 7 2! 9 3! 11 4! 13 5!
†† † †
kk"
45. (a) F(x) t dt error .00052œ á œ á ¸ Ê ¸
'0
xx
Š‹’“
kk
ttt t t t xx
357 21 30 1 30
(0.5)
###
!
(b) error .00089 when F(x) ( 1) kk ¸ ¸á
"
#
"&
33 34 3 4 5 6 7 8 31 32
xxxx x
† ††† †
46. (a) F(x) 1 dt t xœ á œá¸
'0
xx
Š‹’ “
ttt tttt xxxx
23 4 22334455 3 4 5
†††† !#
error .00043ʸkk
(0.5)
6
(b) error .00097 when F(x) x ( 1) kk ¸ ¸á
"
#
$"
32 3 4 31
xxx x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.10 Applications of Power Series 755
47. e (1 x) 1 x 1 x lim
"" "
##
x x 3! 3! 4! x
xxx xx e(1x)
ab
Š‹Š‹
œ á œáÊ
x0Ä
x
lim œáœ
x0ÄŠ‹
""
##
xx
3! 4!
48. e e 1 x 1 x 2x
"" "
##x x !3!4! !3!4! x 3! 5! 7!
xx xxx xxx 2x2x2x
ab
’“Š‹Š‹Š‹
œ á á œ á
2 lim lim 2 2œáÊ œ áœ
2x 2x 2x e e 2x 2x 2x
3! 5! 7! x 3! 5! 7!
x0 x
ÄÄ_
xx
Š‹
49. 1 cos t 1 1 lim
"" "
###
"
tt t
ttttt tt
4! 6! 4! 6! 8!
cos t
Š‹’ “Š‹
œ á œáÊ
t0Ä
Š‹
t
lim œ áœ
t0ÄŠ‹
""
4! 6! 8! 24
tt
50. sin lim
"" "
)) )
) ) )) )) ))
Š‹Š ‹
œ áœáÊ))))
6 6 3! 5! 5! 7! 9!
sin
)Ä0
Š‹
6
lim œ áœ
)Ä0Š‹
""
#5! 7! 9! 1 0
))
51. y tan y y y lim lim
"" " "
"
yy35357 y357
yy yy ytany yy
ab
’“ Š‹Š‹
œ á œáÊ œ á
y0 y0ÄÄ
œ"
3
52. tan y sin y
y cos y y cos y y cos y cos y
yy
áááá
œœœ
ŒŒŒŒ
y y y y y 23y 23y
3 5 3! 5! 6 5! 6 5!
lim lim Êœ œ
y0 y0ÄÄ
tan y sin y
y cos y cos y 6
á "
Œ
65!
23y
53. x 1 e x 1 1 1 lim x e 1
#Î# #Î
"" " " "
##
Š‹ Š‹
ˆ‰
œ áœáÊ
1x 1x
x6x x
x6x
xÄ_
lim 1 1œ áœ
xÄ_ ˆ‰
""
#x6x
54. (x 1) sin (x 1) 1 œ áœá
ˆ‰ Š‹
" """ ""
x 1 x 1 3!(x 1) 5!(x 1) 3!(x 1) 5!(x 1)
lim (x 1) sin lim 1 1Ê œ áœ
xxÄ_ Ä_
ˆ‰ Š‹
"""
x 1 3!(x 1) 5!(x 1)
55. lim lim
ln 1 x ln 1 x
1cos x 1cos x
x1 1
11
ab ab
ŒŒ Œ
Š‹
Š‹ Š‹
á á á
á á
œœÊœ
xx xx xx
33 3
xx
!4! !4!
xx0 x0ÄÄ
!4!
x
á œœ2! 2
56. lim
x4 x2 x4
ln (x 1) ln (x 1)
(x 2)(x 2)
(x 2) 1
á á
œœÊ
’“’“
(x 2) (x 2) (x 2)
33
x2 x2Ä
lim 4œœ
x2Ä
x2
1
á
’“
x2 (x 2)
3
57. ln ln (1 x) ln (1 x) x x 2 x
ˆ‰ Š‹Š ‹Š‹
1x xxx xxx xx
1x 34 34 35
##
œ œ áᜠá
58. ln (1 x) x error when x 0.1;œá áÊ œ œ œ
xxx
3 4 n n n10
(1) x ( ) x
#
"
"
n1n n1n
n
kk
¹¹
n10 10 when n 8 7 terms
"" )
n10 10
n
nÊ Ê
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

756 Chapter 11 Infinite Sequences and Series
59. tan x x error when x 1;
" "
#
"
œá áÊ œ œ œ
xxxx
3579 2n1 2n1 n1
()x (1)x
n12n1 n12n1
kk
¹¹
n 500.5 the first term not used is the 501 we must use 500 terms
""
# #n1 10
1001
Ê œ Ê Ê
st
60. tan x x and lim x lim x
" ##
#
œá á œ œ
xxxx x 2n1 2n1
3579 2n1 2n1x n1
(1) x
n12n1 2n 1
2n 1
nnÄ_ Ä_
¹¹ ¸¸
†
tan x converges for x 1; when x 1 we have which is a convergent series; when x 1Êœ œ
"
kk !
_
œn1
(1)
2n 1
n
we have which is a convergent series the series representing tan x diverges for x 1
!kk
_
œn1
(1)
2n 1
"
n1 Ê
61. tan x x and when the series representing 48 tan has an
" "
"
œá á
xxxx
3579 2n1 18
(1) x
n12n1 ˆ‰
error less than 10 , then the series representing the sum
"'
3†
48 tan 32 tan 20 tan also has an error of magnitude less than 10 ; thus
" " " '
"" "
#
ˆ‰ ˆ‰ ˆ‰
18 57 39
error 48 n 4 using a calculator 4 termskkœÊ Ê
Š‹
18
2n 1
# †
"
n1 310
62. ln (sec x) tan t dt t dtœ œ á ¸á
''
00
xx
Š‹
t2t xx x
315 1245
#
63. (a) 1 x 1 sin x x ; Using the Ratio Test:ab¸Ê ¸
#"
"Î#
#
x3x5x x3x5x
8 16 6 40 112
lim 1 x lim
nnÄ_ Ä_
¹¹¹¹
1 3 5 (2n 1)(2n 1)x 2 4 6 (2n)(2n )
2 4 6 (2n)(2n 2)(2n 3) 1 3 5 (2n 1)x
†† ††
†† ††
â â "
â â
#
2n 3
2n 1
†Ê (2n 1)(2n 1)
(2n 2)
(2n 3)1
x 1 the radius of convergence is 1. See Exercise 69.ÊÊkk
(b) cos x 1 x cos x sin x x x
dx 3x 5x x 3x 5x
dx 6 40 112 6 40 112
abab Š‹
" # " "
"Î#
## #
œ Ê œ ¸ ¸
11 1
64. (a) 1 t (1) (1) tab ab
ˆ‰
¸
# "Î# $Î# #
"Î#
"
##
ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
ab ab
335
(1) t (1) t
!3!
1 sinh x 1 dt xœ Ê ¸ œ
t 3t 3 5t t 3t 5t x 3x 5x
2 2! 2 3! 8 16 6 40 112
##
"
††
†'0
xŠ‹
(b) sinh 0.24746908; the error is less than the absolute value of the first unused
" """
ˆ‰
4 4 384 40,960
3
¸ œ
term, , evaluated at t since the series is alternating error 2.725 10
5x
112 4 112
5
œÊ¸‚
"'
kkˆ‰
4
65. 1 x x x 1 x x x
" " "
#$ #$
1x 1(x) dx 1x 1x dx
d1 d
œ œáÊ œ œ á
ˆ‰ ab
12x3x 4xχ
#$
66. 1 x x x 1 x x x 2x 4x 6x
""
#%' #%' $ &
1x dx1x dx
d2xd
1x
œáÊ œ œ ᜠá
ˆ‰ ab
ab
67. Wallis' formula gives the approximation 4 to produce the table1¸’“
244668 (2n 2)(2n)
335577 (2n 1)(2n 1)
††††† †
††††† †
â
â
n µ1
10 3.221088998
20 3.181104886
30 3.167880758
80 3.151425420
90 3.150331383
93 3.150049112
94 3.149959030
95 3.149870848
100 3.149456425
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 11.11 Fourier Series 757
At n 1929 we obtain the first approximation accurate to 3 decimals: 3.141999845. At n 30,000 we still doœ œ
not obtain accuracy to 4 decimals: 3.141617732, so the convergence to is very slow. Here is a CAS1Maple
procedure to produce these approximations:
pie :=
proc(n)
local i,j;
a(2) := evalf(8/9);
for i from 3 to n do a(i) := evalf(2*(2*i 2)*i/(2*i 1)^2*a(i 1)) od;
[[j,4*a(j)] $ (j = n 5 .. n)]
end
68. ln 1 0; ln 2 ln 2 0.69314; ln 3 ln 2 ln ln 2 ln œ œ ¸ ¸ œ œ
1 1
1 1
3357
3
"
#
Š‹ Š‹ Š‹ Š‹ Š‹
Š‹ Š‹
3 333 5
3 5
ˆ‰
ln 2 2 1.09861; ln 4 2 ln 2 1.38628; ln 5 ln 4 ln ln 4 ln ¸¸œ¸œœ
ˆ‰
"
5357 4
51
1
Š‹ Š‹ Š‹ Š‹
Š‹
555 9
9
1.60943; ln 6 ln 2 ln 3 1.79175; ln 7 ln 6 ln ln 6 ln 1.94591; ln 8 3 ln 2¸ œ¸ œ œ ¸ œ
ˆ‰
7
6
1
1
Š‹
Š‹
13
13
2.07944; ln 9 2 ln 3 2.19722; ln 10 ln 2 ln 5 2.30258¸ œ ¸ œ¸
69. 1 x 1 x (1) (1) xab a b abab ˆ‰
œ œ
# # "Î# $Î# #
"Î# "Î# "
##
ˆ‰ˆ‰ ab
3(1) x
!
11 ᜠáœ
ˆ‰ˆ‰ˆ‰ ab
35
(1) x
3! 2 ! 2 3! n!
x 13x 135x 1 3 5 (2n 1)x
## #
â
†††
†† †
††
!
_
œn1
2n
n
sin x 1 t dt 1 dt x ,Êœ œ œ
" # "Î# â â
##â
''
00
xx
ab Œ
!!
__
œœn1 n1
1 3 5 (2n 1)x 1 3 5 (2n 1)x
n! 4 (2n)(2n 1)
†† ††
††
2n 2n 1
n
where x 1kk
70. tan t tan x dt 1 dtcd –— ˆ‰
" "
_
#
""""
xxx x
œ œ œ œ á
1'' '
dt
1t t t t
t
Š‹
Š‹
1
t
t
1
dt lim œ á œ áœá
'x
b
x
ˆ‰ ‘
"""" " " " " " " " "
t t t t 3t 5t x 3x 5x
t7t7x
bÄ_
tan x , x 1; tan t tan x Ê œá œ œ
" " "
##
"" "1 1
x3x 5x 1t
dt
cd
xx
'
lim tan x ,œ áœáÊ œá
bÄ_ ‘
"""" "" " " "" "
"
#t 3t 5t x 3x 5x x 3x 5x
7t 7x
x
b
1
x1
71. (a) tan tan (n 1) tan (n 1)ab
" "
œ œ œ
tan tan (n 1) tan tan (n 1)
1tantan(n1) tantan(n1) 1(n1)(n1) n
(n 1) (n 1) 2
abab
abab
(b) tan tan (n 1) tan (n 1) tan 2 tan 0 tan 3 tan 1
!!
ˆ‰ c dabab
NN
n1 n1œœ
" " " " " " "
2
nœ œ
tan 4 tan 2 tan (N 1) tan (N 1) tan (N 1) tan N á œ aba b
" " " " " " 1
4
(c) tan lim tan (N 1) tan N
n
!ˆ‰ ‘
_
œn1
" " "
##
2 3
n444
œ œœ
Ä_
1 111 1
11.11 FOURIER SERIES
1. a 1 dx 1, a cos kx dx 0, b sin kx dx 0.
0k k
111 11
2
sin kx cos kx
kk
22
00
œœœ œ œœ œœ
111 11
11
'' '
00 0
22 2
‘ ‘
Thus, the Fourier series for f x is 1.ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
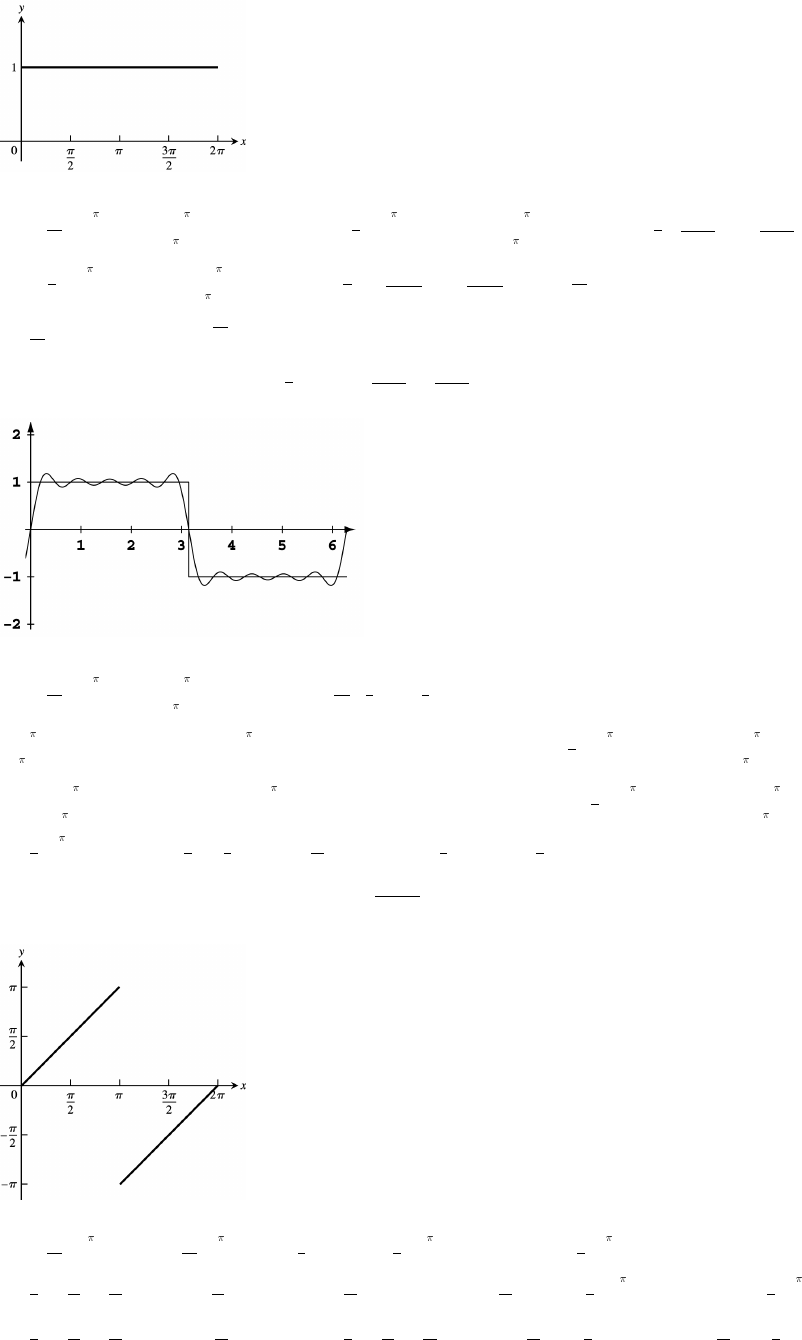
758 Chapter 11 Infinite Sequences and Series
2. a 1 dx 1 dx 0, a cos kx dx cos kx dx 0,
0k
111
2sin kx sin kx
kk
0
2
œœœ œ œ
11 1
11
1
”•” •”•
¹¹
'' ' '
00
22
b sin kx dx sin kx dx cos k 1 cos 2 k cos k
k111
cos kx cos kx
kk
0
2
k
œœ œ
111
11
1
”•”•
¹¹cd
aba b
''
0
2
111
22 cos k .
, k odd
0, k even
œ œ
1
k
4
k
1
1
ab
œ
1
Thus, the Fourier series for f x is .
sin x . . .
ab ‘
4sin 3x sin 5x
35
1
3. a x dx x 2 dx 4 2 0. Note,
011
22
2222
œœœ
11
”•
ab a b
‘
''
0
2
11111
""
##
x 2 cos kx dx u cos ku du (Let u 2 x). So a x cos kx dx x 2 cos kx dx 0.
'' ''
2 2
00
ab ab
”•
œ œœ œ11 1
k1
1
Note, x 2 sin kx dx u sin ku du (Let u 2 x). So b x sin kx dx x 2 sin kx dx
'' ''
2 2
00
ab ab
”•
œ œœ 11 1
k1
1
x sin kx dx cos k 1 .
cos kx sin kx
œœ œœ
22 22
x1
kk
0kk
k1
11
1
'0‘
ab
21
Thus, the Fourier series for f x is 1 .ab a b
!
k1
k1
2 sin kx
k
œ
_
4. a f x dx x dx , a f x cos kx dx x cos kx dx
0k
1111 1
226
22 2
œœœœ œ
11 1 1
'' ' '
00 0 0
22
ab ab1
sin kx x cos kx cos k 1 , b f x sin kx dx x sin kx dxœ œ œ œ œ œ
1x 2 11
kk k k k
0
kk2
111
1
’“Š‹ ab ab
ˆ‰
2
32 2 2
## #
1''
00
2
cos kx x sin kx 1 1 1 1œ œœ
12x 12 1
kk k kk k k k
0
kkk
111
111
’“’“’“Š‹ Š‹ Š ‹
ab ab ab
32 33 3
22
###
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
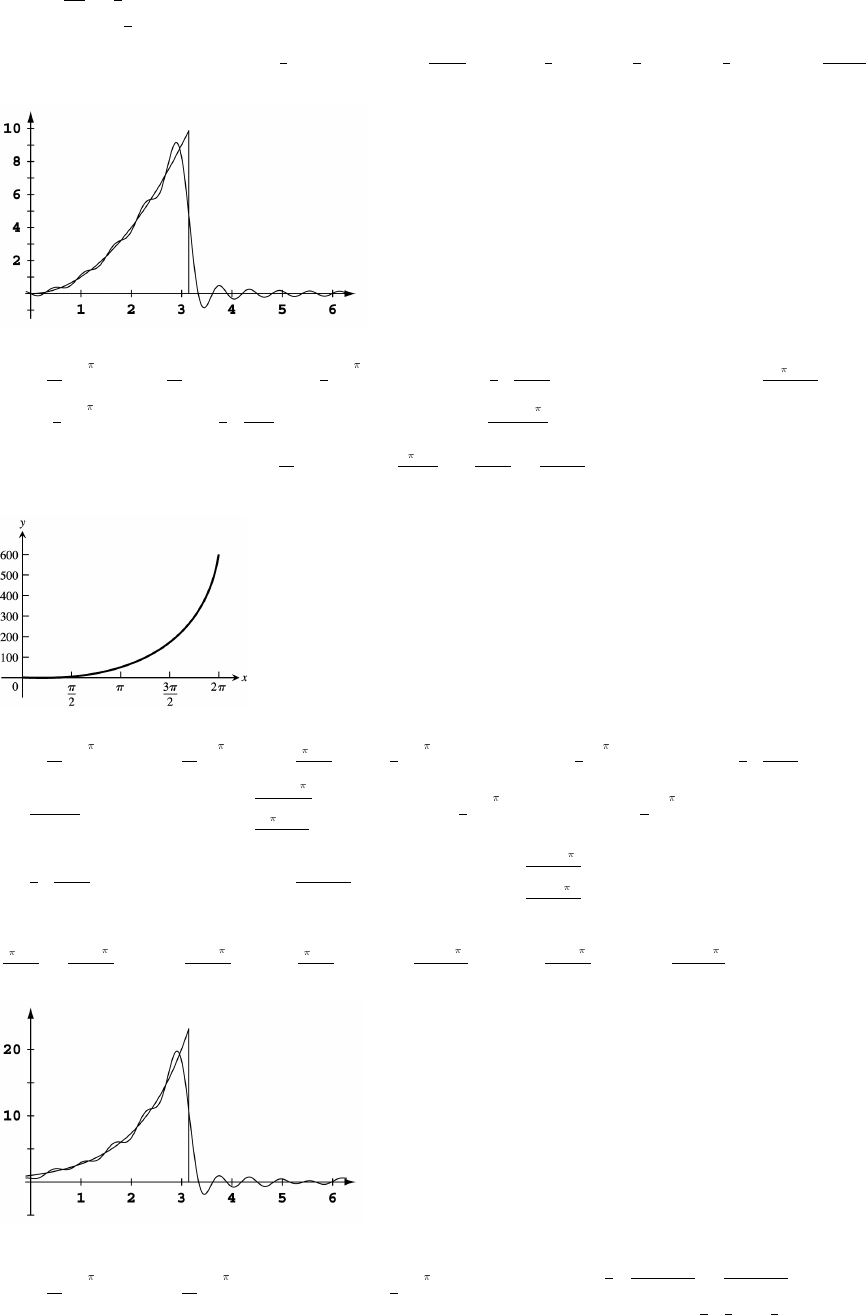
Section 11.11 Fourier Series 759
.
, k odd
, k even
œ
œ4
kk
k
1
1
1
3
Thus, the Fourier series for f x is 2 cos x sin x cos 2x sin 2x cos 3x sin 3x . . .ab Š‹ Š‹
14 294
62927
2
1
111
11
2 2
"
#
5. a e dx e 1 , a e cos kx dx ,
cos kx k sin kx
0k
11 1 1 e1
22 1k
x2 x e
1k 0
2
œœœ œ œ
11 1 1 1
11
''
00
22
ab ‘
ab
x
2
2
2
ab
b e sin kx dx .
sin kx k cos kx
k11
xe
1k 0
2k1 e
1k
œœ œ
11 1
1
'0
2‘
ab
x
2
2
2
ˆ‰
ab
Thus, the Fourier series for f x is e 1 .ab a b !ˆ‰
1 e 1 cos kx k sin kx
21k1k
2
k1
11
1
2
22
œ
_
6. a f x dx e dx , a f x cos kx dx e cos kx dx cos kx k sin kx
0k
11e11 1 1
222
xx
e
1k 0
œœœœ œ œ
1111 1 1
1
'' ' '
00 0 0
22
ab ab ‘
ab
x
2
. b f x sin kx dx e sin kx dx
e1 1 , k odd
, k even
œœ œœ
111
1k
k
1e
1k
e1
1k
kx
111
11
1
ab ab
ab
ab
2
2
2
‘
ab ab
''
00
2
.
sin kx k cos kx e1 1 , k odd
, k even
œœœ
1k
e
1k 01k
k
k1 e
1k
1e
1k
11
111
1
‘‘
abab
x
22
2
2
ab ab
ab
ab
Thus, the Fourier series for f x isab
cos x sin x cos 2x sin 2x cos 3x sin 3x . . .
e1 e1
22 2 5 5 10 10
1e 1e 21e 1e 31e
11 1 1 1 1 1
ab ab ab ab ab
7. a f x dx cos x dx 0, a cos x cos kx dx ,k1
0k
11 1
22
1sink 1x sink 1x
2k 1 2k 1 0
œœ œœ œ Á
11 1
1
1
'' '
00 0
22 2
ab Ú
Û
Ü’“
ab ab
ab ab
x sin 2x , k 1
1
40
1
1
‘
""
#œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
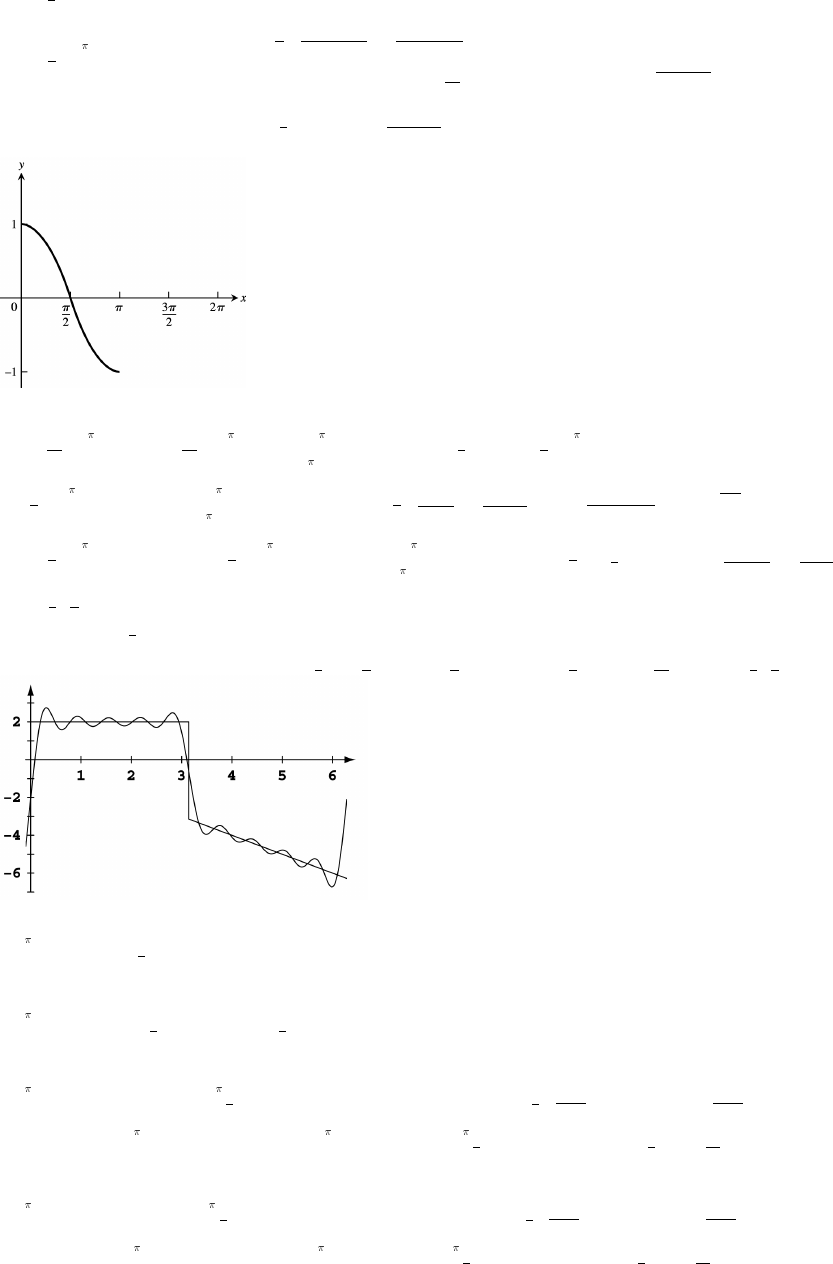
760 Chapter 11 Infinite Sequences and Series
.
,k 1
,k 1
œ!Á
œ
œ"
#
b cos x sin kx dx
,k1
cos 2x , k 1
k1
1cos k 1 x cos k 1 x
2k 1 2k 1 0
1
40
œœ œ
Á
œ
1
1
1
1
1
'0
2Ú
Ý
Û
Ý
Ü’“
¹
ab ab
ab ab
, k odd
, k even .
!
2k
k11ab
2
Thus, the Fourier series for f x is cos x sin kx.ab !
"
#
k even
2k
k11ab
2
8. a f x dx 2 dx x dx 1 , a f x cos kx dx
0 k
11 31
22 4
œœœœ
11 1
''' '
00 0
22 2
ab ab
”•
1
2 cos kx dx x cos kx dx .
, k odd
0, k even
œœ œœ
11
cos kx x sin kx
kk
211
k
2
k
111
1
1
1
”• œ
‘
''
0
2
2
k
2
2
ab
b f x sin kx dx 2 sin kx dx x sin kx dx cos kx
k11 1
2 x cos kx sin kx
kkk
0
2
œœœ
11 1
11
1
'''
00
22
ab ”•”•
¹¹
ˆ‰
2
.
3 , k odd
, k even
œ
ˆ‰
14
k1
k
1
Thus, the Fourier series for f x is 1 cos x 3 sin x sin 2x cos 3x 3 sin 3x . . . .ab ˆ‰ ˆ‰
32 4 2 14
493
111 1 1
"
#
9. cos px dx sin px 0 if p 0.
'0
2œœÁ
1
p
2
0
¹1
10. sin px dx cos px 0 if p 0.
11
'0
2œ œ œ Á
11
pp
2
0
¹cd
1
11. cos px cos qx dx dx 0 if p q.
cos pqxcospqx sin pqx sinpqx
''
00
22
œœ œÁ
""
##
cd
ab ab ‘
ab ab
11
pq pq
2
0
1
If p q then cos px cos qx dx cos px dx 1 cos 2px dx x sin 2px .œœœœœ
'''
000
222
21
2p
2
0
""
##
ab
Š‹
¹1
1
12. sin px sin qx dx dx 0 if p q.
cos pqxcospqx sin pqx sinpqx
''
00
22
œœ œÁ
""
##
cd
ab ab ‘
ab ab
11
pq pq
2
0
1
If p q then sin px sin qx dx sin px dx 1 cos 2px dx x sin 2px .œœœœœ
'''
000
222
21
2p
2
0
""
##
ab
Š‹
¹1
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 11 Practice Exercises 761
13. sin px cos qx dx dx
sin pqxsinpqx cos pqx cospqx
''
00
22
œœ
""
##
cd
ab ab ‘
ab ab
11
pq pq
2
0
1
0. If p q then sin px cos qx dx sin px cos px dx sin 2px dx
11 11
œ œ œ œ œ
" "
# #
‘
ab ab
11
pq pq '''
000
222
cos 2px 1 1 0.œ œ œ
11
44
2
0
11
1
¹ab
14. Yes. Note that if f is continuous at c, then the expression f c since f c f x f c and
fc fc
2xc
ab ab
Ä
œœœab a b ab ablim
f c f x f c . Now since the sum of two piecewise continuous functions on 0, 2 is also continuous on 0, 2 ,ab ab ab
Ä
œ œ ÒÓ ÒÓlim
xc
11
the function f g satisfies the hypothesis of Theorem 24, and so its Fourier series converges to ababababfgc fgc
2
for 0 c 2 . Let s x denote the Fourier series for f x . Then for any c in the interval 0, 211
fab ab a b
sc fgx fgx fx gx fx gx
fg fgc fgc
2xc xc xc xc xc xc
""
##
ÄÄÄÄ ÄÄ
ab ’“’ “
abab abab ab ab ab ab
œœ œ
abababab lim lim lim lim lim lim
+
s c s c , since f and g satisfy the hypothesis of Theorem 24.
fc gc fc gc
œœ
"
#
c d ab ab
ababab ab ab ab fg
15. (a) f x is piecewise continuous on 0, 2 and f x 1 for all x f x is piecewise continuous on 0, 2 . Thenab ab abÒÓ œ ÁÊ ÒÓ11 1
ww
by Theorem 24, the Fourier series for f x converges to f x for all x and converges to f fab ab a bab abÁ111
"
#
0 at x .œ œ œ
"
#ab11 1
(b) The Fourier series for f x is 1 . If we differentiate this series term by term we get the seriesab a b
!
k1
k1
2 sin kx
k
œ
_
1 2 cos kx, which diverges by the n term test for divergence for any x since 1 2 cos kx 0.
!ab ab
k1
k1 k1
th
k
œ
_
Ä_
Álim
16. Since the Fourier series in discontinuous at x , by Theorem 24, the Fourier series will converge to . Thus,œ1fc fc
2
ab ab
at x we have 2 cos x sin x cos 2x sin 2x cos 3x sin 3x . . . .œ œ 11
ff
26 2 9 27
14 294
2
abab11 111
11
"
#
Š‹ Š‹
2 2
2 cos sin cos 2 sin 2 cos 3 sin 3 . . .ʜ
01 4 2 94
26 2 9 27
2
"
#
11 1 1
11
22 2
11 11 11 1
Š‹ Š‹
2 . . . 2 1 . . . 2 2Ê œ œ œ Ê œ
01 2 1 11 1 1 1
26 9 6 49 6 n26 n
22 2
n1 n1
"
#œœ
__
111
222
22
11 1
ˆ‰
!!
22 .
1111
2222
222
26 n3 n6 n
n1 n1 n1
111
œ Êœ Êœ
!!!
œœœ
___
CHAPTER 11 PRACTICE EXERCISES
1. converges to 1, since lim a lim 1 1
nnÄ_ Ä_
n(1)
n
œœ
Š‹
n
2. converges to 0, since 0 a , lim 0 0, lim 0 using the Sandwich Theorem for SequencesŸŸ œ œ
n22
nn
ÈÈ
nnÄ_ Ä_
3. converges to 1, since lim a lim lim 1 1œœœ
nn nÄ_ Ä_ Ä_
n12
2
ˆ‰ ˆ ‰
"
#
n
nn
4. converges to 1, since lim a lim 1 (0.9) 1 0 1
nnÄ_ Ä_
nœ œœcd
n
5. diverges, since sin 0 1 0 1 0 1
˜™
ef
n1
#œ ßßßßßßá
6. converges to 0, since {sin n } {0 0 0 }1œ ßßßá
7. converges to 0, since lim a lim 2 lim 0
nn nÄ_ Ä_ Ä_
nln n
n1
œœ œ
Š‹
n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

762 Chapter 11 Infinite Sequences and Series
8. converges to 0, since lim a lim lim 0
nn nÄ_ Ä_ Ä_
nln (2n )
n1
œœœ
" Š‹
2
2n 1
9. converges to 1, since lim a lim lim 1
nn nÄ_ Ä_ Ä_
nnln n
n1
1
œœœ
ˆ‰
Š‹
n
10. converges to 0, since lim a lim lim lim lim 0
nn n n nÄ_ Ä_ Ä_ Ä_ Ä_
nln 2n 1
n16nn
12n 2
œœœœœ
ab Š‹
6n
2n 1
11. converges to e , since lim a lim lim 1 e by Theorem 5
5 5
n
nn
nn nÄ_ Ä_ Ä_
œœœ
ˆ‰ Š‹
n5
nn
(5)
12. converges to , since lim a lim 1 lim by Theorem 5
""""
ene
n1
nn nÄ_ Ä_ Ä_
œœ œ
ˆ‰
nˆ‰
n
n
13. converges to 3, since lim a lim lim 3 by Theorem 5
nn nÄ_ Ä_ Ä_
n333
n1
1n
n
œœœœ
ˆ‰
n
1n
Î
14. converges to 1, since lim a lim lim 1 by Theorem 5
nn nÄ_ Ä_ Ä_
n331
n1
1n
n
œœœœ
ˆ‰Î1n
1n
15. converges to ln 2, since lim a lim n 2 1 lim lim lim 2 ln 2
nn n n nÄ_ Ä_ Ä_ Ä_ Ä_
n21
œœ œ œab
1n 1n
1n
Š‹
n
2 ln 2
1n
n
n
–—
Š‹
2 ln 2 ln 2œœ
!†
16. converges to 1, since lim a lim 2n 1 lim exp lim exp e 1
nn n nÄ_ Ä_ Ä_ Ä_
nln (2n 1)
n1
œœ œ œœ
ÈŠ‹ Œ
n!
2
2n 1
17. diverges, since lim a lim lim (n 1)
nn nÄ_ Ä_ Ä_
n(n 1)!
n!
œœœ_
18. converges to 0, since lim a lim 0 by Theorem 5
nnÄ_ Ä_
n(4)
n!
œœ
n
19. s
"
# # (2n3)(2n1) n3 2n1 3 5 5 7 n3 2n1 3 2n1
n
œÊœá œ
Š‹ Š‹ Š‹ Š‹ Š‹ Š‹ Š‹ Š‹ Š‹ Š‹
–—–—– —
lim s lim Êœœ
nnÄ_ Ä_
n62n1 6
–—
""
Š‹
20. s lim s
# #
222 22 22 22 22
n(n1) n n1 3 3 4 n n1 n1
n n
œ Êœ á œ Ê
ˆ‰ˆ‰ ˆ ‰ nÄ_
lim 1 1œœ
nÄ_ ˆ‰
2
n1
21. s
9 3 3 333333 3 3
(3n1)(3n2) 3n1 3n2 5 5 8 8 11 3n1 3n2
n
#
œ Êœ á
ˆ‰ˆ‰ˆ‰ ˆ ‰
lim s lim œ Ê œ œ
33 3 3 3
3n 3n 2
n
## # #
nnÄ_ Ä_ ˆ‰
22. s
8 22 222222 22
(4n 3)(4n 1) 4n 3 4n 1 9 13 13 17 17 21 4n 3 4n 1
œ Êœ á
nˆ‰ˆ‰ˆ‰ˆ ‰
lim s lim œ Ê œ œ
22 22 2
94n1 94n1 9
nnÄ_ Ä_
nˆ‰
23. e , a convergent geometric series with r and a 1 the sum is
!!
__
œœn0 n0
"""
n
eee1
1
e
œœœÊœ
nŠ‹
e
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 11 Practice Exercises 763
24. ( 1) a convergent geometric series with r and a the sum is
!!
ˆ‰ˆ‰
__
œœn1 n0
œ œ œÊ
nn
33 3
444 44
n
" "
ˆ‰
ˆ‰
3
4
4
1
3
5
œ
25. diverges, a p-series with p œ"
#
26. 5 , diverges since it is a nonzero multiple of the divergent harmonic series
!!
__
œœn1 n1
"5
nn
œ
27. Since f(x) f (x) 0 f(x) is decreasing a a , and lim a lim 0, the
n
œÊ œÊ Ê œ œ
Ä_
""
w
#
xx n1 n n 1
n
nÄ_ È
series converges by the Alternating Series Test. Since diverges, the given series converges
!!
_ _
œ œn1 n1
()
n n
" "
n
È È
conditionally.
28. converges absolutely by the Direct Comparison Test since for n 1, which is the nth term of a
""
#nn
convergent p-series
29. The given series does not converge absolutely by the Direct Comparison Test since , which is
""
ln (n 1) n 1
the nth term of a divergent series. Since f(x) f (x) 0 f(x) isœÊœ Ê
""
w
ln (x 1) (ln (x 1)) (x 1)
decreasing a a , and lim a lim 0, the given series converges conditionally by theÊ œ œ
n1 n ln (n 1)
"
nnÄ_ Ä_
n
Alternating Series Test.
30. dx lim dx lim (ln x) lim the series
''
22
bb
2
"" """
"
#x(ln x) x(ln x) ln b ln 2 ln
œœœœÊ
bb bÄ_ Ä_ Ä_
cd ˆ‰
converges absolutely by the Integral Test
31. converges absolutely by the Direct Comparison Test since , the nth term of a convergent p-series
ln n n
nnn
œ
"
32. diverges by the Direct Comparison Test for e n ln e ln n n ln n ln n ln (ln n)
nn n n
nn
Ê ÊÊ
ˆ‰
n ln n ln (ln n) , the nth term of the divergent harmonic seriesÊ Ê
ln n
ln (ln n) n
"
33. lim lim 1 1 converges absolutely by the Limit Comparison Test
nnÄ_ Ä_
Š‹
Š‹
nn 1
n
œœœÊ
ÉÈ
n
n1
34. Since f(x) f (x) 0 when x 2 a a for n 2 and lim 0, theœÊœ Ê œ
3x 3n
x1 n1
3x 2 x
x1 n1 n
w
ab
ab nÄ_
series converges by the Alternating Series Test. The series does not converge absolutely: By the Limit
Comparison Test, lim lim 3. Therefore the convergence is conditional.
nnÄ_ Ä_
Š‹
ˆ‰
3n
n 1
n
œœ
3n
n1
35. converges absolutely by the Ratio Test since lim lim 0 1
nnÄ_ Ä_
’“
n2 n! n 2
(n 1)! n 1 (n 1)
†œœ
36. diverges since lim a lim does not exist
nnÄ_ Ä_
n()n 1
2n n 1
œ"
nab
37. converges absolutely by the Ratio Test since lim lim 0 1
nnÄ_ Ä_
’“
3n! 3
(n 1)! 3 n 1
n1
n
†œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

764 Chapter 11 Infinite Sequences and Series
38. converges absolutely by the Root Test since lim a lim lim 0 1
nn nÄ_ Ä_ Ä_
ÈÉ
nnnn
n
nœœœ
23 6
nn
39. converges absolutely by the Limit Comparison Test since lim lim 1
nnÄ_ Ä_
Š‹
Š‹
n
n(n 1)(n 2)
œœ
Én(n 1)(n 2)
n
40. converges absolutely by the Limit Comparison Test since lim lim 1
nnÄ_ Ä_
Š‹
Š‹
n
nn 1
œœ
Énn 1
n
ab
41. lim 1 lim 1 lim 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰
u
u (n 1)3 (x 4) 3 n 1 3
(x 4) n3 n
x4 x4
n1
n
n1
n1 n
n
Ê Ê Ê
†kk kk
x 4 3 3 x 4 3 7 x 1; at x 7 we have , theÊ Ê Ê œ œkk !!
__
œœn1 n1
(1)3 ( )
n3 n
"
nn n
n
alternating harmonic series, which converges conditionally; at x 1 we have , the divergentœ œ
!!
__
œœn1 n1
3
n3 n
n
n"
harmonic series
(a) the radius is 3; the interval of convergence is 7 x 1Ÿ
(b) the interval of absolute convergence is 7 x 1
(c) the series converges conditionally at x 7œ
42. lim 1 lim 1 (x 1) lim 0 1, which holds for
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹
u
u (2n 1)! (x 1) ( n)(2n 1)
(x 1) (2n 1)!
n1
nÊ Ê œ
#
#"
2n
2n 2
†
all x
(a) the radius is ; the series converges for all x_
(b) the series converges absolutely for all x
(c) there are no values for which the series converges conditionally
43. lim 1 lim 1 3x 1 lim 1 3x 1 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
u
u (n 1) (3x 1) (n 1)
(3x 1) nn
n1
n
n1
n
Ê Ê Ê
†
1 3x 1 1 0 3x 2 0 x ; at x 0 we have Ê Ê Ê œ œ
2
3nn
(1) (1) ( )
!!
__
œœn1 n1
"
n1 n 2n1
, a nonzero constant multiple of a convergent p-series, which is absolutely convergent; at x weœ œ
!
_
œn1
"
n 3
2
have , which converges absolutely
!!
__
œœn1 n1
(1) (1) ( )
nn
"
n1 n n1
œ
(a) the radius is ; the interval of convergence is 0 x
"
33
2
ŸŸ
(b) the interval of absolute convergence is 0 xŸŸ
2
3
(c) there are no values for which the series converges conditionally
44. lim 1 lim 1 lim 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ¸¸
u
u 2n3 2 n1 (2x1) 2 2n3 n1
n2 2n1 2 n2 2n
(2x 1) 2x 1
n1
n
n1
n1 n
n
Ê Ê
"
††† †
kk
(1) 1 2x 1 2 2 2x 1 2 3 2x 1 x ; at x we haveÊ Ê Ê Ê Ê œ
kk2x 1 33
### #
"
kk
which diverges by the nth-Term Test for Divergence since
!!
__
œœn1 n1
n1
2n 1 2n 1
(2) ( )(n1)
#
"
†
nn
nœ
lim 0; at x we have , which diverges by the nth-
nÄ_ ˆ‰ !!
n1 n1 2 n
2n 1 2n 1 2n 1
" " "
# # #
œÁ œ œ
__
œœn1 n1
†
n
n
Term Test
(a) the radius is 1; the interval of convergence is x
3
##
"
(b) the interval of absolute convergence is x
3
##
"
(c) there are no values for which the series converges conditionally
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 11 Practice Exercises 765
45. lim 1 lim 1 x lim 1 lim 1
nn n nÄ_ Ä_ Ä_ Ä_
¹¹ ¹ ¹ kk ¸¸ ˆ‰ˆ‰ˆ‰
u
u (n1) x n1 n1 e n1
xn n
nx
n1
n
n1 n
n1 n
Ê Ê Ê
""
†kk
0 1, which holds for all xÊ
kkx
e†
(a) the radius is ; the series converges for all x_
(b) the series converges absolutely for all x
(c) there are no values for which the series converges conditionally
46. lim 1 lim 1 x lim 1 x 1; when x 1 we have
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk kk
É
u
uxn1
xn
n1
n
n1
n
n1
n
Ê Ê Ê œ
ÈÈ
†
, which converges by the Alternating Series Test; when x 1 we have , a divergent
!!
_
œn1
(1)
n n
"
n
È È
œ
n1
p-series
(a) the radius is 1; the interval of convergence is 1 x 1Ÿ
(b) the interval of absolute convergence is 1 x 1
(c) the series converges conditionally at x 1œ
47. lim 1 lim 1 lim 1 3 x 3;
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰ ÈÈ
u
u3(n1)x3n1
(n 2)x 3xn2
n1
n
2n 1
n 1 2n 1
n
Ê Ê Ê
†
the series and , obtained with x 3, both diverge
!! È
__
œœn1 n1
œ„
n1 n1
33
ÈÈ
(a) the radius is 3; the interval of convergence is 3 x 3
ÈÈÈ
(b) the interval of absolute convergence is 3 x 3
ÈÈ
(c) there are no values for which the series converges conditionally
48. lim 1 lim 1 (x 1) lim 1 (x 1) (1) 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ˆ‰
u
u 2n 3 (x 1) 2n 3
(x 1)x 2n 1 2n 1
n1
n
2n 3
2n 1
Ê Ê Ê
##
†
(x 1) 1 x 1 1 1 x 1 1 0 x 2; at x 0 we have Ê Ê Ê Ê œ
#
#
kk !
_
œn1
(1)(1)
n1
n2n1
which converges conditionally by the Alternating Series Test and the factœœ
!!
__
œœn1 n1
(1) (1)
2n 1 2n 1
3n 1 n1
that diverges; at x 2 we have , which also converges
!!!
___
œœœn1 n1 n1
"
2n 1 2n 1 2n 1
(1)(1) (1)
œœ
n2n1 n
conditionally
(a) the radius is 1; the interval of convergence is 0 x 2ŸŸ
(b) the interval of absolute convergence is 0 x 2
(c) the series converges conditionally at x 0 and x 2œœ
49. lim 1 lim 1 x lim 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ kk »»
u
ucsch(n)x
csch (n 1)x
n1
n
n1
n
Ê Ê
Š‹
ˆ‰
2
ee
n1 n1
2
ee
nn
x lim 1 1 e x e; the series e csch n, obtained with x e,ÊÊÊ„ œ„kk a b
¹¹ !
nÄ_
ee
1e e
xn
2n 1
2n 2 kk _
œn1
both diverge since lim e) csch n 0
nÄ_ a„Á
n
(a) the radius is e; the interval of convergence is e x e
(b) the interval of absolute convergence is e x e
(c) there are no values for which the series converges conditionally
50. lim 1 lim 1 x lim 1 x 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ¹ ¹
kk kk
u
ux coth(n) 1e1e
x coth(n1) 1e 1e
n1
n
n1
n2n22n
2n 2 2n
Ê Ê Ê
†
1 x 1; the series 1 coth n, obtained with x 1, both diverge since lim 1 coth n 0Ê „ œ„ „ Á
!ab ab
_
œn1
n n
nÄ_
(a) the radius is 1; the interval of convergence is 1 x 1
(b) the interval of absolute convergence is 1 x 1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

766 Chapter 11 Infinite Sequences and Series
(c) there are no values for which the series converges conditionally
51. The given series has the form 1 x x x ( x) , where x ; the sum is áᜠœ œ
#$ "" "
n
1x 4 5
1
4
ˆ‰
4
52. The given series has the form x ( 1) ln (1 x), where x ; the sum isá ᜠœ
xx x 2
3n 3
n1
#
n
ln 0.510825624
ˆ‰
5
3¸
53. The given series has the form x ( 1) sin x, where x ; the sum isá ᜠœ
xx x
3! 5! (2n 1)!
n2n 1
1
sin 01œ
54. The given series has the form 1 ( 1) cos x, where x ; the sum is cos á ᜠœ œ
xx x
2! 4! (2n)! 3 3
n2n 11"
#
55. The given series has the form 1 x e , where x ln 2; the sum is e 2áᜠœ œ
xx x
2! 3! n!
xln2
nÐÑ
56. The given series has the form x ( 1) tan x, where x ; the sum isá ᜠœ
xx x
35 (2n1)
n
3
2n 1
" "
È
tan" "
Š‹
È36
œ1
57. Consider as the sum of a convergent geometric series with a 1 and r 2x
" "
12x 12x
œœÊ
1 (2x) (2x) (2x) (2x) 2 x where 2x 1 xœáœ œ Ê
#$ "
#
!! kk kk
__
œœn0 n0
nnn
58. Consider as the sum of a convergent geometric series with a 1 and r x
"""
$
1x 1x 1 x
œœÊœ
ab
1 x x x ( 1) x where x 1 x 1 x 1œáœ Ê Êababab kk kk kk
!
$$ $ $ $
#$ _
œn0
n3n
59. sin x sin x œÊœ œ
!!!
___
œœœn0 n0 n0
(1)x (1)(x) (1) x
(2n 1)! (2n 1)! ( n 1)!
#
n2n1 n 2n1 n 2n12n1
111
60. sin x sin œÊœ œ
!!!
___
œœœn0 n0 n0
(1)x (1)2 x
(2n 1)! 3 (2n 1)! 3 ( n 1)!
2x (1)
#
n2n1 n2n12n1
n2n 1
2n 1
Š‹
2x
3
61. cos x cos x œÊœ œ
!!!
ˆ‰
___
œœœn0 n0 n0
(1)x (1)x
(2n)! (2n)! ( n)!
(1) x
&Î#
#
n2n n5n
n2n
ˆ‰
62. cos x cos 5x cos (5x) œÊœ œ œ
!!!
Ȉ‰
___
œœœn0 n0 n0
(1)x (1)5x
(2n)! (2n)! ( n)!
( 1) (5x)
"Î#
#
n2n nnn
n2n
ˆ‰
63. e e
xx2
xx
n! n! n!
n0
œÊœ œ
!!!
__
œœn0 n0
nnn
xn
n
ÐÎÑ _
œ#
11
ˆ‰
64. e e
xx
x
n! n! n!
x(1)x
œÊœ œ
!!!
___
œœœn0 n0 n0
nnn2n
ab
65. f(x) 3 x 3 x f (x) x 3 x f (x) x 3 x 3 xœœ Ê œ Ê œ
Èab ab abab
##w # ww## #
"Î# "Î# $Î# "Î#
f (x) 3x 3 x 3x 3 x ; f( 1) 2, f ( 1) , f ( 1) ,Êœ œœœœ
www $ # # w ww
&Î# $Î# """
##
ab ab 88
3
f ( 1) 3 x 2
www #
œœÊœá
33 9
32 8 32 2 1! 2 2! 2 3!
(x 1) 3(x 1) 9(x 1)
Ȇ† †
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 11 Practice Exercises 767
66. f(x) (1 x) f (x) (1 x) f (x) 2(1 x) f (x) 6(1 x) ; f(2) 1, f (2) 1,œœÊ œÊ œÊ œ œ œ
"
" w # ww $ www % w
1x
f (2) 2, f (2) 6 1 (x 2) (x 2) (x 2)
ww www # $
"
œ œÊ œ á
1x
67. f(x) (x 1) f (x) (x 1) f (x) 2(x 1) f (x) 6(x 1) ; f(3) ,œœÊ œÊ œÊ œ œ
" "
" w # ww $ www %
x1 4
f (3) , f (3) , f (2) (x 3) (x 3) (x 3)
w ww www # $
""""""
œ œ œÊœá
44 x1444
26
44
68. f(x) x f (x) x f (x) 2x f (x) 6x ; f(a) , f (a) , f (a) ,œœ Ê œ Ê œ Ê œ œ œ œ
"""
" w # ww $ www % w ww
xaaa
2
f (a) (x a) (x a) (x a)
www # $
""" " "
œ Êœ á
6
aa
xaa a
69. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na x yÊœ á áÊ
dy dy
dx dx
nn1
"#
a a 2a a x (3a a )x (na a )x 0 a a 0, 2a a 0,œ á áœÊœ œaba b
"! #" $# "! #"
#
nn1
n1
3a a 0 and in general na a 0. Since y 1 when x 0 we have a 1. Therefore a 1,
$# ! "
œ œ œ œ œ œ
nn1
a , a , a , , a
#$%
"" "
##
œœ œœ œœ ᜠœ œ
aaa
21 3 32 4 43 n n (n 1)! n!
na1(1) (1)
††††
n1 nn1
y1xx x x eÊœ á ᜠœ
""
##
#$
3n! n!
(1) (1)x
nx
†
n1 nn
!
_
œn0
70. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na x yÊœ á áÊ
dy dy
dx dx
nn1
"#
a a 2a a x (3a a )x (na a )x 0 a a 0, 2a a 0,œ á áœÊœ œaba b
"! #" $# "! #"
#
nn1
n1
3a a 0 and in general na a 0. Since y 3 when x 0 we have a 3. Therefore a 3,
$# ! "
œ œ œ œ œ œ
nn1
a , a , a y 3 3x x x x
#$
# #
#$
œœ œœ œ œ Êœ á á
aa
2332nn! 213n!
33 3 333
nan
†††
n1
31 x 3 3eœ á á œ œ
Š‹
!
xx x x
!3! n! n!
x
#
nn
_
œn0
71. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na x 2yÊœ á áÊ
dy dy
dx dx
nn1
"#
a 2a 2a 2a x (3a 2a )x (na 2a )x 0. Since y 3 when x 0 weœ á ᜠœ œaba b
"! #" $#
#
nn1
n1
have a 3. Therefore a 2a 2(3) 3(2), a a ( 2 3) 3 , a a
!"! #" $#
## #
œœœœœœœœ
22 2 2
3
†Š‹
3 3 , , a a 3 3œ œ á œ œ œ
22 2 2 2
33nn(n1)!n!
nn1 (1) 2 (1)2
’“Š‹ Š ‹Š‹Š‹ Š ‹
ˆ‰ ˆ‰
##
†
n1n1 nn
y 3 3(2x) 3 x 3 x 3 xÊœá á
(2) (2) ( 1) 2
3n!
n
##
#$
†
nn
3 1 (2x) 3 3eœá ᜠœ
’“
!
(2x) (2x) ( 1) (2x) ( 1) (2x)
2! 3! n! n!
2x
nn nn
_
œn0
72. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na x yÊœ á áÊ
dy dy
dx dx
nn1
"#
a a 2a a x (3a a )x (na a )x 1 a a 1, 2a a 0,œ á áœÊœ œaba b
"! #" $# "! #"
#
nn1
n1
3a a 0 and in general na a 0 for n 1. Since y 0 when x 0 we have a 0. Therefore
$# !
œ œ œ œ œ
nn1
a 1 a 1, a , a , a , , a
"!# $ %
"" "
##
œœ œœ œœ œœ á
aaa
21 3 32 4 43 n
††††
y0x x x xœœ œ Êœá á
""
##
#$
a
n n (n 1)! n! 3 n!
1(1) (1) (1) n
n1 nn1 n1
ˆ‰ †
11 x x x x 1 1 1 eœ á ᜠœ
’“
!
""
##
#$
3n! n!
(1) (1)x
nx
†
nnn
_
œn0
73. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na x yÊœ á áÊ
dy dy
dx dx
nn1
"#
a a 2a a x (3a a )x (na a )x 3x a a 0, 2a a 3,œ á áœÊœ œaba b
"! #" $# "! #"
#
nn1
n1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

768 Chapter 11 Infinite Sequences and Series
3a a 0 and in general na a 0 for n 2. Since y 1 when x 0 we have a 1. Therefore
$# !
œ œ œ œ œ
nn1
a 1, a , a , a , , a
"# $ %
##
œ œ œ œœ œœ á œ œ
3a a a
2332443 nn!
22 2 2
na
†††
n1
y1x x x x xÊœ á á
ˆ‰
232 2
343 n!
n
###
#$ %
†††
21x x x x x 33x 2 33x 2e 3x3œá᜜
ˆ‰
!
"" " "
## #
#$ %
343 n! n!
nx
x
†††
_
œn0
n
74. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na x yÊœ á áÊ
dy dy
dx dx
nn1
"#
a a 2a a x (3a a )x (na a )x x a a 0, 2a a 1,œ á áœÊœ œaba b
"! #" $# "! #"
#
nn1
n1
3a a 0 and in general na a 0 for n 2. Since y 0 when x 0 we have a 0. Therefore
$# !
œ œ œ œ œ
nn1
a 0, a , a , , a
"# $
"
""
#
œœ œ œœáœ œ
aa
2332nn!
na(1)
†
n1 n
y 0 0x x x x 1 x x x x 1 xÊ œ á á œ á á
"" ""
## ##
#$ #$
3n! 3n!
(1) (1)
nn
††
n n
Š‹
1xe x1œœ
!
_
œn0
(1)x
n!
x
nn
75. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na x yÊœ á áÊ
dy dy
dx dx
nn1
"#
a a 2a a x (3a a )x (na a )x x a a 0, 2a a 1,œ á áœÊœ œaba b
"! #" $# "! #"
#
nn1
n1
3a a 0 and in general na a 0 for n 2. Since y 1 when x 0 we have a 1. Therefore
$# !
œ œ œ œ œ
nn1
a 1, a , a , a , , a
"# $ %
##
œœ œ œœ œœ ᜜
1a a a
2332443 nn!
22 2 2
na
†††
n1
y1x x x x xÊœ á á
ˆ‰
222 2
342 n!
n
###
#$ %
†††
21x x x x x 1x2 1x 2e x1œá᜜
ˆ‰
!
"" " "
## #
#$ %
343 n! n!
nx
x
†††
_
œn0
n
76. Assume the solution has the form y a a x a x a x a xœá á
!" #
#
n1 n
n1 n
a 2a x na x yÊœ á áÊ
dy dy
dx dx
nn1
"#
a a 2a a x (3a a )x (na a )x x a a 0, 2a a 1,œ á áœÊ œ œaba b
"! #" $# "! #"
#
nn1
n1
3a a 0 and in general na a 0 for n 2. Since y 2 when x 0 we have a 2. Therefore
$# !
œ œ œ œ œ
nn1
a 2, a , a , a , , a
"# $ %
##
œœ œ œœ œœ ᜜
1a a a
2332443nn!
11 1 1
na
†††
n1
y 2 2x x x x xÊœ á á
11 1 1
343 n!
n
## #
#$ %
†††
1x x x x x 1x 1xe x1œ á ᜠœ
ˆ‰
!
"" " "
## #
#$ %
343 n! n!
nx
x
†††
_
œn0
n
77. exp x dx 1 x dx x
''
00
12 12
ab Š‹’ “
œ á œ á
$$ "Î#
!
xxx x x x x
2! 3! 4! 4 7 2! 10 3! 13 4!
†††
0.484917143¸¸
""""""
###
††† †† †† ††
472!
2 10 3! 2 13 4! 2 16 5!
78. x sin x dx x x dx x dx
'' '
00 0
11 1
ab Š‹Š‹
$$ %
œ á œ á
xxxx xxxx
3! 5! 7! 9! 3! 5! 7! 9!
0.185330149œá¸
’“
xxxxx
5 113! 175! 237! 299!
††††
"
!
79. dx 1 dx x
''
11
12 12
tanx xxxxx xxxx x
x 357911 9254981121
œ á œ á
Š‹’ “
"Î#
!
¸
"""""""""""
## ##
##
9 2 5 9 2 11 2 13 2 15 2 19 21
717
†† †††† ††
††
0.4872223583¸
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 11 Practice Exercises 769
80. dx x dx xxxx dx
'' '
00 0
164 164 164
tanx xxx
xx
357 3 5 7
ÈÈ
œ á œ á
" """
"Î# &Î# *Î# "$Î#
Š‹
ˆ‰
x x x x 0.0013020379œ á œ á ¸
‘ˆ‰
22 2 2 2222
3 1 55 105 3 8 55 8 105 8
21 8
$Î# (Î# ""Î# "&Î#
#
"Î'%
!†††
†
81. lim lim lim
x0 x0 x0ÄÄ Ä
7 sin x 7
e1
2x #
œœœ
7x 71
2x 2
Š‹Š‹
Š‹Š‹
á á
á á
xx xx
3! 5! 3! 5!
2x 2x 2x 2x
2! 3! ! 3!
82. lim lim lim
)) )ÄÄ Ä00 0
ee 2
sin
)
))
œœ
Š‹Š‹Š‹
Š‹ Š‹
1122á á á
á
)))
))
! 3! ! 3! 3! 5!
3! 5! 3! 5! á
lim 2œœ
)Ä0
2Š‹
Š‹
3! 5!
3! 5!
á
á
83. lim lim lim lim
t0 t0 t0 t0ÄÄÄ Ä
ˆ‰
""
#
2 cos t t 2t (1 cos t)
t22 cos t t22 2
2t
œ œ œ
ŒŒ
Š‹
1
11
á
á
tt t
4! 4!
tt
4!
á
á
t
6!
2t
4!
Š‹
t
lim œœ
t0Ä
2
1
Š‹
Š‹
4! 6!
t
2t
4!
á
á1
"
#
84. lim lim
h0 h0ÄÄ
Š‹ ŒŒ
sin h
h
hh hh
3! 5! ! 4!
cos h
hh
œ
11á á
lim lim œ œ áœ
h0 h0ÄÄ
Œ
hhhhhh
!3!5!4!6!7!
á
h ! 3! 5! 4! 6! 7! 3
hhhh
Š‹
"" "
#
85. lim lim lim
z0 z0 z0ÄÄ Ä
"
cos z
ln (1 z) sin z
11z z
zz
œœ
Š‹ Š‹
Š‹Š‹Š ‹
zz
33
zz zz z2zz
33!5! 34
á á
áá á
lim 2œœ
z0Ä
Š‹
Š‹
1á
á
z
3
2z z
34
86. lim lim lim
y0 y0 y0ÄÄ Ä
yy y
cos y cosh y 11
œœ
ŒŒŒ
yyy yyy 2y2y
4!6! !4!6! 6!
á á á
lim 1œœ
y0Ä
"
á
Œ
12y
6!
87. lim s lim s lim s 0
x0 x0 x0ÄÄ Ä
ˆ‰
–—
Š‹
sin 3x r r 3 9 81x r
xx x x x 40 x
3x
œ œ á œ
Š‹
á
#
(3x) (3x)
6 120
0 and s 0 r 3 and sÊœ œÊœ œ
r3 9 9
xx ##
88. (a) csc x csc x sin x¸ Ê ¸ Ê ¸
"
x6 6x 6x
x6x 6x
(b) The approximation sin x is better than¸6x
6x
sin x x.¸
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

770 Chapter 11 Infinite Sequences and Series
89. (a) sin sin sin sin sin sin sin sin sin sin
!ˆ ‰ˆ‰ˆ‰ˆ‰ˆ ‰
_
œn1
" " " " "" "" " "
# # ##2nn1 34567 nn1
œ á
( 1) sin ; f(x) sin f (x) 0 if x 2 sin sin , andá œ œ Ê œ Ê
!
_
œn2
n
nx x n1n
cos
"" ""
w
Š‹
x
lim sin 0 ( 1) sin converges by the Alternating Series Test
nÄ_
""
nn
œÊ
!
_
œn2
n
(b) error sin 0.02381 and the sum is an underestimate because the remainder is positivekk
¸¸
¸
"
42
90. (a) tan tan ( 1) tan (see Exercise 89); f(x) tan f (x) 0
!!
ˆ‰
__
œœn1 n2
"" " "
#
w
2n n 1 n x x
œ œÊœ
nsec ˆ‰
x
tan tan , and lim tan 0 ( 1) tan converges by the Alternating SeriesÊ œÊ
"" " "
n1 n n n
n
nÄ_ !
n2
Test
(b) error tan 0.02382 and the sum is an underestimate because the remainder is positivekk
¸¸
¸
"
42
91. lim 1 x lim 1 x
nnÄ_ Ä_
¹¹
kk kk
¸¸
2 5 8 (3n 1)(3n 2)x 2 4 6 (2n)
4 6 (2n)(2n 2) 5 8 (3n 1)x 2n 2 3
3n 2 2
†† ††
†† ††
â â
#â #â
n1
n
†Ê Ê
the radius of convergence is Ê2
3
92. lim 1 x lim 1 x
nnÄ_ Ä_
¹¹
kk kk
¸¸
3 5 7 (2n 1)(2n 3)(x 1) 4 9 14 (5n 1)
4 9 14 (5n 1)(5n 4) 3 5 7 (2n 1)x 5n 4 2
2n 3 5
†† ††
†† ††
â â
â â
n1
n
†Ê Ê
the radius of convergence is Ê5
2
93. ln 1 ln 1 ln 1 ln (k 1) ln k ln (k 1) ln k
!! !
ˆ‰ ‘ˆ‰ˆ‰ cd
nn n
k2 k2 k2œœ œ
œ œ
"""
kkk
ln 3 ln 2 ln 1 ln 2 ln 4 ln 3 ln 2 ln 3 ln 5 ln 4 ln 3 ln 4 ln 6 ln 5 ln 4 ln 5œ cdcdcdcd
ln (n 1) ln n ln (n 1) ln n ln 1 ln 2 ln (n 1) ln n after cancellationáœcdcdcd
ln 1 ln ln 1 lim ln ln is the sumÊœ Ê œ œ
!!
ˆ‰ˆ‰ ˆ‰ ˆ‰
n
k2 k2œœ
" " "
#k2n k 2n
n1 n 1
nÄ_
94. -
!!
ˆ ‰ ˆ ‰ˆ ‰ˆ ‰ˆ ‰ ˆ ‰
nn
k2 k2œœ
" " " " " " "" "" "" " "
# # # #k 1 k1 k1 1 3 4 3 5 4 6 n n
1
œ œ á
œ œ œ œ
‘ˆ ‰ˆ ‰ˆ‰ ’“
" " """" " " " " "
# # ## #
n1 n1 1 n n1 n n1 2n(n1) 4n(n1)
33nn2
3n(n 1) 2(n 1) 2n
lim Êœ œ
!ˆ‰
k2œ
""
# k1 2nn1 4
31 1 3
nÄ_
95. (a) lim 1 x lim
nnÄ_ Ä_
¹¹
kk
1 4 7 (3n 2)(3n 1)x (3n)! (3n )
(3n 3)! 1 4 7 (3n 2)x (3n 1)(3n 2)(3n 3)
††
††
â "
â
$
3n 3
3n
†Ê
x 0 1 the radius of convergence is œÊ _kk
$†
(b) y 1 x xœ Ê œ
!!
__
œœn1 n1
147 (3n 2) dy 147 (3n 2)
(3n)! dx (3n 1)!
†† ††â â
3n 3n 1
xx xÊœ œ
dy 147 (3n 2) 147 (3n 5)
dx (3n 2)! (3n 3)!
!!
__
œœn1 n2
†† ††â â
3n 2 3n 2
x 1 x xy 0 a 1 and b 0œ œÊœ œ
Œ
!
_
œn1
147 (3n 2)
(3n)!
††â 3n
96. (a) x x ( x) x ( x) x ( x) xxxx (1)x which
xx
1x 1(x)
nn
## # ## $ #$%&
œ œáœáœ
!
_
œn2
converges absolutely for x 1kk
(b) x 1 ( 1) x ( 1) which divergesœÊ œ
!!
__
œœn2 n2
nn n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 11 Practice Exercises 771
97. Yes, the series a b converges as we now show. Since a converges it follows that a 0 a 1
!!
__
œœn1 n1
nn n nn
ÄÊ
for n some index N a b b for n N a b converges by the Direct Comparison Test with bÊÊ
nn n nn n
!!
_ _
œ œn1 n1
98. No, the series a b might diverge (as it would if a and b both equaled n) or it might converge (as it
!
_
œn1
nn n n
would if a and b both equaled ).
nn n
"
99. (x x ) lim (x x ) lim (x x ) lim (x ) x both the series and
!!
__
œœn1 1
n1 n k1 k n1 n1""
œ œ œ Ê
nnnÄ_ Ä_ Ä_
k
sequence must either converge or diverge.
100. It converges by the Limit Comparison Test since lim lim 1 because a converges
nnÄ_ Ä_
Š‹
an
1a
n
n
aœœ
"
1a n
n!
_
œn1
and so a 0.
nÄ
101. Newton's method gives x x x , and if the sequence {x } has the limit L, then
n1 n n n
x1
40 x 1
39
40 40
"
œ œ
ab
ab
n
n
L L L 1 and x converges since 1œÊœ Ö× œ
39 39
40 40 f x 40
nfxf x
"
ÒÓ
¹¹
abab
ab2
102. a a a a a
!ˆ‰ ˆ ‰ ˆ ‰
_
œn1
a
n 3 4 34 5678
aaa
nχ
""#%)
##
" "" """"
a (aaaa ) which is a divergent series á á á
ˆ‰
"" " " "
"' #%)"'
#91011 16
103. a for n 2 a a a , and
nln n ln ln 4 ln 8 ln ln 2 3 ln 2
œ Ê á ᜠá
" """ " " "
#$% ###
1 which diverges so that 1 diverges by the Integral Test.œ á
""" "
##ln 3 n ln n
ˆ‰ !
_
œn2
104. (a) T 0 2 e e e e 0.885660616œ œ¸
84
ˆ‰
##
"""
#"Î# "Î#
Š‹
ˆ‰
(b) x e x 1 x x x x x dx 0.68333
# # #$ #$
## #
"
!
xxx xxxx41
3 4 10 60
œ áœáÊ œ œ œ
Š‹ Š‹’“
'0
1
(c) If the second derivative is positive, the curve is concave upward and the polygonal line segments used in
the trapezoidal rule lie above the curve. The trapezoidal approximation is therefore greater than
the actual area under the graph.
(d) All terms in the Maclaurin series are positive. If we truncate the series, we are omitting positive terms
and hence the estimate is too small.
(e) x e dx x e 2xe 2e e 2e 2e 2 e 2 0.7182818285
'0
1## "
!
xxxx
œ œ œ¸cd
105. a f x dx 1 dx a f x cos kx dx cos kx dx 0.
0k
11 1 1
22
œœœßœ œ œ
11 1 1
'' ' '
00
22 2 2
ab ab
"
#
b f x sin kx dx sin kx dx 1 1 .
, k odd
0, k even
k11cos kx1
kk
2k2
k
œ œ œ œ œ
1111
1
1
1
''
0
22
ab a b
¹Š‹
œ
Thus, the Fourier series of f x is sin kxab !
"
#
k odd
2
k1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
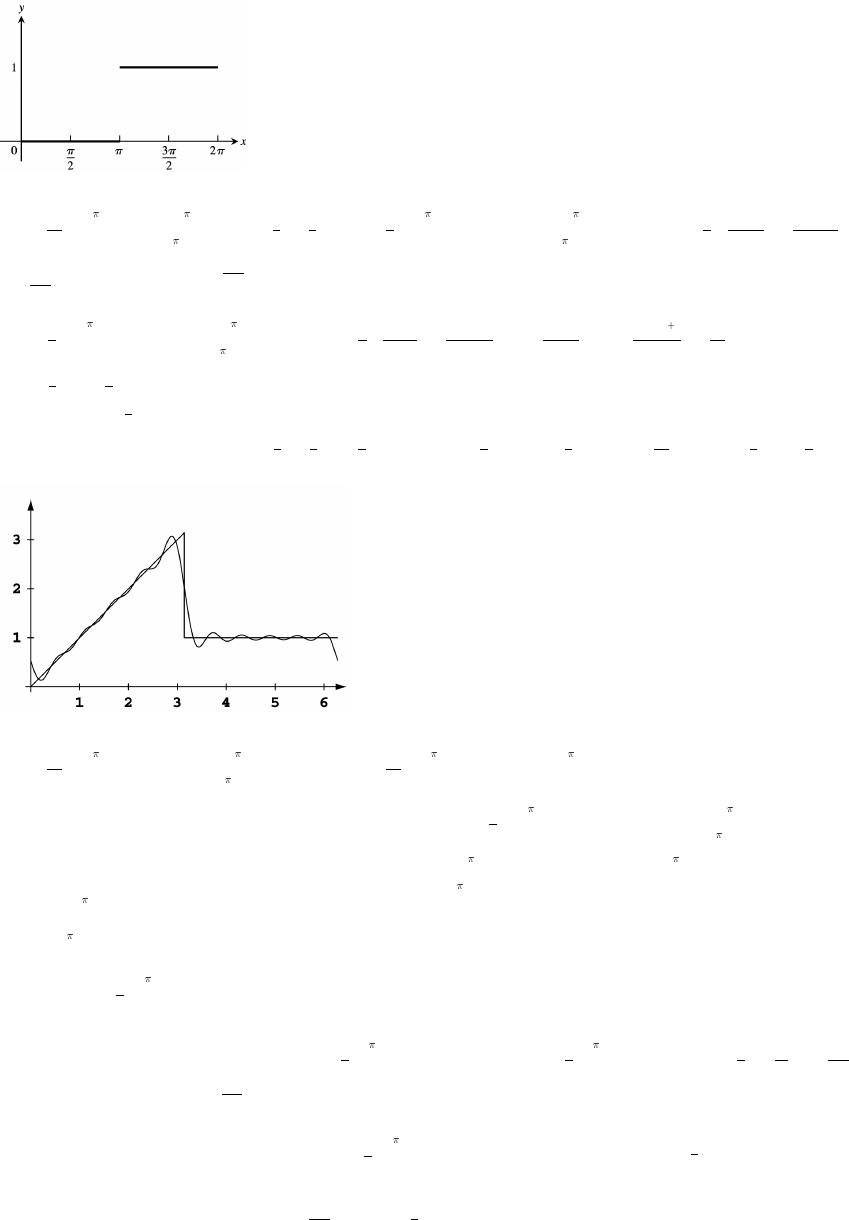
772 Chapter 11 Infinite Sequences and Series
106. a x dx 1 dx , a x cos kx dx cos kx dx
0k
111
24
cos kx x sin kx
kk
0
œœœ œ
111
1
”•” •
‘
'' ' '
00
2 2
""
#12
1 1 .
, k odd
0, k even
œœ
1
k
k2
k
1
1
2
2
Š‹
ab œ
b x sin kx dx sin kx dx 1 1
k11cos kx1
sin kx x cos kx
kk
0kkk
21k
œœ œ
1111
11
1
”•
‘
¹Š‹
ab
''
0
2
2
k1
ab
.
1 , k odd
, k even
œ
ˆ‰
12
k1
k
1
Thus, the Fourier series of f x is cos x 1 sin x sin 2x cos 3x 1 sin 3x . . .ab ˆ‰ ˆ‰
"" "
##
493
22 212
111 1 1
107. a x dx x 2 dx x dx u du 0 where we used the
011
22
œœœ
11
”•
ab a b ab ab
’“
'' ''
000
2
1111
substitution u x in the second integral. We havea x cos kx dx x 2 cos kx dx . Usingœ œ 111
k1
1”•
ab a b
''
0
2
the substitution u x in the second integral gives x 2 cos kx dx u cos ku k duœ œ 1111
''
2
0
ab aba b
.
u cos ku du, k odd
u cos ku du, k even
œ
Ú
Û
Üab
ab
'
'
0
0
1
1
Thus, a .
x cos kx dx, k odd
0, k even
kœ
ab
#
1'0
1
Now, since k is odd, letting v x x cos kx dx v cos kv dv , k odd. (Seeœ Ê œ œ œ11
###
1111
''
00
ab ˆ‰
24
kk
22
Exercise 106). So, a .
, k odd
0, k even
k
4
k
œœ12
Using similar techniques we see that b
u sin ku du, k odd
0, k even
, k odd
0,
k
2
k
œœ
ab œ
#
1'0
1
k even .
Thus, the Fourier series of f x is cos kx sin kx .ab !ˆ‰
k odd
42
kk12
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
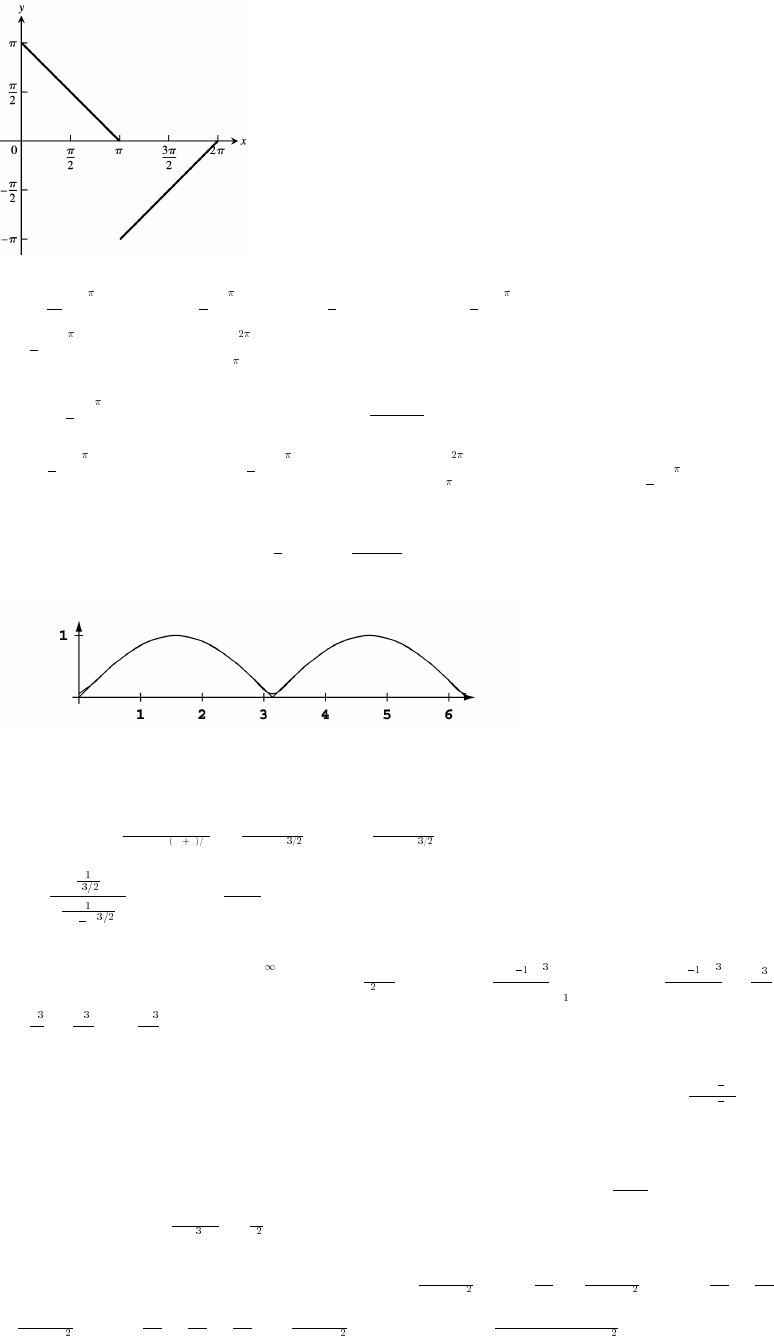
Chapter 11 Additional and Advanced Exercises 773
108. a sin x dx sin x dx . We have a sin x cos kx dx
0k
1121
2
œœœœ
1111
'' '
00 0
2 2
kk kk
sin x cos kx dx sin x cos kx dx . Using techniques similar to those used in Exercise 107, we findœ
1
1’“
''
0
a .
0, k odd
sin x cos kx dx, k even
0, k odd
, k even
k24
k1
œœ
œ
11
'0
ab
2
b sin x sin kx dx sin x sin kx dx sin x sin kx dx 0, k odd
sin x sin kx
k11 2
œœœ
11
1
''' '
00
2
0
kk ’“
dx, k even 0œ
for all k.
Thus, the Fourier series of f x is cos kx .ab !Š‹
24
k even k111
ab
2
CHAPTER 11 ADDITIONAL AND ADVANCED EXERCISES
1. converges since and converges by the Limit Comparison Test:
"" "
# (3n ) (3n 2) (3n 2)
2n 1 2 !
_
œn1
lim lim 3
nnÄ_ Ä_
Š‹
Š‹
n
(3n 2)
œœ
ˆ‰
3n 2
n
$Î# $Î#
2. converges by the Integral Test: tan x lim lim
'1
b
ab ’“ ’ “
" #
dx
x 1 3 3 192
tan x tan b
œœ
bbÄ_ Ä_
ab ab1
œ œ
Š‹
11 1
24 192 192
7
3. diverges by the nth-Term Test since lim a lim ( 1) tanh n lim ( 1) lim ( 1)
nn n
b
Ä_ Ä_ Ä_
Ä_
nnn n
1e
1e
œ œ œ
Š‹
2n
2n
does not exist
4. converges by the Direct Comparison Test: n! n ln (n!) n ln (n) nÊ Ê
nln (n!)
ln (n)
log (n!) n , which is the nth-term of a convergent p-seriesÊÊ
nlog (n!)
nn
n"
5. converges by the Direct Comparison Test: a 1 , a , a
"# $
œœ œ œ œ
12 12 12 23 12
(1)(3)(2) 3 4 (2)(4)(3) 4 5 3 4
†††
†††
ˆ‰ˆ‰
, a , 1 represents theœœ œáÊ
12 34 23 12 2 12
(3)(5)(4) 5 6 4 5 3 4 (4)(6)(5) (n 1)(n 3)(n 2)
%"
ˆ‰ˆ‰ˆ‰ !
†††
†††
_
œn1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

774 Chapter 11 Infinite Sequences and Series
given series and , which is the nth-term of a convergent p-series
12 12
(n 1)(n 3)(n 2) n
6. converges by the Ratio Test: lim lim 0 1
nnÄ_ Ä_
a
a (n 1)(n 1)
n
n1
nœœ
7. diverges by the nth-Term Test since if a L as n , then L L L 1 0 L
n1L
15
ÄÄ_œÊœÊœ
"
#
#„
È
0Á
8. Split the given series into and ; the first subseries is a convergent geometric series and the
!!
__
œœn1 n1
"
33
2n
2n 1 2n
second converges by the Root Test: lim lim 1
nnÄ_ Ä_
É
n
2n
nn
2n 1
3999
2 n
œœœ
ÈÈ""†
9. f(x) cos x with a f 0.5, f , f 0.5, f , f 0.5;œ œ Ê œ œ œ œ œ
11 1 1 1 1
33 3 3 3 3
33
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
w www
##
ww
ÈÈ
4
cos x x x xœ á
""
## #
#$
ÈÈ
33
34 3 1 3
ˆ‰ˆ‰ ˆ‰
11 1
10. f(x) sin x with a 2 f(2 ) 0, f (2 ) 1, f (2 ) 0, f (2 ) 1, f (2 ) 0, f (2 ) 1,œœÊœœœœœœ11 1 1 1 1 1
w www
ww 45
f (2 ) 0, f (2 ) 1; sin x (x 2 )
67
11 1œ œœá
(x 2 ) (x 2 ) (x 2 )
3! 5! 7!
111
11. e 1 x with a 0
xœá œ
xx
!3!
#
12. f(x) ln x with a 1 f(1) 0, f (1) 1, f (1) 1,f (1) 2, f (1) 6;œœÊœœœœœ
w www
ww 4
ln x (x 1)χ
(x 1) (x 1) (x 1)
34
#
13. f(x) cos x with a 22 f(22 ) 1, f (22 ) 0, f (22 ) 1, f (22 ) 0, f (22 ) ,œœÊœœœœœ"11 1 1 1 1
w www
ww 4
f (22 ) 0, f (22 ) 1; cos x 1 (x 22 ) (x 22 ) (x 22 )
56
11 1 1 1œ œ œ á
"" "
#
#%'
4! 6!
14. f(x) tan x with a 1 f(1) , f (1) , f (1) , f (1) ;œœÊœœœœ
" w www
"""
###
ww
1
4
tan x
"
χ
1
42 4 12
(x 1) (x 1) (x 1)
15. Yes, the sequence converges: c a b c b 1 lim c ln b
nœ Êœ Ê œ ab ˆ‰ˆ‰
nn
1n nn
a
bn
n1n
n
ln 1
ÎÎ
Ä_
nÄ_ lim ˆ‰ˆ‰
a
b
n
ln b ln b ln b since 0 a b. Thus, lim c e b.œ œ œ œœlim
n
ln 0 ln
101 nln b
Ä_
†
ˆ‰ ˆ‰ ˆ‰
ˆ‰
aa a
bb b
n
a
b
nnÄ_
16. 1 1 áœ
237237 2 3 7
10 10 10 10 10 10 10 10
10 !!!
__ _
œœ œn1 n1 n1
3n 2 3n 1 3n
1 1œ œ
!!!
__ _
œœ œn0 n0 n0
237
10 10 10 111
3n 1 3n 2 3n 3
2
10
10 10 10
37
10 10
ˆ‰
ˆ‰ ˆ‰ ˆ‰
Š‹ Š‹
1œœ œ
200 30 7 999 237 412
999 999 999 999 333
17. s s s
nn n
dx dx dx dx dx
1 x 1x 1x 1x 1x
œÊœáÊœ
!
n1
k0
œ
'''''
k01n10
k1 1 2 n n
lim s lim tan n tan 0Êœ œ
nnÄ_ Ä_
nab
" "
#
1
18. lim lim lim 1
nn nÄ_ Ä_ Ä_
¹¹ ¹ ¹ ¹ ¹¸¸
u
u (n2)(2x1) nx 2x1 n(n2) 2x1
(n1)x (n1)(2x1) (n1)
xx
n1
n
n1 n
n1 n
œœœ
††
x 2x 1 ; if x 0, x 2x 1 x 2x 1 x 1; if x 0, x 2x 1Ê ÊÊ kk k k kk k k kk k k
"
#
x 2x 1 3x 1 x ; if x , x 2x 1 x 2x 1 x 1. Therefore,Ê Ê Ê Ê Ê
""
#3kk k k
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 11 Additional and Advanced Exercises 775
the series converges absolutely for x 1 and x . "
3
19. (a) Each A fits into the corresponding upper triangular region, whose vertices are:
n1
(n f(n) f(n 1)), (n 1 f(n 1)) and (n f(n)) along the line whose slope is f(n 1) f(n).ß ß ß
All the A 's fit into the first upper triangular region whose area is A
n
n1
f(1) f(2) f(1) f(2)
2n
#
Ê
!
(b) If A f(x) dx, then
kf(k 1) f(k)
œ
#'k
k1
A f(x) dx f(x) dx f(x) dx
!
n1
k1
œ
kf(1) f(2) f(2) f(3) f(3) f(n 1) f(n)
œ á
á
#'' '
12 n1
23 n
f(k) f(x) dx A f(k) f(x) dx , fromœ Êœ
f(1) f(n) f(1) f(n) f(1) f(2)
k
###
!!!
n1 n1 n
k2 k1 k1
œœœ
''
1 1
n n
part (a). The sequence A is bounded above and increasing, so it converges and the limit in
œ
!
n1
k1
œ
k
question must exist.
(c) Let L lim f(k) f(x) dx f 1 f n , which exists by part (b). Since f is positive andœ
nÄ_ ”•
!abab ab
n
k1œ
'1
n"
#
decreasing f n M 0 exists. Thus lim f(k) f(x) dx L f 1 M .lim
nÄ_
"
#
ab a b
”•
!abœ œ
nÄ_
n
k1œ
'1
n
20. The number of triangles removed at stage n is 3 ; the side length at stage n is ; the area of a triangle
n1 b
2
n1
at stage n is .
È3
42
b
ˆ‰
n1
#
(a) b 3 3 3 b b
ÈÈÈÈ È È
3333 3 3
4424 42 4244
bbb 3 3
2
n
##$ ##
ᜠœ
Š‹ Š‹ Š‹ !!
ˆ‰
__
œœn0 n0
n
2n
(b) a geometric series with sum 3b
Š‹
ˆ‰
3
4
3
4
b
1
#
œÈ
(c) No; for instance,the three vertices of the original triangle are not removed. However the total area removed
is 3b which equals the area of the original triangle. Thus the set of points not removed has area 0.
È#
21. (a) No, the limit does not appear to depend on the value of the constant a
(b) Yes, the limit depends on the value of b
(c) s 1 ln s lim ln sœ Ê œ Ê œ
Š‹
cos
n
nln 1
ˆ‰ Œ
ˆ‰
Œ
Š‹
a
n
n
cos a
n
n1cos a
n
n
aa a
nn n
sin cos
n
n
nÄ_
lim 1 lim s e 0.3678794412; similarly,œœœÊœ¸
nnÄ_ Ä_
aa a
nn n
cos a
n
n
sin cos
1
ˆ‰ ˆ‰
01
10
"
lim 1 e
nÄ_ Š‹
œ
cos
bn
n1b
ˆ‰
a
nÎ
22. a converges lim a 0; lim lim
!’“
ˆ‰ ˆ‰
_
œn1
nn
1sin a 1sin a
n1n 1 sin lim a 1sin 0
Êœ œ œ œ
nn nÄ_ Ä_ Ä_
####
Î
nnn
Š‹
n
the series converges by the nth-Root TestœÊ
"
#
23. lim 1 lim 1 bx 1 x 5 b
nnÄ_ Ä_
¹¹ ¹ ¹ kk
u
uln(n1)bx bb5
bx ln n
n1
n
n1n1
nn
Ê Ê ÊœÊœ„
"" "
†
24. A polynomial has only a finite number of nonzero terms in its Taylor series, but the functions sin x, ln x and
e have infinitely many nonzero terms in their Taylor expansions.
x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

776 Chapter 11 Infinite Sequences and Series
25. lim lim
x0 x0ÄÄ
sin (ax) sin x x
xx
ax x x
áá
œŠ‹Š‹
ax x
3! 3!
lim x is finite if a 2 0 a 2;œá œÊœ
x0Ä’“Š‹
a2 a a
x 3!3! 5!5!
" "
#
lim
x0Ä
sin 2x sin x x 2 7
x3!3!6
"
œ œ
26. lim 1 lim 1 lim 1
x0 x0 x0ÄÄ Ä
cos ax b ba ax
xx2x448
1b
"
##
á
œ Ê œ Ê á œ
Œ
ax ax
4! Š‹
b 1 and a 2Êœ œ„
27. (a) 1 C 2 1 and converges
u
un nn n
(n 1) 2
n
n1œœÊœ
""
!
_
œn1
(b) 1 C 1 1 and diverges
u
un nn n
n1 1 0
n
n1œœÊœŸ
"
!
_
œn1
28. 1 1 after long division
u
u (2n 1) 4n 4n 1 n 4n 4n 1 n n
2n(2n 1) 4n 2n 5
n
n1œœ œ œ
Š‹ Š‹ –—
63
4
5n
4n 4n 1
C 1 and f(n) 5 u converges by Raabe's TestÊœ œ œ ŸÊ
35n5
4n 4n 1 4n
#
kk !
Š‹
4
nn
_
œn1
29. (a) a L a a a a L a converges by the Direct Comparison Test
!!!
___
œœœn1 n1 n1
nnnn
nn
œÊ Ÿ œ Ê
##
(b) converges by the Limit Comparison Test: lim lim 1 since a converges and
nnÄ_ Ä_
Š‹
an
1a
n
a1a n
nn
œœ
"
!
_
œn1
therefore lim a 0
xÄ_ nœ
30. If 0 a 1 then ln (1 a ) ln (1 a ) a a a a , œ œ á áœ
nnnn n
aa
31a
nn a
kk nn n
n
#
#$
a positive term of a convergent series, by the Limit Comparison Test and Exercise 29b
31. (1 x) 1 x where x 1 (1 x) nx and when x we haveœ Ê œ œ œ
" "
""
#
!!
kk
__
œœn1 n1
nn1
(1 x) dx
d
412 3 4 nœá á
ˆ‰ ˆ‰ ˆ‰ ˆ‰
"" " "
## # #
#$ n1
32. (a) x (n 1)x n(n 1)x n(n 1)x
!! ! !
__ _ _
œœ œ œn1 n1 n1 n1
n1nn1n
x2xx 2 2x
1 x (1 x) (1 x) (1 x)
œÊ œ Ê œ Ê œ
, x 1Êœœ
!kk
_
œn1
n(n 1)
x(x1)
1
2x
n
2
x
x
Š‹
(b) x x x 3x x 1 0 x 1 1 1œ Êœ Ê œÊœ
!Š‹Š‹
_
œn1
n(n )
x(x1) 9 9
2x 57 57
"
$# "Î$ "Î$
nÈÈ
2.769292, using a CAS or calculator¸
33. The sequence {x } converges to from below so x 0 for each n. By the Alternating Series
nnn
11
##
%œ
Estimation Theorem ( ) with error ( ) , and since the remainder is negative this is an%% %
n1 n n
3! 5!
""
$&
¸kk
overestimate 0 ( ) .Ê %%
n1 n
6
"$
34. Yes, the series ln (1 a ) converges by the Direct Comparison Test: 1 a 1 a
!
_
œn1
á
nnn
aa
!3!
nn
#
1 a e ln (1 a ) aÊ Ê
nnn
an
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 11 Additional and Advanced Exercises 777
35. (a) 1 x x x 1 2x 3x 4x nx
""
#$ # $
(1 x) dx 1 x dx
dd n1
œ œ ᜠáœ
ˆ‰ ab !
_
œn1
(b) from part (a) we have n 6
!ˆ‰ ˆ‰ ˆ‰
’“
_
œn1
5
666
n1
1
2
"""
œœ
ˆ‰
5
6
(c) from part (a) we have np q
!
_
œn1
n1 qq
(1 p) q q
"
œœœ
36. (a) p 2 1 and E(x) kp k2 k2 2
!! ! ! ! ˆ‰
__ _ _ _
œœ œ œ œk1 k1 k1 k1 k1
kk
kk1k
11
œœœ œœ œ œ œ
"""
##
ˆ‰
ˆ‰ ‘ˆ‰
by Exercise 35(a)
(b) p 1 and E(x) kp k k
!! ! ! ! !
ˆ‰ ˆ‰ ˆ‰
’“
__ _ _ _ _
œœ œ œ œ œk1 k1 k1 k1 k1 k1
k k
55 5 5
6 6
56 5 6 6
kk1
1
œœ œ œ œœ œ
k1 k1
k k
5
65
6
"" "
ˆ‰
ˆ‰
6œœ
ˆ‰
""
61
‘ˆ‰
5
6
(c) p lim 1 1 and E(x) kp k
k
!! ! ! !
ˆ‰ ˆ‰ Š‹
__ _ __
œœ œ œœk1 k1 k1 k1 k1
k k
k(k1) k k1 k1 k(k1)
œ œ œ œ œ œ
Ä_
""" " "
, a divergent series so that E(x) does not existœ!
_
œk1
"
k1
37. (a) R C e C e C e R lim R
n
n n
kt 2kt nkt Ce 1 e
1e 1 e e 1
Ce C
œ á œ Êœ œœ
Ä_
!! !
kt nkt
kt kt kt
kt
ˆ‰
(b) R R e 0.36787944 and R 0.58195028;
ne1e e1e
1e 1e
œÊœ¸ œ¸
1n
ab ab
""!
"
R 0.58197671; R R 0.00002643 0.0001œ¸ ¸ Ê
"
"!
e1 R
RR
(c) R , 4.7541659; R
nn
e1e
1e e1 e1 e1
RR1e
œœ¸Ê
11n
11 11
1n
ˆ‰
## # #
"" " "
ˆ‰ ˆ‰ˆ‰
1 e e ln ln n 6.93 n 7Ê Ê Ê Ê Ê Êœ
Î Î
"" " "
## # #
n10 n10 nn
10 10
ˆ‰ ˆ‰
38. (a) R Re R C C e t lnœÊœœÊœÊœ
C
e1
kt kt
HCC
CkC
kt HH
LL
!!
"Š‹
(b) t ln e 20 hrs
!"
œœ
0.05
(c) Give an initial dose that produces a concentration of 2 mg/ml followed every t ln 69.31 hrs
!"
#
œ¸
0.0 0.5
2
ˆ‰
by a dose that raises the concentration by 1.5 mg/ml
(d) t ln 5 ln 6 hrs
!"
œœ¸
0.2 0.03 3
0.1 10
ˆ‰ ˆ‰
39. The convergence of a implies that lim a 0. Let N 0 be such that a 1 a
n
!kk kk kk kk
_
œn1
nn nn
Ä_ œ Ê
""
##
2 a for all n N. Now ln 1 a a aÊ œ ០á
kk
kk
a
1a 34 3 4
nnnn
aaa a a a
n
n
nnn n n n
##
kk k k kkab
¹ ¹ ¹¹ ¹¹ ¹¹
a a a a 2 a . Therefore ln (1 a ) converges by the Directᜠkk kk kk kk kk !
nnnn n n
a
1a
#$%
kk
kk
n
n
_
œn1
Comparison Test since a converges.
!kk
_
œn1
n
40. converges if p 1 and diverges otherwise by the Integral Test: when p 1 we have
!
_
œn3
"
n ln n(ln (ln n))pœ
lim lim ln (ln (ln x)) ; when p 1 we have lim
bb bÄ_ Ä_ Ä_
''
3 3
b b
b
dx dx
x ln x(ln (ln x)) x ln x(ln (ln x))
œœ_Ácd
$p
lim ,if p1
, if p 1
œœ
_
bÄ_ ’“
(ln (ln x))
1p
(ln (ln 3))
1p
p1
p1
b
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

778 Chapter 11 Infinite Sequences and Series
41. (a) s2n 1 ccc ttttt
1 3 2n 1 1 2 3 2n 1
ctt
#
œ á œ á
2n 1 2n 1 2n
t1 t t .œá œ
"#
""" ""
## #
ˆ‰ˆ‰ ˆ ‰ !
3 2n n1 2n1 k(k1) 2n1
2n tt
t
2n 1 2n 1
k
2n
k1œ
(b) c ( 1) convergesef e f !
nn(1)
n
œ Ê
_
œn1
n
(c) c 1 1 1 1 1 1 1 1 1 the series 1 convergesef e f
n34567
œ ßßßßßßßßßá Ê á
""""""
#
42. (a) 1 t t t ( 1) t (1 t) 1 t t t ( 1) t t t t t ( 1) tabá œá á
#$ #$ #$% nn nn nn 1
1(1)t 1tt t (1)tœ Ê á œ
nn 1 nn (1)t
1t 1t
#$
"
nn 1
(b) dt 1 t t ( 1) t dt ln 1 t
''
00
xx x
"
#
!
1t 1t
nn (1) t
œá Ê
’“
cdkk
n1n1
t dt ln 1 xœá Ê
’“kk
tt
2 3 n1 n1
(1)t (1) t
!
nn 1 n 1n 1
x
0
x
'
x R , where R dtœá œ
xx
3n1 n1
(1)x (1) t
n1 n1
#
nn1 n1n1
'0
x
(c) x 0 and R ( 1) dt R dt t dtœ ÊœŸœ
n1 n1
n1 n1
ttx
1t 1t n
#
'''
000
xxx
n1 n2
kk n1
(d) 1 x 0 and R ( 1) dt R dt dt œ Ê œ Ÿ
n1 n1
000
xxx
'''
ttt
1t 1t 1t
n1
n1 n1 n1
kk
¹¹¹¹
dx since 1 t 1 xŸœ
'0
xkk kk
kk a bkk
tx
1x 1x(n2)
n1 n2
kk kk
(e) From part (d) we have R the given series converges sincekk
n1 x
1x(n2)
ŸÊ
kk
abkk
n2
lim 0 R 0 when x 1. If x 1, by part (c) R 0.
nÄ_ kk kk
abkk
x x
1x(n2) n2 n2
n1 n1 1
n2 n2
œÊ Ä œ Ÿ œ Äkk kk kk
Thus the given series converges to ln 1 x for 1 x 1.abŸ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE
12.1 THREE-DIMENSIONAL COORDINATE SYSTEMS
1. The line through the point ( ) parallel to the z-axis#ß $ß !
2. The line through the point ( 1 0 ) parallel to the y-axisß ß!
3. The x-axis
4. The line through the point (1 ) parallel to the z-axisß!ß!
5. The circle x y 4 in the xy-plane
##
œ
6. The circle x y 4 in the plane z = 2
##
œ
7. The circle x z 4 in the xz-plane
##
œ
8. The circle y z 1 in the yz-plane
##
œ
9. The circle y z 1 in the yz-plane
##
œ
10. The circle x z 9 in the plane y 4
##
œ œ
11. The circle x y 16 in the xy-plane
##
œ
12. The circle x z 3 in the xz-plane
##
œ
13. (a) The first quadrant of the xy-plane (b) The fourth quadrant of the xy-plane
14. (a) The slab bounded by the planes x 0 and x 1œœ
(b) The square column bounded by the planes x 0, x 1, y 0, y 1œœœœ
(c) The unit cube in the first octant having one vertex at the origin
15. (a) The solid ball of radius 1 centered at the origin
(b) The exterior of the sphere of radius 1 centered at the origin
16. (a) The circumference and interior of the circle x y 1 in the xy-plane
##
œ
(b) The circumference and interior of the circle x y 1 in the plane z 3
##
œ œ
(c) A solid cylindrical column of radius 1 whose axis is the z-axis
17. (a) The closed upper hemisphere of radius 1 centered at the origin
(b) The solid upper hemisphere of radius 1 centered at the origin
18. (a) The line y x in the xy-planeœ
(b) The plane y x consisting of all points of the form (x x z)œßß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
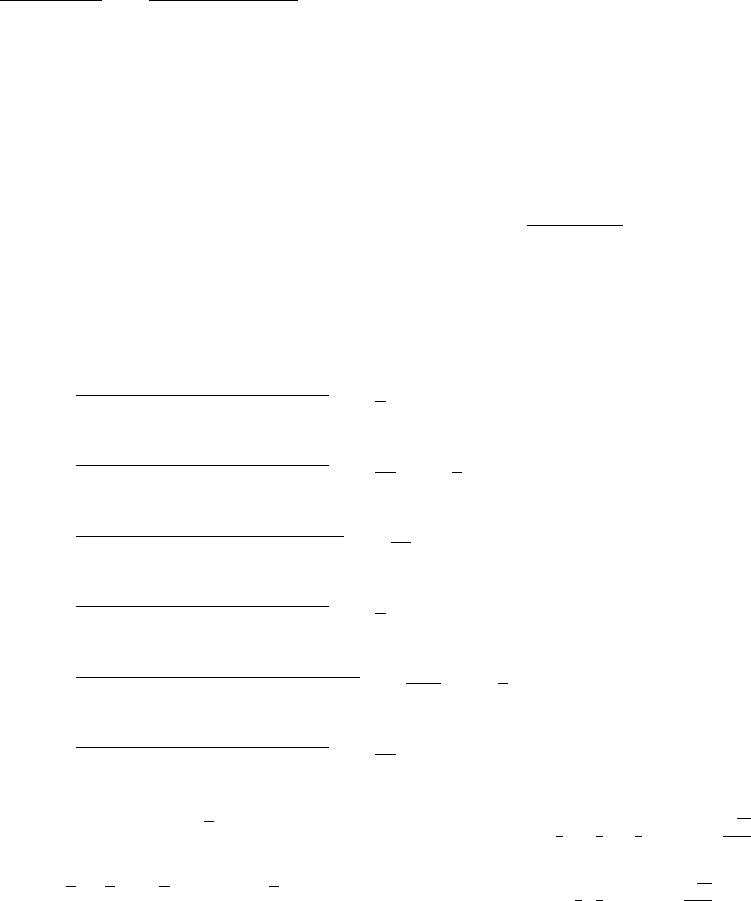
780 Chapter 12 Vectors and the Geometry of Space
19. (a) x 3 (b) y 1 (c) z 2œœœ
20. (a) x 3 (b) y 1 (c) z 2œœœ
21. (a) z 1 (b) x 3 (c) y 1œœœ
22. (a) x y 4, z 0 (b) y z 4, x 0 (c) x z 4, y 0
## ## ##
œ œ œ œ œ œ
23. (a) x (y 2) 4, z 0 (b) (y 2) z 4, x 0 (c) x z 4, y 2
# # ## ##
œ œ œ œ œ œ
24. (a) (x 3) (y 4) 1, z 1 (b) (y 4) (z 1) 1, x 3 œ œ œ œ
## ##
(c) (x 3) (z 1) 1, y 4œ œ
##
25. (a) y 3, z 1 (b) x 1, z 1 (c) x 1, y 3œœ œœ œœ
26. x y z x (y 2) z x y z x (y 2) z y y 4y 4 y 1
ÈÈ
### # ## #### ## ##
œ Ê œ Ê œÊœ
27. x y z 25, z 3 x y 16 in the plane z 3
### ##
œ œÊœ œ
28. x y (z 1) 4 and x y (z 1) 4 x y (z 1) x y (z 1) z 0, x y 3
## # ## # ## # ## # ##
œ œÊ œ Êœ œ
29. 0 z 1 30. 0 x 2, 0 y 2, 0 z 2ŸŸ ŸŸ ŸŸ ŸŸ
31. z 0 32. z 1 x yŸœ
È##
33. (a) (x 1) (y 1) (z 1) 1 (b) (x 1) (y 1) (z 1) 1
### ###
34. 1 x y z 4ŸŸ
###
35. P P 3 1 3 1 0 1 9 3kkababab
ÉÈ
"#
###
œ œ œ
36. P P 2 1 5 1 0 5 50 5 2kkababab
ÉÈÈ
"#
###
œ œ œ
37. P P 4 1 2 4 7 5 49 7kkaba bab
ÉÈ
"#
###
œœ œ
38. P P 2 3 3 4 4 5 3kkababab
ÉÈ
"#
###
œ œ
39. P P 2 0 2 0 2 0 3 4 2 3kkababab
ÉÈÈ
"#
###
œœ†œ
40. P P 0 5 0 3 0 2 38kkababab
ÉÈ
"#
###
œ œ
41. center ( 2 0 2), radius 2 2 42. center , radius ß ß ß ß
Ȉ‰
"""
### #
È21
43. center 2 2 2 , radius 2 44. center , radius
Š‹
ÈÈ È È ˆ‰
ßß !ßß
""
33 3
29
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 12.2 Vectors 781
45. (x 1) (y 2) ( 3) 14 46. x (y 1) (z 5) 4Dœ œ
### ###
47. (x 2) y z 3 48. x (y 7) z 49 œ œ
### # ##
49. x y z 4x 4z 0 x 4x 4 y z 4z 4 4 4
### # # #
œÊ œabab
(x 2) (y 0) (z 2) 8 the center is at ( 2 0 2) and the radius is 8Ê œ Ê ßß
####
Š‹
ÈÈ
50. x y z 6y 8z 0 x y 6y 9 z 8z 16 9 16 (x 0) (y 3) (z 4) 5
### # # # # # # #
œÊ œ Ê œaba b
the center is at (0 3 4) and the radius is 5Êßß
51. 2x 2y 2z x y z 9 x x y y z z
### # # #
"""
####
œ Ê œ
9
xx yy zz x y zÊ œÊœ
ˆ‰ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
Š‹
###
"" "" "" " " "
####
###
#
16 16 16 16 4 4 4 4
93 53
È
the center is at and the radius is Ê ß ß
ˆ‰
"""
444 4
53
È
52. 3x 3y 3z 2y 2z 9 x y y z z 3 x y y z z 3
### ## # ## #
""
œÊœÊ œ
22 2 2 2
33 39 399
ˆ‰ˆ‰
(x 0) y z the center is at 0 and the radius is Ê œ Ê ßß
#"" ""
##
#
ˆ‰ˆ‰ ˆ ‰
Š‹
333 33 3
29 29
ÈÈ
53. (a) the distance between (x y z) and (x 0 0) is y zßß ßß
È##
(b) the distance between (x y z) and (0 y 0) is x zßß ßß
È##
(c) the distance between (x y z) and (0 0 z) is x yßß ßß
È##
54. (a) the distance between (x y z) and (x y 0) is zßß ßß
(b) the distance between (x y z) and (0 y z) is xßß ßß
(c) the distance between (x y z) and (x 0 z) is yßß ßß
55. AB 1 1 1 2 3 1 4 9 4 17kk a ba ba b
Éab ÈÈ
œœœ
###
BC 31 4 1 53 4254 33kkaba bab
Éab ÈÈ
œœœ
###
CA 13 24 15 16416 366kka babab
ÉÈÈ
œœ œ œ
###
Thus the perimeter of triangle ABC is 17 33 6.
ÈÈ
56. PA 2 3 1 1 3 2 1 4 1 6kkaba bab
ÉÈÈ
œœœ
###
PB 43 31 12 141 6kkababab
ÉÈÈ
œ œ œ
###
Thus P is equidistant from A and B.
12.2 VECTORS
1. (a) 3 3 , 3 2 9, 6 2. (a) 2 2 , 2 5 4, 10
¡¡ ¡¡
abab ab abœ œ
(b) 9 6 117 3 13 (b) 4 10 116 2 29
ÉÉ
ab a b
ÈÈ ÈÈ
2 2
2 2
œ œ œ œ
3. (a) 3 2 , 2 5 1, 3 4. (a) 3 2 , 2 5 5, 7
¡¡ ¡¡
ab ab œ œ
(b) 1 3 10 (b) 5 7 74
ÈÈÈ
Éab
22 2 2
œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
782 Chapter 12 Vectors and the Geometry of Space
5. (a) 2 2 3 , 2 2 6, 4 6. (a) 2 2 3 , 2 2 6, 4uuœœ œœ
¡¡ ¡¡
ab a b ab a b
3 3 2 , 3 5 6, 15 5 5 2 , 5 5 10, 25vvœ œ œ œ
¡¡ ¡¡
abab abab
2 3 6 4 , 4 15 12, 19 2 5 6 10 , 4 25 16, 29uv uvœ œ œ œ
¡¡ ¡¡
ab ab
(b) 12 19 505 (b) 16 29 1097
ÉÉ
ab ab
ÈÈ
2 2
22
œ œ
7. (a) 3 , 2 , 8. (a) 3 , 2 ,
3 3 3 9 6 5 5 5 15 10
555 55 13 1313 1313
uuœ œ œ œ
¢£¢£ ¢ £¢£
ab a b ab a b
2, 5 , 4 2, 5 ,
4 4 4 8 12 12 12 24 60
5 5 5 5 13 13 13 13 13
vvœ œ œ œ
¢£¢£ ¢ £¢£
abab abab
, 4 , , 3,
34 9 86 114 5 12 15 241060 70
55 5 55 55 1313 13 131313 13
uv u vœ œ œ œ
¢£¢£ ¢ £¢£
ˆ‰ ˆ‰
(b) (b) 3
ÉÉ
ˆ‰ ˆ‰ ˆ‰
ab
114 70
55 5 13 13
22 2
97 6421
2
œ œ
È È
"
9. 2 1, 1 3 1, 4 10. 0, 0 1, 1
¡¡ ¡
¢£
œ œ
24 3
##
"
ab
11. 0 2, 0 3 2, 3
¡¡
œ
12. AB 2 1, 0 1 1, 1 , CD 2 1 , 2 3 1, 1 , AB CD 0, 0
ÄÄ ÄÄ
œ œ œ œ œ
¡¡ ¡ ¡ ¡
ab ab
13. cos , sin , 14. cos , sin ,
¢£¢£ ¢ £¢£
ˆ‰ˆ‰
22 33
33 2 4 4
3
22
11 11
œ œ
"""
#ÈÈÈ
15. This is the unit vector which makes an angle of 120 90 210 with the positive x-axis;
‰‰ ‰
œ
cos 210 , sin 210 ,
¡
¢£
‰‰ "
#
œ
È3
2
16. cos 135 , sin 135 ,
¡
¢£
‰‰ ""
œ
ÈÈ
22
17. P P 2 5 9 7 2 1 3 2
"#
Äœ œ ababa babij kijk
18. P P 3 1 0 2 5 0 4 2 5
"#
Äœ œ a bababijkijk
19. AB 10 7 8 8 1 1 3 16
Äœ œ abababab abijkij
20. AB 1 1 4 0 5 3 2 4 2
Äœ œ a bababijkijk
21. 5 5 1, 1, 1 2, 0, 3 5, 5, 5 2, 0, 3 5 2, 5 0, 5 3 3, 5, 8 3 5 8uv ijkœ œ œœœ
¡¡¡¡ ¡¡
22. 2 3 2 1, 0, 2 3 1, 1, 1 2, 0, 4 3, 3, 3 5, 3, 1 5 3 œ œ œ œuv ijk
¡¡¡¡¡
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
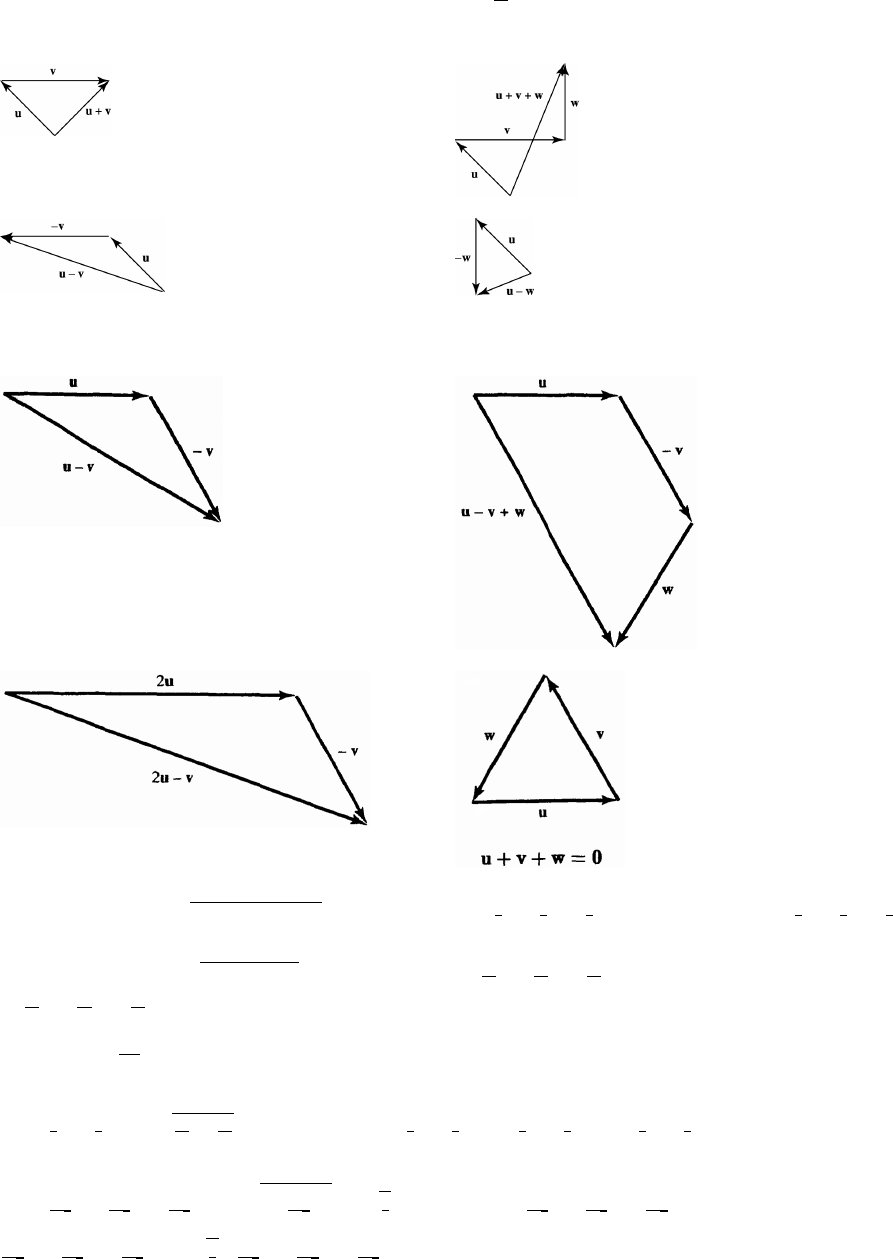
Section 12.2 Vectors 783
23. The vector is horizontal and 1 in. long. The vectors and are in. long. is vertical and makes a 45 angle withvuwwu
"‰
1
16
the horizontal. All vectors must be drawn to scale.
(a) (b)
(c) (d)
24. The angle between the vectors is 120 and vector is horizontal. They are all 1 in. long. Draw to scale.
‰u
(a) (b)
(c) (d)
25. length 2 2 2 1 ( 2) 3, the direction is 2 2 3œ œ œ Êœ kk
Ȉ‰
ij k i j k ij k i j k
## # ""22 22
333 333
26. length 9 2 6 81 4 36 11, the direction is 9 2 6œ œ œ Êkk
È
ijk i j k ijk
926
11 11 11
11œ
ˆ‰
926
11 11 11
ijk
27. length 5 25 5, the direction is 5 5( )œœ œ ÊœkkÈ
kkkk
28. length 1, the direction is 1œ œ œ Êœ
¸¸ ˆ‰
É
34 916 34 34 34
55 2525 55 55 55
ik ik ik ik
29. length 3 , the direction is œ œ œ
¹¹Š‹
ÊÉ
11 11
666 6 333
ÈÈÈ È ÈÈÈ
ijk ijk
""" "
#
#
ʜ
11 11
666 333
ÈÈÈ ÈÈÈ
ijk ijk
"" "
#
ÉŠ‹
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

784 Chapter 12 Vectors and the Geometry of Space
30. length 3 1, the direction is œ œ œ
¹¹Š‹
Ê
11 11
333 3 333
ÈÈÈ È ÈÈÈ
ijk ijk
"" "
#
1ʜ
11 11
333 333
ÈÈÈ ÈÈÈ
ijk ijk
""
Š‹
31. (a) 2 (b) 3 (c) (d) 6 2 3ikjkijk
È32
10 5
32. (a) 7 (b) (c) (d) jikijkijk
32 42
55 43
11 a a a
236
ÈÈ ÈÈÈ
33. 12 5 169 13; (12 5 ) the desired vector is (12 5 )kk ÈÈ
v v ik ikœœ œ œœ Ê
## ""v
vkk 13 13 13
7
34. ; the desired vector is 3kk ÉŠ‹
vijkijkœœ œ Ê
""" """
#444
3111
333 333
Èkk ÈÈÈ ÈÈÈ
v
v
333œ
ÈÈÈ
ijk
35. (a) 3 4 5 5 2 the direction is ijk i j k i j k œ Ê
ÈŠ‹
34 34
52 52 2 52 52 2
ÈÈÈ ÈÈÈ
""
(b) the midpoint is 3
ˆ‰
"
##
ßß
5
36. (a) 3 6 2 7 the direction is ijk i j k i j k œ Ê
ˆ‰
362 362
777 777
(b) the midpoint is 1 6
ˆ‰
5
#ßß
37. (a) 3 the direction is œ Ê ijk i j k i j k
ÈŠ‹
111 111
333 333
ÈÈÈ ÈÈÈ
(b) the midpoint is ˆ‰
579
###
ßß
38. (a) 2 2 2 2 3 the direction is ijk i j k i j k œ Ê
ÈŠ‹
111 111
333 333
ÈÈÈ ÈÈÈ
(b) the midpoint is ( 1)"ß "ß
39. AB (5 a) (1 b) (3 c) 4 2 5 a 1, 1 b 4, and 3 c 2 a 4, b 3, and
Äœ œ Êœ œ œÊœ œijkijk
c 5 A is the point (4 3 5)œÊ ßß
40. AB (a 2) (b 3) (c 6) 7 3 8 a 2 7, b 3 3, and c 6 8 a 9, b 0,
Äœ œ Êœ œ œÊœ œijkijk
and c 14 B is the point ( 9 0 14)œÊ ßß
41. 2 a( ) b( ) (a b) (a b) a b 2 and a b 1 2a 3 a andij ij ij i jœ œ Ê œ œ Ê œ Ê œ
3
#
baœ"œ
"
#
42. 2 a(2 3 ) b( ) (2a b) (3a b) 2a b 1 and 3a b 2 a 3 andij ij ij i j œ œ Ê œ œÊ œ
b 1 a 7 a(2 3 ) 6 9 and b( ) 7œ#œ Ê œ œ œ œuijijuiji7j
"#
43. If x is the magnitude of the x-component, then cos 30° x F cos 30° (10) 5 3 lbkk kk kk Š‹ È
œÊœœœ
kk
kk È
x
F
3
#
53;ÊœFi
xÈ
if y is the magnitude of the y-component, then sin 30° y F sin 30° (10) 5 lb 5 .kk kk kk ˆ‰
œÊœ œ œ Êœ
kk
kk
y
F
1y
#Fj
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
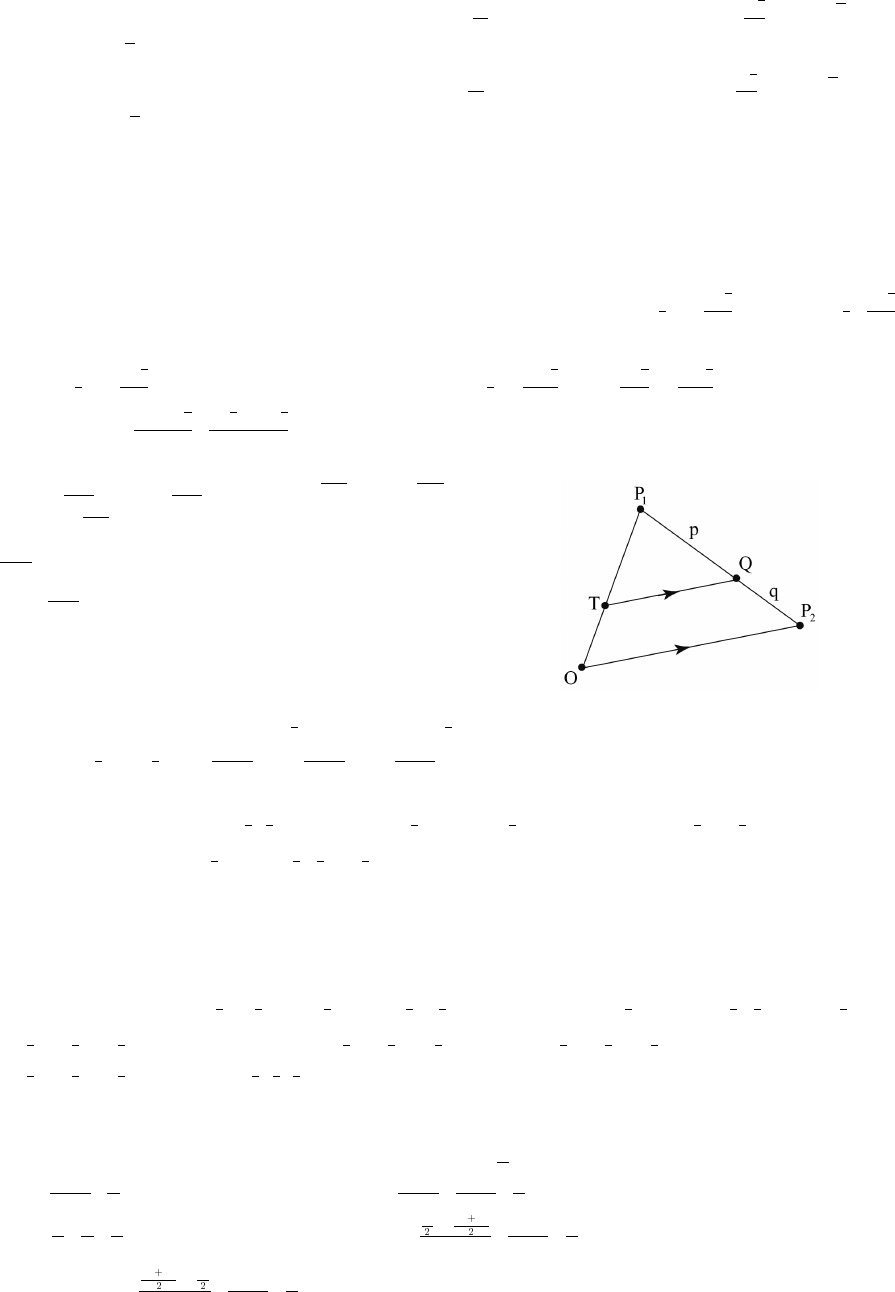
Section 12.2 Vectors 785
44. If x is the magnitude of the x-component, then cos 45° x F cos 45° (12) 6 2 lbkk kk kk Š‹ È
œÊœœœ
kk
kk È
x
F
2
#
6 2 (the negative sign is indicated by the diagram)ÊœFi
xÈ
if y is the magnitude of the y-component, then sin 45° y F sin 45° (12) 6 2 lbkk kk kk Š‹ È
œÊœ œ œ
kk
kk È
y
F
2
#
6 2 (the negative sign is indicated by the diagram)ÊœFj
yÈ
45. 25 west of north is 90 25 115 north of east. 800 cos 155 , sin 115 338.095, 725.046
‰‰‰‰ ‰‰
œ ¸
¡ ¡
46. 10 east of south is 270 10 280 ”north” of east. 600 cos 280 , sin 280 104.189, 590.885
‰‰‰‰ ‰‰
œ ¸
¡¡
47. (a) The tree is located at the tip of the vector OP (5 cos 60°) (5 sin 60°) P
ÄœœÊœßijij
55
53 53
## ##
ÈÈ
Š‹
(b) The telephone pole is located at the point Q, which is the tip of the vector OP PQ
ÄÄ
(10 cos 315°) (10 sin 315°)œ œ
Š‹ Š‹Š ‹
55
2
53 53
10 2 10 2
ij i j i j
ÈÈÈÈ
#####
Q Êœ ß
Š‹
510253102
##
ÈÈ È
48. Let t and s . Choose T on OP so that TQ isœœ
qp
pq pq 1
parallel to OP , so that TP Q is similar to OP P . Then
21 12
˜˜
t OT t OP so that T t x , t y , t z .
kk
kk
OT
OP 1111
1œÊ œ œ
ÄÄ ab
Also, s TQ s OP s x , y , z .
kk
kk
TQ
OP 2222
2œÊ œ œ
ÄÄ
¡
Letting Q x, y, z , we have thatœab
TQ x tx, y ty, z tz sx, y, z
Äœ œ
¡¡
111222
Thus x t x s x , y t y s y , z t z s z .œ œ œ
12 12 12
(Note that if Q is the midpoint, then 1 and t s
p
qœœœ
"
#
so that x x x , y , z so that this result agress with the midpoint formula.)œœ œ œ
""
##
12
xx zz
222
yy
12 12
12
49. (a) the midpoint of AB is M 0 and CM 1 1 ( 3) 3
ˆ‰ ˆ‰ˆ‰
55 5 5 3 3
## # # # #
ßß œ ! œ
Äijkijk
(b) the desired vector is CM 3 2
ˆ‰ ˆ ‰
2233
33
Äœ œ
##
ijkijk
(c) the vector whose sum is the vector from the origin to C and the result of part (b) will terminate
at the center of mass the terminal point of ( 3 ) ( 2 ) 2 2 is the pointÊ œij k ij k i jk
(2 2 1), which is the location of the center of massßß
50. The midpoint of AB is M 0 and CM 1 (0 2) 1 2
ˆ‰ˆ‰ ‘ˆ ‰ˆ‰ ˆ‰
35 2 23 5 25 7
33 3## # # # #
ßß œ œ
Äij kijk
. The terminal point of OC ( 2 )œ œ
Ä
547 547 547
333 333 333
ijk ijk ijk ijk
ˆ‰ˆ‰
is the point which is the location of the intersection of the medians.œ ßß
2 2 4 224
3 3 3 333
ijk ˆ‰
51. Without loss of generality we identify the vertices of the quadrilateral such that A(0 0 0), B(x 0 0),ßß ßß
b
C(x y 0) and D(x y z ) the midpoint of AB is M 0 0 , the midpoint of BC is
cc ddd AB
x
ßß ßß Ê ßß
ˆ‰
b
#
M 0 , the midpoint of CD is M and the midpoint of AD is
BC CD
xx xx z
yyy
ˆ‰ ˆ ‰
bdd
cc
c c d
## # ##
ßß ß ß
M the midpoint of M M is , which is the same as the midpoint
AD AB CD
xz z
yyy
44
ˆ‰ Œ
dd d
d d
c
### #
ßß Ê ß
xxx
bd
c
b
of M M , .
AD BC yy
44
z
ϧ
Œ
xx x
bd
cb
#
cdd
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

786 Chapter 12 Vectors and the Geometry of Space
52. Let V , V , V , , V be the vertices of a regular n-sided polygon and denote the vector from the center to
"#$
áni
v
V for i 1, 2, 3, , n. If and the polygon is rotated through an angle of where
ii i(2 )
n
œá œSv
!
n
i1œ
1
i 1, 2, 3, , n, then would remain the same. Since the vector does not change with these rotations we concludeχ SS
that .S0œ
53. Without loss of generality we can coordinatize the vertices of the triangle such that A(0 0), B(b 0) andßß
C(x y ) a is located at , b is at and c is at 0 . Therefore, Aa ,
cc bx x x
yy y
bb
ßÊ ß ß ß œ
Ä
ˆ‰ˆ‰ ˆ‰ ˆ‰ˆ‰
## ## # ## #
cc c
cc c
ij
Bb b , and Cc x ( y ) Aa Bb Cc .
ÄÄ
œ œ Ê œ
ÄÄÄ
ˆ‰ˆ‰ ˆ‰
xybcc
cc
## #
ij i j 0
54. Let be any unit vector in the plane. If is positioned so that its initial point is at the origin and terminal point is auu t x, y ,ab
then makes an angle with , measured in the counter-clockwise direction. Since 1, we have that x cos andui u) )kkœœ
y sin . Thus cos sin . Since was assumed to be any unit vector in the plane, this holds for unitœœ)))uiju every
vector in the plane.
12.3 THE DOT PRODUCT
NOTE: In Exercises 1-8 below we calculate proj as the vector , so the scalar multiplier of is
vuv v
Š‹
kk
kk
u
v
cos )
the number in column 5 divided by the number in column 2.
cos cos proj vu v u u u†kk kk kk))
v
1. 25 5 5 1 5 2 4 5 ij k
È
2. 3 1 13 3 3
334
13 5 5
ˆ‰
ik
3. 25 15 5 (10 11 2 )
""
339
5ijk
4. 13 15 3 (2 10 11 )
13 13 13
45 15 225 ijk
5. 2 34 3 (5 3 )
ÈÈ 22
334 34 17
ÈÈ È "jk
6. 3 2 2 3 ( )
ÈÈÈ
ÈÈÈ
ÈÈÈ
ÈÈ
32 32 32
32 2
#ij
7. 10 17 26 21 ( 5 )
ÈÈ È10 17 10 17 10 17
546 26 26
ÈÈÈ
ÈÈÈ
ij
8. ,
""""""
#
6665 5
30 30
30 3
ÈÈ ÈÈÈ
¢£
9. cos cos cos cos 0.75 rad)œœ œ œ¸
" " " "
Š‹ Š ‹ Š ‹ Š‹
uv
uv
†
kkkk ÈÈÈÈ
È
(2)(1) (1)(2) (0)( 1)
210 12(1)
44
5 6 30
10. cos cos cos cos 0.84 rad)œœ œ œ¸
" " " "
Š‹ Š ‹ Š ‹ ˆ‰
uv
uv
†
kkkk ÈÈÈÈ
3
(2)(3) ( 2)(0) (1)(4)
2(2)1 304
10 2
9 25
11. cos cos cos)œœ œ
" " "
Š‹ Š ‹
ÎÑ
ÏÒ
uv
uv
†
kkkk Š‹Š‹
ÈÈ
ÊŠ ‹ ÊŠ ‹
ÈÈ ÈÈ
3 3 (7)(1) (0)(2)
3(7)0 3(1)(2)
37
52 8
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 12.3 The Dot Product 787
cos 1.77 radœ¸
"
Š‹
1
26
È
12. cos cos cos)œœ œ
" " "
Š‹ Š ‹
ÎÑ
ÏÒ
uv
uv
†
kkkk Š‹ Š ‹
ÈÈ
ÊŠ‹Š‹
ÈÈ
ÈÈÈ
(1)( 1) 2 (1) 2 (1)
(1) 2 2 ( 1) (1) (1)
1
5 3
cos 1.83 radœ¸
"
Š‹
1
15
È
13. AB 3, 1 , BC 1, 3 , and AC 2, 2 . BA 3, 1 , CB 1, 3 , CA 2, 2 .
ÄÄ Ä Ä ÄÄ
œ œ œ œ œ œ
¡¡ ¡¡¡¡
AB BA 10, BC CB 10, AC CA 2 2,
¹¹¹¹ ¹¹¹¹ ¹¹¹¹
ÈÈ È
ÄÄ ÄÄ ÄÄ
œœ œœ œœ
Angle at A cos cos cos 63.435œœ œ¸
" " " ‰
ÄÄ
ÄÄ
Œ
Š‹
AB AC
AB AC
32 1 2
10 2 2
1
5
†
¹¹¹¹ È
ab a b
Š‹Š‹
ÈÈ
Angle at B cos cos cos 53.130 , andœœ œ¸
" " " ‰
ÄÄ
ÄÄ
Œ
ˆ‰
BC BA
BC BA
13 31
10 10
3
5
†
¹¹¹¹ È È
abababab
Š‹Š‹
Angle at C cos cos cos 63.435œœ œ¸
" " " ‰
ÄÄ
ÄÄ
Œ
Š‹
CB CA
CB CA
12 32
10 2 2
1
5
†
¹¹¹¹ È
ab ab
Š‹Š‹
ÈÈ
14. AC 2, 4 and BD 4, 2 . AC BD 2 4 4 2 0, so the angle measures are all 90 .
ÄÄ
œœ†œœ
ÄÄ
¡ ¡ ab a b ‰
15. (a) cos , cos , cos and!"#œœ œœ œ œ
iv kv
iv v jv v kv v
jv
††
†
kkkk kk kkkk kk kkkk kk
ab c
cos cos cos 1
### ###
!"#œœ œœ
Š‹ Š‹ Š‹
abcabc
kk kk kk kkkk kkkk
kkkk
v v v vv vv
vv
(b) 1 cos a, cos b and cos c are the direction cosines of kkv vœÊ œœ œœ œœ!" #
ab c
kk kk kkvv v
16. 10 2 is parallel to the pipe in the north direction and 10 is parallel to the pipe in the eastuik vjkœ œ
direction. The angle between the two pipes is cos cos 1.55 rad 88.88°.)œœ ¸¸
" "
Š‹ Š ‹
uv
uv
†
kkkk ÈÈ
2
104 101
17. ( ) (3 4 ) ( ) 4 , whereu v u v ij j k ij i j i j kœ œœ
ˆ‰ˆ ‰ ‘ˆ ‰ˆ ‰
vu vu
vv vv
††
††
3 3 33 33
# # ## ##
3 and 2vu vv††œœ
18. ( ) ( ) ( ) ,uvuvvuvijjkijij ijkœ œ œ
ˆ‰ˆ ‰ ‘ˆ ‰ˆ ‰
vu vu
vv vv
††
††
""
# # # # ## ##
œ
ˆ‰
1 1 11 11
where 1 and 2vu vv††œœ
19. ( 2 ) (8 4 12 )uvuvijkijkijkœœ
ˆ‰ˆ ‰ ‘ˆ‰
vu vu
vv vv
††
††
14 14 28 14
3333
, where 28 and 6œ œ œ
ˆ‰ˆ‰
14 28 14 10 16 22
333 333
i j k i j k vu vv††
20. ( ) ( ) ( ( ), where 1 and 1; yesuvuvAijkAi)jk vu vvœœœ œ œ
ˆ‰ˆ ‰ ‘ˆ‰
vu vu
vv vv
††
††
""
11
††
21. The sum of two vectors of equal length is orthogonal to their difference, as we can see from the equationalways
()() 0v v v v vv vv vv vv v v
" # " # "" #" "# ## " #
##
œœœ† ††††kk kk
22. CA CB ( ( )) ( ) 0 because since both equal
ÄÄ
œœœœ œ††††††v u v u vv vu uv uu v u u vkk kk kk kk
##
the radius of the circle. Therefore, CA and CB are orthogonal.
ÄÄ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

788 Chapter 12 Vectors and the Geometry of Space
23. Let and be the sides of a rhombus the diagonals are and uv duvd uvÊœœ
"#
( ) ( ) 0 because , since a rhombusÊ œœœœ œdd uv uv uuuvvuvv v u u v
"#
##
†† ††††kk kk kk kk
has equal sides.
24. Suppose the diagonals of a rectangle are perpendicular, and let and be the sides of a rectangle the diagonals areuv Ê
and . Since the diagonals are perpendicular we have 0duv d uv dd
"# "#
œ œ œ†
( ) ( ) 0 0 0ÍœœÍœÍ œuv uv uuuvvuvv v u v u v u†††††kkkk ababkk kk kk kk
##
0 which is not possible, or 0 which is equivalent to the rectangle is a square.Íœ œ œÊab ab kkkkkk kk kk kkvu vu v u
25. Clearly the diagonals of a rectangle are equal in length. What is not as obvious is the statement that equal
diagonals happen only in a rectangle. We show this is true by letting the adjacent sides of a parallelogram be
the vectors (v v ) and (u u ). The equal diagonals of the parallelogram are
"# "#
ij ij
(v v ) (u u ) and (v v ) (u u ). Hence (v v ) (u u )d ij ij d ij ij d d ij ij
" "# "# # "# "# " # "# "#
œ œ œœ kk kk k k
(v v ) (u u ) (v u ) (v u ) (v u ) (v u )œ Ê œ k kkkkk
" # " # "" ## "" ##
ij ij i j i j
(v u) (v u) (v u) (v u) v 2vu u v 2vu uÊ œ Ê
ÈÈ
"" ## "" ## "" ##
## ##
####
11
v 2vu u v 2vu u 2(vu vu) 2(vu vu) vu vu 0œ Ê œ Ê œ
####
"" ## "" ## "" ## "" ##
11
(v v ) (u u ) 0 the vectors (v v ) and (u u ) are perpendicular and the parallelogramÊ œÊ
"# "# "# "#
ij ij ij ij†
must be a rectangle.
26. If and is the indicated diagonal, then ( )kk kk kk kku v uv uvu uuvu u vu uv vœ œœœ††† ††
##
( ) the angle cos between the diagonal and and the angleœœ Êuv vv u v v u†† † "
Š‹
()
uvu
uvu
†
kkkk
cos between the diagonal and are equal because the inverse cosine function is one-to-one.
"
Š‹
()
uvv
uvv
†
kkkk v
Therefore, the diagonal bisects the angle between and .uv
27. horizontal component: 1200 cos 8 1188 ft/s; vertical component: 1200 sin 8 167 ft/sab ab
‰‰
¸¸
28. cos 33 15 2.5 lb, so . Then cos 33 , sin 33 2.205, 1.432kk a b kk ¡¡
www
‰‰ ‰ ‰
œ œ œ ¸
2.5 lb 2.5 lb
cos 18 cos 18
29. (a) Since cos 1, we have cos (1) .k k k k kkk k kkkk kkkk))ŸŸœuv uv uv uv†œkk
(b) We have equality precisely when cos 1 or when one or both of and is . In the case of nonzerokk)œuv0
vectors, we have equality when 0 or , i.e., when the vectors are parallel.)1œ
30. (x y ) x y cos 0 when . Thisijv ijvœ Ÿ ŸŸ†kkkk))1
1
#
means (x y) has to be a point whose position vector makesß
an angle with that is a right angle or bigger.v
31. (a b ) a b a b( ) a(1) b(0) avu uuuuuuu u uu†††† †
" " # " "" #" " #"
##
œ œ œ œ œkk
32. No, need not equal . For example, 2 but ( ) 1 0 1 andv v ij i j iij iiij
"# Á œ œœ†††
(2) 2 1201.ii j ii ij††††œ œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
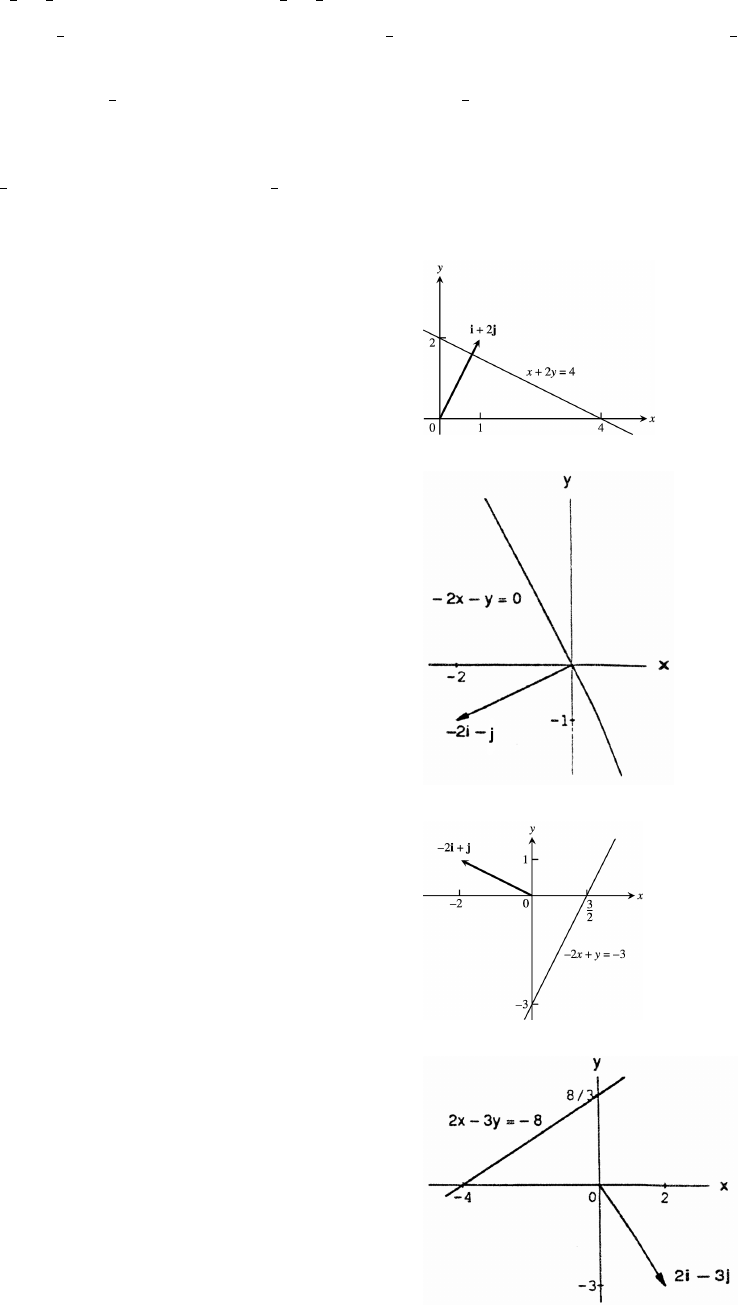
Section 12.3 The Dot Product 789
33. P(x y ) P x , x and Q(x y ) Q x x are any two points P and Q on the line with b 0
"" " " ## # #
ßœ ßœ ß Á
ˆ‰ ˆ‰
ca ca
bb bb
PQ (x x ) (x x ) PQ (x x ) (x x ) (a b ) a(x x ) b (x x )Êœ Ê œ œ
ÄÄ
#" "# #" "# #" "#
ijvijij
aa a
bb b
††
‘ ˆ‰
0 is perpendicular to PQ for b 0. If b 0, then a is perpendicular to the vertical line ax c.œÊ Á œ œ œ
Ä
vvi
Alternatively, the slope of is and the slope of the line ax by c is , so the slopes are negativevba
ab
œ
reciprocals the vector and the line are perpendicular.Êv
34. The slope of is and the slope of bx ay c is , provided that a 0. If a 0, then b is parallel tovvj
bb
aa
œ Á œ œ
the vertical line bx c. In either case, the vector is parallel to the line ax by c.œœv
35. 2 is perpendicular to the line x 2y c;vi jœ œ
P(2 1) on the line 2 2 c x 2y 4ßʜʜ
36. 2 is perpendicular to the line 2x y c;vijœ œ
P( 1 2) on the line ( 2)( 1) 2 cß Ê œ
2x y 0Ê œ
37. 2 is perpendicular to the line 2x y c;vijœ œ
P( 2 7) on the line ( 2)( 2) 7 cß Ê œ
2x y 3Ê œ
38. 2 3 is perpendicular to the line 2x 3y c;vijœ œ
P(11 10) on the line (2)(11) (3)(10) cßÊœ
2x 3y 8ʜ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
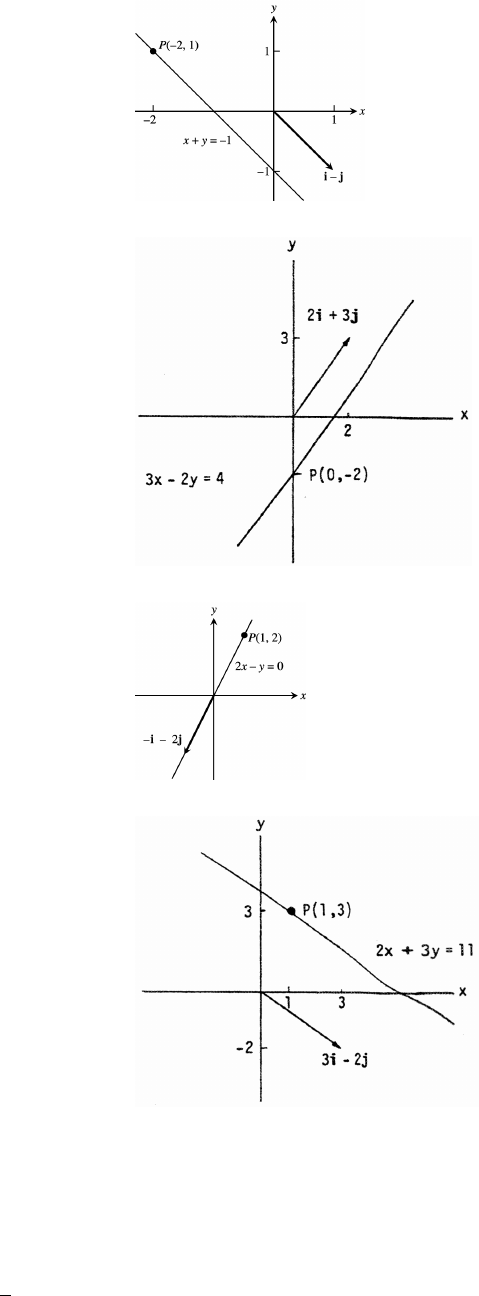
790 Chapter 12 Vectors and the Geometry of Space
39. is parallel to the line x y c;vijœ œ
P( 2 1) on the line 2 1 c x y 1ß Ê œ Ê œab
or x y 1.œ
40. 2 3 is parallel to the line 3x 2y c;vijœ œ
P(0 2) on the line 0 2( 2) c 3x 2y 4ß Ê œ Ê œ
41. 2 is parallel to the line 2x y c;vijœ œ
P(1 2) on the line 2(1) 2 c 2x y 0ßʜʜ
or 2x y 0.œ
42. 3 2 is parallel to the line 2x 3y c;vijœ œ
P(1 3) on the line ( 2)(1) (3)(3) cßÊœ
2x 3y 11 or 2x 3y 11Ê œ œ
43. P(0 0), Q(1 1) and 5 PQ and PQ (5 ) ( ) 5 N m 5 Jßß œÊœ œ œ œ œ
ÄÄ
Fj ij WF jij†† †
44. (distance) cos (602,148 N)(605 km)(cos 0) 364,299,540 N km (364,299,540)(1000) N mWFœœ œ œkk )††
3.6429954 10 Jœ‚
""
45. PQ cos (200)(20)(cos 30°) 2000 3 3464.10 N m 3464.10 JWFœœ œœœ
Ä
kk¹¹ È
)†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 12.3 The Dot Product 791
46. PQ cos (1000)(5280)(cos 60°) 2,640,000 ft lbWFœœ œ
Ä
kk¹¹)†
In Exercises 47-52 we use the fact that a b is normal to the line ax by c.nijœ œ
47. 3 and 2 cos cos cosnijnij
"# " " "
"
œ œÊœ œ œ œ)Š‹ Š ‹ Š‹
nn
nn
†
kkkk ÈÈ È
4
61
10 5 2
1
48. 3 and 3 cos cos cosnijnij
"# " " "
"
œ œ Ê œ œ œ œ
ÈÈ Š‹ Š‹ ˆ‰
)nn
nn
†
kkkk ÈÈ
23
31 2
4 4
1
49. 3 and 3 cos cos cosnijnij
"# " " "
œ œ Êœ œ œ œ
ÈÈ
Š‹ Š ‹ Š‹
)nn
nn
†
kkkk ÈÈ È
ÈÈ
26
33 3
4 4
1
50. 3 and 1 3 1 3 cosni j n i j
"# "
œ œ Ê œ
ÈÈÈ
Š‹Š‹ Š‹
)nn
nn
†
kkkk
cos cos cosœœœœ
" " "
"
Š‹ Š‹
1333
13 12331233
4
28 24
ÈÈ
ÈÉÈÈ ÈÈ
1
51. 3 4 and cos cos cos 0.14 radnijnij
"# " " "
œ œÊœ œ œ ¸)Š‹ Š‹ Š‹
nn
nn
†
kkkk ÈÈÈ
34 7
25 2 5 2
52. 12 5 and 2 2 cos cos cos 1.18 radnijnij
"# " " "
œ œÊœ œ œ ¸)Š‹ Š ‹ Š‹
nn
nn
†
kkkk ÈÈ È
24 10 14
169 8 26 2
53. The angle between the corresponding normals is equal to the angle between the corresponding tangents. The
points of intersection are and . At the tangent line for f(x) x is
Š‹Š‹Š‹
ß ß ß œ
ÈÈ È
33 3
33 3
44 4## #
#
y f x y 3 x y 3x , and the tangent line forœ Ê œ Ê œ
333
444
33 3
w
## #
Š‹Š ‹ Š ‹Š‹ ÈÈ
ÈÈ È
f(x) x is y f x y 3 x 3x . The correspondingœ œ Ê œ œ
ˆ‰ Š‹Š ‹ Š ‹Š‹ ÈÈ
33 39
444
33 3
####
#w
ÈÈ È
normals are 3 and 3 . The angle at is cosnijn ij
"# #
"
œ œ ß œ
ÈÈ Š‹ Š‹
Èkkkk
33
4
)nn
nn
†
cos cos , the angle is and . At the tangent line for f(x) x isœœœ ß œ
" " #
"
##
Š‹ Š‹
ˆ‰
31 2 2 3
4 4 3334
3
ÈÈ È
111
y 3 x 3x and the tangent line for f(x) x is y 3 xœœ œœ
ÈÈ È
Š‹ Š‹
È È
3 3
39 3 3
44 4###
#
3x . The corresponding normals are 3 and 3 . The angle at isœ œ œ ß
ÈÈÈ
Š‹
3 3
4 4
3
nijnij
"# #
È
cos cos cos , the angle is and .)œœœœ
" " "
"
#
Š‹ Š‹ ˆ‰
nn
nn
†
kkkk ÈÈ
333
31 2 2
4 4
111
54. The points of intersection are and . The curve x y has derivative the
Š‹Š ‹
!ß !ß œ œ Ê
ÈÈ
33 3
4dxy
dy
## #
#"
tangent line at is y (x 0) is normal to the curve at that point. The
Š‹
!ß œ Ê œ
ÈÈ
ÈÈ
33
33
##
""
"
nij
curve x y has derivative the tangent line at is y (x 0)œ œ Ê !ß œ
#""
###
3
4dxy
dy 33
3
Š‹
ÈÈ
È
is normal to the curve. The angle between the curves is cosÊœ œnij
#
""
Èkkkk
3
)Š‹
nn
nn
†
cos cos cos and . Because of symmetry the angles betweenœœœœ
" " "
"
#
Š‹ ˆ‰
33
33
2
4
3
1
1 1 33
2
ÉÉ ˆ‰
ˆ‰ 11
the curves at the two points of intersection are the same.
55. The curves intersect when y x y y y 0 or y 1. The points of intersection are ( ) andœ œ œ Ê œ œ !ß !
$# '
$
ab
( ). Note that y 0 since y y . At ( 0) the tangent line for y x is y 0 and the tangent line for"ß " œ !ß œ œ
'$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

792 Chapter 12 Vectors and the Geometry of Space
y x is x 0. Therefore, the angle of intersection at (0 0) is . At (1 1) the tangent line for y x isœœ ß ß œ
È1
#
$
y 3x 2 and the tangent line for y x is y x . The corresponding normal vectors areœ œ œ
È""
##
3 and cos cos , the angle is and .nijn ij
"#
""
#
" "
œ œ Ê œ œ œ)Š‹ Š‹
nn
nn
†
kkkk È
444
2
3111
56. The points of intersection for the curves y x and y x are ( 0) and ( 1 1). At ( 0) the tangentœ œ !ß ß !ß
#$
È
line for y x is y 0 and the tangent line for y x is x 0. Therefore, the angle of intersection at ( 0)œ œ œ œ !ß
#$
È
is . At ( 1 1) the tangent line for y x is y 2x 1 and the tangent line for y x is y x .
1
#
#$"
ß œ œ œ œ
È33
2
The corresponding normal vectors are 2 and cosnijn ij
"#
""
œ œ Êœ
3
)Š‹
nn
nn
†
kkkk
cos cos cos , the angle is and .œœœœ
" " "
"
"
Œ Š‹
25
33
9
5 10
3
ÈɈ‰ È
5 1 2444
3
111
12.4 THE CROSS PRODUCT
1. 3 length 3 and the direction is ;
22
0
uv i j k i j k
ij k
‚œ œ Ê œ
"
""
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰
22 22
333 333
""
( 3 length 3 and the direction is vu uv) i j k i j k‚œ‚ œ Ê œ
ˆ‰
22 22
333 333
""
2. 5( ) length 5 and the direction is
230
10
uv k k
ijk
‚œ œ Ê œ
"
ââ
ââ
ââ
ââ
ââ
ââ
( 5( ) length 5 and the direction is vu uv) k k‚œ‚ œ Ê œ
3. length 0 and has no direction
224
12
uv 0
ijk
‚œ œ Ê œ
"
ââ
ââ
ââ
ââ
ââ
ââ
( length 0 and has no directionvu uv) 0‚œ‚ œ Ê œ
4. length 0 and has no direction
11 1
00 0
uv 0
ij k
‚œ œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ
( length 0 and has no directionvu uv) 0‚œ‚ œ Ê œ
5. 6( ) length 6 and the direction is
200
030
uv k k
ijk
‚œ œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ
( 6( ) length 6 and the direction is vu uv) k k‚œ‚ œ Ê œ
6. ( ) ( ) length 1 and the direction is
001
100
uv ij jk ki j j
ijk
‚œ‚‚‚ œ‚œ œÊ œ
ââ
ââ
ââ
ââ
ââ
ââ
( length 1 and the direction is vu uv) j j‚œ‚ œÊ œ
7. 6 12 length 6 5 and the direction is
824
221
uv i k i k
ijk
‚œ œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ È"
ÈÈ
55
2
( (6 12 length 6 5 and the direction is vu uv) i k) i k‚œ‚ œ Ê œ
È"
ÈÈ
55
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
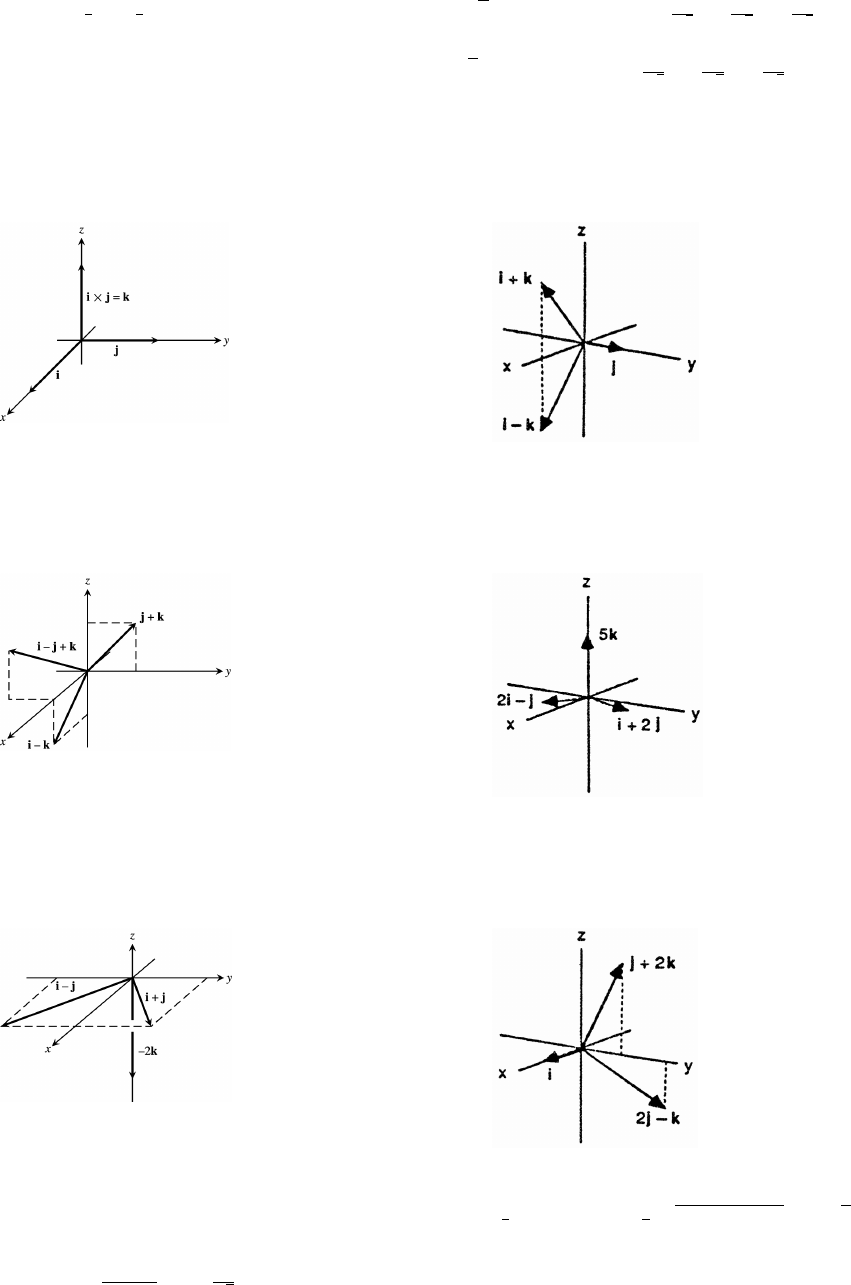
Section 12.4 The Cross Product 793
8. 1 2 2 2 length 2 3 and the direction is
112
uv i j k i j k
ijk
‚œ œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ È
3 1
333
##
"""
ÈÈÈ
( ( 2 2 2 length 2 3 and the direction is vu uv) i j k) i j k‚œ‚ œ Ê œ
È""
ÈÈÈ
333
1
9. 10.
100 10 1
010 01 0
uv k uv ik
ijk ij k
‚œ œ ‚œ œ
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
11. 12. 5
10 1 2 10
01 1 1 2 0
uv ijk uv k
ij k i j k
‚œ œ ‚œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
13. 2 14. 2
110 012
110 100
uv k uv jk
ijk ijk
‚œ œ ‚œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
15. (a) PQ PR 8 4 4 Area PQ PR 64 16 16 2 6
11 3
13 1
ÄÄ
‚ œ œ Ê œ ‚ œ œ
ÄÄ
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
ÈÈ
ijk
ijk ""
##
(b) (2 )uijkœ„ œ„
PQ PR
PQ PR 6
Ä‚Ä
Ä‚Ä
"
¹¹ È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
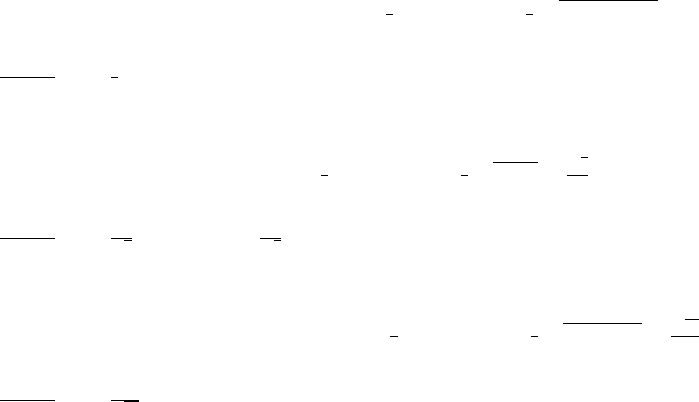
794 Chapter 12 Vectors and the Geometry of Space
16. (a) PQ PR 4 4 2 Area PQ PR 16 16 4 3
102
220
ÄÄ
‚ œ œ Ê œ ‚ œ œ
ÄÄ
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
È
ijk
ijk ""
##
(b) (2 2 )uijkœ„ œ„
PQ PR
PQ PR 3
Ä‚Ä
Ä‚Ä
"
¹¹
17. (a) PQ PR Area PQ PR 1 1
111
110
ÄÄ
‚œ œÊ œ ‚ œ œ
ÄÄ
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
È
ijk
ij ""
###
È2
(b) ( ) ( )uijijœ„ œ„ œ„
PQ PR
PQ PR 22
Ä‚Ä
Ä‚Ä
""
¹¹ ÈÈ
18. (a) PQ PR 2 3 Area PQ PR 4 9 1
211
10 2
ÄÄ
‚ œ œÊ œ ‚ œ œ
ÄÄ
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
È
ij k
ijk ""
## #
È14
(b) (2 3 )uijkœ„ œ„
PQ PR
PQ PR 14
Ä‚Ä
Ä‚Ä
"
¹¹ È
19. If a a a , b b b , and c c c , then ( ) ,
aaa
bbb
ccc
u ijkv ijk w ijk uvwœ œ œ ‚œ
"#$ " # $ "#$
"#$
"#$
"#$
†
ââ
ââ
ââ
ââ
ââ
ââ
( ) and ( ) which all have the same value, since the
bbb ccc
ccc aaa
aaa bbb
vw u wu v††‚œ ‚œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
"#$ "#$
"#$ "#$
"#$ "#$
interchanging of two pair of rows in a determinant does not change its value the volume isÊ
() abs 8
200
020
002
kk
ââ
ââ
ââ
ââ
ââ
ââ
uvw‚œ œ†
20. ( ) abs 4 (for details about verification, see Exercise 19)
111
21 2
12 1
kk
ââ
ââ
ââ
ââ
ââ
ââ
uvw‚œ œ
†
21. ( ) abs 7 7 (for details about verification, see Exercise 19)
210
211
102
kk kk
ââ
ââ
ââ
ââ
ââ
ââ
uvw‚œ œœ
†
22. ( ) abs 8 (for details about verification, see Exercise 19)
11 2
10 1
24 2
kk
ââ
ââ
ââ
ââ
ââ
ââ
uvw‚œ œ
†
23. (a) 6, 81, 18 noneuv uw vw†† †œ œ œ Ê
(b) , ,
511 5 11 015
01 5 153 3 153 3
uv 0uw 0vw 0
ij k i j k i jk
‚œ Á ‚ œ œ ‚ œ Á
ââ â â â â
ââ â â â â
ââ â â â â
ââ â â â â
ââ â â â â
ââ â â â â
and are parallelÊuw
24. (a) 0, 0, 3 , 0, 0, 0 , , , uv u w ur vw vr wr u vu wv wv r†††††œ‚œ œ œ œ œÊ¼¼¼¼1
and wr¼
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 12.4 The Cross Product 795
(b) , ,
12 1 12 1
11 1 10 1
12 1
uv 0uw 0ur 0
ijk ijk ijk
‚œ Á ‚ œ Á ‚œ œ
ââ ââ â â
ââ ââ â â
ââ ââ â â
ââ ââ â â
ââ ââ â â
ââ ââ â â
11
##
1
, ,
111
101
111 1 01
vw 0vr 0wr 0
ijk ijk ijk
‚œ Á ‚œ Á ‚œ Á
ââââââ
ââââââ
ââââââ
ââââââ
ââââââ
ââââââ
11 11
## ##
11
and are parallelÊur
25. PQ PQ sin (60°) 30 ft lb 10 3 ft lb
¹¹¹¹
kk È
ÄÄ
‚œ œ œFF 2
3
3
†† † †
È
#
26. PQ PQ sin (135°) 30 ft lb 10 2 ft lb
¹¹¹¹
kk È
ÄÄ
‚œ œ œFF 2
3
2
†† † †
È
#
27. (a) true, a a akk ÈÈ
uuuœœ
##
#
13
†
(b) not always true, uu u†œkk
#
(c) true, 0 0 0 and 0 0 0
aaa 000
000 aaa
u0 ijk0 0u ijk0
ijk ijk
‚œ œ œ ‚œ œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
"#$
"#$
(d) true, ( ) ( aa aa) ( aa aa) ( aa aa)
aaa
aaa
uu i j k0
ijk
‚ œ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
"#$
"#$
#$ #$ "$ "$ "# "#
(e) not always true, for exampleij k k ji‚œ Áœ‚
(f) true, distributive property of the cross product
(g) true, ( ) ( ) 0uvv uvv u0‚œ‚œœ†† †
(h) true, the volume of a parallelpiped with , , and along the three edges is ( ) ( ) ( ),uv w uvw vwu uvw‚œ‚œ‚†††
since the dot product is commutative.
28. (a) true, a b a b a b b a b a b auv vu††œœœ
"" ## $$ "" ## $$
(b) true, ( )
aaa bbb
bbb aaa
uv vu
ijk ijk
‚ œ œ œ ‚
ââââ
ââââ
ââââ
ââââ
ââââ
ââââ
"#$ "#$
"#$ "#$
(c) true, ( ) ( )
aaa aaa
bbb bbb
‚œ œ œ‚
uv uv
ijk ijk
ââââ
ââââ
ââââ
ââââ
ââââ
ââââ
"#$ "#$
"#$ "#$
(d) true, (c ) (ca )b (ca )b (ca )b a (cb ) a (cb ) a (cb ) (c ) c(a b a b a b )uv u v††œœœ œ
"" ## $$ "" ## $$ "" ## $$
c( )œuv†
(e) true, c( ) c (c ) (c )
a a a ca ca ca a a a
b b b b b b cb cb cb
uv u v u v
ijk i j k i j k
‚œ œ œ ‚œ œ‚
âââ â â â
âââ â â â
âââ â â â
âââ â â â
âââ â â â
âââ â â â
"#$ " # $ " # $
"#$ " # $ " # $
(f) true, aaa aaauu u†œœ œ
### ##
###
13
13
ˆ‰
Èkk
(g) true, ( ) 0uuu 0u‚œœ††
(h) true, and ( ) ( ) 0uv u uv v uvu vuv‚¼ ‚¼ Ê ‚ œ ‚ œ††
29. (a) proj (b) ( ) (c) ( ) (d) ( )
vu v uv uv w uvwœ„‚ „‚‚‚
Š‹ abkk
uv
vv
†
kkkk †
30. (a) ( ) ( )uv uw‚‚‚
(b) ()()() ()uv uv uv u uv v uu vu uv vv ‚ œ ‚ ‚œ‚‚‚‚
2( ), or simply œ‚‚œ ‚ ‚0vuuv0 vu uv
(c) (d) kk k kuuw
v
vkk ‚
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
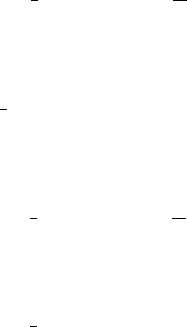
796 Chapter 12 Vectors and the Geometry of Space
31. (a) yes, and are both vectors (b) no, is a vector but is a scalaruv w u vw‚†
(c) yes, and are both vectors (d) no, is a vector but is a scalaruuw u vw‚†
32. ( ) is perpendicular to , and is perpendicular to both and ( ) isuv w uv uv u v uv w‚‚ ‚ ‚ Ê ‚‚
parallel to a vector in the plane of and which means it lies in the plane determined by and .uv uv
The situation is degenerate if and are parallel so and the vectors do not determine a plane.uv uv0‚œ
Similar reasoning shows that ( ) lies in the plane of and provided and are nonparallel.uvw v w v w‚‚
33. No, need not equal . For example, , but ( ) andv w ij ij i ij iiij 0k k Á ‚ œ‚‚ œ œ
() .i ij iiij 0k k‚ œ‚‚ œ œ
34. Yes. If and , then ( ) and ( ) 0. Suppose now that .uv uw uv uw u vw 0 uvw v w‚œ‚ œ ‚ œ œ Á†† †
Then ( ) implies that k for some real number k 0. This in turn implies thatuvw 0 vw u‚ œ œ Á
( ) (k ) k 0, which implies that . Since , it cannot be true that , souv w u u u u 0 u 0 v w††œ œ œ œ Á Ákk
#
.vwœ
35. AB and AD AB AD 2 area AB AD 2
110
110
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
36. AB 7 3 and AD 2 5 AB AD 29 area AB AD 29
730
250
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
37. AB 3 2 and AD 5 AB AD 13 area AB AD 13
320
510
Ä Ä ÄÄ ÄÄ
œ œÊ ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
38. AB 7 4 and AD 2 5 AB AD 43 area AB AD 43
740
250
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
39. AB 2 3 and AC 3 AB AC 11 area AB AC
230
310
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
"
##
11
40. AB 4 4 and AC 3 2 AB AC 4 area AB AC 2
440
320
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
"
#
41. AB 6 5 and AC 11 5 AB AC 25 area AB AC
650
11 5 0
Ä Ä ÄÄ ÄÄ
œ œ Ê ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
"
##
25
42. AB 16 5 and AC 4 4 AB AC 84 area AB AC 42
16 5 0
440
Ä Ä ÄÄ ÄÄ
œ œÊ ‚ œ œ Ê œ ‚ œ
ij ij k
ijk
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
"
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 12.5 Lines and Planes in Space 797
43. If a a and b b , then and the triangle's area is
aa0
bb0
aa
bb
AijBi j AB k
ijk
œ œ ‚œ œ
"# "# "#
"#
"#
"#
ââ
ââ
ââ
ââ
ââ
ââ
ºº
. The applicable sign is ( ) if the acute angle from to runs counterclockwise
aa
bb
""
##
"#
"#
kk ºº
AB AB‚œ„
in the xy-plane, and ( ) if it runs clockwise, because the area must be a nonnegative number.
44. If a a , b b , and c c , then the area of the triangle is AB AC . Now,AijBi jCijœ œ œ ‚
ÄÄ
"# "# "#
"
#¹¹
AB AC AB AC
baba0
caca0
ba ba
ca ca
ÄÄ ÄÄ
‚œ œ Ê ‚
ââ
ââ
ââ
ââ
ââ
ââ
ºº
¹¹
ijk
k
""##
""##
"" ##
"" ##
"
#
(b a )(c a ) (c a )(b a ) a (b c ) a (c b ) (b c c b )œ œ
""
##
""## ""## "## #" " "#"#
kkk k
. The applicable sign ensures the area formula gives a nonnegative number.
aa1
bb1
cc1
œ„
"
#
"#
"#
"#
ââ
ââ
ââ
ââ
ââ
ââ
12.5 LINES AND PLANES IN SPACE
1. The direction and P(3 4 1) x 3 t, y 4 t, z 1 tijk ß ß Ê œ œ œ
2. The direction PQ 2 2 2 and P(1 2 1) x 1 2t, y 2 2t, z 1 2t
Äœ ßß Ê œ œ œijk
3. The direction PQ 5 5 5 and P( 2 0 3) x 2 5t, y 5t, z 3 5t
Äœ ßß Êœ œ œijk
4. The direction PQ and P(1 2 0) x 1, y 2 t, z t
Äœ ß ß Ê œ œ œjk
5. The direction 2 and P( ) x 0, y 2t, z tjk !ß!ß! Ê œ œ œ
6. The direction 2 3 and P(3 2 1) x 3 2t, y 2 t, z 1 3tij k ßß Ê œ œ œ
7. The direction and P(1 1 1) x 1, y 1, z 1 tkßß Ê œ œ œ
8. The direction 3 7 5 and P(2 4 5) x 2 3t, y 4 7t, z 5 5tijk ßß Êœ œ œ
9. The direction 2 2 and P(0 7 0) x t, y 7 2t, z 2tijk ßß Êœ œ œ
10. The direction is 2 4 2 and P( 0) x 2 2t, y 3 4t, z 2t
123
345
AB i j k
ijk
‚ œ œ #ß $ß Ê œ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
11. The direction and P(0 0 0) x t, y 0, z 0ißß Ê œ œ œ
12. The direction and P(0 0 0) x 0, y 0, z tkßß Ê œ œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
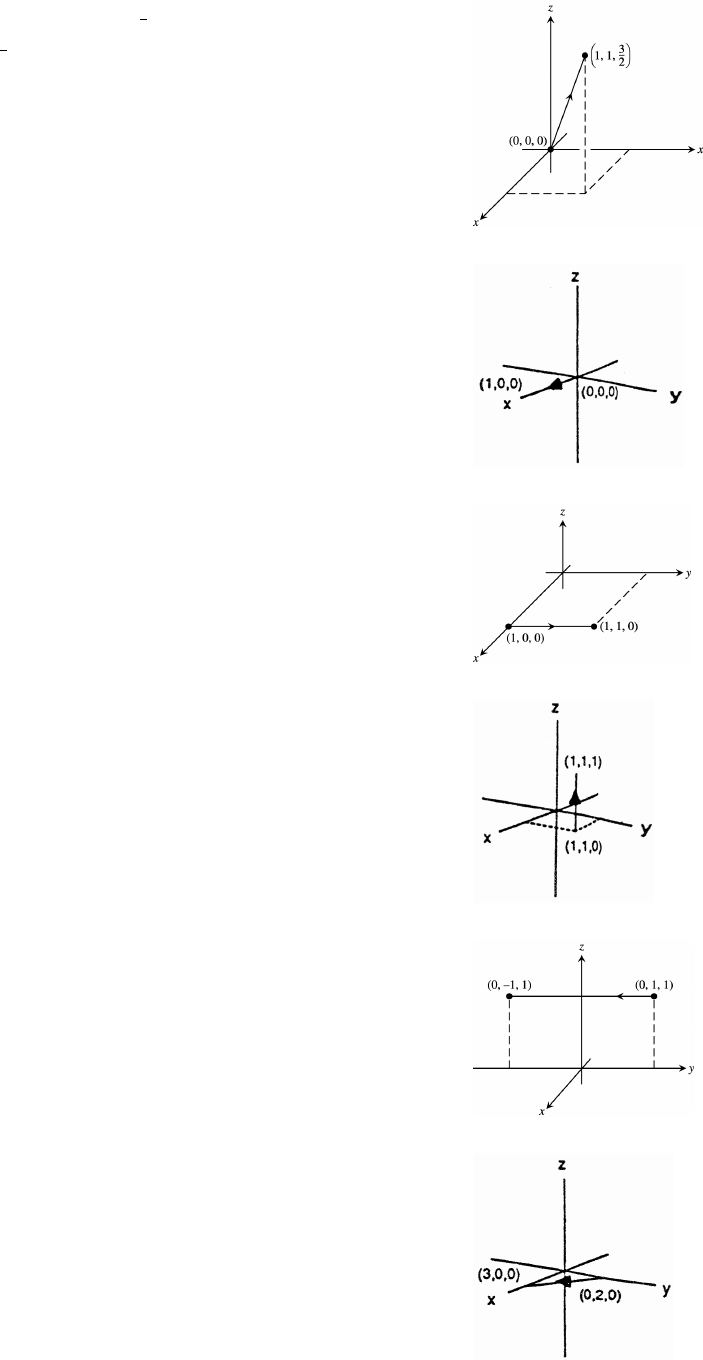
798 Chapter 12 Vectors and the Geometry of Space
13. The direction PQ and P(0 0 0) x t,
Äœ ßß Ê œij k
3
#
y t, z t, where 0 t 1œœ ŸŸ
3
#
14. The direction PQ and P(0 0 0) x t, y 0, z 0,
ÄœßßÊœœœi
where 0 t 1ŸŸ
15. The direction PQ and P(1 1 0) x 1, y 1 t,
ÄœßßÊœœj
z 0, where 1 t 0œŸŸ
16. The direction PQ and P(1 1 0) x 1, y 1, z t,
ÄœßßÊœœœk
where 0 t 1ŸŸ
17. The direction PQ 2 and P(0 1 1) x 0,
Äœ ß ß Ê œj
y 1 2t, z 1, where 0 t 1œ œ ŸŸ
18. The direction PQ 2 and P(0 2 0) x 3t,
Äœ$ ß ß Ê œij
y 2 2t, z 0, where 0 t 1œ œ ŸŸ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
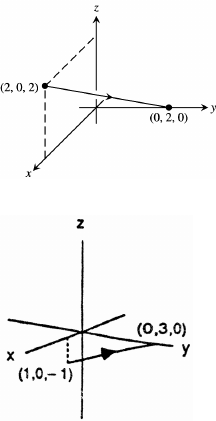
Section 12.5 Lines and Planes in Space 799
19. The direction PQ 2 2 2 and P(2 0 2)
Äœ ß ßijk
x 2 2t, y 2t, z 2 2t, where 0 t 1Êœœœ ŸŸ
20. The direction PQ 3 and P(1 0 1)
Äœ ß ßijk
x 1 t, y 3t, z 1 t, where 0 t 1Êœ œ œ ŸŸ
21. 3(x 0) ( 2)(y 2) ( 1)(z 1) 0 3x 2y z 3 œÊ œ
22. 3(x 1) (1)(y 1) (1)(z 3) 0 3x y z 5 œÊ œ
23. PQ 3 , PS 3 2 PQ PS 7 5 4 is normal to the plane
113
132
ÄÄ ÄÄ
œ œ Ê ‚ œ œ
ij k i j k i j k
ijk
ââ
ââ
ââ
ââ
ââ
ââ
7(x 2) ( 5)(y 0) ( 4)(z 2) 0 7x 5y 4z 6Ê œÊ œ
24. PQ 2 , PS 3 2 3 PQ PS 3 is normal to the plane
112
323
ÄÄ ÄÄ
œ œ Ê ‚ œ œ
ij k i j k i jk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
( 1)(x 1) ( 3)(y 5) (1)(z 7) 0 x 3y z 9Ê œ Ê œ
25. 3 4 , P(2 4 5) (1)(x 2) (3)(y 4) (4)(z 5) 0 x 3y 4z 34ni j kœ ßßœ œÊ œ
26. 2 , P(1 2 1) (1)(x 1) ( 2)(y 2) (1)(z 1) 0 x 2y z 6ni jkœ ßß œ œ Ê œ
27. t 0 and s 1; then z 4t 3 4s 1
x 2t 1 s 2 2t s 1 4t 2s 2
y 3t 2 2s 4 3t 2s 2 3t 2s 2
œœœ
œœ œ œ
œœ œ œ
ÊÊÊœœœœ
4(0) 3 ( 4)( 1) 1 is satisfied the lines do intersect when t 0 and s 1 the point ofÊœ Ê œ œÊ
intersection is x 1, y 2, and z 3 or P(1 2 3). A vector normal to the plane determined by these lines isœœ œ ßß
20 12 , where and are directions of the lines the plane
23 4
12 4
nn i jk n n
ij k
"# " #
‚œ œ Ê
ââ
ââ
ââ
ââ
ââ
ââ
containing the lines is represented by( 20)(x 1) (12)(y 2) (1)(z 3) 0 20x 12y z 7. œÊœ
28. s 1 and t 0; then z t 1 5s 6 0 1 5( 1) 6
x t 2s 2 t 2s 2
yt2 s3 t s1
œœ
œœ œ
œ œ œ
Ê Ê œ œ œœ Ê œ
is satisfied the lines do intersect when s 1 and t 0 the point of intersection is x 0, y 2 and z 1ÊœœÊœœœ
or P(0 2 1). A vector normal to the plane determined by these lines is 11
215
ßß ‚ œ "
nn
ijk
"#
ââ
ââ
ââ
ââ
ââ
ââ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-WesleyCopyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
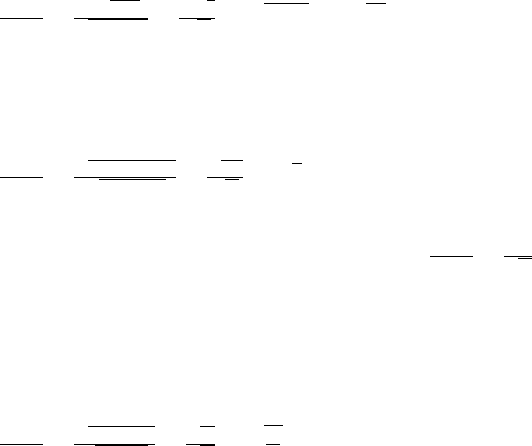
800 Chapter 12 Vectors and the Geometry of Space
6 3 3 , where and are directions of the lines the plane containing the lines is represented byœ Êijk n n
"#
( 6)(x 0) ( 3)(y 2) (3)(z 1) 0 6x 3y 3z 3. œÊ œ
29. The cross product of and 4 2 2 has the same direction as the normal to the planeijk i j k
6 6 . Select a point on either line, such as P( 1 2 1). Since the lines are given
11
42 2
Êœ œ ßß
"
njk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
to intersect, the desired plane is 0(x 1) 6(y 2) 6(z 1) 0 6y 6z 18 y z 3. œÊ œ Êœ
30. The cross product of 3 and has the same direction as the normal to the planeijk ijk
2 2 4 . Select a point on either line, such as P(0 3 2). Since the lines are
131
11 1
nijk
ij k
œœ ßß
ââ
ââ
ââ
ââ
ââ
ââ
given to intersect, the desired plane is ( 2)(x 0) ( 2)(y 3) (4)(z 2) 0 2x 2y 4z 14 œÊœ
xy2z 7.Ê œ
31. 3 3 3 is a vector in the direction of the line of intersection of the planes
21 1
12 1
nn ijk
ij k
"#
‚ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
3(x 2) ( 3)(y 1) 3(z 1) 0 3x 3y 3z 0 x y z 0 is the desired plane containingÊ œÊ œÊœ
P(21 1)
!ßß
32. A vector normal to the desired plane is P P 2 12 2 ; choosing P (1 2 3) as a
20 2
412
"# "
Ä‚œ œ ßß
nijk
ij k
ââ
ââ
ââ
ââ
ââ
ââ
point on the plane ( 2)(x 1) ( 12)(y 2) ( 2)(z 3) 0 2x 12y 2z 32 x 6y z 16Ê œ Ê œ Ê œ
is the desired plane
33. S(0 0 12), P(0 0 0) and 4 2 2 PS 24 48 24( 2 )
0012
422
ßß ßß œ Ê ‚ œ œ œ
Ä
vijk v i j ij
ijk
ââ
ââ
ââ
ââ
ââ
ââ
d 5 24 2 30 is the distance from S to the lineÊœ œ œ œ œ
¹¹
kk ÈÈ
ÈÈ
PS 24 1 4
1644
24 5
24
Ä‚
v
vÈÈ
†
34. S(0 0 0), P(5 5 3) and 3 4 5 PS 13 16 5
553
34 5
ßß ßß œ Ê ‚ œ œ
Ä
vijk v i jk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
d 9 3 is the distance from S to the lineÊœ œ œ œ œ
¹¹
kk ÈÈ
ÈÈ
PS 169 256 25
91625
450
50
Ä‚
v
vÈ
35. S(2 1 3), P(2 1 3) and 2 6 PS d 0 is the distance from S to the lineßß ßß œ Ê ‚ œ Ê œ œ œ
Ä
vij v0 ¹¹
kk È
PS 0
40
Ä‚v
v
(i.e., the point S lies on the line)
36. S(2 1 1), P(0 1 0) and 2 2 2 PS 2 6 4
20 1
22 2
ßß ßß œ Ê ‚œ œ
Ä
vijk v ijk
ij k
ââ
ââ
ââ
ââ
ââ
ââ
d is the distance from S to the lineÊœ œ œ œ
¹¹
kk ÈÈ
ÈÈ
PS 43616
444
56
12
14
3
Ä‚
v
vÉ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
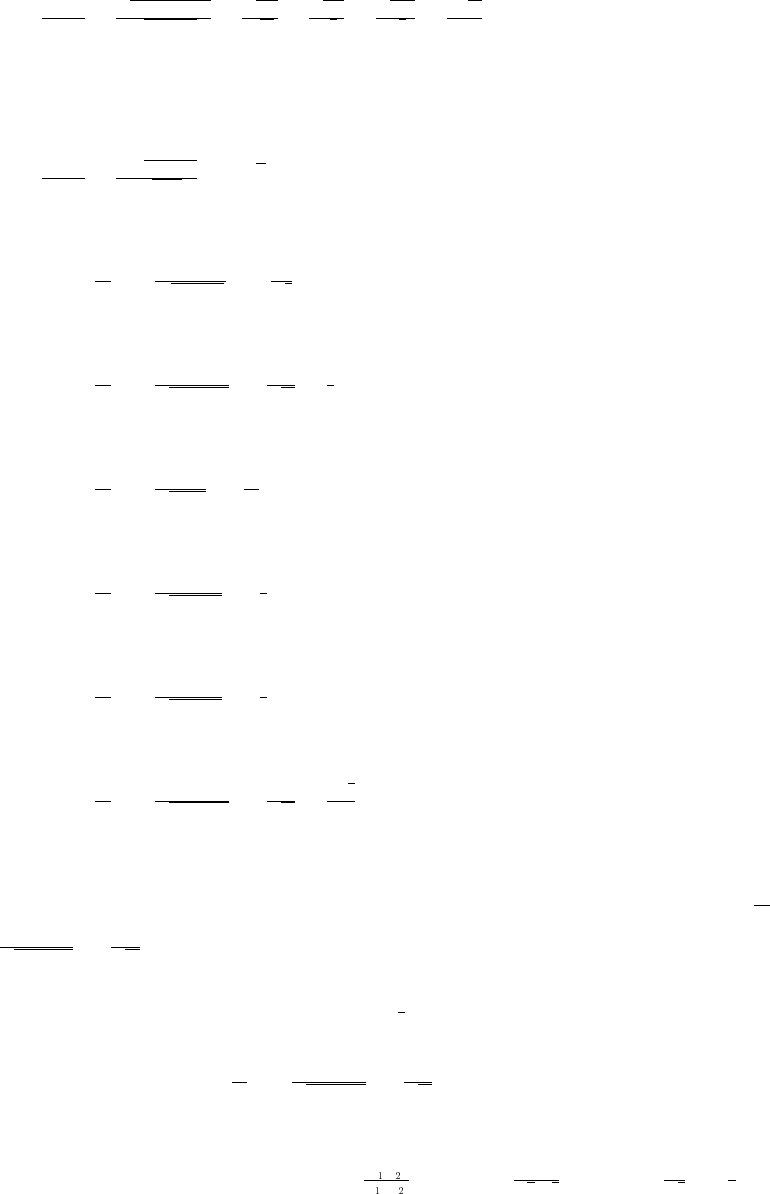
Section 12.5 Lines and Planes in Space 801
37. S(3 1 4), P(4 3 5) and 2 3 PS 30 6 6
149
123
ß ß ß ß œ Ê ‚ œ œ
Ä
v ijk v ijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
d is the distance from S to the lineÊœ œ œœœ œ
¹¹
kk È ÈÈÈ È
ÈÈÈÈ
PS 900 36 36
149
972 486 81 6
14 77
942
7
Ä‚
v
v
†
38. S( 1 4 3), P(10 3 0) and 4 4 PS 28 56 28 28( 2 )
11 7 3
404
ß ß ßß œ Ê ‚ œ œ œ
Ä
vik v i j k ijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
d 7 3 is the distance from S to the lineÊœ œ œ
¹¹
kk È
È
PS 28141
411
Ä‚
v
vÈ
39. S(2 3 4), x 2y 2z 13 and P(13 0 0) is on the plane PS 11 3 4 and 2 2ßß œ ßß Ê œ œ
Äijk nijk
dPS 3Êœ œ œ œ
Ä
¹¹¹ ¹¹¹
†n
nkk ÈÈ
1168 9
144 9
40. S(0 0 0), 3x 2y 6z 6 and P(2 0 0) is on the plane PS 2 and 3 2 6ßß œ ßß Ê œ œ
Äinijk
dPSÊœ œ œ œ
Ä
¹¹¹ ¹
†n
nkk ÈÈ
666
9436 49 7
41. S(0 1 1), 4y 3z 12 and P(0 3 0) is on the plane PS 4 and 4 3ßß œ ßß Ê œ œ
Äjk n j k
dPSÊœ œ œ
Ä
¹¹¹¹
†n
nkk È
16 3 19
16 9 5
42. S(2 2 3), 2x y 2z 4 and P(2 0 0) is on the plane PS 2 3 and 2 2ßß œ ßß Ê œ œ
Äjk nijk
dPSÊœ œ œ
Ä
¹¹¹¹
†n
nkk È26 8
414 3
43. S(0 1 0), 2x y 2z 4 and P(2 0 0) is on the plane PS 2 and 2 2ß ß œ ß ß Ê œ œ
Äij n ij k
dPSÊœ œ œ
Ä
¹¹¹¹
†n
nkk È
410 5
414 3
44. S(1 0 1), 4x y z 4 and P( 1 0 0) is on the plane PS 2 and 4ßß œ ßß Ê œ œ
Äik n ijk
dPSÊœ œ œ œ
Ä
¹¹¹ ¹
†n
nkk ÈÈ
È
#
81 9
1611 18
32
45. The point P(1 0 0) is on the first plane and S(10 0 0) is a point on the second plane PS 9 , andßß ßß Ê œ
Äi
2 6 is normal to the first plane the distance from S to the first plane is d PSni j kœ Ê œÄ
¹¹
†n
nkk
, which is also the distance between the planes.œœ
¹¹
99
1436 41
ÈÈ
46. The line is parallel to the plane since ( 2 6 ) 1 2 3 0. Also the pointvn i j k i j k††œ œœ
ˆ‰
"
#
S(1 0 0) when t 1 lies on the line, and the point P(10 0 0) lies on the plane PS 9 . The distanceßß œ ßß Ê œ
Äi
from S to the plane is d PS , which is also the distance from the line to theœœ œ
Ä
¹¹¹ ¹
†n
nkk ÈÈ
99
1436 41
plane.
47. and 2 2 cos cos cosnij n ijk
"# " " "
"
œ œ Ê œ œ œ œ)Š‹ Š‹ Š‹
nn
nn
†
kkkk ÈÈ
È
4
21
2 9 2
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

802 Chapter 12 Vectors and the Geometry of Space
48. 5 and 2 3 cos cos cos (0)nijknijk
"# " " "
#
œ œ Êœ œ œ œ)Š‹ Š ‹
nn
nn
†
kkkk ÈÈ
523
27 14
1
49. 2 2 2 and 2 2 cos cos cos 1.76 radnijknijk
"# " " "
"
œ œÊœ œ œ ¸)Š‹ Š ‹ Š‹
nn
nn
†
kkkk ÈÈ
È
442
12 9 33
50. and cos cos 0.96 radnijk nk
"#
" "
œ œ Ê œ œ ¸)Š‹ Š‹
nn
nn
†
kkkk ÈÈ
1
3 1
51. 2 2 and 2 cos cos cos 0.82 radn i jk n i jk
"# " " "
œ œÊœ œ œ ¸)Š‹ Š ‹ Š‹
nn
nn
†
kkkk ÈÈ È
241 5
9 6 3 6
52. 4 3 and 3 2 6 cos cos cos 0.73 radnjknijk
"# " " "
œ œ Êœ œ œ ¸)Š‹ Š ‹ ˆ‰
nn
nn
†
kkkk ÈÈ
35
818 26
25 49
53. 2x y 3z 6 2(1 t) (3t) 3(1 t) 6 2t 5 6 t x , y and z œÊ œÊœÊœÊœ œ œ
""
####
33
is the pointÊßß
ˆ‰
33
###
"
54. 6x 3y 4z 12 6(2) 3(3 2t) 4( 2 2t) 12 14t 29 12 t x 2, y 3 , œÊ œ Ê œÊœ Êœ œ
41 41
14 7
and z 2 2 is the pointœ Ê ß ß
41 20 27
777
ˆ‰
55. x y z 2 (1 2t) (1 5t) (3t) 2 10t 2 2 t 0 x 1, y 1 and z 0œÊ œÊ œÊœÊœ œ œ
(1 1 0) is the pointÊßß
56. 2x 3z 7 2( 1 3t) 3(5t) 7 9t 2 7 t 1 x 1 3, y 2 and z 5 œ Ê œ Êœ ÊœÊ œ œ œ
( 4 2 5) is the pointÊ ß ß
57. and , the direction of the desired line; (1 1 1)
111
110
nijk nij nn ij
ijk
"#"#
œ œ Ê ‚ œ œ ßß
ââ
ââ
ââ
ââ
ââ
ââ
is on both planes the desired line is x 1 t, y 1 t, z 1Êœœœ
58. 3 6 2 and 2 14 2 15 , the direction of the
362
21 2
nijknij2knn ijk
ij k
"#"#
œ œ Ê ‚ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
desired line; (1 0 0) is on both planes the desired line is x 1 14t, y 2t, z 15tßß Ê œ œ œ
59. 2 4 and 2 6 3 , the direction of the
124
11 2
nijk nijk nn jk
ij k
"#"#
œ œ Ê ‚ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
desired line; (4 3 1) is on both planes the desired line is x 4, y 3 6t, z 1 3tßß Ê œ œ œ
60. 5 2 and 4 5 10 25 20 , the direction of the
520
04 5
nijnjknn ijk
ij k
"# "#
œ œÊ‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
desired line; (1 3 1) is on both planes the desired line is x 1 10t, y 3 25t, z 1 20tß ß Ê œ œ œ
61. L1 & L2: x 3 2t 1 4s and y 1 4t 1 2s
2t 4s 2 2t 4s 2
4t 2s 2 2t s 1
œ œ œ œ Ê Ê
œ œ
œ œ
œœ
3s 3 s 1 and t 1 on L1, z 1 and on L2, z 1 L1 and L2 intersect at (5 3 1).Ê œ Ê œ œ Ê œ œ Ê ß ß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
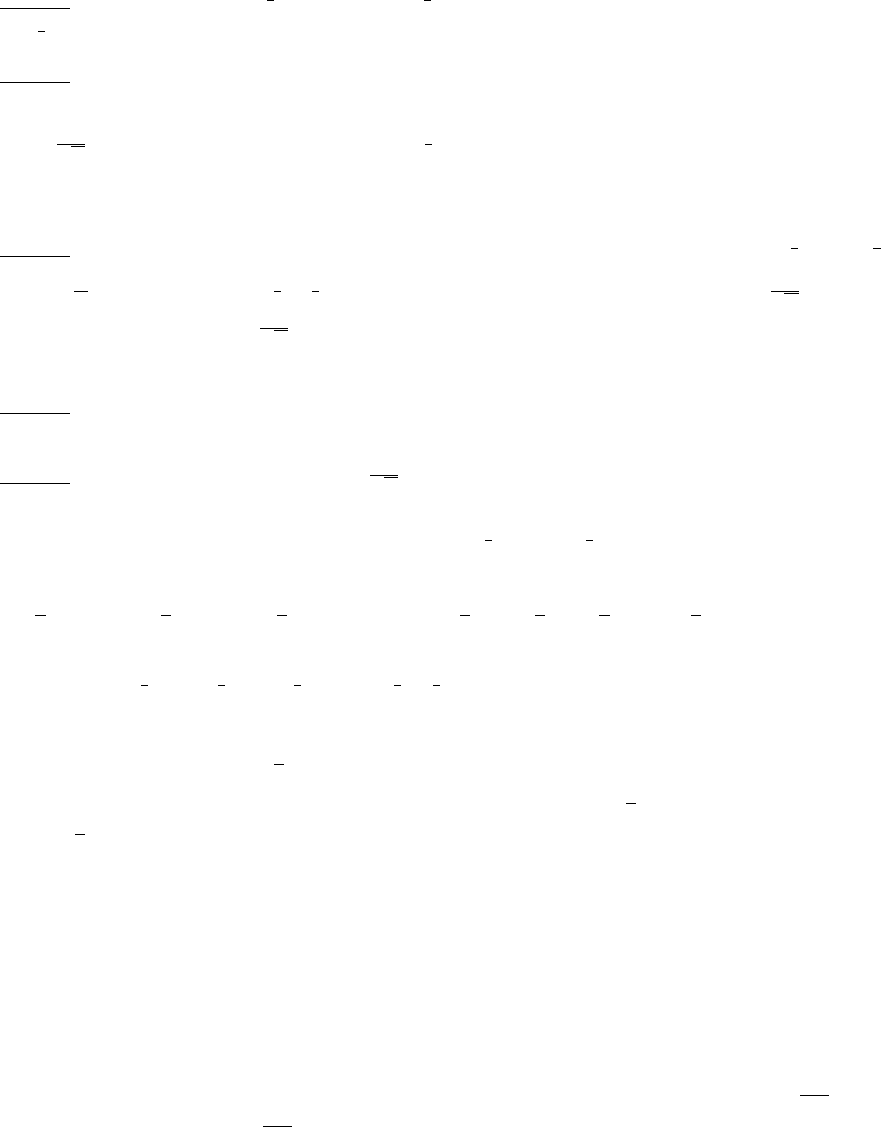
Section 12.5 Lines and Planes in Space 803
L2 & L3: The direction of L2 is (4 2 4 ) (2 2 ) which is the same as the direction
""
63
ijk ijk œ
(2 2 ) of L3; hence L2 and L3 are parallel.
"
3ij k
L1 & L3: x 3 2t 3 2r and y 1 4t 2 r 3t 3
2t 2r 0 t r 0
4t r 3 4t r 3
œ œ œ œÊ Ê Ê œ
œ œ
œ œ
œœ
t 1 and r 1 on L1, z 2 while on L3, z 0 L1 and L2 do not intersect. The direction of L1Êœ œ Ê œ œ Ê
is (2 4 ) while the direction of L3 is (2 2 ) and neither is a multiple of the other; hence
""
È21 3
ijk ijk
L1 and L3 are skew.
62. L1 & L2: x 1 2t 2 s and y 1 t 3s 5s 3 s and t on L1,
2t s 1
t3s1
œ œ œœ Ê Ê œ Ê œ œ Ê
œ
œ
œ34
55
z while on L2, z 1 L1 and L2 do not intersect. The direction of L1 is (2 3 )œœœÊ
12 3 2
555 14
"
Èij k
while the direction of L2 is ( 3 ) and neither is a multiple of the other; hence, L1 and L2 are
"
È11 ijk
skew.
L2 & L3: x 2 s 5 2r and y 3s 1 r 5s 5 s 1 and r 2 on L2,
s2r 3
3s r 1
œœ œ œÊ Ê œ Ê œ œÊ
œ
œ
œ
z 2 and on L3, z 2 L2 and L3 intersect at (1 3 2).œœÊ ßß
L1 & L3: L1 and L3 have the same direction (2 3 ); hence L1 and L3 are parallel.
"
È14 ij k
63. x 2 2t, y 4 t, z 7 3t; x 2 t, y 2 t, z 1 tœ œ œ œ œ œ
"
##
3
64. 1(x 4) 2(y 1) 1(z 5) 0 x 4 2y 2 z 5 0 x 2y z 7; œÊ œÊ œ
2 (x 3) 2 2 (y 2) 2 (z 0) 0 2x 2 2y 2z 7 2 œÊ œ
ÈÈÈ ÈÈÈÈ
65. x 0 t , y , z ; y 0 t 1, x 1, z 3 ( 1 0 3); z 0œ Ê œ œ œ Ê !ß ß œ Ê œ œ œ Ê ß ß œ
"" "
### ##
33
ˆ‰
t 0, x 1, y 1 (1 1 0)ÊœœœÊßß
66. The line contains (0 0 3) and 3 1 3 because the projection of the line onto the xy-plane contains the originßß ßß
Š‹
È
and intersects the positive x-axis at a 30° angle. The direction of the line is 3 0 the line in question
Èij k Ê
is x 3t, y t, z 3.œœœ
È
67. With substitution of the line into the plane we have 2(1 2t) (2 5t) ( 3t) 8 2 4t 2 5t 3t 8œÊœ
4t 4 8 t 1 the point ( 1 7 3) is contained in both the line and plane, so they are not parallel.Ê œÊœÊ ßß
68. The planes are parallel when either vector A B C or A B C is a multiple of the other or
""" ###
ijk ijk
when (A B C ) (A B C 0. The planes are perpendicular when their normals arekk
""" ###
ijk ijk ‚ œ
perpendicular, or(A B C ) (A B C ) 0.
""" ###
ijk ijk Ϡ
69. There are many possible answers. One is found as follows: eliminate t to get t x 1 2 yœœœ
z3
#
x 1 2 y and 2 y x y 3 and 2y z 7 are two such planes.Ê œ œ Ê œ œ
z3
#
70. Since the plane passes through the origin, its general equation is of the form Ax By Cz 0. Since it meetsœ
the plane M at a right angle, their normal vectors are perpendicular 2A 3B C 0. One choice satisfyingʜ
this equation is A 1, B 1 and C 1 x y z 0. Any plane Ax By Cz 0 with 2A 3B C 0œ œ œÊœ œ œ
will pass through the origin and be perpendicular to M.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
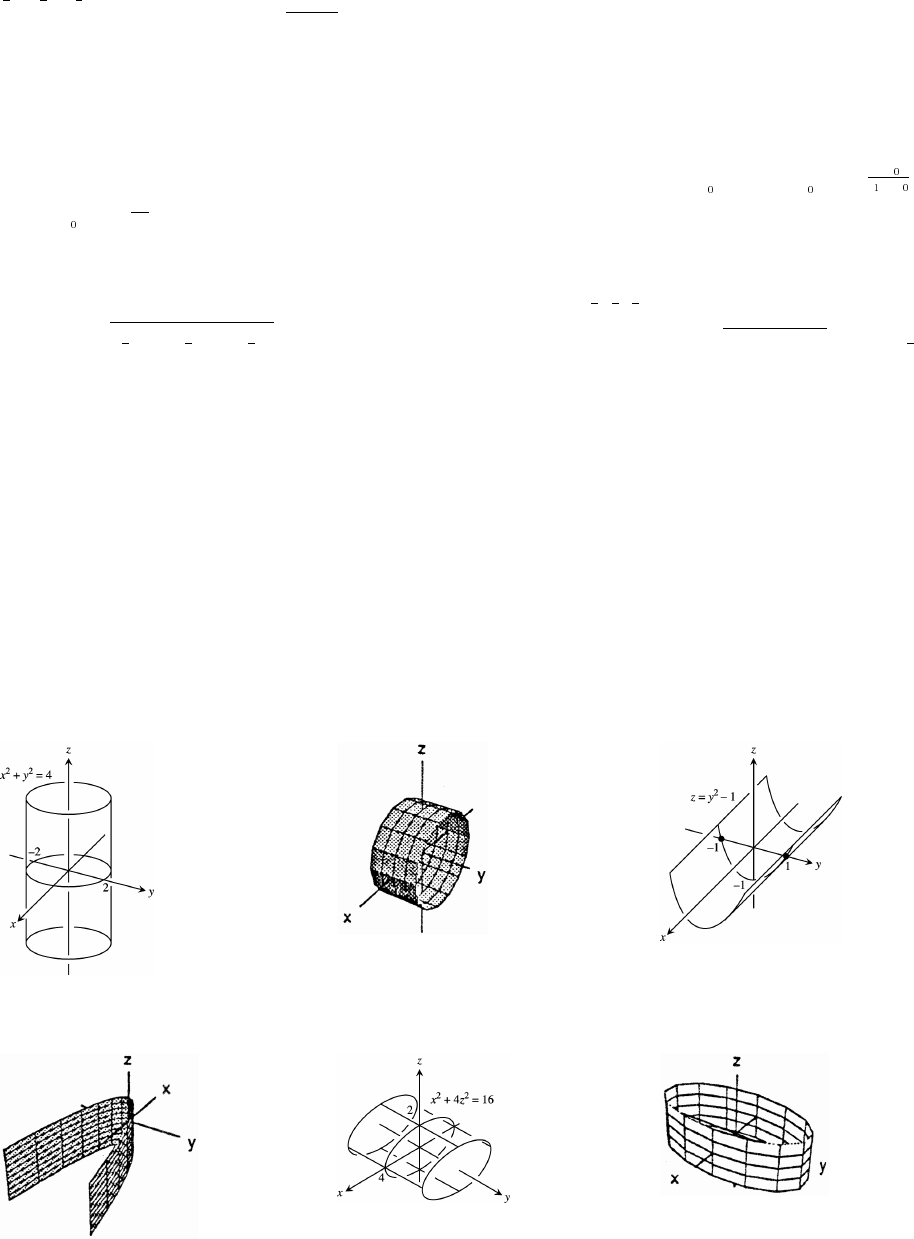
804 Chapter 12 Vectors and the Geometry of Space
71. The points (a 0 0), (0 b 0) and (0 0 c) are the x, y, and z intercepts of the plane. Since a, b, and c are allßß ßß ßß
nonzero, the plane must intersect all three coordinate axes and cannot pass through the origin. Thus,
1 describes all planes except those through the origin or parallel to a coordinate axis.
xz
abc
y
œ
72. Yes. If and are nonzero vectors parallel to the lines, then is perpendicular to the lines.vv vv0
"# "#
‚Á
73. (a) EP cEP x y z c (x x ) y z x c(x x ), y cy and z cz ,
ÄÄ
œÊœÊœœ œ
"! "!"" !"! " "
ijk i j kcd
where c is a positive real number
(b) At x 0 c 1 y y and z z ; at x x x 0, y 0, z 0; lim c lim
""""!!
œÊœÊœ œ œ Ê œ œ œ œ
xxÄ_ Ä_
x
xx
lim 1 c 1 so that y y and z zœœÊÄ ÄÄ
xÄ_
"
""
1
74. The plane which contains the triangular plane is x y z 2. The line containing the endpoints of the lineœ
segment is x 1 t, y 2t, z 2t. The plane and the line intersect at . The visible section of the lineœ œ œ ßß
ˆ‰
222
333
segment is 1 unit in length. The length of the line segment is 1 2 2 3 of
Ɉ‰ ˆ‰ ˆ‰ È
"### ###
333 3
22 2
œ œÊ
the line segment is hidden from view.
12.6 CYLINDERS AND QUADRIC SURFACES
1. d, ellipsoid 2. i, hyperboloid 3. a, cylinder
4. g, cone 5. l, hyperbolic paraboloid 6. e, paraboloid
7. b, cylinder 8. j, hyperboloid 9. k, hyperbolic paraboloid
10. f, paraboloid 11. h, cone 12. c, ellipsoid
13. x y 4 14. x z 4 15. z y 1
## ## #
œ œ œ
16. x y 17. x 4z 16 18. 4x y 36œœœ
#####
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
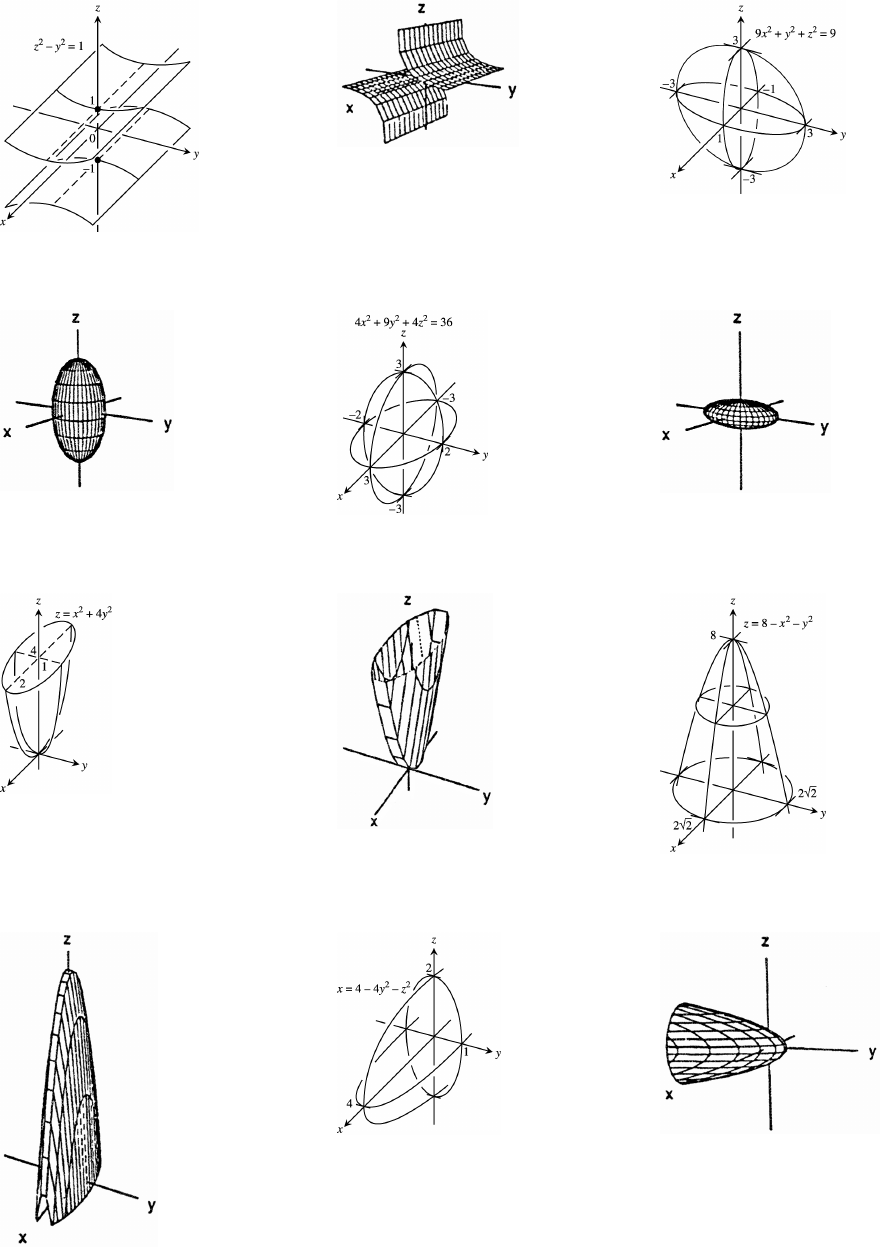
Section 12.6 Cylinders and Quadric Surfaces 805
19. z y 1 20. yz 1 21. 9x y z 9
## ###
œ œ œ
22. 4x 4y z 16 23. 4x 9y 4z 36 24. 9x 4y 36z 36
### ### ## #
œ œ œ
25. x 4y z 26. z x 9y 27. z 8 x y
## ## ##
œ œ œ
28. z 18 x 9y 29. x 4 4y z 30. y 1 x zœ œ œ
# # ## ##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
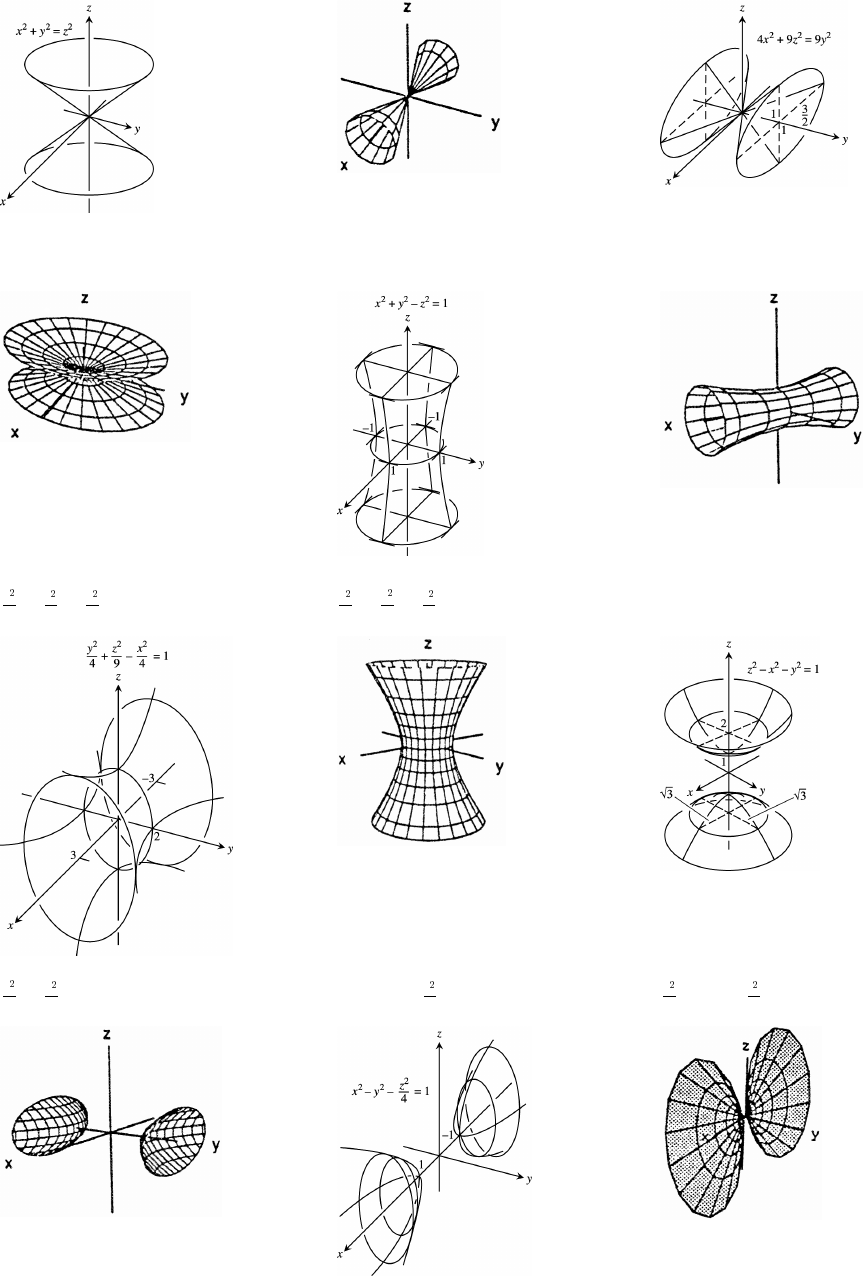
806 Chapter 12 Vectors and the Geometry of Space
31. x y z 32. y z x 33. 4x 9z 9y
### ## # # # #
œ œ œ
34. 9x 4y 36z 35. x y z 1 36. y z x 1
# # # # ## ###
œ œ œ
37. 1 38. 1 39. z x y 1
yy
494 449
zx x z
œ œ œ
###
40. z 1 41. x y 1 42. y 1
y
44 4 4 4
xzxz
œ œ œ
### #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 12.6 Cylinders and Quadric Surfaces 807
43. y x z 44. x y z 45. x y z 4
## # # ###
œ œœ œ
46. 4x 4y z 47. z 1 y x 48. y z 4
### ## ##
œ œ œ
49. y x z 50. z 4x 4y 4 51. 16x 4y 1œ œ œab
## ### ##
52. z x y 1 53. x y z 4 54. x 4 yœ œ œ
## ### #
55. x z y 56. z y 1 57. x z 1
## # # ##
œ œ œ
x
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
808 Chapter 12 Vectors and the Geometry of Space
58. 4x 4y z 4 59. 16y 9z 4x 60. z x y 1
### ## # ##
œ œ œ
61. 9x 4y z 36 62. 4x 9z y 63. x y 16z 16
### ### ## #
œ œ œ
64. z 4y 9 65. z x y 66. y x z 1
# # ## ###
œ œ œab
67. x 4y 1 68. z 4x y 4 69. 4y z 4x 4
## ## ###
œ œ œ
70. z 1 x 71. x y z 72. y z 1œ œ œ
### ##
x
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 12.6 Cylinders and Quadric Surfaces 809
73. yz 1 74. 36x 9y 4z 36 75. 9x 16y 4zœ œ œ
### # ##
76. 4z x y 4
###
œ
77. (a) If x 1 and z c, then x 1 A ab
##
œ œ œ Ê œÊ œ
yyy
49 4 9
z9cx
Š‹’“
9c
9
49 c
9
1
œœ1Š‹Š‹
ÈÈ ab
9c 29c
33 9
29c
1
(b) From part (a), each slice has the area , where 3 z 3. Thus V 2 9 z dz
29z
99
2
11
ab#
Ÿ Ÿ œ
'0
3ab
9 z dz 9z (27 9) 8œœœœ
44z4
9939
111
'0
3ab ’“
#$
!1
(c) 1 1 A
xz x
abc cc
yy
ac z bc z
œÊ œÊ œ
–—–— ÈÈ
ac z bc z
cc
1Š‹Š‹
V 2 c z dz c z c . Note that if r a b c,Êœ œ œ œ œœœ
'0
cc
1111ab 2ab z 2ab 2 4abc
cc3c33
ab ’“ˆ‰
## # $
!
then V , which is the volume of a sphere.œ4r
3
1
78. The ellipsoid has the form 1. To determine c we note that the point (0 r h) lies on the surface
xz
RRc
y
œ ßß
#
of the barrel. Thus, 1 c . We calculate the volume by the disk method:
rh hR
Rc Rr
œÊ œ
#
V y dz. Now, 1 y R 1 R 1 R zœœÊœœœ1'h
h######
y
Rc c hR h
zz Rr
zR r
Š‹’ “ Š‹
ab
V R z dz R z z 2 R h R r h 2Êœ œ œ œ 1111
'h
hh
h
’“’ “ Š‹Š‹ Š‹ ‘
ab
### $###
" "Rr Rr 2Rh rh
h3h 333
R h r h, the volume of the barrel. If r R, then V 2 R h which is the volume of a cylinder ofœ œ œ
42
33
11 1
## #
radius R and height 2h. If r 0 and h R, then V R which is the volume of a sphere.œœ œ
4
31$
79. We calculate the volume by the slicing method, taking slices parallel to the xy-plane. For fixed z, xz
ab c
y
œ
gives the ellipse 1. The area of this ellipse is a b (see Exercise 77a). Hence
xzzabz
y
ccc
Š‹ Š‹
za zb
cc
œ œ1ˆ‰ˆ‰
ÈÈ1
the volume is given by V dz . Now the area of the elliptic base when z h isœœœ œ
'0
hh
111abz abz abh
c2cc
’“
!
A , as determined previously. Thus, V h (base)(altitude), as claimed.œœœœ
111abh abh abh
ccc
""
##
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

810 Chapter 12 Vectors and the Geometry of Space
80. (a) For each fixed value of z, the hyperboloid 1 results in a cross-sectional ellipse
xz
abc
y
œ
1. The area of the cross-sectional ellipse (see Exercise 77a) is
xy
–—–—
ac z bc z
cc
œ
A(z) c z c z c z . The volume of the solid by the method of slices isœ œ1Š‹Š‹
ÈÈ ab
ab ab
cc c
## ## ##
1
V A(z) dz c z dz c z z c h h 3c hœœœœœ
''
00
hh h
11 1 1ab ab ab abh
cc3c33c
ab a b
‘ˆ‰
## # $ # $ # #
""
!
(b) A A(0) ab and A A(h) c h , from part (a) V 3c h
!## ##
œœ œœ Êœ 1h
11ab abh
c3c
ab a b
21 2 2ab c h (2A A)œœœ œ
11 1abh h abh c h h ab h
3c3c3c 3
Š‹Š‹
‘
ab
## !
1h
(c) A A c 4c h (A 4A A )
mmh
œœ œ Ê
ˆ‰ Š‹ab
hab h ab h
c44c 6#
###
!
11
ab 4c h c h c 4c h c h 6c 2hœ œ œ
hab ab abh abh
6c c 6c 6c
‘
ababa ba b111 1 1
## ## # #### # #
3c h V from part (a)œœ
1abh
3c ab
##
81. y y , a parabola in the plane y y vertex when 0 or c 0 x 0œÊœ œÊ œ œœÊœ
""
z x dz dz 2x
cb a dx dx a
y1
Vertex 0 y ; writing the parabola as x z we see that 4p pÊßß œ œÊœ
Š‹
"#
cy a y
bcbc4c
aaa
1 1
Focus 0 yÊßß
Š‹
"cy
b4c
a
1
82. The curve has the general form Ax By Dxy Gx Hy K 0 which is the same form as Eq. (1) in
##
œ
Section 10.3 for a conic section (including the degenerate cases) in the xy-plane.
83. No, it is not mere coincidence. A plane parallel to one of the coordinate planes will set one of the variables
x, y, or z equal to a constant in the general equation Ax By Cz Dxy Eyz Fxz Gx Hy Jz K
###
0 for a quadric surface. The resulting equation then has the general form for a conic in that parallel plane.œ
For example, setting y y results in the equation Ax Cz D x E z Fxz Gx Jz K 0 whereœœ
"##ww w
D Dy , E Ey , and K K By Hy , which is the general form of a conic section in the plane y y
ww w #
"" " "
œœ œ œ
1
by Section 10.3.
84. The trace will be a conic section. To see why, solve the plane's equation Ax By Cz 0 for one of theœ
variables in terms of the other two and substitute into the equation Ax By Cz K 0. The result
###
áœ
will be a second degree equation in the remaining two variables. By Section 10.3, this equation will represent a
conic section. (See also the discussion in Exercises 82 and 83.)
85. z y 86. z 1 yœœ
# #
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 12.6 Cylinders and Quadric Surfaces 811
87. z x yœ
##
88. z x 2yœ
##
(a) (b)
(c) (d)
89-94. Example CAS commands:
:Maple
with( plots );
eq := x^2/9 + y^2/36 = 1 - z^2/25;
implicitplot3d( eq, x=-3..3, y=-6..6, z=-5..5, scaling=constrained,
shading=zhue, axes=boxed, title="#89 (Section 12.6)" );
: (functions and domains may vary):Mathematica
In the following chapter, you will consider contours or level curves for surfaces in three dimensions. For the purposes of
plotting the functions of two variables expressed implicitly in this section, we will call upon the function .ContourPlot3D
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
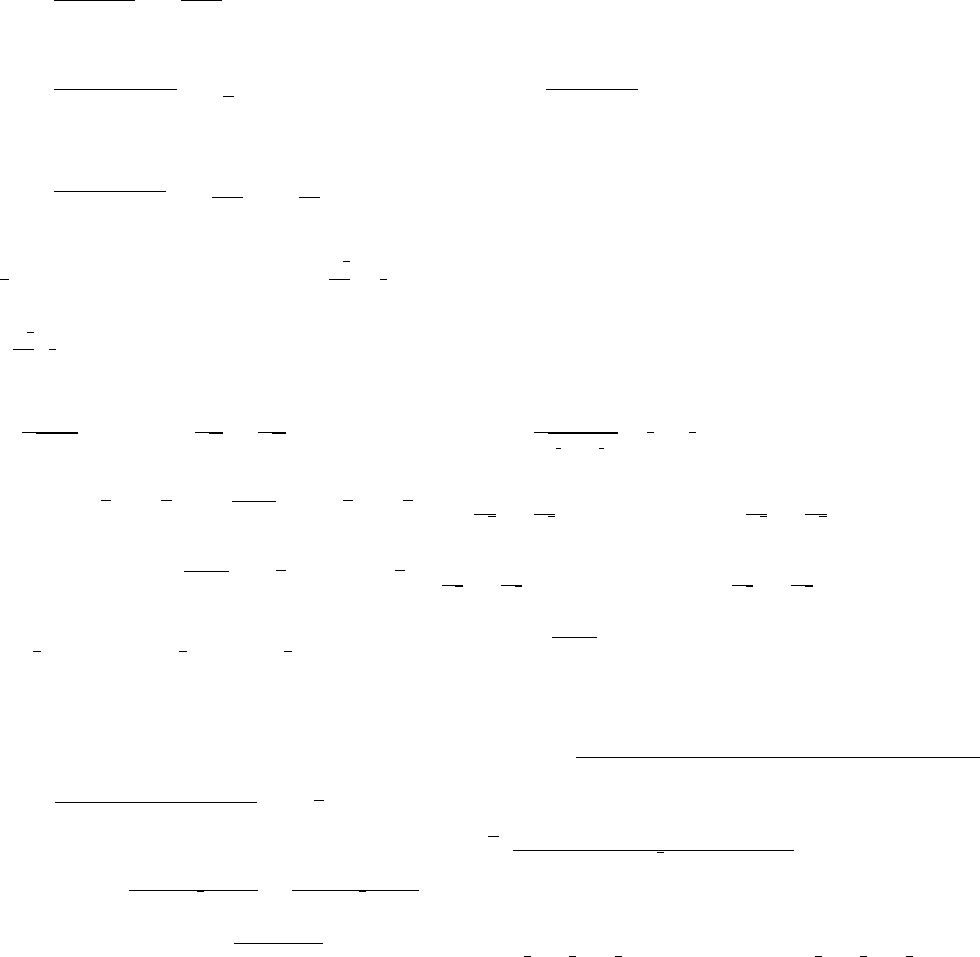
812 Chapter 12 Vectors and the Geometry of Space
To insert the stated function, write all terms on the same side of the equal sign and the default contour equating that
expression to zero will be plotted.
This built-in function requires the loading of a special graphics package.
<<Graphics`ContourPlot3D`
Clear[x, y, z]
ContourPlot3D[x /9 y /16 z /2 1, {x, 9, 9}, {y, 12, 12}, {z, 5, 5},
22 2
Axes True, AxesLabel {x, y, z}, Boxed False,ÄÄÄ
PlotLabel "Elliptic Hyperboloid of Two Sheets"]Ä
Your identification of the plot may or may not be able to be done without considering the graph.
CHAPTER 12 PRACTICE EXERCISES
1. (a) 3 3, 4 4 2, 5 9 8, 12 20 17, 32
¡¡ ¡ ¡
œ œ
(b) 17 32 1313
ÈÈ
22
œ
2. (a) 3 2, 4 5 1, 1 3. (a) 2 3 , 2 4 6, 8
¡¡ ¡¡
ab ab œ œ
(b) 1 1 2 (b) 6 8 10
ÉÉ
abab ab
È
œ œ
22 2
2
4. (a) 5 2 , 5 5 10, 25
¡¡
ab a bœ
(b) 10 25 725 5 29
ÉabÈÈ
22
œ œ
5. radians below the negative x-axis: , [assuming counterclockwise].
1
6
3
¢£
È
##
"
6. ,
¢£
È3
##
"
7. 2 4 8. 5 3 4
Š‹ Š ‹
ab a b
ˆ‰
182 134
41 17 17 55
ÈÈÈ Éˆ ‰ ˆ ‰
22 34
55
22
ij i j i j i jœ œ
9. length 2 2 2 2 2, 2 2 2 the direction is œœœ œ Ê
¹¹ Š‹
ÈÈ ÈÈ
È
ij ij ij ij
"" ""
ÈÈ ÈÈ
22 22
10. length 1 1 2, 2 the direction is œ œ œ œ Ê kk
ÈÈÈ
Š‹
ij ij i j i j
"" ""
ÈÈ ÈÈ
22 22
11. t ( 2 sin ) 2 cos 2 ; length 2 4 0 2; 2 2 the direction isœÊœ œ œ œ œ œÊ
111
222
viji i ii i
ˆ‰ kk ab
È
12. t ln 2 e cos ln 2 e sin ln 2 e sin ln 2 e cos ln 2œÊœ vij
ˆ‰ˆ‰
ab ab ab ab
ln 2 ln 2 ln 2 ln 2
2 cos ln 2 2 sin ln 2 2 sin ln 2 2 cos ln 2 2 cos ln 2 sin ln 2 sin ln 2 cos ln 2
œ œ
ababc dab ab ab ab ababab ab ab ab
ij
ij
length 2 2 cos ln 2 sin ln 2 cos ln 2 sin ln 2
cos ln 2 sin ln 2 sin ln 2 cos ln 2
œœ
k kababc d ab ab ab ab
ababab ab ab ab É
ij 22
2 2cos ln 2 2sin ln 2 2 2;œœ
Èab abÈ
22
222
cos ln 2 sin ln 2 sin ln 2 cos ln 2
cd
ababab ab ab ab ÈŠ‹
œ
ij
ababab ab ab ab
È
cos ln 2 sin ln 2 sin ln 2 cos ln 2
2
ij
directionʜ
ababab ab ab ab
ÈÈ
cos ln 2 sin ln 2 sin ln 2 cos ln 2
22
ij
13. length 2 3 6 4 9 36 7, 2 3 6 7 the direction is œ œ œ œ Ê kk
Ȉ‰
ijk ijk i j k i j k
236 236
777 777
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
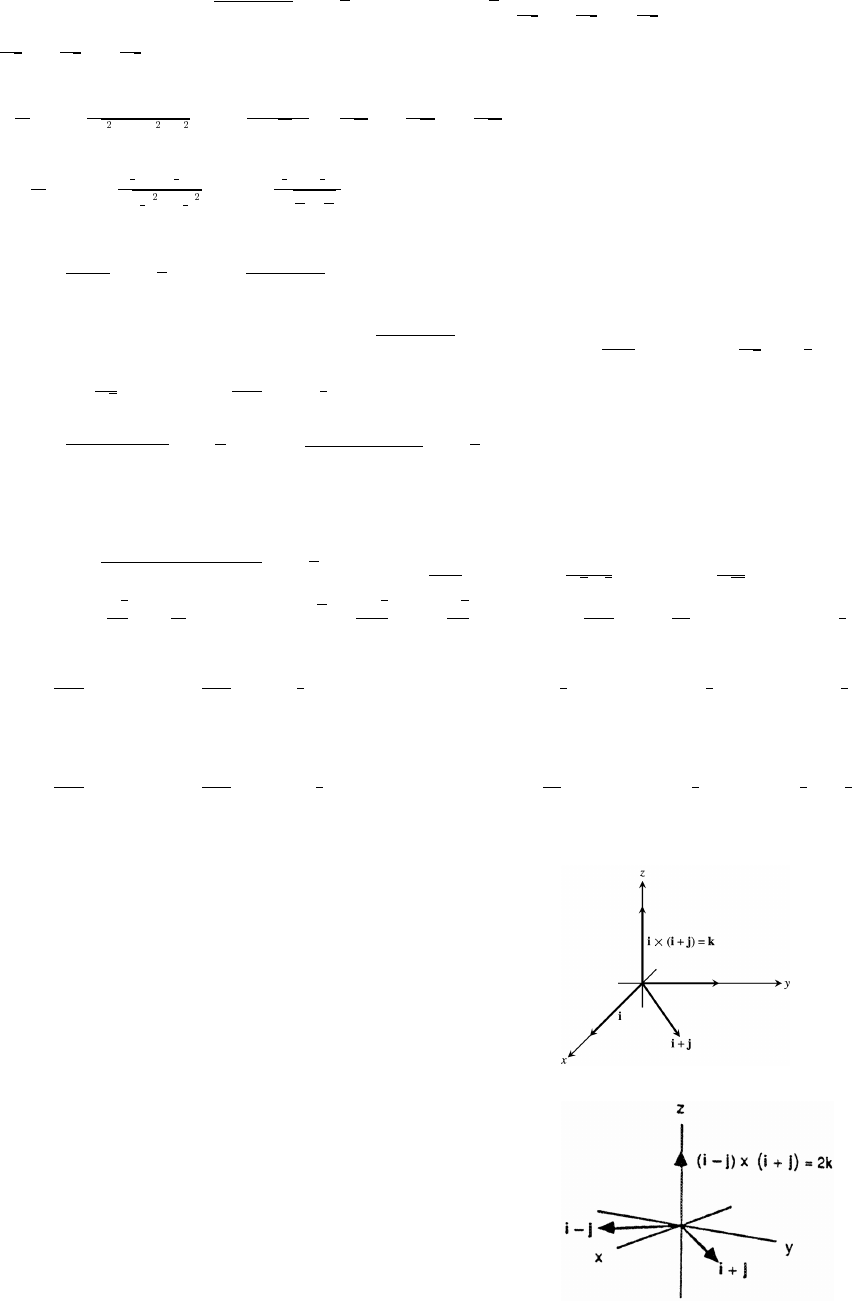
Chapter 12 Practice Exercises 813
14. length 2 1 4 1 6, 2 6 the direction isœ œ œ œ Êkk
ÈÈÈ
Š‹
ijk ijk i j k
121
666
ÈÈÈ
121
666
ÈÈÈ
ijk
15. 2 2 2
v
v
ij k ij k
kk ÈÈÈÈÈ
œ œ œ††
44 44
4(1)4 33 33 33 33
828
ijk
16. 5 5 5 3 4œ œ œ
v
v
ik ik
kk ˆ‰ ˆ‰ ˆ‰ ˆ‰
Ɉ ‰ ˆ ‰ É
††
34 34
55 55
34
55
916
25 25
ik
17. 1 1 2, 4 1 4 3, 3, 3, 2 2 ,
11 0
21 2
kk kk
ÈÈ
Èââ
ââ
ââ
ââ
ââ
ââ
vu vuuvvu ijk
ij k
œœ œœœœ‚œ œ
††
( ) 2 2 , 4 4 1 3, cos cos ,uv vu i jkvu‚œ‚ œ ‚œ œ œ œ œkk
ÈŠ‹ Š‹
)" " "vu
vu
†
kkkk È
4
2
1
cos , proj ( )kkuuvij)œœ
33
22
Èkkkk
vœŠ‹
vu
vv
†
18. 1 1 2 6, ( 1) ( 1) 2, (1)( 1) (1)(0) (2)( 1) 3,kk kk
ÈÈ
ÈÈ
vu vuœœ œœ œ œ
### # # †
3, , ( ) ,
112
10 1
uv v u i j ku v v u i j k
ijk
†œ ‚ œ œ ‚ œ ‚ œ
ââ
ââ
ââ
ââ
ââ
ââ
( 1) ( 1) 1 3, cos cos coskk
ÈÈŠ‹ Š ‹ Š‹
vu‚œ œ œ œ œ
### " " "
)vu
vu
†
kkkk ÈÈÈ
33
6 2 12
cos , cos 2 , proj ( 2 ) ( )œ œ œ † œ œ œ
"
# #
"
Š‹ Š‹
kk È
ÈÈÈ
kkkk
336
5 3
622 6
1uuvijkijk)vœŠ‹
vu
vv
†
19. (2 ) ( 5 ) (2 ) (2 ) (5 11 ),u v u v ijk ij k ijk ijk ij kœŠ‹
vu vu
vv vv
††
kkkk kkkk
œ œ
’“Š‹ ‘
444
3333
"
where 8 and 6vu vv††œœ
20. ( 2 ) ( ) ( 2 ) ( 2 ) ,uvuvijijkijijijkœŠ‹
vu vu
vv vv
††
kkkk kkkk
œ œ
’“Š‹ ‘ˆ‰ˆ‰
11145
33333
where 1 and 3vu vv††œ œ
21. 100
110
uv k
ijk
‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
22. 2
110
110
uv k
ijk
‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

814 Chapter 12 Vectors and the Geometry of Space
23. Let v v v and w w w . Then 2 (v v v ) 2(w w w )vijkw ijk vw ijk ijkœ œ œ
"#$ " # $ "#$ " # $
##
kkk k
(v 2w ) (v 2w ) (v 2w ) (v 2w ) (v 2w ) (v 2w )œ œ kk
ˆ‰
È
"" ## $$ "" ## $$
####
#
ijk
v v v 4(vw vw vw) 4 w w w 4 4 œ œ ab a bkk kk
### # # #
"" ## $$
##
313
vvww†
4 cos 4 4 4(2)(3) cos 36 40 24 40 12 28 2 28œ œ œ œœ Ê œkk kkkk kk k k
ˆ‰ ˆ‰ È
vvw w vw
## "
#
)1
3
27œÈ
24. and are parallel when (4a 40) (20 2a) (0)
24 5
48a
uv uv0 0 i j k0
ijk
‚œ Ê œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ
4a 40 0 and 20 2a 0 a 10Êœ œÊœ
25. (a) area abs 2 3 4 9 1 14
11 1
21 1
œ‚œ œ œ œ
kk k k
ââ
ââ
ââ
ââ
ââ
ââ ÈÈ
uv i jk
ij k
(b) volume ( ) 1(3 2) 1( 1 6) 1( 4 1) 1
11 1
211
123
œ‚œ œœ
uv w†
ââ
ââ
ââ
ââ
ââ
ââ
26. (a) area abs 1
110
010
œ‚œ œ œkk kk
ââ
ââ
ââ
ââ
ââ
ââ
uv k
ijk
(b) volume ( ) 1(1 0) 1(0 0) 0 1
110
010
111
œ ‚ œ œ œuv w†
ââ
ââ
ââ
ââ
ââ
ââ
27. The desired vector is or since is perpendicular to both and and, therefore, also parallel tonv vn nv n v‚‚ ‚
the plane.
28. If a 0 and b 0, then the line by c and are parallel. If a 0 and b 0, then the line ax c and areœÁ œ Áœ œij
parallel. If a and b are both 0, then ax by c contains the points and 0 the vectorÁœ ß!ßÊ
ˆ‰ ˆ‰
cc
ab
ab c(b a ) and the line are parallel. Therefore, the vector b a is parallel to the line
ˆ‰
cc
ab
i j ij ijœ
ax by c in every case.œ
29. The line L passes through the point P(0 0 1) parallel to . With PS 2 2 andßß œ œ
Ä
vijk ijk
PS (2 1) ( 1 2) (2 2) 3 4 , we find the distance
221
111
Ä‚œ œ œ
vijkijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
d.œœ œœ
¹¹
kk ÈÈÈ
ÈÈ
PS 1916
111
26 78
33
Ä‚
v
v
30. The line L passes through the point P(2 2 0) parallel to . With PS 2 2 andßß œ œ
Ä
vijk i jk
PS (2 1) (1 2) ( 2 2) 3 4 , we find the distance
221
111
Ä‚œ œ œ
vijkijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
d.œœ œœ
¹¹
kk ÈÈÈ
ÈÈ
PS 1916
111
26 78
33
Ä‚
v
v
31. Parametric equations for the line are x 1 3t, y 2, z 3 7t.œ œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
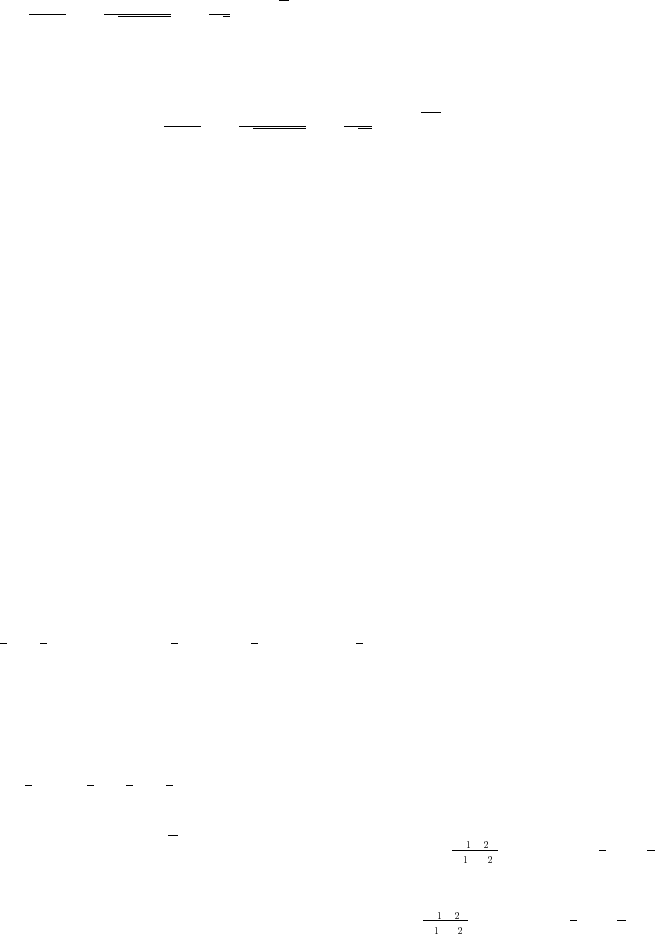
Chapter 12 Practice Exercises 815
32. The line is parallel to PQ 0 and contains the point P(1 2 0) parametric equations are
Äœ ßß Êijk
x 1, y 2 t, z t for 0 t 1.œœœ ŸŸ
33. The point P(4 0 0) lies on the plane x y 4, and PS (6 4) 0 ( 6 0) 2 6 with ßß œ œ œ œ
Äij k ik nij
d2.Êœ œ œ œ
¹¹
kk ÈÈ
n
n
†PS 200 2
110 2
Ä
¹¹ È
34. The point P(0 0 2) lies on the plane 2x 3y z 2, and PS (3 0) (0 0) (10 2) 3 8 withßß œ œ œ
Äij kik
2 3 d 14.nijkœ Êœ œ œ œ
¹¹
kk ÈÈ
n
n
†PS 608 14
491 14
Ä
¹¹ È
35. P(3 2 1) and 2 (2)(x 3) (1)(y ( 2)) (1)(z 1) 0 2x y z 5ßß œ Ê œ Ê œnijk
36. P( 1 6 0) and 2 3 (1)(x ( 1)) ( 2)(y 6) (3)(z 0) 0 x 2y 3z 13ßß œ Ê œÊœni j k
37. P(1 1 2), Q(2 1 3) and R( 1 2 1) PQ 2 , PR 2 3 3 and PQ PRß ß ß ß ß ß Ê œ œ ‚
ÄÄ
ÄÄ
ijk ijk
9 7 is normal to the plane ( 9)(x 1) (1)(y 1) (7)(z 2) 0
121
23 3
œœ Êœ
ââ
ââ
ââ
ââ
ââ
ââ
ijk
ij k
9xy7z 4Ê œ
38. P(1 0 0), Q(0 1 0) and R(0 0 1) PQ , PR and PQ PRßß ßß ßß Ê œ œ ‚
ÄÄ
ÄÄ
ij ik
is normal to the plane (1)(x 1) (1)(y 0) (1)(z 0) 0
110
101
œ œ Ê œ
ââ
ââ
ââ
ââ
ââ
ââ
ijk
ijk
xyz 1Ê œ
39. 0 , since t , y and z when x 0; ( 0 3), since t 1, x 1 and z 3
ˆ‰
ß ß œ œ œ œ "ß ß œ œ œ
"""
## # # #
33
when y 0; (1 1 0), since t 0, x 1 and y 1 when z 0œßß œœ œ œ
40. x 2t, y t, z t represents a line containing the origin and perpendicular to the plane 2x y z 4; thisœ œ œ œ
line intersects the plane 3x 5y 2z 6 when t is the solution of 3(2t) 5( t) 2( t) 6 œ œ
t is the point of intersectionÊœ Ê ßß
2 422
3 333
ˆ‰
41. and 2 the desired angle is cos cosni nij k
"# " " "
#
œ œ Ê œ œ
ÈŠ‹ ˆ‰
nn
nn
†
kkkk 3
1
42. and the desired angle is cos cosnij njk
"# " " "
#
œ œ Ê œ œ
Š‹ ˆ‰
nn
nn
†
kkkk 3
1
43. The direction of the line is 5 3 . Since the point ( 5 3 0) is on
121
112
nn ijk
ijk
"#
‚œ œ ßß
ââ
ââ
ââ
ââ
ââ
ââ
both planes, the desired line is x 5 5t, y 3 t, z 3t.œ œ œ
44. The direction of the intersection is 6 9 12 3(2 3 4 ) and is the
12 2
521
nn ij k ijk
ij k
"#
‚ œ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
same as the direction of the given line.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
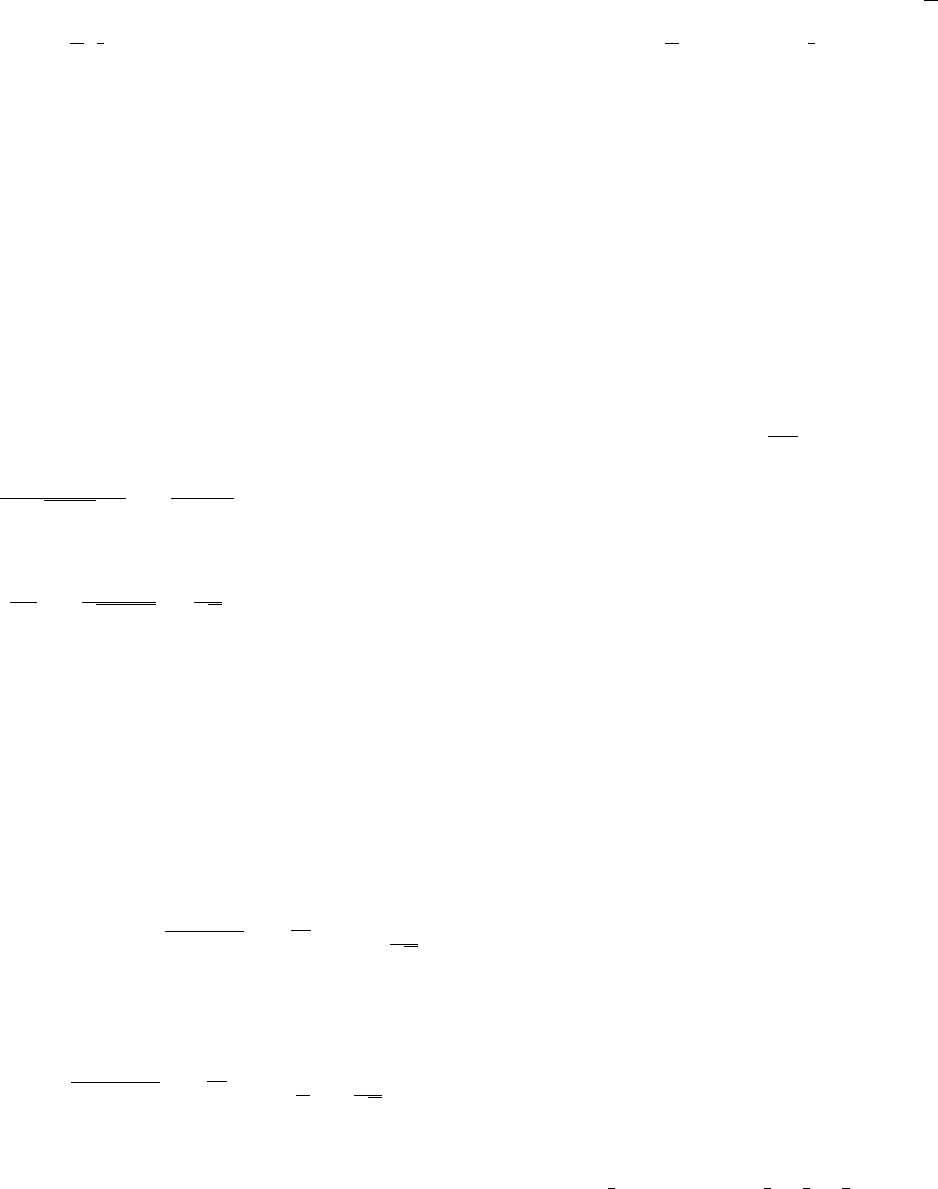
816 Chapter 12 Vectors and the Geometry of Space
45. (a) The corresponding normals are 3 and 2 2 and since niknijk nn
"# "#
œ' œ †
(3)(2) (0)(2) (6)( 1) 6 0 6 0, we have that the planes are orthogonalœ œœ
(b) The line of intersection is parallel to 12 15 6 . Now to find a point in
30 6
22 1
nn i jk
ij k
"#
‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
the intersection, solve 15x 12y 19 x 0 and y
3x 6z 1 3x 6z 1
2x 2y z 3 12x 12y 6z 18
œœ
œ œ
œ œ
Êʜʜœ
19
12
is a point on the line we seek. Therefore, the line is x 12t, y 15t and z 6t.Ê!ßß œ œ œ
ˆ‰
19 19
16 12 6#
" "
46. A vector in the direction of the plane's normal is 7 3 5 and P( 2 3) on
231
112
nuv i j k
ijk
œ‚œ œ "ßß
ââ
ââ
ââ
ââ
ââ
ââ
the plane 7(x 1) 3(y 2) 5(z 3) 0 7x 3y 5z 14.Ê œÊ œ
47. Yes; (2 4 ) (2 0 ) 2 2 4 1 1 0 0 the vector is orthogonal to the plane's normalvn i j k i j k† † †††œ œ œÊ
is parallel to the planeÊv
48. PP 0 represents the half-space of points lying on one side of the plane in the direction which the normal n n†!
Ä
points
49. A normal to the plane is AB AC 2 2 the distance is d
20 1
210
nijk
ij k
œ‚œ œÊ œ
ÄÄ
ââ
ââ
ââ
ââ
ââ
ââ ¹¹
AP
Ä
†n
n
3œœœ
¹¹
¸¸
(4)( 2 )
144
180
3
ij ijk#
†
È
50. P(0 0 0) lies on the plane 2x 3y 5z 0, and PS 2 2 3 with 2 3 5 ßß œ œ œ Ê
Äijk n ijk
dœœ œ
¹¹¹ ¹
n
n
†PS 4615 25
4925 38
Ä
kk ÈÈ
51. 2 is normal to the plane 0 3 3 3 3 is orthogonal
211
11 1
nijk nv ijk jk
ij k
œ Ê‚œ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
to and parallel to the planev
52. The vector is normal to the plane of and ( ) is orthogonal to and parallel to the plane of BC B CABC A B‚Ê‚‚
and :C
5 3 and ( ) 2 3
12 1 2 1 1
11 2 5 3 1
BC i jk A BC i jk
ij k i j k
‚œ œ ‚ ‚ œ œ
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
( ) 4 9 1 14 and ( 2 3 ) is the desired unit vector.Ê‚‚œ œ œ kk
ÈÈ
ABC u i jk
"
È14
53. A vector parallel to the line of intersection is 5 3
121
112
vn n ij k
ijk
œ‚œ œ
"#
ââ
ââ
ââ
ââ
ââ
ââ
25 1 9 35 2 (5 3 ) is the desired vector.Êœ œ Ê œ kk ÈÈŠ‹
vijk
v
vkk È2
35
54. The line containing (0 0 0) normal to the plane is represented by x 2t, y t, and z t. This lineßß œ œ œ
intersects the plane 3x 5y 2z 6 when 3(2t) 5( t) 2( t) 6 t the point is . œ œ Êœ Ê ßß
2 422
3 333
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
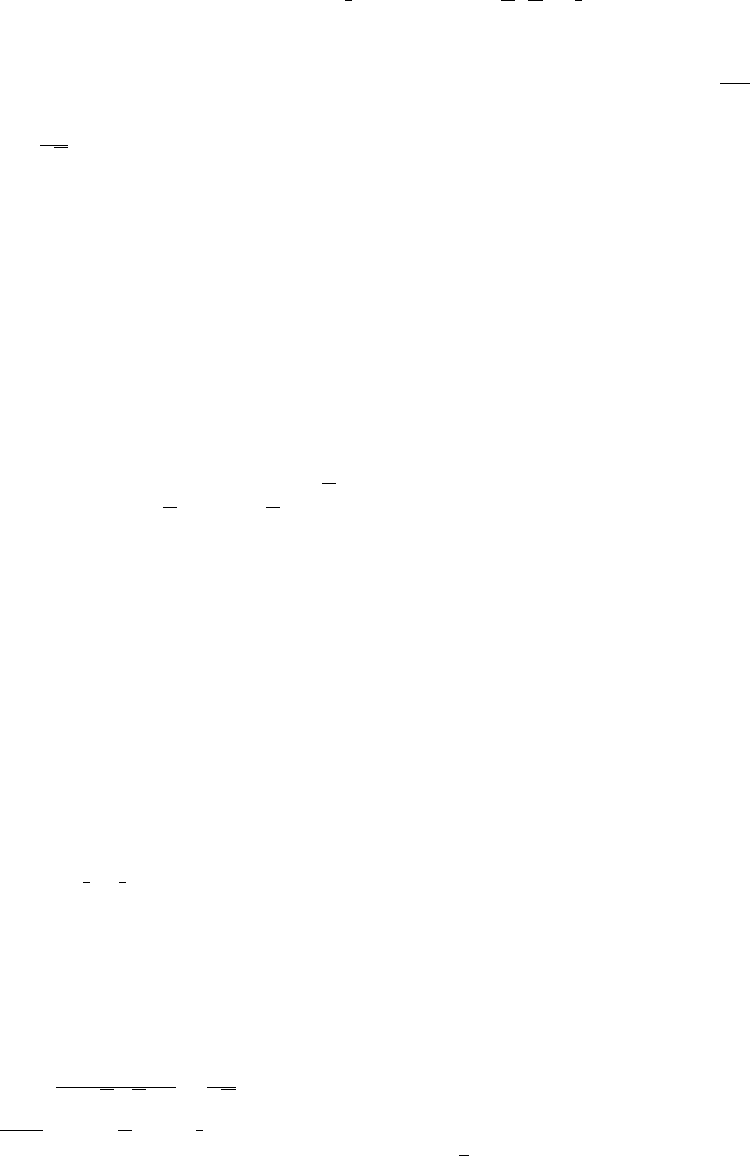
Chapter 12 Practice Exercises 817
55. The line is represented by x 3 2t, y 2 t, and z 1 2t. It meets the plane 2x y 2z 2 whenœ œ œ œ
2(3 2t) (2 t) 2( 2t) 2 t the point is . " œÊœ Ê ßß
811267
9999
ˆ‰
56. The direction of the intersection is 3 5 cos
21 1
11 2
vn n i jk
ij k
œ‚œ œÊœ
"# "
ââ
ââ
ââ
ââ
ââ
ââ Š‹
)vi
vi
†
kkkk
cos 59.5°œ¸
" Š‹
3
35
È
57. The intersection occurs when (3 2t) 3(2t) t 4 t 1 the point is (1 2 1). The required line œÊœÊ ßß
must be perpendicular to both the given line and to the normal, and hence is parallel to 22 1
13 1
ââ
ââ
ââ
ââ
ââ
ââ
ij k
5 3 4 the line is represented by x 1 5t, y 2 3t, and z 1 4t.œ Ê œ œ œ ijk
58. If P(a b c) is a point on the line of intersection, then P lies in both planes a 2b c 3 0 andßß Ê œ
2a b c 1 0 (a 2b c 3) k(2a b c 1) 0 for all k.œ Ê œ
59. The vector AB CD (2 7 2 ) is normal to the plane and A( 2 0 3) lies on the
324
0
ÄÄ
‚œ œ ßß
ââ
ââ
ââ
ââ
ââ
ââ
ij k
ijk
26 26
55
26
5
plane 2(x 2) 7(y 0) 2(z ( 3)) 0 2x 7y 2z 10 0 is an equation of the plane.ʜʜ
60. Yes; the line's direction vector is 2 3 5 which is parallel to the line and also parallel to the normalijk
4 6 10 to the plane the line is orthogonal to the plane. Êij k
61. The vector PQ PR 11 3 is normal to the plane.
213
301
Ä‚œ œ
Ä
ââ
ââ
ââ
ââ
ââ
ââ
ijk
ijk
(a) No, the plane is not orthogonal to PQ PR .
Ä‚Ä
(b) No, these equations represent a line, not a plane.
(c) No, the plane (x 2) 11(y 1) 3z 0 has normal 11 3 which is not parallel to PQ PR . œ ‚
ÄÄ
ijk
(d) No, this vector equation is equivalent to the equations 3y 3z 3, 3x 2z 6, and 3x 2y 4œ œ œ
x t, y t, z 1 t, which represents a line, not a plane.Êœ œ œ
42
33
(e) Yes, this is a plane containing the point R( 2 1 0) with normal PQ PR .ß ß ‚
ÄÄ
62. (a) The line through A and B is x 1 t, y t, z 1 5t; the line through C and D must be parallel andœ œ œ
is L : x 1 t, y 2 t, z 3 5t. The line through B and C is x 1, y 2 2s, z 3 4s; the line
"œ œ œ œ œ œ
through A and D must be parallel and is L : x 2, y 1 2s, z 4 4s. The lines L and L intersect
#"#
œœ œ
at D(2 1 8) where t 1 and s 1.ßß œ œ
(b) cos )œœ
(2 4 ) ( 5 )
20 27 15
3
jkijk†
ÈÈ È
(c) BC BC ( 2 ) where BA 5 and BC 2 4
Š‹
BA BC 18 9
BC BC 20 5
ÄÄ
ÄÄ
†
†
ÄÄ Ä Ä
œ œ œ œ jk ijk jk
(d) area (2 4 ) ( 5 ) 14 4 2 6 6œ‚ œ œkkkk
È
jk ijk ijk
(e) From part (d), 14 4 2 is normal to the plane 14(x 1) 4(y 0) 2(z 1) 0nijkœ Ê œ
7x 2y z 8.ʜ
(f) From part (d), 14 4 2 the area of the projection on the yz-plane is 14; the area of thenijk niœÊ œkk†
projection on the xy-plane is 4; and the area of the projection on the xy-plane is 2.kk kknj nk††œœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
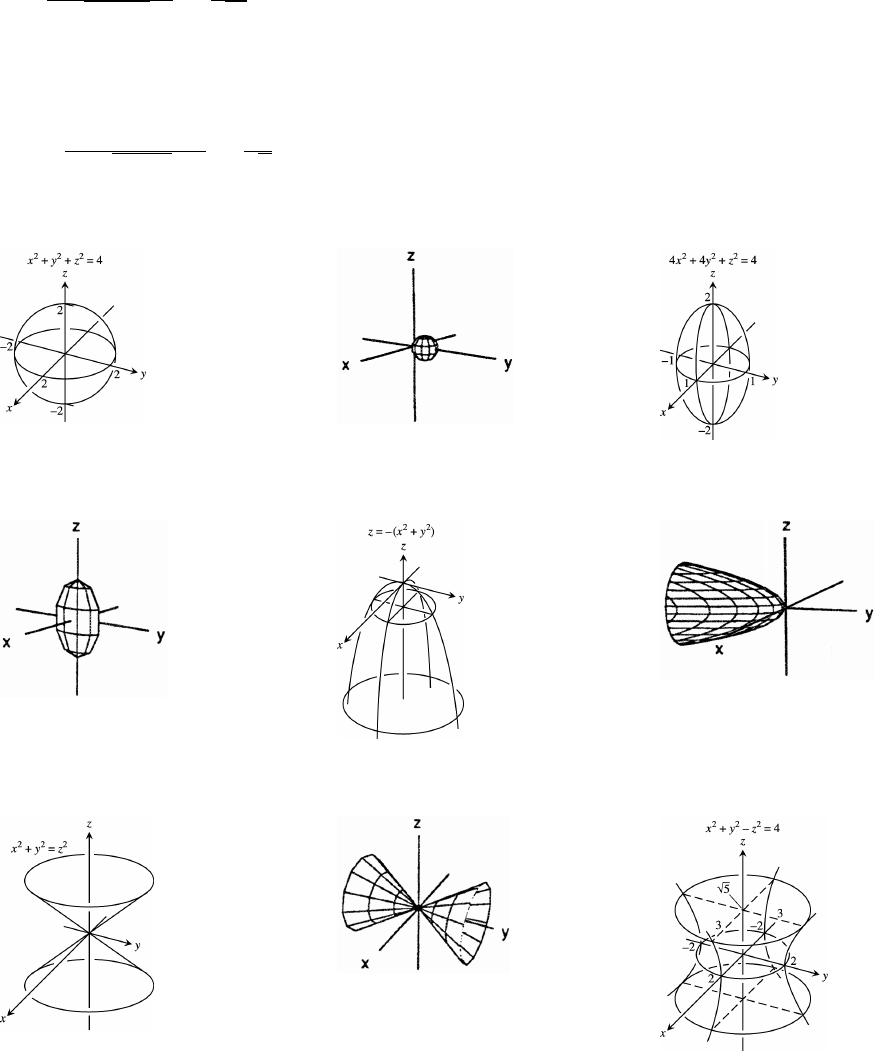
818 Chapter 12 Vectors and the Geometry of Space
63. AB 2 , CD 4 and AC 2 5 9 the distance is
21 1
14 1
ÄÄ Ä
œ œ œ Ê œ Ê
ijk i jk, ij n ij k
ijk
œ
ââ
ââ
ââ
ââ
ââ
ââ
dœœ
¹¹
(2 ) ( 5 9 )
25181
11
107
ij ij k
†
ÈÈ
64. AB 2 4 , CD 2 , and AC 3 3 7 3 2 the distance
24 1
112
ÄÄ Ä
œ œ œ Êœ œ Ê
ijk ijk ij n ijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
is d œœ
¹¹
(3 3)(7 3 2)
4994
12
62
ijijk†
ÈÈ
65. x y z 4 66. x (y 1) z 1 67. 4x 4y z 4
### # ## # ##
œ œ œ
68. 36x 9y 4z 36 69. z x y 70. y x z
### ## ##
œ œ œab ab
71. x y z 72. x z y 73. x y z 4
### ## # ###
œ œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
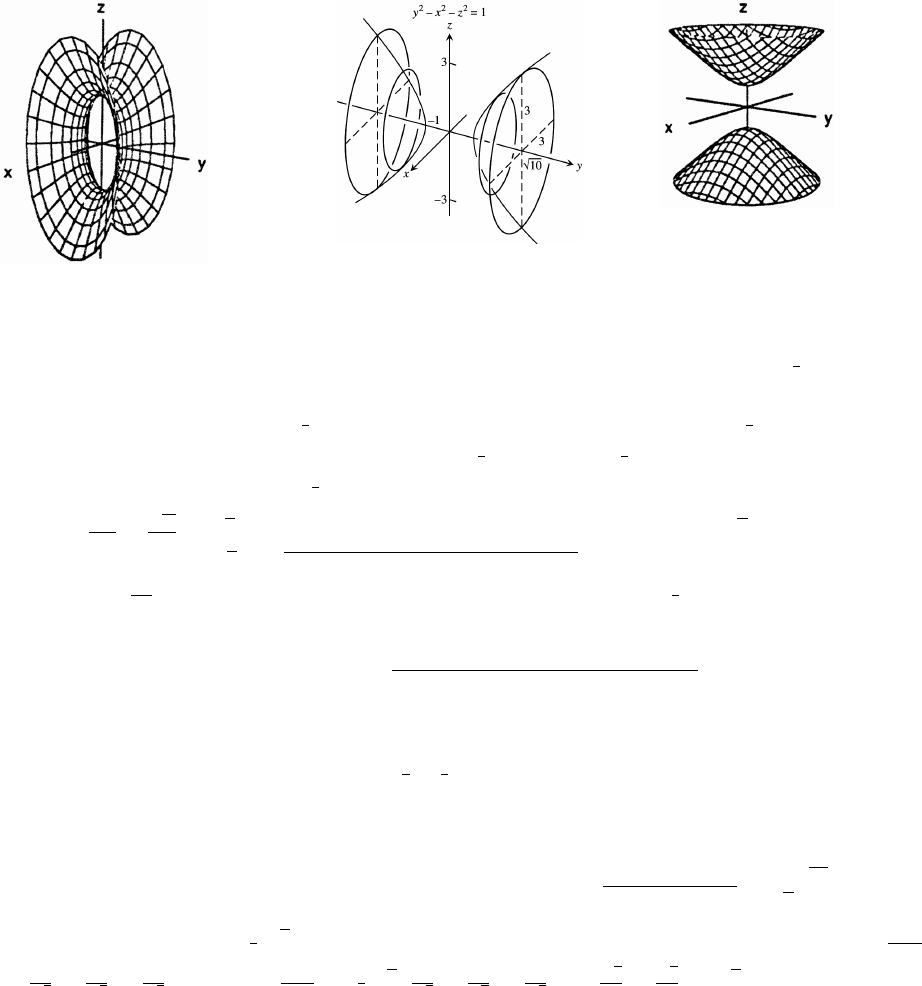
Chapter 12 Additional and Advanced Exercises 819
74. 4y z 4x 4 75. y x z 1 76. z x y 1
## # ### ###
œ œ œ
CHAPTER 12 ADDITIONAL AND ADVANCED EXERCISES
1. Information from ship A indicates the submarine is now on the line L : x 4 2t, y 3t, z t;
""
œœœ
3
information from ship B indicates the submarine is now on the line L : x 18s, y 5 6s, z s. The
#œœœ
current position of the sub is 6 3 and occurs when the lines intersect at t 1 and s . The straight
ˆ‰
ßß œ œ
""
33
line path of the submarine contains both points P 2 1 and Q 6 3 ; the line representing this path
ˆ‰ˆ‰
ß ß ß ß
""
33
is L: x 2 4t, y 1 4t, z . The submarine traveled the distance between P and Q in 4 minutes œ œ œ Ê
"
3
a speed of 2 thousand ft/min. In 20 minutes the submarine will move 20 2 thousand ft from
¹¹ È
PQ
44
32
Ä
œœ
ÈÈ
Q along the line L 20 2 (2 4t 6) ( 1 4t 3) 0 800 16(t 1) 16(t 1) 32(t 1)Ê œ Ê œ œ
ÈÈ### ## #
(t 1) 25 t 6 the submarine will be located at 26 23 in 20 minutes.Ê œ œ ÊœÊ ßß
#"800
32 3
ˆ‰
2. H stops its flight when 6 110t 446 t 4 hours. After 6 hours, H is at P(246 57 9) while H is at
#"#
œÊœ ßß
(446 13 0). The distance between P and Q is (246 446) (57 13) (9 0) 204.98 miles. At 150ßß ¸
È###
mph, it would take about 1.37 hours for H to reach H .
"#
3. Torque PQ 15 ft-lb PQ sin ft 20 lbœ‚Ê œ œ Êœ
ÄÄ
¹¹ ¹¹
kk kk kkFFFF
1
#
3
4†
4. Let be the vector from O to A and 3 2 be the vector from O to B. The vector orthogonal to aijk bi j k v aœ œ
and is parallel to (since the rotation is closkwise). Now 2 ; proj 2 2 2bv ba baij k b a i j kÊ ‚ œ œ œ ‚aab
aa
ˆ‰
†
†
2, 2, 2 is the center of the circular path 1, 3, 2 takes radius 1 1 0 2 arc length perÊÊœœÊab ab ab
ÉÈ
22
2
second covered by the point is 2 units/sec (velocity is constant). A unit vector in the direction of is
3
# ‚
‚
Èkkœvv
ba
bakk
23œ Êœ œ œ
"" ‚ ""
‚#
ÈÈÈ ÈÈÈ
kk ÈÈ
666 666
232
33
22
ijkvv ijk ij kkk
Š‹ Š ‹
ÈÈ
ba
ba
5. (a) If P(x y z) is a point in the plane determined by the three points P (x y z ), P (x y z ) andßß ßß ßß
"" "" ## ##
P (x y z ), then the vectors PP , PP and PP all lie in the plane. Thus PP (PP PP ) 0
$$ $$ " # $ " # $
ßß ‚ œ
ÄÄ Ä Ä Ä Ä
†
0 by the determinant formula for the triple scalar product in Section 10.4.
xxyyzz
xxyyzz
xxyyzz
ʜ
ââ
ââ
ââ
ââ
ââ
ââ
"""
###
$$$
(b) Subtract row 1 from rows 2, 3, and 4 and evaluate the resulting determinant (which has the same value
as the given determinant) by cofactor expansion about column 4. This expansion is exactly the
determinant in part (a) so we have all points P(x y z) in the plane determined by P (x y z ),ßß ß ß
"" ""
P(xyz), and P(xyz).
#### $$$$
ßß ßß
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

820 Chapter 12 Vectors and the Geometry of Space
6. Let L : x a s b , y a s b , z a s b and L : x c t d , y c t d , z c t d . If L L ,
" " " # # $ $ # "" ## $$ "#
œ œ œ œ œ œ ²
then for some k, a kc , i 1, 2, 3 and the determinant
acb d kccb d
acb d kccb d
acb d
ii
œœ œ
âââ â
âââ â
âââ â
âââ â
âââ â
âââ â
""" " "" " "
### # ## # #
$$$ $ kccb d
0,
$$$ $
œ
since the first column is a multiple of the second column. The lines L and L intersect if and only if the
"#
system has a nontrivial solution the determinant of the coefficients i
as ct (b d) 0
as ct (b d) 0
as ct (b d) 0
Ú
Û
Ü
"" ""
## ##
$$ $$
œ
œ
œ
Ís zero.
7. (a) BD AD AB
Ĝ
ÄÄ
(b) AP AB BD AB AD
ÄÄ ÄÄ
œ œ
Ä
""
##
Š‹
(c) AC AB AD, so by part (b), AP AC
ÄÄÄ Ä Ä
œ œ
"
#
8. Extend CD to CG so that CD DG. Then CG t CF CB BG and t CF 3 CE CA, since ACBG is a
ÄÄ ÄÄ Ä ÄÄÄ Ä ÄÄ
œœœœ
parallelogram. If t CF 3 CE CA , then t 3 1 0 t 4, since F, E, and A are collinear.
ÄÄÄ
œ œÊœ0
Therefore, CG 4 CF CD 2 CF F is the midpoint of CD.
ÄÄ ÄÄ
œÊœÊ
9. If Q(x y) is a point on the line ax by c, then P Q (x x ) (y y ) , and a b is normal to theßœœœ
Ä
"""
ijnij
line. The distance is proj P Q
¹¹¹ ¹
n"
Äœœ
[(xx) (yy)](a b)
ab ab
a(x x ) b(y y )
ijij†
ÈÈ
kk
, since c ax by.œœ
kk
È
ax by c
ab
10. (a) Let Q(x y z) be any point on Ax By Cz D 0. Let QP (x x ) (y y ) (z z ) , andßß œ œ
Ä
"" " "
ijk
. The distance is proj QP ((x x ) (y y ) (z z ) )nijkœœ
Ä
ABC ABC
ABC ABC
ijk ijk
""""
È È
¹¹¹ ¹Š‹
n†
.œœ
kkkk
ÈÈ
Ax By Cz (Ax By Cz) Ax By Cz D
ABC ABC
(b) Since both tangent planes are parallel, one-half of the distance between them is equal to the radius of the
sphere, i.e., r 3 (see also Exercise 17a). Clearly, the points (1 2 3) and ( 1 2 3)œ œ ß ß ßß
"
#
kk
È39
111 È
are on the line containing the sphere's center. Hence, the line containing the center is x 1 2t,œ
y 2 4t, z 3 6t. The distance from the plane x y z 3 0 to the center is 3œ œ œ È
3 from part (a) t 0 the center is at (1 2 3). ThereforeʜʜÊßß
kk
È
(1 2t) (2 4t) (3 6t) 3
111
È
an equation of the sphere is (x 1) (y 2) (z 3) 3.œ
###
11. (a) If (x y z ) is on the plane Ax By Cz D , then the distance d between the planes is
""" "
ßß œ
d , since Ax By Cz D , by Exercise 10(a).œœ œ
kkkk
Èkk
Ax By Cz D D D
ABC ABC
""""
ijk
(b) d œœ
kk
ÈÈ
12 6
491
6
14
(c) D 8 or 4 the desired plane is
kkkk
ÈÈ
2(3) ( 1)(2) 2( 1) 4 2(3) ( 1)(2) 2( 1) D
14 14
œÊœÊ
2xy2x 8 œ
(d) Choose the point (2 0 1) on the plane. Then 5 D 3 5 6 the desired planes areßß œ Ê œ „ Ê
kk
È
3D
6
È
x2yz356 and x2yz356.œ œ
ÈÈ
12. Let AB BC and D(x y z) be any point in the plane determined by A, B and C. Then the point D lies innœ‚ ßß
ÄÄ
this plane if and only if AD 0 AD (AB BC) 0.
ÄÄÄÄ
œÍ ‚ œ††n
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 12 Additional and Advanced Exercises 821
13. 2 6 is normal to the plane x 2y 6z 6; 4 5 is parallel to the
111
126
ni j k vn i jk
ijk
œ œ ‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
plane and perpendicular to the plane of and ( ) 32 23 13 is a
126
451
vn wnvn i j k
ijk
Êœ‚‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
vector parallel to the plane x 2y 6z 6 in the direction of the projection vector proj . Therefore,œ Pv
proj proj
Pv vv w w wwijkœ œ œ œ œ œ œ
wŠ‹Š‹ˆ‰
†ww vw
ww w
kk kk kk
†32 23 13 42 32 23 13
32 23 13 1722 41 41 41 41
"
14. proj proj and proj proj ( proj ) proj ( proj ) proj
zz z z zz zz
wvwwvvwwwwvvwœ œ Ê œ œ
2 proj 2 œ œvvv z
zŠ‹
vz
z
†
kk
15. (a) 2 2 4 ( ) ; ( ) ( ) 0 0 ; 4 ( ) ;uv i j k uv C0uwv vwu v u 0vw i u vw 0‚œ ‚ œ Ê ‚ ‚ œ œ œ ‚ œ Ê‚ ‚ œ††
()()00uwv uvw v w 0††œœ
(b) 43 ( ) 1026;
111 143
21 2 12 1
uv ijk uvw ijk
ij k ijk
‚œ œ Ê ‚ ‚ œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
( ) ( ) 4(2 2 ) 2( ) 10 2 6 ;uwv vwu i j k i j k i j k†† œœ
vw i j k u vw i j k
ijk ijk
‚œ œ Ê‚‚ œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
21 2 1 11
12 1 3 4 5
345 ( ) 927;
( ) ( ) 4(2 2 ) ( 1)( 2 ) 9 2 7uwv uvw i j k i j k i j k†† œœ
(c) 2 4 ( ) 4 6 2 ;
210 124
211 102
uv ijk uvw ijk
ijk ij k
‚œ œ Ê ‚ ‚ œ œ
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
( ) ( ) 2(2 ) 4(2 ) 4 6 2 ;uwv vwu i j k i j i j k††œœ
vw i jk u vw i j k
ijk i jk
‚œ œÊ‚‚ œ œ
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
211 210
102 2 31
23 ( ) 24;
( ) ( ) 2(2 ) 3( 2 ) 2 4uwv uvw i j k i k i j k†† œ œ
(d) 3 ( ) 10 10 ;
11 2 131
10 1 2 4 2
uv i jk uv w i k
ijk ijk
‚ œ œ Ê ‚ ‚ œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
( ) ( ) 10( ) 0( 2 ) 10 10 ;uwv vwu ik ij k i k††œœ
vw i j k u vw i j k
ijk ij k
‚œ œ Ê‚‚ œ œ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
ââ ââ
10 1 1 1 2
242 444
4 4 4 ( ) 12 4 8 ;
( ) ( ) 10( ) 1(2 4 2 ) 12 4 8uwv uvw i k i j k i j k††œœ
16. (a) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )uvwvwuwuv uwvuvwvuwvwuwvuwuv0‚‚‚‚‚‚œœ†††† ††
(b) [ ( )] [( ( )] [( ( )] [( ) ] [( ) ] [( ) ]uvii uvjj uvkk uvii uvjj uvkkuv†† † †††‚ ‚ ‚ œ‚ ‚ ‚ œ‚
(c) ( ) ( ) [ ( )] [( ) ( ) ] ( )( ) ( )( )uv wr uv wr u vrw vwr uwvr urvw‚‚œ‚‚œ œ †† †††††††
œºº
uw vw
ur vr
††
††
17. The formula is always true; [ ( )] [( ) ( ) ]uuuvwu uvuuuvw‚‚‚ œ‚ ††††
[( ) ( ) ] œ‚‚œ‚œ‚uvuu uuuvw uuvw uuvw††† ††kk kk
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

822 Chapter 12 Vectors and the Geometry of Space
18. If (cos ) (sin ) and (cos ) (sin ) , where , then sin ( )uijvij uvuv kœ œ ‚œ !! "" "! "!cdkkkk
(cos sin sin cos ) sin ( ) cos sin sin cos , since
cos sin 0
cos sin 0
œœÊœ
ââ
ââ
ââ
ââ
ââ
ââ
ijk
k
!!
""
!" ! " "! !" ! "
1 and 1.kk kkuvœœ
19. If a b and c d , then cos ac bd a b c d cos uij vij uvuvœ œ œ Ê œ †kkkk ÈÈ
))
####
(ac bd) a b c d cos (ac bd) a b c d , since cos 1.Ê œ Ê Ÿ Ÿ
###### ##### #
abab abab))
20. proj and wu vruwu vœ œ œ œ
vŠ‹ Š‹
uv uv
vv vv
††
kk kkkk kk
21. ( ) ( ) 2 2 k k kk kkkk kk a b k k kk kkkk kkuv uv uv uu uvvv u uv v u v uv u vœ œ Ÿ œ ÊŸ
####
††††
22. Let denote the angle between and , and the angle between and . Let a and b . Then!"wu wv u vœœkk kk
cos ,!œœœœœœ
wu vu
wu wu wu wu w w
vuu vuuu vuuu vu
† †
††† †† †
kkkk kkkk kkkk kkkk kk kk
ab
a
(a b ) (a b ) (a b ) aba ba
and likewise, cos . Since the angle between and is always and cos cos , we have"!"œŸœ
uv
w
†
#
ba
kk uv 1
that bisects the angle between and .!"œÊwuv
23. (a b ) (b a ) a b b b a a b a b a b a b av u u v vu uu vv uv uv uu vv uv œœ† † ††† † †††
##
b a a b 0, where a and bœœ œ œ
## ## kk kkuv
24. If a b c , then a b c 0 and 0 iff a b c 0.u i j k uu uuœ œ œ œœœ††
###
25. (a) The vector from (0 d) to (kd 0) is kd d . Theß ß œÊœ Êœrij
k1
dk 1 dk 1
k
kk kk
ab ab
rr
rij
kk
k
"
total force on the mass (0 d) due to the masses Q for k n, n 1, , n 1, n isßœá
k
()Fjœ á
GMm GMm GMm GMm GMm
d2d 5d n1d 2d
2n12
2n
5
Š‹ Š‹ Š ‹ Š ‹
ij ij ij ij
ÈÈ È È
ab
á
GMm GMm
5d n 1 d
2n
5n1
Š‹ Š ‹
ij ij
ÈÈ
ab
The components cancel, givingi
1 the magnitude of the force isFjœ á Ê
GMm 2 2 2
d22 55 n1n1
Š‹
ÈÈ abab
1 .kk Œ
!
Fœ
GMm 2
di1
n
i1œab
(b) Yes, it is finite: lim 1 is finite since converges.
nÄ_ kk Œ
!
Fœ
GMm 2 2
di1 i1
!
_
œ
_
œ
i1 i1
ab ab
26. (a) If x y 0, then x (x y) (x y)x (x x)y (x x)y. This means that
tt t t t ttt ttt ttt
œ ‚‚œœ††††
x y x y (x x) y x 1 y. Since x and y are
tttt ttt t t t t
Šœ œ
""
t
t
c1
x
ccc x
††
É1cxx
cab
kk
Ékk
orthogonal, then x y x 1 y . A calculation will show thatk k kk kk
tt t t
Šœ
## #
t
t
#
kk
Ékk
x
ccc x
x 1 c c . Since y c, then y c sokk kk kk
ttt
œ
# #
t
t
#
## #
kk
Ékk
x
ccc x
1 y 1 c . This means that
kk
t
kk kk
ÉÉ
kk kk
xx
ccc x ccc x
tt
tt
#
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Chapter 12 Additional and Advanced Exercises 823
xy x 1 y x 1 c c.k k kk kk kk
tt t t t
Šœ œ
## ##
tt
tt
##
##
kk kk
ÉÉ
kk kk
xx
ccc x ccc x
We now have x y c , so x y c.kk kk
tt tt
Š Š
##
(b) If x and y are parallel, then x (x y) 0. This gives x y .
tt ttt tt
‚‚œ Šœ
txy
1
tt
xy
c
(i) If x and y have the same direction, then x y and x y .
t t tt tt
Šœ Š œ
xy
11
xy
tt
tt
xy xy
cc cc
††
kk
kk kk
Since y c, x c, we have y 1 c 1 y c xkk kk kk kk kk
Š‹Š‹
tt t t t
Ê
kk kk kkkkxxy x
cc c
tttt
x y c c 1 c. This means that x y c.Ê œ Ê Š
tt tt
kk kk k k
Š‹
kkkk kk kk kk kkx y x y x y
ccc
1
tt t t t t
†xy
cc
†
(ii) If x and y have opposite directions, then x y x y and x y .
tt tt tt tt
œ Š œ†kkkk xy
1
tt
x y
c
Assume x y , then x y . Since x c, we have x 1 c 1kk kk k k kk kkŠ‹Š‹
tt tt t t
Šœ
kkkk kk kkxy y y
1cc
tt t t
x y
c
x c y x y c c 1 c.Ê Ê œ Ê
tttt
kk kk kk kk Š‹
kkkk kkkk kkkk kk kkx y x y x y x y
ccc
1
tt tt tt t t
x y
c
This means that x y c. A similar argument holds if x y .k k kk kk
tt t t
Š
(c) lim x y x y.
cÄ_ tttt
Šœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
824 Chapter 12 Vectors and the Geometry of Space
NOTES:
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
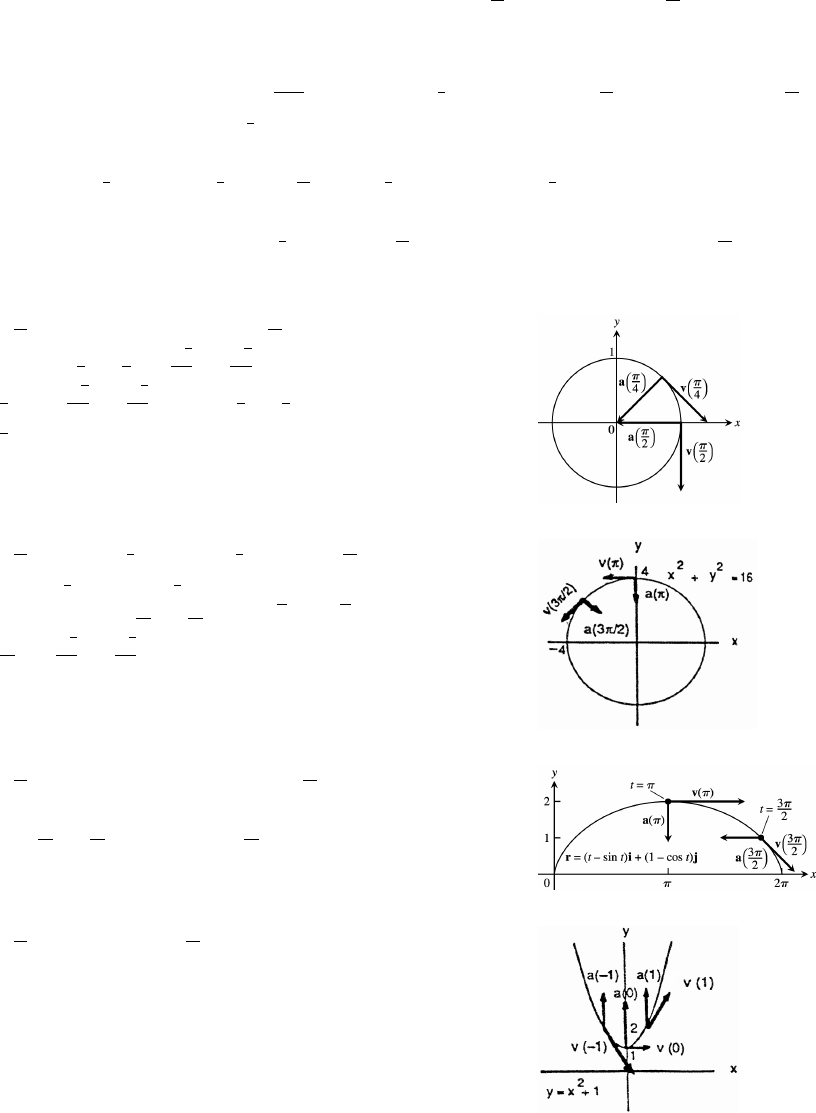
CHAPTER 13 VECTOR-VALUED FUNCTIONS
AND MOTION IN SPACE
13.1 VECTOR FUNCTIONS
1. x t 1 and y t 1 y (x 1) 1 x 2x; 2t 2 2 and 2œ œÊœ œ œ œ Êœ œ Êœ œ
###
vij a jvijaj
dd
dt dt
rv
at t 1œ
2. x t 1 and y 2t 1 x x (y 1) 1; 2t 2 2œ œÊœ "Êœ œ œ Êœ œ
# #
#
#"
ˆ‰
y1
4dt dt
dd
vijai
rv
2 and 2 at tÊœ œ œvi j a i "
#
3. x e and y e y x ; e e e e 3 4 and 3 8 at t ln 3œ œ Êœ œ œ Êœ Êœ œ œ
t2t t2tt2t
22d4 8
99dt9 9
#vijaijvijaij
r
4. x cos 2t and y 3 sin 2t x y 1; ( 2 sin 2t) (6 cos 2t) œœÊœœœÊœ
##
"
9dt dt
dd
vija
rv
( 4 cos 2t) ( 12 sin 2t) 6 and 4 at t 0œ Ê œ œ œijvjai
5. (cos t) (sin t) and (sin t) (cos t)vija ijœœ œœ
dd
dt dt
rv
for t , andÊœ œ
11
44
22
vij
ˆ‰ ÈÈ
##
; for t , andaijvj
ˆ‰ ˆ‰
111
4
22
œ œ œ
ÈÈ
## ##
ai
ˆ‰
1
#œ
6. 2 sin 2 cos and vijaœœ œ
dttd
dt dt
rv
ˆ‰ˆ‰
##
cos sin for t , ( ) 2 andœ Ê œ œ
ˆ‰ˆ‰
tt
##
ij vi11
() ; for t , 2 2 andaj v ij1œ œ œ
3311
##
ˆ‰ ÈÈ
aij
ˆ‰
322
1
###
œ
ÈÈ
7. (1 cos t) (sin t) and vijaœœ œ
dd
dt dt
rv
(sin t) (cos t) for t , ( ) 2 and ( ) ;œ Êœ œ œij viaj11 1
for t , and œœ œ
33 311 1
## #
vija i
ˆ‰ ˆ‰
8. 2t and 2 for t 1,vija jœœ œœ Ê œ
dd
dt dt
rv
( 1) 2 and ( 1) 2 ; for t 0, (0) andvija j viœ œ œ œ
(0) 2 ; for t 1, (1) 2 and (1) 2aj vijajœœœ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

826 Chapter 13 Vector-Valued Functions and Motion in Space
9. (t 1) t 1 2t 2t 2 2 ; Speed: (1) 1 (2(1)) 2 3;ri jkvijka j vœ Ê œ œ Ê œ œ œ œab kk
È
####
dd
dt dt
rr
Direction: (1) 3
vijk
v
(1) 2(1) 2
(1) 3 3 3 3 3 3 3
22 22
kk
œ œ Ê œ
""
ijkv ijk
ˆ‰
10. (1 t) t 2t ; Speed: (1)rijkvijka jk vœ Êœœ Êœ œ
tt d 2t d2
222
3dt dt
ÈÈÈ
rr
#kk
1 (1 ) 2; Direction: (1)œ œ œ œÊ
ÊŠ‹
###
#
## #
"""
2(1) (1)
2 2
(1)
(1 )
È È
kk
v
v
ijk
2(1)
2ijkv
2œ
Š‹
"""
##
ijk
È2
11. (2 cos t) (3 sin t) 4t ( 2 sin t) (3 cos t) 4 ( 2 cos t) (3 sin t) ;rijkv ijka ijœÊœœÊœœ
dd
dt dt
rr
Speed: 2 sin 3 cos 4 2 5; Direction:
¸¸ˆ ‰ˆ ‰ˆ‰ ÉÈ
v111
##
##
#
œ œ
2
v
v
ˆ‰
¸¸ˆ‰
sin cos 2 5œ œ Ê œ
Š‹Š‹ Š ‹
ˆ‰ È
234 2 2
55555 55###
## #
""
ÈÈÈÈÈ ÈÈ
11 1
ijkikv ik
12. (sec t) (tan t) t (sec t tan t) sec t rijkv i jkaœÊœœ Êœ
4d 4d
3dt 3dt
rr
ab
#
sec t tan t sec t 2 sec t tan t ; Speed: sec tan sec 2;œ œ œabab
¸¸ˆ ‰ˆ‰ˆ‰ˆ‰ É
#$ # ##
##
ijv
1111
66663
4
Direction: 2
vijk
v
ˆ‰ ˆ ‰
¸¸ˆ‰
66663
6
4
œ œ Ê œ
sec tan sec
#
""
ˆ‰
333 6 333
22 22
ijkv ijk
ˆ‰ ˆ ‰
1
13. (2 ln (t 1)) t 2t t 2 ;rijkvijka ijkœÊœœ Êœœ
#
td2 d2
2dtt1 dt(t1)
rr
ˆ‰ ’“
Speed: (1) (2(1)) 1 6; Direction: kkɈ‰ È
vœœ œ
2
11 (1)
(1) 2(1) (1)
6
###
v
v
ijk
kk Š‹
È
2
1
(1) 6œ Ê œ
"""
ÈÈÈ ÈÈÈ
666 666
21 2
ijkv ijk
ÈŠ‹
14. e (2 cos 3t) (2 sin 3t) e (6 sin 3t) (6 cos 3t) ri j kv i j kaœ Êœœ Êœab a b
tt
dd
dt dt
rr
e (18 cos 3t) (18 sin 3t) ; Speed: (0) e [ 6 sin 3(0)] [6 cos 3(0)] 37;œ œ œab k k a b
ÉÈ
!##
#
tijkv
Direction: (0) 37
v
v
ij k
(0)
(0)
e 6 sin 3(0) 6 cos 3(0)
37 37 37 37 37
66
kk ab ÈÈÈ ÈÈ
œ œ Êœ
""
ikv ik
ÈŠ‹
15. 3 3 2t and 2 (0) 3 3 and (0) 2 (0) 3 3 0 12 andvi j kak v i ja k vœ œ Ê œ œ Ê œ œ
ÈÈ È
kkÊŠ‹ È
##
#
(0) 2 2; (0) (0) 0 cos 0 kkÈ
avaœ œ œÊ œÊœ
##
†))
1
16. 32t and 32 (0) and (0) 32 (0)vi ja jv ija jvœ œÊ œ œÊ œ
ÈÈ ÈÈ È È
22 22 2 2
## ## # #
##
Š ‹ Š‹Š‹
kkÊ
1 and (0) ( 32) 32; (0) (0) ( 32) 16 2 cos œ œ œ œ œ Ê œ œ Ê œkkÈŠ‹ È
ava
###
†ÈÈÈ
21622
1(32) 4
3
))
1
17. t t 1 and (0) andvij ka i j kvjœ œ Êœ
ˆ‰ˆ‰ ab ’“’“’ “
2t 1 2t 2 2t
t1 t1 t1 t1 t1
#"Î# "
ab ab ab
(0) 2 (0) 1 and (0) 2 1 5; (0) (0) 0 cos 0 aikv a vaœÊ œ œ œ œÊ œÊœkk kkÈÈ
## †))
1
2
18. (1 t) (1 t) and (1 t) (1 t) (0) andvijka i jvijkœ œ Ê œ
22 22
33 33 3 333
"Î# "Î# "Î# "Î#
"" " "
(0) (0) 1 and (0) ; (0) (0)aijv a vaœ Ê œ œ œ œ œ
"" " " "
##
###
33 3 3 3 3 3 3 99
22 22
2
kk kk
ÉÉ
ˆ‰ ˆ ‰ ˆ‰ ˆ‰ ˆ‰ Ȇ
0 cos 0 œÊ œÊœ))
1
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
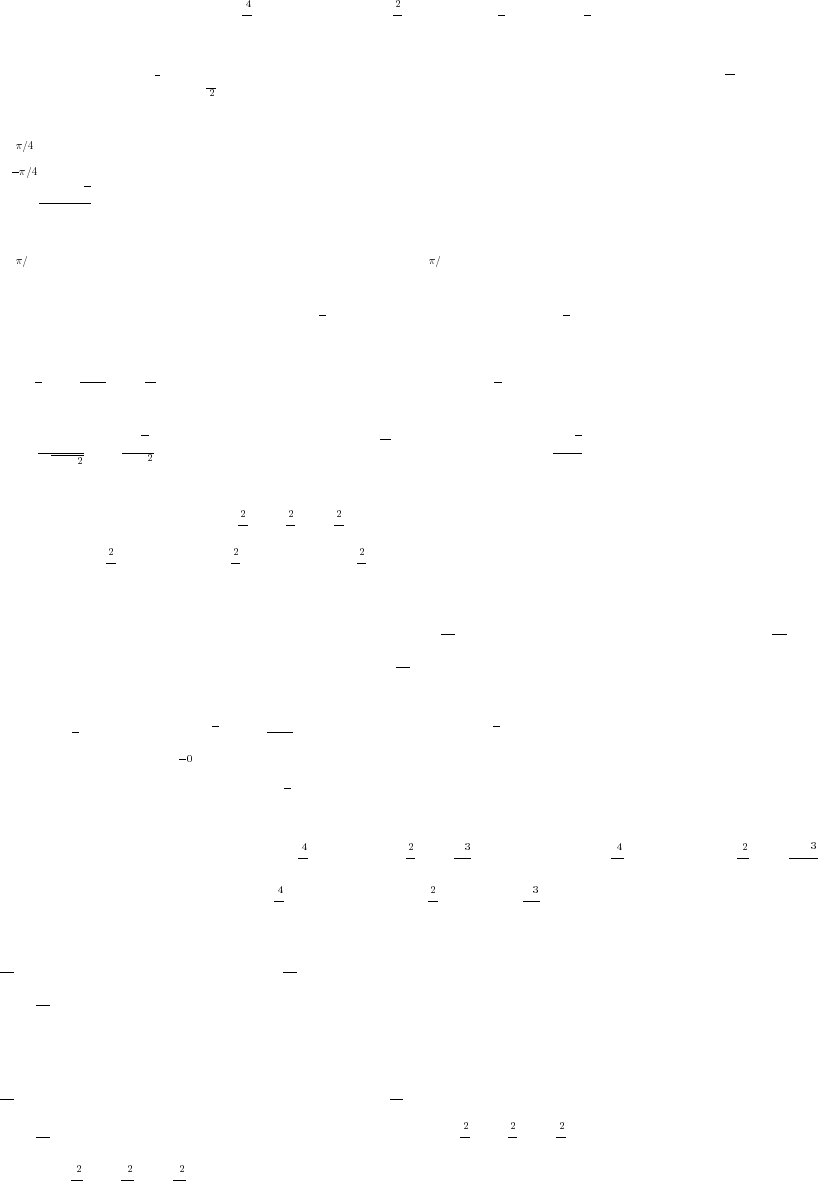
Section 13.1 Vector Functions 827
19. (1 cos t) (sin t) and (sin t) (cos t) (sin t)(1 cos t) (sin t)(cos t) sin t. Thus,vijaijvaœ œ Ê œ œ†
0 sin t 0 t 0, , or 2va†œÊ œÊœ11
20. (cos t) (sin t) and ( sin t) (cos t) sin t cos t sin t cos t 0 for all t 0vijka ikvaœ œ Êœ œ †
21. t 7 (t 1) dt [7t] t 7
'0
1cd
’“ ’ “
$"
""
!!
!"
#
ij k i j k ij k œ œ
tt 3
424
22. (6 6t) 3 t dt 6t 3t 2t 4t 3 4 2 2 2
'1
2‘‘
Ȉ‰ cd cd Š‹
È
œ œ ijk i j ki jk
4
t# $Î# "
#
""
#
"
#
23. (sin t) (1 cos t) sec t dt cos t t sin t tan t
'cdcdcdcdabijk i jk œ
#Î% Î% Î%
Î% Î% Î%
111
111
2œ
Š‹
1
#
22
Èjk
24. (sec t tan t) (tan t) (2 sin t cos t) dt [(sec t tan t) (tan t) (sin 2t) ] dt
''
0 0
3 3
cdij k ij k œ
sec t ln (cos t) cos 2t (ln 2)œ œcd c d ‘
111
Î$ Î$
!!
"
#
Î$
!
ijkijk
3
4
25. dt ln t ln (5 t) ln t (ln 4) (ln 4) (ln 2)
'1
4ˆ‰ ‘
cd c d
"" " "
# #
%%
""
%
"
t5t t
ijk i j k i j k œœ œ
26. dt 2 sin t 3 tan t
'0
1Š‹ ’“
cd
È
2
1t
33
1t 4
ÈÈÈ
" "
"
!
"
!
ik i kikœ œ11
27. ( t t t ) dt ; (0) 0 0 0 2 3 2 3r ijk i j kCr ijkCijk Cijkœ œ œ Ê œ
'ttt
### œ
123Ê œ rijk
Š‹Š‹Š‹
ttt
###
28. (180t) 180t 16t dt 90t 90t t ; (0) 90(0) 90(0) (0)r i j i jCr i jCœœœ
'cdab ˆ‰ ‘
###$ ##$
16 16
33
100 100 90t 90t t 100œÊœ ÊœjC j r i j
##$
ˆ‰
16
3
29. (t 1) e dt (t 1) e ln (t 1) ;rijkijkCœ œ
'‘ˆ‰ˆ‰
3
t1#
"Î# $Î#
"
tt
(0) (0 1) e ln (0 1) rijkCkCijkœ œÊ œ
$Î#
(t 1) 1 1 e [1 ln (t 1)]ʜ rijk
‘
ab
$Î# t
30. t 4t t 2t dt 2t ; (0) 2(0)rijk ijkCr ijkCœ œ œ
'cdab Š‹ ’ “
$## #
tt2t 0 0
423 4 23
2(0)
2t 1 1œ Ê œ Ê œ ij C ij r i j k
Š‹Š‹
tt2t
43
#
#
31. ( 32 ) dt 32t ; (0) 8 8 32(0) 8 8 8 8
dd
dt dt
rr
œ œ œÊ œÊ œ
'kkC ij kCijCij
"""
8 8 32t ; (8 8 32t ) dt 8t 8t 16t ; (0) 100Ê œ œ œ œ
d
dt
rij kr ij k i j kCr k
'##
8(0) 8(0) 16(0) 100 100 8t 8t 100 16tÊ œÊœÊœi j kC kC krij k
# #
## ab
32. ( ) dt (t t t ) ; (0) (0 0 0 )
dd
dt dt
rr
œ œ œÊ œÊ œ
'ijk i j k C 0 i j k C 0 C 0
"""
(t t t ) ; (t t t ) dt ; (0) 10 10 10Ê œ œ œ œ
dttt
dt
rijkr ijk i j k Cr i j k
'Š‹
### #
10 10 10 10 10 10Ê œ Ê œ
Š‹
000
### ##
ijkC ijkC ijk
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

828 Chapter 13 Vector-Valued Functions and Motion in Space
10 10 10Ê œ rijk
Š‹Š‹Š‹
ttt
###
33. (t) (sin t) t cos t e (t) (cos t) (2t sin t) e ; t 0 (t ) andr i jk v i jk v ikœÊœ œÊœab
#!
tt
0
(t ) P (0 1 1) x 0 t t, y 1, and z 1 t are parametric equations of the tangent liner0œœßßÊœœ œ œ
!
34. (t) (2 sin t) 2 cos t 5t (t) (2 cos t) (2 sin t) 5 ; t 4 (t ) 2 5 andrijkv ijk vikœ Êœ œÊœab !10
(t ) P (0 2 20 ) x 0 2t 2t, y 2, and z 20 5t are parametric equations of the tangent liner0œœßß Êœœ œ œ
!11
35. (t) (a sin t) a cos t bt (t) (a cos t) (a sin t) b ; t 2 (t ) a b andrijkv ijk vikœ Êœ œÊœab !10
(t ) P (0 a 2b ) x 0 at at, y a, and z 2 b bt are parametric equations of the tangent liner0œœßß Êœœ œ œ
!11
36. (t) (cos t) sin t (sin 2t) (t) ( sin t) (cos t) (2 cos 2t) ; t (t ) 2 andrijkv ij k vikœ Êœ œÊœab !#
10
(t ) P (0 1 0) x 0 t t, y 1, and z 0 2t 2t are parametric equations of the tangent liner0œœßßÊœœœ œœ
!
37. (a) (t) (sin t) (cos t) (t) (cos t) (sin t) ;vija ijœ Ê œ
(i) (t) ( sin t) (cos t) 1 constant speed;kkÈ
vœ œÊ
##
(ii) (sin t)(cos t) (cos t)(sin t) 0 yes, orthogonal;va†œœÊ
(iii) counterclockwise movement;
(iv) yes, (0) 0rijœ
(b) (t) (2 sin 2t) (2 cos 2t) (t) (4 cos 2t) (4 sin 2t) ;vija ijœ Ê œ
(i) (t) 4 sin 2t 4 cos 2t 2 constant speed;kkÈ
vœœÊ
##
(ii) 8 sin 2t cos 2t 8 cos 2t sin 2t 0 yes, orthogonal;va†œœÊ
(iii) counterclockwise movement;
(iv) yes, (0) 0rijœ
(c) (t) sin t cos t (t) cos t sin t ;vija ijœ Ê œ
ˆ‰ ˆ‰ ˆ‰ ˆ‰
11 11
## ##
(i) (t) sin t cos t 1 constant speed;kkɈ‰ ˆ‰
vœœÊ
##
##
11
(ii) sin t cos t cos t sin t 0 yes, orthogonal;va†œ œÊ
ˆ‰ˆ‰ ˆ‰ˆ‰
11 11
## ##
(iii) counterclockwise movement;
(iv) no, (0) 0 instead of 0rij ijœ
(d) (t) (sin t) (cos t) (t) (cos t) (sin t) ;vija ijœ Ê œ
(i) (t) ( sin t) ( cos t) 1 constant speed;kkÈ
vœ œÊ
##
(ii) (sin t)(cos t) (cos t)(sin t) 0 yes, orthogonal;va†œœÊ
(iii) clockwise movement;
(iv) yes, (0) 0rijœ
(e) (t) (2t sin t) (2t cos t) (t) (2 sin t 2t cos t) (2 cos t 2t sin t) ;vija i jœ Ê œ
(i) (t) (2t cos t) 4t sin t cos t 2 t 2t, t 0
2t sin t
kk c d a b kk
Éab È
vœœœœ
#####
variable speed;Ê
(ii) 4 t sin t t sin t cos t 4 t cos t t cos t sin t 4t 0 in generalva†œ œÁabab
## ##
not orthogonal in general;Ê
(iii) counterclockwise movement;
(iv) yes, (0) 0rijœ
38. Let 2 2 denote the position vector of the point 2, 2, 1 and let, and .pijk u i j v i j kœ œ œab "" """
ÈÈ ÈÈÈ
22 333
Then (t) (cos t) (sin t) . Note that (2 2 1) is a point on the plane and 2 is normal torp u v nijkœ ßß œ
the plane. Moreover, and are orthogonal unit vectors with 0 and are parallel to theuv unvn uv††œœÊ
plane. Therefore, (t) identifies a point that lies in the plane for each t. Also, for each t, (cos t) (sin t)ruv
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
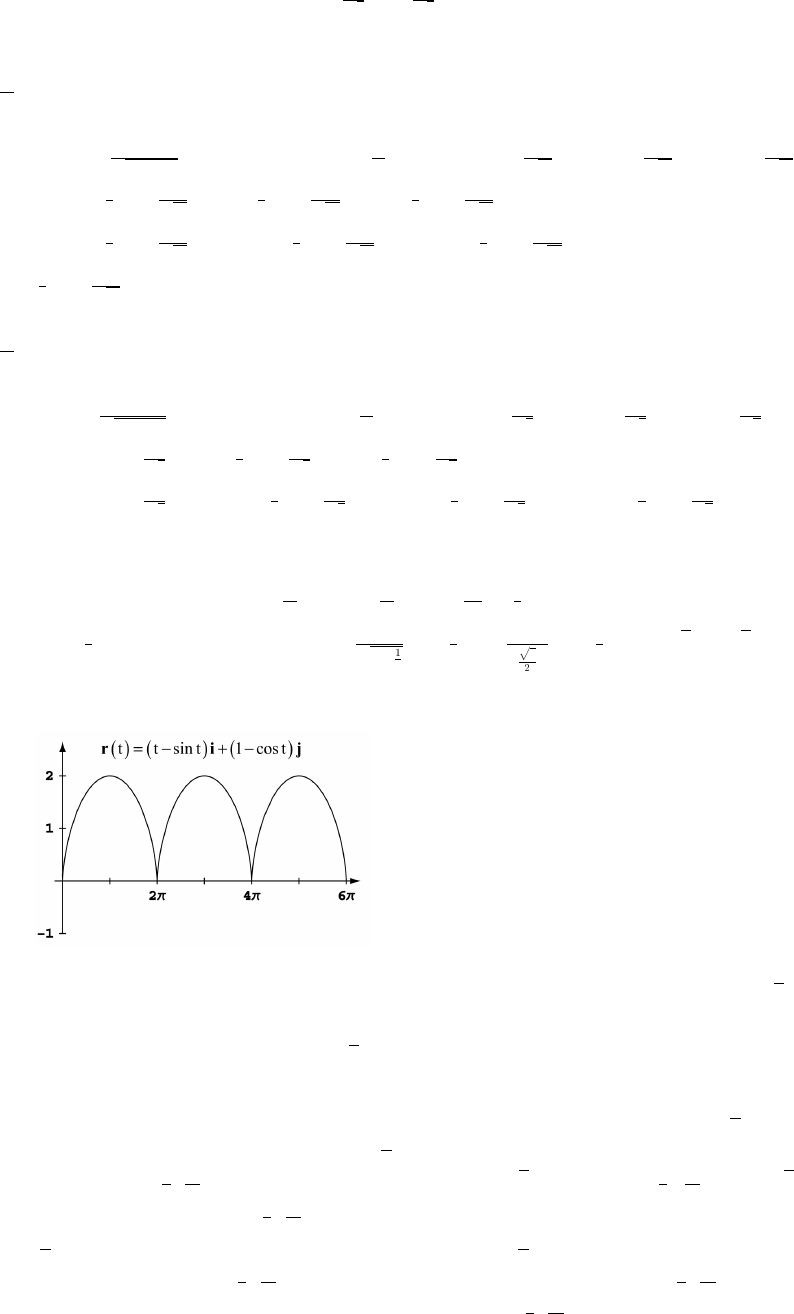
Section 13.1 Vector Functions 829
is a unit vector. Starting at the point 2 , 2 , 1 the vector t traces out a circle of radius 1 and
Š‹
ab
11
22
ÈÈ r
center (2 2 1) in the plane x y 2z 2.ßß œ
39. 3 (t) 3t t t ; the particle travels in the direction of the vector
d
dt
vœœ Ê œ aijk v ijkC
"
(4 1) (1 2) (4 3) 3 (since it travels in a straight line), and at time t 0 it has speed œ œijkijk
2 (0) (3 ) (t) 3t t tÊœ œÊœœ vijkCv ijk
2d622
911 dt 11 11 11
ÈÈÈÈ
"rŠ ‹Š‹Š‹
(t) t t t t t t ; (0) 2 3Êœ œœrijkCrijkC
Š‹Š‹Š‹
36 2 2
11 11 11
###
###
"" ##
ÈÈÈ
(t) t t1 t t2 t t3Êœrijk
Š‹Š‹Š‹
36 2 2
11 11 11
###
###
""
ÈÈÈ
tt(3 )(23)œ
Š‹
"
#
#2
11
Èijk i j k
40. 2 (t) 2t t t ; the particle travels in the direction of the vector
d
dt
vœœ Ê œ aijk v ijkC
"
(3 1) (0 ( 1)) (3 2) 2 (since it travels in a straight line), and at time t 0 it has speed 2 œ œijkijk
(0) (2 ) (t) 2t t tÊœ œÊœœ vijkCvijk
2d422
411 dt 666
ÈÈÈÈ
"rŠ ‹Š‹Š‹
(t) t t t t t t ; (0) 2Ê œ œ œrijkCrijkC
Š‹Š‹Š‹
###
""
## ##
422
666
ÈÈÈ
(t) t t1 t t1 t t2 t t(2 )( 2)Êœ œ rijkijkijk
Š‹Š‹Š‹Š‹
### #
"" "
## #
422 2
666 6
ÈÈÈ È
41. The velocity vector is tangent to the graph of y 2x at the point ( ), has length 5, and a positive
#œ#ß# i
component. Now, y 2x 2y 2 the tangent vector lies in the direction of the
#
Ð#ß#Ñ ##
"
œÊ œÊ œœÊ
dy dy
dx dx 2
2
¹†
vector the velocity vector is 2 5 5ij v ij ij i jÊ œ œ œ
"""
###
55
1
Ɍ
45
ˆ‰ ˆ‰
ÈÈ
42. (a)
(b) (1 cos t) (sin t) and (sin t) (cos t) ; (1 cos t) sin t 2 2 cos t is at a maxvijaijv vœ œ œ œ Êkk kk
##
##
when cos t 1 t , 3 , 5 , etc., and at these values of t, 4 max 4 2; is at a minœ Ê œ œ Ê œ œ111 kk kk kk
È
vvv
##
when cos t 1 t 0, 2 , 4 , etc., and at these values of t, 0 min 0; sin t cos t 1œÊœ œÊ œ œ œ11 kk kk kkvva
##
##
for every t max min 1 1Êœœœkk kk È
aa
43. ( 3 sin t) (2 cos t) and ( 3 cos t) (2 sin t) ; 9 sin t 4 cos t vjka jkv vœ œ œ Êkk kk
ˆ‰
##
##
d
dt
18 sin t cos t 8 cos t sin t 10 sin t cos t; 0 10 sin t cos t 0 sin t 0 or cos t 0œœ œÊ œÊœœ
d
dt ˆ‰
kkv#
t 0, or t , . When t 0, , 4 4 2; when t , , 9 3.Êœ œ œ œ Ê œ œ œ œ œ11
11 11
## ##
#
3 3
kk kk kk
ÈÈ
vv v
Therefore max is 3 when t , , and min 2 when t 0, . Next, 9 cos t 4 sin tkk kk kkvvaœœœœ
11
##
###
31
18 cos t sin t 8 sin t cos t 10 sin t cos t; 0 10 sin t cos t 0 sin t 0 orÊœ œ œÊ œÊœ
d d
dt dt
ˆ‰ ˆ‰
kk kkaa
# #
cos t 0 t 0, or t , . When t 0, , 9 3; when t , , 4 2.œÊœ œ œ œÊœ œ œÊœ11
11 11
## ##
##
33
kk kk kk kkaa aa
Therefore, max 3 when t 0, , and min 2 when t , .kk kkaaœœ œœ111
##
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

830 Chapter 13 Vector-Valued Functions and Motion in Space
44. (a) (t) (r cos ) (r sin ) , and the distance traveled along the circle in time t is t (rate times time)rijœ
!!
)) v
which equals the circular arc length r (t) r cos r sin
!!!
))Êœ Ê œ
vvvttt
rrr
rij
Š‹Š‹
(b) (t) sin cos (t) cos sin vija ijœœ Ê œœ
dtt d t t
dt r r dt r r r r
rv
Š‹Š‹ Š ‹Š ‹
vv
vv vvvv
r cos r sin (t)œ œ
vv vv
rr
tt
rr
’“Š‹Š‹
!!
ijr
(c) m m Fa rœÊ œ Ê œÊœ
Š‹ Š‹
GmM GmM m GM
rrrr
rr
rvv
v#
(d) T is the time for the satellite to complete one full orbit T circumference of circle T 2 rʜ ʜvv1!
(e) Substitute into T T is proportional to r since is avvœœÊœÊœÊ
2r
T r T r GM GM
GM GM 4
4r 4r
111 1
###$
!
constant
45. ( ) 2 2 0 0 is a constant is constant
dddd
dt dt dt dt
vv v v v vv v vv†† † † † † †œœ œœÊ Êœ
vv v kk È
46. (a) ( ) ( ) ( ) ( )
dd dd dd
dt dt dt dt dt dt
uvw vw u vw vw u wv††† ††‚œ ‚ ‚œ ‚ ‚‚
uuvw
ˆ‰
()œ‚‚‚
ddd
dt dt dt
uvw
†††vw u wuv
(b) Each of the determinants is equivalent to each expression in Eq. 7 in part (a) because of the formual in Section 12.4
expressing the triple scalar product as a determinant.
47. , since ( ) 0
d dd d dd d d dd dd
dt dt dt dt dt dt dt dt dt dt dt dt
’ “Š‹Š‹Š‹Š‹Š‹
rrrrAAB††††† †
rr rrr rr rr rr
‚ œ ‚ ‚ ‚œ ‚ ‚œ
and ( ) 0 for any vectors and AB B A B†‚œ
48. a b c with a, b, c real constants 0 0 0uCijk i j k ijk0œœ Ê œ œ œ
ddadbdc
dt dt dt dt
u
49. (a) f(t) g(t) h(t) c cf(t) cg(t) ch(t) (c ) c c c uijku i j k u i j kœ Êœ Ê œ
ddf dh
dt dt dt dt
dg
cc œœ
Š‹
df dh d
dt dt dt dt
dg
ijk u
(b) f(t) g(t) h(t) ( ) f(t) g(t) h(t)ff f f f f f fuijk u i j kœÊœ
ddf dh
dt dt dt dt dt dt dt
dddgd
’“’“’“
ff f
[f(t) g(t) h(t) ]œœ
ddgd
dt dt dt dt dt dt
df dh d
ff
ijk ijk uff
’“
u
50. Let f (t) f (t) f (t) and g (t) g (t) g (t) . Thenuijkv ijkœ œ
"#$ " # $
uv i j kœ [f (t) g (t)] [f (t) g (t)] [f (t) g (t)]
"" ## $$
( ) [f (t) g (t)] [f (t) g (t)] [f (t) g (t)]Ê œ
d
dt uv i j k
ww ww ww
"" ## $$
[f (t) f (t) f (t) ] [g (t) g (t) g (t) ] ;œ œ
www w w w
"$"#$
ijk i j k
dd
dt dt
uv
[f (t) g (t)] [f (t) g (t)] [f (t) g (t)]uv i j kœ
"" ## $$
( ) [f (t) g (t)] [f (t) g (t)] [f (t) g (t)]Ê œ
d
dt uv i j k
ww ww ww
"" ## $$
[f (t) f (t) f (t) ] [g (t) g (t) g (t) ]œ œ
www w w w
"#$ " # $
ijk i j k
dd
dt dt
uv
51. Suppose is continuous at t t . Then lim (t) (t ) lim [f(t) g(t) h(t) ]rrrijkœœÍ
!!
tt ttÄÄ
f(t ) g(t ) h(t ) lim f(t) f(t ), lim g(t) g(t ), and lim h(t) h(t ) f, g, and h areœ œ œ œÍ
!!! ! ! !
ijk Ítt tt ttÄÄ Ä
continuous at t t .œ!
52. lim [ (t) (t)] lim f(t) f(t) f(t)
g(t) g(t) g(t)
lim f (t) lim f (t)
tt tt tt tt
ÄÄ ÄÄ
rr
ijk ijk
"# "#$
"#$
"#
‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
lim f (t)
lim g (t) lim g (t) lim g (t)
tt
tt tt tt
Ä
ÄÄÄ
$
"#$
lim (t) lim (t)œ‚œ‚
tt ttÄÄ
rrAB
"#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 13.1 Vector Functions 831
53. (t ) exists f (t ) g (t ) h (t ) exists f (t ), g (t ), h (t ) all exist f, g, and h are continuous atrijk
w w w w www
! ! ! ! !!!
Ê Ê Ê
t t (t) is continuous at t tœÊ œ
!!
r
54. (a) k (t) dt [kf(t) kg(t) kh(t) ] dt [kf(t)] dt [kg(t)] dt [kh(t)] dt
'' ' ' '
aa a a a
bb b b b
rijk ijkœœ
k f(t) dt g(t) dt h(t) dt k (t) dtœœ
Œ
'' ' '
aa a a
bb b b
ij kr
(b) [ (t) (t)] dt f (t) g (t) h (t) f (t) g (t) h (t) dt
''
aa
bb
rr i j k i j k
"# " " " # # #
„œ „abcdcd
f (t) f (t) [g (t) g (t ] [h (t) h (t)] ) dtœ „ „ „
'a
babcd
"# "# "#
ijk
f (t) f (t) dt g (t) g (t) dt h (t) h (t) dtœ„„ „
'' '
aa a
bb b
cdcdcd
"# "# "#
ij k
f (t) dt f (t) dt g (t) dt g (t) dt h (t) dt h (t) dtœ„„ „
”•”•” •
'' '' ''
aa aa a a
bb bb b b
"# "# " #
ii jj kk
(t) dt (t) dtœ„
''
aa
bb
rr
"#
(c) Let c c c . Then (t) dt c f(t) c g(t) c h(t) dtCijk Crœ œ
"#$ " # $
''
aa
bb
†cd
c f(t) dt c g(t) dt c h(t) dt = (t) dt;œ
"# $
'' ' '
aa a a
bb b b
Cr†
(t) dt c h(t) c g(t) c f(t) c h(t) c g(t) c f(t) dt
''
aa
bb
Cr i j k‚œ cdcdcd
#$ $" "#
c h(t) dt c g(t) dt c f(t) dt c h(t) dt c g(t) dt c f(t) dtœ
”•”•”•
#$ $" "#
'' '' ''
aa aa aa
bb bb bb
ijk
(t) dtœ‚Cr
'a
b
55. (a) Let u and be continuous on [a b]. Then lim u(t) (t) lim [u(t)f(t) u(t)g(t) u(t)h(t) ]rrijkߜ
tt ttÄÄ
u(t )f(t ) u(t )g(t ) u(t )h(t ) u(t ) (t ) u is continuous for every t in [a b].œ œ Ê ß
!! !! !! !! !
ijkrr
(b) Let u and be differentiable. Then (u ) [u(t)f(t) u(t)g(t) u(t)h(t) ]rrijk
dd
dt dt
œ
f(t) u(t) g(t) u(t) h(t) u(t)œ
ˆ‰ ˆ‰
Š‹
du df du du dh
dt dt dt dt dt dt
dg
ijk
[f(t) g(t) h(t) ] u(t) uœ œijk ijkr
du df dh du d
dt dt dt dt dt dt
dg
Š‹
r
56. (a) If (t) and (t) have identical derivatives on I, then RR ijkijk
"# ddfdhdfdh
dt dt dt dt dt dt dt
dg dg
Rœ œ
, , f (t) f (t) c , g (t) g (t) c , h (t) h (t) cœÊœ œ œÊ œ œ œ
ddfdf dhdh
dt dt dt dt dt dt dt
dg dg
R"#"" ##" #$
f (t) g (t) h (t) [f (t) c ] [g (t) c ] [h (t) c ] (t) (t) , whereÊ œÊ œ
""" #"###$ "#
ijk i j kRRC
ccc.Cijkœ
"#$
(b) Let (t) be an antiderivative of (t) on I. Then (t) (t). If (t) is an antiderivative of (t) on I, thenRrRrUr
wœ
(t) (t). Thus (t) (t) on I (t) (t) .Ur UR URC
www
œœÊœ
57. ( ) d [f( ) g( ) h( ) ] d f( ) d g( ) d h( ) d
dd dd d
dt dt dt dt dt
'' '''
aa aaa
tt ttt
rijkijk77 7 7 7 7 77 77 77œœ
f(t) g(t) h(t) (t). Since ( ) d (t), we have that ( ) d is an antiderivative ofœ œ œijkr r r r
d
dt ''
aa
tt
77 77
. If is any antiderivative of , then (t) ( ) d by Exercise 56(b). Then (a) ( ) drR r R r C R r Cœ œ
''
a a
t a
77 77
(a) ( ) d (t) (t) (a) ( ) d (b) (a).œÊ Ê œœ Ê œ 0C C R r R C R R r R Rœ''
aa
tb
77 77
58-61. Example CAS commands:
:Maple
> with( plots );
r := t -> [sin(t)-t*cos(t),cos(t)+t*sin(t),t^2];
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

832 Chapter 13 Vector-Valued Functions and Motion in Space
t0 := 3*Pi/2;
lo := 0;
hi := 6*Pi;
P1 := spacecurve( r(t), t=lo..hi, axes=boxed, thickness=3 ):
display( P1, title="#58(a) (Section 13.1)" );
Dr := unapply( diff(r(t),t), t ); # (b)
Dr(t0); # (c)
q1 := expand( r(t0) + Dr(t0)*(t-t0) );
T := unapply( q1, t );
P2 := spacecurve( T(t), t=lo..hi, axes=boxed, thickness=3, color=black ):
display( [P1,P2], title="#58(d) (Section 13.1)" );
62-63. Example CAS commands:
:Maple
a := 'a'; b := 'b';
r := (a,b,t) -> [cos(a*t),sin(a*t),b*t];
Dr := unapply( diff(r(a,b,t),t), (a,b,t) );
t0 := 3*Pi/2;
q1 := expand( r(a,b,t0) + Dr(a,b,t0)*(t-t0) );
T := unapply( q1, (a,b,t) );
lo := 0;
hi := 4*Pi;
P := NULL:
for a in [ 1, 2, 4, 6 ] do
P1 := spacecurve( r(a,1,t), t=lo..hi, thickness=3 ):
P2 := spacecurve( T(a,1,t), t=lo..hi, thickness=3, color=black ):
P := P, display( [P1,P2], axes=boxed, title=sprintf("#62 (Section 13.1)\n a=%a",a) );
end do:
display( [P], insequence=true );
58-63. Example CAS commands:
: (assigned functions, parameters, and intervals will vary)Mathematica
The x-y-z components for the curve are entered as a list of functions of t. The unit vectors , , are not inserted.ijk
If a graph is too small, highlight it and drag out a corner or side to make it larger.
Only the components of r[t] and values for t0, tmin, and tmax require alteration for each problem.
Clear[r, v, t, x, y, z]
r[t_]={ Sin[t] t Cos[t], Cos[t] t Sin[t], t2}
t0= 3 / 2; tmin= 0; tmax= 6 ;11
ParametricPlot3D[Evaluate[r[t]], {t, tmin, tmax}, AxesLabel {x, y, z}];Ä
v[t_]= r'[t]
tanline[t_]= v[t0] t r[t0]
ParametricPlot3D[Evaluate[{r[t], tanline[t]}], {t, tmin, tmax}, AxesLabel {x, y, z}];Ä
For 62 and 63, the curve can be defined as a function of t, a, and b. Leave a space between a and t and b and t.
Clear[r, v, t, x, y, z, a, b]
r[t_,a_,b_]:={Cos[a t], Sin[a t], b t}
t0= 3 / 2; tmin= 0; tmax= 4 ;11
v[t_,a_,b_]= D[r[t, a, b], t]
tanline[t_,a_,b_]=v[t0, a, b] t r[t0, a, b]
pa1=ParametricPlot3D[Evaluate[{r[t, 1, 1], tanline[t, 1, 1]}], {t,tmin, tmax}, AxesLabel {x, y, z}];Ä
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 13.2 Modeling Projectile Motion 833
pa2=ParametricPlot3D[Evaluate[{r[t, 2, 1], tanline[t, 2, 1]}], {t,tmin, tmax}, AxesLabel {x, y, z}];Ä
pa4=ParametricPlot3D[Evaluate[{r[t, 4, 1], tanline[t, 4, 1]}], {t,tmin, tmax}, AxesLabel {x, y, z}];Ä
pa6=ParametricPlot3D[Evaluate[{r[t, 6, 1], tanline[t, 6, 1]}], {t,tmin, tmax}, AxesLabel {x, y, z}];Ä
Show[GraphicsArray[{pa1, pa2, pa4, pa6}]]
13.2 MODELING PROJECTILE MOTION
1. x (v cos )t (21 km) (840 m/s)(cos 60°)t t 50 secondsœÊ œ Êœ œ
!!ˆ‰
1000 m
1 km (840 m/s)(cos 60°)
21,000 m
2. R sin 2 and maximum R occurs when 45° 24.5 km (sin 90°)œœÊœ
v v
g9.8 m/s
!!
Š‹
v (9.8)(24,500) m /s 490 m/sÊœ œ
!##
È
3. (a) t 72.2 seconds; R sin 2 (sin 90°) 25,510.2 mœœ ¸ œ œ ¸
2v sin
g 9.8 m/s g 9.8 m/s
2(500 m/s)(sin 45°) (500 m/s)
v
!!
(b) x (v cos )t 5000 m (500 m/s)(cos 45°)t t 14.14 s; thus,œÊœ Êœ ¸
!!5000 m
(500 m/s)(cos 45°)
y (v sin )t gt y (500 m/s)(sin 45°)(14.14 s) 9.8 m/s (14.14 s) 4020 mœÊ¸ ¸
!""
##
###
!ab
(c) y 6378 m
max œœ ¸
(v sin ) ((500 m/s)(sin 45°))
2g 2 9.8 m/s
!ab
4. y y (v sin )t gt y 32 ft (32 ft/sec)(sin 30°)t 32 ft/sec t y 32 16t 16t ;œ Êœ Êœ
!! ""
##
####
!ab
the ball hits the ground when y 0 0 32 16t 16t t 1 or t 2 t 2 sec since t 0; thus,œÊœ Êœ œÊœ
#
x (v cos ) t x (32 ft/sec)(cos 30°)t 32 (2) 55.4 ftœÊœ œ ¸
!#
!Š‹
È3
5. x x (v cos )t 0 (44 cos 45°)t 22 2t and y y (v sin )t gt 6.5 (44 sin 45°)t 16tœ œ œ œ œ
!! !! "
#
##
!!
È
6.5 22 2t 16t ; the shot lands when y 0 t 2.135 sec since t 0; thusœ œÊœ ¸
È#„
#
22 2 968 416
3
ÈÈ
x 22 2t 22 2 (2.135) 66.43 ftœ¸ ¸
ÈÈ
Š‹
6. x 0 (44 cos 40°)t 33.706t and y 6.5 (44 sin 40°)t 16t 6.5 28.283t 16t ; y 0œ ¸ œ ¸ œ
##
t 1.9735 sec since t 0; thus x (33.706)(1.9735) 66.52 ft theʸ ¸ ¸ ¸ Ê
28.283 (28.283) 416
3
#
È
difference in distances is about 66.52 66.43 0.09 ft or about 1 inchœ
7. (a) R sin 2 10 m (sin 90°) v 98 m s v 9.9 m/s;œÊœ ʜʸ
vv
g 9.8 m/s
!Š‹ ###
!!
(b) 6m (sin 2 ) sin 2 0.59999 2 36.87° or 143.12° 18.4° or 71.6°¸Ê¸Ê¸ ʸ
(9.9 m/s)
9.8 m/s !! ! !
8. v 5 10 m/s and x 40 cm 0.4 m; thus x (v cos )t 0.4m 5 10 m/s (cos 0°)t
!!
' '
œ‚ œ œ œ Ê œ ‚!ab
t 0.08 10 s 8 10 s; also, y y (v sin )t gtÊœ ‚ œ‚ œ
' ) #
!! "
#
!
y 5 10 m/s (sin 0°) 8 10 s 9.8 m/s 8 10 s 3.136 10 m orÊœ‚ ‚ ‚ œ ‚abababab
' ) # ) "%
"
#
#
3.136 10 cm. Therefore, it drops 3.136 10 cm.‚ ‚
"# "#
9. R sin 2 3(248.8) ft (sin 18°) v 77,292.84 ft /sec v 278.02 ft/sec 190 mphœÊ œ ʸ ʸ ¸
vv
g 32 ft/sec
!Š‹ ###
!!
10. v ft/sec and R 200 ft 200 (sin 2 ) sin 2 0.9 2 64.2° 32.1°; or
!œœÊœÊœÊ¸Ê¸
80 10
332
ÈŠ‹
80 10
3!! ! !
2 115.8° 57.9°; If 32.1 , y 31.4 ft. If 57.9 , y 79.7 ft 75 ft. In!!! !¸Ê¸ ¸ œ ¸ ¸ ¸
‰‰
max max
’“Š‹
80 10
3(sin 32.1°)
2(32)
order to reach the cushion, the angle of elevation will need to be about 32.1°. At this angle, the circus performer will go
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
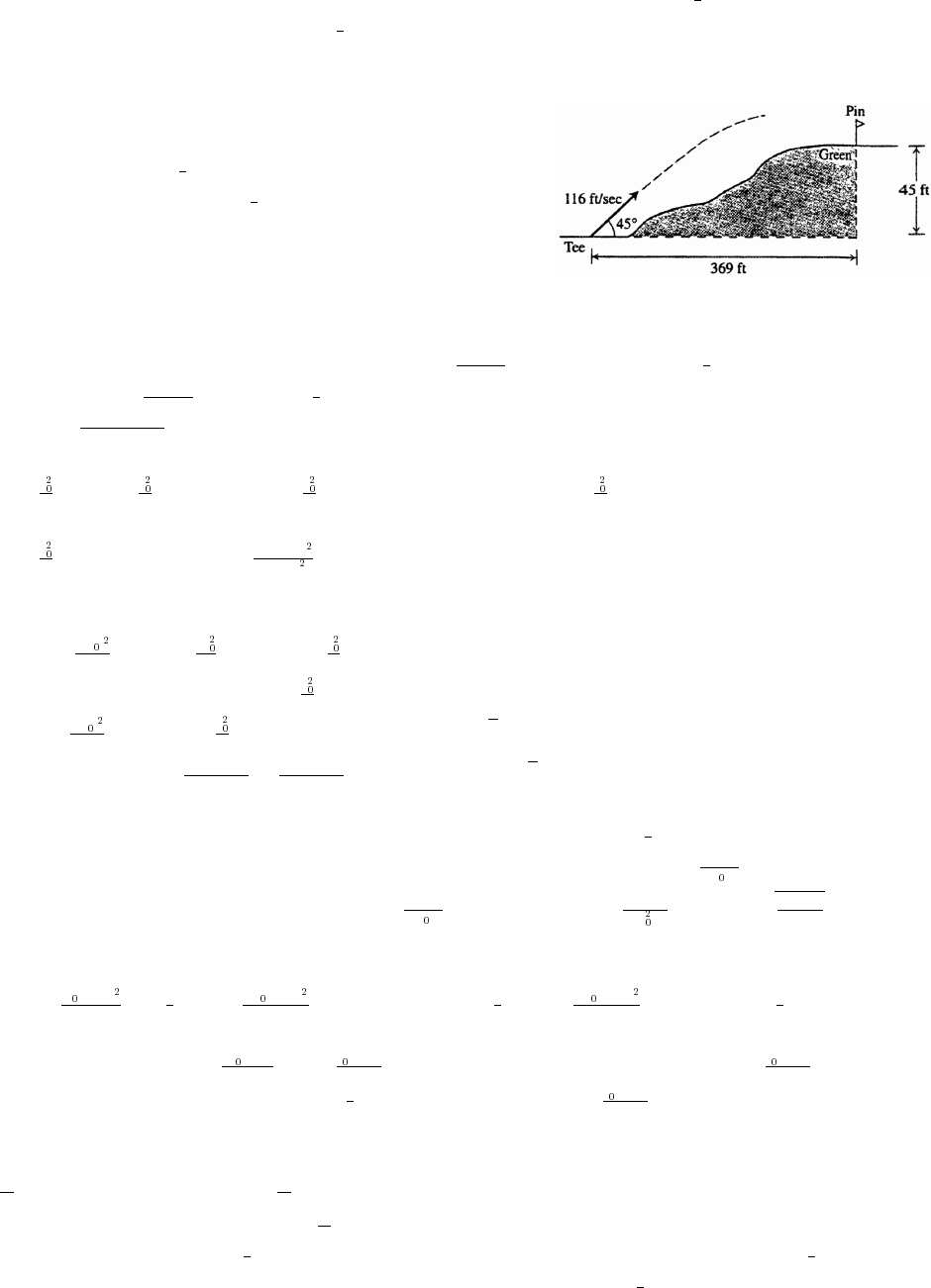
834 Chapter 13 Vector-Valued Functions and Motion in Space
31.4 ft into the air at maximum height and will not strike the 75 ft high ceiling.
11. x (v cos )t 135 ft (90 ft/sec)(cos 30°)t t 1.732 sec; y (v sin )t gtœÊœ ʸ œ
! ! "
#
#
!!
y (90 ft/sec)(sin 30°)(1.732 sec) 32 ft/sec (1.732 sec) y 29.94 ft the golf ball will clipʸ ʸ Ê
"
#
##
ab
the leaves at the top
12. v 116 ft/sec, 45°, and x (v cos )t
!!
œœœ!!
369 (116 cos 45°)t t 4.50 sec;Êœ ʸ
also y (v sin )t gtœ
!"
#
#
!
y (116 sin 45°)(4.50) (32)(4.50)Êœ
"
#
#
45.11 ft. It will take the ball 4.50 sec to travel¸
369 ft. At that time the ball will be 45.11 ft in
the air and will hit the green past the pin.
13. We do part b first.
(b) x (v cos )t 315 ft (v cos 20°)t v ; also y (v sin )t gtœÊœ Êœ œ
!!!!
"
#
#
!!
315
t cos 20°
34 ft (t sin 20°) (32)t 34 315 tan 20° 16t t 5.04 sec t 2.25 secÊœ Êœ ʸ ʸ
ˆ‰
315
t cos 20°
"
#
####
(a) v 149 ft/sec
!œ¸
315
(2.25)(cos 20°)
14. R sin 2 (2 sin cos ) [2 cos (90° ) sin (90° )] [sin 2(90° )]œœ œ œ
vv v v
gg g g
!!! !! !
15. R sin 2 16,000 m sin 2 sin 2 0.98 2 78.5° or 2 101.5° 39.3°œÊœ ʜʸ ¸Ê¸
v
g 9.8 m/s
(400 m/s)
!!!!!!
or 50.7°
16. (a) R sin 2 sin 2 4 sin or 4 times the original range.œœœ
(2v )
gg g
4v v
!! !
Š‹
(b) Now, let the initial range be R sin 2 . Then we want the factor p so that pv will double the rangeœv
g!!
sin 2 2 sin 2 p 2 p 2 or about 141%. The same percentage will approximatelyʜ ʜʜ
(pv )
gg
v
!!
Š‹ È
#
double the height: p 2 p 2.
ababpv sin 2 v sin
2g 2g
00
22
!!
œÊœÊœ
#È
17. x x (v cos )t 0 (v cos 40°)t 0.766 v t and y y (v sin )t gt 6.5 (v sin 40°)t 16tœ œ ¸ œ œ
!! ! ! !! !
"
#
##
!!
6.5 0.643 v t 16t ; now the shot went 73.833 ft 73.833 0.766 v t t sec; the shot lands¸ Ê œ ʸ
! !
#96.383
v
when y 0 0 6.5 (0.643)(96.383) 16 0 68.474 vœÊœ ʸ Ê ¸
Š‹ É
96.383
v 68.474
148,635 148,635
v
#
!
46.6 ft/sec, the shot's initial speed¸
18. y y and y (v sin )t gt (v sin )t gt
max max
(v sin ) 3(v sin ) 3(v sin )
2g 4 8g 8g
3
œÊœ œ Ê œ
!! !
!!
""
##
##
!!
3(v sin ) (8gv sin )t 4g t 4g t (8gv sin )t 3(v sin ) 0 2gt 3v sin 0 orʜʜʜ
!! !! !
##### #
!! !! !
2gt v sin 0 t or t . Since the time it takes to reach y is t ,œÊœ œ œ
!!3v sin v sin v sin
2g 2g g
max max
!! !
then the time it takes the projectile to reach of y is the shorter time t or half the time it takes
3
42g
max v sin
œ!
to reach the maximum height.
19. ( g ) dt gt and (0) (v cos ) (v sin ) g(0) (v cos ) (v sin )
dd
dt dt
rr
œ œ œ Ê œ
'jjC i j jC i j
"!! "!!
!! !!
(v cos ) (v sin ) (v cos ) (v sin gt) ; [(v cos ) (v sin gt) ] dtÊœ Êœ œ Cij i jr i j
"! ! ! ! ! !
!! !! !!
d
dt
r'
(v t cos ) v t sin gt and (0) x y [v (0) cos ] v (0) sin g(0)œœÊ
!! #!!! ! #
" "
# #
# #
!! ! !ijCriji jC
ˆ‰ ‘
x y x y (x v t cos ) y v t sin gt x x v t cos andœ Ê œ Êœ Êœ
!! #!! !! !! !!
"
#
#
ijC ijr i j!! !
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
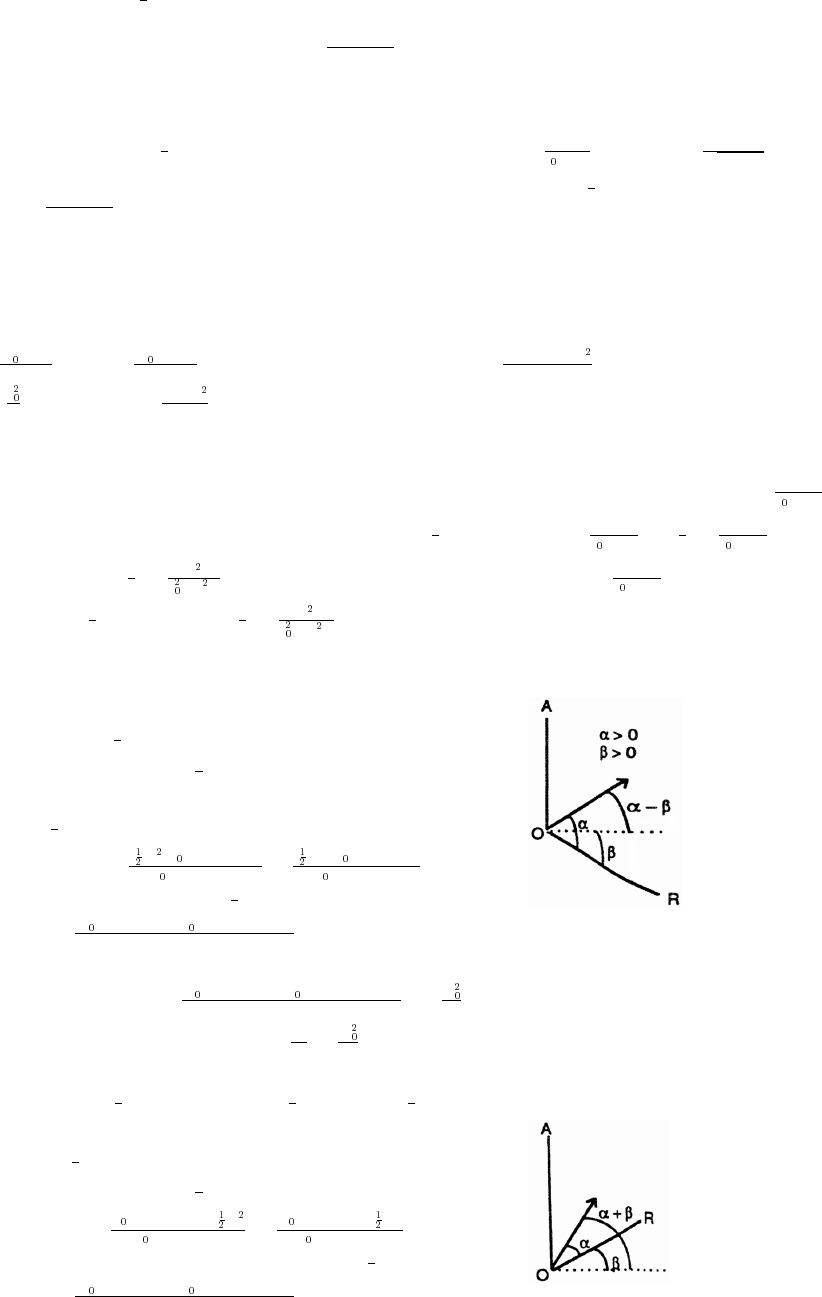
Section 13.2 Modeling Projectile Motion 835
y y v t sin gtœ
!! "
#
#
!
20. From Example 3(b) in the text, v sin (68)(64) v sin 56.5° 65.97 v 79 ft/sec
!!!
!œÊ ¸Ê¸
È
21. The horizontal distance from Rebollo to the center of the cauldron is 90 ft the horizontal distance to theÊ
nearest rim is x 90 (12) 84 84 x (v cos )t 0 t 84 tœ œ Ê œ ¸ Ê œ
"
#!!
!Š‹
90g (90)(32)
v sin (68)(64)
!È
t 1.92 sec. The vertical distance at this time is y y (v sin )t gtÊœ œ
!! "
#
#
!
6 (68)(64) (1.92) 16(1.92) 73.7 ft the arrow clears the rim by 3.7 ft¸ ¸ Ê
È#
22. The projectile rises straight up and then falls straight down, returning to the firing point.
23. Flight time 1 sec and the measure of the angle of elevation is about 64° (using a protractor) so thatœ
t 1 v 17.80 ft/sec. Then y 4.00 ft andœÊœ ʸ œ ¸
2v sin 2v sin 64°
g 32 2(32)
max (17.80 sin 64°)
!!
R sin 2 R sin 128° 7.80 ft the engine traveled about 7.80 ft in 1 sec the engineœÊœ ¸Ê Ê
v
g32
(17.80)
!
velocity was about 7.80 ft/sec
24. When marble A is located R units downrange, we have x (v cos )t R (v cos )t t . AtœÊœÊœ
!!
!!
R
v cos !
that time the height of marble A is y y (v sin )t gt (v sin ) gœ œ
!! !
""
##
##
!!
Š‹Š‹
RR
v cos v cos
!!
y R tan g . The height of marble B at the same time t seconds isÊœ œ!"
#Š‹
RR
v cos v cos
!!
h R tan gt R tan g . Since the heights are the same, the marbles collide regardlessœœ!!
""
##
#Š‹
R
v cos !
of the initial velocity v .
!
25. (a) At the time t when the projectile hits the line OR we
have tan ; x [v cos ( )]t and"!"œœ
y
x!
y [v sin ( )]t gt 0 since R isœ
!"
#
#
!"
below level ground. Therefore let
y gt [v sin ( )]t 0kkœ
"
#
#!!"
so that tan "œœ
‘‘
gt (v sin ( ))t gt v sin ( )
[v cos ( )]t v cos ( )
!" !"
!" !"
v cos ( ) tan gt v sin ( )ʜ
!!
"
#
!" " !"
t , which is the timeʜ
2v sin ( ) 2v cos ( ) tan
g
!" !" "
when the projectile hits the downhill slope. Therefore,
x [v cos ( )] cos ( ) tan sin ( ) cos ( ) . If x isœ œ
! #
!" !" " !" !"
’“
cd
2v sin ( ) 2v cos ( ) tan
gg
2v
!" !" "
maximized, then OR is maximized: [ sin 2( ) tan cos 2( )] 0
dx
dg
2v
!œ œ!" " !"
sin 2( ) tan cos 2( ) 0 tan cot 2( ) 2( ) 90°Ê œÊ œ Ê œ !" " !" " !" !" "
(90° ) (90° ) of AOR.Êœ Êœ œ n!" " ! "
"""
###
(b) At the time t when the projectile hits OR we have
tan ; x [v cos ( )]t and"!"œœ
y
x!
y [v sin ( )]t gtœ
!"
#
#
!"
tan Êœ œ"cd‘
v sin( )t gt v sin( ) gt
[v cos ( )]t v cos ( )
!" !"
!" !"
v cos( ) tan v sin( ) gtʜ
!!
"
#
!" " !"
t , which is the timeʜ
2v sin ( ) 2v cos ( ) tan
g
!" !" "
when the projectile hits the uphill slope. Therefore,
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
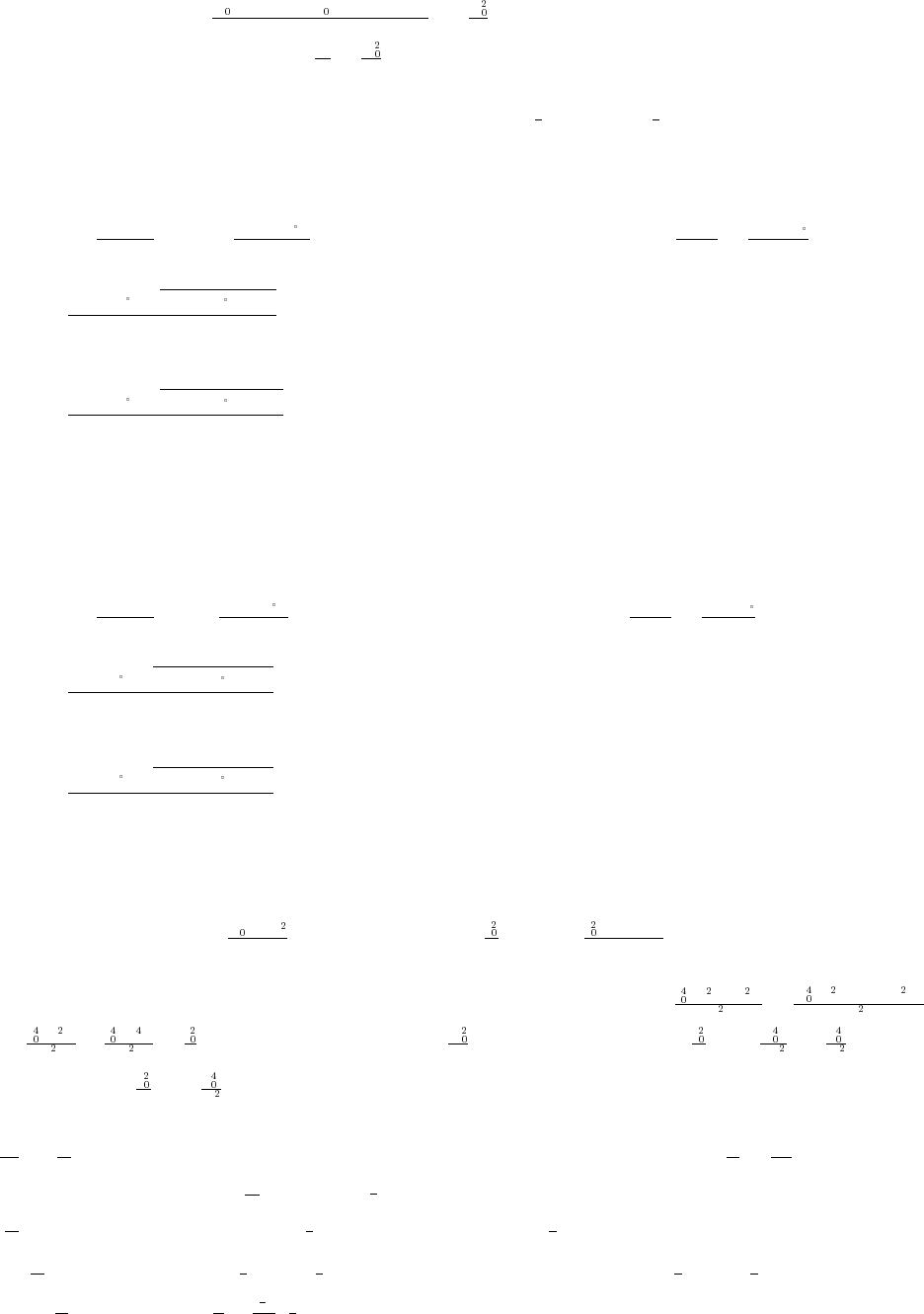
836 Chapter 13 Vector-Valued Functions and Motion in Space
x [v cos ( )] sin ( ) cos ( ) cos ( ) tan . If x isœ œ
! #
!" !" !" !" "
’“
cd
2v sin ( ) 2v cos ( ) tan
gg
2v
!" !" "
maximized, then OR is maximized: [cos 2( ) sin 2( ) tan ] 0
dx
dg
2v
!œœ!" !" "
cos 2( ) sin 2( ) tan 0 cot 2( ) tan cot 2( ) tan Ê œ Ê œ! Ê œ!" !" " !" " !" "
tan ( ) 2( ) 90° ( ) 90° (90° ) of AOR. Therefore v would bisectœÊ œœÊœ œ n"!" " "! "
""
## !
AOR for maximum range uphill.n
26. (a) t x t y t ; where x t 145 cos 23 14 t and y t 2.5 145 sin 23 t 16t .rijab a b a b ab a b ab a bab abœ œ œ
‰‰2
(b) y 2.5 2.5 52.655 feet, which is reached at t 1.771 seconds.
max v sin 145sin 23
2g 64 g 32
vsin 145sin 23
œœ ¸ œœ ¸
ab a b
022 0
!!
(c) For the time, solve y 2.5 145 sin 23 t 16t 0 for t, using the quadratic formulaœ œab
‰2
t 3.585 sec. Then the range at t 3.585 is about x 145 cos 23 14 3.585œ¸ ¸œ
145 sin 23 145 sin 23 160
32
‰
Éab
2abab
428.311 feet.¸
(d) For the time, solve y 2.5 145 sin 23 t 16t 20 for t, using the quadratic formulaœ œab
‰2
t 0.342 and 3.199 seconds. At those times the ball is aboutœ¸
145 sin 23 145 sin 23 1120
32
Éab
2
x 0.342 145 cos 23 14 0.342 40.860 feet from home plate and x 3.199 145 cos 23 14 3.199aba bab aba babœ¸ œ
‰ ‰
382.195 feet from home plate.¸
(e) Yes. According to part (d), the ball is still 20 feet above the ground when it is 382 feet from home plate.
27. (a) (Assuming that "x" is zero at the point of impact:)
t x t y t ; where x t 35 cos 27 t and y t 4 35 sin 27 t 16t .rijab a b a b ab a b ab a bab abœ œ œ
‰‰2
(b) y 4 4 7.945 feet, which is reached at t 0.497 seconds.
max v sin 35sin 27
2g 64 g 32
vsin 35sin 27
œœ ¸ œœ¸
ab a b
022 0
!!
(c) For the time, solve y 4 35 sin 27 t 16t 0 for t, using the quadratic formulaœ œab
‰2
t 1.201 sec. Then the range is about x 1.201 35 cos 27 1.201œ¸ œ
35 sin 27 35 sin 27 256
32
‰
Éab
2aba bab
37.453 feet.¸
(d) For the time, solve y 4 35 sin 27 t 16t 7 for t, using the quadratic formulaœ œab
‰2
t 0.254 and 0.740 seconds. At those times the ball is aboutœ¸
35 sin 27 35 sin 27 192
32
Éab
2
x 0.254 35 cos 27 0.254 7.921 feet and x 0.740 35 cos 27 0.740 23.077 feet the impact point,aba bab aba babœ¸ œ¸
‰‰
or about 37.453 7.921 29.532 feet and 37.453 23.077 14.376 feet from the landing spot.¸ ¸
(e) Yes. It changes things because the ball won't clear the net (y 7.945).
max ¸
28. The maximum height is y and this occurs for x sin 2 . These equations describeœœœ
(v sin )
ggg
v v sin cos
!!!
##
!
parametrically the points on a curve in the xy-plane associated with the maximum heights on the parabolic trajectories in
terms of the parameter (launch angle) . Eliminating the parameter , we have x!!
#
œœ
v sin cos
gg
v sin 1 sin
!! !!
ˆ‰
ab
(2y) (2y) x 4y y 0 x 4 y yœœÊ œÊœ
v sin v sin v 2v v v v
g g g g 2g 16g 4g
!! ### # #
Š‹ ’ “Š‹
x 4 y , where x 0.Ê œ
##
Š‹
vv
4g 4g
29. k g P t k and t g P t dt kt v t e e v t t dt
dd d1
dt dt dt v t
P t dt kt
2
2
rr r
œÊ œ œÊ œ Ê œ œ Ê œjQj Qab ab ab ab ab ab
''
'ab ab
ge e dt ge e , where g ; apply the initial condition:œ œ œ œ
kt kt kt kt
e
k1g
k1
'jjCCC
jC
‘
kt
vcos vsin vcos vsin
d
dt k k
t0 00 0 0
gg
r¹abab ab
ˆ‰
œœœÊœ!! ! !ijjCC i j
v e cos e v sin , dt
v e cos e v sin
Êœ œ
d
dt k k
00
kt kt
gg 00
kt kt
gg
kk
rˆ‰ˆ ‰ˆ‰ˆ‰ˆ ‰ˆ‰
!!
!!
ijr
ij
'cd
; apply the initial condition:
e cos v sin
œ
ˆ‰ ˆ‰
Š‹
v
kkkk
kt gt g
e02
0kt
!!ij
C
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 13.3 Arc Length and the Unit Tangent Vector 837T
0 cos cos
r0 CC
ij ij
ab ˆ‰ˆ ‰ ˆ‰ˆ ‰
œœ Ê œ
v v sin v v sin
kkk kkk
gg
22
00 00
2 2
!!
!!
t
1e cos 1e sin 1kte
ʜ
rij
ab ˆ‰ˆ ‰ˆ‰ ˆ‰ ˆ ‰
vv
kkk
kt kt kt
g
00
2
!!
30. (a) t x t y t ; where x t 1 e cos 20 andrijababab ab a ba bab ab ˆ‰
œ œ
152
0.12
0.12t‰
y t 3 1 e sin 20 1 0.12t eab a ba b a b
ˆ‰ ˆ‰
œ
152 32
0.12 0.12
0.12t 0.12t‰
2
(b) Solve graphically using a calculator or CAS: At t 1.484 seconds the ball reaches a maximum height of about 40.435¸
feet.
(c) Use a graphing calculator or CAS to find that y 0 when the ball has traveled for 3.126 seconds. The range isœ¸
about x 3.126 1 e cos 20 372.311 feet.ab a b
ˆ‰ˆ ‰
œ ¸
152
0.12
0.12 3.126‰ab
(d) Use a graphing calculator or CAS to find that y 30 for t 0.689 and 2.305 seconds, at which times the ball is aboutœ¸
x 0.689 94.454 feet and x 2.305 287.621 feet from home plate.ab ab¸¸
(e) Yes, the batter has hit a home run since a graph of the trajectory shows that the ball is more than 14 feet above the
ground when it passes over the fence.
31. (a) t x t y t ; where x t 1 e 152 cos 20 17.6 andrijababab ab a ba bab ab ˆ‰
œ œ
1
0.08
0.08t‰
y t 3 1 e sin 20 1 0.08t eab a ba b a b
ˆ‰ ˆ‰
œ
152 32
0.08 0.08
0.08t 0.08t‰
2
(b) Solve graphically using a calculator or CAS: At t 1.527 seconds the ball reaches a maximum height of about 41.893¸
feet.
(c) Use a graphing calculator or CAS to find that y 0 when the ball has traveled for 3.181 seconds. The range isœ¸
about x 3.181 1 e 152 cos 20 17.6 351.734 feet.ab a b
ˆ‰ˆ ‰
œ ¸
1
0.08
0.08 3.181‰ab
(d) Use a graphing calculator or CAS to find that y 35 for t 0.877 and 2.190 seconds, at which times the ball is aboutœ¸
x 0.877 106.028 feet and x 2.190 251.530 feet from home plate.ab ab¸¸
(e) No; the range is less than 380 feet. To find the wind needed for a home run, first use the method of part (d) to find that
y 20 at t 0.376 and 2.716 seconds. Then define x w 1 e 152 cos 20 w , and solveœ¸ œ ab a b
ˆ‰ˆ ‰
1
0.08
0.08 2.716‰ab
x w 380 to find w 12.846 ft/sec.abœ¸
13.3 ARC LENGTH AND THE UNIT TANGENT VECTOR T
1. (2 cos t) (2 sin t) 5t ( 2 sin t) (2 cos t) 5rijkv ijkœÊœ
ÈÈ
( 2 sin t) (2 cos t) 5 4 sin t 4 cos t 5 3; Êœ œ œ œkk ÊŠ‹
ÈÈ
vT
## ##
#v
vkk
sin t cos t and Length dt 3 dt 3t 3œ œ œ œ œ
ˆ‰ˆ‰ kk cd
22
33 3
5
ijk v
È''
00
1
!1
2. (6 sin 2t) (6 cos 2t) 5t (12 cos 2t) ( 12 sin 2t) 5rijkv i jkœ Êœ
(12 cos 2t) ( 12 sin 2t) 5 144 cos 2t 144 sin 2t 25 13; Êœ œ œ œkk ÈÈ
v T
##### v
vkk
cos 2t sin 2t and Length dt 13 dt 13t 13œ œœœœ
ˆ‰ˆ‰ kk c d
12 12 5
13 13 13
ijk v
''
00
1
!1
3. t t t 1 t 1 t ; ri k vi k v T i kœ Ê œ Ê œ œ œ œ
2
31t 1t
t
$Î# "Î# # "Î# #"
kk a b
ÉÈv
vkk ÈÈ
È
and Length 1 t dt (1 t)œœœ
'0
8È‘
252
33
$Î# )
!
4. (2 t) (t 1) t 1 ( 1) 1 3 ; rijkvijkv T ijkœ Êœ Ê œ œ œ œ kk ÈÈ
### ""v
vkk ÈÈÈ
333
1
and Length 3 dt 3t 3 3œœœ
'0
3ÈÈÈ
’“
$
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
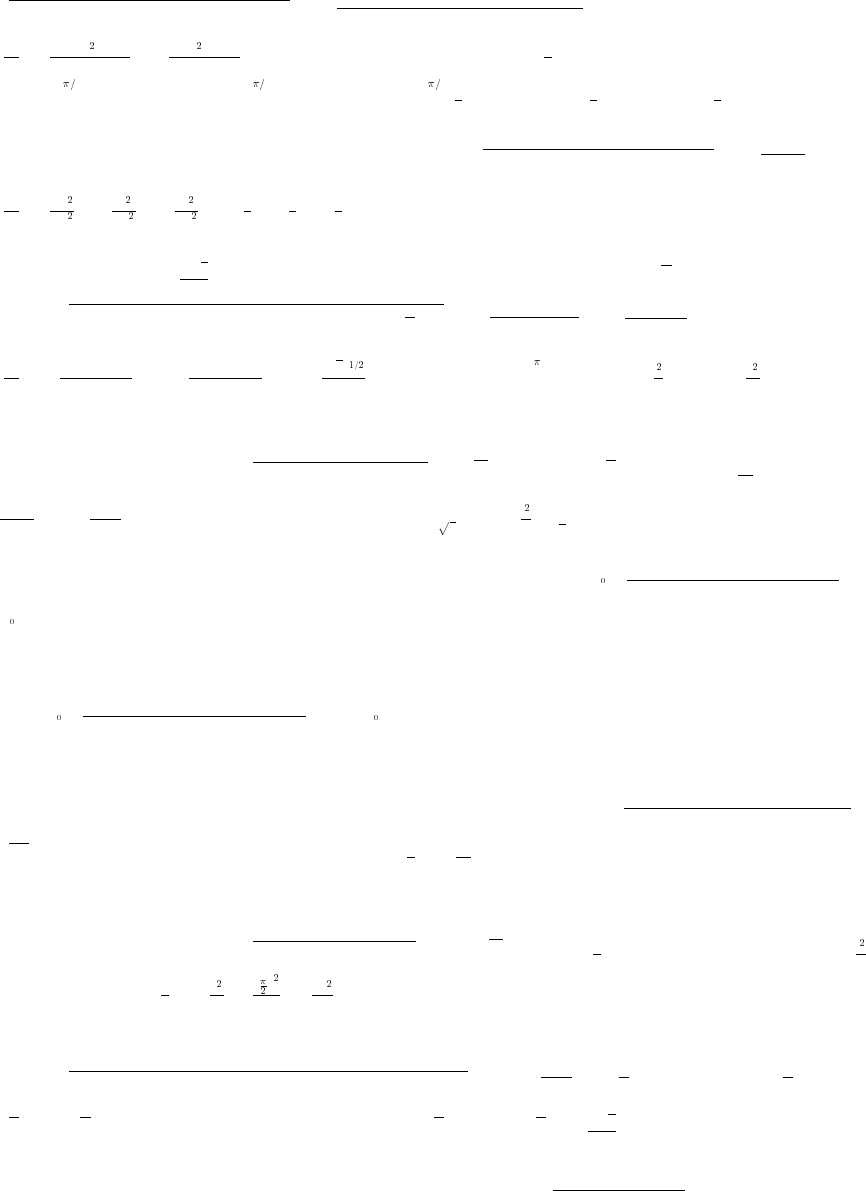
838 Chapter 13 Vector-Valued Functions and Motion in Space
5. cos t sin t 3 cos t sin t 3 sin t cos t rjkv j kvœ Êœ Êabab a ba b kk
$$ # #
3 cos t sin t 3 sin t cos t 9 cos t sin t cos t sin t 3 cos t sin t ;œ œ œ
Éababababkk
È
## ####
##
( cos t) (sin t) , if 0 t , andTjkjkœœ œ ŸŸ
v
vkkkkkk
#
3 cos t sin t 3 sin t cos t
3 cos t sin t 3 cos t sin t
1
Length 3 cos t sin t dt 3 cos t sin t dt sin 2t dt cos 2tœœœœœ
'''
000
222
kk ‘
333
4##
Î#
!
1
6. 6t 2t 3t 18t 6t 9t 18t 6t 9t 441t 21t ;r ijkv ijkvœ Êœ Êœ œ œ
$$$ ### #
### %
###
kk ababab
ÉÈ
and Length 21t dt 7t 49Tijkijkœœ œ œ œ œ
v
vkk "#$
#
"
8t 6t 9t 6 2 3
21t 21t 21t 7 7 7 '1
2cd
7. (t cos t) (t sin t) t (cos t t sin t) (sin t t cos t) 2 trijkv i j kœ Êœ
22
3
È$Î# "Î#
Š‹
È
(cos t t sin t) (sin t t cos t) 2 t 1 t 2t (t 1) t 1 t 1, if t 0;Ê œ œ œ œœ kk kk
ÊŠ‹
ÈÈ È
v## ##
#
and Length (t 1) dt tTijkœœ œœœ
v
vkk È
ˆ‰ˆ‰
Š‹ ’“
cos t t sin t sin t t cos t t
t1 t1 t1 2 2
2t
!
'0
111
8. (t sin t cos t) (t cos t sin t) (sin t t cos t sin t) (cos t t sin t cos t)rijv i jœÊœ
(t cos t) (t sin t) (t cos t) ( t sin t) t t t if 2 t 2; œ Êœ œœœŸŸœijv Tkk kk
ÈÈÈ
### v
vkk
(cos t) (sin t) and Length t dt 1œœ œœœ
ˆ‰ˆ‰ ’“
t cos t t sin t t
tt 2
ijij '2
2#
#
È
9. Let P(t ) denote the point. Then (5 cos t) (5 sin t) 12 and 26 25 cos t 25 sin t 144 dt
!##
vijkœ œ 1'0
tÈ
13 dt 13t t 2 , and the point is P(2 ) (5 sin 2 5 cos 2 24 ) (0 5 24 )œœÊœ œßßœßß
'0
t
!!
111111
10. Let P(t ) denote the point. Then (12 cos t) (12 sin t) 5 and
!vijkœ
13 144 cos t 144 sin t 25 dt 13 dt 13t t , and the point isœ œ œ Êœ11
''
00
tt
È## !!
P( ) (12 sin ( ) 12 cos ( ) 5 ) (0 12 5 ) œ ß ß œ ß ß11111
11. (4 cos t) (4 sin t) 3t ( 4 sin t) (4 cos t) 3 ( 4 sin t) (4 cos t) 3rijkv ijkvœÊœÊœkk È###
25 5 s(t) 5 d 5t Length sœœÊœ œÊ œ œ
Ȉ‰
'0
t
711
##
5
12. (cos t t sin t) (sin t t cos t) ( sin t sin t t cos t) (cos t cos t t sin t)rijv i jœ Êœ
(t cos t) (t sin t) (t cos t) (t cos t) t t, since t s(t) dœ Êœ œœœ ŸŸÊœœijvkk ÈÈ
### ##
1177
'0
tt
Length s( ) sÊœœœ1ˆ‰
11 1
###
ˆ‰ 3
8
13. e cos t e sin t e e cos t e sin t e sin t e cos t er i jk v i jkœÊœabababab
ttt ttttt
e cos t e sin t e sin t e cos t e 3e 3 e s(t) 3 e dÊœ œœ œ Ê œkkababab
ÉÈÈÈ
vtt tt t 2t
t
### '0
t77
3 e 3 Length s(0) s( ln 4) 0 3 e 3œÊ œœ œ
ÈÈ È È
Š‹
tln 4
33
4
È
14. (1 2t) (1 3t) (6 6t) 2 3 6 2 3 ( 6) 7 s(t) 7 d 7trij kvijkvœ Êœ Ê œ œÊ œ œkk È## # '0
t
7
Length s(0) s( 1) 0 ( 7) 7Êœœœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
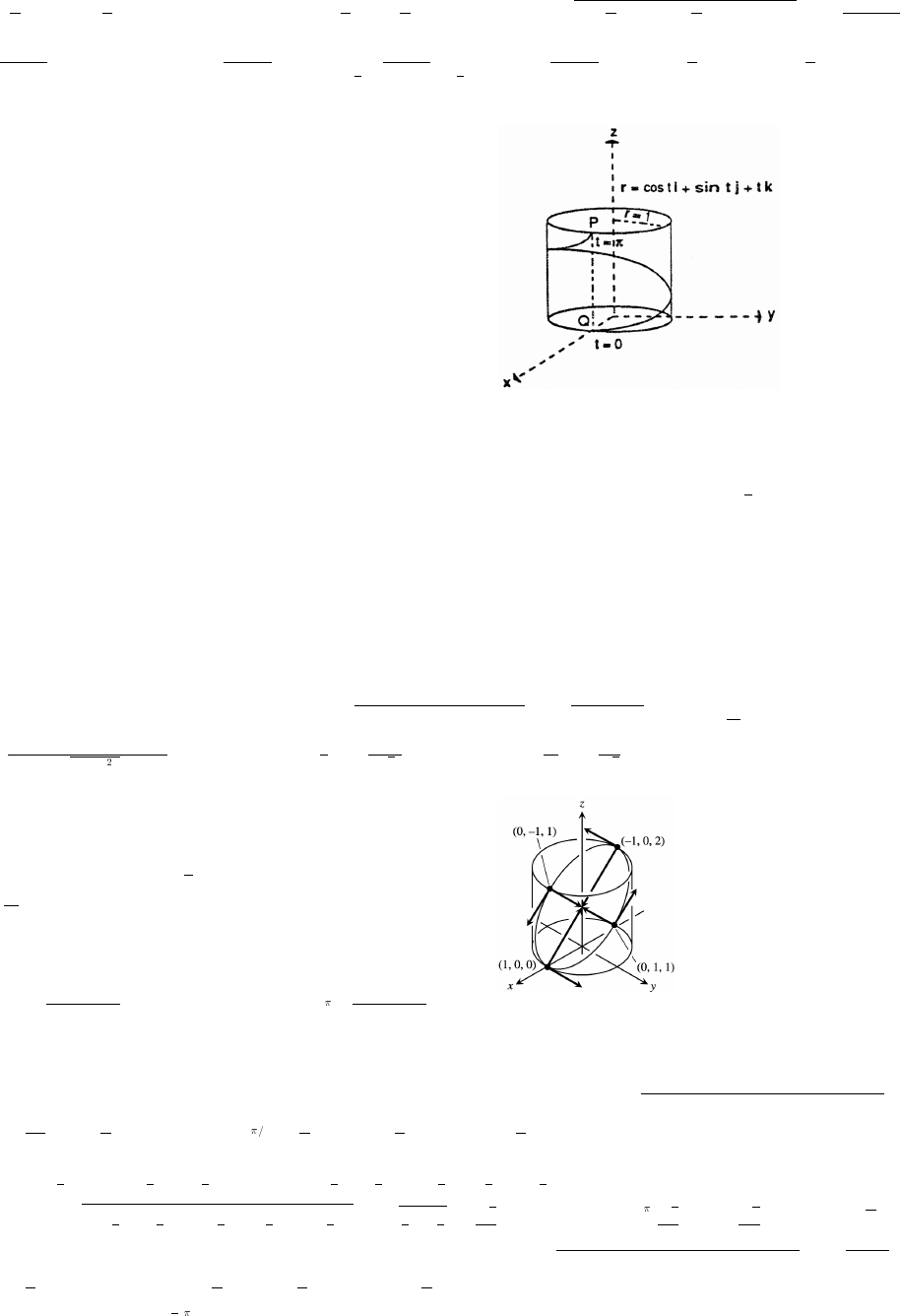
Section 13.3 Arc Length and the Unit Tangent Vector 839T
15. 2t 2t 1 t 2 2 2t 2 2 ( 2t) 4 4trij kvijkvœ ʜʜ œ
Š‹Š‹ Š‹Š‹
ÈÈ ÈÈ ÈÈ È
ab kk
Ê
###
##
2 1 t Length 2 1 t dt 2 1 t ln t 1 t 2 ln 1 2œÊ œ œ œ
ÈÈÈÈÈÈ
’“Š‹Š‹Š‹
####
"
#
"
!
'0
1t
2
16. Let the helix make one complete turn from t 0 to t 2 .œœ1
Note that the radius of the cylinder is 1 theÊ
circumference of the base is 2 . When t 2 , the point P is11œ
(cos 2 sin 2 2 ) (1 0 2 ) the cylinder is 2 units111 1 1ßßœßßÊ
high. Cut the cylinder along PQ and flatten. The resulting
rectangle has a width equal to the circumference of the
cylinder 2 and a height equal to 2 , the height of theœ11
cylinder. Therefore, the rectangle is a square and the portion
of the helix from t 0 to t 2 is its diagonal.œœ1
17. (a) (cos t) (sin t) ( cos t) , 0 t 2 x cos t, y sin t, z 1 cos t x yrij kœ" ŸŸÊœ œœÊ1##
cos t sin t 1, a right circular cylinder with the z-axis as the axis and radius 1. Thereforeœœ œ
##
P(cos t sin t 1 cos t) lies on the cylinder x y 1; t 0 P(1 0 0) is on the curve; t Q( 1 1)ßß œœÊßß œÊ!ßß
##
#
1
is on the curve; t R( 1 0 2) is on the curve. Then PQ and PR 2 2œ Ê ß ß œ œ
ÄÄ
1ijk i k
ik
ijk
Ê PQ PR 2 2 is a vector normal to the plane of P, Q, and R. Then the
1
202
Ä‚œ œ
Ä""
Ô×
ÕØ
plane containing P, Q, and R has an equation 2x 2z 2(1) 2(0) or x z 1. Any point on the curveœ œ
will satisfy this equation since x z cos t (1 cos t) 1. Therefore, any point on the curve lies on theœ œ
intersection of the cylinder x y 1 and the plane x z 1 the curve is an ellipse.
##
œ œÊ
(b) ( sin t) (cos t) (sin t) sin t cos t sin t 1 sin t vijkv Tœ Ê œ œ Ê œkk ÈÈ
### # v
vkk
(0) , , ( ) , œÊœœœœ
( sin t) (cos t) (sin t)
1sint 2 2
3
##
ijk ik ik
ÈÈÈ
TjT T jT
ˆ‰ ˆ‰
11
1
(c) ( cos t) (sin t) (cos t) ; isaijknikœ œ
normal to the plane x z 1 cos t cos tœ Ê œ na†
0 is orthogonal to is parallel to theœÊ Êana
plane; (0) , , ,aika jaikœ œ œ
ˆ‰ ab
1
#1
aj
ˆ‰
31
#œ
(d) 1 sin t (See part (b) L 1 sin t dtkk ÈÈ
vœ Êœ
##
'0
2
(e) L 7.64 (by )¸Mathematica
18. (a) (cos 4t) (sin 4t) 4t ( 4 sin 4t) (4 cos 4t) 4 ( 4 sin 4t) (4 cos 4t) 4rijkv i jkvœÊœ Êœ kk È###
32 4 2 Length 4 2 dt 4 2 t 2 2œœ Ê œ œ œ
ÈÈÈÈÈ
’“
'0
21Î#
!1
(b) cos sin sin cos r i jkv i jkœÊœ
ˆ‰ˆ‰ ˆ ‰ˆ ‰
ttt t t
### #####
"""
sin cos Length dt t 2 2Êœ œ œ Ê œ œ œkk Ɉ‰ˆ‰ˆ‰
É’“ È
v"" """
## # # # # #
### %
!
tt
44 2
222
ÈÈÈ
'0
41
1
(c) (cos t) (sin t) t ( sin t) (cos t) ( sin t) ( cos t) ( 1) 1 1rijkv ijkvœÊœÊœœkk ÈÈ
###
2 Length 2 dt 2 t 2 2œÊ œ œ œ
ÈÈÈÈ
’“
'2
0!
#11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

840 Chapter 13 Vector-Valued Functions and Motion in Space
19. PQB QOB t and PQ arc (AQ) t sincenœnœœœ
PQ length of the unwound string length of arc (AQ);œœ
thus x OB BC OB DP cos t t sin t, andœœœ
y PC QB QD sin t t cos tœœ œ
20. cos t t sin t sin t t cos t sin t t cos t sin t cos t t sin t cos trijv i jœ Êœababa ba babab
t cos t t sin t t cos t t sin t t t t, t 0œÊœ œœœÊœœababkkabab kk
ÉÈ
ijv T ij
22
2t cos t t sin t
tt
v
vkk
cos t sin tœij
13.4 CURVATURE AND THE UNIT NORMAL VECTOR N
1. t ln (cos t) (tan t) 1 ( tan t) sec t sec t sec t, sinceri j vi ji j vœ Ê œ œ Ê œ œ œ œ
ˆ‰ kk k k
ÈÈ
###
sin t
cos t
t (cos t) (sin t) ; ( sin t) (cos t) Ê œ œ œ œ
11
##
"
Tijij ij
vT
vkk ˆ‰ˆ‰
sec t sec t dt
tan t d
( sin t) ( cos t) 1 ( sin t) (cos t) ;Êœ œÊœœ
¸¸È
d
dt
T##
Nij
ˆ‰
¸¸
d
dt
d
dt
T
T
1 cos t.,œ† œ †œ
1d
dt sec tkkv
T
¸¸ "
2. ln (sec t) t (tan t) ( tan t) 1 sec t sec t sec t,r i j v ij ij vœÊœ œÊœ œœœ
ˆ‰ kk k k
ÈÈ
sec t tan t
sec t ## #
since t (sin t) (cos t) ; (cos t) (sin t) Ê œ œ œ œ
11
##
Tijijij
vT
vkk ˆ‰ˆ‰
tan t 1 d
sec t sec t dt
(cos t) ( sin t) 1 (cos t) (sin t) ;Êœ œÊœœ
¸¸È
d
dt
T##
Nij
ˆ‰
¸¸
d
dt
d
dt
T
T
1 cos t.,œ† œ †œ
1d
dt sec tkkv
T
¸¸ "
3. (2t 3) 5 t 2 2t 2 ( 2t) 2 1 t rijvijv T ijœ Êœ Ê œ œ Êœœ ab kk
ÈÈ
### #
v
vkk ÈÈ
22t
21t 21 t
; œ œ Êœ
"" "
##
ÈÈ Š‹Š‹ Š‹ Š‹
ÈÈ È È
1t 1t
td t d t
dt dt
1t 1t 1t 1t
ij i j
TT
¸¸Í
Í
Í
Ì
;œœÊœœ
É"" "
ab ˆ‰
¸¸ ÈÈ
1t 1t
t
1t 1t
Nij
d
dt
d
dt
T
T
,œ† œ † œ
1d
dt 1 t
1t 1t
kk Èab
v
T
¸¸ "" "
# #3/2
4. (cos t t sin t) (sin t t cos t) (t cos t) (t sin t) ( t cos t) (t sin t) t trijvijvœ Êœ Êœ œœkk kk
ÈÈ
###
t, since t 0 (cos t) (sin t) ; ( sin t) (cos t)œÊœœ œ œTijij
vT
v
ij
kk (t cos t) (t sin t)
tdt
d
( sin t) (cos t) 1 ( sin t) (cos t) ; 1Êœ œÊœœ œ†œ†œ
¸¸ ¸¸
È
d1d
dt dt t t
T T
v
## ""
Nij
ˆ‰
¸¸ kk
d
dt
d
dt
T
T,
5. (a) x . Now, f x x 1 fx
,ab ab k k c d
¹¹ ab Éab
œ† œ Ê œ Êœ
1
xdt
dT x 2
kkab ab
v v
v
vi j v T
wwkk
1 f x 1 . Thus x
fx fx
œŠ‹Š‹
œcd abcd ab
ab ab
ww
ÎÎ
w
22
12 12 d
dt
fxfx fx
11
fx fx
ij ij
Tab ab ab
cd cd
ab ab
Š‹Š‹
22
32 32
Êœ œ œ
¹¹
Í
Í
Í
Ì”•
Ë
dx fx
dt
fxf x
1fx
2
1fx
2
fx fx
1
1fx
fx
1fx
Tab ab
ab ab
cd
ab cd
ab cdcd
ab ab
Š‹
cd
ab kkab
¹¹
cd
ab
Š‹ Š‹ Š‹
232
232
22
232
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 13.4 Curvature and the Unit Normal Vector 841N
Thus x,abœ†œ
1
1fx
fx fx
1fx 1fx
ab Š‹
Ò Ó Ò Ó
ab kk kkab ab
kkab cd
ab
212 32
22
(b) y ln (cos x) ( sin x) tan x sec x œÊœœÊœÊœ œ
dy d y
dx cos x dx sec x
sec x
1 ( tan x)
sec x
ˆ‰
"#
,kk
cd
kk
cos x, since xœœ
"
##sec x
11
(c) Note that f (x) 0 at an inflection point.
ww œ
6. (a) f(t) g(t) x y x y x yrijijvijv T i jœ œÊœÊœ Êœœ
ÞÞ Þ Þ ÞÞ
kk È## v
vkk x
xy xy
y
ÈÈ
ÞÞ ÞÞ
dd
dt dt
2
TT
œÊœ
yyx xy xxy yx
xy xy
yyx xy
xy
xxy yx
xy
Þ ÞÞÞ ÞÞÞ Þ ÞÞÞ ÞÞÞ
ÞÞ ÞÞ
ÞÞÞÞ ÞÞÞ
ÞÞ
ÞÞÞÞ ÞÞÞ
ÞÞ
abab
ab ab
ab
ab
ab
ab
3/2 3/2 3/2
ij
¸¸Ê’“’“
3/2
2
3
2
œÊaba b
ab
yxyxxy
xy
ÞÞÞÞÞÞÞÞ
ÞÞ
; .œœ†œ†œ
kk kkkk
kk kk
Èab
yx xy yx xy yx xy
xy xy
1
xy xy
ÞÞÞ ÞÞÞ ÞÞÞ ÞÞÞ ÞÞÞ ÞÞÞ
ÞÞ ÞÞ
ÞÞ
ÞÞ
,1d
dtkkv
T
¸¸ 3/2
(b) (t) t ln (sin t) , 0 t x t and y ln (sin t) x 1, x 0; y cot t, y csc tri jœ Êœ œ Êœ œ œ œ œ
ÞÞÞÞ ÞÞ
1cos t
sin t #
sin tÊœ œ œ,kk
ab
csc t 0
1cott)
csc t
csc t
(c) (t) tan (sinh t) ln (cosh t) x tan (sinh t) and y ln (cosh t) xrijœÊœ œÊœœ
Þ
" "
"cosh t
1sinht cosh t
sech t, x sech t tanh t; y tanh t, y sech t sech tœœ œœœÊœ œ
ÞÞ Þ ÞÞ
sinh t
cosh t sech t tanh t
sech t sech t tanh t
#
,kk
ab
kk
sech tœ
7. (a) (t) f(t) g(t) f (t) g (t) is tangent to the curve at the point (f(t) g(t));rijvijœ Êœ ß
ww
g (t) f (t) f (t) g (t) g (t)f (t) f (t)g (t) 0; ( ) 0; thus,nv i j i j nv nv†† ††œ œ œ œ œcdcd
ww ww wwww
and are both normal to the curve at the pointnn
(b) (t) t e 2e 2e points toward the concave side of the curve; andrijvi jn ij Nœ Ê œ Ê œ œ
2t 2t 2t n
nkk
4e 1 kk È
nNijœÊœ
4t 2e
14e 14e
"
2t
4t 4t
ÈÈ
(c) (t) 4 t t points toward the concave side of the curve;rijvijnijœÊœ Êœ
È#
tt
4t 4t
ÈÈ
and 1 4 t tNn N ijœœœÊœ
n
nkk È
kk ÉŠ‹
È
t2
4t 4t
#
"#
8. (a) (t) t t t t points toward the concave side of the curve when t 0 andri jvijnijœ Ê œ Ê œ
"$##
3
t points toward the concave side when t 0 t for t 0 andœ Ê œ nij N ij
# #
"
È1t
ab
t for t0Nijœ
"
#
È1t
ab
(b) From part (a), 1 t kk ȸ¸É
vTij ijœÊœ Êœ Ê œ
%"
ÈÈ ab ab ab
1t 1t
t d 2t 2t d 4t 4t
dt dt
1t 1t 1t
TT
62
; ; t 0œœœ œ Á
2t
1t
1 t 2t 2t t t
2t 1t 1t t1t t1t
kk ˆ‰
¸¸ kk ab ab kk kk
ÈÈ
Nijij
d
dt
d
dt
T
TŠ‹
does not exist at t 0, where the curve has a point of inflection; 0 so the curvature Nœœœ
¸¸¸
dd
dt ds
TT
t0œ,
0 at t 0 is undefined. Since x t and y t y x , the curve is theœœœÊœ œœÊœ
¸¸
ddt d
dt ds ds 3 3
TT
†N"""
$$
,
cubic power curve which is concave down for x t 0 and concave up for x t 0.œ œ
9. (3 sin t) (3 cos t) 4t (3 cos t) ( 3 sin t) 4 (3 cos t) ( 3 sin t) 4rijkv i jkvœ Êœ Êœ kk È###
25 5 cos t sin t sin t cos tœœÊœœ Êœ
Ȉ‰ˆ‰ ˆ ‰ˆ‰
Tijk ij
vT
vkk 334d33
555dt55
sin t cos t ( sin t) (cos t) ; Ê œ œ Ê œ œ œ†œ
¸¸ ˆ ‰ ˆ ‰
É
d3 33 133
dt 5 5 5 5 5 25
T##
Nij
ˆ‰
¸¸
d
dt
d
dt
T
T,
10. (cos t t sin t) (sin t t cos t) 3 (t cos t) (t sin t) (t cos t) (t sin t) trijkvijvœ Êœ Êœ œkk ÈÈ
###
t t, if t 0 (cos t) (sin t) , t 0 ( sin t) (cos t)œœ Êœ œ Ê œ kk Tij ij
vT
vkk d
dt
( sin t) (cos t) 1 ( sin t) (cos t) ; 1Êœ œÊœœ œ†œ
¸¸È
d
dt tt
T## ""
Nij
ˆ‰
¸¸
d
dt
d
dt
T
T,
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

842 Chapter 13 Vector-Valued Functions and Motion in Space
11. e cos t e sin t 2 e cos t e sin t e sin t e cos t rijkv i jœÊœÊabababab
tt tttt
e cos t e sin t e sin t e cos t 2e e 2 ;kkabab
ÉÈÈ
vœœœ
tt tt 2t
t
##
Tij ijœœ Ê œ
vT
vkk ÈÈ È È
Š‹Š‹ Š ‹Š‹
cos t sin t sin t cos t d sin t cos t cos t sin t
22 2 2
dt
1 ;Êœ œÊœœ
¸¸ÊŠ‹Š‹ Š‹Š‹
d sin t cos t cos t sin t cos t sin t sin t cos t
dt 22 2 2
T
##
ÈÈ È È
ˆ‰
¸¸
Nij
d
dt
d
dt
T
T
1,œ† œ †œ
1d 1 1
dt 22
kk ÈÈ
v
T
¸¸ ee
tt
12. (6 sin 2t) (6 cos 2t) 5t (12 cos 2t) (12 sin 2t) 5rijkv i jkœ Êœ
(12 cos 2t) ( 12 sin 2t) 5 169 13 Êœ œ œÊœkk ÈÈ
vT
### v
vkk
cos 2t sin 2t sin 2t cos 2tœÊœ
ˆ‰ˆ‰ ˆ ‰ˆ‰
12 12 5 d 24 24
13 13 13 dt 13 13
ijk i j
T
sin 2t cos 2t ( sin 2t) (cos 2t) ;Êœ œÊœœ
¸¸ ˆ ‰ ˆ ‰
É
d24 24 24
dt 13 13 13
T##
Nij
ˆ‰
¸¸
d
dt
d
dt
T
T
.,œ† œ†œ
1d 124 24
dt 13 13 169kkv
T
¸¸
13. , t 0 t t t t t t 1, since t 0 rij vijv Tœ ʜʜœ Êœ
Š‹ Š‹ kk ÈÈ
tt
3#
#%# # v
vkk
œ Êœ Êœ
t1d1 t d t
tt t1 dt dt
t1 t1 t1 t1
ÈÈ ab ab ab ab
"
##
ij i j
TT
¸¸ÊŠ‹Š‹
; .œœÊœœ œ†œ†œ
ɸ¸
1t 1 t 1 d 1 1
t1 t1 dt t1
t1 t1 tt1 tt 1
" "
ab ˆ‰
¸¸ ÈÈ È
kk ab
Nij
d
dt
d
dt
T
T,v
T
14. cos t sin t , 0 t 3 cos t sin t 3 sin t cos trij v i jœ Êœ abab a ba b
$$ # #
#
1
3 cos t sin t 3 sin t cos t 9 cos t sin t 9 sin t cos t 3 cos t sin t, since 0 tÊœ œ œ kk a b a b
ÉÈ
v## %#%#
##
#
1
( cos t) (sin t) (sin t) (cos t) sin t cos t 1 Êœœ Ê œ Ê œ œÊœTijij N
vTT
vkk ˆ‰
¸¸
dd
dt dt
¸¸È## d
dt
d
dt
T
T
(sin t) (cos t) ; 1 .œ œ†œ †œij,1d 1 1
dt 3 cos t sin t 3 cos t sin tkkv
T
¸¸
15. t a cosh , a 0 sinh 1 sinh cosh cosh ri j vi j vœ Ê œ Ê œ œ œ
ˆ ‰ ˆ ‰ ˆ‰ ˆ‰
kk ÉÉ
ttttt
aaaaa
##
sech tanh sech tanh sech Êœœ Ê œ Tij ij
vT
vkk ˆ‰ˆ‰ ˆ ‰ˆ ‰
ttd tt t
aadtaaaaa
""
#
sech tanh sech sech tanh sech ;Êœ œ Êœœ
¸ ¸ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ ‰ ˆ ‰
É
dtttt tt
dt a a a a a a a a a
T"""
## % Nij
ˆ‰
¸¸
d
dt
d
dt
T
T
sech sech .,œ† œ † œ
1d 1 t t
dt a a a a
cosh
kkv
T
¸ ¸ ˆ‰ ˆ‰
t
a
""
#
16. (cosh t) (sinh t) t (sinh t) (cosh t) sinh t ( cosh t) 1 2 cosh trijkvijkvœÊœÊœ œkk ÈÈ
##
tanh t sech t sech t sech t tanh tÊœœ Ê œ Tijk i k
vT
vkk ÈÈÈ È È
Š‹ Š‹ Š‹Š ‹
""" " "
#
222 2 2
d
dt
sech t sech t tanh t sech t (sech t) (tanh t) ;Êœ œ Êœœ
¸¸É
d
dt 2
T"" "
##
%##
Ȉ‰
¸¸
Nik
d
dt
d
dt
T
T
sech t sech t.,œ† œ † œ
1d 1
dt 2 cosh t 2
kk ÈÈ
v
T
¸¸ ""
#
#
17. y ax y 2ax y 2a; from Exercise 5(a), (x) 2a 1 4a xœÊœÊœ œ œ
#w ww ##
$Î#
,kk
ab
2a
14ax kka b
(x) 2a 1 4a x 8a x ; thus, (x) 0 x 0. Now, (x) 0 for x 0 and (x) 0 forÊœ œÊœ ,,,,
w###w w w
#
&Î#
3kka b a b
x 0 so that (x) has an absolute maximum at x 0 which is the vertex of the parabola. Since x 0 is theœ œ,
only critical point for (x), the curvature has no minimum value.,
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 13.4 Curvature and the Unit Normal Vector 843N
18. (a cos t) (b sin t) ( a sin t) (b cos t) ( a cos t) (b sin t) r i jv i ja i jvaœ Êœ Êœ Ê‚
ab ab ab, since a b 0; (t)
a sin t b cos t 0
a cos t b sin t 0
œœÊœœœ
ââ
ââ
ââ
ââ
ââ
ââ
kkkk
ijk
kva‚,kk
kk
va
v
‚
ab a sin t b cos t ; (t) (ab) a sin t b cos t 2a sin t cos t 2b sin t cos tœ œ ab aba b
## # # w ## # # # #
$Î# &Î#
#
,3
(ab) a b (sin 2t) a sin t b cos t ; thus, (t) 0 sin 2t 0 t 0, identifyingœ œÊ œÊœ
3
#
## ## ## w
&Î#
aba b ,1
points on the major axis, or t , identifying points on the minor axis. Furthermore, (t) 0 forœ
11
##
w
3,
0 t and for t ; (t) 0 for t and t 2 . Therefore, the points associated
1111
####
w
1, 1 1
33
with t 0 and t on the major axis give absolute maximum curvature and the points associated with tœœ œ11
#
and t on the minor axis give absolute minimum curvature.œ31
#
19. ; 0 a b 0 a b a b since a, b 0. Now, 0 if,œÊœ œÊœÊœ„Êœ
adabd d
a b da da da
ab
##
,, ,
ab
a b and 0 if a b is at a maximum for a b and (b) is the maximum value of .Ê œ œœ
d b
da bb 2b
,,, ,
"
20. (a) From Example 5, the curvature of the helix (t) (a cos t) (a sin t) bt , a, b 0 is ; alsorijkœœ,a
ab
a b . For the helix (t) (3 cos t) (3 sin t) t , 0 t 4 , a 3 and b 1 kk È
vrijkœ œ ŸŸ œ œÊœ œ
##
1,
33
31 10
and 10 K 10 dt tkk ÈÈ
’“
vœÊœ œ œ
'0
43312
10 10 10
ÈÈ
%
!
11
(b) y x x t and y t , t (t) t t 2t 1 4t ;œÊœ œ__Ê œÊœ Ê œ
## # #
rijvijvkk È
; ; . ThusTij i jœ œ œ œ
1 2t d 4t 2 d 16t 4 2
14t 14t dt dt 1 4t
14t 14t 14t
ÈÈ ab ab ab
TT
3/2 3/2
2
3
¸¸É
. Then K 1 4t dt dt,œ†œ œ œ
12 2 2 2
14t 14t 14t
14t 14t
ÈŠ‹
ÈŠ‹
È
#
3''
Š‹
È
lim dt lim dt lim tan 2t lim tan 2tœœ
aa
bb
Ä_ Ä_
Ä_ Ä_
''
a0
0b
a0
b
22
14t 1 4t
" "
!
cd cd
lim tan 2a lim tan 2bœ œœ
ab
Ä_ Ä_
abab
" "
##
111
21. t (sin t) (cos t) 1 (cos t) 1 cos t 1 cos 1; ri j vi j v v Tœ Ê œ Ê œ œ Ê œ œ œkk Èȸ¸ ˆ‰ˆ‰ É
## # #
##
11v
vkk
; œÊœ Êœ œ œœ
ij TTT
œ
cos t
1cost
d sin t cos t sin t d d 1
dt dt 1 cos t dt 1
1cost 1cost
sin t
t
sin
1cos
Èabab kk ¸¸
ˆ‰
222
3/2 3/2 22
2
22
ij
¸¸ ¸¸ 1. Thus 1 1,ˆ‰
1
21
1
œ†œ
1 and the center is 0 x y 1Êœœ ß Ê œ3"
##
##
1ˆ‰ ˆ ‰
11
22. (2 ln t) t 1 1 ;ri jvi jv T ijœÊœÊœœÊœœ
ˆ‰ ˆ‰ˆ‰ ˆ‰
kk É
""
t t t t t t t1 t1
241t12tt1
2
222 22
22
v
vkk
. Thus 1
d4td 21dt22t2
dt dt t 1 dt t 1 t 1 2
2t 1
t1 t1 t1 t1
4 t 1 16t
TT T
v
œ Êœ œ œ†œ†œ Êœ
ˆ‰
ab ab ab ab
ab kk
2
22 2 2
22 42 22 2 2
22
222
ij
¸¸ ¸¸
Êab,,
2. The circle of curvature is tangent to the curve at P(0 2) circle has same tangent as the curveœÊœœ ßÊ
""
#3,
(1) 2 is tangent to the circle the center lies on the y-axis. If t 1 (t 0), then (t 1) 0Êœ Ê Á vi #
t 2t 1 0 t 1 2t 2 since t 0 t 2 t 2 y 2 on bothÊ Ê Ê Ê Ê Ê
##
""t1
ttt
ˆ‰
sides of (0 2) the curve is concave down center of circle of curvature is (0 4) x (y 4) 4ß Ê Ê ß Ê œ
##
is an equation of the circle of curvature
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
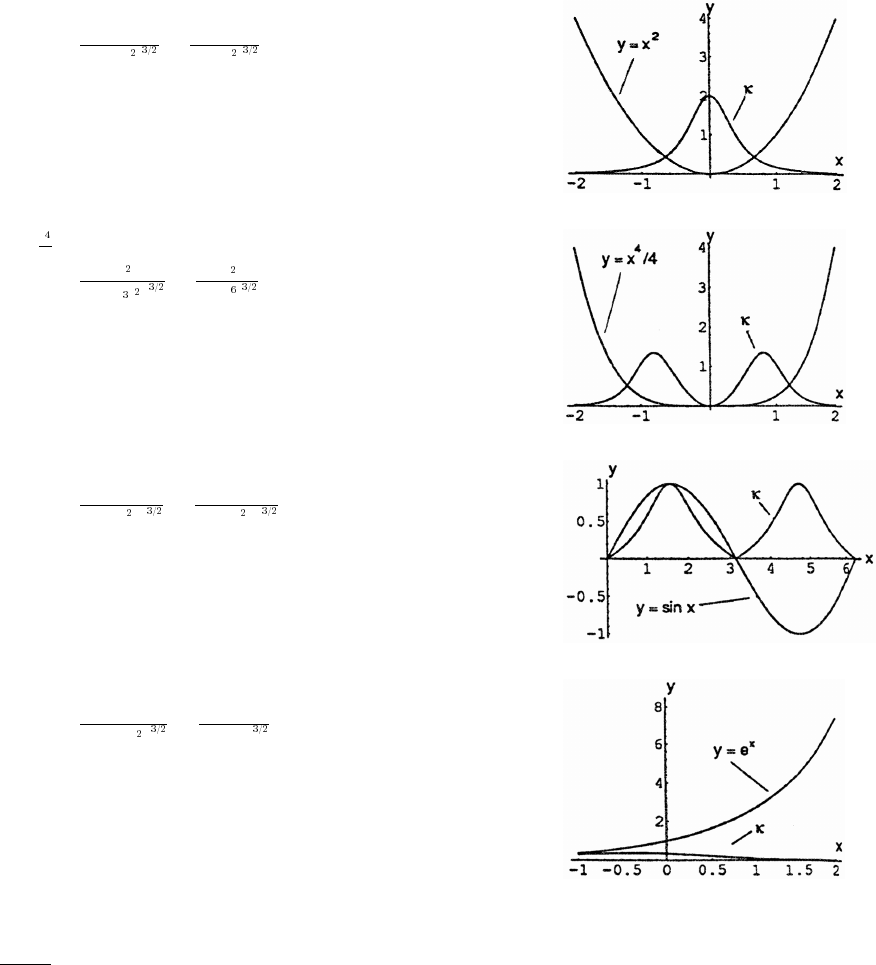
844 Chapter 13 Vector-Valued Functions and Motion in Space
23. y x f (x) 2x and f (x) 2œÊ œ œ
#w ww
Êœ œ,kk
abab
2
1(2x) 14x
2
24. y f (x) x and f (x) 3xœÊ œ œ
x
4w$ww #
Êœ œ,kk
Š‹
ab ab
3x
1x
3x
1x
25. y sin x f (x) cos x and f (x) sin xœÊœ œ
www
Êœ œ,kk kk
abab
sin x sin x
1cosx 1cosx
26. y e f (x) e and f (x) eœÊ œ œ
xxxwww
Êœ œ,kk
Š‹
ˆ‰
e
1
e
1
xx
abee
x2x
27-34. Example CAS commands:
:Maple
with( plots );
r := t -> [3*cos(t),5*sin(t)];
lo := 0;
hi := 2*Pi;
t0 := Pi/4;
P1 := plot( [r(t)[], t=lo..hi] ):
display( P1, scaling=constrained, title="#27(a) (Section 13.4)" );
CURVATURE := (x,y,t) ->simplify(abs(diff(x,t)*diff(y,t,t)-diff(y,t)*diff(x,t,t))/(diff(x,t)^2+diff(y,t)^2)^(3/2));
kappa := eval(CURVATURE(r(t)[],t),t=t0);
UnitNormal := (x,y,t) ->expand( [-diff(y,t),diff(x,t)]/sqrt(diff(x,t)^2+diff(y,t)^2) );
N := eval( UnitNormal(r(t)[],t), t=t0 );
C := expand( r(t0) + N/kappa );
OscCircle := (x-C[1])^2+(y-C[2])^2 = 1/kappa^2;
evalf( OscCircle );
P2 := implicitplot( (x-C[1])^2+(y-C[2])^2 = 1/kappa^2, x=-7..4, y=-4..6, color=blue ):
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 13.5 Torsion and the Unit Binormal Vector 845B
display( [P1,P2], scaling=constrained, title="#27(e) (Section 13.4)" );
: (assigned functions and parameters may vary)Mathematica
In Mathematica, the dot product can be applied either with a period "." or with the word, "Dot".
Similarly, the cross product can be applied either with a very small "x" (in the palette next to the arrow) or with the word,
"Cross". However, the Cross command assumes the vectors are in three dimensions
For the purposes of applying the cross product command, we will define the position vector r as a three dimensional vector
with zero for its z-component. For graphing, we will use only the first two components.
Clear[r, t, x, y]
r[t_]={3 Cos[t], 5 Sin[t] }
t0= /4; tmin= 0; tmax= 2 ;11
r2[t_]= {r[t][[1]], r[t][[2]]}
pp=ParametricPlot[r2[t], {t, tmin, tmax}];
mag[v_]=Sqrt[v.v]
vel[t_]= r'[t]
speed[t_]=mag[vel[t]]
acc[t_]= vel'[t]
curv[t_]= mag[Cross[vel[t],acc[t]]]/speed[t] //Simplify
3
unittan[t_]= vel[t]/speed[t]//Simplify
unitnorm[t_]= unittan'[t] / mag[unittan'[t]]
ctr= r[t0] + (1 / curv[t0]) unitnorm[t0] //Simplify
{a,b}= {ctr[[1]], ctr[[2]]}
To plot the osculating circle, load a graphics package and then plot it, and show it together with the original curve.
<<Graphics`ImplicitPlot`
pc=ImplicitPlot[(x a)2 + (y b)2 == 1/curv[t0] , {x, 8, 8},{y, 8, 8}]
2
radius=Graphics[Line[{{a, b}, r2[t0]}]]
Show[pp, pc, radius, AspectRatio 1]Ä
13.5 TORSION AND THE UNIT BINORMAL VECTOR B
1. By Exercise 9 in Section 13.4, cos t sin t and ( sin t) (cos t) so that Ti jkNijBTNœ œ œ‚
ˆ‰ˆ ‰
334
555
cos t sin t cos t sin t . Also (3 cos t) ( 3 sin t) 4
sin t cos t 0
œ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰ˆ‰
ijk
ijkvi jk
3344 43
5555 55
( 3 sin t) ( 3 cos t) ( 3 cos t) (3 sin t) and 3 cos t 3 sin t 4
3 sin t 3 cos t 0
Êœ Ê œ ‚œ
aij ijva
ijk
d
dt
a
ââ
ââ
ââ
ââ
ââ
ââ
(12 cos t) (12 sin t) 9 12 cos t 12 sin t 9 225. Thusœ Ê ‚ œ œijkvakka ba bab
2###
7œœœœ
ââ
ââ
ââ
ââ
ââ
ââ
ab
3 cos t 3 sin t 4
3 sin t 3 sin t 0
3 cos t 3 sin t 0
225 225 225 25
49 sint9 cost 36 4
†
2. By Exercise 10 in Section 13.4, (cos t) (sin t) and ( sin t) (cos t) ; thus TijN ijBTNœ œ œ‚
cos t sin t . Also (t cos t) (t sin t)
cos t sin t 0
sin t cos t 0
œœœœ
ââ
ââ
ââ
ââ
ââ
ââ
ab
ijk
kk v i j
##
t sin t cos t t cos t sin t t cos t sin t sin t t sin t cos t cos tÊœ Ê œ aij i jababa ba bab d
dt
a
t cos t 2 sin t 2 cos t t sin t . Thus t cos t t sin t 0
t sin t cos t t cos t sin t 0
œ ‚ œ
ababââ
ââ
ââ
ââ
ââ
ââ
abab
ijva
ijk
[(t cos t)(t cos t sin t) (t sin t)( t sin t cos t)] t t t . ThusœœÊ‚œœkk va
##
#
kkab
24
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

846 Chapter 13 Vector-Valued Functions and Motion in Space
07œœœ
ââ
ââ
ââ
ââ
ââ
ââ
t cos t t sin t 0
cos t t sin t sin t t cos t 0
2 sin t t cos t 2 cos t t sin t 0
tt
0
44
3. By Exercise 11 in Section 13.4, and ; ThusTijN i jœ œ
Š‹Š‹ Š ‹Š ‹
cos t sin t sin t cos t cos t sin t sin t cos t
22 2 2
ÈÈ È È
0
0
BTN
ijk
œ‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
’“Š‹Š‹
cos t sin t sin t cos t
22
cos t sin t sin t cos t
22
cos t 2 cos t sin t sin t sin t 2 sin t
2
ÈÈ
ÈÈ
cos t cos t
2
k
. Also, e cos t e sin t e sin t e cos tœ œœ
’“Š‹Š‹ abab
1sin 2t 1sin 2t
22
tt tt
ab ab kk v i j
= 2e sin t 2e cos t
e sin t cos t e cos t sin t e cos t sin t e sin t cos t
ʜ
aijijcdcdabab
a bababab
tt tt tt
2e cos t sin t 2e sin t cos t . Thus 2e
e cos t sin t e sin t cos t 0
2e sin t 2e cos t 0
Êœ ‚œ œ
d
dt
tt 2t
tt
tt
aaba b ââ
ââ
ââ
ââ
ââ
ââ
abab
ijva k
ijk
2e 4e . Thus Ê‚ œ œ œkkabva
22t 4t
cos t sin t sin t cos t 0
2 sin t 2 cos t 0
2 cos t sin t 2 sin t cos
#
7
ââ
ââ
ââ
ââ
ââ
ââ
abab
aba b
ee
ee
ee
tt
tt
tt
t0
4e4t œ0
4. By Exercise 12 in Section 13.4, cos 2t sin 2t and ( sin 2t) (cos 2t) soTijkNijœœ
ˆ‰ˆ‰
12 12 5
13 13 13
cos 2t sin 2t cos 2t sin 2t . Also,
sin 2t cos 2t 0
BTN i j k
ijk
œ‚œ œ
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰ˆ ‰ˆ‰ˆ‰
abab
12 12 5 5 5 12
13 13 13 13 13 13
(12 cos 2t) (12 sin 2t) 5 ( 24 sin 2t) (24 cos 2t) and ( 48 cos 2t) (48 sin 2t)vijka ij ijœÊœ œ
d
dt
a
(120 cos 2t) (120 sin 2t) 288
12 cos 2t 12 sin 2t 5
24 sin 2t 24 cos 2t 0
va i j k va
ijk
‚œ œ Ê ‚
ââ
ââ
ââ
ââ
ââ
ââ kk
2
(120 cos 2t) ( 120 sin 2t) ( 288) 120 cos 2t sin 2t 288 97344. Thusœœœ
#######
ab
7œœœ
ââ
ââ
ââ
ââ
ââ
ââ
ab
12 cos 2t 12 sin 2t 5
24 sin 2t 24 cos 2t 0
48 cos 2t 48 sin 2t 0
97344 97344 169
52448 10
† †
5. By Exercise 13 in Section 13.4, and so that T i j N i j BTNœ œ œ
t1 1t
t1 t1 t1 t1
ab ab ÈÈ
1/2 1/2 ‚
. Also, t t 2t 2 so that 0 0
0
0
tt0
2t 0
200
œœœÊœÊœœÊœ
"
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ijk
kvijaij i
t1
t1 t1
t1 t1
t
d
dt
ÈÈ
ÈÈ
"
#
#
a7
6. By Exercise 14 in Section 13.4, ( cos t) (sin t) and (sin t) (cos t) so that T i j N i j BTNœ œ œ ‚
. Also, 3 cos t sin t 3 sin t cos t
cos t sin t 0
sin t cos t 0
œœœ
ââ
ââ
ââ
ââ
ââ
ââabab
ijk
kv i j
##
3 cos t sin t 3 sin t cos t 3 cos t sin t 3 sin t cos tÊÊaij i jœ œ
ddddd dd
dt dt dt dt dt dt dt
abab abab
ˆ‰ˆ‰
## # #
a
3 cos t sin t 3 sin t cos t 0
3 cos t sin t 3 sin t cos t 0
3 cos t sin t 3 sin t cos
Ê
ââ
ââ
ââ
ââ
ââ
ââ
ââ
abab
ˆ‰ˆ‰
abab
##
##
##
dd
dt dt
dd dd
dt dt dt dt t0
0 0œÊ œ7
7. By Exercise 15 in Section 13.4, sech tanh and tanh sech so that T i j N i j BTNœœ œ œ
v
vkk ˆ‰ˆ‰ ˆ ‰ˆ‰
tt tt
aa aa ‚
. Also, sinh cosh sinh so that
sech tanh 0
tanh sech 0
œœœÊœÊœ
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰ ˆ ‰ ˆ‰
ijk
kvi ja j j
tt
aa
tt
aa
ttdt
aaadtaa
""a
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 13.5 Torsion and the Unit Binormal Vector 847B
0 0
1sinh 0
0 cosh 0
0 sinh 0
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰
ˆ‰
ˆ‰
t
a
aa
t
aa
t
"
"
œÊ œ7
8. By Exercise 16 in Section 13.4, tanh t sech t and (sech t) (tanh t) so thatTijkNikœ œ
Š‹ Š‹
"""
ÈÈÈ
222
tanh t sech t . Also, (sinh t) (cosh t)
tanh t sech t
sech t 0 tanh t
BTN i j k v i jk
ijk
œœ œ œ
‚
ââ
ââ
ââ
ââ
ââ
ââ
ââ
Š‹ Š‹
""" """
ÈÈÈ ÈÈÈ
222 222
(cosh t) (sinh t) (sinh t) (cosh t) and sinh t cosh t 1
cosh t sinh t 0
aij ijva
ijk
œ Êœ ‚œ
d
dt
a
ââ
ââ
ââ
ââ
ââ
ââ
(sinh t) (cosh t) cosh t sinh t (sinh t) (cosh t) sinh t cosh t 1. Thusœ œ Ê‚œij kijkvaab kk
22 ###
.7œœœ
ââ
ââ
ââ
ââ
ââ
ââ
sinh t cosh t 1
cosh t sinh t 0
sinh t cosh t 0
sinh t cosh t 1 sinh t cosh t 1 cosh t
#
" "
9. (a cos t) (a sin t) bt ( a sin t) (a cos t) b ( a sin t) (a cos t) brijkv ijkvœÊœÊœkk È###
a b a 0; ( a cos t) ( a sin t) ( a cos t) ( a sin t) a aœÊœ œœ Êœ œœ
Èkk kk kk
ÈÈ
## ###
Td
dt va i ja
aa0a (0)aaÊœ œ œœÊœ œ
NT
ÉÉ
kk kk kk kk kk kkaaaaTNN
##
##
10. (1 3t) (t 2) 3t 3 3 3 1 ( 3) 19 a 0; rijkvijkv va0œ Êœ Ê œ œ Ê œ œ œkk kk
ÈÈ
## # Td
dt
a a 0 (0) (0)Êœ œÊœ œ
NT
ÉkkaaTN0
##
11. (t 1) 2t t 2 2t 1 2 (2t) 5 4t a 5 4t (8t)rijkvijkvœ Êœ Ê œ œ Êœ
# #
## # # "
#
"Î#
kk a b
ÈÈT
4t 5 4t a (1) ; 2 (1) 2 (1) 2 a a 2œ Ê œœœÊ œÊ œÊœ œ ab kk kk
ÉɈ‰
#"Î# ###
#
T N T
44 4
93 3
Èak a k a a
(1)œœÊœ
É20 4
93 3 3
25 25
ÈÈ
aTN
12. (t cos t) (t sin t) t (cos t t sin t) (sin t t cos t) 2trijkv i jkœÊœ
#
(cos t t sin t) (sin t t cos t) (2t) 5t 1 a 5t 1 (10t)Êœ œ Êœ kk a b
ÈÈ
v####
"
#
#"Î#
T
a (0) 0; ( 2 sin t t cos t) (2 cos t t sin t) 2 (0) 2 2 (0)œÊœœÊœÊ
5t
5t 1
ÈTaijkajkakk
2 2 22 a a 22 0 22 (0) (0) 22 22œœÊœ œ œÊœ œ
ÈÈ È È ÈÈ
Ékk ÊŠ‹
## # #
##
NT
aaTNN
13. t t t t t 2t 1 t 1 t (2t) 1 t 1 tri j kvi j k vœ Êœ Ê œ
#$ $ ##
"" ## #
##
ˆ‰ˆ‰ abab kk abab
É
33
2 t 2t 1 2 1 t a 2t 2 a (0) 0; 2 2t 2t (0) 2 (0) 2œœÊœÊœœÊœÊœ
Èabab kk
ÈÈ
%# #TT
ai j k a i a
a a 2 0 2 (0) (0) 2 2Êœ œ œÊ œ œ
NT
Ékk È
aaTNN
####
14. e cos t e sin t 2e e cos t e sin t e sin t e cos t 2er i jkv i jkœÊœabab abab
ÈÈ
tt t tttt t
e cos t e sin t e sin t e cos t 2e 4e 2e a 2e a (0) 2;Êœ œ œ Êœ Ê œkkabab
ÊŠ‹
ÈÈ
vtt tt t 2t
tt
TT
##
#
e cos t e sin t e sin t e cos t e sin t e cos t e cos t e sin t 2eaijkœ abab
È
t ttt tt t t t
2e sin t 2e cos t 2e (0) 2 2 (0) 2 2 6œ Ê œ Ê œ œabab kk
ÈÈ È
ÊŠ‹È
tt t
ijkajka
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

848 Chapter 13 Vector-Valued Functions and Motion in Space
a a 6 2 2 (0) 2 2Êœ œ œ Ê œ
NT
Ékk ÊŠ‹
ÈÈÈ
aaTN
####
15. (cos t) (sin t) ( sin t) (cos t) ( sin t) (cos t) 1 rijkv ijv TœÊœ Êœ œÊœkk È## v
vkk
( sin t) (cos t) ; ( cos t) (sin t) ( cos t) ( sin t)œ Ê œ œ Ê œ ijT ij ij
ˆ‰ ¸ ¸ È
1
4dt dt
22
dd
ÈÈ
## ##
TT
1 ( cos t) (sin t) ; sin t cos t 0
cos t sin t 0
œÊ œ œ Ê œ œ‚œ œ
NijNijBTN k
ijk
ˆ‰
¸¸ ÈÈ
d
dt
d
dt
T
Tˆ‰ ââ
ââ
ââ
ââ
ââ
ââ
1
4
22
##
, the normal to the osculating plane; P 1 lies on theÊ œ œÊœßßBk r ijk
ˆ‰ ˆ‰ Š‹
11
44
22 22
ÈÈ ÈÈ
## ##
osculating plane 0 x 0 y (z ( 1)) 0 z 1 is the osculating plane; is normalʜʜ
Š‹Š‹
ÈÈ
22
## T
to the normal plane x y 0(z ( 1)) 0 x y 0Ê œÊ œ
Š‹Š‹Š‹Š‹
ÈÈÈÈ ÈÈ
2222 22
#### ##
x y 0 is the normal plane; is normal to the rectifying planeÊ œ N
x y 0(z ( 1)) 0 x y 1 x y 2 is theÊ œ Ê œÊœ
Š‹Š ‹Š‹Š ‹ È
ÈÈ ÈÈ ÈÈ
22 22 22
## ## ##
rectifying plane
16. (cos t) (sin t) t ( sin t) (cos t) sin t cos t 1 2 rijkv ijkv TœÊœÊœ œÊœkk ÈÈ
## v
vkk
sin t cos t cos t sin t œ Ê œ Ê
Š‹Š‹ Š‹Š‹
¸¸
""" " "
ÈÈÈ È È
222 2 2
dd
dt dt
ijk i j
TT
cos t sin t ( cos t) (sin t) ; thus (0) and (0)œœÊœœ œ œ
É"" " ""
##
##
ÈÈÈ
ˆ‰
¸¸
222
NijTjkNi
d
dt
d
dt
T
T
(0) , the normal to the osculating plane; (0) P(1 0 0) lies on
0
10 0
Êœ œ œÊßß
Bjk ri
ijk
ââ
ââ
ââ
ââ
ââ
ââ
ââ
"" ""
ÈÈ ÈÈ
22 22
the osculating plane 0(x 1) (y 0) (z 0) 0 y z 0 is the osculating plane; is normalÊ œÊœ
""
ÈÈ
22 T
to the normal plane 0(x 1) (y 0) (z 0) 0 y z 0 is the normal plane; is normal toÊ œÊœ
""
ÈÈ
22 N
the rectifying plane 1(x 1) 0(y 0) 0(z 0) 0 x 1 is the rectifying planeÊ œÊœ
17. Yes. If the car is moving along a curved path, then 0 and a 0 a a .,,ÁœÁÊœÁ
NTN
kkvaTN0
#
18. constant a 0 a is orthogonal to the acceleration is normal to the pathkk kkvvaNTÊœ œÊœ Ê
TN
d
dt
19. a 0 0 is constantav aT v v¼Ê¼ Ê œÊ œÊ
Td
dt kk kk
20. (t) a a , where a (10) 0 and a 100 0 100 . Now, fromaTN v v aT Nœ œ œ œ œ œ Êœ
TN T N
dd
dt dt
kk kk,, ,
#
Exercise 5(a) Section 13.4, we find for y f(x) x that ; also,œœ œ œ œ
#
,kk
‘
ab cdab
f(x)
1f(x)
22
1(2x) 14x
(t) t t is the position vector of the moving mass 2t 1 4trij vijvœ Ê œ Ê œ
##
kk È
( 2t ). At (0 0): (0) , (0) and (0) 2 m m(100 ) 200m ;Êœ ß œ œ œÊœ œ œTij TiNj Fa Nj
"
È14t ,,
At 2 2 : 2 2 2 , 2 , and 2 m
Š ‹Š‹ Š ‹ Š‹ Š‹
ÈÈ È È È
ßœœ œ œÊœTijijN ij Fa
"" "
333 33 27
22 22 2
ÈÈ
,
m(100 ) m m mœœœ,Nijij
ˆ‰
Š‹
200 200
27 3 3 81 81
2 2 400 2
ÈÈ
"
21. a a , where a (constant) 0 and a m m m aTN v v Fa vN F vœ œ œ œ œ Êœœ Êœ
TN T N
dd
dt dt
kk kk kk kk kk,,,
###
m , a constant multiple of the curvature of the trajectoryœˆ‰
kkv#,,
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 13.5 Torsion and the Unit Binormal Vector 849B
22. a 0 0 0 (since the particle is moving, we cannot have zero speed) the curvature is zero
NœÊ œÊœ Ê,,kkv#
so the particle is moving along a straight line
23. From Example 1, t and a t so that a , t 0 tkk kkvvœœ œÊœœœÁÊœœ
NN
,, 3
#""
at
tt
N
kkv,
24. (x At) (y Bt) (z Ct) A B C 0. Since the curverijkvijka0va0œ Êœ ʜʂœÊ œ
!!! ,
is a plane curve, 0.7œ
25. If a plane curve is sufficiently differentiable the torsion is zero as the following argument shows:
f(t) g(t) f (t) g (t) f (t) g (t) f (t) g (t)rijv i ja i j i jœ Êœ Êœ Êœ
ww w w w w
ww w w
ww
d
dt
a
0Êœ œ7
ââ
ââ
ââ
ââ
ââ
ââ
kk
f (t) g (t) 0
f (t) g (t) 0
f (t) g (t) 0
va‚
26. From Example 2, (b) ; (b) 0 0 a b 0 b a77 7œÊœ œÊ œÊœÊœ„
bab ab
ab ab ab
ww ##
ab ab
b a since a, b 0. Also b a 0 and b a 0 so occurs when b a Êœ Ê Ê œÊ œ777 7
ww
max max a
aa
œ"
2a
27. (t) f(t) g(t) h(t) f (t) g (t) h (t) ; 0 h (t) 0 h(t) Crijkvijkvkœ Êœ œÊ œÊ œ
www w
†
(t) f(t) g(t) C and (a) f(a) g(a) C f(a) 0, g(a) 0 and C 0 h(t) 0.Êœ œ œÊœ œ œÊœr i jkr i jk0
28. From Example 2, (a sin t) (a cos t) b a b vijkv Tœ Ê œ Ê œkk È## v
vkk
(a sin t) (a cos t) b ; (a cos t) (a sin t) œ œ Êœ
""
ÈÈ
ˆ‰
¸¸
ab ab
d
dt
cdcdijk ijN
Td
dt
d
dt
T
T
(cos t) (sin t) ;
cos t sin t 0
œ œ ‚ œ
ijBTN
ijk
ââ
ââ
ââ
ââ
ââ
ââ
ââ
a sin t a cos t b
ab ab ab
ÈÈÈ
(b cos t) (b sin t) œ Êœ Êœ
b sin t b cos t a d d b
ab ab ab ab ab
dt dt
ÈÈÈ È È
"
ijk ijN
BB
cd†
, which is consistent with the result inÊœ œ œ7""
kk ÈÈ
v
B
ˆ‰
Š‹Š‹
dbb
dt a b
ab ab
†N
Example 2.
29-32. Example CAS commands:
:Maple
with( LinearAlgebra );
r := < t*cos(t) | t*sin(t) | t >;
t0 := sqrt(3);
rr := eval( r, t=t0 );
v := map( diff, r, t );
vv := eval( v, t=t0 );
a := map( diff, v, t );
aa := eval( a, t=t0 );
s := simplify(Norm( v, 2 )) assuming t::real;
ss := eval( s, t=t0 );
T := v/s;
TT := vv/ss ;
q1 := map( diff, simplify(T), t ):
NN := simplify(eval( q1/Norm(q1,2), t=t0 ));
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

850 Chapter 13 Vector-Valued Functions and Motion in Space
BB := CrossProduct( TT, NN );
kappa := Norm(CrossProduct(vv,aa),2)/ss^3;
tau := simplify( Determinant(< vv, aa, eval(map(diff,a,t),t=t0) >)/Norm(CrossProduct(vv,aa),2)^3 );
a_t := eval( diff( s, t ), t=t0 );
a_n := evalf[4]( kappa*ss^2 );
: (assigned functions and value for t0 will vary)Mathematica
Clear[t, v, a, t]
mag[vector_]:=Sqrt[vector.vector]
Print["The position vector is ", r[t_]={t Cos[t], t Sin[t], t}]
Print["The velocity vector is ", v[t_]= r'[t]]
Print["The acceleration vector is ", a[t_]= v'[t]]
Print["The speed is ", speed[t_]= mag[v[t]]//Simplify]
Print["The unit tangent vector is ", utan[t_]= v[t]/speed[t] //Simplify]
Print["The curvature is ", curv[t_]= mag[Cross[v[t],a[t]]] / speed[t] //Simplify]
3
Print["The torsion is ", torsion[t_]= Det[{v[t], a[t], a'[t]}] / mag[Cross[v[t],a[t]]] //Simplify]
2
Print["The unit normal vector is ", unorm[t_]= utan'[t] / mag[utan'[t]] //Simplify]
Print["The unit binormal vector is ", ubinorm[t_]= Cross[utan[t],unorm[t]] //Simplify]
Print["The tangential component of the acceleration is ", at[t_]=a[t].utan[t] //Simplify]
Print["The normal component of the acceleration is ", an[t_]=a[t].unorm[t] //Simplify]
You can evaluate any of these functions at a specified value of t.
t0= Sqrt[3]
{utan[t0], unorm[t0], ubinorm[t0]}
N[{utan[t0], unorm[t0], ubinorm[t0]}]
{curv[t0], torsion[t0]}
N[{curv[t0], torsion[t0]}]
{at[t0], an[t0]}
N[{at[t0], an[t0]}]
To verify that the tangential and normal components of the acceleration agree with the formulas in the book:
at[t]== speed'[t] //Simplify
an[t]==curv [t] speed[t] //Simplify
2
13.6 PLANETARY MOTION AND SATELLITES
1. T a T (6,808,000 m)
T4 4 4
aGM GM 6.6726 10 Nm kg 5.975 10 kg
œÊœ Êœ
11 1
#$# $
‚‚abab
3.125 10 sec T 3125 10 sec 55.90 10 sec 93.2 min¸‚ ʸ ‚ ¸‚ ¸
(# #
%#
È
2. e 0.0167 and perihelion distance 149,577,000 km and e 1œœœ
rv
GM
0.0167 1 v 9.03 10 m /secÊœ ʸ‚
(149,577,000,000 m)v
6.6726 10 Nm kg 1.99 10 kg
abab‚‚
#)##
!
v 9.03 10 m /sec 3.00 10 m/secʸ ‚ ¸ ‚
!)# # %
È
3. 92.25 min 5535 sec and a TœœÊœ
T4 GM
aGM 4
1
1
$#
a (5535 sec) 3.094 10 m a 3.094 10 mÊœ œ ‚ ʸ ‚
$##!$
‚‚ #! $
ab
ˆ‰
6.6726 10 Nm kg 5.975 10 kg
41 È
6.764 10 m 6764 km. Note that 6764 km 12,757 km 183 km 589 km .œ‚ ¸ ¸
'"
#ab
4. T 1639 min 98,340 sec and mass of Mars 6.418 10 kg a Tœœ œ‚Êœ
#$ $ #
GM
41
1.049 10 m a 1.049 10 mœ¸‚ʸ‚
abab6.6726 10 Nm kg 6.418 10 kg (98,340 sec)
4
‚‚ ## $ ## $
1È
2.19 10 m 21,900 kmœ‚ œ
(
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 13.6 Planetary Motion and Satellites 851
5. 2a diameter of Mars perigee height apogee height D 1499 km 35,800 kmœœ
2(21,900) km D 37,299 km D 6501 kmʜʜ
6. a 22,030 km 2.203 10 m and T aœœ‚ œ
(#$
4
GM
1
T (2.203 10 m) 9.856 10 secÊœ ‚ ¸ ‚
#($*#
‚‚
4
6.6720 10 Nm kg 6.418 10 kg
1
abab
T 9.856 10 sec 9.928 10 sec 1655 minʸ ‚ ¸ ‚ ¸
È)# %
7. (a) Period of the satellite rotational period of the Earth period of the satellite 1436.1 minœÊœ
86,166 sec; a aœœÊœ
$$
‚‚
GMT
44
6.6726 10 Nm kg 5.975 10 kg (86,166 sec)
11
ab
ˆ‰
7.4980 10 m a 74.980 10 m 4.2168 10 m 42,168 km¸‚ ʸ ‚ ¸‚œ
## $ (
#" $
È
(b) The radius of the Earth is approximately 6379 km the height of the orbit is 42,168 6379 35,789 kmʜ
(c) Symcom 3, GOES 4, and Intelsat 5
8. T 1477.4 min 88,644 sec aœœÊœ
$GMT
41
8.524 10 m a 8.524 10 mœœ‚ʸ‚
abab6.6726 10 Nm kg 6.418 10 kg (88,644 sec)
4
‚‚ #" $ #" $
1È
2.043 10 m 20,430 km¸‚ œ
(
9. Period of the Moon 2.36055 10 sec aœ‚Êœ
'$
GMT
41
5.627 10 m a 5.627 10 mœ¸‚ʸ‚
ab
ˆ‰
6.6726 10 Nm kg 5.975 10 kg (2.36055 10 sec)
4
‚‚‚ #& $ #& $
1È
3.832 10 m 383,200 km from the center of the Earth.¸‚ œ
)
10. r v v 1.9967 10 r m/secœÊœÊœ œ ¸ ‚
GM GM GM
vr r r
6.6726 10 Nm kg 5.975 10 kg
#( "Î#
‚‚
kk ÉÉabab
11. Solar System: 2.97 10 sec /m ;
T4
a 6.6726 10 Nm kg 1.99 10 kg
œ¸‚
1
abab‚‚
"* # $
Earth: 9.902 10 sec /m ;
T4
a6.6726 10 Nm kg 5.975 10 kg
œ¸‚
1
abab‚‚
"% # $
Moon: 8.045 10 sec /m ;
T4
a 6.6726 10 Nm kg 7.354 10 kg
œ¸‚
1
abab‚‚
"# # $
12. e 1 v v ;œ Êœ Êœ
rv
GM r r
GM(e 1) GM(e 1)
#
!
!É
Circle: e 0 vœÊ œ
!ÉGM
r
Ellipse: 0 e 1 v Ê
ÉÉ
GM 2GM
rr
!
Parabola: e 1 vœÊ œ
!É2GM
r
Hyperbola: e 1 vÊ
!É2GM
r
13. r v v which is constant since G, M, and r (the radius of orbit) are constantœÊœÊœ
GM GM GM
vr r
#É
14. A (t t) (t) (t) (t)??œ‚Êœ ‚œ ‚
"""
###
kk
¹¹¹ ¹
rr r r
?
?? ?
??
A
tt t
(t t) (t t) (t) (t)rrrr
(t) (t) (t) (t) lim (t)œ‚‚œ‚Êœ ‚
""" "
###
¹ ¹¹¹ ¹¹
rr rr rr(t t) (t) (t t) (t) (t t) (t)
tt t dt t
dA
???
?? ? ?
rrr r r
?t0Ä
(t) (t) œ‚œ ‚œ‚
"""
###
¸¸¸¸
kk
dd
dt dt
rr
rr rr
Þ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
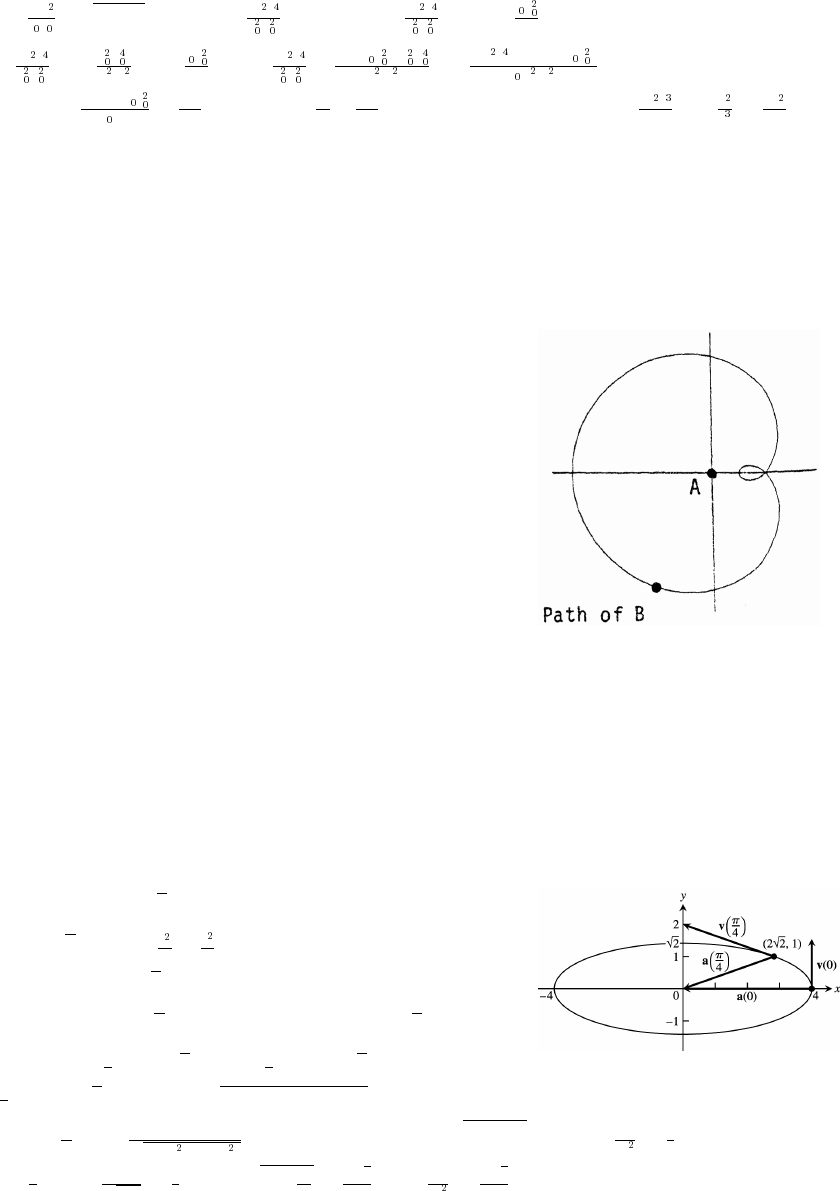
852 Chapter 13 Vector-Valued Functions and Motion in Space
15. T 1 e T 1 e 1 1 (from Equation 32)œÊœœ
Š‹ Š‹ Š‹ Š ‹
Èab ”•
2a 4a 4a
rv GM
rv rv
rv
111
### #
2œ œ œ
Š‹’ “Š‹’ “Š‹
4a 4a
rv rv
rv rv 2GMrv rv
GM GM GM rGM
4a 2GM rv
11
1
ˆ‰
ab
4 a 4 a (from Equation 35) T œœ ʜʜab ab
Š‹
ˆ‰ ˆ‰ˆ‰
11
#% #% #
"
2GM r v
2r GM GM 2a GM GM a GM
22 4aT4
11
16. Let (t) denote the vector from planet A to planet B at time t. Then (t) (t) (t)rrrr
AB AB B A
œ
[3 cos ( t) 2 cos (2 t)] [3 sin ( t) 2 sin (2 t)]œ 11 11ij
3 cos ( t) 2 cos ( t) sin ( t) [3 sin ( t) 4 sin ( t) cos ( t)]œ cdab111 111
##
ij
3 cos ( t) 4 cos ( t) 2 [(3 4 cos ( t)) sin ( t)] parametric equations for the path areœ Êcd11 11
#ij
x(t) 2 [3 4 cos ( t)] cos ( t) and y(t) [3 4 cos ( t)] sin ( t)œ œ 11 11
17. The graph of the path of planet B is the limacon
¸
at the right.
18. (i) Perihelion is the time t such that (t) is a minimum.kkr
(ii) Aphelion is the time t such that (t) is a maximum.kkr
(iii) Equinox is the time t such that (t) 0 .rw†œ
(iv) Summer solstice is the time t such that the angle between (t) and is a maximum.rw
(v) Winter solstice is the time t such that the angle between (t) and is a minimum.rw
CHAPTER 13 PRACTICE EXERCISES
1. (t) (4 cos t) 2 sin t x 4 cos tri jœ Êœ
Š‹
È
and y 2 sin t 1;œÊœ
Èx
16
y
#
vi jœ ( 4 sin t) 2 cos t and
Š‹
È
( 4 cos t) 2 sin t ; (0) 4 , (0) 2 ,ai jrivjœ œ œ
Š‹
ÈÈ
(0) 4; 22 , 22 ,air ijv ijœ œ œ
ˆ‰ ˆ‰
ÈÈ
11
44
2 2 ; 16 sin t 2 cos taijv
ˆ‰ ÈÈ
kk
1
4œ œ
##
a ; at t 0: a 0, a 0 4, 2;Êœ œ œ œ œ œ œ œœ
TN
d 14 sin t cos t 4
dt 2
16 sin t 2 cos t
a
kk kk
É
va
Èkk
#
T,N
v
at t : a , a 9 , œœœœœ œœ
1
439327
77 49
81
42 42
a
TN
ÈÈÈ
kk
É,N
v
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 13 Practice Exercises 853
2. (t) 3 sec t 3 tan t x 3 sec t and y 3 tan t sec t tan t 1;rijœ Êœ œÊœœ
Š‹Š‹
ÈÈ È È
x
33
y##
x y 3; 3 sec t tan t 3 sec tÊœ œ
## #
vij
Š‹Š‹
ÈÈ
and
3 sec t tan t 3 sec t 2 3 sec t tan t ;aijœ
Š‹Š‹
ÈÈÈ
#$ #
(0) 3 , (0) 3 , (0) 3 ;rivjaiœœœ
ÈÈÈ
3 sec t tan t 3 sec tkkvœ
È## %
a ;Êœ œ
Td 6 sec t tan t 18 sec t tan t
dt 2 3 sec t tan t 3 sec t
kkv
È
at t 0: a 0, a 0 3,œœœ œ
TNÉkk È
a#
,œœœ
a3
33
N
kk ÈÈ
v
"
3. t 1 t 1 trijv i jœ Êœ
"
##
$Î# $Î#
ÈÈ
1t 1t
tab ab
t 1 t 1 t . We want to maximize : andÊœ œ œkk ab ab kk
Ê’“’“
vv
##
$Î# $Î#
##
"
1t dt
d 2t
1t
kk ab
v
0 0 t 0. For t 0, 0; for t 0, 0 occurs when
d
dt
2t 2t 2t
1t 1t 1t
kk ab ab ab
vœÊ œÊœ Ê
kkvmax
t0 1œÊ œkkvmax
4. e cos t e sin t e cos t e sin t e sin t e cos trijv i jœ Êœabababab
tt tttt
e cos t e sin t e sin t e cos t e sin t e cos t e cos t e sin tʜ aijabab
t ttt tt t t
2e sin t 2e cos t . Let be the angle between and . Then cosœ œabab Š‹
tt
ij ra))
" ra
ra
†
kkkk
cos cos cos 0 for all tœœœœ
" " "
#
Š‹
2e sin t cos t 2e sin t cos t 0
e cos t e sin t 2e sin t 2e cos t 2e
2t 2t
tt t t 2t
ÉÉ
ababa ba b
1
5. 3 4 and 5 15 25 25; 3 4 5
340
550
vij ai j va k va v
ijk
œ œ Ê‚œ œ Ê œ œ œ
"
ââ
ââ
ââ
ââ
ââ
ââ kk kk
È
‚##
Êœ œœ,kk
kk
va
v
‚"
25
55
6. e 1 e e 1 e e 1 e 2e,œœÊœ
kk
‘
ab
y
1y
x2x x2x x 2x 2x
d3
dx
$Î# $Î# &Î#
#
ab ab abab
’“
,
e 1 e 3e 1 e e 1 e 1 e 3e e 1 e 1 2e ;œ œ œ
x 2x 3x 2x x 2x 2x 2x x 2x 2x
ab ab abc daba bab
$Î# &Î# &Î# &Î#
0 1 2e 0 e 2x ln 2 x ln 2 ln 2 y ; therefore is at a
d
dx
2x 2x
2
,œ Ê œ Ê œ Ê œ Ê œ œ Ê œab È
"""
##
È,
maximum at the point ln 2
Š‹
È
ß
"
È2
7. x y and y y. Since the particle moves around the unit circlerij v i j viœ Êœ œÊ œ
dx dx
dt dt dt
dy †
x y 1, 2x 2y 0 (y) x. Since y and x, we have
##
œ œ Ê œ Ê œ œ œ œ
dx x dx x dx
dt dt dt y dt dt y dt dt
dy dy dy dy
y x at (1 0), and the motion is clockwise.vij v jœ Ê ß œ
8. 9y x 9 3x x . If x y , where x and y are differentiable functions of t,œÊ œ Êœ œ
$# #
"
dy dy
dt dt dt 3 dt
dx dx rij
then . Hence 4 4 and x (3) (4) 12 at (3 3). Also,vij vi vjœ œÊœ œœ œ œ ß
dx dx dx
dt dt dt dt 3 dt 3
dy dy
††
""
##
and x x . Hence 2 2 andaij aiœ œ œÊœ
dx 2 dx dx dx
dt dt dt 3 dt 3 dt dt
dy dy ˆ‰ˆ‰ ˆ ‰
#"#†
(3)(4) (3) ( 2) 26 at the point (x y) (3 3).aj†œœ œ ßœß
dy
dt 3 3
2##
"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
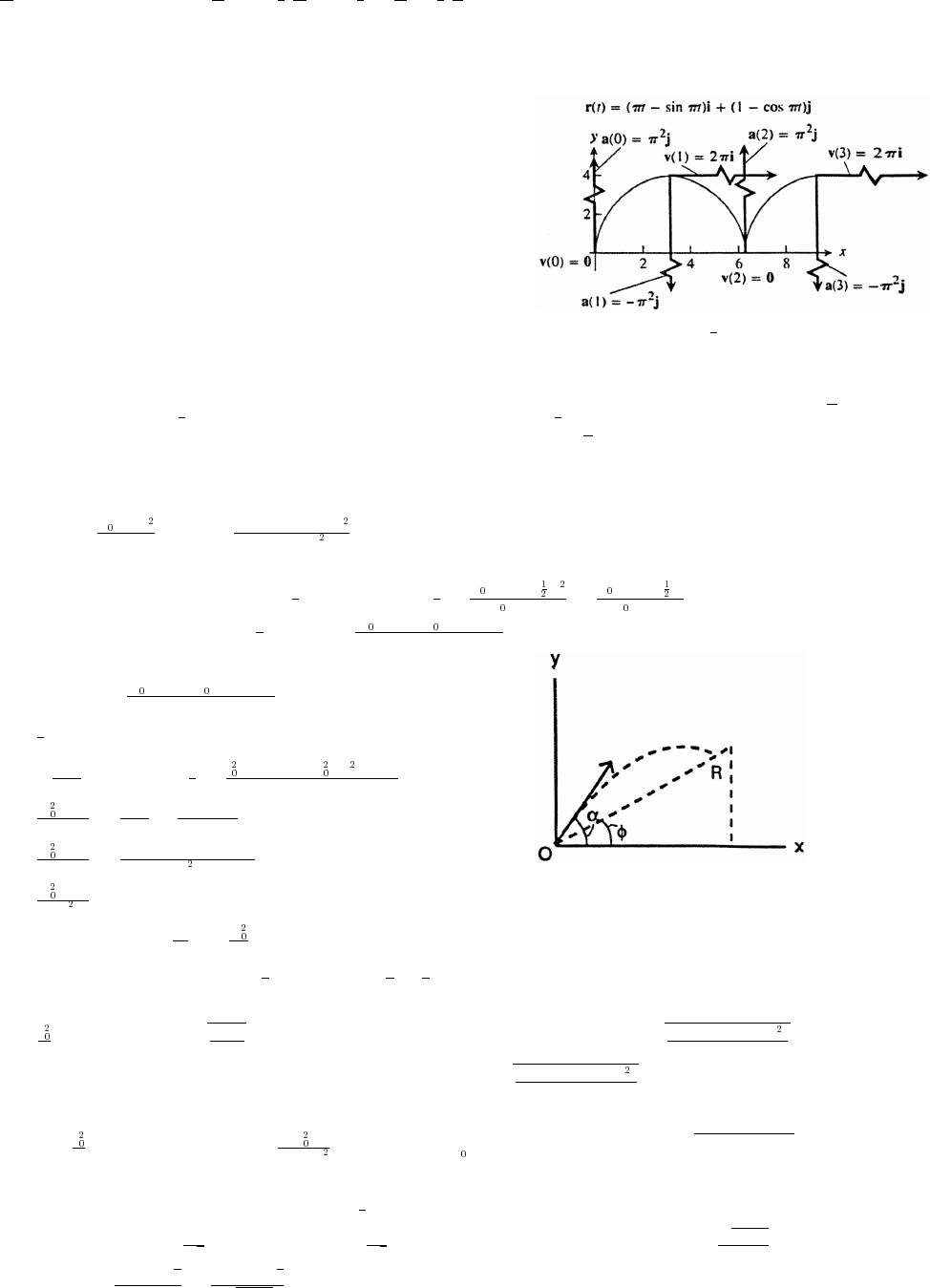
854 Chapter 13 Vector-Valued Functions and Motion in Space
9. orthogonal to 0 ( ) K, a constant. If x y , where
ddddd
dt dt dt dt dt
rrrr
r r r r rr rr r i jÊœ œ œ Ê œ œ††† ††
"""
###
x and y are differentiable functions of t, then x y x y K, which is the equation of a circlerr†œ Ê œ
## ##
centered at the origin.
10. (b) ( cos t) ( sin t)vijœ 11 1 1 1
sin t cos t ;ʜ aijabab11 1 1
##
(0) and (0) ;v0a jœœ1#
(1) 2 and (1) ;via jœœ11
#
(2) and (2) ;v0a jœœ1#
(3) 2 and (3)via jœœ11
#
(c) Forward speed at the topmost point is (1) (3) 2 ft/sec; since the circle makes revolution perkkkkvvœœ1"
#
second, the center moves ft parallel to the x-axis each second the forward speed of C is ft/sec.11Ê
11. y y (v sin )t gt y 6.5 (44 ft/sec)(sin 45°)(3 sec) 32 ft/sec (3 sec) 6.5 66 2 144œ Êœ œ
!! ""
##
###
!ab È
44.16 ft the shot put is on the ground. Now, y 0 6.5 22 2t 16t 0 t 2.13 sec (the¸ Ê œ Ê œ Ê ¸
È#
positive root) x (44 ft/sec)(cos 45°)(2.13 sec) 66.27 ft or about 66 ft, 3 in. from the stopboardʸ ¸
12. y y 7 ft 57 ft
max œ œ ¸
!#
(v sin ) [(80 ft/sec)(sin 45°)]
g (2) 32 ft/sec
!ab
13. x (v cos )t and y (v sin )t gt tan œœÊœœœ
!!
"
#
#
!!9
y
x (v cos )t v cos
(v sin )t gt (v sin ) gt
!!
!!
v cos tan v sin gt t , which is the time when the golf ballʜʜ
!!
"
#
!9 ! 2v sin 2v cos tan
g
!!9
hits the upward slope. At this time
x(v cos )œ!
!Š‹
2v sin 2v cos tan
g
!!9
v sin cos v cos tan . Nowœ
Š‹
ab
2
g###
!!
!! !9
OR ORœÊœ
x2
cos g cos
v sin cos v cos tan
99
!! !9
Š‹Š ‹
œ
Š‹Š ‹
2v cos
gcos cos
sin cos tan
!!
99
!9
œŠ‹Š ‹
2v cos
gcos
sin cos cos sin
!!9 !9
9
[sin ( )]. The distance OR is maximizedœ
Š‹
2v cos
g cos
!
9!9
when x is maximized: (cos 2 sin 2 tan ) 0 (cos 2 sin 2 tan ) 0 cot 2 tan 0
dx
dg
2v
!œœÊœÊœ
Š‹ !!9 !!9 !9
cot 2 tan ( ) 2 ʜʜʜ!9!9!
11
9
##4
14. R sin 2 v ; for 4325 yards: 4325 yards 12,975 ft vœÊœ œÊœ
v
gsin 2 (sin 90°)
Rg (12,975 ft) 32 ft/sec
!! !
ÉÉ
!ab
644 ft/sec; for 4752 yards: 4752 yards 14,256 ft v 675 ft/sec¸œÊœ¸
!É(14,256 ft) 32 ft/sec
(sin 90°)
ab
15. (a) R sin 2 109.5 ft (sin 90°) v 3504 ft /sec v 3504 ft /secœÊœ Êœ Êœ
vv
g 32 ft/sec
!Š‹ È
###
!##
59.19 ft/sec¸
(b) x (v cos )t and y 4 (v sin )t gt ; when the cork hits the ground, x 177.75 ft and y 0œœ œœ
!!
"
#
#
!!
177.75 v t and 0 4 v t 16t 16t 4 177.75 tÊ œ œ Ê œ Êœ
Š‹ Š‹
!!
""
##
ÈÈ È
22
181.75
4
v 74.58 ft/secÊœ œ ¸
!(177.75) 2 4(177.75) 2
t181.75
ÈÈ
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
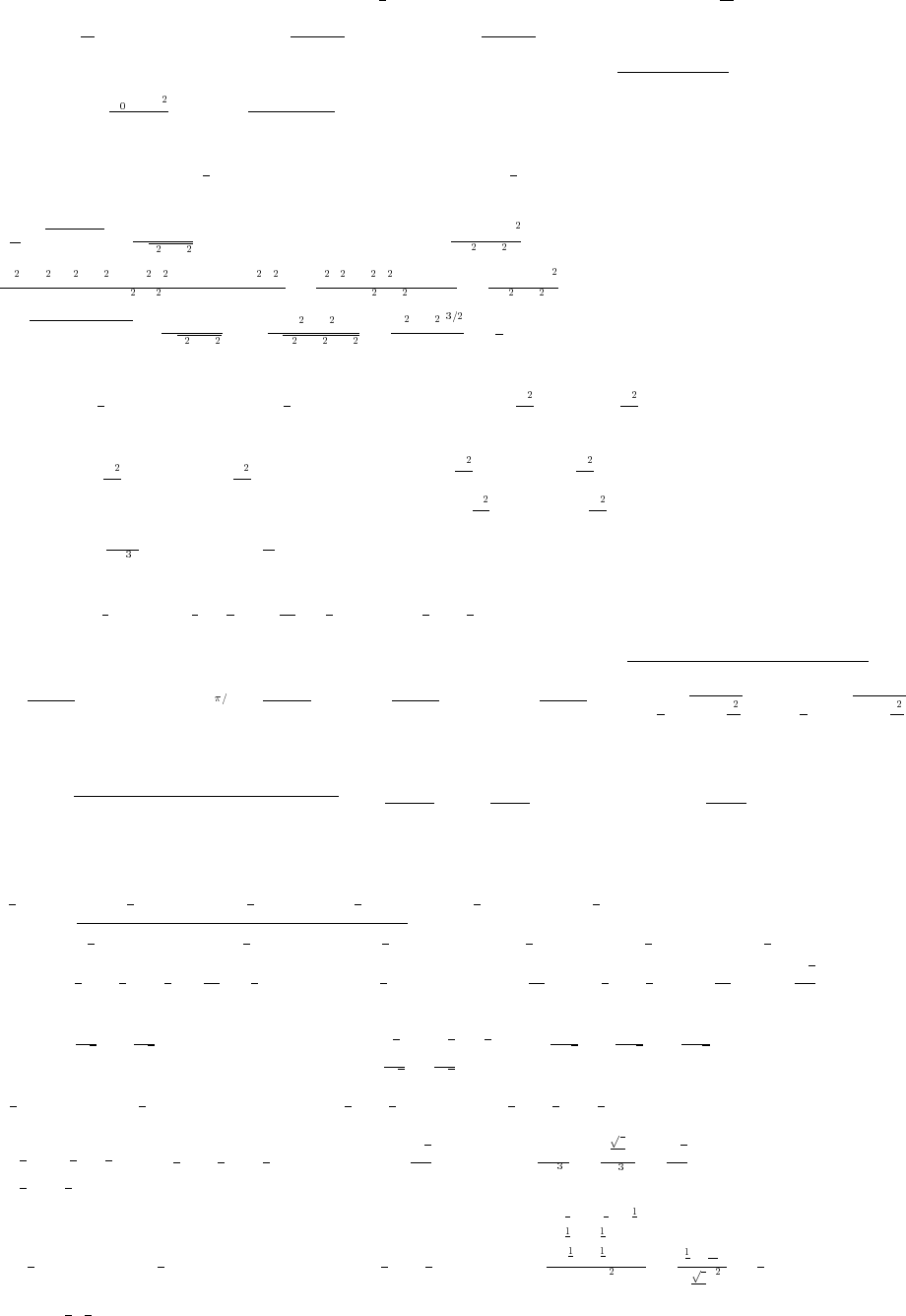
Chapter 13 Practice Exercises 855
16. (a) x v (cos 40°)t and y 6.5 v (sin 40°)t gt 6.5 v (sin 40°)t 16t ; x 262 ft and y 0 ftœœœœœ
!! !
"
#
##
5
12
262 v (cos 40°)t or v and 0 6.5 (sin 40°)t 16t t 14.1684Êœ œ œ Êœ
5 262.4167 262.4167
12 (cos 40°)t (cos 40°)t
!! ##
’“
t 3.764 sec. Therefore, 262.4167 v (cos 40°)(3.764 sec) v v 91 ft/secʸ ¸ Ê ¸ Ê ¸
!!!
262.4167
(cos 40°)(3.764 sec)
(b) y y 6.5 60 ft
max œ ¸ ¸
!(v sin )
2g (2)(32)
(91)(sin 40°)
!ab
2
17. x v cos t and y gt v sin t x y gt v t
# ### # ### # # ##
!! !
""
##
##
œœÊœab ab
ˆ‰ ˆ‰
!!
18. s x y x y s x y
ÞÞ ÞÞ
œœ Êœ
Þ Þ ÞÞ ÞÞ ÞÞ ÞÞ
d
dt È## ## ##
#
xx yy
xy
xx yy
xy
ÞÞÞ ÞÞÞ
ÞÞ
ÞÞÞ ÞÞÞ
ÞÞ
Èab
œœœ
ababa b a bx y x y xx 2xxyyyy xyyx
xy xy xy
x y y x 2x x y y
ÞÞ ÞÞ Þ Þ Þ ÞÞ Þ ÞÞ Þ ÞÞ Þ ÞÞ Þ ÞÞ Þ ÞÞ
ÞÞ ÞÞ ÞÞ
Þ ÞÞ Þ ÞÞ Þ ÞÞ Þ ÞÞ
xys Êœ Ê œ œœ
ÞÞ ÞÞ ÞÞ
È###"
kk ab
ÈÈ kk
xy yx x y
xy
xy
xys xy yx
ÞÞÞ ÞÞÞ Þ Þ
ÞÞ
ÞÞ
ÞÞ ÞÞ
ÞÞ ÞÞÞ ÞÞÞ
,3
19. (t) cos d sin d (t) cos sin 1;rijvijvœ ʜʜ
’ “ ’ “ Š‹ Š‹
ˆ‰ ˆ‰ kk
''
00
tt
""
## ##
##
1) ) 1) ) 11tt
(t) t sin t cos cos sin 0
t sin t cos 0
aijva
ijk
œ Ê ‚ œ
11
11
Š‹ Š‹ ââ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
Š‹ Š‹
Š‹ Š‹
11 11
11
tt tt
tt
## ##
##
t t; (t) 1 s t C; (0) s(0) 0 C 0 sœÊœ œ œœÊœ œÊ œÊœÊœ1, 1 ,1kv r0
kk
kk
va
v
‚kkds
dt
20. s a since a 0œÊœÊœÊœÊœœ )) 9 ,
ss
aadsa aa
d
19
#
"""
¸¸
21. (2 cos t) (2 sin t) t ( 2 sin t) (2 cos t) 2t ( 2 sin t) (2 cos t) (2t)rijkv ijkvœÊœÊœ
####
kk È
2 1 t Length 2 1 t dt t 1 t ln t 1 t 1 ln 1œÊ œ œ œ
ÈÈÈÈ
’“Š‹¹¹
ÉÉ
####
Î%
!
'0
4111 1 1
4164 16
22. (3 cos t) (3 sin t) 2t ( 3 sin t) (3 cos t) 3tr i jkv i jkœÊœ
$Î# "Î#
( 3 sin t) (3 cos t) 3t 9 9t 3 1 t Length 3 1 t dt 2(1 t)Êœ œ œ Ê œ œ kk a b
ÉÈÈ È‘
v# # "Î# #$Î# $
!
'0
3
14œ
23. (1 t) (1 t) t (1 t) (1 t)rijkvijkœ Êœ
44 22
993333
$Î# $Î# "Î# "Î#
""
(1 t) (1 t) 1 (1 t) (1 t)Êœ œÊœ kk É‘ ‘ˆ‰
vTijk
22 22
333333
"Î# "Î#
##
""
#"Î# "Î#
(0) ; (1 t) (1 t) (0) (0)Ê œ œ Ê œ Ê œTijk i j ij
22 d d d
333dt3 3 dt 33 dt 3
2
"" " ""
"Î# "Î#
TTT
¸¸
È
(0) ; (0) (0) (0) ;
0
Êœ œ‚œ œ
NijBTN ijk
ijk
"" " "
"
""
ÈÈ È È È
ÈÈ
2 2 32 32 32
22
333
22
4
ââ
ââ
ââ
ââ
ââ
ââ
ââ
(1 t) (1 t) (0) and (0) (0) (0)aijaijvijk vaœ Ê œ œ Ê ‚
"" "" "
"Î# "Î#
3 3 33 333
22
(0) ;
0
œœÊ‚œÊœœœ
ââ
ââ
ââ
ââ
ââ
ââ kk
ijk
ijk va
22
333
33
999 3 1 3
422
"
""
"" ‚
ÈÈ
kk
kk Š‹
,va
v
2
3
(1 t) (1 t) (0) (0) ;aijaij
ÞÞ
œ Ê œ Ê œ œ œ
"" "" "
$Î# $Î#
‚
66 66 6
0
0
7
ââ
ââ
ââ
ââ
ââ
ââ
ââ
kk ˆ‰ˆ ‰
Š‹
22
333
33
66 318
2
2
3
va
t 0 0 is the point on the curveœÊ ßß
ˆ‰
44
99
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

856 Chapter 13 Vector-Valued Functions and Motion in Space
24. e sin 2t e cos 2t 2e e sin 2t 2e cos 2t e cos 2t 2e sin 2t 2er i jkv i jkœ Êœ abababab
tt ttt tt t
e sin 2t 2e cos 2t e cos 2t 2e sin 2t 2e 3e Êœ œ Êkkababab
É
vT
tt t t t
t
###
œv
vkk
sin 2t cos 2t cos 2t sin 2t (0) ;œ Ê œ
ˆ‰ˆ‰
"" "
33 3 3 3 333
22222
ijkTijk
cos 2t sin 2t sin 2t cos 2t (0) (0) 5
d2 4 2 4 d 24 d 2
dt 3 3 3 3 dt 3 3 dt 3
TTT
œ ʜʜ
ˆ‰ˆ ‰ ¸¸
È
ijij
(0) ; (0) (0) (0) ;
0
Êœ œ œ‚œ œ
NijBTN ijk
ijk
ˆ‰
Š‹ ÈÈ È È È
ÈÈ
24
33
25
3
ij"
"
5 5 35 35 35
2425
212
333
55
2
ââ
ââ
ââ
ââ
ââ
ââ
ââ
4e cos 2t 3e sin 2t 3e cos 2t 4e sin 2t 2e (0) 4 3 2 and (0) 2 2a i jkaijkvijkœ Ê œ œaba b
tt tt t
(0) (0) 8 4 10 64 16 100 6 5 and (0) 3
22
432
Ê ‚ œ œ Ê ‚œ œ œ
"
va ijkva v
ijk
ââ
ââ
ââ
ââ
ââ
ââ kk kk
ÈÈ
(0) ;Êœœ,65 25
39
ÈÈ
4e cos 2t 8e sin 2t 3e sin 2t 6e cos 2t 3e cos 2t 6e sin 2t 4e sin 2t 8e cos 2t 2eai jk
ޜ aba b
t ttt t ttt t
2e cos 2t 11e sin 2t 11 e cos 2t 2e sin 2t 2e (0) 2 11 2œ Ê œ
Þ
abab
tt tt t
ijkaijk
(0) ; t 0 ( 2) is on the curveÊœ œœœÊ!ß"ß7
ââ
ââ
ââ
ââ
ââ
ââ
kk
212
432
2112 80 4
180 9
‚
va
25. t e e 1 e (ln 2) ;ri j vi j v T i j T i jœ Ê œ Ê œ Ê œ Ê œ
"""
#
2t 2t 4t
11 17 17
4
kk ÈÈÈ ÈÈ
ee
e
4t 4t
2t
(ln 2) (ln 2) ;
d2 2 d 328 4
dt dt
11 17 17 17 17 17 17
TT
œ ʜʜ
"
ee
ee
4t 2t
4t 4t
ˆ‰ ˆ‰ ÈÈ ÈÈ
ij ijN ij
(ln 2) (ln 2) (ln 2) ; 2e (ln 2) 8 and (ln 2) 4
0
0
BTN kaja jvij
ijk
œ‚œ œœÊ œ œ
ââ
ââ
ââ
ââ
ââ
ââ
ââ
"
"
ÈÈ
ÈÈ
17 17
4
4
17 17
2t
(ln 2) (ln 2) 8 8 and (ln 2) 17 (ln 2) ; 4e
40
080
Ê‚œ œÊ‚œ œÊ œ œ
"Þ
va kva v aj
ijk
ââ
ââ
ââ
ââ
ââ
ââ kk k k
È,8
17 17
2t
È
(ln 2) 16 (ln 2) 0; t ln 2 (ln 2 2 0) is on the curveʜʜ œœÊßß
Þ
aj7
ââ
ââ
ââ
ââ
ââ
ââ
kk
140
080
0160
va‚
26. (3 cosh 2t) (3 sinh 2t) 6t (6 sinh 2t) (6 cosh 2t) 6rijkvijkœÊœ
36 sinh 2t 36 cosh 2t 36 6 2 cosh 2t tanh 2t sech 2tÊœ œ Êœœ kk ÈÈ
Š‹ Š‹
vTijk
## """v
vkk ÈÈÈ
222
(ln 2) ; sech 2t sech 2t tanh 2t (ln 2)Êœ œ ÊTijk i k
15 8 d 2 2 d
17 2 2 17 2 2 2
dt dt
ÈÈ È È È
"#
TT
Š‹Š ‹
(ln 2)œ œÊœœ
Š‹ Š‹ Š ‹Š ‹
ˆ‰ ˆ‰ˆ‰ ¸ ¸ Ê
2 8 2 8 15 128 240 d 128 240
2 2 289 2 289 2 289 2 289 2
17 17 17 dt 17
82
ÈÈ ÈÈ ÈÈ
È
###
ikik
T
(ln 2) ; (ln 2) (ln 2) (ln 2) ;
0
Êœ œ‚œ œ
NikBTN ijk
ijk
815 15 8
17 17
15 8
17 2 2 17 2
815
17 17
17 2 2 17 2
ââ
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ È ÈÈ È
""
(12 cosh 2t) (12 sinh 2t) (ln 2) 12 12 andaija ijijœ Êœœ
ˆ‰ ˆ‰
17 15 51 45
88##
vijkijkva
ijk
(ln 2) 6 6 6 6 (ln 2) (ln 2) 6
0
œœÊ‚œ
ˆ‰ ˆ‰ ââ
ââ
ââ
ââ
ââ
ââ
15 17 45 51
88 44
45 51
44
51 45
2#
135 153 72 153 2 and (ln 2) 2 (ln 2) ;œ Ê ‚ œ œ Ê œ œijkva vkk k k
ÈÈ
51 32
4 867
153 2
2
,È
Š‹
È
51
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 13 Practice Exercises 857
(24 sinh 2t) (24 cosh 2t) (ln 2) 45 51 (ln 2) ;aijaij
ÞÞ
œ ʜʜœ7
ââ
ââ
ââ
ââ
ââ
ââ
kk
45 51
44
545
22
6
0
45 51 0 32
867
va‚
t ln 2 6 ln 2 is on the curveœÊßß
ˆ‰
51 45
88
27. 2 3t 3t 4t 4t (6 cos t) (3 6t) (4 8t) (6 sin t)rijkvijkœ Êœ abab
##
(3 6t) (4 8t) (6 sin t) 25 100t 100t 36 sin tÊœ œ kk ÈÈ
v### ##
25 100t 100t 36 sin t (100 200t 72 sin t cos t) a (0) (0) 10;Êœ Ê œ œ
d d
dt dt
kk kkv v
"
#
##
"Î#
ab T
6 8 (6 cos t) 6 8 (6 cos t) 100 36 cos t (0) 136aij k a aœ Ê œ œ Ê œkk k k
ÈÈÈ
## # #
a a 136 10 36 6 (0) 10 6Êœ œ œ œÊ œ
NT
Ékk ÈÈ
aaTN
###
28. (2 t) t 2t 1 t (1 4t) 2t 1 (1 4t) (2t)ri j kvi jkvœ Êœ Ê œ abab kk
È
## ###
2 8t 20t 2 8t 20t (8 40t) a (0) 2 2; 4 2œ Ê œ Êœ œ œ
ÈÈ
ab
#"
#
#"Î#
dd
dt dt
kk kkvv
Tajk
4 2 20 a a 20 2 2 12 2 3 (0) 2 2 2 3Êœ œ Êœ œ œ œ Ê œ kk kk
ÈÈÈÈ
ÈÈÈ
ÉÊŠ‹
aa aTN
## #
##
NT
29. (sin t) 2 cos t (sin t) (cos t) 2 sin t (cos t)ri jkv i jkœ Êœ
Š‹ Š‹
ÈÈ
(cos t) 2 sin t (cos t) 2 cos t (sin t) cos t ;Êœ œ Êœœ kk ÊŠ ‹ Š‹ Š‹
ÈÈ
vTijk
##
#""v
vkk ÈÈ
22
sin t (cos t) sin t sin t ( cos t) sin t 1
dd
dt dt
22 2 2
TT
œ Ê œ œ
Š‹ Š‹ Š‹ Š‹
¸¸Ê
"" " "
##
#
ÈÈ È È
ij k
sin t (cos t) sin t ; cos t sin t cos t
sin t cos t sin t
Êœ œ œ‚œ
NijkBTN
ijk
ˆ‰
¸¸ ÈÈ ÈÈ
ÈÈ
d
dt
d
dt
T
TŠ‹ Š‹ ââ
ââ
ââ
ââ
ââ
ââ
ââ
"" ""
""
22 22
22
; ( sin t) 2 cos t (sin t) cos t 2 sin t cos t
sin t 2 cos t sin t
œ œ Ê œ
""
ÈÈ
22
ika i j kva
ijk
Š‹
Èââ
ââ
ââ
ââ
ââ
ââ
È
È
‚
2 2 4 2 ; ( cos t) 2 sin t (cos t)œ Ê‚œœÊœœ œ œ
Þ
ÈÈ È È
kk Š‹
ikva a i j k,kk Š‹
ÈÈ
va
v
‚"
kk
2
22
0Êœ œ œ7
ââ
ââ
ââ
ââ
ââ
ââ
ââ
È
È
È
kk Š‹Š ‹ Š ‹
ÈÈ È
cos t 2 sin t cos t
sin t 2 cos t sin t
cos t 2 sin t cos t (cos t) 2 2 sin t (0) (cos t) 2
4
‚
va
30. (5 cos t) (3 sin t) ( 5 sin t) (3 cos t) ( 5 cos t) (3 sin t)ri jkv j ka jkœ Ê œ Ê œ
25 sin t cos t 9 sin t cos t 16 sin t cos t; 0 16 sin t cos t 0 sin t 0 or cos t 0Ê œ œ œÊ œÊ œ œva va††
t 0, or ʜ 1
#1
31. 2 4 sin 3 0 ( ) 2(1) 4 sin ( 1) 0 2 4 sin sin ri j k rijœ Êœ œ Êœ Ê œÊœ
ˆ‰ˆ‰ ˆ‰
tt t ttt
6######
"
1
1
†
t (for the first time)ʜ
1
3
32. (t) t t t 2t 3t 1 4t 9t (1) 14rijkvijkv vœ Ê œ Ê œ Ê œ
#$ # #%
kk k k
ÈÈ
(1) , which is normal to the normal planeÊœTijk
"
ÈÈÈ
14 14 14
23
(x 1) (y 1) (z 1) 0 or x 2y 3z 6 is an equation of the normal plane. Next weÊ œ œ
"
ÈÈÈ
14 14 14
23
calculate (1) which is normal to the rectifying plane. Now, 2 6t (1) 2 6 (1) (1)Najkajkvaœ Ê œ Ê ‚
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
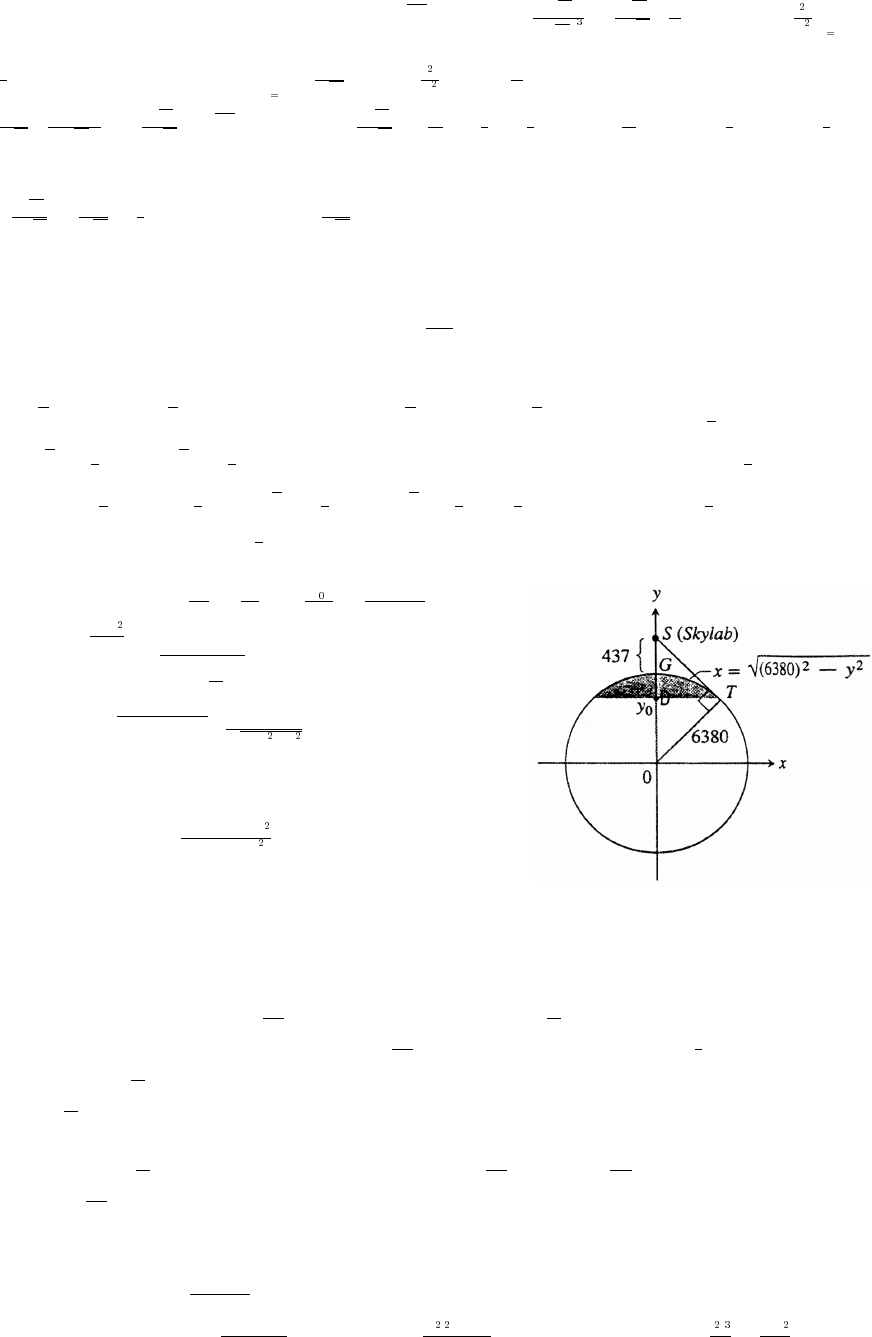
858 Chapter 13 Vector-Valued Functions and Motion in Space
6 6 2 (1) (1) 76 (1) ; (t)
23
026
œ œ Ê ‚ œ Ê œ œ œ Ê
"
ââ
ââ
ââ
ââ
ââ
ââ kk kk
ȹ
ijk
ijk v a v,ÈÈ
Š‹
ÈÈ
76 19
14 714
ds d s
dt dt t1
1 4t 9t 8t 36t , so 2 6œ œ œ Ê
¹
abab ˆ‰
"
#
#% $
"Î# #
t1
22 d s ds
14 dt dt
ÈaT Njk,
14 (x 1) (y 1) (z 1)œ ÊœÊ
22 11 8 9 11 8 9
14 14 7 14
23 14
19
219 777 7 7 7
ÈÈ È È
ÈÈ
Š‹ Š‹
Ȉ‰
ijk #
NN ijk
0 or 11x 8y 9z 10 is an equation of the rectifying plane. Finally, (1) (1) (1)œ œ œ ‚BTN
(3 3 ) 3(x 1) 3(y 1) (z 1) 0 or 3x 3y z
23
11 8 9
œœÊœ
"
Š‹Š‹
ˆ‰ââ
ââ
ââ
ââ
ââ
ââ
È
ÈÈ È
14
219 19
14 7
"" "
ijk
ijk
1 is an equation of the osculating plane.œ
33. e (sin t) ln (1 t) e (cos t) (0) ; (0) (1 0 0) is on the lineri j kvi j kv ijkr iœ Ê œ Ê œ œ Ê ßß
tt
1t
ˆ‰
"
x 1 t, y t, and z t are parametric equations of the lineÊœ œ œ
34. 2 cos t 2 sin t t 2 sin t 2 cos t rijkv ijkvœÊœÊ
Š‹Š‹ Š ‹Š‹
ÈÈ ÈÈ ˆ‰
1
4
2 sin 2 cos is a vector tangent to the helix when t the tangent lineœ œ œ Ê
Š‹Š‹
ÈÈ
11 1
44 4
ijkijk
is parallel to ; also 2 cos 2 sin the point 1 1 is on the linevr i jk
ˆ‰ ˆ‰ ˆ ‰
Š‹Š‹
ÈÈ
11 1 11 1
44 4 44 4
œÊßß
x 1 t, y 1 t, and z t are parametric equations of the lineÊœ œ œ
1
4
35. (a) SOT TOD ??¸ÊœÊœ
DO OT 6380
OT SO 6380 6380 437
y
y y 5971 km;ʜ ʸ
!!
6380
6817
(b) VA 2 x 1 dyœ
'5971
6380
1ÊŠ‹
dx
dy
#
2 6380 y dyœ1'5971
6817ÈŠ‹
##
6380
6380 y
È
2 6380 dy 2 6380yœœ11
'5971
6817 cd
')"(
&*("
16,395,469 km 1.639 10 km ;œ¸‚
#(#
(c) percentage visible 3.21%¸¸
16,395,469 km
4 (6380 km)
1
CHAPTER 13 ADDITIONAL AND ADVANCED EXERCISES
1. (a) The velocity of the boat at (x y) relative to land is the sum of the velocity due to the rower and theß
velocity of the river, or (y 50) 10 20 . Now, 20 y 20t c; y(0) 100vijœ œ Ê œ œ
‘
"#
250 dt
dy
c 100 y 20t 100 ( 20t 50) 10 20 t 8t 20Êœ Êœ Êœ œ vijij
‘ˆ‰
"##
250 5
8
(t) t 4t 20t ; (0) 0 100 100 (t)Êœ œ Ê œÊrijCrijjCr
ˆ‰
8
15 $# ""
t 4t (100 20t)œ
ˆ‰
8
15 $#
ij
(b) The boat reaches the shore when y 0 0 20t 100 from part (a) t 5œÊœ Êœ
(5) 125 4 25 (100 20 5) 100 ; the distance downstream isÊœ œ œrijii
ˆ‰ ˆ‰
8 200 100
15 3 3
†† †
therefore m
100
3
2. (a) Let a b be the velocity of the boat. The velocity of the boat relative to an observer on the bank of theij
river is a b . The distance x of the boat as it crosses the river is related to time byvi jœ
’“
3x(20 x)
100
xat a b a b (t)at bt ;œÊœ œ Ê œ vi ji j r i jC
’“Š‹ Š ‹
3at(20 at)
100 100 100 100
3a t 60at a t 30at
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 13 Additional and Advanced Exercises 859
(0) 0 0 0 (t) at bt . The boat reaches the shore when x 20rijC ri jœ Ê œÊ œ œ
Š‹
a t 30at
100
20 at t and y 0 0 bʜʜ œÊœ œ
20 20 20b
a a 100 a 100a
a 30a (20) 30(20)
ˆ‰ ˆ‰ ˆ‰
20 20
aa
b 2; the speed of the boat is 20 a b a 4 a 16œ Êœ œœœÊœ
2000b 8000 12,000
100a
## # #
Èkk ÈÈ
v
a 4; thus, 4 2 is the velocity of the boatÊœ œvij
(b) (t) at bt 4t 2t by part (a), where 0 t 5ri ji jœ œ ŸŸ
Š‹Š ‹
a t 30at 16t 120t
100 100 100
(c) x 4t and y 2tœœ
16t 120t
100 100
t t 2t t 2t 15t 25œœ
46 2
25 5 25
$# #
ab
t(2t 5)(t 5), which is the graph ofœ
2
25
the cubic displayed here
3. (a) ( ) (a cos ) (a sin ) b [( a sin ) (a cos ) b ] ; 2gzrijk ijkv)))) ) )œÊœ œœ
ddd
dt dt dt
r r)kk ȸ¸
ab 2œ Êœ œ Ê œ œ
ÈÉÉÉÉ
¸
##
œ#
dd d
dt dt a b a b dt a b a b
2gz 2gb 4 gb gb
)) )
)11
)1
(b) dt 2 t C; t 0 0 C 0
dd
dt a b a b a b
2gb 2gb 2gb
))
)
)
œ Ê œ Ê œ œÊœÊ œ
ÉÉ É
"Î#
È))
2 t ; z b zÊœ Êœ œÊœ)))
"Î#
É2gb gbt gb t
a b 2 a b 2 a b
ab ab
(c) (t) [( a sin ) (a cos ) b ] [( a sin ) (a cos ) b ] , from part (b)vijkijkœœ œ
dd
dt dt a b
gbt
r)) ))
)Š‹
(t) ;Êœ œvT
’“Š‹
( a sin ) (a cos ) b gbt gbt
a b a b a b
))i j k
ÈÈÈ
[( a cos ) (a sin ) ] [( a sin ) (a cos ) b ]
dd d
dt dt dt
rœ )) ) )ij i jk
ˆ‰
))
#
[( a cos ) (a sin ) ] [( a sin ) (a cos ) b ]œ
Š‹ Š‹
gbt gb
a b a b
#)) ) )ij i jk
a [( cos ) (sin ) ]œ
’“Š‹Š‹
( a sin ) (a cos ) b gb gbt
a b a b a b
#
))i j k
ÈÈ ))ij
a (there is no component in the direction of ).œ
gb gbt
a b a b
È
#
TN B
Š‹
4. (a) ( ) (a cos ) (a sin ) b [(a cos a sin ) (a sin a cos ) b ] ;rijk i jk) ) ) )) ) ))) )) )œÊœ
d d
dt dt
r)
2gz a a b kk a b
ȸ¸ ˆ‰
vœœœ Êœ
ddd
dt dt dt
2gb
a a b
r####
"Î#
))) )
)
È
È
(b) s dt a a b dt a a b d a a u b duœœ œ œ
'' ' '
00 0 0
tt t
kkabababv#### #### ####
"Î# "Î# "Î#
)))
d
dt
)
a u du a c u du, where cœœ œ
''
00
ÉÈ
a b
aa
a b
###
Èkk
s a c u ln u c u c c ln c c ln cÊœ œ
’“Š ‹
ÈÈÈÈ
¹¹ ¹¹
uc a
## #
## ## ## ##
!
##
)
)) ) )
5. r ; 0 0 (1 e)r (e sin œÊœ œÊ œÊ
(1 e)r (1 e)r (e sin ) (1 e)r (e sin )
1 e cos d (1 e cos ) d (1 e cos )
dr dr
!
)) )) )
))))0œ
sin 0 0 or . Note that 0 when sin 0 and 0 when sin 0. Since sin 0 onʜʜ ))1 ) ) )
dr dr
dd))
0 and sin 0 on 0 , r is a minimum when 0 and r(0) r œ œ œ1) ) )1 ) (1 e)r
1 e cos 0
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

860 Chapter 13 Vector-Valued Functions and Motion in Space
6. (a) f(x) x 1 sin x 0 f(0) 1 and f(2) 2 1 sin 2 since sin 2 1; since f is continuousœ œ Ê œ œ Ÿ
"""
###
kk
on [0 2], the Intermediate Value Theorem implies there is a root between 0 and 2ß
(b) Root 1.4987011335179¸
7. (a) and r [(cos ) (sin ) ] r [( sin ) (cos ) ] andvijvu u i j i jviœ œ œ Ê œ
dx dr d dr d dx
dt dt dt dt dt dt dt
dy
r))
)ˆ‰ ˆ ‰
)) ) ) †
cos r sin cos r sin ; and sin r cos vi vj vj†††œ Êœ œ œ
dr d dx dr d dr d
dt dt dt dt dt dt dt dt
dy
)) )) ) )
)) )
sin r cos ʜ
dy
dt dt dt
dr d
))
)
(b) (cos ) (sin ) cos sin uijvu
rr
œ Êœ )) ) )†dx
dt dt
dy
cos r sin (cos ) sin r cos (sin ) by part (a),œ
ˆ‰ˆ‰
dr d dr d
dt dt dt dt
))) ) ))
))
; therefore, cos sin ;Êœ œ vu†rdr dr dx
dt dt dt dt
dy
))
uijvu
))
œ Ê œ (sin ) (cos ) sin cos )) ) )†dx
dt dt
dy
cos r sin ( sin ) sin r cos (cos ) by part (a) r ;œ Êœ
ˆ‰ˆ‰
dr d dr d d
dt dt dt dt dt
))) ) ))
)) )
)
vu†
therefore, r sin cos
ddx
dt dt dt
dy
)œ ))
8. f( ) f ( ) f ( ) f ( ) ; r rvuuœÊœ Êœ œ)) ))
dr d d r d d dr d
dt dt dt dt dt dt dt
wwww
#
))))
)
ˆ‰ r
cos r sin sin r cos r f f ;œ Êœ œ
ˆ‰ˆ‰ˆ‰ˆ‰ ˆ‰
kk ab
’“’“
)) ) )
dr d dr d dr d d
dt dt dt dt dt dt dt
)) ) )
ijv
##
#w#
"Î# "Î#
#
x y y x , where x r cos and y r sin . Then ( r sin ) (cos ) kkk kva‚œ œ œ œ
ÞÞÞ ÞÞÞ )) ))
dx d dr
dt dt dt
)
( 2 sin ) (r cos ) (r sin ) (cos ) ; (r cos ) (sin ) Êœ œ
dx d dr d d dr d dr
dt dt dt dt dt dt dt dt dt
dy
)))) ))
))) )
ˆ‰
#
(2 cos ) (r sin ) (r cos ) (sin ) . Then Êœ ‚
dy
dt dt dt dt dt dt
ddr d d dr
)) ))
)))
ˆ‰ kk
#va
(after algebra) r r r 2 f f f 2 fœœ†much #ww w
$#$
ˆ‰ ˆ‰ ˆ‰
Š‹
ab
d d dr d d r d dr d
dt dt dt dt dt dt dt dt
22
)))) )
Êœ œ,kk
kk ab
‘
ab
va
v
‚†
f ff 2f
f f
22
9. (a) Let r 2 t and 3t 1 and 3 0. The halfway point is (1 3) t 1;œ œ Ê œ œ Ê œ œ ß Êœ)dr d d r d
dt dt dt dt
))
r (1) 3 ; r r 2 (1) 9 6vu uv uua u ua uuœ Êœ œ Êœ
dr d d r d d dr d
dt dt dt dt dt dt dt
rr r r
))))
)) ) )
’“’ “
ˆ‰
#
(b) It takes the beetle 2 min to crawl to the origin the rod has revolved 6 radiansÊ
L [f( )] f ( ) d 2 d 4 dÊœ œ œ
'' '
00 0
66 6
Écd Ɉ ‰ ˆ ‰ É
))) ) )
#w
##""
#
)))
33 399
4
d ( 6) 1 d ( 6) 1 ln 6 ( 6) 1œ œ œ
''
00
66
ÉÈÈ È
’“
¸¸
37 12
93 3
(6)
" " "
## #
##
'
!
)) )
))) ) ))
37 ln 37 6 6.5 in.œ ¸
ÈÈ
Š‹
"
6
10. (t) (t) m (t) m m ( m ) ( m ) m ; m Lr v vr vvraraFa rœ‚ Êœ‚ ‚ Êœ‚ ‚ œ‚ œ Ê
dd d d c
dt dt dt dt
Lr r L
r
ˆ‰
Š‹ kk
m m ( ) constant vectorœ Ê œ‚ œ‚ œ ‚ œ Ê œararr rr0L
dcc
dt
L
rr
Š‹
kk kk
11. (a) a right-handed frame of unit vectors
cos sin 0
sin cos 0
uu k
ijk
r‚œ œÊ
)
ââ
ââ
ââ
ââ
ââ
ââ
))
))
(b) ( sin ) (cos ) and ( cos ) (sin )
d
dd
d
uu
r
))
)
œ œ œ œ)) ))iju iju
r
(c) From Eq. (7), r r z r r r r r zvu u k av u u u u u kœ Êœœ
ÞÞÞÞÞ
ÞÞÞÞÞ
ÞÞÞ
ÞÞ Þ
rrr
))))
))))
ab
ˆ‰
rr r 2r zœ
ÞÞ Þ
ÞÞÞÞ
ÞÞ
Š‹
ˆ‰
)))
#uuk
r)
12. (a) x r cos dx cos dr r sin d ; y r sin dy sin dr r cos d ; thusœÊœ œÊœ) ) )) ) ) ))
dx cos dr 2r sin cos dr d r sin d and
### ###
œ ))))))
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
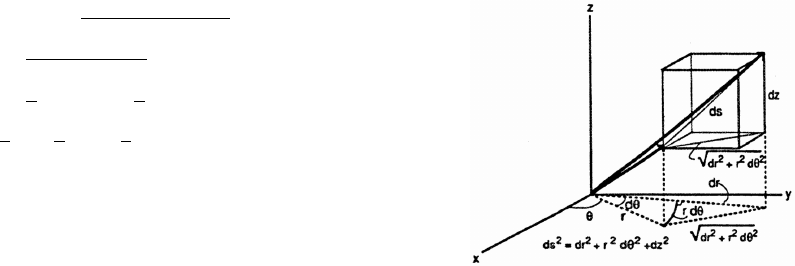
Chapter 13 Additional and Advanced Exercises 861
dy sin dr 2r sin cos dr d r cos d dx dy dz dr r d dz
### ### #######
œ Ê œ )))))) )
(c) r e dr e d œÊœ
))
)
L dr r d dzʜ
'0
ln 8 È### #
)
eee dœ
'0
ln 8È###)))
)
3e d 3 eœœ
'0
ln 8 ln 8
0
ÈÈ
’“
))
)
83 3 73œœ
ÈÈ È
(b)
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
862 Chapter 13 Vector-Valued Functions and Motion in Space
NOTES:
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

CHAPTER 14 PARTIAL DERIVATIVES
14.1 FUNCTIONS OF SEVERAL VARIABLES
1. (a) Domain: all points in the xy-plane
(b) Range: all real numbers
(c) level curves are straight lines y x c parallel to the line y xœ œ
(d) no boundary points
(e) both open and closed
(f) unbounded
2. (a) Domain: set of all (x y) so that y x 0 y xßÊ
(b) Range: z 0
(c) level curves are straight lines of the form y x c where c 0œ
(d) boundary is y x 0 y x, a straight line
Èœ Ê œ
(e) closed
(f) unbounded
3. (a) Domain: all points in the xy-plane
(b) Range: z 0
(c) level curves: for f(x y) 0, the origin; for f(x y) c 0, ellipses with center ( 0) and major and minorßœ ßœ !ß
axes along the x- and y-axes, respectively
(d) no boundary points
(e) both open and closed
(f) unbounded
4. (a) Domain: all points in the xy-plane
(b) Range: all real numbers
(c) level curves: for f(x y) 0, the union of the lines y x; for f(x y) c 0, hyperbolas centered atßœ œ„ ßœÁ
(0 0) with foci on the x-axis if c 0 and on the y-axis if c 0ß
(d) no boundary points
(e) both open and closed
(f) unbounded
5. (a) Domain: all points in the xy-plane
(b) Range: all real numbers
(c) level curves are hyperbolas with the x- and y-axes as asymptotes when f(x y) 0, and the x- and y-axesßÁ
when f(x y) 0ߜ
(d) no boundary points
(e) both open and closed
(f) unbounded
6. (a) Domain: all (x y) (0 y)ßÁß
(b) Range: all real numbers
(c) level curves: for f(x y) 0, the x-axis minus the origin; for f(x y) c 0, the parabolas y cx minus theßœ ßœÁ œ#
origin
(d) boundary is the line x 0œ

864 Chapter 14 Partial Derivatives
(e) open
(f) unbounded
7. (a) Domain: all (x y) satisfying x y 16ß
##
(b) Range: z "
4
(c) level curves are circles centered at the origin with radii r 4
(d) boundary is the circle x y 16
##
œ
(e) open
(f) bounded
8. (a) Domain: all (x y) satisfying x y 9ߟ
##
(b) Range: 0 z 3ŸŸ
(c) level curves are circles centered at the origin with radii r 3Ÿ
(d) boundary is the circle x y 9
##
œ
(e) closed
(f) bounded
9. (a) Domain: (x y) (0 0)ßÁß
(b) Range: all real numbers
(c) level curves are circles with center ( 0) and radii r 0!ß
(d) boundary is the single point (0 0)ß
(e) open
(f) unbounded
10. (a) Domain: all points in the xy-plane
(b) Range: 0 z 1Ÿ
(c) level curves are the origin itself and the circles with center (0 0) and radii r 0ß
(d) no boundary points
(e) both open and closed
(f) unbounded
11. (a) Domain: all (x y) satisfying 1 y x 1ß ŸŸ
(b) Range: zŸŸ
11
##
(c) level curves are straight lines of the form y x c where 1 c 1œ ŸŸ
(d) boundary is the two straight lines y 1 x and y 1 xœ œ
(e) closed
(f) unbounded
12. (a) Domain: all (x y), 0ßBÁ
(b) Range: z
11
##
(c) level curves are the straight lines of the form y cx, c any real number and x 0œÁ
(d) boundary is the line x 0œ
(e) open
(f) unbounded
13. f 14. e 15. a
16. c 17. d 18. b
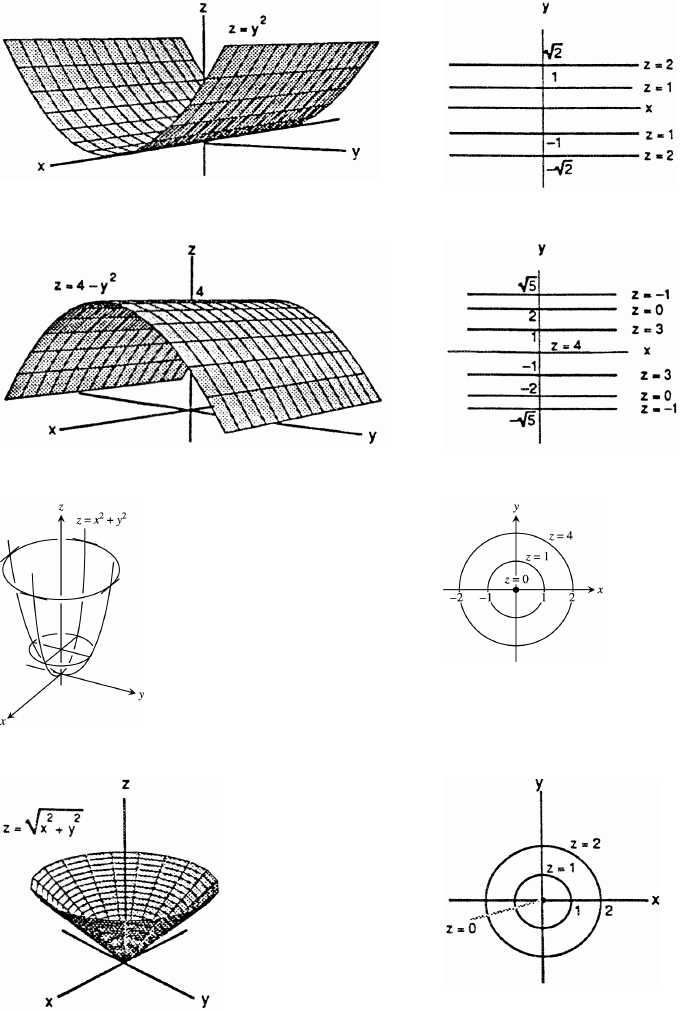
Section 14.1 Functions of Several Variables 865
19. (a) (b)
20. (a) (b)
21. (a) (b)
22. (a) (b)
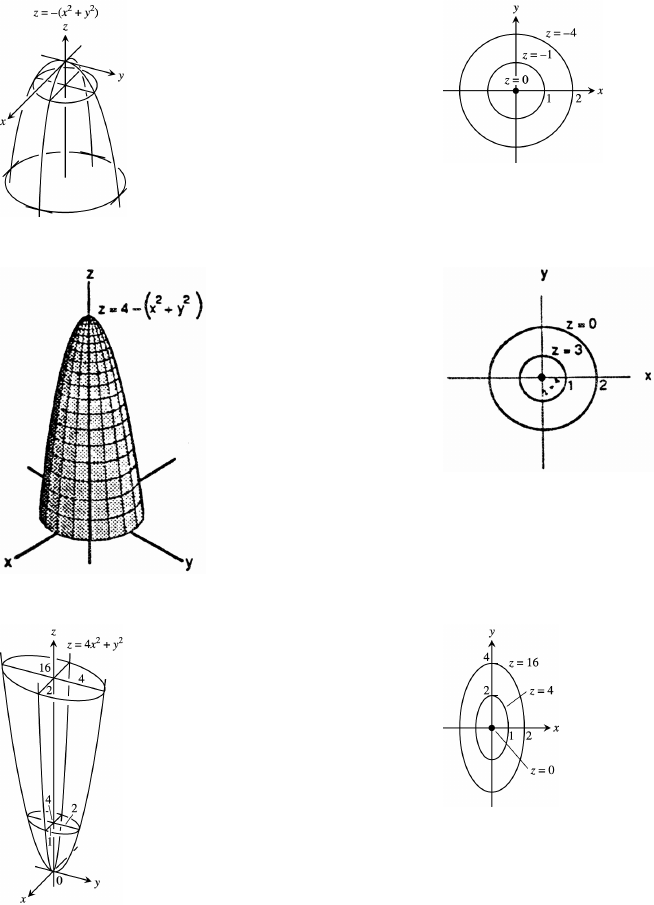
866 Chapter 14 Partial Derivatives
23. (a) (b)
24. (a) (b)
25. (a) (b)
Section 14.1 Functions of Several Variables 867
26. (a) (b)
27. (a) (b)
28. (a) (b)
29. f(x y) 16 x y and 2 2 2 z 16 2 2 2 6 6 16 x y x y 10ßœ ß Êœ œÊœ Ê œ
## ## ##
##
Š‹ Š‹Š‹
ÈÈ È È
30. f(x y) x 1 and (1 0) 1 1 0 x 1 0 x 1 or x 1ßœ ß ÊDœ œÊ œÊœ œ
ÈÈ
##
#
31. f(x y) dt at 2 2 z tan y tan x; at 2 2 z tan 2 tan 2ßœ ß Êœ ß Êœ
'x
y1
1t
" " " "
Š‹ Š‹ Š‹
ÈÈ ÈÈ È È
2 tan 2 tan y tan x 2 tan 2œÊœ
" " " "
ÈÈ
32. f(x y) at (1 2) z ; at (1 2) z 2 2 2y 2x yßœ ßÊœ œ ßÊœ œÊœ Ê œ
!Š‹
n0
n
x2
yyx1yx
1
yy
"
#
Š‹
x
y
y2xʜ
868 Chapter 14 Partial Derivatives
33. 34.
35. 36.
37. 38.
39. 40.
41. f(x y z) x y ln z at (3 1 1) w x y ln z; at (3 1 1) w 3 ( 1) ln 1 2ßßœ ßßÊœ ßßÊœœ
ÈÈ È
xyln z2ʜ
È
Section 14.1 Functions of Several Variables 869
42. f(x y z) ln x y z at ( ) w ln x y z ; at ( ) w ln (1 2 1) ln 4ß ß œ "ß #ß " Ê œ "ß #ß " Ê œ œab ab
## ##
ln 4 ln x y z x y z 4ʜ ʜab
####
43. g(x y z) at (ln 2 ln 4 3) w e ; at (ln 2 ln 4 3) w eßß œ ß ß Ê œ œ ß ß Ê œ
!!
__
œœn0 n0
(x y) (x y)
n! z n! z
bb
nn
nn
Ð ÑÎ Ð ÑÎxy z ln2ln43
e e 2 2 e ln 2œœœÊœ Êœ
ÐÑÎ ÐÑÎ
ln 8 3 ln 2 x y z xy
z
44. g(x y z) at 0 2 w sin sec tßß œ ßß Ê œ
''
x2
yz yz
x2
ddt
1tt1
)
)
ÈÈ
"
#
" "
ˆ‰ cdcd)
sin y sin x sec z sec 2 w sin y sin x sec z ; at 0 2œ Êœ ßß
" " " " " " " "
#
Š‹
Ȉ‰
1
4
w sin sin 0 sec 2 sin y sin x sec zÊœ œÊœ
" " " " " "
"
##
11 1
44
45. f(x y z) xyz and x 20 t, y t, z 20 w (20 t)(t)(20) along the line w 400t 20tßßœ œœœÊœ Êœ
#
400 40t; 0 400 40t 0 t 10 and 40 for all t yes, maximum at t 10Êœ œÊ œÊœ œ Ê œ
dw dw d w
dt dt dt
x 20 10 10, y 10, z 20 maximum of f along the line is f(10 10 20) (10)(10)(20) 2000Êœœ œ œ Ê ßß œ œ
46. f(x y z) xy z and x t 1, y t 2, z t 7 w (t 1)(t 2) (t 7) t 4t 5 along the lineßß œ œ œ œ Ê œ œ
#
2t 4; 0 2t 4 0 t 2 and 2 for all t yes, minimum at t 2 x 2 1 1,Ê œ œ Ê œ Êœ œ Ê œ Ê œœ
dw dw d w
dt dt dt
y 2 2 0, and z 2 7 9 minimum of f along the line is f(1 0 9) (1)(0) 9 9œœ œœ Ê ßß œ œ
47. w 4 4 124.86 km must be (124.86) 63 km south of Nantucketœœ ¸ Ê ¸
ˆ‰ ’“
Th
d5 K/km
(290 K)(16.8 km)
"Î# "Î# "
#
48. The graph of f(xxxx) is a set in a five-dimensional space. It is the set of points
"#$%
ßßß
(xxxxf(xxxx)) for (xxxx) in the domain of f. The graph of f(xxx x) is a set
"#$% "#$% "#$% "#$
ßßßß ßßß ßßß ßßßáß
n
in an (n 1)-dimensional space. It is the set of points (x x x x f(x x x x )) for ßßßáßß ßßßáß
"#$ "#$nn
(x x x x ) in the domain of f.
"#$
ßßßáß
n
49-52. Example CAS commands:
:Maple
with( plots );
f := (x,y) -> x*sin(y/2) + y*sin(2*x);
xdomain := x=0..5*Pi;
ydomain := y=0..5*Pi;
x0,y0 := 3*Pi,3*Pi;
plot3d( f(x,y), xdomain, ydomain, axes=boxed, style=patch, shading=zhue, title="#49(a) (Section 14.1)" );
plot3d( f(x,y), xdomain, ydomain, grid=[50,50], axes=boxed, shading=zhue, style=patchcontour, orientation=[-90,0],
title="#49(b) (Section 14.1)" ); # (b)
L := evalf( f(x0,y0) ); # (c)
plot3d( f(x,y), xdomain, ydomain, grid=[50,50], axes=boxed, shading=zhue, style=patchcontour, contours=[L],
orientation=[-90,0], title="#49(c) (Section 14.1)" );
53-56. Example CAS commands:
:Maple
eq := 4*ln(x^2+y^2+z^2)=1;
implicitplot3d( eq, x=-2..2, y=-2..2, z=-2..2, grid=[30,30,30], axes=boxed, title="#53 (Section 14.1)" );

870 Chapter 14 Partial Derivatives
57-60. Example CAS commands:
:Maple
x := (u,v) -> u*cos(v);
y := (u,v) ->u*sin(v);
z := (u,v) -> u;
plot3d( [x(u,v),y(u,v),z(u,v)], u=0..2, v=0..2*Pi, axes=boxed, style=patchcontour, contours=[($0..4)/2], shading=zhue,
title="#57 (Section 14.1)" );
49-60. Example CAS commands:
: (assigned functions and bounds will vary)Mathematica
For 49 - 52, the command draws 2-dimensional contours that are z-level curves of surfaces z = f(x,y).ContourPlot
Clear[x, y, f]
f[x_, y_]:= x Sin[y/2] y Sin[2x]
xmin= 0; xmax= 5 ; ymin= 0; ymax= 5 ; {x0, y0}={3 , 3 };1111
cp= ContourPlot[f[x,y], {x, xmin, xmax}, {y, ymin, ymax}, ContourShading False];Ä
cp0= ContourPlot[[f[x,y], {x, xmin, xmax}, {y, ymin, ymax}, Contours {f[x0,y0]}, ContourShading False,ÄÄ
PlotStyle {RGBColor[1,0,0]}];Ä
Show[cp, cp0]
For 53 - 56, the command will be used and requires loading a package. Write the function f[x, y, z] so thatContourPlot3D
when it is equated to zero, it represents the level surface given.
For 53, the problem associated with Log[0] can be avoided by rewriting the function as x2 + y2 +z2 - e1/4
<<Graphics`ContourPlot3D`
Clear[x, y, z, f]
f[x_, y_, z_]:= x y z Exp[1/4]
222
ContourPlot3D[f[x, y, z], {x, 5, 5}, {y, 5, 5}, {z, 5, 5}, PlotPoints {7, 7}]; Ä
For 57 - 60, the command ParametricPlot3D will be used and requires loading a package. To get the z-level curves here,
we solve x and y in terms of z and either u or v (v here), create a table of level curves, then plot that table.
<<Graphics`ParametricPlot3D`
Clear[x, y, z, u, v]
ParametricPlot3D[{u Cos[v], u Sin[v], u}, {u, 0, 2}, {v, 0, 2p}];
zlevel= Table[{z Cos[v], z sin[v]}, {z, 0, 2, .1}];
ParametricPlot[Evaluate[zlevel],{v, 0, 2 }];1
14.2 LIMITS AND CONTINUITY
1. lim
Ðß ÑÄÐß Ñxy 00
3x y 5 3(0) 0 5
xy2 002
5
#
œœ
2. lim 0
Ðß ÑÄÐß Ñxy 04
x0
y4
ÈÈ
œœ
3. lim x y 1 3 4 1 24 2 6
Ðß ÑÄÐß Ñxy 34 ÈÈÈ
È
## ##
œ œ œ
4. lim
Ðß ÑÄÐßÑxy 2 3 Š‹
‘ˆ‰ˆ‰
"" " " " "
#
#
##
xy 3 6 36
œ œ œ
5. lim sec x tan y (sec 0) tan (1)(1) 1
Ðß ÑÄ ßxy 0
ˆ‰
4
œœœ
ˆ‰
1
4

Section 14.2 Limits and Continuity 871
6. lim cos cos cos 0 1
Ðß ÑÄÐß Ñxy 00 Š‹Š‹
xy
xy1 001
00
œœœ
7. lim e e e
Ðß ÑÄÐß Ñxy 0ln2
xy 0 ln2 ln "
#
œœœ
ˆ‰
1
2
8. lim ln 1 x y ln 1 (1) (1) ln 2
Ðß ÑÄÐß Ñxy 11 kkk kœ œ
## # #
9. lim lim e e lim 1 1 1
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ä
xy 00 xy 00 x0
e sin x sin x sin x
xxx
y
yœœœœab
ˆ‰ ˆ‰
!††
10. lim cos xy 1 cos (1)(1) 1 cos 0 1
Ðß ÑÄÐß Ñxy 11 ˆ‰ˆ ‰
Èkk È
$$
œ œ œ
11. lim 0
Ðß ÑÄÐß Ñxy 10
x sin y
x1 11 2
1sin 0 0
œœœ
†
12. lim 2
Ðß ÑÄ ßxy 0
ˆ‰
2
cos y 1 (cos 0)
ysin x 1
0sin
11
"
œœœ
ˆ‰
13. lim lim lim (x y) ( 1) 0
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á
xy 11 xy 11 xy 11
xy
x 2xy y (x y)
xy xy
œœœ"œ
14. lim lim lim (x y) (1 1) 2
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á
xy 11 xy 11 xy 11
xy
x y (x y)(x y)
xy xy
œ œ œœ
15. lim lim lim (y 2) (1 2) 1
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
ÁÁ
xy 11 xy 11 xy 11
x1 x1
xyy2x2 (x1)(y2)
x1 x1
œ œ œœ
16. lim lim lim
Ðß ÑÄÐßÑ Ðß ÑÄÐßÑ Ðß ÑÄÐßÑ
Á Á Á Á Á
xy 2 4 xy 2 4 xy 2 4
y 4, xx y 4, xx xx
y4 y4
x y xy 4x 4x x(x 1)(y 4) x(x 1)
1
#
"
œœœ
(2 1)#
"
œ
17. lim lim lim x y 2
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
ÁÁ
xy 00 xy 00 xy 00
xy xy
xy2x2y x y x y2
xy xy
ÈÈÈ
ÈÈÈ
ÈÈ
ÈÈ
ˆ‰ˆ ‰
œœ
ˆ‰
ÈÈ
0022œœ
Š‹
ÈÈ
Note: (x y) must approach (0 0) through the first quadrant only with x y.ßß Á
18. lim lim lim x y 2
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á Á Á
xy 22 xy 22 xy 22
xy4 xy4 xy4
xy4
xy2 xy2
xy2 xy2
ÈÈ
ˆ‰ˆ‰
ÈÈ
œœ
ˆ‰
È
222 22 4œ œœ
Š‹
È
19. lim lim lim
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á Á
xy 20 xy 20 xy 20
2x y 4 2x y 4
ÈÈ
ˆ‰ˆ‰
ÈÈ È
2xy2 2xy2
2xy4 2xy2 2xy2 2xy
#
"
œœ
œœœ
"""
#
È(2)(2) 0 22 4
20. lim lim lim
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á Á
xy 43 xy 43 xy 43
xy1 xy1
ÈÈ
ÈÈ
ˆ‰ˆ‰
ÈÈ È
ÈÈ È
xy1 xy1
xy1 xy1xy1 xy1
"
œœ

872 Chapter 14 Partial Derivatives
œœœ
"""
ÈÈ
43122 4
21. lim
TÄÐßßÑ134 Š‹
""" """
xyz 134 12 12
1243 19
œœ œ
22. lim
TÄÐßßÑ111
2xy yz 2(1)( 1) ( 1)( 1)
xz 1(1) 11
2
#
" "
œœœ
23. lim sin x cos y sec z sin 3 cos 3 sec 0 1 1 2
TÄÐßßÑ330 abab
### ## # #
œ œœ
24. lim tan (xyz) tan 2 tan
TÄ ß ß
ˆ‰
1
42
2
" " "
"
#
œ œ
ˆ‰ˆ‰
44
††
11
25. lim ze cos 2x 3e cos 2 (3)(1)(1) 3
TÄÐßßÑ103
2y 2 0
œœœ1
26. lim ln x y z ln 0 ( 2) 0 ln 4 ln 2
TÄÐßß Ñ020 ÈÈ È
### # ##
œ œ œ
27. (a) All (x y)ß
(b) All (x y) except (0 0)ßß
28. (a) All (x y) so that x yßÁ
(b) All (x y)ß
29. (a) All (x y) except where x 0 or y 0ßœœ
(b) All (x y)ß
30. (a) All (x y) so that x 3x 2 0 (x 2)( 1) 0 x 2 and x 1ßÁÊBÁÊÁÁ
#
(b) All (x y) so that y xßÁ
#
31. (a) All (x y z)ßß
(b) All (x y z) except the interior of the cylinder x y 1ßß œ
##
32. (a) All (x y z) so that xyz 0ßß
(b) All (x y z)ßß
33. (a) All (x y z) with z 0ßß Á
(b) All (x y z) with x z 1ßß Á
##
34. (a) All (x y z) except (x 0 0)ßß ßß
(b) All (x y z) except ( y 0) or (x 0 0)ß ß !ß ß ß ß
35. lim lim lim lim lim ;
Ðß ÑÄÐß Ñ
œ
ÄÄÄÄ
xy 00
along y x
x0
x0 x0 x0 x0
œœœœœ
xxxx
xy xx 2 x 2x 2 2
ÈÈÈÈÈÈ
kk
""
lim lim lim lim
Ðß ÑÄÐß Ñ
œ
ÄÄ Ä
xy 00
along y x
x0
x0 x0 x0
œœœ œ
xxx
xy 2 x 2( x) 2 2
ÈÈÈÈÈ
kk
""

Section 14.2 Limits and Continuity 873
36. lim lim 1; lim lim lim
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
œ
ÄÄÄ
œ
xy 00 xy 00
along y 0
x0 x0 x0
along y x
xx x xx
xy x0 xy 2x
xx
œœ œ œœ
ab "
#
37. lim lim lim different limits for d
Ðß ÑÄÐß Ñ
œ
ÄÄ
xy 00
along y kx
x0 x0
xy
xy xkx
xkx
xkx
xkx 1k
1k
œœœÊ
ab
ab ifferent values of k
38. lim lim lim lim ; if k 0, the limit is 1; but if k
Ðß ÑÄÐß Ñ
œ
Á
ÄÄÄ
xy 00
along y kx
k0
x0 x0 x0
xy x(kx)
xy x(kx) kx k
kx k
kk k k k k kk
œœœ 0, the limit is 1
39. lim lim different limits for different values of k, k 1
Ðß ÑÄÐß Ñ
œ
Á
Ä
xy 00
along y kx
k1
x0
xy
xy xkx 1k
xkx 1k
œœÊ Á
40. lim lim different limits for different values of k, k 1
Ðß ÑÄÐß Ñ
œ
Á
Ä
xy 00
along y kx
k1
x0
xy
xy xkx 1k
xkx 1k
œœÊ Á
41. lim lim different limits for different values of k, k 0
Ðß ÑÄÐß Ñ
œ
Á
Ä
xy 00
along y kx
k0
x0
xy
ykxk
xkx 1k
œœÊ Á
42. lim lim different limits for different values of k, k 1
Ðß ÑÄÐß Ñ
œ
Á
Ä
xy 00
along y kx
k1
x0
xx1
xy xkx 1k
œœÊ Á
43. No, the limit depends only on the values f(x y) has when (x y) (x y )ßßÁß
!!
44. If f is continuous at (x y ), then lim f(x y) must equal f(x y ) 3. If f is not continuous at
!! !!
ßßßœ
Ðß ÑÄÐ ß Ñxy x y
(x y ), the limit could have any value different from 3, and need not even exist.
!!
ß
45. lim 1 1 and lim 1 1 lim 1, by the Sandwich Theorem
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 00 xy 00 xy 00
Š‹
œ œÊ œ
xy tan xy
3xy
46. If xy 0, lim lim lim 2 2 andœœœ
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 00 xy 00 xy 00
2 xy 2xy
xy xy 6
xy
kkŠ‹ Š‹
kk
xy xy
66
ˆ‰
lim lim 2 2; if xy 0, lim lim
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 00 xy 00 xy 00 xy 00
2 xy
xy xy xy
2 xy 2xy
kk
kk kk
kkŠ‹ Š‹
œœ œ
xy xy
66
lim 2 2 and lim 2 lim 2, by the Sandwichœœ œÊ œ
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 00 xy 00 xy 00
ˆ‰
xy
6xy xy
2 xy 44 cos xy
kk
kk kk
Èkk
Theorem
47. The limit is 0 since sin 1 1 sin 1 y y sin y for y 0, and y y sin y for
¸ ¸ ˆ‰ ˆ‰ ˆ‰ˆ‰
"" " "
xx x x
Ÿ ÊŸ Ÿ ÊŸ Ÿ
y 0. Thus as (x y) ( ), both y and y approach 0 y sin 0, by the Sandwich Theorem.ŸßÄ!ß! ÊÄ
ˆ‰
"
x
48. The limit is 0 since cos 1 1 cos 1 x x cos x for x 0, and x x cos x
¹ ¹ Š‹ Š‹ Š‹Š‹
"" " "
yy y y
Ÿ ÊŸ Ÿ ÊŸ Ÿ
for x 0. Thus as (x y) ( ), both x and x approach 0 x cos 0, by the Sandwich Theorem.ŸßÄ!ß! ÊÄ
Š‹
"
y
874 Chapter 14 Partial Derivatives
49. (a) f(x y) sin 2 . The value of f(x y) sin 2 varies with , which is the line'skßœœ œ ßœ
ymxœ
2m 2 tan
1m 1tan
)
))))
angle of inclination.
(b) Since f(x y) sin 2 and since 1 sin 2 1 for every , lim f(x y) varies from 1 to 1kßœ ŸŸ ß
ymxœ)))
Ðß ÑÄÐß Ñxy 00
along y mx.œ
50. xy x y xy x y x y x y x y x y x y x y x yk kkkkkkkkkkk kk kkab ÈÈÈÈ
## ## ## ## ##
## ####
œ Ÿ œ Ÿ
xy xy xy xyœ Ê Ÿ œÊŸ Ÿab ab ab
¹¹
## ## ## ##
#
xyxy xy xyxy
xy xy xy
abab ab
lim xy 0 by the Sandwich Theorem, since lim x y 0; thus, defineÊœ „œ
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 00 xy 00
xy
xy
##
ab
f(0 0) 0ߜ
51. lim lim lim 0
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
xxy
xy r cos r sin 1
r cos (r cos ) r sin r cos cos sin
œœœ
))) )))
))
ab a b
52. lim cos lim cos lim cos cos 0 1
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
Š‹ Š ‹ ’ “
xy
xy r cos r sin 1
r cos r sin rcos sin
œœœœ
))
))
))ab
53. lim lim lim sin sin ; the limit does not exist since sin is between
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
y
xy r
r sin
## #
œœ œ
)ab)) )
0 and 1 depending on )
54. lim lim lim ; the limit does not exist for co
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
2x 2r cos 2 cos 2 cos
x x y r r cos r cos cos
œœœ
)))
))) s 0)œ
55. lim tan lim tan lim tan ;
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
" " "
’“ ’ “ ’ “
kk kk k k k k kka bkkkkx y r cos r sin r cos sin
xy r r
œœ
)) ))
if r 0 , then lim tan lim tan ; if r 0 , thenÄœœÄ
" "
#
rrÄ! Ä!
’“ ’“
kka b k k k kkkkkr cos sin cos sin
rr
)) ))1
lim tan lim tan the limit is
rrÄ! Ä!
" "
# #
’“ Š‹
kka b k k k kkkkkr cos sin cos sin
rr
)) )) 11
œœÊ
56. lim lim lim cos sin lim (cos 2 ) which ranges between
Ðß ÑÄÐß Ñ ÄÄ Ä
xy 00 r0 r0 r0
xy
xy r
r cos r sin
##
œœœ
)) ab)) )
1 and 1 depending on the limit does not existÊ)
57. lim ln lim ln
Ðß ÑÄÐß Ñ Ä
xy 00 r0
Š‹Š ‹
3x x y 3y
xy r
3r cos r cos sin 3r sin
œ))) )
lim ln 3 r cos sin ln 3 define f(0 0) ln 3œ œÊßœ
r0Äab
## #
))
58. lim lim lim 2r cos sin 0 define f(0 0) 0
Ðß ÑÄÐß Ñ ÄÄ
xy 00 r0 r0
2xy
xy r
(2r cos ) r sin
#
œœœÊßœ
))ab ))
59. Let 0.1. Then x y x y 0.1 x y 0.01 x y 0 0.01 f(x y) f( )$$œ Ê ÊÊÊß!ß!
ÈÈ kkk k
## ## ## ##
0.01 .œ%
60. Let 0.05. Then x and y f(x y) f(0 0) 0 y 0.05 .$$$ %œÊßßœœŸœkk kk k k kk
¸¸¸¸
yy
x1 x1
61. Let 0.005. Then x and y f(x y) f(0 0) 0 x y x y$$$œ Ê ß ß œ œ Ÿ kk kk k k k k kk kk
¸¸¸¸
xy xy
x1 x1
0.005 0.005 0.01 .œœ%

Section 14.3 Partial Derivatives 875
62. Let 0.01. Since 1 cos x 1 1 2 cos x 3 1 x y$œŸŸÊŸŸÊŸŸÊŸŸ
""
#
3 cos x 3 2 cos x
xy xy
kk¸¸
kk
x y . Then x and y f(x y) f(0 0) 0 x y 0.01 0.01Ÿ Ê ßßœ œ Ÿ kk kk kk kk k k kk kk
¸¸¸¸
$$ xy xy
2cos x 2cos x
0.02 .œœ%
63. Let 0.015. Then x y z f(x y z) f( 0 0) x y z 0 x y z$$œ Ê ßß!ßß œ œ
ÈÈkkkkkk
### ### ###
x t x 0.015 0.015 .œ œœ
Š‹Š‹
ÈÈ
## #
##
%
64. Let 0.2. Then x , y , and z f(x y z) f( 0 0) xyz 0 xyz x y z (0.2)$$$$œÊßß!ßßœœœkk kk kk k k k k k k kkkkkk $
0.008 .œœ%
65. Let 0.005. Then x , y , and z f(x y z) f( 0 0) 0$$$$œ Ê ß ß !ß ß œ kk kk kk k k ¹¹
xyz
xyz1
x y z x y z 0.005 0.005 0.005 0.015 .œ ŸŸ œ œ
¹¹
k k kk kk kk
xyz
xyz1
%
66. Let tan (0.1). Then x , y , and z f(x y z) f( 0 0) tan x tan y tan z$$$$œÊßß!ßßœ
" ###
kk kk kk k k k k
tan x tan y tan z tan x tan y tan z tan tan tan 0.01 0.01 0.01 0.03Ÿ œ œœkkkkkk
#########
$$$
.œ%
67. lim f(x y z) lim (x y z) x y z f(x y z ) f is continuous at
Ðß ßÑÄÐ ß ß Ñ Ðß ß ÑÄÐ ß ß Ñxyz x y z xyz x y z
ßßœ œœ ßß Ê
!!! !!!
every (x y z )
!!!
ßß
68. lim f(x y z) lim x y z x y z f(x y z ) f is continuous at
Ðß ßÑÄÐ ß ß Ñ Ðß ß ÑÄÐ ß ß Ñxyz x y z xyz x y z
ßßœ œœ ßß Êab
### ###
!!! !!!
every point (x y z )
!!!
ßß
14.3 PARTIAL DERIVATIVES
1. 4x, 3 2. 2x y, x 2y
`` ` `
`` ` `
ff f f
xy x y
œœ œœ
3. 2x(y 2), x 1 4. 5y 14x 3, 5x 2y 6
`` ` `
`` ` `
#
ff f f
xy x y
œ œ œ œ
5. 2y(xy 1), 2x(xy 1) 6. 6(2x 3y) , 9(2x 3y)
`` ` `
`` ` `
##
ff f f
xy x y
œœ œ œ
7. , 8. ,
`` ` `"
`` ` `
fxf f2xf
xy x y
xy xy
y
x3x
œœ œ œ
ÈÈ ÉÉ
ˆ‰ ˆ‰
yy
9. (x y) , (x y)
`"` "`"` "
`` ``
ff
x(xy)x (xy)y(xy)y (xy)
œ œ œ œ††
10. ,
``
``
ff
xy
x y (1) x(2x) x y (0) x(2y)
xy xy xy xy
y x 2xy
œœœœ
ab ab
ab ab ab ab
11. ,
``"
``
"
ffx
x (xy 1) (xy 1) y (xy 1) (xy 1)
(xy 1)(1) (x y)(y) y 1 (xy )(1) (x y)(x)
œœ œ œ œ
12. ,
`"` `"`
`` ``
ff1x
xxx xyyyx xy
11
yy y y
x1 x1
œœœœœœ
ˆ‰ ˆ‰
’“ ’“
ˆ‰ ˆ‰
y y
x x
y y
x x
††
ˆ‰ ˆ‰
13. e (x y 1) e , e (x y 1) e
`` ``
`` ``
ÐÑ ÐÑ ÐÑ ÐÑ
ff
xx yy
xy1 xy1 xy1 xy1
œœœœ††

876 Chapter 14 Partial Derivatives
14. e sin (x y) e cos (x y), e cos (x y)
``
``
ff
xy
xx x
œ œ
15. (x y) , (x y)
`"` "`"` "
`` ``
ff
xxyx xyyxyy xy
œœœœ††
16. e (xy) ln y ye ln y, e (xy) ln y e xe ln y
`` `` "
`` ``
ff e
xx yy y y
xy xy xy xy xy
œœœœ†† †† †
xy
17. 2 sin (x 3y) sin (x 3y) 2 sin (x 3y) cos (x 3y) (x 3y) 2 sin (x 3y) cos (x 3y),
`` `
`` `
f
xx x
œ œ œ ††
2 sin (x 3y) sin (x 3y) 2 sin (x 3y) cos (x 3y) (x 3y) 6 sin (x 3y) cos (x 3y)
`` `
`` `
f
yy y
œ œ œ ††
18. 2 cos 3x y cos 3x y 2 cos 3x y sin 3x y 3x y
`` `
`` `
## ###
f
xx x
œ œ ab ab ababab††
6 cos3xy sin3xy,œ abab
##
2 cos 3x y cos 3x y 2 cos 3x y sin 3x y 3x y
`` `
`` `
## ###
f
yy y
œ œ ab ab ababab††
4y cos 3x y sin 3x yœabab
##
19. yx , x ln x 20. f(x y) and
`` `" `
`` ``
ff ln x f f ln x
xy ln y x x ln y y y(ln y)
œœ ߜʜ œ
y1 y
21. g(x), g(y)
``
``
ff
xy
œ œ
22. f(x y) (xy) , xy 1 f(x y) (1 xy) andßœ Ê ßœ Ê œ œ
!
_
œn0
nkk "` "`
` ` 1 xy x (1 xy) x (1 xy)
fy
†
(1 xy)
`"`
``
fx
y (1 xy) y (1 xy)
œ œ†
23. f 1 y , f 2xy, f 4z 24. f y z, f x z, f y x
x yz xyz
œ œ œ œ œ œ
#
25. f 1, f , f
xy z
y
yz yz
z
œœ œ
ÈÈ
26. f x x y z , f y x y z , f z x y z
xyz
œ œ œ ab ab ab
### ### ###
$Î# $Î# $Î#
27. f , f , f
xyz
yz xy
1 xyz 1 xyz 1 xyz
xz
œœœ
ÈÈÈ
28. f , f , f
xy z
xyz (xyz)1 xyz (xyz) 1 xyz (xyz) 1
zy
œœ œ
"
kk kk kk
ÈÈÈ
29. f , f , f
xyz
œœœ
"
x2y3z x2y3z x2y3z
23
30. f yz (xy) , f z ln (xy) yz ln (xy) z ln (xy) (xy) z ln (xy) z,
xy
xy x xy x y xy y
(yz)(y) yz yz
œœœœœœ†† † †
"` ` `
```
f y ln (xy) yz ln (xy) y ln (xy)
zz
œ œ†`
`
31. f 2xe , f 2ye , f 2ze
xyz
xyz xyz xyz
œ œ œ
ab ab ab
32. f yze , f xze , f xye
xyz
xyz xyz xyz
œ œ œ
33. f sech (x 2y 3z), f 2 sech (x 2y 3z), f 3 sech (x 2y 3z)
xy z
œœ œ
###
34. f y cosh xy z , f x cosh xy z , f 2z cosh xy z
xyz
œœœ ab ab ab
## #

Section 14.3 Partial Derivatives 877
35. 2 sin (2 t ), sin (2 t )
``
``
ff
tœ œ 11! 1!
!
36. v e 2ve , 2ve v e 2ve 2ue
``
`` ` `
# Ð ÎÑ Ð ÎÑ Ð ÎÑ # Ð ÎÑ Ð ÎÑ Ð ÎÑ
``
gg
uuv v vv
2u v 2u v 2u v 2u v 2u v 2u v
2u 2u
œ œ œ œ††
ˆ‰ ˆ‰
37. sin cos , cos cos , sin sin
`` `
`` `
hh h
39 )
œœ œ9) 39) 39)
38. 1 cos , r sin , 1
```
```
ggg
rz
œ œ œ))
)
39. W V, W P , W , W , W
pv v g
v Vv 2Vv Vv Vv
2g 2g 2g g g
œœ œ œœ œ
$$$$
$#
40. m, , , c,
```` `
``#`` ` #
AAAmAkAkmh
chkqmqqq
q
œœœœœ
41. 1 y, 1 x, 0, 0, 1
``````
` ` ``````
ff ffff
x y xyyxxy
œ œ œ œ œ œ
42. y cos xy, x cos xy, y sin xy, x sin xy, cos xy xy sin xy
``` ` ``
````````
##
ff f f ff
xyxyyxxy
œ œ œ œ œ œ
43. 2xy y cos x, x sin y sin x, 2y y sin x, cos y, 2x cos x
`` ````
` ` ` ` `` ``
#
gg gggg
x y x y yx xy
œ œ œ œ œ œ
44. e , xe 1, 0, xe , e
`` `` ``
` ` ` ` `` ``
hh hh hh
x y x y yx xy
œœœœ œœ
yy y y
45. , , , ,
`"`"` "` "` ` "
``` ` ````
rr r r rr
x xy y xy x (xy) y (xy) yx xy (xy)
œœ œ œ œœ
46. , ,
`"` " `"` "
`` ``
ss1x
xxxxxyyyxxxy
1111
yy y y
œœœœœœ
”• ”• ”• ”•
ˆ‰ ˆ ‰ ˆ‰ ˆ‰
ˆ‰ ˆ‰ ˆ‰ ˆ‰
yyyy
xxxx
††
, ,
``
``
ss
xy
y(2x) 2xy x(2y) 2xy
xy xy xy xy
œœ œœ
abab ab ab
``
`` ``
ss
yx xy
x y ( 1) y(2y)
xy xy
yx
œœ œ
ab
ab ab
47. , , , and
` ` ` `
```` ``
w2w3 w 6 w 6
x 2x 3y y 2x 3y y x (2x 3y) x y (2x 3y)
œœ œ œ
48. e ln y , ln x, , and
```""`""
` ` `` ``
wwxw w
x x y y yx y x xy y x
y
œ œ œœ œ
x
49. y 2xy 3x y , 2xy 3x y 4x y , 2y 6xy 12x y , and
`` `
`` ``
# $ #% ## $$ # #$
ww w
xy yx
œ œ œ
2y 6xy 12x y
`
``
##$
w
xyœ
50. sin y y cos x y, x cos y sin x x, cos y cos x 1, and
`` `
````
ww w
xyyx
œ œ œ
cos ycos x1
`
``
w
xyœ
51. (a) x first (b) y first (c) x first (d) x first (e) y first (f) y first
52. (a) y first three times (b) y first three times (c) y first twice (d) x first twice

878 Chapter 14 Partial Derivatives
53. f (1 2) lim lim lim
xf(1 h 2) f(1 2)
hh h
1(1h)26(1h) (26) h612hh 6
ßœ œ œ
h0 h0 h0ÄÄ Ä
ß ß
cd ab
lim lim ( 13 6h) 13,œœœ
h0 h0ÄÄ
13h 6h
h
f (1 2) lim lim lim
yf(1 2 h) f(1 2) (2 6 2h) (2 6)
hh h
11(2h)3(2h) (26)
ßœ œ œ
h0 h0 h0ÄÄ Ä
ß ß
cd
lim ( 2) 2œœ
h0Ä
54. f ( 2 1) lim lim
xf( 2 h 1) f( 2 1)
hh
42(2h)3(2h) (32)
ß œ œ
h0 h0ÄÄ
ß ß cd
lim lim 1 1,œœœ
h0 h0ÄÄ
(2h1h)1
h
f ( 2 1) lim lim
yf( 2 1 h) f( 2 1)
hh
443(1h)2(1h) (32)
ß œ œ
h0 h0ÄÄ
ß ß cd
lim lim lim (1 2h) 1œœœœ
h0 h0 h0ÄÄÄ
ab
33h24h2h 1
hh
h2h
55. f (x y z ) lim ;
zf(xyz h) f(x,yz)
h
!!! ßß ß
ßß œ
h0Ä
f (1 2 3) lim lim lim lim (12 2h) 12
zf(1 2 3 h) f(1, 2 3) 2(3 h) 2(9)
hhh
2h 2h
ßß œ œ œ œ œ
h0 h0 h0 h0ÄÄÄÄ
ßß ß "
56. f (x y z ) lim ;
yf(x y h z ) f(x , y z )
h
!!! ßß ß
ßß œ
h0Ä
f ( 1 0 3) lim lim lim (2h 9) 9
yf( 1h3) f( 1,03)
hh
2h 9h 0
ß ß œ œ œ œ
h0 h0 h0ÄÄÄ
ß ß ß ab
57. y 3z x z 2y 0 3xz 2y y z at (1 1 1) we have (3 2) 1 1 orœÊœÊßß œ
ˆ‰ ab
#$ # $
`` ` `
`` ` `
zz z z
xx x x
2
`
`
z
xœ
58. z x 2x 0 z 2x x at (1 1 3) we have ( 3 1 2) 1 or
ˆ‰ ˆ‰ ˆ ‰
``` ` `
``` ` `
xxx x x
zxzz xz z
yy
œ Ê œ Ê ß ß œ
`"
`
x
z6
œ
59. a b c 2bc cos A 2a (2bc sin A) ; also 0 2b 2c cos A (2bc sin A)
### `` `
`` `
œ Ê œ Ê œ œ
AAa A
a a bc sin A b
2c cos A 2b (2bc sin A) ʜ ʜ
``
``
A A c cos A b
b b bc sin A
60. 0 (sin A) a cos A 0 ; also
ab a aa cos A
sin A sin B sin A x A sin A
(sin A) a cos A
œÊ œÊ œÊœ
a
A``
``
b( csc B cot B) b csc B cot B sin A
ˆ‰
"` `
``sin A B B
aa
œ Ê œ
61. Differentiating each equation implicitly gives 1 v ln u u and 0 u ln v v orœ œ
xxxx
vu
uv
ˆ‰ ˆ‰
v
(ln u) v u 1
v (ln v) u 0 Ÿ
ˆ‰
ˆ‰xx
v
u
u
vxx
0ln v
ln u
ln v
ln v
(ln u)(ln v) 1
œ
œ
Êœ œ
x
ºº
ºº
"
v
u
v
u
u
v
62. Differentiating each equation implicitly gives 1 (2x)x (2y)y and 0 (2x)x y orœ œ
uu uu
x and
(2x)x (2y)y 1
(2x)x y 0
uu
uu
2y
01
2x 2y
2x 1
11
2x 4xy 2x 4xy
œ
œ
Êœ œ œ
u
ºº
ºº
"
y ; next s x y 2x 2y
uœœœœ œÊœ
ºº
2x
2x 0
x 4xy 2x 4xy 2x 4xy 1 2y u u u
2x 2x 1 s x y
"
# ` ` `
``
## `
2x 2yœ œœ
Š‹Š‹
"""
#
2x 4xy 1 2y 1 y 1 2y 1 2y
2y 1 2y
63. 2x, 2y, 4z 2, 2, 4 2 2 ( 4) 0
``` ``` ```
``` ``` ```
fff fff fff
xyz xyz xyz
œœœÊœœœÊœœ

Section 14.3 Partial Derivatives 879
64. 6xz, 6yz, 6z 3 x y , 6z, 6z, 12z
``` ``` ```
``` ``` ```
###
fff fff fff
xyz xyz xyz
œ œ œ œ œ œ Ê ab
6z 6z 12z 0œ œ
65. 2e sin 2x, 2e cos 2x, 4e cos 2x, 4e cos 2x
`` ` ` ``
`` ` ` ``
ffff ff
xy x y xy
œ œ œ œ Ê
2y 2y 2y 2y
4e cos 2x 4e cos 2x 0œ œ
2y 2y
66. , , , 0
``` ` ``
``` ` ``
fxf f f ff
xxyyxyx y x y
yyxxy yxxy
xy xy xy xy
œ œ œ œ Êœœ
ab ab abab
67. x y z (2x) x x y z , x y z (2y)
`" `"
`# `#
### ### ###
$Î# $Î# $Î#
f f
x y
œ œ œ ab ab ab
yxyz , xyz (2z) zxyz ;œ œ œ ab ab ab
### ### ###
$Î# $Î# $Î#
`"
`#
f
z
xyz 3xxyz , xyz 3yxyz ,
``
``
### #### ### ####
$Î# &Î# $Î# &Î#
ff
xy
œ œ abab abab
xyz 3zxyz
````
````
### ####
$Î# &Î#
ffff
zxyz
œ Ê abab
xyz 3xxyz xyz 3yxyzœ
’“’“
abababab
### #### ### ####
$Î# &Î# $Î# &Î#
xyz 3zxyz 3xyz 3x3y3zxyz œ
’“
abababa bab
### #### ### # # ####
$Î# &Î# $Î# &Î#
0œ
68. 3e cos 5z, 4e cos 5z, 5e sin 5z; 9e cos 5z, 16e cos 5z,
``` ` `
``` ` `
fff f f
xyz x y
3x 4y 3x 4y 3x 4y 3x 4y 3x 4y
œœœœ œ
25e cos 5z 9e cos 5z 16e cos 5z 25e cos 5z 0
````
` ```
ffff
z xyz
3x 4y 3x 4y 3x 4y 3x 4y
œ Ê œ œ
69. cos (x ct), c cos (x ct); sin (x ct), c sin (x ct) c [ sin (x ct)]
`` ` ` `
`` ` ` `
##
ww w w w
xt x t t
œ œ œ œ Êœ
c œ#`
`
w
x
70. 2 sin (2x 2ct), 2c sin (2x 2ct); 4 cos (2x 2ct), 4c cos (2x 2ct)
`` ` `
`` ` `
#
ww w w
xt x t
œ œ œ œ
c [ 4 cos (2x 2ct)] cÊœ œ
``
``
##
ww
tx
71. cos (x ct) 2 sin (2x 2ct), c cos (x ct) 2c sin (2x 2ct);
``
``
ww
xt
œ œ
sin (x ct) 4 cos (2x 2ct), c sin (x ct) 4c cos (2x 2ct)
``
``
##
ww
xt
œ œ
c [ sin (x ct) 4 cos (2x 2ct)] c Êœ œ
``
``
##
ww
tx
72. , ; , c c
`"` ` ` ` " `
``` ` ` `
##
wwcw1wcw w
x xct t xct x (xct) t (xct) t (xct) x
œœ œ œÊœ œ
’“
73. 2 sec (2x 2ct), 2c sec (2x 2ct); 8 sec (2x 2ct) tan (2x 2ct),
`` `
`` `
###
ww w
xt x
œœ œ
8c sec (2x 2ct) tan (2x 2ct) c [8 sec (2x 2ct) tan (2x 2ct)] c
`` `
`` `
## # # #
ww w
tt x
œÊœ œ
74. 15 sin (3x 3ct) e , 15c sin (3x 3ct) ce ; 45 cos (3x 3ct) e ,
`` `
`` `
ww w
xt x
œ œ œ
xct xct xct
45c cos (3x 3ct) c e c 45 cos (3x 3ct) e c
`` `
`` `
### #
ww w
tt x
œ Ê œ œ
xct xct
cd
75. (ac) (ac) (ac) a c ; a a a
```` ` ` ````` ` `
```` ` ` `` ``` ` `
##
wfuf w f fwfuf w f
tutu t u uxuxu x u
œœ Êœ œ œœ Êœ
Š‹ Š ‹
††
a ac c a c œÊœ œ œ
######
`` ` ` `
`` ` ` `
fw f f w
ut u u x
Š‹

880 Chapter 14 Partial Derivatives
76. If the first partial derivatives are continuous throughout an open region R, then by Theorem 3 in this section of the
text, f(x y) f(x y ) f (x y ) x f (x y ) y x y, where , 0 as x, y 0. Then asßœßßß Ä Ä
!! !! !! " # "#xy
? ? %? %? % % ? ?
(x y) (x y ), x 0 and y 0 lim f(x y) f(x y ) f is continuous at every pointßÄ ß Ä ÄÊ ßœ ß Ê
!! !!
??Ðß ÑÄÐ ß Ñxy x y
(x y ) in R.
!!
ß
77. Yes, since f , f , f , and f are all continuous on R, use the same reasoning as in Exercise 76 with
xx yy xy yx
f(xy) f(xy) f(xy) x f(xy) y x y and
x x xx xy
ßœßßß
!! !! !! " #
? ? %? %?
f (x y) f (x y ) f (x y ) x f (x y ) y x y. Then lim f (x y) f (x y )
y y yx yy x x
ßœßßß ßœß
ss
!! !! !! " # !!
? ? %? %? Ðß ÑÄÐ ß Ñxy x y
and lim f (x y) f (x y ).
Ðß ÑÄÐ ß Ñxy x y yy
ßœ ß
!!
14.4 THE CHAIN RULE
1. (a) 2x, 2y, sin t, cos t 2x sin t 2y cos t 2 cos t sin t 2 sin t cos t
``
``
w w dx dw
x y dt dt dt
dy
œ œ œ œ Ê œ œ
0; w x y cos t sin t 1 0œ œœ œÊ œ
## # # dw
dt
(b) ( ) 0
dw
dt 1œ
2. (a) 2x, 2y, sin t cos t, sin t cos t
``
``
w w dx dw
x y dt dt dt
dy
œœœ œÊ
(2x)( sin t cos t) (2y)( sin t cos t)œ
2(cos t sin t)(cos t sin t) 2(cos t sin t)(sin t cos t) 2 cos t 2 sin t 2 cos t 2 sin tœ œ abab
## ##
0; w x y (cos t sin t) (cos t sin t) 2 cos t 2 sin t 2 0œ œœ œ œÊ œ
## # # # # dw
dt
(b) (0) 0
dw
dt œ
3. (a) , , , 2 cos t sin t, 2 sin t cos t,
`"`"` "
```
w w w dx dz
x z y z z z dt dt dt t
(x y) dy
œœœ œ œ œ
cos t sin t sin t cos t 1; w t 1Êœ œ œ œœ œÊœ
dw 2 2 cos t sin t x cos t sin t dw
dt z z z t z z dt
xy y
t
Š‹ Š‹ Š‹
ab
ttt
(b) (3) 1
dw
dt œ
4. (a) , , , sin t, cos t, 2t
```
```
"Î#
w2xw w2zdx dz
x xyz y xyz z xyz dt dt dt
2y dy
œœœœœœ
Êœ œ
dw 2x sin t 4zt
dt xyz xyz xyz costsint16t
2y cos t 2 cos t sin t 2 sin t cos t 4 4t t
ˆ‰
; w ln x y z ln cos t sin t 16t ln (1 16t) œœœœÊœ
16 dw 16
1 16t dt 1 16t
### # #
aba b
(b) (3)
dw 16
dt 49
œ
5. (a) 2ye , 2e , , , , e
```" "
```
wwwdx2t dzdw 2ee
x y z z dt t 1 dt t 1 dt dt t 1 t 1 z
xx t
dy 4yte
œœœœœœÊœ
xxt
4t tan t 1; w 2ye ln z 2 tan t t 1 tœœœœ
(4t) tan t t 1 2 t 1
t1 t1 e
ex
a bab ab
" " #
t
tabab
t 1 2 tan t (2t) 1 4t tan t 1Êœ œ
dw 2
dt t 1
ˆ‰
aba b
#" "
(b) (1) (4)(1) 1 1
dw
dt 4
œœ
ˆ‰
11
6. (a) y cos xy, x cos xy, 1, 1, , e y cos xy e
``` "
```
w w w dx dz dw
x y z dt dt t dt dt t
dy x cos xy
œ œ œ œ œ œ Ê œ
t1 t1
(ln t)[cos (t ln t)] e (ln t)[cos (t ln t)] cos (t ln t) e ; w z sin xyœ œ œ
t cos (t ln t)
t
t1 t1
e sin (t ln t) e [cos (t ln t)] ln t t e (1 ln t) cos (t ln t)œ Êœ œ
t1 t1 t1
dw
dt t
‘ˆ‰
"
(b) (1) 1 (1 0)(1) 0
dw
dt œ œ

Section 14.4 The Chain Rule 881
7. (a) 4e ln y (sin v)
````
`````
`
z z x z cos v 4e 4e sin v
uxuyu u cos v y u y
y4e ln y
x
œœ œ ab
ˆ‰
Š‹
xx
x
(4 cos v) ln (u sin v) 4 cos v;œœ
4(u cos v) ln (u sin v) 4(u cos v)(sin v)
uu sin v
4e ln y (u cos v) 4e ln y (tan v)
````
`````
`
z z x z u sin v 4e 4e u cos v
vxvyv u cos v y y
yxx
œœ œ ab ab
ˆ‰
Š‹
xx
[ 4(u cos v) ln (u sin v)](tan v) ( 4u sin v) ln (u sin v) ;œ œ
4(u cos v)(u cos v)
u sin v sin v
4u cos v
z 4e ln y 4(u cos v) ln (u sin v) (4 cos v) ln (u sin v) 4(u cos v)œœ Êœ
xzsin v
uu sin v
`
`ˆ‰
(4 cos v) ln (u sin v) 4 cos v; also ( 4u sin v) ln (u sin v) 4(u cos v)œœ
`
`
zu cos v
vu sin v
ˆ‰
( 4u sin v) ln (u sin v)œ
4u cos v
sin v
(b) At 2 : 4 cos ln 2 sin 4 cos 2 2 ln 2 2 2 2 (ln 2 2);
ˆ‰ ˆ ‰ ÈÈ ÈÈ
ßœ œ œ
1111
4u 4 4 4
z`
`
( 4)(2) sin ln 2 sin 4 2 ln 2 4 2 2 2 ln 2 4 2
`
`
z
v44
(4)(2) cos
sin
œ œ œ
11
ˆ‰ ÈÈ È È È
ˆ‰
ˆ‰
4
4
8. (a) cos v sin v 0;
`
`
zx sin v
uxyxyu
11
y cos v (u sin v)(cos v) (u cos v)(sin v)
œœœ œ
–— –—
Š‹
Š‹ Š‹
Š‹
y
xx
yy
x
y
( u sin v) u cos v
`
`
zxu cos v
vxyxyu
11
yu sin v (u sin v)(u sin v) (u cos v)(u cos v)
œ œœ
–— –—
Š‹
Š‹ Š‹
Š‹
y
xx
yy
x
y
sin v cos v 1; z tan tan (cot v) 0 and csc vœ œ œ œ Ê œ œ
# # " " #
``"
``
Š‹ ˆ‰
ab
xzz
yuv1cotv
1œœ
"
sin v cos v
(b) At 1.3 : 0 and 1
ˆ‰
ßœ œ
1
6u v
zz``
``
9. (a) (y z)(1) (x z)(1) (y x)(v) x y 2z v(y x)
```` ``
```````
`
wwxw wz
uxuyuzu
y
œœœ
(u v) (u v) 2uv v(2u) 2u 4uv; œ œ œ
```` ``
```````
`
wwxw wz
vxvyvzv
y
(y z)(1) (x z)( 1) (y x)(u) y x (y x)u 2v (2u)u 2v 2u ;œ œ œ œ#
w xy yz xz u v u v uv u v uv u v 2u v 2u 4uv andœœ œ Ê œababab
#########`
`
w
u
2v 2u
`
`
#
w
vœ
(b) At 1 : 2 4 (1) 3 and 2(1) 2
ˆ ‰ ˆ‰ ˆ‰ ˆ‰
"` " " ` "
#` # # ` # #
#
ßœ œ œœ
ww3
uv
10. (a) e sin u ue cos u e cos u ue sin u e
`
`
w2x 2z
u xyz xyz xyz
vv v v v
2y
œ
Š‹ Š‹ Š‹
ababab
e sin u ue cos uœ
ˆ‰
ab
2ue sin u
ue sin u ue cos u ue
vv
v
2v 2v 2v
e cos u ue sin u
ˆ‰
ab
2ue cos u
ue sin u ue cos u ue
vv
v
2v 2v 2v
e;œ
ˆ‰
ab
2ue 2
ue sin u ue cos u ue u
v
v
2v 2v 2v
ue sin u ue cos u ue
`
`
w2x 2z
v xyz xyz xyz
vv v
2y
œ
Š‹ Š‹ Š‹
ab ab ab
ue sin uœˆ‰
ab
2ue sin u
ue sin u ue cos u ue
v
v
2v 2v 2v
ue cos uˆ‰
ab
2ue cos u
ue sin u ue cos u ue
v
v
2v 2v 2v
ue 2; w ln u e sin u u e cos u u e ln 2u eœœœ
ˆ‰
ab a b a b
2ue
ue sin u ue cos u ue
v2v2v2v2v
v
2v 2v 2v
### ## #
ln 2 2 ln u 2v and 2œ Êœ œ
``
``
w2 w
uu v
(b) At ( ): 1 and 2#ß ! œ œ œ
``
`# `
w2 w
uv
11. (a) 0;
`````"
```````
` `
uuuur
x p x q x r x qr (qr) (qr) (qr)
p q rp pq qrrppq
œœœ œ
`````"
```````
` `
uuuur
y p y q y r y qr (qr) (qr) (qr) (qr)
p q rp pq qrrppq 2p2r
œœœ œ
; œœœ
(2x2y2z)(2x2y2z) p q
(2z 2y) (z y) z p z q z r z
zuuuur
` `
```````
`````
;œ œ œ œ œ
"
q r (q r) (q r) (q r) (q r) (2z 2y) (z y)
rp pq qrrppq 2q2p 4y y
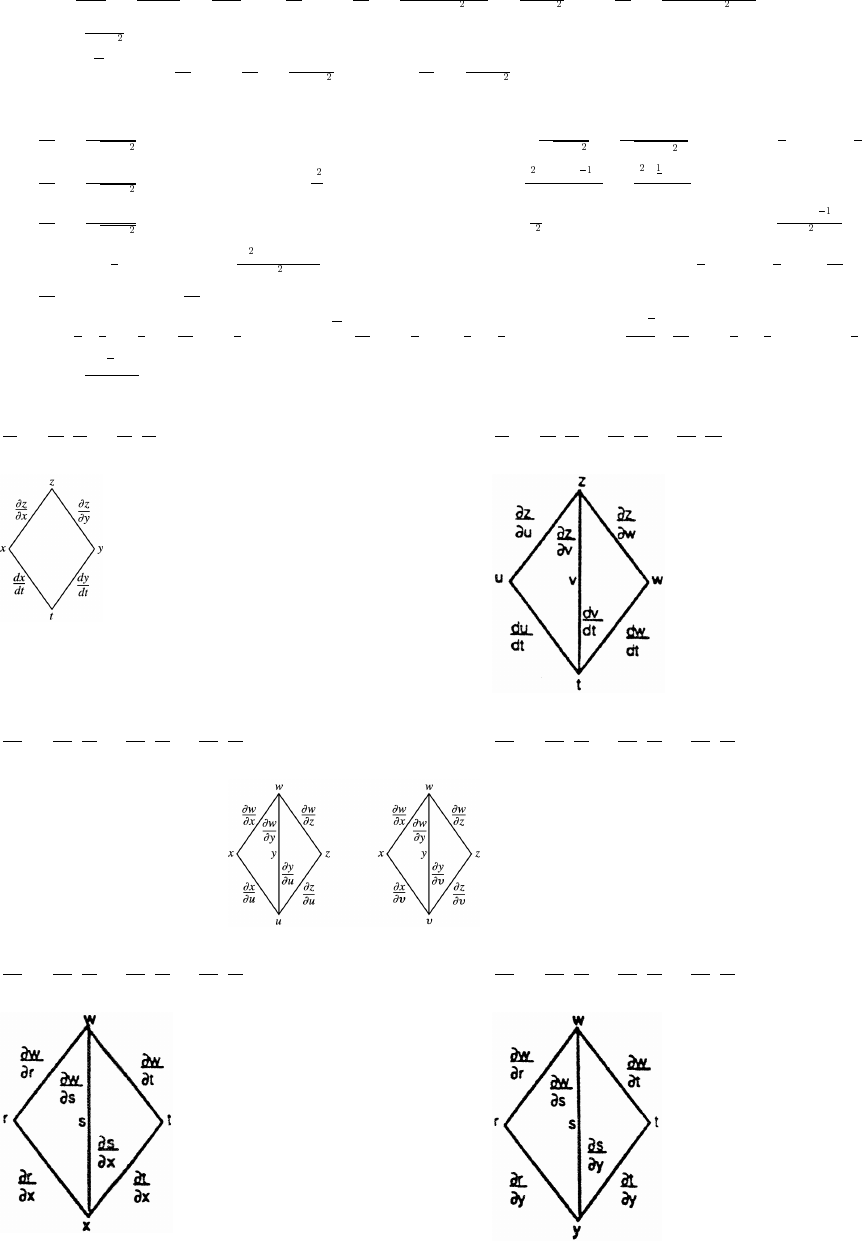
882 Chapter 14 Partial Derivatives
u 0, , and œœ œ Êœ œ œ œ
p q 2y y (z y) y( 1) (z y)(0) y(1)
q r 2z 2y z y x y (z y) (z y) z (z y)
uu z u
` ` `
`` `
œ y
(z y)
(b) At 3 2 1 : 0, 1, and 2
Š‹
Èßß œ œ œ œ œ
``" `
`` `
uu u2
xy(12) z(12)
12. (a) (cos x) re sin p (0) qe sin p (0) y if x ;
`
`##
" "
u e e cos x e cos x
x1p 1p
qr qr z
1sinx
œ œœœ
qr qr z ln y
ÈÈÈ
abab 11
(0) re sin p qe sin p (0) xzy ;
`
`
" "
ue z
yyyy
1p
qr qr z 1
z re sin p zyx
œ œ œœ
qr qr zz
Ȉ‰
abab
Š‹
(0) re sin p (2z ln y) qe sin p 2zre sin p (ln y)
` "
`
" " "
ue
zzz
1p
qr qr qr qe sin p
œ œ
qr qr
Èababa b
ˆ‰
(2z) y x ln y xy ln y; u e sin (sin x) xy if x y ,œœœœŸŸÊœ
ˆ‰
ab
" `
"
##`zz x
zzzlnyz z
z ln y y x u
abab
z11
xzy , and xy ln y from direct calculations
``
``
uu
yz
z1 z
œœœ
(b) At : 2, , ln
ˆ ‰ ˆ‰ ˆ‰ˆ ‰ˆ‰ ˆ‰ˆ‰ ˆ‰
È
111
1
4x y4 4z4
uu u
2
ßß œ œ œ œ œ
""` " ` "" ` " "
##` # ` ## ` # #
"Î# Ð"Î#Ñ" "Î#
È
œ1È2 ln 2
4
13. 14.
dz z dx z dz z du z dv x dw
dt x dt y dt dt u dt v dt w dt
dy
œ œ
`` ```
`` ```
15.
```` `` ```` ``
` `` `` `` ` `` `` ``
` `
wwxw wz wwxw wz
u xu yu zu v xv yv zv
y y
œ œ
16.
``````` ```````
``````` ```````
wwrwswt wwrwswt
xrxsxtx yrysyty
œ œ
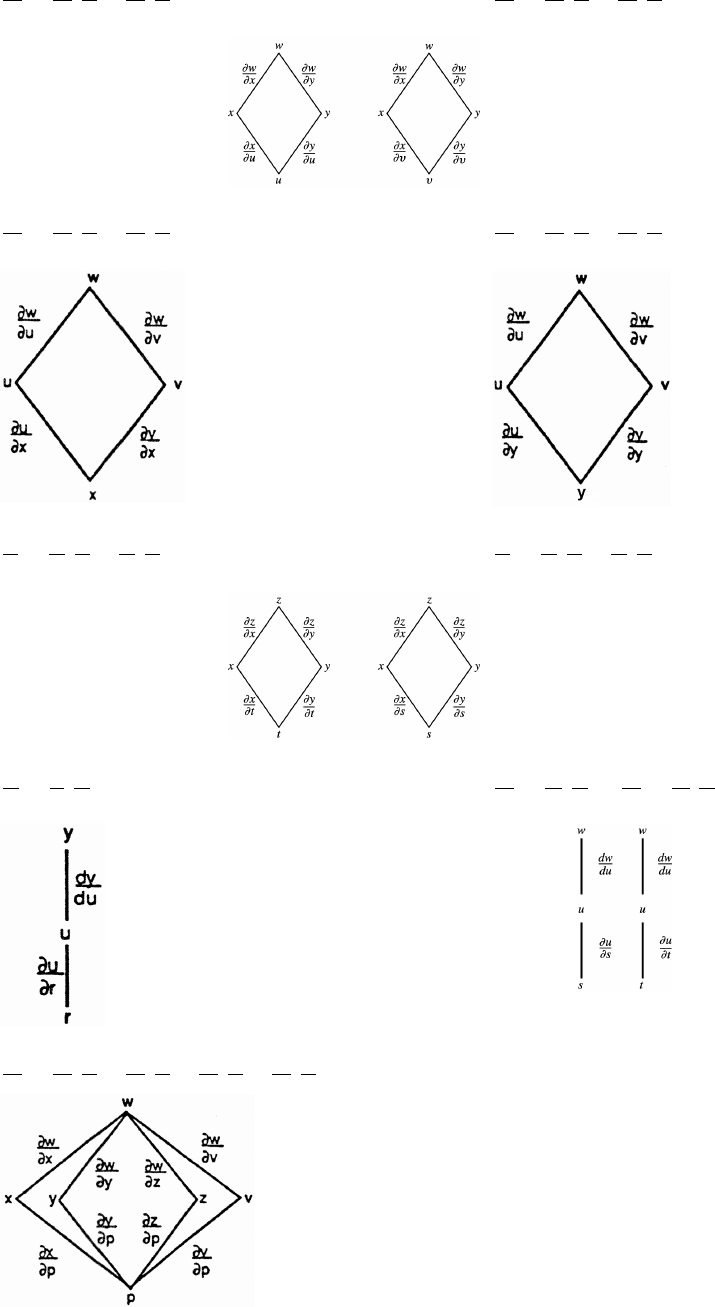
Section 14.4 The Chain Rule 883
17.
```` ````
` `` `` ` `` ``
` `
wwxw wwxw
u xu yu v xv yv
y y
œ œ
18.
` `` `` ` `` ``
` `` `` ` `` ``
w wu wv w wu wv
x ux vx y uy vy
œ œ
19.
```` ````
` `` `` ` `` ``
` `
zzxz zzxz
t xt yt s xs ys
y y
œ œ
20. 21.
`
`` ````
`````
ydy
rdur s dus t dut
u w dw u w dw u
œœœ
22.
```` ````
` ````````
`
wwxw wzwv
p xpypzpvp
y
œ
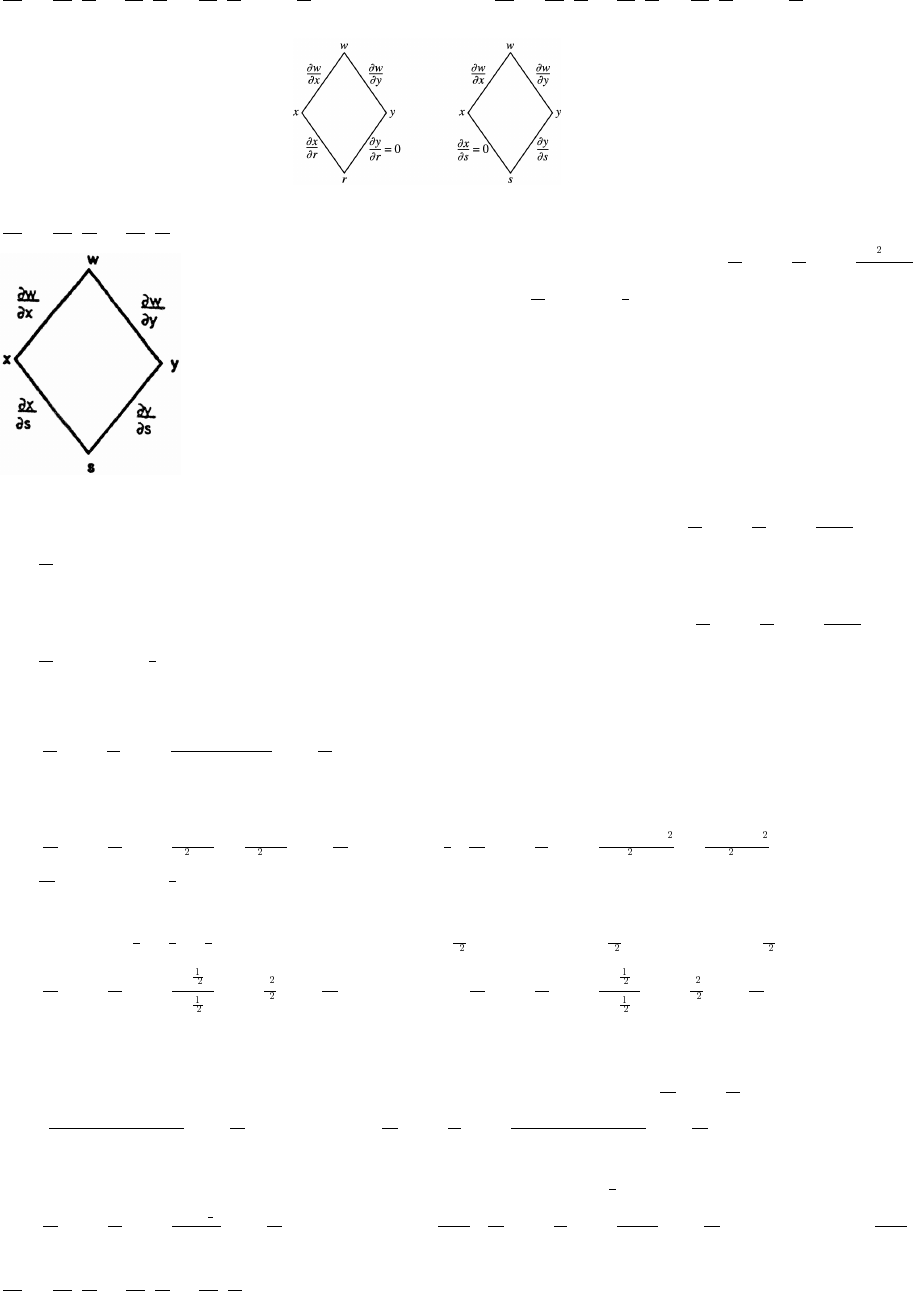
884 Chapter 14 Partial Derivatives
23. since 0 since 0
`` ` ` `` ` `
```` ````
w w dx w w dx w w dx w w dx
r x dr y dr x dr dr s x ds y ds y ds ds
dy dy dy dy
œœ œ œœ œ
24.
````
`````
`
wwxw
sxsys
y
œ
25. Let F(x y) x 2y xy 0 (x y) 3x yßœ œÊJßœ
$# #
x
and F (x y) 4y x
ydy 3x y
dx F ( 4y x)
F
ßœÊ œœ
x
y
(1 1)Êßœ
dy
dx 3
4
26. Let F(x y) xy y 3x 3 0 F (x y) y 3 and F (x y) x 2y ß œ œ Ê ß œ ß œ Ê œ œ
#
xy dy y 3
dx F x 2y
Fx
y
( 1 1) 2Êßœ
dy
dx
27. Let F(x y) x xy y 7 0 F (x y) 2x y and F (x y) x 2y ßœ œÊ ßœ ßœ Ê œœ
##
xy
dy 2x y
dx F x 2y
Fx
y
(1 2)Êßœ
dy
dx 5
4
28. Let F(x y) xe sin xy y ln 2 0 F (x y) e y cos xy and F (x y) xe x sin xy 1ßœ œÊ ßœ ßœ
yyy
xy
( ln 2) (2 ln 2)Ê œ œ Ê !ß œ
dy e y cos xy dy
dx F xe x sin xy 1 dx
Fx
y
y
y
29. Let F(x y z) z xy yz y 2 0 F (x y z) y, F (x y z) x z 3y , F (x y z) 3z yßßœ œ Ê ßßœ ßßœ ßßœ
$$ ##
xy z
(111) ; Ê œ œ œ Ê ß ß œ œ œ œ
``"`
```
zzz
x F 3z y 3z y x 4 y F 3z y 3z y
Fy y xz3y xz3y
F
x
z z
y
(111)Êßßœ
`
`
z3
y4
30. Let F(x y z) 1 0 F (x y z) , F (x y z) , F (x y z)ßß œ œ Ê ßß œ ßß œ ßß œ
""" " " "
xyz x y z
xyz
(236) 9; (236) 4Ê œ œ œ Ê ß ß œ œ œ œ Ê ß ß œ
````
````
zzzzzz
xF xx yF yy
FF
x
z z
x y
z z
y
Š‹ Š‹
Š‹ Š‹
31. Let F(x y z) sin (x y) sin (y z) sin (x z) 0 F (x y z) cos (x y) cos (x z),ßßœœÊßßœ
x
F (x y z) cos (x y) cos (y z), F (x y z) cos (y z) cos (x z)
yz z
xF
F
ßß œ ßß œ Ê œ
`
`
x
z
()1; ()1œ Ê ß ß œ œ œ Ê ß ß œ
cos (x y) cos (x z) cos (x y) cos (y z)
cos (y z) cos (x z) x y F cos (y z) cos (x z) y
zz z
F
` ` `
`` `
111 111
y
z
32. Let F(x y z) xe ye 2 ln x 2 3 ln 2 0 F (x y z) e , F (x y z) xe e , F (x y z) yeßßœ œÊ ßßœ ßßœ ßßœ
yz y yz z
xy z
2
x
(1 ln 2 ln 3) ; (1 ln 2 ln 3)Ê œ œ Ê ß ß œ œ œ Ê ß ß œ
````
````
zz4zxeez5
x F ye x 3 ln 2 y F ye y 3 ln 2
FeF
xx
z z
y2
z z
yyz
ˆ‰
33. 2(x y z)(1) 2(x y z)[ sin (r s)] 2(x y z)[cos (r s)]
```` ``
```````
`
wwxw wz
rxryrzr
y
œ œ
2(x y z)[1 sin (r s) cos (r s)] 2[r s cos (r s) sin (r s)][1 sin (r s) cos (r s)]œ œ

Section 14.4 The Chain Rule 885
2(3)(2) 12Êœœ
¸
`
`
w
rr1s 1œßœ
34. y x(1) (0) (u v) (1)
```` `` " `
``````` `
`
w w x w w z 2v 2v v w 4 4
vxvyvzv u z uu v 1 1
y
œœ œ Ê œ
ˆ‰ ˆ‰ ˆ‰ ¸ ˆ‰ˆ‰
u1v2œ ß œ
8œ
35. 2x ( 2) (1) 2(u 2v 1) ( 2)
```` " "
`````
`
w w x w 2uv2
v x v y v x x (u2v1) u2v1
yy
œœ œ
ˆ‰ˆ‰
’“
7ʜ
¸
`
`
w
vu0v0œßœ
36. (y cos xy sin y)(2u) (x cos xy x cos y)(v)
````
`````
`
zzxz
uxuyu
y
œœ
uv cos u v uv sin uv (2u) u v cos u v uv u v cos uv (v)œcdc dab ababab
$$ ## $$##
0(cos 0cos 0)(1) 2Êœœ
¸
`
`
z
uu0v1œßœ
37. e e (2) 2;
`` `
`` `
zdzx 5 5 z 5
udxu 1x u 1(2)
uu
1eln v
œœ œ Ê œ œ
ˆ‰ ¸
’“ ’“
ab
uuln2v1œßœ
(1) 1
`` " "`
`` `
zdzx 5 5 z 5
vdxv 1xv v v 1(2)
1eln v
œœ œ Ê œ œ
ˆ ‰ˆ‰ ˆ‰ ¸
’“ ’“
ab
uuln2v1œßœ
38.
`" " "
``
`
zdz
udqu q 1u 1u tanu1u
qv3 v3
v3 tanu
œœ œ œ
Š‹Š‹Š ‹Š‹
ÈÈ
Èabab
; Êœ œœœ
¸Š‹Š ‹
`"`"
```
`
z2zdztanu
utan111vdqvq
q
2v3
u1v 2œßœ abab È
1
œœÊœ
Š‹Š‹ ¸
""`"
# ` #
ÈÈ
v3 tanu 2v3
tan u z
(v 3) v u1v 2œßœ
39. V IR R and I; R I 0.01 volts/secœÊ œ œ œ œ Ê
`` ``
`` ``
V V dV V dI V dR dI dR
I R dt I dt R dt dt dt
(600 ohms) (0.04 amps)(0.5 ohms/sec) 0.00005 amps/secœ Êœ
dI dI
dt dt
40. V abc (bc) (ac) (ab)œÊœœ
dV V da V db V dc da db dc
dt a dt b dt c dt dt dt dt
```
```
(2 m)(3 m)(1 m/sec) (1 m)(3 m)(1 m/sec) (1 m)(2 m)( 3 m/sec) 3 m /secÊœ œ
¸
dV
dt a1b2c3œßœßœ
$
and the volume is increasing; S 2ab 2ac 2bc œ Êœ
dS S da S db S dc
dt a dt b dt c dt
```
```
2(b c) 2(a c) 2(a b) œ Ê
da db dc dS
dt dt dt dt ¸a1b2c3œßœßœ
2(5 m)(1 m/sec) 2(4 m)(1 m/sec) 2(3 m)( 3 m/sec) 0 m /sec and the surface area is not changing;œœ
#
D a b c a b c œÊœœ Ê
Ȉ‰¸
### ``` "
```
dD D da D db D dc da db dc dD
dt a dt b dt c dt dt dt dt dt
abc
Èa1b2c3œßœßœ
[(1 m)(1 m/sec) (2 m)(1 m/sec) (3 m)( 3 m/sec)] m/sec 0 the diagonals areœœÊ
Š‹
"
È È
14 m 14
6
decreasing in length
41. (1) (0) ( 1) ,
``````` ` ` ` ``
` `````` ` ` ` ``
ffufvfwf f f ff
x uxvxwx u v w uw
œ œœ
( 1) (1) (0) , and
``````` ` ` ` ``
` `````` ` ` ` ``
ffufvfwf f f ff
y uyvywy u v w uv
œ œ œ
(0) ( 1) (1) 0
``````` ` ` ` `` ```
``````` ` ` ` `` ```
ffufvfwf f f ff fff
z uzvzwz u v w vw xyz
œ œ œÊœ
42. (a) f f f cos f sin and f ( r sin ) f (r cos ) f sin f cos
`` ` "`
``` ` `
`
wx w w
rrr r
xy x y x y x y
y
œœ œ Ê œ )) ) ) ) )
))
(b) sin f sin cos f sin and f sin cos f cos
``
``
##
wcos w
rr
xy xy
))) ) )) )œ œ
ˆ‰
)
)
f (sin ) ; then f cos (sin ) (sin ) f cos Êœ œ Ê
yx x
wcos w w wcos w
rr r rr
)))))
``` ``
``` ` `
ˆ‰ ‘ˆ‰
))
))
sin 1 sin f (cos ) œ œ Êœ
`` ` ` ` ``
`` ` ` ` ``
##
w w sin cos w w sin cos w w sin w
rrr rr rr
x
ab a b
ˆ‰ ˆ‰ ˆ‰
)) )
)) )) )
)))
(c) f cos andab a b
ˆ‰ ˆ ‰ˆ ‰ ˆ‰
Š‹
xw 2 sin cos w w sin w
rrrr
##````
````
##
œ ))) )
))
fsin ffab a b ab ab
ˆ‰ ˆ ‰ˆ ‰ ˆ‰ ˆ‰ ˆ‰
Š‹
yxy
w 2 sin cos w w cos w w w
rrr r rr
###
#```` `"`
```` ``
####
œ Êœ))) )
)) )

886 Chapter 14 Partial Derivatives
43. w x y w x y
xxx
wwuwv w w w w w
x ux vx u v u xu xv
œœœÊœ
` `` `` ` ` ` `` ``
` `` `` ` ` ` `` ``
ˆ‰ ˆ‰
x y x x y y x yœ œ
` ```` ````` `` ``
`````` `````` ``` ```
w wuwv wuwvw ww ww
uuxvux uvxvxu uvu uvv
Š‹Š‹Š‹Š‹
x 2xy y ; w y x œ œœœ
`` ` ` ````` ``
` ` `` ` ` `` `` ` `
##
ww w w wwuwv ww
u u vu v y uy vy u v
y
wy x ʜ
yy wwuwv wuwv
uuyvuy uvyvy
````` ````
`````` `````
Š‹Š‹
y y x x y x y 2xy x ; thusœ œ
``` ``````
` ` `` `` ` ` ` `` `
##
www wwwwww
u u vu uv v u u vu v
Š‹Š‹
w w xy xy xy(w w)0, since w w 0
xx yy uu vv uu vv
ww
uv
œ œ œ œababab
## ## ##
``
``
44. f (u)(1) g (v)(1) f (u) g (v) w f (u)(1) g (v)(1) f (u) g (v);
`
`
w w ww ww w wwww
w
w
xœœÊœ œ
xx
f (u)(i) g (v)( i) w f (u) i g (v) i f (u) g (v) w w 0
`
`
w w ww # ww # ww ww
w
yœÊœ œÊœ
yy xx yy
ab ab
45. f (x y z) cos t, f (x y z) sin t, and f (x y z) t t 2
xy z df f dx f f dz
dt x dt y dt z dt
dy
ßß œ ßß œ ßß œ Ê œ
#```
```
(cos t)( sin t) (sin t)(cos t) t t 2 (1) t t 2; 0 t t 2 0 t 2œ œœÊœÊœab
## #
df
dt
or t 1; t 2 x cos ( 2), y sin ( 2), z 2 for the point (cos ( 2) sin ( 2) 2); t 1 x cos 1,œ œ Ê œ œ œ ß ß œ Ê œ
y sin 1, z 1 for the point (cos 1 sin 1 1)œœ ßß
46. 2xe cos 3z ( sin t) 2x e cos 3z 3x e sin 3z (1)
dw wdx w wdz
dt x dt y dt z dt t
dy 2y 2y 2y
œœ
``` "
``` #
##
aba ba b
ˆ‰
2xe cos 3z sin t 3x e sin 3z; at the point on the curve z 0 t z 0œ œ Ê œ œ
2y 2y
2x e cos 3z
t
2y
#
#
004Êœœ
¸
dw
dt
2(1) (4)(1)
Ðß ßÑ1ln20 #
47. (a) 8x 4y and 8y 4x (8x 4y)( sin t) (8y 4x)(cos t)
`` ``
`` ``
TTdTTdxT
x y dt x dt y dt
dy
œ œ Ê œ œ
(8 cos t 4 sin t)( sin t) (8 sin t 4 cos t)(cos t) 4 sin t 4 cos t 16 sin t cos t;œ œ Êœ
##
dT
dt
0 4 sin t 4 cos t 0 sin t cos t sin t cos t or sin t cos t t , , , on
dT 537
dt 4444
œÊ œÊ œ Ê œ œ Êœ
## ## 1111
the interval 0 t 2 ;ŸŸ1
16 sin cos 0 T has a minimum at (x y) ;
¹Š‹
dT
dt 4 4
22
tœ4
œÊ ßœß
11 ÈÈ
##
16 sin cos 0 T has a maximum at (x y) ;
¹Š‹
dT 3 3
dt 4 4
22
tœ3
4
œÊ ßœß
11 ÈÈ
##
16 sin cos 0 T has a minimum at (x y) ;
¹Š‹
dT 5 5
dt 4 4
22
tœ5
4
œÊ ßœß
11 ÈÈ
##
16 sin cos 0 T has a maximum at (x y)
¹Š‹
dT 7 7
dt 4 4
22
tœ7
4
œÊ ßœß
11 ÈÈ
##
(b) T 4x 4xy 4y 8x 4y, and 8y 4x so the extreme values occur at the four pointsœ Ê œ œ
##
``
``
TT
xy
found in part (a): T T 4 4 4 6, the maximum and
Š‹Š‹
ˆ‰ ˆ ‰ ˆ‰
ß œ ß œ œ
ÈÈ È È
22 2 2
## # # # # #
"""
T T 4 4 4 2, the minimum
Š‹Š ‹
ˆ‰ ˆ‰ ˆ‰
ÈÈ È È
22 2 2
## ## ###
"""
ߜߜ œ
48. (a) y and x y 2 2 sin t x 2 cos t
`` ``
`` ``
TTdTTdxT
x y dt x dt y dt
dy
œ œÊœœ
Š‹Š‹
ÈÈ
2 sin t 2 2 sin t 2 2 cos t 2 cos t 4 sin t 4 cos t 4 sin t 4 1 sin tœ œœ
Š‹Š ‹Š ‹Š‹
ÈÈÈÈ ab
## # #
4 8 sin t 16 sin t cost t; 0 4 8 sin t 0 sin t sin t t ,œ Ê œ œ Ê œ Ê œ Ê œ„ Êœ
###
""
#
dT dT
dt dt 4
2
È1
, , on the interval 0 t 2 ;
357
444
111 ŸŸ1
8 sin 2 8 T has a maximum at (x y) (2 1);
¹ˆ‰
dT
dt 4
tœ4
œ œ Ê ß œ ß
1
8 sin 2 8 T has a minimum at (x y) ( 2 1);
¹ˆ‰
dT 3
dt 4
tœ3
4
œ œ Ê ß œ ß
1
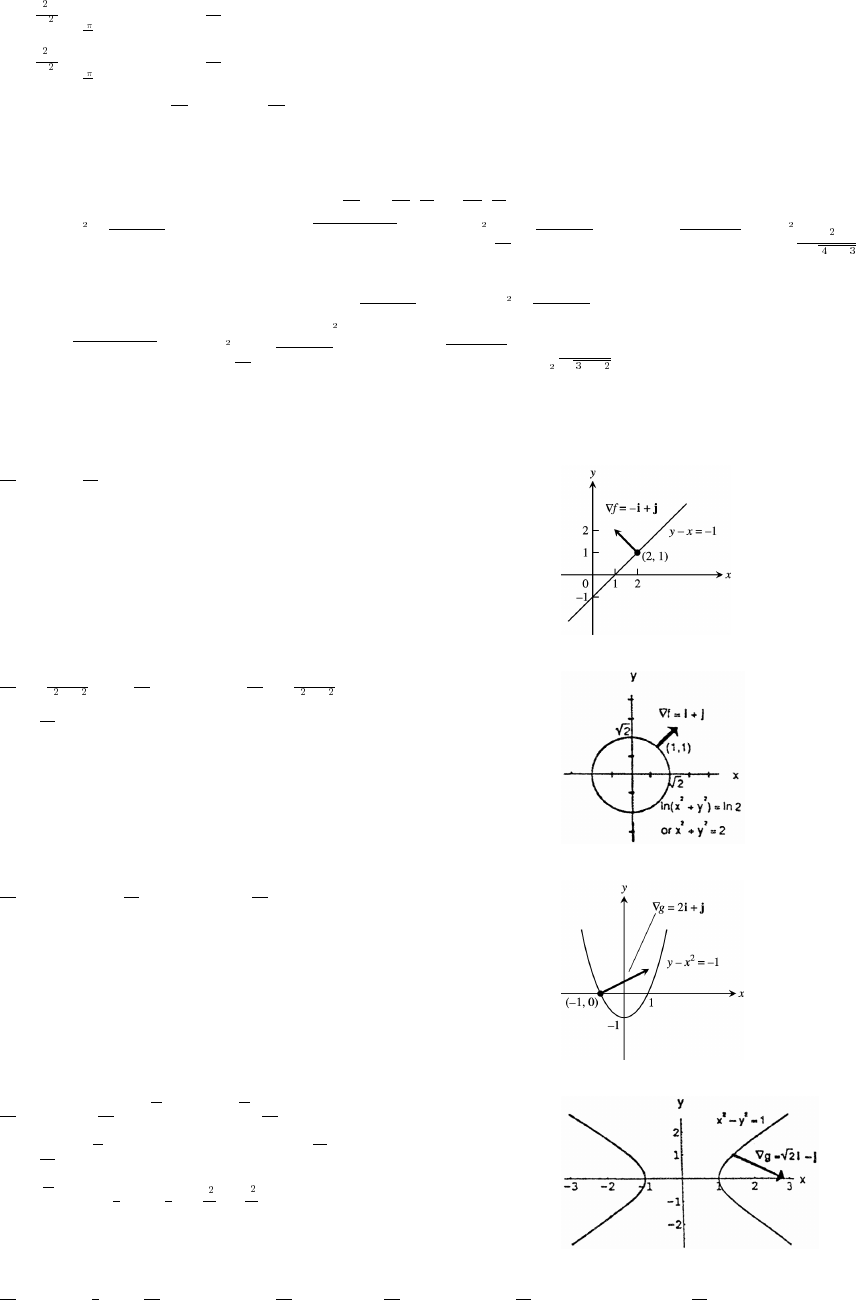
Section 14.5 Directional Derivatives and Gradient Vectors 887
8 sin 2 8 T has a maximum at (x y) ( 2 1);
¹ˆ‰
dT 5
dt 4
tœ5
4
œ œ Ê ß œ ß
1
8 sin 2 8 T has a minimum at (x y) (2 1)
¹ˆ‰
dT 7
dt 4
tœ7
4
œ œ Ê ß œ ß
1
(b) T xy 2 y and x so the extreme values occur at the four points found in part (a):œÊ œ œ
``
``
TT
xy
T(2 1) T( 2 1) 0, the maximum and T( 2 1) T(2 1) 4, the minimumß œ ß œ ß œ ß œ
49. G(u x) g(t x) dt where u f(x) g(u x)f (x) g (t x) dt; thusßœß œÊœœß ß
''
a a
u u
x
dG G du G dx
dx u dx x dx
``
``
w
F(x) t x dt F (x) x x (2x) t x dt 2x x x dtœÊœ œ
'''
000
xxx
ÈÈ
Éab È
%$ # $ %$ )$
w%`
`
x
3x
2t x
È
50. Using the result in Exercise 49, F(x) t x dt t x dt F (x)œœ Ê
''
x1
1x
ÈÈ
$# $# w
xx x dt
xxx tx dt
œœ
’“
Éab ÈÈ
## $#
$#`
`
#'#
''
1
x
x
1
x
x
tx
È
14.5 DIRECTIONAL DERIVATIVES AND GRADIENT VECTORS
1. 1, 1 f ; f(2 1) 1
``
``
ff
xy
œ œ Ê œ ß œ™ij
1 y x is the level curveÊ œ
2. ( ) 1;
```
` ` `
f2x f f
xxy x yxy
2y
œ Ê "ß " œ œ
( ) 1 f ; f(1 1) ln 2 ln 2Ê"ß"œÊ œ ßœ Ê
`
`
f
y™ij
ln x y 2 x y is the level curveœÊœab
## ##
3. 2x ( 1 0) 2; 1
`` `
`` `
gg g
xx y
œ Ê ß œ œ
g2 ; g(10) 1ʜߜ™ij
1 y x is the level curveÊ œ #
4. x 2 2; y
`` `
`` `
gg g
xx y
œÊ ß"œ œ
Š‹
ÈÈ
21 g2;Êß"œÊœ
`
`
g
yŠ‹
ÈÈ
™ij
g 2 or 1 x y is the level
Š‹
Èß" œ Ê œ œ
""
####
##
xy
curve
5. 2x (1 1 1) 3; 2y ( ) 2; 4z ln x ( ) 4;
````` `
````` `
fzf f f f f
xxxyyz z
œ Ê ß ß œ œ Ê "ß "ß " œ œ Ê "ß "ß " œ
thus f 3 2 4™œijk

888 Chapter 14 Partial Derivatives
6. 6xz (1 ) ; 6yz ( ) 6; 6z 3 x y
`````
``#`` `
###
fzf11f f f x
xxz1x y y z xz1
œ Ê ß"ß" œ œ Ê "ß"ß" œ œ ab
( ) ; thus f 6Ê "ß"ß" œ œ
`" "
`# ##
f11
z™ij k
7. ( 1 2 2) ; ( 1 2 2) ;
`"` `"`
````
fx f 26f f 23
xxx27yyy54
xyz xyz
y
œ Ê ß ß œ œ Ê ß ß œ
ab ab
( 1 2 2) ; thus f
`"`
``
fz f 23 262323
zzz54275454
xyz
œ Ê ß ß œ œ
ab ™ijk
8. e cos z 1; e cos z sin x 0 0 ;
````
``#``#
"
ffff
xx6yy6
xy xy
y1
1x
33
œÊ!ß!ßœœÊßßœ
ÈÈÈ
ˆ‰ ˆ‰
11
e sin z ; thus f
``" "
``####
ff
zz6
xy 32 3
œ Ê !ß!ß œ œ
ˆ‰ Š‹
1™ÈÈ
ijk
9. ; f (x y) 2y f (5 5) 10; f (x y) 2x 6y f (5 5) 20uijœœ œ ßœ Ê ßœ ßœ Ê ßœ
v
v
ij
kk È
43
43
43
55
xxy y
f10 20 (Df) f 10 20 4ÊœÊ œ œœ™™†ij u
uP43
55
ˆ‰ ˆ‰
10. ; f (x y) 4x f ( 1 1) 4; f (x y) 2y f ( 1 1) 2uijœœ œ ßœ Êßœ ßœ Êßœ
v
v
ij
kk È34
3(4)
34
55
xxyy
f42 (Df) f 4ÊœÊ œ œœ™™†ij u
uP12 8
55
11. ; g (x y) 1 g (1 1) 3; g (x y)uijœœ œ ßœ Ê ßœ ß
v
v
ij
kk ÈÈ
È
12 5 y
12 5
12 5
13 13 x
xxy
2y 3
2xy 4x y 1
g (1 1) 1 g 3 (D g) gœ Ê ßœÊ œÊ œ œ œ
2y
x13 13 13
2x 3
2xy 4x y 1 yP
36 5 31
È
È™™†ij u
u
12. ; h (x y) h (1 1) ;uijœ œ œ ßœ Ê ßœ
v
v
ij
kk ÈÈÈ Š‹
ˆ‰ ˆ‰
È
ÊŠ‹
32
3(2)
32
13 13 xx
1
3
1
"
#
y
x
y
x
y
xy
4
h (x y) h (1 1) h (D h) h
yy P
1
3
1
33 36
213 213
ßœ Ê ßœ Ê œ Ê œ œ
ˆ‰
ˆ‰ ˆ‰
È
ÊŠ‹ ÈÈ
x
y
x
x
xy
4
###
"
™™†ij u
u
œ 3
213
È
13. ; f (x y z) y z f (1 1 2) 1; f (x y z) x zuijkœœ œ ßßœÊ ßßœ ßßœ
v
v
ijk
kk È36
36(2)
362
777xxy
#
f (1 1 2) 3; f (x y z) y x f (1 1 2) 0 f 3 (D f) f 3Êßßœ ßßœÊßßœÊ œÊ œ œœ
yz z P
318
77
™™†ij u
u
14. ; f (x y z) 2x f (1 1 1) 2; f (x y z) 4yuijkœ œ œ ßß œ Ê ßß œ ßß œ
v
v
ijk
kk ÈÈÈÈ
111
111
333
xxy
f(111) 4; f(xyz) 6z f(111) 6 f 2 4 6 (Df) fÊ ßßœ ßßœ Ê ßßœÊ œ Ê œ
yz z P
™™†ijk u
u
2460œœ
Š‹ Š‹ Š‹
"""
ÈÈÈ
333
15. ; g (x y z) 3e cos yz g (0 0 0) 3; g (x y z) 3ze sin yzuijkœœ œ ßßœ Ê ßßœ ßßœ
v
v
ij k
kk È22
21(2)
212
333 xxy
xx
g (0 0 0) 0; g (x y z) 3ye sin yz g (0 0 0) 0 g 3 (D g) g 2Ê ßßœ ßßœ Ê ßßœÊ œ Ê œ œ
yz z P
x™™†iu
u
16. ; h (x y z) y sin xy h 1 0 1;uijkœœ œ ßßœ Ê ßßœ
v
v
ijk
kk È
""
#
22
122
122
333 x
xx
ˆ‰
h (x y z) x sin xy ze h ; h (x y z) ye h 2 h 2
yyzz
yz yz
z
ß ß œ Ê "ß !ß œ ß ß œ Ê "ß !ß œ Ê œ
ˆ‰ ˆ‰
"" " " "
## # #
™ijk
(D h) h 2Ê œ œœ
uP333
4
™†u""
17. f (2x y) (x 2y) f( 1 1) ; f increases™™œ Ê ßœÊœ œ œ ij iju ij
™
™
f
f(1) 1 22
kk ÈÈÈ
""
ij
most rapidly in the direction and decreases most rapidly in the direction ;uij uijœ œ
"" ""
ÈÈ ÈÈ
22 22
(D f) f f 2 and (D f) 2
uuPP
œœœ œ™† ™ukk
ÈÈ
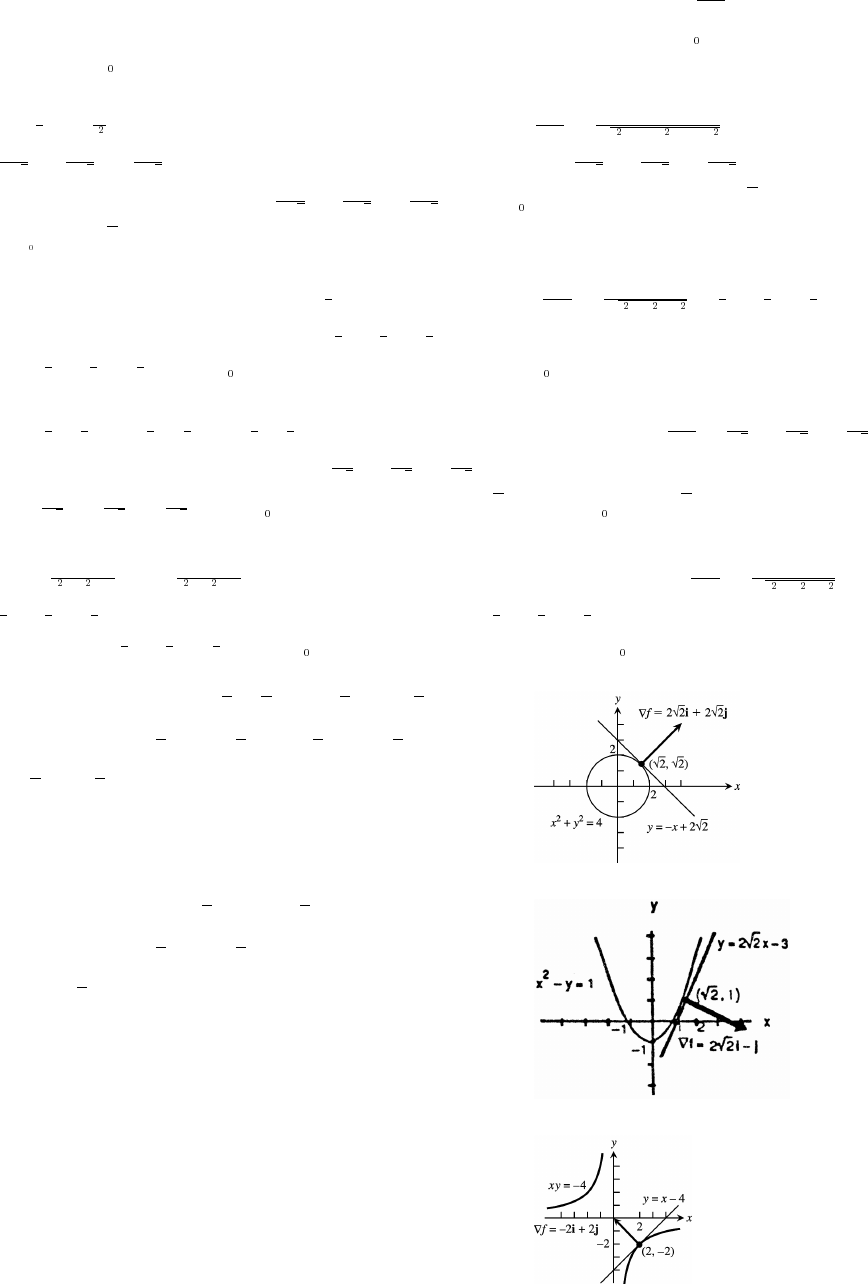
Section 14.5 Directional Derivatives and Gradient Vectors 889
18. f 2xy ye sin y x xe sin y e cos y f(1 0) 2 ; f increases most™™œ Ê ßœÊœœaba b
xy xy xy f
f
ijjuj
#™
™kk
rapidly in the direction and decreases most rapidly in the direction ; (D f) f fuj u j uœœœœ
uP™† ™kk
2 and (D f) 2œœ
uP
19. f z y f(4 ) 5 ™™œ Ê ß "ß " œ Ê œ œ
"
yy f
xf5
1(5)(1)
ijk ijku
Š‹ ™
™kk Èijk
; f increases most rapidly in the direction of and decreasesœ œ
"" ""
33 33 33 33 33 33
5 5
ÈÈÈ ÈÈÈ
ijk u ijk
most rapidly in the direction ; (D f) f f 3 3 andœ œ œ œuijk u
""
33 33 33
5P
ÈÈÈ u™† ™kkÈ
(D f) 3 3
uPœ È
20. g e xe 2z g 1 ln 2 2 2 ;™™œ Ê ß ß œÊœ œ œ
yy g
g333
22
221
22
ijk ijku ijk
ˆ‰
" "
#
™
™kk Èijk
g increases most rapidly in the direction and decreases most rapidly in the directionuijkœ
22
333
"
; (D g) g g 3 and (D g) 3œ œ œ œ œuijk u
22
333 PP
"uu
™† ™kk
21. f f( ) 2 2 2 ;™™œ Ê "ß"ß" œ Ê œ œ
ˆ‰ ˆ‰
Š‹
"" "" "" " " "
xx yy zz f
f
333
ijk ijku ijk
™
™kk ÈÈÈ
f increases most rapidly in the direction and decreases most rapidly in the directionuijkœ
"""
ÈÈÈ
333
; (D f) f f 2 3 and (D f) 2 3œ œ œ œ œuijk u
"""
ÈÈÈ
333 PP
™† ™
uu
kkÈÈ
22. h 1 6 h( 0) 2 3 6 ™™œ Ê "ß"ßœ Êœ œ
Š‹Š ‹
2x
xy1 xy1 h
2y 236
h
236
ijk ijku
™
™kk Èijk
; h increases most rapidly in the direction and decreases most rapidly in theœ œ
236 236
777 777
ijk u ijk
direction ; (D h) h h 7 and (D h) 7œ œ œ œ œuijk u
236
777 PPuu
™† ™kk
23. f 2x 2y f 2 2 2 2 2 2™™œ Ê ß œ ij i j
Š‹
ÈÈ È È
Tangent line: 2 2 x 2 2 2 y 2 0ʜ
ÈÈÈÈ
Š‹Š‹
2x 2y 4ʜ
ÈÈ
24. f 2x f 2 1 2 2™™œÊ ßœ ij i j
Š‹
ÈÈ
Tangent line: 2 2 x 2 (y 1) 0ʜ
ÈÈ
Š‹
y 2 2x 3ʜ
È
25. f y x f(2 2) 2 2™™œ Ê ßœij ij
Tangent line: 2(x 2) 2(y 2) 0ʜ
yx4ʜ

890 Chapter 14 Partial Derivatives
26. f (2x y) (2y x) f( 1 2) 4 5™™œÊ ßœij ij
Tangent line: 4(x 1) 5(y 2) 0ʜ
4x 5y 14 0Ê œ
27. f y (x 2y) f(3 2) 2 7 ; a vector orthogonal to f is 2 ™™ ™œœ Ê ßœ Êœ œi j ij v7ij uv
v
ij
kk È72
7(2)
and are the directions where the derivative is zeroœ œ
72 72
53 53 53 53
ÈÈ ÈÈ
iju ij
28. f f( ) ; a vector orthogonal to f is ™™ ™œ Ê "ß"œ œ
4xy 4x y
xy xy
abab
ij ij vij
and are the directions where the derivative is zeroÊœ œ œ œ uijuij
v
v
ij
kk ÈÈÈ ÈÈ
11 22 22
11 11
29. f (2x 3y) ( 3x 8y) f(1 2) 4 13 f(1 2) ( 4) (13) 185 ; no, the™™™œ Ê ßœ Ê ßœ œij ijkk
ÈÈ
##
maximum rate of change is 185 14
È
30. T 2y (2x z) y T(1 1 1) 2 T(1 1 1) ( 2) 1 1 6 ; no, the™™ ™œ Ê ßßœÊ ßßœœijk ijkkk
ÈÈ
###
minimum rate of change is 6 3
È
31. f f ( ) f ( ) and (D f)(1 2) f (1 2) f (1 2)™œ "ß# "ß# œ œ Ê ß œ ß ß
xy xy
iju ij
"
"" " "
ij
ÈÈÈ È È
11 2 2 2 2
uŠ‹ Š‹
2 2 f (1 2) f (1 2) 4; (D f)(1 2) f (1 2)(0) f (1 2)( 1) 3 f (1 2) 3œ Ê ß ß œ œ Ê ß œ ß ß œ Ê ß œ
Èxy x y y
uj
#u
f (1 2) 3; then f (1 2) 3 4 f (1 2) 1; thus f(1 2) 3 and Êßœ ßœÊßœ ßœ œœ
yx x
™ij uv
v
ij
kk È
2
(1) (2)
(D f) fœ Ê œ œ œ
12 6 7
55 55 5
ÈÈ ÈÈ È
ij u
uP™† "
32. (a) (D f) 2 3 f 2 3; ; thus
uPœ Ê œ œœ œ œ
ÈÈ
kk™uijku
v
v
ijk
kk k k
ÈÈÈÈ
"
11(1)
11
333
f
f
™
™
ff f23 222Ê œ Ê œ œ™™ ™kk ÈŠ‹
uijkijk
"""
ÈÈÈ
333
(b) (D f) f 2 2 2(0) 2 2vij u i j uœÊœœœÊœœœ
v
v
ij
kk ÈÈÈ ÈÈ
"" " "
11 2 2 2 2
uP™† Š‹ Š‹ È
33. The directional derivative is the scalar component. With f evaluated at P , the scalar component of f in™™
!
the direction of is f (D f) .uu™† œuP
34. D f f (f f f ) f ; similarly, D f f f and D f f f
ijk
œœœ œœ œ œ™† † ™† ™†iijki j k
xyz x y z
35. If (x y) is a point on the line, then (x y) (x x ) (y y ) is a vector parallel to the line 0ßßœ ÊœTij TN
!! †
A(x x ) B(y y ) 0, as claimed.ʜ
!!
36. (a) (kf) k k k k k f™ ™œ œ œ œ
```
``` ` ` ` ```
``` ```
(kf) (kf) (kf)
xyz x y z xyz
fff fff
ijk i j k ijk
ˆ‰ ˆ‰
Š‹ Š ‹
(b) (f g)™œ œ
` ` ` ` ` `
``` ``````
```
(f g) (f g) (f g) g g g
xyz xxyyzz
fff
ijk i j k
Š‹Š‹Š‹
fgœ œ œ
`` ` ```
````` ` ``` ```
`` ` ```
ff f fff
xxyyz z xyz xyz
gg g ggg
iijjkk ijk ijk
Š‹Š‹
™™
(c) (f g) f g (Substitute g for g in part (b) above)™™™œ

Section 14.6 Tangent Planes and Differentials 891
(d) (fg) g f g f g f™œ œ
``` ` ` `
``` `` `` ``
```
(fg) (fg) (fg) g g g
xyz xx yy zz
fff
ijk i j k
Š‹Š‹Š‹
gf g fg fœ
ˆ‰ ˆ‰
Š‹Š‹Š‹ Š‹
`` `
``` `` `
```
ff f
xxy yz z
ggg
iijjkk
fgfggfœ œ
Š‹Š‹
```
``` ```
```
ggg
xyz xyz
fff
ijk ijk™™
(e) ™Š‹ Š ‹ Š ‹
Œ
f
gx y z g g g
gf gf
gf
œ œ
```
```
Š‹ Š‹ Š‹
fff
ggg
ijk i j k
ff
xx zz
gg
f
yy
g
œœ
ŒŒ
ggg fff
gggg
gf
fff
xyz xyz
ggg fff
xyz xyz
ggg
ijk ijk ijk ijk
Š‹Š‹
œœ
gf fg gffg
gg g
™™ ™™
14.6 TANTGENT PLANES AND DIFFERENTIALS
1. (a) f 2x 2y 2z f(1 1 1) 2 2 2 Tangent plane: 2(x 1) 2(y 1) 2(z 1) 0™™œ Ê ßßœ Ê œijk ijk
xyz 3;Ê œ
(b) Normal line: x 1 2t, y 1 2t, z 1 2tœ œ œ
2. (a) f 2x 2y 2z f(3 5 4) 6 10 8 Tangent plane: 6(x 3) 10(y 5) 8(z 4) 0™™œ Ê ßßœ Ê œijk ijk
3x 5y 4z 18;Ê œ
(b) Normal line: x 3 6t, y 5 10t, z 4 8tœ œ œ
3. (a) f 2x 2 f(2 0 2) 4 2 Tangent plane: 4(x 2) 2(z 2) 0™™œ Ê ß ß œ Ê œik ik
4x 2z 4 0 2x z 2 0;Ê œÊœ
(b) Normal line: x 2 4t, y 0, z 2 2tœ œ œ
4. (a) f (2x 2y) (2x 2y) 2z f(1 1 3) 4 6 Tangent plane: 4(y 1) 6(z 3) 0™™œ Ê ßßœ Ê œijk jk
2y 3z 7;ʜ
(b) Normal line: x 1, y 1 4t, z 3 6tœœ œ
5. (a) f sin x 2xy ze x z xe y f(0 1 2) 2 2 Tangent plane:™™œ Ê ßßœÊababab11 xz xz
ijk ijk
#
2(x 0) 2(y 1) 1(z 2) 0 2x 2y z 4 0; œÊ œ
(b) Normal line: x 2t, y 1 2t, z 2 tœœœ
6. (a) f (2x y) (x 2y) f(1 1 1) 3 Tangent plane:™™œ Ê ßßœÊijk ijk
1(x 1) 3(y 1) 1(z 1) 0 x 3y z 1; œÊ œ
(b) Normal line: x 1 t, y 1 3t, z 1 tœ œ œ
7. (a) f for all points f(0 1 0) Tangent plane: 1(x 0) 1(y 1) 1(z 0) 0™™œ Ê ßß œ Ê œijk ijk
xyz10;ʜ
(b) Normal line: x t, y 1 t, z tœœœ
8. (a) f (2x 2y 1) (2y 2x 3) f(2 3 18) 9 7 Tangent plane:™™œ Ê ßß œÊijk ijk
9(x 2) 7(y 3) 1(z 18) 0 9x 7y z 21; œ Ê œ
(b) Normal line: x 2 9t, y 3 7t, z 18 tœ œ œ
9. z f(x y) ln x y f (x y) and f (x y) f (1 0) 2 and f (1 0) 0 fromœ ßœ Ê ßœ ßœ Ê ßœ ßœÊab
##
xy xy
2x
xy xy
2y
Eq. (4) the tangent plane at (1 0 0) is 2(x 1) z 0 or 2x z 2 0ßß œ œ

892 Chapter 14 Partial Derivatives
10. z f(x y) e f (x y) 2xe and f (x y) 2ye f (0 0) 0 and f ( ) 0œßœ Ê ßœ ßœ Ê ßœ !ß!œ
ab ab abxy xy xy
xy xy
from Eq. (4) the tangent plane at (0 0 1) is z 1 0 or z 1Êßßœœ
11. z f( y) y x f (x y) (y x) and f (x y) (y x) f (1 2) and f ( )œBßœ Ê ßœ ßœ Ê ßœ "ß#œ
Èxyxy
"" ""
## ##
"Î# "Î#
from Eq. (4) the tangent plane at (1 2 1) is (x 1) (y 2) (z 1) 0 x y 2z 1 0Ê ßß œÊ œ
""
##
12. z f( y) 4x y f (x y) 8x and f (x y) y f (1 1) 8 and f ( 1) from Eq. (4) theœBßœ Ê ßœ ßœ#Ê ßœ "ßœ#Ê
## xy xy
tangent plane at (1 1 5) is 8(x 1) 2(y 1) (z 5) 0 or 8x 2y z 5 0ßß œ œ
13. f 2y 2 f(1 1 1) 2 2 and g for all points; f g™™ ™ ™™œ Ê ßß œ œ œ ‚ijk ijk i v
2 2 Tangent line: x 1, y 1 2t, z 1 2t
22
00
Ê œ œ Ê œ œ œ
"
"
vjk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
14. f yz xz xy f(1 1 1) ; g 2x 4y 6z g(1 1 1) 2 4 6 ;™™™ ™œ Ê ßßœ œ Ê ßßœijk ijk ijk ijk
f g 2 4 2 Tangent line: x 1 2t, y 1 4t, z 1 2t
11
246
Êœ ‚ Ê œ Ê œ œ œ
"
vijk
ijk
™™
ââ
ââ
ââ
ââ
ââ
ââ
15. f 2x 2 2 f 1 1 2 2 2 and g for all points; f g™™ ™ ™™œ Ê ßß œ œ œ ‚ijk ijk j v
ˆ‰
"
#
2 2 Tangent line: x 1 2t, y 1, z 2t
222
010
Êœ œ Ê œ œ œvik
ijk
ââ
ââ
ââ
ââ
ââ
ââ "
#
16. f 2y f 1 2 and g for all points; f g™™ ™ ™™œ Ê ßß œ œ œ ‚ijk ijk j v
ˆ‰
""
##
Tangent line: x t, y 1, z t
121
010
Êœ œÊ œ œ œvik
ijk
ââ
ââ
ââ
ââ
ââ
ââ ""
##
17. f 3x 6xy 4y 6x y 3y 4x 2z f(1 1 3) 13 13 6 ; g 2x 2y 2z™™™œ Ê ßßœ œabab
## ##
ijk ijkijk
g( ) 2 2 6 ; f g 90 90 Tangent line:
313 6
22 6
Ê "ß"ß$ œ œ ‚ Ê œ œ Ê
"
™™™ijkv v i j
ijk
ââ
ââ
ââ
ââ
ââ
ââ
x 1 90t, y 1 90t, z 3œ œ œ
18. f 2x 2y f 2 2 4 2 2 2 2 ; g 2x 2y g 2 2 4™™ ™ ™œ Ê ßßœ œÊ ßßij i j ijk
Š‹ Š‹
ÈÈ È È ÈÈ
22 22 ; f g 22 22 Tangent line:
2222 0
2222 1
œœ‚Êœ œ Ê
ÈÈ ÈÈ
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ
ÈÈ
ijkv v i j
ijk
™™
x222t, y222t, z4œ œ œ
ÈÈ ÈÈ
19. f f(3 4 12) ;™™œ Êßßœ
Š‹Š‹Š‹
xz3412
xyz xyz xyz 169 169 169
y
ijk ijk
f and df ( f ) ds (0.1) 0.0008uijkuuœœ œ Ê œ œ œ ¸
v
v
ijk
kk È362
36(2)
362 9 9
7 7 7 1183 1183
™† ™† ˆ‰
20. f e cos yz ze sin yz ye sin yz f(0 0 0) ; ™™œ Êßßœœœababab
xxx 222
22(2)
ijk iu
v
v
ijk
kk È
f and df ( f ) ds (0.1) 0.0577œ Ê œ œ œ ¸
111 1 1
333 3 3
ÈÈÈ È È
ijk u u™† ™†
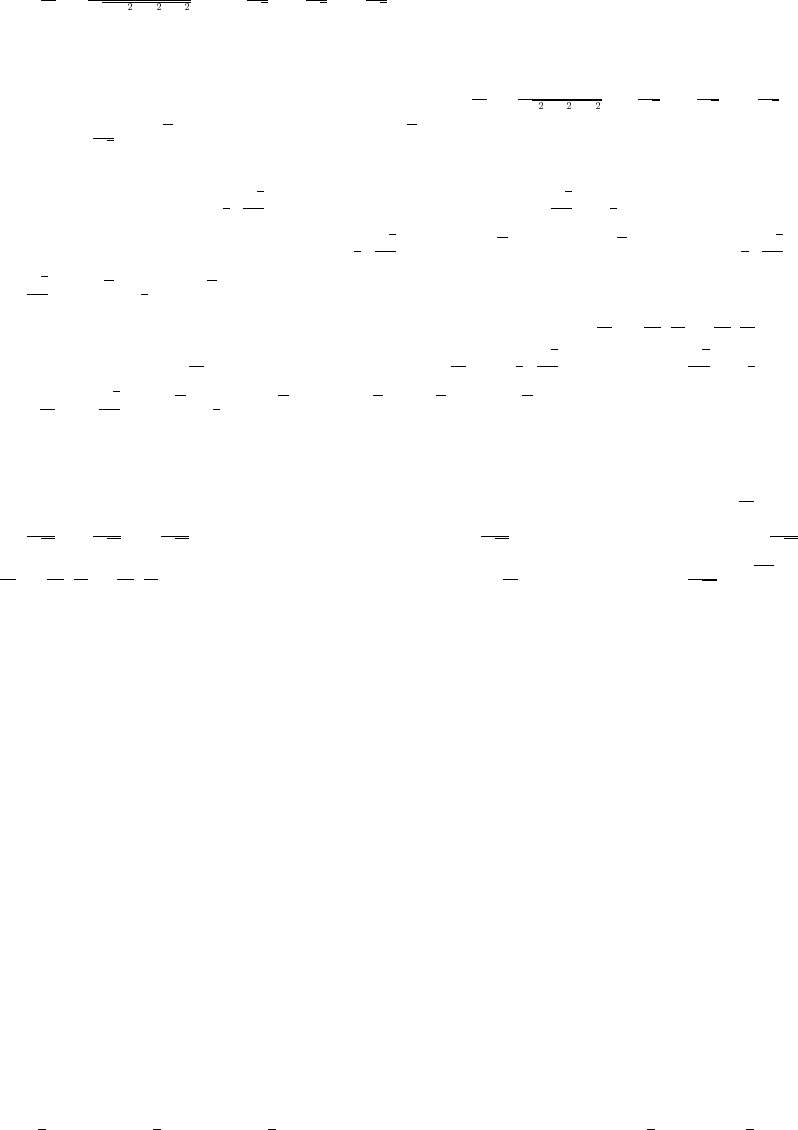
Section 14.6 Tangent Planes and Differentials 893
21. g (1 cos z) (1 sin z) ( x sin z y cos z) g(2 1 0) 2 ; P P 2 2 2™™œ Ê ßßœ œ œ
Ä
ij k ijkA ijk
!"
g 0 and dg ( g ) ds (0)(0.2) 0Êœ œ œ Ê œ œ œ œuijkuu
v
v
ijk
kk ÈÈÈÈ
222
(2) 2 2
111
333 ™† ™†
22. h y sin ( xy) z x sin ( xy) 2xz h( 1 1 1) ( sin 1) ( sin ) 2™™œ Ê ßß œ cdcd11 11 11 11
#ijk ijk
2 ; P P where P ( ) œ œ œ œ!ß!ß!Ê œ œ œ
Ä
ikv ijk u i j k
!" "
v
v
ijk
kk ÈÈÈÈ
111
111
333
h 3 and dh ( h ) ds 3(0.1) 0.1732Êœœ œ œ¸™† ™†uu
3
3
ÈÈÈ
23. (a) The unit tangent vector at in the direction of motion is ;
Š‹
""
## # #
ߜ
ÈÈ
33
uij
T (sin 2y) (2x cos 2y) T sin 3 cos 3 D T T™™ ™†œ Êßœ Êßœij ij u
Š‹Š ‹Š ‹ Š‹
ÈÈ
""
## ##
ÈÈ
33
u
sin 3 cos 3 0.935° C/ftœ¸
È3
##
"
ÈÈ
(b) (t) (sin 2t) (cos 2t) (t) (2 cos 2t) (2 sin 2t) and 2; rijv ijvœ Êœ œœkk dT T dx T
dt x dt y dt
dy
``
``
T T (D T) , where ; at we have from part (a)œœ œ œ ß œ™† ™†vvvu uij
Š‹ Š‹
kk kk
vv
vvkk kk ÈÈ
u""
## # #
33
sin 3 cos 3 2 3 sin 3 cos 3 1.87° C/secÊœ œ ¸
dT
dt
3
Š‹
ÈÈÈÈÈ
È
##
"†
24. (a) T (4x yz) xz xy T(8 6 4) 56 32 48 ; (t) 2t 3t t the particle is™™œ Ê ßßœ œ Êijk ijkr ijk
##
at the point P( 6 4) when t 2; (t) 4t 3 2t (2) 8 3 4 )ßß œ œ Ê œ Êœvijkvijku
v
vkk
D T(8 6 4) T [56 8 32 3 48 ( 4)] ° C/mœ Ê ßßœ œ œ
834 736
89 89 89 89 89
ÈÈÈ È È
ijk u
u™† †††
"
(b) T ( T ) at t 2, D T (2) 89 736° C/sec
dT T dx T dT 736
dt x dt y dt dt
dy
89
œœ œ Êœœ œ œ
``
`` ™† ™†vuv vkk ¸Š‹
È
ut2œÈ
25. (a) f( 0) 1, f (x y) 2x f (0 0) 0, f (x y) 2y f (0 0) 0 L(x y) 1 0(x 0) 0(y 0) 1!ßœ ßœ Ê ßœ ßœ Ê ßœÊ ßœ œ
xxyy
(b) f(1 1) 3, f (1 1) 2, f (1 1) 2 L(x y) 3 2(x 1) 2(y 1) 2x 2y 1ßœ ßœ ßœÊ ßœ œ
xy
26. (a) f( 0) 4, f (x y) 2(x y 2) f (0 0) 4, f (x y) 2(x y 2) f (0 0) 4!ßœ ßœ Ê ßœ ßœ Ê ßœ
xxyy
L(x y) 4 4(x 0) 4(y 0) 4x 4y 4Êßœœ
(b) f(1 2) 25, f (1 2) 10, f (1 2) 10 L(x y) 25 10(x 1) 10(y 2) 10x 10y 5ßœ ßœ ßœ Ê ßœ œ
xy
27. (a) f(0 0) 5, f (x y) 3 for all (x y), f (x y) 4 for all (x y) L(x y) 5 3(x 0) 4(y 0)ßœ ßœ ß ßœ ß Ê ßœ
xy
3x 4y 5œ
(b) f(1 1) 4, f (1 1) 3, f (1 1) 4 L(x y) 4 3(x 1) 4(y 1) 3x 4y 5ßœ ßœ ßœÊ ßœ œ
xy
28. (a) f(1 1) 1, f (x y) 3x y f (1 1) 3, f (x y) 4x y f (1 1) 4ßœ ßœ Ê ßœ ßœ Ê ßœ
xxyy
#% $$
L(x y) 1 3(x 1) 4(y 1) 3x 4y 6Êßœœ
(b) f(0 0) 0, f ( 0) 0, f (0 0) 0 L(x y) 0ßœ !ßœ ßœÊ ßœ
xy
29. (a) f(0 0) 1, f (x y) e cos y f (0 0) 1, f (x y) e sin y f (0 0) 0ßœ ßœ Ê ßœ ßœ Ê ßœ
xxy y
xx
L(x y) 1 1(x 0) 0(y 0) x 1Êßœœ
(b) f 0 0, f 0 0, f 0 1 L(x y) 0 0(x 0) 1 y y
ˆ‰ ˆ‰ ˆ‰ ˆ ‰
ßœ ßœ ßœÊ ßœ œ
111 11
### ##
xy
30. (a) f(0 0) 1, f (x y) e f ( ) 1, f (x y) 2e f (0 0) 2ßœ ßœ Ê !ß!œ ßœ Ê ßœ
xxyy
2y x 2y x
L(xy) 11(x0)2(y0) x2y1Êßœœ
(b) f(12) e, f(12) e, f(12) 2e L(xy) e e(x 1) 2e(y 2)ßœ ßœ ßœ Ê ßœ
$$$ $$$
xy
e x 2e y 2eœ
$$$

894 Chapter 14 Partial Derivatives
31. f(2 1) 3, f (x y) 2x 3y f (2 1) 1, f (x y) 3x f (2 1) 6 L(x y) 3 1(x 2) 6(y 1)ßœ ßœ Ê ßœ ßœ Ê ßœÊ ßœ
xxyy
7 x 6y; f (x y) 2, f (x y) 0, f (x y) 3 M 3; thus E(x y) (3) x 2 y 1œ ߜߜߜʜ ߟ
xx yy xy kk a b
ˆ‰ kkkk
"
#
#
(0.1 0.1) 0.06Ÿœ
ˆ‰
3
#
#
32. f(2 2) 11, f (x y) x y 3 f (2 2) 7, f (x y) x 3 f (2 2) 0ßœ ßœÊ ßœ ßœÊ ßœ
xxy y
y
#
L(x y) 11 7(x 2) 0(y 2) 7x 3; f (x y) 1, f (x y) , f (x y) 1Êßœœ ßœ ßœ ßœ
xx yy xy
"
#
M 1; thus E(x y) (1) x 2 y 2 (0.1 0.1) 0.02Ê œ ß Ÿ Ÿ œkk a b
ˆ‰ ˆ‰
kkkk
"
##
##
1
33. f(0 0) 1, f (x y) cos y f (0 0) 1, f (x y) 1 x sin y f (0 0) 1ßœ ßœ Ê ßœ ßœ Ê ßœ
xxy y
L(x y) 1 1(x 0) 1(y 0) x y 1; f (x y) 0, f (x y) x cos y, f (x y) sin y 1;Ê ßœ œ ßœ ßœ ßœ ÊQœ
xx yy xy
thus E(x y) (1) x y (0.2 0.2) 0.08kk a b
ˆ‰ ˆ‰
kk kkߟ Ÿ œ
"
##
##
1
34. f( ) 6, f (x y) y y sin (x 1) f (1 2) 4, f (x y) 2xy cos (x 1) f (1 2) 5"ß#œ ßœ Ê ßœ ßœ Ê ßœ
xxyy
#
L(x y) 6 4(x 1) 5(y 2) 4x 5y 8; f (x y) y cos (x 1), f (x y) 2x,Ê ßœ œ ßœ ßœ
xx yy
f (x y) 2y sin (x 1); x 1 0.1 0.9 x 1.1 and y 2 0.1 1.9 y 2.1; thus the max of
xy ßœ Ÿ Ê ŸŸ Ÿ Ê ŸŸkk kk
f (x y) on R is 2.1, the max of f (x y) on R is 2.2, and the max of f (x y) on R is 2(2.1) sin (0.9 1)kk kk kk
xx yy xy
ßß ß
4.3 M 4.3; thus E(x y) (4.3) x 1 y 2 (2.15)(0.1 0.1) 0.086Ÿ Ê œ ß Ÿ Ÿ œkk a b
ˆ‰ kkkk
"
#
##
35. f( 0) 1, f (x y) e cos y f (0 0) 1, f (x y) e sin y f (0 0) 0!ßœ ßœ Ê ßœ ßœ Ê ßœ
xxy y
xx
L(x y) 1 1(x 0) 0(y 0) 1 x; f (x y) e cos y, f (x y) e cos y, f (x y) e sin y;Ê ßœ œ ßœ ßœ ßœ
xx yy xy
xxx
x 0.1 0.1 x 0.1 and y 0.1 0.1 y 0.1; thus the max of f (x y) on R is e cos (0.1)kk kk k kŸÊŸŸ ŸÊŸŸ ß
xx 01Þ
1.11, the max of f (x y) on R is e cos (0.1) 1.11, and the max of f (x y) on R is e sin (0.1)Ÿß Ÿ ßkk kk
yy xy
01 01ÞÞ
0.12 M 1.11; thus E(x y) (1.11) x y (0.555)(0.1 0.1) 0.0222ŸÊœ ߟ Ÿ œkk a b
ˆ‰ kk kk
"
#
##
36. f(1 1) 0, f (x y) f (1 1) 1, f (x y) f (1 1) 1 L(x y) 0 1(x 1) 1(y 1)ßœ ßœ Ê ßœ ßœÊ ßœÊ ßœ
xxyy
xy
""
x y 2; f (x y) , f (x y) , f (x y) 0; x 1 0.2 0.98 x 1.2 so the max ofœ ß œ ß œ ß œ Ÿ Ê ŸŸ
xx yy xy
xy
""
kk
f (x y) on R is 1.04; y 1 0.2 0.98 y 1.2 so the max of f (x y) on R iskk kk kk
xx yy
(0.98)
ߟŸÊŸŸ ß
"
1.04 M 1.04; thus E(x y) (1.04) x 1 y 1 (0.52)(0.2 0.2) 0.0832
""
#
##
(0.98) Ÿ Ê œ ß Ÿ Ÿ œkk a b
ˆ‰ kkkk
37. (a) f( ) 3, f (1 1 1) y z 2, f (1 1 1) x z 2, f (1 1 1) y x 2"ß "ß " œ ß ß œ œ ß ß œ œ ß ß œ œkkk
xyz
111 111
111
ÐßßÑ ÐßßÑ
ÐßßÑ
L(x y z) 3 2(x 1) 2(y 1) 2(z 1) 2x 2y 2z 3Ê ßßœœ
(b) f(100) 0, f(100) 0, f(100) 1, f(100) 1 L(xyz) 0 0(x 1) (y 0) (z 0)ßßœ ßßœ ßßœ ßßœÊ ßßœ
xyz
yzœ
(c) f(000) 0, f(000) 0, f(000) 0, f(000) 0 L(xyz) 0ßß œ ßß œ ßß œ ßß œ Ê ßß œ
xyz
38. (a) f(1 1 1) 3, f (1 1 1) 2x 2, f (1 1 1) 2y 2, f (1 1 1) 2z 2ßßœ ßßœ œ ßßœ œ ßßœ œkkk
xyz
Ð"ß"ß"Ñ Ð"ß"ß"Ñ
Ð"ß"ß"Ñ
L(x y z) 3 2(x 1) 2(y 1) 2(z 1) 2x 2y 2z 3Ê ßßœœ
(b) f(0 1 0) 1, f (0 1 0) 0, f ( 1 0) 2, f (0 1 0) 0 L(x y z) 1 0(x 0) 2(y 1) 0(z 0)ßßœ ßßœ !ßßœ ßßœÊ ßßœ
xyz
2y 1œ
(c) f(1 0 0) 1, f (1 0 0) 2, f (1 0 0) 0, f (1 0 0) 0 L(x y z) 1 2(x 1) 0(y 0) 0(z 0)ßß œ ßß œ ßß œ ßß œ Ê ßß œ
xyz
2x 1œ
39. (a) f(1 0 0) 1, f (1 0 0) 1, f (1 0 0) 0,ßßœßßœ œßßœ œ
xy
x
xyz xyz
y
¹¹
ÈÈ
100 100
f (1 0 0) 0 L(x y z) 1 1(x 1) 0(y 0) 0(z 0) x
zz
xyz
ßßœ œÊ ßßœœ
¹
È 100

Section 14.6 Tangent Planes and Differentials 895
(b) f(110) 2, f(110) , f(110) , f(110) 0ßß œ ßß œ ßß œ ßß œ
Èxyz
22
""
ÈÈ
L(x y z) 2 (x 1) (y 1) 0(z 0) x yÊßßœœ
È"" ""
ÈÈ ÈÈ
22 22
(c) f(122) 3, f(122) , f(122) , f(122) L(xyz) 3 (x 1) (y 2) (z 2)ßß œ ßß œ ßß œ ßß œ Ê ßß œ
xyz
3 3 3 333
22 22""
xyzœ
"
333
22
40. (a) f 1 1 1, f 1 1 0, f 1 1 0,
ˆ‰ ˆ‰ ¸ ˆ‰ ¸
11 1
2z z
xy
y cos xy x cos xy
ßßœßßœ œßßœ œ
##
ß"ß" ß"ß"
ˆ‰ ˆ‰
f 1 1 1 L(x y z) 1 0 x 0(y 1) 1(z 1) 2 z
zsin xy
z
ˆ‰ ˆ‰
¹
1 1
# #
ß"ß"
ßß œ œ Ê ßß œ œ
ˆ‰
(b) f(2 0 1) 0, f (2 0 1) 0, f (2 0 1) 2, f (2 0 1) 0 L(x y z) 0 0(x 2) 2(y 0) 0(z 1) 2yßß œ ßß œ ßß œ ßß œ Ê ßß œ œ
xyz
41. (a) f(0 0 0) 2, f (0 0 0) e 1, f (0 0 0) sin (y z) 0,ßßœßßœ œßßœ œ
xy
xkk
Ð!ß!ß!Ñ Ð!ß!ß!Ñ
f (0 0 0) sin (y z) 0 L(x y z) 2 1(x 0) 0(y 0) 0(z 0) 2 x
zßßœ œÊ ßßœœkÐ!ß!ß!Ñ
(b) f 0 0 1, f 0 0 1, f 0 0 1, f 0 0 1 L(x y z)
ˆ‰ ˆ‰ ˆ‰ ˆ‰
ßß œ ßß œ ßß œ ßß œ Ê ßß
111 1
### #
xy z
11(x0)1y 1(z0)xyz 1œ œ
ˆ‰
11
2#
(c) f 0 1, f 0 1, f 0 1, f 0 1 L(x y z)
ˆ‰ ˆ‰ ˆ‰ ˆ‰
ßß œ ßß œ ßß œ ßß œ Ê ßß
11 11 11 11
44 44 44 44
xy z
11(x0)1y 1z xyz 1œ œ
ˆ‰ˆ‰
11 1
44 #
42. (a) f(1 0 0) 0, f (1 0 0) 0, f (1 0 0) 0,ßßœßßœ œßßœ œ
xy
yz
(xyz) 1 (xyz) 1
xz
¹¹
Ð"ß!ß!Ñ Ð"ß!ß!Ñ
f(100) 0 L(xyz) 0
zxy
(xyz) 1
ßß œ œ Ê ßß œ
¹
Ð"ß!ß!Ñ
(b) f(1 1 0) 0, f (1 1 0) 0, f (1 1 0) 0, f (1 1 0) 1 L(x y z) 0 0(x 1) 0(y 1) 1(z 0) zßß œ ßß œ ßß œ ßß œ Ê ßß œ œ
xyz
(c) f(111) , f(111) , f(111) , f(111) L(xyz) (x 1) (y 1) (z 1)ßß œ ßß œ ßß œ ßß œ Ê ßß œ
1 1
4 4
xyz
" " " """
# # # ###
xyzœ
"""
### #
1
4
3
43. f(x y z) xz 3yz 2 at P (1 1 2) f(1 1 2) 2; f z, f 3z, f x 3y L(x y z)ßß œ ßß Ê ßß œ œ œ œ Ê ßß
!xy z
2 2(x 1) 6(y 1) 2(z 2) 2x 6y 2z 6; f 0, f 0, f 0, f 0, f 3œœ œ œ œ œ œ
xx yy zz xy yz
M 3; thus, E(x y z) (3)(0.01 0.01 0.02) 0.0024Êœ ßߟ œkk
ˆ‰
"
#
#
44. f(x y z) x xy yz z at P (1 1 2) f(1 1 2) 5; f 2x y, f x z, f y zßß œ ßß Ê ßß œ œ œ œ
##
" "
!#4xyz
L(x y z) 5 3(x 1) 3(y 1) 2(z 2) 3x 3y 2z 5; f 2, f 0, f , f 1, f 0,Ê ßßœœ œ œ œ œ œ
xx yy zz xy xz
"
#
f 1 M 2; thus E(x y z) (2)(0.01 0.01 0.08) 0.01
yz œÊ œ ßß Ÿ œkk
ˆ‰
"
#
#
45. f(x y z) xy 2yz 3xz at P (1 1 0) f(1 1 0) 1; f y 3z, f x 2z, f 2y 3xßß œ ßß Ê ßß œ œ œ œ
!xyz
L(x y z) 1 (x 1) (y 1) (z 0) x y z 1; f 0, f 0, f 0, f 1, f 3,Ê ßßœœ œ œ œ œ œ
xx yy zz xy xz
f 2 M 3; thus E(x y z) (3)(0.01 0.01 0.01) 0.00135
yz œÊ œ ßß Ÿ œkk
ˆ‰
"
#
#
46. f(x y z) 2 cos x sin (y z) at P 0 0 f 0 0 1; f 2 sin x sin (y z),ßß œ ßß Ê ßß œ œ
ÈÈ
ˆ‰ˆ‰
!11
44
x
f 2 cos x cos (y z), f 2 cos x cos (y z) L(x y z) 1 0(x 0) (y 0) z
yz 4
œ œ Ê ßßœ
ÈÈ ˆ‰
1
y z 1; f 2 cos x sin (y z), f 2 cos x sin (y z), f 2 cos x sin (y z),œ œ œ œ
1
4xx yy zz
ÈÈÈ
f 2 sin x cos (y z), f 2 sin x cos (y z), f 2 cos x sin (y z). The absolute value of
xy xz yz
œ œ œ
ÈÈÈ
each of these second partial derivatives is bounded above by 2 M 2; thus E(x y z)
ÈÈ
kkÊœ ßß
2 (0.01 0.01 0.01) 0.000636.Ÿœ
ˆ‰
Š‹
È
"
#
#

896 Chapter 14 Partial Derivatives
47. T (x y) e e and T (x y) x e e dT T (x y) dx T (x y) dy
xy xy
yy yy
ßœ ßœ Ê œ ß ß
ab
e e dx x e e dy dT 2.5 dx 3.0 dy. If dx 0.1 and dy 0.02, then theœ Ê œ Ÿ Ÿabab k kk kk
yy yy ln 2
Ð#ß Ñ
maximum possible error in the computed value of T is (2.5)(0.1) (3.0)(0.02) 0.31 in magnitude.œ
48. V 2 rh and V r dV V dr V dh dr dh; now 100 1 and
rh rh
dV 2 rh dr r dh 2 dr
Vrhrh r
œœÊœÊœœ Ÿ11
#"11
1¸¸
†
100 1 100 2 (100) (100) 2 100 100 2(1) 1 3 3%
¸¸ ¸¸¸ ¸¸¸¸¸ˆ‰ ˆ‰
dh dV dr dh dr dh
hVrhrh
†† ††ŸÊ Ÿ Ÿ Ÿ œÊ
49. V 2 rh and V r dV V dr V dh dV 2 rh dr r dh dV 120 dr 25 dh;
rh rh 512
œœÊœÊœÊœ11 11 11
##
Ðß Ñ
k
dr 0.1 cm and dh 0.1 cm dV (120 )(0.1) (25 )(0.1) 14.5 cm ; V(5 12) 300 cmkk kkŸŸÊŸœßœ11 1 1
$$
maximum percentage error is 100 4.83%Ê„‚œ„
14.5
300
1
1
50. (a) dR dR dR dR dR dR
""" " " "
"# " #
##
RR R R R R
RR
RR
œ Ê œ Ê œ
Š‹ Š‹
(b) dR R dR dR dR R dR dR R will be moreœÊœÊ
##
"" ""
"# "#
ÐÑ
’“’“Š‹ Š‹ k
RR (100) (400)
100 400
sensitive to a variation in R since
"""
(100) (400)
(c) From part (a), dR dR dR so that R changing from 20 to 20.1 ohms dR 0.1 ohmœ Êœ
Š‹ Š‹
RR
RR
##
"#" "
and R changing from 25 to 24.9 ohms dR 0.1 ohms; R ohms
##
"""
Êœ œÊœ
RR R 9
100
dR (0.1) ( 0.1) 0.011 ohms percentage change is 100Êœ ¸ Ê ‚k¸
ÐÑ Ð
20 25 20 25
ˆ‰ ˆ‰
100 100
99
(20) (25) R
dR
100 0.1%œ‚¸
0.011
ˆ‰
100
9
51. A xy dA x dy y dx; if x y then a 1-unit change in y gives a greater change in dA than a 1-unitœÊ œ
change in x. Thus, pay more attention to y which is the smaller of the two dimensions.
52. (a) f (x y) 2x(y 1) f (1 0) 2 and f (x y) x f (1 0) 1 df 2 dx 1 dy df is more
xxyy
ßœ Ê ßœ ßœ Ê ßœÊ œ Ê
#
sensitive to changes in x
(b) df 0 2 dx dy 0 2 1 0 œÊ œÊ œÊ œ
dx dx
dy dy
"
#
53. (a) r x y 2r dr 2x dx 2y dy dr dx dy dr| 0.01 0.01
### Ð$ß%Ñ
œ Ê œ Ê œ Ê œ „ „
x34
rr 5 5
yˆ‰ ˆ‰
abab
0.014 100 100 0.28%; d dx dyœ„ œ„ Ê ‚ œ „ ‚ œ œ
0.07 dr 0.014
5r5 11
¸¸¸ ¸ )Š‹ Š‹
ˆ‰ ˆ‰
y
x
yy
xx
x
dx dy d | 0.01 0.01œ Êœ„„œ
#
Ð$ß%Ñ „
…
y
y x y x 25 25 25 5
x43 0.03
0.04
)ˆ‰ ˆ‰
abab
maximum change in d occurs when dx and dy have opposite signs (dx 0.01 and dy 0.01 or viceÊœœ)
versa) d 0.0028; tan 0.927255218 100 100Êœ ¸„ œ ¸ Ê ‚ œ ‚))
„ „
#
"
0.07 4 d 0.0028
5 3 0.927255218
ˆ‰ ¸ ¸ ¸ ¸
)
)
0.30%¸
(b) the radius r is more sensitive to changes in y, and the angle is more sensitive to changes in x)
54. (a) V r h dV 2 rh dr r dh at r 1 and h 5 we have dV 10 dr dh the volume isœÊœ Êœ œ œ Ê111 11
##
about 10 times more sensitive to a change in r
(b) dV 0 0 2 rh dr r dh 2h dr r dh 10 dr dh dr dh; choose dh 1.5œÊœ œœÊœ œ11
#"
10
dr 0.15 h 6.5 in. and r 0.85 in. is one solution for V dV 0Êœ Êœ œ ¸ œ?
55. f(a b c d) ad bc f d, f c, f b, f a df d da c db b dc a dd; since
ab
cd
ß ß ß œ œ Ê œ œ œ œ Ê œ
ºº ab c d
a is much greater than b , c , and d , the function f is most sensitive to a change in d.kk kkkk kk

Section 14.7 Extreme Values and Saddle Points 897
56. u e , u xe sin z, u y cos z du e dx xe sin z dy (y cos z) dz
xy z
yy y y
œœ œ Êœ ab
du 3 dx 7 dy 0 dz 3 dx 7 dy magnitude of the maximum possible errorÊ œœ Êk2ln3ßß
2
3(0.2) 7(0.6) 4.8Ÿœ
57. Q , Q , and Q
KM h
œœ œ
"" "
## #
"Î# "Î# "Î#
ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ ‰
2KM 2M 2KM 2K 2KM 2KM
hh hh h h
dQ dK dM dhʜ
"" "
## #
"Î# "Î# "Î#
ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ ‰
2KM 2M 2KM 2K 2KM 2KM
hh hh h h
dK dM dh dQœÊ
"
#
"Î#
ˆ‰ ‘ k
2KM2M2K 2KM
hhhh 22000.05
dK dM dh (0.0125)(800 dK 80 dM 32,000 dh)œœ
"
#
"Î#
’“’ “
(2)(2)(20) (2)(20) (2)(2) (2)(2)(20)
0.05 0.05 0.05 (0.05)
Q is most sensitive to changes in hÊ
58. A ab sin C A b sin C, A a sin C, A ab cos CœÊœ œ œ
""""
####
abc
dA b sin C da a sin C db ab cos C dC; dC 2° 0.0349 radians, da 0.5 ft,Êœ œœ œ
ˆ‰ˆ‰ˆ ‰ kk k k kk
"""
###
db 0.5 ft; at a 150 ft, b 200 ft, and C 60°, we see that the change is approximatelyœœœ œkk
dA (200)(sin 60°) 0.5 (150)(sin 60°) 0.5 (200)(150)(cos 60°) 0.0349 338 ftœ œ„
"""
###
#
kk kk k k
59. z f(x y) g(x y z) f(x y) z 0 g (x y z) f (x y), g (x y z) f (x y) and g (x y z) 1œ ß Ê ßß œ ß œ Ê ßß œ ß ßß œ ß ßß œ
xxyyz
g(x y f(x y)) f(x y), g(x y f(x y)) f(x y) and g(x y f(x y)) 1 the tangentÊ ßßß œ ß ßßß œ ß ßßß œÊ
xxyyz!! !! !! !! !! !! !! !!
plane at the point P is f (x y )(x x ) f (x y )(y y ) [z f(x y )] 0 or
!!! ! !! ! !!xy
ßßßœ
z f (x y )(x x ) f (x y )(y y ) f(x y )œß ß ß
xy!! ! !! ! !!
60. f 2x 2y 2(cos t t sin t) 2(sin t t cos t) and (t cos t) (t sin t) ™œœ œ Êœij i jv i ju
v
vkk
(cos t) (sin t) since t 0 (D f) fœœÊœ
(t cos t) (t sin t)
(t cos t) (t sin t) P
ij u
Èij u™†
2(cos t t sin t)(cos t) 2(sin t t cos t)(sin t) 2œ œ
61. f 2x 2y 2z (2 cos t) (2 sin t) 2t and ( sin t) (cos t) ™œ œ œ Êœijk i jkv i jku
v
vkk
(D f) fœœÊœ
( sin t) (cos t)
(sin t) (cos t) 1
sin t cos t
222 P
"
ijk u
ÈÈÈÈ
Š‹Š‹
ijk u™†
(2 cos t) (2 sin t) (2t) (D f) , (D f)(0) 0 andœœÊœœ
Š‹ Š‹ Š‹ ˆ‰
"sin t cos t 2t
2222 22
4
ÈÈÈÈ È
uu
11
(D f)
uˆ‰
11
422
œÈ
62. r t t (t 3) t t ; t 1 x 1, y 1, z 1 P (1 1 1)œÊœ œÊœœœÊœßß
ÈÈ
ij kv i jk
""""
##
"Î# "Î# !
44
and (1) ; f(x y z) x y z 3 0 f 2x 2yvijk ijkœ ßßœœÊ œ
"""
##
##
4™
f(1 1 1) 2 2 ; therefore ( f) the curve is normal to the surfaceÊ ßßœ œ Ê™™ijk v
"
4
63. r t t (2t 1) t t 2 ; t 1 x 1, y 1, z 1 P (1 1 1) andœ Êœ œÊœ œ œÊ œßß
ÈÈ
ij kv i jk
""
##
"Î# "Î# !
(1) 2 ; f(xyz) x y z 1 0 f 2x 2y f(111) 2 2 ;vijk ijk ijkœ ßßœ œÊ œ Ê ßßœ
""
##
## ™™
now 1 f 1 1 1 0, thus the curve is tangent to the surface when t 1vab a b†™ ßß œ œ
14.7 EXTREME VALUES AND SADDLE POINTS
1. f (x y) 2x y 3 0 and f (x y) x 2y 3 0 x 3 and y 3 critical point is ( 3 3);
xy
ß œ œ ß œ œ Ê œ œ Ê ß
f ( 3 3) 2, f ( 3 3) 2, f ( 3 3) 1 f f f 3 0 and f 0 local minimum of
xx yy xy xx yy xx
xy
ß œ ß œ ß œ Ê œ Ê
#
f( 3 3) 5ß œ

898 Chapter 14 Partial Derivatives
2. f (x y) 2x 3y 6 0 and f (x y) 3x 6y 3 0 x 15 and y 8 critical point is (15 8);
xy
ßœ œ ßœ œÊœ œÊ ß
f (15 8) 2, f (15 8) 6, f (15 8) 3 f f f 3 0 and f 0 local minimum of
xx yy xy xx yy xx
xy
ß œ ß œ ß œ Ê œ Ê
#
f(15 8) 63ß œ
3. f (x y) 2y 10x 4 0 and f (x y) 2x 4y 4 0 x and y critical point is ;
xy 24 24
33 33
ßœ œ ßœ œÊœ œÊ ß
ˆ‰
f 10, f 4, f 2 f f f 36 0 and f 0 local maximum of
xx yy xy xx yy xx
24 24 24
33 33 33 xy
ˆ‰ ˆ‰ ˆ‰
ßœ ßœ ßœÊ œ Ê
#
f0
ˆ‰
24
33
ߜ
4. f (x y) 2y 10x 4 0 and f (x y) 2x 4y 0 x and y critical point is ;
xy
42 42
99 99
ßœ œ ßœœÊœ œÊ ß
ˆ‰
f 10, f 4, f 2 f f f 36 0 and f 0 local maximum of
xx yy xy xx yy xx
42 42 42
99 99 99 xy
ˆ‰ ˆ‰ ˆ‰
ßœ ßœ ßœÊ œ Ê
#
f
ˆ‰
42 28
99 9
ߜ
5. f (x y) 2x y 3 0 and f (x y) x 2 0 x 2 and y 1 critical point is ( 2 1);
xy
ß œ œ ß œœ Ê œ œ Ê ß
f ( 2 1) 2, f ( 2 1) 0, f ( 2 1) 1 f f f 1 0 saddle point
xx yy xy xx yy xy
ß œ ß œ ß œ Ê œ Ê
#
6. f (x y) y 2 0 and f (x y) 2y x 2 0 x 2 and y 2 critical point is ( 2 2);
xy
ßœœ ßœ œÊœ œÊ ß
f ( 2 2) 0, f ( 2 2) 2, f ( 2 2) 1 f f f 1 0 saddle point
xx yy xy xx yy xy
ß œ ß œ ß œ Ê œ Ê
#
7. f (x y) 5y 14x 3 0 and f (x y) 5x 6 0 x and y critical point is ;
xy
669 669
55 525
ßœ œ ßœ œÊœ œ Ê ß
#ˆ‰
f 14, f 0, f 5 f f f 25 0 saddle point
xx yy xy xx yy
669 669 669
525 525 525 xy
ˆ‰ ˆ‰ ˆ‰
ßœ ßœ ßœÊ œÊ
#
8. f (x y) 2y 2x 3 0 and f (x y) 2x 4y 0 x 3 and y critical point is 3 ;
xy 33
2
ßœœ ßœœÊœ œÊ ß
#ˆ‰
f 3 2, f 3 4, f 3 2 f f f 4 0 and f 0 local maximum of
xx yy xy xx yy xx
333
222 xy
ˆ‰ ˆ‰ ˆ‰
ßœ ßœ ßœÊ œ Ê
#
f3
ˆ‰
ߜ
317
##
9. f (x y) 2x 4y 0 and f (x y) 4x 2y 6 0 x 2 and y 1 critical point is (2 1);
xy
ßœœ ßœœÊœ œÊ ß
f (2 1) 2, f (2 1) 2, f (2 1) 4 f f f 12 0 saddle point
xx yy xy xx yy xy
ßœ ßœ ßœÊ œÊ
#
10. f (x y) 6x 6y 2 0 and f (x y) 6x 14y 4 0 x and y critical point is ;
xy 13 3 13 3
14 124
ßœ œ ßœ œÊœ œÊ ß
#ˆ‰
f 6, f 14, f 6 f f f 48 0 and f 0 local minimum of
xx yy xy xx yy xx
13 3 13 3 13 3
14 14 14 xy
ˆ‰ ˆ‰ ˆ‰
## #
#
ß œ ß œ ß œ Ê œ Ê
f
ˆ‰
13 3 31
12 4 1
ß œ #
11. f (x y) 4x 3y 5 0 and f (x y) 3x 8y 2 0 x 2 and y 1 critical point is (2 1);
xy
ßœ œ ßœ œÊœ œÊ ß
f (2 1) 4, f (2 1) 8, f (2 1) 3 f f f 23 0 and f 0 local minimum of
xx yy xy xx yy xx
xy
ß œ ß œ ß œ Ê œ Ê
#
f(2 1) 6ß œ
12. f (x y) 8x 6y 20 0 and f (x y) 6x 10y 26 0 x 1 and y 2 critical point is (1 2);
xy
ßœ œ ßœ œÊœ œÊ ß
f (1 2) 8, f (1 2) 10, f (1 2) 6 f f f 44 0 and f 0 local minimum of
xx yy xy xx yy xx
xy
ß œ ß œ ß œ Ê œ Ê
#
f(1 2) 36ß œ
13. f (x y) 2x 2 0 and f (x y) 2y 4 0 x 1 and y 2 critical point is (1 2); f (1 2) 2,
xy xx
ßœ œ ßœœÊœ œÊ ß ßœ
f (1 2) 2, f (1 2) 0 f f f 4 0 saddle point
yy xy xx yy xy
ßœ ßœÊ œÊ
#
14. f (x y) 2x 2y 2 0 and f (x y) 2x 4y 2 0 x 1 and y 0 critical point is (1 0);
xy
ßœœ ßœœÊœ œÊ ß
f (1 0) 2, f (1 0) 4, f (1 0) 2 f f f 4 0 and f 0 local minimum of
xx yy xy xx yy xx
xy
ßœ ßœ ßœÊ œ Ê
#
f(1 0) 0ߜ

Section 14.7 Extreme Values and Saddle Points 899
15. f (x y) 2x 2y 0 and f (x y) 2x 0 x 0 and y 0 critical point is (0 0); f (0 0) 2,
xy xx
ßœ œ ßœ œÊœ œÊ ß ßœ
f (0 0) 0, f (0 0) 2 f f f 4 0 saddle point
yy xy xx yy xy
ßœ ßœÊ œÊ
#
16. f (x y) 2 4x 2y 0 and f (x y) 2 2x 2y 0 x 0 and y 1 critical point is (0 1);
xy
ßœ œ ßœ œÊœ œÊ ß
f (0 1) 4, f (0 1) 2, f (0 1) 2 f f f 4 0 and f 0 local maximum of f(0 1) 4
xx yy xy xx yy xx
xy
ßœ ßœ ßœÊ œ Ê ßœ
#
17. f (x y) 3x 2y 0 and f (x y) 3y 2x 0 x 0 and y 0, or x and y critical points
xy 22
33
ßœ œ ßœ œÊœ œ œ œÊ
##
are (0 0) and ; for (0 0): f (0 0) 6x 0, f (0 0) 6y 0, f (0 0) 2ß ß ß ßœ œßœœßœ
ˆ‰ kk
22
33 xx yy xy
00 00
ÐßÑ ÐßÑ
f f f 4 0 saddle point; for : f 4, f 4, f 2Ê œ Ê ß ß œ ß œ ß œ
xx yy xx yy xy
xy 22 22 22 22
33 33 33 33
#ˆ‰ˆ‰ ˆ‰ ˆ‰
f f f 12 0 and f 0 local maximum of fÊœ Ê ßœ
xx yy xx
xy 2 2 170
33 27
#ˆ‰
18. f (x y) 3x 3y 0 and f (x y) 3x 3y 0 x 0 and y 0, or x 1 and y 1 critical points
xy
ßœ œ ßœ œÊœ œ œ œÊ
##
are (0 0) and ( 1 1); for ( ): f (0 0) 6x 0, f (0 0) 6y 0, f (0 0) 3 f f fß ß !ß ! ß œ œ ß œ œ ß œ Ê kk
xx yy xy xx yy
00 00 xy
ÐßÑ ÐßÑ #
9 0 saddle point; for ( 1 1): f ( 1 1) 6, f ( 1 1) 6, f ( 1 1) 3 f f fœ Ê ß ß œ ß œ ß œ Ê
xx yy xy xx yy xy
#
27 0 and f 0 local maximum of f( 1 1) 1œ Ê ßœ
xx
19. f (x y) 12x 6x 6y 0 and f (x y) 6y 6x 0 x 0 and y 0, or x 1 and y 1 critical
xy
ßœ œ ßœœÊœ œ œ œÊ
#
points are (0 0) and (1 1); for ( ): f (0 0) 12 12x 12, f (0 0) 6, f (0 0) 6 f f fß ß !ß! ßœ œ ßœ ßœÊ k
xx yy xy xx yy
00 xy
ÐßÑ #
36 0 and f 0 local minimum of f(0 0) 0; for (1 1): f (1 1) 0, f (1 1) 6,œ Ê ß œ ß ß œ ß œ
xx xx yy
f (1 1) 6 f f f 36 0 saddle point
xy xx yy xy
ß œ Ê œ Ê
#
20. f (x y) 6x 6y 0 x y; f (x y) 6y 6y 6x 0 12y 6y 0 6y(2 y) 0 y 0 or
xy
ßœœÊœ ßœ œÊ œÊ œÊœ
##
y 2 (0 0) and (2 2) are the critical points; f (x y) 6, f (x y) 6 12y, f (x y) 6; for (0 0):œÊß ß ßœ ßœ ßœ ß
xx yy xy
f (0 0) 6, f (0 0) 6, f (0 0) 6 f f f 72 0 saddle point; for (2 2): f (2 2) 6,
xx yy xy xx yy xx
xy
ßœ ßœ ßœÊ œÊ ß ßœ
#
f (2 2) 18, f (2 2) 6 f f f 72 0 and f 0 local maximum of f(2 2) 8
yy xy xx yy xx
xy
ßœ ßœÊ œ Ê ßœ
#
21. f (x y) 27x 4y 0 and f (x y) y 4x 0 x 0 and y 0, or x and y critical points are
xy 44
93
ßœ œ ßœ œÊœ œ œ œ Ê
##
(0 0) and ; for ( ): f (0 0) 54x 0, f (0 0) 2y 0, f (0 0) 4 f f fßß!ß!ßœœßœœßœÊ
ˆ‰ kk
44
93 xx yy xy xx yy
00 00 xy
ÐßÑ ÐßÑ #
16 0 saddle point; for : f 24, f , f 4 f f f 48 0œ Ê ß ß œ ß œ ß œ Ê œ
ˆ‰ ˆ‰ ˆ‰ ˆ‰
44 44 44 8 44
93 93 93 3 93
xx yy xy xx yy xy
#
and f 0 local minimum of f
xx 44 64
93 81
Ê ß œ
ˆ‰
22. f (x y) 24x 6y 0 y 4x ; f (x y) 3y 6x 0 3 4x 6x 0 16x 2x 0
xy
ßœ œÊœ ßœ œÊ œÊ œ
####%
#
ab
2x 8x 1 0 x 0 or x ( 0) and 1 are the critical points; f (x y) 48x,Ê œ Ê œ œ Ê !ß ß ß œab ˆ‰
$""
## xx
f (x y) 6y, and f (x y) 6; for (0 0): f (0 0) 0, f (0 0) 0, f (0 0) 6 f f f 36 0
yy xy xx yy xy xx yy xy
ßœ ßœ ß ßœ ßœ ßœÊ œ
#
saddle point; for 1 : f 1 24, f 1 6, f 1 6Ê ß ß œ ß œ ß œ
ˆ‰ˆ‰ ˆ‰ ˆ‰
11 1 1
22 2 2
xx yy xy
f f f 108 0 and f 0 local maximum of f 1 1Êœ Ê ßœ
xx yy xx
xy 1
2
#ˆ‰
23. f (x y) 3x 6x 0 x 0 or x 2; f (x y) 3y 6y 0 y 0 or y 2 the critical points are
xy
ßœ œÊœ œ ßœ œÊœ œÊ
##
(0 0), (0 2), ( 2 0), and ( 2 2); for ( ): f (0 0) 6x 6 6, f (0 0) 6y 6 6,ß ß ß ß !ß! ß œ œ ß œ œkk
xx yy
00 00
ÐßÑ ÐßÑ
f (0 0) 0 f f f 36 0 saddle point; for (0 2): f (0 2) 6, f (0 2) 6, f (0 2) 0
xy xx yy xx yy xy
xy
ßœÊœÊ ß ßœßœßœ
#
f f f 36 0 and f 0 local minimum of f(0 2) 12; for ( 2 0): f ( 2 0) 6,Ê œ Ê ßœ ß ßœ
xx yy xx xx
xy
#
f ( 2 0) 6, f ( 2 0) 0 f f f 36 0 and f 0 local maximum of f( 2 0) 4;
yy xy xx yy xx
xy
ß œ ß œ Ê œ Ê ß œ
#
for ( 2 2): f ( 2 2) 6, f ( 2 2) 6, f ( 2 2) 0 f f f 36 0 saddle pointß ß œ ß œ ß œ Ê œ Ê
xx yy xy xx yy xy
#
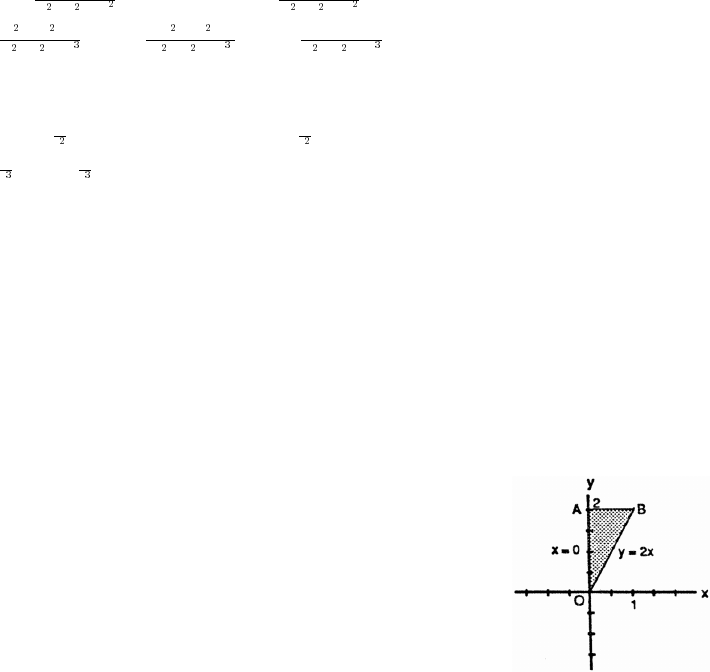
900 Chapter 14 Partial Derivatives
24. f (x y) 6x 18x 0 6x(x 3) 0 x 0 or x 3; f (x y) 6y 6y 12 0 6(y 2)(y 1) 0
x y
ßœ œÊ œÊœ œ ßœ œÊ œ
# #
y 2 or y 1 the critical points are (0 2), (0 1), (3 2), and (3 1); f (x y) 12x 18,Êœ œÊ ß ß ß ß ßœ
xx
f (x y) 12y 6, and f (x y) 0; for ( 2): f (0 2) 18, f (0 2) 18, f (0 2) 0
yy xy xx yy xy
ß œ ß œ !ß ß œ ß œ ß œ
f f f 324 0 and f 0 local maximum of f(0 2) 20; for (0 1): f (0 1) 18,Êœ Ê ßœ ß ßœ
xx yy xx xx
xy
#
f (0 1) 18, f (0 1) 0 f f f 324 0 saddle point; for (3 2): f (3 2) 18,
yy xy xx yy xx
xy
ßœ ßœ Ê œ Ê ß ßœ
#
f (3 2) 18, f (3 2) 0 f f f 324 0 saddle point; for (3 1): f (3 1) 18,
yy xy xx yy xx
xy
ß œ ß œ Ê œ Ê ß ß œ
#
f (3 1) 18, f (3 1) 0 f f f 324 0 and f 0 local minimum of f(3 1) 34
yy xy xx yy xx
xy
ßœ ßœÊ œ Ê ßœ
#
25. f (x y) 4y 4x 0 and f (x y) 4x 4y 0 x y x 1 x 0 x 0, 1, 1 the critical
xy
ßœ œ ßœ œÊœÊ œÊœ Ê
$$ #
ab
points are (0 0), (1 1), and ( 1 1); for ( ): f (0 0) 12x 0, f (0 0) 12y 0,ß ß ß !ß! ßœ œ ßœ œkk
xx yy
00 00
##
ÐßÑ ÐßÑ
f (0 0) 4 f f f 16 0 saddle point; for (1 1): f (1 1) 12, f (1 1) 12, f (1 1) 4
xy xx yy xx yy xy
xy
ß œ Ê œ Ê ß ß œ ß œ ß œ
#
f f f 128 0 and f 0 local maximum of f(1 1) 2; for ( 1 1): f ( 1 1) 12,Êœ Ê ßœ ßßœ
xx yy xx xx
xy
#
f ( 1 1) 12, f ( 1 1) 4 f f f 128 0 and f 0 local maximum of f( 1 1) 2
yy xy xx yy xx
xy
ß œ ß œ Ê œ Ê ß œ
#
26. f (x y) 4x 4y 0 and f (x y) 4y 4x 0 x y x x 0 x 1 x 0 x 0, 1, 1
xy
ßœ œ ßœ œÊœÊœÊ œÊœ
$$ $#
ab
the critical points are (0 0), (1 1), and ( 1 1); f (x y) 12x , f (x y) 12y , and f (x y) 4;Ê ß ß ß ßœ ßœ ßœ
xx yy xy
##
for ( 0): f (0 0) 0, f (0 0) 0, f (0 0) 4 f f f 16 0 saddle point; for (1 1):!ß ßœ ßœ ßœÊ œÊ ß
xx yy xy xx yy xy
#
f (1 1) 12, f (1 1) 12, f (1 1) 4 f f f 128 0 and f 0 local minimum of
xx yy xy xx yy xx
xy
ß œ ß œ ß œ Ê œ Ê
#
f( 1) 2; for ( 1 1): f ( 1 1) 12, f ( 1 1) 12, f ( 1 1) 4 f f f 128 0 and"ßœßߜߜߜʜ
xx yy xy xx yy xy
#
f 0 local minimum of f( 1 1) 2
xx Ê ßœ
27. f (x y) 0 and f (x y) 0 x 0 and y 0 the critical point is ( 0);
xy
2x
xy1 xy1
2y
ßœ œ ßœ œÊœ œÊ !ß
ab ab
f , f , f ; f ( ) 2, f (0 0) 2, f (0 0) 0
xx yy xy xx yy xy
4x 2y 2 2x 4y 2 8xy
xy1 xy1 xy1
œœ œ!ß!œßœßœ
ab ab ab
f f f 4 0 and f 0 local maximum of f(0 0) 1Êœ Ê ßœ
xx yy xx
xy
#
28. f (x y) y 0 and f (x y) x 0 x 1 and y 1 the critical point is (1 1);
xy
11
xy
ßœœ ßœ œÊœ œÊ ß
f , f , f 1; f (1 1) 2, f (1 1) 2, f (1 1) 1 f f f 3 0 and f 2 local
xx yy xy xx yy xy xx yy xx
22
xy xy
œ œ œ ßœ ßœ ßœÊ œ Ê
#
minimum of f(1 1) 3ߜ
29. f (x y) y cos x 0 and f (x y) sin x 0 x n , n an integer, and y 0 the critical points are
xy
ßœ œ ßœ œÊœ œÊ1
(n 0), n an integer (Note: cos x and sin x cannot both be 0 for the same x, so sin x must be 0 and y 0);1ß œ
f y sin x, f 0, f cos x; f (n 0) 0, f (n 0) 0, f (n 0) 1 if n is even and f (n 0) 1
xx yy xy xx yy xy xy
œ œ œ ßœ ßœ ßœ ßœ111 1
if n is odd f f f 1 0 saddle point.ÊœÊ
xx yy xy
#
30. f (x y) 2e cos y 0 and f (x y) e sin y 0 no solution since e 0 for any x and the functions
xy
2x 2x 2x
ßœ œ ßœ œÊ Á
cos y and sin y cannot equal 0 for the same y no critical points no extrema and no saddle pointsÊÊ
31. (i) On OA, f(x y) f(0 y) y 4y 1 on 0 y 2;ßœ ßœ ŸŸ
#
f (0 y) 2y 4 0 y 2;
wßœ œÊœ
f(0 0) 1 and f( ) 3ß œ !ß # œ
(ii) On AB, f(x y) f(x 2) 2x 4x 3 on 0 x 1;ßœ ßœ ŸŸ
#
f (x 2) 4x 4 0 x 1;
wßœ œÊœ
f(0 2) 3 and f(1 ) 5ßœ ß#œ
(iii) On OB, f(x y) f(x 2x) 6x 12x 1 onßœ ß œ
#
0 x 1; endpoint values have been found above;ŸŸ
f (x 2x) 12x 12 0 x 1 and y 2, but ( ) is not an interior point of OB
wßœ œÊœ œ "ß#
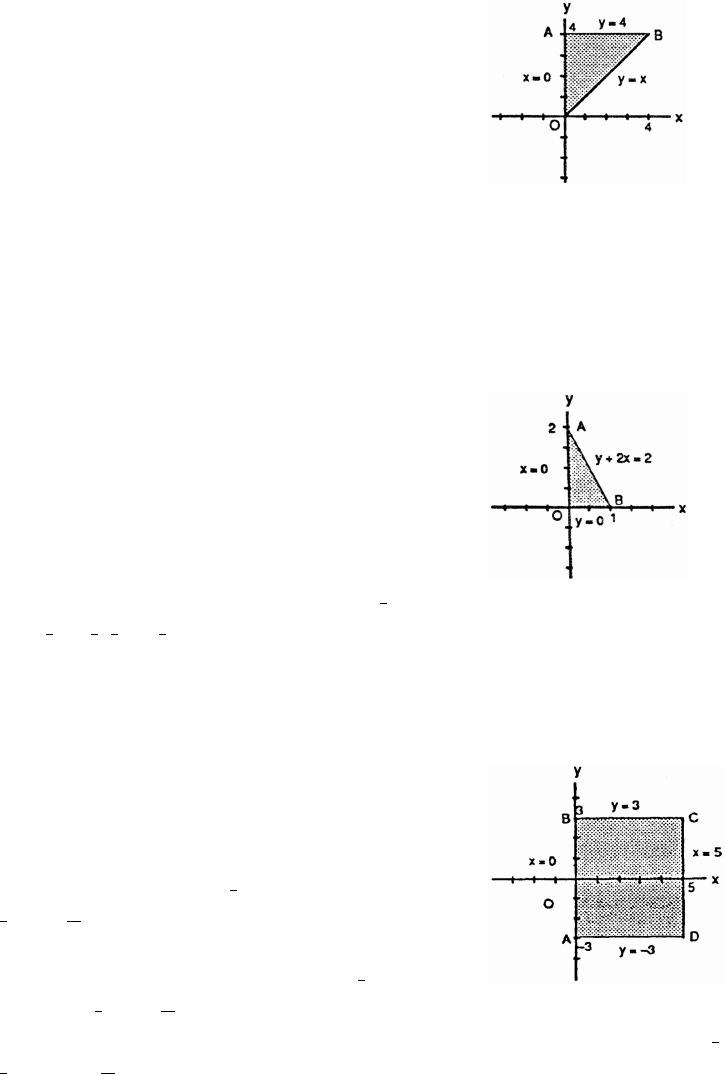
Section 14.7 Extreme Values and Saddle Points 901
(iv) For interior points of the triangular region, f (x y) 4x 4 0 and f (x y) 2y 4 0
xy
ßœ œ ßœ œ
x 1 and y 2, but (1 2) is not an interior point of the region. Therefore, the absolute maximum isÊœ œ ß
1 at (0 0) and the absolute minimum is 5 at ( ).ß "ß #
32. (i) On OA, D(x y) D(0 y) y 1 on 0 y 4;ßœ ßœ ŸŸ
#
D(0y)2y0 y0; D( )1 and
wßœ œÊœ !ß!œ
D( ) 17!ß % œ
(ii) On AB, D(x y) D(x 4) x 4x 17 onߜ ߜ
#
0 x 4; D (x 4) 2x 4 0 x 2 and (2 4)ŸŸ ß œ œ Ê œ ß
w
is an interior point of AB; D( ) 13 and#ß % œ
D( ) D( ) 17%ß % œ !ß % œ
(iii) On OB, D(x y) D(x x) x 1 on 0 x 4;ßœ ßœ ŸŸ
#
D (x x) 2x 0 x 0 and y 0, which is not an interior point of OB; endpoint values have been found
wßœ œÊœ œ
above
(iv) For interior points of the triangular region, f (x y) 2x y 0 and f (x y) x 2y 0 x 0 and y 0,
xy
ßœ œ ßœ œÊœ œ
which is not an interior point of the region. Therefore, the absolute maximum is 17 at ( ) and ( ), and the!ß % %ß %
absolute minimum is 1 at (0 0).ß
33. (i) On OA, f(x y) f( y) y on 0 y 2;ß œ !ß œ Ÿ Ÿ
#
f (0 y) 2y 0 y 0 and x 0; f(0 0) 0 and
wßœ œÊœ œ ßœ
f(0 ) 4ß# œ
(ii) On OB, f(x y) f(x 0) x on 0 x 1;ßœ ßœ ŸŸ
#
f (x 0) 2x 0 x 0 and y 0; f(0 0) 0 and
wßœ œÊœ œ ßœ
f(1 0) 1ߜ
(iii) On AB, f(x y) f(x 2x 2) 5x 8x 4 onߜ ߜ
#
0x1; f(x2x2)10x80 xŸŸ ß œ œÊœ
w4
5
and y ; f ; endpoint values have been found above.œßœ
242 4
555 5
ˆ‰
(iv) For interior points of the triangular region, f (x y) 2x 0 and f (x y) 2y 0 x 0 and y 0, but ( 0) is
xy
ßœ œ ßœ œÊœ œ !ß
not an interior point of the region. Therefore the absolute maximum is 4 at (0 2) and the absolute minimum is 0 atß
(0 0).ß
34. (i) On AB, T(x y) T( y) y on 3 y 3;ßœ!ßœ ŸŸ
#
T(0y)2y0 y0 and x0; T(00)0,
wßœ œÊœ œ ßœ
T( 3) 9, and T( 3) 9!ß œ !ß œ
(ii) On BC, T(x y) T(x 3) x 3x 9 on 0 x 5;ßœ ßœ ŸŸ
#
T (x 3) 2x 3 0 x and y 3;
w
#
ßœ œÊœ œ
3
T 3 and T(5 3) 19
ˆ‰
327
4#ߜ ߜ
(iii) On CD, T(x y) T(5 y) y 5y 5 onߜ ߜ
#
3 y 3;T (5 y) 2y 5 0 y andŸ Ÿ ß œ œ Ê œ
w
#
5
x 5;T 5 , T( 3) 11 and T(5 3) 19œßœ&ßœ ßœ
ˆ‰
545
4#
(iv) On AD, T(x y) T(x 3) x 9x 9 on 0 x 5; T (x 3) 2x 9 0 x and y 3;ߜߜŸŸßœœÊœ œ
#w
#
9
T 3 , T( 3) 9 and T( 3) 11
ˆ‰
945
4#ß œ !ß œ &ß œ
(v) For interior points of the rectangular region, T (x y) 2x y 6 0 and T (x y) x 2y 0 x 4
xy
ßœ œ ßœ œÊœ
and y 2 (4 2) is an interior critical point with T(4 2) 12. Therefore the absolute maximumœ Ê ß ß œ
is 19 at (5 3) and the absolute minimum is 12 at (4 2).ßß

902 Chapter 14 Partial Derivatives
35. (i) On OC, T(x y) T(x 0) x 6x 2 onߜ ߜ
#
0x5; T(x0)2x60 x3 andŸŸ ß œ œ Ê œ
w
y 0; T(3 0) 7, T(0 0) 2, and T(5 0) 3œ ßœ ßœ ßœ
(ii) On CB, T(x y) T(5 y) y 5y 3 onߜ ߜ
#
3 y 0; T (5 y) 2y 5 0 y andŸ Ÿ ß œ œ Ê œ
w
#
5
x 5; T 5 and T(5 3) 9œßœ ßœ
ˆ‰
537
4#
(iii) On AB, T(x y) T(x 3) x 9x 11 onߜ ߜ
#
0x5; T(x3)2x9 0 x andŸŸ ßœ œ Ê œ
w
#
9
y 3; T 3 and T( 3) 11œ ß œ !ß œ
ˆ‰
937
4#
(iv) On AO, T(x y) T( y) y 2 on 3 y 0; T (0 y) 2y 0 y 0 and x 0, but (0 0) isßœ!ßœ ŸŸ ßœ œÊœ œ ß
#w
not an interior point of AO
(v) For interior points of the rectangular region, T (x y) 2x y 6 0 and T (x y) x 2y 0 x 4
xy
ßœ œ ßœ œÊœ
and y 2, an interior critical point with T( 2) 10. Therefore the absolute maximum is 11 atœ %ß œ
( 3) and the absolute minimum is 10 at (4 2).!ß ß
36. (i) On OA, f(x y) f( y) 24y on 0 y 1;ßœ!ßœ ŸŸ
#
f (0 y) 48y 0 y 0 and x 0, but (0 0) is
wßœ œÊœ œ ß
not an interior point of OA; f( 0) 0 and!ß œ
f( 1) 24!ß œ
(ii) On AB, f(x y) f(x 1) 48x 32x 24 onߜ ߜ
$
0 x 1; f (x 1) 48 96x 0 x andŸŸ ß œ œ Ê œ
w#
"
È2
y 1, or x and y 1, but 1 is not inœœ œ ß
""
ÈÈ
22
Š‹
the interior of AB; f 1 16 2 24 and f(1 1) 8
Š‹È
"
È2ßœ ßœ
(iii) On BC, f(x y) f( y) 48y 32 24y on 0 y 1; f ( y) 48 48y 0 y 1 and x 1, butßœ"ßœ ŸŸ "ßœ œÊœ œ
#w
( ) is not an interior point of BC; f( 0) 32 and f( ) 8"ß " "ß œ "ß " œ
(iv) On OC, f(x y) f(x 0) 32x on 0 x 1; f (x 0) 96x 0 x 0 and y 0, but (0 0) is not anßœ ßœ ŸŸ ßœ œÊœ œ ß
$w#
interior point of OC; f( 0) 0 and f( 0) 32!ß œ "ß œ
(v) For interior points of the rectangular region, f (x y) 48y 96x 0 and f (x y) 48x 48y 0
xy
ßœ œ ßœ œ
#
x 0 and y 0, or x and y , but (0 0) is not an interior point of the region; f 2.Êœ œ œ œ ß ß œ
"" ""
## ##
ˆ‰
Therefore the absolute maximum is 2 at and the absolute minimum is 32 at (1 0).
ˆ‰
""
##
ßß
37. (i) On AB, f(x y) f(1 y) 3 cos y on y ;ßœ ßœ ŸŸ
11
44
f (1 y) 3 sin y 0 y 0 and x 1;
wßœ œÊœ œ
f( 0) 3, f 1 , and f 1"ߜ ߜ ߜ
ˆ‰ ˆ‰
11
44
32 32
ÈÈ
##
(ii) On CD, f(x y) f( y) 3 cos y on y ;ßœ$ßœ ŸŸ
11
44
f (3 y) 3 sin y 0 y 0 and x 3;
wßœ œÊœ œ
f(3 0) 3, f 3 and f 3ßœ ß œ ß œ
ˆ‰ ˆ‰
11
44
32 32
ÈÈ
##
(iii) On BC, f(x y) f x 4x x onßœ ß œ
ˆ‰ ab
1
4
2
È
#
#
1 x 3; f x 2(2 x) 0 x 2 and y ; f 2 2 2, f 1 , andŸŸ ß œ œ Ê œ œ ß œ ß œ
w
#
ˆ‰ ˆ‰ ˆ‰
ÈÈ
1111
4444
32
È
f3
ˆ‰
ߜ
1
4
32
È
#
(iv) On AD, f(x y) f x 4x x on 1 x 3; f x 2(2 x) 0 x 2 and y ;ß œ ß œ Ÿ Ÿ ß œ œ Ê œ œ
ˆ‰ ˆ‰
ab È
11 1
44 4
2
È
#
#w
f 2 2 2, f 1 , and f 3
ˆ‰ ˆ‰ ˆ‰
È
ß œ ß œ ß œ
11 1
44 4
32 32
ÈÈ
##
(v) For interior points of the region, f (x y) (4 2x) cos y 0 and f (x y) 4x x sin y 0 x 2
xy
ßœ œ ßœ œÊœab
#
and y 0, which is an interior critical point with f(2 0) 4. Therefore the absolute maximum is 4 atœßœ

Section 14.7 Extreme Values and Saddle Points 903
(2 0) and the absolute minimum is at 3 , 3 , 1 , and 1 .ß ßßß ß
32
44 4 4
È
#ˆ‰ˆ‰ˆ‰ˆ‰
11 1 1
38. (i) On OA, f(x y) f( y) 2y 1 on 0 y 1;ßœ!ßœ ŸŸ
f (0 y) 2 no interior critical points; f(0 0) 1
wßœÊ ßœ
and f(0 1) 3ߜ
(ii) On OB, f(x y) f(x 0) 4x 1 on 0 x 1;ßœ ßœ ŸŸ
f (x 0) 4 no interior critical points; f(1 0) 5
wßœÊ ßœ
(iii) On AB, f(x y) f(x x 1) 8x 6x 3 onߜ ߜ
#
0x1; f(xx1)16x60 xŸŸ ß œ œ Ê œ
w3
8
and y ; f , f(0 1) 3, and f( 0) 5œßœßœ "ßœ
535 15
888 8
ˆ‰
(iv) For interior points of the triangular region, f (x y) 4 8y 0 and f (x y) 8x 2 0
xy
ßœ œ ßœœ
y and x which is an interior critical point with f 2. Therefore the absolute maximum is 5 atÊœ œ ß œ
"" ""
##44
ˆ‰
(1 0) and the absolute minimum is 1 at ( 0).ß!ß
39. Let F(a b) 6 x x dx where a b. The boundary of the domain of F is the line a b in theßœ Ÿ œ
'a
bab
#
ab-plane, and F(a a) 0, so F is identically 0 on the boundary of its domain. For interior critical points weߜ
have: 6 a a 0 a 3, 2 and 6 b b 0 b 3, 2. Since a b, there is only
``
``
##
FF
ab
œ œ Ê œ œ œ Ê œ Ÿab ab
one interior critical point ( 3 2) and F( 3 2) 6 x x dx gives the area under the parabolaß ß œ
'3
2ab
#
y 6 x x that is above the x-axis. Therefore, a 3 and b 2.œ œ œ
#
40. Let F(a b) 24 2x x dx where a b. The boundary of the domain of F is the line a b andßœ Ÿ œ
'a
bab
#"Î$
on this line F is identically 0. For interior critical points we have: 24 2a a 0 a 4, 6
`
`
#"Î$
F
aœ œ Ê œ ab
and 24 2b b 0 b 4, 6. Since a b, there is only one critical point ( 6 4) and
`
`
#"Î$
F
bœ œÊœ Ÿ ßab
F( 6 4) 24 2x x dx gives the area under the curve y 24 2x x that is above the x-axis.ß œ œ
'6
4ab ab
##
"Î$
Therefore, a 6 and b 4.œ œ
41. T (x y) 2x 1 0 and T (x y) 4y 0 x and y 0 with T 0 ; on the boundary
xy 4
ßœ œ ßœ œÊœ œ ß œ
"""
##
ˆ‰
x y 1: T(x y) x x 2 for 1 x 1 T (x y) 2x 1 0 x and y ;
## # w "
##
œ ßœ ŸŸÊ ßœœÊœ œ„
È3
T , T , T( 1 0) 2, and T( 0) 0 the hottest is 2 ° at and
Š‹Š ‹ Š‹
ß œ ß œ ß œ "ß œ Ê ß
"" ""
## # # ##
ÈÈ È
33 3
99
44 4
; the coldest is ° at 0 .
Š‹ ˆ‰
ß ß
"""
## #
È3
4
42. f (x y) y 2 0 and f (x y) x 0 x and y 2; f 2 8,
xy xx
2 2
xy x
2
ßœœ ßœœÊœ œ ß œ œ
"" "
##
ß
ˆ‰ ¸
ˆ‰
1
2
f 2 , f 2 1 f f f 1 0 and f 0 a local minimum of f 2
¹
ˆ‰ ˆ‰ ˆ‰
yy xy xx yy xx
y4
2xy
"" "" "
## #
ß
#
ßœ œ ßœÊ œ Ê ß
ˆ‰
1
2
2 ln 2 ln 2œ œ
"
#
43. (a) f (x y) 2x 4y 0 and f (x y) 2y 4x 0 x 0 and y 0; f (0 0) 2, f (0 0) 2,
x y xx yy
ßœœ ßœœÊœ œ ßœ ßœ
f (0 0) 4 f f f 12 0 saddle point at (0 0)
xy xx yy xy
ßœÊ œÊ ß
#
(b) f (x y) 2x 2 0 and f (x y) 2y 4 0 x 1 and y 2; f (1 2) 2, f (1 2) 2,
x y xx yy
ßœ œ ßœ œÊœ œ ßœ ßœ
f (1 2) 0 f f f 4 0 and f 0 local minimum at ( )
xy xx yy xx
xy
ß œ Ê œ Ê "ß #
#
(c) f (x y) 9x 9 0 and f (x y) 2y 4 0 x 1 and y 2; f (1 2) 18x 18,
xy xx
12
ßœ œ ßœ œÊœ„ œ ßœ œ
#ÐßÑ
k
f (1 2) 2, f (1 2) 0 f f f 36 0 and f 0 local minimum at ( );
yy xy xx yy xx
xy
ß œ ß œ Ê œ Ê "ß#
#
f ( 1 2) 18, f ( 2) 2, f ( 2) 0 f f f 36 0 saddle point at ( 2)
xx yy xy xx yy xy
ß œ "ß œ "ß œ Ê œ Ê "ß
#
904 Chapter 14 Partial Derivatives
44. (a) Minimum at (0 0) since f(x y) 0 for all other (x y)ßß ß
(b) Maximum of 1 at ( ) since f(x y) 1 for all other (x y)!ß ! ß ß
(c) Neither since f(x y) 0 for x 0 and f(x y) 0 for x 0ß ß
(d) Neither since f(x y) 0 for x 0 and f(x y) 0 for x 0ß ß
(e) Neither since f(x y) 0 for x 0 and y 0, but f(x y) 0 for x 0 and y 0ß ß
(f) Minimum at (0 0) since f(x y) 0 for all other (x y)ßß ß
45. If k 0, then f(x y) x y f (x y) 2x 0 and f (x y) 2y 0 x 0 and y 0 ( 0) is the onlyœßœÊßœœßœœÊœœÊ!ß
## xy
critical point. If k 0, f (x y) 2x ky 0 y x; f (x y) kx 2y 0 kx 2 x 0Á ßœœÊœ ßœœÊ œ
xy
22
kk
ˆ‰
kx 0 k x 0 x 0 or k 2 y (0) 0 or y x; in any case (0 0) is aÊ œÊ œÊœ œ„Êœ œ œ„ ß
4x 4 2
kk k
ˆ‰ ˆ‰
critical point.
46. (See Exercise 45 above): f (x y) 2, f (x y) 2, and f (x y) k f f f 4 k ; f will have a
xx yy xy xx yy xy
ßœ ßœ ßœÊ œ
##
saddle point at (0 0) if 4 k 0 k 2 or k 2; f will have a local minimum at (0 0) if 4 k 0ßÊ ß
# #
2 k 2; the test is inconclusive if 4 k 0 k 2.Ê œ Ê œ„
#
47. No; for example f(x y) xy has a saddle point at (a b) (0 0) where f f 0.ßœ ßœß œœ
xy
48. If f (a b) and f (a b) differ in sign, then f (a b) f (a b) 0 so f f f 0. The surface must therefore have a
xx yy xx yy xx yy xy
ßß ßß
#
saddle point at (a b) by the second derivative test.ß
49. We want the point on z 10 x y where the tangent plane is parallel to the plane x 2y 3z 0. Toœ œ
##
find a normal vector to z 10 x y let w z x y 10. Then w 2x 2y is normal toœ œ œ
## ## ™ijk
z 10 x y at (x y). The vector w is parallel to 2 3 which is normal to the plane x 2y 3zœ ß
## ™ijk
0 if 6x 6y 3 2 3 or x and y . Thus the point is 10 or .œ œ œ œ ßß ßßijkijk " " "" " " ""
63 633696336
355
ˆ‰ˆ‰
50. We want the point on z x y 10 where the tangent plane is parallel to the plane x 2y z 0. Letœ œ
##
w z x y 10, then w 2x 2y is normal to z x y 10 at (x y). The vector wœ œ œ ß
## ##
™™ijk
is parallel to 2 which is normal to the plane if x and y 1. Thus the point 1 1 10ijk œ œ ßß
"""
##
ˆ‰
4
or 1 is the point on the surface z x y 10 nearest the plane x 2y z 0.
ˆ‰
"
#
##
ßß œ œ
45
4
51. No, because the domain x 0 and y 0 is unbounded since x and y can be as large as we please. Absolute
extrema are guaranteed for continuous functions defined over closed domains in the plane.and bounded
Since the domain is unbounded, the continuous function f(x y) x y need not have an absolute maximumߜ
(although, in this case, it does have an absolute minimum value of f(0 0) 0).ߜ
52. (a) (i) On x 0, f(x y) f(0 y) y y 1 for 0 y 1; f (0 y) 2y 1 0 y and x 0;œßœßœ ŸŸ ßœœÊœ œ
#w "
#
f 0 , f(0 0) 1, and f(0 1) 1
ˆ‰
ß œ ßœ ßœ
"
#
3
4
(ii) On y 1, f(x y) f(x 1) x x 1 for 0 x 1; f (x 1) 2x 1 0 x and y 1,œßœßœ ŸŸ ßœœÊœ œ
#w "
#
but 1 is outside the domain; f(0 1) 1 and f( ) 3
ˆ‰
ß ß œ "ß"œ
"
#
(iii) On x 1, f(x y) f( y) y y 1 for 0 y 1; f (1 y) 2y 1 0 y and x 1, butœ ß œ"ß œ Ÿ Ÿ ß œ œ Ê œ œ
#w "
#
1 is outside the domain; f(1 0) 1 and f( ) 3
ˆ‰
ß ß œ "ß" œ
"
#
(iv) On y 0, f(x y) f(x 0) x x 1 for 0 x 1; f (x 0) 2x 1 0 x and y 0;œßœßœ ŸŸ ßœœÊœ œ
#w "
#
f 0 ; f(0 0) 1, and f( 0) 1
ˆ‰
"
#ß œ ß œ "ß œ
3
4
(v) On the interior of the square, f (x y) 2x 2y 1 0 and f (x y) 2y 2x 1 0 2x 2y 1
xy
ßœ œ ßœ œÊ œ
(xy) . Then f(xy) x y 2xyxy1(xy) (xy)1 is the absoluteÊ œ ß œ œ œ
"
#
## # 3
4
minimum value when 2x 2y 1.œ
Section 14.7 Extreme Values and Saddle Points 905
(b) The absolute maximum is f( ) 3."ß " œ
53. (a) 2 sin t 2 cos t 0 cos t sin t x y
df f dx f dx
dt x dt y dt dt dt
dy dy
œ œœ œÊ œ Êœ
``
``
(i) On the semicircle x y 4, y 0, we have t and x y 2 f 2 2 2 2. At the
##
œ œ œœ Ê ß œ
1
4ÈÈÈÈ
Š‹
endpoints, f( 2 0) 2 and f( ) 2. Therefore the absolute minimum is f( 2 0) 2 when t ;ß œ #ß! œ ß œ œ1
the absolute maximum is f 2 2 2 2 when t .
Š‹
ÈÈ È
ßœ œ
1
4
(ii) On the quartercircle x y 4, x 0 and y 0, the endpoints give f( 2) 2 and f( 0) 2.
##
œ !ßœ #ßœ
Therefore the absolute minimum is f(2 0) 2 and f( 2) 2 when t 0, respectively; the absoluteßœ !ßœ œ 1
#
maximum is f 2 2 2 2 when t .
Š‹
ÈÈ È
ßœ œ
1
4
(b) y x 4 sin t 4 cos t 0 cos t sin t x y.
dg g g dy dy
dt x dt y dt dt dt
dx dx
œ œœ œÊ œ„ Êœ„
``
``
##
(i) On the semicircle x y 4, y 0, we obtain x y 2 at t and x 2, y 2 at
##
œ œœ œ œ œ
ÈÈÈ
1
4
t . Then g 2 2 2 and g 2 2 2. At the endpoints, g( 2 0) g( 0) 0.œ ß œ ß œ ß œ #ß œ
3
4
1Š‹ Š ‹
ÈÈ ÈÈ
Therefore the absolute minimum is g 2 2 2 when t ; the absolute maximum is
Š‹
ÈÈ
ß œ œ
3
4
1
g22 2 when t .
Š‹
ÈÈ
ßœ œ
1
4
(ii) On the quartercircle x y 4, x 0 and y 0, the endpoints give g( 2) 0 and g( 0) 0.
##
œ !ßœ #ßœ
Therefore the absolute minimum is g(2 0) 0 and g( 2) 0 when t 0, respectively; the absoluteßœ !ßœ œ 1
#
maximum is g 2 2 2 when t .
Š‹
ÈÈ
ßœ œ
1
4
(c) 4x 2y (8 cos t)( 2 sin t) (4 sin t)(2 cos t) 8 cos t sin t 0
dh h dx h dx
dt x dt y dt dt dt
dy dy
œœœ œ œ
``
``
t 0, , yielding the points (2 0), (0 2) for 0 t .Êœ ß ß ŸŸ
1
#11
(i) On the semicircle x y 4, y 0 we have h(2 0) 8, h(0 2) 4, and h( 2 0) 8. Therefore,
##
œ ßœ ßœ ßœ
the absolute minimum is h( 2) 4 when t ; the absolute maximum is h(2 0) 8 and h( 2 0) 8!ß œ œ ß œ ß œ
1
#
when t 0, respectively.œ1
(ii) On the quartercircle x y 4, x 0 and y 0 the absolute minimum is h(0 2) 4 when t ; the
##
#
œ ßœ œ
1
absolute maximum is h(2 0) 8 when t 0.ßœ œ
54. (a) 2 3 6 sin t 6 cos t 0 sin t cos t t for 0 t .
df f dx f dx
dt x dt y dt dt dt 4
dy dy
œœœ œÊœÊœ ŸŸ
``
``
11
(i) On the semi-ellipse, 1, y 0, f(x y) 2x 3y 6 cos t 6 sin t 6 6 6 2
x
94
y22
œ ßœœ œ œ
Š‹ Š‹ È
ÈÈ
##
at t . At the endpoints, f( 3 0) 6 and f(3 0) 6. The absolute minimum is f( 3 0) 6 whenœ ßœ ßœ ßœ
1
4
t ; the absolute maximum is f 2 6 2 when t .œßœœ1Š‹
ÈÈ
32
4
È
#
1
(ii) On the quarter ellipse, at the endpoints f(0 2) 6 and f(3 0) 6. The absolute minimum is f(3 0) 6ߜ ߜ ߜ
and f(0 2) 6 when t 0, respectively; the absolute maximum is f 2 6 2 when t .ßœ œ ß œ œ
1 1
##
Š‹
ÈÈ
32
4
È
(b) y x (2 sin t)( 3 sin t) (3 cos t)(2 cos t) 6 cos t sin t 6 cos 2t 0
dg g g dy dy
dt x dt y dt dt dt
dx dx
œ œœ œ œ œ
``
``
##
ab
t , for 0 t .Êœ ŸŸ
11
44
31
(i) On the semi-ellipse, g(x y) xy 6 sin t cos t. Then g 2 3 when t , andßœ œ ß œ œ
Š‹
È
32
4
È
#
1
g 2 3 when t . At the endpoints, g( 3 0) g( 0) 0. The absolute minimum is
Š‹
È
ß œ œ ß œ $ß œ
32 3
4
È
#
1
g 2 3 when t ; the absolute maximum is g 2 3 when t .
Š‹ Š‹
ÈÈ
ß œ œ ß œ œ
32 32
3
4 4
È È
# #
1 1
(ii) On the quarter ellipse, at the endpoints g( 2) 0 and g( 0) 0. The absolute minimum is g(3 0) 0!ߜ $ߜ ߜ
and g(0 2) 0 at t 0, respectively; the absolute maximum is g 2 3 when t .ßœ œ ß œ œ
1 1
##
Š‹
È
32
4
È

906 Chapter 14 Partial Derivatives
(c) 2x 6y (6 cos t)( 3 sin t) (12 sin t)(2 cos t) 6 sin t cos t 0
dh h dx h dx
dt x dt y dt dt dt
dy dy
œœœ œ œ
``
``
t 0, , for 0 t , yielding the points (3 0), (0 2), and ( 3 0).Êœ ŸŸ ß ß ß
1
#11
(i) On the semi-ellipse, y 0 so that h(3 0) 9, h(0 2) 12, and h( 3 0) 9. The absolute minimum isߜߜߜ
h(3 0) 9 and h( 3 0) 9 when t 0, respectively; the absolute maximum is h( 2) 12 whenß œ ß œ œ !ß œ1
t.œ1
#
(ii) On the quarter ellipse, the absolute minimum is h(3 0) 9 when t 0; the absolute maximum isßœ œ
h( 2) 12 when t .!ß œ œ 1
#
55. y x
df f dx f dx
dt x dt y dt dt dt
dy dy
œœ
``
``
(i) x 2t and y t 1 (t 1)(2) (2t)(1) 4t 2 0 t x 1 and y withœœÊœœœÊœÊœœ
df
dt
""
##
f 1 . The absolute minimum is f 1 when t ; there is no absolute
ˆ‰ ˆ‰
ß œ ß œ œ
"" "" "
## ## #
maximum.
(ii) For the endpoints: t 1 x 2 and y 0 with f( 2 0) 0; t 0 x 0 and y 1 withœÊœ œ ßœ œÊœ œ
f( 1) 0. The absolute minimum is f 1 when t ; the absolute maximum is f(0 1) 0!ß œ ß œ œ ß œ
ˆ‰
"" "
## #
and f( 0) 0 when t 1, 0 respectively.#ß œ œ
(iii) There are no interior critical points. For the endpoints: t 0 x 0 and y 1 with f(0 1) 0;œÊœ œ ßœ
t 1 x 2 and y 2 with f(2 2) 4. The absolute minimum is f(0 1) 0 when t 0; the absoluteœÊœ œ ßœ ßœ œ
maximum is f(2 2) 4 when t 1.ßœ œ
56. (a) 2x 2y
df f dx f dx
dt x dt y dt dt dt
dy dy
œœ
``
``
(i) x t and y 2 2t (2t)(1) 2(2 2t)( 2) 10t 8 0 t x and y withœœÊœœœÊœÊœ œ
df 4 4 2
dt 5 5 5
f . The absolute minimum is f when t ; there is no absolute
ˆ‰ ˆ‰
42 6 4 4 42 4 4
55 5 25 5 55 5 5
ßœœ ßœ œ
"
#
maximum along the line.
(ii) For the endpoints: t 0 x 0 and y 2 with f(0 2) 4; t 1 x 1 and y 0 with f(1 0) 1.œÊœ œ ßœ œÊœ œ ßœ
The absolute minimum is f at the interior critical point when t ; the absolute maximum is
ˆ‰
42 4 4
55 5 5
ßœ œ
f(0 2) 4 at the endpoint when t 0.ßœ œ
(b)
dg g g dy 2y dy
dt x dt y dt dt dt
dx 2x dx
xy xy
œœ
``
``
’“’“
ab ab
(i) x t and y 2 2t x y 5t 8t 4 5t 8t 4 [( 2t)(1) ( 2)(2 2t)( 2)]œœÊœÊœ
## # # #
dg
dt ab
5t 8t 4 ( 10t 8) 0 t x and y with g . The absoluteœ œ Ê œ Ê œ œ ß œ œab ˆ‰
## "44242 5
55555 4
ˆ‰
4
5
maximum is g when t ; there is no absolute minimum along the line since x and y can be
ˆ‰
42 5 4
55 4 5
ßœ œ
as large as we please.
(ii) For the endpoints: t 0 x 0 and y 2 with g(0 2) ; t 1 x 1 and y 0 with g(1 0) 1.œÊœ œ ßœ œÊœ œ ßœ
"
4
The absolute minimum is g(0 2) when t 0; the absolute maximum is g when t .ßœ œ ß œ œ
"
45545
42 5 4
ˆ‰
57. m andœœ
(2)( 1) 3( 4)
(2) 3(10) 13
20
"
b1 (2)œ œ
"
31313
20 9
‘ˆ‰
yx; yÊœ œ
20 9 71
13 13 13
¸x4œ
k x y x x y
112 1 2
20 1 0 0
33 4 9 12
2 1 10 14
kk kk
k
#
D
58. m andœœ
(0)(5) 3(6)
(0) 3(8) 4
3
b5(0)œ œ
"
34 3
35
‘
yx; yÊœ œ
35 14
43 3
¸x4œ
k x y x x y
120 4 0
20 2 0 0
32 3 4 6
058 6
kk kk
k
#
D
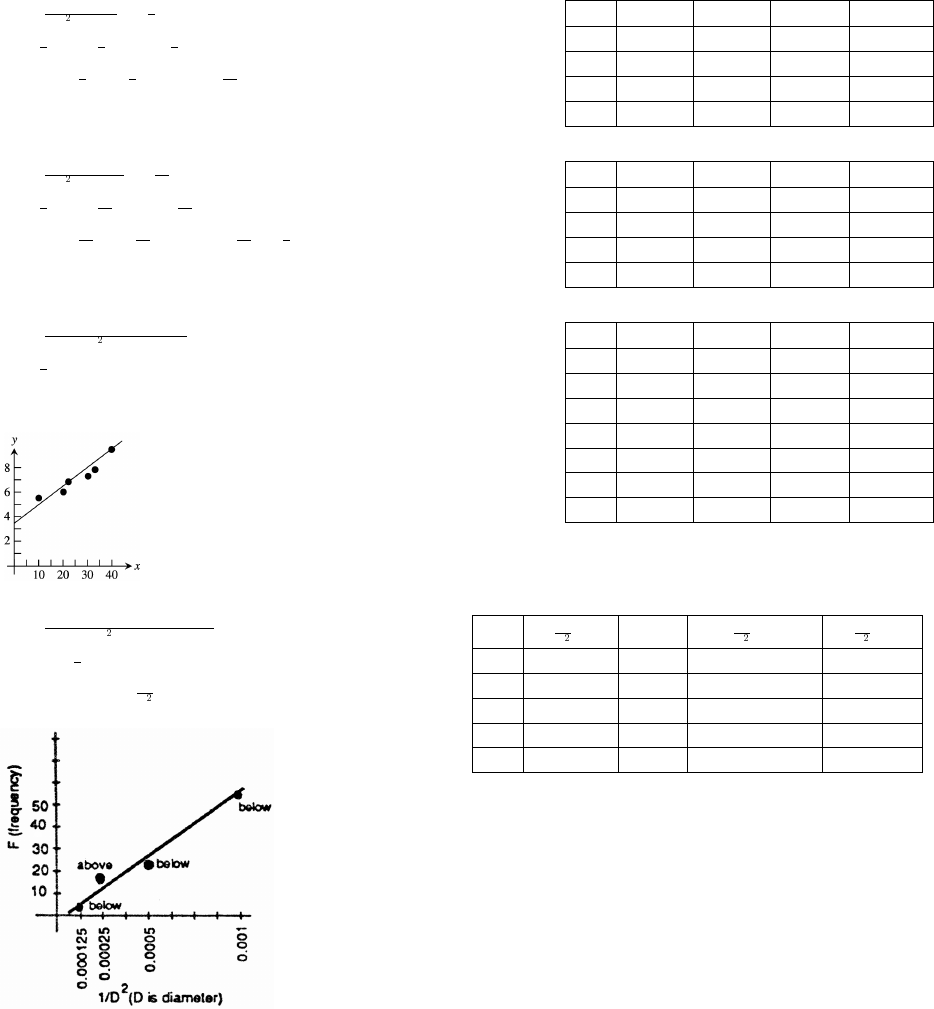
Section 14.7 Extreme Values and Saddle Points 907
59. m andœœ
(3)(5) 3(8)
(3) 3(5) 2
3
b5(3)œ œ
"
32 6
31
‘
yx; yÊœ œ
31 37
26 6
¸x4œ
k x y x x y
10 0 0 0
21 2 1 2
32 3 4 6
355 8
kk kk
k
#
D
60. m andœœ
(5)(5) 3(10)
(5) 3(13) 14
5
b5(5)œ œ
"
314 14
515
‘
yx; yÊœ œ œ
515 355
14 14 14
¸x4œ#
k x y x x y
10 1 0 0
22 2 4 4
33 2 9 6
5 5 13 10
kk kk
k
#
D
61. m 0.122 andœ¸
(162)(41.32) 6(1192.8)
(162) 6(5004)
b 41.32 (0.122)(162) 3.59œ ¸
"
6cd
y 0.122x 3.59ʜ
k x y x x y
1 12 5.27 144 63.24
2 18 5.68 324 102.24
3 24 6.25 576 150
4 30 7.21 900 216.3
5 36 8.20 1296 295.2
6 42 8.7
kk kk
k
#
1 1764 365.82
162 41.32 5004 1192.8D
62. m 51,545œ¸
(0.001863)(91) 4(0.065852)
(0.001863) 4(0.000001323)
and b (91 51,545(0.001863)) 1.26œ ¸
"
4
F 51,545 1.26ʜ
"
D
k F F
1 0.001 51 0.000001 0.051
2 0.0005 22 0.00000025 0.011
3 0.00024 14 0.0000000576 0.00336
40.
ˆ‰ ˆ‰ ˆ‰
"""
#
DDD
kkk
kk
000123 4 0.0000000153 0.000492
0.001863 91 0.000001323 0.065852D
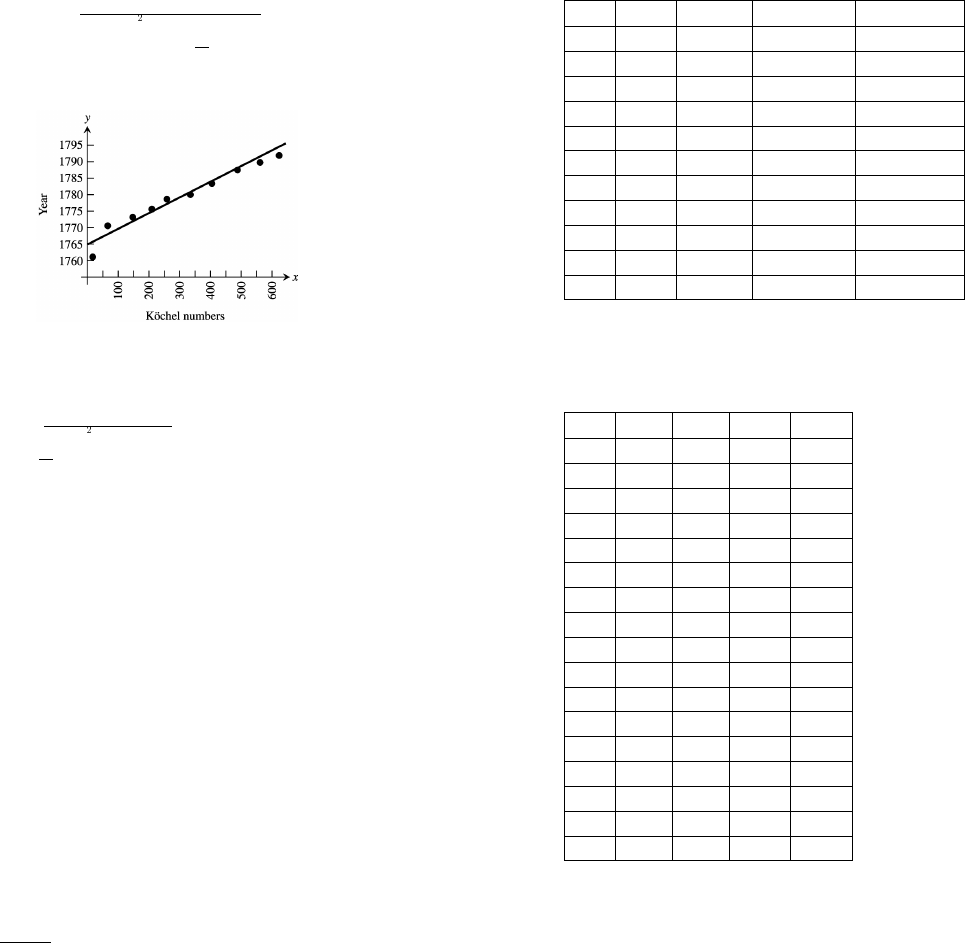
908 Chapter 14 Partial Derivatives
63. (b) m œ(3201)(17,785) 10(5,710,292)
(3201) 10(1,430,389)
0.0427 and b [17,785 (0.0427)(3201)]¸œ
"
10
1764.8 y 0.0427K 1764.8¸Êœ
(c) K 364 y (0.0427)(364)œÊœ
y (0.0427)(364) 1764.8 1780Êœ ¸
k K y K K y
1 1 1761 1 1761
2 75 1771 5625 132,825
3 155 1772 24,025 274,660
4 219 1775 47,961 388,725
5 271 1777
kk kk
#
73,441 481,567
6 351 1780 123,201 624,780
7 425 1783 180,625 757,775
8 503 1786 253,009 898,358
9 575 1789 330,625 1,028,675
10 626 1791 391,876 1,121,166
D3201 17,785 1,430,389 5,710,292
64. m 1.04 andœ¸
(123)(140) 16(1431)
(123) 16(1287)
b [140 (1.04)(123)] 0.755œ ¸
"
16
y 1.04x 0.755ʜ
k x y x x y
13399
22244
3461624
42346
5542520
6532515
7 9 11 81 99
8 12 9 144 108
9 8 10 64 80
10 13 16 169 208
11 14 13 196 182
12 3 5 9 15
13 4 6
kk kk
k
#
16 24
14 13 19 169 247
15 10 15 100 150
16 16 15 256 240
123 140 1287 1431D
65-70. Example CAS commands:
:Maple
f := (x,y) -> x^2+y^3-3*x*y;
x0,x1 := -5,5;
y0,y1 := -5,5;
plot3d( f(x,y), x=x0..x1, y=y0..y1, axes=boxed, shading=zhue, title="#65(a) (Section 14.7)" );
plot3d( f(x,y), x=x0..x1, y=y0..y1, grid=[40,40], axes=boxed, shading=zhue, style=patchcontour, title="#65(b)
(Section 14.7)" );
fx := D[1](f); # (c)
fy := D[2](f);
crit_pts := solve( {fx(x,y)=0,fy(x,y)=0}, {x,y} );
fxx := D[1](fx); # (d)
fxy := D[2](fx);
fyy := D[2](fy);
discr := unapply( fxx(x,y)*fyy(x,y)-fxy(x,y)^2, (x,y) );
for CP in {crit_pts} do # (e)
eval( [x,y,fxx(x,y),discr(x,y)], CP );
Section 14.8 Lagrange Multipliers 909
end do;
# (0,0) is a saddle point
# ( 9/4, 3/2) is a local minimum
: (assigned functions and bounds will vary)Mathematica
Clear[x,y,f]
f[x_,y_]:= x y 3x y
23
xmin= 5; xmax= 5; ymin= 5; ymax= 5;
Plot3D[f[x,y], {x, xmin, xmax}, {y, ymin, ymax}, AxesLabel {x, y, z}]Ä
ContourPlot[f[x,y], {x, xmin, xmax}, {y, ymin, ymax}, ContourShading False, Contours 40]ÄÄ
fx= D[f[x,y], x];
fy= D[f[x,y], y];
critical=Solve[{fx==0, fy==0},{x, y}]
fxx= D[fx, x];
fxy= D[fx, y];
fyy= D[fy, y];
discriminant= fxx fyy fxy2
{{x, y}, f[x, y], discriminant, fxx} /.critical
14.8 LAGRANGE MULTIPLIERS
1. f y x and g 2x 4y so that f g y x (2x 4y ) y 2x and x 4y™™ ™™œ œ œ Ê œ Êœ œij i j ij i j-- --
x 8x or x 0.Êœ Êœ„ œ--
#È2
4
CASE 1: If x 0, then y 0. But (0 0) is not on the ellipse so x 0.œœß Á
CASE 2: x 0 x 2y 2y 2y 1 y .ÁÊœ„ Êœ„ Ê„ œÊœ„-È2
4ÈÈ
Š‹
##"
#
Therefore f takes on its extreme values at and . The extreme values of f on the ellipse
Š‹Š ‹
„ß „ß
ÈÈ
22
22
""
##
are .„È2
#
2. f y x and g 2x 2y so that f g y x (2x 2y ) y 2x and x 2y™™ ™™œ œ œ Ê œ Êœ œij i j ij i j-- --
x 4x x 0 or .Êœ Êœ œ„--
#1
2
CASE 1: If x 0, then y 0. But (0 0) is not on the circle x y 10 0 so x 0.œœß œÁ
##
CASE 2: x 0 y 2x x x x 10 0 x 5 y 5.ÁÊœ„Êœ „ œ„Ê „ œÊœ„ Êœ„-1
2ˆ‰ ab ÈÈ
"
#
##
Therefore f takes on its extreme values at 5 5 and 5 5 . The extreme values of f on the
Š‹Š ‹
ÈÈ È È
„ß „ß
circle are 5 and 5.
3. f 2x 2y and g 3 so that f g 2x 2y ( 3 ) x and y™™™™œ œ œ Ê œ Ê œ œij ij ijij--
--
##
3
3 10 2 x 1 and y 3 f takes on its extreme value at (1 3) on the line.Ê œ Ê œÊ œ œ Ê ß
ˆ‰ˆ‰
--
##
3-
The extreme value is f( ) 49 1 9 39."ß $ œ œ
4. f 2xy x and g so that f g 2xy x ( ) 2xy and x™™™™œ œ œ Ê œÊœ œij ij ij ij
###
----
2xy x x 0 or 2y x.ʜʜ œ
#
CASE 1: If x 0, then x y 3 y 3.œœÊœ
CASE 2: If x 0, then 2y x so that x y 3 2y y 3 y 1 x 2.Á œ œÊ œÊœÊœ
Therefore f takes on its extreme values at ( 3) and ( ). The extreme values of f are f(0 3) 0 and!ß #ß " ß œ
f( 1) 4.#ß œ

910 Chapter 14 Partial Derivatives
5. We optimize f(x y) x y , the square of the distance to the origin, subject to the constraintߜ
##
g(x y) xy 54 0. Thus f 2x 2y and g y 2xy so that f g 2x 2yßœ œ œ œ œ Ê
##
™™ ™™ij i j ij-
y 2xy 2x y and 2y 2 xy.œ Êœ œ---ab
##
ij
CASE 1: If y 0, then x 0. But (0 0) does not satisfy the constraint xy 54 so y 0.œœß œÁ
#
CASE 2: If y 0, then 2 2 x x 2 y y . Then xy 54 54ÁœÊœÊœÊœ œÊ œ--
"" "
## #
-- - --
ˆ‰ ˆ‰ˆ‰
22
x 3 and y 18 x 3 and y 3 2.ʜʜʜ œÊœ œ„--
$#
""
27 3 È
Therefore 3 2 are the points on the curve xy 54 nearest the origin (since xy 54 has points
Š‹
È
$ß „ œ œ
##
increasingly far away as y gets close to 0, no points are farthest away).
6. We optimize f(x y) x y , the square of the distance to the origin subject to the constraint g(x y)ßœ ß
##
x y 2 0. Thus f 2x 2y and g 2xy x so that f g 2x 2xy and 2y xœœ œ œ œ Êœ œ
###
™™ ™™ij ij ---
, since x 0 y 0 (but g(0 0) 0). Thus x 0 and 2x 2xy x 2yÊœ œÊœ ßÁ Á œ Ê œ-2y 2y
x x
ˆ‰ ##
2y y 2 0 y 1 (since y 0) x 2 . Therefore 2 1 are the points on the curveʜʜ Êœ„ „ßab ÈÈ
Š‹
#
x y 2 nearest the origin (since x y 2 has points increasingly far away as x gets close to 0, no points are
##
œœ
farthest away).
7. (a) f and g y x so that f g (y x ) 1 y and 1 x y and™™ ™™œ œ œ Ê œ Ê œ œ Ê œij i j ij i j-- --
"
-
x 16 . Use since x 0 and y 0. Then x 4 and y 4 the minimumœÊ œ Êœ„ œ œ œÊ
"" " "
-- --
44
value is 8 at the point (4 4). Now, xy 16, x 0, y 0 is a branch of a hyperbola in the first quadrantߜ
with the x-and y-axes as asymptotes. The equations x y c give a family of parallel lines with m 1.œ œ
As these lines move away from the origin, the number c increases. Thus the minimum value of c occurs
where x y c is tangent to the hyperbola's branch.œ
(b) f y x and g so that f g y x ( ) y x y y 16 y 8™™ ™™œ œ œ Ê œ Êœœ œ Êœij ij ij ij---
x 8 f( ) 64 is the maximum value. The equations xy c (x 0 and y 0 or x 0 and y 0ÊœÊ)ß)œ œ
to get a maximum value) give a family of hyperbolas in the first and third quadrants with the x- and y-
axes as asymptotes. The maximum value of c occurs where the hyperbola xy c is tangent to the lineœ
x y 16.œ
8. Let f(x y) x y be the square of the distance from the origin. Then f 2x 2y andßœ œ
## ™ij
g (2x y) (2y x) so that f g 2x (2x y) and 2y (2y x) ™™™œ œ Êœ œÊ œij -- - -
2y
2y x
2x (2x y) x(2y x) y(2x y) x y y x.Ê œ Ê œ Ê œ Êœ„
Š‹
2y
2y x
##
CASE 1: y x x x(x) x 1 0 x and y x.œÊ œÊœ„ œ
## "
È3
CASE 2: y x x x( x) ( x) 1 0 x 1 and y x. Thus fœ Ê œ Ê œ „ œ ß œ
## ""
Š‹
ÈÈ
33
2
3
f and f(1 1) 2 f( 1 1).œ ß ß œ œ ß
Š‹
""
ÈÈ
33
Therefore the points (1 1) and ( 1 1) are the farthest away; and are the closestß ß ß ß
Š‹Š ‹
"" " "
ÈÈ È È
33 3 3
points to the origin.
9. V r h 16 r h 16 r h g(r h) r h 16; S 2 rh 2 r S (2 h 4 r) 2 r andœÊœÊœÊßœœÊ œ111 11 111
### # #
™ij
g 2rh r so that S g (2 rh 4 r) 2 r 2rh r 2 rh 4 r 2rh and™™™œ œ Ê œ Ê œij i j ij
# #
-111- 11-ab
2 r r r 0 or . But r 0 gives no physical can, so r 0 2 h 4 r1- - - 1 1œÊœ œ œ ÁÊœÊ
#22
rr
11
2rh 2r h 16 r (2r) r 2 h 4; thus r 2 cm and h 4 cm give the only extremeœ Ê œÊ œ ʜʜ œ œ
ˆ‰
2
r
1#
surface area of 24 cm . Since r 4 cm and h 1 cm V 16 cm and S 40 cm , which is a larger111
#$#
œœÊœ œ
surface area, then 24 cm must be the minimum surface area.1#

Section 14.8 Lagrange Multipliers 911
10. For a cylinder of radius r and height h we want to maximize the surface area S 2 rh subject to the constraintœ1
g(r h) r a 0. Thus S 2 h 2 r and g 2r so that S g 2 h 2 r andßœ œ œ œ œ Ê œ
##
# #
#
ˆ‰
h h
™™™™11 - 1-ij ij
2 r and 2 r 4r h h 2r r a 2r a r1-1œ Ê œ œ Ê œÊœÊœÊ œÊœ
-1 1hh hh 4r a
rr 4 2
##
## # # ##
ˆ‰ˆ‰ È
h a 2 S 2 a 2 2 a .Êœ Êœ œ
ÈÈ
Š‹Š ‹
11
a
2
È#
11. A (2x)(2y) 4xy subject to g(x y) 1 0; A 4y 4x and g so that Aœœ ßœœœ œ
xx
16 9 8 9
y2y
™™ ™ij i j
g 4y 4x 4y and 4x and 4xœÊœÊœ œÊœ œ-- ---™ij i j
ˆ ‰ ˆ‰ ˆ‰ ˆ‰ˆ‰
xx
89 8 9 x 9x
2y 2y 32y 2y 32y
y x 1 x 8 x 2 2 . We use x 2 2 since x represents distance.Êœ„ Ê œÊ œÊœ„ œ
3x
4169
x
ˆ‰
3
4#ÈÈ
Then y 2 2 , so the length is 2x 4 2 and the width is 2y 3 2.œœ œ œ
3
4
32
Š‹
ÈÈÈ
È
#
12. P 4x 4y subject to g(x y) 1 0; P 4 4 and g so that P gœ ßœœ œ œ œ
x2x
ab a b
y2y
™™ ™™ij i j -
4 and 4 and 4 y x 1 Êœ œ Êœ œ Êœ Ê œÊ
ˆ‰ ˆ‰ ˆ‰
Š‹ Š‹
2x 2a 2a b x x b x
abxbxaaba
2y 2y x
a
--- Š‹
b
a
1 a b x a x , since x 0 y x width 2xœÊ œ Êœ Êœ œ Ê œ œab Š‹
###%
abb2a
ab ab ab
a
ÈÈÈ
and height 2y perimeter is P 4x 4y 4 a bœœ Ê œœ œ
2b 4a 4b
ab ab
ÈÈ
##
È
13. f 2x 2y and g (2x 2) (2y 4) so that f g 2x 2y [(2x 2) (2y 4) ]™™ ™™œ œ œ œ œ ij i j ij i j--
2x (2x 2) and 2y (2y 4) x and y , 1 y 2x x 2x (2x) 4(2x)Êœ œ Êœ œ ÁÊœÊ -- -
--
--
##
11
2
0 x 0 and y 0, or x 2 and y 4. Therefore f(0 0) 0 is the minimum value and f(2 4) 20 is theœÊœœœœ ßœ ßœ
maximum value. (Note that 1 gives 2x 2x 2 or 2, which is impossible.)-œœ!œ
14. f 3 and g 2x 2y so that f g 3 2 x and 1 2 y and 1 2 y™™ ™™œ œ œ Êœ œ Ê œ œij i j ----
33
2x 2x
ˆ‰
y x 4 10x 36 x x and y , or x andÊœÊ œÊ œ Êœ„ Êœ œ œ
xx 66 26
33 10 10 10 10
##
#
ˆ‰ ÈÈ È È
y . Therefore f 6 2 10 6 12.325 is the maximum value, andœ ß œ œ ¸
26220
10 10 10 10
ÈÈÈÈ
Š‹ È
f 2 10 6 0.325 is the minimum value.
Š‹
È
ß œ ¸
62
10 10
ÈÈ
15. T (8x 4y) ( 4x 2y) and g(x y) x y 25 0 g 2x 2y so that T g™™™™œ ßœœÊ œ œij ij
## -
(8x 4y) ( 4x 2y) (2x 2y ) 8x 4y 2 x and 4x 2y 2 y y , 1Êœ Êœ œ Êœ Áijij----
2x
1-
8x 4 2 x x 0, or 0, or 5.Ê œÊœœœ
ˆ‰
2x
1----
CASE 1: x 0 y 0; but (0 0) is not on x y 25 so x 0.œÊœ ß œ Á
##
CASE 2: 0 y 2x x (2x) 25 x 5 and y 2x.-œÊœ Ê œ Êœ„ œ
## È
CASE 3: 5 y x 25 x 2 5 x 2 5 and y 5, or x 2 5-œ Ê œ œ Ê œ Ê œ „ Ê œ œ œ
##
##
2x x x
4ˆ‰ ÈÈ È È
and y 5 .œÈ
Therefore T 5 2 5 0° T 5 2 5 is the minimum value and T 2 5 5 125°
Š‹Š ‹ Š ‹
ÈÈ È È ÈÈ
ß œ œ ß ß œ
T 2 5 5 is the maximum value. (Note: 1 x 0 from the equation 4x 2y 2 y; but weœ ß œÊœ œ
Š‹
ÈÈ --
found x 0 in CASE 1.)Á
16. The surface area is given by S 4 r 2 rh subject to the constraint V(r h) r r h 8000. Thusœ ßœ œ11 11
#$#
4
3
S (8 r 2 h) 2 r and V 4 r 2 rh r so that S V (8 r 2 h) 2 r™™ ™™œ œ œ œ 11 1 1 1 1 - 11 1ij ij ijab
##
4r 2rh r 8r 2h 4r 2rh and 2r r r 0 or 2 r. But r 0œÊœ œÊœœ Á-1 1 1 1 1 -1 1 1 -1 -cdabab
## # #
ij
so 2 r 4r h 2r rh h 0 the tank is a sphere (there is no cylindrical part) andœÊœÊœ ÊœÊ--
22
rr
ab
#
r 8000 r 10 .
46
31$"Î$
œÊœ
ˆ‰
1

912 Chapter 14 Partial Derivatives
17. Let f(x y z) (x 1) (y 1) (z 1) be the square of the distance from (1 1 1). Thenßß œ ßß
###
f 2(x 1) 2(y 1) 2(z 1) and g 2 3 so that f g™™™™œ œ œijk ijk -
2(x 1) 2(y 1) 2(z 1) ( 2 3 ) 2(x 1) , 2(y 1) 2 , 2(z 1) 3Ê œ Ê œ œ œijkijk----
2(y 1) 2[2(x 1)] and 2(z 1) 3[2(x 1)] x z 2 3 or z ; thusÊœ œ Êœ Êœ œ
y1 y1 3y1
###
ˆ‰
2y 3 13 0 y 2 x and z . Therefore the point 2 is closest (since no
y1 3y1 35 35
## ## ##
œÊœÊœ œ ßß
ˆ‰ ˆ ‰
point on the plane is farthest from the point (1 1 1)).ßß
18. Let f(x y z) (x 1) (y 1) (z 1) be the square of the distance from (1 1 1). Thenßß œ ßß
###
f 2(x 1) 2(y 1) 2(z 1) and g 2x 2y 2z so that f g x 1 x, y 1 y™™™™œ œ œ Êœ œijk ijk ---
and z 1 z x , y , and z for 1 4œ Ê œ œ œ Á Ê œ--
"" " """
###
1 1 1 111- - - ---
ˆ‰ˆ‰ˆ‰
x , y , z or x , y , z . The largest value of fÊœ„Êœ œ œ œ œ œ
"
"-
2222 222
3333 333
ÈÈÈÈ ÈÈÈ
occurs where x 0, y 0, and z 0 or at the point on the sphere. ßß
Š‹
22 2
33 3
ÈÈ È
19. Let f(x y z) x y z be the square of the distance from the origin. Then f 2x 2y 2z andßßœ œ
### ™ijk
g 2x 2y 2z so that f g 2x 2y 2z (2x 2y 2z ) 2x 2x , 2y 2y ,™™™œ œ Ê œ Êœ œijk ijk ijk-- --
and 2z 2z x 0 or 1.œ Ê œ œ--
CASE 1: 1 2y 2y y 0; 2z 2z z 0 x 1 0 x 1 and y z 0.-œ Ê œ Ê œ œ Ê œ Ê œ Ê œ „ œ œ
#
CASE 2: x 0 y z 1, which has no solution.œÊœ
##
Therefore the points on the unit circle x y 1, are the points on the surface x y z 1 closest to the origin
## ###
œ œ Þ
The minimum distance is 1.
20. Let f(x y z) x y z be the square of the distance to the origin. Then f 2x 2y 2z andßßœ œ
### ™ijk
g y x so that f g 2x 2y 2z (y x ) 2x y, 2y x, and 2z™™™œ œ Ê œ Ê œ œ œijk i j k ijk-----
x 2y y 0 or 2.Êœ Ê œ Êœ œ„
--yy
##
--
Š‹
CASE 1: y 0 x 0 z 1 0 z 1.œÊœÊœÊœ
CASE 2: 2 x y and z 1 x ( 1) 1 0 x 2 0, so no solution.-œÊœ œÊ œÊ œ
##
CASE 3: 2 x y and z 1 ( y)y 1 1 0 y 0, again.-œ Ê œ œ Ê œ Ê œ
Therefore (0 0 1) is the point on the surface closest to the origin since this point gives the only extreme valueßß
and there is no maximum distance from the surface to the origin.
21. Let f(x y z) x y z be the square of the distance to the origin. Then f 2x 2y 2z andßßœ œ
### ™ijk
g y x 2z so that f g 2x 2y 2z ( y x 2z ) 2x y , 2y x , and™™™œ œ Ê œ Ê œ œij k i j k ij k-- --
2z 2z 1 or z 0.œÊœ œ--
CASE 1: 1 2x y and 2y x y 0 and x 0 z 4 0 z 2 and x y 0.-œ Ê œ œ Ê œ œ Ê œ Ê œ „ œ œ
#
CASE 2: z 0 xy 4 0 y . Then 2x , and x xœ Ê œ Ê œ œ Ê œ œ Ê œ
44x8 8x
xx x x
-- -
##
Š‹
x 16 x 2. Thus, x 2 and y 2, or x = 2 and y 2.ʜʜ„ œ œ œ
%
Therefore we get four points: ( 2 0), ( 2 2 0), (0 0 2) and ( 0 2). But the points ( 0 2) and ( 2)#ß ß ß ß ß ß !ß ß !ß ß !ß !ß
are closest to the origin since they are 2 units away and the others are 2 2 units away.
È
22. Let f(x y z) x y z be the square of the distance to the origin. Then f 2x 2y 2z andßßœ œ
### ™ijk
g yz xz xy so that f g 2x yz, 2y xz, and 2z xy 2x xyz and 2y yxz™™™œ œ Êœ œ œ Ê œ œijk ------
##
x y y x z x x x x 1 x 1 the points are (1 1 1), ( 1 1),Ê œ Êœ„Êœ„Ê „ „œÊœ„Ê ßß "ßß
## abab
( ), and ( 1 1, 1)."ß "ß " ß
23. f 2 5 and g 2x 2y 2z so that f g 2 5 (2x 2y 2z ) 1 2x ,™™ ™™œ œ œ Êœ Êœijk i j k ijk i j k-- -
2 2y , and 5 2z x , y 2x, and z 5x x ( 2x) (5x) 30 x 1.œ œ Ê œ œ œ œ œ Ê œ Ê œ„--
""
##
###
-- -
5

Section 14.8 Lagrange Multipliers 913
Thus, x 1, y 2, z 5 or x 1, y 2, z 5. Therefore f(1 2 5) 30 is the maximum value andœœœ œœœ ßßœ
f( 1 2 5) 30 is the minimum value.ß ß œ
24. f 2 3 and g 2x 2y 2z so that f g 2 3 (2x 2y 2z ) 1 2x ,™™ ™™œ œ œ Êœ Êœijk i j k ijk i j k-- -
2 2y , and 3 2z x , y 2x, and z 3x x (2x) (3x) 25 x .œ œ Êœ œœ œ œ Ê œ Êœ„--
""
##
###
-- -
35
14
È
Thus, x , y , z or x , y , z . Therefore fœœœ œœœ ßß
5 10 15 5 10 15 5 10 15
14 14 14 14 14 14 14 14 14
È È È È È È ÈÈÈ
Š‹
5 14 is the maximum value and f , 5 14 is the minimum value.œßœ
ÈÈ
Š‹
51015
14 14 14
ÈÈÈ
25. f(x y z) x y z and g(x y z) x y z 9 0 f 2x 2y 2z and g so thatßßœ ßßœœÊ œ œ
### ™™ijk ijk
f g 2x 2y 2z ( ) 2x , 2y , and 2z xyz xxx90™™œ Ê œ Ê œ œ œ Ê œœÊœ-----ijkijk
x 3, y 3, and z 3.Êœ œ œ
26. f(x y z) xyz and g(x y z) x y z 16 0 f yz xz xy and g 2z so thatßßœ ßßœœÊ œ œ
#™™ijk ijk
f g yz xz xy ( 2z ) yz , xz , and xy 2z yz xz z 0 or y x.™™œÊœÊœœ œÊœÊœœ-----ijkijk
But z 0 so that y x x 2z and xz . Then x 2z(xz) x 0 or x 2z . But x 0 so thatœÊœ œ œÊœœ
## #
--
x 2z y 2z 2z 2z z 16 z . We use z since z 0. Then x and yœÊœÊœÊœ„ œ œ œ
##### 4 4 32 32
55 55
ÈÈ
which yields f .
Š‹
32 32 4 4096
55 5255
ßß œ
ÈÈ
27. V 6xyz and g(x y z) x y z 1 0 V 6yz 6xz 6xy and g 2x 2y 2z so thatœ ßßœœÊ œ œ
### ™™ijk ijk
V g 3yz x, 3xz y, and 3xy z 3xyz x and 3xyz y y x z x™™œÊœ œ œÊœ œÊœ„Êœ„------
##
x x x 1 x since x 0 the dimensions of the box are by by for maximumʜʜ Ê
### "
È ÈÈÈ
3 333
222
volume. (Note that there is no minimum volume since the box could be made arbitrarily thin.)
28. V xyz with x y z all positive and 1; thus V xyz and g(x y z) bcx acy abz abc 0œ ßß œ œ ßßœ œ
xz
abc
y
V yz xz xy and g bc ac ab so that V g yz bc, xz ac, and xy abÊ œ œ œ Êœ œ œ™™ ™™ijk ijk ----
xyz bcx, xyz acy, and xyz abz 0. Also, bcx acy abz bx ay, cy bz, andÊœ œ œ ÊÁ œ œ Êœ œ-- -- ---
cx az y x and z x. Then 1 x x 1 1 xœ Êœ œ œÊ œÊ œÊœ
bcxcxbc 3x a
aaabzabaca a 3
y""
ˆ‰ ˆ‰
y and z V xyz is the maximum volume. (Note thatÊœ œ œ œÊ œ œ œ
ˆ‰ˆ‰ ˆ‰ˆ‰ ˆ‰ˆ‰ˆ‰
ba b ca c abc abc
a3 3 a3 3 333 27
there is no minimum volume since the box could be made arbitrarily thin.)
29. T 16x 4z (4y 16) and g 8x 2y 8z so that T g 16x 4z (4y 16)™™™™œ œ œ Ê ij k ijk ij k-
(8x 2y 8z ) 16x 8x , 4z 2y , and 4y 16 8z 2 or x 0.œÊœ œ œÊœ œ-----ijk
CASE 1: 2 4z 2y(2) z y. Then 4z 16 16z z y . Then-œÊ œ Êœ œ ʜʜ
44
33
4x 4 16 x .
###
œ Ê œ„
ˆ‰ ˆ‰
44 4
33 3
CASE 2: x 0 4y 16 8z y 4y 4z 4(0) y y 4y 16 0œÊœ Ê œ Ê œ Ê œ-2z 2z
yy
Š‹ ab
#####
y 2y 8 0 (y 4)(y 2) 0 y 4 or y 2. Now y 4 4z 4 4(4)ÊœÊ œÊœ œ œÊ œ
###
z 0 and y 2 4z ( 2) 4( 2) z 3.Êœ œÊ œ Êœ„
## È
The temperatures are T 642 , T(0 4 0) 600°, T 0 2 3 600 24 3 , and
ˆ‰ Š‹Š ‹
ÈÈ
„ßß œ ßß œ ßß œ
444 2
333 3
°°
T 0 2 3 600 24 3 641.6°. Therefore are the hottest points on the space probe.
Š‹Š‹
ÈÈ ˆ‰
ß ß œ ¸ „ ß ß
°444
333
30. T 400yz 400xz 800xyz and g 2x 2y 2z so that T g™™™™œ œ œ
##
ijk ijk -
400yz 400xz 800xyz (2x 2y 2z ) 400yz 2x , 400xz 2y , and 800xyz 2z .Ê œÊœ œ œ
## # #
ijkijk----
Solving this system yields the points 1 0 , 1 0 0 , and . The correspondingabab
Š‹
!ß„ß „ßß „ß„ß„
""
## #
È2
914 Chapter 14 Partial Derivatives
temperatures are T 1 0 0, T 1 0 0 0, and T 50. Therefore 50 is theabab Š‹
!ß „ ß œ „ ß ß œ „ ß „ ß „ œ „
""
## #
È2
maximum temperature at and ; 50 is the minimum temperature at
Š‹Š ‹
"" " "
## # # # #
ßß„ ßß„
ÈÈ
22
and .
Š‹Š‹
"" ""
## # ## #
ßß„ ßß„
ÈÈ
22
31. U (y 2) x and g 2 so that U g (y 2) x (2 ) y 2 and™™™™œ œ œ Ê œ Ê#œij ij ij ij---
x y 2 2x y 2x 2 2x (2x 2) 30 x 8 and y 14. Therefore U(8 14) $128œÊœÊœÊœÊœ œ ßœ-
is the maximum value of U under the constraint.
32. M (6 z) 2y x and g 2x 2y 2z so that M g (6 z) 2y x™™™™œ œ œ Êijk ijk ijk-
(2x 2y 2z ) 6 z 2x , 2y 2y , x 2z 1 or y 0.œÊœœ œÊœœ-----ijk
CASE 1: 1 6 z 2x and x 2z 6 z 2( 2z) z 2 and x 4. Then-œ Ê œ œ Ê œ Ê œ œ
(4)y2360 y 4. œÊœ„
###
CASE 2: y 0, 6 z 2x , and x 2z 6 z 2x 6z z xœœ œ ʜʜ Êœ---
xx
2z 2z
ˆ‰ ##
6z z 0 z 36 z 6 or z 3. Now z 6 x 0 x 0; z 3Ê œ Êœ œ œÊ œÊœ œab
### #
x 27 x 3 3.ʜʜ„
#È
Therefore we have the points 3 3 0 3 , (0 0 6), and 4 4 2 . Then M 3 3 0 3
Š‹ Š‹
ÈÈ
ab„ßß ßß ß„ß ßß
27 3 60 106.8, M 3 3 0 3 60 27 3 13.2, M(0 0 6) 60, and M( 4 4 2) 12œ ¸ ßß œ ¸ ßß œ ßß œ
ÈÈÈ
Š‹
M( 4 4 2). Therefore, the weakest field is at 4 4 2 .œßß ß„ßab
33. Let g (x y z) 2x y 0 and g (x y z) y z 0 g 2 , g , and f 2x 2 2z
"# "#
ßß œ œ ßß œ œ Ê œ œ œ ™™ ™ij jk i j k
so that f g g 2x 2 2z (2 ) ( ) 2x 2 2z 2 ( )™™ ™œ ʜʜ-. - . -.-.
"#
ij k ij jk ij k i j k
2x 2 , 2 , and 2z x . Then 2 2z x x 2z 2 so that 2x y 0Ê œ œ œ Ê œ œ Ê œ œ-.- . -
2( 2z 2) y 0 4z 4 y 0. This equation coupled with y z 0 implies z and y .ʜʜ œ œ œ
44
33
Then x so that is the point that gives the maximum value f 2œßß ßßœ
2244 244244
3333 333333
ˆ‰ ˆ‰ˆ‰ˆ‰ˆ‰
##
.œ4
3
34. Let g (x y z) x 2y 3z 6 0 and g (x y z) x 3y 9z 9 0 g 2 3 ,
"# "
ßß œ œ ßß œ œ Ê œ ™ijk
g 3 9 , and f 2x 2y 2z so that f g g 2x 2y 2z™™ ™™™
#"#
œ œ œ Ê ijk i j k i j k-.
( 2 3 ) ( 3 9 ) 2x , 2y 2 3 , and 2z 3 9 . Then 0 x 2y 3z 6œ Ê œ œ œ œ- . -. -. -.ijk ijk
( ) (2 3 ) 6 7 17 6; 0 x 3y 9z 9œ Êœœ
"
###
-. - . - . - .
ˆ‰
927
( ) 3 9 34 91 18. Solving these two equations for and givesÊ Êœ
"
####
-. - . - . - . - .
ˆ‰ˆ ‰
92781
and x , y , and z . The minimum value is-.œ œÊœœœœ œœ
240 78 81 123 9
59 59 59 59 59
23 39-. -. -.
## #
f . (Note that there is no value of f subject to the constraints because
ˆ‰
81 123 9 369
59 59 59 59 59
21,771
ßß œ œ maximum
at least one of the variables x, y, or z can be made arbitrary and assume a value as large as we please.)
35. Let f(x y z) x y z be the square of the distance from the origin. We want to minimize f(x y z) subjectßß œ ßß
###
to the constraints g (x y z) y 2z 12 0 and g (x y z) x y 6 0. Thus f 2x 2y 2z ,
"#
ßß œ œ ßß œœ œ ™ijk
g 2 , and g so that f g g 2x , 2y , and 2z 2 . Then™™™™™
"# "#
œ œ œ Ê œ œ œjk ij -. .-. -
0 y 2z 12 2 12 12 5 24; 0 x y 6 6œœ Ê œ Ê œ œœ
ˆ‰ ˆ‰
- -
...
## # # # ##
"
--.-.
5
6 12. Solving these two equations for and gives 4 and 4 x 2,Ê œÊ#œ œ œÊœœ
"
# #
-. - . - . - . .
y 4, and z 4. The point (2 4 4) on the line of intersection is closest to the origin. (There is noœœ œœ ßß
-.
#-
maximum distance from the origin since points on the line can be arbitrarily far away.)
36. The maximum value is f from Exercise 33 above.
ˆ‰
24 4 4
33 3 3
ßß œ
Section 14.8 Lagrange Multipliers 915
37. Let g (x y z) z 1 0 and g (x y z) x y z 10 0 g , g 2x 2y 2z , and
"# "#
###
ßßœœ ßßœœÊ œ œ™™kijk
f 2xyz x z x y so that f g g 2xyz x z x y ( ) (2x 2y 2z )™™™™œ œ Ê œijk ijkk ijk
## ##
"#
-. -.
2xyz 2x , x z 2y , and x y 2z xyz x x 0 or yz y since z 1.Êœ œ œÊœÊœ œÊœ œ.. .- . ..
##
CASE 1: x 0 and z 1 y 9 0 (from g ) y 3 yielding the points 0 3 1 .œœÊœ Êœ„ ß„ß
##ab
CASE 2: y x z 2y x 2y (since z 1) 2y y 1 10 0 (from g ) 3y 9 0.œÊ œ Ê œ œ Ê œ Ê œ
#### ## #
#
y 3 x 2 3 x 6 yielding the points 6 3 .Êœ„ Ê œ „ Êœ„ „ ß„ ß"
ÈÈÈ ÈÈ
Š‹ Š ‹
##
Now f 3 1 1 and f 6 3 6 3 1 1 6 3. Therefore the maximum of f isab Š‹Š‹
ÈÈ È È
!ß„ß œ „ ß„ ß"œ „ œ„
1 6 3 at 6 3 1 , and the minimum of f is 1 6 3 at 6 3 .„ßß „ßß"
ÈÈÈ ÈÈÈ
Š‹ Š ‹
38. (a) Let g (x y z) x y z 40 0 and g (x y z) x y z 0 g , g , and
"#"#
ßß œ œ ßß œ œ Ê œ œ™™ijk ijk
w yz xz xy so that w g g yz xz xy ( ) ( )™™™™œ œ Ê œijk ijk ijk ijk-. - .
"#
yz , xz , and xy yz xz z 0 or y x.Êœ œ œÊœÊœ œ-. -. -.
CASE 1: z 0 x y 40 and x y 0 no solution.œ Ê œ œ Ê
CASE 2: x y 2x z 40 0 and 2x z 0 z 20 x 10 and y 10 w (10)(10)(20)œÊ œ œÊœ Êœ œ Ê œ
2000œ
(b) 2 2 is parallel to the line of intersection the line is x 2t 10,
nij
ij k
œ œ Ê œ
"" "
"""
ââ
ââ
ââ
ââ
ââ
ââ
y 2t 10, z 20. Since z 20, we see that w xyz ( 2t 10)(2t 10)(20) 4t 100 (20)œ œ œ œ œ œ ab
#
which has its maximum when t 0 x 10, y 10, and z 20.œÊœ œ œ
39. Let g ( y z) y x 0 and g (x y z) x y z 4 0. Then f y x 2z , g , and
"# "
###
Bßß œœ ßß œ œ œ œ™™ij k ij
g 2x2y2z so that f g g yx2z ( ) (2x2y2z)™™™
#"#
œ ™œ Ê œ ijk ijk ij ijk-. - .
y 2x , x 2y , and 2z 2z z 0 or 1.Êœ œ œ Êœ œ-.-. . .
CASE 1: z 0 x y 4 0 2x 4 0 (since x y) x 2 and y 2 yielding the pointsœÊ œÊ œ œ Êœ„ œ„
## # ÈÈ
22.
Š‹
ÈÈ
„ß„ß!
CASE 2: 1 y 2x and x 2y x y 2(x y) 2x 2(2x) since x y x 0 y 0.--œ Ê œ œ Ê œ Ê œ œÊœÊœ
z 4 0 z 2 yielding the points 2 .Ê œ Ê œ „ !ß !ß „
#ab
Now, f 2 4 and f 2 2 2. Therefore the maximum value of f is 4 at 2 and theab ab
Š‹
ÈÈ
!ß !ß „ œ „ ß „ ß ! œ !ß !ß „
minimum value of f is 2 at 2 2 .
Š‹
ÈÈ
„ß„ß!
40. Let f(x y z) x y z be the square of the distance from the origin. We want to minimize f(x y z) subjectßß œ ßß
###
to the constraints g (x y z) 2y 4z 5 0 and g (x y z) 4x 4y z 0. Thus f 2x 2y 2z ,
"#
###
ßß œ œ ßß œ œ œ ™ijk
g 2 4 , and g 8x 8y 2z so that f g g 2x 2y 2z™™ ™™™
"# "#
œ œ œ Ê jk i j k i j k-.
(2 4 ) (8x 8y 2z ) 2x 8x , 2y 2 8y , and 2z 4 2z x 0 or .œ Êœ œ œÊœ œ-. .-.-. .jk i j k "
4
CASE 1: x 0 4(0) 4y z 0 z 2y 2y 4(2y) 5 0 y , or 2y 4( 2y) 5 0œÊ œÊœ„ Ê œÊœ œ
### "
#
y yielding the points and .Êœ !ßß" !ßß
555
663
ˆ‰ˆ ‰
"
#
CASE 2: y y 0 2z 4(0) 2z z 0 2y 4(0) 5 y and.--œÊœÊœÊ œ ÊœÊ œÊœ
""
#44
5
ˆ‰
(0) 4x 4 no solution.
##
#
#
œ Ê
ˆ‰
5
Then f 1 and f 25 the point 1 is closest to the origin.
ˆ‰ ˆ ‰ˆ‰ ˆ‰
!ß ß œ !ß ß œ œ Ê !ß ß
""""
# #
5 5 5 125
46336936
41. f and g y x so that f g (y x ) 1 y and 1 x y x™™ ™™œ œ œ Ê œ Ê œ œ Ê œij i j ij i j-- --
y 16 y 4 (4 4) and ( 4) are candidates for the location of extreme values. But as x ,Ê œ Ê œ „ Ê ß %ß Ä _
#
y and f(x y) ; as x , y 0 and f(x y) . Therefore no maximum or minimum valueÄ_ ß Ä_ Ä_ Ä ß Ä_
exists subject to the constraint.

916 Chapter 14 Partial Derivatives
42. Let f(A B C) (Ax By C z ) C (B C 1) (A B C 1) (A C 1) . We wantßß œ œ
!
4
k1œ
kk k
## # # #
to minimize f. Then f (A B C) 4A 2B 4C, f (A B C) 2A 4B 4C 4, and
AB
ßßœ ßßœ
f (A B C) 4A 4B 8C 2. Set each partial derivative equal to 0 and solve the system to get A ,
Cßßœ œ
"
#
B , and C or the critical point of f is .œ œ ßß
33
44###
"""
ˆ‰
43. (a) Maximize f(a b c) a b c subject to a b c r . Thus f 2ab c 2a bc 2a b c andßßœ œ œ
### # # # # ## # # ##
™ijk
g 2a 2b 2c so that f g 2ab c 2a , 2a bc 2b , and 2a b c 2c™™™œ œ Ê œ œ œijk ----
## # # ##
2a b c 2a 2b 2c 0 or a b c .ÊœœœÊœœœ
### # # # # # #
----
CASE 1: 0 a b c 0.-œÊ œ
###
CASE 2: a b c f(abc) aaa and 3a r f(abc) is the maximum value.
# # # ### # # $
œœ Ê ßßœ œÊ ßßœ
Š‹
r
3
(b) The point a b c is on the sphere if a b c r . Moreover, by part (a), abc f a b c
Š‹ Š‹
ÈÈ ÈÈ
È È
ß ß œ œ ß ß
#
(abc) , as claimed.ŸÊ Ÿœ
Š‹
rrabc
333
$"Î$
44. Let f(x x x ) a x a x a x a x and g(x x x ) x x x 1. Then we
" # "" ## " # ## #
ßßáß œ œ á ßßáß œ á
nii nn n n
!
n
i1œ
want f g a (2x ), a (2x ), , a (2x ), 0 x 1™™œÊœ œáœ ÁÊœÊáœ--- --
""##nn i
a
244 4
aa a
i
--- -
n
4 a 2 a f(x x x ) a x a a a isÊœ Êœ Êßßáßœ œ œ œ--
## # ##
"Î# "Î#
"# ##
"
!! !!!!
Œ Œ
ˆ‰
n
i1
ii ii
niii
nnnnn
i1 i1 i1 i1 i1œœœœœ
ai
--
the maximum value.
45-50. Example CAS commands:
:Maple
f := (x,y,z) -> x*y+y*z;
g1 := (x,y,z) -> x^2+y^2-2;
g2 := (x,y,z) -> x^2+z^2-2;
h := unapply( f(x,y,z)-lambda[1]*g1(x,y,z)-lambda[2]*g2(x,y,z), (x,y,z,lambda[1],lambda[2]) ); # (a)
hx := diff( h(x,y,z,lambda[1],lambda[2]), x ); #(b)
hy := diff( h(x,y,z,lambda[1],lambda[2]), y );
hz := diff( h(x,y,z,lambda[1],lambda[2]), z );
hl1 := diff( h(x,y,z,lambda[1],lambda[2]), lambda[1] );
hl2 := diff( h(x,y,z,lambda[1],lambda[2]), lambda[2] );
sys := { hx=0, hy=0, hz=0, hl1=0, hl2=0 };
q1 := solve( sys, {x,y,z,lambda[1],lambda[2]} ); # (c)
q2 := map(allvalues,{q1});
for p in q2 do # (d)
eval( [x,y,z,f(x,y,z)], p );
``=evalf(eval( [x,y,z,f(x,y,z)], p ));
end do;
Mathematica: (assigned functions will vary)
Clear[x, y, z, lambda1, lambda2]
f[x_,y_,z_]:= x y y z
g1[x_,y_,z_]:= x y 2
22
g2[x_,y_,z_]:= x z 2
22
h = f[x, y, z] lambda1 g1[x, y, z] lambda2 g2[x, y, z];
hx= D[h, x]; hy= D[h, y]; hz= D[h,z]; hL1=D[h, lambda1]; hL2= D[h, lambda2];
critical=Solve[{hx==0, hy==0, hz==0, hL1==0, hL2==0, g1[x,y,z]==0, g2[x,y,z]==0},
Section 14.9 Partial Derivatives with Constrained Variables 917
{x, y, z, lambda1, lambda2}]//N
{{x, y, z}, f[x, y, z]}/.critical
14.9 PARTIAL DERIVATIVES WITH CONSTRAINED VARIABLES
1. w x y z and z x y :œ œ
### ##
(a) w ; 0 and 2x 2y
y
z
xx(yz)
yy
zz
Œ ÎÑ
ÏÒŠ‹
ÄÄÊœœœ
ϧ
œ
œ
```` ``` ` `
```````` ` ``
``
wwxw wzz z x
yxyyyzyy y yy
yy
z
2x 2y 0 2x 2y (2x) (2y)(1) (2z)(0) 2y 2y 0œÊœÊœÊ œœœ
````
````
xxxw
yyyxyx
yy
Š‹ ˆ‰
z
(b) w ; 0 and 2x 2y
x
z
xx
yy(xz)
zz
Œ ÎÑ
ÏÒˆ‰
ÄÄÊœœœ
œ
ϧ
œ
```` ``` ` `
```````` ` ` `
``
wwxw wzx z x
zxzyzzzz z z z
yy
x
1 2y (2x)(0) (2y) (2z)(1) 1 2zÊœ Ê œ Ê œ œ
``
``# `
"` "
yy
zzy z 2y
w
ˆ‰ Š‹
x
(c) w ; 0 and 2x 2y
y
z
xx(yz)
yy
zz
Œ ÎÑ
ÏÒˆ‰
ÄÄÊœœœ
ϧ
œ
œ
```` `` ` `
```````` ` ` `
`` `
wwxw wz z x
zxzyzzzz z z z
yy y
y
1 2x (2x) (2y)(0) (2z)(1) 1 2zʜʜʜ œ
`` ` "
`` ` #
xx1 w
zz2x z x
ˆ‰ ˆ‰
y
2. w x y z sin t and x y t:œ œ
#
(a) w ; 0, 0, and
x
y
z
xx
yy
zz
txy
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ Š‹
Ä ÄÊ œ œœ
œ
œ
œ
œ
``````````
```````````
`
wwxwwzwtxz
yxyyyzytyyy
y
xz
1 (2x)(0) (1)(1) ( 1)(0) (cos t)(1) 1 cos t 1 cos (x y)
``
``
tw
yy
œÊ œ œ œ
Š‹
xt
(b) w ; 0 and 0
y
z
t
xty
yy
zz
tt
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ Š‹
Ä ÄÊ œ œ œ
œ
œ
œ
œ
````````` `
`````````` `
`
wwxwwzwtz t
yxyyyzytyy y
y
zt
1 (2x)( 1) (1)(1) ( 1)(0) (cos t)(0) 1 2 t y 1 2y 2tÊ œœÊ œ œœ
`` `
``` `
`
xt w
yyy y
yŠ‹ ab
zt
(c) w ; 0 and 0
x
y
z
xx
yy
zz
txy
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ ˆ‰
ÄÄÊœœœ
œ
œ
œ
œ
`````````
`````````` `
``
wwxwwzwtx
zxzyzzztzz z
yy
xy
(2x)(0) (1)(0) ( 1)(1) (cos t)(0) 1Êœ œ
ˆ‰
`
`
w
zxy
(d) w ; 0 and 0
y
z
t
xty
yy
zz
tt
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ ˆ‰
ÄÄÊœœœ
œ
œ
œ
œ
```````` `
`````````` `
``
wwxwwzwt t
zxzyzzztzz z
yy
yt
(2x)(0) (1)(0) ( 1)(1) (cos t)(0) 1Êœ œ
ˆ‰
`
`
w
zyt
(e) w ; 0 and 0
x
z
t
xx
ytx
zz
tt
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ ˆ‰
ÄÄÊœœœ
œ
œ
œ
œ
` `` ` `` ``` `
`````````` `
`
w wx w wz wt x z
txtytztttt t
y
xz
(2x)(0) (1)(1) ( 1)(0) (cos t)(1) 1 cos tÊœ œ
ˆ‰
`
`
w
txz
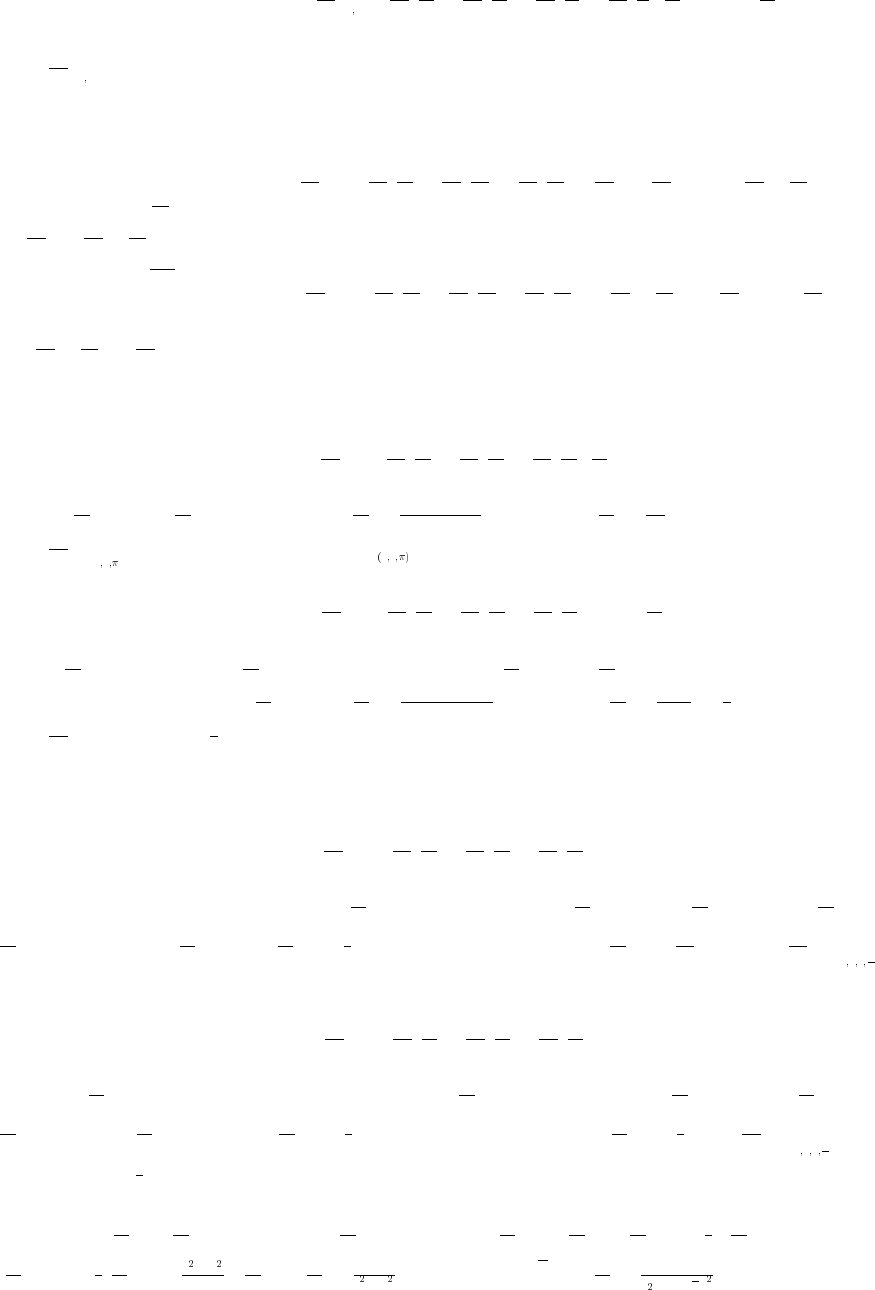
918 Chapter 14 Partial Derivatives
(f) w ; 0 and 0
y
z
t
xty
yy
zz
tt
ÎÑ
ÏÒ ÎÑ
ÐÓ
ÐÓ
ÏÒ ˆ‰
ÄÄÊœœœ
œ
œ
œ
œ
` `` ` `` `` `
`````````` `
``
w wx w wz wt z
txtytztttt t
yy
yz
(2x)(1) (1)(0) ( 1)(0) (cos t)(1) cos t 2x cos t 2(t y)Ê œ œœ
ˆ‰
`
`
w
tyz
3. U f(P V T) and PV nRTœßß œ
(a) U (0)
P
V
PP
VV
T
Œ ÎÑ
ÏÒ ˆ‰ ˆ‰ ˆ‰ˆ‰
ÄÄÊœœ
œ
œ
œPV
nR
UUPUVUTUU UV
PPPVPTPPV TnR
````````` `
````````` `
V
œ
``
``
UUV
PTnR
ˆ‰ˆ‰
(b) U (0)
V
T
P
VV
TT
Œ ÎÑ
ÏÒ ˆ‰ ˆ‰ˆ‰ˆ‰
ÄÄÊœœ
œ
œ
œ
nRT
VUUPUVUTUnRU U
TPTVTTTPVV T
```````` ` `
```````` ` `
V
œ
ˆ‰ˆ‰
``
``
UnR U
PV T
4. w x y z and y sin z z sin x 0œ œ
###
(a) w ; 0 and
x
y
xx
yy
zz(xy)
Œ ÎÑ
ÏÒˆ‰
ÄÄÊœœ
œ
œ
ϧ
```` ``
````````
``
wwxw wz
xxxyxzxx
yy
y
(y cos z) (sin x) z cos x 0 . At (0 1 ),
`` ` `
`` ` `
zz zz cos x z
xx xy cos zsin x x1
œÊœ ßßœœ11
1
(2x)(1) (2y)(0) (2z)( ) 2Êœ œ
ˆ‰ k
`
`
#
w
xk
y(0 1 ) 01
11
(b) w (2x) (2y)(0) (2z)(1)
y
z
xx(yz)
yy
zz
Œ ÎÑ
ÏÒˆ‰
ÄÄÊœœ
ϧ
œ
œ
```` `` `
``````` `
`
wwxw wz x
zxzyzzz z
y
y
(2x) 2z. Now (sin z) y cos z sin x (z cos x) 0 and 0œ œ œ
``
`` ``
``
xx
zz zz
yy
y cos z sin x (z cos x) 0 . At ( ), Ê œ Ê œ !ß "ß œ œ
`` `"
`` `
xx x10
z z z cos x z ( )(1)
y cos z sin x 111
2(0) 2 2Êœœ
ˆ‰ ˆ‰
`"
`C!"ß Ñ
w
z(,
k1111
5. w x y yz z and x y z 6œ œ
## $ # # #
(a) w
x
y
xx
yy
zz(xy)
Œ ÎÑ
ÏÒŠ‹
ÄÄÊœ
œ
œ
ϧ
```` ``
```````
`
wwxw wz
yxyyyzy
y
x
2xy (0) 2x y z (1) y 3z 2x y z y 3z . Now (2x) 2y (2z) 0 andœœ œaba bab ab
## ## #
````
````
zzxz
yyyy
0 2y (2z) 0 . At (w x y z) (4 2 1 1), 1
``` `"`
``` ``
xzz zw
yyyz y1y
y
œ Ê œ Ê œ ßßß œ ßßß œ œ Ê ¹Š‹
x(421 1)
(2)(2) (1) ( 1) 1 3( 1) (1) 5œœcdcd
##
(b) w
y
z
xx(yz)
yy
zz
Œ ÎÑ
ÏÒŠ‹
ÄÄÊœ
ϧ
œ
œ
```` ``
```````
`
wwxw wz
yxyyyzy
y
z
2xy 2x y z (1) y 3z (0) 2x y 2x y z. Now (2x) 2y (2z) 0 andœœ œab a b a b ab
## ###
````
````
xxxz
yyyy
0 (2x) 2y 0 . At (w x y z) (4 2 1 1),
`` ` `"`
`` ` ``
zx x xw
y y yx y2 y
y
(
œ Ê œ Ê œ ßßß œ ßßß œ Ê ¹Š‹
z421 1)
(2)(2)(1) (2)(2) (1) ( 1) 5œœ
##
"
#
ˆ‰
6. y uv 1 v u ; x u v and 0 0 2u 2v 1œÊœ œ œÊœ Êœ Ê
`` ` ` `` `
`` ` ` `` `
##
uv x u v v uu
yy y y y y vy
ˆ‰
v u . At (u v) 2 1 , 1œ œ Êœ ßœ ß œ œ
```` `"
`` `` `
uuuvuuuv u
yvyvyyvu y
12
Š‹Š‹ Š‹
ÈŠ‹
È

Section 14.10 Taylor's Formula for Two Variables 919
1ʜ
Š‹
`
`
u
yx
7. cos ; x y r 2x 2y 2r and 0 2x 2r
rxr cos
y r sin
Œ Œ ˆ‰
))
))ÄÊœœÊœœÊœ
œ
œ
```
`````
### ``
xrr
rxxxx
yy
)
ÊœÊ œ
``
``
rx r x
xr x xy
ˆ‰
yÈ
8. If x, y, and z are independent, then
ˆ‰
````````
`````````
`
wwxwwzwt
xxxyxzxtx
y
yz œ
(2x)(1) ( 2y)(0) (4)(0) (1) 2x . Thus x 2z t 25 1 0 0 1œ œ œÊœÊœ
ˆ‰
`` ``
`` ``
tt tt
xx xx
2x 1. On the other hand, if x, y, and t are independent, then ʜ
ˆ‰ ˆ‰
` `
` `
w w
x x
yz yt
(2x)(1) ( 2y)(0) 4 (1)(0) 2x 4 . Thus, x 2z t 25œœ œ œ
`` ` `` `` ` `
`` `` `` `` ` `
`
wx w wz w t z z
xx yx zx tx x x
y
12 0 0 2x4 2x2.Ê œÊ œÊ œ œ
``"` "
``#` #
zzw
xxx
ˆ‰ ˆ‰
yt
9. If x is a differentiable function of y and z, then f(x y z) 0 0 0ßßœÊ œÊ œ
`` ` `` ` `
`` `` `` ` ``
``
fx f fz f f
xx yx zx x yx
yy
. Similarly, if y is a differentiable function of x and z, and if z is aÊœ œ
Š‹ Š‹
```
``` ```
`` `
xf/ z
yf/z zf/x
f/ y y
z x
differentiable function of x and y, . Then
ˆ‰ ˆ‰
Š‹Š‹
``` ` `
``` ```
`
zf/x x z
xf/y yzx
y
yy
zx
œ
1.œœ
Š‹ Š‹
ˆ‰
``
`` `` ``
`` ``
f/ y
f/ z f/ x f/ y
f/ z f/ x
10. z z f(u) and u xy 1 1 y ; also 0 x so that x y œ œ Ê œ œ œ œ
`` `` ``
`` `` ``
zdfu dfzdfudf zz
xdux duyduydu xy
x1 y yx xœ œ
ˆ‰ˆ‰
df df
du du
11. If x and y are independent, then g(x y z) 0 0 and 0 0ßß œ Ê œ œ Ê œ
` ``` ``
`` `` `` ` ` ``
``` `
g gyg gg
xy yy zy y y zy
xzx z
, as claimed.ʜ
Š‹
`
```
``
z
yg/z
g/ y
x
12. Let x and y be independent. Then f(x y z w) 0, g(x y z w) 0 and 0ßßß œ ßßß œ œ
`
`
y
x
0 andÊœœ
`` ` `` ` ` ` `` ` `
`` `` `` ` ` ` `` ` `
`
fx f fz fw f fz f w
xx yx zx wx x zx wx
y
0 imply
````` `` `
`` `` `` ` ` ` `` ` `
`````
ggygg gg g
xx yx zx wx x zx wx
xzwzw
œ œ
ˆ‰
`` `` `
`` ` ` `
`` `
`` ` ` `
``
`
`
fz fw f
zx wx x
gg g
zx wx x
zw
z
x
œ
œ
Êœ œ
y
»»
»»
c
c
ff
xw
gg
xw
ff
zw
gg
zw
ff
xw xw
gg
f
z
gg g g
wzw zwwz
fff
ff
xw wx
gg
œ , as claimed.
Likewise, f(x y z w) 0, g(x y z w) 0 and 0 ßßß œ ßßß œ œ Ê
````````
` ````````
`
xfxffzfw
y xyyyzywy
y
0 and (similarly) 0 implyœ œ œ
``` `` ` `
````` `````
`` `
ffzfw z w
yzywy yzywy
gg g
Š‹
`` `` `
`` ` ` `
`` `
`` ` ` `
``
`
`
fz fw f
zy wy y
gg g
zy wy y
zw
w
y
œ
œ
Êœ œ
x
»»
»»
ff
zy
gg
zy
ff
zw
gg
zw
c
cff
zy zy
gg
f
z
gg g g
wzw zwwz
fff
ff
zy yz
gg
œ , as claimed.
14.10 TAYLOR'S FORMULA FOR TWO VARIABLES
1. f(x y) xe f e , f xe , f 0, f e , f xeßœ Ê œ œ œ œ œ
yyy yy
x y xx xy yy
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
0 x 1 y 0 x 0 2xy 1 y 0 x xy quadratic approximation;œ œ†† † † †
"
#
##
ab
f 0, f 0, f e , f xe
xxx xxy xyy yyy
yy
œœœ œ

920 Chapter 14 Partial Derivatives
f(x y) quadratic x f ( ) 3x yf (0 0) 3xy f ( ) y f (0 0)Ê ß ¸ !ß ! ß !ß ! ß
"$# #$
6xxx xxy xyy yyy
cd
x xy x 0 3x y 0 3xy 1 y 0 x xy xy , cubic approximationœ œ
""
$# #$ #
#6ab††††
2. f(x y) e cos y f e cos y, f e sin y, f e cos y, f e sin y, f e cos yßœ Ê œ œ œ œ œ
xxxxxx
x y xx xy yy
f(x y) f(0 0) xf (0 0) yf ( 0) x f ( ) 2xyf ( ) y f (0 0)Ê ß ¸ ß ß !ß !ß ! !ß ! ß
x y xx xy yy
"
#
##
cd
1 x 1 y 0 x 1 2xy 0 y ( 1) 1 x x y , quadratic approximation;œ œ †† † † †
""
##
## ##
cdab
f e cos y, f e sin y, f e cos y, f e sin y
xxx xxy xyy yyy
xxxx
œœœœ
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
1 x x y x 1 3x y 0 3xy ( 1) y 0œ
""
#
## $ # # $
abc d
6††† †
1 x x y x 3xy , cubic approximationœ
""
#
## $ #
aba b
6
3. f(x y) y sin x f y cos x, f sin x, f y sin x, f cos x, f 0ßœ Ê œ œ œ œ œ
x y xx xy yy
f(x y) f(0 0) xf (0 0) yf ( 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê ß¸ ß ß !ß ß ß ß
x y xx xy yy
"
#
##
cd
0 x 0 y 0 x 0 2xy 1 y 0 xy, quadratic approximation;œ œ†† † † †
"
#
##
ab
f y cos x, f sin x, f 0, f 0
xxx xxy xyy yyy
œ œ œ œ
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
xy x 0 3x y 0 3xy 0 y 0 xy, cubic approximationœ œ
"$# #$
6ab††††
4. f(x y) sin x cos y f cos x cos y, f sin x sin y, f sin x cos y, f cos x sin y,ß œ Ê œ œ œ œ
x y xx xy
f sin x cos y f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)
yy x y xx xy yy
œ Ê߸ßßß ß ß ß
"
#
##
cd
0 x 1 y 0 x 0 2xy 0 y 0 x, quadratic approximation;œ œ†† † † †
"
#
##
ab
f cos x cos y, f sin x sin y, f cos x cos y, f sin x sin y
xxx xxy xyy yyy
œ œ œ œ
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
x x ( 1) 3x y 0 3xy ( 1) y 0 x x 3xy , cubic approximationœ œ
""
$##$ $#
66
cdab††††
5. f(x y) e ln (1 y) f e ln (1 y), f , f e ln (1 y), f , fßœ Ê œ œ œ œ œ
xx x
x y xx xy yy
eee
1 y 1 y (1 y)
xxx
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
0 x 0 y 1 x 0 2xy 1 y ( 1) y 2xy y , quadratic approximation;œ œ †† † † †
""
##
## #
cdab
f e ln (1 y), f , f , f
xxx xxy xyy yyy
xee2e
1 y (1 y) (1 y)
œœ œ œ
xxx
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
y 2xy y x 0 3x y 1 3xy ( 1) y 2œ
""
#$ # # $
26
abc d††† †
y 2xy y 3x y 3xy 2y , cubic approximationœ
""
#
###$
aba b
6
6. f(x y) ln (2x y 1) f , f , f , f ,ßœ Ê œ œ œ œ
xyxx xy
242
2x y 1 x y 1 (2x y 1) (2x y 1) #
"
f f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)
yy x y xx xy yy
(2x y 1)
œ Ê ß¸ ß ß ß ß ß ß
" "
#
##
cd
0 x 2 y 1 x ( 4) 2xy ( 2) y ( 1) 2x y 4x 4xy yœ œ †† † † †
""
##
## ##
cdab
(2x y) (2x y) , quadratic approximation;œ
"
#
#
f, f, f, f
xxx xxy xyy yyy
16842
(2x y 1) (2x y 1) (2x y 1) (2x y 1)
œœœœ
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
(2x y) (2x y) x 16 3x y 8 3xy 4 y 2œ
""
#
#$ # # $
6ab††††
(2x y) (2x y) 8x 12x y 6xy yœ
""
#
#$###
3ab
(2x y) (2x y) (2x y) , cubic approximationœ
""
#
#$
3
7. f(x y) sin x y f 2x cos x y , f 2y cos x y , f 2 cos x y 4x sin x y ,ߜʜœœ ab ab ab ab ab
## ## ## ## # ##
xyxx
f 4xy sin x y , f 2 cos x y 4y sin x y
xy yy
œ œ ab ab ab
## ## # ##

Section 14.10 Taylor's Formula for Two Variables 921
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
0 x 0 y 0 x 2 2xy 0 y 2 x y , quadratic approximation;œ œ†† † † †
"
#
####
ab
f 12x sin x y 8x cos x y , f 4y sin x y 8x y cos x y ,
xxx xxy
œ œ ab ab ab ab
## $ ## ## # ##
f 4x sin x y 8xy cos x y , f 12y sin x y 8y cos x y
xyy yyy
œ œ ab ab ab ab
## # ## ## $ ##
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
x y x 0 3x y 0 3xy 0 y 0 x y , cubic approximationœ œ
## $ # # $ ##
"
6ab††††
8. f(x y) cos x y f 2x sin x y , f 2y sin x y ,ßœ Ê œ œ ab ab ab
## ## ##
xy
f 2 sin x y 4x cos x y , f 4xy cos x y , f 2 sin x y 4y cos x y
xx xy yy
œ œ œ ab ab ab ab ab
## # ## ## ## # ##
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
1 x 0 y 0 x 0 2xy 0 y 0 1, quadratic approximation;œ œ†† † † †
"
#
##
cd
f 12x cos x y 8x sin x y , f 4y cos x y 8x y sin x y ,
xxx xxy
œ œ ab ab ab ab
## $ ## ## # ##
f 4x cos x y 8xy sin x y , f 12y cos x y 8y sin x y
xyy yyy
œ œ ab ab ab ab
## # ## ## $ ##
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
1 x 0 3x y 0 3xy 0 y 0 1, cubic approximationœ œ
"$# #$
6ab††††
9. f(x y) f f , f f fßœ Ê œ œ œ œ œ
""
1 x y (1 x y) (1 x y)
x y xx xy yy
2
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
1 x 1 y 1 x 2 2xy 2 y 2 1 (x y) x 2xy yœ œ†† † † †
"
#
## ##
abab
1 (x y) (x y) , quadratic approximation; f f f fœ œ œ œ œ
#
xxx xxy xyy yyy
6
(1 x y)
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
1(xy)(xy) x63xy63xy6y6œ
#$ # # $
"
6ab††††
1 (x y) (x y) x 3x y 3xy y 1 (x y) (x y) (x y) , cubic approximationœ œ
#$ # #$ # $
ab
10. f(x y) f , f , f ,ßœ Ê œ œ œ
"
"
1 x y xy (1 x y xy) ( x y xy) (1 x y xy)
xyxx
1 y 2(1 y)
1 x
f, f
xy yy
1
( x y xy) (1 x y xy)
2( x)
œœ
"
"
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
1x1y1 x22xy1y2 1xyx xyy, quadratic approximation;œ œ†† † † †
"
#
## ##
ab
f, f ,
xxx xxy
6(1 y) [ 4(1 x y xy) 6(1 y)(1 x)](1 y)
(1 x y xy) (1 x y xy)
œœ
f, f
xyy yyy
[ 4(1 x y xy) 6(1 x)(1 y)](1 x) 6(1 x)
(1 x y xy) (1 x y xy)
œœ
f(x y) quadratic x f (0 0) 3x yf ( 0) 3xy f (0 0) y f (0 0)Ê߸ ß !ß ß ß
"$# #$
6xxx xxy xyy yyy
cd
1xyx xyy x63xy23xy2y6œ
##$# #$
"
6ab††††
1xyx xyy x xyxy y, cubic approximationœ
# #$# #$
11. f(x y) cos x cos y f sin x cos y, f cos x sin y, f cos x cos y, f sin x sin y,ßœ Ê œ œ œ œ
xyxx xy
f cos x cos y f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)
yy x y xx xy yy
œ Ê߸ßßß ß ß ß
"
#
##
cd
1 x 0 y 0 x ( 1) 2xy 0 y ( 1) 1 , quadratic approximation. Since all partialœ œ†† † † †
"
###
##
cd
xy
derivatives of f are products of sines and cosines, the absolute value of these derivatives is less than or equal
to 1 E(x y) (0.1) 3(0.1) 3(0.1) 0.1) 0.00134.Êߟ Ÿ
"$$$$
6cd
12. f(x y) e sin y f e sin y, f e cos y, f e sin y, f e cos y, f e sin yߜʜœœœœ
xxxxxx
x y xx xy yy
f(x y) f(0 0) xf (0 0) yf (0 0) x f (0 0) 2xyf (0 0) y f (0 0)Ê߸ßßß ß ß ß
x y xx xy yy
"
#
##
cd
0 x 0 y 1 x 0 2xy 1 y 0 y xy , quadratic approximation. Now, f e sin y,œ œ œ†† † † †
"
#
##
ab xxx x
f e cos y, f e sin y, and f e cos y. Since x 0.1, e sin y e sin 0.1 0.11 and
xxy xyy yyy
xx x x01
œœ œ Ÿ Ÿ¸kk k k k k
Þ
e cos y e cos 0.1 1.11. Therefore,kkk k
x01
Ÿ¸
Þ
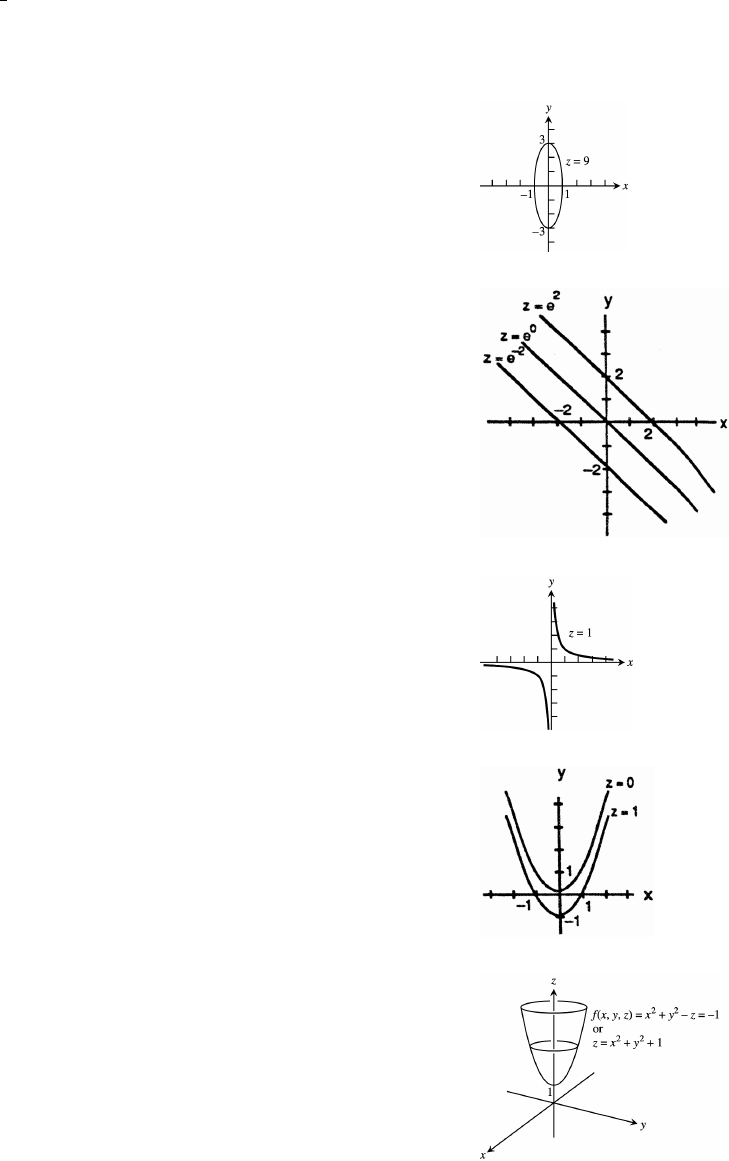
922 Chapter 14 Partial Derivatives
E(x y) (0.11)(0.1) 3(1.11)(0.1) 3(0.11)(0.1) (1.11)(0.1) 0.000814.ߟ Ÿ
"$$$$
6cd
CHAPTER 14 PRACTICE EXERCISES
1. Domain: All points in the xy-plane
Range: z 0
Level curves are ellipses with major axis along the y-axis
and minor axis along the x-axis.
2. Domain: All points in the xy-plane
Range: 0 z_
Level curves are the straight lines x y ln z withœ
slope 1, and z 0.
3. Domain: All (x y) such that x 0 and y 0ßÁÁ
Range: z 0Á
Level curves are hyperbolas with the x- and y-axes
as asymptotes.
4. Domain: All (x y) so that x y 0ß
#
Range: z 0
Level curves are the parabolas y x c, c 0.œ
#
5. Domain: All points (x y z) in spaceßß
Range: All real numbers
Level surfaces are paraboloids of revolution with
the z-axis as axis.
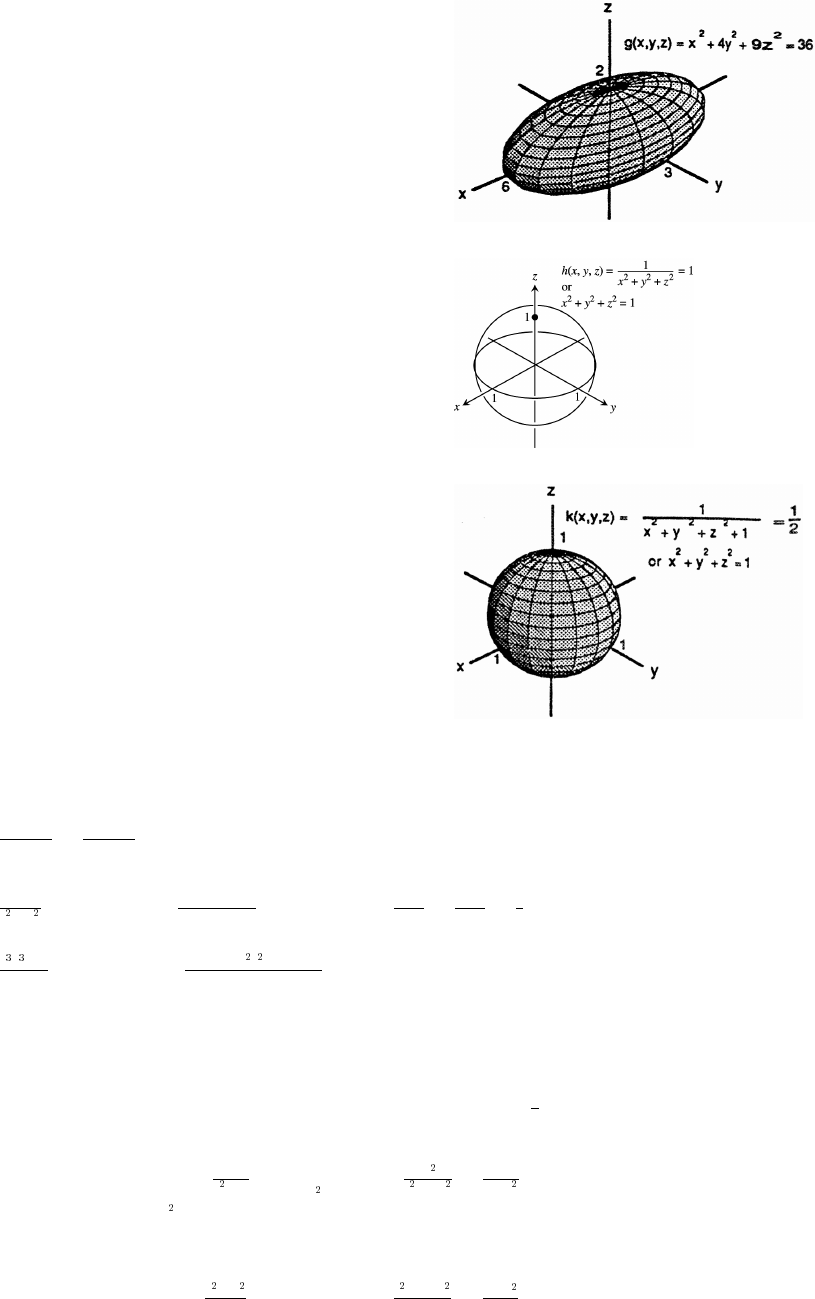
Chapter 14 Practice Exercises 923
6. Domain: All points (x y z) in spaceßß
Range: Nonnegative real numbers
Level surfaces are ellipsoids with center (0 0 0).ßß
7. Domain: All (x y z) such that (x y z) (0 0)ßß ßß Á ß!ß
Range: Positive real numbers
Level surfaces are spheres with center (0 0 0) andßß
radius r 0.
8. Domain: All points (x y z) in spaceßß
Range: (0 1]ß
Level surfaces are spheres with center (0 0 0) andßß
radius r 0.
9. lim e cos x e cos (2)( 1) 2
Ðß ÑÄÐß Ñxy ln21
yln2
œœœ1
10. lim 2
Ðß ÑÄÐß Ñxy 00
2y
xcos y 0cos 0
20
œœ
11. lim lim lim
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ
Á„ Á„
xy 11 xy 11 xy 11
xy xy
xy xy
x y (x y)(x y) x y 1 1
1
#
""
œœœœ
12. lim lim lim x y xy 1 1 1 1 1 1 3
Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñ Ðß ÑÄÐß Ñxy 11 xy 11 xy 11
xy 1
xy 1 xy 1
(xy1)xy xy1
## # #
œœœœ
ab ab††
13. lim ln x y z ln 1 ( 1) e ln e 1
P11eÄÐ ß ß Ñ kkk k œ œ œ
14. lim tan (x y z) tan (1 ( 1) ( 1)) tan ( 1)
P 111Ä Ð ß ß Ñ
" " "
œ œ œ
1
4
15. Let y kx , k 1. Then lim lim which gives different limits forœÁ œ œ
#
Ðß ÑÄÐß Ñ
Á
ßÄÐßÑ
xy 00
yx
xkx 00
y
xy xkx 1k
kx k
ab
different values of k the limit does not exist.Ê
16. Let y kx, k 0. Then lim lim which gives different limits forœÁ œ œ
Ðß ÑÄÐß Ñ ß ÑÄÐß Ñ
Á
xy 00 (xkx 00
xy 0
xy x(kx)
xy x(kx) k
1k

924 Chapter 14 Partial Derivatives
different values of k the limit does not exist.Ê
17. Let y kx. Then lim which gives different limits for different valuesœœœ
Ðß ÑÄÐß Ñxy 00
xy
xy xkx 1k
xkx 1k
of k the limit does not exist so f(0 0) cannot be defined in a way that makes f continuous at the origin.Êß
18. Along the x-axis, y 0 and lim lim , so the limit fails to exist
1, x 0
, x 0
œœœ
"
Ðß ÑÄÐß Ñ Ä
xy 00 x0
sin (x y)
xy x
sin x
kk kk œ
f is not continuous at (0 0).Êß
19. cos sin , r sin r cos
``
``
gg
rœ œ )) ) )
)
20. ,
`"
`#
f2x x
xxy xyxyxy
1
yxy
œ œœ
Š‹
Š‹
ˆ‰
y
x
y
x
`"
`#
fx
yxy xyxyxy
2y y x y
1
œ œœ
Š‹
Š‹
ˆ‰
1
x
y
x
21. , ,
`"`"`"
```
fff
RRR
RRR
œ œ œ
22. h (x y z) 2 cos (2 x y 3z), h (x y z) cos (2 x y 3z), h (x y z) 3 cos (2 x y 3z)
xyz
ßß œ ßß œ ßß œ 11 1 1
23. , , ,
````
````
P RT P nT P nR P nRT
nVRVTVV V
œœœœ
24. f (r T w) , f (r T w) , f (r T w)
r T
ßjß ß œ ßjß ß œ ßjß ß œ
"""""
j#j#j
j
2r w r w r
TT
w2T
ÉÉ
ˆ‰
Š‹Š‹
11
1
ÈÈ
, f (r T w) wœœ ßjßßœ œ
"" " " " "
jj #j# j
$Î#
4r T w 4r T w r 4r w w
TT T
ÉÉ É É
ˆ‰ ˆ ‰
11 1 1
w
25. , 1 0, ,
`` `` ``
` ` ` ` `` ``
" "
gg gg gg
xyy y x y yyx xy y
x2x
œœÊœœ œœ
26. g (x y) e y cos x, g (x y) sin x g (x y) e y sin x, g (x y) 0, g (x y) g (x y) cos x
x y xx yy xy yx
xx
ßœ ßœ Ê ßœ ßœ ßœ ßœ
27. 1 y 15x , x 30x , 0, 1
``````
````````
#
f2xff22xfff
x x 1 y x y yx xy
x1
œ œ Ê œ œ œ œ
ab
28. f (x y) 3y, f (x y) 2y 3x sin y 7e f (x y) 0, f (x y) 2 cos y 7e , f (x y) f (x y)
x y xx yy xy yx
yy
ßœ ßœ Ê ßœ ßœ ßœ ß
3œ
29. y cos (xy ), x cos (xy ), e ,
`` "
``
wwdx
x y dt dt t 1
dy
œœœœ11
t
[y cos (xy )]e [x cos (xy )] ; t 0 x 1 and y 0Êœ œÊœ œ
dw
dt t 1
11
tˆ‰
"
0 1 [1 ( 1)] 1Êœ œ
¸ˆ‰
dw
dt 0 1
t0œ†† "
30. e , xe sin z, y cos z sin z, t , 1 ,
`` ` "
`` `
"Î#
ww w dx dz
xy z dt dttdt
dy
œœ œ œ œœ
yy 1
e t xe sin z 1 (y cos z sin z) ; t 1 x 2, y 0, and zÊœ œÊœ œ œ
dw
dt t
yy"Î# "
ab
ˆ‰ 11
1 1 (2 1 0)(2) (0 0) 5Êœœ
¸
dw
dt t1œ†† 1
31. 2 cos (2x y), cos (2x y), 1, cos s, s, r
`` ``
`` ````
``
ww xx
xy rsrs
yy
œœœœœœ
[2 cos (2x y)](1) [ cos (2x y)](s); r and s 0 x and y 0Êœ œ œÊœ œ
`
`
w
r11

Chapter 14 Practice Exercises 925
(2 cos 2 ) (cos 2 )(0) 2; [2 cos (2x y)](cos s) [ cos (2x y)](r)Êœ œœ
¸
``
``
ww
rs
011
(2 cos 2 )(cos 0) (cos 2 )( ) 2Êœ œ
¸
`
`
w
s01111
32. 2e cos v ; u v 0 x 2 (2) ;
`` " ` "
`` `
wdwx x w 2 2
udxu 1xx1 u 55 5
œ œ œœÊœÊ œ œ
ˆ‰ ¸ˆ‰
ab
u
00
2e sin v (0) 0
`` " ` "
`` `
wdwx x w 2
vdxv 1xx1 v 55
œœ Ê œœ
ˆ‰ ¸ˆ‰
ab
u
00
33. y z, x z, y x, sin t, cos t, 2 sin 2t
```
```
fffdx dz
x y z dt dt dt
dy
œ œ œ œ œ œ
(y z)(sin t) (x z)(cos t) 2(y x)(sin 2t); t 1 x cos 1, y sin 1, and z cos 2Êœ œÊœ œ œ
df
dt
(sin 1 cos 2)(sin 1) (cos 1 cos 2)(cos 1) 2(sin 1 cos 1)(sin 2)ʜ
¸
df
dt t1œ
34. (5) and (1) 5 5 5 0
`` `` ``
`` `` ``
w dw s dw w dw s dw dw w w dw dw
x ds x ds y ds y ds ds x y ds ds
œœ œœ œÊœœ
35. F(x y) 1 x y sin xy F 1 y cos xy and F 2y x cos xy ßœ Ê œ œ Ê œœ
#
xy
dy 1 y cos xy
dx F 2y x cos xy
Fx
y
at (x y) ( 1) we have 1œ Ê ß œ !ß œ œ
1 y cos xy dy
2y x cos xy dx 2
1
"
¹ÐßÑ01
36. F(x y) 2xy e 2 F 2y e and F 2x e ß œ Ê œ œ Ê œ œ
xy xy xy
xy
dy 2y e
dx F 2x e
F
x
y
xy
xy
at (x y) ( ln 2) we have (ln 2 1)Êßœ!ß œ œ
¹
dy
dx 0 2
2 ln 2 2
Ðß Ñ0ln2
37. f ( sin x cos y) (cos x sin y) f f ;™™™œ Ê œ Ê œ œ œij ijkkk
Ɉ‰ˆ‰
44
"" " " "
## # # #
##
ÈÈ
2
2
f increases most rapidly in the direction and decreases mostuij uijœœ Ê œ
™
™
f
f
22 22
kk ÈÈ ÈÈ
## ##
rapidly in the direction ; (D f) f and (D f) ;œ œ œ œuij
ÈÈ È È
22 2 2
## # #
uuPP
kk™
(D f) fuiju
""
""
##
œœ œ Ê œ œ œ
v
v
ij
kk È
34
34
34 3 4 7
55 5 5 10
uP™† ˆ‰ˆ‰ˆ‰ˆ‰
38. f 2xe 2x e f f 2 ( 2) 2 2; ™™™œ Ê œ##Êœœ œœ
2y 2y
10
ij ij u ij
###
kkk
ÈÈ™
™
f
f
11
22
kk ÈÈ
f increases most rapidly in the direction and decreases most rapidly in the directionÊœuij
11
22
ÈÈ
; (D f) f 2 2 and (D f) 2 2 ; œ œ œ œ œ œ œ uij u ij
11 11
22 11 2 2
ÈÈ ÈÈÈ
kk
uuPP
kkÈÈ
™"
v
v
ij
(D f) f (2) ( 2) 0Êœ œ œ
uP™†u"""
Š‹ Š‹
ÈÈ
22
39. f f 2 3 6 ;™™œ Êœ
Š‹Š‹Š‹ k
236
2x 3y 6z 2x 3y 6z 2x 3y 6z
ijk ijk
111
f increases most rapidly in the direction andu ijk u ijkœ œ œ Ê œ
™
™
f
f777 777
236
236
236 236
kk Èijk
decreases most rapidly in the direction ; (D f) f 7, (D f) 7;œ œ œ œuijk
236
777 uuPP
kk™
(D f) (D f) 7uijk
"œœ Ê œ œ
v
vkk 236
777 uuPP
40. f (2x 3y) (3x 2) (1 2z) f 2 ; f increases most™™œ Ê œ œ œ Êijk jku jkk000
™
™
f
f
2
55
kk ÈÈ
"
rapidly in the direction and decreases most rapidly in the direction ;ujk u jkœ œ
2 2
55 55
ÈÈ ÈÈ
" "
(D f) f 5 and (D f) 5 ;
uuPP
œ œ œ œœ œkk
ÈÈ
™"
"""
uijk
v
v
ijk
kk ÈÈÈÈ
111 333
(D f) f (0) (2) (1) 3Êœœœœ
uP™†u""""
Š‹ Š‹ Š‹ È
ÈÈÈÈ
3333
3
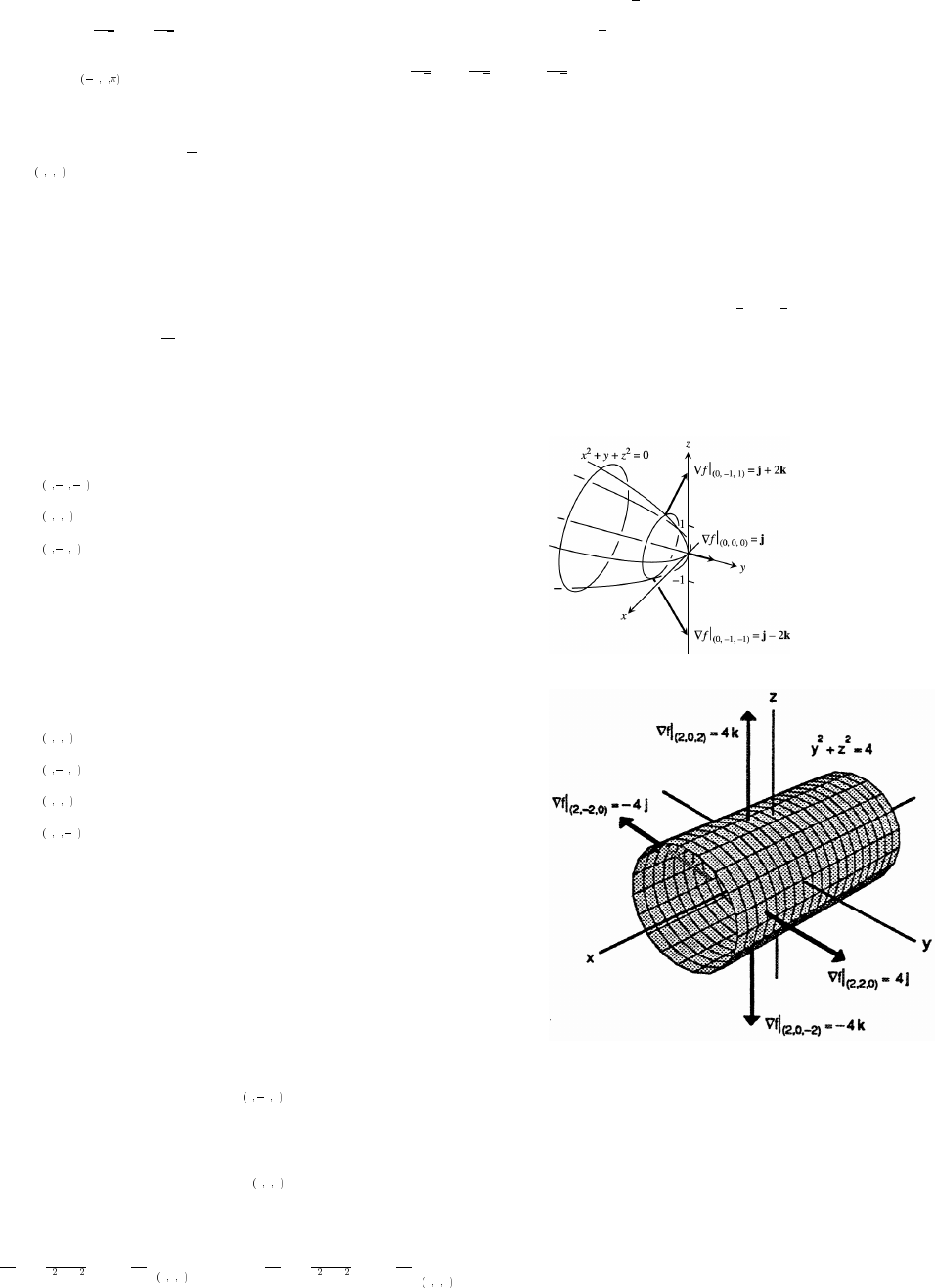
926 Chapter 14 Partial Derivatives
41. (cos 3t) (sin 3t) 3t (t) ( 3 sin 3t) (3 cos 3t) 3 3 3rijkv i jkvjkœÊœ Êœ
ˆ‰
1
3
; f(x y z) xyz f yz xz xy ; t yields the point on the helix ( 1 0 )Ê œ ßß œ Ê œ œ ßßujk ijk
""
ÈÈ
22 3
™11
f f()ʜʜœkŠ‹
™™††
10 11j ujjk
""
ÈÈ È
22 2
1
42. f(x y z) xyz f yz xz xy ; at (1 1 1) we get f the maximum value ofßß œ Ê œ ßß œ Ê™™ijk ijk
Df f 3kkk
È
u111 œœ™
43. (a) Let f a b at (1 2). The direction toward (2 2) is determined by (2 1) (2 2)™œ ß ß œ œœij v i jiu
"
so that f 2 a 2. The direction toward (1 1) is determined by (1 1) (1 2)™†uvijjuœÊœ ß œ œœ
#
so that f 2 b 2 b 2. Therefore f 2 2 ; f 1, 2 f 1, 2 2.™† ™uijœ Ê œ Ê œ œ œ œ
xy
ab ab
(b) The direction toward (4 6) is determined by (4 1) (6 2) 3 4 ßœœÊœvijijuij
$34
55
f.Êœ™†u14
5
44. (a) True (b) False (c) True (d) True
45. f 2x 2z ™œ Êij k
f2,k™011œjk
f,k™000 œj
f2k™011œjk
46. f 2y 2z ™œ Êjk
f4,k™220 œj
f4,k™220œ j
f4,k™202 œk
f4k™20 2 œ k
47. f 2x 5 f 4 5 Tangent Plane: 4(x 2) (y 1) 5(z 1) 0™™œ Ê œ Ê œij k ij kk211
4x y 5z 4; Normal Line: x 2 4t, y 1 t, z 1 5tÊœ œ œœ
48. f 2x 2y f 2 2 Tangent Plane: 2(x 1) 2(y 1) (z 2) 0™™œÊ œÊ œijk ijkk112
2x 2y z 6 0; Normal Line: x 1 2t, y 1 2t, z 2 tÊœ œ œ œ
49. 0 and 2; thus the tangent plane is
`` ``
` ` ` `
z2x z z z
xxy x yxy y
2y
œÊ œ œÊ œ
¸¹
010 010
2(y 1) (z 0) 0 or 2y z 2 0œ œ
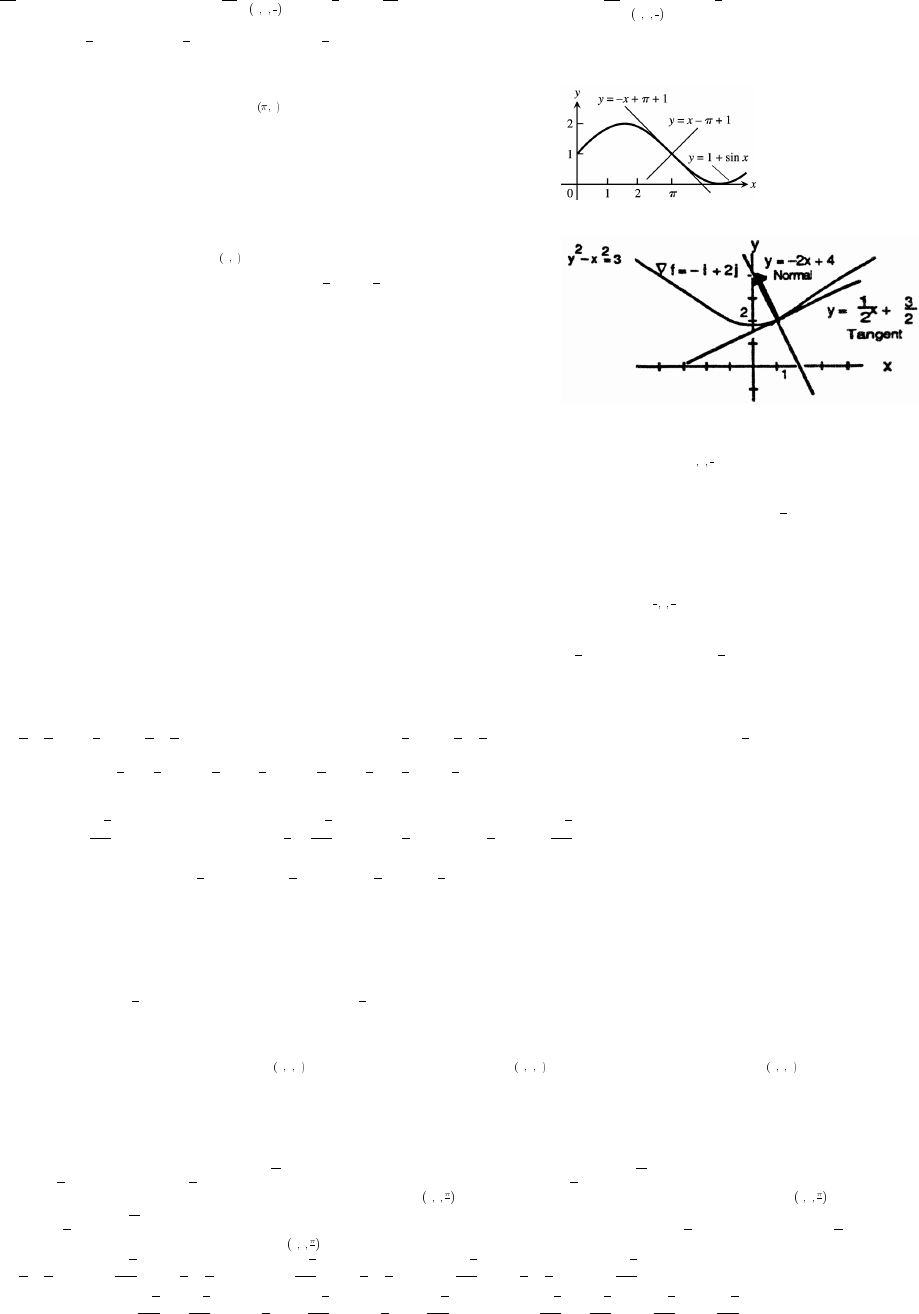
Chapter 14 Practice Exercises 927
50. 2x x y and 2y x y ; thus the tangent
``"``"
``#``#
## ##
# #
zzzz
xxyy
œ Ê œ œ Ê œab ab
¸¹
11 11
1
21
2
plane is (x 1) (y 1) z 0 or x y 2z 3 0œ œ
"" "
## #
ˆ‰
51. f ( cos x) f the tangent™™œ Ê œ Êij ijk1
line is (x ) (y 1) 0 x y 1; theœÊœ11
normal line is y 1 1(x ) y x 1œ Ê œ11
52. f x y f 2 the tangent™™œ Ê œ Êij ijk12
line is (x 1) 2(y 2) 0 y x ; the normal œÊœ
"
##
3
line is y 2 2(x 1) y 2x 4œ Êœ
53. Let f(x y z) x 2y 2z 4 and g(x y z) y 1. Then f 2x 2 2 2 2 2ßß œ ßß œ œ œ
#k™ijk ijk
ab111
2
and g f g 2 2 the line is x 1 2t, y 1, z 2t
222
00
™™™œÊ ‚ œ œ Ê œ œ œ
"
jik
ijk
ââ
ââ
ââ
ââ
ââ
ââ "
#
54. Let f(x y z) x y z 2 and g(x y z) y 1. Then f 2y 2 andßß œ ßß œ œ œ
#k™ijk ijk
ab
11
22
1
g f g the line is x t, y 1, z t
121
00
™™™œÊ ‚ œ œ Ê œ œ œ
"
jik
ijk
ââ
ââ
ââ
ââ
ââ
ââ ""
##
55. f , f cos x cos y , f sin x sin y
ˆ‰ ˆ‰ ˆ‰
kk
11 11 11
11 11
44 44 44
xy
44 44
ßœ ßœ œ ßœ œ
"" "
## #
ÐÎßÎÑ ÐÎßÎÑ
L(x y) x y x y; f (x y) sin x cos y, f (x y) sin x cos y, andÊßœ œ ßœ ßœ
"" " "" "
## # ## #
ˆ‰ˆ‰
11
44 xx yy
f (x y) cos x sin y. Thus an upper bound for E depends on the bound M used for f , f , and f .
xy xx xy yy
ߜ kkkk kk
With M we have E(x y) x y (0.2) 0.0142;œßŸŸŸ
ÈÈ È
22 2
444###
"##
kk
Š‹
ˆ‰¸¸¸¸
11
with M 1, E(x y) (1) x y (0.2) 0.02.œßŸ œ œkk ˆ‰¸¸¸¸
""
##
##
11
44
56. f(1 1) 0, f (1 1) y 1, f (1 1) x 6y 5 L(x y) (x 1) 5(y 1) x 5y 4;ßœ ßœ œ ßœ œÊ ßœ œ kk
xy
11 11
ÐßÑ ÐßÑ
f (x y) 0, f (x y) 6, and f (x y) 1 maximum of f , f , and f is 6 M 6
xx yy xy xx yy xy
ßœ ßœ ßœÊ Ê œkkkk kk
E(x y) (6) x 1 y 1 (6)(0.1 0.2) 0.27Ê ß Ÿ œ œkk a bkkkk
""
##
##
57. f(1 0 0) 0, f (1 0 0) y 3z 0, f (1 0 0) x 2z 1, f (1 0 0) 2y 3x 3ßß œ ßß œ œ ßß œ œ ßß œ œkk k
xyz
100 100
100
L(x y z) 0(x 1) (y 0) 3(z 0) y 3z; f(1 1 0) 1, f (1 1 0) 1, f (1 1 0) 1, f ( ) 1Ê ßßœ œ ßßœ ßßœ ßßœ "ß"ß!œ
xyz
L(x y z) 1 (x 1) (y 1) 1(z 0) x y z 1Ê ßßœ œ
58. f 0 1, f 0 2 sin x sin (y z) 0, f 0 2 cos x cos (y z) 1,
ˆ‰ ˆ‰ ˆ‰
¹¹
ÈÈ
ß!ßœ !ßßœ œ !ßßœ œ
11 1
44 4
x y
00 00
4 4
f 0 2 cos x cos (y z) 1 L(x y z) 1 1(y 0) 1 z 1 y z ;
z00
ˆ‰ ˆ‰
¹
È
!ß ß œ œ Ê ß ß œ œ
111
444
4
f 0 , f 0 , f 0 , f 0
ˆ‰ ˆ‰ ˆ‰ ˆ‰
11 11 11 11
44 44 44 44
2222
ßßœ ßßœ ßßœ ßßœ
ÈÈÈÈ
####
xyz
L(xyz) x y (z 0) x y zÊßßœœ
ÈÈÈÈÈÈÈÈ
22222222
44########
ˆ‰ ˆ‰
11

928 Chapter 14 Partial Derivatives
59. V r h dV 2 rh dr r dh dV 2 (1.5)(5280) dr (1.5) dh 15,840 dr 2.25 dh.kœÊœ Ê œ œ 111 1 1 11
## #
155280
You should be more careful with the diameter since it has a greater effect on dV.
60. df (2x y) dx ( x 2y) dy df 3 dy f is more sensitive to changes in y; in fact, near the pointkœ Ê œ Ê
12
(1 2) a change in x does not change f.ß
61. dI dV dR dI dV dR dI 0.01 (480)(.0001) 0.038,
¸¸
œ Ê œ Ê œ œ
""
R R 100 100
V24
24 100 dV 1 dR 20œ ß œ
or increases by 0.038 amps; % change in V (100) 4.17%; % change in R (100) 20%;œ ¸ œ œ
ˆ‰ ˆ ‰
"
24 100
20
I 0.24 estimated % change in I 100 100 15.83% more sensitive to voltage change.œœ Ê œ‚œ ‚¸ Ê
24 dI 0.038
100 I 0.24
62. A ab dA b da a db dA 16 da 10 db; da 0.1 and db 0.1kœÊœ Ê œ œ„ œ„111 11
10 16
dA 26 (0.1) 2.6 and A (10)(16) 160 100 100 1.625%Êœ„ œ„ œ œ Ê‚œ ‚¸111 1
¸¸¸ ¸
dA 2.6
A 160
1
1
63. (a) y uv dy v du u dv; percentage change in u 2% du 0.02, and percentage change in v 3%œÊœ Ÿ Ê Ÿ Ÿkk
dv 0.03; 100 100 100 100 100ÊŸ œ œÊ‚œ‚‚Ÿ‚‚kk ¹¹
¸ ¸¸¸¸¸
dy dy
yuvuvy u v u v
v du u dv du dv du dv du dv
2% 3% 5%Ÿœ
(b) z u v (since u 0, v 0)œÊœ œŸ
dz du dv du dv du dv
zuvuvuvuv
100 100 100 100Ê ‚ Ÿ‚ ‚ œ‚
¸¸¸ ¸
¹¹
dz du dv
zuvy
dy
64. C C and CœÊœ œ
7
71.84w h 71.84w h 71.84w h
wh
( 0.425)(7) ( 0.725)(7)
0 425 0 725 1 425 0 725 0 425 1 725
dC dw dh; thus when w 70 and h 180 we haveÊœ œ œ
2.975 5.075
71.84w h 71.84w h
1 425 0 725 0 425 1 725
dC (0.00000225) dw (0.00000149) dh 1 kg error in weight has more effectkÐß Ñ70 180 ¸ Ê
65. f (x y) 2x y 2 0 and f (x y) x 2y 2 0 x 2 and y 2 ( 2 2) is the critical point;
xy
ß œ œ ß œ œ Ê œ œ Ê ß
f ( 2 2) 2, f ( 2) 2, f ( 2) 1 f f f 3 0 and f 0 local minimum value
xx yy xy xx yy xx
xy
ßœ #ßœ #ßœÊ œ Ê
#
of f( 2) 8#ß œ
66. f (x y) 10x 4y 4 0 and f (x y) 4x 4y 4 0 x 0 and y 1 (0 1) is the critical point;
xy
ßœ œ ßœ œÊœ œÊß
f (0 1) 10, f (0 1) 4, f (0 1) 4 f f f 56 0 saddle point with f(0 1) 2
xx yy xy xx yy xy
ßœ ßœ ßœ Ê œ Ê ßœ
#
67. f (x y) 6x 3y 0 and f (x y) 3x 6y 0 y 2x and 3x 6 4x 0 x 1 8x 0
xy
ßœ œ ßœ œÊœ œÊ œ
###%$
ab a b
x 0 and y 0, or x and y the critical points are (0 0) and . For ( ):Ê œ œ œ œ Ê ß ß !ß !
"" ""
## ##
ˆ‰
f ( ) 12x 0, f ( ) 12y 0, f ( 0) 3 f f f 9 0 saddle point withkk
xx yy xy xx yy
00 00 xy
!ß ! œ œ !ß ! œ œ !ß œ Ê œ Ê
ÐßÑ ÐßÑ #
f(0 0) 0. For : f 6, f 6, f 3 f f f 27 0 and f 0 local maximumßœ ß œœœÊ œ Ê
ˆ‰
""
##
#
xx yy xy xx yy xx
xy
value of f ˆ‰
ß œ
"" "
## 4
68. f (x y) 3x 3y 0 and f (x y) 3y 3x 0 y x and x x 0 x x 1 0 the critical
xy
ßœ œ ßœ œÊœ œÊ œÊ
###%$
ab
points are (0 0) and (1 1) . For ( ): f ( ) 6x 0, f ( ) 6y 0, f ( 0) 3ß ß !ß ! !ß ! œ œ !ß ! œ œ !ß œ kk
xx yy xy
00 00
ÐßÑ ÐßÑ
f f f 9 0 saddle point with f(0 0) 15. For (1 1): f (1 1) 6, f (1 1) 6, f (1 1) 3Ê œ Ê ß œ ß ß œ ß œ ß œ
xx yy xx yy xy
xy
#
f f f 27 0 and f 0 local minimum value of f(1 1) 14Êœ Ê ßœ
xx yy xx
xy
#
69. f (x y) 3x 6x 0 and f (x y) 3y 6y 0 x(x 2) 0 and y(y 2) 0 x 0 or x 2 and
xy
ßœ œ ßœ œÊ œ œÊœ œ
##
y 0 or y 2 the critical points are (0 0), (0 2), ( 2 0), and ( 2 2) . For ( ): f ( ) 6x 6œ œ Ê ß ß ß ß !ß ! !ß ! œ k
xx 00ÐßÑ
6, f ( ) 6y 6 6, f ( 0) 0 f f f 36 0 saddle point with f(0 0) 0. Forœ !ß ! œ œ !ß œ Ê œ Ê ß œk
yy xy xx yy
00 xy
ÐßÑ #
(0 2): f ( 2) 6, f (0 ) 6, f ( 2) 0 f f f 36 0 and f 0 local minimum value ofß !ßœ ß#œ !ßœÊ œ Ê
xx yy xy xx yy xx
xy
#
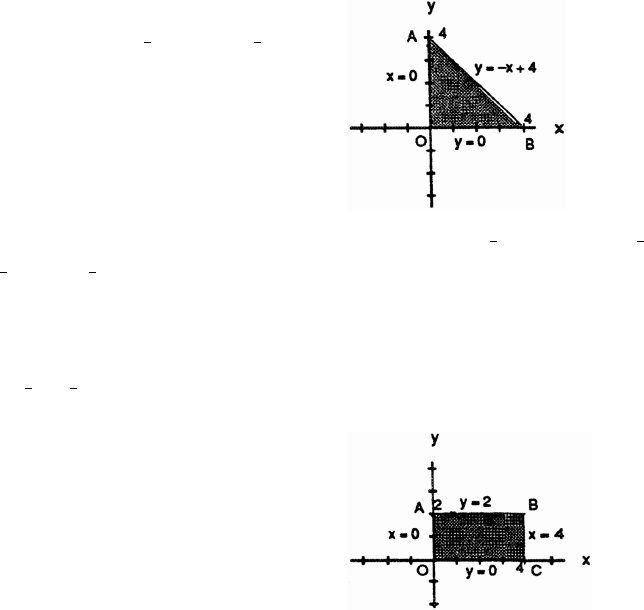
Chapter 14 Practice Exercises 929
f( 2) 4. For ( 0): f ( 2 0) 6, f ( 0) 6, f ( 2 0) 0 f f f 36 0 and f 0!ß œ #ß ß œ #ß œ ß œ Ê œ
xx yy xy xx yy xx
xy
#
local maximum value of f( 2 0) 4. For ( 2 2): f ( 2 2) 6, f ( 2 2) 6, f ( 2 2) 0Ê ß œ ß ß œ ß œ ß œ
xx yy xy
f f f 36 0 saddle point with f( 2 2) 0.ÊœÊ ßœ
xx yy xy
#
70. f (x y) 4x 16x 0 4x x 4 0 x 0, 2, 2; f (x y) 6y 6 0 y 1. Therefore the critical
x y
ßœ œÊ œÊœ ßœ œÊœ
$#
ab
points are (0 1), (2 1), and ( 2 1). For ( 1): f ( 1) 12x 16 16, f ( 1) 6, f ( 1) 0ß ß ß !ß !ß œ œ !ß œ !ß œk
xx yy xy
01
#ÐßÑ
f f f 96 0 saddle point with f(0 1) 3. For (2 1): f (2 1) 32, f (2 1) 6,Ê œÊ ßœ ß ßœ ßœ
xx yy xx yy
xy
#
f (2 1) 0 f f f 192 0 and f 0 local minimum value of f(2 1) 19. For ( 1):
xy xx yy xx
xy
ßœÊ œ Ê ßœ #ß
#
f ( 2 1) 32, f ( 1) 6, f ( 2 1) 0 f f f 192 0 and f 0 local minimum value of
xx yy xy xx yy xx
xy
ß œ #ß œ ß œ Ê œ Ê
#
f( 2 1) 19.ß œ
71. (i) On OA, f(x y) f(0 y) y 3y for 0 y 4ßœ ßœ ŸŸ
#
f ( y) 2y 3 0 y . But Ê!ßœœÊœ !ß
w
##
33
ˆ‰
is not in the region.
Endpoints: f(0 0) 0 and f(0 4) 28.ߜ ߜ
(ii) On AB, f(x y) f(x x 4) x 10x 28ߜ ߜ
#
for 0 x 4 f(xx4) 2x100ŸŸÊ ßœœ
w
x 5, y 1. But (5 1) is not in the region.Êœ œ ß
Endpoints: f(4 0) 4 and f( 4) 28.ß œ !ß œ
(iii) On OB, f(x y) f(x 0) x 3x for 0 x 4 f (x 0) 2x 3 x and y 0 0 is aßœ ßœ ŸŸ Ê ßœ Êœ œÊ ß
#w
##
33
ˆ‰
critical point with f .
ˆ‰
39
4#ß! œ
Endpoints: f(0 0) 0 and f( 0) 4.ß œ %ß œ
(iv) For the interior of the triangular region, f (x y) 2x y 3 0 and f (x y) x 2y 3 0 x 3
xy
ß œ œ ß œ œ Ê œ
and y 3. But (3 3) is not in the region. Therefore the absolute maximum is 28 at (0 4) and theœ ß ß
absolute minimum is at .ß!
93
4ˆ‰
#
72. (i) On OA, f(x y) f(0 y) y 4y 1 forߜ ߜ
#
0 y 2 f ( y) 2y 4 0 y 2 andŸŸ Ê !ß œ œ Ê œ
w
x 0. But (0 2) is not in the interior of OA.ϧ
Endpoints: f(0 0) 1 and f(0 2) 5.ߜ ߜ
(ii) On AB, f(x y) f(x 2) x 2x 5 for 0 x 4ßœ ßœ ŸŸ
#
f (x 2) 2x 2 0 x 1 and y 2ÊßœœÊœ œ
w
(1 2) is an interior critical point of AB withÊß
f(1 2) 4. Endpoints: f(4 2) 13 and f( 2) 5.ߜ ߜ !ߜ
(iii) On BC, f(x y) f(4 y) y 4y 9 for 0 y 2 f (4 y) 2y 4 0 y and x 4. Butßœ ßœ ŸŸ Ê ßœœÊœ# œ
#w
(4 2) is not in the interior of BC. Endpoints: f(4 0) 9 and f( 2) 13.ßßœ%ßœ
(iv) On OC, f(x y) f(x 0) x 2x 1 for 0 x 4 f (x 0) 2x 2 0 x 1 and y 0 (1 0)ßœ ßœ ŸŸÊ ßœ œÊœ œÊß
#w
is an interior critical point of OC with f(1 0) 0. Endpoints: f(0 0) 1 and f(4 0) 9.ߜ ߜ ߜ
(v) For the interior of the rectangular region, f (x y) 2x 2 0 and f (x y) 2y 4 0 x 1 and
xy
ßœ œ ßœœÊœ
y 2. But (1 2) is not in the interior of the region. Therefore the absolute maximum is 13 at (4 2)œß ß
and the absolute minimum is 0 at (1 0).ß
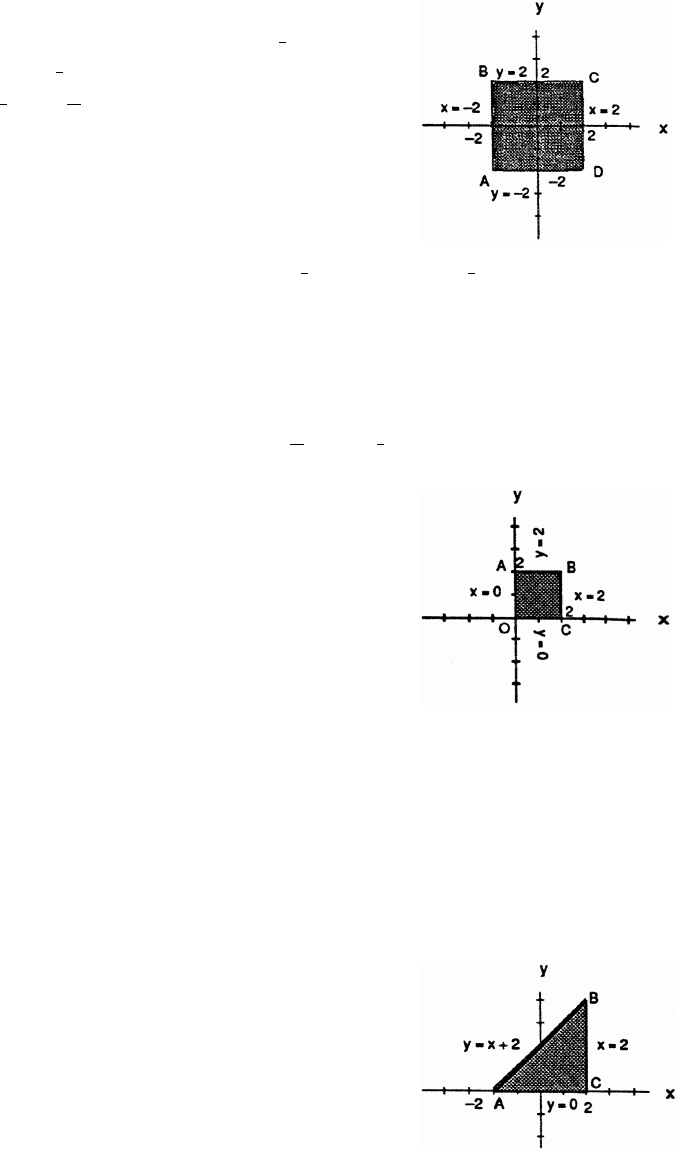
930 Chapter 14 Partial Derivatives
73. (i) On AB, f(x y) f( 2 y) y y 4 forߜߜ
#
2y2 f(2y)2y1 y andŸ Ÿ Ê ß œ Ê œ
w"
#
x 2 2 is an interior critical point in ABœ Ê ß
ˆ‰
"
#
with f 2 . Endpoints: f( 2 2) 2 and
ˆ‰
ß œ ß œ
"
#
17
4
f(2 2) 2.ߜ
(ii) On BC, f(x y) f(x 2) 2 for 2 x 2ßœ ßœ ŸŸ
f (x 2) 0 no critical points in the interior ofÊßœÊ
w
BC. Endpoints: f( 2 2) 2 and f(2 2) 2.ß œ ß œ
(iii) On CD, f(x y) f(2 y) y 5y 4 forߜ ߜ
#
2 y 2 f (2 y) 2y 5 0 y and x 2. But is not in the region.Ÿ Ÿ Ê ß œ œ Ê œ œ #ß
w
##
55
ˆ‰
Endpoints: f(2 2) 18 and f(2 2) 2.ß œ ß œ
(iv) On AD, f(x y) f(x 2) 4x 10 for 2 x 2 f (x 2) 4 no critical points in the interiorß œ ß œ Ÿ Ÿ Ê ß œ Ê
w
of AD. Endpoints: f( 2 2) 2 and f(2 2) 18.ß œ ß œ
(v) For the interior of the square, f (x y) y 2 0 and f (x y) 2y x 3 0 y 2 and x 1
xy
ßœœ ßœ œÊœ œ
(1 2) is an interior critical point of the square with f(1 2) 2. Therefore the absolute maximumÊß ßœ
is 18 at (2 2) and the absolute minimum is at .ß #ß
17
4ˆ‰
"
#
74. (i) On OA, f(x y) f(0 y) 2y y for 0 y 2ßœ ßœ ŸŸ
#
f ( y) 2 2y 0 y 1 and x 0 Ê!ßœœÊœ œÊ
w
( 1) is an interior critical point of OA with!ß
f(0 1) 1. Endpoints: f(0 0) 0 and f(0 2) 0.ߜ ߜ ߜ
(ii) On AB, f(x y) f(x 2) 2x x for 0 x 2ßœ ßœ ŸŸ
#
f (x 2) 2 2x 0 x 1 and y 2ÊßœœÊœ œ
w
(1 2) is an interior critical point of AB withÊß
f(1 2) 1. Endpoints: f(0 2) 0 and f(2 2) 0.ߜ ߜ ߜ
(iii) On BC, f(x y) f(2 y) 2y y for 0 y 2ßœ ßœ ŸŸ
#
f (2 y) 2 2y 0 y 1 and x 2ÊßœœÊœ œ
w
(2 1) is an interior critical point of BC with f(2 1) 1. Endpoints: f(2 0) 0 and f(2 2) 0.Êß ßœ ßœ ßœ
(iv) On OC, f(x y) f(x 0) 2x x for 0 x 2 f (x 0) 2 2x 0 x 1 and y 0 (1 0)ßœ ßœ ŸŸÊ ßœ œÊœ œÊß
#w
is an interior critical point of OC with f(1 0) 1. Endpoints: f(0 0) 0 and f(0 2) 0.ߜ ߜ ߜ
(v) For the interior of the rectangular region, f (x y) 2 2x 0 and f (x y) 2 2y 0 x 1 and
xy
ßœ œ ßœ œÊœ
y 1 (1 1) is an interior critical point of the square with f(1 1) 2. Therefore the absolute maximumœÊß ßœ
is 2 at (1 1) and the absolute minimum is 0 at the four corners (0 0), (0 2), (2 2), and (2 0).ß ßßß ß
75. (i) On AB, f(x y) f(x x 2) 2x 4 forߜ ߜ
2 x 2 f (x x 2) 2 0 no criticalŸ Ÿ Ê ß œœ Ê
w
points in the interior of AB. Endpoints: f( 2 0) 8ß œ
and f(2 4) 0.ߜ
(ii) On BC, f(x y) f(2 y) y 4y for 0 y 4ßœ ßœ ŸŸ
#
f (2 y) 2y 4 0 y 2 and x 2ÊßœœÊœ œ
w
(2 2) is an interior critical point of BC withÊß
f(2 2) 4. Endpoints: f(2 0) 0 and f(2 4) 0.ߜ ߜ ߜ
(iii) On AC, f(x y) f(x 0) x 2x for 2 x 2ßœ ßœ ŸŸ
#
f (x 0) 2x 2 x 1 and y 0 (1 0) is an interior critical point of AC with f(1 0) 1.Êߜʜ œÊß ßœ
w
Endpoints: f( 2 0) 8 and f(2 0) 0.ß œ ß œ
(iv) For the interior of the triangular region, f (x y) 2x 2 0 and f (x y) 2y 4 0 x 1 and
xy
ßœ œ ßœœÊœ
y 2 (1 2) is an interior critical point of the region with f(1 2) 3. Therefore the absolute maximumœÊß ßœ
is 8 at ( 2 0) and the absolute minimum is 1 at (1 0).ß ß
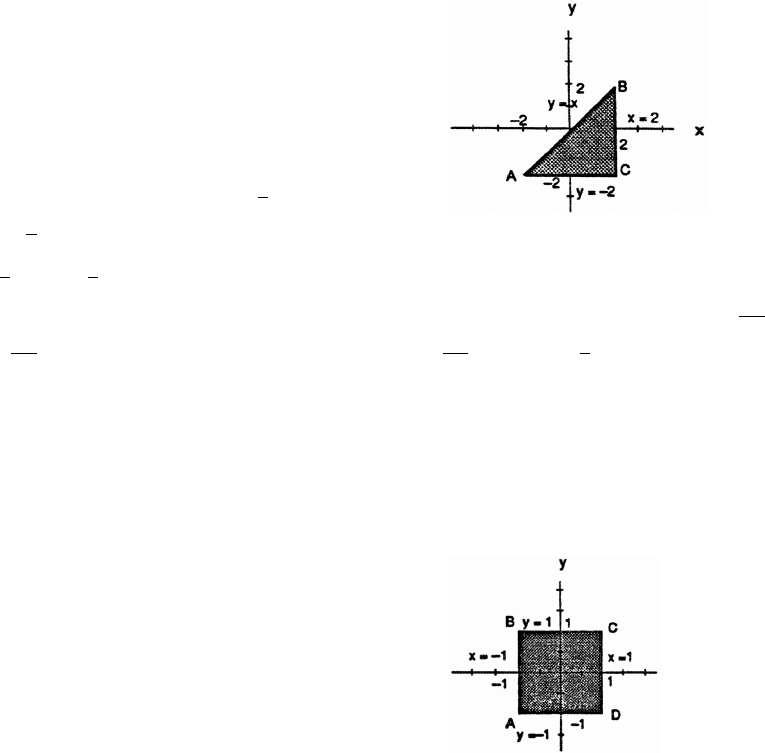
Chapter 14 Practice Exercises 931
76. (i) On AB, f(x y) f(x x) 4x 2x 16 forߜ ߜ
#%
2x2 f(xx)8x8x 0 x0Ÿ Ÿ Ê ß œ œ Ê œ
w$
and y 0, or x 1 and y 1, or x 1 and y 1œœ œœœ
(0 0), ( 1), ( 1 1) are all interior points of ABÊ ß "ß ß
with f(0 0) 16, f(1 1) 18, and f( 1 1) 18.ߜ ߜ ߜ
Endpoints: f( 2 2) 0 and f(2 2) 0.ß œ ß œ
(ii) On BC, f(x y) f(2 y) 8y y for 2 y 2ßœ ßœ ŸŸ
%
f (2 y) 8 4y 0 y 2 and x 2ÊßœœÊœ œ
w$
$
È
2 2 is an interior critical point of BC withÊß
Š‹
È
$
f 2 2 6 2. Endpoints: f(2 2) 32 and f(2 2) 0.
Š‹
ÈÈ
ߜ ߜ ߜ
$$
(iii) On AC, f(x y) f(x 2) 8x x for 2 x 2 f (x 2) 8 4x 0 x 2 and y 2ß œ ß œ Ÿ Ÿ Ê ß œ œ Ê œ œ
%w$
$
È
2 2 is an interior critical point of AC with f 2 2 6 . Endpoints:Êß ßœ#
Š‹ Š‹
ÈÈ
È
$$$
f( 2 2) 0 and f(2 2) 32.ß œ ß œ
(iv) For the interior of the triangular region, f (x y) 4y 4x 0 and f (x y) 4x 4y 0 x 0 and
xy
ßœ œ ßœ œÊœ
$$
y 0, or x 1 and y 1 or x 1 and y 1. But neither of the points (0 0) and (1 1), or ( 1 1) are interiorœœ œœœ ß ßß
to the region. Therefore the absolute maximum is 18 at (1 1) and ( 1 1), and the absolute minimum is 32 atßß
(2 2).ß
77. (i) On AB, f(x y) f( 1 y) y 3y 2 forߜߜ
$#
1y1 f(1y)3y 6y0 y0ŸŸÊ ß œ œ Ê œ
w#
and x 1, or y 2 and x 1 ( 1 0) is anœ œ œ Ê ß
interior critical point of AB with f( 1 0) 2; ( 1 2)ß œ ß
is outside the boundary. Endpoints: f( 1 1) 2ß œ
and f( 1 1) 0.ß œ
(ii) On BC, f(x y) f(x 1) x 3x 2 forߜ ߜ
$#
1x1 f(x1)3x 6x0 x0Ÿ Ÿ Ê ß œ œ Ê œ
w#
and y 1, or x 2 and y 1 (0 1) is anœœœÊß
interior critical point of BC with f( 1) 2; ( 2 1) is outside the boundary. Endpoints: f( 1) 0 and!ß œ ß "ß œ
f( 1) 2."ß œ
(iii) On CD, f(x y) f( y) y 3y 4 for 1 y 1 f ( y) 3y 6y 0 y 0 and x 1, orßœ"ßœ ŸŸÊ "ßœ œÊœ œ
$# w #
y 2 and x 1 ( 0) is an interior critical point of CD with f( 0) 4; (1 2) is outside the boundary.œœÊ"ß "ßœß
Endpoints: f(1 1) 2 and f( 1) 0.ߜ "ߜ
(iv) On AD, f(x y) f(x 1) x 3x 4 for 1 x 1 f (x 1) 3x 6x 0 x 0 and y 1,ßœ ßœ ŸŸÊ ßœ œÊœ œ
$# w #
or x 2 and y 1 (0 1) is an interior point of AD with f(0 1) 4; ( 1) is outside theœ œ Ê ß ß œ #ß
boundary. Endpoints: f( 1 1) 2 and f( 1) 0.ß œ "ß œ
(v) For the interior of the square, f (x y) 3x 6x 0 and f (x y) 3y 6y 0 x 0 or x 2, and
xy
ßœ œ ßœ œÊœ œ
##
y 0 or y 2 (0 0) is an interior critical point of the square region with f( 0) 0; the points (0 2),œœÊß !ßœ ß
( 2 0), and ( 2 2) are outside the region. Therefore the absolute maximum is 4 at (1 0) and theß ß ß
absolute minimum is 4 at (0 1).ß

932 Chapter 14 Partial Derivatives
78. (i) On AB, f(x y) f( 1 y) y 3y for 1 y 1ߜߜ ŸŸ
$
f ( 1 y) 3y 3 0 y 1 and x 1Êßœ œÊœ„ œ
w#
yielding the corner points ( 1 1) and ( 1 1) withß ß
f( 1 1) 2 and f( 1 1) 2.ß œ ß œ
(ii) On BC, f(x y) f(x 1) x 3x 2 forߜ ߜ
$
1 x 1 f (x 1) 3x 3 0 noŸ Ÿ Ê ß œ œ Ê
w#
solution. Endpoints: f( 1) 2 and f( 1) 6."ߜ "ߜ
(iii) On CD, f(x y) f( y) y 3y 2 forß œ "ß œ
$
1 y 1 f ( y) 3y 3 0 noŸŸÊ "ßœ œÊ
w#
solution. Endpoints: f(1 1) 6 and f( 1) 2.ß œ "ß œ
(iv) On AD, f(x y) f(x 1) x 3x for 1 x 1 f (x 1) 3x 3 0 x 1 and y 1ß œ ß œ Ÿ Ÿ Ê ß œ œ Ê œ „ œ
$w#
yielding the corner points ( 1 1) and (1 1) with f( 1 1) 2 and f(1 1) 2ß ß ß œ ß œ
(v) For the interior of the square, f (x y) 3x 3y 0 and f (x y) 3y 3x 0 y x and
xy
ßœ œ ßœ œÊœ
###
x x 0 x 0 or x 1 y 0 or y 1 ( 0) is an interior critical point of the square
%œÊœ œÊœ œÊ!ß
region with f(0 0) 1; ( 1 1) is on the boundary. Therefore the absolute maximum is 6 at ( 1) andßœ ß "ß
the absolute minimum is 2 at (1 1) and ( 1 1).ß ß
79. f 3x 2y and g 2x 2y so that f g 3x 2y (2x 2y ) 3x 2x and™™ ™™œ œ œ Ê œ Êœ
###
ij ij ij ij-- -
2y 2y 1 or y 0.œÊœ œ--
CASE 1: 1 3x 2x x 0 or x ; x 0 y 1 yielding the points (0 1) and ( 1); x-œÊ œ Êœ œ œÊœ„ ß !ß œ
#2 2
3 3
y yielding the points and .Êœ„ ß ß
ÈÈÈ
555
33333
22
Š‹Š ‹
CASE 2: y 0 x 1 0 x 1 yielding the points (1 0) and ( 1 0).œÊ œÊœ„ ß ß
#
Evaluations give f 1 1, f , f( 0) 1, and f( 0) 1. Therefore the absoluteabŠ‹
!ß„œ ß„ œ "ßœ "ßœ
223
33 27
5
È
maximum is 1 at 1 and (1 0), and the absolute minimum is 1 at ( ).ab!ß „ ß "ß !
80. f y x and g 2x 2y so that f g y x (2x 2y ) y 2 x and™™ ™™œ œ œ Ê œ Êœij i j ij i j-- -
xy 2 y x 2 (2 x) 4 x x 0 or 4 1.œÊœ œ Êœ œ---- -
##
CASE 1: x 0 y 0 but (0 0) does not lie on the circle, so no solution.œÊœ ß
CASE 2: 4 1 or . For , y x 1 x y 2x x yielding the--- -
### #
"" " "
## #
œÊœ œ œ œÊœœ ÊœCœ„
È2
points and , . For , y x 1 x y 2x x and
Š‹Š ‹
"" " " " "
#
## #
ÈÈ È È È
22 2 2 2
ß œ œÊœœ Êœ„-
y x yielding the points and , .œ ß
Š‹Š‹
"" " "
ÈÈ È È
22 2 2
Evaluations give the absolute maximum value f f and the absolute minimum
Š‹Š ‹
"" " " "
#
ÈÈ È È
22 2 2
ߜߜ
value f f .
Š‹Š‹
ß œ ß œ
"" " " "
#
ÈÈ È È
22 2 2
81. (i) f(x y) x 3y 2y on x y 1 f 2x (6y 2) and g 2x 2y so that f gßœ œÊ œ œ œ
## ## ™™™™ij ij -
2x (6y 2) (2x 2y ) 2x 2x and 6y 2 2y 1 or x 0.Êœ Êœ œ Êœ œijij----
CASE 1: 1 6y 2 2y y and x yielding the points .-œÊ œ Êœ œ„ „ ß
""
## ##
ÈÈ
33
Š‹
CASE 2: x 0 y 1 y 1 yielding the points 1 .œÊ œÊœ„ !ß„
#ab
Evaluations give f , f(0 1) 5, and f( 1) 1. Therefore and 5 are the extreme
Š‹
„ßœ ßœ !ßœ
È3
### #
"" "
values on the boundary of the disk.
(ii) For the interior of the disk, f (x y) 2x 0 and f (x y) 6y 2 0 x 0 and y
xy
ßœ œ ßœ œÊœ œ
"
3
is an interior critical point with f . Therefore the absolute maximum of f on theÊ !ß !ß œ
ˆ‰ ˆ‰
1
333
""
disk is 5 at (0 1) and the absolute minimum of f on the disk is at .ß !ß
""
33
ˆ‰
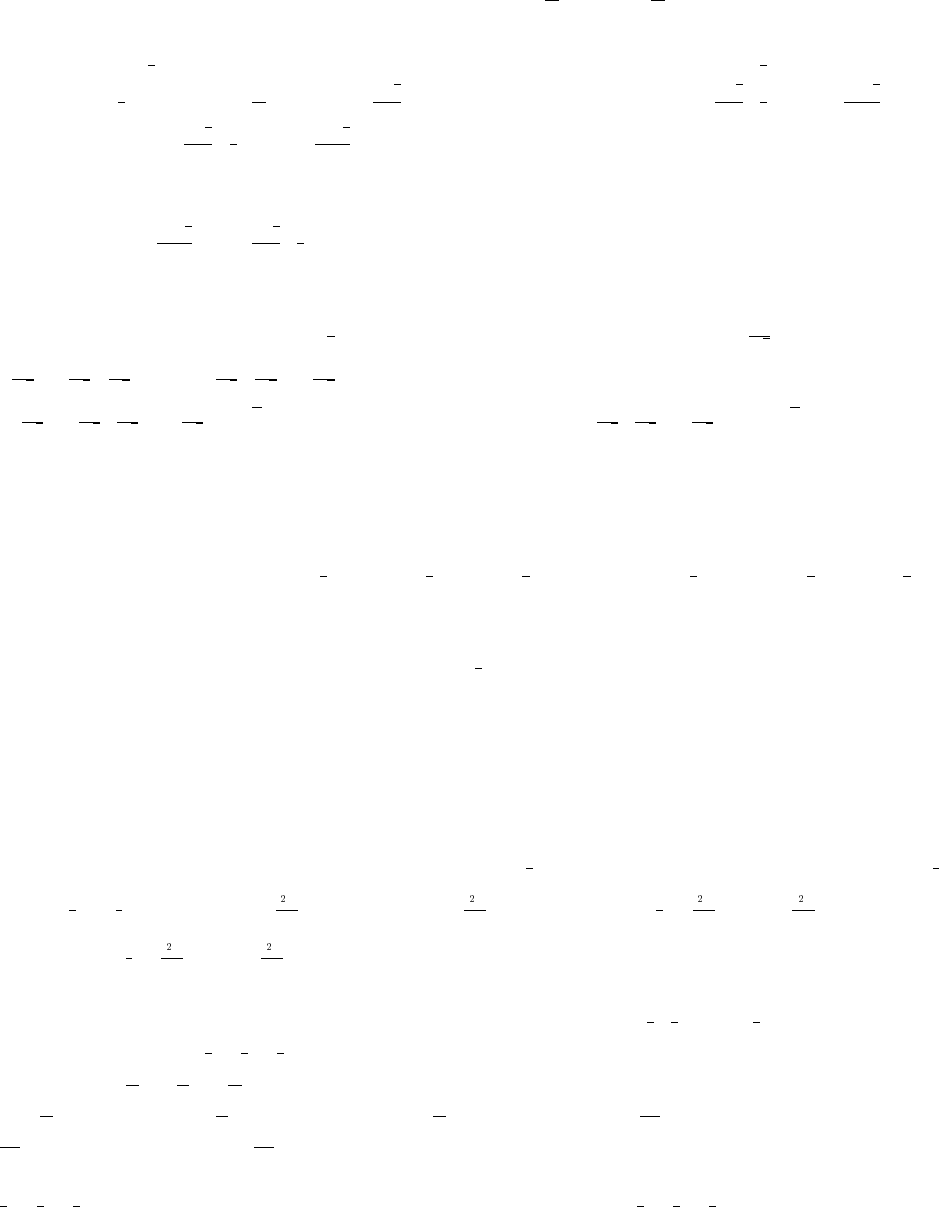
Chapter 14 Practice Exercises 933
82. (i) f(x y) x y 3x xy on x y 9 f (2x 3 y) (2y x) and g 2x 2y so thatßœ œÊ œ œ
## ## ™™ij ij
f g (2x 3 y) (2y x) (2x 2y ) 2x 3 y 2x and 2y x 2y™™œ Ê œ Ê œ œ----ijij
2x( ) y 3 and x 2y(1 ) 0 1 and (2x) y 3 x y 3yÊ"œ œÊœ œÊœ---
xx
2y 2y
Š‹ ##
x y 3y. Thus, 9 x y y 3y y 2y 3y 9 0 (2y 3)(y 3) 0Ê œ œœ Ê œÊ œ
## ### # #
y 3, . For y 3, x y 9 x 0 yielding the point (0 3). For y , x y 9Êœ œ œÊœ ß œ œ
3 3
# #
## ##
x 9 x x . Evaluations give f(0 3) 9, f 9ʜʜʜ„ ßœ ßœ
##
###
927 3
44 4
33 33 273
ÈÈÈ
Š‹
20.691, and f , 9 2.691.¸œ¸
Š‹
33 273
3
4
ÈÈ
##
(ii) For the interior of the disk, f (x y) 2x 3 y 0 and f (x y) 2y x 0 x 2 and y 1
xy
ßœ œ ßœ œÊœ œ
(2 1) is an interior critical point of the disk with f(2 1) 3. Therefore, the absolute maximum of f onÊß ßœ
the disk is 9 at and the absolute minimum of f on the disk is 3 at (2 1).ß ß
27 3 3 3
4
3
ÈÈ
Š‹
##
83. f and g 2x 2y 2z so that f g (2x 2y 2z ) 1 2x ,™™ ™™œ œ œ Ê œ Ê œijk i j k ijk i j k-- -
1 2y , 1 2z x y z . Thus x y z 1 3x 1 x yielding the pointsœ œ Êœœœ œÊ œÊœ„-- ""
### #
-È3
, and , , . Evaluations give the absolute maximum value of
Š‹Š ‹
""" """
ÈÈÈ ÈÈÈ
333 333
ß
f 3 and the absolute minimum value of f 3.
Š‹ Š ‹
ÈÈ
""" "" "
ÈÈÈ È ÈÈÈ
333 3 333
3
ßßœœ ßßœ
84. Let f(x y z) x y z be the square of the distance to the origin and g(x y z) z xy 4. Thenßß œ ßß œ
### #
f 2x 2y 2z and g y x 2z so that f g 2x y, 2y x, and 2z 2 z™™ ™™œ œ œ Ê œ œ œijk ijk ----
z 0 or 1.Êœ œ-
CASE 1: z 0 xy 4 x and y 2 y and 2 x y and xœ Ê œ Ê œ œ Ê œ œ Ê œ œ
444 4 88
yxy x
Š‹ ˆ‰
--
--
##
y x y x. But y x x 4 leads to no solution, so y x x 4 x 2ʜʜ„ œÊœ œÊœÊœ„
## # #
yielding the points ( 2 2 0) and (2 2 0).ß ß ßß
CASE 2: 1 2x y and 2y x 2y 4y y y 0 x 0 z 4 0 z 2-œ Ê œ œ Ê œ Ê œ Ê œ Ê œ Ê œ Ê œ „
ˆ‰
y
#
#
yielding the points (0 0 2) and ( 0 2).ßß !ßß
Evaluations give f( 2 2 0) f(2 2 0) 8 and f( 2) f( 2) 4. Thus the points ( 2) and ß ß œ ß ß œ !ß !ß œ !ß !ß œ !ß !ß
( 2) on the surface are closest to the origin.!ß !ß
85. The cost is f(x y z) 2axy 2bxz 2cyz subject to the constraint xyz V. Then f gßß œ œ œ™™-
2ay 2bz yz, 2ax 2cz xz, and 2bx 2cy xy 2axy 2bxz xyz, 2axy 2cyz xyz, andÊœ œ œ Ê œ œ-- - - -
2bxz 2cyz xyz 2axy 2bxz 2axy 2cyz y x. Also 2axy 2bxz 2bxz 2cyz z x.œ Ê œ Êœ œ Êœ-ˆ‰ ˆ‰
ba
cc
Then x x x V x width x , Depth y , and
ˆ‰ˆ‰ ˆ‰
Š‹ Š‹ Š‹
b a cV cV b cV bV
c c ab ab c ab ac
œ Ê œ Ê œœ œœ œ
$"Î$ "Î$ "Î$
Height z .œœ œ
ˆ‰
Š‹ Š‹
acV aV
cab bc
"Î$ "Î$
86. The volume of the pyramid in the first octant formed by the plane is V(a b c) ab c abc. The pointßß œ œ
"" "
#36
ˆ‰
(2 1 2) on the plane 1. We want to minimize V subject to the constraint 2bc ac 2ab abc.ßß Ê œ œ
22
abc
"
Thus, V and g (c 2b bc) (2c 2a ac) (2b a ab) so that V g™™ ™™œ œ œ
bc ac ab
666
ijk i j k -
(c 2b bc), (2c 2a ac), and (2b a ab) (ac 2ab abc),Êœ œ œ Ê œ
bc ac ab abc
66 6 6
-- - -
(2bc 2ab abc), and (2bc ac abc) ac 2 bc and 2 ab 2 bc. Now 0 since
abc abc
66
œ œÊœ œ Á-------
a 0, b 0, and c 0 ac 2bc and ab bc a 2b c. Substituting into the constraint equation givesÁÁ ÁÊœ œÊœœ
1 a 6 b 3 and c 6. Therefore the desired plane is 1 or x 2y z 6.
222 xz
aaa 636
y
œÊœÊœ œ œ œ
87. f (y z) x x , g 2x 2y , and h z x so that f g h™™™™™™œ œ œ œ ijk i j ik -.
(y z) x x (2x 2y ) (z x ) y z 2 x z, x 2 y, x x x 0Êœ Êœ œ œ Êœijk i j ik-. -.-.

934 Chapter 14 Partial Derivatives
or 1..œ
CASE 1: x 0 which is impossible since xz 1.œœ
CASE 2: 1 y z 2 x z y 2 x and x 2 y y (2 )(2 y) y 0 or.-----œÊœ Êœ œ Êœ Êœ
4 1. If y 0, then x 1 x 1 so with xz 1 we obtain the points (1 0 1)-##
œœ œÊœ„ œ ßß
and ( 1 0 1). If 4 1, then . For , y x so x y 1 xß ß œ œ„ œ œ œ Ê œ-- -
####
"" "
## #
x with xz 1 z 2, and we obtain the points 2 andÊœ„ œÊœ„ ß ß
"""
ÈÈÈ
222
ÈÈ
Š‹
2 . For , y x x x with xz 1 z 2,
Š‹
ÈÈ
ß ß œ œÊ œÊœ„ œÊœ„
"" " " "
##
#
ÈÈ È
22 2
-
and we obtain the points , 2 and 2 .
Š‹Š ‹
ÈÈ
"" " "
ÈÈ È È
22 2 2
ß ß ß
Evaluations give f(1 0 1) 1, f( 1 0 1) 1, f 2 , f , 2 ,ßß œ ßß œ ß ß œ ß œ
Š‹Š ‹
ÈÈ
"" " "" "
##
ÈÈ ÈÈ
22 22
f 2 , and f 2 . Therefore the absolute maximum is at
Š‹Š ‹
ÈÈ
"" " "
## #
ÈÈ È È
22 2 2
33 3
ß ß œ ß ß œ
2 and 2 , and the absolute minimum is at 2 and
Š‹Š ‹ Š ‹
ÈÈ È
"" " " " ""
#
ÈÈ È È ÈÈ
22 2 2 22
ßß ßß ßß
2.
Š‹
È
""
ÈÈ
22
ß ß
88. Let f(x y z) x y z be the square of the distance to the origin. Then f 2x 2y 2z ,ßßœ œ
### ™ijk
g , and h 4x 4y 2z so that f g h 2x 4x , 2y 4y ,™™ ™™™œ œ œ Ê œ œ ijk i j k - . -. -.
and 2z 2z 2x(1 2 ) 2y(1 2 ) 2z(1 2 ) x y or .œ Êœ œ œ Êœ œ-.- . . . .
"
#
CASE 1: x y z 4x z 2x so that x y z 1 x x 2x 1 or x x 2x 1œ Ê œ Ê œ„ œ Ê œ œ
##
(impossible) x y and z yielding the point .ʜʜ œ ßß
" " " """
##44 44
ˆ‰
CASE 2: 0 0 2z(1 1) z 0 so that 2x 2y 0 x y 0. But the origin.-œÊœÊœ Êœ œÊœœ
"
#
##
( 0 0) fails to satisfy the first constraint x y z 1.!ßß œ
Therefore, the point on the curve of intersection is closest to the origin.
ˆ‰
"""
#44
ßß
89. (a) y, z are independent with w x e and z x y œœÊœ
###
```` ``
```````
`
yz wwxw wz
yxyyyzy
y
2xe zx e (1) yx e (0); z x y 0 2x 2y ; therefore,œ œÊœÊœab a b a b
yz yz yz
```
```
## ##
xxx
yyyx
y
2xe zx e 2y zx e
Š‹ ab a b
ˆ‰
`
`
##
w
yx
y
z
yz yz yz
œœ
(b) z, x are independent with w x e and z x y œœÊœ
###
```` ``
```````
`
yz wwxw wz
zxzyzzz
y
2xe (0) zx e yx e (1); z x y 1 0 2y ; therefore,œ œÊœÊœab a b a b
yz yz yz## ##
```
```#
"
yyy
zzzy
zxe yxe xe y
ˆ‰ ab
Š‹ Š ‹
`
`
###
w1 z
z2y 2y
x
yz yz yz
œœ
(c) z, y are independent with w x e and z x y œœÊœ
###
```` ``
```````
`
yz wwxw wz
zxzyzzz
y
2xe zx e (0) yx e (1); z x y 1 2x 0 ; therefore,œ œÊœÊœab a b a b
yz yz yz
```"
```#
####
xxx
zzzx
2xe yx e 1 x y e
ˆ‰ ˆ‰
ab a b
`
`
##
w1
z2x
y
yz yz yz
œœ
90. (a) T, P are independent with U f(P V T) and PV nRT œßß œ Ê œ
```````
```````
UUPUVUT
TPTVTTT
(0) (1); PV nRT P nR ; therefore,œ œÊœÊœ
ˆ‰ ˆ‰ˆ‰ˆ‰
```` ` `
```` ` `
UUVU V VnR
PVTT T TP
ˆ‰ ˆ‰ˆ‰
`` `
`` `
UUnRU
TVPT
Pœ
(b) V, T are independent with U f(P V T) and PV nRT œßß œ Ê œ
```````
```````
UUPUVUT
VPVVVTV
(1) (0); PV nRT V P (nR) 0 ; therefore,œ œÊœœÊœ
ˆ‰ˆ‰ˆ‰ ˆ‰ ˆ‰
`` ` ` ` ` `
`` ` ` ` ` `
UP U U P T P P
PV V T V V V V
ˆ‰ ˆ‰ˆ ‰
`` `
`` `
UUPU
VPVV
Tœ
91. Note that x r cos and y r sin r x y and tan . Thus,œœÊœœ)) )
Ȉ‰
## " y
x
(cos ) ;
````` ` ` ` `
````` ` ` ` `
wwrw w x w wsin w
xrx x r xy r r
xy
y
œœ œ
)) )
) )
ˆ‰ ˆ‰ ˆ ‰
Š‹ Š‹
È)

Chapter 14 Practice Exercises 935
(sin )
````` ` ` ` `
```` ` ` ` `
wwrw w w x wcos w
yry y r xy r r
y
xy
œœ œ
)) ) )
) )
ˆ‰ ˆ‰ ˆ ‰
Š‹ Š‹
È)
92. z f f af af , and z f f bf bf
xu v u v yu v u v
œœ œœ
`` ``
`` ``
uv uv
xx yy
93. b and a a and b and
` ` `` `` "` "`
` ` `` `` ` `
u u wdwu dw wdwu dw wdw wdw
y x x du x du y du y du a x du b y du
œœÊœœ œœÊœ œ
b a ʜʜ
"` "` ` `
`` ``ax by x y
ww ww
94. - , ,
`"`
` `#
w2x w rs
x x y 2z (rs) (rs) 4rs 2r 2rss rs y x y 2z (rs) (rs)
2(r s) 2(r s) 2y 2(r s)
œœ œ œœœœ
ab
and (2s)
`"``````""
` ```````
`
w 2 w w x w w z r s 2r 2s
z x y 2z (r s) r x r y r z r r s (r s) (r s) (r s)
y
œœÊœœ œ
’“
and (2r)œœœ œ
2wwxwwz rs 2
rs s x s y s z s rs (rs) (rs) rs
y
` `` `` ``
```` `` " "
`’“
95. e cos v x 0 e cos v e sin v 1; e sin v y 0 e sin v e cos v 0.
uuuuuu
uv u v
xx x x
œ Ê œ œ Ê œabab abab
`` ` `
`` ` `
Solving this system yields e cos v and e sin v. Similarly, e cos v x 0
``
``
uv
xx
uuu
œœ œ
e cos v e sin v 0 and e sin v y 0 e sin v e cos v 1. Solving thisÊœœÊœabab abab
uu u uu
uv u v
yy y y
`` ` `
`` ` `
second system yields e sin v and e cos v. Therefore
` ` `` ``
` ` `` ``
u v uu vv
y y xy xy
uu
œœ
Š‹Š‹
ij ij†
e cos v e sin v e sin v e cos v 0 the vectors are orthogonal the angleœ œÊ Êcdc dababa bab
uu uu
ij i j†
between the vectors is the constant .
1
#
96. ( r sin ) (r cos )
``
````` ` `
`` ` ` `
gy
fx f f f
xy x y)))
œœ ))
( r sin ) (r cos ) (r cos ) (r sin ) ʜ
`` `
` ` ` ``` ` ``` ` ` `
`` ` ` ` ` ` `
gy y
fx f f f x f f
xyx x xyy y))) ))
))))
Š‹ Š‹
( r sin ) (r cos ) (r cos ) (r sin )œ ))))
Š‹ Š‹
``
`` ``
``
xx
yy
)) ))
( r sin r cos )( r sin r cos ) (r cos r sin ) ( 2)( 2) (0 2) 4 2 2 atœ œ œ œ)))) ))
(r ) 2 .ßœß)ˆ‰
1
#
97. (y z) (z x) 16 f 2(z x) 2(y z) 2(y 2z x) ; if the normal line is parallel to theœÊ œ
## ™ij k
yz-plane, then x is constant 0 2(z x) 0 z x (y z) (z z) 16 y z 4.ʜʜʜʜʜ„
`
`
##
f
x
Let x t z t y t 4. Therefore the points are (t t 4 t), t a real number.œÊ œÊ œ„ ß„ß
98. Let f(x y z) xy yz zx x z 0. If the tangent plane is to be parallel to the xy-plane, then f isßßœ œ
#™
perpendicular to the xy-plane f 0 and f 0. Now f (y z 1) (x z) (y x 2z)Ê œ œ œ ™† ™† ™ij ijk
so that f y z 1 0 y z 1 y 1 z, and f x z 0 x z. Then™† ™†ijœœ Ê œ Ê œ œœ Ê œ
z(1 z) ( z)z z( z) ( z) z 0 z 2z 0 z or z 0. Now z x and y " œ Ê œ Ê œ œ œ Ê œ œ
##
""""
####
is one desired point; z 0 x 0 and y 1 (0 1 0) is a second desired point.Êßß œ Ê œ œ Ê ßß
ˆ‰
"""
###
99. f (x y z ) x f(x y z) x g(y z) for some function g y™œÊœÊßßœ ß Êœœ--- -ijk `" `
`# ``
#`
f f
xyy
g
g(y z) y h(z) for some function h z h (z) h(z) z C for some arbitraryÊßœ Êœœœ Ê œ
"`"
#``#
#w#
`
-- -
f
zz
g
constant C g(y z) y z C f(x y z) x y z C f(0 0 a) a CÊßœ ÊßßœÊßßœ
" " """ "
# # ### #
## ### #
- - --- -
ˆ‰
and f(0 0 a) ( a) C f(0 0 a) f(0 0 a) for any constant a, as claimed.ßß œ Ê ßß œ ßß
"
#
#
-
100. lim , s 0
s0
ˆ‰
df
ds
f(0su0su0su)f(000)
u(000) œ
Ä
ßß ßß
s
lim , s 0
s0
œ
Ä
Ésu su su 0
s

936 Chapter 14 Partial Derivatives
lim lim 1;
s0 s0
œœœ
ÄÄ
su u u
É
skku
however, f fails to exist at the origin (0 0 0)™œ ßß
xz
xyz xyz xyz
y
ÈÈÈ
ijk
101. Let f(x y z) xy z 2 f y x . At (1 1 1), we have f the normal line isßß œ Ê œ ßß œ Ê™™ijk ijk
x 1 t, y 1 t, z 1 t, so at t 1 x 0, y 0, z 0 and the normal line passes through theœ œ œ œÊ œ œ œ
origin.
102. (b) f(x y z) x y z 4ßßœœ
###
f 2x 2y 2z at (2 3 3)Ê œ Ê ßß™ijk
the gradient is f 4 6 6 which is™œijk
normal to the surface
(c) Tangent plane: 4x 6y 6z 8 orœ
2x 3y 3z 4œ
Normal line: x 2 4t, y 3 6t, z 3 6tœ œ œ
CHAPTER 14 ADDITIONAL AND ADVANCED EXERCISES
1. By definition, f ( 0) lim so we need to calculate the first partial derivatives in the
xy !ß œ h0Ä
f(0h) f(00)
h
xx
ß ß
numerator. For (x y) (0 0) we calculate f (x y) by applying the differentiation rules to the formula forßÁß ß
x
f(x y): f (x y) (xy) f (0 h) h.ß ßœ œ Êßœœ
x x
xy y xy y 4xy
xy xy h
x y (2x) x y (2x)
xy xy
h
abab
ab ab
For (x y) (0 0) we apply the definition: f ( 0) lim lim 0. Then by definitionßœß !ßœ œ œ
xh0 h0ÄÄ
f(h 0) f(0 0)
hh
00
ß ß
f (0 0) lim 1. Similarly, f (0 0) lim , so for (x y) (0 0) we have
xy yx
ßœ œ ßœ ßÁß
h0 h0ÄÄ
ß!ß
h0
hh
f(h0) f( 0)
yy
f (x y) f (h 0) h; for (x y) (0 0) we obtain f (0 0) lim
y y
ßœ Ê ßœ œ ßœß ßœ
xxy 4xy f(0 h) f( 0)
xy h h
xy yh
ß!ß
ab h0Ä
lim 0. Then by definition f (0 0) lim 1. Note that f (0 0) f (0 0) in this case.œœ ßœœ ßÁß
h0 h0ÄÄ
00 h0
hh
xy yx
yx
2. 1 e cos y w x e cos y g(y); e sin y g (y) 2y e sin y g (y) 2y
``
``
ww
ww
xy
xx x x
œ Ê œ œ œ Ê œ
g(y) y C; w ln 2 when x ln 2 and y 0 ln 2 ln 2 e cos 0 0 C 0 2 CÊœœ œ œÊœ Êœ
# #ln 2
C 2. Thus, w x e cos y g(y) x e cos y y 2.Êœ œ œ
xx#
3. Substitution of u u(x) and v v(x) in g(u v) gives g(u(x) v(x)) which is a function of the independentœß ß
variable x. Then, g(u v) f(t) dt f(t) dt f(t) dt ßœ Êœœ
'''
uuu
vvv
dg g g
dx u dx v dx u dx v dx
du dv du dv
``
`` ` `
``
Š‹Š‹
f(t) dt f(t) dt f(u(x)) f(v(x)) f(v(x)) f(u(x)) œ œœ
Š‹Š‹
``
``u dx v dx dx dx dx dx
du dv du dv dv du
''
vu
uv
4. Applying the chain rules, f f . Similarly, f and
xxx yy
œÊœ œ
df r d f r df r d f r df r
dr x dr x dr x dr y dr y
``` ``
``` ``
##
Š‹ Š‹Š‹
ˆ‰
f . Moreover, ;
zz œ œÊœ œ
Š‹
ˆ‰
df r df r r x r r
dr z dr z x x y
xyz xyz
yz y
xyz
`` ` ` `
`` ` ` `
#
ÈÈ
ˆ‰
È3
; and . Next, f f f 0Êœ œ Êœ œ
` ` `
```
rxz r z r
yzz
xyz xyz
xyz
xy xx yy zz
ˆ‰ ˆ‰
ÈÈ
È
3 3
Ê
Š‹Š ‹ Š‹Š ‹
ˆ‰ ˆ‰
Œ Œ
df x df df df x z
dr x y z dr dr x y z dr
yz y
xyz xyz
ˆ‰ ˆ‰
ÈÈ
3 3

Chapter 14 Practice Exercises 937
0 0 0 œÊœÊœ
Š‹Š ‹ Š ‹
ˆ‰
Œ
df z df df 2 df df 2 df
dr x y z dr dr dr dr r dr
xy
xyz xyz
ˆ‰
ÈÈ
3
(f ) f , where f ln f 2 ln r ln C f Cr , orÊœ œÊœÊœÊœ
d 2 df df 2 dr
dr r dr f r
www w w#
ˆ‰
Cr f(r) b b for some constants a and b (setting a C)
df C a
dr r r
œÊœœ œ
#
5. (a) Let u tx, v ty, and w f(u v) f(u(t x) v(t y)) f(tx ty) t f(x y), where t, x, and y areœ œ œßœßßߜߜß
n
independent variables. Then nt f(x y) x y . Now,
n1 ßœœœ
````` ` `
````` ` `
wwuwv w w
tutvt u v
(t) (0) t . Likewise,
````` ` ` ` ` "`
````` ` ` ` ` `
wwuwv w w w w w
xuxvx u v u utx
œœ œÊœ
ˆ‰ ˆ‰ ˆ‰ˆ‰
(0) (t) . Therefore,
````` ` ` ` "`
````` ` ` ` `
wwuwv w w w w
yuyvy u v vty
œœ Êœ
ˆ‰ ˆ‰ ˆ‰
Š‹
nt f(x y) x y . When t 1, u x, v y, and w f(x y)
n1 ßœœ œœœ œß
`` ` `
`` ` `
wwxw w
uvtxty
y
ˆ‰ˆ ‰ ˆ‰
Š‹
and nf(x y) x y , as claimed.Êœ œÊ ßœ
`` `` ` `
`` `` ` `
wf wf f f
xx yx x y
(b) From part (a), nt f(x y) x y . Differentiating with respect to t again we obtain
n1 ߜ
``
``
ww
uv
n(n 1)t f(x y) x x y y x 2xy y .ßœœ
n2 `` `` `` `` ` ` `
`` ``` ``` `` ` `` `
##
wu wv wu wv w w w
ut vut uvt vt u uv v
Also from part (a), t t t t ,
``` `` ```` ````
``` `` ````` ````
#
ww wwuwvww w
xxx xu uxvux uyyy
œœ œ œ œ
ˆ‰ ˆ ‰ Š‹
t t t t , and t t t œ œ œ œœ œ
`` `` `` ` ` `` `` `` ``
` ` `` ` ` ` ` `` ` ` ` ` ` ` `` `
#
y v uv y v y v yx y x y u u y vu y
wwuwvww w wwuwv
ˆ‰ ˆ‰ ˆ‰
t , , and œÊ œ œ œ
#`"``"`` "``
`` ` ` ` ` `` ``
wwwww ww
vu t x u t y v t yx vu
ˆ‰ ˆ‰ ˆ‰
n(n 1)t f(x y) for t 0. When t 1, w f(x y) andÊ ßœ Á œ œß
n2 Š‹Š ‹ Š ‹ Š‹Š ‹
ˆ‰
xw w w
tx tyx ty
2xy y
```
````
we have n(n 1)f(x y) x 2xy y as claimed.ߜ
##
```
````
Š‹ Š ‹ Š‹
fff
xxyy
6. (a) lim lim 1, where t 6r
r0 t0ÄÄ
sin 6r sin t
6r t
œœ œ
(b) f (0 0) lim lim lim lim
rßœ œ œ œ
h0 h0 h0 h0ÄÄÄÄ
f(0 h 0) f(0 0)
h h 6h 12h
1sin 6h 6h 6 cos 6h 6
ß ß
ˆ‰
sin 6h
6h
lim 0 (applying l'Hopital's rule twice)œœ s
h0Ä
36 sin 6h
12
(c) f (r ) lim lim lim 0ßœ œ œ œ)h0 h0 h0ÄÄÄ
f(r h) f(r )
hhh
0
ß ß
)) ˆ‰ˆ‰
sin 6r sin 6r
6r 6r
7. (a) x y z r x y z and rrijk r i j kœ Êœ œ œ kk È###
™xz
xyz xyz xyz
y
ÈÈÈ
œr
r
(b) r x y z
nn
œ
ˆ‰
È###
r nxxyz nyxyz nzxyzÊ œ ™abababab
nn2 1 n2 1 n2 1
### ### ###
Ðijk
nrœn2
r
(c) Let n 2 in part (b). Then r r x y z is the function.œœÊœÊœ
"""
####
## ###
™™ab a b
ˆ‰
rr
r
(d) d dx dy dz d x dx y dy z dz, and dr r dx r dy r dz dx dy dzrijkrrœ Ê œ œ œ †xyz
xz
rrr
y
r dr x dx y dy z dz dÊœœrr†
(e) a b c ax by cz ( ) a b cA i j k Ar Ar i j k Aœ Ê œ Ê œœ†™†
8. f(g(t) h(t)) c 0 , where is the tangent vectorߜʜœœ
df f dx f f f dx dx
dt x dt y dt x y dt dt dt dt
dy dy dy
`` ``
`` ``
Š‹Š‹
ij ij ij†
f is orthogonal to the tangent vectorÊ™
9. f(x y z) xz yz cos xy 1 f z y sin xy ( z x sin xy) (2xz y) f(0 0 1)ßß œ Ê œ Ê ßß œ
##
™™abijk ij
the tangent plane is x y 0; (ln t) (t ln t) t (ln t 1) ; x y 0, z 1ÊœœÊœœœœri jkri jk
w"
ˆ‰
t
t 1 (1) . Since ( ) ( ) r (1) f 0, is parallel to the plane, andÊ œ Ê œ œ œrijk ijkij r
ww
††™
(1) 0 0 is contained in the plane.rijkrœÊ

938 Chapter 14 Partial Derivatives
10. Let f(x y z) x y z xyz f 3x yz 3y xz 3z xy f(0 1 1) 3 3ßßœ Ê œ Ê ßßœ
$$$ ###
™™abababijk ijk
the tangent plane is x 3y 3z 0; 2 3 (cos (t 2))Ê œ œ rij k
Š‹
ˆ‰
t4
4t
(sin (t 2)) ; x 0, y 1, z 1 t 2 (2) 3 . SinceÊ œ œ œ œÊœÊ œrij k rij
w w
Š‹ ˆ‰
3t 4
4t
(2) f 0 is parallel to the plane, and (2) is contained in the plane.rr rikr
w†™ œÊ œÊ
11. 3x 9y 0 and 3y 9x 0 y x and 3 x 9x 0 x 9x 0
`` """
``
####%
#
zz
xy 333
œ œ œ œÊœ œÊ œ
ˆ‰
x x 27 0 x 0 or x 3. Now x 0 y 0 or ( 0) and x 3 y 3 or (3 3). NextÊ œÊœ œ œÊœ !ß œÊœ ßab
$
6x, 6y, and 9. For ( 0), 81 no extremum (a saddle point),
`` ` ```
` ` `` ` ` ``
#
zz z zzz
x y xy x y xy
œœ œ!ß œÊ
Š‹
and for (3 3), 243 0 and 18 0 a local minimum.ßœœÊ
`` ` `
`` `` `
#
zz z z
xy xy x
Š‹
12. f(x y) 6xye f (x y) 6y(1 2x)e 0 and f (x y) 6x(1 3y)e 0 x 0 andßœ Êßœ œ ßœ œÊœ
Ð Ñ Ð Ñ Ð Ñ2x 3y 2x 3y 2x 3y
xy
y 0, or x and y . The value f(0 0) 0 is on the boundary, and f . On the positive y-axis,œœ œ ßœ ßœ
"" """
# #33e
ˆ‰2
f(0 y) 0, and on the positive x-axis, f(x 0) 0. As x or y we see that f(x y) 0. Thus theßœ ßœ Ä_ Ä_ ß Ä
absolute maximum of f in the closed first quadrant is at the point .
"""
#e3
2ˆ‰
ß
13. Let f(x y z) 1 f an equation of the plane tangent at the pointßß œ Ê œ Ê
x z 2x 2z
abc a b c
y2y
™ijk
P (x y y ) is x y z 2 or x y z 1.
!!!!
ßß œ œ œ
ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰ ˆ‰
2x 2z x z
abcabc abc
2y y
2x 2y 2z
The intercepts of the plane are 0 0 , 0 0 and . The volume of the tetrahedron formed
Š‹Š‹Š‹
ab c
xy z
ß ß ß ß !ß !ß
by the plane and the coordinate planes is V we need to maximizeœÊ
ˆ‰ˆ‰
Š‹Š‹Š‹
""
#3 xyz
abc
V(x y z) (xyz) subject to the constraint f(x y z) 1. Thus,ßß œ ßß œ œ
(abc) y
6abc
xz
"
, , and . Multiply the first equation
’“Š‹ ’“Š‹ ’“Š‹
œœœ
(abc) (abc) 2y (abc)
6 x yz a 6 xy z b 6 xyz c
2x 2z
"" "
-- -
by a yz, the second by b xz, and the third by c xy. Then equate the first and second a y b x
## # ####
ʜ
y x, x 0; equate the first and third a z c x z x, x 0; substitute into f(x y z) 0Êœ Ê œ Êœ ßßœ
b c
a a
## ##
x y z V abc.Êœ Êœ Êœ Ê œ
abc
333
3
ÈÈÈ È
#
14. 2(x u) , 2(y v) , 2(x u) , and 2(y v) 2 v x u v y, x u , and œ œ œ œ Ê œ œ-- . . .
#
y v v x u v v or 0. œ Ê œ œ Ê œ œ.. .
.
##
"
CASE 1: 0 x u, y v, and 0; then y x 1 v u 1 and v u v v 1.-œÊœ œ œ œÊœ œÊœ
##
v v 1 0 v no real solution.ʜʜ Ê
#„
#
114
È
CASE 2: v and u v u ; x y and y x 1 x x 2xœ œ Ê œ œ œ Ê œ Ê œ
"""" """
## #
#44 4 4
x y . Then f 2 the minimum distanceÊ œ Ê œ ßßß œ œ Ê
"""""""
##
##
#
88 884 848 8
77 73
ˆ ‰ˆ ‰ˆ‰ˆ‰
is 2. (Notice that f has no maximum value.)
3
8È
15. Let (x y ) be any point in R. We must show lim f(x y) f(x y ) or, equivalently that
!! !!
ßßœß
Ðß ÑÄÐ ß Ñxy x y
lim f(x h y k) f(x y ) 0. Consider f(x h y k) f(x y )
Ðß ÑÄÐß Ñhk 00 kk
!! !! !! !!
ß ß œ ß ß
[f(x h y k) f(x y k)] [f(x y k) f(x y )]. Let F(x) f(x y k) and apply the Mean Valueœ ß ß ß ß œ ß
! ! !! !! !! !
Theorem: there exists with x x h such that F ( )h F(x h) F(x ) hf ( y k)00 0 0
!! ! ! !
w
œ Ê ß
x
f(x h y k) f(x y k). Similarly, k f (x ) f(x y k) f(x y ) for some withœßß ßœßß
!! !! ! !! !!y((
y y k. Then f(x h y k) f(x y ) hf ( y k) kf (x ) . If M, N are positive real
!! !! !! ! !
ß ß Ÿ ß ß(0(kkkkkk
xy
numbers such that f M and f N for all (x y) in the xy-plane, then f(x h y k) f(x y )kk kk k k
xy
ŸŸ ß ßß
!! !!
M h N k . As (h k) 0, f(x h y k) f(x y ) 0 lim f(x h y k) f(x y )Ÿ ßÄ ßßÄÊ ßßkkkkkkkk
!! !! !! !!
Ðß ÑÄÐß Ñhk 00

Chapter 14 Practice Exercises 939
0 f is continuous at (x y ).œÊ ß
!!
16. At extreme values, f and are orthogonal because f 0 by the First Derivative Theorem for™™†vœœœ
ddfd
dt dt dt
rr
Local Extreme Values.
17. 0 f(x y) h(y) is a function of y only. Also, 0 g(x y) k(x) is a function of x only.
` `
```
`
f f
xyx
g
œÊ ßœ œ œÊ ßœ
Moreover, h (y) k (x) for all x and y. This can happen only if h (y) k (x) c is a constant.
`
``
`ww ww
f
yx
g
œÊ œ œ œ
Integration gives h(y) cy c and k(x) cx c , where c and c are constants. Therefore f(x y) cy cœ œ ßœ
"#"# "
and g(x y) cx c . Then f(1 2) g(1 2) 5 5 2c c c c , and f(0 0) 4 c 4 cßœ ßœ ߜʜ œ ßœÊ œÊœ
#"#"
"
#
c . Thus, f(x y) y 4 and g(x y) x .ʜ ߜ ߜ
### ##
""99
18. Let g(x y) D f(x y) f (x y)a f (x y)b. Then D g(x y) g (x y)a g (x y)bßœ ßœ ß ß ßœ ß ß
uuxy x y
f (x y)a f (x y)ab f (x y)ba f (x y)b f (x y)a 2f (x y)ab f (x y)b .œßß ß ß œß ß ß
xx yx xy yy xx xy yy
####
19. Since the particle is heat-seeking, at each point (x y) it moves in the direction of maximal temperatureß
increase, that is in the direction of T(x y) e sin x 2e cos x . Since T(x y) is parallel to™™ßœ ßaba b
2y 2y
ij
the particle's velocity vector, it is tangent to the path y f(x) of the particle f (x) 2 cot x.œÊœœ
w2e cos x
e sin x
2y
2y
Integration gives f(x) 2 ln sin x C and f 0 0 2 ln sin C C 2 ln lnœ œÊœ Êœœkk ˆ‰ ¸ ¸ Š‹
11
44
22
2
ÈÈ
#
#
ln 2. Therefore, the path of the particle is the graph of y 2 ln sin x ln 2.œœkk
20. The line of travel is x t, y t, z 30 5t, and the bullet hits the surface z 2x 3y whenœœœ œ
##
30 5t 2t 3t t t 6 0 (t 3)(t 2) 0 t 2 (since t 0). Thus the bullet hits theœ Ê œÊ œÊœ
## #
surface at the point (2 2 20). Now, the vector 4x 6y is normal to the surface at any (x y z), so thatßß ßßijk
8 12 is normal to the surface at (2 2 20). If 5 , then the velocity of the particleni jk vijkœ ßß œ
after the ricochet is 2 proj ( 5 )wv vv nv n ij k i j kœ œ œ œ
nŠ‹ ˆ‰ ˆ ‰
2 2 25 400 600 50
209 209 209 209
vn
n
††
kk
.œ
191 391 995
209 209 209
ijk
21. (a) is a vector normal to z 10 x y at the point ( 0 10). So directions tangential to S at ( 0 10) willkœ !ß ß !ß ß
##
be unit vectors a b . Also, T(x y z) (2xy 4) x 2yz 14 y 1uij i j kœ ßßœ ™abab
##
T( 0 10) 4 14 . We seek the unit vector a b such that D T(0 0 10)Ê!ßßœ œ ßß™ijk uij u
(4 14 ) (a b ) (4 14 ) (a b ) is a maximum. The maximum will occur when a bœ œ ijkij ijij ij††
has the same direction as 4 14 , or (2 7 ).iju ijœ
"
È53
(b) A vector normal to S at (1 1 8) is 2 2 . Now, T(1 1 8) 6 31 2 and we seek the unitßß œ ßßœ nijk i jk™
vector such that D T(1 1 8) T has its largest value. Now write T , where is paralleluu vwv
ußß œ œ ™† ™
to T and is orthogonal to T. Then D T T ( ) . Thus™™™†††††w u vwuvuwuwu
uœœœœ
D T(1 1 8) is a maximum when has the same direction as . Now, T
ußß œ uwwn™Š‹
™†Tn
nkk
(6 31 2 ) (2 2 ) 6 31 2œ œ ijk ijk i j k
ˆ‰ ˆ‰ˆ‰ˆ‰
12 62 2 152 152 76
441 9 9 9
(98 127 58 ).œ Ê œ œ
98 127 58
999 29,097
ijku ijk
w
wkk È"
22. Suppose the surface (boundary) of the mineral deposit is the graph of z f(x y) (where the z-axis points upϧ
into the air). Then is an outer normal to the mineral deposit at (x y) and points in ß
`` ``
`` ``
ff ff
xy xy
ijk ij
the direction of steepest ascent of the mineral deposit. This is in the direction of the vector at (0 0)
``
``
ff
xy
ijß
(the location of the 1st borehole) that the geologists should drill their fourth borehole. To approximate this
vector we use the fact that (0 0 1000), (0 100 950), and (100 1025) lie on the graph of z f(x y).ß ß ß ß ß!ß œ ß
The plane containing these three points is a good approximation to the tangent plane to z f(x y) at the pointϧ

940 Chapter 14 Partial Derivatives
(0 0 0). A normal to this plane is 2500 5000 10,000 , or 2 4 . So at
00050
00 0 25
ßß œ
"
"
ââ
ââ
ââ
ââ
ââ
ââ
ijk
ij kijk
( 0) the vector is approximately 2 . Thus the geologists should drill their fourth borehole!ß
``
``
ff
xy
ij ij
in the direction of ( 2 ) from the first borehole.
"
È5ij
23. w e sin x w re sin x and w e cos x w e sin x; w w , where c is theœÊœ œ Êœ œ
rt rt rt rt
t x xx xx t
c
111111
##
"
positive constant determined by the material of the rod e sin x re sin xÊ œ11 1
#"
rt rt
cab
r c e sin x 0 r c w e sin xÊ œÊœ Êœab
## ##
11 1 1
rt c t1
24. w e sin kx w re sin kx and w ke cos kx w k e sin kx; w wœÊœ œ Êœ œ
rt rt rt rt
t x xx xx t
c
#"
k e sin kx re sin kx r c k e sin kx 0 r c k w e sin kx.Ê œ Ê œ Ê œ Ê œ
#####
"
rt rt rt c k t
cabab
Now, w(L t) 0 e sin kL 0 kL n for n an integer k w e sin x .ßœ Ê œ Ê œ Ê œ Ê œ
Îckt cn tL
nn
LL
111
1ˆ‰
As t , w 0 since sin x 1 and e 0.Ä_ Ä Ÿ Ä
¸¸ˆ‰
n
L
cn tL
11Î
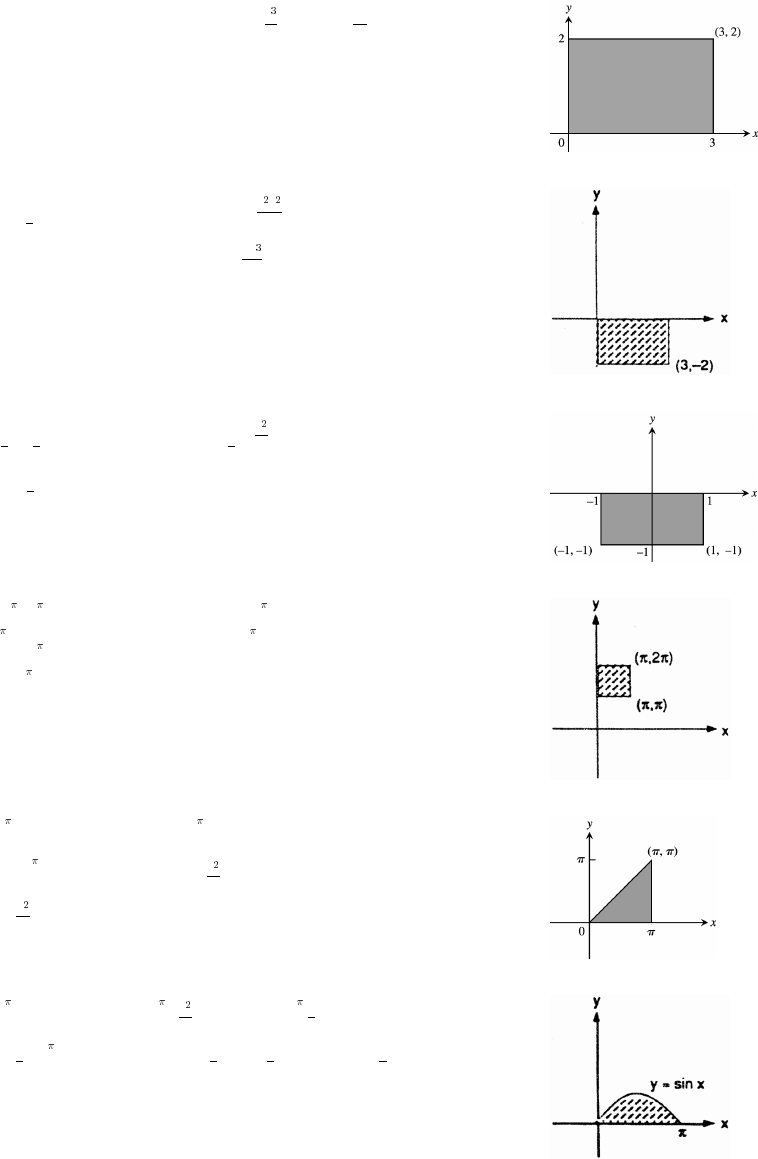
CHAPTER 15 MULTIPLE INTEGRALS
15.1 DOUBLE INTEGRALS
1. 4 y dy dx 4y dx dx 16
'' ' '
00 0 0
32 3 3
ab ’“
œœœ
##
!
y
33
16
2. (x y 2xy dy dx xy dx
'' '
02 0
30 3
ab ’“
##
!
#
œ
xy
2
4x 2x dx 2x 0œ œœ
'0
3ab
’“
##
$
!
2x
3
3. (x y 1) dx dy yx x dy
'' '
11 1
01 0
œ
’“
x
2
"
"
(2y 2) dy y 2y 1œœœ
'1
0cd
#!
"
4. (sin x cos y) dx dy ( cos x) (cos y)x dy
'' '
22
0œcd
1
!
( cos y 2) dy sin y 2y 2œœœ
'2
11 1cd
#1
1
5. (x sin y) dy dx x cos y dx
'' '
00 0
xx
œcd
!
(x x cos x) dx (cos x x sin x)œ œ
'0’“
x
2
1
!
2œ
1
#
6. y dy dx dx sin x dx
'' ' '
00 0 0
sin x sin x
œœ
’“
y
2!
"
#
#
(1 cos 2x) dx x sin 2xœ œ œ
"""
!
4424
'0‘
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
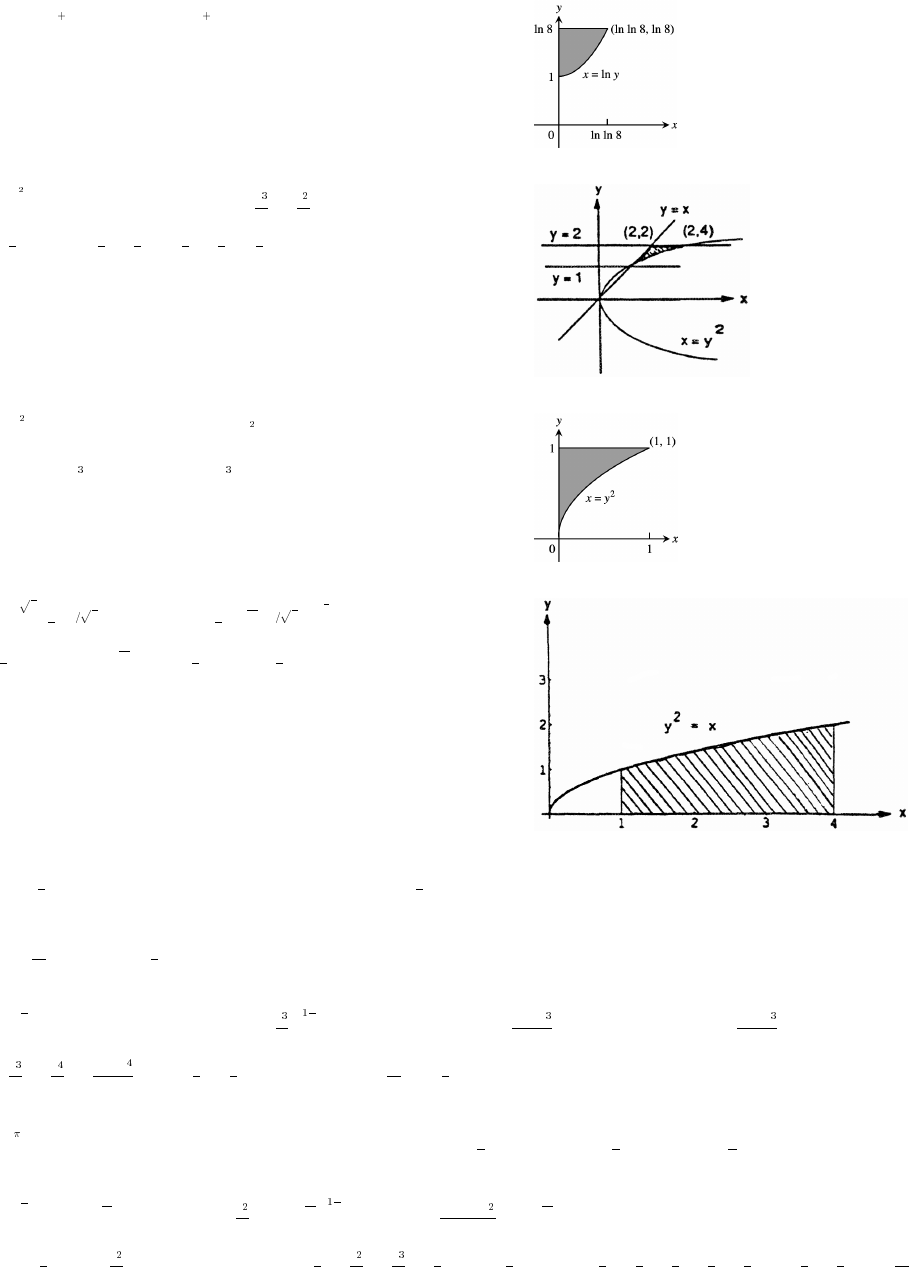
942 Chapter 15 Multiple Integrals
7. e dx dy e dy ye e dy
'' ' '
10 1 1
ln 8 ln y ln 8 ln 8
xy xy y y
ln y
œœcd a b
!
(y 1)e e 8(ln 8 1) 8 eœ œ cd
yy
ln 8
1
8 ln 816eœ
8. dx dy y y dy
'' '
1y 1
2y 2
œœab’“
#
#
#
"
yy
3
2œ œœ
ˆ‰ˆ‰
8735
3336
""
##
9. 3y e dx dy 3y e dy
'' '
00 0
11
0
yy
$#xy xy
œcd
3y e 3y dy e y e 2œœœ
'0
1Š‹’“
## $
"
!
yy
10. e dy dx x e dx
'' '
10 1
4x 4
yx yx x
0
33
2#œ‘
ÈÈ
(e 1) x dx (e 1) x 7(e 1)œ œ œ
332
23#
$Î# %
"
'1
4È‘ˆ‰
11. dy dx x ln y dx (ln 2) x dx ln 2
'' ' '
1x 1 1
22x 2 2
2x
x
x3
yœœœcd #
12. dy dx (ln 2 ln 1) dx (ln 2) dx (ln 2)
'' ' '
11 1 1
22 2 2
1
xy x
œœ œ
"#
13. x y dy dx x y dx x (1 x) dx x x dx
'' ' ' '
00 0 0 0
11x 1 1 1
x
0
ab ’“ ’ “ ’ “
## # # #$
œœ œ
y (1x) (1x)
333
000œ œ œ
’“
ˆ‰ˆ‰
xx
34 1 34 1 6
(1 x)
##
"
!
"" " "
14. y cos xy dx dy sin xy dy sin y dy cos y ( 1 1)
'' ' '
00 0 0
111
œœœœœcd ‘
1
111
!""
"
!
11 2
15. v u dv du v u du u(1 u) du
'' ' '
00 0 0
11u 1 1
u
0
ˆ‰
ÈÈ È
’“ ’ “
œ œ
v12uu
2
#
uuu du uuœ œ œœœ
'0
1Š‹’ “
"""" " "
## # ## #
"Î# $Î# $Î# &Î# "
!
u uuu2 2 22 2
2 6 3 5 635 5 10
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
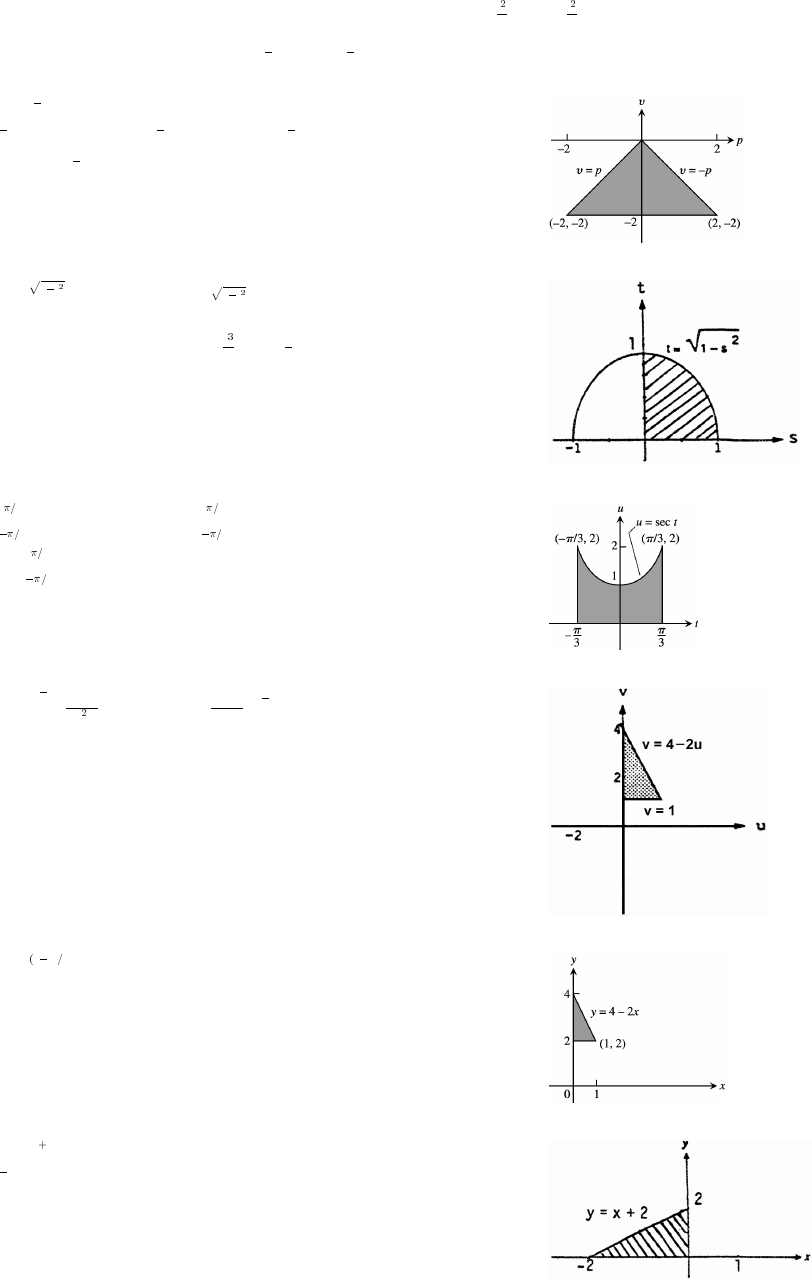
Section 15.1 Double Integrals 943
16. e ln t ds dt e ln t dt (t ln t ln t) dt ln t t ln t t
'' ' '
10 1 1
2lnt 2 2
ln t
0
ss tt
24
œœœcd ’“
#
"
(2 ln 212 ln 22) 1œœ
ˆ‰
""
44
17. 2 dp dv 2 p dv 2 2v dv
'' ' '
2v 2 2
0v 0 0
v
v
œœcd
2v 8œ œcd
#0
2
18. 8t dt ds 4t ds
'' '
00 0
11s 1 1s
0
œcd
#
41 s ds 4sœœœ
'0
1ab ’“
#"
!
s8
33
19. 3 cos t du dt (3 cos t)u
'' '
30 3
3sect 3 sec t
0
œcd
3 dt 2œœ
'3
3
1
20. dv du du
'' '
01 0
342u 3 42u
1
42u 2u4
vv
œ‘
(3 u) du 3u uœ#œœ!
'0
3cd
#$
!
21. dx dy
''
20
44y)2
22. dy dx
''
20
0x2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
944 Chapter 15 Multiple Integrals
23. dy dx
''
0x
1x
24. dx dy
''
01y
11y
25. dx dy
''
1lny
e1
26. dy dx
''
10
2lnx
27. 16x dx dy
''
00
99y
1
2
28. y dy dx
''
00
44x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 15.1 Double Integrals 945
29. 3y dy dx
''
10
11x
30. 6x dx dy
''
20
24y
31. dy dx dx dy sin y dy 2
'' '' '
0x 00 0
y
sin y sin y
yy
œœœ
32. 2y sin xy dy dx 2y sin xy dx dy
'' ''
0x 00
22 2y
##
œ
2y cos xy dy 2y cos y 2y dyœ œ
''
00
22
y
0
cda b
#
sin y y 4 sin 4œ œ cd
##
#
!
33. x e dx dy x e dy dx xe dx
'' '' '
0y 00 0
11 1x 1
xy xy xy x
0
##
œœ cd
xe x dx eœœœ
'0
1xx
ab
’“
"
##
"
!
2
xe2
34. dy dx dx dy
'' ''
00 00
24x 4 4y
xe xe
4y 4y
2y 2y
œ
dy dyœœœœ
''
00
44
4y
0
’“ ’“
xe e e e
(4 y) 4 4
2y 2y 2y
# #
%
!
"
35. e dx dy e dy dx
'' ''
0y/2 00
2 ln 3 ln 3 ln 3 2x
xx
œ
2xe dx e e 1 2œœœœ
'0
ln 3 xx ln3
ln 3
0
cd
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
946 Chapter 15 Multiple Integrals
36. e dy dx e dx dy
'' ''
0x3 00
31 13y
yy
œ
3y e dy e e 1œœœ
'0
1yy
#"
!
cd
37. cos 16 x dx dy cos 16 x dy dx
'' ''
0y 00
11612 12x
ab ab11
&&
œ
x cos 16 x dxœœœ
'0
12 %& "Î#
!
"
ab’“
1sin 16 x
80 80
ab1
11
38. dy dx dx dy
'' ''
0x 00
82 2y
""
y1 y1
œ
dy ln y 1œœœ
'0
2y
y1 44
ln 17
"%#
!
cdab
39. y 2x dA
''
Rab#
y 2x dy dx y 2x dy dxœ
'' ''
1x1 0x1
0x1 11x
ab ab
##
y 2x y dx y 2x y dxœ
''
10
01
x1x
x1 x1
‘ ‘
""
## ##
22
(x 1) 2x (x 1) ( x 1) 2x ( x 1) dxœ
'1
0‘
""
##
## ##
(1 x) 2x (1 x) (x 1) 2x (x 1) dx
'0
1‘
""
##
## ##
4 x x dx 4 x x dxœ
''
10
01
ab ab
$# $#
444 48œ œ œ œ œ
’“’“’ “
ˆ‰ˆ ‰
xx xx 34 8 2
4 3 4 3 4 3 4 3 12 12 12 3
(1) (1)
0
1
"
!
""
40. xy dA xy dy dx xy dy dx
''
R
œ
'' ''
0x 23x
23 2x 1 2 x
xy dx xy dxœ
''
023
23 1
2x 2 x
xx
‘ ‘
""
##
22
2x x dx x(2 x) x dxœ
''
023
23 1
ˆ‰ ‘
$$ #$
"""
###
x dx 2x x dxœ
''
023
23 1
3
#
$#
ab
xxx 1œœ œœ
‘ ‘ ˆ‰ˆ‰ˆ ‰ ‘ ˆ ‰ˆ‰ˆ ‰
3 2 3 16 2 4 2 8 6 27 36 16 13
8 3 8 81 3 9 3 27 81 81 81 81 81
%#$
"
#Î$
23
0
41. V x y dy dx x y dx 2x dxœœœœ
'' ' '
0x 0 0
12x 1 1
2x
x
ab ’“ ’ “’ “
## # #
"
!
y (2x) (2x)
3 3 3 3 12 12
7x 2x 7x
00œ œ
ˆ‰ˆ‰
27 16 4
31212 12 3
"
42. V x dy dx x y dx 2x x x dx x x xœœœœ
'' ' '
2x 2 2
12x 1 1
2x
x
# # #%$ $ & %
"
#
cd a b ‘
211
354
œœ œœ
ˆ‰ˆ ‰ˆ ‰ˆ ‰
2 16 32 16 40 12 15 320 384 240 189 63
3 5 4 3 5 4 60 60 60 60 60 60 60 20
""
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 15.1 Double Integrals 947
43. V (x 4) dy dx xy 4y dx x 4 x 4 4 x 3x 12x dxœœœ
'' ' '
43x 4 4
14x 1 1
4x
3x
cd c dabab
###
x 7x 8x 16 dx x x 4x 16x 12 64œ œ œ
'4
1ab
‘ˆ‰ˆ‰
$# % $# "
%
"17 7 64
43 43 3
œœ
157 625
3412
"
44. V (3 y) dy dx 3y dx 3 4 x dxœœœ
'' ' '
00 0 0
24x 2 2
4x
0
’“ ’ “
ÈŠ‹
y
2
4x
#
#
x4 x 6 sin 2x 6 4 3œ œœœ
’“
Ȉ‰ ˆ‰
3xx81698
26663
#"
##
#
!
11
1
45. V 4 y dx dy 4x y x dy 12 3y dy 12y y 24 8 16œ œœœœœ
'' ' '
00 0 0
23 2 2
ab cd abcd
## #$
$
!!
#
46. V 4 x y dy dx 4 x y dx 4 x dx 8 4x dxœœœœ
'' ' ' '
00 0 0 0
24x 2 2 2
4x
a b ab ab
’“ Š‹
## ##
"
##
#
y
2
x
8x x x 16œ œœ œ
‘
4 32 32 480 320 96 128
3 10 3 10 30 15
$&
"
#
!
47. V 12 3y dy dx 12y y dx 24 12x (2 x) dxœœœ
'' ' '
00 0 0
22x 2 2
ab cd c d
#$ $
#
!
x
24x 6x 20œ œ
’“
##
!
(2 x)
4
48. V (3 3x) dy dx (3 3x) dy dx 6 1 x dx 6 (1 x) dx 4 2 6œ œ œœ
'' '' ' '
1x1 0x1 1 0
0x1 11x 0 1
ab
##
49. V (x 1) dy dx xy y dx 1 1 2 1 dxœœœœ
'' ' ' '
11x 1 1 1
21x 2 2 2
1x
1x
cd ‘ˆ‰ˆ‰
"" "
xx x
2 x ln x 2(1 ln 2)œ œcd
#
"
50. V 4 1 y dy dx 4 y dx 4 sec x dxœœœ
'' ' '
00 0 0
3 sec x 3 3
sec x
0
ab ’“ Š ‹
#y
33
sec x
7 ln sec x tan x sec x tan x 7 ln 2 3 2 3œ œ
22
33
cdkk ’“Š‹
ÈÈ
1Î$
!
51. dy dx dx dx lim lim 1 1
'' ' '
1e 1 1
1
e
b
1
xx
"""
"
xy x x x b
ln y x
œœœœœ
’“ ˆ‰ ‘ ˆ ‰
bbÄ_ Ä_
52. (2y 1) dy dx y y dx dx 4 lim sin x
'' ' '
11/1x 1 1
11/1x 1 1
1/ 1 x
1/ 1 x
b
œ œ œcd cd
º
#"
!
1
1
2
1x
Èb1Ä
4 lim sin b 0 2œœ
b1Äcd
" 1
53. -dx dy 2 lim tan b tan 0 dy 2 lim dy
'' ' '
" "
" "
ababx1y1 y1 y1
2
œœ
0 0
b
Š‹Š ‹
bbÄ_ Ä_
1
2 lim tan b tan 0 (2 )œœœ111
Š‹
ˆ‰
bÄ_
" " #
#
1
54. xe dx dy e lim xe e dy e lim be e 1 dy
'' ' '
00 0 0
x2y 2y x x 2y b b
b
0
œœ
bbÄ_ Ä_
cd a b
e dy lim e 1œœœ
'0
2y 2b
""
##
bÄ_ ab
55. f(x y) dA f 0 f(0 0) f 0 f 0 f f f
''
R
߸ßßßßß!ßß
""" """"""""""""
######488444884
ˆ ‰ ˆ‰ ˆ‰ ˆ ‰ ˆ‰ ˆ‰
00œ œ
""" " ""
## #484416
33
ˆ‰ˆ ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

948 Chapter 15 Multiple Integrals
56. f(x y) dA f f ffff ff
''
R
ß ¸ ß ß ß ß ß ß ß ß
"
44444444444 444444
79 99 511 711 911 1111 513 713
ˆ‰ˆ‰ˆ ‰ˆ ‰ˆ ‰ˆ ‰ˆ ‰ˆ ‰
ff ff
‘ˆ‰ˆ ‰ˆ‰ˆ‰
ß ßßß
913 1113 715 915
44 4 4 44 44
(252727293133313335373739) 24œ œ œ
"
16 16
384
57. The ray meets the circle x y 4 at the point 3 1 the ray is represented by the line y .)œœßÊ œ
1
6
x
3
## Š‹
ÈÈ
Thus, f(x y) dA 4 x dy dx 4 x 4 x dx 4x
''
R
ßœ œ œ
'' '
0x3 0
34x 3
3
3
0
ÈÈ
’“
ab ”•
##
#
xx
3
4x
33
ab
È
œ20 3
9
È
58. dy dx dx dx 6
'' ' ' '
20 2 2 2
22
0
"
ab ab
xx(y1)
3(y 1)
xx xx xx x(x1)
33 dx
œœœ
’“ ˆ‰
6 lim dx 6 lim ln (x 1) ln x 6 lim [ln (b 1) ln b ln 1 ln 2]œ œ œ
bb bÄ_ Ä_ Ä_
'2
bb
2
ˆ‰ cd
""
x1 x
6 lim ln 1 ln 2 6 ln 2œœ
’“
ˆ‰
bÄ_
"
b
59. V x y dy dx x y dxœœ
'' '
0x 0
12x 1 2x
x
ab ’“
## # y
3
2x dxœ œ
'0
1’“’“
#
"
!
7x 2x 7x
33 31212
(2 x) (2 x)
00œ œ
ˆ‰ˆ‰
27 16 4
3121 12 3
"
#
60. tan x tan x dx dy dx dx dy dx dy
'''''''
00x0y2y
22x2y22
ab
" " "" "
1œ œ
1y 1y 1y
dy dy ln 1 y 2 tan y ln 1 yœœ
''
02
22 2
2
ˆ‰ ˆ‰
1y 2
1y 1y 2
#
#
" "
#" #
!
yˆ‰ ‘
cd abab
1
11
ln 5 2 tan 2 ln 1 4 2 tan 2 ln 5œ
ˆ‰ ab
1
11 1
" "
" # "
#
1
22
11
2 tan 2 2 tan 2 ln 1 4œ
" " #
"
#
11
2
ln 5
1ab
61. To maximize the integral, we want the domain to include all points where the integrand is positive and to
exclude all points where the integrand is negative. These criteria are met by the points (x y) such thatß
4 x 2y 0 or x 2y 4, which is the ellipse x 2y 4 together with its interior. Ÿ œ
## ## ##
62. To minimize the integral, we want the domain to include all points where the integrand is negative and to
exclude all points where the integrand is positive. These criteria are met by the points (x y) such thatß
x y 9 0 or x y 9, which is the closed disk of radius 3 centered at the origin.
## ##
Ÿ Ÿ
63. No, it is not possible By Fubini's theorem, the two orders of integration must give the same result.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 15.1 Double Integrals 949
64. One way would be to partition R into two triangles with the
line y 1. The integral of f over R could then be writtenœ
as a sum of integrals that could be evaluated by integrating
first with respect to x and then with respect to y:
f(x y) dA
''
R
ß
f(x y) dx dy f(x y) dx dy.œßß
'' ''
022y 1y1
12y2 22y2
Partitioning R with the line x 1 would let us write theœ
integral of f over R as a sum of iterated integrals with
order dy dx.
65. e dx dy e e dx dy e e dx dy e dx e dy
'' '' ' ' ' '
bb bb b b b b
bb bb b b b b
xy y x y x x y
œœ œ
ŒŒŒ
e dx 2 e dx 4 e dx ; taking limits as b gives the stated result.œœ œ Ä_
ŒŒ Œ
'''
b0 0
bbb
xxx
###
66. dy dx dx dy dy
'' '' ' '
00 00 0 0
13 31 3 3
xx x
(y 1) (y 1) (y 1) (y 1)
33
dy
""
"
!
œœœ
’“
lim lim lim (y 1) lim (y 1)œ œ
""
"Î$ "Î$
33
dy dy
(y 1) (y 1)
b1 b1
b1 b1
ÄÄ
ÄÄ
''
0b
b3 b3
0b
‘ ‘
lim (b 1) ( 1) lim (b 1) (2) (0 1) 0 2 1 2œœœ
’“’“Š‹
ÈÈ
b1 b1
ÄÄ
"Î$ "Î$ "Î$ "Î$ $$
67-70. Example CAS commands:
:Maple
f := (x,y) -> 1/x/y;
q1 := Int( Int( f(x,y), y=1..x ), x=1..3 );
evalf( q1 );
value( q1 );
evalf( value(q1) );
71-76. Example CAS commands:
:Maple
f := (x,y) -> exp(x^2);
c,d := 0,1;
g1 := y ->2*y;
g2 := y -> 4;
q5 := Int( Int( f(x,y), x=g1(y)..g2(y) ), y=c..d );
value( q5 );
plot3d( 0, x=g1(y)..g2(y), y=c..d, color=pink, style=patchnogrid, axes=boxed, orientation=[-90,0],
scaling=constrained, title="#71 (Section 15.1)" );
r5 := Int( Int( f(x,y), y=0..x/2 ), x=0..2 ) + Int( Int( f(x,y), y=0..1 ), x=2..4 );
value( r5);
value( q5-r5 );
67-76. Example CAS commands:
: (functions and bounds will vary)Mathematica
You can integrate using the built-in integral signs or with the command . In the command, theIntegrate Integrate
integration begins with the variable on the right. (In this case, y going from 1 to x).
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
950 Chapter 15 Multiple Integrals
Clear[x, y, f]
f[x_, y_]:= 1 / (x y)
Integrate[f[x, y], {x, 1, 3}, {y, 1, x}]
To reverse the order of integration, it is best to first plot the region over which the integration extends. This can be done
with ImplicitPlot and all bounds involving both x and y can be plotted. A graphics package must be loaded. Remember to
use the double equal sign for the equations of the bounding curves.
Clear[x, y, f]
<<Graphics`ImplicitPlot`
ImplicitPlot[{x==2y, x==4, y==0, y==1},{x, 0, 4.1}, {y, 0, 1.1}];
f[x_, y_]:=Exp[x ]
2
Integrate[f[x, y], {x, 0, 2}, {y, 0, x/2}] Integrate[f[x, y], {x, 2, 4}, {y, 0, 1}]
To get a numerical value for the result, use the numerical integrator, . Verify that this equals the original.NIntegrate
Integrate[f[x, y], {x, 0, 2}, {y, 0, x/2}] NIntegrate[f[x, y], {x, 2, 4}, {y, 0, 1}]
NIntegrate[f[x, y], {y, 0, 1},{x, 2y, 4}]
Another way to show a region is with the FilledPlot command. This assumes that functions are given as y = f(x).
Clear[x, y, f]
<<Graphics`FilledPlot`
FilledPlot[{x , 9},{x, 0,3}, AxesLabels {x, y}];
2Ä
f[x_, y_]:= x Cos[y ]
2
Integrate[f[x, y], {y, 0, 9}, {x, 0, Sqrt[y]}]
67. dy dx 0.603 68. e dy dx 0.558
'' ''
11 00
3x 11 xy
"
xy ¸¸
69. tan xy dy dx 0.233 70. 3 1 x y dy dx 3.142
'' ''
00 10
11 11x
" ##
¸¸
È
71. Evaluate the integrals:
e dx dy
''
02y
14
x
e dy dx e dy dxœ
'' ''
00 20
2x/2 41
xx
e 2 erfi 2 2 erfi 4œ
""
44
4
ˆ‰ÈÈ
ab ab11
1.1494 10¸‚
6
The following graphs was generated using
Mathematica.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
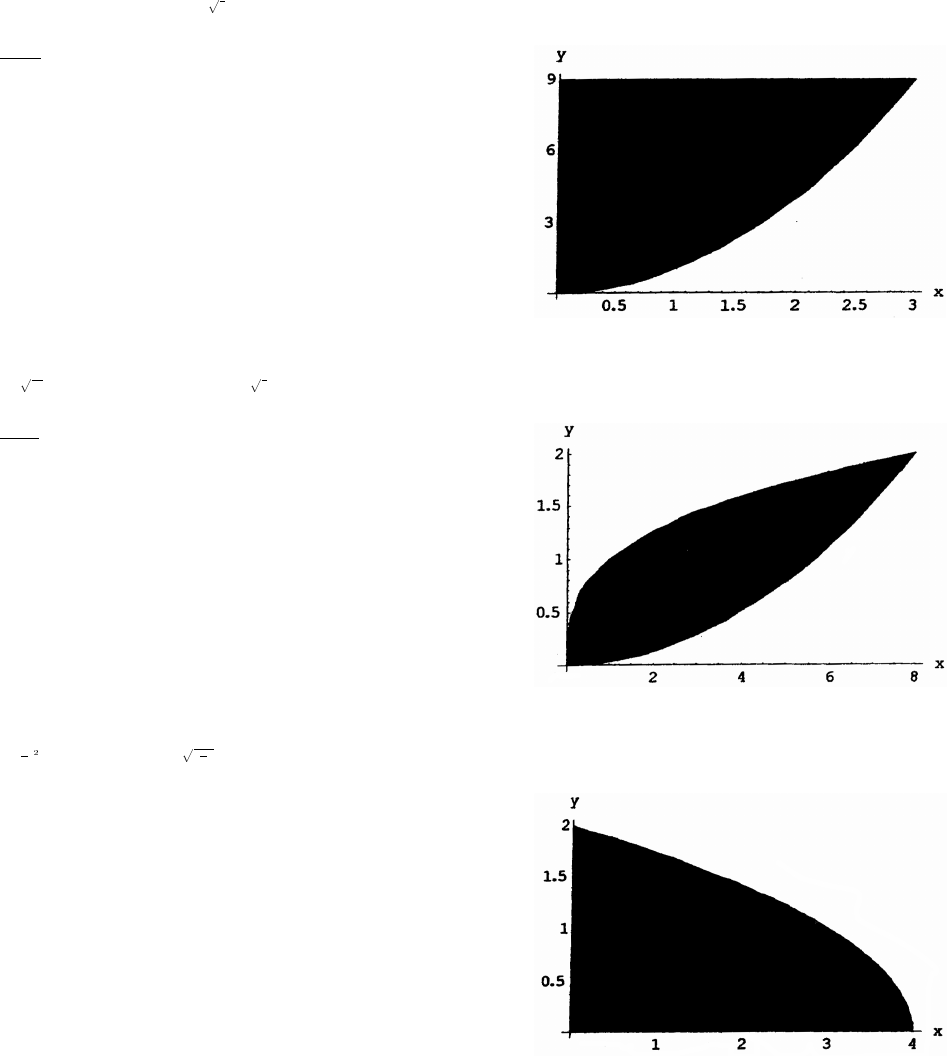
Section 15.2 Areas, Moments, and Centers of Mass 951
72. Evaluate the integrals:
x cos y dy dx x cos y dx dy
'' ''
0x 00
39 9 y
22
2ab abœ
0.157472œ¸
sin 81
4
ab
The following graphs was generated using
Mathematica.
73. Evaluate the integrals:
x y xy dx dy x y xy dy dx
'' ''
0y 0x/32
242y 8 x
22 22
32
3
ab abœ
97.4315œ¸
67,520
693
The following graphs was generated using
Mathematica.
74. Evaluate the integrals:
e dx dy e dy dx
'' ''
00 00
24y 4 4x
xy xy
œ
20.5648¸
The following graphs was generated using
Mathematica.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
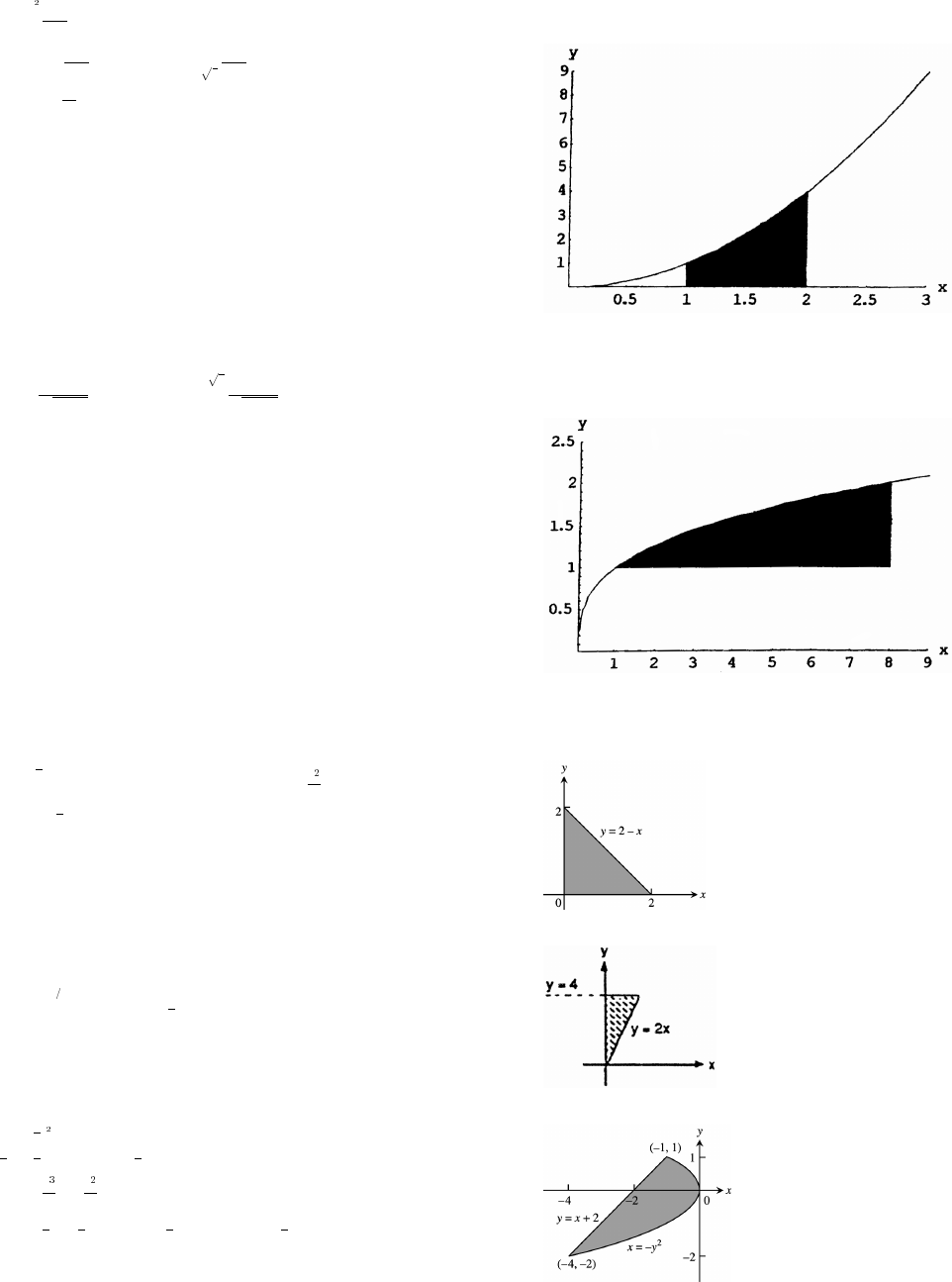
952 Chapter 15 Multiple Integrals
75. Evaluate the integrals:
dy dx
''
10
2x
1
xy
dx dy dx dyœ
'' ''
01 1 y
12 42
11
xy xy
1 ln 0.909543 ¸
ˆ‰
27
4
The following graphs was generated using
Mathematica.
76. Evaluate the integrals:
dx dy dy dx
'' ''
1y 11
28 8 x
3
3
11
xy xy
ÈÈ
22 22
œ
0.866649¸
The following graphs was generated using
Mathematica.
15.2 AREAS, MOMENTS, AND CENTERS OF MASS
1. dy dx (2 x) dx 2x 2,
'' '
00 0
22x 2
œœœ
’“
x
2
#
!
or dx dy (2 y) dy 2
'' '
00 0
22y 2
œœ
2. dy dx (4 2x) dx 4x x 4,
'' '
02x 0
24 2 2
0
œ œœcd
#
or dx dy dy 4
'' '
00 0
4y2 4
œœ
y
#
3. dx dy y y 2 dy
'' '
2y2 2
1y 1
œab
#
2yœ
’“
yy
3#
"
#
224œ œ
ˆ‰ˆ‰
""
##33
89
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
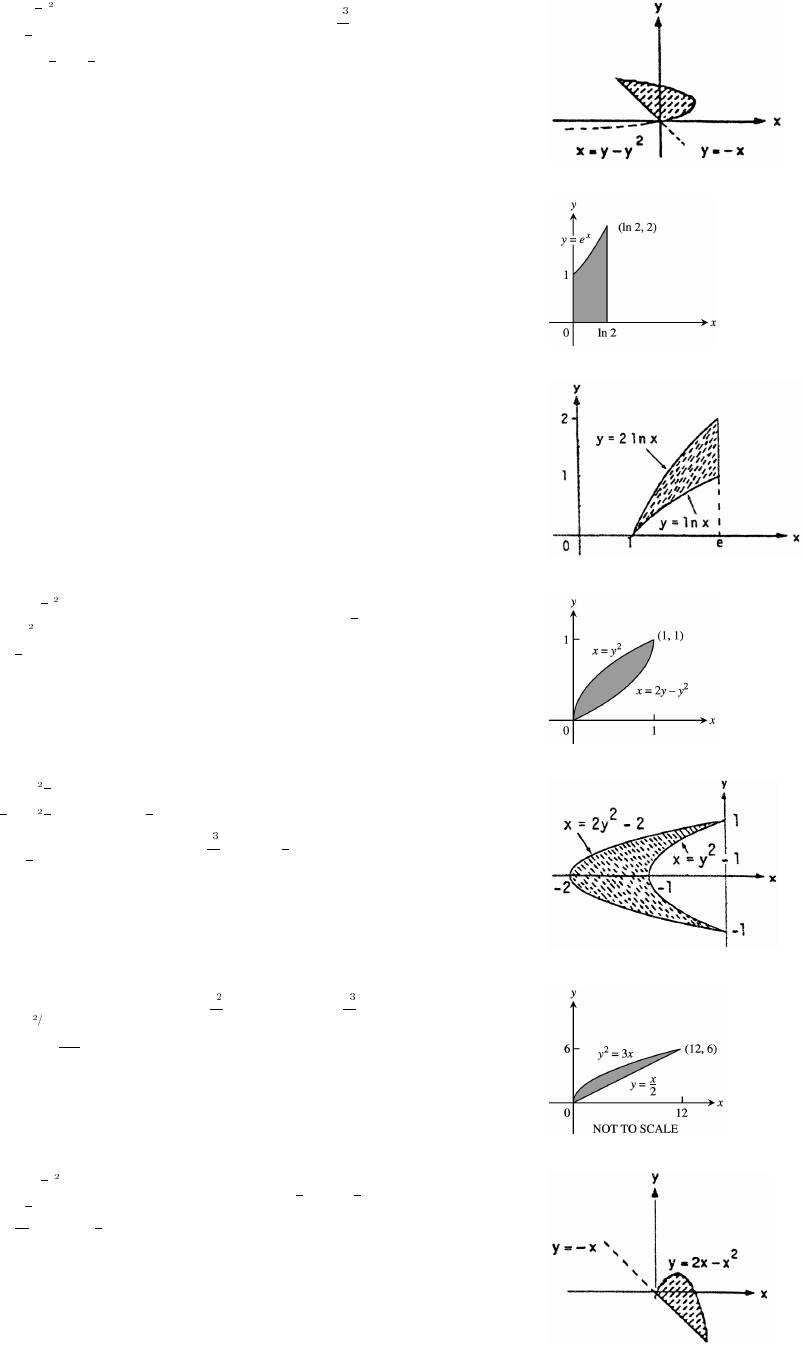
Section 15.2 Areas, Moments, and Centers of Mass 953
4. dx dy 2y y dy y
'' '
0y 0
2yy 2
œœab
’“
##
#
!
y
3
4œ œ
84
33
5. dy dx e dx e 2 1 1
'' '
00 0
ln 2 e ln 2 xx
ln 2
0
x
œ œ œœcd
6. dy dx ln x dx x ln x x
'' '
1ln x 1
e2 ln x e e
1
œœcd
(e e) (0 1) 1œœ
7. dx dy 2y 2y dy y y
'' '
0y 0
12yy 1
œ œab
‘
##$
"
!
2
3
œ"
3
8. dx dy y 1 2y 2 dy
'' '
12y2 1
1y1 1
œab
##
1 y dy yœ œœ
'1
1ab’“
#"
"
y
33
4
9. dx dy 2y dy y
'' '
0y3 0
62y 6
œœ
Š‹’“
yy
39
#'
!
36 12œ œ
216
9
10. dy dx 3x x dx x x
'' '
0x 0
32xx 3
œœab
‘
##$
"$
!
3
23
9œœ
27 9
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
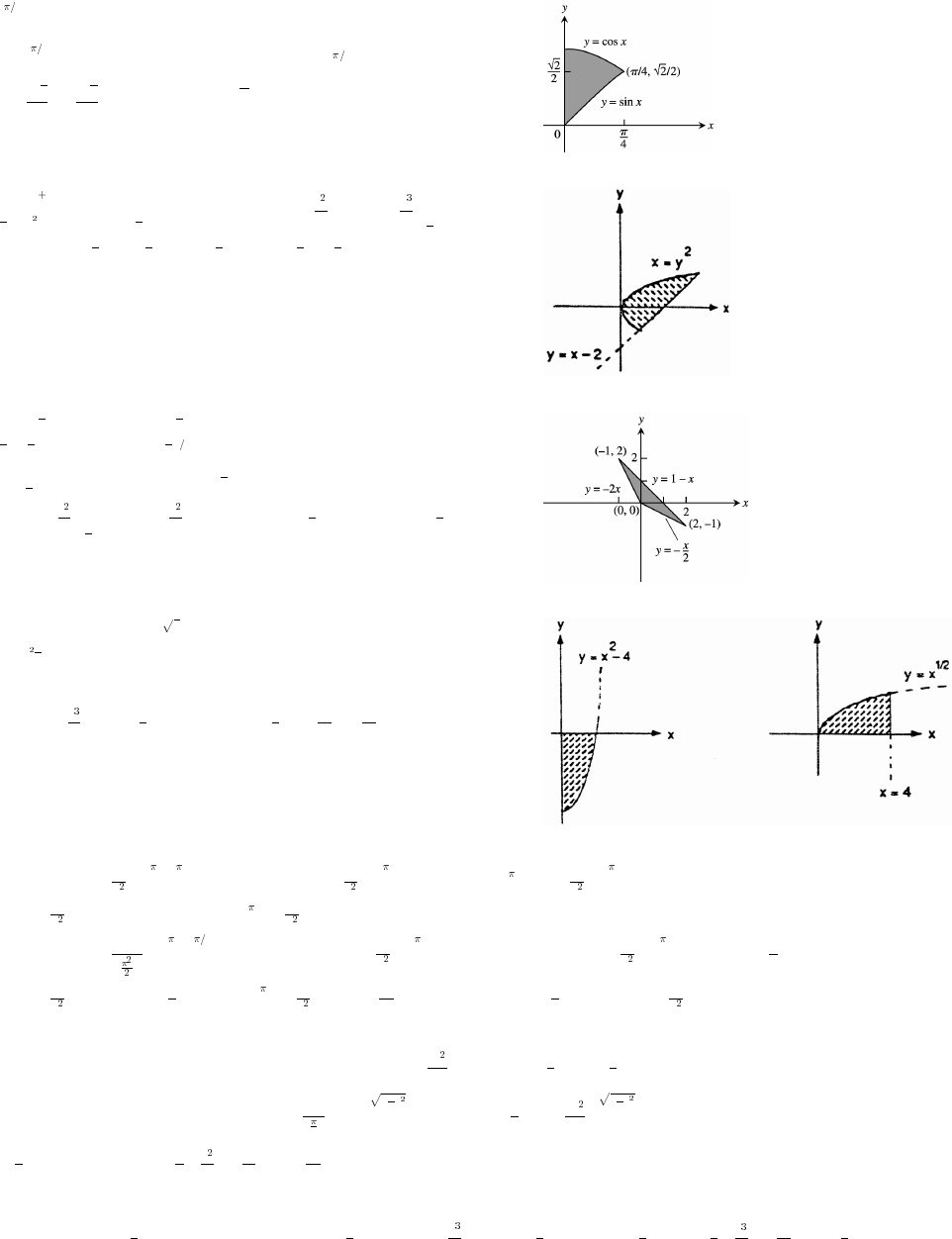
954 Chapter 15 Multiple Integrals
11. dy dx
''
0sin x
4cos x
(cos x sin x) dx sin x cos xœœ
'0
44
0
cd
(0 1) 2 1œœ
Š‹ È
ÈÈ
22
##
12. dx dy y 2 y dy 2y
'' '
1y 1
2y2 2 2
1
œ œab
’“
#yy
23
24 2 5œœœ
ˆ‰ˆ‰
89
33
"" "
###
13. dy dx dy dx
'' ''
12x 0 x2
01x 21x
(1 x) dx 1 dxœ
''
10
02
ˆ‰
x
#
xx 1(21)œ œœ
’“’“ˆ‰
xx 3
24
02
10
"
##
14. dy dx dy dx
'' ''
0x4 00
20 4 x
4 x dx x dxœ
''
00
24
ab
# "Î#
4x x 8œ œœ
’“
‘ˆ‰
x2 81632
33 333
2
0
4
0
$Î#
15. (a) average sin (x y) dy dx cos (x y) dx [ cos (x ) cos x] dxœœœ
"""
111
'' ' '
00 0 0
0
cd 1
sin (x ) sin x [( sin 2 sin ) ( sin sin 0)] 0œ œ œ
""
11
cd1111
0
(b) average sin (x y) dy dx cos (x y) dx cos x cos x dxœœœ
"Î#
!#
Š‹
'' ' '
00 0 0
222
11
11
cd ‘ˆ‰
sin x sin x sin sin sin sin 0œ œ œ
223 4
11 1
111
‘ ‘ˆ‰ ˆ ‰ˆ ‰
###
01
16. average value over the square xy dy dx dx dx 0.25;œœœœœ
'' ' '
00 0 0
11 1 1
’“
xy
24
x
"
!#
"
average value over the quarter circle xy dy dx dxœœ
"
ˆ‰
4'' '
00 0
11x 1 1x
0
4xy
21’“
x x dx 0.159. The average value over the square is larger.œœœ¸
22xx
24111
'0
1ab ’“
$"
!
"
#
4
17. average height x y dy dx x y dx 2x dxœœœœœ
""""
## # #
##
!!
#44343333
y8x4x8
''''
0000
2222
ab ’“ ’“
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 15.2 Areas, Moments, and Centers of Mass 955
18. average dy dx dxœœ
"""
(ln 2) xy (ln 2) x
ln y
'' '
ln 2 ln 2 ln 2
2 ln 2 2 ln 2 2 ln 2 2 ln 2
ln 2
’“
(ln 2 ln ln 2 ln ln 2) dx ln xœœœ
"" " "
#(ln 2) x ln 2 x ln
dx
''
ln 2 ln 2
2 ln 2 2 ln 2 2 ln 2
ln 2
ˆ‰ ˆ‰
cd
(ln 2 ln ln 2 ln ln 2) 1œœ
ˆ‰
"
#ln
19. M 3 dy dx 3 2 x x dx ; M 3x dy dx 3 xy dxœœœœ œ
'' ' '' '
0x 0 0x 0
12x 1 12x 1
y
2x
x
ab cd
#
#
7
3 2x x x dx ; M 3y dy dx y dx 4 5x x dxœ œœ œ œ œ
'''''
00x00
112x11
x
2x
x
ab cd ab
$# # #%
##
53319
4 5
x and yÊœ œ
538
14 35
20. M dy dx 3 dx 9 ; I y dy dx dx 27 ; R 3;œœœœ œœœœ$$$$ $ $
'' ' '' '
00 0 00 0
33 3 33 3
x x
3
0
#’“ ÉÈ
y
3M
Ix
I x dy dx x y dx 3x dx 27 ; R 3
y y
00 0 0
33 3 3
œœœœœœ$$$$
'' ' '
## #
$
!
cd ÉÈ
I
M
y
21. M dx dy 4 y dy ; M x dx dy x dyœœœœ œ
'' ' '' '
0y2 0 0y2 0
24y 2 24y 2
y
4y
y2
Š‹ cd
y14
3
##
"#
16 8y y dy ; M y dx dy 4y y dyœœœ œœ
"
# #
##
''''
00y20
224y2
x
Š‹ Š‹
yy
415 3
128 10
x and yÊœ œ
64 5
35 7
22. M dy dx (3 x) dx ; M x dy dx xy dx 3x x dxœœœœ œœœ
'' ' ' ' ' '
00 0 0 0 0 0
33x 3 3 3x 3 3
y
3x
0
9 9
# #
#
cd a b
x 1 and y 1, by symmetryÊœ œ
23. M 2 dy dx 2 1 x dx 2 ; M 2 y dy dx y dxœœœœœ œ
'' ' '' '
00 0 00 0
11x 1 11x 1
x
1x
0
Ȉ‰ cd
##
#
11
4
1 x dx x y and x 0, by symmetryœ œœÊœ œ
'0
1ab’“
#"
!
x2 4
33 3
1
24. M ; M x dy dx xy dx 5x x dx ;œœ œ œ œ
125 625
6 1
$ $
y0x 0 0
56xx 5 5
6x x
x
$$$
'' ' '
cd a b
#$
#
M y dy dx y dx 35x 12x x dx x and y 5
x0x 0 0
56xx 5 5
6x x
x
œœœœÊœœ$'' ' '
$$ $
## #
##$%
cd a b 625 5
6
25. M dy dx ; M x dy dx xy dx x a x dxœœœ œœœ
'' '' ' '
00 00 0 0
aax aax a a
y
ax
0
1a a
4 3
cd È##
x y , by symmetryÊœœ
4a
31
26. M dy dx sin x dx 2; M y dy dx y dx sin x dxœœœœ œ œ
'' ' '' ' '
00 0 00 0 0
sin x sin x
x
sin x
0
""
##
##
cd
(1 cos 2x) dx x and yœ œÊœ œ
"
#448
'0
111
27. I y dy dx dx 4 x dx 4 ; I 4 , by symmetry;
x y
24x 2 2
24x 2 2
4x
4x
œœœœœ
'' ' '
##
$Î#
’“ ab
y
33
211
III8
oxy
œœ1
28. I x dy dx sin x 0 dx (1 cos 2x) dx
y
2sinxx 2 2
0
œœœœ
'' ' '
##
"
##
ab 1
29. M dy dx e dx lim e dx 1 lim e 1; M x dy dx xe dxœœœ œœœ œ
'' ' ' '' '
0e 0 0 0e 0
0b 0
xx b x
y
x x
bbÄ_ Ä_
lim xe dx lim xe e 1 lim be e 1; M y dy dxœœœœœ
bb bÄ_ Ä_ Ä_
'''
b 0
00e
xxx bb
0
bx
cd ab x
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

956 Chapter 15 Multiple Integrals
e dx lim e dx x 1 and yœœ œÊœœ
"" " "
##
''
00
2x 2x
b
bÄ_ 44
30. M x dy dx lim xe dx lim 1 1
y00 0
eb
x2 b
0
œœ œœ
'' '
x2
x2
bbÄ_ Ä_ ‘
"
e
31. M (x y) dx dy xy dy 2y 2y dy ;œœœœœ
'' ' '
0y 0 0
2yy 2 2
yy
y
’“ Š ‹’ “
x 8
22 10315
yyy2y
$#
#
#
!
I y (x y) dx dy xy dy 2y 2y dy ;
x0y 0 0
2yy 2 2
yy
y
œœœœ
'' ' '
#$&%
’“ Š ‹
xy y
2 2 105
64
R2
xœœœ
ÉÉÉ
I
M7 7
82
x
32. M 5x dx dy 5 dy 12 4y 16y dy 23 3œœœœ
'' ' '
32 4y 32 32
32 12 4y 32 32
12 4y
4y
’“ ab
È
x5
2#
#%
33. M (6x 3y 3) dy dx 6xy y 3y dx 12 12x dx 8;œœœœ
'' ' '
0x 0 0
12x 1 1
2x
x
‘
ab
3
#
##
M x(6x 3y 3) dy dx 12x 12x dx 3; M y(6x 3y 3) dy dx
y x
0x 0 0x
12x 1 12x
œœœœ
'' ' ''
ab
$
14 6x 6x 2x dx x and yœ œÊœ œ
'0
1ab
#$
#
17 3 17
816
34. M (y 1) dx dy 2y 2y dy ; M y(y 1) dx dy 2y 2y dy ;œœœœ œœ
'' ' '' '
0y 0 0y 0
12yy 1 12yy 1
x
ab a b
$#%
"
#
4
15
M x(y 1) dx dy 2y 2y dy x and y ; I y (y 1) dx dy
y0y 0 0y
12yy 1 12yy
œœœÊœœœ
'' ' ''
ab
#% #
488
15 15 15 x
2 y y dyœœ
'0
1ab
$& "
6
35. M (x y 1) dx dy (6y 24) dy 27; M y(x y 1) dx dy y(6y 24) dy 14;œ œœœ œœ
'' ' '' '
00 0 00 0
16 1 16 1
x
M x(x y 1) dx dy (18y 90) dy 99 x and y ; I x (x y 1) dx dy
y y
00 0 00
16 1 16
œœœÊœœœ
'' ' ''
11 14
327 #
216 dy 432; R 4œœœœ
'0
1
y
ˆ‰ É
y
36 M
11 Iy
36. M (y 1) dy dx x dx ; M y(y 1) dy dx dxœœœœ œ
'' ' '' '
1x 1 1x 1
11 1 11 1
x
Š‹ Š‹
x332 5xx
15 6 3
## #
#
; M x(y 1) dy dx x dx 0 x 0 and y ; I x (y 1) dy dxœœ œ œÊœ œœ
48 3x x 9
35 14
y y
1x 1 1x
11 1 11
'' ' ''
Š‹
##
$#
x dx ; Rœœœœ
'1
1
y
Š‹ ÉÉ
3x x 16 3
22 35 M 14
I
%y
37. M (7y 1) dy dx x dx ; M y(7y 1) dy dx dx ;œœœœ œœ
'' ' '' '
10 1 10 1
1x 1 1x 1
x
Š‹ Š‹
7x 31 7x x 13
15 3 2 15
#
#
M x(7y 1) dy dx x dx 0 x 0 and y ; I x (7y 1) dy dx
y y
10 1 10
1x 1 1x
œœœÊœœœ
'' ' ''
Š‹
7x 13
31
#
$#
x dx ; Rœœœœ
'1
1
y
Š‹ ÉÉ
7x 7 21
5M31
I
#
%y
38. M 1 dy dx 2 dx 60; M y 1 dy dx 1 dx 0;œœœœ œ œ
'' ' '' '
01 0 01 0
20 1 20 20 1 20
x
ˆ‰ ˆ‰ ˆ‰ ˆ‰
’“Š‹
xx x x
20 10 20 0
y
##
"
"
M x 1 dy dx 2x dx x and y 0; I y 1 dy dx
y x
01 0 01
20 1 20 20 1
œœœÊœœœ
'' ' ''
ˆ‰ ˆ‰
Š‹
x x 2000 100 x
20 10 3 9 20
#
1 dx 20; Rœœœœ
2x
320 M3
I
'0
20
x
ˆ‰ ÉÉ
x"
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 15.2 Areas, Moments, and Centers of Mass 957
39. M (y 1) dx dy 2y 2y dy ; M y(y 1) dx dy 2 y y dy ;œœœœ œœ
'' ' ''
0y 0 0y
1y 1 1y
x
1
0
ab ab
'
#$#
57
36
M x(y 1) dx dy 0 dy 0 x 0 and y ; I y (y 1) dx dy 2y 2y dy
y x
0y 0 0y 0
1y 1 1y 1
œœœÊœœœ œ
'' ' '' '
7
10 #%$
ab
R ; I x (y 1) dx dy 2y 2y dy R ;œÊœ œ œ œ œÊœ œ
9 3
10 M 10 3 10 M 10
I36 I32
xy y
0y 0
1y 1
Éab É
xÈ È
'' '
#%$
"y
III R
oxy
œœ Ê œ œ
6
5M5
I32
!ÉoÈ
40. M 3x 1 dx dy 2y 2y dy ; M y 3x 1 dx dy 2y 2y dy ;œœœœ œœ
'' ' '' '
0y 0 0y 0
1y 1 1y 1
x
ab a b ab a b
#$ # %#
#
316
15
M x 3x 1 dx dy 0 x 0 and y ; I y 3x 1 dx dy 2y 2y dy
y x
0y 0y 0
1y 1y 1
œœÊœœœ œœ
'' '' '
ab ab a b
###&$
32 5
45 6
R ; I x 3x 1 dx dy 2 y y dy R ;Êœ œ œ œ œÊœ œ
xy y
0y 0
1y 1
Éab ˆ‰ ÉÉ
I
M3 5 3 30 M 45
5311 11
I
xÈ'' '
## & $
"y
III R
oxy o
œœ Ê œ œ
62
5M
I
5
ÉoÈ
41. dy dx 10,000 1 e 10,000 1 e
'' ' ' '
52 5 5
50 5 5
10,000e
11
dx dx dx
11
y
# #
xx
xx
œ œ ab ab
’“
10,000 1 e 2 ln 1 10,000 1 e 2 ln 1œ ab ab
‘ ‘ˆ‰ ˆ‰
22
xx
##
!&
& !
10,000 1 e 2 ln 1 10,000 1 e 2 ln 1 40,000 1 e ln 43,329œ œ ¸ab ab ab
‘ ‘ ˆ‰ˆ‰ ˆ‰
# # #
##
557
2
42. 100(y 1) dx dy 100(y 1)x dy 100(y 1) 2y 2y dy 200 y y dy
'' ' ' '
0y 0 0 0
12yy 1 1 1
2y y
y
œ œ œ cd ab ab
#$
200 (200) 50œœ œ
’“ ˆ‰
yy
24 4
"
!
"
43. M dy dx 2a 1 x dx 2a x ; M y dy dxœœœœœ
'' ' ''
10 0 10
1a1x 1 1a1x
x
ab ’“
#"
!
x4a
33
1 2x x dx a x y . The angle between theœœœÊœœœ
2a 2x x 8a 2a
35 15 M 5
M
#
#% # "
!
'0
1ab
’“ xŠ‹
Š‹
8a
15
4a
3
)
x-axis and the line segment from the fulcrum to the center of mass on the y-axis plus 45° must be no more than
90° if the center of mass is to lie on the left side of the line x 1 tan a .œÊŸ Ê Ÿ ÊŸ)11 1
454
2a 5
##
" ˆ‰
Thus, if 0 a , then the appliance will have to be tipped more than 45° to fall over.Ÿ
5
#
44. f(a) I (y a) dy dx dx (2 a) a ; thus f (a) 0 4(2 a) 4aœœ œ œ œ Ê
a00 0
42 4
'' '
#$$w##
’“
cd
(2 a)
33 3
a4
0 a (2 a) 0 4 4a 0 a 1. Since f (a) 8(2 a) 8a 16 0, a 1 gives aœÊ œÊ œÊœ œ œ œ
## w
w
minimum value of I .
a
45. M dy dx dx 2 sin x 2 0 ; M x dy dxœœœœœœ
'' ' ''
011x 0 011x
111x 1 111x
y
2
1x
È
" "
!#
cd
ˆ‰
11
dx 2 1 x 2 x and y 0 by symmetryœœœÊœœ
'0
12x 2
1x
È
#"Î# "
!
’“
ab 1
46. (a) I x dx RœœÊœœ
'L2
L2
$#"$$
$
LLL
12 12 L 23
ɆÈ
(b) I x dx RœœÊœœ
'0
L
$#"$$
$
LLL
33L
3
ɆÈ
47. (a) M dx dy 2 y y dy 2 2
" "
# #
#"
!
œœ œ œ œ œÊœ
'' '
0y 0
12yy 1
$$ $ $ $ab ’“ˆ‰
yy
23 6 3
3
$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

958 Chapter 15 Multiple Integrals
(b) average value , so the values are the sameœœœœ
''
''
0y
12yy
0y
12yy
(y 1) dx dy
dx dy
bŠ‹
Š‹
3
3
#$
48. Let (x y ) be the location of the weather station in county i for i 1 254. The average temperature
ii
ßœßáß
in Texas at time t is approximately , where T(x y ) is the temperature at time t at the
! !
ß
!
254
i1
T(x y ) A
Aii
ii i
?
ß
weather station in county i, A is the area of county i, and A is the area of Texas.?i
49. (a) x 0 M x (x y) dy dx 0œœÊ œ ß œ
M
M
y
y''
R
$
(b) I (x h) (x y) dA x (x y) dA 2hx (x y) dA h (x y) dA
Lœ ßœ ß ß ß
'' '' '' ''
RRRR
## #
$$ $$
I 0 h (x y) dA I mhœ ß œ
ycm
##
''
R
$
50. (a) I I mh I I mh 14 ; I I mh 12 14
cm L x5/7y y1114x
œ Ê œ œ œ œ œ œ
## #
œ
##
39 523 1147
5 7 35 14 14
ˆ‰ ˆ‰
(b) I I mh 14 ; I I mh 14 24
x1 x57 y2
œœ œ œ œ œ
##
##
23 2 9 47 17
35 7 5 14 14
ˆ‰ ˆ‰
y1114œÎ
51. M y dA y dA M M x ; likewise, y ;
xpp
œ'' ''
RR
"#
œÊœ œ
xx
MM MM
mm mm
xx yy
thus x y M M M M mx mx my mycij i j i jœœ œ
""
"" ## " #
"#
mm mm
xx yy
cdc dabab a ba b
mx y mx yœœ
"
"" ##
"#
mm mm
mm
cdababij ij cc
52. From Exercise 51 we have that Pappus's formula is true for n 2. Assume that Pappus's formula is true forœ
n k 1, i.e., that (k 1) . The first moment about x of k nonoverlapping plates isœ œc
!
!
k1
i1
k1
i1
m
m
ii
i
c
y dA y dA M M x ; similarly, y ;
!
k1
i1
œ
'' ''
RR
ik
ikxx
MM MM
mm mm
œÊœ œ
c
cc
k1 k
xx yy
k1 k1
kk
ik ik
!!
k1 k1
i1 i1
thus (k) x y M M M Mcij i jœœ
"
!
k
i1
i
k1 k k1 k
m ‘ˆ‰ˆ‰
xx yy
cc
m x m x m y myœ
"
!
k
i1
i
m ”•ŒŒŒ Œ
!!
k1 k1
i1 i1
œœ
ikk ik
k
cc
ij
mx y mx yœœ
"
!!
!
kk1
i1 i1
k1
i1
m m
ikk
k
m(k1)m
i i
ikk
–—
abab
!
k1
i1
œ
cc
cc
ij ij
, and by mathematical induction the statement follows.œmm m m
mm m m
cc c c á
á
k1k1 kk
k1 k
53. (a) x and ycœœÊœœ
8( 3 ) 2(3 3.5 ) 14 31
82 10 5 10
731
ij i j i j
(b) x and ycœœÊœœ
8( 3 ) 6(5 2 ) 38 36
14 14 7 7
19 18
ij i j i j
(c) x and ycœœÊœœ
2(3 3.5 ) 6(5 2 ) 36 19
8828
919
ij ij ij
(d) x and ycœœÊœœ
8( 3 ) 2(3 3.5 ) 6(5 2 ) 44 43
16 16 4 16
11 43
ij i j ij i j
54. cœœ œœ
15 7 48(12 )
15 48 4 63 4 63 4 7
15(3 28 ) 48(48 4 ) 2349 612 261 68
ˆ‰
3
4ij ij ij ij i j ij
†††
x and yÊœ œ
261 17
87#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 15.3 Double Integrals in Polar Form 959
55. Place the midpoint of the triangle's base at the origin and above the semicircle. Then the center of
mass of the triangle is 0 , and the center of mass of the disk is 0 from Exercise 25. From
ˆ‰ ˆ ‰
ßß
h4a
331
Pappus's formula, , so the centroid is on the boundarycœœ
(ah)
ah ah
ˆ‰ ˆ ‰
Š‹ Š ‹
Š‹ Š‹
h a 4a ah 2a
323 3
aa
jj j
if ah 2a 0 h 2a h a 2 . In order for the center of mass to be inside T we must have
#$ # #
œÊœ Êœ
È
ah 2a 0 or h a 2.
#$
È
56. Place the midpoint of the triangle's base at the origin and above the square. From Pappus's formula,
, so the centroid is on the boundary if 0 h 3s 0 h s 3.cœœÊœÊœ
Š‹Š‹ ˆ‰
Š‹
sh h s
32
sh
jj
#
##
ssh s
6
c
sÈ
15.3 DOUBLE INTEGRALS IN POLAR FORM
1. dy dx r dr d d
'' '' '
10 0 0 0
11x 1
œœœ))
"
##
1
2. dy dx r dr d d
'' '' '
11x 00 0
11x 21 2
œœœ))1
"
#
3. x y dx dy r dr d d
'' ' ' '
00 0 0 0
11y 21 2
ab
## $ "
œ œ œ))
48
1
4. x y dx dy r dr d d
'' '' '
11y 00 0
11y 21 2
ab
## $ "
#
œ œœ))
4
1
5. dy dx r dr d d a
'' '' '
aax 00 0
aax 2a 2
œœœ))1
a
2#
6. x y dx dy r dr d 4 d 2
'' ' ' '
00 0 0 0
24y 22 2
ab
## $
œ œ œ))1
7. x dx dy r cos dr d 72 cot csc d 36 cot 36
'' ' ' '
00 40 4
6y 26 csc 2 2
4
œœœœ
###
)) ) )) )cd
8. y dy dx r sin dr d tan sec d
'' ' ' '
00 0 0 0
2x 42 sec 4
œœœ
##
)) ) ))
84
33
9. dy dx dr d 2 1 dr d 2 (1 ln 2) d
'' '' '' '
11x 0 0
0 0 32 1 32 1 32
22r
1xy 1r 1r
"
Èœœœ)))
ˆ‰
(1 ln 2)œ 1
10. dx dy dr d 4 1 dr d 4 1 d
'' '' '' '
11y 20 20 2
1 0 32 1 32 1 32
4x y
1x y 1 r 1 r 4
4r
È
"
œœœ)))
ˆ‰ ˆ‰
1
4œ11
#
11. e dx dy re dr d (2 ln 2 1) d (2 ln 2 1)
'' '' '
00 00 0
ln 2 (ln 2) y 2 ln 2 2
r
Èxy
œœœ))
1
#
12. e dy dx re dr d 1 d
'' ' ' '
00 0 0 0
11x 21 2
xy
œœœ
""
#
r
e4e
(e 1)
))
ˆ‰ 1
13. dy dx r dr d 2 cos 2 sin cos d
'' ' ' '
00 0 0 0
21(x1) 22 cos 2
x y r(cos sin )
xy r
#
œœ
)) )))))ab
sin 1œ œ œ
‘
))
sin 2 2
2
)11
#
##
2
0
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

960 Chapter 15 Multiple Integrals
14. xy dx dy sin cos r dr d sin cos d sin
'' ' ' '
01(y1) 20 2
2 0 2 sin
2
##%()
œœœœ)) ) ))) )
32 4 4
555
cd
15. ln x y 1 dx dy 4 ln r 1 r dr d 2 (ln 4 1) d (ln 4 1)
'' ' ' '
11y 00 0
11y 21 2
ab ab
## #
œ œ œ ))1
16. dy dx 4 dr d 4 d 2 d
'' ' ' ' '
11x 00 0 0
11x 21 2 2
22r
1x y 1r 1r
ab ab
"
"
!
œœœœ)))1
‘
17. r dr d 2 (2 sin 2 ) d 2( 1)
'' '
00 0
222sin 2 2
)))1œ œ
18. A 2 r dr d 2 cos cos dœœœ
'' '
01 0
21cos 2
))))ab
#8
4
1
19. A 2 r dr d 144 cos 3 d 12œœœ
'' '
00 0
6 12 cos 3 6
)))1
#
20. A r dr d dœœœ
'' '
00 0
243 2
)))
864
927
#1
21. A r dr d 2 sin d 1œœœ
'' '
00 0
21sin 2
)))
13 cos 2 3
28
ˆ‰
##
)1
22. A 4 r dr d 2 2 cos d 4œœœ
'' '
00 0
21cos 2
)))
ˆ‰
3cos 23
2##
)1
23. M 3r sin dr d (1 cos ) sin d 4
x00 0
1cos
œœœ
'' '
#$
)) ) ))
24. I y k x y dy dx k r sin dr d d ;
xaax 00 0
aax 2a 2
œœ œœ
'' '' '
### &#
#
cdab )) )
ka 1 cos 2 ka
66
)1
I k x y dy dx k r dr d d
oaax 00 0
aax 2a 2
œœœœ
'' ' ' '
ab
## &
#))
ka ka
63
1
25. M 2 dr d 2 (6 sin 3) d 6 2 cos 6 3 2œœœœ
'' '
63 6
26 sin 2 2
6
)))))1cd
È
26. I r dr d cos 2 cos d 2 sin 2
o21 2
32 1cos 32 32
2
œœœœ
'' '
)))) )
""
###
#
ab
‘
sin 2
44
)) 1
27. M 2 r dr d (1 cos ) d ; M 2 r cos dr dœœœœ
'' ' ''
00 0 00
1cos 1cos
y
))) ))
##
#
31
2 cos 2 sin cos d x and y 0, by symmetryœœÊœœ
'0ˆ‰
4 cos 15 cos 4 5 5
324 4 4 6
))1
))) )
#
28. I r dr d (1 cos ) d
o00 0
21cos 2
œœœ
'' '
$%
"
)))
416
351
29. average r a r dr d a dœœœ
442a
a3a311
'' '
00 0
2a 2
È## $
))
30. average r dr d a dœœœ
442a
a3a311
'' '
00 0
2a 2
#$
))
31. average x y dy dx r dr d dœœœœ
""
## #
111aa33
a2a
'' ' ' '
aax 00 0
aax 2a 2
È))
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 15.3 Double Integrals in Polar Form 961
32. average (1 x) y dy dx (1 r cos ) r sin r dr dœœ
""
## ###
11
''
Rcd c d
''
00
21
)))
r 2r cos r dr d dœœœœ
"""
$#
#111
))
'' '
00 0
21 2 2
0
ab
ˆ‰ ‘
)) ))
3 2 cos 3 2 sin 3
43 4 3
33. r dr d 2 ln r dr d 2 r ln r r d 2 e 1 1 d 2 2 e
'' '' ' '
01 01 0 0
2e 2e 2 2
e
1
Š‹ cd ÈÈ
‘ˆ‰ˆ‰
ln r
r)) ) )1œœœœ
"
#
34. dr d dr d (ln r) d d 2
'' '' ' '
01 01 0 0
2e 2e 2 2
e
1
Š‹ ˆ‰ cd
ln r 2 ln r
rr
))))1œœœœ
#
35. V 2 r cos dr d 3 cos 3 cos cos dœœ
'' '
01 0
21cos 2
##$%
)) ) ) ))
2
3ab
sin 2 3 sin sinœ œ
25 sin 4 4 5
38 32 3 8
‘
"$
))1
))) 2
0
36. V 4 r 2 r dr d (2 2 cos 2 ) 2 dœœ
'' '
00 0
42 cos 2 4
È‘
#$Î# $Î#
)))
4
3
1 cos sin d cos œ œ œ
22 22 6240264
33 333 9
32 32 cos
111
)
ÈÈÈÈ
'0
44
0
ab ’“
#
))) )
37. (a) I e dx dy e r dr d lim re dr d
#
œœ œ
'' ' ' ' '
00 0 0 0 0
22b
abxy Š‹ ”•
rr
))
bÄ_
lim e 1 d d Iœ œ œ Ê œ
""
###
''
00
22
bÄ_ Š‹
b
4
))
11
È
(b) lim dt e dt 1, from part (a)
xÄ_ ''
00
x2e 2 2
t
t
ÈÈ È
È
11 1
1
œœœ
#
Š‹Š‹
38. dx dy dr d lim dr lim
'' ' ' '
00 0 0 0
2bb
0
" "
#
a b ab ab1x y 1r 1r
rr
41r
œœ œ)11
bbÄ_ Ä_ ‘
lim 1œœ
11
41b4
bÄ_ ˆ‰
"
39. Over the disk x y : dA dr d ln 1 r d
## #
""
Ÿ œ œ
3r
41xy 1r 2
''
R
'' '
00 0
232 2 32
0
))
‘
ab
ln d (ln 2) d ln 4œ œ œ
''
00
22
ˆ‰
""
#4))1
Over the disk x y 1: dA dr d lim dr d
## "
Ÿ œ œ
''
Ra1
1x y 1r 1r
rr
'' ' '
00 0 0
21 2 a
))
’“
Ä
lim ln 1 a d 2 lim ln 1 a 2 , so the integral does not exist overœœœ_
'0
2
a1 a1ÄÄ
‘ ‘
ab ab
""
##
##
)1 1††
xy1
##
Ÿ
40. The area in polar coordinates is given by A r dr d d f ( ) d r d ,œœœœ
'' ' ' '
0
ff
0
)))))
’“
r
2
""
##
##
where r f( )œ)
41. average (r cos h) r sin r dr d r 2r h cos rh dr dœœ
""
### $ # #
11aa
'' ''
00 00
2a 2a
cdab))) ))
d dœœœ
"""
###111
)))))
a43 43 43
a 2a h cos a h a 2ah cos h a 2ah sin h
''
00
22 2
0
Š‹Š‹’“
))
a2hœ
"
#
##
ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
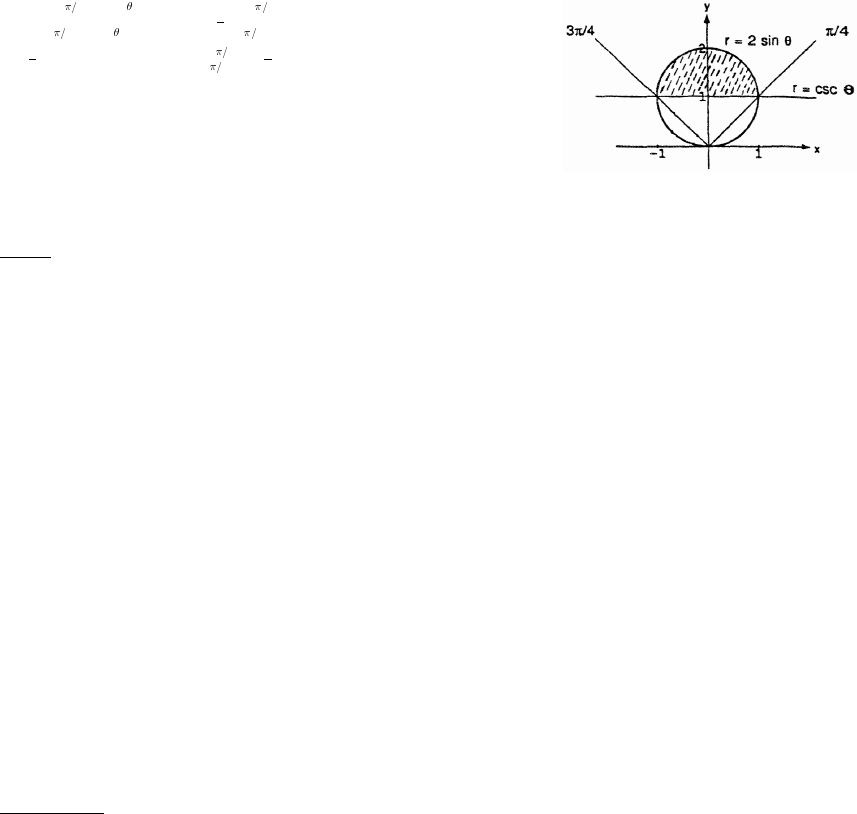
962 Chapter 15 Multiple Integrals
42. A r dr d 4 sin csc dœœ
'' '
4csc 4
3 4 2 sin 3 4
))))
"
#
##
ab
2sin 2cot œ œ
"
##
cd)))
34
4
1
44-46. Example CAS commands:
:Maple
f := (x,y) -> y/(x^2+y^2);
a,b := 0,1;
f1 := x -> x;
f2 := x -> 1;
plot3d( f(x,y), y=f1(x)..f2(x), x=a..b, axes=boxed, style=patchnogrid, shading=zhue, orientation=[0,180], title="#43(a)
(Section 15.3)" ); # (a)
q1 := eval( x=a, [x=r*cos(theta),y=r*sin(theta)] ); # (b)
q2 := eval( x=b, [x=r*cos(theta),y=r*sin(theta)] );
q3 := eval( y=f1(x), [x=r*cos(theta),y=r*sin(theta)] );
q4 := eval( y=f2(x), [x=r*cos(theta),y=r*sin(theta)] );
theta1 := solve( q3, theta );
theta2 := solve( q1, theta );
r1 := 0;
r2 := solve( q4, r );
plot3d(0,r=r1..r2, theta=theta1..theta2, axes=boxed, style=patchnogrid, shading=zhue, orientation=[-90,0],
title="#43(c) (Section 15.3)" );
fP := simplify(eval( f(x,y), [x=r*cos(theta),y=r*sin(theta)] )); # (d)
q5 := Int( Int( fP*r, r=r1..r2 ), theta=theta1..theta2 );
value( q5 );
: (functions and bounds will vary)Mathematica
For 43 and 44, begin by drawing the region of integration with the command.FilledPlot
Clear[x, y, r, t]
<<Graphics`FilledPlot`
FilledPlot[{x, 1}, {x, 0, 1}, AspectRatio 1, AxesLabel {x,y}];ÄÄ
The picture demonstrates that r goes from 0 to the line y=1 or r = 1/ Sin[t], while t goes from /4 to /2.11
f:= y / (x y )
22
topolar={x r Cos[t], y r Sin[t]};ÄÄ
fp= f/.topolar //Simplify
Integrate[r fp, {t, /4, /2}, {r, 0, 1/Sin[t]}]11
For 45 and 46, drawing the region of integration with the ImplicitPlot command.
Clear[x, y]
<<Graphics`ImplicitPlot`
ImplicitPlot[{x==y, x==2 y, y==0, y==1}, {x, 0, 2.1}, {y, 0, 1.1}];
The picture shows that as t goes from 0 to /4, r goes from 0 to the line x=2 y. will find the bound for r.1Solve
bdr=Solve[r Cos[t]==2 r Sin[t], r]//Simplify
f:=Sqrt[x y]
topolar={x r Cos[t], y r Sin[t]};ÄÄ
fp= f/.topolar //Simplify
Integrate[r fp, {t, 0, /4}, {r, 0, bdr[[1, 1, 2]]}]1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
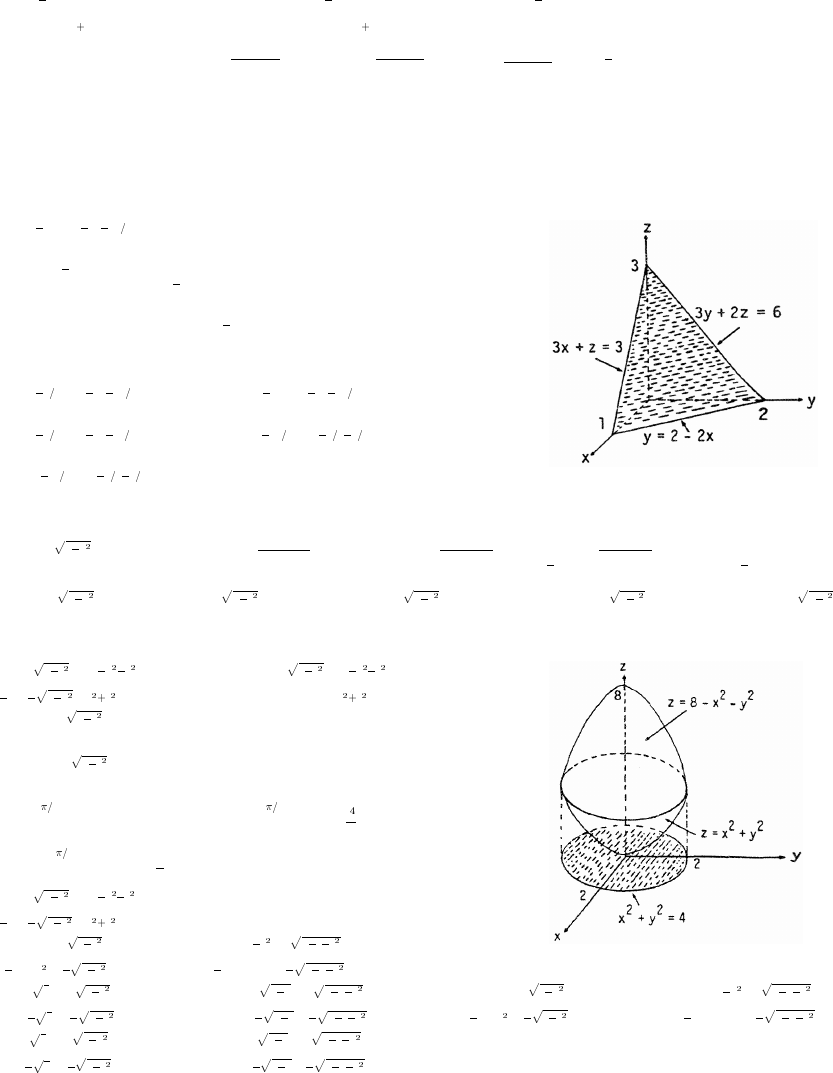
Section 15.4 Triple Integrals in Rectangular Coordinates 963
15.4 TRIPLE INTEGRALS IN RECTANGULAR COORDINATES
1. F x, y, z dy dz dx dy dz dx 1 x z dz dx
'' ' '' ' ''
00 xz 00 xz 00
11x1 11x1 11x
ab a bœœ
1x x1x dx dxœ œ œ œ
''
00
11
’“’“
abab
ab ab ab
1x 1x
22 6
1x
60
1
"
22
3
2. dz dy dx 3 dy dx 6 dx 6, dz dx dy, dx dy dz, dx dz dy,
''' '' ' ''' ''' '''
000 00 0 000 000 000
123 12 1 213 321 231
œœœ
dy dx dz, dy dz dx
''' '''
000 000
312 132
3. dz dy dx
'' '
00 0
1 22x 33x3y2
3 3x y dy dxœ
''
00
122x
ˆ‰
3
2
3(1 x) 2(1 x) 4(1 x) dxœ
'0
1‘
††
3
4#
3 (1 x) dx (1 x) 1,œœœ
'0
1#$
"
!
cd
dz dx dy, dy dz dx,
'' ' '' '
00 0 00 0
2 1y2 33x3y2 1 33x 22x2z3
dy dx dz, dx dz dy,
'' ' '' '
00 0 00 0
31z322x2z3 233y21y2z3
dx dy dz
'' '
00 0
322z31y2z3
4. dz dy dx 4 x dy dx 3 4 x dx x 4 x 4 sin 6 sin 1 3 ,
''' '' '
000 00 0
23 4x 23 2 2
0
œœœ œœ
ÈÈÈ
’“
###
##
" "
3x
1
dz dx dy, dy dz dx, dy dx dz, dx dy dz, dx dz dy
''' '' ' '' ' ''' '''
0 00 00 0 00 0 000 000
3 2 4x 2 4x 3 2 4z 3 2 3 4z 3 2 4z
5. dz dy dx 4 dz dy dx
'' ' '' '
24xxy 00 xy
2 4x 8xy 2 4x 8xy
œ
4 8 2 x y dy dxœ
''
00
24x
cdab
##
8 4 x y dy dxœ
''
00
24x
ab
##
8 4 r r dr d 8 2r dœœ
'' '
00 0
22 2
ab ’“
##
#
!
))
r
4
32 d 32 16 ,œœœ
'0
2
)1
ˆ‰
1
#
dz dx dy,
'' '
24yxy
24y8xy
dx dz dy dx dz dy,
''' '' '
2y zy 24 8zy
2 4 zy 2 8y 8zy
dx dy dz dx dy dz, dy dz dx dy dz
'' ' '' ' ''' '' '
0 z zy 4 8z 8zy 2 x zx 2 4 8zx
4 z zy 8 8z 8zy 2 4 zx 2 8x 8zx
dx,
dy dx dz dy dx dz
'' ' '' '
0zzx 48z8zx
4z zx 88z 8zx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

964 Chapter 15 Multiple Integrals
6. The projection of D onto the xy-plane has the boundary
x y 2y x (y 1) 1, which is a circle.
## # #
œ Ê œ
Therefore the two integrals are:
dz dx dy and dz dy dx
'' ' '' '
0 2yy xy 11 1x xy
2 2y y 2y 1 1 1 x 2y
7. x y z dz dy dx x y dy dx x dx 1
''' '' '
000 00 0
111 11 1
ab ˆ‰ˆ‰
### ## #
"
œ œ œ
33
2
8. dz dx dy 8 2x 4y dx dy 8x x 4xy dy
''' '' '
00x3y 00 0
23y8xy 23y 2 3y
0
œœab‘
## $ #
2
3
24y 18y 12y dy 12y y 24 30 6œ œ œœ
'0
22
0
ab
‘
$$ # %
"5
2
9. dx dy dz dy dz dy dz dz dz 1
''' '' '' ' '
111 11 11 1 1
eee ee ee e e
ee
11
"""
xyz yz yz z z
ln x ln y
œœœœœ
’“ ’“
10. dz dy dx (3 3x y) dy dx (3 3x) (3 3x) dx (1 x) dx
'' ' '' ' '
00 0 00 0 0
1 33x 33xy 1 33x 1 1
œœœ
‘
## #
"
##
9
(1 x)œ œ
33
##
$"
!
cd
11. y sin z dx dy dz y sin z dy dz sin z dz (1 cos 1)
''' '' '
000 00 0
111
œœœ 111
##
12. (x y z) dy dx dz xy y zy dx dz (2x 2z) dx dz x 2zx dz
''' '' '' '
111 11 11 1
111 11 11 1
œ œ œ
‘ cd
"##
"
"
"
"
2
4z dz 0œœ
'1
1
13. dz dy dx 9 x dy dx 9 x dx 9x 18
'' ' '' '
00 0 00 0
39x 9x 39x 3
œœœœ
Èab’“
##$
!
x
3
14. dz dx dy (2x y) dx dy x xy dy 4 y (2y) dy
'' ' '' ' '
04y0 04y 0 0
24y 2xy 24y 2 2
4y
4y
œœœcd ab
##
"Î#
4y (4)œ œ œ
’“
ab
2216
333
# $Î#
$Î# #
!
15. dz dy dx (2 x y) dy dx (2 x) (2 x) dx (2 x) dx
'' ' '' ' '
00 0 00 0 0
12x2xy 12x 1 1
œœœ
‘
## #
""
##
(2 x)œ œ œ
‘
""
$"
!
6666
87
16. x dz dy dx x 1 x y dy dx x 1 x 1 x dx x 1 x dx
'' ' '' ' '
00 3 00 0 0
11x 4xy 11x 1 1
œœœa b abab ab
’“
####
##
""
##
1xœ œ
’“
ab
""
#$"
!
12 12
17. cos (u v w) du dv dw [sin (w v ) sin (w v)] dv dw
''' ''
000 00
œ 1
[( cos (w 2 ) cos (w )) (cos (w ) cos w)] dwœ
'0
11 1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 15.4 Triple Integrals in Rectangular Coordinates 965
sin (w 2 ) sin (w ) sin w sin (w ) 0œ œcd11 1
1
!
18. ln r ln s ln t dt dr ds (ln r ln s) t ln t t dr ds (ln s) r ln r r ds s ln s s 1
''' '' '
111 11 1
eee ee e
eee
111
œœœœcd cdcd
19. e dx dt dv lim e e dt dv e dt dv e dv
'' ' '' '' '
00 00 00 0
4 ln sec v 2t 4 ln sec v 4 ln sec v 4
x 2t b 2t 2 ln sec v
œœœ
bÄ_ ab ˆ‰
""
##
dvœœœ
'0
4Š‹
‘
sec v tan v v
22 8
## #
""
Î%
!
11
20. dp dq dr dq dr 4 q dr dr
''' '' ' '
000 00 0 0
72 4q 72 7 7
q
r1 r1 3(r1) 3 r1
q4q 8
""
#$Î# #
!
œœœ
È’“
ab
8 ln 2œœ
8 ln 8
3
21. (a) dy dz dx (b) dy dx dz (c) dx dy dz
'' ' '' ' '' '
10 x 0 1z x 0 0 y
1 1x 1z 1 1z 1z 1 1z y
(d) dx dz dy (e) dz dx dy
'' ' '' '
00 y 0 y 0
11yy 1y1y
22. (a) dy dz dx (b) dy dx dz (c) dx dy dz
''' ''' ' ' '
00 1 00 1 0 1 0
11 z 11 z 1 z1
(d) dx dz dy (e) dz dx dy
''' '''
10 0 10 0
0y1 01y
23. V dz dy dx y dy dx dxœœœœ
''' '' '
010 01 0
11 y 11 1
#22
33
24. V dy dz dx (2 2z) dz dx 2z z dx 1 x dx xœœœœœœ
'' ' '' ' '
00 0 00 0 0
11x22z 11x 1 1
1x
0
cd ab
’“
##
"
!
x2
33
25. V dz dy dx (2 y) dy dx 2 4 x dxœœœ
'' ' '' '
00 0 00 0
44x2y 44x 4
’“
Ȉ‰
4x
#
(4 x) (4 x) (4) (16) 4œ œ œ œ
‘
4 4 32 20
34 3433
$Î# # $Î#
""
%
!
26. V 2 dz dy dx 2 y dy dx 1 x dxœœœœ
'' ' ' ' '
01x0 0 1x 0
10 y 1 0 1
ab
#2
3
27. V dz dy dx 3 3x y dy dx 6(1 x) 4(1 x) dxœœœ
'' ' '' '
00 0 00 0
1 22x 33x3y2 1 22x 1
ˆ‰ ‘
33
4#
##
†
3(1 x) dx (1 x) 1œœœ
'0
1#$
"
!
cd
28. V dz dy dx cos dy dx cos (1 x) dxœœœ
'' ' '' '
00 0 00 0
11xcosx2 11x 1
ˆ‰ ˆ ‰
11xx
##
cos dx x cos dx sin u cos u du cos u u sin uœ œ œ
'' '
00 0
11 2 2
0
ˆ‰ ˆ‰ ‘ cd
111
11 11
xx2x4 24
###
"
!
1œ œ
24 4
11 1
1
ˆ‰
#
29. V 8 dz dy dx 8 1 x dy dx 8 1 x dxœœœœ
'' ' '' '
00 0 00 0
11x 1x 11x 1
Èab
##16
3
30. V dz dy dx 4 x y dy dx 4 x 4 x dxœœœ
'' ' '' '
00 0 00 0
24x 4xy 24x 2
a b abab
’“
###
##
"
#
4 x dx 8 4x dxœœœ
"
##
##
#
''
00
22
ab Š‹
x 128
15
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

966 Chapter 15 Multiple Integrals
31. V dx dz dy (4 y) dz dy (4 y) dyœœœ
'' ' '' '
00 0 00 0
416y24y 416y2 4
È16 y
#
2 16 y dy y 16 y dy y 16 y 16 sin 16 yœ œ
''
00
44
ÈÈÈ
‘
’“
ab
###
""
#
" #
%
!
$Î# %
!
y
46
16 (16) 8œ œ
ˆ‰
1
#
"$Î#
63
32
1
32. V dz dy dx (3 x) dy dx 2 (3 x) 4 x dxœœœ
'' ' '' '
24x0 24x 2
24x3x 24x 2 È#
3 2 4 x dx 2 x 4 x dx 3 x 4 x 4 sin 4 xœ œ
''
22
22
ÈÈÈ
’“’“
ab
###
" #
##
# #
$Î#
x2
23
12 sin 1 12 sin ( 1) 12 12 12œœœ
" "
##
ˆ‰ ˆ ‰
11
1
33. dz dy dx 3 dy dx
'' ' ''
0 0 2xy2 0 0
22x42x2y 22x
œ
ˆ‰
3x 3y
##
3 1 (2 x) (2 x) dxœ
'0
2‘ˆ‰
x3
4#
#
66x dxœ
'0
2’“
3x 3(2 x)
4
#
6x3x (121240) 2œ œœ
’“
##
!
x2
24 4
(2 x)
34. V dx dy dz (8 2z) dy dz (8 2z)( z) dz 64 24z 2z dzœœœ)œ
''' '' ' '
0zz 0z 0 0
488z 48 4 4
ab
#
64z 12z zœ œ
‘
#$
%
!
2 320
33
35. V 2 dz dy dx 2 (x 2) dy dx (x 2) 4 x dxœœœ
'' ' '' '
20 0 20 2
24x2x2 24x2 2 È#
24 x dx x4 x dx x4 x 4 sin 4 xœ œ
''
22
22
ÈÈÈ
’“’“
ab
###
" #
#
##
# #
"$Î#
x
3
44 4œœ
ˆ‰ ˆ ‰
11
##
1
36. V 2 dz dx dy 2 x y dx dy 2 xy dyœœœ
'' ' '' '
00 0 00 0
11y xy 11y 1 1y
0
ab ’“
## #
x
3
2 1 y 1 y y dy 2 1 y y y dy 1 y dyœ œ œ
'''
000
111
abab ab ab
’“ ˆ‰
### ##% '
""""
#
33333
2
yœ œ œ
2264
37 377
y
’“
ˆ‰ˆ‰
"
!
37. average x 9 dz dy dx 2x 18 dy dx 4x 36 dxœœœœ
"""
###
8883
31
''' '' '
000 00 0
222 22 2
ab ab ab
38. average (x y z) dz dy dx (2x 2y 2) dy dx (2x 1) dx 0œœœœ
"""
222
''' '' '
000 00 0
112 11 1
39. average x y z dz dy dx x y dy dx x dx 1œœœœ
''' '' '
000 00 0
111 11 1
ab ˆ‰ˆ‰
### ## #
"
33
2
40. average xyz dz dy dx xy dy dx x dx 1œœœœ
"""
842
''' '' '
000 00 0
222 22 2
41. dx dy dz dy dx dz dx dz z dz
''' ''' '' '
002y 00 0 00 0
412 42 x2 42 4
4 cos x 4 cos x x cos x
2z 2z z
sin 4
ab ab ab
ÈÈÈ
œœœ
ˆ‰
#
"Î#
(sin 4)z 2 sin 4œœ
‘
"Î# %
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 15.4 Triple Integrals in Rectangular Coordinates 967
42. 12xz e dy dx dz 12xz e dx dy dz 6yz e dy dz 3e dz
''' ''' '' '
00x 000 00 0
111 11 y 11 1
zy zy zy zy
œœœ
’“
"
!
3ez dz3e1 3e6œœœ
'0
1zz
ab cd
"
!
43. dx dy dz dy dz dz dy
''' '' ''
0z0 0z 00
11 ln 3 11 1y
1 1 11 11e sin y 4 sin y 4 sin y
yyy
2x ab ab ab
œœ
4 y sin y dy 2 cos y 2( 1) 2(1) 4œœœœ
'0
1
11 1ab c dab
##
"
!
44. dy dz dx dz dx x dx dz (4 z) dz
'' ' '' '' '
00 0 00 00 0
24x x 24x 4 4z 4
sin 2z x sin 2z sin 2z sin 2z
4z 4z 4z 4z#
"
œœ œ
ˆ‰ ˆ‰
cos 2z sin zœ œ œ
‘ ‘
"""
%%
!##
#
!
44
sin 4
45. dz dy dx 4 x y a dy dx
'' ' ''
00 a 00
1 4ax 4x y 1 4ax
œÊ œ
44
15 15
ab
#
4 a x 4 a x dx 4 a x dx (4 a) 2x (4 a) x dxÊ œ Ê œ Ê
'''
000
111
’“
abab ab c d
## # ##%
## #
""
##
44
15 15
(4 a) x x (4 a) (4 a) (4 a) 15(4 a) 10(4 a) 5 0œ Ê œ Ê œ Ê œ
82x828
15 3 5 15 3 5 15
’“
#$ # #
"
!
"
3(4 a) 2(4 a) 1 0 [3(4 a) 1][(4 a) 1] 0 4 a or 4 a 1 a or a 3ÊœÊ œÊœ œÊœ œ
#"
33
13
46. The volume of the ellipsoid 1 is so that 8 c 3.
x z 4abc
abc 3 3
y 4(1)(2)(c)
œ œ Êœ
111
47. To minimize the integral, we want the domain to include all points where the integrand is negative and to
exclude all points where it is positive. These criteria are met by the points (x y z) such thatßß
4x 4y z 4 0 or 4x 4y z 4, which is a solid ellipsoid centered at the origin.
### ###
Ÿ Ÿ
48. To maximize the integral, we want the domain to include all points where the integrand is positive and to
exclude all points where it is negative. These criteria are met by the points (x y z) such thatßß
1 x y z 0 or x y z 1, which is a solid sphere of radius 1 centered at the origin. Ÿ
### ###
49-52. Example CAS commands:
:Maple
F := (x,y,z) -> x^2*y^2*z;
q1 := Int( Int( Int( F(x,y,z), y=-sqrt(1-x^2)..sqrt(1-x^2) ), x=-1..1 ), z=0..1 );
value( q1 );
: (functions and bounds will vary)Mathematica
Due to the nature of the bounds, cylindrical coordinates are appropriate, although Mathematica can do it as is also.
Clear[f, x, y, z];
f:= x y z
22
Integrate[f, {x, 1,1}, {y, Sqrt[1 x ], Sqrt[1 x ]}, {z, 0, 1}]
22
N[%]
topolar={x r Cos[t], y r Sin[t]};ÄÄ
fp= f/.topolar //Simplify
Integrate[r fp, {t, 0, 2 }, {r, 0, 1},{z, 0, 1}]1
N[%]
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

968 Chapter 15 Multiple Integrals
15.5 MASSES AND MOMENTS IN THREE DIMENSIONS
1. I y z dx dy dz a y z dy dz a yz dz
xc2 b2 a2 c2 b2 c2
c2 b2 a2 c2 b2 c2 b2
b2
œœœ
''' '' '
ab ab ’“
## ## #
y
3
a bz dz ab z ab b c b c ;œœœœœ
'c2
c2 c2
c2
Š‹’“Š‹
abab
bbzbccabcM
12 12 3 12 12 1 12
#####
#
R ; likewise R and R , by symmetry
xyz
œœœ
ÉÉÉ
bc ac ab
12 12 12
2. The plane z is the top of the wedge I y z dz dy dxœÊœ
42y
3
##
x3243
34 42y3
''' ab
dy dx dx 208; I x z dz dy dxœœœœ
'' ' '''
32 3 3243
34 3 34 42y3
y
’“ ab
8y 2y 8(2 y)
3 3 81 81 3
64 104
##
dy dx 12x dx 280;œœœ
'' '
32 3
34 3
’“
ˆ‰
(4 2y) x (4 2y)
81 3 3 81 3
4x 64 32
#
I x y dz dy dx x y dy dx 12 x 2 dx 360
z3243 32 3
34 42y3 34 3
œœœœ
''' '' '
ab ab ab
ˆ‰
## ## #
8
33
2y
3. I y z dz dy dx cy dy dx dx
x000 00 0
abc ab a
œœœœ
''' '' '
ab Š‹ Š‹
## #
ccbcb
3333
abc b c
ab
b c where M abc; I a c and I a b , by symmetryœ œ œ œ
MMM
333
ab ab ab
## ## ##
yz
4. (a) M dz dy dx (1 x y) dy dx x dx ;œœœœ
'' ' '' '
00 0 00 0
11x1xy 11x 1
Š‹
x
6
##
""
M x dz dy dx x(1 x y) dy dx x 2x x dx
yz 00 0 00 0
11x1xy 11x 1
œœœœ
'' ' '' '
""
#
$#
ab
24
x y z , by symmetry; I y z dz dy dxÊœœœ œ
"##
4x00 0
11x1xy
'' ' ab
y xy y dy dx (1 x) dx I I , by symmetryœ œœÊœœ
'' '
00 0
11x 1
yx
’“
##$ %
"""
(1xy)
3 6 30 30
(b) R 0.4472; the distance from the centroid to the x-axis is 0
xœœœ¸ œœ
ÉÉÉÉ
I
M55 16 16 8 4
52
x""" "
#
È È
0.3536¸
5. M 4 dz dy dx 4 4 4y dy dx 16 dx ; M 4 z dz dy dxœœœœœ
''' '' ' '''
004y 00 0 004y
114 11 1 114
xy
ab
#232
33
2 16 16y dy dx dx z , and x y 0, by symmetry;œœœÊœœœ
'' '
00 0
11 1
ab
%128 128 12
555
I 4 y z dz dy dx 4 4y 4y dy dx 4 dx ;
x004y 00 0
114 11 1
œœœœ
''' '' '
ab ’“
ˆ‰
Š‹
## # %
64 1976 7904
3 3 105 105
64y
I 4 x z dz dy dx 4 4x 4x y dy dx 4 x dx
y004y 00 0
114 11 1
œœœ
''' '' '
ab ’“
ˆ‰ ˆ ‰
Š‹
## # ## #
64 8 128
33 37
64y
; I 4 x y dz dy dx 16 x x y y y dy dxœœ œ
4832
63 z004y 00
114 11
''' ''
ab a b
## ####%
16 dxœœ
'0
1Š‹
2x 2 256
315 45
6. (a) M dz dy dx (2 x) dy dx (2 x) 4 x dx 4 ;œœœœ
'' ' '' '
24x20 24x2 2
24x22x 24x2 2 Š‹
È#1
M x dz dy dx x(2 x) dy dx x(2 x) 4 x dx 2 ;
yz 24x20 24x2 2
24x22x 24x2 2
œœœœ
'' ' '' ' Š‹
È#1
M y dz dy dx y(2 x) dy dx
xz 24x20 24x2
24x22x 24x2
œœ
'' ' ''
(2 x) dx 0 x and y 0œ œÊœœ
" "
##
'2
2’“
4x 4x
44
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 15.5 Masses and Moments in Three Dimensions 969
(b) M z dz dy dx (2 x) dy dx (2 x) 4 x dx
xy 24x20 24x2 2
24x22x 24x2 2
œœœ
'' ' '' '
""
##
##
#
Š‹
È
5 zœÊœ15
4
7. (a) M 4 dz dy dx 4 r dz dr d 4 4r r dr d 4 4 d 8 ;œœœœœ
'' ' ' '' ' ' '
00 xy 0 0r 0 0 0
2 4x 4 224 22 2
)))1ab
$
M zr dz dr d 16 r dr d d z , and x y 0,
xy 00r 00 0
224 22 2
œœœœÊœœœ
''' '' '
)))
r32648
333#
%
ab 1
by symmetry
(b) M 8 4 r dz dr d cr r dr d d c 8 c 2 2,œÊœ œ œ œ ʜʜ11 ) ) )
'' ' '' '
00 r 0 0 0
2cc 2 c 2
ab È
$#
#
cc
4
1
since c 0
8. M 8; M z dz dy dx dy dx 0; M x dz dy dxœœ œ œœ
xy yz
13 1 13 13 1
151 15 151
''' '' '''
’“
z
2
"
"
2 x dy dx 4 x dx 0; M y dz dy dx 2 y dy dx 16 dx 32œœœœ œ œœ
'' ' ''' '' '
13 1 13 1 13 1
15 1 151 15 1
xz
x 0, y 4, z 0; I y z dz dy dx 2y dy dx 100 dx ;Êœ œ œ œ œ œ œ
x13 1 13 1
151 15 1
''' '' '
ab ˆ‰
## #
2 2 400
33 3
I x z dz dy dx 2x dy dx 3x 1 dx ;
y13 1 13 1
151 15 1
œœœœ
''' '' '
ab ab
ˆ‰
## # #
24 16
33 3
I x y dz dy dx 2 x y dy dx 2 2x dx R R
zxz
13 1 13 1
151 15 1
œœœœÊœœ
''' '' '
ab ab ˆ‰ É
## ## #
98 400 50
33 3
and Ryσ2
3
9. The plane y 2z 2 is the top of the wedge I (y 6) z dz dy dxœ Êœ
L221
24 2y2
''' cd
##
dy dx; let t 2 y I 4 5t 16t dt 1386;œœÊœœ
'' '
22 2
24 4
L
’“ Š‹
(y 6) (4 y) (2 y)
24 3 24 3
13t 49
#
"#
M (3)(6)(4) 36 RœœÊœœ
"
##
LÉÉ
I
M
77
L
10. The plane y 2z 2 is the top of the wedge I (x 4) y dz dy dxœ Êœ
L221
24 2y2
''' cd
##
x 8x 16 y (4 y) dy dx 9x 72x 162 dx 696; M (3)(6)(4) 36œ œ œ œ œ
" "
# #
## #
'' '
22 2
24 2
ab ab
RÊœ œ
LÉÉ
I
M3
58
L
11. M 8; I z (y 2) dz dy dx y 4y dy dx dxœœ œ œ œ
L000 00 0
421 42 4
''' '' '
cd ˆ‰
## #
13 10 40
333
RÊœ œ
LÉÉ
I
M3
5
L
12. M 8; I (x 4) y dz dy dx (x 4) y dy dx 2(x 4) dxœ œ œ œ œ
L000 00 0
421 42 4
''' '' '
cd cd
‘
## ## #
8 160
33
RÊœ œ
LÉÉ
I
M3
20
L
13. (a) M 2x dz dy dx 4x 2x 2xy dy dx x 4x 4x dxœœœœ
'' ' '' '
00 0 00 0
22x2xy 22x 2
abab
#$#
4
3
(b) M 2xz dz dy dx x(2 x y) dy dx dx ; M by
xy xz
00 0 00 0
22x2xy 22x 2
œœœœœ
'' ' '' '
#x(2 x)
31515
88
symmetry; M 2x dz dy dx 2x (2 x y) dy dx 2x x dx
yz 00 0 00 0
22x2xy 22x 2
œœœœ
'' ' '' '
## #
#
ab16
15
x , and y zÊœ œœ
42
55
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

970 Chapter 15 Multiple Integrals
14. (a) M kxy dz dy dx k xy 4 x dy dx 4x x dxœœœœ
'' ' '' '
00 0 00 0
2x4x 2x 2
ab a b
##%
#
k 32k
15
(b) M kx y dz dy dx k x y 4 x dy dx 4x x dx
yz 00 0 00 0
2x4x 2x 2
œœœœ
'' ' '' '
###$&
#
ab a b
k8k
3
x ; M kxy dz dy dx k xy 4 x dy dx 4x x dxÊœ œ œ œ
5 k
4 3
xz 00 0 00 0
2x4x 2x 2
'' ' '' '
# # # &Î# *Î#
ab ˆ‰
y ; M kxyz dz dy dx xy 4 x dy dxœÊœ œ œ
256 2k 40 2
231 77
ÈÈ
xy 00 0 00
2x4x 2x
'' ' '' ab
##
16x 8x x dx zœœÊœ
k 256k 8
4 105 7
'0
2ab
#%'
15. (a) M (x y z 1) dz dy dx x y dy dx (x 2) dxœœœœ
''' '' '
000 00 0
111 11 1
ˆ‰
35
##
(b) M z(x y z 1) dz dy dx x y dy dx x dx
xy 000 00 0
111 11 1
œœœœ
''' '' '
""
##
ˆ‰ ˆ‰
5134
363
M M M , by symmetry x y zÊœœœ Êœœœ
xy yz xz 48
315
(c) I x y (x y z 1) dz dy dx x y x y dy dx
z000 00
111 11
œœ
''' ''
ab ab
ˆ‰
## ##
#
3
x 2x x dx I I I , by symmetryœœÊœœœ
'0
1
xyz
ˆ‰
$#
"
34 6 6
311 11
(d) R R R
xyz I
M15
11
œœœ œ
ÉÉ
z
16. The plane y 2z 2 is the top of the wedge.œ
(a) M (x 1) dz dy dx (x 1) 2 dy dx 18œœœ
''' ''
121 12
14 2y2 14 ˆ‰
y
#
(b) M x(x 1) dz dy dx x(x 1) 2 dy dx 6;
yz 121 12
14 2y2 14
œœœ
''' '' ˆ‰
y
#
M y(x 1) dz dy dx y(x 1) 2 dy dx 0;
xz 121 12
14 2y2 14
œœœ
''' '' ˆ‰
y
#
M z(x 1) dz dy dx (x 1) y dy dx 0 x , and y z 0
xy 121 12
14 2y2 14
œœœÊœœœ
''' ''
"
#Š‹
y
43
1
(c) I (x 1) y z dz dy dx (x 1) 2y dy dx 45;
x121 12
14 2y2 14
œœ"œ
''' ''
ab ’“
ˆ‰
## #
""
#
$
332
yy
I (x 1) x z dz dy dx (x 1) 2x dy dx 15;
y121 12
14 2y2 14
œœ"œ
''' ''
ab ’“
ˆ‰
## #
""
#
$
332
xy y
I (x 1) x y dz dy dx (x 1) 2 x y dy dx 42
z121 12
14 2y2 14
œœœ
''' ''
ab ab
ˆ‰
## ##
#
y
(d) R R and R
xy z
II
MM6M3
55 7
I
œœßœœß œœ
ÉÉ
ÉÉ É
É
x z
y
#
17. M (2y 5) dy dx dz z 5 z dx dz 2 z 5 z (1 z) dzœœœ
'' ' '' '
0z10 0z1 0
11z z 11z 1
ˆ‰ ˆ‰
ÈÈ
2 5z z 5z z dz 2 z z 2z z 2 3œ œ œœ
'0
1ˆ‰ ‘ˆ‰
"Î# $Î# # $Î# # &Î# $
""
##
"
!
10 9 3
333
18. M x y dz dy dx x y 16 4 x y dy dxœœ
'' ' ''
24x2xy 24x
24x162xy 24x
ÈÈ
cdab
## ## ##
4 r 4 r r dr d 4 d 4 dœœœœ
'' ' '
00 0 0
22 2 2
ab ’“
##
!
)))
4r r 64 512
3 5 15 15
1
19. (a) Let V be the volume of the ith piece, and let (x y z ) be a point in the ith piece. Then the work done?iiii
ßß
by gravity in moving the ith piece to the xy-plane is approximately W m gz (x y z 1)g V z
iiiiii ii
œœ?
the total work done is the triple integral W (x y z 1)gz dz dy dxʜ
'''
000
111
g xz yz z z dy dx g x y dy dx g xy y y dxœœœ
'' '' '
00 00 0
11 11 1
‘ˆ‰‘
"""" "" ""
## # ##
# #$# #
" "
! !
36246
55
g x dx g x g gœœœœ
'0
1ˆ‰ ˆ‰
’“
"
#
"
!
13 x 13 16 4
12 4 12 12 3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 15.5 Masses and Moments in Three Dimensions 971
(b) From Exercise 15 the center of mass is and the mass of the liquid is the work done by
ˆ‰
888 5
15 15 15
ßß Ê
#
gravity in moving the center of mass to the xy-plane is W mgd (g) g, which is the same asœœ œ
ˆ‰ ˆ‰
584
2153
the work done in part (a).
20. (a) From Exercise 19(a) we see that the work done is W g kxyz dz dy dxœ'' '
00 0
2x4x
kg xy 4 x dy dx x 4 x dx 16x 8x x dxœœœ
'' ' '
00 0 0
2x 2 2
"
#
####%'
##
ab ab a b
kg kg
44
xxxœœ
kg 256k g
4 3 5 7 105
16 8
‘
$&(
"#
!
†
(b) From Exercise 14 the center of mass is and the mass of the liquid is the work done by
Š‹
5 8 32k
4777 15
40 2
ßß Ê
È
gravity in moving the center of mass to the xy-plane is W mgd (g)œœ œ
ˆ‰ˆ‰
32k 8
15 7 105
256k g†
21. (a) x 0 x (x y z) dx dy dz 0 M 0œœÊ ßß œÊ œ
M
M
yz '''
R
$yz
(b) I h dm (x h) y dm x 2xh h y dm
Lœœ œ
''' ''' '''
DD D
kk k k a bvi ij
##
###
x y dm 2h x dm h dm I 0 h m I h mœ œœ
''' ''' '''
DDD
ab
## # # #
xcm
22. I I mh ma ma ma
Lcm
œ œ œ
####
27
55
23. (a) (x y z) I I abc I Ißß œ ß ß Ê œ Ê œ
ˆ‰ Š‹
É
abc a b
44 4
cm z abc a b
###
#
ÞÞ
zcm ab
; Rœœ œœ
abc a b abc a b abc a b
341 M12
cm Iab
ab ab ab
#ÞÞ
ÉÉ
cm
(b) I I abc 2b
Lcm ab
41241
abc a b abc a 9b abc 4a 28b
œ œ œ
ÞÞ ##
##
Œ
Ɉ ‰ ab a b a b
; Rœœœ
abc a 7b
3M3
LIa7b
ab
ÉÉ
L
24. M dz dy dx (4 y) dy dx 4y dx 12 dx 72;œ œ œœœ
''' '' ' '
3243 32 3 3
34 42y3 34 3 3
22
332
y
’“
%
#
x y z 0 from Exercise 2 I I 72 0 0 I I I 72 16œœœ Ê œ œ Ê œ
xcmL
16
9
cm cmÞÞ ÞÞ
Š‹ Š‹
ÈÉ
##
#
ÞÞ
#
208 72 1488œ œ
ˆ‰
160
9
25. M x dV x dV M M x M M ; similarly,
yz yz yz yz yz m m
BBœœÊœ
''' '''
BB
"#
ÐÑ ÐÑ ÐÑ ÐÑ
y M M and z M M x y zœ œ Êœ
ÐÑ ÐÑ ÐÑ ÐÑ xz xz m m xy xy m m cijk
MM MM MMœ
"
ÐÑ ÐÑ ÐÑ ÐÑ ÐÑ ÐÑ
mm yz yz xz xz xy xy
‘ˆ‰ˆ‰ˆ‰
ijk
mx mx my my mz mzœ
"
"" ## " # "" ##
"#
mm
cdabababijk
mx y z mx y zœœ
"
"" " ## #
"#
mm mm
mm
cdababijk ijk cc
26. (a) 12 2 4 12 2 x , y , zcijk ijkœ œ Êœ œ œ
ˆ‰ˆ ‰
313 13 13
2714714
13
""
##
13 13
2
ij k
(b) 12 12 12 12 x 1, y , zcijk ijkœ œ Êœœœ
ˆ‰ˆ ‰
311 71
2224
27
##
"ij k
1
2
(c) 2 4 12 2 12 x , y , zcijkijkœœ Êœœœ
ˆ‰ˆ‰
"" "
## ##
11 13 37 5
13 74 5
14 14 7 14
ijk
(d) 12 2 4 12 12 2 12 x , y , zcijk ijk ijkœ œ Êœœ œ
ˆ‰ˆ ‰ˆ ‰
311 25467
226 26 13 26
25 92 7
"" "
## ##
ijk
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
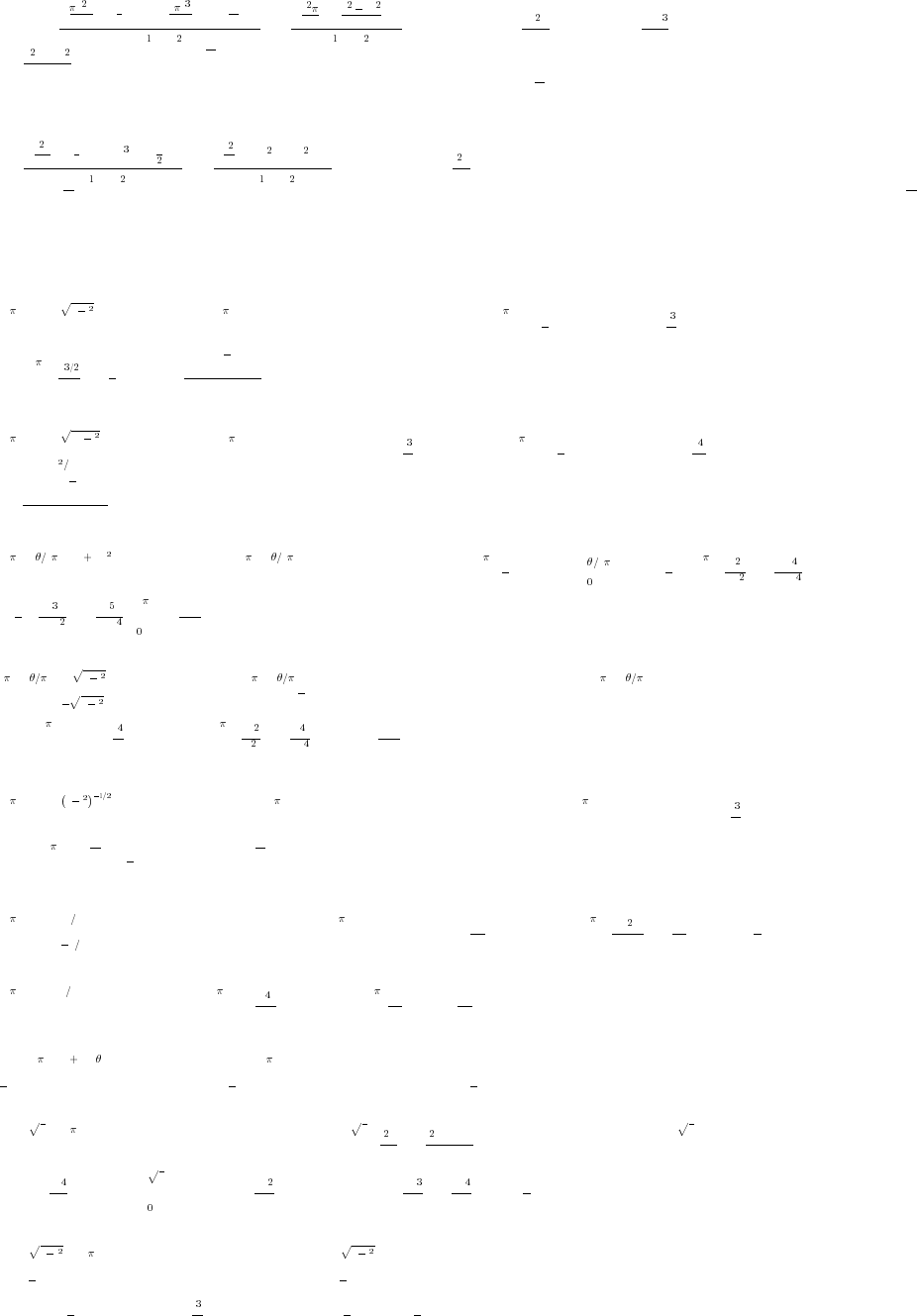
972 Chapter 15 Multiple Integrals
27. (a) , where m and m ; ifcœœœœ
Š‹
ah h 2a 3a
34 3 8 ah3a
34
Š‹Š ‹Š ‹ Š‹Š ‹
kk
"#
c
mm mm 3 3
ah 2 a
k11
0, or h a 3, then the centroid is on the common base
h3a
4
œœ
È
(b) See the solution to Exercise 55, Section 15.2, to see that h a 2.œÈ
28. , where m and m s ; if h 6s 0,cœœ œœœ
Š‹ ˆ‰ ab
sh h s
34 s
12
Š‹ Š‹
‘
kk
"#
$##
sh6s
c
c
mm mm 3
sh
k
or h 6s, then the centroid is in the base of the pyramid. The corresponding result in 15.2, Exercise 56, is h 3s.œ œ
È È
15.6 TRIPLE INTEGRALS IN CYLINDRICAL AND SPHERICAL COORDINATES
1. dz r dr d r 2 r r dr d 2 r d
''' '' '
00r 00 0
21 2r 21 2
)))œœ
’“’ “
ab ab
## #
"Î# $Î#
""
!
33
r
dœœ
'0
2Š‹
22
33 3
42
)1Š‹
È"
2. dz r dr d r 18 r dr d 18 r d
''' '' '
00r3 00 0
23 18r 23 2
)))œœ
’“’ “
ab ab
##
"Î# $Î#
"$
!
rr
3312
œ9827
2
1Š‹
È
3. dz r dr d 3r 24r dr d r 6r d d
'' ' '' ' '
00 0 00 0 0
22324r 22 2 2
2
))))œœœab ‘ Š‹
$#%
#
334
24
16
))
11
œœ
317
12 5
20
#’“
)) 1
11
2
4. z dz r dr d 9 4 r 4 r r dr d 4 4r r dr d
'' ' '' ''
00 4r 00 00
34r
)))œœ
"
#
## $
cdababab
4 2r 4 dœœ œ
''
00
’“ Š ‹
#Î
!
r2 37
415
4
)1 )) 1
11)
5. 3 dz r dr d 3 r 2 r r dr d 3 2 r d
''' '' '
00r 00 0
212r 21 2
)))œœ
’“’“
ab ab
## #
"Î# "Î# "
!
r
3
3 2 d 6 2 8œœ
'0
2Š‹Š ‹
ÈÈ
4
3)1
6. r sin z dz r dr d r sin dr d d
''' '' '
00 12 00 0
2112 21 2
ab ˆ‰Š‹
## # $# "
)) )) )œ œœ
rsin
12 4 24 3
)1
7. r dr dz d dz d d
''' '' '
000 00 0
23z3 23 2
$)))œœœ
z33
324 20 10
1
8. 4r dr d dz 2(1 cos ) d dz 6 d 12
''' '' '
10 0 10 1
12 1cos 12 1
)))1)1œ œœ
#
9. r cos z r d dr dz z r dr dz r 2 rz dr dz
'' ' '' ''
00 0 00 00
1z2 1z 1z
ab ab
’“
## # # $ #
#
!
)) ) 11œ œ
rr sin 2
24
)) 1
r z dz z dzœ œ œœ
''
00
11
z
’“Š‹’“
11111rzzz
441243
11
## $ "
!
10. (r sin 1) r d dz dr 2 r dz dr 2 r 4 r r 2r dr
'' ' '' '
0r2 0 0r2 0
24r2 24r 2
)) 1 1œ œ
’“
ab
##
"Î#
24r r2 4(4)8œ œ œ111
’“
ab ‘
""
# # $Î#
$Î# #
!
33 33
r8
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
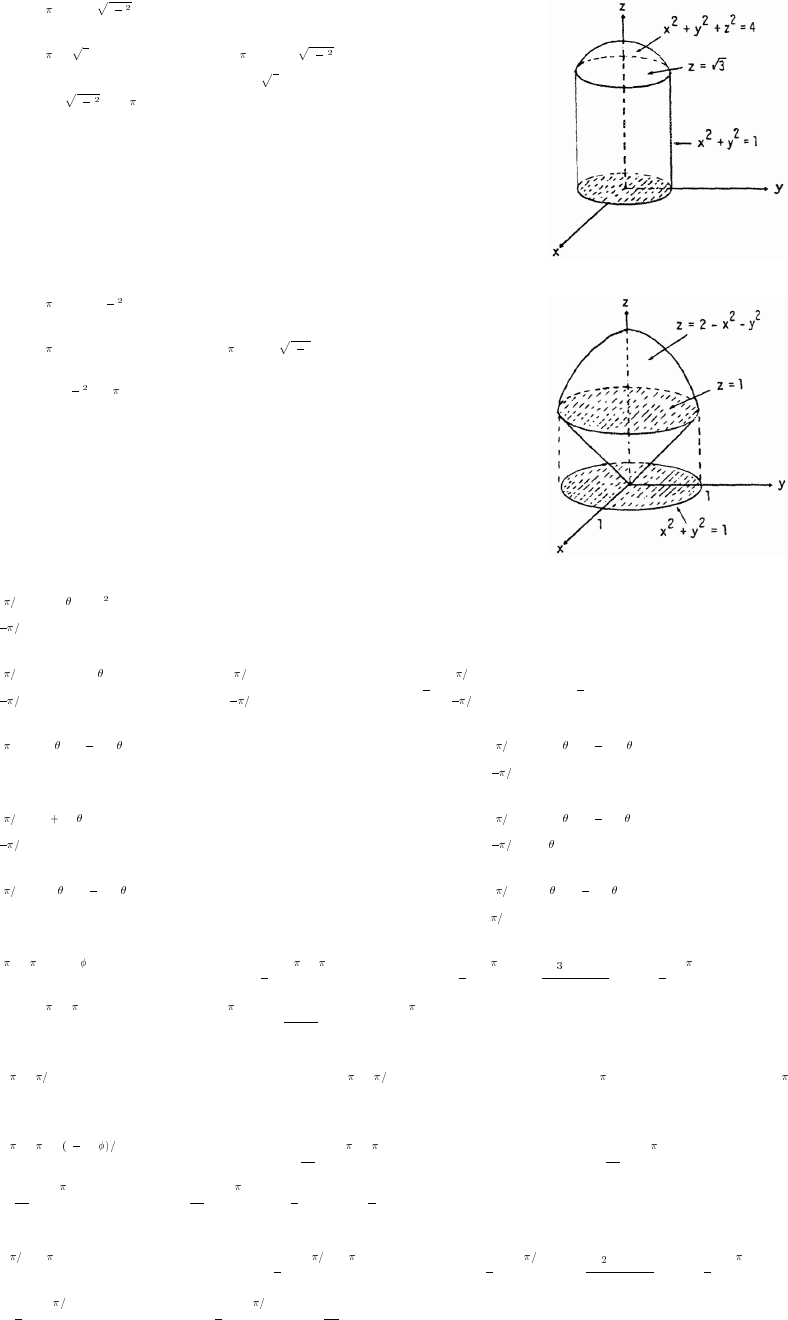
Section 15.6 Triple Integrals in Cylindrical and Spherical Coordinates 973
11. (a) dz r dr d
'''
000
21 4r
)
(b) r dr dz d r dr dz d
'' ' '''
00 0 0 30
231 224z
))
(c) r d dz dr
'' '
00 0
14r2
)
12. (a) dz r dr d
'''
00r
212r
)
(b) r dr dz d r dr dz d
''' '''
000 010
21z 22 2z
))
(c) r d dz dr
'' '
0r 0
12r 2
)
13. f(r z) dz r dr d
'''
20 0
2 cos 3r
ßß))
14. r dz dr d r cos dr d cos d
''' '' '
20 0 20 2
21r cos 21 2
$%
"
)))))œœœ
55
2
15. f(r z) dz r dr d 16. f(r z) dz r dr d
'' ' ' ' '
00 0 20 0
2 sin 4 r sin 2 3 cos 5 r cos
ßß ßß)) ))
17. f(r z) dz r dr d 18. f(r z) dz r dr d
'' ' '' '
21 0 2cos 0
21cos 4 2 2 cos 3 r sin
ßß ßß)) ))
19. f(r z) dz r dr d 20. f(r z) dz r dr d
'' ' '' '
00 0 40 0
4 sec 2 r sin 2 csc 2 r sin
ßß ßß)) ))
21. sin d d d sin d d sin d d
''' '' ' '
000 00 0 0
2 sin
3 939) 99) 99 )
#% #
!
œœ
88 3
3344
sin cos
Š‹’“
99
1
2 sin d d d dœœœœ
'' ' '
00 0 0
##
#!
99) ) ) 1) 1
‘
sin 2)1
22. ( cos ) sin d d d 4 cos sin d d 2 sin d d 2
'' ' '' ' '
00 0 00 0 0
242 24 2 2
3 93 939) 9 99) 9 ) ) 1
# # Î%
!
œœœœcd
1
23. sin d d d (1 cos ) sin d d (1 cos ) d
''' '' '
000 00 0
21cos 2 2 2
3 939) 9 99) 9 )
#$%
""
!
œ œ
24 96 cd
1
20 d d (2)œœœœ
""
%
96 96 6 3
16
''
00
22
ab))1
1
24. 5 sin d d d sin d d sin d d
''' '' ' '
000 00 0 0
32 1 32 32
3939) 99) 99)
$$ $
!
œœ
55 2
4433
sin cos
Š‹’“
99
1
cos d dœ œ œ
555
63
''
00
32 32
cd9) )
11
!#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

974 Chapter 15 Multiple Integrals
25. 3 sin d d d 8 sec sin d d 8 cos sec d
'' ' '' '
00 sec 00 0
232 23 2
3939) 999) 9 9 )
#$ #
"Î$
!
œ œab ‘
2
1
(4 2) 8 d d 5œ œ œ
''
00
22
‘ˆ‰
"
##
))1
5
26. sin cos d d d tan sec d d tan d
'' ' '' '
00 0 00 0
24sec 24 2
39939) 999) 9 )
$##
"""
Î%
!
œœ
442
‘
1
dœœ
"
84
'0
2
)1
27. sin 2 d d d d d d d d
'' ' '' '' '
04 0 0 0
20 2 20 20 2
3 99)3 3 )3 )3 3
$$
Î#
Î% ##
œ œ œ
‘
cos 2
2
91
1
331
2œœ
’“
13
8
#
!1
28. sin d d d 2 sin d d sin d
'' ' '' '
6 csc 0 6 csc 6
3 2 csc 2 3 2 csc 3 2 csc
csc
39)391 3939 39 9
##$
œœ
2
3
1cd
csc dœœ
14 28
333
11
'6
3#99 È
29. 12 sin d d d 12 8 sin d d d
''' '' '
000 00 0
14 1 4
3 99)3 3 3 99 )3
$Î%
!
œ
Œ
’“
sin cos
3
99
1
8 cos dd 8 dd 8 d 4œ œ œ œ
'' '' '
00 00 0
111
Š ‹ Š‹ Š‹’ “
cd
210105
2222
3333
1
ÈÈÈÈ
39)3 3)313313
Î%
!#"
!
œŠ‹
ÈÈ
425
2
1
30. 5 sin d d d 32 csc sin d d 32 sin csc d d
''' '' ''
62csc 62 62
222 22 22
393)9 99)9 9 9)9
%$ & $ $ #
œ œ ab a b
32 sin csc d sin d cot œœ 19991 9919
''
6 6
2 2
ab cd
’“
$# Î#
Î'
Î#
Î'
32 sin cos
33
64
99
1
1
11
1
cos 3 11 3œ œ œœ1911 1
Š‹ Š‹ Š‹
cd ÈÈ
ˆ‰
32 3 3 3 33 3
24 3 3 3 3
64 64
ÈÈÈÈ
11
1
1
1
Î#
Î' #
31. (a) x y 1 sin 1, and sin 1 csc ; thus
## ##
œÊ œ œÊœ39 39 3 9
sin d d d sin d d d
'' ' '' '
00 0 0 60
262 22csc
3939) 3939)
##
(b) sin d d d sin d d d
''' '''
01 6 000
22sin1 22 6
3993) 3993)
##
32. (a) sin d d d
'' '
00 0
2 4 sec
3939)
#
(b) sin d d d
'''
000
21 4
3993)
#
sin d d d'' '
01 cos
224
3993)
#
33. V sin d d d 8 cos sin d dœœ
'' ' ''
00 cos 00
222 22
3939) 999)
#$
"
3ab
8 cos d 8 d (2 )œ œ œ œ
"""
Î#
!
3434126
cos 31 31
''
00
22
’“
ˆ‰ˆ‰
9) )1
911
34. V sin d d d 3 cos 3 cos cos sin d dœœ
'' ' ''
00 1 00
221cos 22
3939) 9 9 999)
##$
"
3ab
cos cos cos d 1 d d (2 )œ œ œ œ œ
"""
#
#$ %
Î#
!
3432412126
31 3111111
'''
000
222
‘ˆ‰ˆ‰
99 9) ) ) 1
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 15.6 Triple Integrals in Cylindrical and Spherical Coordinates 975
35. V sin d d d (1 cos ) sin d d dœœœ
''' '' '
000 00 0
21cos 2 2
3939) 9 99) )
#$
""
"
!
334
(cos )
’“
91
(2) d (2 )œœœ
"%
12 3 3
48
'0
2
)1
1
36. V sin d d d (1 cos ) sin d d dœœœ
'' ' '' '
00 0 00 0
221cos 22 2
3939) 9 99) )
#$
""
" Î#
!
334
(cos )
’“
91
d(2)œœœ
""
12 12 6
'0
2
)1
1
37. V sin d d d cos sin d d dœœœ
'' ' '' '
040 04 0
222 cos 22 2
3939) 999) )
#$ Î#
Î%
88
334
cos
’“
91
1
d(2)œœœ
ˆ‰ˆ‰
8
316 6 3
""
'0
2
)1
1
38. V sin d d d sin d d cos d dœœœœœ
'' ' '' ' '
030 03 0 0
222 22 2 2
3939) 99) 9 ) )
#Î#
Î$
8848
3333
cd
1
1
1
39. (a) 8 sin d d d (b) 8 dz r dr d
''' '''
000 000
222 22 4r
3939) )
#
(c) 8 dz dy dx
'' '
00 0
24x 4xy
40. (a) dz r dr d (b) sin d d d
'' ' '''
00 r 000
232 9r 2 43
)3939)
#
(c) sin d d d 9 sin d d 9 1 d
''' '' '
000 00 0
243 24 2
3939) 99) )
#"
œœœ
Š‹
ÈŠ‹
È
2
92 2
4
1
41. (a) V sin d d d (b) V dz r dr dœœ
'' ' '' '
0 0 sec 00 1
232 234r
3939) )
#
(c) V dz dy dxœ'' '
33x1
33x 4xy
(d) V r 4 r r dr d d dœœœ
'' ' '
00 0 0
23 2 2
’“ Š‹
ab ”•
#"Î#
##
$
!
"
)))
ab È
4r
333
r34
dœœ
55
63
'0
2
)1
42. (a) I r dz r dr d
z000
21 1r
œ''' #)
(b) I sin sin d d d , since r x y sin cos sin sin
z00 0
221
œ œœ
'' 'abab393939) 39)39)
## # # # # ## # ## #
sinœ39
##
(c) I sin d d sin d d cos d
z00 0 0 0
22 2 2 2
œœœ
'' ' ' '
""
$Î#
!
Î#
!
5533 15
sin cos 22
99) 99 ) 9 )
Œ
’“ cd
99
11
(2 )œœ
24
15 15
11
43. V 4 dz r dr d 4 5r 4r r dr d 4 1 dœœœ
''' '' '
00r1 00 0
2144r 21 2
)))ab ˆ‰
$&
#
"5
6
4 dœœ
'0
2
)8
3
1
44. V 4 dz r dr d 4 r r r 1 r dr d 4 1 r dœœœ
''' '' '
00 1r 00 0
211r 21 2
)) )
Š‹’ “
Èab
##
#"$Î# "
!
rr
233
4 d2d2œ œ œœ
''
00
22
ˆ‰ ˆ‰
"""
##33
)) 1
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
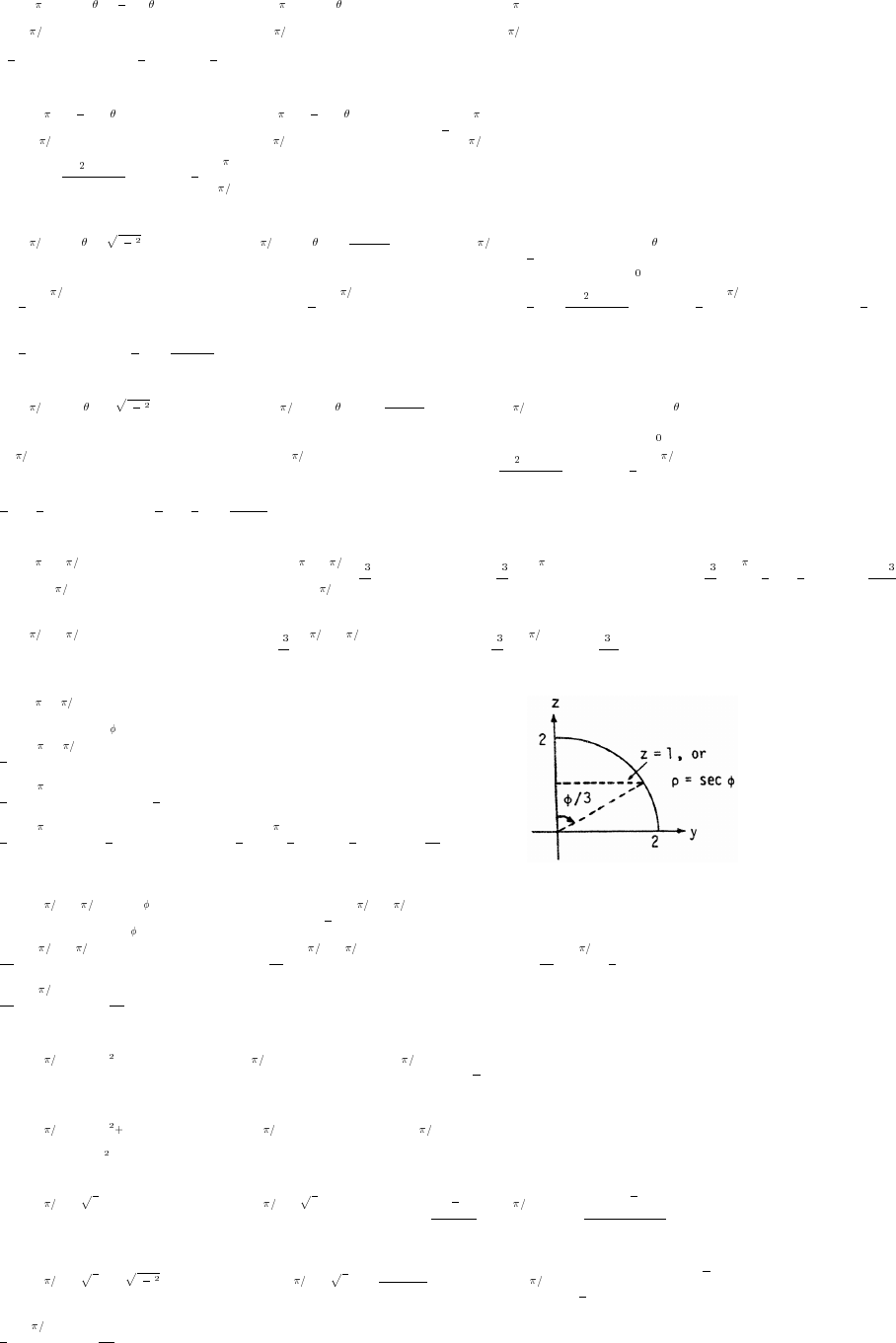
976 Chapter 15 Multiple Integrals
45. V dz r dr d r sin dr d 9 cos (sin ) dœœœ
'' ' '' '
32 0 0 32 0 32
2 3 cos r sin 2 3 cos 2
))))))
#$
ab
cos 0œœœ
‘
999
444
%#
$Î#
)1
1
46. V 2 dz r dr d 2 r dr d 27 cos dœœœ
'' ' '' '
20 0 20 2
3 cos r 3 cos
))))
#$
2
3
18 cos d 12 sin 12œ œ œ
Œ
’“ cd
cos sin 2
33
))
1
1
1
1
Î# Î#
'2)) )
47. V dz r dr d r 1 r dr d 1 r dœœœ
''' '' '
00 0 00 0
2sin 1r 2sin 2 sin
)) )
È’“
ab
#"#$Î#
3
1 sin 1 d cos 1 d cos dœ œ œ
"""
#$
$Î# Î#
!
Î#
!
333333
cos sin 2
'' '
00 0
22 2
’“ ’“
ab abŒ
‘
)) )) ))
)) )
11
sin œ œ
243
9618
cd)111
Î#
!
48. V dz r dr d 3r 1 r dr d 1 r dœœœ
'' ' '' '
00 0 00 0
2cos 1r 2cos 2 cos
3
)) ) È’“
ab
##$Î#
1 cos 1 d 1 sin d sin dœ œ œ
'' '
00 0
22 2
’“ ’“
ab ab
#$
$Î# Î#
!
)) ))) ))
sin cos 2
33
))
1
cos œ œœ
111
1
##
Î#
!2234
336
cd)
49. V sin d d d sin d d cos d dœœœœœ
'' ' '' ' '
030 03 0 0
223a 223 2 2
3939) 99) 9 ) )
##Î$
Î$
""
##
aa a 2a
33 3 3
cd ˆ‰
1
1
1
50. V sin d d d sin d d dœœœœ
''' '' '
000 00 0
62a 62 6
3939) 99) )
#aaa
3318
1
51. V sin d d dœ'' '
0 0 sec
232
3939)
#
8 sin tan sec d dœ
"#
3''
00
23
ab9999)
8 cos tan dœ
""
#Î$
!
32
'0
2‘
99)
1
4 (3) 8 d d (2 )œœ œœ
"" "
##3363
55 5
''
00
22
‘
))1
1
52. V 4 sin d d d 8 sec sec sin d dœœ
''' ''
00sec 00
242 sec 24
3939) 9 999)
#$$
4
3ab
sec sin d d tan sec d d tan dœœœ
28 28 28
3332
'' '' '
00 00 0
24 24 2
$##
"Î%
!
9 99) 9 99) 9 )
‘
1
dœœ
14 7
33
'0
2
)1
53. V 4 dz r dr d 4 r dr d dœœœœ
''' '' '
000 00 0
21r 21 2
)))
$
#
1
54. V 4 dz r dr d 4 r dr d 2 dœœœœ
''' '' '
00r 00 0
21r1 21 2
)))1
55. V 8 dz r dr d 8 r dr d 8 dœœœœ
''' '' '
010 01 0
22r 22 2
)) )
#" "
Š‹
22
33
422
ÈŠ‹
È
1
56. V 8 dz r dr d 8 r 2 r dr d 8 2 r dœœœ
'' ' '' '
01 0 01 0
22 2r 22 2
)) )
È’“
ab
#"#$Î# #
31
È
dœœ
84
33
'0
2
)1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 15.6 Triple Integrals in Cylindrical and Spherical Coordinates 977
57. V dz r dr d 4r r sin dr d 8 1 d 16œœœœ
''' '' '
000 00 0
224r sin 22 2
))))1ab ˆ‰
#sin
3
)
58. V dz r dr d 4r r (cos sin ) dr d (3 cos sin ) d 16œœœœ
''' '' '
000 00 0
2 2 4 r cos r sin 2 2 2
)))))))1cd
#8
3
59. The paraboloids intersect when 4x 4y 5 x y x y 1 and z 4
# # ## ##
œÊœ œ
V 4 dz r dr d 4 5r 5r dr d 20 d 5 dÊœ œ œ œ œ
''' '' ' '
004r 00 0 0
215r 21 2 2
))))ab ’“
$"
!#
rr 5
24
1
60. The paraboloid intersects the xy-plane when 9 x y 0 x y 9 œÊ œÊ
## ##
V 4 dz r dr d 4 9r r dr d 4 d 4 dœœœœ
''' '' ' '
010 01 0 0
23 9r 23 2 2
))))ab ’“ ˆ‰
$$
"
9r r 81 17
24 44
64 d 32œœ
'0
2
)1
61. V 8 dz r dr d 8 r 4 r dr d 8 4 r dœœœ
''' '' '
000 00 0
21 4r 21 2
)) )ab ab
’“
##
"Î# $Î#
""
!
3
38 dœ œ
8
33
4833
'0
2ˆ‰
$Î#
)1Š‹
È
62. The sphere and paraboloid intersect when x y z 2 and z x y z z 2 0
### ## #
œ œ Ê œ
(z 2)(z 1) 0 z 1 or z 2 z 1 since z 0. Thus, x y 1 and the volume isÊ œÊœ œÊœ œ
##
given by the triple integral V 4 dz r dr d 4 r 2 r r dr dœœ
''' ''
00r 00
21 2r 21
))
’“
ab
#$
"Î#
4 2 r d 4 dœ œ œ
''
00
22
’“Š‹
ab
"#$Î# "
!
34 3126
r7
22 827
))
ÈŠ‹
È
1
63. average r dz dr d 2r dr d dœœœœ
"""
##
##
111
''' '' '
00 1 00 0
211 21 2
)))
33
2
64. average r dz dr d 2r 1 r dr dœœ
"##
#
ˆ‰
4
3''' ''
00 1r 00
21 1r 21
))
3
41È
sin r r 1 r 1 2r d 0 d d (2 )œœœœœ
33333
28 8 16 32 32 1611
11
'''
000
222
’“
Èab ˆ‰ ˆ‰
""
" #
#"
!#
)))1
65. average sin d d d sin d d dœœœœ
"$
ˆ‰
4
3''' '' '
000 00 0
21 2 2
3939) 99) )
333
16 8 411
66. average cos sin d d d cos sin d d dœœœ
"$Î#
!
ˆ‰
2
3'' ' '' '
00 0 00 0
221 22 2
3 9 939) 9 99) )
33
882
sin
11
91
’“
d(2)œœœ
333
16 16 811
'0
2
)1
ˆ‰
67. M 4 dz r dr d 4 r dr d d ; M z dz r dr dœœœœœ
''' '' ' '''
000 00 0 000
21 r 21 2 2 1r
xy
))) )
#42
33
1
r dr d d z , and x y 0, by symmetryœœœÊœœœœœ
"
#
$
'' '
00 0
21 2
))
133
84M428
M
11
1
xy ˆ‰ˆ‰
68. M dz r dr d r dr d d ; M x dz r dr dœœœœœ
''' '' ' '''
000 00 0 000
22r 22 2 22 r
yz
))) )
#84
33
1
r cos dr d 4 cos d 4; M y dz r dr d r sin dr dœœœœ œ
'' ' ''' ''
00 0 000 00
2 2 2 22r 22
xz
$ $
)) )) ) ))
4 sin d 4; M z dz r dr d r dr d 2 d x ,œœœ œ œœÊœœ
'''''''
0000000
222r222
xy
)) ) ) ) 1
"
#
$M
M
3
yz
1
y , and zœœ œœ
M
MM4
33
M
xz xy
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

978 Chapter 15 Multiple Integrals
69. M ; M z sin d d d cos sin d d d 4 cos sin d dœœ œ œ
8
3
1xy 030 030 03
222 222 22
'' ' '' ' ''
3 939) 3 9 939) 9 99 )
#$
4 d 4 d d z ( ) , and x y 0,œœœœÊœœœœœ
'''
000
222
’“ ˆ‰ ˆ‰
sin
28 M88
333
M
91
11
Î#
Î$
""
##
)))11
xy
by symmetry
70. M sin d d d sin d d d ;œœœœ
'' ' '' '
00 0 00 0
24a 24 2
3939) 99) )
#
#
aa
333
22 a2 2
ÈŠ‹
È
1
M sin cos d d d sin cos d d d
xy 00 0 0 0 0
24a 2 4 2
œœœœ
'' ' ' ' '
3 9 939) 9 99) )
$aaa
4168
1
z , and x y 0, by symmetryÊœ œ œ œ œœ
M
M8 8 16
a3 3a
a2 2
22 32 2a
xy Š‹ Š ‹
–—
ˆ‰
1
1Š‹
ÈÈŠ‹
È
#
71. M dz r dr d r dr d d ; M z dz r dr dœœœœœ
''' '' ' '''
000 00 0 000
24 r 24 2 24 r
xy
))) )
$Î# 64 128
55
1
r dr d d z , and x y 0, by symmetryœœœÊœœœœ
"
#
#
'' '
00 0
24 2
))
32 64 5
33M6
M
1xy
72. M dz r dr d 2r 1 r dr d 1 r dœœœ
''' '' '
30 1r 30 3
31 1r 31 3
)) )
È’“
ab
##$Î# "
!
2
3
d ; M r cos dz dr d 2 r 1 r cos dr dœœœœ œ
2224
3339
''''''
3301r30
3311r31
yz
)))))
ˆ‰ˆ ‰ È
11 ##
#
2 sin r r 1 r 1 2r cos d cos d sin 2œœœœœ
''
3 3
3 3 3
3
’“ Š‹
Èab cdˆ‰
1
88 8 8 8 8
33
" #
"#"
!#
)) )) )
111
1
†ÈÈ
x , and y z 0, by symmetryÊœ œ œœ
M
M32
93
yz È
73. I x y dz r dr d 4 r dr d 15 d 30 ; M dz r dr d
z010 01 0 010
224 22 2 224
œœ œœœ
''' '' ' '''
ab
## $
)))1 )
4r dr d 6 d 12 RœœœÊœœ
'' '
01 0
22 2
))1
zI
M
5
ÉÉ
z
#
74. (a) I r dz dr d 2 r dr d d
z00 1 00 0
211 21 2
œœœœ
''' '' '
$$
"
#
)))1
(b) I r sin z dz r dr d 2 2r sin dr d d
x00 1 00 0
211 21 2
œœœ
''' '' '
ab ˆ‰
Š‹
## # $#
#
"
)) )) )
2r sin
33
)
œ œœ
‘
))) 111
1
483 36
sin 2 2 7
#
!#
75. We orient the cone with its vertex at the origin and axis along the z-axis . We use the the x-axisʜ91
4
which is through the vertex and parallel to the base of the cone I r sin z dz r dr dʜ
x00r
211
'''
ab
## #
))
r sin r sin dr d dœœœœœ
'' '
00 0
21 2
Š‹Š‹
‘
$# %# "#
!#
)) ) )
rr sin sin 2
3 3 20 10 40 80 10 0 5 4
))))111
1
76. I r dz dr d 2r a r dr d 2 a r d
z00 00 0
2a 2a 2
ar
ar
a
œœœ
'' '' '
'È’“Š‹
ab
$$ ##
## $Î#
!
)) )
r2a
515
2 a dœœ
'0
228a
15 15
&)1
77. I x y dz r dr d r dz dr d hr dr d
z00 r 00 00
2ah 2a h 2a
h
œœ œ
''' '' ' ''
hhr
a a
hr
a
ab 'Š‹
## $ $
)) )
hr
a
h dh d dœœœ œ
'' '
00 0
22 2
a
’“ Š‹
r r a a ha ha
4 5a 4 5a 20 10
!)))
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 15.6 Triple Integrals in Cylindrical and Spherical Coordinates 979
78. (a) M z dz r dr d r dr d d ; M z dz r dr dœœœœœ
''' '' ' '''
000 00 0 000
21r 21 2 21r
xy
))) )
""
#
&#
12 6
1
r dr d d z , and x y 0, by symmetry;œœœÊœœœ
"" "
(
#32412
'' '
00 0
21 2
))
1
I zr dz dr d r dr d d R
z z
000 00 0
21r 21 2
œœœœÊœœ
''' '' '
$(
""
##
)))
16 8 M
I3
1ÉzÈ
(b) M r dz dr d r dr d d ; M zr dz dr dœœœœœ
''' '' ' '''
000 00 0 000
21r 21 2 21r
xy
#% #
"
))) )
55
21
r dr d d z , and x y 0, by symmetry; I r dz dr dœœœÊœœœ œ
""
' %
214714
5
'' ' '''
00 0 000
21 2 21r
z
)) )
1
r dr d d RœœœÊœœ
'' '
00 0
21 2
z
'"
))
77 M7
25
I
1ÉÉ
z
79. (a) M z dz r dr d r r dr d d ; M z dz r dr dœœœœœ
''' '' ' '''
00r 00 0 00r
211 21 2 211
xy
))) )
""
#
$#
ab 84
1
r r dr d d z , and x y 0, by symmetry; I zr dz dr dœœœÊœœœ œ
""
% $
31055
4
'' ' '''
00 0 00r
21 2 211
z
ab)) )
1
r r dr d d RœœœÊœœ
"" "
#
$&
'' '
00 0
21 2
ab ÉÉ
))
24 12 M 3
zI
1z
(b) M z dz r dr d from part (a); M z dz r dr d r r dr dœœœœ
''' ''' ''
00r 00r 00
211 211 21
xy
#$&
"
)))
1
54
ab
d z , and x y 0, by symmetry; I z r dz dr d r r dr dœœÊœœœ œ œ
" "
#$ $ '
12 6 6 3
5
''''''
000r 00
2211 21
z
)))
1ab
d RœœÊœœ
"
28 14 M 14
zI5
'0
2
)1ÉÉ
z
80. (a) M sin d d d sin d d d ;œœœœ
''' '' '
000 00 0
2a 2 2
3939) 99) )
%a2a4a
555
1
I sin d d d 1 cos sin d d cos d
z000 00 0
2a 2 2
œœœ
''' '' '
3939) 999) 9 )
'$ #
!
aa
773
cos
ab ’“
91
d R aœœÊœœ
4a 8a 10
121 M21
zI
#'0
2
)1ÉÉ
z
(b) M sin d d d d d d ;œœœœ
''' '' '
000 00 0
2a 2 2
3939) 9) )
$#
#
aaa
484
(1 cos 2 )
911
I sin d d d sin d d
z000 00
2a 2
œœ
''' ''
3939) 99)
&% %
a
6
sin d d d dœœœ
a3a a
644 8416
sin cos sin 2
''' '
000 0
222
Š‹’“ ‘
!
#
#!
99 9 9
111
99 ) ) )
RœÊœ œ
aa
8M
zI
2
1ÉzÈ
81. M dz r dr d r a r dr d a r dœœœ
''' '' '
000 00 0
2a ar 2a 2
h
a)) )
hh
aa3
a
È’“
ab
## "##
$Î#
!
d ; M z dz r dr d a r r dr dœœœ œ
h a 2ha h
a3 3 2a
'''' ''
0000 00
22a ar2a
xy
)))
1
h
aab
#$
d z h, and x y 0, by symmetryœœÊœ œœœ
haa ah ah33
2a 4 4 4 2ha 8
'0
2Š‹ Š‹
ˆ‰
#)11
1
82. Let the base radius of the cone be a and the height h, and place the cone's axis of symmetry along the z-axis
with the vertex at the origin. Then M and M z dz r dr d h r r dr dœœ œ
1ah h
3 a
xy 00 r 0 0
2ah 2 a
''' ' '
h
a
))
"
#
#$
Š‹
d d d z h, andœœœ œÊœœ œ
h r r h a a ha ha ha 3 3
24a 4 8 4 M 4 ah 4
aM
###
!
'''
000
222
’“ Š‹ Š‹
ˆ‰
)))
11
1
xy
x y 0, by symmetry the centroid is one fourth of the way from the base to the vertexœœ Ê
83. M (z 1) dz r dr d h r dr d d ;œœœ œ
''' '' '
000 00 0
2ah 2a 2
)))
Š‹
hah 2h ah 2h
4
##
ab ab1
M z z dz r dr d r dr d d
xy 000 00 0
2ah 2a 2
œœœ œ
''' '' '
ab Š‹
#
#
)))
hh
3126
a 2h 3h a 2h 3h
ab ab1
z , and x y 0, by symmetry;Êœ œ œœ
’“’“
1
1
a2h 3h
6ah2h3h6
22h3h
abab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
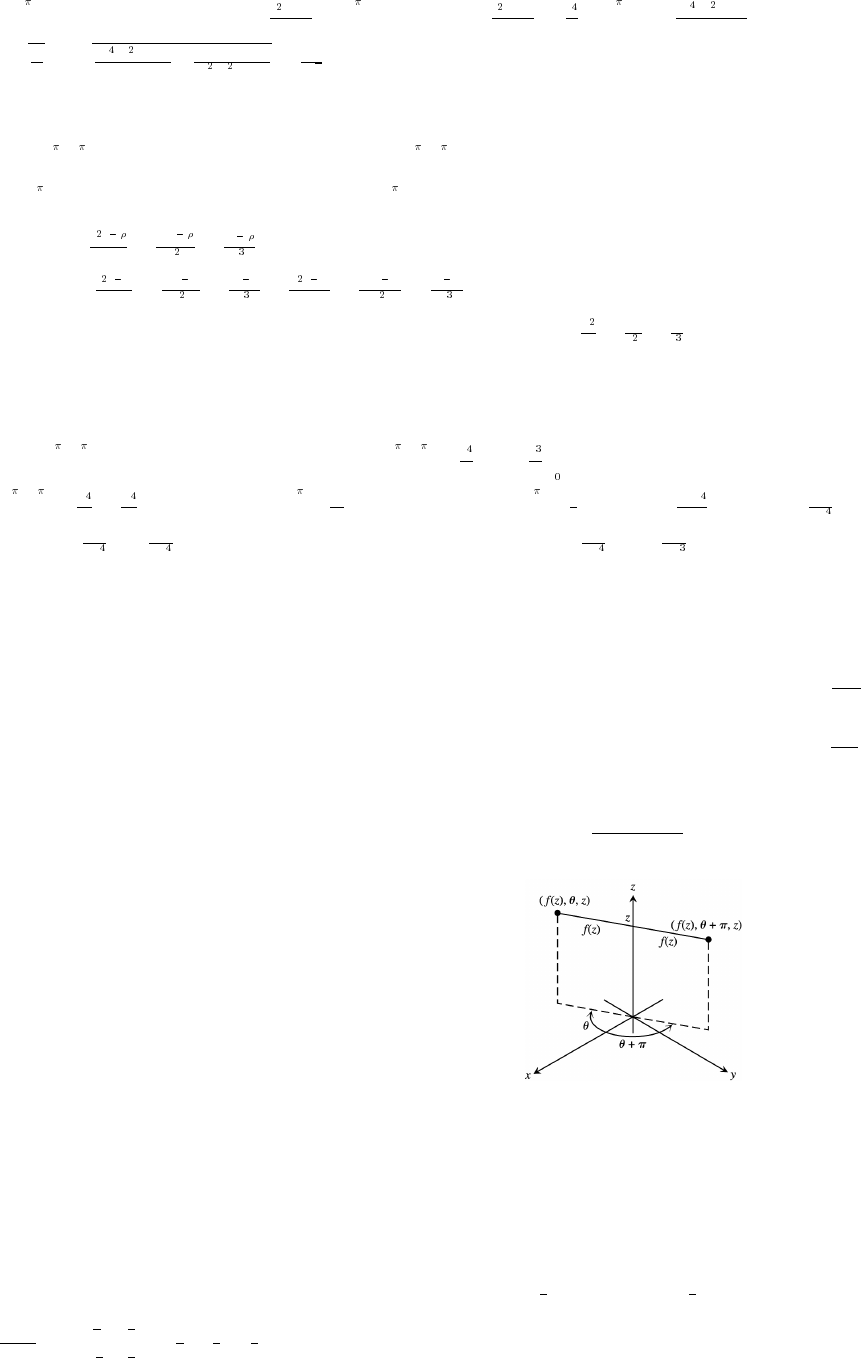
980 Chapter 15 Multiple Integrals
I (z 1)r dz dr d r dr d d ;
z000 00 0
2ah 2a 2
œœ œ œ
''' '' '
$$
##
)))
Š‹ Š‹Š‹
h2h h2h a
44
ah 2h
1ab
R
zœœ œ
ÉÉ
I
M4ah2h
ah 2h 2a
2
z1
1
abab
È
†
84. The mass of the plant's atmosphere to an altitude h above the surface of the planet is the triple integral
M(h) e sin d d d e sin d d dœœ
''' '''
00R R00
2h h2
. 3 939) . 3 99)3
!!
Ð Ñ # Ð Ñ #cR cR33
e ( cos ) dd 2 e e dd 4 e e dœœ œ
'' '' '
R0 R0 R
h2 h2 h
‘
.39)3 .3)31. 33
!!!
Ð Ñ # # #
!
cR cRc cR c333
1
4 e (by parts)œ1.!cR e2e
ccc
2e h
R
’“
33
cc
c
4e .œ1.!cR h e 2he 2e R e 2Re 2e
ccc c c c
Š‹
ch ch ch cR cR cR
The mass of the planet's atmosphere is therefore M lim M(h) 4 .œœ
hÄ_ 1.!Š‹
R2R2
ccc
85. The density distribution function is linear so it has the form ( ) k C, where is the distance from the$3 3 3œ
center of the planet. Now, (R) 0 kR C 0, and ( ) k kR. It remains to determine the constant$$33œÊ œ œ
k: M (k kR) sin d d d k kR sin d dœ œ
''' ''
000 00
2R 2 R
3 3 939) 99)
#’“
33
43
k sin d d R cos d R d kœ œœœÊœ
'' ' '
00 0 0
222
Š‹ cd
RR k k kR 3M
43 1 6 3 R
99) 9 ) )
#
%%
!
11
1
( ) R . At the center of the planet 0 (0) R .Êœ œÊœ œ$3 3 3 $
3M 3M 3M 3M
RR R R
11 1 1
ˆ‰
86. x y a sin cos sin sin a sin cos sin a sin a
222 2 22 2 2 2 22 2
22
œÊ œÊ œÊ œabababa b39) 39) 39 ) ) 39
sin a or sin a sin a or a csc , since 0 and 0.Êœ œÊœœ ŸŸ 39 39 39 3 9 91 3
87. (a) A plane perpendicular to the x-axis has the form x a in rectangular coordinates r cos a rœÊœÊœ)a
cos )
r a sec , in cylindrical coordinates.ʜ )
(b) A plane perpendicular to the y-axis has the form y b in rectangular coordinates r sin b rœÊœÊœ)b
sin )
r b csc , in cylindrical coordinates.ʜ )
88. ax by c a r cos b r sin c r a cos b sin c r .œÊ œÊ œÊœabab a b)) )) c
a cos b sin ))
89. The equation r f z implies that the point r, , zœab a b)
f z , , z will lie on the surface for all . In particularœabab))
f z , , z lies on the surface whenever f z , , z doesab abab ab)1 )
the surface is symmetric with respect to the z-axis.Ê
90. The equation f implies that the point , , f , , lies on the surface for all . In particular, if39 39) 99) )œœab a b a bab
f , , lies on the surface, then f , , lies on the surface, so the surface is symmetric wiith respect to theab a bab ab99) 99) 1
z-axis.
15.7 SUBSTITUTIONS IN MULTIPLE INTEGRALS
1. (a) x y u and 2x y v 3x u v and y x u x (u v) and y ( 2u v);œ œ Ê œ œ Ê œ œ
""
33
`ß
`ß
""
"
""
(x y)
(u v) 9 9 3
33
2
33
2
œ œœ
»»
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
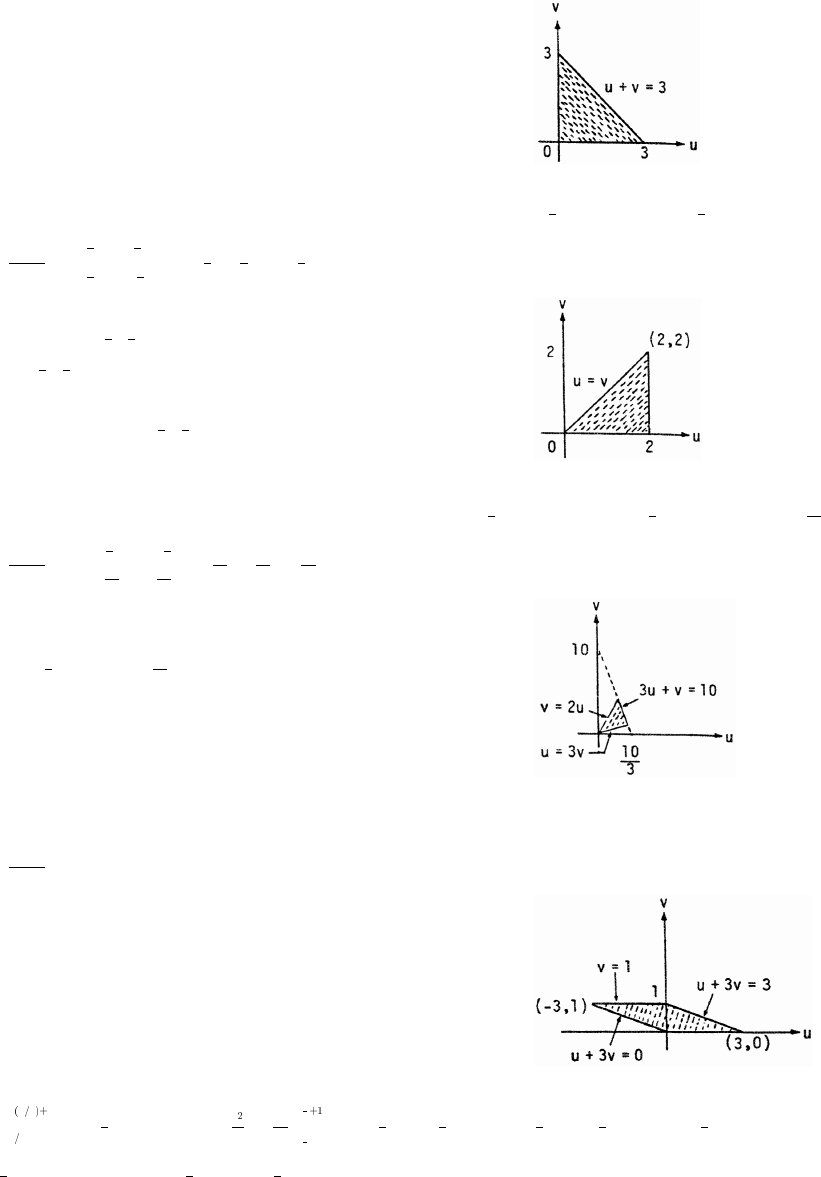
Section 15.6 Triple Integrals in Cylindrical and Spherical Coordinates 981
(b) The line segment y x from ( 0) to (1 1) is x y 0œ!ßßœ
u 0; the line segment y 2x from (0 0) toÊœ œ ß
(1 2) is 2x y 0 v 0; the line segment x 1ß œ Ê œ œ
from (1 1) to ( 2) is (x y) (2x y) 3ß"ß œ
u v 3. The transformed region is sketched at theʜ
right.
2. (a) x 2y u and x y v 3y u v and x v y y (u v) and x (u 2v);œ œÊœ œÊœ œ
""
33
`ß
`ß
"
"
""
(x y)
(u v) 9 9 3
33
2
1
33
2
œœœ
»»
(b) The triangular region in the xy-plane has vertices (0 0),ß
(2 0), and . The line segment y x from (0 0)ßß œß
ˆ‰
22
33
to is x y 0 v 0; the line segment
ˆ‰
22
33
ߜʜ
y 0 from (0 0) to ( 0) u v; the line segmentœß#ßÊœ
x 2y 2 from to (2 0) u 2. Theœ ß ßÊœ
ˆ‰
22
33
transformed region is sketched at the right.
3. (a) 3x 2y u and x 4y v 5x 2u v and y (u 3x) x (2u v) and y (3v u);œ œÊœ œ Êœ œ
"""
#510
`ß
`ß
"
(x y)
(u v) 50 50 10
21
55
13
10 10
61
œ œœ
»»
(b) The x-axis y 0 u 3v; the y-axis x 0œÊœ œ
v 2u; the line x y 1Êœ œ
(2u v) (3v u) 1ʜ
""
510
2(2u v) (3v u) 10 3u v 10. Theʜʜ
transformed region is sketched at the right.
4. (a) 2x 3y u and x y v x u 3v and y v x x u 3v and y u 2v;œœÊœœÊœœ
23 1
3
12
`ß
`ß
(x y)
(u v) œ œœ
"
ºº
(b) The line x 3 u 3v 3 or u 3v 3;œ Ê œ œ
x0 u3v0; yx v0; yx1œÊ œ œÊœ œ
v 1. The transformed region is the parallelogramʜ
sketched at the right.
5. x dx dy dy 1 1 y y dy
'' ' '
0y2 0 0
4y21 4 4
ˆ‰ ˆ‰ˆ‰ˆ‰ˆ‰
’“ ’ “
œ œ
yxyyyyy
x
2#######
"##
y
2
y
2
(y 1 y) dy dy (4) 2œœ œœ
"""
###
''
00
44
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
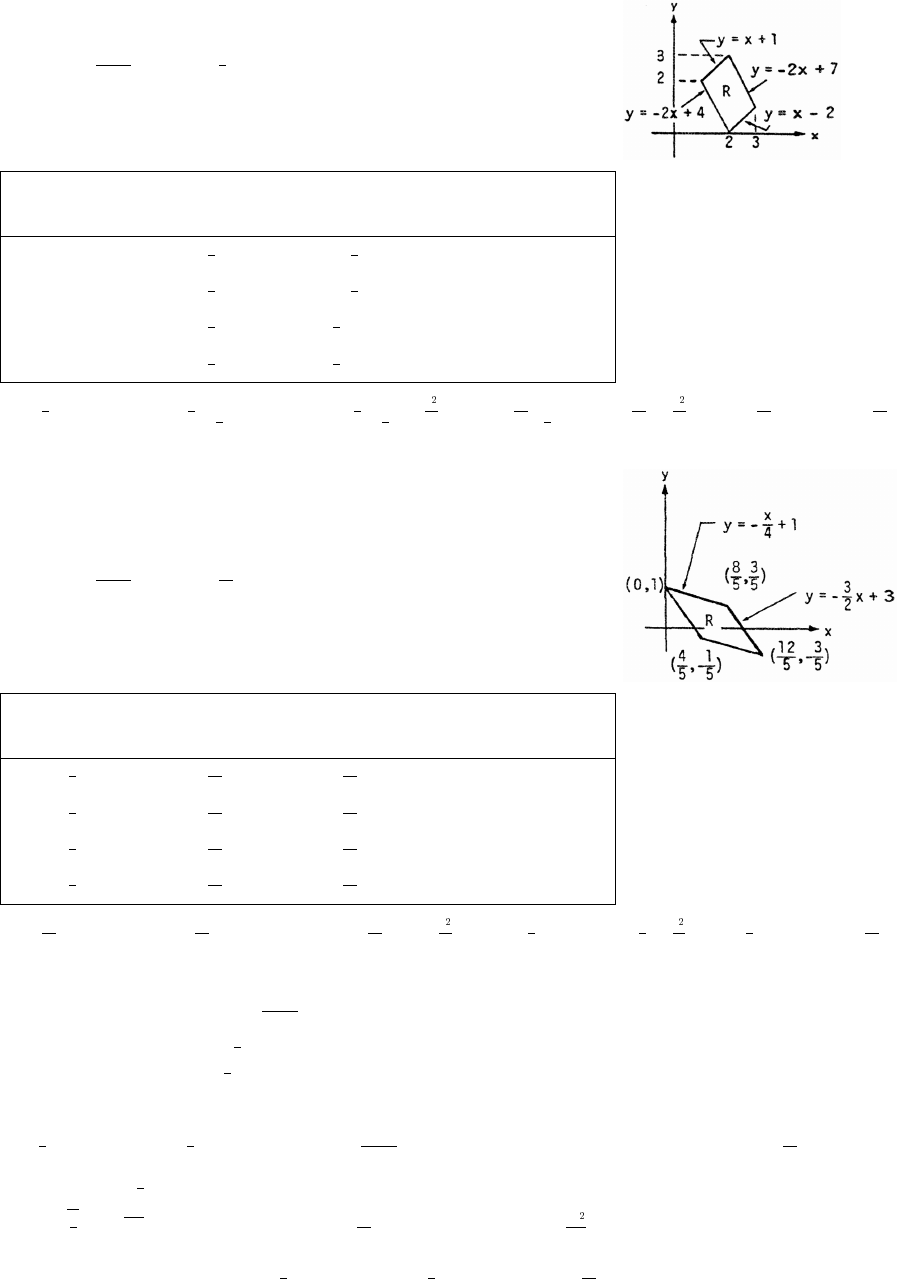
982 Chapter 15 Multiple Integrals
6. 2x xy y dx dy (x y)(2x y) dx dy
'' ''
RR
ab
##
œ
uv du dv uv du dv;œœ
'' ''
GG
¹¹
`ß
`ß
"
(x y)
(u v) 3
We find the boundaries of G from the boundaries of R,
shown in the accompanying figure:
xy-equations for Corresponding uv-equations Simplified
the boundary of R for the boundary of G uv-equations
y2x4œ "
3(2uv) (uv)4 v 4
y 2x7 (2uv) (uv)7 v7
y x 2 ( 2u v) (u v) 2 u 2
y x 1 ( 2u v) (u v) 1 u 1
œ œ
œ œ œ
œ œ œ
œ œ œ
2
3
33
2
33
1
33
1
"
"
"
uv du dv uv dv du u du u du (4 1)Êœ œ œœœœ
"" "
(#
%"
##33 32 244
v 11 11 u 11 33
''
G'' ' '
14 1 1
27 2 2
’“ ’“
ˆ‰ ˆ‰
7. 3x 14xy 8y dx dy
''
Rab
##
(3x 2y)(x 4y) dx dyœ
''
R
uv du dv uv du dv;œœ
'' ''
GG
¹¹
`ß
`ß
"
(x y)
(u v) 10
We find the boundaries of G from the boundaries of R,
shown in the accompanying figure:
xy-equations for Corresponding uv-equations Simplified
the boundary of R for the boundary of G uv-equations
yx1œ
3
#
"
10 10
3
33
10 10
41020
1
41020
1
(3v u) (2u v) 1 u 2
y x 3 (3v u) (2u v) 3 u 6
y x (3v u) (2u v) v 0
y x 1 (3v u) (2u v) 1 v 4
œ œ
œ œ œ
œ œ œ
œ œ œ
#
"
""
""
uv du dv uv dv du u du u du (18 2)Êœ œœœœœ
"" "
%'
!#
10 10 10 2 5 5 2 5 5
v4 4u4 64
''
G'' ' '
20 2 2
64 6 6
’“ ’“
ˆ‰ ˆ‰
8. 2(x y) dx dy 2v du dv 2v du dv; the region G is sketched in Exercise 4
'' '' ''
RGG
œ œ
¹¹
`ß
`ß
(x y)
(u v)
2v du dv 2v du dv 2v(3 3v 3v) dv 6v dv 3v 3Ê œ œ œ œ œ
''
G
'' ' '
03v 0 0
133v 1 1 cd
#"
!
9. x and y uv v and xy u ; J(u v) v u v u ;
vuv
vu
œ œÊœ œ œßœ œœ
u2u
vx (uv) v
y(xy)
# # " "
`ß
`ß
" #
ºº
y x uv v 1, and y 4x v 2; xy 1 u 1, and xy 9 u 3; thusœÊ œÊœ œ Êœ œÊœ œÊœ
u
v
xy dx dy (v u) dv du 2u dv du 2uv 2u ln v du
''
RŠ‹ Š‹
ÉȈ‰ cd
y
xvv
2u 2u
œ œœ
'' '' '
11 11 1
32 32 3 ##
"
2u 2u ln 2 du u u ln 2 8 (26)(ln 2) 8 (ln 2)œ œ œ œ
'1
3ab
‘
###
$
"
22 52
33 3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
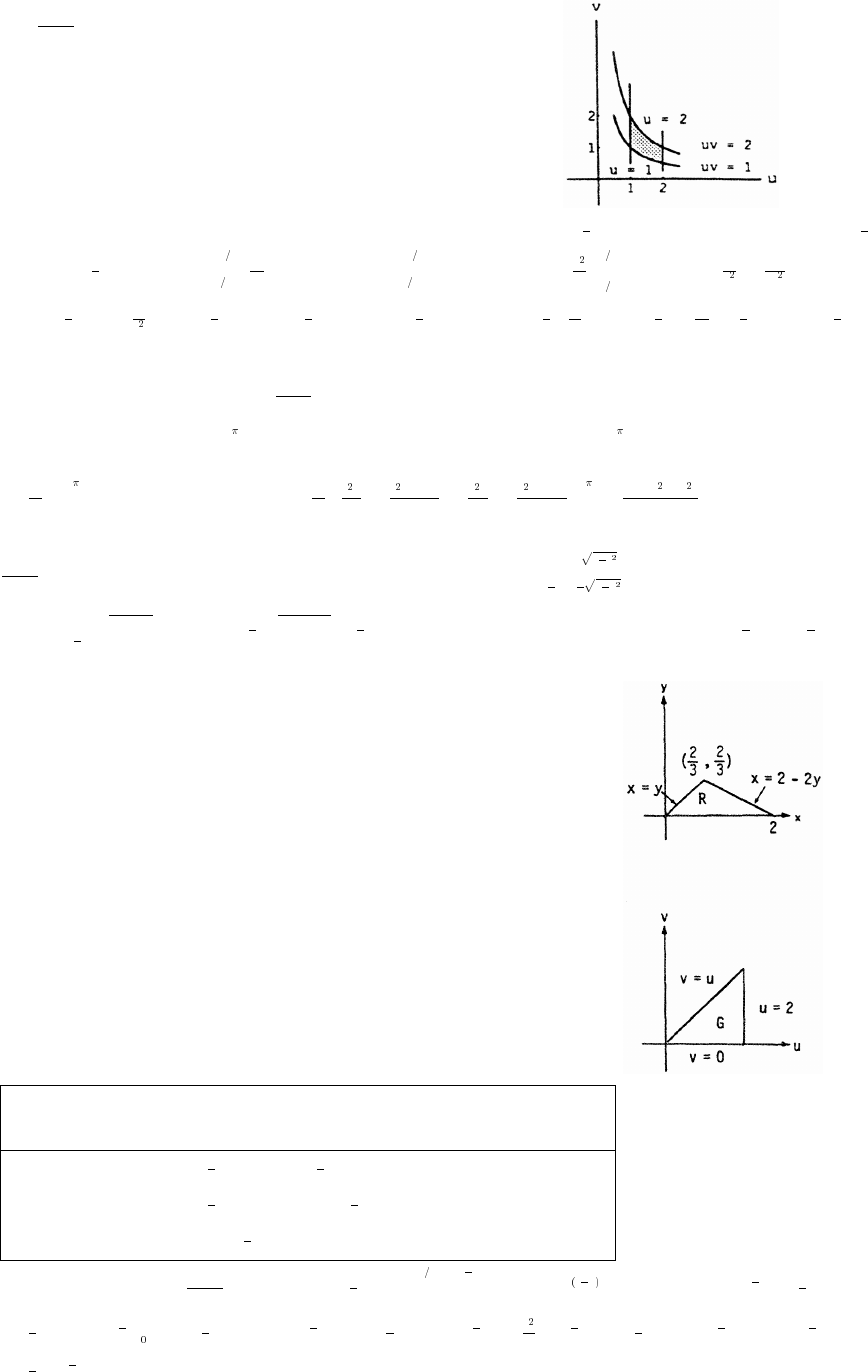
Section 15.6 Triple Integrals in Cylindrical and Spherical Coordinates 983
10. (a) J(u v) u, and
0
vu
`ß
`ß
(x y)
(u v) œßœ œ
"
ºº
the region G is sketched at the right
(b) x 1 u 1, and x 2 u 2; y 1 uv 1 v , and y 2 uv 2 v ; thus,œÊœ œÊœ œÊ œÊœ œÊ œÊœ
"
uu
2
dy dx u dv du uv dv du u du u du
'' '' '' ' '
11 11u 11u 1 1
22 22u 22u 2 2
2u
1u
y
xu 2u2u
uv v 2
œœœœ
ˆ‰ ˆ ‰
’“ "
u du ln u ln 2; dy dx dx ln x ln 2œœœ œ†œœœ
333 13dx33
uxx2x
yy
### ###
"# #
" "
'''''
11111
22222
2
1
ˆ‰ cd cd
’“
2
11. x ar cos and y ar sin J(r ) abr cos abr sin abr;
a cos ar sin
b sin br cos
œœÊœßœ œœ
)) ) ))
))
))
`ß
`ß
##
(x y)
(r ))ºº
I x y dA r a cos b sin J(r ) dr d abr a cos b sin dr d
!## ### ## $## ##
œœ ß œ
''
Rababkkab
'' ''
00 00
21 21
)))) )))
a cos b sin dœœœ
ab ab a a sin 2 b b sin 2
4424244
ab a b
'0
22
ab
’“
## ##
!
)))
))))
1ab
12. J(u v) ab; A dy dx ab du dv ab dv du
a0
0b
`ß
`ß
(x y)
(u v) œßœ œ œ œ œ
ºº '' ''
RG''
11u
11u
2ab 1 u du 2ab 1 u sin u ab sin 1 sin ( 1) ab abœœ œœœ
'1
1ÈÈ
’“
cd
‘ˆ‰
##
"
###
" " "
"
"
u
2
11 1
13. The region of integration R in the xy-plane is
sketched in the figure at the right. The
boundaries of the image G are obtained as
follows, with G sketched at the right:
xy-equations for Corresponding uv-equations Simplified
the boundary of R for the boundary of G uv-equations
xy (u2œ
"
3v) (u v) v 0
x 2 2y (u 2v) 2 (u v) u 2
y0 0 (uv) vu
œ œ
œ œ œ
œœ œ
1
3
33
2
1
3
"
Also, from Exercise 2, J(u v) (x 2y) e dx dy ue dv du
`ß
`ß
""
(x y)
(u v) 3 3
œßœÊ œ
'' ''
0y 00
23 2 2y 2 u
yx v
¸¸
u e du u1 e du uu e e 22 e 2 e 1œœ œœ
"" " "
#
#
!
33 3 3
u
''
00
22
vuuu22
u
cd ab ab c d
’“
ab
3e 1 0.4687œ¸
"
3ab
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

984 Chapter 15 Multiple Integrals
14. x u and y v 2x y (2u v) v 2u andœ œ Ê œ œ
v
#
J(u v) 1; next, u x
0
`ß
`ß #
"
#
(x y)
(u v)
v
œßœ œ œ
"
"
ºº
x and v y, so the boundaries of the region ofœ œ
y
#
integration R in the xy-plane are transformed to the
boundaries of G:
xy-equations for Corresponding uv-equations Simplified
the boundary of R for the boundary of G uv-equations
xuœœ
yv
##
v
yvv
#
###
u0
x2 u 2 u2
y0 v0 v0
y2 v2 v2
œ
œ œ œ
œœ œ
œœ œ
y (2x y) e dx dy v (2u) e du dv v e dv v e 1 dvÊœ œ œ
'' '' ' '
0y2 00 0 0
2y22 22 2 2 16
$ÐÑ $ $ $
""
#
!
2x y 4u 4u
44
’“ ab
e1 e1œ œ
"#
!
44
v
ab
’“
16 16
15. (a) x u cos v and y u sin v u cos v u sin v u
cos v u sin v
sin v u cos v
œœÊœ œœ
`ß
`ß
##
(x y)
(u v) ºº
(b) x u sin v and y u cos v u sin v u cos v u
sin v u cos v
cos v u sin v
œœÊœ œœ
`ß
`ß
##
(x y)
(u v) ºº
16. (a) x u cos v, y u sin v, z w u cos v u sin v u
cos v u sin v 0
sin v u cos v 0
00
œœœÊœ œœ
"
`ßß
`ßß
##
(xyz)
(uvw)
ââ
ââ
ââ
ââ
ââ
ââ
(b) x 2u 1, y 3v 4, z (w 4) (2)(3) 3
200
030
00
œ œ œ Ê œ œ œ
""
#`ßß #
`ßß
"
#
(xyz)
(uvw)
ââ
ââ
ââ
ââ
ââ
â∉
17.
sin cos cos cos sin sin
sin sin cos sin sin cos
cos sin 0
ââ
ââ
ââ
ââ
ââ
ââ
9)39)39)
9)3 9)39 )
939
(cos ) ( sin )
cos cos sin sin sin cos sin sin
cos sin sin cos sin sin sin cos
œ
939
39)39) 9)39)
39)39) 9)39)
ºººº
cos sin cos cos sin cos sin sin sin cos sin sinœaba baba b3 9 99 ) 99)39 9 ) 9)
########
sin cos sin sin cos sin sin œœ œ3 9 93 93 9 9 93 9
###$# ###
aba b
18. Let u g(x) J(x) g (x) f(u) du f(g(x))g (x) dx in accordance with Theorem 6 inœÊœœ Ê œ
du
dx ww
''
ag(a)
bg(b)
Section 5.6. Note that g (x) represents the Jacobian of the transformation u g(x) or x g (u).
w"
œœ
19. dx dy dz dy dz (y 1) dy dz
''' '' ''
00y2 00 00
341y2 34 34
y2
y2
ˆ‰ ‘
’“
2x y xy y
zxxz z
323 3
####
"Ð "
œ œ
dz dz 2 dz 2z 12œœœœœ
'''
000
333
’“ ’“
ˆ‰ˆ‰
(y 1) y yz
443 434 3 3
94z 4z 2z
% $
! !
"
20. J(u v w) abc; the transformation takes the ellipsoid region 1 in xyz-space
a00
0b0
00c
ßß œ œ Ÿ
ââ
ââ
ââ
ââ
ââ
ââ xz
abc
y
into the spherical region u v w 1 in uvw-space which has volume V
## #
Ÿ œ
ˆ‰
4
31
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 15 Practice Exercises 985
V dx dy dz abc du dv dwÊœ œ œ
''' '''
RG
4abc
3
1
21. J(u v w) abc; for R and G as in Exercise 19, xyz dx dy dz
a00
0b0
00c
ßß œ œ
ââ
ââ
ââ
ââ
ââ
ââ kk
'''
R
a b c uvw dw dv du 8a b c ( sin cos )( sin sin )( cos ) sin d d dœœ
'''
G
### ### #
'''
000
221
39 )39)3 93 939)ab
sin cos sin cos d d sin cos dœœœ
4abc abc abc
336
'' '
00 0
22 2
)) 999) )))
$
22. u x, v xy, and w 3z x u, y , and z w J(u v w) ;
100
0
00
œœ œÊœœ œ Êßßœ œ
v
u3 3u
v
uu
3
""
"
"
ââ
ââ
ââ
ââ
ââ
ââ
x y 3xyz dx dy dz u 3u J(u v w) du dv dw v du dv dw
''' '''
RG
ab kk
‘ ˆ‰ˆ‰ ˆ‰ˆ‰
## "
œ ßßœ
vvw vw
uu3 3 u
'''
001
322
(v vw ln 2) dv dw (1 w ln 2) dw (1 w ln 2) dw w ln 2œ œ œ œ
""
#$
!!
332332
v2 2w
'' ' '
00 0 0
32 3 3
’“ ’ “
3 ln 2 2 3 ln 2 2 ln 8œ œ œ
29
3ˆ‰
#
23. The first moment about the xy-coordinate plane for the semi-ellipsoid, 1 using the
xz
abc
y
œ
transformation in Exercise 21 is, M z dz dy dx cw J(u v w) du dv dw
xy œœßß
''' '''
DGkk
abc w du dv dw abc M of the hemisphere x y z 1, z 0 ;œ œ œ œ
## ###
'''
Gaba b†xy abc
4
1
the mass of the semi-ellipsoid is z c
2abc abc 3 3
3 4 2abc 8
11
1
Êœ œ
Š‹
ˆ‰
24. A solid of revolutions is symmetric about the axis of revolution, therefore, the height of the solid is solely a function of r.
That is, y f x f r . Using cylindrical coordinates with x r cos , y y and z r sin , we haveœœ œ œ œab ab ))
V r dyddr r dyddr ddr r fr ddr dr
r y r f r
œœ œ œ œ
'''
G
))))
)
'' ' '' '' '
a0 0 a0 a0 a
b2 b2 b2 b 2
fr
00
fr
ab ab
cd ab c d
ab
rf r dr. In the last integral, r is a dummy or stand-in variable and as such it can be replaced by any variable name.
'a
b
21ab
Choosing x instead of r we have V xf x dx, which is the same result obtained using the shell method.œ'a
b
21ab
CHAPTER 15 PRACTICE EXERCISES
1. ye dx dy e dy
'' '
10 1
10 1 y 10 y
xy xy
œcd
"
(e 1) dy 9e 9œœ
'1
10
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
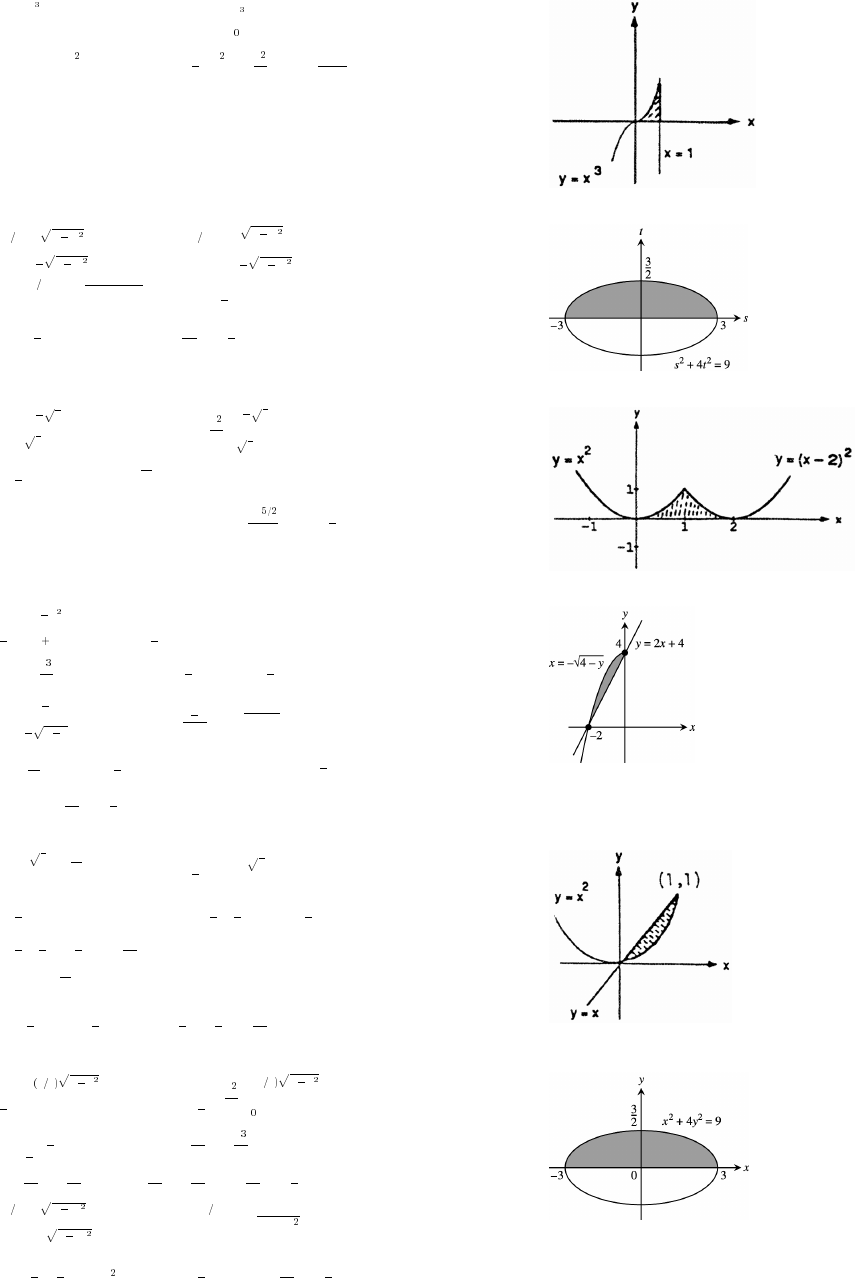
986 Chapter 15 Multiple Integrals
2. e dy dx x e dx
'' '
00 0
1x 1 x
yx yxÎÎ
œ‘
xe x dx eœœœ
'0
1Š‹’ “
xx
2
xe2
"
##
"
!
3. t ds dt ts dt
'' '
094t 0
32 9 4t 32 94t
94t
œcd
2t 9 4t dt 9 4tœœ
'0
32 È’“
ab
#"#$Î# $Î#
!
6
09œ œ œ
"$Î# $Î#
#66
27 9
ˆ‰
4. xy dx dy y dy
'' '
0y 0
12y 1 2y
y
œ’“
x
2
y44yyy dyœ
"
#'0
1ˆ‰
È
2y 2y dy yœ œœ
'0
1ˆ‰
’“
$Î# # "
!
"
4y
55
5. dy dx x 2x dx
'' '
22x4 2
04x 0
œab
#
x4œ œ œ
’“
ˆ‰
x84
333
#!
#
dx dy dy
'' '
04y 0
4y4)/2 4
y4
2
(
œˆ‰
È4y
48 4
2y 4 y
œœ†
’“
ab
y3/2
23
23/2 4
0
2
3
2
4œ œ
16 4
33
6. x dx dy x dy
'' '
0y 0
1y 1 y
y
È‘
œ2
3$Î#
y y dy y yœœ
2242
3375
'0
1ˆ‰ ‘
$Î% $Î# (Î% &Î# "
!
œœ
24 2 4
37 5 35
ˆ‰
x dy dx x x x dx x x dx
'' ' '
0x 0 0
1x 1 1
2 Èab ˆ‰
œœ
1/2 2 3/2 5/2
xxœ œœ
‘
22 224
57 5735
5/2 7/2
0
1
7. y dy dx dx
'' '
30 3
3129x 3 12 9 x
œ’“
y
2
Ð
9 x dxœœ
'3
3"#$
$
8824
9x x
ab’“
œœœ
ˆ‰ˆ ‰
27 27 27 27 27 9
824 824 6 #
y dx dy 2y dy
'' '
094y 0
32 9 4y 32
œÈ94y
9œ † œ † œ œ
""
#43 6 6
2279
3/2
0
3/2
3/2
ab
º
94y
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
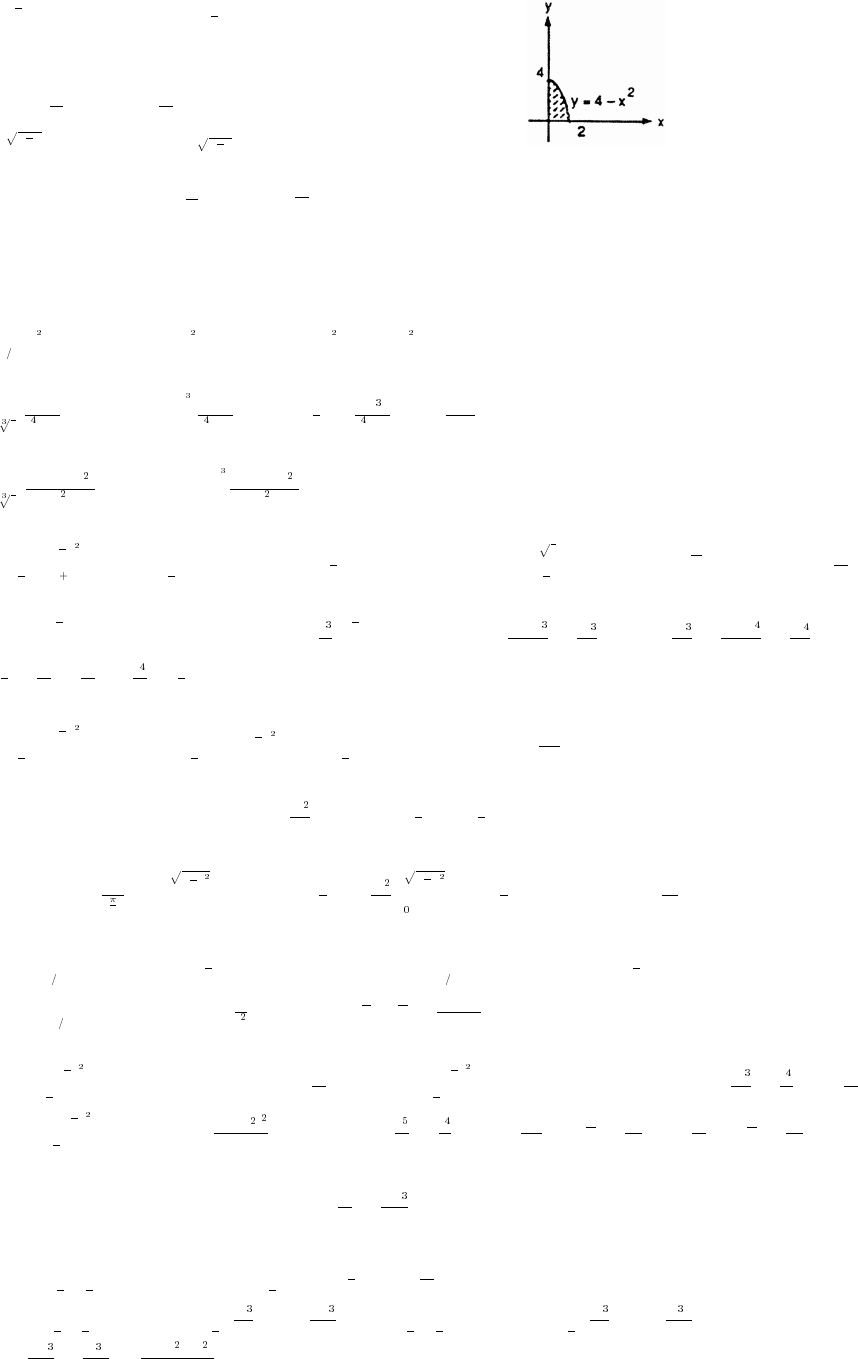
Chapter 15 Practice Exercises 987
8. 2x dy dx 2xy dx
'' '
00 0
24x 2 4x
0
22
œcd
2x 4 dx 8x 2 dxœœ
''
00
22
23
abababxx
4168œ œœ
’“
x2
2
x16
22
4
!
2x dx dy x dy
'' '
00 0
44y 4 4y
0
œcd
2
4 y dy 16 8
4y
œœ œœ
'0
4ab’“
y
20
416
2
2
9. 4 cos x dx dy 4 cos x dy dx 2x cos x dx sin x sin 4
'' '' '
02y 00 0
12 2x/2 2
ab ab ab c dab
####
#
!
œœœœ
10. e dx dy e dy dx 2xe dx e e 1
'' '' '
0y2 00 0
21 12x 1
xxxx
œœœœcd
"
!
11. dy dx dx dy dy
'' '' '
0x 00 0
82 2y 2
"""
y1 y1 y1
44
4y ln 17
œœœ
12. dx dy dy dx 2 x sin x dx cos x ( 1) ( 1) 2
'' '' '
0y 00 0
11 1x 1
2 sin x 2 sin x
xx
11 11ab ab
œœœœœ11 1ab c dab
##
"
!
13. A dy dx x 2x dx 14. A dx dy y 2 y dyœœœ œœœ
'' ' '' '
2 2x4 2 1 2y 1
04x 0 4 y 4
ab ˆ‰
È
#437
3 6
15. V x y dy dx x y dx 2x dxœ œ œœ
'' ' '
0x 0 0
12x 1 1
2x
x
ab ’“ ’ “’ “
## # #
"
!
y (2x) (2x)
3 3 3 3 12 12
7x 2x 7x
œ œ
ˆ‰
2724
31212 12 3
"
16. V x dy dx x y dx 6x x x dxœœœœ
'' ' '
3x 3 3
26x 2 2
6x
x
# # #%$
cd a b 125
4
17. average value xy dy dx dx dxœœœœ
'' ' '
00 0 0
11 1 1
’“
xy
224
x
"
!
"
18. average value xy dy dx dx x x dxœœœœ
" "
$
#
ˆ‰
4'' ' '
00 0 0
11x 1 1
1x
42
xy
2111
’“ ab
19. M dy dx 2 dx 2 ln 4; M x dy dx x 2 dx 1;œœœœ œœ
'' ' '' '
12x 1 12x 1
22 2 22 2
y
ˆ‰ ˆ‰
22
xx
M y dy dx 2 dx 1 x y
x12x 1
22 2
œœœÊœœ
'' 'ˆ‰
2
xln 4
"
#
20. M dx dy 4y y dy ; M y dx dy 4y y dy ;œ œœ œ œ œœ
'' ' '' '
02y 0 02y 0
42yy 4 42yy 4
x
ab a b
’“
##$
%
!
32 64
3343
4y y
M x dx dy 2y dy x and y 2
y02y 0
42yy 4
œœœœÊœœœœ
'' '’“’“
ab2y y yy
10 2 5 M 5 M
128 12
MM
#
#%
!
yx
21. I x y (3) dy dx 3 4x dx 104
o02x 0
24 2
œ œ œ
'' '
ab Š‹
## #
64 14x
33
22. (a) I x y dy dx 2x dx
o240
33
œœœ
'' '
21 2
21 2
ab ˆ‰
## #
(b) I y dy dx dx ; I x dx dy dy I I I
xy oxy
2b 4ab 2a 4a b
33 33
œœœœ œœÊœ
'' ' '' '
ab a ba b
ab a ba b
##
œœ
4ab 4a b
33 3
4ab b a
ab
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

988 Chapter 15 Multiple Integrals
23. M dy dx dx 3 ; I y dy dx x dx 2 Rœœœœ œœœÊœ$$$$ $
'' ' '' '
00 0 00 0
32x3 3 32x3 3
2x 8 8 3 2
3818143
x x
#$
$$
ˆ‰
Š‹ É
24. M (x 1) dy dx x x dx ; M y(x 1) dy dx xxxx dx ;œ œ œ œ œ œ
'' ' '' '
0x 0 0x 0
1x 1 1x 1
ab a b
$$&#%
"""
#4120
x3
M x(x 1) dy dx x x dx x and y ; I y (x 1) dy dx
y x
2813
15 15 30
œœœÊœœœ
'' ' ''
0x 0 0x
1x 1 1x
ab
#% #
xxxx dx R ; I x(x1) dydx xx dxœ œ Ê œ œ œ œ
"%($' # $&
3 280 M 70
17 17
xy
I
''''
00x 0
11x 1
ab ab
ÉÉ
x
RœÊ œ œ
11
12 M 3
yI
ÉÉ
y
25. M x y dy dx 2x dx 4; M y x y dy dx 0 dx 0;œ œœœ œœ
'' ' '' '
11 1 11 1
11 1 11 1
ˆ‰ˆ‰ ˆ‰
## # ##
" "
33 3
4x
M x x y dy dx 2x x dx 0
y33
4
œœœ
'' '
11 1
11 1
ˆ‰ˆ‰
## $
"
26. Place the ABC with its vertices at A(0 0), B(b 0) and C(a h). The line through the points A and C is?ßß ß
y x; the line through the points C and B is y (x b). Thus, M dx dyœœœ
hh
aab''
0ayh
habyhb
$
b 1 dy ; I y dx dy b y dy ; Rœœœ œ œœœ$$$
''''
00ayh0
hhabyhbh
x
ˆ‰ Š‹ É
y y
hh1 M
bh bh h
xI
6
$ $
# #
## xÈ
27. dy dx dr d d d
'' '' ' '
11x 00 0 0
11x 21 2 2
22r
1x y 1r
1r
ab ab
#
""
"
!
œœœœ)))1
‘
28. ln x y 1 dx dy r ln r 1 dr d ln u du d u ln u u d
'' '' '' '
11y 00 01 0
11y 21 22 2
ab ab cd
## # ""
##
#
"
œ œ œ )) )
(2 ln 2 1) d [ln (4) 1]œœ
"
#'0
2
)1
29. M r dr d d 3 ; M r cos dr d 9 cos d 9 3 x ,œœœœ œ œÊœ
'' ' '' '
30 3 30 3
33 3 33 3
y
))1 )) ))
933
#
#ÈÈ
1
and y 0 by symmetryœ
30. M r dr d 4 d 2 ; M r cos dr d cos d x , andœœœœ œ œÊœ
'' ' '' '
01 0 01 0
23 2 23 2
y
))1 )) ))
#26 26 13
3331
y by symmetryœ13
31
31. (a) M 2 r dr d œ''
01
21cos
)
2 cos d ;œœ
'0
2ˆ‰
))
1cos 2 8
4
#
)1
M (r cos ) r dr d
y21
21cos
œ''
))
cos cos dœ
'2
2Š‹
#$
)) )
cos
3
)
x , andœÊœ
32 15 15 32
24 6 48
11
1
y 0 by symmetryœ
(b)
32. (a) M r dr d d a ; M (r cos ) r dr d dœœœœ œœ
'' ' '' '
00
aa
y
))! )) )
a a cos 2a sin
33
#
#)!
x , and y 0 by symmetry; lim x lim 0Êœ œ œ œ
2a sin 2a sin
33
!!
!!
!1 !1ÄÄ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 15 Practice Exercises 989
(b) x and y 0œœ
2a
51
33. x y x y 0 r r cos 2 0 r cos 2 so the integral is dr dabab
## ## %# #
#
œÊ œÊœ)) )
''
40
4cos 2 r
1rab
1 d 1 dœ œ
'''
444
444
cos 2
’“ ˆ‰ ˆ‰
""""
##2 1 r 1 cos 2 cosab
È d )œ))
))
1 dœœœ
""
###
'4
44
4
Š‹‘
sec tan 2
24
))1
))
34. (a) dx dy dr d d
''
R
""
!
ab ab ab
1x y 1r
r
21 r
œœ
'' '
00 0
3 sec 3 sec
))
’“
d d ;
utan
du sec d
œ œ Ä
œ
œ
'' '
00 0
33 3
’“ ”•
"" " "
## # #
#
ab1sec 1sec 2u
sec du
))
)
))
)
))
tan tan œœ
""
##
" "
$
!
’“ É
ÈÈ
ÈÈ
22
u3
2
4
(b) dx dy dr d lim d
''
Rb
" "
ab ab ab
1x y 1r
r
21 r 0
b
œœ
'' '
00 0
22
))
Ä_ ’“
lim d dœœœ
''
00
22
bÄ_ ’“
"" "
## #ab1b 4
))
1
35. cos (x y z) dx dy dz [sin (z y ) sin (z y)] dy dz
''' ''
000 00
œ 1
[ cos (z 2 ) cos (z ) cos z cos (z )] dz 0œ œ
'011 1
36. e dz dy dx e dy dx e dx 1
''' '' '
ln 6 0 ln 4 ln 6 0 ln 6
ln 7 ln 2 ln 5 ln 7 ln 2 ln 7
ÐÑ ÐÑxyz xy x
œœœ
37. (2x y z) dz dy dx dy dx dx
'' ' '' '
00 0 00 0
1x xy 1x 1
œ œ œ
Š‹ Š‹
3x 3x x 8
3y
35
## ##
38. dy dz dx dz dx ln x dx x ln x x 1
''' '' '
110 11 1
exz ex e e
1
2y
zz
œœœœ
"cd
39. V 2 dz dx dy 2 2x dx dy 2 cos y dy 2œœœœœ
'' ' '' '
0cos y0 0cos y 0
20 2x 20 2 2
#
#
’“
ysin 2y
24
1
40. V 4 dz dy dx 4 4 x dy dx 4 4 x dxœœœ
'' ' '' '
00 0 00 0
24x4x 24x 2
ab ab
##
$Î#
x 4 x 6x 4 x 24 sin 24 sin 1 12œ œ œ
’“
ab È
#""
$Î# ##
!
x
21
41. average 30xz x y dz dy dx 15x x y dy dx 15x x y dx dyœœœ
"""
###
333
''' '' ''
000 00 00
131 13 31
ÈÈÈ
5 x y dy 5(1 y) 5y dy 2(1 y) 2y 2(4) 2(3) 2œœœœ
"" ""
# $Î# $Î# &Î# &Î# &Î# &Î#
$Î# "
!
$
!
33 33
''
00
33
’“
ab ‘‘ ‘
231 3œ
"&Î#
3‘ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

990 Chapter 15 Multiple Integrals
42. average sin d d d sin d d dœœœœ
33a3a3a
4a 16 8 4111
''' '' '
000 00 0
2a 2 2
3939) 99) )
$
43. (a) 3 dz dx dy
'' '
22yxy
22y 4xy
(b) 3 sin d d d
'' '
00 0
242
3939)
#
(c) 3 dz r dr d 3 r 4 r r dr d 3 4 r d
'' ' '' '
00 r 00 0
224r 22 2
)))œœ
’“’ “
ab ab
## #
"Î# $Î#
"#
!
33
rÈ
224 d842d2842œ œ œ
''
00
22
ˆ‰
Š‹ Š‹
ÈÈ
$Î# $Î# $Î# ))1
44. (a) 21(r cos )(r sin ) dz r dr d 21r cos sin dz r dr d
''' '''
20 r 20 r
21r 21r
)) ) )) )
#$#
œ
(b) 21r cos sin dz r dr d 84 r sin cos dr d 12 sin cos d 4
''' '' '
20 r 0 0 0
21r 21 2
$# '# #
)) ) ))) )))œœœ
45. (a) sin d d d
'' '
00 0
2 4 sec
3939)
#
(b) sin d d d (sec )(sec tan ) d d tan d d
'' ' '' ' '
00 0 00 0 0
24sec 24 2 2
4
3939) 9 999) 9 ) )
# #
""""
Î
œœœœ
33263
‘
11
46. (a) (6 4y) dz dy dx (b) (6 4r sin ) dz r dr d
'' ' ' ''
00 0 000
1 1x xy 21r
))
(c) (6 4 sin sin ) sin d d d
'''
040
2 2 csc
39)3 939)ab
#
(d) (6 4r sin ) dz r dr d 6r 4r sin dr d 2r r sin d
''' '' '
000 00 0
21r 21 2
œœ)) )) ))abcd
#$ $% "
!
(2 sin ) d 2 cos 1œ œ œ
'0
2
)) ) ) 1cd
1Î#
!
47. z yx dz dy dx z yx dz dy dx
'' ' ' ' '
01x1 10 1
13x 4xy 33x 4xy
##
48. (a) Bounded on the top and bottom by the sphere x y z 4, on the right by the right circular
###
œ
cylinder (x 1) y 1, on the left by the plane y 0œ œ
##
(b) dz r dr d
'' '
00 4r
22 cos 4r
)
49. (a) V dz r dr d r 8 r 2r dr d 8 r r dœœœ
''' '' '
002 00 0
22 8r 22 2
)))
Š‹’ “
Èab
#"##
$Î# #
!
3
(4) 4 (8) d 2328 d 425 dœ œ œ œ
'' '
00 0
22 2
‘
Š‹Š‹
ÈÈ
""
$Î# $Î#
33 3 3 3
44
8425
)))
1Š‹
È
(b) V sin d d d 2 2 sin sec sin d dœœ
'' ' ''
00 2 sec 00
248 24
3939) 9 999)
#$
8
3Š‹
È
2 2 sin tan sec d d 2 2 cos tan dœœ
88
33
'' '
00 0
24 2
Š‹’“
ÈÈ
9999) 9 9)
##
"
#
Î%
!
1
222 d dœ œ œ
88
333
542 8425
''
00
22
Š‹Š‹
È
"
##
))
ÈŠ‹
È
1
50. I ( sin ) sin d d d sin d d d
z00 0 00 0
232 232
œœ
'' ' '' '
393 939) 3 939)
## % $
ab
sin cos sin d d cos dœ œœ
32 32 8
5533
cos
'' '
00 0
23 2
ab
’“
9999) 9 )
#Î$
!
911
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
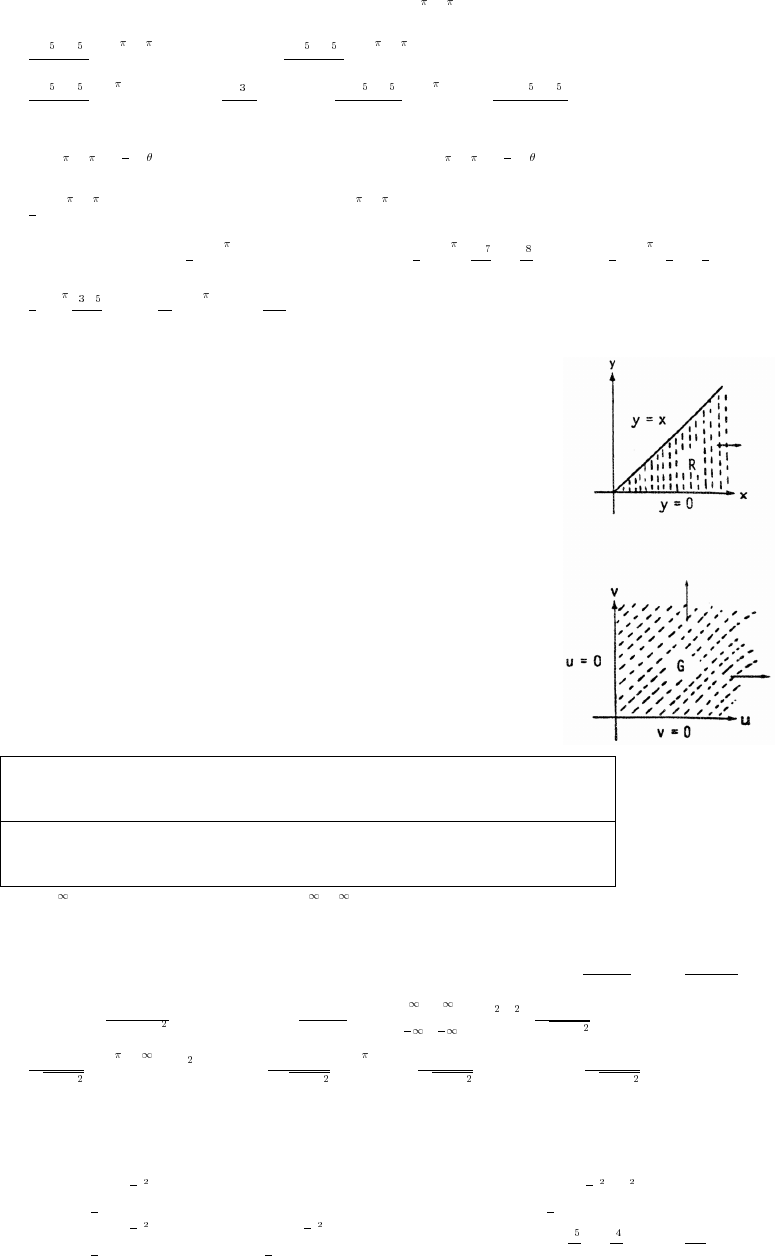
Chapter 15 Additional and Advanced Exercises 991
51. With the centers of the spheres at the origin, I ( sin ) sin d d d
z00a
2b
œ'''$3 9 3 9 3 9 )
##
ab
sin d d sin cos sin d dœœ
$$ab abba ba
55
$#
'' ''
00 00
22
99) 9 9 9 9)ab
cos d dœœ œ
$$1$
91
ab ab abba 4ba 8 ba
5 3 15 15
cos
!
''
00
22
’“
9) )
52. I ( sin ) sin d d d sin d d d
z000 000
21cos 21cos
œœ
''' '''
393 939) 3 939)
## % $
ab
(1 cos ) sin d d (1 cos ) (1 cos ) sin d d ;œ œ
"&$ '
5'' ''
00 00
22
999) 9 999)
u(2u) dud d 2 d
u1cos
du sin d
”• ’“ ˆ‰
œ
œÄœœ
9
99 )))
"""""
' )
#
!
5578578
2u u
'' ' '
00 0 0
22 2 2
d dœœœ
"
556 35 35
2 2 32 64
''
00
22
†))
1
53. x u y and y v x u v and y vœ œ Ê œ œ
J(u v) 1; the boundary of the
0
Êßœ œ
""
"
ºº
image G is obtained from the boundary of R as
follows:
xy-equations for Corresponding uv-equations Simplified
the boundary of R for the boundary of G uv-equations
yx vuv uœœ œ
œœ œ
0
y0 v0 v0
e f(x y y) dy dx e f(u v) du dvÊßœ ß
'' ''
00 00
xÐÑsx s u v
54. If s x y and t x y where ( ) ac b , then x , y ,œ œ œ œ œ!" #$ !$"#
##
$"
!$ "# !$ "#
#!
st st
and J(s t) e ds dtßœ œ Ê
"" "
()
st
ac b
!$ "# !$ "#
ºº
$"
#! '' ab
È
re dr d d . Therefore, 1 ac b .œœœ œÊœ
""
#
##
ÈÈÈÈ
acb acb acb acb
r
'' '
00 0
22
)) 1
11
CHAPTER 15 ADDITIONAL AND ADVANCED EXERCISES
1. (a) V x dy dx (b) V dz dy dxœœ
'' '' '
3x 3x 0
26x 26x x
#
(c) V x dy dx 6x x x dx 2xœœœœ
'' ''
3x 3x
26x 26x
# #%$ $ #
$
ab
’“
x x 125
54 4
2. Place the sphere's center at the origin with the surface of the water at z 3. Thenœ
9 25 x y x y 16 is the projection of the volume of water onto the xy-planeœ Ê œ
## ##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
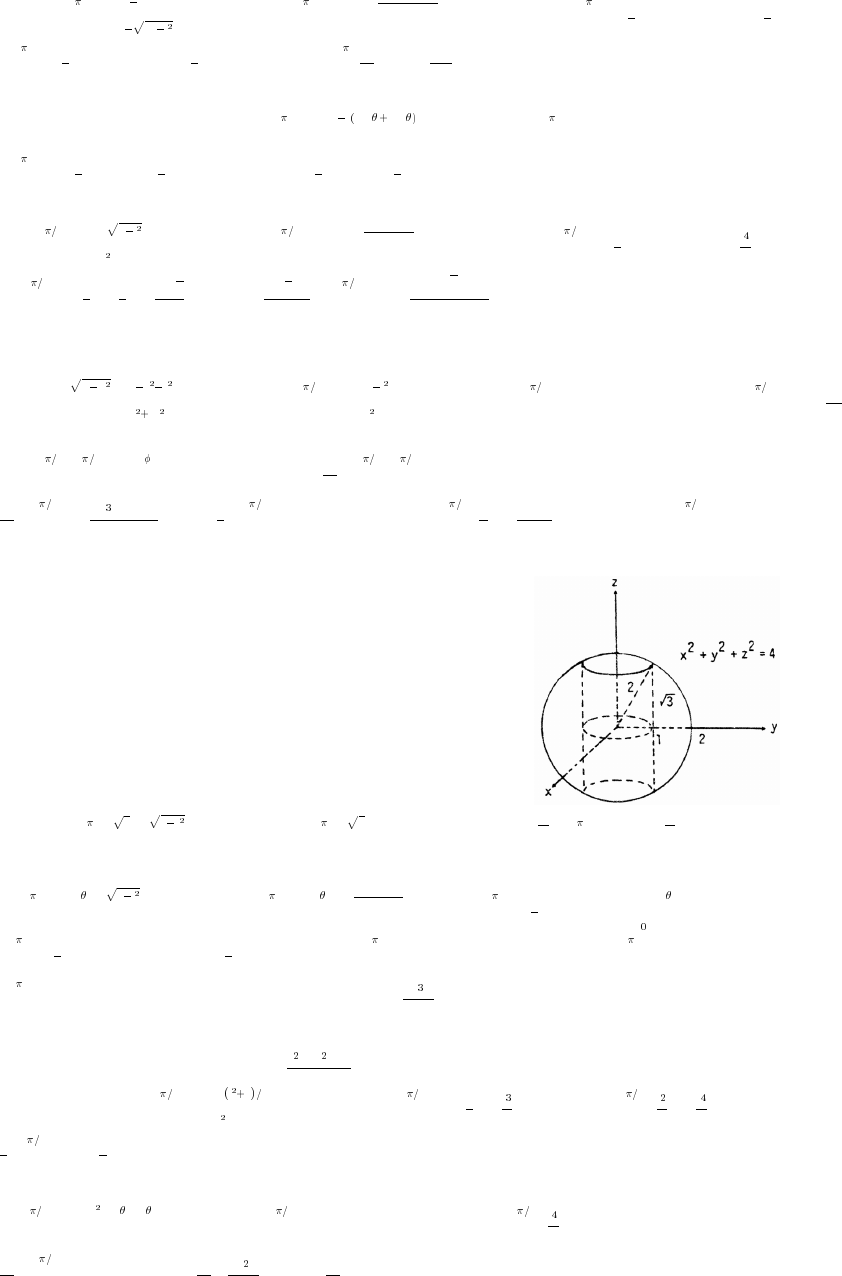
992 Chapter 15 Multiple Integrals
V dz r dr d r 25 r 3r dr d 25 r r dÊœ œ œ
''' '' '
00 25r 00 0
24 3 24 2
)) )
Š‹’ “
Èab
#"##
$Î#
#
%
!
3
3
(9) 24 (25) d dœ œ œ
''
00
22
‘
""
$Î# $Î#
33 33
26 52
))
1
3. Using cylindrical coordinates, V dz r dr d 2r r cos r sin dr dœœ
''' ''
000 00
2 1 2 r cos sin 2 1
))))ab
##
1 cos sin d sin cos 2œ œ œ
'0
2ˆ‰‘
"" ""
#
!
33 33
))))) )1
1
4. V 4 dz r dr d 4 r 2 r r dr d 4 2 r dœœœ
''' '' '
00r 00 0
21 2r 21 2
)))
Š‹’ “
Èab
#$#
"$Î# "
!
34
r
4 d dœ œ œ
''
00
22
Š‹Š‹
""
34 3 3 6
22 827 827
ÈÈ Š‹
È
))
1
5. The surfaces intersect when 3 x y 2x 2y x y 1. Thus the volume isœ Ê œ
## # # ##
V 4 dz dy dx 4 dz r dr d 4 3r 3r dr d 3 dœœœœœ
'' ' ' '' ' ' '
0 0 2x 2y 0 0 2r 0 0 0
1 1x 3xy 213r 21 2
)))ab
$
#
31
6. V 8 sin d d d sin d dœœ
''' ''
000 00
222 sin 22
3939) 99)
#%
64
3
sin d d 16 d 4 d 2œ œ œ œ
64 3
344 24
sin cos sin 2
''' '
000 0
222 2
”•
¹‘
99 9 9
11
Î#
!
# #
Î#
!
99 ) ) 1 ) 1
7. (a) The radius of the hole is 1, and the
radius of the sphere is 2.
(b) V 2 r dr dz d 3 z dz d 2 3 d 4 3œœœœ
'' ' '' '
00 1 00 0
234z 23 2
)))1ab ÈÈ
#
8. V dz r dr d r 9 r dr d 9 r dœœœ
'' ' '' '
00 0 00 0
3 sin 9 r 3 sin 3 sin
)) )
È’“
ab
#"#$Î#
3
9 9 sin (9) d 9 1 1 sin d 9 1 cos dœ œ œ
'''
000
’“’“
ab ab ab
""
# $Î# # $
$Î# $Î#
33
)) )) ))
1 cos sin cos d 9 sin 9œ œ œ
'0ab
’“
)))))) 1
#
!
sin
3
)1
9. The surfaces intersect when x y x y 1. Thus the volume in cylindrical
## ##
#
œ Ê œ
xy1
coordinates is V 4 dz r dr d 4 dr d 4 dœ œ œ
''' '' '
00r 00 0
21 r12 21 2
)))
Š‹ ’“
rr r r
48##
"
!
dœœ
"
#'0
2
)1
4
10. V dz r dr d r sin cos dr d sin cos dœœœ
''' '' '
010 01 0
22r sin cos 22 2
)))))))
$#
"
’“
r
4
sin cos dœœœ
15 15 sin 15
4428
'0
2
))) ’“
)1Î#
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
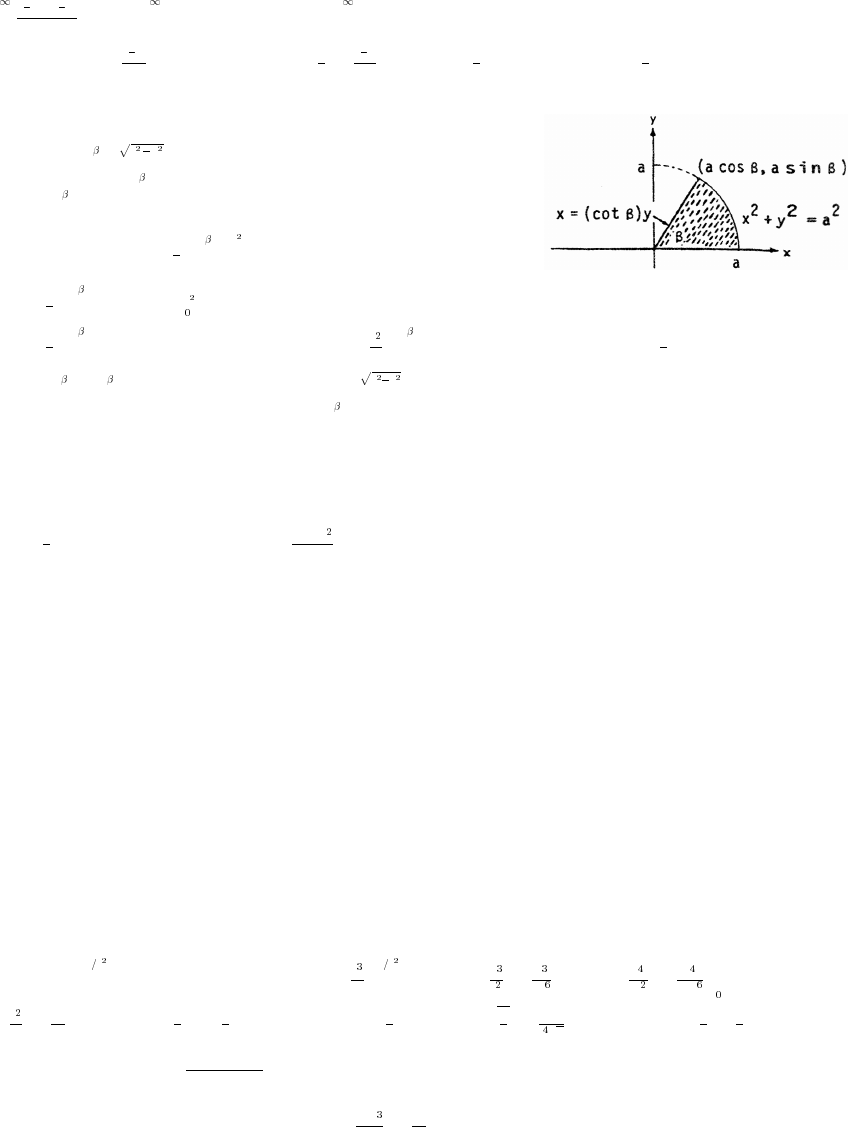
Chapter 15 Additional and Advanced Exercises 993
11. dx e dy dx e dx dy lim e dx dy
'''''''
00aa0a0
bb bt
ee
x
xy xy xy
ax bx
œœœ
Š‹
tÄ_
lim dy lim dy dy ln y lnœœ œœœ
'' '
aa a
bb b
tb
a
ttÄ_ Ä_
’“ Š ‹ cd ˆ‰
ee b
yyyya
xy yt
!
""
12. (a) The region of integration is sketched at the right
ln x y dx dyÊ
''
0y cot
a sin a y ab
##
r ln r dr d ;œ''
00
aab
#)
ln u du d
ur
du 2r dr
”•
œ
π
#"
#''
00
a
)
[u ln u u] dœ
"
#'0
a)
2a ln a a lim t ln t d (2 ln a 1) d a ln aœ œœ
" "
###
## #
''
00
’“ ˆ‰
t0Ä))"
a
(b) ln x y dy dx ln x y dy dx
'' ''
0 0 a cos 0
a cos (tan )x a a x
ab ab
## ##
13. e f(t) dt du e f(t) du dt (x t)e f(t) dt; also
'' '' '
00 0t 0
xu xx x
mx t mx t mx tÐÑ ÐÑ ÐÑ
œœ
e f(t) dt du dv e f(t) du dv dt (v t)e f(t) dv dt
''' ''' ''
000 0t t 0t
xvu xxv xx
mx t mx t mx tÐÑ ÐÑ ÐÑ
œœ
(v t) e f(t) dt e f(t) dtœ œ
''
00
xx
x
t
‘
"#ÐÑ ÐÑ
#2
mx t mx t
(x t)
14. f(x) g(x y)f(y) dy dx g(x y)f(x)f(y) dy dx
'' ''
00 00
1x 1x
Š‹
œ
g(x y)f(x)f(y) dx dy f(y) g(x y)f(x) dx dy;œ œ
'' ' '
0y 0 y
11 1 1
Œ
g x y f(x)f(y) dx dy g(x y)f(x)f(y) dy dx g(y x)f(x)f(y) dy dx
'' '' ''
00 00 0x
11 1x 11
abkkœ
g(x y)f(x)f(y) dx dy g(y x)f(x)f(y) dy dxœ
'' ''
0y 0x
11 11
g(x y)f(x)f(y) dx dy g(x y)f(y)f(x) dx dyœ
'' ''
0y 0y
11 11
ðóóóóóóóóóóóóñóóóóóóóóóóóóò
simply interchange x and y
variable names
2 g(x y)f(x)f(y) dx dy, and the statement now follows.œ
''
0y
11
15. I (a) x y dy dx x y dx dx
o00 0 0
axa a a
xa a
œœœœ
'' ' '
ab ’“ Š‹’ “
## #
!
y
3 a 3a 4a 12a
xx x x
a ; I (a) a a 0 a a . Since I (a) a 0, theœ œ œÊ œÊœ œ œ
a
41 6 3 3 3
""" """ ""
## ##
# w $ % ww %
%
o o
ÉÈ
value of a does provide a for the polar moment of inertia I (a).minimum o
16. I x y (3) dy dx 3 4x dx 104
o02x 0
24 2
œ œ œ
'' '
ab Š‹
## #
14x 64
33
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

994 Chapter 15 Multiple Integrals
17. M r dr d sec dœœ
'' '
b sec
a
)))
Š‹
ab
##
#
a b tan a cos bœ œ
## #" #
)) ˆ‰ Š‹
b
ab
ab
È
a cos b a b ; I r dr dœœ
#" $
##
ˆ‰ È
b
aob sec
a
'' )
ab sec dœ
"%%%
4'ab))
ab1tan sec dœ
"%% # #
4'cdabab)))
a b tan œ
"%%
43
b tan
’“
))
))
)
œ
a b tan b tan
6
)) )
##
a cos b a b b a bœ
"""
##
%" $ $# #
## $Î#
ˆ‰ Èab
b
a6
18. M dx dy 1 dy y ; M x dx dyœœœœœ
'' ' ''
21y4 2 21y4
22y2 2 22y2
y
Š‹’“
yy
4123
8
#
#
dy 4 y dy 16 8y y dy 16yœœœœ
'' '
22 2
22 2
2y2
1y4
’“ ’ “
ab a b
x33 3
23232 1635
8y y
##% #
!
32 x , and y 0 by symmetryœœ œÊœœ œ œ
36432332848 4836
16 3 5 16 15 15 M 15 8 5
M
ˆ ‰ ˆ‰ˆ ‰ ˆ‰ˆ‰
†y
19. e dy dx e dy dx e dx dy
'' '' ''
00 00 00
ab abxa bayb
max b x a y b x a yabߜ
x e dx y e dy e e e 1 e 1œœœ
''
00
ab ab
ˆ‰ ˆ‰ ’“’“Š‹Š‹
ba
a b 2ab 2ba ab ab
bx ay bx ay ba ab
""" "
!!
##
e1œ
"
ab
ab
Š‹
20. dx dy dy dx F(x y) F(x y)
'' ' '
yx y y
yx y y
x
x
y
y
`ß `ß `ß `ß
`` ` ` ` "!
F(x y) F(x y) F(x y) F(x y)
xy y y y
œœœßß
’“ ’ “cd
F(x y ) F(x y ) F(x y ) F(x y )œßßßß
"" !" "! !!
21. (a) (i) Fubini's Theorem
(ii) Treating G(y) as a constant
(iii) Algebraic rearrangement
(iv) The definite integral is a constant number
(b) e cos y dy dx e dx cos y dy e e sin sin 0 (1)(1) 1
'' ' '
00 0 0
ln 2 2 ln 2 2
xx ln 20
œœœœ
ŒŒ
ab
ˆ‰
1
#
(c) dx dy dy x dx 1 0
'' ' '
11 1 1
21 2 1
xx
yy y2
œœœœ
ŒŒ
’“’“ ˆ‰ˆ‰
"""""
#"
"" ###
22. (a) f x y D f u x u y; the area of the region of integration is ™œ Ê œ ij u"# "
#
average 2 (u x u y) dy dx 2 u x(1 x) u (1 x) dxÊœ œ
'' '
00 0
11x 1
"# " #
"
#
#
‘
2u u 2 u u (u u)œ œœ
’“Š‹
ˆ‰ ˆ ‰
"# "#"#
""""
#
"
!
xx
23 3 6 6 3
(1 x)
(b) average (u x u y) dA x dA y dA u u u x u yœœ œœ
""# " # "#
area area area M M
uu MM
'' '' ''
RRR
Š‹ ˆ‰
yx
23. (a) I e dx dy e r dr d lim re dr d
#œœœ
'' ' ' ' '
00 0 0 0 0
xy r r
22b
ab ”•
))
bÄ_
lim e 1 d d Iœ œ œ Ê œ
""
###
''
00
22
b
bÄ_ ab))
11
4È
(b) t e dt y e (2y) dy 2 e dy 2 , where y t> 1
ˆ‰ È
ab Š‹ È
"
# #
"Î# #
"Î#
œœ œœœœ
'' '
00 0
tyy
È1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
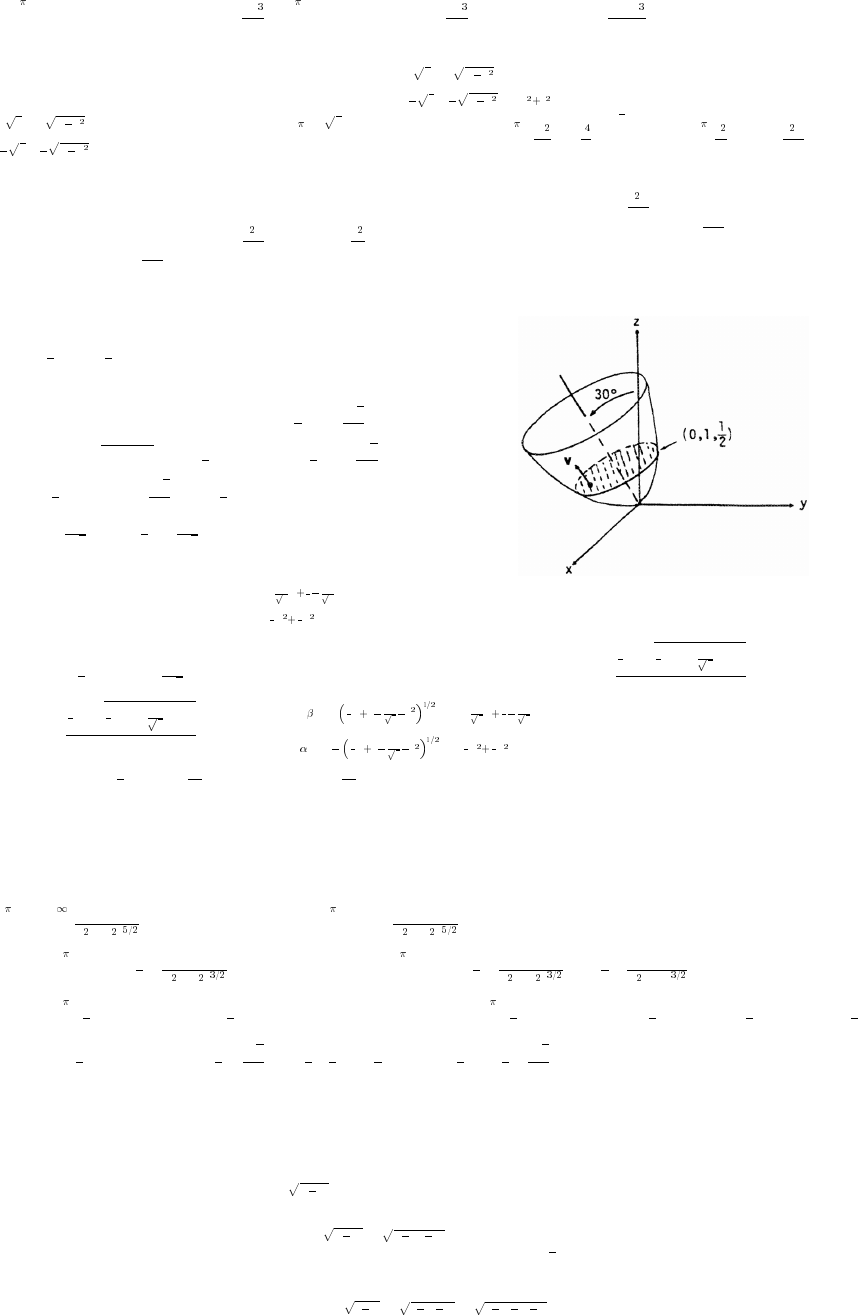
Chapter 15 Additional and Advanced Exercises 995
24. Q kr (1 sin ) dr d (1 sin ) d cos œœœœ
'' '
00 0
2R 2
##
!
)) )) ) )
kR kR 2 kR
333
cd
11
25. For a height h in the bowl the volume of water is V dz dy dxœ'' '
hhxxy
hhx h
h x y dy dx h r r dr d d d .œœœœœ
'' '' ' '
hhx 00 0 0
hhx 2 h 2 2
h
ab ab ’“
## #
!#
)))
hr r h h
24 4
È1
Since the top of the bowl has area 10 , then we calibrate the bowl by comparing it to a right circular cylinder1
whose cross sectional area is 10 from z 0 to z 10. If such a cylinder contains cubic inches of water1œœ h1
#
to a depth w then we have 10 w w . So for 1 inch of rain, w 1 and h 20; for 3 inches of1œÊœ œ œ
hh
20
1
#È
rain, w 3 and h 60.œœ
È
26. (a) An equation for the satellite dish in standard position
is z x y . Since the axis is tilted 30°, a unitœ
""
##
##
vector 0 a b normal to the plane of thevijkœ
water level satisfies b cosœœ œvk†ˆ‰
1
6
3
È
#
a1b Êœ œÊœ
È#""
###
vjk
È3
(y 1) z 0Ê œ
""
###
È3ˆ‰
zyʜ
"""
#
ÈÈ
33
Š‹
is an equation of the plane of the water level. Therefore
the volume of water is V dz dy dx, where R is the interior of the ellipseœ'''
R
11
22
111
33
2
xy
y
x y y 1 0. When x 0, then y or y , where
##
#
œ œ œ œ œ
22
33
41
ÈÊŠ‹
!"!
24 2
39 3
and V 1 dz dx dy"œÊœ
24 2
39 3
#
ÊŠ‹
41 '' '
22 11
322
3
22 111
32
333
y1 y x y
y1 y y
(b) x 0 z y and y; y 1 1 the tangent line has slope 1 or a 45° slantœÊœ œ œÊ œÊ
"
#
#dz dz
dy dy
at 45° and thereafter, the dish will not hold water.Ê
27. The cylinder is given by x y 1 from z 1 to z r z dV
## ##
&Î#
œ œ _Ê
'''
Dab
dz r dr d lim dz dr dœœ
''' '''
001 001
21 21a
zrz
rz rzab ab
))
aÄ_
lim dr d lim dr dœ œ
aaÄ_ Ä_
'' ''
00 00
21 21
a
1
’“ ’ “
ˆ‰ ˆ‰ ˆ‰
"""
333
rrr
rz ra r1ab ab ab
))
lim r a r 1 d lim 1 a 2 a dœœ
aaÄ_ Ä_
''
0 0
2 2
’“’ “
ab ab ab ab
ˆ‰
"" """"
# # # # "Î# #
"Î# "Î# "Î# "Î#
"
!
33 3333
))
lim 2 1 a 2 .œœ
aÄ_ 11
’“’“
ab Š‹ ˆ‰ ˆ‰
"""""""
#"Î#
##333a333
22
ÈÈ
28. Let's see?
The length of the "unit" line segment is: L 2 dx 2.œœ
'0
1
The area of the unit circle is: A 4 dy dx .œœ
''
00
11x
2
1
The volume of the unit sphere is: V 8 dz dy dx .œœ
'' '
00 0
11x 1xy
222
4
31
Therefore, the hypervolume of the unit 4-sphere should be:
V 16 dw dz dy dx.
hyper œ'' ' '
00 0 0
11x 1xy 1xyz
222222
Mathematica is able to handle this integral, but we'll use the brute force approach.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
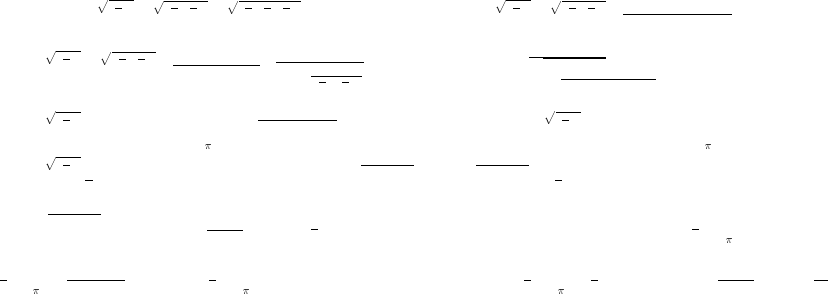
996 Chapter 15 Multiple Integrals
V 16 dw dz dy dx 16 dz dy dx
hyper œœ
'' ' ' '' '
00 0 0 00 0
11x 1xy 1xyz 11x 1xy
222
222222 222
È1xyz
16 dz dy dx cos
dz 1 x y sin d
œœ
œ
œ
'' '
00 0
11x 1xy
22 z
1x y
222
2
22
ÈÉ
1x y1 –—
Èz
1x y
22
È
22 )
))
16 1 x y 1 cos sin d dy dx 16 1 x y sin d dy dxœ œ
'' ' '' '
00 /2 00 /2
11x 0 11x 0
2 2
ab ab
È
22 22 2
2))) ))
16 1 x y dy dx 4 1 x x 1 x 1 x dxœ œ
'' '
00 0
11x 1
2
1
4 3
22 2 2
22
3/2
ab ab
Š‹
ÈÈ
1"
4 1 x dx 1 x dx sin d
1x x cos
dx sin d
œ œœ œ
œ
œ
11 1))
)
))
'' '
00 /2
11 0
È‘
ab ab ”•
221x 88
33
24
3/2
$
3
d 1 2 cos 2 cos 2 d 2 cos 2 dœ œ œ œ
81cos 2 2 23 cos 4
32 3 3 22
22
1)1)))1))
'' '
/2 /2 /2
00 0
ˆ‰ ˆ ‰
ab
#
))1
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

CHAPTER 16 INTEGRATION IN VECTOR FIELDS
16.1 LINE INTEGRALS
1. t ( t) x t and y 1 t y 1 x (c)ri jœ" Ê œ œÊ œÊ
2. t x 1, y 1, and z t (e)rij kœ Ê œ œ œ Ê
3. (2 cos t) (2 sin t) x 2 cos t and y 2 sin t x y 4 (g)rijœ Êœ œÊœÊ
##
4. t x t, y 0, and z 0 (a)riœÊœ œ œÊ
5. t t t x t, y t, and z t (d)rijkœ Ê œ œ œÊ
6. t (2 2t) y t and z 2 2t z 2 2y (b)rj kœ Ê œ œ Ê œ Ê
7. t 1 2t y t 1 and z 2t y 1 (f)rjkœ Êœ œÊœÊab
## z
4
8. (2 cos t) (2 sin t) x 2 cos t and z 2 sin t x z 4 (h)rikœ Êœ œÊœÊ
##
9. (t) t (1 t) , 0 t 1 2 ; x t and y 1 t x y t ( t) 1ri j ij jœ ŸŸ Ê œÊ œ œ œÊ œ"œ
dd
dt dt
rr
¸¸ È
f(x y z) ds f(t 1 t 0) dt (1) 2 dt 2 t 2Êßßœßß œ œ œ
'' '
C0 0
11
¸¸ Š‹ ’ “
ÈÈÈ
d
dt
r"
!
10. (t) t (1 t) , 0 t 1 2; x t, y 1 t, and z 1 x y z 2ri jk ijœ ŸŸ Ê œÊ œ œ œ œ Ê
dd
dt dt
rr
¸¸ È
t (1 t) 1 2 2t 2 f(x y z) ds (2t 2) 2 dt 2 t 2t 2œ œ Ê ßß œ œ œ
''
C0
1ÈÈ È
cd
#"
!
11. (t) 2t t (2 2t) , 0 t 1 2 2 4 1 4 3; xy y zrij k ijkœ ŸŸÊ œ Ê œ œ
dd
dt dt
rr
¸¸ È
(2t)t t (2 2t) f(x y z) ds 2t t 2 3 dt 3 t t 2t 3 2œÊ ßß œ œ œœ
''
C0
1ab
‘ˆ‰
#$#
""
###
"
!
2213
33
12. (t) (4 cos t) (4 sin t) 3t , 2 t 2 ( 4 sin t) (4 cos t) 3rijk ijkœŸŸÊœ11
d
dt
r
16 sin t 16 cos t 9 5; x y 16 cos t 16 sin t 4 f(x y z) ds (4)(5) dtÊœ œ œ œÊ ßßœ
¸¸ ÈÈ
È
d
dt
r## ## ## ''
C2
2
20t 80œœcd
#
#
1
11
13. (t) ( 2 3 ) t( 3 2 ) (1 t) (2 3t) (3 2t) , 0 t 1 3 2r ijk ijk i j k ijkœ œ ŸŸÊ œ
d
dt
r
194 14; xyz(1t)(23t)(32t) 66t f(xyz) dsÊ œ œ œ œ Ê ßß
¸¸ ÈÈ
d
dt
r'C
(6 6t) 14 dt 6 14 t 6 14 3 14œ œ œ œ
'0
1ÈÈ È È
’“Š‹
ˆ‰
t
2
"
!
"
#
14. (t) t t t , 1 t 3 ; rijk ijkœ ŸŸ_Ê œ Ê œ œ œ
dd
dt dt x y z t t t 3t
333
rr
¸¸ ÈÈÈÈ
f(x y z) ds 3 dt lim 1 1Êßßœ œœ œ
''
C1
Š‹
È‘ ˆ ‰
È3
3t t b
1_
"
"
bÄ_
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

998 Chapter 16 Integration in Vector Fields
15. C : (t) t t , 0 t 1 2t 1 4t ; x y z t t 0 t t 2t
"# #
##
rij ijœ ŸŸ Ê œ Ê œ œ œ œ
dd
dt dt
rr
¸¸ ÈÈÈkk
since t 0 f(x y z) ds 2t 1 4t dt 4t (5) 5 5 1 ;Ê ßß œ œ " œ œ
''
C0
1È’“ Š‹
ab È
#""""
# $Î#
$Î# "
!
6666
C : (t) t , 0 t 1 1; x y z 1 1 t 2 t
####
rijk kœ ŸŸ Ê œ Ê œ œ œ
dd
dt dt
rr
¸¸ ÈÈ
f(x y z) ds 2 t (1) dt 2t t 2 ; therefore f(x y z) dsÊßßœ œœœ ßß
'' '
C0 C
1ab ‘
#$
""
"
!
333
5
f(x y z) ds f(x y z) ds 5œßßßßœ
''
CC
53
6È#
16. C : (t) t , 0 t 1 1; x y z 0 0 t t
"###
rk kœŸŸÊœÊœœœ
dd
dt dt
rr
¸¸ ÈÈ
f(x y z) ds t (1) dt ;Êßßœ œœ
''
C0
1ab ’“
#"
!
"t
33
C : (t) t , 0 t 1 1; x y z 0 t 1 t 1
##
rjk jœ ŸŸ Ê œ Ê œ œ œ
dd
dt dt
rr
¸¸ ÈÈÈ
f(x y z) ds t 1 (1) dt t t 1 ;Êßßœ œœœ
''
C0
1ˆ‰ ‘
È22
333
$Î# "
!
"
C : (t) t , 0 t 1 1; x y z t 1 1 t
$#
rijk iœ ŸŸÊ œÊ œ œ œ
dd
dt dt
rr
¸¸ ÈÈ
f(x y z) ds (t)(1) dt f(x y z) ds f ds f ds f dsÊ ßßœ œ œÊ ßßœ œ
' ' ' '''
C 0 C CCC
1’“ ˆ‰
t
233
"
!
""""
# #
œ"
6
17. (t) t t t , 0 a t b 3 ; rijk ijkœ ŸŸ Ê œ Ê œ œ œ
d d ttt 1
dt dt x y z t t t t
xyz
rr
¸¸ È
f(x y z) ds 3 dt 3 ln t 3 ln , since 0 a bÊßßœ œ œ Ÿ
''
Ca
bb
a
ˆ‰ ˆ‰
ÈÈ È
’“
kk
1b
ta
18. (t) (a cos t) (a sin t) , 0 t 2 ( a sin t) (a cos t) a sin t a cos t a ;rjk jkœ ŸŸÊœ Êœ œ1dd
dt dt
rr
¸¸ Èkk
## # #
x z 0 a sin t f(x y z) ds a sin t dt a sin t dt
a sin t, 0 t
a sin t, t 2
œ œ Ê ßß œ
ŸŸ
ŸŸ
ÈÈ œkk
kk kk kk
## ## ##
1
11
'' '
C0
2
a cos t a cos t a ( 1) a a a ( 1) 4aœ œ œcdcdc dc d
## #### #
!
#11
1
19. (x) x y x , 0 x 2 x 1 x ; f(x y) f x 2x f dsrijij ijœœ ŸŸÊ œ Ê œ ßœ ß œ œ Ê
xdd xx
dx dx
# #
#
rr
¸¸ ÈŠ‹Š‹
x'C
(2x) 1 x dx 1 x 5 1œœœœ
'0
2È’“
ab ˆ‰
## $Î#
$Î# #
!
22
333
10 5 2
È
20. (t) 1 t 1 t , 0 t 1 1 1 t ; f(x y) f 1 t 1 trijœ ŸŸÊ œ ßœ ß œabab ab abab
¸¸ ÉŠ‹
1d 1
2 2
dt
1t 1t
11t
# #
#
rabab
Éab
1
4
4
f ds 1 1 t dt 1 t 1 t dt 1 t 1 tÊœ œœ
'' '
C0 0
11
abab
Éab
1t 1t
11t
11
420
425
#"
#
"
!
1
4
4Éab abab ab ab
Š‹’ “
0œ œ
ˆ‰
""
## #00
11
21. (t) (2 cos t) (2 sin t) , 0 t ( 2 sin t) (2 cos t) 2; f(x y) f(2 cos t 2 sin t)rij ijœ ŸŸÊœ ʜߜß
1
#
dd
dt dt
rr
¸¸
2 cos t 2 sin t f ds (2 cos t 2 sin t)(2) dt 4 sin t 4 cos t 4 ( 4) 8œÊ œ œ œœ
''
C0
2cd
1Î#
!
22. (t) (2 sin t) (2 cos t) , 0 t (2 cos t) ( 2 sin t) 2; f(x y) f(2 sin t 2 cos t)rij ijœ ŸŸÊœ ʜߜß
1
4dt dt
ddrr
¸¸
4 sin t 2 cos t f ds 4 sin t 2 cos t (2) dt 4t 2 sin 2t 4 sin tœ Ê œ œ
## Î%
''
C0
4
0
abc d
1
21 2œ 1Š‹
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.1 Line Integrals 999
23. (t) t 1 2t , 0 t 1 2t 2 2 t 1; M (x y z) ds (t) 2 t 1 dtrjk jkœ ŸŸÊ œÊ œ œ ßß œ ab ¸¸ ÈÈ
Š‹
###
dd
dt dt
rr ''
C0
1
$$
t2t1 dt t1 2 1221œœœœ
'0
1ˆ‰
Š‹’“
ÈÈ
ab
33/2
### $Î#
"
!
24. (t) t 1 2t , 1 t 1 2t 2rjk jkœ ŸŸÊ œab
#d
dt
r
2 t 1; M (x y z) dsÊœ œ ßß
¸¸ È'
d
dt
r#
C
$
15 t 1 2 2 t 1 dtœ
'1
1ˆ‰
ÈabŠ‹
È
##
30 t 1 dt 30 t 60 1 80;œœœœ
'1
1ab’“Š‹ ˆ‰
#"
"
"t
33
M y (x y z) ds t 1 30 t 1 dt
xz C1
1
œßßœ
''
$abc dab
##
30 t 1 dt 30 t 60 1œœœ
'1
1ab’“Š‹ ˆ‰
%"
"
"t
55
48 y ; M x (x y z) ds 0 ds 0 x 0; z 0 by symmetry (since isœ Ê œ œ œ œ ß ß œ œ Ê œ œ
M
M805
48 3 yz
xz ''
CC
$$ $
independent of z) (x y z) 0Êßßœ!ßß
ˆ‰
3
5
25. (t) 2t 2t 4 t , 0 t 1 2 2 2t 2 2 4t 2 1 t ;rij k ijkœ ŸŸÊœÊœœ
ÈÈ ÈÈ È È
ab ¸¸
###
dd
dt dt
rr
(a) M ds (3t) 2 1 t dt 2 1 t 2 2 1 4 2 2œœ œ œœ
''
C0
1
$Š‹’ “
ÈÈ
ab ˆ‰
## $Î#
$Î# "
!
(b) M ds (1) 2 1 t dt t 1 t ln t 1 t 2 ln 1 2 (0 ln 1)œ œ œ œ
''
C0
1
$Š‹’ “’ “
ÈÈ ÈÈÈ
Š‹ Š‹
## #
"
!
2ln1 2œ
ÈÈ
Š‹
26. (t) t 2t t , 0 t 2 2 t 1 4 t 5 t;rij k ijkœ ŸŸ Ê œ Ê œ œ
2d d
3dt dt
$Î# "Î#
rr
¸¸ ÈÈ
M ds 3 5 t 5 t dt 3(5 t) dt (5 t) 7 5 (24) 36;œœ œœœœœ
'' '
C0 0
22
$ˆ‰ˆ‰ ‘
ÈÈ ab
333
2###
#
!##
M x ds t[3(5 t)] dt 15t 3t dt t t 30 8 38;
yz 5
2
œœœœœœ
'' '
C0 0
22
$ab
‘
##$
"#
!
M y ds 2t[3(5 t)] dt 2 15t 3t dt 76; M z ds t [3(5 t)] dt
xz xy 2
3
œœ œ œœ œ
'' ' ' '
C0 0 C 0
22 2
$$ab
# $Î#
10t 2t dt 4t t 4(2) (2) 16 2 2 2 xœœœœœÊœ
'0
2ˆ‰‘ ÈÈ È
$Î# &Î# &Î# (Î# &Î# (Î#
#
!
4 4 32 144
7777M
Myz
, y , and z 2œœ œ œœ œ œ œ
38 19 76 19 4
36 18 M 36 9 M 7 36 7
MM144 2
xz xy È
†È
27. Let x a cos t and y a sin t, 0 t 2 . Then a sin t, a cos t, 0œœŸŸœœœ1dx dz
dt dt dt
dy
dt a dt; I x y ds a sin t a cos t a dtÊœœœ
ʈ‰ ˆ‰
Š‹ ab a b
dx dz
dt dt dt
dy z
##
### ## ##
''
C0
2
$$
a dt 2 a ; M (x y z) ds a dt 2 a R a.œœœßßœœÊœœœ
'''
0C0
22
$$
$1$ $ $ 1$ zI
M2a
2a
ÉÉ
z1$
1$
28. (t) t (2 2t) , 0 t 1 2 5; M ds 5 dt 5;rj k jkœ ŸŸ Ê œ Ê œ œ œ œ
dd
dt dt
rr
¸¸ ÈÈÈ
''
C0
1
$$ $
I y z ds t (2 2t) 5 dt 5t 8t 4 5 dt 5 t 4t 4t 5 ;
x55
33
œ œ œ œ œ
'' '
C0 0
11
ab c d a b
ÈÈÈÈ
‘
## # # # $ # "
!
$$ $$ $
I x z ds 0 (2 2t) 5 dt 4t 8t 4 5 dt 5 t 4t 4t 5 ;
y44
33
œ œ œ œ œ
'' '
C0 0
11
ab c d a b
ÈÈÈÈ
‘
## # # # $ # "
!
$$ $$ $
I x y ds 0 t 5 dt 5 5 R , R ,
zC0
1
œ œ œ œ Êœœ œœœ
''
ab ab
ÈÈ È
’“ ÉÉÉ
É
## ## "
!
"
$$$$
t542
33 M3 M3
xy
II
3
xyÈ
and RzI
M3
œœ
Éz"
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
1000 Chapter 16 Integration in Vector Fields
29. (t) (cos t) (sin t) t , 0 t 2 ( sin t) (cos t) sin t cos t 1 2;rijk ijkœŸŸÊœÊœ œ1dd
dt dt
rr
¸¸ ÈÈ
##
(a) M ds 2 dt 2 2; I x y ds cos t sin t 2 dt 2 2œœ œ œœ œ
'' ' '
C0 C 0
2 2
z
$ $ 1$ $ $ 1$
ÈÈ ÈÈ
ab a b
## # #
R1Êœ œ
zI
M
Éz
(b) M (x y z) ds 2 dt 4 2 and I x y ds 2 dt 4 2œßßœ œ œ œ œ
'' ' '
C0 C 0
4 4
z
$ $ 1$ $ $ 1$
ÈÈ ÈÈ
ab
##
R1Êœ œ
zI
M
Éz
30. (t) (t cos t) (t sin t) t , 0 t 1 (cos t t sin t) (sin t t cos t) 2t rijk i jkœ ŸŸÊœ
22
3dt
d
È$Î# rÈ
(t 1) t 1 for 0 t 1; M ds (t 1) dt (t 1) 2 1 ;Êœœ ŸŸœ œœ œ œ
¸¸ ‘
Èab
d 3
dt 2
r#""
###
"
!##
''
C0
1
$
M z ds t (t 1) dt t t dt t t
xy 22 22 22
33 375
22
œœ œ œ
'' '
C0 0
11
$Š‹ ˆ‰ ‘
ÈÈ È
$Î# &Î# $Î# (Î# &Î# "
!
z ; I x y dsœœ œÊœœ œ œ
22 22 162 162 322
3 7 5 3 35 35 M 35 3 105
22 24 2
Mz
ÈÈÈ ÈÈ
ˆ‰ ˆ‰ ˆ‰
Š‹ ab
xy 'C
##
$
t cos t t sin t (t 1) dt t t dt Rœ œ œ œœ Ê œ œ
''
00
11
abab
’“ ÉÉ
## ## $# "
!
""tt 7 7
43 4312 M 18
zIz
31. (x y z) 2 z and (t) (cos t) (sin t) , 0 t M 2 2 as found in Example 4 of the text;$11ßß œ œ Ÿ Ÿ Ê œ rjk
also 1; I y z ds cos t sin t (2 sin t) dt (2 sin t) dt 2 2 R
¸¸ ab a b É
d
dt M
x x I
rœœ œ œ œÊœ
'' '
C0 0
## # #
$1
x
1œ
32. (t) t t , 0 t 2 2 t t 1 2t t (1 t) 1 t forri jk i jkœ ŸŸ Ê œ Ê œ œ œ
22
3dtdt
td d
È$Î# "Î#
###
rr
ÈÈ
¸¸ È
0 t 2; M ds (1 t) dt dt 2; M x ds t (1 t) dt 2;ŸŸ œ œ œ œ œ œ œ œ
'' ' ' '
C0 0 C 0
22 2
yz
$$
ˆ‰ ˆ‰ ’“
""
#
!
t1 t1 2
t
M y ds t dt t ; M z ds dt x 1,
xz 22 42
31515 63M
32 t t M
œœ œ œœœœœÊœœ
'' ''
C0 C0
2 2
xy
$$
ÈÈ
$Î# &Î# ##
!!
#
%
’“ ’“ yz
y , and z ; I y z ds t t dt t ;œ œ œ œ œ œ œ œœ
M
M15 M3 9 4 9 20 92045
16 8 2 t 32 32 232
Mx
xz xy #"
## $ % % #
!
''
C0
2
ab ˆ‰
’“
$
I x z ds t t dt ; I x y ds
y z
C0 C
2
œ œ œœœœ
'' '
ab ab
ˆ‰
’“
## # % ##
"#
!
$$
432032015
tt 83264
t t dt t R , R , andœ œ œœÊœœ œœ
'0
2ˆ‰
’“ ÉÉÉ
É
#$ %
#
!
8 t 2 8 32 56 2 29 32
939399 M35M15
xy
II
xy
R7
zI
M3
2
œœ
ÉÈ
z
33-36. Example CAS commands:
:Maple
f := (x,y,z) -> sqrt(1+30*x^2+10*y);
g := t -> t;
h := t -> t^2;
k := t -> 3*t^2;
a,b := 0,2;
ds := ( D(g)^2 + D(h)^2 + D(k)^2 )^(1/2): # (a)
'ds' = ds(t)*'dt';
F := f(g,h,k): # (b)
'F(t)' = F(t);
Int( f, s=C..NULL ) = Int( simplify(F(t)*ds(t)), t=a..b ); # (c)
`` = value(rhs(%));
: (functions and domains may vary)Mathematica
Clear[x, y, z, r, t, f]
f[x_,y_,z_]:= Sqrt[1 30x 10y]
2
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.2 Vector Fields, Work, Circulation, and Flux 1001
{a,b}= {0, 2};
x[t_]:= t
y[t_]:= t2
z[t_]:= 3t2
r[t_]:= {x[t], y[t], z[t]}
v[t_]:= D[r[t], t]
mag[vector_]:=Sqrt[vector.vector]
Integrate[f[x[t],y[t],z[t]] mag[v[t]], {t, a, b}]
N[%]
16.2 VECTOR FIELDS, WORK, CIRCULATION, AND FLUX
1. f(xyz)xyz xyz (2x) xxyz ; similarly,ß ß œ Ê œ œ ab ab ab
### ### ###
"Î# $Î# $Î#
`"
`#
f
x
yxyz and zxyz f
``
``
### ###
$Î# $Î#
ff
yz
xyz
xyz
œ œ Ê œab ab™ijk
ab
2. f(x y z) ln x y z ln x y z (2x) ;ßßœ œ Ê œ œ
ÈabŠ‹
###
"`""
#`#
### fx
x xyz x y z
similarly, and f
``
` `
ffz
y xyz z xyz xyz
yxyz
œœÊœ™ijk
3. g(x y z) e ln x y , and eß ß œ Ê œ œ œ
z z
gg2yg
xxyyxy z
2x
ab
## `` `
```
geÊœ™Š‹Š‹
2x
xy xy
2y
ijk
z
4. g(x y z) xy yz xz y z, x z, and y x g (y z) ( z) (x y)ßß œ Ê œ œ œ Ê œ B
`` `
`` `
gg g
xy z ™ijk
5. inversely proportional to the square of the distance from (x y) to the origin (M(x y)) (N(x y))kk È
FßÊßß
##
, k 0; points toward the origin is in the direction of œ Ê œ
k x
xy xy xy
y
FFnij
ÈÈ
a , for some constant a 0. Then M(x y) and N(x y)ʜ ߜ ߜFn
ax
xy xy
ay
ÈÈ
(M(x y)) (N(x y)) a a , for any constant k 0Êßߜʜʜ
È##
kkx
xy xy xy
ky
Fij
ab ab
6. Given x y a b , let x a b cos t and y a b sin t. Then
#### ## ##
œ œ œ
ÈÈ
a b cos t a b sin t traces the circle in a clockwise direction as t goes from 0 to 2rijœ
Š‹Š‹
ÈÈ
## ## 1
a b sin t a b cos t is tangent to the circle in a clockwise direction. Thus, letʜ vij
Š‹Š‹
ÈÈ
## ##
y x and (0 0) .Fv F i j F 0œÊ œ ßœ
7. Substitute the parametric representations for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate the work W .FFœ'C†d
dt
r
(a) 3t 2t 4t and 9t W 9t dtFijk ijkFœ œÊ œÊ œ œ
dd 9
dt dt
rr
†'0
1
#
(b) 3t 2t 4t and 2t 4t 7t 16t W 7t 16t dt t 2tFijk ijkFœ œ Ê œ Êœ œ
#% $ #( #($)
"
!
dd 7
dt dt 3
rr
†'0
1ab
‘
2œœ
713
33
(c) t t and t ; 3t 2t and 5t W 5t dt ;r i j r ij kF i j ij F
"# " " "
#
œ œ œ œ Ê œ Ê œ œ
dd
dt dt
5
rr
†'0
1
3 2 4t and 4t W 4t dt 2 W W WFijk kF
###"#
#
œ œÊ œ Ê œ œÊ œ œ
dd
dt dt
9
rr
†'0
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1002 Chapter 16 Integration in Vector Fields
8. Substitute the parametric representation for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate the work W .FFœ'C†d
dt
r
(a) and W dt tan tFjijkFœ œ Ê œ Ê œ œ œ
ˆ‰ cd
"""
" "
!
t1 dt dt t1 t1 4
dd
rr
†'0
11
(b) and 2t 4t W dt ln t 1 ln 2FjijkFœœÊœÊœœœ
ˆ‰ cdab
"
$#
"
!
t1 dt dt t1 t1
d d 2t 2t
rr
†'0
1
(c) t t and t ; and ; and rijrijkF j ijF F j k
"# " " #
"""
#
œ œ œ œ Ê œ œ œ
ˆ‰
t 1 dt dt t 1 dt
dd d
rr r
†
0 W dtʜʜ œF#"
†d
dt t 1 4
r'0
11
9. Substitute the parametric representation for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate the work W .FFœ'C†d
dt
r
(a) t 2t t and 2 t 2t W 2 t 2t dt t tFijk ijkFœ œ Ê œ Ê œ œ œ
ÈÈ È È
ˆ‰‘
dd 4
dt dt 3 3
rr
†'0
1$Î# # "
!
"
(b) t 2t t and 2t 4t 4t 3t W 4t 3t dt t tFijk ij kFœ œ Ê œ Ê œ œ œ
# $ %# %# &$
"
!
"dd 4
dt dt 5 5
rr
†'0
1ab
‘
(c) t t and t ; 2t t and 2t W 2t dtr i j r ij kF j k ij F
"# " " "
œ œ œ œ Ê œ Ê œ
Èdd
dt dt
rr
†'0
1
1; t 2 and 1 W dt 1 W W W 0œ œ œÊ œÊ œ œÊœœFijk kF
###"#
Èdd
dt dt
rr
†'0
1
10. Substitute the parametric representation for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate the work W .FFœ'C†d
dt
r
(a) t t t and 3t W 3t dt 1Fijk ijkFœ œÊ œ Ê œ œ
### # #
dd
dt dt
rr
†'0
1
(b) t t t and 2t 4t t 2t 4t W t 2t 4t dtFijk ij kFœ œ Ê œ Ê œ
$'& $ $() $()
dd
dt dt
rr
†'0
1ab
tœ œ
’“
tt4 17
449 18
*"
!
(c) t t and t ; t and t W t dt ;rijrijkF i ijF
"# " " "
###
"
œ œ œ œ Ê œ Ê œ œ
dd
dt dt 3
rr
†'0
1
t t and t W t dt W W WFijk k F
###"#
"
#
œ œÊ œÊ œ œÊœœ
dd
dt dt 6
5
rr
†'0
1
11. Substitute the parametric representation for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate the work W .FFœ'C†d
dt
r
(a) 3t 3t 3t and 3t 1 W 3t 1 dt t t 2FijkijkFœ œ Ê œ Ê œ œ œab abcd
###$
"
!
dd
dt dt
rr
†'0
1
(b) 3t 3t 3t and 2t 4t 6t 4t 3t 3tFijkijkFœ œ Ê œab
# % $ &$#
dd
dt dt
rr
†
W 6t4t3t3t dt ttt tÊ œ œ œ
'0
1ab
‘
&$# '%$ #
##
"
!
33
(c) t t and t ; 3t 3t and 3t 3tr i j r ij kF ik ij F
"# " "
##
œ œ œ œ Ê œ ab dd
dt dt
rr
†
W 3t 3t dt t t ; 3t and 1 W dt 1Êœ œ œ œ œÊ œÊœ œ
"###
#$#
"
!
"
#
''
0 0
1 1
ab
‘
3
2dtdt
dd
Fjk kF
rr
†
WW WÊœœ
"#
1
2
12. Substitute the parametric representation for (t) x(t) y(t) z(t) representing each path into the vectorrijkœ
field , and calculate the work W .FFœ'C†d
dt
r
(a) 2t 2t 2t and 6t W 6t dt 3t 3Fijk ijkFœ œÊ œÊ œ œ œ
dd
dt dt
rr
†'0
1cd
#"
!
(b) t t t t t t and 2t 4t 6t 5t 3tFijkijkFœ œ Ê œ a babab
#% % # $ &%#
dd
dt dt
rr
†
W 6t5t3t dtttt 3Êœ œ œ
'0
1abcd
&%# '&$
"
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.2 Vector Fields, Work, Circulation, and Flux 1003
(c) t t and t ; t t 2t and 2t W 2t dt ;rijrijkFijk ijF
"# " " "
œ œ œ œÊ œ Ê œ œ"
dd
dt dt
rr
†'0
1
(1 t) (t 1) 2 and 2 W 2 dt 2 W W W 3FijkkF
###"#
œ œÊ œÊ œ œÊ œ œ
dd
dt dt
rr
†'0
1
13. t t t , 0 t 1, and xy y yz t t t and 2tri jk F i j k F i j k i jkœ ŸŸ œ Êœ œ
#$#$
d
dt
r
2t work 2t dtʜʜ œF†d
dt
r$$
"
#
'0
1
14. (cos t) (sin t) , 0 t 2 , and 2y 3x (x y)rijk Fij kœ ŸŸ œ
t
61
(2 sin t) (3 cos t) (cos t sin t) and ( sin t) (cos t) Êœ œ ÊFij k ijkF
dd
dt 6 dt
rr"†
3 cos t 2sin t cos t sin t work 3 cos t 2 sin t cos t sin t dtœÊœ
##
"" ""
22
66 66
'0
2ˆ‰
t sin 2t t sin t cos tœ œ
‘
3 3 sin 2t
24 2 6 6
""
#
!
11
15. (sin t) (cos t) t , 0 t 2 , and z x y t (sin t) (cos t) andrijk FijkFijkœ ŸŸ œÊœ1
(cos t) (sin t) t cos t sin t cos t work t cos t sin t cos t dt
dd
dt dt
rr
œÊœÊœ ijkF†##
'0
2ab
cos t t sin t sin tœ œ
‘
tsin 2t
24
#
!
11
16. (sin t) (cos t) , 0 t 2 , and 6z y 12x t cos t (12 sin t) andrijk FijkFi j kœ ŸŸ œÊœ
t
61##
ab
(cos t) (sin t) t cos t sin t cos t 2 sin t
dd
dt 6 dt
rr
œÊœ ijkF
"#
†
work t cos t sin t cos t 2 sin t dt cos t t sin t cos t 2 cos t 0Êœ œ œ
'0
2ab
‘
#$
#
!
1
3
1
17. x t and y x t t t , 1 t 2, and xy (x y) t t t andœœœÊœŸŸ œÊœ
## # $ #
ri j F i j F i jab
2t t 2t 2t 3t 2t xy dx (x y) dy dt 3t 2t dt
dd d
dt dt dt
rr r
œ Ê œ œ Ê œ œ ijF F††
$#$ $# $#
ab ab
'''
CC
tt 12œ œ œœ
‘ˆ‰ˆ‰
3 2 16 3 2 45 18 69
43 3 43434
%$
#
"
18. Along (0 0) to (1 0): t , 0 t 1, and (x y) (x y) t t and t;ßßœŸŸ œÊœ œÊœri F i j Fij i F
dd
dt dt
rr
†
Along (1 0) to (0 1): (1 t) t , 0 t 1, and (x y) (x y) (1 2t) andß ß œ ŸŸ œ Êœ rij F i jF ij
2t;
dd
dt dt
rr
œ Ê œij F†
Along (0 1) to (0 0): (1 t) , 0 t 1, and (x y) (x y) (t 1) (1 t) andß ß œ ŸŸ œ Êœ rj F i jFij
t 1 (x y) dx (x y) dy t dt 2t dt (t 1) dt (4t 1) dt
dd
dt dt
rr
œ Ê œ Ê œ œ jF†'''''
C0000
11 1 1
2t t 2 1 1œ œœcd
#"
!
19. x y y y , 2 y 1, and x y y y 2y and 2y yr ij ij F ij ij ij Fœœ œ œ Ê œ œ
##% &
dd
dy dy
rr
†
ds dy 2y y dy y yÊœ œœœœœ
'' '
C2 2
11
FT F††
d64 4 3 63 39
dy 3 3 3 3
rab
‘ˆ‰ˆ‰
&'#
"" ""
#####
"
#
20. (cos t) (sin t) , 0 t , and y x (sin t) (cos t) and ( sin t) (cos t)rij FijFij ijœ ŸŸ œÊœ œ
1
#
d
dt
r
FFrʆ †
d
dt
rœ œ Ê œ œsin t cos t 1 d ( 1) dt
##
#
''
C0
21
21. ( ) t( 2 ) (1 t) (1 2t) , 0 t 1, and xy (y x) 1 3t 2t t andrij ij i j F i j F ijœ œ ŸŸ œ Ê œ ab
#
2 1 5t 2t work dt 1 5t 2t dt t t t
dd d 5225
dt dt dt 2 3 6
rr r
œ Ê œ Ê œ œ œ œij F F††
###$
"
!
''
C0
1ab
‘
22. (2 cos t) (2 sin t) , 0 t 2 , and f 2(x y) 2(x y)rij F ijœ ŸŸ œœ1™
4(cos t sin t) 4(cos t sin t) and ( 2 sin t) (2 cos t) Êœ œ ÊFij ijF
dd
dt dt
rr
†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1004 Chapter 16 Integration in Vector Fields
8 sin t cos t sin t 8 cos t cos t sin t 8 cos t sin t 8 cos 2t work f dœ œ œ Ê œababab
## ## 'C™†r
dt 8 cos 2t dt 4 sin 2t 0œœ œœ
''
C0
2
F†d
dt
rcd
#
!
1
23. (a) (cos t) (sin t) , 0 t 2 , x y , and y x ( sin t) (cos t) ,rij FijFij ijœ ŸŸœ œÊœ1"#d
dt
r
(cos t) (sin t) , and ( sin t) (cos t) 0 and sin t cos t 1FijF ijF F
"# "#
##
œ œ Ê œ œœ††
dd
dt dt
rr
Circ 0 dt 0 and Circ dt 2 ; (cos t) (sin t) cos t sin t 1 andÊœ œ œ œœ Ê œœ
"# "
##
''
00
22
1nijFn†
0 Flux dt 2 and Flux 0 dt 0Fn
#" #
†œÊ œ œ œ œ
''
00
22
1
(b) (cos t) (4 sin t) , 0 t 2 ( sin t) (4 cos t) , (cos t) (4 sin t) , andri j i jF i jœ ŸŸÊœ œ1d
dt
r"
( 4 sin t) (cos t) 15 sin t cos t and 4 Circ 15 sin t cos t dtFijF F
#"#"
œ Ê œ œ Ê œ††
dd
dt dt
rr
'0
2
sin t 0 and Circ 4 dt 8 ; cos t sin t œœœœœ Ê
‘ Š‹Š‹
" "
##
!# "
54
217 17
1'0
2
1nijFn
ÈÈ †
cos t sin t and sin t cos t Flux ( ) dt 17 dtœ œ Êœ œ
44 15 4
17 17 17 17
ÈÈ È È
##
#""
Fn Fnv††
''
00
22
kk Š‹
È
8 and Flux ( ) dt sin t cos t 17 dt sin t 0œœ œ œœ1## ##
!
''
00
22
Fnv†kk Š‹
È‘
15 15
17 2
È1
24. (a cos t) (a sin t) , 0 t 2 , 2x 3y , and 2x (x y) ( a sin t) (a cos t) ,rij FijFij ijœ ŸŸ œ œ Êœ 1"# d
dt
r
(2a cos t) (3a sin t) , and (2a cos t) (a cos t a sin t) (a cos t) (a sin t) ,FijFi jnvij
"#
œ œÊœkk
2a cos t 3a sin t, and 2a cos t a sin t cos t a sin tFnv Fnv
"#
## ## ## # ##
††kk kkœ œ
Flux 2a cos t 3a sin t dt 2a 3a a , andÊœ œ œ
"## ## # # #
##
!!
'0
2ab
‘‘
tsin 2t tsin 2t
24 24
11
1
Flux 2a cos t a sin t cos t a sin t dt 2a sin t a a
### # ## # # # #
##
!!
#
#
!
œœœ
'0
2abcd
‘ ‘
t sin 2t a t sin 2t
24 24
11
11
25. (a cos t) (a sin t) , ( a sin t) (a cos t) 0 Circ 0; M a cos t,Fij ijF
""""
œ œ ʜʜœ
dd
dt dt
rr
†
N a sin t, dx a sin t dt, dy a cos t dt Flux M dy N dx a cos t a sin t dt
""""
## ##
œœ œÊœœ
''
C0
ab
a dt a ;œœ
'0
##
1
t , t Circ t dt 0; M t, N 0, dx dt, dy 0 FluxFi iF
##### #
œœÊ œÊœ œœœœœÊ
dd
dt dt
rr
†'a
a
M dy N dx 0 dt 0; therefore, Circ Circ Circ 0 and Flux Flux Flux aœ œ œ œœ œ œ
''
Ca
a
## "# "#
#1
26. a cos t a sin t , ( a sin t) (a cos t) a sin t cos t a cos t sin tFij ijF
" "
#### $#$#
œ œÊœ abab
dd
dt dt
rr
†
Circ a sin t cos t a cos t sin t dt ; M a cos t, N a sin t, dy a cos t dt,Êœ œ œ œ œ
"""
$#$# ## ##
'0ab
2a
3
dx a sin t dt Flux M dy N dx a cos t a sin t dt a ;œ Ê œ œ œ
""" $$ $$ $
''
C0
ab
4
3
t , t Circ t dt ; M t , N 0, dy 0, dx dtFi iF
### ##
####
œ œÊ œÊ œ œ œ œœœ
dd
dt dt 3
2a
rr
†'a
a
Flux M dy N dx 0; therefore, Circ Circ Circ 0 and Flux Flux Flux aÊ œ œ œœ œ œ
### "# "#
$
'C
4
3
27. ( a sin t) (a cos t) , ( a sin t) (a cos t) a sin t a cos t aFij ijF
" " ## # # #
œ œ Ê œ œ
dd
dt dt
rr
†
Circ a dt a ; M a sin t, N a cos t, dx a sin t dt, dy a cos t dtÊœ œ œ œ œ œ
"""
##
'01
Flux M dy N dx a sin t cos t a sin t cos t dt 0; t , 0Êœ œ œœœÊ œ
""" # #
##
''
C0
abFj iF
dd
dt dt
rr
†
Circ 0; M 0, N t, dx dt, dy 0 Flux M dy N dx t dt 0; therefore,ÊœœœœœÊ œ œœ
### # ##
''
Ca
a
Circ Circ Circ a and Flux Flux Flux 0œœ œ œ
"# " #
#1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.2 Vector Fields, Work, Circulation, and Flux 1005
28. a sin t a cos t , ( a sin t) (a cos t) a sin t a cos tFij ijF
" "
## # # $$ $ $
œ œ Ê œ abab
dd
dt dt
rr
†
Circ a sin t a cos t dt a ; M a sin t, N a cos t, dy a cos t dt, dx a sin t dtÊ œ œ œ œ œ œ
"""
$$ $ $ $ ## # #
'0ab
4
3
Flux M dy N dx a cos t sin t a sin t cos t dt a ; t , 0Êœ œ œ œ œÊ œ
""" # #
$#$# $#
''
C0
ab
2
3dtdt
dd
Fj iF
rr
†
Circ 0; M 0, N t , dy 0, dx dt Flux M dy N dx t dt a ; therefore,ÊœœœœœÊ œ œœ
### # ##
##$
''
Ca
a2
3
Circ Circ Circ a and Flux Flux Flux 0œœ œ œ
"# " #
$
4
3
29. (a) (cos t) (sin t) , 0 t , and (x y) x y ( sin t) (cos t) andrij F i j ijœ ŸŸ œÊœ1ab
## d
dt
r
(cos t sin t) cos t sin t sin t cos t sin t cos t dsFi jF FTœ Ê œ Êab
## #
††
d
dt
r'C
sin t cos t sin t cos t dt sin t sin tœ œ œ
'0ab
‘
##
"
##
!
24
tsin 2t 11
(b) (1 2t) , 0 t 1, and (x y) x y 2 and (1 2t) (1 2t) ri Fi j iFi jœ ŸŸ œ Ê œ œ Êab
## #
d
dt
r
4t 2 ds (4t 2) dt 2t 2t 0FFT††
d
dt
rœÊ œ œ œ
''
C0
1cd
#"
!
(c) (1 t) t , 0 t 1, and (x y) x y and (1 2t) 1 2t 2trij Fi j ijFi j
"## #
œ ŸŸ œ Ê œ œ ab a b
d
dt
r
(2t 1) 1 2t 2t 2t Flow 2t dt ; t (t 1) ,ÊœœÊœ œ œœFFrij††
d d
dt dt 3
2
r r
ab
## #
"#
''
C0
1
0 t 1, and (x y) x y and t t 2t 1ŸŸ œ Ê œ œ Fi j ijFi jab a b
## ##
d
dt
r
2t 2t 1 1 2t 2t 1 2t 2t Flow 2t 2t dtœ Ê œ œ Ê œ œ ijF Fab ab ab
### #
#
††
d d
dt dt
r r
''
C0
1
t t Flow Flow Flow 1œ œ Ê œ œœ
‘
#$
"
!
""
"#
22
33 33
30. From (1 0) to (0 1): (1 t) t , 0 t 1, and (x y) x y ,ß ß œ ŸŸ œ Ê œrij Fi j ij
"##
abd
dt
r
1 2t 2t , and 2t 2t Flux 2t 2t dtFi j nv ij Fnvœ œ Ê œ Ê œ abkk kk ab
###
"" " "
†"'0
1
tt ;œ œ
‘
#$
"
!
"2
33
From (0 1) to ( 1 0): t (1 t) , 0 t 1, and (x y) x y ,ßß œŸŸ œÊœri j F i j ij
###
abd
dt
r
(1 2t) 1 2t 2t , and (2t 1) 1 2t 2t 2 4t 2tFi jnvijFnvœ œ Ê œ œ a b kk kk a b
###
## ##
†
Flux 2 4t 2t dt 2t 2t t ;Êœœœ
###$
"
!
'0
1ab
‘
22
33
From ( 1 0) to (1 0): ( 1 2t) , 0 t 1, and (x y) x y 2 ,ß ß œ Ÿ Ÿ œ Ê œri Fiji
$##
abd
dt
r
( 1 2t) 1 4t 4t , and 2 2 1 4t 4tFi jnvjFnvœ œ Ê œ a b kk kk a b
##
$$ $$
†
Flux 2 1 4t 4t dt 2 t 2t t Flux Flux Flux FluxÊ œ œ œ Ê œ œœ
$"#$
##$
"
!
""
'0
1ab
‘
42 22
3 3 333 3
31. on x y 4;Fijœ œ
y
xy xy
x
ÈÈ
##
at (2 0), ; at (0 2), ; at ( 2 0),ßœ ßœßFj F i
; at ( 2), ; at 2 2 , ;Fj Fi F ijœ !ß œ ß œ
Š‹
ÈÈ È3
##
"
at 2 2 , ; at 2 2 ,
Š‹ Š‹
ÈÈ ÈÈ
ß œ ßFij
È3
##
"
; at 2 2 , Fij Fijœ ß œ
ÈÈ
33
## ##
""
Š‹
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
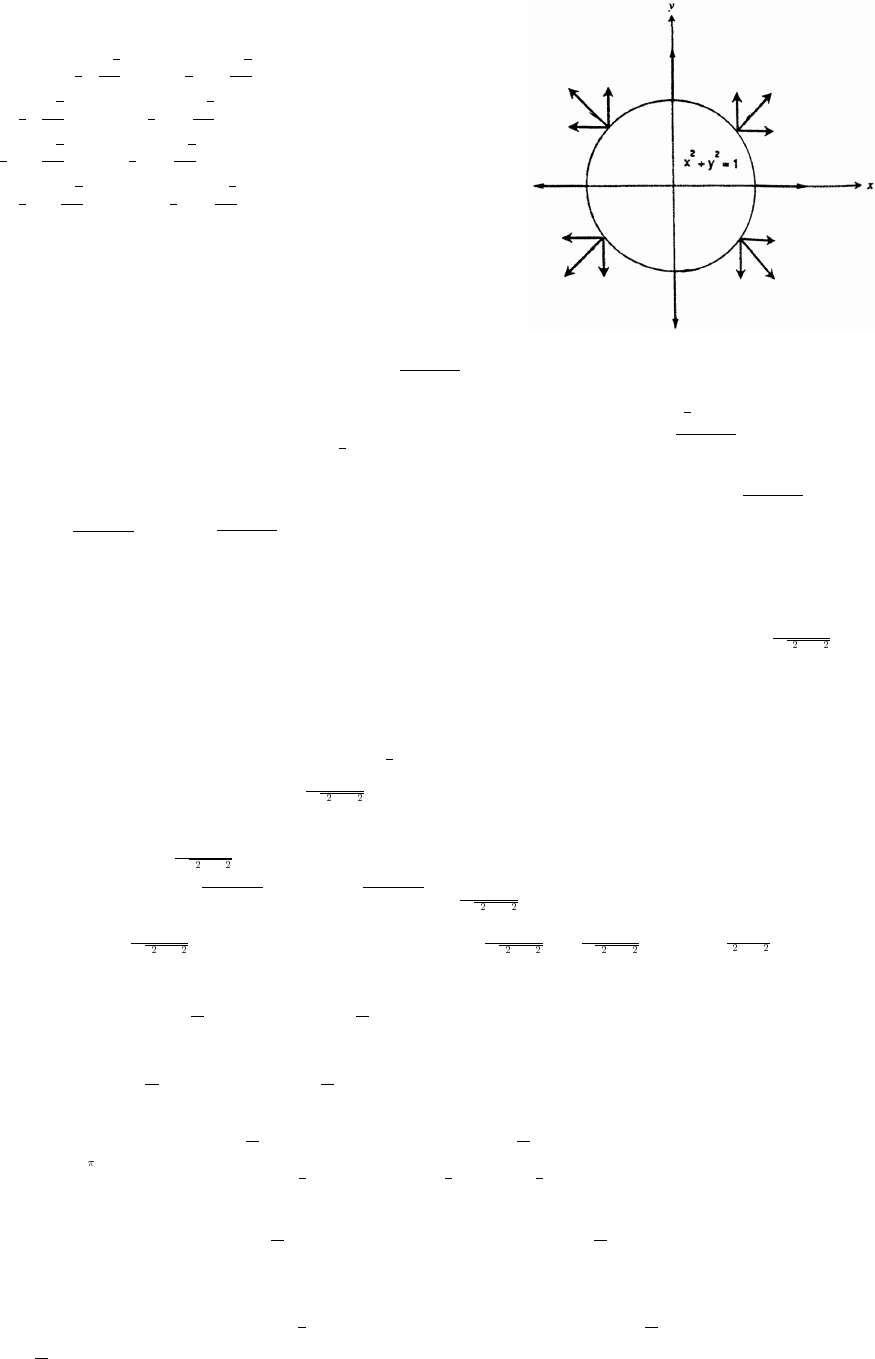
1006 Chapter 16 Integration in Vector Fields
32. x y on x y 1; at (1 0), ;Fij Fiœ œ ß œ
##
at ( 1 0), ; at (0 1), ; at (0 1),ß œ ß œ ßFi Fj
; at , ;Fj Fi jœ ß œ
Š‹
""
## # #
ÈÈ
33
at , ;
Š‹
ß œ
""
## # #
ÈÈ
33
Fij
at , ;
Š‹
""
## # #
ß œ
ÈÈ
33
Fi j
at , .
Š‹
ß œ
""
## # #
ÈÈ
33
Fij
33. (a) P(x y) Q(x y) is to have a magnitude a b and to be tangent to x y a b in aGijœß ß œ
È## ####
counterclockwise direction. Thus x y a b 2x 2yy 0 y is the slope of the tangent
#### w w
œ Ê œÊ œ
x
y
line at any point on the circle y at (a b). Let b a a b , with in aÊœ ß œÊ œ
w##
a
bvijv vkk È
counterclockwise direction and tangent to the circle. Then let P(x y) y and Q(x y) xߜ ߜ
y x for (a b) on x y a b we have b a and a b .Ê œ Ê ß œ œ œ Gij GijG
#### ##
kk È
(b) x y a b .GF Fœœ
ˆ‰
ÈŠ‹
È
## ##
34. (a) From Exercise 33, part a, y x is a vector tangent to the circle and pointing in a counterclockwiseij
direction y x is a vector tangent to the circle pointing in a clockwise direction Ê Êœij G y x
x y
i j
È
is a unit vector tangent to the circle and pointing in a clockwise direction.
(b) GFœ
35. The slope of the line through (x y) and the origin is x y is a vector parallel to that line andßÊœ
y
xvij
pointing away from the origin is the unit vector pointing toward the origin.ÊœFx y
x y
i j
È
36. (a) From Exercise 35, is a unit vector through (x y) pointing toward the origin and we wantß
x y
x y
i j
È
to have magnitude x y x y x y .kk ÈÈ
Š‹
FFij
## ##
Êœ œ
x y
x y
i j
È
(b) We want where C 0 is a constant C .kk Š‹Š‹
FFœ Á Êœœ
CC
x y x y x y
x y x y
x y
ÈÈÈ
i j i j
37. 4t 8t 2 and 2t 12t Flow 12t dt 3t 48Fijk ijFœ œ Ê œ Ê œ œ œ
$# $ $ %
#
!
dd
dt dt
rr
†'0
2cd
38. 12t 9t and 3 4 72t Flow 72t dt 24t 24Fjk jkFœ œÊ œÊ œ œ œ
## # # $
"
!
dd
dt dt
rr
†'0
1cd
39. (cos t sin t) (cos t) and ( sin t) (cos t) sin t cos t 1Fik ikFœ œ Ê œ
dd
dt dt
rr
†
Flow ( sin t cos t 1) dt cos t t 0Êœ œ œœ
'0‘ˆ‰ˆ‰
"""
#
!##2
111
40. ( 2 sin t) (2 cos t) 2 and (2 sin t) (2 cos t) 2 4 sin t 4 cos t 4 0Fijk ijkFœ œ Ê œ œ
dd
dt dt
rr
†##
Flow 0ʜ
41. C : (cos t) (sin t) t , 0 t (2 cos t) 2t (2 sin t) and ( sin t) (cos t)
"#
rijk F ij k ijkœŸŸÊœ œ
1d
dt
r
2 cos t sin t 2t cos t 2 sin t sin 2t 2t cos t 2 sin tÊœ œ F†d
dt
r
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.2 Vector Fields, Work, Circulation, and Flux 1007
Flow ( sin 2t 2t cos t 2 sin t) dt cos 2t 2t sin t 2 cos t 2 cos t 1 ;Êœ œ œ
""Î#
!
'0
2‘
2
11
C : (1 t) , 0 t 1 (1 t) 2 and
## #
rj k F j k k Fœ ŸŸ Ê œ œ Ê œ
1 1
11
dd
dt dt
rr
†
Flow dt t ;Êœœœ
#"
!
'0
1
111cd
C : t (1 t) , 0 t 1 2t 2(1 t) and 2t
$ri j F i k ij Fœ ŸŸ Ê œ œÊ œ
dd
dt dt
rr
†
Flow 2t dt t 1 Circulation ( 1 ) 1 0Êœ œœÊ œœ
$#"
!
'0
1cd 11
42. x y z , where f(x y z) x y x f tFFr† †
d dx dz f dx f f dz d d
dt dt dt dt x dt y dt z dt dt dt
dy dy
r r
œœ ßßœ Ê œ
``` "
``` #
###
ab ababab
by the chain rule Circulation dt f t dt f b f a . Since C is an entire ellipse,Êœœ œ
''
Ca
b
Frrr†dd
dt dt
rabababab ab abab
b a , thus the Circulation 0.rrab abœœ
43. Let x t be the parameter y x t and z x t t t t , 0 t 1 from (0 0 0) to (1 1 1)œ Êœœ œœÊœ ŸŸ ßß ßß
## #
ri jk
2t and xy y yz t t t t 2t t 2t Flow 2t dtÊ œ œ œ Ê œ œ Ê œ
d d
dt dt
r r
ijkF ij kijkF
$#$ $ $$ $ $
†'0
1
œ"
#
44. (a) xy z , where f(x y z) xy z dtFF FœÊœœ ßߜʙ† †ab
#$ #$
```
```
d f dx f z dz df d
dt x dt y dt z dt dt dt
dy
r r
)C
f t dt f b f a 0 since C is an entire ellipse.œœœ
'a
bd
dt abababab ab ababrrr
(b) xy z dt xy z (2)(1) ( 1) (1)(1) (1) 2 1 3
''
C 111
21 1
F†dd
dt dt
rœœœœœabcd
#$ #$ # $ # $
Ð#ß"ß"Ñ
Ð"ß"ß"Ñ
45. Yes. The work and area have the same numerical value because work d y dœœ
''
CC
Fr ir††
[f(t) ] dt [On the path, y equals f(t)]œ
'b
a
ii j†‘
df
dt
f(t) dt Area under the curve [because f(t) 0]œœ
'a
b
46. x y x f(x) f (x) ; (x y ) has constant magnitude k and points awayriji j i jF ijœœ Ê œ œ
dk
dx x y
rw
È
from the origin k x [f(x)] , by the chain ruleÊœœ œ F†dkx d
dx dx
x y x y x [f(x)]
k y f (x) kx k f(x) f (x)
rÈÈ È
†† † † ##
È
ds dx k x [f(x)] dx k x [f(x)]Êœ œ œ
'' '
CC a
bb
a
FT F††
dd
dx dx
rÈÈ
‘
## ##
k b [f(b)] a [f(a)] , as claimed.œ
ˆ‰
ÈÈ
####
47-52. Example CAS commands:
:Maple
with( LinearAlgebra );#47
F := r -> < r[1]*r[2]^6 | 3*r[1]*(r[1]*r[2]^5+2) >;
r := t -> < 2*cos(t) | sin(t) >;
a,b := 0,2*Pi;
dr := map(diff,r(t),t); # (a)
F(r(t)); # (b)
q1 := simplify( F(r(t)) . dr ) assuming t::real; # (c)
q2 := Int( q1, t=a..b );
value( q2 );
: (functions and bounds will vary):Mathematica
Exercises 47 and 48 use vectors in 2 dimensions
Clear[x, y, t, f, r, v]
f[x_, y_]:= {x y , 3x (x y 2)}
65
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
1008 Chapter 16 Integration in Vector Fields
{a, b}={0, 2 };1
x[t_]:= 2 Cos[t]
y[t_]:= Sin[t]
r[t_]:={x[t], y[t]}
v[t_]:= r'[t]
integrand= f[x[t], y[t]] . v[t] //Simplify
Integrate[integrand,{t, a, b}]
N[%]
If the integration takes too long or cannot be done, use NIntegrate to integrate numerically. This is suggested for exercises
49 - 52 that use vectors in 3 dimensions. Be certain to leave spaces between variables to be multiplied.
Clear[x, y, z, t, f, r, v]
f[x_, y_, z_]:= {y y z Cos[x y z], x x z Cos[x y z], z x y Cos[x y z]}
2
{a, b}={0, 2 };1
x[t_]:= 2 Cos[t]
y[t_]:= 3 Sin[t]
z[t_]:= 1
r[t_]:={x[t], y[t], z[t]}
v[t_]:= r'[t]
integrand= f[x[t], y[t],z[t]] . v[t] //Simplify
NIntegrate[integrand,{t, a, b}]
16.3 PATH INDEPENDENCE, POTENTIAL FUNCTIONS, AND CONSERVATIVE FIELDS
1. x , y , z Conservative
``` ```
``````
PNMPNM
yzzxxy
œœ œœ œœ Ê
2. x cos z , y cos z , sin z Conservative
``` ```
``````
PNMPNM
yzzxxy
œœ œœœœÊ
3. 1 1 Not Conservative 4. 1 1 Not Conservative
`` ` `
`` ` `
PN NM
yz x y
œ Á œ Ê œ Á œ Ê
5. 0 1 Not Conservative
``
``
NM
xy
œÁœ Ê
6. 0 , 0 , e sin y Conservative
``` `` `
````` `
PNMPN M
yzzxx y
x
œœ œœ œ œ Ê
7. 2x f(x y z) x g(y z) 3y g(y z) h(z) f(x y z) x h(z)
``
```##
# #
`
ff
xyy
g3y 3y
œÊßßœßÊœœÊßœ Êßßœ
h (z) 4z h(z) 2z C f(x y z) x 2z CÊœ œÊ œÊßßœ
`
` #
w###
f
z
3y
8. y z f(x y z) (y z)x g(y z) x x z z g(y z) zy h(z)
``
````
``
ff
xyyy
gg
œ Ê ßß œ ß Ê œ œ Ê œ Ê ß œ
f(x y z) (y z)x zy h(z) x y h (z) x y h (z) 0 h(z) C f(x y z)Êßßœ Êœ œÊ œÊ œÊßß
`
`
ww
f
z
(yz)xzyCœ
9. e f(x y z) xe g(y z) xe xe 0 f(x y z)
``
````
``
ff
xyyy
y 2z y 2z y 2z y 2z
gg
œÊßßœßÊœœ ÊœÊßß
xe h(z) 2xe h (z) 2xe h (z) 0 h(z) C f(x y z) xe CœÊœ œ ʜʜÊßßœ
y 2z y 2z y 2z y 2z
f
z
ww
`
`
10. y sin z f(x y z) xy sin z g(y z) x sin z x sin z 0 g(y z) h(z)
``
````
``
ff
xyyy
gg
œÊßßœ ßÊœœÊœÊßœ
f(x y z) xy sin z h(z) xy cos z h (z) xy cos z h (z) 0 h(z) C f(x y z)Êßßœ Êœ œ Ê œÊ œÊßß
`
`
ww
f
z
xy sin z Cœ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.3 Path Independence, Potential Functions, and Conservative Fields 1009
11. f(x y z) ln y z g(x y) ln x sec (x y) g(x y)
`" `
` # ``
## #
`
fz f
zyz x x
g
œÊßßœ ßÊœœÊßab
(x ln x x) tan (x y) h(y) f(x y z) ln y z (x ln x x) tan (x y) h(y)œ Êßßœ
"
#
##
ab
sec (x y) h (y) sec (x y) h (y) 0 h(y) C f(x y z)Êœ œ Ê œÊ œÊßß
`
`
#w# w
f
yyz yz
yy
ln y z (x ln x x) tan (x y) Cœ
"
#
##
ab
12. f(x y z) tan (xy) g(y z)
``
` ` `
" `
ffxxz
x1xy y1xy y1xy
y g
1yz
œ Êßßœ ßÊœœ
È
g(y z) sin (yz) h(z) f(x y z) tan (xy) sin (yz) h(z)Êœ Êßœ Êßßœ
`
`
" " "
g
y
z
1yz
È
h (z) h (z) h(z) ln z CÊÊœ œ Ê œÊ œ
`""
`
ww
f
zzz
yy
1yz 1yz
ÈÈ kk
f(x y z) tan (xy) sin (yz) ln z CÊßßœ
" " kk
13. Let (x y z) 2x 2y 2z 0 , 0 , 0 M dx N dy P dz isFijkßßœ Êœœ œœ œœ Ê
``` `` `
````` `
PNMPNM
yzz xx y
exact; 2x f(x y z) x g(y z) 2y g(y z) y h(z) f(x y z) x y h(z)
``
```
####
`
ff
xyy
g
œ Ê ßßœ ßÊ œ œ Ê ßœ Ê ßßœœ
h (z) 2z h(z) z C f(x y z) x y z C 2x dx 2y dy 2z dzÊ œ œ Ê œÊ ßßœÊ
`
`
w# ###
f
z'000
23 6
f(2 3 6) f( ) 2 3 ( 6) 49œ ß ß !ß!ß! œ œ
## #
14. Let (x y z) yz xz xy x , y , z M dx N dy P dz isFijkßßœ Ê œœ œœ œœ Ê
``` ```
``````
PNMPNM
yzzxxy
exact; yz f(x y z) xyz g(y z) xz xz 0 g(y z) h(z) f(x y z)
``
````
``
ff
xyyy
gg
œÊßßœ ßÊœœÊœÊ ßœ Êßß
xyz h(z) xy h (z) xy h (z) 0 h(z) C f(x y z) xyz Cœ Êœ œÊ œÊ œÊßßœ
`
`
ww
f
z
yz dx xz dy xy dz f(3 5 0) f(1 1 2) 0 2 2Ê œ ßß ßß œœ
'112
350
15. Let (x y z) 2xy x z 2yz 2z , 0 , 2xFijkßß œ Ê œ œ œ œ œ œab
## ``````
``````
PNMPNM
yzzxxy
M dx N dy P dz is exact; 2xy f(x y z) x y g(y z) x x z zÊ œÊßßœßÊœœÊœ
``
````
#####
``
ff
xyyy
gg
g(y z) yz h(z) f(x y z) x y yz h(z) 2yz h (z) 2yz h (z) 0 h(z) CÊ ß œ Ê ß ß œ Ê œ œ Ê œ Ê œ
### ww
`
`
f
z
f(x y z) x y yz C 2xy dx x z dy 2yz dz f( ) f( ) 2 2(3) 16Ê ß ß œ Ê œ "ß#ß$ !ß!ß! œ œ
## ## #
'000
123 ab
16. Let (x y z) 2x y 0 , 0 , 0Fijkßß œ Ê œœ œœ œœ
#
``````
``` `` `
ˆ‰
4PNMPNM
1z y z z x x y
M dx N dy P dz is exact; 2x f(x y z) x g(y z) y g(y z) h(z)Ê œ Ê ß ß œ ß Ê œ œ Ê ß œ
``
```
##
`
ff
xyy3
gy
f(x y z) x h(z) h (z) h(z) 4 tan z C f(x y z)Êßßœ Êœ œ Ê œ Êßß
#w "
`
`
y
3z1z
f4
x 4 tan z C 2x dx y dy dz f(3 3 1) f( )œ Ê œ ß ß !ß!ß!
#" #
y
31z
4
'000
331
94(0)œ !! œ
ˆ‰
27
34
†11
17. Let (x y z) (sin y cos x) (cos y sin x) 0 , 0 , cos y cos xFijkßߜʜœœœœœ
``` `` `
````` `
PNMPN M
yzzxx y
M dx N dy P dz is exact; sin y cos x f(x y z) sin y sin x g(y z) cos y sin xÊ œ Êßßœ ßÊœ
` `
```
`
f f
xyy
g
cos y sin x 0 g(y z) h(z) f(x y z) sin y sin x h(z) h (z) 1 h(z) z Cœ Ê œÊ ßœ Ê ßßœ Ê œ œÊ œ
`
` `
`w
g
y z
f
f(x y z) sin y sin x z C sin y cos x dx cos y sin x dy dz f(0 1 1) f(1 )Ê ßßœ Ê œ ßß ß!ß!
'100
011
(0 1) (0 0) 1œœ
18. Let (x y z) (2 cos y) 2x sin y 0 , 0 , 2 sin yFijkßß œ Ê œ œ œ œ œ œ
Š‹
ˆ‰
""``````
````` `yzyzzxxy
PNMPN M
M dx N dy P dz is exact; 2 cos y f(x y z) 2x cos y g(y z) 2x sin yÊ œ Êßßœ ßÊœ
``
```
`
ff
xyy
g
2x sin y g(y z) ln y h(z) f(x y z) 2x cos y ln y h(z) h (z)œ Ê œ Ê ß œ Ê ßß œ Ê œ œ
"" `"
`
` `
w
yyy zz
gf
kk kk
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1010 Chapter 16 Integration in Vector Fields
h(z) ln z C f(x y z) 2x cos y ln y ln z CÊœ Êßßœ kk kk kk
2 cos y dx 2x sin y dy dz f 1 2 f( )Ê œ ß ß !ß #ß "
'021
122 Š‹ ˆ‰
""
#yz
1
2 0 ln ln 2 (0 cos 2 ln 2 ln 1) ln œ œ
ˆ‰
††
11
##
19. Let (x y z) 3x (2z ln y) , 0 , 0Fijkßß œ Ê œ œ œœ œœ
#``````
``````
Š‹
zP2zNMPNM
yyyzzxxy
M dx N dy P dz is exact; 3x f(x y z) x g(y z) g(y z) z ln y h(z)Ê œ Ê ßßœ ß Ê œ œ Ê ßœ
``
```
#$ #
`
ffz
xyyy
g
f(x y z) x z ln y h(z) 2z ln y h (z) 2z ln y h (z) 0 h(z) C f(x y z)Êßßœ Êœ œ Ê œÊ œÊßß
$# w w
`
`
f
z
x z ln y C 3x dx dy 2z ln y dz f(1 2 3) f( )œ Ê œ ß ß "ß "ß "
$# #
'111
123 z
y
(1 9 ln 2 C) (1 0 C) 9 ln 2œ œ
20. Let (x y z) (2x ln y yz) xz (xy) x , y , zFijkßß œ Ê œ œ œ œ œ œ
Š‹
xPNMPN2xM
yyzzxxyy
``` `` `
````` `
M dx N dy P dz is exact; 2x ln y yz f(x y z) x ln y xyz g(y z) xzÊ œ Êßßœ ßÊœ
` `
```
#`
ffx
xyy y
g
xz 0 g(y z) h(z) f(x y z) x ln y xyz h(z) xy h (z) xy h (z) 0œÊ œÊ ßœ Ê ßßœ Ê œ œÊ œ
x f
yy z
g
`
` `
#ww
`
h(z) C f(x y z) x ln y xyz C (2x ln y yz) dx xz dy xy dzÊœÊßßœ Ê
#'121
211 Š‹
x
y
f(2 1 1) f( 2 1) (4 ln 1 2 C) (ln 2 2 C) ln 2œ ß ß "ß ß œ œ
21. Let (x y z) , 0 , Fijkßß œ Ê œ œ œ œ œ œ
Š‹ Š ‹ ˆ‰
"`"`````
````` `yzy z yzzz xxyy
1x P NM PN 1 M
y
M dx N dy P dz is exact; f(x y z) g(y z) Ê œÊßßœßÊœœ
`" ` "
```
`
fxfxx
xy y y y yzy
g
g(y z) h(z) f(x y z) h(z) h (z) h (z) 0 h(z) CÊ œÊ ßœ Ê ßßœ Ê œ œ Ê œÊ œ
`
` `
" ` ww
gy y yy
yz z yz z z z
xf
f(x y z) C dx dy dz f(2 2 2) f( 1 1) C CÊ ßßœÊ œ ßß"ßßœ
x1x 22
yz y zy z 11
yy
'111
222 """
##
Š‹ ˆ‰ˆ‰
0œ
22. Let (x y z) and let x y z , , Fßßœ œÊœœœ
2x 2y 2z y
xyz x y z
xz
ijk
` ` `
#### ```
Š‹
3333
333
, , M dx N dy P dz is exact;Êœœ œœ œœ Ê
``` `` `
````` `
P N M 4xz P N M
yzzxx y
4yz 4xy
333
f(xyz) lnx y z g(yz)
` `
` ``
### `
f2x f
x xyz y xyz y xyz
2y g 2y
œÊßßœßÊœœab
0 g(y z) h(z) f(x y z) ln x y z h(z) h (z)ÊœÊßœ Êßßœ Êœ
`
``
### w
`
g
yz xyz
f2z
ab
h (z) 0 h(z) C f(x y z) ln x y z CœÊœÊœÊßßœ
2z
xyz
w###
ab
f(2 2 2) f( 1 1) ln 12 ln 3 ln 4Êœßß"ßßœœ
'111
222 2x dx 2y dy 2z dz
xyz
23. ( ) t( 2 2 ) (1 t) (1 2t) (1 2t) , 0 t 1 dx dt, dy 2 dt, dz 2 dtrijk ijk i j kœ œ ŸŸÊ œ œ œ
y dx x dy 4 dz (2t 1) dt (t 1)(2 dt) 4( 2) dt (4t 5) dt 2t 5t 3Ê œ œ œœ
'' '
111 0 0
23 1 1 1 cd
#"
!
24. t(3 4 ), 0 t 1 dx 0, dy 3 dt, dz 4 dt x dx yz dy dzrjkœ ŸŸÊœ œ œ Ê
'000
034 #
#
Š‹
y
12t (3 dt) (4 dt) 54t dt 18t 18œœœœ
''
00
11
ab cd
Š‹
###
#
"
!
9t
25. 0 , 2z , 0 M dx N dy P dz is exact is conservative
``` `` `
``` `` `
PNM PNM
yzz xx y
œœ œ œ œœ Ê ÊF
path independenceÊ
26. , ,
``` `` `
````` `
PNMxzPNM
yzzxx y
yz xy
xyz xyz xyz
œ œ œ œ œ œ
ˆ‰ ˆ‰ ˆ‰
ÈÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 16.3 Path Independence, Potential Functions, and Conservative Fields 1011
M dx N dy P dz is exact is conservative path independenceÊ Ê ÊF
27. 0 , 0 , is conservative there exists an f so that f;
``` `` `
````` `
PNMPN2xM
yzzxxyy
œœ œœ œ œ Ê Ê œFF™
f(x y) g(y) g (y) g (y) g(y) C
``""
``
ww
f2x x f x 1x
xy y y y y y y
œÊßœ Êœ œ Ê œÊ œ
f(x y) C Êߜʜ
xx1
yy y
"
F™Š‹
28. cos z , 0 , is conservative there exists an f so that f;
``````
``````
PNMPNeM
yzzxxyy
œœ œœ œœÊ Ê œ
xFF™
e ln y f(x y z) e ln y g(y z) sin z sin z g(y z)
``
````
``
ffee
xyyyyy
xx gg
œ Ê ßßœ ß Ê œ œ Ê œ Ê ß
xx
y sin z h(z) f(x y z) e ln y y sin z h(z) y cos z h (z) y cos z h (z) 0œÊßߜʜ œ Êœ
xf
z
`
`
ww
h(z) C f(x y z) e ln y y sin z C e ln y y sin zÊœÊßßœ Êœ
xx
F™ab
29. 0 , 0 , 1 is conservative there exists an f so that f;
``` `` `
````` `
PNMPNM
yzz xx y
œœ œœ œœ Ê Ê œFF™
x y f(x y z) x xy g(y z) x y x y g(y z) y h(z)
`"` "
````
#$ ##$
``
ff
x3yyy3
gg
œÊ ßßœ ßÊ œ œÊ œ Ê ßœ
f(x y z) x xy y h(z) h (z) ze h(z) ze e C f(x y z)Êßßœ Êœ œ Ê œÊßß
"" `
$$ w
`33 z
fzzz
xxy yzeeC xxy yzeeœÊœ
"" ""
$$ $$
33 33
zz zz
F™ˆ‰
(a) work dt d x xy y ze e 0 0 e e 0 0 1œ œ œ œ
''
AA
BB
FFr††
d
dt 3 3 3 3
zz
r‘ˆ‰ˆ‰
"" " "
$$ Ð"ß!ß"Ñ
Ð"ß!ß!Ñ
1œ
(b) work d x xy y ze e 1œœœ
'A
B
Fr†‘
""
$$ Ð"ß!ß"Ñ
Ð"ß!ß!Ñ
33
zz
(c) work d x xy y ze e 1œœœ
'A
B
Fr†‘
""
$$ Ð"ß!ß"Ñ
Ð"ß!ß!Ñ
33
zz
: Since is conservative, d is independent of the path from (1 0 0) to (1 0 1).Note FFr
'A
B
†ßß ßß
30. xe xyze cos y , ye , ze is conservative there exists an f so
``````
``````
PNMPNM
yzzxxy
yz yz yz yz
œ œ œœ œœÊ ÊF
that f; e f(x y z) xe g(y z) xze xze z cos y z cos yFœœÊßßœßÊœœÊœ™``
````
``
ff
xyyy
yz yz yz yz
gg
g(y z) z sin y h(z) f(x y z) xe z sin y h(z) xye sin y h (z) xye sin yÊßœ Êßßœ Êœ œ
yz yz yz
f
z
`
`
w
h (z) 0 h(z) C f(x y z) xe z sin y C xe z sin yʜʜÊßßœ Êœ
wyz yz
F™ab
(a) work d xe z sin y (1 0) (1 0) 0œ œ œœ
'A
B
Fr†cd
yz Ð"ß Î#ß!Ñ
Ð"ß!ß"Ñ
1
(b) work d xe z sin y 0œœ œ
'A
B
Fr†cd
yz Ð"ß Î#ß!Ñ
Ð"ß!ß"Ñ
1
(c) work d xe z sin y 0œœ œ
'A
B
Fr†cd
yz Ð"ß Î#ß!Ñ
Ð"ß!ß"Ñ
1
: Since is conservative, d is independent of the path from (1 0 1) to 1 0 .Note FFr
'A
B
†ßß ß ß
ˆ‰
1
#
31. (a) x y 3x y 2x y ; let C be the path from ( 1 1) to (0 0) x t 1 andFFijœÊœ ßßÊœ™ab
$# ## $ "
y t 1, 0 t 1 3(t 1) ( t 1) 2(t 1) ( t 1) 3(t 1) 2(t 1)œ Ÿ Ÿ Ê œ œ Fijij
## $ % %
and (t 1) ( t 1) d dt dt d 3(t 1) 2(t 1) dtri jrijFr
"""
%%
œ Ê œ Ê œ
''
C0
1
†cd
5(t 1) dt (t 1) 1; let C be the path from (0 0) to (1 1) x t and y t,œœœ ßßÊœ œ
'0
1%&
"
!#
cd
0 t 1 3t 2t and t t d dt dt d 3t 2t dtŸŸ Ê œ œ Ê œ Ê œ Fijrijr ij Fr
%% %%
## #
''
C0
1
†ab
5t dt 1 d d d 2œœÊœ œ
''''
0CCC
1%"#
Fr Fr Fr†† †
(b) Since f(x y) x y is a potential function for , d f(1 1) f( 1 1) 2ßœ œ ßßœ
$# FFr
'11
11
†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1012 Chapter 16 Integration in Vector Fields
32. 0 , 0 , 2x sin y is conservative there exists an f so that f;
``` `` `
````` `
PNMPN M
yzzxx y
œœ œœ œ œ Ê Ê œFF™
2x cos y f(x y z) x cos y g(y z) x sin y x sin y 0 g(y z) h(z)
``
````
###
``
ff
xyyy
gg
œÊßßœßÊœœÊœÊßœ
f(x y z) x cos y h(z) h (z) 0 h(z) C f(x y z) x cos y C x cos yÊßßœ Êœ œÊ œÊßßœ Êœ
#w # #
`
`
f
zF™ab
(a) 2x cos y dx x sin y dy x cos y 0 1 1
'C œ œœ
##
Ð!ß"Ñ
Ð"ß!Ñ
cd
(b) 2x cos y dx x sin y dy x cos y 1 ( 1) 2
'Cœ œœ
##
Ð"ß!Ñ
Ð"ß Ñ
cd
1
(c) 2x cos y dx x sin y dy x cos y 1 1 0
'C œ œœ
##
Ð"ß!Ñ
Ð"ß!Ñ
cd
(d) 2x cos y dx x sin y dy x cos y 1 1 0
'C œ œœ
##
Ð"ß!Ñ
Ð"ß!Ñ
cd
33. (a) If the differential form is exact, then 2ay cy for all y 2a c, 2cx 2cx for
`` ` `
`` ``
PN MP
yz zx
œÊ œ Êœ œÊ œ
all x, and by 2ay for all y b 2a and c 2a
``
``
NM
xy
œÊœ Êœ œ
(b) f the differential form with a 1 in part (a) is exact b 2 and c 2FœÊ œ Êœ œ™
34. f g(x y z) d f d f(x y z) f(0 0 0) 0, 0, andFFrrœ Ê ßß œ œ œ ßß ßß Ê œ œ ™†™†
''
000 000
xyz xyz ``
`` ``
``
gg
xx yy
ff
0 g f , as claimed
`
``
`
g
zz
f
œÊ œ œ™™F
35. The path will not matter; the work along any path will be the same because the field is conservative.
36. The field is not conservative, for otherwise the work would be the same along C and C .
"#
37. Let the coordinates of points A and B be x , y , z and x , y , z , respectively. The force a b c isabab
AAA BBB Fijkœ
conservative because all the partial derivatives of M, N, and P are zero. Therefore, the potential function is
f x, y, z ax by cz C, and the work done by the force in moving a particle along any path from A to B isabœ
f B f A f x , y , z f x , y , z ax by cz C ax by cz Cab ab a b a b a b a bœ œ
BBB AAA B B B A A A
ax x by y cz z BAœœ†
Ä
ababab
BA BA BAF
38. (a) Let GmM C CœÊœ Fijk
’“
xz
xyz xyz xyz
y
ababab
, , f forÊœ œ œ œ œ œ Êœ
````` `
````` `
P N M 3xzC P N M
yzzxx y
3yzC 3xyC
xyz xyz xyzab ab ab F™
some f; f(x y z) g(y z)
` `
```
`
fxC C f
xyy
xyz xyz xyz
yC g
œÊßßœßÊœ
ab ab ab
0 g(y z) h(z) h (z)œÊœÊߜʜœ
yC g
xyz xyz xyz
yz
fzC zC
ab ab ab
`
``
`w
h(z) C f(x y z) C . Let C 0 f(x y z) is a potentialÊœÊßßœ œÊßßœ
"""
CGmM
xyz xyzab ab
function for .F
(b) If s is the distance of (x y z) from the origin, then s x y z . The work done by the gravitational fieldßß œ
È###
is work d GmM , as claimed.FFrœ œ œœ
'P
P
†’“ Š‹
GmM GmM GmM
xyz
È
T
T
""
ss ss
16.4 GREEN'S THEOREM IN THE PLANE
1. M y a sin t, N x a cos t, dx a sin t dt, dy a cos t dt 0, 1, 1, andœ œ œ œ œ œ Ê œ œ œ
`` `
`` `
MM N
xy x
0;
`
`
N
yœ
Equation (11): M dy N dx [( a sin t)(a cos t) (a cos t)( a sin t)] dt 0 dt 0;
)' '
C0 0
2 2
œ œ œ
dx dy 0 dx dy 0, Flux
'' ''
RR
Š‹
``
``
MN
xy
œ œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Section 16.4 Green's Theorem in the Plane 1013
Equation (12): M dx N dy [( a sin t)( a sin t) (a cos t)(a cos t)] dt a dt 2 a ;
)' '
C0 0
2 2
œ œ œ
##
1
dx dy 2 dy dx 4 a x dx 4 a x sin
''
RŠ‹ ’ “
ÈÈ
``
`` #
## ## "
NM xax
xy 2a
œ œœ
'' '
ac a
aax a a
a
2a 2a , Circulationœœ
##
##
ˆ‰
11 1
2. M y a sin t, N 0, dx a sin t dt, dy a cos t dt 0, 1, 0, and 0;œœ œ œ œ Ê œ œ œ œ
``` `
``` `
MMN N
xyx y
Equation (11): M dy N dx a sin t cos t dt a sin t 0; 0 dx dy 0, Flux
)'
C0
2
œ œ œ œ
###
"#
!
‘
2
1''
R
Equation (12): M dx N dy a sin t dt a a ; dx dy
)'
C0
2
œ œ œ ab‘ Š‹
## # #
#
!
``
``
tsin 2t N M
24 xy
11''
R
1 dx dy r dr d d a , Circulationœ œ œ œ
''
R'' '
00 0
2a 2
))1
a
#
#
3. M 2x 2a cos t, N 3y 3a sin t, dx a sin t dt, dy a cos t dt 2, 0, 0, andœ œ œ œ œ œ Ê œ œ œ
```
```
MMN
xyx
3;
`
`
N
yœ
Equation (11): M dy N dx [(2a cos t)(a cos t) (3a sin t)( a sin t)] dt
)'
C0
2
œ
2a cos t 3a sin t dt 2a 3a 2 a 3 a a ;œ œ œœ
'0
2ab
‘‘
## ## # # # # #
##
!!
tsin 2t tsin 2t
24 24
11
11 1
1 dx dy r dr d d a , Flux
'' ''
RR
Š‹
``
`` #
#
MN a
xy
œ œ œ œ
'' '
00 0
2a 2
))1
Equation (12): M dx N dy [(2a cos t)( a sin t) ( 3a sin t)(a cos t)] dt
)'
C0
2
œ
2a sin t cos t 3a sin t cos t dt 5a sin t 0; 0 dx dy 0, Circulationœ œ œ œ
'0
2ab
‘
## ##
#
!
1
2
1''
R
4. M x y a cos t, N xy a cos t sin t, dx a sin t dt, dy a cos t dtœ œ œ œ œ œ
#$# #$ #
2xy, x , y , and 2xy;Êœ œ œ œ
``` `
``` `
#
MMN N
xyx y
2
Equation (11): M dy N dx a cos t sin t a cos t sin t cos t sin t 0;
)'
C0
2
œ œ œab
’“
%$ % $ % %
#
!
aa
44
1
dx dy ( 2xy 2xy) dx dy 0, Flux
'' ''
RR
Š‹
``
``
MN
xy
œœ
Equation (12): M dx N dy a cos t sin t a cos t sin t dt 2a cos t sin t dt
)' '
C0 0
22
œ œabab
%# # %# # %# #
a sin 2t dt sin u du ; dx dy y x dx dyœœœœœ
''
00
24
"``
##``
%# # ##
%
!
aausin 2uaNM
4424 xy
‘ Š‹ ab
11'' ''
RR
r r dr d d , Circulationœœœ
'' '
00 0
2a 2
#
#
†))
aa
4
1
5. M x y, N y x 1, 1, 1, 1 Flux 2 dx dy 2 dx dy 2;œ œ Ê œ œ œ œ Ê œ œ œ
`` ` `
`` ` `
MM N N
xy x y ''
R''
00
11
Circ [ 1 ( 1)] dx dy 0œ œ
''
R
6. M x 4y, N x y 2x, 4, 1, 2y Flux (2x 2y) dx dyœœÊœ œœœÊœ
##
````
````
MMNN
xyxy ''
R
(2x 2y) dx dy x 2xy dy (1 2y) dy y y 2; Circ (1 4) dx dyœœœœœœ
'' ' '
00 0 0
11 1 1
cd cd
##
""
!!
''
R
3 dx dy 3œ œ
''
00
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1014 Chapter 16 Integration in Vector Fields
7. M y x , N x y 2x, 2y, 2x, 2y Flux ( 2x 2y) dx dyœ œ Ê œ œ œ œ Ê œ
## ## ````
````
MMNN
xyxy ''
R
( 2x 2y) dy dx 2x x dx x 9; Circ (2x 2y) dx dyœ œœœœ
'' '
00 0
3x 3
ab
‘
## $
"$
!
3''
R
(2x 2y) dy dx x dx 9œœœ
'' '
00 0
3x 3
#
8. M x y, N x y 1, 1, 2x, 2y Flux (1 2y) dx dyœ œ Ê œ œ œ œ Ê œ ab
## ``` `
``` `
MMN N
xyx y ''
R
(1 2y) dy dx x x dx ; Circ ( 2x 1) dx dy ( 2x 1) dy dxœ œœœœ
'' ' ''
00 0 00
1x 1 1x
ab
#"
6''
R
2x x dxœ œ
'0
1ab
#7
6
9. M x e sin y, N x e cos y 1 e sin y, e cos y, 1 e cos y, e sin yœ œ Ê œ œ œ œ
xx xx xx
MMN N
xyxy
````
````
Flux dx dy r dr d cos 2 d sin 2 ;Êœ œ œ œ œ
''
R'' '
40 4
4cos2 4
))))
ˆ‰‘
"""
##
Î%
Î%
4
1
1
Circ 1 e cos y e cos y dx dy dx dy r dr d cos 2 dœ œ œ œ œ
'' ''
RR
ab ˆ‰
xx '' '
40 4
4cos2 4
)))
""
##
10. M tan , N ln x y , , , œ œÊœ œœœ
" # # ````
````
yy 2y
x x xy y xy x xy y xy
MMxN2xN
ab
Flux dx dy r dr d sin d 2;Êœ œ œ œ
''
RŠ‹ ˆ‰
y2y
xy xy r
r sin
'' '
01 0
2))))
Circ dx dy r dr d cos d 0œ œ œ œ
''
RŠ‹ ˆ‰
2x x r cos
xy xy r
'' '
01 0
2))))
11. M xy, N y y, x, 0, 2y Flux (y 2y) dy dx 3y dy dxœœÊœ œœœÊœ œ
#````
````
MMNN
xyxy ''
R
''
0x
1x
dx ; Circ x dy dx x dy dx x x dxœ œ œœœœ
''''
00x 0
11x 1
Š‹ ab
3x 3x
5 1
## #
" "
#$
''
R
12. M sin y, N x cos y 0, cos y, cos y, x sin yœ œ Ê œ œ œ œ
`` ` `
`` ` `
MM N N
xy x y
Flux ( x sin y) dx dy ( x sin y) dx dy sin y dy ;Êœœœœ
''
R'' '
00 0
22 2
Š‹
11
88
Circ [cos y ( cos y)] dx dy 2 cos y dx dy cos y dy sin yœ œ œ œ œ
''
R'' '
00 0
22 2
111cd
1Î#
!
13. M 3xy , N e tan y 3y , œ œ Êœ œ
xMN
1y x 1y y 1y
x
``
" `"`"
Flux 3y dx dy 3y dx dy (3r sin ) r dr dÊœ œ œ
'' ''
RR
Š‹
""
1y 1y ''
00
2a1cos
))
a (1 cos ) (sin ) d (1 cos ) 4a 4a 0œ œ œœ
'0
2$$ %$$
#
!
))) )
’“
ab
a
4
1
14. M y e ln y, N 1 , Circ 1 dx dy ( 1) dx dyœ œ Ê œ œ Ê œ œ
xeM eNe e e
yy yxy y y
xxx xx
``
`` '' ''
RR
’“Š‹
dy dx 3 x x 1 dx x x 2 dxœ œ œ œ
'' ' '
1x 1 1 1
13x 1 1
cdababab
#% %# 44
15
15. M 2xy , N 4x y 6xy , 8xy work 2xy dx 4x y dy 8xy 6xy dx dyœœÊœ œÊœ œ
$## # # $## ##
``
``
MN
yx )C''
Rab
2xy dy dx x dxœœœ
'' '
00 0
1x 1
#"!
22
333
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.4 Green's Theorem in the Plane 1015
16. M 4x 2y, N 2x 4y 2, 2 work (4x 2y) dx (2x 4y) dyœ œ Ê œ œÊ œ
``
``
MN
yx )C
[2 ( 2)] dx dy 4 dx dy 4(Area of the circle) 4( 4) 16œ œ œ œ œ
'' ''
RR
11†
17. M y , N x 2y, 2x y dx x dy (2x 2y) dy dxœœÊœ œÊ œ
## ##
``
``
MN
yx )C''
R
(2x 2y) dy dx 3x 4x 1 dx x 2x x 1 2 1 0œœœœœ
'' '
00 0
11x 1
abcd
#$#
"
!
18. M 3y, N 2x 3, 2 3y dx 2x dy (2 3) dx dy 1 dy dxœœÊœœÊ œ œ
``
``
MN
yx )''
C00
sin x
''
R
sin x dx 2œ œ
'0
19. M 6y x, N y 2x 6, 2 (6y x) dx (y 2x) dy (2 6) dy dxœ œ Ê œ œÊ œ
``
``
MN
yx )C''
R
4(Area of the circle) 16œ œ 1
20. M 2x y , N 2xy 3y 2y, 2y 2x y dx (2xy 3y) dy (2y 2y) dx dy 0œ œ Ê œ œ Ê œ œ
# #
``
``
MN
yx )Cab ''
R
21. M x a cos t, N y a sin t dx a sin t dt, dy a cos t dt Area x dy y dxœœ œœ Ê œ œ Ê œ
"
#)C
a cos t a sin t dt a dt aœ œœ
""
##
## ## # #
''
00
22
ab 1
22. M x a cos t, N y b sin t dx a sin t dt, dy b cos t dt Area x dy y dxœœ œœ Ê œ œ Ê œ
"
#)C
ab cos t ab sin t dt ab dt abœ œœ
""
##
##
''
00
22
ab 1
23. M x a cos t, N y sin t dx 3 cos t sin t dt, dy 3 sin t cos t dt Area x dy y dxœœ œœ Ê œ œ Ê œ
$$ # # "
#)C
3 sin t cos t cos t sin t dt 3 sin t cos t dt sin 2t dt sin u duœœœœ
""
##
## # # ## # #
''''
0000
2224
ababab
33
816
œ œ
3 u sin 2u 3
16 2 4 8
‘
%
!
11
24. M x t , N y t dx 2t dt, dy t 1 dt Area x dy y dxœœ œœ Ê œ œ Ê œ
##
"
#
t
3ab )C
t t 1 t (2t) dt t t dt t t 9 3 15 3œœœœ
""" "
##
## % # & $ $
$
''
33
33
’“ Š‹
ab
Š‹ ˆ‰ ‘ ÈÈ
t111
33215315
ÈÈ
3œ8
5È
25. (a) M f(x), N g(y) 0, 0 f(x) dx g(y) dy dx dyœœÊœœÊ œ
`` ``
`` ``
MN NM
yx xy
)C''
RŠ‹
0 dx dy 0œœ
''
R
(b) M ky, N hx k, h ky dx hx dy dx dyœœÊœœÊ œ
`` ``
`` ``
MN NM
yx xy
)C''
RŠ‹
(h k) dx dy (h k)(Area of the region)œ œ
''
R
26. M xy , N x y 2x 2xy, 2xy 2 xy dx x y 2x dy dx dyœœÊœ œÊ œ
## # #
`` ``
`` ``
MN NM
yx xy
)Cab Š‹
''
R
(2xy 2 2xy) dx dy 2 dx dy 2 times the area of the squareœ œ œ
'' ''
RR
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
1016 Chapter 16 Integration in Vector Fields
27. The integral is 0 for any simple closed plane curve C. The reasoning: By the tangential form of Green's
Theorem, with M 4x y and N x , 4x y dx x dy x 4x y dx dyœœ œ
$%$% %$
``
``
)C''
R’“
ab a b
xy
4x 4x dx dy 0.œ œ
''
Rðóóñóóò
ab
$$
0
28. The integral is 0 for any simple closed curve C. The reasoning: By the normal form of Green's theorem, with
M x and N y , y dy x dx y x dx dy 0.œœœ œ
$$$$ $$
``
``
)C''
R”•
ðñò
ab ab
ï
xy
0 0
29. Let M x and N 0 1 and 0 M dy N dx dx dy x dyœœÊœ œÊ œ Ê
`` ``
`` ``
MN MN
xy xy
))
C C
''
RŠ‹
(1 0) dx dy Area of R dx dy x dy; similarly, M y and N 0 1 andœ Ê œ œ œ œÊœ
'' ''
RR
)C
`
`
M
y
0 M dx N dy dy dx y dx (0 1) dy dx y dx
```
```
NNM
xxy
œÊ œ Ê œ Ê
)))
CCC
'' ''
RR
Š‹
dx dy Area of Rœœ
''
R
30. f(x) dx Area of R y dx, from Exercise 29
')
aC
b
œœ
31. Let (x y) 1 x Ax x dA (x 0) dx dy$ߜʜ œ œ œ Ê œ œ
M
MA
x (x y) dA x dA x dA
(x y) dA dA
y
'' '' ''
'' ''
RRR
RR
$
$
ß
ß'' ''
RR
dy, Ax x dA (0 x) dx dy xy dx, and Ax x dA x x dx dyœœœœ œœ
)CC
x 2
33
#
"
'' '' ''
RR R
R
)''
ˆ‰
x dy xy dx x dy xy dx x dy xy dx AxœÊ œœœ
))))
CCCC
"" " "
## #
#33 3
32. If (x y) 1, then I x (x y) dA x dA x 0 dy dx x dy,$$ßœ œ ß œ œ œ
yC
'' '' ''
RRR
### $
"
ab 3)
x dA 0 x dy dx x y dx, and x dA x x dy dx
'' '' '' ''
RR RR
######
"
œ œ œ ab ˆ‰
)C
3
44
x dy x y dx x dy x y dx x dy x y dx x dy x y dx IœœÊ œœœ
)))))
CCCCC
y
"" " " "
$ # $# $ # $#
44 4 3 4
33. M , N , dx dy dx dy 0 for suchœœÊœ œÊ œ œ
```````` ``
```````` ``
ffMfNfff ff
yxyyxxyx xy
)C''
RŠ‹
curves C
34. M x y y , N x x y , 1 Curl 1 x y 0 in the interior ofœ œÊ œ œÊ œ œ
"" ` ` `` "
# $ ## ##
`` ``43 y4 x xy 4
M1 N N M ˆ‰
the ellipse x y 1 work d 1 x y dx dy will be maximized on the region
""
## ##
44
œÊ œ œ
'CFr†''
Rˆ‰
R {(x y) | curl } 0 or over the region enclosed by 1 x yœß œ F"##
4
35. (a) f M , N ; since M, N are discontinuous at (0 0), we™œ Êœœ ß
Š‹Š‹
2x 2x
xy xy xy xy
2y 2y
ij
compute f ds directly since Green's Theorem does not apply. Let x a cos t, y a sin t dx a sin t dt,
'C™†nœœÊœ
dy a cos t dt, M cos t, N sin t, 0 t 2 , so f ds M dy N dxœœœŸŸ œ
22
aa 1''
CC
™†n
cos t a cos t sin t a sin t dt 2 cos t sin t dt 4 . Note that this holds for anyœœœ
''
0 0
2 2
‘ˆ‰ ˆ‰
ab a b a b
22
aa
22 1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.4 Green's Theorem in the Plane 1017
a 0, so f ds 4 for any circle C centered at 0, 0 traversed counterclockwise and f ds 4œ œ
''
C C
™† ™†n n1 1ab
if C is traversed clockwise.
(b) If K does not enclose the point (0 0) we may apply Green's Theorem: f ds M dy N dxߜ
''
CC
™†n
dx dy dx dy 0 dx dy 0. If K does enclose the pointœ œ œ œ
'' '' ''
RR R
Š‹ Š ‹
``
``
MN
xy
2y x 2x y
xy xy
ˆ‰ˆ‰
abab
22 22
22 22
22
(0 0) we proceed as in Example 6:ß
Choose a small enough so that the circle C centered at (0 0) of radius a lies entirely within K. Green's Theoremß
applies to the region R that lies between K and C. Thus, as before, 0 dx dy
R
œ
''Š‹
``
``
MN
xy
M dy N dx M dy N dx where K is traversed counterclockwise and C is traversed clockwise.œ
''
KC
Hence by part (a) 0 4 4 f ds. We have shown:
M dy N dx M dy N dx
œÊœœ
’“
''
'
KK
K
11 ™†n
f ds 0 if (0 0) lies inside K
4 if (0 0) lies outside K
'K™†nœß
ß
œ1
36. Assume a particle has a closed trajectory in R and let C be the path C encloses a simply connected region
""
Ê
R C is a simple closed curve. Then the flux over R is ds 0, since the velocity vectors are
"" "
ʜ
)CFn F†
tangent to C . But 0 ds M dy N dx dx dy M N 0, which is a
"``
``
œœœÊœ
))
CC xy
Fn†''
RŠ‹
MN
xy
contradiction. Therefore, C cannot be a closed trajectory.
"
37. dx dy N(g (y) y) N(g (y) y) dx dy [N(g (y) y) N(g (y) y)] dy
''''
gy cgy c
gy dgy d
``
``
#" #"
NN
xx
œßßÊ œ ßß
ˆ‰
N(g (y) y) dy N(g (y) y) dy N(g (y) y) dy N(g (y) y) dy N dy N dyœßßœßßœ
''''''
cc cdCC
dd dc
#" #"
dy N dy dx dy
R
œÊ œ
))
CC
'' `
`
N
x
38. dy dx [M(x d) M(x c)] dx M(x d) dx M(x c) dx M dx M dx.
'' ' ' ' ' '
ac a a a C C
bd b b b
`
`
M
yœßßœßßœ
3
Because x is constant along C and C , M dx M dx 0
#%
''
CC
œœ
M dx M dx M dx M dx M dx dy dx M dx.Ê œÊ œ
Š‹
'''' ) '' )
CCCC C ac C
bd
`
`
M
y
39. The curl of a conservative two-dimensional field is zero. The reasoning: A two-dimensional field M NFijœ
can be considered to be the restriction to the xy-plane of a three-dimensional field whose k component is zero,
and whose and components are independent of z. For such a field to be conservative, we must haveij
by the component test in Section 16.3 curl 0.
`` ``
`` ``
NM NM
xy xy
œÊœœF
40. Green's theorem tells us that the circulation of a conservative two-dimensional field around any simple closed
curve in the xy-plane is zero. The reasoning: For a conservative field M N , we have Fijœ œ
``
``
NM
xy
(component test for conservative fields, Section 16.3, Eq. (2)), so curl 0. By Green's theorem,Fœ œ
``
``
NM
xy
the counterclockwise circulation around a simple closed plane curve C must equal the integral of curl over theF
region R enclosed by C. Since curl 0, the latter integral is zero and, therefore, so is the circulation.Fœ
The circulation ds is the same as the work d done by around C, so our observation that
))
CC
FT F r F††
circulation of a conservative two-dimensional field is zero agrees with the fact that the work done by a
conservative field around a closed curve is always 0.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1018 Chapter 16 Integration in Vector Fields
41-44. Example CAS commands:
:Maple
with( plots );#41
M := (x,y) -> 2*x-y;
N := (x,y) -> x+3*y;
C := x^2 + 4*y^2 = 4;
implicitplot( C, x=-2..2, y=-2..2, scaling=constrained, title="#41(a) (Section 16.4)" );
curlF_k := D[1](N) - D[2](M): # (b)
'curlF_k' = curlF_k(x,y);
top,bot := solve( C, y ); # (c)
left,right := -2, 2;
q1 := Int( Int( curlF_k(x,y), y=bot..top ), x=left..right );
value( q1 );
: (functions and bounds will vary)Mathematica
The command will be useful for 41 and 42, but is not needed for 43 and 44. In 44, the equation of the lineImplicitPlot
from (0, 4) to (2, 0) must be determined first.
Clear[x, y, f]
<<Graphics`ImplicitPlot`
f[x_, y_]:= {2x y, x 3y}
curve= x 4y ==4
22
ImplicitPlot[curve, {x, 3, 3},{y, 2, 2}, AspectRatio Automatic, AxesLabel {x, y}]; Ä Ä
ybounds= Solve[curve, y]
{y1, y2}=y/.ybounds;
integrand:=D[f[x,y][[2]], x] D[f[x,y][[1]], y]//Simplify
Integrate[integrand, {x, 2, 2}, {y, y1, y2}]
N[%]
Bounds for y are determined differently in 43 and 44. In 44, note equation of the line from (0, 4) to (2, 0).
Clear[x, y, f]
f[x_, y_]:= {x Exp[y], 4x Log[y]}
2
ybound = 4 2x
Plot[{0, ybound}, {x, 0,2. 1}, AspectRatio Automatic, AxesLabel {x, y}];ÄÄ
integrand:=D[f[x, y][[2]], x] D[f[x, y][[1]], y]//Simplify
Integrate[integrand, {x, 0, 2}, {y, 0, ybound}]
N[%]
16.5 SURFACE AREA AND SURFACE INTEGRALS
1. , f 2x 2y f (2x) (2y) ( 1) 4x 4y 1 and f 1;pk i jk pœ œÊ œ œ œ™™ ™†kk k k
ÈÈ
## # ##
z 2 x y 2; thus S dA 4x 4y 1 dx dyœÊ œ œ œ
## ##
'' ''
RR
kk
kk
™
™†
f
fpÈ
4r cos 4r sin 1 r dr d 4r 1 r dr d 4r 1 dœ œ œ
''
RÈÈ
’“
ab
## ## # "#$Î# #
!
))) ) )
'' '
00 0
22 2
12
È
dœœ
'0
213 13
63
)1
2. , f 2x 2y f 4x 4y 1 and f 1; 2 x y 6pk i jk pœ œÊ œ œ ŸŸ™™ ™†kk k k
È## ##
S dA 4x 4y 1 dx dy 4r 1 r dr d 4r 1 r dr dÊœ œ œ œ
'' '' ''
RR R
kk
kk
™
™†
f
fpÈÈÈ
## # #
))
''
02
26
4r 1 d dœ œœ
''
00
22
’“
ab
"#$Î# '
#
12 6 3
49 49
È
È))1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.5 Surface Area and Surface Integrals 1019
3. , f 2 2 f 3 and f 2; x y and x 2 y intersect at (1 1) and (1 1)pk i j k pœœÊœ œœ œ ß ß™™™†kk k k ##
S dA dx dy dx dy 3 3y dy 4Êœ œ œ œ œ
'' ''
RR
kk
kk
™
™†
f
f
33
p##
#
'' '
1y 1
12y 1
ab
4. , f 2x 2 f 4x 4 2 x 1 and f 2 S dApk i k pœ œÊ œœ œÊœ™™ ™†kk k k
ÈÈ
## ''
R
kk
kk
™
™†
f
fp
dx dy x 1 dy dx x x 1 dx x 1 (4)œœœœœœ
''
R
2x 1
3333
7
ÈÈ
###
"""
# $Î#
$Î# $
!
'' '
00 0
3x 3
ÈÈ
’“
ab
5. , f 2x 2 2 f (2x) ( 2) ( 2) 4x 8 2 x 2 and f 2pk i j k pœ œ Ê œ œ œ œ™™ ™†kk k k
ÈÈÈ
### # #
S dA dx dy x 2 dy dx 3x x 2 dx x 2Êœ œ œ œ œ
'' ''
RR
kk
kk È
™
™†
f
f
2x 2
p
###
#$Î# #
!
'' '
00 0
23x 2
ÈÈ
’“
ab
66 22œ
ÈÈ
6. , f 2x 2y 2z f 4x 4y 4z 8 2 2 and f 2z; x y z 2 andpk i j k pœ œ Ê œ œ œ œ œ™™ ™†kk k k
ÈÈÈ
### ###
z x y x y 1; thus, S dA dA 2 dAœÊœ œ œ œ
ÈÈ
## ##
#
"
'' '' ''
RR R
kk
kk È
™
™†
f
fz z
22
p
2 dA 2 2 1 2 d 2 2 2œœœœ
ÈÈÈÈÈ
Š‹Š‹
''
R
"
ÈÈ
ab2xy
r dr d
2r
'' '
00 0
21 2
))1
7. , f c f c 1 and f 1 S dA c 1 dx dypk ik pœ œÊ œ œÊœ œ ™™ ™†kk k k
ÈÈ
# #
'' ''
RR
kk
kk
™
™†
f
fp
c 1 r dr d d c 1œœ œ
'' '
00 0
21 2
ÈÈ
##
#
))1
Èc1
8. , f 2x 2z f (2x) (2z) 2 and f 2z for the upper surface, z 0pk i j pœœÊœœ œ ™™ ™†kk k k
È##
S dA dA dy dx 2 dy dx dxÊœ œ œ œ œ
'' '' ''
RRR
kk
kk ÈÈÈ
™
™†
f
fz
21
1x 1x 1x
p#
""
'' '
12 0 12
12 12 12
sin xœœœcd ˆ‰
" "Î#
"Î#
111
663
9. , f 2y 2z f 1 (2y) (2z) 1 4y 4z and f 1; 1 y z 4pi i j k pœ œÊ œœ œŸŸ™™ ™†kk k k
ÈÈ
### ## ##
S dA 1 4y 4z dy dz 1 4r cos 4r sin r dr dÊœ œ œ
'' ''
RR
kk
kk
™
™†
f
fpÈÈ
## ## ##
''
01
22
)))
14r r drd 14r d 171755 d 171755œœ œ œ
'' ' '
01 0 0
22 2 2
È’“Š‹Š‹
ab ÈÈ
ÈÈ
#""
#$Î# #
"#
)) )
12 1 6
1
10. , f 2x 2z f 4x 4z 1 and f 1; y 0 and x y z 2 x z 2;pj ij k pœœÊœ œœ œÊœ™™ ™†kk k k
È## ## ##
thus, S dA 4x 4z 1 dx dz 4r 1 r dr d dœœœ œœ
'' ''
RR
kk
kk
™
™†
f
f63
13 13
pÈÈ
## #
'' '
00 0
22 2
))1
11. , f 2x 15 f 2x 15 ( 1) 4x 8 2xpk i jkœœÊœ œœ™™
ˆ‰ ˆ‰ ˆ‰
ÈÈ
kk
ÊŠ‹ ÉÉ
22 42
xx xx
##
###
2x , on 1 x 2 and f 1 S dA 2x 2x dx dyœ ŸŸ œÊœ œ
2
xf
f
kk a b™†p'' ''
RR
kk
kk
™
™†p
"
2x 2x dx dy x 2 ln x dy (3 2 ln 2) dy 3 2 ln 2œ œ œœ
'' ' '
01 0 0
12 1 1
ab cd
" # #
"
12. , f 3 x 3 y 3 f 9x 9y 9 3 x y 1 and f 3pk i j k pœ œÊ œœ œ™™ ™†
ÈÈkk k k
ÈÈ
S dA x y 1 dx dy x y 1 dx dy (x y 1) dyÊœ œ œ œ
'' ''
RR
kk
kk
™
™†
f
f 3
2
pÈÈ
‘
'' '
00 0
11 1 $Î# "
!
(y 2) (y 1) dy (y 2) (y 1) (3) (2) (2) 1œ œ œ
'0
1‘ ‘‘
22 4 4 4
3 3 15 15 15
$Î# $Î# &Î# &Î# &Î# &Î# &Î#
"
!
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1020 Chapter 16 Integration in Vector Fields
93 82 1œ
4
15 Š‹
ÈÈ
13. The bottom face S of the cube is in the xy-plane z 0 g(x y 0) x y and f(x y z) z 0 ÊœÊ ßßœ ßßœœÊœpk
and f f 1 and f 1 d dx dy g d (x y) dx dy™™ ™†œÊ œ œÊ œ Ê œ kpkk k k 55
'' ''
SR
(x y) dx dy ay dy a . Because of symmetry, we also get a over the face of the cubeœœœ
'' '
00 0
aa a
Š‹
a
#
$$
in the xz-plane and a over the face of the cube in the yz-plane. Next, on the top of the cube, g(x y z)
$ßß
g(x y a) x y a and f(x y z) z a and f f 1 and f 1 d dx dyœßßœ ßßœœÊœ œÊ œ œÊœpk k p™™ ™†kk k k 5
g d (x y a) dx dy (x y a) dx dy (x y) dx dy a dx dy 2a .
'' ''
SR
5œ œ œ œ
'' '' ''
00 00 00
aa aa aa $
Because of symmetry, the integral is also 2a over each of the other two faces. Therefore,
$
(xyz) d 3a 2a 9a.
''
cube
œ œ5ab
$$ $
14. On the face S in the xz-plane, we have y 0 f(x y z) y 0 and g(x y z) g(x 0 z) z andœ Ê ßß œ œ ßß œ ßß œ Ê œpj
f f 1 and f 1 d dx dz g d (y z) d z dx dz 2z dz™™ ™†œÊ œ œ Ê œ Ê œ œ œjpkk k k 555
'' ''
SS '' '
00 0
12 1
1.œ
On the face in the xy-plane, we have z 0 f(x y z) z 0 and g(x y z) g(x y 0) y andœ Ê ßß œ œ ßß œ ßß œ Ê œpk
f f 1 and f 1 d dx dy g d y d y dx dy 1.™™ ™†œÊ œ œÊ œ Ê œ œ œkpkk k k 555
'' ''
SS
''
00
12
On the triangular face in the plane x 2 we have f(x y z) x 2 and g(x y z) g(2 y z) y z andœ ßßœœ ßßœ ßßœÊ œpi
f f 1 and f 1 d dz dy g d (y z) d (y z) dz dy™™ ™†œÊ œ œ Ê œ Ê œ œ ipkk k k 555
'' ''
SS ''
00
11y
1 y dy .œœ
'0
1""
#
#
ab3
On the triangular face in the yz-plane, we have x 0 f(x y z) x 0 and g(x y z) g(0 y z) y zœ Ê ßß œ œ ßß œ ßß œ
and f f 1 and f 1 d dz dy g d (y z) dÊœ œÊ œ œÊ œ Ê œ pi i p™™ ™†kk k k 555
'' ''
SS
(y z) dz dy .œœ
''
00
11y "
3
Finally, on the sloped face, we have y z 1 f(x y z) y z 1 and g(x y z) y z 1 andœ Ê ßß œœ ßß œœ Ê œpk
f f 2 and f 1 d 2 dx dy g d (y z) d™™™†œ Ê œ œ Ê œ Ê œ jk pkk k k
ÈÈ
555
'' ''
SS
2 dx dy 2 2. Therefore, g(x y z) d 1 1 2 2 2 2œ œ ßß œ œ
''
00
12
ÈÈ ÈÈ
''
wedge
5""
33 3
8
15. On the faces in the coordinate planes, g(x y z) 0 the integral over these faces is 0.ßß œ Ê
On the face x a, we have f(x y z) x a and g(x y z) g(a y z) ayz and f f 1œ ßßœœ ßßœ ßßœ Ê œ œÊ œpi i™™kk
and f 1 d dy dz g d ayz d ayz dy dz .kk™†pœÊ œ Ê œ œ œ555
'' ''
SS ''
00
cb ab c
4
On the face y b, we have f(x y z) y b and g(x y z) g(x b z) bxz and f f 1œ ßßœœ ßßœ ßßœ Ê œ œÊ œpj j™™kk
and f 1 d dx dz g d bxz d bxz dx dz .kk™†pœÊ œ Ê œ œ œ555
'' ''
SS ''
00
ca abc
4
On the face z c, we have f(x y z) z c and g(x y z) g(x y c) cxy and f f 1œ ßßœœ ßßœ ßßœ Ê œ œ Ê œpk k™™kk
and f 1 d dy dx g d cxy d cxy dx dy . Therefore,kk™†pœÊ œ Ê œ œ œ555
'' ''
SS ''
00
ba abc
4
g(xyz) d .
''
S
ßß œ5abc(ab ac bc)
4
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.5 Surface Area and Surface Integrals 1021
16. On the face x a, we have f(x y z) x a and g(x y z) g(a y z) ayz and f f 1œ ßßœœ ßßœ ßßœ Ê œ œÊ œpi i™™kk
and f 1 d dz dy g d ayz d ayz dz dy 0. Because of the symmetrykk™†pœÊ œ Ê œ œ œ555
'' ''
SS ''
bc
bc
of g on all the other faces, all the integrals are 0, and g(x y z) d 0.
''
S
ßß œ5
17. f(x y z) 2x 2y z 2 f 2 2 and g(x y z) x y (2 2x 2y) 2 x y ,ßßœ œÊ œ ßßœ œÊœ™ijk pk
f 3 and f 1 d 3 dy dx; z 0 2x 2y 2 y 1 x g d (2 x y) dkk k k™™†œ œ Ê œ œ Ê œÊœÊ œ p555
'' ''
SS
3 (2 x y) dy dx 3 (2 x)(1 x) (1 x) dx 3 2x dx 2œœœœ
'' ' '
00 0 0
11x 1 1
‘
Š‹
"
###
#3x
18. f(x y z) y 4z 16 f 2y 4 f 4y 16 2 y 4 and f 4ßß œ œ Ê œ Ê œ œ œ Ê œ
###
™™ ™†jk pk pkk k k
ÈÈ
d dx dy g d x y 4 dx dy dx dyÊœ Ê œ œ55
2y 4 y 4
4
xy 4
ÈÈ
ab
###
''
S'' ''
40 40
41 41
ˆ‰
ÈŠ‹
y 4 dy 4y 16œœœœ
'4
4"""
#
##
%
!
4333
y64 56
ab ’“
ˆ‰
19. g(x y z) z, g g 1 and g 1 Flux d ( ) dAßß œ œ Ê œ Ê œ œ Ê œ œp k k p Fn Fk™™ ™† † †kk k k '' ''
SR
5
3 dy dx 18œœ
''
00
23
20. g(x y z) y, g g 1 and g 1 Flux d ( ) dAßß œ œ Ê œ Ê œ œ Ê œ œ pj j p Fn Fj™™ ™† † †kk k k '' ''
SR
5
2 dz dx 2(7 2) dx 10(2 1) 30œœœœ
'' '
12 1
27 2
21. g 2x 2y 2z g 4x 4y 4z 2a; ;™™ †œ Ê œ œ œ œ Ê œijk n Fnkk
È###
#
2x 2y 2z x y z
xyz aa
z
ijk ijk
È
g 2z d dA Flux dA z dA a x y dx dykk ab
Š‹
ˆ‰ È
™†kœÊ œ Ê œ œ œ 52a z a
2z a z
'' '' ''
RRR
###
a r r dr dœœ
''
00
2a
È## )1a
6
22. g 2x 2y 2z g 4x 4y 4z 2a; ™™ †œ Ê œ œ œ œ Ê œ ijk n Fnkk
È###
#
2x 2y 2z x y z xy xy
xyz aaa
ijk ijk
È
0; g 2z d dA Flux d 0 d 0œœÊœÊœ œœkk™† †kFn555
2a
2z '' ''
SS
23. From Exercise 21, and d dA Flux dAnFnœœÊœœÊœ
xyz xy xy
az aaaa az
azzza
ijk 5†''
Rˆ‰ˆ‰
1 dAœœ
''
R
1a
4
24. From Exercise 21, and d dA z aznFnœœÊœœœ
xyz zy xyz
az aaaa
azxz
ijk
5†Š‹
Flux (za) dx dy a dx dy a (Area of R) aÊœ œ œ œ
'' ''
RR
ˆ‰
a
z4
## %
"1
25. From Exercise 21, and d dA a FluxnFnœœÊœœÊ
xyz y
az aaa
axz
ijk 5†
a dA dA dA r dr dœœœ œ
'' '' ''
RRR
ˆ‰
aa a a
zz
axy ar
ÈÈ
ab
''
00
2a
)
aar dœœ
'0
2a
###
!#
’“
È)1a
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1022 Chapter 16 Integration in Vector Fields
26. From Exercise 21, and d dA 1nFnœœÊœœœ
xyz
az a
a
xyz
ijk
5†Š‹ Š‹
Œ
ÈŠ‹
xz
aaa
ya
a
Flux dx dy dx dy r dr dÊœ œ œ œ
'' ''
RR
aa aa
zaxy ar
ÈÈ
ab
#
''
00
2a
)1
27. g(x y z) y z 4 g 2y g 4y 1 ßß œ œ Ê œ Ê œ Ê œ
##
™™jk nkk
È2y
4y 1
jk
È
; g 1 d 4y 1 dA FluxÊœ œÊ œÊœ ÊFn p k p†™†
2xy 3z
4y 1
#
Èkk È
5
4y 1 dA (2xy 3z) dA; z 0 and z 4 y y 4œœœœÊœ
''
RR
Š‹
È''
2xy 3z
4y 1
###
È
Flux 2xy 3 4 y dA 2xy 12 3y dy dx xy 12y y dxÊœ œ œ
''
Rcdabcdab
###$
#
#
'' '
02 0
12 1
32 dx 32œ œ
'0
1
28. g(x y z) x y z 0 g 2x 2y g 4x 4y 1 4 x y 1ßßœœÊ œÊ œ œ
## ## ##
™™ijkkk a b
ÈÈ
; g 1 d 4 x y 1 dAÊœ Ê œ œÊ œÊ œ nFnpkp
2x 2y 8x 8y 2
4x y 1 4x y 1
ijk
##
ÈÈ
ab ab
†™†kk ab
È
5
Flux 4 x y 1 dA 8x 8y 2 dA; z 1 and x y zÊœ œ œ œ
'' ''
RR
Š‹
Èab a b
8x 8y 2
4x y 1
## ## ##
Èab
x y 1 Flux 8r 2 r dr d 2ÊœÊ œ œ
## #
''
00
21
ab)1
29. g(x y z) y e 0 g e g e 1 ; ßß œ œ Ê œ Ê œ Ê œ Ê œ œ
xx 2x e2e2y
e1 e1
™™ †ij n Fn p ikk
Èxx
2x 2x
ij
ÈÈ
g e d dA Flux dA dAʜʜ Êœ œkk Š‹Š‹
™†pxe1 e 1
eee
2e 2y
e1
2e 2e
5ÈÈ
È
2x 2x
xxx
x
2x
xx
'' ''
RR
4 dA 4 dy dz 4œ œ œ
''
R''
01
12
30. g(x y z) y ln x 0 g g 1 since 1 x eßß œ œ Ê œ Ê œ œ Ÿ Ÿ™™
""
xxx
1x
ij kk
ÉÈ
; g 1 d dAÊœ œ Ê œ œÊ œÊ œnFnpjp
Š‹
Œ
ÈÈ È
x
1x
x
ij ij
x 2xy 1 x
1x 1x x
†™†kk 5
Flux dA 2y dx dz 2 ln x dz dx 2 ln x dxÊœ œ œ œ
''
RŠ‹Š‹
2xy 1 x
1x x
ÈÈ
'' '' '
01 10 1
1e e1 e
2 x ln x x 2(e e) 2(0 1) 2œ œœcd
e
"
31. On the face z a: g(x y z) z g g 1; 2xz 2ax since z a;œßßœÊœÊ œœÊœœ œ™™ †knkFnkk
d dx dy Flux 2ax dx dy 2ax dx dy a .5œÊœ œ œ
''
R''
00
aa %
On the face z 0: g(x y z) z g g 1; 2xz 0 since z 0;œßßœÊœÊ œœÊœœ œ™™ †knkFnkk
d dx dy Flux 0 dx dy 0.5œÊœ œ
''
R
On the face x a: g(x y z) x g g 1; 2xy 2ay since x a;œßßœÊœÊ œœÊœœ œ™™ †iniFnkk
d dy dz Flux 2ay dy dz a .5œÊœ œ
''
00
aa %
On the face x 0: g(x y z) x g g 1; 2xy 0 since x 0œßßœÊœÊ œœÊœœ œ™™ †iniFnkk
Flux 0.ʜ
On the face y a: g(x y z) y g g 1; 2yz 2az since y a;œßßœÊœÊ œœÊœœ œ™™ †jnjFnkk
d dz dx Flux 2az dz dx a .5œÊœ œ
''
00
aa %
On the face y 0: g(x y z) y g g 1; 2yz 0 since y 0œßßœÊœÊ œœÊœœ œ™™ †jnjFnkk
Flux 0. Therefore, Total Flux 3a .Êœ œ
%
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.5 Surface Area and Surface Integrals 1023
32. Across the cap: g(x y z) x y z 25 g 2x 2y 2z g 4x 4y 4z 10ßßœœ Ê œ Ê œ œ
### ###
™™ijkkk
È
; g 2z since z 0 d dAÊœ œ Ê œ œÊ œ Ê œnFnpkp
™
™
g
g5 555 2z
xyz yz
xz z 10
kk ijk †™†kk 5
Flux d dA x y 1 dx dy r 1 r dr dÊœ œ œ œ
cap 00
24
'' '' ''
cap RR
Fn†5 )
Š‹
ˆ‰ ab ab
xz z 5
555z
yz ## #
''
72 d 144 .œœ
'0
2
)1
Across the bottom: g(x y z) z 3 g g 1 1; g 1ßß œ œ Ê œ Ê œ Ê œ Ê œ œ Ê œ™™ † ™†knkFnpkpkk k k
d dA Flux d 1 dA 1(Area of the circular region) 16 . Therefore,Ê œ Ê œ œ œ œ55 1
bottom '' ''
bottom R
Fn†
Flux Flux Flux 128œ œ
cap bottom 1
33. f 2x 2y 2z f 4x 4y 4z 2a; f 2z since z 0 d dA™™ ™†œ Ê œ œ œÊ œ Êœijk pk pkk k k
È### 52a
2z
dA; M d (surface area of sphere) ; M z d z dAœœ œ œ œ œ
aaa
z8 z
xy
'' '' ''
SS
R
$5 $5 $
$$1
#ˆ‰
a dA a r dr d z . Because of symmetry, x yœœ œÊœœ œ œ$$ )
'' Š‹
ˆ‰
R''
00
2a $1 $1
$1
aa2a
4M4a
Mxy
#
the centroid is .œÊ ßß
a aaa
2ˆ‰
###
34. f 2y 2z f 4y 4z 4 y z 6; f 2z since z 0 d dA™™ ™†œ Ê œ œ œ œÊ œ Êœjk pk kkk a b k k
ÈÈ
## ## 56
2z
dA; M 1 d dx dy dx dy 9 ; M z dœœ œ œ œœ
333
zz
9y xy
'' ''
S S
515
'' ''
30 30
33 33
È
z dx dy 54; M y d y dx dy dx dy 0;œœœœœ œ
'' '' ''
30 30 30
33 33 33
ˆ‰ ˆ‰
33
zz
xz 3y
9y
''
S
5È
M x d dx dy . Therefore, x , y 0, and z
yz 3x 27 3 54 6
9y 99
œœ œ œœœœœ
''
S
51
''
30
33
ÈŠ‹
##
27 1
111
35. Because of symmetry, x y 0; M d d (Area of S) 3 2 ; f 2x 2y 2zœœœœœ œ œ
'' ''
SS
$5 $ 5 $ 1 $
șijk
f 4x4y4z2xyz; f 2z d dAÊ œ œ œÊ œÊœkk k k
ÈÈ
™™†
### ###
#
pk p 52xyz
z
È
dA dA M z dAœœÊœ
ÈÈ È
ab ÈÈ
xy xy
zz z
2x y 2x y
xy
$''
RŠ‹
2 x y dA 2 r dr d zœœ œÊœœ$$)$
''
RÈÈ
È## #
''
01
22 14 2
39
32
14
1$
1$
Ȍ
È
14 2
3
x y z 0 0 . Next, I x y d x y dAÊßßœßß œ œ ab ab ab
ˆ‰ Š‹
14
9 z
z2x y
'' ''
SR
## ##
$5 $
ÈÈ
2 x y dA 2 r dr d Rœœ œÊœœ$$)$
ÈÈ
ab É
''
R
## $
##
''
01
22
z
15 2 I
M
10
1ÈÈ
z
36. f(x y z) 4x 4y z 0 f 8x 8y 2z f 64x 64y 4zßßœ œÊ œ Ê œ
### ###
™™ijkkk
È
2 16x 16y z 2 4z z 2 5 z since z 0; f 2z d dA 5 dAœ œ œ œÊ œ Ê œ œ
ÈÈÈÈ
kk
### ## pk p™† 525z
2z
È
I x y d 5 x y dx dy 5 r dr dÊœ œ œ œ
z35
'' ''
SR
ab ab
ÈÈ
## ## $
#
$5 $ $ )
''
20
22cos È1$
37. (a) Let the diameter lie on the z-axis and let f(x y z) x y z a , z 0 be the upper hemisphereßßœœ
####
f 2x 2y 2z f 4x 4y 4z 2a, a 0; f 2z since z 0Ê œ Ê œ œ œÊ œ ™™ ™†ijk pk pkk k k
È###
d dA I x y d a dA a r dr dÊœ Êœ œ œ5$5$ $)
aa r
zz
xy
axy ar
z00
2a
'' ab
ˆ‰
SR
##
''ÈÈ
ab ''
a r a r a r d a a d a the moment of inertia is a forœ œ œÊ$)$)$$
''
0 0
2 2
a
’“
Èab
### $% %
## $Î#
!
224 8
333 3
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1024 Chapter 16 Integration in Vector Fields
the whole sphere
(b) I I mh , where m is the mass of the body and h is the distance between the parallel lines; now,
Lc.m.
œ
#
I a (from part a) and d dA a dy dx
c.m. 8ma
3z
axy
œœœœ
1%
#
"
$$5$$
'' '' ''
SRR
ˆ‰ Èab
a r dr d a a r d a a d 2 a and h aœœœœœ$)$ )$)1$
'' ' '
00 0 0
2a 2 2
a
"
##
!
#
Èar ’“
È
Ia4aa aÊœ œ
L820
33
11
%##%
$1$ $
38. (a) Let z x y be the cone from z 0 to z h, h 0. Because of symmetry, x 0 and y 0;œ œœ œ œ
h
aÈ##
z x y f(x y z) x y z 0 f 2zœ Êßßœ œÊœ
h h 2xh
aa aa
2yh
Èab
## ## # ™ijk
f 4z 2 xy xy 2 xy 1Êœ œ œ kk abab ab
ÉÉÉ
ˆ‰ ˆ ‰
™4x h h h h h
aa a
4y h
aaa
##### ##
2 z h a since z 0; f 2z d dAœœœÊœÊœ
Ɉ‰ˆ‰
Èkk
###
ha 2z
aa 2z
ha
pk p™† 5ˆ‰
È
2z
a
dA; M d dA a a h a ;œœœ œœ
ÈÈÈ
ha ha ha
aaa
###
'' ''
SR
511ab È
M z d z dA x y dx dy r dr d
xy 00
2a
œœ œ œ
'' '' ''
SRR
5 )
Š‹ È
ÈÈ È
ha ha hha
aaa a
h
## #
''
z the centroid is 0 0œÊœœÊ ßß
2ah h a
3M3 3
M2h 2h
1Èxy ˆ‰
(b) The base is a circle of radius a and center at (0 0 h) (0 0 h) is the centroid of the base and the mass isßß Ê ßß
M d a . In Pappus' formula, let , h , m a h a , and m aœœ œ œœ œ
''
S
51 1 1
# #
"#" #
##
ckck
2h
3È
the centroid is Ê œ œ Ê !ß !ßck
11
11
ah a ah
ah a a
2h h a 3ah 2h h a 3ah
3haa 3haa
ÈŠ‹
ÈÈÈ
Š‹ Š‹
ÈÈ
2h
3kk
(c) If the hemisphere is sitting so its base is in the plane z h, then its centroid is 0 0 h and its mass isœßß
ˆ‰
a
#
2 a . In Pappus' formula, let , h , m a h a , and m 2 a111
# #
"# " #
###
ckc kœœ œ œ
2h a
3ˆ‰ È
the centroid isÊœ œ Êck
11
11
ah a 2ah
ah a 2a
2h h a 6ah 3a
3ha2a
Ȉ‰ ˆ ‰
ÈÈŠ‹
È
2h
3kk
a
. Thus, for the centroid to be in the plane of the bases we must have z h
!ß !ß œ
2h h a 6ah 3a
3ha2a
ÈŠ‹
È
h 2h h a 6ah 3a 3h h a 6ah 3a h h aʜʜʜ
2h h a 6ah 3a
3ha2a
ÈŠ‹
È
## ## ##
##
ÈÈÈ
9a h h a h a h 9a 0 h (the positive root) h aʜ ʜʜ ʜ
% ### %## % # "
##
ab Š‹ É
ÈÈ
37 a 2372
39. f (x y) 2x, f (x y) 2y f f 1 4x 4y 1 Area 4x 4y 1 dx dy
xy xy
ßœ ßœ Ê œ Ê œ
ÉÈÈ
## ## ##
''
R
4r 1 r dr d 13 13 1œœ
''
00
23
ÈŠ‹
È
#)1
6
40. f (y z) 2y, f (y z) 2z f f 1 4y 4z 1 Area 4y 4z 1 dy dz
yz yz
ßœ ßœÊ œ Ê œ
ÉÈÈ
## ## ##
''
R
4r 1 r dr d 5 5 1œœ
''
00
21
ÈŠ‹
È
#)1
6
41. f (x y) , f (x y) f f 1 1 2
xy
xx
xy xy
yy
xy xy xy
ßœ ßœ Ê œ œ
ÈÈ
##
ÉÉÈ
Area 2 dx dy 2(Area between the ellipse and the circle) 2(6 ) 5 2Êœ œ œ œ
''
Rxy ÈÈ È È
11 1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.6 Parameterized Surfaces 1025
42. Over R : z 2 x 2y f (x y) , f (x y) 2 f f 1 4 1
xy x y
22 47
33 93
xy
œ Ê ß œ ß œÊ œ œ
ÉÉ
##
Area dA (Area of the shadow triangle in the xy-plane) .Êœ œ œ œ
''
Rxy
77 737
33 3
ˆ‰ˆ‰
##
Over R : y 1 x z f (x z) , f (x z) f f 1 1
xz x z
11 17
33 946
xz
œ Ê ß œ ß œ Ê œ œ
"""
##
##
ÈÉ
Area dA (Area of the shadow triangle in the xz-plane) (3) .Êœ œ œ œ
''
Rxz
77 7 7
66 6
ˆ‰ #
Over R : x 3 3y z f (y z) 3, f (y z) f f 1 9 1
yz y z
3397
yz 4
œ Ê ß œ ß œ Ê œ œ
## #
##
ÉÉ
Area dA (Area of the shadow triangle in the yz-plane) (1) .Êœ œ œ œ
''
Ryz
77 7 7
22 2
ˆ‰ #
43. y z f (x z) 0, f (x z) z f f 1 z 1 ; y z z 4œ Ê ßœ ßœ Ê œ œ Ê œ Êœ
216 16 2
3333
xz xz
$Î# "Î# $Î#
##
ÈÈ
Area z 1 dx dz z 1 dz 5 5 1Êœ œ œ
'' '
00 0
41 4
ÈÈ
Š‹
È
2
3
44. y 4 z f (x z) 0, f (x z) 1 f f 1 2 Area 2 dA 2 dx dzœ Ê ß œ ß œÊ œ Ê œ œ
xz xz
ÈÈÈÈ
## ''
Rxz
00
24z
''
2 4 z dzœœ
Èab
'0
2#16 2
3
È
16.6 PARAMETRIZED SURFACES
1. In cylindrical coordinates, let x r cos , y r sin , z x y r . Thenœœœœ))
ˆ‰
È##
##
(r ) (r cos ) (r sin ) r , 0 r 2, 0 2 .rijkßœ ŸŸ ŸŸ))) )1
#
2. In cylindrical coordinates, let x r cos , y r sin , z 9 x y 9 r . Thenœœœœ)) ## #
(r ) (r cos ) (r sin ) 9 r ; z 0 9 r 0 r 9 3 r 3, 0 2 . Butrijkßœ ÊÊ ŸÊŸŸ ŸŸ))) )1ab
###
3 r 0 gives the same points as 0 r 3, so let 0 r 3.ŸŸ ŸŸ Ÿ Ÿ
3. In cylindrical coordinates, let x r cos , y r sin , z z . ThenœœœÊœ))
Èxy r
##
(r ) (r cos ) (r sin ) . For 0 z 3, 0 3 0 r 6; to get only the first octant, letrijkßœ ŸŸ ŸŸÊŸŸ)))
ˆ‰
rr
##
0.ŸŸ)1
#
4. In cylindrical coordinates, let x r cos , y r sin , z 2 x y z 2r. ThenœœœÊœ))
È##
(r ) (r cos ) (r sin ) 2r . For 2 z 4, 2 2r 4 1 r 2, and let 0 2 .rijkßœ ŸŸ Ÿ ŸÊŸŸ ŸŸ))) )1
5. In cylindrical coordinates, let x r cos , y r sin since x y r z 9 x y 9 rœœ œÊœœ))
## # ## #2ab
z 9 r , z 0. Then (r ) (r cos ) (r sin ) 9 r . Let 0 2 . For the domainÊœ ßœ ŸŸ
ÈÈ
# #
rijk))) )1
of r: z x y and x y z 9 x y x y 9 2 x y 9 2r 9œ œÊ œÊ œÊ œ
ÈÈ
ˆ‰ ab
## ##
### ## ## #
#
r 0 r .Êœ Ê ŸŸ
33
22
ÈÈ
6. In cylindrical coordinates, (r ) (r cos ) (r sin ) 4 r (see Exercise 5 above with x y z 4,rijkßœ œ)))
È####
instead of x y z 9). For the first octant, let 0 . For the domain of r: z x y and
###
###
œ ŸŸ œ )1È
x y z 4 x y x y 4 2 x y 4 2r 4 r 2. Thus, let 2 r 2
### ## ## #
##
#
œÊ œÊ œÊ œÊœ ŸŸ
ˆ‰
Èab ÈÈ
(to get the portion of the sphere between the cone and the xy-plane).
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1026 Chapter 16 Integration in Vector Fields
7. In spherical coordinates, x sin cos , y sin sin , x y z 3 3œœœÊœÊœ39 ) 39)3 3 3
ÈÈ
### #
z 3 cos for the sphere; z 3 cos cos ; z 3 cos Êœ œ œ Ê œ Ê œ œ Ê œ
ÈÈ È
9999 9
ÈÈÈ
333
3####
"1
cos . Then ( ) 3 sin cos 3 sin sin 3 cos ,ʜʜ ߜ 99 9) 9) 9) 9
"
#
2
3
1rijk
Š‹Š‹Š‹
ÈÈÈ
and 0 2 .
11
33
2
ŸŸ ŸŸ9)1
8. In spherical coordinates, x sin cos , y sin sin , x y z 8 8 2 2œœœÊœÊœœ39 ) 39)3 3 3
ÈÈÈ
### #
x 2 2 sin cos , y 2 2 sin sin , and z 2 2 cos . Thus letÊœ œ œ
ÈÈ È
9) 9) 9
( ) 2 2 sin cos 2 2 sin sin 2 2 cos ; z 2 2 2 2 cos rijk9) 9 ) 9 ) 9 9ßœ œÊœ
Š‹Š‹Š‹
ÈÈÈ È
cos ; z 2 2 2 2 2 2 cos cos 1 0. Thus 0 andʜʜœÊœ ʜʜ ŸŸ99 999 9
"
È2
3 3
4 4
1 1
ÈÈÈ
02.ŸŸ)1
9. Since z 4 y , we can let be a function of x and y (x y) x y 4 y . Then z 0œ Ê ßœ œ
# #
rrijkab
0 4 y y 2. Thus, let 2 y 2 and 0 x 2.Êœ Êœ„ ŸŸ ŸŸ
#
10. Since y x , we can let be a function of x and z (x z) x x z . Then y 2œÊßœœ
# #
rrijk
x 2 x 2. Thus, let 2 x 2 and 0 z 3.ʜʜ„ ŸŸ ŸŸ
#ÈÈÈ
11. When x 0, let y z 9 be the circular section in the yz-plane. Use polar coordinates in the yz-planeœœ
##
y 3 cos and z 3 sin . Thus let x u and v (u,v) u (3 cos v) (3 sin v) whereÊœ œ œ œÊ œ )) )ri j k
0 u 3, and 0 v 2 .ŸŸ ŸŸ1
12. When y 0, let x z 4 be the circular section in the xz-plane. Use polar coordinates in the xz-planeœœ
##
x 2 cos and z 2 sin . Thus let y u and v (u,v) (2 cos v) u (3 sin v) whereÊœ œ œ œÊ œ )) )rijk
2 u 2, and 0 v (since we want the portion the xy-plane).Ÿ Ÿ Ÿ Ÿ1above
13. (a) x y z 1 z 1 x y. In cylindrical coordinates, let x r cos and y r sin œ Êœ œ œ))
z 1 r cos r sin (r ) (r cos ) (r sin ) (1 r cos r sin ) , 0 2 andÊœ Ê ß œ ŸŸ))))) )))1rij k
0r3.ŸŸ
(b) In a fashion similar to cylindrical coordinates, but working in the yz-plane instead of the xy-plane, let
y u cos v, z u sin v where u y z and v is the angle formed by (x y z), (x 0 0), and (x y 0)œ œ œ ßß ßß ßß
È##
with (x 0 0) as vertex. Since x y z 1 x 1 y z x 1 u cos v u sin v, then is aßß œ Ê œ Ê œ r
function of u and v (u v) (1 u cos v u sin v) (u cos v) (u sin v) , 0 u 3 and 0 v 2 .Êßœ ŸŸ ŸŸrijk1
14. (a) In a fashion similar to cylindrical coordinates, but working in the xz-plane instead of the xy-plane, let
x u cos v, z u sin v where u x z and v is the angle formed by (x y z), (y 0 0), and (x y 0)œ œ œ ßß ßß ßß
È##
with vertex (y 0 0). Since x y 2z 2 y x 2z 2, then (u v)ßß œ Ê œ ßr
(u cos v) (u cos v 2u sin v 2) (u sin v) , 0 u 3 and 0 v 2 .œ ŸŸ ŸŸijk
È1
(b) In a fashion similar to cylindrical coordinates, but working in the yz-plane instead of the xy-plane, let
y u cos v, z u sin v where u y z and v is the angle formed by (x y z), (x 0 0), and (x y 0)œ œ œ ßß ßß ßß
È##
with vertex (x 0 0). Since x y 2z 2 x y 2z 2, then (u v)ßß œ Ê œ ßr
(u cos v 2u sin v 2) (u cos v) (u sin v) , 0 u 2 and 0 v 2 .œ ŸŸ ŸŸijk
È1
15. Let x w cos v and z w sin v. Then (x 2) z 4 x 4x z 0 w cos v 4w cos v w sin vœ œ œÊ œÊ
## # # ## ##
0 w 4w cos v 0 w 0 or w 4 cos v 0 w 0 or w 4 cos v. Now w 0 x 0 and y 0,œÊ œÊ œ œ Ê œ œ œ Ê œ œ
#
which is a line not a cylinder. Therefore, let w 4 cos v x (4 cos v)(cos v) 4 cos v and z 4 cos v sin v.œÊœ œ œ
#
Finally, let y u. Then (u v) 4 cos v u (4 cos v sin v) , v and 0 u 3.œ ß œ ŸŸ ŸŸrijkab
#
##
11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.6 Parameterized Surfaces 1027
16. Let y w cos v and z w sin v. Then y (z 5) 25 y z 10z 0œœ œÊœ
## ##
w cos v w sin v 10w sin v 0 w 10w sin v 0 w(w 10 sin v) 0 w 0 orʜʜʜʜ
## ## #
w 10 sin v. Now w 0 y 0 and z 0, which is a line not a cylinder. Therefore, let w 10 sin vœœÊœœ œ
y 10 sin v cos v and z 10 sin v. Finally, let x u. Then (u v) u (10 sin v cos v) 10 sin v ,Êœ œ œ ßœ
# #
ri j kab
0 u 10 and 0 v .ŸŸ ŸŸ1
17. Let x r cos and y r sin . Then (r ) (r cos ) (r sin ) , 0 r 1 and 0 2œœ ßœ ŸŸŸŸ) ) ))) )1rijk
ˆ‰
2r sin
#
)
(cos ) (sin ) and ( r sin ) (r cos )Êœ œ rijkr i jk
rsin r cos
)) ) )
ˆ‰ ˆ ‰
))
)
##
cos sin
r sin r cos
Ê‚œ
rr
ijk
rsin
r cos
))
)
ââ
ââ
ââ
ââ
ââ
ââ
))
))
#
#
r cos r sin rœ œ
Š‹Š‹
ab
## ## #
##
r sin cos r sin r cos r
(sin )(r cos )
)) ) )
))
ij kjk))
r A dr d d dÊ‚œ œ Êœ œ œ œkk
É’“
rr
rr
44
5r 5r 5r 5
)1
### #
"
!
ÈÈÈ È
'' ' '
00 0 0
21 2 2
)))
18. Let x r cos and y r sin z x r cos , 0 r 2 and 0 2 . ThenœœÊœœŸŸŸŸ)) ) )1
(r ) (r cos ) (r sin ) (r cos ) (cos ) (sin ) (cos ) andrijkrijkßœ Ê œ ))) ) )))
r
( r sin ) (r cos ) (r sin )rijk
)œ )))
cos sin cos
r sin r cos r sin
Ê‚œ
rr
ijk
r)
ââ
ââ
ââ
ââ
ââ
ââ
)) )
)))
r sin r cos (r sin cos r sin cos ) r cos r sin r rœ œab ab
## ##
) ) )) )) ) )ijkik
r r r 2 A r 2 dr d d 2 2 d 4 2Ê‚œ œ Êœ œ œ œkk
ÈÈ È ÈÈ
’“
rr
rr2
2
)## #
!
'' ' '
00 0 0
22 2 2
)))1
È
19. Let x r cos and y r sin z 2 x y 2r, 1 r 3 and 0 2 . ThenœœÊœœŸŸŸŸ)) )1
È##
(r ) (r cos ) (r sin ) 2r (cos ) (sin ) 2 and ( r sin ) (r cos )rijkrijkrijßœ Ê œ œ ))) )) ) )
r)
( 2r cos ) (2r sin ) r cos r sin
cos sin 2
r sin r cos 0
Ê‚œ œ
rr i j k
ijk
r)
ââ
ââ
ââ
ââ
ââ
ââ ab
))
))
))))
##
( 2r cos ) (2r sin ) r 4r cos 4r sin r 5r r 5œ Ê ‚ œ œ œ)) ))ijkrrkk
ÈÈÈ
r)## ## # #
A r 5 dr d d 4 5 d 8 5Êœ œ œ œ
'' ' '
01 0 0
23 2 2
ÈÈÈ
’“
)))1
r5
2
È$
"
20. Let x r cos and y r sin z , 3 r 4 and 0 2 . ThenœœÊœœŸŸŸŸ)) )1
Èxy
33
r
(r ) (r cos ) (r sin ) (cos ) (sin ) and ( r sin ) (r cos )r i jkr i jkr i jßœ Ê œ œ ))) )) ) )
ˆ‰ ˆ‰
r
33
r")
cos sin r cos r sin r cos r sin
r sin r cos 0
Ê‚œ œ
rr i j k
ijk
r33 3
)
ââ
ââ
ââ
ââ
ââ
ââ
ˆ‰ˆ‰
ab)) ) ) ) )
))
"" " ##
r cos r sin r r cos r sin rœ Ê ‚ œ œ œ
ˆ‰ˆ‰kk
ÉÉ
"" ""
## ## #
33 99 93
r10r r10
)) ))ijkrr
)È
A dr d d dÊœ œ œ œ
'' ' '
03 0 0
24 2 2
r 10 r 10 7 10 7 10
3663
ÈÈÈÈ
)))
’“
%
$
1
21. Let x r cos and y r sin r x y 1, 1 z 4 and 0 2 . Thenœ œ Ê œœ ŸŸ ŸŸ)) )1
###
(z ) (cos ) (sin ) z and ( sin ) (cos )rijkrkrijßœ Ê œ œ ))) ) )
z)
(cos ) (sin ) cos sin 1
sin cos 0
001
Ê‚œ œ Ê‚œ œ
rr i j rr
ijk
) )z z
ââ
ââ
ââ
ââ
ââ
ââ kk
È
)) )) ))
##
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1028 Chapter 16 Integration in Vector Fields
A 1 dr d 3 d 6Êœ œ œ
'' '
01 0
24 2
))1
22. Let x u cos v and z u sin v u x z 10, 1 y 1, 0 v 2 . ThenœœÊœœŸŸŸŸ
### 1
(y v) (u cos v) y (u sin v) 10 cos v y 10 sin vrijk ijkßœ œ
Š‹Š‹
ÈÈ
10 sin v 10 cos v and 10 sin v 0 10 cos v
010
Êœ œÊ‚œ
rikrjrr
ijk
vyvy
Š‹Š‹
ÈÈ ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ
10 cos v 10 sin v 10 A 10 du dv 10u dvœ Ê ‚ œ Ê œ œ
Š‹Š‹ ’“
ÈÈ È È È
kkikrr
vy 01 0
21 2
'' ' "
"
2 10 dv 4 10œœ
'0
2ÈÈ
1
23. z 2 x y and z x y z 2 z z z 2 0 z 2 or z 1. Since z x y 0,œ œ Ê œ Ê œ Ê œ œ œ
## # #
## ##
ÈÈ
we get z 1 where the cone intersects the paraboloid. When x 0 and y 0, z 2 the vertex of theœœœœÊ
paraboloid is (0 0 2). Therefore, z ranges from 1 to 2 on the “cap" r ranges from 1 (when x y 1) to 0ßß Ê œ
##
(when x 0 and y 0 at the vertex). Let x r cos , y r sin , and z 2 r . Thenœœ œ œ œ)) #
(r ) (r cos ) (r sin ) 2 r , 0 r 1, 0 2 (cos ) (sin ) 2r andrijk rijkßœ ŸŸ ŸŸ Ê œ ))) )1 ))ab
#r
( r sin ) (r cos ) cos sin 2r
r sin r cos 0
rijrr
ijk
))
œ Ê ‚ œ
)) ))
))
r
ââ
ââ
ââ
ââ
ââ
ââ
2r cos 2r sin r 4r cos 4r sin r r 4r 1œÊ‚œ œabab kk
ÈÈ
## %# %# # #
)) ))ijkrr
r)
A r 4r 1 dr d 4r 1 d d 5 5 1Êœ œ œ œ
'' ' '
00 0 0
21 2 2
È’“Š‹Š‹
ab È
#"#$Î# "
!
"
#
)))
12 1 6
55
È1
24. Let x r cos , y r sin and z x y r . Then (r ) (r cos ) (r sin ) r , 1 r 2,œ œ œœ ßœ ŸŸ) ) )))
### #
rijk
0 2 (cos ) (sin ) 2r and ( r sin ) (r cos )ŸŸ Ê œ œ )1 ) ) ) )rijkr i j
r)
2r cos 2r sin r
cos sin 2r
r sin r cos 0
Ê‚œ œ Ê ‚
rr i jk rr
ijk
r r) )
ââ
ââ
ââ
ââ
ââ
ââ
ababkk
))
))
))
##
4r cos 4r sin r r 4r 1 A r 4r 1 dr d 4r 1 dœœÊœ œ
ÈÈÈ
’“
ab
%# %# # # # "#$Î# #
"
)) ) )
'' '
01 0
22 2
12
d171755œœ
'0
2Š‹Š ‹
ÈÈ
17 17 5 5
16
ÈÈ
#)1
25. Let x sin cos , y sin sin , and z cos x y z 2 on the sphere. Next,œ œ œ Êœ œ39 ) 39) 3 9 3
ÈÈ
###
x y z 2 and z x y z z 2 z 1 z 1 since z 0 . For the lower
### ## #
##
œ œ Ê œÊ œÊœ Ê œ
È91
4
portion of the sphere cut by the cone, we get . Then91œ
( ) 2 sin cos 2 sin sin 2 cos , , 0 2rijk9) 9 ) 9 ) 9 9 1 ) 1ßœ ŸŸ ŸŸ
Š‹Š‹Š‹
ÈÈÈ
1
4
2 cos cos 2 cos sin 2 sin and 2 sin sin 2 sin cos Êœ œ rijkr ij
9 )
Š‹Š‹Š‹Š ‹Š‹
ÈÈÈ ÈÈ
9) 9) 9 9) 9)
2 cos cos 2 cos sin 2 sin
2 sin sin 2 sin cos 0
Ê‚œ
rr
ijk
9)
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ È
ÈÈ
9) 9) 9
9) 9 )
2 sin cos 2 sin sin (2 sin cos )œabab
##
9) 9) 99ijk
4 sin cos 4 sin sin 4 sin cos 4 sin 2 sin 2 sin Ê‚œ œ œ œkk kk
ÈÈ
rr
9) %# %# ## #
9) 9) 99 9 9 9
A 2 sin d d 2 2 d 4 2 2Êœ œ œ
'' '
04 0
22
99) ) 1
Š‹Š ‹
ÈÈ
26. Let x sin cos , y sin sin , and z cos x y z 2 on the sphere. Next,œ œ œ Êœ œ39 ) 39) 3 9 3
È###
z 1 1 2 cos cos ; z 3 3 2 cos cos . Thenœ Ê œ Ê œ Ê œ œ Ê œ Ê œ Ê œ99 9 99 9
"
# #
2
3 6
3
1 1
ÈÈ È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.6 Parameterized Surfaces 1029
( ) (2 sin cos ) (2 sin sin ) (2 cos ) , , 0 2rijk9) 9 ) 9 ) 9 9 ) 1ßœ ŸŸ ŸŸ
11
63
2
(2 cos cos ) (2 cos sin ) (2 sin ) andʜ rijk
99) 9) 9
( 2 sin sin ) (2 sin cos )rij
)œ 9) 9 )
2 cos cos 2 cos sin 2 sin
2 sin sin 2 sin cos 0
Ê‚œ
rr
ijk
9)
ââ
ââ
ââ
ââ
ââ
ââ
9) 9) 9
9) 9 )
4 sin cos 4 sin sin (4 sin cos )œabab
##
9) 9) 99ijk
16 sin cos 16 sin sin 16 sin cos 16 sin 4 sin 4 sin Ê‚œ œ œ œkk kk
ÈÈ
rr
9) %# %# ## #
9) 9) 99 9 9 9
A 4 sin d d 2 2 3 d 4 4 3Êœ œ œ
'' '
06 0
223 2
99) ) 1
Š‹Š‹
ÈÈ
27. Let the parametrization be (x z) x x z 2x and 12x0
00
rijkrijrkrr
ijk
ßœ Ê œ œ Ê ‚œ
"
#xzxz
ââ
ââ
ââ
ââ
ââ
ââ
2x 4x 1 G(x y z) d x 4x 1 dx dz 4x 1 dzœÊ‚œ Ê ßß œ œ ij r rkk a b
ÈÈ
’“
xz 00 0
32 3
##
"#$Î# #
!
''
S
5'' ' 12
17 17 1 dzœœ
'0
3"
#
"
14
17 17
Š‹
ÈÈ
28. Let the parametrization be (x y) x y 4 y , 2 y 2 and rij k rirj kßœ ŸŸÊ œ œ
È#
xy
y
4y
È
1
10 0
01
Ê‚œ œ Ê ‚œ œ
rr jk rr
ij k
xy xy
ââ
ââ
ââ
ââ
ââ
ââ kk
É
y
4y
yy
4y 4y
4y
2
ÈÈÈ
G(x y z) d 4 y dy dx 24Êßßœ œ
''
S
5''
12
42
ÈŠ‹
#
2
4y
È
29. Let the parametrization be ( ) (sin cos ) (sin sin ) (cos ) (spherical coordinates with 1rijk9) 9 ) 9 ) 9 3ßœ œ
on the sphere), 0 , 0 2 (cos cos ) (cos sin ) (sin ) andŸŸ ŸŸ Ê œ 91 ) 1 9 ) 9 ) 9rijk
9
( sin sin ) (sin cos ) cos cos cos sin sin
sin sin sin cos 0
rijrr
ijk
)9)
œ Ê ‚ œ
9) 9 ) 9) 9) 9
9) 9 )
ââ
ââ
ââ
ââ
ââ
ââ
sin cos sin sin (sin cos ) sin cos sin sin sin cosœÊ‚œ abab kk
È
## %# %# ##
9) 9) 99 9 ) 9 ) 9 9ijkrr
9)
sin ; x sin cos G(x y z) cos sin G(x y z) d cos sin (sin ) d dœœ Êßßœ Êßßœ99) )9 5 )999)
## ##
''
S''
00
2ab
cos 1 cos (sin ) d d ; cos u 1 du d
u cos
du sin d
œ Ä
œ
œ
'' ''
00 01
221
aba b abab
”•
## ##
)999) ) )
9
99
cos u d cos dœœœœ
''
00
22
ab
’“ ‘
##
"
"
#
!
))))
u4 4sin 24
33 3243
)) 1
1
30. Let the parametrization be ( ) (a sin cos ) (a sin sin ) (a cos ) (spherical coordinates withrijk9) 9 ) 9 ) 9ߜ
a, a 0, on the sphere), 0 (since z 0), 0 239)1œ ŸŸ ŸŸ
1
#
(a cos cos ) (a cos sin ) (a sin ) andʜ rijk
99) 9) 9
( a sin sin ) (a sin cos ) a cos cos a cos sin a sin
a sin sin a sin cos 0
rijrr
ijk
)9)
œ Ê ‚ œ
9) 9 ) 9) 9) 9
9) 9 )
ââ
ââ
ââ
ââ
ââ
ââ
a sin cos a sin sin (a sin cos )œabab
## ## #
9) 9) 99ijk
a sin cos a sin sin a sin cos a sin ; z a cos Ê‚œ œ œkk
È
rr
9) %% # %% # %# # #
9) 9) 99 9 9
G(x y z) a cos G(x y z) d a cos a sin d d aÊßßœ Ê ßß œ œ
## ## # %
95 999)1
''
S''
00
22
abab2
3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1030 Chapter 16 Integration in Vector Fields
31. Let the parametrization be (x y) x y (4 x y) and rij krikrjkßœ Ê œ œ
xy
3 F(x y z) d (4 x y) 3 dy dx
10 1
01
Ê ‚ œ œ Ê ‚ œ Ê ßß œ
"
rr ijk rr
ij k
xy xy
ââ
ââ
ââ
ââ
ââ
ââ kk
ÈÈ
''
S
5''
00
11
3 4y xy dx 3 x dx 3 x 3 3œœœœ
''
00
11
ÈÈÈÈ
’“ ’“
ˆ‰
y
22
77x
""
!!
##
32. Let the parametrization be (r ) (r cos ) (r sin ) r , 0 r 1 (since 0 z 1) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
(cos ) (sin ) and ( r sin ) (r cos ) cos sin
r sin r cos 0
Êœ œ Ê‚œ "
rijkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
( r cos ) (r sin ) r ( r cos ) ( r sin ) r r 2; z r and x r cos œ Ê ‚ œ œ œ œ)) ) ) )ijkrrkk
ÈÈ
r)###
F(x y z) r r cos F(x y z) d (r r cos ) r 2 dr d 2 (1 cos ) r dr dÊßßœ Ê ßß œ œ )5 )) ))
''
S'' ''
00 00
21 21
Š‹
ÈÈ #
œ22
3
1È
33. Let the parametrization be (r ) (r cos ) (r sin ) 1 r , 0 r 1 (since 0 z 1) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1ab
#
(cos ) (sin ) 2r and ( r sin ) (r cos ) cos sin 2r
r sin r cos 0
Êœ œ Ê‚œ
r i jkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
2r cos 2r sin r 2r cos 2r sin r r 1 4r ; z 1 r andœÊ‚œ œœabab kkabab
ÉÈ
## #
####
#
)) ))ijkrr
r)
x r cos H(xyz) r cos 1 4r H(xyz) dœÊßßœ Ê ßß)) 5ab
È
## #''
S
r cos 1 4r r 1 4r dr d r 1 4r cos dr dœœœ
'' ''
00 00
21 21
ab ab
Š‹Š‹
ÈÈ
## $ # #
##
))))
11
12
1
34. Let the parametrization be ( ) (2 sin cos ) (2 sin sin ) (2 cos ) (spherical coordinates withrijk9) 9 ) 9 ) 9ߜ
2 on the sphere), 0 ; x y z 4 and z x y z z 4 z 2 z 2 (since39œ ŸŸ œ œ Ê œÊ œÊœ
1
4### ## #
##
ÈÈ
z 0) 2 cos 2 cos , 0 2 ; (2 cos cos ) (2 cos sin ) (2 sin )Ê œ Ê œ Êœ ŸŸ œ 999)19)9)9
ÈÈ2
4#
19
rijk
and r ( 2 sin sin ) (2 sin cos ) 2 cos cos 2 cos sin 2 sin
2 sin sin 2 sin cos 0
)9)
œ Ê ‚ œ
9) 9 ) 9) 9) 9
9) 9 )
ijrr
ijk
ââ
ââ
ââ
ââ
ââ
ââ
4 sin cos 4 sin sin (4 sin cos )œabab
##
9) 9) 99ijk
16 sin cos 16 sin sin 16 sin cos 4 sin ; y 2 sin sin andÊ‚œ œ œkk
È
rr
9) %# %# ##
9) 9) 99 9 9)
z 2 cos H(x y z) 4 cos sin sin H(x y z) d (4 cos sin sin )(4 sin ) d dœ Ê ßß œ Ê ßß œ9 99) 5 99) 99)
''
S''
00
24
16 sin cos sin d d 0œœ
''
00
24 #99)9)
35. Let the parametrization be (x y) x y 4 y , 0 x 1, 2 y 2; z 0 0 4 yrij kßœ ŸŸŸŸ œÊœab
##
y 2; and 2y 2y d
10 0
01 2y
Êœ„ œ œ Ê ‚œ œ Ê
ri rj k rr jk Fn
ij k
xy xy
ââ
ââ
ââ
ââ
ââ
ââ †5
dy dx (2xy 3z) dy dx 2xy 3 4 y dy dx dœ‚œœÊFrr Fn††
rr
rr
xy
xy
‚
‚
#
kk
kk c dab
xy ''
S
5
2xy 3y 12 dy dx xy y 12y dx 32 dx 32œœœœ
'' ' '
02 0 0
12 1 1
abcd
##$
#
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
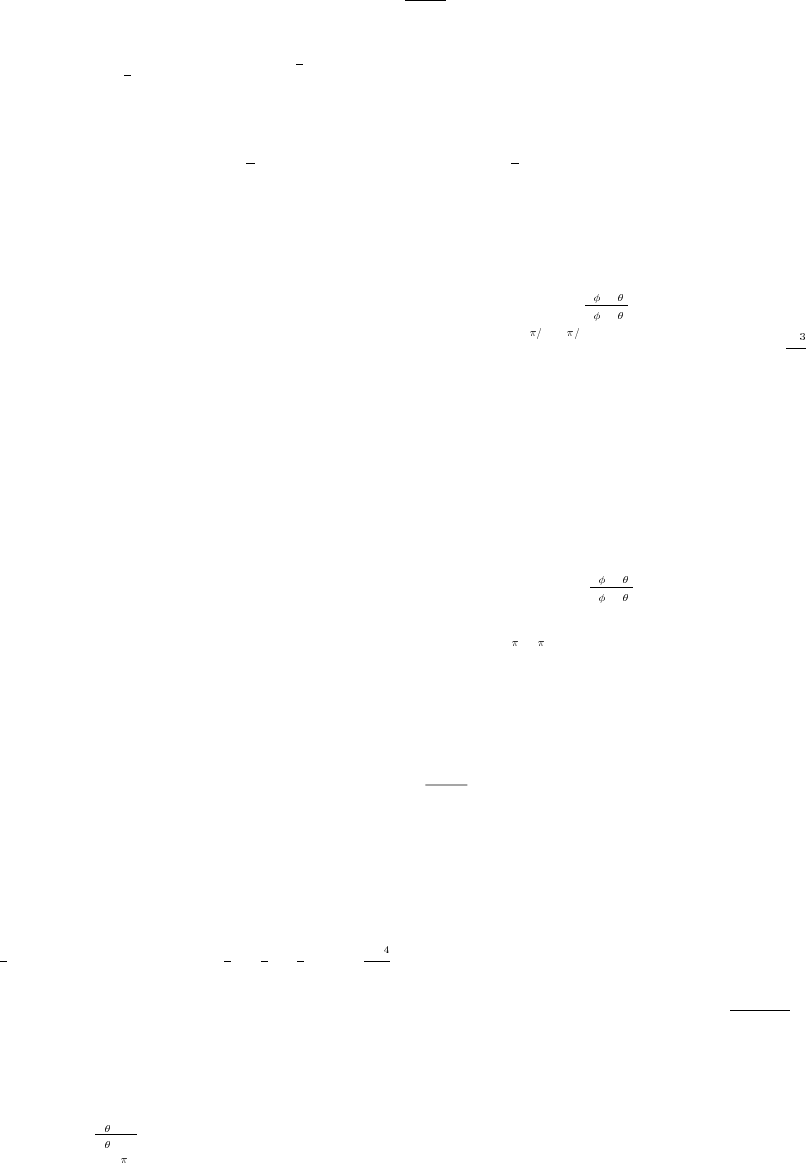
Section 16.6 Parameterized Surfaces 1031
36. Let the parametrization be (x y) x x z , 1 x 1, 0 z 2 2x and rijk rijrkßœ ŸŸ ŸŸÊ œ œ
#xz
2x d dz dx x dz dx
12x0
001
Ê‚œ œ Ê œ ‚ œrr ij Fn F rr
ijk
xz xz
ââ
ââ
ââ
ââ
ââ
ââ kk††5rr
rr
xz
xz
‚
‚
#
kk
d x dz dxÊœœ
''
S
Fn†5''
10
12 #4
3
37. Let the parametrization be ( ) (a sin cos ) (a sin sin ) (a cos ) (spherical coordinates withrijk9) 9 ) 9 ) 9ߜ
a, a 0, on the sphere), 0 (for the first octant) 0 (for the first octant)39)œ ŸŸ ߟŸ
11
##
(a cos cos ) (a cos sin ) (a sin ) and ( a sin sin ) (a sin cos )Êœ œ rijkr ij
9 )
9) 9) 9 9) 9)
a cos cos a cos sin a sin
a sin sin a sin cos 0
Ê‚œ
rr
ijk
9)
ââ
ââ
ââ
ââ
ââ
ââ
9) 9) 9
9) 9 )
a sin cos a sin sin a sin cos d d dœ Êœ‚ababab kk
## ## # ‚
‚
9) 9) 99 5 )9ijkFnFrr††
rr
rr
kk
9)
a cos sin d d since z (a cos ) d a cos sin d dœœœÊœ œ
$# $#
99)9 9 5 999)Fk k Fn
''
S
†''
00
22 1a
6
38. Let the parametrization be ( ) (a sin cos ) (a sin sin ) (a cos ) (spherical coordinates withrijk9) 9 ) 9 ) 9ߜ
a, a 0, on the sphere), 0 , 0 2391)1œ ŸŸ ŸŸ
(a cos cos ) (a cos sin ) (a sin ) and ( a sin sin ) (a sin cos )Êœ œ rijkr ij
9 )
9) 9) 9 9) 9)
a cos cos a cos sin a sin
a sin sin a sin cos 0
Ê‚œ
rr
ijk
9)
ââ
ââ
ââ
ââ
ââ
ââ
9) 9) 9
9) 9 )
a sin cos a sin sin a sin cos d d dœ Êœ‚ababab kk
## ## # ‚
‚
9) 9) 99 5 )9ijkFnFrr††
rr
rr
kk
9)
a sin cos a sin sin a sin cos d d a sin d d since x y zœ œ œab
$$ # $$ # $ # $
99 9) 99)9 9)9 Fijk
(a sin cos ) (a sin sin ) (a cos ) d a sin d d 4 aœÊœ œ9) 9) 9 5 99)1ijkFn
''
S
†''
00
2$$
39. Let the parametrization be (x y) x y (2a x y) , 0 x a, 0 y a and rij k rikrjkßœ ŸŸ ŸŸÊ œ œ
xy
d dy dx
10 1
01 1
Ê ‚ œ œ Ê œ ‚
rr ijk Fn F rr
ij k
xy xy
ââ
ââ
ââ
ââ
ââ
ââ kk††5rr
rr
xy
xy
‚
‚kk
[2xy 2y(2a x y) 2x(2a x y)] dy dx since 2xy 2yz 2xzœ œFijk
2xy 2y(2a x y) 2x(2a x y) dœ ÊijkFn
''
S
†5
[2xy 2y(2a x y) 2x(2a x y)] dy dx 4ay 2y 4ax 2x 2xy dy dxœ œ
'' ''
00 00
aa aa
ab
##
a 3a x 2ax dx aœœœ
'0
aˆ‰ˆ‰
4 432 13a
3336
$# # %
#
40. Let the parametrization be ( z) (cos ) (sin ) z , 0 z a, 0 2 (where r x y 1 onrijk))) )1ßœ ŸŸ ŸŸ œ œ
È##
the cylinder) ( sin ) (cos ) and (cos ) (sin )
sin cos 0
001
Êœ œÊ‚œ œ
rijrkrr ij
ijk
))
)) ))
))
zz
ââ
ââ
ââ
ââ
ââ
ââ
d dz d cos sin dz d dz d , since (cos ) (sin ) zÊœ ‚œ œ œFn F r r F i j k††5)))))))
rr
rr
‚
‚
##
z
z
kk
kk a b
)z
d 1 dz d 2 aÊœ œ
''
S
Fn†5)1
''
00
2a
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1032 Chapter 16 Integration in Vector Fields
41. Let the parametrization be (r ) (r cos ) (r sin ) r , 0 r 1 (since 0 z 1) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
(cos ) (sin ) and ( r sin ) (r cos ) r sin r cos 0
cos sin 1
Êœ œ Ê‚œ
rijkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
(r cos ) (r sin ) r d d dr r sin cos r d dr sinceœÊœ ‚œ )) 5 ) )))ijkFnFrr††
rr
rr
‚
‚
$##
r
r
kk
kk a b
)r
FikFnœÊœ œ ab a bˆ‰
r sin cos r d r sin cos r dr d sin cos d
#$###
""
)) 5 ) ) ) ) ) )
''
S
†'' '
00 0
21 2
43
cosœ œ
‘
"$#
!
12 3 3
2
))1
1
42. Let the parametrization be (r ) (r cos ) (r sin ) 2r , 0 r 1 (since 0 z 2) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
(cos ) (sin ) 2 and ( r sin ) (r cos ) r sin r cos 0
cos sin 2
Êœ œ Ê‚œ
rijkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
(2r cos ) (2r sin ) r d d drœÊœ ‚)) 5 )ijkFnFrr††
rr
rr
‚
‚
r
r
kk
kk
)r
2r sin cos 4r cos sin r d dr sinceœab
$# $
)) )) )
Fi jkFnœ Ê œ abab a br sin 2r cos d 2r sin cos 4r cos sin r dr d
## # $# $
)) 5 )))))
''
S
†''
00
21
sin cos cos sin d sin sinœœœ
'0
2ˆ‰‘
""""
#$#
#
#
!
2262
1
)) )) ) ) ) ) 1
1
43. Let the parametrization be (r ) (r cos ) (r sin ) r , 1 r 2 (since 1 z 2) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
(cos ) (sin ) and ( r sin ) (r cos ) r sin r cos 0
cos sin 1
Êœ œ Ê‚œ
rijkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
(r cos ) (r sin ) r d d dr r cos r sin r d drœÊœ ‚œ)) 5 ) )))ijkFnFrr††
rr
rr
‚
‚
## ## $
r
r
kk
kk a b
)r
r r d dr since ( r cos ) (r sin ) r d r r dr dœ œ Ê œ œab ab
#$ # #$
))) 5 )FijkFn
''
S
†''
01
22 73
6
1
44. Let the parametrization be (r ) (r cos ) (r sin ) r , 0 r 1 (since 0 z 1) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
#
(cos ) (sin ) 2r and ( r sin ) (r cos ) r sin r cos 0
cos sin 2r
Êœ œ Ê‚œ
r i jkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
2r cos 2r sin r d d dr 8r cos 8r sin 2r d drœÊœ ‚œabab kka b
## $# $#
‚
‚
)) 5 ) )))ijkFnFrr††
rr
rr
r
r
kk
)r
8r 2r d dr since (4r cos ) (4r sin ) 2 d 8r 2r dr d 2œ œ Ê œ œab ab
$ $
))) 5 )1FijkFn
''
S
†''
00
21
45. Let the parametrization be ( ) (a sin cos ) (a sin sin ) (a cos ) , 0 , 0rijk9) 9 ) 9 ) 9 9 )ßœ ŸŸ ŸŸ
11
##
(a cos cos ) (a cos sin ) (a sin ) and ( a sin sin ) (a sin cos )Êœ œ rijkr ij
9 )
9) 9) 9 9) 9)
a cos cos a cos sin a sin
a sin sin a sin cos 0
Ê‚œ
rr
ijk
9)
ââ
ââ
ââ
ââ
ââ
ââ
9) 9) 9
9) 9 )
a sin cos a sin sin a sin cos œababab
## ## #
9) 9) 99ijk
a sin cos a sin sin a sin cos a sin a sin . The mass isÊ‚œ œ œkk
ÈÈ
rr
9) %% # %% # %# # %# #
9) 9) 99 9 9
M d a sin d d ; the first moment is M x dœœ œ œ
'' ''
S S
599) 5
''
00
22
yz
ab
#
#
a1
(a sin cos ) a sin d d x the centroid is located at , , byœœÊœœÊ
''
00
22
9) 99)ab ˆ‰
#
# ###
aa aaa
4
1Š‹
Š‹
a
4
a
symmetry
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
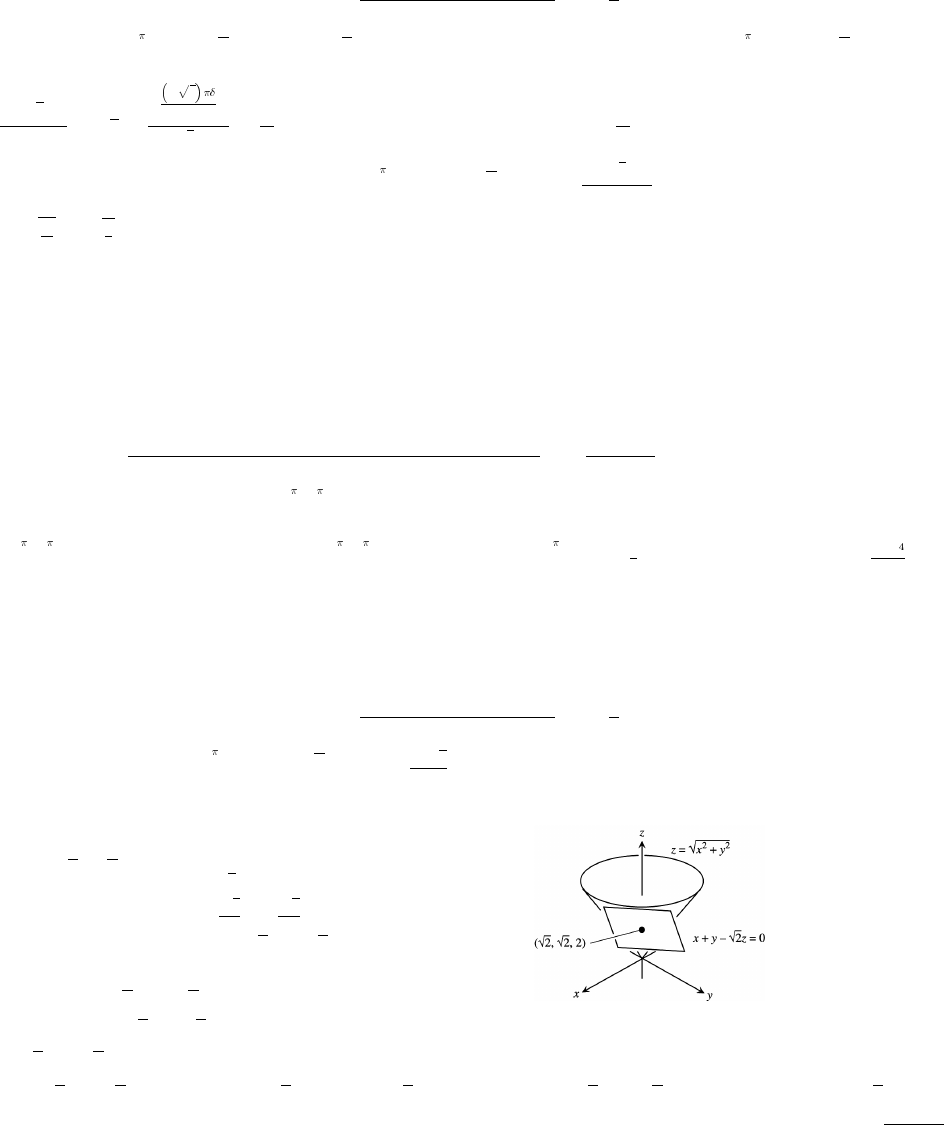
Section 16.6 Parameterized Surfaces 1033
46. Let the parametrization be (r ) (r cos ) (r sin ) r , 1 r 2 (since 1 z 2) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
(cos ) (sin ) and ( r sin ) (r cos ) r sin r cos 0
cos sin 1
Êœ œ Ê‚œ
rijkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
(r cos ) (r sin ) r r cos r sin r r 2. The mass isœÊ‚œ œ)) ))ijkrrkk
ÈÈ
)r## ## #
M d r 2 dr d 3 2 ; the first moment is M z d r r 2 dr dœœ œ œ œ
'' ''
S S
$5 $ ) 1$ $ 5 $ )
'' ''
01 01
22 22
y
ÈÈ È
Š‹ Š‹
x
z the center of mass is located at 0 0 by symmetry. TheœÊœ œÊ ßß
Š‹
È
Š‹
È
14 2
39 9
32
14 14
1$
1$
14 2
3ˆ‰
moment of inertia is I x y d r r 2 dr d the radius of gyration is
z01
22
œœ œ Ê
''
S
$5$ )ab Š‹
È
## #
#
'' Š‹
È
15 2 1$
R
zI
M
5
œœ
ÉÉ
z
#
47. Let the parametrization be ( ) (a sin cos ) (a sin sin ) (a cos ) , 0 , 0 2rijk9) 9 ) 9 ) 9 9 1 ) 1ßœ ŸŸ ŸŸ
(a cos cos ) (a cos sin ) (a sin ) and ( a sin sin ) (a sin cos )Êœ œ rijkr ij
9 )
9) 9) 9 9) 9)
a cos cos a cos sin a sin
a sin sin a sin cos 0
Ê‚œ
rr
ijk
9)
ââ
ââ
ââ
ââ
ââ
ââ
9) 9) 9
9) 9 )
a sin cos a sin sin a sin cos œababab
## ## #
9) 9) 99ijk
a sin cos a sin sin a sin cos a sin a sin . The moment ofÊ‚œ œ œkk
ÈÈ
rr
9) %% # %% # %# # %# #
9) 9) 99 9 9
inertia is I x y d (a sin cos ) (a sin sin ) a sin d d
z00
2
œœ
''
S
$5$9)9)99)ab c dab
## # ##
''
a sin a sin d d a sin d d a cos sin 2 dœœœœ
'' '' '
00 00 0
222
$999) $99)$ 99 )abab a b
‘ˆ‰
## # %$ % #
"
!
33
8a
1$1
48. Let the parametrization be (r ) (r cos ) (r sin ) r , 0 r 1 (since 0 z 1) and 0 2rijkßœ ŸŸ ŸŸ ŸŸ))) )1
(cos ) (sin ) and ( r sin ) (r cos ) r sin r cos 0
cos sin 1
Êœ œ Ê‚œ
rijkr i jrr
ijk
r r
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
(r cos ) (r sin ) r r cos r sin r r 2. The moment of inertia isœÊ‚œ œ)) ))ijkrrkk
ÈÈ
)r## ## #
I x y d r r 2 dr d
z00
21
œœ œ
''
S
$5$ )ab Š‹
È
## #
#
'' 1$È2
49. The parametrization (r ) (r cos ) (r sin ) rrijkߜ )))
at P 2 2 2 , r 2,
!œßßÊœœ
Š‹
ÈÈ )1
4
(cos ) (sin ) andrijkijk
r22
œ œ)) ÈÈ
##
( r sin ) (r cos ) 2 2rijij
)œ œ ))
ÈÈ
2/2 2/2 1
220
Ê‚œ
rr
ijk
r)
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ
ÈÈ
2 2 2 the tangent plane isœ Ê
ÈÈ
ijk
0 2 2 2 x 2 y 2 (z 2) 2x 2y 2z 0, or x y 2z 0.œ Êœ œ
Š‹’ “
ÈÈ È È ÈÈ È
Š‹Š‹
ijk i j k†
The parametrization (r ) x r cos , y r sin and z r x y r z the surface is z x y .rßÊœ œ œÊ œœ Ê œ ))) #### ##
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
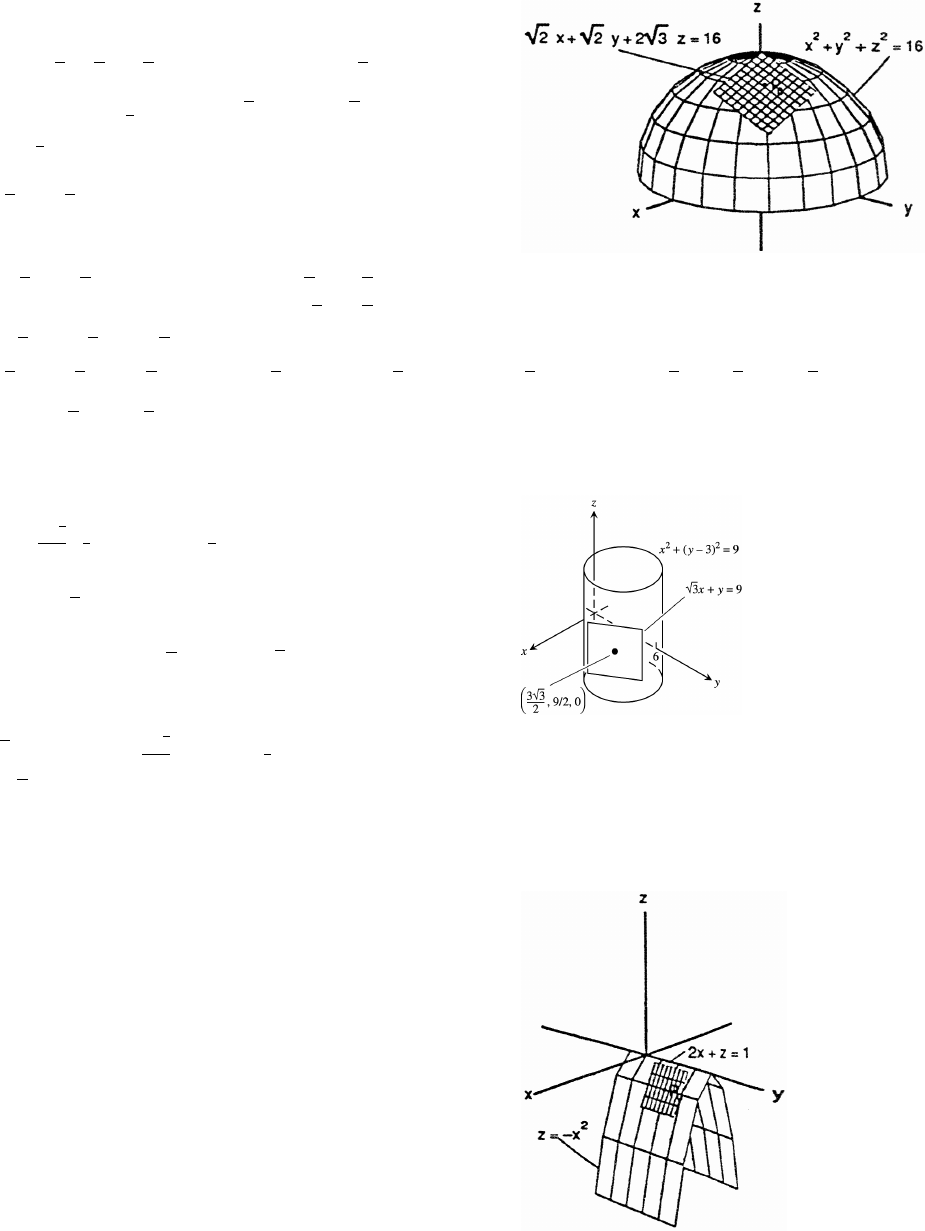
1034 Chapter 16 Integration in Vector Fields
50. The parametrization ( )r9)ß
(4 sin cos ) (4 sin sin ) (4 cos )œ9) 9) 9ijk
at P 2 2 2 3 4 and z 2 3
!œßß Êœ œ
Š‹
ÈÈ ÈÈ
3
4 cos ; also x 2 and y 2œÊœ œ œ99
1
6ÈÈ
. Then ʜ)19
4r
(4 cos cos ) (4 cos sin ) (4 sin )œ9) 9) 9ijk
662 andœ
ÈÈ
ijk
( 4 sin sin ) (4 sin cos )rij
)œ 9) 9 )
22 at P 662
220
œ Ê ‚ œ
ÈÈ ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ
ÈÈ
ij rr
ijk
! 9)
2 2 2 2 4 3 the tangent plane isœ Ê
ÈÈÈ
ijk
22 22 43 x 2 y 2 z 23 0 2x 2y 23z 16,
Š‹’ “
ÈÈ È È ÈÈ
ÈÈÈ
Š‹Š‹Š ‹
ijk i j k œÊ œ†
or x y 6z 8 2. The parametrization x 4 sin cos , y 4 sin sin , z 4 cos œ Ê œ œ œ
ÈÈ9) 9) 9
the surface is x y z 16, z 0.Ê œ
###
51. The parametrization ( z) (3 sin 2 ) 6 sin zrijk)))ߜ ab
#
at P 0 and z 0. Then
!##
œßßÊœ œ
Š‹
33 9
3
È)1
(6 cos 2 ) (12 sin cos )ri j
)œ)))
3 3 3 and at Pœ œijrk
Èz!
33 3
3330
001
Ê‚œ œ
rr ij
ijk
)z
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ
the tangent plane isÊ
33 3 x y (z 0) 0
Š‹’ “
ÈŠ‹
ˆ‰
ij i j kϠ33 9
È
##
3x y 9. The parametrization x 3 sin 2ʜ ʜ
È)
and y 6 sin x y 9 sin 2 6 sinœÊœ
#### #
#
)))ab
9 4 sin cos 36 sin 6 6 sin 6y x y 6y 9 9 x (y 3) 9œœœÊœÊœab ab
## % # ## # #
)) ) )
52. The parametrization (x y) x y x atrijkߜ
#
P (1 2 1) 2x 2 and at P
! !
œßß Ê œ œ œri kik rj
xy
2 the tangent plane
10 2
00
Ê‚œ œÊ
"
rr ik
ij k
xy
ââ
ââ
ââ
ââ
ââ
ââ
is (2 ) [(x 1) (y 2) (z 1) ] 0ik i j kϠ
2x z 1. The parametrization x x, y y andÊœ Êœ œ
z x the surface is z xœ Ê œ
##
53. (a) An arbitrary point on the circle C is (x z) (R r cos u, r sin u) (x y z) is on the torus withßœ Ê ßß
x (R r cos u) cos v, y (R r cos u) sin v, and z r sin u, 0 u 2 , 0 v 2œ œ œ ŸŸ ŸŸ11
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.7 Stoke's Theorem 1035
(b) ( r sin u cos v) (r sin u sin v) (r cos u) and ( (R r cos u) sin v) ((R r cos u) cos v)rijkr i j
uv
œ œ
r sin u cos v r sin u sin v r cos u
(R r cos u) sin v (R r cos u) cos v 0
Ê‚œ
rr
ijk
uv
ââ
ââ
ââ
ââ
ââ
ââ
(R r cos u)(r cos v cos u) (R r cos u)(r sin v cos u) ( r sin u)(R r cos u)œ ijk
(R r cos u) r cos v cos u r sin v cos u r sin u r(R r cos u)Ê‚ œ Ê‚œkk a bkkrr rr
uv uv
### # # # # # # #
A rR r cos u du dv 2 rR dv 4 rRÊœ œ œ
'' '
00 0
22 2
ab
##
11
54. (a) The point (x y z) is on the surface for fixed x f(u) when y g(u) sin v and z g(u) cos vßß œ œ œ
ˆ‰ ˆ‰
11
##
x f(u), y g(u) cos v, and z g(u) sin v (u v) f(u) (g(u) cos v) (g(u) sin v) , 0 v 2 ,Êœ œ œ Ê ßœ ŸŸri j k1
aubŸŸ
(b) Let u y and x u f(u) u and g(u) u (u v) u (u cos v) (u sin v) , 0 v 2 , 0 uœœÊœ œÊßœ ŸŸŸ
## #
ri j k 1
55. (a) Let w 1 where w cos and sin cos cos cos and cos sin
# #
œ œ œ Ê œ Êœ œ
zzxx
ccabab
yy
99 9 9) 9)
x a cos cos , y b sin cos , and z c sin Êœ œ œ)9 )9 9
( ) (a cos cos ) (b sin cos ) (c sin )Êßœ rijk)9 )9 )9 9
(b) ( a sin cos ) (b cos cos ) and ( a cos sin ) (b sin sin ) (c cos )rijrijk
)9
œ œ )9 )9 )9 )9 9
a sin cos b cos cos 0
a cos sin b sin sin c cos
Ê‚œ
rr
ijk
)9
ââ
ââ
ââ
ââ
ââ
ââ
)9 )9
)9 )9 9
bc cos cos ac sin cos (ab sin cos )œabab)9 )9 99
##
ijk
b c cos cos a c sin cos a b sin cos , and the result follows.Ê‚ œ kkrr
)9
### # % ## # % ## # #
)9 )9 99
A d d d d
a b sin cos b c cos cos a c sin cos
Ê‚œ
'' ''
00 00
22 1/2
kk c drr
)9
9) 9)
99 )9 )9
## # # ## # % ## # %
56. (a) ( u) (cosh u cos ) (cosh u sin ) (sinh u)rijk)))ߜ
(b) ( u) (a cosh u cos ) (b cosh u sin ) (c sinh u)rijk)))ߜ
57. ( u) (5 cosh u cos ) (5 cosh u sin ) (5 sinh u) ( 5 cosh u sin ) (5 cosh u cos ) andrijkrij))) ))ßœ Ê œ
)
(5 sinh u cos ) (5 sinh u sin ) (5 cosh u)rijk
uœ))
r 5 cosh u sin 5 cosh u cos 0
5 sinh u cos 5 sinh u sin 5 cosh u
Ê‚œ
)r
ijk
u
ââ
ââ
ââ
ââ
ââ
ââ
))
))
25 cosh u cos 25 cosh u sin (25 cosh u sinh u) . At the point (x y 0), where x y 25œ ßßœabab
## ##
!!
))ijk 00
we have 5 sinh u 0 u 0 and x 25 cos , y 25 sin the tangent plane isœÊœ œ œ Ê
!!
))
5(x y ) [(x x) (y y) z ] 0 xx x yy y 0 xx yy 25
!! ! ! ! ! ! !
##
ij i jkœÊœÊœ†00
58. Let w 1 where cosh u and w sinh u w w cos and w sin
zz xx
cc abab
yy
œ œ œ Ê œÊœ œ
##
))
x a sinh u cos , y b sinh u sin , and z c cosh uÊœ œ œ))
( u) (a sinh u cos ) (b sinh u sin ) (c cosh u) , 0 2 , uÊßœ ŸŸ__rijk))) )1
16.7 STOKES' THEOREM
1. curl 0 0 (2 0) 2 and curl 2 d dx dy
x2xz
FF ijkknkFn
ijk
œ ‚œ œ œ œÊ œÊ œ™†
ââ
ââ
ââ
ââ
ââ
ââ
```
```
##
xyz 5
d 2 dA 2(Area of the ellipse) 4Êœ œ œ
)CFr†''
R
1
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1036 Chapter 16 Integration in Vector Fields
2. curl 0 0 (3 2) and curl 1 d dx dy
2y 3x z
F F i j kk nk Fn
ij k
œ ‚œ œ œ œÊ œÊ œ
™†
ââ
ââ
ââ
ââ
ââ
ââ
`` `
`` `
#
xy z 5
d dx dy Area of circle 9Êœ œ œ
)CFr†''
R
1
3. curl x 2x (z 1) and curl
yxzx
FF ijkn Fn
ijk
œ‚œ œ œ Ê™†
ââ
ââ
ââ
ââ
ââ
ââ
```
```
#
xyz 3
ijk
È
( x 2x z 1) d dA d ( 3x z 1) 3 dAœÊœ Ê œ
" "
È È
È
3 3
3
1
5)CFr†''
RÈ
[ 3x (1 x y) 1] dy dx ( 4x y) dy dx 4x(1 x) (1 x) dxœ œ œ
'' '' '
00 00 0
11x 11x 1‘
"
#
#
3x x dxœ œ
'0
1ˆ‰
"
##
#
75
6
4. curl (2y 2z) (2z 2x) (2x 2y) and
yzxzxy
FF i j kn
ijk
œ‚œ œ œ
™
ââ
ââ
ââ
ââ
ââ
ââ
```
```
######
xyz 3
ijk
È
curl (2y 2z 2z 2x 2x 2y) 0 d 0 d 0Ê œ œÊ œ œFn F r††
"
È3)C''
S
5
5. curl 2y (2z 2x) (2x 2y) and
yzxyxy
FF i j knk
ijk
œ‚œ œ œ
™
ââ
ââ
ââ
ââ
ââ
ââ
```
```
######
xyz
curl 2x 2y d dx dy d (2x 2y) dx dy x 2xy dyʜʜʜ œFn F r††5)'' '
C11 1
11 1
cd
#"
"
4y dy 0œ œ
'1
1
6. curl 0 0 3x y and
xy 1 z
FF ijkn
ijk
œ ‚œ œ œ œ™
ââ
ââ
ââ
ââ
ââ
ââ
```
```
#$
##
xyz
2x 2y 2z x y z
2xyz 4
ijk ijk
È
curl x y z; d dA (Section 16.5, Example 5, with a 4) dÊœ œ œÊFn F r††
34
4z
## 5)C
x y z dA 3 r cos r sin r dr d 3 (cos sin ) dœ œ œ
''
Rˆ‰ˆ‰ abab ’“
34 r
4z 6
## # # # # #
#
!
'' '
00 0
22 2
))) )))
32 sin 2 d 4 sin u du 4 8œ œ œ œ
''
00
24
"## %
!
424
usin 2u
)) 1
‘
1
7. x 3 cos t and y 2 sin t (2 sin t) 9 cos t 9 cos t 16 sin t sin e at theœœÊœFi j kaba b
##%6 sin t cos t 0
base of the shell; (3 cos t) (2 sin t) d ( 3 sin t) (2 cos t) 6 sin t 18 cos trijr ijFœ Êœ Êœ†d
dt
r#$
d 6 sin t 18 cos t dt 3t sin 2t 6(sin t) cos t 2 6Ê‚œ œ œ
''
S
™†Fn5 1
'0
2ab ab
‘
#$ #
#
!
3
2
1
8. curl 2 ; f(x y z) 4x y z f 8x 2z
ztanyx
FF j ijk
ijk
œ‚œ œ ßßœÊ œ
™ ™
ââ
ââ
ââ
ââ
ââ
ââ
ââ
```
```
""
#
"
##
xyz
x4z
and f 1 d dA f dA; ( 2 f)Êœ œÊ œÊ œ œ ‚ œ œnpjp Fnj
™
™™†™™
™
f
ffff
f2
kk k k kk kk
kk
kk kk™† ™ ™ † †™5p
"
d 2 dA d 2 dA 2(Area of R) 2( 1 2) 4 , where RÊ ‚ œ Ê ‚ œ œ œ œ™† ™† ††Fn Fn55 11
'' ''
SR
is the elliptic region in the xz-plane enclosed by 4x z 4.
##
œ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
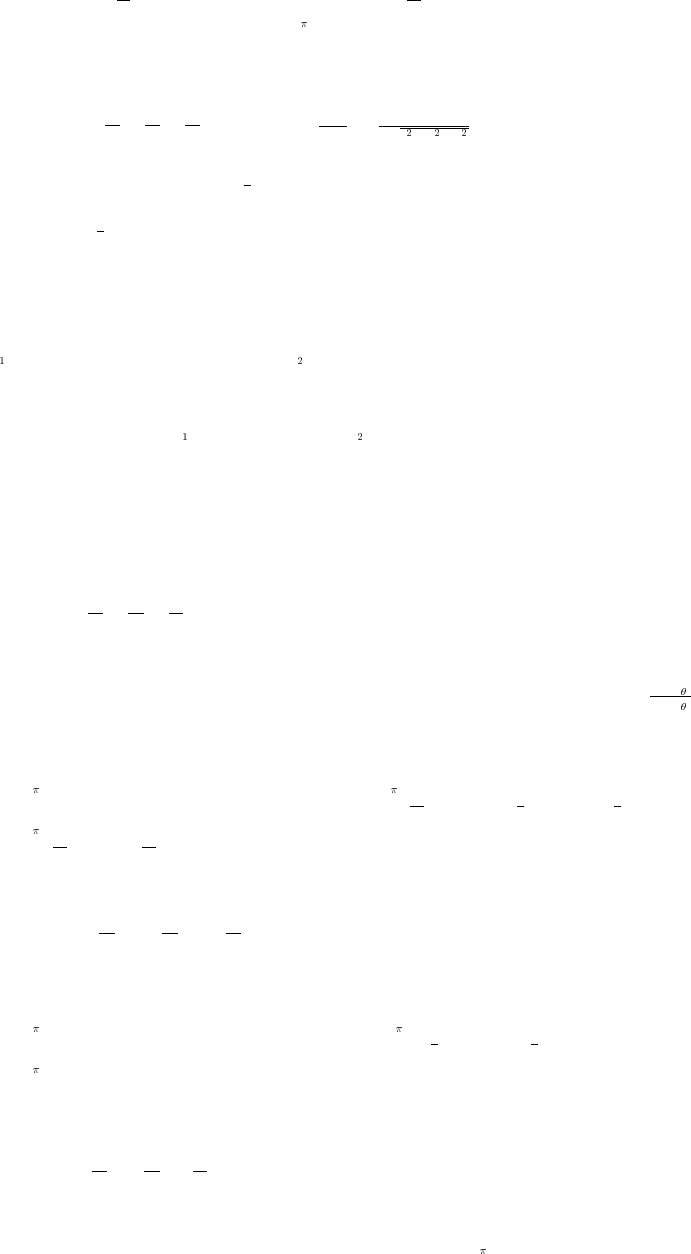
Section 16.7 Stoke's Theorem 1037
9. Flux of d d , so let C be parametrized by (a cos t) (a sin t) ,™™† †‚œ ‚ œ œ FFnFr rij
''
S
5)C
0 t 2 ( a sin t) (a cos t) ay sin t ax cos t a sin t a cos t aŸŸ Ê œ Ê œ œ œ1dd
dt dt
rr
ijF†## # # #
Flux of d a dt 2 aÊ‚œœœ™†FFr
)'
C0
2##
1
10. (y ) ; x y z
y00
™‚ œ œ œ œ œikn ijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
```
```
xyz
f
f
2x 2y 2z
2xyz
™
™kk È
ijk
(y ) z; d dA (Section 16.5, Example 5, with a 1) (y ) dÊ‚ œ œ œÊ ‚™† ™†in in55
"
z''
S
( z) dA dA , where R is the disk x y 1 in the xy-plane.œ œ œ Ÿ
'' ''
RR
ˆ‰
"##
z1
11. Let S and S be oriented surfaces that span C and that induce the same positive direction on C. Then
"#
d d d
'' ''
SS
™† † ™†‚œœ‚Fn F r Fn
"" ##
55
)C
12. d d d , and since S and S are joined by the simple
'' '' ''
SSS
™† ™† ™†‚œ‚‚Fn Fn Fn555
"#
closed curve C, each of the above integrals will be equal to a circulation integral on C. But for one surface
the circulation will be counterclockwise, and for the other surface the circulation will be clockwise. Since the
integrands are the same, the sum will be 0 d 0.Ê‚œ
''
S
™†Fn5
13. 5 2 3 ; (cos ) (sin ) 2r and ( r sin ) (r cos )
2z 3x 5y
™‚œ œ œ œ Fijkrijkrij
ijk
ââ
ââ
ââ
ââ
ââ
ââ
```
```xyz r)) ) )
)
2r cos 2r sin r ; and d dr d
cos sin 2r
r sin r cos 0
Ê‚œ œ œ œ‚
rr i jkn rr
ijk
r r) )
ââ
ââ
ââ
ââ
ââ
ââ
abab kk
))
))
)) 5 )
## ‚
‚
rr
rr
r
r
kk
d ( ) ( ) dr d 10r cos 4r sin 3r dr d dÊ‚ œ‚ ‚ œ Ê ‚™† ™ † ™†Fn F r r Fn5))))5
r)ab
## ''
S
10r cos 4r sin 3r dr d r cos r sin r dœœ
'' '
00 0
22 2
ab
‘
## $ $ #
"
#
#
!
))) ) ) )
043
33
cos sin 6 d 6(2 ) 12œœœ
'0
2ˆ‰
80 32
33
)))11
14. 2 2 ; 2r cos 2r sin r and
yzzxxz
™‚œ œ ‚ œ
Fijkrrijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ abab
```
``` ##
xyz r)))
d ( ) ( ) dr d (see Exercise 13 above) d™† ™ † ™†‚œ‚‚ Ê‚Fn F r r Fn5) 5
r)''
S
2r cos 4r sin 2r dr d r cos r sin r dœ œ
'' '
00 0
23 2
ab
‘
## $ $#
$
!
))) ) ))
24
33
18 cos 36 sin 9 d 9(2 ) 18œ œ œ
'0
2ab)))11
15. 2y 0 x ;
x y 2y z 3z
cos sin 1
r sin r cos 0
™‚œ œ ‚ œ
Fijkrr
ijk ijk
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
```
```
#$
$#
xyz r)))
))
( r cos ) (r sin ) r and d ( ) ( ) dr d (see Exercise 13 above)œ ‚ œ ‚ ‚)) 5 )ijkFn Frr™† ™ †
r)
d 2ry cos rx dr d 2r sin cos r cos dr dÊ‚œ œ
'' ''
SR
™†Fn5)) ))))aba b
$# % $#
''
00
21 3
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
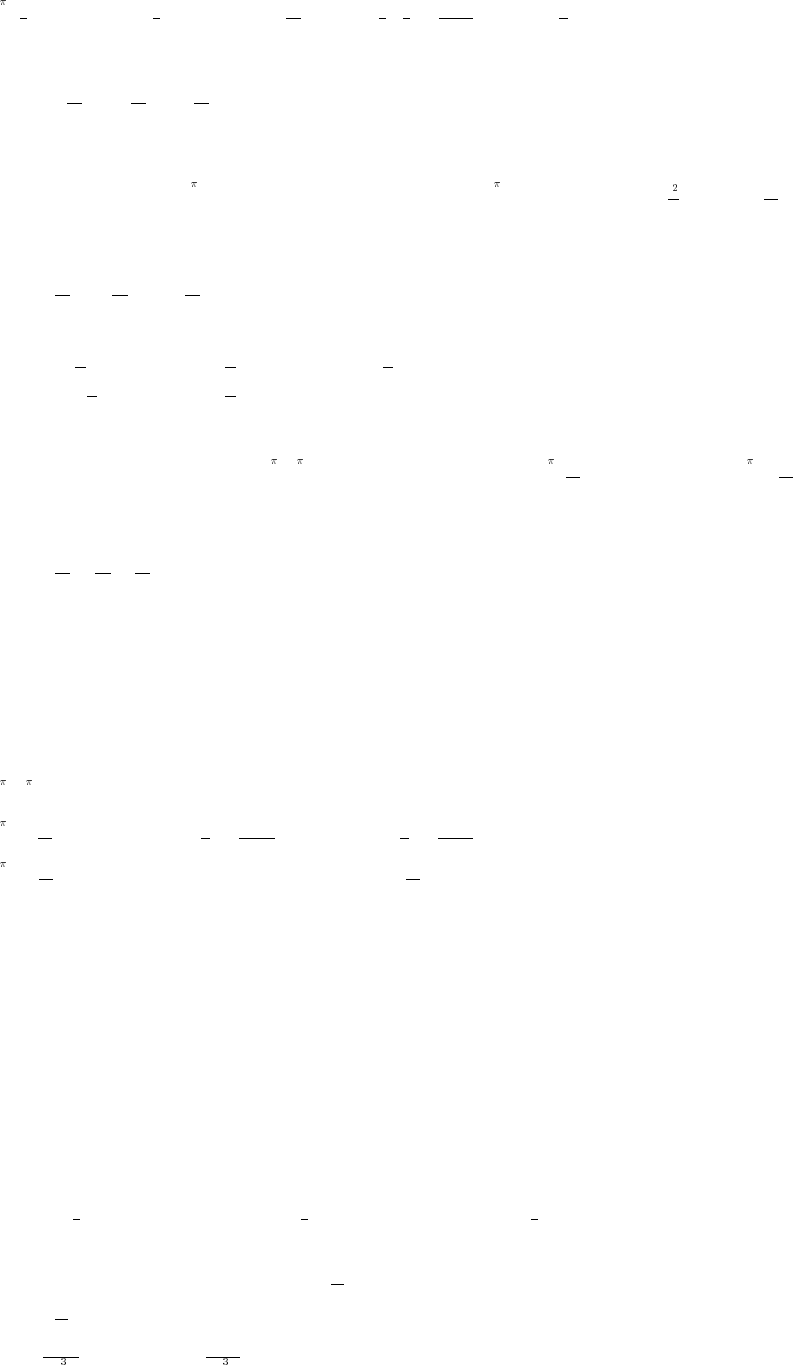
1038 Chapter 16 Integration in Vector Fields
sin cos cos d sinœœœ
'0
2ˆ‰‘ˆ‰
2sin 2
5410444
34
)) )) )
"""
#
#
#
!
)) 1
1
16. ;
xyyzzx
cos sin 1
r sin r cos 0
™‚ œ œ ‚ œ
Fijkrr
ijk ijk
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
ââ â â
```
```xyz r)))
))
(r cos ) (r sin ) r and d ( ) ( ) dr d (see Exercise 13 above)œ ‚œ‚‚)) 5 )ijkFn Frr™† ™ †
r)
d (r cos r sin r) dr d (cos sin 1) d (2 ) 25Ê‚œ œ œ œ
''
S
™†Fn5))))))11
'' '
00 0
25 2
’“
ˆ‰
r25
##
&
!
17. 0 0 5 ;
3y 5 2x z 2
™‚œ œ
Fijk
ij k
ââ
ââ
ââ
ââ
ââ
ââ
`` `
`` `
#
xy z
3 cos cos 3 cos sin 3 sin
3 sin sin 3 sin cos 0
rr
ijk
9)
‚œ
ââ
ââ
ââ
ââ
ââ
ââ
ÈÈ È
ÈÈ
9) 9) 9
9) 9 )
3 sin cos 3 sin sin (3 sin cos ) ; d ( ) ( ) d d (see Exerciseœ ‚œ‚‚abab
##
9) 9) 99 5 9)ijkFnFrr™† ™ †
9)
13 above) d 15 cos sin d d cos d d 15Ê‚œ œ œœ
''
S
™†Fn5999)9))1
'' ' '
00 0 0
2/2 2 2
‘
15 15
2#Î#
!#
1
18. 2z 2y ;
yz x
™‚œ œ Fijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
```
```
##
xyz
2 cos cos 2 cos sin 2 sin
2 sin sin 2 sin cos 0
rr
ijk
9)
‚œ
ââ
ââ
ââ
ââ
ââ
ââ
9) 9) 9
9) 9 )
4 sin cos 4 sin sin (4 sin cos ) ; d ( ) ( ) d d (see Exerciseœ ‚œ‚‚abab
##
9) 9) 99 5 9)ijkFnFrr™† ™ †
9)
13 above) d 8z sin cos 4 sin sin 8y sin cos d dÊ‚œ
'' ''
SR
™†Fn59)9)9)9)ab
##
16 sin cos cos 4 sin sin 16 sin sin cos d dœ
''
00
2/2
ab
###
9 9 ) 9) 9) )9)
sin cos 4 (sin ) 16 (sin cos ) dœ
'0
2‘ˆ‰ ˆ‰
"$
##
Î#
!
6
344
sin 2 sin 2
9) ) )) )
99 99 1
cos sin 4 sin cos d sin cos 2 sin 0œ œ œ
'0
2ˆ‰‘
16 6
33
)1 ) 1 ) )) )1 ) 1 )
"##
!
1
19. (a) 2x 2y 2z curl d d 0 d 0Fijk F0 Fr Fnœ Ê œÊ œ ‚ œ œ
)C†™†
'' ''
SS
55
(b) Let f(x y z) x y z f curl d dßß œ Ê ‚ œ ‚ œ Ê œ Ê œ ‚
##$ ™™™ † ™†F0F0FrFn
)C''
S
5
0 d 0œœ
''
S
5
(c) (x y z ) d d 0 d 0Fijk0F0Fr Fnœ‚œÊ ‚œÊ œ ‚ œ œ™™†™†
)C'' ''
SS
55
(d) f f d d 0 d 0FF0FrFnœÊ‚œ‚œÊ œ ‚ œ œ™™ ™™ † ™†
)C'' ''
SS
55
20. f x y z (2x) x y z (2y) x y z (2z)Fijkœœ ™"""
###
### ### ###
$Î# $Î# $Î#
ab ab ab
xxyz yxyz zxyzœ ababab
### ### ###
$Î# $Î# $Î#
ijk
(a) (a cos t) (a sin t) , 0 t 2 ( a sin t) (a cos t)rij ijœ ŸŸÊœ1d
dt
r
xxyz (a sin t)yxyz (a cos t)Êœ F†d
dt
rab ab
### ###
$Î# $Î#
( a sin t) (a cos t) 0 d 0œ œ Ê œ
ˆ‰ ˆ‰
a cos t a sin t
aa )CFr†
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.8 The Divergence Theorem and a Unified Theory 1039
(b) d d f d d 0 d 0
)CFr Fn n 0n†™† ™™† †œ‚ œ‚ œ œ œ
'' '' '' ''
SS SS
5555
21. Let 2y 3z x 3 2 ;
2y 3z x
F i jk F ijkn
ijk
œÊ ‚œ œ œ
™
ââ
ââ
ââ
ââ
ââ
ââ
`` `
`` `
xy z
22
3
ijk
2 2y dx 3z dy x dz d d 2 dÊ™ † † ™ † Fn F r Fn‚œÊ œ œ ‚ œ
))
CC
'' ''
SS
55
2 d , where d is the area of the region enclosed by C on the plane S: 2x 2y z 2œ œ
'' ''
SS
55
22. 0
xyz
™‚œ œF
ijk
ââ
ââ
ââ
ââ
ââ
ââ
```
```xyz
23. Suppose M N P exists such that Fijk F i j kœ ‚œ ™Š‹ Š‹
ˆ‰
`` ` ` ` `
`` `` ` `
PN MP NM
yz zx x y
x y z . Then (x) 1. Likewise, (y)œ œ Ê œ œijk `` ` ` ` ` `` ` `
` ` ` ` `` `` ` ` ` `x y z x xy xz y z x y
PN P N MP
Š‹ ˆ‰
1 and (z) 1. Summing the calculated equationsÊœ œ Êœ
`` ``` ` ``
`` `` ` ` ` ` `` ``
MP NM NM
yz yx z x y z zx zy
Š‹
3 or 0 3 (assuming the second mixed partials areÊ œœ
Š‹Š‹Š‹
`` `` ``
`` `` `` `` `` ``
PP NN MM
xy yx zx xz yz zy
equal). This result is a contradiction, so there is no field such that curl x y z .FFijkœ
24. Yes: If , then the circulation of around the boundary C of any oriented surface S in the domain of™‚œF0 F
is zero. The reason is this: By Stokes's theorem, circulation d d dFFrFn0nœœ‚œ
)C†™† †
'' ''
SS
55
0.œ
25. r x y r x y r 4x x y 4y x y M NœÊœÊœ œ œ
Èab ababab
## % ## % ## ##
#Fijij™
r ds ds M dy N dx dx dyÊœœœ
)))
CCC
™† †ab Š‹
%``
``
nFn ''
R
MN
xy
4 x y 8x 4 x y 8y dA 16 x y dA 16 x dA 16 y dAœœ œ
'' cdabab ab
RRRR
## # ## # ## # #
'' '' ''
16I 16I .œ
yx
26. 0, 0, 0, 0, , curl .
`` ` `` `
`` ``` `
PNMPN M
yz zxx y
yx yx yx yx
xy xy xy xy
œœœœœ œ Ê œ œ
ab ab abab
Fk0
’“
However, x y 1 (cos t) (sin t) ( sin t) (cos t)
##
œÊœ Ê œ rij ij
d
dt
r
sin t cos t sin t cos t 1 d 1 dt 2 which isÊœ Ê œ œÊ œ œFijF Frabab ††
d
dt
r## ))
C1
not zero.
16.8 THE DIVERGENCE THEOREM AND A UNIFIED THEORY
1. div 0 2. x y div 1 1 2FF FijFœ Ê œ œ œ Ê œœ
y x xy xy
xy xy
ij
Èab
3. div GMFFœ Ê œ
GM(x y z )
xyz
xyz 3xxyz
xyz
ijk
ab abab
ab
”•
GM GM
”•”•
abab abab
ab ab
xyz 3yxyz xyz 3zxyz
xyz xyz
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1040 Chapter 16 Integration in Vector Fields
GM 0œ œ
’“
3xyz 3xyz xyz
xyz
ababab
ab
4. z a r in cylindrical coordinates z a x y a x y div 0œ Êœ Êœ Ê œ
## # ## ###
ab a bvkv
5. (y x) 1, (z y) 1, (y x) 0 2 Flux 2 dx dy dz 2 2
```
```
$
xyz
œ œ œÊ œÊ œ œ™†F'''
111
111 ab
16œ
6. x 2x, y 2y, z 2z 2x 2y 2z
```
```
###
xyx
ab ab abœœœÊœ™†F
(a) Flux (2x 2y 2z) dx dy dz x 2x(y z) dy dz (1 2y 2z) dy dzœœœ
''' '' ''
000 00 00
111 11 11
cd
#"
!
y(1 2z) y dz (2 2z) dz 2z z 3œœœœ
''
00
11
cd cd
##
""
!!
(b) Flux (2x 2y 2z) dx dy dz x 2x(y z) dy dz (4y 4z) dy dzœœœ
''' '' ''
111 11 11
111 11 11
cd
#"
"
2y 4yz dz 8z dz 4z 0œ œ œœ
''
11
11
cd cd
##
""
" "
(c) In cylindrical coordinates, Flux (2x 2y 2z) dx dy dzœ
'''
D
(2r cos 2r sin 2z) r dr d dz r cos r sin zr d dzœœ
''' ''
000 00
122 12
)) ) ) ) )
‘
22
33
$$#
#
!
cos sin 4z d dz sin cos 4z dz 8 z dz 4 z 4œœœœœ
'' ' '
00 0 0
12 1 1
ˆ‰ ‘
cd
16 16 6 16
33 33
))) ) )) 111
"#
!
#"
!
1
7. (y) 0, (xy) x, ( z) 1 x 1; z x y z r in cylindrical coordinates
`` `
`` `
## #
xy z
œœœÊœœÊœ™†F
Flux (x 1) dz dy dx (r cos 1) dz r dr d r cos r r dr dÊœ œ œ
'''
D''' ''
000 00
22r 22
)) ))ab
$#
cos d cos 4 d sin 4 8œœ œœ
''
00
22
’“ˆ‰‘
r r 32 32
54 5 5
)) )) )) 1
#
!
#
!
1
8. x 2x, (xz) 0, (3z) 3 2x 3 Flux (2x 3) dV
```
```
#
xyz
abœœœÊœÊœ™†F'''
D
(2 sin cos 3) sin d d d sin cos sin d dœœ
''' ''
000 00
22 2
3 9 ) 3 9 39) 9 ) 3 99)ab ’“
#$
#
!
3
2
(8 sin cos 8) sin d d 8 cos 8 cos d (4 cos 16) dœœœ
'' ' '
00 0 0
22 2
9) 99) ) 9) 1) )
‘ˆ‰
99 1
24
sin 2
!
32œ1
9. x 2x, ( 2xy) 2x, (3xz) 3x Flux 3x dx dy dz
`` `
`` `
#
xy z
abœœ œÊœ
'''
D
(3 sin cos ) sin d d d 12 sin cos d d 3 cos d 3œœœœ
''' '' '
000 00 0
222 22 2
3 9 ) 3 9 39) 9 )9) 1 )) 1ab
##
10. 6x 2xy 12x 2y, 2y x z 2, 4x y 0 12x 2y 2
```
```
###$
xyz
ab ababœ œ œÊ œ™†F
Flux (12x 2y 2) dV (12r cos 2r sin 2) r dr d dzÊœ œ
'''
D'' '
00 0
322
)) )
32 cos sin 4 d dz 32 2 dz 112 6œœœ
'' '
00 0
32 3
ˆ‰ˆ‰
))) 1 1
16 16
33
11. (2xz) 2z, ( xy) x, z 2z x Flux x dV
`` `
`` `
#
xy z
œ œ œ Ê œ Ê œ ab ™†F'''
D
x dz dy dx (xy 4x) dy dx x 16 4x 4x 16 4x dxœœœ
'' ' ' ' '
00 0 0 0 0
2 16 4x 4 y 2 16 4x 2’“
ab
È
1
2##
4x x 16 4xœ œ
’“
ab
#% #
"" $Î# #
!
23 3
40
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Section 16.8 The Divergence Theorem and a Unified Theory 1041
12. x 3x , y 3y , z 3z 3x 3y 3z Flux 3 x y z dV
```
```
$#$#$# ### ###
xyz
ab ab ab a b
'''
œœœÊœÊœ™†F
D
3 sin d d d 3 sin d d 3 dœœœœ
''' '' '
000 00 0
2a 2 2
33 9 39) 99) )
##
ab a2a12a
555
1
13. Let x y z . Then , , ( x) x , ( y) y333333œ œœœÊ œ œ œ
ÈŠ‹ Š‹
### ``` ` `
``` ` ` ` `
``
333 3 3
333 3xyz x x y y
xz x
y
, ( z) z 3 4 , since x y zœ œ œÊ œ œ œ
y xyz
zz
z
333
3
33 3 3 33 3
`
``
` ###
Š‹ È
™†F
Flux 4 dV (4 ) sin d d d 3 sin d d 6 d 12Êœ œ œ œ œ
'''
D
333939)99))1
''' '' '
001 00 0
22 2 2
ab
#
14. Let x y z . Then , , . Similarly,3œ œœœÊ œ œ
ÈŠ‹ Š‹
### ``` `
``` ` `
`"
333 3
333 333 33xyz x x
xzxx1x
y
and
`" `"
``
yz
y y xyz
zz 3 2
Š‹ Š‹
333 333 3 3 3
œ œ Ê œ œ™†F
Flux dV sin d d d 3 sin d d 6 d 12Êœ œ œ œ œ
'''
D
22
33
''' '' '
001 00 0
22 2 2
Š‹
ab3939) 99) ) 1
#
15. 5x 12xy 15x 12y , y e sin z 3y e sin z, 5z e cos z 15z e sin z
`` `
`` `
$###$ # $ #
xy z
yy y y
ab ab a bœ œ œ
15x 15y 15z 15 Flux 15 dV 15 sin d d dÊ œœ Ê œ œ™†F### # # ##
33 33939)
'''
D'''
001
22
aba b
12 2 3 sin d d 24 2 6 d 48 2 12œœœ
'' '
00 0
22
Š‹ Š‹Š ‹
ÈÈÈ
99) ) 1
16. ln x y , tan , z x y x y
`` `
`` `
## "
## ##
xxyyxxx xyz
2x 2z 2z 2z
y
1
cdab ˆ‰ˆ‰ ˆ‰
–— ÈÈ
œ œ œ œ
Š‹
ˆ‰
x
y
x
x y Flux x y dz dy dxʜʜ ™†F2x 2z 2x 2z
xy xy xy xy
## ##
ÈÈ
Š‹
'''
D
r dz r dr d 6 cos 3r dr dœœ
'' ' ''
01 1 0 1
222 2 2
ˆ‰ ˆ ‰
2r cos 2z 3
rr r
))))
#
6 21 cos 3 ln 2221 d 2 ln 2221œœ
'0
2’“Š‹Š‹
ÈÈÈ È
))1
3
#
17. (a) M N P curl Gijk G G i k k Gœ Ê ‚œ œ Ê ‚™ ™†™
Š‹ Š‹
ˆ‰
`` ` ` ` `
`` `` ` `
PN MP NM
yz z x x y
div(curl )œœG`` ` `` ` `` `
`` ` `` ` `` `xy z yz x zx y
PN MP NM
Š‹ Š‹
ˆ‰
0 if all first and second partial derivatives are continuousœœ
``` ```
`` `` `` `` `` ``
PNMPNM
xy xz yz yx zx zy
(b) By the Divergence Theorem, the outward flux of across a closed surface is zero because™‚G
outward flux of ( ) d™™†‚œ ‚GGn
''
S
5
dV [Divergence Theorem with ]œ‚ œ‚
'''
D
™†™ ™GFG
(0) dV 0 [by part (a)]œœ
'''
D
18. (a) Let M N P and M N P a bFijkFijkFF
"""" #### " #
œ œ Ê
(aM bM ) (aN bN ) (aP bP ) (a b )œ Ê
"# "# "# "#
ijkFF™†
a b a b a bœ
ˆ‰ ˆ‰
Š‹
`` `` ``
`` `` ``
MM NN PP
xx yy zz
aba()b()œœ
Š‹Š‹
``` ```
``` ``` "#
MNP MNP
xyz xyz ™† ™†FF
(b) Define and as in part a (a b )FF FF
"# "#
Ê‚™
ab a b a b abœ
’“Š‹
ˆ‰ ‘ˆ‰ˆ‰
`` ` ` ` ` ``
`` ` ` ` ` ``
PP NN MM PP
yy z z z z xx
ij
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1042 Chapter 16 Integration in Vector Fields
ab a b a œ
’“’ “
ˆ‰ ˆ‰
Š‹Š‹ Š‹
`` ` ` `` `` ``
`` ` ` `` `` ``
NN MM PN MP NM
xx y y yz zx xy
kijk
bab œ‚‚
’“Š‹ Š‹
ˆ‰
`` ` ` ` `
`` `` ` ` "#
PN MP NM
yz z x x y
ij kFF™™
(c) (N P P N ) (M P P M ) (M N N M ) ( )
MNP
MNP
FF i j k FF
ijk
" # "# " # "# " # " # " # " #
"""
###
‚œ œ Ê ‚
ââ
ââ
ââ
ââ
ââ
ââ ™†
[(N P P N ) (M P P M ) (M N N M ) ]œ™† "# " # "# " # " # " #
ij k
(N P P N ) (M P P M ) (M N N M ) P N N Pœ œ
`` `
`` ` ````
"# " # "# " # " # " # # " # "
````
xy z xxxx
NPPN
ˆ‰
MPPM MNNM
Š‹
ˆ‰
"#"# "#"#
`` ` ` ` ` ` `
`` ` ` ` ` ` `
PMMP NMMN
yy y y z z z z
MNP MNœ
### ""
`` ` ` `` `` ``
`` `` ` ` `` ``
Š‹ Š‹Š‹
ˆ‰ ˆ‰
PN MP NM NP PM
yz z x x y zy xz
Pœ‚‚
"#""#
``
``
Š‹
MN
yx
FFFF†™ †™
19. (a) div(g ) g (gM) (gN) (gP) g M g N g PFFœœœ™† ``` ` ` `
``` ``````
```
xyz xxyyzz
MNP
ggg
Š‹Š‹Š‹
MNP g g gœœ
Š‹Š‹
```
``` ```
```
ggg
xyz xyz
MNP ™† ™ †FF
(b) (g ) (gP) (gN) (gM) (gP) (gN) (gM)™‚œ Fijk
’“ ’“
‘
`` ` ` ` `
`` ` ` ` `yz z x x y
PgNg Mg Pg Ng Mgœ
Š‹Š‹Š ‹
`` `` ` `
`` `` ` ` `` `` ` `
`` `` ` `
gg gg g g
yy z z z z xx xx y y
PN MP N M
ij k
PN gg MP g g NMœ
Š‹Š‹Š‹ Š‹
ˆ‰
`` `` ` `
`` `` `` `` ` `
`` ` `
gg gg g g
yz yz zx zx x y
PN MP
ii jj k
gg g g œ‚‚
Š‹
``
``
NM
xy
kFF™™
20. Let M N P and M N P .FijkFijk
"""" ####
œ œ
(a) (N P P N ) (P M M P ) (M N N M ) ( )FF i j k FF
" # "# " # " # "# " # " # " #
‚œ Ê ‚ ‚™
(M N N M ) (P M M P ) (N P P N ) (M N N M )œ
’“
‘
`` ``
`` ``
"# "# "# "# "# "# "# "#
yz zx
ij
(P M M P ) (N P P N )
’“
``
``
" # "# "# " #
xy
k
and consider the -component only: (M N N M ) (P M M P )i``
``
"# "# "# "#
yz
NMMN MPP Mœ
#"#"#"#"
````````
````````
MNNMPMMP
yyyyzzzz
NP NP M Mœ
Š‹Š‹Š‹Š‹
## "" " #
`` `` `` ``
`` ```` ``
MM MM NP NP
yz yzyz yz
MNP MNP Mœ
Š‹Š‹Š‹
### """ "
``` ``````
``` ``````
MMM MMMMNP
xyz xyzxyz
M . Now, -comp of ( ) M N P M œ
Š‹ Š ‹
```
``` ` ` `
##"###"
```
MNP
xyz x y z
iFF†™
M N P ; likewise, -comp of ( ) M N P ;œ œ
Š‹ Š‹
### "#"""
``` ```
``` ```
MMM MMM
xyz xyz
iFF†™
-comp of ( ) M and -comp of ( ) M .iFF iFF™† ™†
#" " "# #
``` ```
``` ```
œ œ
Š‹ Š‹
MNP MNP
xyz xyz
Similar results hold for the and components of ( ). In summary, since the correspondingjk FF™‚‚
"#
components are equal, we have the result
()()()()()™ †™†™™†™†‚‚œFFFFFF FF FF
"##""# #" "#
(b) Here again we consider only the -component of each expression. Thus, the -comp of ( )iiFF™†
"#
(MM NN PP) M M N N P Pœ œ
`
```````
"# "# "# " # " # " #
``````
xxxxxxx
MMNNPP
ˆ‰
-comp of ( ) M N P ,iFF
"#" " "
```
```
†™ œ
Š‹
MMM
xyz
-comp of ( ) M N P ,iFF
#"# # #
```
```
†™ œ
Š‹
MMM
xyz
-comp of ( ) N P , andiF F
"#" "
`` ` `
`` ``
‚‚œ ™Š‹
ˆ‰
NM MP
xy zx
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
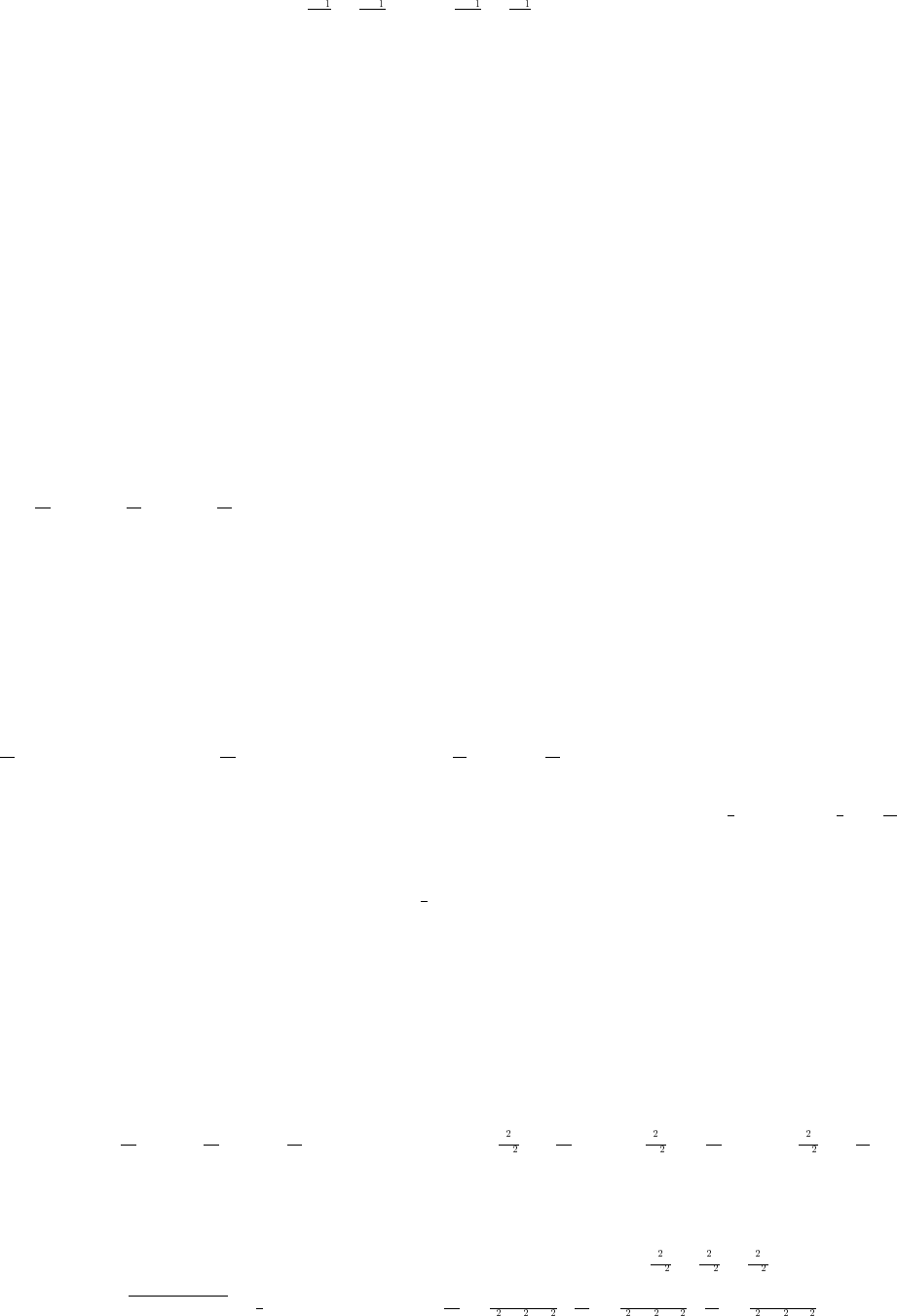
Section 16.8 The Divergence Theorem and a Unified Theory 1043
-comp of ( ) N P .iF F
#"# #
`` ` `
`` ``
‚‚œ ™Š‹
ˆ‰
NM MP
xy zx
Since corresponding components are equal, we see that
( ) ( ) ( ) ( ) ( ), as claimed.™ † †™ †™ ™ ™FFFFFFF FF F
"#"##"" ## "
œ‚‚‚‚
21. The integral's value never exceeds the surface area of S. Since 1, we have (1)(1) 1 andkk k k kkkkFFnFnŸœŸœ†
d d [Divergence Theorem]
''' ''
DS
™† †FFn55œ
d [A property of integrals]Ÿ''
SkkFn†5
(1) d 1ŸŸ
''
S
5cdkkFn†
Area of S.œ
22. Yes, the outward flux through the top is 5. The reason is this: Since (x 2y (z 3)™† ™†Fijkœ
1 2 1 0, the outward flux across the closed cubelike surface is 0 by the Divergence Theorem. The fluxœœ
across the top is therefore the negative of the flux across the sides and base. Routine calculations show that
the sum of these latter fluxes is 5. (The flux across the sides that lie in the xz-plane and the yz-plane are 0, while the flux
across the xy-plane is 3.) Therefore the flux across the top is 5.
23. (a) (x) 1, (y) 1, (z) 1 3 Flux 3 dV 3 dV
```
```xyz
œ œ œÊ œÊ œ œ™†F''' '''
DD
3(Volume of the solid)œ
(b) If is orthogonal to at every point of S, then 0 everywhere Flux d 0.F n Fn Fn††œÊœœ
''
S
5
But the flux is 3(Volume of the solid) 0, so is not orthogonal to at every point.ÁFn
24. 2x 4y 6z 12 Flux ( 2x 4y 6z 12) dz dy dx™†Fœ Ê œ
'''
000
ab1
( 2x 4y 9) dy dx 2xb 2b 9b dx a b 2ab 9ab ab( a 2b 9) f(a b);œ œ œ œ œß
'' '
00 0
ab a
ab
###
2ab 2b 9b and a 4ab 9a so that 0 and 0 b( 2a 2b 9) 0 and
`` ``
`` ``
##
ff ff
ab ab
œ œ œ œ Ê œ
a( a 4b 9) 0 b 0 or 2a 2b 9 0, and a 0 or a 4b 9 0. Now b 0 or a 0 œ Ê œ œ œ œ œ œ
Flux 0; 2a 2b 9 0 and a 4b 9 0 3a 9 0 a 3 b so that f 3 is theÊ œ œ œ Ê œ Ê œ Ê œ ß œ
3327
###
ˆ‰
maximum flux.
25. d dV 3 dV d dV Volume of D
'' ''' ''' '' '''
SS
DD D
Fn F Fn†™† †55œœÊœœ
"
3
26. 0 Flux d dV 0 dV 0FC F Fn FœÊ œÊ œ œ œ œ™† † ™†
'' ''' '''
SDD
5
27. (a) From the Divergence Theorem, f d f dV f dV 0 dV 0
'' ''' ''' '''
SDDD
™ † ™†™ ™n5œœœœ
#
(b) From the Divergence Theorem, f f d f f dV. Now,
'' '''
SD
™† ™†™n5œ
ff f f f ff f f f™™†™œ Ê œ
ˆ‰ ˆ‰ ˆ‰ ˆ‰
Š‹ ’ “ Š‹ ’ “
”•
``` `` `` ``
``` `` `` ``
##
#
fff ff ff ff
xyz xx yy zz
ijk
f f f 0 f since f is harmonic f f d f dV, as claimed.œ œ Ê œ™™ ™ ™† ™
### #
kk kk kk
'' '''
SD
n5
28. From the Divergence Theorem, f d f dV dV. Now,
'' ''' '''
SDD
™ † ™†™n5œœ
Š‹
```
```
fff
xyz
f(x y z) ln x y z ln x y z , , ßßœ œ Ê œ œ œ
Èab
###
"```
#```
### fxf fz
x xyz y xyz z xyz
y
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1044 Chapter 16 Integration in Vector Fields
, , , Êœ œ œ Ê
``` ```
``` ```
fff fff
xyz xyz
x y z xyz xyz
xyz xyz xyzab ab ab
f d dddœœÊ œ œ
xyz
xyz xyz xyz
dV sin
"
ab '' '''
SD
™†n539)
'''
000
22a
39
3
a sin d d a cos d a dœœœœ
'' ' '
00 0 0
22 2 2
99) 9 ) )cd
11
Î#
!#
a
29. f g d f g dV f f f dV
'' ''' '''
SDD
™† ™†™ ™†nijk5œœ
Š‹
```
```
ggg
xyz
f f f dVœ
'''
DŠ‹
``````
``` ``` ```
```
gggggg
xxx yyy zzz
fff
f dV f g f g dVœœ
''' '''
D D
’“Š‹Š ‹ab
``` ` ` `
` ` ` ``````
``` #
ggg g g g
x y z xxyyzz
fff ™™†™
30. By Exercise 29, f g d f g f g dV and by interchanging the roles of f and g,
'' '''
SD
™† ™ ™†™n5œab
#
g f d g f g f dV. Subtracting the second equation from the first yields:
'' '''
SD
™† ™ ™ †™n5œab
#
f g g f d f g g f dV since f g g f
'' '''
SD
ab a b™™† ™ ™ ™†™™†™œ œÞn5##
31. (a) The integral p(t x y z) dV represents the mass of the fluid at any time t. The equation says that
'''
D
ßßß
the instantaneous rate of change of mass is flux of the fluid through the surface S enclosing the region D:
the mass decreases if the flux is outward (so the fluid flows out of D), and increases if the flow is inward
(interpreting as the outward pointing unit normal to the surface).n
(b) dV p dV p d p dV p
''' ''' '' '''
DD D
S
`
` `
`
p
tdt t
d
œœœ Êœvn v v†™† ™†53
Since the law is to hold for all regions D, p 0, as claimed™† vœ
`
`
p
t
32. (a) T points in the direction of maximum change of the temperature, so if the solid is heating up at the™
point the temperature is greater in a region surrounding the point T points away from the pointÊ™
T points toward the point T points in the direction the heat flows.Ê Ê™™
(b) Assuming the Law of Conservation of Mass (Exercise 31) with k T p and c T p, we haveœ œ™v3
c T dV k T d the continuity equation, ( k T) (c T) 0
d
dt t
''' ''
DS
35 3œ Ê œ™† ™† ™n`
`
c ( k T) k T T K T, as claimedÊœ œ Êœ œ3``
``
###
TTk
ttc
™† ™ ™ ™ ™
3
CHAPTER 16 PRACTICE EXERCISES
1. Path 1: t t t x t, y t, z t, 0 t 1 f(g(t) h(t) k(t)) 3 3t and 1, 1,rijkœ Ê œ œ œ ŸŸ Ê ß ß œ œ œ
#dx
dt dt
dy
1 dt 3 dt f(x y z) ds 3 3 3t dt 2 3
dz dx dz
dt dt dt dt
dy
œÊ œ Ê ßß œ œ
ʈ‰ ˆ‰
Š‹ ÈÈÈ
ab
##
##
''
C0
1
Path 2: t t , 0 t 1 x t, y t, z 0 f(g(t) h(t) k(t)) 2t 3t 3 and 1, 1,rij
"#
œ ŸŸ Ê œ œ œ Ê ß ß œ œ œ
dx
dt dt
dy
0 dt 2 dt f(x y z) ds 2 2t 3t 3 dt 3 2 ;
dz dx dz
dt dt dt dt
dy
œÊ œ Ê ßß œ œ
ʈ‰ ˆ‰
Š‹ ÈÈÈ
'ab
##
##
C0
1
'
t x 1, y 1, z t f(g(t) h(t) k(t)) 2 2t and 0, 0, 1rijk
#œ Ê œ œ œ Ê ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds (2 2t) dt 1ÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz
dt dt dt
dy
##
#''
C0
1
f(xyz) ds f(xyz) ds f(xyz) 3 2 1Êßßœßßßßœ
'''
CCC
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 16 Practice Exercises 1045
2. Path 1: t x t, y 0, z 0 f(g(t) h(t) k(t)) t and 1, 0, 0ri
"#
œÊœ œ œÊ ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds t dt ;ÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz
dt dt dt 3
dy
##
##"
''
C0
1
t x 1, y t, z 0 f(g(t) h(t) k(t)) 1 t and 0, 1, 0rij
#œ Ê œ œ œ Ê ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds (1 t) dt ;ÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz 3
dt dt dt 2
dy
##
#''
C0
1
t x 1, y 1, z t f(g(t) h(t) k(t)) 2 t and 0, 0, 1rijk
$œ Ê œ œ œ Ê ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds (2 t) dtÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz 3
dt dt dt 2
dy
##
#''
C0
1
f(xyz) ds f(xyz) ds f(xyz) ds f(xyz) dsÊ ßß œ ßß ßß ßß œ
''''
Path 1 C C C
10
3
Path 2: t t x t, y t, z 0 f(g(t) h(t) k(t)) t t and 1, 1, 0rij
%#
œ Ê œ œ œ Ê ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt 2 dt f(x y z) ds 2 t t dt 2;ÊœÊßßœ œ
ʈ‰ ˆ‰
Š‹ ÈÈÈ
ab
dx dz 5
dt dt dt 6
dy
##
##
''
C0
1
t (see above) f(x y z) dsrijk
$œ Ê ßß œ
'C
3
2
f(x y z) ds f(x y z) ds f(x y z) ds 2Ê ßßœ ßß ßßœ œ
'''
Path 2 C C
53
66
529
È#
È
Path 3: t x 0, y 0, z t, 0 t 1 f(g(t) h(t) k(t)) t and 0, 0, 1rk
&œÊœ œ œ ŸŸÊ ßß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds t dt ;ÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz
dt dt dt 2
dy
##
#"
''
C0
1
t x 0, y t, z 1, 0 t 1 f(g(t) h(t) k(t)) t 1 and 0, 1, 0rjk
'œ Ê œ œ œ ŸŸ Ê ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds (t 1) dt ;ÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz 1
dt dt dt 2
dy
##
#''
C0
1
t x t, y 1, z 1, 0 t 1 f(g(t) h(t) k(t)) t and 1, 0, 0rijk
(#
œÊœ œ œ ŸŸÊ ß ß œ œ œ œ
dx dz
dt dt dt
dy
dt dt f(x y z) ds t dtÊœÊßßœœ
ʈ‰ ˆ‰
Š‹
dx dz 1
dt dt dt 3
dy
##
##
''
C0
1
f(xyz) ds f(xyz) ds f(xyz) ds f(xyz) dsÊ ßß œ ßß ßß ßß œ œ
''''
Path 3 C C C
"""
##33
2
3. (a cos t) (a sin t) x 0, y a cos t, z a sin t f g(t) h(t) k(t) a sin t a sin t andrjkœ ÊœœœÊßßœ œab kk
È##
0, a sin t, a cos t dt a dt
dx dz dx dz
dt dt dt dt dt dt
dy dy
œœ œ Ê œ
ʈ‰ ˆ‰
Š‹
##
#
f(x y z) ds a sin t dt a sin t dt a sin t dt 4aÊßßœ œ œ
'' ''
C0 0
22
## ##
kk
4. (cos t t sin t) (sin t t cos t) x cos t t sin t, y sin t t cos t, z 0rijœ Êœ œ œ
f g(t) h(t) k(t) (cos t t sin t) (sin t t cos t) 1 t and sin t sin t t cos tÊßßœ œ œab
ÈÈ
###
dx
dt
t cos t, cos t cos t t sin t t sin t, 0 dtœœœœÊ
dy dy
dt dt dt dt dt
dz dx dz
ʈ‰ ˆ‰
Š‹
##
#
t cos t t sin t dt t dt t dt since 0 t 3 f(x y z) ds t 1 t dtœœœ ŸŸÊßßœœ
È È
kk È
## ## #
''
C0
37
3
5. (xyz) , (xyz) , (xyz)
`" `` " `` " `
`# `` # `` # `
$Î# $Î# $Î#
PNMPNM
yzzxx y
œ œ œ œ œ œ
M dx N dy P dz is exact; f(x y z) 2 x y z g(y z) Ê œ ÊßßœßÊœ
`" `"
```
`
f f
xyy
xyz xyz
g
È È
È
0 g(y z) h(z) f(x y z) 2 x y z h(z) h (z)œ Ê œÊ ßœ Ê ßßœ Ê œ
"`"
`
` `
w
È È
xyz xyz
g
y z
f
È
h (x) 0 h(z) C f(x y z) 2 x y z C œÊœÊœÊßßœÊ
"
w
È È
xyz xyz
dx dy dz
È'111
430
f(4 3 0) f( 1 1 1) 2 1 2 1 0œßßßßœœ
ÈÈ
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1046 Chapter 16 Integration in Vector Fields
6. , 0 , 0 M dx N dy dz is exact; 1 f(x y z)
`"`` `` ` `
`# `` `` ` `
PNMPNM f
yyzzz xx y x
œ œ œ œ œ œ Ê T œ Ê ß ß
È
x g(y z) g(y z) 2 yz h(z) f(x y z) x 2 yz h(z)œ ß Ê œ œ Ê ßœ Ê ßßœ
`
``
`
fz
yy y
gÉÈÈ
h (z) h (z) 0 h(z) C f(x y z) x 2 yz CÊœ œ Ê œÊ œÊßßœ
`
`
ww
f
zz z
yy
ÉÉ È
dx dy dz f(10 3 3) f(1 1 1) (10 2 3) (1 2 1) 4 1 5Ê œßßßßœœœ
'111
1033 ÉÉ
z
yz
y††
7. y cos z y cos z is not conservative; 2 cos t 2 sin t , 0 t 2
``
``
MP
zx
œ Á œ Ê œ Ÿ ŸFrijkabab 1
d 2 sin t 2 cos t d 2 cos t sin 1 2 cos t dt
2 sin t sin 1 2 sin t
Êœ Ê œ
rijFrabab c d
abababab aba ba bab
''
C0
2
†
4 sin 1 sin t cos t dt 8 sin 1œœab a b ab
'0
222 1
8. 0 , 0 , 3x is conservative d 0
``` `` `
````` `
#
PNMPN M
yzzxx y
œœ œœ œ œ Ê Ê œFFr
'C†
9. Let M 8x sin y and N 8y cos x 8x cos y and 8y sin x 8x sin y dx 8y cos x dyœœÊœ œÊ
``
``
MN
yx
'C
(8y sin x 8x cos y) dy dx (8y sin x 8x cos y) dy dx sin x 8x dxœ œ œ
''
R'' '
00 0
/2 /2 /2ab1#
0œ œ11
##
10. Let M y and N x 2y and 2x y dx x dy (2x 2y) dx dyœœÊœ œÊœ
## ##
``
``
MN
yx
'C''
R
(2r cos 2r sin ) r dr d (cos sin ) d 0œœœ
'' '
00 0
22 2
))) )))
16
3
11. Let z 1 x y f (x y) 1 and f (x y) 1 f f 1 3 Surface Area 3 dx dyœ Ê ß œ ß œÊ œ Ê œ
xy xy
ÉÈÈ
## ''
R
3(Area of the circular region in the xy-plane) 3œœ
ÈÈ
1
12. f 3 2y 2z , f 9 4y 4z and f 3™™™†œ œ Ê œ œijkpi pkk k k
È##
Surface Area dy dz r dr d 21 d 7 21 9Êœ œ œ œ
''
R
ÈÈ
94y 4z
333446
94r 79
"
'' '
00 0
23 2
))
Š‹Š‹
ÈÈ
1
13. f 2x 2y 2z , f 4x 4y 4z 2 x y z 2 and f 2z 2z since™™ ™†œ œÊ œ œ œ œ œijkpk pkk k kkk
ÈÈ
### ###
z 0 Surface Area dA dA dx dy r dr dÊ œ œ œ œ
'' '' ''
RRR
2
2z z 1x y 1r
"" "
ÈÈ
''
00
212
)
1 r d 1 d 2 1
''
00
22
’ “ Š‹ Š‹
È
œ œ
#"Î #
!
""
ÈÈÈ
))1
22
14. (a) f 2x 2y 2z , f 4x 4y 4z 2 x y z 4 and f 2z since™™ ™†œ œÊ œ œ œ œijkpk pkk k k
ÈÈ
### ###
z 0 Surface Area dA dA 2 r dr d 4 8Ê œ œ œ œ
'' ''
RR
42 2
2z z 4r
''
00
/2 2 cos È)1
(b) 2 cos d 2 sin d ; ds r d dr (Arc length in polar coordinates)rrœÊœ œ))))
### #
ds (2 cos ) d dr 4 cos d 4 sin d 4 d ds 2 d ; the height of theÊœ œ œ Êœ
# ## # ## ## #
) ) )) )) ) )
cylinder is z 4 r 4 4 cos 2 sin 2 sin if 0œœ œ œ ŸŸ
ÈÈkk
## #
))))
1
Surface Area h ds 2 (2 sin )(2 d ) 8Êœœ œ
''
20
/2 /2
))
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 16 Practice Exercises 1047
15. f(x y z) 1 f f and fßßœœÊ œ Ê œ œÊ œ
xz
abc a b c a b c c
y™™ ™†
ˆ‰ ˆ‰ ˆ‰ kk k k
É
""" """ "
ijk pk p
since c 0 Surface Area dA c dA abc ,Ê œ œ œ
'' ''
RR
ÉŠ‹
abc
c
""" " """
#
ÉÉ
abc abc
since the area of the triangular region R is ab. To check this result, let a c and a b ; the area can be
"
#vik w ijœ œ
found by computing .
"
#kkvw‚
16. (a) f 2y , f 4y 1 and f 1 d 4y 1 dx dy™™™†œœÊ œ œÊœjkp k pkk k k
ÈÈ
##
5
g(x y z) d 4y 1 dx dy y y 1 dx dy y y dx dyÊßßœ œ œ
'' '' ''
SRR
5yz
4y 1
È
##$
Èab ab
''
10
13
3y y dy 3 0œœœ
'1
1ab ’“
$
#
"
"
yy
4
(b) g(x y z) d 4y 1 dx dy y 1 dx dy 3 y 1 dy
'' ''
SR
ßß œ œ œ 5z
4y 1
È
###
Èab ab
'' '
10 1
13 1
3y 4œœ
’“
y
3
"
"
17. f 2y 2z , f 4y 4z 2 y z 10 and f 2z since z 0™™ ™†œ œÊ œœœ œ jkpk pkk k k
ÈÈ
## ##
d dx dy dx dy g(x y z) d x y y z dx dyÊœ œ œ ßß œ 55
10 5 5
2z z z
'' ''
SRaba b
ˆ‰
%##
x y (25) dx dy x dx dy dy 50œœœœ
''
Rab Š‹
%%
5
25 y 25 y 25 y
125y 25y
ÈÈÈ
'' '
00 0
41 4
18. Define the coordinate system so that the origin is at the center of the earth, the z-axis is the earth's axis (north
is the positive z direction), and the xz-plane contains the earth's prime meridian. Let S denote the surface
which is Wyoming so then S is part of the surface z R x y . Let R be the projection of S ontoœab
###
"Î#
xy
the xy-plane. The surface area of Wyoming is 1 d 1 dA
'' ''
SR
5œ
xy ʈ‰ Š‹
``
``
##
zz
xy
1 dA dA R R r r dr d
'' ''
RR
xy xy
R sin 45°
Rsin 49°
Éab
xR
Rxy Rxy
y
Rxy
##
"Î#
œ œ
ab'' )
(where and are the radian equivalent to 104°3 and 111°3 , respectively)))
"# ww
R R r R R R sin 45° R R R sin 49° dœ œ
''
¹
ab abab
## # ## # ##
"Î# "Î# "Î#
Rsin 49°
R sin 45°
)
( )R (cos 45° cos 49°) R (cos 45° cos 49°) (3959) (cos 45° cos 49°)œ œ œ ))
#"
## #
77
180 180
11
97,751 sq. mi.¸
19. A possible parametrization is ( ) (6 sin cos ) (6 sin sin ) (6 cos ) (spherical coordinates);rijk9) 9 ) 9 ) 9ߜ
now 6 and z 3 3 6 cos cos and z 3 3 3 3 6 cos 3999 9œœÊœ ʜʜ œÊœ
"
#
2
3
1ÈÈ
cos ; also 0 2ʜʜʟŸ ŸŸ99 9 )1
È3
66 3
2
#
11 1
20. A possible parametrization is (r ) (r cos ) (r sin ) (cylindrical coordinates);rijkߜ )))
Š‹
r
#
now r x y z and 2 z 0 2 0 4 r 0 0 r 2 since r 0;œÊœ ŸŸÊŸŸÊÊŸŸ
È## ##
#
rr
also 0 2ŸŸ)1
21. A possible parametrization is (r ) (r cos ) (r sin ) (1 r) (cylindrical coordinates);rijkߜ )))
now r x y z 1 r and 1 z 3 1 1 r 3 0 r 2; also 0 2œ Êœ ŸŸÊŸŸÊŸŸ ŸŸ
È## )1
22. A possible parametrization is (x y) x y 3 x for 0 x 2 and 0 y 2rij kßœ ŸŸ ŸŸ
ˆ‰
y
#
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1048 Chapter 16 Integration in Vector Fields
23. Let x u cos v and z u sin v, where u x z and v is the angle in the xz-plane with the x-axisœœ œ
È##
(u v) (u cos v) 2u (u sin v) is a possible parametrization; 0 y 2 2u 2 u 1Ê ßœ ŸŸÊ ŸÊ Ÿrijk
###
0 u 1 since u 0; also, for just the upper half of the paraboloid, 0 vÊŸŸ ŸŸ1
24. A possible parametrization is 10 sin cos 10 sin sin 10 cos ) , 0 and
Š‹Š‹Š
ÈÈÈ
9) 9) 9 9ijkŸŸ
1
2
0 ŸŸ)1
#
25. , 2 6
0
rijrijk rr ijk rr
ijk
u v uv uv
œ œ Ê ‚ œ œ Ê ‚ œ
""
"""
ââ
ââ
ââ
ââ
ââ
ââ kk
È
Surface Area du dv 6 du dv 6Êœ‚œ œ
''
Ruv
00
11
kk ÈÈ
rr
uv ''
26. xy z d (u v)(u v) v 6 du dv 6 u 2v du dv
''
Sab c d a b
ÈÈ
œ œ
####
5'' ''
00 00
11 11
6 2uv dv 6 2v dv 6 v vœ œ œ œ œ
ÈÈÈ
’“ ˆ‰ ‘ É
''
00
11
u22
333333
6
##$
"
!
""
"
!È
27. (cos ) (sin ) , ( r sin ) (r cos ) cos sin 0
r sin r cos
rijr i jkrr
ijk
r r
œ œ Ê‚œ
"
)) ) ) ))
))
))
ââ
ââ
ââ
ââ
ââ
ââ
(sin ) (cos ) r sin cos r 1 r Surface Area dr dœ Ê‚œ œÊ œ ‚)) )) )ijkrr rrkk kk
ÈÈ
r r) )
### # ''
Rr
1 r dr d 1 r ln r 1 r d 2 ln 1 2 dœœœ
'' ' '
00 0 0
21 2 2
ÈÈÈ ÈÈ
’“’“Š‹ Š‹
###
"""
###
"
!
)))
r
2
2ln1 2œ1’“
ÈÈ
Š‹
28. x y 1 d r cos r sin 1 1 r dr d 1 r dr d
''
SÈÈÈ
ab
## ## ## # #
œ œ 5))) )
'' ''
00 00
21 21
r d dœ œ œ
''
00
22
’“
r48
333
"
!))1
29. 0 , 0 , 0 Conservative
``` `` `
````` `
PNMPNM
yzz xx y
œœ œœ œœ Ê
30. , , Conservative
````` `
````` `
P N M 3xz P N M
yzz xx y
3zy 3xy
xyz xyz xyz
œœœœœœÊ
ab ab ab
31. 0 ye Not Conservative
``
``
PN
yz
œÁ œ Ê
z
32. , , Conservative
``` ```
` `` `` `
Px NM PN z M
y (xyz) z z (xyz) x x (xyz) y
y
œœ œœœœÊ
33. 2 f(x y z) 2x g(y z) 2y z g(y z) y zy h(z)
``
```
`#
ff
xyy
g
œÊ ßßœ ß Ê œ œ Ê ßœ
f(x y z) 2x y zy h(z) y h (z) y 1 h (z) 1 h(z) z CÊ ßß œ Ê œ œ Ê œ Ê œ
#ww
`
`
f
z
f(xyz) 2x y zy z CÊßßœ
#
34. z cos xz f(x y z) sin xz g(y z) e g(y z) e h(z)
``
```
`
ff
xyy
gyy
œÊßßœßÊœœÊßœ
f(x y z) sin xz e h(z) x cos xz h (z) x cos xz h (z) 0 h(z) CÊßßœ Êœ œ Ê œÊ œ
yf
z
`
`
ww
f(x y z) sin xz e CÊßßœ
y
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

Chapter 16 Practice Exercises 1049
35. Over Path 1: t t t , 0 t 1 x t, y t, z t and d ( ) dt 2t trijk rijk F ij kœ ŸŸ Ê œ œ œ œ Ê œ
##
d 3t 1 dt Work 3t 1 dt 2;ʜʜ œFr†ab ab
##
'0
1
Over Path 2: t t , 0 t 1 x t, y t, z 0 and d ( ) dt 2t trij rij F ijk
"""
##
œ ŸŸ Ê œ œ œ œ Ê œ
d 2t 1 dt Work 2t 1 dt ; t , 0 t 1 x 1, y 1, z t andÊ œ Ê œ œ œ ŸŸ Ê œ œ œFr rijk
"" " #
##
†ab ab
'0
15
3
d dt 2 d dt Work dt 1 Work Work Work 1rk F ijk Fr
## ## # "#
œÊœÊ œÊ œœÊœœœ†'0
158
33
36. Over Path 1: t t t , 0 t 1 x t, y t, z t and d ( ) dt 2t tr i j k r ijk F i jkœ ŸŸ Ê œ œ œ œ Ê œ
##
d 3t 1 dt Work 3t 1 dt 2;ʜʜ œFr†ab ab
##
'0
1
Over Path 2: Since f is conservative, d 0 around any simple closed curve C. Thus consider
)CFr†œ
d d d , where C is the path from (0 0 0) to (1 1 0) to ( ) and C is the path
'''
curve C C
Fr Fr Fr†††œ ß ß ß ß "ß "ß "
"#
from (1 1 1) to ( ). Now, from Path 1 above, d 2 0 d d ( 2)ß ß !ß !ß ! œ Ê œ œ
'''
C curve C
Fr Fr Fr†††
d2ʜ
'CFr†
37. (a) e cos t e sin t x e cos t, y e sin t from (1 0) to e 0 0 t 2rijœ Êœœ ßßÊŸŸabab ab
tt tt 211
e cos t e sin t e sin t e cos t and Êœ œ œ
d
dt
tt tt xy
xy
e cos t e sin t
e cost e sint
rij ij
ababijF
ab abab
ab
tt
2t 2t
eœ Êœ œ
ˆ‰ˆ‰ Š‹
cos t sin t d cos t sin t cos t sin t sin t cos t
ee dteeee
t
2t 2t t t t t
ijF†r
Work e dt 1 eÊœ œ
'0
2t21
(b) f(x y z) x y g(y z) FœÊœÊßßœßÊœ
xy yg
xy xy xy
fx f
xyy
ij `
` `
```
##
"Î#
ab ab ab
ab
g(y z) C f(x y z) x y is a potential function for dœ Ê ßœ Ê ßßœ Ê
y
xyab
##
"Î#
ab FFr
'C†
fe 0 f(10) 1 eœßßœab
2211
38. (a) x ze is conservative d 0 for closed path CFF FrœÊ Êœ™†ab
#y)Cany
(b) d x ze d x ze x ze 2 0 2
''
C 100
102
Fr r†™†œœœœab k kab ab
## #
Ð"ß!ß# Ñ Ð"ß!ß!Ñ
yy y
111
39. 2y ; unit normal to the plane is
yy3z
™‚œ œ œ œ
Fk nijk
ijk
ââ
ââ
ââ
ââ
ââ
ââ
`` `
`` `
##
xy z
263
4369
263
777
ijk
È
y; and f(x y z) 2x 6y 3z f 3 d dA dAÊ‚ œ œ ßßœÊ œÊœ œ™† ™†Fn p k p
6 7
7f3
f
kk 5kk
kk
™
™†p
d y d y dA 2y dA 2r sin r dr d sin d 0Êœ œ œ œ œ œ
)'''
C00 0
21 2
Fr†'' '' ''
RR R
667 2
773 3
5))))
ˆ‰ˆ ‰
40. 8y ; the circle lies in the plane f(x y z) y z 0 with unit normal
x y x y 4y z
™‚œ œ ßßœœ
Fi
ijk
ââ
ââ
ââ
ââ
ââ
ââ
`` `
`` `
##
xy z
0 d d 0 d 0njk Fn Fr Fnœ Ê‚ œÊ œ ‚ œ œ
""
ÈÈ
22 ™† † ™†
)C'' ''
RR
55
41. (a) 2t 2t 4 t , 0 t 1 x 2t, y 2t, z 4 t 2, 2, 2trij kœ ŸŸÊœ œ œÊœ œ œ
ÈÈ È È È È
ab
##
dx dz
dt dt dt
dy
dt 4 4t dt M (x y z) ds 3t 4 4t dt (4 4t)ʜʜßßœ œ
ʈ‰ ˆ‰ ‘
Š‹ ÈÈ
dx dz
dt dt dt 4
dy
##
###
"$Î# "
!
''
C0
1
$
42 2œ
È
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1050 Chapter 16 Integration in Vector Fields
(b) M (x y z) ds 4 4t dt t 1 t ln t 1 t 2 ln 1 2œßßœœœ
''
C0
1
$ÈÈ ÈÈÈ
’“Š‹Š‹
## #
"
!
42. t 2t t , 0 t 2 x t, y 2t, z t 1, 2, tri j kœ ŸŸ Ê œ œ œ Ê œ œ œ
2 2 dx dz
3 3 dt dt dt
dy
$Î# $Î# "Î#
dt t 5 dt M (x y z) ds 3 5 t t 5 dtʜʜßßœ
ʈ‰ ˆ‰
Š‹ ÈÈÈ
dx dz
dt dt dt
dy
##
#''
C0
2
$
3(t 5) dt 36; M x ds 3t(t 5) dt 38; M y ds 6t(t 5) dt 76;œœœ œœœ œœ
'''''
0C0 C0
22 2
yz xz
$$
M z ds 2t (t 5) dt 2 x , y , z
xy 144 38 19 76 19
7 M 36 18 M 36 9 M 36
MM
M2
œœ œÊœœœœœœœœ
''
C0
2
$$Î# Èyz xy
xz
144
7
Š‹
È
2œ4
7È
43. t t , 0 t 2 x t, y t , z 1, 2 t , tri j kœ ŸŸ Ê œ œ œ Ê œ œ œ
Š‹Š‹ È
22 22 dy
3 3 dt dt dt
t t dx dz
ÈÈ
$Î# $Î# "Î#
##
dt 1 2t t dt (t 1) dt t 1 dt (t 1) dt on the domain given.Êœœœœ
ʈ‰ ˆ‰
Š‹ ÈÈkk
dx dz
dt dt dt
dy
##
###
Then M ds (t 1) dt dt 2; M x ds t (t 1) dt t dt 2;œœ œœœ œ œœ
'' ' ' ' '
C0 0 C 0 0
22 2 2
$$
ˆ‰ ˆ‰
""
t1 t1
yz
M y ds t (t 1) dt t dt ; M z ds
xz xy
22 22
3t1 3 15
32
œœ œ œœ
'' ' '
C0 0 C
22
$$
Š‹
ˆ‰
ÈÈ
$Î# $Î#
"
(t 1) dt dt x 1; y ; zœœœÊœœœœœœœ
''
00
22
Š‹
ˆ‰
tt4216
t1 3 M M 15 M
MM
M
# # # #
"yz xy
xz
32
15
ˆ‰
; I y z ds t dt ; I x z ds t dt ;œœ œ œ œ œ œ œ
ˆ‰
4
3
#
## $ ## #
2 8 t 232 t 64
39445 415
xy
'' ''
C0 C0
2 2
ab ab
Š‹ Š‹
$$
I y x ds t t dt ; R ; R ;
zxy
856
99 M M
I229
35 15
I42
œ œ œœœ œ œœ œ
''
C0
2
ab ˆ‰ ÉÊÊ
É
## # $
##
$xy
Š‹ Š‹
ÈÈ
ÈÈ
232 64
45 15
R
zI
M3
27
œœ œ
ÉÊ
zŠ‹ È
56
9
#
44. z 0 because the arch is in the xy-plane, and x 0 because the mass is distributed symmetrically with respectœœ
to the y-axis; (t) (a cos t) (a sin t) , 0 t ds dtrijœ ŸŸÊœ1ʈ‰ ˆ‰
Š‹
dx dz
dt dt dt
dy
##
#
( a sin t) (a cos t) dt a dt, since a 0; M ds (2a y) ds (2a a sin t) a dtœ œ œ œ œ
È## '' '
CC 0
$
2a 2a ; M y dt y(2a y) ds (a sin t)(2a a sin t) dt 2a sin t a sin t dtœ œ œ œ œ
21$
####
xz CC 0 0
'' ' '
ab
2a cos t a 4a y x y z 0 0œ œ Ê œ œ Ê ßß œ ß ß
‘ ˆ‰ˆ‰ ab
## #
!#
tsin 2t a 8 8
2 4 2a 2a 4 4 4 4
4a
1111
11 1
Š‹
a
45. (t) e cos t e sin t e , 0 t ln 2 x e cos t, y e sin t, z e e cos t e sin t ,rijkœŸŸÊœœœÊœabab a b
ttt ttt tt
dx
dt
e sin t e cos t , e dt
dy dy
dt dt dt dt dt
tt t
dz dx dz
œ œÊ ab
ʈ‰ ˆ‰
Š‹
##
#
e cos t e sin t e sin t e cos t e dt 3e dt 3 e dt; M ds 3 e dtœœœ œœ
Éababab
ÈÈÈ
tt tt t 2t tt
### ''
C0
ln 2
$
3; M z ds 3 e e dt 3 e dt z ;œœœ œ œÊœœœ
ÈÈÈ
Š‹
ab
xy tt 2t 33 M
M3
3
'' '
C0 0
ln 2 ln 2
$Ȍ
È
##
xy
33
I x y ds e cos t e sin t 3 e dt 3 e dt R
z z
2t 2t t 3t 73
3M
I
œ œ œ œÊœ
'' '
C0 0
ln 2 ln 2
ab a b
Š‹
ÈÈ É
## # #
$Èz
œœ
ÊÉ
73
33
7
3
È
È
46. (t) (2 sin t) (2 cos t) 3t , 0 t 2 x 2 sin t, y 2 cos t, z 3t 2 cos t, 2 sin t,rijkœ ŸŸÊœ œ œÊœ œ1dx
dt dt
dy
3 dt 4 9 dt 13 dt; M ds 13 dt 2 13;
dz dx dz
dt dt dt dt
dy
œÊ œ œ œ œ œ
ʈ‰ ˆ‰
Š‹ ÈÈÈÈ
##
#''
C0
2
$$ 1$
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
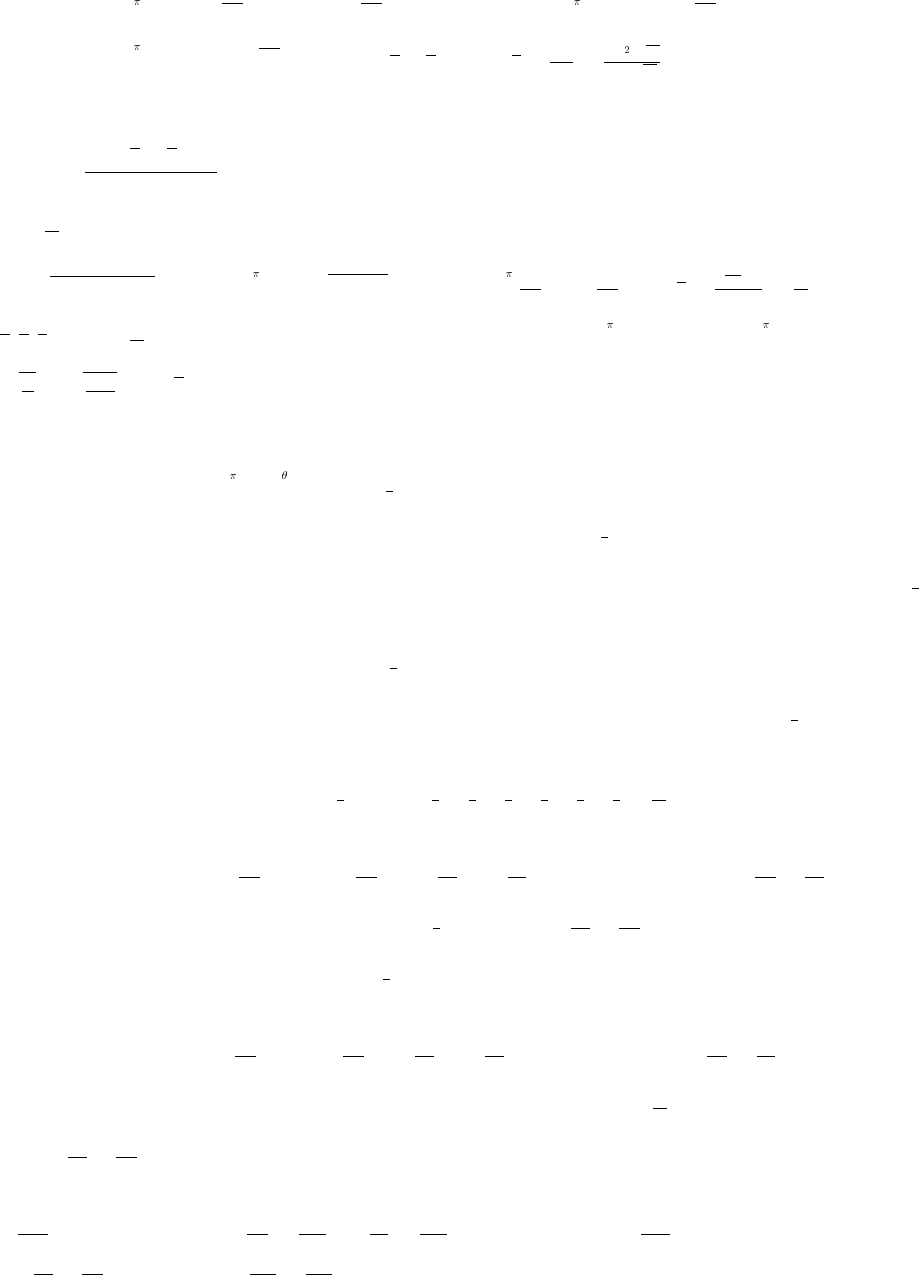
Chapter 16 Practice Exercises 1051
M z ds (3t) 13 dt 6 13; M x ds (2 sin t) 13 dt 0;
xy yz
œœ œ œœ œ
'' ''
C0 C0
2 2
$$$1 $ $
Š‹ Š‹
ÈÈ È
#
M y ds (2 cos t) 13 dt 0 x y 0 and z 3 ( 3 ) is the
xz M
M
613
213
œ œ œ Ê œ œ œ œ œ Ê !ß !ß
''
C0
2
$$ 11
Š‹
Èxy $1
$1
È
È
center of mass
47. Because of symmetry x y 0. Let f(x y z) x y z 25 f 2x 2y 2zœœ ßßœœ Ê œ
### ™ijk
f 4x 4y 4z 10 and f 2z, since z 0 M (x y z) dÊ œ œ œÊ œ Êœ ßßkk k k
È
™™†
### pk p ''
R
$5
z dA 5 dA 5(Area of the circular region) 80 ; M z d 5z dAœœœ œœœ
'' '' '' ''
RR RR
ˆ‰
10
zxy
#1$5
5 25 x y dx dy 5 25 r r dr d d zœœ œœÊœœ
''
RÈŠ‹
È
## #
'' '
00 0
24 2
))1
490 980 49
3 3 80 12
Š‹
980
31
1
x y z 0 ; I x y d 5 x y dx dy 5r dr d 320 d 640 ;Êßßœß!ß œ œ œ œ œab ab ab
ˆ‰
49
12 z'' ''
RR
## ## $
$5 ) ) 1
'' '
00 0
24 2
R22
zœœ œ
ÉÉÈ
I
M80
640
z1
1
48. On the face z 1: g(x y z) z 1 and g g 1 and g 1 d dAœßßœœ œÊœÊ œ œÊœpk k p™™ ™†kk k k 5
I x y dA 2 r dr d ; On the face z 0: g(x y z) z 0 g and Êœ œ œ œ ßßœœ Ê œ œ
''
Rab
## $
''
00
/4 sec
)2
3™kpk
g 1 g 1 d dA I x y dA ; On the face y 0: g(x y z) y 0ÊœÊ œÊœÊœ œ œßßœœkk k k a b™™†p5''
R
## 2
3
g and g 1 g 1 d dA I x 0 dA x dx dz ;Ê œ œÊ œÊ œÊ œ Êœ œ œ™™™†jpj pkk k k a b5''
R
##
"
''
00
11
3
On the face y 1: g(x y z) y 1 g and g 1 g 1 d dAœßßœœÊœ œÊ œÊ œÊœ™™™†jpj pkk k k 5
I x 1 dA x 1 dx dz ; On the face x 1: g(x y z) x 1 g and Êœ œ œ œ ßßœœ Ê œ œ
''
Rab ab
## #
''
00
11 4
3™ipi
g 1 g 1 d dA I 1 y dA 1 y dy dz ; On the faceÊœÊ œÊœÊœœ œkk k k a b a b™™†p5''
R
## #
''
00
11 4
3
x 0: g(x y z) x 0 g and g 1 g 1 d dAœßßœœÊœ œÊ œÊ œÊœ™™™†ipi pkk k k 5
I 0 y dA y dy dz IÊ œ œ œ Ê œœ
''
Rab
## # ""
''
00
11
z
1224414
3 333333 3
49. M 2xy x and N xy y 2y 1, 2x, y, x 1 Flux dx dyœ œÊœ œ œ œÊ œ
```` ``
```` ``
MMNN MN
xyxy xy
''
RŠ‹
(2y1x1) dydx (2yx) dydx ; Circ dxdyœ œ œ œ
'' ''
R R
''
00
11 3NM
xy#``
``
Š‹
(y 2x) dy dx (y 2x) dy dxœ œ œ
''
R''
00
11 "
#
50. M y 6x and N x y 12x, 1, 1, 2y Flux dx dyœ œ Ê œ œ œ œ Ê œ
##
```` ``
```` ``
MMNN MN
xyxy xy
''
RŠ‹
( 12x 2y) dx dy ( 12x 2y) dx dy 4y 2y 6 dy ;œ œ œ œ
''
R'' '
0y 0
11 1
ab
#11
3
Circ dx dy (1 1) dx dy 0œ œœ
'' ''
RR
Š‹
``
``
NM
xy
51. M and N ln x sin y and ln x sin y dy dxœ œ Ê œ œ Ê
cos y sin y sin y cos y
xyxxxx
MN``
``
)C
dx dy dx dy 0œ œ œ
'' ''
RR
Š‹ Š ‹
``
``
NM
xy x x
sin y sin y
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
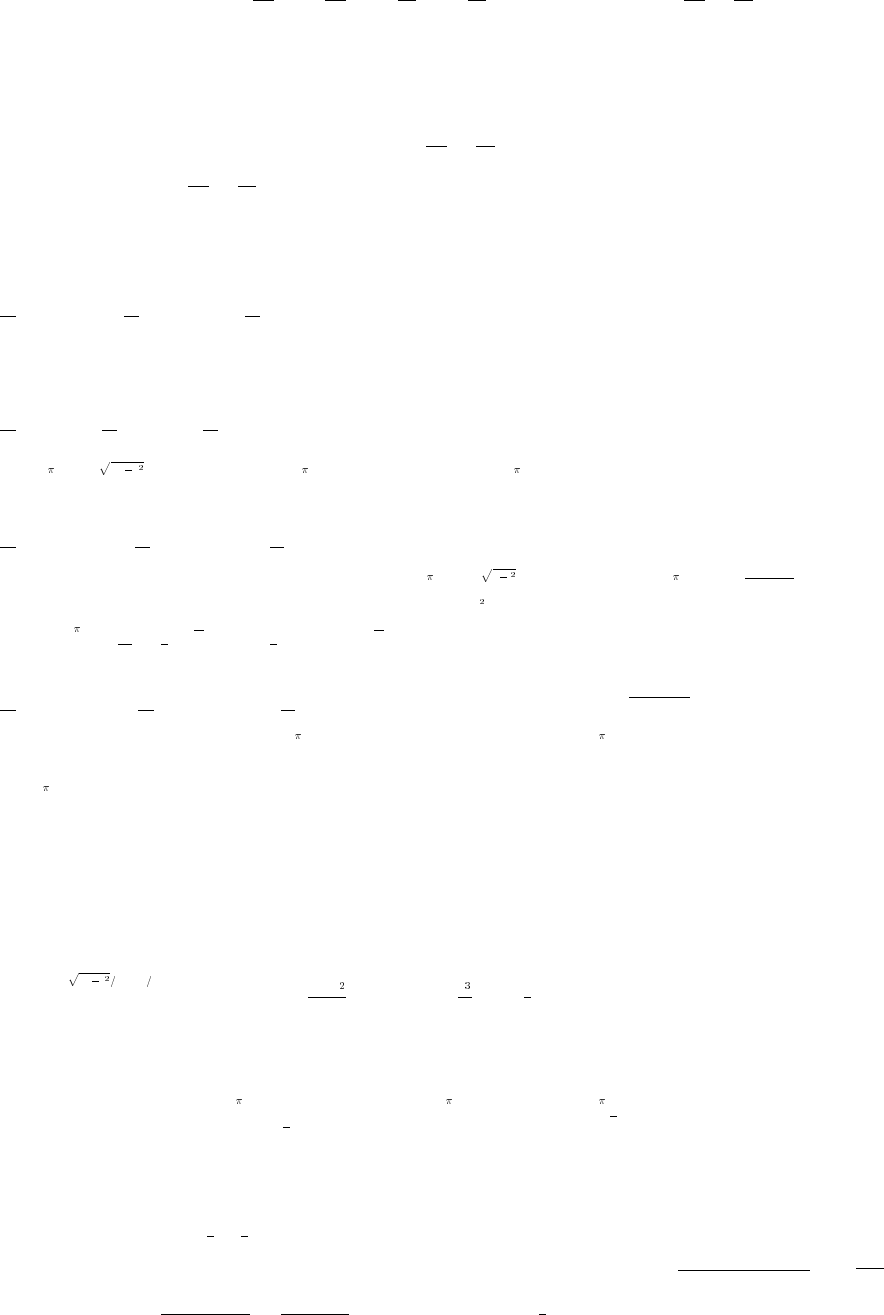
1052 Chapter 16 Integration in Vector Fields
52. (a) Let M x and N y 1, 0, 0, 1 Flux dx dyœ œÊœ œœœÊœ
```` ``
```` ``
MMNN MN
xyxy xy
''
RŠ‹
(1 1) dx dy 2 dx dy 2(Area of the region)œ œ œ
'' ''
RR
(b) Let C be a closed curve to which Green's Theorem applies and let be the unit normal vector to C. Letn
x y and assume is orthogonal to at every point of C. Then the flux density of at every pointFij F n Fœ
of C is 0 since 0 at every point of C 0 at every point of CFn†œÊœ
``
``
MN
xy
Flux dx dy 0 dx dy 0. But part (a) above states that the flux isÊœ œ œ
'' ''
RR
Š‹
``
``
MN
xy
2(Area of the region) the area of the region would be 0 contradiction. Therefore, cannot beÊÊF
orthogonal to at every point of C.n
53. (2xy) 2y, (2yz) 2z, (2xz) 2x 2y 2z 2x Flux (2x 2y 2z) dV
```
```xyz
œœœÊœÊœ™†F'''
D
(2x 2y 2z) dx dy dz (1 2y 2z) dy dz (2 2z) dz 3œœœœ
''' '' '
000 00 0
111 11 1
54. (xz) z, (yz) z, (1) 0 2z Flux 2z r dr d dz
```
```xyz
œœœÊœÊœ™†F'''
D
)
2z dz r dr d r 16 r dr d 64 d 128œœœœ
''' '' '
003 0 0 0
24 25r 2 4 2
)))1ab
#
55. ( 2x) 2, ( 3y) 3, (z) 1 4; x y z 2 and x y z z 1
```
```
### ##
xyz
œ œ œ Ê œ œ œ Ê œ™†F
x y 1 Flux 4 dV 4 dz r dr d 4 r 2 r r dr dÊ œ Ê œ œ œ
## $
#
'''
D''' ''
00r 00
21 2r 21
))
Š‹
È
42 d782œ œ
'0
2Š‹Š‹
ÈÈ
72 2
12 3 3
)1
56. (6x y) 6, ( x z) 0, (4yz) 4y 6 4y; z x y r
`` `
`` ` ##
xy z
œ œ œ Ê œ œ œ™†FÈ
Flux (6 4y) dV (6 4r sin ) dz r dr d 6r 4r sin dr dÊœ œ œ
'''
D''' ''
000 00
/21r /21
)) ))ab
#$
(2 sin ) d 1œ œ
'0
/2
)) 1
57. y z x 0 Flux d dV 0Fijk F Fn Fœ Ê œÊ œ œ œ™† † ™†
'' '''
SD
5
58. 3xz y z 3z 1 3z 1 Flux d dVFijk F Fn Fœ Ê œœÊ œ œ
#$ ##
™† † ™†
'' '''
SD
5
1 dz dy dx dx xœœœœ
'' ' '
00 0 0
416x2y2 4
Š‹ ’ “
16 x x 8
16 48 3
%
!
59. xy x y y y x 0 Flux d dVFijk F Fn FœÊ œÊ œ œ
## ##
™† † ™†
'' '''
SD
5
x y dV r dz r dr d 2r dr d dœœ œ œœ
'''
Dab
## # $ "
#
''' '' '
00 1 00 0
211 21 2
)))1
60. (a) (3z 1) 3 Flux across the hemisphere d dVFkF Fn Fœ Ê œÊ œ œ™† † ™†
'' '''
SD
5
3 dV 3 a 2 aœœ œ
'''
Dˆ‰ˆ ‰
"
#
$$
4
311
(b) f(xyz)xyza 0 f2x2y2z f 4x4y4z 4a2a sinceßßœœÊ œ Ê œ œ œ
#### ### #
™™ijkkk
ÈÈ
a0 (3z1) ; f f 2zÊœ œ Ê œ œÊ œ œnFnpkpk
2x 2y 2z x y z
aa a
z
ijk ijk
#†™†™†
ˆ‰
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
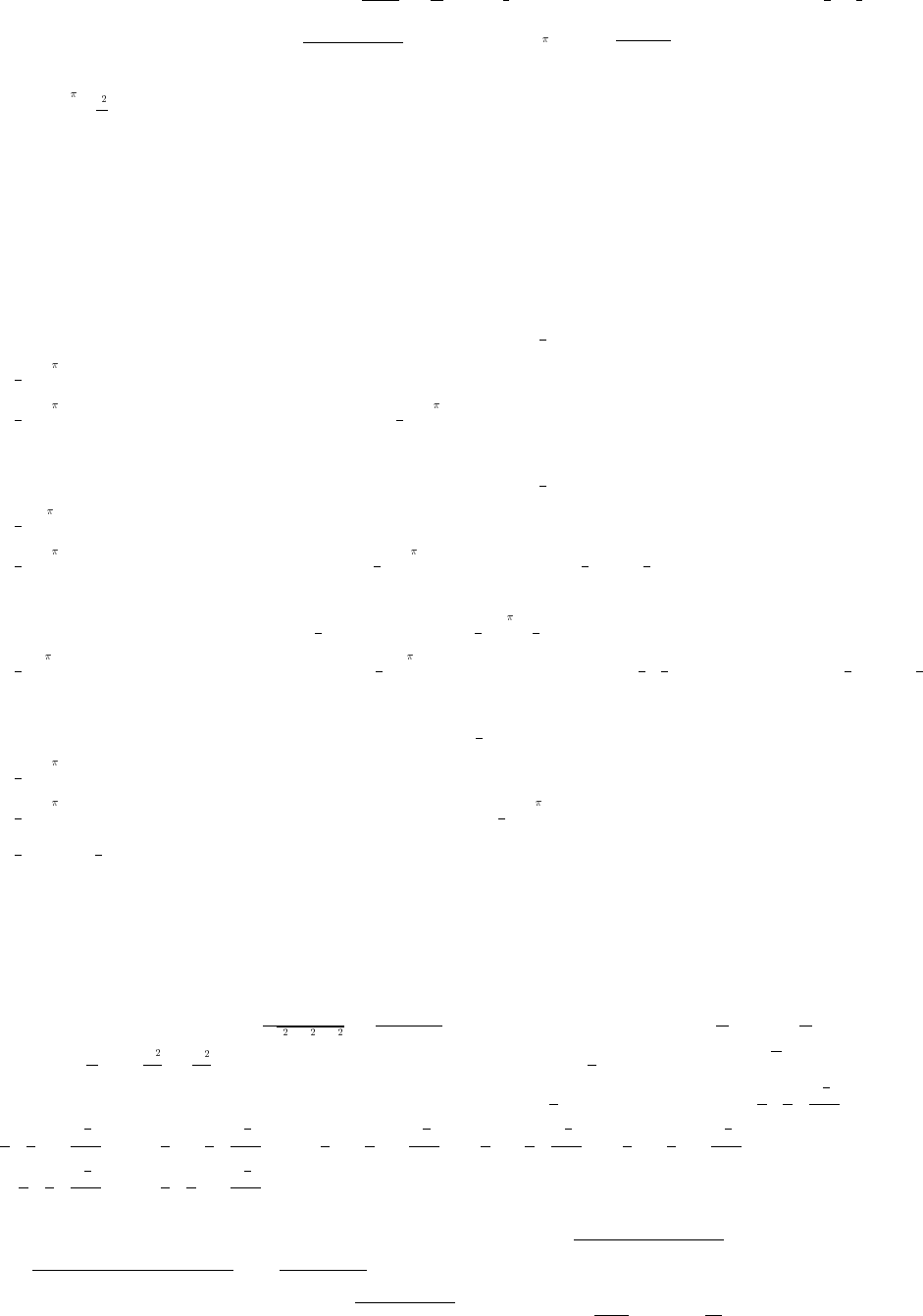
Chapter 16 Additional and Advanced Exercises 1053
f 2z since z 0 d dA dA d (3z 1) dAʜʜœœÊ œkk ˆ‰ˆ‰
™† †pFn55
kk
kk
™
™†
f
f2z z az
2a a z a
p'' ''
SRxy
(3z 1) dx dy 3 a x y 1 dx dy 3 a r 1 r dr dœ œ œ
'' ''
RR
xy xy
00
2a
ˆ‰
ÈŠ‹
È
### ##
'' )
a d a 2 a , which is the flux across the hemisphere. Across the base we findœœ
'0
2Š‹
a
#
$#$
)1 1
[3(0) 1] since z 0 in the xy-plane (outward normal) 1 Flux acrossFkk nk Fnœœ œ Êœ Ê œÊ†
the base d 1 dx dy a . Therefore, the total flux across the closed surface isœœœ
'' ''
SR
Fn†51
xy
#
a2a a 2a.ab111 1
#$# $
œ
CHAPTER 16 ADDITIONAL AND ADVANCED EXERCISES
1. dx ( 2 sin t 2 sin 2t) dt and dy (2 cos t 2 cos 2t) dt; Area x dy y dxœ œ œ
"
#)C
[(2 cos t cos 2t)(2 cos t 2 cos 2t) (2 sin t sin 2t)( 2 sin t 2 sin 2t)] dtœ
"
#'0
2
[6 (6 cos t cos 2t 6 sin t sin 2t)] dt (6 6 cos t) dt 6œ œ œ
""
##
''
0 0
2 2
1
2. dx ( 2 sin t 2 sin 2t) dt and dy (2 cos t 2 cos 2t) dt; Area x dy y dxœ œ œ
"
#)C
[(2 cos t cos 2t)(2 cos t 2 cos 2t) (2 sin t sin 2t)( 2 sin t 2 sin 2t)] dtœ
"
#'0
2
[2 2(cos t cos 2t sin t sin 2t)] dt (2 2 cos 3t) dt 2t sin 3t 2œ œ œ œ
"""
###
#
!
''
0 0
2 2 ‘
2
3
11
3. dx cos 2t dt and dy cos t dt; Area x dy y dx sin 2t cos t sin t cos 2t dtœœœœ
"""
###
)'
C0
ˆ‰
sin t cos t (sin t) 2 cos t 1 dt sin t cos t sin t dt cos t cos t 1œœœœœ
"""""
###
## # $
!
''
0 0
cdabab ‘
333
2
1
4. dx ( 2a sin t 2a cos 2t) dt and dy (b cos t) dt; Area x dy y dxœ œ œ
"
#)C
2ab cos t ab cos t sin 2t 2ab sin t 2ab sin t cos 2t dtœ
"
#
##
'0
2cdaba b
2ab 2ab cos t sin t 2ab(sin t) 2 cos t 1 dt 2ab 2ab cos t sin t 2ab sin t dtœ œ
" "
# #
## #
''
0 0
2 2
cdabab
2abt ab cos t 2ab cos t 2 abœ œ
"
#
$#
!
‘
2
3
11
5. (a) (x y z) z x y is only at the point (0 0 0), and curl (x y z) is never .Fijk0 Fijk0ßßœ ßß ßßœ
(b) (x y z) z y is only on the line x t, y 0, z 0 and curl (x y z) is never .Fik0 Fij0ßßœ œ œ œ ßßœ
(c) (x y z) z is only when z 0 (the xy-plane) and curl (x y z) is never .Fi0 Fj0ßß œ œ ßß œ
6. yz xz 2xyz and , so is parallel to when yz , xz ,Fij kn F nœ œ œ œ œ
## ##
xyz xyz cy
xyz RRR
cx
ijk ijk
È
and 2xyz 2xy y x y x and z 2x z 2x. Also,œÊ œœ ʜʜ„ œ„œ Êœ„
cz xz c
Rxy R
yz ## # # È
x y z R x x 2x R 4x R x . Thus the points are: ,
#### ## ## ##
####
œ Ê œ Ê œ Êœ„ ßß
RRR
2R
Š‹
È
, , , , ,
Š‹Š ‹Š ‹Š‹Š ‹
RR RR RR RR RR
2R 2R 2R 2R 2R
## # # ## # # # # ## # # #
ß ß ß ß ß ß ß ß ß ß
ÈÈ ÈÈÈ
,
Š‹Š ‹
ßß ßß
RR RR
2R 2R
## # ## #
ÈÈ
7. Set up the coordinate system so that (a b c) (0 R 0) (x y z) x (y R) zßß œ ß ß Ê ßß œ $È###
x y z 2Ry R 2R 2Ry ; let f(x y z) x y z R and œœ ßßœ œ
ÈÈ
### # # ### # pi
f 2x 2y 2z f 2 x y z 2R d dz dy dz dyÊ œ Ê œ œ Ê œ œ™™ijkkkÈ### 5kk
kk
™
™†
f
f2x
2R
i
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1054 Chapter 16 Integration in Vector Fields
Mass (x y z) d 2R 2Ry dz dy R dz dyÊœ ßßœ œ
'' '' ''
SRR
$5
yz yz
Ȉ‰
#
R
x
2R 2Ry
Ryz
È
È
4R dz dy 4R 2R 2Ry sin dyœœ
'' '
R0 R
RRy R
0
Ry
È
ÈÈ
2R 2Ry
Ryz
21z
Ry
ÉŠ‹
»
22
2 R 2R 2Ry dy 2 R 2R 2Ryœœœ11
'R
R3/2
R
R
É»
2116R
3R 3
2
ˆ‰
ab
1
8. (r ) (r cos ) (r sin ) , 0 r 1, 0 2 cos sin 0
r sin r cos
rijk rr
ijk
ßœ ŸŸ ŸŸ Ê ‚œ
"
)))) )1 ))
))
r)
ââ
ââ
ââ
ââ
ââ
ââ
(sin ) (cos ) r 1 r ; 2 x y 2 r cos r sin 2rœ Ê‚œœœ œ)) $ ) )ijkrrkk
ÈÈ
È
r)#######
Mass (x y z) d 2r 1 r dr d 1 r d 2 2 1 dÊœ ßßœ œ œ
''
S
$5 ) ) )
'' ' '
00 0 0
21 2 2
ÈÈ
’“ Š‹
ab
##$Î# "
!
22
33
22 1œ
4
3
1Š‹
È
9. M x 4xy and N 6y 2x 4y and 6 Flux (2x 4y 6) dx dyœ œ Ê œ œÊ œ
#``
``
MN
xx ''
00
ba
a 4ay 6a dy a b 2ab 6ab. We want to minimize f(a b) a b 2ab 6ab ab(a 2b 6).œ œ ßœœ
'0
bab
### ##
Thus, f (a b) 2ab 2b 6b 0 and f (a b) a 4ab 6a 0 b(2a 2b 6) 0 b 0 or
ab
ßœ œ ßœ œÊ œÊœ
##
b a 3. Now b 0 a 6a 0 a 0 or a 6 (0 0) and (6 0) are critical points. On the otherœ œ Ê œ Ê œ œ Ê ß ß
#
hand, b a 3 a 4a( a 3) 6a 0 3a 6a 0 a 0 or a 2 (0 3) and ( ) are alsoœÊ œÊ œÊœ œÊß #ß"
##
critical points. The flux at (0 0) 0, the flux at (6 0) 0, the flux at (0 3) 0 and the flux at (2 1) 4.ߜ ߜ ߜ ߜ
Therefore, the flux is minimized at (2 1) with value 4.ß
10. A plane through the origin has equation ax by cz 0. Consider first the case when c 0. Assume the plane is givenœ Á
by z ax by and let f(x y z) x y z 4. Let C denote the circle of intersection of the plane with the sphere.œ ßßœœ
###
By Stokes's Theorem, d d , where is a unit normal to the plane. Let
S
)''
CFr Fn n†™†œ‚5
(x y) x y (ax by) be a parametrization of the surface. Then a b
0a
0b
rij k rr ijk
ijk
ßœ ‚œ œ
"
"
xy
ââ
ââ
ââ
ââ
ââ
ââ
d dx dy a b 1 dx dy. Also, and
zxy
Ê œ ‚ œ ‚ œ œ œ5kk Èââ
ââ
ââ
ââ
ââ
ââ
rr F ijk n
ijk
xy xyz
ab
ab1
## ```
```
™ijk
È
d a b 1 dx dy (a b 1) dx dy (a b 1) dx dy. NowÊ‚œ œœ
'' '' '' ''
SRRR
™†Fn5
xy xy xy
ab1
ab1
##
ÈÈ
x y (ax by) 4 x y xy 1 the region R is the interior of the
## # # #
#
œÊ œÊ
Š‹Š‹ˆ‰
a1 b1 ab
44 xy
ellipse Ax Bxy Cy 1 in the xy-plane, where A , B , and C . By Exercise 47 in
##
#
œ œ œ œ
a1 ab b1
44
Section 10.3, the area of the ellipse is d h(a b) .
24
4AC B ab1 ab1
4(a b 1)
11 1
ÈÈ È
œÊœßœ
)CFr†
Thus we optimize H(a b) : 0 andßœ œ œ
(a b 1)
ab1 a
H2(a b 1) b 1 a ab
ab1
`
`
ab
ab
2
0 a b 1 0, or b 1 a ab 0 and a 1 b ab 0
`
`
##
H
b
2(a b 1) a 1 b ab
ab1
œ œ Ê œ œ œ
ab
ab
2
a b 1 0, or a b (b a) 0 a b 1 0, or (a b)(a b 1) 0 a b 1 0 or a b.Êœ œÊœ œ Êœ œ
##
The critical values a b 1 0 give a saddle. If a b, then 0 b 1 a ab a 1 a a 0 œ œ œ Ê œ
###
a 1 b 1. Thus, the point (a b) ( 1 1) gives a local extremum for d z x yÊ œ Ê œ ß œ ß Ê œ
)CFr†
x y z 0 is the desired plane, if c 0.Ê œ Á
: Since h( 1 1) is negative, the circulation about is , so is the correct pointing normal forNote clockwiseß nn
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
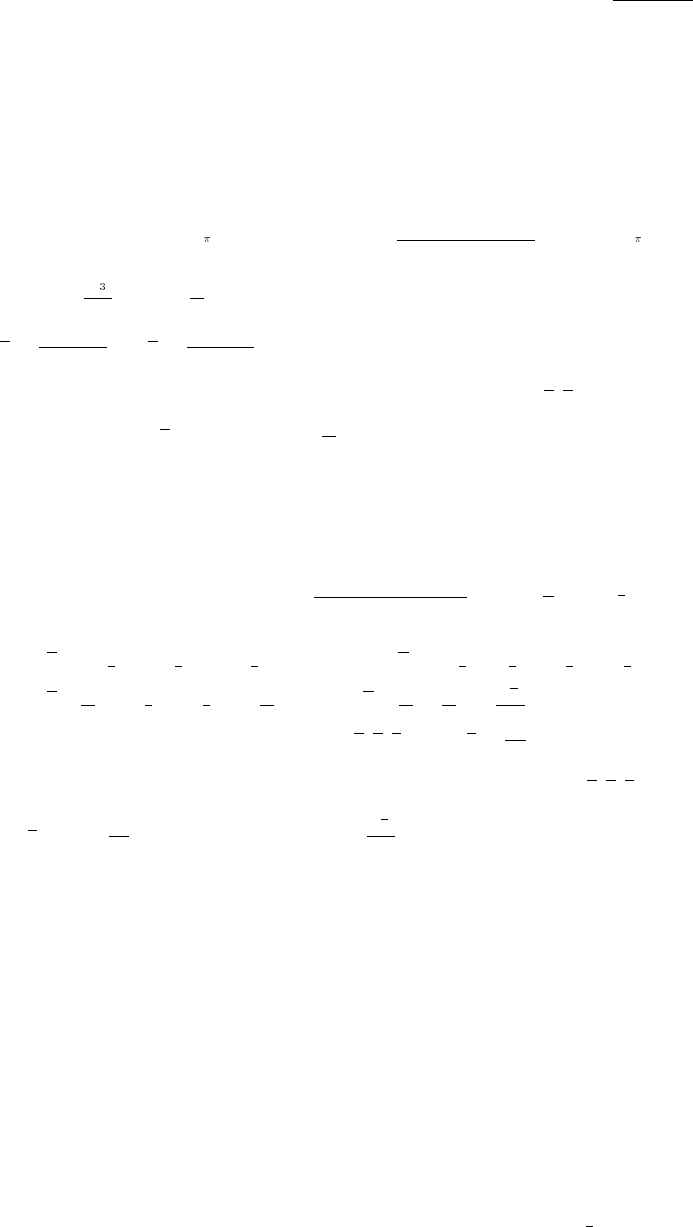
Chapter 16 Additional and Advanced Exercises 1055
the counterclockwise circulation. Thus ( ) d actually gives the circulation.
''
S
™†‚Fn5maximum
If c 0, one can see that the corresponding problem is equivalent to the calculation above when b 0, which does notœ œ
lead to a local extreme.
11. (a) Partition the string into small pieces. Let s be the length of the i piece. Let (x y ) be a point in the?iii
th ß
i piece. The work done by gravity in moving the i piece to the x-axis is approximately
th th
W (gx y s)y where x y s is approximately the mass of the i piece. The total work done by
i iii i iii th
œ??
gravity in moving the string to the x-axis is W gx y s Work gxy dsDD?
ii
iii
iC
œÊœ
##
'
(b) Work gxy ds g(2 cos t) 4 sin t 4 sin t 4 cos t dt 16g cos t sin t dtœœ œ
'' '
C0 0
/2 /2
## #
##
ab
È
16g gœœ
’“Š‹
sin t 16
33
1Î#
!
(c) x and y ; the mass of the string is xy ds and the weight of the string isœœ
''
''
CC
CC
x(xy) ds y(xy) ds
xy ds xy ds 'C
g xy ds. Therefore, the work done in moving the point mass at x y to the x-axis is
'Cabß
W g xy ds y g xy ds g.œœœ
Š‹
''
CC
#16
3
12. (a) Partition the sheet into small pieces. Let be the area of the i piece and select a point (x y z ) in?5
iiii
th ßß
the i piece. The mass of the i piece is approximately x y . The work done by gravity in moving the
th th ii i
?5
i piece to the xy-plane is approximately (gx y )z gx y z Work gxyz d .
th ii i i iii i
?5 ?5 5œÊœ
''
S
(b) gxyz d g xy(1 x y) 1 ( 1) ( 1) dA 3g xy x y xy dy dx
'' ''
SR
5œœ
xy
00
11x
ÈÈab
## ##
''
3g xy x y xy dx 3g x x x x dxœ œ
ÈÈ
‘ ‘
''
00
11
x
" " " """"
### $ #$%
###
"
!
23 6 6
3gxxx x 3gœ œ œ
ÈÈ
‘ˆ‰
"""" ""
#$% &
"
!#126630 13020
3g
È
(c) The center of mass of the sheet is the point x y z where z with M xyz d andabßß œ œ
M
M
xy
xy ''
S
5
M xy d . The work done by gravity in moving the point mass at x y z to the xy-plane isœßß
''
S
5ab
gMz gM gM gxyz d .œœœ œ
Š‹
M
M20
3g
xy
xy ''
S
5È
13. (a) Partition the sphere x y (z 2) 1 into small pieces. Let be the surface area of the i piece
## #
œ ?5
ith
and let (x y z ) be a point on the i piece. The force due to pressure on the i piece is approximately
iii th th
ßß
w(4 z ) . The total force on S is approximately w(4 z ) . This gives the actual force to be
ii ii
?5 D ?5
i
w(4 z) d .
''
S
5
(b) The upward buoyant force is a result of the -component of the force on the ball due to liquid pressure.k
The force on the ball at (x y z) is w(4 z)( ) w(z 4) , where is the outer unit normal at (x y z).ßß œ ßßnnn
Hence the -component of this force is w(z 4) w(z 4) . The (magnitude of the) buoyant forceknkknœ††
on the ball is obtained by adding up all these -components to obtain w(z 4) d .kkn
''
S
†5
(c) The Divergence Theorem says w(z 4) d div(w(z 4) ) dV w dV, where D
'' ''' '''
SDD
œ œkn k†5
is x y (z 2) 1 w(z 4) d w 1 dV w, the weight of the fluid if it
## #
ŸÊ œ œ
'' '''
SD
kn†51
4
3
were to occupy the region D.
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley

1056 Chapter 16 Integration in Vector Fields
14. The surface S is z x y from z 1 to z 2. Partition S into small pieces and let be the area of theœ œ œ
È## ?5
i
i piece. Let (x y z ) be a point on the i piece. Then the magnitude of the force on the i piece due to
th th th
iii
ßß
liquid pressure is approximately F w(2 z ) the total force on S is approximately
iii
œ Ê?5
F w(2 z ) the actual force is w(2 z) d w 2 x y 1 dADD ?5 5
iSR
iii
xy
œ Ê œ
'' '' ˆ‰
ÈÉ
##
x
xy xy
y
2 w 2 x y dA 2w(2 r) r dr d 2w r r d dœœ œœ
''
Rxy
01 0 0
22 2 2
ÈÈÈ
ˆ‰ ‘
È## #$
"#
"
'' ' '
)))
33
22w
È
œ42w
3
È1
15. Assume that S is a surface to which Stokes's Theorem applies. Then d ( ) d
)CEr En†™†œ‚
''
S
5
d d . Thus the voltage around a loop equals the negative of the rateœ œ
'' ''
SS
``
``
B
tt
††nBn55
of change of magnetic flux through the loop.
16. According to Gauss's Law, d 4 GmM for any surface enclosing the origin. But if
''
S
Fn F H†™51œœ‚
then the integral over such a closed surface would have to be 0 by the Divergence Theorem since div 0.Fœ
17. f g d (f g) d (Stokes's Theorem)
)C™† ™ ™ †rnœ‚
''
S
5
(f g f g) d (Section 16.8, Exercise 19b)œ‚‚
''
S
™™ ™ ™†n5
[(f)( ) f g] d (Section 16.7, Equation 8)œ‚
''
S
0n™™†5
( f g) dœ‚
''
S
™™†n5
18. ( ) is conservative f; also, ™ ™ ™ ™ ™† ™†‚œ ‚Ê ‚ œÊ Êœ œFF FF0FF FF FF
" # #" #" #" " #
( ) 0 f 0 (so f is harmonic). Finally, on the surface S, f ( )ʜʜ œ™† ™ ™ † †FF nFFn
#" #"
#
0. Now, (f f) f f f f so the Divergence Theorem givesœœ œ FnFn
#" #
† † ™† ™ ™ †™ ™
f dV f f dV (f f) dV f f d 0, and since f 0 we have
''' ''' ''' ''
DDD S
kk™™™†™™† ™
## #
œ œœ œn5
f dV 0 0 dV 0 , as claimed.
''' '''
DD
kk k k™##
#" #" # "
œ Ê œ Ê œ Ê œ FF FF 0 F F
19. False; let y x (y) (x) 0 and 0 0 0
xy0
Fij0 F F ijk0
ijk
œÁÊ œ œ ‚œ œ œ™† ™
``
``
```
```
xy xyz
ââ
ââ
ââ
ââ
ââ
ââ
20. sin 1 cos cos ( )k k kkkk kkkka b kkkk kkkk kkkkrr rr rr rr rr rr rr
uv uv uv uv uv uv uv
‚œ œ œ œ
### ## #### ##
## # #
)) )†
EG F d du dv EG F du dvÊ‚ œ Êœ‚ œ kk kk
ÈÈ
rr rr
uv uv
###
5
21. x y z 1 1 1 3 dV 3 dV 3V V dVrijk r r rœ Ê œœÊ œ œ Ê œ™† ™† ™†
''' ''' '''
DD D
"
3
d , by the Divergence Theoremœ"
3''
S
rn†5
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley
Chapter 16 Additional and Advanced Exercises 1057
NOTES:
Copyright (c) 2006 Pearson Education, Inc., publishing as Pearson Addison-Wesley