VARIFORC User Manual: Chapter 8 (FORC Tutorial) Manual Chapter08 Tutorial
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 45

VARIFORC User Manual: 8. FORC tutorial 8.1
VARIFORC User Manual
Chapter 8:
FORC tutorial
M
0
M
1
M
2
M
3
0
0
H
H
H
(M1
−
M0)′
(M2
−
M1)′
(M3
−
M2)′
µ0Hc
µ0Hb
1,1
2,1
2,2
3,1
3,2
3,3
1,1
1,1
2,1
2,1
3,1
2,2
2,2
3,2
3,3

VARIFORC User Manual: 8. FORC tutorial 8.2
© 2014 by Ramon Egli and Michael Winklhofer. Provided for non-commercial research
and educaonal use only.

VARIFORC User Manual: 8. FORC tutorial 8.3
This chapter is based on contribuons by Ramon Egli and Michael Winklhofer to the Inter-
naonal Workshop on Paleomagnesm and Rock Magnesm (Kazan Instute of Geology and
Petroleum Technology, Russia, October 7-12, 2013), summarized in the following conference
proceeding arcle:
Recent developments on processing and interpretaon aspects of
first-order reversal curves (FORC)
Ramon Egli
Central Instute for Meteorology and Geodynamics, Hohe Warte 38, 1190 Vienna, Austria
(r.egli@zamg.ac.at)
Michael Winklhofer
Department for Earth and Environmental Sciences, Munich University, Theresienstrasse 41,
80333 Munich, Germany (michael@geophysik.uni-muenchen.de)
Abstract Several recent developments in paleo- and environmental magnesm have been based on
measurement of first-order reversal curves (FORC). Most notable examples are related to the detec-
on of fossil magnetosomes produced by magnetotacc bacteria and to absolute paleointensity es-
mates for temperature-sensive samples, such as meteorites. Future developments in these scienfic
disciplines rely on improved characterizaon of natural magnec mineral assemblages. Promising
results have been obtained in several cases with the parallel development of FORC processing proto-
cols on one hand, and models for idealized magnec systems on the others. Unl now, FORC diagrams
have been used mainly as a qualitave tool for the idenficaon of magnec domain state fingerprints,
with missing quantave links to other magnec parameters. This arcle bridges FORC measurements
and convenonal hysteresis parameters on the basis of three types of FORC-related magnezaons
and corresponding coercivity distribuons. One of them is the well-known saturaon remanence, with
corresponding coercivity distribuon derived from backfield demagnezaon data in zero-field FORC
measurements. The other two magnezaon types are related to irreversible processes occurring
along hysteresis branches and to the inversion symmetry of magnec states in isolated parcles, res-
pecvely. All together, these magnezaons provide precise informaon about magnezaon proces-
ses in single-domain, pseudo-single-domain, and muldomain parcles. Unlike hysteresis parameters
used in the so-called Day diagram, these magnezaons are unaffected by reversible processes (e.g.
superparamagnesm), and therefore well suited for reliable characterizaon of remanent magneza-
on carriers. The soware package VARIFORC has been developed with the purpose of performing
detailed FORC analyses and calculate the three types of coercivity distribuons described above. Key
examples of such analyses are presented in this arcle, and are available for download along with the
VARIFORC package.

VARIFORC User Manual: 8. FORC tutorial 8.4

VARIFORC User Manual: 8. FORC tutorial 8.5
8.1 Introducon
Several measurement protocols have been developed over the last 50 years for under-
standing complex magnezaon processes related to technological applicaons [Chikazumi,
1997; Coey, 2009], the origin and stability of rock magnezaons [Dunlop and Özdemir, 1997;
Tauxe, 2010], and environment-sensive magnec minerals in sediments [Evans and Heller,
2003; Liu et al., 2012]. First-order reversal curves (FORC) provide one of the most advanced
protocols for probing hysteresis processes and represent them in a two-dimensional parame-
ter space (i.e. coercivity field c
H and bias field b
H). The interpretaon of hysteresis has evol-
ved from mathemacal formalisms based on the superposion of elemental source contribu-
ons, called hysterons [Preisach, 1935; Mayergoyz, 1986; Hejda and Zelinka, 1990; Fabian and
Dobeneck, 1997], toward physical models of specific magnec systems, such as non-interac-
ng [Newell, 2005; Egli et al., 2010] and interacng [Woodward and Della Torre, 1960; Basso
and Berto, 1994; Pike et al., 1999; Muxworthy and Williams, 2005; Egli, 2006a] single-do-
main (SD) parcles, pseudo-single-domain (PSD) parcles [Muxworthy and Dunlop, 2002; Car-
vallo et al., 2003; Winklhofer et al., 2008], muldomain (MD) crystals [Pike et al., 2001b;
Church et al., 2011], and spin glasses [Katzgraber et al., 2002]. These models provide proto-
type signatures for specific magnezaon processes (e.g. switching, vortex nucleaon, do-
main wall pinning), which can be recognized in FORC diagrams of geologic samples [Roberts
et al., 2000, 2006]. Some of these signatures occur within a limited subset of FORC space, as
for instance along c0H» (viscosity and MD processes) or along b0H» (weakly interacng
SD parcles). Therefore, it is possible to idenfy the corresponding sources in FORC diagrams
of samples containing complex magnec mineral mixtures [e.g. Roberts et al., 2012], and, in
some cases, to esmate the abundance of magnec parcles associated with these processes
[Roberts et al., 2011; Yamazaki and Ikehara, 2012; Egli, 2013; Ludwig et al., 2013]. Up to the
few examples menoned above, FORC diagrams of geologic materials are mostly interpreted
in a qualitave manner. Furthermore, only loose connecons have been established with mo-
re common magnec parameters, such as isothermal and anhysterec remanent magneza-
ons and domain state-sensive raos, although some of these parameters can be directly
derived from FORC subsets [e.g. Fabian and Dobeneck, 1997; Winklhofer and Zimanyi, 2006;
Egli et al., 2010].
Quantave interpretaon of FORC measurements is based on the calculaon of magnec
parameters associated with specific magnezaon processes. Some of these processes pro-
duce FORC signatures that are representable only in terms of non-regular funcons, whose
appearance in the FORC diagram depends strongly on data processing. A meanwhile well-
known example of non-regular FORC signatures is represented by the so-called central ridge
produced by non-interacng SD parcles [Egli et al., 2010; Egli, 2013]. Magnec viscosity is
another example associated with a vercal ridge near c0H= [Pike et al., 2001a]. On the other
hand, most magnec processes in weakly magnec natural samples produce connuous FORC

VARIFORC User Manual: 8. FORC tutorial 8.6
contribuons with very low amplitudes, which are below the significance threshold aainable
with convenonal FORC processing [Egli, 2013]. Since the introducon of FORC measurements
to rock magnesm [Pike et al., 1999; Roberts et al., 2000], some studies have been dedicated
to selected aspects of FORC processing, such as computaonal opmizaon [Heslop and Mux-
worthy, 2005], locally weighted regression [Harrison and Feinberg, 2008], error calculaon
[Heslop and Roberts, 2012], and variable polynomial regression smoothing [Egli, 2013]. These
improvements have been merged into a single FORC processing procedure called VARIFORC
(VARIable FORC smoothing) [Egli, 2013]. The principal advantage of VARIFORC consists in the
possibility of processing FORC data containing high-amplitude, non-regular FORC signatures
as well as low-amplitude, connuous backgrounds, using a local compromise between high
resoluon and noise suppression requirements. First applicaons of this technique enabled
full characterizaon of SD signatures in pelagic carbonates [Ludwig et al., 2013].
Meanwhile, VARIFORC has been complemented with rounes for the automac separa-
on of different FORC contribuons, and the calculaon of corresponding magnezaons and
coercivity distribuons. The full VARIFORC package, including a detailed user manual, is availa-
ble at hp://www.conrad-observatory.at/cmsjoomla/en/download. VARIFORC runs on Wol-
fram MathemacaTM and Wofram PlayerProTM (see Chapter 2). Applicaon examples of quan-
tave FORC analysis performed with VARIFORC are discussed in this paper.
VARIFORC User Manual: 8. FORC tutorial 8.7
8.2 A brief introducon to FORC diagrams
8.2.1 Reversible and irreversible hysteresis processes
Ferrimagnec materials are characterized by complex magnec properes that depend on
their past magnec and thermal history. Memory of previously applied fields gives raise to the
well-known phenomenon of magnec hysteresis. The discovery magnec hysteresis is credi-
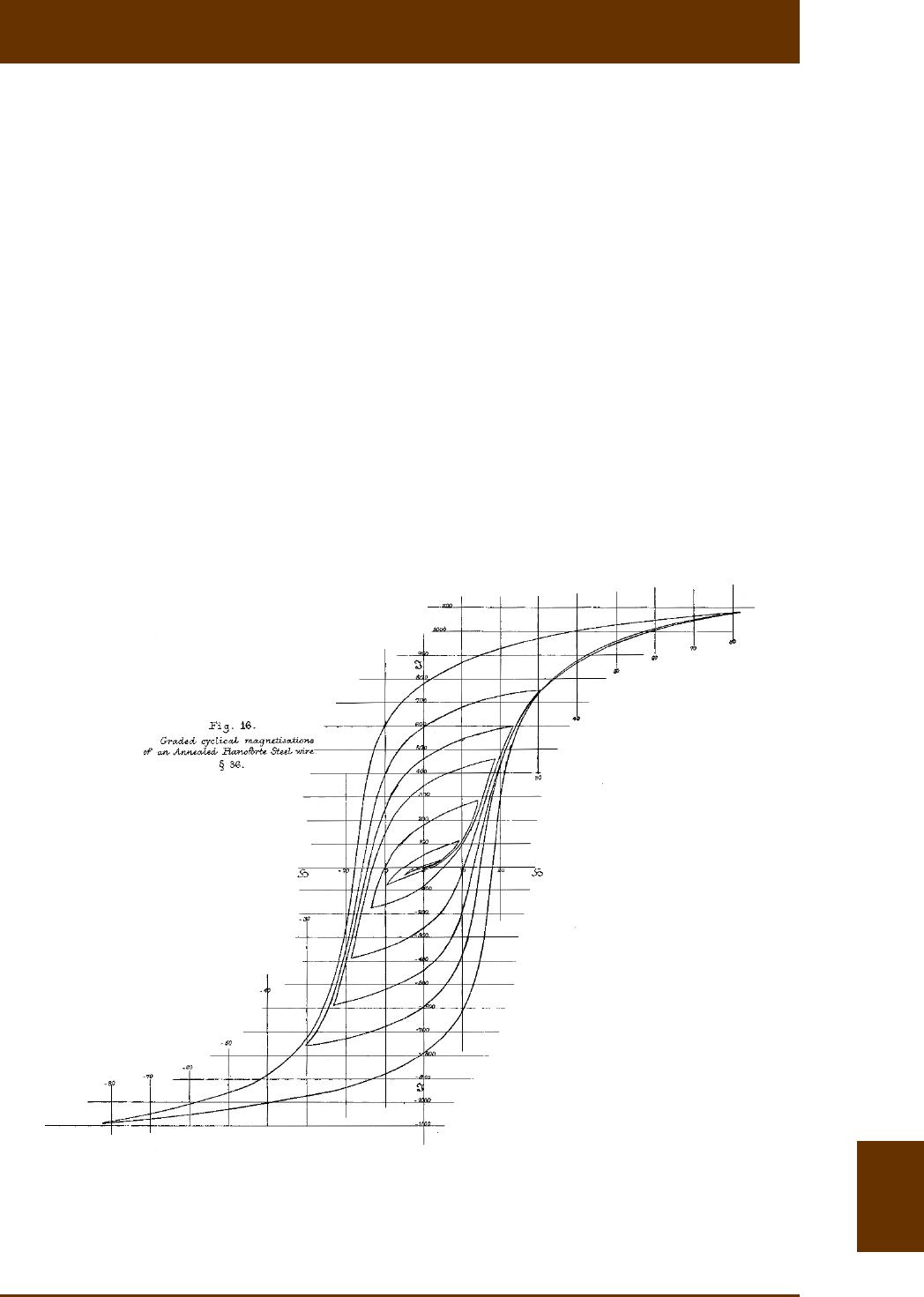
ted to Sir Alfred James Ewing (1855-1955), who measured the first hysteresis loop (Fig. 8.1)
on a piano wire [Ewing, 1885]. While the main characteriscs of a hysteresis loop are summari-
zed by four magnec parameters yielding the well-known Day diagram [Day et al., 1977;
Dunlop, 2002a,b], much more detailed informaon on magnezaon processes can be obtai-
ned by accessing the inner area of hysteresis loops. This is possible by in-field measuring pro-
tocols involving a sequence of field sweep reversals. The oldest example of such sequences is
the alternang-field (AF) demagnezaon [Chikazumi, 1997], in which the field sweep is rever-
sed at increasingly small field amplitudes, unl a demagnezed, so-called anhysterec state
0HM== is reached (Fig. 8.1).
Fig. 8.1: Original figure from Ewing [1885] showing the hysteresis measurement of a piano wire (see
the IRM Quarterly Vol. 22 for a story about Sir Alfred Ewing’s first hysteresis measurements). The
measurement shown here represents an AF demagnezaon curve, as a possible method for accessing
the inner area of hysteresis loops.

VARIFORC User Manual: 8. FORC tutorial 8.8
Other measuring protocols for accessing the inner area of a hysteresis loop are possible,
and the FORC protocol described by Pike et al. [1999] is just one of them. All protocols start
from a well-defined magnec state obtained by saturang the sample in a large field. The first
magnezaon curve obtained by sweeping the magnec field from posive or negave satu-
raon coincides with one of the two major hysteresis loop branches ()MH
. Hysteresis bran-
ches are also known as a zero-order curves, because they originate directly from a saturated
state. If the field sweep producing a zero-order curve is reversed at a reversal field r
H, before
saturaon is reached, a new magnezaon curve r
(,)MH H originates from the major hyste-
resis loop (Fig. 8.2a). This curve represents a first-order magnezaon, also known as first-
order reversal curve in case of FORC measurements. A set of first-order curves branching from
the major hysteresis loop at different reversal fields covers the enre area enclosed by the
loop, accessing a much larger number of magnezaon states that cannot be obtained with
simple hysteresis measurements. If the field sweep is reversed again while a first-order curve
is measured, a second-order curve is obtained, and so on. Within this context, AF demagne-
zaon is a sequence of nested magnezaon curves with increasing order.
When describing magnezaon curves, an important disncon is made between mag-
nezaon changes due to reversible and irreversible processes. The two types of processes
occurring along any magnezaon curve are disnguished by comparing a small poron
A
B
MM of the curve between close fields
A
H and B
H with the magnezaon
A
M* obtained
by sweeping the field from B
H back to
A
H (Fig. 8.2a). Hysteresis, known in this context as
magnec memory, ensures that BA
MM
*
does not follow the same path as
A
B
MM , in
which case
A
A
MM
*¹ [Mayergoyz, 1986]. The difference
A
A
MM
*- is the irreversible magne-
zaon change occurring when sweeping the field from
A
H to B
H, while BA
MM
*
- is the rever-
sible change. The sum of the two contribuons gives BA
MM-, as expected.
8.2.2 Preisach diagrams
Because n-th order magnezaon curves depend on 1n+ parameters (i.e. n reversal
fields and one measuring field), interpretaon of first- and higher order curves requires a para-
meter space model. The best known bivariate hysteresis model has been implemented by
Preisach [1935] for the characterizaon of transformer steel. The Preisach model assumes that
magnezaon curves are the result of magnec switching in elemental rectangular hysteresis
loops (so-called hysterons). Hysterons are characterized by two switching fields AB
HH£ whe-
re the magnezaon jumps disconnuously from the lower to the upper branch and vice-
versa (Fig. 8.2b). Each hysteron is thus represented by a point in AB
(,)HH-space, and macro-
scopic magnec volumes or magnec parcle assemblages are described by a bivariate sta-
scal distribuon AB
(,)PH H of hysteron switching fields, known as the Preisach distribuon.
VARIFORC User Manual: 8. FORC tutorial 8.9
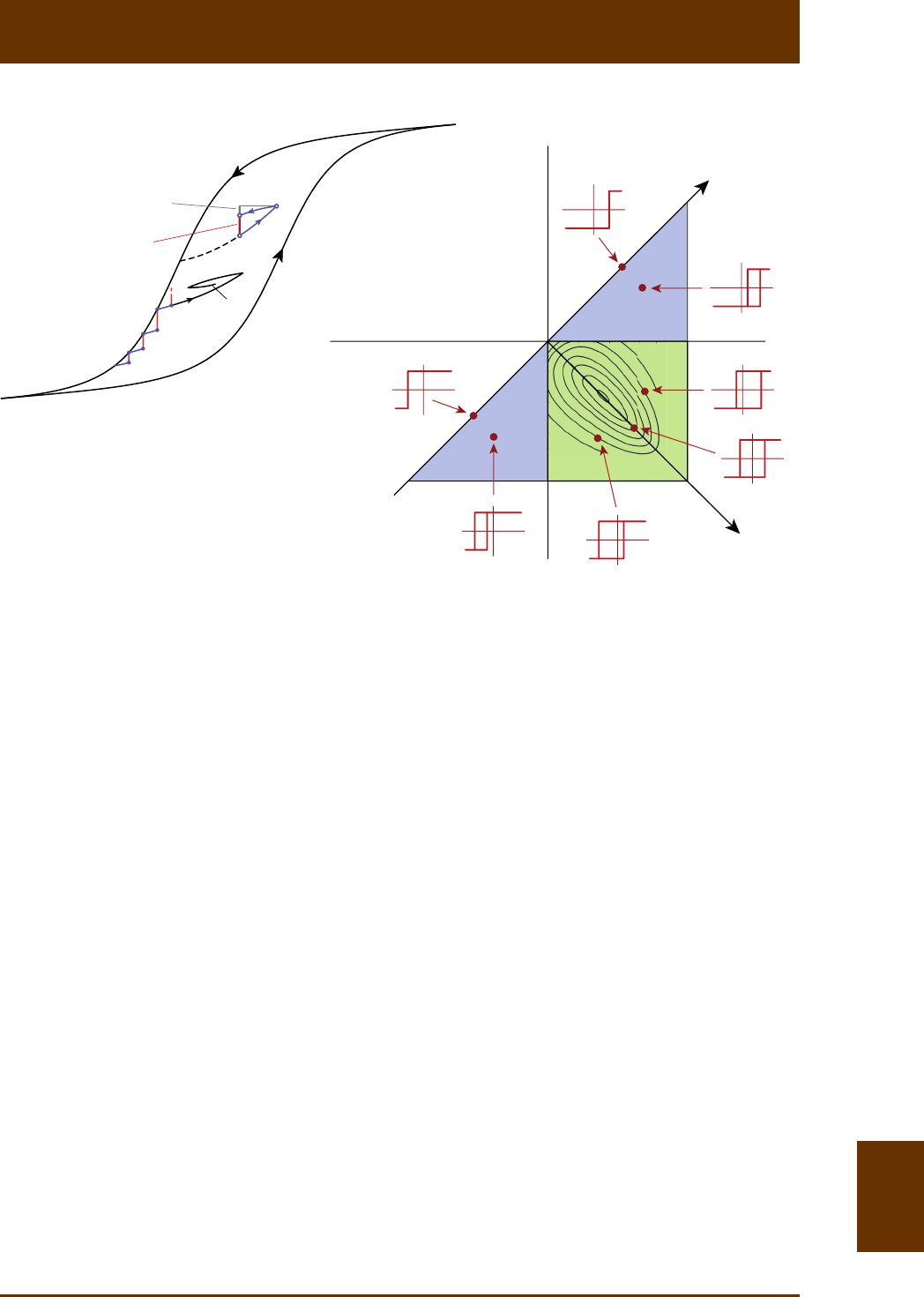
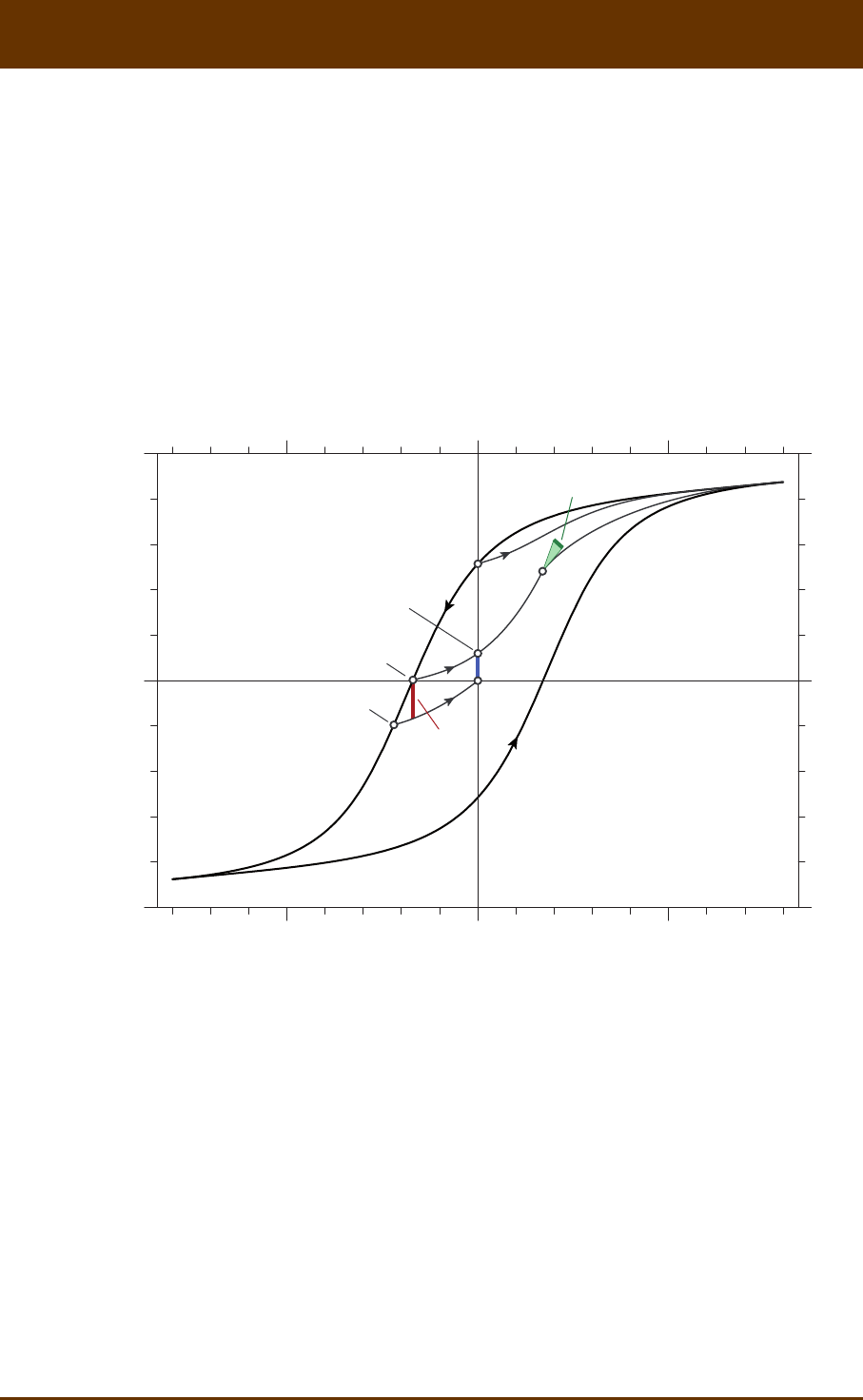
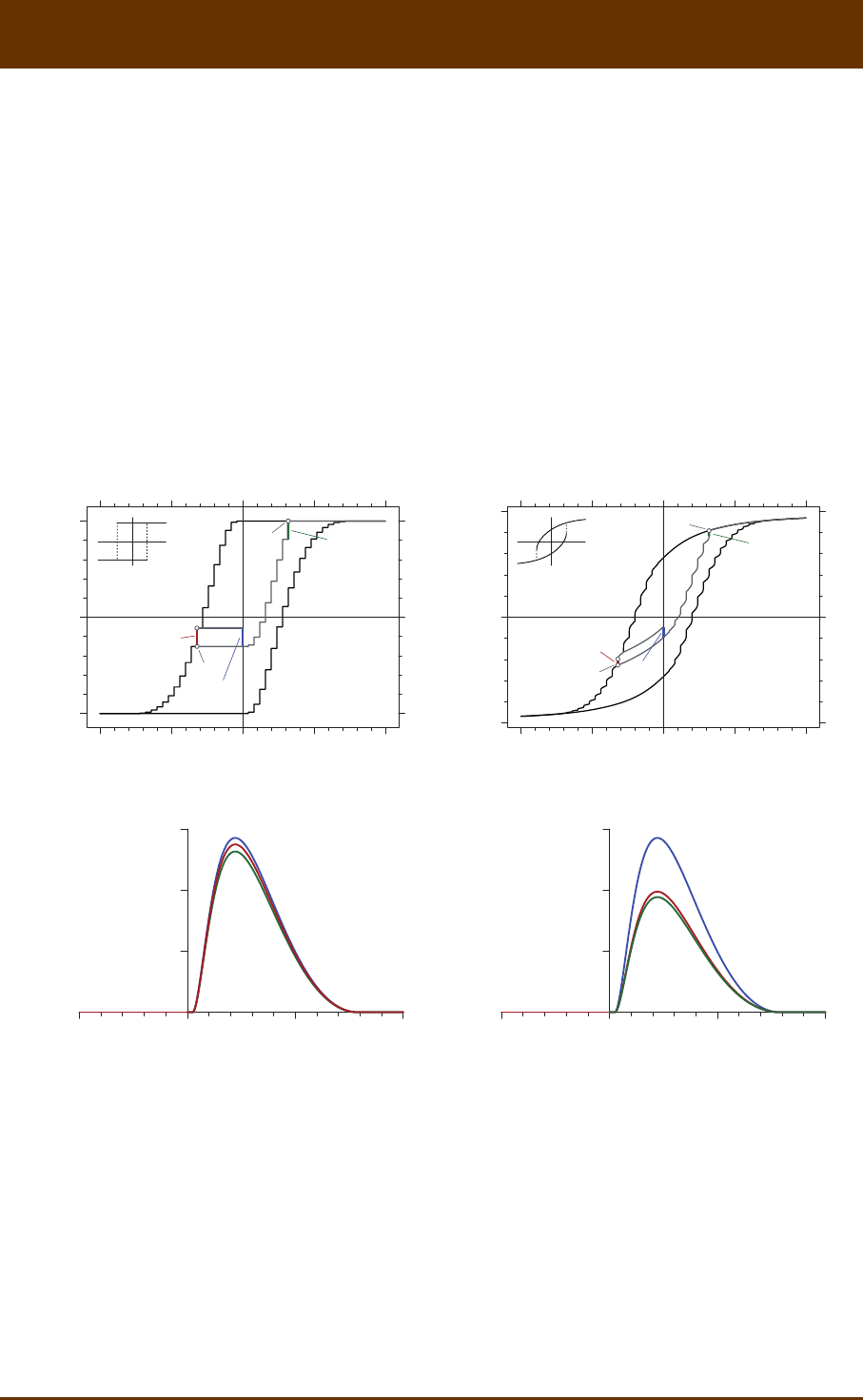
Fig. 8.2: Preisach theory in a nutshell. (a) The major hysteresis loop (black lines with large arrows) is
composed of two zero-order magnezaon curves starng from posive and negave saturaon,
respecvely. First-order magnezaon curves originate from the major hysteresis if the field sweep is
reversed (black curve labeled with 1st). Higher-order magnezaon curves (curves labeled with 2nd and
3rd) are obtained aer successive field sweep reversals. Any point inside the major hysteresis loop can
be accessed by first-order magnezaon curves (dashed black line). For any of these points (e.g. point
A at the end of the dashed line), magnezaon changes can be decomposed into a reversible ( rev
ΔM)
and an irreversible ( irr
ΔM) component by sweeping the field a lile further to point B and then back
to the original field, ending with point A*, which, because of irr
ΔM, does not coincide with A. The
inial parts of first-order curves originang from the upper hysteresis branch (blue segments) define
the irreversible component (red bars) of magnezaon changes along this branch. (b) The Preisach
diagram is a representaon of hysteresis processes as the sum of elemental contribuons from rectan-
gular hysteresis loops (hysterons, sketched in red) with switching fields A
H and B
H. Because BA
HH³
by definion, hysteron coordinates AB
(,)HH plot below the AB
HH= diagonal, over a triangular area
(colored) limited by the saturaon field sat
H above which magnec hysteresis is fully reversible.
Further disncons can be made between (1) closed hysterons with AB
HH=, (2) hysterons with only
one possible state in zero field (posive or negave saturaon, blue areas), and (3) hysterons with two
possible states in zero field (so-called magnec remanence carriers, green square). The Preisach space
can also be expressed in transformed coordinates represenng coercivity (i.e. hysteron opening
cBA
()/2HHH=- ) and the bias field (i.e. hysteron horizontal shis b
H= BA
()/2HH+). Hysteron
examples (red) are given for selected points of the Preisach space, which can be understood as samples
of the Preisach distribuon. Contour lines over the region occupied by remanence-carrying hysterons
(green) represent a Preisach distribuon obtained for interacng SD parcles by Dunlop et al. [1990].
In the Preisach-Néel model, c
H- and b
H-coordinates coincide with coercivies and interacon fields
of real SD parcles, respecvely.
1
st
2
nd
3
rd
A
B
A*
A
BA*
∆M
irr
∆M
rev
H
b
H
c
H
A
H
B
(a) (b)
−H
sat
H
sat

VARIFORC User Manual: 8. FORC tutorial 8.10
Hysterons are merely a mathemacal construct and do generally not correspond to dis-
crete parcles or sample volumes. Nevertheless, the bivariate Preisach distribuon provides
intrinsically more informaon than any one-dimensional magnezaon curve. The simplest
physical interpretaon of a Preisach distribuon has been proposed by Néel [1958] with what
is known as the Preisach-Néel model of single-domain (SD) parcles. This model relies on the
resemblance between hysteresis loops of individual SD parcles with uniaxial anisotropy [Sto-
ner and Wohlfarth, 1948] on one hand, and symmetric Preisach hysterons (i.e. AB
HH=- ) on
the other hand. Both are characterized by only two magnezaon states (one for each hyste-
resis branch) with disconnuous transions at Ac
HH=- and Bc
HH=+ . The Preisach distri-
buon of isolated SD parcles is thus concentrated along the AB
HH=- diagonal of the Prei-
sach space and coincides with the well-known coercivity or switching field distribuon.
In interacng SD parcle assemblages, magnec switching of individual parcles occur in
a total field given by the sum of the applied field and an internal, so-called interacon field
b
H, which is the sum of dipole fields produced by the magnec moments of the other par-
cles. Whenever b0H¹, elemental hysteresis loops are shied horizontally, so that magnec
switching occurs at Abc
HHH=- and B
H
=
bc
HH+. Because the interacon field is a local
variable determined by the spaal arrangement and magnezaon of neighbor parcles, the
Preisach distribuon of interacng SD parcles can be represented as the product of a coer-
civity distribuon c
()
f
H and an interacon field distribuon b
()gH :
cb
()()PfHgH= (8.1)
with cBA
()/2HHH=- and bBA
()/2HHH=+ (Fig. 8.2b). More generally, c
H and b
H are
known as the coercivity field and the bias field of hysterons. The appealing simplicity of the
Preisach-Néel model has promoted the use of the transformed coordinates cb
(,)HH (whereby
b
H is also called u
H or i
H), instead of the original Preisach fields A
H and B
H.
The Preisach space spanned by hysteresis processes that are saturated in fields sat
||HH<
is a triangular region delimited by the diagonal line BA
HH³ (by definion of hysteron swit-
ching fields), and by Asat
HH>- , Bsat
HH<+ , respecvely (Fig. 8.2b). This space can be further
subdivided into a square region with A0H< and B0H> where hysterons can have two mag-
nezaon states in zero field, and the remaining space where hysterons are negavely or posi-
vely saturated when no external fields are applied. The square region is parcularly relevant
to paleo- and rock magnesm, because remanent magnezaons originate only from hyste-
rons located within it. In parcular, the saturaon remanent magnezaon rs
M corresponds
to the integral of the Preisach funcon over this region, i.e.
sat
AsatB
0
rs A B A B
0(,)dd
H
HHH
MPHHHH
+
=- =
=òò (8.2)
On the other hand, the saturaon magnezaon s
M corresponds to the integral of the
Preisach funcon over the enre domain defined by BA
HH³.

VARIFORC User Manual: 8. FORC tutorial 8.11
8.2.3 The FORC distribuon
Several measurement protocols have been developed in order to obtain experimental
Preisach funcon esmates. What is nowadays known as the FORC protocol has been first
described by Hejda and Zelinka [1990]. With this protocol, first-order magnezaon curves
r
(,)MH H , measured upon posive sweeps of H (i.e. H increases) from reversal fields r
H, de-
fine the so-called FORC funcon
2
r
r
1
(,) 2
M
ρH H HH
=-
(8.3)
[Pike, 2003]. This funcon coincides with the Preisach distribuon in case of measurements
performed on samples that are correctly described by the Preisach model. Because real sam-
ples rarely sasfy this condion, empirical distribuons such as eq. (3) do generally not coin-
cide with the Preisach distribuon up to few excepons [e.g. Carvallo et al., 2005]. For exam-
ple, the Preisach distribuon is a strictly posive probability funcon, while FORC diagrams
can have negave amplitudes [Newell, 2005]. Several modificaons of the original Preisach
model have been developed in order to account for such differences. So-called moving Prei-
sach models [Vajda and Della Torre, 1991] take the effect of macroscopic magnezaon states
on the intrinsic hysteron properes into account, and are used for instance to describe mag-
nezaon-dependent interacon fields. Magnec viscosity, on the other hand, is accounted
by Preisach models with stochasc inputs simulang thermal fluctuaons of switching fields
[Mitchler et al., 1996; Borcia et al., 2002].
Modificaons of the Preisach formalism are not sufficient to explain all aspects of FORC
funcons, especially in case of non-SD magnec systems. Therefore, physical FORC models
have been developed in order to properly interpret magnec processes in isolated [Newell,
2005] and interacng [Muxworthy and Williams, 2005; Egli, 2006] SD parcles, nucleaon of
magnec vorces in PSD parcles [Carvallo et al., 2003; Winklhofer et al., 2008], domain wall
displacement in MD crystals [Pike et al., 2001b; Church et al., 2011], and magnec viscosity
[Pike et al., 2001a]. Magnec models of idealized systems yield characterisc signatures of the
FORC funcon that can be used as fingerprints for the idenficaon of magnec minerals in
geologic samples [Roberts et al., 2000]. In some cases, these signatures are precisely determi-
ned to the point that quantave analysis is possible [Winklhofer and Zimanyi, 2006; Egli et
al., 2010; Ludwig et al., 2013].
The remaining part of this secon is dedicated to the implementaon of a general FORC
model that will be used to interpret the properes of SD, PSD, and MD samples presented in
this arcle. For this purpose, a relavely simple magnec system with few magnezaon sta-
tes is considered. This system corresponds to the micromagnec hysteresis simulaon of a
cluster of seven strongly interacng SD parcles (Fig. 8.3). The upper branch of the major hys-
teresis loop contains three magnezaon jumps produced by abrupt transions between four
VARIFORC User Manual: 8. FORC tutorial 8.12
magnec states with magnezaons 0
M, 1
M, 2
M, and 3
M. These states represent con-
nuous segments of the upper hysteresis branch.
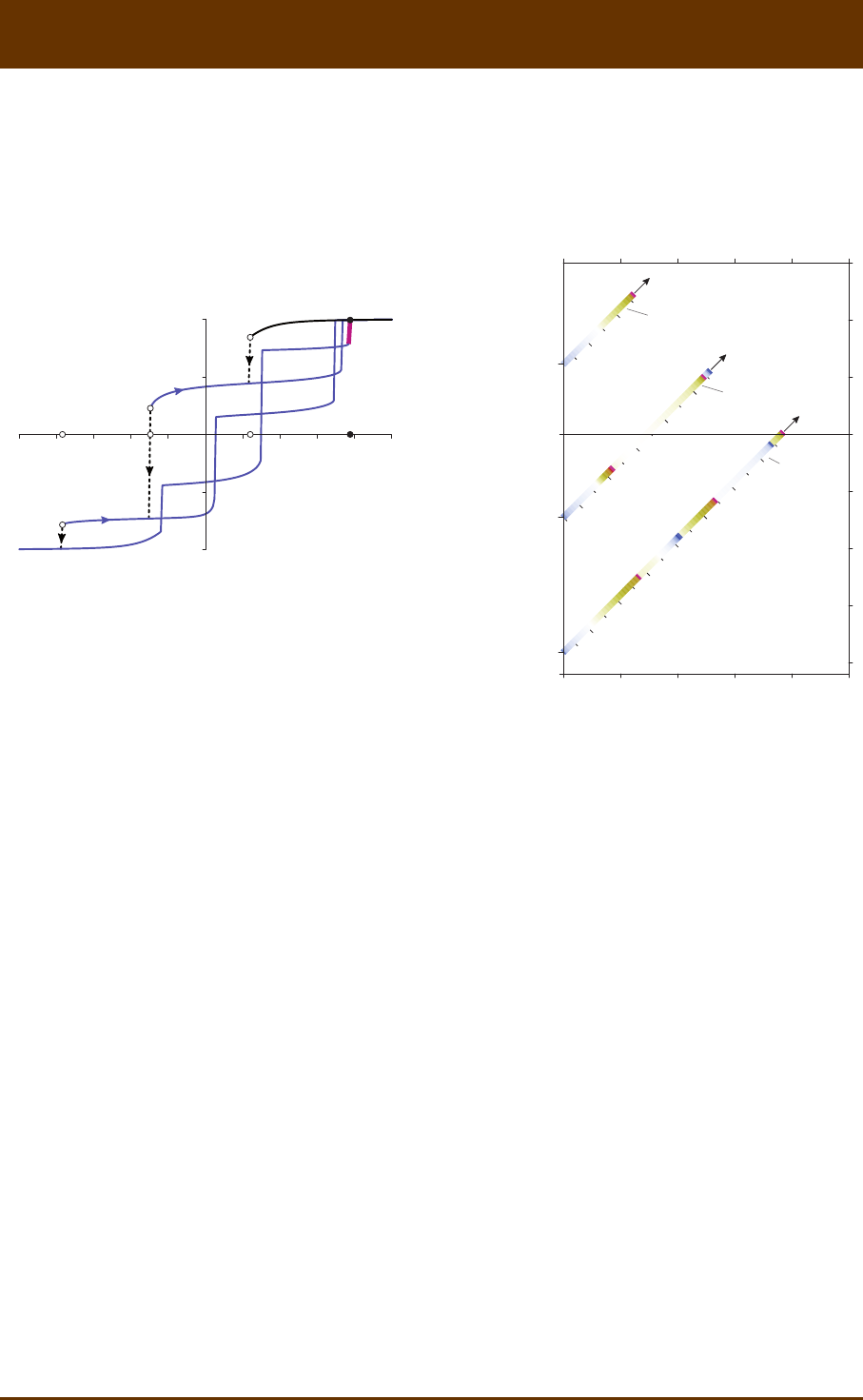
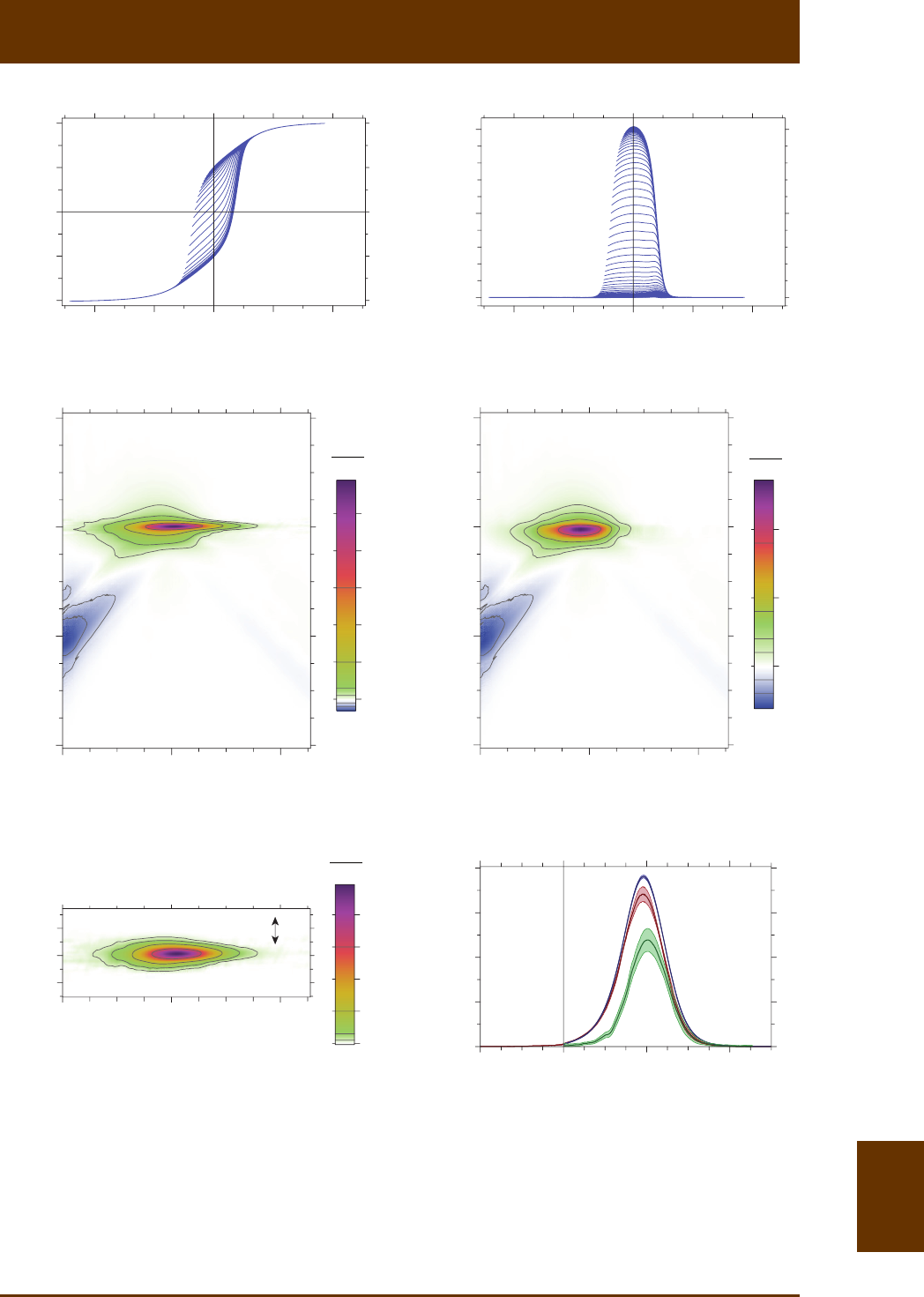
Fig. 8.3: FORC model of a linear chain of 7 SD magnete parcles with elongaon 1.3e= and long
axes perpendicular to the chain axis. This model represents the simulaon of a collapsed magnetosome
chain according to Fig. 9a in Shcherbakov et al. [1997]. In this example, the chain axis forms an angle
of 75° with the applied field direcon. Magnezaon jumps along the upper branch of the major
hysteresis loop are indicated by dashed lines. Cursive number pairs are used to count disconnuies
of first-order curves 1
M, 2
M, and 3
M (blue lines). For example, (2,2) is the second jump (counted from
the right) occurring along 2
M. Any measurable FORC coincide with 0
M, 1
M, 2
M, or 3
M. The amplitude
of the last magnezaon jump on 3
M (magenta) defines the contribuon cr
M of the central ridge to
the FORC diagram shown in (b). (b) FORC diagram calculated from (a), consisng of three diagonal
ridges defined by first derivaves 1
()
ii
MM
-¢
- of differences between 0
M, 1
M, 2
M, and 3
M. The
ridges width is exaggerated in order to show the color coding for posive (orange to magenta) and
negave (blue) contribuons. Cursive number pairs indicate peaks of the FORC funcon produced by
magnezaon jumps with same labels as in (a). One of the peaks, labeled with CR, contributes to the
central ridge and is generated by the last magnezaon jump (i.e. 3,1) of the last FORC (i.e. 3
M). All
FORC contribuons are enclosed in a triangular region defined by verces with coordinates sat
(0, )H
and sat
(,0)H, where sat 40 mTH» is the field above which hysteresis becomes fully reversible.
02040
+50 mT−50
M
0
M
1
M
2
M
3
H
r,1
H
r,2
H
r,3
0
0
20 30
0102030−10
20
10
0
−10
−20
−30
H
H
H
(M
1
− M
0
)′
(M
2
− M
1
)′
(M
3
− M
2
)′
µ
0Hc [mT]
µ0Hb [mT]
(a) (b)
1,1
2,1
2,2
3,1
3,2
3,3
H
r,1
H
r,2
H
r,3
1,1
1,1
2,1
2,1
3,1
2,2
2,2
3,2
3,3
−H
r,3

VARIFORC User Manual: 8. FORC tutorial 8.13
If the field sweep is reversed within the posively saturated state 0
M, the resulng first-
order magnezaon curves will always coincide with 0
M. Because these curves are idencal,
r
/0MH= and no contribuon to the FORC funcon is obtained. If the reversal field is de-
creased below the first magnezaon jump at r,1
H, first-order curves will start from 1
M
in-
stead of 0
M, and connue along 1
M unl a magnezaon jump (labeled with ‘1,1’ in Fig. 8.3a)
will bring the magnezaon 1
M back to posive saturaon (i.e. 0
M). The finite difference
between the last first-order curve coinciding with 0
M and the first one coinciding with 1
M
creates a contribuon
rr,1 1 0
1()( )
2
ρ
δH H M M
H
=- -
(8.4)
to the FORC distribuon, where rr,1
()δH H- is the Dirac impulse funcon accounng for the
magnezaon jump at r,1
H. Because rr,1
()
δ
HH- is zero everywhere, except for rr,1
HH-=
0, eq. (8.4) produces a diagonal ridge in FORC space (Fig. 8.3b). Using the coordinate transfor-
maons cr
()/2HHH=- and br
()/2HHH=+ , the ridge locaon is given by a line with equa-
on br,1c
HH H=+. FORC contribuons along this line are proporonal to the derivave of
10
MM- and are of two fundamental types. The first type occurs at points where 0
M and 1
M
are connuous, and is proporonal to differences between their slopes. Such FORC contribu-
ons are magnecally reversible, because a small change of the applied field H does not nu-
cleate magnec state transions. On the other hand, magnecally irreversible contribuons
occur at magnezaon jumps occurring along 1
M
(e.g. jump ‘1,1’ in Fig. 8.3b). In this case, the
derivave of 10
MM- is a Dirac impulse with amplitude 1,1
ΔM, contribung with a point peak
1,1 r r,1 1,1
1()()
2
ρ
MδH H δHHΔ=--
(8.5)
to the FORC distribuon. Equaons (8.4-5) can be generalized to any pair of first-order curves,
giving raise to as many diagonal ridges in FORC space, as discrete magnezaon jumps are
encountered along the upper hysteresis branch. The FORC funcon is thus fully described by
the sum of all diagonal ridges, i.e.
rr, 1
1
1()( )
2
n
iii
i
ρδHHMM
H-
=
=- -
å
(8.6)
An important characteriscs of this FORC model is that both reversible and irreversible con-
tribuons can have posive and negave amplitudes, depending on the slopes of first-order
curves, and on whether a magnezaon jump occurs along i
M or 1i
M-.
The FORC funcon of a simple system with few magnezaon states, such as in the exam-
ple of Fig. 8.3, is given by a certain number of infinite, isolated peaks corresponding to discrete
transions between magnec states. Each peak is preceded by a sort of diagonal “shadow”
produced by the pronounced curvature of magnezaon curves in proximity of magnec state

VARIFORC User Manual: 8. FORC tutorial 8.14
transions. Peak posions define so-called switching or nucleaon fields in which magnec
state transions occur. Small modificaons of the magnec system, as for instance the intro-
ducon of an addional parcle in the SD cluster model of Fig. 8.3, modify crical fields and
eventually produce addional magnezaon states with corresponding transions. Therefore,
samples containing large numbers of heterogeneous magnec parcles generate a dense
“cloud” of peaks merging into a connuous FORC distribuon. Because individual peaks can
be posive or negave, some regions of the FORC diagram might be characterized by negave
amplitudes. In general, all FORC contribuons are contained within a triangular region defined
by verces with coordinates sat
(0, )H and sat
(,0)H.
An important characterisc of the general FORC model described above is related to the
inversion symmetry of magnec states. This symmetry ensures that the last magnezaon
jump along the upper branch (i.e. the transion from 2
M to 3
M in Fig. 8.3a) is always ac-
companied by an idencal jump along the following first-order curve, which coincides with
the lower hysteresis branch (i.e. jump ‘3,1’ in Fig. 8.3a). This jump produces an infinite peak
on the last diagonal ridge of the FORC diagram (Fig. 8.3b), which is located exactly at b0H=.
This is because the last diagonal ridge starts at a certain negave reversal field r,last
H and ends
with a jump occurring at r,last
HH=- , so that b r,last r,last 0HH H=-=. While other peaks can
occur everywhere in FORC space, the peak associated with r,last
H is always placed exactly at
b0H=.
A sample containing many isolated (i.e. non-interacng) parcles with few magnec states
will produce a corresponding number of FORC peaks along b0H=, while other peaks contri-
bute to a distributed background. The superposion of all peaks with b0H= appears as an
infinitely sharp, so-called central ridge [Egli et al., 2010]. Its existence has been first predicted
for non-interacng uniaxial SD parcles [Newell, 2005], which represent the simplest possible
case of parcles with two magnec states, and observed for a magnetofossil-bearing lake sedi-
ment [Egli et al., 2010]. Because of the theorecally infinite sharpness of the central ridge,
high-resoluon FORC measurements and proper processing are necessary for its idenfica-
on. Since its first observaon, the central ridge has been found to be a widespread signature
of freshwater and marine sediments containing magnetofossils [Roberts et al., 2012]. Two
condions must be met for the existence of a central ridge: first, magnec parcles should not
interact with each other, since the presence of an interacon field destroys the inversion sym-
metry of single parcle hysteresis loops by shiing them horizontally. Second, individual par-
cles should have only few magnezaon states, so that the lower hysteresis branch merges
directly with the upper branch, without joining any other first-order curve. For example, MD
parcles with many domain wall pinning sites produce a large number of individual FORC
peaks, none of which must forcedly occur at b0H= (Fig. 8.4).
VARIFORC User Manual: 8. FORC tutorial 8.15
In any case, the central ridge is not an exclusive feature of SD parcles, as it can occur in
ensembles of non-interacng parcles with few magnezaon states (e.g. PSD). Some exam-
ples will be provided with the discussion of PSD magnezaon processes in secon 8.4.2.
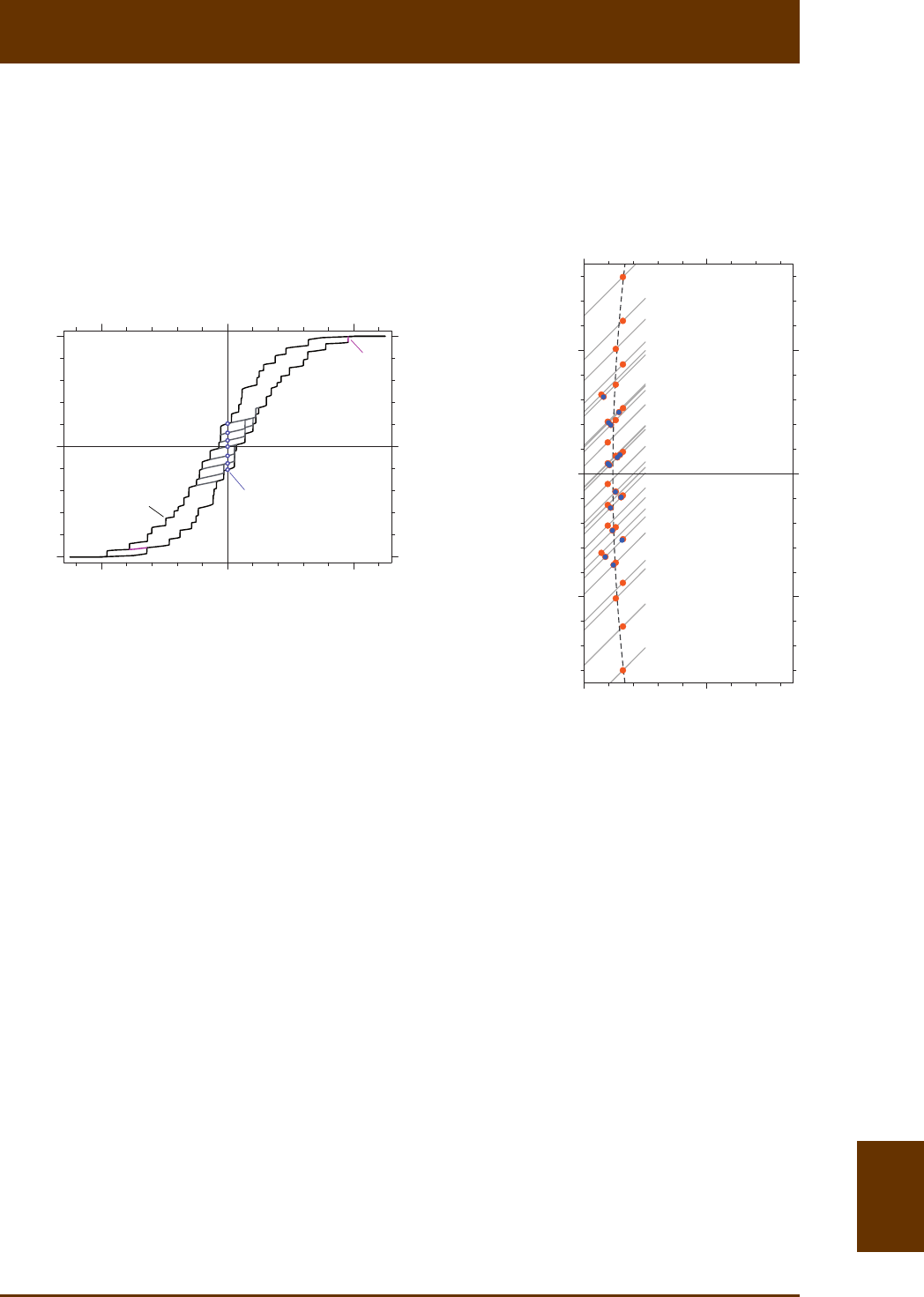
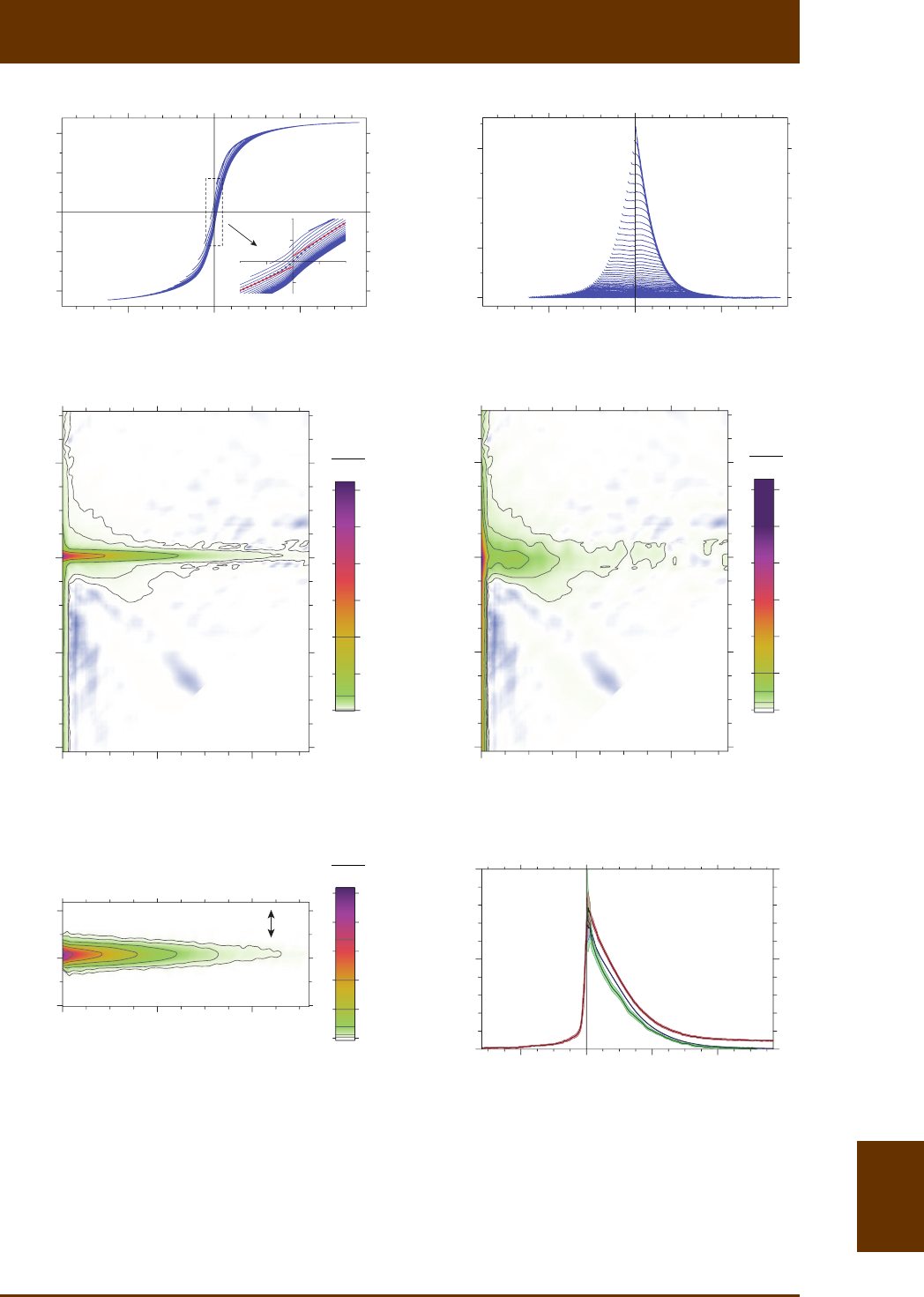
Fig. 8.4: (a) Model hysteresis loop (black) and FORCs (gray) generated by three MD parcles with
demagnezing factors of 0.1, 0.2, and 0.3, respecvely, calculated according to Pike et al. [2001b]. Only
FORCs necessary for measurement of the backfield demagnezaon curve bf
M (blue dots) are shown
for clarity. The last FORC 1n
M- that does not coincide with the lower hysteresis branch is show in
purple. It merges with the lower hysteresis branch before the last magnezaon jump Δ n
M has occur-
red, so that no central ridge contribuons are produced. (b) FORC diagram corresponding to the MD
hysteresis model shown in (a). Gray diagonal lines are individual FORC trajectories along which irrever-
sible magnezaon processes are recorded as posive (orange dots) and negave (blue dots) peaks.
The dashed line is a quadrac fit to the dots showing clustering around the crest of a ‘crescent-shaped’
distribuon as discussed in Church et al. [2011].
−100 0 +100
Mbf
+1
−1
0
µ0H [mT]
norm. magnetization
(a)
M+
Mn−1
0 +50
−50
0
+50
µ0Hc [mT]
µ0Hb [mT]
(b)
∆Mn
VARIFORC User Manual: 8. FORC tutorial 8.16
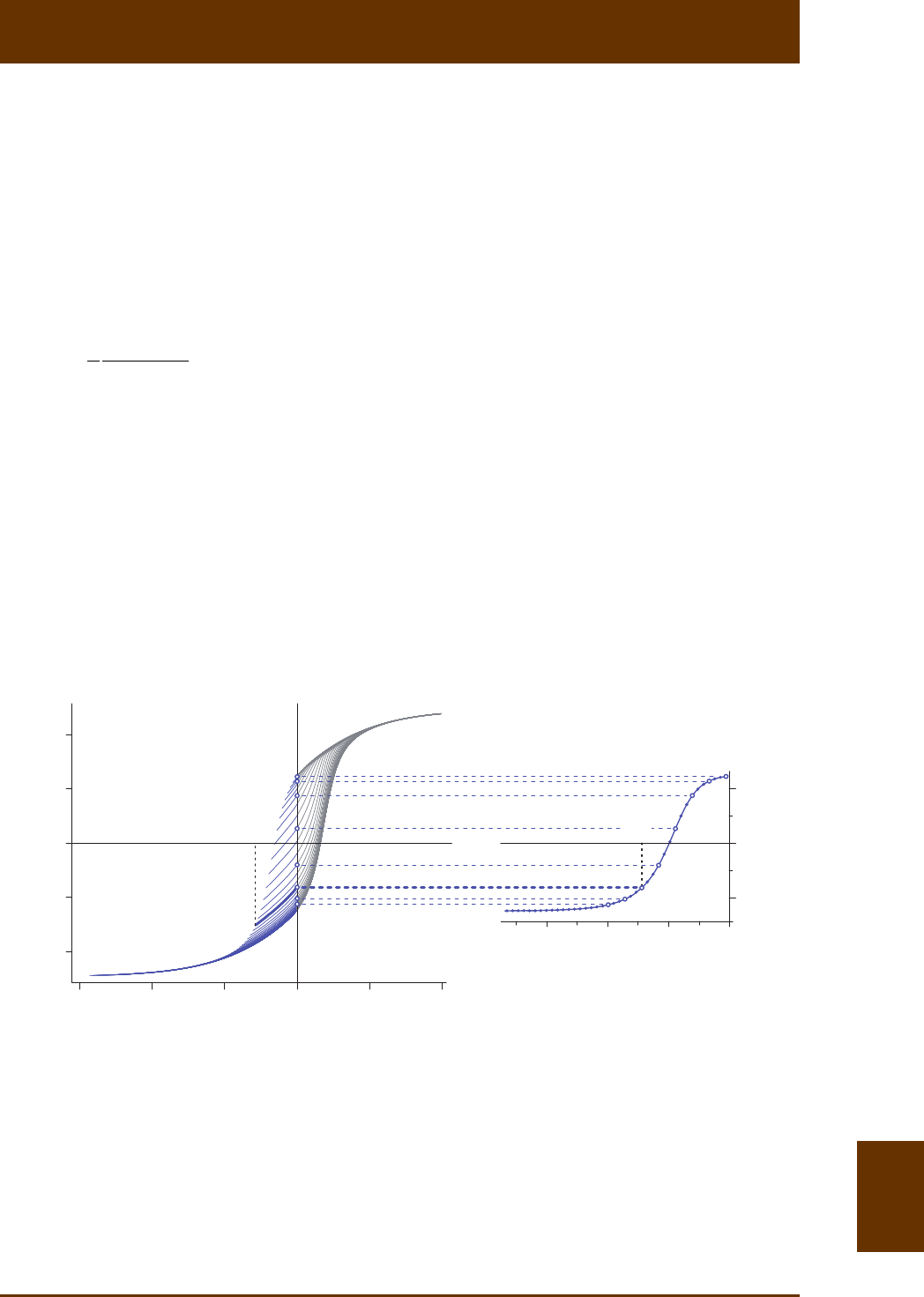
8.3 Coercivity distribuons derived from FORC measurements
FORC measurements subsets define three types of coercivity distribuons that provide a
bridge with convenonal parameters used in rock magnesm since several decades. These
coercivity distribuons originate from three parcular FORC segments (Fig. 8.5): (1) the inial
part rr
(, )MH H H of each curve and its departure from the upper hysteresis branch, (2) the
remanent magnezaon r
(,0)MH of each curve, and (3) the point r
HH=- of each curve
where the applied field equals the reversal field amplitude. These regions define magneza-
on curves that will be discussed in the following.
Fig. 8.5: Relevant magnezaon processes captured by FORCs. irr
ΔM (red bar) is the irreversible mag-
nezaon change along the upper hysteresis branch, defined by the inial difference between FORCs
originang at consecuve reversal fields r
H. In this example, r
H-values have been chosen to coincide
with the coercivity c
H and the coercivity of remanence cr
H for didacc purposes. The difference
between the same two FORCs in zero field ( 0H=, blue bar) defines a contribuon bf
ΔM to the back-
field demagnezaon curve. Finally, the abrupt slope change of FORCs at r
HH= defines the contribu-
on cr
ΔM (green) to the central ridge. The FORC starng at r0H=, where rs
MM=, is called satura-
on inial curve [Fabian, 2003]. In ensembles of non-interacng SD parcles, this curve coincides with
the upper hysteresis branch because negave fields are required to switch them from posive satura-
on.
∆M
irr
∆M
bf
H
r
=H
cr
−H
r
M
rs
−50 0 +50
0
−1
+1
field µ0H [mT]
norm. magnetization M/Ms
H=0
H
r
=H
c
∆M
bf
VARIFORC User Manual: 8. FORC tutorial 8.17
8.3.1 Backfield coercivity distribuon
Backfield or DC demagnezaon of a posively saturated sample is obtained by measuring
its remanent magnezaon aer applicaon of increasingly large negave fields [Wohlfarth,
1958]. The applied negave fields are equivalent to reversal fields r
H of the FORC protocol
(Fig. 8.6), so that the backfield demagnezaon curve is given by FORC remanent magne-
zaons r
(,0)MH . The corresponding backfield coercivity distribuon is defined as the first
derivave of r
(,0)MH , i.e.
bf
1d ( ,0)
() 2d
Mx
fx
x
-
=- (8.7)
The backfield coercivity distribuon can be determined very precisely with the same polyno-
mial regression method used to calculate FORC diagrams. The factor ½ in eq. (8.7) ensures
that the integral of bf
f
over all fields yields the saturaon remanence rs
M of the sample.
Moreover, bf
f
is defined only for posive arguments, which correspond to negave reversal
fields, because the remanent magnezaon of curves starng at r0H> cannot be measured.
Within the Preisach model, the argument of bf
f
coincides with the coercivity field c
H of hyste-
rons, and bf c c
()d
f
HH
coincides with the rs
M-contribuon of all hysterons with coercivies
comprised between c
H and cc
dHH+.
Fig. 8.6: Construcon of a backfield demagnezaon curve (right) from FORC measurements (le) of
a magnetofossil-bearing pelagic carbonate. FORC porons that are actually swept during backfield
measurements are shown in blue, and some zero-field measurements are highlighted with blue circles.
Remanent magnezaon measurements rr
(,0)MMH= on FORCs beginning at r
H- define the back-
field curve coordinates rr
(, )HM.
–100 0 +100
–2
0
+2
–60 –40 –20 0
–1
0
+1
H
, mT
M
, μAm2
Hr
, mT
M
(Hr, 0)
H
r,nH
r,n

VARIFORC User Manual: 8. FORC tutorial 8.18
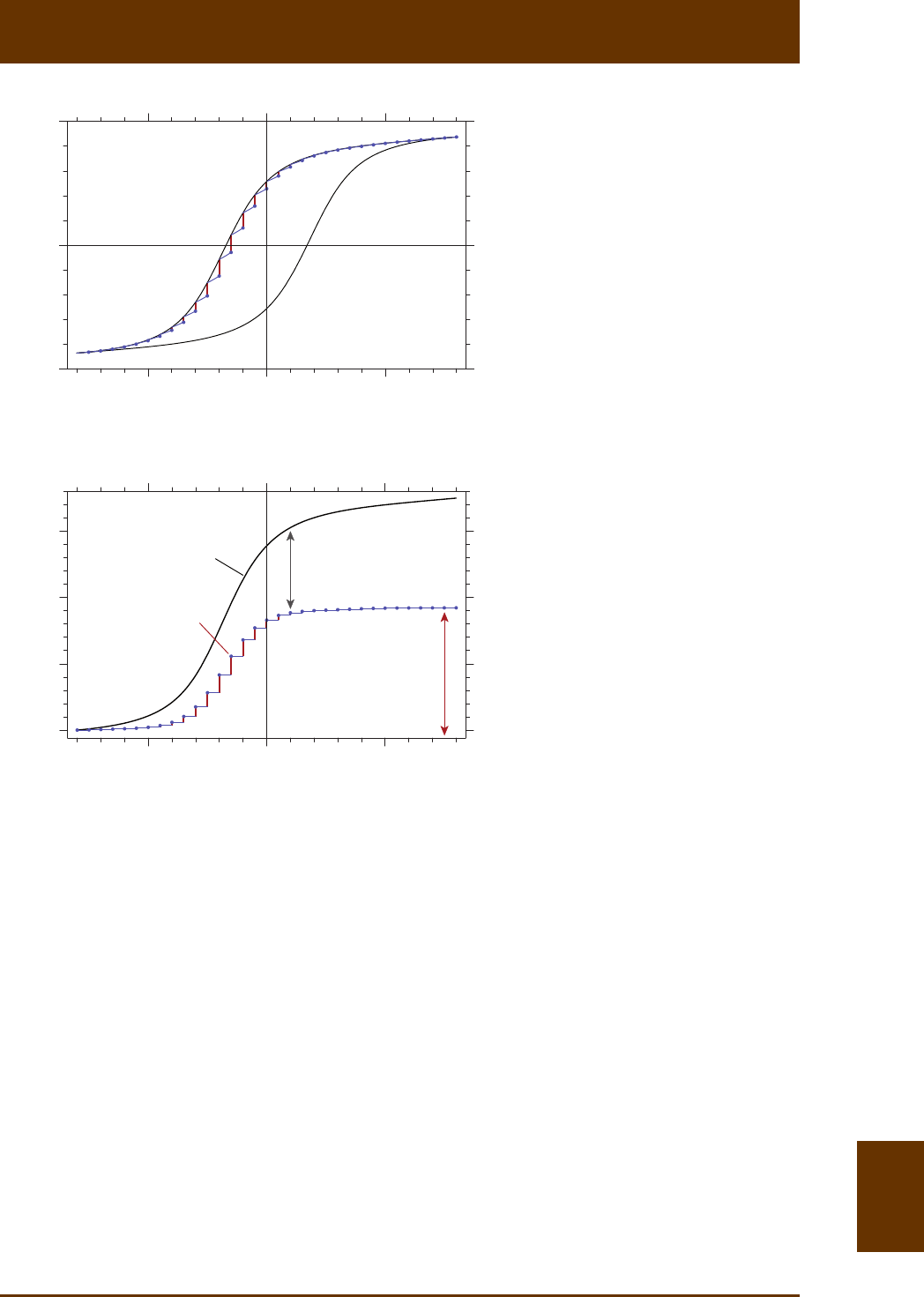
8.3.2 Reversal coercivity distribuon
Inial FORC slopes can be used to calculate irreversible magnezaon changes
irr r r r r
Δ(,)(,)M MHδHHδHMHHδH=+ +- + (8.8)
along the upper hysteresis branch (Fig. 8.7), where
δ
H is the (constant) field increment used
for the measurements. The sum of all irr
ΔM’s obtained from consecuve FORCs starng at
reversal fields r
Hx£ defines a magnezaon curve irr ()Mx with the following meaning: if
reversible magnezaon processes are removed from the upper hysteresis branch, the re-
sulng ‘irreversible hysteresis’ branch would coincide with irr
M up to a constant (Fig. 8.7b).
The so-called reversal coercivity distribuon is defined by analogy with backfield demagne-
zaon as
r
irr r
irr
r
1d ( ) 1 ( , )
() 2d 2 HH x
Mx MHH
fx xH
==-
-
=- =-
. (8.9)
The factor ½ in eq. (8.9) has been introduced to ensure that the total integral irs
M of irr
f
is a
magnezaon with the following properes: irs s
0MM<£
for any sample, and irs s
MM= in
absence of reversible processes. Unlike rs
M, the parameter irs
M includes all irreversible pro-
cesses occurring along the major hysteresis loop and shall therefore be called irreversible satu-
raon magnezaon.
A fundamental property of irs
M is that it coincides with the total integral of the FORC
funcon, because, using eq. (8.6):
r,
r
rr 1 irs
,11
11
(,)dd ( ) Δ
22
i
nn
ii i
HH
HH ii
ρ
HH H H M M M M
-=
==
=-==
åå
òò (8.10)
This important result implies that, while reversible magnezaon processes can contribute
locally to the FORC funcon, these local contribuons cancel each other out upon integraon
in FORC space.
The definions of bf
f
and irr
f
are analogous, since they both rely on differences between
consecuve FORCs evaluated at 0H= and r
HH=, respecvely, and are both related to the
FORC starng at r
Hx
=-
(Fig. 8.5). An important difference, on the other hand, is that the
argument of irr
f
can be posive as well as negave, unlike other coercivity distribuons.
Posive arguments of irr
f
correspond to measurements of the upper hysteresis branch in ne-
gave fields and vice versa. Similarly, posive arguments of bf
f
correspond to negave fields
used for DC demagnezaon. Furthermore, irr bf
(0) (0)
f
f= by the definions given with eq.
(8.7) and eq. (8.9).
VARIFORC User Manual: 8. FORC tutorial 8.19
Fig. 8.7: Construcon of the magne-
zaon curve corresponding to irre-
versible processes along the upper
hysteresis branch. (a) Irreversible
magnezaon changes irr
ΔM (red)
defined by the inial parts of all
FORCs (blue). (b) Upper hysteresis
branch M+ (black curve) aer ad-
ding the saturaon magnezaon
s
M, and irreversible magnezaon
curve irr ()MH
reconstructed by in-
tegrang all magnezaon steps
irr
ΔM shown in (a). The saturaon
value irr ()MH ¥ is the total irre-
versible magnezaon irs
2M of the
hysteresis branch.
8.3.3 Central ridge coercivity distribuon
The central ridge coercivity distribuon is best explained by considering an isolated mag-
nec parcle with any domain state. A first-order curve starng from the upper hysteresis
branch just aer a magnezaon jump has occurred at r0H< will contribute to the central
ridge if another magnezaon jump is encountered at r
HH=- while sweeping the field back
towards posive values, before merging with the previous FORC. Usually, magnezaon
jumps can occur at any field and there is no parcular reason for having one exactly at H=
r
H-. In this case FORC contribuons accumulate at b0H= as over any other place in FORC
space, generang a connuous FORC distribuon. An excepon is provided by the FORC ori-
ginang from the upper hysteresis branch just aer the last magnezaon jump. This curve
coincides by definion with the lower hysteresis branch. Because of inversion symmetry, the
lower branch will contain a symmetric magnezaon jump at r
HH=- . If the lower branch
−50 0 +50
0
1
0
−1
+1
−50 0 +50
∆Mirr
µ
0
H [mT]
MM + Ms
µ
0
H [mT]
(a)
(b)
M+(H) + Ms
Mirr(H)
Mirr(H)
2Mirs
∆Mirr
M+
M−

VARIFORC User Manual: 8. FORC tutorial 8.20
merges with the previous FORC curve before r
HH=- is reached, as it is commonly the case
for MD hysteresis (Fig. 8.4a), the jump at r
HH=- will not contribute to the FORC diagram,
because the two curves are idencal and
r
/0MH= . Otherwise, there will be a contribuon
to the central ridge in form of a peak with FORC coordinates cb r
(,)( ,0)HH H=- (Fig. 8.3).
Because these contribuons are placed exactly at b0H=, they produce a ridge of the form
cr c b cr c b
1
(,) ()()
2
ρ
HH f HδH= (8.11)
where cr
f
is the so-called central ridge coercivity distribuon [Egli et al., 2010]. In FORC dia-
grams obtained from real measurements, the infinite sharpness of cr
ρ
is regularized by re-
placing the Dirac impulse with an appropriate funcon of b
H that takes the smoothing effects
of measurements performed with finite field increments into account. A rigorous treatment
of such effects is given in Egli [2013]. The central ridge coercivity distribuon is obtained from
real measurements in two steps: first, the central ridge contribuon cr
ρ
to the FORC diagram
is isolated from the connuous background produced by other processes, then cr
ρ
is integra-
ted over b
H so that
cr c cr c b b
() (, )dfH
ρ
HH H
+¥
-¥
=ò. (8.12)
While the amplitude of cr
ρ
depends on the resoluon of FORC measurements and on FORC
processing, cr
f
is independent of any measuring and processing parameter and reflects intrin-
sic magnec properes. The complex operaon of isolang the central ridge and calculang
cr
f
is performed automacally by VARIFORC with few controlling parameters described in this
user manual (Chapter 6).
The total magnezaon cr
M associated with the central ridge is obtained by integrang
cr
f
over c
H and represents the total contribuon of last magnezaon jumps in isolated
magnec parcles. Accordingly, cr irs
/MM
is the rao between the last magnezaon jump
n
ΔM of a hysteresis branch and the sum of all magnezaon jumps over the same branch. In
case of non-interacng, uniaxial SD parcles, n1
ΔΔMM= is the only magnezaon jump of
single parcle hysteresis, so that cr irs
/1MM=. As soon as addional magnec states begin to
exist in small PSD parcles, the relave amplitude of n
ΔM decreases with respect to the sum
irs
M of all magnezaon jumps, and cr irs
/1MM<, unl cr 0M= is reached in MD-like sys-
tems.
VARIFORC User Manual: 8. FORC tutorial 8.21
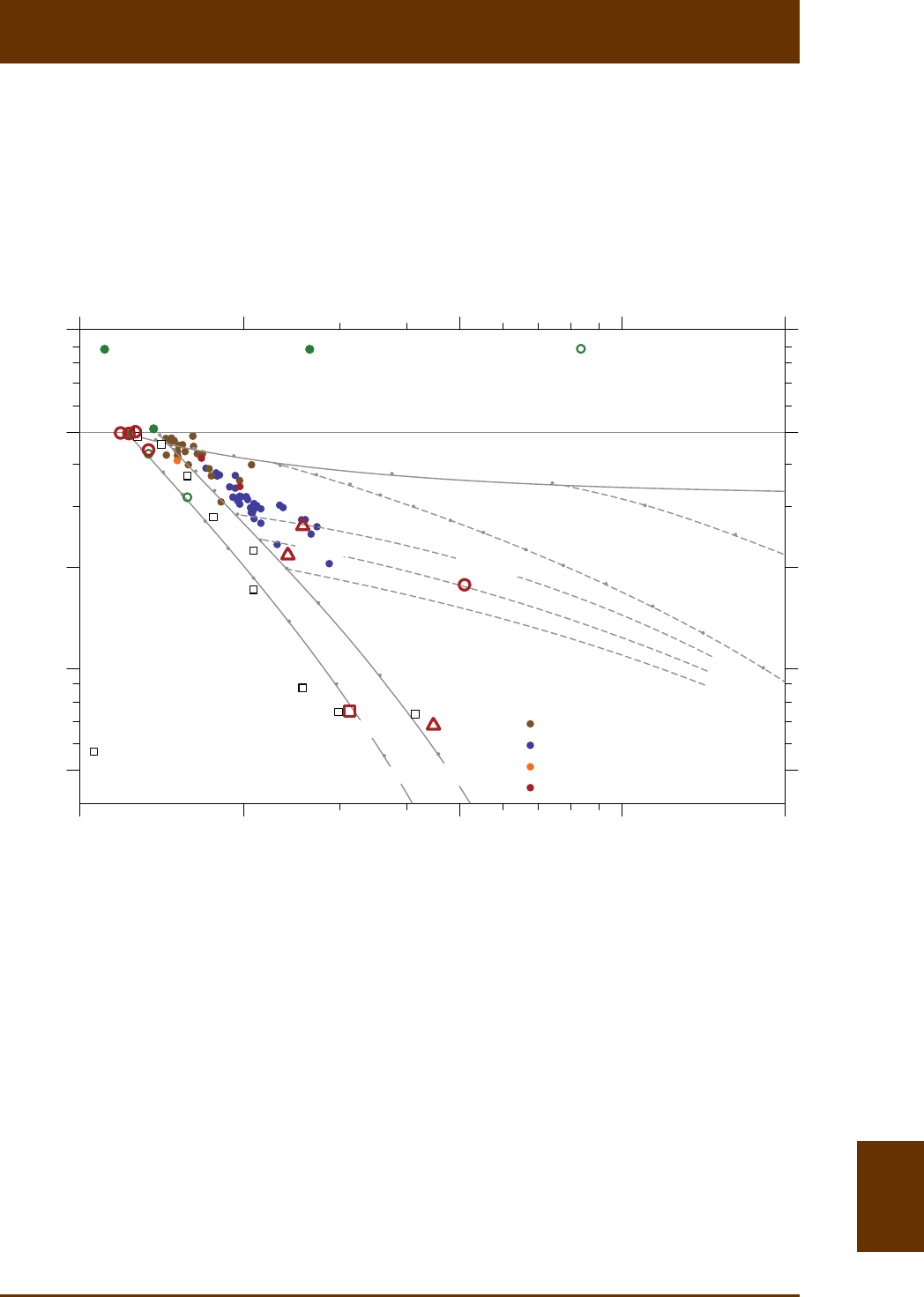
8.4 Examples
The physical meaning of FORC diagrams and derived coercivity distribuons is best illus-
trated with topic examples related to SD, PSD, and MD magnec parcle assemblages. The
hysteresis properes of samples discussed in this secon are summarized by the Day diagram
of Fig. 8.8.
Fig. 8.8: Day diagram summarizing the hysteresis properes of samples discussed in this paper (red
circles for SD samples, red triangles for PSD samples, red squares for MD samples), compared with
properes of magnetofossil-bearing sediments (colored dots). The Day diagram with mixing curves
between domain states (gray) is drawn from Dunlop [2002b]. Cultured magnetotacc bacteria (‘cul-
tured MB’) plot exactly on the expected spot for non-interacng uniaxial SD parcles. The effect of
magnetostac interacons on such parcles is shown with models from Muxworthy et al. [2003] and
with disrupted magnetosome chains (green circle, from Li et al., 2012]). In general, interacng SD par-
cles follow the SD+MD mixing curve. Magnetofossil-bearing sediments follow a different trend with
end-members defined by CBD-extractable magnec minerals on one hand (red circle labeled as ‘CBD
extr.’, from Ludwig et al. [2013]) and the central region of the diagram on the other hand, possibly
represented by a clay mineral dispersion of SDS-treated Magnetospirillum cells (red circle labeled as
‘MS disp.’). Iron nanodots with single-vortex states (red triangle labeled as AV-109, from Winklhofer et
al. [2008]) do not plot on the expected trend line for PSD parcles.
SD+MD mixing curves
20%
40%
50%
60%
70%
80%
SP+PSD
mixing curves
SP saturation envelope
10% 20%
30%
30%
40%
50%
60%
SP+SD
mixing curves
70%
80%
10 nm
40%
50%
15 nm
1251020
1
0.5
0.2
0.1
0.05
Hcr/Hc
Mrs/Ms
interacting uniaxial
SD particles
[Muxworthy et al., 2003]
uncultured MB
(mainly cocci with double chains)
[Pan et al., 2005]
P
L
PL uncultured cocci
[Lin and Pan, 2009]
AMB-1 intact and collapsed
[Li et al., 2012]
Gehring et al., 2011
Abrajevitch and Kodama, 2011
Roberts et al., 2011
magnetofossil-rich sediments:
this study
cultured MB
MS disp.
CBD
extr.
AV-109
EF-3
volc. ash
MD-20
VARIFORC User Manual: 8. FORC tutorial 8.22
8.4.1 SD magnec assemblages
The first example is a conceptual model of a sample containing a small number of non-
interacng, uniaxial SD parcles with rectangular (Fig. 8.9a) and curved (Fig. 8.9c) single-par-
cle hysteresis loops. Reversible processes (i.e. magnec moment rotaon in the applied field)
are absent in the first case. The SD parcles have two stable magnezaon states in fields
s
HH||< , where s
H is a parcle-specific switching field. Transions from one magnezaon
state to the other in individual parcles once their specific s
H-values have been reached is
seen in Fig. 8.9 as a series of magnezaon jumps. These jumps represent irreversible magne-
zaon processes, while reversible magnec moment rotaons (Fig. 8.9c) occur along con-
nuous segments of the magnezaon curves.
Fig. 8.9: Modeled FORC properes of few uniaxial, non-interacng SD parcles. Switching of individual
parcles appears as magnezaon jumps. (a) Preisach-Néel model with rectangular single parcle hys-
teresis loops (inset). This case is characterized by irr bf cr
ΔΔΔMMM==, so that the coercivity distribu-
ons in (b) are idencal. irr
ΔM and cr
ΔM are magnezaon jumps produced by the same parcle in
r
H and r
H-, respecvely. (c) Model with Stoner-Wohlfarth single parcle hysteresis loops (inset).
Magnezaon jumps occur at same fields as in (a), but their size is smaller, because magnezaon
changes are caused in part by magnec moment rotaons over the connuous segments. Because
magnezaon jump sizes of single parcle hysteresis loops are smaller than saturaon remanent mag-
nezaons, irr cr bf
ΔΔΔMMM=<, and the backfield coercivity distribuon is larger than the other two
coercivity distribuons, as shown in (d).
−0.1 0 +0.1
∆M
irr
∆M
bf
H
r
−H
r
+0.5
−0.5
0
∆M
irr
∆M
bf
H
r
−H
r
µ
0H [T]
norm. magnetization
−0.1 0 +0.1
+1
−1
0
µ0H [T]
norm. magnetization
(a) (c)
M
+
(H)
M
+
(H)
∆M
cr
∆M
cr
µ
0H [T]
(b)
+0.1+0.050−0.05
f
bf
=
f
irr
=
f
cr
f
bf
f
irr
=
f
cr
µ
0H [T]
+0.1+0.050−0.05
(d)

VARIFORC User Manual: 8. FORC tutorial 8.23
Each magnezaon jump along the upper hysteresis branch is the starng point of a FORC
that does not coincide with the previous one, while all FORCs starng from the same con-
nuous hysteresis segment are idencal.
Non-interacng, uniaxial SD parcles have relavely simple FORC properes. First, no swit-
ching occurs when the field is reduced from posive saturaon to zero. Therefore, all FORCs
r
(0,)MH H³ starng at posive reversal fields are idencal to the upper branch M+ of the
major hysteresis loop and their shape is enrely determined by reversible magnec moment
rotaon. Departure from M+ of the FORC (0, )MH
originang at r0H= (called saturaon
inial curve si
M), can be used as a measure of how much real hysteresis loops differ from the
ideal non-interacng SD case characterized by si
MM
+
= [Fabian, 2003]. As soon as negave
fields are reached along r
()MH
+, all parcles with sr
HH>- are switched: accordingly, FORCs
starng at r0H< are produced by a mixture of switched and unswitched parcles. While the
applied field is increased from r0H< to 0H=, magnec moments rotate reversibly without
further switching. Moreover, the remanent magnezaon bf
M= r
(,0)MH obtained at 0H=
reflects the same configuraon of switched parcles created at the beginning of the corres-
ponding FORC.
In both examples of Fig. 8.9, the last magnezaon jump of each FORC contributes to the
central ridge and has the same amplitude as the magnezaon jump on ()MH
+ from which
the FORC is branching, because both jumps are produced by the two switching fields s
H of
same parcles. Therefore, the coercivity distribuons associated with r
()MH
+ and with the
central ridge are idencal, i.e. cr irr
() ()
f
xfx= over 0
x
³ and irr (0)0
f
x<= (Fig. 8.9b,d). The
backfield coercivity distribuon, on the other hand, is based on magnezaon differences
measured in zero field instead of the switching fields, and is therefore disnct from the other
two coercivity distribuons in case of SD parcles with curved elemental hysteresis loops, such
as Stoner-Wohlfarth parcles (Fig. 8.9c,d). In case of randomly oriented Stoner-Wohlfarth par-
cles, the mean size of magnezaon jumps in single-parcle hysteresis is irs rs
/SMM==
cr rs
/ 0.5436MM= [Egli et al., 2010], and rs s
/0.5MM=. Single-parcle hysteresis loops be-
come much closer to rectangular loops as soon as thermal acvaons are taken into conside-
raon, because switching occurs in smaller fields where reversible magnec moment rotaon
is less pronounced. FORC measurements yield 0.8-0.9S» for SD parcles in a pelagic carbo-
nate [Ludwig et al., 2013].
The FORC properes discussed above are important for the idenficaon of SD parcles
in geologic samples, notably magnetofossils in freshwater and marine sediment, but also well-
dispersed SD parcles in rocks. In parcular, the occurrence of sedimentary SD parcles in
isolated form or as linear chains produced by magnetotacc bacteria is the maer of an on-
going debate. For example, the unusually strong SD signature of sediments from the Paleo-
cene-Eocene thermal maximum (PETM) has been aributed to magnetofossils produced by
magnetotacc bacteria thriving in a parcularly favorable environment [Kopp et al., 2007;

VARIFORC User Manual: 8. FORC tutorial 8.24
Lippert and Zachos, 2007], as well as, at least in part, to isolated SD parcles produced by a
cometary impact [Wang et al., 2013]. In the following, some examples of FORC and coercivity
distribuon signatures of sedimentary SD parcles are discussed.
The first example is based on high-resoluon FORC measurements by Wang et al. [2013]
of a pure culture of the magnetotacc bacterium MV-1, which produces single chains of pris-
mac 3553 nm magnete crystals [Sparks et al., 1990]. The original measurements have
been reprocessed with VARIFORC and results are shown in Fig. 8.10. Isolated magnetosome
chains behave as a whole like SD parcles with uniaxial anisotropy, because the magnec
moments of individual crystal are switched in unison due to strong magnetostac coupling
[Jacobs and Bean, 1955; Egli et al., 2010]. Magnetostac interacons between chains, on the
other hand, are minimized by the good separaon naturally provided by the much larger cell
volume.
Because of intrinsic magnetosome elongaon and well-constrained dimensions, MV-1 cul-
tures provide a close analogue to random dispersions of nearly idencal, uniaxial SD parcles.
The resulng coercivity distribuons are relavely narrow with virtually no contribuons at
c0H= (Fig. 8.10f), as expected for SD parcles with minimum uniaxial anisotropy provided
by crystal elongaon and chain geometry. Hysteresis parameters (rs s
/0.496MM=, cr c
/HH=
1.19, Fig. 8.8) praccally coincide with those of randomly oriented Stoner-Wohlfarth parcles.
Lack of strong magnetostac interacons is confirmed by the negligible intrinsic vercal exten-
sion of the central ridge, as predicted by theorecal calculaons [Newell, 2005].
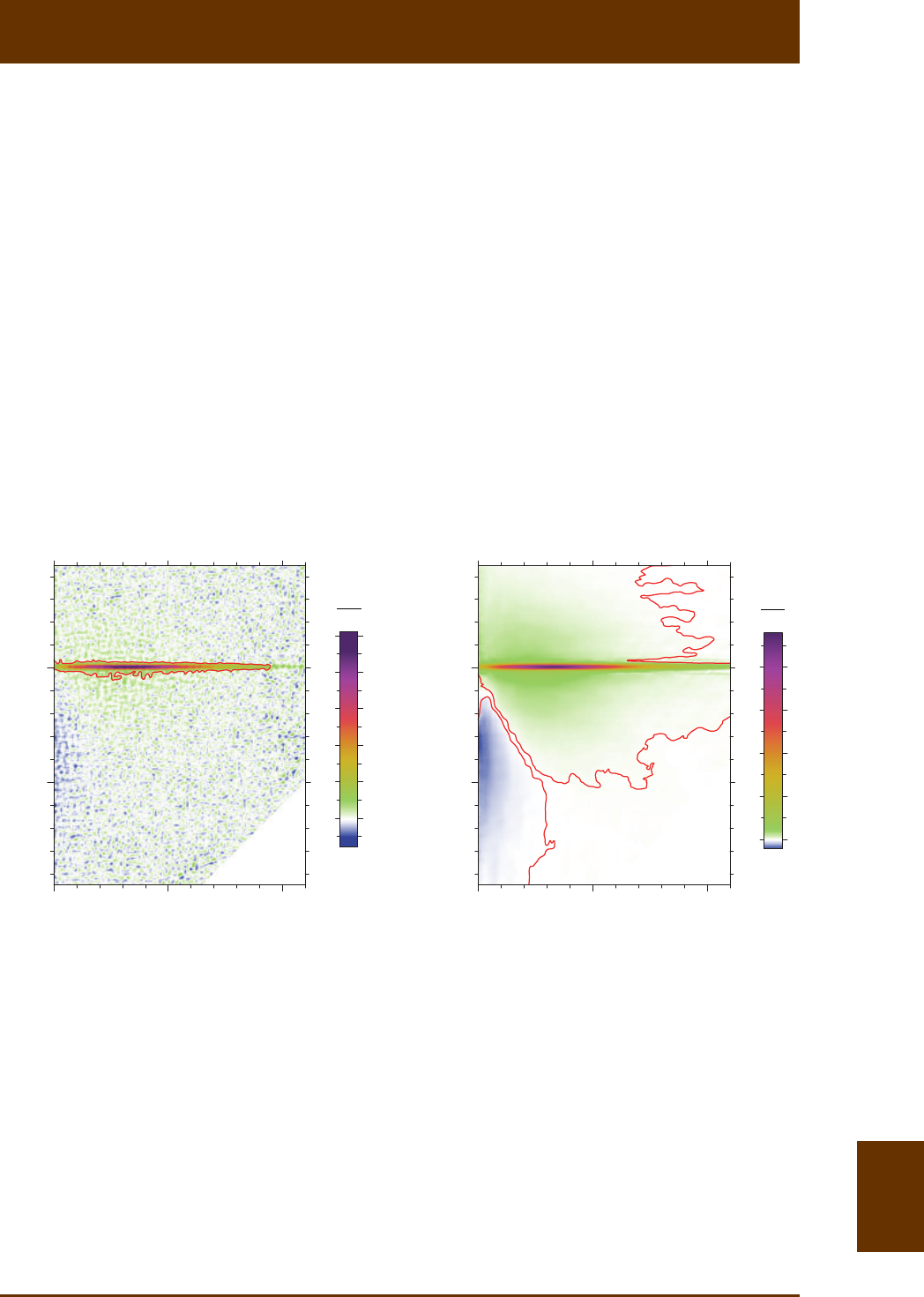
Fig. 8.10 (front page): Cultures of the magnetotacc bacterium MV-1 represent one of the best
material realizaons of non-interacng SD parcle assemblages with minimum uniaxial magnec ani-
sotropy. These bacteria contain a single chain of SD magnete crystals that switch in unison, behaving
effecvely as an equivalent SD parcle with elongaon along the chain axis. (a) Set of FORC measu-
rements where every 4th curve is ploed for clarity. (b) Same as (a), aer subtracng the lower hyste-
resis branch from each curve. Every 2nd curve is shown for clarity. The bell-shaped envelope of all
curves is the difference between upper and lower hysteresis branches, i.e. the even component
rh ()/2MMM
+-
=- of the hysteresis loop mulplied by a factor 2 [Fabian and Dobeneck, 1997]. (c)
FORC diagram calculated with VARIFORC from the measurements shown in (a). (d) Same as (c), aer
subtracon of the central ridge. Most contribuons in this diagram are due to reversible magnezaon
processes (i.e. in-field magnec moment rotaons). (e) Central ridge isolated from (c) and ploed with
a 2 vercal exaggeraon. Zero-coercivity contribuons are completely absent, as expected for a
system of parcles with intrinsic shape anisotropy along chain axes. The central ridge’s vercal exten-
sion slightly exceeds the minimum extension expected from data processing of an ideal ridge, revealing
residual magnetostac interacons between magnetosome chains. The associated interacon field
amplitudes are <0.5 mT.
VARIFORC User Manual: 8. FORC tutorial 8.25
Fig. 8.10 (connued): (f) Coercivity distribuons derived from FORC measurements and corresponding
magnezaons calculated by integraon of the distribuons over all fields. The condion irs cr
MM=
expected for these parcles is not exactly met, because of residual FORC contribuons not correspon-
ding to non-interacng, uniaxial SD parcles. On the other hand, irr (0)0fx<=, as expected from
posively saturated SD parcles that cannot be switched in posive fields. High-resoluon FORC mea-
surements have been kindly provided by Wang et al. [2013].
–2
0
+2
0
2
4
0.0
0.5
1.0
0
2
4
0
20
40
+2000
H
, mT
M
, μAm
2
0
1
–200 +2000
H
, mT
∆M, μAm
2
04080
H
c
, mT
0
–40
H
b
, mT
+40
–80
04080
H
c
, mT
0
–40
H
b
, mT
+40
–80
04080
H
c
, mT
0
–5
H
b
, mT
+5
04080
−H
r
or H
c
, mT
–40
dM/dH
, μAm
2
/T
(a) (b)
(c) (d)
(e) (f)
–200
2
2
2
mAm
T
2
2
mAm
T
2
2
mAm
T
2×
μAm
2
:
M
rs
= 1.01
M
irs
= 0.889
M
cr
= 0.568
f
bf
f
cr
f
irr

VARIFORC User Manual: 8. FORC tutorial 8.26
Ideally, the three types of coercivity distribuons shown in Fig. 8.10f should be characte-
rized by irr cr bk
f
ffº£ and irr () 0
f
x= for negave arguments, so that cr irs
/1MM=. The mea-
sured rao cr irs
/0.64MM= reflects residual FORC contribuons of unspecified nature clearly
visible over b0H>, where 0
ρ
= is expected from non-interacng SD parcles [Newell, 2005].
These contribuons are probably associated with a small fracon of collapsed magnetosome
chains (Fig. 8.10d).
The second example is also based on a magnetotacc bacteria sample, but its magnec
properes are less straighorward. The sample is a synthec sediment analogue obtained by
dispersing cultured cells of the magnetotacc bacterium Magnetospirillum magnetotaccum
MS-1 in a clay slurry (kaolinite) while dissolving the cell material with addion of 2% sodium
dodecyl sulfate (SDS) during connuous srring. The purpose of this experiment was to check
the stability of magnetosome chains in sediment once the cell material is dissolved. Analogous
experiments performed directly in aqueous soluon yielded strongly interacng magneto-
some clusters [Kobayashi et al., 2006]. FORC analysis of this sample (Fig. 8.11) poses a formi-
dable problem in terms of data processing, because of the simultaneous presence of (1) a
sharp superparamagnec (SP) overprint, and (2) a double disconnuity at r0HH==, due to
the overlap of a central ridge and a vercal ridge in the FORC diagram.
Fig. 8.11 (front page): FORC measurements of a specially prepared sample containing equidimensional
magnete magnetosomes. The sample was obtained by dispersing a Magnetospirillum culture in clay
(kaolinite) with subsequent 2% SDS addion under connuous srring. Dissoluon of cell material by
SDS is expected to produce clay-magnetosomes aggregates of some form. (a) Set of FORC measu-
rements where every 12th curve is ploed for clarity. The insert shows a zoom around the origin, where
a sigmoidal SP contribuon is recognizable. The SP signature saturates in <2 mT, and, although not
contribung to the FORC diagram, it poses a processing problem, because polynomial regression pro-
vides a correct fit only if unsuitably small smoothing factors are chosen (SF = 2 in this case). (b) Same
as (a), aer subtracng the lower hysteresis branch from each curve. Every 3rd curve is shown for cla-
rity. The exponenal-like envelope of all curves is the difference between the upper and lower hyste-
resis branches, and the cusp at 0H= denotes a system with zero-coercivity contribuons. The SP
contribuon shown in the inset of (a) is naturally eliminated from measurement differences, which
therefore no longer pose FORC processing problems. (c) FORC diagram calculated with VARIFORC from
the measurement differences shown in (b). The only significant contribuons are the central ridge,
indicave of non-interacng SD parcles, and a vercal ridge at c0H=, which is produced by magnec
viscosity. The absence of other significant FORC contribuons, and in parcular the typical signature
for reversible magnec moment rotaon, indicate that single-parcle hysteresis loops are praccally
rectangular. (d) Same as (c), aer subtracon of the central ridge. Residual contribuons around the
former central ridge locaon reveal addional magnezaon processes, which, given the SD nature of
the sample, must arise from magnetostac interacons. (e) Central ridge isolated from (c) and ploed
with a 3 vercal exaggeraon. The central ridge peak at c0H= denotes a system containing SD par-
cles with vanishing coercivity.
VARIFORC User Manual: 8. FORC tutorial 8.27
Fig. 8.11 (connued): (f) Coercivity distribuons derived from FORC measurements and corresponding
magnezaons calculated by integraon of the distribuons over all fields. The condion irs rs
MM»»
cr
M met by this sample is typical for non-interacng SD parcles with squared hysteresis loops and
represents a physical realizaon of a Preisach-Néel system. Residual irr
f-contribuons over negave
arguments are caused by non-zero FORC amplitudes over b0H> in (d).
–0.4
0
+0.4
0
1
2
3
0
0.2
0.4
0.6
0
1
2
0
5
10
–50 +500
H
, mT
M
, μAm
2
0
0.1
–50 +500
H
, mT
∆M, μAm
2
02040
H
c
, mT
0
–20
H
b
, mT
+20
–40
02040
H
c
, mT
0
–20
H
b
, mT
+20
–40
02040
H
c
, mT
0
–5
H
b
, mT
+5
02040
−H
r
or H
c
, mT
–20
dM/dH
, μAm
2
/T
(a) (b)
(c) (d)
(e) (f)
2
2
mAm
T
2
2
mAm
T
2
2
mAm
T
−4 +4
0.2
3×
μAm
2
:
M
rs
= 80
M
irs
= 120
M
cr
= 74
f
bf
f
cr
f
irr

VARIFORC User Manual: 8. FORC tutorial 8.28
Because the sigmoidal SP overprint extends only over few measurement points, saturang
in <2 mT (Fig. 8.11a), it cannot be adequately fied by polynomial regression with smoothing
factors required for adequate measurement noise suppression [Egli, 2013]. The SP overprint
is eliminated by subtracng the lower branch of the major hysteresis loop from all curves, in
which case no parcular features are seen at 0H= (Fig. 8.11b). This operaon does not affect
FORC calculaons, because the r
H-derivave of any magnezaon curve added or subtracted
to all measurements is zero. For this reason, subtracon of the lower hysteresis branch is an
opon provided by VARIFORC for processing quasi-disconnuous measurements. Moreover,
FORC measurement differences reveal details that are oen completely hidden in hysteresis
loops with rs s
/0MM and/or large paramagnec contribuons.
The hysteresis loop of this sample is clearly constricted at 0H=, in what is oen called a
‘wasp-waisted’ shape [Tauxe et al., 2006]. The interpretaon of corresponding Day diagram
parameters ( rs s
/0.177MM=,cr c
/5.12HH=, Fig. 8.8) is ambiguous, because it involves mix-
tures of SD, PSD, and SP parcles. On the other hand, the FORC diagram (Fig. 8.11c), contains
two precisely interpretable signatures, namely a central ridge, as expected for non-interacng
SD parcles, and a vercal ridge due to magnec viscosity. Addional FORC contribuons out-
side of the two ridges are very weak (Fig. 8.11d). Coercivity distribuons (Fig. 8.11f) are charac-
terized by exponenal-like funcons peaking at c0H=. Because this is also true for cr
f
, many
parcles must have vanishingly small switching fields. Such features can be explained by a
combinaon of thermal acvaon effects and the absence of chain-derived uniaxial aniso-
tropy, as expected for equidimensional MS-1 magnetosomes if their original arrangement is
destroyed. On the other hand, the presence of magnetosome clusters similar to those obtai-
ned from cell disrupon in aqueous soluons [Kobayashi et al., 2006] can be excluded, be-
cause of the absence of magnetostac interacon signatures otherwise reported with FORC
diagrams of extracted magnetosomes [e.g. Chen et al., 2007; Wang et al., 2013]. The apparent
contradicon between lack of uniaxial chain anisotropy and magnetostac interacon signa-
tures can be reconciled by assuming that magnetosomes have been individually dispersed in
the clay matrix.
The three coercivity distribuons derived from FORC measurements are almost idencal;
approaching the limit case bk cr irr
f
ff== predicted for non-interacng SD parcles with rec-
tangular single-parcle hysteresis loops. Rectangular loops can be explained by the strong
switching field reducon in thermally acvated SD parcles close to the SD/SP threshold. This
example demonstrates the level of detailed informaon that is provided by high-resoluon
FORC measurements. Results shown in Fig. 8.10 and Fig. 8.11 can be considered represen-
tave for well dispersed SD parcles with and without minimum uniaxial shape anisotropies.
The effect of shape anisotropy is much less evident with samples of interacng SD parcles,
because local interacon fields act as an addional magnec anisotropy source.
VARIFORC User Manual: 8. FORC tutorial 8.29
The third SD example is based on high-resoluon FORC measurements of a magnetofossil-
bearing pelagic carbonate from the Equatorial Pacific [Ludwig et al., 2013]. Typical sediment
magnezaons of the order of few mAm2/kg, as for this sample, yield FORC measurements
with important noise contribuons that need to be adequately suppressed in order to obtain
useful FORC diagrams. FORC processing becomes crical in such cases, as shown in Fig. 8.12.
Convenonal data processing based on constant smoothing factors yields significant values of
the FORC distribuon only over a limited region around the central ridge (Fig. 8.12a), unless
the high resoluon required in proximity of b0H= and c0H= is sacrificed. The VARIFORC
variable smoothing algorithm, on the other hand, finds a locally opmized compromise be-
tween resoluon preservaon and noise suppression. With this approach, significant domains
of the FORC distribuon are dramacally expanded (Fig. 8.12b), revealing a broad, connuous
background around the central ridge, as well as negave FORC amplitudes characterisc for
SD parcles.
Fig. 8.12: Example showing the importance of proper FORC processing for extracng detailed infor-
maon from weak natural samples. The two FORC diagrams have been obtained from the same set of
high-resoluon measurements (field step size: 0.5 mT) of a pelagic carbonate from the Equatorial Paci-
fic [Ludwig et al., 2013]. The red contour(s) enclose significant regions of the FORC diagram, i.e. regions
where the FORC funcon is not zero at a 95% confidence level according to the error calculaon me-
thod implemented by Heslop and Roberts [2012]. (a) Convenonal FORC processing with a constant
smoothing factor SF = 4. The central ridge is the only significant FORC feature that can be resolved.
Larger smoothing factors would extend the significant region at the cost of blurring the central ridge
to the point where it can no longer be idenfied as such (see Fig. 1 in Egli [2013]). (b) VARIFORC pro-
cessing obtained with a variable smoothing factor opmized for the best compromise between noise
suppression and detail preservaon. Low-amplitude features, such as negave contribuons, are now
significant over large porons of the whole FORC space.
0
4
8
0 50 100
H
c
, mT
0
–50
H
b
, mT
2
2
Am
Tkg
0 50 100
H
c
, mT
0
–50
H
b
, mT
0
4
8
2
2
Am
Tkg
(a) (b)
SF = 4 variable smoothing

VARIFORC User Manual: 8. FORC tutorial 8.30
The last example of this secon (Fig. 8.13) is based on a special technique used to isolate
the contribuon of secondary SD magnete parcles from the same pelagic carbonate sample
of Fig. 8.12. For this purpose, idencal FORC measurements has been performed before and
aer treang homogenized sediment material with a citrate-bicarbonate-dithionite (CBD) so-
luon for selecve magnetofossil dissoluon [Ludwig et al., 2013]. Large magnete crystals,
as well as SD parcles embedded in a silicate matrix, are not affected by this treatment. There-
fore, differences shown in Fig. 8.13 between the two sets of measurements represent the
intrinsic magnec signature of CBD-extractable parcles. Hysteresis properes ( rs s
/MM=
0.44, cr c
/1.34HH=, Fig. 8.8) are close to the limit case of randomly oriented, non-interacng
SD parcles with uniaxial anisotropy, despite evident magnetostac interacon signatures
deducible from posive FORC contribuons over the upper quadrant (Fig. 8.13d). Interpreta-
on of interacon signatures in terms of collapsed magnetosome chains or authigenic SD mag-
nete clusters requires further invesgaon [Ludwig et al., 2013]. Coercivity distribuons (Fig.
8.13f) display minor contribuons near c0H=, and their overall shape is beer associable
with intact magnetotacc bacteria cultures (Fig. 8.10) than dispersed magnetosomes in clay
(Fig. 8.11). Coercivity distribuons of magnetofossil-bearing sediment are wider than those of
individual bacterial strains, because of the natural diversity of magnetosome and chain mor-
phologies. On the other hand, no systemac differences are observed between FORC-related
magnezaon raos (Table 8.1), as long as chain integrity is not evidently compromised. In
parcular, FORC properes of PETM sediment appear to be compable with those of similar
magnetofossil-bearing samples, rather than dispersions of equidimensional SD parcles.
Fig. 8.13 (front page): FORC analysis of a pelagic carbonate sample from the Equatorial Pacific, ob-
tained from differences between idencal measurements of the same material before and aer selec-
ve SD magnete dissoluon [Ludwig et al., 2013]. This approach, combined with the fact that the
main magnezaon carriers are magnetofossils, ensures that results shown here represent the uncon-
taminated signature of secondary SD minerals. (a) Set of FORC measurements where every 8th curve is
ploed for clarity. (b) Same as (a), aer subtracng the lower hysteresis branch from each curve. Every
4th curve is shown for clarity. The bell-shaped envelope of all curves is the difference between the
upper and lower hysteresis branches. Its shape is intermediate between the examples shown in Fig.
8.10-11, albeit closer to Fig. 8.10b. (c) FORC diagram calculated with VARIFORC from the measure-
ments shown in (a). The central ridge is overlaid to addional low-amplitude contribuons (<10% of
the central ridge peak), which, because of their extension over the FORC space, represent as much as
50% of the total magnezaon irs
M ‘seen’ by the measurements. (d) Same as (c), aer subtracon
of the central ridge. The lower quadrant partly coincides with the signature of reversible magnec
moment rotaons as predicted by Newell [2005]. Because non-SD contribuons are excluded by the
special preparaon procedure, posive FORC amplitudes over b0H> must represent the signature of
magnetostac interacons between SD parcles. (e) Central ridge isolated from (c) and ploed with a
3 vercal exaggeraon.
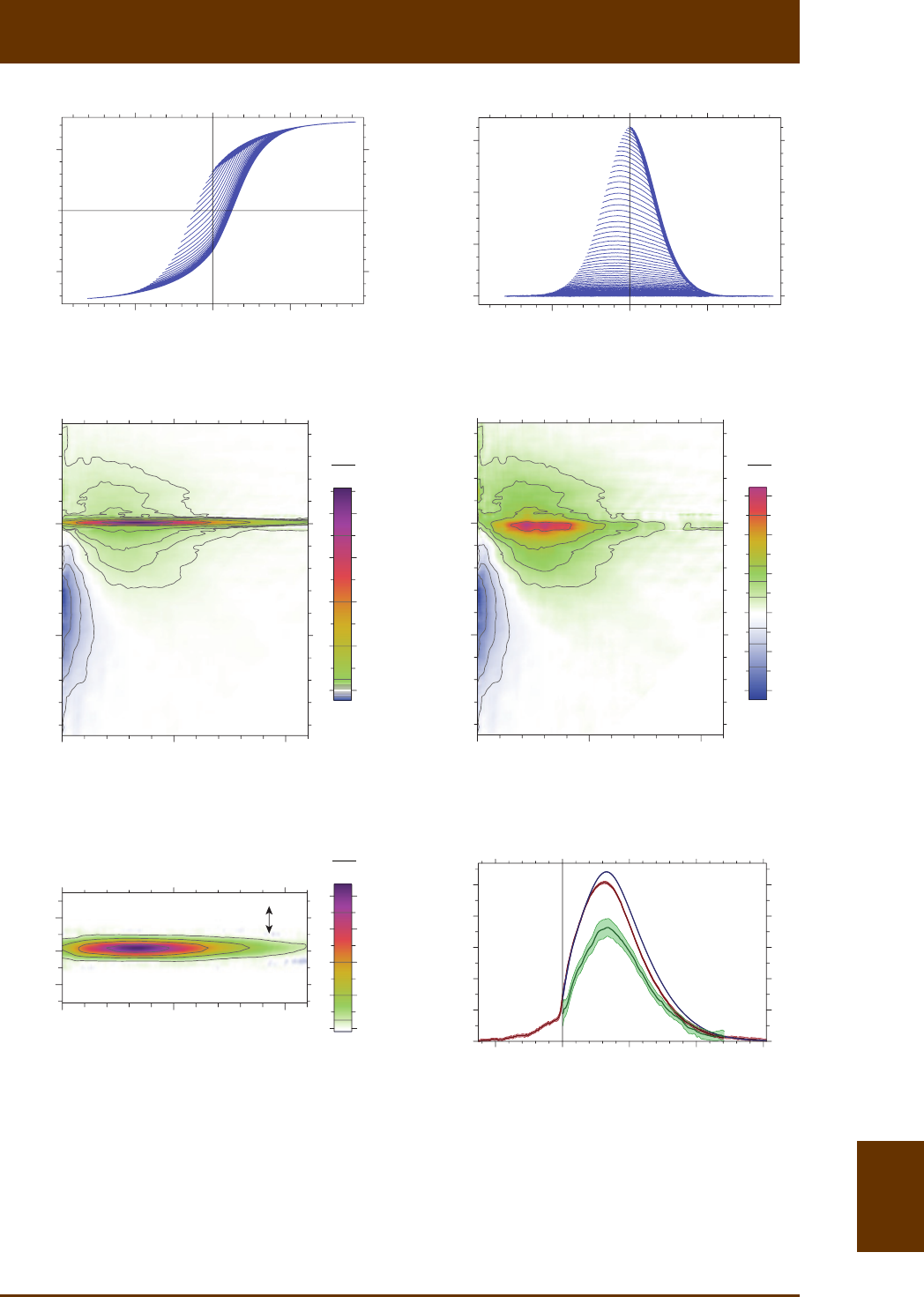
VARIFORC User Manual: 8. FORC tutorial 8.31
Fig. 8.13 (connued): (f) Coercivity distribuons derived from FORC measurements and corresponding
magnezaons calculated by integraon of the distribuons over all fields. Magnezaon raos (e.g.
irs rs
/MM
, cr irs
/MM
, Table 8.1) are similar to those of the MV-1 example in Fig. 8.10 and represen-
tave for magnetofossil-bearing sediment.
–5
0
+5
0
4
8
0
–0.4
0.4
0
4
8
0
20
–100 +1000
H , mT
M , mAm2/kg
0
2
–100 +1000
H , mT
∆M , mAm2/kg
0 50 100
Hc , mT
0
–50
Hb , mT
0 50 100
Hc , mT
0
–50
Hb , mT
0 50 100
Hc , mT
0
–5
Hb , mT
+5
0 50 100
−Hr or Hc , mT
–50
dM/dH, mAm2/(Tkg)
(a) (b)
(c) (d)
(e) (f)
4
6
150
40
2
2
Am
Tk
g
2
2
Am
Tk
g
2
2
Am
Tkg
mAm
2
/kg:
M
rs
= 3.25
M
irs
= 3.18
M
cr
= 2.12
3×
fbf
fcr
firr

VARIFORC User Manual: 8. FORC tutorial 8.32
Table 8.1: Hysteresis parameters cr c
/HH
and rs s
/MM
, and raos between FORC-derived magneza-
ons rs
M, irs
M, and cr
M, for samples described in this arcle.
Material cr c
/HH
rs s
/MM
irs rs
/MM cr rs
/MM
cr irs
/MM
Strictly SD examples
MS-1 dispersion in clay
MS-1
AMB-1 a
MV-1 b
CBD-extractable in pelagic carbonate c
Magnetofossil-rich sediments
Pelagic carbonate c
PETM b
Soppensee d
PSD examples
AV-109 e
EF-3
Volcanic ash b
MD parcles
MD20
5.12
1.233
1.267
1.190
1.340
1.690
1.677
1.503
2.578
4.489
2.421
3.147
0.177
0.494
0.500
0.496
0.442
0.399
0.418
0.411
0.267
0.069
0.219
0.075
1.397
0.928
0.893
0.879
0.815
1.011
0.953
1.066
1.856
2.500
1.976
2.873
0.885
0.510
0.698
0.561
0.651
0.569
0.550
0.387
0.598
0.097
0.024
0
0.633
0.550
0.782
0.638
0.667
0.563
0.576
0.364
0.322
0.039
0.012
0
a FORC data kindly provided by Li et al. [2012].
b FORC data kindly provided by Wang et al. [2013].
c FORC data from Ludwig et al. [2013].
d FORC data from Kind et al. [2011].
e FORC data from Winklhofer et al. [2008].
8.4.2 PSD magnec assemblages
The next two FORC examples are based on PSD parcle assemblages, starng with the
simplest case of an array of idencal, weakly interacng Fe nanoparcles with grain sizes sligh-
tly larger than the upper SD limit [Winklhofer et al., 2008]. These parcles can have two pairs
of anparallel magnec states: so-called ‘flower’ states with nearly homogenous magneza-
on and SD-like magnec moments (SD+ and SD), and single vortex states with nearly zero
magnec moments (SV+ and SV). Hysteresis properes are shaped by the transion sequen-
ces SD+ SV+ SD and SD SV SD+ between posive and negave saturaon. Similar
transions in magnete cubes have been modeled micromagnecally [Newell and Merrill,
2000], yielding the single-parcle hysteresis loops shown in Fig. 8.14.
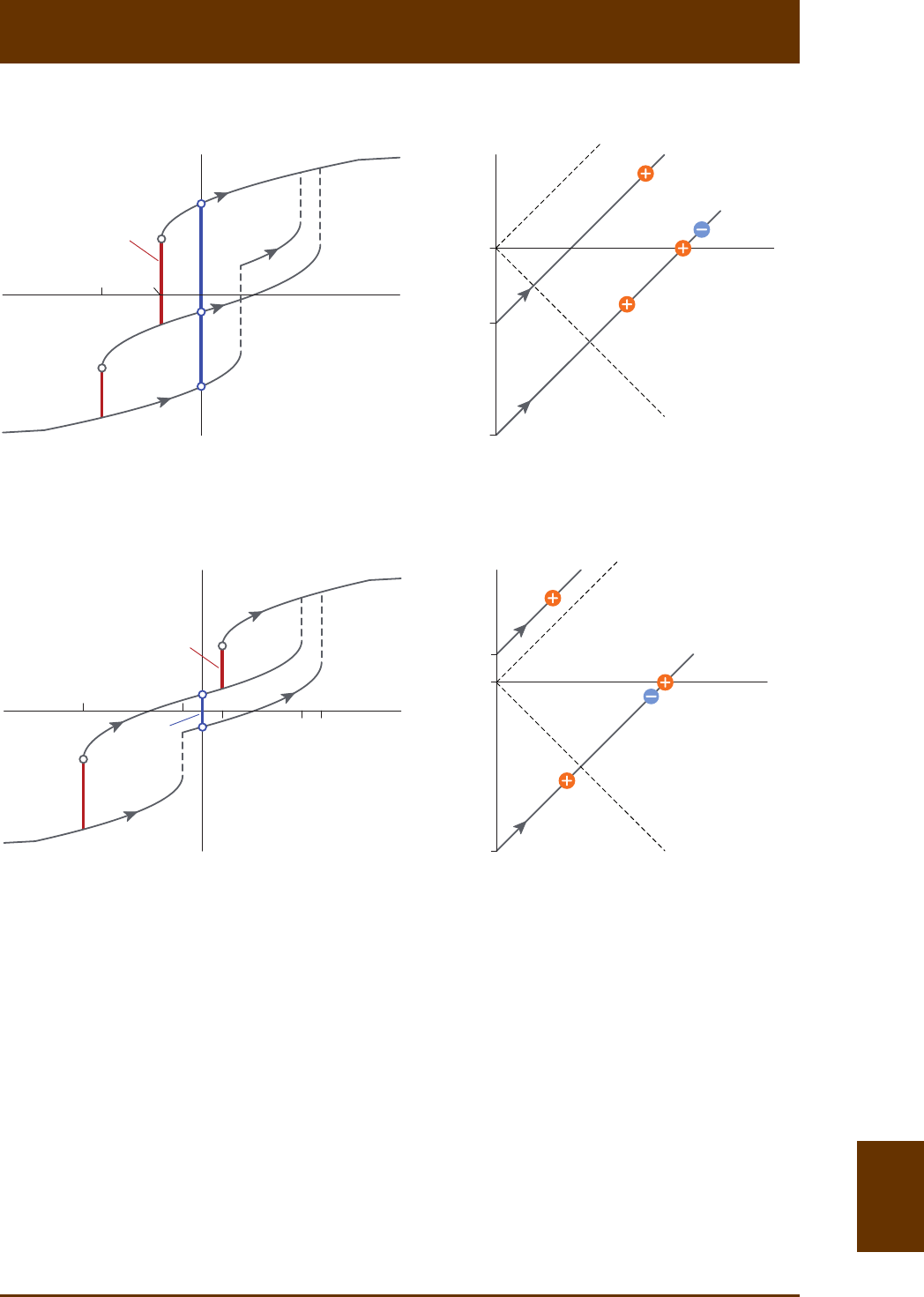
VARIFORC User Manual: 8. FORC tutorial 8.33
Fig. 8.14: Two examples of single parcle hysteresis loops (le plots) and corresponding FORC dia-
grams (right plots), generated by micromagnec simulaons of 0.1 µm (a) and 0.11 µm (c) magnete
cubes by Newell and Merrill [2000]. In both cases, the parcles have two SD-like (SD) and two vortex-
like (SV) magnezaon states. SD-like states in (c) exist only in sufficiently large applied fields and
cannot contribute to remanent magnezaons. Transions between magnec states occur at magne-
zaon jumps (dashed lines and red lines), defining three groups of idencal FORCs 0
M, 1
M and 2
M.
Magnezaon jumps relevant for FORC calculaons are labeled by number pairs like in Fig. 8.3. Corres-
ponding posive and negave peaks of the FORC funcon (b,d) are shown with ‘+’ and ‘’ symbols,
respecvely. Gray diagonal lines with arrows are the only FORC trajectories producing non-zero contri-
buons. Only peaks located to the right of the dashed lines contribute to the backfield demagnezaon
curve and thus to rs
M, determining large differences in magnec remanence properes of otherwise
similar FORC diagrams.
M
0
M
1
M
2
∆M
irr
∆M
irr
∆M
bf
∆M
bf
1,1
2,1
2,2
H
r2
SD
+
SV
+
SV
−
SD
−
(1,1)− M
0
(2,1)− M
1
M
2
−(1,1)
H
r2
H
r1
21
MM
′
(−)
0
∆M
irr
∆M
irr
∆M
bf
H
r2
H
r1
M
0
M
1
M
2
SD
+
SD
−
SV
−
SV
+
2,1
1,1
2,2
10
MM
′
(−)
21
MM
′
(−)
H
r2
H
r1
0
H
c
H
c
H
b
H
b
H
H
M
M
(a) (b)
(c) (d)
H
r1
(2,2)− M
1
(1,1)− M
0
(2,1)− M
1
M
2
−(1,1)
(2,2)− M
1
10
MM
′
(−)

VARIFORC User Manual: 8. FORC tutorial 8.34
The complex FORC signature of Fe nanoparcles (Fig. 8.15) can explained by a combinaon
of the two micromagnec models in Fig. 8.14, with individual peaks corresponding to magnec
transions between SD and SV states. The SV SD+ transion along the lower hysteresis
branch produces a central ridge peaking at c0.15 TH». Addional pairs of posive FORC
peaks at c0.06 TH» and negave peaks just above and below the central ridge are produced
by the remaining transions, while negave FORC amplitudes peaking at b0.15 TH»- can
be explained by reversible magnezaon changes of the SV
+-state in proximity of its de-
nucleaon field. All relevant FORC contribuons occur at or in proximity of SV nucleaon in
±0.01 T and SV denucleaon in ±0.15 T (Fig. 8.15c), producing a constricted hysteresis loop
(Fig. 8.15a) and bimodal coercivity distribuons (Fig. 8.15f).
Unlike the case of isolated SD parcles, magnec state transions from posive saturaon
(i.e. SD+) occur already in posive fields. These transions (e.g. SV nucleaon) are not captured
by remanent demagnezaon measurements, therefore contribung to irr (0)
f
x<, but not to
bk
f. In the example of Fig. 8.15, SV denucleaon is the only process captured by the central
ridge, so that cr
f is characterized by a single peak at c0.15 TH», instead of two peaks, as for
the other two coercivity distribuons.
Fig. 8.15 (front page): FORC analysis of Fe nanodots [Winklhofer et al., 2008]. The arficial sample (AV-
109) is a two-dimensional, quasi-hexagonal array of polycrystalline Fe nanodots with a diameter of
6713 nm and 20 nm thickness. The nanodots center-to-center spacing is 2 dot diameters [Dumas et
al., 2007]. FORC measurements have been performed in the array plane. (a) Set of FORC measure-
ments where every 2nd curve is ploed for clarity. (b) Same as (a), aer subtracng the lower hysteresis
branch from each curve. Every 2nd curve is shown for clarity. Hysteresis loop constricon at 0H= and
the double peak of the curve envelope in (b) are produced by a bimodal distribuon of nucleaon
fields. As evident in (b), some FORCs cross each other, as well as the lower hysteresis branch. This
means that regions outside the major hysteresis loop can in principle be accessed by FORC measure-
ments (e.g. Fig. 8.14a), albeit rarely seen with natural samples and impossible with non-interacng SD
parcles. (c) FORC diagram calculated with VARIFORC from the measurements shown in (a), featuring
localized peaks typical for magnec transions between four magnec states: two SD-like states with
large magnec moments, and two states corresponding to a single magnec vortex with small net
magnec moment. Because magnec parcles in this sample are praccally idencal, magnec tran-
sions occur collecvely, appearing as disnct FORC funcon peaks. In case of less homogenous sam-
ples, FORC peaks would merge into a connuous background with triangular contour lines, as com-
monly seen with natural PSD assemblages. The dashed lines mark the rectangular domain of FORC
amplitudes associated with remanent magnezaons. Accordingly, only about half of the two peaks
at c
H» 0.06 T contribute to rs
M. (d) Same as (c), aer subtracon of the central ridge. The two
negave peaks around the central ridge in (c) now appear as a single contribuon produced by vortex
denucleaon. (e) Central ridge isolated from (c) and ploed with a 2 vercal exaggeraon, featuring
a single peak at 0.15 T.
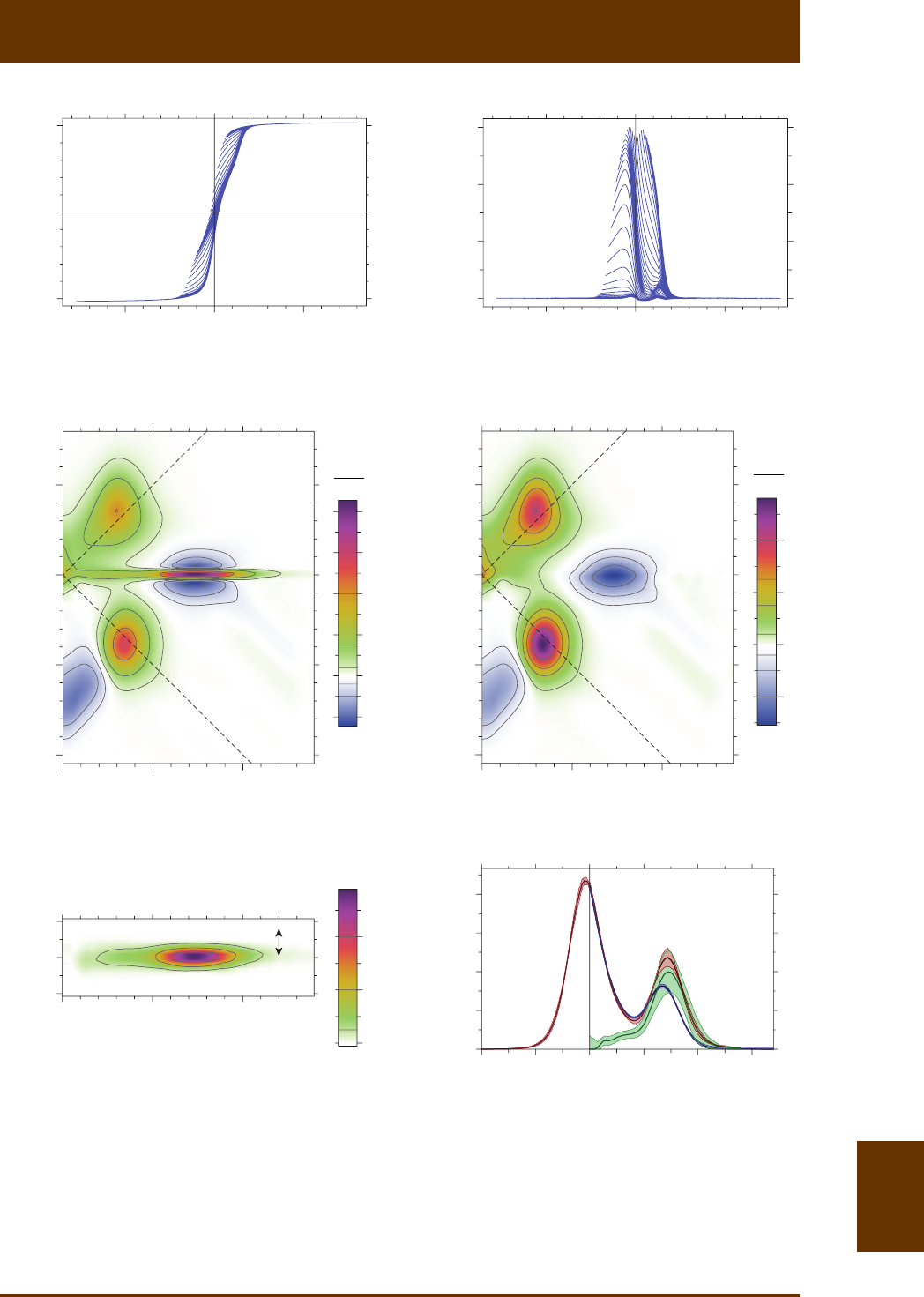
VARIFORC User Manual: 8. FORC tutorial 8.35
Fig. 8.15 (connued): (f) Coercivity distribuons derived from FORC measurements and corresponding
magnezaons calculated by integraon of the distribuons over all fields. The bimodal character of
irr
f and bf
f arises from the existence of two different fields for nucleaon (±0.01 T) and denucleaon
(±0.15 T) of vortex states, producing the constricted hysteresis loop seen in (a). Only vortex denuclea-
on is captured by the central ridge, so that cr
f consists of a single peak.
–0.1
0
+0.1
0
4
8
0
2
4
0
4
8
0
0.2
0.4
+0.50
H
, T
M
, μAm
2
0
20
–0.5 +0.50
H
, T
∆M, nAm
2
0 0.1 0.2
H
c
, T
0
–0.1
H
b
, T
+0.1
–0.2
0 0.1 0.2
H
c
, T
H
b
, T
0 0.1 0.2
H
c
, T
0
H
b
, mT
+20
00.2
−H
r
or H
c
, mT
–0.2
dM/dH
, μAm
2
/T
(a) (b)
(c) (d)
(e) (f)
–0.5
40
60
0
–0.1
+0.1
–0.2
–2
–20
2
2
μAm
T
2
2
μAm
T
2×
μAm
2
:
M
rs
= 28.8
M
irs
= 53.5
M
cr
= 17.5
f
bf
f
cr
f
irr

VARIFORC User Manual: 8. FORC tutorial 8.36
Hysteresis parameters of small PSD crystals are very sensive to vortex nucleaon fields:
if nucleaon from posive saturaon occurs in negave fields, SD-like values of rs s
/MM
are
obtained from SD states that are stable in zero fields. If, on the contrary, vortex states can
nucleate from SD+ in posive fields, rs s
/MM
drops well below 0.5, because of their small net
magnec moment. On the other hand, PSD parcles are always characterized by cr bk
MM<
irs
M<, unlike the case of non-interacng SD parcles, where bk irs
MM³.
The FORC diagram in Fig. 8.15c does not resemble the typical signature of PSD magnete
in synthec and geologic samples, which consists of a unimodal distribuon peaking near
cb
0HH==
, with triangular contour lines having their maximum vercal extension at c0H=
[Roberts et al., 2000; Muxworthy and Dunlop, 2002]. This signature is explainable on the basis
of the abovemenoned PSD processes by taking the following factors into consideraon: first,
magnec states of small PSD parcles are very sensive to grain sizes and shapes, so that
magnezaon jumps of single-parcle hysteresis generate disnct FORC peaks only in case of
exceponally homogeneous samples, such as the Fe nanoparcles discussed above. Second,
the number of possible magnec states grows rapidly with increasing grain size, along with
the number of FORC peaks, which eventually merge into a unimodal funcon. As discussed in
secon 3, the FORC funcon occupies a triangular area of the FORC space limited by verces
with coordinates sat
(0, )H and sat
(,0)H, where sat
H is the field in which the two branches of
the hysteresis loop merge. This limit is consequently imposed to the shape of contour lines.
Finally, the central ridge is broadened by magnetostac interacons, which are probably not
negligible in most synthec magnete powders.
Some natural materials, such as olivine-hosted Fe-Ni parcles in chondric meteorites
[Lappe et al., 2011], contain weakly interacng PSD parcles with sufficiently homogeneous
properes for producing FORC diagrams with disnguishable contribuons from vortex nu-
cleaon and denucleaon. In such cases, high-resoluon measurements are essenal for cap-
turing details of PSD magnezaon processes. Faint evidence of such processes persists in
FORC diagrams of many natural rocks (Fig. 8.16).
Fig. 8.16 (front page): Two FORC examples based on natural samples containing PSD parcle assembla-
ges, i.e. (a-c) basalt (sample EF-3), and (d-f) volcanic ash [Ludwig et al., 2013]. (a,d) FORC measure-
ments, with results aer lower hysteresis branch subtracon shown in the insets. (b,e) FORC diagrams
calculated with VARIFORC from the measurements shown in (a,d). Some features typical for single-
vortex PSD parcles (Fig. 8.15) can be recognized, namely the existence of a central ridge, albeit much
weaker, and the influence of localized negave FORC amplitudes (labeled with a minus sign) on the
overall shape of contour lines. Furthermore, two nearly symmetric posive peaks above and below the
central ridge are disnguishable in (b). Unlike the example of Fig. 8.15, the existence of such contri-
buons cannot be directly inferred from the hysteresis loop. The vercal ridge along c0H= in (e) is a
signature of magnec viscosity.
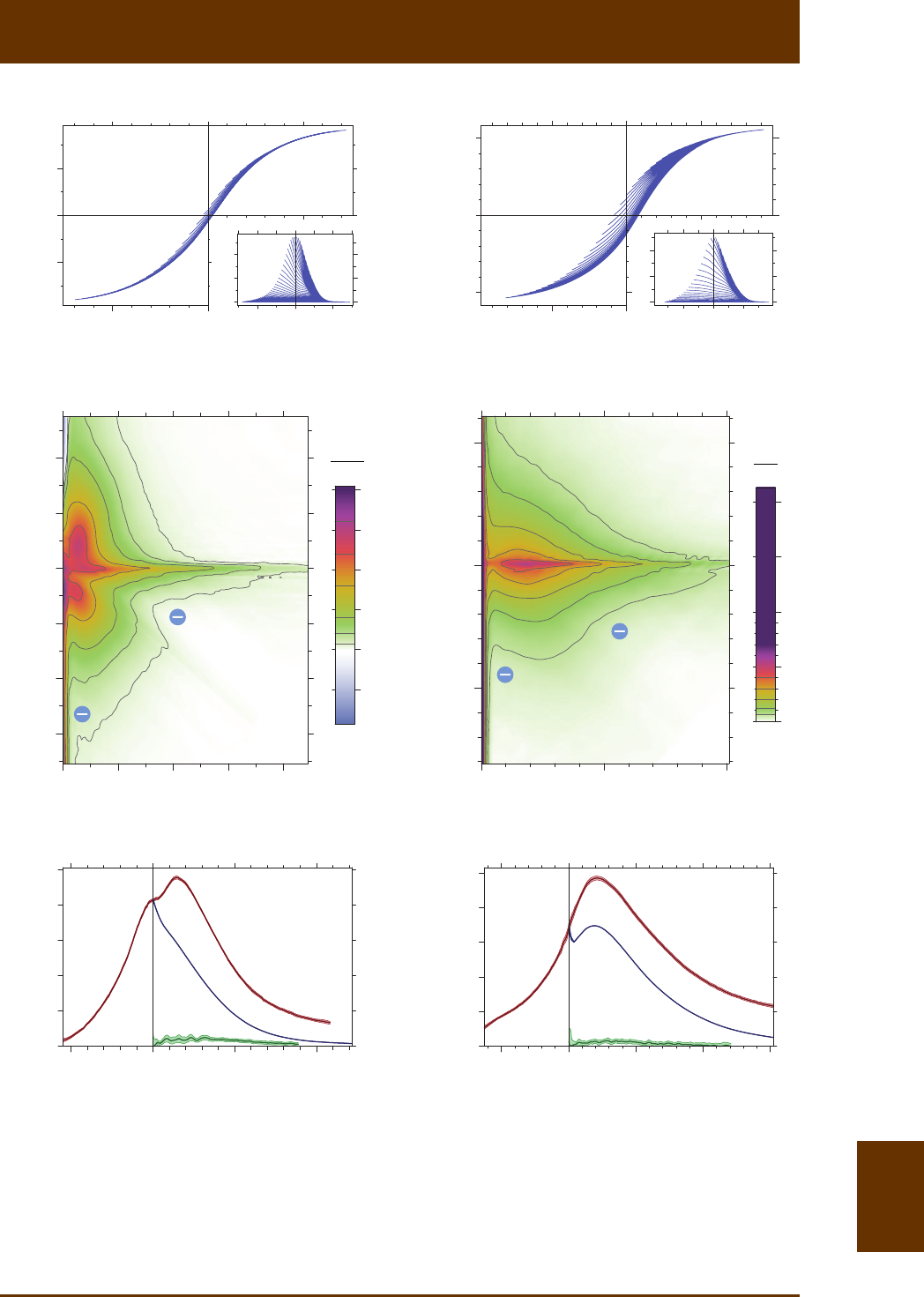
VARIFORC User Manual: 8. FORC tutorial 8.37
Fig. 8.16 (connued): (c,f) Coercivity distribuons derived from the FORC measurements shown in
(b,e). Residual bimodality is sll recognizable for irr
f and bf
f in (c). The central ridge distribuon cr
f is
much smaller than the other two, but significantly 0. Unlike the case of SD parcles, the contribuon
of irr
f over negave arguments is not negligible, as expected from large posive FORC amplitudes over
the upper quadrant.
0
10
20
0
10
20
04080
H
c
, T
0
–40
H
b
, T
+40
0 50 100
H
c
, T
0
–50
H
b
, T
+50
2
2
Am
Tkg
2
2
mAm
T
0
0.2
0.4
050
−H
r
or H
c
, mT
–50
dM/dH
, mAm
2
/T
100
0
0.2
0.4
050
−H
r
or H
c
, mT
–50
dM/dH
, mAm
2
/(Tkg)
100 150
–0.1
0
+0.1
+0.1
0
H
, T
M
, mAm2
(a)
–0.1 –0.1
0.02
0
0
H
, T
–0.1
–50
0
+50
M
, mAm2/kg
+0.1–0.1
20
0
(d)
(b) (e)
(c) (f)
μAm
2
:
Mrs = 13.5
Mirs = 33.7
Mcr = 1.3
f
bf
f
cr
f
irr
f
bf
f
cr
f
irr
mAm
2
/kg:
Mrs = 12.7
Mirs = 25.1
Mcr = 0.3

VARIFORC User Manual: 8. FORC tutorial 8.38
Because of its sharpness, the central ridge remains disnguishable even with contribuons
as low as few % of irs
M. Localized negave amplitudes over the lower quadrant, on the other
hand, produce characterisc contour line indentaons when overlaid to a posive back-
ground. Resoluon of such signatures in PSD samples can benefit paleomagnec applicaons,
where FORC analysis has been proposed as a selecon [Wehland et al., 2005; Carvallo et al.,
2006; Acton et al., 2007] and modeling [Muxworthy et al., 2011a,b] tool for paleointensity
determinaons. For example, cr irs
/MM
is a measure for the relave magnezaon of vortex
states, which probably represent the preferenal PSD contribuon to natural remanent mag-
nezaons.
8.4.3 MD parcles
Domain wall displacement models [Pike et al., 2001b; Church et al., 2011] explain the ideal
hysteresis properes and FORC signature of MD parcles (Fig. 8.4). These properes are met
by annealed magnete crystals [Pike et al., 2001b], while FORC diagrams of unannealed par-
cles (Fig. 8.17) can be explained by the superposion of MD and PSD signatures. As far as
coercivity distribuons are concerned, ideal MD properes are characterized by hysteresis
branches and corresponding irreversible contribuons being are quasi-symmetric about H=
0, which means that irr irr
() ( )
f
xf x»-
. The typical irr
f
-shape of MD parcles resembles a
Laplace (double exponenal) distribuon (Fig. 8.17c). Because the magnezaon of ideal
crystals with weak domain wall pinning is almost completely reversible, irreversible processes,
which occur in form of so-called Barkhausen magnezaon jumps, represent only a small frac-
on of the saturaon magnezaon, i.e. irs s
/1MM. For example, irs s
/0.22MM= for the
20-25 µm magnete crystals of Fig. 8.17. Only a small fracon of all Barkhausen jumps yield a
remanent magnezaon, so that rs irs
/1MM ( rs irs
/0.35MM= for the example of Fig. 8.17).
Since bk irr
(0) (0)ff=, the backfield coercivity distribuon is a funcon that decays much more
rapidly than irr
f
to zero for posive arguments. Finally, cr 0f= because of the absence of a
central ridge.
In summary, ideal MD crystals without strong domain wall pinning are characterized by
cr 0M= and rs irs s
MM M
. For comparison, PSD and SD parcles yield rs irs
MM< and
rs irs
MM³, respecvely. Therefore, the rao rs irs
/MM can be considered as a sort of domain
state indicator analogous to rs s
/MM
, with the important advantage that rs irs
/MM is insensive
to reversible magnezaon processes (e.g. SP contribuons).
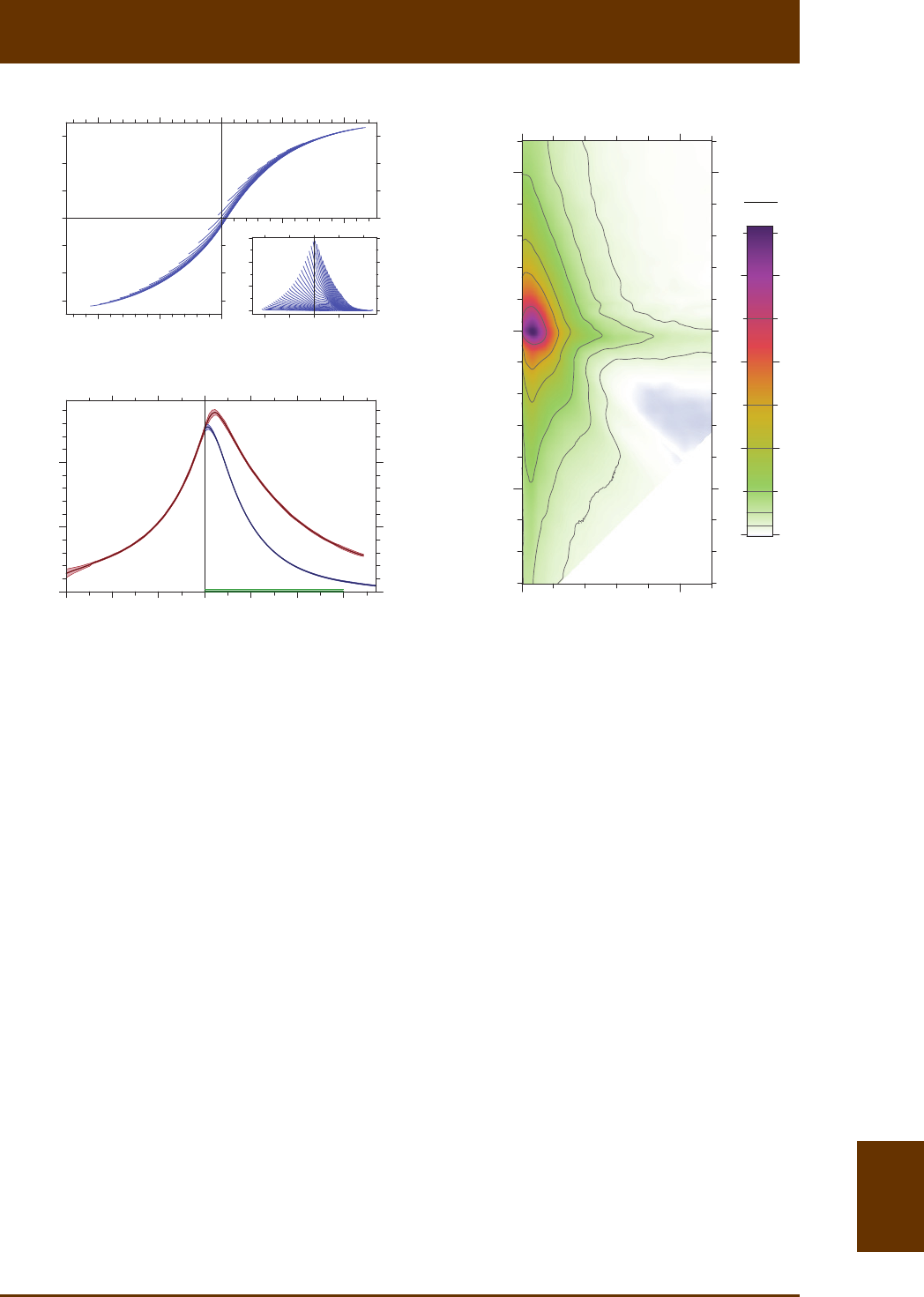
VARIFORC User Manual: 8. FORC tutorial 8.39
Fig. 8.17: FORC analysis of synthec MD magnete parcles with 20-25 µm mean grain size. (a) Set of
FORC measurements where every 8th curve is ploed for clarity. The inset shows the same set of curves
(every 4th is ploed) aer subtracon of the lower hysteresis branch. Measurement details are recog-
nizable only in this plot, because of the very small hysteresis loop opening. (b) FORC diagram obtained
with VARIFORC from the FORC measurements shown in (a). The MD nature of this sample is determi-
ned by the large vercal spread of the FORC funcon in proximity of c0H=. Addional PSD signatures
are recognizable over b0H< and along a sort of blurred central ridge. These features are typical of
unannealed MD crystals. (c) Coercivity distribuons derived from the FORC measurements shown in
(c). irr
f is a quasi-even funcon with similar contribuons over negave and posive field, as expected
for MD parcles. The central ridge does not exist, so that cr 0f=.
–0.2
0
+0.2
+0.1
0
H
, T
M
, mAm
2
(a)
–0.1 –0.1
0.04
0
0
20
40
60
050
H
c
, T
0
–50
H
b
, T
+50
2
2
mAm
T
0
0.5
1.0
020
−H
r
or H
c
, mT
–60
dM/dH
, mAm
2
/T
60
(c)
40–40 –20
(b)
f
bf
f
cr
f
irr
μAm2:
M
rs
= 28.4
M
irs
= 81.7
M
cr
≈ 0

VARIFORC User Manual: 8. FORC tutorial 8.40
8.5 Conclusions
FORC diagrams are two-dimensional parameter representaons of hysteresis processes
providing a lot more details than the convenonal bulk hysteresis parameters rs s
/MM
and
cr c
/HH
. The simplest interpretaon of FORC diagrams is based on Preisach theories, which,
however, rarely describes real magnezaon processes. Dedicated models have been develo-
ped for explaining the FORC properes of ideal SD, PSD, and MD parcle assemblages. Such
models describe ‘end-member’ FORC signatures that can be used for qualitave interpretaon
of FORC diagrams in terms of domain states. This has been the first rock magnec applicaon
of FORC measurements. Meanwhile, connuous modeling improvements and the use of high-
resoluon measurements resulted in first quantave FORC analyses of samples containing
non-interacng SD parcles.
An important forward step in FORC analysis consists in overcoming the quantave gap
with convenonal magnec parameters. As shown in this arcle, FORC measurements define
three different types of irreversible magnezaons and corresponding coercivity distribu-
ons: the first type is represented by the well-known saturaon remanence rs
M and asso-
ciated coercivity distribuon derived from backfield demagnezaon. The second magne-
zaon type defined by FORC measurements is the irreversible saturaon magnezaon irs
M,
which is the sum of all irreversible magnezaon changes occurring along the upper or lower
branch of the hysteresis loop. irs
M is also the total integral of the FORC funcon. The coercivity
distribuon associated with irs
M represents irreversible processes occurring on the upper
hysteresis branch at a given field. The third, so-called central ridge magnezaon cr
M is gene-
rated by the last magnezaon jump occurring in single parcle hysteresis loops of isolated
SD and small PSD magnec parcles. The central ridge coercivity distribuon is derived from
the corresponding signature of the FORC funcon along b0H=.
Unlike rs s
/MM
and cr c
/HH
, these magnezaons are unaffected by reversible magne-
zaons and provide more robust domain state informaon than the Day diagram. For exam-
ple, the Day diagram characteriscs of clay-dispersed, SDS-treated magnetosome chains (Fig.
8.8) suggest a mixture of SD, SP, and PSD parcles. In reality, as seen with FORC diagram mea-
surements, the whole remanent magnezaon of this sample is produced by non-interacng
SD parcles. This sample represents a possible end-member of a trend defined by magneto-
fossil-bearing sediments on the Day diagram. The magnec properes of these sediments are
therefore not necessarily interpretable as mixtures of magnetofossils on one hand, and SP and
PSD parcles on the other. Another example is represented by the Day diagram properes of
small PSD parcles (Fig. 8.15), which plots on the same trend defined by sediments, while its
purely PSD nature is clearly recognizable on the basis of irs rs
/MM
and cr irs
/MM
.
All FORC processing aspects described in this paper, including the calculaon of FORC-
related magnezaons and coercivity distribuons, have been implemented in the VARIFORC
soware package, so that they can become a roune magnec analysis tool.

VARIFORC User Manual: 8. FORC tutorial 8.41
8.6 Literature
Acton, G., Q.-Z. Yin, K.L. Verosub, L. Jovane, A. Roth, B. Jacobsen, and D.S. Ebel (2007). Micromagnec
coercivity distribuons and interacons in chondrules with implicaons for paleointensies of the
early solar system, Journal of Geophysical Research, 112, doi:10.1029/2006JB 004655.
Basso, V., and G. Berto (1994). Descripon of magnec interacons and Henkel plots by the Preisach
hysteresis model, IEEE Transacons on Magnesm, 30, 64-72.
Borcia, I.D., L. Spinu, and A. Stancu (2002). A Preisach-Néel model with thermally variable variance,
IEEE Transacons on Magnesm, 38, 2415-2417.
Carvallo, C., A.R. Muxworthy, D.J. Dunlop, and W. Williams (2003). Micromagnec modeling of first-
order reversal curve (FORC) diagrams for single-domain and pseudo-single-domain magnete,
Earth and Planetary Science Leers, 213, 375-390.
Carvallo, C., D.J. Dunlop, and Ö. Özdemir (2005). Experimental comparison of FORC and remanent
Preisach diagrams, Geophysical Journal Internaonal, 162, 747-754.
Carvallo, C., A. P. Roberts, R. Leonhardt, C. Laj, C. Kissel, M. Perrin, and P. Camps (2006). Increasing the
efficiency of paleointensity analyses by selecon of samples using first-order reversal curve dia-
grams, Journal of Geophysical Research, 111, B12103, doi:10.1029/2005JB 004126.
Chen, A.P., R. Egli, and B.M. Moskowitz (2007). First-order reversal curve (FORC) of natural and cul-
tured biogenic magnete, Journal of Geophysical Research, 112, B08S90, doi:10.1029/2006JB
004575.
Chikazumi, S. (1997). Physics of ferromagnesm, Oxford University Press, New York, 655 pp.
Church, N., J.M. Feinberg, and R. Harrison (2011). Low-temperature domain wall pinning in tanomag-
nete: Quantave modeling of muldomain first-order reversal curve diagrams and AC suscep-
bility, Geochemistry, Geophysics, Geosystems, 12, Q07Z27, doi:10.1029/GC003538.
Coey, J.M.D. (2009). Magnesm and Magnec Materials, Cambridge University Press, Cambridge, 614
pp.
Day, R., M. Fuller, and V.A. Schmidt (1977). Hysteresis properes of tanomagnetes: grain size and
composion dependence, Physics of the Earth and Planetary Interiors, 13, 260-267.
Dunlop, D.J., and Ö. Özdemir (1997). Rock Magnesm: Fundamentals and Froners, Cambridge
University Press, Cambridge, 573.
Dunlop, D.J., M.F. Wesco-Lewis, and M.E. Bailey (1990). Preisach diagrams and anhysteresis: do they
measure interacons?, Physics of the Earth and Planetary Interiors, 65, 62-77.
Dunlop, D.J. (2002a). Theory and applicaon of the Day plot (Mrs/Ms versus Hcr/Hc), 1: Theorecal cur-
ves and tests using tanomagnete data, Journal of Geophysical Research, 107, doi: 10.1029/
2001JB000486.
Dunlop, D.J. (2002b). Theory and applicaon of the Day plot (Mrs/Ms versus Hcr/Hc), 2: Applicaon to
data for rocks, sediments, and soils, Journal of Geophysical Research, 107, doi:10.1029/2001JB
000487.
Dumas, R.K., C.-P. Li, I.V. Roshchin, I.K. Schuller, and K. Liu (2007). Magnec fingerprints of sub-100 nm
Fe dots, Physical Review B, 75, 134405.

VARIFORC User Manual: 8. FORC tutorial 8.42
Egli, R. (2006). Theorecal aspects of dipolar interacons and their appearance in first-order reversal
curves of thermally acvated single-domain parcles, Journal of Geophysical Research, 111,
B12S17, doi:10.1029/2006JB004567.
Egli, R., A.P. Chen, M. Winklhofer, K.P. Kodama, and C.-S. Horng (2010). Detecon of non-interacng
single domain parcles using first-order reversal curve diagrams, Geochemistry, Geophysics, Geo-
systems, 11, Q01Z11, doi:10.1029/2009GC002916.
Egli, R. (2013). VARIFORC: an opmized protocol for the calculaon of non-regular first-order reversal
curve (FORC) diagrams, Global and Planetary Change, 110, 302-320.
Evans, M.E., and F. Heller (2003). Environmental Magnesm: Principles and Applicaons of Enviro-
magnecs, Academic Press, Elsevier, 293 pp.
Ewing, J.A. (1885). Experimental research in magnesm, Philosophical Transacons of the Royal Society
of London, 176, 523-640.
Fabian, K., and T. von Dobeneck (1997). Isothermal magnezaon of samples with stable Preisach
funcon: A survey of hysteresis, remanence, and rock magnec parameters, Journal of Geophysical
Research, 102, 17659-17677.
Fabian, K. (2003). Some addional parameters to esmate domain state from isothermal magne-
zaon measurements, Earth and Planetary Science Leers, 213, 337-345.
Harrison, R.J., and J.M. Feinberg (2008). FORCinel: An improved algorithm for calculang first-order
reversal curve distribuons using locally weighted regression smoothing, Geochemistry, Geo-
physics, Geosystems, 9, Q05016, doi:10.1029/2008GC001987.
Hejda, P., and T. Zelinka (1990). Modeling of hysteresis processes in magnec rock samples using the
Preisach diagram, Physics of the Earth and Planetary Interiors, 63, 32-40.
Heslop, D., and A. Muxworthy (2005). Aspects of calculang first-order reversal curve distribuons,
Journal of Magnesm and Magnec Materials, 288, 155-167.
Heslop, D., and A.P. Roberts (2012). Esmaon of significance levels and confidence intervals for first-
order reversal curve distribuons, Geochemistry, Geophysics, Geosystems, 13, Q12Z40, doi:
10.1029/2012GC004115.
Jacobs, I.S., and C.P. Bean (1955). An approach to elongated fine-parcle magnets, Physical Review,
100, 1060-1067.
Katzgraber, H.G., F. Pázmándi, C.R. Pike, K. Liu, R.T. Scalear, K.L. Verosub, and G.T. Zimányi (2002).
Reversal-field memory in the hysteresis of spin glasses, Physical Review Leers, 89, 257202.
Kind, K., Gehring A.U., Winklhofer, M., Hirt, A.M. (2011). Combined use of magnetometry and spectro-
scopy for idenfying magnetofossils in sediments, Geochemistry, Geophysics, Geosystems, 12,
Q08008, doi:10.1029/2011GC003633.
Kobayashi, A., J.L. Krischvink, C.Z. Nash, R.E. Kopp, D.A. Sauer, L.E. Bertani, W.F. Voorhout, and T.
Taguchi (2006). Experimental observaon of magnetosome chain collapse in magnetotacc bac-
teria: Sedimentological, paleomagnec, and evoluonary implicaons, Earth and Planetary Science
Leers, 245, 538-550.
Kopp, R.E. et al. (2007). Magnetofossil spike during the Paleocene-Eocene thermal maximum: Ferro-
magnec resonance, rock magnec, and electron microscopy evidence from Ancora, New Jersey,
United States, Paleoceanograpy, 22, PA4103, doi:10.1029/2007PA001473.

VARIFORC User Manual: 8. FORC tutorial 8.43
Lappe, S.-C., N.S. Church, T. Kasama, A. Bastos da Silva Fanta, G. Bromiley, R.E. Dunin-Borkowski, J.M.
Feinberg, S. Russell, and R.J. Harrison (2011). Mineral magnesm of dusty olivine: A credible re-
corder of pre-accreonary remanence, Geochemistry, Geophysics, Geosystems, 12, Q12Z35, doi:
10.1029/2011GC003811.
Li, J., W. Wu, Q. Liu, and Y. Pan (2012). Magnec anisotropy, magnetostac interacons, and iden-
ficaon of magnetofossils, Geochemistry, Geophysics, Geosystems, 13, Q10Z51, doi: 10.1029/
2012GC0043 84.
Lippert, P.C., and J.C. Zachos (2007). A biogenic origin for anomalous fine-grained magnec material at
the Paleocene-Eocene boundary at Wilson Lake, New Jersey, Paleoceanography, 22, PA4104,
doi:10.1029/2007PA001471.
Liu, Q., A.P. Robersts, J.C. Larrasoaña, S.K. Banerjee, Y. Guyodo, L. Tauxe, and F. Oldfield (2012).
Environmental magnesm: Principles and applicalons, Reviews of Geophysics, 50, RG4002, doi:
10.1029/ 2012RG000393.
Ludwig, P., R. Egli, S. Bishop, V. Chernenko, T. Frederichs, G. Rugel, and S. Merchel (2013). Charac-
terizaon of primary and secondary magnete in marine sediment by combining chemical and
magnec unmixing techniques, Global and Planetary Change, 110, 321-339.
Mayergoyz, I.D. (1986). Mathemacal models of hysteresis, Physical Review Leers, 56, 1518-1521.
Mitchler, P.D., E. Dan Dahlberg, E.E. Wesseling, and R.M. Roshko (1996). Henkel plots in a temperature
and me dependent Preisach model, IEEE Transacons on Magnesm, 32, 3185-3194.
Muxworthy, A.R., and D.J. Dunlop (2002). First-order reversal curve (FORC) diagrams for pseudo-single-
domain magnetes at high temperature, Earth and Planetary Science Leers, 203, 369-382.
Muxworthy, A., W. Williams, and D. Virdee (2003). Effect of magnetostac interacons on the hyste-
resis parameters of single-domain and pseudo-single-domain grains, Journal of Geophysical Re-
search, 108, 2517, doi: 10.1029/2003JB002588.
Muxworthy, A.R., and W. Williams (2005). Magnetostac interacon fields in first-order-reversal curve
diagrams, Journal of Applied Physics, 97, 063905.
Muxworthy, A.R., and D. Heslop (2011a). A Preisach method for esmang absolute paleofield inten-
sity under the constraint of using only isothermal measurements: 1. Theorecal framework, Journal
of Geophysical Research, 116, B04102, doi: 10.1029/2010JB007843.
Muxworthy, A.R., D. Heslop, G.A. Paterson, and D. Michalk (2011b). A Preisach method for esmang
absolute paleofield intensity under the constraint of using only isothermal measurements: 2. Expe-
rimental tesng, Journal of Geophysical Research, 116, B04103, doi:10.1029/2010 JB007844.
Néel, L. (1958). Sur les effets d’un couplage entre grains ferromagnéques, Comptes Rendus de l’Aca-
démie des Sciences, 246, 2313-2319.
Newell, A.J., and R.T. Merrill (2000). Nucleaon and stability of ferromagnec states, Journal of Geo-
physical Research, 105, 19377-19391.
Newell, A.J. (2005). A high-precision model of first-order reversal curve (FORC) funcons for single-
domain ferromagnets with uniaxial anisotropy, Geochemistry, Geophysics, Geosystems, 6, Q05010,
doi: 10. 1029/2004GC000877.
Pike, C.R., A.P. Roberts, and K.L. Verosub (1999). Characterizing interacons in fine magnec parcle
systems using first order reversal curves, Journal of Applied Physics, 85, 6660-6667.

VARIFORC User Manual: 8. FORC tutorial 8.44
Pike, C.R., A.P. Roberts, and K.L. Verosub (2001a). First-order reversal curve diagrams and thermal
relaxaon effects in magnec parcles, Geophysical Journal Internaonal, 145, 721-730.
Pike, C.R., A.P. Roberts, M.J. Dekkers, and K.L. Verosub (2001b). An invesgaon of mul-domain
hysteresis mechanism using FORC diagrams, Physics of the Earth and Planetary Interiors, 126, 11-
25.
Pike, C.R. (2003). First-order reversal-curve diagrams and reversible magnezaon, Physical Review B,
68, 104424.
Preisach, F. (1935). Über die magnesche Nachwirkung, Zeitschri für Physik, 94, 277-302.
Roberts, A.P., C.R. Pike, and K.L. Verosub (2000). First-order reversal curve diagrams: A new tool for
characterizing the magnec properes of natural samples, Journal of Geophysical Research, 105,
28461-28475.
Roberts, A.P., Q. Liu, C.J. Rowan, L. Chang, C. Carvallo, J. Torrent, an C.-H. Horng (2006). Characte-
rizaon of hemate (α-Fe2O3), goethite (α-FeOOH), greigite (Fe3S4), and pyrrhote (Fe
7S8) using
first-order reversal curve diagrams, Journal of Geophysical Research, 111, B12S35, doi:10.1029/
2006JB004715.
Roberts, A.P., F. Florindo, G. Villa, L. Chang, L. Jovine, S.M. Bohaty, J.C. Larrasoaña, D. Heslop, and J.D.
Fitz Gerald (2011). Magnetotacc bacterial abundance in pelagic marine environments is limited by
organic carbon flux and availability of dissolved iron, Earth and Planetary Science Leers, 310, 441-
452.
Roberts, A.P., L. Chang, D. Heslop, F. Florindo, and J.C. Larrasoaña (2012). Searching for single domain
magnete in the ‘pseudo-single-domain’ sedimentary haystack: Implicaons of biogenic magnete
preservaon for sediment magnesm and relave paleointensity determinaons, Journal of Geo-
physical Research, 117: B08104, doi: 10.1029/2012JB 009412.
Shcherbakov, V.P., M. Winklhofer, M. Hanzlik, and N. Petersen (1997). Elasc stability of chains of
magnetosomes in magnetotacc bacteria, European Biophysical Journal, 26, 319-326.
Sparks, N.H.C., S. Mann, D.A. Bazylinski, D.R. Lovley, H.W. Jannash, and R.B. Frankel (1990). Structure
and morphology of magnete anaerobically-produced by a marine magnetotacc bacterium and a
dissimilatory iron-reducing bacterium, Earth and Planetary Science Leers, 98, 14-22.
Stoner, E.C., and E.P. Wohlfarth (1948). A mechanism of magnec hysteresis in heterogeneous alloys,
Philosophical Transacons of the Royal Society of London, A240, 599-642
Tauxe, L., T.A.T. Mullender, and R. Pick (1996). Potbellies, wasp-waists, and superparamagnesm in
magnec hysteresis, Journal of Geophysical Research, 101, 571-583.
Tauxe, L. (2010). Essenals of Paleomagnesm, University of California Press, 489 pp.
Vajda F., and E. Della Torre (1991). Measurements of output-dependent Preisach funcons, IEEE
Transacons on Magnesm, 27, 4757-4762.
Wang, H., Kent, D.V., and M.J. Jackson (2013). Evidence for abundant isolated magnec nanoparcles
at the Paleocene-Eocene boundary, Proceedings of the Naonal Academy of Sciences of the United
States, 110, 425-430.
Winklhofer, M., and G.T. Zimanyi (2006). Extracng the intrinsic switching field distribuon in perpen-
dicular media: A comparave analysis, Journal of Applied Physics, 99, 08E710.

VARIFORC User Manual: 8. FORC tutorial 8.45
Winklhofer, M., Dumas, R.K., and K. Liu (2008). Idenfying reversible and irreversible magnezaon
changes in prototype paerned media using first- and second-order reversal curves, Journal of Ap-
plied Physics, 103, 07C518.
Wehland, F., R. Leonhardt, F. Vadeboin, and E. Appel (2005). Magnec interacon analysis of basalc
samples and pre-selecon for absolute paleointensity measurements, Geophysical Journal Interna-
onal, 162, 315-320.
Wohlfarth, E.P. (1958). Relaons between different modes of acquision of the remanent magne-
zaon of ferromagnec parcles, Journal of Applied Physics, 29, 595-596.
Woodward, J.G., and E. Della Torre (1960). Parcle interacon in magnec recording tapes, Journal of
Applied Physics, 31, 56-62.
Yamazaki, T., and M. Ikehara (2012). Origin of magnec mineral concentraon variaon in the Sou-
thern Ocean, Paleoceanography, 27, PA2206, doi: 10.1029/2011PA002271.