Efficient Design Of Adaptive Complex Narrowband IIR Filters COZ 1 Cr1485

User Manual: COZ-1

Open the PDF directly: View PDF .
Page Count: 4

EFFICIENT DESIGN OF ADAPTIVE COMPLEX NARROWBAND IIR FILTERS

Georgi Iliev1, Zlatka Nikolova2, Georgi Stoyanov2, Karen Egiazarian1

1 Institute of Signal Processing, Tampere University of Technology

P.O. Box 527, 33101 Tampere, Finland

phone: +358 3 3115 4329, fax: +358 3 3115 3817, email: iliev@cs.tut.fi

2 Department of Telecommunications, Technical University of Sofia

8 Kliment Ohridski St, 1000 Sofia, Bulgaria

phone: +359 2 965 3255, fax: +359 2 68 60 89, email: zvv@tu-sofia.bg

ABSTRACT

In this paper a new adaptive complex digital filter structure

is proposed. First, a very low sensitivity second-order com-

plex bandpass (BP) filter section with independent tuning of

the central frequency and the bandwidth (BW) is developed

(the low sensitivity of the narrow-band realization is ensur-

ing a higher BW-tuning accuracy or better precision in a

severe coefficient quantization). Then, a BP/Bandstop (BS)

adaptive filter structure is formed around this section, using

LMS algorithm to adapt the central frequency. The devel-

oped filter circuit is providing a low computational com-

plexity and a very fast convergence, and is convenient for

cancellation/enhancement of complex sinusoids or narrow-

band signals. All theoretical results in the work are verified

experimentally.

1.INTRODUCTION

The area of narrowband signal elimination/enhancement has

been widely investigated during the last years. A great num-

ber of realizations for real narrowband filters has been pro-

posed [1] – [4]. At the same time only a few complex coun-

terparts have been developed and completely studied [5],

[6]. In this work a new digital adaptive complex narrowband

filter is proposed and investigated.

First, very low magnitude sensitivity narrowband first-

order lowpass (LP) filter section is selected. Then, using a

general rotation transformation, second-order complex coef-

ficient bandpass (BP) section is obtained and its central fre-

quency is made variable without limitations by tuning the

transformation factor θ. The bandwidth (BW) of the section

is made tunable by using the spectral LP to LP transforma-

tion followed by truncated Taylor series expansion. The new

complex filter conducts well in finite wordlength environ-

ment and demonstrates very-low coefficient sensitivity.

Having in mind above-mentioned good characteristics of

this particular type of complex filter, we use it for the design

of an adaptive complex narrowband filter. The behaviour of

the filter has been tested with different values of the main

filter parameters, namely, step of adaptation and filter band-

width.

2.COMPLEX DIGITAL FILTER CIRCUIT

In [7], a new method of designing complex coefficient BP

and BS filters with independently tunable center frequency

and bandwidth is proposed. This method ensures wider

range of tuning of the bandwidth, lower stopband sensitivity,

reduced complexity and higher freedom of tuning compared

to the other well-known methods. We apply this method to

obtain a new complex digital adaptive narrow-band second

order filter section.

It is well known that if the variable z in a given real digi-

tal N-order transfer function H(z) is substituted by

]H] θ−

= or 11 )sincos( −− θ+θ= ]M] , (1)

the new complex coefficient transfer function H(e–jθ) will be

a 2N-order BP/BS filter. The complex circuit realizations

always have two inputs and two outputs (both real and

imaginary), i.e. it is described by 4 transfer functions:

+(]) = +(]) and +(]) = –+(]). (2)

If the starting function H(z) is LP, then all transfer func-

tions (2) are of BP type. If the initial function H(z) is of HP-

type, then some of transfer functions (2) are of BS type. The

new complex filter may have its central frequency every-

where on the frequency axis (0-π) tuned by changing of θ.

The filter’s bandwidth will be tuned in some limits using the

LP to LP spectral transformations of Constantinides

)(

1]7

]

χ−

→−

−

−, (3)

followed by truncated Taylor series expansion in order to

avoid delay-free loops. But we can avoid the usage of trun-

cated Taylor series if we can tune directly the BW of the ini-

tial LP/HP filter by trimming a single multiplier coefficient.

When transformation (1) is applied, it was shown in [8]

that all the properties (including sensitivity) of the prototype

LP/HP structures will be inherited by the new complex

BP/BS filter. Therefore we shall try first to develop or select

a very low-sensitivity prototype for a given pole-disposition

1597

and then to apply transformation (1) in order to obtain a

complex BP section with high accuracy of tuning of the BW.

It is well known that mainly narrow-band BP/BS filters

are of practical importance. Such filters are obtained starting

from very narrow-band LP and wide-band HP prototypes.

As we need a narrow-band BP complex structure, a nar-

row-band (having poles near z = +1) LP structure with very

low-sensitivity has to be develop or found.

After sensitivities investigation of the most often used

first-order sections, it was found that one of the best appli-

cant for LP prototype circuit appeared to be our section LS1

(Fig.1a), proposed in [8]. It has a canonical number of multi-

pliers and delay elements and a unity DC gain. The transfer

function of this section is:

)21(1

)1(

)( −

−

β−−

β= ]

]

]+ (4)

Applying the circuit transformation proposed by Wata-

nabe and Nishihara [9] on this LS1 section, a BP second-

order complex realization is obtained (Fig.1b). This trans-

formation guarantees also a canonical number of elements

for the complex structure.

Out

(a)

In Re

Out Re In Im

Out Im

cos

sin

cos

(b)

Figure 1: (a) Low-sensitivity first order LP section LS1; (b)

Second-order low-sensitivity complex BP structure realiza-

tion.

The transfer functions of the low-sensitivity prototype-

based complex section (Fig. 1b) are:

)12(cos)12(21

sin)1(2

)()(

;

2(cos)12(21

2(cos21

)()(

221

−−

−

−−

−β+θ−β+

θβ−

β=−=

−+−+

−++

]]

]

]+]+

]]

]+]+

(5)

All these transfer functions are of BP type.

In Fig.2a it is shown how the central frequency of the

magnitude response of HRR(z) (5) of the narrow-band second-

order sections of Fig. 1b is tuned by trimming of θ (for fixed

β). The results for the bandwidth tuning by changing β (for

fixed θ) are shown in Fig. 2b. It is seen that the bandwidth is

tuned without problem over a wide frequency range and the

shape of the magnitude is almost not varying in the tuning

process.

The behavior of the filter in a limited word-length envi-

ronment also was investigated. Due to the very low coeffi-

cient sensitivity of the initial section, our filter is behaving

very well even when the coefficients are severely quantized.

(a)

(b)

Figure 2: Magnitude responses of variable BP complex sec-

ond-order filter (a) for different values of θ; (b) for different

values of β.

3.ADAPTIVE COMPLEX NARROWBAND

FILTERING

In Fig. 3 the block-diagram of our narrowband filter section

is shown. In the following we consider the input/output rela-

tions for corresponding BP/BS filters (Eq.(6)-(13)).

1598

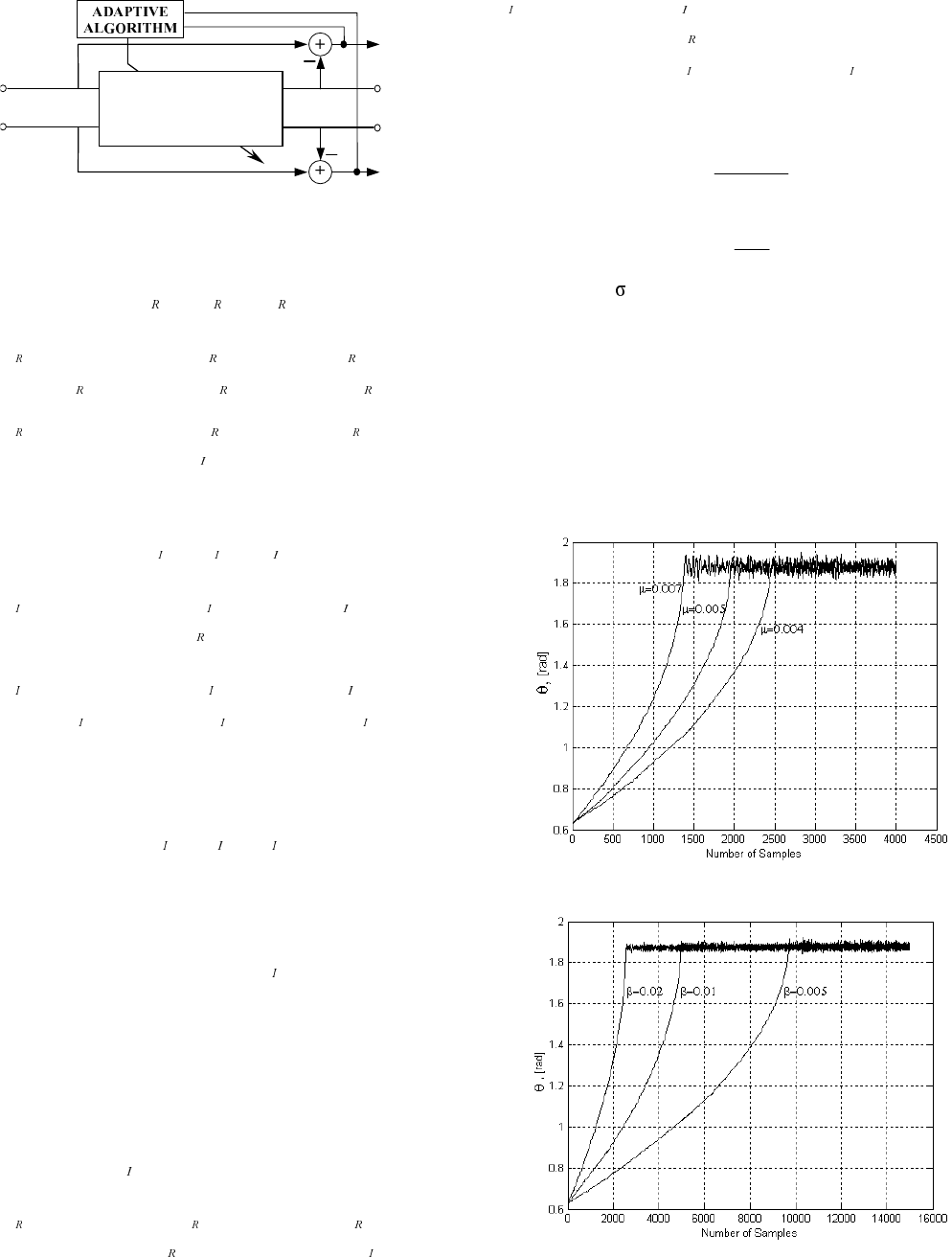
SECOND-ORDER

COMPLEX

FILTER

(n)

Figure 3: Block-diagram of a BP/BS adaptive complex filter

section.

For the BP filter we have the following real output:

)()()( 21 Q\Q\Q\

, (6)

where

)2()12(2)1()(cos4)(2

)2()12()1()(cos)12(2)(

−−ββ+−θβ+β+

+−−β−−θ−β−=

Q[Q[QQ[

Q\Q\QQ\ (7)

).1()(sin)1(4

)2()12()1()(cos)12(2)( 2

−θβ−β−

−−−β−−θ−β−=

Q[Q

Q\Q\QQ\ (8)

The imaginary output is given by the following equa-

tion:

)()()( 21 Q\Q\Q\

, (9)

where

)1()(sin)1(4

)2()12()1()(cos)12(2)( 1

−θβ−β+

+−−β−−θ−β−=

Q[Q

Q\Q\QQ\ (10)

and

).2()12(2)1()(cos4)(2

)2()12()1()(cos)12(2)(

−−ββ+−θβ+β+

+−−β−−θ−β−=

Q[Q[QQ[

Q\Q\QQ\ (11)

For the bandstop filter we have the real output

)()()( Q\Q[QH

−

, (12)

and the imaginary output

)()()( Q\Q[QH

−

. (13)

The cost-function is the power of bandstop filter output

signal:

)]()([ QHQH ∗, (14)

where

)()()( QMHQHQH

. (15)

We apply a Least Mean Squares (LMS) algorithm to up-

date the filter coefficient responsible for the central fre-

quency as follows:

)]()(Re[)()1( ’Q\QHQQ ∗

µ+θ=+θ . (16)

Where µ is the step size controlling the speed of conver-

gence, (*) denotes complex-conjugate, y

′

(n) is a derivative of

)()()( QM\Q\Q\

with respect to the coefficient - subject

of adaptation,

)1()(cos)1(4)1()(sin)12(2

)1()(sin4)1()(sin)12(2)(

’

−θβ−β−−θ−β+

+−θβ−−θ−β=

Q[QQ\Q

Q[QQ\QQ\ (17)

and

).1()(sin4)1()(sin)12(2

)1()(cos)1(4

)1()(sin)12(2)(

’

−θβ−−θ−β+

+−θβ−β+

+−θ−β=

Q[QQ\Q

Q[Q

Q\QQ\

(18)

In order to ensure the stability of the adaptive algorithm

we should set the range of the step size µ. We use the results

reported in [10]:

)R(Trace

0<µ< , (19)

or in a more convenient form:

<µ< 2

0. (20)

,QRXUFDVH 2 is the power of the signal y

′

(n), L is the fil-

ter order and K is a constant depending on the statistical

characteristics of the input signal. In most of the practical

situations K is approximately equal to 0.1.

4.SIMULATION RESULTS

We test our filter for elimination/enhancement of narrow-

band complex signals. Input signal is a mixture of white

noise and complex (analytic) sinusoidal signal.

(a)

(b)

1599

(c)

Figure 4: Trajectories of filter coefficient DIRUGLIIHUHQW

VWHS VL]H  EIRU GLIIHUHQW EDQGZLGWK  F IRU GLIIHUHQW

frequency f.

In Figure 4a the learning curves for different values of

VWHSVL]H DUHVKRZQ,WFDQEHREVHUYHGWKDWWKHODUJHUis the

step size the higher speed of adaptation could be achieved. In

Figure 4b the results for different filter bandwidth are pre-

sented. It is obvious that by narrowing the filter bandwidth

we make the process of convergence slower. Finally, in Fig-

ure 4c we show the behaviour of our filter for a wide range of

sinusoidal frequencies. In all the cases our filter converges to

the proper frequency value.

In the next experiment we investigate the dependence on

 DQG LWV GHELDVLQJ effect. Parameter  GHILQHV WKH ILOWHU

EDQGZLGWK DQG IRU  §  WKH UHVXOWLQJ ILOWHU LV D JRRG

approximation of an ideal notch filter. For the purpose of this

study, the input signal consists of a complex sinusoid at a

frequency of 0DQGZKLWHQRLVH6WHSVL]H LVVHWWR

We have conducted 30 independent trials with a data-length

of  7KH UHVXOWV IRU   ZKLFK WUXH YDOXH LV   DUH

summarized in Table 1. It can be seen that the estimates

improve continuRXVO\ZLWK Dpproaching 0.004.

Table 1: Simulation results for one complex sinusoid in white

QRLVHDVDIXQFWLRQRI DQGIRUDGDWDOHQJWKRI.

[rad]

mean standard deviation

0.050

0.045

0.040

0.035

0.030

0.025

0.020

0.015

0.010

0.005

0.5603

0.5533

0.5471

0.5411

0.5351

0.5278

0.5207

0.5139

0.5074

0.5004

0.0086

0.0075

0.0065

0.0057

0.0051

0.0042

0.0031

0.0026

0.0018

0.0011

5.CONCLUSIONS

A very low sensitivity real LP filter section was transformed

in this work to a complex BP section permitting a very pre-

cise tuning of the BW in much wider frequency range com-

pared to other known sections (based on truncated Taylor

series). The transformation factor θ is used to tune (also

adaptively, by applying an LMS algorithm) the central fre-

quency of the complex BP filter so obtained. The conver-

gence of the algorithm for the developed adaptive complex

filter circuit is investigated experimentally and the efficiency

of the adaptation is clearly demonstrated.

The main advantages of the proposed adaptive structure

are in its low computational complexity, fast convergence

(less than 100 iterations) and the convenience for implemen-

tation with CORDIC processors. The very low sensitivity of

the initial LP section ensures a high tuning accuracy even

with severely quantized multiplier coefficients.

REFERENCES

[1] G. Stoyanov and M. Kawamata, “Variable digital filters,”

Journal of Signal Processing, vol. 1, No 4, pp. 275–290,

July 1997.

[2] J. Chicharo and T. Ng, “Gradient-based adaptive IIR

notch filtering for frequency estimation”, IEEE Trans. on

ASSP, pp. 769 – 777, May 1990.

[3] R. Kumar and R. Pal, “A gradient algorithm for center-

frequency adaptive recursive bandpass filters”, Proc.

IEEE, pp. 371 – 372, Feb. 1985.

[4] A. Nehorai, “A minimal parameter adaptive notch filter

with constrained poles and zeros,” IEEE Trans. on ASSP,

pp. 983–996, Aug. 1985.

[5] S. Nishimura and Hai-Yun Jiang, “Gradient-based com-

plex adaptive IIR notch filters for frequency estimation”,

in Proc. of IEEE Asia Pacific Conference on Circuits and

Systems ’96, Seul, Korea, Nov. 1996, pp. 235–238.

[6] S. Nishimura and Hai-Yun Jiang, “Convergence analysis

of complex adaptive IIR notch filters”, in Proc. of ISCAS

’97, Hong Kong, June. 1997, pp. 2325 –2328.

[7] G. Stoyanov and Zl. Nikolova, “Improved method of de-

sign of complex coefficients variable IIR digital filters”,

in Proc. TELECOM’99, Varna, Bulgaria, vol. 2, Oct.

1999, pp.40–46.

[8] G. Stoyanov, M. Kawamata, Zl. Valkova, “New first and

second-order very low-sensitivity bandpass/ bandstop

complex digital filter sections. ” in Proc. IEEE 1997 Re-

gion 10th Annual Conf. "TENCON’97", Brisbane, Austra-

lia, vol. 1, Dec. 1997, pp. 61–64.

[9] E. Watanabe and A. Nishihara, “A Synthesis of a class of

complex digital filters based on circuitry transforma-

tions”, IEICE Trans., vol. E-74, No.11, pp. 3622 – 3624,

1991.

[10] S. Douglas, “Adaptive filtering,” in Digital Signal Proc-

essing Handbook. D. Williams and V. Madisetti, Eds.

Boca Raton: CRC Press LLC, 1999, pp. 451–619.

1600

Efficient Design Of Adaptive Complex Narrowband IIR Filters COZ 1 Cr1485

Navigation menu

Versions of this User Manual:

Views

Navigation