Idas Guide
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 232 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- List of Tables
- List of Figures
- Introduction
- Mathematical Considerations
- Code Organization
- Using IDAS for IVP Solution
- Access to library and header files
- Data types
- Header files
- A skeleton of the user's main program
- User-callable functions
- IDAS initialization and deallocation functions
- IDAS tolerance specification functions
- Linear solver specification functions
- Initial condition calculation function
- Rootfinding initialization function
- IDAS solver function
- Optional input functions
- Interpolated output function
- Optional output functions
- IDAS reinitialization function
- User-supplied functions
- Residual function
- Error message handler function
- Error weight function
- Rootfinding function
- Jacobian information (direct method with dense Jacobian)
- Jacobian information (direct method with banded Jacobian)
- Jacobian information (direct method with sparse Jacobian)
- Jacobian information (matrix-vector product)
- Preconditioning (linear system solution)
- Preconditioning (Jacobian data)
- Integration of pure quadrature equations
- A parallel band-block-diagonal preconditioner module
- Using IDAS for Forward Sensitivity Analysis
- A skeleton of the user's main program
- User-callable routines for forward sensitivity analysis
- Forward sensitivity initialization and deallocation functions
- Forward sensitivity tolerance specification functions
- Forward sensitivity initial condition calculation function
- IDAS solver function
- Forward sensitivity extraction functions
- Optional inputs for forward sensitivity analysis
- Optional outputs for forward sensitivity analysis
- User-supplied routines for forward sensitivity analysis
- Integration of quadrature equations depending on forward sensitivities
- Sensitivity-dependent quadrature initialization and deallocation
- IDAS solver function
- Sensitivity-dependent quadrature extraction functions
- Optional inputs for sensitivity-dependent quadrature integration
- Optional outputs for sensitivity-dependent quadrature integration
- User-supplied function for sensitivity-dependent quadrature integration
- Note on using partial error control
- Using IDAS for Adjoint Sensitivity Analysis
- A skeleton of the user's main program
- User-callable functions for adjoint sensitivity analysis
- Adjoint sensitivity allocation and deallocation functions
- Adjoint sensitivity optional input
- Forward integration function
- Backward problem initialization functions
- Tolerance specification functions for backward problem
- Linear solver initialization functions for backward problem
- Initial condition calculation functions for backward problem
- Backward integration function
- Optional input functions for the backward problem
- Optional output functions for the backward problem
- Backward integration of quadrature equations
- User-supplied functions for adjoint sensitivity analysis
- DAE residual for the backward problem
- DAE residual for the backward problem depending on the forward sensitivities
- Quadrature right-hand side for the backward problem
- Sensitivity-dependent quadrature right-hand side for the backward problem
- Jacobian information for the backward problem (direct method with dense Jacobian)
- Jacobian information for the backward problem (direct method with banded Jacobian)
- Jacobian information for the backward problem (direct method with sparse Jacobian)
- Jacobian information for the backward problem (matrix-vector product)
- Preconditioning for the backward problem (linear system solution)
- Preconditioning for the backward problem (Jacobian data)
- Using the band-block-diagonal preconditioner for backward problems
- Description of the NVECTOR module
- Providing Alternate Linear Solver Modules
- General Use Linear Solver Components in SUNDIALS
- SUNDIALS Package Installation Procedure
- IDAS Constants
- Bibliography
- Index

User Documentation for idas v1.3.0
(sundials v2.7.0)
Radu Serban, Cosmin Petra, and Alan C. Hindmarsh
Center for Applied Scientific Computing
Lawrence Livermore National Laboratory
September 26, 2016
UCRL-SM-208112
DISCLAIMER
This document was prepared as an account of work sponsored by an agency of the United States
government. Neither the United States government nor Lawrence Livermore National Security, LLC,
nor any of their employees makes any warranty, expressed or implied, or assumes any legal liability or
responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or
process disclosed, or represents that its use would not infringe privately owned rights. Reference herein
to any specific commercial product, process, or service by trade name, trademark, manufacturer, or
otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by
the United States government or Lawrence Livermore National Security, LLC. The views and opinions
of authors expressed herein do not necessarily state or reflect those of the United States government
or Lawrence Livermore National Security, LLC, and shall not be used for advertising or product
endorsement purposes.
This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore
National Laboratory under Contract DE-AC52-07NA27344.
Approved for public release; further dissemination unlimited
Contents
List of Tables vii
List of Figures ix
1 Introduction 1
1.1 Changes from previous versions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 ReadingthisUserGuide................................... 3
1.3 SUNDIALSReleaseLicense................................. 4
1.3.1 CopyrightNotices .................................. 4
1.3.1.1 SUNDIALS Copyright . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.3.1.2 ARKodeCopyright ............................ 5
1.3.2 BSDLicense ..................................... 5
2 Mathematical Considerations 7
2.1 IVPsolution ......................................... 7
2.2 Preconditioning........................................ 11
2.3 Rootfinding .......................................... 11
2.4 Purequadratureintegration................................. 12
2.5 Forward sensitivity analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.5.1 Forward sensitivity methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.5.2 Selection of the absolute tolerances for sensitivity variables . . . . . . . . . . . 14
2.5.3 Evaluation of the sensitivity right-hand side . . . . . . . . . . . . . . . . . . . . 15
2.5.4 Quadratures depending on forward sensitivities . . . . . . . . . . . . . . . . . . 16
2.6 Adjoint sensitivity analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
2.6.1 Sensitivity of G(p) .................................. 16
2.6.2 Sensitivity of g(T, p) ................................. 17
2.6.3 Checkpointingscheme ................................ 18
2.7 Second-order sensitivity analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3 Code Organization 21
3.1 SUNDIALSorganization................................... 21
3.2 IDASorganization ...................................... 21
4 Using IDAS for IVP Solution 25
4.1 Access to library and header files . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
4.2 Datatypes .......................................... 26
4.3 Headerfiles .......................................... 26
4.4 A skeleton of the user’s main program . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
4.5 User-callablefunctions.................................... 30
4.5.1 IDAS initialization and deallocation functions . . . . . . . . . . . . . . . . . . . 30
4.5.2 IDAS tolerance specification functions . . . . . . . . . . . . . . . . . . . . . . . 31
4.5.3 Linear solver specification functions . . . . . . . . . . . . . . . . . . . . . . . . 32
4.5.4 Initial condition calculation function . . . . . . . . . . . . . . . . . . . . . . . . 37
iii
4.5.5 Rootfinding initialization function . . . . . . . . . . . . . . . . . . . . . . . . . 38
4.5.6 IDASsolverfunction................................. 38
4.5.7 Optional input functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
4.5.7.1 Main solver optional input functions . . . . . . . . . . . . . . . . . . . 40
4.5.7.2 Dense/band direct linear solvers optional input functions . . . . . . . 46
4.5.7.3 Sparse direct linear solvers optional input functions . . . . . . . . . . 47
4.5.7.4 Iterative linear solvers optional input functions . . . . . . . . . . . . . 49
4.5.7.5 Initial condition calculation optional input functions . . . . . . . . . . 51
4.5.7.6 Rootfinding optional input functions . . . . . . . . . . . . . . . . . . . 53
4.5.8 Interpolated output function . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
4.5.9 Optional output functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
4.5.9.1 Main solver optional output functions . . . . . . . . . . . . . . . . . . 55
4.5.9.2 Initial condition calculation optional output functions . . . . . . . . . 62
4.5.9.3 Rootfinding optional output functions . . . . . . . . . . . . . . . . . . 62
4.5.9.4 Dense/band direct linear solvers optional output functions . . . . . . 63
4.5.9.5 Sparse direct linear solvers optional output functions . . . . . . . . . 65
4.5.9.6 Iterative linear solvers optional output functions . . . . . . . . . . . . 65
4.5.10 IDAS reinitialization function . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
4.6 User-suppliedfunctions ................................... 69
4.6.1 Residualfunction................................... 69
4.6.2 Error message handler function . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
4.6.3 Errorweightfunction ................................ 71
4.6.4 Rootfindingfunction................................. 71
4.6.5 Jacobian information (direct method with dense Jacobian) . . . . . . . . . . . 71
4.6.6 Jacobian information (direct method with banded Jacobian) . . . . . . . . . . 73
4.6.7 Jacobian information (direct method with sparse Jacobian) . . . . . . . . . . . 74
4.6.8 Jacobian information (matrix-vector product) . . . . . . . . . . . . . . . . . . . 75
4.6.9 Preconditioning (linear system solution) . . . . . . . . . . . . . . . . . . . . . . 76
4.6.10 Preconditioning (Jacobian data) . . . . . . . . . . . . . . . . . . . . . . . . . . 76
4.7 Integration of pure quadrature equations . . . . . . . . . . . . . . . . . . . . . . . . . . 77
4.7.1 Quadrature initialization and deallocation functions . . . . . . . . . . . . . . . 78
4.7.2 IDASsolverfunction................................. 79
4.7.3 Quadrature extraction functions . . . . . . . . . . . . . . . . . . . . . . . . . . 80
4.7.4 Optional inputs for quadrature integration . . . . . . . . . . . . . . . . . . . . . 81
4.7.5 Optional outputs for quadrature integration . . . . . . . . . . . . . . . . . . . . 82
4.7.6 User-supplied function for quadrature integration . . . . . . . . . . . . . . . . . 83
4.8 A parallel band-block-diagonal preconditioner module . . . . . . . . . . . . . . . . . . 83
5 Using IDAS for Forward Sensitivity Analysis 89
5.1 A skeleton of the user’s main program . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
5.2 User-callable routines for forward sensitivity analysis . . . . . . . . . . . . . . . . . . . 91
5.2.1 Forward sensitivity initialization and deallocation functions . . . . . . . . . . . 91
5.2.2 Forward sensitivity tolerance specification functions . . . . . . . . . . . . . . . 94
5.2.3 Forward sensitivity initial condition calculation function . . . . . . . . . . . . . 95
5.2.4 IDASsolverfunction................................. 95
5.2.5 Forward sensitivity extraction functions . . . . . . . . . . . . . . . . . . . . . . 95
5.2.6 Optional inputs for forward sensitivity analysis . . . . . . . . . . . . . . . . . . 97
5.2.7 Optional outputs for forward sensitivity analysis . . . . . . . . . . . . . . . . . 99
5.2.7.1 Main solver optional output functions . . . . . . . . . . . . . . . . . . 99
5.2.7.2 Initial condition calculation optional output functions . . . . . . . . . 102
5.3 User-supplied routines for forward sensitivity analysis . . . . . . . . . . . . . . . . . . 102
5.4 Integration of quadrature equations depending on forward sensitivities . . . . . . . . . 103
5.4.1 Sensitivity-dependent quadrature initialization and deallocation . . . . . . . . . 104
5.4.2 IDASsolverfunction................................. 106
iv

5.4.3 Sensitivity-dependent quadrature extraction functions . . . . . . . . . . . . . . 106
5.4.4 Optional inputs for sensitivity-dependent quadrature integration . . . . . . . . 108
5.4.5 Optional outputs for sensitivity-dependent quadrature integration . . . . . . . 109
5.4.6 User-supplied function for sensitivity-dependent quadrature integration . . . . 110
5.5 Note on using partial error control . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
6 Using IDAS for Adjoint Sensitivity Analysis 113
6.1 A skeleton of the user’s main program . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
6.2 User-callable functions for adjoint sensitivity analysis . . . . . . . . . . . . . . . . . . . 116
6.2.1 Adjoint sensitivity allocation and deallocation functions . . . . . . . . . . . . . 116
6.2.2 Adjoint sensitivity optional input . . . . . . . . . . . . . . . . . . . . . . . . . . 117
6.2.3 Forward integration function . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
6.2.4 Backward problem initialization functions . . . . . . . . . . . . . . . . . . . . . 118
6.2.5 Tolerance specification functions for backward problem . . . . . . . . . . . . . . 121
6.2.6 Linear solver initialization functions for backward problem . . . . . . . . . . . 121
6.2.7 Initial condition calculation functions for backward problem . . . . . . . . . . . 122
6.2.8 Backward integration function . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
6.2.9 Optional input functions for the backward problem . . . . . . . . . . . . . . . . 125
6.2.9.1 Main solver optional input functions . . . . . . . . . . . . . . . . . . . 125
6.2.9.2 Denselinearsolver............................. 125
6.2.9.3 Bandlinearsolver ............................. 126
6.2.9.4 Sparse linear solvers . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
6.2.9.5 SPILS linear solvers . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
6.2.10 Optional output functions for the backward problem . . . . . . . . . . . . . . . 131
6.2.10.1 Main solver optional output functions . . . . . . . . . . . . . . . . . . 131
6.2.10.2 Initial condition calculation optional output function . . . . . . . . . 131
6.2.11 Backward integration of quadrature equations . . . . . . . . . . . . . . . . . . . 132
6.2.11.1 Backward quadrature initialization functions . . . . . . . . . . . . . . 132
6.2.11.2 Backward quadrature extraction function . . . . . . . . . . . . . . . . 133
6.2.11.3 Optional input/output functions for backward quadrature integration 134
6.3 User-supplied functions for adjoint sensitivity analysis . . . . . . . . . . . . . . . . . . 134
6.3.1 DAE residual for the backward problem . . . . . . . . . . . . . . . . . . . . . . 134
6.3.2 DAE residual for the backward problem depending on the forward sensitivities 135
6.3.3 Quadrature right-hand side for the backward problem . . . . . . . . . . . . . . 136
6.3.4 Sensitivity-dependent quadrature right-hand side for the backward problem . . 137
6.3.5 Jacobian information for the backward problem (direct method with dense Ja-
cobian) ........................................ 137
6.3.6 Jacobian information for the backward problem (direct method with banded
Jacobian) ....................................... 139
6.3.7 Jacobian information for the backward problem (direct method with sparse
Jacobian) ....................................... 142
6.3.8 Jacobian information for the backward problem (matrix-vector product) . . . . 144
6.3.9 Preconditioning for the backward problem (linear system solution) . . . . . . . 145
6.3.10 Preconditioning for the backward problem (Jacobian data) . . . . . . . . . . . 147
6.4 Using the band-block-diagonal preconditioner for backward problems . . . . . . . . . . 148
6.4.1 Usage of IDABBDPRE for the backward problem . . . . . . . . . . . . . . . . 149
6.4.2 User-supplied functions for IDABBDPRE . . . . . . . . . . . . . . . . . . . . . 150
7 Description of the NVECTOR module 153
7.1 The NVECTOR SERIAL implementation . . . . . . . . . . . . . . . . . . . . . . . . . 158
7.2 The NVECTOR PARALLEL implementation . . . . . . . . . . . . . . . . . . . . . . . 160
7.3 The NVECTOR OPENMP implementation . . . . . . . . . . . . . . . . . . . . . . . . 163
7.4 The NVECTOR PTHREADS implementation . . . . . . . . . . . . . . . . . . . . . . 165
7.5 The NVECTOR PARHYP implementation . . . . . . . . . . . . . . . . . . . . . . . . 167
v

7.6 The NVECTOR PETSC implementation . . . . . . . . . . . . . . . . . . . . . . . . . 169
7.7 NVECTORExamples .................................... 170
7.8 NVECTOR functions used by IDAS . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172
8 Providing Alternate Linear Solver Modules 175
8.1 Initializationfunction .................................... 176
8.2 Setupfunction ........................................ 176
8.3 Solvefunction......................................... 177
8.4 Performance monitoring function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177
8.5 Memory deallocation function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178
9 General Use Linear Solver Components in SUNDIALS 179
9.1 The DLS modules: DENSE and BAND . . . . . . . . . . . . . . . . . . . . . . . . . . 180
9.1.1 TypeDlsMat ..................................... 180
9.1.2 Accessor macros for the DLS modules . . . . . . . . . . . . . . . . . . . . . . . 183
9.1.3 Functions in the DENSE module . . . . . . . . . . . . . . . . . . . . . . . . . . 183
9.1.4 Functions in the BAND module . . . . . . . . . . . . . . . . . . . . . . . . . . . 186
9.2 TheSLSmodule ....................................... 187
9.2.1 TypeSlsMat ..................................... 188
9.2.2 Functions in the SLS module . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191
9.2.3 TheKLUsolver ................................... 192
9.2.4 TheSUPERLUMTsolver.............................. 192
9.3 The SPILS modules: SPGMR, SPFGMR, SPBCG, and SPTFQMR . . . . . . . . . . 192
9.3.1 TheSPGMRmodule................................. 192
9.3.2 TheSPFGMRmodule................................ 193
9.3.3 TheSPBCGmodule................................. 194
9.3.4 TheSPTFQMRmodule............................... 194
A SUNDIALS Package Installation Procedure 195
A.1 CMake-basedinstallation .................................. 196
A.1.1 Configuring, building, and installing on Unix-like systems . . . . . . . . . . . . 196
A.1.2 Configuration options (Unix/Linux) . . . . . . . . . . . . . . . . . . . . . . . . 198
A.1.3 Configurationexamples ............................... 201
A.1.4 Working with external Libraries . . . . . . . . . . . . . . . . . . . . . . . . . . 202
A.2 Building and Running Examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203
A.3 Configuring, building, and installing on Windows . . . . . . . . . . . . . . . . . . . . . 203
A.4 Installed libraries and exported header files . . . . . . . . . . . . . . . . . . . . . . . . 204
B IDAS Constants 207
B.1 IDASinputconstants .................................... 207
B.2 IDASoutputconstants.................................... 207
Bibliography 213
Index 215
vi
List of Tables
4.1 sundials linear solver interfaces and vector implementations that can be used for each. 29
4.2 Optional inputs for idas,idadls,idasls, and idaspils ................. 41
4.3 Optional outputs from idas,idadls,idasls, and idaspils ............... 56
5.1 Forward sensitivity optional inputs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
5.2 Forward sensitivity optional outputs . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
7.1 Vector Identifications associated with vector kernels supplied with sundials. ..... 155
7.2 Description of the NVECTOR operations . . . . . . . . . . . . . . . . . . . . . . . . . 155
7.3 List of vector functions usage by idas codemodules ................... 173
A.1 sundials librariesandheaderfiles ............................. 205
A.2 sundials libraries and header files (cont.) . . . . . . . . . . . . . . . . . . . . . . . . . 206
vii
List of Figures
2.1 Illustration of the checkpointing algorithm for generation of the forward solution during
the integration of the adjoint system. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.1 Organization of the SUNDIALS suite . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
3.2 Overall structure diagram of the idas package....................... 23
9.1 Diagram of the storage for a banded matrix of type DlsMat ............... 182
9.2 Diagram of the storage for a compressed-sparse-column matrix of type SlsMat .... 190
A.1 Initial ccmake configurationscreen ............................. 197
A.2 Changing the instdir ..................................... 198
ix
Chapter 1
Introduction
idas is part of a software family called sundials: SUite of Nonlinear and DIfferential/ALgebraic
equation Solvers [19]. This suite consists of cvode,arkode,kinsol, and ida, and variants of these
with sensitivity analysis capabilities, cvodes and idas.
idas is a general purpose solver for the initial value problem (IVP) for systems of differential-
algebraic equations (DAEs). The name IDAS stands for Implicit Differential-Algebraic solver with
Sensitivity capabilities. idas is an extension of the ida solver within sundials, itself based on
daspk [5,6]; however, like all sundials solvers, idas is written in ANSI-standard C rather than
Fortran77. Its most notable features are that, (1) in the solution of the underlying nonlinear system
at each time step, it offers a choice of Newton/direct methods and a choice of Inexact Newton/Krylov
(iterative) methods; (2) it is written in a data-independent manner in that it acts on generic vectors
without any assumptions on the underlying organization of the data; and (3) it provides a flexible,
extensible framework for sensitivity analysis, using either forward or adjoint methods. Thus idas
shares significant modules previously written within CASC at LLNL to support the ordinary differen-
tial equation (ODE) solvers cvode [21,12] and pvode [8,9], the DAE solver ida [24] on which idas
is based, the sensitivity-enabled ODE solver cvodes [22,32], and also the nonlinear system solver
kinsol [13].
The Newton/Krylov methods in idas are: the GMRES (Generalized Minimal RESidual) [31],
Bi-CGStab (Bi-Conjugate Gradient Stabilized) [34], and TFQMR (Transpose-Free Quasi-Minimal
Residual) linear iterative methods [17]. As Krylov methods, these require almost no matrix storage
for solving the Newton equations as compared to direct methods. However, the algorithms allow for a
user-supplied preconditioner matrix, and for most problems preconditioning is essential for an efficient
solution.
For very large DAE systems, the Krylov methods are preferable over direct linear solver methods,
and are often the only feasible choice. Among the three Krylov methods in idas, we recommend
GMRES as the best overall choice. However, users are encouraged to compare all three, especially
if encountering convergence failures with GMRES. Bi-CGFStab and TFQMR have an advantage in
storage requirements, in that the number of workspace vectors they require is fixed, while that number
for GMRES depends on the desired Krylov subspace size.
idas is written with a functionality that is a superset of that of ida. Sensitivity analysis capabili-
ties, both forward and adjoint, have been added to the main integrator. Enabling forward sensitivity
computations in idas will result in the code integrating the so-called sensitivity equations simultane-
ously with the original IVP, yielding both the solution and its sensitivity with respect to parameters
in the model. Adjoint sensitivity analysis, most useful when the gradients of relatively few functionals
of the solution with respect to many parameters are sought, involves integration of the original IVP
forward in time followed by the integration of the so-called adjoint equations backward in time. idas
provides the infrastructure needed to integrate any final-condition ODE dependent on the solution of
the original IVP (in particular the adjoint system).
There are several motivations for choosing the Clanguage for idas. First, a general movement away
from Fortran and toward Cin scientific computing was apparent. Second, the pointer, structure,
2 Introduction
and dynamic memory allocation features in Care extremely useful in software of this complexity,
with the great variety of method options offered. Finally, we prefer Cover C++ for idas because of
the wider availability of Ccompilers, the potentially greater efficiency of C, and the greater ease of
interfacing the solver to applications written in extended Fortran.
1.1 Changes from previous versions
Changes in v1.3.0
Two additional nvector implementations were added – one for Hypre (parallel) ParVector vectors,
and one for PetSC vectors. These additions are accompanied by additions to various interface functions
and to user documentation.
Each nvector module now includes a function, N VGetVectorID, that returns the nvector
module name.
An optional input function was added to set a maximum number of linesearch backtracks in
the initial condition calculation, and four user-callable functions were added to support the use of
LAPACK linear solvers in solving backward problems for adjoint sensitivity analysis.
For each linear solver, the various solver performance counters are now initialized to 0 in both the
solver specification function and in solver linit function. This ensures that these solver counters are
initialized upon linear solver instantiation as well as at the beginning of the problem solution.
A bug in for-loop indices was fixed in IDAAckpntAllocVectors. A bug was fixed in the interpo-
lation functions used in solving backward problems.
A memory leak was fixed in the banded preconditioner interface. In addition, updates were done
to return integers from linear solver and preconditioner ’free’ functions.
In interpolation routines for backward problems, added logic to bypass sensitivity interpolation if
input sensitivity argument is NULL.
The Krylov linear solver Bi-CGstab was enhanced by removing a redundant dot product. Various
additions and corrections were made to the interfaces to the sparse solvers KLU and SuperLU MT,
including support for CSR format when using KLU.
New examples were added for use of the openMP vector and for use of sparse direct solvers within
sensitivity integrations.
Minor corrections and additions were made to the idas solver, to the examples, to installation-
related files, and to the user documentation.
Changes in v1.2.0
Two major additions were made to the linear system solvers that are available for use with the idas
solver. First, in the serial case, an interface to the sparse direct solver KLU was added. Second,
an interface to SuperLU MT, the multi-threaded version of SuperLU, was added as a thread-parallel
sparse direct solver option, to be used with the serial version of the NVECTOR module. As part of
these additions, a sparse matrix (CSC format) structure was added to idas.
Otherwise, only relatively minor modifications were made to idas:
In IDARootfind, a minor bug was corrected, where the input array rootdir was ignored, and a
line was added to break out of root-search loop if the initial interval size is below the tolerance ttol.
In IDALapackBand, the line smu = MIN(N-1,mu+ml) was changed to smu = mu + ml to correct an
illegal input error for DGBTRF/DGBTRS.
An option was added in the case of Adjoint Sensitivity Analysis with dense or banded Jacobian:
With a call to IDADlsSetDenseJacFnBS or IDADlsSetBandJacFnBS, the user can specify a user-
supplied Jacobian function of type IDADls***JacFnBS, for the case where the backward problem
depends on the forward sensitivities.
A minor bug was fixed regarding the testing of the input tstop on the first call to IDASolve.
For the Adjoint Sensitivity Analysis case in which the backward problem depends on the forward
sensitivities, options have been added to allow for user-supplied pset,psolve, and jtimes functions.

1.2 Reading this User Guide 3
In order to avoid possible name conflicts, the mathematical macro and function names MIN,MAX,
SQR,RAbs,RSqrt,RExp,RPowerI, and RPowerR were changed to SUNMIN,SUNMAX,SUNSQR,SUNRabs,
SUNRsqrt,SUNRexp,SRpowerI, and SUNRpowerR, respectively. These names occur in both the solver
and in various example programs.
In the User Guide, a paragraph was added in Section 6.2.1 on IDAAdjReInit, and a paragraph
was added in Section 6.2.9 on IDAGetAdjY.
Two new nvector modules have been added for thread-parallel computing environments — one
for openMP, denoted NVECTOR OPENMP, and one for Pthreads, denoted NVECTOR PTHREADS.
With this version of sundials, support and documentation of the Autotools mode of installation
is being dropped, in favor of the CMake mode, which is considered more widely portable.
Changes in v1.1.0
One significant design change was made with this release: The problem size and its relatives, band-
width parameters, related internal indices, pivot arrays, and the optional output lsflag have all
been changed from type int to type long int, except for the problem size and bandwidths in user
calls to routines specifying BLAS/LAPACK routines for the dense/band linear solvers. The function
NewIntArray is replaced by a pair NewIntArray/NewLintArray, for int and long int arrays, re-
spectively. In a minor change to the user interface, the type of the index which in IDAS was changed
from long int to int.
Errors in the logic for the integration of backward problems were identified and fixed.
A large number of minor errors have been fixed. Among these are the following: A missing
vector pointer setting was added in IDASensLineSrch. In IDACompleteStep, conditionals around
lines loading a new column of three auxiliary divided difference arrays, for a possible order increase,
were fixed. After the solver memory is created, it is set to zero before being filled. In each linear solver
interface function, the linear solver memory is freed on an error return, and the **Free function now
includes a line setting to NULL the main memory pointer to the linear solver memory. A memory leak
was fixed in two of the IDASp***Free functions. In the rootfinding functions IDARcheck1/IDARcheck2,
when an exact zero is found, the array glo of gvalues at the left endpoint is adjusted, instead of
shifting the tlocation tlo slightly. In the installation files, we modified the treatment of the macro
SUNDIALS USE GENERIC MATH, so that the parameter GENERIC MATH LIB is either defined
(with no value) or not defined.
1.2 Reading this User Guide
The structure of this document is as follows:
•In Chapter 2, we give short descriptions of the numerical methods implemented by idas for
the solution of initial value problems for systems of DAEs, continue with short descriptions of
preconditioning (§2.2) and rootfinding (§2.3), and then give an overview of the mathematical
aspects of sensitivity analysis, both forward (§2.5) and adjoint (§2.6).
•The following chapter describes the structure of the sundials suite of solvers (§3.1) and the
software organization of the idas solver (§3.2).
•Chapter 4is the main usage document for idas for simulation applications. It includes a complete
description of the user interface for the integration of DAE initial value problems. Readers that
are not interested in using idas for sensitivity analysis can then skip the next two chapters.
•Chapter 5describes the usage of idas for forward sensitivity analysis as an extension of its IVP
integration capabilities. We begin with a skeleton of the user main program, with emphasis
on the steps that are required in addition to those already described in Chapter 4. Following
that we provide detailed descriptions of the user-callable interface routines specific to forward
sensitivity analysis and of the additonal optional user-defined routines.

4 Introduction
•Chapter 6describes the usage of idas for adjoint sensitivity analysis. We begin by describing
the idas checkpointing implementation for interpolation of the original IVP solution during
integration of the adjoint system backward in time, and with an overview of a user’s main
program. Following that we provide complete descriptions of the user-callable interface routines
for adjoint sensitivity analysis as well as descriptions of the required additional user-defined
routines.
•Chapter 7gives a brief overview of the generic nvector module shared amongst the various
components of sundials, as well as details on the nvector implementations provided with
sundials: a serial implementation (§7.1), a distributed memory parallel implementation based
on MPI (§7.2), and two thread-parallel implementations based on openMP (§7.3) and Pthreads
(§7.4), respectively.
•Chapter 8describes the specifications of linear solver modules as supplied by the user.
•Chapter 9describes in detail the generic linear solvers shared by all sundials solvers.
•Finally, in the appendices, we provide detailed instructions for the installation of idas, within
the structure of sundials (Appendix A), as well as a list of all the constants used for input to
and output from idas functions (Appendix B).
The reader should be aware of the following notational conventions in this user guide: program
listings and identifiers (such as IDAInit) within textual explanations appear in typewriter type style;
fields in Cstructures (such as content) appear in italics; and packages or modules, such as idadense,
are written in all capitals. Usage and installation instructions that constitute important warnings are
marked with a triangular symbol in the margin.
!
1.3 SUNDIALS Release License
The SUNDIALS packages are released open source, under a BSD license. The only requirements of
the BSD license are preservation of copyright and a standard disclaimer of liability. Our Copyright
notice is below along with the license.
**PLEASE NOTE** If you are using SUNDIALS with any third party libraries linked in (e.g.,
!
LaPACK, KLU, SuperLU MT, petsc, or hypre), be sure to review the respective license of the package
as that license may have more restrictive terms than the SUNDIALS license. For example, if someone
builds SUNDIALS with a statically linked KLU, the build is subject to terms of the LGPL license
(which is what KLU is released with) and *not* the SUNDIALS BSD license anymore.
1.3.1 Copyright Notices
All SUNDIALS packages except ARKode are subject to the following Copyright notice.
1.3.1.1 SUNDIALS Copyright
Copyright (c) 2002-2016, Lawrence Livermore National Security. Produced at the Lawrence Livermore
National Laboratory. Written by A.C. Hindmarsh, D.R. Reynolds, R. Serban, C.S. Woodward, S.D.
Cohen, A.G. Taylor, S. Peles, L.E. Banks, and D. Shumaker.
UCRL-CODE-155951 (CVODE)
UCRL-CODE-155950 (CVODES)
UCRL-CODE-155952 (IDA)
UCRL-CODE-237203 (IDAS)
LLNL-CODE-665877 (KINSOL)
All rights reserved.

1.3 SUNDIALS Release License 5
1.3.1.2 ARKode Copyright
ARKode is subject to the following joint Copyright notice. Copyright (c) 2015-2016, Southern
Methodist University and Lawrence Livermore National Security Written by D.R. Reynolds, D.J.
Gardner, A.C. Hindmarsh, C.S. Woodward, and J.M. Sexton.
LLNL-CODE-667205 (ARKODE)
All rights reserved.
1.3.2 BSD License
Redistribution and use in source and binary forms, with or without modification, are permitted
provided that the following conditions are met:
1. Redistributions of source code must retain the above copyright notice, this list of conditions
and the disclaimer below.
2. Redistributions in binary form must reproduce the above copyright notice, this list of conditions
and the disclaimer (as noted below) in the documentation and/or other materials provided with the
distribution.
3. Neither the name of the LLNS/LLNL nor the names of its contributors may be used to endorse
or promote products derived from this software without specific prior written permission.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS
”AS IS” AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED
TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTIC-
ULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL LAWRENCE LIVERMORE NA-
TIONAL SECURITY, LLC, THE U.S. DEPARTMENT OF ENERGY OR CONTRIBUTORS BE
LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CON-
SEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUB-
STITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS IN-
TERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN
CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE)
ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE
POSSIBILITY OF SUCH DAMAGE.
Additional BSD Notice
1. This notice is required to be provided under our contract with the U.S. Department of Energy
(DOE). This work was produced at Lawrence Livermore National Laboratory under Contract
No. DE-AC52-07NA27344 with the DOE.
2. Neither the United States Government nor Lawrence Livermore National Security, LLC nor any
of their employees, makes any warranty, express or implied, or assumes any liability or respon-
sibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or
process disclosed, or represents that its use would not infringe privately-owned rights.
3. Also, reference herein to any specific commercial products, process, or services by trade name,
trademark, manufacturer or otherwise does not necessarily constitute or imply its endorsement,
recommendation, or favoring by the United States Government or Lawrence Livermore National
Security, LLC. The views and opinions of authors expressed herein do not necessarily state or
reflect those of the United States Government or Lawrence Livermore National Security, LLC,
and shall not be used for advertising or product endorsement purposes.
Chapter 2
Mathematical Considerations
idas solves the initial-value problem (IVP) for a DAE system of the general form
F(t, y, ˙y)=0, y(t0) = y0,˙y(t0) = ˙y0,(2.1)
where y, ˙y, and Fare vectors in RN,tis the independent variable, ˙y=dy/dt, and initial values y0,
˙y0are given. (Often tis time, but it certainly need not be.)
Additionally, if (2.1) depends on some parameters p∈RNp, i.e.
F(t, y, ˙y, p)=0
y(t0) = y0(p),˙y(t0) = ˙y0(p),(2.2)
idas can also compute first order derivative information, performing either forward sensitivity analysis
or adjoint sensitivity analysis. In the first case, idas computes the sensitivities of the solution with
respect to the parameters p, while in the second case, idas computes the gradient of a derived function
with respect to the parameters p.
2.1 IVP solution
Prior to integrating a DAE initial-value problem, an important requirement is that the pair of vectors
y0and ˙y0are both initialized to satisfy the DAE residual F(t0, y0,˙y0) = 0. For a class of problems that
includes so-called semi-explicit index-one systems, idas provides a routine that computes consistent
initial conditions from a user’s initial guess [6]. For this, the user must identify sub-vectors of y(not
necessarily contiguous), denoted ydand ya, which are its differential and algebraic parts, respectively,
such that Fdepends on ˙ydbut not on any components of ˙ya. The assumption that the system is
“index one” means that for a given tand yd, the system F(t, y, ˙y) = 0 defines yauniquely. In this
case, a solver within idas computes yaand ˙ydat t=t0, given ydand an initial guess for ya. A
second available option with this solver also computes all of y(t0) given ˙y(t0); this is intended mainly
for quasi-steady-state problems, where ˙y(t0) = 0 is given. In both cases, idas solves the system
F(t0, y0,˙y0) = 0 for the unknown components of y0and ˙y0, using Newton iteration augmented with
a line search global strategy. In doing this, it makes use of the existing machinery that is to be used
for solving the linear systems during the integration, in combination with certain tricks involving the
step size (which is set artificially for this calculation). For problems that do not fall into either of
these categories, the user is responsible for passing consistent values, or risks failure in the numerical
integration.
The integration method used in idas is the variable-order, variable-coefficient BDF (Backward
Differentiation Formula), in fixed-leading-coefficient form [3]. The method order ranges from 1 to 5,
with the BDF of order qgiven by the multistep formula
q
X
i=0
αn,iyn−i=hn˙yn,(2.3)

8 Mathematical Considerations
where ynand ˙ynare the computed approximations to y(tn) and ˙y(tn), respectively, and the step size
is hn=tn−tn−1. The coefficients αn,i are uniquely determined by the order q, and the history of the
step sizes. The application of the BDF (2.3) to the DAE system (2.1) results in a nonlinear algebraic
system to be solved at each step:
G(yn)≡F tn, yn, h−1
n
q
X
i=0
αn,iyn−i!= 0 .(2.4)
Regardless of the method options, the solution of the nonlinear system (2.4) is accomplished with
some form of Newton iteration. This leads to a linear system for each Newton correction, of the form
J[yn(m+1) −yn(m)] = −G(yn(m)),(2.5)
where yn(m)is the m-th approximation to yn. Here Jis some approximation to the system Jacobian
J=∂G
∂y =∂F
∂y +α∂F
∂˙y,(2.6)
where α=αn,0/hn. The scalar αchanges whenever the step size or method order changes.
For the solution of the linear systems within the Newton corrections, idas provides several choices,
including the option of an user-supplied linear solver module. The linear solver modules distributed
with sundials are organized in three families, a direct family comprising direct linear solvers for dense
or banded matrices, a sparse family comprising direct linear solvers for matrices stored in compressed-
sparse-column format, and a spils family comprising scaled preconditioned iterative (Krylov) linear
solvers. The methods offered through these modules are as follows:
•dense direct solvers, using either an internal implementation or a Blas/Lapack implementation
(serial or threaded vector modules only),
•band direct solvers, using either an internal implementation or a Blas/Lapack implementation
(serial or threaded vector modules only),
•sparse direct solver interfaces, using either the KLU sparse solver library [14,1], or the thread-
enabled SuperLU MT sparse solver library [27,15,2] (serial or threaded vector modules only)
[Note that users will need to download and install the KLU or SuperLU MT packages indepen-
dent of idas],
•spgmr, a scaled preconditioned GMRES (Generalized Minimal Residual method) solver without
restarts,
•spbcg, a scaled preconditioned Bi-CGStab (Bi-Conjugate Gradient Stable method) solver, or
•sptfqmr, a scaled preconditioned TFQMR (Transpose-Free Quasi-Minimal Residual method)
solver.
For large stiff systems, where direct methods are not feasible, the combination of a BDF integrator
and any of the preconditioned Krylov methods (spgmr,spbcg, or sptfqmr) yields a powerful tool
because it combines established methods for stiff integration, nonlinear iteration, and Krylov (linear)
iteration with a problem-specific treatment of the dominant source of stiffness, in the form of the
user-supplied preconditioner matrix [4]. For the spils linear solvers, preconditioning is allowed only
on the left (see §2.2). Note that the direct linear solvers (dense, band, and sparse) can only be used
with serial or threaded vector representations.
In the process of controlling errors at various levels, idas uses a weighted root-mean-square norm,
denoted k · kWRMS, for all error-like quantities. The multiplicative weights used are based on the
current solution and on the relative and absolute tolerances input by the user, namely
Wi= 1/[rtol · |yi|+atoli].(2.7)

2.1 IVP solution 9
Because 1/Wirepresents a tolerance in the component yi, a vector whose norm is 1 is regarded as
“small”. For brevity, we will usually drop the subscript WRMS on norms in what follows.
In the case of a direct linear solver (dense, band, or sparse), the nonlinear iteration (2.5) is a
Modified Newton iteration, in that the Jacobian Jis fixed (and usually out of date), with a coefficient
¯αin place of αin J. When using one of the Krylov methods spgmr,spbcg, or sptfqmr as the linear
solver, the iteration is an Inexact Newton iteration, using the current Jacobian (through matrix-free
products Jv), in which the linear residual J∆y+Gis nonzero but controlled. The Jacobian matrix
J(direct cases) or preconditioner matrix P(spgmr/spbcg/sptfqmr case) is updated when:
•starting the problem,
•the value ¯αat the last update is such that α/¯α < 3/5 or α/¯α > 5/3, or
•a non-fatal convergence failure occurred with an out-of-date Jor P.
The above strategy balances the high cost of frequent matrix evaluations and preprocessing with
the slow convergence due to infrequent updates. To reduce storage costs on an update, Jacobian
information is always reevaluated from scratch.
The stopping test for the Newton iteration in idas ensures that the iteration error yn−yn(m)is
small relative to yitself. For this, we estimate the linear convergence rate at all iterations m > 1 as
R=δm
δ11
m−1
,
where the δm=yn(m)−yn(m−1) is the correction at iteration m= 1,2, . . .. The Newton iteration is
halted if R > 0.9. The convergence test at the m-th iteration is then
Skδmk<0.33 ,(2.8)
where S=R/(R−1) whenever m > 1 and R≤0.9. The user has the option of changing the constant
in the convergence test from its default value of 0.33. The quantity Sis set to S= 20 initially and
whenever Jor Pis updated, and it is reset to S= 100 on a step with α6= ¯α. Note that at m= 1, the
convergence test (2.8) uses an old value for S. Therefore, at the first Newton iteration, we make an
additional test and stop the iteration if kδ1k<0.33 ·10−4(since such a δ1is probably just noise and
therefore not appropriate for use in evaluating R). We allow only a small number (default value 4)
of Newton iterations. If convergence fails with Jor Pcurrent, we are forced to reduce the step size
hn, and we replace hnby hn/4. The integration is halted after a preset number (default value 10)
of convergence failures. Both the maximum allowable Newton iterations and the maximum nonlinear
convergence failures can be changed by the user from their default values.
When spgmr,spbcg, or sptfqmr is used to solve the linear system, to minimize the effect of linear
iteration errors on the nonlinear and local integration error controls, we require the preconditioned
linear residual to be small relative to the allowed error in the Newton iteration, i.e., kP−1(Jx +G)k<
0.05 ·0.33. The safety factor 0.05 can be changed by the user.
In the direct linear solver cases, the Jacobian Jdefined in (2.6) can be either supplied by the user or
have idas compute one internally by difference quotients. In the latter case, we use the approximation
Jij = [Fi(t, y +σjej,˙y+ασjej)−Fi(t, y, ˙y)]/σj,with
σj=√Umax {|yj|,|h˙yj|,1/Wj}sign(h˙yj),
where Uis the unit roundoff, his the current step size, and Wjis the error weight for the component
yjdefined by (2.7). In the spgmr/spbcg/sptfqmr case, if a routine for Jv is not supplied, such
products are approximated by
Jv = [F(t, y +σv, ˙y+ασv)−F(t, y, ˙y)]/σ ,
where the increment σis 1/kvk. As an option, the user can specify a constant factor that is inserted
into this expression for σ.

10 Mathematical Considerations
We note that with the sparse direct solvers, the Jacobian must be supplied by a user routine in
compressed-sparse-column format.
During the course of integrating the system, idas computes an estimate of the local truncation
error, LTE, at the n-th time step, and requires this to satisfy the inequality
kLTEkWRMS ≤1.
Asymptotically, LTE varies as hq+1 at step size hand order q, as does the predictor-corrector difference
∆n≡yn−yn(0). Thus there is a constant Csuch that
LTE = C∆n+O(hq+2),
and so the norm of LTE is estimated as |C| · k∆nk. In addition, idas requires that the error in the
associated polynomial interpolant over the current step be bounded by 1 in norm. The leading term
of the norm of this error is bounded by ¯
Ck∆nkfor another constant ¯
C. Thus the local error test in
idas is
max{|C|,¯
C}k∆nk ≤ 1.(2.9)
A user option is available by which the algebraic components of the error vector are omitted from the
test (2.9), if these have been so identified.
In idas, the local error test is tightly coupled with the logic for selecting the step size and order.
First, there is an initial phase that is treated specially; for the first few steps, the step size is doubled
and the order raised (from its initial value of 1) on every step, until (a) the local error test (2.9) fails,
(b) the order is reduced (by the rules given below), or (c) the order reaches 5 (the maximum). For
step and order selection on the general step, idas uses a different set of local error estimates, based
on the asymptotic behavior of the local error in the case of fixed step sizes. At each of the orders q0
equal to q,q−1 (if q > 1), q−2 (if q > 2), or q+ 1 (if q < 5), there are constants C(q0) such that the
norm of the local truncation error at order q0satisfies
LTE(q0) = C(q0)kφ(q0+ 1)k+O(hq0+2),
where φ(k) is a modified divided difference of order kthat is retained by idas (and behaves asymp-
totically as hk). Thus the local truncation errors are estimated as ELTE(q0) = C(q0)kφ(q0+ 1)kto
select step sizes. But the choice of order in idas is based on the requirement that the scaled derivative
norms, khky(k)k, are monotonically decreasing with k, for knear q. These norms are again estimated
using the φ(k), and in fact
khq0+1y(q0+1)k ≈ T(q0)≡(q0+ 1)ELTE(q0).
The step/order selection begins with a test for monotonicity that is made even before the local error
test is performed. Namely, the order is reset to q0=q−1 if (a) q= 2 and T(1) ≤T(2)/2, or (b) q > 2
and max{T(q−1), T (q−2)} ≤ T(q); otherwise q0=q. Next the local error test (2.9) is performed,
and if it fails, the step is redone at order q←q0and a new step size h0. The latter is based on the
hq+1 asymptotic behavior of ELTE(q), and, with safety factors, is given by
η=h0/h = 0.9/[2 ELTE(q)]1/(q+1) .
The value of ηis adjusted so that 0.25 ≤η≤0.9 before setting h←h0=ηh. If the local error test
fails a second time, idas uses η= 0.25, and on the third and subsequent failures it uses q= 1 and
η= 0.25. After 10 failures, idas returns with a give-up message.
As soon as the local error test has passed, the step and order for the next step may be adjusted.
No such change is made if q0=q−1 from the prior test, if q= 5, or if qwas increased on the previous
step. Otherwise, if the last q+ 1 steps were taken at a constant order q < 5 and a constant step size,
idas considers raising the order to q+ 1. The logic is as follows: (a) If q= 1, then reset q= 2 if
T(2) < T (1)/2. (b) If q > 1 then
•reset q←q−1 if T(q−1) ≤min{T(q), T (q+ 1)};

2.2 Preconditioning 11
•else reset q←q+ 1 if T(q+ 1) < T (q);
•leave qunchanged otherwise [then T(q−1) > T (q)≤T(q+ 1)].
In any case, the new step size h0is set much as before:
η=h0/h = 1/[2 ELTE(q)]1/(q+1) .
The value of ηis adjusted such that (a) if η > 2, ηis reset to 2; (b) if η≤1, ηis restricted to
0.5≤η≤0.9; and (c) if 1 < η < 2 we use η= 1. Finally his reset to h0=ηh. Thus we do not
increase the step size unless it can be doubled. See [3] for details.
idas permits the user to impose optional inequality constraints on individual components of the
solution vector y. Any of the following four constraints can be imposed: yi>0, yi<0, yi≥0,
or yi≤0. The constraint satisfaction is tested after a successful nonlinear system solution. If any
constraint fails, we declare a convergence failure of the Newton iteration and reduce the step size.
Rather than cutting the step size by some arbitrary factor, idas estimates a new step size h0using a
linear approximation of the components in ythat failed the constraint test (including a safety factor
of 0.9 to cover the strict inequality case). These additional constraints are also imposed during the
calculation of consistent initial conditions.
Normally, idas takes steps until a user-defined output value t=tout is overtaken, and then
computes y(tout) by interpolation. However, a “one step” mode option is available, where control
returns to the calling program after each step. There are also options to force idas not to integrate
past a given stopping point t=tstop.
2.2 Preconditioning
When using a Newton method to solve the nonlinear system (2.5), idas makes repeated use of a linear
solver to solve linear systems of the form J∆y=−G. If this linear system solve is done with one of
the scaled preconditioned iterative linear solvers, these solvers are rarely successful if used without
preconditioning; it is generally necessary to precondition the system in order to obtain acceptable
efficiency. A system Ax =bcan be preconditioned on the left, on the right, or on both sides. The
Krylov method is then applied to a system with the matrix P−1A, or AP −1, or P−1
LAP −1
R, instead
of A. However, within idas, preconditioning is allowed only on the left, so that the iterative method
is applied to systems (P−1J)∆y=−P−1G. Left preconditioning is required to make the norm of the
linear residual in the Newton iteration meaningful; in general, kJ∆y+Gkis meaningless, since the
weights used in the WRMS-norm correspond to y.
In order to improve the convergence of the Krylov iteration, the preconditioner matrix Pshould in
some sense approximate the system matrix A. Yet at the same time, in order to be cost-effective, the
matrix Pshould be reasonably efficient to evaluate and solve. Finding a good point in this tradeoff be-
tween rapid convergence and low cost can be very difficult. Good choices are often problem-dependent
(for example, see [4] for an extensive study of preconditioners for reaction-transport systems).
Typical preconditioners used with idas are based on approximations to the Newton iteration matrix
of the systems involved; in other words, P≈∂F
∂y +α∂F
∂˙y, where αis a scalar inversely proportional to
the integration step size h. Because the Krylov iteration occurs within a Newton iteration and further
also within a time integration, and since each of these iterations has its own test for convergence, the
preconditioner may use a very crude approximation, as long as it captures the dominant numerical
feature(s) of the system. We have found that the combination of a preconditioner with the Newton-
Krylov iteration, using even a fairly poor approximation to the Jacobian, can be surprisingly superior
to using the same matrix without Krylov acceleration (i.e., a modified Newton iteration), as well as
to using the Newton-Krylov method with no preconditioning.
2.3 Rootfinding
The idas solver has been augmented to include a rootfinding feature. This means that, while inte-
grating the Initial Value Problem (2.1), idas can also find the roots of a set of user-defined functions

12 Mathematical Considerations
gi(t, y, ˙y) that depend on t, the solution vector y=y(t), and its t−derivative ˙y(t). The number of
these root functions is arbitrary, and if more than one giis found to have a root in any given interval,
the various root locations are found and reported in the order that they occur on the taxis, in the
direction of integration.
Generally, this rootfinding feature finds only roots of odd multiplicity, corresponding to changes in
sign of gi(t, y(t),˙y(t)), denoted gi(t) for short. If a user root function has a root of even multiplicity (no
sign change), it will probably be missed by idas. If such a root is desired, the user should reformulate
the root function so that it changes sign at the desired root.
The basic scheme used is to check for sign changes of any gi(t) over each time step taken, and then
(when a sign change is found) to home in on the root (or roots) with a modified secant method [18].
In addition, each time gis computed, idas checks to see if gi(t) = 0 exactly, and if so it reports this as
a root. However, if an exact zero of any giis found at a point t,idas computes gat t+δfor a small
increment δ, slightly further in the direction of integration, and if any gi(t+δ) = 0 also, idas stops
and reports an error. This way, each time idas takes a time step, it is guaranteed that the values of
all giare nonzero at some past value of t, beyond which a search for roots is to be done.
At any given time in the course of the time-stepping, after suitable checking and adjusting has
been done, idas has an interval (tlo, thi] in which roots of the gi(t) are to be sought, such that thi is
further ahead in the direction of integration, and all gi(tlo)6= 0. The endpoint thi is either tn, the end
of the time step last taken, or the next requested output time tout if this comes sooner. The endpoint
tlo is either tn−1, or the last output time tout (if this occurred within the last step), or the last root
location (if a root was just located within this step), possibly adjusted slightly toward tnif an exact
zero was found. The algorithm checks gat thi for zeros and for sign changes in (tlo, thi). If no sign
changes are found, then either a root is reported (if some gi(thi) = 0) or we proceed to the next time
interval (starting at thi). If one or more sign changes were found, then a loop is entered to locate the
root to within a rather tight tolerance, given by
τ= 100 ∗U∗(|tn|+|h|) (U= unit roundoff) .
Whenever sign changes are seen in two or more root functions, the one deemed most likely to have
its root occur first is the one with the largest value of |gi(thi)|/|gi(thi)−gi(tlo)|, corresponding to the
closest to tlo of the secant method values. At each pass through the loop, a new value tmid is set,
strictly within the search interval, and the values of gi(tmid) are checked. Then either tlo or thi is reset
to tmid according to which subinterval is found to have the sign change. If there is none in (tlo, tmid)
but some gi(tmid) = 0, then that root is reported. The loop continues until |thi −tlo|< τ, and then
the reported root location is thi.
In the loop to locate the root of gi(t), the formula for tmid is
tmid =thi −(thi −tlo)gi(thi)/[gi(thi)−αgi(tlo)] ,
where αa weight parameter. On the first two passes through the loop, αis set to 1, making tmid
the secant method value. Thereafter, αis reset according to the side of the subinterval (low vs high,
i.e. toward tlo vs toward thi) in which the sign change was found in the previous two passes. If the
two sides were opposite, αis set to 1. If the two sides were the same, αis halved (if on the low
side) or doubled (if on the high side). The value of tmid is closer to tlo when α < 1 and closer to thi
when α > 1. If the above value of tmid is within τ/2 of tlo or thi, it is adjusted inward, such that its
fractional distance from the endpoint (relative to the interval size) is between .1 and .5 (.5 being the
midpoint), and the actual distance from the endpoint is at least τ/2.
2.4 Pure quadrature integration
In many applications, and most notably during the backward integration phase of an adjoint sensitivity
analysis run (see §2.6) it is of interest to compute integral quantities of the form
z(t) = Zt
t0
q(τ, y(τ),˙y(τ), p)dτ . (2.10)

2.5 Forward sensitivity analysis 13
The most effective approach to compute z(t) is to extend the original problem with the additional
ODEs (obtained by applying Leibnitz’s differentiation rule):
˙z=q(t, y, ˙y, p), z(t0)=0.(2.11)
Note that this is equivalent to using a quadrature method based on the underlying linear multistep
polynomial representation for y(t).
This can be done at the “user level” by simply exposing to idas the extended DAE system
(2.2)+(2.10). However, in the context of an implicit integration solver, this approach is not desir-
able since the nonlinear solver module will require the Jacobian (or Jacobian-vector product) of this
extended DAE. Moreover, since the additional states zdo not enter the right-hand side of the ODE
(2.10) and therefore the residual of the extended DAE system does not depend on z, it is much more
efficient to treat the ODE system (2.10) separately from the original DAE system (2.2) by “taking
out” the additional states zfrom the nonlinear system (2.4) that must be solved in the correction step
of the LMM. Instead, “corrected” values znare computed explicitly as
zn=1
αn,0 hnq(tn, yn,˙yn, p)−
q
X
i=1
αn,izn−i!,
once the new approximation ynis available.
The quadrature variables zcan be optionally included in the error test, in which case corresponding
relative and absolute tolerances must be provided.
2.5 Forward sensitivity analysis
Typically, the governing equations of complex, large-scale models depend on various parameters,
through the right-hand side vector and/or through the vector of initial conditions, as in (2.2). In
addition to numerically solving the DAEs, it may be desirable to determine the sensitivity of the results
with respect to the model parameters. Such sensitivity information can be used to estimate which
parameters are most influential in affecting the behavior of the simulation or to evaluate optimization
gradients (in the setting of dynamic optimization, parameter estimation, optimal control, etc.).
The solution sensitivity with respect to the model parameter piis defined as the vector si(t) =
∂y(t)/∂piand satisfies the following forward sensitivity equations (or sensitivity equations for short):
∂F
∂y si+∂F
∂˙y˙si+∂F
∂pi
= 0
si(t0) = ∂y0(p)
∂pi
,˙si(t0) = ∂˙y0(p)
∂pi
,
(2.12)
obtained by applying the chain rule of differentiation to the original DAEs (2.2).
When performing forward sensitivity analysis, idas carries out the time integration of the combined
system, (2.2) and (2.12), by viewing it as a DAE system of size N(Ns+ 1), where Nsis the number
of model parameters pi, with respect to which sensitivities are desired (Ns≤Np). However, major
improvements in efficiency can be made by taking advantage of the special form of the sensitivity
equations as linearizations of the original DAEs. In particular, the original DAE system and all
sensitivity systems share the same Jacobian matrix Jin (2.6).
The sensitivity equations are solved with the same linear multistep formula that was selected
for the original DAEs and the same linear solver is used in the correction phase for both state and
sensitivity variables. In addition, idas offers the option of including (full error control) or excluding
(partial error control) the sensitivity variables from the local error test.
2.5.1 Forward sensitivity methods
In what follows we briefly describe three methods that have been proposed for the solution of the
combined DAE and sensitivity system for the vector ˆy= [y, s1, . . . , sNs].

14 Mathematical Considerations
•Staggered Direct In this approach [11], the nonlinear system (2.4) is first solved and, once an
acceptable numerical solution is obtained, the sensitivity variables at the new step are found
by directly solving (2.12) after the BDF discretization is used to eliminate ˙si. Although the
system matrix of the above linear system is based on exactly the same information as the
matrix Jin (2.6), it must be updated and factored at every step of the integration, in contrast
to an evaluation of Jwhich is updated only occasionally. For problems with many parameters
(relative to the problem size), the staggered direct method can outperform the methods described
below [26]. However, the computational cost associated with matrix updates and factorizations
makes this method unattractive for problems with many more states than parameters (such as
those arising from semidiscretization of PDEs) and is therefore not implemented in idas.
•Simultaneous Corrector In this method [28], the discretization is applied simultaneously to both
the original equations (2.2) and the sensitivity systems (2.12) resulting in an “extended” non-
linear system ˆ
G(ˆyn) = 0 where ˆyn= [yn, . . . , si, . . .]. This combined nonlinear system can be
solved using a modified Newton method as in (2.5) by solving the corrector equation
ˆ
J[ˆyn(m+1) −ˆyn(m)] = −ˆ
G(ˆyn(m)) (2.13)
at each iteration, where
ˆ
J=
J
J1J
J20J
.
.
..
.
.......
JNs0. . . 0J
,
Jis defined as in (2.6), and Ji= (∂/∂y) [Fysi+F˙y˙si+Fpi]. It can be shown that 2-step
quadratic convergence can be retained by using only the block-diagonal portion of ˆ
Jin the
corrector equation (2.13). This results in a decoupling that allows the reuse of Jwithout
additional matrix factorizations. However, the sum Fysi+F˙y˙si+Fpimust still be reevaluated
at each step of the iterative process (2.13) to update the sensitivity portions of the residual ˆ
G.
•Staggered corrector In this approach [16], as in the staggered direct method, the nonlinear system
(2.4) is solved first using the Newton iteration (2.5). Then, for each sensitivity vector ξ≡si, a
separate Newton iteration is used to solve the sensitivity system (2.12):
J[ξn(m+1) −ξn(m)] =
−"Fy(tn, yn,˙yn)ξn(m)+F˙y(tn, yn,˙yn)·h−1
n αn,0ξn(m)+
q
X
i=1
αn,iξn−i!+Fpi(tn, yn,˙yn)#.
(2.14)
In other words, a modified Newton iteration is used to solve a linear system. In this approach,
the matrices ∂F/∂y,∂F/∂ ˙yand vectors ∂F/∂pineed be updated only once per integration step,
after the state correction phase (2.5) has converged.
idas implements both the simultaneous corrector method and the staggered corrector method.
An important observation is that the staggered corrector method, combined with a Krylov linear
solver, effectively results in a staggered direct method. Indeed, the Krylov solver requires only the
action of the matrix Jon a vector and this can be provided with the current Jacobian information.
Therefore, the modified Newton procedure (2.14) will theoretically converge after one iteration.
2.5.2 Selection of the absolute tolerances for sensitivity variables
If the sensitivities are included in the error test, idas provides an automated estimation of absolute
tolerances for the sensitivity variables based on the absolute tolerance for the corresponding state
variable. The relative tolerance for sensitivity variables is set to be the same as for the state variables.

2.5 Forward sensitivity analysis 15
The selection of absolute tolerances for the sensitivity variables is based on the observation that
the sensitivity vector siwill have units of [y]/[pi]. With this, the absolute tolerance for the j-th
component of the sensitivity vector siis set to atolj/|¯pi|, where atoljare the absolute tolerances for
the state variables and ¯pis a vector of scaling factors that are dimensionally consistent with the model
parameters pand give an indication of their order of magnitude. This choice of relative and absolute
tolerances is equivalent to requiring that the weighted root-mean-square norm of the sensitivity vector
siwith weights based on sibe the same as the weighted root-mean-square norm of the vector of scaled
sensitivities ¯si=|¯pi|siwith weights based on the state variables (the scaled sensitivities ¯sibeing
dimensionally consistent with the state variables). However, this choice of tolerances for the simay
be a poor one, and the user of idas can provide different values as an option.
2.5.3 Evaluation of the sensitivity right-hand side
There are several methods for evaluating the residual functions in the sensitivity systems (2.12):
analytic evaluation, automatic differentiation, complex-step approximation, and finite differences (or
directional derivatives). idas provides all the software hooks for implementing interfaces to automatic
differentiation (AD) or complex-step approximation; future versions will include a generic interface
to AD-generated functions. At the present time, besides the option for analytical sensitivity right-
hand sides (user-provided), idas can evaluate these quantities using various finite difference-based
approximations to evaluate the terms (∂F/∂y)si+ (∂F/∂ ˙y) ˙siand (∂F/∂pi), or using directional
derivatives to evaluate [(∂F/∂y)si+ (∂F/∂ ˙y) ˙si+ (∂F/∂pi)]. As is typical for finite differences, the
proper choice of perturbations is a delicate matter. idas takes into account several problem-related
features: the relative DAE error tolerance rtol, the machine unit roundoff U, the scale factor ¯pi, and
the weighted root-mean-square norm of the sensitivity vector si.
Using central finite differences as an example, the two terms (∂F/∂y)si+ (∂F/∂ ˙y) ˙siand ∂F/∂pi
in (2.12) can be evaluated either separately:
∂F
∂y si+∂F
∂˙y˙si≈F(t, y +σysi,˙y+σy˙si, p)−F(t, y −σysi,˙y−σy˙si, p)
2σy
,(2.15)
∂F
∂pi≈F(t, y, ˙y, p +σiei)−F(t, y, ˙y, p −σiei)
2σi
,(2.15’)
σi=|¯pi|pmax(rtol, U ), σy=1
max(1/σi,ksikWRMS/|¯pi|),
or simultaneously:
∂F
∂y si+∂F
∂˙y˙si+∂F
∂pi≈F(t, y +σsi,˙y+σ˙si, p +σei)−F(t, y −σsi,˙y−σ˙si, p −σei)
2σ,(2.16)
σ= min(σi, σy),
or by adaptively switching between (2.15)+(2.15’) and (2.16), depending on the relative size of the
two finite difference increments σiand σy. In the adaptive scheme, if ρ= max(σi/σy, σy/σi), we use
separate evaluations if ρ>ρmax (an input value), and simultaneous evaluations otherwise.
These procedures for choosing the perturbations (σi,σy,σ) and switching between derivative
formulas have also been implemented for one-sided difference formulas. Forward finite differences can
be applied to (∂F/∂y)si+ (∂F/∂ ˙y) ˙siand ∂F
∂piseparately, or the single directional derivative formula
∂F
∂y si+∂F
∂˙y˙si+∂F
∂pi≈F(t, y +σsi,˙y+σ˙si, p +σei)−F(t, y, ˙y, p)
σ
can be used. In idas, the default value of ρmax = 0 indicates the use of the second-order centered
directional derivative formula (2.16) exclusively. Otherwise, the magnitude of ρmax and its sign (pos-
itive or negative) indicates whether this switching is done with regard to (centered or forward) finite
differences, respectively.

16 Mathematical Considerations
2.5.4 Quadratures depending on forward sensitivities
If pure quadrature variables are also included in the problem definition (see §2.4), idas does not carry
their sensitivities automatically. Instead, we provide a more general feature through which integrals
depending on both the states yof (2.2) and the state sensitivities siof (2.12) can be evaluated. In
other words, idas provides support for computing integrals of the form:
¯z(t) = Zt
t0
¯q(τ, y(τ),˙y(τ), s1(τ), . . . , sNp(τ), p)dτ .
If the sensitivities of the quadrature variables zof (2.10) are desired, these can then be computed
by using:
¯qi=qysi+q˙y˙si+qpi, i = 1, . . . , Np,
as integrands for ¯z, where qy,q˙y, and qpare the partial derivatives of the integrand function qof
(2.10).
As with the quadrature variables z, the new variables ¯zare also excluded from any nonlinear solver
phase and “corrected” values ¯znare obtained through explicit formulas.
2.6 Adjoint sensitivity analysis
In the forward sensitivity approach described in the previous section, obtaining sensitivities with
respect to Nsparameters is roughly equivalent to solving an DAE system of size (1 + Ns)N. This
can become prohibitively expensive, especially for large-scale problems, if sensitivities with respect
to many parameters are desired. In this situation, the adjoint sensitivity method is a very attractive
alternative, provided that we do not need the solution sensitivities si, but rather the gradients with
respect to model parameters of a relatively few derived functionals of the solution. In other words, if
y(t) is the solution of (2.2), we wish to evaluate the gradient dG/dp of
G(p) = ZT
t0
g(t, y, p)dt , (2.17)
or, alternatively, the gradient dg/dp of the function g(t, y, p) at the final time t=T. The function g
must be smooth enough that ∂g/∂y and ∂g/∂p exist and are bounded.
In what follows, we only sketch the analysis for the sensitivity problem for both Gand g. For
details on the derivation see [10].
2.6.1 Sensitivity of G(p)
We focus first on solving the sensitivity problem for G(p) defined by (2.17). Introducing a Lagrange
multiplier λ, we form the augmented objective function
I(p) = G(p)−ZT
t0
λ∗F(t, y, ˙y, p)dt.
Since F(t, y, ˙y, p) = 0, the sensitivity of Gwith respect to pis
dG
dp =dI
dp =ZT
t0
(gp+gyyp)dt −ZT
t0
λ∗(Fp+Fyyp+F˙y˙yp)dt, (2.18)
where subscripts on functions such as For gare used to denote partial derivatives. By integration
by parts, we have
ZT
t0
λ∗F˙y˙ypdt = (λ∗F˙yyp)|T
t0−ZT
t0
(λ∗F˙y)0ypdt,

2.6 Adjoint sensitivity analysis 17
where (···)0denotes the t−derivative. Thus equation (2.18) becomes
dG
dp =ZT
t0
(gp−λ∗Fp)dt −ZT
t0
[−gy+λ∗Fy−(λ∗F˙y)0]ypdt −(λ∗F˙yyp)|T
t0.(2.19)
Now by requiring λto satisfy
(λ∗F˙y)0−λ∗Fy=−gy,(2.20)
we obtain
dG
dp =ZT
t0
(gp−λ∗Fp)dt −(λ∗F˙yyp)|T
t0.(2.21)
Note that ypat t=t0is the sensitivity of the initial conditions with respect to p, which is easily ob-
tained. To find the initial conditions (at t=T) for the adjoint system, we must take into consideration
the structure of the DAE system.
For index-0 and index-1 DAE systems, we can simply take
λ∗F˙y|t=T= 0,(2.22)
yielding the sensitivity equation for dG/dp
dG
dp =ZT
t0
(gp−λ∗Fp)dt + (λ∗F˙yyp)|t=t0.(2.23)
This choice will not suffice for a Hessenberg index-2 DAE system. For a derivation of proper final
conditions in such cases, see [10].
The first thing to notice about the adjoint system (2.20) is that there is no explicit specification
of the parameters p; this implies that, once the solution λis found, the formula (2.21) can then be
used to find the gradient of Gwith respect to any of the parameters p. The second important remark
is that the adjoint system (2.20) is a terminal value problem which depends on the solution y(t) of
the original IVP (2.2). Therefore, a procedure is needed for providing the states yobtained during
a forward integration phase of (2.2) to idas during the backward integration phase of (2.20). The
approach adopted in idas, based on checkpointing, is described in §2.6.3 below.
2.6.2 Sensitivity of g(T, p)
Now let us consider the computation of dg/dp(T). From dg/dp(T)=(d/dT )(dG/dp) and equation
(2.21), we have
dg
dp = (gp−λ∗Fp)(T)−ZT
t0
λ∗
TFpdt + (λ∗
TF˙yyp)|t=t0−d(λ∗F˙yyp)
dT (2.24)
where λTdenotes ∂λ/∂T . For index-0 and index-1 DAEs, we obtain
d(λ∗F˙yyp)|t=T
dT = 0,
while for a Hessenberg index-2 DAE system we have
d(λ∗F˙yyp)|t=T
dT =−d(gya(CB)−1f2
p)
dt t=T
.
The corresponding adjoint equations are
(λ∗
TF˙y)0−λ∗
TFy= 0.(2.25)
For index-0 and index-1 DAEs (as shown above, the index-2 case is different), to find the boundary
condition for this equation we write λas λ(t, T ) because it depends on both tand T. Then
λ∗(T, T )F˙y|t=T= 0.

18 Mathematical Considerations
Taking the total derivative, we obtain
(λt+λT)∗(T, T )F˙y|t=T+λ∗(T, T )dF ˙y
dt |t=T= 0.
Since λtis just ˙
λ, we have the boundary condition
(λ∗
TF˙y)|t=T=−λ∗(T, T )dF ˙y
dt +˙
λ∗F˙y|t=T.
For the index-one DAE case, the above relation and (2.20) yield
(λ∗
TF˙y)|t=T= [gy−λ∗Fy]|t=T.(2.26)
For the regular implicit ODE case, F˙yis invertible; thus we have λ(T, T ) = 0, which leads to λT(T) =
−˙
λ(T). As with the final conditions for λ(T) in (2.20), the above selection for λT(T) is not sufficient
for index-two Hessenberg DAEs (see [10] for details).
2.6.3 Checkpointing scheme
During the backward integration, the evaluation of the right-hand side of the adjoint system requires,
at the current time, the states ywhich were computed during the forward integration phase. Since
idas implements variable-step integration formulas, it is unlikely that the states will be available at
the desired time and so some form of interpolation is needed. The idas implementation being also
variable-order, it is possible that during the forward integration phase the order may be reduced as
low as first order, which means that there may be points in time where only yand ˙yare available.
These requirements therefore limit the choices for possible interpolation schemes. idas implements
two interpolation methods: a cubic Hermite interpolation algorithm and a variable-degree polynomial
interpolation method which attempts to mimic the BDF interpolant for the forward integration.
However, especially for large-scale problems and long integration intervals, the number and size
of the vectors yand ˙ythat would need to be stored make this approach computationally intractable.
Thus, idas settles for a compromise between storage space and execution time by implementing a so-
called checkpointing scheme. At the cost of at most one additional forward integration, this approach
offers the best possible estimate of memory requirements for adjoint sensitivity analysis. To begin
with, based on the problem size Nand the available memory, the user decides on the number Nd
of data pairs (y, ˙y) if cubic Hermite interpolation is selected, or on the number Ndof yvectors in
the case of variable-degree polynomial interpolation, that can be kept in memory for the purpose of
interpolation. Then, during the first forward integration stage, after every Ndintegration steps a
checkpoint is formed by saving enough information (either in memory or on disk) to allow for a hot
restart, that is a restart which will exactly reproduce the forward integration. In order to avoid storing
Jacobian-related data at each checkpoint, a reevaluation of the iteration matrix is forced before each
checkpoint. At the end of this stage, we are left with Nccheckpoints, including one at t0. During the
backward integration stage, the adjoint variables are integrated backwards from Tto t0, going from
one checkpoint to the previous one. The backward integration from checkpoint i+ 1 to checkpoint i
is preceded by a forward integration from ito i+ 1 during which the Ndvectors y(and, if necessary
˙y) are generated and stored in memory for interpolation1
This approach transfers the uncertainty in the number of integration steps in the forward inte-
gration phase to uncertainty in the final number of checkpoints. However, Ncis much smaller than
the number of steps taken during the forward integration, and there is no major penalty for writ-
ing/reading the checkpoint data to/from a temporary file. Note that, at the end of the first forward
1The degree of the interpolation polynomial is always that of the current BDF order for the forward interpolation at
the first point to the right of the time at which the interpolated value is sought (unless too close to the i-th checkpoint, in
which case it uses the BDF order at the right-most relevant point). However, because of the FLC BDF implementation
(see §2.1), the resulting interpolation polynomial is only an approximation to the underlying BDF interpolant.
The Hermite cubic interpolation option is present because it was implemented chronologically first and it is also used
by other adjoint solvers (e.g. daspkadjoint). The variable-degree polynomial is more memory-efficient (it requires only
half of the memory storage of the cubic Hermite interpolation) and is more accurate.

2.7 Second-order sensitivity analysis 19
t0t1t2t3tf
k3
k2
k1
k0
Forward pass
Backward pass
. . . .
. . .
Figure 2.1: Illustration of the checkpointing algorithm for generation of the forward solution during
the integration of the adjoint system.
integration stage, interpolation data are available from the last checkpoint to the end of the interval
of integration. If no checkpoints are necessary (Ndis larger than the number of integration steps
taken in the solution of (2.2)), the total cost of an adjoint sensitivity computation can be as low as
one forward plus one backward integration. In addition, idas provides the capability of reusing a set
of checkpoints for multiple backward integrations, thus allowing for efficient computation of gradients
of several functionals (2.17).
Finally, we note that the adjoint sensitivity module in idas provides the necessary infrastructure
to integrate backwards in time any DAE terminal value problem dependent on the solution of the
IVP (2.2), including adjoint systems (2.20) or (2.25), as well as any other quadrature ODEs that may
be needed in evaluating the integrals in (2.21). In particular, for DAE systems arising from semi-
discretization of time-dependent PDEs, this feature allows for integration of either the discretized
adjoint PDE system or the adjoint of the discretized PDE.
2.7 Second-order sensitivity analysis
In some applications (e.g., dynamically-constrained optimization) it may be desirable to compute
second-order derivative information. Considering the DAE problem (2.2) and some model output
functional2g(y), the Hessian d2g/dp2can be obtained in a forward sensitivity analysis setting as
d2g
dp2=gy⊗INpypp +yT
pgyyyp,
where ⊗is the Kronecker product. The second-order sensitivities are solution of the matrix DAE
system:
F˙y⊗INp·˙ypp +Fy⊗INp·ypp +IN⊗˙yT
p·(F˙y˙y˙yp+Fy˙yyp) + IN⊗yT
p·(Fy˙y˙yp+Fyyyp)=0
ypp(t0) = ∂2y0
∂p2,˙ypp(t0) = ∂2˙y0
∂p2,
where ypdenotes the first-order sensitivity matrix, the solution of Npsystems (2.12), and ypp is a
third-order tensor. It is easy to see that, except for situations in which the number of parameters Np
is very small, the computational cost of this so-called forward-over-forward approach is exorbitant as
it requires the solution of Np+N2
padditional DAE systems of the same dimension as (2.2).
A much more efficient alternative is to compute Hessian-vector products using a so-called forward-
over-adjoint approach. This method is based on using the same “trick” as the one used in computing
gradients of pointwise functionals with the adjoint method, namely applying a formal directional for-
ward derivation to the gradient of (2.21) (or the equivalent one for a pointwise functional g(T, y(T))).
2For the sake of simplifity in presentation, we do not include explicit dependencies of gon time tor parameters p.
Moreover, we only consider the case in which the dependency of the original DAE (2.2) on the parameters pis through
its initial conditions only. For details on the derivation in the general case, see [29].

20 Mathematical Considerations
With that, the cost of computing a full Hessian is roughly equivalent to the cost of computing the gra-
dient with forward sensitivity analysis. However, Hessian-vector products can be cheaply computed
with one additional adjoint solve.
As an illustration3, consider the ODE problem
˙y=f(t, y), y(t0) = y0(p),
depending on some parameters pthrough the initial conditions only and consider the model functional
output G(p) = Rtf
t0g(t, y)dt. It can be shown that the product between the Hessian of G(with respect
to the parameters p) and some vector ucan be computed as
∂2G
∂p2u=λT⊗INpyppu+yT
pµt=t0,
where λand µare solutions of
−˙µ=fT
yµ+λT⊗Infyy s;µ(tf)=0
−˙
λ=fT
yλ+gT
y;λ(tf)=0
˙s=fys;s(t0) = y0pu.
(2.27)
In the above equation, s=ypuis a linear combination of the columns of the sensitivity matrix yp.
The forward-over-adjoint approach hinges crucially on the fact that scan be computed at the cost of
a forward sensitivity analysis with respect to a single parameter (the last ODE problem above) which
is possible due to the linearity of the forward sensitivity equations (2.12).
Therefore (and this is also valid for the DAE case), the cost of computing the Hessian-vector
product is roughly that of two forward and two backward integrations of a system of DAEs of size
N. For more details, including the corresponding formulas for a pointwise model functional output,
see the work by Ozyurt and Barton [29] who discuss this problem for ODE initial value problems. As
far as we know, there is no published equivalent work on DAE problems. However, the derivations
given in [29] for ODE problems can be extended to DAEs with some careful consideration given to
the derivation of proper final conditions on the adjoint systems, following the ideas presented in [10].
To allow the foward-over-adjoint approach described above, idas provides support for:
•the integration of multiple backward problems depending on the same underlying forward prob-
lem (2.2), and
•the integration of backward problems and computation of backward quadratures depending on
both the states yand forward sensitivities (for this particular application, s) of the original
problem (2.2).
3The derivation for the general DAE case is too involved for the purposes of this discussion.

Chapter 3
Code Organization
3.1 SUNDIALS organization
The family of solvers referred to as sundials consists of the solvers cvode and arkode (for ODE
systems), kinsol (for nonlinear algebraic systems), and ida (for differential-algebraic systems). In
addition, sundials also includes variants of cvode and ida with sensitivity analysis capabilities
(using either forward or adjoint methods), called cvodes and idas, respectively.
The various solvers of this family share many subordinate modules. For this reason, it is organized
as a family, with a directory structure that exploits that sharing (see Fig. 3.1). The following is a list
of the solver packages presently available, and the basic functionality of each:
•cvode, a solver for stiff and nonstiff ODE systems dy/dt =f(t, y) based on Adams and BDF
methods;
•cvodes, a solver for stiff and nonstiff ODE systems with sensitivity analysis capabilities;
•arkode, a solver for ODE systems Mdy/dt =f(t, y) based on additive Runge-Kutta methods;
•ida, a solver for differential-algebraic systems F(t, y, ˙y) = 0 based on BDF methods;
•idas, a solver for differential-algebraic systems with sensitivity analysis capabilities;
•kinsol, a solver for nonlinear algebraic systems F(u) = 0.
3.2 IDAS organization
The idas package is written in the ANSI Clanguage. The following summarizes the basic structure
of the package, although knowledge of this structure is not necessary for its use.
The overall organization of the idas package is shown in Figure 3.2. The central integration
module, implemented in the files idas.h,idas impl.h, and idas.c, deals with the evaluation of
integration coefficients, the Newton iteration process, estimation of local error, selection of stepsize
and order, and interpolation to user output points, among other issues. Although this module contains
logic for the basic Newton iteration algorithm, it has no knowledge of the method being used to solve
the linear systems that arise. For any given user problem, one of the linear system modules is specified,
and is then invoked as needed during the integration.
In addition, if forward sensitivity analysis is turned on, the main module will integrate the forward
sensitivity equations simultaneously with the original IVP. The sensitivity variables may be included
in the local error control mechanism of the main integrator. idas provides two different strategies
for dealing with the correction stage for the sensitivity variables: IDA SIMULTANEOUS IDA STAGGERED
(see §2.5). The idas package includes an algorithm for the approximation of the sensitivity equations
residuals by difference quotients, but the user has the option of supplying these residual functions
directly.
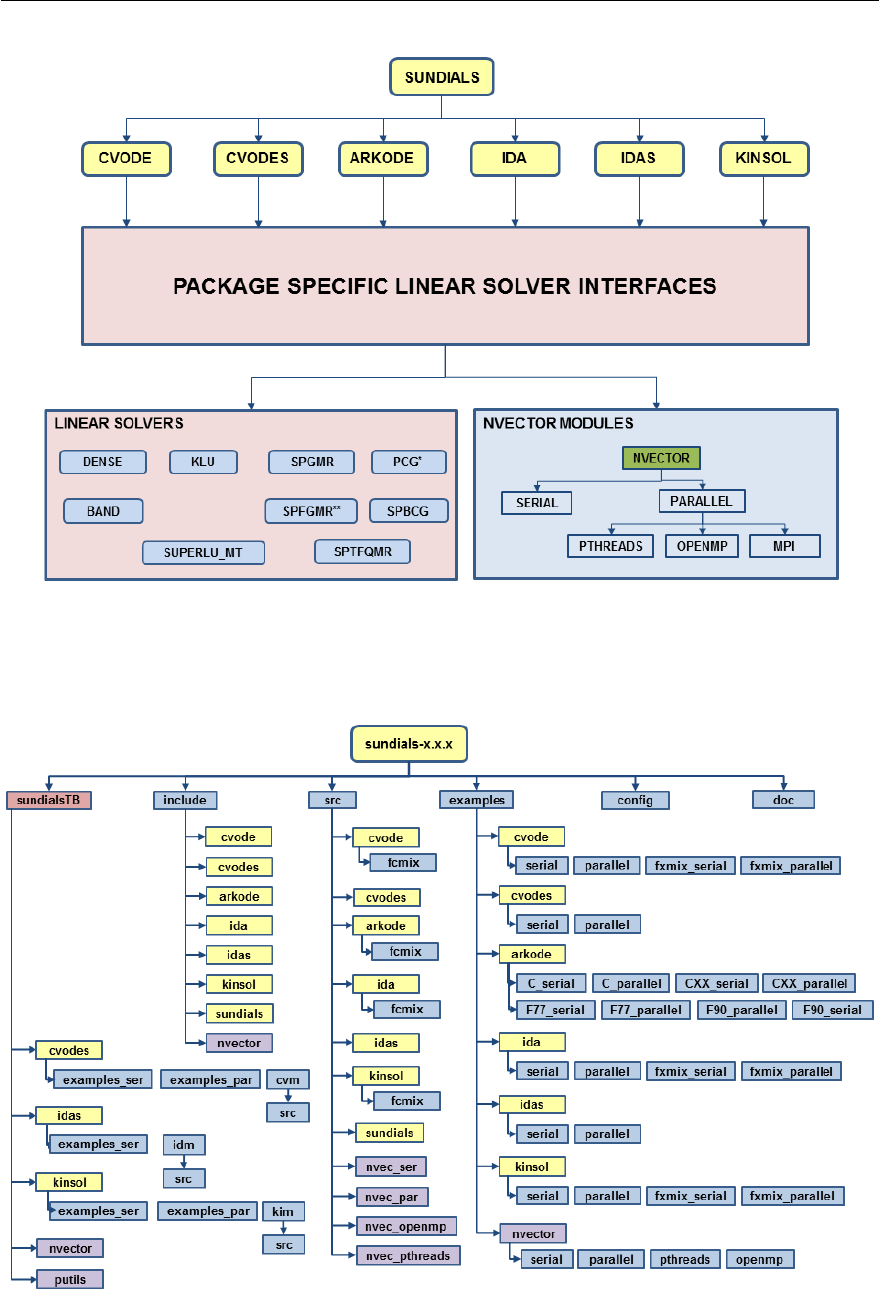
22 Code Organization
(a) High-level diagram (note that none of the Lapack-based linear solver modules are represented.)
* only applies to arkode
** only applies to arkode and kinsol
(b) Directory structure of the source tree
Figure 3.1: Organization of the SUNDIALS suite
3.2 IDAS organization 23
LINEAR SOLVER
INTERFACES
GENERIC
LINEAR SOLVERS
SUNDIALS
DENSE
SPGMR SPBCG
BAND
SERIAL
NVECTOR
IDASPTFQMR
SPTFQMR
PARALLEL
IDAS
IDAADJOINT
NVECTOR
MODULES
PRECONDITIONER
MODULES
IDABAND
IDASPGMR
IDADENSE
IDASPBCG
IDABBDPRE
Figure 3.2: Overall structure diagram of the idas package. Modules specific to idas are distinguished
by rounded boxes, while generic solver and auxiliary modules are in square boxes. Note that the
direct linear solvers using Lapack implementations are not explicitly represented. Note also that the
KLU and SuperLU MT support is through interfaces to packages. Users will need to download and
compile those packages independently.
The adjoint sensitivity module (file idaa.c) provides the infrastructure needed for the backward
integration of any system of DAEs which depends on the solution of the original IVP, in particular the
adjoint system and any quadratures required in evaluating the gradient of the objective functional.
This module deals with the setup of the checkpoints, the interpolation of the forward solution during
the backward integration, and the backward integration of the adjoint equations.
At present, the package includes the following seven idas linear algebra modules, organized into
two families. The direct family of linear solvers provides solvers for the direct solution of linear systems
with dense or banded matrices and includes:
•idadense: LU factorization and backsolving with dense matrices (using either an internal im-
plementation or Blas/Lapack);
•idaband: LU factorization and backsolving with banded matrices (using either an internal
implementation or Blas/Lapack);
•idaklu: LU factorization and backsolving with compressed-sparse-column (CSC) matrices using
the KLU linear solver library [14,1] (KLU to be downloaded and compiled by user independent
of ida);
•idasuperlumt: LU factorization and backsolving with compressed-sparse-column (CSC) ma-
trices using the threaded SuperLU MT linear solver library [27,15,2] (SuperLU MT to be
downloaded and compiled by user independent of ida).
The spils family of linear solvers provides scaled preconditioned iterative linear solvers and includes:
•idaspgmr: scaled preconditioned GMRES method;
•idaspbcg: scaled preconditioned Bi-CGStab method;

24 Code Organization
•idasptfqmr: scaled preconditioned TFQMR method.
The set of linear solver modules distributed with idas is intended to be expanded in the future as
new algorithms are developed. Note that users wishing to employ KLU or SuperLU MT will need to
download and install these libraries independent of sundials.sundials provides only the interfaces
between itself and these libraries.
In the case of the direct methods idadense and idaband the package includes an algorithm for the
approximation of the Jacobian by difference quotients, but the user also has the option of supplying
the Jacobian (or an approximation to it) directly. When using the sparse direct linear solvers idaklu
and idasuperlumt the user must supply a routine for the Jacobian (or an approximation to it) in
CSC format, since standard difference quotient approximations do not leverage the inherent sparsity of
the problem. In the case of the Krylov iterative methods idaspgmr,idaspbcg, and idasptfqmr, the
package includes an algorithm for the approximation by difference quotients of the product between
the Jacobian matrix and a vector of appropriate length. Again, the user has the option of providing
a routine for this operation. When using any of the Krylov methods, the user must supply the
preconditioning in two phases: a setup phase (preprocessing of Jacobian data) and a solve phase.
While there is no default choice of preconditioner analogous to the difference quotient approximation
in the direct case, the references [4,7], together with the example and demonstration programs
included with idas, offer considerable assistance in building preconditioners.
Each idas linear solver module consists of five routines, devoted to (1) memory allocation and
initialization, (2) setup of the matrix data involved, (3) solution of the system, (4) monitoring perfor-
mance, and (5) freeing of memory. The setup and solution phases are separate because the evaluation
of Jacobians and preconditioners is done only periodically during the integration, as required to achieve
convergence. The call list within the central idas module to each of the five associated functions is
fixed, thus allowing the central module to be completely independent of the linear system method.
These modules are also decomposed in another way. Each of the linear solver modules (idadense
etc.) consists of an interface built on top of a generic linear system solver (dense etc.). The inter-
face deals with the use of the particular method in the idas context, whereas the generic solver is
independent of the context. While some of the generic linear system solvers (dense,band,spgmr,
spbcg, and sptfqmr) were written with sundials in mind, they are intended to be usable anywhere
as general-purpose solvers. This separation also allows for any generic solver to be replaced by an
improved version, with no necessity to revise the idas package elsewhere.
idas also provides a preconditioner module, idabbdpre, that works in conjunction with nvec-
tor parallel and generates a preconditioner that is a block-diagonal matrix with each block being
a band matrix.
All state information used by idas to solve a given problem is saved in a structure, and a pointer
to that structure is returned to the user. There is no global data in the idas package, and so, in this
respect, it is reentrant. State information specific to the linear solver is saved in a separate structure,
a pointer to which resides in the idas memory structure. The reentrancy of idas was motivated by
the situation where two or more problems are solved by intermixed calls to the package from one user
program.
Chapter 4
Using IDAS for IVP Solution
This chapter is concerned with the use of idas for the integration of DAEs. The following sections
treat the header files, the layout of the user’s main program, description of the idas user-callable
functions, and description of user-supplied functions. This usage is essentially equivalent to using
ida [24].
The sample programs described in the companion document [33] may also be helpful. Those codes
may be used as templates (with the removal of some lines involved in testing), and are included in
the idas package.
The user should be aware that not all linear solver modules are compatible with all nvector
implementations. For example, nvector parallel is not compatible with the direct dense, direct
band or direct sparse linear solvers, since these linear solver modules need to form the complete
system Jacobian. The idadense and idaband modules (using either the internal implementation or
Lapack), as well as the idaklu and idasuperlumt modules can only be used with nvector serial,
nvector openmp and nvector pthreads. It is not recommended to use a threaded vector module
with SuperLU MT unless it is the nvector openmp module and SuperLU MT is also compiled with
openMP. The preconditioner module idabbdpre can only be used with nvector parallel.
idas uses various constants for both input and output. These are defined as needed in this chapter,
but for convenience are also listed separately in Appendix B.
4.1 Access to library and header files
At this point, it is assumed that the installation of idas, following the procedure described in Appendix
A, has been completed successfully.
Regardless of where the user’s application program resides, its associated compilation and load
commands must make reference to the appropriate locations for the library and header files required
by idas. The relevant library files are
•libdir/libsundials idas.lib,
•libdir/libsundials nvec*.lib (one to four files),
where the file extension .lib is typically .so for shared libraries and .a for static libraries. The relevant
header files are located in the subdirectories
•incdir/include/idas
•incdir/include/sundials
•incdir/include/nvector
The directories libdir and incdir are the install library and include directories, respectively. For
a default installation, these are instdir/lib and instdir/include, respectively, where instdir is the
directory where sundials was installed (see Appendix A).

26 Using IDAS for IVP Solution
Note that an application cannot link to both the ida and idas libraries because both contain
user-callable functions with the same names (to ensure that idas is backward compatible with ida).
Therefore, applications that contain both DAE problems and DAEs with sensitivity analysis, should
use idas.
4.2 Data types
The sundials types.h file contains the definition of the type realtype, which is used by the sundials
solvers for all floating-point data. The type realtype can be float,double, or long double, with
the default being double. The user can change the precision of the sundials solvers arithmetic at
the configuration stage (see §A.1.2).
Additionally, based on the current precision, sundials types.h defines BIG REAL to be the largest
value representable as a realtype,SMALL REAL to be the smallest value representable as a realtype,
and UNIT ROUNDOFF to be the difference between 1.0 and the minimum realtype greater than 1.0.
Within sundials, real constants are set by way of a macro called RCONST. It is this macro that
needs the ability to branch on the definition realtype. In ANSI C, a floating-point constant with no
suffix is stored as a double. Placing the suffix “F” at the end of a floating point constant makes it a
float, whereas using the suffix “L” makes it a long double. For example,
#define A 1.0
#define B 1.0F
#define C 1.0L
defines Ato be a double constant equal to 1.0, Bto be a float constant equal to 1.0, and Cto be
along double constant equal to 1.0. The macro call RCONST(1.0) automatically expands to 1.0 if
realtype is double, to 1.0F if realtype is float, or to 1.0L if realtype is long double.sundials
uses the RCONST macro internally to declare all of its floating-point constants.
A user program which uses the type realtype and the RCONST macro to handle floating-point
constants is precision-independent except for any calls to precision-specific standard math library
functions. (Our example programs use both realtype and RCONST.) Users can, however, use the type
double,float, or long double in their code (assuming that this usage is consistent with the typedef
for realtype). Thus, a previously existing piece of ANSI Ccode can use sundials without modifying
the code to use realtype, so long as the sundials libraries use the correct precision (for details see
§A.1.2).
4.3 Header files
The calling program must include several header files so that various macros and data types can be
used. The header file that is always required is:
•idas.h, the header file for idas, which defines the several types and various constants, and
includes function prototypes.
Note that idas.h includes sundials types.h, which defines the types realtype and booleantype
and the constants FALSE and TRUE.
The calling program must also include an nvector implementation header file, of the form
nvector ***.h. See Chapter 7for the appropriate name. This file in turn includes the header
file sundials nvector.h which defines the abstract N Vector data type.
Finally, a linear solver module header file is required. The header files corresponding to the various
linear solver options in idas are as follows:
•idas dense.h, which is used with the dense direct linear solver;
•idas band.h, which is used with the band direct linear solver;

4.4 A skeleton of the user’s main program 27
•idas lapack.h, which is used with Lapack implementations of dense or band direct linear
solvers;
•idas klu.h, which is used with the KLU sparse direct linear solver;
•idas superlumt.h, which is used with the SuperLU MT threaded sparse direct linear solver;
•idas spgmr.h, which is used with the scaled, preconditioned GMRES Krylov linear solver
spgmr;
•idas spbcgs.h, which is used with the scaled, preconditioned Bi-CGStab Krylov linear solver
spbcg;
•idas sptfqmr.h, which is used with the scaled, preconditioned TFQMR Krylov solver sptfqmr.
The header files for the dense and banded linear solvers (both internal and Lapack) include the file
idas direct.h, which defines common functions. This in turn includes a file (sundials direct.h)
which defines the matrix type for these direct linear solvers (DlsMat), as well as various functions and
macros acting on such matrices.
The header files for the KLU and SuperLU MT sparse linear solvers include the file idas sparse.h,
which defines common functions. This in turn includes a file (sundials sparse.h) which defines the
matrix type for these sparse direct linear solvers (SlsMat), as well as various functions and macros
acting on such matrices.
The header files for the Krylov iterative solvers include idas spils.h which defines common
functions and which in turn includes a header file (sundials iterative.h) which enumerates the
kind of preconditioning and (for the spgmr solver only) the choices for the Gram-Schmidt process.
Other headers may be needed, according to the choice of preconditioner, etc. For example, in the
idasFoodWeb kry p example (see [33]), preconditioning is done with a block-diagonal matrix. For
this, even though the idaspgmr linear solver is used, the header sundials dense.h is included for
access to the underlying generic dense linear solver.
4.4 A skeleton of the user’s main program
The following is a skeleton of the user’s main program (or calling program) for the integration of a
DAE IVP. Most of the steps are independent of the nvector implementation used. For the steps
that are not, refer to Chapter 7for the specific name of the function to be called or macro to be
referenced.
1. Initialize parallel or multi-threaded environment, if appropriate
For example, call MPI Init to initialize MPI if used, or set num threads, the number of threads
to use within the threaded vector functions, if used.
2. Set problem dimensions etc.
This generally includes the problem size N, and may include the local vector length Nlocal.
Note: The variables Nand Nlocal should be of type long int.
3. Set vectors of initial values
To set the vectors y0 and yp0 to initial values for yand ˙y, use the appropriate functions defined
by the particular nvector implementation.
For native sundials vector implementations, use a call of the form y0 = N VMake ***(...,
ydata) if the realtype array ydata containing the initial values of yalready exists. Otherwise,
create a new vector by making a call of the form y0 = N VNew ***(...), and then set its elements
by accessing the underlying data with a call of the form ydata = N VGetArrayPointer ***(y0).
See §7.1-7.4 for details.

28 Using IDAS for IVP Solution
For the hypre and petsc vector wrappers, first create and initialize the underlying vector and
then create nvector wrapper with a call of the form y0 = N VMake ***(yvec), where yvec is a
hypre or petsc vector. Note that calls like N VNew ***(...) and N VGetArrayPointer ***(...)
are not available for these vector wrappers. See §7.5 and §7.6 for details.
Set the vector yp0 of initial conditions for ˙ysimilarly.
4. Create idas object
Call ida mem = IDACreate() to create the idas memory block. IDACreate returns a pointer to
the idas memory structure. See §4.5.1 for details. This void * pointer must then be passed as
the first argument to all subsequent idas function calls.
5. Initialize idas solver
Call IDAInit(...) to provide required problem specifications (residual function, initial time, and
initial conditions), allocate internal memory for idas, and initialize idas.IDAInit returns an
error flag to indicate success or an illegal argument value. See §4.5.1 for details.
6. Specify integration tolerances
Call IDASStolerances(...) or IDASVtolerances(...) to specify, respectively, a scalar relative
tolerance and scalar absolute tolerance, or a scalar relative tolerance and a vector of absolute
tolerances. Alternatively, call IDAWFtolerances to specify a function which sets directly the
weights used in evaluating WRMS vector norms. See §4.5.2 for details.
7. Set optional inputs
Optionally, call IDASet* functions to change from their default values any optional inputs that
control the behavior of idas. See §4.5.7.1 for details.
8. Attach linear solver module
Initialize the linear solver module with one of the following calls (for details see §4.5.3):
flag = IDADense(...);
flag = IDABand(...);
flag = IDALapackDense(...);
flag = IDALapackBand(...);
flag = IDAKLU(...);
flag = IDASuperLUMT(...);
flag = IDASpgmr(...);
flag = IDASpbcg(...);
flag = IDASptfqmr(...);
NOTE: The direct (dense or band) and sparse linear solver options are usable only in a serial
environment.
9. Set linear solver optional inputs
Optionally, call IDA*Set* functions from the selected linear solver module to change optional
inputs specific to that linear solver. See §4.5.7.2 and §4.5.7.4 for details.
10. Correct initial values
Optionally, call IDACalcIC to correct the initial values y0 and yp0 passed to IDAInit. See §4.5.4.
Also see §4.5.7.5 for relevant optional input calls.
11. Specify rootfinding problem

4.4 A skeleton of the user’s main program 29
Optionally, call IDARootInit to initialize a rootfinding problem to be solved during the integration
of the DAE system. See §4.5.5 for details, and see §4.5.7.6 for relevant optional input calls.
12. Advance solution in time
For each point at which output is desired, call flag = IDASolve(ida mem, tout, &tret, yret,
ypret, itask). Here itask specifies the return mode. The vector yret (which can be the same
as the vector y0 above) will contain y(t), while the vector ypret will contain ˙y(t). See §4.5.6 for
details.
13. Get optional outputs
Call IDA*Get* functions to obtain optional output. See §4.5.9 for details.
14. Deallocate memory for solution vectors
Upon completion of the integration, deallocate memory for the vectors yret and ypret (or yand
yp) by calling the appropriate destructor function defined by the nvector implementation:
N VDestroy ***(yret);
and similarly for ypret.
15. Free solver memory
IDAFree(&ida mem) to free the memory allocated for idas.
16. Finalize MPI, if used
Call MPI Finalize() to terminate MPI.
sundials provides some linear solvers only as a means for users to get problems running and not
as highly efficient solvers. For example, if solving a dense system, we suggest using the Lapack solvers
if the size of the linear system is >50,000. (Thanks to A. Nicolai for his testing and recommen-
dation.) Table 4.1 shows the linear solver interfaces available in sundials packages and the vector
implementations required for use. As an example, one cannot use the sundials package specific dense
direct solver interfaces with the MPI-based vector implementation. However, as discussed in Chapter
9the direct dense, direct band, and iterative spils solvers provided with sundials are written in a
way that allows a user to develop their own solvers around them should a user so desire.
Table 4.1: sundials linear solver interfaces and vector implementations that can be used for each.
Linear Solver
Interface
Serial Parallel
(MPI)
OpenMP pThreads hypre
Vector
petsc
Vector
User
Supplied
Dense X X X X
Band X X X X
LapackDense X X X X
LapackBand X X X X
klu X X X X
superlumt X X X X
spgmr X X X X X X X
spfgmr X X X X X X X
spbcg X X X X X X X
sptfqmr XXXXXXX
User supplied XXXXXXX
30 Using IDAS for IVP Solution
4.5 User-callable functions
This section describes the idas functions that are called by the user to set up and solve a DAE. Some of
these are required. However, starting with §4.5.7, the functions listed involve optional inputs/outputs
or restarting, and those paragraphs can be skipped for a casual use of idas. In any case, refer to §4.4
for the correct order of these calls.
On an error, each user-callable function returns a negative value and sends an error message to
the error handler routine, which prints the message on stderr by default. However, the user can set
a file as error output or can provide his own error handler function (see §4.5.7.1).
4.5.1 IDAS initialization and deallocation functions
The following three functions must be called in the order listed. The last one is to be called only after
the DAE solution is complete, as it frees the idas memory block created and allocated by the first
two calls.
IDACreate
Call ida mem = IDACreate();
Description The function IDACreate instantiates an idas solver object.
Arguments IDACreate has no arguments.
Return value If successful, IDACreate returns a pointer to the newly created idas memory block (of
type void *). Otherwise it returns NULL.
IDAInit
Call flag = IDAInit(ida mem, res, t0, y0, yp0);
Description The function IDAInit provides required problem and solution specifications, allocates
internal memory, and initializes idas.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
res (IDAResFn) is the Cfunction which computes the residual function Fin the
DAE. This function has the form res(t, yy, yp, resval, user data). For
full details see §4.6.1.
t0 (realtype) is the initial value of t.
y0 (N Vector) is the initial value of y.
yp0 (N Vector) is the initial value of ˙y.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAInit was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.
IDA MEM FAIL A memory allocation request has failed.
IDA ILL INPUT An input argument to IDAInit has an illegal value.
Notes If an error occurred, IDAInit also sends an error message to the error handler function.
IDAFree
Call IDAFree(&ida mem);
Description The function IDAFree frees the pointer allocated by a previous call to IDACreate.
Arguments The argument is the pointer to the idas memory block (of type void *).
Return value The function IDAFree has no return value.
4.5 User-callable functions 31
4.5.2 IDAS tolerance specification functions
One of the following three functions must be called to specify the integration tolerances (or directly
specify the weights used in evaluating WRMS vector norms). Note that this call must be made after
the call to IDAInit.
IDASStolerances
Call flag = IDASStolerances(ida mem, reltol, abstol);
Description The function IDASStolerances specifies scalar relative and absolute tolerances.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
reltol (realtype) is the scalar relative error tolerance.
abstol (realtype) is the scalar absolute error tolerance.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDASStolerances was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.
IDA NO MALLOC The allocation function IDAInit has not been called.
IDA ILL INPUT One of the input tolerances was negative.
IDASVtolerances
Call flag = IDASVtolerances(ida mem, reltol, abstol);
Description The function IDASVtolerances specifies scalar relative tolerance and vector absolute
tolerances.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
reltol (realtype) is the scalar relative error tolerance.
abstol (N Vector) is the vector of absolute error tolerances.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDASVtolerances was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.
IDA NO MALLOC The allocation function IDAInit has not been called.
IDA ILL INPUT The relative error tolerance was negative or the absolute tolerance had
a negative component.
Notes This choice of tolerances is important when the absolute error tolerance needs to be
different for each component of the state vector y.
IDAWFtolerances
Call flag = IDAWFtolerances(ida mem, efun);
Description The function IDAWFtolerances specifies a user-supplied function efun that sets the
multiplicative error weights Wifor use in the weighted RMS norm, which are normally
defined by Eq. (2.7).
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
efun (IDAEwtFn) is the Cfunction which defines the ewt vector (see §4.6.3).
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAWFtolerances was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.

32 Using IDAS for IVP Solution
IDA NO MALLOC The allocation function IDAInit has not been called.
General advice on choice of tolerances. For many users, the appropriate choices for tolerance
values in reltol and abstol are a concern. The following pieces of advice are relevant.
(1) The scalar relative tolerance reltol is to be set to control relative errors. So reltol=10−4
means that errors are controlled to .01%. We do not recommend using reltol larger than 10−3.
On the other hand, reltol should not be so small that it is comparable to the unit roundoff of the
machine arithmetic (generally around 10−15).
(2) The absolute tolerances abstol (whether scalar or vector) need to be set to control absolute
errors when any components of the solution vector ymay be so small that pure relative error control
is meaningless. For example, if y[i] starts at some nonzero value, but in time decays to zero, then
pure relative error control on y[i] makes no sense (and is overly costly) after y[i] is below some
noise level. Then abstol (if scalar) or abstol[i] (if a vector) needs to be set to that noise level. If
the different components have different noise levels, then abstol should be a vector. See the example
idasRoberts dns in the idas package, and the discussion of it in the idas Examples document [33].
In that problem, the three components vary between 0 and 1, and have different noise levels; hence the
abstol vector. It is impossible to give any general advice on abstol values, because the appropriate
noise levels are completely problem-dependent. The user or modeler hopefully has some idea as to
what those noise levels are.
(3) Finally, it is important to pick all the tolerance values conservatively, because they control the
error committed on each individual time step. The final (global) errors are a sort of accumulation of
those per-step errors. A good rule of thumb is to reduce the tolerances by a factor of .01 from the actual
desired limits on errors. So if you want .01% accuracy (globally), a good choice is reltol= 10−6. But
in any case, it is a good idea to do a few experiments with the tolerances to see how the computed
solution values vary as tolerances are reduced.
Advice on controlling unphysical negative values. In many applications, some components
in the true solution are always positive or non-negative, though at times very small. In the numerical
solution, however, small negative (hence unphysical) values can then occur. In most cases, these values
are harmless, and simply need to be controlled, not eliminated. The following pieces of advice are
relevant.
(1) The way to control the size of unwanted negative computed values is with tighter absolute
tolerances. Again this requires some knowledge of the noise level of these components, which may or
may not be different for different components. Some experimentation may be needed.
(2) If output plots or tables are being generated, and it is important to avoid having negative
numbers appear there (for the sake of avoiding a long explanation of them, if nothing else), then
eliminate them, but only in the context of the output medium. Then the internal values carried by
the solver are unaffected. Remember that a small negative value in yret returned by idas, with
magnitude comparable to abstol or less, is equivalent to zero as far as the computation is concerned.
(3) The user’s residual routine res should never change a negative value in the solution vector yy
to a non-negative value, as a ”solution” to this problem. This can cause instability. If the res routine
cannot tolerate a zero or negative value (e.g. because there is a square root or log of it), then the
offending value should be changed to zero or a tiny positive number in a temporary variable (not in
the input yy vector) for the purposes of computing F(t, y, ˙y).
(4) idas provides the option of enforcing positivity or non-negativity on components. Also, such
constraints can be enforced by use of the recoverable error return feature in the user-supplied residual
function. However, because these options involve some extra overhead cost, they should only be
exercised if the use of absolute tolerances to control the computed values is unsuccessful.
4.5.3 Linear solver specification functions
As previously explained, Newton iteration requires the solution of linear systems of the form (2.5).
There are seven idas linear solvers currently available for this task: idadense,idaband,idaklu,
idasuperlumt,idaspgmr,idaspbcg, and idasptfqmr.
The first two linear solvers are direct and derive their names from the type of approximation
4.5 User-callable functions 33
used for the Jacobian J=∂F/∂y +α∂F/∂ ˙y.idadense and idaband work with dense and banded
approximations to J, respectively. The sundials suite includes both internal implementations of
these two linear solvers and interfaces to Lapack implementations. Together, these linear solvers are
referred to as idadls (from Direct Linear Solvers).
The second two linear solvers are sparse direct solvers based on Gaussian elimination, and require
user-supplied routines to construct the Jacobian J=∂F/∂y +α∂F/∂ ˙yin compressed-sparse-column
format. The sundials suite does not include internal implementations of these solver libraries, instead
requiring compilation of sundials to link with existing installations of these libraries (if either is
missing, sundials will install without the corresponding interface routines). Together, these linear
solvers are referred to as cvsls (from Sparse Linear Solvers).
The remaining three idas linear solvers, idaspgmr,idaspbcg, and idasptfqmr, are Krylov
iterative solvers. The spgmr,spbcg, and sptfqmr in the names indicate the scaled preconditioned
GMRES, scaled preconditioned Bi-CGStab, and scaled preconditioned TFQMR methods, respectively.
Together, they are referred to as idaspils (from Scaled Preconditioned Iterative Linear Solvers).
When using any of the Krylov linear solvers, preconditioning (on the left) is permitted, and in fact
encouraged, for the sake of efficiency. A preconditioner matrix Pmust approximate the Jacobian J,
at least crudely. For the specification of a preconditioner, see §4.5.7.4 and §4.6.
To specify an idas linear solver, after the call to IDACreate but before any calls to IDASolve, the
user’s program must call one of the functions IDADense/IDALapackDense,IDABand/IDALapackBand,
IDAKLU,IDASuperLUMT,IDASpgmr,IDASpbcg, or IDASptfqmr, as documented below. The first argu-
ment passed to these functions is the idas memory pointer returned by IDACreate. A call to one
of these functions links the main idas integrator to a linear solver and allows the user to specify
parameters which are specific to a particular solver, such as the bandwidths in the idaband case.
The use of each of the linear solvers involves certain constants and possibly some macros, that are
likely to be needed in the user code. These are available in the corresponding header file associated
with the linear solver, as specified below.
In each case the linear solver module used by idas is actually built on top of a generic linear
system solver, which may be of interest in itself. These generic solvers, denoted dense,band,klu,
superlumt,spgmr,spbcg, and sptfqmr, are described separately in Chapter 9.
IDADense
Call flag = IDADense(ida mem, N);
Description The function IDADense selects the idadense linear solver and indicates the use of the
internal direct dense linear algebra functions.
The user’s main program must include the idas dense.h header file.
Arguments ida mem (void *) pointer to the idas memory block.
N(long int) problem dimension.
Return value The return value flag (of type int) is one of
IDADLS SUCCESS The idadense initialization was successful.
IDADLS MEM NULL The ida mem pointer is NULL.
IDADLS ILL INPUT The idadense solver is not compatible with the current nvector
module.
IDADLS MEM FAIL A memory allocation request failed.
Notes The idadense linear solver is not compatible with all implementations of the nvector
module. Of the nvector modules provided with sundials, only nvector serial,
nvector openmp, and nvector pthreads are compatible.
IDALapackDense
Call flag = IDALapackDense(ida mem, N);

34 Using IDAS for IVP Solution
Description The function IDALapackDense selects the idadense linear solver and indicates the use
of Lapack functions.
The user’s main program must include the idas lapack.h header file.
Arguments ida mem (void *) pointer to the idas memory block.
N(int) problem dimension.
Return value The values of the returned flag (of type int) are identical to those of IDADense.
Notes Note that Nis restricted to be of type int here, because of the corresponding type
restriction in the Lapack solvers.
IDABand
Call flag = IDABand(ida mem, N, mupper, mlower);
Description The function IDABand selects the idaband linear solver and indicates the use of the
internal direct band linear algebra functions.
The user’s main program must include the idas band.h header file.
Arguments ida mem (void *) pointer to the idas memory block.
N(long int) problem dimension.
mupper (long int) upper half-bandwidth of the problem Jacobian (or of the approx-
imation of it).
mlower (long int) lower half-bandwidth of the problem Jacobian (or of the approxi-
mation of it).
Return value The return value flag (of type int) is one of
IDABAND SUCCESS The idaband initialization was successful.
IDABAND MEM NULL The ida mem pointer is NULL.
IDABAND ILL INPUT The idaband solver is not compatible with the current nvector
module, or one of the Jacobian half-bandwidths is outside its valid
range (0 . . . N−1).
IDABAND MEM FAIL A memory allocation request failed.
Notes The idaband linear solver is not compatible with all implementations of the nvector
module. Of the nvector modules provided with sundials, only nvector serial,
nvector openmp and nvector pthreads are compatible. The half-bandwidths are
to be set so that the nonzero locations (i, j) in the banded (approximate) Jacobian
satisfy −mlower ≤j−i≤mupper.
IDALapackBand
Call flag = IDALapackBand(ida mem, N, mupper, mlower);
Description The function IDALapackBand selects the idaband linear solver and indicates the use of
Lapack functions.
The user’s main program must include the idas lapack.h header file.
Arguments The input arguments are identical to those of IDABand, except that N,mupper, and
mlower are of type int here.
Return value The values of the returned flag (of type int) are identical to those of IDABand.
Notes Note that N,mupper, and mlower are restricted to be of type int here, because of the
corresponding type restriction in the Lapack solvers.
4.5 User-callable functions 35
IDAKLU
Call flag = IDAKLU(ida mem, NP, NNZ, sparsetype);
Description The function IDAKLU selects the idaklu linear solver and indicates the use of sparse
direct linear algebra functions.
The user’s main program must include the idas sparse.h header file.
Arguments ida mem (void *) pointer to the idas memory block.
NP (int) problem dimension.
NNZ (int) maximum number of nonzero entries in the system Jacobian.
sparsetype (int) sparse storage type of the system Jacobian. If sparsetype is set
to CSC MAT the solver will expect the Jacobian to be stored as a compressed
sparse column matrix, and if sparsetype=CSR MAT the solver will expect a
compressed sparse row matrix. If neither option is chosen, the solver will exit
with error.
Return value The return value flag (of type int) is one of
IDASLS SUCCESS The idaklu initialization was successful.
IDASLS MEM NULL The ida mem pointer is NULL.
IDASLS ILL INPUT The idaklu solver is not compatible with the current nvector
module.
IDASLS MEM FAIL A memory allocation request failed.
IDASLS PACKAGE FAIL A call to the KLU library returned a failure flag.
Notes The idaklu linear solver is not compatible with all implementations of the nvector
module. Of the nvector modules provided with sundials, only nvector serial,
nvector openmp and nvector pthreads are compatible.
IDASuperLUMT
Call flag = IDASuperLUMT(ida mem, num threads, N, NNZ);
Description The function IDASuperLUMT selects the idasuperlumt linear solver and indicates the
use of sparse direct linear algebra functions.
The user’s main program must include the idas superlumt.h header file.
Arguments ida mem (void *) pointer to the idas memory block.
num threads (int) the number of threads to use when factoring/solving the linear
systems. Note that SuperLU MT is thread-parallel only in the factorization
routine.
N(int) problem dimension.
NNZ (int) maximum number of nonzero entries in the system Jacobian.
Return value The return value flag (of type int) is one of
IDASLS SUCCESS The idasuperlumt initialization was successful.
IDASLS MEM NULL The ida mem pointer is NULL.
IDASLS ILL INPUT The idasuperlumt solver is not compatible with the current nvec-
tor module.
IDASLS MEM FAIL A memory allocation request failed.
IDASLS PACKAGE FAIL A call to the SuperLU MT library returned a failure flag.
Notes The idasuperlumt linear solver is not compatible with all implementations of the
nvector module. Of the nvector modules provided with sundials, only nvec-
tor serial,nvector openmp and nvector pthreads are compatible.
Performance will significantly degrade if the user applies the SuperLU MT package
!
36 Using IDAS for IVP Solution
compiled with PThreads while using the nvector openmp module. If a user wants to
use a threaded vector kernel with this thread-parallel solver, then SuperLU MT should
be compiled with openMP and the nvector openmp module should be used. Also,
note that the expected benefit of using the threaded vector kernel is minimal compared
to the potential benefit of the threaded solver, unless very long (greater than 100,000
entries) vectors are used.
IDASpgmr
Call flag = IDASpgmr(ida mem, maxl);
Description The function IDASpgmr selects the idaspgmr linear solver.
The user’s main program must include the idas spgmr.h header file.
Arguments ida mem (void *) pointer to the idas memory block.
maxl (int) maximum dimension of the Krylov subspace to be used. Pass 0 to use
the default value IDA SPILS MAXL= 5.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The idaspgmr initialization was successful.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS MEM FAIL A memory allocation request failed.
IDASpbcg
Call flag = IDASpbcg(ida mem, maxl);
Description The function IDASpbcg selects the idaspbcg linear solver.
The user’s main program must include the idas spbcgs.h header file.
Arguments ida mem (void *) pointer to the idas memory block.
maxl (int) maximum dimension of the Krylov subspace to be used. Pass 0 to use
the default value IDA SPILS MAXL= 5.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The idaspbcg initialization was successful.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS MEM FAIL A memory allocation request failed.
IDASptfqmr
Call flag = IDASptfqmr(ida mem, maxl);
Description The function IDASptfqmr selects the idasptfqmr linear solver.
The user’s main program must include the idas sptfqmr.h header file.
Arguments ida mem (void *) pointer to the idas memory block.
maxl (int) maximum dimension of the Krylov subspace to be used. Pass 0 to use
the default value IDA SPILS MAXL= 5.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The idasptfqmr initialization was successful.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS MEM FAIL A memory allocation request failed.

4.5 User-callable functions 37
4.5.4 Initial condition calculation function
IDACalcIC calculates corrected initial conditions for the DAE system for certain index-one problems
including a class of systems of semi-implicit form. (See §2.1 and Ref. [6].) It uses Newton iteration
combined with a linesearch algorithm. Calling IDACalcIC is optional. It is only necessary when
the initial conditions do not satisfy the given system. Thus if y0 and yp0 are known to satisfy
F(t0, y0,˙y0) = 0, then a call to IDACalcIC is generally not necessary.
A call to the function IDACalcIC must be preceded by successful calls to IDACreate and IDAInit
(or IDAReInit), and by a successful call to the linear system solver specification function. The call to
IDACalcIC should precede the call(s) to IDASolve for the given problem.
IDACalcIC
Call flag = IDACalcIC(ida mem, icopt, tout1);
Description The function IDACalcIC corrects the initial values y0 and yp0 at time t0.
Arguments ida mem (void *) pointer to the idas memory block.
icopt (int) is one of the following two options for the initial condition calculation.
icopt=IDA YA YDP INIT directs IDACalcIC to compute the algebraic compo-
nents of yand differential components of ˙y, given the differential components
of y. This option requires that the N Vector id was set through IDASetId,
specifying the differential and algebraic components.
icopt=IDA Y INIT directs IDACalcIC to compute all components of y, given
˙y. In this case, id is not required.
tout1 (realtype) is the first value of tat which a solution will be requested (from
IDASolve). This value is needed here only to determine the direction of inte-
gration and rough scale in the independent variable t.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS IDASolve succeeded.
IDA MEM NULL The argument ida mem was NULL.
IDA NO MALLOC The allocation function IDAInit has not been called.
IDA ILL INPUT One of the input arguments was illegal.
IDA LSETUP FAIL The linear solver’s setup function failed in an unrecoverable man-
ner.
IDA LINIT FAIL The linear solver’s initialization function failed.
IDA LSOLVE FAIL The linear solver’s solve function failed in an unrecoverable man-
ner.
IDA BAD EWT Some component of the error weight vector is zero (illegal), either
for the input value of y0 or a corrected value.
IDA FIRST RES FAIL The user’s residual function returned a recoverable error flag on
the first call, but IDACalcIC was unable to recover.
IDA RES FAIL The user’s residual function returned a nonrecoverable error flag.
IDA NO RECOVERY The user’s residual function, or the linear solver’s setup or solve
function had a recoverable error, but IDACalcIC was unable to
recover.
IDA CONSTR FAIL IDACalcIC was unable to find a solution satisfying the inequality
constraints.
IDA LINESEARCH FAIL The linesearch algorithm failed to find a solution with a step
larger than steptol in weighted RMS norm, and within the
allowed number of backtracks.
IDA CONV FAIL IDACalcIC failed to get convergence of the Newton iterations.
38 Using IDAS for IVP Solution
Notes All failure return values are negative and therefore a test flag <0 will trap all
IDACalcIC failures.
Note that IDACalcIC will correct the values of y(t0) and ˙y(t0) which were specified
in the previous call to IDAInit or IDAReInit. To obtain the corrected values, call
IDAGetconsistentIC (see §4.5.9.2).
4.5.5 Rootfinding initialization function
While integrating the IVP, idas has the capability of finding the roots of a set of user-defined functions.
To activate the rootfinding algorithm, call the following function. This is normally called only once,
prior to the first call to IDASolve, but if the rootfinding problem is to be changed during the solution,
IDARootInit can also be called prior to a continuation call to IDASolve.
IDARootInit
Call flag = IDARootInit(ida mem, nrtfn, g);
Description The function IDARootInit specifies that the roots of a set of functions gi(t, y, ˙y) are to
be found while the IVP is being solved.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
nrtfn (int) is the number of root functions gi.
g(IDARootFn) is the Cfunction which defines the nrtfn functions gi(t, y, ˙y)
whose roots are sought. See §4.6.4 for details.
Return value The return value flag (of type int) is one of
IDA SUCCESS The call to IDARootInit was successful.
IDA MEM NULL The ida mem argument was NULL.
IDA MEM FAIL A memory allocation failed.
IDA ILL INPUT The function gis NULL, but nrtfn>0.
Notes If a new IVP is to be solved with a call to IDAReInit, where the new IVP has no
rootfinding problem but the prior one did, then call IDARootInit with nrtfn= 0.
4.5.6 IDAS solver function
This is the central step in the solution process, the call to perform the integration of the DAE. One
of the input arguments (itask) specifies one of two modes as to where idas is to return a solution.
But these modes are modified if the user has set a stop time (with IDASetStopTime) or requested
rootfinding.
IDASolve
Call flag = IDASolve(ida mem, tout, &tret, yret, ypret, itask);
Description The function IDASolve integrates the DAE over an interval in t.
Arguments ida mem (void *) pointer to the idas memory block.
tout (realtype) the next time at which a computed solution is desired.
tret (realtype) the time reached by the solver (output).
yret (N Vector) the computed solution vector y.
ypret (N Vector) the computed solution vector ˙y.
itask (int) a flag indicating the job of the solver for the next user step. The
IDA NORMAL task is to have the solver take internal steps until it has reached or
just passed the user specified tout parameter. The solver then interpolates in
order to return approximate values of y(tout) and ˙y(tout). The IDA ONE STEP
option tells the solver to just take one internal step and return the solution at
the point reached by that step.

4.5 User-callable functions 39
Return value IDASolve returns vectors yret and ypret and a corresponding independent variable
value t=tret, such that (yret,ypret) are the computed values of (y(t), ˙y(t)).
In IDA NORMAL mode with no errors, tret will be equal to tout and yret =y(tout),
ypret = ˙y(tout).
The return value flag (of type int) will be one of the following:
IDA SUCCESS IDASolve succeeded.
IDA TSTOP RETURN IDASolve succeeded by reaching the stop point specified through
the optional input function IDASetStopTime.
IDA ROOT RETURN IDASolve succeeded and found one or more roots. In this case,
tret is the location of the root. If nrtfn >1, call IDAGetRootInfo
to see which giwere found to have a root. See §4.5.9.3 for more
information.
IDA MEM NULL The ida mem argument was NULL.
IDA ILL INPUT One of the inputs to IDASolve was illegal, or some other input
to the solver was either illegal or missing. The latter category
includes the following situations: (a) The tolerances have not been
set. (b) A component of the error weight vector became zero during
internal time-stepping. (c) The linear solver initialization function
(called by the user after calling IDACreate) failed to set the linear
solver-specific lsolve field in ida mem. (d) A root of one of the
root functions was found both at a point tand also very near t. In
any case, the user should see the printed error message for details.
IDA TOO MUCH WORK The solver took mxstep internal steps but could not reach tout.
The default value for mxstep is MXSTEP DEFAULT = 500.
IDA TOO MUCH ACC The solver could not satisfy the accuracy demanded by the user for
some internal step.
IDA ERR FAIL Error test failures occurred too many times (MXNEF = 10) during
one internal time step or occurred with |h|=hmin.
IDA CONV FAIL Convergence test failures occurred too many times (MXNCF = 10)
during one internal time step or occurred with |h|=hmin.
IDA LINIT FAIL The linear solver’s initialization function failed.
IDA LSETUP FAIL The linear solver’s setup function failed in an unrecoverable man-
ner.
IDA LSOLVE FAIL The linear solver’s solve function failed in an unrecoverable manner.
IDA CONSTR FAIL The inequality constraints were violated and the solver was unable
to recover.
IDA REP RES ERR The user’s residual function repeatedly returned a recoverable error
flag, but the solver was unable to recover.
IDA RES FAIL The user’s residual function returned a nonrecoverable error flag.
IDA RTFUNC FAIL The rootfinding function failed.
Notes The vector yret can occupy the same space as the vector y0 of initial conditions that
was passed to IDAInit, and the vector ypret can occupy the same space as yp0.
In the IDA ONE STEP mode, tout is used on the first call only, and only to get the
direction and rough scale of the independent variable.
All failure return values are negative and therefore a test flag <0 will trap all IDASolve
failures.
On any error return in which one or more internal steps were taken by IDASolve, the
returned values of tret,yret, and ypret correspond to the farthest point reached in
the integration. On all other error returns, these values are left unchanged from the
previous IDASolve return.
40 Using IDAS for IVP Solution
4.5.7 Optional input functions
There are numerous optional input parameters that control the behavior of the idas solver. idas
provides functions that can be used to change these optional input parameters from their default
values. Table 4.2 lists all optional input functions in idas which are then described in detail in the
remainder of this section. For the most casual use of idas, the reader can skip to §4.6.
We note that, on an error return, all these functions also send an error message to the error handler
function. We also note that all error return values are negative, so a test flag <0 will catch any
error.
4.5.7.1 Main solver optional input functions
The calls listed here can be executed in any order. However, if the user’s program calls either
IDASetErrFile or IDASetErrHandlerFn, then that call should appear first, in order to take effect for
any later error message.
IDASetErrFile
Call flag = IDASetErrFile(ida mem, errfp);
Description The function IDASetErrFile specifies the pointer to the file where all idas messages
should be directed when the default idas error handler function is used.
Arguments ida mem (void *) pointer to the idas memory block.
errfp (FILE *) pointer to output file.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes The default value for errfp is stderr.
Passing a value NULL disables all future error message output (except for the case in
which the idas memory pointer is NULL). This use of IDASetErrFile is strongly dis-
couraged.
If IDASetErrFile is to be called, it should be called before any other optional input
!
functions, in order to take effect for any later error message.
IDASetErrHandlerFn
Call flag = IDASetErrHandlerFn(ida mem, ehfun, eh data);
Description The function IDASetErrHandlerFn specifies the optional user-defined function to be
used in handling error messages.
Arguments ida mem (void *) pointer to the idas memory block.
ehfun (IDAErrHandlerFn) is the user’s Cerror handler function (see §4.6.2).
eh data (void *) pointer to user data passed to ehfun every time it is called.
Return value The return value flag (of type int) is one of
IDA SUCCESS The function ehfun and data pointer eh data have been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes Error messages indicating that the idas solver memory is NULL will always be directed
to stderr.
4.5 User-callable functions 41
Table 4.2: Optional inputs for idas,idadls,idasls, and idaspils
Optional input Function name Default
IDAS main solver
Pointer to an error file IDASetErrFile stderr
Error handler function IDASetErrHandlerFn internal fn.
User data IDASetUserData NULL
Maximum order for BDF method IDASetMaxOrd 5
Maximum no. of internal steps before tout IDASetMaxNumSteps 500
Initial step size IDASetInitStep estimated
Maximum absolute step size IDASetMaxStep ∞
Value of tstop IDASetStopTime ∞
Maximum no. of error test failures IDASetMaxErrTestFails 10
Maximum no. of nonlinear iterations IDASetMaxNonlinIters 4
Maximum no. of convergence failures IDASetMaxConvFails 10
Maximum no. of error test failures IDASetMaxErrTestFails 7
Coeff. in the nonlinear convergence test IDASetNonlinConvCoef 0.33
Suppress alg. vars. from error test IDASetSuppressAlg FALSE
Variable types (differential/algebraic) IDASetId NULL
Inequality constraints on solution IDASetConstraints NULL
Direction of zero-crossing IDASetRootDirection both
Disable rootfinding warnings IDASetNoInactiveRootWarn none
IDAS initial conditions calculation
Coeff. in the nonlinear convergence test IDASetNonlinConvCoefIC 0.0033
Maximum no. of steps IDASetMaxNumStepsIC 5
Maximum no. of Jacobian/precond. evals. IDASetMaxNumJacsIC 4
Maximum no. of Newton iterations IDASetMaxNumItersIC 10
Max. linesearch backtracks per Newton iter. IDASetMaxBacksIC 100
Turn off linesearch IDASetLineSearchOffIC FALSE
Lower bound on Newton step IDASetStepToleranceIC uround2/3
IDADLS linear solvers
Dense Jacobian function IDADlsSetDenseJacFn DQ
Band Jacobian function IDADlsSetBandJacFn DQ
IDASLS linear solvers
Sparse Jacobian function IDASlsSetSparseJacFn none
Sparse matrix ordering algorithm IDAKLUSetOrdering 1 for COLAMD
Sparse matrix ordering algorithm IDASuperLUMTSetOrdering 3 for COLAMD
IDASPILS linear solvers
Preconditioner functions IDASpilsSetPreconditioner NULL, NULL
Jacobian-times-vector function IDASpilsSetJacTimesVecFn DQ
Factor in linear convergence test IDASpilsSetEpsLin 0.05
Factor in DQ increment calculation IDASpilsSetIncrementFactor 1.0
Maximum no. of restarts (idaspgmr)IDASpilsSetMaxRestarts 5
Type of Gram-Schmidt orthogonalization (a)IDASpilsSetGSType Modified GS
Maximum Krylov subspace size(b)IDASpilsSetMaxl 5
(a)Only for idaspgmr
(b)Only for idaspbcg and idasptfqmr

42 Using IDAS for IVP Solution
IDASetUserData
Call flag = IDASetUserData(ida mem, user data);
Description The function IDASetUserData specifies the user data block user data and attaches it
to the main idas memory block.
Arguments ida mem (void *) pointer to the idas memory block.
user data (void *) pointer to the user data.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes If specified, the pointer to user data is passed to all user-supplied functions that have
it as an argument. Otherwise, a NULL pointer is passed.
If user data is needed in user linear solver or preconditioner functions, the call to
!
IDASetUserData must be made before the call to specify the linear solver.
IDASetMaxOrd
Call flag = IDASetMaxOrd(ida mem, maxord);
Description The function IDASetMaxOrd specifies the maximum order of the linear multistep method.
Arguments ida mem (void *) pointer to the idas memory block.
maxord (int) value of the maximum method order. This must be positive.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT The input value maxord is ≤0, or larger than its previous value.
Notes The default value is 5. If the input value exceeds 5, the value 5 will be used. Since
maxord affects the memory requirements for the internal idas memory block, its value
cannot be increased past its previous value.
IDASetMaxNumSteps
Call flag = IDASetMaxNumSteps(ida mem, mxsteps);
Description The function IDASetMaxNumSteps specifies the maximum number of steps to be taken
by the solver in its attempt to reach the next output time.
Arguments ida mem (void *) pointer to the idas memory block.
mxsteps (long int) maximum allowed number of steps.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes Passing mxsteps = 0 results in idas using the default value (500).
Passing mxsteps <0 disables the test (not recommended).
IDASetInitStep
Call flag = IDASetInitStep(ida mem, hin);
Description The function IDASetInitStep specifies the initial step size.
Arguments ida mem (void *) pointer to the idas memory block.
4.5 User-callable functions 43
hin (realtype) value of the initial step size to be attempted. Pass 0.0 to have
idas use the default value.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes By default, idas estimates the initial step as the solution of kh˙ykWRMS = 1/2, with an
added restriction that |h| ≤ .001|tout - t0|.
IDASetMaxStep
Call flag = IDASetMaxStep(ida mem, hmax);
Description The function IDASetMaxStep specifies the maximum absolute value of the step size.
Arguments ida mem (void *) pointer to the idas memory block.
hmax (realtype) maximum absolute value of the step size.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT Either hmax is not positive or it is smaller than the minimum allowable
step.
Notes Pass hmax= 0 to obtain the default value ∞.
IDASetStopTime
Call flag = IDASetStopTime(ida mem, tstop);
Description The function IDASetStopTime specifies the value of the independent variable tpast
which the solution is not to proceed.
Arguments ida mem (void *) pointer to the idas memory block.
tstop (realtype) value of the independent variable past which the solution should
not proceed.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT The value of tstop is not beyond the current tvalue, tn.
Notes The default, if this routine is not called, is that no stop time is imposed.
IDASetMaxErrTestFails
Call flag = IDASetMaxErrTestFails(ida mem, maxnef);
Description The function IDASetMaxErrTestFails specifies the maximum number of error test
failures in attempting one step.
Arguments ida mem (void *) pointer to the idas memory block.
maxnef (int) maximum number of error test failures allowed on one step (>0).
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes The default value is 7.
44 Using IDAS for IVP Solution
IDASetMaxNonlinIters
Call flag = IDASetMaxNonlinIters(ida mem, maxcor);
Description The function IDASetMaxNonlinIters specifies the maximum number of nonlinear solver
iterations at one step.
Arguments ida mem (void *) pointer to the idas memory block.
maxcor (int) maximum number of nonlinear solver iterations allowed on one step
(>0).
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes The default value is 3.
IDASetMaxConvFails
Call flag = IDASetMaxConvFails(ida mem, maxncf);
Description The function IDASetMaxConvFails specifies the maximum number of nonlinear solver
convergence failures at one step.
Arguments ida mem (void *) pointer to the idas memory block.
maxncf (int) maximum number of allowable nonlinear solver convergence failures on
one step (>0).
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes The default value is 10.
IDASetNonlinConvCoef
Call flag = IDASetNonlinConvCoef(ida mem, nlscoef);
Description The function IDASetNonlinConvCoef specifies the safety factor in the nonlinear con-
vergence test; see Chapter 2, Eq. (2.8).
Arguments ida mem (void *) pointer to the idas memory block.
nlscoef (realtype) coefficient in nonlinear convergence test (>0.0).
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT The value of nlscoef is <= 0.0.
Notes The default value is 0.33.
IDASetSuppressAlg
Call flag = IDASetSuppressAlg(ida mem, suppressalg);
Description The function IDASetSuppressAlg indicates whether or not to suppress algebraic vari-
ables in the local error test.
Arguments ida mem (void *) pointer to the idas memory block.
suppressalg (booleantype) indicates whether to suppress (TRUE) or not (FALSE) the
algebraic variables in the local error test.
Return value The return value flag (of type int) is one of
4.5 User-callable functions 45
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes The default value is FALSE.
If suppressalg=TRUE is selected, then the id vector must be set (through IDASetId)
to specify the algebraic components.
In general, the use of this option (with suppressalg = TRUE) is discouraged when solv-
ing DAE systems of index 1, whereas it is generally encouraged for systems of index 2
or more. See pp. 146-147 of Ref. [3] for more on this issue.
IDASetId
Call flag = IDASetId(ida mem, id);
Description The function IDASetId specifies algebraic/differential components in the yvector.
Arguments ida mem (void *) pointer to the idas memory block.
id (N Vector) state vector. A value of 1.0 indicates a differential variable, while
0.0 indicates an algebraic variable.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes The vector id is required if the algebraic variables are to be suppressed from the lo-
cal error test (see IDASetSuppressAlg) or if IDACalcIC is to be called with icopt =
IDA YA YDP INIT (see §4.5.4).
IDASetConstraints
Call flag = IDASetConstraints(ida mem, constraints);
Description The function IDASetConstraints specifies a vector defining inequality constraints for
each component of the solution vector y.
Arguments ida mem (void *) pointer to the idas memory block.
constraints (N Vector) vector of constraint flags. If constraints[i] is
0.0 then no constraint is imposed on yi.
1.0 then yiwill be constrained to be yi≥0.0.
−1.0 then yiwill be constrained to be yi≤0.0.
2.0 then yiwill be constrained to be yi>0.0.
−2.0 then yiwill be constrained to be yi<0.0.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT The constraints vector contains illegal values.
Notes The presence of a non-NULL constraints vector that is not 0.0 in all components will
cause constraint checking to be performed. However, a call with 0.0 in all components
of constraints will result in an illegal input return.
46 Using IDAS for IVP Solution
4.5.7.2 Dense/band direct linear solvers optional input functions
The idadense solver needs a function to compute a dense approximation to the Jacobian matrix
J(t, y, ˙y). This function must be of type IDADlsDenseJacFn. The user can supply his/her own dense
Jacobian function, or use the default internal difference quotient approximation that comes with the
idadense solver. To specify a user-supplied Jacobian function djac,idadense provides the function
IDADlsSetDenseJacFn. The idadense solver passes the pointer user data to the dense Jacobian
function. This allows the user to create an arbitrary structure with relevant problem data and access
it during the execution of the user-supplied Jacobian function, without using global data in the
program. The pointer user data may be specified through IDASetUserData.
IDADlsSetDenseJacFn
Call flag = IDADlsSetDenseJacFn(ida mem, djac);
Description The function IDADlsSetDenseJacFn specifies the dense Jacobian approximation func-
tion to be used.
Arguments ida mem (void *) pointer to the idas memory block.
djac (IDADlsDenseJacFn) user-defined dense Jacobian approximation function.
Return value The return value flag (of type int) is one of
IDADLS SUCCESS The optional value has been successfully set.
IDADLS MEM NULL The ida mem pointer is NULL.
IDADLS LMEM NULL The idadense linear solver has not been initialized.
Notes By default, idadense uses an internal difference quotient function. If NULL is passed to
djac, this default function is used.
The function type IDADlsDenseJacFn is described in §4.6.5.
The idaband solver needs a function to compute a banded approximation to the Jacobian matrix
J(t, y, ˙y). This function must be of type IDADlsBandJacFn. The user can supply his/her own banded
Jacobian approximation function, or use the default difference quotient function that comes with the
idaband solver. To specify a user-supplied Jacobian function bjac,idaband provides the function
IDADlsSetBandJacFn. The idaband solver passes the pointer user data to the banded Jacobian
approximation function. This allows the user to create an arbitrary structure with relevant problem
data and access it during the execution of the user-supplied Jacobian function, without using global
data in the program. The pointer user data may be specified through IDASetUserData.
IDADlsSetBandJacFn
Call flag = IDADlsSetBandJacFn(ida mem, bjac);
Description The function IDADlsSetBandJacFn specifies the banded Jacobian approximation func-
tion to be used.
Arguments ida mem (void *) pointer to the idas memory block.
bjac (IDADlsBandJacFn) user-defined banded Jacobian approximation function.
Return value The return value flag (of type int) is one of
IDADLS SUCCESS The optional value has been successfully set.
IDADLS MEM NULL The ida mem pointer is NULL.
IDADLS LMEM NULL The idaband linear solver has not been initialized.
Notes By default, idaband uses an internal difference quotient function. If NULL is passed to
bjac, this default function is used.
The function type IDADlsBandJacFn is described in §4.6.6.
4.5 User-callable functions 47
4.5.7.3 Sparse direct linear solvers optional input functions
The idaklu and idasuperlumt solvers require a function to compute a compressed-sparse-column
approximation ot the Jacobian matrix J(t, y, ˙y). This function must be of type IDASlsSparseJacFn.
The user must supply a custom sparse Jacobian function since a difference quotient approximation
would not leverage the underlying sparse matrix structure of the problem. To specify a user-supplied
Jacobian function sjac,idaklu and idasuperlumt provide the function IDASlsSetSparseJacFn.
The idaklu and idasuperlumt solvers pass the pointer user data to the sparse Jacobian function.
This mechanism allows the user to create an arbitrary structure with relevant problem data and
access it during the execution of the user-supplied Jacobian function, without using global data in the
program. The pointer user data may be specified through IDASetUserData.
IDASlsSetSparseJacFn
Call flag = IDASlsSetSparseJacFn(ida mem, sjac);
Description The function IDASlsSetSparseJacFn specifies the sparse Jacobian approximation func-
tion to be used.
Arguments ida mem (void *) pointer to the idas memory block.
sjac (IDASlsSparseJacFn) user-defined sparse Jacobian approximation function.
Return value The return value flag (of type int) is one of
IDASLS SUCCESS The optional value has been successfully set.
IDASLS MEM NULL The ida mem pointer is NULL.
IDASLS LMEM NULL The idaklu or idasuperlumt linear solver has not been initialized.
Notes The function type IDASlsSparseJacFn is described in §4.6.7.
When using a sparse direct solver, there may be instances when the number of state variables does
not change, but the number of nonzeroes in the Jacobian does change. In this case, for the idaklu
solver, we provide the following reinitialization function. This function reinitializes the Jacobian
matrix memory for the new number of nonzeroes and sets flags for a new factorization (symbolic and
numeric) to be conducted at the next solver setup call. This routine is useful in the cases where the
number of nonzeroes has changed, or where the structure of the linear system has changed, requiring
a new symbolic (and numeric) factorization.
IDAKLUReInit
Call flag = IDAKLUReInit(ida mem, n, nnz, reinit type);
Description The function IDAKLUReInit reinitializes Jacobian matrix memory and flags for new
symbolic and numeric KLU factorizations.
Arguments ida mem (void *) pointer to the ida memory block.
n(int) number of state variables in the system.
nnz (int) number of nonzeroes in the Jacobian matrix.
reinit type (int) type of reinitialization:
1 The Jacobian matrix will be destroyed and a new one will be allocated
based on the nnz value passed to this call. New symbolic and numeric
factorizations will be completed at the next solver setup.
2 Only symbolic and numeric factorizations will be completed. It is assumed
that the Jacobian size has not exceeded the size of nnz given in the prior
call to idaklu.
Return value The return value flag (of type int) is one of
IDASLS SUCCESS The reinitialization succeeded.
IDASLS MEM NULL The ida mem pointer is NULL.
48 Using IDAS for IVP Solution
IDASLS LMEM NULL The idaklu linear solver has not been initialized.
IDASLS ILL INPUT The given reinit type has an illegal value.
IDASLS MEM FAIL A memory allocation failed.
Notes The default value for reinit type is 2.
Both the idaklu and idasuperlumt solvers can apply reordering algorithms to minimize fill-in for the
resulting sparse LU decomposition internal to the solver. The approximate minimal degree ordering
for nonsymmetric matrices given by the COLAMD algorithm is the default algorithm used within both
solvers, but alternate orderings may be chosen through one of the following two functions. The input
values to these functinos are the numeric values used in the respective packages, and the user-supplied
value will be passed directly to the package.
IDAKLUSetOrdering
Call flag = IDAKLUSetOrdering(ida mem, ordering choice);
Description The function IDAKLUSetOrdering specifies the ordering algorithm used by idaklu for
reducing fill.
Arguments ida mem (void *) pointer to the idas memory block.
ordering choice (int) flag denoting algorithm choice:
0AMD
1COLAMD
2 natural ordering
Return value The return value flag (of type int) is one of
IDASLS SUCCESS The optional value has been successfully set.
IDASLS MEM NULL The ida mem pointer is NULL.
IDASLS ILL INPUT The supplied value of ordering choice is illegal.
Notes The default ordering choice is 1 for COLAMD.
IDASuperLUMTSetOrdering
Call flag = IDASuperLUMTSetOrdering(ida mem, ordering choice);
Description The function IDASuperLUMTSetOrdering specifies the ordering algorithm used by ida-
superlumt for reducing fill.
Arguments ida mem (void *) pointer to the idas memory block.
ordering choice (int) flag denoting algorithm choice:
0 natural ordering
1 minimal degree ordering on JTJ
2 minimal degree ordering on JT+J
3COLAMD
Return value The return value flag (of type int) is one of
IDASLS SUCCESS The optional value has been successfully set.
IDASLS MEM NULL The ida mem pointer is NULL.
IDASLS ILL INPUT The supplied value of ordering choice is illegal.
Notes The default ordering choice is 3 for COLAMD.
4.5 User-callable functions 49
4.5.7.4 Iterative linear solvers optional input functions
If preconditioning is to be done with one of the idaspils linear solvers, then the user must supply a pre-
conditioner solve function psolve and specify its name through a call to IDASpilsSetPreconditioner.
The evaluation and preprocessing of any Jacobian-related data needed by the user’s preconditioner
solve function is done in the optional user-supplied function psetup. Both of these functions are
fully specified in §4.6. If used, the name of the psetup function should be specified in the call to
IDASpilsSetPreconditioner.
The pointer user data received through IDASetUserData (or a pointer to NULL if user data was
not specified) is passed to the preconditioner psetup and psolve functions. This allows the user to
create an arbitrary structure with relevant problem data and access it during the execution of the
user-supplied preconditioner functions without using global data in the program.
The idaspils solvers require a function to compute an approximation to the product between
the Jacobian matrix J(t, y) and a vector v. The user can supply his/her own Jacobian-times-vector
approximation function, or use the default internal difference quotient function that comes with the
idaspils solvers. A user-defined Jacobian-vector function must be of type IDASpilsJacTimesVecFn
and can be specified through a call to IDASpilsSetJacTimesVecFn (see §4.6.8 for specification details).
As with the preconditioner user-supplied functions, a pointer to the user-defined data structure,
user data, specified through IDASetUserData (or a NULL pointer otherwise) is passed to the Jacobian-
times-vector function jtimes each time it is called.
IDASpilsSetPreconditioner
Call flag = IDASpilsSetPreconditioner(ida mem, psetup, psolve);
Description The function IDASpilsSetPreconditioner specifies the preconditioner setup and solve
functions.
Arguments ida mem (void *) pointer to the idas memory block.
psetup (IDASpilsPrecSetupFn) user-defined preconditioner setup function. Pass NULL
if no setup is to be done.
psolve (IDASpilsPrecSolveFn) user-defined preconditioner solve function.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional values have been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
Notes The function type IDASpilsPrecSolveFn is described in §4.6.9. The function type
IDASpilsPrecSetupFn is described in §4.6.10.
IDASpilsSetJacTimesVecFn
Call flag = IDASpilsSetJacTimesVecFn(ida mem, jtimes);
Description The function IDASpilsSetJacTimesFn specifies the Jacobian-vector function to be used.
Arguments ida mem (void *) pointer to the idas memory block.
jtimes (IDASpilsJacTimesVecFn) user-defined Jacobian-vector product function.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
Notes By default, the idaspils solvers use the difference quotient function. If NULL is passed
to jtimes, this default function is used.
The function type IDASpilsJacTimesVecFn is described in §4.6.8.
50 Using IDAS for IVP Solution
IDASpilsSetGSType
Call flag = IDASpilsSetGSType(ida mem, gstype);
Description The function IDASpilsSetGSType specifies the Gram-Schmidt orthogonalization to be
used. This must be one of the enumeration constants MODIFIED GS or CLASSICAL GS.
These correspond to using modified Gram-Schmidt and classical Gram-Schmidt, respec-
tively.
Arguments ida mem (void *) pointer to the idas memory block.
gstype (int) type of Gram-Schmidt orthogonalization.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASPILS ILL INPUT The value of gstype is not valid.
Notes The default value is MODIFIED GS.
This option is available only for the idaspgmr linear solver.
!
IDASpilsSetMaxRestarts
Call flag = IDASpilsSetMaxRestarts(ida mem, maxrs);
Description The function IDASpilsSetMaxRestarts specifies the maximum number of restarts to
be used in the GMRES algorithm.
Arguments ida mem (void *) pointer to the idas memory block.
maxrs (int) maximum number of restarts.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASPILS ILL INPUT The maxrs argument is negative.
Notes The default value is 5. Pass maxrs = 0 to specify no restarts.
This option is available only for the idaspgmr linear solver.
!
IDASpilsSetEpsLin
Call flag = IDASpilsSetEpsLin(ida mem, eplifac);
Description The function IDASpilsSetEpsLin specifies the factor by which the Krylov linear solver’s
convergence test constant is reduced from the Newton iteration test constant. (See §2.1).
Arguments ida mem (void *) pointer to the idas memory block.
eplifac (realtype) linear convergence safety factor (>= 0.0).
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASPILS ILL INPUT The value of eplifac is negative.
Notes The default value is 0.05.
Passing a value eplifac= 0.0 also indicates using the default value.

4.5 User-callable functions 51
IDASpilsSetIncrementFactor
Call flag = IDASpilsSetIncrementFactor(ida mem, dqincfac);
Description The function IDASpilsSetIncrementFactor specifies a factor in the increments to y
used in the difference quotient approximations to the Jacobian-vector products. (See
§2.1). The increment used to approximate Jv will be σ=dqincfac/kvk.
Arguments ida mem (void *) pointer to the idas memory block.
dqincfac (realtype) difference quotient increment factor.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASPILS ILL INPUT The increment factor was non-positive.
Notes The default value is dqincfac = 1.0.
IDASpilsSetMaxl
Call flag = IDASpilsSetMaxl(ida mem, maxl);
Description The function IDASpilsSetMaxl resets the maximum Krylov subspace dimension for the
Bi-CGStab or TFQMR methods.
Arguments ida mem (void *) pointer to the idas memory block.
maxl (int) maximum dimension of the Krylov subspace.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
Notes The maximum subspace dimension is initially specified in the call to the linear solver
specification function (see §4.5.3). This function call is needed only if maxl is being
changed from its previous value.
An input value maxl ≤0 will result in the default value, 5.
This option is available only for the idaspbcg and idasptfqmr linear solvers.
!
4.5.7.5 Initial condition calculation optional input functions
The following functions can be called just prior to calling IDACalcIC to set optional inputs controlling
the initial condition calculation.
IDASetNonlinConvCoefIC
Call flag = IDASetNonlinConvCoefIC(ida mem, epiccon);
Description The function IDASetNonlinConvCoefIC specifies the positive constant in the Newton
iteration convergence test within the initial condition calculation.
Arguments ida mem (void *) pointer to the idas memory block.
epiccon (realtype) coefficient in the Newton convergence test (>0).
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT The epiccon factor is <= 0.0.
52 Using IDAS for IVP Solution
Notes The default value is 0.01 ·0.33.
This test uses a weighted RMS norm (with weights defined by the tolerances). For
new initial value vectors yand ˙yto be accepted, the norm of J−1F(t0, y, ˙y) must be ≤
epiccon, where Jis the system Jacobian.
IDASetMaxNumStepsIC
Call flag = IDASetMaxNumStepsIC(ida mem, maxnh);
Description The function IDASetMaxNumStepsIC specifies the maximum number of steps allowed
when icopt=IDA YA YDP INIT in IDACalcIC, where happears in the system Jacobian,
J=∂F/∂y + (1/h)∂F/∂ ˙y.
Arguments ida mem (void *) pointer to the idas memory block.
maxnh (int) maximum allowed number of values for h.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT maxnh is non-positive.
Notes The default value is 5.
IDASetMaxNumJacsIC
Call flag = IDASetMaxNumJacsIC(ida mem, maxnj);
Description The function IDASetMaxNumJacsIC specifies the maximum number of the approximate
Jacobian or preconditioner evaluations allowed when the Newton iteration appears to
be slowly converging.
Arguments ida mem (void *) pointer to the idas memory block.
maxnj (int) maximum allowed number of Jacobian or preconditioner evaluations.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT maxnj is non-positive.
Notes The default value is 4.
IDASetMaxNumItersIC
Call flag = IDASetMaxNumItersIC(ida mem, maxnit);
Description The function IDASetMaxNumItersIC specifies the maximum number of Newton itera-
tions allowed in any one attempt to solve the initial conditions calculation problem.
Arguments ida mem (void *) pointer to the idas memory block.
maxnit (int) maximum number of Newton iterations.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT maxnit is non-positive.
Notes The default value is 10.
4.5 User-callable functions 53
IDASetMaxBacksIC
Call flag = IDASetMaxBacksIC(ida mem, maxbacks);
Description The function IDASetMaxBacksIC specifies the maximum number of linesearch back-
tracks allowed in any Newton iteration, when solving the initial conditions calculation
problem.
Arguments ida mem (void *) pointer to the ida memory block.
maxbacks (int) maximum number of linesearch backtracks per Newton step.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT maxbacks is non-positive.
Notes The default value is 100.
If IDASetMaxBacksIC is called in a Forward Sensitivity Analysis, the the limit maxbacks
applies in the calculation of both the initial state values and the initial sensititivies.
IDASetLineSearchOffIC
Call flag = IDASetLineSearchOffIC(ida mem, lsoff);
Description The function IDASetLineSearchOffIC specifies whether to turn on or off the linesearch
algorithm.
Arguments ida mem (void *) pointer to the idas memory block.
lsoff (booleantype) a flag to turn off (TRUE) or keep (FALSE) the linesearch algo-
rithm.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes The default value is FALSE.
IDASetStepToleranceIC
Call flag = IDASetStepToleranceIC(ida mem, steptol);
Description The function IDASetStepToleranceIC specifies a positive lower bound on the Newton
step.
Arguments ida mem (void *) pointer to the idas memory block.
steptol (int) Minimum allowed WRMS-norm of the Newton step (>0.0).
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT The steptol tolerance is <= 0.0.
Notes The default value is (unit roundoff)2/3.
4.5.7.6 Rootfinding optional input functions
The following functions can be called to set optional inputs to control the rootfinding algorithm.
54 Using IDAS for IVP Solution
IDASetRootDirection
Call flag = IDASetRootDirection(ida mem, rootdir);
Description The function IDASetRootDirection specifies the direction of zero-crossings to be lo-
cated and returned to the user.
Arguments ida mem (void *) pointer to the idas memory block.
rootdir (int *) state array of length nrtfn, the number of root functions gi, as spec-
ified in the call to the function IDARootInit. A value of 0 for rootdir[i]
indicates that crossing in either direction should be reported for gi. A value
of +1 or −1 indicates that the solver should report only zero-crossings where
giis increasing or decreasing, respectively.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT rootfinding has not been activated through a call to IDARootInit.
Notes The default behavior is to locate both zero-crossing directions.
IDASetNoInactiveRootWarn
Call flag = IDASetNoInactiveRootWarn(ida mem);
Description The function IDASetNoInactiveRootWarn disables issuing a warning if some root func-
tion appears to be identically zero at the beginning of the integration.
Arguments ida mem (void *) pointer to the idas memory block.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes idas will not report the initial conditions as a possible zero-crossing (assuming that one
or more components giare zero at the initial time). However, if it appears that some gi
is identically zero at the initial time (i.e., giis zero at the initial time and after the first
step), idas will issue a warning which can be disabled with this optional input function.
4.5.8 Interpolated output function
An optional function IDAGetDky is available to obtain additional output values. This function must be
called after a successful return from IDASolve and provides interpolated values of yor its derivatives
of order up to the last internal order used for any value of tin the last internal step taken by idas.
The call to the IDAGetDky function has the following form:
IDAGetDky
Call flag = IDAGetDky(ida mem, t, k, dky);
Description The function IDAGetDky computes the interpolated values of the kth derivative of yfor
any value of tin the last internal step taken by idas. The value of kmust be non-
negative and smaller than the last internal order used. A value of 0 for kmeans that
the yis interpolated. The value of tmust satisfy tn−hu≤t≤tn, where tndenotes
the current internal time reached, and huis the last internal step size used successfully.
Arguments ida mem (void *) pointer to the idas memory block.
t(realtype) time at which to interpolate.
k(int) integer specifying the order of the derivative of ywanted.
dky (N Vector) vector containing the interpolated kth derivative of y(t).
4.5 User-callable functions 55
Return value The return value flag (of type int) is one of
IDA SUCCESS IDAGetDky succeeded.
IDA MEM NULL The ida mem argument was NULL.
IDA BAD T t is not in the interval [tn−hu, tn].
IDA BAD K k is not one of {0,1, . . . , klast}.
IDA BAD DKY dky is NULL.
Notes It is only legal to call the function IDAGetDky after a successful return from IDASolve.
Functions IDAGetCurrentTime,IDAGetLastStep and IDAGetLastOrder (see §4.5.9.1)
can be used to access tn,huand klast.
4.5.9 Optional output functions
idas provides an extensive list of functions that can be used to obtain solver performance information.
Table 4.3 lists all optional output functions in idas, which are then described in detail in the remainder
of this section.
Some of the optional outputs, especially the various counters, can be very useful in determining
how successful the idas solver is in doing its job. For example, the counters nsteps and nrevals
provide a rough measure of the overall cost of a given run, and can be compared among runs with
differing input options to suggest which set of options is most efficient. The ratio nniters/nsteps
measures the performance of the Newton iteration in solving the nonlinear systems at each time step;
typical values for this range from 1.1 to 1.8. The ratio njevals/nniters (in the case of a direct
linear solver), and the ratio npevals/nniters (in the case of an iterative linear solver) measure the
overall degree of nonlinearity in these systems, and also the quality of the approximate Jacobian
or preconditioner being used. Thus, for example, njevals/nniters can indicate if a user-supplied
Jacobian is inaccurate, if this ratio is larger than for the case of the corresponding internal Jacobian.
The ratio nliters/nniters measures the performance of the Krylov iterative linear solver, and thus
(indirectly) the quality of the preconditioner.
4.5.9.1 Main solver optional output functions
idas provides several user-callable functions that can be used to obtain different quantities that may
be of interest to the user, such as solver workspace requirements, solver performance statistics, as well
as additional data from the idas memory block (a suggested tolerance scaling factor, the error weight
vector, and the vector of estimated local errors). Also provided are functions to extract statistics
related to the performance of the idas nonlinear solver being used. As a convenience, additional
extraction functions provide the optional outputs in groups. These optional output functions are
described next.
IDAGetWorkSpace
Call flag = IDAGetWorkSpace(ida mem, &lenrw, &leniw);
Description The function IDAGetWorkSpace returns the idas real and integer workspace sizes.
Arguments ida mem (void *) pointer to the idas memory block.
lenrw (long int) number of real values in the idas workspace.
leniw (long int) number of integer values in the idas workspace.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes In terms of the problem size N, the maximum method order maxord, and the number
nrtfn of root functions (see §4.5.5), the actual size of the real workspace, in realtype
words, is given by the following:

56 Using IDAS for IVP Solution
Table 4.3: Optional outputs from idas,idadls,idasls, and idaspils
Optional output Function name
IDAS main solver
Size of idas real and integer workspace IDAGetWorkSpace
Cumulative number of internal steps IDAGetNumSteps
No. of calls to residual function IDAGetNumResEvals
No. of calls to linear solver setup function IDAGetNumLinSolvSetups
No. of local error test failures that have occurred IDAGetNumErrTestFails
Order used during the last step IDAGetLastOrder
Order to be attempted on the next step IDAGetCurrentOrder
Order reductions due to stability limit detection IDAGetNumStabLimOrderReds
Actual initial step size used IDAGetActualInitStep
Step size used for the last step IDAGetLastStep
Step size to be attempted on the next step IDAGetCurrentStep
Current internal time reached by the solver IDAGetCurrentTime
Suggested factor for tolerance scaling IDAGetTolScaleFactor
Error weight vector for state variables IDAGetErrWeights
Estimated local errors IDAGetEstLocalErrors
No. of nonlinear solver iterations IDAGetNumNonlinSolvIters
No. of nonlinear convergence failures IDAGetNumNonlinSolvConvFails
Array showing roots found IDAGetRootInfo
No. of calls to user root function IDAGetNumGEvals
Name of constant associated with a return flag IDAGetReturnFlagName
IDAS initial conditions calculation
Number of backtrack operations IDAGetNumBacktrackops
Corrected initial conditions IDAGetConsistentIC
IDADLS linear solver
Size of real and integer workspace IDADlsGetWorkSpace
No. of Jacobian evaluations IDADlsGetNumJacEvals
No. of residual calls for finite diff. Jacobian evals. IDADlsGetNumResEvals
Last return from a linear solver function IDADlsGetLastFlag
Name of constant associated with a return flag IDADlsGetReturnFlagName
IDASLS linear solver
No. of Jacobian evaluations IDASlsGetNumJacEvals
Last return from a linear solver function IDASlsGetLastFlag
Name of constant associated with a return flag IDASlsGetReturnFlagName
IDASPILS linear solvers
Size of real and integer workspace IDASpilsGetWorkSpace
No. of linear iterations IDASpilsGetNumLinIters
No. of linear convergence failures IDASpilsGetNumConvFails
No. of preconditioner evaluations IDASpilsGetNumPrecEvals
No. of preconditioner solves IDASpilsGetNumPrecSolves
No. of Jacobian-vector product evaluations IDASpilsGetNumJtimesEvals
No. of residual calls for finite diff. Jacobian-vector evals. IDASpilsGetNumResEvals
Last return from a linear solver function IDASpilsGetLastFlag
Name of constant associated with a return flag IDASpilsGetReturnFlagName
4.5 User-callable functions 57
•base value: lenrw = 55 + (m+ 6) ∗Nr+ 3∗nrtfn;
•with IDASVtolerances:lenrw =lenrw +Nr;
•with constraint checking (see IDASetConstraints): lenrw =lenrw +Nr;
•with id specified (see IDASetId): lenrw =lenrw +Nr;
where m= max(maxord,3), and Nris the number of real words in one N Vector (≈N).
The size of the integer workspace (without distinction between int and long int words)
is given by:
•base value: leniw = 38 + (m+ 6) ∗Ni+nrtfn;
•with IDASVtolerances:leniw =leniw +Ni;
•with constraint checking: lenrw =lenrw +Ni;
•with id specified: lenrw =lenrw +Ni;
where Niis the number of integer words in one N Vector (= 1 for nvector serial
and 2*npes for nvector parallel on npes processors).
For the default value of maxord, with no rootfinding, no id, no constraints, and with
no call to IDASVtolerances, these lengths are given roughly by: lenrw = 55 + 11N,
leniw = 49.
Note that additional memory is allocated if quadratures and/or forward sensitivity
integration is enabled. See §4.7.1 and §5.2.1 for more details.
IDAGetNumSteps
Call flag = IDAGetNumSteps(ida mem, &nsteps);
Description The function IDAGetNumSteps returns the cumulative number of internal steps taken
by the solver (total so far).
Arguments ida mem (void *) pointer to the idas memory block.
nsteps (long int) number of steps taken by idas.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDAGetNumResEvals
Call flag = IDAGetNumResEvals(ida mem, &nrevals);
Description The function IDAGetNumResEvals returns the number of calls to the user’s residual
evaluation function.
Arguments ida mem (void *) pointer to the idas memory block.
nrevals (long int) number of calls to the user’s res function.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes The nrevals value returned by IDAGetNumResEvals does not account for calls made to
res from a linear solver or preconditioner module.
58 Using IDAS for IVP Solution
IDAGetNumLinSolvSetups
Call flag = IDAGetNumLinSolvSetups(ida mem, &nlinsetups);
Description The function IDAGetNumLinSolvSetups returns the cumulative number of calls made
to the linear solver’s setup function (total so far).
Arguments ida mem (void *) pointer to the idas memory block.
nlinsetups (long int) number of calls made to the linear solver setup function.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDAGetNumErrTestFails
Call flag = IDAGetNumErrTestFails(ida mem, &netfails);
Description The function IDAGetNumErrTestFails returns the cumulative number of local error
test failures that have occurred (total so far).
Arguments ida mem (void *) pointer to the idas memory block.
netfails (long int) number of error test failures.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDAGetLastOrder
Call flag = IDAGetLastOrder(ida mem, &klast);
Description The function IDAGetLastOrder returns the integration method order used during the
last internal step.
Arguments ida mem (void *) pointer to the idas memory block.
klast (int) method order used on the last internal step.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDAGetCurrentOrder
Call flag = IDAGetCurrentOrder(ida mem, &kcur);
Description The function IDAGetCurrentOrder returns the integration method order to be used on
the next internal step.
Arguments ida mem (void *) pointer to the idas memory block.
kcur (int) method order to be used on the next internal step.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
4.5 User-callable functions 59
IDAGetLastStep
Call flag = IDAGetLastStep(ida mem, &hlast);
Description The function IDAGetLastStep returns the integration step size taken on the last internal
step.
Arguments ida mem (void *) pointer to the idas memory block.
hlast (realtype) step size taken on the last internal step by ida, or last artificial
step size used in IDACalcIC, whichever was called last.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDAGetCurrentStep
Call flag = IDAGetCurrentStep(ida mem, &hcur);
Description The function IDAGetCurrentStep returns the integration step size to be attempted on
the next internal step.
Arguments ida mem (void *) pointer to the idas memory block.
hcur (realtype) step size to be attempted on the next internal step.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDAGetActualInitStep
Call flag = IDAGetActualInitStep(ida mem, &hinused);
Description The function IDAGetActualInitStep returns the value of the integration step size used
on the first step.
Arguments ida mem (void *) pointer to the idas memory block.
hinused (realtype) actual value of initial step size.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes Even if the value of the initial integration step size was specified by the user through
a call to IDASetInitStep, this value might have been changed by idas to ensure that
the step size is within the prescribed bounds (hmin ≤h0≤hmax), or to meet the local
error test.
IDAGetCurrentTime
Call flag = IDAGetCurrentTime(ida mem, &tcur);
Description The function IDAGetCurrentTime returns the current internal time reached by the
solver.
Arguments ida mem (void *) pointer to the idas memory block.
tcur (realtype) current internal time reached.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.

60 Using IDAS for IVP Solution
IDAGetTolScaleFactor
Call flag = IDAGetTolScaleFactor(ida mem, &tolsfac);
Description The function IDAGetTolScaleFactor returns a suggested factor by which the user’s
tolerances should be scaled when too much accuracy has been requested for some internal
step.
Arguments ida mem (void *) pointer to the idas memory block.
tolsfac (realtype) suggested scaling factor for user tolerances.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDAGetErrWeights
Call flag = IDAGetErrWeights(ida mem, eweight);
Description The function IDAGetErrWeights returns the solution error weights at the current time.
These are the Wigiven by Eq. (2.7) (or by the user’s IDAEwtFn).
Arguments ida mem (void *) pointer to the idas memory block.
eweight (N Vector) solution error weights at the current time.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes The user must allocate space for eweight.
!
IDAGetEstLocalErrors
Call flag = IDAGetEstLocalErrors(ida mem, ele);
Description The function IDAGetEstLocalErrors returns the estimated local errors.
Arguments ida mem (void *) pointer to the idas memory block.
ele (N Vector) estimated local errors at the current time.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes The user must allocate space for ele.
!
The values returned in ele are only valid if IDASolve returned a non-negative value.
The ele vector, togther with the eweight vector from IDAGetErrWeights, can be used
to determine how the various components of the system contributed to the estimated
local error test. Specifically, that error test uses the RMS norm of a vector whose
components are the products of the components of these two vectors. Thus, for example,
if there were recent error test failures, the components causing the failures are those
with largest values for the products, denoted loosely as eweight[i]*ele[i].
IDAGetIntegratorStats
Call flag = IDAGetIntegratorStats(ida mem, &nsteps, &nrevals, &nlinsetups,
&netfails, &klast, &kcur, &hinused,
&hlast, &hcur, &tcur);
Description The function IDAGetIntegratorStats returns the idas integrator statistics as a group.
Arguments ida mem (void *) pointer to the idas memory block.
4.5 User-callable functions 61
nsteps (long int) cumulative number of steps taken by idas.
nrevals (long int) cumulative number of calls to the user’s res function.
nlinsetups (long int) cumulative number of calls made to the linear solver setup
function.
netfails (long int) cumulative number of error test failures.
klast (int) method order used on the last internal step.
kcur (int) method order to be used on the next internal step.
hinused (realtype) actual value of initial step size.
hlast (realtype) step size taken on the last internal step.
hcur (realtype) step size to be attempted on the next internal step.
tcur (realtype) current internal time reached.
Return value The return value flag (of type int) is one of
IDA SUCCESS the optional output values have been successfully set.
IDA MEM NULL the ida mem pointer is NULL.
IDAGetNumNonlinSolvIters
Call flag = IDAGetNumNonlinSolvIters(ida mem, &nniters);
Description The function IDAGetNumNonlinSolvIters returns the cumulative number of nonlinear
(functional or Newton) iterations performed.
Arguments ida mem (void *) pointer to the idas memory block.
nniters (long int) number of nonlinear iterations performed.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDAGetNumNonlinSolvConvFails
Call flag = IDAGetNumNonlinSolvConvFails(ida mem, &nncfails);
Description The function IDAGetNumNonlinSolvConvFails returns the cumulative number of non-
linear convergence failures that have occurred.
Arguments ida mem (void *) pointer to the idas memory block.
nncfails (long int) number of nonlinear convergence failures.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDAGetNonlinSolvStats
Call flag = IDAGetNonlinSolvStats(ida mem, &nniters, &nncfails);
Description The function IDAGetNonlinSolvStats returns the idas nonlinear solver statistics as a
group.
Arguments ida mem (void *) pointer to the idas memory block.
nniters (long int) cumulative number of nonlinear iterations performed.
nncfails (long int) cumulative number of nonlinear convergence failures.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.

62 Using IDAS for IVP Solution
IDAGetReturnFlagName
Call name = IDAGetReturnFlagName(flag);
Description The function IDAGetReturnFlagName returns the name of the idas constant correspond-
ing to flag.
Arguments The only argument, of type int, is a return flag from an idas function.
Return value The return value is a string containing the name of the corresponding constant.
4.5.9.2 Initial condition calculation optional output functions
IDAGetNumBcktrackOps
Call flag = IDAGetNumBacktrackOps(ida mem, &nbacktr);
Description The function IDAGetNumBacktrackOps returns the number of backtrack operations done
in the linesearch algorithm in IDACalcIC.
Arguments ida mem (void *) pointer to the idas memory block.
nbacktr (long int) the cumulative number of backtrack operations.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDAGetConsistentIC
Call flag = IDAGetConsistentIC(ida mem, yy0 mod, yp0 mod);
Description The function IDAGetConsistentIC returns the corrected initial conditions calculated
by IDACalcIC.
Arguments ida mem (void *) pointer to the idas memory block.
yy0 mod (N Vector) consistent solution vector.
yp0 mod (N Vector) consistent derivative vector.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA ILL INPUT The function was not called before the first call to IDASolve.
IDA MEM NULL The ida mem pointer is NULL.
Notes If the consistent solution vector or consistent derivative vector is not desired, pass NULL
for the corresponding argument.
The user must allocate space for yy0 mod and yp0 mod (if not NULL).
!
4.5.9.3 Rootfinding optional output functions
There are two optional output functions associated with rootfinding.
IDAGetRootInfo
Call flag = IDAGetRootInfo(ida mem, rootsfound);
Description The function IDAGetRootInfo returns an array showing which functions were found to
have a root.
Arguments ida mem (void *) pointer to the idas memory block.

4.5 User-callable functions 63
rootsfound (int *) array of length nrtfn with the indices of the user functions gi
found to have a root. For i= 0,...,nrtfn −1, rootsfound[i]6= 0 if gihas a
root, and = 0 if not.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output values have been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes Note that, for the components gifor which a root was found, the sign of rootsfound[i]
indicates the direction of zero-crossing. A value of +1 indicates that giis increasing,
while a value of −1 indicates a decreasing gi.
The user must allocate memory for the vector rootsfound.
!
IDAGetNumGEvals
Call flag = IDAGetNumGEvals(ida mem, &ngevals);
Description The function IDAGetNumGEvals returns the cumulative number of calls to the user root
function g.
Arguments ida mem (void *) pointer to the idas memory block.
ngevals (long int) number of calls to the user’s function gso far.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
4.5.9.4 Dense/band direct linear solvers optional output functions
The following optional outputs are available from the idadls modules: workspace requirements,
number of calls to the Jacobian routine, number of calls to the residual routine for finite-difference
Jacobian approximation, and last return value from an idadls function. Note that, where the name
of an output would otherwise conflict with the name of an optional output from the main solver, a
suffix LS (for Linear Solver) has been added here (e.g. lenrwLS).
IDADlsGetWorkSpace
Call flag = IDADlsGetWorkSpace(ida mem, &lenrwLS, &leniwLS);
Description The function IDADlsGetWorkSpace returns the sizes of the real and integer workspaces
used by an idadls linear solver (idadense or idaband).
Arguments ida mem (void *) pointer to the idas memory block.
lenrwLS (long int) the number of real values in the idadls workspace.
leniwLS (long int) the number of integer values in the idadls workspace.
Return value The return value flag (of type int) is one of
IDADLS SUCCESS The optional output value has been successfully set.
IDADLS MEM NULL The ida mem pointer is NULL.
IDADLS LMEM NULL The idadls linear solver has not been initialized.
Notes For the idadense linear solver, in terms of the problem size N, the actual size of the real
workspace is 2N2realtype words, while the actual size of the integer workspace is Nin-
teger words. For the idaband linear solver, in terms of Nand Jacobian half-bandwidths,
the actual size of the real workspace is N(2 mupper+3 mlower +2) realtype words,
while the actual size of the integer workspace is Ninteger words.
64 Using IDAS for IVP Solution
IDADlsGetNumJacEvals
Call flag = IDADlsGetNumJacEvals(ida mem, &njevals);
Description The function IDADlsGetNumJacEvals returns the cumulative number of calls to the
idadls (dense or banded) Jacobian approximation function.
Arguments ida mem (void *) pointer to the idas memory block.
njevals (long int) the cumulative number of calls to the Jacobian function (total so
far).
Return value The return value flag (of type int) is one of
IDADLS SUCCESS The optional output value has been successfully set.
IDADLS MEM NULL The ida mem pointer is NULL.
IDADLS LMEM NULL The idadense linear solver has not been initialized.
IDADlsGetNumResEvals
Call flag = IDADlsGetNumResEvals(ida mem, &nrevalsLS);
Description The function IDADlsGetNumResEvals returns the cumulative number of calls to the user
residual function due to the finite difference (dense or band) Jacobian approximation.
Arguments ida mem (void *) pointer to the idas memory block.
nrevalsLS (long int) the cumulative number of calls to the user residual function.
Return value The return value flag (of type int) is one of
IDADLS SUCCESS The optional output value has been successfully set.
IDADLS MEM NULL The ida mem pointer is NULL.
IDADLS LMEM NULL The idadense linear solver has not been initialized.
Notes The value nrevalsLS is incremented only if the default internal difference quotient
function is used.
IDADlsGetLastFlag
Call flag = IDADlsGetLastFlag(ida mem, &lsflag);
Description The function IDADlsGetLastFlag returns the last return value from an idadls routine.
Arguments ida mem (void *) pointer to the idas memory block.
lsflag (long int) the value of the last return flag from an idadls function.
Return value The return value flag (of type int) is one of
IDADLS SUCCESS The optional output value has been successfully set.
IDADLS MEM NULL The ida mem pointer is NULL.
IDADLS LMEM NULL The idadense linear solver has not been initialized.
Notes If the idadense setup function failed (i.e., IDASolve returned IDA LSETUP FAIL), the
value lsflag is equal to the column index (numbered from one) at which a zero diagonal
element was encountered during the LU factorization of the (dense or band) Jacobian
matrix. For all other failures, the value of lsflag is negative.
IDADlsGetReturnFlagName
Call name = IDADlsGetReturnFlagName(lsflag);
Description The function IDADlsGetReturnFlagName returns the name of the idadls constant cor-
responding to lsflag.
Arguments The only argument, of type long int, is a return flag from an idadls function.
Return value The return value is a string containing the name of the corresponding constant. If 1 ≤
lsflag ≤N(LU factorization failed), this function returns “NONE”.
4.5 User-callable functions 65
4.5.9.5 Sparse direct linear solvers optional output functions
The following optional outputs are available from the idasls modules: number of calls to the Jacobian
routine and last return value from an idasls function.
IDASlsGetNumJacEvals
Call flag = IDASlsGetNumJacEvals(ida mem, &njevals);
Description The function IDASlsGetNumJacEvals returns the cumulative number of calls to the
idasls sparse Jacobian approximation function.
Arguments ida mem (void *) pointer to the idas memory block.
njevals (long int) the cumulative number of calls to the Jacobian function (total so
far).
Return value The return value flag (of type int) is one of
IDASLS SUCCESS The optional output value has been successfully set.
IDASLS MEM NULL The ida mem pointer is NULL.
IDASLS LMEM NULL The idasls linear solver has not been initialized.
IDASlsGetLastFlag
Call flag = IDASlsGetLastFlag(ida mem, &lsflag);
Description The function IDASlsGetLastFlag returns the last return value from an idasls routine.
Arguments ida mem (void *) pointer to the idas memory block.
lsflag (long int) the value of the last return flag from an idasls function.
Return value The return value flag (of type int) is one of
IDASLS SUCCESS The optional output value has been successfully set.
IDASLS MEM NULL The ida mem pointer is NULL.
IDASLS LMEM NULL The idasls linear solver has not been initialized.
Notes
IDASlsGetReturnFlagName
Call name = IDASlsGetReturnFlagName(lsflag);
Description The function IDASlsGetReturnFlagName returns the name of the idasls constant cor-
responding to lsflag.
Arguments The only argument, of type long int, is a return flag from an idasls function.
Return value The return value is a string containing the name of the corresponding constant.
4.5.9.6 Iterative linear solvers optional output functions
The following optional outputs are available from the idaspils modules: workspace requirements,
number of linear iterations, number of linear convergence failures, number of calls to the preconditioner
setup and solve routines, number of calls to the Jacobian-vector product routine, number of calls to
the residual routine for finite-difference Jacobian-vector product approximation, and last return value
from a linear solver function. Note that, where the name of an output would otherwise conflict with
the name of an optional output from the main solver, a suffix LS (for Linear Solver) has been added
here (e.g. lenrwLS).
66 Using IDAS for IVP Solution
IDASpilsGetWorkSpace
Call flag = IDASpilsGetWorkSpace(ida mem, &lenrwLS, &leniwLS);
Description The function IDASpilsGetWorkSpace returns the global sizes of the idaspils real and
integer workspaces.
Arguments ida mem (void *) pointer to the idas memory block.
lenrwLS (long int) global number of real values in the idaspils workspace.
leniwLS (long int) global number of integer values in the idaspils workspace.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional output value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
Notes In terms of the problem size Nand maximum subspace size maxl, the actual size of the
real workspace is roughly:
N∗(maxl +5)+ maxl ∗(maxl +4) + 1 realtype words for idaspgmr,
10 ∗Nrealtype words for idaspbcg,
and 13 ∗Nrealtype words for idasptfqmr.
In a parallel setting, the above values are global, summed over all processors.
IDASpilsGetNumLinIters
Call flag = IDASpilsGetNumLinIters(ida mem, &nliters);
Description The function IDASpilsGetNumLinIters returns the cumulative number of linear itera-
tions.
Arguments ida mem (void *) pointer to the idas memory block.
nliters (long int) the current number of linear iterations.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional output value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASpilsGetNumConvFails
Call flag = IDASpilsGetNumConvFails(ida mem, &nlcfails);
Description The function IDASpilsGetNumConvFails returns the cumulative number of linear con-
vergence failures.
Arguments ida mem (void *) pointer to the idas memory block.
nlcfails (long int) the current number of linear convergence failures.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional output value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASpilsGetNumPrecEvals
Call flag = IDASpilsGetNumPrecEvals(ida mem, &npevals);
Description The function IDASpilsGetNumPrecEvals returns the cumulative number of precondi-
tioner evaluations, i.e., the number of calls made to psetup.
4.5 User-callable functions 67
Arguments ida mem (void *) pointer to the idas memory block.
npevals (long int) the cumulative number of calls to psetup.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional output value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASpilsGetNumPrecSolves
Call flag = IDASpilsGetNumPrecSolves(ida mem, &npsolves);
Description The function IDASpilsGetNumPrecSolves returns the cumulative number of calls made
to the preconditioner solve function, psolve.
Arguments ida mem (void *) pointer to the idas memory block.
npsolves (long int) the cumulative number of calls to psolve.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional output value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASpilsGetNumJtimesEvals
Call flag = IDASpilsGetNumJtimesEvals(ida mem, &njvevals);
Description The function IDASpilsGetNumJtimesEvals returns the cumulative number of calls
made to the Jacobian-vector function, jtimes.
Arguments ida mem (void *) pointer to the idas memory block.
njvevals (long int) the cumulative number of calls to jtimes.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional output value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASpilsGetNumResEvals
Call flag = IDASpilsGetNumResEvals(ida mem, &nrevalsLS);
Description The function IDASpilsGetNumResEvals returns the cumulative number of calls to the
user residual function for finite difference Jacobian-vector product approximation.
Arguments ida mem (void *) pointer to the idas memory block.
nrevalsLS (long int) the cumulative number of calls to the user residual function.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional output value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
Notes The value nrevalsLS is incremented only if the default IDASpilsDQJtimes difference
quotient function is used.

68 Using IDAS for IVP Solution
IDASpilsGetLastFlag
Call flag = IDASpilsGetLastFlag(ida mem, &lsflag);
Description The function IDASpilsGetLastFlag returns the last return value from an idaspils
routine.
Arguments ida mem (void *) pointer to the idas memory block.
lsflag (long int) the value of the last return flag from an idaspils function.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional output value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
Notes If the idaspils setup function failed (IDASolve returned IDA LSETUP FAIL), lsflag will
be SPGMR PSET FAIL UNREC,SPBCG PSET FAIL UNREC, or SPTFQMR PSET FAIL UNREC.
If the idaspgmr solve function failed (IDASolve returned IDA LSOLVE FAIL), lsflag
contains the error return flag from SpgmrSolve and will be one of: SPGMR MEM NULL,
indicating that the spgmr memory is NULL;SPGMR ATIMES FAIL UNREC, indicating an
unrecoverable failure in the J∗vfunction; SPGMR PSOLVE FAIL UNREC, indicating that
the preconditioner solve function psolve failed unrecoverably; SPGMR GS FAIL, indicat-
ing a failure in the Gram-Schmidt procedure; or SPGMR QRSOL FAIL, indicating that the
matrix Rwas found to be singular during the QR solve phase.
If the idaspbcg solve function failed (IDASolve returned IDA LSOLVE FAIL), lsflag
contains the error return flag from SpbcgSolve and will be one of: SPBCG MEM NULL,
indicating that the spbcg memory is NULL;SPBCG ATIMES FAIL UNREC, indicating an
unrecoverable failure in the J∗vfunction; or SPBCG PSOLVE FAIL UNREC, indicating that
the preconditioner solve function psolve failed unrecoverably.
If the idasptfqmr solve function failed (IDASolve returned IDA LSOLVE FAIL), lsflag
contains the error flag from SptfqmrSolve and will be one of: SPTFQMR MEM NULL,
indicating that the sptfqmr memory is NULL;SPTFQMR ATIMES FAIL UNREC, indicating
an unrecoverable failure in the J∗vfunction; or SPTFQMR PSOLVE FAIL UNREC, indicating
that the preconditioner solve function psolve failed unrecoverably.
IDASpilsGetReturnFlagName
Call name = IDASpilsGetReturnFlagName(lsflag);
Description The function IDASpilsGetReturnFlagName returns the name of the idaspils constant
corresponding to lsflag.
Arguments The only argument, of type long int, is a return flag from an idaspils function.
Return value The return value is a string containing the name of the corresponding constant.
4.5.10 IDAS reinitialization function
The function IDAReInit reinitializes the main idas solver for the solution of a new problem, where
a prior call to IDAInit has been made. The new problem must have the same size as the previous
one. IDAReInit performs the same input checking and initializations that IDAInit does, but does
no memory allocation, as it assumes that the existing internal memory is sufficient for the new prob-
lem. A call to IDAReInit deletes the solution history that was stored internally during the previous
integration. Following a successful call to IDAReInit, call IDASolve again for the solution of the new
problem.
The use of IDAReInit requires that the maximum method order, maxord, is no larger for the new
problem than for the problem specified in the last call to IDAInit. In addition, the same nvector
module set for the previous problem will be reused for the new problem.
4.6 User-supplied functions 69
If there are changes to the linear solver specifications, make the appropriate IDA*** calls, as
described in §4.5.3. If there are changes to any optional inputs, make the appropriate IDASet***
calls, as described in §4.5.7. Otherwise, all solver inputs set previously remain in effect.
One important use of the IDAReInit function is in the treating of jump discontinuities in the
residual function. Except in cases of fairly small jumps, it is usually more efficient to stop at each point
of discontinuity and restart the integrator with a readjusted DAE model, using a call to IDAReInit.
To stop when the location of the discontinuity is known, simply make that location a value of tout. To
stop when the location of the discontinuity is determined by the solution, use the rootfinding feature.
In either case, it is critical that the residual function not incorporate the discontinuity, but rather have
a smooth extention over the discontinuity, so that the step across it (and subsequent rootfinding, if
used) can be done efficiently. Then use a switch within the residual function (communicated through
user data) that can be flipped between the stopping of the integration and the restart, so that the
restarted problem uses the new values (which have jumped). Similar comments apply if there is to be
a jump in the dependent variable vector.
IDAReInit
Call flag = IDAReInit(ida mem, t0, y0, yp0);
Description The function IDAReInit provides required problem specifications and reinitializes idas.
Arguments ida mem (void *) pointer to the idas memory block.
t0 (realtype) is the initial value of t.
y0 (N Vector) is the initial value of y.
yp0 (N Vector) is the initial value of ˙y.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAReInit was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.
IDA NO MALLOC Memory space for the idas memory block was not allocated through a
previous call to IDAInit.
IDA ILL INPUT An input argument to IDAReInit has an illegal value.
Notes If an error occurred, IDAReInit also sends an error message to the error handler func-
tion.
4.6 User-supplied functions
The user-supplied functions consist of one function defining the DAE residual, (optionally) a function
that handles error and warning messages, (optionally) a function that provides the error weight vector,
(optionally) a function that provides Jacobian-related information for the linear solver (if Newton
iteration is chosen), and (optionally) one or two functions that define the preconditioner for use in
any of the Krylov iteration algorithms.
4.6.1 Residual function
The user must provide a function of type IDAResFn defined as follows:
IDAResFn
Definition typedef int (*IDAResFn)(realtype tt, N Vector yy, N Vector yp,
N Vector rr, void *user data);
Purpose This function computes the problem residual for given values of the independent variable
t, state vector y, and derivative ˙y.
Arguments tt is the current value of the independent variable.
70 Using IDAS for IVP Solution
yy is the current value of the dependent variable vector, y(t).
yp is the current value of ˙y(t).
rr is the output residual vector F(t, y, ˙y).
user data is a pointer to user data, the same as the user data parameter passed to
IDASetUserData.
Return value An IDAResFn function type should return a value of 0 if successful, a positive value
if a recoverable error occurred (e.g. yy has an illegal value), or a negative value if a
nonrecoverable error occurred. In the last case, the integrator halts. If a recoverable
error occurred, the integrator will attempt to correct and retry.
Notes A recoverable failure error return from the IDAResFn is typically used to flag a value
of the dependent variable ythat is “illegal” in some way (e.g., negative where only a
non-negative value is physically meaningful). If such a return is made, idas will attempt
to recover (possibly repeating the Newton iteration, or reducing the step size) in order
to avoid this recoverable error return.
For efficiency reasons, the DAE residual function is not evaluated at the converged solu-
tion of the nonlinear solver. Therefore, in general, a recoverable error in that converged
value cannot be corrected. (It may be detected when the right-hand side function is
called the first time during the following integration step, but a successful step cannot
be undone.) However, if the user program also includes quadrature integration, the
state variables can be checked for legality in the call to IDAQuadRhsFn, which is called
at the converged solution of the nonlinear system, and therefore idas can be flagged to
attempt to recover from such a situation. Also, if sensitivity analysis is performed with
the staggered method, the DAE residual function is called at the converged solution of
the nonlinear system, and a recoverable error at that point can be flagged, and idas
will then try to correct it.
Allocation of memory for yp is handled within idas.
4.6.2 Error message handler function
As an alternative to the default behavior of directing error and warning messages to the file pointed to
by errfp (see IDASetErrFile), the user may provide a function of type IDAErrHandlerFn to process
any such messages. The function type IDAErrHandlerFn is defined as follows:
IDAErrHandlerFn
Definition typedef void (*IDAErrHandlerFn)(int error code, const char *module,
const char *function, char *msg,
void *eh data);
Purpose This function processes error and warning messages from idas and its sub-modules.
Arguments error code is the error code.
module is the name of the idas module reporting the error.
function is the name of the function in which the error occurred.
msg is the error message.
eh data is a pointer to user data, the same as the eh data parameter passed to
IDASetErrHandlerFn.
Return value A IDAErrHandlerFn function has no return value.
Notes error code is negative for errors and positive (IDA WARNING) for warnings. If a function
that returns a pointer to memory encounters an error, it sets error code to 0.

4.6 User-supplied functions 71
4.6.3 Error weight function
As an alternative to providing the relative and absolute tolerances, the user may provide a function of
type IDAEwtFn to compute a vector ewt containing the multiplicative weights Wiused in the WRMS
norm kvkWRMS =q(1/N )PN
1(Wi·vi)2. These weights will used in place of those defined by Eq.
(2.7). The function type IDAEwtFn is defined as follows:
IDAEwtFn
Definition typedef int (*IDAEwtFn)(N Vector y, N Vector ewt, void *user data);
Purpose This function computes the WRMS error weights for the vector y.
Arguments yis the value of the dependent variable vector at which the weight vector is
to be computed.
ewt is the output vector containing the error weights.
user data is a pointer to user data, the same as the user data parameter passed to
IDASetUserData.
Return value An IDAEwtFn function type must return 0 if it successfully set the error weights and −1
otherwise.
Notes Allocation of memory for ewt is handled within idas.
The error weight vector must have all components positive. It is the user’s responsiblity
!
to perform this test and return −1 if it is not satisfied.
4.6.4 Rootfinding function
If a rootfinding problem is to be solved during the integration of the DAE system, the user must
supply a Cfunction of type IDARootFn, defined as follows:
IDARootFn
Definition typedef int (*IDARootFn)(realtype t, N Vector y, N Vector yp,
realtype *gout, void *user data);
Purpose This function computes a vector-valued function g(t, y, ˙y) such that the roots of the
nrtfn components gi(t, y, ˙y) are to be found during the integration.
Arguments tis the current value of the independent variable.
yis the current value of the dependent variable vector, y(t).
yp is the current value of ˙y(t), the t−derivative of y.
gout is the output array, of length nrtfn, with components gi(t, y, ˙y).
user data is a pointer to user data, the same as the user data parameter passed to
IDASetUserData.
Return value An IDARootFn should return 0 if successful or a non-zero value if an error occurred (in
which case the integration is halted and IDASolve returns IDA RTFUNC FAIL).
Notes Allocation of memory for gout is handled within idas.
4.6.5 Jacobian information (direct method with dense Jacobian)
If the direct linear solver with dense treatment of the Jacobian is used (i.e. either IDADense or
IDALapackDense is called in Step 8of §4.4), the user may provide a function of type IDADlsDenseJacFn
defined by

72 Using IDAS for IVP Solution
IDADlsDenseJacFn
Definition typedef int (*IDADlsDenseJacFn)(long int Neq, realtype tt, realtype cj,
N Vector yy, N Vector yp, N Vector rr,
DlsMat Jac, void *user data,
N Vector tmp1, N Vector tmp2, N Vector tmp3);
Purpose This function computes the dense Jacobian Jof the DAE system (or an approximation
to it), defined by Eq. (2.6).
Arguments Neq is the problem size (number of equations).
tt is the current value of the independent variable t.
cj is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
yy is the current value of the dependent variable vector, y(t).
yp is the current value of ˙y(t).
rr is the current value of the residual vector F(t, y, ˙y).
Jac is the output (approximate) Jacobian matrix, J=∂F/∂y +cj ∂F/∂ ˙y.
user data is a pointer to user data, the same as the user data parameter passed to
IDASetUserData.
tmp1
tmp2
tmp3 are pointers to memory allocated for variables of type N Vector which can
be used by IDADlsDenseJacFn as temporary storage or work space.
Return value An IDADlsDenseJacFn function type should return 0 if successful, a positive value if a
recoverable error occurred, or a negative value if a nonrecoverable error occurred.
In the case of a recoverable eror return, the integrator will attempt to recover by reducing
the stepsize, and hence changing αin (2.6).
Notes A user-supplied dense Jacobian function must load the Neq ×Neq dense matrix Jac
with an approximation to the Jacobian matrix J(t, y, ˙y) at the point (tt,yy,yp). Only
nonzero elements need to be loaded into Jac because Jac is set to the zero matrix before
the call to the Jacobian function. The type of Jac is DlsMat (described below and in
§9.1).
The accessor macros DENSE ELEM and DENSE COL allow the user to read and write dense
matrix elements without making explicit references to the underlying representation of
the DlsMat type. DENSE ELEM(Jac, i, j) references the (i,j)-th element of the dense
matrix Jac (i,j= 0 . . . Neq−1). This macro is for use in small problems in which effi-
ciency of access is not a major concern. Thus, in terms of indices mand nrunning from
1 to Neq, the Jacobian element Jm,n can be loaded with the statement DENSE ELEM(Jac,
m-1, n-1) = Jm,n. Alternatively, DENSE COL(Jac, j) returns a pointer to the storage
for the jth column of Jac (j= 0 . . . Neq−1), and the elements of the j-th column are
then accessed via ordinary array indexing. Thus Jm,n can be loaded with the state-
ments col n = DENSE COL(Jac, n-1); col n[m-1] = Jm,n. For large problems, it is
more efficient to use DENSE COL than to use DENSE ELEM. Note that both of these macros
number rows and columns starting from 0, not 1.
The DlsMat type and the accessor macros DENSE ELEM and DENSE COL are documented
in §9.1.
If the user’s IDADlsDenseJacFn function uses difference quotient approximations, it
may need to access quantities not in the call list. These include the current stepsize,
the error weights, etc. To obtain these, the user will need to add a pointer to ida mem to
user data and then use the IDAGet* functions described in §4.5.9.1. The unit roundoff
can be accessed as UNIT ROUNDOFF defined in sundials types.h.
4.6 User-supplied functions 73
For the sake of uniformity, the argument Neq is of type long int, even in the case that
the Lapack dense solver is to be used.
4.6.6 Jacobian information (direct method with banded Jacobian)
If the direct linear solver with banded treatment of the Jacobian is used (i.e. either IDABand or
IDALapackBand is called in Step 8of §4.4), the user may provide a function of type IDADlsBandJacFn
defined as follows:
IDADlsBandJacFn
Definition typedef int (*IDADlsBandJacFn)(long int Neq, long int mupper,
long int mlower, realtype tt, realtype cj,
N Vector yy, N Vector yp, N Vector rr,
DlsMat Jac, void *user data,
N Vector tmp1, N Vector tmp2,N Vector tmp3);
Purpose This function computes the banded Jacobian Jof the DAE system (or a banded ap-
proximation to it), defined by Eq. (2.6).
Arguments Neq is the problem size.
mupper
mlower are the upper and lower half bandwidth of the Jacobian.
tt is the current value of the independent variable.
yy is the current value of the dependent variable vector, y(t).
yp is the current value of ˙y(t).
rr is the current value of the residual vector F(t, y, ˙y).
cj is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
Jac is the output (approximate) Jacobian matrix, J=∂F/∂y +cj ∂F/∂ ˙y.
user data is a pointer to user data, the same as the user data parameter passed to
IDASetUserData.
tmp1
tmp2
tmp3 are pointers to memory allocated for variables of type N Vector which can
be used by IDADlsBandJacFn as temporary storage or work space.
Return value A IDADlsBandJacFn function type should return 0 if successful, a positive value if a
recoverable error occurred, or a negative value if a nonrecoverable error occurred.
In the case of a recoverable eror return, the integrator will attempt to recover by reducing
the stepsize, and hence changing αin (2.6).
Notes A user-supplied band Jacobian function must load the band matrix Jac of type DlsMat
with the elements of the Jacobian J(t, y, ˙y) at the point (tt,yy,yp). Only nonzero
elements need to be loaded into Jac because Jac is preset to zero before the call to the
Jacobian function.
The accessor macros BAND ELEM,BAND COL, and BAND COL ELEM allow the user to read
and write band matrix elements without making specific references to the underlying
representation of the DlsMat type. BAND ELEM(Jac, i, j) references the (i,j)th ele-
ment of the band matrix Jac, counting from 0. This macro is for use in small problems
in which efficiency of access is not a major concern. Thus, in terms of indices mand
nrunning from 1 to Neq with (m, n) within the band defined by mupper and mlower,
the Jacobian element Jm,n can be loaded with the statement BAND ELEM(Jac, m-1,
n-1) = Jm,n. The elements within the band are those with -mupper ≤m-n ≤mlower.
Alternatively, BAND COL(Jac, j) returns a pointer to the diagonal element of the jth
74 Using IDAS for IVP Solution
column of Jac, and if we assign this address to realtype *col j, then the ith element
of the jth column is given by BAND COL ELEM(col j, i, j), counting from 0. Thus for
(m, n) within the band, Jm,n can be loaded by setting col n = BAND COL(Jac, n-1);
BAND COL ELEM(col n, m-1, n-1) = Jm,n. The elements of the jth column can also
be accessed via ordinary array indexing, but this approach requires knowledge of the
underlying storage for a band matrix of type DlsMat. The array col n can be indexed
from −mupper to mlower. For large problems, it is more efficient to use the combination
of BAND COL and BAND COL ELEM than to use the BAND ELEM. As in the dense case, these
macros all number rows and columns starting from 0, not 1.
The DlsMat type and the accessor macros BAND ELEM,BAND COL, and BAND COL ELEM
are documented in §9.1.
If the user’s IDADlsBandJacFn function uses difference quotient approximations, it may
need to access quantities not in the call list. These include the current stepsize, the
error weights, etc. To obtain these, the user will need to add a pointer to ida mem to
user data and then use the IDAGet* functions described in §4.5.9.1. The unit roundoff
can be accessed as UNIT ROUNDOFF defined in sundials types.h.
For the sake of uniformity, the arguments Neq,mlower, and mupper are of type long
int, even in the case that the Lapack band solver is to be used.
4.6.7 Jacobian information (direct method with sparse Jacobian)
If the direct linear solver with sparse treatment of the Jacobian is used (i.e. either IDAKLU or
IDASuperLUMT is called in Step 8of §4.4), the user must provide a function of type IDASlsSparseJacFn
defined as follows:
IDASlsSparseJacFn
Definition typedef int (*IDASlsSparseJacFn)(realtype t, realtype c j,
N Vector y, N Vector yp, N Vector r,
SlsMat Jac, void *user data,
N Vector tmp1, N Vector tmp2,N Vector tmp3);
Purpose This function computes the sparse Jacobian Jof the DAE system (or an approximation
to it), defined by Eq. (2.6).
Arguments tis the current value of the independent variable.
yis the current value of the dependent variable vector, y(t).
yp is the current value of ˙y(t).
ris the current value of the residual vector F(t, y, ˙y).
c j is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
Jac is the output (approximate) Jacobian matrix, J=∂F/∂y +cj ∂F/∂ ˙y.
user data is a pointer to user data, the same as the user data parameter passed to
IDASetUserData.
tmp1
tmp2
tmp3 are pointers to memory allocated for variables of type N Vector which can
be used by IDASlsSparseJacFn as temporary storage or work space.
Return value A IDASlsSparseJacFn function type should return 0 if successful, a positive value if a
recoverable error occurred, or a negative value if a nonrecoverable error occurred.
In the case of a recoverable error return, the integrator will attempt to recover by
reducing the stepsize, and hence changing αin (2.6).
4.6 User-supplied functions 75
Notes A user-supplied sparse Jacobian function must load the compressed-sparse-column ma-
trix Jac with the elements of the Jacobian J(t, y, ˙y) at the point (t,y,yp). Storage
for Jac already exists on entry to this function, although the user should ensure that
sufficient space is allocated in Jac to hold the nonzero values to be set; if the existing
space is insufficient the user may reallocate the data and row index arrays as needed.
The type of Jac is SlsMat, and the amount of allocated space is available within the
SlsMat structure as NNZ. The SlsMat type is further documented in the Section §9.2.
If the user’s IDASlsSparseJacFn function uses difference quotient approximations to
set the specific nonzero matrix entries, then it may need to access quantities not in
the argument list. These include the current step size, the error weights, etc. To
obtain these, the user will need to add a pointer to ida mem to user data and then
use the IDAGet* functions described in §4.5.9.1. The unit roundoff can be accessed as
UNIT ROUNDOFF defined in sundials types.h.
4.6.8 Jacobian information (matrix-vector product)
If one of the Krylov iterative linear solvers spgmr,spbcg, or sptfqmr is selected (IDASp* is called
in step 8of §4.4), the user may provide a function of type IDASpilsJacTimesVecFn, described below,
to compute matrix-vector products Jv. If such a function is not supplied, the default is a difference
quotient approximation to these products.
IDASpilsJacTimesVecFn
Definition typedef int (*IDASpilsJacTimesVecFn)(realtype tt, N Vector yy,
N Vector yp, N Vector rr,
N Vector v, N Vector Jv,
realtype cj, void *user data,
N Vector tmp1, N Vector tmp2);
Purpose This function computes the product Jv of the DAE system Jacobian J(or an approxi-
mation to it) and a given vector v, where Jis defined by Eq. (2.6).
Arguments tt is the current value of the independent variable.
yy is the current value of the dependent variable vector, y(t).
yp is the current value of ˙y(t).
rr is the current value of the residual vector F(t, y, ˙y).
vis the vector by which the Jacobian must be multiplied to the right.
Jv is the computed output vector.
cj is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
user data is a pointer to user data, the same as the user data parameter passed to
IDASetUserData.
tmp1
tmp2 are pointers to memory allocated for variables of type NVector which can
be used by IDASpilsJacTimesVecFn as temporary storage or work space.
Return value The value to be returned by the Jacobian-times-vector function should be 0 if successful.
A nonzero value indicates that a nonrecoverable error occurred.
Notes If the user’s IDASpilsJacTimesVecFn function uses difference quotient approximations,
it may need to access quantities not in the call list. These include the current stepsize,
the error weights, etc. To obtain these, the user will need to add a pointer to ida mem to
user data and then use the IDAGet* functions described in §4.5.9.1. The unit roundoff
can be accessed as UNIT ROUNDOFF defined in sundials types.h.

76 Using IDAS for IVP Solution
4.6.9 Preconditioning (linear system solution)
If preconditioning is used, then the user must provide a Cfunction to solve the linear system P z =r
where Pis a left preconditioner matrix which approximates (at least crudely) the Jacobian matrix
J=∂F/∂y +cj ∂F/∂ ˙y. This function must be of type IDASpilsPrecSolveFn, defined as follows:
IDASpilsPrecSolveFn
Definition typedef int (*IDASpilsPrecSolveFn)(realtype tt, N Vector yy,
N Vector yp, N Vector rr,
N Vector rvec, N Vector zvec,
realtype cj, realtype delta,
void *user data, N Vector tmp);
Purpose This function solves the preconditioning system P z =r.
Arguments tt is the current value of the independent variable.
yy is the current value of the dependent variable vector, y(t).
yp is the current value of ˙y(t).
rr is the current value of the residual vector F(t, y, ˙y).
rvec is the right-hand side vector rof the linear system to be solved.
zvec is the computed output vector.
cj is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
delta is an input tolerance to be used if an iterative method is employed in the
solution. In that case, the residual vector Res =r−P z of the system should
be made less than delta in weighted l2norm, i.e., pPi(Resi·ewti)2<
delta. To obtain the N Vector ewt, call IDAGetErrWeights (see §4.5.9.1).
user data is a pointer to user data, the same as the user data parameter passed to
the function IDASetUserData.
tmp is a pointer to memory allocated for a variable of type N Vector which can
be used for work space.
Return value The value to be returned by the preconditioner solve function is a flag indicating whether
it was successful. This value should be 0 if successful, positive for a recoverable error
(in which case the step will be retried), negative for an unrecoverable error (in which
case the integration is halted).
4.6.10 Preconditioning (Jacobian data)
If the user’s preconditioner requires that any Jacobian-related data be evaluated or preprocessed, then
this needs to be done in a user-supplied Cfunction of type IDASpilsPrecSetupFn, defined as follows:
IDASpilsPrecSetupFn
Definition typedef int (*IDASpilsPrecSetupFn)(realtype tt, N Vector yy,
N Vector yp, N Vector rr,
realtype cj, void *user data,
N Vector tmp1, N Vector tmp2,
N Vector tmp3);
Purpose This function evaluates and/or preprocesses Jacobian-related data needed by the pre-
conditioner.
Arguments The arguments of an IDASpilsPrecSetupFn are as follows:
tt is the current value of the independent variable.
yy is the current value of the dependent variable vector, y(t).
4.7 Integration of pure quadrature equations 77
yp is the current value of ˙y(t).
rr is the current value of the residual vector F(t, y, ˙y).
cj is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
user data is a pointer to user data, the same as the user data parameter passed to
the function IDASetUserData.
tmp1
tmp2
tmp3 are pointers to memory allocated for variables of type N Vector which can
be used by IDASpilsPrecSetupFn as temporary storage or work space.
Return value The value to be returned by the preconditioner setup function is a flag indicating
whether it was successful. This value should be 0 if successful, positive for a recov-
erable error (in which case the step will be retried), negative for an unrecoverable error
(in which case the integration is halted).
Notes The operations performed by this function might include forming a crude approximate
Jacobian, and performing an LU factorization on the resulting approximation.
Each call to the preconditioner setup function is preceded by a call to the IDAResFn
user function with the same (tt,yy,yp) arguments. Thus the preconditioner setup
function can use any auxiliary data that is computed and saved during the evaluation
of the DAE residual.
This function is not called in advance of every call to the preconditioner solve function,
but rather is called only as often as needed to achieve convergence in the Newton
iteration.
If the user’s IDASpilsPrecSetupFn function uses difference quotient approximations, it
may need to access quantities not in the call list. These include the current stepsize, the
error weights, etc. To obtain these, the user will need to add a pointer to ida mem to
user data and then use the IDAGet* functions described in §4.5.9.1. The unit roundoff
can be accessed as UNIT ROUNDOFF defined in sundials types.h.
4.7 Integration of pure quadrature equations
idas allows the DAE system to include pure quadratures. In this case, it is more efficient to treat
the quadratures separately by excluding them from the nonlinear solution stage. To do this, begin
by excluding the quadrature variables from the vectors yy and yp and the quadrature equations from
within res. Thus a separate vector yQ of quadrature variables is to satisfy (d/dt)yQ =fQ(t, y, ˙y). The
following is an overview of the sequence of calls in a user’s main program in this situation. Steps that
are unchanged from the skeleton program presented in §4.4 are grayed out.
1. Initialize parallel or multi-threaded environment, if appropriate
2. Set problem dimensions, etc.
This generally includes N, the problem size N(excluding quadrature variables), Nq, the number
of quadrature variables, and may include the local vector length Nlocal (excluding quadrature
variables), and local number of quadrature variables Nqlocal.
3. Set vectors of initial values
4. Create idas object
5. Allocate internal memory
6. Set optional inputs
78 Using IDAS for IVP Solution
7. Attach linear solver module
8. Set linear solver optional inputs
9. Set vector of initial values for quadrature variables
Typically, the quadrature variables should be initialized to 0.
10. Initialize quadrature integration
Call IDAQuadInit to specify the quadrature equation right-hand side function and to allocate
internal memory related to quadrature integration. See §4.7.1 for details.
11. Set optional inputs for quadrature integration
Call IDASetQuadErrCon to indicate whether or not quadrature variables should be used in the
step size control mechanism. If so, one of the IDAQuad*tolerances functions must be called to
specify the integration tolerances for quadrature variables. See §4.7.4 for details.
12. Advance solution in time
13. Extract quadrature variables
Call IDAGetQuad or IDAGetQuadDky to obtain the values of the quadrature variables or their
derivatives at the current time. See §4.7.3 for details.
14. Get optional outputs
15. Get quadrature optional outputs
Call IDAGetQuad* functions to obtain optional output related to the integration of quadratures.
See §4.7.5 for details.
16. Deallocate memory for solution vectors and for the vector of quadrature variables
17. Free solver memory
18. Finalize MPI, if used
IDAQuadInit can be called and quadrature-related optional inputs (step 11 above) can be set, any-
where between steps 4and 12.
4.7.1 Quadrature initialization and deallocation functions
The function IDAQuadInit activates integration of quadrature equations and allocates internal mem-
ory related to these calculations. The form of the call to this function is as follows:
IDAQuadInit
Call flag = IDAQuadInit(ida mem, rhsQ, yQ0);
Description The function IDAQuadInit provides required problem specifications, allocates internal
memory, and initializes quadrature integration.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
rhsQ (IDAQuadRhsFn) is the Cfunction which computes fQ, the right-hand side of
the quadrature equations. This function has the form fQ(t, yy, yp, rhsQ,
user data) (for full details see §4.7.6).
yQ0 (N Vector) is the initial value of yQ.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAQuadInit was successful.
4.7 Integration of pure quadrature equations 79
IDA MEM NULL The idas memory was not initialized by a prior call to IDACreate.
IDA MEM FAIL A memory allocation request failed.
Notes If an error occurred, IDAQuadInit also sends an error message to the error handler
function.
In terms of the number of quadrature variables Nqand maximum method order maxord, the size of
the real workspace is increased as follows:
•Base value: lenrw =lenrw + (maxord+5)Nq
•If IDAQuadSVtolerances is called: lenrw =lenrw +Nq
and the size of the integer workspace is increased as follows:
•Base value: leniw =leniw + (maxord+5)Nq
•If IDAQuadSVtolerances is called: leniw =leniw +Nq
The function IDAQuadReInit, useful during the solution of a sequence of problems of same size,
reinitializes the quadrature-related internal memory and must follow a call to IDAQuadInit (and
maybe a call to IDAReInit). The number Nq of quadratures is assumed to be unchanged from the
prior call to IDAQuadInit. The call to the IDAQuadReInit function has the following form:
IDAQuadReInit
Call flag = IDAQuadReInit(ida mem, yQ0);
Description The function IDAQuadReInit provides required problem specifications and reinitializes
the quadrature integration.
Arguments ida mem (void *) pointer to the idas memory block.
yQ0 (N Vector) is the initial value of yQ.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAReInit was successful.
IDA MEM NULL The idas memory was not initialized by a prior call to IDACreate.
IDA NO QUAD Memory space for the quadrature integration was not allocated by a prior
call to IDAQuadInit.
Notes If an error occurred, IDAQuadReInit also sends an error message to the error handler
function.
IDAQuadFree
Call IDAQuadFree(ida mem);
Description The function IDAQuadFree frees the memory allocated for quadrature integration.
Arguments The argument is the pointer to the idas memory block (of type void *).
Return value The function IDAQuadFree has no return value.
Notes In general, IDAQuadFree need not be called by the user as it is invoked automatically
by IDAFree.
4.7.2 IDAS solver function
Even if quadrature integration was enabled, the call to the main solver function IDASolve is exactly the
same as in §4.5.6. However, in this case the return value flag can also be one of the following:
IDA QRHS FAIL The quadrature right-hand side function failed in an unrecoverable man-
ner.
IDA FIRST QRHS ERR The quadrature right-hand side function failed at the first call.
80 Using IDAS for IVP Solution
IDA REP QRHS ERR Convergence test failures occurred too many times due to repeated recov-
erable errors in the quadrature right-hand side function. This value will
also be returned if the quadrature right-hand side function had repeated
recoverable errors during the estimation of an initial step size (assuming
the quadrature variables are included in the error tests).
4.7.3 Quadrature extraction functions
If quadrature integration has been initialized by a call to IDAQuadInit, or reinitialized by a call to
IDAQuadReInit, then idas computes both a solution and quadratures at time t. However, IDASolve
will still return only the solution yin y. Solution quadratures can be obtained using the following
function:
IDAGetQuad
Call flag = IDAGetQuad(ida mem, &tret, yQ);
Description The function IDAGetQuad returns the quadrature solution vector after a successful return
from IDASolve.
Arguments ida mem (void *) pointer to the memory previously allocated by IDAInit.
tret (realtype) the time reached by the solver (output).
yQ (N Vector) the computed quadrature vector.
Return value The return value flag of IDAGetQuad is one of:
IDA SUCCESS IDAGetQuad was successful.
IDA MEM NULL ida mem was NULL.
IDA NO QUAD Quadrature integration was not initialized.
IDA BAD DKY yQ is NULL.
The function IDAGetQuadDky computes the k-th derivatives of the interpolating polynomials for the
quadrature variables at time t. This function is called by IDAGetQuad with k=0and with the current
time at which IDASolve has returned, but may also be called directly by the user.
IDAGetQuadDky
Call flag = IDAGetQuadDky(ida mem, t, k, dkyQ);
Description The function IDAGetQuadDky returns derivatives of the quadrature solution vector after
a successful return from IDASolve.
Arguments ida mem (void *) pointer to the memory previously allocated by IDAInit.
t(realtype) the time at which quadrature information is requested. The time
tmust fall within the interval defined by the last successful step taken by idas.
k(int) order of the requested derivative. This must be ≤klast.
dkyQ (N Vector) the vector containing the derivative. This vector must be allocated
by the user.
Return value The return value flag of IDAGetQuadDky is one of:
IDA SUCCESS IDAGetQuadDky succeeded.
IDA MEM NULL The pointer to ida mem was NULL.
IDA NO QUAD Quadrature integration was not initialized.
IDA BAD DKY The vector dkyQ is NULL.
IDA BAD K k is not in the range 0,1, ..., klast.
IDA BAD T The time tis not in the allowed range.

4.7 Integration of pure quadrature equations 81
4.7.4 Optional inputs for quadrature integration
idas provides the following optional input functions to control the integration of quadrature equa-
tions.
IDASetQuadErrCon
Call flag = IDASetQuadErrCon(ida mem, errconQ);
Description The function IDASetQuadErrCon specifies whether or not the quadrature variables are
to be used in the step size control mechanism within idas. If they are, the user must
call either IDAQuadSStolerances or IDAQuadSVtolerances to specify the integration
tolerances for the quadrature variables.
Arguments ida mem (void *) pointer to the idas memory block.
errconQ (booleantype) specifies whether quadrature variables are included (TRUE) or
not (FALSE) in the error control mechanism.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL
IDA NO QUAD Quadrature integration has not been initialized.
Notes By default, errconQ is set to FALSE.
It is illegal to call IDASetQuadErrCon before a call to IDAQuadInit.
!
If the quadrature variables are part of the step size control mechanism, one of the following
functions must be called to specify the integration tolerances for quadrature variables.
IDAQuadSStolerances
Call flag = IDAQuadSVtolerances(ida mem, reltolQ, abstolQ);
Description The function IDAQuadSStolerances specifies scalar relative and absolute tolerances.
Arguments ida mem (void *) pointer to the idas memory block.
reltolQ (realtype) is the scalar relative error tolerance.
abstolQ (realtype) is the scalar absolute error tolerance.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional value has been successfully set.
IDA NO QUAD Quadrature integration was not initialized.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT One of the input tolerances was negative.
IDAQuadSVtolerances
Call flag = IDAQuadSVtolerances(ida mem, reltolQ, abstolQ);
Description The function IDAQuadSVtolerances specifies scalar relative and vector absolute toler-
ances.
Arguments ida mem (void *) pointer to the idas memory block.
reltolQ (realtype) is the scalar relative error tolerance.
abstolQ (N Vector) is the vector absolute error tolerance.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional value has been successfully set.
IDA NO QUAD Quadrature integration was not initialized.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT One of the input tolerances was negative.

82 Using IDAS for IVP Solution
4.7.5 Optional outputs for quadrature integration
idas provides the following functions that can be used to obtain solver performance information
related to quadrature integration.
IDAGetQuadNumRhsEvals
Call flag = IDAGetQuadNumRhsEvals(ida mem, &nrhsQevals);
Description The function IDAGetQuadNumRhsEvals returns the number of calls made to the user’s
quadrature right-hand side function.
Arguments ida mem (void *) pointer to the idas memory block.
nrhsQevals (long int) number of calls made to the user’s rhsQ function.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO QUAD Quadrature integration has not been initialized.
IDAGetQuadNumErrTestFails
Call flag = IDAGetQuadNumErrTestFails(ida mem, &nQetfails);
Description The function IDAGetQuadNumErrTestFails returns the number of local error test fail-
ures due to quadrature variables.
Arguments ida mem (void *) pointer to the idas memory block.
nQetfails (long int) number of error test failures due to quadrature variables.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO QUAD Quadrature integration has not been initialized.
IDAGetQuadErrWeights
Call flag = IDAGetQuadErrWeights(ida mem, eQweight);
Description The function IDAGetQuadErrWeights returns the quadrature error weights at the cur-
rent time.
Arguments ida mem (void *) pointer to the idas memory block.
eQweight (N Vector) quadrature error weights at the current time.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO QUAD Quadrature integration has not been initialized.
Notes The user must allocate memory for eQweight.
!
If quadratures were not included in the error control mechanism (through a call to
IDASetQuadErrCon with errconQ = TRUE), IDAGetQuadErrWeights does not set the
eQweight vector.

4.8 A parallel band-block-diagonal preconditioner module 83
IDAGetQuadStats
Call flag = IDAGetQuadStats(ida mem, &nrhsQevals, &nQetfails);
Description The function IDAGetQuadStats returns the idas integrator statistics as a group.
Arguments ida mem (void *) pointer to the idas memory block.
nrhsQevals (long int) number of calls to the user’s rhsQ function.
nQetfails (long int) number of error test failures due to quadrature variables.
Return value The return value flag (of type int) is one of
IDA SUCCESS the optional output values have been successfully set.
IDA MEM NULL the ida mem pointer is NULL.
IDA NO QUAD Quadrature integration has not been initialized.
4.7.6 User-supplied function for quadrature integration
For integration of quadrature equations, the user must provide a function that defines the right-hand
side of the quadrature equations (in other words, the integrand function of the integral that must be
evaluated). This function must be of type IDAQuadRhsFn defined as follows:
IDAQuadRhsFn
Definition typedef int (*IDAQuadRhsFn)(realtype t, N Vector yy, N Vector yp,
N Vector rhsQ, void *user data);
Purpose This function computes the quadrature equation right-hand side for a given value of the
independent variable tand state vectors yand ˙y.
Arguments tis the current value of the independent variable.
yy is the current value of the dependent variable vector, y(t).
yp is the current value of the dependent variable derivative vector, ˙y(t).
rhsQ is the output vector fQ(t, y, ˙y).
user data is the user data pointer passed to IDASetUserData.
Return value A IDAQuadRhsFn should return 0 if successful, a positive value if a recoverable error
occurred (in which case idas will attempt to correct), or a negative value if it failed
unrecoverably (in which case the integration is halted and IDA QRHS FAIL is returned).
Notes Allocation of memory for rhsQ is automatically handled within idas.
Both yand rhsQ are of type N Vector, but they typically have different internal repre-
sentations. It is the user’s responsibility to access the vector data consistently (including
the use of the correct accessor macros from each nvector implementation). For the
sake of computational efficiency, the vector functions in the two nvector implementa-
tions provided with idas do not perform any consistency checks with respect to their
N Vector arguments (see §7.1 and §7.2).
There is one situation in which recovery is not possible even if IDAQuadRhsFn function
returns a recoverable error flag. This is when this occurs at the very first call to the
IDAQuadRhsFn (in which case idas returns IDA FIRST QRHS ERR).
4.8 A parallel band-block-diagonal preconditioner module
A principal reason for using a parallel DAE solver such as idas lies in the solution of partial differential
equations (PDEs). Moreover, the use of a Krylov iterative method for the solution of many such
problems is motivated by the nature of the underlying linear system of equations (2.5) that must be
solved at each time step. The linear algebraic system is large, sparse, and structured. However, if a
Krylov iterative method is to be effective in this setting, then a nontrivial preconditioner needs to be

84 Using IDAS for IVP Solution
used. Otherwise, the rate of convergence of the Krylov iterative method is usually unacceptably slow.
Unfortunately, an effective preconditioner tends to be problem-specific.
However, we have developed one type of preconditioner that treats a rather broad class of PDE-
based problems. It has been successfully used for several realistic, large-scale problems [25] and is
included in a software module within the idas package. This module works with the parallel vector
module nvector parallel and generates a preconditioner that is a block-diagonal matrix with each
block being a band matrix. The blocks need not have the same number of super- and sub-diagonals
and these numbers may vary from block to block. This Band-Block-Diagonal Preconditioner module
is called idabbdpre.
One way to envision these preconditioners is to think of the domain of the computational PDE
problem as being subdivided into Mnon-overlapping sub-domains. Each of these sub-domains is then
assigned to one of the Mprocessors to be used to solve the DAE system. The basic idea is to isolate the
preconditioning so that it is local to each processor, and also to use a (possibly cheaper) approximate
residual function. This requires the definition of a new function G(t, y, ˙y) which approximates the
function F(t, y, ˙y) in the definition of the DAE system (2.1). However, the user may set G=F.
Corresponding to the domain decomposition, there is a decomposition of the solution vectors yand ˙y
into Mdisjoint blocks ymand ˙ym, and a decomposition of Ginto blocks Gm. The block Gmdepends
on ymand ˙ym, and also on components of ym0and ˙ym0associated with neighboring sub-domains
(so-called ghost-cell data). Let ¯ymand ¯
˙ymdenote ymand ˙ym(respectively) augmented with those
other components on which Gmdepends. Then we have
G(t, y, ˙y)=[G1(t, ¯y1,¯
˙y1), G2(t, ¯y2,¯
˙y2), . . . , GM(t, ¯yM,¯
˙yM)]T,(4.1)
and each of the blocks Gm(t, ¯ym,¯
˙ym) is uncoupled from the others.
The preconditioner associated with this decomposition has the form
P=diag[P1, P2, . . . , PM] (4.2)
where
Pm≈∂Gm/∂ym+α∂Gm/∂ ˙ym(4.3)
This matrix is taken to be banded, with upper and lower half-bandwidths mudq and mldq defined as
the number of non-zero diagonals above and below the main diagonal, respectively. The difference
quotient approximation is computed using mudq +mldq +2 evaluations of Gm, but only a matrix of
bandwidth mukeep +mlkeep +1 is retained.
Neither pair of parameters need be the true half-bandwidths of the Jacobians of the local block of
G, if smaller values provide a more efficient preconditioner. Such an efficiency gain may occur if the
couplings in the DAE system outside a certain bandwidth are considerably weaker than those within
the band. Reducing mukeep and mlkeep while keeping mudq and mldq at their true values, discards
the elements outside the narrower band. Reducing both pairs has the additional effect of lumping the
outer Jacobian elements into the computed elements within the band, and requires more caution and
experimentation.
The solution of the complete linear system
P x =b(4.4)
reduces to solving each of the equations
Pmxm=bm(4.5)
and this is done by banded LU factorization of Pmfollowed by a banded backsolve.
Similar block-diagonal preconditioners could be considered with different treatment of the blocks
Pm. For example, incomplete LU factorization or an iterative method could be used instead of banded
LU factorization.
The idabbdpre module calls two user-provided functions to construct P: a required function
Gres (of type IDABBDLocalFn) which approximates the residual function G(t, y, ˙y)≈F(t, y, ˙y) and
which is computed locally, and an optional function Gcomm (of type IDABBDCommFn) which performs
4.8 A parallel band-block-diagonal preconditioner module 85
all inter-process communication necessary to evaluate the approximate residual G. These are in
addition to the user-supplied residual function res. Both functions take as input the same pointer
user data as passed by the user to IDASetUserData and passed to the user’s function res. The user
is responsible for providing space (presumably within user data) for components of yy and yp that
are communicated by Gcomm from the other processors, and that are then used by Gres, which should
not do any communication.
IDABBDLocalFn
Definition typedef int (*IDABBDLocalFn)(long int Nlocal, realtype tt,
N Vector yy, N Vector yp, N Vector gval,
void *user data);
Purpose This Gres function computes G(t, y, ˙y). It loads the vector gval as a function of tt,
yy, and yp.
Arguments Nlocal is the local vector length.
tt is the value of the independent variable.
yy is the dependent variable.
yp is the derivative of the dependent variable.
gval is the output vector.
user data is a pointer to user data, the same as the user data parameter passed to
IDASetUserData.
Return value An IDABBDLocalFn function type should return 0 to indicate success, 1 for a recoverable
error, or -1 for a non-recoverable error.
Notes This function must assume that all inter-processor communication of data needed to
calculate gval has already been done, and this data is accessible within user data.
The case where Gis mathematically identical to Fis allowed.
IDABBDCommFn
Definition typedef int (*IDABBDCommFn)(long int Nlocal, realtype tt,
N Vector yy, N Vector yp, void *user data);
Purpose This Gcomm function performs all inter-processor communications necessary for the ex-
ecution of the Gres function above, using the input vectors yy and yp.
Arguments Nlocal is the local vector length.
tt is the value of the independent variable.
yy is the dependent variable.
yp is the derivative of the dependent variable.
user data is a pointer to user data, the same as the user data parameter passed to
IDASetUserData.
Return value An IDABBDCommFn function type should return 0 to indicate success, 1 for a recoverable
error, or -1 for a non-recoverable error.
Notes The Gcomm function is expected to save communicated data in space defined within the
structure user data.
Each call to the Gcomm function is preceded by a call to the residual function res with
the same (tt,yy,yp) arguments. Thus Gcomm can omit any communications done by
res if relevant to the evaluation of Gres. If all necessary communication was done in
res, then Gcomm =NULL can be passed in the call to IDABBDPrecInit (see below).
Besides the header files required for the integration of the DAE problem (see §4.3), to use the
idabbdpre module, the main program must include the header file idas bbdpre.h which declares
the needed function prototypes.

86 Using IDAS for IVP Solution
The following is a summary of the usage of this module and describes the sequence of calls in
the user main program. Steps that are unchanged from the user main program presented in §4.4 are
grayed-out.
1. Initialize MPI
2. Set problem dimensions
3. Set vector of initial values
4. Create idas object
5. Allocate internal memory
6. Set optional inputs
7. Attach iterative linear solver, one of:
(a) flag = IDASpgmr(ida mem, maxl);
(b) flag = IDASpbcg(ida mem, maxl);
(c) flag = IDASptfqmr(ida mem, maxl);
8. Initialize the idabbdpre preconditioner module
Specify the upper and lower bandwidths mudq,mldq and mukeep,mlkeep and call
flag = IDABBDPrecInit(ida mem, Nlocal, mudq, mldq,
mukeep, mlkeep, dq rel yy, Gres, Gcomm);
to allocate memory and initialize the internal preconditioner data. The last two arguments of
IDABBDPrecInit are the two user-supplied functions described above.
9. Set linear solver optional inputs
Note that the user should not overwrite the preconditioner setup function or solve function through
calls to idaspils optional input functions.
10. Correct initial values
11. Specify rootfinding problem
12. Advance solution in time
13. Get optional outputs
Additional optional outputs associated with idabbdpre are available by way of two routines
described below, IDABBDPrecGetWorkSpace and IDABBDPrecGetNumGfnEvals.
14. Deallocate memory for solution vector
15. Free solver memory
16. Finalize MPI
The user-callable functions that initialize (step 8above) or re-initialize the idabbdpre preconditioner
module are described next.
IDABBDPrecInit
Call flag = IDABBDPrecInit(ida mem, Nlocal, mudq, mldq,
mukeep, mlkeep, dq rel yy, Gres, Gcomm);

4.8 A parallel band-block-diagonal preconditioner module 87
Description The function IDABBDPrecInit initializes and allocates (internal) memory for the id-
abbdpre preconditioner.
Arguments ida mem (void *) pointer to the idas memory block.
Nlocal (long int) local vector dimension.
mudq (long int) upper half-bandwidth to be used in the difference-quotient Ja-
cobian approximation.
mldq (long int) lower half-bandwidth to be used in the difference-quotient Jaco-
bian approximation.
mukeep (long int) upper half-bandwidth of the retained banded approximate Ja-
cobian block.
mlkeep (long int) lower half-bandwidth of the retained banded approximate Jaco-
bian block.
dq rel yy (realtype) the relative increment in components of yused in the difference
quotient approximations. The default is dq rel yy=√unit roundoff, which
can be specified by passing dq rel yy= 0.0.
Gres (IDABBDLocalFn) the Cfunction which computes the local residual approx-
imation G(t, y, ˙y).
Gcomm (IDABBDCommFn) the optional Cfunction which performs all inter-process
communication required for the computation of G(t, y, ˙y).
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The call to IDABBDPrecInit was successful.
IDASPILS MEM NULL The ida mem pointer was NULL.
IDASPILS MEM FAIL A memory allocation request has failed.
IDASPILS LMEM NULL An idaspils linear solver memory was not attached.
IDASPILS ILL INPUT The supplied vector implementation was not compatible with
block band preconditioner.
Notes If one of the half-bandwidths mudq or mldq to be used in the difference-quotient cal-
culation of the approximate Jacobian is negative or exceeds the value Nlocal−1, it is
replaced by 0 or Nlocal−1 accordingly.
The half-bandwidths mudq and mldq need not be the true half-bandwidths of the Jaco-
bian of the local block of G, when smaller values may provide a greater efficiency.
Also, the half-bandwidths mukeep and mlkeep of the retained banded approximate
Jacobian block may be even smaller, to reduce storage and computation costs further.
For all four half-bandwidths, the values need not be the same on every processor.
The idabbdpre module also provides a reinitialization function to allow for a sequence of problems
of the same size with idaspgmr/idabbdpre,idaspbcg/idabbdpre, or idasptfqmr/idabbdpre,
provided there is no change in local N,mukeep, or mlkeep. After solving one problem, and after calling
IDAReInit to re-initialize idas for a subsequent problem, a call to IDABBDPrecReInit can be made
to change any of the following: the half-bandwidths mudq and mldq used in the difference-quotient
Jacobian approximations, the relative increment dq rel yy, or one of the user-supplied functions Gres
and Gcomm.
IDABBDPrecReInit
Call flag = IDABBDPrecReInit(ida mem, mudq, mldq, dq rel yy);
Description The function IDABBDPrecReInit reinitializes the idabbdpre preconditioner.
Arguments ida mem (void *) pointer to the idas memory block.
mudq (long int) upper half-bandwidth to be used in the difference-quotient Ja-
cobian approximation.
88 Using IDAS for IVP Solution
mldq (long int) lower half-bandwidth to be used in the difference-quotient Jaco-
bian approximation.
dq rel yy (realtype) the relative increment in components of yused in the difference
quotient approximations. The default is dq rel yy =√unit roundoff, which
can be specified by passing dq rel yy = 0.0.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The call to IDABBDPrecReInit was successful.
IDASPILS MEM NULL The ida mem pointer was NULL.
IDASPILS LMEM NULL An idaspils linear solver memory was not attached.
IDASPILS PMEM NULL The function IDABBDPrecInit was not previously called.
Notes If one of the half-bandwidths mudq or mldq is negative or exceeds the value Nlocal−1,
it is replaced by 0 or Nlocal−1, accordingly.
The following two optional output functions are available for use with the idabbdpre module:
IDABBDPrecGetWorkSpace
Call flag = IDABBDPrecGetWorkSpace(ida mem, &lenrwBBDP, &leniwBBDP);
Description The function IDABBDPrecGetWorkSpace returns the local sizes of the idabbdpre real
and integer workspaces.
Arguments ida mem (void *) pointer to the idas memory block.
lenrwBBDP (long int) local number of real values in the idabbdpre workspace.
leniwBBDP (long int) local number of integer values in the idabbdpre workspace.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional output value has been successfully set.
IDASPILS MEM NULL The ida mem pointer was NULL.
IDASPILS PMEM NULL The idabbdpre preconditioner has not been initialized.
Notes In terms of the local vector dimension Nl, and smu = min(Nl−1,mukeep +mlkeep),
the actual size of the real workspace is Nl(2 mlkeep +mukeep +smu +2) realtype
words. The actual size of the integer workspace is Nlinteger words.
IDABBDPrecGetNumGfnEvals
Call flag = IDABBDPrecGetNumGfnEvals(ida mem, &ngevalsBBDP);
Description The function IDABBDPrecGetNumGfnEvals returns the cumulative number of calls to
the user Gres function due to the finite difference approximation of the Jacobian blocks
used within idabbdpre’s preconditioner setup function.
Arguments ida mem (void *) pointer to the idas memory block.
ngevalsBBDP (long int) the cumulative number of calls to the user Gres function.
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional output value has been successfully set.
IDASPILS MEM NULL The ida mem pointer was NULL.
IDASPILS PMEM NULL The idabbdpre preconditioner has not been initialized.
In addition to the ngevalsBBDP Gres evaluations, the costs associated with idabbdpre also include
nlinsetups LU factorizations, nlinsetups calls to Gcomm,npsolves banded backsolve calls, and
nrevalsLS residual function evaluations, where nlinsetups is an optional idas output (see §4.5.9.1),
and npsolves and nrevalsLS are linear solver optional outputs (see §4.5.9.6).

Chapter 5
Using IDAS for Forward Sensitivity
Analysis
This chapter describes the use of idas to compute solution sensitivities using forward sensitivity anal-
ysis. One of our main guiding principles was to design the idas user interface for forward sensitivity
analysis as an extension of that for IVP integration. Assuming a user main program and user-defined
support routines for IVP integration have already been defined, in order to perform forward sensitivity
analysis the user only has to insert a few more calls into the main program and (optionally) define
an additional routine which computes the residuals for sensitivity systems (2.12). The only departure
from this philosophy is due to the IDAResFn type definition (§4.6.1). Without changing the definition
of this type, the only way to pass values of the problem parameters to the DAE residual function is
to require the user data structure user data to contain a pointer to the array of real parameters p.
idas uses various constants for both input and output. These are defined as needed in this chapter,
but for convenience are also listed separately in Appendix B.
We begin with a brief overview, in the form of a skeleton user program. Following that are detailed
descriptions of the interface to the various user-callable routines and of the user-supplied routines that
were not already described in Chapter 4.
5.1 A skeleton of the user’s main program
The following is a skeleton of the user’s main program (or calling program) as an application of idas.
The user program is to have these steps in the order indicated, unless otherwise noted. For the sake
of brevity, we defer many of the details to the later sections. As in §4.4, most steps are independent
of the nvector implementation used. For the steps that are not, refer to Chapter 7for the specific
names. Differences between the user main program in §4.4 and the one below start only at step (11).
Steps that are unchanged from the skeleton program presented in §4.4 are grayed out.
First, note that no additional header files need be included for forward sensitivity analysis beyond
those for IVP solution (§4.4).
1. Initialize parallel or multi-threaded environment
2. Set problem dimensions etc.
3. Set initial values
4. Create idas object
5. Allocate internal memory
6. Specify integration tolerances
90 Using IDAS for Forward Sensitivity Analysis
7. Set optional inputs
8. Attach linear solver module
9. Set linear solver optional inputs
10. Initialize quadrature problem, if not sensitivity-dependent
11. Define the sensitivity problem
•Number of sensitivities (required)
Set Ns =Ns, the number of parameters with respect to which sensitivities are to be computed.
•Problem parameters (optional)
If idas is to evaluate the residuals of the sensitivity systems, set p, an array of Np real
parameters upon which the IVP depends. Only parameters with respect to which sensitivities
are (potentially) desired need to be included. Attach pto the user data structure user data.
For example, user data->p = p;
If the user provides a function to evaluate the sensitivity residuals, pneed not be specified.
•Parameter list (optional)
If idas is to evaluate the sensitivity residuals, set plist, an array of Ns integers to specify the
parameters pwith respect to which solution sensitivities are to be computed. If sensitivities
with respect to the j-th parameter p[j] (0 ≤j<Np) are desired, set plisti=j, for some
i= 0, . . . , Ns−1.
If plist is not specified, idas will compute sensitivities with respect to the first Ns parame-
ters; i.e., plisti=i(i= 0, . . . , Ns−1).
If the user provides a function to evaluate the sensitivity residuals, plist need not be spec-
ified.
•Parameter scaling factors (optional)
If idas is to estimate tolerances for the sensitivity solution vectors (based on tolerances for
the state solution vector) or if idas is to evaluate the residuals of the sensitivity systems
using the internal difference-quotient function, the results will be more accurate if order of
magnitude information is provided.
Set pbar, an array of Ns positive scaling factors. Typically, if pi6= 0, the value ¯pi=|pplisti|
can be used.
If pbar is not specified, idas will use ¯pi= 1.0.
If the user provides a function to evaluate the sensitivity residual and specifies tolerances for
the sensitivity variables, pbar need not be specified.
Note that the names for p,pbar,plist, as well as the field pof user data are arbitrary, but they
must agree with the arguments passed to IDASetSensParams below.
12. Set sensitivity initial conditions
Set the Ns vectors yS0[i] and ypS0[i] of initial values for sensitivities (for i= 0,..., Ns −1),
using the appropriate functions defined by the particular nvector implementation chosen.
First, create an array of Ns vectors by making the appropriate call
yS0 = N VCloneVectorArray ***(Ns, y0);
or
yS0 = N VCloneVectorArrayEmpty ***(Ns, y0);
Here the argument y0 serves only to provide the N Vector type for cloning.
Then, for each i= 0,...,Ns −1, load initial values for the i-th sensitivity vector yS0[i].
Set the initial conditions for the Ns sensitivity derivative vectors ypS0 of ˙ysimilarly.

5.2 User-callable routines for forward sensitivity analysis 91
13. Activate sensitivity calculations
Call flag = IDASensInit(...); to activate forward sensitivity computations and allocate inter-
nal memory for idas related to sensitivity calculations (see §5.2.1).
14. Set sensitivity tolerances
Call IDASensSStolerances,IDASensSVtolerances, or IDASensEEtolerances. See §5.2.2.
15. Set sensitivity analysis optional inputs
Call IDASetSens* routines to change from their default values any optional inputs that control
the behavior of idas in computing forward sensitivities. See §5.2.6.
16. Correct initial values
17. Specify rootfinding problem
18. Advance solution in time
19. Extract sensitivity solution
After each successful return from IDASolve, the solution of the original IVP is available in the y
argument of IDASolve, while the sensitivity solution can be extracted into yS and ypS (which can
be the same as yS0 and ypS0, respectively) by calling one of the following routines: IDAGetSens,
IDAGetSens1,IDAGetSensDky or IDAGetSensDky1 (see §5.2.5).
20. Deallocate memory for solutions vector
21. Deallocate memory for sensitivity vectors
Upon completion of the integration, deallocate memory for the vectors contained in yS0 and ypS0:
N VDestroyVectorArray ***(yS0, Ns);
and similarly for ypS0.
If yS was created from realtype arrays yS i, it is the user’s responsibility to also free the space
for the arrays yS i, and likewise for ypS.
22. Free user data structure
23. Free solver memory
24. Free vector specification memory
25. Finalize MPI, if used
5.2 User-callable routines for forward sensitivity analysis
This section describes the idas functions, in addition to those presented in §4.5, that are called by
the user to set up and solve a forward sensitivity problem.
5.2.1 Forward sensitivity initialization and deallocation functions
Activation of forward sensitivity computation is done by calling IDASensInit. The form of the call
to this routine is as follows:
IDASensInit
Call flag = IDASensInit(ida mem, Ns, ism, resS, yS0, ypS0);

92 Using IDAS for Forward Sensitivity Analysis
Description The routine IDASensInit activates forward sensitivity computations and allocates in-
ternal memory related to sensitivity calculations.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
Ns (int) the number of sensitivities to be computed.
ism (int) a flag used to select the sensitivity solution method. Its value can be
either IDA SIMULTANEOUS or IDA STAGGERED:
•In the IDA SIMULTANEOUS approach, the state and sensitivity variables are
corrected at the same time. If IDA NEWTON was selected as the nonlinear
system solution method, this amounts to performing a modified Newton
iteration on the combined nonlinear system;
•In the IDA STAGGERED approach, the correction step for the sensitivity
variables takes place at the same time for all sensitivity equations, but
only after the correction of the state variables has converged and the state
variables have passed the local error test;
resS (IDASensResFn) is the Cfunction which computes the residual of the sensitiv-
ity DAE. For full details see §5.3.
yS0 (N Vector *) a pointer to an array of Ns vectors containing the initial values
of the sensitivities of y.
ypS0 (N Vector *) a pointer to an array of Ns vectors containing the initial values
of the sensitivities of ˙y.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDASensInit was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.
IDA MEM FAIL A memory allocation request has failed.
IDA ILL INPUT An input argument to IDASensInit has an illegal value.
Notes Passing resS=NULL indicates using the default internal difference quotient sensitivity
residual routine.
If an error occurred, IDASensInit also prints an error message to the file specified by
the optional input errfp.
In terms of the problem size N, number of sensitivity vectors Ns, and maximum method order maxord,
the size of the real workspace is increased as follows:
•Base value: lenrw =lenrw + (maxord+5)NsN
•With IDASensSVtolerances:lenrw =lenrw +NsN
the size of the integer workspace is increased as follows:
•Base value: leniw =leniw + (maxord+5)NsNi
•With IDASensSVtolerances:leniw =leniw +NsNi,
where Niis the number of integer words in one N Vector.
The routine IDASensReInit, useful during the solution of a sequence of problems of same size,
reinitializes the sensitivity-related internal memory and must follow a call to IDASensInit (and maybe
a call to IDAReInit). The number Ns of sensitivities is assumed to be unchanged since the call to
IDASensInit. The call to the IDASensReInit function has the form:

5.2 User-callable routines for forward sensitivity analysis 93
IDASensReInit
Call flag = IDASensReInit(ida mem, ism, yS0, ypS0);
Description The routine IDASensReInit reinitializes forward sensitivity computations.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
ism (int) a flag used to select the sensitivity solution method. Its value can be
either IDA SIMULTANEOUS or IDA STAGGERED.
yS0 (N Vector *) a pointer to an array of Ns variables of type N Vector containing
the initial values of the sensitivities of y.
ypS0 (N Vector *) a pointer to an array of Ns variables of type N Vector containing
the initial values of the sensitivities of ˙y.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAReInit was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.
IDA NO SENS Memory space for sensitivity integration was not allocated through a
previous call to IDASensInit.
IDA ILL INPUT An input argument to IDASensReInit has an illegal value.
IDA MEM FAIL A memory allocation request has failed.
Notes All arguments of IDASensReInit are the same as those of IDASensInit.
If an error occurred, IDASensReInit also prints an error message to the file specified
by the optional input errfp.
To deallocate all forward sensitivity-related memory (allocated in a prior call to IDASensInit), the
user must call
IDASensFree
Call IDASensFree(ida mem);
Description The function IDASensFree frees the memory allocated for forward sensitivity compu-
tations by a previous call to IDASensInit.
Arguments The argument is the pointer to the idas memory block (of type void *).
Return value The function IDASensFree has no return value.
Notes In general, IDASensFree need not be called by the user as it is invoked automatically
by IDAFree.
After a call to IDASensFree, forward sensitivity computations can be reactivated only
by calling IDASensInit again.
To activate and deactivate forward sensitivity calculations for successive idas runs, without having
to allocate and deallocate memory, the following function is provided:
IDASensToggleOff
Call IDASensToggleOff(ida mem);
Description The function IDASensToggleOff deactivates forward sensitivity calculations. It does
not deallocate sensitivity-related memory.
Arguments ida mem (void *) pointer to the memory previously allocated by IDAInit.
Return value The return value flag of IDASensToggle is one of:
IDA SUCCESS IDASensToggleOff was successful.
IDA MEM NULL ida mem was NULL.
Notes Since sensitivity-related memory is not deallocated, sensitivities can be reactivated at
a later time (using IDASensReInit).
94 Using IDAS for Forward Sensitivity Analysis
5.2.2 Forward sensitivity tolerance specification functions
One of the following three functions must be called to specify the integration tolerances for sensitivities.
Note that this call must be made after the call to IDASensInit.
IDASensSStolerances
Call flag = IDASensSStolerances(ida mem, reltolS, abstolS);
Description The function IDASensSStolerances specifies scalar relative and absolute tolerances.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
reltolS (realtype) is the scalar relative error tolerance.
abstolS (realtype*) is a pointer to an array of length Ns containing the scalar absolute
error tolerances.
Return value The return flag flag (of type int) will be one of the following:
IDA SUCCESS The call to IDASStolerances was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.
IDA NO SENS The sensitivity allocation function IDASensInit has not been called.
IDA ILL INPUT One of the input tolerances was negative.
IDASensSVtolerances
Call flag = IDASensSVtolerances(ida mem, reltolS, abstolS);
Description The function IDASensSVtolerances specifies scalar relative tolerance and vector abso-
lute tolerances.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
reltolS (realtype) is the scalar relative error tolerance.
abstolS (N Vector*) is an array of Ns variables of type N Vector. The N Vector from
abstolS[is] specifies the vector tolerances for is-th sensitivity.
Return value The return flag flag (of type int) will be one of the following:
IDA SUCCESS The call to IDASVtolerances was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.
IDA NO SENS The sensitivity allocation function IDASensInit has not been called.
IDA ILL INPUT The relative error tolerance was negative or one of the absolute tolerance
vectors had a negative component.
Notes This choice of tolerances is important when the absolute error tolerance needs to be
different for each component of any vector yS[i].
IDASensEEtolerances
Call flag = IDASensEEtolerances(ida mem);
Description When IDASensEEtolerances is called, idas will estimate tolerances for sensitivity vari-
ables based on the tolerances supplied for states variables and the scaling factors ¯p.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
Return value The return flag flag (of type int) will be one of the following:
IDA SUCCESS The call to IDASensEEtolerances was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.
IDA NO SENS The sensitivity allocation function IDASensInit has not been called.
5.2 User-callable routines for forward sensitivity analysis 95
5.2.3 Forward sensitivity initial condition calculation function
IDACalcIC also calculates corrected initial conditions for sensitivity variables of a DAE system. When
used for initial conditions calculation of the forward sensitivities, IDACalcIC must be preceded by
successful calls to IDASensInit (or IDASensReInit) and should precede the call(s) to IDASolve. For
restrictions that apply for initial conditions calculation of the state variables, see §4.5.4.
Calling IDACalcIC is optional. It is only necessary when the initial conditions do not satisfy the
sensitivity systems. Even if forward sensitivity analysis was enabled, the call to the initial conditions
calculation function IDACalcIC is exactly the same as for state variables.
flag = IDACalcIC(ida_mem, icopt, tout1);
See §4.5.4 for a list of possible return values.
5.2.4 IDAS solver function
Even if forward sensitivity analysis was enabled, the call to the main solver function IDASolve is
exactly the same as in §4.5.6. However, in this case the return value flag can also be one of the
following:
IDA SRES FAIL The sensitivity residual function failed in an unrecoverable manner.
IDA REP SRES ERR The user’s residual function repeatedly returned a recoverable error flag, but the
solver was unable to recover.
5.2.5 Forward sensitivity extraction functions
If forward sensitivity computations have been initialized by a call to IDASensInit, or reinitialized by
a call to IDASensReInit, then idas computes both a solution and sensitivities at time t. However,
IDASolve will still return only the solutions yand ˙yin yret and ypret, respectively. Solution
sensitivities can be obtained through one of the following functions:
IDAGetSens
Call flag = IDAGetSens(ida mem, &tret, yS);
Description The function IDAGetSens returns the sensitivity solution vectors after a successful return
from IDASolve.
Arguments ida mem (void *) pointer to the memory previously allocated by IDAInit.
tret (realtype) the time reached by the solver (output).
yS (N Vector *) the array of Ns computed forward sensitivity vectors.
Return value The return value flag of IDAGetSens is one of:
IDA SUCCESS IDAGetSens was successful.
IDA MEM NULL ida mem was NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
IDA BAD DKY yS is NULL.
Notes Note that the argument tret is an output for this function. Its value will be the same
as that returned at the last IDASolve call.
The function IDAGetSensDky computes the k-th derivatives of the interpolating polynomials for the
sensitivity variables at time t. This function is called by IDAGetSens with k= 0, but may also be
called directly by the user.
96 Using IDAS for Forward Sensitivity Analysis
IDAGetSensDky
Call flag = IDAGetSensDky(ida mem, t, k, dkyS);
Description The function IDAGetSensDky returns derivatives of the sensitivity solution vectors after
a successful return from IDASolve.
Arguments ida mem (void *) pointer to the memory previously allocated by IDAInit.
t(realtype) specifies the time at which sensitivity information is requested.
The time tmust fall within the interval defined by the last successful step
taken by idas.
k(int) order of derivatives.
dkyS (N Vector *) array of Ns vectors containing the derivatives on output. The
space for dkyS must be allocated by the user.
Return value The return value flag of IDAGetSensDky is one of:
IDA SUCCESS IDAGetSensDky succeeded.
IDA MEM NULL ida mem was NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
IDA BAD DKY dkyS or one of the vectors dkyS[i] is NULL.
IDA BAD K k is not in the range 0,1, ..., klast.
IDA BAD T The time tis not in the allowed range.
Forward sensitivity solution vectors can also be extracted separately for each parameter in turn
through the functions IDAGetSens1 and IDAGetSensDky1, defined as follows:
IDAGetSens1
Call flag = IDAGetSens1(ida mem, &tret, is, yS);
Description The function IDAGetSens1 returns the is-th sensitivity solution vector after a successful
return from IDASolve.
Arguments ida mem (void *) pointer to the memory previously allocated by IDAInit.
tret (realtype *) the time reached by the solver (output).
is (int) specifies which sensitivity vector is to be returned (0 ≤is< Ns).
yS (N Vector) the computed forward sensitivity vector.
Return value The return value flag of IDAGetSens1 is one of:
IDA SUCCESS IDAGetSens1 was successful.
IDA MEM NULL ida mem was NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
IDA BAD IS The index is is not in the allowed range.
IDA BAD DKY yS is NULL.
IDA BAD T The time tis not in the allowed range.
Notes Note that the argument tret is an output for this function. Its value will be the same
as that returned at the last IDASolve call.
IDAGetSensDky1
Call flag = IDAGetSensDky1(ida mem, t, k, is, dkyS);
Description The function IDAGetSensDky1 returns the k-th derivative of the is-th sensitivity solu-
tion vector after a successful return from IDASolve.
Arguments ida mem (void *) pointer to the memory previously allocated by IDAInit.

5.2 User-callable routines for forward sensitivity analysis 97
t(realtype) specifies the time at which sensitivity information is requested.
The time tmust fall within the interval defined by the last successful step
taken by idas.
k(int) order of derivative.
is (int) specifies the sensitivity derivative vector to be returned (0 ≤is< Ns).
dkyS (N Vector) the vector containing the derivative on output. The space for dkyS
must be allocated by the user.
Return value The return value flag of IDAGetSensDky1 is one of:
IDA SUCCESS IDAGetQuadDky1 succeeded.
IDA MEM NULL ida mem was NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
IDA BAD DKY dkyS is NULL.
IDA BAD IS The index is is not in the allowed range.
IDA BAD K k is not in the range 0,1, ..., klast.
IDA BAD T The time tis not in the allowed range.
5.2.6 Optional inputs for forward sensitivity analysis
Optional input variables that control the computation of sensitivities can be changed from their default
values through calls to IDASetSens* functions. Table 5.1 lists all forward sensitivity optional input
functions in idas which are described in detail in the remainder of this section.
IDASetSensParams
Call flag = IDASetSensParams(ida mem, p, pbar, plist);
Description The function IDASetSensParams specifies problem parameter information for sensitivity
calculations.
Arguments ida mem (void *) pointer to the idas memory block.
p(realtype *) a pointer to the array of real problem parameters used to evalu-
ate F(t, y, ˙y, p). If non-NULL,pmust point to a field in the user’s data structure
user data passed to the user’s residual function. (See §5.1).
pbar (realtype *) an array of Ns positive scaling factors. If non-NULL,pbar must
have all its components >0.0. (See §5.1).
plist (int *) an array of Ns non-negative indices to specify which components of p
to use in estimating the sensitivity equations. If non-NULL,plist must have
all components ≥0. (See §5.1).
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
IDA ILL INPUT An argument has an illegal value.
Notes This function must be preceded by a call to IDASensInit.
!
Table 5.1: Forward sensitivity optional inputs
Optional input Routine name Default
Sensitivity scaling factors IDASetSensParams NULL
DQ approximation method IDASetSensDQMethod centered,0.0
Error control strategy IDASetSensErrCon FALSE
Maximum no. of nonlinear iterations IDASetSensMaxNonlinIters 3
98 Using IDAS for Forward Sensitivity Analysis
IDASetSensDQMethod
Call flag = IDASetSensDQMethod(ida mem, DQtype, DQrhomax);
Description The function IDASetSensDQMethod specifies the difference quotient strategy in the case
in which the residual of the sensitivity equations are to be computed by idas.
Arguments ida mem (void *) pointer to the idas memory block.
DQtype (int) specifies the difference quotient type and can be either IDA CENTERED or
IDA FORWARD.
DQrhomax (realtype) positive value of the selection parameter used in deciding switch-
ing between a simultaneous or separate approximation of the two terms in the
sensitivity residual.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA ILL INPUT An argument has an illegal value.
Notes If DQrhomax = 0.0, then no switching is performed. The approximation is done simul-
taneously using either centered or forward finite differences, depending on the value of
DQtype. For values of DQrhomax ≥1.0, the simultaneous approximation is used when-
ever the estimated finite difference perturbations for states and parameters are within
a factor of DQrhomax, and the separate approximation is used otherwise. Note that a
value DQrhomax <1.0 will effectively disable switching. See §2.5 for more details.
The default value are DQtype=IDA CENTERED and DQrhomax= 0.0.
IDASetSensErrCon
Call flag = IDASetSensErrCon(ida mem, errconS);
Description The function IDASetSensErrCon specifies the error control strategy for sensitivity vari-
ables.
Arguments ida mem (void *) pointer to the idas memory block.
errconS (booleantype) specifies whether sensitivity variables are included (TRUE) or
not (FALSE) in the error control mechanism.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes By default, errconS is set to FALSE. If errconS=TRUE then both state variables and
sensitivity variables are included in the error tests. If errconS=FALSE then the sensi-
tivity variables are excluded from the error tests. Note that, in any event, all variables
are considered in the convergence tests.
IDASetSensMaxNonlinIters
Call flag = IDASetSensMaxNonlinIters(ida mem, maxcorS);
Description The function IDASetSensMaxNonlinIters specifies the maximum number of nonlinear
solver iterations for sensitivity variables per step.
Arguments ida mem (void *) pointer to the idas memory block.
maxcorS (int) maximum number of nonlinear solver iterations allowed per step (>0).
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
Notes The default value is 3.

5.2 User-callable routines for forward sensitivity analysis 99
5.2.7 Optional outputs for forward sensitivity analysis
5.2.7.1 Main solver optional output functions
Optional output functions that return statistics and solver performance information related to forward
sensitivity computations are listed in Table 5.2 and described in detail in the remainder of this section.
IDAGetSensNumResEvals
Call flag = IDAGetSensNumResEvals(ida mem, &nfSevals);
Description The function IDAGetSensNumResEvals returns the number of calls to the sensitivity
residual function.
Arguments ida mem (void *) pointer to the idas memory block.
nfSevals (long int) number of calls to the sensitivity residual function.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
IDAGetNumResEvalsSens
Call flag = IDAGetNumResEvalsSens(ida mem, &nfevalsS);
Description The function IDAGetNumResEvalsSEns returns the number of calls to the user’s residual
function due to the internal finite difference approximation of the sensitivity residuals.
Arguments ida mem (void *) pointer to the idas memory block.
nfevalsS (long int) number of calls to the user residual function for sensitivity resid-
uals.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
Notes This counter is incremented only if the internal finite difference approximation routines
are used for the evaluation of the sensitivity residuals.
Table 5.2: Forward sensitivity optional outputs
Optional output Routine name
No. of calls to sensitivity residual function IDAGetSensNumResEvals
No. of calls to residual function for sensitivity IDAGetNumResEvalsSens
No. of sensitivity local error test failures IDAGetSensNumErrTestFails
No. of calls to lin. solv. setup routine for sens. IDAGetSensNumLinSolvSetups
Sensitivity-related statistics as a group IDAGetSensStats
Error weight vector for sensitivity variables IDAGetSensErrWeights
No. of sens. nonlinear solver iterations IDAGetSensNumNonlinSolvIters
No. of sens. convergence failures IDAGetSensNumNonlinSolvConvFails
Sens. nonlinear solver statistics as a group IDAGetSensNonlinSolvStats
100 Using IDAS for Forward Sensitivity Analysis
IDAGetSensNumErrTestFails
Call flag = IDAGetSensNumErrTestFails(ida mem, &nSetfails);
Description The function IDAGetSensNumErrTestFails returns the number of local error test fail-
ures for the sensitivity variables that have occurred.
Arguments ida mem (void *) pointer to the idas memory block.
nSetfails (long int) number of error test failures.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
Notes This counter is incremented only if the sensitivity variables have been included in the
error test (see IDASetSensErrCon in §5.2.6). Even in that case, this counter is not
incremented if the ism=IDA SIMULTANEOUS sensitivity solution method has been used.
IDAGetSensNumLinSolvSetups
Call flag = IDAGetSensNumLinSolvSetups(ida mem, &nlinsetupsS);
Description The function IDAGetSensNumLinSolvSetups returns the number of calls to the linear
solver setup function due to forward sensitivity calculations.
Arguments ida mem (void *) pointer to the idas memory block.
nlinsetupsS (long int) number of calls to the linear solver setup function.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
Notes This counter is incremented only if Newton iteration has been used and staggered sensi-
tivity solution method (ism=IDA STAGGERED) was specified in the call to IDASensInit
(see §5.2.1).
IDAGetSensStats
Call flag = IDAGetSensStats(ida mem, &nfSevals, &nfevalsS, &nSetfails,
&nlinsetupsS);
Description The function IDAGetSensStats returns all of the above sensitivity-related solver statis-
tics as a group.
Arguments ida mem (void *) pointer to the idas memory block.
nfSevals (long int) number of calls to the sensitivity residual function.
nfevalsS (long int) number of calls to the user-supplied residual function.
nSetfails (long int) number of error test failures.
nlinsetupsS (long int) number of calls to the linear solver setup function.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output values have been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
5.2 User-callable routines for forward sensitivity analysis 101
IDAGetSensErrWeights
Call flag = IDAGetSensErrWeights(ida mem, eSweight);
Description The function IDAGetSensErrWeights returns the sensitivity error weight vectors at the
current time. These are the reciprocals of the Wiof (2.7) for the sensitivity variables.
Arguments ida mem (void *) pointer to the idas memory block.
eSweight (N Vector S) pointer to the array of error weight vectors.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
Notes The user must allocate memory for eweightS.
IDAGetSensNumNonlinSolvIters
Call flag = IDAGetSensNumNonlinSolvIters(ida mem, &nSniters);
Description The function IDAGetSensNumNonlinSolvIters returns the number of nonlinear itera-
tions performed for sensitivity calculations.
Arguments ida mem (void *) pointer to the idas memory block.
nSniters (long int) number of nonlinear iterations performed.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
Notes This counter is incremented only if ism was IDA STAGGERED in the call to IDASensInit
(see §5.2.1).
IDAGetSensNumNonlinSolvConvFails
Call flag = IDAGetSensNumNonlinSolvConvFails(ida mem, &nSncfails);
Description The function IDAGetSensNumNonlinSolvConvFails returns the number of nonlinear
convergence failures that have occurred for sensitivity calculations.
Arguments ida mem (void *) pointer to the idas memory block.
nSncfails (long int) number of nonlinear convergence failures.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
Notes This counter is incremented only if ism was IDA STAGGERED in the call to IDASensInit
(see §5.2.1).
IDAGetSensNonlinSolvStats
Call flag = IDAGetSensNonlinSolvStats(ida mem, &nSniters, &nSncfails);
Description The function IDAGetSensNonlinSolvStats returns the sensitivity-related nonlinear
solver statistics as a group.
Arguments ida mem (void *) pointer to the idas memory block.
nSniters (long int) number of nonlinear iterations performed.

102 Using IDAS for Forward Sensitivity Analysis
nSncfails (long int) number of nonlinear convergence failures.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output values have been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
5.2.7.2 Initial condition calculation optional output functions
The sensitivity consistent initial conditions found by idas (after a successful call to IDACalcIC) can
be obtained by calling the following function:
IDAGetSensConsistentIC
Call flag = IDAGetSensConsistentIC(ida mem, yyS0 mod, ypS0 mod);
Description The function IDAGetSensConsistentIC returns the corrected initial conditions calcu-
lated by IDACalcIC for sensitivities variables.
Arguments ida mem (void *) pointer to the idas memory block.
yyS0 mod (N Vector *) a pointer to an array of Ns vectors containing consistent sensi-
tivity vectors.
ypS0 mod (N Vector *) a pointer to an array of Ns vectors containing consistent sensi-
tivity derivative vectors.
Return value The return value flag (of type int) is one of
IDA SUCCESS IDAGetSensConsistentIC succeeded.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS The function IDASensInit has not been previously called.
IDA ILL INPUT IDASolve has been already called.
Notes If the consistent sensitivity vectors or consistent derivative vectors are not desired, pass
NULL for the corresponding argument.
The user must allocate space for yyS0 mod and ypS0 mod (if not NULL).
!
5.3 User-supplied routines for forward sensitivity analysis
In addition to the required and optional user-supplied routines described in §4.6, when using idas for
forward sensitivity analysis, the user has the option of providing a routine that calculates the residual
of the sensitivity equations (2.12).
By default, idas uses difference quotient approximation routines for the residual of the sensitivity
equations. However, idas allows the option for user-defined sensitivity residual routines (which also
provides a mechanism for interfacing idas to routines generated by automatic differentiation).
The user may provide the residuals of the sensitivity equations (2.12), for all sensitivity parameters
at once, through a function of type IDASensResFn defined by:
IDASensResFn
Definition typedef int (*IDASensResFn)(int Ns, realtype t,
N Vector yy, N Vector yp, N Vector resval,
N Vector *yS, N Vector *ypS,
N Vector *resvalS, void *user data,
N Vector tmp1, N Vector tmp2, N Vector tmp3);
Purpose This function computes the sensitivity residual for all sensitivity equations. It must com-
pute the vectors (∂F/∂y)si(t)+(∂F/∂ ˙y) ˙si(t)+(∂F/∂pi) and store them in resvalS[i].
5.4 Integration of quadrature equations depending on forward sensitivities 103
Arguments tis the current value of the independent variable.
yy is the current value of the state vector, y(t).
yp is the current value of ˙y(t).
resval contains the current value Fof the original DAE residual.
yS contains the current values of the sensitivities si.
ypS contains the current values of the sensitivity derivatives ˙si.
resvalS contains the output sensitivity residual vectors.
user data is a pointer to user data.
tmp1
tmp2
tmp3 are N Vectors of length Nwhich can be used as temporary storage.
Return value An IDASensResFn should return 0 if successful, a positive value if a recoverable error
occurred (in which case idas will attempt to correct), or a negative value if it failed
unrecoverably (in which case the integration is halted and IDA SRES FAIL is returned).
Notes There is one situation in which recovery is not possible even if IDASensResFn function
returns a recoverable error flag. That is when this occurs at the very first call to the
IDASensResFn, in which case idas returns IDA FIRST RES FAIL.
5.4 Integration of quadrature equations depending on forward
sensitivities
idas provides support for integration of quadrature equations that depends not only on the state
variables but also on forward sensitivities.
The following is an overview of the sequence of calls in a user’s main program in this situation.
Steps that are unchanged from the skeleton program presented in §5.1 are grayed out. See also §4.7.
1. Initialize parallel or multi-threaded environment
2. Set problem dimensions, etc.
3. Set vectors of initial values
4. Create idas object
5. Allocate internal memory
6. Set optional inputs
7. Attach linear solver module
8. Set linear solver optional inputs
9. Initialize sensitivity-independent quadrature problem
10. Define the sensitivity problem
11. Set sensitivity initial conditions
12. Activate sensitivity calculations
13. Set sensitivity analysis optional inputs
14. Set vector of initial values for quadrature variables
Typically, the quadrature variables should be initialized to 0.

104 Using IDAS for Forward Sensitivity Analysis
15. Initialize sensitivity-dependent quadrature integration
Call IDAQuadSensInit to specify the quadrature equation right-hand side function and to allocate
internal memory related to quadrature integration. See §5.4.1 for details.
16. Set optional inputs for sensitivity-dependent quadrature integration
Call IDASetQuadSensErrCon to indicate whether or not quadrature variables should be used in
the step size control mechanism. If so, one of the IDAQuadSens*tolerances functions must be
called to specify the integration tolerances for quadrature variables. See §5.4.4 for details.
17. Advance solution in time
18. Extract sensitivity-dependent quadrature variables
Call IDAGetQuadSens,IDAGetQuadSens1,IDAGetQuadSensDky or IDAGetQuadSensDky1 to obtain
the values of the quadrature variables or their derivatives at the current time. See §5.4.3 for details.
19. Get optional outputs
20. Extract sensitivity solution
21. Get sensitivity-dependent quadrature optional outputs
Call IDAGetQuadSens* functions to obtain optional output related to the integration of sensitivity-
dependent quadratures. See §5.4.5 for details.
22. Deallocate memory for solutions vector
23. Deallocate memory for sensitivity vectors
24. Deallocate memory for sensitivity-dependent quadrature variables
25. Free solver memory
26. Finalize MPI, if used
Note: IDAQuadSensInit (step 15 above) can be called and quadrature-related optional inputs (step
16 above) can be set, anywhere between steps 10 and 17.
5.4.1 Sensitivity-dependent quadrature initialization and deallocation
The function IDAQuadSensInit activates integration of quadrature equations depending on sensitiv-
ities and allocates internal memory related to these calculations. If rhsQS is input as NULL, then
idas uses an internal function that computes difference quotient approximations to the functions
¯qi= (∂q/∂y)si+ (∂q/∂ ˙y) ˙si+∂q/∂pi, in the notation of (2.10). The form of the call to this function
is as follows:
IDAQuadSensInit
Call flag = IDAQuadSensInit(ida mem, rhsQS, yQS0);
Description The function IDAQuadSensInit provides required problem specifications, allocates in-
ternal memory, and initializes quadrature integration.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
rhsQS (IDAQuadSensRhsFn) is the Cfunction which computes fQS , the right-hand
side of the sensitivity-dependent quadrature equations (for full details see
§5.4.6).
yQS0 (N Vector *) contains the initial values of sensitivity-dependent quadratures.
Return value The return value flag (of type int) will be one of the following:

5.4 Integration of quadrature equations depending on forward sensitivities 105
IDA SUCCESS The call to IDAQuadSensInit was successful.
IDA MEM NULL The idas memory was not initialized by a prior call to IDACreate.
IDA MEM FAIL A memory allocation request failed.
IDA NO SENS The sensitivities were not initialized by a prior call to IDASensInit.
IDA ILL INPUT The parameter yQS0 is NULL.
Notes Before calling IDAQuadSensInit, the user must enable the sensitivites by calling
!
IDASensInit.
If an error occurred, IDAQuadSensInit also sends an error message to the error handler
function.
In terms of the number of quadrature variables Nqand maximum method order maxord, the size of
the real workspace is increased as follows:
•Base value: lenrw =lenrw + (maxord+5)Nq
•If IDAQuadSensSVtolerances is called: lenrw =lenrw +NqNs
and the size of the integer workspace is increased as follows:
•Base value: leniw =leniw + (maxord+5)Nq
•If IDAQuadSensSVtolerances is called: leniw =leniw +NqNs
The function IDAQuadSensReInit, useful during the solution of a sequence of problems of same
size, reinitializes the quadrature related internal memory and must follow a call to IDAQuadSensInit.
The number Nq of quadratures as well as the number Ns of sensitivities are assumed to be unchanged
from the prior call to IDAQuadSensInit. The call to the IDAQuadSensReInit function has the form:
IDAQuadSensReInit
Call flag = IDAQuadSensReInit(ida mem, yQS0);
Description The function IDAQuadSensReInit provides required problem specifications and reini-
tializes the sensitivity-dependent quadrature integration.
Arguments ida mem (void *) pointer to the idas memory block.
yQS0 (N Vector *) contains the initial values of sensitivity-dependent quadratures.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAQuadSensReInit was successful.
IDA MEM NULL The idas memory was not initialized by a prior call to IDACreate.
IDA NO SENS Memory space for the sensitivity calculation was not allocated by a
prior call to IDASensInit.
IDA NO QUADSENS Memory space for the sensitivity quadratures integration was not
allocated by a prior call to IDAQuadSensInit.
IDA ILL INPUT The parameter yQS0 is NULL.
Notes If an error occurred, IDAQuadSensReInit also sends an error message to the error
handler function.
IDAQuadSensFree
Call IDAQuadSensFree(ida mem);
Description The function IDAQuadSensFree frees the memory allocated for sensitivity quadrature
integration.
Arguments The argument is the pointer to the idas memory block (of type void *).
Return value The function IDAQuadSensFree has no return value.
Notes In general, IDAQuadSensFree need not be called by the user as it is called automatically
by IDAFree.
106 Using IDAS for Forward Sensitivity Analysis
5.4.2 IDAS solver function
Even if quadrature integration was enabled, the call to the main solver function IDASolve is exactly the
same as in §4.5.6. However, in this case the return value flag can also be one of the following:
IDA QSRHS FAIL The sensitivity quadrature right-hand side function failed in an unrecoverable
manner.
IDA FIRST QSRHS ERR The sensitivity quadrature right-hand side function failed at the first call.
IDA REP QSRHS ERR Convergence test failures occurred too many times due to repeated recover-
able errors in the quadrature right-hand side function. The IDA REP RES ERR
will also be returned if the quadrature right-hand side function had repeated
recoverable errors during the estimation of an initial step size (assuming the
sensitivity quadrature variables are included in the error tests).
5.4.3 Sensitivity-dependent quadrature extraction functions
If sensitivity-dependent quadratures have been initialized by a call to IDAQuadSensInit, or reinitial-
ized by a call to IDAQuadSensReInit, then idas computes a solution, sensitivities, and quadratures
depending on sensitivities at time t. However, IDASolve will still return only the solutions yand ˙y.
Sensitivity-dependent quadratures can be obtained using one of the following functions:
IDAGetQuadSens
Call flag = IDAGetQuadSens(ida mem, &tret, yQS);
Description The function IDAGetQuadSens returns the quadrature sensitivity solution vectors after
a successful return from IDASolve.
Arguments ida mem (void *) pointer to the memory previously allocated by IDAInit.
tret (realtype) the time reached by the solver (output).
yQS (N Vector *) array of Ns computed sensitivity-dependent quadrature vectors.
Return value The return value flag of IDAGetQuadSens is one of:
IDA SUCCESS IDAGetQuadSens was successful.
IDA MEM NULL ida mem was NULL.
IDA NO SENS Sensitivities were not activated.
IDA NO QUADSENS Quadratures depending on the sensitivities were not activated.
IDA BAD DKY yQS or one of the yQS[i] is NULL.
The function IDAGetQuadSensDky computes the k-th derivatives of the interpolating polynomials for
the sensitivity-dependent quadrature variables at time t. This function is called by IDAGetQuadSens
with k=0, but may also be called directly by the user.
IDAGetQuadSensDky
Call flag = IDAGetQuadSensDky(ida mem, t, k, dkyQS);
Description The function IDAGetQuadSensDky returns derivatives of the quadrature sensitivities
solution vectors after a successful return from IDASolve.
Arguments ida mem (void *) pointer to the memory previously allocated by IDAInit.
t(realtype) the time at which information is requested. The time tmust fall
within the interval defined by the last successful step taken by idas.
k(int) order of the requested derivative.
dkyQS (N Vector *) array of Ns vectors containing the derivatives. This vector array
must be allocated by the user.
Return value The return value flag of IDAGetQuadSensDky is one of:
IDA SUCCESS IDAGetQuadSensDky succeeded.
5.4 Integration of quadrature equations depending on forward sensitivities 107
IDA MEM NULL ida mem was NULL.
IDA NO SENS Sensitivities were not activated.
IDA NO QUADSENS Quadratures depending on the sensitivities were not activated.
IDA BAD DKY dkyQS or one of the vectors dkyQS[i] is NULL.
IDA BAD K k is not in the range 0,1, ..., klast.
IDA BAD T The time tis not in the allowed range.
Quadrature sensitivity solution vectors can also be extracted separately for each parameter in turn
through the functions IDAGetQuadSens1 and IDAGetQuadSensDky1, defined as follows:
IDAGetQuadSens1
Call flag = IDAGetQuadSens1(ida mem, &tret, is, yQS);
Description The function IDAGetQuadSens1 returns the is-th sensitivity of quadratures after a
successful return from IDASolve.
Arguments ida mem (void *) pointer to the memory previously allocated by IDAInit.
tret (realtype) the time reached by the solver (output).
is (int) specifies which sensitivity vector is to be returned (0 ≤is< Ns).
yQS (N Vector) the computed sensitivity-dependent quadrature vector.
Return value The return value flag of IDAGetQuadSens1 is one of:
IDA SUCCESS IDAGetQuadSens1 was successful.
IDA MEM NULL ida mem was NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
IDA NO QUADSENS Quadratures depending on the sensitivities were not activated.
IDA BAD IS The index is is not in the allowed range.
IDA BAD DKY yQS is NULL.
IDAGetQuadSensDky1
Call flag = IDAGetQuadSensDky1(ida mem, t, k, is, dkyQS);
Description The function IDAGetQuadSensDky1 returns the k-th derivative of the is-th sensitivity
solution vector after a successful return from IDASolve.
Arguments ida mem (void *) pointer to the memory previously allocated by IDAInit.
t(realtype) specifies the time at which sensitivity information is requested.
The time tmust fall within the interval defined by the last successful step
taken by idas.
k(int) order of derivative.
is (int) specifies the sensitivity derivative vector to be returned (0 ≤is< Ns).
dkyQS (N Vector) the vector containing the derivative. The space for dkyQS must be
allocated by the user.
Return value The return value flag of IDAGetQuadSensDky1 is one of:
IDA SUCCESS IDAGetQuadDky1 succeeded.
IDA MEM NULL ida mem was NULL.
IDA NO SENS Forward sensitivity analysis was not initialized.
IDA NO QUADSENS Quadratures depending on the sensitivities were not activated.
IDA BAD DKY dkyQS is NULL.
IDA BAD IS The index is is not in the allowed range.
IDA BAD K k is not in the range 0,1, ..., klast.
IDA BAD T The time tis not in the allowed range.

108 Using IDAS for Forward Sensitivity Analysis
5.4.4 Optional inputs for sensitivity-dependent quadrature integration
idas provides the following optional input functions to control the integration of sensitivity-dependent
quadrature equations.
IDASetQuadSensErrCon
Call flag = IDASetQuadSensErrCon(ida mem, errconQS)
Description The function IDASetQuadSensErrCon specifies whether or not the quadrature variables
are to be used in the local error control mechanism. If they are, the user must specify
the error tolerances for the quadrature variables by calling IDAQuadSensSStolerances,
IDAQuadSensSVtolerances, or IDAQuadSensEEtolerances.
Arguments ida mem (void *) pointer to the idas memory block.
errconQS (booleantype) specifies whether sensitivity quadrature variables are included
(TRUE) or not (FALSE) in the error control mechanism.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Sensitivities were not activated.
IDA NO QUADSENS Quadratures depending on the sensitivities were not activated.
Notes By default, errconQS is set to FALSE.
It is illegal to call IDASetQuadSensErrCon before a call to IDAQuadSensInit.
!
If the quadrature variables are part of the step size control mechanism, one of the following
functions must be called to specify the integration tolerances for quadrature variables.
IDAQuadSensSStolerances
Call flag = IDAQuadSensSVtolerances(ida mem, reltolQS, abstolQS);
Description The function IDAQuadSensSStolerances specifies scalar relative and absolute toler-
ances.
Arguments ida mem (void *) pointer to the idas memory block.
reltolQS (realtype) is the scalar relative error tolerance.
abstolQS (realtype*) is a pointer to an array containing the Ns scalar absolute error
tolerances.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Sensitivities were not activated.
IDA NO QUADSENS Quadratures depending on the sensitivities were not activated.
IDA ILL INPUT One of the input tolerances was negative.
IDAQuadSensSVtolerances
Call flag = IDAQuadSensSVtolerances(ida mem, reltolQS, abstolQS);
Description The function IDAQuadSensSVtolerances specifies scalar relative and vector absolute
tolerances.
Arguments ida mem (void *) pointer to the idas memory block.
reltolQS (realtype) is the scalar relative error tolerance.
abstolQS (N Vector*) is an array of Ns variables of type N Vector. The N Vector from
abstolS[is] specifies the vector tolerances for is-th quadrature sensitivity.
5.4 Integration of quadrature equations depending on forward sensitivities 109
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional value has been successfully set.
IDA NO QUAD Quadrature integration was not initialized.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Sensitivities were not activated.
IDA NO QUADSENS Quadratures depending on the sensitivities were not activated.
IDA ILL INPUT One of the input tolerances was negative.
IDAQuadSensEEtolerances
Call flag = IDAQuadSensEEtolerances(ida mem);
Description The function IDAQuadSensEEtolerances specifies that the tolerances for the sensitivity-
dependent quadratures should be estimated from those provided for the pure quadrature
variables.
Arguments ida mem (void *) pointer to the idas memory block.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO SENS Sensitivities were not activated.
IDA NO QUADSENS Quadratures depending on the sensitivities were not activated.
Notes When IDAQuadSensEEtolerances is used, before calling IDASolve, integration of pure
quadratures must be initialized (see 4.7.1) and tolerances for pure quadratures must be
also specified (see 4.7.4).
5.4.5 Optional outputs for sensitivity-dependent quadrature integration
idas provides the following functions that can be used to obtain solver performance information
related to quadrature integration.
IDAGetQuadSensNumRhsEvals
Call flag = IDAGetQuadSensNumRhsEvals(ida mem, &nrhsQSevals);
Description The function IDAGetQuadSensNumRhsEvals returns the number of calls made to the
user’s quadrature right-hand side function.
Arguments ida mem (void *) pointer to the idas memory block.
nrhsQSevals (long int) number of calls made to the user’s rhsQS function.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO QUADSENS Sensitivity-dependent quadrature integration has not been initialized.
IDAGetQuadSensNumErrTestFails
Call flag = IDAGetQuadSensNumErrTestFails(ida mem, &nQSetfails);
Description The function IDAGetQuadSensNumErrTestFails returns the number of local error test
failures due to quadrature variables.
Arguments ida mem (void *) pointer to the idas memory block.
nQSetfails (long int) number of error test failures due to quadrature variables.
Return value The return value flag (of type int) is one of:
110 Using IDAS for Forward Sensitivity Analysis
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO QUADSENS Sensitivity-dependent quadrature integration has not been initialized.
IDAGetQuadSensErrWeights
Call flag = IDAGetQuadSensErrWeights(ida mem, eQSweight);
Description The function IDAGetQuadSensErrWeights returns the quadrature error weights at the
current time.
Arguments ida mem (void *) pointer to the idas memory block.
eQSweight (N Vector *) array of quadrature error weight vectors at the current time.
Return value The return value flag (of type int) is one of:
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO QUADSENS Sensitivity-dependent quadrature integration has not been initialized.
Notes The user must allocate memory for eQSweight.
!
If quadratures were not included in the error control mechanism (through a call to
IDASetQuadSensErrCon with errconQS=TRUE), IDAGetQuadSensErrWeights does not
set the eQSweight vector.
IDAGetQuadSensStats
Call flag = IDAGetQuadSensStats(ida mem, &nrhsQSevals, &nQSetfails);
Description The function IDAGetQuadSensStats returns the idas integrator statistics as a group.
Arguments ida mem (void *) pointer to the idas memory block.
nrhsQSevals (long int) number of calls to the user’s rhsQS function.
nQSetfails (long int) number of error test failures due to quadrature variables.
Return value The return value flag (of type int) is one of
IDA SUCCESS the optional output values have been successfully set.
IDA MEM NULL the ida mem pointer is NULL.
IDA NO QUADSENS Sensitivity-dependent quadrature integration has not been initialized.
5.4.6 User-supplied function for sensitivity-dependent quadrature integra-
tion
For the integration of sensitivity-dependent quadrature equations, the user must provide a function
that defines the right-hand side of the sensitivity quadrature equations. For sensitivities of quadratures
(2.10) with integrands q, the appropriate right-hand side functions are given by ¯qi= (∂q/∂y)si+
(∂q/∂ ˙y) ˙si+∂q/∂pi. This user function must be of type IDAQuadSensRhsFn, defined as follows:
IDAQuadSensRhsFn
Definition typedef int (*IDAQuadSensRhsFn)(int Ns, realtype t, N Vector yy,
N Vector yp, N Vector *yyS, N Vector *ypS,
N Vector rrQ, N Vector *rhsvalQS,
void *user data, N Vector tmp1,
N Vector tmp2, N Vector tmp3)
Purpose This function computes the sensitivity quadrature equation right-hand side for a given
value of the independent variable tand state vector y.

5.5 Note on using partial error control 111
Arguments Ns is the number of sensitivity vectors.
tis the current value of the independent variable.
yy is the current value of the dependent variable vector, y(t).
yp is the current value of the dependent variable vector, ˙y(t).
yyS is an array of Ns variables of type N Vector containing the dependent sen-
sitivity vectors si.
ypS is an array of Ns variables of type N Vector containing the dependent sen-
sitivity derivatives ˙si.
rrQ is the current value of the quadrature right-hand side q.
rhsvalQS contains the Ns output vectors.
user data is the user data pointer passed to IDASetUserData.
tmp1
tmp2
tmp3 are N Vectors which can be used as temporary storage.
Return value An IDAQuadSensRhsFn should return 0 if successful, a positive value if a recoverable
error occurred (in which case idas will attempt to correct), or a negative value if it failed
unrecoverably (in which case the integration is halted and IDA QRHS FAIL is returned).
Notes Allocation of memory for rhsvalQS is automatically handled within idas.
Both yy and yp are of type N Vector and both yyS and ypS are pointers to an array
containing Ns vectors of type N Vector. It is the user’s responsibility to access the vector
data consistently (including the use of the correct accessor macros from each nvector
implementation). For the sake of computational efficiency, the vector functions in the
two nvector implementations provided with idas do not perform any consistency
checks with respect to their N Vector arguments (see §7.1 and §7.2).
There is one situation in which recovery is not possible even if IDAQuadSensRhsFn
function returns a recoverable error flag. That is when this occurs at the very first call
to the IDAQuadSensRhsFn, in which case idas returns IDA FIRST QSRHS ERR).
5.5 Note on using partial error control
For some problems, when sensitivities are excluded from the error control test, the behavior of idas
may appear at first glance to be erroneous. One would expect that, in such cases, the sensitivity
variables would not influence in any way the step size selection.
The short explanation of this behavior is that the step size selection implemented by the error
control mechanism in idas is based on the magnitude of the correction calculated by the nonlinear
solver. As mentioned in §5.2.1, even with partial error control selected in the call to IDASensInit,
the sensitivity variables are included in the convergence tests of the nonlinear solver.
When using the simultaneous corrector method (§2.5), the nonlinear system that is solved at each
step involves both the state and sensitivity equations. In this case, it is easy to see how the sensitivity
variables may affect the convergence rate of the nonlinear solver and therefore the step size selection.
The case of the staggered corrector approach is more subtle. The sensitivity variables at a given
step are computed only once the solver for the nonlinear state equations has converged. However, if
the nonlinear system corresponding to the sensitivity equations has convergence problems, idas will
attempt to improve the initial guess by reducing the step size in order to provide a better prediction
of the sensitivity variables. Moreover, even if there are no convergence failures in the solution of the
sensitivity system, idas may trigger a call to the linear solver’s setup routine which typically involves
reevaluation of Jacobian information (Jacobian approximation in the case of idadense and idaband,
or preconditioner data in the case of the Krylov solvers). The new Jacobian information will be used
by subsequent calls to the nonlinear solver for the state equations and, in this way, potentially affect
the step size selection.

112 Using IDAS for Forward Sensitivity Analysis
When using the simultaneous corrector method it is not possible to decide whether nonlinear solver
convergence failures or calls to the linear solver setup routine have been triggered by convergence
problems due to the state or the sensitivity equations. When using one of the staggered corrector
methods, however, these situations can be identified by carefully monitoring the diagnostic information
provided through optional outputs. If there are no convergence failures in the sensitivity nonlinear
solver, and none of the calls to the linear solver setup routine were made by the sensitivity nonlinear
solver, then the step size selection is not affected by the sensitivity variables.
Finally, the user must be warned that the effect of appending sensitivity equations to a given system
of DAEs on the step size selection (through the mechanisms described above) is problem-dependent
and can therefore lead to either an increase or decrease of the total number of steps that idas takes to
complete the simulation. At first glance, one would expect that the impact of the sensitivity variables,
if any, would be in the direction of increasing the step size and therefore reducing the total number
of steps. The argument for this is that the presence of the sensitivity variables in the convergence
test of the nonlinear solver can only lead to additional iterations (and therefore a smaller iteration
error), or to additional calls to the linear solver setup routine (and therefore more up-to-date Jacobian
information), both of which will lead to larger steps being taken by idas. However, this is true only
locally. Overall, a larger integration step taken at a given time may lead to step size reductions at
later times, due to either nonlinear solver convergence failures or error test failures.
Chapter 6
Using IDAS for Adjoint Sensitivity
Analysis
This chapter describes the use of idas to compute sensitivities of derived functions using adjoint sensi-
tivity analysis. As mentioned before, the adjoint sensitivity module of idas provides the infrastructure
for integrating backward in time any system of DAEs that depends on the solution of the original IVP,
by providing various interfaces to the main idas integrator, as well as several supporting user-callable
functions. For this reason, in the following sections we refer to the backward problem and not to the
adjoint problem when discussing details relevant to the DAEs that are integrated backward in time.
The backward problem can be the adjoint problem (2.20) or (2.25), and can be augmented with some
quadrature differential equations.
idas uses various constants for both input and output. These are defined as needed in this chapter,
but for convenience are also listed separately in Appendix B.
We begin with a brief overview, in the form of a skeleton user program. Following that are detailed
descriptions of the interface to the various user-callable functions and of the user-supplied functions
that were not already described in Chapter 4.
6.1 A skeleton of the user’s main program
The following is a skeleton of the user’s main program as an application of idas. The user program
is to have these steps in the order indicated, unless otherwise noted. For the sake of brevity, we defer
many of the details to the later sections. As in §4.4, most steps are independent of the nvector
implementation used. Where this is not the case, refer to Chapter 7for specific names. Steps that
are unchanged from the skeleton programs presented in §4.4,§5.1, and §5.4, are grayed out.
1. Include necessary header files
The idas.h header file also defines additional types, constants, and function prototypes for the
adjoint sensitivity module user-callable functions. In addition, the main program should include
an nvector implementation header file (for the particular implementation used) and, if Newton
iteration was selected, the main header file of the desired linear solver module.
2. Initialize parallel or multi-threaded environment
Forward problem
3. Set problem dimensions etc. for the forward problem
4. Set initial conditions for the forward problem
5. Create idas object for the forward problem

114 Using IDAS for Adjoint Sensitivity Analysis
6. Allocate internal memory for the forward problem
7. Specify integration tolerances for forward problem
8. Set optional inputs for the forward problem
9. Attach linear solver module for the forward problem
10. Set linear solver optional inputs for the forward problem
11. Initialize quadrature problem or problems for forward problems, using IDAQuadInit
and/or IDAQuadSensInit.
12. Initialize forward sensitivity problem
13. Specify rootfinding
14. Allocate space for the adjoint computation
Call IDAAdjInit() to allocate memory for the combined forward-backward problem (see §6.2.1
for details). This call requires Nd, the number of steps between two consecutive checkpoints.
IDAAdjInit also specifies the type of interpolation used (see §2.6.3).
15. Integrate forward problem
Call IDASolveF, a wrapper for the idas main integration function IDASolve, either in IDA NORMAL
mode to the time tout or in IDA ONE STEP mode inside a loop (if intermediate solutions of the
forward problem are desired (see §6.2.3)). The final value of tret is then the maximum allowable
value for the endpoint Tof the backward problem.
Backward problem(s)
16. Set problem dimensions etc. for the backward problem
This generally includes NB, the number of variables in the backward problem and possibly the
local vector length NBlocal.
17. Set initial values for the backward problem
Set the endpoint time tB0 =T, and set the corresponding vectors yB0 and ypB0 at which the
backward problem starts.
18. Create the backward problem
Call IDACreateB, a wrapper for IDACreate, to create the idas memory block for the new backward
problem. Unlike IDACreate, the function IDACreateB does not return a pointer to the newly
created memory block (see §6.2.4). Instead, this pointer is attached to the internal adjoint memory
block (created by IDAAdjInit) and returns an identifier called which that the user must later
specify in any actions on the newly created backward problem.
19. Allocate memory for the backward problem
Call IDAInitB (or IDAInitBS, when the backward problem depends on the forward sensitivi-
ties). The two functions are actually wrappers for IDAInit and allocate internal memory, specify
problem data, and initialize idas at tB0 for the backward problem (see §6.2.4).
20. Specify integration tolerances for backward problem
Call IDASStolerancesB(...) or IDASVtolerancesB(...) to specify a scalar relative tolerance
and scalar absolute tolerance, or a scalar relative tolerance and a vector of absolute tolerances,
respectively. The functions are wrappers for IDASStolerances(...) and IDASVtolerances(...)

6.1 A skeleton of the user’s main program 115
but they require an extra argument which, the identifier of the backward problem returned by
IDACreateB. See §6.2.5 for more information.
21. Set optional inputs for the backward problem
Call IDASet*B functions to change from their default values any optional inputs that control the
behavior of idas. Unlike their counterparts for the forward problem, these functions take an extra
argument which, the identifier of the backward problem returned by IDACreateB (see §6.2.9).
22. Attach linear solver module for the backward problem
Initialize the linear solver module for the backward problem by calling the appropriate wrapper
function: IDADenseB,IDABandB,IDALapackDenseB,IDALapackBandB,IDAKLUB,IDASuperLUMTB,
IDASpgmrB,IDASpbcgB, or IDASptfqmrB (see §6.2.6). Note that it is not required to use the
same linear solver module for both the forward and the backward problems; for example, the
forward problem could be solved with the idadense linear solver and the backward problem with
idaspgmr.
23. Initialize quadrature calculation
If additional quadrature equations must be evaluated, call IDAQuadInitB or IDAQuadInitBS (if
quadrature depends also on the forward sensitivities) as shown in §6.2.11.1. These functions are
wrappers around IDAQuadInit and can be used to initialize and allocate memory for quadrature
integration. Optionally, call IDASetQuad*B functions to change from their default values optional
inputs that control the integration of quadratures during the backward phase.
24. Integrate backward problem
Call IDASolveB, a second wrapper around the idas main integration function IDASolve, to inte-
grate the backward problem from tB0 (see §6.2.8). This function can be called either in IDA NORMAL
or IDA ONE STEP mode. Typically, IDASolveB will be called in IDA NORMAL mode with an end time
equal to the initial time t0of the forward problem.
25. Extract quadrature variables
If applicable, call IDAGetQuadB, a wrapper around IDAGetQuad, to extract the values of the quadra-
ture variables at the time returned by the last call to IDASolveB. See §6.2.11.2.
26. Deallocate memory
Upon completion of the backward integration, call all necessary deallocation functions. These
include appropriate destructors for the vectors yand yB, a call to IDAFree to free the idas
memory block for the forward problem. If one or more additional adjoint sensitivity analyses are
to be done for this problem, a call to IDAAdjFree (see §6.2.1) may be made to free and deallocate
the memory allocated for the backward problems, followed by a call to IDAAdjInit.
27. Finalize MPI, if used
The above user interface to the adjoint sensitivity module in idas was motivated by the desire to
keep it as close as possible in look and feel to the one for DAE IVP integration. Note that if steps
(16)-(25) are not present, a program with the above structure will have the same functionality as one
described in §4.4 for integration of DAEs, albeit with some overhead due to the checkpointing scheme.
If there are multiple backward problems associated with the same forward problem, repeat steps
(16)-(25) above for each successive backward problem. In the process, each call to IDACreateB creates
a new value of the identifier which.
116 Using IDAS for Adjoint Sensitivity Analysis
6.2 User-callable functions for adjoint sensitivity analysis
6.2.1 Adjoint sensitivity allocation and deallocation functions
After the setup phase for the forward problem, but before the call to IDASolveF, memory for the
combined forward-backward problem must be allocated by a call to the function IDAAdjInit. The
form of the call to this function is
IDAAdjInit
Call flag = IDAAdjInit(ida mem, Nd, interpType);
Description The function IDAAdjInit updates idas memory block by allocating the internal memory
needed for backward integration. Space is allocated for the Nd =Ndinterpolation data
points, and a linked list of checkpoints is initialized.
Arguments ida mem (void *) is the pointer to the idas memory block returned by a previous
call to IDACreate.
Nd (long int) is the number of integration steps between two consecutive
checkpoints.
interpType (int) specifies the type of interpolation used and can be IDA POLYNOMIAL
or IDA HERMITE, indicating variable-degree polynomial and cubic Hermite
interpolation, respectively (see §2.6.3).
Return value The return value flag (of type int) is one of:
IDA SUCCESS IDAAdjInit was successful.
IDA MEM FAIL A memory allocation request has failed.
IDA MEM NULL ida mem was NULL.
IDA ILL INPUT One of the parameters was invalid: Nd was not positive or interpType
is not one of the IDA POLYNOMIAL or IDA HERMITE.
Notes The user must set Nd so that all data needed for interpolation of the forward problem
solution between two checkpoints fits in memory. IDAAdjInit attempts to allocate
space for (2Nd+3) variables of type N Vector.
If an error occurred, IDAAdjInit also sends a message to the error handler function.
IDAAdjReInit
Call flag = IDAAdjReInit(ida mem);
Description The function IDAAdjReInit reinitializes the idas memory block for ASA, assuming
that the number of steps between check points and the type of interpolation remain
unchanged.
Arguments ida mem (void *) is the pointer to the idas memory block returned by a previous call
to IDACreate.
Return value The return value flag (of type int) is one of:
IDA SUCCESS IDAAdjReInit was successful.
IDA MEM NULL ida mem was NULL.
IDA NO ADJ The function IDAAdjInit was not previously called.
Notes The list of check points (and associated memory) is deleted.
The list of backward problems is kept. However, new backward problems can be added
to this list by calling IDACreateB. If a new list of backward problems is also needed, then
free the adjoint memory (by calling IDAAdjFree) and reinitialize ASA with IDAAdjInit.
The idas memory for the forward and backward problems can be reinitialized separately
by calling IDAReInit and IDAReInitB, respectively.
6.2 User-callable functions for adjoint sensitivity analysis 117
IDAAdjFree
Call IDAAdjFree(ida mem);
Description The function IDAAdjFree frees the memory related to backward integration allocated
by a previous call to IDAAdjInit.
Arguments The only argument is the idas memory block pointer returned by a previous call to
IDACreate.
Return value The function IDAAdjFree has no return value.
Notes This function frees all memory allocated by IDAAdjInit. This includes workspace
memory, the linked list of checkpoints, memory for the interpolation data, as well as
the idas memory for the backward integration phase.
Unless one or more further calls to IDAAdjInit are to be made, IDAAdjFree should not
be called by the user, as it is invoked automatically by IDAFree.
6.2.2 Adjoint sensitivity optional input
At any time during the integration of the forward problem, the user can disable the checkpointing of
the forward sensitivities by calling the following function:
IDAAdjSetNoSensi
Call flag = IDAAdjSetNoSensi(ida mem);
Description The function IDAAdjSetNoSensi instructs IDASolveF not to save checkpointing data
for forward sensitivities any more.
Arguments ida mem (void *) pointer to the idas memory block.
Return value The return flag (of type int) is one of:
IDA SUCCESS The call to IDACreateB was successful.
IDA MEM NULL The ida mem was NULL.
IDA NO ADJ The function IDAAdjInit has not been previously called.
6.2.3 Forward integration function
The function IDASolveF is very similar to the idas function IDASolve (see §4.5.6) in that it integrates
the solution of the forward problem and returns the solution (y, ˙y). At the same time, however,
IDASolveF stores checkpoint data every Nd integration steps. IDASolveF can be called repeatedly
by the user. Note that IDASolveF is used only for the forward integration pass within an Adjoint
Sensitivity Analysis. It is not for use in Forward Sensitivity Analysis; for that, see Chapter 5. The
call to this function has the form
IDASolveF
Call flag = IDASolveF(ida mem, tout, &tret, yret, ypret, itask, &ncheck);
Description The function IDASolveF integrates the forward problem over an interval in tand saves
checkpointing data.
Arguments ida mem (void *) pointer to the idas memory block.
tout (realtype) the next time at which a computed solution is desired.
tret (realtype) the time reached by the solver (output).
yret (N Vector) the computed solution vector y.
ypret (N Vector) the computed solution vector ˙y.
118 Using IDAS for Adjoint Sensitivity Analysis
itask (int) a flag indicating the job of the solver for the next step. The IDA NORMAL
task is to have the solver take internal steps until it has reached or just passed
the user-specified tout parameter. The solver then interpolates in order to
return an approximate value of y(tout) and ˙y(tout). The IDA ONE STEP option
tells the solver to take just one internal step and return the solution at the
point reached by that step.
ncheck (int) the number of (internal) checkpoints stored so far.
Return value On return, IDASolveF returns vectors yret,ypret and a corresponding independent
variable value t=tret, such that yret is the computed value of y(t) and ypret the
value of ˙y(t). Additionally, it returns in ncheck the number of internal checkpoints
saved; the total number of checkpoint intervals is ncheck+1. The return value flag (of
type int) will be one of the following. For more details see §4.5.6.
IDA SUCCESS IDASolveF succeeded.
IDA TSTOP RETURN IDASolveF succeeded by reaching the optional stopping point.
IDA ROOT RETURN IDASolveF succeeded and found one or more roots. In this case,
tret is the location of the root. If nrtfn >1, call IDAGetRootInfo
to see which giwere found to have a root.
IDA NO MALLOC The function IDAInit has not been previously called.
IDA ILL INPUT One of the inputs to IDASolveF is illegal.
IDA TOO MUCH WORK The solver took mxstep internal steps but could not reach tout.
IDA TOO MUCH ACC The solver could not satisfy the accuracy demanded by the user for
some internal step.
IDA ERR FAILURE Error test failures occurred too many times during one internal
time step or occurred with |h|=hmin.
IDA CONV FAILURE Convergence test failures occurred too many times during one in-
ternal time step or occurred with |h|=hmin.
IDA LSETUP FAIL The linear solver’s setup function failed in an unrecoverable man-
ner.
IDA LSOLVE FAIL The linear solver’s solve function failed in an unrecoverable manner.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA MEM FAIL A memory allocation request has failed (in an attempt to allocate
space for a new checkpoint).
Notes All failure return values are negative and therefore a test flag<0 will trap all IDASolveF
failures.
At this time, IDASolveF stores checkpoint information in memory only. Future versions
will provide for a safeguard option of dumping checkpoint data into a temporary file as
needed. The data stored at each checkpoint is basically a snapshot of the idas internal
memory block and contains enough information to restart the integration from that
time and to proceed with the same step size and method order sequence as during the
forward integration.
In addition, IDASolveF also stores interpolation data between consecutive checkpoints
so that, at the end of this first forward integration phase, interpolation information is
already available from the last checkpoint forward. In particular, if no checkpoints were
necessary, there is no need for the second forward integration phase.
It is illegal to change the integration tolerances between consecutive calls to IDASolveF,
!
as this information is not captured in the checkpoint data.
6.2.4 Backward problem initialization functions
The functions IDACreateB and IDAInitB (or IDAInitBS) must be called in the order listed. They
instantiate an idas solver object, provide problem and solution specifications, and allocate internal
6.2 User-callable functions for adjoint sensitivity analysis 119
memory for the backward problem.
IDACreateB
Call flag = IDACreateB(ida mem, &which);
Description The function IDACreateB instantiates an idas solver object for the backward problem.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
which (int) contains the identifier assigned by idas for the newly created backward
problem. Any call to IDA*B functions requires such an identifier.
Return value The return flag (of type int) is one of:
IDA SUCCESS The call to IDACreateB was successful.
IDA MEM NULL The ida mem was NULL.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA MEM FAIL A memory allocation request has failed.
There are two initialization functions for the backward problem – one for the case when the
backward problem does not depend on the forward sensitivities, and one for the case when it does.
These two functions are described next.
The function IDAInitB initializes the backward problem when it does not depend on the for-
ward sensitivities. It is essentially wrapper for IDAInit with some particularization for backward
integration, as described below.
IDAInitB
Call flag = IDAInitB(ida mem, which, resB, tB0, yB0, ypB0);
Description The function IDAInitB provides problem specification, allocates internal memory, and
initializes the backward problem.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
which (int) represents the identifier of the backward problem.
resB (IDAResFnB) is the Cfunction which computes fB, the residual of the back-
ward DAE problem. This function has the form resB(t, y, yp, yB, ypB,
resvalB, user dataB) (for full details see §6.3.1).
tB0 (realtype) specifies the endpoint Twhere final conditions are provided for the
backward problem, normally equal to the endpoint of the forward integration.
yB0 (N Vector) is the initial value (at t=tB0) of the backward solution.
ypB0 (N Vector) is the initial derivative value (at t=tB0) of the backward solution.
Return value The return flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAInitB was successful.
IDA NO MALLOC The function IDAInit has not been previously called.
IDA MEM NULL The ida mem was NULL.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA BAD TB0 The final time tB0 was outside the interval over which the forward
problem was solved.
IDA ILL INPUT The parameter which represented an invalid identifier, or one of yB0,
ypB0,resB was NULL.
Notes The memory allocated by IDAInitB is deallocated by the function IDAAdjFree.
For the case when backward problem also depends on the forward sensitivities, user must call
IDAInitBS instead of IDAInitB. Only the third argument of each function differs between these
functions.
120 Using IDAS for Adjoint Sensitivity Analysis
IDAInitBS
Call flag = IDAInitBS(ida mem, which, resBS, tB0, yB0, ypB0);
Description The function IDAInitBS provides problem specification, allocates internal memory, and
initializes the backward problem.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
which (int) represents the identifier of the backward problem.
resBS (IDAResFnBS) is the Cfunction which computes f B, the residual or the back-
ward DAE problem. This function has the form resBS(t, y, yp, yS, ypS,
yB, ypB, resvalB, user dataB) (for full details see §6.3.2).
tB0 (realtype) specifies the endpoint Twhere final conditions are provided for
the backward problem.
yB0 (N Vector) is the initial value (at t=tB0) of the backward solution.
ypB0 (N Vector) is the initial derivative value (at t=tB0) of the backward solution.
Return value The return flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAInitB was successful.
IDA NO MALLOC The function IDAInit has not been previously called.
IDA MEM NULL The ida mem was NULL.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA BAD TB0 The final time tB0 was outside the interval over which the forward
problem was solved.
IDA ILL INPUT The parameter which represented an invalid identifier, or one of yB0,
ypB0,resB was NULL, or sensitivities were not active during the forward
integration.
Notes The memory allocated by IDAInitBS is deallocated by the function IDAAdjFree.
The function IDAReInitB reinitializes idas for the solution of a series of backward problems, each
identified by a value of the parameter which.IDAReInitB is essentially a wrapper for IDAReInit, and
so all details given for IDAReInit in §4.5.10 apply here. Also, IDAReInitB can be called to reinitialize
a backward problem even if it has been initialized with the sensitivity-dependent version IDAInitBS.
Before calling IDAReInitB for a new backward problem, call any desired solution extraction functions
IDAGet** associated with the previous backward problem. The call to the IDAReInitB function has
the form
IDAReInitB
Call flag = IDAReInitB(ida mem, which, tB0, yB0, ypB0)
Description The function IDAReInitB reinitializes an idas backward problem.
Arguments ida mem (void *) pointer to idas memory block returned by IDACreate.
which (int) represents the identifier of the backward problem.
tB0 (realtype) specifies the endpoint Twhere final conditions are provided for
the backward problem.
yB0 (N Vector) is the initial value (at t=tB0) of the backward solution.
ypB0 (N Vector) is the initial derivative value (at t=tB0) of the backward solution.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAReInitB was successful.
IDA NO MALLOC The function IDAInit has not been previously called.
IDA MEM NULL The ida mem memory block pointer was NULL.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA BAD TB0 The final time tB0 is outside the interval over which the forward problem
was solved.
6.2 User-callable functions for adjoint sensitivity analysis 121
IDA ILL INPUT The parameter which represented an invalid identifier, or one of yB0,
ypB0 was NULL.
6.2.5 Tolerance specification functions for backward problem
One of the following two functions must be called to specify the integration tolerances for the backward
problem. Note that this call must be made after the call to IDAInitB or IDAInitBS.
IDASStolerancesB
Call flag = IDASStolerances(ida mem, which, reltolB, abstolB);
Description The function IDASStolerancesB specifies scalar relative and absolute tolerances.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
which (int) represents the identifier of the backward problem.
reltolB (realtype) is the scalar relative error tolerance.
abstolB (realtype) is the scalar absolute error tolerance.
Return value The return flag (of type int) will be one of the following:
IDA SUCCESS The call to IDASStolerancesB was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.
IDA NO MALLOC The allocation function IDAInit has not been called.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA ILL INPUT One of the input tolerances was negative.
IDASVtolerancesB
Call flag = IDASVtolerancesB(ida mem, which, reltolB, abstolB);
Description The function IDASVtolerancesB specifies scalar relative tolerance and vector absolute
tolerances.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
which (int) represents the identifier of the backward problem.
reltol (realtype) is the scalar relative error tolerance.
abstol (N Vector) is the vector of absolute error tolerances.
Return value The return flag (of type int) will be one of the following:
IDA SUCCESS The call to IDASVtolerancesB was successful.
IDA MEM NULL The idas memory block was not initialized through a previous call to
IDACreate.
IDA NO MALLOC The allocation function IDAInit has not been called.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA ILL INPUT The relative error tolerance was negative or the absolute tolerance had
a negative component.
Notes This choice of tolerances is important when the absolute error tolerance needs to be
different for each component of the DAE state vector y.
6.2.6 Linear solver initialization functions for backward problem
All idas linear solver modules available for forward problems provide additional specification func-
tions for backward problems. The initialization functions described in §4.5.3 cannot be directly used
since the optional user-defined Jacobian-related functions have different prototypes for the backward
problem than for the forward problem (see §6.3).
122 Using IDAS for Adjoint Sensitivity Analysis
The following wrapper functions can be used to initialize one of the linear solver modules for the
backward problem. Their arguments are identical to those of the functions in §4.5.3 with the exception
of the additional second argument, which, the identifier of the backward problem.
flag = IDADenseB(ida_mem, which, nB);
flag = IDABandB(ida_mem, which, nB, mupperB, mlowerB);
flag = IDALapackDenseB(ida_mem, which, nB);
flag = IDALapackBandB(ida_mem, which, nB, mupperB, mlowerB);
flag = IDAKLUB(ida_mem, which, nB, nnzB, sparsetype);
flag = IDASuperLUMTB(ida_mem, which, num_threads, nB, nnzB);
flag = IDASpgmrB(ida_mem, which, maxlB);
flag = IDASpbcgB(ida_mem, which, maxlB);
flag = IDASptfqmrB(ida_mem, which, maxlB);
Their return value flag (of type int) can have any of the return values of their counterparts. If the
ida mem argument was NULL,flag will be IDADLS MEM NULL,IDASLS MEM NULL or IDASPILS MEM NULL.
Also, if which is not a valid identifier, the functions will return IDADLS ILL INPUT,IDASLS ILL INPUT
or IDASPILS ILL INPUT.
6.2.7 Initial condition calculation functions for backward problem
idas provides support for calculation of consistent initial conditions for certain backward index-one
problems of semi-implicit form through the functions IDACalcICB and IDACalcICBS. Calling them is
optional. It is only necessary when the initial conditions do not satisfy the adjoint system.
The above functions provide the same functionality for backward problems as IDACalcIC with
parameter icopt =IDA YA YDP INIT provides for forward problems (see §4.5.4): compute the algebraic
components of yB and differential components of ˙yB, given the differential components of yB. They
require that the IDASetIdB was previously called to specify the differential and algebraic components.
Both functions require forward solutions at the final time tB0.IDACalcICBS also needs forward
sensitivities at the final time tB0.
IDACalcICB
Call flag = IDACalcICB(ida mem, which, tBout1, N Vector yfin, N Vector ypfin);
Description The function IDACalcICB corrects the initial values yB0 and ypB0 at time tB0 for the
backward problem.
Arguments ida mem (void *) pointer to the idas memory block.
which (int) is the identifier of the backward problem.
tBout1 (realtype) is the first value of tat which a solution will be requested (from
IDASolveB). This value is needed here only to determine the direction of inte-
gration and rough scale in the independent variable t.
yfin (N Vector) the forward solution at the final time tB0.
ypfin (N Vector) the forward solution derivative at the final time tB0.
Return value The return value flag (of type int) can be any that is returned by IDACalcIC (see
§4.5.4). However IDACalcICB can also return one of the following:
IDA NO ADJ IDAAdjInit has not been previously called.
IDA ILL INPUT Parameter which represented an invalid identifier.
Notes All failure return values are negative and therefore a test flag <0 will trap all
IDACalcICB failures.
Note that IDACalcICB will correct the values of yB(tB0) and ˙yB(tB0) which were
specified in the previous call to IDAInitB or IDAReInitB. To obtain the corrected values,
call IDAGetconsistentICB (see §6.2.10.2).

6.2 User-callable functions for adjoint sensitivity analysis 123
In the case where the backward problem also depends on the forward sensitivities, user must call
the following function to correct the initial conditions:
IDACalcICBS
Call flag = IDACalcICBS(ida mem, which, tBout1, N Vector yfin, N Vector ypfin,
N Vector ySfin, N Vector ypSfin);
Description The function IDACalcICBS corrects the initial values yB0 and ypB0 at time tB0 for the
backward problem.
Arguments ida mem (void *) pointer to the idas memory block.
which (int) is the identifier of the backward problem.
tBout1 (realtype) is the first value of tat which a solution will be requested (from
IDASolveB).This value is needed here only to determine the direction of inte-
gration and rough scale in the independent variable t.
yfin (N Vector) the forward solution at the final time tB0.
ypfin (N Vector) the forward solution derivative at the final time tB0.
ySfin (N Vector *) a pointer to an array of Ns vectors containing the sensitivities
of the forward solution at the final time tB0.
ypSfin (N Vector *) a pointer to an array of Ns vectors containing the derivatives of
the forward solution sensitivities at the final time tB0.
Return value The return value flag (of type int) can be any that is returned by IDACalcIC (see
§4.5.4). However IDACalcICBS can also return one of the following:
IDA NO ADJ IDAAdjInit has not been previously called.
IDA ILL INPUT Parameter which represented an invalid identifier, sensitivities were not
active during forward integration, or IDAInitBS (or IDAReInitBS) has
not been previously called.
Notes All failure return values are negative and therefore a test flag <0 will trap all
IDACalcICBS failures.
Note that IDACalcICBS will correct the values of yB(tB0) and ˙yB(tB0) which were
specified in the previous call to IDAInitBS or IDAReInitBS. To obtain the corrected
values, call IDAGetConsistentICB (see §6.2.10.2).
6.2.8 Backward integration function
The function IDASolveB performs the integration of the backward problem. It is essentially a wrapper
for the idas main integration function IDASolve and, in the case in which checkpoints were needed,
it evolves the solution of the backward problem through a sequence of forward-backward integration
pairs between consecutive checkpoints. In each pair, the first run integrates the original IVP forward
in time and stores interpolation data; the second run integrates the backward problem backward in
time and performs the required interpolation to provide the solution of the IVP to the backward
problem.
The function IDASolveB does not return the solution yB itself. To obtain that, call the function
IDAGetB, which is also described below.
The IDASolveB function does not support rootfinding, unlike IDASoveF, which supports the finding
of roots of functions of (t, y, ˙y). If rootfinding was performed by IDASolveF, then for the sake of
efficiency, it should be disabled for IDASolveB by first calling IDARootInit with nrtfn = 0.
The call to IDASolveB has the form
IDASolveB
Call flag = IDASolveB(ida mem, tBout, itaskB);
Description The function IDASolveB integrates the backward DAE problem.

124 Using IDAS for Adjoint Sensitivity Analysis
Arguments ida mem (void *) pointer to the idas memory returned by IDACreate.
tBout (realtype) the next time at which a computed solution is desired.
itaskB (int) a flag indicating the job of the solver for the next step. The IDA NORMAL
task is to have the solver take internal steps until it has reached or just passed
the user-specified value tBout. The solver then interpolates in order to return
an approximate value of yB(tBout). The IDA ONE STEP option tells the solver
to take just one internal step in the direction of tBout and return.
Return value The return value flag (of type int) will be one of the following. For more details see
§4.5.6.
IDA SUCCESS IDASolveB succeeded.
IDA MEM NULL The ida mem was NULL.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA NO BCK No backward problem has been added to the list of backward prob-
lems by a call to IDACreateB
IDA NO FWD The function IDASolveF has not been previously called.
IDA ILL INPUT One of the inputs to IDASolveB is illegal.
IDA BAD ITASK The itaskB argument has an illegal value.
IDA TOO MUCH WORK The solver took mxstep internal steps but could not reach tBout.
IDA TOO MUCH ACC The solver could not satisfy the accuracy demanded by the user for
some internal step.
IDA ERR FAILURE Error test failures occurred too many times during one internal
time step.
IDA CONV FAILURE Convergence test failures occurred too many times during one in-
ternal time step.
IDA LSETUP FAIL The linear solver’s setup function failed in an unrecoverable man-
ner.
IDA SOLVE FAIL The linear solver’s solve function failed in an unrecoverable manner.
IDA BCKMEM NULL The idas memory for the backward problem was not created with
a call to IDACreateB.
IDA BAD TBOUT The desired output time tBout is outside the interval over which
the forward problem was solved.
IDA REIFWD FAIL Reinitialization of the forward problem failed at the first checkpoint
(corresponding to the initial time of the forward problem).
IDA FWD FAIL An error occurred during the integration of the forward problem.
Notes All failure return values are negative and therefore a test flag<0 will trap all IDASolveB
failures.
In the case of multiple checkpoints and multiple backward problems, a given call to
IDASolveB in IDA ONE STEP mode may not advance every problem one step, depending
on the relative locations of the current times reached. But repeated calls will eventually
advance all problems to tBout.
To obtain the solution yB to the backward problem, call the function IDAGetB as follows:
IDAGetB
Call flag = IDAGetB(ida mem, which, &tret, yB, ypB);
Description The function IDAGetB provides the solution yB of the backward DAE problem.
Arguments ida mem (void *) pointer to the idas memory returned by IDACreate.
which (int) the identifier of the backward problem.
tret (realtype) the time reached by the solver (output).

6.2 User-callable functions for adjoint sensitivity analysis 125
yB (N Vector) the backward solution at time tret.
ypB (N Vector) the backward solution derivative at time tret.
Return value The return value flag (of type int) will be one of the following.
IDA SUCCESS IDAGetB was successful.
IDA MEM NULL ida mem is NULL.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA ILL INPUT The parameter which is an invalid identifier.
Notes The user must allocate space for yB and ypB.
!
6.2.9 Optional input functions for the backward problem
6.2.9.1 Main solver optional input functions
The adjoint module in idas provides wrappers for most of the optional input functions defined in
§4.5.7.1. The only difference is that the user must specify the identifier which of the backward
problem within the list managed by idas.
The optional input functions defined for the backward problem are:
flag = IDASetUserDataB(ida_mem, which, user_dataB);
flag = IDASetMaxOrdB(ida_mem, which, maxordB);
flag = IDASetMaxNumStepsB(ida_mem, which, mxstepsB);
flag = IDASetInitStepB(ida_mem, which, hinB)
flag = IDASetMaxStepB(ida_mem, which, hmaxB);
flag = IDASetSuppressAlgB(ida_mem, which, suppressalgB);
flag = IDASetIdB(ida_mem, which, idB);
flag = IDASetConstraintsB(ida_mem, which, constraintsB);
Their return value flag (of type int) can have any of the return values of their counterparts, but it
can also be IDA NO ADJ if IDAAdjInit has not been called, or IDA ILL INPUT if which was an invalid
identifier.
6.2.9.2 Dense linear solver
Optional inputs for the idadense linear solver module can be set for the backward problem through
the following two functions:
IDADlsSetDenseJacFnB
Call flag = IDADlsSetDenseJacFnB(ida mem, which, jacB);
Description The function IDADlsSetDenseJacFnB specifies the dense Jacobian approximation func-
tion to be used for the backward problem.
Arguments ida mem (void *) pointer to the idas memory returned by IDACreate.
which (int) represents the identifier of the backward problem.
jacB (IDADlsDenseJacFnB) user-defined dense Jacobian approximation function.
Return value The return value flag (of type int) is one of:
IDADLS SUCCESS IDADlsSetDenseJacFnB succeeded.
IDADLS MEM NULL The ida mem was NULL.
IDADLS NO ADJ The function IDAAdjInit has not been previously called.
IDADLS LMEM NULL The linear solver has not been initialized with a call to IDADenseB
or IDALapackDenseB.
IDADLS ILL INPUT The parameter which represented an invalid identifier.
Notes The function type IDADlsDenseJacFnB is described in §6.3.5.
126 Using IDAS for Adjoint Sensitivity Analysis
IDADlsSetDenseJacFnBS
Call flag = IDADlsSetDenseJacFnBS(ida mem, which, jacBS);
Description The function IDADlsSetDenseJacFnBS specifies the dense Jacobian approximation func-
tion to be used for the backward problem, in the case where the backward problem
depends on the forward sensitivities.
Arguments ida mem (void *) pointer to the idas memory returned by IDACreate.
which (int) represents the identifier of the backward problem.
jacBS (IDADlsDenseJacFnBS) user-defined dense Jacobian approximation function.
Return value The return value flag (of type int) is one of:
IDADLS SUCCESS IDADlsSetDenseJacFnBS succeeded.
IDADLS MEM NULL The ida mem was NULL.
IDADLS NO ADJ The function IDAAdjInit has not been previously called.
IDADLS LMEM NULL The linear solver has not been initialized with a call to IDADenseB
or IDALapackDenseB.
IDADLS ILL INPUT The parameter which represented an invalid identifier.
Notes The function type IDADlsDenseJacFnBS is described in §6.3.5.
6.2.9.3 Band linear solver
Optional inputs for the idaband linear solver module can be set for the backward problem through
the following two functions:
IDADlsSetBandJacFnB
Call flag = IDADlsSetBandJacFnB(ida mem, which, jacB);
Description The function IDADlsSetBandJacFnB specifies the banded Jacobian approximation func-
tion to be used for the backward problem.
Arguments ida mem (void *) pointer to the idas memory returned by IDACreate.
which (int) represents the identifier of the backward problem.
jacB (IDADlsBandJacFnB) user-defined banded Jacobian approximation function.
Return value The return value flag (of type int) is one of:
IDADLS SUCCESS IDADlsSetBandJacFnB succeeded.
IDADLS MEM NULL The ida mem was NULL.
IDADLS NO ADJ The function IDAAdjInit has not been previously called.
IDADLS LMEM NULL The linear solver has not been initialized with a call to IDABandB or
IDALapackBandB.
IDADLS ILL INPUT The parameter which represented an invalid identifier.
Notes The function type IDADlsBandJacFnB is described in §6.3.6.
IDADlsSetBandJacFnBS
Call flag = IDADlsSetBandJacFnBS(ida mem, which, jacBS);
Description The function IDADlsSetBandJacFnBS specifies the banded Jacobian approximation func-
tion to be used for the backward problem, in the case where the backward problem
depends on the forward sensitivities.
Arguments ida mem (void *) pointer to the idas memory returned by IDACreate.
which (int) represents the identifier of the backward problem.
jacBS (IDADlsBandJacFnBS) user-defined banded Jacobian approximation function.
6.2 User-callable functions for adjoint sensitivity analysis 127
Return value The return value flag (of type int) is one of:
IDADLS SUCCESS IDADlsSetBandJacFnBS succeeded.
IDADLS MEM NULL The ida mem was NULL.
IDADLS NO ADJ The function IDAAdjInit has not been previously called.
IDADLS LMEM NULL The linear solver has not been initialized with a call to IDABandB or
IDALapackBandB.
IDADLS ILL INPUT The parameter which represented an invalid identifier.
Notes The function type IDADlsBandJacFnBS is described in §6.3.6.
6.2.9.4 Sparse linear solvers
Optional inputs for the idaklu and idasuperlumt linear solver modules can be set for the backward
problem through the following functions.
The following wrapper functions can be used to to set the fill-reducing ordering and, in the case
of KLU, reinitialize the sparse solver in the sparse linear solver modules for the backward problem.
Their arguments are identical to those of the functions in §4.5.3 with the exception of the additional
second argument, which, the identifier of the backward problem.
flag = IDAKLUReInitB(ida_mem, which, nB, nnzB, reinit_typeB);
flag = IDAKLUSetOrderingB(ida_mem, which, ordering_choiceB);
flag = IDASuperLUMTSetOrderingB(ida_mem, which, num_threads, ordering_choiceB);
Their return value flag (of type int) can have any of the return values of their counterparts. If
the ida mem argument was NULL,flag will be IDASLS MEM NULL. Also, if which is not a valid identifier,
the functions will return IDASLS ILL INPUT.
IDASlsSetSparseJacFnB
Call flag = IDASlsSetSparseJacFnB(ida mem, which, jacB);
Description The function IDASlsSetSparseJacFnB specifies the sparse Jacobian approximation func-
tion to be used for the backward problem.
Arguments ida mem (void *) pointer to the idas memory returned by IDACreate.
which (int) represents the identifier of the backward problem.
jacB (IDASlsSparseJacFnB) user-defined sparse Jacobian approximation function.
Return value The return value flag (of type int) is one of:
IDASLS SUCCESS IDASlsSetSparseJacFnB succeeded.
IDASLS MEM NULL The ida mem was NULL.
IDASLS NO ADJ The function IDAAdjInit has not been previously called.
IDASLS LMEM NULL The linear solver has not been initialized with a call to IDAKLUB or
IDASuperLUMTB.
IDASLS ILL INPUT The parameter which represented an invalid identifier.
Notes The function type IDASlsSparseJacFnB is described in §6.3.7.
IDASlsSetSparseJacFnBS
Call flag = IDASlsSetSparseJacFnBS(ida mem, which, jacBS);
Description The function IDASlsSetSparseJacFnBS specifies the sparse Jacobian approximation
function to be used for the backward problem, in the case where the backward problem
depends on the forward sensitivities.
Arguments ida mem (void *) pointer to the idas memory returned by IDACreate.
which (int) represents the identifier of the backward problem.
128 Using IDAS for Adjoint Sensitivity Analysis
jacBS (IDASlsSparseJacFnBS) user-defined sparse Jacobian approximation function.
Return value The return value flag (of type int) is one of:
IDASLS SUCCESS IDASlsSetSparseJacFnBS succeeded.
IDASLS MEM NULL The ida mem was NULL.
IDASLS NO ADJ The function IDAAdjInit has not been previously called.
IDASLS LMEM NULL The linear solver has not been initialized with a call to IDAKLUB or
IDASuperLUMTB.
IDASLS ILL INPUT The parameter which represented an invalid identifier.
Notes The function type IDASlsSparseJacFnBS is described in §6.3.7.
6.2.9.5 SPILS linear solvers
Optional inputs for the idaspils linear solver module can be set for the backward problem through
the following functions:
IDASpilsSetPreconditionerB
Call flag = IDASpilsSetPreconditionerB(ida mem, which, psetupB, psolveB);
Description The function IDASpilsSetPrecSolveFnB specifies the preconditioner setup and solve
functions for the backward integration.
Arguments ida mem (void *) pointer to the idas memory block.
which (int) the identifier of the backward problem.
psetupB (IDASpilsPrecSetupFnB) user-defined preconditioner setup function.
psolveB (IDASpilsPrecSolveFnB) user-defined preconditioner solve function.
Return value The return value flag (of type int) is one of:
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL The ida mem memory block pointer was NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASPILS NO ADJ The function IDAAdjInit has not been previously called.
IDASPILS ILL INPUT The parameter which represented an invalid identifier.
Notes The function types IDASpilsPrecSolveFnB and IDASpilsPrecSetupFnB are described
in §6.3.9 and §6.3.10, respectively. The psetupB argument may be NULL if no setup
operation is involved in the preconditioner.
IDASpilsSetPreconditionerBS
Call flag = IDASpilsSetPreconditionerBS(ida mem, which, psetupBS, psolveBS);
Description The function IDASpilsSetPrecSolveFnBS specifies the preconditioner setup and solve
functions for the backward integration, in the case where the backward problem depends
on the forward sensitivities.
Arguments ida mem (void *) pointer to the idas memory block.
which (int) the identifier of the backward problem.
psetupBS (IDASpilsPrecSetupFnBS) user-defined preconditioner setup function.
psolveBS (IDASpilsPrecSolveFnBS) user-defined preconditioner solve function.
Return value The return value flag (of type int) is one of:
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL The ida mem memory block pointer was NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
6.2 User-callable functions for adjoint sensitivity analysis 129
IDASPILS NO ADJ The function IDAAdjInit has not been previously called.
IDASPILS ILL INPUT The parameter which represented an invalid identifier.
Notes The function types IDASpilsPrecSolveFnBS and IDASpilsPrecSetupFnBS are described
in §6.3.9 and §6.3.10, respectively. The psetupBS argument may be NULL if no setup
operation is involved in the preconditioner.
IDASpilsSetJacTimesVecFnB
Call flag = IDASpilsSetJacTimesVecFnB(ida mem, which, jtvB);
Description The function IDASpilsSetJacTimesVecFnB specifies the Jacobian-vector product func-
tion to be used.
Arguments ida mem (void *) pointer to the idas memory block.
which (int) the identifier of the backward problem.
jtvB (IDASpilsJacTimesVecFnB) user-defined Jacobian-vector product function.
Return value The return value flag (of type int) is one of:
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL The ida mem memory block pointer was NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASPILS NO ADJ The function IDAAdjInit has not been previously called.
IDASPILS ILL INPUT The parameter which represented an invalid identifier.
Notes The function type IDASpilsJacTimesVecFnB is described in §6.3.8.
IDASpilsSetJacTimesVecFnBS
Call flag = IDASpilsSetJacTimesVecFnBS(ida mem, which, jtvBS);
Description The function IDASpilsSetJacTimesVecFnBS specifies the Jacobian-vector product func-
tion to be used, in the case where the backward problem depends on the forward sen-
sitivities.
Arguments ida mem (void *) pointer to the idas memory block.
which (int) the identifier of the backward problem.
jtvBS (IDASpilsJacTimesVecFnBS) user-defined Jacobian-vector product function.
Return value The return value flag (of type int) is one of:
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL The ida mem memory block pointer was NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASPILS NO ADJ The function IDAAdjInit has not been previously called.
IDASPILS ILL INPUT The parameter which represented an invalid identifier.
Notes The function type IDASpilsJacTimesVecFnBS is described in §6.3.8.
IDASpilsSetGSTypeB
Call flag = IDASpilsSetGSType(ida mem, which, gstypeB);
Description The function IDASpilsSetGSTypeB specifies the type of Gram-Schmidt orthogonal-
ization to be used with idaspgmr. This must be one of the enumeration constants
MODIFIED GS or CLASSICAL GS. These correspond to using modified Gram-Schmidt and
classical Gram-Schmidt, respectively.
Arguments ida mem (void *) pointer to the idas memory block.
which (int) the identifier of the backward problem.
130 Using IDAS for Adjoint Sensitivity Analysis
gstypeB (int) type of Gram-Schmidt orthogonalization.
Return value The return value flag (of type int) is one of:
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL ida mem was NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASPILS NO ADJ The function IDAAdjInit has not been previously called.
IDASPILS ILL INPUT The parameter which represented an invalid identifier or the value
of gstypeB was not valid.
Notes The default value is MODIFIED GS.
This option is available only with idaspgmr.
!
IDASpilsSetMaxlB
Call flag = IDASpilsSetMaxlB(ida mem, which, maxlB);
Description The function IDASpilsSetMaxlB resets maximum Krylov subspace dimension for the
Bi-CGStab or TFQMR methods.
Arguments ida mem (void *) pointer to the idas memory block.
which (int) the identifier of the backward problem.
maxlB (realtype) maximum dimension of the Krylov subspace.
Return value The return value flag (of type int) is one of:
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL ida mem was NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASPILS NO ADJ The function IDAAdjInit has not been previously called.
IDASPILS ILL INPUT The parameter which represented an invalid identifier.
Notes The maximum subspace dimension is initially specified in the call to IDASpbcgB or
IDASptfqmrB. The call to IDASpilsSetMaxlB is needed only if maxlB is being changed
from its previous value.
This option is available only for the idaspbcg and idasptfqmr linear solvers.
!
IDASpilsSetEpsLinB
Call flag = IDASpilsSetEpsLinB(ida mem, eplifacB);
Description The function IDASpilsSetEpsLinB specifies the factor by which the Krylov linear
solver’s convergence test constant is reduced from the Newton iteration test constant.
(See §2.1).
Arguments ida mem (void *) pointer to the idas memory block.
eplifacB (realtype) linear convergence safety factor (>= 0.0).
Return value The return value flag (of type int) is one of
IDASPILS SUCCESS The optional value has been successfully set.
IDASPILS MEM NULL The ida mem pointer is NULL.
IDASPILS LMEM NULL The idaspils linear solver has not been initialized.
IDASPILS NO ADJ The function IDAAdjInit has not been previously called.
IDASPILS ILL INPUT The value of eplifacB is negative.
Notes The default value is 0.05.
Passing a value eplifacB= 0.0 also indicates using the default value.

6.2 User-callable functions for adjoint sensitivity analysis 131
6.2.10 Optional output functions for the backward problem
6.2.10.1 Main solver optional output functions
The user of the adjoint module in idas has access to any of the optional output functions described
in §4.5.9, both for the main solver and for the linear solver modules. The first argument of these
IDAGet* and IDA*Get* functions is the pointer to the idas memory block for the backward problem.
In order to call any of these functions, the user must first call the following function to obtain this
pointer:
IDAGetAdjIDABmem
Call ida memB = IDAGetAdjIDABmem(ida mem, which);
Description The function IDAGetAdjIDABmem returns a pointer to the idas memory block for the
backward problem.
Arguments ida mem (void *) pointer to the idas memory block created by IDACreate.
which (int) the identifier of the backward problem.
Return value The return value, ida memB (of type void *), is a pointer to the idas memory for the
backward problem.
Notes The user should not modify ida memB in any way.
!
Optional output calls should pass ida memB as the first argument; thus, for example, to
get the number of integration steps: flag = IDAGetNumSteps(idas memB,&nsteps).
To get values of the forward solution during a backward integration, use the following function.
The input value of twould typically be equal to that at which the backward solution has just been
obtained with IDAGetB. In any case, it must be within the last checkpoint interval used by IDASolveB.
IDAGetAdjY
Call flag = IDAGetAdjY(ida mem, t, y, yp);
Description The function IDAGetAdjY returns the interpolated value of the forward solution yand
its derivative during a backward integration.
Arguments ida mem (void *) pointer to the idas memory block created by IDACreate.
t(realtype) value of the independent variable at which yis desired (input).
y(N Vector) forward solution y(t).
yp (N Vector) forward solution derivative ˙y(t).
Return value The return value flag (of type int) is one of:
IDA SUCCESS IDAGetAdjY was successful.
IDA MEM NULL ida mem was NULL.
IDA GETY BADT The value of twas outside the current checkpoint interval.
Notes The user must allocate space for yand yp.
!
6.2.10.2 Initial condition calculation optional output function
IDAGetConsistentICB
Call flag = IDAGetConsistentICB(ida mem, which, yB0 mod, ypB0 mod);
Description The function IDAGetConsistentICB returns the corrected initial conditions for back-
ward problem calculated by IDACalcICB.
Arguments ida mem (void *) pointer to the idas memory block.
which is the identifier of the backward problem.

132 Using IDAS for Adjoint Sensitivity Analysis
yB0 mod (N Vector) consistent initial vector.
ypB0 mod (N Vector) consistent initial derivative vector.
Return value The return value flag (of type int) is one of
IDA SUCCESS The optional output value has been successfully set.
IDA MEM NULL The ida mem pointer is NULL.
IDA NO ADJ IDAAdjInit has not been previously called.
IDA ILL INPUT Parameter which did not refer a valid backward problem identifier.
Notes If the consistent solution vector or consistent derivative vector is not desired, pass NULL
for the corresponding argument.
The user must allocate space for yB0 mod and ypB0 mod (if not NULL).
!
6.2.11 Backward integration of quadrature equations
Not only the backward problem but also the backward quadrature equations may or may not depend on
the forward sensitivities. Accordingly, one of the IDAQuadInitB or IDAQuadInitBS should be used to
allocate internal memory and to initialize backward quadratures. For any other operation (extraction,
optional input/output, reinitialization, deallocation), the same function is called regardless of whether
or not the quadratures are sensitivity-dependent.
6.2.11.1 Backward quadrature initialization functions
The function IDAQuadInitB initializes and allocates memory for the backward integration of quadra-
ture equations that do not depende on forward sensititvities. It has the following form:
IDAQuadInitB
Call flag = IDAQuadInitB(ida mem, which, rhsQB, yQB0);
Description The function IDAQuadInitB provides required problem specifications, allocates internal
memory, and initializes backward quadrature integration.
Arguments ida mem (void *) pointer to the idas memory block.
which (int) the identifier of the backward problem.
rhsQB (IDAQuadRhsFnB) is the Cfunction which computes f QB, the residual of the
backward quadrature equations. This function has the form rhsQB(t, y, yp,
yB, ypB, rhsvalBQ, user dataB) (see §6.3.3).
yQB0 (N Vector) is the value of the quadrature variables at tB0.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAQuadInitB was successful.
IDA MEM NULL ida mem was NULL.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA MEM FAIL A memory allocation request has failed.
IDA ILL INPUT The parameter which is an invalid identifier.
The function IDAQuadInitBS initializes and allocates memory for the backward integration of
quadrature equations that depend on the forward sensitivities.
IDAQuadInitBS
Call flag = IDAQuadInitBS(ida mem, which, rhsQBS, yQBS0);
Description The function IDAQuadInitBS provides required problem specifications, allocates internal
memory, and initializes backward quadrature integration.
Arguments ida mem (void *) pointer to the idas memory block.

6.2 User-callable functions for adjoint sensitivity analysis 133
which (int) the identifier of the backward problem.
rhsQBS (IDAQuadRhsFnBS) is the Cfunction which computes f QBS, the residual of
the backward quadrature equations. This function has the form rhsQBS(t,
y, yp, yS, ypS, yB, ypB, rhsvalBQS, user dataB) (see §6.3.4).
yQBS0 (N Vector) is the value of the sensitivity-dependent quadrature variables at
tB0.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAQuadInitBS was successful.
IDA MEM NULL ida mem was NULL.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA MEM FAIL A memory allocation request has failed.
IDA ILL INPUT The parameter which is an invalid identifier.
The integration of quadrature equations during the backward phase can be re-initialized by calling
the following function. Before calling IDAQuadReInitB for a new backward problem, call any desired
solution extraction functions IDAGet** associated with the previous backward problem.
IDAQuadReInitB
Call flag = IDAQuadReInitB(ida mem, which, yQB0);
Description The function IDAQuadReInitB re-initializes the backward quadrature integration.
Arguments ida mem (void *) pointer to the idas memory block.
which (int) the identifier of the backward problem.
yQB0 (N Vector) is the value of the quadrature variables at tB0.
Return value The return value flag (of type int) will be one of the following:
IDA SUCCESS The call to IDAQuadReInitB was successful.
IDA MEM NULL ida mem was NULL.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA MEM FAIL A memory allocation request has failed.
IDA NO QUAD Quadrature integration was not activated through a previous call to
IDAQuadInitB.
IDA ILL INPUT The parameter which is an invalid identifier.
Notes IDAQuadReInitB can be used after a call to either IDAQuadInitB or IDAQuadInitBS.
6.2.11.2 Backward quadrature extraction function
To extract the values of the quadrature variables at the last return time of IDASolveB,idas provides
a wrapper for the function IDAGetQuad (see §4.7.3). The call to this function has the form
IDAGetQuadB
Call flag = IDAGetQuadB(ida mem, which, &tret, yQB);
Description The function IDAGetQuadB returns the quadrature solution vector after a successful
return from IDASolveB.
Arguments ida mem (void *) pointer to the idas memory.
tret (realtype) the time reached by the solver (output).
yQB (N Vector) the computed quadrature vector.
Return value
!
Notes T
he user must allocate space for yQB. The return value flag of IDAGetQuadB is one of:

134 Using IDAS for Adjoint Sensitivity Analysis
IDA SUCCESS IDAGetQuadB was successful.
IDA MEM NULL ida mem is NULL.
IDA NO ADJ The function IDAAdjInit has not been previously called.
IDA NO QUAD Quadrature integration was not initialized.
IDA BAD DKY yQB was NULL.
IDA ILL INPUT The parameter which is an invalid identifier.
6.2.11.3 Optional input/output functions for backward quadrature integration
Optional values controlling the backward integration of quadrature equations can be changed from
their default values through calls to one of the following functions which are wrappers for the corre-
sponding optional input functions defined in §4.7.4. The user must specify the identifier which of the
backward problem for which the optional values are specified.
flag = IDASetQuadErrConB(ida_mem, which, errconQ);
flag = IDAQuadSStolerancesB(ida_mem, which, reltolQ, abstolQ);
flag = IDAQuadSVtolerancesB(ida_mem, which, reltolQ, abstolQ);
Their return value flag (of type int) can have any of the return values of its counterparts, but it
can also be IDA NO ADJ if the function IDAAdjInit has not been previously called or IDA ILL INPUT
if the parameter which was an invalid identifier.
Access to optional outputs related to backward quadrature integration can be obtained by calling
the corresponding IDAGetQuad* functions (see §4.7.5). A pointer ida memB to the idas memory block
for the backward problem, required as the first argument of these functions, can be obtained through
a call to the functions IDAGetAdjIDABmem (see §6.2.10).
6.3 User-supplied functions for adjoint sensitivity analysis
In addition to the required DAE residual function and any optional functions for the forward problem,
when using the adjoint sensitivity module in idas, the user must supply one function defining the
backward problem DAE and, optionally, functions to supply Jacobian-related information and one
or two functions that define the preconditioner (if one of the idaspils solvers is selected) for the
backward problem. Type definitions for all these user-supplied functions are given below.
6.3.1 DAE residual for the backward problem
The user must provide a resB function of type IDAResFnB defined as follows:
IDAResFnB
Definition typedef int (*IDAResFnB)(realtype t, N Vector y, N Vector yp,
N Vector yB, N Vector ypB,
N Vector resvalB, void *user dataB);
Purpose This function evaluates the residual of the backward problem DAE system. This could
be (2.20) or (2.25).
Arguments tis the current value of the independent variable.
yis the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the output vector containing the residual for the backward DAE problem.
user dataB is a pointer to user data, same as passed to IDASetUserDataB.

6.3 User-supplied functions for adjoint sensitivity analysis 135
Return value An IDAResFnB should return 0 if successful, a positive value if a recoverable error oc-
curred (in which case idas will attempt to correct), or a negative value if an unre-
coverabl failure occurred (in which case the integration stops and IDASolveB returns
IDA RESFUNC FAIL).
Notes Allocation of memory for resvalB is handled within idas.
The y,yp,yB,ypB, and resvalB arguments are all of type N Vector, but yB,ypB, and
resvalB typically have different internal representations from yand yp. It is the user’s
responsibility to access the vector data consistently (including the use of the correct
accessor macros from each nvector implementation). For the sake of computational
efficiency, the vector functions in the two nvector implementations provided with idas
do not perform any consistency checks with respect to their N Vector arguments (see
§7.1 and §7.2).
The user dataB pointer is passed to the user’s resB function every time it is called and
can be the same as the user data pointer used for the forward problem.
Before calling the user’s resB function, idas needs to evaluate (through interpolation)
!
the values of the states from the forward integration. If an error occurs in the inter-
polation, idas triggers an unrecoverable failure in the residual function which will halt
the integration and IDASolveB will return IDA RESFUNC FAIL.
6.3.2 DAE residual for the backward problem depending on the forward
sensitivities
The user must provide a resBS function of type IDAResFnBS defined as follows:
IDAResFnBS
Definition typedef int (*IDAResFnBS)(realtype t, N Vector y, N Vector yp,
N Vector *yS, N Vector *ypS,
N Vector yB, N Vector ypB,
N Vector resvalB, void *user dataB);
Purpose This function evaluates the residual of the backward problem DAE system. This could
be (2.20) or (2.25).
Arguments tis the current value of the independent variable.
yis the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yS a pointer to an array of Ns vectors containing the sensitivities of the forward
solution.
ypS a pointer to an array of Ns vectors containing the derivatives of the forward
sensitivities.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the output vector containing the residual for the backward DAE problem.
user dataB is a pointer to user data, same as passed to IDASetUserDataB.
Return value An IDAResFnBS should return 0 if successful, a positive value if a recoverable error
occurred (in which case idas will attempt to correct), or a negative value if an unre-
coverable error occurred (in which case the integration stops and IDASolveB returns
IDA RESFUNC FAIL).
Notes Allocation of memory for resvalB is handled within idas.
The y,yp,yB,ypB, and resvalB arguments are all of type N Vector, but yB,ypB,
and resvalB typically have different internal representations from yand yp. Likewise

136 Using IDAS for Adjoint Sensitivity Analysis
for each yS[i] and ypS[i]. It is the user’s responsibility to access the vector data
consistently (including the use of the correct accessor macros from each nvector im-
plementation). For the sake of computational efficiency, the vector functions in the two
nvector implementations provided with idas do not perform any consistency checks
with respect to their N Vector arguments (see §7.1 and §7.2).
The user dataB pointer is passed to the user’s resBS function every time it is called
and can be the same as the user data pointer used for the forward problem.
Before calling the user’s resBS function, idas needs to evaluate (through interpolation)
!
the values of the states from the forward integration. If an error occurs in the inter-
polation, idas triggers an unrecoverable failure in the residual function which will halt
the integration and IDASolveB will return IDA RESFUNC FAIL.
6.3.3 Quadrature right-hand side for the backward problem
The user must provide an fQB function of type IDAQuadRhsFnB defined by
IDAQuadRhsFnB
Definition typedef int (*IDAQuadRhsFnB)(realtype t, N Vector y, N Vector yp,
N Vector yB, N Vector ypB,
N Vector rhsvalBQ, void *user dataB);
Purpose This function computes the quadrature equation right-hand side for the backward prob-
lem.
Arguments tis the current value of the independent variable.
yis the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
rhsvalBQ is the output vector containing the residual for the backward quadrature
equations.
user dataB is a pointer to user data, same as passed to IDASetUserDataB.
Return value An IDAQuadRhsFnB should return 0 if successful, a positive value if a recoverable er-
ror occurred (in which case idas will attempt to correct), or a negative value if it
failed unrecoverably (in which case the integration is halted and IDASolveB returns
IDA QRHSFUNC FAIL).
Notes Allocation of memory for rhsvalBQ is handled within idas.
The y,yp,yB,ypB, and rhsvalBQ arguments are all of type N Vector, but they typi-
cally all have different internal representations. It is the user’s responsibility to access
the vector data consistently (including the use of the correct accessor macros from each
nvector implementation). For the sake of computational efficiency, the vector func-
tions in the two nvector implementations provided with idas do not perform any
consistency checks with repsect to their N Vector arguments (see §7.1 and §7.2).
The user dataB pointer is passed to the user’s fQB function every time it is called and
can be the same as the user data pointer used for the forward problem.
Before calling the user’s fQB function, idas needs to evaluate (through interpolation) the
!
values of the states from the forward integration. If an error occurs in the interpolation,
idas triggers an unrecoverable failure in the quadrature right-hand side function which
will halt the integration and IDASolveB will return IDA QRHSFUNC FAIL.

6.3 User-supplied functions for adjoint sensitivity analysis 137
6.3.4 Sensitivity-dependent quadrature right-hand side for the backward
problem
The user must provide an fQBS function of type IDAQuadRhsFnBS defined by
IDAQuadRhsFnBS
Definition typedef int (*IDAQuadRhsFnBS)(realtype t, N Vector y, N Vector yp,
N Vector *yS, N Vector *ypS,
N Vector yB, N Vector ypB,
N Vector rhsvalBQS, void *user dataB);
Purpose This function computes the quadrature equation residual for the backward problem.
Arguments tis the current value of the independent variable.
yis the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yS a pointer to an array of Ns vectors containing the sensitivities of the forward
solution.
ypS a pointer to an array of Ns vectors containing the derivatives of the forward
sensitivities.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
rhsvalBQS is the output vector containing the residual for the backward quadrature
equations.
user dataB is a pointer to user data, same as passed to IDASetUserDataB.
Return value An IDAQuadRhsFnBS should return 0 if successful, a positive value if a recoverable er-
ror occurred (in which case idas will attempt to correct), or a negative value if it
failed unrecoverably (in which case the integration is halted and IDASolveB returns
IDA QRHSFUNC FAIL).
Notes Allocation of memory for rhsvalBQS is handled within idas.
The y,yp,yB,ypB, and rhsvalBQS arguments are all of type N Vector, but they typically
do not all have the same internal representations. Likewise for each yS[i] and ypS[i].
It is the user’s responsibility to access the vector data consistently (including the use
of the correct accessor macros from each nvector implementation). For the sake
of computational efficiency, the vector functions in the two nvector implementations
provided with idas do not perform any consistency checks with repsect to their N Vector
arguments (see §7.1 and §7.2).
The user dataB pointer is passed to the user’s fQBS function every time it is called and
can be the same as the user data pointer used for the forward problem.
Before calling the user’s fQBS function, idas needs to evaluate (through interpolation)
!
the values of the states from the forward integration. If an error occurs in the interpo-
lation, idas triggers an unrecoverable failure in the quadrature right-hand side function
which will halt the integration and IDASolveB will return IDA QRHSFUNC FAIL.
6.3.5 Jacobian information for the backward problem (direct method with
dense Jacobian)
If the direct linear solver with dense treatment of the Jacobian is selected for the backward problem
(i.e. IDADenseB or IDALapackDenseB is called in step 22 of §6.1), the user may provide, through a call
to IDADlsSetDenseJacFnB or IDADlsSetDenseJacFnBS (see §6.2.9), a function of one of the following
two types:

138 Using IDAS for Adjoint Sensitivity Analysis
IDADlsDenseJacFnB
Definition typedef int (*IDADlsDenseJacFnB)(long int NeqB, realtype tt,
realtype cjB, N Vector yy, N Vector yp,
N Vector yB, N Vector ypB,
N Vector resvalB,
DlsMat JacB, void *user dataB,
N Vector tmp1B, N Vector tmp2B,
N Vector tmp3B);
Purpose This function computes the dense Jacobian of the backward problem (or an approxima-
tion to it).
Arguments NeqB is the backward problem size (number of equations).
tt is the current value of the independent variable.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
yy is the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the current value of the residual for the backward problem.
JacB is the output approximate dense Jacobian matrix.
user dataB is a pointer to user data — the parameter passed to IDASetUserDataB.
tmp1B
tmp2B
tmp3B are pointers to memory allocated for variables of type N Vector which can
be used by IDADlsDenseJacFnB as temporary storage or work space.
Return value An IDADlsDenseJacFnB should return 0 if successful, a positive value if a recover-
able error occurred (in which case idas will attempt to correct, while idadense sets
last flag to IDADLS JACFUNC RECVR), or a negative value if it failed unrecoverably (in
which case the integration is halted, IDASolveB returns IDA LSETUP FAIL and idadense
sets last flag to IDADLS JACFUNC UNRECVR).
Notes A user-supplied dense Jacobian function must load the NeqB by NeqB dense matrix JacB
with an approximation to the Jacobian matrix at the point (tt,yy,yB), where yy is the
solution of the original IVP at time tt and yB is the solution of the backward problem
at the same time. Only nonzero elements need to be loaded into JacB as this matrix is
set to zero before the call to the Jacobian function. The type of JacB is DlsMat. The
user is referred to §4.6.5 for details regarding accessing a DlsMat object.
Before calling the user’s IDADlsDenseJacFnB,idas needs to evaluate (through interpo-
!
lation) the values of the states from the forward integration. If an error occurs in the
interpolation, idas triggers an unrecoverable failure in the Jacobian function which will
halt the integration (IDASolveB returns IDA LSETUP FAIL and idadense sets last flag
to IDADLS JACFUNC UNRECVR).
IDADlsDenseJacFnBS
Definition typedef int (*IDADlsDenseJacFnBS)(long int NeqB, realtype tt,
realtype cjB, N Vector yy, N Vector yp,
N Vector *yS, N Vector *ypS,
N Vector yB, N Vector ypB,
N Vector resvalB,
DlsMat JacB, void *user dataB,
N Vector tmp1B, N Vector tmp2B,
N Vector tmp3B);

6.3 User-supplied functions for adjoint sensitivity analysis 139
Purpose This function computes the dense Jacobian of the backward problem (or an approxima-
tion to it), in the case where the backward problem depends on the forward sensitivities.
Arguments NeqB is the backward problem size (number of equations).
tt is the current value of the independent variable.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
yy is the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yS a pointer to an array of Ns vectors containing the sensitivities of the forward
solution.
ypS a pointer to an array of Ns vectors containing the derivatives of the forward
solution sensitivities.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the current value of the residual for the backward problem.
JacB is the output approximate dense Jacobian matrix.
user dataB is a pointer to user data — the parameter passed to IDASetUserDataB.
tmp1B
tmp2B
tmp3B are pointers to memory allocated for variables of type N Vector which can
be used by IDADlsDenseJacFnBS as temporary storage or work space.
Return value An IDADlsDenseJacFnBS should return 0 if successful, a positive value if a recover-
able error occurred (in which case idas will attempt to correct, while idadense sets
last flag to IDADLS JACFUNC RECVR), or a negative value if it failed unrecoverably (in
which case the integration is halted, IDASolveB returns IDA LSETUP FAIL and idadense
sets last flag to IDADLS JACFUNC UNRECVR).
Notes A user-supplied dense Jacobian function must load the NeqB by NeqB dense matrix JacB
with an approximation to the Jacobian matrix at the point (tt,yy,yS,yB), where yy is
the solution of the original IVP at time tt,yS is the array of forward sensitivities at
time tt, and yB is the solution of the backward problem at the same time. Only nonzero
elements need to be loaded into JacB as this matrix is set to zero before the call to the
Jacobian function. The type of JacB is DlsMat. The user is referred to §4.6.5 for details
regarding accessing a DlsMat object.
Before calling the user’s IDADlsDenseJacFnBS,idas needs to evaluate (through inter-
!
polation) the values of the states from the forward integration. If an error occurs in the
interpolation, idas triggers an unrecoverable failure in the Jacobian function which will
halt the integration (IDASolveB returns IDA LSETUP FAIL and idadense sets last flag
to IDADLS JACFUNC UNRECVR).
6.3.6 Jacobian information for the backward problem (direct method with
banded Jacobian)
If the direct linear solver with banded treatment of the Jacobian is selected for the backward problem
(i.e. IDABandB or IDALapackBandB is called in step 22 of §6.1), the user may provide, through a call
to IDADlsSetBandJacFnB or IDADlsSetBandJacFnBS (see §6.2.9), a function of one of the following
two types:
IDADlsBandJacFnB

140 Using IDAS for Adjoint Sensitivity Analysis
Definition typedef int (*IDADlsBandJacFnB)(long int NeqB,
long int mupperB, long int mlowerB,
realtype tt, realtype cjB,
N Vector yy, N Vector yp,
N Vector yB, N Vector ypB,
N Vector resvalB, DlsMat JacB,
void *user dataB,
N Vector tmp1B, N Vector tmp2B,
N Vector tmp3B);
Purpose This function computes the banded Jacobian of the backward problem (or a banded
approximation to it).
Arguments NeqB is the backward problem size.
mlowerB
mupperB are the lower and upper half-bandwidth of the Jacobian.
tt is the current value of the independent variable.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
yy is the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the current value of the residual for the backward problem.
JacB is the output approximate band Jacobian matrix.
user dataB is a pointer to user data — the parameter passed to IDASetUserDataB.
tmp1B
tmp2B
tmp3B are pointers to memory allocated for variables of type NVector which can
be used by IDADlsBandJacFnB as temporary storage or work space.
Return value An IDADlsBandJacFnB should return 0 if successful, a positive value if a recoverable er-
ror occurred (in which case idas will attempt to correct, while idaband sets last flag
to IDADLS JACFUNC RECVR), or a negative value if it failed unrecoverably (in which
case the integration is halted, IDASolveB returns IDA LSETUP FAIL and idadense sets
last flag to IDADLS JACFUNC UNRECVR).
Notes A user-supplied band Jacobian function must load the band matrix JacB (of type
DlsMat) with the elements of the Jacobian at the point (tt,yy,yB), where yy is the
solution of the original IVP at time tt and yB is the solution of the backward problem
at the same time. Only nonzero elements need to be loaded into JacB because JacB
is preset to zero before the call to the Jacobian function. More details on the acces-
sor macros provided for a DlsMat object and on the rest of the arguments passed to a
function of type IDADlsBandJacFnB are given in §4.6.6.
Before calling the user’s IDADlsBandJacFnB,idas needs to evaluate (through interpo-
!
lation) the values of the states from the forward integration. If an error occurs in the
interpolation, idas triggers an unrecoverable failure in the Jacobian function which will
halt the integration (IDASolveB returns IDA LSETUP FAIL and idaband sets last flag
to IDADLS JACFUNC UNRECVR).
IDADlsBandJacFnBS

6.3 User-supplied functions for adjoint sensitivity analysis 141
Definition typedef int (*IDADlsBandJacFnBS)(long int NeqB,
long int mupperB, long int mlowerB,
realtype tt, realtype cjB,
N Vector yy, N Vector yp,
N Vector *yS, N Vector *ypS,
N Vector yB, N Vector ypB,
N Vector resvalB, DlsMat JacB,
void *user dataB,
N Vector tmp1B, N Vector tmp2B,
N Vector tmp3B);
Purpose This function computes the banded Jacobian of the backward problem (or a banded
approximation to it), in the case where the backward problem depends on the forward
sensitivities.
Arguments NeqB is the backward problem size.
mlowerB
mupperB are the lower and upper half-bandwidth of the Jacobian.
tt is the current value of the independent variable.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
yy is the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yS a pointer to an array of Ns vectors containing the sensitivities of the forward
solution.
ypS a pointer to an array of Ns vectors containing the derivatives of the forward
sensitivities.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the current value of the residual for the backward problem.
JacB is the output approximate band Jacobian matrix.
user dataB is a pointer to user data — the parameter passed to IDASetUserDataB.
tmp1B
tmp2B
tmp3B are pointers to memory allocated for variables of type N Vector which can
be used by IDADlsBandJacFnBS as temporary storage or work space.
Return value An IDADlsBandJacFnBS should return 0 if successful, a positive value if a recoverable er-
ror occurred (in which case idas will attempt to correct, while idaband sets last flag
to IDADLS JACFUNC RECVR), or a negative value if it failed unrecoverably (in which
case the integration is halted, IDASolveB returns IDA LSETUP FAIL and idadense sets
last flag to IDADLS JACFUNC UNRECVR).
Notes A user-supplied band Jacobian function must load the band matrix JacB (of type
DlsMat) with the elements of the Jacobian at the point (tt,yy,yS,yB), where yy is
the solution of the original IVP at time tt,yS is the array of forward sensitivities at
time tt, and yB is the solution of the backward problem at the same time. Only nonzero
elements need to be loaded into JacB because JacB is preset to zero before the call to the
Jacobian function. More details on the accessor macros provided for a DlsMat object
and on the rest of the arguments passed to a function of type IDADlsBandJacFnBS are
given in §4.6.6.
Before calling the user’s IDADlsBandJacFnBS,idas needs to evaluate (through interpo-
!
lation) the values of the states from the forward integration. If an error occurs in the
interpolation, idas triggers an unrecoverable failure in the Jacobian function which will

142 Using IDAS for Adjoint Sensitivity Analysis
halt the integration (IDASolveB returns IDA LSETUP FAIL and idaband sets last flag
to IDADLS JACFUNC UNRECVR).
6.3.7 Jacobian information for the backward problem (direct method with
sparse Jacobian)
If the direct linear solver with sparse treatment of the Jacobian is selected for the backward problem
(i.e. IDAKLUB or IDASuperLUMTB is called in step 22 of §6.1), the user must provide, through a call to
IDASlsSetSparseJacFnB or IDASlsSetSparseJacFnBS (see §6.2.9), a function of one of the following
two types:
IDASlsSparseJacFnB
Definition typedef int (*IDASlsSparseJacFnB)(realtype tt, realtype cjB,
N Vector yy, N Vector yp,
N Vector yB, N Vector ypB,
N Vector rrB, SlsMat JacB,
void *user dataB, N Vector tmp1B,
N Vector tmp2B, N Vector tmp3B);
Purpose This function computes the sparse Jacobian of the backward problem (or an approxi-
mation to it).
Arguments tt is the current value of the independent variable.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
yy is the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
rrB is the current value of the residual for the backward problem.
JacB is the output approximate sparse Jacobian matrix.
user dataB is a pointer to user data — the parameter passed to IDASetUserDataB.
tmp1B
tmp2B
tmp3B are pointers to memory allocated for variables of type N Vector which can
be used by IDASlsSparseJacFnB as temporary storage or work space.
Return value An IDASlsSparseJacFnB should return 0 if successful, a positive value if a recoverable
error occurred (in which case idas will attempt to correct, while idaklu or idasuper-
lumt sets last flag to IDASLS JACFUNC RECVR), or a negative value if it failed unre-
coverably (in which case the integration is halted, IDASolveB returns IDA LSETUP FAIL
and idaklu or idasuperlumt sets last flag to IDASLS JACFUNC UNRECVR).
Notes A user-supplied sparse Jacobian function must load the compressed-sparse-column ma-
trix JacB with an approximation to the Jacobian matrix at the point (tt,yy,yB), where
yy is the solution of the original IVP at time tt and yB is the solution of the backward
problem at the same time. Storage for JacB already exists on entry to this function,
although the user should ensure that sufficient space is allocated in JacB to hold the
nonzero values to be set; if the existing space is insufficient the user may reallocate the
data and row index arrays as needed. The type of JacB is SlsMat, and the amount of
allocated space is available within the SlsMat structure as NNZ. The SlsMat type is fur-
ther documented in the Section §9.2. The user is referred to §4.6.7 for details regarding
accessing a SlsMat object.
Before calling the user’s IDASlsSparseJacFnB,idas needs to evaluate (through inter-
!
6.3 User-supplied functions for adjoint sensitivity analysis 143
polation) the values of the states from the forward integration. If an error occurs in
the interpolation, idas triggers an unrecoverable failure in the Jacobian function which
will halt the integration (IDASolveB returns IDA LSETUP FAIL and idaklu or idasu-
perlumt sets last flag to IDASLS JACFUNC UNRECVR).
IDASlsSparseJacFnBS
Definition typedef int (*IDASlsSparseJacFnBS)(realtype tt, realtype cjB,
N Vector yy, N Vector yp,
N Vector *yS, N Vector *ypS,
N Vector yB, N Vector ypB,
N Vector rrB, SlsMat JacB,
void *user dataB, N Vector tmp1B,
N Vector tmp2B, N Vector tmp3B);
Purpose This function computes the sparse Jacobian of the backward problem (or an approxima-
tion to it), in the case where the backward problem depends on the forward sensitivities.
Arguments tt is the current value of the independent variable.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
yy is the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yS a pointer to an array of Ns vectors containing the sensitivities of the forward
solution.
ypS a pointer to an array of Ns vectors containing the derivatives of the forward
solution sensitivities.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
rrB is the current value of the residual for the backward problem.
JacB is the output approximate sparse Jacobian matrix.
user dataB is a pointer to user data — the parameter passed to IDASetUserDataB.
tmp1B
tmp2B
tmp3B are pointers to memory allocated for variables of type N Vector which can
be used by IDASlsSparseJacFnBS as temporary storage or work space.
Return value An IDASlsSparseJacFnBS should return 0 if successful, a positive value if a recoverable
error occurred (in which case idas will attempt to correct, while idaklu or idasuper-
lumt sets last flag to IDASLS JACFUNC RECVR), or a negative value if it failed unre-
coverably (in which case the integration is halted, IDASolveB returns IDA LSETUP FAIL
and idaklu or idasuperlumt sets last flag to IDASLS JACFUNC UNRECVR).
Notes A user-supplied sparse Jacobian function must load the compressed-sparse-column ma-
trix JacB with an approximation to the Jacobian matrix at the point (tt,yy,yS,yB),
where yy is the solution of the original IVP at time tt,yS is the array of forward
sensitivities at time tt, and yB is the solution of the backward problem at the same
time. Storage for JacB already exists on entry to this function, although the user should
ensure that sufficient space is allocated in JacB to hold the nonzero values to be set; if
the existing space is insufficient the user may reallocate the data and row index arrays
as needed. The type of JacB is SlsMat, and the amount of allocated space is available
within the SlsMat structure as NNZ. The SlsMat type is further documented in the
Section §9.2. The user is referred to §4.6.7 for details regarding accessing a SlsMat
object.
144 Using IDAS for Adjoint Sensitivity Analysis
Before calling the user’s IDASlsSparseJacFnBS,idas needs to evaluate (through in-
!
terpolation) the values of the states from the forward integration. If an error occurs
in the interpolation, idas triggers an unrecoverable failure in the Jacobian function
which will halt the integration (IDASolveB returns IDA LSETUP FAIL and idaklu or
idasuperlumt sets last flag to IDASLS JACFUNC UNRECVR).
6.3.8 Jacobian information for the backward problem (matrix-vector prod-
uct)
If one of the Krylov iterative linear solvers spgmr,spbcg, or sptfqmr is selected (IDASp*B is called
in step 22 of §6.1), the user may provide a function of one of the following two forms:
IDASpilsJacTimesVecFnB
Definition typedef int (*IDASpilsJacTimesVecFnB)(realtype t,
N Vector yy, N Vector yp,
N Vector yB, N Vector ypB,
N Vector resvalB,
N Vector vB, N Vector JvB,
realtype cjB, void *user dataB,
N Vector tmp1B, N Vector tmp2B);
Purpose This function computes the action of the backward problem Jacobian JB on a given
vector vB.
Arguments tis the current value of the independent variable.
yy is the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the current value of the residual for the backward problem.
vB is the vector by which the Jacobian must be multiplied.
JvB is the computed output vector, JB*vB.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
user dataB is a pointer to user data — the same as the user dataB parameter passed
to IDASetUserDataB.
tmp1B
tmp2B are pointers to memory allocated for variables of type N Vector which can
be used by IDASpilsJacTimesVecFnB as temporary storage or work space.
Return value The return value of a function of type IDASpilsJtimesFnB should be 0 if successful or
nonzero if an error was encountered, in which case the integration is halted.
Notes A user-supplied Jacobian-vector product function must load the vector JvB with the
product of the Jacobian of the backward problem at the point (t,y,yB) and the vector
vB. Here, yis the solution of the original IVP at time tand yB is the solution of the
backward problem at the same time. The rest of the arguments are equivalent to those
passed to a function of type IDASpilsJacTimesVecFn (see §4.6.8). If the backward
problem is the adjoint of ˙y=f(t, y), then this function is to compute −(∂f/∂y)TvB.
IDASpilsJacTimesVecFnBS
6.3 User-supplied functions for adjoint sensitivity analysis 145
Definition typedef int (*IDASpilsJacTimesVecFnBS)(realtype t,
N Vector yy, N Vector yp,
N Vector *yyS, N Vector *ypS,
N Vector yB, N Vector ypB,
N Vector resvalB,
N Vector vB, N Vector JvB,
realtype cjB, void *user dataB,
N Vector tmp1B, N Vector tmp2B);
Purpose This function computes the action of the backward problem Jacobian JB on a given
vector vB, in the case where the backward problem depends on the forward sensitivities.
Arguments tis the current value of the independent variable.
yy is the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yyS a pointer to an array of Ns vectors containing the sensitivities of the forward
solution.
ypS a pointer to an array of Ns vectors containing the derivatives of the forward
sensitivities.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the current value of the residual for the backward problem.
vB is the vector by which the Jacobian must be multiplied.
JvB is the computed output vector, JB*vB.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
user dataB is a pointer to user data — the same as the user dataB parameter passed
to IDASetUserDataB.
tmp1B
tmp2B are pointers to memory allocated for variables of type N Vector which
can be used by IDASpilsJacTimesVecFnBS as temporary storage or work
space.
Return value The return value of a function of type IDASpilsJtimesFnBS should be 0 if successful
or nonzero if an error was encountered, in which case the integration is halted.
Notes A user-supplied Jacobian-vector product function must load the vector JvB with the
product of the Jacobian of the backward problem at the point (t,y,yB) and the vector
vB. Here, yis the solution of the original IVP at time tand yB is the solution of the
backward problem at the same time. The rest of the arguments are equivalent to those
passed to a function of type IDASpilsJacTimesVecFn (see §4.6.8).
6.3.9 Preconditioning for the backward problem (linear system solution)
If preconditioning is used during integration of the backward problem, then the user must provide a
Cfunction to solve the linear system P z =r, where Pis a left preconditioner matrix. This function
must have one of the following two forms:
IDASpilsPrecSolveFnB

146 Using IDAS for Adjoint Sensitivity Analysis
Definition typedef int (*IDASpilsPrecSolveFnB)(realtype t,
N Vector yy, N Vector yp,
N Vector yB, N Vector ypB,
N Vector resvalB,
N Vector rvecB, N Vector zvecB,
realtype cjB, realtype deltaB,
void *user dataB, N Vector tmpB);
Purpose This function solves the preconditioning system P z =rfor the backward problem.
Arguments tis the current value of the independent variable.
yy is the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the current value of the residual for the backward problem.
rvecB is the right-hand side vector rof the linear system to be solved.
zvecB is the computed output vector.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
deltaB is an input tolerance to be used if an iterative method is employed in the
solution.
user dataB is a pointer to user data — the same as the user dataB parameter passed
to the function IDASetUserDataB.
tmpB is a pointer to memory allocated for a variable of type N Vector which can
be used for work space.
Return value The return value of a preconditioner solve function for the backward problem should be
0 if successful, positive for a recoverable error (in which case the step will be retried),
or negative for an unrecoverable error (in which case the integration is halted).
IDASpilsPrecSolveFnBS
Definition typedef int (*IDASpilsPrecSolveFnBS)(realtype t,
N Vector yy, N Vector yp,
N Vector *yyS, N Vector *ypS,
N Vector yB, N Vector ypB,
N Vector resvalB,
N Vector rvecB, N Vector zvecB,
realtype cjB, realtype deltaB,
void *user dataB, N Vector tmpB);
Purpose This function solves the preconditioning system P z =rfor the backward problem, for
the case in which the backward problem depends on the forward sensitivities.
Arguments tis the current value of the independent variable.
yy is the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yyS a pointer to an array of Ns vectors containing the sensitivities of the forward
solution.
ypS a pointer to an array of Ns vectors containing the derivatives of the forward
sensitivities.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the current value of the residual for the backward problem.
6.3 User-supplied functions for adjoint sensitivity analysis 147
rvecB is the right-hand side vector rof the linear system to be solved.
zvecB is the computed output vector.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
deltaB is an input tolerance to be used if an iterative method is employed in the
solution.
user dataB is a pointer to user data — the same as the user dataB parameter passed
to the function IDASetUserDataB.
tmpB is a pointer to memory allocated for a variable of type N Vector which can
be used for work space.
Return value The return value of a preconditioner solve function for the backward problem should be
0 if successful, positive for a recoverable error (in which case the step will be retried),
or negative for an unrecoverable error (in which case the integration is halted).
6.3.10 Preconditioning for the backward problem (Jacobian data)
If the user’s preconditioner requires that any Jacobian-related data be preprocessed or evaluated, then
this needs to be done in a user-supplied Cfunction of one of the following two types:
IDASpilsPrecSetupFnB
Definition typedef int (*IDASpilsPrecSetupFnB)(realtype t,
N Vector yy, N Vector yp,
N Vector yB, N Vector ypB,
N Vector resvalB,
realtype cjB, void *user dataB,
N Vector tmp1B, N Vector tmp2B,
N Vector tmp3B);
Purpose This function preprocesses and/or evaluates Jacobian-related data needed by the pre-
conditioner for the backward problem.
Arguments The arguments of an IDASpilsPrecSetupFnB are as follows:
tis the current value of the independent variable.
yy is the current value of the forward solution vector.
yp is the current value of the forward solution vector.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the current value of the residual for the backward problem.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
user dataB is a pointer to user data — the same as the user dataB parameter passed
to the function IDASetUserDataB.
tmp1B
tmp2B
tmp3B are pointers to memory allocated for vectors which can be used as tempo-
rary storage or work space.
Return value The return value of a preconditioner setup function for the backward problem should
be 0 if successful, positive for a recoverable error (in which case the step will be retried),
or negative for an unrecoverable error (in which case the integration is halted).

148 Using IDAS for Adjoint Sensitivity Analysis
IDASpilsPrecSetupFnBS
Definition typedef int (*IDASpilsPrecSetupFnBS)(realtype t,
N Vector yy, N Vector yp,
N Vector *yyS, N Vector *ypS,
N Vector yB, N Vector ypB,
N Vector resvalB,
realtype cjB, void *user dataB,
N Vector tmp1B, N Vector tmp2B,
N Vector tmp3B);
Purpose This function preprocesses and/or evaluates Jacobian-related data needed by the pre-
conditioner for the backward problem, in the case where the backward problem depends
on the forward sensitivities.
Arguments The arguments of an IDASpilsPrecSetupFnBS are as follows:
tis the current value of the independent variable.
yy is the current value of the forward solution vector.
yp is the current value of the forward solution vector.
yyS a pointer to an array of Ns vectors containing the sensitivities of the forward
solution.
ypS a pointer to an array of Ns vectors containing the derivatives of the forward
sensitivities.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
resvalB is the current value of the residual for the backward problem.
cjB is the scalar in the system Jacobian, proportional to the inverse of the step
size (αin Eq. (2.6) ).
user dataB is a pointer to user data — the same as the user dataB parameter passed
to the function IDASetUserDataB.
tmp1B
tmp2B
tmp3B are pointers to memory allocated for vectors which can be used as tempo-
rary storage or work space.
Return value The return value of a preconditioner setup function for the backward problem should
be 0 if successful, positive for a recoverable error (in which case the step will be retried),
or negative for an unrecoverable error (in which case the integration is halted).
6.4 Using the band-block-diagonal preconditioner for back-
ward problems
As on the forward integration phase, the efficiency of Krylov iterative methods for the solution of
linear systems can be greatly enhanced through preconditioning. The band-block-diagonal precondi-
tioner module idabbdpre, provides interface functions through which it can be used on the backward
integration phase.
The adjoint module in idas offers an interface to the band-block-diagonal preconditioner module
idabbdpre described in section §4.8. This generates a preconditioner that is a block-diagonal matrix
with each block being a band matrix and can be used with one of the Krylov linear solvers and with
the MPI-parallel vector module nvector parallel.
In order to use the idabbdpre module in the solution of the backward problem, the user must
define one or two additional functions, described at the end of this section.

6.4 Using the band-block-diagonal preconditioner for backward problems 149
6.4.1 Usage of IDABBDPRE for the backward problem
The idabbdpre module is initialized by calling the following function, after one of the idaspils linear
solvers has been specified, by calling the appropriate function (see §6.2.6).
IDABBDPrecInitB
Call flag = IDABBDPrecInitB(ida mem, which, NlocalB, mudqB, mldqB,
mukeepB, mlkeepB, dqrelyB, GresB, GcommB);
Description The function IDABBDPrecInitB initializes and allocates memory for the idabbdpre
preconditioner for the backward problem.
Arguments ida mem (void *) pointer to the idas memory block.
which (int) the identifier of the backward problem.
NlocalB (long int) local vector dimension for the backward problem.
mudqB (long int) upper half-bandwidth to be used in the difference-quotient Jaco-
bian approximation.
mldqB (long int) lower half-bandwidth to be used in the difference-quotient Jaco-
bian approximation.
mukeepB (long int) upper half-bandwidth of the retained banded approximate Jaco-
bian block.
mlkeepB (long int) lower half-bandwidth of the retained banded approximate Jaco-
bian block.
dqrelyB (realtype) the relative increment in components of yB used in the difference
quotient approximations. The default is dqrelyB=√unit roundoff, which can
be specified by passing dqrely= 0.0.
GresB (IDABBDLocalFnB) the Cfunction which computes GB(t, y, ˙y, yB,˙yB), the func-
tion approximating the residual of the backward problem.
GcommB (IDABBDCommFnB) the optional Cfunction which performs all interprocess com-
munication required for the computation of GB.
Return value If successful, IDABBDPrecInitB creates, allocates, and stores (internally in the idas
solver block) a pointer to the newly created idabbdpre memory block. The return
value flag (of type int) is one of:
IDASPILS SUCCESS The call to IDABBDPrecInitB was successful.
IDASPILS MEM FAIL A memory allocation request has failed.
IDASPILS MEM NULL The ida mem argument was NULL.
IDASPILS LMEM NULL No linear solver has been attached.
IDASPILS ILL INPUT An invalid parameter has been passed.
To reinitialize the idabbdpre preconditioner module for the backward problem, possibly with a change
in mudqB,mldqB, or dqrelyB, call the following function:
IDABBDPrecReInitB
Call flag = IDABBDPrecReInitB(ida mem, which, mudqB, mldqB, dqrelyB);
Description The function IDABBDPrecReInitB reinitializes the idabbdpre preconditioner for the
backward problem.
Arguments ida mem (void *) pointer to the idas memory block returned by IDACreate.
which (int) the identifier of the backward problem.
mudqB (long int) upper half-bandwidth to be used in the difference-quotient Jaco-
bian approximation.
mldqB (long int) lower half-bandwidth to be used in the difference-quotient Jaco-
bian approximation.
150 Using IDAS for Adjoint Sensitivity Analysis
dqrelyB (realtype) the relative increment in components of yB used in the difference
quotient approximations.
Return value The return value flag (of type int) is one of:
IDASPILS SUCCESS The call to IDABBDPrecReInitB was successful.
IDASPILS MEM FAIL A memory allocation request has failed.
IDASPILS MEM NULL The ida mem argument was NULL.
IDASPILS PMEM NULL The IDABBDPrecInitB has not been previously called.
IDASPILS LMEM NULL No linear solver has been attached.
IDASPILS ILL INPUT An invalid parameter has been passed.
For more details on idabbdpre see §4.8.
6.4.2 User-supplied functions for IDABBDPRE
To use the idabbdpre module, the user must supply one or two functions which the module calls
to construct the preconditioner: a required function GresB (of type IDABBDLocalFnB) which approxi-
mates the residual of the backward problem and which is computed locally, and an optional function
GcommB (of type IDABBDCommFnB) which performs all interprocess communication necessary to evaluate
this approximate residual (see §4.8). The prototypes for these two functions are described below.
IDABBDLocalFnB
Definition typedef int (*IDABBDLocalFnB)(long int NlocalB, realtype t,
N Vector y, N Vector yp,
N Vector yB, N Vector ypB,
N Vector gB, void *user dataB);
Purpose This GresB function loads the vector gB, an approximation to the residual of the back-
ward problem, as a function of t,y,yp, and yB and ypB.
Arguments NlocalB is the local vector length for the backward problem.
tis the value of the independent variable.
yis the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
gB is the output vector, GB(t, y, ˙y, yB,˙yB).
user dataB is a pointer to user data — the same as the user dataB parameter passed
to IDASetUserDataB.
Return value An IDABBDLocalFnB should return 0 if successful, a positive value if a recoverable er-
ror occurred (in which case idas will attempt to correct), or a negative value if it
failed unrecoverably (in which case the integration is halted and IDASolveB returns
IDA LSETUP FAIL).
Notes This routine must assume that all interprocess communication of data needed to calcu-
late gB has already been done, and this data is accessible within user dataB.
Before calling the user’s IDABBDLocalFnB,idas needs to evaluate (through interpola-
!
tion) the values of the states from the forward integration. If an error occurs in the
interpolation, idas triggers an unrecoverable failure in the preconditioner setup function
which will halt the integration (IDASolveB returns IDA LSETUP FAIL).

6.4 Using the band-block-diagonal preconditioner for backward problems 151
IDABBDCommFnB
Definition typedef int (*IDABBDCommFnB)(long int NlocalB, realtype t,
N Vector y, N Vector yp,
N Vector yB, N Vector ypB,
void *user dataB);
Purpose This GcommB function performs all interprocess communications necessary for the exe-
cution of the GresB function above, using the input vectors y,yp,yB and ypB.
Arguments NlocalB is the local vector length.
tis the value of the independent variable.
yis the current value of the forward solution vector.
yp is the current value of the forward solution derivative vector.
yB is the current value of the backward dependent variable vector.
ypB is the current value of the backward dependent derivative vector.
user dataB is a pointer to user data — the same as the user dataB parameter passed
to IDASetUserDataB.
Return value An IDABBDCommFnB should return 0 if successful, a positive value if a recoverable er-
ror occurred (in which case idas will attempt to correct), or a negative value if it
failed unrecoverably (in which case the integration is halted and IDASolveB returns
IDA LSETUP FAIL).
Notes The GcommB function is expected to save communicated data in space defined within
the structure user dataB.
Each call to the GcommB function is preceded by a call to the function that evaluates the
residual of the backward problem with the same t,y,yp,yB and ypB arguments. If there
is no additional communication needed, then pass GcommB =NULL to IDABBDPrecInitB.

Chapter 7
Description of the NVECTOR
module
The sundials solvers are written in a data-independent manner. They all operate on generic vectors
(of type N Vector) through a set of operations defined by the particular nvector implementation.
Users can provide their own specific implementation of the nvector module, or use one of four
provided within sundials – a serial implementation and three parallel implementations. The generic
operations are described below. In the sections following, the implementations provided with sundials
are described.
The generic N Vector type is a pointer to a structure that has an implementation-dependent
content field containing the description and actual data of the vector, and an ops field pointing to a
structure with generic vector operations. The type N Vector is defined as
typedef struct _generic_N_Vector *N_Vector;
struct _generic_N_Vector {
void *content;
struct _generic_N_Vector_Ops *ops;
};
The generic N Vector Ops structure is essentially a list of pointers to the various actual vector
operations, and is defined as
struct _generic_N_Vector_Ops {
N_Vector_ID (*nvgetvectorid)(N_Vector);
N_Vector (*nvclone)(N_Vector);
N_Vector (*nvcloneempty)(N_Vector);
void (*nvdestroy)(N_Vector);
void (*nvspace)(N_Vector, long int *, long int *);
realtype* (*nvgetarraypointer)(N_Vector);
void (*nvsetarraypointer)(realtype *, N_Vector);
void (*nvlinearsum)(realtype, N_Vector, realtype, N_Vector, N_Vector);
void (*nvconst)(realtype, N_Vector);
void (*nvprod)(N_Vector, N_Vector, N_Vector);
void (*nvdiv)(N_Vector, N_Vector, N_Vector);
void (*nvscale)(realtype, N_Vector, N_Vector);
void (*nvabs)(N_Vector, N_Vector);
void (*nvinv)(N_Vector, N_Vector);
void (*nvaddconst)(N_Vector, realtype, N_Vector);
realtype (*nvdotprod)(N_Vector, N_Vector);
realtype (*nvmaxnorm)(N_Vector);
154 Description of the NVECTOR module
realtype (*nvwrmsnorm)(N_Vector, N_Vector);
realtype (*nvwrmsnormmask)(N_Vector, N_Vector, N_Vector);
realtype (*nvmin)(N_Vector);
realtype (*nvwl2norm)(N_Vector, N_Vector);
realtype (*nvl1norm)(N_Vector);
void (*nvcompare)(realtype, N_Vector, N_Vector);
booleantype (*nvinvtest)(N_Vector, N_Vector);
booleantype (*nvconstrmask)(N_Vector, N_Vector, N_Vector);
realtype (*nvminquotient)(N_Vector, N_Vector);
};
The generic nvector module defines and implements the vector operations acting on N Vector.
These routines are nothing but wrappers for the vector operations defined by a particular nvector
implementation, which are accessed through the ops field of the N Vector structure. To illustrate
this point we show below the implementation of a typical vector operation from the generic nvector
module, namely N VScale, which performs the scaling of a vector xby a scalar c:
void N_VScale(realtype c, N_Vector x, N_Vector z)
{
z->ops->nvscale(c, x, z);
}
Table 7.2 contains a complete list of all vector operations defined by the generic nvector module.
Finally, note that the generic nvector module defines the functions N VCloneVectorArray and
N VCloneVectorArrayEmpty. Both functions create (by cloning) an array of count variables of type
N Vector, each of the same type as an existing N Vector. Their prototypes are
N_Vector *N_VCloneVectorArray(int count, N_Vector w);
N_Vector *N_VCloneVectorArrayEmpty(int count, N_Vector w);
and their definitions are based on the implementation-specific N VClone and N VCloneEmpty opera-
tions, respectively.
An array of variables of type N Vector can be destroyed by calling N VDestroyVectorArray, whose
prototype is
void N_VDestroyVectorArray(N_Vector *vs, int count);
and whose definition is based on the implementation-specific N VDestroy operation.
A particular implementation of the nvector module must:
•Specify the content field of N Vector.
•Define and implement the vector operations. Note that the names of these routines should be
unique to that implementation in order to permit using more than one nvector module (each
with different N Vector internal data representations) in the same code.
•Define and implement user-callable constructor and destructor routines to create and free an
N Vector with the new content field and with ops pointing to the new vector operations.
•Optionally, define and implement additional user-callable routines acting on the newly defined
N Vector (e.g., a routine to print the content for debugging purposes).
•Optionally, provide accessor macros as needed for that particular implementation to be used to
access different parts in the content field of the newly defined N Vector.
Each nvector implementation included in sundials has a unique identifier specified in enumer-
ation and shown in Table 7.1. It is recommended that a user-supplied nvector implementation use
the SUNDIALS NVEC CUSTOM identifier.
155
Table 7.1: Vector Identifications associated with vector kernels supplied with sundials.
Vector ID Vector type ID Value
SUNDIALS NVEC SERIAL Serial 0
SUNDIALS NVEC PARALLEL Distributed memory parallel (MPI) 1
SUNDIALS NVEC OPENMP OpenMP shared memory parallel 2
SUNDIALS NVEC PTHREADS PThreads shared memory parallel 3
SUNDIALS NVEC PARHYP hypre ParHyp parallel vector 4
SUNDIALS NVEC PETSC petsc parallel vector 5
SUNDIALS NVEC CUSTOM User-provided custom vector 6
Table 7.2: Description of the NVECTOR operations
Name Usage and Description
N VGetVectorID id = N VGetVectorID(w);
Returns the vector type identifier for the vector w. It is used to deter-
mine the vector implementation type (e.g. serial, parallel,. . . ) from the
abstract N Vector interface. Returned values are given in Table 7.1.
N VClone v = N VClone(w);
Creates a new N Vector of the same type as an existing vector wand sets
the ops field. It does not copy the vector, but rather allocates storage
for the new vector.
N VCloneEmpty v = N VCloneEmpty(w);
Creates a new N Vector of the same type as an existing vector wand
sets the ops field. It does not allocate storage for data.
N VDestroy N VDestroy(v);
Destroys the N Vector v and frees memory allocated for its internal
data.
N VSpace N VSpace(nvSpec, &lrw, &liw);
Returns storage requirements for one N Vector.lrw contains the num-
ber of realtype words and liw contains the number of integer words.
This function is advisory only, for use in determining a user’s total space
requirements; it could be a dummy function in a user-supplied nvector
module if that information is not of interest.
continued on next page
156 Description of the NVECTOR module
continued from last page
Name Usage and Description
N VGetArrayPointer vdata = N VGetArrayPointer(v);
Returns a pointer to a realtype array from the N Vector v. Note
that this assumes that the internal data in N Vector is a contiguous
array of realtype. This routine is only used in the solver-specific in-
terfaces to the dense and banded (serial) linear solvers, the sparse lin-
ear solvers (serial and threaded), and in the interfaces to the banded
(serial) and band-block-diagonal (parallel) preconditioner modules pro-
vided with sundials.
N VSetArrayPointer N VSetArrayPointer(vdata, v);
Overwrites the data in an N Vector with a given array of realtype.
Note that this assumes that the internal data in N Vector is a contigu-
ous array of realtype. This routine is only used in the interfaces to
the dense (serial) linear solver, hence need not exist in a user-supplied
nvector module for a parallel environment.
N VLinearSum N VLinearSum(a, x, b, y, z);
Performs the operation z=ax +by, where aand bare realtype scalars
and xand yare of type N Vector:zi=axi+byi, i = 0, . . . , n −1.
N VConst N VConst(c, z);
Sets all components of the N Vector z to realtype c:zi=c, i =
0, . . . , n −1.
N VProd N VProd(x, y, z);
Sets the N Vector z to be the component-wise product of the N Vector
inputs xand y:zi=xiyi, i = 0, . . . , n −1.
N VDiv N VDiv(x, y, z);
Sets the N Vector z to be the component-wise ratio of the N Vector
inputs xand y:zi=xi/yi, i = 0, . . . , n −1. The yimay not be tested
for 0 values. It should only be called with a ythat is guaranteed to have
all nonzero components.
N VScale N VScale(c, x, z);
Scales the N Vector x by the realtype scalar cand returns the result
in z:zi=cxi, i = 0, . . . , n −1.
N VAbs N VAbs(x, z);
Sets the components of the N Vector z to be the absolute values of the
components of the N Vector x:yi=|xi|, i = 0, . . . , n −1.
continued on next page

157
continued from last page
Name Usage and Description
N VInv N VInv(x, z);
Sets the components of the N Vector z to be the inverses of the compo-
nents of the N Vector x:zi= 1.0/xi, i = 0, . . . , n −1. This routine may
not check for division by 0. It should be called only with an xwhich is
guaranteed to have all nonzero components.
N VAddConst N VAddConst(x, b, z);
Adds the realtype scalar bto all components of xand returns the result
in the N Vector z:zi=xi+b, i = 0, . . . , n −1.
N VDotProd d = N VDotProd(x, y);
Returns the value of the ordinary dot product of xand y:d=Pn−1
i=0 xiyi.
N VMaxNorm m = N VMaxNorm(x);
Returns the maximum norm of the N Vector x:m= maxi|xi|.
N VWrmsNorm m = N VWrmsNorm(x, w)
Returns the weighted root-mean-square norm of the N Vector x with
realtype weight vector w:m=rPn−1
i=0 (xiwi)2/n.
N VWrmsNormMask m = N VWrmsNormMask(x, w, id);
Returns the weighted root mean square norm of the N Vector x with
realtype weight vector wbuilt using only the elements of xcorrespond-
ing to nonzero elements of the N Vector id:
m=rPn−1
i=0 (xiwisign(idi))2/n.
N VMin m = N VMin(x);
Returns the smallest element of the N Vector x:m= minixi.
N VWL2Norm m = N VWL2Norm(x, w);
Returns the weighted Euclidean `2norm of the N Vector x with
realtype weight vector w:m=qPn−1
i=0 (xiwi)2.
N VL1Norm m = N VL1Norm(x);
Returns the `1norm of the N Vector x:m=Pn−1
i=0 |xi|.
N VCompare N VCompare(c, x, z);
Compares the components of the N Vector x to the realtype scalar c
and returns an N Vector z such that: zi= 1.0 if |xi| ≥ cand zi= 0.0
otherwise.
continued on next page

158 Description of the NVECTOR module
continued from last page
Name Usage and Description
N VInvTest t = N VInvTest(x, z);
Sets the components of the N Vector z to be the inverses of the com-
ponents of the N Vector x, with prior testing for zero values: zi=
1.0/xi, i = 0, . . . , n −1. This routine returns a boolean assigned to TRUE
if all components of xare nonzero (successful inversion) and returns
FALSE otherwise.
N VConstrMask t = N VConstrMask(c, x, m);
Performs the following constraint tests: xi>0 if ci= 2, xi≥0 if ci= 1,
xi≤0 if ci=−1, xi<0 if ci=−2. There is no constraint on xiif
ci= 0. This routine returns a boolean assigned to FALSE if any element
failed the constraint test and assigned to TRUE if all passed. It also
sets a mask vector m, with elements equal to 1.0 where the constraint
test failed, and 0.0 where the test passed. This routine is used only for
constraint checking.
N VMinQuotient minq = N VMinQuotient(num, denom);
This routine returns the minimum of the quotients obtained by term-
wise dividing numiby denomi. A zero element in denom will be skipped.
If no such quotients are found, then the large value BIG REAL (defined
in the header file sundials types.h) is returned.
7.1 The NVECTOR SERIAL implementation
The serial implementation of the nvector module provided with sundials,nvector serial, defines
the content field of N Vector to be a structure containing the length of the vector, a pointer to the
beginning of a contiguous data array, and a boolean flag own data which specifies the ownership of
data.
struct _N_VectorContent_Serial {
long int length;
booleantype own_data;
realtype *data;
};
The header file to be included when using this module is nvector serial.h.
The following five macros are provided to access the content of an nvector serial vector. The
suffix Sin the names denotes the serial version.
•NV CONTENT S
This routine gives access to the contents of the serial vector N Vector.
The assignment v cont =NV CONTENT S(v) sets v cont to be a pointer to the serial N Vector
content structure.
Implementation:
#define NV_CONTENT_S(v) ( (N_VectorContent_Serial)(v->content) )
•NV OWN DATA S,NV DATA S,NV LENGTH S
These macros give individual access to the parts of the content of a serial N Vector.
The assignment v data = NV DATA S(v) sets v data to be a pointer to the first component of
the data for the N Vector v. The assignment NV DATA S(v) = v data sets the component array
of vto be v data by storing the pointer v data.
7.1 The NVECTOR SERIAL implementation 159
The assignment v len = NV LENGTH S(v) sets v len to be the length of v. On the other hand,
the call NV LENGTH S(v) = len v sets the length of vto be len v.
Implementation:
#define NV_OWN_DATA_S(v) ( NV_CONTENT_S(v)->own_data )
#define NV_DATA_S(v) ( NV_CONTENT_S(v)->data )
#define NV_LENGTH_S(v) ( NV_CONTENT_S(v)->length )
•NV Ith S
This macro gives access to the individual components of the data array of an N Vector.
The assignment r = NV Ith S(v,i) sets rto be the value of the i-th component of v. The
assignment NV Ith S(v,i) = r sets the value of the i-th component of vto be r.
Here iranges from 0 to n−1 for a vector of length n.
Implementation:
#define NV_Ith_S(v,i) ( NV_DATA_S(v)[i] )
The nvector serial module defines serial implementations of all vector operations listed in Ta-
ble 7.2. Their names are obtained from those in Table 7.2 by appending the suffix Serial (e.g.
N VDestroy Serial). The module nvector serial provides the following additional user-callable
routines:
•N VNew Serial
This function creates and allocates memory for a serial N Vector. Its only argument is the
vector length.
N_Vector N_VNew_Serial(long int vec_length);
•N VNewEmpty Serial
This function creates a new serial N Vector with an empty (NULL) data array.
N_Vector N_VNewEmpty_Serial(long int vec_length);
•N VMake Serial
This function creates and allocates memory for a serial vector with user-provided data array.
(This function does not allocate memory for v data itself.)
N_Vector N_VMake_Serial(long int vec_length, realtype *v_data);
•N VCloneVectorArray Serial
This function creates (by cloning) an array of count serial vectors.
N_Vector *N_VCloneVectorArray_Serial(int count, N_Vector w);
•N VCloneVectorArrayEmpty Serial
This function creates (by cloning) an array of count serial vectors, each with an empty (NULL)
data array.
N_Vector *N_VCloneVectorArrayEmpty_Serial(int count, N_Vector w);
•N VDestroyVectorArray Serial
This function frees memory allocated for the array of count variables of type N Vector created
with N VCloneVectorArray Serial or with N VCloneVectorArrayEmpty Serial.
void N_VDestroyVectorArray_Serial(N_Vector *vs, int count);
•N VGetLength Serial
This function returns the number of vector elements.
long int N_VGetLength_Serial(N_Vector v);

160 Description of the NVECTOR module
•N VPrint Serial
This function prints the content of a serial vector to stdout.
void N_VPrint_Serial(N_Vector v);
Notes
•When looping over the components of an N Vector v, it is more efficient to first obtain the
component array via v data = NV DATA S(v) and then access v data[i] within the loop than
it is to use NV Ith S(v,i) within the loop.
•N VNewEmpty Serial,N VMake Serial, and N VCloneVectorArrayEmpty Serial set the field
!
own data =FALSE.N VDestroy Serial and N VDestroyVectorArray Serial will not attempt
to free the pointer data for any N Vector with own data set to FALSE. In such a case, it is the
user’s responsibility to deallocate the data pointer.
•To maximize efficiency, vector operations in the nvector serial implementation that have
!
more than one N Vector argument do not check for consistent internal representation of these
vectors. It is the user’s responsibility to ensure that such routines are called with N Vector
arguments that were all created with the same internal representations.
For solvers that include a Fortran interface module, the nvector serial module also includes
a Fortran-callable function FNVINITS(code, NEQ, IER), to initialize this nvector serial module.
Here code is an input solver id (1 for cvode, 2 for ida, 3 for kinsol, 4 for arkode); NEQ is the
problem size (declared so as to match C type long int); and IER is an error return flag equal 0 for
success and -1 for failure.
7.2 The NVECTOR PARALLEL implementation
The nvector parallel implementation of the nvector module provided with sundials is based on
MPI. It defines the content field of N Vector to be a structure containing the global and local lengths
of the vector, a pointer to the beginning of a contiguous local data array, an MPI communicator, and
a boolean flag own data indicating ownership of the data array data.
struct _N_VectorContent_Parallel {
long int local_length;
long int global_length;
booleantype own_data;
realtype *data;
MPI_Comm comm;
};
The header file to be included when using this module is nvector parallel.h.
The following seven macros are provided to access the content of a nvector parallel vector.
The suffix Pin the names denotes the distributed memory parallel version.
•NV CONTENT P
This macro gives access to the contents of the parallel vector N Vector.
The assignment v cont = NV CONTENT P(v) sets v cont to be a pointer to the N Vector content
structure of type struct N VectorContent Parallel.
Implementation:
#define NV_CONTENT_P(v) ( (N_VectorContent_Parallel)(v->content) )

7.2 The NVECTOR PARALLEL implementation 161
•NV OWN DATA P,NV DATA P,NV LOCLENGTH P,NV GLOBLENGTH P
These macros give individual access to the parts of the content of a parallel N Vector.
The assignment v data = NV DATA P(v) sets v data to be a pointer to the first component of
the local data for the N Vector v. The assignment NV DATA P(v) = v data sets the component
array of vto be v data by storing the pointer v data.
The assignment v llen = NV LOCLENGTH P(v) sets v llen to be the length of the local part of
v. The call NV LENGTH P(v) = llen v sets the local length of vto be llen v.
The assignment v glen = NV GLOBLENGTH P(v) sets v glen to be the global length of the vector
v. The call NV GLOBLENGTH P(v) = glen v sets the global length of vto be glen v.
Implementation:
#define NV_OWN_DATA_P(v) ( NV_CONTENT_P(v)->own_data )
#define NV_DATA_P(v) ( NV_CONTENT_P(v)->data )
#define NV_LOCLENGTH_P(v) ( NV_CONTENT_P(v)->local_length )
#define NV_GLOBLENGTH_P(v) ( NV_CONTENT_P(v)->global_length )
•NV COMM P
This macro provides access to the MPI communicator used by the nvector parallel vectors.
Implementation:
#define NV_COMM_P(v) ( NV_CONTENT_P(v)->comm )
•NV Ith P
This macro gives access to the individual components of the local data array of an N Vector.
The assignment r = NV Ith P(v,i) sets rto be the value of the i-th component of the local
part of v. The assignment NV Ith P(v,i) = r sets the value of the i-th component of the local
part of vto be r.
Here iranges from 0 to n−1, where nis the local length.
Implementation:
#define NV_Ith_P(v,i) ( NV_DATA_P(v)[i] )
The nvector parallel module defines parallel implementations of all vector operations listed in
Table 7.2 Their names are obtained from those in Table 7.2 by appending the suffix Parallel
(e.g. N VDestroy Parallel). The module nvector parallel provides the following additional
user-callable routines:
•N VNew Parallel
This function creates and allocates memory for a parallel vector.
N_Vector N_VNew_Parallel(MPI_Comm comm,
long int local_length,
long int global_length);
•N VNewEmpty Parallel
This function creates a new parallel N Vector with an empty (NULL) data array.
N_Vector N_VNewEmpty_Parallel(MPI_Comm comm,
long int local_length,
long int global_length);

162 Description of the NVECTOR module
•N VMake Parallel
This function creates and allocates memory for a parallel vector with user-provided data array.
(This function does not allocate memory for v data itself.)
N_Vector N_VMake_Parallel(MPI_Comm comm,
long int local_length,
long int global_length,
realtype *v_data);
•N VCloneVectorArray Parallel
This function creates (by cloning) an array of count parallel vectors.
N_Vector *N_VCloneVectorArray_Parallel(int count, N_Vector w);
•N VCloneVectorArrayEmpty Parallel
This function creates (by cloning) an array of count parallel vectors, each with an empty (NULL)
data array.
N_Vector *N_VCloneVectorArrayEmpty_Parallel(int count, N_Vector w);
•N VDestroyVectorArray Parallel
This function frees memory allocated for the array of count variables of type N Vector created
with N VCloneVectorArray Parallel or with N VCloneVectorArrayEmpty Parallel.
void N_VDestroyVectorArray_Parallel(N_Vector *vs, int count);
•N VGetLength Parallel
This function returns the number of vector elements (global vector length).
long int N_VGetLength_Parallel(N_Vector v);
•N VGetLocalLength Parallel
This function returns the local vector length.
long int N_VGetLocalLength_Parallel(N_Vector v);
•N VPrint Parallel
This function prints the content of a parallel vector to stdout.
void N_VPrint_Parallel(N_Vector v);
Notes
•When looping over the components of an N Vector v, it is more efficient to first obtain the local
component array via v data = NV DATA P(v) and then access v data[i] within the loop than
it is to use NV Ith P(v,i) within the loop.
•N VNewEmpty Parallel,N VMake Parallel, and N VCloneVectorArrayEmpty Parallel set the
!
field own data =FALSE.N VDestroy Parallel and N VDestroyVectorArray Parallel will not
attempt to free the pointer data for any N Vector with own data set to FALSE. In such a case,
it is the user’s responsibility to deallocate the data pointer.
•To maximize efficiency, vector operations in the nvector parallel implementation that have
!
more than one N Vector argument do not check for consistent internal representation of these
vectors. It is the user’s responsibility to ensure that such routines are called with N Vector
arguments that were all created with the same internal representations.

7.3 The NVECTOR OPENMP implementation 163
For solvers that include a Fortran interface module, the nvector parallel module also includes
a Fortran-callable function FNVINITP(COMM, code, NLOCAL, NGLOBAL, IER), to initialize this nvec-
tor parallel module. Here COMM is the MPI communicator, code is an input solver id (1 for cvode,
2 for ida, 3 for kinsol, 4 for arkode); NLOCAL and NGLOBAL are the local and global vector sizes,
respectively (declared so as to match C type long int); and IER is an error return flag equal 0 for suc-
cess and -1 for failure. NOTE: If the header file sundials config.h defines SUNDIALS MPI COMM F2C
!
to be 1 (meaning the MPI implementation used to build sundials includes the MPI Comm f2c func-
tion), then COMM can be any valid MPI communicator. Otherwise, MPI COMM WORLD will be used, so
just pass an integer value as a placeholder.
7.3 The NVECTOR OPENMP implementation
In situations where a user has a multi-core processing unit capable of running multiple parallel threads
with shared memory, sundials provides an implementation of nvector using OpenMP, called nvec-
tor openmp, and an implementation using Pthreads, called nvector pthreads. Testing has shown
that vectors should be of length at least 100,000 before the overhead associated with creating and
using the threads is made up by the parallelism in the vector calculations.
The OpenMP nvector implementation provided with sundials,nvector openmp, defines the
content field of N Vector to be a structure containing the length of the vector, a pointer to the
beginning of a contiguous data array, a boolean flag own data which specifies the ownership of data,
and the number of threads. Operations on the vector are threaded using OpenMP.
struct _N_VectorContent_OpenMP {
long int length;
booleantype own_data;
realtype *data;
int num_threads;
};
The header file to be included when using this module is nvector openmp.h.
The following six macros are provided to access the content of an nvector openmp vector. The
suffix OMP in the names denotes the OpenMP version.
•NV CONTENT OMP
This routine gives access to the contents of the OpenMP vector N Vector.
The assignment v cont =NV CONTENT OMP(v) sets v cont to be a pointer to the OpenMP
N Vector content structure.
Implementation:
#define NV_CONTENT_OMP(v) ( (N_VectorContent_OpenMP)(v->content) )
•NV OWN DATA OMP,NV DATA OMP,NV LENGTH OMP,NV NUM THREADS OMP
These macros give individual access to the parts of the content of a OpenMP N Vector.
The assignment v data = NV DATA OMP(v) sets v data to be a pointer to the first component
of the data for the N Vector v. The assignment NV DATA OMP(v) = v data sets the component
array of vto be v data by storing the pointer v data.
The assignment v len = NV LENGTH OMP(v) sets v len to be the length of v. On the other
hand, the call NV LENGTH OMP(v) = len v sets the length of vto be len v.
The assignment v num threads = NV NUM THREADS OMP(v) sets v num threads to be the num-
ber of threads from v. On the other hand, the call NV NUM THREADS OMP(v) = num threads v
sets the number of threads for vto be num threads v.
Implementation:
#define NV_OWN_DATA_OMP(v) ( NV_CONTENT_OMP(v)->own_data )

164 Description of the NVECTOR module
#define NV_DATA_OMP(v) ( NV_CONTENT_OMP(v)->data )
#define NV_LENGTH_OMP(v) ( NV_CONTENT_OMP(v)->length )
#define NV_NUM_THREADS_OMP(v) ( NV_CONTENT_OMP(v)->num_threads )
•NV Ith OMP
This macro gives access to the individual components of the data array of an N Vector.
The assignment r = NV Ith OMP(v,i) sets rto be the value of the i-th component of v. The
assignment NV Ith OMP(v,i) = r sets the value of the i-th component of vto be r.
Here iranges from 0 to n−1 for a vector of length n.
Implementation:
#define NV_Ith_OMP(v,i) ( NV_DATA_OMP(v)[i] )
The nvector openmp module defines OpenMP implementations of all vector operations listed in
Table 7.2. Their names are obtained from those in Table 7.2 by appending the suffix OpenMP (e.g.
N VDestroy OpenMP). The module nvector openmp provides the following additional user-callable
routines:
•N VNew OpenMP
This function creates and allocates memory for a OpenMP N Vector. Arguments are the vector
length and number of threads.
N_Vector N_VNew_OpenMP(long int vec_length, int num_threads);
•N VNewEmpty OpenMP
This function creates a new OpenMP N Vector with an empty (NULL) data array.
N_Vector N_VNewEmpty_OpenMP(long int vec_length, int num_threads);
•N VMake OpenMP
This function creates and allocates memory for a OpenMP vector with user-provided data array.
(This function does not allocate memory for v data itself.)
N_Vector N_VMake_OpenMP(long int vec_length, realtype *v_data, int num_threads);
•N VCloneVectorArray OpenMP
This function creates (by cloning) an array of count OpenMP vectors.
N_Vector *N_VCloneVectorArray_OpenMP(int count, N_Vector w);
•N VCloneVectorArrayEmpty OpenMP
This function creates (by cloning) an array of count OpenMP vectors, each with an empty
(NULL) data array.
N_Vector *N_VCloneVectorArrayEmpty_OpenMP(int count, N_Vector w);
•N VDestroyVectorArray OpenMP
This function frees memory allocated for the array of count variables of type N Vector created
with N VCloneVectorArray OpenMP or with N VCloneVectorArrayEmpty OpenMP.
void N_VDestroyVectorArray_OpenMP(N_Vector *vs, int count);
•N VGetLength OpenMP
This function returns number of vector elements.
long int N_VGetLength_OpenMP(N_Vector v);
•N VPrint OpenMP
This function prints the content of a OpenMP vector to stdout.
void N_VPrint_OpenMP(N_Vector v);

7.4 The NVECTOR PTHREADS implementation 165
Notes
•When looping over the components of an N Vector v, it is more efficient to first obtain the
component array via v data = NV DATA OMP(v) and then access v data[i] within the loop
than it is to use NV Ith OMP(v,i) within the loop.
•N VNewEmpty OpenMP,N VMake OpenMP, and N VCloneVectorArrayEmpty OpenMP set the field
!
own data =FALSE.N VDestroy OpenMP and N VDestroyVectorArray OpenMP will not attempt
to free the pointer data for any N Vector with own data set to FALSE. In such a case, it is the
user’s responsibility to deallocate the data pointer.
•To maximize efficiency, vector operations in the nvector openmp implementation that have
!
more than one N Vector argument do not check for consistent internal representation of these
vectors. It is the user’s responsibility to ensure that such routines are called with N Vector
arguments that were all created with the same internal representations.
For solvers that include a Fortran interface module, the nvector openmp module also includes a
Fortran-callable function FNVINITOMP(code, NEQ, NUMTHREADS, IER), to initialize this nvector openmp
module. Here code is an input solver id (1 for cvode, 2 for ida, 3 for kinsol, 4 for arkode); NEQ
is the problem size (declared so as to match C type long int); NUMTHREADS is the number of
threads; and IER is an error return flag equal 0 for success and -1 for failure.
7.4 The NVECTOR PTHREADS implementation
In situations where a user has a multi-core processing unit capable of running multiple parallel threads
with shared memory, sundials provides an implementation of nvector using OpenMP, called nvec-
tor openmp, and an implementation using Pthreads, called nvector pthreads. Testing has shown
that vectors should be of length at least 100,000 before the overhead associated with creating and
using the threads is made up by the parallelism in the vector calculations.
The Pthreads nvector implementation provided with sundials, denoted nvector pthreads,
defines the content field of N Vector to be a structure containing the length of the vector, a pointer
to the beginning of a contiguous data array, a boolean flag own data which specifies the ownership
of data, and the number of threads. Operations on the vector are threaded using POSIX threads
(Pthreads).
struct _N_VectorContent_Pthreads {
long int length;
booleantype own_data;
realtype *data;
int num_threads;
};
The header file to be included when using this module is nvector pthreads.h.
The following six macros are provided to access the content of an nvector pthreads vector.
The suffix PT in the names denotes the Pthreads version.
•NV CONTENT PT
This routine gives access to the contents of the Pthreads vector N Vector.
The assignment v cont =NV CONTENT PT(v) sets v cont to be a pointer to the Pthreads
N Vector content structure.
Implementation:
#define NV_CONTENT_PT(v) ( (N_VectorContent_Pthreads)(v->content) )
•NV OWN DATA PT,NV DATA PT,NV LENGTH PT,NV NUM THREADS PT
These macros give individual access to the parts of the content of a Pthreads N Vector.
166 Description of the NVECTOR module
The assignment v data = NV DATA PT(v) sets v data to be a pointer to the first component
of the data for the N Vector v. The assignment NV DATA PT(v) = v data sets the component
array of vto be v data by storing the pointer v data.
The assignment v len = NV LENGTH PT(v) sets v len to be the length of v. On the other hand,
the call NV LENGTH PT(v) = len v sets the length of vto be len v.
The assignment v num threads = NV NUM THREADS PT(v) sets v num threads to be the number
of threads from v. On the other hand, the call NV NUM THREADS PT(v) = num threads v sets
the number of threads for vto be num threads v.
Implementation:
#define NV_OWN_DATA_PT(v) ( NV_CONTENT_PT(v)->own_data )
#define NV_DATA_PT(v) ( NV_CONTENT_PT(v)->data )
#define NV_LENGTH_PT(v) ( NV_CONTENT_PT(v)->length )
#define NV_NUM_THREADS_PT(v) ( NV_CONTENT_PT(v)->num_threads )
•NV Ith PT
This macro gives access to the individual components of the data array of an N Vector.
The assignment r = NV Ith PT(v,i) sets rto be the value of the i-th component of v. The
assignment NV Ith PT(v,i) = r sets the value of the i-th component of vto be r.
Here iranges from 0 to n−1 for a vector of length n.
Implementation:
#define NV_Ith_PT(v,i) ( NV_DATA_PT(v)[i] )
The nvector pthreads module defines Pthreads implementations of all vector operations listed
in Table 7.2. Their names are obtained from those in Table 7.2 by appending the suffix Pthreads
(e.g. N VDestroy Pthreads). The module nvector pthreads provides the following additional
user-callable routines:
•N VNew Pthreads
This function creates and allocates memory for a Pthreads N Vector. Arguments are the vector
length and number of threads.
N_Vector N_VNew_Pthreads(long int vec_length, int num_threads);
•N VNewEmpty Pthreads
This function creates a new Pthreads N Vector with an empty (NULL) data array.
N_Vector N_VNewEmpty_Pthreads(long int vec_length, int num_threads);
•N VMake Pthreads
This function creates and allocates memory for a Pthreads vector with user-provided data array.
(This function does not allocate memory for v data itself.)
N_Vector N_VMake_Pthreads(long int vec_length, realtype *v_data, int num_threads);
•N VCloneVectorArray Pthreads
This function creates (by cloning) an array of count Pthreads vectors.
N_Vector *N_VCloneVectorArray_Pthreads(int count, N_Vector w);
•N VCloneVectorArrayEmpty Pthreads
This function creates (by cloning) an array of count Pthreads vectors, each with an empty
(NULL) data array.
N_Vector *N_VCloneVectorArrayEmpty_Pthreads(int count, N_Vector w);
7.5 The NVECTOR PARHYP implementation 167
•N VDestroyVectorArray Pthreads
This function frees memory allocated for the array of count variables of type N Vector created
with N VCloneVectorArray Pthreads or with N VCloneVectorArrayEmpty Pthreads.
void N_VDestroyVectorArray_Pthreads(N_Vector *vs, int count);
•N VGetLength Pthreads
This function returns the number of vector elements.
long int N_VGetLength_Pthreads(N_Vector v);
•N VPrint Pthreads
This function prints the content of a Pthreads vector to stdout.
void N_VPrint_Pthreads(N_Vector v);
Notes
•When looping over the components of an N Vector v, it is more efficient to first obtain the
component array via v data = NV DATA PT(v) and then access v data[i] within the loop than
it is to use NV Ith PT(v,i) within the loop.
•N VNewEmpty Pthreads,N VMake Pthreads, and N VCloneVectorArrayEmpty Pthreads set the
!
field own data =FALSE.N VDestroy Pthreads and N VDestroyVectorArray Pthreads will not
attempt to free the pointer data for any N Vector with own data set to FALSE. In such a case,
it is the user’s responsibility to deallocate the data pointer.
•To maximize efficiency, vector operations in the nvector pthreads implementation that have
!
more than one N Vector argument do not check for consistent internal representation of these
vectors. It is the user’s responsibility to ensure that such routines are called with N Vector
arguments that were all created with the same internal representations.
For solvers that include a Fortran interface module, the nvector pthreads module also includes
a Fortran-callable function FNVINITPTS(code, NEQ, NUMTHREADS, IER), to initialize this nvector pthreads
module. Here code is an input solver id (1 for cvode, 2 for ida, 3 for kinsol, 4 for arkode); NEQ
is the problem size (declared so as to match C type long int); NUMTHREADS is the number of
threads; and IER is an error return flag equal 0 for success and -1 for failure.
7.5 The NVECTOR PARHYP implementation
The nvector parhyp implementation of the nvector module provided with sundials is a wrapper
around hypre’s ParVector class. Most of the vector kernels simply call hypre vector operations. The
implementation defines the content field of N Vector to be a structure containing the global and local
lengths of the vector, a pointer to an object of type hypre ParVector, an MPI communicator, and a
boolean flag own parvector indicating ownership of the hypre parallel vector object x.
struct _N_VectorContent_ParHyp {
long int local_length;
long int global_length;
booleantype own_parvector;
MPI_Comm comm;
hypre_ParVector *x;
};
The header file to be included when using this module is nvector parhyp.h. Unlike native sundials
vector types, nvector parhyp does not provide macros to access its member variables.
The nvector parhyp module defines implementations of all vector operations listed in Table
7.2, except for N VSetArrayPointer and N VGetArrayPointer, because accessing raw vector data is
168 Description of the NVECTOR module
handled by low-level hypre functions. As such, this vector is not available for use with sundials
Fortran interfaces. When access to raw vector data is needed, one should extract hypre vector first,
and then use hypre methods to access the data. Usage examples of nvector parhyp are provided in
the cvAdvDiff non ph.c example program for cvode [20] and the ark diurnal kry ph.c example
program for arkode [30].
The names of parhyp methods are obtained from those in Table 7.2 by appending the suffix
ParHyp (e.g. N VDestroy ParHyp). The module nvector parhyp provides the following additional
user-callable routines:
•N VNewEmpty ParHyp
This function creates a new parhyp N Vector with the pointer to the hypre vector set to NULL.
N_Vector N_VNewEmpty_ParHyp(MPI_Comm comm,
long int local_length,
long int global_length);
•N VMake ParHyp
This function creates an N_Vector wrapper around an existing hypre parallel vector. It does
not allocate memory for xitself.
N_Vector N_VMake_ParHyp(hypre_ParVector *x);
•N VGetVector ParHyp
This function returns a pointer to the underlying hypre vector.
hypre_ParVector *N_VGetVector_ParHyp(N_Vector v);
•N VCloneVectorArray ParHyp
This function creates (by cloning) an array of count parallel vectors.
N_Vector *N_VCloneVectorArray_ParHyp(int count, N_Vector w);
•N VCloneVectorArrayEmpty ParHyp
This function creates (by cloning) an array of count parallel vectors, each with an empty (NULL)
data array.
N_Vector *N_VCloneVectorArrayEmpty_ParHyp(int count, N_Vector w);
•N VDestroyVectorArray ParHyp
This function frees memory allocated for the array of count variables of type N Vector created
with N VCloneVectorArray ParHyp or with N VCloneVectorArrayEmpty ParHyp.
void N_VDestroyVectorArray_ParHyp(N_Vector *vs, int count);
•N VPrint ParHyp
This function prints the content of a parhyp vector to stdout.
void N_VPrint_ParHyp(N_Vector v);

7.6 The NVECTOR PETSC implementation 169
Notes
•When there is a need to access components of an N Vector ParHyp,v, it is recommended to
extract the hypre vector via x vec = N VGetVector ParHyp(v) and then access components
using appropriate hypre functions.
•N VNewEmpty ParHyp,N VMake ParHyp, and N VCloneVectorArrayEmpty ParHyp set the field
!
own parvector to FALSE.N VDestroy ParHyp and N VDestroyVectorArray ParHyp will not at-
tempt to delete an underlying hypre vector for any N Vector with own parvector set to FALSE.
In such a case, it is the user’s responsibility to delete the underlying vector.
•To maximize efficiency, vector operations in the nvector parhyp implementation that have
!
more than one N Vector argument do not check for consistent internal representations of these
vectors. It is the user’s responsibility to ensure that such routines are called with N Vector
arguments that were all created with the same internal representations.
7.6 The NVECTOR PETSC implementation
The nvector petsc module is an nvector wrapper around the petsc vector. It defines the content
field of a N Vector to be a structure containing the global and local lengths of the vector, a pointer
to the petsc vector, an MPI communicator, and a boolean flag own data indicating ownership of the
wrapped petsc vector.
struct _N_VectorContent_Petsc {
long int local_length;
long int global_length;
booleantype own_data;
Vec *pvec;
MPI_Comm comm;
};
The header file to be included when using this module is nvector petsc.h. Unlike native sundials
vector types, nvector petsc does not provide macros to access its member variables. Note that
nvector petsc requires sundials to be built with MPI support.
The nvector petsc module defines implementations of all vector operations listed in Table 7.2,
except for N_VGetArrayPointer and N_VSetArrayPointer. As such, this vector cannot be used
with sundials Fortran interfaces. When access to raw vector data is needed, it is recommended to
extract the petsc vector first, and then use petsc methods to access the data. Usage examples of
nvector petsc are provided in example programs for ida [23].
The names of vector operations are obtained from those in Table 7.2 by appending the suffix
Petsc (e.g. N VDestroy Petsc). The module nvector petsc provides the following additional
user-callable routines:
•N VNewEmpty Petsc
This function creates a new nvector wrapper with the pointer to the wrapped petsc vector
set to (NULL). It is used by the N VMake Petsc and N VClone Petsc implementations.
N_Vector N_VNewEmpty_Petsc(MPI_Comm comm,
long int local_length,
long int global_length);
•N VMake Petsc
This function creates and allocates memory for an nvector petsc wrapper around a user-
provided petsc vector. It does not allocate memory for the vector pvec itself.

170 Description of the NVECTOR module
N_Vector N_VMake_Petsc(Vec *pvec);
•N VGetVector Petsc
This function returns a pointer to the underlying petsc vector.
Vec *N_VGetVector_Petsc(N_Vector v);
•N VCloneVectorArray Petsc
This function creates (by cloning) an array of count nvector petsc vectors.
N_Vector *N_VCloneVectorArray_Petsc(int count, N_Vector w);
•N VCloneVectorArrayEmpty Petsc
This function creates (by cloning) an array of count nvector petsc vectors, each with pointers
to petsc vectors set to (NULL).
N_Vector *N_VCloneEmptyVectorArray_Petsc(int count, N_Vector w);
•N VDestroyVectorArray Petsc
This function frees memory allocated for the array of count variables of type N Vector created
with N VCloneVectorArray Petsc or with N VCloneVectorArrayEmpty Petsc.
void N_VDestroyVectorArray_Petsc(N_Vector *vs, int count);
•N VPrint Petsc
This function prints the content of a wrapped petsc vector to stdout.
void N_VPrint_Petsc(N_Vector v);
Notes
•When there is a need to access components of an N Vector Petsc,v, it is recommeded to
extract the petsc vector via x vec = N VGetVector Petsc(v) and then access components
using appropriate petsc functions.
•The functions NVNewEmpty Petsc,N VMake Petsc, and N VCloneVectorArrayEmpty Petsc set
!
the field own data to FALSE.N VDestroy Petsc and N VDestroyVectorArray Petsc will not
attempt to free the pointer pvec for any N Vector with own data set to FALSE. In such a case,
it is the user’s responsibility to deallocate the pvec pointer.
•To maximize efficiency, vector operations in the nvector petsc implementation that have
!
more than one N Vector argument do not check for consistent internal representations of these
vectors. It is the user’s responsibility to ensure that such routines are called with N Vector
arguments that were all created with the same internal representations.
7.7 NVECTOR Examples
There are NVector examples that may be installed for each implementation: serial, parallel, OpenMP,
and Pthreads. Each implementation makes use of the functions in test nvector.c. These example
functions show simple usage of the NVector family of functions. The input to the examples are the
vector length, number of threads (if threaded implementation), and a print timing flag.
The following is a list of the example functions in test nvector.c:
•Test N VClone: Creates clone of vector and checks validity of clone.

7.7 NVECTOR Examples 171
•Test N VCloneEmpty: Creates clone of empty vector and checks validity of clone.
•Test N VCloneVectorArray: Creates clone of vector array and checks validity of cloned array.
•Test N VCloneVectorArray: Creates clone of empty vector array and checks validity of cloned
array.
•Test N VGetArrayPointer: Get array pointer.
•Test N VSetArrayPointer: Allocate new vector, set pointer to new vector array, and check
values.
•Test N VLinearSum Case 1a: Test y = x + y
•Test N VLinearSum Case 1b: Test y = -x + y
•Test N VLinearSum Case 1c: Test y = ax + y
•Test N VLinearSum Case 2a: Test x = x + y
•Test N VLinearSum Case 2b: Test x = x - y
•Test N VLinearSum Case 2c: Test x = x + by
•Test N VLinearSum Case 3: Test z = x + y
•Test N VLinearSum Case 4a: Test z = x - y
•Test N VLinearSum Case 4b: Test z = -x + y
•Test N VLinearSum Case 5a: Test z = x + by
•Test N VLinearSum Case 5b: Test z = ax + y
•Test N VLinearSum Case 6a: Test z = -x + by
•Test N VLinearSum Case 6b: Test z = ax - y
•Test N VLinearSum Case 7: Test z = a(x + y)
•Test N VLinearSum Case 8: Test z = a(x - y)
•Test N VLinearSum Case 9: Test z = ax + by
•Test N VConst: Fill vector with constant and check result.
•Test N VProd: Test vector multiply: z = x * y
•Test N VDiv: Test vector division: z = x / y
•Test N VScale: Case 1: scale: x = cx
•Test N VScale: Case 2: copy: z = x
•Test N VScale: Case 3: negate: z = -x
•Test N VScale: Case 4: combination: z = cx
•Test N VAbs: Create absolute value of vector.
•Test N VAddConst: add constant vector: z = c + x
•Test N VDotProd: Calculate dot product of two vectors.
•Test N VMaxNorm: Create vector with known values, find and validate max norm.

172 Description of the NVECTOR module
•Test N VWrmsNorm: Create vector of known values, find and validate weighted root mean square.
•Test N VWrmsNormMask: Case 1: Create vector of known values, find and validate weighted root
mean square using all elements.
•Test N VWrmsNormMask: Case 2: Create vector of known values, find and validate weighted root
mean square using no elements.
•Test N VMin: Create vector, find and validate the min.
•Test N VWL2Norm: Create vector, find and validate the weighted Euclidean L2 norm.
•Test N VL1Norm: Create vector, find and validate the L1 norm.
•Test N VCompare: Compare vector with constant returning and validating comparison vector.
•Test N VInvTest: Test z[i] = 1 / x[i]
•Test N VConstrMask: Test mask of vector x with vector c.
•Test N VMinQuotient: Fill two vectors with known values. Calculate and validate minimum
quotient.
7.8 NVECTOR functions used by IDAS
In Table 7.3 below, we list the vector functions used in the nvector module used by the idas
package. The table also shows, for each function, which of the code modules uses the function. The
idas column shows function usage within the main integrator module, while the remaining five columns
show function usage within each of the five idas linear solvers, the idabbdpre preconditioner module,
and the idas adjoint sensitivity module (denoted here by idaa). Here idadls stands for idadense
and idaband;idaspils stands for idaspgmr,idaspbcg, and idasptfqmr; and idasls stands for
idaklu and idasuperlumt.
There is one subtlety in the idaspils column hidden by the table, explained here for the case of
the idaspgmr module. The N VDotProd function is called both within the interface file ida spgmr.c
and within the implementation files sundials spgmr.c and sundials iterative.c for the generic
spgmr solver upon which the idaspgmr solver is built. Also, although N VDiv and N VProd are
not called within the interface file ida spgmr.c, they are called within the implementation file
sundials spgmr.c, and so are required by the idaspgmr solver module. Analogous statements ap-
ply to the idaspbcg and idasptfqmr modules, except that they do not use sundials iterative.c.
This issue does not arise for the direct idas linear solvers because the generic dense and band solvers
(used in the implementation of idadense and idaband) do not make calls to any vector functions.
Of the functions listed in Table 7.2,N VWL2Norm,N VL1Norm,N VCloneEmpty, and N VInvTest
are not used by idas. Therefore a user-supplied nvector module for idas could omit these four
functions.
7.8 NVECTOR functions used by IDAS 173
Table 7.3: List of vector functions usage by idas code modules
idas
idadls
idaspils
idasls
idabbdpre
idaa
N VGetVectorID
N VClone X X X X
N VDestroy X X X X
N VCloneVectorArray X X
N VDestroyVectorArray X X
N VSpace X
N VGetArrayPointer X X X
N VSetArrayPointer X
N VLinearSum X X X X
N VConst X X X
N VProd X X
N VDiv X X
N VScale X X X X X X
N VAbs X
N VInv X
N VAddConst X
N VDotProd X
N VMaxNorm X
N VWrmsNorm X X
N VMin X
N VMinQuotient X
N VConstrMask X
N VWrmsNormMask X
N VCompare X
Chapter 8
Providing Alternate Linear Solver
Modules
The central idas module interfaces with a linear solver module by way of calls to five functions. These
are denoted here by linit,lsetup,lsolve,lperf, and lfree. Briefly, their purposes are as follows:
•linit: initialize memory specific to the linear solver;
•lsetup: evaluate and preprocess the Jacobian or preconditioner;
•lsolve: solve the linear system;
•lperf: monitor performance and issue warnings;
•lfree: free the linear solver memory.
A linear solver module must also provide a user-callable specification function (like those described
in §4.5.3) which will attach the above five functions to the main idas memory block. The idas memory
block is a structure defined in the header file idas impl.h. A pointer to such a structure is defined as
the type IDAMem. The five fields in an IDAMem structure that must point to the linear solver’s functions
are ida linit,ida lsetup,ida lsolve,ida lperf, and ida lfree, respectively. Note that of the
five interface functions, only lsolve is required. The lfree function must be provided only if the
solver specification function makes any memory allocation. For any of the functions that are not
provided, the corresponding field should be set to NULL. The linear solver specification function must
also set the value of the field ida setupNonNull in the idas memory block — to TRUE if lsetup is
used, or FALSE otherwise.
Typically, the linear solver will require a block of memory specific to the solver, and a principal
function of the specification function is to allocate that memory block, and initialize it. Then the
field ida lmem in the idas memory block is available to attach a pointer to that linear solver memory.
This block can then be used to facilitate the exchange of data between the five interface functions.
If the linear solver involves adjustable parameters, the specification function should set the default
values of those. User-callable functions may be defined that could, optionally, override the default
parameter values.
We encourage the use of performance counters in connection with the various operations involved
with the linear solver. Such counters would be members of the linear solver memory block, would
be initialized in the linit function, and would be incremented by the lsetup and lsolve functions.
Then, user-callable functions would be needed to obtain the values of these counters.
For consistency with the existing idas linear solver modules, we recommend that the return value
of the specification function be 0 for a successful return, and a negative value if an error occurs.
Possible error conditions include: the pointer to the main idas memory block is NULL, an input is
illegal, the nvector implementation is not compatible, or a memory allocation fails.
176 Providing Alternate Linear Solver Modules
To be used during the backward integration with the idas module, a linear solver module must
also provide an additional user-callable specification function (like those described in §6.2.6) which
will attach the five functions to the idas memory block for each backward integration. Note that
this block, of type IDAMem, is not directly accessible to the specification function, but rather is itself
a field in the idas memory block. For a given backward problem identifier which, the corresponding
memory block must be located in the linked list starting at ida mem->ida adj mem->IDAB mem; see for
example the function IDADenseB for specific details. This specification function must also allocate the
linear solver memory for the backward problem, and attach that, as well as a corresponding memory
free function, to the above block IDAB mem, of type struct IDABMemRec. The specification function
for backward integration should return a negative value if it encounters an illegal input, if backward
integration has not been initialized, or if its memory allocation failed.
These five functions, which interface between idas and the linear solver module, necessarily have
fixed call sequences. Thus a user wishing to implement another linear solver within the idas package
must adhere to this set of interfaces. The following is a complete description of the call list for each of
these functions. Note that the call list of each function includes a pointer to the main idas memory
block, by which the function can access various data related to the idas solution. The contents of
this memory block are given in the file idas impl.h (but not reproduced here, for the sake of space).
8.1 Initialization function
The type definition of linit is
linit
Definition int (*linit)(IDAMem IDA mem);
Purpose The purpose of linit is to complete initializations for the specific linear solver, such
as counters and statistics. It should also set pointers to data blocks that will later be
passed to functions associated with the linear solver. The linit function is called once
only, at the start of the problem, during the first call to IDASolve.
Arguments IDA mem is the idas memory pointer of type IDAMem.
Return value An linit function should return 0 if it has successfully initialized the idas linear solver
and a negative value otherwise.
8.2 Setup function
The type definition of lsetup is
lsetup
Definition int (*lsetup)(IDAMem IDA mem, N Vector yyp, N Vector ypp, N Vector resp,
N Vector vtemp1, N Vector vtemp2, N Vector vtemp3);
Purpose The job of lsetup is to prepare the linear solver for subsequent calls to lsolve, in the
solution of systems Mx =b, where Mis some approximation to the system Jacobian,
J=∂F/∂y +cj ∂F/∂ ˙y. (See Eqn. (2.6), in which α=cj). Here cj is available as
IDA mem->ida cj.
The lsetup function may call a user-supplied function, or a function within the linear
solver module, to compute Jacobian-related data that is required by the linear solver.
It may also preprocess that data as needed for lsolve, which may involve calling a
generic function (such as for LU factorization). This data may be intended either for
direct use (in a direct linear solver) or for use in a preconditioner (in a preconditioned
iterative linear solver).
8.3 Solve function 177
The lsetup function is not called at every time step, but only as frequently as the solver
determines that it is appropriate to perform the setup task. In this way, Jacobian-related
data generated by lsetup is expected to be used over a number of time steps.
Arguments IDA mem is the idas memory pointer of type IDAMem.
yyp is the predicted yvector for the current idas internal step.
ypp is the predicted ˙yvector for the current idas internal step.
resp is the value of the residual function at yyp and ypp, i.e. F(tn, ypred,˙ypred).
vtemp1
vtemp2
vtemp3 are temporary variables of type N Vector provided for use by lsetup.
Return value The lsetup function should return 0 if successful, a positive value for a recoverable
error, and a negative value for an unrecoverable error. On a recoverable error return,
the solver will attempt to recover by reducing the step size.
8.3 Solve function
The type definition of lsolve is
lsolve
Definition int (*lsolve)(IDAMem IDA mem, N Vector b, N Vector weight,
N Vector ycur, N Vector ypcur, N Vector rescur);
Purpose The lsolve function must solve the linear system, Mx =b, where Mis some approxi-
mation to the system Jacobian, J=∂F/∂y+cj ∂F/∂ ˙y(see Eqn. (2.6), in which α=cj),
and the right-hand side vector, b, is input. Here cj is available as IDA mem->ida cj.
lsolve is called once per Newton iteration, hence possibly several times per time step.
If there is an lsetup function, this lsolve function should make use of any Jacobian
data that was computed and preprocessed by lsetup, either for direct use, or for use
in a preconditioner.
Arguments IDA mem is the idas memory pointer of type IDAMem.
bis the right-hand side vector b. The solution is to be returned in the vector b.
weight is a vector that contains the error weights. These are the Wiof (2.7). This
weight vector is included here to enable the computation of weighted norms
needed to test for the convergence of iterative methods (if any) within the
linear solver.
ycur is a vector that contains the solver’s current approximation to y(tn).
ypcur is a vector that contains the solver’s current approximation to ˙y(tn).
rescur is a vector that contains the current residual, F(tn,ycur,ypcur).
Return value The lsolve function should return a positive value for a recoverable error and a neg-
ative value for an unrecoverable error. Success is indicated by a 0 return value. On
a recoverable error return, the solver will attempt to recover, such as by calling the
lsetup function with current arguments.
8.4 Performance monitoring function
The type definition of lperf is

178 Providing Alternate Linear Solver Modules
lperf
Definition int (*lperf)(IDAMem IDA mem, int perftask);
Purpose The lperf function is to monitor the performance of the linear solver. It can be used to
compute performance metrics related to the linear solver and issue warnings if these in-
dicate poor performance of the linear solver. The lperf function is called with perftask
= 0 at the start of each call to IDASolve, and then is called with perftask = 1 just
before each internal time step.
Arguments IDA mem is the idas memory pointer of type IDAMem.
perftask is a task flag. perftask = 0 means initialize needed counters. perftask =
1 means evaluate performance and issue warnings if needed. Counters that
are used to compute performance metrics (e.g. counts of iterations within the
lsolve function) should be initialized here when perftask = 0, and used for
the calculation of metrics when perftask = 1.
Return value The lperf return value is ignored.
8.5 Memory deallocation function
The type definition of lfree is
lfree
Definition int (*lfree)(IDAMem IDA mem);
Purpose The lfree function should free up any memory allocated by the linear solver.
Arguments The argument IDA mem is the idas memory pointer of type IDAMem.
Return value The lfree function should return 0 if successful, or a nonzero if not.
Notes This function is called once a problem has been completed and the linear solver is no
longer needed.

Chapter 9
General Use Linear Solver
Components in SUNDIALS
In this chapter, we describe linear solver code components that are included in sundials, but which
are of potential use as generic packages in themselves, either in conjunction with the use of sundials
or separately.
These generic modules in sundials are organized in three families, the dls family, which includes
direct linear solvers appropriate for sequential computations; the sls family, which includes sparse
matrix solvers; and the spils family, which includes scaled preconditioned iterative (Krylov) linear
solvers. The solvers in each family share common data structures and functions.
The dls family contains the following two generic linear solvers:
•The dense package, a linear solver for dense matrices either specified through a matrix type
(defined below) or as simple arrays.
•The band package, a linear solver for banded matrices either specified through a matrix type
(defined below) or as simple arrays.
Note that this family also includes the Blas/Lapack linear solvers (dense and band) available to the
sundials solvers, but these are not discussed here.
The sls family contains a sparse matrix package and interfaces between it and two sparse direct
solver packages:
•The klu package, a linear solver for compressed-sparse-column matrices, [1,14].
•The superlumt package, a threaded linear solver for compressed-sparse-column matrices, [2,
27,15].
The spils family contains the following generic linear solvers:
•The spgmr package, a solver for the scaled preconditioned GMRES method.
•The spfgmr package, a solver for the scaled preconditioned Flexible GMRES method.
•The spbcg package, a solver for the scaled preconditioned Bi-CGStab method.
•The sptfqmr package, a solver for the scaled preconditioned TFQMR method.
For reasons related to installation, the names of the files involved in these packages begin with the
prefix sundials . But despite this, each of the dls and spils solvers is in fact generic, in that it is
usable completely independently of sundials.
For the sake of space, the functions for the dense and band modules that work with a matrix
type, and the functions in the spgmr,spfgmr,spbcg, and sptfqmr modules are only summarized
briefly, since they are less likely to be of direct use in connection with a sundials solver. However, the

180 General Use Linear Solver Components in SUNDIALS
functions for dense matrices treated as simple arrays and sparse matrices are fully described, because
we expect that they will be useful in the implementation of preconditioners used with the combination
of one of the sundials solvers and one of the spils linear solvers.
9.1 The DLS modules: DENSE and BAND
The files comprising the dense generic linear solver, and their locations in the sundials srcdir, are
as follows:
•header files (located in srcdir/include/sundials)
sundials direct.h,sundials dense.h,
sundials types.h,sundials math.h,sundials config.h
•source files (located in srcdir/src/sundials)
sundials direct.c,sundials dense.c,sundials math.c
The files comprising the band generic linear solver are as follows:
•header files (located in srcdir/include/sundials)
sundials direct.h,sundials band.h,
sundials types.h,sundials math.h,sundials config.h
•source files (located in srcdir/src/sundials)
sundials direct.c,sundials band.c,sundials math.c
Only two of the preprocessing directives in the header file sundials config.h are relevant to the
dense and band packages by themselves.
•(required) definition of the precision of the sundials type realtype. One of the following lines
must be present:
#define SUNDIALS DOUBLE PRECISION 1
#define SUNDIALS SINGLE PRECISION 1
#define SUNDIALS EXTENDED PRECISION 1
•(optional) use of generic math functions: #define SUNDIALS USE GENERIC MATH 1
The sundials types.h header file defines the sundials realtype and booleantype types and the
macro RCONST, while the sundials math.h header file is needed for the macros SUNMIN and SUNMAX,
and the function SUNRabs.
The files listed above for either module can be extracted from the sundials srcdir and compiled
by themselves into a separate library or into a larger user code.
9.1.1 Type DlsMat
The type DlsMat, defined in sundials direct.h is a pointer to a structure defining a generic matrix,
and is used with all linear solvers in the dls family:
typedef struct _DlsMat {
int type;
long int M;
long int N;
long int ldim;
long int mu;
long int ml;
long int s_mu;
realtype *data;
long int ldata;
realtype **cols;
} *DlsMat;

9.1 The DLS modules: DENSE and BAND 181
For the dense module, the relevant fields of this structure are as follows. Note that a dense matrix
of type DlsMat need not be square.
type -SUNDIALS DENSE (=1)
M- number of rows
N- number of columns
ldim - leading dimension (ldim ≥M)
data - pointer to a contiguous block of realtype variables
ldata - length of the data array (= ldim·N). The (i,j)-th element of a dense matrix Aof type DlsMat
(with 0 ≤i<Mand 0 ≤j<N) is given by the expression (A->data)[0][j*M+i]
cols - array of pointers. cols[j] points to the first element of the j-th column of the matrix in the
array data. The (i,j)-th element of a dense matrix Aof type DlsMat (with 0 ≤i<Mand 0 ≤
j<N) is given by the expression (A->cols)[j][i]
For the band module, the relevant fields of this structure are as follows (see Figure 9.1 for a diagram
of the underlying data representation in a banded matrix of type DlsMat). Note that only square
band matrices are allowed.
type -SUNDIALS BAND (=2)
M- number of rows
N- number of columns (N=M)
mu - upper half-bandwidth, 0 ≤mu <min(M,N)
ml - lower half-bandwidth, 0 ≤ml <min(M,N)
s mu - storage upper bandwidth, mu ≤s mu <N. The LU decomposition routine writes the LU
factors into the storage for A. The upper triangular factor U, however, may have an upper
bandwidth as big as min(N-1,mu+ml) because of partial pivoting. The s mu field holds the upper
half-bandwidth allocated for A.
ldim - leading dimension (ldim ≥s mu)
data - pointer to a contiguous block of realtype variables. The elements of a banded matrix of type
DlsMat are stored columnwise (i.e. columns are stored one on top of the other in memory). Only
elements within the specified half-bandwidths are stored. data is a pointer to ldata contiguous
locations which hold the elements within the band of A.
ldata - length of the data array (= ldim·(s mu+ml+1)
cols - array of pointers. cols[j] is a pointer to the uppermost element within the band in the j-th
column. This pointer may be treated as an array indexed from s mu−mu (to access the uppermost
element within the band in the j-th column) to s mu+ml (to access the lowest element within the
band in the j-th column). Indices from 0 to s mu−mu−1 give access to extra storage elements
required by the LU decomposition function. Finally, cols[j][i-j+s mu] is the (i, j)-th element,
j−mu ≤i≤j+ml.
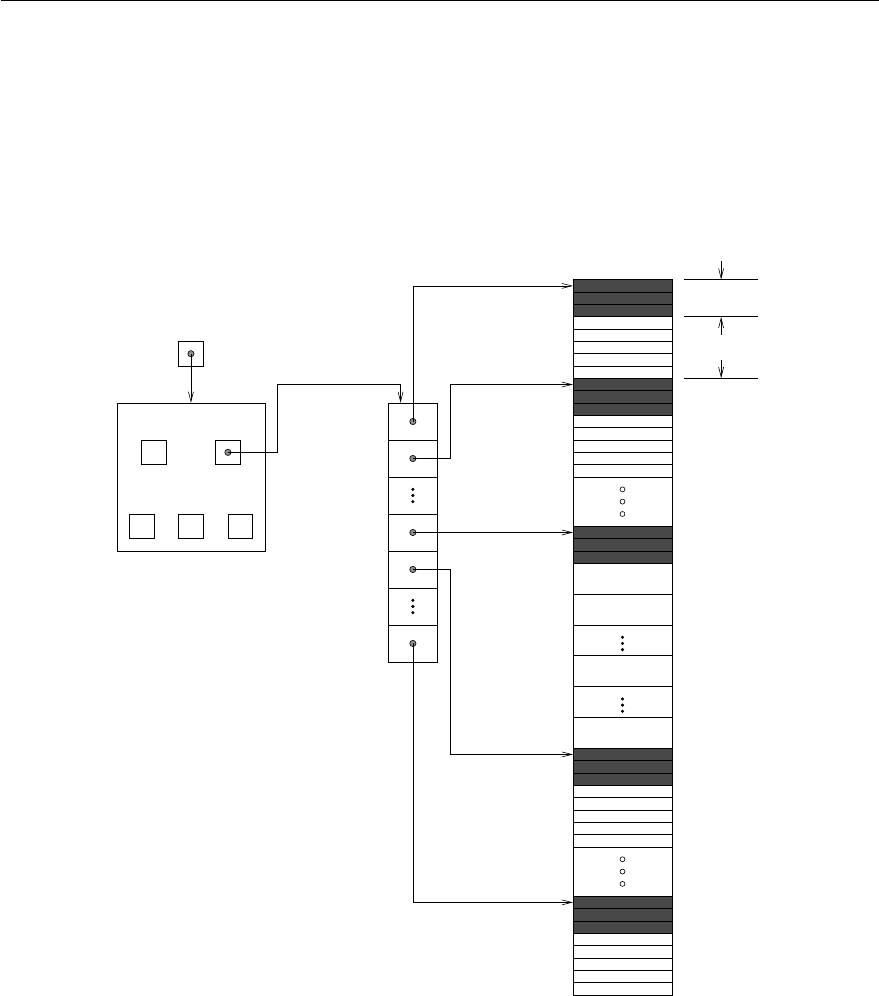
182 General Use Linear Solver Components in SUNDIALS
A (type BandMat)
size data
N
mu ml smu
data[0]
data[1]
data[j]
data[j+1]
data[N−1]
data[j][smu−mu]
data[j][smu]
data[j][smu+ml]
mu+ml+1
smu−mu
A(j−mu−1,j)
A(j−mu,j)
A(j,j)
A(j+ml,j)
Figure 9.1: Diagram of the storage for a banded matrix of type DlsMat. Here Ais an N×Nband
matrix of type DlsMat with upper and lower half-bandwidths mu and ml, respectively. The rows and
columns of Aare numbered from 0 to N−1 and the (i, j)-th element of Ais denoted A(i,j). The
greyed out areas of the underlying component storage are used by the BandGBTRF and BandGBTRS
routines.
9.1 The DLS modules: DENSE and BAND 183
9.1.2 Accessor macros for the DLS modules
The macros below allow a user to efficiently access individual matrix elements without writing out
explicit data structure references and without knowing too much about the underlying element storage.
The only storage assumption needed is that elements are stored columnwise and that a pointer to the
j-th column of elements can be obtained via the DENSE COL or BAND COL macros. Users should use
these macros whenever possible.
The following two macros are defined by the dense module to provide access to data in the DlsMat
type:
•DENSE ELEM
Usage : DENSE ELEM(A,i,j) = a ij; or a ij = DENSE ELEM(A,i,j);
DENSE ELEM references the (i,j)-th element of the M×NDlsMat A, 0 ≤i< M , 0 ≤j< N.
•DENSE COL
Usage : col j = DENSE COL(A,j);
DENSE COL references the j-th column of the M×NDlsMat A, 0 ≤j< N . The type of the
expression DENSE COL(A,j) is realtype * . After the assignment in the usage above, col j
may be treated as an array indexed from 0 to M−1. The (i,j)-th element of Ais referenced
by col j[i].
The following three macros are defined by the band module to provide access to data in the DlsMat
type:
•BAND ELEM
Usage : BAND ELEM(A,i,j) = a ij; or a ij = BAND ELEM(A,i,j);
BAND ELEM references the (i,j)-th element of the N×Nband matrix A, where 0 ≤i,j≤N−1.
The location (i,j) should further satisfy j−(A->mu) ≤i≤j+(A->ml).
•BAND COL
Usage : col j = BAND COL(A,j);
BAND COL references the diagonal element of the j-th column of the N×Nband matrix A, 0 ≤
j≤N−1. The type of the expression BAND COL(A,j) is realtype *. The pointer returned by
the call BAND COL(A,j) can be treated as an array which is indexed from −(A->mu) to (A->ml).
•BAND COL ELEM
Usage : BAND COL ELEM(col j,i,j) = a ij; or a ij = BAND COL ELEM(col j,i,j);
This macro references the (i,j)-th entry of the band matrix Awhen used in conjunction with
BAND COL to reference the j-th column through col j. The index (i,j) should satisfy j−(A->mu)
≤i≤j+(A->ml).
9.1.3 Functions in the DENSE module
The dense module defines two sets of functions with corresponding names. The first set contains
functions (with names starting with a capital letter) that act on dense matrices of type DlsMat. The
second set contains functions (with names starting with a lower case letter) that act on matrices
represented as simple arrays.
The following functions for DlsMat dense matrices are available in the dense package. For full
details, see the header files sundials direct.h and sundials dense.h.
•NewDenseMat: allocation of a DlsMat dense matrix;
•DestroyMat: free memory for a DlsMat matrix;

184 General Use Linear Solver Components in SUNDIALS
•PrintMat: print a DlsMat matrix to standard output.
•NewLintArray: allocation of an array of long int integers for use as pivots with DenseGETRF
and DenseGETRS;
•NewIntArray: allocation of an array of int integers for use as pivots with the Lapack dense
solvers;
•NewRealArray: allocation of an array of realtype for use as right-hand side with DenseGETRS;
•DestroyArray: free memory for an array;
•SetToZero: load a matrix with zeros;
•AddIdentity: increment a square matrix by the identity matrix;
•DenseCopy: copy one matrix to another;
•DenseScale: scale a matrix by a scalar;
•DenseGETRF: LU factorization with partial pivoting;
•DenseGETRS: solution of Ax =busing LU factorization (for square matrices A);
•DensePOTRF: Cholesky factorization of a real symmetric positive matrix;
•DensePOTRS: solution of Ax =busing the Cholesky factorization of A;
•DenseGEQRF: QR factorization of an m×nmatrix, with m≥n;
•DenseORMQR: compute the product w=Qv, with Qcalculated using DenseGEQRF;
•DenseMatvec: compute the product y=Ax, for an Mby Nmatrix A;
The following functions for small dense matrices are available in the dense package:
•newDenseMat
newDenseMat(m,n) allocates storage for an mby ndense matrix. It returns a pointer to the newly
allocated storage if successful. If the memory request cannot be satisfied, then newDenseMat
returns NULL. The underlying type of the dense matrix returned is realtype**. If we allocate
a dense matrix realtype** a by a = newDenseMat(m,n), then a[j][i] references the (i,j)-th
element of the matrix a, 0 ≤i<m, 0 ≤j< n, and a[j] is a pointer to the first element in
the j-th column of a. The location a[0] contains a pointer to m×ncontiguous locations which
contain the elements of a.
•destroyMat
destroyMat(a) frees the dense matrix aallocated by newDenseMat;
•newLintArray
newLintArray(n) allocates an array of nintegers, all long int. It returns a pointer to the first
element in the array if successful. It returns NULL if the memory request could not be satisfied.
•newIntArray
newIntArray(n) allocates an array of nintegers, all int. It returns a pointer to the first element
in the array if successful. It returns NULL if the memory request could not be satisfied.
•newRealArray
newRealArray(n) allocates an array of n realtype values. It returns a pointer to the first
element in the array if successful. It returns NULL if the memory request could not be satisfied.

9.1 The DLS modules: DENSE and BAND 185
•destroyArray
destroyArray(p) frees the array pallocated by newLintArray,newIntArray, or newRealArray;
•denseCopy
denseCopy(a,b,m,n) copies the mby ndense matrix ainto the mby ndense matrix b;
•denseScale
denseScale(c,a,m,n) scales every element in the mby ndense matrix aby the scalar c;
•denseAddIdentity
denseAddIdentity(a,n) increments the square nby ndense matrix aby the identity matrix
In;
•denseGETRF
denseGETRF(a,m,n,p) factors the mby ndense matrix a, using Gaussian elimination with row
pivoting. It overwrites the elements of awith its LU factors and keeps track of the pivot rows
chosen in the pivot array p.
A successful LU factorization leaves the matrix aand the pivot array pwith the following
information:
1. p[k] contains the row number of the pivot element chosen at the beginning of elimination
step k,k= 0,1, ...,n−1.
2. If the unique LU factorization of ais given by P a =LU , where Pis a permutation matrix,
Lis an mby nlower trapezoidal matrix with all diagonal elements equal to 1, and Uis an
nby nupper triangular matrix, then the upper triangular part of a(including its diagonal)
contains Uand the strictly lower trapezoidal part of acontains the multipliers, I−L. If a
is square, Lis a unit lower triangular matrix.
denseGETRF returns 0 if successful. Otherwise it encountered a zero diagonal element during
the factorization, indicating that the matrix adoes not have full column rank. In this case
it returns the column index (numbered from one) at which it encountered the zero.
•denseGETRS
denseGETRS(a,n,p,b) solves the nby nlinear system ax =b. It assumes that a(of size
n×n) has been LU-factored and the pivot array phas been set by a successful call to
denseGETRF(a,n,n,p). The solution xis written into the barray.
•densePOTRF
densePOTRF(a,m) calculates the Cholesky decomposition of the mby mdense matrix a, assumed
to be symmetric positive definite. Only the lower triangle of ais accessed and overwritten with
the Cholesky factor.
•densePOTRS
densePOTRS(a,m,b) solves the mby mlinear system ax =b. It assumes that the Cholesky
factorization of ahas been calculated in the lower triangular part of aby a successful call to
densePOTRF(a,m).
•denseGEQRF
denseGEQRF(a,m,n,beta,wrk) calculates the QR decomposition of the mby nmatrix a(m≥
n) using Householder reflections. On exit, the elements on and above the diagonal of acontain
the nby nupper triangular matrix R; the elements below the diagonal, with the array beta,
represent the orthogonal matrix Qas a product of elementary reflectors. The real array wrk, of
length m, must be provided as temporary workspace.

186 General Use Linear Solver Components in SUNDIALS
•denseORMQR
denseORMQR(a,m,n,beta,v,w,wrk) calculates the product w=Qv for a given vector vof length
n, where the orthogonal matrix Qis encoded in the mby nmatrix aand the vector beta of
length n, after a successful call to denseGEQRF(a,m,n,beta,wrk). The real array wrk, of length
m, must be provided as temporary workspace.
•denseMatvec
denseMatvec(a,x,y,m,n) calculates the product y=ax for a given vector xof length n, and m
by nmatrix a.
9.1.4 Functions in the BAND module
The band module defines two sets of functions with corresponding names. The first set contains
functions (with names starting with a capital letter) that act on band matrices of type DlsMat. The
second set contains functions (with names starting with a lower case letter) that act on matrices
represented as simple arrays.
The following functions for DlsMat banded matrices are available in the band package. For full
details, see the header files sundials direct.h and sundials band.h.
•NewBandMat: allocation of a DlsMat band matrix;
•DestroyMat: free memory for a DlsMat matrix;
•PrintMat: print a DlsMat matrix to standard output.
•NewLintArray: allocation of an array of int integers for use as pivots with BandGBRF and
BandGBRS;
•NewIntArray: allocation of an array of int integers for use as pivots with the Lapack band
solvers;
•NewRealArray: allocation of an array of realtype for use as right-hand side with BandGBRS;
•DestroyArray: free memory for an array;
•SetToZero: load a matrix with zeros;
•AddIdentity: increment a square matrix by the identity matrix;
•BandCopy: copy one matrix to another;
•BandScale: scale a matrix by a scalar;
•BandGBTRF: LU factorization with partial pivoting;
•BandGBTRS: solution of Ax =busing LU factorization;
•BandMatvec: compute the product y=Ax, for a square band matrix A;
The following functions for small band matrices are available in the band package:
•newBandMat
newBandMat(n, smu, ml) allocates storage for an nby nband matrix with lower half-bandwidth
ml.
•destroyMat
destroyMat(a) frees the band matrix aallocated by newBandMat;

9.2 The SLS module 187
•newLintArray
newLintArray(n) allocates an array of nintegers, all long int. It returns a pointer to the first
element in the array if successful. It returns NULL if the memory request could not be satisfied.
•newIntArray
newIntArray(n) allocates an array of nintegers, all int. It returns a pointer to the first element
in the array if successful. It returns NULL if the memory request could not be satisfied.
•newRealArray
newRealArray(n) allocates an array of n realtype values. It returns a pointer to the first
element in the array if successful. It returns NULL if the memory request could not be satisfied.
•destroyArray
destroyArray(p) frees the array pallocated by newLintArray,newIntArray, or newRealArray;
•bandCopy
bandCopy(a,b,n,a smu, b smu,copymu, copyml) copies the nby nband matrix ainto the n
by nband matrix b;
•bandScale
bandScale(c,a,n,mu,ml,smu) scales every element in the nby nband matrix aby c;
•bandAddIdentity
bandAddIdentity(a,n,smu) increments the nby nband matrix aby the identity matrix;
•bandGETRF
bandGETRF(a,n,mu,ml,smu,p) factors the nby nband matrix a, using Gaussian elimination
with row pivoting. It overwrites the elements of awith its LU factors and keeps track of the
pivot rows chosen in the pivot array p.
•bandGETRS
bandGETRS(a,n,smu,ml,p,b) solves the nby nlinear system ax =b. It assumes that a(of
size n×n) has been LU-factored and the pivot array phas been set by a successful call to
bandGETRF(a,n,mu,ml,smu,p). The solution xis written into the barray.
•bandMatvec
bandMatvec(a,x,y,n,mu,ml,smu) calculates the product y=ax for a given vector xof length
n, and nby nband matrix a.
9.2 The SLS module
sundials provides a compressed-sparse-column matrix type and sparse matrix support functions. In
addition, sundials provides interfaces to the publically available KLU and SuperLU MT sparse direct
solver packages. The files comprising the sls matrix module, used in the klu and superlumt linear
solver packages, and their locations in the sundials srcdir, are as follows:
•header files (located in srcdir/include/sundials)
sundials sparse.h,sundials klu impl.h,
sundials superlumt impl.h,sundials types.h,
sundials math.h,sundials config.h
•source files (located in srcdir/src/sundials)
sundials sparse.c,sundials math.c

188 General Use Linear Solver Components in SUNDIALS
Only two of the preprocessing directives in the header file sundials config.h are relevant to the sls
package by itself:
•(required) definition of the precision of the sundials type realtype. One of the following lines
must be present:
#define SUNDIALS DOUBLE PRECISION 1
#define SUNDIALS SINGLE PRECISION 1
#define SUNDIALS EXTENDED PRECISION 1
•(optional) use of generic math functions: #define SUNDIALS USE GENERIC MATH 1
The sundials types.h header file defines the sundials realtype and booleantype types and the
macro RCONST, while the sundials math.h header file is needed for the macros SUNMIN and SUNMAX,
and the function SUNRabs.
9.2.1 Type SlsMat
sundials supports operations with compressed-sparse-column (CSC) and compressed-sparse-row (CSR)
matrices. For convenience integer sparse matrix identifiers are defined as:
#define CSC MAT 0
#define CSR MAT 1
The type SlsMat, defined in sundials sparse.h is a pointer to a structure defining generic CSC
and CSR matrix formats, and is used with all linear solvers in the sls family:
typedef struct _SlsMat {
int M;
int N;
int NNZ;
int NP;
realtype *data;
int sparsetype;
int *indexvals;
int *indexptrs;
int **rowvals;
int **colptrs;
int **colvals;
int **rowptrs;
} *SlsMat;
The fields of this structure are as follows (see Figure 9.2 for a diagram of the underlying compressed-
sparse-column representation in a sparse matrix of type SlsMat). Note that a sparse matrix of type
SlsMat need not be square.
M- number of rows
N- number of columns
NNZ - maximum number of nonzero entries in the matrix (allocated length of data and rowvals
arrays)
NP - number of index pointers (e.g. number of column pointers for CSC matrix). For CSC matrices
NP =N, and for CSR matrices NP =M. This value is set automatically based the input for
sparsetype.
data - pointer to a contiguous block of realtype variables (of length NNZ), containing the values of
the nonzero entries in the matrix
sparsetype - type of the sparse matrix (CSC MAT or CSR MAT)

9.2 The SLS module 189
indexvals - pointer to a contiguous block of int variables (of length NNZ), containing the row indices
(if CSC) or column indices (if CSR) of each nonzero matrix entry held in data
indexptrs - pointer to a contiguous block of int variables (of length NP+1). For CSC matrices each
entry provides the index of the first column entry into the data and indexvals arrays, e.g. if
indexptr[3]=7, then the first nonzero entry in the fourth column of the matrix is located in
data[7], and is located in row indexvals[7] of the matrix. The last entry contains the total
number of nonzero values in the matrix and hence points one past the end of the active data in
the data and indexvals arrays. For CSR matrices, each entry provides the index of the first
row entry into the data and indexvals arrays.
The following pointers are added to the SlsMat type for user convenience, to provide a more intuitive
interface to the CSC and CSR sparse matrix data structures. They are set automatically by the
SparseNewMat function, based on the sparse matrix storage type.
rowvals - pointer to indexvals when sparsetype is CSC MAT, otherwise set to NULL.
colptrs - pointer to indexptrs when sparsetype is CSC MAT, otherwise set to NULL.
colvals - pointer to indexvals when sparsetype is CSR MAT, otherwise set to NULL.
rowptrs - pointer to indexptrs when sparsetype is CSR MAT, otherwise set to NULL.
For example, the 5 ×4 CSC matrix
0310
3002
0700
1009
0005
could be stored in a SlsMat structure as either
M = 5;
N = 4;
NNZ = 8;
NP = N;
data = {3.0, 1.0, 3.0, 7.0, 1.0, 2.0, 9.0, 5.0};
sparsetype = CSC_MAT;
indexvals = {1, 3, 0, 2, 0, 1, 3, 4};
indexptrs = {0, 2, 4, 5, 8};
rowvals = &indexvals;
colptrs = &indexptrs;
colvals = NULL;
rowptrs = NULL;
or
M = 5;
N = 4;
NNZ = 10;
NP = N;
data = {3.0, 1.0, 3.0, 7.0, 1.0, 2.0, 9.0, 5.0, *, *};
sparsetype = CSC_MAT;
indexvals = {1, 3, 0, 2, 0, 1, 3, 4, *, *};
indexptrs = {0, 2, 4, 5, 8};
...
where the first has no unused space, and the second has additional storage (the entries marked with
*may contain any values). Note in both cases that the final value in indexptrs is 8. The work
associated with operations on the sparse matrix is proportional to this value and so one should use
the best understanding of the number of nonzeroes here.
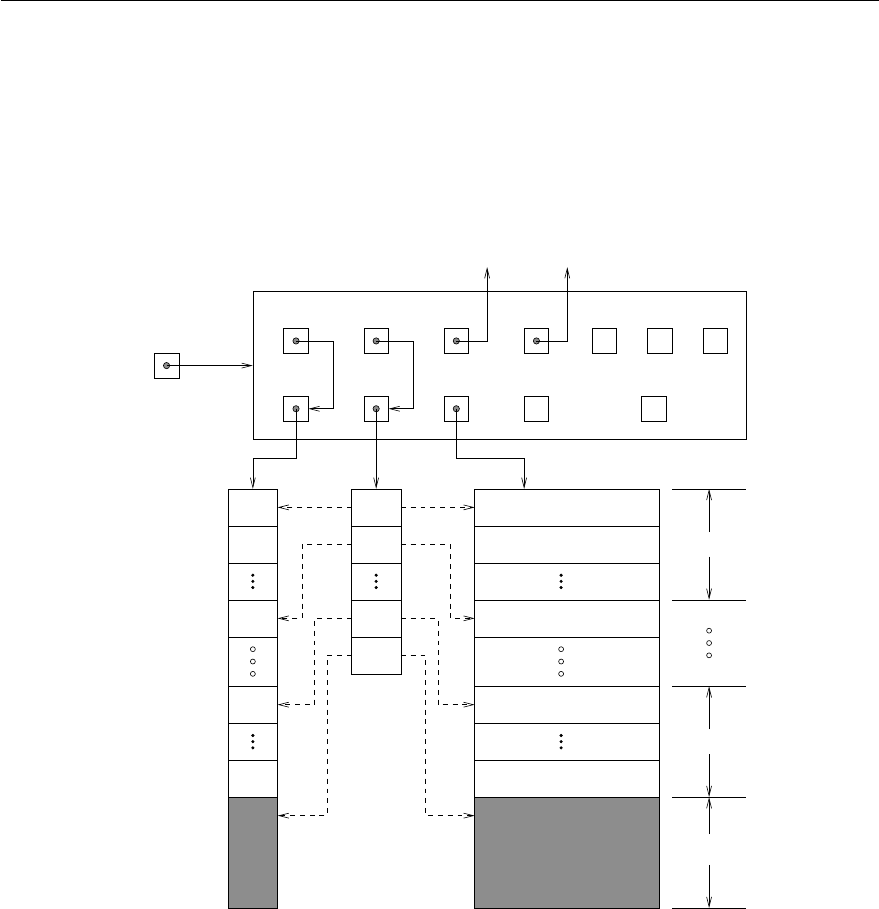
190 General Use Linear Solver Components in SUNDIALS
data
A (type SlsMat)
k
nz
0
j column 0
unused
storage
rowvals colptrs
indexvals indexptrs
colvals rowptrs
NULL NULL
A(*rowvals[j],1)
A(*rowvals[1],0)
A(*rowvals[0],0)
A(*rowvals[k],NP−1)
A(*rowvals[nz−1],NP−1)
column NP−1
NNZ
M
sparsetype=CSC_MAT
NNP = N
Figure 9.2: Diagram of the storage for a compressed-sparse-column matrix of type SlsMat. Here A
is an M×Nsparse matrix of type SlsMat with storage for up to NNZ nonzero entries (the allocated
length of both data and indexvals). The entries in indexvals may assume values from 0 to M−1,
corresponding to the row index (zero-based) of each nonzero value. The entries in data contain the
values of the nonzero entries, with the row i, column jentry of A(again, zero-based) denoted as
A(i,j). The indexptrs array contains N+ 1 entries; the first Ndenote the starting index of each
column within the indexvals and data arrays, while the final entry points one past the final nonzero
entry. Here, although NNZ values are allocated, only nz are actually filled in; the greyed-out portions
of data and indexvals indicate extra allocated space.

9.2 The SLS module 191
9.2.2 Functions in the SLS module
The sls module defines functions that act on sparse matrices of type SlsMat. For full details, see the
header file sundials sparse.h.
•SparseNewMat
SparseNewMat(M, N, NNZ, sparsetype) allocates storage for an Mby Nsparse matrix, with
storage for up to NNZ nonzero entries and sparsetype storage type (CSC MAT or CSR MAT).
•SparseFromDenseMat
SparseFromDenseMat(A) converts a dense or band matrix Aof type DlsMat into a new CSC
matrix of type SlsMat by retaining only the nonzero values of the matrix A.
•SparseDestroyMat
SparseDestroyMat(A) frees the memory for a sparse matrix Aallocated by either SparseNewMat
or SparseFromDenseMat.
•SparseSetMatToZero(A) zeros out the SlsMat matrix A. The storage for Ais left unchanged.
•SparseCopyMat
SparseCopyMat(A, B) copies the SlsMat A into the SlsMat B. It is assumed that the matrices
have the same row/column dimensions and storage type. If Bhas insufficient storage to hold all
the nonzero entries of A, the data and index arrays in Bare reallocated to match those in A.
•SparseScaleMat
SparseScaleMat(c, A) scales every element in the SlsMat A by the realtype scalar c.
•SparseAddIdentityMat
SparseAddIdentityMat(A) increments the SlsMat A by the identity matrix. If Ais not square,
only the existing diagonal values are incremented. Resizes the data and rowvals arrays of Ato
allow for new nonzero entries on the diagonal.
•SparseAddMat
SparseAddMat(A, B) adds two SlsMat matrices Aand B, placing the result back in A. Resizes
the data and rowvals arrays of Aupon completion to exactly match the nonzero storage for
the result. Upon successful completion, the return value is zero; otherwise -1 is returned. It is
assumed that both matrices have the same size and storage type.
•SparseReallocMat
SparseReallocMat(A) eliminates unused storage in the SlsMat A by resizing the internal data
and rowvals arrays to contain exactly colptrs[N] values.
•SparseMatvec
SparseMatvec(A, x, y) computes the sparse matrix-vector product, y=Ax. If the SlsMat A
is a sparse matrix of dimension M×N, then it is assumed that xis a realtype array of length
N, and yis a realtype array of length M. Upon successful completion, the return value is zero;
otherwise -1 is returned.
•SparsePrintMat
SparsePrintMat(A) Prints the SlsMat matrix Ato standard output.

192 General Use Linear Solver Components in SUNDIALS
9.2.3 The KLU solver
klu is a sparse matrix factorization and solver library written by Tim Davis [1,14]. klu has a
symbolic factorization routine that computes the permutation of the linear system matrix to block
triangular form and the permutations that will pre-order the diagonal blocks (the only ones that need
to be factored) to reduce fill-in (using AMD, COLAMD, CHOLAMD, natural, or an ordering given
by the user). Note that SUNDIALS uses the COLAMD ordering by default with klu.
klu breaks the factorization into two separate parts. The first is a symbolic factorization and the
second is a numeric factorization that returns the factored matrix along with final pivot information.
klu also has a refactor routine that can be called instead of the numeric factorization. This routine
will reuse the pivot information. This routine also returns diagnostic information that a user can
examine to determine if numerical stability is being lost and a full numerical factorization should be
done instead of the refactor.
The klu interface in sundials will perform the symbolic factorization once. It then calls the
numerical factorization once and will call the refactor routine until estimates of the numerical condi-
tioning suggest a new factorization should be completed. The klu interface also has a ReInit routine
that can be used to force a full refactorization at the next solver setup call.
In order to use the sundials interface to klu, it is assumed that klu has been installed on the
system prior to installation of sundials, and that sundials has been configured appropriately to link
with klu (see Appendix Afor details).
Designed for serial calculations only, klu is supported for calculations employing sundials’ serial
or shared-memory parallel nvector modules (see Sections 7.1,7.3 and 7.4 for details).
9.2.4 The SUPERLUMT solver
superlumt is a threaded sparse matrix factorization and solver library written by X. Sherry Li
[2,27,15]. The package performs matrix factorization using threads to enhance efficiency in shared
memory parallel environments. It should be noted that threads are only used in the factorization step.
In order to use the sundials interface to superlumt, it is assumed that superlumt has been
installed on the system prior to installation of sundials, and that sundials has been configured
appropriately to link with superlumt (see Appendix Afor details).
Designed for serial and threaded calculations only, superlumt is supported for calculations em-
ploying sundials’ serial or shared-memory parallel nvector modules (see Sections 7.1,7.3 and 7.4
for details).
9.3 The SPILS modules: SPGMR, SPFGMR, SPBCG, and
SPTFQMR
The spils modules contain implementations of some of the most commonly use scaled preconditioned
Krylov solvers. A linear solver module from the spils family can be used in conjunction with any
nvector implementation library.
9.3.1 The SPGMR module
The spgmr package, in the files sundials spgmr.h and sundials spgmr.c, includes an implemen-
tation of the scaled preconditioned GMRES method. A separate code module, implemented in
sundials iterative.(h,c), contains auxiliary functions that support spgmr, as well as the other
Krylov solvers in sundials (spfgmr,spbcg, and sptfqmr). For full details, including usage instruc-
tions, see the header files sundials spgmr.h and sundials iterative.h.
The files comprising the spgmr generic linear solver, and their locations in the sundials srcdir,
are as follows:
•header files (located in srcdir/include/sundials)
sundials spgmr.h,sundials iterative.h,sundials nvector.h,
9.3 The SPILS modules: SPGMR, SPFGMR, SPBCG, and SPTFQMR 193
sundials types.h,sundials math.h,sundials config.h
•source files (located in srcdir/src/sundials)
sundials spgmr.c,sundials iterative.c,sundials nvector.c
Only two of the preprocessing directives in the header file sundials config.h are required to use the
spgmr package by itself:
•(required) definition of the precision of the sundials type realtype. One of the following lines
must be present:
#define SUNDIALS DOUBLE PRECISION 1
#define SUNDIALS SINGLE PRECISION 1
#define SUNDIALS EXTENDED PRECISION 1
•(optional) use of generic math functions:
#define SUNDIALS USE GENERIC MATH 1
The sundials types.h header file defines the sundials realtype and booleantype types and the
macro RCONST, while the sundials math.h header file is needed for the macros SUNMIN,SUNMAX, and
SUNSQR, and the functions SUNRabs and SUNRsqrt.
The generic nvector files, sundials nvector.(h,c) are needed for the definition of the generic
N Vector type and functions. The nvector functions used by the spgmr module are: N VDotProd,
N VLinearSum,N VScale,N VProd,N VDiv,N VConst,N VClone,N VCloneVectorArray,N VDestroy,
and N VDestroyVectorArray.
The nine files listed above can be extracted from the sundials srcdir and compiled by themselves
into an spgmr library or into a larger user code.
The following functions are available in the spgmr package:
•SpgmrMalloc: allocation of memory for SpgmrSolve;
•SpgmrSolve: solution of Ax =bby the spgmr method;
•SpgmrFree: free memory allocated by SpgmrMalloc.
The following functions are available in the support package sundials iterative.(h,c):
•ModifiedGS: performs modified Gram-Schmidt procedure;
•ClassicalGS: performs classical Gram-Schmidt procedure;
•QRfact: performs QR factorization of Hessenberg matrix;
•QRsol: solves a least squares problem with a Hessenberg matrix factored by QRfact.
9.3.2 The SPFGMR module
The spfgmr package, in the files sundials spfgmr.h and sundials spfgmr.c, includes an imple-
mentation of the scaled preconditioned Flexible GMRES method. For full details, including usage
instructions, see the file sundials spfgmr.h.
The files needed to use the spfgmr module by itself are the same as for the spgmr module, but
with sundials spfgmr.(h,c) in place of sundials spgmr.(h,c).
The following functions are available in the spfgmr package:
•SpfgmrMalloc: allocation of memory for SpfgmrSolve;
•SpfgmrSolve: solution of Ax =bby the spfgmr method;
•SpfgmrFree: free memory allocated by SpfgmrMalloc.

194 General Use Linear Solver Components in SUNDIALS
9.3.3 The SPBCG module
The spbcg package, in the files sundials spbcgs.h and sundials spbcgs.c, includes an implemen-
tation of the scaled preconditioned Bi-CGStab method. For full details, including usage instructions,
see the file sundials spbcgs.h.
The files needed to use the spbcg module by itself are the same as for the spgmr module, but
with sundials spbcgs.(h,c) in place of sundials spgmr.(h,c).
The following functions are available in the spbcg package:
•SpbcgMalloc: allocation of memory for SpbcgSolve;
•SpbcgSolve: solution of Ax =bby the spbcg method;
•SpbcgFree: free memory allocated by SpbcgMalloc.
9.3.4 The SPTFQMR module
The sptfqmr package, in the files sundials sptfqmr.h and sundials sptfqmr.c, includes an imple-
mentation of the scaled preconditioned TFQMR method. For full details, including usage instructions,
see the file sundials sptfqmr.h.
The files needed to use the sptfqmr module by itself are the same as for the spgmr module, but
with sundials sptfqmr.(h,c) in place of sundials spgmr.(h,c).
The following functions are available in the sptfqmr package:
•SptfqmrMalloc: allocation of memory for SptfqmrSolve;
•SptfqmrSolve: solution of Ax =bby the sptfqmr method;
•SptfqmrFree: free memory allocated by SptfqmrMalloc.

Appendix A
SUNDIALS Package Installation
Procedure
The installation of any sundials package is accomplished by installing the sundials suite as a whole,
according to the instructions that follow. The same procedure applies whether or not the downloaded
file contains one or all solvers in sundials.
The sundials suite (or individual solvers) are distributed as compressed archives (.tar.gz).
The name of the distribution archive is of the form solver-x.y.z.tar.gz, where solver is one of:
sundials,cvode,cvodes,arkode,ida,idas, or kinsol, and x.y.z represents the version number
(of the sundials suite or of the individual solver) . To begin the installation, first uncompress and
expand the sources, by issuing
% tar xzf solver-x.y.z.tar.gz
This will extract source files under a directory solver-x.y.z.
Starting with version 2.6.0 of sundials, CMake is the only supported method of installation.
The explanations on the installation procedure begins with a few common observations:
•The remainder of this chapter will follow these conventions:
srcdir is the directory solver-x.y.z created above; i.e., the directory containing the sundials
sources.
builddir is the (temporary) directory under which sundials is built.
instdir is the directory under which the sundials exported header files and libraries will be
installed. Typically, header files are exported under a directory instdir/include while
libraries are installed under instdir/lib, with instdir specified at configuration time.
•For sundials CMake-based installation, in-source builds are prohibited; in other words, the
build directory builddir can not be the same as srcdir and such an attempt will lead to an error.
This prevents “polluting” the source tree and allows efficient builds for different configurations
and/or options.
•The installation directory instdir can not be the same as the source directory srcdir.
!
•By default, only the libraries and header files are exported to the installation directory instdir.
If enabled by the user (with the appropriate toggle for CMake), the examples distributed with
sundials will be built together with the solver libraries but the installation step will result
in exporting (by default in a subdirectory of the installation directory) the example sources
and sample outputs together with automatically generated configuration files that reference the
installed sundials headers and libraries. As such, these configuration files for the sundials ex-
amples can be used as ”templates” for your own problems. CMake installs CMakeLists.txt files
and also (as an option available only under Unix/Linux) Makefile files. Note this installation

196 SUNDIALS Package Installation Procedure
approach also allows the option of building the sundials examples without having to install
them. (This can be used as a sanity check for the freshly built libraries.)
•Even if generation of shared libraries is enabled, only static libraries are created for the FCMIX
modules. (Because of the use of fixed names for the Fortran user-provided subroutines, FCMIX
shared libraries would result in ”undefined symbol” errors at link time.)
A.1 CMake-based installation
CMake-based installation provides a platform-independent build system. CMake can generate Unix
and Linux Makefiles, as well as KDevelop, Visual Studio, and (Apple) XCode project files from the
same configuration file. In addition, CMake also provides a GUI front end and which allows an
interactive build and installation process.
The sundials build process requires CMake version 2.8.1 or higher and a working compiler. On
Unix-like operating systems, it also requires Make (and curses, including its development libraries, for
the GUI front end to CMake, ccmake), while on Windows it requires Visual Studio. While many Linux
distributions offer CMake, the version included is probably out of date. Many new CMake features
have been added recently, and you should download the latest version from http://www.cmake.org.
Build instructions for CMake (only necessary for Unix-like systems) can be found on the CMake
website. Once CMake is installed, Linux/Unix users will be able to use ccmake, while Windows users
will be able to use CMakeSetup.
As previously noted, when using CMake to configure, build and install sundials, it is always
required to use a separate build directory. While in-source builds are possible, they are explicitly
prohibited by the sundials CMake scripts (one of the reasons being that, unlike autotools, CMake
does not provide a make distclean procedure and it is therefore difficult to clean-up the source tree
after an in-source build). By ensuring a separate build directory, it is an easy task for the user to
clean-up all traces of the build by simply removing the build directory. CMake does generate a make
clean which will remove files generated by the compiler and linker.
A.1.1 Configuring, building, and installing on Unix-like systems
The default CMake configuration will build all included solvers and associated examples and will build
static and shared libraries. The installdir defaults to /usr/local and can be changed by setting the
CMAKE INSTALL PREFIX variable. Support for FORTRAN and all other options are disabled.
CMake can be used from the command line with the cmake command, or from a curses-based
GUI by using the ccmake command. Examples for using both methods will be presented. For the
examples shown it is assumed that there is a top level sundials directory with appropriate source,
build and install directories:
% mkdir (...)sundials/instdir
% mkdir (...)sundials/builddir
% cd (...)sundials/builddir
Building with the GUI
Using CMake with the GUI follows this general process:
•Select and modify values, run configure (ckey)
•New values are denoted with an asterisk
•To set a variable, move the cursor to the variable and press enter
–If it is a boolean (ON/OFF) it will toggle the value
–If it is string or file, it will allow editing of the string
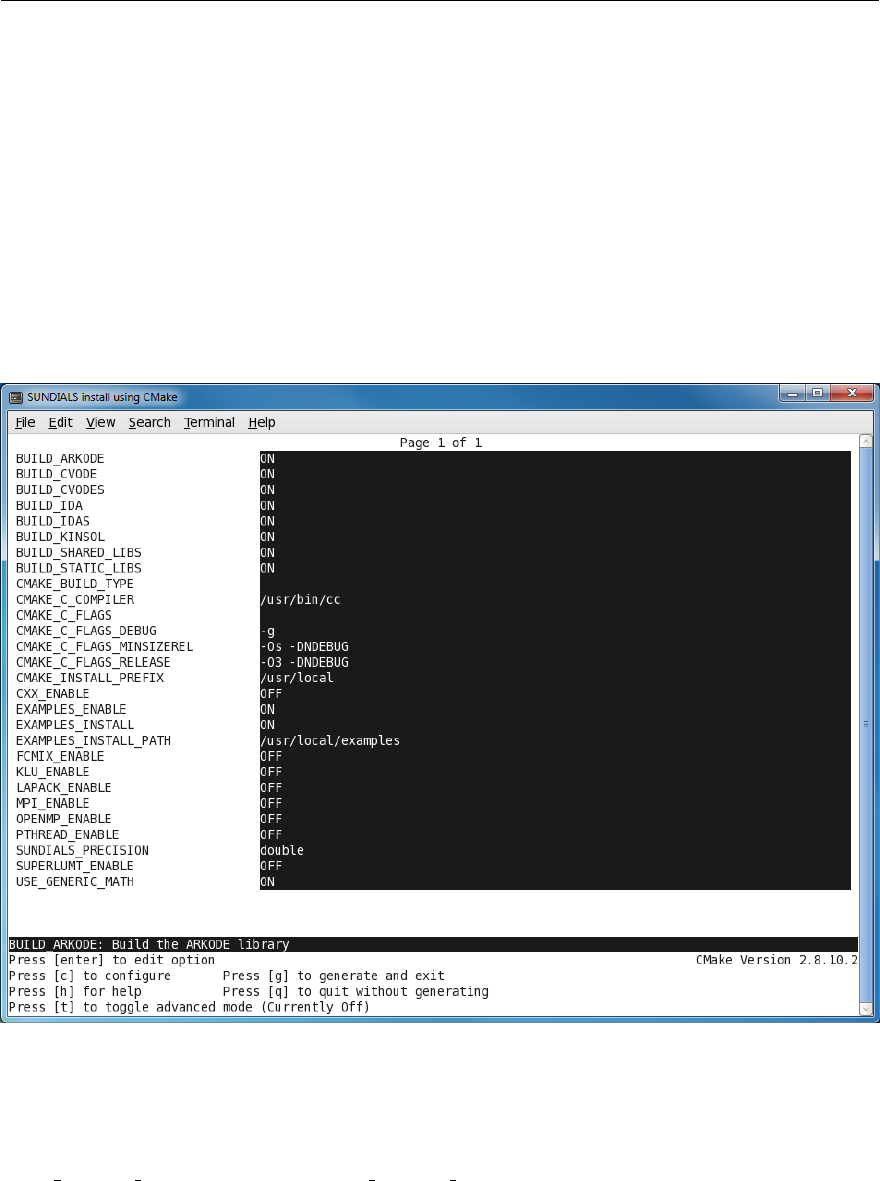
A.1 CMake-based installation 197
–For file and directories, the <tab> key can be used to complete
•Repeat until all values are set as desired and the generate option is available (gkey)
•Some variables (advanced variables) are not visible right away
•To see advanced variables, toggle to advanced mode (tkey)
•To search for a variable press /key, and to repeat the search, press the nkey
To build the default configuration using the GUI, from the builddir enter the ccmake command
and point to the srcdir:
% ccmake ../srcdir
The default configuration screen is shown in Figure A.1.
Figure A.1: Default configuration screen. Note: Initial screen is empty. To get this default config-
uration, press ’c’ repeatedly (accepting default values denoted with asterisk) until the ’g’ option is
available.
The default instdir for both sundials and corresponding examples can be changed by setting the
CMAKE INSTALL PREFIX and the EXAMPLES INSTALL PATH as shown in figure A.2.
Pressing the (gkey) will generate makefiles including all dependencies and all rules to build sun-
dials on this system. Back at the command prompt, you can now run:
% make
To install sundials in the installation directory specified in the configuration, simply run:
% make install
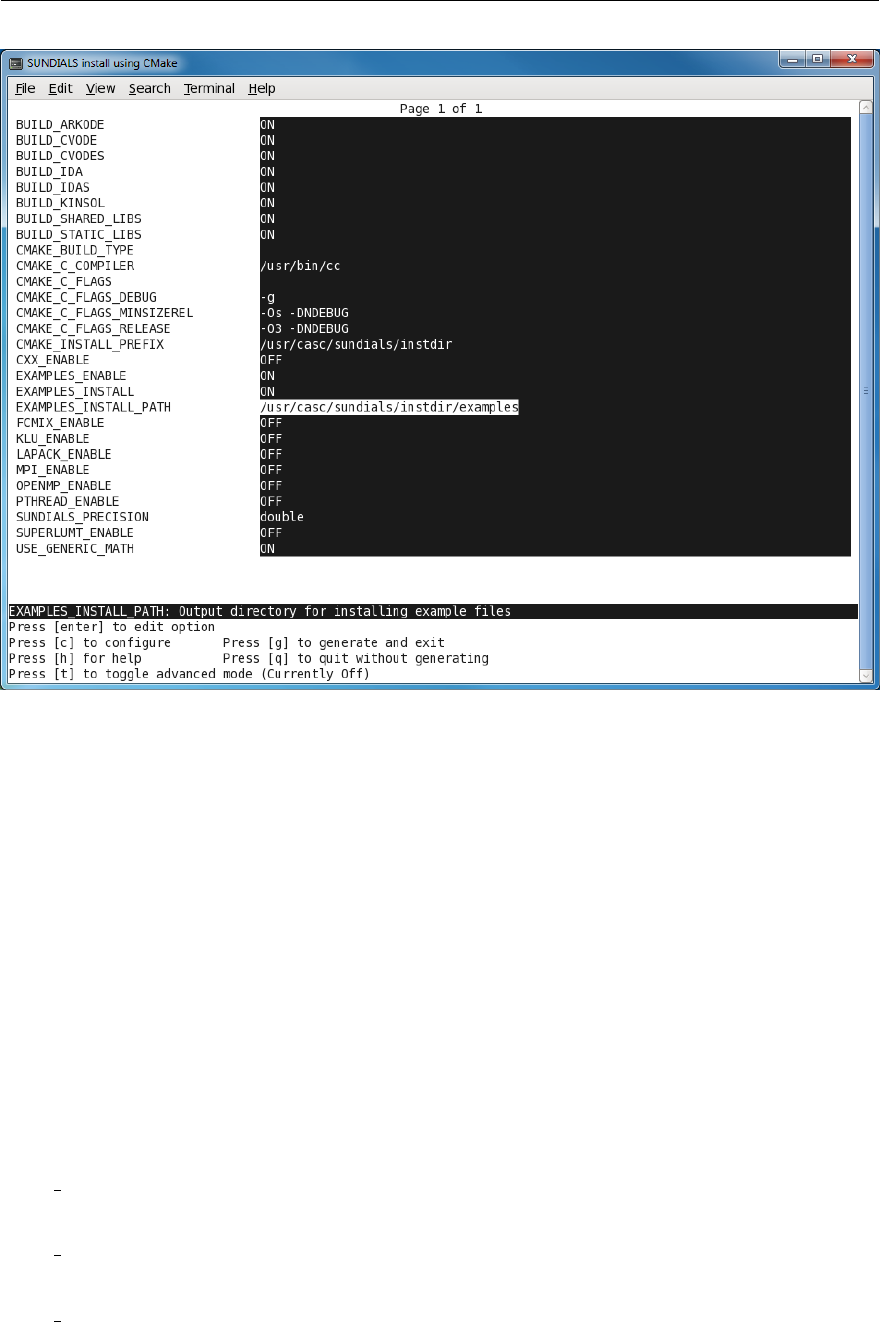
198 SUNDIALS Package Installation Procedure
Figure A.2: Changing the instdir for sundials and corresponding examples
Building from the command line
Using CMake from the command line is simply a matter of specifying CMake variable settings with
the cmake command. The following will build the default configuration:
% cmake -DCMAKE_INSTALL_PREFIX=/home/myname/sundials/instdir \
> -DEXAMPLES_INSTALL_PATH=/home/myname/sundials/instdir/examples \
> ../srcdir
% make
% make install
A.1.2 Configuration options (Unix/Linux)
A complete list of all available options for a CMake-based sundials configuration is provide below.
Note that the default values shown are for a typical configuration on a Linux system and are provided
as illustration only.
BUILD ARKODE - Build the ARKODE library
Default: ON
BUILD CVODE - Build the CVODE library
Default: ON
BUILD CVODES - Build the CVODES library
Default: ON

A.1 CMake-based installation 199
BUILD IDA - Build the IDA library
Default: ON
BUILD IDAS - Build the IDAS library
Default: ON
BUILD KINSOL - Build the KINSOL library
Default: ON
BUILD SHARED LIBS - Build shared libraries
Default: OFF
BUILD STATIC LIBS - Build static libraries
Default: ON
CMAKE BUILD TYPE - Choose the type of build, options are: None (CMAKE C FLAGS used) Debug
Release RelWithDebInfo MinSizeRel
Default:
CMAKE C COMPILER - C compiler
Default: /usr/bin/cc
CMAKE C FLAGS - Flags for C compiler
Default:
CMAKE C FLAGS DEBUG - Flags used by the compiler during debug builds
Default: -g
CMAKE C FLAGS MINSIZEREL - Flags used by the compiler during release minsize builds
Default: -Os -DNDEBUG
CMAKE C FLAGS RELEASE - Flags used by the compiler during release builds
Default: -O3 -DNDEBUG
CMAKE Fortran COMPILER - Fortran compiler
Default: /usr/bin/gfortran
Note: Fortran support (and all related options) are triggered only if either Fortran-C support is
enabled (FCMIX ENABLE is ON) or Blas/Lapack support is enabled (LAPACK ENABLE is ON).
CMAKE Fortran FLAGS - Flags for Fortran compiler
Default:
CMAKE Fortran FLAGS DEBUG - Flags used by the compiler during debug builds
Default:
CMAKE Fortran FLAGS MINSIZEREL - Flags used by the compiler during release minsize builds
Default:
CMAKE Fortran FLAGS RELEASE - Flags used by the compiler during release builds
Default:
CMAKE INSTALL PREFIX - Install path prefix, prepended onto install directories
Default: /usr/local
Note: The user must have write access to the location specified through this option. Exported
sundials header files and libraries will be installed under subdirectories include and lib of
CMAKE INSTALL PREFIX, respectively.
EXAMPLES ENABLE - Build the sundials examples
Default: ON
200 SUNDIALS Package Installation Procedure
EXAMPLES INSTALL - Install example files
Default: ON
Note: This option is triggered only if building example programs is enabled (EXAMPLES ENABLE
ON). If the user requires installation of example programs then the sources and sample output
files for all sundials modules that are currently enabled will be exported to the directory
specified by EXAMPLES INSTALL PATH. A CMake configuration script will also be automatically
generated and exported to the same directory. Additionally, if the configuration is done under
a Unix-like system, makefiles for the compilation of the example programs (using the installed
sundials libraries) will be automatically generated and exported to the directory specified by
EXAMPLES INSTALL PATH.
EXAMPLES INSTALL PATH - Output directory for installing example files
Default: /usr/local/examples
Note: The actual default value for this option will an examples subdirectory created under
CMAKE INSTALL PREFIX.
FCMIX ENABLE - Enable Fortran-C support
Default: OFF
HYPRE ENABLE - Enable hypre support
Default: OFF
HYPRE INCLUDE DIR - Path to hypre header files
HYPRE LIBRARY - Path to hypre installed library
KLU ENABLE - Enable KLU support
Default: OFF
KLU INCLUDE DIR - Path to SuiteSparse header files
KLU LIBRARY DIR - Path to SuiteSparse installed library files
LAPACK ENABLE - Enable Lapack support
Default: OFF
Note: Setting this option to ON will trigger the two additional options see below.
LAPACK LIBRARIES - Lapack (and Blas) libraries
Default: /usr/lib/liblapack.so;/usr/lib/libblas.so
Note: CMake will search for these libraries in your LD LIBRARY PATH prior to searching default
system paths.
MPI ENABLE - Enable MPI support
Default: OFF
Note: Setting this option to ON will trigger several additional options related to MPI.
MPI MPICC -mpicc program
Default:
MPI RUN COMMAND - Specify run command for MPI
Default: mpirun
Note: This can either be set to mpirun for OpenMPI or srun if jobs are managed by SLURM -
Simple Linux Utility for Resource Management as exists on LLNL’s high performance computing
clusters.
MPI MPIF77 -mpif77 program
Default:
Note: This option is triggered only if using MPI compiler scripts (MPI USE MPISCRIPTS is ON)
and Fortran-C support is enabled (FCMIx ENABLE is ON).

A.1 CMake-based installation 201
OPENMP ENABLE - Enable OpenMP support
Default: OFF
Turn on support for the OpenMP based nvector.
PETSC ENABLE - Enable PETSc support
Default: OFF
PETSC INCLUDE DIR - Path to PETSc header files
PETSC LIBRARY DIR - Path to PETSc installed library files
PTHREAD ENABLE - Enable Pthreads support
Default: OFF
Turn on support for the Pthreads based nvector.
SUNDIALS PRECISION - Precision used in sundials, options are: double, single or extended
Default: double
SUPERLUMT ENABLE - Enable SUPERLU MT support
Default: OFF
SUPERLUMT INCLUDE DIR - Path to SuperLU MT header files (typically SRC directory)
SUPERLUMT LIBRARY DIR - Path to SuperLU MT installed library files
SUPERLUMT THREAD TYPE - Must be set to Pthread or OpenMP
USE GENERIC MATH - Use generic (stdc) math libraries
Default: ON
A.1.3 Configuration examples
The following examples will help demonstrate usage of the CMake configure options.
To configure sundials using the default C and Fortran compilers, and default mpicc and mpif77
parallel compilers, enable compilation of examples, and install libraries, headers, and example sources
under subdirectories of /home/myname/sundials/, use:
% cmake \
> -DCMAKE_INSTALL_PREFIX=/home/myname/sundials/instdir \
> -DEXAMPLES_INSTALL_PATH=/home/myname/sundials/instdir/examples \
> -DMPI_ENABLE=ON \
> -DFCMIX_ENABLE=ON \
> /home/myname/sundials/srcdir
%
% make install
%
To disable installation of the examples, use:
% cmake \
> -DCMAKE_INSTALL_PREFIX=/home/myname/sundials/instdir \
> -DEXAMPLES_INSTALL_PATH=/home/myname/sundials/instdir/examples \
> -DMPI_ENABLE=ON \
> -DFCMIX_ENABLE=ON \
> -DEXAMPLES_INSTALL=OFF \
> /home/myname/sundials/srcdir
%
% make install
%

202 SUNDIALS Package Installation Procedure
A.1.4 Working with external Libraries
The sundials Suite contains many options to enable implementation flexibility when developing
solutions. The following are some notes addressing specific configurations when using the supported
third party libraries.
Building with LAPACK and BLAS
To enable LAPACK and BLAS libraries, set the LAPACK ENABLE option to ON. If the directory contain-
ing the LAPACK and BLAS libraries is in the LD LIBRARY PATH environment variable, CMake will
set the LAPACK LIBRARIES variable accordingly, otherwise CMake will attemp to find the LAPACK
and BLAS libraries in standard system locations. To explicitly tell CMake what libraries to use, the
LAPACK LIBRARIES varible can be set to the desired libraries. Example:
% cmake \
> -DCMAKE_INSTALL_PREFIX=/home/myname/sundials/instdir \
> -DEXAMPLES_INSTALL_PATH=/home/myname/sundials/instdir/examples \
> -DLAPACK_LIBRARIES=/mypath/lib/liblapack.so;/mypath/lib/libblas.so \
> /home/myname/sundials/srcdir
%
% make install
%
Building with KLU
The KLU libraries are part of SuiteSparse, a suite of sparse matrix software, available from the Texas
A&M University website: http://faculty.cse.tamu.edu/davis/suitesparse.html.sundials has
been tested with SuiteSparse version 4.5.3. To enable KLU, set KLU ENABLE to ON, set KLU INCLUDE DIR
to the include path of the KLU installation and set KLU LIBRARY DIR to the lib path of the KLU
installation. The CMake configure will result in populating the following variables: AMD LIBRARY,
AMD LIBRARY DIR,BTF LIBRARY,BTF LIBRARY DIR,COLAMD LIBRARY,COLAMD LIBRARY DIR, and
KLU LIBRARY
Building with SuperLU MT
The SuperLU MT libraries are available for download from the Lawrence Berkeley National Labo-
ratory website: http://crd-legacy.lbl.gov/∼xiaoye/SuperLU/#superlu mt.sundials has been
tested with SuperLU MT version 3.1. To enable SuperLU MT, set SUPERLUMT ENABLE to ON, set
SUPERLUMT INCLUDE DIR to the SRC path of the SuperLU MT installation, and set the variable
SUPERLUMT LIBRARY DIR to the lib path of the SuperLU MT installation. At the same time, the
variable SUPERLUMT THREAD TYPE must be set to either Pthread or OpenMP.
Do not mix thread types when building sundials solvers. If threading is enabled for sundials by
having either OPENMP ENABLE or PTHREAD ENABLE set to ON then SuperLU MT should be set to use
the same threading type.
!
Building with PETSc
The PETSc libraries are available for download from the Argonne National Laboratory website:
http://www.mcs.anl.gov/petsc.sundials has been tested with PETSc version 3.7.2. To en-
able PETSc, set PETSC ENABLE to ON, set PETSC INCLUDE DIR to the include path of the PETSc
installation, and set the variable PETSC LIBRARY DIR to the lib path of the PETSc installation.
Building with hypre
The hypre libraries are available for download from the Lawrence Livermore National Laboratory web-
site: http://computation.llnl.gov/projects/hypre-scalable-linear-solvers-multigrid-methods.

A.2 Building and Running Examples 203
sundials has been tested with hypre version 2.11.1. To enable hypre, set HYPRE ENABLE to ON, set
HYPRE INCLUDE DIR to the include path of the hypre installation, and set the variable HYPRE LIBRARY DIR
to the lib path of the hypre installation.
A.2 Building and Running Examples
Each of the sundials solvers is distributed with a set of examples demonstrating basic usage. To
build and install the examples, set both EXAMPLES ENABLE and EXAMPLES INSTALL to ON. Specify the
installation path for the examples with the variable EXAMPLES INSTALL PATH. CMake will generate
CMakeLists.txt configuration files (and Makefile files if on Linux/Unix) that reference the installed
sundials headers and libraries.
Either the CMakeLists.txt file or the traditional Makefile may be used to build the examples as
well as serve as a template for creating user developed solutions. To use the supplied Makefile simply
run make to compile and generate the executables. To use CMake from within the installed example
directory, run cmake (or ccmake to use the GUI) followed by make to compile the example code.
Note that if CMake is used, it will overwrite the traditional Makefile with a new CMake-generated
Makefile. The resulting output from running the examples can be compared with example output
bundled in the sundials distribution.
NOTE: There will potentially be differences in the output due to machine architecture, compiler
versions, use of third party libraries etc.
!
A.3 Configuring, building, and installing on Windows
CMake can also be used to build sundials on Windows. To build sundials for use with Visual
Studio the following steps should be performed:
1. Unzip the downloaded tar file(s) into a directory. This will be the srcdir
2. Create a separate builddir
3. Open a Visual Studio Command Prompt and cd to builddir
4. Run cmake-gui ../srcdir
(a) Hit Configure
(b) Check/Uncheck solvers to be built
(c) Change CMAKE INSTALL PREFIX to instdir
(d) Set other options as desired
(e) Hit Generate
5. Back in the VS Command Window:
(a) Run msbuild ALL BUILD.vcxproj
(b) Run msbuild INSTALL.vcxproj
The resulting libraries will be in the instdir. The sundials project can also now be opened in Visual
Studio. Double click on the ALL BUILD.vcxproj file to open the project. Build the whole solution to
create the sundials libraries. To use the sundials libraries in your own projects, you must set the
include directories for your project, add the sundials libraries to your project solution, and set the
sundials libraries as dependencies for your project.
204 SUNDIALS Package Installation Procedure
A.4 Installed libraries and exported header files
Using the CMake sundials build system, the command
% make install
will install the libraries under libdir and the public header files under includedir. The values for these
directories are instdir/lib and instdir/include, respectively. The location can be changed by setting
the CMake variable CMAKE INSTALL PREFIX. Although all installed libraries reside under libdir/lib,
the public header files are further organized into subdirectories under includedir/include.
The installed libraries and exported header files are listed for reference in Tables A.1 and A.2.
The file extension .lib is typically .so for shared libraries and .a for static libraries. Note that, in the
Tables, names are relative to libdir for libraries and to includedir for header files.
A typical user program need not explicitly include any of the shared sundials header files from
under the includedir/include/sundials directory since they are explicitly included by the appropriate
solver header files (e.g.,cvode dense.h includes sundials dense.h). However, it is both legal and
safe to do so, and would be useful, for example, if the functions declared in sundials dense.h are to
be used in building a preconditioner.

A.4 Installed libraries and exported header files 205
Table A.1: sundials libraries and header files
shared Libraries n/a
Header files sundials/sundials config.h sundials/sundials types.h
sundials/sundials math.h
sundials/sundials nvector.h sundials/sundials fnvector.h
sundials/sundials direct.h sundials/sundials lapack.h
sundials/sundials dense.h sundials/sundials band.h
sundials/sundials sparse.h
sundials/sundials iterative.h sundials/sundials spgmr.h
sundials/sundials spbcgs.h sundials/sundials sptfqmr.h
sundials/sundials pcg.h sundials/sundials spfgmr.h
nvector serial Libraries libsundials nvecserial.lib libsundials fnvecserial.a
Header files nvector/nvector serial.h
nvector parallel Libraries libsundials nvecparallel.lib libsundials fnvecparallel.a
Header files nvector/nvector parallel.h
nvector openmp Libraries libsundials nvecopenmp.lib libsundials fnvecopenmp.a
Header files nvector/nvector openmp.h
nvector pthreads Libraries libsundials nvecpthreads.lib libsundials fnvecpthreads.a
Header files nvector/nvector pthreads.h
cvode Libraries libsundials cvode.lib libsundials fcvode.a
Header files cvode/cvode.h cvode/cvode impl.h
cvode/cvode direct.h cvode/cvode lapack.h
cvode/cvode dense.h cvode/cvode band.h
cvode/cvode diag.h
cvode/cvode sparse.h cvode/cvode klu.h
cvode/cvode superlumt.h
cvode/cvode spils.h cvode/cvode spgmr.h
cvode/cvode sptfqmr.h cvode/cvode spbcgs.h
cvode/cvode bandpre.h cvode/cvode bbdpre.h
cvodes Libraries libsundials cvodes.lib
Header files cvodes/cvodes.h cvodes/cvodes impl.h
cvodes/cvodes direct.h cvodes/cvodes lapack.h
cvodes/cvodes dense.h cvodes/cvodes band.h
cvodes/cvodes diag.h
cvodes/cvodes sparse.h cvodes/cvodes klu.h
cvodes/cvodes superlumt.h
cvodes/cvodes spils.h cvodes/cvodes spgmr.h
cvodes/cvodes sptfqmr.h cvodes/cvodes spbcgs.h
cvodes/cvodes bandpre.h cvodes/cvodes bbdpre.h
arkode Libraries libsundials arkode.lib libsundials farkode.a
Header files arkode/arkode.h arkode/arkode impl.h
arkode/arkode direct.h arkode/arkode lapack.h
arkode/arkode dense.h arkode/arkode band.h
arkode/arkode sparse.h arkode/arkode klu.h
arkode/arkode superlumt.h
arkode/arkode spils.h arkode/arkode spgmr.h
arkode/arkode sptfqmr.h arkode/arkode spbcgs.h
arkode/arkode pcg.h arkode/arkode spfgmr.h
arkode/arkode bandpre.h arkode/arkode bbdpre.h

206 SUNDIALS Package Installation Procedure
Table A.2: sundials libraries and header files (cont.)
ida Libraries libsundials ida.lib libsundials fida.a
Header files ida/ida.h ida/ida impl.h
ida/ida direct.h ida/ida lapack.h
ida/ida dense.h ida/ida band.h
ida/ida sparse.h ida/ida klu.h
ida/ida superlumt.h
ida/ida spils.h ida/ida spgmr.h
ida/ida spbcgs.h ida/ida sptfqmr.h
ida/ida bbdpre.h
idas Libraries libsundials idas.lib
Header files idas/idas.h idas/idas impl.h
idas/idas direct.h idas/idas lapack.h
idas/idas dense.h idas/idas band.h
idas/idas sparse.h idas/idas klu.h
idas/idas superlumt.h
idas/idas spils.h idas/idas spgmr.h
idas/idas spbcgs.h idas/idas sptfqmr.h
idas/idas bbdpre.h
kinsol Libraries libsundials kinsol.lib libsundials fkinsol.a
Header files kinsol/kinsol.h kinsol/kinsol impl.h
kinsol/kinsol direct.h kinsol/kinsol lapack.h
kinsol/kinsol dense.h kinsol/kinsol band.h
kinsol/kinsol sparse.h kinsol/kinsol klu.h
kinsol/kinsol superlumt.h
kinsol/kinsol spils.h kinsol/kinsol spgmr.h
kinsol/kinsol spbcgs.h kinsol/kinsol sptfqmr.h
kinsol/kinsol bbdpre.h kinsol/kinsol spfgmr.h
Appendix B
IDAS Constants
Below we list all input and output constants used by the main solver and linear solver modules,
together with their numerical values and a short description of their meaning.
B.1 IDAS input constants
idas main solver module
IDA NORMAL 1 Solver returns at specified output time.
IDA ONE STEP 2 Solver returns after each successful step.
IDA SIMULTANEOUS 1 Simultaneous corrector forward sensitivity method.
IDA STAGGERED 2 Staggered corrector forward sensitivity method.
IDA CENTERED 1 Central difference quotient approximation (2nd order) of the
sensitivity RHS.
IDA FORWARD 2 Forward difference quotient approximation (1st order) of the
sensitivity RHS.
IDA YA YDP INIT 1 Compute yaand ˙yd, given yd.
IDA Y INIT 2 Compute y, given ˙y.
idas adjoint solver module
IDA HERMITE 1 Use Hermite interpolation.
IDA POLYNOMIAL 2 Use variable-degree polynomial interpolation.
Iterative linear solver module
PREC NONE 0 No preconditioning
PREC LEFT 1 Preconditioning on the left.
MODIFIED GS 1 Use modified Gram-Schmidt procedure.
CLASSICAL GS 2 Use classical Gram-Schmidt procedure.
B.2 IDAS output constants
idas main solver module
208 IDAS Constants
IDA SUCCESS 0 Successful function return.
IDA TSTOP RETURN 1IDASolve succeeded by reaching the specified stopping point.
IDA ROOT RETURN 2IDASolve succeeded and found one or more roots.
IDA WARNING 99 IDASolve succeeded but an unusual situation occurred.
IDA TOO MUCH WORK -1 The solver took mxstep internal steps but could not reach
tout.
IDA TOO MUCH ACC -2 The solver could not satisfy the accuracy demanded by the
user for some internal step.
IDA ERR FAIL -3 Error test failures occurred too many times during one inter-
nal time step or minimum step size was reached.
IDA CONV FAIL -4 Convergence test failures occurred too many times during one
internal time step or minimum step size was reached.
IDA LINIT FAIL -5 The linear solver’s initialization function failed.
IDA LSETUP FAIL -6 The linear solver’s setup function failed in an unrecoverable
manner.
IDA LSOLVE FAIL -7 The linear solver’s solve function failed in an unrecoverable
manner.
IDA RES FAIL -8 The user-provided residual function failed in an unrecoverable
manner.
IDA REP RES FAIL -9 The user-provided residual function repeatedly returned a re-
coverable error flag, but the solver was unable to recover.
IDA RTFUNC FAIL -10 The rootfinding function failed in an unrecoverable manner.
IDA CONSTR FAIL -11 The inequality constraints were violated and the solver was
unable to recover.
IDA FIRST RES FAIL -12 The user-provided residual function failed recoverably on the
first call.
IDA LINESEARCH FAIL -13 The line search failed.
IDA NO RECOVERY -14 The residual function, linear solver setup function, or linear
solver solve function had a recoverable failure, but IDACalcIC
could not recover.
IDA MEM NULL -20 The ida mem argument was NULL.
IDA MEM FAIL -21 A memory allocation failed.
IDA ILL INPUT -22 One of the function inputs is illegal.
IDA NO MALLOC -23 The idas memory was not allocated by a call to IDAInit.
IDA BAD EWT -24 Zero value of some error weight component.
IDA BAD K -25 The k-th derivative is not available.
IDA BAD T -26 The time tis outside the last step taken.
IDA BAD DKY -27 The vector argument where derivative should be stored is
NULL.
IDA NO QUAD -30 Quadratures were not initialized.
IDA QRHS FAIL -31 The user-provided right-hand side function for quadratures
failed in an unrecoverable manner.
IDA FIRST QRHS ERR -32 The user-provided right-hand side function for quadratures
failed in an unrecoverable manner on the first call.
IDA REP QRHS ERR -33 The user-provided right-hand side repeatedly returned a re-
coverable error flag, but the solver was unable to recover.
B.2 IDAS output constants 209
IDA NO SENS -40 Sensitivities were not initialized.
IDA SRES FAIL -41 The user-provided sensitivity residual function failed in an
unrecoverable manner.
IDA REP SRES ERR -42 The user-provided sensitivity residual function repeatedly re-
turned a recoverable error flag, but the solver was unable to
recover.
IDA BAD IS -43 The sensitivity identifier is not valid.
IDA NO QUADSENS -50 Sensitivity-dependent quadratures were not initialized.
IDA QSRHS FAIL -51 The user-provided sensitivity-dependent quadrature right-
hand side function failed in an unrecoverable manner.
IDA FIRST QSRHS ERR -52 The user-provided sensitivity-dependent quadrature right-
hand side function failed in an unrecoverable manner on the
first call.
IDA REP QSRHS ERR -53 The user-provided sensitivity-dependent quadrature right-
hand side repeatedly returned a recoverable error flag, but
the solver was unable to recover.
idas adjoint solver module
IDA NO ADJ -101 The combined forward-backward problem has not been ini-
tialized.
IDA NO FWD -102 IDASolveF has not been previously called.
IDA NO BCK -103 No backward problem was specified.
IDA BAD TB0 -104 The desired output for backward problem is outside the in-
terval over which the forward problem was solved.
IDA REIFWD FAIL -105 No checkpoint is available for this hot start.
IDA FWD FAIL -106 IDASolveB failed because IDASolve was unable to store data
between two consecutive checkpoints.
IDA GETY BADT -107 Wrong time in interpolation function.
idadls linear solver modules
IDADLS SUCCESS 0 Successful function return.
IDADLS MEM NULL -1 The ida mem argument was NULL.
IDADLS LMEM NULL -2 The idadls linear solver has not been initialized.
IDADLS ILL INPUT -3 The idadls solver is not compatible with the current nvec-
tor module.
IDADLS MEM FAIL -4 A memory allocation request failed.
IDADLS JACFUNC UNRECVR -5 The Jacobian function failed in an unrecoverable manner.
IDADLS JACFUNC RECVR -6 The Jacobian function had a recoverable error.
IDADLS NO ADJ -101 The combined forward-backward problem has not been ini-
tialized.
IDADLS LMEMB NULL -102 The linear solver was not initialized for the backward phase.
idasls linear solver module

210 IDAS Constants
IDASLS SUCCESS 0 Successful function return.
IDASLS MEM NULL -1 The ida mem argument was NULL.
IDASLS LMEM NULL -2 The idasls linear solver has not been initialized.
IDASLS ILL INPUT -3 The idasls solver is not compatible with the current nvec-
tor module or other input is invalid.
IDASLS MEM FAIL -4 A memory allocation request failed.
IDASLS JAC NOSET -5 The Jacobian evaluation routine was not been set before the
linear solver setup routine was called.
IDASLS PACKAGE FAIL -6 An external package call return a failure error code.
IDASLS JACFUNC UNRECVR -7 The Jacobian function failed in an unrecoverable manner.
IDASLS JACFUNC RECVR -8 The Jacobian function had a recoverable error.
IDASLS NO ADJ -101 The combined forward-backward problem has not been ini-
tialized.
IDASLS LMEMB NULL -102 The linear solver was not initialized for the backward phase.
idaspils linear solver modules
IDASPILS SUCCESS 0 Successful function return.
IDASPILS MEM NULL -1 The ida mem argument was NULL.
IDASPILS LMEM NULL -2 The idaspils linear solver has not been initialized.
IDASPILS ILL INPUT -3 The idaspils solver is not compatible with the current nvec-
tor module.
IDASPILS MEM FAIL -4 A memory allocation request failed.
IDASPILS PMEM NULL -5 The preconditioner module has not been initialized.
IDASPILS NO ADJ -101 The combined forward-backward problem has not been ini-
tialized.
IDASPILS LMEMB NULL -102 The linear solver was not initialized for the backward phase.
spgmr generic linear solver module
SPGMR SUCCESS 0 Converged.
SPGMR RES REDUCED 1 No convergence, but the residual norm was reduced.
SPGMR CONV FAIL 2 Failure to converge.
SPGMR QRFACT FAIL 3 A singular matrix was found during the QR factorization.
SPGMR PSOLVE FAIL REC 4 The preconditioner solve function failed recoverably.
SPGMR ATIMES FAIL REC 5 The Jacobian-times-vector function failed recoverably.
SPGMR PSET FAIL REC 6 The preconditioner setup routine failed recoverably.
SPGMR MEM NULL -1 The spgmr memory is NULL
SPGMR ATIMES FAIL UNREC -2 The Jacobian-times-vector function failed unrecoverably.
SPGMR PSOLVE FAIL UNREC -3 The preconditioner solve function failed unrecoverably.
SPGMR GS FAIL -4 Failure in the Gram-Schmidt procedure.
SPGMR QRSOL FAIL -5 The matrix Rwas found to be singular during the QR solve
phase.

B.2 IDAS output constants 211
SPGMR PSET FAIL UNREC -6 The preconditioner setup routine failed unrecoverably.
spfgmr generic linear solver module (only available in kinsol and arkode)
SPFGMR SUCCESS 0 Converged.
SPFGMR RES REDUCED 1 No convergence, but the residual norm was reduced.
SPFGMR CONV FAIL 2 Failure to converge.
SPFGMR QRFACT FAIL 3 A singular matrix was found during the QR factorization.
SPFGMR PSOLVE FAIL REC 4 The preconditioner solve function failed recoverably.
SPFGMR ATIMES FAIL REC 5 The Jacobian-times-vector function failed recoverably.
SPFGMR PSET FAIL REC 6 The preconditioner setup routine failed recoverably.
SPFGMR MEM NULL -1 The spfgmr memory is NULL
SPFGMR ATIMES FAIL UNREC -2 The Jacobian-times-vector function failed unrecoverably.
SPFGMR PSOLVE FAIL UNREC -3 The preconditioner solve function failed unrecoverably.
SPFGMR GS FAIL -4 Failure in the Gram-Schmidt procedure.
SPFGMR QRSOL FAIL -5 The matrix Rwas found to be singular during the QR solve
phase.
SPFGMR PSET FAIL UNREC -6 The preconditioner setup routine failed unrecoverably.
spbcg generic linear solver module
SPBCG SUCCESS 0 Converged.
SPBCG RES REDUCED 1 No convergence, but the residual norm was reduced.
SPBCG CONV FAIL 2 Failure to converge.
SPBCG PSOLVE FAIL REC 3 The preconditioner solve function failed recoverably.
SPBCG ATIMES FAIL REC 4 The Jacobian-times-vector function failed recoverably.
SPBCG PSET FAIL REC 5 The preconditioner setup routine failed recoverably.
SPBCG MEM NULL -1 The spbcg memory is NULL
SPBCG ATIMES FAIL UNREC -2 The Jacobian-times-vector function failed unrecoverably.
SPBCG PSOLVE FAIL UNREC -3 The preconditioner solve function failed unrecoverably.
SPBCG PSET FAIL UNREC -4 The preconditioner setup routine failed unrecoverably.
sptfqmr generic linear solver module
SPTFQMR SUCCESS 0 Converged.
SPTFQMR RES REDUCED 1 No convergence, but the residual norm was reduced.
SPTFQMR CONV FAIL 2 Failure to converge.
SPTFQMR PSOLVE FAIL REC 3 The preconditioner solve function failed recoverably.
SPTFQMR ATIMES FAIL REC 4 The Jacobian-times-vector function failed recoverably.
SPTFQMR PSET FAIL REC 5 The preconditioner setup routine failed recoverably.
SPTFQMR MEM NULL -1 The sptfqmr memory is NULL
SPTFQMR ATIMES FAIL UNREC -2 The Jacobian-times-vector function failed.
SPTFQMR PSOLVE FAIL UNREC -3 The preconditioner solve function failed unrecoverably.
SPTFQMR PSET FAIL UNREC -4 The preconditioner setup routine failed unrecoverably.

Bibliography
[1] KLU Sparse Matrix Factorization Library. http://faculty.cse.tamu.edu/davis/suitesparse.html.
[2] SuperLU MT Threaded Sparse Matrix Factorization Library. http://crd-legacy.lbl.gov/ xiaoye/-
SuperLU/.
[3] K. E. Brenan, S. L. Campbell, and L. R. Petzold. Numerical Solution of Initial-Value Problems
in Differential-Algebraic Equations. SIAM, Philadelphia, Pa, 1996.
[4] P. N. Brown and A. C. Hindmarsh. Reduced Storage Matrix Methods in Stiff ODE Systems. J.
Appl. Math. & Comp., 31:49–91, 1989.
[5] P. N. Brown, A. C. Hindmarsh, and L. R. Petzold. Using Krylov Methods in the Solution of
Large-Scale Differential-Algebraic Systems. SIAM J. Sci. Comput., 15:1467–1488, 1994.
[6] P. N. Brown, A. C. Hindmarsh, and L. R. Petzold. Consistent Initial Condition Calculation for
Differential-Algebraic Systems. SIAM J. Sci. Comput., 19:1495–1512, 1998.
[7] G. D. Byrne. Pragmatic Experiments with Krylov Methods in the Stiff ODE Setting. In J.R.
Cash and I. Gladwell, editors, Computational Ordinary Differential Equations, pages 323–356,
Oxford, 1992. Oxford University Press.
[8] G. D. Byrne and A. C. Hindmarsh. User Documentation for PVODE, An ODE Solver for Parallel
Computers. Technical Report UCRL-ID-130884, LLNL, May 1998.
[9] G. D. Byrne and A. C. Hindmarsh. PVODE, An ODE Solver for Parallel Computers. Intl. J.
High Perf. Comput. Apps., 13(4):254–365, 1999.
[10] Y. Cao, S. Li, L. R. Petzold, and R. Serban. Adjoint Sensitivity Analysis for Differential-Algebraic
Equations: The Adjoint DAE System and its Numerical Solution. SIAM J. Sci. Comput.,
24(3):1076–1089, 2003.
[11] M. Caracotsios and W. E. Stewart. Sensitivity Analysis of Initial Value Problems with Mixed
ODEs and Algebraic Equations. Computers and Chemical Engineering, 9:359–365, 1985.
[12] S. D. Cohen and A. C. Hindmarsh. CVODE, a Stiff/Nonstiff ODE Solver in C. Computers in
Physics, 10(2):138–143, 1996.
[13] A. M. Collier, A. C. Hindmarsh, R. Serban, and C.S. Woodward. User Documentation for
KINSOL v2.7.0. Technical Report UCRL-SM-208116, LLNL, 2011.
[14] T. A. Davis and P. N. Ekanathan. Algorithm 907: KLU, a direct sparse solver for circuit
simulation problems. ACM Trans. Math. Softw., 37(3), 2010.
[15] J. W. Demmel, J. R. Gilbert, and X. S. Li. An asynchronous parallel supernodal algorithm for
sparse gaussian elimination. SIAM J. Matrix Analysis and Applications, 20(4):915–952, 1999.
[16] W. F. Feehery, J. E. Tolsma, and P. I. Barton. Efficient Sensitivity Analysis of Large-Scale
Differential-Algebraic Systems. Applied Numer. Math., 25(1):41–54, 1997.

214 BIBLIOGRAPHY
[17] R. W. Freund. A Transpose-Free Quasi-Minimal Residual Algorithm for Non-Hermitian Linear
Systems. SIAM J. Sci. Comp., 14:470–482, 1993.
[18] K. L. Hiebert and L. F. Shampine. Implicitly Defined Output Points for Solutions of ODEs.
Technical Report SAND80-0180, Sandia National Laboratories, February 1980.
[19] A. C. Hindmarsh, P. N. Brown, K. E. Grant, S. L. Lee, R. Serban, D. E. Shumaker, and C. S.
Woodward. SUNDIALS, suite of nonlinear and differential/algebraic equation solvers. ACM
Trans. Math. Softw., (31):363–396, 2005.
[20] A. C. Hindmarsh and R. Serban. Example Programs for CVODE v2.7.0. Technical report, LLNL,
2011. UCRL-SM-208110.
[21] A. C. Hindmarsh and R. Serban. User Documentation for CVODE v2.7.0. Technical Report
UCRL-SM-208108, LLNL, 2011.
[22] A. C. Hindmarsh and R. Serban. User Documentation for CVODES v2.6.0. Technical report,
LLNL, 2011. UCRL-SM-208111.
[23] A. C. Hindmarsh, R. Serban, and A. Collier. Example Programs for IDA v2.7.0. Technical Report
UCRL-SM-208113, LLNL, 2011.
[24] A. C. Hindmarsh, R. Serban, and A. Collier. User Documentation for IDA v2.7.0. Technical
Report UCRL-SM-208112, LLNL, 2011.
[25] A. C. Hindmarsh and A. G. Taylor. PVODE and KINSOL: Parallel Software for Differential
and Nonlinear Systems. Technical Report UCRL-ID-129739, LLNL, February 1998.
[26] S. Li, L. R. Petzold, and W. Zhu. Sensitivity Analysis of Differential-Algebraic Equations: A
Comparison of Methods on a Special Problem. Applied Num. Math., 32:161–174, 2000.
[27] X. S. Li. An overview of SuperLU: Algorithms, implementation, and user interface. ACM Trans.
Math. Softw., 31(3):302–325, September 2005.
[28] T. Maly and L. R. Petzold. Numerical Methods and Software for Sensitivity Analysis of
Differential-Algebraic Systems. Applied Numerical Mathematics, 20:57–79, 1997.
[29] D.B. Ozyurt and P.I. Barton. Cheap second order directional derivatives of stiff ODE embedded
functionals. SIAM J. of Sci. Comp., 26(5):1725–1743, 2005.
[30] Daniel R. Reynolds. Example Programs for ARKODE v1.1.0. Technical report, Southern
Methodist University, 2016.
[31] Y. Saad and M. H. Schultz. GMRES: A Generalized Minimal Residual Algorithm for Solving
Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comp., 7:856–869, 1986.
[32] R. Serban and A. C. Hindmarsh. CVODES, the sensitivity-enabled ODE solver in SUNDIALS.
In Proceedings of the 5th International Conference on Multibody Systems, Nonlinear Dynamics
and Control, Long Beach, CA, 2005. ASME.
[33] R. Serban and A. C. Hindmarsh. Example Programs for IDAS v1.1.0. Technical Report LLNL-
TR-437091, LLNL, 2011.
[34] H. A. Van Der Vorst. Bi-CGSTAB: A Fast and Smoothly Converging Variant of Bi-CG for the
Solution of Nonsymmetric Linear Systems. SIAM J. Sci. Stat. Comp., 13:631–644, 1992.
Index
adjoint sensitivity analysis
checkpointing, 18
implementation in idas,19,21–23
mathematical background, 16–19
quadrature evaluation, 136
residual evaluation, 134,135
sensitivity-dependent quadrature evaluation,
137
band generic linear solver
functions, 186
small matrix, 186–187
macros, 183
type DlsMat,180–183
BAND COL,73,183
BAND COL ELEM,73,183
BAND ELEM,73,183
bandAddIdentity,187
bandCopy,187
bandGETRF,187
bandGETRS,187
bandMatvec,187
bandScale,187
Bi-CGStab method, 51,130,194
BIG REAL,26,158
CLASSICAL GS,50,129
CSC MAT,35
dense generic linear solver
functions
large matrix, 183–184
small matrix, 184–186
macros, 183
type DlsMat,180–183
DENSE COL,72,183
DENSE ELEM,72,183
denseAddIdentity,185
denseCopy,185
denseGEQRF,185
denseGETRF,185
denseGETRS,185
denseMatvec,186
denseORMQR,186
densePOTRF,185
densePOTRS,185
denseScale,185
destroyArray,185,187
destroyMat,184,186
DlsMat,72,73,138–141,180
eh data,70
error control
sensitivity variables, 14
error messages, 40
redirecting, 40
user-defined handler, 40,70
FGMRES method, 193
forward sensitivity analysis
absolute tolerance selection, 14–15
correction strategies, 13–14,21,92,93
mathematical background, 13–16
residual evaluation, 102
right hand side evaluation, 15
right-hand side evaluation, 15
generic linear solvers
band,180
dense,180
klu,187
sls,187
spbcg,194
spfgmr,193
spgmr,192
sptfqmr,194
superlumt,187
use in idas,24
GMRES method, 192
Gram-Schmidt procedure, 50,129
half-bandwidths, 34,73–74,86
header files, 26,85
IDA BAD DKY,55,80,95–97,107
IDA BAD EWT,37
IDA BAD IS,96,97,107
IDA BAD ITASK,124

216 INDEX
IDA BAD K,55,80,96,97,107
IDA BAD T,55,80,96,97,107
IDA BAD TB0,119,120
IDA BAD TBOUT,124
IDA BCKMEM NULL,124
IDA CENTERED,98
IDA CONSTR FAIL,37,39
IDA CONV FAIL,37,39
IDA CONV FAILURE,118,124
IDA ERR FAIL,39
IDA ERR FAILURE,118,124
IDA FIRST QRHS ERR,79,83
IDA FIRST QSRHS ERR,106,111
IDA FIRST RES FAIL,37,103
IDA FORWARD,98
IDA FWD FAIL,124
IDA GETY BADT,131
IDA HERMITE,116
IDA ILL INPUT,30,31,37,39,42–45,51–54,62,
69,81,92–94,97,98,102,105,108,109,
116,118–121,124,125,132–134
IDA LINESEARCH FAIL,37
IDA LINIT FAIL,37,39
IDA LSETUP FAIL,37,39,118,124,138–143,150,
151
IDA LSOLVE FAIL,37,39,118
IDA MEM FAIL,30,79,92,93,105,116,118,119,
132,133
IDA MEM NULL,30,31,37,39,40,42–45,51–55,
57–63,69,79–83,92–102,105,107–110,
117,119–121,124,125,131–134
IDA NO ADJ,116–125,132–134
IDA NO BCK,124
IDA NO FWD,124
IDA NO MALLOC,31,32,37,69,118–121
IDA NO QUAD,79–83,109,133
IDA NO QUADSENS,105–110
IDA NO RECOVERY,37
IDA NO SENS,93–97,99–102,105,107
IDA NORMAL,38,114,118,124
IDA ONE STEP,38,114,118,124
IDA POLYNOMIAL,116
IDA QRHS FAIL,79,83,111
IDA QRHSFUNC FAIL,136,137
IDA QSRHS FAIL,106
IDA REIFWD FAIL,124
IDA REP QRHS ERR,80
IDA REP QSRHS ERR,106
IDA REP RES ERR,39
IDA REP SRES ERR,95
IDA RES FAIL,37,39
IDA RESFUNC FAIL,135
IDA ROOT RETURN,39,118
IDA RTFUNC FAIL,39,71
IDA SIMULTANEOUS,21,92
IDA SOLVE FAIL,124
IDA SRES FAIL,95,103
IDA STAGGERED,21,92
IDA SUCCESS,30,31,37,39,40,42–45,51–55,
63,69,78–83,92–102,104–110,116–121,
124,125,131–133
IDA TOO MUCH ACC,39,118,124
IDA TOO MUCH WORK,39,118,124
IDA TSTOP RETURN,39,118
IDA WARNING,70
IDA Y INIT,37
IDA YA YDP INIT,37
IDAAdjFree,117
IDAAdjInit,114,116
IDAAdjReInit,116
IDAAdjSetNoSensi,117
idaband linear solver
Jacobian approximation used by, 46
memory requirements, 63
nvector compatibility, 34
optional input, 46,126–127
optional output, 63–64
selection of, 34
IDABand,28,33,34,73
IDABAND ILL INPUT,34
IDABAND MEM FAIL,34
IDABAND MEM NULL,34
IDABAND SUCCESS,34
IDABandB,139
idabbdpre preconditioner
description, 84
optional output, 88
usage, 85–86
usage with adjoint module, 148–151
user-callable functions, 86–88,149–150
user-supplied functions, 84–85,150–151
IDABBDPrecGetNumGfnEvals,88
IDABBDPrecGetWorkSpace,88
IDABBDPrecInit,87
IDABBDPrecInitB,149
IDABBDPrecReInit,87
IDABBDPrecReInitB,149
IDACalcIC,37
IDACalcICB,122
IDACalcICBS,122,123
IDACreate,30
IDACreateB,114,119
idadense linear solver
Jacobian approximation used by, 46
memory requirements, 63
nvector compatibility, 33
optional input, 46,125–126
optional output, 63–64

INDEX 217
selection of, 33
IDADense,28,33,71
IDADenseB,137
IDADLS ILL INPUT,33,125–127
IDADLS JACFUNC RECVR,138–141
IDADLS JACFUNC UNRECVR,138–142
IDADLS LMEM NULL,46,63,64,125–127
IDADLS MEM FAIL,33
IDADLS MEM NULL,33,46,63,64,125–127
IDADLS NO ADJ,125–127
IDADLS SUCCESS,33,46,64,125–127
IDADlsBandJacFn,73
IDADlsDenseJacFn,71
IDADlsGetLastFlag,64
IDADlsGetNumJacEvals,64
IDADlsGetNumResEvals,64
IDADlsGetReturnFlagName,64
IDADlsGetWorkSpace,63
IDADlsSetBandJacFn,46
IDADlsSetBandJacFnB,126
IDADlsSetBandJacFnBS,126
IDADlsSetDenseJacFn,46
IDADlsSetDenseJacFnB,125
IDADlsSetDenseJacFnBS,126
IDAErrHandlerFn,70
IDAEwtFn,71
IDAFree,29,30
IDAGetActualInitStep,59
IDAGetAdjIDABmem,131
IDAGetAdjY,131
IDAGetB,124
IDAGetConsistentIC,62
IDAGetConsistentICB,131
IDAGetCurrentOrder,58
IDAGetCurrentStep,59
IDAGetCurrentTime,59
IDAGetDky,54
IDAGetErrWeights,60
IDAGetEstLocalErrors,60
IDAGetIntegratorStats,60
IDAGetLastOrder,58
IDAGetLastStep,59
IDAGetNonlinSolvStats,61
IDAGetNumBacktrackOps,62
IDAGetNumErrTestFails,58
IDAGetNumGEvals,63
IDAGetNumLinSolvSetups,58
IDAGetNumNonlinSolvConvFails,61
IDAGetNumNonlinSolvIters,61
IDAGetNumResEvals,57
IDAGetNumResEvalsSEns,99
IDAGetNumSteps,57
IDAGetQuad,80,133
IDAGetQuadB,115,133
IDAGetQuadDky,80
IDAGetQuadErrWeights,82
IDAGetQuadNumErrTestFails,82
IDAGetQuadNumRhsEvals,82
IDAGetQuadSens,106
IDAGetQuadSens1,107
IDAGetQuadSensDky,106
IDAGetQuadSensDky1,107
IDAGetQuadSensErrWeights,110
IDAGetQuadSensNumErrTestFails,109
IDAGetQuadSensNumRhsEvals,109
IDAGetQuadSensStats,110
IDAGetQuadStats,83
IDAGetReturnFlagName,62
IDAGetRootInfo,62
IDAGetSens,91,95
IDAGetSens1,91,96
IDAGetSensConsistentIC,102
IDAGetSensDky,91,95,96
IDAGetSensDky1,91,96
IDAGetSensErrWeights,101
IDAGetSensNonlinSolvStats,101
IDAGetSensNumErrTestFails,100
IDAGetSensNumLinSolvSetups,100
IDAGetSensNumNonlinSolvConvFails,101
IDAGetSensNumNonlinSolvIters,101
IDAGetSensNumResEvals,99
IDAGetSensStats,100
IDAGetTolScaleFactor,60
IDAGetWorkSpace,55
IDAInit,30,68
IDAInitB,114,119
IDAInitBS,114,120
IDAKLU,28,33,35,74
idaklu linear solver
Jacobian approximation used by, 47
matrix reordering algorithm specification, 48
nvector compatibility, 34
optional input, 47–48,127–128
optional output, 65
reinitialization, 47
selection of, 34
IDAKLUB,142
IDAKLUReInit,47
IDAKLUSetOrdering,48
IDALapackBand,28,33,34,73
IDALapackBandB,139
IDALapackDense,28,33,34,71
IDALapackDenseB,137
IDAQuadFree,79
IDAQuadInit,78,79
IDAQuadInitB,132
IDAQuadInitBS,132
IDAQuadReInit,79

218 INDEX
IDAQuadReInitB,133
IDAQuadRhsFn,78,83
IDAQuadRhsFnB,132,136
IDAQuadRhsFnBS,133,137
IDAQuadSensEEtolerances,109
IDAQuadSensFree,105
IDAQuadSensInit,104,105
IDAQuadSensReInit,105
IDAQuadSensRhsFn,104,110
IDAQuadSensSStolerances,108
IDAQuadSensSVtolerances,108
IDAQuadSStolerances,81
IDAQuadSVtolerances,81
IDAReInit,68,69
IDAReInitB,120
IDAResFn,30,69
IDAResFnB,119,134
IDAResFnBS,120,135
IDARootFn,71
IDARootInit,38
idas
motivation for writing in C, 1–2
package structure, 21
relationship to ida,1
idas linear solvers
built on generic solvers, 33
header files, 26
idaband,34
idadense,33
idaklu,34
idaspbcg,36
idaspgmr,36
idasptfqmr,36
idasuperlumt,35
implementation details, 24
list of, 23–24
nvector compatibility, 25
selecting one, 33
usage with adjoint module, 121
idas.h,26
idas band.h,26
idas dense.h,26
idas klu.h,27
idas lapack.h,27
idas spbcgs.h,27
idas spgmr.h,27
idas sptfqmr.h,27
idas superlumt.h,27
IDASensEEtolerances,94
IDASensFree,93
IDASensInit,91,92
IDASensReInit,92,93
IDASensResFn,92,102
IDASensSStolerances,94
IDASensSVtolerances,94
IDASensToggleOff,93
IDASetConstraints,45
IDASetErrFile,40
IDASetErrHandlerFn,40
IDASetId,45
IDASetInitStep,42
IDASetLineSearchOffIC,53
IDASetMaxBacksIC,53
IDASetMaxConvFails,44
IDASetMaxErrTestFails,43
IDASetMaxNonlinIters,44
IDASetMaxNumItersIC,52
IDASetMaxNumJacsIC,52
IDASetMaxNumSteps,42
IDASetMaxNumStepsIC,52
IDASetMaxOrd,42
IDASetMaxStep,43
IDASetNoInactiveRootWarn,54
IDASetNonlinConvCoef,44
IDASetNonlinConvCoefIC,51
IDASetQuadErrCon,81
IDASetQuadSensErrCon,108
IDASetRootDirection,54
IDASetSensDQMethod,98
IDASetSensErrCon,98
IDASetSensMaxNonlinIters,98
IDASetSensParams,97
IDASetStepToleranceIC,53
IDASetStopTime,43
IDASetSuppressAlg,44
IDASetUserData,42
IDASLS ILL INPUT,35,48,127,128
IDASLS JACFUNC RECVR,142,143
IDASLS JACFUNC UNRECVR,142–144
IDASLS LMEM NULL,47,48,65,127,128
IDASLS MEM FAIL,35,48
IDASLS MEM NULL,35,47,48,65,127,128
IDASLS NO ADJ,127,128
IDASLS PACKAGE FAIL,35
IDASLS SUCCESS,35,47,48,65,127,128
IDASlsGetLastFlag,65
IDASlsGetNumJacEvals,65
IDASlsGetReturnFlagName,65
IDASlsSetSparseJacFn,47
IDASlsSetSparseJacFnB,127
IDASlsSetSparseJacFnBS,127
IDASlsSparseJacFn,74
IDASolve,29,38,109
IDASolveB,115,123
IDASolveF,114,117
idaspbcg linear solver
Jacobian approximation used by, 49
memory requirements, 65
INDEX 219
optional input, 49–51,128–130
optional output, 65–68
preconditioner setup function, 49,76,147
preconditioner solve function, 49,76,145
selection of, 36
IDASpbcg,28,33,36
idaspgmr linear solver
Jacobian approximation used by, 49
memory requirements, 65
optional input, 49–51,128–130
optional output, 65–68
preconditioner setup function, 49,76,147
preconditioner solve function, 49,76,145
selection of, 36
IDASpgmr,28,33,36
IDASPILS ILL INPUT,50,51,87,128–130,149,
150
IDASPILS LMEM NULL,49–51,66–68,87,88,128–
130,149,150
IDASPILS MEM FAIL,36,87,149,150
IDASPILS MEM NULL,36,49–51,66–68,128–130,
149,150
IDASPILS NO ADJ,128–130
IDASPILS PMEM NULL,88,150
IDASPILS SUCCESS,36,49–51,68,128–130,149,
150
IDASpilsGetLastFlag,68
IDASpilsGetNumConvFails,66
IDASpilsGetNumJtimesEvals,67
IDASpilsGetNumLinIters,66
IDASpilsGetNumPrecEvals,66
IDASpilsGetNumPrecSolves,67
IDASpilsGetNumResEvals,67
IDASpilsGetReturnFlagName,68
IDASpilsGetWorkSpace,66
IDASpilsJacTimesVecFn,75
IDASpilsPrecSetupFn,76
IDASpilsPrecSolveFn,76
IDASpilsSetEpsLin,50
IDASpilsSetEpsLinB,130
IDASpilsSetGSType,50
IDASpilsSetGSTypeB,129
IDASpilsSetIncrementFactor,51
IDASpilsSetJacTimesFn,49
IDASpilsSetJacTimesVecFnB,129
IDASpilsSetJacTimesVecFnBS,129
IDASpilsSetMaxl,51
IDASpilsSetMaxlB,130
IDASpilsSetMaxRestarts,50
IDASpilsSetPreconditioner,49
IDASpilsSetPrecSolveFnB,128
IDASpilsSetPrecSolveFnBS,128
idasptfqmr linear solver
Jacobian approximation used by, 49
memory requirements, 65
optional input, 49–51,128–130
optional output, 65–68
preconditioner setup function, 49,76,147
preconditioner solve function, 49,76,145
selection of, 36
IDASptfqmr,28,33,36
IDASStolerances,31
IDASStolerancesB,121
idasuperlumt linear solver
Jacobian approximation used by, 47
matrix reordering algorithm specification, 48
nvector compatibility, 35
optional input, 47–48,127–128
optional output, 65
selection of, 35
IDASuperLUMT,28,33,35,74
IDASuperLUMTB,142
IDASuperLUMTSetOrdering,48
IDASVtolerances,31
IDASVtolerancesB,121
IDAWFtolerances,31
itask,38,118
Jacobian approximation function
band
difference quotient, 46
user-supplied, 46,73–74
user-supplied (backward), 126,139
dense
difference quotient, 46
user-supplied, 46,71–73
user-supplied (backward), 125,137,138
Jacobian times vector
difference quotient, 49
user-supplied, 49,75
Jacobian-vector product
user-supplied (backward), 129,144
sparse
user-supplied, 47,74–75
user-supplied (backward), 127,142,143
klu sparse linear solver
type SlsMat,188
maxl,36
maxord,68
memory requirements
idaband linear solver, 63
idabbdpre preconditioner, 88
idadense linear solver, 63
idas solver, 79,92,105
idas solver, 55
idaspgmr linear solver, 65
MODIFIED GS,50,129
220 INDEX
MPI, 4
N VCloneVectorArray,154
N VCloneVectorArray OpenMP,164
N VCloneVectorArray Parallel,162
N VCloneVectorArray ParHyp,168
N VCloneVectorArray Petsc,170
N VCloneVectorArray Pthreads,166
N VCloneVectorArray Serial,159
N VCloneVectorArrayEmpty,154
N VCloneVectorArrayEmpty OpenMP,164
N VCloneVectorArrayEmpty Parallel,162
N VCloneVectorArrayEmpty ParHyp,168
N VCloneVectorArrayEmpty Petsc,170
N VCloneVectorArrayEmpty Pthreads,166
N VCloneVectorArrayEmpty Serial,159
N VDestroyVectorArray,154
N VDestroyVectorArray OpenMP,164
N VDestroyVectorArray Parallel,162
N VDestroyVectorArray ParHyp,168
N VDestroyVectorArray Petsc,170
N VDestroyVectorArray Pthreads,167
N VDestroyVectorArray Serial,159
N Vector,26,153
N VGetLength OpenMP,164
N VGetLength Parallel,162
N VGetLength Pthreads,167
N VGetLength Serial,159
N VGetLocalLength Parallel,162
N VGetVector ParHyp,168
N VGetVector Petsc,170
N VMake OpenMP,164
N VMake Parallel,162
N VMake ParHyp,168
N VMake Petsc,169
N VMake Pthreads,166
N VMake Serial,159
N VNew OpenMP,164
N VNew Parallel,161
N VNew Pthreads,166
N VNew Serial,159
N VNewEmpty OpenMP,164
N VNewEmpty Parallel,161
N VNewEmpty ParHyp,168
N VNewEmpty Petsc,169
N VNewEmpty Pthreads,166
N VNewEmpty Serial,159
N VPrint OpenMP,164
N VPrint Parallel,162
N VPrint ParHyp,168
N VPrint Petsc,170
N VPrint Pthreads,167
N VPrint Serial,160
newBandMat,186
newDenseMat,184
newIntArray,184,187
newLintArray,184,187
newRealArray,184,187
NV COMM P,161
NV CONTENT OMP,163
NV CONTENT P,160
NV CONTENT PT,165
NV CONTENT S,158
NV DATA OMP,163
NV DATA P,161
NV DATA PT,165
NV DATA S,158
NV GLOBLENGTH P,161
NV Ith OMP,164
NV Ith P,161
NV Ith PT,166
NV Ith S,159
NV LENGTH OMP,163
NV LENGTH PT,165
NV LENGTH S,158
NV LOCLENGTH P,161
NV NUM THREADS OMP,163
NV NUM THREADS PT,165
NV OWN DATA OMP,163
NV OWN DATA P,161
NV OWN DATA PT,165
NV OWN DATA S,158
NVECTOR module, 153
openMP, 4
optional input
backward solver, 125
band linear solver, 46,126–127
dense linear solver, 46,125–126
forward sensitivity, 97–98
initial condition calculation, 51–53
iterative linear solver, 49–51,128–130
quadrature integration, 81,134
rootfinding, 53–54
sensitivity-dependent quadrature integration,
108–109
solver, 40–45
sparse linear solver, 47–48,127–128
optional output
backward initial condition calculation, 131–
132
backward solver, 131
band linear solver, 63–64
band-block-diagonal preconditioner, 88
dense linear solver, 63–64
forward sensitivity, 99–102
initial condition calculation, 62,102
interpolated quadratures, 80

INDEX 221
interpolated sensitivities, 95
interpolated sensitivity-dep. quadratures, 106
interpolated solution, 54
iterative linear solver, 65–68
quadrature integration, 82–83,134
sensitivity-dependent quadrature integration,
109–110
solver, 55–62
sparse linear solver, 65
output mode, 118,124
partial error control
explanation of idas behavior, 111
portability, 26
preconditioning
advice on, 11,24
band-block diagonal, 84
setup and solve phases, 24
user-supplied, 49,76,128–129,145,147
Pthreads, 4
quadrature integration, 12
forward sensitivity analysis, 16
RCONST,26
realtype,26
reinitialization, 68,120
residual function, 69
backward problem, 134,135
forward sensitivity, 102
quadrature backward problem, 136
sensitivity-dep. quadrature backward prob-
lem, 137
right-hand side function
quadrature equations, 83
sensitivity-dependent quadrature equations,
110
Rootfinding, 28,38
rootfinding, 11
second-order sensitivity analysis, 19
support in idas,20
sls sparse linear solver
functions
small matrix, 191
SlsMat,188
SMALL REAL,26
SparseAddIdentityMat,191
SparseAddMat,191
SparseCopyMat,191
SparseDestroyMat,191
SparseFromDenseMat,191
SparseMatvec,191
SparseNewMat,191
SparsePrintMat,191
SparseReallocMat,191
SparseScaleMat,191
sparsetype,35
sparsetype=CSR MAT,35
spbcg generic linear solver
description of, 194
functions, 194
spfgmr generic linear solver
description of, 193
functions, 193
spgmr generic linear solver
description of, 192
functions, 193
support functions, 193
sptfqmr generic linear solver
description of, 194
functions, 194
step size bounds, 43
sundials nvector.h,26
sundials types.h,26
superlumt sparse linear solver
type SlsMat,188
TFQMR method, 51,130,194
tolerances, 8,32,71,81,108
UNIT ROUNDOFF,26
User main program
Adjoint sensitivity analysis, 113
forward sensitivity analysis, 89
idabbdpre usage, 86
idas usage, 27
integration of quadratures, 77
integration of sensitivitiy-dependent quadra-
tures, 103
user data,42,70,71,83,85,111
user dataB,150,151
weighted root-mean-square norm, 8–9