Air Hogs Ornithopter Kpeterson Iros11

User Manual: Air Hogs Ornithopter

Open the PDF directly: View PDF .
Page Count: 7

Experimental Dynamics of Wing Assisted Running for a Bipedal

Ornithopter

Kevin Peterson and Ronald S. Fearing

Abstract— BOLT is a lightweight bipedal ornithopter capa-

ble of high-speed dynamic running and effecting transitions

between aerial and terrestrial locomotion modes. The gait

dynamics of both quasi-static and dynamic locomotion are

examined through the use of an on-board accelerometer, part

of a one gram electronics package also containing a processor

and radio. We discuss the accelerations in the context of the

traditional spring-loaded inverted pendulum model seen in

nearly all legged locomotion in organisms. Flapping wings are

shown to provide damping along with propulsive force. The

aerodynamic forces of the flapping wings also impart passive

stability to the robot, enabling it to run bipedally with only

a single actuator. BOLT transitions from ground running to

aerial hovering in as little as one meter of runway. Overall, the

advantages provided by wings in terrestrial locomotion, coupled

with aerial capabilities, allow BOLT to navigate complex

three dimensional environments, switching between locomotion

modes when necessary.

I. INTRODUCTION

Navigating complex three dimensional environments is an

ability that is seemingly trivial for small animals, yet pro-

vides significant challenges for robots today. Small, mobile

robots (mass on the order of grams, linear dimensions on

the order of centimeters) provide many advantages when

exploring an environment, and are capable of operating in

small spaces unreachable by a larger robot. In addition,

their small size allows multiple robots to be transported and

deployed, greatly increasing the amount of area they can

cover.

While there are many advantages to small robots, there are

also many obstacles they have trouble navigating. Obstacles

much larger than the robot present a significant challenge

in legged locomotion, and even robots with the ability to

climb up obstacles would be impeded when confronted with

an aquatic obstacle. In confined spaces, aerial robots are

often unable to navigate, giving an advantage to a terrestrial

robot. Flying also requires a large amount of energy, and no

robot can stay aloft indefinitely. Terrestrial locomotion may

be more energy efficient for shorter distances, and would

allow for locomotion even if the energy for flight is spent.

By being capable of both aerial and terrestrial locomotion,

This work was supported by the United States Army Research Labora-

tory under the Micro Autonomous Science and Technology Collaborative

Technology Alliance

Kevin Peterson is with Department of Electrical Engineering and

Computer Sciences, University of California, Berkeley, CA 94720, USA

kevincp@eecs.berkeley.edu

Ronald S. Fearing is with Department of Electrical Engineering and

Computer Sciences, University of California, Berkeley, CA 94720, USA

ronf@eecs.berkeley.edu

Fig. 1. BOLT: a bipedal ornithopter capable of both arial and terrestrial

locomotion.

a hybrid robot could choose the best mode of locomotion

given the obstacles confronting it.

Many successful small terrestrial robots have been pre-

viously developed, including DASH [1], DynaRoACH [2],

Mini-Whegs [3], Sprawlita [4], iSprawl [5], and RHex [6].

With the exception of Mini-Whegs, these robots all use

six legs arranged in an alternating tripod configuration for

passive stability when running. In contrast, dynamic bipedal

running has generally required a complex controller and

multiple actuators to maintain stability. Dynamic bipedal

running has been previously demonstrated by RHex [7],

along with an extensive list of larger bipedal robots. At the

very small scale, dynamic bipedal running can be seen in the

cockroach Periplaneta americana when it is running at its

fastest speeds [8]. The locomotion dynamics of these robots

is characterized by the spring loaded inverted pendulum

model (SLIP) [9], a pattern exhibited by nearly all legged

organisms despite widely varying leg numbers [10].

There have also been many ornithopters capable of hov-

ering in an indoor environment, namely DelFly II [11], a

hummingbird sized ornithopter developed by Nathan Chro-

nister [12], and the Aerovironment Nano Hummingbird

[13]. Previous work on small hybrid robots includes MALV

[14] and its descendant MMALV [15], the SkyhopperTMby

WowWeeTM, and the EPFL microglider [16] currently under

development. Work has also been done on aerial-terrestrial

transitions, with [17] and [18] both capable of wall perching.

Other hybrid robots which have been developed primarily

focus on terrestrial and aquatic locomotion such as Boxybot

[19] and AQUA, a waterproof version of RHex [20].

The Bipedal Ornithopter for Locomotion Transitioning, or

BOLT (Fig. 1), is a small lightweight robot capable of both

aerial and terrestrial locomotion modes. The integration of an

electronics package allows two-way communication and the

investigation of the robot dynamics with a six-axis inertial

measurement unit (IMU). BOLT has a total weight of 11.4

grams, with a wingspan of 28 cm and a length of 17.5 cm.

The robot is capable of dynamic high-speed bipedal loco-

motion by exploiting its aerodynamic properties for stability.

The use of aerodynamics during bipedal locomotion has been

previously seen in some birds [21], although generally only

in inclined running. BOLT can transition from terrestrial

locomotion to hovering in as little as one meter of space,

and has demonstrated the ability to takeoff on smooth tile,

foam, carpeted flooring, and plywood. BOLT can also take

off from inclined ledges, with up to a 45 degree slope tested.

The Smart Composite Microstructures (SCM) [22] process

allows the integration of a lightweight leg structure with the

rest of the body, comprised mainly of carbon fiber spars.

II. MECHANICAL DESIGN

The primary design goal for BOLT is developing a plat-

form capable of both terrestrial and aerial locomotion. To ac-

complish this goal, we combine the gearbox and wings from

a commercial ornithopter (Air HogsTMV-wing AvengerTM)

with a custom airframe, leg design, and electronics package.

Because of the desire for stable hovering flight, weight and

weight distribution are a key consideration in all design

decisions. A single motor drives both the leg and the wings,

allowing sufficiently high power density to maintain hovering

flight.

A. Airframe Design

BOLT’s airframe uses carbon fiber spars for structural

rigidity. The lightweight properties of carbon fiber make

it ideal for use in a flying platform. A rigid airframe is

critical in preventing serial compliance from reducing the

wing thrust. To create a lightweight tail, carbon fiber spars

are placed in a cardboard pattern and a 12.7 µmfilm of

polyethylene terephthalate (PET) is overlaid and attached to

the spars with cyanoacrylate (Fig. 2(a)). The construction

materials of the tail are similar to those used in [11], a

successful ornithopter on the same size scale as BOLT.

The center of mass location of the robot is important for

determining the posture of the robot when it is in the air.

We place the battery at the very posterior of the robot on the

tail, while the controller board is placed within the airframe.

This gives the robot a vertical posture, with the majority of

the wing thrust directed downward. By adjusting the position

of the controller board, the robot can be set to either hover

in place or fly forward at a slow rate. The airframe of the

robot also protects the controller board during operation.

Directly mounting the controller board to the rigid carbon

fiber airframe overwhelms the accelerometer due to the high

(a) (b)

Fig. 2. (a) shows the tail of the robot, constructed from carbon fiber spars

and 12.7 micron thick PET film. The battery is placed at the back of the

tail to maintain proper weight distribution. (b) shows the controller board

mounted on small foam offsets. The foam offsets are critical for dampening

the high frequency vibrations of the body.

frequency vibrations produced by the motor transmission.

To accurately study the dynamics of the robot, the board is

moved forward and placed on foam mounts (Fig. 2(b)) to

dampen the vibration noise and improve the quality of the

acceleration measurements.

A critical feature enabling ground-to-air transitions of the

robot is the angle of attack of the wings. The clap-and-peel

design of the wings produces force directed perpendicularly

to the stroke plane. On the initial iterations of BOLT, the

wings had a low angle of attack, directing propulsive force

horizontally when running along the ground. This robot was

capable of flight, but could only takeoff by running from

a one meter or higher ledge. Once in the air, the center of

mass location caused the tail to swing under the robot and it

entered a stable flight posture. Increasing the wing angle of

attack allows the robot to build lift as the forward speed

increases, eventually causing the robot to pitch upwards,

directing the main flapping force downwards. This leads to

takeoff from the ground and the robot entering a stable flight

posture due to the center of mass location with respect to

the center of lift. On BOLT, the angle of attack is set to 28

degrees. This value was chosen experimentally to provide a

balance between the robot’s maximum terrestrial speed, and

the distance required for takeoff.

B. Leg Design

BOLT has a bipedal leg design, with each leg going

through a symmetrical motion 180 degrees out of phase with

the another. The legs are built using the SCM process [22],

which allows the implementation of a lightweight structure

that transforms the output of the motor to the desired leg

trajectory. Four layers of unidirectional carbon fiber pre-

preg are sandwiched around 50.8 µmPET to create the leg

structure. The layers of the unidirectional carbon fiber are

arranged crosswise to provide stiffness in two directions,

and are mirrored across the flexure layer. The structure is

designed to provide protection to the hips in case of high

velocity impacts, while allowing the legs to still extend in

front and below the body.

Fig. 3 shows a simplified version of the mechanisms that

transform the rotation of the motor in the transverse plane

of the robot to the desired leg trajectories. A set of parallel

four-bars drives the vertical motion of the legs (Fig. 3(a)),

FRONT

VIEW

Top

Bottom

(a)

Front

Back

TOP

VIEW

(b)

Fig. 3. Simplified representation of the mechanisms that enable the (a)

vertical motion and (b) fore-aft motion of the legs.

TABLE I

PHYSICAL PARAMETERS AND COMPONENTS OF BOLT

Total Mass 11.4 grams

Body Size 17.5 x 28 x 15 cm

Battery Full River 60 mAh lithium polymer

Micro-controller Microchip dsPIC33F

Communications Atmel AT86RF231

Accelerometer Analog Devices ADXL345

Gyroscope Invensense ITG-3200

while a crank-slider mechanism drives the fore-aft motion of

the legs (Fig. 3(b)). One revolution of the motor output gear

(hereafter referred to as a single motor cycle) corresponds to

a full left and right leg stride, and a single complete wing

beat (opening stroke and closing stroke). In implementing the

mechanisms shown in Fig. 3, several implementation details

are necessary due to the properties of the SCM process. The

structure is designed such that each of the flexures is in a

straight default configuration, reducing the effect of off-axis

forces and minimizing the strain of the PET (Fig. 4(a)). The

motion of the legs is shown in Fig. 4, and in the companion

video.

C. Power, Communications, and Control

BOLT uses a custom electronics package (ImageProc 2.2)

that incorporates a 40 MHz dsPIC processor with a motor

driver, six-axis IMU, and 1 MB of Flash memory (Table

I) [23]. In addition, the board has an Atmel 802.15.4 radio

for communication with a laptop. A Python interface sends

commands to the robot and receives data from the board’s

sensors. A 60 mAh battery powers the electronics board and

motor.

III. METHODS AND RESULTS

BOLT has two regimes of operation when locomoting

terrestrially, a quasi-static gait (9 Hz) and a dynamic gait

(12.5 Hz). To study the dynamics in each of these modes,

we use the accelerometer to examine the intra-stride forces

at steady-state velocity. The rate gyroscope allows the accel-

eration data to be corrected for the pitch and roll of the body,

(a) (b) θ=0◦

(c) θ=135◦(d) θ=205◦

Fig. 4. The implementation of the mechanism described in Fig. 3 is shown

by (a). Here, the movable flexures have been straightened, reducing the

strain and the effect of off-axis forces. (b)-(d) show screenshots from the

companion video of the left leg moving through its stride. The right leg

exhibits similar motion in anti-phase with the left.

aligning the acceleration components in the horizontal and

vertical directions. We use the maximum velocity obtained

by the robot as a relative measure of the maximum effective

locomotive force on the robot. The data are parameterized

by the output gear phase, obtained by integrating the highly

periodic back EMF signal. By performing the tests on carpet,

we ensure the legs have good traction with the ground during

the trials.

We consider two control cases to distinguish between the

force contributions of the flapping wings and the legs when

running along the ground. We replace the legs on BOLT with

lightweight wheels (Fig. 5(a)) to isolate the effects of the

flapping wings (wings-only, WO). In this configuration, the

flapping wings supply all of the locomotive force. Removing

the linkage driving the wings (Fig. 5(b)) reduces the wings to

a passive element with the locomotive force coming entirely

from the legs, (wings-passive, WP). This configuration also

allows the differentiation between the effects of flapping the

wings and the passive properties of the airfoil.

(a) Wings-Only (WO) (b) Wings-Passive (WP)

Fig. 5. (a) shows the first control case, the robot with wheels instead of

legs, allowing the investigation of the wing effects alone. For the second

control case (b), we disconnect the linkage driving the wings, removing any

active effects from flapping.

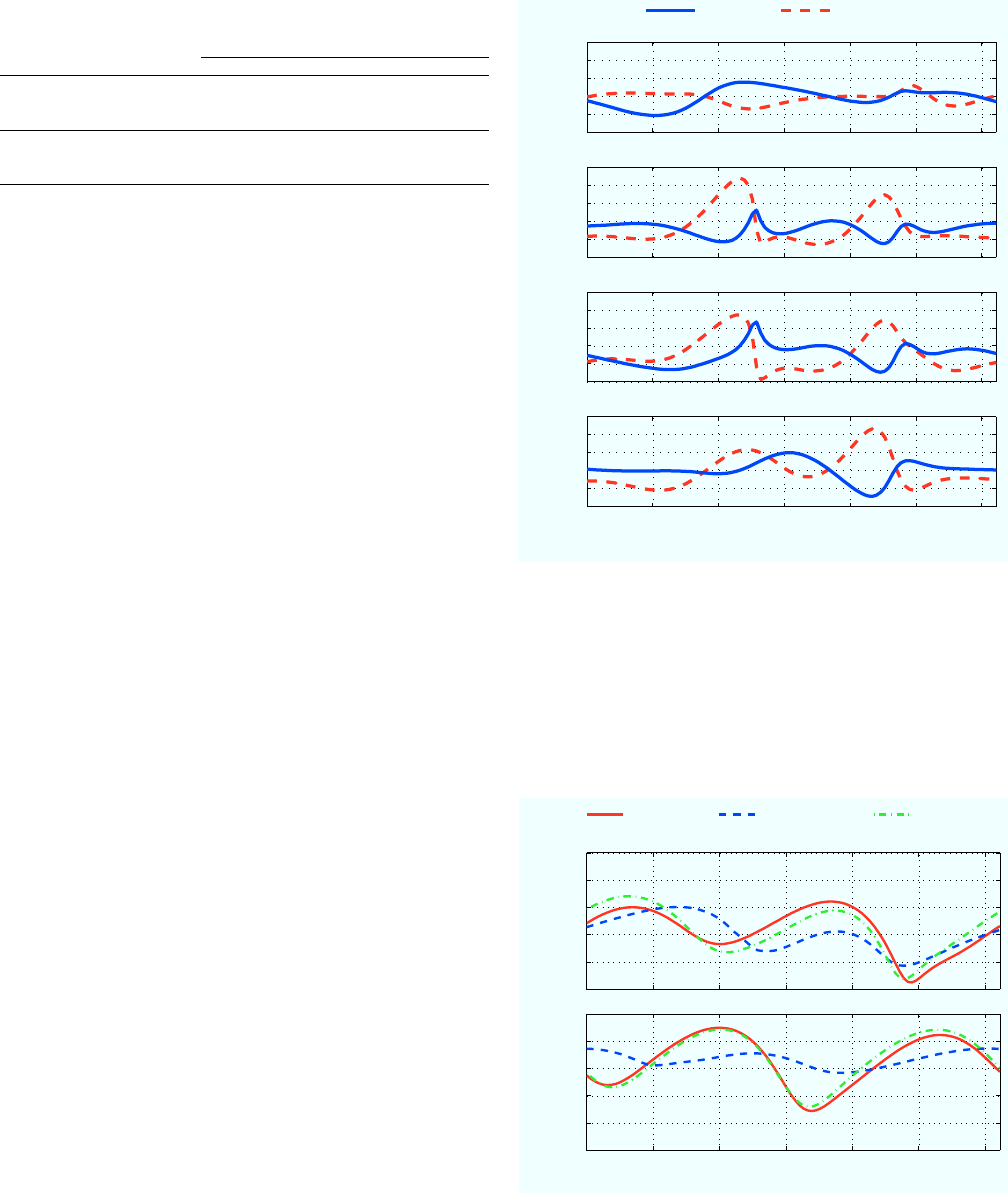
TABLE II

FORWARD VELOCITY (m/s), MOTOR INPUT POWER (W), AND COST OF

TRANSPORT (J/(kg ·m))FOR DIFFERENT CONFIGURATIONS AND GAITS

Gait Configuration

(frequency) Wings-Passive Wings-Only Hybrid

Quasi-static

(9 Hz)

Velocity 0.33 0.17 0.50

Power 0.36 0.65 0.89

COT 96.8 337.4 155.8

Dynamic

(12.5 Hz)

Velocity 0.35 1.5 1.5

Power 0.36 0.79 0.91

COT 89.7 45.9 53.1

A. Quasi-static Terrestrial Locomotion

BOLT exhibits a quasi-static walking gait when running

at a flapping frequency of 9 Hz. The aerodynamic effects

of the flapping wings are minimal in this gait, with the WO

robot reaching a maximum velocity of 0.17 m/s. In contrast,

the legs of the WP robot propel it at 0.33 m/s. Overall, the

hybrid robot reaches 0.5 m/s, suggesting a superposition of

the leg and wing thrust components may explain the hybrid

gait.

Fig. 6 shows the fore-aft and vertical accelerations of the

robot over a representative cycle. We show the accelerations

for the WO robot, the WP robot, the superposition of the WO

and WP robots, and the hybrid robot. The accelerations of the

hybrid robot are similar in both magnitude and shape to the

superposition of the WO and WP robots, suggesting a lower

degree of interaction between the leg and wing forces in this

gait. An effect of leg/wing force coupling that can be seen

is the smoother accelerations of the hybrid robot compared

to those the WO+WP model predicts. The flapping wings

provide a higher amount of dampening on the impulsive leg

forces the robot generates than the passive wings.

The motor velocity over a representative cycle of the

quasi-static gait is shown in Fig. 7. The robot uses constant

PWM control for the motor, causing the motor velocity to

vary dependent upon load. Over a single cycle, the effect of

the varying load due to the flapping wings or legs is seen

clearly from the change in motor velocity. The variation in

motor velocity for the hybrid robot and the WO robot is

nearly identical, implying a similar load in the two cases.

Thus, despite the wings ineffectiveness in this gait they are

responsible for the majority of the power consumption of the

motor. Table II shows the WO robot consumes 80% more

power than the WP robot despite traveling at only half the

speed. This is reflected by the cost of transport: the WP robot

is the most efficient while the WO robot is the least efficient.

The hybrid robot has an efficiency between the two controls.

B. Dynamic Locomotion

The second running gait of BOLT is dynamic bipedal

locomotion, seen at a flapping frequency of 12.5 Hz. The

aerodynamic force the flapping wings provide increases

greatly, with the WO robot running at 1.5 m/s. The hybrid

robot also runs at 1.5 m/s, while the WP robot is only capable

−20

0

30

Wings−Only

Fore−Aft Vertical

−20

0

30 Wings−Passive

Acceleration (m/s 2)

0123456

−20

0

30 Hybrid

Phase (rad)

−20

0

30 Wings−Only + Wings−Passive

Fig. 6. Fore-aft and vertical accelerations shown over a single representative

cycle when running at 9 Hz at a steady state velocity. At slow frequencies the

robot exhibits quasi-static motion. In this regime, the forces on the hybrid

robot are consistent with the superposition model of the individual leg and

wing forces.

0123456

20

40

60

80

100

120

Phase (rad)

Dynamic Gait

Wings−Only Passive Wings Hybrid

20

40

60

80

100

120

Motor Velocity (rad/s)

Quasi−static Gait

Fig. 7. Motor velocity over a representative cycle for both the quasi-static

gait (9 Hz) and the dynamic gait (12.5 Hz).

of 0.35 m/s. In this gait, there is a strong interaction between

the wing and leg dynamics.

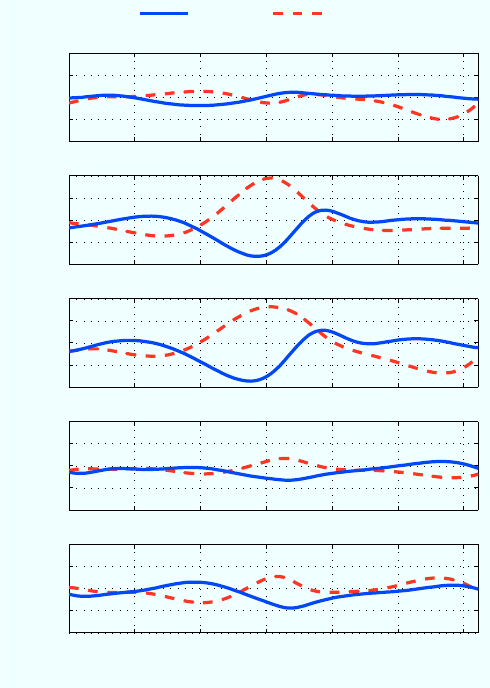
The acceleration plots of Fig. 8 show the same four cases

as above (WO, WP, WO+WP, Hybrid), along with a fifth

case: the WO case subtracted from the hybrid case. For

this gait, the WO+WP model is a poor predictor of the

hybrid accelerations, predicting magnitudes over double the

measured values.

The WP case shows one overly large single acceleration

caused by a footfall centered at a phase of π, propelling the

robot into the air preventing the next footfall from generating

the same amount of force. Between footfalls, the robot is

in free-fall, with zero fore-aft acceleration, and a vertical

acceleration of −9.8m/s2. The high accelerations and gait

asymmetry of the WP case are generally indicative of poor

leg tuning on a robot with a traditional SLIP gait. The

hybrid robot uses the same legs as the WP robot at the same

frequency, but the accelerations experienced by the robot are

much lower. We again see the effect of the flapping wings

dampening the leg impulses from the quasi-static case, but

to a higher degree now. The hybrid robot does not have the

free-fall state shown by the WP robot; stopping this free-fall

leads to the high accelerations seen in the WP case. The

hybrid robot is “flying between footfalls” instead of falling,

greatly reducing the accelerations that must be effected by

the legs.

The WO robot and the hybrid robot both run at the same

forward velocity and motor frequency (see Fig. 7). This leads

to the assumption that the wing forces are nearly the same

in both cases regardless of the ground contacts. Subtracting

the WO case from the hybrid case shows the leg forces for

the hybrid robot. While they still differ from a traditional

SLIP gait due to the leg/wing interactions, the legs no longer

appear poorly tuned. From this data, we conclude a flapping

wing robot should use stiffer legs than would normally be

expected for a robot running with legs alone.

The motor velocities, and thus the dynamic loading, are

nearly identical between the hybrid robot and the WO robot

during the dynamic gait (Fig. 7). As in the quasi-static case,

the WP robot uses the least amount of power, followed by the

WO robot with the hybrid robot consuming the most power

(see Table II). Due to the differing forward speeds the COT

relationship is now markedly different, with the WO case

the most efficient and the WP case the least efficient. Once

again, the hybrid provides a compromise between the cases.

C. Terrestrial to Aerial Transitions

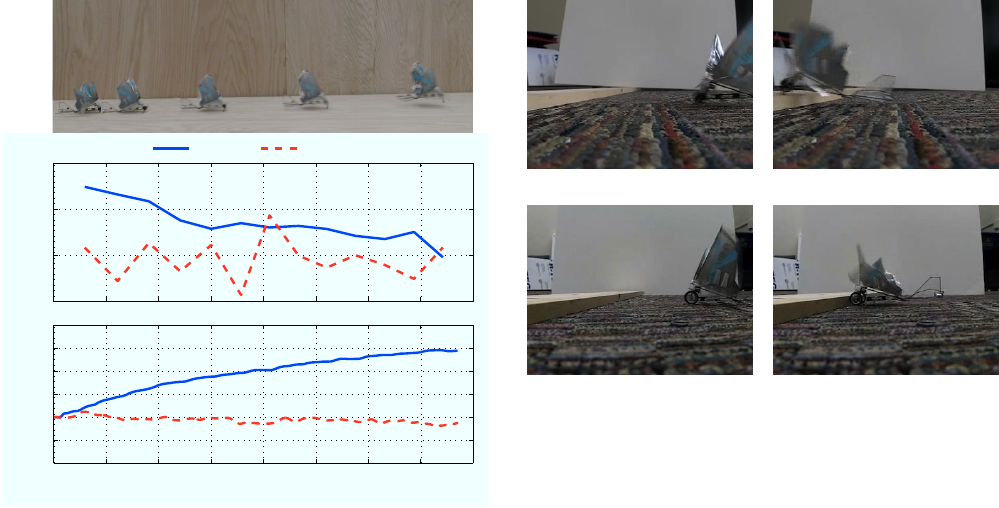
By running along the ground at a high speed, BOLT can

generate enough aerodynamic lift to take off. Depending

upon the center of mass location, BOLT requires between

one and two meters of runway space. Fig. 9 shows the robot

during a takeoff maneuver with the controller board mounted

forward, causing a takeoff distance just under 2 meters when

flapping at 18 Hz. The average acceleration for each stride

is shown, along with the instantaneous velocity obtained by

integrating the accelerometer data. BOLT accelerates very

quickly from a standstill, reaching 1 m/s in 0.14 s and 2

−50

0

50

Wings−Only

Fore−Aft Vertical

−50

0

50 Wings−Passive

−50

0

50 Hybrid

−50

0

50 Wings−Only + Wings−Passive

Acceleration (m/s 2)

0123456

−50

0

50 Hybrid − Wings−Only

Phase (rad)

Fig. 8. Fore-aft and vertical accelerations shown over a single representative

cycle when running at 12.5 Hz. At high speeds, a simple superposition of

the leg and wing forces does not accurately predict the overall force on

BOLT. The interactions between the legs and the wings are an important

component of the forces during dynamic locomotion, altering the range of

leg stiffnesses that give stable locomotion.

m/s in 0.38 s. Upon reaching a velocity of 2.5 m/s, BOLT

has taken off and is no longer touching the ground. The

robot continues to accelerate until reaching 3 m/s. At this

point the tail begins to swing under the robot and it enters

a vertical flight posture. The vertical accelerations oscillate

around zero throughout the maneuver as the robot bounces

along the runway. The total vertical velocity stays very near

zero however, as the accelerometer does not pick up the slow

movement upwards of the robot.

By moving the location of the controller board (and the

center of mass), BOLT can be configured to have different

transition properties. Moving the controller board forward

increases the distance required for takeoff (∼2 m), but also

increases the maximum terrestrial speed (2.5 m/s). Addi-

tionally, it allows the board to be placed on foam offsets,

improving the IMU measurements. When the board is moved

to the back of the airframe, the takeoff distance is reduced

to 1 meter. The speed where takeoff occurs is also reduced

to 1.75 m/s.

−5

0

5

10

Acceleration (m/s 2)

Fore−Aft Vertical

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

−1

0

1

2

3

Velocity (m/s)

Time (s)

A B C D E

A B C D E

Fig. 9. BOLT transitioning from terrestrial locomotion to aerial locomotion.

The average acceleration of each stride/wingbeat is plotted, along with the

velocity obtained by integrating the accelerometer data. The robot quickly

builds speed (A-C), lifting off at 2.5 m/s (D) and continuing to accelerate

until it reaches 3 m/s (E). The vertical acceleration oscillates around zero,

giving near zero vertical velocity throughout the run.

IV. DISCUSSION

The method BOLT uses to maintain stability when running

differ between the quasi-static and dynamic gait. At low

speeds, the tail of the robot remains in contact with the

ground and provides an extra point of stability. At higher

speeds, the tail of the robot lifts off of the ground, and

the robot is truly bipedal. The aerodynamic forces from

the flapping wings and the tail allow the robot to maintain

passive stability despite its bipedal locomotion in the absence

of any closed loop control. The sprawled posture of the

legs and low-to-the-ground design help the robot maintain

stability during both modes of locomotion.

By using the flapping wings to provide additional thrust,

the terrestrial speed of the robot is significantly increased

from a legged robot. With a quasi-static gait, the wings-

passive robot has the best COT, while the wings-only robot

performed best at a dynamic gait. The hybrid robot provides

a compromise between the two, allowing more efficient

locomotion when a range of speeds is necessary. At slow

speeds legs provide more efficient thrust than wing flapping;

at high speeds the wings allow the robot to “fly” along the

ground, dramatically reducing the cost of transport.

BOLT has also shown the ability to clear terrestrial obsta-

cles, both with a running start and from standstill. Fig. 10

shows BOLT clearing a 2 cm obstacle, the highest obstacle

it can clear with a purely terrestrial gait. In the wings-only

configuration the robot is unable to clear the 2 cm obstacle,

clearly showing the necessity of the legs. The wings-passive

(a) BOLT (b) BOLT

(c) Wings-only (d) Wings-only

Fig. 10. (a-b) show BOLT running at a 2 cm obstacle and easily clearing

the top of it. By contrast, (c-d) show the wings-only robot incapable of

getting over the barrier. The wings-passive robot is capable of clearing the

barrier, but is not always successful.

robot can clear the obstacle, but does so inconsistently. BOLT

has shown two methods of clearing this obstacle, depending

on the initial condition when first encountering the obstacle.

If the obstacle is encountered at the low point in the stride,

the robot will run at the obstacle for a few strides until its

legs are able to pull it over the top. During the high point of

its stride, the robot simply leaps over the obstacle without

stopping. These scenarios are shown in the accompanying

video.

V. CONCLUSIONS AND FUTURE WORK

BOLT achieves its goal of being capable of both aerial

and terrestrial locomotion, and transitioning between the

two in an indoor environment. During dynamic running,

BOLT uses a unique method for maintaining passively stable

bipedal locomotion, exploiting the aerodynamic effects of its

flapping wings. Because of the aerodynamic forces present

on the robot, BOLT does not run using a traditional SLIP

gait. Despite this fact, the robot is capable of high speed

locomotion, “flying” along the ground using a combination

of aerodynamic forces and ground reaction forces to propel

itself. The hybrid robot also provides a compromise in

efficiency across a range of speeds, when compared to the

wings-only and wings-passive robots. The legs and wings

hybrid configuration is also particularly adept at crossing

low obstacles placed in its path without needing to resort

to aerial locomotion.

While not the first hybrid aerial/terrestrial robot, BOLT is

currently the smallest. Its ability to transition from terrestrial

locomotion to aerial locomotion in a small space enables it to

take advantage of both modes of transportation, especially in

a confined environment. The key contribution setting BOLT

apart is the integration of a smart electronics package capable

of measuring the dynamics of a fully capable hybrid plat-

form. BOLT has begun to provide insights into the dynamics

of wing assisted locomotion, and allows the interactions

between legs and wings to be examined.

Future work on BOLT will further explore the dynamics

of running with flapping wings, attempting to determine

the proper leg stiffness to achieve a stable gait with high

efficiency in a terrestrial mode where SLIP does not apply.

Additionally, a transmission capable of selectively driving

the legs or wings would further improve the efficiency of

the robot. By turning off the wings at low terrestrial speeds,

or disengaging the legs when flying, the robot can minimize

the power lost to unnecessary appendages. Techniques for

steering, both in aerial and terrestrial locomotion modes also

bear further investigation.

ACKNOWLEDGMENTS

The authors gratefully thank Stan Baek for his design of

the ImageProc 2.2 electronics board, and Stan and Aaron

Hoover for their diligent work developing the drivers for the

electronics board.

REFERENCES

[1] P. Birkmeyer, K. Peterson, and R. Fearing, “DASH: A dynamic 16g

hexapedal robot,” in IEEE/RSJ International Conference on Intelligent

Robots and Systems, October 2009, pp. 2683–2689.

[2] A. Hoover, S. Burden, X. Fu, S. Sastry, and R. Fearing, “Bio-inspired

design and dynamic maneuverability of a minimally actuated six-

legged robot,” in 3rd IEEE RAS and EMBS International Conference

on Biomedical Robotics and Biomechatronics (BioRob), September

2010, pp. 869–876.

[3] J. M. Morrey, B. Lambrecht, A. D. Horchler, R. E. Ritzmann, and

R. D. Quinn, “Highly mobile and robust small quadruped robot,” in

IEEE/RSJ International Conference on Intelligent Robots and Systems,

October 2003, pp. 82–87.

[4] J. G. Cham, S. A. Bailey, J. E. Clark, R. J. Full, and M. R.

Cutkosky, “Fast and robust: Hexapedal robots via shape deposition

manufacturing,” International Journal of Robotics Research, vol. 21,

no. 10, 2002.

[5] S. Kim, J. E. Clark, and M. R. Cutkosky, “isprawl: Design and tuning

for high-speed autonomous open-loop running,” International Journal

of Robotics Research, vol. 25, no. 9, pp. 903–912, 2006.

[6] U. Saranli, M. Buehler, and D. E. Koditschek, “Rhex: A simple

and highly mobile hexapod robot,” International Journal of Robotics

Research, vol. 20, no. 7, pp. 616 – 631, July 2001.

[7] N. Neville, M. Buehler, and I. Sharf, “A bipedal running robot with

one actuator per leg,” in IEEE International Conference on Robotics

and Automation, May 2006, pp. 848 –853.

[8] R. Full and M. Tu, “Mechanics of rapid running insects: two-, four-

, and six-legged locomotion,” Journal of Experimental Biology, vol.

156, pp. 215–231, 1991.

[9] P. Holmes, R. J. Full, D. Koditschek, and J. Guckenheimer, “The

dynamics of legged locomotion: Models, analyses, and challenges,”

SIAM Review, vol. 48, no. 2, pp. 207–304, 2006.

[10] R. Blickhan and R. J. Full, “Similarity in multilegged locomotion:

Bouncing like a monopode,” Journal of Comparative Physiology A:

Neuroethology, Sensory, Neural, and Behavioral Physiology, vol. 173,

no. 5, pp. 509–517, November 1993.

[11] D. Lentink, S. Jongerius, and N. Bradshaw, “The scalable design of

flapping micro-air vehicles inspired by insect flight,” Flying Insects

and Robots, p. 185, 2009.

[12] (2011). [Online]. Available: http://www.ornithopter.org/

[13] (2011). [Online]. Available: http://www.avinc.com/nano

[14] R. J. Bachmann, F. J. Boria, R. Vaidyanathan, P. G. Ifju, and R. D.

Quinn, “A biologically inspired micro-vehicle capable of aerial and

terrestrial locomotion,” Mechanism and Machine Theory, vol. 44,

no. 3, pp. 513 – 526, 2009, special issue on Bio-Inspired Mechanism

Engineering.

[15] F. Boria, R. Bachmann, P. Ifju, R. Quinn, R. Vaidyanathan, C. Perry,

and J. Wagener, “A sensor platform capable of aerial and terrestrial

locomotion,” in IEEE/RSJ International Conference on Intelligent

Robots and Systems, August 2005, pp. 3959–3964.

[16] M. Kovac, J. Zufferey, and D. Floreano, “Towards a self-deploying

and gliding robot,” Flying Insects and Robots, 2009.

[17] M. Kovac¸, J. Germann, C. Hrzeler, R. Siegwart, and D. Floreano, “A

perching mechanism for micro aerial vehicles,” Journal of Micro-Nano

Mechatronics, vol. 5, pp. 77–91, 2009.

[18] A. Lussier Desbiens, A. Asbeck, and M. Cutkosky, “Landing, perching

and taking off from vertical surfaces,” The International Journal of

Robotics Research, vol. 30, no. 3, p. 355, 2011.

[19] D. Lachat, A. Crespi, and A. Ijspeert, “Boxybot: a swimming and

crawling fish robot controlled by a central pattern generator,” in

The First IEEE/RAS-EMBS International Conference on Biomedical

Robotics and Biomechatronics (BioRob), February 2006, pp. 643–648.

[20] C. Georgiades, A. German, A. Hogue, H. Liu, C. Prahacs, A. Ripsman,

R. Sim, L. Torres, P. Zhang, M. Buehler et al., “AQUA: an aquatic

walking robot,” in IEEE/RSJ International Conference on Intelligent

Robots and Systems, vol. 4, September 2004, pp. 3525–3531.

[21] M. Bundle and K. Dial, “Mechanics of wing-assisted incline running

(WAIR),” Journal of Experimental Biology, vol. 206, no. 24, pp. 4553–

4564, 2003.

[22] R. Wood, S. Avadhanula, R. Sahai, E. Steltz, and R. Fearing, “Micro-

robot design using fiber reinforced composites,” Journal of Mechanical

Design, vol. 130, p. 052304, 2008.

[23] S. Baek, F. G. Bermudez, and R. Fearing, “Flight control for target

seeking by 13 gram ornithopter,” in IEEE International Conference

on Intelligent RObots and Systems(IROS), September 2011.