Kupdf.net Practical Guide To Cluster Analysis In R Unsupervised Machine Learning

(Multivariate%20Analysis%201)%20Alboukadel%20Kassambara-Practical%20Guide%20to%20Cluster%20Analysis%20in%20R.%20Unsupervised%20M

User Manual:

Open the PDF directly: View PDF .
Page Count: 187 [warning: Documents this large are best viewed by clicking the View PDF Link!]

2015

Multivariate

Analysis I

Alboukadel Kassambara

 Practical Guide To

Cluster Analysis in R

Edition 1 sthda.com

Unsupervised Machine Learning

Published by STHDA (http://www.sthda.com), Alboukadel Kassambara

Contact: Alboukadel Kassambara <alboukadel.kassambara@gmail.com>

No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form

or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, without the prior

written permission of the Publisher. Requests to the Publisher for permission should

be addressed to STHDA (http://www.sthda.com).

Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best eﬀorts in

preparing this book, they make no representations or warranties with respect to the accuracy or

completeness of the contents of this book and speciﬁcally disclaim any implied warranties of

merchantability or ﬁtness for a particular purpose. No warranty may be created or extended by sales

representatives or written sales materials.

Neither the Publisher nor the authors, contributors, or editors,

assume any liability for any injury and/or damage

to persons or property as a matter of products liability,

negligence or otherwise, or from any use or operation of any

methods, products, instructions, or ideas contained in the material herein.

For general information contact Alboukadel Kassambara <alboukadel.kassambara@gmail.com>.

0.1. PREFACE 3

0.1 Preface

Large amounts of data are collected every day from satellite images, bio-medical,

security, marketing, web search, geo-spatial or other automatic equipment. Mining

knowledge from these big data far exceeds human’s abilities.

Clustering

is one of the important data mining methods for discovering knowledge

in multidimensional data. The goal of clustering is to identify pattern or groups of

similar objects within a data set of interest.

In the litterature, it is referred as “pattern recognition” or “unsupervised machine

learning” - “unsupervised” because we are not guided by a priori ideas of which

variables or samples belong in which clusters. “Learning” because the machine

algorithm “learns” how to cluster.

Cluster analysis is popular in many ﬁelds, including:

•

In cancer research for classifying patients into subgroups according their gene

expression proﬁle. This can be useful for identifying the molecular proﬁle of

patients with good or bad prognostic, as well as for understanding the disease.

•

In marketing for market segmentation by identifying subgroups of customers with

similar proﬁles and who might be receptive to a particular form of advertising.

•

In City-planning for identifying groups of houses according to their type, value

and location.

This book provides a practical guide to unsupervised machine learning or cluster

analysis using R software. Additionally, we developped an R package named factoextra

to create, easily, a ggplot2-based elegant plots of cluster analysis results. Factoextra

oﬃcial online documentation: http://www.sthda.com/english/rpkgs/factoextra

0.2 About the author

Alboukadel Kassambara is a PhD in Bioinformatics and Cancer Biology. He works since

many years on genomic data analysis and visualization. He created a bioinformatics

tool named GenomicScape (www.genomicscape.com) which is an easy-to-use web tool

for gene expression data analysis and visualization.

He developed also a website called STHDA (Statistical Tools for High-throughput Data

Analysis, www.sthda.com/english), which contains many tutorials on data analysis

and visualization using R software and packages.

He is the author of the R packages

survminer

(for analyzing and drawing survival

curves),

ggcorrplot

(for drawing correlation matrix using ggplot2) and

factoextra

(to easily extract and visualize the results of multivariate analysis such PCA, CA,

MCA and clustering). You can learn more about these packages at: http://www.

sthda.com/english/wiki/r-packages

Recently, he published two books on data visualization:

1. Guide to Create Beautiful Graphics in R (at: https://goo.gl/vJ0OYb).

2. Complete Guide to 3D Plots in R (at: https://goo.gl/v5gwl0).

Contents

0.1 Preface................................... 3

0.2 Abouttheauthor............................. 4

0.3 Key features of this book . . . . . . . . . . . . . . . . . . . . . . . . . 9

0.4 How this book is organized? . . . . . . . . . . . . . . . . . . . . . . . 10

0.5 Bookwebsite ............................... 16

0.6 Executing the R codes from the PDF . . . . . . . . . . . . . . . . . . 16

I Basics 17

1 Introduction to R 18

1.1 InstallRandRStudio .......................... 18

1.2 Installing and loading R packages . . . . . . . . . . . . . . . . . . . . 19

1.3 Getting help with functions in R . . . . . . . . . . . . . . . . . . . . . 20

1.4 Importing your data into R . . . . . . . . . . . . . . . . . . . . . . . 20

1.5 Demodatasets .............................. 22

1.6 Close your R/RStudio session . . . . . . . . . . . . . . . . . . . . . . 22

2 Data Preparation and R Packages 23

2.1 Datapreparation ............................. 23

2.2 RequiredRPackages........................... 24

3 Clustering Distance Measures 25

3.1 Methods for measuring distances . . . . . . . . . . . . . . . . . . . . 25

3.2 What type of distance measures should we choose? . . . . . . . . . . 27

3.3 Datastandardization........................... 28

3.4 Distance matrix computation . . . . . . . . . . . . . . . . . . . . . . 29

3.5 Visualizing distance matrices . . . . . . . . . . . . . . . . . . . . . . . 32

3.6 Summary ................................. 33

6CONTENTS

II Partitioning Clustering 34

4 K-Means Clustering 36

4.1 K-meansbasicideas ........................... 36

4.2 K-meansalgorithm ............................ 37

4.3 Computing k-means clustering in R . . . . . . . . . . . . . . . . . . . 38

4.4 K-means clustering advantages and disadvantages . . . . . . . . . . . 46

4.5 Alternative to k-means clustering . . . . . . . . . . . . . . . . . . . . 47

4.6 Summary ................................. 47

5 K-Medoids 48

5.1 PAMconcept ............................... 49

5.2 PAMalgorithm .............................. 49

5.3 ComputingPAMinR .......................... 50

5.4 Summary ................................. 56

6 CLARA - Clustering Large Applications 57

6.1 CLARAconcept ............................. 57

6.2 CLARAAlgorithm ............................ 58

6.3 ComputingCLARAinR......................... 58

6.4 Summary ................................. 63

III Hierarchical Clustering 64

7 Agglomerative Clustering 67

7.1 Algorithm ................................. 67

7.2 Steps to agglomerative hierarchical clustering . . . . . . . . . . . . . 68

7.3 Verify the cluster tree . . . . . . . . . . . . . . . . . . . . . . . . . . . 73

7.4 Cut the dendrogram into diﬀerentgroups................ 74

7.5 ClusterRpackage............................. 77

7.6 Application of hierarchical clustering to gene expression data analysis 77

7.7 Summary ................................. 78

8 Comparing Dendrograms 79

8.1 Datapreparation ............................. 79

8.2 Comparing dendrograms . . . . . . . . . . . . . . . . . . . . . . . . . 80

9 Visualizing Dendrograms 84

9.1 Visualizing dendrograms . . . . . . . . . . . . . . . . . . . . . . . . . 85

9.2 Case of dendrogram with large data sets . . . . . . . . . . . . . . . . 90

CONTENTS 7

9.3 Manipulating dendrograms using dendextend . . . . . . . . . . . . . . 94

9.4 Summary ................................. 96

10 Heatmap: Static and Interactive 97

10.1 R Packages/functions for drawing heatmaps . . . . . . . . . . . . . . 97

10.2Datapreparation ............................. 98

10.3 R base heatmap: heatmap() . . . . . . . . . . . . . . . . . . . . . . . 98

10.4 Enhanced heat maps: heatmap.2() . . . . . . . . . . . . . . . . . . . 101

10.5 Pretty heat maps: pheatmap() . . . . . . . . . . . . . . . . . . . . . . 102

10.6 Interactive heat maps: d3heatmap() . . . . . . . . . . . . . . . . . . . 103

10.7 Enhancing heatmaps using dendextend . . . . . . . . . . . . . . . . . 103

10.8Complexheatmap............................. 104

10.9 Application to gene expression matrix . . . . . . . . . . . . . . . . . . 114

10.10Summary ................................. 116

IV Cluster Validation 117

11 Assessing Clustering Tendency 119

11.1RequiredRpackages ........................... 119

11.2Datapreparation ............................. 120

11.3 Visual inspection of the data . . . . . . . . . . . . . . . . . . . . . . . 120

11.4 Why assessing clustering tendency? . . . . . . . . . . . . . . . . . . . 121

11.5 Methods for assessing clustering tendency . . . . . . . . . . . . . . . 123

11.6Summary ................................. 127

12 Determining the Optimal Number of Clusters 128

12.1Elbowmethod............................... 129

12.2 Average silhouette method . . . . . . . . . . . . . . . . . . . . . . . . 130

12.3Gapstatisticmethod........................... 130

12.4 Computing the number of clusters using R . . . . . . . . . . . . . . . 131

12.5Summary ................................. 137

13 Cluster Validation Statistics 138

13.1 Internal measures for cluster validation . . . . . . . . . . . . . . . . . 139

13.2 External measures for clustering validation . . . . . . . . . . . . . . . 141

13.3 Computing cluster validation statistics in R . . . . . . . . . . . . . . 142

13.4Summary ................................. 150

14 Choosing the Best Clustering Algorithms 151

14.1 Measures for comparing clustering algorithms . . . . . . . . . . . . . 151

8CONTENTS

14.2 Compare clustering algorithms in R . . . . . . . . . . . . . . . . . . . 152

14.3Summary ................................. 155

15 Computing P-value for Hierarchical Clustering 156

15.1Algorithm ................................. 156

15.2Requiredpackages ............................ 157

15.3Datapreparation ............................. 157

15.4 Compute p-value for hierarchical clustering . . . . . . . . . . . . . . . 158

V Advanced Clustering 161

16 Hierarchical K-Means Clustering 163

16.1Algorithm ................................. 163

16.2Rcode................................... 164

16.3Summary ................................. 166

17 Fuzzy Clustering 167

17.1RequiredRpackages ........................... 167

17.2 Computing fuzzy clustering . . . . . . . . . . . . . . . . . . . . . . . 168

17.3Summary ................................. 170

18 Model-Based Clustering 171

18.1 Concept of model-based clustering . . . . . . . . . . . . . . . . . . . . 171

18.2 Estimating model parameters . . . . . . . . . . . . . . . . . . . . . . 173

18.3 Choosing the best model . . . . . . . . . . . . . . . . . . . . . . . . . 173

18.4 Computing model-based clustering in R . . . . . . . . . . . . . . . . . 173

18.5 Visualizing model-based clustering . . . . . . . . . . . . . . . . . . . 175

19 DBSCAN: Density-Based Clustering 177

19.1WhyDBSCAN?.............................. 178

19.2Algorithm ................................. 180

19.3Advantages ................................ 181

19.4Parameterestimation........................... 182

19.5ComputingDBSCAN........................... 182

19.6 Method for determining the optimal eps value . . . . . . . . . . . . . 184

19.7 Cluster predictions with DBSCAN algorithm . . . . . . . . . . . . . . 185

20 References and Further Reading 186

0.3. KEY FEATURES OF THIS BOOK 9

0.3 Key features of this book

Although there are several good books on unsupervised machine learning/clustering

and related topics, we felt that many of them are either too high-level, theoretical

or too advanced. Our goal was to write a practical guide to cluster analysis, elegant

visualization and interpretation.

The main parts of the book include:

•distance measures,

•partitioning clustering,

•hierarchical clustering,

•cluster validation methods, as well as,

•

advanced clustering methods such as fuzzy clustering, density-based clustering

and model-based clustering.

The book presents the basic principles of these tasks and provide many examples in

R. This book oﬀers solid guidance in data mining for students and researchers.

Key features:

•Covers clustering algorithm and implementation

•Key mathematical concepts are presented

•

Short, self-contained chapters with practical examples. This means that, you

don’t need to read the diﬀerent chapters in sequence.

At the end of each chapter, we present R lab sections in which we systematically

work through applications of the various methods discussed in that chapter.

10 CONTENTS

0.4 How this book is organized?

This book contains 5 parts. Part I (Chapter 1 - 3) provides a quick introduction to

R (chapter 1) and presents required R packages and data format (Chapter 2) for

clustering analysis and visualization.

The classiﬁcation of objects, into clusters, requires some methods for measuring the

distance or the (dis)similarity between the objects. Chapter 3 covers the common

distance measures used for assessing similarity between observations.

Part II starts with partitioning clustering methods, which include:

•K-means clustering (Chapter 4),

•K-Medoids or PAM (partitioning around medoids) algorithm (Chapter 5) and

•CLARA algorithms (Chapter 6).

Partitioning clustering approaches subdivide the data sets into a set of k groups, where

k is the number of groups pre-speciﬁed by the analyst.

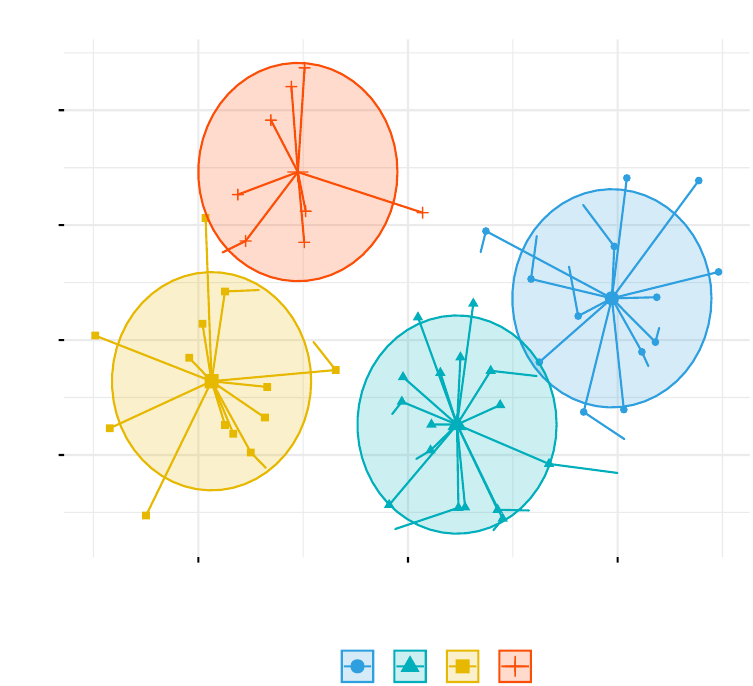
0.4. HOW THIS BOOK IS ORGANIZED? 11

Alabama

Alaska

Arizona

Arkansas

California Colorado Connecticut

Delaware

Florida

Georgia

Hawaii

Idaho

Illinois

Indiana

Iowa

Kansas

Kentucky

Louisiana Maine

Maryland

Massachusetts

Michigan

Minnesota

Mississippi

Missouri

Montana

Nebraska

Nevada

New Hampshire

New Jersey

New Mexico

New York

North Carolina

North Dakota

Ohio

Oklahoma

Oregon Pennsylvania

Rhode Island

South Carolina

South Dakota

Tennessee

Texas

Utah

Vermont

Virginia

Washington

West Virginia

Wisconsin

Wyoming

-1

-2 0 2

Dim1 (62%)

Dim2 (24.7%)

cluster aaaa

1234

Partitioning Clustering Plot

In Part III, we consider agglomerative hierarchical clustering method, which is an

alternative approach to partitionning clustering for identifying groups in a data set.

It does not require to pre-specify the number of clusters to be generated. The result

of hierarchical clustering is a tree-based representation of the objects, which is also

known as dendrogram (see the ﬁgure below).

In this part, we describe how to compute, visualize, interpret and compare dendro-

grams:

•Agglomerative clustering (Chapter 7)

–Algorithm and steps

–Verify the cluster tree

–Cut the dendrogram into diﬀerent groups

•Compare dendrograms (Chapter 8)

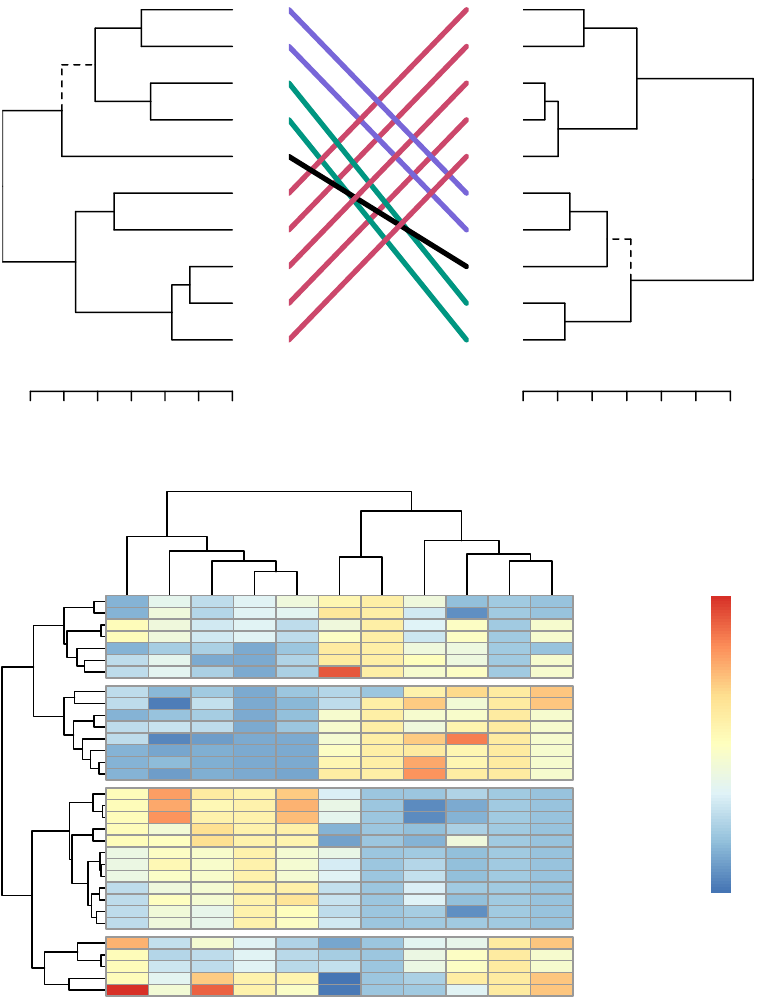
–Visual comparison of two dendrograms

–Correlation matrix between a list of dendrograms

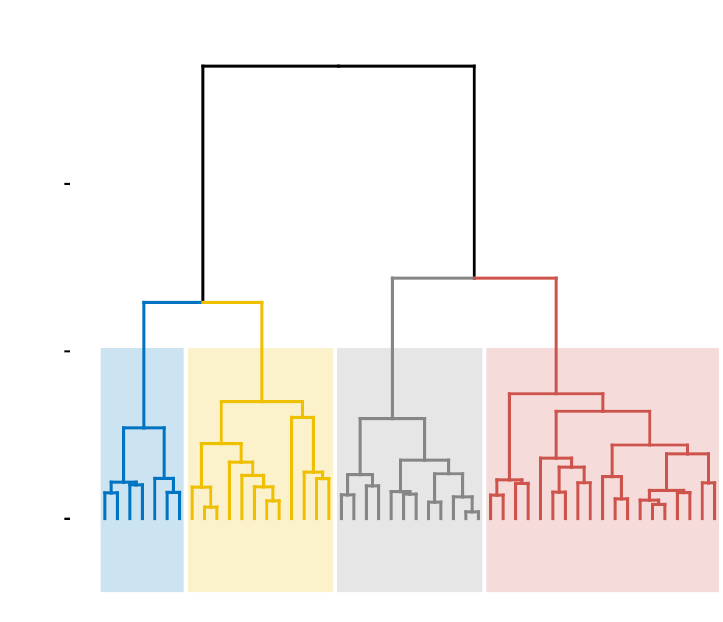
12 CONTENTS

•Visualize dendrograms (Chapter 9)

–Case of small data sets

–Case of dendrogram with large data sets: zoom, sub-tree, PDF

–Customize dendrograms using dendextend

•Heatmap: static and interactive (Chapter 10)

–R base heat maps

–Pretty heat maps

–Interactive heat maps

–Complex heatmap

–Real application: gene expression data

In this section, you will learn how to generate and interpret the following plots.

•Standard dendrogram with ﬁlled rectangle around clusters:

Alabama

Louisiana

Georgia

Tennessee

North Carolina

Mississippi

South Carolina

Texas

Illinois

New York

Florida

Arizona

Michigan

Maryland

New Mexico

Alaska

Colorado

California

Nevada

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

Height

Cluster Dendrogram

0.4. HOW THIS BOOK IS ORGANIZED? 13

•Compare two dendrograms:

3.0 2.0 1.0 0.0

Maine

Iowa

Wisconsin

Rhode Island

Utah

Mississippi

Maryland

Arizona

Tennessee

Virginia

0123456

Maryland

Arizona

Mississippi

Tennessee

Virginia

Maine

Iowa

Wisconsin

Rhode Island

Utah

•Heatmap:

carb

cyl

disp

qsec

mpg

drat

gear

Hornet 4 Drive

Valiant

Merc 280

Merc 280C

Toyota Corona

Merc 240D

Merc 230

Porsche 914−2

Lotus Europa

Datsun 710

Volvo 142E

Honda Civic

Fiat X1−9

Fiat 128

Toyota Corolla

Chrysler Imperial

Cadillac Fleetwood

Lincoln Continental

Duster 360

Camaro Z28

Merc 450SLC

Merc 450SE

Merc 450SL

Hornet Sportabout

Pontiac Firebird

Dodge Challenger

AMC Javelin

Ferrari Dino

Mazda RX4

Mazda RX4 Wag

Ford Pantera L

Maserati Bora

−1

14 CONTENTS

Part IV describes clustering validation and evaluation strategies, which consists of

measuring the goodness of clustering results. Before applying any clustering algorithm

to a data set, the ﬁrst thing to do is to assess the clustering tendency. That is,

whether applying clustering is suitable for the data. If yes, then how many clusters

are there. Next, you can perform hierarchical clustering or partitioning clustering

(with a pre-speciﬁed number of clusters). Finally, you can use a number of measures,

described in this chapter, to evaluate the goodness of the clustering results.

The diﬀerent chapters included in part IV are organized as follow:

•Assessing clustering tendency (Chapter 11)

•Determining the optimal number of clusters (Chapter 12)

•Cluster validation statistics (Chapter 13)

•Choosing the best clustering algorithms (Chapter 14)

•Computing p-value for hierarchical clustering (Chapter 15)

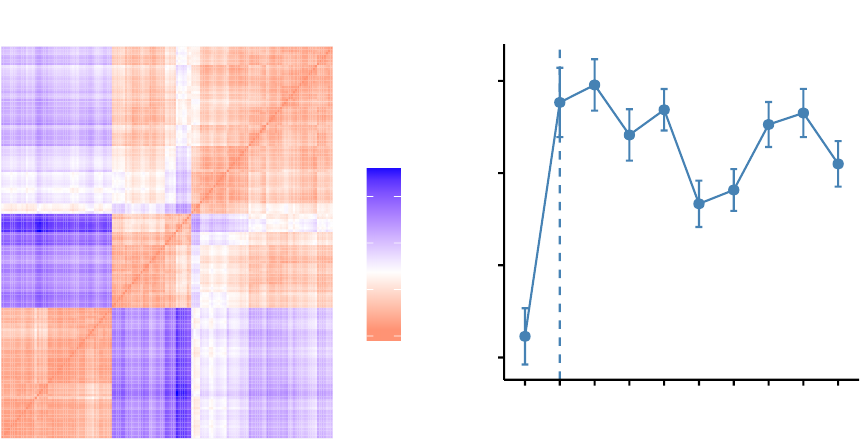
In this section, you’ll learn how to create and interpret the plots hereafter.

•Visual assessment of clustering tendency

(left panel): Clustering tendency

is detected in a visual form by counting the number of square shaped dark blocks

along the diagonal in the image.

•Determine the optimal number of clusters

(right panel) in a data set using

the gap statistics.

value

Clustering tendency

0.2

0.3

0.4

0.5

1 2 3 4 5 6 7 8 9 10

Number of clusters k

Gap statistic (k)

Optimal number of clusters

0.4. HOW THIS BOOK IS ORGANIZED? 15

•

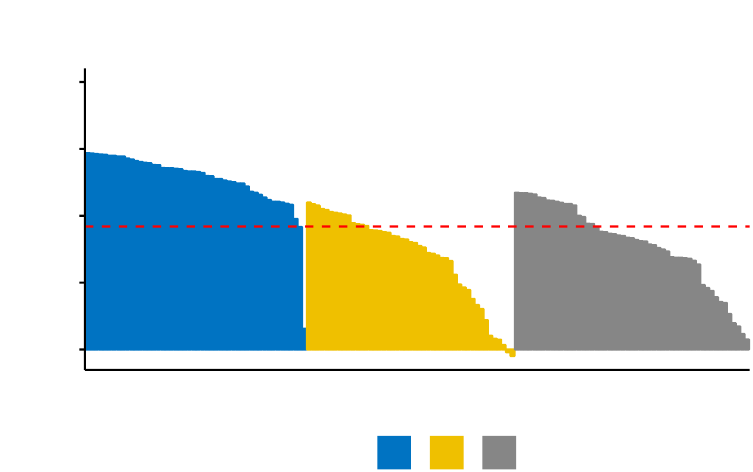
Cluster validation using the silhouette coeﬃcient (Si): A value of Si close to 1

indicates that the object is well clustered. A value of Si close to -1 indicates

that the object is poorly clustered. The ﬁgure below shows the silhouette plot

of a k-means clustering.

0.00

0.25

0.50

0.75

1.00

Silhouette width Si

cluster 123

Clusters silhouette plot

Average silhouette width: 0.46

Part V presents advanced clustering methods, including:

•Hierarchical k-means clustering (Chapter 16)

•Fuzzy clustering (Chapter 17)

•Model-based clustering (Chapter 18)

•DBSCAN: Density-Based Clustering (Chapter 19)

The hierarchical k-means clustering is an hybrid approach for improving k-means

results.

In Fuzzy clustering, items can be a member of more than one cluster. Each item has a

set of membership coeﬃcients corresponding to the degree of being in a given cluster.

In model-based clustering, the data are viewed as coming from a distribution that is

mixture of two ore more clusters. It ﬁnds best ﬁt of models to data and estimates the

number of clusters.

The density-based clustering (DBSCAN is a partitioning method that has been intro-

duced in Ester et al. (1996). It can ﬁnd out clusters of diﬀerent shapes and sizes from

data containing noise and outliers.

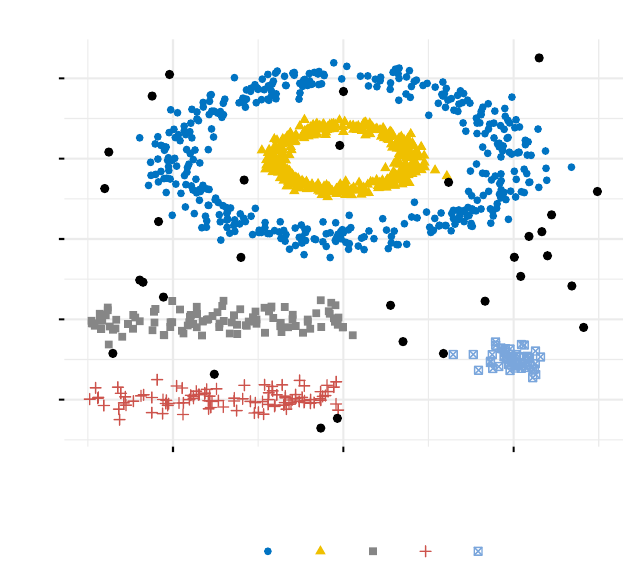
16 CONTENTS

-3

-2

-1

-1 0 1

x value

y value

cluster 12345

Density-based clustering

0.5 Book website

The website for this book is located at : http://www.sthda.com/english/. It contains

number of ressources.

0.6 Executing the R codes from the PDF

For a single line R code, you can just copy the code from the PDF to the R console.

For a multiple-line R codes, an error is generated, sometimes, when you copy and

paste directly the R code from the PDF to the R console. If this happens, a solution

is to:

•Paste ﬁrstly the code in your R code editor or in your text editor

•Copy the code from your text/code editor to the R console

Part I

Basics

Chapter 1

Introduction to R

is a free and powerful statistical software for

analyzing

and

visualizing

data. If

you want to learn easily the essential of R programming, visit our series of tutorials

available on STHDA: http://www.sthda.com/english/wiki/r-basics-quick-and-easy.

In this chapter, we provide a very brief introduction to

, for installing R/RStudio as

well as importing your data into R.

1.1 Install R and RStudio

R and RStudio can be installed on Windows, MAC OSX and Linux platforms. RStudio

is an integrated development environment for R that makes using R easier. It includes

a console, code editor and tools for plotting.

R can be downloaded and installed from the Comprehensive R Archive Network

(CRAN) webpage (http://cran.r-project.org/).

After installing R software, install also the RStudio software available at:

http://www.rstudio.com/products/RStudio/.

3. Launch RStudio and start use R inside R studio.

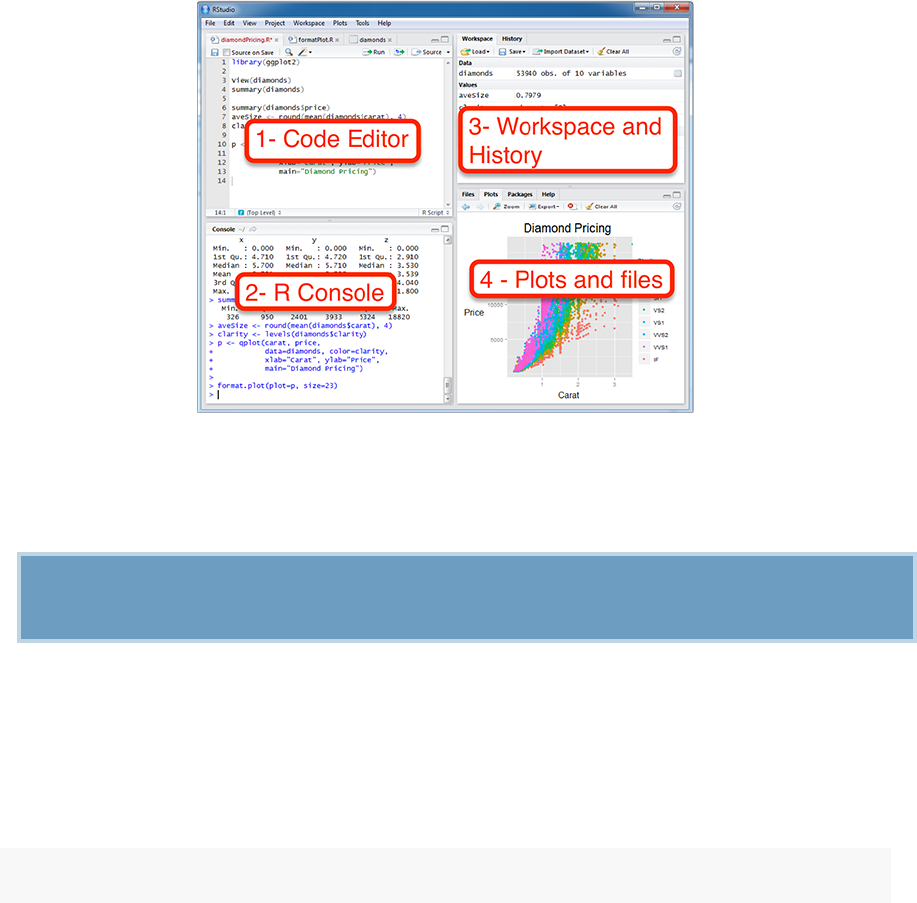
1.2. INSTALLING AND LOADING R PACKAGES 19

RStudio screen:

1.2 Installing and loading R packages

R package

is an extension of R containing data sets and speciﬁc R functions to

solve speciﬁc questions.

For example, in this book, you’ll learn how to compute easily clustering algorithm

using the cluster R package.

There are thousands other R packages available for download and installation from

CRAN, Bioconductor(biology related R packages) and GitHub repositories.

1. How to install packages from CRAN? Use the function install.packages():

install.packages("cluster")

How to install packages from GitHub? You should ﬁrst install devtools if you

don’t have it already installed on your computer:

For example, the following R code installs the latest version of factoextra R pack-

age developed by A. Kassambara (https://github.com/kassambara/facoextra) for

multivariate data analysis and elegant visualization..

20 CHAPTER 1. INTRODUCTION TO R

install.packages("devtools")

devtools::install_github("kassambara/factoextra")

Note that, GitHub contains the developmental version of R packages.

After installation, you must ﬁrst load the package for using the functions in the

package. The function library() is used for this task.

library("cluster")

Now, we can use R functions in the cluster package for computing clustering algo-

rithms, such as PAM (Partitioning Around Medoids).

1.3 Getting help with functions in R

If you want to learn more about a given function, say kmeans(), type this:

?kmeans

1.4 Importing your data into R

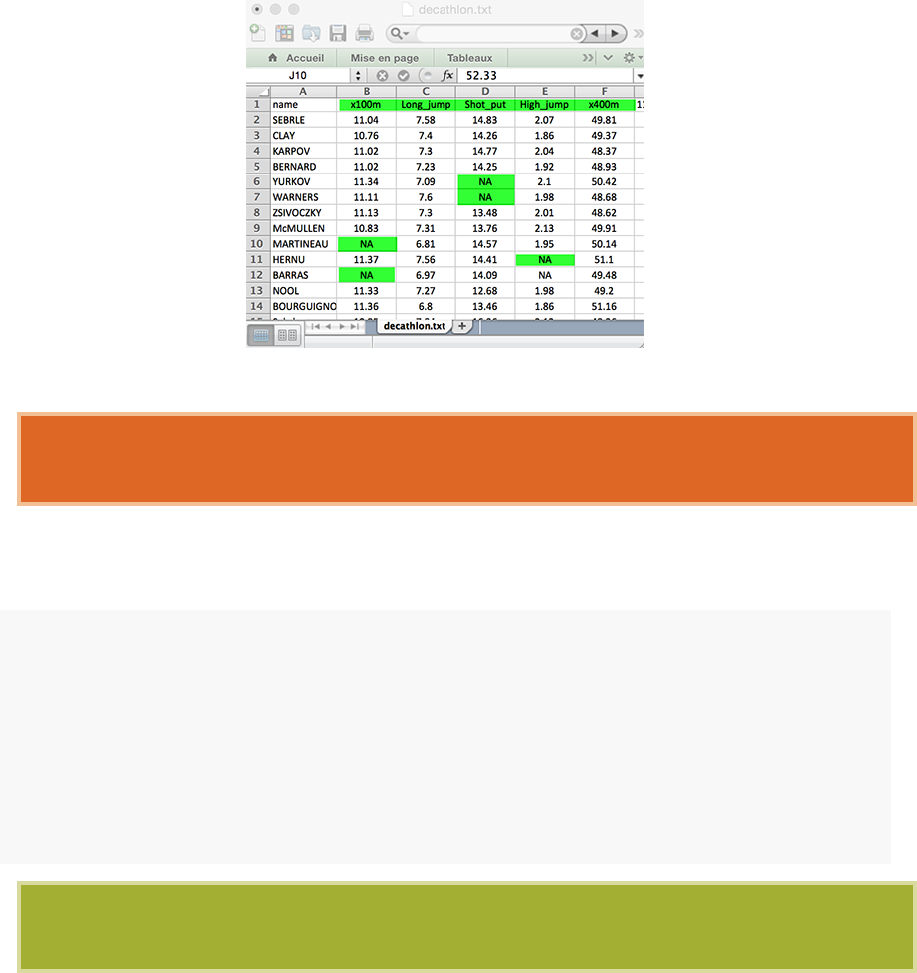
1. Prepare your ﬁle as follow:

•Use the ﬁrst row as column names. Generally, columns represent variables

•Use the ﬁrst column as row names. Generally rows represent observations.

•Each row/column name should be unique, so remove duplicated names.

•

Avoid names with blank spaces. Good column names: Long_jump or Long.jump.

Bad column name: Long jump.

•

Avoid names with special symbols: ?, $, *, +, #, (, ), -, /, }, {, |, >, < etc.

Only underscore can be used.

•

Avoid beginning variable names with a number. Use letter instead. Good column

names: sport_100m or x100m. Bad column name: 100m

•R is case sensitive. This means that Name is diﬀerent from Name or NAME.

•Avoid blank rows in your data

•Delete any comments in your ﬁle

1.4. IMPORTING YOUR DATA INTO R 21

•Replace missing values by NA (for not available)

•

If you have a column containing date, use the four digit format. Good format:

01/01/2016. Bad format: 01/01/16

2. Our ﬁnal ﬁle should look like this:

3. Save your ﬁle

We recommend to save your ﬁle into

.txt

(tab-delimited text ﬁle) or

.csv

(comma

separated value ﬁle) format.

4. Get your data into R:

Use the R code below. You will be asked to choose a ﬁle:

# .txt file: Read tab separated values

my_data <- read.delim(file.choose())

# .csv file: Read comma (",") separated values

my_data <- read.csv(file.choose())

# .csv file: Read semicolon (";") separated values

my_data <- read.csv2(file.choose())

You can read more about how to import data into R at this link:

http://www.sthda.com/english/wiki/importing-data-into-r

22 CHAPTER 1. INTRODUCTION TO R

1.5 Demo data sets

comes with several built-in data sets, which are generally used as demo data for

playing with R functions. The most used R demo data sets include:

USArrests

iris

and mtcars. To load a demo data set, use the function data() as follow:

data("USArrests")# Loading

head(USArrests, 3)# Print the first 3 rows

## Murder Assault UrbanPop Rape

## Alabama 13.2 236 58 21.2

## Alaska 10.0 263 48 44.5

## Arizona 8.1 294 80 31.0

If you want learn more about USArrests data sets, type this:

?USArrests

USArrests data set is an object of class data frame.

To select just certain columns from a data frame, you can either refer to the columns

by name or by their location (i.e., column 1, 2, 3, etc.).

# Access the data in Murdercolumn

# dollar sign is used

head(USArrests$Murder)

## [1] 13.2 10.0 8.1 8.8 9.0 7.9

# Or use this

USArrests[, Murder]

1.6 Close your R/RStudio session

Each time you close R/RStudio, you will be asked whether you want to save the data

from your R session. If you decide to save, the data will be available in future R

sessions.

Chapter 2

Data Preparation and R Packages

2.1 Data preparation

To perform a cluster analysis in R, generally, the data should be prepared as follow:

1. Rows are observations (individuals) and columns are variables

2. Any missing value in the data must be removed or estimated.

The data must be standardized (i.e., scaled) to make variables comparable. Recall

that, standardization consists of transforming the variables such that they have

mean zero and standard deviation one. Read more about data standardization

in chapter 3.

Here, we’ll use the built-in R data set “USArrests”, which contains statistics in arrests

per 100,000 residents for assault, murder, and rape in each of the 50 US states in 1973.

It includes also the percent of the population living in urban areas.

data("USArrests")# Load the data set

df <- USArrests # Use df as shorter name

1. To remove any missing value that might be present in the data, type this:

df <- na.omit(df)

As we don’t want the clustering algorithm to depend to an arbitrary variable

unit, we start by scaling/standardizing the data using the R function scale():

24 CHAPTER 2. DATA PREPARATION AND R PACKAGES

df <- scale(df)

head(df, n=3)

## Murder Assault UrbanPop Rape

## Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473

## Alaska 0.50786248 1.1068225 -1.2117642 2.484202941

## Arizona 0.07163341 1.4788032 0.9989801 1.042878388

2.2 Required R Packages

In this book, we’ll use mainly the following R packages:

•cluster for computing clustering algorithms, and

•factoextra

for ggplot2-based elegant visualization of clustering results. The

oﬃcial online documentation is available at: http://www.sthda.com/english/

rpkgs/factoextra.

factoextra contains many functions for cluster analysis and visualization, including:

Functions Description

dist(fviz_dist, get_dist) Distance Matrix Computation and Visualization

get_clust_tendency Assessing Clustering Tendency

fviz_nbclust(fviz_gap_stat) Determining the Optimal Number of Clusters

fviz_dend Enhanced Visualization of Dendrogram

fviz_cluster Visualize Clustering Results

fviz_mclust Visualize Model-based Clustering Results

fviz_silhouette Visualize Silhouette Information from Clustering

hcut Computes Hierarchical Clustering and Cut the Tree

hkmeans Hierarchical k-means clustering

eclust Visual enhancement of clustering analysis

To install the two packages, type this:

install.packages(c("cluster","factoextra"))

Chapter 3

Clustering Distance Measures

The classiﬁcation of observations into groups requires some methods for computing

the

distance

or the (dis)

similarity

between each pair of observations. The result of

this computation is known as a dissimilarity or distance matrix.

There are many methods to calculate this distance information. In this article, we

describe the common distance measures and provide R codes for computing and

visualizing distances.

3.1 Methods for measuring distances

The choice of distance measures is a critical step in clustering. It deﬁnes how the

similarity of two elements (x, y) is calculated and it will inﬂuence the shape of the

clusters.

The classical methods for distance measures are Euclidean and Manhattan distances,

which are deﬁned as follow:

1. Euclidean distance:

deuc(x, y)=ˆ

i=1

(xi≠yi)2

2. Manhattan distance:

26 CHAPTER 3. CLUSTERING DISTANCE MEASURES

dman(x, y)=

i=1

|(xi≠yi)|

Where, xand yare two vectors of length n.

Other dissimilarity measures exist such as

correlation-based distances

, which is

widely used for gene expression data analyses. Correlation-based distance is deﬁned by

subtracting the correlation coeﬃcient from 1. Diﬀerent types of correlation methods

can be used such as:

1. Pearson correlation distance:

dcor(x, y)=1≠

i=1(xi≠¯x)(yi≠¯y)

Ûn

i=1(xi≠¯x)2n

i=1(yi≠¯y)2

Pearson correlation measures the degree of a linear relationship between two proﬁles.

2. Eisen cosine correlation distance (Eisen et al., 1998):

It’s a special case of Pearson’s correlation with ¯xand ¯yboth replaced by zero:

deisen(x, y)=1≠----

i=1 xiyi----

Ûn

i=1 x2

i=1 y2

3. Spearman correlation distance:

The spearman correlation method computes the correlation between the rank of x and

the rank of y variables.

dspear(x, y)=1≠

i=1(xÕ

i≠¯

xÕ)(yÕ

i≠¯

yÕ)

Ûn

i=1(xÕ

i≠¯

xÕ)2n

i=1(yÕ

i≠¯

yÕ)2

Where xÕ

i=rank(xi)and yÕ

i=rank(y).

3.2. WHAT TYPE OF DISTANCE MEASURES SHOULD WE CHOOSE? 27

4. Kendall correlation distance:

Kendall correlation method measures the correspondence between the ranking of x

and y variables. The total number of possible pairings of x with y observations is

(

n≠

2, where n is the size of x and y. Begin by ordering the pairs by the x values.

If x and y are correlated, then they would have the same relative rank orders. Now,

for each

, count the number of

yj>y

(concordant pairs (c)) and the number of

yj<y

i(discordant pairs (d)).

Kendall correlation distance is deﬁned as follow:

dkend(x, y)=1≠nc≠nd

2n(n≠1)

Where,

•nc: total number of concordant pairs

•nd: total number of discordant pairs

•n: size of x and y

Note that,

- Pearson correlation analysis is the most commonly used method. It is

also known as a parametric correlation which depends on the distribution of the

data.

- Kendall and Spearman correlations are non-parametric and they are used to

perform rank-based correlation analysis.

In the formula above,

and

are two vectors of length

and, means

¯x

and

¯y

respectively. The distance between x and y is denoted d(x, y).

3.2 What type of distance measures should we

choose?

The choice of distance measures is very important, as it has a strong inﬂuence on the

clustering results. For most common clustering software, the default distance measure

is the Euclidean distance.

28 CHAPTER 3. CLUSTERING DISTANCE MEASURES

Depending on the type of the data and the researcher questions, other dissimilarity

measures might be preferred. For example, correlation-based distance is often used in

gene expression data analysis.

Correlation-based distance considers two objects to be similar if their features are

highly correlated, even though the observed values may be far apart in terms of

Euclidean distance. The distance between two objects is 0 when they are perfectly

correlated. Pearson’s correlation is quite sensitive to outliers. This does not matter

when clustering samples, because the correlation is over thousands of genes. When

clustering genes, it is important to be aware of the possible impact of outliers. This

can be mitigated by using Spearman’s correlation instead of Pearson’s correlation.

If we want to identify clusters of observations with the same overall proﬁles regardless

of their magnitudes, then we should go with correlation-based distance as a dissimilarity

measure. This is particularly the case in gene expression data analysis, where we

might want to consider genes similar when they are “up” and “down” together. It is

also the case, in marketing if we want to identify group of shoppers with the same

preference in term of items, regardless of the volume of items they bought.

If Euclidean distance is chosen, then observations with high values of features will be

clustered together. The same holds true for observations with low values of features.

3.3 Data standardization

The value of distance measures is intimately related to the scale on which measurements

are made. Therefore, variables are often scaled (i.e. standardized) before measuring the

inter-observation dissimilarities. This is particularly recommended when variables are

measured in diﬀerent scales (e.g: kilograms, kilometers, centimeters, . . . ); otherwise,

the dissimilarity measures obtained will be severely aﬀected.

The goal is to make the variables comparable. Generally variables are scaled to have

i) standard deviation one and ii) mean zero.

The standardization of data is an approach widely used in the context of gene expression

data analysis before clustering. We might also want to scale the data when the mean

and/or the standard deviation of variables are largely diﬀerent.

When scaling variables, the data can be transformed as follow:

xi≠center(x)

scale(x)

3.4. DISTANCE MATRIX COMPUTATION 29

Where

center

(

)can be the mean or the median of x values, and

scale

(

)can be

the standard deviation (SD), the interquartile range, or the MAD (median absolute

deviation).

The R base function scale() can be used to standardize the data. It takes a numeric

matrix as an input and performs the scaling on the columns.

Standardization makes the four distance measure methods - Euclidean, Manhattan,

Correlation and Eisen - more similar than they would be with non-transformed data.

Note that, when the data are standardized, there is a functional relation-

ship between the Pearson correlation coeﬃcient

(

x, y

)and the Euclidean distance.

With some maths, the relationship can be deﬁned as follow:

deuc(x, y)=Ò2m[1 ≠r(x, y)]

Where x and y are two standardized m-vectors with zero mean and unit length.

Therefore, the result obtained with Pearson correlation measures and stan-

dardized Euclidean distances are comparable.

3.4 Distance matrix computation

3.4.1 Data preparation

We’ll use the USArrests data as demo data sets. We’ll use only a subset of the data

by taking 15 random rows among the 50 rows in the data set. This is done by using

the function sample(). Next, we standardize the data using the function scale():

# Subset of the data

set.seed(123)

ss <- sample(1:50,15)# Take 15 random rows

df <- USArrests[ss, ] # Subset the 15 rows

df.scaled <- scale(df) # Standardize the variables

30 CHAPTER 3. CLUSTERING DISTANCE MEASURES

3.4.2 R functions and packages

There are many R functions for computing distances between pairs of observations:

1. dist() R base function [stats package]: Accepts only numeric data as an input.

get_dist() function [factoextra package]: Accepts only numeric data as an input.

Compared to the standard dist() function, it supports correlation-based distance

measures including “pearson”, “kendall” and “spearman” methods.

daisy() function [cluster package]: Able to handle other variable types (e.g. nom-

inal, ordinal, (a)symmetric binary). In that case, the Gower’s coeﬃcient will

be automatically used as the metric. It’s one of the most popular measures of

proximity for mixed data types. For more details, read the R documentation of

the daisy() function (?daisy).

All these functions compute distances between rows of the data.

3.4.3 Computing euclidean distance

To compute Euclidean distance, you can use the R base dist() function, as follow:

dist.eucl <- dist(df.scaled, method = "euclidean")

Note that, allowed values for the option method include one of: “euclidean”, “maxi-

mum”, “manhattan”, “canberra”, “binary”, “minkowski”.

To make it easier to see the distance information generated by the dist() function, you

can reformat the distance vector into a matrix using the as.matrix() function.

# Reformat as a matrix

# Subset the first 3 columns and rows and Round the values

round(as.matrix(dist.eucl)[1:3,1:3], 1)

## Iowa Rhode Island Maryland

## Iowa 0.0 2.8 4.1

## Rhode Island 2.8 0.0 3.6

## Maryland 4.1 3.6 0.0

3.4. DISTANCE MATRIX COMPUTATION 31

In this matrix, the value represent the distance between objects. The values on the

diagonal of the matrix represent the distance between objects and themselves (which

are zero).

In this data set, the columns are variables. Hence, if we want to compute pairwise

distances between variables, we must start by transposing the data to have variables

in the rows of the data set before using the dist() function. The function t() is used

for transposing the data.

3.4.4 Computing correlation based distances

Correlation-based distances are commonly used in gene expression data analysis.

The function get_dist()[factoextra package] can be used to compute correlation-based

distances. Correlation method can be either pearson,spearman or kendall.

# Compute

library("factoextra")

dist.cor <- get_dist(df.scaled, method = "pearson")

# Display a subset

round(as.matrix(dist.cor)[1:3,1:3], 1)

## Iowa Rhode Island Maryland

## Iowa 0.0 0.4 1.9

## Rhode Island 0.4 0.0 1.5

## Maryland 1.9 1.5 0.0

3.4.5 Computing distances for mixed data

The function daisy() [cluster package] provides a solution (Gower’s metric) for com-

puting the distance matrix, in the situation where the data contain no-numeric

columns.

The R code below applies the daisy() function on ﬂower data which contains factor,

ordered and numeric variables:

32 CHAPTER 3. CLUSTERING DISTANCE MEASURES

library(cluster)

# Load data

data(flower)

head(flower, 3)

## V1 V2 V3 V4 V5 V6 V7 V8

## 1 0 1 1 4 3 15 25 15

## 2 1 0 0 2 1 3 150 50

## 3 0 1 0 3 3 1 150 50

# Data structure

str(flower)

## data.frame:18obs.of8variables:

## $ V1: Factor w/ 2 levels "0","1": 1 2 1 1 1 1 1 1 2 2 ...

## $ V2: Factor w/ 2 levels "0","1": 2 1 2 1 2 2 1 1 2 2 ...

## $ V3: Factor w/ 2 levels "0","1": 2 1 1 2 1 1 1 2 1 1 ...

## $ V4: Factor w/ 5 levels "1","2","3","4",..: 4 2 3 4 5 4 4 2 3 5 ...

## $ V5: Ord.factor w/ 3 levels "1"<"2"<"3": 3 1 3 2 2 3 3 2 1 2 ...

## $ V6: Ord.factor w/ 18 levels "1"<"2"<"3"<"4"<..: 15 3 1 16 2 12 13 7 4 14 ...

## $ V7: num 25 150 150 125 20 50 40 100 25 100 ...

## $ V8: num 15 50 50 50 15 40 20 15 15 60 ...

# Distance matrix

dd <- daisy(flower)

round(as.matrix(dd)[1:3,1:3], 2)

## 1 2 3

## 1 0.00 0.89 0.53

## 2 0.89 0.00 0.51

## 3 0.53 0.51 0.00

3.5 Visualizing distance matrices

A simple solution for visualizing the distance matrices is to use the function fviz_dist()

[factoextra package]. Other specialized methods, such as agglomerative hierarchical

clustering (Chapter 7) or heatmap (Chapter 10) will be comprehensively described in

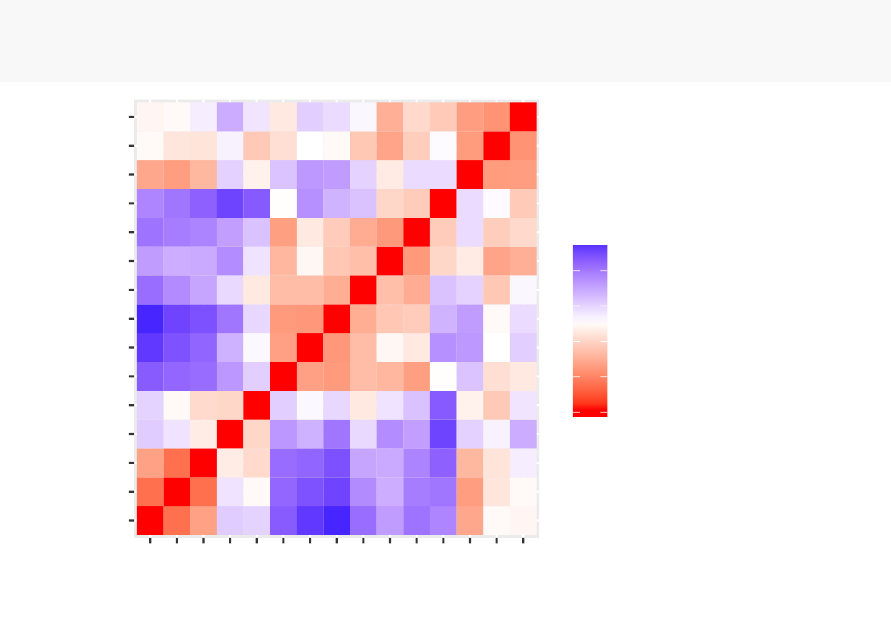
3.6. SUMMARY 33

the dedicated chapters.

To use fviz_dist() type this:

library(factoextra)

fviz_dist(dist.eucl)

Maine-

Iowa-

Wisconsin-

Rhode Island-

Utah-

Maryland-

Arizona-

Michigan-

Texas-

Tennessee-

Louisiana-

Mississippi-

Montana-

Virginia-

Arkansas-

Maine-

Iowa-

Wisconsin-

Rhode Island-

Utah-

Maryland-

Arizona-

Michigan-

Texas-

Tennessee-

Louisiana-

Mississippi-

Montana-

Virginia-

Arkansas-

value

•Red: high similarity (ie: low dissimilarity) | Blue: low similarity

The color level is proportional to the value of the dissimilarity between observations:

pure red if

dist

(

xi,x

)=0and pure blue if

dist

(

xi,x

)=1. Objects belonging to the

same cluster are displayed in consecutive order.

3.6 Summary

We described how to compute distance matrices using either Euclidean or correlation-

based measures. It’s generally recommended to standardize the variables before

distance matrix computation. Standardization makes variable comparable, in the

situation where they are measured in diﬀerent scales.

Part II

Partitioning Clustering

Partitioning clustering

are clustering methods used to classify observations, within

a data set, into multiple groups based on their similarity. The algorithms require the

analyst to specify the number of clusters to be generated.

This chapter describes the commonly used partitioning clustering, including:

•K-means clustering

(MacQueen, 1967), in which, each cluster is represented

by the center or means of the data points belonging to the cluster. The K-means

method is sensitive to anomalous data points and outliers.

•K-medoids clustering

PAM

(Partitioning Around Medoids, Kaufman &

Rousseeuw, 1990), in which, each cluster is represented by one of the objects in

the cluster. PAM is less sensitive to outliers compared to k-means.

•CLARA algorithm

(Clustering Large Applications), which is an extension to

PAM adapted for large data sets.

For each of these methods, we provide:

•the basic idea and the key mathematical concepts

•the clustering algorithm and implementation in R software

•R lab sections with many examples for cluster analysis and visualization

The following R packages will be used to compute and visualize partitioning clustering:

•stats package for computing K-means

•cluster package for computing PAM and CLARA algorithms

•factoextra for beautiful visualization of clusters

Chapter 4

K-Means Clustering

K-means clustering

(MacQueen, 1967) is the most commonly used unsupervised

machine learning algorithm for partitioning a given data set into a set of k groups (i.e.

k clusters), where k represents the number of groups pre-speciﬁed by the analyst. It

classiﬁes objects in multiple groups (i.e., clusters), such that objects within the same

cluster are as similar as possible (i.e., high intra-class similarity), whereas objects

from diﬀerent clusters are as dissimilar as possible (i.e., low inter-class similarity).

In k-means clustering, each cluster is represented by its center (i.e, centroid) which

corresponds to the mean of points assigned to the cluster.

In this article, we’ll describe the

k-means algorithm

and provide practical examples

using Rsoftware.

4.1 K-means basic ideas

The basic idea behind k-means clustering consists of deﬁning clusters so that the total

intra-cluster variation (known as total within-cluster variation) is minimized.

There are several k-means algorithms available. The standard algorithm is the

Hartigan-Wong algorithm (1979), which deﬁnes the total within-cluster variation as

the sum of squared distances Euclidean distances between items and the corresponding

centroid:

4.2. K-MEANS ALGORITHM 37

W(Ck)= ÿ

xiœCk

(xi≠µk)2

•xidesign a data point belonging to the cluster Ck

•µkis the mean value of the points assigned to the cluster Ck

Each observation (

) is assigned to a given cluster such that the sum of squares (SS)

distance of the observation to their assigned cluster centers µkis a minimum.

We deﬁne the total within-cluster variation as follow:

tot.withinss =

k=1

W(Ck)=

k=1 ÿ

xiœCk

(xi≠µk)2

The total within-cluster sum of square measures the compactness (i.e goodness) of the

clustering and we want it to be as small as possible.

4.2 K-means algorithm

The ﬁrst step when using k-means clustering is to indicate the number of clusters (k)

that will be generated in the ﬁnal solution.

The algorithm starts by randomly selecting k objects from the data set to serve as the

initial centers for the clusters. The selected objects are also known as cluster means

or centroids.

Next, each of the remaining objects is assigned to it’s closest centroid, where closest is

deﬁned using the Euclidean distance (Chapter 3) between the object and the cluster

mean. This step is called “cluster assignment step”. Note that, to use correlation

distance, the data are input as z-scores.

After the assignment step, the algorithm computes the new mean value of each cluster.

The term cluster “centroid update” is used to design this step. Now that the centers

have been recalculated, every observation is checked again to see if it might be closer

to a diﬀerent cluster. All the objects are reassigned again using the updated cluster

means.

The cluster assignment and centroid update steps are iteratively repeated until the

cluster assignments stop changing (i.e until convergence is achieved). That is, the

38 CHAPTER 4. K-MEANS CLUSTERING

clusters formed in the current iteration are the same as those obtained in the previous

iteration.

K-means algorithm can be summarized as follow:

1. Specify the number of clusters (K) to be created (by the analyst)

Select randomly k objects from the data set as the initial cluster centers or means

Assigns each observation to their closest centroid, based on the Euclidean

distance between the object and the centroid

For each of the k clusters update the cluster centroid by calculating the new

mean values of all the data points in the cluster. The centoid of a

Kth

cluster

is a vector of length

containing the means of all variables for the observations

in the kth cluster; pis the number of variables.

Iteratively minimize the total within sum of square. That is, iterate steps 3

and 4 until the cluster assignments stop changing or the maximum number of

iterations is reached. By default, the R software uses 10 as the default value

for the maximum number of iterations.

4.3 Computing k-means clustering in R

4.3.1 Data

We’ll use the demo data sets “USArrests”. The data should be prepared as described

in chapter 2. The data must contains only continuous variables, as the k-means

algorithm uses variable means. As we don’t want the k-means algorithm to depend to

an arbitrary variable unit, we start by scaling the data using the R function scale() as

follow:

data("USArrests")# Loading the data set

df <- scale(USArrests) # Scaling the data

# View the firt 3 rows of the data

head(df, n=3)

4.3. COMPUTING K-MEANS CLUSTERING IN R 39

## Murder Assault UrbanPop Rape

## Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473

## Alaska 0.50786248 1.1068225 -1.2117642 2.484202941

## Arizona 0.07163341 1.4788032 0.9989801 1.042878388

4.3.2 Required R packages and functions

The standard R function for k-means clustering is kmeans() [stats package], which

simpliﬁed format is as follow:

kmeans(x, centers, iter.max = 10,nstart = 1)

•x: numeric matrix, numeric data frame or a numeric vector

•centers

: Possible values are the number of clusters (k) or a set of initial (distinct)

cluster centers. If a number, a random set of (distinct) rows in x is chosen as

the initial centers.

•iter.max: The maximum number of iterations allowed. Default value is 10.

•nstart

: The number of random starting partitions when centers is a number.

Trying nstart > 1 is often recommended.

To create a beautiful graph of the clusters generated with the kmeans() function, will

use the factoextra package.

•Installing factoextra package as:

install.packages("factoextra")

•Loading factoextra:

library(factoextra)

4.3.3 Estimating the optimal number of clusters

The k-means clustering requires the users to specify the number of clusters to be

generated.

One fundamental question is: How to choose the right number of expected clusters

(k)?

40 CHAPTER 4. K-MEANS CLUSTERING

Diﬀerent methods will be presented in the chapter “cluster evaluation and validation

statistics”.

Here, we provide a simple solution. The idea is to compute k-means clustering using

diﬀerent values of clusters k. Next, the wss (within sum of square) is drawn according

to the number of clusters. The location of a bend (knee) in the plot is generally

considered as an indicator of the appropriate number of clusters.

The R function fviz_nbclust() [in factoextra package] provides a convenient solution

to estimate the optimal number of clusters.

library(factoextra)

fviz_nbclust(df, kmeans, method = "wss")+

geom_vline(xintercept = 4,linetype = 2)

100

150

200

123456 7 8 9 10

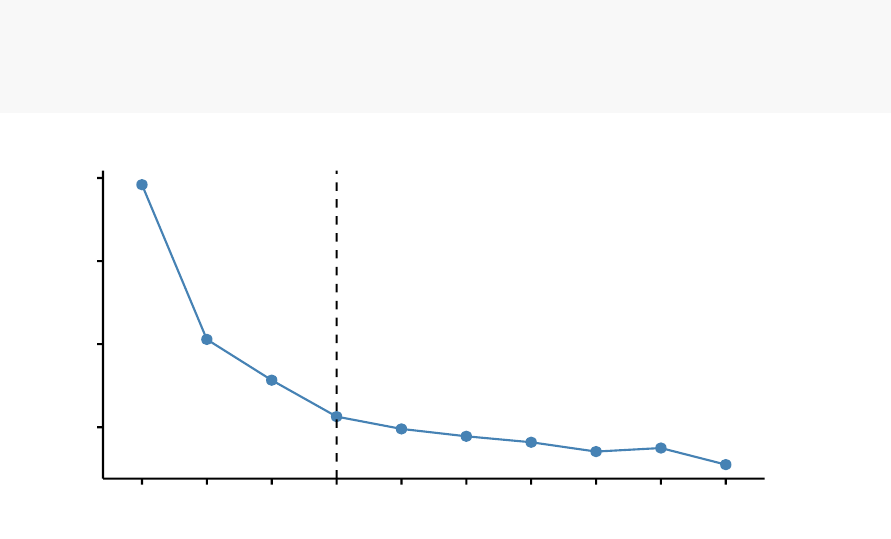
Number of clusters k

Total Within Sum of Square

Optimal number of clusters

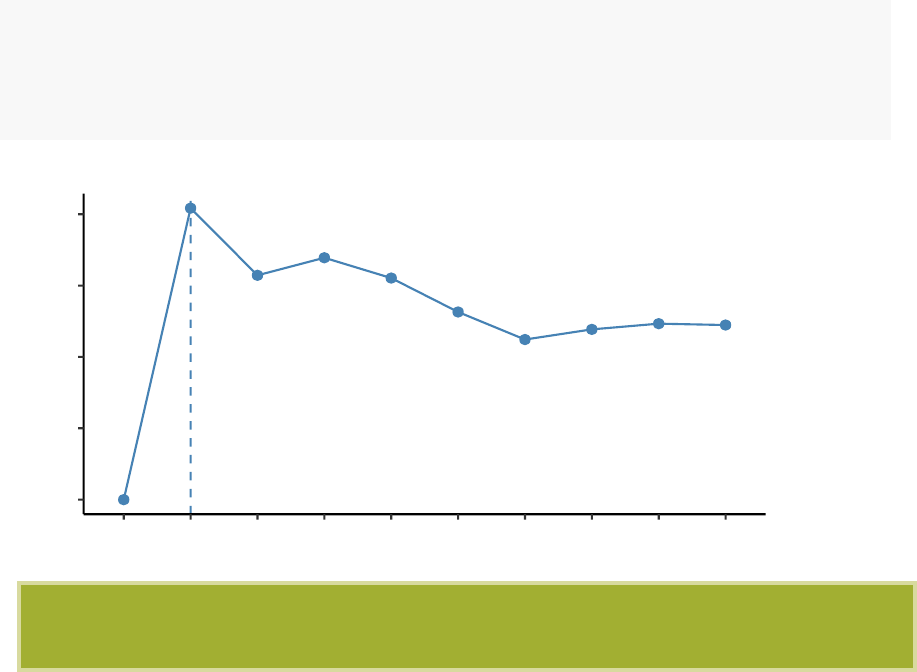
The plot above represents the variance within the clusters. It decreases as k increases,

but it can be seen a bend (or “elbow”) at k = 4. This bend indicates that additional

clusters beyond the fourth have little value.. In the next section, we’ll classify the

observations into 4 clusters.

4.3.4 Computing k-means clustering

As k-means clustering algorithm starts with k randomly selected centroids, it’s always

recommended to use the set.seed() function in order to set a seed for R’s random

4.3. COMPUTING K-MEANS CLUSTERING IN R 41

number generator. The aim is to make reproducible the results, so that the reader of

this article will obtain exactly the same results as those shown below.

The R code below performs k-means clustering with k = 4:

# Compute k-means with k = 4

set.seed(123)

km.res <- kmeans(df, 4,nstart = 25)

As the ﬁnal result of k-means clustering result is sensitive to the random starting

assignments, we specify nstart = 25. This means that R will try 25 diﬀerent random

starting assignments and then select the best results corresponding to the one with

the lowest within cluster variation. The default value of nstart in R is one. But, it’s

strongly recommended to compute k-means clustering with a large value of nstart

such as 25 or 50, in order to have a more stable result.

# Print the results

print(km.res)

## K-means clustering with 4 clusters of sizes 13, 16, 13, 8

## Cluster means:

## Murder Assault UrbanPop Rape

## 1 -0.9615407 -1.1066010 -0.9301069 -0.96676331

## 2 -0.4894375 -0.3826001 0.5758298 -0.26165379

## 3 0.6950701 1.0394414 0.7226370 1.27693964

## 4 1.4118898 0.8743346 -0.8145211 0.01927104

## Clustering vector:

## Alabama Alaska Arizona Arkansas California

##43343

## Colorado Connecticut Delaware Florida Georgia

##32234

## Hawaii Idaho Illinois Indiana Iowa

##21321

## Kansas Kentucky Louisiana Maine Maryland

##21413

## Massachusetts Michigan Minnesota Mississippi Missouri

##23143

## Montana Nebraska Nevada New Hampshire New Jersey

42 CHAPTER 4. K-MEANS CLUSTERING

##11312

## New Mexico New York North Carolina North Dakota Ohio

##33412

## Oklahoma Oregon Pennsylvania Rhode Island South Carolina

##22224

## South Dakota Tennessee Texas Utah Vermont

##14321

## Virginia Washington West Virginia Wisconsin Wyoming

##22112

## Within cluster sum of squares by cluster:

## [1] 11.952463 16.212213 19.922437 8.316061

## (between_SS / total_SS = 71.2 %)

## Available components:

## [1] "cluster" "centers" "totss" "withinss"

## [5] "tot.withinss" "betweenss" "size" "iter"

## [9] "ifault"

The printed output displays:

•

the cluster means or centers: a matrix, which rows are cluster number (1 to 4)

and columns are variables

•

the clustering vector: A vector of integers (from 1:k) indicating the cluster to

which each point is allocated

It’s possible to compute the mean of each variables by clusters using the original data:

aggregate(USArrests, by=list(cluster=km.res$cluster), mean)

## cluster Murder Assault UrbanPop Rape

## 1 1 3.60000 78.53846 52.07692 12.17692

## 2 2 5.65625 138.87500 73.87500 18.78125

## 3 3 10.81538 257.38462 76.00000 33.19231

## 4 4 13.93750 243.62500 53.75000 21.41250

If you want to add the point classiﬁcations to the original data, use this:

4.3. COMPUTING K-MEANS CLUSTERING IN R 43

dd <- cbind(USArrests, cluster = km.res$cluster)

head(dd)

## Murder Assault UrbanPop Rape cluster

## Alabama 13.2 236 58 21.2 4

## Alaska 10.0 263 48 44.5 3

## Arizona 8.1 294 80 31.0 3

## Arkansas 8.8 190 50 19.5 4

## California 9.0 276 91 40.6 3

## Colorado 7.9 204 78 38.7 3

4.3.5 Accessing to the results of kmeans() function

kmeans() function returns a list of components, including:

•cluster

: A vector of integers (from 1:k) indicating the cluster to which each

point is allocated

•centers: A matrix of cluster centers (cluster means)

•totss

: The total sum of squares (TSS), i.e

q(xi≠¯x)2

. TSS measures the total

variance in the data.

•withinss: Vector of within-cluster sum of squares, one component per cluster

•tot.withinss: Total within-cluster sum of squares, i.e. sum(withinss)

•betweenss: The between-cluster sum of squares, i.e. totss ≠tot.withinss

•size: The number of observations in each cluster

These components can be accessed as follow:

# Cluster number for each of the observations

km.res$cluster

head(km.res$cluster, 4)

## Alabama Alaska Arizona Arkansas

## 4 3 3 4

. . . ..

# Cluster size

km.res$size

44 CHAPTER 4. K-MEANS CLUSTERING

## [1] 13 16 13 8

# Cluster means

km.res$centers

## Murder Assault UrbanPop Rape

## 1 -0.9615407 -1.1066010 -0.9301069 -0.96676331

## 2 -0.4894375 -0.3826001 0.5758298 -0.26165379

## 3 0.6950701 1.0394414 0.7226370 1.27693964

## 4 1.4118898 0.8743346 -0.8145211 0.01927104

4.3.6 Visualizing k-means clusters

It is a good idea to plot the cluster results. These can be used to assess the choice of

the number of clusters as well as comparing two diﬀerent cluster analyses.

Now, we want to visualize the data in a scatter plot with coloring each data point

according to its cluster assignment.

The problem is that the data contains more than 2 variables and the question is what

variables to choose for the xy scatter plot.

A solution is to reduce the number of dimensions by applying a dimensionality reduction

algorithm, such as

Principal Component Analysis (PCA)

, that operates on the

four variables and outputs two new variables (that represent the original variables)

that you can use to do the plot.

In other words, if we have a multi-dimensional data set, a solution is to perform

Principal Component Analysis (PCA) and to plot data points according to the ﬁrst

two principal components coordinates.

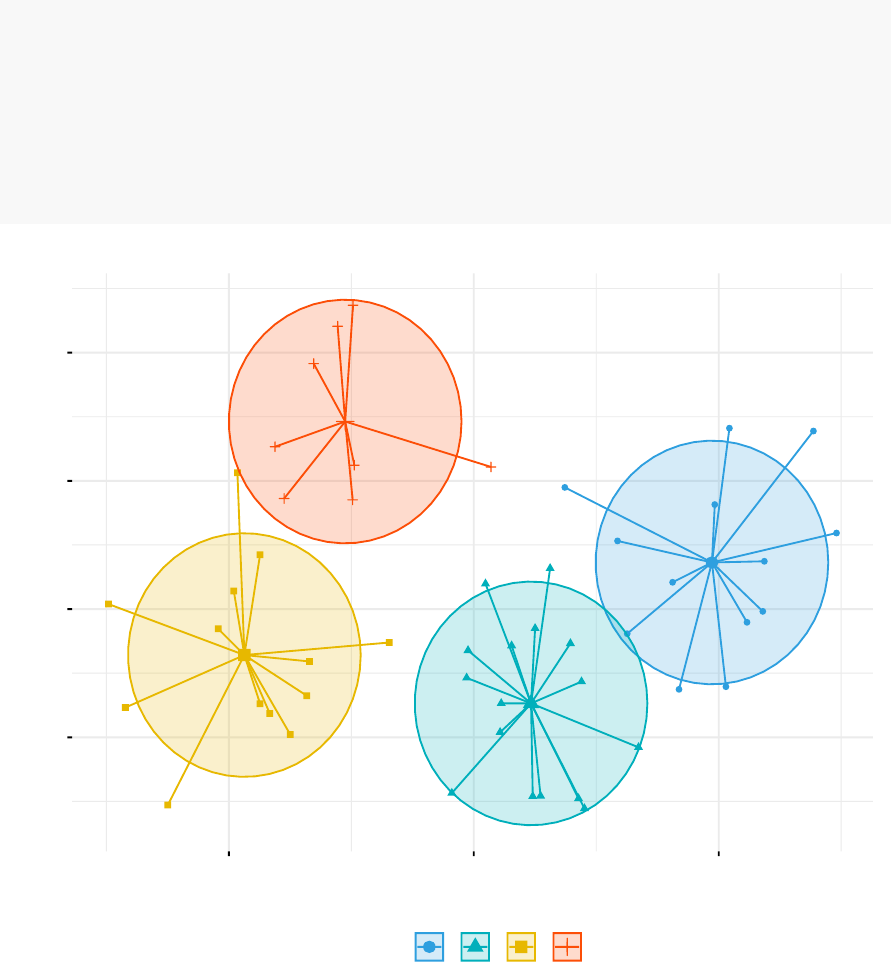
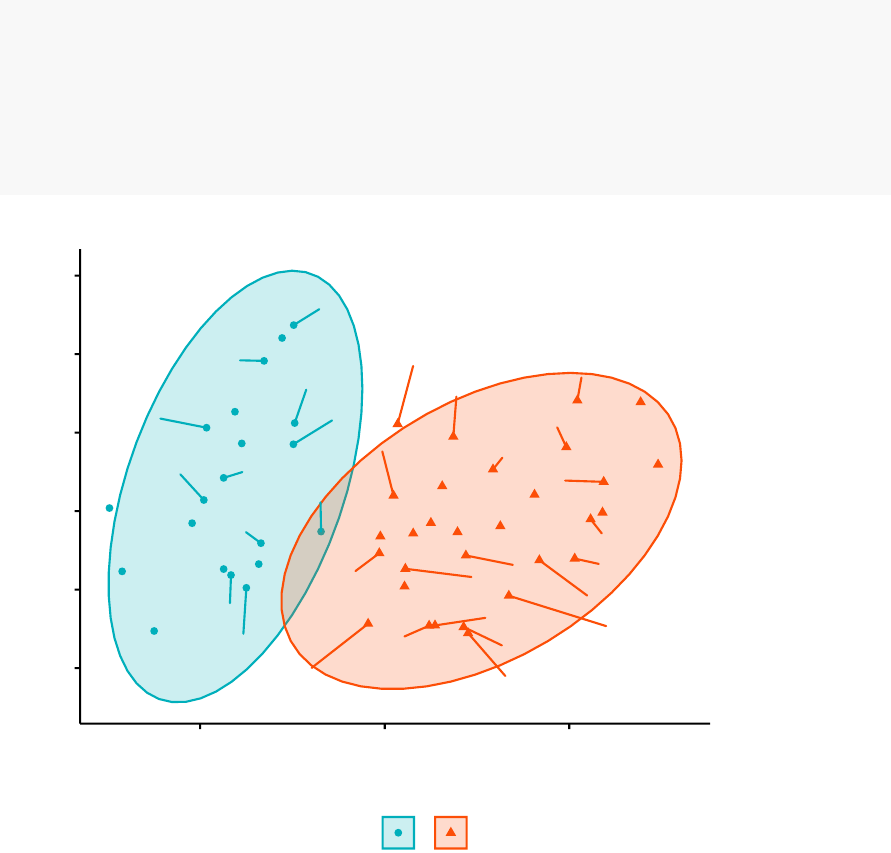
The function fviz_cluster() [factoextra package] can be used to easily visualize k-means

clusters. It takes k-means results and the original data as arguments. In the resulting

plot, observations are represented by points, using principal components if the number

of variables is greater than 2. It’s also possible to draw concentration ellipse around

each cluster.

4.3. COMPUTING K-MEANS CLUSTERING IN R 45

fviz_cluster(km.res, data = df,

palette = c("#2E9FDF","#00AFBB","#E7B800","#FC4E07"),

ellipse.type = "euclid",# Concentration ellipse

star.plot = TRUE,# Add segments from centroids to items

repel = TRUE,# Avoid label overplotting (slow)

ggtheme = theme_minimal()

)

Alabama

Alaska

Arizona

Arkansas

California

Colorado Connecticut

Delaware

Florida

Georgia

Hawaii

Idaho

Illinois

Indiana

Iowa

Kansas

Kentucky

Louisiana

Maine

Maryland

Massachusetts

Michigan

Minnesota

Mississippi

Missouri

Montana

Nebraska

Nevada

New Hampshire

New Jersey

New Mexico

New York

North Carolina

North Dakota

Ohio

Oklahoma

Oregon Pennsylvania

Rhode Island

South Carolina

South Dakota

Tennessee

Texas

Utah

Vermont

Virginia

Washington

West Virginia

Wisconsin

Wyoming

-1

-2 0 2

Dim1 (62%)

Dim2 (24.7%)

cluster aaaa

1234

Cluster plot

46 CHAPTER 4. K-MEANS CLUSTERING

4.4 K-means clustering advantages and disadvan-

tages

K-means clustering is very simple and fast algorithm. It can eﬃciently deal with very

large data sets. However there are some weaknesses, including:

It assumes prior knowledge of the data and requires the analyst to choose the

appropriate number of cluster (k) in advance.

The ﬁnal results obtained is sensitive to the initial random selection of cluster

centers. Why is this a problem? Because, for every diﬀerent run of the

algorithm on the same data set, you may choose diﬀerent set of initial centers.

This may lead to diﬀerent clustering results on diﬀerent runs of the algorithm.

3. It’s sensitive to outliers.

If you rearrange your data, it’s very possible that you’ll get a diﬀerent solution

every time you change the ordering of your data.

Possible solutions to these weaknesses, include:

Solution to issue 1: Compute k-means for a range of k values, for example

by varying k between 2 and 10. Then, choose the best k by comparing the

clustering results obtained for the diﬀerent k values.

Solution to issue 2: Compute K-means algorithm several times with diﬀerent

initial cluster centers. The run with the lowest total within-cluster sum of

square is selected as the ﬁnal clustering solution.

To avoid distortions caused by excessive outliers, it’s possible to use PAM

algorithm, which is less sensitive to outliers.

4.5. ALTERNATIVE TO K-MEANS CLUSTERING 47

4.5 Alternative to k-means clustering

A robust alternative to k-means is PAM, which is based on medoids. As discussed

in the next chapter, the PAM clustering can be computed using the function pam()

[cluster package]. The function pamk( ) [fpc package] is a wrapper for PAM that also

prints the suggested number of clusters based on optimum average silhouette width.

4.6 Summary

K-means clustering can be used to classify observations into k groups, based on their

similarity. Each group is represented by the mean value of points in the group, known

as the cluster centroid.

K-means algorithm requires users to specify the number of cluster to generate. The R

function kmeans() [stats package] can be used to compute k-means algorithm. The

simpliﬁed format is kmeans(x, centers), where “x” is the data and centers is the

number of clusters to be produced.

After, computing k-means clustering, the R function fviz_cluster() [factoextra package]

can be used to visualize the results. The format is fviz_cluster(km.res, data), where

km.res is k-means results and data corresponds to the original data sets.

Chapter 5

K-Medoids

The

k-medoids algorithm

is a clustering approach related to k-means clustering

(chapter 4) for partitioning a data set into k groups or clusters. In k-medoids clustering,

each cluster is represented by one of the data point in the cluster. These points are

named cluster medoids.

The term medoid refers to an object within a cluster for which average dissimilarity

between it and all the other the members of the cluster is minimal. It corresponds to

the most centrally located point in the cluster. These objects (one per cluster) can

be considered as a representative example of the members of that cluster which may

be useful in some situations. Recall that, in k-means clustering, the center of a given

cluster is calculated as the mean value of all the data points in the cluster.

K-medoid is a robust alternative to k-means clustering. This means that, the algorithm

is less sensitive to noise and outliers, compared to k-means, because it uses medoids

as cluster centers instead of means (used in k-means).

The k-medoids algorithm requires the user to specify k, the number of clusters to be

generated (like in k-means clustering). A useful approach to determine the optimal

number of clusters is the silhouette method, described in the next sections.

The most common k-medoids clustering methods is the

PAM

algorithm (

Partitioning

Around Medoids, Kaufman & Rousseeuw, 1990).

In this article, We’ll describe the PAM algorithm and provide practical examples

using

software. In the next chapter, we’ll also discuss a variant of PAM named

CLARA

(Clustering Large Applications) which is used for analyzing large data

sets.

5.1. PAM CONCEPT 49

5.1 PAM concept

The use of means implies that k-means clustering is highly sensitive to outliers. This

can severely aﬀects the assignment of observations to clusters. A more robust algorithm

is provided by the PAM algorithm.

5.2 PAM algorithm

The PAM algorithm is based on the search for k representative objects or medoids

among the observations of the data set.

After ﬁnding a set of k medoids, clusters are constructed by assigning each observation

to the nearest medoid.

Next, each selected medoid m and each non-medoid data point are swapped and the

objective function is computed. The objective function corresponds to the sum of the

dissimilarities of all objects to their nearest medoid.

The SWAP step attempts to improve the quality of the clustering by exchanging

selected objects (medoids) and non-selected objects. If the objective function can

be reduced by interchanging a selected object with an unselected object, then the

swap is carried out. This is continued until the objective function can no longer be

decreased. The goal is to ﬁnd k representative objects which minimize the sum of the

dissimilarities of the observations to their closest representative object.

In summary, PAM algorithm proceeds in two phases as follow:

50 CHAPTER 5. K-MEDOIDS

Select k objects to become the medoids, or in case these objects were provided

use them as the medoids;

2. Calculate the dissimilarity matrix if it was not provided;

3. Assign every object to its closest medoid;

For each cluster search if any of the object of the cluster decreases the

average dissimilarity coeﬃcient; if it does, select the entity that decreases this

coeﬃcient the most as the medoid for this cluster;

5. If at least one medoid has changed go to (3), else end the algorithm.

As mentioned above, the PAM algorithm works with a matrix of dissimilarity, and to

compute this matrix the algorithm can use two metrics:

1. The euclidean distances, that are the root sum-of-squares of diﬀerences;

2. And, the Manhattan distance that are the sum of absolute distances.

Note that, in practice, you should get similar results most of the time, using either

euclidean or Manhattan distance. If your data contains outliers, Manhattan distance

should give more robust results, whereas euclidean would be inﬂuenced by unusual

values.

Read more on distance measures in Chapter 3.

5.3 Computing PAM in R

5.3.1 Data

We’ll use the demo data sets “USArrests”, which we start by scaling (Chapter 2) using

the R function scale() as follow:

data("USArrests")# Load the data set

df <- scale(USArrests) # Scale the data

head(df, n=3)# View the firt 3 rows of the data

5.3. COMPUTING PAM IN R 51

## Murder Assault UrbanPop Rape

## Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473

## Alaska 0.50786248 1.1068225 -1.2117642 2.484202941

## Arizona 0.07163341 1.4788032 0.9989801 1.042878388

5.3.2 Required R packages and functions

The function pam() [cluster package] and pamk() [fpc package] can be used to compute

PAM.

The function pamk() does not require a user to decide the number of clusters K.

In the following examples, we’ll describe only the function pam(), which simpliﬁed

format is:

pam(x, k, metric = "euclidean",stand = FALSE)

•x: possible values includes:

–

Numeric data matrix or numeric data frame: each row corresponds to an

observation, and each column corresponds to a variable.

–

Dissimilarity matrix: in this case x is typically the output of

daisy()

dist()

•k: The number of clusters

•metric

: the distance metrics to be used. Available options are “euclidean” and

“manhattan”.

•stand

: logical value; if true, the variables (columns) in x are standardized before

calculating the dissimilarities. Ignored when x is a dissimilarity matrix.

To create a beautiful graph of the clusters generated with the pam() function, will use

the factoextra package.

1. Installing required packages:

install.packages(c("cluster","factoextra"))

2. Loading the packages:

library(cluster)

library(factoextra)

52 CHAPTER 5. K-MEDOIDS

5.3.3 Estimating the optimal number of clusters

To estimate the optimal number of clusters, we’ll use the average silhouette method.

The idea is to compute PAM algorithm using diﬀerent values of clusters k. Next,

the average clusters silhouette is drawn according to the number of clusters. The

average silhouette measures the quality of a clustering. A high average silhouette

width indicates a good clustering. The optimal number of clusters k is the one that

maximize the average silhouette over a range of possible values for k (Kaufman and

Rousseeuw [1990]).

The R function fviz_nbclust() [factoextra package] provides a convenient solution to

estimate the optimal number of clusters.

library(cluster)

library(factoextra)

fviz_nbclust(df, pam, method = "silhouette")+

theme_classic()

0.0

0.1

0.2

0.3

0.4

123456789 10

Number of clusters k

Average silhouette width

Optimal number of clusters

From the plot, the suggested number of clusters is 2. In the next section, we’ll

classify the observations into 2 clusters.

5.3. COMPUTING PAM IN R 53

5.3.4 Computing PAM clustering

The R code below computes PAM algorithm with k = 2:

pam.res <- pam(df, 2)

print(pam.res)

## Medoids:

## ID Murder Assault UrbanPop Rape

## New Mexico 31 0.8292944 1.3708088 0.3081225 1.1603196

## Nebraska 27 -0.8008247 -0.8250772 -0.2445636 -0.5052109

## Clustering vector:

## Alabama Alaska Arizona Arkansas California

##11121

## Colorado Connecticut Delaware Florida Georgia

##12211

## Hawaii Idaho Illinois Indiana Iowa

##22122

## Kansas Kentucky Louisiana Maine Maryland

##22121

## Massachusetts Michigan Minnesota Mississippi Missouri

##21211

## Montana Nebraska Nevada New Hampshire New Jersey

##22122

## New Mexico New York North Carolina North Dakota Ohio

##11122

## Oklahoma Oregon Pennsylvania Rhode Island South Carolina

##22221

## South Dakota Tennessee Texas Utah Vermont

##21122

## Virginia Washington West Virginia Wisconsin Wyoming

##22222

## Objective function:

## build swap

## 1.441358 1.368969

## Available components:

## [1] "medoids" "id.med" "clustering" "objective" "isolation"

## [6] "clusinfo" "silinfo" "diss" "call" "data"

54 CHAPTER 5. K-MEDOIDS

The printed output shows:

•

the cluster medoids: a matrix, which rows are the medoids and columns are

variables

•

the clustering vector: A vector of integers (from 1:k) indicating the cluster to

which each point is allocated

If you want to add the point classiﬁcations to the original data, use this:

dd <- cbind(USArrests, cluster = pam.res$cluster)

head(dd, n=3)

## Murder Assault UrbanPop Rape cluster

## Alabama 13.2 236 58 21.2 1

## Alaska 10.0 263 48 44.5 1

## Arizona 8.1 294 80 31.0 1

5.3.5 Accessing to the results of the pam() function

The function pam() returns an object of class pam which components include:

•medoids: Objects that represent clusters

•clustering: a vector containing the cluster number of each object

These components can be accessed as follow:

# Cluster medoids: New Mexico, Nebraska

pam.res$medoids

## Murder Assault UrbanPop Rape

## New Mexico 0.8292944 1.3708088 0.3081225 1.1603196

## Nebraska -0.8008247 -0.8250772 -0.2445636 -0.5052109

# Cluster numbers

head(pam.res$clustering)

## Alabama Alaska Arizona Arkansas California Colorado

##111211

5.3. COMPUTING PAM IN R 55

5.3.6 Visualizing PAM clusters

To visualize the partitioning results, we’ll use the function fviz_cluster() [factoextra

package]. It draws a scatter plot of data points colored by cluster numbers. If the data

contains more than 2 variables, the Principal Component Analysis (PCA) algorithm

is used to reduce the dimensionality of the data. In this case, the ﬁrst two principal

dimensions are used to plot the data.

fviz_cluster(pam.res,

palette = c("#00AFBB","#FC4E07"), # color palette

ellipse.type = "t",# Concentration ellipse

repel = TRUE,# Avoid label overplotting (slow)

ggtheme = theme_classic()

)

Alabama

Alaska

Arizona

Arkansas

California Colorado Connecticut

Delaware

Florida

Georgia

Hawaii

Idaho

Illinois

Indiana

Iowa

Kansas

Kentucky

Louisiana

Maine

Maryland

Massachusetts

Michigan

Minnesota

Mississippi

Missouri

Montana

Nebraska

Nevada

New Hampshire

New Jersey

New Mexico

New York

North Carolina

North Dakota

Ohio

Oklahoma

Oregon Pennsylvania

Rhode Island

South Carolina

South Dakota

Tennessee

Texas

Utah

Vermont

Virginia

Washington

West Virginia

Wisconsin

Wyoming

-2

-1

-2 0 2

Dim1 (62%)

Dim2 (24.7%)

cluster aa

Cluster plot

56 CHAPTER 5. K-MEDOIDS

5.4 Summary

The K-medoids algorithm, PAM, is a robust alternative to k-means for partitioning a

data set into clusters of observation.

In k-medoids method, each cluster is represented by a selected object within the

cluster. The selected objects are named medoids and corresponds to the most centrally

located points within the cluster.

The PAM algorithm requires the user to know the data and to indicate the appro-

priate number of clusters to be produced. This can be estimated using the function

fviz_nbclust [in factoextra R package].

The R function pam() [cluster package] can be used to compute PAM algorithm. The

simpliﬁed format is pam(x, k), where “x” is the data and k is the number of clusters

to be generated.

After, performing PAM clustering, the R function fviz_cluster() [

factoextra

package]

can be used to visualize the results. The format is fviz_cluster(pam.res), where

pam.res is the PAM results.

Note that, for large data sets, pam() may need too much memory or too much

computation time. In this case, the function clara() is preferable. This should not

be a problem for modern computers.

Chapter 6

CLARA - Clustering Large

Applications

CLARA

(Clustering Large Applications, Kaufman and Rousseeuw (1990)) is an

extension to k-medoids methods (Chapter 5) to deal with data containing a large

number of objects (more than several thousand observations) in order to reduce

computing time and RAM storage problem. This is achieved using the sampling

approach.

6.1 CLARA concept

Instead of ﬁnding medoids for the entire data set, CLARA considers a small sample

of the data with ﬁxed size (sampsize) and applies the PAM algorithm (Chapter 5) to

generate an optimal set of medoids for the sample. The quality of resulting medoids

is measured by the average dissimilarity between every object in the entire data set

and the medoid of its cluster, deﬁned as the cost function.

CLARA repeats the sampling and clustering processes a pre-speciﬁed number of times

in order to minimize the sampling bias. The ﬁnal clustering results correspond to the

set of medoids with the minimal cost. The CLARA algorithm is summarized in the

next section.

58 CHAPTER 6. CLARA - CLUSTERING LARGE APPLICATIONS

6.2 CLARA Algorithm

The algorithm is as follow:

1. Split randomly the data sets in multiple subsets with ﬁxed size (sampsize)

Compute PAM algorithm on each subset and choose the corresponding k

representative objects (medoids). Assign each observation of the entire data

set to the closest medoid.

Calculate the mean (or the sum) of the dissimilarities of the observations to

their closest medoid. This is used as a measure of the goodness of the clustering.

Retain the sub-data set for which the mean (or sum) is minimal. A further

analysis is carried out on the ﬁnal partition.

Note that, each sub-data set is forced to contain the medoids obtained from the best

sub-data set until then. Randomly drawn observations are added to this set until

sampsize has been reached.

6.3 Computing CLARA in R

6.3.1 Data format and preparation

To compute the CLARA algorithm in R, the data should be prepared as indicated in

Chapter 2.

Here, we’ll generate use a random data set. To make the result reproducible, we start

by using the function set.seed().

set.seed(1234)

# Generate 500 objects, divided into 2 clusters.

df <- rbind(cbind(rnorm(200,0,8), rnorm(200,0,8)),

cbind(rnorm(300,50,8), rnorm(300,50,8)))

# Specify column and row names

colnames(df) <- c("x","y")

6.3. COMPUTING CLARA IN R 59

rownames(df) <- paste0("S",1:nrow(df))

# Previewing the data

head(df, nrow = 6)

## x y

## S1 -9.656526 3.881815

## S2 2.219434 5.574150

## S3 8.675529 1.484111

## S4 -18.765582 5.605868

## S5 3.432998 2.493448

## S6 4.048447 6.083699

6.3.2 Required R packages and functions

The function clara() [cluster package] can be used to compute CLARA. The simpliﬁed

format is as follow:

clara(x, k, metric = "euclidean",stand = FALSE,

samples = 5,pamLike = FALSE)

•x

: a numeric data matrix or data frame, each row corresponds to an observation,

and each column corresponds to a variable. Missing values (NAs) are allowed.

•k: the number of clusters.

•metric

: the distance metrics to be used. Available options are “euclidean” and

“manhattan”. Euclidean distances are root sum-of-squares of diﬀerences, and

manhattan distances are the sum of absolute diﬀerences. Read more on distance

measures (Chapter 3). Note that, manhattan distance is less sensitive to outliers.

•stand

: logical value; if true, the variables (columns) in x are standardized before

calculating the dissimilarities. Note that, it’s recommended to standardize

variables before clustering.

•samples

: number of samples to be drawn from the data set. Default value is 5

but it’s recommended a much larger value.

•pamLike

: logical indicating if the same algorithm in the

pam

() function should

be used. This should be always true.

To create a beautiful graph of the clusters generated with the pam() function, will use

the factoextra package.

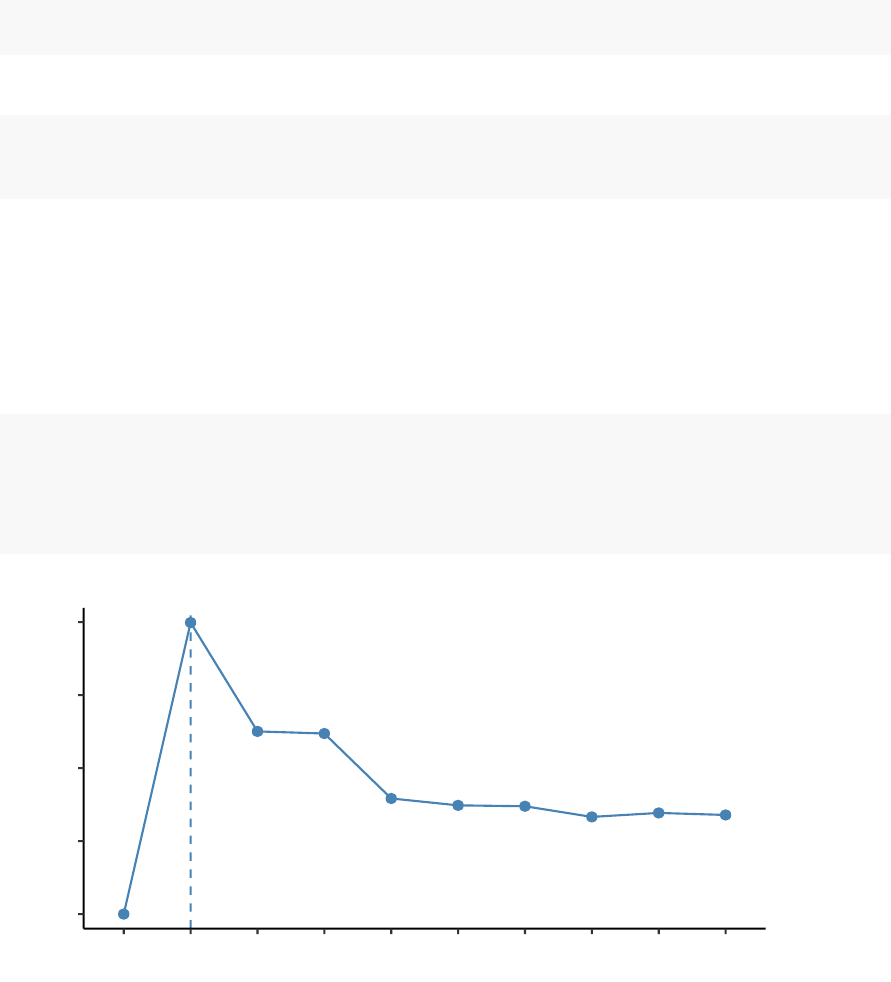
60 CHAPTER 6. CLARA - CLUSTERING LARGE APPLICATIONS

1. Installing required packages:

install.packages(c("cluster","factoextra"))

2. Loading the packages:

library(cluster)

library(factoextra)

6.3.3 Estimating the optimal number of clusters

To estimate the optimal number of clusters in your data, it’s possible to use the

average silhouette method as described in PAM clustering chapter (Chapter 5). The R

function fviz_nbclust() [factoextra package] provides a solution to facilitate this step.

library(cluster)

library(factoextra)

fviz_nbclust(df, clara, method = "silhouette")+

theme_classic()

0.0

0.2

0.4

0.6

0.8

123456789 10

Number of clusters k

Average silhouette width

Optimal number of clusters

From the plot, the suggested number of clusters is 2. In the next section, we’ll classify

the observations into 2 clusters.

6.3. COMPUTING CLARA IN R 61

6.3.4 Computing CLARA

The R code below computes PAM algorithm with k = 2:

# Compute CLARA

clara.res <- clara(df, 2,samples = 50,pamLike = TRUE)

# Print components of clara.res

print(clara.res)

## Call: clara(x = df, k = 2, samples = 50, pamLike = TRUE)

## Medoids:

## x y

## S121 -1.531137 1.145057

## S455 48.357304 50.233499

## Objective function: 9.87862

## Clustering vector: Named int [1:500] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ...

## - attr(*, "names")= chr [1:500] "S1" "S2" "S3" "S4" "S5" "S6" "S7" ...

## Cluster sizes: 200 300

## Best sample:

## [1] S37 S49 S54 S63 S68 S71 S76 S80 S82 S101 S103 S108 S109 S118

## [15] S121 S128 S132 S138 S144 S162 S203 S210 S216 S231 S234 S249 S260 S261

## [29] S286 S299 S304 S305 S312 S315 S322 S350 S403 S450 S454 S455 S456 S465

## [43] S488 S497

## Available components:

## [1] "sample" "medoids" "i.med" "clustering" "objective"

## [6] "clusinfo" "diss" "call" "silinfo" "data"

The output of the function clara() includes the following components:

•medoids: Objects that represent clusters

•clustering: a vector containing the cluster number of each object

•sample

: labels or case numbers of the observations in the best sample, that is,

the sample used by the clara algorithm for the ﬁnal partition.

If you want to add the point classiﬁcations to the original data, use this:

dd <- cbind(df, cluster = clara.res$cluster)

head(dd, n=4)

62 CHAPTER 6. CLARA - CLUSTERING LARGE APPLICATIONS

## x y cluster

## S1 -9.656526 3.881815 1

## S2 2.219434 5.574150 1

## S3 8.675529 1.484111 1

## S4 -18.765582 5.605868 1

You can access to the results returned by clara() as follow:

# Medoids

clara.res$medoids

## x y

## S121 -1.531137 1.145057

## S455 48.357304 50.233499

# Clustering

head(clara.res$clustering, 10)

## S1 S2 S3 S4 S5 S6 S7 S8 S9 S10

##1111111111

The medoids are S121, S455

6.3.5 Visualizing CLARA clusters

To visualize the partitioning results, we’ll use the function fviz_cluster() [factoextra

package]. It draws a scatter plot of data points colored by cluster numbers.

fviz_cluster(clara.res,

palette = c("#00AFBB","#FC4E07"), # color palette

ellipse.type = "t",# Concentration ellipse

geom = "point",pointsize = 1,

ggtheme = theme_classic()

)

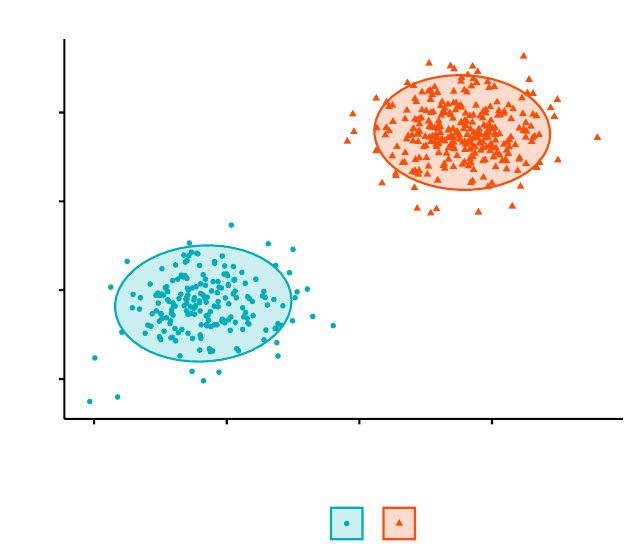
6.4. SUMMARY 63

-2

-1

-2 -1 0 1

x value

y value

cluster 12

Cluster plot

6.4 Summary

The CLARA (Clustering Large Applications) algorithm is an extension to the PAM

(Partitioning Around Medoids) clustering method for large data sets. It intended to

reduce the computation time in the case of large data set.

As almost all partitioning algorithm, it requires the user to specify the appropri-

ate number of clusters to be produced. This can be estimated using the function

fviz_nbclust [in factoextra R package].

The R function clara() [cluster package] can be used to compute CLARA algorithm.

The simpliﬁed format is clara(x, k, pamLike = TRUE), where “x” is the data and k is

the number of clusters to be generated.

After, computing CLARA, the R function fviz_cluster() [factoextra package] can be

used to visualize the results. The format is fviz_cluster(clara.res), where clara.res is

the CLARA results.

Part III

Hierarchical Clustering

Hierarchical clustering

[or

hierarchical cluster analysis

(

HCA

)] is an alter-

native approach to partitioning clustering (Part II) for grouping objects based on

their similarity. In contrast to partitioning clustering, hierarchical clustering does not

require to pre-specify the number of clusters to be produced.

Hierarchical clustering can be subdivided into two types:

•

Agglomerative clustering in which, each observation is initially considered as a

cluster of its own (leaf). Then, the most similar clusters are successively merged

until there is just one single big cluster (root).

•

Divise clustering, an inverse of agglomerative clustering, begins with the root,

in witch all objects are included in one cluster. Then the most heterogeneous

clusters are successively divided until all observation are in their own cluster.

The result of hierarchical clustering is a tree-based representation of the objects, which

is also known as dendrogram (see the ﬁgure below).

Alabama

Louisiana

Georgia

Tennessee

North Carolina

Mississippi

South Carolina

Texas

Illinois

New York

Florida

Arizona

Michigan

Maryland

New Mexico

Alaska

Colorado

California

Nevada

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

Height

Hierarchical Clustering

The dendrogram is a multilevel hierarchy where clusters at one level are joined together

to form the clusters at the next levels. This makes it possible to decide the level at

which to cut the tree for generating suitable groups of a data objects.

In previous chapters, we deﬁned several methods for measuring distances (Chapter

3) between objects in a data matrix. In this chapter, we’ll show how to visualize the

dissimilarity between objects using dendrograms.

We start by describing hierarchical clustering algorithms and provide R scripts

for computing and visualizing the results of hierarchical clustering. Next, we’ll

demonstrate how to cut dendrograms into groups. We’ll show also how to compare

two dendrograms. Additionally, we’ll provide solutions for handling dendrograms of

large data sets.

Chapter 7

Agglomerative Clustering

The

agglomerative clustering

is the most common type of hierarchical clustering

use to group objects in clusters based on their similarity. It’s also known as AGNES

(Agglomerative Nesting). The algorithm starts by treating each object as a single-

ton cluster. Next, pairs of clusters are successively merged until all clusters have

been merged into one big cluster containing all objects. The result is a tree-based

representation of the objects, named dendrogram.

In this article we start by describing the agglomerative clustering algorithms. Next, we

provide R lab sections with many examples for computing and visualizing hierarchical

clustering. We continue by explaining how to interpret dendrogram. Finally, we

provide R codes for cutting dendrograms into groups.

7.1 Algorithm

Agglomerative clustering works in a “bottom-up” manner. That is, each object is

initially considered as a single-element cluster (leaf). At each step of the algorithm,

the two clusters that are the most similar are combined into a new bigger cluster

(nodes). This procedure is iterated until all points are member of just one single big

cluster (root) (see ﬁgure below).

The inverse of agglomerative clustering is divisive clustering, which is also known as

DIANA (Divise Analysis) and it works in a “top-down” manner. It begins with the

root, in which all objects are included in a single cluster. At each step of iteration,

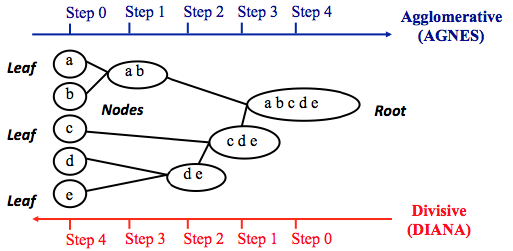
68 CHAPTER 7. AGGLOMERATIVE CLUSTERING

the most heterogeneous cluster is divided into two. The process is iterated until all

objects are in their own cluster (see ﬁgure below).

Note that, agglomerative clustering is good at identifying small clusters. Divisive

clustering is good at identifying large clusters. In this article, we’ll focus mainly on

agglomerative hierarchical clustering.

7.2 Steps to agglomerative hierarchical clustering

We’ll follow the steps below to perform agglomerative hierarchical clustering using R

software:

1. Preparing the data

Computing (dis)similarity information between every pair of objects in the data

set.

Using linkage function to group objects into hierarchical cluster tree, based on

the distance information generated at step 1. Objects/clusters that are in close

proximity are linked together using the linkage function.

Determining where to cut the hierarchical tree into clusters. This creates a

partition of the data.

We’ll describe each of these steps in the next section.

7.2.1 Data structure and preparation

The data should be a numeric matrix with:

•rows representing observations (individuals);

7.2. STEPS TO AGGLOMERATIVE HIERARCHICAL CLUSTERING 69

•and columns representing variables.

Here, we’ll use the R base USArrests data sets.

Note that, it’s generally recommended to standardize variables in the data set before

performing subsequent analysis. Standardization makes variables comparable, when

they are measured in diﬀerent scales. For example one variable can measure the

height in meter and another variable can measure the weight in kg. The R function

scale() can be used for standardization, See ?scale documentation.

# Load the data

data("USArrests")

# Standardize the data

df <- scale(USArrests)

# Show the first 6 rows

head(df, nrow = 6)

## Murder Assault UrbanPop Rape

## Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473

## Alaska 0.50786248 1.1068225 -1.2117642 2.484202941

## Arizona 0.07163341 1.4788032 0.9989801 1.042878388

## Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602

## California 0.27826823 1.2628144 1.7589234 2.067820292

## Colorado 0.02571456 0.3988593 0.8608085 1.864967207

7.2.2 Similarity measures

In order to decide which objects/clusters should be combined or divided, we need

methods for measuring the similarity between objects.

There are many methods to calculate the (dis)similarity information, including Eu-

clidean and manhattan distances (Chapter 3). In R software, you can use the function

dist() to compute the distance between every pair of object in a data set. The results

of this computation is known as a distance or dissimilarity matrix.

By default, the function dist() computes the Euclidean distance between objects;

however, it’s possible to indicate other metrics using the argument method. See ?dist

70 CHAPTER 7. AGGLOMERATIVE CLUSTERING

for more information.

For example, consider the R base data set USArrests, you can compute the distance

matrix as follow:

# Compute the dissimilarity matrix

# df = the standardized data

res.dist <- dist(df, method = "euclidean")

Note that, the function dist() computes the distance between the rows of a data

matrix using the speciﬁed distance measure method.

To see easily the distance information between objects, we reformat the results of the

function dist() into a matrix using the as.matrix() function. In this matrix, value in

the cell formed by the row i, the column j, represents the distance between object i

and object j in the original data set. For instance, element 1,1 represents the distance

between object 1 and itself (which is zero). Element 1,2 represents the distance

between object 1 and object 2, and so on.

The R code below displays the ﬁrst 6 rows and columns of the distance matrix:

as.matrix(res.dist)[1:6,1:6]

## Alabama Alaska Arizona Arkansas California Colorado

## Alabama 0.000000 2.703754 2.293520 1.289810 3.263110 2.651067

## Alaska 2.703754 0.000000 2.700643 2.826039 3.012541 2.326519

## Arizona 2.293520 2.700643 0.000000 2.717758 1.310484 1.365031

## Arkansas 1.289810 2.826039 2.717758 0.000000 3.763641 2.831051

## California 3.263110 3.012541 1.310484 3.763641 0.000000 1.287619

## Colorado 2.651067 2.326519 1.365031 2.831051 1.287619 0.000000

7.2.3 Linkage

The linkage function takes the distance information, returned by the function dist(),

and groups pairs of objects into clusters based on their similarity. Next, these newly

formed clusters are linked to each other to create bigger clusters. This process is

iterated until all the objects in the original data set are linked together in a hierarchical

tree.

7.2. STEPS TO AGGLOMERATIVE HIERARCHICAL CLUSTERING 71

For example, given a distance matrix “res.dist” generated by the function dist(), the

R base function hclust() can be used to create the hierarchical tree.

hclust() can be used as follow:

res.hc <- hclust(d=res.dist, method = "ward.D2")

•d: a dissimilarity structure as produced by the dist() function.

•method

: The agglomeration (linkage) method to be used for computing distance

between clusters. Allowed values is one of “ward.D”, “ward.D2”, “single”,

“complete”, “average”, “mcquitty”, “median” or “centroid”.

There are many cluster agglomeration methods (i.e, linkage methods). The most

common linkage methods are described below.

•

Maximum or complete linkage: The distance between two clusters is deﬁned as

the maximum value of all pairwise distances between the elements in cluster 1

and the elements in cluster 2. It tends to produce more compact clusters.

•

Minimum or single linkage: The distance between two clusters is deﬁned

as the minimum value of all pairwise distances between the elements in

cluster 1 and the elements in cluster 2. It tends to produce long, "loose" clusters.

•

Mean or average linkage: The distance between two clusters is deﬁned as the

average distance between the elements in cluster 1 and the elements in cluster 2.

•

Centroid linkage: The distance between two clusters is deﬁned as the distance

between the centroid for cluster 1 (a mean vector of length p variables) and

the centroid for cluster 2.

•

Ward’s minimum variance method: It minimizes the total within-cluster vari-

ance. At each step the pair of clusters with minimum between-cluster distance

are merged.

Note that, at each stage of the clustering process the two clusters, that have the

smallest linkage distance, are linked together.

Complete linkage and Ward’s method are generally preferred.

72 CHAPTER 7. AGGLOMERATIVE CLUSTERING

7.2.4 Dendrogram

Dendrograms correspond to the graphical representation of the hierarchical tree

generated by the function hclust(). Dendrogram can be produced in R using the

base function plot(res.hc), where res.hc is the output of hclust(). Here, we’ll use the

function fviz_dend()[ in factoextra R package] to produce a beautiful dendrogram.

First install factoextra by typing this: install.packages(“factoextra”); next visualize

the dendrogram as follow:

# cex: label size

library("factoextra")

fviz_dend(res.hc, cex = 0.5)

Alabama

Louisiana

Georgia

Tennessee

North Carolina

Mississippi

South Carolina

Texas

Illinois

New York

Florida

Arizona

Michigan

Maryland

New Mexico

Alaska

Colorado

California

Nevada

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

Height

Cluster Dendrogram

In the dendrogram displayed above, each leaf corresponds to one object. As we move

up the tree, objects that are similar to each other are combined into branches, which

are themselves fused at a higher height.

The height of the fusion, provided on the vertical axis, indicates the (dis)similarity/distance

between two objects/clusters. The higher the height of the fusion, the less similar the

objects are. This height is known as the cophenetic distance between the two objects.

7.3. VERIFY THE CLUSTER TREE 73

Note that, conclusions about the proximity of two objects can be drawn only based on

the height where branches containing those two objects ﬁrst are fused. We cannot use

the proximity of two objects along the horizontal axis as a criteria of their similarity.

In order to identify sub-groups, we can cut the dendrogram at a certain height as

described in the next sections.

7.3 Verify the cluster tree

After linking the objects in a data set into a hierarchical cluster tree, you might want

to assess that the distances (i.e., heights) in the tree reﬂect the original distances

accurately.

One way to measure how well the cluster tree generated by the hclust() function

reﬂects your data is to compute the correlation between the cophenetic distances and

the original distance data generated by the dist() function. If the clustering is valid,

the linking of objects in the cluster tree should have a strong correlation with the

distances between objects in the original distance matrix.

The closer the value of the correlation coeﬃcient is to 1, the more accurately the

clustering solution reﬂects your data. Values above 0.75 are felt to be good. The

“average” linkage method appears to produce high values of this statistic. This may

be one reason that it is so popular.

The R base function cophenetic() can be used to compute the cophenetic distances for

hierarchical clustering.

# Compute cophentic distance

res.coph <- cophenetic(res.hc)

# Correlation between cophenetic distance and

# the original distance

cor(res.dist, res.coph)

## [1] 0.6975266

Execute the hclust() function again using the average linkage method. Next, call

cophenetic() to evaluate the clustering solution.

74 CHAPTER 7. AGGLOMERATIVE CLUSTERING

res.hc2 <- hclust(res.dist, method = "average")

cor(res.dist, cophenetic(res.hc2))

## [1] 0.7180382

The correlation coeﬃcient shows that using a diﬀerent linkage method creates a tree

that represents the original distances slightly better.

7.4 Cut the dendrogram into diﬀerent groups

One of the problems with hierarchical clustering is that, it does not tell us how many

clusters there are, or where to cut the dendrogram to form clusters.

You can cut the hierarchical tree at a given height in order to partition your data

into clusters. The R base function cutree() can be used to cut a tree, generated by

the hclust() function, into several groups either by specifying the desired number of

groups or the cut height. It returns a vector containing the cluster number of each

observation.

# Cut tree into 4 groups

grp <- cutree(res.hc, k=4)

head(grp, n=4)

## Alabama Alaska Arizona Arkansas

## 1 2 2 3

# Number of members in each cluster

table(grp)

## grp

## 1 2 3 4

## 7 12 19 12

# Get the names for the members of cluster 1

rownames(df)[grp == 1]

## [1] "Alabama" "Georgia" "Louisiana" "Mississippi"

7.4. CUT THE DENDROGRAM INTO DIFFERENT GROUPS 75

## [5] "North Carolina" "South Carolina" "Tennessee"

The result of the cuts can be visualized easily using the function fviz_dend() [in

factoextra]:

# Cut in 4 groups and color by groups

fviz_dend(res.hc, k=4,# Cut in four groups

cex = 0.5,# label size

k_colors = c("#2E9FDF","#00AFBB","#E7B800","#FC4E07"),

color_labels_by_k = TRUE,# color labels by groups

rect = TRUE # Add rectangle around groups

)

Alabama

Louisiana

Georgia

Tennessee

North Carolina

Mississippi

South Carolina

Texas

Illinois

New York

Florida

Arizona

Michigan

Maryland

New Mexico

Alaska

Colorado

California

Nevada

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

Height

Cluster Dendrogram

Using the function fviz_cluster() [in factoextra], we can also visualize the result in

a scatter plot. Observations are represented by points in the plot, using principal

components. A frame is drawn around each cluster.

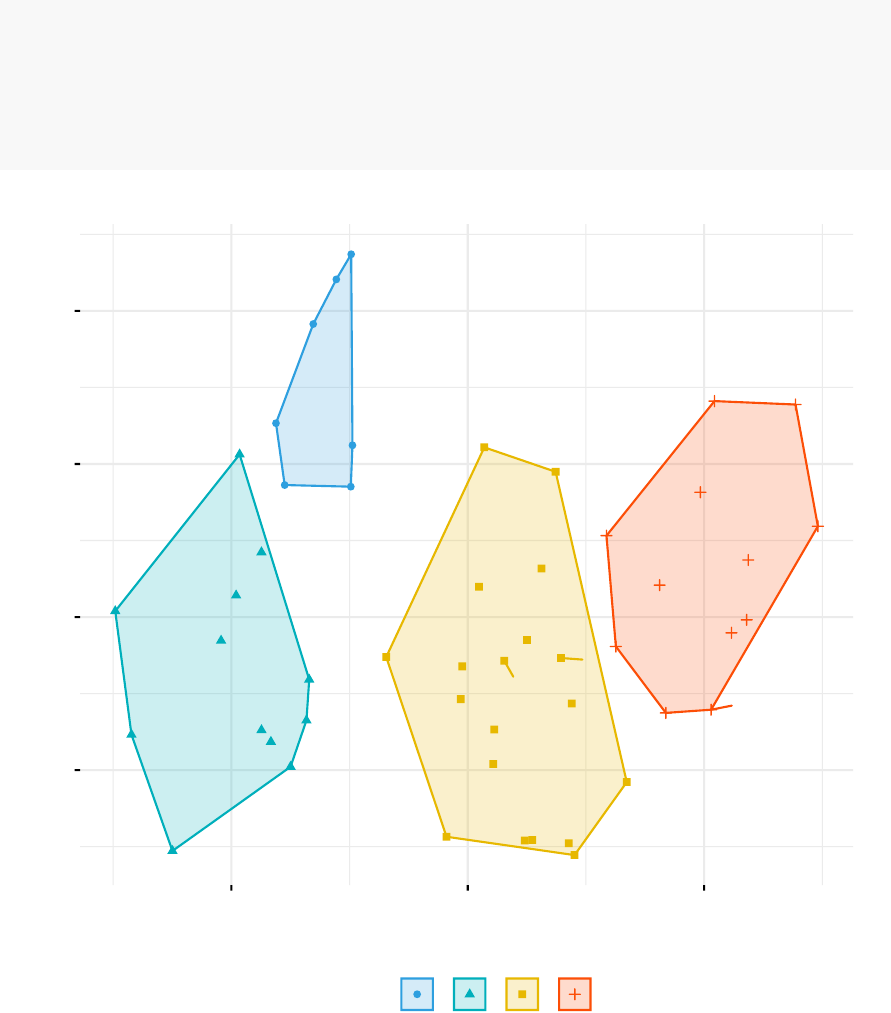
76 CHAPTER 7. AGGLOMERATIVE CLUSTERING

fviz_cluster(list(data = df, cluster = grp),

palette = c("#2E9FDF","#00AFBB","#E7B800","#FC4E07"),

ellipse.type = "convex",# Concentration ellipse

repel = TRUE,# Avoid label overplotting (slow)

show.clust.cent = FALSE,ggtheme = theme_minimal())

Alabama

Alaska

Arizona

Arkansas

California

Colorado Connecticut

Delaware

Florida

Georgia

Hawaii

Idaho

Illinois

Indiana

Iowa

Kansas

Kentucky

Louisiana

Maine

Maryland

Massachusetts

Michigan

Minnesota

Mississippi

Missouri

Montana

Nebraska

Nevada

New Hampshire

New Jersey

New Mexico

New York

North Carolina

North Dakota

Ohio

Oklahoma

Oregon

Pennsylvania

Rhode Island

South Carolina

South Dakota

Tennessee

Texas

Utah

Vermont

Virginia

Washington

West Virginia

Wisconsin

Wyoming

-1

-2 0 2

Dim1 (62%)

Dim2 (24.7%)

cluster aaaa

1234

Cluster plot

7.5. CLUSTER R PACKAGE 77

7.5 Cluster R package

The R package cluster makes it easy to perform cluster analysis in R. It provides

the function agnes() and diana() for computing agglomerative and divisive clustering,

respectively. These functions perform all the necessary steps for you. You don’t need

to execute the scale(), dist() and hclust() function separately.

The functions can be executed as follow:

library("cluster")

# Agglomerative Nesting (Hierarchical Clustering)

res.agnes <- agnes(x=USArrests, # data matrix

stand = TRUE,# Standardize the data

metric = "euclidean",# metric for distance matrix

method = "ward" # Linkage method

)

# DIvisive ANAlysis Clustering

res.diana <- diana(x=USArrests, # data matrix

stand = TRUE,# standardize the data

metric = "euclidean" # metric for distance matrix

)

After running agnes() and diana(), you can use the function fviz_dend()[in factoextra]

to visualize the output:

fviz_dend(res.agnes, cex = 0.6,k=4)

7.6 Application of hierarchical clustering to gene

expression data analysis

In gene expression data analysis,clustering is generaly used as one of the ﬁrst step to

explore the data. We are interested in whether there are groups of genes or groups of

samples that have similar gene expression patterns.

Several distance measures (Chapter 3) have been described for assessing the similarity

or the dissimilarity between items, in order to decide which items have to be grouped

78 CHAPTER 7. AGGLOMERATIVE CLUSTERING

together or not. These measures can be used to cluster genes or samples that are

similar.

For most common clustering softwares, the default distance measure is the Euclidean

distance. The most popular methods for gene expression data are to use log2(expression

+ 0.25), correlation distance and complete linkage clustering agglomerative-clustering.

Single and Complete linkage give the same dendrogram whether you use the raw data,

the log of the data or any other transformation of the data that preserves the order

because what matters is which ones have the smallest distance. The other methods

are sensitive to the measurement scale.

Note that, when the data are scaled, the Euclidean distance of the z-scores is the

same as correlation distance.

Pearson’s correlation is quite sensitive to outliers. When clustering genes,

it is important to be aware of the possible impact of outliers. An alternative option

is to use Spearman’s correlation instead of Pearson’s correlation.

In principle it is possible to cluster all the genes, although visualizing a huge den-

drogram might be problematic. Usually, some type of preliminary analysis, such as

diﬀerential expression analysis is used to select genes for clustering.

Selecting genes based on diﬀerential expression analysis removes genes which are likely

to have only chance patterns. This should enhance the patterns found in the gene

clusters.

7.7 Summary

Hierarchical clustering is a cluster analysis method, which produce a tree-based

representation (i.e.: dendrogram) of a data. Objects in the dendrogram are linked

together based on their similarity.

To perform hierarchical cluster analysis in R, the ﬁrst step is to calculate the pairwise

distance matrix using the function dist(). Next, the result of this computation is used

by the hclust() function to produce the hierarchical tree. Finally, you can use the

function fviz_dend() [in factoextra R package] to plot easily a beautiful dendrogram.

It’s also possible to cut the tree at a given height for partitioning the data into multiple

groups (R function cutree()).

Chapter 8

Comparing Dendrograms

After showing how to compute hierarchical clustering (Chapter 7), we describe, here,

how to compare two dendrograms using the dendextend R package.

The dendextend package provides several functions for comparing dendrograms. Here,

we’ll focus on two functions:

•tanglegram() for visual comparison of two dendrograms

•and cor.dendlist() for computing a correlation matrix between dendrograms.

8.1 Data preparation

We’ll use the R base USArrests data sets and we start by standardizing the variables

using the function scale() as follow:

df <- scale(USArrests)

To make readable the plots, generated in the next sections, we’ll work with a small

random subset of the data set. Therefore, we’ll use the function sample() to randomly

select 10 observations among the 50 observations contained in the data set:

# Subset containing 10 rows

set.seed(123)

ss <- sample(1:50,10)

df <- df[ss,]

80 CHAPTER 8. COMPARING DENDROGRAMS

8.2 Comparing dendrograms

We start by creating a list of two dendrograms by computing hierarchical clustering

(HC) using two diﬀerent linkage methods (“average” and “ward.D2”). Next, we

transform the results as dendrograms and create a list to hold the two dendrograms.

library(dendextend)

# Compute distance matrix

res.dist <- dist(df, method = "euclidean")

# Compute 2 hierarchical clusterings

hc1 <- hclust(res.dist, method = "average")

hc2 <- hclust(res.dist, method = "ward.D2")

# Create two dendrograms

dend1 <- as.dendrogram (hc1)

dend2 <- as.dendrogram (hc2)

# Create a list to hold dendrograms

dend_list <- dendlist(dend1, dend2)

8.2.1 Visual comparison of two dendrograms

To visually compare two dendrograms, we’ll use the tanglegram() function [dendextend

package], which plots the two dendrograms, side by side, with their labels connected

by lines.

The quality of the alignment of the two trees can be measured using the function

entanglement(). Entanglement is a measure between 1 (full entanglement) and 0 (no

entanglement). A lower entanglement coeﬃcient corresponds to a good alignment.

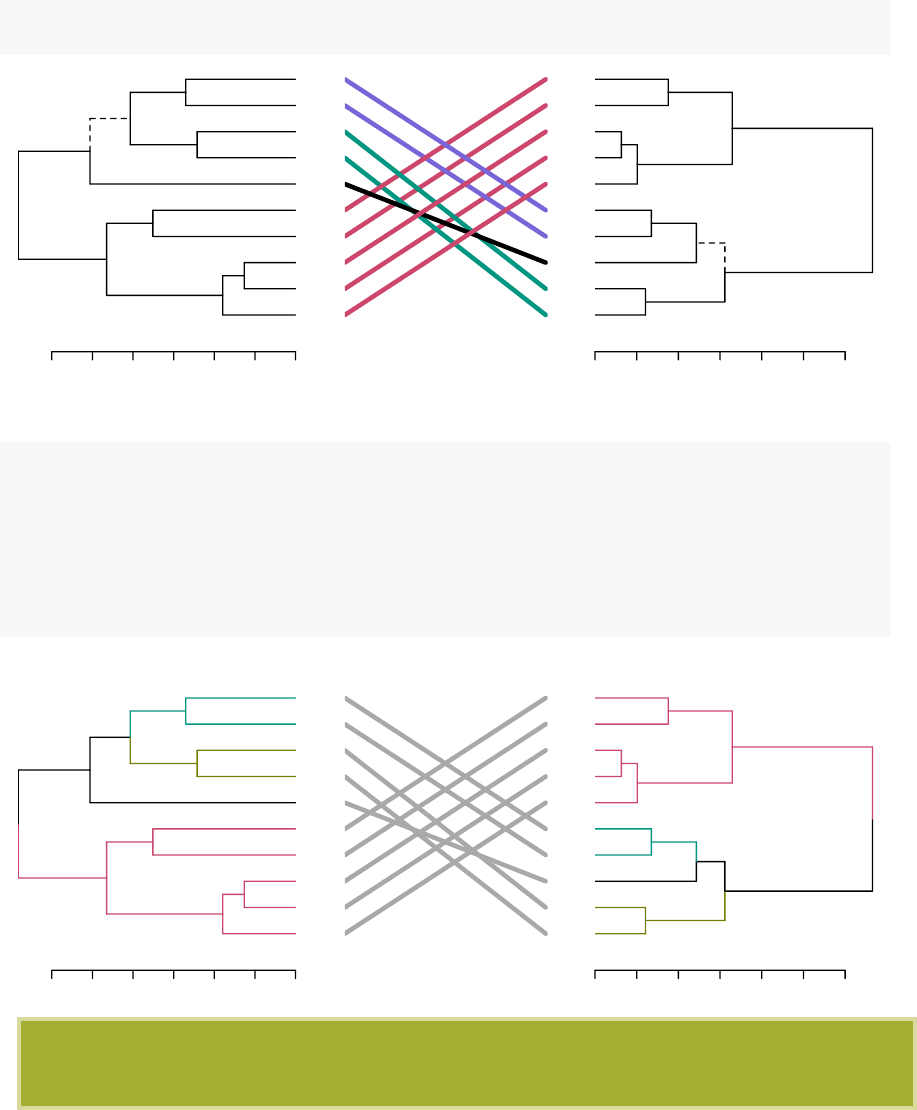
8.2. COMPARING DENDROGRAMS 81

•Draw a tanglegram:

tanglegram(dend1, dend2)

3.0 2.5 2.0 1.5 1.0 0.5 0.0

Maine

Iowa

Wisconsin

Rhode Island

Utah

Mississippi

Maryland

Arizona

Tennessee

Virginia

0123456

Maryland

Arizona

Mississippi

Tennessee

Virginia

Maine

Iowa

Wisconsin

Rhode Island

Utah

•Customized the tanglegram using many other options as follow:

tanglegram(dend1, dend2,

highlight_distinct_edges = FALSE,# Turn-off dashed lines

common_subtrees_color_lines = FALSE,# Turn-off line colors

common_subtrees_color_branches = TRUE,# Color common branches

main = paste("entanglement =",round(entanglement(dend_list), 2))

)

3.0 2.5 2.0 1.5 1.0 0.5 0.0

Maine

Iowa

Wisconsin

Rhode Island

Utah

Mississippi

Maryland

Arizona

Tennessee

Virginia

entanglement = 0.9

0123456

Maryland

Arizona

Mississippi

Tennessee

Virginia

Maine

Iowa

Wisconsin

Rhode Island

Utah

Note that "unique" nodes, with a combination of labels/items not present in the

other tree, are highlighted with dashed lines.

82 CHAPTER 8. COMPARING DENDROGRAMS

8.2.2 Correlation matrix between a list of dendrograms

The function cor.dendlist() is used to compute “Baker”or“Cophenetic” correlation

matrix between a list of trees. The value can range between -1 to 1. With near 0

values meaning that the two trees are not statistically similar.

# Cophenetic correlation matrix

cor.dendlist(dend_list, method = "cophenetic")

## [,1] [,2]

## [1,] 1.0000000 0.9646883

## [2,] 0.9646883 1.0000000

# Baker correlation matrix

cor.dendlist(dend_list, method = "baker")

## [,1] [,2]

## [1,] 1.0000000 0.9622885

## [2,] 0.9622885 1.0000000

The correlation between two trees can be also computed as follow:

# Cophenetic correlation coefficient

cor_cophenetic(dend1, dend2)

## [1] 0.9646883

# Baker correlation coefficient

cor_bakers_gamma(dend1, dend2)

## [1] 0.9622885

It’s also possible to compare simultaneously multiple dendrograms. A chaining operator

%>% is used to run multiple function at the same time. It’s useful for simplifying the

code:

8.2. COMPARING DENDROGRAMS 83

# Create multiple dendrograms by chaining

dend1 <- df %>% dist %>% hclust("complete")%>%as.dendrogram

dend2 <- df %>% dist %>% hclust("single")%>%as.dendrogram

dend3 <- df %>% dist %>% hclust("average")%>%as.dendrogram

dend4 <- df %>% dist %>% hclust("centroid")%>%as.dendrogram

# Compute correlation matrix

dend_list <- dendlist("Complete" =dend1, "Single" =dend2,

"Average" =dend3, "Centroid" =dend4)

cors <- cor.dendlist(dend_list)

# Print correlation matrix

round(cors, 2)

## Complete Single Average Centroid

## Complete 1.00 0.76 0.99 0.75

## Single 0.76 1.00 0.80 0.84

## Average 0.99 0.80 1.00 0.74

## Centroid 0.75 0.84 0.74 1.00

# Visualize the correlation matrix using corrplot package

library(corrplot)

corrplot(cors, "pie","lower")

-1 -0.8-0.6-0.4-0.2 00.20.40.60.8 1

Complete

Single

Average

Centroid

Complete

Single

Average

Centroid

Chapter 9

Visualizing Dendrograms

As described in previous chapters, a

dendrogram

is a tree-based representation of a

data created using hierarchical clustering methods (Chapter 7). In this article, we

provide R code for

visualizing

and customizing dendrograms. Additionally, we show

how to save and to zoom a large dendrogram.

We start by computing hierarchical clustering using the USArrests data sets:

# Load data

data(USArrests)

# Compute distances and hierarchical clustering

dd <- dist(scale(USArrests), method = "euclidean")

hc <- hclust(dd, method = "ward.D2")

To visualize the dendrogram, we’ll use the following R functions and packages:

•

fviz_dend()[in factoextra R package] to create easily a ggplot2-based beautiful

dendrogram.

•dendextend package to manipulate dendrograms

Before continuing, install the required package as follow:

install.packages(c("factoextra","dendextend"))

9.1. VISUALIZING DENDROGRAMS 85

9.1 Visualizing dendrograms

We’ll use the function fviz_dend()[in factoextra R package] to create easily a beautiful

dendrogram using either the R base plot or ggplot2. It provides also an option for

drawing circular dendrograms and phylogenic-like trees.

To create a basic dendrograms, type this:

library(factoextra)

fviz_dend(hc, cex = 0.5)

You can use the arguments main, sub, xlab, ylab to change plot titles as follow:

fviz_dend(hc, cex = 0.5,

main = "Dendrogram - ward.D2",

xlab = "Objects",ylab = "Distance",sub = "")

To draw a horizontal dendrogram, type this:

fviz_dend(hc, cex = 0.5,horiz = TRUE)

It’s also possible to cut the tree at a given height for partitioning the data into multiple

groups as described in the previous chapter: Hierarchical clustering (Chapter 7). In

this case, it’s possible to color branches by groups and to add rectangle around each

group.

For example:

fviz_dend(hc, k=4,# Cut in four groups

cex = 0.5,# label size

k_colors = c("#2E9FDF","#00AFBB","#E7B800","#FC4E07"),

color_labels_by_k = TRUE,# color labels by groups

rect = TRUE,# Add rectangle around groups

rect_border = c("#2E9FDF","#00AFBB","#E7B800","#FC4E07"),

rect_fill = TRUE)

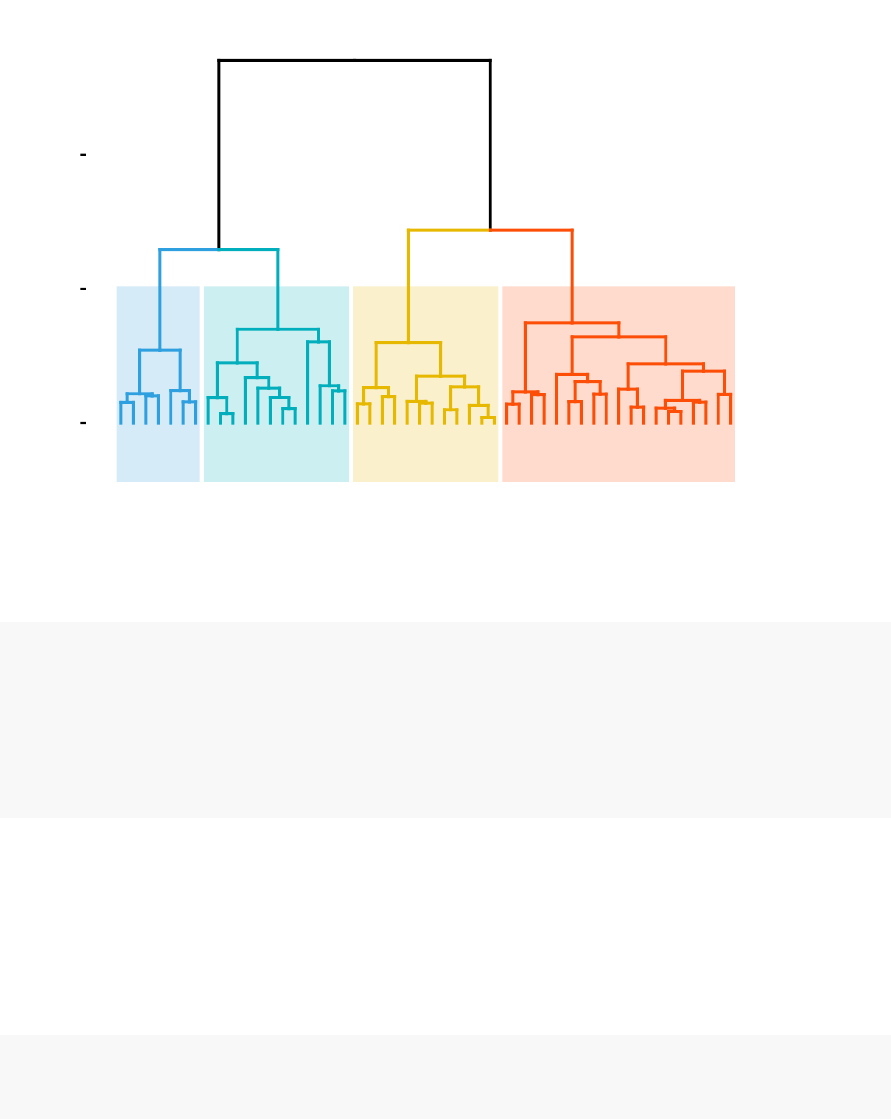
86 CHAPTER 9. VISUALIZING DENDROGRAMS

Alabama

Louisiana

Georgia

Tennessee

North Carolina

Mississippi

South Carolina

Texas

Illinois

New York

Florida

Arizona

Michigan

Maryland

New Mexico

Alaska

Colorado

California

Nevada

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

Height

Cluster Dendrogram

To change the plot theme, use the argument ggtheme, which allowed values include gg-

plot2 oﬃcial themes [ theme_gray(), theme_bw(), theme_minimal(), theme_classic(),

theme_void()] or any other user-deﬁned ggplot2 themes.

fviz_dend(hc, k=4,# Cut in four groups

cex = 0.5,# label size

k_colors = c("#2E9FDF","#00AFBB","#E7B800","#FC4E07"),

color_labels_by_k = TRUE,# color labels by groups

ggtheme = theme_gray() # Change theme

)

Allowed values for k_color include brewer palettes from RColorBrewer Package (e.g.

“RdBu”, “Blues”, “Dark2”, “Set2”, . . . ; ) and scientiﬁc journal palettes from ggsci R

package (e.g.: “npg”, “aaas”, “lancet”, “jco”, “ucscgb”, “uchicago”, “simpsons” and

“rickandmorty”).

In the R code below, we’ll change group colors using “jco” (journal of clinical oncology)

color palette:

fviz_dend(hc, cex = 0.5,k=4,# Cut in four groups

k_colors = "jco")

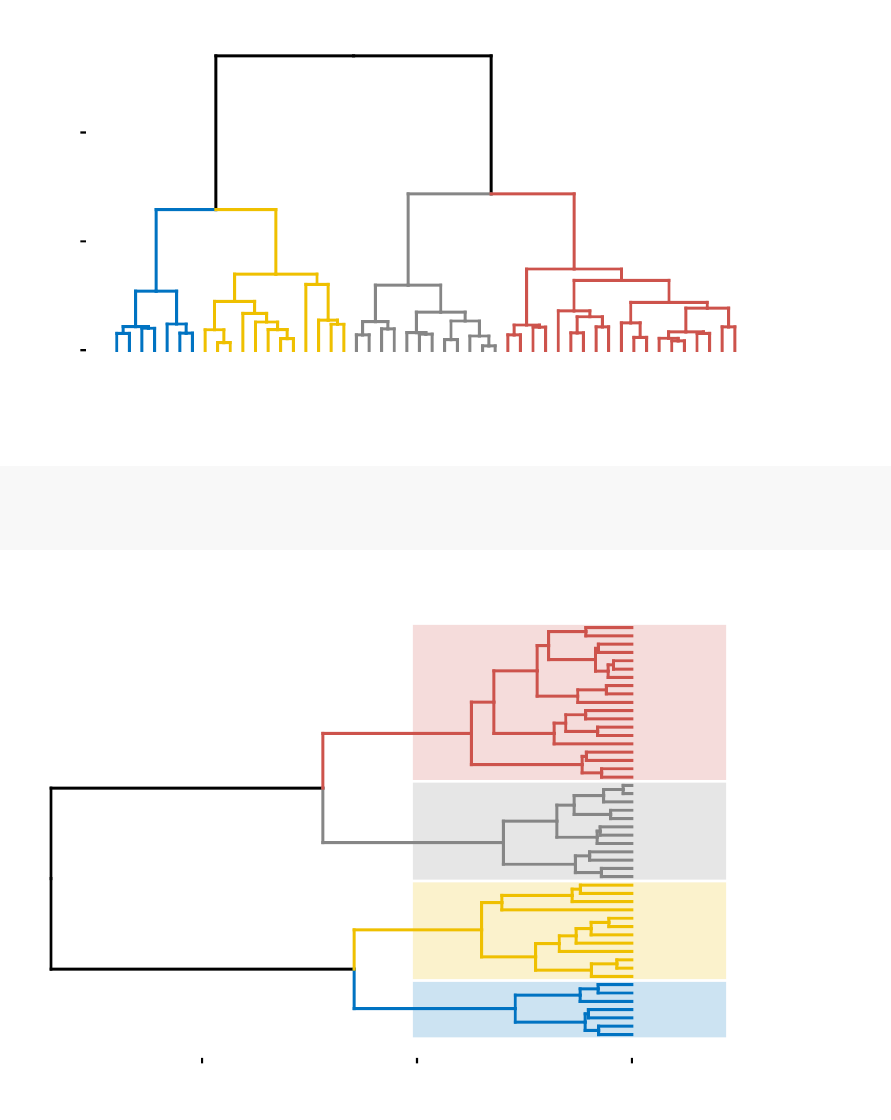
9.1. VISUALIZING DENDROGRAMS 87

Alabama

Louisiana

Georgia

Tennessee

North Carolina

Mississippi

South Carolina

Texas

Illinois

New York

Florida

Arizona

Michigan

Maryland

New Mexico

Alaska

Colorado

California

Nevada

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

Height

Cluster Dendrogram

If you want to draw a horizontal dendrogram with rectangle around clusters, use this:

fviz_dend(hc, k=4,cex = 0.4,horiz = TRUE,k_colors = "jco",

rect = TRUE,rect_border = "jco",rect_fill = TRUE)

Alabama

Louisiana

Georgia

Tennessee

North Carolina

Mississippi

South Carolina

Texas

Illinois

New York

Florida

Arizona

Michigan

Maryland

New Mexico

Alaska

Colorado

California

Nevada

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

0510

Height

Cluster Dendrogram

88 CHAPTER 9. VISUALIZING DENDROGRAMS

Additionally, you can plot a circular dendrogram using the option type = “circular”.

fviz_dend(hc, cex = 0.5,k=4,

k_colors = "jco",type = "circular")

Alabama

Louisiana

Georgia

Tennessee

North Carolina

Mississippi

South Carolina

Texas

Illinois

New York

Florida

Arizona

Michigan

Maryland

New Mexico

Alaska

Colorado

California

Nevada

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

To plot a phylogenic-like tree, use type = “phylogenic” and repel = TRUE (to avoid

labels overplotting). This functionality requires the R package igraph. Make sure that

it’s installed before typing the following R code.

require("igraph")

fviz_dend(hc, k=4,k_colors = "jco",

type = "phylogenic",repel = TRUE)

9.1. VISUALIZING DENDROGRAMS 89

Alabama

Alaska

Arizona

Arkansas

California

Colorado

Connecticut

Delaware

Florida

Georgia

Hawaii

Idaho

Illinois

Indiana

Iowa

Kansas

Kentucky

Louisiana

Maine

Maryland

Massachusetts

Michigan

Minnesota

Mississippi

Missouri

Montana

Nebraska

Nevada

New Hampshire

New Jersey

New Mexico

New York

North Carolina

North Dakota

Ohio

Oklahoma

Oregon

Pennsylvania

Rhode Island

South Carolina

South Dakota

Tennessee

Texas

Utah

Vermont

Virginia

Washington

West Virginia

Wisconsin

Wyoming

The default layout for phylogenic trees is “layout.auto”. Allowed values are one of:

c(“layout.auto”, “layout_with_drl”, “layout_as_tree”, “layout.gem”, “layout.mds”,

“layout_with_lgl”). To read more about these layouts, read the documentation of the

igraph R package.

Let’s try phylo.layout = “layout.gem”:

require("igraph")

fviz_dend(hc, k=4,# Cut in four groups

k_colors = "jco",

type = "phylogenic",repel = TRUE,

phylo_layout = "layout.gem")

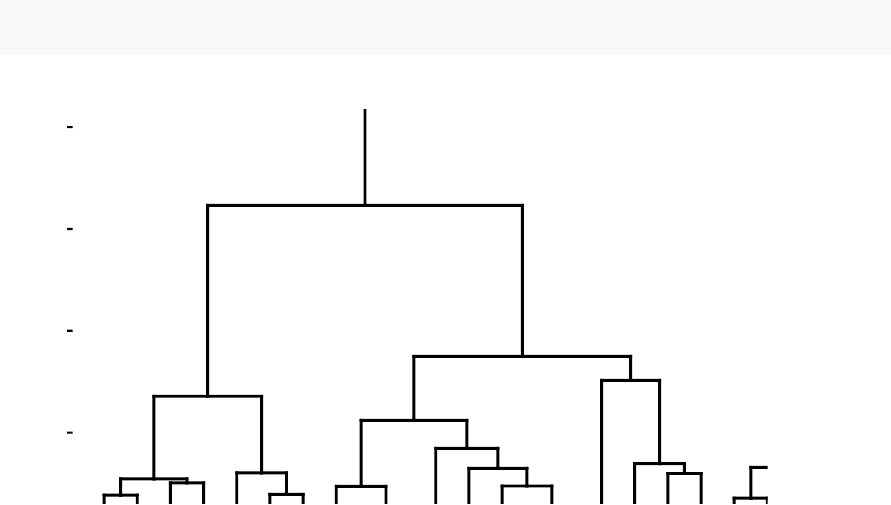
90 CHAPTER 9. VISUALIZING DENDROGRAMS

9.2 Case of dendrogram with large data sets

If you compute hierarchical clustering on a large data set, you might want to zoom in

the dendrogram or to plot only a subset of the dendrogram.

Alternatively, you could also plot the dendrogram to a large page on a PDF, which

can be zoomed without loss of resolution.

9.2.1 Zooming in the dendrogram

If you want to zoom in the ﬁrst clusters, its possible to use the option xlim and ylim

to limit the plot area. For example, type the code below:

fviz_dend(hc, xlim = c(1,20), ylim = c(1,8))

Height

Cluster Dendrogram

9.2.2 Plotting a sub-tree of dendrograms

To plot a sub-tree, we’ll follow the procedure below:

Create the whole dendrogram using fviz_dend() and save the result into an

object, named dend_plot for example.

9.2. CASE OF DENDROGRAM WITH LARGE DATA SETS 91

Use the R base function cut.dendrogram() to cut the dendrogram, at a given

height (h), into multiple sub-trees. This returns a list with components $upper

and $lower, the ﬁrst is a truncated version of the original tree, also of class

dendrogram, the latter a list with the branches obtained from cutting the tree,

each a dendrogram.

3. Visualize sub-trees using fviz_dend().

The R code is as follow.

•Cut the dendrogram and visualize the truncated version:

# Create a plot of the whole dendrogram,

# and extract the dendrogram data

dend_plot <- fviz_dend(hc, k=4,# Cut in four groups

cex = 0.5,# label size

k_colors = "jco"

)

dend_data <- attr(dend_plot, "dendrogram")# Extract dendrogram data

# Cut the dendrogram at height h = 10

dend_cuts <- cut(dend_data, h=10)

# Visualize the truncated version containing

# two branches

fviz_dend(dend_cuts$upper)

Branch 1

Branch 2

Height

Cluster Dendrogram

•Plot dendrograms sub-trees:

92 CHAPTER 9. VISUALIZING DENDROGRAMS

# Plot the whole dendrogram

print(dend_plot)

Alabama

Louisiana

Georgia

Tennessee

North Carolina

Mississippi

South Carolina

Texas

Illinois

New York

Florida

Arizona

Michigan

Maryland

New Mexico

Alaska

Colorado

California

Nevada

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

Height

Cluster Dendrogram

# Plot subtree 1

fviz_dend(dend_cuts$lower[[1]], main = "Subtree 1")

# Plot subtree 2

fviz_dend(dend_cuts$lower[[2]], main = "Subtree 2")

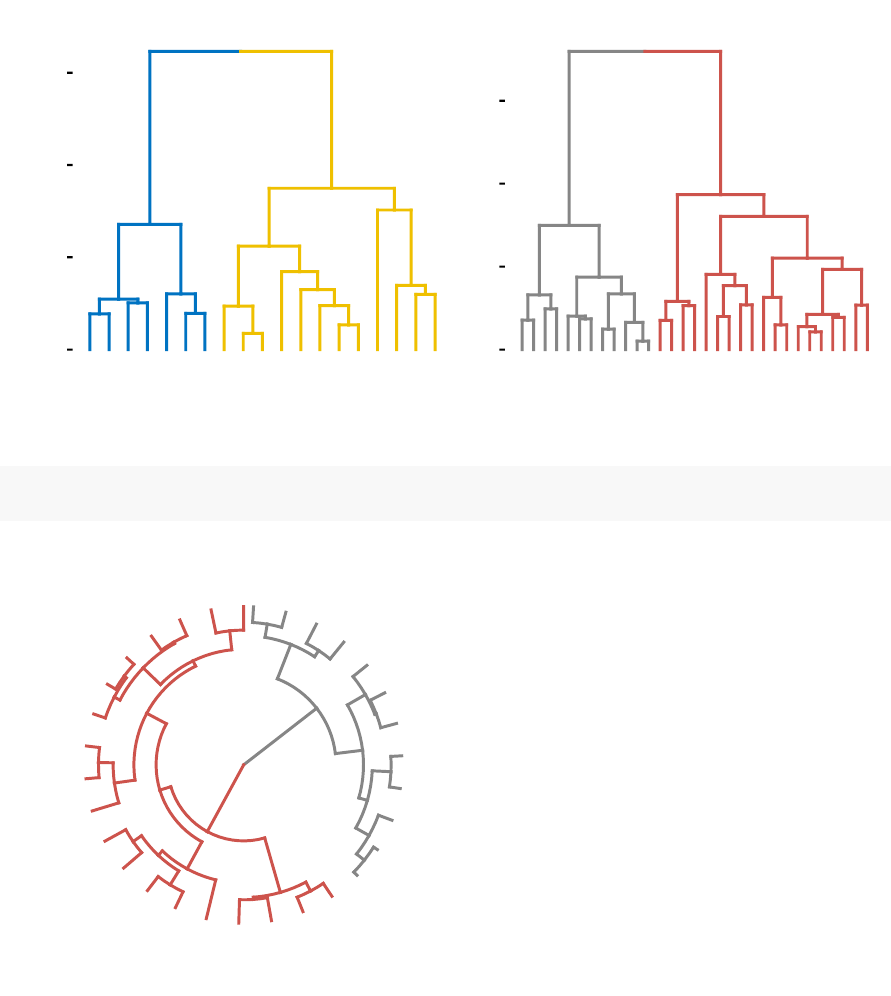
9.2. CASE OF DENDROGRAM WITH LARGE DATA SETS 93

Alabama

Louisiana

Georgia

Tennessee

North Carolina

Mississippi

South Carolina

Texas

Illinois

New York

Florida

Arizona

Michigan

Maryland

New Mexico

Alaska

Colorado

California

Nevada

Height

Subtree 1

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

Height

Subtree 2

You can also plot circular trees as follow:

fviz_dend(dend_cuts$lower[[2]], type = "circular")

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

94 CHAPTER 9. VISUALIZING DENDROGRAMS

9.2.3 Saving dendrogram into a large PDF page

If you have a large dendrogram, you can save it to a large PDF page, which can be

zoomed without loss of resolution.

pdf("dendrogram.pdf",width=30,height=15)# Open a PDF

p<-fviz_dend(hc, k=4,cex = 1,k_colors = "jco" )# Do plotting

print(p)

dev.off() # Close the PDF

9.3 Manipulating dendrograms using dendextend

The package dendextend provide functions for changing easily the appearance of a

dendrogram and for comparing dendrograms.

In this section we’ll use the chaining operator (%>%) to simplify our code. The

chaining operator turns x %>% f(y) into f(x, y) so you can use it to rewrite multiple

operations such that they can be read from left-to-right, top-to-bottom. For instance,

the results of the two R codes below are equivalent.

•Standard R code for creating a dendrogram:

data <- scale(USArrests)

dist.res <- dist(data)

hc <- hclust(dist.res, method = "ward.D2")

dend <- as.dendrogram(hc)

plot(dend)

•R code for creating a dendrogram using chaining operator:

library(dendextend)

dend <- USArrests[1:5,] %>% # data

scale %>% # Scale the data

dist %>% # calculate a distance matrix,

hclust(method = "ward.D2")%>%# Hierarchical clustering

as.dendrogram # Turn the object into a dendrogram.

plot(dend)

9.3. MANIPULATING DENDROGRAMS USING DENDEXTEND 95

•

Functions to customize dendrograms: The function set() [in dendextend package]

can be used to change the parameters of a dendrogram. The format is:

set(object, what, value)

1. object: a dendrogram object

2. what

: a character indicating what is the property of the tree that should be

set/updated

3. value

: a vector with the value to set in the tree (the type of the value depends

on the “what”).

Possible values for the argument what include:

Value for the argument what Description

labels set the labels

labels_colors and labels_cex Set the color and the size of

labels, respectively

leaves_pch,leaves_cex and

leaves_col

set the point type, size and color

for leaves, respectively

nodes_pch,nodes_cex and

nodes_col

set the point type, size and color

for nodes, respectively

hang_leaves hang the leaves

branches_k_color color the branches

branches_col,branches_lwd ,

branches_lty

Set the color, the line width and

the line type of branches,

respectively

by_labels_branches_col,

by_labels_branches_lwd and

by_labels_branches_lty

Set the color, the line width and

the line type of branches with

speciﬁc labels, respectively

clear_branches and

clear_leaves

Clear branches and leaves,

respectively

96 CHAPTER 9. VISUALIZING DENDROGRAMS

•Examples:

library(dendextend)

# 1. Create a customized dendrogram

mycols <- c("#2E9FDF","#00AFBB","#E7B800","#FC4E07")

dend <- as.dendrogram(hc) %>%

set("branches_lwd",1)%>%# Branches line width

set("branches_k_color",mycols,k=4)%>%# Color branches by groups

set("labels_colors",mycols,k=4)%>% # Color labels by groups

set("labels_cex",0.5)# Change label size

# 2. Create plot

fviz_dend(dend)

9.4 Summary

We described functions and packages for visualizing and customizing dendrograms

including:

•

fviz_dend() [in factoextra R package], which provides convenient solutions for

plotting easily a beautiful dendrogram. It can be used to create rectangular and

circular dendrograms, as well as, a phylogenic tree.

•

and the dendextend package, which provides a ﬂexible methods to customize

dendrograms.

Additionally, we described how to plot a subset of large dendrograms.

Chapter 10

Heatmap: Static and Interactive

heatmap

(or

heat map

) is another way to visualize hierarchical clustering. It’s

also called a false colored image, where data values are transformed to color scale.

Heat maps allow us to simultaneously visualize clusters of samples and features. First

hierarchical clustering is done of both the rows and the columns of the data matrix.

The columns/rows of the data matrix are re-ordered according to the hierarchical

clustering result, putting similar observations close to each other. The blocks of ‘high’

and ‘low’ values are adjacent in the data matrix. Finally, a color scheme is applied for

the visualization and the data matrix is displayed. Visualizing the data matrix in this

way can help to ﬁnd the variables that appear to be characteristic for each sample

cluster.

Previously, we described how to visualize dendrograms (Chapter 9). Here, we’ll

demonstrate how to draw and arrange a heatmap in R.

10.1 R Packages/functions for drawing heatmaps

There are a multiple numbers of R packages and functions for drawing interactive and

static heatmaps, including:

•heatmap() [R base function, stats package]: Draws a simple heatmap

•

heatmap.2 () [gplots R package]: Draws an enhanced heatmap compared to the

R base function.

98 CHAPTER 10. HEATMAP: STATIC AND INTERACTIVE

•

pheatmap() [pheatmap R package]: Draws pretty heatmaps and provides more

control to change the appearance of heatmaps.

•d3heatmap() [d3heatmap R package]: Draws an interactive/clickable heatmap

•

Heatmap() [ComplexHeatmap R/Bioconductor package]: Draws, annotates and

arranges complex heatmaps (very useful for genomic data analysis)

Here, we start by describing the 5 R functions for drawing heatmaps. Next, we’ll

focus on the ComplexHeatmap package, which provides a ﬂexible solution to arrange

and annotate multiple heatmaps. It allows also to visualize the association between

diﬀerent data from diﬀerent sources.

10.2 Data preparation

We use mtcars data as a demo data set. We start by standardizing the data to make

variables comparable:

df <- scale(mtcars)

10.3 R base heatmap: heatmap()

The built-in R heatmap() function [in stats package] can be used.

A simpliﬁed format is:

heatmap(x, scale = "row")

•x: a numeric matrix

•scale

: a character indicating if the values should be centered and scaled in

either the row direction or the column direction, or none. Allowed values are in

c(“row”, “column”, “none”). Default is “row”.

# Default plot

heatmap(df, scale = "none")

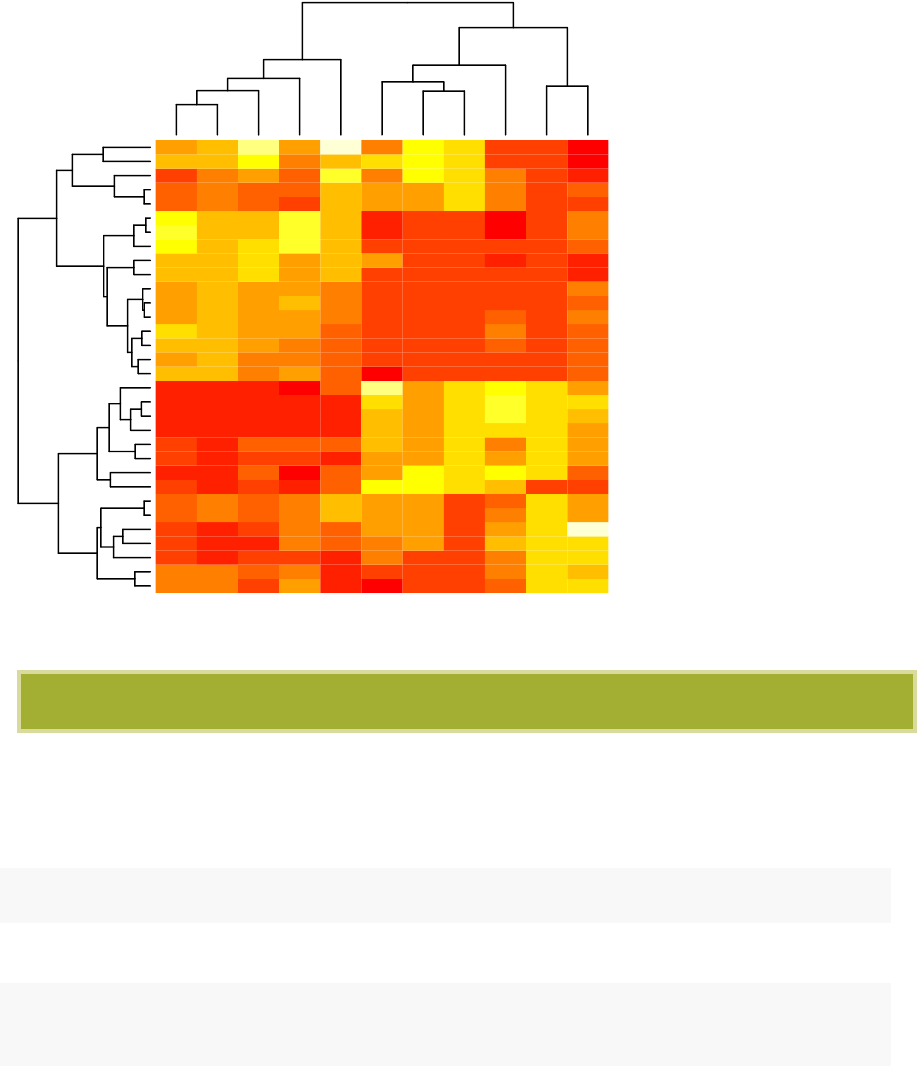
10.3. R BASE HEATMAP: HEATMAP() 99

disp

cyl

carb

drat

gear

mpg

qsec

Valiant

Hornet 4 Drive

Toyota Corona

Merc 240D

Merc 230

Merc 280

Merc 280C

Porsche 914-2

Lotus Europa

Datsun 710

Volvo 142E

Fiat X1-9

Fiat 128

Toyota Corolla

Honda Civic

Dodge Challenger

AMC Javelin

Hornet Sportabout

Pontiac Firebird

Merc 450SL

Merc 450SE

Merc 450SLC

Duster 360

Camaro Z28

Chrysler Imperial

Cadillac Fleetwood

Lincoln Continental

Mazda RX4

Mazda RX4 Wag

Ferrari Dino

Ford Pantera L

Maserati Bora

In the plot above, high values are in red and low values are in yellow.

It’s possible to specify a color palette using the argument col, which can be deﬁned as

follow:

•Using custom colors:

col<- colorRampPalette(c("red","white","blue"))(256)

•Or, using RColorBrewer color palette:

library("RColorBrewer")

col <- colorRampPalette(brewer.pal(10,"RdYlBu"))(256)

Additionally, you can use the argument RowSideColors and ColSideColors to annotate

rows and columns, respectively.

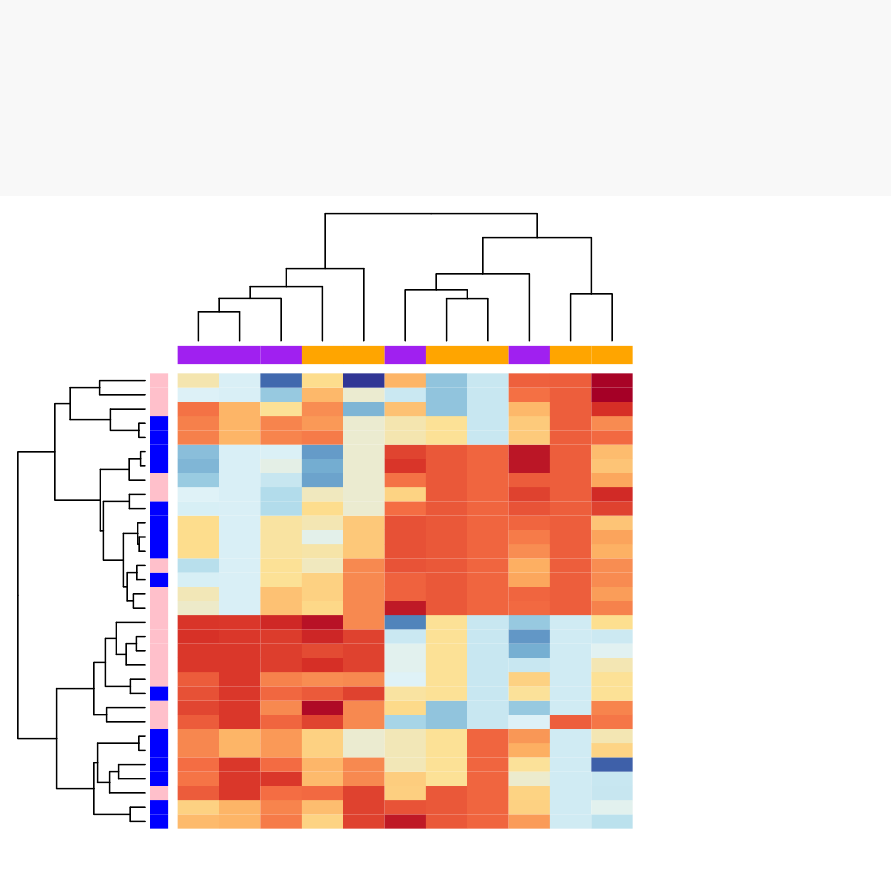
100 CHAPTER 10. HEATMAP: STATIC AND INTERACTIVE

For example, in the the R code below will customize the heatmap as follow:

1. An RColorBrewer color palette name is used to change the appearance

The argument RowSideColors and ColSideColors are used to annotate rows

and columns respectively. The expected values for these options are a vector

containing color names specifying the classes for rows/columns.

# Use RColorBrewer color palette names

library("RColorBrewer")

col <- colorRampPalette(brewer.pal(10,"RdYlBu"))(256)

heatmap(df, scale = "none",col = col,

RowSideColors = rep(c("blue","pink"), each = 16),

ColSideColors = c(rep("purple",5), rep("orange",6)))

disp

cyl

carb

drat

gear

mpg

qsec

Valiant

Hornet 4 Drive

Toyota Corona

Merc 240D

Merc 230

Merc 280

Merc 280C

Porsche 914-2

Lotus Europa

Datsun 710

Volvo 142E

Fiat X1-9

Fiat 128

Toyota Corolla

Honda Civic

Dodge Challenger

AMC Javelin

Hornet Sportabout

Pontiac Firebird

Merc 450SL

Merc 450SE

Merc 450SLC

Duster 360

Camaro Z28

Chrysler Imperial

Cadillac Fleetwood

Lincoln Continental

Mazda RX4

Mazda RX4 Wag

Ferrari Dino

Ford Pantera L

Maserati Bora

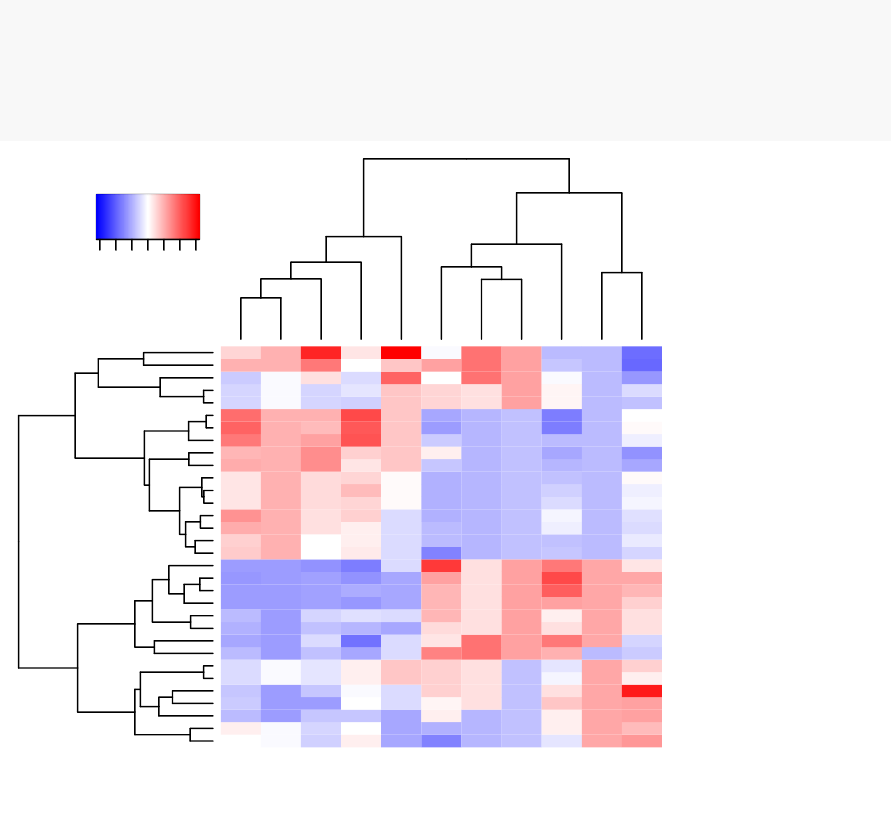
10.4. ENHANCED HEAT MAPS: HEATMAP.2() 101

10.4 Enhanced heat maps: heatmap.2()

The function heatmap.2 () [in gplots package] provides many extensions to the standard

Rheatmap() function presented in the previous section.

# install.packages("gplots")

library("gplots")

heatmap.2(df, scale = "none",col = bluered(100),

trace = "none",density.info = "none")

disp

cyl

carb

drat

gear

mpg

qsec

Valiant

Hornet 4 Drive

Toyota Corona

Merc 240D

Merc 230

Merc 280

Merc 280C

Porsche 914-2

Lotus Europa

Datsun 710

Volvo 142E

Fiat X1-9

Fiat 128

Toyota Corolla

Honda Civic

Dodge Challenger

AMC Javelin

Hornet Sportabout

Pontiac Firebird

Merc 450SL

Merc 450SE

Merc 450SLC

Duster 360

Camaro Z28

Chrysler Imperial

Cadillac Fleetwood

Lincoln Continental

Mazda RX4

Mazda RX4 Wag

Ferrari Dino

Ford Pantera L

Maserati Bora

-3 -1 1 3

Value

Color Key

Other arguments can be used including:

•labRow,labCol

•hclustfun: hclustfun=function(x) hclust(x, method=“ward”)

In the R code above, the bluered() function [in gplots package] is used to generate

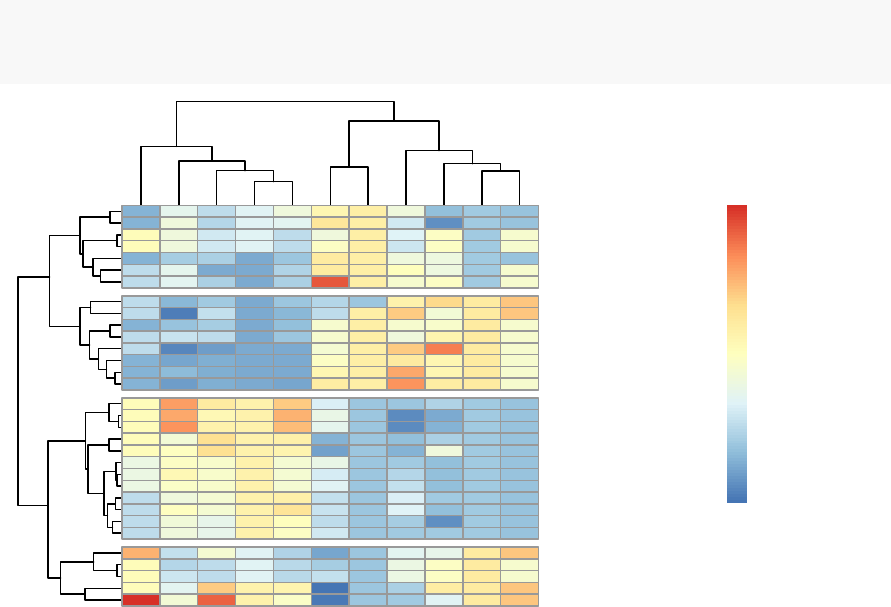
102 CHAPTER 10. HEATMAP: STATIC AND INTERACTIVE

a smoothly varying set of colors. You can also use the following color generator

functions:

•colorpanel(n, low, mid, high)

–n: Desired number of color elements to be generated

–

low, mid, high: Colors to use for the Lowest, middle, and highest values.

mid may be omitted.

•redgreen(n), greenred(n), bluered(n) and redblue(n)

10.5 Pretty heat maps: pheatmap()

First, install the pheatmap package: install.packages(“pheatmap”); then type this:

library("pheatmap")

pheatmap(df, cutree_rows = 4)

carb

cyl

disp

qsec

mpg

drat

gear

Hornet 4 Drive

Valiant

Merc 280

Merc 280C

Toyota Corona

Merc 240D

Merc 230

Porsche 914−2

Lotus Europa

Datsun 710

Volvo 142E

Honda Civic

Fiat X1−9

Fiat 128

Toyota Corolla

Chrysler Imperial

Cadillac Fleetwood

Lincoln Continental

Duster 360

Camaro Z28

Merc 450SLC

Merc 450SE

Merc 450SL

Hornet Sportabout

Pontiac Firebird

Dodge Challenger

AMC Javelin

Ferrari Dino

Mazda RX4

Mazda RX4 Wag

Ford Pantera L

Maserati Bora

−1

Arguments are available for changing the default clustering metric (“euclidean”) and

method (“complete”). It’s also possible to annotate rows and columns using grouping

variables.

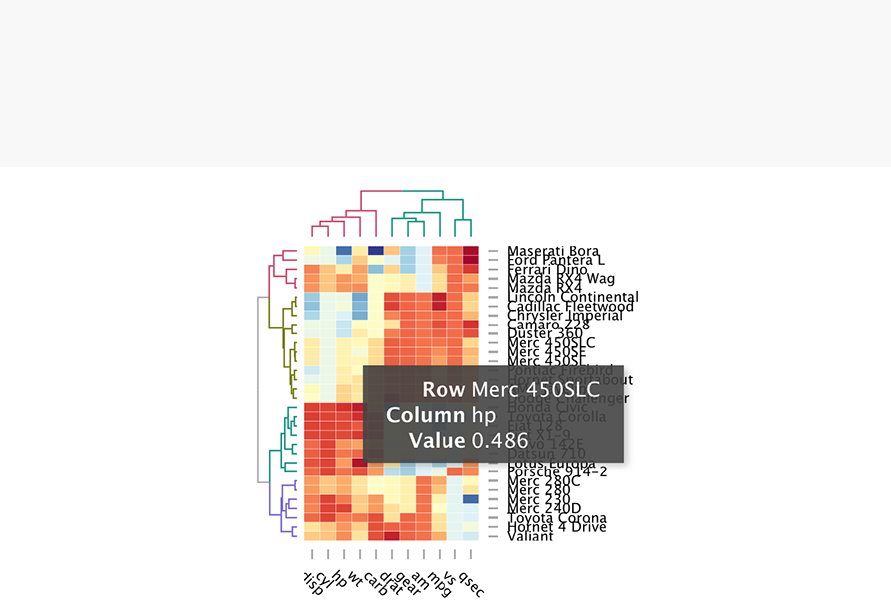
10.6. INTERACTIVE HEAT MAPS: D3HEATMAP() 103

10.6 Interactive heat maps: d3heatmap()

First, install the d3heatmap package: install.packages(“d3heatmap”); then type this:

library("d3heatmap")

d3heatmap(scale(mtcars), colors = "RdYlBu",

k_row = 4,# Number of groups in rows

k_col = 2# Number of groups in columns

)

The d3heamap() function makes it possible to:

•

Put the mouse on a heatmap cell of interest to view the row and the column

names as well as the corresponding value.

•

Select an area for zooming. After zooming, click on the heatmap again to go

back to the previous display

10.7 Enhancing heatmaps using dendextend

The package dendextend can be used to enhance functions from other packages. The

mtcars data is used in the following sections. We’ll start by deﬁning the order and the

appearance for rows and columns using dendextend. These results are used in others

functions from others packages.

104 CHAPTER 10. HEATMAP: STATIC AND INTERACTIVE

The order and the appearance for rows and columns can be deﬁned as follow:

library(dendextend)

# order for rows

Rowv <- mtcars %>% scale %>% dist %>% hclust %>% as.dendrogram %>%

set("branches_k_color",k=3)%>%set("branches_lwd",1.2)%>%

ladderize

# Order for columns: We must transpose the data

Colv <- mtcars %>% scale %>% t%>%dist %>% hclust %>% as.dendrogram %>%

set("branches_k_color",k=2,value = c("orange","blue")) %>%

set("branches_lwd",1.2)%>%

ladderize

The arguments above can be used in the functions below:

1. The standard heatmap() function [in stats package]:

heatmap(scale(mtcars), Rowv = Rowv, Colv = Colv,

scale = "none")

2. The enhanced heatmap.2 () function [in gplots package]:

library(gplots)

heatmap.2(scale(mtcars), scale = "none",col = bluered(100),

Rowv = Rowv, Colv = Colv,

trace = "none",density.info = "none")

The interactive heatmap generator d3heatmap() function [in d3heatmap package]:

library("d3heatmap")

d3heatmap(scale(mtcars), colors = "RdBu",

Rowv = Rowv, Colv = Colv)

10.8 Complex heatmap

ComplexHeatmap

is an R/bioconductor package, developed by Zuguang Gu, which

provides a ﬂexible solution to arrange and annotate multiple heatmaps. It allows also

to visualize the association between diﬀerent data from diﬀerent sources.

10.8. COMPLEX HEATMAP 105

It can be installed as follow:

source("https://bioconductor.org/biocLite.R")

biocLite("ComplexHeatmap")

10.8.1 Simple heatmap

You can draw a simple heatmap as follow:

library(ComplexHeatmap)

Heatmap(df,

name = "mtcars",#title of legend

column_title = "Variables",row_title = "Samples",

row_names_gp = gpar(fontsize = 7)# Text size for row names

)

Variables

Samples

Maserati Bora

Ford Pantera L

Ferrari Dino

Mazda RX4 Wag

Mazda RX4

Lincoln Continental

Cadillac Fleetwood

Chrysler Imperial

Camaro Z28

Duster 360

Merc 450SLC

Merc 450SE

Merc 450SL

Pontiac Firebird

Hornet Sportabout

AMC Javelin

Dodge Challenger

Honda Civic

Toyota Corolla

Fiat 128

Fiat X1-9

Volvo 142E

Datsun 710

Lotus Europa

Porsche 914-2

Merc 280C

Merc 280

Merc 230

Merc 240D

Toyota Corona

Hornet 4 Drive

Valiant

disp

cyl

carb

drat

gear

mpg

qsec

mtcars

-1

-2

Additional arguments:

show_row_names, show_column_names: whether to show row and column

106 CHAPTER 10. HEATMAP: STATIC AND INTERACTIVE

names, respectively. Default value is TRUE

show_row_hclust, show_column_hclust: logical value; whether to show row

and column clusters. Default is TRUE

clustering_distance_rows, clustering_distance_columns: metric for clustering:

“euclidean”, “maximum”, “manhattan”, “canberra”, “binary”, “minkowski”,

“pearson”, “spearman”, “kendall”)

clustering_method_rows, clustering_method_columns: clustering methods:

“ward.D”, “ward.D2”, “single”, “complete”, “average”, . . . (see ?hclust).

To specify a custom colors, you must use the the colorRamp2 () function [circlize

package], as follow:

library(circlize)

mycols <- colorRamp2(breaks = c(-2,0,2),

colors = c("green","white","red"))

Heatmap(df, name = "mtcars",col = mycols)

It’s also possible to use RColorBrewer color palettes:

library("circlize")

library("RColorBrewer")

Heatmap(df, name = "mtcars",

col = colorRamp2(c(-2,0,2), brewer.pal(n=3,name="RdBu")))

We can also customize the appearance of dendograms using the function

color_branches() [dendextend package]:

library(dendextend)

row_dend = hclust(dist(df)) # row clustering

col_dend = hclust(dist(t(df))) # column clustering

Heatmap(df, name = "mtcars",

row_names_gp = gpar(fontsize = 6.5),

cluster_rows = color_branches(row_dend, k=4),

cluster_columns = color_branches(col_dend, k=2))

10.8. COMPLEX HEATMAP 107

Hornet 4 Drive

Valiant

Merc 280

Merc 280C

Toyota Corona

Merc 240D

Merc 230

Porsche 914-2

Lotus Europa

Datsun 710

Volvo 142E

Honda Civic

Fiat X1-9

Fiat 128

Toyota Corolla

Chrysler Imperial

Cadillac Fleetwood

Lincoln Continental

Duster 360

Camaro Z28

Merc 450SLC

Merc 450SE

Merc 450SL

Hornet Sportabout

Pontiac Firebird

Dodge Challenger

AMC Javelin

Ferrari Dino

Mazda RX4

Mazda RX4 Wag

Ford Pantera L

Maserati Bora

disp

cyl

carb

drat

gear

mpg

qsec

mtcars

-1

-2

10.8.2 Splitting heatmap by rows

You can split the heatmap using either the k-means algorithm or a grouping variable.

It’s important to use the set.seed() function when performing k-means so that the

results obtained can be reproduced precisely at a later time.

•To split the dendrogram using k-means, type this:

# Divide into 2 groups

set.seed(2)

Heatmap(df, name = "mtcars",k=2)

•

To split by a grouping variable, use the argument split. In the following example

we’ll use the levels of the factor variable cyl [in mtcars data set] to split the

heatmap by rows. Recall that the column cyl corresponds to the number of

cylinders.

108 CHAPTER 10. HEATMAP: STATIC AND INTERACTIVE

# split by a vector specifying rowgroups

Heatmap(df, name = "mtcars",split = mtcars$cyl,

row_names_gp = gpar(fontsize = 7))

468

Honda Civic

Toyota Corolla

Fiat 128

Fiat X1-9

Volvo 142E

Datsun 710

Lotus Europa

Porsche 914-2

Merc 230

Merc 240D

Toyota Corona

Ferrari Dino

Mazda RX4 Wag

Mazda RX4

Merc 280C

Merc 280

Hornet 4 Drive

Valiant

Maserati Bora

Ford Pantera L

Lincoln Continental

Cadillac Fleetwood

Chrysler Imperial

Camaro Z28

Duster 360

Merc 450SLC

Merc 450SE

Merc 450SL

Pontiac Firebird

Hornet Sportabout

AMC Javelin

Dodge Challenger

disp

cyl

carb

drat

gear

mpg

qsec

mtcars

-1

-2

Note that, split can be also a data frame in which diﬀerent combinations of levels

split the rows of the heatmap.

# Split by combining multiple variables

Heatmap(df, name ="mtcars",

split = data.frame(cyl = mtcars$cyl, am = mtcars$am))

10.8.3 Heatmap annotation

The HeatmapAnnotation class is used to deﬁne annotation on row or column. A

simpliﬁed format is:

10.8. COMPLEX HEATMAP 109

HeatmapAnnotation(df, name, col, show_legend)

•df: a data.frame with column names

•name: the name of the heatmap annotation

•col: a list of colors which contains color mapping to columns in df

For the example below, we’ll transpose our data to have the observations in columns

and the variables in rows.

df <- t(df)

10.8.3.1 Simple annotation

A vector, containing discrete or continuous values, is used to annotate rows or columns.

We’ll use the qualitative variables cyl (levels = “4”, “5” and “8”) and am (levels = “0”

and “1”), and the continuous variable mpg to annotate columns.

For each of these 3 variables, custom colors are deﬁned as follow:

# Annotation data frame

annot_df <- data.frame(cyl = mtcars$cyl, am = mtcars$am,

mpg = mtcars$mpg)

# Define colors for each levels of qualitative variables

# Define gradient color for continuous variable (mpg)

col = list(cyl = c("4" ="green","6" ="gray","8" ="darkred"),

am = c("0" ="yellow","1" ="orange"),

mpg = circlize::colorRamp2(c(17,25),

c("lightblue","purple")) )

# Create the heatmap annotation

ha <- HeatmapAnnotation(annot_df, col = col)

# Combine the heatmap and the annotation

Heatmap(df, name = "mtcars",

top_annotation = ha)

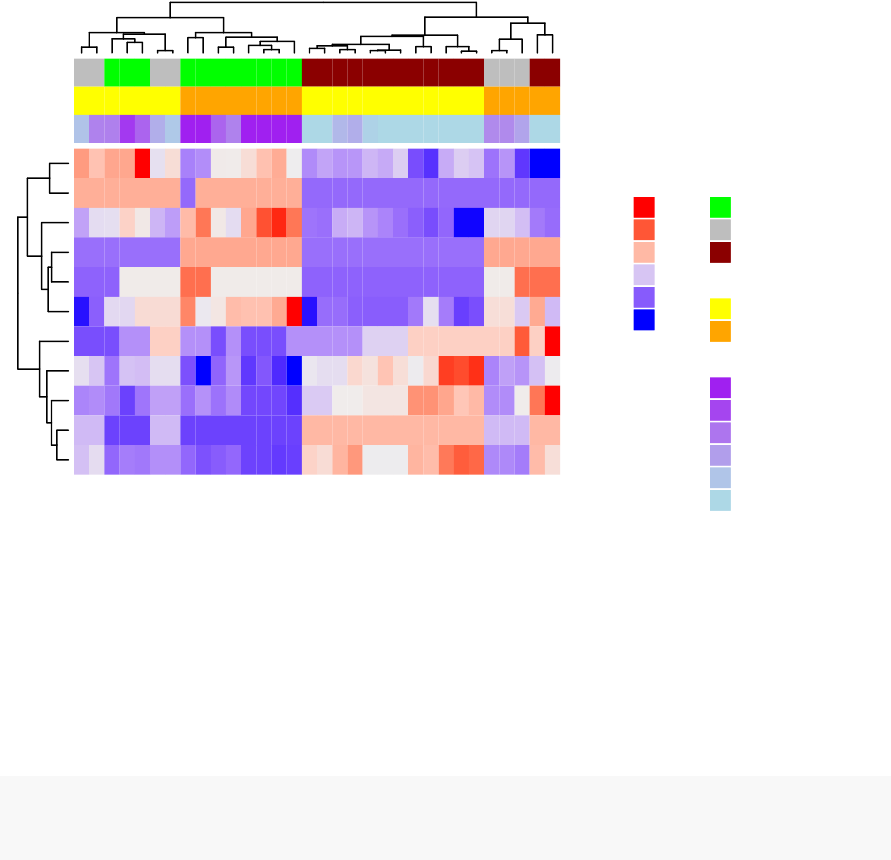
110 CHAPTER 10. HEATMAP: STATIC AND INTERACTIVE

qsec

mpg

gear

drat

carb

cyl

disp

Valiant

Hornet 4 Drive

Toyota Corona

Merc 240D

Merc 230

Merc 280

Merc 280C

Porsche 914-2

Lotus Europa

Datsun 710

Volvo 142E

Fiat X1-9

Fiat 128

Toyota Corolla

Honda Civic

Dodge Challenger

AMC Javelin

Hornet Sportabout

Pontiac Firebird

Merc 450SL

Merc 450SE

Merc 450SLC

Duster 360

Camaro Z28

Chrysler Imperial

Cadillac Fleetwood

Lincoln Continental

Mazda RX4

Mazda RX4 Wag

Ferrari Dino

Ford Pantera L

Maserati Bora

mtcars

-1

-2

cyl

mpg

It’s possible to hide the annotation legend using the argument show_legend = FALSE

as follow:

ha <- HeatmapAnnotation(annot_df, col = col, show_legend = FALSE)

Heatmap(df, name = "mtcars",top_annotation = ha)

10.8.3.2 Complex annotation

In this section we’ll see how to combine heatmap and some basic graphs to show

the data distribution. For simple annotation graphics, the following functions

can be used: anno_points(), anno_barplot(), anno_boxplot(), anno_density() and

anno_histogram().

An example is shown below:

10.8. COMPLEX HEATMAP 111

# Define some graphics to display the distribution of columns

.hist = anno_histogram(df, gp = gpar(fill = "lightblue"))

.density = anno_density(df, type = "line",gp = gpar(col = "blue"))

ha_mix_top = HeatmapAnnotation(hist = .hist, density = .density)

# Define some graphics to display the distribution of rows

.violin = anno_density(df, type = "violin",

gp = gpar(fill = "lightblue"), which = "row")

.boxplot = anno_boxplot(df, which = "row")

ha_mix_right = HeatmapAnnotation(violin = .violin, bxplt = .boxplot,

which = "row",width = unit(4,"cm"))

# Combine annotation with heatmap

Heatmap(df, name = "mtcars",

column_names_gp = gpar(fontsize = 8),

top_annotation = ha_mix_top,

top_annotation_height = unit(3.8,"cm")) + ha_mix_right

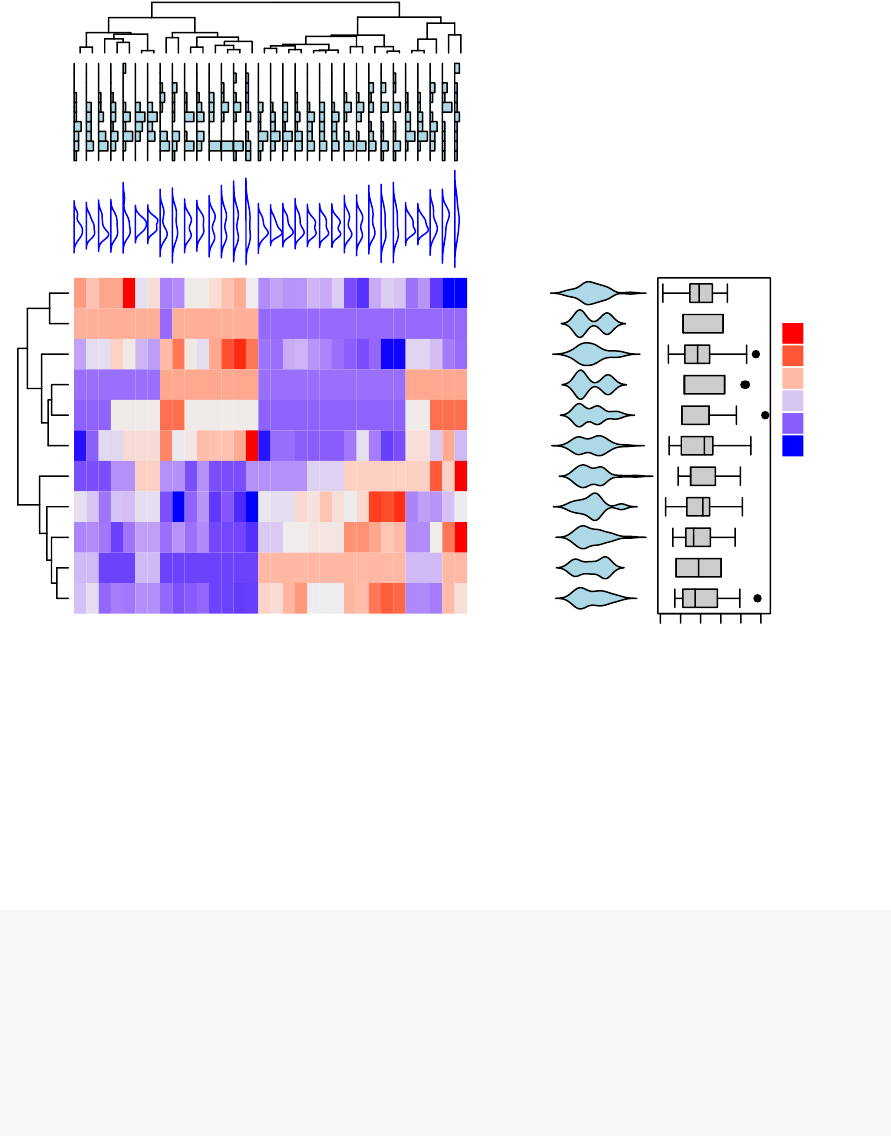
112 CHAPTER 10. HEATMAP: STATIC AND INTERACTIVE

qsec

mpg

gear

drat

carb

cyl

disp

Valiant

Hornet 4 Drive

Toyota Corona

Merc 240D

Merc 230

Merc 280

Merc 280C

Porsche 914-2

Lotus Europa

Datsun 710

Volvo 142E

Fiat X1-9

Fiat 128

Toyota Corolla

Honda Civic

Dodge Challenger

AMC Javelin

Hornet Sportabout

Pontiac Firebird

Merc 450SL

Merc 450SE

Merc 450SLC

Duster 360

Camaro Z28

Chrysler Imperial

Cadillac Fleetwood

Lincoln Continental

Mazda RX4

Mazda RX4 Wag

Ferrari Dino

Ford Pantera L

Maserati Bora

-2 -1 0 1 2 3

mtcars

-1

-2

10.8.3.3 Combining multiple heatmaps

Multiple heatmaps can be arranged as follow:

# Heatmap 1

ht1 = Heatmap(df, name = "ht1",km = 2,

column_names_gp = gpar(fontsize = 9))

# Heatmap 2

ht2 = Heatmap(df, name = "ht2",

col = circlize::colorRamp2(c(-2,0,2), c("green","white","red")),

column_names_gp = gpar(fontsize = 9))

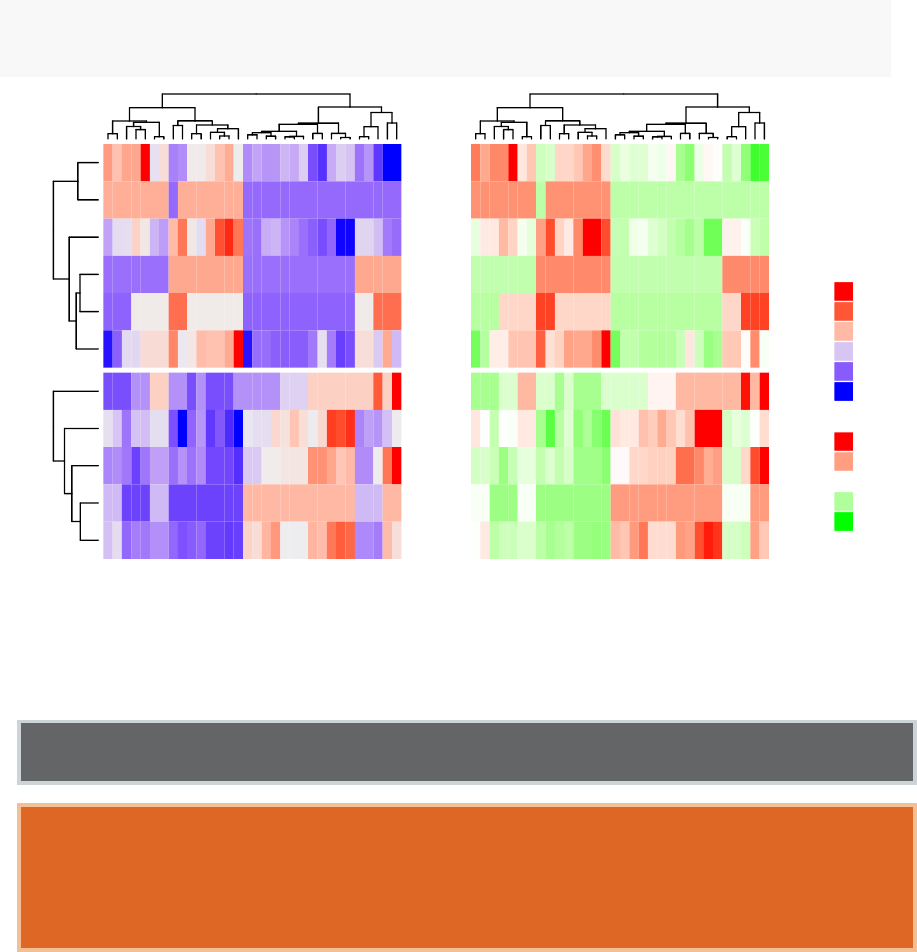
10.8. COMPLEX HEATMAP 113

# Combine the two heatmaps

ht1 + ht2

cluster1cluster2

qsec

mpg

gear

drat

carb

cyl

disp

Valiant

Hornet 4 Drive

Toyota Corona

Merc 240D

Merc 230

Merc 280

Merc 280C

Porsche 914-2

Lotus Europa

Datsun 710

Volvo 142E

Fiat X1-9

Fiat 128

Toyota Corolla

Honda Civic

Dodge Challenger

AMC Javelin

Hornet Sportabout

Pontiac Firebird

Merc 450SL

Merc 450SE

Merc 450SLC

Duster 360

Camaro Z28

Chrysler Imperial

Cadillac Fleetwood

Lincoln Continental

Mazda RX4

Mazda RX4 Wag

Ferrari Dino

Ford Pantera L

Maserati Bora

qsec

mpg

gear

drat

carb

cyl

disp

Valiant

Hornet 4 Drive

Toyota Corona

Merc 240D

Merc 230

Merc 280

Merc 280C

Porsche 914-2

Lotus Europa

Datsun 710

Volvo 142E

Fiat X1-9

Fiat 128

Toyota Corolla

Honda Civic

Dodge Challenger

AMC Javelin

Hornet Sportabout

Pontiac Firebird

Merc 450SL

Merc 450SE

Merc 450SLC

Duster 360

Camaro Z28

Chrysler Imperial

Cadillac Fleetwood

Lincoln Continental

Mazda RX4

Mazda RX4 Wag

Ferrari Dino

Ford Pantera L

Maserati Bora

ht1

-1

-2

ht2

-1

-2

You can use the option width = unit(3, "cm")) to control the size of the heatmaps.

Note that when combining multiple heatmaps, the ﬁrst heatmap is considered as

the main heatmap. Some settings of the remaining heatmaps are auto-adjusted

according to the setting of the main heatmap. These include: removing row clusters

and titles, and adding splitting.

114 CHAPTER 10. HEATMAP: STATIC AND INTERACTIVE

The draw() function can be used to customize the appearance of the ﬁnal image:

draw(ht1 + ht2,

row_title = "Two heatmaps, row title",

row_title_gp = gpar(col = "red"),

column_title = "Two heatmaps, column title",

column_title_side = "bottom",

# Gap between heatmaps

gap = unit(0.5,"cm"))

Legends can be removed using the arguments show_heatmap_legend = FALSE,

show_annotation_legend = FALSE.

10.9 Application to gene expression matrix

In gene expression data, rows are genes and columns are samples. More information

about genes can be attached after the expression heatmap such as gene length and

type of genes.

expr <- readRDS(paste0(system.file(package = "ComplexHeatmap"),

"/extdata/gene_expression.rds"))

mat <- as.matrix(expr[, grep("cell",colnames(expr))])

type <- gsub("s\\d+_","",colnames(mat))

ha = HeatmapAnnotation(df = data.frame(type = type))

Heatmap(mat, name = "expression",km = 5,top_annotation = ha,

top_annotation_height = unit(4,"mm"),

show_row_names = FALSE,show_column_names = FALSE)+

Heatmap(expr$length, name = "length",width = unit(5,"mm"),

col = circlize::colorRamp2(c(0,100000), c("white","orange"))) +

Heatmap(expr$type, name = "type",width = unit(5,"mm")) +

Heatmap(expr$chr, name = "chr",width = unit(5,"mm"),

col = circlize::rand_color(length(unique(expr$chr))))

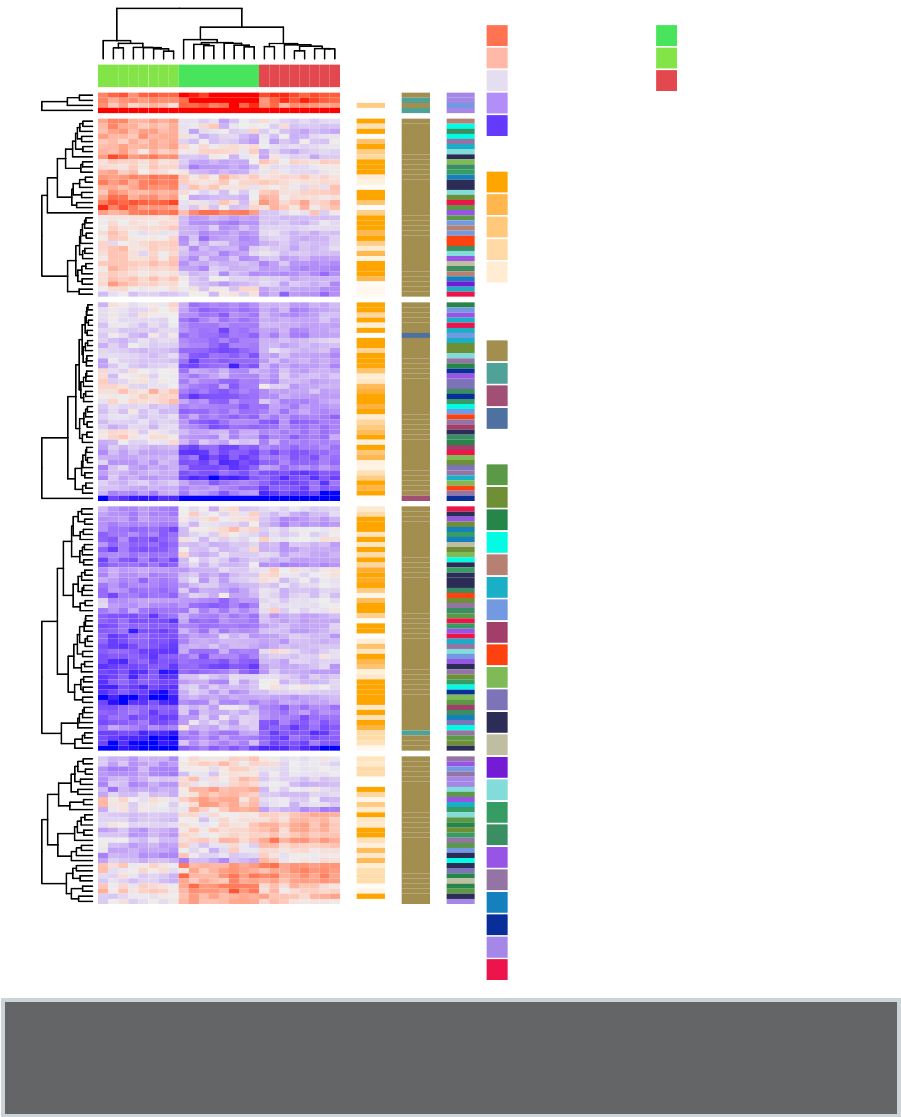
10.9. APPLICATION TO GENE EXPRESSION MATRIX 115

cluster1cluster2cluster3cluster4cluster5

length

type

chr

expression

length

1e+05

80000

60000

40000

20000

type

protein_coding

others

antisense

pseudogene

chr

chr1

chr10

chr11

chr12

chr13

chr14

chr15

chr16

chr17

chr18

chr19

chr2

chr20

chr22

chr3

chr4

chr5

chr6

chr7

chr8

chr9

chrM

chrX

type

cell01

cell02

cell03

It’s also possible to visualize genomic alterations and to integrate diﬀerent molecular

levels (gene expression, DNA methylation, ...). Read the vignette, on Bioconductor,

for further examples.

116 CHAPTER 10. HEATMAP: STATIC AND INTERACTIVE

10.10 Summary

We described many functions for drawing heatmaps in R (from basic to complex

heatmaps). A basic heatmap can be produced using either the R base function

heatmap() or the function heatmap.2 () [in the gplots package].

The pheatmap() function, in the package of the same name, creates pretty heatmaps,

where ones has better control over some graphical parameters such as cell size.

The Heatmap() function [in ComplexHeatmap package] allows us to easily, draw,

annotate and arrange complex heatmaps. This might be very useful in genomic ﬁelds.

Part IV

Cluster Validation

117

118

The

cluster validation

consists of measuring the goodness of clustering results.

Before applying any clustering algorithm to a data set, the ﬁrst thing to do is to

assess the clustering tendency. That is, whether applying clustering is suitable for the

data. If yes, then how many clusters are there. Next, you can perform hierarchical

clustering or partitioning clustering (with a pre-speciﬁed number of clusters). Finally,

you can use a number of measures, described in this part, to evaluate the goodness of

the clustering results.

Contents:

•Assessing clustering tendency (Chapter 11)

•Determining the optimal number of clusters (Chapter 12)

•Cluster validation statistics (Chapter 13)

•Choosing the best clustering algorithms (Chapter 14)

•Computing p-value for hierarchical clustering (Chapter 15)

Chapter 11

Assessing Clustering Tendency

Before applying any clustering method on your data, it’s important to evaluate whether

the data sets contains meaningful clusters (i.e.: non-random structures) or not. If

yes, then how many clusters are there. This process is deﬁned as the assessing of

clustering tendency or the feasibility of the clustering analysis.

A big issue, in cluster analysis, is that clustering methods will return clusters even

if the data does not contain any clusters. In other words, if you blindly apply a

clustering method on a data set, it will divide the data into clusters because that is

what it supposed to do.

In this chapter, we start by describing why we should evaluate the clustering tendency

before applying any clustering method on a data. Next, we provide statistical and

visual methods for assessing the clustering tendency.

11.1 Required R packages

•factoextra for data visualization

•clustertend for statistical assessment clustering tendency

To install the two packages, type this:

install.packages(c("factoextra","clustertend"))

119

120 CHAPTER 11. ASSESSING CLUSTERING TENDENCY

11.2 Data preparation

We’ll use two data sets:

•the built-in R data set iris.

•and a random data set generated from the iris data set.

The iris data sets look like this:

head(iris, 3)

## Sepal.Length Sepal.Width Petal.Length Petal.Width Species

## 1 5.1 3.5 1.4 0.2 setosa

## 2 4.9 3.0 1.4 0.2 setosa

## 3 4.7 3.2 1.3 0.2 setosa

We start by excluding the column “Species” at position 5

# Iris data set

df <- iris[, -5]

# Random data generated from the iris data set

random_df <- apply(df, 2,

function(x){runif(length(x), min(x), (max(x)))})

random_df <- as.data.frame(random_df)

# Standardize the data sets

df <- iris.scaled <- scale(df)

random_df <- scale(random_df)

11.3 Visual inspection of the data

We start by visualizing the data to assess whether they contains any meaningful

clusters.

As the data contain more than two variables, we need to reduce the dimensionality

in order to plot a scatter plot. This can be done using principal component analysis

(PCA) algorithm (R function: prcomp()). After performing PCA, we use the function

fviz_pca_ind() [factoextra R package] to visualize the output.

The iris and the random data sets can be illustrated as follow:

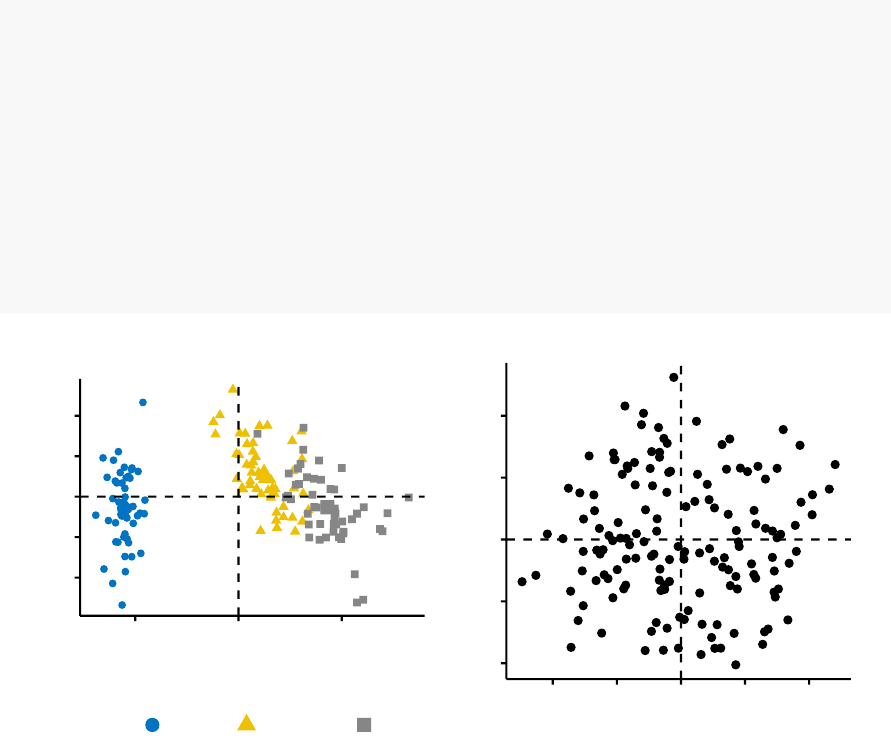
11.4. WHY ASSESSING CLUSTERING TENDENCY? 121

library("factoextra")

# Plot faithful data set

fviz_pca_ind(prcomp(df), title = "PCA - Iris data",

habillage = iris$Species, palette = "jco",

geom = "point",ggtheme = theme_classic(),

legend = "bottom")

# Plot the random df

fviz_pca_ind(prcomp(random_df), title = "PCA - Random data",

geom = "point",ggtheme = theme_classic())

-2

-1

-2 0 2

Dim1 (73%)

Dim2 (22.9%)

Groups setosa versicolor virginica

PCA - Iris data

-2

-1

-2 -1 0 1 2

Dim1 (29.4%)

Dim2 (26.5%)

PCA - Random data

It can be seen that the iris data set contains 3 real clusters. However the randomly

generated data set doesn’t contain any meaningful clusters.

11.4 Why assessing clustering tendency?

In order to illustrate why it’s important to assess cluster tendency, we start by

computing k-means clustering (Chapter 4) and hierarchical clustering (Chapter 7) on

the two data sets (the real and the random data). The function fviz_cluster() and

fviz_dend() [in factoextra R package] will be used to visualize the results.

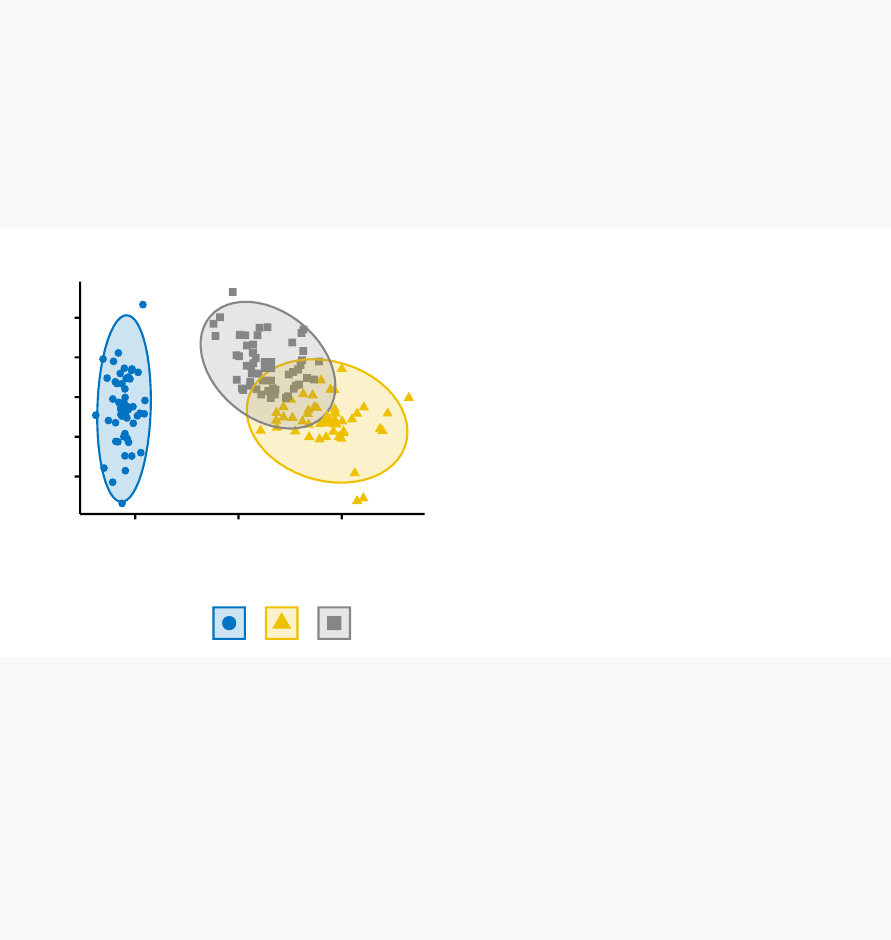
122 CHAPTER 11. ASSESSING CLUSTERING TENDENCY

library(factoextra)

set.seed(123)

# K-means on iris dataset

km.res1 <- kmeans(df, 3)

fviz_cluster(list(data = df, cluster = km.res1$cluster),

ellipse.type = "norm",geom = "point",stand = FALSE,

palette = "jco",ggtheme = theme_classic())

-2

-1

-2 0 2

Dim1 (73%)

Dim2 (22.9%)

cluster 123

Cluster plot

# K-means on the random dataset

km.res2 <- kmeans(random_df, 3)

fviz_cluster(list(data = random_df, cluster = km.res2$cluster),

ellipse.type = "norm",geom = "point",stand = FALSE,

palette = "jco",ggtheme = theme_classic())

# Hierarchical clustering on the random dataset

fviz_dend(hclust(dist(random_df)), k=3,k_colors = "jco",

as.ggplot = TRUE,show_labels = FALSE)

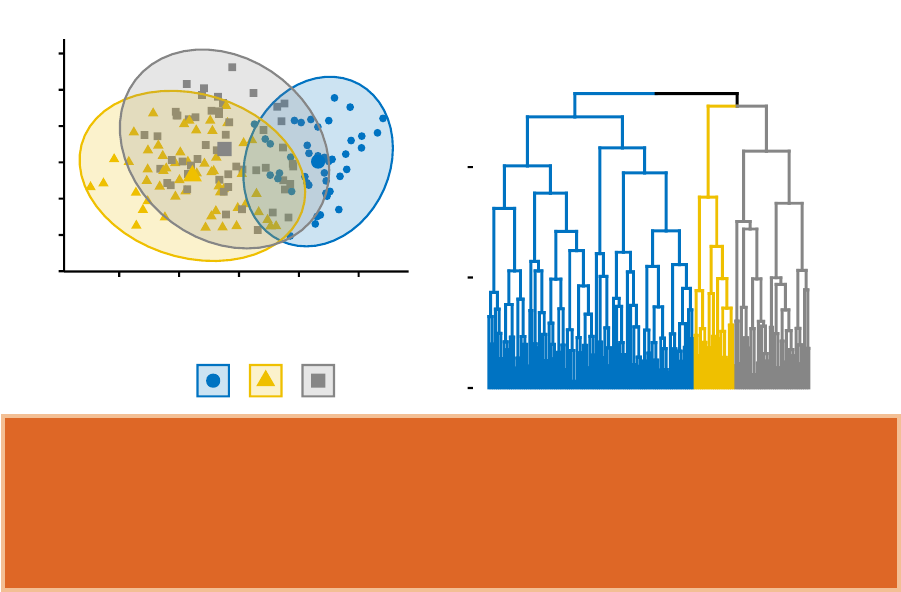
11.5. METHODS FOR ASSESSING CLUSTERING TENDENCY 123

-3

-2

-1

-2 -1 0 1 2

Dim1 (29.4%)

Dim2 (26.5%)

cluster 123

Cluster plot

Height

Cluster Dendrogram

It can be seen that the k-means algorithm and the hierarchical clustering impose

a classiﬁcation on the random uniformly distributed data set even if there are no

meaningful clusters present in it. This is why, clustering tendency assessment methods

should be used to evaluate the validity of clustering analysis. That is, whether a

given data set contains meaningful clusters.

11.5 Methods for assessing clustering tendency

In this section, we’ll describe two methods for evaluating the clustering tendency: i) a

statistical (Hopkins statistic) and ii) a visual methods (Visual Assessment of cluster

Tendency (VAT) algorithm).

11.5.1 Statistical methods

The Hopkins statistic is used to assess the clustering tendency of a data set by

measuring the probability that a given data set is generated by a uniform data

distribution. In other words, it tests the spatial randomness of the data.

For example, let D be a real data set. The Hopkins statistic can be calculated as

follow:

124 CHAPTER 11. ASSESSING CLUSTERING TENDENCY

1. Sample uniformly npoints (p1,..., pn)fromD.

2. For each point

piœD

, ﬁnd it’s nearest neighbor

; then compute the

distance between piand pjand denote it as xi=dist(pi,p

3. Generate a simulated data set (

randomD

) drawn from a random uni-

form distribution with

points (

,...,

) and the same variation as the original real

data set D.

3. For each point

qiœrandomD

, ﬁnd it’s nearest neighbor

in D; then

compute the distance between qiand qjand denote it yi=dist(qi,q

4. Calculate the Hopkins statistic (H) as the mean nearest neighbor dis-

tance in the random data set divided by the sum of the mean nearest neighbor

distances in the real and across the simulated data set.

The formula is deﬁned as follow:

i=1 yi

i=1 xi+n

i=1 yi

A value of H about 0.5 means that

i=1 yi

and

i=1 xi

are close to each other, and thus

the data D is uniformly distributed.

The null and the alternative hypotheses are deﬁned as follow:

•Null hypothesis

: the data set D is uniformly distributed (i.e., no meaningful

clusters)

•Alternative hypothesis

: the data set D is not uniformly distributed (i.e.,

contains meaningful clusters)

If the value of Hopkins statistic is close to zero, then we can reject the null hypothesis

and conclude that the data set D is signiﬁcantly a clusterable data.

The R function hopkins() [in clustertend package] can be used to statistically evaluate

clustering tendency in R. The simpliﬁed format is:

11.5. METHODS FOR ASSESSING CLUSTERING TENDENCY 125

hopkins(data, n)

•data: a data frame or matrix

•n: the number of points to be selected from the data

library(clustertend)

# Compute Hopkins statistic for iris dataset

set.seed(123)

hopkins(df, n=nrow(df)-1)

## $H

## [1] 0.1815219

# Compute Hopkins statistic for a random dataset

set.seed(123)

hopkins(random_df, n=nrow(random_df)-1)

## $H

## [1] 0.4868278

It can be seen that the iris data set is highly clusterable (the

value = 0.18 which

is far below the threshold 0.5). However the random_df data set is not clusterable

(H=0.50)

11.5.2 Visual methods

The algorithm of the visual assessment of cluster tendency (VAT) approach (Bezdek

and Hathaway, 2002) is as follow:

The algorithm of VAT is as follow:

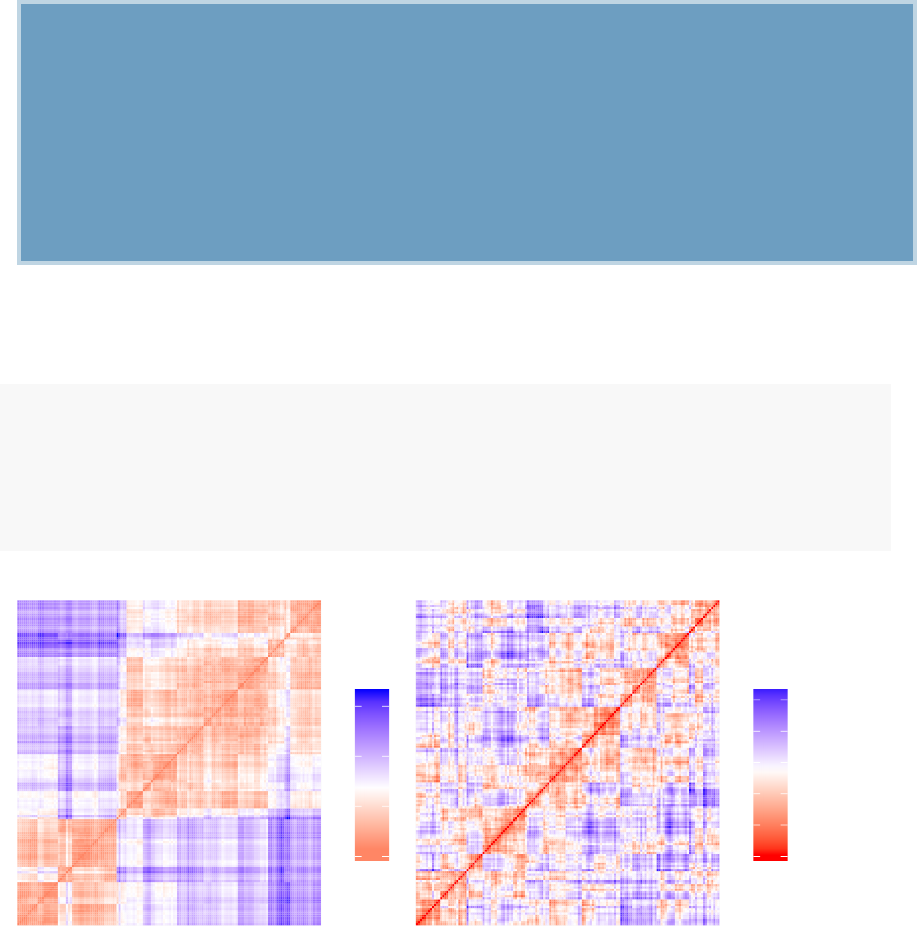
126 CHAPTER 11. ASSESSING CLUSTERING TENDENCY

1. Compute the dissimilarity (DM) matrix between the objects in the data set using

the Euclidean distance measure (3)

2. Reorder the DM so that similar objects are close to one another. This

process create an ordered dissimilarity matrix (ODM)

3. The ODM is displayed as an ordered dissimilarity image (ODI), which is

the visual output of VAT

For the visual assessment of clustering tendency, we start by computing the dissimilarity

matrix between observations using the function dist(). Next the function fviz_dist()

[factoextra package] is used to display the dissimilarity matrix.

fviz_dist(dist(df), show_labels = FALSE)+

labs(title = "Iris data")

fviz_dist(dist(random_df), show_labels = FALSE)+

labs(title = "Random data")

value

Iris data

value

Random data

•Red: high similarity (ie: low dissimilarity) | Blue: low similarity

The color level is proportional to the value of the dissimilarity between observations:

pure red if

dist

(

xi,x

)=0and pure blue if

dist

(

xi,x

)=1. Objects belonging to the

same cluster are displayed in consecutive order.

The dissimilarity matrix image conﬁrms that there is a cluster structure in the iris

data set but not in the random one.

11.6. SUMMARY 127

The VAT detects the clustering tendency in a visual form by counting the number of

square shaped dark blocks along the diagonal in a VAT image.

11.6 Summary

In this article, we described how to assess clustering tendency using the Hopkins

statistics and a visual method. After showing that a data is clusterable, the next step

is to determine the number of optimal clusters in the data. This will be described in

the next chapter.

Chapter 12

Determining the Optimal Number

of Clusters

Determining the optimal number of clusters in a data set

is a fundamental

issue in partitioning clustering, such as k-means clustering (Chapter 4), which requires

the user to specify the number of clusters k to be generated.

Unfortunately, there is no deﬁnitive answer to this question. The optimal number

of clusters is somehow subjective and depends on the method used for measuring

similarities and the parameters used for partitioning.

A simple and popular solution consists of inspecting the dendrogram produced using

hierarchical clustering (Chapter 7) to see if it suggests a particular number of clusters.

Unfortunately, this approach is also subjective.

In this chapter, we’ll describe diﬀerent methods for determining the optimal number

of clusters for k-means, k-medoids (PAM) and hierarchical clustering.

These methods include direct methods and statistical testing methods:

Direct methods: consists of optimizing a criterion, such as the within cluster

sums of squares or the average silhouette. The corresponding methods are named

elbow and silhouette methods, respectively.

Statistical testing methods: consists of comparing evidence against null hypoth-

esis. An example is the gap statistic.

In addition to elbow,silhouette and gap statistic methods, there are more than thirty

other indices and methods that have been published for identifying the optimal number

128

12.1. ELBOW METHOD 129

of clusters. We’ll provide R codes for computing all these 30 indices in order to decide

the best number of clusters using the “majority rule”.

For each of these methods:

•We’ll describe the basic idea and the algorithm

•

We’ll provide easy-o-use R codes with many examples for determining the

optimal number of clusters and visualizing the output.

12.1 Elbow method

Recall that, the basic idea behind partitioning methods, such as k-means clustering

(Chapter 4), is to deﬁne clusters such that the total intra-cluster variation [or total

within-cluster sum of square (WSS)] is minimized. The total WSS measures the

compactness of the clustering and we want it to be as small as possible.

The Elbow method looks at the total WSS as a function of the number of clusters:

One should choose a number of clusters so that adding another cluster doesn’t improve

much better the total WSS.

The optimal number of clusters can be deﬁned as follow:

1. Compute clustering algorithm (e.g., k-means clustering) for diﬀerent values of k.

For instance, by varying k from 1 to 10 clusters.

2. For each k, calculate the total within-cluster sum of square (wss).

3. Plot the curve of wss according to the number of clusters k.

4. The location of a bend (knee) in the plot is generally considered as an

indicator of the appropriate number of clusters.

Note that, the elbow method is sometimes ambiguous. An alternative is the average

silhouette method (Kaufman and Rousseeuw [1990]) which can be also used with

any clustering approach.

130 CHAPTER 12. DETERMINING THE OPTIMAL NUMBER OF CLUSTERS

12.2 Average silhouette method

The average silhouette approach we’ll be described comprehensively in the chapter

cluster validation statistics (Chapter 13). Brieﬂy, it measures the quality of a clustering.

That is, it determines how well each object lies within its cluster. A high average

silhouette width indicates a good clustering.

Average silhouette method computes the average silhouette of observations for diﬀerent

values of k. The optimal number of clusters k is the one that maximize the average

silhouette over a range of possible values for k (Kaufman and Rousseeuw [1990]).

The algorithm is similar to the elbow method and can be computed as follow:

1. Compute clustering algorithm (e.g., k-means clustering) for diﬀerent values of k.

For instance, by varying k from 1 to 10 clusters.

2. For each k, calculate the average silhouette of observations (avg.sil).

3. Plot the curve of avg.sil according to the number of clusters k.

4. The location of the maximum is considered as the appropriate number

of clusters.

12.3 Gap statistic method

The gap statistic has been published by R. Tibshirani, G. Walther, and T. Hastie

(Standford University, 2001). The approach can be applied to any clustering method.

The gap statistic compares the total within intra-cluster variation for diﬀerent values

of k with their expected values under null reference distribution of the data. The

estimate of the optimal clusters will be value that maximize the gap statistic (i.e, that

yields the largest gap statistic). This means that the clustering structure is far away

from the random uniform distribution of points.

The algorithm works as follow:

12.4. COMPUTING THE NUMBER OF CLUSTERS USING R 131

1. Cluster the observed data, varying the number of clusters from k = 1, ...,

kmax

and compute the corresponding total within intra-cluster variation Wk.

2. Generate B reference data sets with a random uniform distribution. Cluster each

of these reference data sets with varying number of clusters k = 1, ...,

kmax

, and

compute the corresponding total within intra-cluster variation Wkb.

3. Compute the estimated gap statistic as the deviation of the observed

value from

its expected value

Wkb

under the null hypothesis:

Gap

(

b=1

log

(

Wú

)

≠log

(

Compute also the standard deviation of the statistics.

4. Choose the number of clusters as the smallest value of k such that the gap statistic

is within one standard deviation of the gap at k+1: Gap(k)ØGap(k+1)≠sk+1.

Note that, using B = 500 gives quite precise results so that the gap plot is basically

unchanged after an another run.

12.4 Computing the number of clusters using R

In this section, we’ll describe two functions for determining the optimal number of

clusters:

fviz_nbclust() function [in factoextra R package]: It can be used to compute the

three diﬀerent methods [elbow, silhouette and gap statistic] for any partitioning

clustering methods [K-means, K-medoids (PAM), CLARA, HCUT]. Note that the

hcut() function is available only in factoextra package.It computes hierarchical

clustering and cut the tree in k pre-speciﬁed clusters.

NbClust() function [ in NbClust R package] (Charrad et al., 2014): It provides

30 indices for determining the relevant number of clusters and proposes to users

the best clustering scheme from the diﬀerent results obtained by varying all

combinations of number of clusters, distance measures, and clustering methods.

It can simultaneously computes all the indices and determine the number of

clusters in a single function call.

132 CHAPTER 12. DETERMINING THE OPTIMAL NUMBER OF CLUSTERS

12.4.1 Required R packages

We’ll use the following R packages:

•

factoextra to determine the optimal number clusters for a given clustering

methods and for data visualization.

•

NbClust for computing about 30 methods at once, in order to ﬁnd the optimal

number of clusters.

To install the packages, type this:

pkgs <- c("factoextra","NbClust")

install.packages(pkgs)

Load the packages as follow:

library(factoextra)

library(NbClust)

12.4.2 Data preparation

We’ll use the USArrests data as a demo data set. We start by standardizing the data

to make variables comparable.

# Standardize the data

df <- scale(USArrests)

head(df)

## Murder Assault UrbanPop Rape

## Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473

## Alaska 0.50786248 1.1068225 -1.2117642 2.484202941

## Arizona 0.07163341 1.4788032 0.9989801 1.042878388

## Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602

## California 0.27826823 1.2628144 1.7589234 2.067820292

## Colorado 0.02571456 0.3988593 0.8608085 1.864967207

12.4. COMPUTING THE NUMBER OF CLUSTERS USING R 133

12.4.3 fviz_nbclust() function: Elbow, Silhouhette and Gap

statistic methods

The simpliﬁed format is as follow:

fviz_nbclust(x, FUNcluster, method = c("silhouette","wss","gap_stat"))

•x: numeric matrix or data frame

•FUNcluster

: a partitioning function. Allowed values include kmeans, pam,

clara and hcut (for hierarchical clustering).

•method

: the method to be used for determining the optimal number of clusters.

The R code below determine the optimal number of clusters for k-means clustering:

# Elbow method

fviz_nbclust(df, kmeans, method = "wss")+

geom_vline(xintercept = 4,linetype = 2)+

labs(subtitle = "Elbow method")

# Silhouette method

fviz_nbclust(df, kmeans, method = "silhouette")+

labs(subtitle = "Silhouette method")

# Gap statistic

# nboot = 50 to keep the function speedy.

# recommended value: nboot= 500 for your analysis.

# Use verbose = FALSE to hide computing progression.

set.seed(123)

fviz_nbclust(df, kmeans, nstart = 25,method = "gap_stat",nboot = 50)+

labs(subtitle = "Gap statistic method")

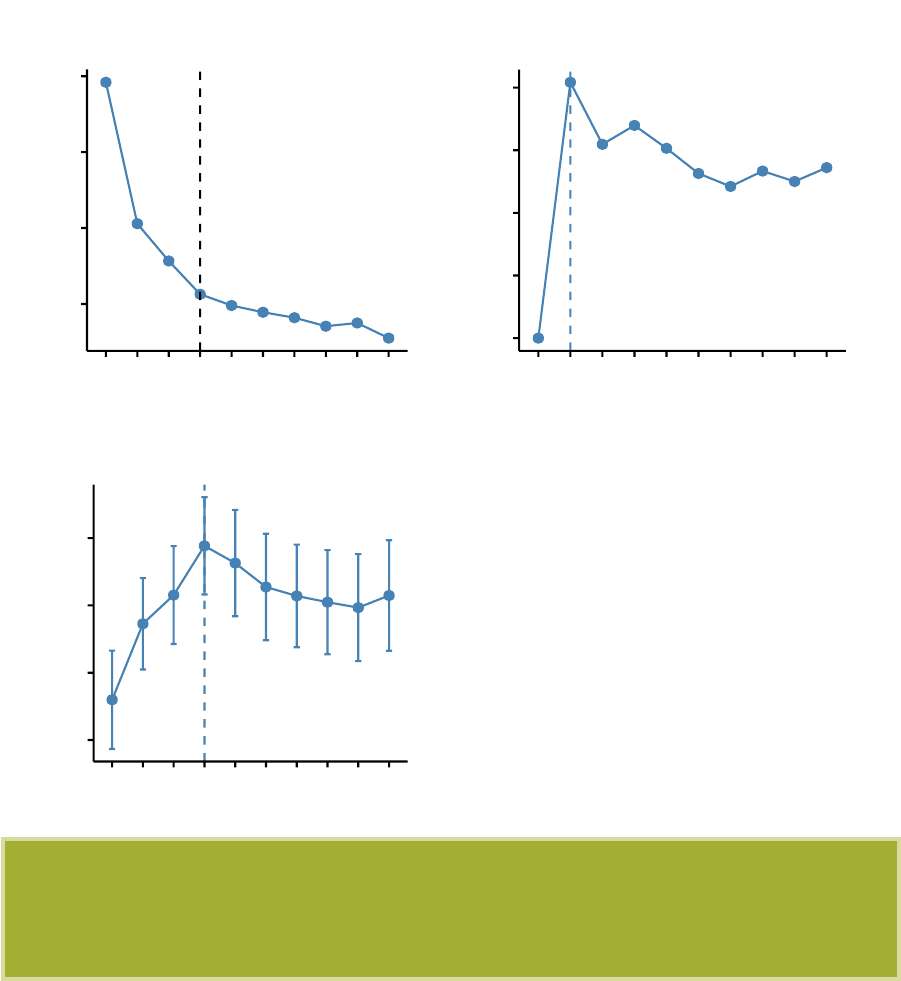
134 CHAPTER 12. DETERMINING THE OPTIMAL NUMBER OF CLUSTERS

100

150

200

12345678910

Number of clusters k

Total Within Sum of Square

Elbow method

Optimal number of clusters

0.0

0.1

0.2

0.3

0.4

12345678910

Number of clusters k

Average silhouette width

Silhouette method

Optimal number of clusters

0.15

0.20

0.25

0.30

1 2 3 4 5 6 7 8 9 10

Number of clusters k

Gap statistic (k)

Gap statistic method

Optimal number of clusters

- Elbow method: 4 clusters solution suggested

- Silhouette method: 2 clusters solution suggested

- Gap statistic method: 4 clusters solution suggested

According to these observations, it’s possible to deﬁne k = 4 as the optimal number

of clusters in the data.

12.4. COMPUTING THE NUMBER OF CLUSTERS USING R 135

The disadvantage of elbow and average silhouette methods is that, they measure

a global clustering characteristic only. A more sophisticated method is to use the

gap statistic which provides a statistical procedure to formalize the elbow/silhouette

heuristic in order to estimate the optimal number of clusters.

12.4.4 NbClust() function: 30 indices for choosing the best

number of clusters

The simpliﬁed format of the function NbClust() is:

NbClust(data = NULL,diss = NULL,distance = "euclidean",

min.nc = 2,max.nc = 15,method = NULL)

•data: matrix

•diss

: dissimilarity matrix to be used. By default, diss=NULL, but if it is

replaced by a dissimilarity matrix, distance should be “NULL”

•distance

: the distance measure to be used to compute the dissimilarity matrix.

Possible values include “euclidean”, “manhattan” or “NULL”.

•min.nc, max.nc: minimal and maximal number of clusters, respectively

•method

: The cluster analysis method to be used including “ward.D”, “ward.D2”,

“single”, “complete”, “average”, “kmeans” and more.

•To compute NbClust() for kmeans, use method = “kmeans”.

•

To compute NbClust() for hierarchical clustering, method should be one of

c(“ward.D”, “ward.D2”, “single”, “complete”, “average”).

The R code below computes NbClust() for k-means:

library("NbClust")

nb <- NbClust(df, distance = "euclidean",min.nc = 2,

max.nc = 10,method = "kmeans")

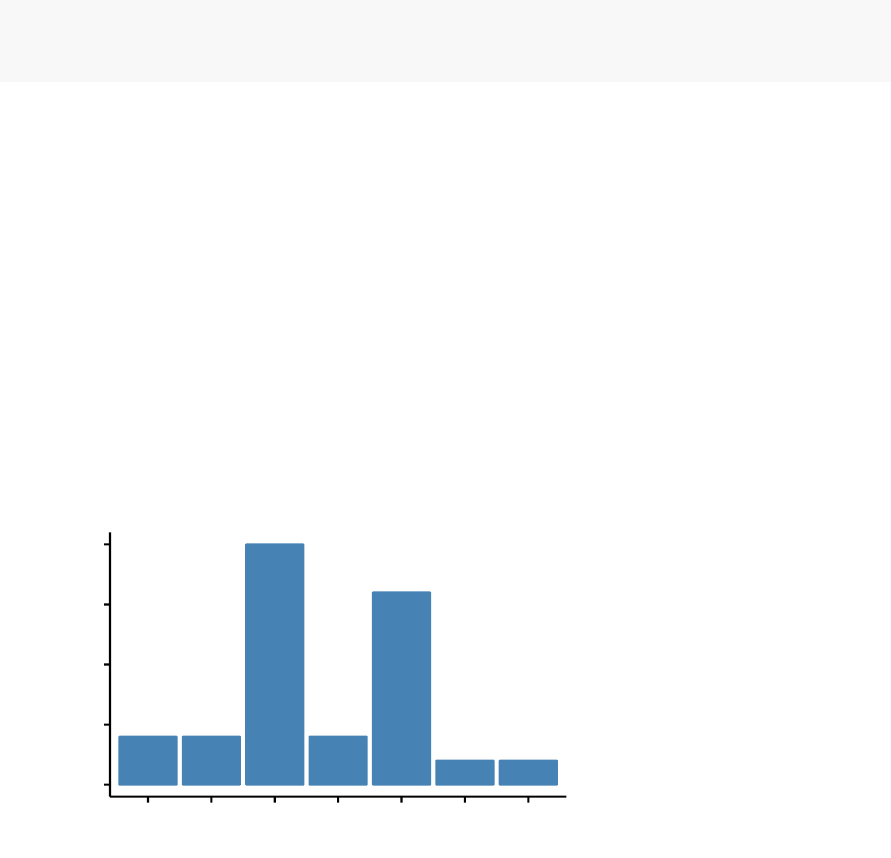
136 CHAPTER 12. DETERMINING THE OPTIMAL NUMBER OF CLUSTERS

The result of NbClust using the function fviz_nbclust() [in factoextra], as follow:

library("factoextra")

fviz_nbclust(nb)

## Among all indices:

## ===================

## * 2 proposed 0 as the best number of clusters

## * 10 proposed 2 as the best number of clusters

## * 2 proposed 3 as the best number of clusters

## * 8 proposed 4 as the best number of clusters

## * 1 proposed 5 as the best number of clusters

## * 1 proposed 8 as the best number of clusters

## * 2 proposed 10 as the best number of clusters

## Conclusion

## =========================

## * According to the majority rule, the best number of clusters is 2 .

0.0

2.5

5.0

7.5

10.0

0 10 2 3 4 5 8

Number of clusters k

Frequency among all indices

Optimal number of clusters - k = 2

12.5. SUMMARY 137

- ....

- 2 proposed 0 as the best number of clusters

- 10 indices proposed 2 as the best number of clusters.

- 2 proposed 3 as the best number of clusters.

- 8 proposed 4 as the best number of clusters.

According to the majority rule, the best number of clusters is 2.

12.5 Summary

In this article, we described diﬀerent methods for choosing the optimal number of

clusters in a data set. These methods include the elbow, the silhouette and the gap

statistic methods.

We demonstrated how to compute these methods using the R function fviz_nbclust()

[in factoextra R package]. Additionally, we described the package NbClust(), which can

be used to compute simultaneously many other indices and methods for determining

the number of clusters.

After choosing the number of clusters k, the next step is to perform partitioning

clustering as described at: k-means clustering (Chapter 4).

Chapter 13

Cluster Validation Statistics

The term

cluster validation

is used to design the procedure of evaluating the

goodness of clustering algorithm results. This is important to avoid ﬁnding patterns in

a random data, as well as, in the situation where you want to compare two clustering

algorithms.

Generally, clustering validation statistics can be categorized into 3 classes (Theodoridis

and Koutroubas, 2008; G. Brock et al., 2008, Charrad et al., 2014):

1. Internal cluster validation

, which uses the internal information of the cluster-

ing process to evaluate the goodness of a clustering structure without reference

to external information. It can be also used for estimating the number of clusters

and the appropriate clustering algorithm without any external data.

2. External cluster validation

, which consists in comparing the results of a

cluster analysis to an externally known result, such as externally provided class

labels. It measures the extent to which cluster labels match externally supplied

class labels. Since we know the “true” cluster number in advance, this approach

is mainly used for selecting the right clustering algorithm for a speciﬁc data set.

3. Relative cluster validation

, which evaluates the clustering structure by vary-

ing diﬀerent parameter values for the same algorithm (e.g.,: varying the number

of clusters k). It’s generally used for determining the optimal number of clusters.

In this chapter, we start by describing the diﬀerent methods for clustering validation.

Next, we’ll demonstrate how to compare the quality of clustering results obtained

with diﬀerent clustering algorithms. Finally, we’ll provide R scripts for validating

clustering results.

138

13.1. INTERNAL MEASURES FOR CLUSTER VALIDATION 139

In all the examples presented here, we’ll apply k-means, PAM and hierarchical

clustering. Note that, the functions used in this article can be applied to evaluate

the validity of any other clustering methods.

13.1 Internal measures for cluster validation

In this section, we describe the most widely used clustering validation indices. Recall

that the goal of partitioning clustering algorithms (Part II) is to split the data set

into clusters of objects, such that:

•the objects in the same cluster are similar as much as possible,

•and the objects in diﬀerent clusters are highly distinct

That is, we want the average distance within cluster to be as small as possible; and

the average distance between clusters to be as large as possible.

Internal validation measures reﬂect often the

compactness

, the

connectedness

and

the separation of the cluster partitions.

Compactness

or cluster cohesion: Measures how close are the objects within

the same cluster. A lower

within-cluster variation

is an indicator of a good

compactness (i.e., a good clustering). The diﬀerent indices for evaluating the

compactness of clusters are base on distance measures such as the cluster-wise within

average/median distances between observations.

Separation

: Measures how well-separated a cluster is from other clus-

ters. The indices used as separation measures include:

- distances between cluster centers

- the pairwise minimum distances between objects in diﬀerent clusters

Connectivity

: corresponds to what extent items are placed in the same

cluster as their nearest neighbors in the data space. The connectivity has a value

between 0 and inﬁnity and should be minimized.

140 CHAPTER 13. CLUSTER VALIDATION STATISTICS

Generally most of the indices used for internal clustering validation combine compact-

ness and separation measures as follow:

Index =(–◊Separation)

(—◊Compactness)

Where –and —are weights.

In this section, we’ll describe the two commonly used indices for assessing the

goodness of clustering: the

silhouette width

and the

Dunn index

. These internal

measure can be used also to determine the optimal number of clusters in the data.

13.1.1 Silhouette coeﬃcient

The silhouette analysis measures how well an observation is clustered and it estimates

the

average distance between clusters

. The silhouette plot displays a measure of

how close each point in one cluster is to points in the neighboring clusters.

For each observation i, the silhouette width siis calculated as follows:

For each observation

, calculate the average dissimilarity

between

and all

other points of the cluster to which i belongs.

For all other clusters

, to which i does not belong, calculate the average

dissimilarity

(

i, C

)of

to all observations of C. The smallest of these

(

i, C

)

is deﬁned as

minCd

(

i, C

). The value of

can be seen as the dissimilarity

between

and its “neighbor” cluster, i.e., the nearest one to which it does not

belong.

Finally the silhouette width of the observation

is deﬁned by the formula:

Si=(bi≠ai)/max(ai,b

i).

Silhouette width can be interpreted as follow:

13.2. EXTERNAL MEASURES FOR CLUSTERING VALIDATION 141

- Observations with a large Si(almost 1) are very well clustered.

- A small

(around 0) means that the observation lies between two clus-

ters.

- Observations with a negative

are probably placed in the wrong cluster.

13.1.2 Dunn index

The

Dunn index

is another internal clustering validation measure which can be

computed as follow:

For each cluster, compute the distance between each of the objects in the cluster

and the objects in the other clusters

Use the minimum of this pairwise distance as the inter-cluster separation

(min.separation)

For each cluster, compute the distance between the objects in the same cluster.

Use the maximal intra-cluster distance (i.e maximum diameter) as the intra-

cluster compactness

5. Calculate the Dunn index (D) as follow:

D=min.separation

max.diameter

If the data set contains compact and well-separated clusters, the diameter of the

clusters is expected to be small and the distance between the clusters is expected to

be large. Thus, Dunn index should be maximized.

13.2 External measures for clustering validation

The aim is to compare the identiﬁed clusters (by k-means, pam or hierarchical

clustering) to an external reference.

142 CHAPTER 13. CLUSTER VALIDATION STATISTICS

It’s possible to quantify the agreement between partitioning clusters and external

reference using either the corrected Rand index and Meila’s variation index VI, which

are implemented in the R function cluster.stats()[fpc package].

The corrected Rand index varies from -1 (no agreement) to 1 (perfect agreement).

External clustering validation, can be used to select suitable clustering algorithm for

a given data set.

13.3 Computing cluster validation statistics in R

13.3.1 Required R packages

The following R packages are required in this chapter:

•factoextra for data visualization

•fpc for computing clustering validation statistics

•NbClust for determining the optimal number of clusters in the data set.

•Install the packages:

install.packages(c("factoextra","fpc","NbClust"))

•Load the packages:

library(factoextra)

library(fpc)

library(NbClust)

13.3.2 Data preparation

We’ll use the built-in R data set iris:

# Excluding the column "Species" at position 5

df <- iris[, -5]

13.3. COMPUTING CLUSTER VALIDATION STATISTICS IN R 143

# Standardize

df <- scale(df)

13.3.3 Clustering analysis

We’ll use the function eclust() [enhanced clustering, in factoextra] which provides

several advantages:

•It simpliﬁes the workﬂow of clustering analysis

•

It can be used to compute hierarchical clustering and partitioning clustering in

a single line function call

•

Compared to the standard partitioning functions (kmeans, pam, clara and fanny)

which requires the user to specify the optimal number of clusters, the function

eclust() computes automatically the gap statistic for estimating the right number

of clusters.

•

It provides silhouette information for all partitioning methods and hierarchical

clustering

•It draws beautiful graphs using ggplot2

The simpliﬁed format the eclust() function is as follow:

eclust(x, FUNcluster = "kmeans",hc_metric = "euclidean",...)

•x: numeric vector, data matrix or data frame

•FUNcluster

: a clustering function including “kmeans”, “pam”, “clara”, “fanny”,

“hclust”, “agnes” and “diana”. Abbreviation is allowed.

•hc_metric

: character string specifying the metric to be used for calculating

dissimilarities between observations. Allowed values are those accepted by the

function dist() [including “euclidean”, “manhattan”, “maximum”, “canberra”,

“binary”, “minkowski”] and correlation based distance measures [“pearson”,

“spearman” or “kendall”]. Used only when FUNcluster is a hierarchical clustering

function such as one of “hclust”, “agnes” or “diana”.

•...: other arguments to be passed to FUNcluster.

The function

eclust()

returns an object of class

eclust

containing the result of the

standard function used (e.g., kmeans, pam, hclust, agnes, diana, etc.).

It includes also:

•cluster: the cluster assignment of observations after cutting the tree

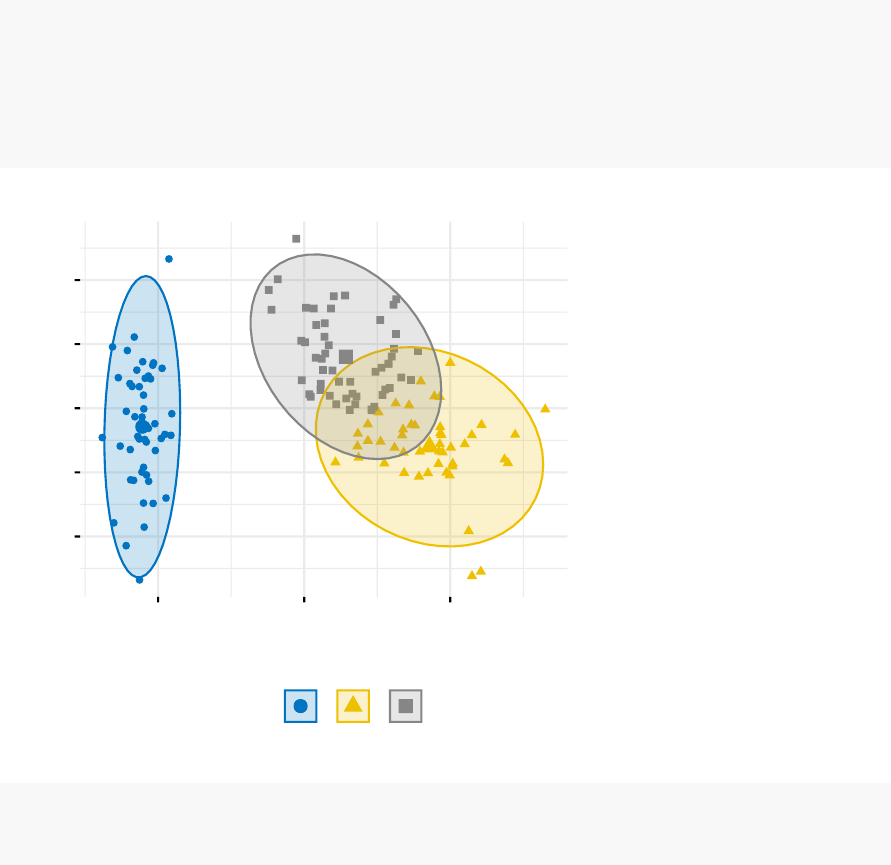
144 CHAPTER 13. CLUSTER VALIDATION STATISTICS

•nbclust: the number of clusters

•silinfo: the silhouette information of observations

•size: the size of clusters

•data

: a matrix containing the original or the standardized data (if stand =

TRUE)

•gap_stat: containing gap statistics

To compute a partitioning clustering, such as k-means clustering with k = 3, type

this:

# K-means clustering

km.res <- eclust(df, "kmeans",k=3,nstart = 25,graph = FALSE)

# Visualize k-means clusters

fviz_cluster(km.res, geom = "point",ellipse.type = "norm",

palette = "jco",ggtheme = theme_minimal())

-2

-1

-2 0 2

Dim1 (73%)

Dim2 (22.9%)

cluster 123

Cluster plot

To compute a hierarchical clustering, use this:

# Hierarchical clustering

hc.res <- eclust(df, "hclust",k=3,hc_metric = "euclidean",

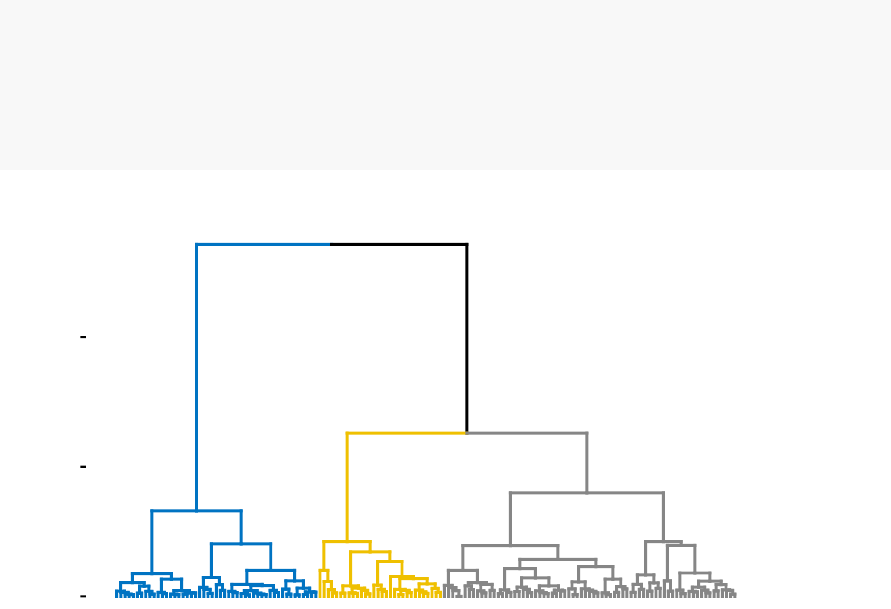
13.3. COMPUTING CLUSTER VALIDATION STATISTICS IN R 145

hc_method = "ward.D2",graph = FALSE)

# Visualize dendrograms

fviz_dend(hc.res, show_labels = FALSE,

palette = "jco",as.ggplot = TRUE)

Height

Cluster Dendrogram

13.3.4 Cluster validation

13.3.4.1 Silhouette plot

Recall that the silhouette coeﬃcient (

) measures how similar an object

is to the

the other objects in its own cluster versus those in the neighbor cluster.

values

range from 1 to - 1:

•

A value of

close to 1 indicates that the object is well clustered. In the other

words, the object iis similar to the other objects in its group.

•

A value of

close to -1 indicates that the object is poorly clustered, and that

assignment to some other cluster would probably improve the overall results.

It’s possible to draw silhouette coeﬃcients of observations using the function

fviz_silhouette() [factoextra package], which will also print a summary of the silhouette

analysis output. To avoid this, you can use the option print.summary = FALSE.

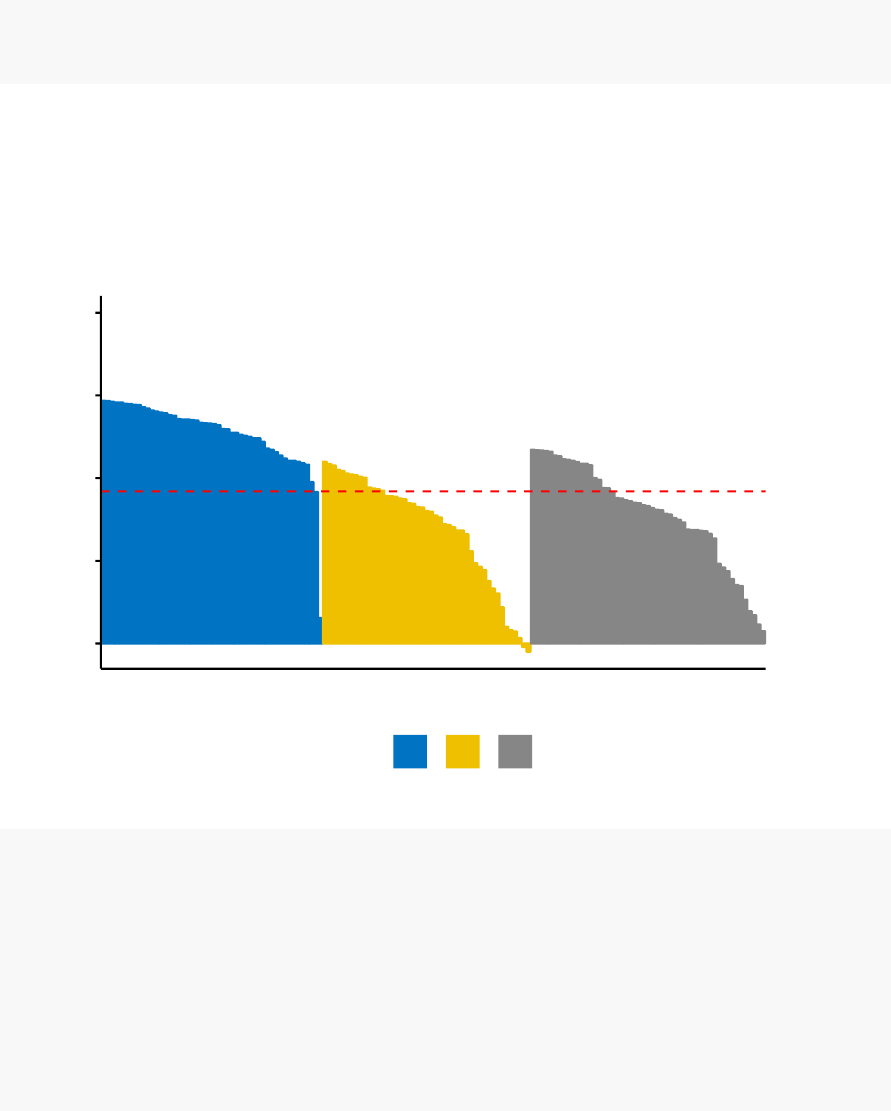
146 CHAPTER 13. CLUSTER VALIDATION STATISTICS

fviz_silhouette(km.res, palette = "jco",

ggtheme = theme_classic())

## cluster size ave.sil.width

## 1 1 50 0.64

## 2 2 47 0.35

## 3 3 53 0.39

0.00

0.25

0.50

0.75

1.00

Silhouette width Si

cluster 123

Clusters silhouette plot

Average silhouette width: 0.46

Silhouette information can be extracted as follow:

# Silhouette information

silinfo <- km.res$silinfo

names(silinfo)

# Silhouette widths of each observation

head(silinfo$widths[, 1:3], 10)

# Average silhouette width of each cluster

silinfo$clus.avg.widths

# The total average (mean of all individual silhouette widths)

silinfo$avg.width

13.3. COMPUTING CLUSTER VALIDATION STATISTICS IN R 147

# The size of each clusters

km.res$size

It can be seen that several samples, in cluster 2, have a negative silhouette coeﬃcient.

This means that they are not in the right cluster. We can ﬁnd the name of these

samples and determine the clusters they are closer (neighbor cluster), as follow:

# Silhouette width of observation

sil <- km.res$silinfo$widths[, 1:3]

# Objects with negative silhouette

neg_sil_index <- which(sil[, sil_width]<0)

sil[neg_sil_index, , drop = FALSE]

## cluster neighbor sil_width

## 112 2 3 -0.01058434

## 128 2 3 -0.02489394

13.3.4.2 Computing Dunn index and other cluster validation statistics

The function cluster.stats() [fpc package] and the function NbClust() [in NbClust

package] can be used to compute Dunn index and many other indices.

The simpliﬁed format is:

cluster.stats(d=NULL,clustering,al.clustering = NULL)

•d: a distance object between cases as generated by the dist() function

•clustering: vector containing the cluster number of each observation

•alt.clustering

: vector such as for clustering, indicating an alternative clustering

The function cluster.stats() returns a list containing many components useful for

analyzing the intrinsic characteristics of a clustering:

•cluster.number: number of clusters

•cluster.size: vector containing the number of points in each cluster

•average.distance

median.distance

: vector containing the cluster-wise within

average/median distances

•average.between

: average distance between clusters. We want it to be as large

as possible

148 CHAPTER 13. CLUSTER VALIDATION STATISTICS

•average.within

: average distance within clusters. We want it to be as small as

possible

•clus.avg.silwidths

: vector of cluster average silhouette widths. Recall that, the

silhouette width

is also an estimate of the average distance between clusters.

Its value is comprised between 1 and -1 with a value of 1 indicating a very good

cluster.

•within.cluster.ss

: a generalization of the within clusters sum of squares (k-

means objective function), which is obtained if d is a Euclidean distance matrix.

•dunn, dunn2: Dunn index

•corrected.rand, vi

: Two indexes to assess the similarity of two clustering: the

corrected Rand index and Meila’s VI

All the above elements can be used to evaluate the internal quality of clustering.

In the following sections, we’ll compute the clustering quality statistics for k-means.

Look at the

within.cluster.ss

(within clusters sum of squares), the

average.within

(average distance within clusters) and

clus.avg.silwidths

(vector of cluster average

silhouette widths).

library(fpc)

# Statistics for k-means clustering

km_stats <- cluster.stats(dist(df), km.res$cluster)

# Dun index

km_stats$dunn

## [1] 0.02649665

To display all statistics, type this:

km_stats

Read the documentation of cluster.stats() for details about all the available indices.

13.3.5 External clustering validation

Among the values returned by the function

cluster.stats

(), there are two indexes to

assess the similarity of two clustering, namely the corrected Rand index and Meila’s

VI.

13.3. COMPUTING CLUSTER VALIDATION STATISTICS IN R 149

We know that the iris data contains exactly 3 groups of species.

Does the K-means clustering matches with the true structure of the data?

We can use the function cluster.stats() to answer to this question.

Let start by computing a cross-tabulation between k-means clusters and the reference

Species labels:

table(iris$Species, km.res$cluster)

## 1 2 3

## setosa 50 0 0

## versicolor 0 11 39

## virginica 0 36 14

It can be seen that:

•All setosa species (n = 50) has been classiﬁed in cluster 1

•

A large number of versicor species (n = 39 ) has been classiﬁed in cluster 3.

Some of them ( n = 11) have been classiﬁed in cluster 2.

•

A large number of virginica species (n = 36 ) has been classiﬁed in cluster 2.

Some of them (n = 14) have been classiﬁed in cluster 3.

It’s possible to quantify the agreement between Species and k-means clusters using

either the corrected Rand index and Meila’s VI provided as follow:

library("fpc")

# Compute cluster stats

species <- as.numeric(iris$Species)

clust_stats <- cluster.stats(d=dist(df),

species, km.res$cluster)

# Corrected Rand index

clust_stats$corrected.rand

## [1] 0.6201352

# VI

clust_stats$vi

## [1] 0.7477749

150 CHAPTER 13. CLUSTER VALIDATION STATISTICS

The corrected

Rand index

provides a measure for assessing the similarity between

two partitions, adjusted for chance. Its range is -1 (no agreement) to 1 (perfect

agreement). Agreement between the specie types and the cluster solution is 0.62

using Rand index and 0.748 using Meila’s VI

The same analysis can be computed for both PAM and hierarchical clustering:

# Agreement between species and pam clusters

pam.res <- eclust(df, "pam",k=3,graph = FALSE)

table(iris$Species, pam.res$cluster)

cluster.stats(d=dist(iris.scaled),

species, pam.res$cluster)$vi

# Agreement between species and HC clusters

res.hc <- eclust(df, "hclust",k=3,graph = FALSE)

table(iris$Species, res.hc$cluster)

cluster.stats(d=dist(iris.scaled),

species, res.hc$cluster)$vi

External clustering validation, can be used to select suitable clustering algorithm for

a given data set.

13.4 Summary

We described how to validate clustering results using the silhouette method and the

Dunn index. This task is facilitated using the combination of two R functions: eclust()

and fviz_silhouette in the factoextra package We also demonstrated how to assess the

agreement between a clustering result and an external reference.

In the next chapters, we’ll show how to i) choose the appropriate clustering algorithm

for your data; and ii) computing p-values for hierarchical clustering.

Chapter 14

Choosing the Best Clustering

Algorithms

Choosing the best clustering method

for a given data can be a hard task for

the analyst. This article describes the R package

clValid

(G. Brock et al., 2008),

which can be used to compare simultaneously multiple clustering algorithms in a single

function call for identifying the best clustering approach and the optimal number of

clusters.

We’ll start by describing the diﬀerent measures in the clValid package for comparing

clustering algorithms. Next, we’ll present the function *clValid*(). Finally, we’ll

provide R scripts for validating clustering results and comparing clustering algorithms.

14.1 Measures for comparing clustering algo-

rithms

The clValid package compares clustering algorithms using two cluster validation

measures:

Internal measures, which uses intrinsic information in the data to assess the qual-

ity of the clustering. Internal measures include the connectivity, the silhouette

coeﬃcient and the Dunn index as described in Chapter 13 (Cluster Validation

Statistics).

151

152 CHAPTER 14. CHOOSING THE BEST CLUSTERING ALGORITHMS

Stability measures, a special version of internal measures, which evaluates the

consistency of a clustering result by comparing it with the clusters obtained

after each column is removed, one at a time.

Cluster stability measures include:

•The average proportion of non-overlap (APN)

•The average distance (AD)

•The average distance between means (ADM)

•The ﬁgure of merit (FOM)

The APN, AD, and ADM are all based on the cross-classiﬁcation table of the original

clustering on the full data with the clustering based on the removal of one column.

•

The APN measures the average proportion of observations not placed in the

same cluster by clustering based on the full data and clustering based on the

data with a single column removed.

•

The AD measures the average distance between observations placed in the same

cluster under both cases (full data set and removal of one column).

•

The ADM measures the average distance between cluster centers for observations

placed in the same cluster under both cases.

•

The FOM measures the average intra-cluster variance of the deleted column,

where the clustering is based on the remaining (undeleted) columns.

The values of APN, ADM and FOM ranges from 0 to 1, with smaller value corre-

sponding with highly consistent clustering results. AD has a value between 0 and

inﬁnity, and smaller values are also preferred.

Note that, the clValid package provides also biological validation measures, which

evaluates the ability of a clustering algorithm to produce biologically meaningful clus-

ters. An application is microarray or RNAseq data where observations corresponds

to genes.

14.2 Compare clustering algorithms in R

We’ll use the function

clValid

() [in the clValid package], which simpliﬁed format is

as follow:

14.2. COMPARE CLUSTERING ALGORITHMS IN R 153

clValid(obj, nClust, clMethods = "hierarchical",

validation = "stability",maxitems = 600,

metric = "euclidean",method = "average")

•obj

: A numeric matrix or data frame. Rows are the items to be clustered and

columns are samples.

•nClust

: A numeric vector specifying the numbers of clusters to be evaluated.

e.g., 2:10

•clMethods

: The clustering method to be used. Available options are “hierar-

chical”, “kmeans”, “diana”, “fanny”, “som”, “model”, “sota”, “pam”, “clara”,

and “agnes”, with multiple choices allowed.

•validation

: The type of validation measures to be used. Allowed values are

“internal”, “stability”, and “biological”, with multiple choices allowed.

•maxitems

: The maximum number of items (rows in matrix) which can be

clustered.

•metric

: The metric used to determine the distance matrix. Possible choices are

“euclidean”, “correlation”, and “manhattan”.

•method

: For hierarchical clustering (hclust and agnes), the agglomeration

method to be used. Available choices are “ward”, “single”, “complete” and

“average”.

For example, consider the iris data set, the clValid() function can be used as follow.

We start by cluster internal measures, which include the connectivity, silhouette width

and Dunn index. It’s possible to compute simultaneously these internal measures for

multiple clustering algorithms in combination with a range of cluster numbers.

library(clValid)

# Iris data set:

# - Remove Species column and scale

df <- scale(iris[, -5])

# Compute clValid

clmethods <- c("hierarchical","kmeans","pam")

intern <- clValid(df, nClust = 2:6,

clMethods = clmethods, validation = "internal")

# Summary

summary(intern)

154 CHAPTER 14. CHOOSING THE BEST CLUSTERING ALGORITHMS

## Clustering Methods:

## hierarchical kmeans pam

## Cluster sizes:

## 2 3 4 5 6

## Validation Measures:

## 23456

## hierarchical Connectivity 0.9762 5.5964 7.5492 18.0508 24.7306

## Dunn 0.2674 0.1874 0.2060 0.0700 0.0762

## Silhouette 0.5818 0.4803 0.4067 0.3746 0.3248

## kmeans Connectivity 0.9762 23.8151 25.9044 40.3060 40.1385

## Dunn 0.2674 0.0265 0.0700 0.0808 0.0808

## Silhouette 0.5818 0.4599 0.4189 0.3455 0.3441

## pam Connectivity 0.9762 23.0726 31.8067 35.7964 44.5413

## Dunn 0.2674 0.0571 0.0566 0.0642 0.0361

## Silhouette 0.5818 0.4566 0.4091 0.3574 0.3400

## Optimal Scores:

## Score Method Clusters

## Connectivity 0.9762 hierarchical 2

## Dunn 0.2674 hierarchical 2

## Silhouette 0.5818 hierarchical 2

It can be seen that hierarchical clustering with two clusters performs the best in

each case (i.e., for connectivity, Dunn and Silhouette measures). Regardless of the

clustering algorithm, the optimal number of clusters seems to be two using the three

measures.

The stability measures can be computed as follow:

# Stability measures

clmethods <- c("hierarchical","kmeans","pam")

stab <- clValid(df, nClust = 2:6,clMethods = clmethods,

validation = "stability")

# Display only optimal Scores

optimalScores(stab)

14.3. SUMMARY 155

## Score Method Clusters

## APN 0.003266667 hierarchical 2

## AD 1.004288856 pam 6

## ADM 0.016087089 hierarchical 2

## FOM 0.455750052 pam 6

For the APN and ADM measures, hierarchical clustering with two clusters again

gives the best score. For the other measures, PAM with six clusters has the best

score.

14.3 Summary

Here, we described how to compare clustering algorithms using the clValid R package.

Chapter 15

Computing P-value for

Hierarchical Clustering

Clusters can be found in a data set by chance due to clustering noise or sampling error.

This article describes the R package

pvclust

(Suzuki et al., 2004) which uses bootstrap

resampling techniques to compute p-value for each hierarchical clusters.

15.1 Algorithm

Generated thousands of bootstrap samples by randomly sampling elements of

the data

2. Compute hierarchical clustering on each bootstrap copy

3. For each cluster:

•

compute the bootstrap probability (BP) value which corresponds to the

frequency that the cluster is identiﬁed in bootstrap copies.

•

Compute the approximately unbiased (AU) probability values (p-values) by

multiscale bootstrap resampling

Clusters with AU >= 95% are considered to be strongly supported by data.

156

15.2. REQUIRED PACKAGES 157

15.2 Required packages

1. Install pvclust:

install.packages("pvclust")

2. Load pvclust:

library(pvclust)

15.3 Data preparation

We’ll use lung data set [in pvclust package]. It contains the gene expression proﬁle of

916 genes of 73 lung tissues including 67 tumors. Columns are samples and rows are

genes.

library(pvclust)

# Load the data

data("lung")

head(lung[, 1:4])

## fetal_lung 232-97_SCC 232-97_node 68-96_Adeno

## IMAGE:196992 -0.40 4.28 3.68 -1.35

## IMAGE:587847 -2.22 5.21 4.75 -0.91

## IMAGE:1049185 -1.35 -0.84 -2.88 3.35

## IMAGE:135221 0.68 0.56 -0.45 -0.20

## IMAGE:298560 NA 4.14 3.58 -0.40

## IMAGE:119882 -3.23 -2.84 -2.72 -0.83

# Dimension of the data

dim(lung)

## [1] 916 73

We’ll use only a subset of the data set for the clustering analysis. The R function

sample() can be used to extract a random subset of 30 samples:

158CHAPTER 15. COMPUTING P-VALUE FOR HIERARCHICAL CLUSTERING

set.seed(123)

ss <- sample(1:73,30)# extract 20 samples out of

df <- lung[, ss]

15.4 Compute p-value for hierarchical clustering

15.4.1 Description of pvclust() function

The function pvclust() can be used as follow:

pvclust(data, method.hclust = "average",

method.dist = "correlation",nboot = 1000)

Note that, the computation time can be strongly decreased using parallel computation

version called parPvclust(). (Read ?parPvclust() for more information.)

parPvclust(cl=NULL,data,method.hclust = "average",

method.dist = "correlation",nboot = 1000,

iseed = NULL)

•data: numeric data matrix or data frame.

•method.hclust

: the agglomerative method used in hierarchical clustering.

Possible values are one of “average”, “ward”, “single”, “complete”, “mcquitty”,

“median” or “centroid”. The default is “average”. See method argument in

?hclust.

•method.dist

: the distance measure to be used. Possible values are one of

“correlation”, “uncentered”, “abscor” or those which are allowed for

method

argument in dist() function, such “euclidean” and “manhattan”.

•nboot: the number of bootstrap replications. The default is 1000.

•iseed

: an integrer for random seeds. Use iseed argument to achieve reproducible

results.

The function pvclust() returns an object of class pvclust containing many elements

including hclust which contains hierarchical clustering result for the original data

generated by the function hclust().

15.4. COMPUTE P-VALUE FOR HIERARCHICAL CLUSTERING 159

15.4.2 Usage of pvclust() function

pvclust() performs clustering on the columns of the data set, which correspond to

samples in our case. If you want to perform the clustering on the variables (here,

genes) you have to transpose the data set using the function t().

The R code below computes pvclust() using 10 as the number of bootstrap replications

(for speed):

library(pvclust)

set.seed(123)

res.pv <- pvclust(df, method.dist="cor",

method.hclust="average",nboot = 10)

# Default plot

plot(res.pv, hang = -1,cex = 0.5)

pvrect(res.pv)

132-95_Adeno

181-96_Adeno

320-00_Adeno_p

265-98_Adeno

306-99_node

306-99_Adeno

165-96_Adeno

313-99MT_Adeno

313-99PT_Adeno

6-00_LCLC

222-97_normal

219-97_normal

68-96_Adeno

137-96_Adeno

207-97_SCLC

314-99_SCLC

315-99_node

59-96_SCC

139-97_LCLC

234-97_Adeno

184-96_Adeno

184-96_node

157-96_SCC

219-97_SCC

3-SCC

232-97_node

246-97_SCC_c

245-97_node

220-97_SCC

239-97_SCC

0.0 0.4 0.8

Cluster dendrogram with AU/BP values (%)

Cluster method: average

Distance: correlation

Height

100 100 100

100

100 73

100 79

100 69

57 51

68 100

89 26 31

92 40 54

62 60

100 100 100

100

100 76

100 50

100 42

90 83

54 100

66 35 77

65 14 50

38 40

123

10 11

14 15

16 17

18 19 20

23 24 25

27 28

edge #

160CHAPTER 15. COMPUTING P-VALUE FOR HIERARCHICAL CLUSTERING

Values on the dendrogram are AU p-values (Red, left), BP values (green, right),

and

clusterlabels

(grey, bottom). Clusters with AU > = 95% are indicated by the

rectangles and are considered to be strongly supported by data.

To extract the objects from the signiﬁcant clusters, use the function pvpick():

clusters <- pvpick(res.pv)

clusters

Parallel computation can be applied as follow:

# Create a parallel socket cluster

library(parallel)

cl <- makeCluster(2,type = "PSOCK")

# parallel version of pvclust

res.pv <- parPvclust(cl, df, nboot=1000)

stopCluster(cl)

Part V

Advanced Clustering

161

162

Contents:

•Hierarchical k-means clustering (Chapter 16)

•Fuzzy clustering (Chapter 17)

•Model-based clustering (Chapter 18)

•DBSCAN: Density-Based Clustering (Chapter 19)

Chapter 16

Hierarchical K-Means Clustering

K-means (Chapter 4) represents one of the most popular clustering algorithm. However,

it has some limitations: it requires the user to specify the number of clusters in advance

and selects initial centroids randomly. The ﬁnal k-means clustering solution is very

sensitive to this initial random selection of cluster centers. The result might be

(slightly) diﬀerent each time you compute k-means.

In this chapter, we described an hybrid method, named

hierarchical k-means

clustering (hkmeans), for improving k-means results.

16.1 Algorithm

The algorithm is summarized as follow:

1. Compute hierarchical clustering and cut the tree into k-clusters

2. Compute the center (i.e the mean) of each cluster

Compute k-means by using the set of cluster centers (deﬁned in step 2) as the

initial cluster centers

Note that, k-means algorithm will improve the initial partitioning generated at the

step 2 of the algorithm. Hence, the initial partitioning can be slightly diﬀerent from

the ﬁnal partitioning obtained in the step 4.

163

164 CHAPTER 16. HIERARCHICAL K-MEANS CLUSTERING

16.2 R code

The R function hkmeans() [in factoextra], provides an easy solution to compute the

hierarchical k-means clustering. The format of the result is similar to the one provided

by the standard kmeans() function (see Chapter 4).

To install factoextra, type this: install.packages(“factoextra”).

We’ll use the USArrest data set and we start by standardizing the data:

df <- scale(USArrests)

# Compute hierarchical k-means clustering

library(factoextra)

res.hk <-hkmeans(df, 4)

# Elements returned by hkmeans()

names(res.hk)

## [1] "cluster" "centers" "totss" "withinss"

## [5] "tot.withinss" "betweenss" "size" "iter"

## [9] "ifault" "data" "hclust"

To print all the results, type this:

# Print the results

res.hk

# Visualize the tree

fviz_dend(res.hk, cex = 0.6,palette = "jco",

rect = TRUE,rect_border = "jco",rect_fill = TRUE)

16.2. R CODE 165

Alabama

Louisiana

Georgia

Tennessee

North Carolina

Mississippi

South Carolina

Texas

Illinois

New York

Florida

Arizona

Michigan

Maryland

New Mexico

Alaska

Colorado

California

Nevada

South Dakota

West Virginia

North Dakota

Vermont

Idaho

Montana

Nebraska

Minnesota

Wisconsin

Maine

Iowa

New Hampshire

Virginia

Wyoming

Arkansas

Kentucky

Delaware

Massachusetts

New Jersey

Connecticut

Rhode Island

Missouri

Oregon

Washington

Oklahoma

Indiana

Kansas

Ohio

Pennsylvania

Hawaii

Utah

Height

Cluster Dendrogram

# Visualize the hkmeans final clusters

fviz_cluster(res.hk, palette = "jco",repel = TRUE,

ggtheme = theme_classic())

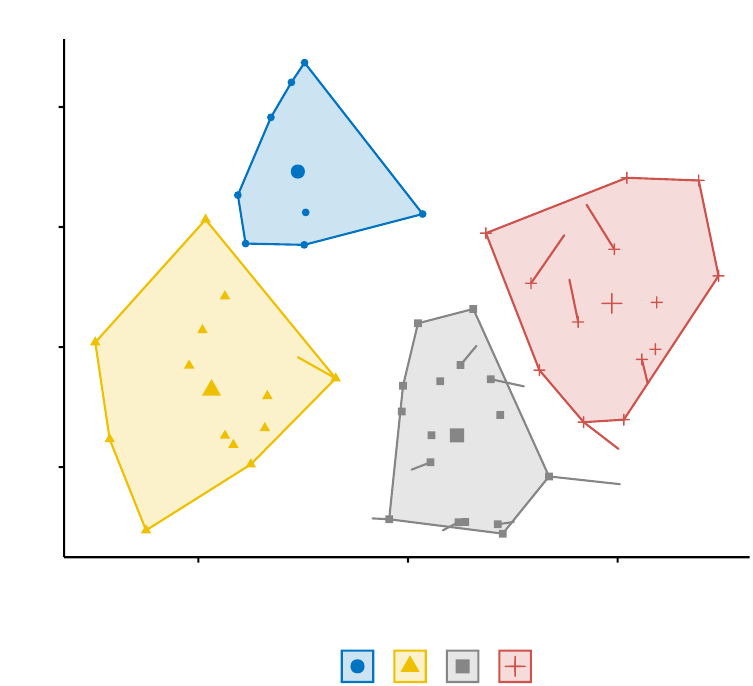
166 CHAPTER 16. HIERARCHICAL K-MEANS CLUSTERING

Alabama

Alaska

Arizona

Arkansas

California

Colorado Connecticut

Delaware

Florida

Georgia

Hawaii

Idaho

Illinois

Indiana

Iowa

Kansas

Kentucky

Louisiana

Maine

Maryland

Massachusetts

Michigan

Minnesota

Mississippi

Missouri

Montana

Nebraska

Nevada

New Hampshire

New Jersey

New Mexico

New York

North Carolina

North Dakota

Ohio

Oklahoma

Oregon Pennsylvania

Rhode Island

South Carolina

South Dakota

Tennessee

Texas

Utah

Vermont

Virginia

Washington

West Virginia

Wisconsin

Wyoming

-1

-2 0 2

Dim1 (62%)

Dim2 (24.7%)

cluster aaaa

1234

Cluster plot

16.3 Summary

We described hybrid

hierarchical k-means clustering

for improving k-means re-

sults.

Chapter 17

Fuzzy Clustering

The

fuzzy clustering

is considered as soft clustering, in which each element has a

probability of belonging to each cluster. In other words, each element has a set of

membership coeﬃcients corresponding to the degree of being in a given cluster.

This is diﬀerent from k-means and k-medoid clustering, where each object is aﬀected

exactly to one cluster. K-means and k-medoids clustering are known as hard or

non-fuzzy clustering.

In fuzzy clustering, points close to the center of a cluster, may be in the cluster to a

higher degree than points in the edge of a cluster. The degree, to which an element

belongs to a given cluster, is a numerical value varying from 0 to 1.

The

fuzzy c-means

(FCM) algorithm is one of the most widely used fuzzy clustering

algorithms. The centroid of a cluster is calculated as the mean of all points, weighted

by their degree of belonging to the cluster:

In this article, we’ll describe how to compute fuzzy clustering using the R software.

17.1 Required R packages

We’ll use the following R packages: 1) cluster for computing fuzzy clustering and 2)

factoextra for visualizing clusters.

167

168 CHAPTER 17. FUZZY CLUSTERING

17.2 Computing fuzzy clustering

The function fanny() [cluster R package] can be used to compute fuzzy clustering.

FANNY stands for fuzzy analysis clustering. A simpliﬁed format is:

fanny(x, k, metric = "euclidean",stand = FALSE)

•x: A data matrix or data frame or dissimilarity matrix

•k: The desired number of clusters to be generated

•metric: Metric for calculating dissimilarities between observations

•stand

: If TRUE, variables are standardized before calculating the dissimilarities

The function fanny() returns an object including the following components:

•membership

: matrix containing the degree to which each observation belongs

to a given cluster. Column names are the clusters and rows are observations

•coeﬀ

: Dunn’s partition coeﬃcient F(k) of the clustering, where k is the number

of clusters. F(k) is the sum of all squared membership coeﬃcients, divided by

the number of observations. Its value is between 1/k and 1. The normalized

form of the coeﬃcient is also given. It is deﬁned as (

(

)

≠

)

≠

), and

ranges between 0 and 1. A low value of Dunn’s coeﬃcient indicates a very fuzzy

clustering, whereas a value close to 1 indicates a near-crisp clustering.

•clustering

: the clustering vector containing the nearest crisp grouping of

observations

For example, the R code below applies fuzzy clustering on the USArrests data set:

library(cluster)

df <- scale(USArrests) # Standardize the data

res.fanny <- fanny(df, 2)# Compute fuzzy clustering with k = 2

The diﬀerent components can be extracted using the code below:

head(res.fanny$membership, 3)# Membership coefficients

## [,1] [,2]

## Alabama 0.6641977 0.3358023

## Alaska 0.6098062 0.3901938

## Arizona 0.6862278 0.3137722

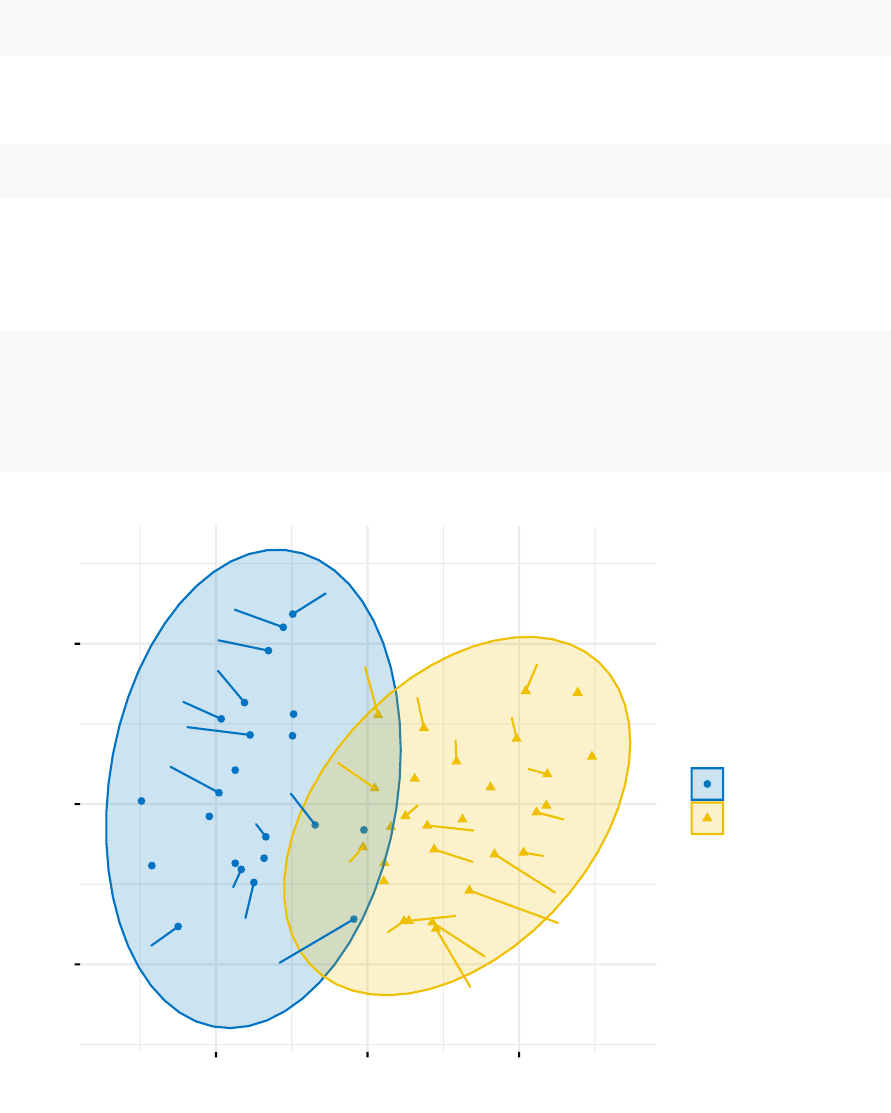
17.2. COMPUTING FUZZY CLUSTERING 169

res.fanny$coeff # Dunns partition coefficient

## dunn_coeff normalized

## 0.5547365 0.1094731

head(res.fanny$clustering) # Observation groups

## Alabama Alaska Arizona Arkansas California Colorado

##111211

To visualize observation groups, use the function fviz_cluster() [factoextra package]:

library(factoextra)

fviz_cluster(res.fanny, ellipse.type = "norm",repel = TRUE,

palette = "jco",ggtheme = theme_minimal(),

legend = "right")

Alabama

Alaska

Arizona

Arkansas

California

Colorado Connecticut

Delaware

Florida

Georgia

Hawaii

Idaho

Illinois

Indiana

Iowa

Kansas

Kentucky

Louisiana

Maine

Maryland

Massachusetts

Michigan

Minnesota

Mississippi

Missouri

Montana

Nebraska

Nevada

New Hampshire

New Jersey

New Mexico

New York

North Carolina

North Dakota

Ohio

Oklahoma

Oregon Pennsylvania

Rhode Island

South Carolina

South Dakota

Tennessee

Texas

Utah

Vermont

Virginia

Washington

West Virginia

Wisconsin

Wyoming

-2

-2 0 2

Dim1 (62%)

Dim2 (24.7%)

cluster

Cluster plot

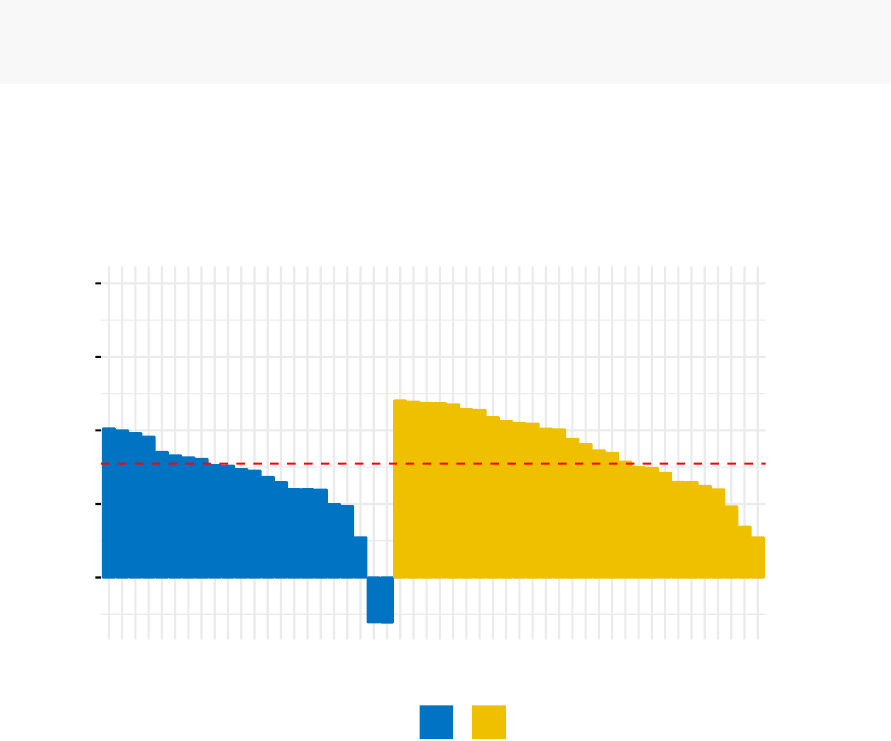
170 CHAPTER 17. FUZZY CLUSTERING

To evaluate the goodnesss of the clustering results, plot the silhouette coeﬃcient as

follow:

fviz_silhouette(res.fanny, palette = "jco",

ggtheme = theme_minimal())

## cluster size ave.sil.width

## 1 1 22 0.32

## 2 2 28 0.44

0.00

0.25

0.50

0.75

1.00

Silhouette width Si

cluster 12

Clusters silhouette plot

Average silhouette width: 0.39

17.3 Summary

Fuzzy clustering is an alternative to k-means clustering, where each data point has

membership coeﬃcient to each cluster. Here, we demonstrated how to compute and

visualize fuzzy clustering using the combination of cluster and factoextra R packages.

Chapter 18

Model-Based Clustering

The traditional clustering methods, such as hierarchical clustering (Chapter 7) and

k-means clustering (Chapter 4), are heuristic and are not based on formal models.

Furthermore, k-means algorithm is commonly randomnly initialized, so diﬀerent runs

of k-means will often yield diﬀerent results. Additionally, k-means requires the user to

specify the the optimal number of clusters.

An alternative is

model-based clustering

, which consider the data as coming from

a distribution that is mixture of two or more clusters (Chris Fraley and Adrian E.

Raftery, 2002 and 2012). Unlike k-means, the model-based clustering uses a soft

assignment, where each data point has a probability of belonging to each cluster.

In this chapter, we illustrate model-based clustering using the R package mclust.

18.1 Concept of model-based clustering

In model-based clustering, the data is considered as coming from a mixture of density.

Each component (i.e. cluster) k is modeled by the normal or Gaussian distribution

which is characterized by the parameters:

•µk: mean vector,

•qk: covariance matrix,

•

An associated probability in the mixture. Each point has a probability of

belonging to each cluster.

171

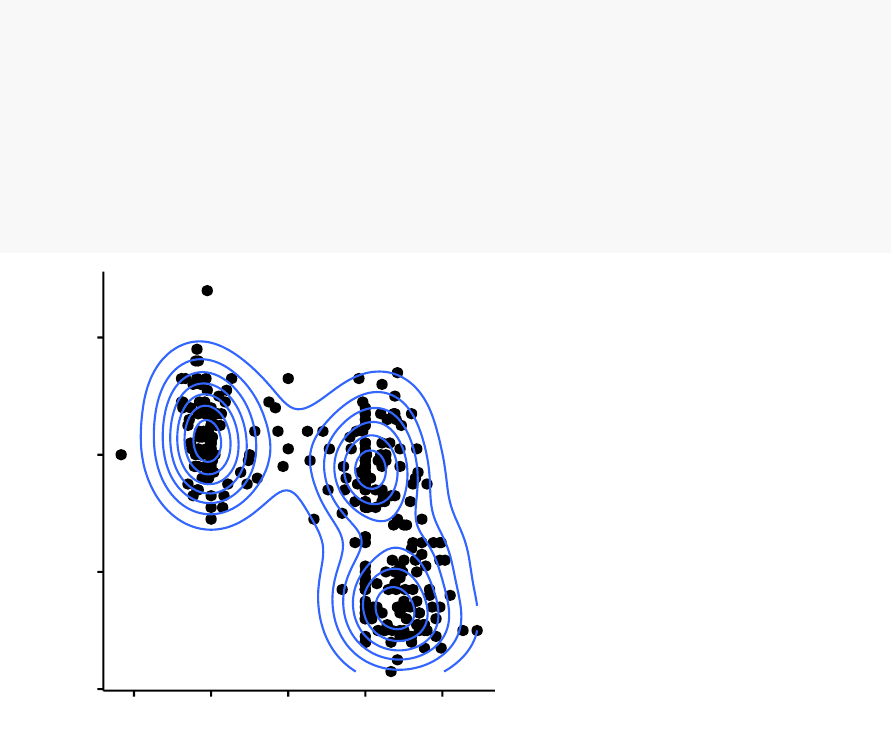
172 CHAPTER 18. MODEL-BASED CLUSTERING

For example, consider the “old faithful geyser data” [in MASS R package], which can

be illustrated as follow using the ggpubr R package:

# Load the data

library("MASS")

data("geyser")

# Scatter plot

library("ggpubr")

ggscatter(geyser, x="duration",y="waiting")+

geom_density2d() # Add 2D density

100

12345

duration

waiting

The plot above suggests at least 3 clusters in the mixture. The shape of each of the

3 clusters appears to be approximately elliptical suggesting three bivariate normal

distributions. As the 3 ellipses seems to be similar in terms of volume, shape and

orientation, we might anticipate that the three components of this mixture might have

homogeneous covariance matrices.

18.2. ESTIMATING MODEL PARAMETERS 173

18.2 Estimating model parameters

The model parameters can be estimated using the Expectation-Maximization (EM)

algorithm initialized by hierarchical model-based clustering. Each cluster k is centered

at the means µk, with increased density for points near the mean.

Geometric features (shape, volume, orientation) of each cluster are determined by the

covariance matrix qk.

Diﬀerent possible parameterizations of

are available in the R package mclust (see

?mclustModelNames).

The available model options, in mclust package, are represented by identiﬁers including:

EII, VII, EEI, VEI, EVI, VVI, EEE, EEV, VEV and VVV.

The ﬁrst identiﬁer refers to volume, the second to shape and the third to orientation.

E stands for “equal”, V for “variable” and I for “coordinate axes”.

For example:

•

EVI denotes a model in which the volumes of all clusters are equal (E), the

shapes of the clusters may vary (V), and the orientation is the identity (I) or

“coordinate axes.

•

EEE means that the clusters have the same volume, shape and orientation in

p-dimensional space.

•

VEI means that the clusters have variable volume, the same shape and orientation

equal to coordinate axes.

18.3 Choosing the best model

The Mclust package uses maximum likelihood to ﬁt all these models, with diﬀerent

covariance matrix parameterizations, for a range of k components.

The best model is selected using the Bayesian Information Criterion or BIC. A large

BIC score indicates strong evidence for the corresponding model.

18.4 Computing model-based clustering in R

We start by installing the mclust package as follow: install.packages(“mclust”)

174 CHAPTER 18. MODEL-BASED CLUSTERING

Note that, model-based clustering can be applied on univariate or multivariate data.

Here, we illustrate model-based clustering on the diabetes data set [mclust package]

giving three measurements and the diagnosis for 145 subjects described as follow:

library("mclust")

data("diabetes")

head(diabetes, 3)

## class glucose insulin sspg

## 1 Normal 80 356 124

## 2 Normal 97 289 117

## 3 Normal 105 319 143

•

class: the diagnosis: normal, chemically diabetic, and overtly diabetic. Excluded

from the cluster analysis.

•glucose: plasma glucose response to oral glucose

•insulin: plasma insulin response to oral glucose

•sspg: steady-state plasma glucose (measures insulin resistance)

Model-based clustering can be computed using the function Mclust() as follow:

library(mclust)

df <- scale(diabetes[, -1]) # Standardize the data

mc <- Mclust(df) # Model-based-clustering

summary(mc) # Print a summary

## ----------------------------------------------------

## Gaussian finite mixture model fitted by EM algorithm

## ----------------------------------------------------

## Mclust VVV (ellipsoidal, varying volume, shape, and orientation) model with 3 components:

## log.likelihood n df BIC ICL

## -169.0918 145 29 -482.5089 -501.4368

## Clustering table:

##123

## 81 36 28

18.5. VISUALIZING MODEL-BASED CLUSTERING 175

For this data, it can be seen that model-based clustering selected a model with three

components (i.e. clusters). The optimal selected model name is VVV model. That

is the three components are ellipsoidal with varying volume, shape, and orientation.

The summary contains also the clustering table specifying the number of observations

in each clusters.

You can access to the results as follow:

mc$modelName # Optimal selected model ==> "VVV"

mc$G # Optimal number of cluster => 3

head(mc$z, 30)# Probality to belong to a given cluster

head(mc$classification, 30)# Cluster assignement of each observation

18.5 Visualizing model-based clustering

Model-based clustering results can be drawn using the base function plot.Mclust() [in

mclust package]. Here we’ll use the function fviz_mclust() [in factoextra package] to

create beautiful plots based on ggplot2.

In the situation, where the data contain more than two variables, fviz_mclust() uses

a principal component analysis to reduce the dimensionnality of the data. The ﬁrst

two principal components are used to produce a scatter plot of the data. How-

ever, if you want to plot the data using only two variables of interest, let say here

c(“insulin”, “sspg”), you can specify that in the fviz_mclust() function using the

argument choose.vars = c(“insulin”, “sspg”).

library(factoextra)

# BIC values used for choosing the number of clusters

fviz_mclust(mc, "BIC",palette = "jco")

# Classification: plot showing the clustering

fviz_mclust(mc, "classification",geom = "point",

pointsize = 1.5,palette = "jco")

# Classification uncertainty

fviz_mclust(mc, "uncertainty",palette = "jco")

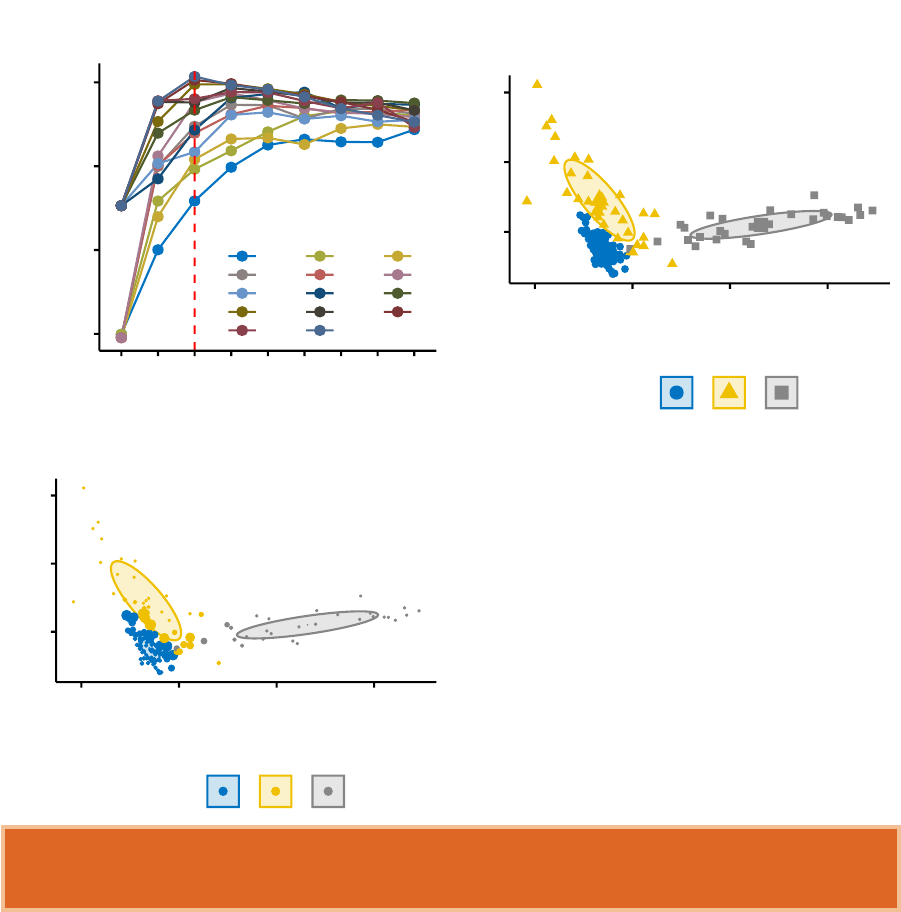
176 CHAPTER 18. MODEL-BASED CLUSTERING

-1250

-1000

-750

-500

123456789

Number of components

BIC

EII VII EEI

VEI EVI VVI

EEE EVE VEE

VVE EEV VEV

EVV VVV

Best model: VVV | Optimal clusters: n = 3

Model selection

-2 0 2 4

Dim1 (73.2%)

Dim2 (25.6%)

cluster 123

Classification

Cluster plot

-2 0 2 4

Dim1 (73.2%)

Dim2 (25.6%)

cluster 123

Uncertainty

Cluster plot

Note that, in the uncertainty plot, larger symbols indicate the more uncertain

observations.

Chapter 19

DBSCAN: Density-Based

Clustering

DBSCAN

(

Density-Based Spatial Clustering and Application with Noise

is a

density-based clusering

algorithm, introduced in Ester et al. 1996, which can

be used to identify clusters of any shape in a data set containing noise and outliers.

The basic idea behind the density-based clustering approach is derived from a human

intuitive clustering method. For instance, by looking at the ﬁgure below, one can

easily identify four clusters along with several points of noise, because of the diﬀerences

in the density of points.

Clusters are dense regions in the data space, separated by regions of lower density of

points. The DBSCAN algorithm is based on this intuitive notion of “clusters” and

“noise”. The key idea is that for each point of a cluster, the neighborhood of a given

radius has to contain at least a minimum number of points.

177

178 CHAPTER 19. DBSCAN: DENSITY-BASED CLUSTERING

(From Ester et al. 1996)

In this chapter, we’ll describe the DBSCAN algorithm and demonstrate how to

compute DBSCAN using the *fpc* R package.

19.1 Why DBSCAN?

Partitioning methods (K-means, PAM clustering) and hierarchical clustering are

suitable for ﬁnding spherical-shaped clusters or convex clusters. In other words, they

work well only for compact and well separated clusters. Moreover, they are also

severely aﬀected by the presence of noise and outliers in the data.

Unfortunately, real life data can contain: i) clusters of arbitrary shape such as those

shown in the ﬁgure below (oval, linear and “S” shape clusters); ii) many outliers and

noise.

The ﬁgure below shows a data set containing nonconvex clusters and outliers/noises.

The simulated data set multishapes [in factoextra package] is used.

19.1. WHY DBSCAN? 179

-3

-2

-1

-1 0 1

The plot above contains 5 clusters and outliers, including:

•2 ovales clusters

•2 linear clusters

•1 compact cluster

Given such data, k-means algorithm has diﬃculties for identifying theses clusters with

arbitrary shapes. To illustrate this situation, the following R code computes k-means

algorithm on the multishapes data set. The function fviz_cluster()[factoextra package]

is used to visualize the clusters.

First, install factoextra: install.packages(“factoextra”); then compute and visualize

k-means clustering using the data set multishapes:

library(factoextra)

data("multishapes")

df <- multishapes[, 1:2]

set.seed(123)

km.res <- kmeans(df, 5,nstart = 25)

fviz_cluster(km.res, df, geom = "point",

ellipse= FALSE,show.clust.cent = FALSE,

palette = "jco",ggtheme = theme_classic())

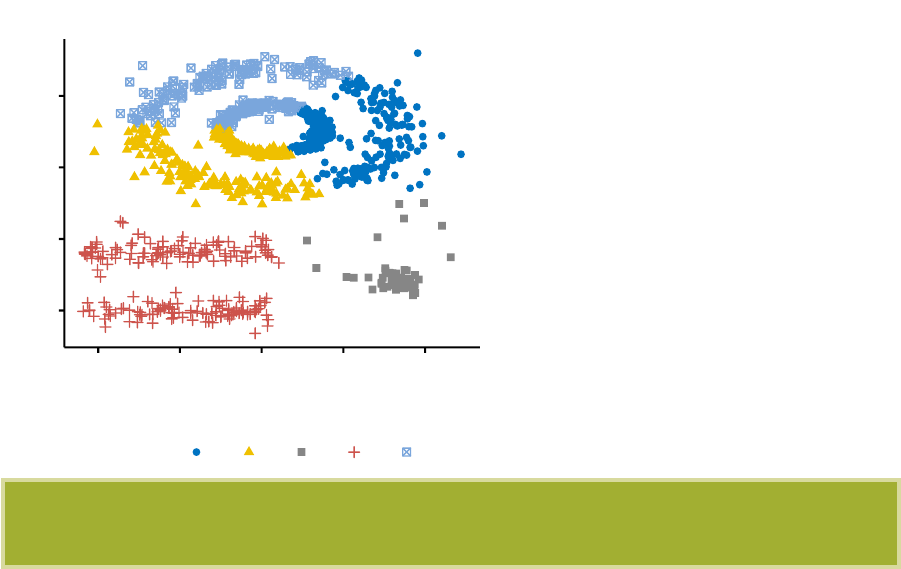
180 CHAPTER 19. DBSCAN: DENSITY-BASED CLUSTERING

-2

-1

-2 -1 0 1 2

x value

y value

cluster 12345

Cluster plot

We know there are 5 ﬁve clusters in the data, but it can be seen that k-means method

inaccurately identify the 5 clusters.

19.2 Algorithm

The goal is to identify dense regions, which can be measured by the number of objects

close to a given point.

Two important parameters are required for DBSCAN: epsilon (“eps”) and minimum

points (“MinPts”). The parameter eps deﬁnes the radius of neighborhood around

a point x. It’s called called the

‘

-neighborhood of x. The parameter MinPts is the

minimum number of neighbors within “eps” radius.

Any point x in the data set, with a neighbor count greater than or equal to MinPts, is

marked as a core point. We say that x is border point, if the number of its neighbors is

less than MinPts, but it belongs to the

‘

-neighborhood of some core point z. Finally,

if a point is neither a core nor a border point, then it is called a noise point or an

outlier.

The ﬁgure below shows the diﬀerent types of points (core, border and outlier points)

using MinPts = 6. Here x is a core point because

neighbours‘

(

)=6, y is a border

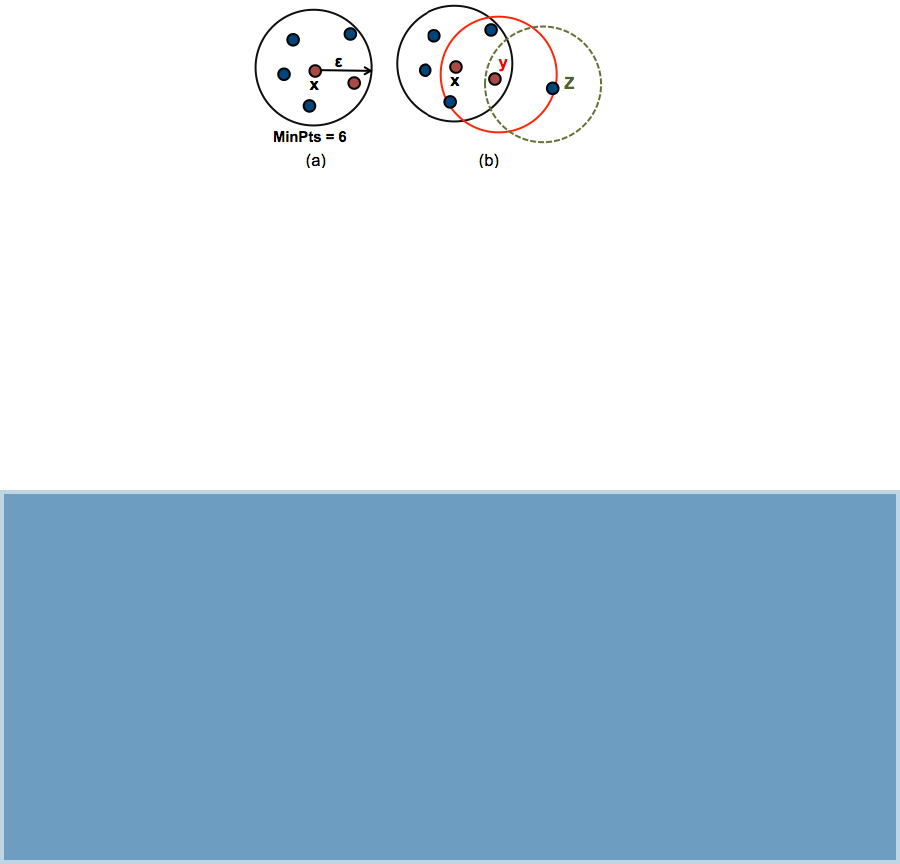
19.3. ADVANTAGES 181

point because

neighbours‘

(

)

< MinP ts

, but it belongs to the

‘

-neighborhood of the

core point x. Finally, z is a noise point.

We start by deﬁning 3 terms, required for understanding the DBSCAN algorithm:

•

Direct density reachable: A point “A” is directly density reachable from another

point “B” if: i) “A” is in the

‘

-neighborhood of “B” and ii) “B” is a core point.

•

Density reachable: A point “A” is density reachable from “B” if there are a set

of core points leading from “B” to “A.

•

Density connected: Two points “A” and “B” are density connected if there are a

core point “C”, such that both “A” and “B” are density reachable from “C”.

A density-based cluster is deﬁned as a group of density connected points. The algorithm

of density-based clustering (DBSCAN) works as follow:

1. For each point

, compute the distance between

and the other points. Finds

all neighbor points within distance eps of the starting point (

). Each point, with a

neighbor count greater than or equal to MinPts, is marked as core point or visited.

2. For each core point, if it’s not already assigned to a cluster, create a

new cluster. Find recursively all its density connected points and assign them to the

same cluster as the core point.

3. Iterate through the remaining unvisited points in the data set.

Those points that do not belong to any cluster are treated as outliers or

noise.

19.3 Advantages

Unlike K-means, DBSCAN does not require the user to specify the number of

clusters to be generated

182 CHAPTER 19. DBSCAN: DENSITY-BASED CLUSTERING

DBSCAN can ﬁnd any shape of clusters. The cluster doesn’t have to be circular.

3. DBSCAN can identify outliers

19.4 Parameter estimation

•

MinPts: The larger the data set, the larger the value of minPts should be chosen.

minPts must be chosen at least 3.

•‘

: The value for

‘

can then be chosen by using a k-distance graph, plotting the

distance to the k = minPts nearest neighbor. Good values of

‘

are where this

plot shows a strong bend.

19.5 Computing DBSCAN

Here, we’ll use the R package fpc to compute DBSCAN. It’s also possible to use the

package dbscan, which provides a faster re-implementation of DBSCAN algorithm

compared to the fpc package.

We’ll also use the factoextra package for visualizing clusters.

First, install the packages as follow:

install.packages("fpc")

install.packages("dbscan")

install.packages("factoextra")

The R code below computes and visualizes DBSCAN using multishapes data set

[factoextra R package]:

# Load the data

data("multishapes",package = "factoextra")

df <- multishapes[, 1:2]

# Compute DBSCAN using fpc package

library("fpc")

set.seed(123)

db <- fpc::dbscan(df, eps = 0.15,MinPts = 5)

19.5. COMPUTING DBSCAN 183

# Plot DBSCAN results

library("factoextra")

fviz_cluster(db, data = df, stand = FALSE,

ellipse = FALSE,show.clust.cent = FALSE,

geom = "point",palette = "jco",ggtheme = theme_classic())

-3

-2

-1

-1 0 1

x value

y value

cluster 12345

Cluster plot

Note that, the function fviz_cluster() uses diﬀerent point symbols for core points

(i.e, seed points) and border points. Black points correspond to outliers. You can

play with eps and MinPts for changing cluster conﬁgurations.

It can be seen that DBSCAN performs better for these data sets and can identify

the correct set of clusters compared to k-means algorithms.

The result of the fpc::dbscan() function can be displayed as follow:

print(db)

## dbscan Pts=1100 MinPts=5 eps=0.15

## 0 1 2 3 4 5

## border 31 24 1 5 7 1

184 CHAPTER 19. DBSCAN: DENSITY-BASED CLUSTERING

## seed 0 386 404 99 92 50

## total 31 410 405 104 99 51

In the table above, column names are cluster number. Cluster 0 corresponds to outliers

(black points in the DBSCAN plot). The function print.dbscan() shows a statistic of

the number of points belonging to the clusters that are seeds and border points.

# Cluster membership. Noise/outlier observations are coded as 0

# A random subset is shown

db$cluster[sample(1:1089,20)]

## [1] 1 3 2 4 3 1 2 4 2 2 2 2 2 2 1 4 1 1 1 0

DBSCAN algorithm requires users to specify the optimal eps values and the parameter

MinPts. In the R code above, we used eps = 0.15 and MinPts = 5. One limitation of

DBSCAN is that it is sensitive to the choice of

‘

, in particular if clusters have diﬀerent

densities. If

‘

is too small, sparser clusters will be deﬁned as noise. If

‘

is too large,

denser clusters may be merged together. This implies that, if there are clusters with

diﬀerent local densities, then a single ‘value may not suﬃce.

A natural question is:

How to deﬁne the optimal value of eps?

19.6 Method for determining the optimal eps

value

The method proposed here consists of computing the k-nearest neighbor distances in

a matrix of points.

The idea is to calculate, the average of the distances of every point to its k nearest

neighbors. The value of k will be speciﬁed by the user and corresponds to MinPts.

Next, these k-distances are plotted in an ascending order. The aim is to determine

the “knee”, which corresponds to the optimal eps parameter.

A knee corresponds to a threshold where a sharp change occurs along the k-distance

curve.

19.7. CLUSTER PREDICTIONS WITH DBSCAN ALGORITHM 185

The function kNNdistplot() [in dbscan package] can be used to draw the k-distance

plot:

dbscan::kNNdistplot(df, k= 5)

abline(h=0.15,lty = 2)

0 1000 3000 5000

0.0 0.2 0.4 0.6

Points (sample) sorted by distance

5-NN distance

It can be seen that the optimal eps value is around a distance of 0.15.

19.7 Cluster predictions with DBSCAN algorithm

The function predict.dbscan(object, data, newdata) [in fpc package] can be used to

predict the clusters for the points in newdata. For more details, read the documentation

(?predict.dbscan).

Chapter 20

References and Further Reading

This book was written in R Markdown inside RStudio. knitr and pandoc converted

the raw Rmarkdown to pdf. This version of the book was built with

(ver. x86_64-

apple-darwin13.4.0, x86_64, darwin13.4.0, x86_64, darwin13.4.0, , 3, 3.2, 2016, 10,

31, 71607, R, R version 3.3.2 (2016-10-31), Sincere Pumpkin Patch),

factoextra

(ver.

1.0.3.900) and ggplot2 (ver. 2.2.1)

References:

•

Brock, G., Pihur, V., Datta, S. and Datta, S. (2008) clValid: An R Package for

Cluster Validation Journal of Statistical Software 25(4).http://www.jstatsoft.

org/v25/i04

•

Charrad M., Ghazzali N., Boiteau V., Niknafs A. (2014). NbClust: An R Package

for Determining the Relevant Number of Clusters in a Data Set. Journal of

Statistical Software, 61(6), 1-36.

•

Chris Fraley, A. E. Raftery, T. B. Murphy and L. Scrucca (2012). mclust Version

4 for R: Normal Mixture Modeling for Model-Based Clustering, Classiﬁcation,

and Density Estimation. Technical Report No. 597, Department of Statistics,

University of Washington. pdf

•

Chris Fraley and A. E. Raftery (2002). Model-based clustering, discriminant

analysis, and density estimation. Journal of the American Statistical Association

97:611:631.

•

Ranjan Maitra. Model-based clustering. Department of Statistics Iowa State

University. http://www.public.iastate.edu/~maitra/stat501/lectures/

•

Kaufman, L. and Rousseeuw, P.J. (1990). Finding Groups in Data: An Intro-

duction to Cluster Analysis. Wiley, New York.

•

Hartigan, J. A. and Wong, M. A. (1979). A K-means clustering algorithm.

186

187

Applied Statistics 28, 100–108.

•

J. C. Dunn (1973): A Fuzzy Relative of the ISODATA Process and Its Use in

Detecting Compact Well-Separated Clusters. Journal of Cybernetics 3: 32-57.

•

J. C. Bezdek (1981): Pattern Recognition with Fuzzy Objective Function Algo-

rithms. Plenum Press, New York Tariq Rashid: “Clustering”.

•

MacQueen, J. (1967) Some methods for classiﬁcation and analysis of multivariate

observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical

Statistics and Probability, eds L. M. Le Cam & J. Neyman, 1, pp. 281–297.

Berkeley, CA: University of California Press.

•

Malika Charrad, Nadia Ghazzali, Veronique Boiteau, Azam Niknafs (2014).

NbClust: An R Package for Determining the Relevant Number of Clusters in

a Data Set. Journal of Statistical Software, 61(6), 1-36. URL http://www.

jstatsoft.org/v61/i06/.

•

Martin Ester, Hans-Peter Kriegel, Joerg Sander, Xiaowei Xu (1996). A Density-

Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise.

Institute for Computer Science, University of Munich. Proceedings of 2nd

International Conference on Knowledge Discovery and Data Mining (KDD-96)

•

Suzuki, R. and Shimodaira, H. An application of multiscale bootstrap resampling

to hierarchical clustering of microarray data: How accurate are these clusters?.

The Fifteenth International Conference on Genome Informatics 2004, P034.

•

Suzuki R1, Shimodaira H. Pvclust: an R package for assessing the uncertainty

in hierarchical clustering. Bioinformatics. 2006 Jun 15;22(12):1540-2. Epub

2006 Apr 4.

•

Theodoridis S, Koutroubas K (2008). Pattern Recognition. 4th edition. Aca-

demic Press.

•

Tibshirani, R., Walther, G. and Hastie, T. (2001). Estimating the number of

data clusters via the Gap statistic. Journal of the Royal Statistical Society B,

63, 411–423. PDF

Kupdf.net Practical Guide To Cluster Analysis In R Unsupervised Machine Learning

(Multivariate%20Analysis%201)%20Alboukadel%20Kassambara-Practical%20Guide%20to%20Cluster%20Analysis%20in%20R.%20Unsupervised%20M

(Multivariate%20Analysis%201)%20Alboukadel%20Kassambara-Practical%20Guide%20to%20Cluster%20Analysis%20in%20R.%20Unsupervised%20M

Navigation menu

Versions of this User Manual:

Views

Navigation