Simpcomp Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 226 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Introduction
- Theoretical foundations
- The new GAP object types of simpcomp
- Functions and operations for the GAP object type SCPolyhedralComplex
- The GAP object types SCSimplicialComplex and SCNormalSurface
- Functions and operations for SCSimplicialComplex
- Creating an SCSimplicialComplex object from a facet list
- Isomorphism signatures
- Generating some standard triangulations
- Generating infinite series of transitive triangulations
- A census of regular and chiral maps
- Generating new complexes from old
- Simplicial complexes from transitive permutation groups
- The classification of cyclic combinatorial 3-manifolds
- Computing properties of simplicial complexes
- Operations on simplicial complexes
- Functions and operations for SCNormalSurface
- (Co-)Homology of simplicial complexes
- Bistellar flips
- Simplicial blowups
- Polyhedral Morse theory
- Forman's discrete Morse theory
- Library and I/O
- Interfaces to other software packages
- Miscellaneous functions
- Property handlers
- A demo session with simpcomp
- simpcomp internals
- References
- Index

simpcomp 2
Abstract
simpcomp is an extension (a so called package) to GAP for working with simplicial complexes in the context
of combinatorial topology. The package enables the user to compute numerous properties of (abstract) sim-
plicial complexes (such as the f-, g- and h-vectors, the face lattice, the fundamental group, the automorphism
group, (co-)homology with explicit basis computation, etc.). It provides functions to generate simplicial
complexes from facet lists, orbit representatives or difference cycles. Moreover, a variety of infinite series of
combinatorial manifolds and pseudomanifolds (such as the simplex, the cross polytope, transitive handle bodies
and sphere bundles, etc.) is given and it is possible to create new complexes from existing ones (links and stars,
connected sums, simplicial cartesian products, handle additions, bistellar flips, etc.). simpcomp ships with
an extensive library of known triangulations of manifolds and a census of all combinatorial 3-manifolds with
transitive cyclic symmetry up to 22 vertices. Furthermore, it provides the user with the possibility to create
own complex libraries. In addition, functions related to slicings and polyhedral Morse theory as well as a
combinatorial version of algebraic blowups and the possibility to resolve isolated singularities of 4-manifolds
are implemented.
simpcomp caches computed properties of a simplicial complex, thus avoiding unnecessary computations,
internally handles the vertex labeling of the complexes and insures the consistency of a simplicial complex
throughout all operations.
If possible, simpcomp makes use of the GAP package homology [DHSW11] for its homology computation
but also provides the user with own (co-)homology algorithms. For automorphism group computation the GAP
package GRAPE [Soi12] is used, which in turn uses the program by Brendan McKay [MP14]. An
internal automorphism group calculation algorithm is used as fallback if the GRAPE package is not available.
Copyright
© 2018 Felix Effenberger and Jonathan Spreer. Permission is granted to copy, distribute and/or modify this
document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published
by the Free Software Foundation, see for a copy.
simpcomp is free software. The code of simpcomp is released under the GPL version 2 or later
(at your preference). For the text of the GPL see the file in the simpcomp directory or
.
Acknowledgements
A few functions of simpcomp are based on code from other authors. The bistellar flips implementation, the al-
gorithm to collapse bounded simplicial complexes as well as the classification algorithm for transitive triangula-
tions is based upon work of Frank Lutz (see [Lut03] and the GAP programs BISTELLAR and MANIFOLD_VT
from [Lut]). Some functions were carried over from the homology package by Dumas et al. [DHSW11] – these
functions are marked in the documentation and the source code. The internal (co-)homology algorithms were
implemented by Armin Weiss.
Most of the complexes in the simplicial complex library are taken from the "Manifold Page" by Frank Lutz
[Lut].
The authors acknowledge support by the Deutsche Forschungsgemeinschaft (DFG): simpcomp has been
developed within the DFG projects Ku 1203/5-2 and Ku 1203/5-3.
simpcomp 3

Contents
1Introduction 7
1.1 Whatisnew.......................................... 7
1.2 simpcomp benefits...................................... 7
1.3 How to save time reading this document . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.4 Organization of this document . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
1.5 How to assure simpcomp works correctly . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.6 Controlling simpcomp log messages . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.7 How to cite simpcomp ................................... 10
2Theoretical foundations 11
2.1 Polytopes and polytopal complexes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.2 Simplices and simplicial complexes . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.3 From geometry to combinatorics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
2.4 Discrete Normal surfaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.5 Polyhedral Morse theory and slicings . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2.6 Discrete Morse theory . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.7 Tightness and tight triangulations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.8 Simplicial blowups . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3The new GAP object types of simpcomp 21
3.1 Accessing properties of a object . . . . . . . . . . . . . . . . 22
4Functions and operations for the GAP object type 24
4.1 Computing properties of objects of type . . . . . . . . . . . . 24
4.2 Vertex labelings and label operations . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
4.3 Operations on objects of type . . . . . . . . . . . . . . . . . . 29
5The GAP object types and 35
5.1 The object type . . . . . . . . . . . . . . . . . . . . . . . . . . 35
5.2 Overloaded operators of . . . . . . . . . . . . . . . . . . . . . 37
5.3 as a subtype of . . . . . . . . . . . . . . . . . . . . . . . 40
5.4 The object type . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
5.5 Overloaded operators of . . . . . . . . . . . . . . . . . . . . . . . . 43
5.6 as a subtype of . . . . . . . . . . . . . . . . . . . . . . . . . . 44
4

simpcomp 5
6Functions and operations for 46
6.1 Creating an object from a facet list . . . . . . . . . . . . . . . 46
6.2 Isomorphism signatures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
6.3 Generating some standard triangulations . . . . . . . . . . . . . . . . . . . . . . . . . . 50
6.4 Generating infinite series of transitive triangulations . . . . . . . . . . . . . . . . . . . 55
6.5 A census of regular and chiral maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
6.6 Generating new complexes from old . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
6.7 Simplicial complexes from transitive permutation groups . . . . . . . . . . . . . . . . 77
6.8 The classification of cyclic combinatorial 3-manifolds . . . . . . . . . . . . . . . . . . 80
6.9 Computing properties of simplicial complexes . . . . . . . . . . . . . . . . . . . . . . 82
6.10 Operations on simplicial complexes . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
7Functions and operations for 119
7.1 Creating an object . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
7.2 Generating new objects from discrete normal surfaces . . . . . . . . . . . . . . . . . . 122
7.3 Properties of objects . . . . . . . . . . . . . . . . . . . . . . . . . . 123
8(Co-)Homology of simplicial complexes 133
8.1 Homology computation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133
8.2 Cohomology computation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135
9Bistellar flips 143
9.1 Theory............................................. 143
9.2 Functions for bistellar flips . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
10 Simplicial blowups 156
10.1 Theory............................................. 156
10.2 Functions related to simplicial blowups . . . . . . . . . . . . . . . . . . . . . . . . . . 156
11 Polyhedral Morse theory 159
11.1 Polyhedral Morse theory related functions . . . . . . . . . . . . . . . . . . . . . . . . . 159
12 Forman’s discrete Morse theory 166
12.1 Functions using discrete Morse theory . . . . . . . . . . . . . . . . . . . . . . . . . . . 166
13 Library and I/O 175
13.1 Simplicial complex library . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175
13.2 simpcomp input / output functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 182
14 Interfaces to other software packages 187
14.1 Interface to the GAP-package homalg ........................... 187
15 Miscellaneous functions 191
15.1 simpcomp logging...................................... 191
15.2 Email notification system . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 192
15.3 Testing the functionality of simpcomp .......................... 194

simpcomp 6
16 Property handlers 195
16.1 Property handlers of . . . . . . . . . . . . . . . . . . . . . . . 195
16.2 Property handlers of . . . . . . . . . . . . . . . . . . . . . . . 196
16.3 Property handlers of . . . . . . . . . . . . . . . . . . . . . . . . . . 199
16.4 Property handlers of . . . . . . . . . . . . . . . . . . . . . . . . . . 199
17 A demo session with simpcomp 200
17.1 Creating a object . . . . . . . . . . . . . . . . . . . . . . . . . 200
17.2 Working with a object . . . . . . . . . . . . . . . . . . . . . . 202
17.3 Calculating properties of a object . . . . . . . . . . . . . . . 202
17.4 Creating new complexes from a object . . . . . . . . . . . . 204
17.5 Homology related calculations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205
17.6 Bistellar flips . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 207
17.7 Simplicial blowups . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209
17.8 Discrete normal surfaces and slicings . . . . . . . . . . . . . . . . . . . . . . . . . . . . 211
18 simpcomp internals 213
18.1 The GAP object type . . . . . . . . . . . . . . . . . . . . . . . . 213
18.2 Example of a common attribute . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 215
18.3 Writing a method for an attribute . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 217
References 222
Index 223

Chapter 1
Introduction
simpcomp is a GAP package that provides the user with functions to do calculations and construc-
tions with simplicial complexes in the context of combinatorial topology (see abstract). If possible, it
makes use of the GAP packages homology [DHSW11] by J.-G. Dumas et al. and GRAPE [Soi12]
by L. Soicher.
Most parts of this manual can be accessed directly from within GAP using its internal help system.
1.1 What is new
simpcomp is a package for working with simplicial complexes. It claims to provide the user with a
broad spectrum of functionality regarding simplicial constructions.
simpcomp allows the user to interactively construct complexes and to compute their properties
in the GAP shell. Furthermore, it makes use of GAP’s expertise in groups and group operations. For
example, automorphism groups and fundamental groups of complexes can be computed and exam-
ined further within the GAP system. Apart from supplying a facet list, the user can as well construct
simplicial complexes from a set of generators and a prescribed automorphism group – the latter form
being the common in which a complex is presented in a publication. This feature is to our knowl-
edge unique to simpcomp. Furthermore, simpcomp as of Version 1.3.0 supports the construction
of simplicial complexes of prescribed dimension, vertex number and transitive automorphism group
as described in [Lut03], [CK01] and a number of functions (function prefix ) provide
infinite series of combinatorial manifolds with transitive automorphism group.
As of Version 1.4.0, simpcomp provides the possibility to perform a combinatorial version of al-
gebraic blowups, so-called simplicial blowups, for combinatorial 4-manfolds as described in [SK11]
and [Spr11a]. The implementation can be used as well to resolve isolated singularities of combinato-
rial 4-pseudomanifolds. It seems that this feature, too, is unique to simpcomp.
Starting from Version 1.5.4, simpcomp comes with more efficient code to perform bistellar moves
implemented in (see function (9.2.15)). However, this feature is completely
optional.
1.2 simpcomp benefits
The origin of simpcomp is a collection of scripts of the two authors [Eff11a], [Spr11a] that
provide basic and often-needed functions and operations for working with simplicial complexes.
Apart from some optional code dealing with bistellar moves (see Section 9and in particular
7

simpcomp 8
(9.2.15)), it is written entirely in the GAP scripting language, thus giving
the user the possibility to see behind the scenes and to customize or alter simpcomp functions if
needed.
The main benefit when working with simpcomp over implementing the needed functions from
scratch is that simpcomp encapsulates all methods and properties of a simplicial complex in a new
GAP object type (as an abstract data type). This way, among other things, simpcomp can transpar-
ently cache properties already calculated, thus preventing unnecessary double calculations. It also
takes care of the error-prone vertex labeling of a complex. As of Version 1.5, simpcomp makes use
of GAP’s caching mechanism (as described in [BL98]) to cache all known properties of a simplicial
complex. In addition, a customized data structure is provided to organize the complex library and to
cache temporary information about a complex.
simpcomp provides the user with functions to save and load the simplicial complexes to and
from files and to import and export a complex in various formats (e.g. from and to polymake/TOPAZ
[GJ00], SnapPea [Wee99] and Regina [BBP+14] (via the SnapPea file format), Macaulay2 [GS],
LaTeX, etc.).
In contrast to the software package polymake [GJ00] providing the most efficient algorithms
for each task in form of a heterogeneous package (where algorithms are implemented in various
languages), the primary goal when developing simpcomp was not efficiency (this is already limited
by the GAP scripting language), but rather ease of use and ease of extensibility by the user in the
GAP language with all its mathematical and algebraic capabilities. Extending simpcomp is possible
directly from within GAP, without having to compile anything, see Chapter 18.
1.3 How to save time reading this document
The core component in simpcomp is the newly defined object types and its de-
rived subtype . When working with this package it is important to understand
how objects of these types can be created, accessed and modified. The reader is therefore advised to
first skim over the Chapters 3and 5.
The impatient reader may then directly skip to Chapter 17 to see simpcomp in action.
The next advised step is to have a look at the functions for creating objects of type
, see the first section of Chapter 6.
The rest of Chapter 6contains most of the functions that simpcomp provides, except for the func-
tions related to (co-)homology, bistellar flips, simplicial blowups, polyhedral Morse theory, slicings
(discrete normal surfaces) and the simplicial complex library that are described in the Chapters 8to
13. Functions for the more general GAP object type are described in Chapter
4.
1.4 Organization of this document
This manual accompanying simpcomp is organized as follows.
• Chapter 2provides a short introduction into the theory of simplicial complexes and PL-
topology.
• Chapter 3gives a short overview about the newly defined GAP object types simpcomp is
working with.

simpcomp 9
• Chapter 4is devoted to the description of the GAP object type that is
defined by simpcomp.
• Chapter 5introduce the GAP object types and
which are both derived from .
• In Chapter 6functions for working with simplicial complexes are described.
• Chapter 7gives an overview over functions related to slicings / discrete normal surfaces.
• Chapter 8describes the homology- and cohomology-related functions of simpcomp.
• Chapter 9contains a description of the functions related to bistellar flips provided by simp-
comp.
• In Chapter 10 simplicial blowups and resolutions of singularities of combinatorial 4-
pseudomanifolds are explained.
• In Chapter 11 polyhedral Morse theory is discussed.
• In Chapter 13 the simplicial complex library and the input output functionality that simpcomp
provides is described in detail.
• Chapter 15 contains descriptions of functions not fitting in the other chapters, such as the error
handling and the email notification system of simpcomp.
• Chapter 16 contains a list of all property handlers allowing to access properties of a
object, a object or a object via
the dot operator (pseudo object orientation).
• Chapter 17 contains the transcript of a demo session with simpcomp showing some of the con-
structions and calculations with simplicial complexes that can also be used as a first overview
of things possible with this package.
• Finally, Chapter 18 focuses on the description of the internal structure of simpcomp and deals
with aspects of extending the functionality of the package.
1.5 How to assure simpcomp works correctly
As with all software, it is important to test whether simpcomp functions correctly on your system
after installing it. GAP has an internal testing mechanism and simpcomp ships with a short testing
file that does some sample computations and verifies that the results are correct.
To test the functionality of simpcomp you can run the function (15.3.1) from the
GAP console:
(15.3.1) should return , otherwise the correct functionality of simpcomp cannot be
guaranteed.
simpcomp 10
1.6 Controlling simpcomp log messages
Note that the verbosity of the output of information to the screen during calls to functions of the pack-
age simpcomp can be controlled by setting the info level parameter via the function
(15.1.1).
1.7 How to cite simpcomp
If you would like to cite simpcomp using BibTeX, you can use the following BibTeX entry for the
current simpcomp version (remember to include the package in your L
A
T
EX document):
If you are not using BibTeX, you can use the following entry inside the bibliography environment of
LaTeX.

Chapter 2
Theoretical foundations
The purpose of this chapter is to recall some basic definitions regarding polytopes, triangula-
tions, polyhedral Morse theory, discrete normal surfaces, slicings, tight triangulations and simplicial
blowups. The expert in these fields may well skip to the next chapter.
For a more detailed look the authors recommend the books [Hud69], [RS72] on PL-topology and
[Zie95], [Grü03] on the theory of polytopes.
An overview of the more recent developments in the field of combinatorial topology can be found
in [Lut05] and [Dat07].
2.1 Polytopes and polytopal complexes
A convex d-polytope is the convex hull of npoints pi∈Edin the d-dimensional euclidean space:
P=conv
{v1,...,vn}⊂Ed,where the v1,...,vndo not lie in a hyperplane of Ed.
From now on when talking about polytopes in this document always convex polytopes are meant
unless explicitly stated otherwise.
For any supporting hyperplane h⊂Ed,P∩his called a k-face of Pif dim(P∩h)=k. The 0-faces
are called vertices, the 1-faces edges and the (d−1)-faces are called facets of P.
Ad-polytope Pfor which all facets are congruent regular (d−1)-polytopes and for which all
vertex links are congruent regular (d−1)-polytopes is called regular, where the regular 2-polytopes
are regular polygons.
Figure 1 below shows the only five regular convex 3-polytopes (also known as platonic solids).
Figure 1. The platonic solids as the five regular convex 3-polytopes.
The set of all k-faces of Pis called the k-skeleton of P, written as skelk(P).
11
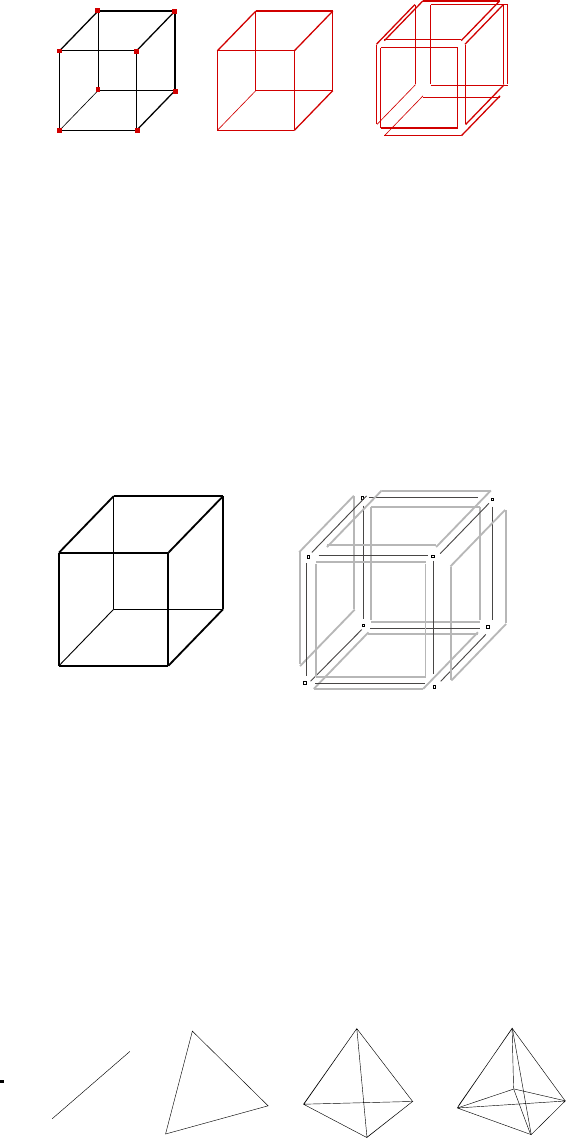
simpcomp 12
Figure 2. From left to right, drawn in grey: the 0-skeleton, the 1-skeleton and the 2-skeleton of the cube.
Apolytopal complex C is a finite collection of polytopes P
i, 1 ≤i≤nfor which the intersection of
any two polytopes P
i∩Pjis either empty or a common face of P
iand Pj. The polytopes of maximal
dimension are called the facets of C. The dimension of a polytopal complex Cis defined as the
maximum over all dimensions of its facets.
For every d-dimensional polytopal complex the (d+1)-tuple, containing its number of i-faces in
the i-th entry is called the f -vector of the polytopal complex.
Every polytope Pgives rise to a polytopal complex consisting of all the proper faces of P. This
polytopal complex is called the boundary complex C(∂P)of the polytope P.
Figure 2 below shows the boundary complex of the cube.
Figure 3. The 3-cube (left) and its boundary complex (right) where the 0-faces shown in black, the 1-faces
dark gray and the 2-faces in light gray.
2.2 Simplices and simplicial complexes
Ad-dimensional simplex or d-simplex for short is the convex hull of d+1 points in Edin general
position. Thus the d-simplex is the smallest (with respect to the number of vertices) possible d-
polytope. Every face of the d-simplex is a m-simplex, m≤d.
A 0-simplex is a point, a 1-simplex is a line segment, a 2-simplex is a triangle, a 3-simplex a
tetrahedron, and so on.
Figure 4. From left to right: a 0-simplex, a 1-simplex, a 2-simplex, a 3-simplex and a Schlegel diagram of a
4-simplex.
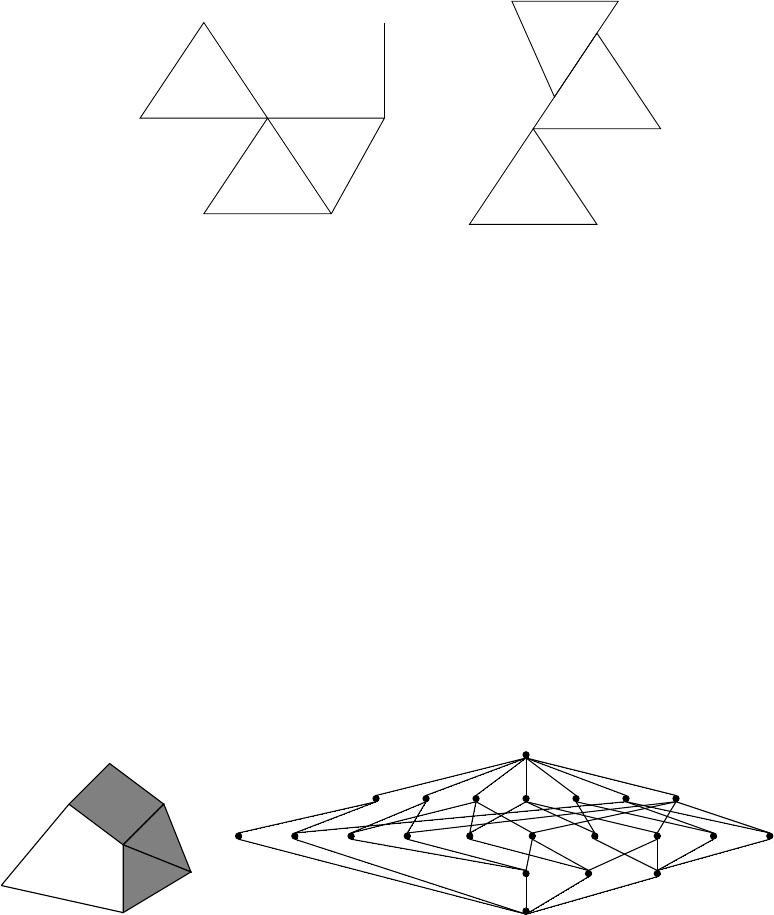
simpcomp 13
A polytopal complex which entirely consists of simplices is called a simplicial complex (for this it
actually suffices that the facets (i. e., the faces that are not included in any other face of the complex)
of a polytopal complex are simplices).
Figure 4. A simplicial complex (left) and a collection of simplices that does not form a simplicial complex
(right).
The dimension of a simplicial complex is the maximal dimension of a facet. A simplicial complex
is said to be pure if all facets are of the same dimension. A pure simplicial complex of dimension d
satisfies the weak pseudomanifold property if every (d−1)-face is part of exactly two facets.
Since simplices are polytopes and, hence, simplicial complexes are polytopal complexes all of the
terminology regarding simplicial complexes can be transfered from polytope theory.
2.3 From geometry to combinatorics
Every d-simplex has an underlying set in Ed, as the set of all points of that simplex. In the same way
one can define the underlying set Cof a simplicial complex C. If the underlying set of a simplicial
complex Cis a topological manifold, then Cis called triangulated manifold (or triangulation of C).
One can also go the other way and assign an abstract simplicial complex to a geometrical one by
identifying each simplex with its vertex set. This obviously defines a set of sets with a natural partial
ordering given by the inclusion (a socalled poset).
1
6
5
4
7
2
3
{1} {2}
{12} {16} {23} {27}
{3}
{34}
ø
{37}
{4} {5} {6} {7}
{47}{45}
{237} {347}
C
{4567}
{56} {67}
Figure 5. A geometrical polytopal complex (left) and its abstract version in form of a poset (right).
Let vbe a vertex of C. The set of all facets that contain vis called star of v in C and is denoted by
starC(v). The subcomplex of starC(v)that contains all faces not containing vis called link of v in C,
written as lkC(v).
Acombinatorial d-manifold is a d-dimensional simplicial complex whose vertex links are all tri-
angulated (d−1)-dimensional spheres with standard PL-structure. A combinatorial pseudomanifold
is a simplicial complex whose vertex links are all combinatorial (d−1)-manifolds.
simpcomp 14
1
2
3
1
1
2
3
1
4 5
4 5
6
7
Figure 6. A simplicial complex that is a vertex-minimal combinatorial triangulation of the torus T2(so called
Möbius’ torus) – each vertex link is a hexagon.
Note that every combinatorial manifold is a triangulated manifold. The opposite is wrong: for
example, there exists a triangulation of the 5-sphere that is not combinatorial, the so called Edward’s
sphere, see [BL00].
A combinatorial manifold carries an induced PL-structure and can be understood in terms of an
abstract simplicial complex. If the complex has dvertices there exists a natural embedding of Cinto
the (d−1)simplex and, thus, into Ed−1. In general, there is no canonical embedding into any lower
dimensional space. However, combinatorial methods allow to examine a given simplicial complex
independently from an embedding and, in particular, independently from vertex coordinates.
Some fundamental properties of an abstract simplicial complex Care the following:
Dimensionality.
The dimension of C.
f,gand h-vector.
The f-vector ( fkequals the number of k-faces of a simplicial complex), the g- and h-vector can
be obtained from the f-vector via linear transformations.
(Co-)Homology.
The simplicical (co-)homology groups and Betti numbers.
Euler characteristic
The Euler characteristic as the alternating sum over the Betti numbers / the f-vector.
Connectedness and closedness.
Whether Cis strongly connected, path connected, has a boundary or not.
Symmetries.
The automorphism group, i. e. the group of all permutations on the set of vertex labels that do
not change the complex as a whole.
All of those properties and many more can be computed on a strictly combinatorial basis.
simpcomp 15
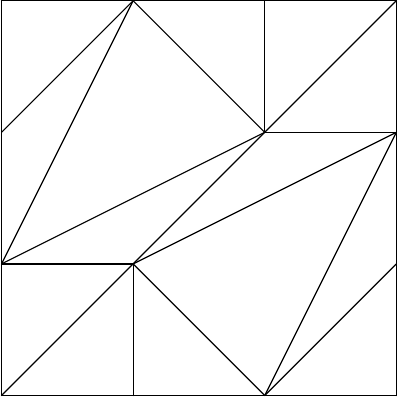
2.4 Discrete Normal surfaces
The concept of normal surfaces is originally due to Kneser [Kne29] and Haken [Hak61]: A surface S,
properly embedded into a 3-manifold M, is said to be normal, if it respects a given cell decomposition
of Min the following sense: It does not intersect any vertex nor touch any 3-cell of the manifold and
does not intersect with any 2-cell in a circle or an arc starting and ending in a point of the same edge.
Here we will look at normal surfaces in the case that Mis given as a combinatorial 3-manifold and
we will call the corresponding objects discrete normal surfaces. In order to do this let us first define:
DEFINITION
Apolytopal manifold is a polytopal complex Msuch that there exists a simplicial subdivision of M
which is a combinatorial manifold. If Mis a surface we will call it a polytopal map. If, in addition M
entirely consists of m-gons, we call it a polytopal m-gon map.
DEFINITION (Discrete Normal surface, [Spr11b])
Let Mbe a combinatorial 3-manifold (3-pseudomanifold), ∆∈Mone of its tetrahedra and Pthe
intersection of ∆with a plane that does not include any vertex of ∆. Then Pis called a normal subset
of ∆. Up to an isotopy that respects the face lattice of ∆,Pis equal to one of the triangles P
i, 1 ≤i≤4,
or quadrilaterals P
i, 5 ≤i≤7, shown in Figure 7.
A polyhedral map S⊂Mthat entirely consists of facets P
isuch that every tetrahedron contains
at most one facet is called discrete normal surface of M.
The second author has recently investigated on the combinatorial theory of discrete normal
surfaces, see [Spr11b].
P5P6
P7
P1
P2
P3
P4
(1;0;0;0;0;0;0) (0;1;0;0;0;0;0) (0;0;1;0;0;0;0) (0;0;0;1;0;0;0)
(0;0;0;0;1;0;0) (0;0;0;0;0;1;0) (0;0;0;0;0;0;1) (0;1;0;0;0;0;2)
2 2 2 2
2 2 2 2
4 4 4 4
4 4 4 4
3 3 3 3
3 3 3 3
1 1 1 1
1 1 1 1
Figure 7. The seven different normal subsets of the tetrahedron. Note that the rightmost picture of the bottom
row can not be part of a discrete normal surface.
2.5 Polyhedral Morse theory and slicings
In the field of PL-topology Kühnel developed what one might call a polyhedral Morse theory
(compare [Küh95], not to be confused with Forman’s discrete Morse theory for cell complexes which
simpcomp 16
is decribed in Section 2.6):
Let Mbe a combinatorial d-manifold. A function f∶M→Ris called regular simplexwise lin-
ear (rsl) if f(v)≠f(w)for any two vertices w≠vand if fis linear when restricted to an arbitrary
simplex of the triangulation.
A vertex x∈Mis said to be critical for an rsl-function f∶M→R, if H⋆(Mx,Mx{x},F)≠0
where Mx∶={y∈Mf(y)≤f(x)} and Fis a field.
It follows that no point of Mcan be critical except possibly the vertices. In arbitrary dimen-
sions we define:
DEFINITION (Slicing, [Spr11b])
Let Mbe a combinatorial pseudomanifold of dimension dand f∶M→Ran rsl-function. Then we
call the pre-image f−1(α)aslicing of Mwhenever α≠f(v)for any vertex v∈M.
By construction, a slicing is a polytopal (d−1)-manifold and for any ordered pair α≤βwe
have f−1(α)≅f−1(β)whenever f−1([α,β]) contains no vertex of M. In particular, a slicing Sof
a closed combinatorial 3-manifold Mis a discrete normal surface: It follows from the simplexwise
linearity of fthat the intersection of the pre-image with any tetrahedron of Meither forms a single
triangle or a single quadrilateral. In addition, if two facets of Slie in adjacent tetrahedra they ei-
ther are disjoint or glued together along the intersection line of the pre-image and the common triangle.
Any partition of the set of vertices V=V1˙
∪V2of Malready determines a slicing: Just define
an rsl-function f∶M→Rwith f(v)≤f(w)for all v∈V1and w∈V2and look at a suitable pre-image.
In the following we will write S(V1,V2)for the slicing defined by the vertex partition V=V1˙
∪V2.
Every vertex of a slicing is given as an intersection point of the corresponding pre-image with
an edge u,wof the combinatorial manifold. Since there is at most one such intersection point per
edge, we usually label this vertex of the slicing according to the vertices of the corresponding edge,
that is u
wwith u∈V1and w∈V2.
Every slicing decomposes the surrounding combinatorial manifold Minto at least 2 pieces (an
upper part M+and a lower part M−). This is not the case for discrete normal surfaces (see 2.4) in
general. However, we will focus on the case where discrete normal surfaces are slicings and we will
apply the above notation for both types of objects.
Since every combinatorial pseudomanifold Mhas a finite number of vertices, there exist only
a finite number of slicings of M. Hence, if fis chosen carefully, the induced slicings admit a useful
visualization of M, c.f. [SK11].
simpcomp 17
12
3
4
1
32
3
1
42
4
f−1(α)
fα
S2R
Figure 8. One dimensional slicing of the 2-sphere (represented as the boundary of the 3-simplex) seen as a
level set of a regular point of a simplicial Morse function.
1
4
1
5
1
6
1
4
2
4
2
5
2
62
4
3
4
3
5
3
63
4
1
4
1
5
1
6
1
4
Figure 9. Handlebody decomposition of genus 1 of a 6-vertex 3-sphere - a 3×3-grid torus.
2
5
2
8
4
5
4
8
2
7
3
7
3
8
1
7
3
6
1
5
1
6
4
6
Figure 10. Separating sphere of an 8-vertex cylinder S2
4×[0,1]- A cuboctahedron (drawn as a Schlegel
diagram of a quadrilateral face).
simpcomp 18
2.6 Discrete Morse theory
For an introduction into Forman’s discrete Morse theory see [For95], not to be confused with
Banchoff and Kühnel’s theory of regular simplexwise linear functions which is described in Section
2.5).
2.7 Tightness and tight triangulations
Tightness is a notion developed in the field of differential geometry as the equality of the (normalized)
total absolute curvature of a submanifold with the lower bound sum of the Betti numbers [Kui84],
[BK97]. It was first studied by Alexandrov, Milnor, Chern and Lashof and Kuiper and later
extended to the polyhedral case by Banchoff [Ban65], Kuiper [Kui84] and Kühnel [Küh95]. From a
geometrical point of view, tightness can be understood as a generalization of the concept of convexity
that applies to objects other than topological balls and their boundary manifolds since it roughly
means that an embedding of a submanifold is “as convex as possible” according to its topology. The
usual definition is the following:
DEFINITION (Tightness, [Küh95])
Let Fbe a field. An embedding M→ENof a compact manifold is called k-tight with respect to Fif
for any open or closed halfspace h⊂ENthe induced homomorphism
Hi(M∩h;F)Ð→ Hi(M;F)
is injective for all i≤k.Mis called F-tight if it is k-tight for all k. The standard choice for the field of
coefficients is F2and an F2-tight embedding is called tight.
With regard to PL embeddings of PL manifolds tightness of combinatorial manifolds can also
be defined via a purely combinatorial condition as follows. For an introduction to PL topology see
[RS72].
DEFINITION (Tight triangulation [Küh95])
Let Fbe a field. A combinatorial manifold Kon nvertices is called (k-) tight w.r.t. Fif its canonical
embedding K⊂∆n−1⊂En−1is (k-)tight w.r.t. F, where ∆n−1denotes the (n−1)-dimensional simplex.
In dimension d=2 the following are equivalent for a triangulated surface Son nvertices: (i)
Shas a complete edge graph Kn, (ii) Sappears as a so called regular case in Heawood’s Map Color
Theorem [Rin74], compare [Küh95] and (iii) the induced piecewise linear embedding of Sinto
Euclidean (n−1)-space has the two-piece property [Ban74], and it is tight [Küh95].
Kühnel investigated the tightness of combinatorial triangulations of manifolds also in higher
dimensions and codimensions, see [Küh94]. It turned out that the tightness of a combinatorial
triangulation is closely related to the concept of Hamiltonicity of a polyhedral complexes (see
[Küh95]): A subcomplex Aof a polyhedral complex Kis called k-Hamiltonian if Acontains the
full k-dimensional skeleton of K(not to be confused with the notion of a k-Hamiltonian graph).
This generalization of the notion of a Hamiltonian circuit in a graph seems to be due to C.Schulz

simpcomp 19
[Sch94]. A Hamiltonian circuit then becomes a special case of a 0-Hamiltonian subcomplex of a
1-dimensional graph or of a higher-dimensional complex.
A triangulated 2k-manifold that is a k-Hamiltonian subcomplex of the boundary complex of
some higher dimensional simplex is a tight triangulation as Kühnel [Küh95] showed. Such a
triangulation is also called (k+1)-neighborly triangulation since any k+1 vertices in a k-dimensional
simplex are common neighbors. Moreover, (k+1)-neighborly triangulations of 2k-manifolds are also
referred to as super-neighborly triangulations – in analogy with neighborly polytopes the boundary
complex of a (2k+1)-polytope can be at most k-neighborly unless it is a simplex. Notice here that
combinatorial 2k-manifolds can go beyond k-neighborliness, depending on their topology.
Whereas in the 2-dimensional case all tight triangulations of surfaces were classified by Ringel and
Jungerman and Ringel, in dimensions d≥3 there exist only a finite number of known examples of
tight triangulations (see [KL99] for a census) apart from the trivial case of the boundary of a simplex
and an infinite series of triangulations of sphere bundles over the circle due to Kühnel [Küh95],
[Küh86].
2.8 Simplicial blowups
The blowing up process or Hopf σ-process can be described as the resolution of nodes or ordinary
double points of a complex algebraic variety. This was described by H. Hopf in [Hop51], compare
[Hir53] and [Hau00]. From the topological point of view the process consists of cutting out some
subspace and gluing in some other subspace. In complex algebraic geometry one point is replaced by
the projective line CP1≅S2of all complex lines through that point. This is often called blowing up
of the point or just blowup. In general the process can be applied to non-singular 4-manifolds and
yields a transformation of a manifold Mto M#(+CP2)or M#(−CP2), depending on the choice of an
orientation. The same construction is possible for nodes or ordinary double points (a special type of
singularities), and also the ambiguity of the orientation is the same for the blowup process of a node.
Similarly it has been used in arbitrary even dimension by Spanier [Spa56] as a so-called dilatation
process.
A PL version of the blowing up process is the following: We cut out the star of one of the
singular vertices which is, in the case of an ordinary double point, nothing but a cone over a
triangulated RP3. The boundary of the resulting space is this triangulated RP3. Now we glue back in
a triangulated version Cof a complex projective plane with a 4-ball removed where antipodal points
of the boundary are identified. Cis called a triangulated mapping cylinder and by construction its
boundary is PL homeomorphic to RP3.
For a combinatorial version with concrete triangulations, however, we face the problem that
these two triangulations are not isomorphic. This implies that before cutting out and gluing in we
have to modify the triangulations by bistellar moves until they coincide:
DEFINITION (Simplicial blowup, [SK11])
Let vbe a vertex of a combinatorial 4-pseudomanifold Mwhose link is isomorphic with the particular
11-vertex triangulation of RP3which is given by the boundary complex of the triangulated Cgiven
in [SK11]. Let ψ∶lk(v)→∂Cdenote such an isomorphism. A simplicial resolution of the singularity

Chapter 3
The new GAP object types of simpcomp
In order to meet the particular requirements of piecewise linear geometric objects and their invariants,
simpcomp defines a number of new GAP object types.
All new object types are derived from the object type which is a subtype
of . It is a GAP object consisting of permanent and temporary attributes. While simpcomp
makes use of GAP’s internal attribute caching mechanism for permanent attributes (see below), this
is not the case for temporary ones.
The temporary properties of a can be accessed directly with the functions
and changed with . But this direct access to property
objects is discouraged when working with simpcomp, as the internal consistency of the objects cannot
be guaranteed when the properties of the objects are modified in this way.
Important note: The temporary properties of are not used to hold properties
(in the GAP sense) of simplicial complexes or other geometric objects. This is done by the GAP4 type
system [BL98]. Instead, the properties handled by simpcomp’s own caching mechanism are used to
store changing information, e.g. the complex library (see Section 13) of the package or any other data
which possibly is subject to changes (and thus not suited to be stored by the GAP type system).
To realize its complex library (see Section 13), simpcomp defines a GAP object type
which provides the possibility to store, load, etc. any defined geometric object
to and from the build-in complex library as well as customized user libraries. In addition, a searching
mechanism is provided.
Geometric objects are represented by the GAP object type , which as well
is a subtype of . is designed to represent any kind of
piecewise linear geometric object given by a certain cell decomposition. Here, as already mentioned,
the GAP4 type system [BL98] is used to cache properties of the object. In this way, a property is not
calculated multiple times in case the object is not altered (see (5.1.4) for a
way of dropping previously calculated properties).
As of Version 1.4, simpcomp makes use of two different subtypes of :
to handle simplicial complexes and to deal with dis-
crete normal surfaces (slicings of dimension 2). Whenever possible, only one method per opera-
tions is implemented to deal with all subtypes of , these functions are de-
scribed in Chapter 4. For all other operations, the different methods for and
are documented separately.
21

simpcomp 22
3.1 Accessing properties of a object
As described above the object type (and thus also the GAP object types
and ) has properties that are handled by the GAP4 type
system. Hence, GAP takes care of the internal consistency of objects of type .
There are two ways of accessing properties of a object. The first is
to call a property handler function of the property one wishes to calculate. The first argument of
such a property handler function is always the simplicial complex for which the property should be
calculated, in some cases followed by further arguments of the property handler function. An example
would be:
Here the functions and are the property handler functions, see Chapter 16 for a list
of all property handlers of a , or
object. Apart from this (standard) method of calling the property handlers directly with a
object, simpcomp provides the user with another more object oriented
method which calls property handlers of a object indirectly and more conve-
niently:
Note that the code in this example calculates the same properties as in the first example above, but
the properties of a object are accessed via the operator (the record access
operator).
For each property handler of a object the object oriented form of this
property handler equals the name of the corresponding operation. However, in most cases abbrevi-
ations are available: Usually the prefix “ ” can be dropped, in other cases even shorter names are
available. See Chapter 16 for a complete list of all abbreviations available.
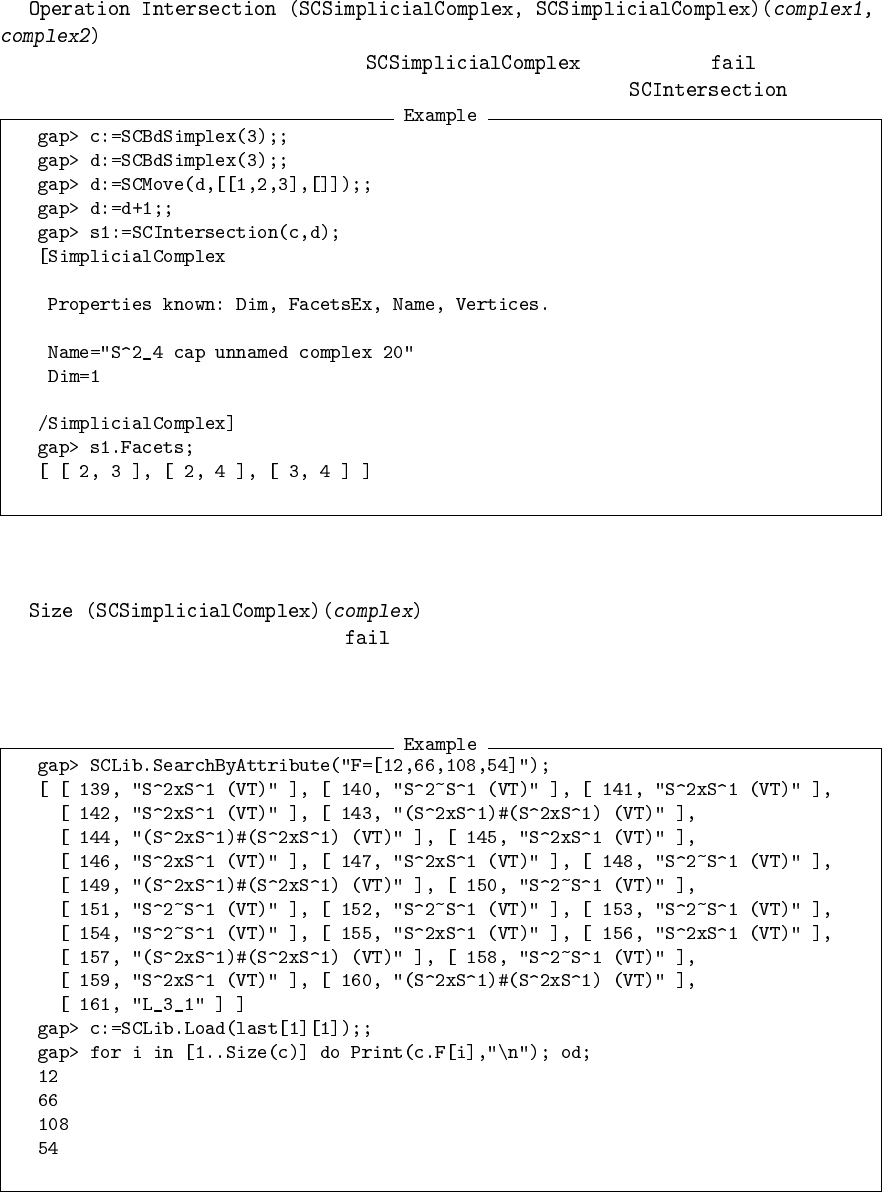
simpcomp 23
SCPropertyObject
SCLibRepository SCPolyhedralComplex
SCNormalSurface SCSimplicialComplex
Figure 11. Overview over all GAP object types defined by simpcomp.
Chapter 4
Functions and operations for the GAP
object type
In the following all operations for the GAP object type are listed. I. e. for
the following operations only one method is implemented to deal with all geometric objects derived
from this object type.
4.1 Computing properties of objects of type
The following functions compute basic properties of objects of type (and
thus also of objects of type and ). None of these functions
alter the complex. All properties are returned as immutable objects (this ensures data consistency of
the cached properties of a simplicial complex). Use or the internal simpcomp function
to get a mutable copy.
Note: every object is internally stored with the standard vertex labeling from 1 to nand a maptable
to restore the original vertex labeling. Thus, we have to relabel some of the complex properties (facets,
etc...) whenever we want to return them to the user. As a consequence, some of the functions exist
twice, one of them with the appendix "Ex". These functions return the standard labeling whereas the
other ones relabel the result to the original labeling.
4.1.1 SCFacets
▷(method)
Returns: a facet list upon success, otherwise.
Returns the facets of a simplicial complex in the original vertex labeling.
4.1.2 SCFacetsEx
▷(method)
Returns: a facet list upon success, otherwise.
24

simpcomp 25
Returns the facets of a simplicial complex as they are stored, i. e. with standard vertex labeling
from 1 to n.
4.1.3 SCVertices
▷(method)
Returns: a list of vertex labels of upon success, otherwise.
Returns the vertex labels of a simplicial complex .
4.1.4 SCVerticesEx
▷(method)
Returns: [1,...,n]upon success, otherwise.
Returns [1,...,n], where nis the number of vertices of a simplicial complex .
4.2 Vertex labelings and label operations
This section focuses on functions operating on the labels of a complex such as the name or the vertex
labeling.
Internally, simpcomp uses the standard labeling [1,...,n]. It is recommended to use simple ver-
tex labels like integers and, whenever possible, the standard labeling, see also
(4.2.7).
4.2.1 SCLabelMax
▷(method)
Returns: vertex label of (an integer, a short list, a character, a short string) upon
success, otherwise.
The maximum over all vertex labels is determined by the GAP function .

simpcomp 26
4.2.2 SCLabelMin
▷(method)
Returns: vertex label of (an integer, a short list, a character, a short string) upon
success, otherwise.
The minimum over all vertex labels is determined by the GAP function .
4.2.3 SCLabels
▷(method)
Returns: a list of vertex labels of (a list of integers, short lists, characters, short strings,
...) upon success, otherwise.
Returns the vertex labels of as a list. This is a synonym of (4.1.3).
4.2.4 SCName
▷(operation)
Returns: a string upon success, otherwise.
Returns the name of a simplicial complex .

simpcomp 27
4.2.5 SCReference
▷(operation)
Returns: a string upon success, otherwise.
Returns a literature reference of a polyhedral complex .
4.2.6 SCRelabel
▷(method)
Returns: upon success, otherwise.
has to be a list of length nwhere nis the number of vertices of . The function
maps the i-th entry of to the i-th entry of the current vertex labels. If has the
standard vertex labeling [1,...,n]the vertex label iis mapped to .
Note that the elements of must admit a total ordering. Hence, following Section 4.11
of the GAP manual, they must be members of one of the following families: rationals , cyclo-
tomics , finite field elements , permutations , booleans , charac-
ters and lists (strings) .
Internally the property “SCVertices” of is replaced by

simpcomp 28
4.2.7 SCRelabelStandard
▷(method)
Returns: upon success, otherwise.
Maps vertex labels v1,...,vnof to [1,...,n]. Internally the property "SCVertices" is
replaced by [1,...,n].
4.2.8 SCRelabelTransposition
▷(method)
Returns: upon success, otherwise.
Permutes vertex labels of a single pair of vertices. has to be a list of length 2 and a sublist
of the property “SCVertices”.
The function is equivalent to (4.2.6) with =
[SCVertices[1],...,SCVertices[j],...,SCVertices[i],...,SCVertices[n]] if =
[SCVertices[j],SCVertices[i]],j≤i,j≠i.
4.2.9 SCRename
▷(method)
Returns: upon success, otherwise.
Renames a polyhedral complex. The argument has to be given in form of a string.

simpcomp 29
4.2.10 SCSetReference
▷(method)
Returns: upon success, otherwise.
Sets the literature reference of a polyhedral complex. The argument has to be given in form
of a string.
4.2.11 SCUnlabelFace
▷(method)
Returns: a list upon success, otherwise.
Computes the standard labeling of in .
4.3 Operations on objects of type
The following functions perform operations on objects of type and all of its
subtypes. Most of them return simplicial complexes. Thus, this section is closely related to the Sec-
tions 6.6 (for objects of type ), ”Generate new complexes from old”. How-
ever, the data generated here is rather seen as an intrinsic attribute of the original complex and not as
an independent complex.
4.3.1 SCAntiStar
▷(method)
Returns: simplicial complex of type upon success, otherwise .
Computes the anti star of (a face given as a list of vertices or a scalar interpreted as vertex)
in , i. e. the complement of in .

simpcomp 30
4.3.2 SCLink
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Computes the link of (a face given as a list of vertices or a scalar interpreted as vertex) in
a polyhedral complex , i. e. all facets containing , reduced by . if is
pure, the resulting complex is of dimension dim( ) - dim( ) −1. If is not a face of
the empty complex is returned.
4.3.3 SCLinks
▷(method)
Returns: a list of simplicial complexes of type upon success,
otherwise.
Computes the link of all -faces of the polyhedral complex and returns them as a list of
simplicial complexes. Internally calls (4.3.2) for every -face of .

simpcomp 31

simpcomp 32

simpcomp 33
4.3.4 SCStar
▷(method)
Returns: simplicial complex of type upon success, otherwise .
Computes the star of (a face given as a list of vertices or a scalar interpreted as vertex) in a
polyhedral complex , i. e. the set of facets of that contain .
4.3.5 SCStars
▷(method)
Returns: a list of simplicial complexes of type upon success,
otherwise.
Computes the star of all -faces of the polyhedral complex and returns them as a list of
simplicial complexes. Internally calls (4.3.4) for every -face of .

simpcomp 34

Chapter 5
The GAP object types
and
Currently, the GAP package simpcomp supports data structures for two different kinds of geo-
metric objects, namely simplicial complexes ( ) and discrete normal surfaces
( ) which are both subtypes of the GAP object type
5.1 The object type
A major part of simpcomp deals with the object type . For a complete
list of properties that handles, see Chapter 6. For a few fundamental
methods and functions (such as checking the object class, copying objects of this type, etc.) for
see below.
5.1.1 SCIsSimplicialComplex
▷(filter)
Returns: or upon success, otherwise.
Checks if is of type . The object type is
derived from the object type .
5.1.2 SCCopy
▷(method)
Returns: a copy of upon success, otherwise.
Makes a “deep copy” of – this is a copy such that all properties of the copy can be altered
without changing the original complex.
35

simpcomp 36
5.1.3 ShallowCopy (SCSimplicialComplex)
▷(method)
Returns: a copy of upon success, otherwise.
Makes a copy of . This is actually a “deep copy” such that all properties of the copy can
be altered without changing the original complex. Internally calls (7.2.1).
5.1.4 SCPropertiesDropped
▷(function)
Returns: a object of type upon success, otherwise.
An object of the type caches its previously calculated properties such
that each property only has to be calculated once. This function returns a copy of with all
properties (apart from Facets, Dim and Name) dropped, clearing all previously computed properties.
See also (18.1.8) and (18.1.13).

simpcomp 37
5.2 Overloaded operators of
simpcomp overloads some standard operations for the object type if this
definition is intuitive and mathematically sound. See a list of overloaded operators below.
5.2.1 Operation + (SCSimplicialComplex, Integer)
▷(method)
Returns: the simplicial complex passed as argument upon success, otherwise.
Positively shifts the vertex labels of (provided that all labels satisfy the property
) by the amount specified in .
5.2.2 Operation - (SCSimplicialComplex, Integer)
▷(method)
Returns: the simplicial complex passed as argument upon success, otherwise.
Negatively shifts the vertex labels of (provided that all labels satisfy the property
) by the amount specified in .
5.2.3 Operation mod (SCSimplicialComplex, Integer)
▷(method)
Returns: the simplicial complex passed as argument upon success, otherwise.

simpcomp 38
Takes all vertex labels of modulo the value specified in (provided that all labels
satisfy the property ). Warning: this might result in different vertices being
assigned the same label or even in invalid facet lists, so be careful.
5.2.4 Operation (SCSimplicialComplex, Integer)
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Forms the -th simplicial cartesian power of , i.e. the -fold cartesian
product of copies of . The complex passed as argument is not altered. Internally calls
(6.6.1).
5.2.5 Operation + (SCSimplicialComplex, SCSimplicialComplex)
▷
(method)
Returns: simplicial complex of type upon success, otherwise.
Forms the connected sum of and . Uses the lexicographically first facets of
both complexes to do the gluing. The complexes passed as arguments are not altered. Internally calls
(6.6.5).

simpcomp 39
5.2.6 Operation - (SCSimplicialComplex, SCSimplicialComplex)
▷
(method)
Returns: simplicial complex of type upon success, otherwise.
Calls (6.10.5)( , )
5.2.7 Operation * (SCSimplicialComplex, SCSimplicialComplex)
▷
(method)
Returns: simplicial complex of type upon success, otherwise.
Forms the simplicial cartesian product of and . Internally calls
(6.6.2).
5.2.8 Operation = (SCSimplicialComplex, SCSimplicialComplex)
▷
(method)
Returns: or upon success, otherwise.
Calculates whether two simplicial complexes are isomorphic, i.e. are equal up to a relabeling of
the vertices.

simpcomp 40
5.3 as a subtype of
Apart from being a subtype of , an object of type also
behaves like a GAP type. The elements of the set are given by the facets of the simplical complex,
grouped by their dimensionality, i.e. if is an object of type ,
refers to the 0-faces of , to the 1-faces, etc.
5.3.1 Operation Union (SCSimplicialComplex, SCSimplicialComplex)
▷
(method)
Returns: simplicial complex of type upon success, otherwise.
Computes the union of two simplicial complexes by calling (7.3.16).
5.3.2 Operation Difference (SCSimplicialComplex, SCSimplicialComplex)
▷
(method)
Returns: simplicial complex of type upon success, otherwise.
Computes the “difference” of two simplicial complexes by calling (6.10.5).
simpcomp 41
5.3.3 Operation Intersection (SCSimplicialComplex, SCSimplicialComplex)
▷
(method)
Returns: simplicial complex of type upon success, otherwise.
Computes the “intersection” of two simplicial complexes by calling (6.10.8).
5.3.4 Size (SCSimplicialComplex)
▷(method)
Returns: an integer upon success, otherwise.
Returns the “size” of a simplicial complex. This is d+1, where dis the dimension of the complex.
d+1 is returned instead of d, as all lists in GAP are indexed beginning with 1 – thus this also holds
for all the face lattice related properties of the complex.

simpcomp 42
5.3.5 Length (SCSimplicialComplex)
▷(method)
Returns: an integer upon success, otherwise.
Returns the “size” of a simplicial complex by calling .
5.3.6 Operation [] (SCSimplicialComplex)
▷(method)
Returns: a list of faces upon success, otherwise.
Returns the (pos −1)-dimensional faces of as a list. If pos ≥d+2, where dis the
dimension of , the empty set is returned. Note that must be ≥1.
5.3.7 Iterator (SCSimplicialComplex)
▷(method)
Returns: an iterator on the face lattice of upon success, otherwise.
Provides an iterator object for the face lattice of a simplicial complex.
simpcomp 43
5.4 The object type
The GAP object type is designed to describe slicings (level sets of discrete Morse
functions) of combinatorial 3-manifolds, i. e. discrete normal surfaces. Internally
is a subtype of and, thus, mostly behaves like a
object (see Section 5.1). For a very short introduction to normal surfaces see 2.4, for a more
thorough introduction to the field see [Spr11b]. For some fundamental methods and functions for
see below. For more functions related to the object type see
Chapter 7.
5.5 Overloaded operators of
As with the object type , simpcomp overloads some standard operations for
the object type . See a list of overloaded operators below.
5.5.1 Operation + (SCNormalSurface, Integer)
▷(method)
Returns: the discrete normal surface passed as argument upon success, otherwise.
Positively shifts the vertex labels of (provided that all labels satisfy the property
) by the amount specified in .
5.5.2 Operation - (SCNormalSurface, Integer)
▷(method)
Returns: the discrete normal surface passed as argument upon success, otherwise.
Negatively shifts the vertex labels of (provided that all labels satisfy the property
) by the amount specified in .

simpcomp 44
5.5.3 Operation mod (SCNormalSurface, Integer)
▷(method)
Returns: the discrete normal surface passed as argument upon success, otherwise.
Takes all vertex labels of modulo the value specified in (provided that all labels
satisfy the property ). Warning: this might result in different vertices being
assigned the same label or even invalid facet lists, so be careful.
5.6 as a subtype of
Like objects of type , an object of type behaves like a
GAP type. The elements of the set are given by the facets of the normal surface, grouped by their
dimensionality and type, i.e. if is an object of type , refers to the
0-faces of , to the 1-faces, to the triangles and to the quadrilaterals. See
below for some examples and Section 5.3 for details.
5.6.1 Operation Union (SCNormalSurface, SCNormalSurface)
▷
(method)
Returns: discrete normal surface of type upon success, otherwise.
Computes the union of two discrete normal surfaces by calling (7.3.16).

simpcomp 45

Chapter 6
Functions and operations for
6.1 Creating an object from a facet list
This section contains functions to generate or to construct new simplicial complexes. Some of them
obtain new complexes from existing ones, some generate new complexes from scratch.
6.1.1 SCFromFacets
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Constructs a simplicial complex object from the given facet list. The facet list has to
be a duplicate free list (or set) which consists of duplicate free entries, which are in turn lists or
sets. For the vertex labels (i. e. the entries of the list items of ) an ordering via the less-
operator has to be defined. Following Section 4.11 of the GAP manual this is the case for objects
of the following families: rationals , cyclotomics , finite field elements ,
permutations , booleans , characters and lists (strings) .
Internally the vertices are mapped to the standard labeling 1..n, where nis the number of
vertices of the complex and the vertex labels of the original complex are stored in the property
”VertexLabels”, see (4.2.3) and the functions like (4.2.6) or
(4.2.7).
46

simpcomp 47
6.1.2 SC
▷(method)
Returns: simplicial complex of type upon success, otherwise.
A shorter function to create a simplicial complex from a facet list, just calls
(6.1.1)( ).
6.1.3 SCFromDifferenceCycles
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Creates a simplicial complex object from the list of difference cycles provided. If
is of length 1 the computation is equivalent to the one in (6.6.8). Oth-
erwise the induced modulus (the sum of all entries of a difference cycle) of all cycles has to be equal
and the union of all expanded difference cycles is returned.
An-dimensional difference cycle D=(d1∶...∶dn+1)induces a simplex ∆=(v1,...,vn+1)by v1=
d1,vi=vi−1+diand a cyclic group action by Zσwhere σ=∑diis the modulus of D. The function
returns the Zσ-orbit of ∆.
Note that modulo operations in GAP are often a little bit cumbersome, since all integer ranges
usually start from 1.

simpcomp 48
6.1.4 SCFromGenerators
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Constructs a simplicial complex object from the set of on which the group
acts, i.e. a complex which has as a subgroup of the automorphism group and a facet list that
consists of the -orbits specified by the list of representatives passed in . Note that
is not stored as an attribute of the resulting complex as it might just be a subgroup of the actual
automorphism group. Internally calls and (6.1.1).
6.2 Isomorphism signatures
This section contains functions to construct simplicial complexes from isomorphism signatures and
to compress closed and strongly connected weak pseudomanifolds to strings.
The isomorphism signature of a closed and strongly connected weak pseudomanifold is a rep-
resentation which is invariant under relabelings of the underlying complex and thus unique for a
combinatorial type, i.e. two complexes are isomorphic iff they have the same isomorphism signature.

simpcomp 49
To compute the isomorphism signature of a closed and strongly connected weak pseudomanifold
Pwe have to compute all canonical labelings of Pand chose the one that is lexicographically minimal.
A canonical labeling of Pis determined by chosing a facet ∆∈Pand a numbering 1,2,...,d+1
of the vertices of ∆(which in turn determines a numbering of the co-dimension one faces of ∆by
identifying each face with its opposite vertex). This numbering can then be uniquely extended to a
numbering (and thus a labeling) on all vertices of Pby the weak pseudomanifold property: start at
face 1 of ∆and label the opposite vertex of the unique other facet δmeeting face 1 by d+2, go on
with face 2 of ∆and so on. After finishing with the first facet we now have a numbering on δ, repeat
the procedure for δ, etc. Whenever the opposite vertex of a face is already labeled (and also, if the
vertex occurs for the first time) we note this label. Whenever a facet is already visited we skip this step
and keep track of the number of skippings between any two newly discovered facets. This results in
a sequence of m−1 vertex labels together with m−1 skipping numbers (where mdenotes the number
of facets in P) which then can by encoded by characters via a lookup table.
Note that there are precisely (d+1)!mcanonical labelings we have to check in order to find
the lexicographically minimal one. Thus, computing the isomorphism signature of a large or highly
dimensional complex can be time consuming. If you are not interested in the isomorphism signature
but just in the compressed string representation use (6.2.1) which just computes
the first canonical labeling of the complex provided as argument and returns the resulting string.
Note: Another way of storing and loading complexes is provided by simpcomp’s library function-
ality, see Section 13.1 for details.
6.2.1 SCExportToString
▷(function)
Returns: string upon success, otherwise.
Computes one string representation of a closed and strongly connected weak pseudomanifold.
Compare (6.2.2), which returns the lexicographically minimal string representa-
tion.
6.2.2 SCExportIsoSig
▷(method)
Returns: string upon success, otherwise.
Computes the isomorphism signature of a closed, strongly connected weak pseudomanifold. The
isomorphism signature is stored as an attribute of the complex.

simpcomp 50
6.2.3 SCFromIsoSig
▷(method)
Returns: a SCSimplicialComplex object upon success, otherwise.
Computes a simplicial complex from its isomorphism signature. If a file with isomorphism signa-
tures is provided a list of all complexes is returned.
6.3 Generating some standard triangulations
6.3.1 SCBdCyclicPolytope
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates the boundary complex of the -dimensional cyclic polytope (a combinatorial d−1-
sphere) on vertices, where n≥d+2.

simpcomp 51
6.3.2 SCBdSimplex
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates the boundary of the d-simplex ∆d, a combinatorial d−1-sphere.
6.3.3 SCEmpty
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates an empty complex (of dimension −1), i. e. a object with empty
facet list.

simpcomp 52
6.3.4 SCSimplex
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates the -simplex.
6.3.5 SCSeriesTorus
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates the d-torus described in [Küh86].
6.3.6 SCSurface
▷(function)
Returns: simplicial complex of type upon success, otherwise.

simpcomp 53
Generates the surface of genus where the boolean argument specifies whether the sur-
face is orientable or not. The surfaces have transitive cyclic group actions and can be described using
the minimum amount of O(log(g)) memory. If is and ≥50 or if is and
≥100 only the difference cycles of the surface are returned

simpcomp 54
6.3.7 SCFVectorBdCrossPolytope
▷(function)
Returns: a list of integers of size upon success, otherwise.
Computes the f-vector of the d-dimensional cross polytope without generating the underlying
complex.
6.3.8 SCFVectorBdCyclicPolytope
▷(function)
Returns: a list of integers of size upon success, otherwise.
Computes the f-vector of the -dimensional cyclic polytope on vertices, n≥d+2, without
generating the underlying complex.
6.3.9 SCFVectorBdSimplex
▷(function)
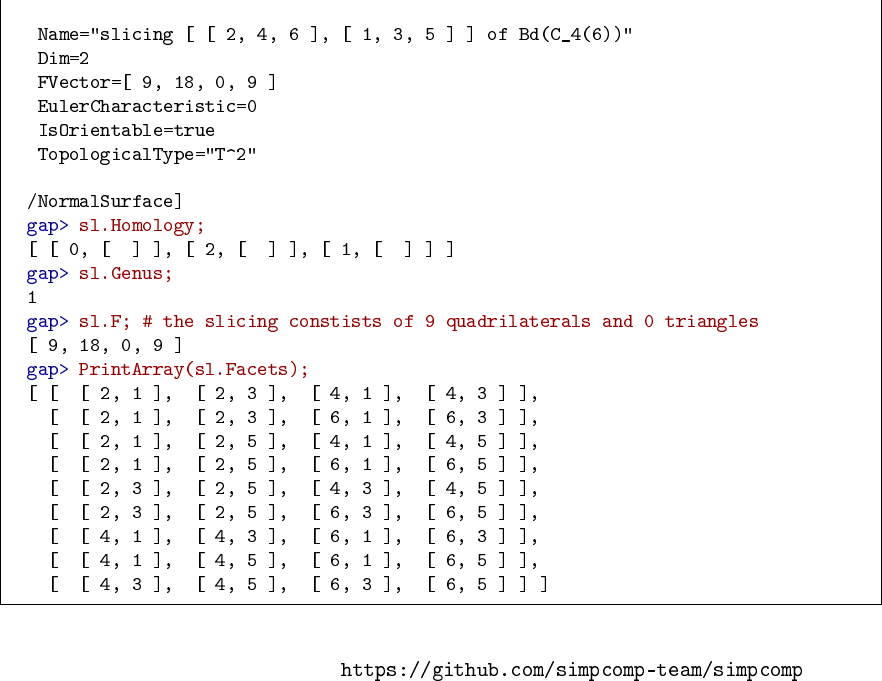
Returns: a list of integers of size upon success, otherwise.
Computes the f-vector of the d-simplex without generating the underlying complex.

simpcomp 55
6.4 Generating infinite series of transitive triangulations
6.4.1 SCSeriesAGL
▷(function)
Returns: a permutation group and a list of 5-tuples of integers upon success, otherwise.
For a given prime the automorphism group (AGL(1,p)) and the generators of all members of
the series of 2-transitive combinatorial 4-pseudomanifolds with vertices from [Spr11a], Section 5.2,
is computed. The affine linear group AGL(1,p)is returned as the first argument. If no member of the

simpcomp 56
series with vertices exists only the group is returned.
6.4.2 SCSeriesBrehmKuehnelTorus
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates a neighborly 3-torus with vertices if is odd and a centrally symmetric 3-torus if
is even ( ≥15 . The triangulations are taken from [BK12]

simpcomp 57
6.4.3 SCSeriesBdHandleBody
▷(function)
Returns: simplicial complex of type upon success, otherwise.
generates a transitive d-dimensional sphere bundle (d≥2) with n
vertices (n≥2d+3) which coincides with the boundary of (6.4.9) . The
sphere bundle is orientable if dis even or if dis odd and nis even, otherwise it is not orientable.
Internally calls (6.1.3).

simpcomp 58
6.4.4 SCSeriesBid
▷(function)
Returns: a simplicial complex upon success, otherwise.
Constructs the complex B(i,d)as described in [KN12], cf. [Eff11a], [Spa99]. The complex
B(i,d)is a i-Hamiltonian subcomplex of the d-cross polytope and its boundary topologically is a
sphere product Si×Sd−i−2with vertex transitive automorphism group.
6.4.5 SCSeriesC2n
▷(function)
Returns: simplicial complex of type upon success, otherwise.

simpcomp 59
Generates the combinatorial 3-manifold C2n,n≥8, with 2nvertices from [Spr11a], Section 4.5.3
and Section 5.2. The complex is homeomorphic to S2×S1for nodd and homeomorphic to S2"S1
in case nis an even number. In the latter case C2nis isomorphic to D2nfrom (6.4.8).
The complexes are believed to appear as the vertex links of some of the members of the series of 2-
transitive 4-pseudomanifolds from (6.4.1). Internally calls
(6.1.3).
6.4.6 SCSeriesConnectedSum
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates a combinatorial manifold of type (S2xS1)kfor keven. The complex is a combinatorial
3-manifold with transitive cyclic symmetry as described in [BS14].

simpcomp 61
6.4.8 SCSeriesD2n
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates the combinatorial 3-manifold D2n,n≥8, n≠9, with 2nvertices from [Spr11a], Section
4.5.3 and Section 5.2. The complex is homeomorphic to S2"S1. In the case that nis even D2nis
isomorphic to C2nfrom (6.4.5). The complexes are believed to appear as the vertex
links of some of the members of the series of 2-transitive 4-pseudomanifolds from
(6.4.1). Internally calls (6.1.3).

simpcomp 62
6.4.9 SCSeriesHandleBody
▷(function)
Returns: simplicial complex of type upon success, otherwise.
generates a transitive d-dimensional handle body (d≥3) with nver-
tices (n≥2d+1). The handle body is orientable if dis odd or if dand nare even, otherwise it is not
orientable. The complex equals the difference cycle (1∶... ∶1∶n−d)To obtain the boundary com-
plexes of use the function (6.4.3). Internally
calls (6.1.3).
6.4.10 SCSeriesHomologySphere
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates a combinatorial Brieskorn homology sphere of type Σ(p,q,r),p,qand rpairwise co-
prime. The complex is a combinatorial 3-manifold with transitive cyclic symmetry as described in
[BS14].

simpcomp 63
6.4.11 SCSeriesK
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates the -th member (k≥0) of the series (1 ≤i≤396) from [Spr11a]. The 396 series
describe a complete classification of all dense series (i. e. there is a member of the series for every
integer, f0(Ki(k+1)) =f0(Ki(k))+1) of cyclic 3-manifolds with a fixed number of difference cycles
and at least one member with less than 23 vertices. See (6.4.13) for a list of series of order
2.
6.4.12 SCSeriesKu
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Computes the symmetric orientable sphere bundle Ku(n)with 4nvertices from [Spr11a], Section
4.5.2. The series is defined as a generalization of the slicings from [Spr11a], Section 3.3.

simpcomp 64
6.4.13 SCSeriesL
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates the -th member (k≥0) of the series , 1 ≤i≤18 from [Spr11a]. The 18 series
describe a complete classification of all series of cyclic 3-manifolds with a fixed number of difference
cycles of order 2 (i. e. there is a member of the series for every second integer, f0(Li(k+1)) =
f0(Li(k))+2) and at least one member with less than 15 vertices where each series does not appear
as a sub series of one of the series Kifrom (6.4.11).

simpcomp 65
6.4.14 SCSeriesLe
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates the -th member (k≥7) of the series from [Spr11a], Section 4.5.1. The series can
be constructed as the generalization of the boundary of a genus 1 handlebody decomposition of the
manifold from the classification in [Lut03].
6.4.15 SCSeriesLensSpace
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates the lens space L(p,q)whenever p=(k+2)2−1 and q=k+2 or p=2k+3 and q=1 for
ak≥0 and otherwise. All complexes have a transitive cyclic automorphism group.

simpcomp 66
6.4.16 SCSeriesPrimeTorus
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates the well known triangulated torus {(l∶j∶p−l−j),(l∶p−l−j∶j)} with pvertices, 3p
edges and 2ptriangles where jhas to be greater than land pmust be any prime number greater than
6.
6.4.17 SCSeriesSeifertFibredSpace
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates a combinatorial Seifert fibred space of type
SFS[(T2)(a−1)(b−1)∶(pa,b1)b,(qb,b2)a,(rab,b3)]
where pand qare co-prime, a=gcd(p,r),b=gcd(p,r), and the biare given by the identity
b1
p+b2
q+b3
r=±ab
pqr .
This 3-parameter family of combinatorial 3-manifolds contains the families generated
by (6.4.10), (6.4.6) and parts of
(6.4.15), internally calls .
The complexes are combinatorial 3-manifolds with transitive cyclic symmetry as described in
[BS14].

simpcomp 67
6.4.18 SCSeriesS2xS2
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Generates a combinatorial version of (S2×S2)#k.
6.5 A census of regular and chiral maps
6.5.1 SCChiralMap
▷(function)
Returns: a object upon success, otherwise.
Returns the (hyperbolic) chiral map of vertex valence and genus if existent and other-
wise. The list was generated with the help of the classification of regular maps by Marston Conder
[Con09]. Use (6.5.2) to get a list of all chiral maps available.

simpcomp 68
6.5.2 SCChiralMaps
▷(function)
Returns: a list of lists upon success, otherwise.
Returns a list of all simplicial (hyperbolic) chiral maps of orientable genus up to 100. The list
was generated with the help of the classification of regular maps by Marston Conder [Con09]. Every
chiral map is given by a 2-tuple (m,g)where mis the vertex valence and gis the genus of the map.
Use the 2-tuples of the list together with (6.5.1) to get the corresponding triangulations.
6.5.3 SCChiralTori
▷(function)
Returns: a object upon success, otherwise.
Returns a list of chiral triangulations of the torus with nvertices. See [BK08] for details.

simpcomp 69
6.5.4 SCNrChiralTori
▷(function)
Returns: an integer upon success, otherwise.
Returns the number of simplicial chiral maps on the torus with nvertices, cf. [BK08] for details.
6.5.5 SCNrRegularTorus
▷(function)
Returns: an integer upon success, otherwise.
Returns the number of simplicial regular maps on the torus with nvertices, cf. [BK08] for details.
6.5.6 SCRegularMap
▷(function)
Returns: a object upon success, otherwise.

simpcomp 70
Returns the (hyperbolic) regular map of vertex valence , genus and orientability if
existent and otherwise. The triangulations were generated with the help of the classification of
regular maps by Marston Conder [Con09]. Use (6.5.7) to get a list of all regular
maps available.
6.5.7 SCRegularMaps
▷(function)
Returns: a list of lists upon success, otherwise.
Returns a list of all simplicial (hyperbolic) regular maps of orientable genus up to 100 or non-
orientable genus up to 200. The list was generated with the help of the classification of regular maps
by Marston Conder [Con09]. Every regular map is given by a 3-tuple (m,g,or)where mis the vertex
valence, gis the genus and or is a boolean stating if the map is orientable or not. Use the 3-tuples of
the list together with (6.5.6) to get the corresponding triangulations. g

simpcomp 71
6.5.8 SCRegularTorus
▷(function)
Returns: a object upon success, otherwise.
Returns a list of regular triangulations of the torus with nvertices (the length of the list will be at
most 1). See [BK08] for details.
6.5.9 SCSeriesSymmetricTorus
▷(function)
Returns: a object upon success, otherwise.
Returns the equivarient triangulation of the torus {3,6}(p,q)with fundamental domain (p,q)on
the 2-dimensional integer lattice. See [BK08] for details.

simpcomp 72
See also (6.3.6) for example triangulations of all compact closed surfaces with transi-
tive cyclic automorphism group.
6.6 Generating new complexes from old
6.6.1 SCCartesianPower
▷(method)
Returns: simplicial complex of type upon success, otherwise.
The new complex is PL-homeomorphic to ntimes the cartesian product of , of dimen-
sions n⋅dand has fn
d⋅n⋅2n−1
2n−1! facets where ddenotes the dimension and fddenotes the number of
facets of . Note that the complex returned by the function is not the n-fold cartesian product
nof (which, in general, is not simplicial) but a simplicial subdivision of n.
6.6.2 SCCartesianProduct
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Computes the simplicial cartesian product of and where and
are pure, simplicial complexes. The original vertex labeling of and
is changed into the standard one. The new complex has vertex labels of type [vi,vj]where viis a
vertex of and vjis a vertex of .
If ni,i=1,2, are the number facets and di,i=1,2, are the dimensions of , then the new
complex has n1⋅n2⋅d1+d2
d1facets. The number of vertices of the new complex equals the product of
the numbers of vertices of the arguments.

simpcomp 73
6.6.3 SCConnectedComponents
▷(method)
Returns: a list of simplicial complexes of type upon success,
otherwise.
Computes all connected components of an arbitrary simplicial complex.

simpcomp 74
6.6.4 SCConnectedProduct
▷(method)
Returns: simplicial complex of type upon success, otherwise.
If n≥2, the function internally calls 1×(6.6.5) and (n−2)×
(6.6.6).
6.6.5 SCConnectedSum
▷(method)
Returns: simplicial complex of type upon success, otherwise.
In a lexicographic ordering the smallest facet of both and is removed and the
complexes are glued together along the resulting boundaries. The bijection used to identify the vertices
of the boundaries differs from the one chosen in (6.6.6) by a transposition.
Thus, the topological type of is different from the one of
(6.6.6) whenever and do not allow an orientation reversing homeomorphism.

simpcomp 75
6.6.6 SCConnectedSumMinus
▷(method)
Returns: simplicial complex of type upon success, otherwise.
In a lexicographic ordering the smallest facet of both and is removed and
the complexes are glued together along the resulting boundaries. The bijection used to identify the
vertices of the boundaries differs from the one chosen in (6.6.5) by a transposition.
Thus, the topological type of is different from the one of
(6.6.5) whenever and do not allow an orientation reversing homeomorphism.

simpcomp 76
6.6.7 SCDifferenceCycleCompress
▷(function)
Returns: list with possibly duplicate entries upon success, otherwise.
A difference cycle is returned, i. e. a list of integer values of length (d+1), if dis the di-
mension of , and a sum equal to . In some sense this is the inverse operation of
(6.6.8).

simpcomp 77
6.6.8 SCDifferenceCycleExpand
▷(function)
Returns: simplicial complex of type upon success, otherwise.
induces a simplex ∆=(v1,...,vn+1)by v1=,vi=vi−1+
and a cyclic group action by Zσwhere σ=∑is the modulus of . The
function returns the Zσ-orbit of ∆.
Note that modulo operations in GAP are often a little bit cumbersome, since all integer ranges
usually start from 1.
6.6.9 SCStronglyConnectedComponents
▷(method)
Returns: a list of simplicial complexes of type upon success,
otherwise.
Computes all strongly connected components of a pure simplicial complex.
6.7 Simplicial complexes from transitive permutation groups
Beginning from Version 1.3.0, simpcomp is able to generate triangulations from a prescribed tran-
sitive group action on its set of vertices. Note that the corresponding group is a subgroup of the full

simpcomp 78
automorphism group, but not necessarily the full automorphism group of the triangulations obtained
in this way. The methods and algorithms are based on the works of Frank H. Lutz [Lut03], [Lut] and
in particular his program .
6.7.1 SCsFromGroupExt
▷
(function)
Returns: a list of simplicial complexes of type upon success,
otherwise.
Computes all combinatorial -pseudomanifolds, d=2 / all strongly connected combinatorial -
pseudomanifolds, d≥3, as a union of orbits of the group action of on -tuples on the set of
vertices, see [Lut03]. The integer argument specifies, whether complexes exceeding
the maximal size of each vertex link for combinatorial manifolds are sorted out ( )
or not ( , in this case some combinatorial pseudomanifolds won’t be found, but no
combinatorial manifold will be sorted out). The integer argument specifies if the orbits are
held in memory during the computation, a value of means that the orbits are discarded, trading
speed for memory, any other value means that they are kept, trading memory for speed. The boolean
argument specifies whether the results are checked for combinatorial iso-
morphism, preventing isomorphic entries. The argument specifies an output file containing
all complexes found by the algorithm, if is anything else than a string, not output file is
generated. The argument determines a maximal link size of any output complex. If
=0 or if is anything else than an integer the argument is ignored. The
argument specifies a set of orbits (given by a list of indices of ) which have to be
contained in any output complex. If is anything else than a subset of
the argument is ignored.

simpcomp 79
6.7.2 SCsFromGroupByTransitivity
▷
(function)
Returns: a list of simplicial complexes of type upon success,
otherwise.
Computes all combinatorial -pseudomanifolds, d=2 / all strongly connected combinatorial -
pseudomanifolds, d≥3, as union of orbits of group actions for all -transitive groups on -tuples
on the set of vertices, see [Lut03]. The boolean argument specifies, whether the resulting
complexes should be listed separately by combinatorial manifolds, combinatorial pseudomanifolds
and complexes where the verification that the object is at least a combinatorial pseudomanifold failed.
The boolean argument specifies whether or not the real automorphism group
should be computed (note that a priori the generating group is just a subgroup of the automorphism
group). The boolean argument specifies whether the results are checked
for combinatorial isomorphism, preventing isomorphic entries. Internally calls
(6.7.1) for every group.

simpcomp 80
6.8 The classification of cyclic combinatorial 3-manifolds
This section contains functions to access the classification of combinatorial 3-manifolds with transitive
cyclic symmetry and up to 22 vertices as presented in [Spr14].
6.8.1 SCNrCyclic3Mflds
▷(function)
Returns: integer upon success, otherwise.
Returns the number of combinatorial 3-manifolds with transitive cyclic symmetry with vertices.
See [Spr14] for more about the classification of combinatorial 3-manifolds with transitive cyclic sym-
metry up to 22 vertices.
6.8.2 SCCyclic3MfldTopTypes
▷(function)
Returns: a list of strings upon success, otherwise.
Returns a list of all topological types that occur in the classification combinatorial 3-manifolds
with transitive cyclic symmetry with vertices. See [Spr14] for more about the classification of
combinatorial 3-manifolds with transitive cyclic symmetry up to 22 vertices.
6.8.3 SCCyclic3Mfld
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Returns the th combinatorial 3-manifold with vertices in the classification of combinatorial
3-manifolds with transitive cyclic symmetry. See [Spr14] for more about the classification of combi-
natorial 3-manifolds with transitive cyclic symmetry up to 22 vertices.

simpcomp 81
6.8.4 SCCyclic3MfldByType
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Returns the smallest combinatorial 3-manifolds in the classification of combinatorial 3-manifolds
with transitive cyclic symmetry of topological type . See [Spr14] for more about the classifica-
tion of combinatorial 3-manifolds with transitive cyclic symmetry up to 22 vertices.
6.8.5 SCCyclic3MfldListOfGivenType
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Returns a list of indices {(i1,j1),(i1,j1),...(in,jn)} of all combinatorial 3-manifolds in the clas-
sification of combinatorial 3-manifolds with transitive cyclic symmetry of topological type .
Complexes can be obtained by calling (6.8.3) using these indices. See [Spr14] for
more about the classification of combinatorial 3-manifolds with transitive cyclic symmetry up to 22
vertices.

simpcomp 82
6.9 Computing properties of simplicial complexes
The following functions compute basic properties of simplicial complexes of type
. None of these functions alter the complex. All properties are re-
turned as immutable objects (this ensures data consistency of the cached properties of a simplicial
complex). Use or the internal simpcomp function to get a
mutable copy.
Note: every simplicial complex is internally stored with the standard vertex labeling from 1 to n
and a maptable to restore the original vertex labeling. Thus, we have to relabel some of the complex
properties (facets, face lattice, generators, etc...) whenever we want to return them to the user. As a
consequence, some of the functions exist twice, one of them with the appendix "Ex". These functions
return the standard labeling whereas the other ones relabel the result to the original labeling.
6.9.1 SCAltshulerSteinberg
▷(method)
Returns: a non-negative integer upon success, otherwise.
Computes the Altshuler-Steinberg determinant.
Definition: Let vi, 1 ≤i≤nbe the vertices and let Fj, 1 ≤j≤mbe the facets of a pure simplicial
complex C, then the determinant of AS ∈Zn×m,ASi j =1 if vi∈Fj,ASi j =0 otherwise, is called the
Altshuler-Steinberg matrix. The Altshuler-Steinberg determinant is the determinant of the quadratic
matrix AS ⋅AST.
The Altshuler-Steinberg determinant is a combinatorial invariant of Cand can be checked before
searching for an isomorphism between two simplicial complexes.
6.9.2 SCAutomorphismGroup
▷(method)
Returns: aGAP permutation group upon success, otherwise.
Computes the automorphism group of a strongly connected pseudomanifold , i. e. the
group of all automorphisms on the set of vertices of that do not change the complex as a
whole. Necessarily the group is a subgroup of the symmetric group Snwhere nis the number of
vertices of the simplicial complex.

simpcomp 83
The function uses an efficient algorithm provided by the package GRAPE (see [Soi12], which is
based on the program by Brendan McKay [MP14]). If the package GRAPE is not available,
this function call falls back to (6.9.3).
The position of the group in the GAP libraries of small groups, transitive groups or primitive
groups is given. If the group is not listed, its structure description, provided by the GAP function
, is returned as the name of the group. Note that the latter form is not
always unique, since every non trivial semi-direct product is denoted by ” ”.
6.9.3 SCAutomorphismGroupInternal
▷(method)
Returns: aGAP permutation group upon success, otherwise.
Computes the automorphism group of a strongly connected pseudomanifold , i. e. the
group of all automorphisms on the set of vertices of that do not change the complex as a
whole. Necessarily the group is a subgroup of the symmetric group Snwhere nis the number of
vertices of the simplicial complex.
The position of the group in the GAP libraries of small groups, transitive groups or primitive
groups is given. If the group is not listed, its structure description, provided by the GAP function
, is returned as the name of the group. Note that the latter form is not
always unique, since every non trivial semi-direct product is denoted by ” ”.
6.9.4 SCAutomorphismGroupSize
▷(method)
Returns: a positive integer group upon success, otherwise.
Computes the size of the automorphism group of a strongly connected pseudomanifold ,
see (6.9.2).

simpcomp 84
6.9.5 SCAutomorphismGroupStructure
▷(method)
Returns: the GAP structure description upon success, otherwise.
Computes the GAP structure description of the automorphism group of a strongly connected
pseudomanifold , see (6.9.2).
6.9.6 SCAutomorphismGroupTransitivity
▷(method)
Returns: a positive integer upon success, otherwise.
Computes the transitivity of the automorphism group of a strongly connected pseudomanifold
, i. e. the maximal integer tsuch that for any two ordered t-tuples T1and T2of vertices of
, there exists an element gin the automorphism group of for which gT1=T2, see
[Hup67].
6.9.7 SCBoundary
▷(method)
Returns: simplicial complex of type upon success, otherwise.
The function computes the boundary of a simplicial complex satisfying the weak pseu-
domanifold property and returns it as a simplicial complex. In addition, it is stored as a property of
.
The boundary of a simplicial complex is defined as the simplicial complex consisting of all d−1-
faces that are contained in exactly one facet.
If does not fulfill the weak pseudomanifold property (i. e. if the valence of any d−1-face
exceeds 2) the function returns .

simpcomp 85
6.9.8 SCDehnSommervilleCheck
▷(method)
Returns: or upon success, otherwise.
Checks if the simplicial complex fulfills the Dehn Sommerville equations: hj−hd+1−j=
(−1)d+1−jd+1
j(χ(M)−2)for 0 ≤j≤d
2and deven, and hj−hd+1−j=0 for 0 ≤j≤d−1
2and dodd.
Where hjis the jth component of the h-vector, see (6.9.26).

simpcomp 86
6.9.9 SCDehnSommervilleMatrix
▷(method)
Returns: a×matrix with integer entries upon success, otherwise.
Computes the coefficients of the Dehn Sommerville equations for dimension : hj−hd+1−j=
(−1)d+1−jd+1
j(χ(M)−2)for 0 ≤j≤d
2and deven, and hj−hd+1−j=0 for 0 ≤j≤d−1
2and dodd.
Where hjis the jth component of the h-vector, see (6.9.26).
6.9.10 SCDifferenceCycles
▷(method)
Returns: a list of lists upon success, otherwise.
Computes the difference cycles of in standard labeling if is invariant under a
shift of the vertices of type v↦v+1 mod n. The function returns the difference cycles as lists where
the sum of the entries equals the number of vertices nof .
6.9.11 SCDim
▷(method)
Returns: an integer ≥−1 upon success, otherwise.
Computes the dimension of a simplicial complex. If the complex is not pure, the dimension of the
highest dimensional simplex is returned.

simpcomp 87
6.9.12 SCDualGraph
▷(method)
Returns: 1-dimensional simplicial complex of type upon success,
otherwise.
Computes the dual graph of the pure simplicial complex .
6.9.13 SCEulerCharacteristic
▷(method)
Returns: integer upon success, otherwise.
Computes the Euler characteristic χ(C)=d
∑
i=0(−1)ifiof a simplicial complex C, where fidenotes
the i-th component of the f-vector.
6.9.14 SCFVector
▷(method)
Returns: a list of non-negative integers upon success, otherwise.

simpcomp 88
Computes the f-vector of the simplicial complex , i. e. the number of i-dimensional
faces for 0 ≤i≤d, where dis the dimension of . A memory-saving implicit algorithm is used
that avoids calculating the face lattice of the complex. Internally calls (6.9.52).
6.9.15 SCFaceLattice
▷(method)
Returns: a list of face lists upon success, otherwise.
Computes the entire face lattice of a d-dimensional simplicial complex, i. e. all of its i-skeletons
for 0 ≤i≤d. The faces are returned in the original labeling.
6.9.16 SCFaceLatticeEx
▷(method)
Returns: a list of face lists upon success, otherwise.
Computes the entire face lattice of a d-dimensional simplicial complex, i. e. all of its i-skeletons
for 0 ≤i≤d. The faces are returned in the standard labeling.
6.9.17 SCFaces
▷(method)
Returns: a face list upon success, otherwise.
This is a synonym of the function (7.3.13).
6.9.18 SCFacesEx
▷(method)
Returns: a face list upon success, otherwise.
This is a synonym of the function (7.3.14).

simpcomp 89
6.9.19 SCFacets
▷(method)
Returns: a facet list upon success, otherwise.
Returns the facets of a simplicial complex in the original vertex labeling.
6.9.20 SCFacetsEx
▷(method)
Returns: a facet list upon success, otherwise.
Returns the facets of a simplicial complex as they are stored, i. e. with standard vertex labeling
from 1 to n.
6.9.21 SCFpBettiNumbers
▷(method)
Returns: a list of non-negative integers upon success, otherwise.
Computes the Betti numbers of a simplicial complex with respect to the field Fpfor any prime
number .
6.9.22 SCFundamentalGroup
▷(method)
Returns: aGAP fp group upon success, otherwise.
Computes the first fundamental group of , which must be a connected simplicial com-
plex, and returns it in form of a finitely presented group. The generators of the group are given
as 2-tuples that correspond to the edges of in standard labeling. You can use GAP’s
to simplify the group presenation.

simpcomp 90
6.9.23 SCGVector
▷(method)
Returns: a list of integers upon success, otherwise.
Computes the g-vector of a simplicial complex. The g-vector is defined as follows:

simpcomp 91
Let hbe the h-vector of a d-dimensional simplicial complex C, then gi∶=hi+1−hi;d
2≥i≥0 is
called the g-vector of C. For the definition of the h-vector see (6.9.26). The information
contained in gsuffices to determine the f-vector of C.
6.9.24 SCGenerators
▷(method)
Returns: a list of pairs of the form upon success, otherwise.
Computes the generators of a simplicial complex in the original vertex labeling.
The generating set of a simplicial complex is a list of simplices that will generate the complex by
uniting their G-orbits if Gis the automorphism group of .
The function returns the simplices together with the length of their orbits.

simpcomp 92
6.9.25 SCGeneratorsEx
▷(method)
Returns: a list of pairs of the form upon success, otherwise.
Computes the generators of a simplicial complex in the standard vertex labeling.
The generating set of a simplicial complex is a list of simplices that will generate the complex by
uniting their G-orbits if Gis the automorphism group of .
The function returns the simplices together with the length of their orbits.

simpcomp 93
6.9.26 SCHVector
▷(method)
Returns: a list of integers upon success, otherwise.
Computes the h-vector of a simplicial complex. The h-vector is defined as hk∶=
k−1
∑
i=−1(−1)k−i−1d−i−1
k−i−1fifor 0 ≤k≤d, where f−1∶=1. For all simplicial complexes we have h0=1,
hence the returned list starts with the second entry of the h-vector.

simpcomp 94
6.9.27 SCHasBoundary
▷(method)
Returns: or upon success, otherwise.
Checks if a simplicial complex that fulfills the weak pseudo manifold property has a
boundary, i. e. d−1-faces of valence 1. If is closed is returned, if does not
fulfill the weak pseudomanifold property, is returned, otherwise is returned.
6.9.28 SCHasInterior
▷(method)
Returns: or upon success, otherwise.
Returns if a simplicial complex that fulfills the weak pseudomanifold property has
at least one d−1-face of valence 2, i. e. if there exist at least one d−1-face that is not in the boundary
of , if no such face can be found is returned. It does not fulfill the weak
pseudomanifold property is returned.
6.9.29 SCHeegaardSplittingSmallGenus
▷(method)
Returns: a list of an integer, a list of two sublists and a string upon success, otherwise.
Computes a Heegaard splitting of the combinatorial 3-manifold of small genus. The function
returns the genus of the Heegaard splitting, the vertex partition of the Heegaard splitting and informa-
tion whether the splitting is minimal or just small (i. e. the Heegaard genus could not be determined).
See also (6.9.30) for a faster computation of a Heegaard splitting of arbitrary
genus and (6.9.40) for a test whether or not a given splitting defines a
Heegaard splitting.

simpcomp 95
6.9.30 SCHeegaardSplitting
▷(method)
Returns: a list of an integer, a list of two sublists and a string upon success, otherwise.
Computes a Heegaard splitting of the combinatorial 3-manifold . The function returns the genus
of the Heegaard splitting, the vertex partition of the Heegaard splitting and a note, that splitting is ar-
bitrary and in particular possibly not minimal. See also (6.9.29)
for the calculation of a Heegaard splitting of small genus and (6.9.40) for
a test whether or not a given splitting defines a Heegaard splitting.
6.9.31 SCHomologyClassic
▷(function)
Returns: a list of pairs of the form .
Computes the integral simplicial homology groups of a simplicial complex (internally
calls the function from the homology package, see
[DHSW11]).
If the homology package is not available, this function call falls back to
(8.1.5). The output is a list of homology groups of the form [H0,....,Hd], where dis the dimension of
. The format of the homology groups Hiis given in terms of their maximal cyclic subgroups,
i.e. a homology group Hi≅Zf+Zt1Z×⋅⋅⋅×ZtnZis returned in form of a list [f,[t1,...,tn]], where f
is the (integer) free part of Hiand tidenotes the torsion parts of Hiordered in weakly increasing size.

simpcomp 96
6.9.32 SCIncidences
▷(method)
Returns: a list of face lists upon success, otherwise.
Returns a list of all -faces of the simplicial complex . The list is sorted by the valence
of the faces in the +1-skeleton of the complex, i. e. the i-th entry of the list contains all -faces of
valence i. The faces are returned in the original labeling.
6.9.33 SCIncidencesEx
▷(method)
Returns: a list of face lists upon success, otherwise.
Returns a list of all -faces of the simplicial complex . The list is sorted by the valence
of the faces in the +1-skeleton of the complex, i. e. the i-th entry of the list contains all -faces of
valence i. The faces are returned in the standard labeling.

simpcomp 97
6.9.34 SCInterior
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Computes all d−1-faces of valence 2 of a simplicial complex that fulfills the weak
pseudomanifold property, i. e. the function returns the part of the d−1-skeleton of Cthat is not part
of the boundary.
6.9.35 SCIsCentrallySymmetric
▷(method)
Returns: or upon success, otherwise.
Checks if a simplicial complex is centrally symmetric, i. e. if its automorphism group
contains a fixed point free involution.
6.9.36 SCIsConnected
▷(method)
Returns: or upon success, otherwise.
Checks if a simplicial complex is connected.

simpcomp 98
6.9.37 SCIsEmpty
▷(method)
Returns: or upon success, otherwise.
Checks if a simplicial complex is the empty complex, i. e. a
object with empty facet list.
6.9.38 SCIsEulerianManifold
▷(method)
Returns: or upon success, otherwise.
Checks whether a given simplicial complex is a Eulerian manifold or not, i. e. checks if
all vertex links of have the Euler characteristic of a sphere. In particular the function returns
in case has a non-empty boundary.

simpcomp 99
6.9.39 SCIsFlag
▷(method)
Returns: or upon success, otherwise.
Checks if is flag. A connected simplicial complex of dimension at least one is a flag
complex if all cliques in its 1-skeleton span a face of the complex (cf. [Fro08]).
6.9.40 SCIsHeegaardSplitting
▷(method)
Returns: or upon success, otherwise.
Checks whether defines a Heegaard splitting of or not. See also
(6.9.30) and (6.9.29) for functions to compute Heegaard split-
tings.

simpcomp 100
6.9.41 SCIsHomologySphere
▷(method)
Returns: or upon success, otherwise.
Checks whether a simplicial complex is a homology sphere, i. e. has the homology of a
sphere, or not.
6.9.42 SCIsInKd
▷(method)
Returns: / upon success, otherwise.
Checks whether the simplicial complex that must be a combinatorial d-manifold is in
the class Kk(d), 1 ≤k≤d+1
2, of simplicial complexes that only have k-stacked spheres as vertex
links, see [Eff11b]. Note that it is not checked whether is a combinatorial manifold – if not,
the algorithm will not succeed. Returns / upon success. If is returned this means
that is at least -stacked and thus that the complex is in the class Kk(d), i.e. all vertex
links are -stacked spheres. If is returnd the complex cannot be -stacked. In some cases the
question can not be decided. In this case is returned.
Internally calls (9.2.5) for all links. Please note that this is a radomized
algorithm that may give an indefinite answer to the membership problem.
6.9.43 SCIsKNeighborly
▷(method)
Returns: or upon success, otherwise.

simpcomp 101
6.9.44 SCIsOrientable
▷(method)
Returns: or upon success, otherwise.
Checks if a simplicial complex , satisfying the weak pseudomanifold property, is ori-
entable.
6.9.45 SCIsPseudoManifold
▷(method)
Returns: or upon success, otherwise.
Checks if a simplicial complex fulfills the weak pseudomanifold property, i. e. if every
d−1-face of is contained in at most 2 facets.
6.9.46 SCIsPure
▷(method)
Returns: a boolean upon success, otherwise.
Checks if a simplicial complex is pure.
6.9.47 SCIsShellable
▷(method)
Returns: or upon success, otherwise.

simpcomp 102
The simplicial complex must be pure, strongly connected and must fulfill the weak
pseudomanifold property with non-empty boundary (cf. (6.9.7)).
The function checks whether is shellable or not. An ordering (F1,F2,...,Fr)on the facet
list of a simplicial complex is called a shelling if and only if Fi∩(F1∪...∪Fi−1)is a pure simplicial
complex of dimension d−1 for all i=1,...,r. A simplicial complex is called shellable, if at least one
shelling exists.
See [Zie95], [Pac87] to learn more about shellings.
6.9.48 SCIsStronglyConnected
▷(method)
Returns: or upon success, otherwise.
Checks if a simplicial complex is strongly connected, i. e. if for any pair of facets (ˆ
∆,˜
∆)
there exists a sequence of facets (∆1,...,∆k)with ∆1=ˆ
∆and ∆k=˜
∆and dim(∆i,∆i+1)=d−1 for all
1≤i≤k−1.
6.9.49 SCMinimalNonFaces
▷(method)
Returns: a list of face lists upon success, otherwise.
Computes all missing proper faces of a simplicial complex by calling
(6.9.50). The simplices are returned in the original labeling of .

simpcomp 103
6.9.50 SCMinimalNonFacesEx
▷(method)
Returns: a list of face lists upon success, otherwise.
Computes all missing proper faces of a simplicial complex , i.e. the missing (i+1)-tuples
in the i-dimensional skeleton of a . A missing i+1-tuple is not listed if it only consists of
missing i-tuples. Note that whenever is k-neighborly the first k+1 entries are empty. The
simplices are returned in the standard labeling 1,...,n, where nis the number of vertices of .
6.9.51 SCNeighborliness
▷(method)
Returns: a positive integer upon success, otherwise.
Returns kif a simplicial complex is k-neighborly but not (k+1)-neighborly. See also
(6.9.43).
Note that every complex is at least 1-neighborly.
6.9.52 SCNumFaces
▷(method)
Returns: an integer or a list of integers upon success, otherwise.
If is not specified the function computes the f-vector of the simplicial complex (cf.
(7.3.4)). If the optional integer parameter is passed, only the -th position of the f-

simpcomp 104
vector of is calculated. In any case a memory-saving implicit algorithm is used that avoids
calculating the face lattice of the complex.
6.9.53 SCOrientation
▷(method)
Returns: a list of the type {±1}fdor upon success, otherwise.
This function tries to compute an orientation of a pure simplicial complex that fulfills
the weak pseudomanifold property. If is orientable, an orientation in form of a list of orien-
tations for the facets of is returned, otherwise an empty set.
6.9.54 SCSkel
▷(method)
Returns: a face list or a list of face lists upon success, otherwise.
If is an integer, the -skeleton of a simplicial complex , i. e. all -faces of ,
is computed. If is a list, a list of all -faces of for each entry (which has to be
an integer) is returned. The faces are returned in the original labeling.
6.9.55 SCSkelEx
▷(method)
Returns: a face list or a list of face lists upon success, otherwise.
If is an integer, the -skeleton of a simplicial complex , i. e. all -faces of ,
is computed. If is a list, a list of all -faces of for each entry (which has to be
an integer) is returned. The faces are returned in the standard labeling.

simpcomp 105
6.9.56 SCSpanningTree
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Computes a spanning tree of a connected simplicial complex using a greedy algorithm.
6.10 Operations on simplicial complexes
The following functions perform operations on simplicial complexes. Most of them return simplicial
complexes. Thus, this section is closely related to the Sections 6.6 ”Generate new complexes from
old”. However, the data generated here is rather seen as an intrinsic attribute of the original complex
and not as an independent complex.
6.10.1 SCAlexanderDual
▷(method)
Returns: simplicial complex of type upon success, otherwise.
The Alexander dual of a simplicial complex with set of vertices Vis the simplicial
complex where any subset of Vspans a face if and only if its complement in Vis a non-face of
.

simpcomp 106
6.10.2 SCClose
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Closes a simplicial complex by building a cone over its boundary. If is specified it
is assigned to the apex of the cone and the original vertex labeling of is preserved, otherwise
an arbitrary vertex label is chosen and is returned in the standard labeling.
6.10.3 SCCone
▷(function)
Returns: simplicial complex of type upon success, otherwise.
If the second argument is passed every facet of the simplicial complex is united with
. If not, an arbitrary vertex label vis used (which is not a vertex of ). In the first case
the vertex labeling remains unchanged. In the second case the function returns the new complex in
the standard vertex labeling from 1 to n+1 and the apex of the cone is n+1.
If called with a facet list instead of a object and is not specified,
internally falls back to the homology package [DHSW11], if available.

simpcomp 107
6.10.4 SCDeletedJoin
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Calculates the simplicial deleted join of the simplicial complexes and . If
called with a facet list instead of a object, the function internally falls back
to the homology package [DHSW11], if available.

simpcomp 108
6.10.5 SCDifference
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Forms the “difference” of two simplicial complexes and as the simpli-
cial complex formed by the difference of the face lattices of minus . The
two arguments are not altered. Note: for the difference process the vertex labelings of the
complexes are taken into account, see also
(5.3.2).
6.10.6 SCFillSphere
▷(function)
Returns: simplicial complex of type upon success, otherwise .
Fills the given simplicial sphere by forming the suspension of the anti star of
over . This is a triangulated (d+1)-ball with the boundary , see [BD08]. If the
optional argument is not supplied, the first vertex of is chosen.
Note that it is not checked whether really is a simplicial sphere – this has to be done by
the user!

simpcomp 109
6.10.7 SCHandleAddition
▷(method)
Returns: simplicial complex of type , otherwise.
Returns a simplicial complex obtained by identifying the vertices of facet with the ones from
facet in . A combinatorial handle addition is possible, whenever we have d(v,w)≥3 for
any two vertices v∈and w∈, where d(⋅,⋅)is the length of the shortest path from vto w. This
condition is not checked by this algorithm. See [BD11] for further information.
6.10.8 SCIntersection
▷(method)
Returns: simplicial complex of type upon success, otherwise.

simpcomp 110
Forms the “intersection” of two simplicial complexes and as the simpli-
cial complex formed by the intersection of the face lattices of and . The
two arguments are not altered. Note: for the intersection process the vertex labelings of the com-
plexes are taken into account. See also
(5.3.3).
6.10.9 SCIsIsomorphic
▷(method)
Returns: or upon success, otherwise.
The function returns , if the simplicial complexes and are combinato-
rially isomorphic, if not.
6.10.10 SCIsSubcomplex
▷(method)
Returns: or upon success, otherwise.
Returns if the simplicial complex is a sub-complex of simplicial complex ,
otherwise. If dim( ) ≤dim( ) the facets of are compared with the dim( )-skeleton of
. Only works for pure simplicial complexes. Note: for the intersection process the vertex labelings
of the complexes are taken into account.

simpcomp 111
6.10.11 SCIsomorphism
▷(method)
Returns: a list of pairs of vertex labels or upon success, otherwise.
Returns an isomorphism of simplicial complex to simplicial complex in
the standard labeling if they are combinatorially isomorphic, otherwise. Internally calls
(6.10.12).
6.10.12 SCIsomorphismEx
▷(method)
Returns: a list of pairs of vertex labels or upon success, otherwise.
Returns an isomorphism of simplicial complex to simplicial complex in
the standard labeling if they are combinatorially isomorphic, otherwise. If the f-vector and
the Altshuler-Steinberg determinant of and are equal, the internal function
is called.
6.10.13 SCJoin
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Calculates the simplicial join of the simplicial complexes and . If facet lists
instead of objects are passed as arguments, the function internally falls back

simpcomp 112
to the homology package [DHSW11], if available. Note that the vertex labelings of the complexes
passed as arguments are not propagated to the new complex.
6.10.14 SCNeighbors
▷(method)
Returns: a list of faces upon success, otherwise.
In a simplicial complex all neighbors of the -face , i. e. all -faces distinct from
intersecting with in a common (k−1)-face, are returned in the original labeling.

simpcomp 113
6.10.15 SCNeighborsEx
▷(method)
Returns: a list of faces upon success, otherwise.
In a simplicial complex all neighbors of the -face , i. e. all -faces distinct from
intersecting with in a common (k−1)-face, are returned in the standard labeling.
6.10.16 SCShelling
▷(method)
Returns: a facet list or upon success, otherwise.
The simplicial complex must be pure, strongly connected and must fulfill the weak
pseudomanifold property with non-empty boundary (cf. (6.9.7)).
An ordering (F1,F2,...,Fr)on the facet list of a simplicial complex is a shelling if and only if
Fi∩(F1∪...∪Fi−1)is a pure simplicial complex of dimension d−1 for all i=1,...,r.
The function checks whether is shellable or not. In the first case a permuted version of
the facet list of is returned encoding a shelling of , otherwise is returned.
Internally calls (6.10.17) . To learn more about shellings
see [Zie95], [Pac87].

simpcomp 114
6.10.17 SCShellingExt
▷(method)
Returns: a list of facet lists (if ) or or (if is not
empty), otherwise.
The simplicial complex must be pure of dimension d, strongly connected and must fulfill
the weak pseudomanifold property with non-empty boundary (cf. (6.9.7)).
An ordering (F1,F2,...,Fr)on the facet list of a simplicial complex is a shelling if and only if
Fi∩(F1∪...∪Fi−1)is a pure simplicial complex of dimension d−1 for all i=1,...,r.
If is set to all possible shellings of are computed. If is set to , at
most one shelling is computed.
Every shelling is represented as a permuted version of the facet list of . The list
encodes a shelling in a shorter form. It only contains the indices of the facets. If
an order of indices is assigned to the function tests whether it is a valid shelling or not.
See [Zie95], [Pac87] to learn more about shellings.
6.10.18 SCShellings
▷(method)
Returns: a list of facet lists upon success, otherwise.
The simplicial complex must be pure, strongly connected and must fulfill the weak
pseudomanifold property with non-empty boundary (cf. (6.9.7)).
An ordering (F1,F2,...,Fr)on the facet list of a simplicial complex is a shelling if and only if
Fi∩(F1∪...∪Fi−1)is a pure simplicial complex of dimension d−1 for all i=1,...,r.
The function checks whether is shellable or not. In the first case a list of permuted
facet lists of is returned containing all possible shellings of , otherwise is
returned.
Internally calls (6.10.17) . To learn more about shellings
see [Zie95], [Pac87].

simpcomp 115
6.10.19 SCSpan
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Computes the reduced face lattice of all faces of a simplicial complex that are spanned
by , a subset of the set of vertices of .

simpcomp 116
6.10.20 SCSuspension
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Calculates the simplicial suspension of the simplicial complex . Internally falls back to
the homology package [DHSW11] (if available) if a facet list is passed as argument. Note that the
vertex labelings of the complexes passed as arguments are not propagated to the new complex.

simpcomp 117
6.10.21 SCUnion
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Forms the union of two simplicial complexes and as the simplicial complex
formed by the union of their facets sets. The two arguments are not altered. Note: for the union
process the vertex labelings of the complexes are taken into account, see also
(5.3.1). Facets occurring in both arguments
are treated as one facet in the new complex.
6.10.22 SCVertexIdentification
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Identifies vertex with vertex in a simplicial complex and returns the result as
a new object. A vertex identification of and is possible whenever d( , ) ≥3. This is not
checked by this algorithm.
6.10.23 SCWedge
▷(method)
Returns: simplicial complex of type upon success, otherwise.
simpcomp 118
Calculates the wedge product of the complexes supplied as arguments. Note that the vertex label-
ings of the complexes passed as arguments are not propagated to the new complex.

Chapter 7
Functions and operations for
7.1 Creating an object
This section contains functions to construct discrete normal surfaces that are slicings from a list of
2-dimensional facets (triangles and quadrilaterals) or combinatorial 3-manifolds.
For a very short introduction to the theory of discrete normal surfaces and slicings see Section
2.4 and Section 2.5, for an introduction to the GAP object type see 5.4, for more
information see the article [Spr11b].
7.1.1 SCNSEmpty
▷(function)
Returns: discrete normal surface of type upon success, otherwise.
Generates an empty complex (of dimension −1), i. e. an object of type with
empty facet list.
7.1.2 SCNSFromFacets
▷(method)
Returns: discrete normal surface of type upon success, otherwise.
Constructor for a discrete normal surface from a facet list, see (6.1.1) for details.
119

simpcomp 120
7.1.3 SCNS
▷(method)
Returns: discrete normal surface of type upon success, otherwise.
Internally calls (7.1.2).
7.1.4 SCNSSlicing
▷(function)
Returns: discrete normal surface of type upon success, otherwise.
Computes a slicing defined by a partition of the set of vertices of the 3-dimensional
combinatorial pseudomanifold . In particular, has to be a pair of lists of vertex
labels and has to contain all vertex labels of .

simpcomp 121

simpcomp 122
7.2 Generating new objects from discrete normal surfaces
simpcomp provides the possibility to copy and / or triangulate normal surfaces. Note that other
constructions like the connected sum or the cartesian product do not make sense for (embedded)
normal surfaces in general.
7.2.1 SCCopy
▷(method)
Returns: discrete normal surface of type upon success, otherwise.
Copies a GAP object of type (cf. ).

simpcomp 123
7.2.2 SCNSTriangulation
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Computes a simplicial subdivision of a slicing without introducing new vertices. The subdi-
vision is stored as a property of and thus is returned as an immutable object. Note that symmetry
may be lost during the computation.
7.3 Properties of objects
Although some properties of a discrete normal surface can be computed by using the functions for
simplicial complexes, there is a variety of properties needing specially designed functions. See below
for a list.
7.3.1 SCConnectedComponents
▷(method)
Returns: a list of simplicial complexes of type upon success, otherwise.
Computes all connected components of an arbitrary normal surface.

simpcomp 124
7.3.2 SCDim
▷(method)
Returns: an integer upon success, otherwise.
Computes the dimension of a discrete normal surface (which is always 2 if the slicing is not
empty).
7.3.3 SCEulerCharacteristic
▷(method)
Returns: an integer upon success, otherwise.
Computes the Euler characteristic of a discrete normal surface , cf. .

simpcomp 125
7.3.4 SCFVector
▷(method)
Returns: a 1, 3 or 4 tuple of (non-negative) integer values upon success, otherwise.
Computes the f-vector of a discrete normal surface, i. e. the number of vertices, edges, triangles
and quadrilaterals of , cf. .
7.3.5 SCFaceLattice
▷(method)
Returns: a list of facet lists upon success, otherwise.
Computes the face lattice of a discrete normal surface in the original labeling. Triangles and
quadrilaterals are stored separately (cf. (7.3.13)).
7.3.6 SCFaceLatticeEx
▷(method)
Returns: a list of face lists upon success, otherwise.

simpcomp 126
Computes the face lattice of a discrete normal surface in the standard labeling. Triangles and
quadrilaterals are stored separately (cf. (7.3.14)).
7.3.7 SCFpBettiNumbers
▷(method)
Returns: a list of non-negative integers upon success, otherwise.
Computes the Betti numbers modulo of a slicing . Internally, is triangulated (using
(7.2.2)) and the Betti numbers are computed via using
the triangulation.
7.3.8 SCGenus
▷(method)
Returns: a non-negative integer upon success, otherwise.
Computes the genus of a discrete normal surface .

simpcomp 127
7.3.9 SCHomology
▷(method)
Returns: a list of homology groups upon success, otherwise.
Computes the homology of a slicing . Internally, is triangulated (cf.
(7.2.2)) and simplicial homology is computed via using the triangulation.
7.3.10 SCIsConnected
▷(method)
Returns: or upon success, otherwise.
Checks if a normal surface is connected.

simpcomp 128
7.3.11 SCIsEmpty
▷(method)
Returns: or upon success, otherwise.
Checks if a normal surface is the empty complex, i. e. a object with
empty facet list.
7.3.12 SCIsOrientable
▷(method)
Returns: or upon success, otherwise.
Checks if a discrete normal surface is orientable.

simpcomp 129
7.3.13 SCSkel
▷(method)
Returns: a face list (of tuples) or a list of face lists upon success, otherwise.
Computes all faces of cardinality in the original labeling: =0 computes the vertices, =1
computes the edges, =2 computes the triangles, =3 computes the quadrilaterals.
If is a list (necessarily a sublist of ) all faces of all cardinalities contained in are
computed.
7.3.14 SCSkelEx
▷(method)
Returns: a face list (of tuples) or a list of face lists upon success, otherwise.

simpcomp 130
Computes all faces of cardinality in the standard labeling: =0 computes the vertices, =1
computes the edges, =2 computes the triangles, =3 computes the quadrilaterals.
If is a list (necessarily a sublist of ) all faces of all cardinalities contained in are
computed.
7.3.15 SCTopologicalType
▷(method)
Returns: a string upon success, otherwise.
Determines the topological type of via the classification theorem for closed compact surfaces.
If is not connected, the topological type of each connected component is computed.

simpcomp 131
7.3.16 SCUnion
▷(method)
Returns: normal surface of type upon success, otherwise.
Forms the union of two normal surfaces and as the normal surface formed
by the union of their facet sets. The two arguments are not altered. Note: for the union pro-
cess the vertex labelings of the complexes are taken into account, see also
(5.6.1). Facets occurring in both arguments are treated
as one facet in the new complex.

simpcomp 132

Chapter 8
(Co-)Homology of simplicial complexes
By default, simpcomp uses an algorithm based on discrete Morse theory (see Chapter 12,
(12.1.12)) for its homology computations. However, some additional (co-)homology
related functionality cannot be realised using this algorithm. For this, simpcomp contains an addi-
tional (co-)homology algorithm (cf. (8.1.5)), which will be presented in this
chapter.
Furthermore, whenever possible simpcomp makes use of the GAP package ”homology”
[DHSW11], for an alternative method to calculate homology groups (cf.
(6.9.31)) which sometimes is much faster than the built-in discrete Morse theory algorithm.
8.1 Homology computation
Apart from calculating boundaries of simplices, boundary matrices or the simplicial homology of a
given complex, simpcomp is also able to compute a basis of the homology groups.
8.1.1 SCBoundaryOperatorMatrix
▷(method)
Returns: a rectangular matrix upon success, otherwise.
Calculates the matrix of the boundary operator ∂of a simplicial complex . Note that
each column contains the boundaries of a +1-simplex as a list of oriented -simplices and that the
matrix is stored as a list of row vectors (as usual in GAP).
133

simpcomp 134
8.1.2 SCBoundarySimplex
▷(function)
Returns: a list upon success, otherwise.
Calculates the boundary of a given . If the flag is set to , the function
returns the boundary as a list of oriented simplices of the form [ ORIENTATION, SIMPLEX ], where
ORIENTATION is either +1 or -1 and a value of +1 means that SIMPLEX is positively oriented and a
value of -1 that SIMPLEX is negatively oriented. If is set to , an unoriented list
of simplices is returned.
8.1.3 SCHomologyBasis
▷(method)
Returns: a list of pairs of the form
upon success, otherwise.
Calculates a set of basis elements for the -dimensional homology group (with integer coeffi-
cients) of a simplicial complex . The entries of the returned list are of the form [ MODU-
LUS, [ BASEELM1, BASEELM2, ...] ], where the value MODULUS is 1 for the basis elements of
the free part of the -th homology group and q≥2 for the basis elements of the q-torsion part. In
contrast to the function (8.1.4) the basis elements are stored as lists
of coefficient-index pairs referring to the simplices of the complex, i.e. a basis element of the form
[[λ1,i],[λ2,j],...]... encodes the linear combination of simplices of the form λ1∗∆1+λ2∗∆2with
∆1= , ∆2= and so on.
8.1.4 SCHomologyBasisAsSimplices
▷(method)
Returns: a list of pairs of the form
upon success, otherwise.
Calculates a set of basis elements for the -dimensional homology group (with integer coeffi-
cients) of a simplicial complex . The entries of the returned list are of the form [ MODU-
LUS, [ BASEELM1, BASEELM2, ...] ], where the value MODULUS is 1 for the basis elements of
the free part of the -th homology group and q≥2 for the basis elements of the q-torsion part. In

simpcomp 135
contrast to the function (8.1.3) the basis elements are stored as lists of coefficient-
simplex pairs, i.e. a basis element of the form [[λ1,∆1],[λ2,∆2],...]encodes the linear combination
of simplices of the form λ1∗∆1+λ2∗∆2+....
8.1.5 SCHomologyInternal
▷(function)
Returns: a list of pairs of the form upon success, otherwise.
This function computes the reduced simplicial homology with integer coefficients of a given sim-
plicial complex with integer coefficients. It uses the algorithm described in [DKT08].
The output is a list of homology groups of the form [H0,....,Hd], where dis the dimension of
. The format of the homology groups Hiis given in terms of their maximal cyclic subgroups,
i.e. a homology group Hi≅Zf+Zt1Z×⋅⋅⋅×ZtnZis returned in form of a list [f,[t1,...,tn]], where
fis the (integer) free part of Hiand tidenotes the torsion parts of Hiordered in weakly incresing size.
See also (12.1.12) and (6.9.31).
8.2 Cohomology computation
simpcomp can also compute the cohomology groups of simplicial complexes, bases of these coho-
mology groups, the cup product of two cocycles and the intersection form of (orientable) 4-manifolds.
8.2.1 SCCoboundaryOperatorMatrix
▷(method)
Returns: a rectangular matrix upon success, otherwise.
Calculates the matrix of the coboundary operator das a list of row vectors.

simpcomp 136
8.2.2 SCCohomology
▷(method)
Returns: a list of pairs of the form upon success, otherwise.
This function computes the simplicial cohomology groups of a given simplicial complex
with integer coefficients. It uses the algorithm described in [DKT08].
The output is a list of cohomology groups of the form [H0,....,Hd], where dis the dimension of
. The format of the cohomology groups Hiis given in terms of their maximal cyclic sub-
groups, i.e. a cohomology group Hi≅Zf+Zt1Z×⋅⋅⋅×ZtnZis returned in form of a list [f,[t1, ...,tn]],
where fis the (integer) free part of Hiand tidenotes the torsion parts of Hiordered in weakly in-
creasing size.
8.2.3 SCCohomologyBasis
▷(method)
Returns: a list of pairs of the form
upon success, otherwise.
Calculates a set of basis elements for the -dimensional cohomology group (with integer coeffi-
cients) of a simplicial complex . The entries of the returned list are of the form [ MODU-
LUS, [ BASEELM1, BASEELM2, ...] ], where the value MODULUS is 1 for the basis elements of

simpcomp 137
the free part of the -th homology group and q≥2 for the basis elements of the q-torsion part. In
contrast to the function (8.2.4) the basis elements are stored as
lists of coefficient-index pairs referring to the linear forms dual to the simplices in the k-th cochain
complex of , i.e. a basis element of the form [[λ1,i],[λ2,j],...]... encodes the linear com-
bination of simplices (or their dual linear forms in the corresponding cochain complex) of the form
λ1∗∆1+λ2∗∆2with ∆1= , ∆2= and so on.
8.2.4 SCCohomologyBasisAsSimplices
▷(method)
Returns: a list of pars of the form upon
success, otherwise.
Calculates a set of basis elements for the -dimensional cohomology group (with integer coeffi-
cients) of a simplicial complex . The entries of the returned list are of the form [ MODULUS,
[ BASEELM1, BASEELM2, ...] ], where the value MODULUS is 1 for the basis elements of the free
part of the -th homology group and q≥2 for the basis elements of the q-torsion part. In contrast to
the function (8.2.3) the basis elements are stored as lists of coefficient-simplex
pairs referring to the linear forms dual to the simplices in the k-th cochain complex of , i.e.
a basis element of the form [[λ1,∆i],[λ2,∆j],...]... encodes the linear combination of simplices (or
their dual linear forms in the corresponding cochain complex) of the form λ1∗∆1+λ2∗∆2+....

simpcomp 138

simpcomp 139
8.2.5 SCCupProduct
▷(function)
Returns: a list of pairs of the form upon success, otherwise.
The cup product is a method of adjoining two cocycles of degree pand qto form a composite
cocycle of degree p+q. It endows the cohomology groups of a simplicial complex with the structure
of a ring.
The construction of the cup product starts with a product of cochains: if is a p-
cochain and is a q-cochain of a simplicial complex (given as list of oriented
p- (q-)simplices), then
⌣(σ)=(σ○ι0,1,...p)⋅(σ○ιp,p+1,...,p+q)
where σis a p+q-simplex and ιS,S⊂{0,1,..., p+q}is the canonical embedding of the simplex
spanned by Sinto the (p+q)-standard simplex.
σ○ι0,1,...,pis called the p-th front face and σ○ιp,p+1,...,p+qis the q-th back face of σ, respectively.
Note that this function only computes the cup product in the case that is an orientable
weak pseudomanifold of dimension 2kand p=q=k. Furthermore, must be given in stan-
dard labeling, with sorted facet list and and must be given in simplex notation
and labeled accordingly. Note that the latter condition is usually fulfilled in case the cocycles were
computed using (8.2.4).
8.2.6 SCIntersectionForm
▷(method)
Returns: a square matrix of integer values upon success, otherwise.
For 2k-dimensional orientable manifolds Mthe cup product (see (8.2.5)) defines
a bilinear form
Hk(M)×Hk(M)→H2k(M),(a,b)↦a∪b
called the intersection form of M. This function returns the intersection form of an orientable com-
binatorial 2k-manifold in form of a matrix with respect to the basis of Hk(M)
computed by (8.2.4). The matrix entry equals the
intersection number of the -th base element with the -th base element of Hk(M).

simpcomp 140
8.2.7 SCIntersectionFormParity
▷(method)
Returns: or upon success, otherwise.
Computes the parity of the intersection form of a combinatorial manifold (see
(8.2.6)). If the intersection for is even (i. e. all diagonal entries are even
numbers) is returned, otherwise is returned.
8.2.8 SCIntersectionFormDimensionality
▷(method)
Returns: an integer upon success, otherwise.
Returns the dimensionality of the intersection form of a combinatorial manifold , i. e.
the length of a minimal generating set of Hk(M)(where 2kis the dimension of ). See
(8.2.6) for further details.

simpcomp 141
8.2.9 SCIntersectionFormSignature
▷(method)
Returns: a triple of integers upon success, otherwise.
Computes the dimensionality (see (8.2.8)) and the sig-
nature of the intersection form of a combinatorial manifold as a 3-tuple that contains the
dimensionality in the first entry and the number of positive / negative eigenvalues in the second and
third entry. See (8.2.6) for further details.
Internally calls the GAP-functions and
to compute the number of positive / negative eigenvalues of
the intersection form.

simpcomp 142
Chapter 9
Bistellar flips
9.1 Theory
Since two combinatorial manifolds are already considered distinct to each other as soon as they
are not combinatorially isomorphic, a topological PL-manifold is represented by a whole class of
combinatorial manifolds. Thus, a frequent question when working with combinatorial manifolds is
whether two such objects are PL-homeomorphic or not. One possibility to approach this problem,
i. e. to find combinatorially distinct members of the class of a PL-manifold, is a heuristic algorithm
using the concept of bistellar moves.
DEFINITION (Bistellar moves [Pac87])
Let Mbe a combinatorial d-manifold (d-pseudomanifold), γ=v0,...,vkak-face and
δ=w0,...,wd−ka(d−k+1)-tuple of vertices of Mthat does not span a (d−k)-face in M,
0≤k≤d, such that {v0,...,vk}∩{w0,...,wd−k}=∅and {v0,...,vk,w0,...wk−d}spans exactly
d−k+1 facets. Then the operation
κ(γ,δ)(M)=M∖(γ⋆∂ δ )∪(∂ γ ⋆δ)
is called a bistellar (d−k)-move.
In other words: If there exists a bouquet D⊂Mof d−k+1 facets on a subset of vertices
W⊂Vof order d+2 with a common k-face γand the complement δof the vertices of γin Wdoes
not span a (d−k)-face in Mwe can remove Dand replace it by a bouquet of k+1 facets E⊂Mwith
vertex set Wwith a common face spanned by δ. By construction ∂D=∂Eand the altered complex
is again a combinatorial d-manifold (d-pseudomanifold). See Fig. 11 for a bistellar 1-move of a
2-dimensional complex, see Fig. 12 for all bistellar moves in dimension 3.
143
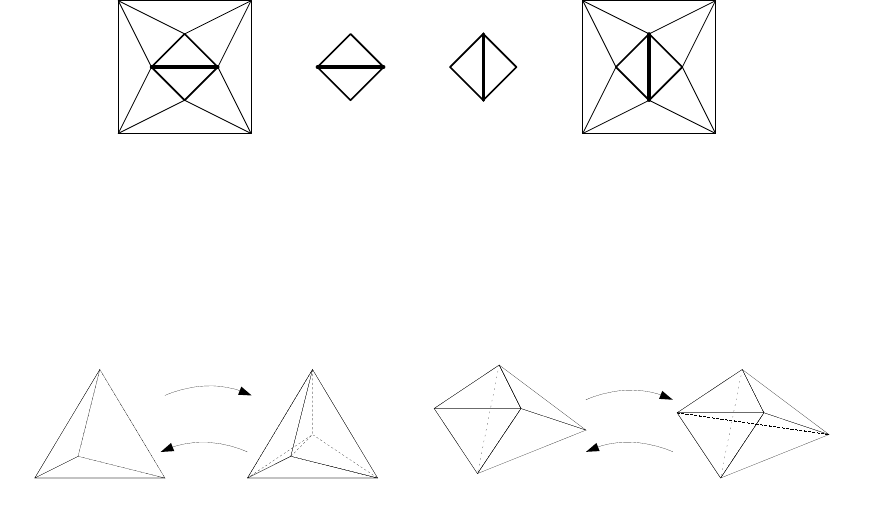
simpcomp 144
\∪=
γ ⋆ ∂δ δ ⋆ ∂γ
M:= hh1,2,3i,h1,2,5i,h1,3,4i,h1,4,8i,h1,5,8i,h2,3,6i,h2,5,6i,h3,4,7i,h3,6,7i,h4,7,8ii;
γ:= hh1,3ii;δ:= hh2,4ii;
κ(γ,δ)(M) = hh1,2,4i,h1,2,5i,h2,3,4i,h1,4,8i,h1,5,8i,h2,3,6i,h2,5,6i,h3,4,7i,h3,6,7i,h4,7,8ii;
5
6 7
8
2
3
4
1
2
3
4
1
2
3
4
1
5
6 7
8
2
3
4
1
Figure 11. Bistellar 1-move in dimension 2 with W={1,2,3,4}.
1 1
2
3
2
3
4
((5),(1,2,3,4))
((1,2,3,4),(5)) ((1,2,3),(4,5))
((4,5),(1,2,3))
2
1
4
3
4
5
2
1
4
3
5
5
Figure 12. Bistellar moves in dimension d=3 with W={1,2,3,4,5}. On the left side a bistellar 0- and a
bistellar 3-move, on the right side a bistellar 1- and a bistellar 2-move.
A bistellar 0-move is a stellar subdivision, i. e. the subdivision of a facet δinto d+1 new
facets by introducing a new vertex at the center of δ(cf. Fig. 12 on the left). In particular, the
vertex set of a combinatorial manifold (pseudomanifold) is not invariant under bistellar moves.
For any bistellar (d−k)-move κ(γ,δ)we have an inverse bistellar k-move κ−1
(γ,δ)=κ(δ,γ)such that
κ(δ,γ)(κ(γ,δ)(M)) =M. If for two combinatorial manifolds Mand Nthere exist a sequence of
bistellar moves that transforms one into the other, Mand Nare called bistellarly equivalent. So
far bistellar moves are local operations on combinatorial manifolds that change its combinatorial
type. However, the strength of the concept in combinatorial topology is a consequence of the following
THEOREM (Bistellar moves [Pac87])
Two combinatorial manifolds (pseudomanifolds) Mand Nare PL homeomorphic if and only if they
are bistellarly equivalent.
Unfortunately Pachners theorem does not guarantee that the search for a connecting sequence
of bistellar moves between Mand Nterminates. Hence, using bistellar moves, we can not prove that
Mand Nare not PL-homeomorphic. However, there is a very effective simulated annealing approach
that is able to give a positive answer in a lot of cases. The heuristic was first implemented by Bjoerner
and Lutz in [BL00]. The functions presented in this chapter are based on this code which can be used
for several tasks:
• Decide, whether two combinatorial manifolds are PL-homeomorphic,

simpcomp 145
• for a given triangulation of a PL-manifold, try to find a smaller one with less vertices,
• check, if an abstract simplicial complex is a combinatorial manifold by reducing all vertex links
to the boundary of the d-simplex (this can also be done using discrete Morse theory, see Chapter
<Ref Chap="chap:DMT" />, <Ref Meth="SCBistellarIsManifold" />).
In many cases the heuristic reduces a given triangulation but does not reach a minimal triangula-
tion after a reasonable amount of flips. Thus, we usually can not expect the algorithm to terminate.
However, in some cases the program normally stops after a small number of flips:
• Whenever d=1 (in this case the approach is deterministic),
• whenever a complex is PL-homeomorphic to the boundary of the d-simplex,
• in the case of some 3-manifolds, namely S2"S1,S2×S1or RP3.
Technical note: Since bistellar flips do not respect the combinatorial properties of a complex, no
attention to the original vertex labels is payed, i. e. the flipped complex will be relabeled whenever its
vertex labels become different from the standard labeling (for example after every reverse 0-move).
9.2 Functions for bistellar flips
9.2.1 SCBistellarOptions
▷(global variable)
Record of global variables to adjust output an behavior of bistellar moves in
(9.2.4) and (9.2.14) respectively.
1. : determines the length of the relaxation period. Default: 3
2. : determines the length of the heating period. Default: 4
3. : value of the current relaxation period. Default: 0
4. : value of the current heating period. Default: 0
5. : maximal over all number of bistellar flips that will be performed. Default: 500000
6. : maximal number of bistellar flips that will be performed without a change of
the f-vector of the moved complex. Default: 100000
7. : flip mode, 0=reducing, 1=comparing, 2=reduce as sub-complex, 3=randomize. Default:
0
8. : 0=no output, 1=storing of every vertex minimal complex to user library, 2=e-mail
notification. Default: 1
9. : (minimum) number of seconds between two e-mail notifications. De-
fault: 24⋅60 ⋅60 (one day)

simpcomp 146
10. : maximal number of bistellar flips that will be performed without a
change of the f-vector of a vertex link while trying to prove that the complex is a combinatorial
manifold. Default: 5000
11. : number of flips performed to create a randomized sphere.
Default: 50
9.2.2 SCEquivalent
▷(method)
Returns: or upon success, or a list of type
otherwise.
Checks if the simplicial complex (which has to fulfill the weak pseudomanifold prop-
erty with empty boundary) can be reduced to the simplicial complex via bistellar moves, i.
e. if and are PL-homeomorphic. Note that in general the problem is undecid-
able. In this case is returned.
It is recommended to use a minimal triangulation for the check if possible.
Internally calls (9.2.14)

simpcomp 147
9.2.3 SCExamineComplexBistellar
▷(method)
Returns: simplicial complex passed as argument with additional properties upon success,
otherwise.
Computes the face lattice, the f-vector, the AS-determinant, the dimension and the maximal vertex
label of .
9.2.4 SCIntFunc.SCChooseMove
▷(function)
Returns: a bistellar move, i. e. a pair of lists upon success, otherwise.
Since the problem of finding a bistellar flip sequence that reduces a simplicial complex is unde-
cidable, we have to use an heuristic approach to choose the next move.
The implemented strategy first tries to directly remove vertices,
edges, i-faces in increasing dimension etc. If this is not possible it inserts high dimensional faces in
decreasing co-dimension. To do this in an efficient way a number of parameters have to be adjusted,
namely and . See
(9.2.1) for further options.
If this strategy does not work for you, just implement a customized strategy and pass it to
(9.2.14).
See (9.2.10) for further information.

simpcomp 148
9.2.5 SCIsKStackedSphere
▷(method)
Returns: a list upon success, otherwise.
Checks, whether the given simplicial complex that must be a PL d-sphere is a -stacked
sphere with 1 ≤k≤d+2
2using a randomized algorithm based on bistellar moves (see [Eff11b],
[Eff11a]). Note that it is not checked whether is a PL sphere – if not, the algorithm will
not succeed. Returns a list upon success: the first entry is a boolean, where means that the com-
plex is -stacked and means that the complex cannot be -stacked. A value of -1 means that
the question could not be decided. The second argument contains a simplicial complex that, in case
of success, contains the trigangulated (d+1)-ball Bwith ∂B=Sand skeld−k(B)=skeld−k(S), where
Sdenotes the simplicial complex passed in .
Internally calls (9.2.14).
9.2.6 SCBistellarIsManifold
▷(method)
Returns: or upon success, otherwise.
Tries to prove that a closed simplicial d-pseudomanifold is a combinatorial manifold by reducing
its vertex links to the boundary of the d-simplex.

simpcomp 149
is returned if it can be proven that there exists a vertex link which is not PL-homeomorphic
to the standard PL-sphere, is returned if all vertex links are bistellarly equivalent to the bound-
ary of the simplex, is returned if the algorithm does not terminate after the number of rounds
indicated by .
Internally calls (9.2.14)
for every link of . Note that is returned in case of a bounded manifold.
See (12.1.18) and (12.1.17) for alternative methods for mani-
fold verification.
9.2.7 SCIsMovableComplex
▷(method)
Returns: or upon success, otherwise.
Checks if a simplicial complex can be modified by bistellar moves, i. e. if it is a pure
simplicial complex which fulfills the weak pseudomanifold property with empty boundary.
Complex with non-empty boundary:
9.2.8 SCMove
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Applies the bistellar move to a simplicial complex . is given as a (r+1)-tuple
together with a (d+1−r)-tuple if dis the dimension of and if is a r-move. See
(9.2.10) for detailed information about bistellar r-moves.
Note: and should be given in standard labeling to ensure a correct result.

simpcomp 150
9.2.9 SCMoves
▷(method)
Returns: a list of list of pairs of lists upon success, otherwise.
See (9.2.10) for further information.
9.2.10 SCRMoves
▷(method)
Returns: a list of pairs of the form , otherwise.
A bistellar r-move of a d-dimensional combinatorial manifold is a r-face m1together
with a d−r-tuple m2where m1is a common face of exactly (d+1−r)facets and m2is not a face of
.
The r-move removes all facets containing m1and replaces them by the (r+1)faces obtained by
uniting m2with any subset of m1of order r.
The resulting complex is PL-homeomorphic to .

simpcomp 151
9.2.11 SCRandomize
▷(function)
Returns: a simplicial complex upon success, otherwise.
Randomizes the given simplicial complex via bistellar moves chosen at random. By
passing the optional array , which has to be a dense array of integer values of
length , certain moves can be allowed or forbidden in the proccess. An entry
allows (i−1)-moves and an entry forbids (i−1)-moves
in the randomization process.
With optional positive integer argument , the amount of randomization can be
controlled. The higher the value of , the more bistellar moves will be ran-
domly performed on . Note that the argument overrides the global setting
(this value is used, if is not specified). In-
ternally calls (9.2.14).
9.2.12 SCReduceAsSubcomplex
▷(method)
Returns: : a triple of the form
upon termination of the algorithm.
: A library of simplicial complexes with a number of
complexes from the reducing process and (upon termination) a triple of the form
.
: A mail in case a smaller version of was
found, a library of simplicial complexes with a number of complexes from the reducing process and
(upon termination) a triple of the form
.
Returns upon an error.

simpcomp 152
Reduces a simplicial complex (satisfying the weak pseudomanifold property with
empty boundary) as a sub-complex of the simplicial complex .
Main application: Reduce a sub-complex of the cross polytope without introducing diagonals.
Internally calls (9.2.14)
9.2.13 SCReduceComplex
▷(method)
Returns: : a triple of the form
upon termination of the algorithm.
: A library of simplicial complexes with a number of
complexes from the reducing process and (upon termination) a triple of the form
.
: A mail in case a smaller version of was
found, a library of simplicial complexes with a number of complexes from the reducing process and
(upon termination) a triple of the form
.
Returns upon an error..
Reduces a pure simplicial complex satisfying the weak pseudoman-
ifold property via bistellar moves. Internally calls (9.2.14)

simpcomp 153
9.2.14 SCReduceComplexEx
▷(function)
Returns: : a triple of the form
upon termination of the algorithm.
: A library of simplicial complexes with a number of
complexes from the reducing process and (upon termination) a triple of the form
.
: A mail in case a smaller version of was
found, a library of simplicial complexes with a number of complexes from the reducing process and
(upon termination) a triple of the form .
Returns upon an error.
Reduces a pure simplicial complex satisfying the weak pseudomanifold property via bis-
tellar moves , compares it to the simplicial complex ( ) or reduces
it as a sub-complex of ( ).
is a function containing a flip strategy, see also (9.2.4).
The currently smallest complex is stored to the variable , the currently smallest f-
vector to . Note that in general the algorithm will not stop until the maximum number of rounds
is reached. You can adjust the maximum number of rounds via the property
(9.2.1). The number of rounds performed is returned in the third entry of the triple returned by this
function.
This function is called by
1. (9.2.13),
2. (9.2.2),
3. (9.2.12),
4. (9.2.6).
5. (9.2.11).
Please see (15.2.3) for further information about the email notification system in
case is set to 2.
simpcomp 154
Content of sent mail:

Chapter 10
Simplicial blowups
10.1 Theory
In this chapter functions are provided to perform simplicial blowups as well as the resolution of
isolated singularities of certain types of combinatorial 4-manifolds. As of today singularities where
the link is homeomorphic to RP3,S2×S1,S2"S1and the lens spaces L(k,1)are supported. In addition,
the program provides the possibility to hand over additional types of mapping cylinders to cover other
types of singularities.
Please note that the program is based on a heuristic algorithm using bistellar moves. Hence, the
search for a suitable sequence of bistellar moves to perform the blowup does not always terminate.
However, especially in the case of ordinary double points (singularities of type RP3), a lot of blowups
have already been successful. For a very short introduction to simplicial blowups see 2.8, for further
information see [SK11].
10.2 Functions related to simplicial blowups
10.2.1 SCBlowup
▷(property)
Returns: simplicial complex of type upon success, otherwise.
If is an ordinary double point of a combinatorial 4-pseudomanifold
(lk( )=RP3) the blowup of at is
computed. If it is a singularity of type S2×S1,S2"S1or L(k,1),k≤4, the canonical resolution of
is computed using the bounded complexes provided in the source code below.
If the optional argument of type is given, this complex
will be used to to resolve the singularity .
Note that bistellar moves do not necessarily preserve any orientation. Thus, the orientation of the
blowup has to be checked in order to verify which type of blowup was performed. Normally, repeated
computation results in both versions.
156
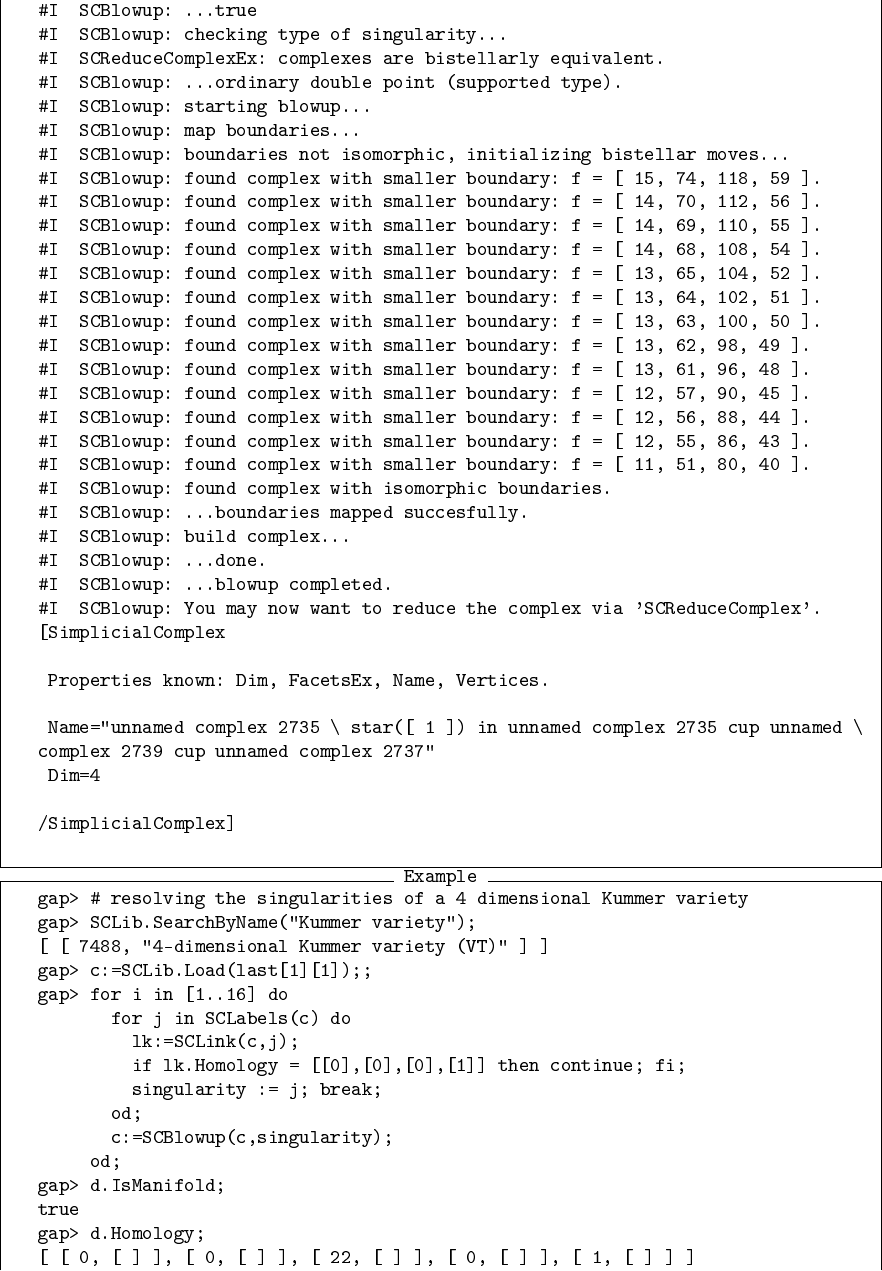
simpcomp 157

Chapter 11
Polyhedral Morse theory
In this chapter we present some useful functions dealing with polyhedral Morse theory. See Section
2.5 for a very short introduction to the field, see [Küh95] for more information. Note: this is not
to be confused with Robin Forman’s discrete Morse theory for cell complexes which is described in
Chapter 12.
If Mis a combinatorial d-manifold with n-vertices a rsl-function will be represented as an ordering
on the set of vertices, i. e. a list of length ncontaining all vertex labels of the corresponding simplicial
complex.
11.1 Polyhedral Morse theory related functions
11.1.1 SCIsTight
▷(method)
Returns: or upon success, otherwise.
Checks whether a simplicial complex ( must satisfy the weak pseudomanifold
property and must be closed) is a tight triangulation (with respect to the field with two elements)
or not. A simplicial complex with nvertices is said to be a tight triangulation if it can be tightly
embedded into the (n−1)-simplex. See Section 2.7 for a short introduction to the field of tightness.
First, if is a (k+1)-neighborly 2k-manifold (cf. [Küh95], Corollary 4.7), or
is of dimension d≥4, 2-neighborly and all its vertex links are stacked spheres (i.e. the complex is in
Walkup’s class K(d), see [Eff11b]) is returned as the complex is a tight triangulation in these
cases. If is of dimension d=3, is returned if and only if is 2-neighborly and
stacked (i.e. tight-neighbourly, see [BDSS15]), otherwise is returned, see [BDS].
Note that, for dimension d≥4, it is not computed whether or not is a combinatorial man-
ifold as this computation might take a long time. Hence, only if the manifold flag of the complex is set
(this can be achieved by calling (12.1.17) and the complex indeed is a combinatorial
manifold) these checks are performed.
In a second step, the algorithm first checks certain rsl-functions allowing slicings between minimal
non faces and the rest of the complex. In most cases where is not tight at least one of these
rsl-functions is not perfect and thus is returned as the complex is not a tight triangulation.
If the complex passed all checks so far, the remaining rsl-functions are checked for being per-
fect functions. As there are “only” 2ndifferent multiplicity vectors, but n! different rsl-functions, a
lookup table containing all possible multiplicity vectors is computed first. Note that nonetheless the
159

simpcomp 161

simpcomp 162

simpcomp 163
11.1.2 SCMorseIsPerfect
▷(method)
Returns: or upon success, otherwise.
Checks whether the rsl-function is perfect on the simplicial complex or not. A rsl-function is
said to be perfect, if it has the minimum number of critical points, i. e. if the sum of its critical points
equals the sum of the Betti numbers of .
11.1.3 SCSlicing
▷(method)
Returns: a facet list of a polyhedral complex or a object upon success,
otherwise.

simpcomp 164
Returns the pre-image f−1(α)of a rsl-function fon the simplicial complex where fis
given in the second argument by a partition of the set of vertices =[V1,V2]such
that f(v1)(f(v2)) is smaller (greater) than αfor all v1∈V1(v2∈V2).
If is of dimension 3, a GAP object of type is returned. Otherwise
only the facet list is returned. See also (7.1.4).
The vertex labels of the returned slicing are of the form (v1,v2)where v1∈V1and v2∈V2. They
represent the center points of the edges v1,v2defined by the intersection of with .
11.1.4 SCMorseMultiplicityVector
▷(method)
Returns: a list of (d+1)-tuples if is a d-dimensional simplicial complex upon success,
otherwise.
Computes all multiplicity vectors of a rsl-function on a simplicial complex . is given as an
ordered list (v1,...vn)of all vertices of where is defined by (vi)=i−1
n−1. The i-th entry of the
returned list denotes the multiplicity vector of vertex vi.

simpcomp 165
11.1.5 SCMorseNumberOfCriticalPoints
▷(method)
Returns: an integer and a list upon success, otherwise.
Computes the number of critical points of each index of a rsl-function on a simplicial complex
as well as the total number of critical points.
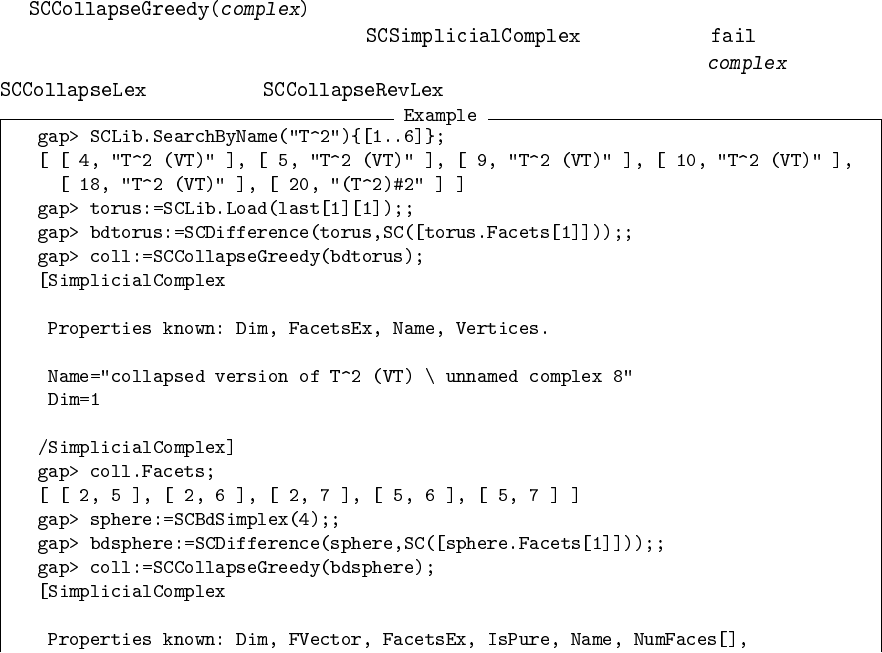
Chapter 12
Forman’s discrete Morse theory
In this chapter a framework is provided to use Forman’s discrete Morse theory [For95] within simp-
comp. See Section 2.6 for a brief introduction.
Note: this is not to be confused with Banchoff and Kühnel’s theory of regular simplexwise linear
functions which is described in Chapter 11.
12.1 Functions using discrete Morse theory
12.1.1 SCCollapseGreedy
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Employs a greedy collapsing algorithm to collapse the simplicial complex . See also
(12.1.2) and (12.1.3).
166
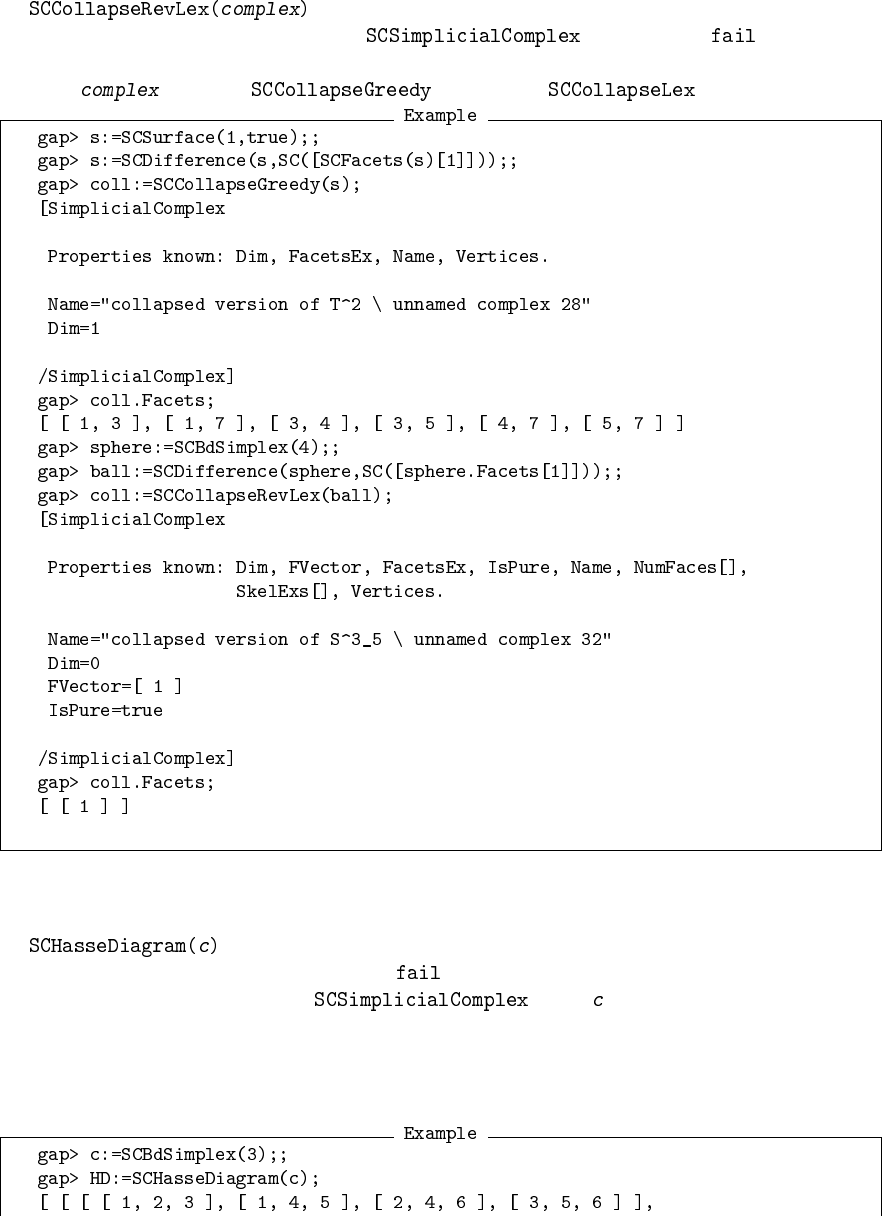
simpcomp 168
12.1.3 SCCollapseRevLex
▷(method)
Returns: simplicial complex of type upon success, otherwise.
Employs a greedy collapsing algorithm in reverse lexicographical order to collapse the simplicial
complex . See also (12.1.1) and (12.1.2).
12.1.4 SCHasseDiagram
▷(function)
Returns: two lists of lists upon success, otherweise.
Computes the Hasse diagram of object . The Hasse diagram is returned
as two sets of lists. The first set of lists contains the upward part of the Hasse diagram, the second set
of lists contains the downward part of the Hasse diagram.
The i-th list of each set of lists represents the incidences between the (i−1)-faces and the i-faces.
The faces are given by their indices of the face lattice.

simpcomp 169
12.1.5 SCMorseEngstroem
▷(function)
Returns: two lists of small integer lists upon success, otherweise.
Builds a discrete Morse function following the Engstroem method by reducing the input complex
to smaller complexes defined by minimal link and deletion operations. See [Eng09] for details.
12.1.6 SCMorseRandom
▷(function)
Returns: two lists of small integer lists upon success, otherweise.
Builds a discrete Morse function following Lutz and Benedetti’s random discrete Morse theory
approach: Faces are paired with free co-dimension one faces until now free faces remain. Then a
critical face is removed at random. See [BL14] for details.
12.1.7 SCMorseRandomLex
▷(function)
Returns: two lists of small integer lists upon success, otherweise.
Builds a discrete Morse function following Adiprasito, Benedetti and Lutz’ lexicographic random
discrete Morse theory approach. See [BL14], [KAL14] for details.

simpcomp 170
12.1.8 SCMorseRandomRevLex
▷(function)
Returns: two lists of small integer lists upon success, otherweise.
Builds a discrete Morse function following Adiprasito, Benedetti and Lutz’ reverse lexicographic
random discrete Morse theory approach. See [BL14], [KAL14] for details.
12.1.9 SCMorseSpec
▷(function)
Returns: a list upon success, otherweise.
Computes versions of a discrete Morse function of using a randomised method
specified by (default choice is (12.1.6), other randomised methods avail-
able are (12.1.7) (12.1.8), and (12.1.10)).
The result is referred to by the Morse spectrum of and is returned in form of a list containing
all Morse vectors sorted by number of critical points together with the actual vector of critical points
and how often they ocurred (see [BL14] for details).
12.1.10 SCMorseUST
▷(function)
Returns: a random Morse function of a simplicial complex and a list of critical faces.
Builds a random Morse function by removing a uniformly sampled spanning tree from the dual
1-skeleton followed by a collapsing approach. needs to be a closed weak pseudomanifold
for this to work. For details of the algorithm, see [PS15].

simpcomp 171
12.1.11 SCSpanningTreeRandom
▷(function)
Returns: a list of edges upon success, otherweise.
Computes a uniformly sampled spanning tree of the complex belonging to the Hasse diagram
using Wilson’s algorithm (see [Wil96]). If the output is a spanning tree of the dual graph
of the underlying complex. If the output is a spanning tree of the primal graph (i.e., the
1-skeleton.
12.1.12 SCHomology
▷(method)
Returns: a list of pairs of the form upon success
Computes the homology groups of a given simplicial complex using
(12.1.6) to obtain a Morse function and . Use
(12.1.13) to use alternative methods to compute discrete Morse functions (such as
(12.1.5), or (12.1.10)) or the Smith normal form.
The output is a list of homology groups of the form [H0,....,Hd], where dis the dimension of
. The format of the homology groups Hiis given in terms of their maximal cyclic subgroups,
i.e. a homology group Hi≅Zf+Zt1Z×⋅⋅⋅×ZtnZis returned in form of a list [f,[t1,...,tn]], where f
is the (integer) free part of Hiand tidenotes the torsion parts of Hiordered in weakly increasing size.
12.1.13 SCHomologyEx
▷(method)
Returns: a list of pairs of the form upon success, fail otherwise.
Computes the homology groups of a given simplicial complex using the function
for discrete Morse function computations and for Smith normal form computations.

simpcomp 172
The output is a list of homology groups of the form [H0,....,Hd], where dis the dimension of
. The format of the homology groups Hiis given in terms of their maximal cyclic subgroups,
i.e. a homology group Hi≅Zf+Zt1Z×⋅⋅⋅×ZtnZis returned in form of a list [f,[t1,...,tn]], where f
is the (integer) free part of Hiand tidenotes the torsion parts of Hiordered in weakly increasing size.
12.1.14 SCIsSimplyConnected
▷(function)
Returns: a boolean value upon success, otherweise.
Computes if the object is simply connected. The algorithm is a heuris-
tic method and is described in [PS15]. Internally calls (12.1.15).
12.1.15 SCIsSimplyConnectedEx
▷(function)
Returns: a boolean value upon success, otherweise.

simpcomp 173
Computes if the object is simply connected. The optional boolean
argument determines whether a spanning graph in the dual or the primal graph of will be used
for a collapsing sequence. The optional positive integer argument determines the number of
times the algorithm will try to find a collapsing sequence. The algorithm is a heuristic method and is
described in [PS15].
12.1.16 SCIsSphere
▷(function)
Returns: a boolean value upon success, otherweise.
Determines whether the object is a topological sphere. In dimension
≠4 the algorithm determines whether is PL-homeomorphic to the standard sphere. In dimension 4
the PL type is not specified. The algorithm uses a result due to [KS77] stating that, in dimension ≠4,
any simply connected homology sphere with PL structure is a standard PL sphere. The function calls
(12.1.14) which uses a heuristic method described in [PS15].
12.1.17 SCIsManifold
▷(function)
Returns: a boolean value upon success, otherweise.
The algorithm is a heuristic method and is described in [PS15] in more detail. Internally calls
(12.1.18).
12.1.18 SCIsManifoldEx
▷(function)
Returns: a boolean value upon success, otherweise.

simpcomp 174
If the boolean argument is the automorphism group is computed and only one link
per orbit is checked to be a sphere. If is not provided symmetry information is only used if
the automorphism group is already known. If the boolean argument is the algorithm
returns whether or not is a combinatorial manifold. If is the 4-dimensional links are not
verified to be standard PL 4-spheres and is a combinatorial manifold modulo the smooth Poincare
conjecture. By default is set to . The algorithm is a heuristic method and is described in
[PS15] in more detail.
See (9.2.6) for an alternative method for manifold verification.

Chapter 13
Library and I/O
13.1 Simplicial complex library
simpcomp contains a library of simplicial complexes on few vertices, most of them (combinatorial)
triangulations of manifolds and pseudomanifolds. The user can load these known triangulations from
the library in order to study their properties or to construct new triangulations out of the known ones.
For example, a user could determine the topological type of a given triangulation – which can be quite
tedious if done by hand – by establishing a PL equivalence to a complex in the library.
Among other known triangulations, the library contains all of the vertex transitive triangulations
of combinatorial manifolds with up to 15 vertices (for d∈{2,3,9,10,11,12}) and up to 13 vertices (for
d∈{4,5,6,7,8}) and all of the vertex transitive combinatorial pseudomanifolds with up to 15 vertices
(for d=3) and up to 13 vertices (for d∈{4,5,6,7}) classified by Frank Lutz that can be found on
his “Manifold Page” , along with some
triangulations of sphere bundles and some bounded triangulated PL-manifolds.
See (13.1.2) for a naming convention used for the global library of simpcomp. Note:
Another way of storing and loading complexes is provided by the functions (6.2.2),
(6.2.1) and (6.2.3), see Section 6.2 for details.
13.1.1 SCIsLibRepository
▷(filter)
Returns: or upon success, otherwise.
Filter for the category of a library repository used by the simpcomp library.
The category is derived from the category .
13.1.2 SCLib
▷(global variable)
175

simpcomp 176
The global variable contains the library object of the global library of simp-
comp through which the user can access the library. The path to the global library is
.
The naming convention in the global library is the following: complexes are usually named by
their topological type. As usual, ‘ Sˆd’ denotes a d-sphere, ‘T’ a torus, ‘x’ the cartesian product, ‘˜’
the twisted product and ‘#’ the connected sum. The Klein Bottle is denoted by ‘K’ or ‘Kˆ2’.

simpcomp 177
13.1.3 SCLibAdd
▷(function)
Returns: upon success, otherwise.
Adds a given simplicial complex to a given repository of type
. is saved to a file with suffix in the repositories base path, where
the file name is either formed from the optional argument and the current time or taken from the
name of the complex, if it is named.
13.1.4 SCLibAllComplexes
▷(function)
Returns: list of entries of the form upon success, otherwise.
Returns a list with entries of the form of all the complexes in the given repository
of type .

simpcomp 178
13.1.5 SCLibDelete
▷(function)
Returns: upon success, otherwise.
Deletes the simplicial complex with the given id from the given repository . Apart
from deleting the complexes’ index entry, the associated file is also deleted.
13.1.6 SCLibDetermineTopologicalType
▷(function)
Returns: simplicial complex of type or a list of integers upon success,
otherwise.
Tries to determine the topological type of a given complex by first looking for com-
plexes with matching homology in the library repository (if no repository is passed, the
global repository is used) and either returns a simplicial complex object (that is combinatori-
ally isomorphic to the complex given) or a list of library ids of complexes in the library with the same
homology as the complex provided.
The ids obtained in this way can then be used to compare the corresponding complexes with
via the function (9.2.2).
If is a combinatorial manifold of dimension 1 or 2 its topological type is computed,
stored to the property and is returned.
If no complexes with matching homology can be found, the empty set is returned.

simpcomp 179
13.1.7 SCLibFlush
▷(function)
Returns: upon success, otherwise.
Completely empties a given repository . The index and all simplicial complexes in
this repository are deleted. The second argument, , must be the string in order to
confirm the deletion.
13.1.8 SCLibInit
▷(function)
Returns: library repository of type upon success, otherwise.
This function initializes a library repository object for the given directory (which has to be
provided in form of a GAP object of type or ) and returns that library repository
object in case of success. The returned object then provides a mean to access the library repository
via the -functions of simpcomp.
The global library repository of simpcomp is loaded automatically at startup and is stored in the
variable . User repositories can be created by calling with a desired destination
directory. Note that each repository must reside in a different path since otherwise data may get lost.
The function first tries to load the repository index for the given directory to rebuild it (by calling
) if loading the index fails. The library index of a library repository is stored in its base
path in the XML file , the complexes are stored in files with suffix , also in XML
format.

simpcomp 180
13.1.9 SCLibIsLoaded
▷(function)
Returns: or upon succes, otherwise.
Returns when a given library repository is in loaded state. This means that
the directory of this repository is accessible and a repository index file for this repository exists in the
repositories’ path. If this is not the case is returned.
13.1.10 SCLibSearchByAttribute
▷(function)
Returns: A list of items of the form upon success, otherwise.
Searches a given repository for complexes for which the boolean expression ,
passed as string, evaluates to and returns a list of complexes with entries of the form
or upon error. The expression may use all GAP functions and can access all the indexed
attributes of the complexes in the given repository for the query. The standard attributes are: Dim
(Dimension), F (f-vector), G (g-vector), H (h-vector), Chi (Euler characteristic), Homology, Name,
IsPM, IsManifold. See for the set of indexed attributes of the global library of simpcomp.
13.1.11 SCLibSearchByName
▷(function)
Returns: A list of items of the form upon success, otherwise.
Searches a given repository for complexes that contain the string as a substring
of their name attribute and returns a list of the complexes found with entries of the form .
See (13.1.2) for a naming convention used for the global library of simpcomp.

simpcomp 181
13.1.12 SCLibSize
▷(function)
Returns: integer upon success, otherwise.
Returns the number of complexes contained in the given repository . Fails if the
library repository was not previously loaded with .
13.1.13 SCLibUpdate
▷(function)
Returns: library repository of type upon success, otherwise.
Recreates the index of a given repository (either via a repository object or a base path of a repos-
itory ) by scanning the base path for all files containing simplicial complexes of
the repository. Returns a repository object with the newly created index on success or in case
of an error. The optional boolean argument forces simpcomp to recompute all the indexed
properties (such as f-vector, homology, etc.) of the simplicial complexes in the repository if set to
.
13.1.14 SCLibStatus
▷(function)
Returns: library repository of type upon success, otherwise.
Lets GAP print the status of a given library repository . is the
list of attributes indexed for this repository. If is true, the index at-
tributes for a complex added to the library are calculated automatically upon addition of the complex,
otherwise this is left to the user and only pre-calculated attributes are indexed.

simpcomp 182
13.2 simpcomp input / output functions
This section contains a description of the input/output-functionality provided by simpcomp. The
package provides the functionality to save and load simplicial complexes (and their known properties)
to, respectively from files in XML format. Furthermore, it provides the user with functions to export
simplicial complexes into polymake format (for this format there also exists rudimentary import func-
tionality), as JavaView geometry or in form of a L
A
T
EX table. For importing more complex polymake
data the package polymaking [R¨
13] can be used.
13.2.1 SCLoad
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Loads a simplicial complex stored in a binary format (using ) from a file specified in
(as string). If does not end in , this suffix is appended to the file name.

simpcomp 183
13.2.2 SCLoadXML
▷(function)
Returns: simplicial complex of type upon success, otherwise.
Loads a simplicial complex stored in XML format from a file specified in (as string).
If does not end in , this suffix is appended to the file name.
13.2.3 SCSave
▷(function)
Returns: upon success, otherwise.
Saves a simplicial complex in a binary format (using ) to a file specified in
(as string). If does not end in , this suffix is appended to the file name.

simpcomp 184
13.2.4 SCSaveXML
▷(function)
Returns: upon success, otherwise.
Saves a simplicial complex to a file specified by (as string) in XML format.
If does not end in , this suffix is appended to the file name.
13.2.5 SCExportMacaulay2
▷(function)
Returns: upon success, otherwise.
Exports the facet list of a given simplicial complex in format to a file speci-
fied by . The argument can either be the ring of integers (specified by ) or
the ring of rationals (sepcified by ). The optional boolean argument labels
the complex with characters from a,...,zin the exported file if a value of is supplied, while
the standard labeling of the vertices is v1,...,vnwhere nis the number of vertices of . If
has more than 26 vertices, the argument is ignored.
13.2.6 SCExportPolymake
▷(function)
Returns: upon success, otherwise.
Exports the facet list with vertex labels of a given simplicial complex in
format to a file specified by . Currently, only the export in the format of version
2.3 is supported.
13.2.7 SCImportPolymake
▷(function)
Returns: simplicial complex of type upon success, otherwise.

simpcomp 185
Imports the facet list of a file specified by (discarding any vertex
labels) and creates a simplicial complex object from these facets.
13.2.8 SCExportLatexTable
▷(function)
Returns: on success, otherwise.
Exports the facet list of a given simplicial complex (or any list given as first argument)
in form of a L
A
T
EX table to a file specified by . The argument specifies how
many columns the exported table should have. The faces are exported in the format v1,...,vk.
13.2.9 SCExportJavaView
▷(function)
Returns: on success, otherwise.
Exports the 2-skeleton of the given simplicial complex (or the facets if the complex is of
dimension 2 or less) in format (file name suffix ) to a file specified by (as
string). The list must contain a 3-tuple of real coordinates for each vertex of , either
as tuple of length three containing the coordinates (Warning: as GAP only has rudimentary support
for floating point values, currently only integer numbers can be used as coordinates when providing
as list of 3-tuples) or as string of the form with decimal numbers , ,
for the three coordinates (i.e. ).

simpcomp 186
13.2.10 SCExportPolymake
▷(function)
Returns: upon success, otherwise.
Exports the gluings of the tetrahedra of a given combinatorial 3-manifold in a format
compatible with Matveev’s 3-manifold software .
13.2.11 SCExportSnapPy
▷(function)
Returns: upon success, otherwise.
Exports the facet list and orientability of a given combinatorial 3-pseudomanifold in
format to a file specified by .

Chapter 14
Interfaces to other software packages
simpcomp contains various interfaces to other software packages (see Chapter 13 for file-related
export and import formats). In this chapter, some more sophisticated interfaces to other software
packages are described.
Note that this chapter is subject to change and extension as it is planned to expand simpcomp’s
functionality in this area in the course of the next versions.
14.1 Interface to the GAP-package homalg
As of Version 1.5, simpcomp is equipped with an interface to the GAP-package homalg [BR08]
by Mohamed Barakat. This allows to use homalg’s powerful capabilities in the field of homological
algebra to compute topological properties of simplicial complexes.
For the time being, the only functions provided are ones allowing to compute the homology and
cohomology groups of simplicial complexes with arbitrary coefficients. It is planned to extend the
functionality in future releases of simpcomp. See below for a list of functions that provide an inter-
face to homalg.
14.1.1 SCHomalgBoundaryMatrices
▷(method)
Returns: a list of homalg objects upon success, otherwise.
This function computes the boundary operator matrices for the simplicial complex with
a ring of coefficients as specified by : a value of yields Q-matrices, a value of yields
Z-matrices and a value of , q a prime or a prime power, computes the Fq-matrices.
187

simpcomp 188
14.1.2 SCHomalgCoboundaryMatrices
▷(method)
Returns: a list of homalg objects upon success, otherwise.
This function computes the coboundary operator matrices for the simplicial complex
with a ring of coefficients as specified by : a value of yields Q-matrices, a value of yields
Z-matrices and a value of , q a prime or a prime power, computes the Fq-matrices.
14.1.3 SCHomalgHomology
▷(method)
Returns: a list of integers upon success, otherwise.
This function computes the ranks of the homology groups of with a ring of coefficients as
specified by : a value of computes the Q-homology, a value of computes the Z-homology
and a value of , q a prime or a prime power, computes the Fq-homology ranks.
Note that if you are interested not only in the ranks of the homology groups, but rather their full
structure, have a look at the function (14.1.4).
14.1.4 SCHomalgHomologyBasis
▷(method)
Returns: ahomalg object upon success, otherwise.
This function computes the homology groups (including explicit bases of the modules involved) of
with a ring of coefficients as specified by : a value of computes the Q-homology,
a value of computes the Z-homology and a value of , q a prime or a prime power, computes the
Fq-homology groups.
The k-th homology group can be obtained by calling ,
where is the homalg object returned by this function. The generators of can then be
obtained via .

simpcomp 189
Note that if you are only interested in the ranks of the homology groups, then it is better to use the
funtion (14.1.3) which is way faster.
14.1.5 SCHomalgCohomology
▷(method)
Returns: a list of integers upon success, otherwise.
This function computes the ranks of the cohomology groups of with a ring of coefficients
as specified by : a value of computes the Q-cohomology, a value of computes the Z-
cohomology and a value of , q a prime or a prime power, computes the Fq-cohomology ranks.
Note that if you are interested not only in the ranks of the cohomology groups, but rather their full
structure, have a look at the function (14.1.6).
14.1.6 SCHomalgCohomologyBasis
▷(method)
Returns: ahomalg object upon success, otherwise.
This function computes the cohomology groups (including explicit bases of the modules involved)
of with a ring of coefficients as specified by : a value of computes the Q-
cohomology, a value of computes the Z-cohomology and a value of , q a prime or a prime power,
computes the Fq-homology groups.
The k-th cohomology group can be obtained by calling
, where is the homalg object returned
by this function. The generators of can then be obtained via .
Note that if you are only interested in the ranks of the cohomology groups, then it is better to use
the funtion (14.1.5) which is way faster.

simpcomp 190

Chapter 15
Miscellaneous functions
The behaviour of simpcomp can be changed by setting cetain global options. This can be achieved
by the functions described in the following.
15.1 simpcomp logging
The verbosity of the output of information to the screen during calls to functions of the package sim-
pcomp can be controlled by setting the info level parameter via the function (15.1.1).
15.1.1 SCInfoLevel
▷(function)
Returns:
Sets the logging verbosity of simpcomp. A level of 0 suppresses all output, a level of 1 lets sim-
pcomp output normal running information, whereas levels of 2 and higher display verbose running
information. Examples of functions using more verbose logging are bistellar flip-related functions.
191

simpcomp 192
15.2 Email notification system
simpcomp comes with an email notification system that can be used for being notified of the progress
of lengthy computations (such as reducing a complex via bistellar flips). See below for a description
of the mail notification related functions. Note that this might not work on non-Unix systems.
See (9.2.14) for an example computation using the email notification sys-
tem.
15.2.1 SCMailClearPending
▷(function)
Returns: nothing.
Clears a pending mail message.
15.2.2 SCMailIsEnabled
▷(function)
Returns: or upon success, otherwise.
Returns when the mail notification system of simpcomp is enabled, otherwise. De-
fault setting is .
15.2.3 SCMailIsPending
▷(function)
Returns: or upon success, otherwise.
Returns when an email of the simpcomp email notification system is pending, oth-
erwise.

simpcomp 193
15.2.4 SCMailSend
▷(function)
Returns: when the message was sent, if it was not send, upon an error.
Tries to send an email to the address specified by (15.2.6) using the Unix
program . The optional parameter specifies the starting time (as the integer Unix
timestamp) a calculation was started (then the duration of the calculation is included in the email),
the optional boolean parameter can be used to force the sending of an email, even if this
violates the minimal email sending interval, see (15.2.8).
15.2.5 SCMailSendPending
▷(function)
Returns: upon success, otherwise.
Tries to send a pending email of the simpcomp email notification system. Returns on
success or if there was no mail pending.
15.2.6 SCMailSetAddress
▷(function)
Returns: upon success, otherwise.
Sets the email address that should be used to send notification messages and enables the mail
notification system by calling (15.2.7)( ).
15.2.7 SCMailSetEnabled
▷(function)
Returns: upon success, otherwise.
Enables or disables the mail notification system of simpcomp. By default it is disabled. Returns
if no email message was previously set with (15.2.6).

simpcomp 194
15.2.8 SCMailSetMinInterval
▷(function)
Returns: upon success, otherwise.
Sets the minimal time interval in seconds that mail messages can be sent by simpcomp. This
prevents a flooding of the specified email address with messages sent by simpcomp. Default is 3600,
i.e. one hour.
15.3 Testing the functionality of simpcomp
simpcomp makes use of the GAP internal testing mechanisms and provides the user with a function
to test the functionality of the package.
15.3.1 SCRunTest
▷(function)
Returns: upon success, otherwise.
Test whether the package simpcomp is functional by calling
. The returned value of GAP4stones is a measure of your system per-
formance and differs from system to system.
On a modern computer, the function should take about a minute to complete when the
packages GRAPE [Soi12] and homology [DHSW11] are available. If these packages are missing,
the testing will take slightly longer.

Chapter 16
Property handlers
As explained in Chapter 5, objects of the types , and
provide a set of property handlers for ease of access to simpcomp functions
using these objects. Accessing these property handlers is possible via the .-operator.
For example, the f-vector of a simplicial complex that is stored as a
object can be accessed via the statement instead of writing the longer .
See below for a list of all properties supported by objects of the types ,
, and (Note that the property handlers
of can be used by both and ).
16.1 Property handlers of
This section contains a table of all property handlers of a object.
PROPERTY HANDLER FUNCTION CALLED
AntiStar (4.3.1)
Ast (4.3.1)
Facets (6.9.19)
FacetsEx (6.9.20)
LabelMax (4.2.1)
LabelMin (4.2.2)
Labels (4.2.3)
Lk (4.3.2)
Link (4.3.2)
Links (4.3.3)
Lks (4.3.3)
Name (4.2.4)
Reference (4.2.5)
Relabel (4.2.6)
RelabelStandard (4.2.7)
RelabelTransposition (4.2.8)
Rename (4.2.9)
SetReference (4.2.10)
195

simpcomp 196
Star (4.3.4)
Str (4.3.4)
Stars (4.3.5)
Strs (4.3.5)
UnlabelFace (4.2.11)
Vertices (4.1.3)
VerticesEx (4.1.4)
16.2 Property handlers of
This section contains a table of all property handlers of a object.
PROPERTY HANDLER FUNCTION CALLED
ASDet (6.9.1)
AlexanderDual (6.10.1)
AutomorphismGroup (6.9.2)
AutomorphismGroupInternal (6.9.3)
AutomorphismGroupSize (6.9.4)
AutomorphismGroupStructure (6.9.5)
AutomorphismGroupTransitivity (6.9.6)
Bd (6.9.7)
Boundary (6.9.7)
BoundaryOperatorMatrix (8.1.1)
Chi (7.3.3)
CoboundaryOperatorMatrix (8.2.1)
Cohomology (8.2.2)
CohomologyBasis (8.2.3)
CohomologyBasisAsSimplices (8.2.4)
CollapseGreedy (12.1.1)
Cone (6.10.3)
ConnectedComponents (7.3.1)
Copy (7.2.1)
CupProduct (8.2.5)
DehnSommervilleCheck (6.9.8)
DeletedJoin (6.10.4)
DetermineTopologicalType (13.1.6)
Difference (6.10.5)
DifferenceCycles (6.9.10)
Dim (7.3.2)
DualGraph (6.9.12)
Equivalent (9.2.2)
EulerCharacteristic (7.3.3)
ExportJavaView (13.2.9)
ExportLatexTable (13.2.8)
ExportPolymake (13.2.10)

simpcomp 197
F (7.3.4)
FaceLattice (7.3.5)
FaceLatticeEx (7.3.6)
Faces (6.9.17)
FacesEx (6.9.18)
FillSphere (6.10.6)
FpBetti (7.3.7)
FundamentalGroup (6.9.22)
G (6.9.23)
Generators (6.9.24)
GeneratorsEx (6.9.25)
H (6.9.26)
HandleAddition (6.10.7)
HasBd (6.9.27)
HasBoundary (6.9.27)
HasInt (6.9.28)
HasInterior (6.9.28)
HasseDiagram (12.1.4)
Homology (12.1.12)
HomologyBasis (8.1.3)
HomologyBasisAsSimplices (8.1.4)
HomologyInternal (8.1.5)
Incidences (6.9.32)
IncidencesEx (6.9.33)
Interior (6.9.34)
Intersection (6.10.8)
IntersectionForm (8.2.6)
IntersectionFormDimensionality (8.2.8)
IntersectionFormParity (8.2.7)
IntersectionFormSignature (8.2.9)
IsCentrallySymmetric (6.9.35)
IsConnected (7.3.10)
IsEmpty (7.3.11)
IsEulerianManifold (6.9.38)
IsFlag (6.9.39)
IsHomologySphere (6.9.41)
IsInKd (6.9.42)
IsIsomorphic (6.10.9)
IsKNeighborly (6.9.43)
IsKStackedSphere (9.2.5)

simpcomp 198
IsManifold (12.1.17)
IsMovable (9.2.7)
Isomorphism (6.10.11)
IsomorphismEx (6.10.12)
IsOrientable (7.3.12)
IsPM (6.9.45)
IsPure (6.9.46)
IsSC (12.1.14)
IsSimplyConnected (12.1.14)
IsShellable (6.9.47)
IsSphere (12.1.16)
IsStronglyConnected (6.9.48)
IsSubcomplex (6.10.10)
IsTight (11.1.1)
Join (6.10.13)
Load (13.2.1)
MinimalNonFaces (6.9.49)
MinimalNonFacesEx (6.9.50)
MorseIsPerfect (11.1.2)
MorseMultiplicityVector (11.1.4)
MorseNumberOfCriticalPoints (11.1.5)
Move (9.2.8)
Moves (9.2.9)
Neighborliness (6.9.51)
Neighbors (6.10.14)
NeighborsEx (6.10.15)
NumFaces (6.9.52)
Orientation (6.9.53)
PropertiesDropped (5.1.4)
Randomize (9.2.11)
RMoves (9.2.10)
Reduce (9.2.13)
ReduceAsSubcomplex (9.2.12)
ReduceEx (9.2.14)
Save (13.2.3)
Shelling (6.10.16)
ShellingExt (6.10.17)
Shellings (6.10.18)
Skel (7.3.13)
SkelEx (7.3.14)
Slicing (11.1.3), (7.1.4)
Span (6.10.19)
SpanningTree (6.9.56)
StronglyConnectedComponents (6.6.9)
Suspension (6.10.20)
Transitivity (6.9.6)
Union (7.3.16)
VertexIdentification (6.10.22)
Wedge (6.10.23)

simpcomp 199
16.3 Property handlers of
This section contains a table of all property handlers of a object.
PROPERTY HANDLER FUNCTION CALLED
Betti (7.3.7)
ConnectedComponents (7.3.1)
FpBettiNumbers (7.3.7)
Chi (7.3.3)
EulerCharacteristic (7.3.3)
Connected (7.3.10)
IsConnected (7.3.10)
Copy (7.2.1)
D (7.3.2)
Dim (7.3.2)
F (7.3.4)
FVector (7.3.4)
FaceLattice (7.3.5)
Faces (7.3.13)
Genus (7.3.8)
Homology (12.1.12)
IsEmpty (7.3.11)
Name (4.2.4)
Triangulation (7.2.2)
TopologicalType (7.3.15)
16.4 Property handlers of
This section contains a table of all property handlers of a object.
PROPERTY HANDLER FUNCTION CALLED
Update (13.1.13)
IsLoaded (13.1.9)
Size (13.1.12)
Status (13.1.14)
Flush (13.1.7)
Add (13.1.3)
Delete (13.1.5)
All (13.1.4)
SearchByName (13.1.11)
SearchByAttribute (13.1.10)
DetermineTopologicalType (13.1.6)

Chapter 17
A demo session with simpcomp
This chapter contains the transcript of a demo session with simpcomp that is intended to give an
insight into what things can be done with this package.
Of course this only scratches the surface of the functions provided by simpcomp. See Chapters 4
through 15 for further functions provided by simpcomp.
17.1 Creating a object
Simplicial complex objects can either be created from a facet list (complex below), orbit represen-
tatives together with a permutation group (complex ) or difference cycles (complex , see Section
6.1), from a function generating triangulations of standard complexes (complex , see Section 6.3)
or from a function constructing infinite series for combinatorial (pseudo)manifolds (complexes ,
, , see Section 6.4 and the function prefix ). There are also functions creating new
simplicial complexes from old, see Section 6.6, which will be described in the next sections.
200

simpcomp 201

simpcomp 202
17.2 Working with a object
As described in Section 3.1 there are two several ways of accessing an object of type
. An example for the two equivalent ways is given below. The preference
will be given to the object oriented notation in this demo session. The code listed below
is equivalent to
17.3 Calculating properties of a object
simpcomp provides a variety of functions for calculating properties of simplicial complexes, see
Section 6.9. All these properties are only calculated once and stored in the
object.
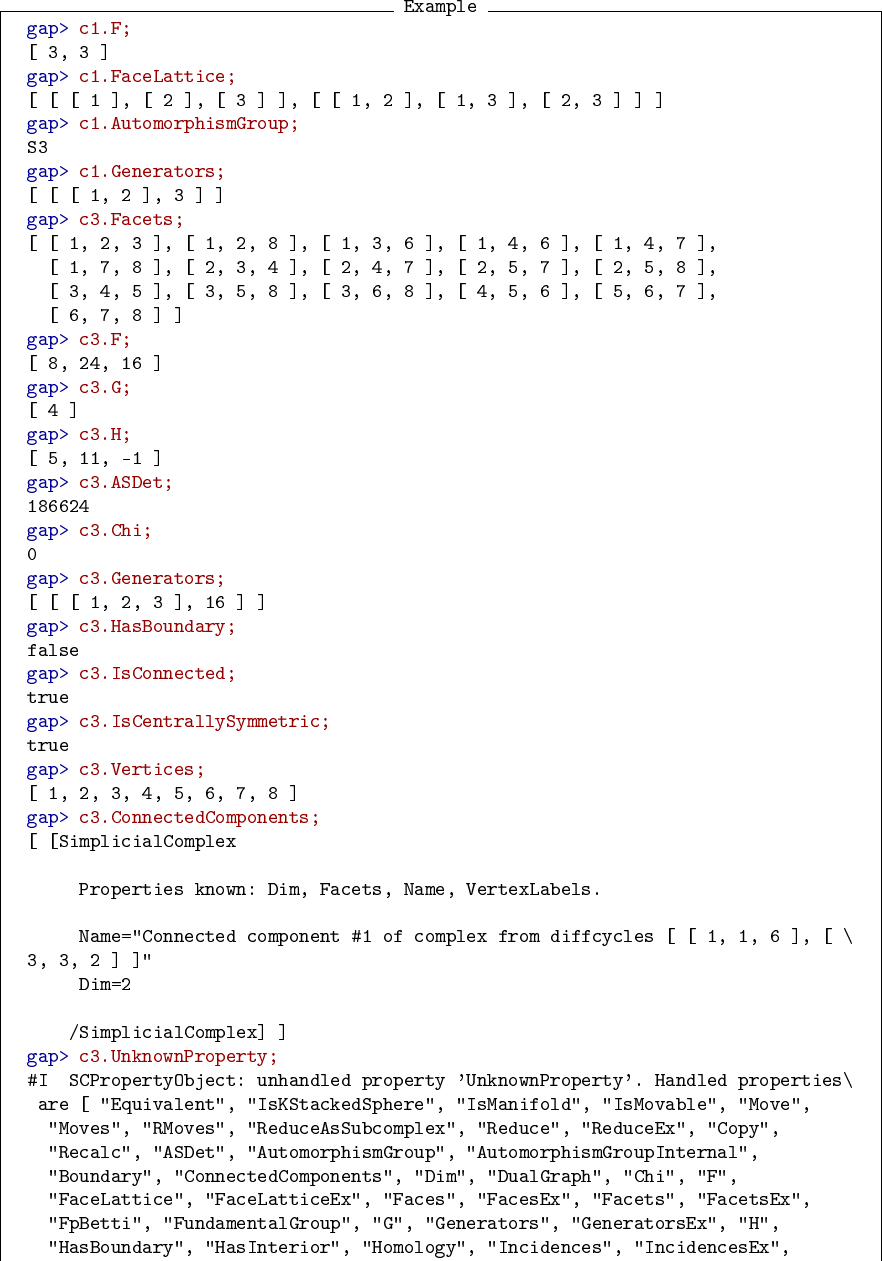
simpcomp 203

simpcomp 206
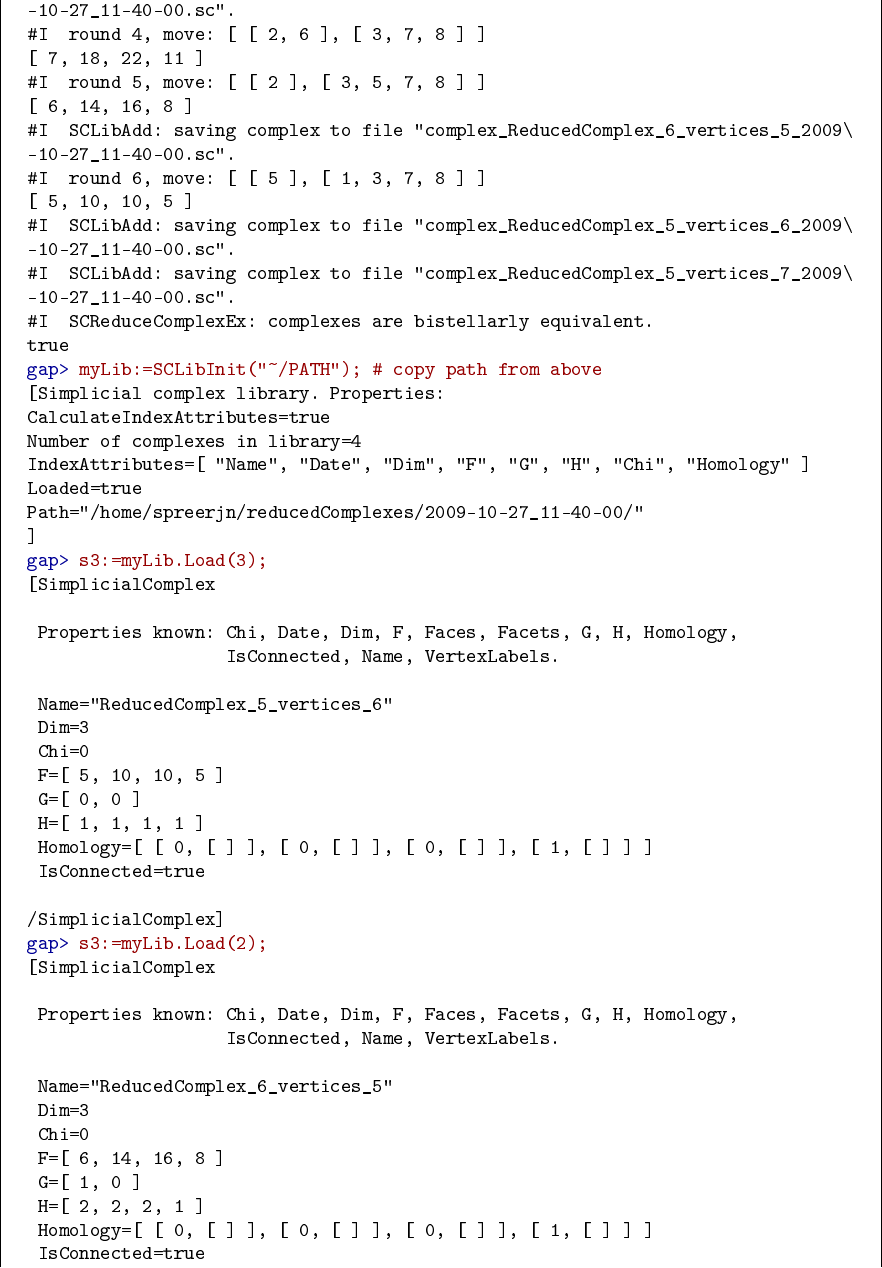
simpcomp 208

simpcomp 210

Chapter 18
simpcomp internals
The package simpcomp works with geometric objects for which the GAP object types
and are defined and calculates properties of these ob-
jects via so called property handlers. This chapter describes how to extend simpcomp by writing
own property handlers.
If you extended simpcomp and want to share your extension with other users please send your
extension to one of the authors and we will consider including it (of course with giving credit) in a
future release of simpcomp.
18.1 The GAP object type
In the following, we present a number of functions to manage a GAP object of type
. Since most properties of , and
are managed by the GAP4 type system (cf. [BL98]), the functions described be-
low are mainly used by the object type and to store temporary properties.
18.1.1 SCProperties
▷(method)
Returns: a record upon success.
Returns the record of all stored properties of the .
18.1.2 SCPropertiesFlush
▷(method)
Returns: upon success.
Drops all properties and temporary properties of the .
18.1.3 SCPropertiesManaged
▷(method)
Returns: a list of managed properties upon success, otherwise.
Returns a list of all properties that are managed for the via property
handler functions. See (18.1.9).
213

simpcomp 214
18.1.4 SCPropertiesNames
▷(method)
Returns: a list upon success.
Returns a list of all the names of the stored properties of the . These can
be accessed via (18.1.10) and (18.1.8).
18.1.5 SCPropertiesTmp
▷(method)
Returns: a record upon success.
Returns the record of all stored temporary properties (these are mutable in contrast to regular
properties and not serialized when the object is serialized to XML) of the .
18.1.6 SCPropertiesTmpNames
▷(method)
Returns: a list upon success.
Returns a list of all the names of the stored temporary properties of the .
These can be accessed via (18.1.14) and (18.1.13).
18.1.7 SCPropertyByName
▷(method)
Returns: any value upon success, otherwise.
Returns the value of the property with name of the if this property
is known for and otherwise. The names of known properties can be accessed via the function
(18.1.4)
18.1.8 SCPropertyDrop
▷(method)
Returns: upopn success, otherwise
Drops the property with name of the . Returns if the property
is successfully dropped and if a property with that name did not exist.
18.1.9 SCPropertyHandlersSet
▷(method)
Returns:
Sets the property handling functions for a SCPropertyObject to the functions described
in the record . The record has to contain entries of the following struc-
ture: . For
for example simpcomp defines (among many others): . See
the file .

simpcomp 215
18.1.10 SCPropertySet
▷(method)
Returns: upon success.
Sets the value of the property with name of the to . Note
that the argument becomes immutable. If this behaviour is not desired, use
(18.1.11) instead.
18.1.11 SCPropertySetMutable
▷(method)
Returns: upon success.
Sets the value of the property with name of the to . Note
that the argument does not become immutable. If this behaviour is not desired, use
(18.1.10) instead.
18.1.12 SCPropertyTmpByName
▷(method)
Returns: any value upon success, otherwise.
Returns the value of the temporary property with the name of the
if this temporary property is known for and otherwise. The names of known temporary
properties can be accessed via the function (18.1.6)
18.1.13 SCPropertyTmpDrop
▷(method)
Returns: upon success, otherwise
Drops the temporary property with name of the . Returns if
the property is successfully dropped and if a temporary property with that name did not exist.
18.1.14 SCPropertyTmpSet
▷(method)
Returns: upon success.
Sets the value of the temporary property with name of the to .
Note that the argument does not become immutable. This is the standard behaviour for temporary
properties.
18.2 Example of a common attribute
In this section we will have a look at the property handler (7.3.3) in order
to explain the inner workings of property handlers. This is the code of the property handler for
calculating the Euler characteristic of a complex in simpcomp:

simpcomp 216
When looking at the code one already sees the structure that such a handler needs to have:
1. Each property handler (a GAP operation) needs to be defined. This is done by the first
line of code. Once an operation is defined, multiple methods can by implemented for var-
ious types of GAP objects (here two methods are implemented for the GAP object types
and ).
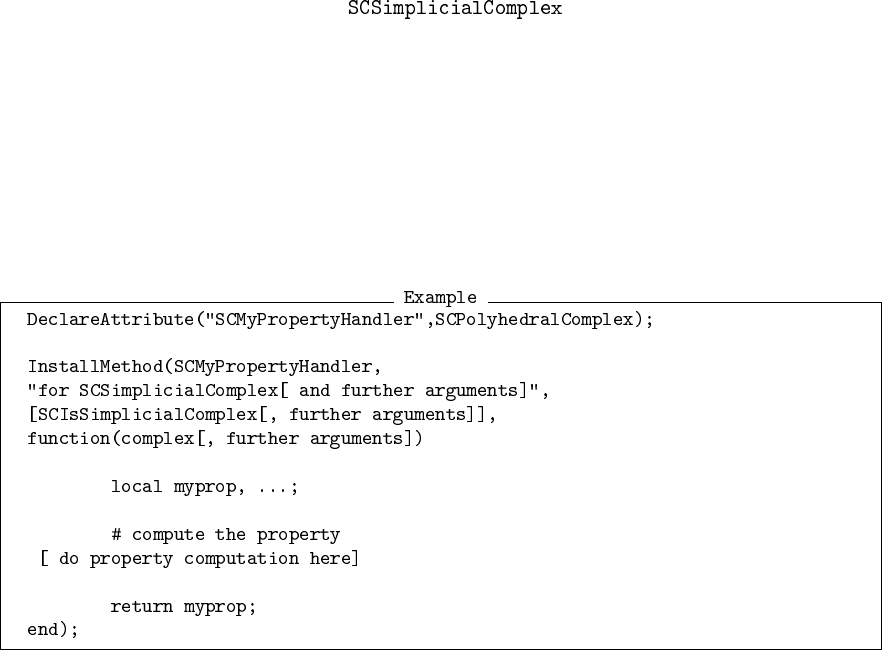
simpcomp 217
2. First note that the validity of the arguments is checked by GAP. For example, the first method
only accepts an argument of type .
3. If the property was already computed, the GAP4 type system automatically returns the cached
property avoiding unnecessary double calculations.
4. If the property is not already known. it is computed and returned (and automatically cached by
the GAP4 type system).
18.3 Writing a method for an attribute
This section provides the skeleton of a method that can be used when writing own methods:
References
[Ban65] Thomas F. Banchoff. Tightly embedded 2-dimensional polyhedral manifolds. Amer. J.
Math., 87:462–472, 1965. 18
[Ban74] Thomas F. Banchoff. Tight polyhedral Klein bottles, projective planes, and Möbius
bands. Math. Ann., 207:233–243, 1974. 18
[BBP+14] B. A. Burton, Ryan Budney, William Pettersson, et al. Regina: normal surface and 3-
manifold topology software, version 4.97. , 1999–
2014. 8
[BD08] Bhaskar Bagchi and Basudeb Datta. Lower bound theorem for normal pseudomanifolds.
Expo. Math., 26(4):327–351, 2008. 108
[BD11] Bhaskar Bagchi and Basudeb Datta. On Walkup’s class K(d)and a minimal triangulation
of (S3×
–S1)#3.Discrete Math., 311(12):989–995, 2011. 109
[BDS] B. Bagchi, B. Datta, and J. Spreer. A characterization of tightly triangulated 3-manifolds.
159
[BDSS15] Benjamin A. Burton, Basudeb Datta, Nitin Singh, and Jonathan Spreer. Separation index
of graphs and stacked 2-spheres. J. Combin. Theory Ser. A, 136:184–197, 2015. 159
[BK97] Thomas F. Banchoff and Wolfgang Kühnel. Tight submanifolds, smooth and polyhedral.
In Tight and taut submanifolds (Berkeley, CA, 1994), volume 32 of Math. Sci. Res. Inst.
Publ., pages 51–118. Cambridge Univ. Press, Cambridge, 1997. 18
[BK08] Ulrich Brehm and Wolfgang Kühnel. Equivelar maps on the torus. European J. Combin.,
29(8):1843–1861, 2008. 68,69,71
[BK12] Ulrich Brehm and Wolfgang Kühnel. Lattice triangulations of E3and of the 3-torus.
Israel J. Math., 189:97–133, 2012. 56
[BL98] Thomas Breuer and Steve Linton. The gap 4 type system: organising algebraic algo-
rithms. In Proceedings of the 1998 international symposium on Symbolic and algebraic
computation, ISSAC ’98, pages 38–45, New York, NY, USA, 1998. ACM. 8,21,213
[BL00] Anders Björner and Frank H. Lutz. Simplicial manifolds, bistellar flips and a 16-vertex
triangulation of the Poincaré homology 3-sphere. Experiment. Math., 9(2):275–289,
2000. 14,144
[BL14] Bruno Benedetti and Frank H. Lutz. Random discrete Morse theory and a new library of
triangulations. Exp. Math., 23(1):66–94, 2014. 169,170
218

simpcomp 219
[BR08] Mohamed Barakat and Daniel Robertz. : a meta-package for homological alge-
bra. J. Algebra Appl., 7(3):299–317, 2008. 187
[BS14] B. A. Burton and J. Spreer. Combinatorial seifert fibred spaces with transitive cyclic
automorphism group. , 2014. 26 pages, 10 figures. To
appear in Israel Journal of Mathematics. 59,62,66
[CK01] Mario Casella and Wolfgang Kühnel. A triangulated K3 surface with the minimum num-
ber of vertices. Topology, 40(4):753–772, 2001. 7
[Con09] Marston D. E. Conder. Regular maps and hypermaps of Euler characteristic −1 to −200.
J. Combin. Theory Ser. B, 99(2):455–459, 2009. 67,68,70
[Dat07] Basudeb Datta. Minimal triangulations of manifolds. J. Indian Inst. Sci., 87(4):429–449,
2007. 11
[DHSW11] J.-G. Dumas, F. Heckenbach, B. D. Saunders, and V. Welker. Simplicial Homology, v.
1.4.5. , 2001–2011. 2,7,95,106,
107,112,116,133,194,205
[DKT08] Mathieu Desbrun, Eva Kanso, and Yiying Tong. Discrete differential forms for compu-
tational modeling. In Discrete differential geometry, volume 38 of Oberwolfach Semin.,
pages 287–324. Birkhäuser, Basel, 2008. 135,136
[Eff11a] Felix Effenberger. Hamiltonian submanifolds of regular polytopes. Logos Verlag, Berlin,
2011. Dissertation, University of Stuttgart, 2010. 7,58,148
[Eff11b] Felix Effenberger. Stacked polytopes and tight triangulations of manifolds. Journal of
Combinatorial Theory, Series A, 118(6):1843 – 1862, 2011. 100,148,159
[Eng09] Alexander Engström. Discrete Morse functions from Fourier transforms. Experiment.
Math., 18(1):45–53, 2009. 169
[For95] Robin Forman. A discrete Morse theory for cell complexes. In Geometry, topology,
& physics, Conf. Proc. Lecture Notes Geom. Topology, IV, pages 112–125. Int. Press,
Cambridge, MA, 1995. 18,166
[Fro08] Andrew Frohmader. Face vectors of flag complexes. Israel J. Math., 164:153–164, 2008.
99
[GJ00] Ewgenij Gawrilow and Michael Joswig. polymake: a framework for analyzing con-
vex polytopes. In Polytopes—combinatorics and computation (Oberwolfach, 1997), vol-
ume 29 of DMV Sem., pages 43–73. Birkhäuser, Basel, 2000. 8
[Grü03] Branko Grünbaum. Convex polytopes, volume 221 of Graduate Texts in Mathematics.
Springer-Verlag, New York, second edition, 2003. Prepared and with a preface by Volker
Kaibel, Victor Klee and Günter M. Ziegler. 11
[GS] Daniel R. Grayson and Michael E. Stillman. Macaulay2, a software system for research
in algebraic geometry. Available at http://www.math.uiuc.edu/Macaulay2/. 8
[Hak61] Wolfgang Haken. Theorie der Normalflächen. Acta Math., 105:245–375, 1961. 15

simpcomp 220
[Hau00] Herwig Hauser. Resolution of singularities 1860–1999. In Resolution of singularities
(Obergurgl, 1997), volume 181 of Progr. Math., pages 5–36. Birkhäuser, Basel, 2000. 19
[Hir53] Friedrich E. P. Hirzebruch. über vierdimensionale riemannsche flächen mehrdeutiger
analytischer funktionen von zwei komplexen veränderlichen. Math. Ann., 126:1 – 22,
1953. 19
[Hop51] Heinz Hopf. Über komplex-analytische Mannigfaltigkeiten. Univ. Roma. Ist. Naz. Alta
Mat. Rend. Mat. e Appl. (5), 10:169–182, 1951. 19
[Hud69] John F. P. Hudson. Piecewise linear topology. University of Chicago Lecture Notes
prepared with the assistance of J. L. Shaneson and J. Lees. W. A. Benjamin, Inc., New
York-Amsterdam, 1969. 11
[Hup67] Bertram Huppert. Endliche Gruppen. I. Die Grundlehren der Mathematischen Wis-
senschaften, Band 134. Springer-Verlag, Berlin, 1967. 84
[KAL14] B. Benedetti K. Adiprasito and F. H. Lutz. Random discrete morse theory ii and a col-
lapsible 5-manifold different from the 5-ball. , 20 pages,
6 figures, 2 tables, 2014. 169,170
[KL99] Wolfgang Kühnel and Frank H. Lutz. A census of tight triangulations. Period. Math.
Hungar., 39(1-3):161–183, 1999. Discrete geometry and rigidity (Budapest, 1999). 19
[KN12] Steven Klee and Isabella Novik. Centrally symmetric manifolds with few vertices. Adv.
Math., 229(1):487–500, 2012. 58
[Kne29] Hellmuth Kneser. Geschlossene Flächen in dreidimensionalen Mannigfaltigkeiten.
Jahresbericht der deutschen Mathematiker-Vereinigung, 38:248–260, 1929. 15
[KS77] Robion C. Kirby and Laurence C. Siebenmann. Foundational essays on topological
manifolds, smoothings, and triangulations. Princeton University Press, Princeton, N.J.;
University of Tokyo Press, Tokyo, 1977. With notes by John Milnor and Michael Atiyah,
Annals of Mathematics Studies, No. 88. 173
[Küh86] Wolfgang Kühnel. Higher dimensional analogues of Császár’s torus. Results Math.,
9:95–106, 1986. 19,52
[Küh94] Wolfgang Kühnel. Manifolds in the skeletons of convex polytopes, tightness, and gen-
eralized Heawood inequalities. In Polytopes: abstract, convex and computational (Scar-
borough, ON, 1993), volume 440 of NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., pages
241–247. Kluwer Acad. Publ., Dordrecht, 1994. 18
[Küh95] Wolfgang Kühnel. Tight polyhedral submanifolds and tight triangulations, volume 1612
of Lecture Notes in Mathematics. Springer-Verlag, Berlin, 1995. 15,18,19,159
[Kui84] Nicolaas H. Kuiper. Geometry in total absolute curvature theory. In Perspectives in
mathematics, pages 377–392. Birkhäuser, Basel, 1984. 18
[Lut] Frank H. Lutz. The Manifold Page.
.2,78

simpcomp 221
[Lut03] Frank H. Lutz. Triangulated Manifolds with Few Vertices and Vertex-Transitive Group
Actions. PhD thesis, TU Berlin, 2003. 2,7,65,78,79
[Lut05] Frank H. Lutz. Triangulated Manifolds with Few Vertices: Combinatorial Manifolds.
, Preprint, 37 pages, 2005. 11
[MP14] Brendan D. McKay and Adolfo Piperno. Practical graph isomorphism, {II}. Journal of
Symbolic Computation, 60(0):94 – 112, 2014. 2,83
[Pac87] Udo Pachner. Konstruktionsmethoden und das kombinatorische Homöomorphieproblem
für Triangulierungen kompakter semilinearer Mannigfaltigkeiten. Abh. Math. Sem. Uni.
Hamburg, 57:69–86, 1987. 102,113,114,143,144
[PS15] J. Paixão and J. Spreer. Random collapsibility and 3-sphere recognition.
, 2015. Preprint, 18 pages, 6 figures. 170,172,173,
174
[R¨
13] Marc Röder. GAP package polymaking.
, 2013. 182
[Rin74] Gerhard Ringel. Map color theorem. Springer-Verlag, New York, 1974. Die Grundlehren
der mathematischen Wissenschaften, Band 209. 18
[RS72] Colin P. Rourke and Brian J. Sanderson. Introduction to piecewise-linear topology.
Springer-Verlag, New York, 1972. Ergebnisse der Mathematik und ihrer Grenzgebiete,
Band 69. 11,18
[Sch94] Christoph Schulz. Polyhedral manifolds on polytopes. Rend. Circ. Mat. Palermo (2)
Suppl., (35):291–298, 1994. First International Conference on Stochastic Geometry,
Convex Bodies and Empirical Measures (Palermo, 1993). 19
[SK11] Jonathan Spreer and Wolfgang Kühnel. Combinatorial properties of the K3 surface:
Simplicial blowups and slicings. Experiment. Math., 20(2):201–216, 2011. 7,16,19,20,
156,158
[Soi12] Leonard H. Soicher. GRAPE - GRaph Algorithms using PErmutation groups.
, 2012. Version 4.6.1. 2,7,83,194
[Spa56] Edwin H. Spanier. The homology of Kummer manifolds. Proc. AMS, 7:155–160, 1956.
19
[Spa99] Eric Sparla. A new lower bound theorem for combinatorial 2k-manifolds. Graphs Com-
bin., 15(1):109–125, 1999. 58
[Spr11a] J. Spreer. Blowups, slicings and permutation groups in combinatorial topology. PhD
thesis, University of Stuttgart, 2011. Ph.D. thesis. 7,55,59,61,63,64,65,212
[Spr11b] Jonathan Spreer. Normal surfaces as combinatorial slicings. Discrete Math.,
311(14):1295–1309, 2011. . 15,16,43,119
[Spr12] J. Spreer. Partitioning the triangles of the cross polytope into surfaces. Beitr. Algebra
Geom. / Contributions to Algebra and Geometry, 53(2):473–486, 2012. 60

simpcomp 222
[Spr14] Jonathan Spreer. Combinatorial 3-manifolds with transitive cyclic symmetry. Discrete
Comput. Geom., 51(2):394–426, 2014. 80,81
[Wee99] Jeff Weeks. SnapPea (Software for hyperbolic 3-manifolds), 1999.
.8
[Wil96] David Bruce Wilson. Generating random spanning trees more quickly than the cover
time. In Proceedings of the Twenty-eighth Annual ACM Symposium on the Theory of
Computing (Philadelphia, PA, 1996), pages 296–303. ACM, New York, 1996. 171
[Zie95] Günter M. Ziegler. Lectures on polytopes, volume 152 of Graduate Texts in Mathematics.
Springer-Verlag, New York, 1995. 11,102,113,114
simpcomp 224
,85
,86
,107
,108
,76
,77
,86
,86,124
,87
,51
,146
,87,124
,147
,49
,185
,185
,184
,184,186
,186
,49
,88,125
,88,125
,88
,88
,24,89
,24,89
,108
,89,126
,47
,46
,48
,50
,89
,87,125
,54
,54
,54
,91
,92
,126
,90
,109
,94
,94
,168
,95
,94
,187
,188
,189
,189
,188
,188
,127,171
,134
,134
,95
,171
,135
,93
,184
,96
,96
,191
,97
,109
,139
,140
,140
,141
,147
,97
,97,127
,98,128
,98
,99
,99
,100
,100
,110
,100
,148
,175
,173
,173
,149
,111
,111
,101,128
,101
,101
,101
,35
,172
simpcomp 225
,172
,173
,102
,110
,159
,111
,25
,26
,26
,175
,177
,177
,178
,178
,179
,179
,180
,180
,180
,181
,181
,181
,30
,30
,182
,183
,192
,192
,192
,193
,193
,193
,193
,194
,158
,102
,103
,169
,163
,164
,165
,169
,169
,170
,170
,170
,149
,150
,26
,103
,112
,113
,69
,80
,69
,120
,119
,119
,120
,123
,103
,104
,213
,36
,213
,213
,214
,214
,214
,214
,214
,214
,215
,215
,215
,215
,215
,151
,151
,152
,153
,155
,27
,69
,70
,71
,27
,28
,28
,28
,150
,194
,183
,184