Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 42
- Plantillas
- Cosas para tener en cuenta
- Grafos
- Teoría de números
- Programación Dinámica
- Longest increasing subsequence
- Problema de la mochila
- Edit distance
- Formas de sumar un número
- Longest Common Substring
- Longest Common Subsequence
- Shortest Common Supersequence
- Maximum subarray (non-adjacent) sum (1D)
- Maximum subarray sum (1D) - Kadane's Algorithm
- Maximum subrectangle sum (2D)
- Maximum subrectangle sum (3D)
- Partition problem
- Longest Palindromic Substring
- Longest Palindromic Subsequence
- Text Justification
- Burst Balloons
- Wildcard Matching
- Maximum profit - Best time to buy and sell stock
- Geometría
- Strings
- Otros
- Struct
- C++
- Java
- Varios

Manual de algoritmos para maratones de programaci´on
Just Code It. Bodhert
16 de noviembre de 2017
´
Indice
1. Plantillas 2
2. Cosas para tener en cuenta 3
3. Grafos 3
3.1. BFS .................................. 3
3.2. DFS .................................. 4
3.3. Ordenamiento topol´ogico . . . . . . . . . . . . . . . . . . . . . . 4
3.4. Componentes fuertemente conexas . . . . . . . . . . . . . . . . . 4
3.4.1. Kosaraju’s algorithm . . . . . . . . . . . . . . . . . . . . . 5
3.4.2. Tarjan’s algorithm . . . . . . . . . . . . . . . . . . . . . . 5
3.5. Algoritmo de Dijkstra . . . . . . . . . . . . . . . . . . . . . . . . 6
3.6. Algoritmo de Bellman-Ford . . . . . . . . . . . . . . . . . . . . . 7
3.7. Algoritmo de Floyd-Warshall . . . . . . . . . . . . . . . . . . . . 7
3.7.1. Clausura transitiva . . . . . . . . . . . . . . . . . . . . . . 7
3.7.2. Minimax ........................... 8
3.7.3. Maximin ........................... 8
3.8. AlgoritmodePrim .......................... 8
3.9. Algoritmo de Kruskal . . . . . . . . . . . . . . . . . . . . . . . . 8
3.9.1. Union-Find .......................... 8
3.9.2. Algoritmo de Kruskal . . . . . . . . . . . . . . . . . . . . 9
3.9.3. Algoritmo de Kruskal CP3 . . . . . . . . . . . . . . . . . 9
3.10. Algoritmo de m´aximo flujo . . . . . . . . . . . . . . . . . . . . . 11
3.11.TeoremadeKonig .......................... 12
3.11.1. Ejemplo, aplicaci´on Max Flow - Mimimum Vertex Cover
- Maximum Matching Size . . . . . . . . . . . . . . . . . . 12
4. Teor´ıa de n´umeros 13
4.1. N´umerosromanos .......................... 13
4.1.1. ´
ArabeaRomano....................... 13
4.1.2. Romano a ´
Arabe....................... 14
4.2. Divisores de un n´umero . . . . . . . . . . . . . . . . . . . . . . . 14
4.3. M´aximo com´un divisor y m´ınimo com´un m´ultiplo . . . . . . . . . 14
4.4. Criba de Erat´ostenes . . . . . . . . . . . . . . . . . . . . . . . . . 14
4.5. Factorizaci´on prima de un n´umero . . . . . . . . . . . . . . . . . 15
4.6. Exponenciaci´on logar´ıtmica . . . . . . . . . . . . . . . . . . . . . 15
4.6.1. Propiedades de la operaci´on m´odulo . . . . . . . . . . . . 15
4.6.2. Bigmod............................ 15
4.7. Combinatoria............................. 15
4.7.1. Coeficientes binomiales . . . . . . . . . . . . . . . . . . . 15
4.7.2. Propiedades de combinatoria . . . . . . . . . . . . . . . . 16
5. Programaci´on Din´amica 16
5.1. Longest increasing subsequence . . . . . . . . . . . . . . . . . . . 16
5.1.1. Orden cuadr´atico . . . . . . . . . . . . . . . . . . . . . . . 16
5.1.2. Orden logar´ıtmico imprimiendo s´olo longitud . . . . . . . 16
5.1.3. Orden logar´ıtmico imprimiendo la secuencia . . . . . . . . 17
5.2. Problema de la mochila . . . . . . . . . . . . . . . . . . . . . . . 18
5.3. Editdistance ............................. 18
5.4. Formas de sumar un n´umero . . . . . . . . . . . . . . . . . . . . 19
5.5. Longest Common Substring . . . . . . . . . . . . . . . . . . . . . 19
5.6. Longest Common Subsequence . . . . . . . . . . . . . . . . . . . 20
5.7. Shortest Common Supersequence . . . . . . . . . . . . . . . . . . 20
5.8. Maximum subarray (non-adjacent) sum (1D) . . . . . . . . . . . 20
5.9. Maximum subarray sum (1D) - Kadane’s Algorithm . . . . . . . 21
5.9.1. Maximum circular subarray sum . . . . . . . . . . . . . . 21
5.10. Maximum subrectangle sum (2D) . . . . . . . . . . . . . . . . . . 21
5.10.1. Na¨ıve solution - O(n4).................... 21
5.10.2. Using Kadane’s - O(n3) ................... 21
5.11. Maximum subrectangle sum (3D) . . . . . . . . . . . . . . . . . . 22
5.12. Partition problem . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
5.13. Longest Palindromic Substring . . . . . . . . . . . . . . . . . . . 23
5.14. Longest Palindromic Subsequence . . . . . . . . . . . . . . . . . . 25
5.15. Text Justification . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
1

5.16.BurstBalloons ............................ 27
5.17. Wildcard Matching . . . . . . . . . . . . . . . . . . . . . . . . . . 27
5.18. Maximum profit - Best time to buy and sell stock . . . . . . . . . 27
6. Geometr´ıa 28
6.1. Closest pair of points in a plane . . . . . . . . . . . . . . . . . . . 28
7. Strings 30
7.1. AlgoritmodeKMP.......................... 30
7.2. Algoritmo de Booth - Lexicographically minimal string rotation . 30
7.3. sufix/trie/array ........................... 31
7.3.1. suffixtrie ........................... 31
7.3.2. suffixarray .......................... 31
7.3.3. String Matching . . . . . . . . . . . . . . . . . . . . . . . 32
7.3.4. Longest Common Prefix (LCP) . . . . . . . . . . . . . . . 33
7.3.5. Longest Repeated Substring) . . . . . . . . . . . . . . . . 34
7.4. Formatos de impresi´on . . . . . . . . . . . . . . . . . . . . . . . . 34
7.4.1. N´umeros............................ 34
7.4.2. Strings............................. 34
7.4.3. Formato en Java . . . . . . . . . . . . . . . . . . . . . . . 35
8. Otros 35
8.1. BinarySearch............................. 35
8.1.1. Traditional algorithm . . . . . . . . . . . . . . . . . . . . 35
8.1.2. Lowerbound ......................... 36
8.1.3. Upperbound ......................... 36
8.2. Binary Search Tree (BST) . . . . . . . . . . . . . . . . . . . . . . 36
8.2.1. Largest BST in a Binary Tree . . . . . . . . . . . . . . . . 36
8.3. Build Binary Tree from PreOrder and InOrder . . . . . . . . . . 37
8.4. Build Binary Tree from PosOrder and InOrder . . . . . . . . . . 38
8.5. BitSet ................................. 38
8.6. M´aximo orden dado un n...................... 38
8.7. Suma de grandes n´umeros en C++ . . . . . . . . . . . . . . . . . 38
8.8. Largest Rectangle in a Histogram . . . . . . . . . . . . . . . . . . 39
9. Struct 39
9.1. Funci´on de comparaci´on . . . . . . . . . . . . . . . . . . . . . . . 39
9.2. Radixsort............................... 40
10.C++ 40
10.1. Strings con arreglo de caracteres . . . . . . . . . . . . . . . . . . 40
10.2.miselanea ............................... 41
11.Java 41
11.1.FileReader .............................. 41
11.2.Baseconverter ............................ 41
12.Varios 42
1. Plantillas
#include <algorithm>
#include <iostream>
#include <iterator>
#include <numeric>
#include <sstream>
#include <fstream>
#include <cassert>
#include <climits>
#include <cstdlib>
#include <cstring>
#include <string>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <deque>
#include <stack>
#include <list>
#include <map>
#include <set>
#include <bitset>
#define D(x) cout << "DEBUG: " << #x " = " << x << endl
using namespace std;
const double EPS = 1e-9;
const double PI = acos(-1.0);
template <class T> string toStr(const T &x)
{ stringstream s; s << x; return s.str(); }
template <class T> int toInt(const T &x)
{ stringstream s; s << x; int r; s >> r; return r; }
2

int
main() {
return 0;
}
.............................................................................
/*
la mayoria de los jueces, no requieren de estas lineas
debido a que leen de consola, NO OLVIDAR comentar
las lineas para abrir y escribir en archivos,
y evitar WA cuando se envie el ejercicio, debido a que
esta hecho con el propositio de ahorrarnos tiempo al ingresar
los datos de prueba.
PROG: el programa lee dos enteros de un archivo llamado in.in y
los escribe en un archivo out.out
*/
#include <bits/stdc++.h> // si no compila,hacer
//includes necesarios
#define D(x) cout << "DEBUG: " << #x "=" << x << endl;
using namespace std;
typedef pair<int, int> ii;
typedef vector<ii> vii;
typedef vector<int> vi;
int main()
{
//ofstream fout ("out.out");
//ifstream fin ("in.in");
freopen("in.in","r",stdin); // directamente cin y cout,
freopen("out.out","w",stdout); // y scanf.
int a, b;
//fin >> a >> b;
//fout << a << " " << b << endl;
cin >> a >> b;
cout << a << " " << b << endl;
return 0;
}
/*
es importante resaltar que el archivo "in.in" debe de estar en
la misma carpeta del programa
*/
.............................................................................
2. Cosas para tener en cuenta
Si la respuesta de un problema es un n´umero de punto flotante redondeado
y est´a dando W rongAnswer, ensayar sumarle un ´epsilon a la respuesta, es
decir, sumarle EPS (siendo EPS por lo general 1e-9).
Recordar que para redondear un n´umero de punto flotante se debe usar el
par´ametro %.xf (donde x es la cantidad de cifras) en la funci´on printf .
En problemas que se trabajen n´umeros de punto flotante y enteros a la vez,
es recomendable mutiplicar por 1.0 cuando se est´en haciendo operaciones
con ambos tipos de datos. Con esto se evitar´an problemas de conversi´on.
3. Grafos
3.1. BFS
Algoritmo de recorrido de grafos en anchura que empieza desde una fuente
sy visita todos los nodos alcanzables desde s.
El BFS tambi´en halla la distancia m´as corta entre sy los dem´as nodos si las
aristas tienen todas peso 1.
Complejidad: O(n+m) donde nes el n´umero de nodos y mes el n´umero de
aristas.
vector <int> g[MAXN]; // La lista de adyacencia
int d[MAXN]; // Distancia de la fuente a cada nodo
void bfs(int s, int n){ // s = fuente, n = n´umero de nodos
for (int i = 0; i <= n; ++i) d[i] = -1;
queue <int> q;
q.push(s);
d[s] = 0;
while (q.size() > 0){
3

int cur = q.front();
q.pop();
for (int i = 0; i < g[cur].size(); ++i){
int next = g[cur][i];
if (d[next] == -1){
d[next] = d[cur] + 1;
q.push(next);
}
}
}
}
.............................................................................
3.2. DFS
Algoritmo de recorrido de grafos en profundidad que empieza visita todos
los nodos del grafo.
El algoritmo puede ser modificado para que retorne informaci´on de los nodos
seg´un la necesidad del problema.
El grafo tiene un ciclo ↔si en alg´un momento se llega a un nodo marcado
como gris.
Complejidad: O(n+m) donde nes el n´umero de nodos y mes el n´umero de
aristas.
vector <int> g[MAXN]; // La lista de adyacencia
int color[MAXN]; // El arreglo de visitados
enum {WHITE, GRAY, BLACK}; // WHITE = 1, GRAY = 2, BLACK = 3
// Visita el nodo u y todos sus vecinos empezando por
// los m´as profundos
void dfs(int u){
color[u] = GRAY; // Marcar el nodo como semi-visitado
for (int i = 0; i < g[u].size(); ++i){
int v = g[u][i];
if (color[v] == WHITE) dfs(v); // Visitar los vecinos
}
color[u] = BLACK; // Marcar el nodo como visitado
}
// Llama la funci´on dfs para los nodos 0 a n-1
void call_dfs(int n){
for (int u = 0; u < n; ++u) color[u] = WHITE;
for (int u = 0; u < n; ++u)
if (color[u] == WHITE) dfs(u);
}
.............................................................................
3.3. Ordenamiento topol´ogico
Dado un grafo no c´ıclico y dirigido (DAG), ordena los nodos linealmente de
tal forma que si existe una arista entre los nodos uyventonces uaparece antes
que ven el ordenamiento.
Este ordenamiento se puede ver como una forma de poner todos los nodos en
una l´ınea recta y que las aristas vayan todas de izquierda a derecha.
Complejidad: O(n+m) donde nes el n´umero de nodos y mes el n´umero de
aristas.
vector <int> g[MAXN]; // La lista de adyacencia
bool seen[MAXN]; // El arreglo de visitados para el dfs
vector <int> topo_sort; // El vector del ordemamiento
void dfs(int u){
seen[u] = true;
for (int i = 0; i < g[u].size(); ++i){
int v = g[u][i];
if (!seen[v]) dfs(v);
}
topo_sort.push_back(u); // Agregar el nodo al ordenamiento
}
void topological(int n){ // n = n´umero de nodos
topo_sort.clear();
for (int i = 0; i < n; ++i) seen[i] = false;
for (int i = 0; i < n; ++i) if (!seen[i]) dfs(i);
reverse(topo_sort.begin(), topo_sort.end());
}
.............................................................................
3.4. Componentes fuertemente conexas
Dado un grafo dirigido, calcula la componente fuertemente conexa (SCC) a
la que pertenece cada nodo.
Para cada pareja de nodos u, v que pertenecen a una misma SCC se cumple
que hay un camino de uavy de vau.
Si se comprime el grafo dejando como nodos cada una de las componentes se
4
quedar´a con un DAG.
3.4.1. Kosaraju’s algorithm
Complejidad: O(n+m) donde nes el n´umero de nodos y mes el n´umero de
aristas.
vector <int> g[MAXN]; // El grafo
vector <int> grev[MAXN]; // El grafo con las aristas reversadas
vector <int> topo_sort; // El "ordenamiento topologico" del grafo
int scc[MAXN]; // La componente a la que pertenece cada nodo
bool seen[MAXN]; // El arreglo de visitado para el primer DFS
// DFS donde se halla el ordenamiento topol´ogico
void dfs1(int u){
seen[u] = true;
for (int i = 0; i < g[u].size(); ++i){
int v = g[u][i];
if (!seen[v]) dfs1(v);
}
topo_sort.push_back(u);
}
// DFS donde se hallan las componentes
void dfs2(int u, int comp){
scc[u] = comp;
for (int i = 0; i < grev[u].size(); ++i){
int v = grev[u][i];
if (scc[v] == -1) dfs2(v, comp);
}
}
// Halla las componentes fuertemente conexas del grafo usando
// el algoritmo de Kosaraju. Retorna la cantidad de componentes
int find_scc(int n){ // n = n´umero de nodos
// Crear el grafo reversado
for (int u = 0; u < n; ++u){
for (int i = 0; i < g[u].size(); ++i){
int v = g[u][i];
grev[v].push_back(u);
}
}
// Llamar el primer dfs
for (int i = 0; i < n; ++i){
if (!seen[i]) dfs1(i);
}
reverse(topo_sort.begin(), topo_sort.end());
// Llamar el segundo dfs
int comp = 0;
for (int i = 0; i < n; ++i){
int u = topo_sort[i];
if (scc[u] == -1) dfs2(u, comp++);
}
return comp;
}
.............................................................................
3.4.2. Tarjan’s algorithm
d[i] = Tiempo de descubrimiento del nodo i. (Inicializar con -1)
low[i] = Menor tiempo de descubrimiento alcanzable desde el nodo i. (No
inicializar)
scc[i] = Componente a la que pertenece el nodo i. (No inicializar)
s= Pila usada por el algoritmo (Inicializar vac´ıa)
stacked[i] = true si el nodo i est´a en la pila. (Inicializar con falso)
ticks = Reloj usado para los tiempos de descubrimiento (Inicializar en 0)
currentscc = id de la componente actual siendo descubierta. (Inicializar
en 0)
vector <int> g[MAXN];
int d[MAXN], low[MAXN], scc[MAXN];
bool stacked[MAXN];
stack <int> s;
int ticks, current_scc;
// Check initializations.
void tarjan(int u) {
d[u] = low[u] = ticks++;
s.push(u);
5

stacked[u] = true;
for (int k = 0; k < g[u].size(); ++k) {
int v = g[u][k];
if (d[v] == -1) {
tarjan(v);
low[u] = min(low[u], low[v]);
}
else if (stacked[v]) low[u] = min(low[u], low[v]);
}
if (d[u] == low[u]) {
int v;
do {
v = s.top();
s.pop();
stacked[v] = false;
scc[v] = current_scc;
}
while (u != v);
current_scc++;
}
}
.........................................................................
3.5. Algoritmo de Dijkstra
Dado un grafo con pesos no negativos en las aristas, halla la m´ınima
distancia entre una fuente sy los dem´as nodos.
Al heap se inserta primero la distancia y luego en nodo al que se llega. Si se
quieren modificar los pesos por long long o por double se debe cambiar en
los tipos de dato dist_node yedge.
Complejidad: O((n+m) log n) donde nes el n´umero de nodos y mes el n´umero
de aristas.
const int MAXN = 100005;
const int INF = 1 << 30; // Usar 1LL << 60 para long long
typedef pair <int, int> dist_node; // Datos del heap (dist, nodo)
typedef pair <int, int> edge; // Dato de las arista (nodo, peso)
vector <edge> g[MAXN]; // g[u] = (v = nodo, w = peso)
int d[MAXN]; // d[u] La distancia m´as corta de s a u
int p[MAXN]; // p[u] El predecesor de u en el camino m´as corto
// La funci´on recibe la fuente s y el n´umero total de nodos n
void dijkstra(int s, int n){
for (int i = 0; i <= n; ++i){
d[i] = INF; p[i] = -1;
}
priority_queue < dist_node, vector <dist_node>,
greater<dist_node> > q;
d[s] = 0;
q.push(dist_node(0, s));
while (!q.empty()){
int dist = q.top().first;
int cur = q.top().second;
q.pop();
if (dist > d[cur]) continue;
for (int i = 0; i < g[cur].size(); ++i){
int next = g[cur][i].first;
int w_extra = g[cur][i].second;
if (d[cur] + w_extra < d[next]){
d[next] = d[cur] + w_extra;
p[next] = cur;
q.push(dist_node(d[next], next));
}
}
}
}
// La funci´on que retorna los nodos del camino m´as corto de s a t
// Primero hay que correr dijktra desde s.
// Eliminar si no se necesita hallar el camino.
vector <int> find_path (int t){
vector <int> path;
int cur = t;
while(cur != -1){
path.push_back(cur);
cur = p[cur];
}
reverse(path.begin(), path.end());
return path;
}
.............................................................................
6

3.6. Algoritmo de Bellman-Ford
Dado un grafo con pesos cualquiera, halla la m´ınima distancia entre una
fuente sy los dem´as nodos.
Si hay un ciclo de peso negativo en el grafo, el algoritmo lo indica.
Complejidad: O(n×m) donde nes el n´umero de nodos y mes el n´umero de
aristas.
Tener en cuenta que si el nodo es inalcanzable la distancia que resulta en dicho
nodo siempre ser´a infinito.
Si el problema es como Haunted Graveyard, donde los ni˜nos querian salir
del cementerio lo m´as r´apido posible (no querian quedarse dando vueltas as´ı
fueran ciclos negativos) entonces no deberia poner aristas en el nodo de salida.
const int MAXN = 105;
const int INF = 1 << 30; // Para long long INF = 1LL << 60
typedef pair <int, int> edge; // Modificar seg´un el problema
vector <edge> g[MAXN]; // g[u] = (v = nodo, w = peso)
int d[MAXN]; // d[u] = distancia m´as corta de s a u
// Retorna verdadero si el grafo tiene un ciclo de peso negativo
// alcanzable desde s y falso si no es as´ı.
// Al finalizar el algoritmo, si no hubo ciclo de peso negativo,
// la distancia m´as corta entre s y u est´a almacenada en d[u]
bool bellman_ford(int s, int n){ // s = fuente, n = n´umero nodos
for (int u = 0; u <= n; ++u) d[u] = INF;
d[s] = 0;
for (int i = 1; i <= n - 1; ++i){
for (int u = 0; u < n; ++u){
for (int k = 0; k < g[u].size(); ++k){
int v = g[u][k].first;
int w = g[u][k].second;
d[v] = min(d[v], d[u] + w);
}
}
}
for (int u = 0; u < n; ++u){
for (int k = 0; k < g[u].size(); ++k){
int v = g[u][k].first;
int w = g[u][k].second;
if (d[v] > d[u] + w) return true;
}
}
return false;
}
.............................................................................
3.7. Algoritmo de Floyd-Warshall
Dado un grafo con pesos cualquiera, halla la m´ınima distancia entre cualquier
para de nodos.
Si este algoritmo es muy lento para el problema ejecutar nveces el algoritmo
de Dijkstra o de Bellman-Ford seg´un el caso.
Complejidad: O(n3) donde nes el n´umero de nodos.
Casos base: d[i][j] =
0 si i=j
wi,j si existe una arista entre iyj
+∞en otro caso
Nota: Utilizar el tipo de dato apropiado (int,long long,double) para dy
para +∞seg´un el problema.
// Los nodos est´an numerados de 0 a n-1
for (int k = 0; k < n; ++k){
for (int i = 0; i < n; ++i){
for (int j = 0; j < n; ++j){
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
// Ac´a d[i][j] es la m´ınima distancia entre el nodo i y el j
.............................................................................
3.7.1. Clausura transitiva
Dado un grafo cualquiera, hallar si existe un camino desde ihasta jpara
cualquier pareja de nodos i, j
Casos base: d[i][j] =
true si i=j
true si existe una arista entre iyj
false en otro caso
Caso recursivo: d[i][j] = d[i][j] or (d[i][k] and d[k][j]);
7

3.7.2. Minimax
Dado un grafo con pesos, hallar el camino de ihasta jdonde la arista m´as
grande del camino sea lo m´as peque˜na posible.
Ejemplos: Que el peaje m´as caro sea lo m´as barato posible, que la autopista
m´as larga sea lo m´as corta posible.
Casos base: d[i][j] =
0 si i=j
wi,j si existe una arista entre iyj
+∞en otro caso
Caso recursivo: d[i][j] = min( d[i][j], max (d[i][k], d[k][j]) );
3.7.3. Maximin
Dado un grafo con pesos, hallar el camino de ihasta jdonde la arista m´as
peque˜na del camino sea lo m´as grande posible.
Ejemplos: Que el trayecto menos seguro sea lo m´as seguro posible, que la
autopista de menos carriles tenga la mayor cantidad de carriles.
Casos base: d[i][j] =
+∞si i=j
wi,j si existe una arista entre iyj
−∞ en otro caso
Caso recursivo: d[i][j] = max( d[i][j] , min(d[i][k], d[k][j]) )
3.8. Algoritmo de Prim
Dado un grafo no dirigido y conexo, retorna el costo del ´arbol de m´ınima
expansi´on de ese grafo.
El costo del ´arbol de m´ınima expansi´on tambi´en se puede ver como el m´ınimo
costo de las aristas de manera que haya un camino entre cualquier par de
nodos.
Complejidad: O(mlog n) donde nes el n´umero de nodos y mes el n´umero de
aristas.
const int MAXN = 10005;
typedef pair <int, int> edge; // Pareja (nodo, peso)
typedef pair <int, int> weight_node; // Pareja (peso, nodo)
vector <edge> g[MAXN]; // Lista de adyacencia
bool visited[MAXN];
// Retorna el costo total del MST
int prim(int n){ // n = n´umero de nodos
for (int i = 0; i <= n; ++i) visited[i] = false;
int total = 0;
priority_queue<weight_node, vector <weight_node>,
greater<weight_node> > q;
// Empezar el MST desde 0 (cambiar si el nodo 0 no existe)
q.push(weight_node(0, 0));
while (!q.empty()){
int u = q.top().second;
int w = q.top().first;
q.pop();
if (visited[u]) continue;
visited[u] = true;
total += w;
for (int i = 0; i < g[u].size(); ++i){
int v = g[u][i].first;
int next_w = g[u][i].second;
if (!visited[v]){
q.push(weight_node(next_w, v));
}
}
}
return total;
}
.............................................................................
3.9. Algoritmo de Kruskal
3.9.1. Union-Find
Union-Find es una estructura de datos para almacenar una colecci´on con-
juntos disjuntos (no tienen elementos en com´un) que cambian din´amicamente.
Identifica en cada conjunto un “padre” que es un elemento al azar de ese
conjunto y hace que todos los elementos del conjunto “apunten” hacia ese
padre.
Inicialmente se tiene una colecci´on donde cada elemento es un conjunto
unitario.
Complejidad aproximada: O(m) donde mel n´umero total de operaciones de
initialize,union yjoin realizadas.
8

const int MAXN = 100005;
int p[MAXN];// El padre del conjunto al que pertenece cada nodo
// Inicializar cada conjunto como unitario
void initialize(int n){
for (int i = 0; i <= n; ++i) p[i] = i;
}
// Encontrar el padre del conjunto al que pertenece u
int find(int u){
if (p[u] == u) return u;
return p[u] = find(p[u]);
}
// Unir los conjunto a los que pertenecen u y v
void join(int u, int v){
int a = find(u);
int b = find(v);
if (a == b) return;
p[a] = b;
}
.............................................................................
3.9.2. Algoritmo de Kruskal
Dado un grafo no dirigido y conexo, retorna el costo del ´arbol de m´ınima
expansi´on de ese grafo.
El costo del ´arbol de m´ınima expansi´on tambi´en se puede ver como el m´ınimo
costo de las aristas de manera que haya un camino entre cualquier par de
nodos.
Utiliza Union-Find para ver r´apidamente qu´e aristas generan ciclos.
Complejidad: O(mlog n) donde nes el n´umero de nodos y mes el n´umero de
aristas.
struct edge{
int start, end, weight;
edge(int u, int v, int w){
start = u; end = v; weight = w;
}
bool operator < (const edge &other) const{
return weight < other.weight;
}
};
const int MAXN = 100005;
vector <edge> edges; // Lista de aristas y no lista de adyacencia
int p[MAXN]; // El padre de cada conjunto (union-find)
// Incluir las operaciones de Union-Find (initialize, find, join)
int kruskal(int n){
initialize(n);
sort(edges.begin(), edges.end());
int total = 0;
for (int i = 0; i < edges.size(); ++i){
int u = edges[i].start;
int v = edges[i].end;
int w = edges[i].weight;
if (find(u) != find(v)){
total += w;
join(u, v);
}
}
return total;
}
.............................................................................
3.9.3. Algoritmo de Kruskal CP3
#include <algorithm>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
typedef pair<int, int> ii;
typedef vector<int> vi;
typedef vector<ii> vii;
// Union-Find Disjoint Sets Library written in OOP manner,
// using both path compression and union by rank heuristics
class UnionFind
9

// OOP style
{
private:
vi p, rank, setSize; // remember: vi is vector<int>
int numSets;
public:
UnionFind(int N)
{
setSize.assign(N, 1); numSets = N; rank.assign(N, 0);
p.assign(N, 0); for (int i = 0; i < N; i++) p[i] = i;
}
int findSet(int i) { return (p[i] == i) ?
i : (p[i] = findSet(p[i])); }
bool isSameSet(int i, int j) {return findSet(i) == findSet(j);}
void unionSet(int i, int j)
{
if (!isSameSet(i, j))
{
numSets--;
int x = findSet(i), y = findSet(j);
// rank is used to keep the tree short
if (rank[x] > rank[y])
{ p[y] = x; setSize[x] += setSize[y]; }
else
{
p[x] = y; setSize[y] += setSize[x];
if (rank[x] == rank[y]) rank[y]++;
}
}
}
int numDisjointSets() { return numSets; }
int sizeOfSet(int i) { return setSize[findSet(i)]; }
};
vector<vii> AdjList;
vi taken;
// global boolean flag to avoid cycle
priority_queue<ii> pq;
// priority queue to help choose shorter edges
// sort by (inc) weight then by (inc) id
int main() {
int V, E, u, v, w;
scanf("%d %d", &V, &E);
// Kruskal’s algorithm merged with Prim’s algorithm
AdjList.assign(V, vii());
vector< pair<int, ii> > EdgeList;
// (weight, two vertices) of the edge
for (int i = 0; i < E; i++)
{
scanf("%d %d %d", &u, &v, &w); // read the triple: (u, v, w)
EdgeList.push_back(make_pair(w, ii(u, v))); // (w, u, v)
}
sort(EdgeList.begin(), EdgeList.end());
// sort by edge weight O(E log E)
// note: pair object has built-in comparison function
int mst_cost = 0;
UnionFind UF(V); // all V are disjoint sets initially
for (int i = 0; i < E; i++)
{// for each edge, O(E)
pair<int, ii> front = EdgeList[i];
if (!UF.isSameSet(front.second.first, front.second.second))
{ // check
mst_cost += front.first; // add the weight of e to MST
UF.unionSet(front.second.first, front.second.second);// link them
}
}
// note: the runtime cost of UFDS is very light
// note: the number of disjoint sets must eventually
// be 1 for a valid MST
printf("MST cost = %d (Kruskal’s)\n", mst_cost);
return 0;
}
.............................................................................
10

3.10. Algoritmo de m´aximo flujo
Dado un grafo con capacidades enteras, halla el m´aximo flujo entre una
fuente sy un sumidero t.
Como el m´aximo flujo es igual al m´ınimo corte, halla tambi´en el m´ınimo costo
de cortar aristas de manera que sytqueden desconectados.
Si hay varias fuentes o varios sumideros poner una s´uper-fuente / s´uper-
sumidero que se conecte a las fuentes / sumideros con capacidad infinita.
Si los nodos tambi´en tienen capacidad, dividir cada nodo en dos nodos: uno
al que lleguen todas las aristas y otro del que salgan todas las aristas y
conectarlos con una arista que tenga la capacidad del nodo.
Complejidad: O(n·m2) donde nes el n´umero de nodos y mes el n´umero de
aristas.
const int MAXN = 105;
// Lista de adyacencia de la red residual
vector <int> g [MAXN];
// Capacidad de aristas de la red de flujos
int c [MAXN][MAXN];
// El flujo de cada arista
int f [MAXN][MAXN];
//El predecesor de cada nodo en el camino de aumentaci´on de s a t
int prev [MAXN];
void connect (int i, int j, int cap){
// Agregar SIEMPRE las dos aristas a g (red residual) as´ı el
// grafo sea dirigido. Esto es porque g representa la red
// residual que tiene aristas en los dos sentidos.
g[i].push_back(j);
g[j].push_back(i);
c[i][j] += cap;
// Omitir esta l´ınea si el grafo es dirigido
c[j][i] += cap;
}
// s = fuente, t = sumidero, n = n´umero de nodos
int maxflow(int s, int t, int n){
for (int i = 0; i <= n; i++){
for (int j = 0; j <= n; j++){
f[i][j] = 0;
}
}
int flow = 0;
while (true){
for (int i = 0; i <= n; i++) prev[i] = -1;
queue <int> q;
q.push(s);
prev[s] = -2;
while (q.size() > 0){
int u = q.front(); q.pop();
if (u == t) break;
for (int i = 0; i < g[u].size(); ++i){
int v = g[u][i];
if (prev[v] == -1 and c[u][v] - f[u][v] > 0){
q.push(v);
prev[v] = u;
}
}
}
if (prev[t] == -1) break;
int extra = 1 << 30;
int end = t;
while (end != s){
int start = prev[end];
extra = min(extra, c[start][end] - f[start][end]);
end = start;
}
end = t;
while (end != s){
int start = prev[end];
f[start][end] += extra;
f[end][start] = -f[start][end];
end = start;
}
flow += extra;
}
return flow;
}
11

.............................................................................
3.11. Teorema de Konig
3.11.1. Ejemplo, aplicaci´on Max Flow - Mimimum Vertex Cover -
Maximum Matching Size
El algoritmo de m´aximo flujo es equivalente al problema de
MinimumV ertexCover en un grafo bipartito, pero como el Vertex Cover es
NP-hard, entonces el teorema de Konig nos dice que el M inimumV ertexCover
es igual al MaximumM atchingSize, el cual puede ser encontrado por un
m´aximo flujo est´andar.
A continuaci´on se presenta un problema para esta aplicaci´on.
As an example, one year there were six interns: Stephen Cook, Vinton Cerf,
Edmund Clarke, Judea Pearl, Shafi Goldwasser, and Silvio Micali. They were
able to self-organize into three teams:
Stephen Cook, Vinton Cerf, and Edmund Clarke (whose last names all
begin with C)
Shafi Goldwasser and Silvio Micali (whose first names begin with S)
Judea Pearl (not an interesting group, but everyone’s first name in this
group starts with J)
As a historical note, the company was eventually shut down due to a rather
strange (and illegal) hiring practice—they refused to hire any interns whose
last names began with the letter S, T, U, V, W, X, Y, or Z. (First names were
not subject to such a whim, which was fortunate for our friend Vinton Cerf.)
Input: Each year’s group of interns is considered as a separate trial. A trial
begins with a line containing a single integer N, such that 1 ≤N≤300,
designating the number of interns that year. Following that are N lines—one
for each intern—with a line having a first and last name separated by one
space. Names will not have any punctuation, and both the first name and
last name will begin with an uppercase letter. In the case of last names, that
letter will have an additional constraint that it be in the range from ’A’ to ’R’
inclusive. The end of the input is designated by a line containing the value 0.
There will be at most 20 trials.
Output: For each trial, output a single integer, k, designating the minimum
number of teams that were necessary.
La entrada y saida ejemplo es:
Entonces la soluci´on ser´ıa, utilizando M axF low:
const int MAXN = 55; //26 letras nombres +
//26 letras apellidos + 3
int n;
vector <int> g[MAXN];
int c[MAXN][MAXN];
int f[MAXN][MAXN];
int prev[MAXN];
void
connect (int i, int j) {
g[i].push_back(j);
g[j].push_back(i);
c[i][j] = 1;
}
int
maxflow(int s, int t) {
for (int i = 0; i < MAXN; i++) {
12

for (int j = 0; j < MAXN; j++) {
f[i][j] = 0;
}
}
int flow = 0;
while (true) {
for (int i = 0; i < MAXN; i++) prev[i] = -1;
queue <int> q;
q.push(s);
prev[s] = -2;
while (!q.empty()) {
int u = q.front(); q.pop();
if (u == t) break;
for (int i = 0; i < g[u].size(); i++) {
int v = g[u][i];
if (prev[v] == -1 and c[u][v] - f[u][v] > 0) {
q.push(v);
prev[v] = u;
}
}
}
if (prev[t] == -1) break;
int extra = 1 << 30;
int end = t;
while (end != s) {
int start = prev[end];
extra = min(extra, c[start][end] - f[start][end]);
end = start;
}
end = t;
while (end != s) {
int start = prev[end];
f[start][end] += extra;
f[end][start] = -f[start][end];
end = start;
}
flow += extra;
}
return flow;
}
void
limpiar() {
for (int i = 0; i < MAXN; i++) {
g[i].clear();
}
}
int
main() {
while (cin >> n && n) {
limpiar();
for (int i = 0; i < n; i++) {
string nombre, apellido;
cin >> nombre >> apellido;
if (apellido[0] == ’S’ || apellido[0] == ’T’ ||
apellido[0] == ’U’ || apellido[0] == ’V’ ||
apellido[0] == ’W’ || apellido[0] == ’X’ ||
apellido[0] == ’Y’ || apellido[0] == ’Z’) continue;
int nodoNombre, nodoApellido;
nodoNombre = nombre[0] - ’A’ + 1; //A = 1
nodoApellido = apellido[0] - ’A’ + 27; //Z = 52
connect(nodoNombre, nodoApellido);
connect(0, nodoNombre);
connect(nodoApellido, 53);
}
cout << maxflow(0, 53) << endl;
}
return 0;
}
.............................................................................
4. Teor´ıa de n´umeros
4.1. N´umeros romanos
A continuaci´on est´an las funciones para pasar del sistema romano a ´arabe.
Valores: I = 1, V = 5, X = 10, L = 50, C = 100, D = 500 y M = 1000;
4.1.1. ´
Arabe a Romano
OJO: Tener en cuenta que el rango de conversi´on es 1 - 3999
13

string
arabicToRoman(int num) {
string uni[10] = {"", "I", "II", "III", "IV", "V",
"VI", "VII", "VIII", "IX"};
string deci[10]={"", "X", "XX", "XXX", "XL", "L",
"LX", "LXX", "LXXX", "XC"};
string cen[10]={"", "C", "CC", "CCC", "CD", "D",
"DC", "DCC", "DCCC", "CM"};
string mil[4]={"", "M", "MM", "MMM"};
int nUni = num % 10;
int nDec = (num / 10) % 10;
int nCen = ((num / 10) / 10) % 10;
int nMil = (((num / 10) / 10) / 10) % 10;
string ans = mil[nMil];
ans += cen[nCen];
ans += deci[nDec];
ans += uni[nUni];
return ans;
}
.............................................................................
4.1.2. Romano a ´
Arabe
OJO: Tener en cuenta que el rango de conversi´on es 1 - 3999
int
romanToArabic(string num) {
map <char, int> RtoA;
RtoA[’I’] = 1; RtoA[’V’] = 5; RtoA[’X’] = 10; RtoA[’L’] = 50;
RtoA[’C’] = 100;RtoA[’D’] = 500;RtoA[’M’] = 1000;
int value = 0;
for (int i = 0; num[i]; i++) {
if (num[i+1] && RtoA[num[i]] < RtoA[num[i+1]]) {
value += RtoA[num[i+1]] - RtoA[num[i]];
i++;
}
else value += RtoA[num[i]];
}
return value;
}
.............................................................................
4.2. Divisores de un n´umero
Imprime los divisores de un n´umero (cuidado que no lo hace en orden).
Complejidad: O(√n) donde nes el n´umero.
void divisors(int n){
int i;
for (i = 1; i * i < n; ++i){
if (n % i == 0) printf("%d\n%d\n", i, n/i);
}
// Si existe, imprimir su raiz cuadrada una sola vez
if (i * i == n) printf("%d\n", i);
}
.............................................................................
4.3. M´aximo com´un divisor y m´ınimo com´un m´ultiplo
Para hallar el m´aximo com´un divisor entre dos n´umeros aybejecutar el
comando __gcd(a, b).
Para hallar el m´ınimo com´un m´ultiplo: lcm(a, b) = |a·b|
gcd(a, b)
4.4. Criba de Erat´ostenes
Encuentra los primos desde 1 hasta un l´ımite n.
sieve[i] es falso s´ı y solo s´ı i es un n´umero primo.
Complejidad: O(n) donde nes el l´ımite superior.
const int MAXN = 1000000;
bool sieve[MAXN + 5];
vector <int> primes;
void build_sieve(){
memset(sieve, false, sizeof(sieve));
sieve[0] = sieve[1] = true;
for (int i = 2; i * i <= MAXN; ++i){
if (!sieve[i]){
for (int j = i * i; j <= MAXN; j += i){
sieve[j] = true;
}
}
14

}
for (int i = 2; i <= MAXN; ++i){
if (!sieve[i]) primes.push_back(i);
}
}
.............................................................................
4.5. Factorizaci´on prima de un n´umero
Halla la factorizaci´on prima de un n´umero apositivo. Si aes negativo llamar
el algoritmo con |a|y agregarle -1 a la factorizaci´on.
Se asume que ya se ha ejecutado el algoritmo para generar los primos hasta al
menos √a.
El algoritmo genera la lista de primos en orden de menor a mayor.
Utiliza el hecho de que en la factorizaci´on prima de aaparece m´aximo un
primo mayor a √a.
Complejidad aproximada: O(√a)
const int MAXN = 1000000; // MAXN > sqrt(a)
bool sieve[MAXN + 5];
vector <int> primes;
vector <long long> factorization(long long a){
// Se asume que se tiene y se llam´o la funci´on build_sieve()
vector <long long> ans;
long long b = a;
for (int i = 0; 1LL * primes[i] * primes[i] <= a; ++i){
int p = primes[i];
while (b % p == 0){
ans.push_back(p);
b /= p;
}
}
if (b != 1) ans.push_back(b);
return ans;
}
.............................................................................
4.6. Exponenciaci´on logar´ıtmica
4.6.1. Propiedades de la operaci´on m´odulo
(amod n) mod n=amod n
(a+b) mod n= ((amod n)+(bmod n)) mod n
(a·b) mod n= ((amod n)·(bmod n)) mod n
a
bmod n6=amod n
bmod nmod n
4.6.2. Big mod
Halla r´apidamente el valor de bpmod mpara 0 ≤b, p, m ≤2147483647
Si se cambian los valores por long long los l´ımites se cambian por
0≤b, p ≤9223372036854775807 y 1 ≤m≤3037000499.
Complejidad: O(log p)
int bigmod(int b, int p, int m){
if (p == 0) return 1;
if (p % 2 == 0){
int mid = bigmod(b, p/2, m);
return (1LL * mid * mid) % m;
}else{
int mid = bigmod(b, p-1, m);
return (1LL * mid * b) % m;
}
}
.............................................................................
4.7. Combinatoria
4.7.1. Coeficientes binomiales
Halla el valor de n
kpara 0 ≤k≤n≤66. Para n > 66 los valores comienzan
a ser muy grandes y no caben en un long long.
Complejidad: O(n2)
const int MAXN = 66;
unsigned long long choose[MAXN+5][MAXN+5];
void binomial(int N){
15
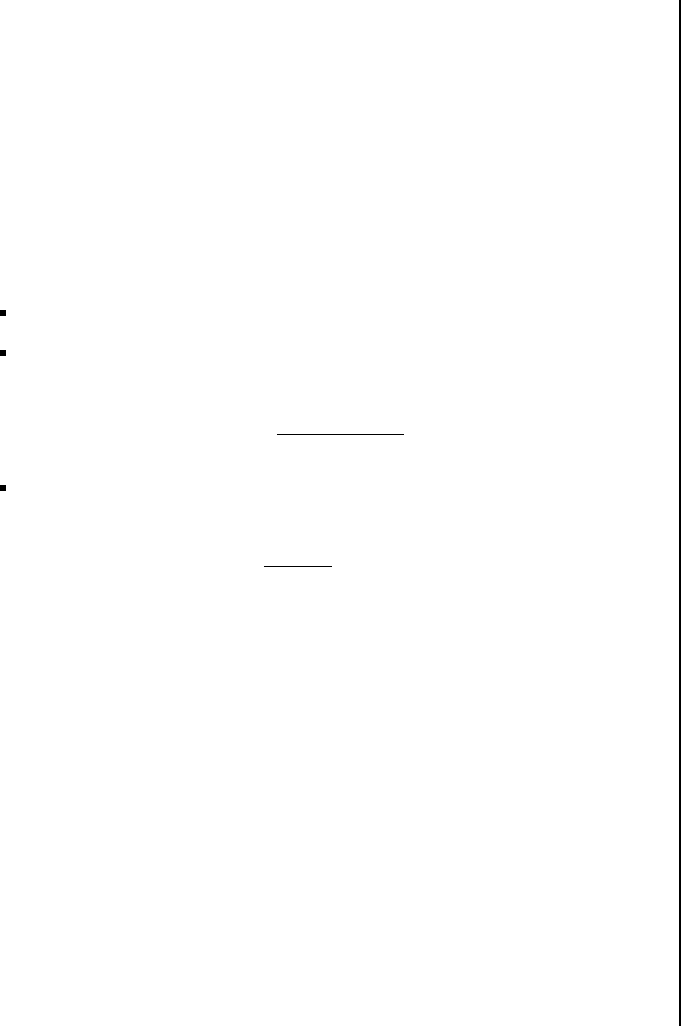
for (int n = 0; n <= N; ++n) choose[n][0] = choose[n][n] = 1;
for (int n = 1; n <= N; ++n){
for (int k = 1; k < n; ++k){
choose[n][k] = choose[n-1][k-1] + choose[n-1][k];
}
}
}
.............................................................................
4.7.2. Propiedades de combinatoria
El n´umero de permutaciones de nelementos diferentes es n!
El n´umero de permutaciones de nelementos donde hay m1elementos re-
petidos de tipo 1, m2elementos repetidos de tipo 2, . . . , mkelementos
repetidos de tipo kes
n!
m1!m2!···mk!
El n´umero de permutaciones de kelementos diferentes tomados de un
conjunto de nelementos es
n!
(n−k)! =k!n
k
5. Programaci´on Din´amica
5.1. Longest increasing subsequence
Halla la longitud de la subsecuencia creciente m´as larga que hay en un arreglo
(tambi´en se puede usar con strings).
5.1.1. Orden cuadr´atico
Retorna un vector con los elementos que componen la subsecuencia cre-
ciente m´as larga del arreglo arr.
Si se necesita s´olo la longitud de la subsecuencia ignorar las l´ıneas que tienen
comentado un ∗y retornar lo que se requiera.
Complejidad: O(n2) donde nes la longitud de arr.
const int MAXN = 1005;
int dp[MAXN];
int prev[MAXN]; //*
int arr[MAXN];
vector <int>
lis(int n) {
int maxi = 1;
int indexMaxi = 0; //*
dp[0] = 1;
prev[0] = -1; //*
for (int i = 1; i < n; i++) {
dp[i] = 1;
prev[i] = -1; //*
for (int j = i - 1; j >= 0; j--) {
//> estrictamente creciente
//>= dos elementos iguales son ambos inclu´ıdos
if (arr[i] > arr[j] && dp[j] + 1 > dp[i]) {
dp[i] = dp[j] + 1;
prev[i] = j; //*
if (dp[i] > maxi) {
maxi = dp[i];
indexMaxi = i; //*
}
}
}
}
//Si se necesita s´olo el tama~no retornar maxi aqu´ı
vector <int> seq;
for (int i = indexMaxi; i >= 0; i = prev[i]) {
seq.push_back(arr[i]);
}
reverse(seq.begin(), seq.end());
return seq;
}
.............................................................................
5.1.2. Orden logar´ıtmico imprimiendo s´olo longitud
Retorna el tama˜no de la longitud de la subsecuencia creciente m´as larga del
arreglo arr.
Complejidad: O(nlog2n) donde nes la longitud de arr.
const int MAXN = 100005;
int arr[MAXN]; //Almacena los elementos
int dp[MAXN]; //Almacena la secuencia creciente m´as larga
16

int
binarySearch(int low, int high, int key) {
while (high - low + 1 > 1) {
int mid = low + (high-low) / 2;
(arr[mid] >= key ? high : low) = mid;
}
return high;
}
int
lis(int n) {
int pointer = 1; //Siempre apunta un lugar vac´ıo
memset(dp, 0, sizeof(dp[0]) * n);
dp[0] = arr[0];
pointer = 1;
for (int i = 1; i < n; i++) {
if (arr[i] < dp[0])
dp[0] = arr[i]; //Nuevo valor m´as peque~no
else if (arr[i] > dp[pointer - 1])
//Quiere extender la secuencia
dp[pointer++] = arr[i];
else {
//Quiere ser el actual candidate de una secuencia
//existente, reemplazar´a un valor piso de la tabla dp
int index = binarySearch(0, pointer - 1, arr[i]);
dp[index] = arr[i];
}
}
return pointer;
}
.............................................................................
5.1.3. Orden logar´ıtmico imprimiendo la secuencia
Retorna un vector con los elementos que componen la subsecuencia cre-
ciente m´as larga del arreglo arr.
Complejidad: O(nlog2n) donde nes la longitud de arr.
const int MAXN = 100005;
int arr[MAXN]; //Almacena los n´umeros
int dp[MAXN]; //Almacena ´ındices de los n´umeros
int prev[MAXN]; //Almacena ´ındices de los antecesores
//OJO: Este binarySearch cambia con respecto al anterior
int
binarySearch(int low, int high, int key) {
while (high - low + 1 > 1) {
int mid = low + (high-low) / 2;
if (arr[dp[mid]] > key) high = mid;
else low = mid + 1;
}
return high;
}
vector <int>
lis(int n) {
memset(dp, 0, sizeof(dp[0]) * n);
//memset(prev, 0xFF, sizeof(prev[0]) * n);
dp[0] = 0;
prev[0] = -1;
int pointer = 1; //Siempre apunta a una posici´on vac´ıa
for (int i = 1; i < n; i++) {
if (arr[i] < arr[dp[0]]) {
//Nuevo valor m´as peque~no
dp[0] = i; //Almaceno el index
prev[i] = -1; //El 0xFF del memset ya tiene un -1
}
else if (arr[i] > arr[dp[pointer - 1]]) {
//Quiere extender la secuencia
prev[i] = dp[pointer - 1];
dp[pointer++] = i;
}
else {
//Quiere ser un candidato potencial de una secuencia futura
//Va a reemplazar un valor piso en la tabla dp
int index = binarySearch(0, pointer - 1, arr[i]);
prev[i] = dp[index - 1];
dp[index] = i;
}
}
vector <int> sec;
for (int i = dp[pointer - 1]; i >= 0; i = prev[i]) {
sec.push_back(arr[i]);
}
17

reverse(sec.begin(), sec.end());
return sec;
}
.............................................................................
5.2. Problema de la mochila
Halla el valor m´aximo que se puede obtener al empacar un subconjunto de
nobjetos en una mochila de tama˜no Wcuando se conoce el valor y el tama˜no
de cada objeto.
Complejidad: O(n×W) donde nes el n´umero de objetos y Wes la capacidad
de la mochila.
// M´aximo n´umero de objetos
const int MAXN = 2005;
// M´aximo tama~no de la mochila
const int MAXW = 2005;
// w[i] = peso del objeto i (i comienza en 1)
int w[MAXN];
// v[i] = valor del objeto i (i comienza en 1)
int v[MAXN];
// dp[i][j] m´axima ganancia si se toman un subconjunto de los
// objetos 1 .. i y se tiene una capacidad de j
int dp[MAXN][MAXW];
int knapsack(int n, int W){
for (int j = 0; j <= W; ++j) dp[0][j] = 0;
for (int i = 1; i <= n; ++i){
for (int j = 0; j <= W; ++j){
dp[i][j] = dp[i-1][j];
if (j - w[i] >= 0){
dp[i][j] = max(dp[i][j], dp[i-1][j-w[i]] + v[i]);
}
}
}
return dp[n][W];
}
.............................................................................
5.3. Edit distance
Calcula cual es el m´ınimo costo de convertir de un string sal string t, utili-
zando las operaciones de reemplazar,insertar yborrar.
Complejidad: O(n×m) donde nymson los tama˜nos de los string.
const int MAXN = 5005;
int dp[MAXN][MAXN];
// dp[i][j] = Min cost of turning s[0..i) into t[0..j)
// Allowed operations are deletion, insertion and
// substitution (in the string s) .Note that the same
// result can be achieved deleting from s or inserting in t
// and viceversa
int
solve(string s, string t, int n, int m) {
// Turn the empty string into t[0..j), add to s all
// of the characters in t
for (int j = 0; j <= m; j++) dp[0][j] = j;
// Turn s[0..i) into the empty string, delete all
// of the characters in s
for (int i = 0; i <= n; i++) dp[i][0] = i;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
// Turn s[0..i) into t[0..j)
// If the characters match, keep going
if (s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1];
else {
int substituteCost, insertCost, deleteCost;
substituteCost = insertCost = deleteCost = 1;
// Try substituting s[i-1] for t[j-1] and turn
// s[0..i-1) into t[0..j-1)
dp[i][j] = dp[i - 1][j - 1] + substituteCost;
// Try deleting character s[i-1] and turn
// s[0..i-1) into t[0..j)
dp[i][j] = min(dp[i][j], dp[i - 1][j] + deleteCost);
// Try inserting character t[j-1] and turn
// s[0..i) into t[0..j-1)
dp[i][j] = min(dp[i][j], dp[i][j - 1] + insertCost);
}
18

}
}
return dp[n][m];
}
.............................................................................
5.4. Formas de sumar un n´umero
Calcula la cantidad de formas en la que puedo obtener un n´umero ncon k
sumandos.
Complejidad O(MAXN2) asumiendo, que la ny la ktienen el mismo l´ımite
m´aximo.
Notar que al inicio del main estamos construyendo la matriz, si no es necesario
construirla toda, sino hasta la nykque me den, entonces lo hago.
const int MAXN = 105;
//El n´umero puede ser demasiado grande
const int MOD = 1000000;
// n: n´umero que quiero hallar
// k: con cu´antos sumandos
int n, k;
// Filas: k, Columnas: n
int dp[MAXK][MAXN];
void
build() {
//Para cualquier n, si tengo 1 sumando, s´olo tengo una opci´on
//Para cualquier j, si tengo que sumar 0, s´olo tengo una opci´on
for (int j = 1; j < MAXN; j++) dp[1][j] = 1, dp[j][0] = 1;
for (int i = 2; i < MAXN; i++) {
for (int j = 1; j < MAXN; j++) {
dp[i][j] = (dp[i-1][j] + dp[i][j-1]) % MOD;
}
}
}
int
main() {
build();
while (cin >> n >> k && n && k) {
//Al final, la respuesta est´a en dp[k][n]
cout << dp[k][n] << endl;
}
return 0;
}
.............................................................................
5.5. Longest Common Substring
Permite hallar la subcadena com´un m´as larga, estrictamente continua, entre
dos strings syt.
El ejemplo actual tambi´en tiene el m´etodo backtrack que permite reconstruir
la soluci´on. Complejidad O(n×m) donde nymson los tama˜nos del string.
const int MAXN = 1005;
int dp[MAXN][MAXN];
string
backtrack(const string &s, int i, int j, string p) {
if (dp[i][j] == 0) {
reverse(p.begin(), p.end());
return p;
}
else {
p += s[i-1];
return backtrack(s, i-1, j-1, p);
}
}
string
lcsubstr(const string &s, const string &t, int n, int m) {
for (int i = 0; i <= n; i++) dp[i][0] = 0;
for (int j = 0; j <= m; j++) dp[0][j] = 0;
string ret = "";
int maxi = 0;
int maxI = -1, maxJ = -1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (s[i-1] == t[j-1]) {
dp[i][j] = dp[i-1][j-1] + 1;
if (dp[i-1][j-1] + 1 > maxi) {
maxI = i;
maxJ = j;
19

maxi = dp[i-1][j-1] + 1;
}
}
else dp[i][j] = 0;
}
}
if (maxI != -1 && maxJ != -1) {
//Reconstruimos el longest common substring
ret = backtrack(s, maxI, maxJ, "");
}
return ret;
}
int
main() {
string s, t;
cin >> s >> t;
string lcsstring = lcsubstr(s, t, s.size(), t.size());
if (lcsstring == "") printf("No common sequence.\n");
else cout << lcsstring << endl;
return 0;
}
.............................................................................
5.6. Longest Common Subsequence
Halla la longitud de la m´axima subsecuencia (no substring) de dos cadenas
syt.
Una subsecuencia de una secuencia ses una secuencia que se puede obtener
de sal borrarle algunos de sus elementos (probablemente todos) sin cambiar
el orden de los elementos restantes.
El algoritmo tambi´en se puede aplicar para vectores de elementos, no s´olo para
strings.
Complejidad: O(n×m) donde nes la longitud de symes la longitud de t.
const int MAXN = 1005;
int dp[MAXN][MAXN];
int
lcs(const string &s, const string &t) {
int n = s.size(), m = t.size();
for (int j = 0; j <= m; j++) dp[0][j] = 0;
for (int i = 0; i <= n; i++) dp[i][0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
}
return dp[n][m];
}
.............................................................................
5.7. Shortest Common Supersequence
El Shortest Common Supersequence es el string m´as corto ztal que los
strings sytsean subsecuencias de z.
Para hallar esto, simplemente es ejecutar el Longest Common Subsequence
entre los strings syt, y el tama˜no de la supersecuencia m´as corta ser´a (n+m)
-lcs(s, t), donde nymson los tama˜nos de los strings sytrespectivamente.
5.8. Maximum subarray (non-adjacent) sum (1D)
Dado un arreglo con n´umeros positivos, encontrar la m´axima suma de una
subsecuencia, teniendo en cuenta que los n´umeros de dicha secuencia no pueden
ser adyacentes.
Por ejemplo 32710deber´ıa retornar 13 (suma de 3 y 10), 325107de-
ber´ıa retornar 15 (suma de 3, 5 y 7).
Complejidad: O(n) donde nes el tama˜no del arreglo.
vector <int> arr;
int
findMaxSum(int n) {
int incl = arr[0];
int excl = 0;
int excl_new;
for (int i = 1; i < n; i++) {
// Current max excluding i.
excl_new = (incl > excl) ? incl : excl;
// Current max including i.
incl = excl + arr[i];
excl = excl_new;
20

}
// Return max of incl and excl
return ((incl > excl) ? incl : excl);
}
.............................................................................
5.9. Maximum subarray sum (1D) - Kadane’s Algorithm
Encuentra el subarreglo continuo (que contiene al menos un entero positivo)
con la suma m´as grande.
Complejidad: O(n) donde nes el tama˜no del arreglo.
int
kadane(vector <int> a, int n) {
int max_so_far = 0, max_ending_here = 0;
for(int i = 0; i < n; i++) {
max_ending_here = max_ending_here + a[i];
if(max_ending_here < 0) max_ending_here = 0;
if(max_so_far < max_ending_here) max_so_far = max_ending_here;
}
return max_so_far;
}
.............................................................................
5.9.1. Maximum circular subarray sum
Si el arreglo es circular y queremos hallar la suma m´as grande se hace el
siguiente procedimiento:
Aplicamos Kadane0sal arreglo sin modificar, y se almacena como m´aximo:
maxi.
Se itera sobre el arreglo para calcular la suma acumulada acc e invertir los
valores del arreglo: a inv[i] = -a[i].
La respuesta es el m´aximo entre el valor del punto 1 y la suma acumulada
m´as el resultado de un nuevo llamado al algoritmo con el arreglo invertido:
max(maxi, acc + kadane(a inv))
5.10. Maximum subrectangle sum (2D)
Permite hallar el sub-rect´angulo de una matriz con la mayor suma, la suma de
un rect´angulo es la suma de todos sus elementos. Un sub-rect´angulo es cualquier
sub-arreglo continuo de tama˜no 1 ×1 o mayor, localizado dentro del toda la
matriz.
5.10.1. Na¨ıve solution - O(n4)
Complejidad: O(n4) donde nes el tama˜no de un lado de la matriz (asumiendo
que son iguales).
Cuidado que puede no pasar con 100. Lo idea ser´ıa MAXN =4
√106
const int MAXN = 105;
const int INF = 1 << 30;
int n;
int arr[MAXN][MAXN];
int
main() {
cin >> n;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> arr[i][j];
if (i > 0) arr[i][j] += arr[i-1][j];
if (j > 0) arr[i][j] += arr[i][j-1];
if (i > 0 && j > 0) arr[i][j] -= arr[i-1][j-1];
}
}
int maxi = -1*INF;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
for (int k = i; k < n; k++) {
for (int l = j; l < n; l++) {
int sub = arr[k][l];
if (i > 0) sub -= arr[i-1][l];
if (j > 0) sub -= arr[k][j-1];
if (i > 0 && j > 0) sub += arr[i-1][j-1];
maxi = max(maxi, sub);
}
}
}
}
cout << maxi << endl;
return 0;
}
.............................................................................
5.10.2. Using Kadane’s - O(n3)
const int ROW = 105;
21

const int COL = 105;
int M[ROW][COL];
int arr[ROW];
int start, finish;
int n;
int
kadane() {
int sum = 0, maxSum = INT_MIN, i;
finish = -1;
int local_start = 0;
for (i = 0; i < n; ++i) {
sum += arr[i];
if (sum < 0) {
sum = 0;
local_start = i + 1;
}
else if (sum > maxSum) {
maxSum = sum;
start = local_start;
finish = i;
}
}
if (finish != -1) return maxSum;
// Special Case: When all numbers in arr are negative
maxSum = arr[0];
start = finish = 0;
// Find the maximum element in array
for (i = 1; i < n; i++) {
if (arr[i] > maxSum) {
maxSum = arr[i];
start = finish = i;
}
}
return maxSum;
}
void
findMaxSum() {
// Variables to store the final output
int maxSum = INT_MIN, finalLeft, finalRight, finalTop, finalBottom;
int left, right, i;
int sum;
for (left = 0; left < COL; ++left) {
memset(arr, 0, sizeof(arr));
for (right = left; right < COL; ++right) {
for (i = 0; i < ROW; ++i) arr[i] += M[i][right];
sum = kadane();
if (sum > maxSum) {
maxSum = sum;
finalLeft = left;
finalRight = right;
finalTop = start;
finalBottom = finish;
}
}
}
printf("(Top, Left) (%d, %d)\n", finalTop, finalLeft);
printf("(Bottom, Right) (%d, %d)\n", finalBottom, finalRight);
printf("Max sum is: %d\n", maxSum);
}
.............................................................................
5.11. Maximum subrectangle sum (3D)
Permite hallar la mayor suma en un arreglo 3D. Complejidad O(n6) donde
nes el tama˜no de uno de los lados del cubo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.12. Partition problem
Determina si un arreglo de n´umeros puede ser particionado en dos conjuntos
tal que la suma de ambos sea la misma.
Complejidad: O(sum ∗n), donde nes el tama˜no del arreglo y sum es la suma
de cada conjunto. (notar que este algoritmo no es eficiente para arreglos con
grandes sumas, para ese caso intentar una soluci´on recursiva O(2n))
vector <int> arr;
/* part[i][j] = true if a subset of {arr[0], arr[1], ..arr[j-1]}
has sum equal to i, otherwise false */
bool findPartiion (int n) {
int sum = 0;
int i, j;
for (i = 0; i < n; i++) sum += arr[i];
if (sum % 2 != 0) return false;
22

bool part[sum / 2 + 1][n + 1];
// Initialize top row as true
for (i = 0; i <= n; i++) part[0][i] = true;
// Initialize leftmost column, except part[0][0], as 0
for (i = 1; i <= sum / 2; i++) part[i][0] = false;
// Fill the partition table in botton up manner
for (i = 1; i <= sum/2; i++) {
for (j = 1; j <= n; j++) {
part[i][j] = part[i][j-1];
if (i >= arr[j-1])
part[i][j] = part[i][j] || part[i - arr[j-1]][j-1];
}
}
/* Uncomment this part to print table.
for (i = 0; i <= sum/2; i++)
{
for (j = 0; j <= n; j++)
printf ("%4d", part[i][j]);
printf("\n");
} */
return part[sum/2][n];
}
.............................................................................
5.13. Longest Palindromic Substring
Dado un string, encontrar el substring (estrictamente continuo) m´as largo que
sea pal´ındromo. Por ejemplo si tenemos "forgeeksskeegfor" la salida deber´ıa
ser: "geeksskeeg"
Complejidad: Creo que el primer m´etodo O(n3), el segundo O(n) y el tercero
O(n2).
/**
* Date 07/29/2015
* @author Tushar Roy
* Given a string find longest palindromic substring in this string.
*/
public class LongestPalindromeSubstring {
// I think this takes O(n^3)
public int longestPalindromeSubstringEasy(char arr[]) {
int longest_substring = 1;
for (int i = 0; i < arr.length; i++) {
int x, y;
int palindrome;
x = i;
y=i+1;
palindrome = 0;
while (x >= 0 && y < arr.length && arr[x] == arr[y]) {
x--;
y++;
palindrome += 2;
}
longest_substring = Math.max(longest_substring, palindrome);
x=i-1;
y=i+1;
palindrome = 1;
while (x >= 0 && y < arr.length && arr[x] == arr[y]) {
x--;
y++;
palindrome += 2;
}
longest_substring = Math.max(longest_substring, palindrome);
}
return longest_substring;
}
/**
* Linear time Manacher’s algorithm to find longest palindromic
substring.
* There are 4 cases to handle
* Case 1 : Right side palindrome is totally contained under
current palindrome. In this case do not consider this as
center.
* Case 2 : Current palindrome is proper suffix of input.
Terminate the loop in this case.
No better palindrom will be found on right.
* Case 3 : Right side palindrome is proper suffix and its
corresponding left side
palindrome is proper prefix of current palindrome.
Make largest such point as
* next center.
* Case 4 : Right side palindrome is proper suffix but its
left corresponding palindrome is be beyond current
palindrome. Do not consider this as center because
it will not extend at all.
*
23

* To handle even size palindromes replace input string with
one containing $ between every
input character and in start and end.
*/
public int longestPalindromicSubstringLinear(char input[]) {
int index = 0;
// preprocess the input to convert it into type abc -> $a$b$c$
// to handle even length case.
// Total size will be 2*n + 1 of this new array.
char newInput[] = new char[2*input.length + 1];
for(int i=0; i < newInput.length; i++) {
if(i % 2 != 0) {
newInput[i] = input[index++];
} else {
newInput[i] = ’$’;
}
}
// create temporary array for holding largest palindrome at
// every point.
// There are 2*n + 1 such points.
int T[] = new int[newInput.length];
int start = 0;
int end = 0;
//here i is the center.
for(int i=0; i < newInput.length; ) {
//expand around i. See how far we can go.
while(start >0 && end < newInput.length-1 &&
newInput[start-1] == newInput[end+1]) {
start--;
end++;
}
//set the longest value of palindrome around center i at T[i]
T[i] = end - start + 1;
// this is case 2. Current palindrome is proper suffix of input.
// No need to proceed. Just break out of loop.
if(end == T.length -1) {
break;
}
// Mark newCenter to be either end or end + 1 depending on if we
// dealing with even or old number input.
int newCenter = end + (i%2 ==0 ? 1 : 0);
for(int j = i + 1; j <= end; j++) {
// i - (j - i) is left mirror. Its possible left mirror might
// go beyond current center palindrome. So take minimum of
// either left side palindrome or distance of j to end.
T[j] = Math.min(T[i - (j - i)], 2 * (end - j) + 1);
// Only proceed if we get case 3. This check is to make sure
// we do not pick j as new center for case 1 or case 4.
// As soon as we find a center lets break out of this inner
// while loop.
if(j + T[i - (j - i)]/2 == end) {
newCenter = j;
break;
}
}
// make i as newCenter. Set right and left to atleast the value
// we already know should be matching based of left side
// palindrome.
i = newCenter;
end = i + T[i]/2;
start = i - T[i]/2;
}
//find the max palindrome in T and return it.
int max = Integer.MIN_VALUE;
for(int i = 0; i < T.length; i++) {
int val;
/*if(i%2 == 0) {
val = (T[i] -1)/2;
} else {
val = T[i]/2;
}*/
val = T[i]/2;
if(max < val) {
max = val;
}
}
return max;
}
// I think this takes O(n^2)
public int longestPalindromeDynamic(char []str){
boolean T[][] = new boolean[str.length][str.length];
for(int i=0; i < T.length; i++){
24

T[i][i] = true;
}
int max = 1;
for(int l = 2; l <= str.length; l++){
int len = 0;
for(int i=0; i < str.length-l+1; i++){
int j = i + l-1;
len = 0;
if(l == 2){
if(str[i] == str[j]){
T[i][j] = true;
len = 2;
}
}
else{
if(str[i] == str[j] && T[i+1][j-1]){
T[i][j] = true;
len = j -i + 1;
}
}
if(len > max) {
max = len;
}
}
}
return max;
}
public static void main(String args[]) {
LongestPalindromeSubstring lps = new LongestPalindromeSubstring();
System.out.println(lps
.longestPalindromicSubstringLinear("abba"
.toCharArray()));
System.out.println(lps
.longestPalindromicSubstringLinear("abbababba"
.toCharArray()));
System.out.println(lps
.longestPalindromicSubstringLinear("babcbaabcbaccba"
.toCharArray()));
System.out.println(lps
.longestPalindromicSubstringLinear("cdbabcbabdab"
.toCharArray()));
}
}
.............................................................................
5.14. Longest Palindromic Subsequence
Dado un string, encontrar el tama˜no de la subsecuencia (no necesariamente
continua). Por ejemplo para BBABCBCAB la respuesta es 7, porque BABCBAB es la
subsecuencia palindr´omica m´as larga.
int lps(const string &str) {
int n = str.size();
int i, j, cl;
int L[n][n];
for (i = 0; i < n; i++) L[i][i] = 1;
for (cl = 2; cl <= n; cl++) {
for(i=0;i<n-cl+1;i++){
j=i+cl-1;
if (str[i] == str[j] && cl == 2) L[i][j] = 2;
else if (str[i] == str[j]) L[i][j] = L[i+1][j-1] + 2;
else L[i][j] = max(L[i][j-1], L[i+1][j]);
}
}
return L[0][n-1];
}
.............................................................................
5.15. Text Justification
Dada una secuencia de palabras y un n´umero l´ımite de caracteres que pue-
den escribirse en una l´ınea, poner los fin de l´ıneas en la secuencia dada tal
que las l´ıneas queden impresas equitativamente (En cuanto espacios en blanco)
Complejidad: O(n2).
/**
* Date 05/07/2015
* @author tusroy
*
* Video link - https://youtu.be/RORuwHiblPc
*
* Given a sequence of words, and a limit on the number of
* characters that can be put in one line (line width). Put line
* breaks in the given sequence such that the lines are printed
25

* neatly
*
* Solution:
* Badness - We define badness has square of empty spaces in
* every line. So 2 empty space on one line gets penalized as 4
* (2^2) while 1 each empty space on 2 lines gets penalized as
* 2(1 + 1). So we prefer 1 empty space on different lines over 2
* empty space on one line.
*
* For every range i,j(words from i to j) find the cost of
* putting them on one line. If words * from i to j cannot fit
* in one line cost will be infinite. Cost is calculated as square
* of empty space left in line after fitting words from i to j.
*
* Then apply this formula to get places where words need to be
* going on new line. minCost[i] = minCost[j] + cost[i][j-1]
* Above formula will try every value of j from i to len and see
* which one gives minimum cost to split words from i to len.
*
* Space complexity is O(n^2)
* Time complexity is O(n^2)
*
* References:
* http://www.geeksforgeeks.org/dynamic-programming-set-18-word
* -wrap/
*/
public class TextJustification {
public String justify(String words[], int width) {
int cost[][] = new int[words.length][words.length];
// next 2 for loop is used to calculate cost of putting
// words from i to j in one line. If words don’t fit in
// one line then we put Integer.MAX_VALUE there.
for(int i=0 ; i < words.length; i++){
cost[i][i] = width - words[i].length();
for(int j=i+1; j < words.length; j++){
cost[i][j] = cost[i][j-1] - words[j].length() - 1;
}
}
for(int i=0; i < words.length; i++){
for(int j=i; j < words.length; j++){
if(cost[i][j] < 0){
cost[i][j] = Integer.MAX_VALUE;
}else{
cost[i][j] = (int)Math.pow(cost[i][j], 2);
}
}
}
//minCost from i to len is found by trying
//j between i to len and checking which
//one has min value
int minCost[] = new int[words.length];
int result[] = new int[words.length];
for(int i = words.length-1; i >= 0 ; i--){
minCost[i] = cost[i][words.length-1];
result[i] = words.length;
for(int j=words.length-1; j > i; j--){
if(cost[i][j-1] == Integer.MAX_VALUE){
continue;
}
if(minCost[i] > minCost[j] + cost[i][j-1]){
minCost[i] = minCost[j] + cost[i][j-1];
result[i] = j;
}
}
}
int i = 0;
int j;
System.out.println("Minimum cost is " + minCost[0]);
System.out.println("\n");
//finally put all words with new line added in
//string buffer and print it.
StringBuilder builder = new StringBuilder();
do{
j = result[i];
for(int k=i; k < j; k++){
builder.append(words[k] + " ");
}
builder.append("\n");
i = j;
}while(j < words.length);
26

return builder.toString();
}
public static void main(String args[]){
String words1[] = {"Tushar","likes","to","write","code",
"at", "free", "time"};
TextJustification awl = new TextJustification();
System.out.println(awl.justify(words1, 12));
}
}
.............................................................................
5.16. Burst Balloons
Dados nglobos, numerados de 0 a n−1, cada globo tiene un n´umero. Si se
explota el globo i, se obtiene puntaje de nums[i−1] ∗nums[i]∗nums[i+ 1].
Cuando se explota el globo i, los globos i−1 y i+ 1 pasan a ser adyacentes.
Encontrar el m´aximo puntaje que se puede obtener explotando los globos en
un determinado orden.
Complejidad: Tiempo - O(n3), espacio - O(n2).
int max_score(vector<int>& nums) {
int n = nums.size();
int dp[n][n];
for (int l = 0; l < n; ++l) {
for (int i = 0, j = l; j < n; ++i, ++j) {
dp[i][j] = -1;
for (int k = i; k <= j; ++k) {
int cur_ans = k - 1 < i ? 0 : dp[i][k - 1];
cur_ans += k + 1 > j ? 0 : dp[k + 1][j];
cur_ans += burst(nums, k, i - 1, j + 1);
dp[i][j] = max(dp[i][j], cur_ans);
}
}
}
return n == 0 ? 0 : dp[0][n - 1];
}
int burst(const vector <int> &nums, int ind, int left, int right) {
int score = nums[ind];
score *= left < 0 ? 1 : nums[left];
score *= right >= nums.size() ? 1 : nums[right];
return score;
}
.............................................................................
5.17. Wildcard Matching
Determina si un texto cumple con un patr´on que puede contener ? y ∗, donde:
?matchea cualquier caracter (exactamente uno).
∗matchea cualquier secuencia de caracteres. (Incluyendo vac´ıo)
Complejidad: Tiempo - O(n×m), espacio - O(n). Donde nes el tama˜no del
texto y mel tama˜no del patr´on.
NOTA: Se puede aplicar un preprocesamiento para quitar ∗consecutivos.
bool is_match(const string &s, const string &p) {
int n = s.size(), m = p.size();
bool dp[2][m + 1];
dp[0][0] = true;
for (int j = 1; j <= m; ++j)
dp[0][j] = p[j - 1] == ’*’ ? dp[0][j - 1] : false;
for (int i = 1; i <= n; ++i) {
dp[i % 2][0] = false;
for (int j = 1; j <= m; ++j) {
if (s[i - 1] == p[j - 1] || p[j - 1] == ’?’)
dp[i % 2][j] = dp[1 - (i % 2)][j - 1];
else if (p[j - 1] == ’*’)
dp[i % 2][j] = dp[1 - (i % 2)][j] || dp[i % 2][j - 1];
else dp[i % 2][j] = false;
}
}
return dp[n % 2][m];
}
.............................................................................
5.18. Maximum profit - Best time to buy and sell stock
Se tiene un arreglo donde el ith elemento es el precio de un stock en el d´ıa
i. Determina la ganancia m´axima cuando se pueden completar a lo sumo k
transacciones.
27

NOTA: Antes de comprar un stock se tiene que vender lo que se ha comprado.
Es decir, si el n´umero m´aximo de transacciones es 1, la ganancia es 0 (solo se
podr´ıa comprar sin vender, entonces mejor no compro ni mierda).
Complejidad: Tiempo - O(days2), espacio - O(days). Hint: si kes mayor a los
d´ıas, no va a mejorar la respuesta, por eso se toma kcomo m´aximo el n´umero
de d´ıas.
int maxProfit(int k, const vector<int> &prices) {
int n = prices.size();
if (n == 0) return 0;
int dp[2][n];
k = min(k, n);
for (int j = 0; j < n; ++j) dp[0][j] = 0;
for (int i = 1; i <= k; ++i) {
dp[i % 2][0] = 0;
int max_diff = -prices[1 - (i % 2)];
for (int j = 1; j < n; ++j) {
max_diff = max(max_diff, dp[1 - (i % 2)][j - 1] - prices[j - 1]);
dp[i % 2][j] = max(dp[i % 2][j - 1], max_diff + prices[j]);
}
}
return dp[k % 2][n - 1];
}
.............................................................................
6. Geometr´ıa
6.1. Closest pair of points in a plane
Finds the smallest distance from a given set of points.
// A divide and conquer program in C++ to find the smallest
// distance from a given set of points.
#include <iostream>
#include <float.h>
#include <stdlib.h>
#include <math.h>
using namespace std;
// A structure to represent a Point in 2D plane
struct Point
{
int x, y;
};
// Following two functions are needed for library function qsort().
// Refer: http://www.cplusplus.com/reference/clibrary/cstdlib/qsort/
// Needed to sort array of points according to X coordinate
int compareX(const void* a, const void* b)
{
Point *p1 = (Point *)a, *p2 = (Point *)b;
return (p1->x - p2->x);
}
// Needed to sort array of points according to Y coordinate
int compareY(const void* a, const void* b)
{
Point *p1 = (Point *)a, *p2 = (Point *)b;
return (p1->y - p2->y);
}
// A utility function to find the distance between two points
float dist(Point p1, Point p2)
{
return sqrt( (p1.x - p2.x)*(p1.x - p2.x) +
(p1.y - p2.y)*(p1.y - p2.y)
);
}
// A Brute Force method to return the smallest distance between
// two points in P[] of size n
float bruteForce(Point P[], int n)
{
float min = FLT_MAX;
for (int i = 0; i < n; ++i)
for (int j = i+1; j < n; ++j)
if (dist(P[i], P[j]) < min)
min = dist(P[i], P[j]);
return min;
}
// A utility function to find minimum of two float values
float min(float x, float y)
{
28

return (x < y)? x : y;
}
// A utility function to find the distance beween the closest
// points of strip of given size. All points in strip[] are sorted
// accordint to y coordinate. They all have an upper bound on
// minimum distance as d. Note that this method seems to be a
// O(n^2) method, but it’s a O(n) method as the inner loop runs
// at most 6 times
float stripClosest(Point strip[], int size, float d)
{
float min = d; // Initialize the minimum distance as d
// Pick all points one by one and try the next points till
// the difference between y coordinates is smaller than d.
// This is a proven fact that this loop runs at most 6 times
for (int i = 0; i < size; ++i)
for (int j = i+1; j < size &&
(strip[j].y - strip[i].y) < min; ++j)
if (dist(strip[i],strip[j]) < min)
min = dist(strip[i], strip[j]);
return min;
}
// A recursive function to find the smallest distance. The array
// Px contains all points sorted according to x coordinates and
// Py contains all points sorted according to y coordinates
float closestUtil(Point Px[], Point Py[], int n)
{
// If there are 2 or 3 points, then use brute force
if (n <= 3)
return bruteForce(Px, n);
// Find the middle point
int mid = n/2;
Point midPoint = Px[mid];
// Divide points in y sorted array around the vertical line.
// Assumption: All x coordinates are distinct.
Point Pyl[mid+1];// y sorted points on left of vertical line
Point Pyr[n-mid-1];// y sorted points on right of vertical line
int li = 0, ri = 0;// indexes of left and right subarrays
for (int i = 0; i < n; i++)
{
if (Py[i].x <= midPoint.x)
Pyl[li++] = Py[i];
else
Pyr[ri++] = Py[i];
}
// Consider the vertical line passing through the middle point
// calculate the smallest distance dl on left of middle point
// and dr on right side
float dl = closestUtil(Px, Pyl, mid);
float dr = closestUtil(Px + mid, Pyr, n-mid);
// Find the smaller of two distances
float d = min(dl, dr);
// Build an array strip[] that contains points close (closer
// than d) to the line passing through the middle point
Point strip[n];
int j = 0;
for (int i = 0; i < n; i++)
if (abs(Py[i].x - midPoint.x) < d)
strip[j] = Py[i], j++;
// Find the closest points in strip. Return the minimum of
// d and closest distance is strip[]
return min(d, stripClosest(strip, j, d) );
}
// The main functin that finds the smallest distance
// This method mainly uses closestUtil()
float closest(Point P[], int n)
{
Point Px[n];
Point Py[n];
for (int i = 0; i < n; i++)
{
Px[i] = P[i];
Py[i] = P[i];
}
29

qsort(Px, n, sizeof(Point), compareX);
qsort(Py, n, sizeof(Point), compareY);
// Use recursive function closestUtil() to find the smallest
// distance
return closestUtil(Px, Py, n);
}
// Driver program to test above functions
int main()
{
Point P[] = {{2, 3}, {12, 30}, {40, 50}, {5, 1}, {12, 10},
{3, 4}};
int n = sizeof(P) / sizeof(P[0]);
cout << "The smallest distance is " << closest(P, n);
return 0;
}
.............................................................................
7. Strings
7.1. Algoritmo de KMP
Encuentra si el string needle aparece en en string haystack.
Si no se retorna directamente true cuando se halla la primera ocurrencia, el
algoritmo encuentra todas las ocurrencias de needle en haystack.
La primera parte del algoritmo llena el arreglo border donde border[i] es
la longitud del borde del prefijo de needle que termina en la posici´on i. Un
borde de una cadena ses la cadena m´as larga que es a la vez prefijo y sufijo
de spero que es diferente de s.
Complejidad: O(n) donde nes el tama˜no de haystack.
bool kmp(const string &needle, const string &haystack){
int m = needle.size();
vector<int> border(m);
border[0] = 0;
for (int i = 1; i < m; ++i) {
border[i] = border[i - 1];
while (border[i] > 0 and needle[i] != needle[border[i]])
border[i] = border[border[i] - 1];
if (needle[i] == needle[border[i]]) border[i]++;
}
int n = haystack.size();
int seen = 0;
for (int i = 0; i < n; ++i){
while (seen > 0 and haystack[i] != needle[seen])
seen = border[seen - 1];
if (haystack[i] == needle[seen]) seen++;
if (seen == m) return true; // Ocurre entre [i - m + 1, i]
}
return false;
}
.............................................................................
7.2. Algoritmo de Booth - Lexicographically minimal
string rotation
Encuentra la rotaci´on de un string que contiene el menor orden lexicogr´afico
de todas las rotaciones posibles. Por ejemplo, la menor rotaci´on lexicogr´afica
de bbaaccaadd ser´ıa aaccaaddbb, y de abcdeabcdea ser´ıa aabcdeabcde.
El algoritmo concatena el string a s´ı mismo y computa una tabla bas´andose en
el algoritmo de KMP.
El m´etodo devuelve el ´ındice en base 0 a primera letra correspondiente a
la mejor rotaci´on, si se necesita el string completo se deber´a utilizar substring
para reconstruirlo: str.substr(ind, str.size()) + str.substr(0, ind)
Complejidad: O(n) donde nes el tama˜no del string.
int
booth(const string &str) {
string s = str + str;
int n = s.size();
vector <int> f(n, -1);
int k = 0;
for (int j = 1; j < n; ++j) {
int i = f[j - k - 1];
while (i != -1 && s[j] != s[k + i + 1]) {
if(s[j]<s[k+i+1])k=j-i-1;
i = f[i];
}
if (i == -1 && s[j] != s[k + i + 1]) {
if (s[j] < s[k + i + 1]) k = j;
30

f[j - k] = -1;
}
else f[j - k] = i + 1;
}
return k;
}
.............................................................................
7.3. sufix /trie/array
Estructura de datos que maneja eficientemente strings, y operaciones sobre la
misma se tratara las siguientes implementaciones implementaciones suffix trie
ysuffix array
7.3.1. suffix trie
#include<bits/stdc++.h>
using namespace std;
struct node{
int count;
node *next[26];
node()
{
count = 0;
for(int i = 0; i<26; i++)
next[i] = NULL;
}
}*root;
void add(string name)
{
node *current = root;
current->count++;
for(int i = 0; i<name.size(); i++)
{
char nw = name[i];
if(current->next[(int)nw - ’a’] == NULL)
current->next[(int) nw - ’a’] = new node();
current = current->next[(int) nw - ’a’];
current->count++;
}
}
int main()
{
add(str);
}
.............................................................................
7.3.2. suffix array
la construccion del sufix array es compleja de entender , se recomienda, apren-
der mas a manejar esta estructura, que entender las optimizaciones que tiene
#include <bits/stdc++.h>
using namespace std;
#define MAX_N 100010 // second approach: \
// O(n log n)
char T[MAX_N]; // the input string, up
// to 100K characters
int n; // the length of input string
int RA[MAX_N], tempRA[MAX_N]; // rank array and temporary
// rank array
int SA[MAX_N], tempSA[MAX_N]; // suffix array and temporary
// suffix array for
//counting/radix sort
int c[MAX_N];
void countingSort(int k)
{ // O(n)
int i, sum, maxi = max(300, n);
// up to 255 ASCII chars or length of n
memset(c, 0, sizeof c);
// clear frequency table
for (i = 0; i < n; i++)
// count the frequency of each integer rank
c[i + k < n ? RA[i + k] : 0]++;
for (i = sum = 0; i < maxi; i++)
{
int t = c[i];
c[i] = sum;
sum += t;
}
31

for (i = 0; i < n; i++) // shuffle the suffix array if
// necessary
tempSA[c[SA[i] + k < n ? RA[SA[i] + k] : 0]++] = SA[i];
for (i = 0; i < n; i++) // update the suffix array SA
SA[i] = tempSA[i];
}
void constructSA()
{ // this version can go up to 100000 characters
int i, k, r;
for (i = 0; i < n; i++)
RA[i] = T[i]; // initial rankings
for (i = 0; i < n; i++)
SA[i] = i; // initial SA: {0, 1, 2, ..., n-1}
for (k = 1; k < n; k <<= 1)
{ // repeat sorting process log n times
countingSort(k);
// actually radix sort: sort based on the
//second item
countingSort(0); // then (stable) sort
// based on the first
//item
tempRA[SA[0]] = r = 0; // re-ranking; start from
//rank r = 0
for (i = 1; i < n; i++) // compare adjacent
// suffixes
// if same pair => same
// rank r;
// otherwise,increase r
tempRA[SA[i]] =
( RA[SA[i]] == RA[SA[i - 1]] && RA[SA[i] + k]
== RA[SA[i - 1] + k]) ? r : ++r;
for (i = 0; i < n; i++) // update the rank array RA
RA[i] = tempRA[i];
if (RA[SA[n - 1]] == n - 1)
break; // nice optimization trick
}
}
int main()
{
strcpy(T, "GATAGACA");
n = (int)strlen(T);
T[n++] = ’$’;
constructSA(); // O(n log n)
printf("\nThe Suffix Array of string T = ’%s’
is shown below (O(n log n)
version) :\n ", T);
printf("i\tSA[i]\tSuffix\n");
for (int i = 0; i < n; i++)
printf("%2d\t%2d\t%s\n", i, SA[i], T + SA[i]);
return 0;
}
.............................................................................
7.3.3. String Matching
Despues de haber construido el sufix array de Tpodemos buscar un patr´on
Pen O(mlogn)
typedef pair<int, int> ii;
char P[MAX_N]; // the pattern string (for string matching)
int m; // the length of pattern string
ii stringMatching()
{ // string matching in O(m log n)
int lo = 0, hi = n - 1, mid = lo; // valid matching
//= [0..n-1]
while (lo < hi)
{ // find lower bound
mid = (lo + hi) / 2; // this is round down
int res = strncmp(T + SA[mid], P, m);
// try to find P in suffix ’mid’
if (res >= 0)
hi = mid;
// prune upper half (notice the >= sign)
else
lo = mid + 1;
// prune lower half including mid
} // observe ‘=’ in "res >= 0" above
if (strncmp(T + SA[lo], P, m) != 0)
return ii(-1, -1); // if not found
ii ans;
32

ans.first = lo;
lo = 0;
hi=n-1;
mid = lo;
while (lo < hi)
{ // if lower bound is found, find upper bound
mid = (lo + hi) / 2;
int res = strncmp(T + SA[mid], P, m);
if (res > 0)
hi = mid; // prune upper half
else
lo = mid + 1;
// prune lower half including mid
} // (notice the selected branch when res == 0)
if (strncmp(T + SA[hi], P, m) != 0)
hi--; // special case
ans.second = hi;
return ans;
} // return lower/upperbound as first/second item of
// the pair, respectively
int main()
{
// stringMatching demo
//printf("\nNow, enter a string P below,
//we will try to find P in T:\n");
strcpy(P, "A");
m = (int)strlen(P);
// if ’\n’ is read, uncomment the next line
//P[m-1] = 0; m--;
ii pos = stringMatching();
if (pos.first != -1 && pos.second != -1)
{
printf("%s is found SA[%d..%d] of %s\n", P,
pos.first, pos.second, T);
printf("They are:\n");
for (int i = pos.first; i <= pos.second; i++)
printf(" %s\n", T + SA[i]);
}
else
printf("%s is not found in %s\n", P, T);
return 0;
}
.............................................................................
7.3.4. Longest Common Prefix (LCP)
Se puede hallar el LCP entre sufijos consecutivos en O(n)
int Phi[MAX_N]; // for computing longest common prefix
int PLCP[MAX_N];
int LCP[MAX_N]; // LCP[i] stores the LCP between
// previous suffix T+SA[i-1]
// and current suffix T+SA[i]
char P[MAX_N]; // the pattern string (for string matching)
int m; // the length of pattern string
int n; // the length of input string
// returns what string is the owner of
// the suffix, if there are more than two
// string this line has to be modified to the num of
// strings in the input
int owner(int idx) { return (idx < n - m - 1) ? 1 : 2; }
void computeLCP()
{
int i, L;
Phi[SA[0]] = -1; // default value
for (i = 1; i < n; i++) // compute Phi in O(n)
Phi[SA[i]] = SA[i - 1]; // remember which suffix
// is behind
// this suffix
for (i = L = 0; i < n; i++)
{ // compute Permuted LCP in O(n)
if (Phi[i] == -1)
{
PLCP[i] = 0;
continue;
} // special case
while (T[i + L] == T[Phi[i] + L])
L++; // L increased max n times
PLCP[i] = L;
L = max(L - 1, 0); // L decreased max n times
}
33

for (i = 0; i < n; i++) // compute LCP in O(n)
LCP[i] = PLCP[SA[i]]; // put the permuted LCP to the
// correct position
}
int main()
{
computeLCP(); // O(n)
printf("\nThe LCP information of ’T+P’ = ’%s’:\n", T);
printf("i\tSA[i]\tLCP[i]\tOwner\tSuffix\n");
for (int i = 0; i < n; i++)
printf("%2d\t%2d\t%2d\t%2d\t%s\n", i,
SA[i], LCP[i], owner(SA[i]), T + SA[i]);
return 0;
}
.............................................................................
7.3.5. Longest Repeated Substring
typedef pair<int, int> ii;
ii LRS()
{ // returns a pair (the LRS length and its index)
int i, idx = 0, maxLCP = -1;
for (i = 1; i < n; i++) // O(n), start from i = 1
if (LCP[i] > maxLCP)
maxLCP = LCP[i], idx = i;
return ii(maxLCP, idx);
}
int main()
{
// LRS demo
ii ans = LRS();
// find the LRS of the first input string
char lrsans[MAX_N];
strncpy(lrsans, T + SA[ans.second], ans.first);
printf("\nThe LRS is ’%s’ with length = %d\n\n",
lrsans, ans.first);
}
.............................................................................
7.4. Formatos de impresi´on
7.4.1. N´umeros
Con la funci´on printf podemos dar distintos formatos de impresi´on, por
ejemplo justificar, ceros o espacios iniciales, etc.
int
main() {
//Width 3
printf("%3d\n", 45);
//Width 3 leading 0’s
printf("%03d\n", 45);
//Width 6, after point precision 2
printf("%6.2f\n", 4.123);
//Width 6 leading 0’s, after point precision 2
printf("%06.2f\n", 4.123);
printf("%x\n", 255); //Prints in hexa lowercase
printf("%X\n", 255); //Prints in hexa uppercase
printf("%o\n", 16); //Prints in octal
return 0;
}
.............................................................................
7.4.2. Strings
The printf(“ %s”, “Hello, world!”); statement prints the string (nothing
special happens.)
The printf(“ %15s”, “Hello, world!”); statement prints the string, but print
15 characters. If the string is smaller the “empty” positions will be filled
with “whitespace.”
The printf(“ %.10s”, “Hello, world!”); statement prints the string, but print
only 10 characters of the string.
The printf(“ %-10s”, “Hello, world!”); statement prints the string, but
prints at least 10 characters. If the string is smaller “whitespace” is ad-
ded at the end. (See next example.)
The printf(“ %-15s”, “Hello, world!”); statement prints the string, but
prints at least 15 characters. The string in this case is shorter than the
defined 15 character, thus “whitespace” is added at the end (defined by
the minus sign.)
34
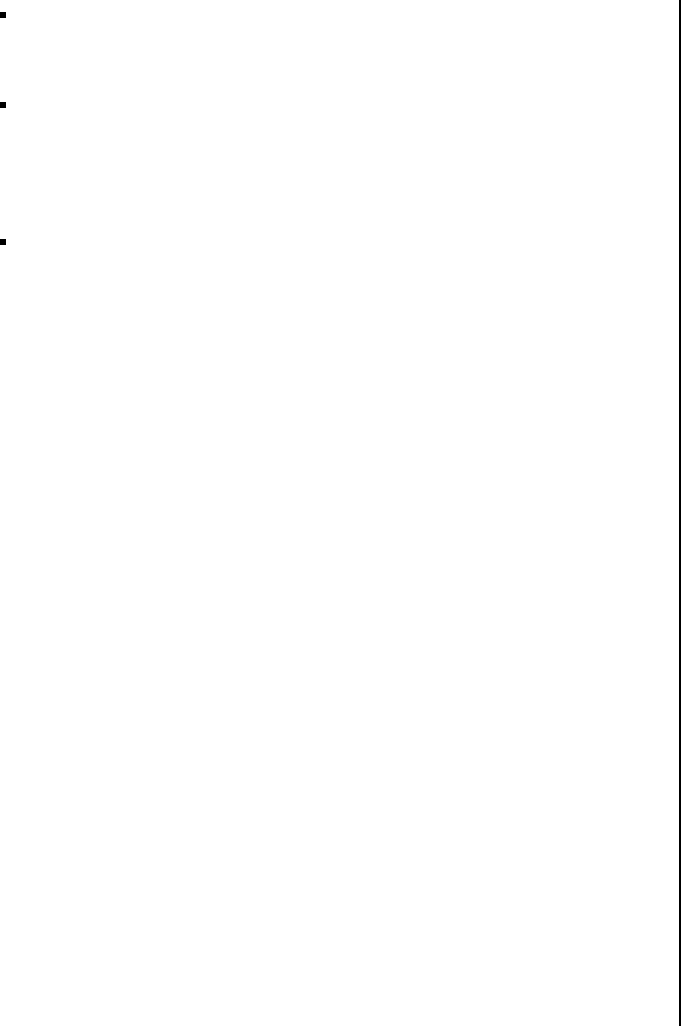
The printf(“ %.15s”, “Hello, world!”); statement prints the string, but print
only 15 characters of the string. In this case the string is shorter than 15,
thus the whole string is printed.
The printf(“ %15.10s”, “Hello, world!”); statement prints the string, but
print 15 characters. If the string is smaller the “empty” positions will be
filled with “whitespace.” But it will only print a maximum of 10 characters,
thus only part of new string (old string plus the whitespace positions) is
printed.
The printf(“ %-15.10s”, “Hello, world!”); statement prints the string, but
it does the exact same thing as the previous statement, accept the “whi-
tespace” is added at the end.
7.4.3. Formato en Java
Para utilizar formatos de impresi´on en Java se debe usar System.out.format
y darle formatos muy parecidos a los de C++, ac´a podemos ver varios ejemplos.
Se pueden dar incluso formatos para impresi´on de Calendar.
import java.util.Calendar;
import java.util.Locale;
public class Main {
public static void main(String[] args) {
long n = 461012;
System.out.format("%d%n", n); // --> "461012"
System.out.format("%08d%n", n); // --> "00461012"
System.out.format("%+8d%n", n); // --> " +461012"
System.out.format("%,8d%n", n); // --> " 461,012"
System.out.format("%+,8d%n%n", n); // --> "+461,012"
double pi = Math.PI;
System.out.format("%f%n", pi); // --> "3.141593"
System.out.format("%.3f%n", pi); // --> "3.142"
System.out.format("%10.3f%n", pi); // --> " 3.142"
System.out.format("%-10.3f%n", pi); // --> "3.142"
System.out.format(Locale.ENGLISH,
"%-10.4f%n%n", pi); // --> "3.1416"
Calendar c = Calendar.getInstance();
// --> "September 3, 2014"
System.out.format("%tB %te, %tY%n", c, c, c);
// --> "3:21 am"
System.out.format("%tl:%tM %tp%n", c, c, c);
// --> "09/03/14"
System.out.format("%tD%n", c);
}
}
.............................................................................
8. Otros
8.1. Binary Search
Permite buscar un elemento (key) en un arreglo ordenado (arr). Compleji-
dad: O(nlog2n) donde nes la cantidad de elementos del arreglo.
8.1.1. Traditional algorithm
Returns the index of some element that is equal to the given value (if there
are multiple elements, it returns some arbitrary one).
// invariants: value > arr[i] for all i < low
// value < arr[i] for all i > high
// or <= and => if mutiple elements of
// the same value are allowed.
int binary_search(vector <int> arr, int value) {
int n = arr.size();
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (arr[mid] > value) high = mid - 1;
else if (arr[mid] < value) low = mid + 1;
else return mid;
}
return low; // I didn’t find the value.
// so it would be inserted at low index.
}
.............................................................................
35

8.1.2. Lower bound
Returns the leftmost place where the given element can be correctly inserted.
// invariants: value > arr[i] for all i < low
// value <= arr[i] for all i > high
int lower_bound(vector <int> arr, int value) {
int n = arr.size();
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = (low + high) / 2;
if (arr[mid] >= value) high = mid - 1;
else low = mid + 1;
}
return low;
}
.............................................................................
8.1.3. Upper bound
Returns the rightmost place where the given element can be correctly inser-
ted.
// invariants: value >= arr[i] for all i < low
// value < arr[i] for all i > high
int upper_bound(vector <int> arr, int value) {
int n = arr.size();
int low = 0;
int high = n - 1;
while (low <= high) {
int mid = (low + high) / 2;
// Comparing with > instead of >=
if (arr[mid] > value) high = mid - 1;
else low = mid + 1;
}
return low;
}
.............................................................................
8.2. Binary Search Tree (BST)
8.2.1. Largest BST in a Binary Tree
Dado un ´arbol binario, encontrar el tama˜no del BST m´as grande en ese ´arbol.
/**
* Date 07/20/2014
* @author tusroy
*
* Video link - https://youtu.be/4fiDs7CCxkc
*
* Given a binary tree, find size of largest binary search
* subtree in this binary tree.
*
* Traverse tree in post order fashion. Left and right nodes
* return 4 piece of information to root which isBST, size of max
* BST, min and max in those subtree.
* If both left and right subtree are BST and this node data is
* greater than max of left and less than min of right then it
* returns to above level left size + right size + 1 and new min
* will be min of left side and new max will be max of right side.
*
* References:
* http://www.geeksforgeeks.org/find-the-largest-subtree-in-a-
* tree-that-is-also-a-bst/
*/
public class LargestBSTInBinaryTree {
public int largestBST(Node root){
MinMax m = largest(root);
return m.size;
}
private MinMax largest(Node root){
// if root is null return min as Integer.MAX and max as
// Integer.MIN
if(root == null){
return new MinMax();
}
//postorder traversal of tree. First visit left and right
//then use information of left and right to calculate
//largest BST.
MinMax leftMinMax = largest(root.left);
MinMax rightMinMax =largest(root.right);
MinMax m = new MinMax();
36

// if either of left or right subtree says its not BST or
// the data of this node is not greater/equal than max of
// left and less than min of right then subtree with this
// node as root will not be BST. Return false and max
// size of left and right subtree to parent
if (leftMinMax.isBST == false ||
rightMinMax.isBST == false ||
(leftMinMax.max > root.data ||
rightMinMax.min <= root.data)) {
m.isBST = false;
m.size = Math.max(leftMinMax.size,
rightMinMax.size);
return m;
}
// if we reach this point means subtree with this node as
// root is BST. Set isBST as true. Then set size as size
// of left + size of right + 1. Set min and max to be
// returned to parent
m.isBST = true;
m.size = leftMinMax.size + rightMinMax.size + 1;
//if root.left is null then set root.data as min else
//take min of left side as min
m.min = root.left != null ? leftMinMax.min : root.data;
//if root.right is null then set root.data as max else
//take max of right side as max.
m.max = root.right != null ? rightMinMax.max : root.data;
return m;
}
public static void main(String args[]){
LargestBSTInBinaryTree lbi = new LargestBSTInBinaryTree();
ConstructTreeFromInOrderPreOrder ctf =
new ConstructTreeFromInOrderPreOrder();
//this is just to create a binary tree.
int inorder[]={-7,-6,-5,-4,-3,-2,1,2,3,16,6,10,11,12,14};
int preorder[]={3,-2,-3,-4,-5,-6,-7,1,2,16,10,6,12,11,14};
Node root = ctf.createTree(inorder, preorder);
int largestBSTSize = lbi.largestBST(root);
System.out.println("Size of largest BST is " +
largestBSTSize);
assert largestBSTSize == 8;
}
}
/**
* Object of this class holds information which child passes back
* to parent node.
*/
class MinMax{
int min;
int max;
boolean isBST;
int size ;
MinMax(){
min = Integer.MAX_VALUE;
max = Integer.MIN_VALUE;
isBST = true;
size = 0;
}
}
.............................................................................
8.3. Build Binary Tree from PreOrder and InOrder
Permite crear un Binary Tree partiendo de los valores de PreOrden e InOrder
del BT, el resultado sera un String con el posOrder del BT.
string pre, in;
string reconstruct(int stpre, int epre, int stin, int ein) {
if(stpre > epre || stin > ein) return "";
char currRoot = pre[stpre];
int pos = 0;
for(int i = 0; i < in.size(); ++i) {
if(currRoot == in[i]) {
pos = i;
break;
}
}
string left = reconstruct(stpre + 1, stpre + (pos - stin),
stin, pos - 1);
37

string right = reconstruct(stpre + (pos - stin) + 1, epre,
pos + 1, ein);
return (left + right) + currRoot;
}
.............................................................................
8.4. Build Binary Tree from PosOrder and InOrder
Permite crear un Binary Tree partiendo de los valores de PosOrden e InOrder
del BT, el resultado sera un String con el inOrder del BT.
string buildTree(int inStart, int inEnd, int postStart, int postEnd) {
if (inStart > inEnd || postStart > postEnd) return "";
char rootValue = postorder[postEnd];
int k = 0;
for (int i = 0; i < inorder.size(); i++) {
if (inorder[i] == rootValue) {
k = i;
break;
}
}
string left = buildTree(inorder, inStart, k - 1, postorder,
postStart, postStart + k - (inStart + 1));
// Becuase k is not the length, it it need to -(inStart+1)
// to get the length
string right = buildTree(inorder, k + 1, inEnd, postorder,
postStart + k- inStart, postEnd - 1);
// postStart+k-inStart = postStart+k-(inStart+1) +1
return left + root + right;
}
.............................................................................
8.5. BitSet
Almacena bits, simula un array de booleanos, optimizando el espacio, cada
elemento puede ser accedido por el operador [ ]
int
main() {
bitset<16> set1; //Inicializa todo en 0
bitset<16> set2(0xFA2); //Inicializa con valor hex
bitset<16> set3(string("0101101")); //Inicializa a partir
//del string
cout << set3.count() << endl; //Imrpime 4
cout << set3.test(0) << endl; //Imprime true
cout << set3.test(1) << endl; //Imprime false
cout << set1.any() << endl; //False porque set1 no tiene
//bits en 1
cout << set1.none() << endl; //True
//cout << set2.all() << endl; //False, almenos hay
//un bit apagado
cout << set1.set() << endl; //Poner todos en 1
cout << set1.set(2) << endl; //Poner pos 2 en 1
cout << set1.reset(1) << endl; //Apaga el pos 1
cout << set1.flip(2) << endl; //Hacer flip al pos 2
string s = set1.to_string <char, string::traits_type,
string::allocator_type>();
cout << s << endl;
cout << set1.to_ulong() << endl;
return 0;
}
.............................................................................
8.6. M´aximo orden dado un n
En la siguiente tabla se encuentran los l´ımites de orden m´aximo respecto a
un n´umero de elementos ndel problema.
8.7. Suma de grandes n´umeros en C++
Como sabemos, en C++ los enteros (int) tienen un rango de (231) −1, y los
longlong tienen un rango de (264)−1, por esto no podemos almacenar n´umeros
de m´as de 18 19 n´umeros, para esto se debe usar la clase BigInteger en Java, o
si no hay que preocuparse por tiempo, podemos representar los n´umeros como
string y utilizar la siguiente funciones como la siguiente:
38

string
sumar(const string &a, const string &b) {
int ia = a.size() - 1, ib = b.size() - 1;
int llevo = 0;
string ans = "";
while (ia >= 0 || ib >= 0) {
int sum = (ia >= 0 ? toInt(a[ia--]) : 0)
+ (ib >= 0 ? toInt(b[ib--]) : 0);
sum += llevo;
llevo = sum / 10;
ans += toStr(sum % 10);
}
if (llevo) ans += toStr(llevo);
reverse(ans.begin(), ans.end());
return ans;
}
.............................................................................
8.8. Largest Rectangle in a Histogram
Encuentra el ´area rectangular m´as grande posible en un histograma, donde
el rect´angulo es determinado por un n´umero de barras continuas. Se asume que
todas las barras tienen el mismo ancho de 1 unidad.
Complejidad: O(n) donde nes la cantidad de barras en el histograma.
const int MAXN = 100005;
typedef long long ll;
int n;
ll h[MAXN];
stack <int> s;
/* DO NOT call this. Call largest_rectangle */
ll
calc(int i) {
int smallest = s.top(); s.pop();
ll cur = h[smallest] * (s.empty() ? i : i - s.top() - 1);
return cur;
}
/* h[i] = height of the bar i.
n = total number of bars in the histogram.
s = an empty stack. */
ll
largest_rectangle() {
ll ans = 0LL;
int i = 0;
while (i < n) {
if (s.empty() || h[s.top()] <= h[i]) s.push(i++);
else ans = max(ans, calc(i));
}
while (!s.empty()) ans = max(ans, calc(i));
return ans;
}
.............................................................................
9. Struct
Las estructuras en C++ son muy ´utiles a la hora de hacer alg´un tipo de dato
muy espec´ıfico o usar funciones de comparaci´on personalizadas
9.1. Funci´on de comparaci´on
En este caso tenemos una funci´on de comparaci´on que involucra los dos atri-
butos xyyde la estructura dato
struct dato {
//x tiene m´as prioridad que y, (Ver abajo la funcion <)
int x, y;
dato (int X, int Y) : x(X), y(Y) {}
//Funci´on que reemplaza el operador < entre dos ’dato’
//retorna true si this es menor, false de lo contrario.
bool operator < (const dato &otro) const {
if (x < otro.x) return true;
else if (x == otro.x) {
//Como las x son iguales, entro a preguntar por las y
if (y < otro.y) return true;
else return false;
}
else { //x > otro.x
return false;
}
}
};
39

int
main() {
int x, y;
vector <dato> v;
while (cin >> x >> y && x) {
v.push_back(dato(x, y));
}
sort(v.begin(), v.end());
cout << "Ordenados: " << endl;
for (int i = 0; i < v.size(); i++) {
cout << v[i].x << " " << v[i].y << endl;
}
return 0;
}
.............................................................................
9.2. Radix sort
Complejidad: O(w×n) donde nes la cantidad de elementos del arreglo y w
la longitud del mayor n´umero.
int getMax(int arr[], int n) {
int max = arr[0];
for (int i = 1; i < n; i++)
if (arr[i] > max) max = arr[i];
return max;
}
/*
* count sort of arr[]
*/
void countSort(int arr[], int n, int exp) {
int output[n];
int i, count[10] = {0};
for (i = 0; i < n; i++) count[(arr[i] / exp) % 10]++;
for (i = 1; i < 10; i++) count[i] += count[i - 1];
for (i = n - 1; i >= 0; i--) {
output[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
for (i = 0; i < n; i++) arr[i] = output[i];
}
/*
* sorts arr[] of size n using Radix Sort
*/
void radixsort(int arr[], int n) {
int m = getMax(arr, n);
for (int exp = 1; m / exp > 0; exp *= 10)
countSort(arr, n, exp);
}
.............................................................................
10. C++
10.1. Strings con arreglo de caracteres
Para lograr una implementaci´on eficiente, se pueden trabajar los strings como
arreglo de caracteres, es decir, como en C, existen varias funciones que pueden
ser ´utiles, NOTA: no todas las funciones se encuentran en el ejemplo.
#include <iostream>
#include <stdio.h>
#include <string>
using namespace std;
const int MAXN = 1005;
char s[MAXN];
string cs;
int
main() {
while (true) {
scanf("%s", s); //Only a token stored in char array
cout << "scanf: |" << s << "|" << endl;
gets(s); //Until end of line or EOF stored in char array
cout << "gets: |" << s << "|" << endl;
getline(cin, cs); //Until end of line or EOF stored in string
cout << "getline: |" << cs << "|" << endl;
// ---------------------------------------
for (int i = 0; i < strlen(s); i++) cout << s[i] << " - ";
cout << endl;
char dest[MAXN];
strncpy(dest, s, 5); //Dest, source, length (size_t)
dest[5] = ’\0’; //ALWAYS ADD NULL CHARACTER AT END POSITION
40

cout << "cpyDest: |" << dest << "|" << endl;
strncat(dest, s, 3); //Dest, source, length (size_t)
cout << "catDest: |" << dest << "|" << endl;
dest[4] = ’\0’; //Cut string, result length 5
if (strncmp(s, dest, 5) == 0) cout << "equals 5" << endl;
if (strncmp(s, dest, 4) == 0) cout << "equals 4" << endl;
}
return 0;
}
.............................................................................
10.2. miselanea
Las siguientes dos lineas son dos artima˜nas para cuando queremos optimizar
tiempos en ejecucion. mas informacion sobre que hacen las siguientes lineas
en https://stackoverflow.com/questions/31162367/significance-of-ios-basesync-
with-stdiofalse-cin-tienull
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(NULL)
/*
programa ...
*/
}
.............................................................................
11. Java
11.1. File Reader
Forma de leer e imprimir en un archivo
import java.io.*;
import java.util.*;
class Reader
{
public static void main(String[] args) throws FileNotFoundException
{
System.setIn(new FileInputStream("in.in"));
System.setOut(new PrintStream("out.out"));
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
System.out.println(n);
}
}
.............................................................................
11.2. Base converter
Dado en un numero en una base convertir ese numero a otra base, el siguiente
ejemplo convierte los numeros del 1 al 300 dada una base b, leida desde un
archivo
import java.io.*;
import java.util.StringTokenizer;
class palsquare
{
public static void main(String[] args) throws IOException
{
BufferedReader f =
new BufferedReader(new FileReader("palsquare.in"));
PrintWriter out =
new PrintWriter
(new BufferedWriter(new FileWriter("palsquare.out")));
StringTokenizer st =
new StringTokenizer(f.readLine());
int base = Integer.parseInt(st.nextToken());
for(int i = 1; i <= 300; ++i)
{
//Integer.toString
//(Integer.parseInt(number, base1), base2);
41

String numBaseChanger =
Integer.toString
(Integer.parseInt
(Integer.toString(i),10),base);
out.println(numBaseChanger.toUpperCase());
}
out.close();
}
}
.............................................................................
12. Varios
42