Manual
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 134 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Introduction
- The physical equations of Fluid Dynamics
- The building blocks of the Finite Element Method
- Solving the Stokes equations with the FEM
- Solving the elastic equations with the FEM
- Additional techniques
- Picard and Newton
- The SUPG formulation for the energy equation
- Tracking materials and/or interfaces
- Dealing with a free surface
- Convergence criterion for nonlinear iterations
- Static condensation
- The method of manufactured solutions
- Assigning values to quadrature points
- Matrix (Sparse) storage
- Mesh generation
- Visco-Plasticity
- Pressure smoothing
- Pressure scaling
- Pressure normalisation
- The choice of solvers
- The GMRES approach
- The consistent boundary flux (CBF)
- The value of the timestep
- mappings
- Exporting data to vtk format
- List of tutorials
- fieldstone_01: simple analytical solution
- fieldstone_02: Stokes sphere
- fieldstone_03: Convection in a 2D box
- fieldstone_04: The lid driven cavity
- fieldstone_05: SolCx benchmark
- fieldstone_06: SolKz benchmark
- fieldstone_07: SolVi benchmark
- fieldstone_08: the indentor benchmark
- fieldstone_09: the annulus benchmark
- fieldstone_10: Stokes sphere (3D) - penalty
- fieldstone_11: stokes sphere (3D) - mixed formulation
- fieldstone_12: consistent pressure recovery
- fieldstone_13: the Particle in Cell technique (1) - the effect of averaging
- fieldstone_f14: solving the full saddle point problem
- fieldstone_f15: saddle point problem with Schur complement approach - benchmark
- fieldstone_f16: saddle point problem with Schur complement approach - Stokes sphere
- fieldstone_17: solving the full saddle point problem in 3D
- fieldstone_18: solving the full saddle point problem with Q2Q1 elements
- fieldstone_19: solving the full saddle point problem with Q3Q2 elements
- fieldstone_20: the Busse benchmark
- fieldstone_21: The non-conforming Q1 P0 element
- fieldstone_22: The stabilised Q1 Q1 element
- fieldstone_23: compressible flow (1) - analytical benchmark
- fieldstone_24: compressible flow (2) - convection box
- fieldstone_25: Rayleigh-Taylor instability (1) - instantaneous
- fieldstone_26: Slab detachment benchmark (1) - instantaneous
- fieldstone: Gravity: buried sphere
The Finite Element Method in Geodynamics
C. Thieulot
January 21, 2019
Contents
1 Introduction 4
1.1 Philosophy ............................................ 4
1.2 Acknowledgments......................................... 4
1.3 Essentialliterature........................................ 4
1.4 Installation ............................................ 4
2 The physical equations of Fluid Dynamics 5
2.1 The heat transport equation - energy conservation equation . . . . . . . . . . . . . . . . . 5
2.2 The momentum conservation equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.3 The mass conservation equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.4 The equations in ASPECT manual . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.5 the Boussinesq approximation: an Incompressible flow . . . . . . . . . . . . . . . . . . . . 8
3 The building blocks of the Finite Element Method 9
3.1 Numericalintegration ...................................... 9
3.1.1 in1D-theory ...................................... 9
3.1.2 in1D-examples..................................... 11
3.1.3 in2D/3D-theory .................................... 12
3.2 Themesh ............................................. 12
3.3 AbitofFEterminology..................................... 12
3.4 Elements and basis functions in 1D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.4.1 Linear basis functions (Q1) ............................... 13
3.4.2 Quadratic basis functions (Q2) ............................. 13
3.4.3 Cubic basis functions (Q3) ............................... 14
3.5 Elements and basis functions in 2D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
3.5.1 Bilinear basis functions in 2D (Q1)........................... 17
3.5.2 Biquadratic basis functions in 2D (Q2)......................... 19
3.5.3 Bicubic basis functions in 2D (Q3) ........................... 20
4 Solving the Stokes equations with the FEM 22
4.1 strongandweakforms...................................... 22
4.2 Thepenaltyapproach ...................................... 22
4.3 ThemixedFEM ......................................... 25
5 Solving the elastic equations with the FEM 26
6 Additional techniques 27
6.1 PicardandNewton........................................ 27
6.2 The SUPG formulation for the energy equation . . . . . . . . . . . . . . . . . . . . . . . . 27
6.3 Tracking materials and/or interfaces . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
6.4 Dealingwithafreesurface.................................... 27
6.5 Convergence criterion for nonlinear iterations . . . . . . . . . . . . . . . . . . . . . . . . . 27
6.6 Staticcondensation........................................ 27
1

6.7 The method of manufactured solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
6.8 Assigning values to quadrature points . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
6.9 Matrix(Sparse)storage ..................................... 32
6.9.1 2D domain - One degree of freedom per node . . . . . . . . . . . . . . . . . . . . . 32
6.9.2 2D domain - Two degrees of freedom per node . . . . . . . . . . . . . . . . . . . . 33
6.9.3 infieldstone........................................ 34
6.10Meshgeneration ......................................... 35
6.11Visco-Plasticity.......................................... 38
6.11.1 Tensorinvariants..................................... 38
6.11.2 Scalarviscoplasticity................................... 39
6.11.3 about the yield stress value Y.............................. 39
6.12Pressuresmoothing........................................ 40
6.13Pressurescaling.......................................... 42
6.14Pressurenormalisation...................................... 43
6.15Thechoiceofsolvers....................................... 44
6.15.1 The Schur complement approach . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
6.16TheGMRESapproach...................................... 48
6.17 The consistent boundary flux (CBF) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
6.18Thevalueofthetimestep .................................... 50
6.19mappings ............................................. 51
6.20 Exporting data to vtk format . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
7 List of tutorials 55
8fieldstone 01: simple analytical solution 56
9fieldstone 02: Stokes sphere 59
10 fieldstone 03: Convection in a 2D box 60
11 fieldstone 04: The lid driven cavity 63
11.1 the lid driven cavity problem (ldc=0) ............................. 63
11.2 the lid driven cavity problem - regularisation I (ldc=1).................... 63
11.3 the lid driven cavity problem - regularisation II (ldc=2) ................... 63
12 fieldstone 05: SolCx benchmark 65
13 fieldstone 06: SolKz benchmark 67
14 fieldstone 07: SolVi benchmark 68
15 fieldstone 08: the indentor benchmark 70
16 fieldstone 09: the annulus benchmark 72
17 fieldstone 10: Stokes sphere (3D) - penalty 74
18 fieldstone 11: stokes sphere (3D) - mixed formulation 75
19 fieldstone 12: consistent pressure recovery 76
20 fieldstone 13: the Particle in Cell technique (1) - the effect of averaging 78
21 fieldstone f14: solving the full saddle point problem 82
22 fieldstone f15: saddle point problem with Schur complement approach - benchmark
84
2

23 fieldstone f16: saddle point problem with Schur complement approach - Stokes
sphere 87
24 fieldstone 17: solving the full saddle point problem in 3D 89
24.0.1 Constantviscosity .................................... 91
24.0.2 Variableviscosity..................................... 92
25 fieldstone 18: solving the full saddle point problem with Q2×Q1elements 94
26 fieldstone 19: solving the full saddle point problem with Q3×Q2elements 96
27 fieldstone 20: the Busse benchmark 98
28 fieldstone 21: The non-conforming Q1×P0element 100
29 fieldstone 22: The stabilised Q1×Q1element 101
30 fieldstone 23: compressible flow (1) - analytical benchmark 102
31 fieldstone 24: compressible flow (2) - convection box 105
31.1Thephysics ............................................ 105
31.2Thenumerics ........................................... 105
31.3Theexperimentalsetup ..................................... 107
31.4Scaling............................................... 107
31.5Conservationofenergy1..................................... 108
31.5.1 under BA and EBA approximations . . . . . . . . . . . . . . . . . . . . . . . . . . 108
31.5.2 under no approximation at all . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
31.6Conservationofenergy2..................................... 109
31.7 The problem of the onset of convection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
31.8 results - BA - Ra = 104..................................... 112
31.9 results - BA - Ra = 105..................................... 114
31.10results - BA - Ra = 106..................................... 115
31.11results - EBA - Ra = 104.................................... 116
31.12results - EBA - Ra = 105.................................... 118
31.13Onsetofconvection........................................ 119
32 fieldstone 25: Rayleigh-Taylor instability (1) - instantaneous 121
33 fieldstone 26: Slab detachment benchmark (1) - instantaneous 123
34 fieldstone: Gravity: buried sphere 125
3

WARNING: this is work in progress
1 Introduction
1.1 Philosophy
This document was writing with my students in mind, i.e. 3rd and 4th year Geology/Geophysics stu-
dents at Utrecht University. I have chosen to use jargon as little as possible unless it is a term that is
commonly found in the geodynamics literature (methods paper as well as application papers). There is
no mathematical proof of any theorem or statement I make. These are to be found in generic Numerical
Analysic, Finite Element and Linear Algebra books.
The codes I provide here are by no means optimised as I value code readability over code efficiency. I
have also chosen to avoid resorting to multiple code files or even functions to favour a sequential reading of
the codes. These codes are not designed to form the basis of a real life application: Existing open source
highly optimised codes shoud be preferred, such as ASPECT, CITCOM, LAMEM, PTATIN, PYLITH,
...
All kinds of feedback is welcome on the text (grammar, typos, ...) or on the code(s). You will have
my eternal gratitude if you wish to contribute an example, a benchmark, a cookbook.
All the python scripts and this document are freely available at
https://github.com/cedrict/fieldstone
1.2 Acknowledgments
I have benefitted from many discussions, lectures, tutorials, coffee machine discussions, debugging ses-
sions, conference poster sessions, etc ... over the years. I wish to name these instrumental people in
particular and in alphabetic order: Wolfgang Bangerth, Jean Braun, Philippe Fullsack, Menno Fraters,
Anne Glerum, Timo Heister, Robert Myhill, John Naliboff, Lukas van de Wiel, Arie van den Berg, and
the whole ASPECT family/team.
I wish to acknowledge many BSc and MSc students for their questions and feedback. and wish to
mention Job Mos in particular who wrote the very first version of fieldstone as part of his MSc thesis.
and Tom Weir for his contributions to the compressible formulations.
1.3 Essential literature
1.4 Installation
python3.6 -m pip install --user numpy scipy matplotlib
4

2 The physical equations of Fluid Dynamics
Symbol meaning unit
tTime s
x, y, z Cartesian coordinates m
vvelocity vector m·s−1
ρmass density kg/m3
ηdynamic viscosity Pa·s
λpenalty parameter Pa·s
Ttemperature K
∇gradient operator m−1
∇·divergence operator m−1
ppressure Pa
˙
ε(v) strain rate tensor s−1
αthermal expansion coefficient K−1
kthermal conductivity W/(m ·K)
CpHeat capacity J/K
Hintrinsic specific heat production W/kg
βTisothermal compressibility Pa−1
τdeviatoric stress tensor Pa
σfull stress tensor Pa
2.1 The heat transport equation - energy conservation equation
Let us start from the heat transport equation as shown in Schubert, Turcotte and Olson [75]:
ρCp
DT
Dt −αT Dp
Dt =∇·k∇T+Φ+ρH
with D/Dt being the total derivatives so that
DT
Dt =∂T
∂t +v·∇TDp
Dt =∂p
∂t +v·∇p
Solving for temperature, this equation is often rewritten as follows:
ρCp
DT
Dt −∇·k∇T=αT Dp
Dt +Φ+ρH
A note on the shear heating term Φ: In many publications, Φ is given by Φ = τij ∂jui=τ:∇v.
Φ = τij ∂jui
= 2η˙εd
ij ∂jui
= 2η1
2˙εd
ij ∂jui+ ˙εd
ji∂iuj
= 2η1
2˙εd
ij ∂jui+ ˙εd
ij ∂iuj
= 2η˙εd
ij
1
2(∂jui+∂iuj)
= 2η˙εd
ij ˙εij
= 2η˙
εd:˙
ε
= 2η˙
εd:˙
εd+1
3(∇·v)1
= 2η˙
εd:˙
εd+ 2η˙
εd:1(∇·v)
= 2η˙
εd:˙
εd(1)
Finally
Φ = τ:∇v= 2η˙
εd:˙
εd= 2η( ˙εd
xx)2+ ( ˙εd
yy)2+ 2( ˙εd
xy)2
5

2.2 The momentum conservation equations
Because the Prandlt number is virtually zero in Earth science applications the Navier Stokes equations
reduce to the Stokes equation:
∇·σ+ρg= 0
Since
σ=−p1+τ
it also writes
−∇p+∇·τ+ρg= 0
Using the relationship τ= 2η˙
εdwe arrive at
−∇p+∇·(2η˙
εd) + ρg= 0
2.3 The mass conservation equations
The mass conservation equation is given by
Dρ
Dt +ρ∇·v= 0
or,
∂ρ
∂t +∇·(ρv)=0
In the case of an incompressible flow, then ∂ρ/∂t = 0 and ∇ρ= 0, i.e. Dρ/Dt = 0 and the remaining
equation is simply:
∇·v= 0
2.4 The equations in ASPECT manual
The following is lifted off the ASPECT manual. We focus on the system of equations in a d= 2- or
d= 3-dimensional domain Ω that describes the motion of a highly viscous fluid driven by differences in
the gravitational force due to a density that depends on the temperature. In the following, we largely
follow the exposition of this material in Schubert, Turcotte and Olson [75].
Specifically, we consider the following set of equations for velocity u, pressure pand temperature T:
−∇ · 2η˙ε(v)−1
3(∇ · v)1+∇p=ρgin Ω,(2)
∇ · (ρv) = 0 in Ω,(3)
ρCp∂T
∂t +v· ∇T−∇·k∇T=ρH
+ 2η˙ε(v)−1
3(∇ · v)1:˙ε(v)−1
3(∇ · v)1(4)
+αT (v· ∇p)
in Ω,
where ˙
ε(u) = 1
2(∇u+∇uT) is the symmetric gradient of the velocity (often called the strain rate).
In this set of equations, (104) and (105) represent the compressible Stokes equations in which v=
v(x, t) is the velocity field and p=p(x, t) the pressure field. Both fields depend on space xand time
t. Fluid flow is driven by the gravity force that acts on the fluid and that is proportional to both the
density of the fluid and the strength of the gravitational pull.
Coupled to this Stokes system is equation (106) for the temperature field T=T(x, t) that contains
heat conduction terms as well as advection with the flow velocity v. The right hand side terms of this
equation correspond to
6

•internal heat production for example due to radioactive decay;
•friction (shear) heating;
•adiabatic compression of material;
In order to arrive at the set of equations that ASPECT solves, we need to
•neglect the ∂p/∂t.WHY?
•neglect the ∂ρ/∂t .WHY?
from equations above.
—————————————-
Also, their definition of the shear heating term Φ is:
Φ = kB(∇·v)2+ 2η˙
εd:˙
εd
For many fluids the bulk viscosity kBis very small and is often taken to be zero, an assumption known
as the Stokes assumption: kB=λ+ 2η/3 = 0. Note that ηis the dynamic viscosity and λthe second
viscosity. Also,
τ= 2η˙
ε+λ(∇·v)1
but since kB=λ+ 2η/3 = 0, then λ=−2η/3 so
τ= 2η˙
ε−2
3η(∇·v)1= 2η˙
εd
7

2.5 the Boussinesq approximation: an Incompressible flow
[from aspect manual] The Boussinesq approximation assumes that the density can be considered constant
in all occurrences in the equations with the exception of the buoyancy term on the right hand side of
(104). The primary result of this assumption is that the continuity equation (105) will now read
∇·v= 0
This implies that the strain rate tensor is deviatoric. Under the Boussinesq approximation, the equations
are much simplified:
−∇ · [2η˙
ε(v)] + ∇p=ρgin Ω,(5)
∇ · (ρv) = 0 in Ω,(6)
ρ0Cp∂T
∂t +v· ∇T−∇·k∇T=ρH in Ω (7)
Note that all terms on the rhs of the temperature equations have disappeared, with the exception of the
source term.
8
3 The building blocks of the Finite Element Method
3.1 Numerical integration
As we will see later, using the Finite Element method to solve problems involves computing integrals
which are more often than not too complex to be computed analytically/exactly. We will then need to
compute them numerically.
[wiki] In essence, the basic problem in numerical integration is to compute an approximate solution
to a definite integral Zb
a
f(x)dx
to a given degree of accuracy. This problem has been widely studied [?] and we know that if f(x) is a
smooth function, and the domain of integration is bounded, there are many methods for approximating
the integral to the desired precision.
There are several reasons for carrying out numerical integration.
•The integrand f(x) may be known only at certain points, such as obtained by sampling. Some
embedded systems and other computer applications may need numerical integration for this reason.
•A formula for the integrand may be known, but it may be difficult or impossible to find an an-
tiderivative that is an elementary function. An example of such an integrand is f(x) = exp(−x2),
the antiderivative of which (the error function, times a constant) cannot be written in elementary
form.
•It may be possible to find an antiderivative symbolically, but it may be easier to compute a numerical
approximation than to compute the antiderivative. That may be the case if the antiderivative is
given as an infinite series or product, or if its evaluation requires a special function that is not
available.
3.1.1 in 1D - theory
The simplest method of this type is to let the interpolating function be a constant function (a polynomial
of degree zero) that passes through the point ((a+b)/2, f((a+b)/2)).
This is called the midpoint rule or rectangle rule.
Zb
a
f(x)dx '(b−a)f(a+b
2)
insert here figure
The interpolating function may be a straight line (an affine function, i.e. a polynomial of degree 1)
passing through the points (a, f(a)) and (b, f(b)).
This is called the trapezoidal rule.
Zb
a
f(x)dx '(b−a)f(a) + f(b)
2
insert here figure
For either one of these rules, we can make a more accurate approximation by breaking up the interval
[a, b] into some number n of subintervals, computing an approximation for each subinterval, then adding
up all the results. This is called a composite rule, extended rule, or iterated rule. For example, the
composite trapezoidal rule can be stated as
Zb
a
f(x)dx 'b−a
n f(a)
2+
n−1
X
k=1
f(a+kb−a
n) + f(b)
2!
where the subintervals have the form [kh, (k+ 1)h], with h= (b−a)/n and k= 0,1,2, . . . , n −1.
9
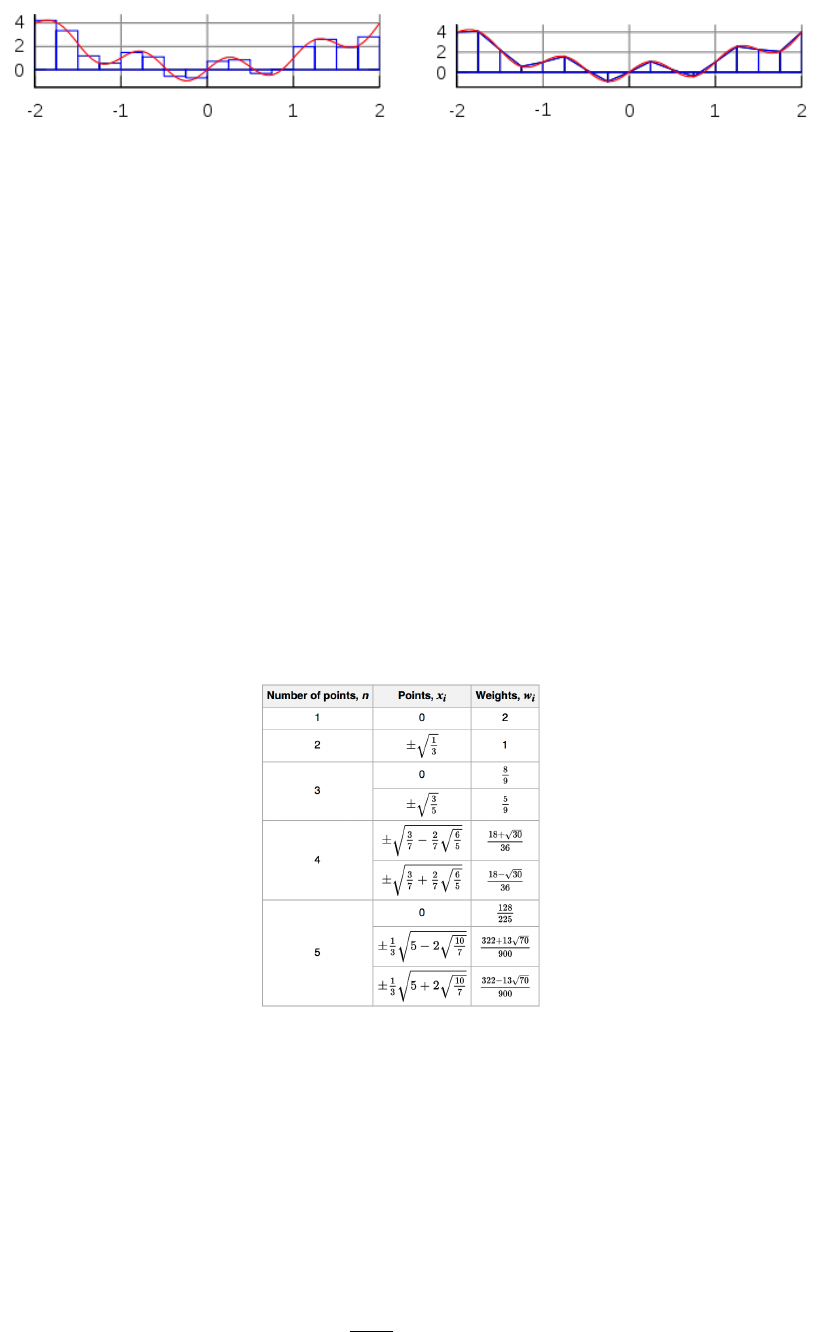
a) b)
The interval [−2,2] is broken into 16 sub-intervals. The blue lines correspond to the approximation of
the red curve by means of a) the midpoint rule, b) the trapezoidal rule.
There are several algorithms for numerical integration (also commonly called ’numerical quadrature’,
or simply ’quadrature’) . Interpolation with polynomials evaluated at equally spaced points in [a, b] yields
the NewtonCotes formulas, of which the rectangle rule and the trapezoidal rule are examples. If we allow
the intervals between interpolation points to vary, we find another group of quadrature formulas, such
as the Gauss(ian) quadrature formulas. A Gaussian quadrature rule is typically more accurate than a
NewtonCotes rule, which requires the same number of function evaluations, if the integrand is smooth
(i.e., if it is sufficiently differentiable).
An n−point Gaussian quadrature rule, named after Carl Friedrich Gauss, is a quadrature rule con-
structed to yield an exact result for polynomials of degree 2n−1 or less by a suitable choice of the points
xiand weights wifor i= 1, . . . , n.
The domain of integration for such a rule is conventionally taken as [−1,1], so the rule is stated as
Z+1
−1
f(x)dx =
n
X
iq=1
wiqf(xiq)
In this formula the xiqcoordinate is the i-th root of the Legendre polynomial Pn(x).
It is important to note that a Gaussian quadrature will only produce good results if the function f(x)
is well approximated by a polynomial function within the range [−1,1]. As a consequence, the method
is not, for example, suitable for functions with singularities.
Gauss-Legendre points and their weights.
As shown in the above table, it can be shown that the weight values must fulfill the following condition:
X
iq
wiq= 2 (8)
and it is worth noting that all quadrature point coordinates are symmetrical around the origin.
Since most quadrature formula are only valid on a specific interval, we now must address the problem
of their use outside of such intervals. The solution turns out to be quite simple: one must carry out a
change of variables from the interval [a, b] to [−1,1].
We then consider the reduced coordinate r∈[−1,1] such that
r=2
b−a(x−a)−1
10
This relationship can be reversed such that when ris known, its equivalent coordinate x∈[a, b] can be
computed:
x=b−a
2(1 + r) + a
From this it follows that
dx =b−a
2dr
and then Zb
a
f(x)dx =b−a
2Z+1
−1
f(r)dr 'b−a
2
n
X
iq=1
wiqf(riq)
3.1.2 in 1D - examples
example 1 Since we know how to carry out any required change of variables, we choose for simplicity
a=−1, b= +1. Let us take for example f(x) = π. Then we can compute the integral of this function
over the interval [a, b] exactly:
I=Z+1
−1
f(x)dx =πZ+1
−1
dx = 2π
We can now use a Gauss-Legendre formula to compute this same integral:
Igq =Z+1
−1
f(x)dx =
nq
X
iq=1
wiqf(xiq) =
nq
X
iq=1
wiqπ=π
nq
X
iq=1
wiq
| {z }
=2
= 2π
where we have used the property of the weight values of Eq.(8). Since the actual number of points was
never specified, this result is valid for all quadrature rules.
example 2 Let us now take f(x) = mx +pand repeat the same exercise:
I=Z+1
−1
f(x)dx =Z+1
−1
(mx +p)dx = [1
2mx2+px]+1
−1= 2p
Igq =Z+1
−1
f(x)dx=
nq
X
iq=1
wiqf(xiq)=
nq
X
iq=1
wiq(mxiq+p)= m
nq
X
iq=1
wiqxiq
| {z }
=0
+p
nq
X
iq=1
wiq
| {z }
=2
= 2p
since the quadrature points are symmetric w.r.t. to zero on the x-axis. Once again the quadrature is able
to compute the exact value of this integral: this makes sense since an n-point rule exactly integrates a
2n−1 order polynomial such that a 1 point quadrature exactly integrates a first order polynomial like
the one above.
example 3 Let us now take f(x) = x2. We have
I=Z+1
−1
f(x)dx =Z+1
−1
x2dx = [1
3x3]+1
−1=2
3
and
Igq =Z+1
−1
f(x)dx=
nq
X
iq=1
wiqf(xiq)=
nq
X
iq=1
wiqx2
iq
•nq= 1: x(1)
iq = 0, wiq= 2. Igq = 0
•nq= 2: x(1)
q=−1/√3, x(2)
q= 1/√3, w(1)
q=w(2)
q= 1. Igq =2
3
•It also works ∀nq>2 !
11
3.1.3 in 2D/3D - theory
Let us now turn to a two-dimensional integral of the form
I=Z+1
−1Z+1
−1
f(x, y)dxdy
The equivalent Gaussian quadrature writes:
Igq '
nq
X
iq=1
nq
X
jq
f(xiq, yjq)wiqwjq
3.2 The mesh
3.3 A bit of FE terminology
We introduce here some terminology for efficient element descriptions [38]:
•For triangles/tetrahedra, the designation Pm×Pnmeans that each component of the velocity is
approximated by continuous piecewise complete Polynomials of degree mand pressure by continuous
piecewise complete Polynomials of degree n. For example P2×P1means
u∼a1+a2x+a3y+a4xy +a5x2+a6y2
with similar approximations for v, and
p∼b1+b2x+b3y
Both velocity and pressure are continuous across element boundaries, and each triangular element
contains 6 velocity nodes and three pressure nodes.
•For the same families, Pm×P−nis as above, except that pressure is approximated via piecewise
discontinuous polynomials of degree n. For instance, P2×P−1is the same as P2P1except that
pressure is now an independent linear function in each element and therefore discontinuous at
element boundaries.
•For quadrilaterals/hexahedra, the designation Qm×Qnmeans that each component of the velocity
is approximated by a continuous piecewise polynomial of degree min each direction on the quadri-
lateral and likewise for pressure, except that the polynomial is of degree n. For instance, Q2×Q1
means
u∼a1+a2x+a3y+a4xy +a5x2+a6y2+a7x2y+a8xy2+a9x2y2
and
p∼b1+b2x+b3y+b4xy
•For these same families, Qm×Q−nis as above, except that the pressure approximation is not
continuous at element boundaries.
•Again for the same families, Qm×P−nindicates the same velocity approximation with a pressure
approximation that is a discontinuous complete piecewise polynomial of degree n(not of degree n
in each direction !)
•The designation P+
mor Q+
mmeans that some sort of bubble function was added to the polynomial
approximation for the velocity. You may also find the term ’enriched element’ in the literature.
•Finally, for n= 0, we have piecewise-constant pressure, and we omit the minus sign for simplicity.
Another point which needs to be clarified is the use of so-called ’conforming elements’ (or ’non-
conforming elements’). Following again [38], conforming velocity elements are those for which the
basis functions for a subset of H1for the continuous problem (the first derivatives and their squares are
integrable in Ω). For instance, the rotated Q1×P0element of Rannacher and Turek (see section ??) is
such that the velocity is discontinous across element edges, so that the derivative does not exist there.
Another typical example of non-conforming element is the Crouzeix-Raviart element [19].
12
3.4 Elements and basis functions in 1D
3.4.1 Linear basis functions (Q1)
Let f(r) be a C1function on the interval [−1 : 1] with f(−1) = f1and f(1) = f2.
Let us assume that the function f(r) is to be approximated on [−1,1] by the first order polynomial
f(r) = a+br (9)
Then it must fulfill
f(r=−1) = a−b=f1
f(r= +1) = a+b=f2
This leads to
a=1
2(f1+f2)b=1
2(−f1+f2)
and then replacing a, b in Eq. (9) by the above values on gets
f(r) = 1
2(1 −r)f1+1
2(1 + r)f2
or
f(r) =
2
X
i=1
Ni(r)f1
with
N1(r) = 1
2(1 −r)
N2(r) = 1
2(1 + r) (10)
3.4.2 Quadratic basis functions (Q2)
Let f(r) be a C1function on the interval [−1 : 1] with f(−1) = f1,f(0) = f2and f(1) = f3.
Let us assume that the function f(r) is to be approximated on [−1,1] by the second order polynomial
f(r) = a+br +cr2(11)
Then it must fulfill
f(r=−1) = a−b+c=f1
f(r= 0) = a=f2
f(r= +1) = a+b+c=f3
13

This leads to
a=f2b=1
2(−f1 + f3) c=1
2(f1+f3−2f2)
and then replacing a, b, c in Eq. (11) by the above values on gets
f(r) = 1
2r(r−1)f1+ (1 −r2)f2+1
2r(r+ 1)f3
or,
f(r) =
3
X
i=1
Ni(r)fi
with
N1(r) = 1
2r(r−1)
N2(r) = (1 −r2)
N3(r) = 1
2r(r+ 1) (12)
3.4.3 Cubic basis functions (Q3)
The 1D basis polynomial is given by
f(r) = a+br +cr2+dr3
with the nodes at position -1,-1/3, +1/3 and +1.
f(−1) = a−b+c−d=f1
f(−1/3) = a−b
3+c
9−d
27 =f2
f(+1/3) = a−b
3+c
9−d
27 =f3
f(+1) = a+b+c+d=f4
Adding the first and fourth equation and the second and third, one arrives at
f1+f4= 2a+ 2c f2+f3= 2a+2c
9
and finally:
a=1
16 (−f1+ 9f2+ 9f3−f4)
c=9
16 (f1−f2−f3+f4)
Combining the original 4 equations in a different way yields
2b+ 2d=f4−f1
2b
3+2d
27 =f3−f2
so that
b=1
16 (f1−27f2+ 27f3−f4)
d=9
16 (−f1+ 3f2−3f3+f4)
Finally,
14

f(r) = a+b+cr2+dr3
=1
16(−1 + r+ 9r2−9r3)f1
+1
16(9 −27r−9r2+ 27r3)f2
+1
16(9 + 27r−9r2−27r3)f3
+1
16(−1−r+ 9r2+ 9r3)f4
=
4
X
i=1
Ni(r)fi
where
N1=1
16(−1 + r+ 9r2−9r3)
N2=1
16(9 −27r−9r2+ 27r3)
N3=1
16(9 + 27r−9r2−27r3)
N4=1
16(−1−r+ 9r2+ 9r3)
Verification:
•Let us assume f(r) = C, then
ˆ
f(r) = XNi(r)fi=X
i
NiC=CX
i
Ni=C
so that a constant function is exactly reproduced, as expected.
•Let us assume f(r) = r, then f1=−1, f2=−1/3, f3= 1/3 and f4= +1. We then have
ˆ
f(r) = XNi(r)fi
=−N1(r)−1
3N2(r) + 1
3N3(r) + N4(r)
= [−(−1 + r+ 9r2−9r3)
−1
3(9 −27r−9r2−27r3)
+1
3(9 + 27r−9r2+ 27r3)
+(−1−r+ 9r2+ 9r3)]/16
= [−r+ 9r+ 9r−r]/16 + ...0...
=r(13)
The basis functions derivative are given by
15
∂N1
∂r =1
16(1 + 18r−27r2)
∂N2
∂r =1
16(−27 −18r+ 81r2)
∂N3
∂r =1
16(+27 −18r−81r2)
∂N4
∂r =1
16(−1 + 18r+ 27r2)
Verification:
•Let us assume f(r) = C, then
∂ˆ
f
∂r =X
i
∂Ni
∂r fi
=CX
i
∂Ni
∂r
=C
16[(1 + 18r−27r2)
+(−27 −18r+ 81r2)
+(+27 −18r−81r2)
+(−1 + 18r+ 27r2)]
= 0
•Let us assume f(r) = r, then f1=−1, f2=−1/3, f3= 1/3 and f4= +1. We then have
∂ˆ
f
∂r =X
i
∂Ni
∂r fi
=1
16[−(1 + 18r−27r2)
−1
3(−27 −18r+ 81r2)
+1
3(+27 −18r−81r2)
+(−1 + 18r+ 27r2)]
=1
16[−2 + 18 + 54r2−54r2]
= 1
3.5 Elements and basis functions in 2D
Let us for a moment consider a single quadrilateral element in the xy-plane, as shown on the following
figure:
16
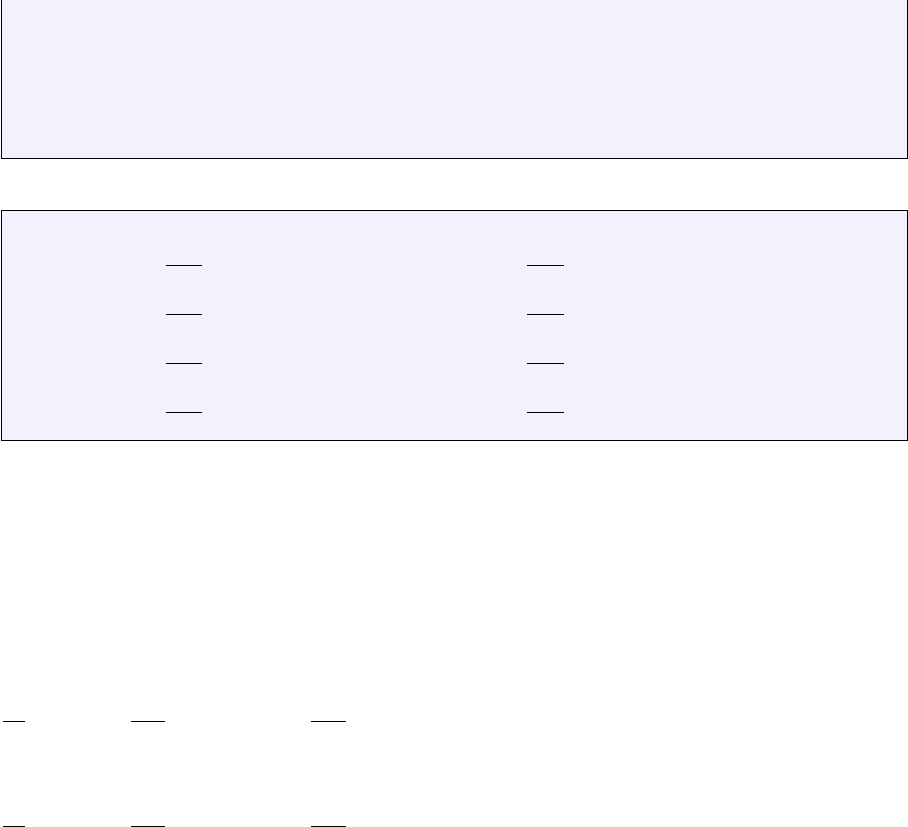
Let us assume that we know the values of a given field uat the vertices. For a given point Minside
the element in the plane, what is the value of the field uat this point? It makes sense to postulate that
uM=u(xM, yM) will be given by
uM=φ(u1, u2, u3, u4, xM, yM)
where φis a function to be determined. Although φis not unique, we can decide to express the value
uMas a weighed sum of the values at the vertices ui. One option could be to assign all four vertices the
same weight, say 1/4 so that uM= (u1+u2+u3+u4)/4, i.e. uMis simply given by the arithmetic mean
of the vertices values. This approach suffers from a major drawback as it does not use the location of
point Minside the element. For instance, when (xM, yM)→(x2, y2) we expect uM→u2.
In light of this, we could now assume that the weights would depend on the position of Min a
continuous fashion:
u(xM, yM) =
4
X
i=1
Ni(xM, yM)ui
where the Niare continous (”well behaved”) functions which have the property:
Ni(xj, yj) = δij
or, in other words:
N3(x1, y1) = 0 (14)
N3(x2, y2) = 0 (15)
N3(x3, y3) = 1 (16)
N3(x4, y4) = 0 (17)
The functions Niare commonly called basis functions.
Omitting the Msubscripts for any point inside the element, the velocity components uand vare
given by:
ˆu(x, y) =
4
X
i=1
Ni(x, y)ui(18)
ˆv(x, y) =
4
X
i=1
Ni(x, y)vi(19)
Rather interestingly, one can now easily compute velocity gradients (and therefore the strain rate tensor)
since we have assumed the basis functions to be ”well behaved” (in this case differentiable):
˙xx(x, y) = ∂u
∂x =
4
X
i=1
∂Ni
∂x ui(20)
˙yy(x, y) = ∂v
∂y =
4
X
i=1
∂Ni
∂y vi(21)
˙xy(x, y) = 1
2
∂u
∂y +1
2
∂v
∂x =1
2
4
X
i=1
∂Ni
∂y ui+1
2
4
X
i=1
∂Ni
∂x vi(22)
How we actually obtain the exact form of the basis functions is explained in the coming section.
3.5.1 Bilinear basis functions in 2D (Q1)
In this section, we place ourselves in the most favorables case, i.e. the element is a square defined by
−1< r < 1, −1< s < 1 in the Cartesian coordinates system (r, s):
17
3===========2
| | (r_0,s_0)=(-1,-1)
| | (r_1,s_1)=(+1,-1)
| | (r_2,s_2)=(+1,+1)
| | (r_3,s_3)=(-1,+1)
| |
0===========1
This element is commonly called the reference element. How we go from the (x, y) coordinate system
to the (r, s) once and vice versa will be dealt later on. For now, the basis functions in the above reference
element and in the reduced coordinates system (r, s) are given by:
N1(r, s)=0.25(1 −r)(1 −s)
N2(r, s)=0.25(1 + r)(1 −s)
N3(r, s)=0.25(1 + r)(1 + s)
N4(r, s)=0.25(1 −r)(1 + s)
The partial derivatives of these functions with respect to rans sautomatically follow:
∂N1
∂r (r, s) = −0.25(1 −s)∂N1
∂s (r, s) = −0.25(1 −r)
∂N2
∂r (r, s) = +0.25(1 −s)∂N2
∂s (r, s) = −0.25(1 + r)
∂N3
∂r (r, s) = +0.25(1 + s)∂N3
∂s (r, s) = +0.25(1 + r)
∂N4
∂r (r, s) = −0.25(1 + s)∂N4
∂s (r, s) = +0.25(1 −r)
Let us go back to Eq.(19). And let us assume that the function v(r, s) = Cso that vi=Cfor
i= 1,2,3,4. It then follows that
ˆv(r, s) =
4
X
i=1
Ni(r, s)vi=C
4
X
i=1
Ni(r, s) = C[N1(r, s) + N2(r, s) + N3(r, s) + N4(r, s)] = C
This is a very important property: if the vfunction used to assign values at the vertices is constant, then
the value of ˆvanywhere in the element is exactly C. If we now turn to the derivatives of vwith respect
to rand s:
∂ˆv
∂r (r, s) =
4
X
i=1
∂Ni
∂r (r, s)vi=C
4
X
i=1
∂Ni
∂r (r, s) = C[−0.25(1 −s)+0.25(1 −s)+0.25(1 + s)−0.25(1 + s)] = 0
∂ˆv
∂s (r, s) =
4
X
i=1
∂Ni
∂s (r, s)vi=C
4
X
i=1
∂Ni
∂s (r, s) = C[−0.25(1 −r)−0.25(1 + r)+0.25(1 + r)+0.25(1 −r)] = 0
We reassuringly find that the derivative of a constant field anywhere in the element is exactly zero.
18
If we now choose v(r, s) = ar +bs with aand btwo constant scalars, we find:
ˆv(r, s) =
4
X
i=1
Ni(r, s)vi(23)
=
4
X
i=1
Ni(r, s)(ari+bsi) (24)
=a
4
X
i=1
Ni(r, s)ri
| {z }
r
+b
4
X
i=1
Ni(r, s)si
| {z }
s
(25)
=a[0.25(1 −r)(1 −s)(−1) + 0.25(1 + r)(1 −s)(+1) + 0.25(1 + r)(1 + s)(+1) + 0.25(1 −r)(1 + s)(−1)]
+b[0.25(1 −r)(1 −s)(−1) + 0.25(1 + r)(1 −s)(−1) + 0.25(1 + r)(1 + s)(+1) + 0.25(1 −r)(1 + s)(+1)]
=a[−0.25(1 −r)(1 −s)+0.25(1 + r)(1 −s)+0.25(1 + r)(1 + s)−0.25(1 −r)(1 + s)]
+b[−0.25(1 −r)(1 −s)−0.25(1 + r)(1 −s)+0.25(1 + r)(1 + s)+0.25(1 −r)(1 + s)]
=ar +bs (26)
verify above eq. This set of bilinear shape functions is therefore capable of exactly representing a bilinear
field. The derivatives are:
∂ˆv
∂r (r, s) =
4
X
i=1
∂Ni
∂r (r, s)vi(27)
=a
4
X
i=1
∂Ni
∂r (r, s)ri+b
4
X
i=1
∂Ni
∂r (r, s)si(28)
=a[−0.25(1 −s)(−1) + 0.25(1 −s)(+1) + 0.25(1 + s)(+1) −0.25(1 + s)(−1)]
+b[−0.25(1 −s)(−1) + 0.25(1 −s)(−1) + 0.25(1 + s)(+1) −0.25(1 + s)(+1)]
=a
4[(1 −s) + (1 −s) + (1 + s) + (1 + s)]
+b
4[(1 −s)−(1 −s) + (1 + s)−(1 + s)]
=a(29)
Here again, we find that the derivative of the bilinear field inside the element is exact: ∂ˆv
∂r =∂v
∂r .
However, following the same methodology as above, one can easily prove that this is no more true
for polynomials of degree strivtly higher than 1. This fact has serious consequences: if the solution to
the problem at hand is for instance a parabola, the Q1shape functions cannot represent the solution
properly, but only by approximating the parabola in each element by a line. As we will see later, Q2
basis functions can remedy this problem by containing themselves quadratic terms.
3.5.2 Biquadratic basis functions in 2D (Q2)
Inside an element the local numbering of the nodes is as follows:
3=====6=====2
| | | (r_0,s_0)=(-1,-1) (r_4,s_4)=( 0,-1)
| | | (r_1,s_1)=(+1,-1) (r_5,s_5)=(+1, 0)
7=====8=====5 (r_2,s_2)=(+1,+1) (r_6,s_6)=( 0,+1)
| | | (r_3,s_3)=(-1,+1) (r_7,s_7)=(-1, 0)
| | | (r_8,s_8)=( 0, 0)
0=====4=====1
The velocity shape functions are then given by:
19
N0(r, s) = 1
2r(r−1)1
2s(s−1)
N1(r, s) = 1
2r(r+ 1)1
2s(s−1)
N2(r, s) = 1
2r(r+ 1)1
2s(s+ 1)
N3(r, s) = 1
2r(r−1)1
2s(s+ 1)
N4(r, s) = (1 −r2)1
2s(s−1)
N5(r, s) = 1
2r(r+ 1)(1 −s2)
N6(r, s) = (1 −r2)1
2s(s+ 1)
N7(r, s) = 1
2r(r−1)(1 −s2)
N8(r, s) = (1 −r2)(1 −s2)
and their derivatives by:
∂N0
∂r =1
2(2r−1)1
2s(s−1) ∂N0
∂s =1
2r(r−1)1
2(2s−1)
∂N1
∂r =1
2(2r+ 1)1
2s(s−1) ∂N1
∂s =1
2r(r+ 1)1
2(2s−1)
∂N2
∂r =1
2(2r+ 1)1
2s(s+ 1) ∂N2
∂s =1
2r(r+ 1)1
2(2s+ 1)
∂N3
∂r =1
2(2r−1)1
2s(s+ 1) ∂N3
∂s =1
2r(r−1)1
2(2s+ 1)
∂N4
∂r = (−2r)1
2s(s−1) ∂N4
∂s = (1 −r2)1
2(2s−1)
∂N5
∂r =1
2(2r+ 1)(1 −s2)∂N5
∂s =1
2r(r+ 1)(−2s)
∂N6
∂r = (−2r)1
2s(s+ 1) ∂N6
∂s = (1 −r2)1
2(2s+ 1)
∂N7
∂r =1
2(2r−1)(1 −s2)∂N7
∂s =1
2r(r−1)(−2s)
∂N8
∂r = (−2r)(1 −s2)∂N8
∂s = (1 −r2)(−2s)
3.5.3 Bicubic basis functions in 2D (Q3)
Inside an element the local numbering of the nodes is as follows:
12===13===14===15 (r,s)_{00}=(-1,-1) (r,s)_{08}=(-1,+1/3)
|| || || || (r,s)_{01}=(-1/3,-1) (r,s)_{09}=(-1/3,+1/3)
08===09===10===11 (r,s)_{02}=(+1/3,-1) (r,s)_{10}=(+1/3,+1/3)
|| || || || (r,s)_{03}=(+1,-1) (r,s)_{11}=(+1,+1/3)
04===05===06===07 (r,s)_{04}=(-1,-1/3) (r,s)_{12}=(-1,+1)
|| || || || (r,s)_{05}=(-1/3,-1/3) (r,s)_{13}=(-1/3,+1)
00===01===02===03 (r,s)_{06}=(+1/3,-1/3) (r,s)_{14}=(+1/3,+1)
(r,s)_{07}=(+1,-1/3) (r,s)_{15}=(+1,+1)
20

The velocity shape functions are given by:
N1(r)=(−1 + r+ 9r2−9r3)/16 N1(t)=(−1 + t+ 9t2−9t3)/16
N2(r) = (+9 −27r−9r2+ 27r3)/16 N2(t) = (+9 −27t−9t2+ 27t3)/16
N3(r) = (+9 + 27r−9r2−27r3)/16 N3(t) = (+9 + 27t−9t2−27t3)/16
N4(r)=(−1−r+ 9r2+ 9r3)/16 N4(t)=(−1−t+ 9t2+ 9t3)/16
N01(r, s) = N1(r)N1(s)=(−1 + r+ 9r2−9r3)/16 ∗(−1 + t+ 9s2−9s3)/16
N02(r, s) = N2(r)N1(s) = (+9 −27r−9r2+ 27r3)/16 ∗(−1 + t+ 9s2−9s3)/16
N03(r, s) = N3(r)N1(s) = (+9 + 27r−9r2−27r3)/16 ∗(−1 + t+ 9s2−9s3)/16
N04(r, s) = N4(r)N1(s)=(−1−r+ 9r2+ 9r3)/16 ∗(−1 + t+ 9s2−9s3)/16
N05(r, s) = N1(r)N2(s) = (−1 + r+ 9r2−9r3)/16 ∗(9 −27s−9s2+ 27s3)/16
N06(r, s) = N2(r)N2(s) = (+9 −27r−9r2+ 27r3)/16 ∗(9 −27s−9s2+ 27s3)/16
N07(r, s) = N3(r)N2(s) = (+9 + 27r−9r2−27r3)/16 ∗(9 −27s−9s2+ 27s3)/16
N08(r, s) = N4(r)N2(s)=(−1−r+ 9r2+ 9r3)/16 ∗(9 −27s−9s2+ 27s3)/16
N09(r, s) = N1(r)N3(s) = (30)
N10(r, s) = N2(r)N3(s) = (31)
N11(r, s) = N3(r)N3(s) = (32)
N12(r, s) = N4(r)N3(s) = (33)
N13(r, s) = N1(r)N4(s) = (34)
N14(r, s) = N2(r)N4(s) = (35)
N15(r, s) = N3(r)N4(s) = (36)
N16(r, s) = N4(r)N4(s) = (37)
21

4 Solving the Stokes equations with the FEM
In the case of an incompressible flow, we have seen that the continuity (mass conservation) equation takes
the simple form ∇·v= 0. In other word flow takes place under the constraint that the divergence of its
velocity field is exactly zero eveywhere (solenoidal constraint), i.e. it is divergence free.
We see that the pressure in the momentum equation is then a degree of freedom which is needed to
satisfy the incompressibilty constraint (and it is not related to any constitutive equation) [26]. In other
words the pressure is acting as a Lagrange multiplier of the incompressibility constraint.
Various approaches have been proposed in the literature to deal with the incompressibility constraint
but we will only focus on the penalty method (section 4.2) and the so-called mixed finite element method
4.3.
4.1 strong and weak forms
The strong form consists of the governing equation and the boundary conditions, i.e. the mass, momentum
and energy conservation equations supplemented with Dirichlet and/or Neumann boundary conditions
on (parts of) the boundary.
To develop the finite element formulation, the partial differential equations must be restated in an
integral form called the weak form. In essence the PDEs are first multiplied by an arbitrary function and
integrated over the domain.
4.2 The penalty approach
In order to impose the incompressibility constraint, two widely used procedures are available, namely
the Lagrange multiplier method and the penalty method [6, 42]. The latter is implemented in elefant,
which allows for the elimination of the pressure variable from the momentum equation (resulting in a
reduction of the matrix size).
Mathematical details on the origin and validity of the penalty approach applied to the Stokes problem
can for instance be found in [20], [67] or [40].
The penalty formulation of the mass conservation equation is based on a relaxation of the incompress-
ibility constraint and writes
∇·v+p
λ= 0 (38)
where λis the penalty parameter, that can be interpreted (and has the same dimension) as a bulk
viscosity. It is equivalent to say that the material is weakly compressible. It can be shown that if one
chooses λto be a sufficiently large number, the continuity equation ∇·v= 0 will be approximately
satisfied in the finite element solution. The value of λis often recommended to be 6 to 7 orders of
magnitude larger than the shear viscosity [28, 43].
Equation (38) can be used to eliminate the pressure in Eq. (??) so that the mass and momentum
conservation equations fuse to become :
∇·(2η˙ε(v)) + λ∇(∇·v) = ρg= 0 (39)
[56] have established the equivalence for incompressible problems between the reduced integration of
the penalty term and a mixed Finite Element approach if the pressure nodes coincide with the integration
points of the reduced rule.
In the end, the elimination of the pressure unknown in the Stokes equations replaces the original
saddle-point Stokes problem [7] by an elliptical problem, which leads to a symmetric positive definite
(SPD) FEM matrix. This is the major benefit of the penalized approach over the full indefinite solver
with the velocity-pressure variables. Indeed, the SPD character of the matrix lends itself to efficient
solving stragegies and is less memory-demanding since it is sufficient to store only the upper half of the
matrix including the diagonal [37] . list codes which
use this ap-
proach
list codes which
use this ap-
proach
The stress tensor σis symmetric (i.e. σij =σji). For simplicity I will now focus on a Stokes flow in
two dimensions.
22
Since the penalty formulation is only valid for incompressible flows, then ˙
=˙
dso that the dsuper-
script is ommitted in what follows. The stress tensor can also be cast in vector format:
σxx
σyy
σxy
=
−p
−p
0
+ 2η
˙xx
˙yy
˙xy
=λ
˙xx + ˙yy
˙xx + ˙yy
0
+ 2η
˙xx
˙yy
˙xy
=
λ
110
110
000
| {z }
K
+η
200
020
001
| {z }
C
·
∂u
∂x
∂v
∂y
∂u
∂y +∂v
∂x
Remember that
∂u
∂x =
4
X
i=1
∂Ni
∂x ui
∂v
∂y =
4
X
i=1
∂Ni
∂y vi
∂u
∂y +∂v
∂x =
4
X
i=1
∂Ni
∂y ui+
4
X
i=1
∂Ni
∂x vi
so that
∂u
∂x
∂v
∂y
∂u
∂y +∂v
∂x
=
∂N1
∂x 0∂N2
∂x 0∂N3
∂x 0∂N4
∂x 0
0∂N1
∂y 0∂N2
∂y 0∂N3
∂y 0∂N4
∂y
∂N1
∂y
∂N1
∂x
∂N2
∂y
∂N2
∂x
∂N3
∂y
∂N3
∂x
∂N3
∂y
∂N4
∂x
| {z }
B
·
u1
v1
u2
v2
u3
v3
u4
v4
| {z }
V
Finally,
σ =
σxx
σyy
σxy
= (λK+ηC)·B·V
We will now establish the weak form of the momentum conservation equation. We start again from
∇·σ+b=0
For the Ni’s ’regular enough’, we can write:
ZΩe
Ni∇·σdΩ + ZΩe
NibdΩ=0
We can integrate by parts and drop the surface term1:
ZΩe
∇Ni·σdΩ = ZΩe
NibdΩ
or,
ZΩe
∂Ni
∂x 0∂Ni
∂y
0∂Ni
∂y
∂Ni
∂x
·
σxx
σyy
σxy
dΩ = ZΩe
NibdΩ
1We will come back to this at a later stage
23

Let i= 1,2,3,4 and stack the resulting four equations on top of one another.
ZΩe
∂N1
∂x 0∂N1
∂y
0∂N1
∂y
∂N1
∂x
·
σxx
σyy
σxy
dΩ = ZΩe
N1bx
bydΩ (40)
ZΩe
∂N2
∂x 0∂N2
∂y
0∂N2
∂y
∂N2
∂x
·
σxx
σyy
σxy
dΩ = ZΩe
Nibx
bydΩ (41)
ZΩe
∂N3
∂x 0∂N3
∂y
0∂N3
∂y
∂N3
∂x
·
σxx
σyy
σxy
dΩ = ZΩe
N3bx
bydΩ (42)
ZΩe
∂N4
∂x 0∂N4
∂y
0∂N4
∂y
∂N4
∂x
·
σxx
σyy
σxy
dΩ = ZΩe
N4bx
bydΩ (43)
We easily recognize BTinside the integrals! Let us define
NT
b= (N1bx, N1by, ...N4bx, N4by)
then we can write
ZΩe
BT·
σxx
σyy
σxy
dΩ = ZΩe
NbdΩ
and finally: ZΩe
BT·[λK+ηC]·B·VdΩ = ZΩe
NbdΩ
Since Vcontains the velocities at the corners, it does not depend on the xor ycoordinates so it can be
taking outside of the integral:
ZΩe
BT·[λK+ηC]·BdΩ
| {z }
Ael(8×8)
·V
|{z}
(8x1)
=ZΩe
NbdΩ
| {z }
Bel(8×1)
or,
ZΩe
λBT·K·BdΩ
| {z }
Aλ
el(8×8)
+ZΩe
ηBT·C·BdΩ
| {z }
Aη
el(8×8)
·V
|{z}
(8x1)
=ZΩe
NbdΩ
| {z }
Bel(8×1)
INTEGRATION - MAPPING
reduced integration [43]
1. partition domain Ω into elements Ωe,e= 1, ...nel.
2. loop over elements and for each element compute Ael,Bel
3. a node belongs to several elements
→need to assemble Ael and Bel in A,B
4. apply boundary conditions
5. solve system: x=A−1·B
6. visualise/analyse x
24
4.3 The mixed FEM
25
5 Solving the elastic equations with the FEM
26
6 Additional techniques
6.1 Picard and Newton
6.2 The SUPG formulation for the energy equation
6.3 Tracking materials and/or interfaces
6.4 Dealing with a free surface
6.5 Convergence criterion for nonlinear iterations
6.6 Static condensation
27
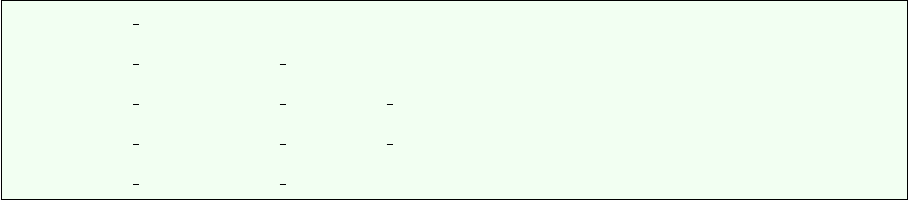
6.7 The method of manufactured solutions
The method of manufactured solutions is a relatively simple way of carrying out code verification. In
essence, one postulates a solution for the PDE at hand (as well as the proper boundary conditions),
inserts it in the PDE and computes the corresponding source term. The same source term and boundary
conditions will then be used in a numerical simulation so that the computed solution can be compared
with the (postulated) true analytical solution.
Examples of this approach are to be found in [26, 14, ?].
python codes/fieldstone
python codes/fieldstone saddlepoint
python codes/fieldstone saddlepoint q2q1
python codes/fieldstone saddlepoint q3q2
python codes/fieldstone burstedde
28

6.8 Assigning values to quadrature points
As we have seen in Section ??, the building of the elemental matrix and rhs requires (at least) to assign
a density and viscosity value to each quadrature point inside the element. Depending on the type of
modelling, this task can prove more complex than one might expect and have large consequences on the
solution accuracy.
Here are several options:
•The simplest way (which is often used for benchmarks) consists in computing the ’real’ coordinates
(xq, yq, zq) of a given quadrature point based on its reduced coordinates (rq, sq, tq), and passing these
coordinates to a function which returns density and/or viscosity at this location. For instance, for
the Stokes sphere:
def rho(x,y):
if (x-.5)**2+(y-0.5)**2<0.123**2:
val=2.
else:
val=1.
return val
def mu(x,y):
if (x-.5)**2+(y-0.5)**2<0.123**2:
val=1.e2
else:
val=1.
return val
This is very simple, but it has been shown to potentially be problematic. In essence, it can introduce
very large contrasts inside a single element and perturb the quadrature. Please read section 3.3
of [41] and/or have a look at the section titled ”Averaging material properties” in the ASPECT
manual.
•another similar approach consists in assigning a density and viscosity value to the nodes of the FE
mesh first, and then using these nodal values to assign values to the quadrature points. Very often
,and quite logically, the shape functions are used to this effect. Indeed we have seen before that for
any point (r, s, t) inside an element we have
fh(r, s, t) =
m
X
i
fiNi(r, s, t)
where the fiare the nodal values and the Nithe corresponding basis functions.
In the case of linear elements (Q1basis functions), this is straightforward. In fact, the basis functions
Nican be seen as moving weights: the closer the point is to a node, the higher the weight (basis
function value).
However, this is quite another story for quadratic elements (Q2basis functions). In order to
illustrate the problem, let us consider a 1D problem. The basis functions are
N1(r) = 1
2r(r−1) N2(r)=1−r2N3(r) = 1
2r(r+ 1)
Let us further assign: ρ1=ρ2= 0 and ρ3= 1. Then
ρh(r) =
m
X
i
ρiNi(r) = N3(r)
There lies the core of the problem: the N3(r) basis function is negative for r∈[−1,0]. This means
that the quadrature point in this interval will be assigned a negative density, which is nonsensical
and numerically problematic!
use 2X Q1. write about it !
29
The above methods work fine as long as the domain contains a single material. As soon as there are
multiple fluids in the domain a special technique is needed to track either the fluids themselves or their
interfaces. Let us start with markers. We are then confronted to the infernal trio (a menage a trois?)
which is present for each element, composed of its nodes, its markers and its quadrature points.
Each marker carries the material information (density and viscosity). This information must ul-
timately be projected onto the quadrature points. Two main options are possible: an algorithm is
designed and projects the marker-based fields onto the quadrature points directly or the marker fields
are first projected onto the FE nodes and then onto the quadrature points using the techniques above.
————————–
At a given time, every element econtains nemarkers. During the FE matrix building process, viscosity
and density values are needed at the quadrature points. One therefore needs to project the values carried
by the markers at these locations. Several approaches are currently in use in the community and the
topic has been investigated by [24] and [29] for instance.
elefant adopts a simple approach: viscosity and density are considered to be elemental values, i.e.
all the markers within a given element contribute to assign a unique constant density and viscosity value
to the element by means of an averaging scheme.
While it is common in the literature to treat the so-called arithmetic, geometric and harmonic means
as separate averagings, I hereby wish to introduce the notion of generalised mean, which is a family of
functions for aggregating sets of numbers that include as special cases the arithmetic, geometric and
harmonic means.
If pis a non-zero real number, we can define the generalised mean (or power mean) with exponent p
of the positive real numbers a1, ... anas:
Mp(a1, ...an) = 1
n
n
X
i=1
ap
i!1/p
(44)
and it is trivial to verify that we then have the special cases:
M−∞ = lim
p→−∞ Mp= min(a1, ...an) (minimum) (45)
M−1=n
1
a1+1
a2+··· +1
an
(harm.avrg.) (46)
M0= lim
p→0Mp=n
Y
i=1
ai1/n
(geom.avrg.) (47)
M+1 =1
n
n
X
i=1
ai(arithm.avrg.) (48)
M+2 =v
u
u
t1
n
n
X
i=1
a2
i(root mean square) (49)
M+∞= lim
p→+∞Mp= max(a1, ...an) (maximum) (50)
Note that the proofs of the limit convergence are given in [13].
An interesting property of the generalised mean is as follows: for two real values pand q, if p < q
then Mp≤Mq. This property has for instance been illustrated in Fig. 20 of [73].
One can then for instance look at the generalised mean of a randomly generated set of 1000 viscosity
values within 1018P a.s and 1023P a.s for −5≤p≤5. Results are shown in the figure hereunder and the
arithmetic, geometric and harmonic values are indicated too. The function Mpassumes an arctangent-
like shape: very low values of p will ultimately yield the minimum viscosity in the array while very high
values will yield its maximum. In between, the transition is smooth and occurs essentially for |p| ≤ 5.
30
1e+18
1e+19
1e+20
1e+21
1e+22
1e+23
-4 -2 0 2 4
M(p)
p
geom.
arithm.
harm.
python codes/fieldstone markers avrg
31
6.9 Matrix (Sparse) storage
The FE matrix is the result of the assembly process of all elemental matrices. Its size can become quite
large when the resolution is being increased (from thousands of lines/columns to tens of millions).
One important property of the matrix is its sparsity. Typically less than 1% of the matrix terms is
not zero and this means that the matrix storage can and should be optimised. Clever storage formats
were designed early on since the amount of RAM memory in computers was the limiting factor 3 or 4
decades ago. [69]
There are several standard formats:
•compressed sparse row (CSR) format
•compressed sparse column format (CSC)
•the Coordinate Format (COO)
•Skyline Storage Format
•...
I focus on the CSR format in what follows.
6.9.1 2D domain - One degree of freedom per node
Let us consider again the 3 ×2 element grid which counts 12 nodes.
8=======9======10======11
||||
| (3) | (4) | (5) |
||||
4=======5=======6=======7
||||
| (0) | (1) | (2) |
||||
0=======1=======2=======3
In the case there is only a single degree of freedom per node, the assembled FEM matrix will look
like this:
X X X X
X X X X X X
X X X X X X
X X X X
X X X X X X
X X X X X X X X X
X X X X X X X X X
X X X X X X
X X X X
X X X X X X
X X X X X X
X X X X
where the Xstand for non-zero terms. This matrix structure stems from the fact that
•node 0 sees nodes 0,1,4,5
•node 1 sees nodes 0,1,2,4,5,6
•node 2 sees nodes 1,2,3,5,6,7
•...
32

•node 5 sees nodes 0,1,2,4,5,6,8,9,10
•...
•node 10 sees nodes 5,6,7,9,10,11
•node 11 sees nodes 6,7,10,11
In light thereof, we have
•4 corner nodes which have 4 neighbours (counting themselves)
•2(nnx-2) nodes which have 6 neighbours
•2(nny-2) nodes which have 6 neighbours
•(nnx-2)×(nny-2) nodes which have 9 neighbours
In total, the number of non-zero terms in the matrix is then:
NZ = 4 ×4+4×6+2×6+2×9 = 70
In general, we would then have:
NZ = 4 ×4 + [2(nnx −2) + 2(nny −2)] ×6+(nnx −2)(nny −2) ×9
Let us temporarily assume nnx =nny =n. Then the matrix size (total number of unknowns) is
N=n2and
NZ = 16 + 24(n−2) + 9(n−2)2
A full matrix array would contain N2=n4terms. The ratio of NZ (the actual number of reals to store)
to the full matrix size (the number of reals a full matrix contains) is then
R=16 + 24(n−2) + 9(n−2)2
n4
It is then obvious that when nis large enough R∼1/n2.
CSR stores the nonzeros of the matrix row by row, in a single indexed array A of double precision
numbers. Another array COLIND contains the column index of each corresponding entry in the A array.
A third integer array RWPTR contains pointers to the beginning of each row, which an additional pointer
to the first index following the nonzeros of the matrix A. A and COLIND have length NZ and RWPTR
has length N+1.
In the case of the here-above matrix, the arrays COLIND and RWPTR will look like:
COLIND = (0,1,4,5,0,1,2,4,5,6,1,2,3,5,6,7, ..., 6,7,10,11)
RW P T R = (0,4,10,16, ...)
6.9.2 2D domain - Two degrees of freedom per node
When there are now two degrees of freedom per node, such as in the case of the Stokes equation in
two-dimensions, the size of the Kmatrix is given by
NfemV=nnp∗ndofV
In the case of the small grid above, we have NfemV=24. Elemental matrices are now 8 ×8 in size.
We still have
•4 corner nodes which have 4 ,neighbours,
•2(nnx-2) nodes which have 6 neighbours
•2(nny-2) nodes which have 6 neighbours
33

•(nnx-2)x(nny-2) nodes which have 9 neighbours,
but now each degree of freedom from a node sees the other two degrees of freedom of another node too.
In that case, the number of nonzeros has been multiplied by four and the assembled FEM matrix looks
like:
X X X X X X X X
X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X
X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X X X X X X X X X X X
X X X X X X X X X X X X X X X X X X
X X X X X X X X X X X X X X X X X X
X X X X X X X X X X X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X
X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X X X X X
X X X X X X X X
X X X X X X X X
Note that the degrees of freedom are organised as follows:
(u0, v0, u1, v1, u2, v2, ...u11, v11)
In general, we would then have:
NZ = 4 [4 ×4 + [2(nnx −2) + 2(nny −2)] ×6+(nnx −2)(nny −2) ×9]
and in the case of the small grid, the number of non-zero terms in the matrix is then:
NZ = 4 [4 ×4+4×6+2×6+2×9] = 280
In the case of the here-above matrix, the arrays COLIND and RWPTR will look like:
COLIND = (0,1,2,3,8,9,10,11,0,1,2,3,8,9,10,11, ...)
RW P T R = (0,8,16,28, ...)
6.9.3 in fieldstone
The majority of the codes have the FE matrix being a full array
a mat = np . z e r o s ( ( Nfem , Nfem) , dtype=np . f l o a t 6 4 )
and it is converted to CSR format on the fly in the solve phase:
s o l = s p s . l i n a l g . s p s o l v e ( sp s . c s r m a t r i x ( a mat ) , r hs )
Note that linked list storages can be used (lil matrix). Substantial memory savings but much longer
compute times.
34

6.10 Mesh generation
Before basis functions can be defined and PDEs can be discretised and solved we must first tesselate the
domain with polygons, e.g. triangles and quadrilaterals in 2D, tetrahedra, prisms and hexahedra in 3D.
When the domain is itself simple (e.g. a rectangle, a sphere, ...) the mesh (or grid) can be (more
or less) easily produced and the connectivity array filled with straightforward algorithms [83]. However,
real life applications can involve etremely complex geometries (e.g. a bridge, a human spine, a car chassis
and body, etc ...) and dedicated algorithms/softwares must be used (see [85, 32, 91]).
We usually distinguish between two broad classes of grids: structured grids (with a regular connec-
tivity) and unstructured grids (with an irregular connectivity).
On the following figure are shown various triangle- tetrahedron-based meshes. These are obviously
better suited for simulations of complex geometries:
add more examples coming from geo
Let us now focus on the case of a rectangular computational domain of size Lx ×Ly with a regular
mesh composed of nelx×nely=nel quadrilaterals. There are then nnx×nny=nnp grid points. The
elements are of size hx×hy with hx=Lx/nelx.
We have no reason to come up with an irregular/ilogical node numbering so we can number nodes
row by row or column by column as shown on the example hereunder of a 3×2 grid:
8=======9======10======11 2=======5=======8======11
||||||||
| (3) | (4) | (5) | | (1) | (3) | (5) |
||||||||
4=======5=======6=======7 1=======4=======7======10
||||||||
| (0) | (1) | (2) | | (0) | (2) | (4) |
||||||||
0=======1=======2=======3 0=======3=======6=======9
"row by row" "column by column"
The numbering of the elements themselves could be done in a somewhat chaotic way but we follow
the numbering of the nodes for simplicity. The row by row option is the adopted one in fieldstoneand
the coordinates of the points are computed as follows:
x = np . empty (nnp , dtype=np . f l o a t 6 4 )
y = np . empty (nnp , dtype=np . f l o a t 6 4 )
35

co u nt er = 0
f o r jin range ( 0 , nny ) :
f o r ii n r an ge ( 0 , nnx ) :
x [ co unt er ]= i ∗hx
y [ co unt er ]= j ∗hy
co u nt er += 1
The inner loop has iranging from 0to nnx-1 first for j=0, 1, ... up to nny-1 which indeed corresponds
to the row by row numbering.
We now turn to the connectivity. As mentioned before, this is a structured mesh so that the so-called
connectivity array, named icon in our case, can be filled easily. For each element we need to store the
node identities of its vertices. Since there are nel elements and m=4 corners, this is a m×nel array. The
algorithm goes as follows:
i c o n =np . z e r o s ( (m, n e l ) , d type=np . i n t 1 6 )
co u nt er = 0
f o r jin range ( 0 , n e l y ) :
f o r ii n r an ge ( 0 , n e l x ) :
i c o n [ 0 , c o u nt e r ] = i + j ∗nnx
i c o n [ 1 , c o u nt e r ] = i + 1 + j ∗nnx
i c o n [ 2 , c o u nt e r ] = i + 1 + ( j + 1 ) ∗nnx
i c o n [ 3 , c o u nt e r ] = i + ( j + 1 ) ∗nnx
co u nt er += 1
In the case of the 3×2 mesh, the icon is filled as follows:
element id→0 1 2 3 4 5
node id↓
0 0 1 2 4 5 6
1 1 2 3 5 6 7
2 56791011
3 4 5 6 8 9 10
It is to be understood as follows: element #4 is composed of nodes 5, 6, 10 and 9. Note that nodes are
always stored in a counter clockwise manner, starting at the bottom left. This is very important since
the corresponding basis functions and their derivatives will be labelled accordingly.
In three dimensions things are very similar. The mesh now counts nelx×nely×nelz=nel elements
which represent a cuboid of size Lx×Ly×Lz. The position of the nodes is obtained as follows:
x = np . empty (nnp , dtype=np . f l o a t 6 4 )
y = np . empty (nnp , dtype=np . f l o a t 6 4 )
z = np . empty (nnp , dtype=np . f l o a t 6 4 )
co u nt er=0
f o r iin range ( 0 , nnx ) :
f o r jin range ( 0 , nny ) :
f o r kin range ( 0 , nnz ) :
x [ co unt er ]= i ∗hx
y [ co unt er ]= j ∗hy
z [ co unt er ]=k∗hz
co u nt er += 1
The connectivity array is now of size m×nel with m=8:
i c o n =np . z e r o s ( (m, n e l ) , d type=np . i n t 1 6 )
co u nt er = 0
f o r iin range ( 0 , n e l x ) :
f o r jin range ( 0 , n e l y ) :
f o r kin range ( 0 , n e l z ) :
i c o n [ 0 , c o un t e r ]= nny ∗nnz∗( i )+nnz ∗( j )+k
i c o n [ 1 , c o un t e r ]= nny ∗nnz∗( i +1)+nnz ∗( j )+k
i c o n [ 2 , c o un t e r ]= nny ∗nnz∗( i +1)+nnz ∗( j +1)+k
i c o n [ 3 , c o un t e r ]= nny ∗nnz∗( i )+nnz ∗( j +1)+k
i c o n [ 4 , c o un t e r ]= nny ∗nnz∗( i )+nnz ∗( j )+k+1
i c o n [ 5 , c o un t e r ]= nny ∗nnz∗( i +1)+nnz ∗( j )+k+1
i c o n [ 6 , c o un t e r ]= nny ∗nnz∗( i +1)+nnz ∗( j +1)+k+1
i c o n [ 7 , c o un t e r ]= nny ∗nnz∗( i )+nnz ∗( j +1)+k+1
co u nt er += 1
36

produce drawing of node numbering
37
6.11 Visco-Plasticity
6.11.1 Tensor invariants
Before we dive into the world of nonlinear rheologies it is necessary to introduce the concept of tensor
invariants since they are needed further on. Unfortunately there are many different notations used in the
literature and these can prove to be confusing.
Given a tensor T, one can compute its (moment) invariants as follows:
•first invariant :
TI|2D=T r[T] = Txx +Tyy
TI|3D=T r[T] = Txx +Tyy +Tzz
•second invariant :
TII |2D=1
2T r[T2] = 1
2X
ij
Tij Tji =1
2(T2
xx +T2
yy) + T2
xy
TII |3D=1
2T r[T2] = 1
2X
ij
Tij Tji =1
2(T2
xx +T2
yy +T2
yy) + T2
xy +T2
xz +T2
yz
•third invariant :
TIII =1
3T r[T3] = 1
3X
ijk
Tij TjkTki
The implementation of the plasticity criterions relies essentially on the second invariants of the (de-
viatoric) stress τand the (deviatoric) strainrate tensors ˙
ε:
τII |2D=1
2(τ2
xx +τ2
yy) + τ2
xy
=1
4(σxx −σyy)2+σ2
xy
=1
4(σ1−σ2)2
τII |3D=1
2(τ2
xx +τ2
yy +τ2
zz) + τ2
xy +τ2
xz +τ2
yz
=1
6(σxx −σyy )2+ (σyy −σzz)2+ (σxx −σzz)2+σ2
xy +σ2
xz +σ2
yz
=1
6(σ1−σ2)2+ (σ2−σ3)2+ (σ1−σ3)2
εII |2D=1
2( ˙εd
xx)2+ ( ˙εd
yy)2+ ( ˙εd
xy)2
=1
21
4( ˙εxx −˙εyy)2+1
4( ˙εyy −˙εxx)2+ ˙ε2
xy
=1
4( ˙εxx −˙εyy)2+ ˙ε2
xy
εII |3D=1
2( ˙εd
xx)2+ ( ˙εd
yy)2+ ( ˙εd
zz)2+ ( ˙εd
xy)2+ ( ˙εd
xz)2+ ( ˙εd
yz)2
=1
6(˙xx −˙yy)2+ ( ˙yy −˙zz)2+ ( ˙xx −˙zz)2+ ˙2
xy + ˙2
xz + ˙2
yz
Note that these (second) invariants are almost always used under a square root so we define:
38

τII =√τII ˙εII =p˙εII
Note that these quantities have the same dimensions as their tensor counterparts, i.e. Pa for stresses and
s−1for strain rates.
6.11.2 Scalar viscoplasticity
This formulation is quite easy to implement. It is widely used, e.g. [90, 84, 76], and relies on the
assumption that a scalar quantity ηp(the ’effective plastic viscosity’) exists such that the deviatoric
stress tensor
τ= 2ηp˙
ε(51)
is bounded by some yield stress value Y. From Eq. (51) it follows that τII = 2ηp˙εII =Ywhich yields
ηp=Y
2˙εII
This approach has also been coined the Viscosity Rescaling Method (VRM) [47].
insert here the rederivation 2.1.1 of spmw16
It is at this stage important to realise that (i) in areas where the strainrate is low, the resulting effective
viscosity will be large, and (ii) in areas where the strainrate is high, the resulting effective viscosity will be
low. This is not without consequences since (effective) viscosity contrasts up to 8-10 orders of magnitude
have been observed/obtained with this formulation and it makes the FE matrix very stiff, leading to
(iterative) solver convergence issues. In order to contain these viscosity contrasts one usually resorts to
viscosity limiters ηmin and ηmax such that
ηmin ≤ηp≤ηmax
Caution must be taken when choosing both values as they may influence the final results.
python codes/fieldstone indentor
6.11.3 about the yield stress value Y
In geodynamics the yield stress value is often given as a simple function. It can be constant (in space
and time) and in this case we are dealing with a von Mises plasticity yield criterion. . We simply assume
YvM =Cwhere Cis a constant cohesion independent of pressure, strainrate, deformation history, etc ...
Another model is often used: the Drucker-Prager plasticity model. A friction angle φis then intro-
duced and the yield value Ytakes the form
YDP =psin φ+Ccos φ
and therefore depends on the pressure p. Because φis with the range [0◦,45◦], Yis found to increase
with depth (since the lithostatic pressure often dominates the overpressure).
Note that a slightly modified verion of this plasticity model has been used: the total pressure pis
then replaced by the lithostatic pressure plith.
39

6.12 Pressure smoothing
It has been widely documented that the use of the Q1×P0element is not without problems. Aside from
the consequences it has on the FE matrix properties, we will here focus on another unavoidable side
effect: the spurious pressure checkerboard modes.
These modes have been thoroughly analysed [39, 16, 70, 71]. They can be filtered out [16] or simply
smoothed [51].
On the following figure (a,b), pressure fields for the lid driven cavity experiment are presented for
both an even and un-even number of elements. We see that the amplitude of the modes can sometimes
be so large that the ’real’ pressure is not visible and that something as simple as the number of elements
in the domain can trigger those or not at all.
a) b)
c)
a) element pressure for a 32x32 grid and for a 33x33 grid;
b) image from [26, p307] for a manufactured solution;
c) elemental pressure and smoothed pressure for the punch experiment [84]
The easiest post-processing step that can be used (especially when a regular grid is used) is explained in
[84]: ”The element-to-node interpolation is performed by averaging the elemental values from elements
common to each node; the node-to-element interpolation is performed by averaging the nodal values
element-by-element. This method is not only very efficient but produces a smoothing of the pressure that
is adapted to the local density of the octree. Note that these two steps can be repeated until a satisfying
level of smoothness (and diffusion) of the pres- sure field is attained.”
In the codes which rely on the Q1×P0element, the (elemental) pressure is simply defined as
p=np . ze r o s ( nel , dtype=np . f l o a t 6 4 )
while the nodal pressure is then defined as
q=np . ze r o s ( nnp , dtype=np . f l o a t 6 4 )
The element-to-node algorithm is then simply (in 2D):
cou nt=np . z e r o s ( nnp , dtype=np . i n t 1 6 )
f o r i e l in range ( 0 , n e l ) :
q [ i co n [ 0 , i e l ]]+=p [ i e l ]
q [ i co n [ 1 , i e l ]]+=p [ i e l ]
q [ i co n [ 2 , i e l ]]+=p [ i e l ]
q [ i co n [ 3 , i e l ]]+=p [ i e l ]
co un t [ i c o n [ 0 , i e l ]]+=1
co un t [ i c o n [ 1 , i e l ]]+=1
co un t [ i c o n [ 2 , i e l ]]+=1
co un t [ i c o n [ 3 , i e l ]]+=1
q=q/ count
40

6.13 Pressure scaling
As perfectly explained in the step 32 of deal.ii2, we often need to scale the Gterm since it is many orders
of magnitude smaller than K, which introduces large inaccuracies in the solving process to the point that
the solution is nonsensical. This scaling coefficient is η/L. We start from
K G
GT0·V
P=f
h
and introduce the scaling coefficient as follows (which in fact does not alter the solution at all):
Kη
LG
η
LGT0·V
L
ηP=f
η
Lh
We then end up with the modified Stokes system:
K G
GT0·V
P=f
h
where
G=η
LGP=L
ηPh=η
Lh
After the solve phase, we recover the real pressure with P=η
LP0.
2https://www.dealii.org/9.0.0/doxygen/deal.II/step 32.html
42

6.14 Pressure normalisation
When Dirichlet boundary conditions are imposed everywhere on the boundary, pressure is only present
by its gradient in the equations. It is thus determined up to an arbitrary constant. In such a case, one
commonly impose the average of the pressure over the whole domain or on a subsect of the boundary to
be have a zero average, i.e. ZΩ
pdV = 0
Another possibility is to impose the pressure value at a single node.
Let us assume that we are using Q1×P0elements. Then the pressure is constant inside each element.
The integral above becomes:
ZΩ
pdV =X
eZΩe
pdV =X
e
peZΩe
dV =X
e
peAe=
where the sum runs over all elements eof area Ae. This can be rewritten
LTP= 0
and it is a constraint on the pressure. As we have seen before ??, we can associate to it a Lagrange
multiplier λso that we must solve the modified Stokes system:
K G 0
GT0L
0LT0
·
V
P
λ
=
f
h
0
When higher order spaces are used for pressure (continuous or discontinuous) one must then carry out
the above integration numerically by means of (usually) a Gauss-Legendre quadrature.
python codes/fieldstone stokes sphere 3D saddlepoint/
python codes/fieldstone burstedde/
python codes/fieldstone busse/
python codes/fieldstone RTinstability1/
python codes/fieldstone saddlepoint q2q1/
python codes/fieldstone compressible2/
python codes/fieldstone compressible1/
python codes/fieldstone saddlepoint q3q2/
43

6.15 The choice of solvers
Let us first look at the penalty formulation. In this case we are only solving for velocity since pressure is
recovered in a post-processing step. We also know that the penalty factor is many orders of magnitude
higher than the viscosity and in combination with the use of the Q1×P0element the resulting matrix
condition number is very high so that the use of iterative solvers in precluded. Indeed codes such as
SOPALE [33], DOUAR [10], or FANTOM [82] relying on the penalty formulation all use direct solvers
(BLKFCT, MUMPS, WSMP).
The main advantage of direct solvers is used in this case: They can solve ill-conditioned matrices.
However memory requirements for the storage of number of nonzeros in the Cholesky matrix grow very fast
as the number of equations/grid size increases, especially in 3D, to the point that even modern computers
with tens of Gb of RAM cannot deal with a 1003element mesh. This explains why direct solvers are
often used for 2D problems and rarely in 3D with noticeable exceptions [84, 92, 11, 55, 2, 3, 4, 89, 61].
In light of all this, let us start again from the (full) Stokes system:
K G
GT0·V
P=f
h
We need to solve this system in order to obtain the solution, i.e. the Vand Pvectors. But how?
Unfortunately, this question is not simple to answer and the ’right’ depends on many parameters.
How big is the matrix ? what is the condition number of the matrix K? Is it symmetric ? (i.e. how are
compressible terms handled?).
6.15.1 The Schur complement approach
Let us write the above system as two equations:
KV+GP=f(52)
GTV=h(53)
The first line can be re-written V=K−1(f−GP) and can be inserted in the second:
GTV=GT[K−1(f−GP)] = h
or,
GTK−1GP=GTK−1f−h
The matrix S=GTK−1Gis called the Schur complement. It is Symmetric (since Kis symmetric) and
Postive-Definite3(SPD) if Ker(G) = 0. look in donea-huerta book for details Having solved this equation
(we have obtained P), the velocity can be recovered by solving KV=f−GP. For now, let us assume
that we have built the Smatrix and the right hand side ˜
f=GTK−1f−h. We must solve SP=˜
f.
Since Sis SPD, the Conjugate Gradient (CG) method is very appropriate to solve this system. Indeed,
looking at the definition of Wikipedia: In mathematics, the conjugate gradient method is an algorithm for
the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric
and positive-definite. The conjugate gradient method is often implemented as an iterative algorithm,
applicable to sparse systems that are too large to be handled by a direct implementation or other direct
methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving
partial differential equations or optimization problems.
The Conjugate Gradient algorithm is as follows:
3Mpositive definite ⇐⇒ xTM x > 0∀x∈Rn\0
44

Algorithm obtained from https://en.wikipedia.org/wiki/Conjugate_gradient_method
Let us look at this algorithm up close. The parts which may prove to be somewhat tricky are those
involving the matrix (in our case the Schur complement). We start the iterations with a guess pressure
P0( and an initial guess velocity which could be obtained by solving KV0=f−GP0).
r0=˜
f−SP0(54)
=GTK−1f−h−(GTK−1G)P0(55)
=GTK−1(f−GP0)−h(56)
=GTK−1KV0−h(57)
=GTV0−h(58)
(59)
We now turn to the αkcoefficient:
αk=rT
krk
pkSpk
=rT
krk
pkGTK−1Gpk
=rT
krk
(Gpk)TK−1(Gpk)
We then define ˜pk=Gpk, so that αkcan be computed as follows:
1. compute ˜pk=Gpk
2. solve Kdk= ˜pk
3. compute αk= (rT
krk)/(˜pT
kdk)
Then we need to look at the term Spk:
Spk=GTK−1Gpk=GTK−1˜pk=GTdk
We can then rewrite the CG algorithm as follows [97]:
•r0=GTV0−h
•if r0is sufficiently small, then return (V0,P0) as the result
•p0=r0
•k= 0
•repeat
–compute ˜pk=Gpk
–solve Kdk= ˜pk
–compute αk= (rT
krk)/(˜pT
kdk)
45

–Pk+1 =Pk+αkpk
–rk+1 =rk−αkGTdk
–if rk+1 is sufficiently small, then exit loop
–βk= (rT
k+1rk+1)/(rT
krk)
–pk+1 =rk+1 +βkpk
–k=k+ 1
•return Pk+1 as result
We see that we have managed to solve the Schur complement equation with the Conjugate Gradient
method without ever building the matrix S. Having obtained the pressure solution, we can easily recover
the corresponding velocity with KVk+1 =f−GPk+1. However, this is rather unfortunate because it
requires yet another solve with the Kmatrix. As it turns out, we can slightly alter the above algorithm
to have it update the velocity as well so that this last solve is unnecessary.
We have
Vk+1 =K−1(f−GPp+1) = K−1(f−G(Pk+αkpk)) = K−1(f−GPk)−αkK−1Gpk=V−αkK−1˜pk=Vk−αkdk
and we can insert this minor extra calculation inside the algorithm and get the velocity solution nearly
for free. The final CG algorithm is then
solver cg:
•compute V0=K−1(f−GP0)
•r0=GTV0−h
•if r0is sufficiently small, then return (V0,P0) as the result
•p0=r0
•k= 0
•repeat
–compute ˜pk=Gpk
–solve Kdk= ˜pk
–compute αk= (rT
krk)/(˜pT
kdk)
–Pk+1 =Pk+αkpk
–Vk+1 =Vk−αkdk
–rk+1 =rk−αkGTdk
–if rk+1 is sufficiently small (|rk+1|2/|r0|2< tol), then exit loop
–βk= (rT
k+1rk+1)/(rT
krk)
–pk+1 =rk+1 +βkpk
–k=k+ 1
•return Pk+1 as result
This iterative algorithm will converge to the solution with a rate which depends on the condition
number of the Smatrix, which is not easily obtainable since Sis never built. Also, we know that large
viscosity contrasts in the domain will influence this too. Finally, we notice that this algorithm requires
one solve with matrix Kper iteration but says nothing about the method employed to do so.
One thing we know improves the convergence of any iterative solver is the use of a preconditioner
matrix and therefore use the Preconditioned Conjugate Gradient method:
46

Algorithm obtained from https://en.wikipedia.org/wiki/Conjugate_gradient_method
In the algorithm above the preconditioner matrix Mhas to be symmetric positive-definite and fixed,
i.e., cannot change from iteration to iteration.
We see that this algorithm introduces an additional vector zand a solve with the matrix Mat each
iteration, which means that Mmust be such that solving M x =fwhere fis a given rhs vector must be
cheap. Ultimately, the PCG algorithm applied to the Schur complement equation takes the form:
solver pcg:
•compute V0=K−1(f−GP0)
•r0=GTV0−h
•if r0is sufficiently small, then return (V0,P0) as the result
•z0=M−1r0
•p0=z0
•k= 0
•repeat
–compute ˜pk=Gpk
–solve Kdk= ˜pk
–compute αk= (rT
kzk)/(˜pT
kdk)
–Pk+1 =Pk+αkpk
–Vk+1 =Vk−αkdk
–rk+1 =rk−αkGTdk
–if rk+1 is sufficiently small (|rk+1|2/|r0|2< tol), then exit loop
–zk+1 =M−1rk+1
–βk= (zT
k+1rk+1)/(zT
krk)
–pk+1 =zk+1 +βkpk
–k=k+ 1
•return Pk+1 as result
47

how to compute Mfor the Schur complement ?
6.16 The GMRES approach
48

6.18 The value of the timestep
The chosen time step dt used for time integration is chosen to comply with the Courant-Friedrichs-Lewy
condition [5].
δt =Cmin h
max |v|,h2
κ
where his a measure of the element size, κ=k/ρcpis the thermal diffusivity and C is the so-called CFL
number chosen in [0,1[.
In essence the CFL condition arises when solving hyperbolic PDEs . It limits the time step in many
explicit time-marching computer simulations so that the simulation does not produce incorrect results.
This condition is not needed when solving the Stokes equation but it is mandatory when solving
the heat transport equation or any kind of advection-diffusion equation. Note that any increase of grid
resolution (i.e. hbecomes smaller) yields an automatic decrease of the time step value.
50
6.19 mappings
The name isoparametric derives from the fact that the same (’iso’) functions are used as basis functions
and for the mapping to the reference element.
51

6.20 Exporting data to vtk format
This format seems to be the universally accepted format for 2D and 3D visualisation in Computational
Geodynamics. Such files can be opened with free softwares such as Paraview 4, MayaVi 5or Visit 6.
Unfortunately it is my experience that no simple tutorial exists about how to build such files. There
is an official document which describes the vtk format7but it delivers the information in a convoluted
way. I therefore describe hereafter how fieldstone builds the vtk files.
I hereunder show vtk file corresponding to the 3x2 grid presented earlier 6.10. In this particular
example there are:
•12 nodes and 6 elements
•1 elemental field: the pressure p)
•2 nodal fields: 1 scalar (the smoothed pressure q), 1 vector (the velocity field u,v,0)
Note that vtk files are inherently 3D so that even in the case of a 2D simulation the z-coordinate of the
points and for instance their z-velocity component must be provided. The file, usually called solution.vtu
starts with a header:
<VTKFile typ e= ’ U ns tr u ct u re d Gr i d ’ v e r s i o n= ’ 0 . 1 ’ b y t e o r d e r= ’ BigE ndi an ’>
<UnstructuredGrid>
<P i e c e Numb erOfP oints= ’ 1 2 ’ Num berO fCe lls= ’ 6 ’>
We then proceed to write the node coordinates as follows:
<Poi nts >
<DataArray t ype= ’ F lo at 32 ’ NumberOfComponents= ’ 3 ’ Format= ’ a s c i i ’>
0. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
3.333333e−01 0 .0 00 0 00 e+00 0 .0 00 00 0 e+00
6.666667e−01 0 .0 00 0 00 e+00 0 .0 00 00 0 e+00
1. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
0. 000 000 e+00 5 .0 00 000 e −01 0 .0 0 00 00 e+00
3.333333e−01 5 .0 00 000 e −01 0 . 00 00 00 e+00
6.666667e−01 5 .0 00 000 e −01 0 . 00 00 00 e+00
1. 000 000 e+00 5 .0 00 000 e −01 0 .0 0 00 00 e+00
0. 0 00 00 0 e+00 1 .0 00 00 0 e+00 0 . 00 00 00 e+00
3.333333e−01 1 .0 00 0 00 e+00 0 .0 00 00 0 e+00
6.666667e−01 1 .0 00 0 00 e+00 0 .0 00 00 0 e+00
1. 0 00 00 0 e+00 1 .0 00 00 0 e+00 0 . 00 00 00 e+00
</DataArray>
</Po ints >
These are followed by the elemental field(s):
<Ce ll Dat a S c a l a r s= ’ s c a l a r s ’>
<DataArray t ype= ’ F lo at 32 ’ Name= ’ p ’ Format=’ a s c i i ’>
−1.333333 e+00
−3. 104414 e −10
1. 3 33 33 3 e+00
−1.333333 e+00
8.278417e−17
1. 3 33 33 3 e+00
</DataArray>
</CellData>
Nodal quantities are written next:
<Poi ntData S c a l a r s= ’ s c a l a r s ’>
<DataArray t ype= ’ F lo at 32 ’ NumberOfComponents= ’ 3 ’ Name= ’ v e l o c i t y ’ Format= ’ a s c i i ’>
0. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
0. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
0. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
0. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
4https://www.paraview.org/
5https://docs.enthought.com/mayavi/mayavi/
6https://wci.llnl.gov/simulation/computer-codes/visit/
7https://www.vtk.org/wp-content/uploads/2015/04/file-formats.pdf
52

0. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
8.888885e−08 −8.278 405 e −24 0 . 0 0 00 00 e+00
8.888885e−08 1 .6 55 682 e −23 0 . 00 00 00 e+00
0. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
1. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
1. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
1. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
1. 0 00 00 0 e+00 0 .0 00 00 0 e+00 0 . 00 00 00 e+00
</DataArray>
<DataArray t ype= ’ F lo at 32 ’ NumberOfComponents= ’ 1 ’ Name= ’ q ’ Format= ’ a s c i i ’>
−1.333333 e+00
−6. 666664 e −01
6.666664e−01
1. 3 33 33 3 e+00
−1.333333 e+00
−6. 666664 e −01
6.666664e−01
1. 3 33 33 3 e+00
−1.333333 e+00
−6. 666664 e −01
6.666664e−01
1. 3 33 33 3 e+00
</DataArray>
</PointData>
To these informations we must append 3 more datasets. The first one is the connectivity, the second
one is the offsets and the third one is the type. The first one is trivial since said connectivity is needed
for the Finite Elements. The second must be understood as follows: when reading the connectivity
information in a linear manneer the offset values indicate the beginning of each element (omitting the
zero value). The third simply is the type of element as given in the vtk format document (9 corresponds
to a generic quadrilateral with an internal numbering consistent with ours).
<Cells>
<DataArray t ype= ’ I nt 32 ’ Name= ’ c o n n e c t i v i t y ’ Format= ’ a s c i i ’>
0 1 5 4
1 2 6 5
2 3 7 6
4 5 9 8
5 6 10 9
6 7 11 10
</DataArray>
<DataArray t ype= ’ In t3 2 ’ Name= ’ o f f s e t s ’ Format= ’ a s c i i ’>
4
8
12
16
20
24
</DataArray>
<DataArray t ype= ’ In t3 2 ’ Name= ’ ty pe s ’ Format= ’ a s c i i ’>
9
9
9
9
9
9
</DataArray>
</C e l l s >
The file is then closed with
</Pi ece >
</UnstructuredGrid>
</VTKFile>
The solution.vtu file can then be opened with ParaView, MayaVi or Visit and the reader is advised
to find tutorials online on how to install and use these softwares.
53
To Do:
•write about impose bc on el matrix
•full compressible
•total energy calculations
•constraints
•compositions, marker chain
•free-slip bc on annulus and sphere . See for example p540 Gresho and Sani book.
•non-linear rheologies (two layer brick spmw16, tosn15)
•Picard vs Newton
•periodic boundary conditions
•open boundary conditions
•free surface
•zaleski disk advection
•cvi !!!
•TOSI !!!!
•matrix singular annulus conv
•pure elastic
•including phase changes (w. R. Myhill)
•discontinuous galerkin
•nonlinear poiseuille
•formatting of code style
•navier-stokes ? (LUKAS)
•compute strainrate in middle of element or at quad point for punch?
•GEO1442 code
•GEO1442 indenter setup in plane ?
•in/out flow on sides for lith modelling
•Fehlberg RK advection
Problems to solve:
colorscale
better yet simple matrix storage ?
write Scott about matching compressible2 setup with his paper
deal with large matrices.
54

7 List of tutorials
tutorial number
element outer solver formulation physical problem
ndim
temperature
time stepping
nonlinear
compressible
1Q1×P0penalty analytical benchmark 2
2Q1×P0penalty Stokes sphere 2
3Q1×P0penalty Convection box 2 † †
4Q1×P0penalty Lid driven cavity 2
5Q1×P0penalty SolCx benchmark 2
6Q1×P0penalty SolKz benchmark 2
7Q1×P0penalty SolVi benchmark 2
8Q1×P0penalty Indentor 2 †
9Q1×P0penalty annulus benchmark 2
10 Q1×P0penalty Stokes sphere 3
11 Q1×P0saddle point mixed Stokes sphere 3
+ full matrix
12 Q1×P0penalty analytical benchmark 2
+ consistent press recovery
13 Q1×P0penalty Stokes sphere 2
+ markers averaging
14 Q1×P0saddle point mixed analytical benchmark 2
+ full matrix
15 Q1×P0saddle point mixed analytical benchmark 2
+ Schur
comp. CG
16 Q1×P0saddle point mixed Stokes sphere 2
+ Schur
comp. PCG
17 Q2×Q1saddle point mixed Burstedde benchmark 3
+ full matrix
18 Q2×Q1saddle point mixed analytical benchmark 2
+ full matrix
19 Q3×Q2saddle point mixed analytical benchmark 2
+ full matrix
20 Q1×P0penalty Busse convection 3 † †
21 Rannacher-
Turek
penalty analytical benchmark 2
22 Q1×Q1-
stab
saddle point mixed analytical benchmark 2
+ full matrix
23 Q1×P0mixed analytical benchmark 2 †
24 Q1×P0mixed convection box 2 † † †
25 Q1×P0saddle point mixed Rayleigh-Taylor instability 2
+ full matrix
26 Q1×P0saddle point mixed Slab detachment 2 †
+ full matrix
55

8fieldstone 01: simple analytical solution
From [26]. In order to illustrate the behavior of selected mixed finite elements in the solution of stationary
Stokes flow, we consider a two-dimensional problem in the square domain Ω = [0,1]×[0,1], which possesses
a closed-form analytical solution. The problem consists of determining the velocity field v= (u, v) and
the pressure psuch that
−ν∆v+∇p=bin Ω
∇·v= 0 in Ω
v=0on Γ
where the fluid viscosity is taken as ν= 1. The components of the body force bare prescribed as
bx= (12 −24y)x4+ (−24 + 48y)x3+ (−48y+ 72y2−48y3+ 12)x2
+(−2 + 24y−72y2+ 48y3)x+ 1 −4y+ 12y2−8y3
by= (8 −48y+ 48y2)x3+ (−12 + 72y−72y2)x2
+(4 −24y+ 48y2−48y3+ 24y4)x−12y2+ 24y3−12y4
With this prescribed body force, the exact solution is
u(x, y) = x2(1 −x)2(2y−6y2+ 4y3)
v(x, y) = −y2(1 −y)2(2x−6x2+ 4x3)
p(x, y) = x(1 −x)−1/6
Note that the pressure obeys RΩp dΩ=0
features
•Q1×P0element
•incompressible flow
•penalty formulation
•Dirichlet boundary conditions (no-slip)
•direct solver
•isothermal
•isoviscous
•analytical solution
56
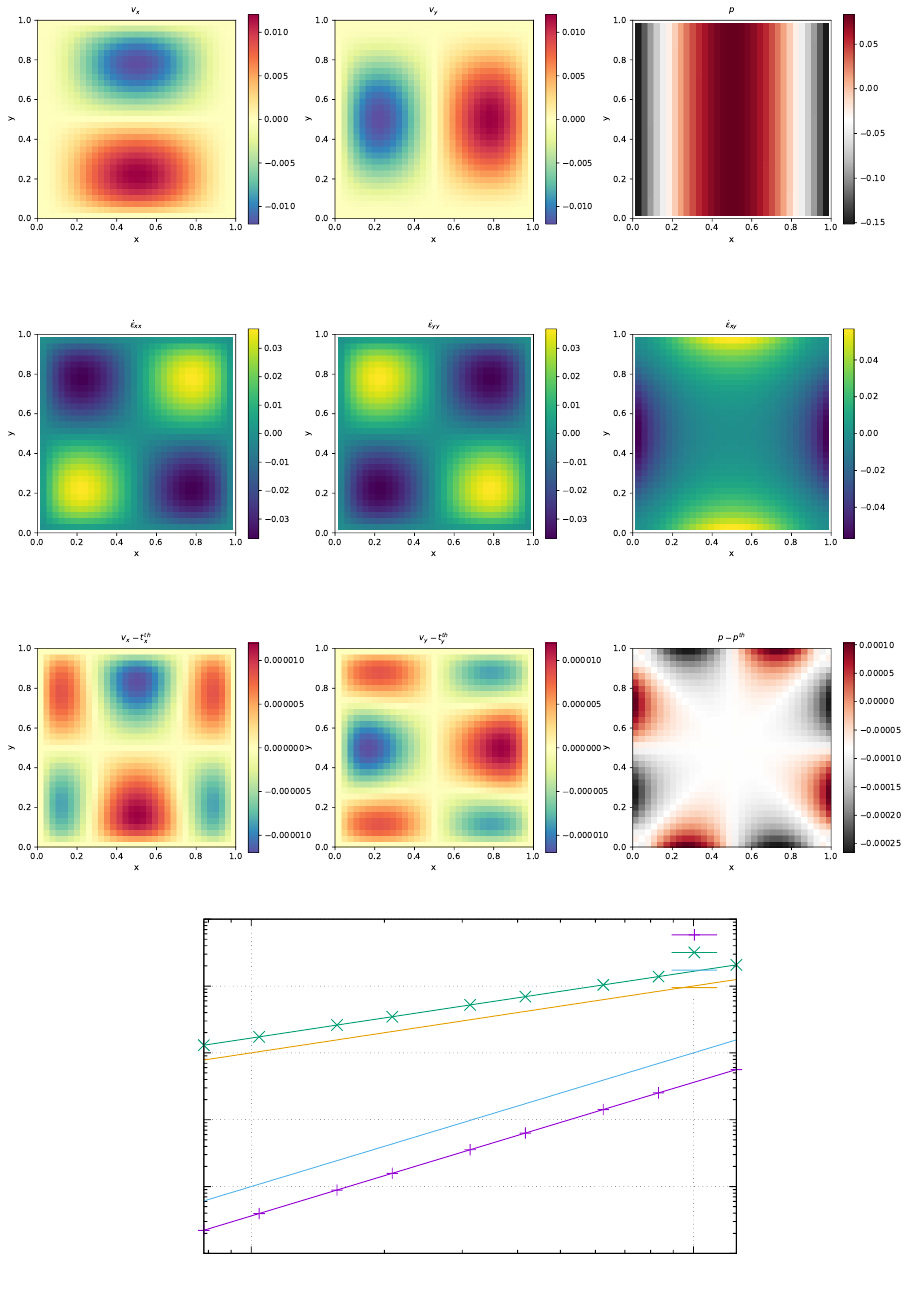
0.000001
0.000010
0.000100
0.001000
0.010000
0.100000
0.01 0.1
error
h
velocity
pressure
x2
x1
Quadratic convergence for velocity error, linear convergence for pressure error, as expected.
57
ToDo:
pressure normalisation?
different cmat, a la schmalholz
To go further:
1. make your own analytical solution
58
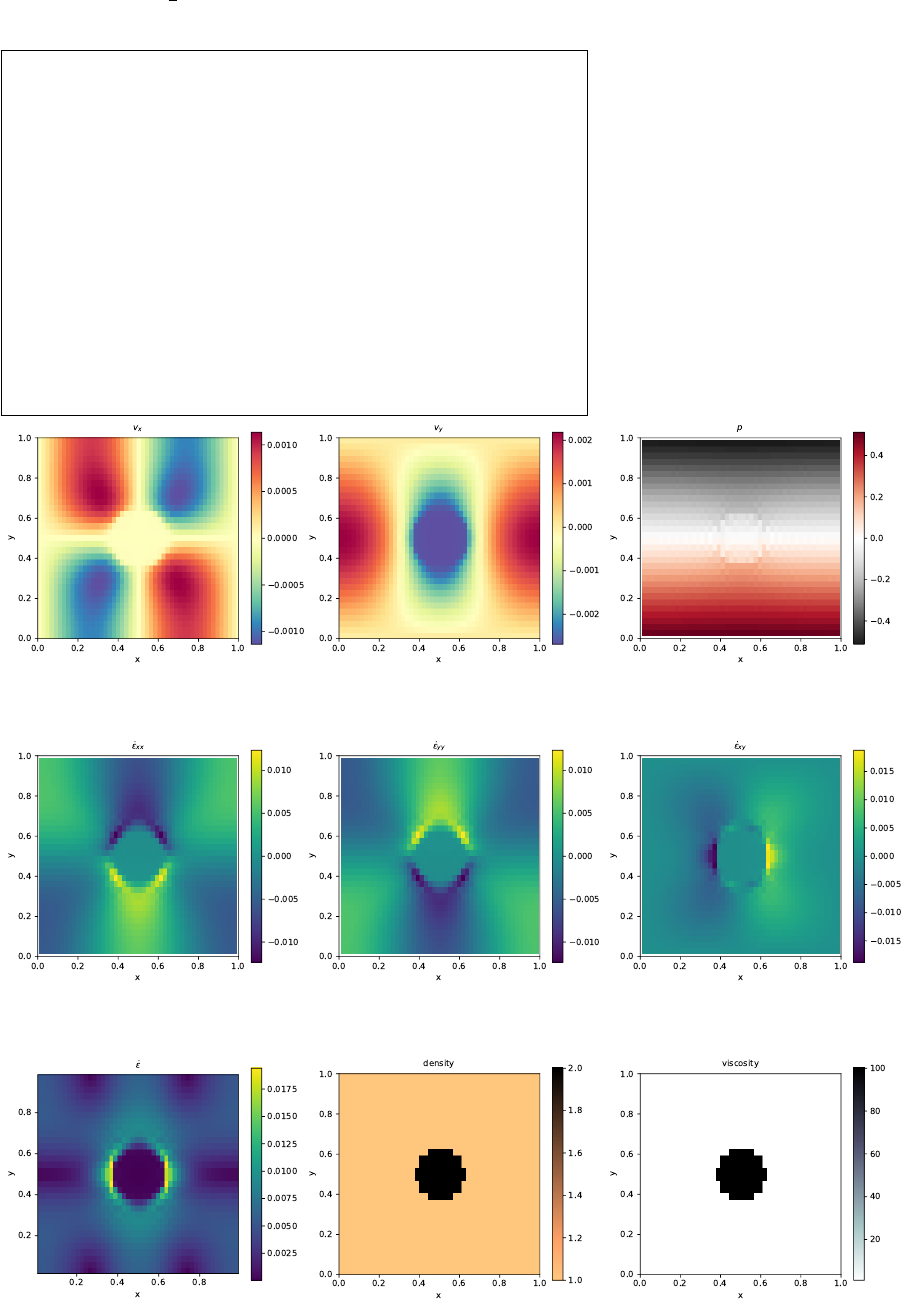
9fieldstone 02: Stokes sphere
Viscosity and density directly computed at the quadrature points.
features
•Q1×P0element
•incompressible flow
•penalty formulation
•Dirichlet boundary conditions (free-slip)
•isothermal
•non-isoviscous
•buoyancy-driven flow
•Stokes sphere
59

10 fieldstone 03: Convection in a 2D box
This benchmark deals with the 2-D thermal convection of a fluid of infinite Prandtl number in a rectan-
gular closed cell. In what follows, I carry out the case 1a, 1b, and 1c experiments as shown in [9]: steady
convection with constant viscosity in a square box.
The temperature is fixed to zero on top and to ∆Tat the bottom, with reflecting symmetry at the
sidewalls (i.e. ∂xT= 0) and there are no internal heat sources. Free-slip conditions are implemented on
all boundaries.
The Rayleigh number is given by
Ra =αgy∆T h3
κν =αgy∆T h3ρ2cp
kµ (60)
In what follows, I use the following parameter values: Lx=Ly= 1,ρ0=cP=k=µ= 1, T0= 0,
α= 10−2,g= 102Ra and I run the model with Ra = 104,105and 106.
The initial temperature field is given by
T(x, y) = (1 −y)−0.01 cos(πx) sin(πy) (61)
The perturbation in the initial temperature fields leads to a perturbation of the density field and sets the
fluid in motion.
Depending on the initial Rayleigh number, the system ultimately reaches a steady state after some
time.
The Nusselt number (i.e. the mean surface temperature gradient over mean bottom temperature) is
computed as follows [9]:
Nu =LyR∂T
∂y (y=Ly)dx
RT(y= 0)dx (62)
Note that in our case the denominator is equal to 1 since Lx= 1 and the temperature at the bottom is
prescribed to be 1.
Finally, the steady state root mean square velocity and Nusselt number measurements are indicated
in Table ?? alongside those of [9] and [78]. (Note that this benchmark was also carried out and published
in other publications [86, 1, 35, 21, 53] but since they did not provide a complete set of measurement
values, they are not included in the table.)
Blankenbach et al Tackley [78]
Ra = 104Vrms 42.864947 ±0.000020 42.775
Nu 4.884409 ±0.000010 4.878
Ra = 105Vrms 193.21454 ±0.00010 193.11
Nu 10.534095 ±0.000010 10.531
Ra = 106Vrms 833.98977 ±0.00020 833.55
Nu 21.972465 ±0.000020 21.998
Steady state Nusselt number N u and Vrms measurements as reported in the literature.
60
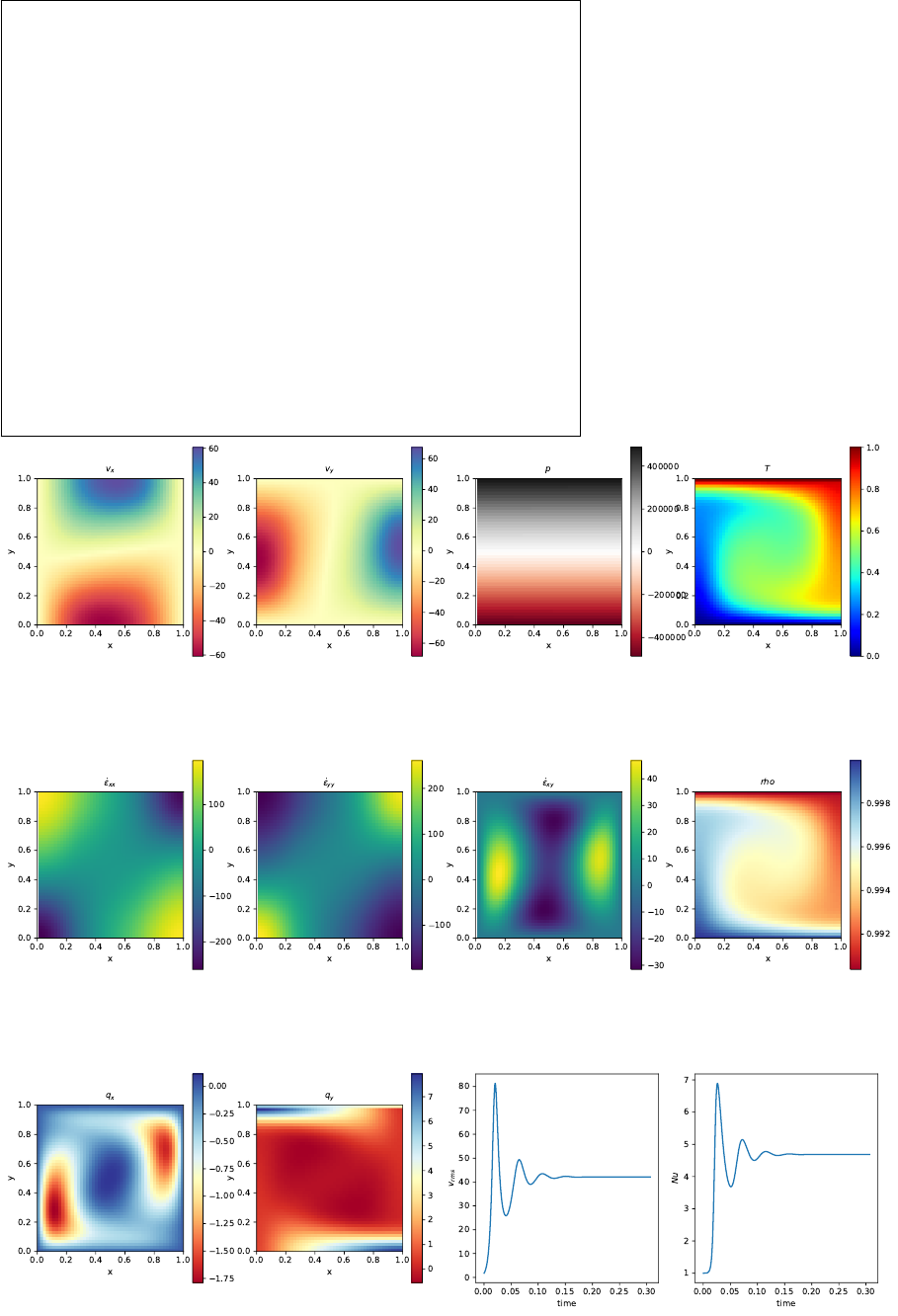
features
•Q1×P0element
•incompressible flow
•penalty formulation
•Dirichlet boundary conditions (free-slip)
•Boussinesq approximation
•direct solver
•non-isothermal
•buoyancy-driven flow
•isoviscous
•CFL-condition
61
ToDo:
implement steady state criterion
reach steady state
do Ra=1e4, 1e5, 1e6
plot against blankenbach paper and aspect
look at critical Ra number
62

11 fieldstone 04: The lid driven cavity
The lid driven cavity is a famous Computational Fluid Dynamics test case and has been studied in
countless publications with a wealth of numerical techniques (see [31] for a succinct review) and also in
the laboratory [49].
It models a plane flow of an isothermal isoviscous fluid in a rectangular (usually square) lid-driven
cavity. The boundary conditions are indicated in the Fig. ??a. The gravity is set to zero.
11.1 the lid driven cavity problem (ldc=0)
In the standard case, the upper side of the cavity moves in its own plane at unit speed, while the other
sides are fixed. This thereby introduces a discontinuity in the boundary conditions at the two upper
corners of the cavity and yields an uncertainty as to which boundary (side or top) the corner points
belong to. In this version of the code the top corner nodes are considered to be part of the lid. If these
are excluded the recovered pressure showcases and extremely large checkboard pattern.
This benchmark is usually dicussed in the context of low to very high Reynolds number with the full
Navier-Stokes equations being solved (with the noticeable exception of [70, 71, 16, 30] which focus on
the Stokes equation). In the case of the incompressible Stokes flow, the absence of inertia renders this
problem instantaneous so that only one time step is needed.
11.2 the lid driven cavity problem - regularisation I (ldc=1)
We avoid the top corner nodes issue altogether by prescribing the horizontal velocity of the lid as follows:
u(x) = x2(1 −x)2.(63)
In this case the velocity and its first derivative is continuous at the corners. This is the so-called regularised
lid-driven cavity problem [64].
11.3 the lid driven cavity problem - regularisation II (ldc=2)
Another regularisation was presented in [23]. Here, a regularized lid driven cavity is studied which is
consistent in the sense that ∇·v= 0 holds also at the corners of the domain. There are no-slip conditions
at the boundaries x= 0, x= 1, and y= 0.
The velocity at y= 1 is given by
u(x)=1−1
41−cos(x1−x
x1
π)2
x∈[0, x1]
u(x)=1 x∈[x1,1−x1]
u(x)=1−1
41−cos(x−(1 −x1)
x1
π)2
x∈[1 −x1,1] (64)
Results are obtained with x1= 0.1.
features
•Q1×P0element
•incompressible flow
•penalty formulation
•isothermal
•isoviscous
63
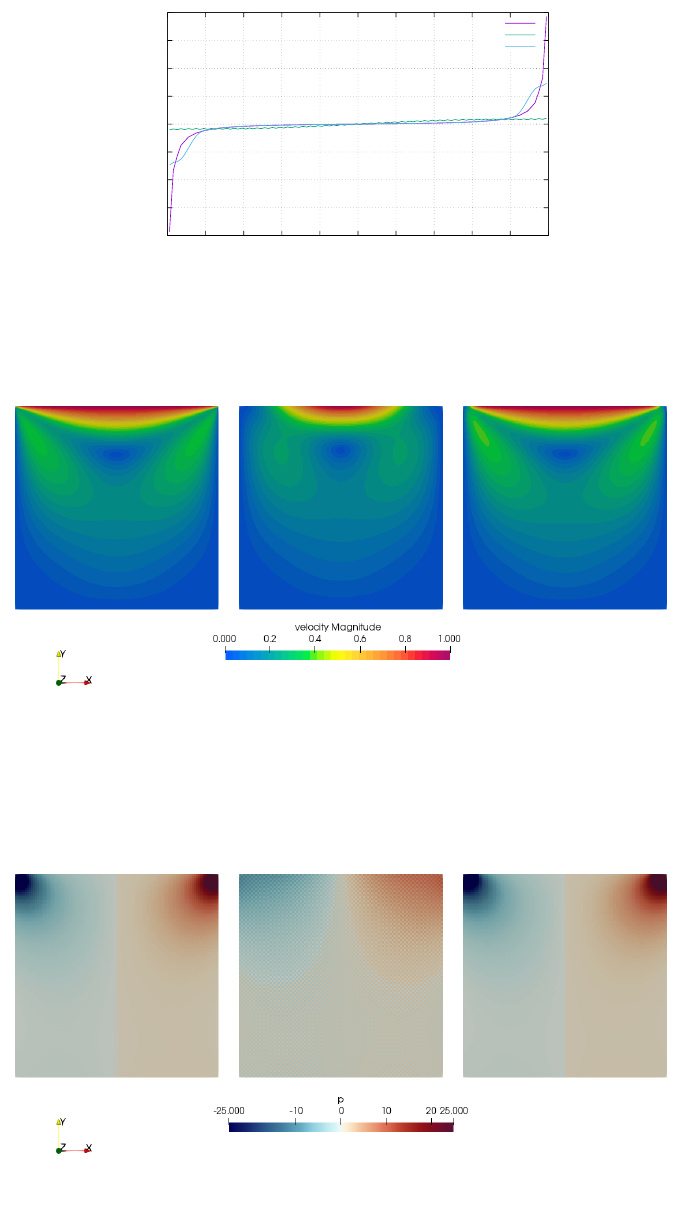
A 100x100 element grid is used. No-slip boundary conditions are prescribed on sides and bottom. A
zero vertical velocity is prescribed at the top and the exact form of the prescribed horizontal velocity is
controlled by the ldc parameter.
-200
-150
-100
-50
0
50
100
150
200
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
pressure
x
ldc0
ldc1
ldc2
64
12 fieldstone 05: SolCx benchmark
The SolCx benchmark is intended to test the accuracy of the solution to a problem that has a large jump
in the viscosity along a line through the domain. Such situations are common in geophysics: for example,
the viscosity in a cold, subducting slab is much larger than in the surrounding, relatively hot mantle
material.
The SolCx benchmark computes the Stokes flow field of a fluid driven by spatial density variations,
subject to a spatially variable viscosity. Specifically, the domain is Ω = [0,1]2, gravity is g= (0,−1)T
and the density is given by
ρ(x, y) = sin(πy) cos(πx) (65)
Boundary conditions are free slip on all of the sides of the domain and the temperature plays no role in
this benchmark. The viscosity is prescribed as follows:
µ(x, y) = 1for x < 0.5
106for x > 0.5(66)
Note the strongly discontinuous viscosity field yields a stagnant flow in the right half of the domain and
thereby yields a pressure discontinuity along the interface.
The SolCx benchmark was previously used in [29] (references to earlier uses of the benchmark are
available there) and its analytic solution is given in [94]. It has been carried out in [50] and [36]. Note that
the source code which evaluates the velocity and pressure fields for both SolCx and SolKz is distributed
as part of the open source package Underworld ([60], http://underworldproject.org).
In this particular example, the viscosity is computed analytically at the quadrature points (i.e. tracers
are not used to attribute a viscosity to the element). If the number of elements is even in any direction,
all elements (and their associated quadrature points) have a constant viscosity(1 or 106). If it is odd, then
the elements situated at the viscosity jump have half their integration points with µ= 1 and half with
µ= 106(which is a pathological case since the used quadrature rule inside elements cannot represent
accurately such a jump).
features
•Q1×P0element
•incompressible flow
•penalty formulation
•Dirichlet boundary conditions (free-slip)
•direct solver
•isothermal
•non-isoviscous
•analytical solution
65
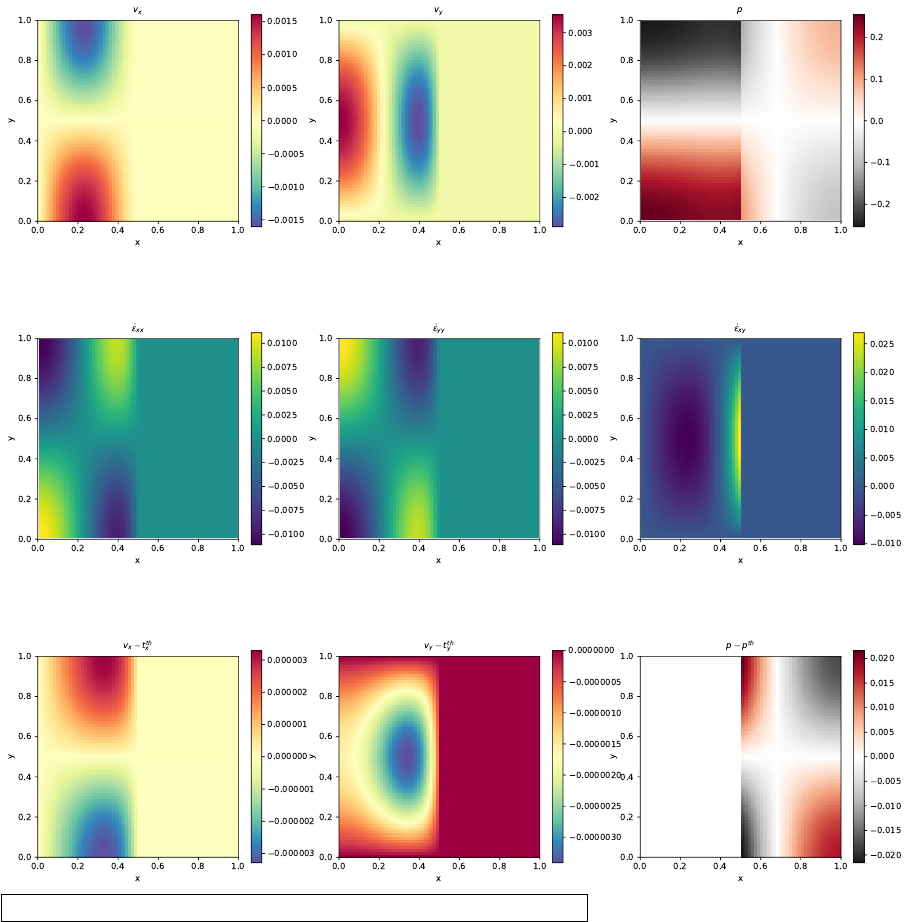
What we learn from this
66
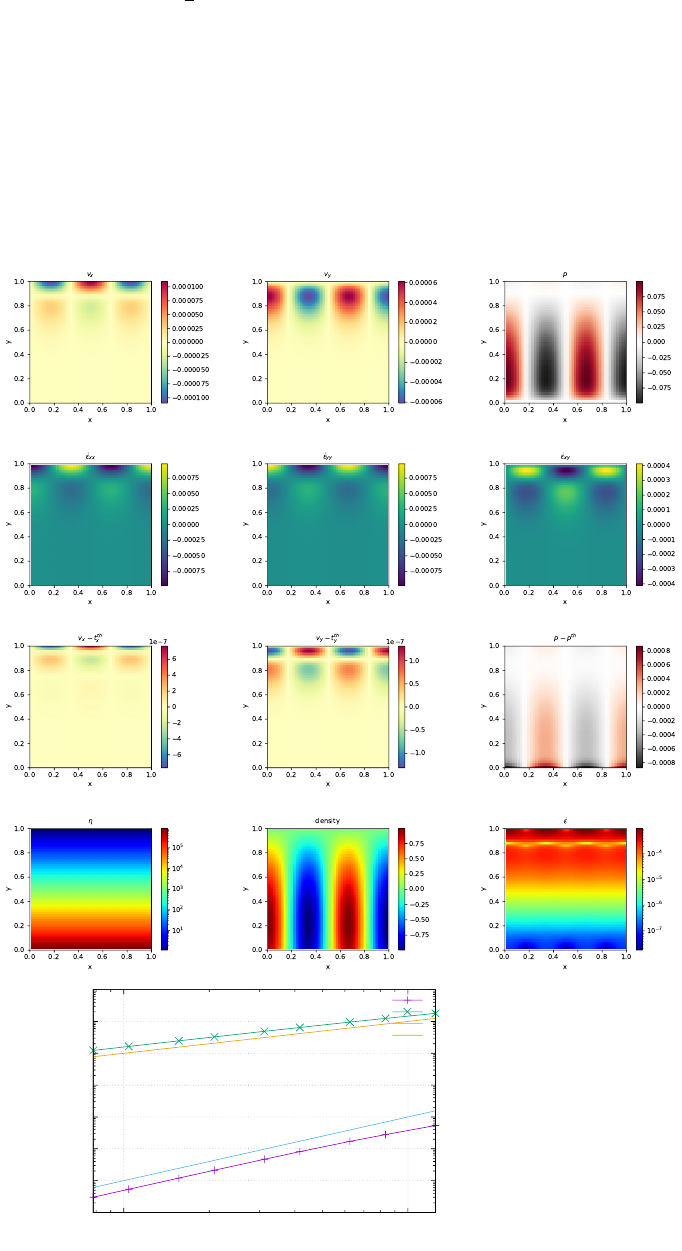
13 fieldstone 06: SolKz benchmark
The SolKz benchmark [68] is similar to the SolCx benchmark. but the viscosity is now a function of the
space coordinates:
µ(y) = exp(By) with B= 13.8155 (67)
It is however not a discontinuous function but grows exponentially with the vertical coordinate so that
its overall variation is again 106. The forcing is again chosen by imposing a spatially variable density
variation as follows:
ρ(x, y) = sin(2y) cos(3πx) (68)
Free slip boundary conditions are imposed on all sides of the domain. This benchmark is presented in
[94] as well and is studied in [29] and [36].
0.00000001
0.00000010
0.00000100
0.00001000
0.00010000
0.00100000
0.01000000
0.10000000
0.01 0.1
error
h
velocity
pressure
x2
x1
67

14 fieldstone 07: SolVi benchmark
Following SolCx and SolKz, the SolVi inclusion benchmark solves a problem with a discontinuous viscosity
field, but in this case the viscosity field is chosen in such a way that the discontinuity is along a circle.
Given the regular nature of the grid used by a majority of codes and the present one, this ensures that the
discontinuity in the viscosity never aligns to cell boundaries. This in turns leads to almost discontinuous
pressures along the interface which are difficult to represent accurately. [74] derived a simple analytic
solution for the pressure and velocity fields for a circular inclusion under simple shear and it was used in
[24], [77], [29], [50] and [36].
Because of the symmetry of the problem, we only have to solve over the top right quarter of the
domain (see Fig. ??a).
The analytical solution requires a strain rate boundary condition (e.g., pure shear) to be applied far
away from the inclusion. In order to avoid using very large domains and/or dealing with this type of
boundary condition altogether, the analytical solution is evaluated and imposed on the boundaries of
the domain. By doing so, the truncation error introduced while discretizing the strain rate boundary
condition is removed.
A characteristic of the analytic solution is that the pressure is zero inside the inclusion, while outside
it follows the relation
pm= 4˙µm(µi−µm)
µi+µm
r2
i
r2cos(2θ) (69)
where µi= 103is the viscosity of the inclusion and µm= 1 is the viscosity of the background media,
θ= tan−1(y/x), and ˙= 1 is the applied strain rate.
[24] thoroughly investigated this problem with various numerical methods (FEM, FDM), with and
without tracers, and conclusively showed how various averagings lead to different results. [29] obtained a
first order convergence for both pressure and velocity, while [50] and [36] showed that the use of adaptive
mesh refinement in respectively the FEM and FDM yields convergence rates which depend on refinement
strategies.
68
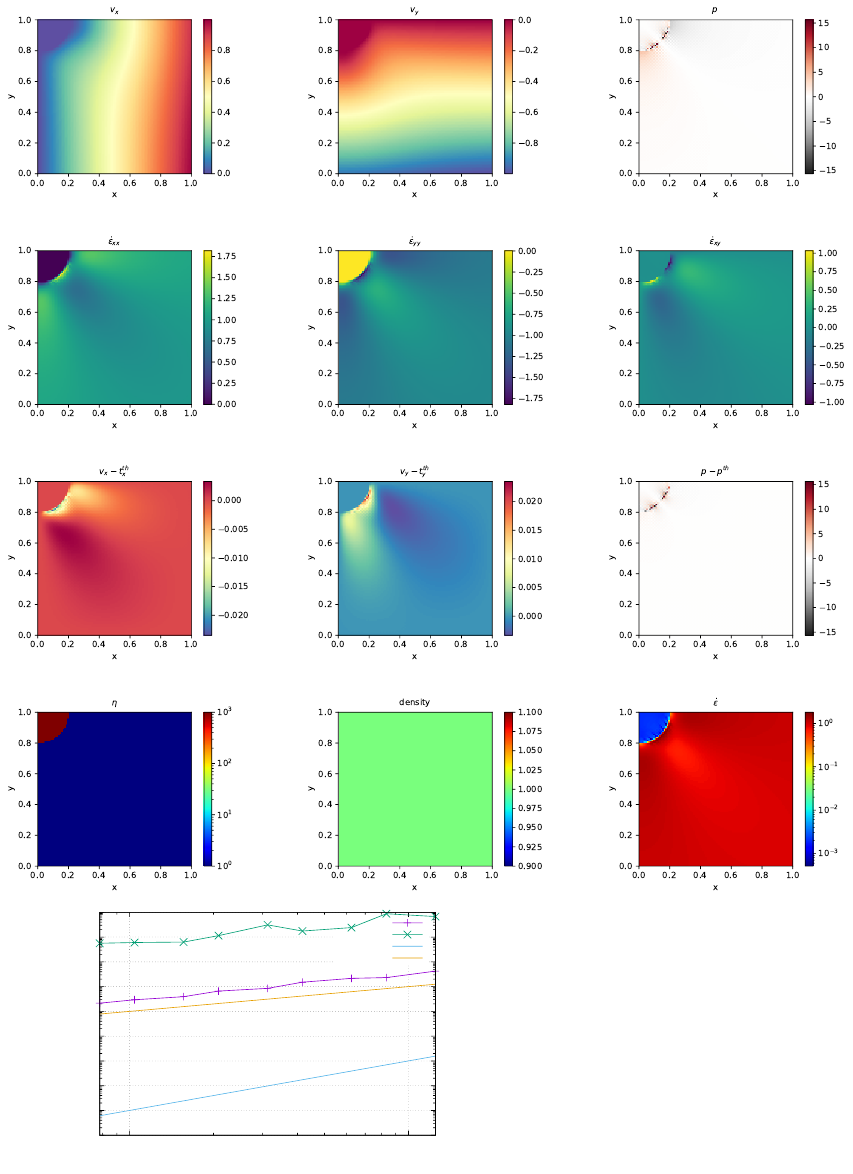
0.00000001
0.00000010
0.00000100
0.00001000
0.00010000
0.00100000
0.01000000
0.10000000
1.00000000
10.00000000
0.01 0.1
error
h
velocity
pressure
x2
x1
69

15 fieldstone 08: the indentor benchmark
The punch benchmark is one of the few boundary value problems involving plastic solids for which there
exists an exact solution. Such solutions are usually either for highly simplified geometries (spherical or
axial symmetry, for instance) or simplified material models (such as rigid plastic solids) [47].
In this experiment, a rigid punch indents a rigid plastic half space; the slip line field theory gives exact
solutions as shown in Fig. ??a. The plane strain formulation of the equations and the detailed solution
to the problem were derived in the Appendix of [84] and are also presented in [34].
The two dimensional punch problem has been extensively studied numerically for the past 40 years
[100, 99, 18, 17, 44, 93, 12, 66] and has been used to draw a parallel with the tectonics of eastern China
in the context of the India-Eurasia collision [80, 59]. It is also worth noting that it has been carried out
in one form or another in series of analogue modelling articles concerning the same region, with a rigid
indenter colliding with a rheologically stratified lithosphere [63, 22, 46].
Numerically, the one-time step punch experiment is performed on a two-dimensional domain of purely
plastic von Mises material. Given that the von Mises rheology yield criterion does not depend on pressure,
the density of the material and/or the gravity vector is set to zero. Sides are set to free slip boundary
conditions, the bottom to no slip, while a vertical velocity (0,−vp) is prescribed at the top boundary for
nodes whose xcoordinate is within [Lx/2−δ/2, Lx/2 + δ/2].
The following parameters are used: Lx= 1, Ly= 0.5, µmin = 10−3,µmax = 103,vp= 1, δ=
0.123456789 and the yield value of the material is set to k= 1.
The analytical solution predicts that the angle of the shear bands stemming from the sides of the
punch is π/4, that the pressure right under the punch is 1 + π, and that the velocity of the rigid blocks
on each side of the punch is vp/√2 (this is simply explained by invoking conservation of mass).
70
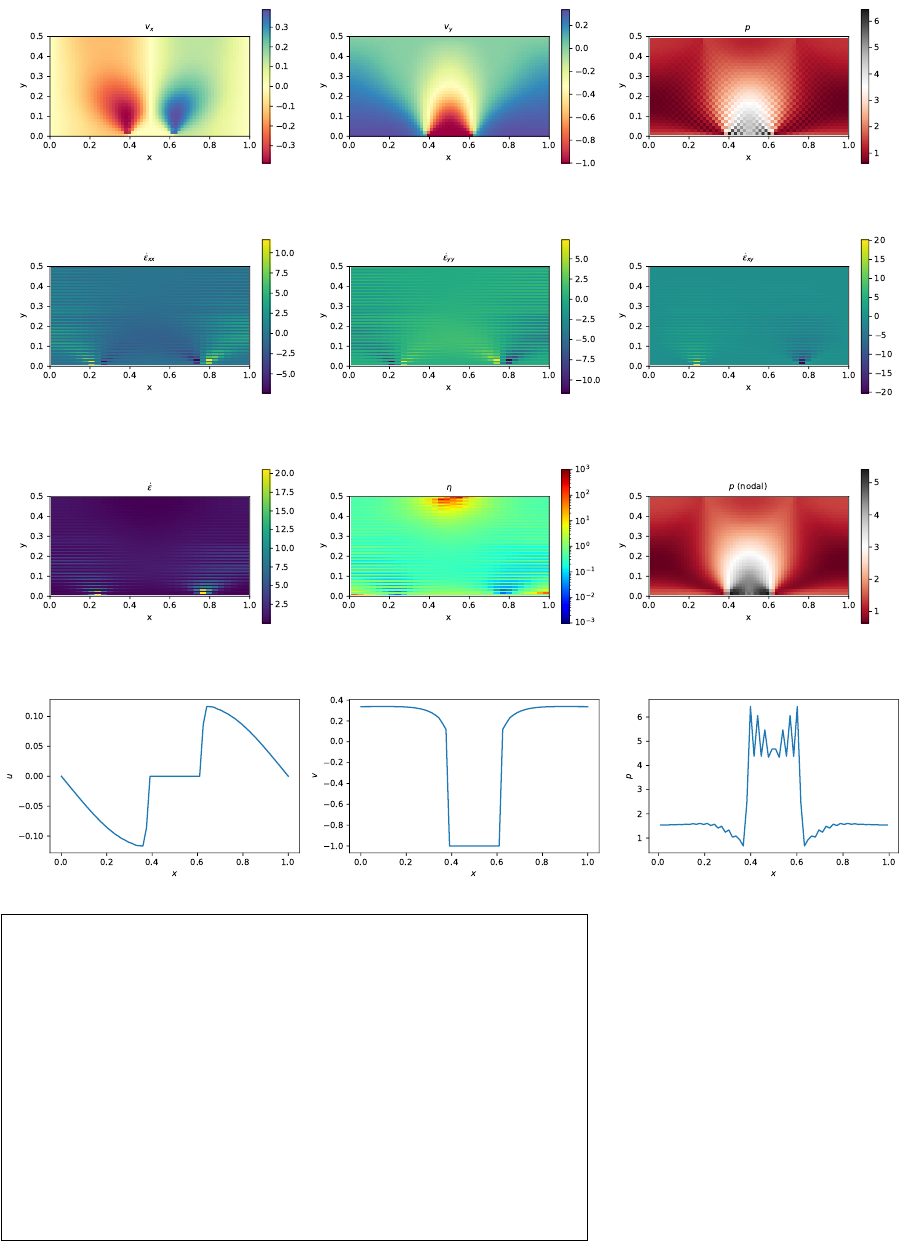
ToDo: smooth punch
features
•Q1×P0element
•incompressible flow
•penalty formulation
•Dirichlet boundary conditions (no-slip)
•isothermal
•non-isoviscous
•nonlinear rheology
71

16 fieldstone 09: the annulus benchmark
This benchmark is based on Thieulot & Puckett [Subm.] in which an analytical solution to the isoviscous
incompressible Stokes equations is derived in an annulus geometry. The velocity and pressure fields are
as follows:
vr(r, θ) = g(r)ksin(kθ),(70)
vθ(r, θ) = f(r) cos(kθ),(71)
p(r, θ) = kh(r) sin(kθ),(72)
ρ(r, θ) = ℵ(r)ksin(kθ),(73)
with
f(r) = Ar +B/r, (74)
g(r) = A
2r+B
rln r+C
r,(75)
h(r) = 2g(r)−f(r)
r,(76)
ℵ(r) = g00 −g0
r−g
r2(k2−1) + f
r2+f0
r,(77)
A=−C2(ln R1−ln R2)
R2
2ln R1−R2
1ln R2
,(78)
B=−CR2
2−R2
1
R2
2ln R1−R2
1ln R2
.(79)
The parameters Aand Bare chosen so that vr(R1) = vr(R2) = 0, i.e. the velocity is tangential to
both inner and outer surfaces. The gravity vector is radial and of unit length. In the present case, we
set R1= 1, R2= 2 and C=−1.
features
•Q1×P0element
•incompressible flow
•penalty formulation
•Dirichlet boundary conditions
•direct solver
•isothermal
•isoviscous
•analytical solution
•annulus geometry
•elemental boundary conditions
72
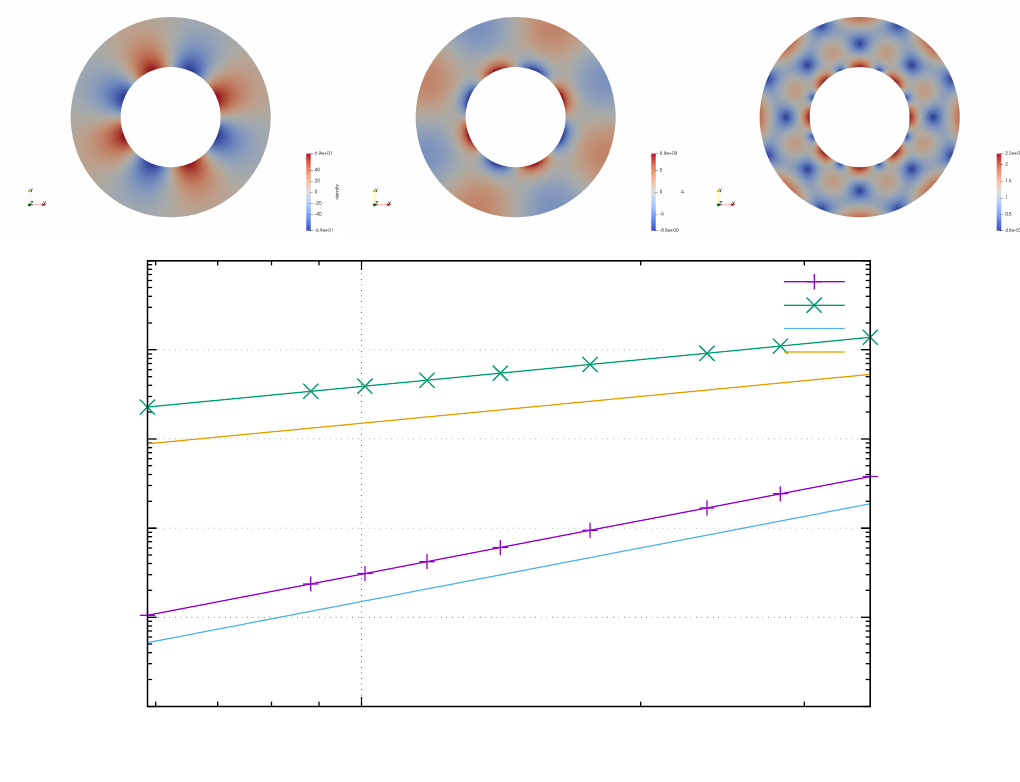
0.0001
0.001
0.01
0.1
1
10
0.01
error
h
velocity
pressure
x2
x1
73
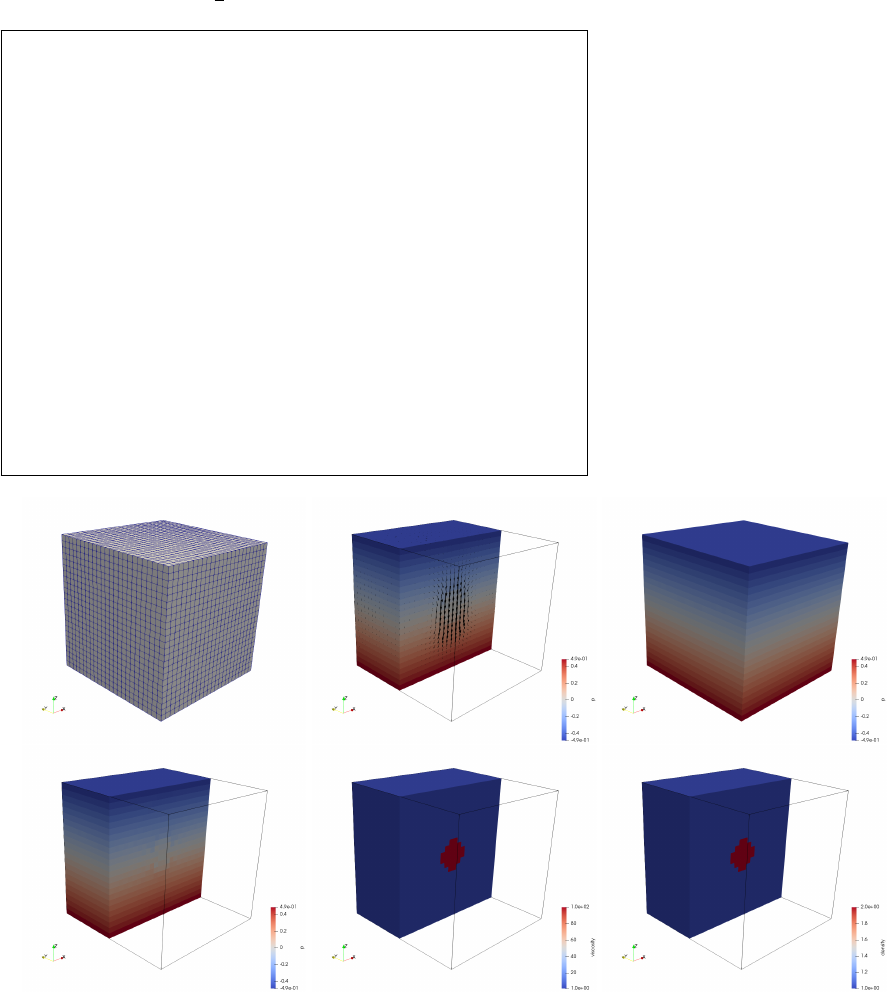
17 fieldstone 10: Stokes sphere (3D) - penalty
features
•Q1×P0element
•incompressible flow
•penalty formulation
•Dirichlet boundary conditions (free-slip)
•direct solver
•isothermal
•non-isoviscous
•3D
•elemental b.c.
•buoyancy driven
resolution is 24x24x24
74

19 fieldstone 12: consistent pressure recovery
What follows is presented in [98]. The second part of their paper wishes to establish a simple and effective
numerical method to calculate variables eliminated by the penalisation process. The method involves an
additional finite element solution for the nodal pressures using the same finite element basis and numerical
quadrature as used for the velocity.
Let us start with:
p=−λ∇·v
which lead to
(q, p) = −λ(q, ∇·v)
and then ZN N dΩ·P=−λZN∇NdΩ·V
or,
M·P=−D·V
and finally
P=−M−1·D·V
with Mof size (np ×np), Dof size (np ∗ndof ×np ∗ndof) and Vof size (np ∗ndof). The vector P
contains the np nodal pressure values directly, with no need for a smoothing scheme. The mass matrix
Mis to be evaluated at the full integration points, while the constraint part (the right hand side of the
equation) is to be evaluated at the reduced integration point.
As noted by [98], it is interesting to note that when linear elements are used and the lumped matrices
are used for the Mthe resulting algebraic equation is identical to the smoothing scheme based on the
averaging method only if the uniform square finite element mesh is used. In this respect this method is
expected to yield different results when elements are not square or even rectangular.
——-
q1is smoothed pressure obtained with the center-to-node approach.
q2is recovered pressure obtained with [98].
All three fulfill the zero average condition: RpdΩ = 0.
76
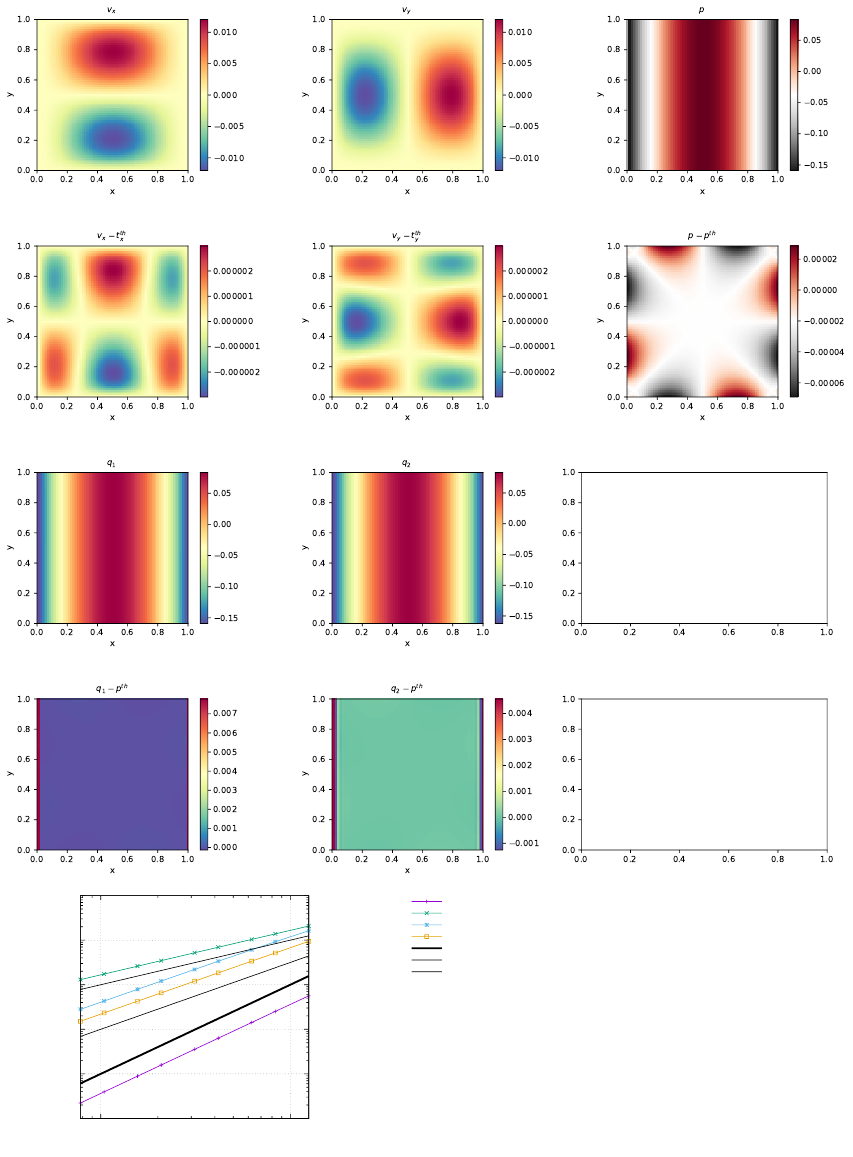
0.000001
0.000010
0.000100
0.001000
0.010000
0.100000
0.01 0.1
error
h
velocity
pressure (el)
pressure (q1)
pressure (q2)
x2
x1.5
x1
In terms of pressure error, q2is better than q1which is better than elemental.
QUESTION: why are the averages exactly zero ?!
TODO:
•add randomness to internal node positions.
•look at elefant algorithms
77
20 fieldstone 13: the Particle in Cell technique (1) - the effect
of averaging
features
•Q1×P0element
•incompressible flow
•penalty formulation
•Dirichlet boundary conditions (no-slip)
•isothermal
•non-isoviscous
•particle-in-cell
After the initial setup of the grid, markers can then be generated and placed in the domain. One
could simply randomly generate the marker positions in the whole domain but unless a very large number
of markers is used, the chance that an element does not contain any marker exists and this will prove
problematic. In order to get a better control over the markers spatial distribution, one usually generates
the marker per element, so that the total number of markers in the domain is the product of the number
of elements times the user-chosen initial number of markers per element.
Our next concern is how to actually place the markers inside an element. Two methods come to mind:
on a regular grid, or in a random manner, as shown on the following figure:
In both cases we make use of the basis shape functions: we generate the positions of the markers
(random or regular) in the reference element first (rim, sim), and then map those out to the real element
as follows:
xim =
m
X
i
Ni(rim, sim)xiyim =
m
X
i
Ni(rim, sim)yi
where xi, yiare the coordinates of the vertices of the element.
When using active markers, one is faced with the problem of transferring the properties they carry to
the mesh on which the PDEs are to be solved. As we have seen, building the FE matrix involves a loop
over all elements, so one simple approach consists of assigning each element a single property computed as
the average of the values carried by the markers in that element. Often in colloquial language ”average”
refers to the arithmetic mean:
hφiam =1
n
n
X
k
φi
where < φ >am is the arithmetic average of the nnumbers φi. However, in mathematics other means
are commonly used, such as the geometric mean:
hφigm = n
Y
i
φi!
78
and the harmonic mean:
hφihm = 1
n
n
X
i
1
φi!−1
Furthermore, there is a well known inequality for any set of positive numbers,
hφiam ≥ hφigm ≥ hφihm
which will prove to be important later on.
Let us now turn to a simple concrete example: the 2D Stokes sphere. There are two materials
in the domain, so that markers carry the label ”mat=1” or ”mat=2”. For each element an average
density and viscosity need to be computed. The majority of elements contains markers with a single
material label so that the choice of averaging does not matter (it is trivial to verify that if φi=φ0then
hφiam =hφigm =hφihm =φ0. Remain the elements crossed by the interface between the two materials:
they contain markers of both materials and the average density and viscosity inside those depends on 1)
the total number of markers inside the element, 2) the ratio of markers 1 to markers 2, 3) the type of
averaging.
This averaging problem has been studied and documented in the literature [73, 24, 81, 65]
Nodal projection. Left: all markers inside elements to which the green node belongs to are taken into
account. Right: only the markers closest to the green node count.
The setup is identical as the Stokes sphere experiment. The bash script runall runs the code for many
resolutions, both initial marker distribution and all three averaging types. The viscosity of the sphere has
been set to 103while the viscosity of the surrounding fluid is 1. The average density is always computed
with an arithmetic mean. Root mean square velocity results are shown hereunder:
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.01
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
vrms
h
random markers, elemental proj
am, 09 m
am, 16 m
am, 25 m
am, 36 m
am, 48 m
am, 64 m
gm, 09 m
gm, 16 m
gm, 25 m
gm, 36 m
gm, 48 m
gm, 64 m
hm, 09 m
hm, 16 m
hm, 25 m
hm, 36 m
hm, 48 m
hm, 64 m
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.01
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
vrms
h
regular markers, elemental proj
am, 09 m
am, 16 m
am, 25 m
am, 36 m
am, 48 m
am, 64 m
gm, 09 m
gm, 16 m
gm, 25 m
gm, 36 m
gm, 48 m
gm, 64 m
hm, 09 m
hm, 16 m
hm, 25 m
hm, 36 m
hm, 48 m
hm, 64 m
79
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.01
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
vrms
h
random markers, nodal proj
am, 09 m
am, 16 m
am, 25 m
am, 36 m
am, 48 m
am, 64 m
gm, 09 m
gm, 16 m
gm, 25 m
gm, 36 m
gm, 48 m
gm, 64 m
hm, 09 m
hm, 16 m
hm, 25 m
hm, 36 m
hm, 48 m
hm, 64 m
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.01
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
vrms
h
regular markers, nodal proj
am, 09 m
am, 16 m
am, 25 m
am, 36 m
am, 48 m
am, 64 m
gm, 09 m
gm, 16 m
gm, 25 m
gm, 36 m
gm, 48 m
gm, 64 m
hm, 09 m
hm, 16 m
hm, 25 m
hm, 36 m
hm, 48 m
hm, 64 m
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.01
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
vrms
h
random markers, nodal proj
am, 09 m
am, 16 m
am, 25 m
am, 36 m
am, 48 m
am, 64 m
gm, 09 m
gm, 16 m
gm, 25 m
gm, 36 m
gm, 48 m
gm, 64 m
hm, 09 m
hm, 16 m
hm, 25 m
hm, 36 m
hm, 48 m
hm, 64 m
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.01
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
vrms
h
regular markers, nodal proj
am, 09 m
am, 16 m
am, 25 m
am, 36 m
am, 48 m
am, 64 m
gm, 09 m
gm, 16 m
gm, 25 m
gm, 36 m
gm, 48 m
gm, 64 m
hm, 09 m
hm, 16 m
hm, 25 m
hm, 36 m
hm, 48 m
hm, 64 m
Left column: random markers. Right column: regular markers. Top row: elemental projection. Middle
row: nodal 1 projection. Bottom row: nodal 2 projection.
Conclusions:
•With increasing resolution (h→0) vrms values seem to converge towards a single value, irrespective
of the number of markers.
•At low resolution, say 32x32 (i.e. h=0.03125), vrms values for the three averagings differ by about
10%. At higher resolution, say 128x128, vrms values are still not converged.
80
•The number of markers per element plays a role at low resolution, but less and less with increasing
resolution.
•Results for random and regular marker distributions are not identical but follow a similar trend
and seem to converge to the same value.
•At low resolutions, elemental values yield better results.
•harmonic mean yields overal the best results
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.01
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
vrms
h
64 markers per element
am, reg, el
gm, reg, el
hm, reg, el
am, rand, el
gm, rand, el
hm, rand, el
am, reg, nod1
gm, reg, nod1
hm, reg, nod1
am, rand, nod1
gm, rand, nod1
hm, rand, nod1
am, reg, nod2
gm, reg, nod2
hm, reg, nod2
am, rand, nod2
gm, rand, nod2
hm, rand, nod2
81
21 fieldstone f14: solving the full saddle point problem
The details of the numerical setup are presented in Section ??.
The main difference is that we no longer use the penalty formulation and therefore keep both velocity
and pressure as unknowns. Therefore we end up having to solve the following system:
K G
GT0·V
P=f
hor,A·X=rhs
Each block K,Gand vector f,hare built separately in the code and assembled into the matrix A
and vector rhs afterwards. Aand rhs are then passed to the solver. We will see later that there are
alternatives to solve this approach which do not require to build the full Stokes matrix A.
Each element has m= 4 vertices so in total ndofV ×m= 8 velocity dofs and a single pressure
dof, commonly situated in the center of the element. The total number of velocity dofs is therefore
NfemV =nnp ×ndofV while the total number of pressure dofs is NfemP =nel. The total number of
dofs is then Nfem =NfemV +N femP .
As a consequence, matrix Khas size N femV, N femV and matrix Ghas size N femV, N femP . Vector
fis of size NfemV and vector his of size N femP .
features
•Q1×P0element
•incompressible flow
•mixed formulation
•Dirichlet boundary conditions (no-slip)
•direct solver (?)
•isothermal
•isoviscous
•analytical solution
•pressure smoothing
82
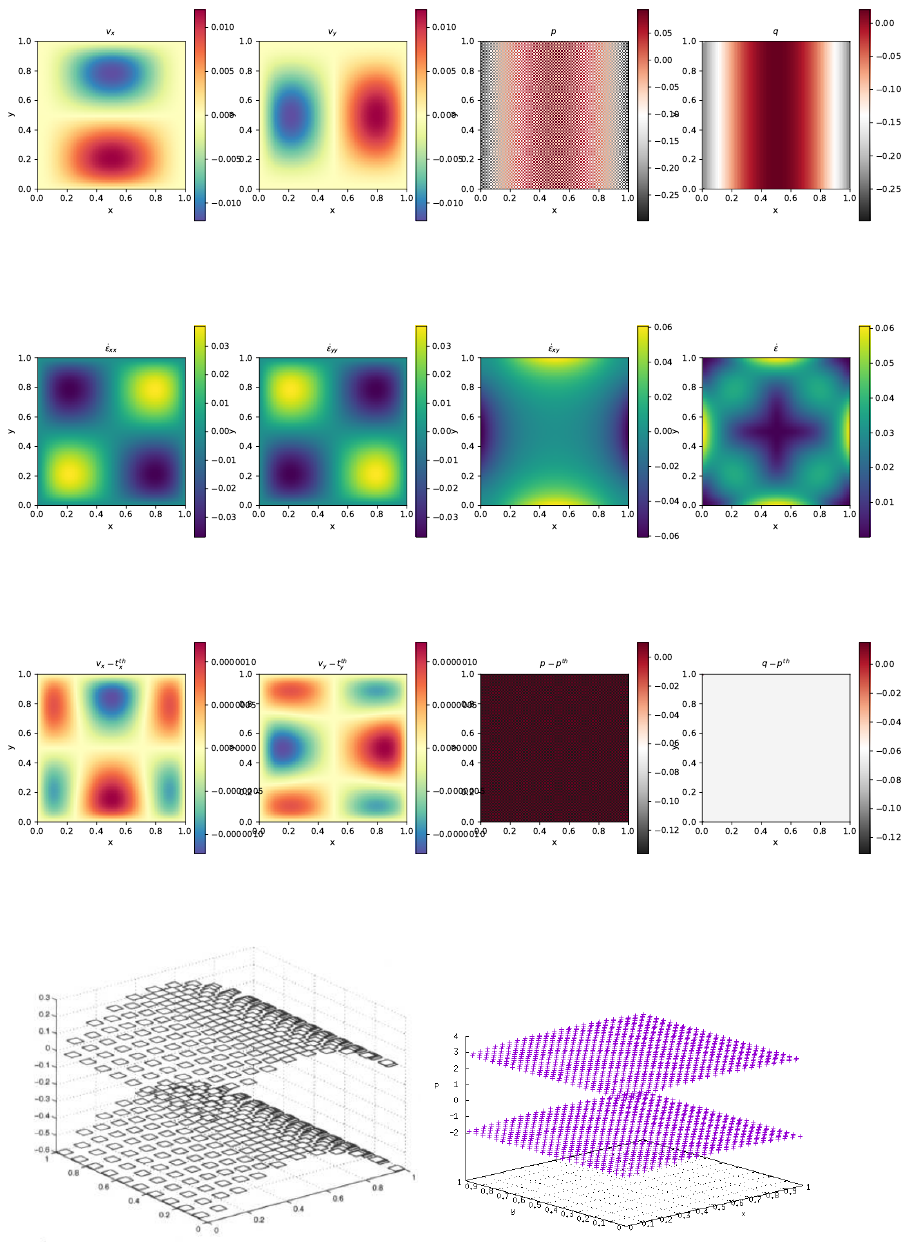
Unlike the results obtained with the penalty formualtion (see Section ??), the pressure showcases a
very strong checkerboard pattern, similar to the one in [27].
Left: pressure solution as shown in [27]; Right: pressure solution obtained with fieldstone.
Rather interestingly, the nodal pressure (obtained with a simple center-to-node algorithm) fails to
recover a correct pressure at the four corners.
83
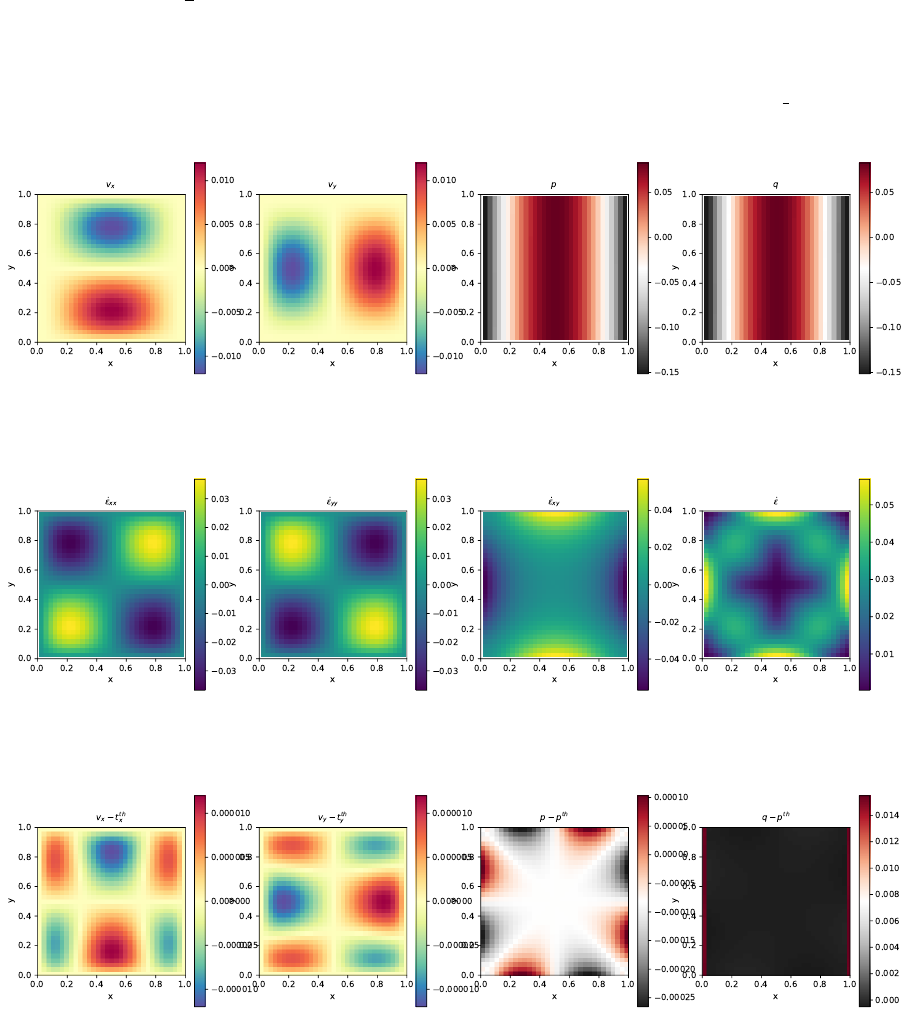
22 fieldstone f15: saddle point problem with Schur comple-
ment approach - benchmark
The details of the numerical setup are presented in Section ??. The main difference resides in the Schur
complement approach to solve the Stokes system, as presented in Section 6.15 (see solver cg). This
iterative solver is very easy to implement once the blocks Kand G, as well as the rhs vectors fand h
have been built.
Rather interestingly the pressure checkerboard modes are not nearly as present as in Section ?? which
uses a full matrix approach.
Looking at the discretisation errors for velocity and pressure, we of course recover the same rates and
values as in the full matrix case.
84
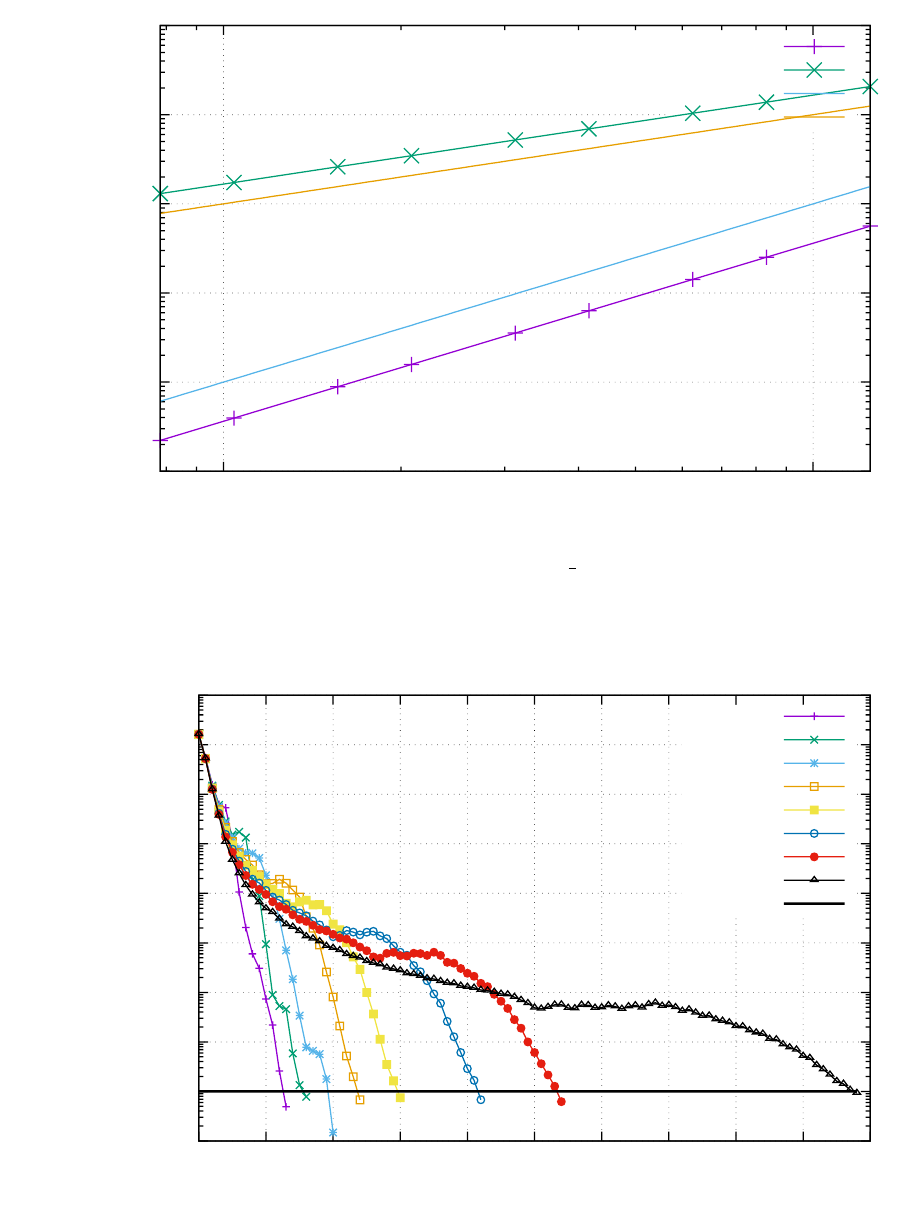
0.000001
0.000010
0.000100
0.001000
0.010000
0.100000
0.01 0.1
error
h
velocity
pressure
x2
x1
Finally, for each experiment the normalised residual (see solver cg) was recorded. We see that all
things equal the resolution has a strong influence on the number of iterations the solver must perform to
reach the required tolerance. This is one of the manifestations of the fact that the Q1×P0element is
not a stable element: the condition number of the matrix increases with resolution. We will see that this
is not the case of stable elements such as Q2×Q1.
0.000000001
0.000000010
0.000000100
0.000001000
0.000010000
0.000100000
0.001000000
0.010000000
0.100000000
1.000000000
0 10 20 30 40 50 60 70 80 90 100
normalised residual
# iteration
8x8
12x12
16x16
24x24
32x32
48x48
64x64
128x128
1e-8
85

features
•Q1×P0element
•incompressible flow
•mixed formulation
•Schur complement approach
•isothermal
•isoviscous
•analytical solution
build S and
have python
compute its
smallest and
largest eigenval-
ues as a func-
tion of resolu-
tion?
build S and
have python
compute its
smallest and
largest eigenval-
ues as a func-
tion of resolu-
tion?
86
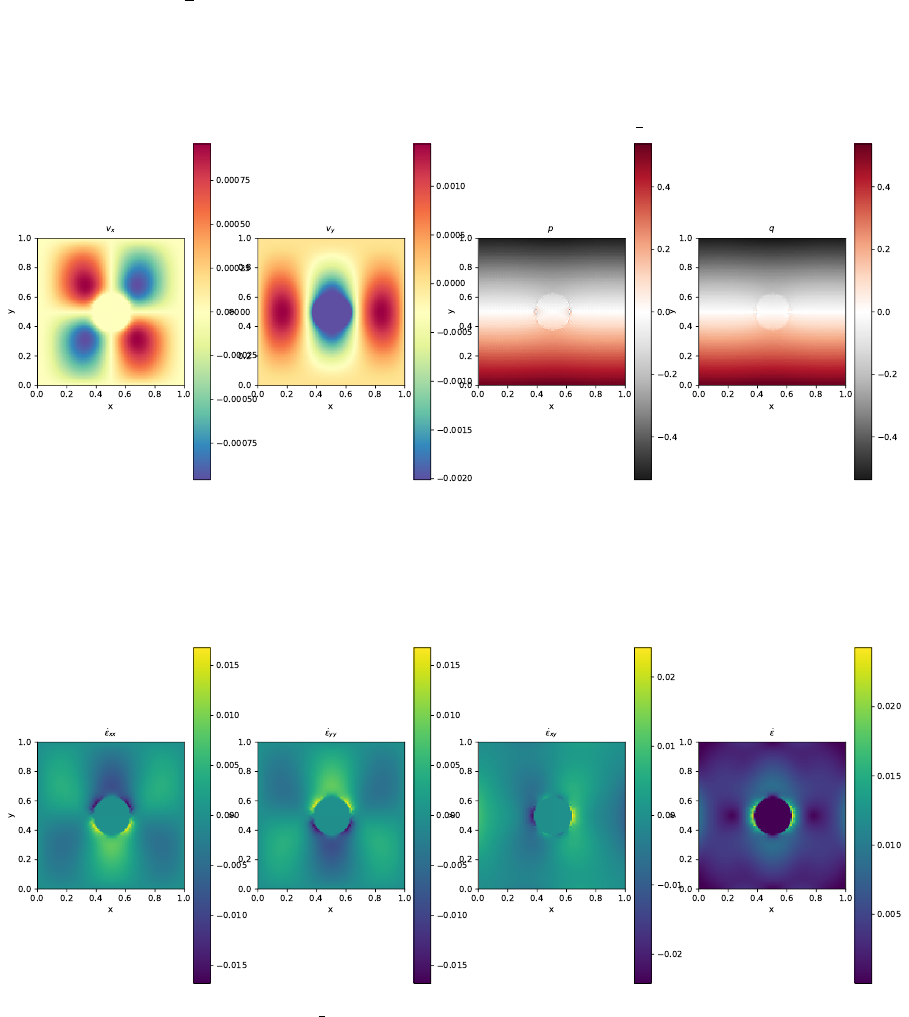
23 fieldstone f16: saddle point problem with Schur comple-
ment approach - Stokes sphere
We are revisiting the 2D Stokes sphere problem, but this time we use the Schur complement approach
to solve the Stokes system, Because there are viscosity contrasts in the domain, it is advisable to use the
Preconditioned Conjugate Gradient as presented in Section 6.15 (see solver pcg).
The normalised residual (see solver pcg) was recorded. We see that all things equal the resolution
has a strong influence on the number of iterations the solver must perform to reach the required tolerance.
However, we see that the use of the preconditioner can substantially reduce the number of iterations inside
the Stokes solver. At resolution 128x128, this number is halved.
87
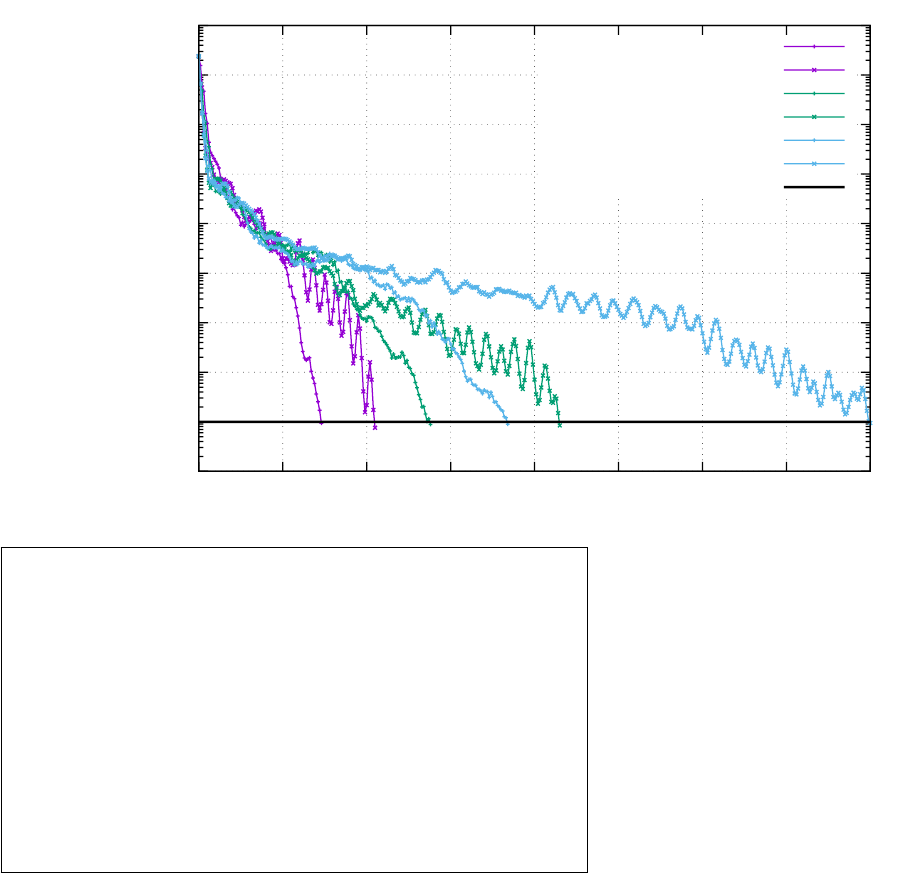
0.000000001
0.000000010
0.000000100
0.000001000
0.000010000
0.000100000
0.001000000
0.010000000
0.100000000
1.000000000
0 50 100 150 200 250 300 350 400
normalised residual
# iteration
32x32 (prec.)
32x32 (no prec.)
64x64 (prec.)
64x64 (no prec.)
128x128 (prec.)
128x128 (no prec.)
1e-8
features
•Q1×P0element
•incompressible flow
•mixed formulation
•Schur complement approach
•isothermal
•non-isoviscous
•Stokes sphere
88

24 fieldstone 17: solving the full saddle point problem in 3D
When using Q1×P0elements, this benchmark fails because of the Dirichlet b.c. on all 6 sides and all
three components. However, as we will see, it does work well with Q2×Q1elements. .
This benchmark begins by postulating a polynomial solution to the 3D Stokes equation [25]:
v=
x+x2+xy +x3y
y+xy +y2+x2y2
−2z−3xz −3yz −5x2yz
(80)
and
p=xyz +x3y3z−5/32 (81)
While it is then trivial to verify that this velocity field is divergence-free, the corresponding body force
of the Stokes equation can be computed by inserting this solution into the momentum equation with a
given viscosity µ(constant or position/velocity/strain rate dependent). The domain is a unit cube and
velocity boundary conditions simply use Eq. (80). Following [14], the viscosity is given by the smoothly
varying function
µ= exp(1 −β(x(1 −x) + y(1 −y) + z(1 −z))) (82)
One can easily show that the ratio of viscosities µ?in the system follows µ?= exp(−3β/4) so that
choosing β= 10 yields µ?'1808 and β= 20 yields µ?'3.269 ×106.
We start from the momentum conservation equation:
−∇p+∇·(2µ˙
) = f
The x-component of this equation writes
fx=−∂p
∂x +∂
∂x (2µ˙xx) + ∂
∂y (2µ˙xy) + ∂
∂z (2µ˙xz ) (83)
=−∂p
∂x + 2µ∂
∂x ˙xx + 2µ∂
∂y ˙xy + 2µ∂
∂z ˙xz + 2 ∂µ
∂x ˙xx + 2 ∂µ
∂y ˙xy + 2 ∂µ
∂z ˙xz (84)
Let us compute all the block separately:
˙xx = 1 + 2x+y+ 3x2y
˙yy = 1 + x+ 2y+ 2x2y
˙zz =−2−3x−3y−5x2y
2˙xy = (x+x3)+(y+ 2xy2) = x+y+ 2xy2+x3
2˙xz = (0) + (−3z−10xyz) = −3z−10xyz
2˙yz = (0) + (−3z−5x2z) = −3z−5x2z
89
In passing, one can verify that ˙xx + ˙yy + ˙zz = 0. We further have
∂
∂x 2 ˙xx = 2(2 + 6xy)
∂
∂y 2 ˙xy = 1 + 4xy
∂
∂z 2 ˙xz =−3−10xy
∂
∂x 2 ˙xy = 1 + 2y2+ 3x2
∂
∂y 2 ˙yy = 2(2 + 2x2)
∂
∂z 2 ˙yz =−3−5x2
∂
∂x 2 ˙xz =−10yz
∂
∂y 2 ˙yz = 0
∂
∂z 2 ˙zz = 2(0)
∂p
∂x =yz + 3x2y3z(85)
∂p
∂y =xz + 3x3y2z(86)
∂p
∂z =xy +x3y3(87)
Pressure normalisation Here again, because Dirichlet boundary conditions are prescribed on all
sides the pressure is known up to an arbitrary constant. This constant can be determined by (arbitrarily)
choosing to normalised the pressure field as follows:
ZΩ
p dΩ = 0 (88)
This is a single constraint associated to a single Lagrange multiplier λand the global Stokes system takes
the form
K G 0
GT0C
0CT0
V
P
λ
In this particular case the constraint matrix Cis a vector and it only acts on the pressure degrees of
freedom because of Eq.(88). Its exact expression is as follows:
ZΩ
p dΩ = X
eZΩe
p dΩ = X
eZΩeX
i
Np
ipidΩ = X
eX
iZΩe
Np
idΩpi=X
eCe·pe
where peis the list of pressure dofs of element e. The elemental constraint vector contains the correspond-
ing pressure basis functions integrated over the element. These elemental constraints are then assembled
into the vector C.
90

24.0.1 Constant viscosity
Choosing β= 0 yields a constant velocity µ(x, y, z) = exp(1) '2.718 (and greatly simplifies the right-
hand side) so that
∂
∂x µ(x, y, z) = 0 (89)
∂
∂y µ(x, y, z) = 0 (90)
∂
∂z µ(x, y, z) = 0 (91)
and
fx=−∂p
∂x + 2µ∂
∂x ˙xx + 2µ∂
∂y ˙xy + 2µ∂
∂z ˙xz
=−(yz + 3x2y3z) + 2(2 + 6xy) + (1 + 4xy)+(−3−10xy)
=−(yz + 3x2y3z) + µ(2 + 6xy)
fy=−∂p
∂y + 2µ∂
∂x ˙xy + 2µ∂
∂y ˙yy + 2µ∂
∂z ˙yz
=−(xz + 3x3y2z) + µ(1 + 2y2+ 3x2) + µ2(2 + 2x2) + µ(−3−5x2)
=−(xz + 3x3y2z) + µ(2 + 2x2+ 2y2)
fz=−∂p
∂z + 2µ∂
∂x ˙xz + 2µ∂
∂y ˙yz + 2µ∂
∂z ˙zz
=−(xy +x3y3) + µ(−10yz)+0+0
=−(xy +x3y3) + µ(−10yz)
Finally
f=−
yz + 3x2y3z
xz + 3x3y2z
xy +x3y3
+µ
2+6xy
2+2x2+ 2y2
−10yz
Note that there seems to be a sign problem with Eq.(26) in [14].
91
0.00001
0.00010
0.00100
0.01000
0.1
error
h
velocity
pressure
x3
x2
24.0.2 Variable viscosity
The spatial derivatives of the viscosity are then given by
∂
∂x µ(x, y, z) = −(1 −2x)βµ(x, y, z)
∂
∂y µ(x, y, z) = −(1 −2y)βµ(x, y, z)
∂
∂z µ(x, y, z) = −(1 −2z)βµ(x, y, z)
92

and thr right-hand side by
f=−
yz + 3x2y3z
xz + 3x3y2z
xy +x3y3
+µ
2+6xy
2+2x2+ 2y2
−10yz
(92)
−(1 −2x)βµ(x, y, z)
2˙xx
2˙xy
2˙xz
−(1 −2y)βµ(x, y, z)
2˙xy
2˙yy
2˙yz
−(1 −2z)βµ(x, y, z)
2˙xz
2˙yz
2˙zz
=−
yz + 3x2y3z
xz + 3x3y2z
xy +x3y3
+µ
2+6xy
2+2x2+ 2y2
−10yz
−(1 −2x)βµ
2+4x+ 2y+ 6x2y
x+y+ 2xy2+x3
−3z−10xyz
−(1 −2y)βµ
x+y+ 2xy2+x3
2+2x+ 4y+ 4x2y
−3z−5x2z
−(1 −2z)βµ
−3z−10xyz
−3z−5x2z
−4−6x−6y−10x2y
Note that at (x, y, z) = (0,0,0), µ= exp(1), and at (x, y, z) = (0.5,0.5,0.5), µ= exp(1 −3β/4) so
that the maximum viscosity ratio is given by
µ?=exp(1 −3β/4)
exp(1) = exp(−3β/4)
By varying βbetween 1 and 22 we can get up to 7 orders of magnitude viscosity difference.
features
•Q1×P0element
•incompressible flow
•saddle point system
•Dirichlet boundary conditions (free-slip)
•direct solver
•isothermal
•non-isoviscous
•3D
•elemental b.c.
•analytical solution
93
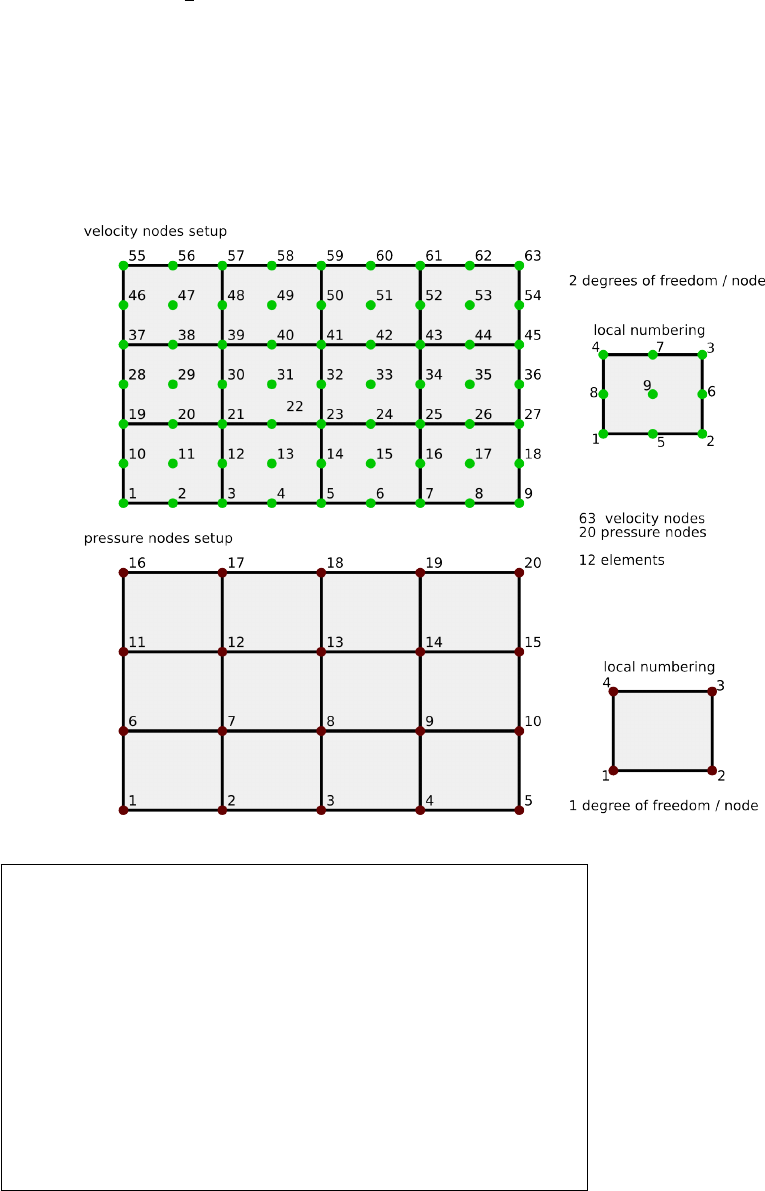
25 fieldstone 18: solving the full saddle point problem with
Q2×Q1elements
The details of the numerical setup are presented in Section ??.
Each element has mV= 9 vertices so in total ndofV×mV= 18 velocity dofs and ndofP∗mP= 4
pressure dofs. The total number of velocity dofs is therefore NfemV =nnp ×ndofV while the total
number of pressure dofs is N femP =nel. The total number of dofs is then N fem =NfemV +NfemP .
As a consequence, matrix Khas size N femV, N femV and matrix Ghas size N femV, N femP . Vector
fis of size NfemV and vector his of size N femP .
renumber all nodes to start at zero!! Also internal numbering does not work here
features
•Q2×Q1element
•incompressible flow
•mixed formulation
•Dirichlet boundary conditions (no-slip)
•isothermal
•isoviscous
•analytical solution
94
0.0000001
0.0000010
0.0000100
0.0001000
0.0010000
0.0100000
0.1
error
h
velocity
pressure
x3
x2
95

26 fieldstone 19: solving the full saddle point problem with
Q3×Q2elements
The details of the numerical setup are presented in Section ??.
Each element has mV= 16 vertices so in total ndofV×mV= 32 velocity dofs and ndofP∗mP= 9
pressure dofs. The total number of velocity dofs is therefore NfemV =nnp ×ndofV while the total
number of pressure dofs is N femP =nel. The total number of dofs is then N fem =NfemV +NfemP .
As a consequence, matrix Khas size N femV, N femV and matrix Ghas size N femV, N femP . Vector
fis of size NfemV and vector his of size N femP .
60===61===62===63===64===65===66===67===68===70
|| || || ||
50 51 52 53 54 55 56 57 58 59
|| || || ||
40 41 42 43 44 45 46 47 48 49
|| || || ||
30===31===32===33===34===35===36===37===38===39
|| || || ||
20 21 22 23 24 25 26 27 28 29
|| || || ||
10 11 12 13 14 15 16 17 18 19
|| || || ||
00===01===02===03===04===05===06===07===08===09
Example of 3x2 mesh. nnx=10, nny=7, nnp=70, nelx=3, nely=2, nel=6
12===13===14===15 06=====07=====08
|| || || || || || ||
08===09===10===11 || || ||
|| || || || 03=====04=====05
04===05===06===07 || || ||
|| || || || || || ||
00===01===02===03 00=====01=====02
Velocity (Q3) Pressure (Q2)
(r,s)_{00}=(-1,-1) (r,s)_{00}=(-1,-1)
(r,s)_{01}=(-1/3,-1) (r,s)_{01}=(0,-1)
(r,s)_{02}=(+1/3,-1) (r,s)_{02}=(+1,-1)
(r,s)_{03}=(+1,-1) (r,s)_{03}=(-1,0)
(r,s)_{04}=(-1,-1/3) (r,s)_{04}=(0,0)
(r,s)_{05}=(-1/3,-1/3) (r,s)_{05}=(+1,0)
(r,s)_{06}=(+1/3,-1/3) (r,s)_{06}=(-1,+1)
(r,s)_{07}=(+1,-1/3) (r,s)_{07}=(0,+1)
(r,s)_{08}=(-1,+1/3) (r,s)_{08}=(+1,+1)
(r,s)_{09}=(-1/3,+1/3)
(r,s)_{10}=(+1/3,+1/3)
(r,s)_{11}=(+1,+1/3)
(r,s)_{12}=(-1,+1)
(r,s)_{13}=(-1/3,+1)
(r,s)_{14}=(+1/3,+1)
(r,s)_{15}=(+1,+1)
Write about 4 point quadrature.
96
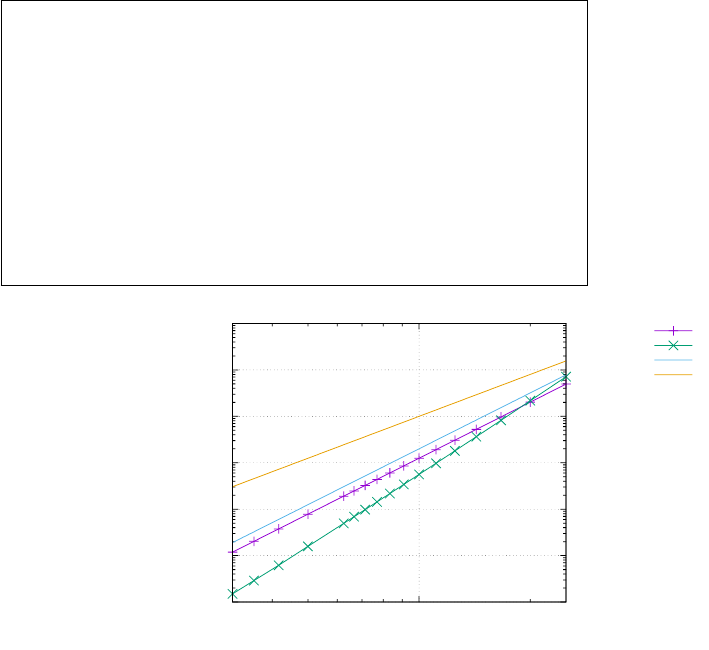
features
•Q3×Q2element
•incompressible flow
•mixed formulation
•isothermal
•isoviscous
•analytical solution
1x10-10
1x10-9
1x10-8
1x10-7
1x10-6
1x10-5
0.0001
0.1
error
h
velocity
pressure
x4
x3
velocity error rate is cubic, pressure superconvergent since the pressure field is quadratic and therefore
lies into the Q2 space.
97
27 fieldstone 20: the Busse benchmark
This three-dimensional benchmark was first proposed by [15]. It has been subsequently presented in
[78, 86, 1, 62, 21, 50]. We here focus on Case 1 of [15]: an isoviscous bimodal convection experiment at
Ra = 3 ×105.
The domain is of size a×b×hwith a= 1.0079h,b= 0.6283hwith h= 2700km. It is filled
with a Newtonian fluid characterised by ρ0= 3300kg.m−3,α= 10−5K−1,µ= 8.0198 ×1023Pa.s,
k= 3.564W.m−1.K−1,cp= 1080J.K−1.kg−1. The gravity vector is set to g= (0,0,−10)T. The
temperature is imposed at the bottom (T= 3700◦C) and at the top (T= 0◦C).
The various measurements presented in [15] are listed hereafter:
•The Nusselt number N u computed at the top surface following Eq. (62):
Nu =LzRRz=Lz
∂T
∂y dxdy
RRz=0 T dxdy
•the root mean square velocity vrms and the temperature mean square velocity Trms
•The vertical velocity wand temperature Tat points x1= (0,0, Lz/2), x2= (Lx,0, Lz/2), x3=
(0, Ly, Lz/2) and x4= (Lx, Ly, Lz/2);
•the vertical component of the heat flux Qat the top surface at all four corners.
The values plotted hereunder are adimensionalised by means of a reference temperature (3700K), a
reference lengthscale 2700km, and a reference time L2
z/κ.
0.0001
0.0002
0.0003
0.0004
0.0005
0.0006
0.0007
0.0008
0.0009
0 2x108 4x108 6x108 8x108 1x109 1.2x109
1.4x109
1.6x109
vrms
time/year
2115
2116
2117
2118
2119
2120
2121
2122
2123
2124
0 2x108 4x108 6x108 8x108 1x109 1.2x109
1.4x109
1.6x109
<T>
time/year
98
-0.002
-0.0015
-0.001
-0.0005
0
0.0005
0.001
0.0015
0.002
0 2x108 4x108 6x108 8x108 1x109 1.2x109
1.4x109
1.6x109
w at Lz/2
time/year
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
1x108 1.5x108 2x108 2.5x108 3x108 3.5x108
heat flux
time/year
features
•Q1×P0element
•incompressible flow
•mixed formulation
•Dirichlet boundary conditions (free-slip)
•direct solver
•isothermal
•non-isoviscous
•3D
•elemental b.c.
•buoyancy driven
ToDo: look at energy conservation. run to steady state and make sure the expected values are
retrieved.
99

28 fieldstone 21: The non-conforming Q1×P0element
features
•Non-conforming Q1×P0element
•incompressible flow
•mixed formulation
•isothermal
•non-isoviscous
•analytical solution
•pressure smoothing
try Q1 mapping instead of isoparametric.
100

29 fieldstone 22: The stabilised Q1×Q1element
The details of the numerical setup are presented in Section ??.
101

30 fieldstone 23: compressible flow (1) - analytical benchmark
This work is part of the MSc thesis of T. Weir (2018).
We first start with an isothermal Stokes flow, so that we disregard the heat transport equation and
the equations we wish to solve are simply:
−∇ · 2η˙ε(v)−1
3(∇ · v)1+∇p=ρgin Ω,(93)
∇ · (ρv) = 0 in Ω (94)
The second equation can be rewritten ∇ · (ρv) = ρ∇ · v+v·∇ρ= 0 or,
∇ · v+1
ρv·∇ρ= 0
Note that this presupposes that the density is not zero anywhere in the domain.
We use a mixed formulation and therefore keep both velocity and pressure as unknowns. We end up
having to solve the following system:
K G
GT+Z0·V
P=f
hor,A·X=rhs
Where Kis the stiffness matrix, Gis the discrete gradient operator, GTis the discrete divergence operator,
Vthe velocity vector, Pthe pressure vector. Note that the term ZVderives from term v·∇ρin the
continuity equation.
Each block K,G,Zand vectors fand hare built separately in the code and assembled into the
matrix Aand vector rhs afterwards. Aand rhs are then passed to the solver. We will see later that
there are alternatives to solve this approach which do not require to build the full Stokes matrix A.
Remark: the term ZVis often put in the rhs (i.e. added to h) so that the matrix Aretains the same
structure as in the incompressible case. This is indeed how it is implemented in ASPECT. This however
requires more work since the rhs depends on the solution and some form of iterations is needed.
In the case of a compressible flow the strain rate tensor and the deviatoric strain rate tensor are no
more equal (since ∇·v6= 0). The deviatoric strainrate tensor is given by8
˙
d(v) = ˙
(v)−1
3T r(˙
)1=˙
(v)−1
3(∇·v)1
In that case:
˙d
xx =∂u
∂x −1
3∂u
∂x +∂v
∂y =2
3
∂u
∂x −1
3
∂v
∂y (95)
˙d
yy =∂v
∂y −1
3∂u
∂x +∂v
∂y =−1
3
∂u
∂x +2
3
∂v
∂y (96)
2˙d
xy =∂u
∂y +∂v
∂x (97)
and then
˙
d(v) =
2
3
∂u
∂x −1
3
∂v
∂y
1
2
∂u
∂y +1
2
∂v
∂x
1
2
∂u
∂y +1
2
∂v
∂x −1
3
∂u
∂x +2
3
∂v
∂y
From τ = 2ηdwe arrive at:
τxx
τyy
τxy
= 2η
˙d
xx
˙d
yy
˙d
xy
= 2η
2/3−1/3 0
−1/3 2/3 0
0 0 1/2
·
∂u
∂x
∂v
∂y
∂u
∂y +∂v
∂x
=η
4/3−2/3 0
−2/3 4/3 0
0 0 1
·
∂u
∂x
∂v
∂y
∂u
∂y +∂v
∂x
or,
τ =CηBV
8See the ASPECT manual for a justification of the 3 value in the denominator in 2D and 3D.
102
In order to test our implementation we have created a few manufactured solutions:
•benchmark #1 (ibench=1)): Starting from a density profile of:
ρ(x, y) = xy (98)
We derive a velocity given by:
vx(x, y) = Cx
x, vy(x, y) = Cy
y(99)
With gx(x, y) = 1
xand gy(x, y) = 1
y, this leads us to a pressure profile:
p=−η4Cx
3x2+4Cy
3y2+xy +C0(100)
This gives us a strain rate:
˙xx =−Cx
x2˙yy =−Cy
y2˙xy = 0
In what follows, we choose η= 1 and Cx=Cy= 1 and for a unit square domain [1 : 2] ×[1 : 2] we
compute C0so that the pressure is normalised to zero over the whole domain and obtain C0=−1.
•benchmark #2 (ibench=2): Starting from a density profile of:
ρ= cos(x) cos(y) (101)
We derive a velocity given by:
vx=Cx
cos(x), vy=Cy
cos(y)(102)
With gx=1
cos(y)and gy=1
cos(x), this leads us to a pressure profile:
p=η 4Cxsin(x)
3 cos2(x)+4Cysin(y)
3 cos2(y)!+ (sin(x) + sin(y)) + C0(103)
˙xx =Cx
sin(x)
cos2(x)˙yy =Cy
sin(y)
cos2(y)˙xy = 0
We choose η= 1 and Cx=Cy= 1. The domain is the unit square [0 : 1] ×[0 : 1] and we obtain C0
as before and obtain
C0= 2 −2 cos(1) + 8/3( 1
cos(1) −1) '3.18823730
(thank you WolframAlpha)
•benchmark #3 (ibench=3)
•benchmark #4 (ibench=4)
•benchmark #5 (ibench=5)
features
•Q1×P0element
•incompressible flow
•mixed formulation
•Dirichlet boundary conditions (no-slip)
•isothermal
•isoviscous
•analytical solution
•pressure smoothing
103
ToDo:
•pbs with odd vs even number of elements
•q is ’fine’ everywhere except in the corners - revisit pressure smoothing paper?
•redo A v d Berg benchmark (see Tom Weir thesis)
104

31 fieldstone 24: compressible flow (2) - convection box
This work is part of the MSc thesis of T. Weir (2018).
31.1 The physics
Let us start with some thermodynamics. Every material has an equation of state. The equilibrium
thermodynamic state of any material can be constrained if any two state variables are specified. Examples
of state variables include the pressure pand specific volume ν= 1/ρ, as well as the temperature T.
After linearisation, the density depends on temperature and pressure as follows:
ρ(T, p) = ρ0((1 −α(T−T0) + βTp)
where αis the coefficient of thermal expansion, also called thermal expansivity:
α=−1
ρ∂ρ
∂T p
αis the percentage increase in volume of a material per degree of temperature increase; the subscript p
means that the pressure is held fixed.
βTis the isothermal compressibility of the fluid, which is given by
βT=1
K=1
ρ∂ρ
∂P T
with Kthe bulk modulus. Values of βT= 10−12 −10−11 Pa−1are reasonable for Earth’s mantle, with
values decreasing by about a factor of 5 between the shallow lithosphere and core-mantle boundary. This
is the percentage increase in density per unit change in pressure at constant temperature. Both the
coefficient of thermal expansion and the isothermal compressibility can be obtained from the equation of
state.
The full set of equations we wish to solve is given by
−∇ · 2η˙
d(v)+∇p=ρ0((1 −α(T−T0) + βTp)gin Ω (104)
∇ · v+1
ρv·∇ρ= 0 in Ω (105)
ρCp∂T
∂t +v· ∇T−∇·k∇T=ρH + 2η˙
d:˙
d+αT ∂p
∂t +v· ∇pin Ω,(106)
Note that this presupposes that the density is not zero anywhere in the domain.
31.2 The numerics
We use a mixed formulation and therefore keep both velocity and pressure as unknowns. We end up
having to solve the following system:
K G +W
GT+Z0·V
P=f
hor,A·X=rhs
Where Kis the stiffness matrix, Gis the discrete gradient operator, GTis the discrete divergence operator,
Vthe velocity vector, Pthe pressure vector. Note that the term ZVderives from term v·∇ρin the
continuity equation.
As perfectly explained in the step 32 of deal.ii9, we need to scale the Gterm since it is many orders
of magnitude smaller than K, which introduces large inaccuracies in the solving process to the point that
the solution is nonsensical. This scaling coefficient is η/L. After building the Gblock, it is then scaled
as follows: G0=η
LGso that we now solve
9https://www.dealii.org/9.0.0/doxygen/deal.II/step 32.html
105

K G0+W
G0T+Z0·V
P0=f
h
After the solve phase, we recover the real pressure with P=η
LP0.
adapt notes since I should scale Wand Ztoo.hshould be caled too !!!!!!!!!!!!!!!
Each block K,G,Zand vectors fand hare built separately in the code and assembled into the
matrix Aand vector rhs afterwards. Aand rhs are then passed to the solver. We will see later that
there are alternatives to solve this approach which do not require to build the full Stokes matrix A.
Remark 1: the terms ZVand WPare often put in the rhs (i.e. added to h) so that the matrix
Aretains the same structure as in the incompressible case. This is indeed how it is implemented in
ASPECT, see also appendix A of [52]. This however requires more work since the rhs depends on the
solution and some form of iterations is needed.
Remark 2: Very often the adiabatic heating term αT (v· ∇p) is simplified as follows: If you assume
the vertical component of the gradient of the dynamic pressure to be small compared to the gradient of
the total pressure (in other words, the gradient is dominated by the gradient of the hydrostatic pressure),
then −ρg'∇pand then αT (v· ∇p)' −αρT v·g. We will however not be using this approximation in
what follows.
We have already established that
τ =CηBV
The following measurements are carried out:
•The root mean square velocity (vrms):
vrms =s1
VZV
v2dV
•The average temperature (Tavrg):
< T >=1
VZV
T dV
•The total mass (mass):
M=ZV
ρdV
•The Nusselt number (Nu):
Nu =−1
Lx
1
∆TZLx
0
∂T (x, y =Ly)
∂y dx
•The kinetic energy (EK):
EK=ZV
1
2ρv2dV
•The work done against gravity
< W >=−ZV
ρgyvydV
•The total viscous dissipation (visc diss)
<Φ>=ZΦdV =1
VZ2η˙
ε:˙
εdV
•The gravitational potential energy (EG)
EG=ZV
ρgy(Ly−y)dV
106

•The internal thermal energy (ET)
ET=ZV
ρ(0)CpT dV
Remark 3: Measuring the total mass can be misleading: indeed because ρ=ρ0(1 −αT ), then
measuring the total mass amounts to measuring a constant minus the volume-integrated tempera-
ture, and there is no reason why the latter should be zero, so that there is no reason why the total
mass should be zero...!
31.3 The experimental setup
The setup is as follows: the domain is Lx =Ly = 3000km. Free slip boundary conditions are imposed
on all four sides. The initial temperature is given by:
T(x, y) = Ly−y
Ly −0.01 cos(πx
Lx
) sin( πy
Ly )∆T+Tsurf
with ∆T= 4000K, Tsurf =T0= 273.15K. The temperature is set to ∆T+Tsurf at the bottom and
Tsurf at the top. We also set k= 3, Cp= 1250, |g|= 10, ρ0= 3000 and we keep the Rayleigh number
Ra and dissipation number Di as input parameters:
Ra =αg∆T L3ρ2
0Cp
ηk Di =αgL
Cp
From the second equation we get α=DiCp
gL , which we can insert in the first one:
Ra =DiC2
p∆T L2ρ2
0
ηk or, η =DiC2
p∆T L2ρ2
0
Ra k
For instance, for Ra = 104and Di = 0.75, we obtain α'3·10−5and η'1025 which are quite reasonable
values.
31.4 Scaling
Following [48], we non-dimensionalize the equations using the reference values for density ρr, thermal
expansivity αr, temperature contrast ∆Tr(refTemp), thermal conductivity kr, heat capacity Cp, depth
of the fluid layer Land viscosity ηr. The non-dimensionalization for velocity, ur, pressure prand time,
trbecome
ur=kr
ρrCpL(refvel)
pr=ηrkr
ρrCpL2(refpress)
tr=ρrCpL2
kr
(reftime)
In the case of the setup described hereabove, and when choosing Ra = 104and Di = 0.5, we get:
alphaT 2.083333e-05
eta 8.437500e+24
reftime 1.125000e+19
refvel 2.666667e-13
refPress 7.500000e+05
107

31.5 Conservation of energy 1
31.5.1 under BA and EBA approximations
Following [52], we take the dot product of the momentum equation with the velocity vand integrate over
the whole volume10:ZV
[−∇ · τ+∇p]·vdV =ZV
ρg·vdV
or,
−ZV
(∇ · τ)·vdV +ZV
∇p·vdV =ZV
ρg·vdV
Let us look at each block separately:
−ZV
(∇ · τ)·vdV =−ZS
τ v ·n
|{z}
=0 (b.c.)
dS +ZV
τ:∇vdV =ZV
τ:˙
εdV =ZV
ΦdV
which is the volume integral of the shear heating. Then,
ZV
∇p·vdV =ZS
pv·n
|{z}
=0 (b.c.)
dS −ZV
∇·v
|{z}
=0 (incomp.)
pdV = 0
which is then zero in the case of an incompressible flow. And finally
ZV
ρg·vdV =W
which is the work against gravity.
Conclusion for an incompressible fluid: we should have
ZV
ΦdV =ZV
ρg·vdV (107)
This formula is hugely problematic: indeed, the term ρin the rhs is the full density. We know that to the
value of ρ0corresponds a lithostatic pressure gradient pL=ρ0gy. In this case one can write ρ=ρ0+ρ0
and p=pL+p0so that we also have
ZV
[−∇ · τ+∇p0]·vdV =ZV
ρ0g·vdV
which will ultimately yield
ZV
ΦdV =ZV
ρ0g·vdV =ZV
(ρ−ρ0)g·vdV (108)
Obviously Eqs.(107) and (108) cannot be true at the same time. The problem comes from the nature
of the (E)BA approximation: ρ=ρ0in the mass conservation equation but it is not constant in the
momentum conservation equation, which is of course inconsistent. Since the mass conservation equation
is ∇·v= 0 under this approximation then the term RV∇p·vdV is always zero for any pressure (full
pressure p, or overpressure p−pL), hence the paradox. This paradox will be lifted when a consistent set
of equations will be used (compressible formulation). On a practical note, Eqs.(107) is not verified by
the code, while (108) is.
In the end: ZV
ΦdV
| {z }
visc diss
=ZV
(ρ−ρ0)g·vdV
| {z }
work grav
(109)
10Check: this is akin to looking at the power, force*velocity, says Arie
108
31.5.2 under no approximation at all
ZV
∇p·vdV =ZS
pv·n
|{z}
=0 (b.c.)
dS −ZV
∇·vpdV = 0 (110)
=ZV
1
ρv·∇ρ pdV = 0 (111)
(112)
ToDo:see section 3 of [52] where this is carried out with the Adams-Williamson eos.
31.6 Conservation of energy 2
Also, following the Reynold’s transport theorem [57],p210, we have for a property A(per unit mass)
d
dt ZV
AρdV =ZV
∂
∂t (Aρ)dV +ZS
Aρv·ndS
Let us apply to this to A=CpTand compute the time derivative of the internal energy:
d
dt ZV
ρCpT dV =ZV
∂
∂t (ρCpT)dV +ZS
Aρ v·n
|{z}
=0 (b.c.)
dS =ZV
CpT∂ρ
∂t dV
| {z }
I
+ZV
ρCp
∂T
∂t dV
| {z }
II
(113)
In order to expand I, the mass conservation equation will be used, while the heat transport equation
will be used for II:
I=ZV
CpT∂ρ
∂t dV =−ZV
CpT∇·(ρv)dV =−ZV
CpT ρ v·n
|{z}
=0 (b.c.)
dS +ZV
ρCp∇T·vdV (114)
II =ZV
ρCp
∂T
∂t dV =ZV−ρCpv·∇T+∇·k∇T+ρH +Φ+αT ∂p
∂t +v·∇pdV (115)
=ZV−ρCpv·∇T+ρH +Φ+αT ∂p
∂t +v·∇pdV +ZV
∇·k∇T dV(116)
=ZV−ρCpv·∇T+ρH +Φ+αT ∂p
∂t +v·∇pdV +ZS
k∇T·ndS(117)
=ZV−ρCpv·∇T+ρH +Φ+αT ∂p
∂t +v·∇pdV −ZS
q·ndS (118)
Finally:
I+II =d
dt ZV
ρCpT dV
| {z }
ET
=ZVρH +Φ+αT ∂p
∂t +v·∇pdV −ZS
q·ndS (119)
=ZV
ρHdV +ZV
ΦdV
| {z }
visc diss
+ZV
αT ∂p
∂t dV
| {z }
extra
+ZV
αT v·∇pdV
| {z }
adiab heating
−ZS
q·ndS
| {z }
heatflux boundary
(120)
This was of course needlessly complicated as the term ∂ρ/∂t is always taken to be zero, so that I= 0
automatically. The mass conservation equation is then simply ∇·(ρv) = 0. Then it follows that
0 = ZV
CpT∇·(ρv)dV =−ZV
CpT ρ v·n
|{z}
=0 (b.c.)
dS +ZV
ρCp∇T·vdV (121)
=ZV
ρCp∇T·vdV (122)
so that the same term in Eq.(118) vanishes too, and then Eq.(120) is always valid, although one should
be careful when computing ETin the BA and EBA cases as it should use ρ0and not ρ.
109
31.7 The problem of the onset of convection
[wiki] In geophysics, the Rayleigh number is of fundamental importance: it indicates the presence and
strength of convection within a fluid body such as the Earth’s mantle. The mantle is a solid that behaves
as a fluid over geological time scales.
The Rayleigh number essentially is an indicator of the type of heat transport mechanism. At low
Rayleigh numbers conduction processes dominate over convection ones. At high Rayleigh numbers it is
the other way around. There is a so-called critical value of the number with delineates the transition
from one regime to the other.
This problem has been studied and approached both theoretically and numerically [87, e.g.] and it
was found that the critical Rayleigh number Racis
Rac= (27/4)π4'657.5
in setups similar to ours.
VERY BIG PROBLEM
The temperature setup is built as follows: Tsurf is prescribed at the top, Tsurf + ∆Tis prescribed
at the bottom. The initial temperature profile is linear between these two values. In the case of BA, the
actual value of Tsurf is of no consequence. However, for the EBA the full temperature is present in the
adiabatic heating term on the rhs of the hte, and the value of Tsurf will therefore influence the solution
greatly. This is very problematic as there is no real way to arrive at the surface temperature from the
King paper. On top of this, the density uses a reference temperature T0which too will influence the
solution without being present in the controlling Ra and Di numbers!!
In light thereof, it will be very difficult to recover the values of King et al for EBA!
features
•Q1×P0element
•compressible flow
•mixed formulation
•Dirichlet boundary conditions (no-slip)
•isoviscous
•analytical solution
•pressure smoothing
Relevant literature: [8, 45, 79, 52, 48, 53, 54, 41]
ToDo:
•heat flux is at the moment elemental, so Nusselt and heat flux on boundaries measurements not as
accurate as could be.
110
31.8 results - BA - Ra = 104
These results were obtained with a 64x64 resolution, and CFL number of 1. Steady state was reached
after about 1250 timesteps.
(a)
0
1x10-6
2x10-6
3x10-6
4x10-6
5x10-6
6x10-6
7x10-6
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
EK
time (Myr)
(b)
7.67188x1022
7.67188x1022
7.67188x1022
7.67188x1022
7.67188x1022
7.67188x1022
7.67188x1022
7.67188x1022
7.67188x1022
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
ET
time (Myr)
(c)
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
EG
time (Myr)
(d)
2273.15
2273.15
2273.15
2273.15
2273.15
2273.15
2273.15
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
<T>
time (Myr)
(e)
0
500
1000
1500
2000
2500
3000
3500
4000
4500
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
Temperature
time (Myr)
min(T)
max(T)
(f)
-0.0015
-0.001
-0.0005
0
0.0005
0.001
0.0015
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
velocity
time (Myr)
min(u)
max(u)
min(v)
max(v)
(g)
-80000
-70000
-60000
-50000
-40000
-30000
-20000
-10000
0
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
adiabatic heating
time (Myr)
(h)
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
viscous dissipation
time (Myr)
(i)
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
work against gravity
time (Myr)
(j)
-5x10-8
-4x10-8
-3x10-8
-2x10-8
-1x10-8
0
1x10-8
2x10-8
3x10-8
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
heat flux
time (Myr)
(k)
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
vrms (cm/yr)
time (Myr)
(l)
0
1
2
3
4
5
6
7
8
0 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000
Nu
time (Myr)
4.88
(l)
-6x10-7
-4x10-7
-2x10-7
0
2x10-7
4x10-7
6x10-7
8x10-7
0 1x1010
2x1010
3x1010
4x1010
5x1010
6x1010
7x1010
8x1010
9x1010
1x1011
time (Myr)
0
HF
dETdt
(m)
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
0 1x1010
2x1010
3x1010
4x1010
5x1010
6x1010
7x1010
8x1010
9x1010
1x1011
time (Myr)
VD
WG
AH: adiabatic heating, VD: viscous dissipation, HF: heat flux, WG: work against gravity
Eq.(120) is verified by (l) and Eq.(109) is verified by (m).
112
(a) (b) (c)
(d) (e) (f)
(g) (h) (i)
113
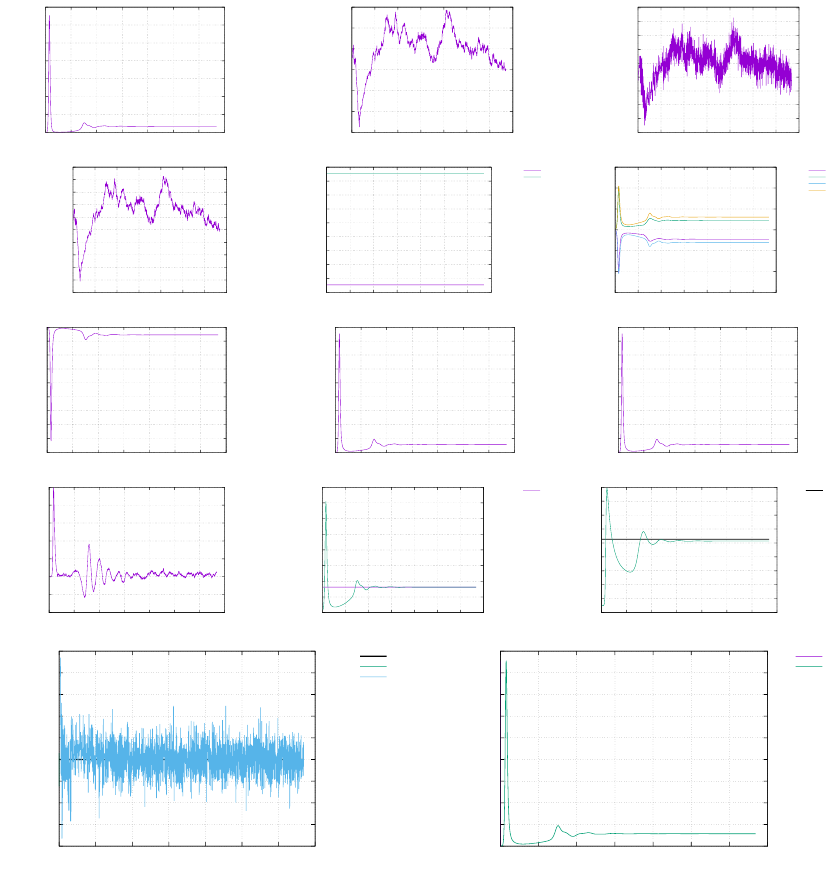
31.9 results - BA - Ra = 105
These results were obtained with a 64x64 resolution, and CFL number of 1. Steady state was reached
after about 1250 timesteps.
(a)
0
0.0001
0.0002
0.0003
0.0004
0.0005
0.0006
0.0007
0 5000 10000 15000 20000 25000 30000 35000
EK
time (Myr)
(b)
7.67188x1022
7.67188x1022
7.67188x1022
7.67188x1022
7.67188x1022
7.67188x1022
7.67188x1022
0 5000 10000 15000 20000 25000 30000 35000
ET
time (Myr)
(c)
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
-7.73687x1023
0 5000 10000 15000 20000 25000 30000 35000
EG
time (Myr)
(d)
2273.149999999
2273.149999999
2273.149999999
2273.150000000
2273.150000000
2273.150000000
2273.150000000
2273.150000000
2273.150000001
2273.150000001
2273.150000001
0 5000 10000 15000 20000 25000 30000 35000
<T>
time (Myr)
(e)
0
500
1000
1500
2000
2500
3000
3500
4000
4500
0 5000 10000 15000 20000 25000 30000 35000
Temperature
time (Myr)
min(T)
max(T)
(f)
-0.015
-0.01
-0.005
0
0.005
0.01
0.015
0 5000 10000 15000 20000 25000 30000 35000
velocity
time (Myr)
min(u)
max(u)
min(v)
max(v)
(g)
-900000
-800000
-700000
-600000
-500000
-400000
-300000
-200000
-100000
0
0 5000 10000 15000 20000 25000 30000 35000
adiabatic heating
time (Myr)
(h)
0
100000
200000
300000
400000
500000
600000
700000
800000
900000
0 5000 10000 15000 20000 25000 30000 35000
viscous dissipation
time (Myr)
(i)
0
100000
200000
300000
400000
500000
600000
700000
800000
900000
0 5000 10000 15000 20000 25000 30000 35000
work against gravity
time (Myr)
(j)
-1x10-6
-5x10-7
0
5x10-7
1x10-6
1.5x10-6
2x10-6
2.5x10-6
0 5000 10000 15000 20000 25000 30000 35000
heat flux
time (Myr)
(k)
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0 5000 10000 15000 20000 25000 30000 35000
vrms (cm/yr)
time (Myr)
193.2150
(l)
0
2
4
6
8
10
12
14
16
18
0 5000 10000 15000 20000 25000 30000 35000
Nu
time (Myr)
10.53
(l)
-8x10-6
-6x10-6
-4x10-6
-2x10-6
0
2x10-6
4x10-6
6x10-6
8x10-6
1x10-5
0 5x109 1x1010
1.5x1010
2x1010
2.5x1010
3x1010
3.5x1010
time (Myr)
0
HF
dETdt
(m)
0
100000
200000
300000
400000
500000
600000
700000
800000
900000
0 5x109 1x1010 1.5x1010 2x1010 2.5x1010 3x1010 3.5x1010
time (Myr)
VD
WG
AH: adiabatic heating, VD: viscous dissipation, HF: heat flux, WG: work against gravity
Eq.(120) is verified by (l) and Eq.(109) is verified by (m).
114
31.10 results - BA - Ra = 106
115
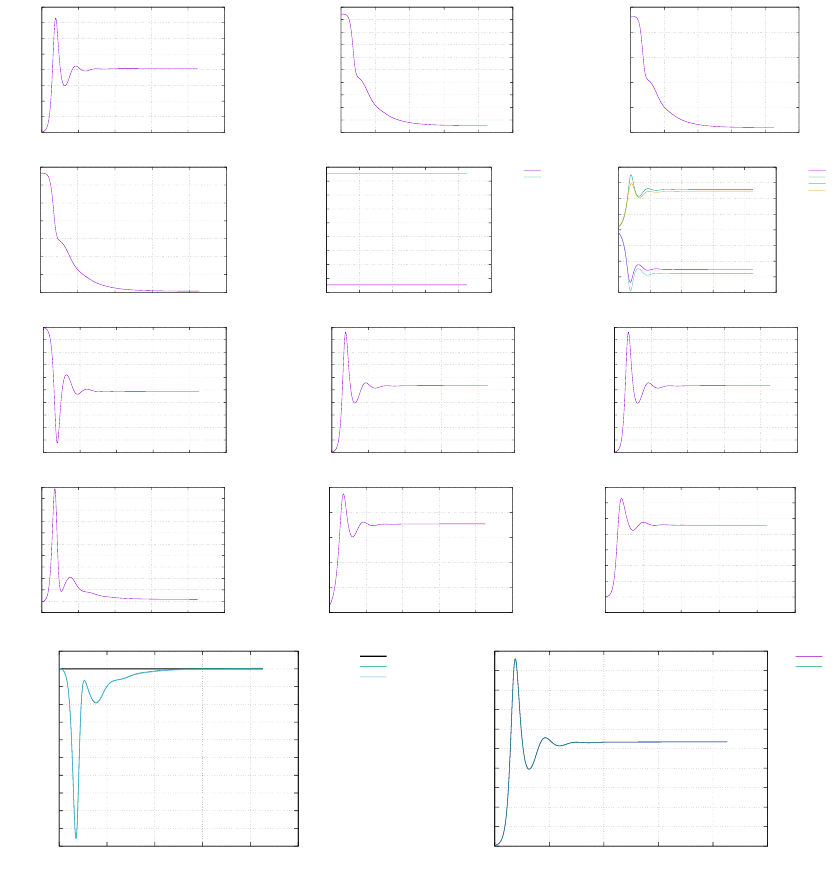
31.11 results - EBA - Ra = 104
These results were obtained with a 64x64 resolution, and CFL number of 1. Steady state was reached
after about 2500 timesteps
(a)
0
1x10-7
2x10-7
3x10-7
4x10-7
5x10-7
6x10-7
7x10-7
8x10-7
0 50000 100000 150000 200000 250000
EK
time (Myr)
(b)
7.2x1022
7.25x1022
7.3x1022
7.35x1022
7.4x1022
7.45x1022
7.5x1022
7.55x1022
7.6x1022
7.65x1022
7.7x1022
0 50000 100000 150000 200000 250000
ET
time (Myr)
(c)
-7.76x1023
-7.755x1023
-7.75x1023
-7.745x1023
-7.74x1023
-7.735x1023
0 50000 100000 150000 200000 250000
EG
time (Myr)
(d)
2140
2160
2180
2200
2220
2240
2260
2280
0 50000 100000 150000 200000 250000
<T>
time (Myr)
(e)
0
500
1000
1500
2000
2500
3000
3500
4000
4500
0 50000 100000 150000 200000 250000
Temperature
time (Myr)
min(T)
max(T)
(f)
-0.0004
-0.0003
-0.0002
-0.0001
0
0.0001
0.0002
0.0003
0.0004
0 50000 100000 150000 200000 250000
velocity
time (Myr)
min(u)
max(u)
min(v)
max(v)
(g)
-10000
-9000
-8000
-7000
-6000
-5000
-4000
-3000
-2000
-1000
0
0 50000 100000 150000 200000 250000
adiabatic heating
time (Myr)
(h)
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
0 50000 100000 150000 200000 250000
viscous dissipation
time (Myr)
(i)
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
0 50000 100000 150000 200000 250000
work against gravity
time (Myr)
(j)
-1000
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
0 50000 100000 150000 200000 250000
heat flux
time (Myr)
(k)
0
0.005
0.01
0.015
0.02
0.025
0 50000 100000 150000 200000 250000
vrms (cm/yr)
time (Myr)
(l)
0.8
1
1.2
1.4
1.6
1.8
2
2.2
2.4
0 50000 100000 150000 200000 250000
Nu
time (Myr)
(l)
-10000
-9000
-8000
-7000
-6000
-5000
-4000
-3000
-2000
-1000
0
1000
0 50000 100000 150000 200000 250000
time (Myr)
0
AH+VD+HF
dETdt
(m)
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
0 50000 100000 150000 200000 250000
time (Myr)
VD
WG
AH: adiabatic heating, VD: viscous dissipation, HF: heat flux, WG: work against gravity
Eq.(120) is verified by (l) and Eq.(109) is verified by (m).
116
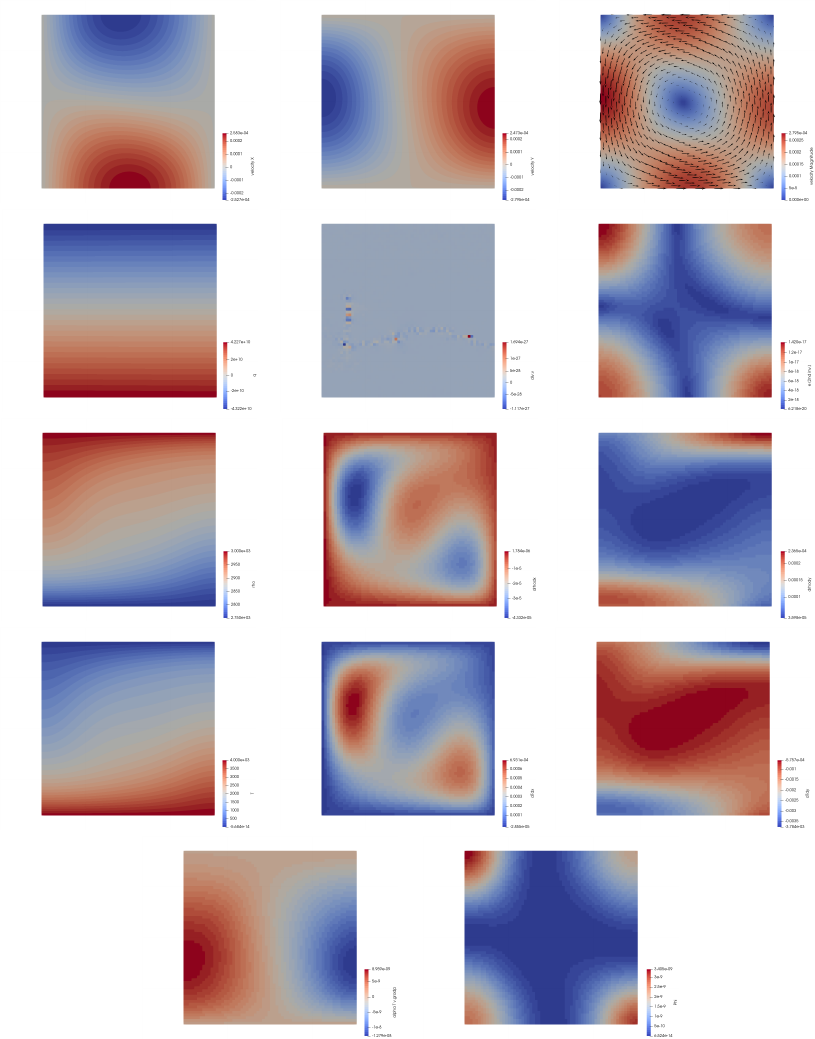
a) b) c)
d) e) f)
g) h) i)
j) k) l)
m) n)
117
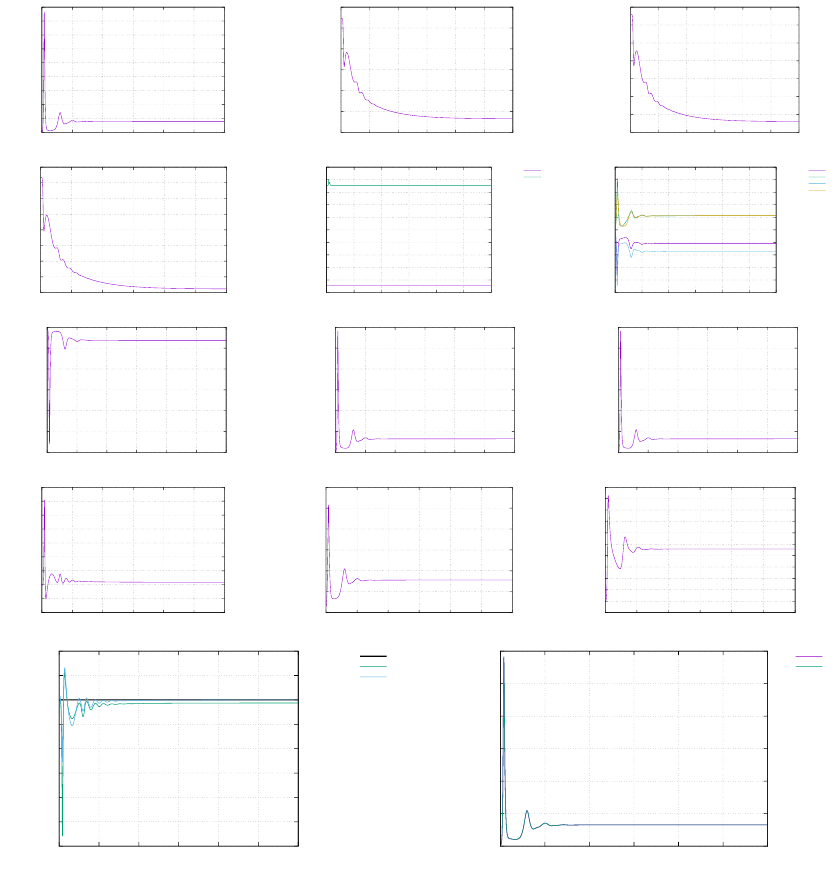
31.12 results - EBA - Ra = 105
These results were obtained with a 64x64 resolution, and CFL number of 1. Simulation was stopped after
about 4300 timesteps.
(a)
0
1x10-5
2x10-5
3x10-5
4x10-5
5x10-5
6x10-5
7x10-5
8x10-5
9x10-5
0 20000 40000 60000 80000 100000 120000
EK
time (Myr)
(b)
7.4x1022
7.45x1022
7.5x1022
7.55x1022
7.6x1022
7.65x1022
7.7x1022
0 20000 40000 60000 80000 100000 120000
ET
time (Myr)
(c)
-7.75x1023
-7.748x1023
-7.746x1023
-7.744x1023
-7.742x1023
-7.74x1023
-7.738x1023
-7.736x1023
0 20000 40000 60000 80000 100000 120000
EG
time (Myr)
(d)
2200
2210
2220
2230
2240
2250
2260
2270
2280
0 20000 40000 60000 80000 100000 120000
<T>
time (Myr)
(e)
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
0 20000 40000 60000 80000 100000 120000
Temperature
time (Myr)
min(T)
max(T)
(f)
-0.005
-0.004
-0.003
-0.002
-0.001
0
0.001
0.002
0.003
0.004
0.005
0 20000 40000 60000 80000 100000 120000
velocity
time (Myr)
min(u)
max(u)
min(v)
max(v)
(g)
-120000
-100000
-80000
-60000
-40000
-20000
0
0 20000 40000 60000 80000 100000 120000
adiabatic heating
time (Myr)
(h)
0
20000
40000
60000
80000
100000
120000
0 20000 40000 60000 80000 100000 120000
viscous dissipation
time (Myr)
(i)
0
20000
40000
60000
80000
100000
120000
0 20000 40000 60000 80000 100000 120000
work against gravity
time (Myr)
(j)
-20000
-10000
0
10000
20000
30000
40000
50000
60000
70000
0 20000 40000 60000 80000 100000 120000
heat flux
time (Myr)
(k)
0
0.05
0.1
0.15
0.2
0.25
0.3
0 20000 40000 60000 80000 100000 120000
vrms (cm/yr)
time (Myr)
(l)
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
0 20000 40000 60000 80000 100000 120000
Nu
time (Myr)
(l)
-60000
-50000
-40000
-30000
-20000
-10000
0
10000
20000
0 20000 40000 60000 80000 100000 120000
time (Myr)
0
AH+VD+HF
dETdt
(m)
0
20000
40000
60000
80000
100000
120000
0 20000 40000 60000 80000 100000 120000
time (Myr)
VD
WG
AH: adiabatic heating, VD: viscous dissipation, HF: heat flux, WG: work against gravity
118
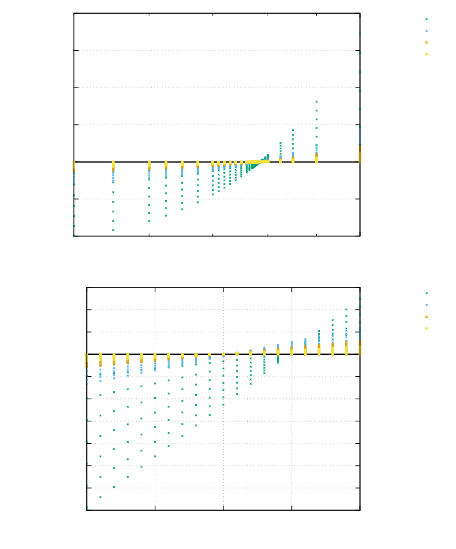
31.13 Onset of convection
The code can be run for values of Ra between 500 and 1000, at various resolutions for the BA formulation.
The value vrms(t)−vrms(0) is plotted as a function of Ra and for the 10 first timesteps. If the vrms is
found to decrease, then the Rayleigh number is not high enough to allow for convection and the initial
temperature perturbation relaxes by diffusion (and then vrms(t)−vrms(0) <0. If the vrms is found to
increase, then vrms(t)−vrms(0) >0 and the system is going to showcase convection. The zero value of
vrms(t)−vrms(0) gives us the critical Rayleigh number, which is found between 775 and 790.
-4x10-15
-2x10-15
0
2x10-15
4x10-15
6x10-15
8x10-15
1000
vrms trend
Ra
16x16
32x32
48x48
64x64
-3.5x10-16
-3x10-16
-2.5x10-16
-2x10-16
-1.5x10-16
-1x10-16
-5x10-17
0
5x10-17
1x10-16
1.5x10-16
770 775 780 785 790
vrms trend
Ra
16x16
32x32
48x48
64x64
119

Appendix: Looking for the right combination of parameters for the King benchmark.
I run a quadruple do loop over L, ∆T,ρ0and η0between plausible values (see code targets.py) and
write in a file only the combination which yields the required Rayleigh and Dissipation number values
(down to 1% accuracy).
alp ha=3e−5
g=10
hcapa =1250
hcond=3
DTmin=1000 ; DTmax=4000 ; DTnpts=251
Lmin=1e6 ; Lmax=3e6 ; Lnpts =251
rhomin =3000 ; rhomax=3500 ; r hon pt s=41
etam in =19 ; etamax=25 ; e t a n p t s =100
On the following plots the ’winning’ combinations of these four parameters are shown:
0.24
0.245
0.25
0.255
0.26
9600 9800 10000 10200 10400
Di
Ra
1x106
1.005x106
1.01x106
1.015x106
1.02x106
1.025x106
1.03x106
1.035x106
1.04x106
1.045x106
1.05x106
500 1000 1500 2000 2500 3000 3500 4000 4500
L
DT
1x1023
2x1023
3x1023
4x1023
5x1023
6x1023
7x1023
8x1023
9x1023
2800 3000 3200 3400 3600 3800 4000 4200
eta
rho
We see that:
•the parameter L(being to the 3rd power in the Ra number) cannot vary too much. Although it is
varied between 1000 and 3000km there seems to be a ’right’ value at about 1040 km. (why?)
•viscosities are within 1023 and 1024 which are plausible values (although a bit high?).
•densities can be chosen freely between 3000 and 3500
•∆Tseems to be the most problematic value since it can range from 1000 to 4000K ...
120
32 fieldstone 25: Rayleigh-Taylor instability (1) - instantaneous
This numerical experiment was first presented in [88]. It consists of an isothermal Rayleigh-Taylor
instability in a two-dimensional box of size Lx = 0.9142 and Ly= 1.
Two Newtonian fluids are present in the system: the buoyant layer is placed at the bottom of the
box and the interface between both fluids is given by y(x)=0.2+0.02 cos πx
LxThe bottom fluid is
parametrised by its mass density ρ1and its viscosity µ1, while the layer above is parametrised by ρ2and
µ2.
No-slip boundary conditions are applied at the bottom and at the top of the box while free-slip
boundary conditions are applied on the sides.
In the original benchmark the system is run over 2000 units of dimensionless time and the timing
and position of various upwellings/downwellings is monitored. In this present experiment only the root
mean square velocity is measured at t= 0: the code is indeed not yet foreseen of any algorithm capable
of tracking deformation.
Another approach than the ones presented in the extensive literature which showcases results of this
benchmark is taken. The mesh is initially fitted to the fluids interface and the resolution is progressively
increased. This results in the following figure:
0.00001
0.00010
0.00100
0.01000
0.01 0.1
vrms
hx
The green line indicates results obtained with my code ELEFANT with grids up to 2000x2000 with the
exact same methodology.
121
features
•Q1×P0element
•incompressible flow
•mixed formulation
•isothermal
•numerical benchmark
122
33 fieldstone 26: Slab detachment benchmark (1) - instanta-
neous
As in [72], the computational domain is 1000km ×660km. No-slip boundary conditions are imposed on
the sides of the system while free-slip boundary conditions are imposed at the top and bottom. Two
materials are present in the domain: the lithosphere (mat.1) and the mantle (mat.2). The overriding
plate (mat.1) is 80km thick and is placed at the top of the domain. An already subducted slab (mat.1)
of 250km length hangs vertically under this plate. The mantle occupies the rest of the domain.
The mantle has a constant viscosity η0= 1021P a.s and a density ρ= 3150kg/m3. The slab has a
density ρ= 3300kg/m3and is characterised by a power-law flow law so that its effective viscosity depends
on the second invariant of the strainrate I2as follows:
ηeff =1
2A−1/nsI1/ns−1
2=1
2[(2 ×4.75×1011)−ns]−1/nsI1/ns−1
2= 4.75×1011I1/ns−1
2=η0I1/ns−1
2(123)
with ns= 4 and A= (2 ×4.75×1011)−ns, or η0= 4.75 ×1011.
Fields at convergence for 151x99 grid.
1x1020
1x1021
1x1022
1x1023
1x1024
0 100 200 300 400 500 600 700 800 900 1000
viscosity (Pa.s)
x (km)
nelx=32
nelx=48
nelx=51
nelx=64
nelx=100
nelx=128
nelx=151
1x1020
1x1021
1x1022
1x1023
1x1024
400 450 500 550 600
viscosity (Pa.s)
x (km)
nelx=32
nelx=48
nelx=51
nelx=64
nelx=100
nelx=128
nelx=151
1x1020
1x1021
1x1022
1x1023
1x1024
1x1025
1x1026
0 100 200 300 400 500 600 700
viscosity (Pa.s)
y (km)
nelx=32
nelx=48
nelx=51
nelx=64
nelx=100
nelx=128
nelx=151
0.0000001
0.0000010
0.0000100
0.0001000
0.0010000
0.0100000
0.1000000
1.0000000
0 5 10 15 20 25 30 35 40 45
normalised nonlinear residual
y (km)
nelx=32
nelx=48
nelx=51
nelx=64
nelx=100
nelx=128
nelx=151
1e-7
-8x10-16
-6x10-16
-4x10-16
-2x10-16
0
2x10-16
4x10-16
0 100 200 300 400 500 600 700 800 900 1000
exx
x (km)
nelx=32
nelx=48
nelx=51
nelx=64
nelx=100
nelx=128
nelx=151
-4x10-16
-2x10-16
0
2x10-16
4x10-16
6x10-16
8x10-16
1x10-15
0 100 200 300 400 500 600 700 800 900 1000
eyy
x (km)
nelx=32
nelx=48
nelx=51
nelx=64
nelx=100
nelx=128
nelx=151
-1.5x10-15
-1x10-15
-5x10-16
0
5x10-16
1x10-15
1.5x10-15
0 100 200 300 400 500 600 700 800 900 1000
exy
x (km)
nelx=32
nelx=48
nelx=51
nelx=64
nelx=100
nelx=128
nelx=151
123
Along the horizontal line
-1x10-15
-8x10-16
-6x10-16
-4x10-16
-2x10-16
0
2x10-16
4x10-16
0 100 200 300 400 500 600 700
exx
y (km)
nelx=32
nelx=48
nelx=51
nelx=64
nelx=100
nelx=128
nelx=151
-4x10-16
-2x10-16
0
2x10-16
4x10-16
6x10-16
8x10-16
1x10-15
0 100 200 300 400 500 600 700
eyy
y (km)
nelx=32
nelx=48
nelx=51
nelx=64
nelx=100
nelx=128
nelx=151
-6x10-17
-4x10-17
-2x10-17
0
2x10-17
4x10-17
6x10-17
8x10-17
0 100 200 300 400 500 600 700
exy
y (km)
nelx=32
nelx=48
nelx=51
nelx=64
nelx=100
nelx=128
nelx=151
Along the vertical line
features
•Q1×P0element
•incompressible flow
•mixed formulation
•isothermal
•nonlinear rheology
•nonlinear residual
Todo: nonlinear mantle, pressure normalisation
124

34 fieldstone: Gravity: buried sphere
Before you proceed further, please read :
http://en.wikipedia.org/wiki/Gravity_anomaly
http://en.wikipedia.org/wiki/Gravimeter
Let us consider a vertical domain Lx ×Ly where Lx= 1000km and Ly = 500km. This domain
is discretised by means of a grid which counts nnp =nnx ×nny nodes. This grid then counts nel =
nelx ×nely = (nnx −1) ×(nny −1) cells. The horizontal spacing between nodes is hx and the vertical
spacing is hy.
Assume that this domain is filled with a rock type which mass density is given by ρmedium =
3000kg/m3, and that there is a circular inclusion of another rock type (ρsphere = 3200kg/m3) at lo-
cation (xsphere,ysphere) of radius rsphere. The density in the system is then given by
ρ(x, y) = ρsphere inside the circle
ρmedium outside the circle
Let us now assume that we place nsurf gravimeters at the surface of the model. These are placed
equidistantly between coordinates x= 0 and coordinates x=Lx. We will use the arrays xsurf and ysurf
to store the coordinates of these locations. The spacing between the gravimeters is δx=Lx/(nsurf −1).
At any given point (xi, yi) in a 2D space, one can show that the gravity anomaly due to the presence
of a circular inclusion can be computed as follows:
g(xi, yi)=2πG(ρsphere −ρ0)R2yi−ysphere
(xi−xsphere)2+ (yi−ysphere)2(124)
where rsphere is the radius of the inclusion, (xsphere, ysphere) are the coordinates of the center of the
inclusion, and ρ0is a reference density.
However, the general formula to compute the gravity anomaly at a given point (xi, yi) in space due
to a density anomaly of any shape is given by:
g(xi, yi)=2GZ ZΩ
∆ρ(x, y)(y−yi)
(x−xi)2+ (y−yi)2dxdy (125)
where Ω is the area of the domain on which the integration is to be carried out. Furthermore the density
anomaly can be written : ∆ρ(x, y) = ρ(x, y)−ρ0. We can then carry out the integration for each cell
and sum their contributions:
g(xi, yi)=2G
nel
X
ic=1 Z ZΩe
(ρ(x, y)−ρ0)(y−yi)
(x−xi)2+ (y−yi)2dxdy (126)
where Ωeis now the area of a single cell. Finally, one can assume the density to be constant within each
cell so that ρ(x, y)→ρ(ic) and RRΩedxdy →hx ×hy and then
g(xi, yi) = 2G
nel
X
ic=1
(ρ(ic)−ρ0)(y(ic)−yi)
(x(ic)−xi)2+ (y(ic)−yi)2sxsy(127)
We will then use the array gsurf to store the value of the gravity anomaly measured at each gravimeter
at the surface.
125
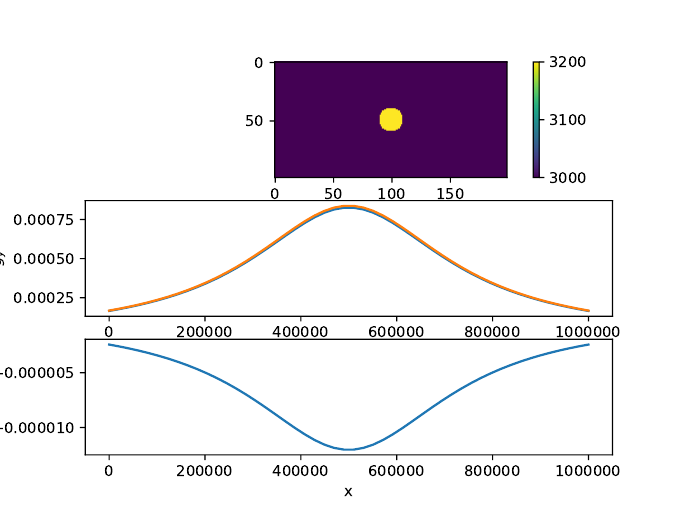
To go further
•explore the effect of the size of the inclusion on the gravity profile.
•explore the effect of the ρ0value.
•explore the effect of the grid resolution.
•measure the time that is required to compute the gravity. How does this time vary with nsurf ?
how does it vary when the grid resolution is doubled ?
•Assume now that ρ2< ρ1. What does the gravity profile look like ?
•what happens when the gravimeters are no more at the surface of the Earth but in a satellite ?
•if you feel brave, redo the whole exercise in 3D...
126
References
[1] M. Albers. A local mesh refinement multigrid method for 3D convection problems with strongly
variable viscosity. J. Comp. Phys., 160:126–150, 2000.
[2] V. Allken, R. Huismans, and C. Thieulot. Three dimensional numerical modelling of upper crustal
extensional systems. J. Geophys. Res., 116:B10409, 2011.
[3] V. Allken, R. Huismans, and C. Thieulot. Factors controlling the mode of rift interaction in brittle-
ductile coupled systems: a 3d numerical study. Geochem. Geophys. Geosyst., 13(5):Q05010, 2012.
[4] V. Allken, R.S. Huismans, H. Fossen, and C. Thieulot. 3D numerical modelling of graben interaction
and linkage: a case study of the Canyonlands grabens, Utah. Basin Research, 25:1–14, 2013.
[5] J.D. Anderson. Computational Fluid Dynamics. McGraw-Hill, 1995.
[6] K.-J. Bathe. Finite Element Procedures in Engineering Analysis. Prentice-Hall, 1982.
[7] M. Benzi, G.H. Golub, and J. Liesen. Numerical solution of saddle point problems. Acta Numerica,
14:1–137, 2005.
[8] D. Bercovici, G. Schubert, and G.A. Glatzmaier. Three-dimensional convection of an infinite
Prandtl-number compressible fluid in a basally heated spherical shell. J. Fluid Mech., 239:683–
719, 1992.
[9] B. Blankenbach, F. Busse, U. Christensen, L. Cserepes, D. Gunkel, U. Hansen, H. Harder, G. Jarvis,
M. Koch, G. Marquart, D. Moore, P. Olson, H. Schmeling, and T. Schnaubelt. A benchmark
comparison for mantle convection codes. Geophys. J. Int., 98:23–38, 1989.
[10] J. Braun, C. Thieulot, P. Fullsack, M. DeKool, and R.S. Huismans. DOUAR: a new three-
dimensional creeping flow model for the solution of geological problems. Phys. Earth. Planet. Inter.,
171:76–91, 2008.
[11] J. Braun and P. Yamato. Structural evolution of a three-dimensional, finite-width crustal wedge.
Tectonophysics, 484:181–192, doi:10.1016/j.tecto.2009.08.032, 2009.
[12] H.H. Bui, R. Fukugawa, K. Sako, and S. Ohno. Lagrangian meshfree particles method (SPH) for
large deformation and failure flows of geomaterial using elasticplastic soil constitutive model. Int.
J. Numer. Anal. Geomech., 32(12):1537–1570, 2008.
[13] P.S. Bullen. Handbook of Means and Their Inequalities. Springer; 2nd edition, 2003.
[14] C. Burstedde, G. Stadler, L. Alisic, L.C. Wilcox, E. Tan, M. Gurnis, and O. Ghattas. Large-scale
adaptive mantle convection simulation. Geophy. J. Int., 192:889–906, 2013.
[15] F.H. Busse, U. Christensen, R. Clever, L. Cserepes, C. Gable, E. Giannandrea, L. Guillou, G. House-
man, H.-C. Nataf, M. Ogawa, M. Parmentier, C. Sotin, and B. Travis. 3D convection at infinite
Prandtl number in Cartesian geometry - a benchmark comparison. Geophys. Astrophys. Fluid
Dynamics, 75:39–59, 1993.
[16] J.S. Chen, C. Pan, and T.Y.P. Chang. On the control of pressure oscillation in bilinear-displacement
constant-pressure element. Comput. Methods Appl. Mech. Engrg., 128:137–152, 1995.
[17] Edmund Christiansen and Knud D. Andersen. Computation of collapse states with von mises type
yield condition. International Journal for Numerical Methods in Engineering, 46:1185–1202, 1999.
[18] Edmund Christiansen and Ole S. Pedersen. Automatic mesh refinement in limit analysis. Interna-
tional Journal for Numerical Methods in Engineering, 50:1331–1346, 2001.
[19] M. crouzeix and P.A. Raviart. Conforming and non-conforming finite element methods for solving
the stationary Stokes equations. RAIRO, 7:33–76, 1973.
127
[20] C. Cuvelier, A. Segal, and A.A. van Steenhoven. Finite Element Methods and Navier-Stokes Equa-
tions. D. Reidel Publishing Company, 1986.
[21] D.R. Davies, C.R. Wilson, and S.C. Kramer. Fluidity: A fully unstructured anisotropic adaptive
mesh computational modeling framework for geodynamics. Geochem. Geophys. Geosyst., 12(6),
2011.
[22] P. Davy and P. Cobbold. Indentation tectonics in nature and experiment. 1. experiments scaled for
gravity. Bulletin of the Geological Institutions of Uppsala, 14:129–141, 1988.
[23] J. de Frutos, V. John, and J. Novo. Projection methods for incompressible ow problems with
WENO nite difference schemes. J. Comp. Phys., 309:368–386, 2016.
[24] Y. Deubelbeiss and B.J.P. Kaus. Comparison of Eulerian and Lagrangian numerical techniques for
the Stokes equations in the presence of strongly varying viscosity. Phys. Earth Planet. Interiors,
171:92–111, 2008.
[25] C.R. Dohrmann and P.B. Bochev. A stabilized finite element method for the Stokes problem based
on polynomial pressure projections. Int. J. Num. Meth. Fluids, 46:183–201, 2004.
[26] J. Donea and A. Huerta. Finite Element Methods for Flow Problems. 2003.
[27] J. Donea and A. Huerta. Finite Element Methods for Flow Problems. John Wiley & Sons, 2003.
[28] Jean Donea and Antonio Huerta. Finite Element Methods for Flow Problems. John Wiley & Sons,
2003.
[29] T. Duretz, D.A. May, T.V. Gerya, and P.J. Tackley. Discretization errors and free surface stabilisa-
tion in the finite difference and marker-in-cell method for applied geodynamics: A numerical study.
Geochem. Geophys. Geosyst., 12(Q07004), 2011.
[30] R. Eid. Higher order isoparametric finite element solution of Stokes flow . Applied Mathematics
and Computation, 162:1083–1101, 2005.
[31] E. Erturk. Discussions on Driven Cavity Flow. Int. J. Num. Meth. Fluids, 60:275–294, 2009.
[32] P.J. Frey and P.-L. George. Mesh generation. Hermes Science, 2000.
[33] P. Fullsack. An arbitrary Lagrangian-Eulerian formulation for creeping flows and its application in
tectonic models. Geophy. J. Int., 120:1–23, 1995.
[34] M. Gerbault, A.N.B. Poliakov, and M. Daignieres. Prediction of faulting from the theories of
elasticity and plasticity: what are the limits? Journal of Structural Geology, 20:301–320, 1998.
[35] Taras Gerya. Numerical Geodynamic Modelling. Cambridge University Press, 2010.
[36] T.V. Gerya, D.A. May, and T. Duretz. An adaptive staggered grid finite difference method for
modeling geodynamic Stokes flows with strongly variable viscosity. Geochem. Geophys. Geosyst.,
14(4), 2013.
[37] G.H. Golub and C.F. van Loan. Matrix Computations, 4th edition. John Hopkins University Press,
2013.
[38] P.M. Gresho and R.L. Sani. Incompressible flow and the Finite Element Method, vol II. John Wiley
and Sons, Ltd, 2000.
[39] D. Griffiths and D. Silvester. Unstable modes of the q1-p0 element. Technical Report 257, University
of MAnchester/UMIST, 1994.
[40] M. Gunzburger. Finite Element Methods for Viscous Incompressible Flows: A Guide to Theory,
Practice and Algorithms. Academic, Boston, 1989.
128
[41] T. Heister, J. Dannberg, R. Gassm¨oller, and W. Bangerth. High Accuracy Mantle Convection
Simulation through Modern Numerical Methods. II: Realistic Models and Problems. Geophy. J. Int.,
210(2):833–851, 2017.
[42] T.J.R. Hughes. The Finite Element Method. Linear Static and Dynamic Finite Element Analysis.
Dover Publications, Inc., 2000.
[43] T.J.R. Hughes, W.K. Liu, and A. Brooks. Finite element analysis of incompressible viscous flows
by the penalty function formulation. J. Comp. Phys., 30:1–60, 1979.
[44] Hoon Huh, Choong Ho Lee, and Wei H. Yang. A general algorithm for plastic flow simulation by
finite element limit analysis. International Journal of Solids and Structures, 36:1193–1207, 1999.
[45] J. Ita and S.D. King. Sensitivity of convection with an endothermic phase change to the form of gov-
erning equations, initial conditions, boundary conditions, and equation of state. J. Geophys. Res.,
99(B8):15,919–15,938, 1994.
[46] L. Jolivet, P. Davy, and P. Cobbold. Right-lateral shear along the Northwest Pacific margin and
the India-Eurasia collision. Tectonics, 9(6):1409–1419, 1990.
[47] L.M. Kachanov. Fundamentals of the Theory of Plasticity. Dover Publications, Inc., 2004.
[48] S. King, C. Lee, P. van Keken, W. Leng, S. Zhong, E. Tan, N. Tosi, and M. Kameyama. A commu-
nity benchmark for 2D Cartesian com- pressible convection in the Earths mantle. Geophy. J. Int.,
180:7387, 2010.
[49] J.R. Koseff and R.L. Street. The Lid-Driven Cavity Flow: A Synthesis of Qualitative and Quanti-
tative Observations. J. Fluids Eng, 106:390–398, 1984.
[50] M. Kronbichler, T. Heister, and W. Bangerth. High accuracy mantle convection simulation through
modern numerical methods . Geophy. J. Int., 191:12–29, 2012.
[51] R. Lee, P. Gresho, and R. Sani. Smooting techniques for certain primitive variable solutions of the
Navier-Stokes equations. . Int. Journal for Numerical Methods in Engineering, 14:1785–1804, 1979.
[52] W. Leng and S. Zhong. Viscous heating, adiabatic heating and energetic consistency in compressible
mantle convection. Geophy. J. Int., 173:693–702, 2008.
[53] W. Leng and S. Zhong. Implementation and application of adaptive mesh refinement for thermo-
chemical mantle convection studies. Geochem. Geophys. Geosyst., 12(4), 2011.
[54] X. Liu and S. Zhong. Analyses of marginal stability, heat transfer and boundary layer properties for
thermal convection in a compressible fluid with infinite Prandtl number. Geophy. J. Int., 194:125–
144, 2013.
[55] C. Loiselet, J. Braun, L. Husson, C. Le Carlier de Veslud, C. Thieulot, P. Yamato, and
D. Grujic. Subducting slabs: Jellyfishes in the Earth’s mantle. Geochem. Geophys. Geosyst.,
11(8):doi:10.1029/2010GC003172, 2010.
[56] D.S. Malkus and T.J.R. Hughes. Mixed finite element methods - reduced and selective integration
techniques: a unification of concepts. Comput. Meth. Appl. Mech. Eng., 15:63–81, 1978.
[57] L.E. Malvern. Introduction to the mechanics of a continuous medium. Prentice-Hall, Inc., 1969.
[58] A. Mizukami. A mixed finite element method for boundary flux computation. Computer Methods
in Applied Mechanics and Engineering, 57:239–243, 1986.
[59] P. Molnar and P. Tapponnier. Relation of the tectonics of eastern China to the India-Eurasia
collision: Application of the slip-line field theory to large-scale continental tectonics. Geology,
5:212–216, 1977.
129
[60] L. Moresi, S. Quenette, V. Lemiale, C. M´eriaux, B. Appelbe, and H.-B. M¨uhlhaus. Computational
approaches to studying non-linear dynamics of the crust and mantle. Phys. Earth. Planet. Inter.,
163:69–82, 2007.
[61] M. Nettesheim, T.A. Ehlers, D.M. Whipp, and A. Koptev. The influence of upper-plate advance
and erosion on overriding plate deformation in orogen syntaxes. Solid Earth, 9:1207–1224, 2018.
[62] C. O’Neill, L. Moresi, D. M¨uller, R. Albert, and F. Dufour. Ellipsis 3D: a particle-in-cell finite
element hybrid code for modelling mantle convection and lithospheric deformation. Computers and
Geosciences, 32:1769–1779, 2006.
[63] G. Peltzer and P. Tapponnier. Formation and evolution of strike-slip faults, rifts, and basins during
the india-asia collision: an experimental approach. J. Geophys. Res., 93(B12):15085–15177, 1988.
[64] A. Pinelli and A. Vacca. Chebyshev collocation method and multidomain decomposition for the
incompressible Navier-Stokes equations. International Journal for numerical methods in fluids,
18:781–799, 1994.
[65] A.E. Pusok, B.J.P. Kaus, and A.A. Popov. On the Quality of Velocity Interpolation
Schemes for Marker-in-Cell Method and Staggered Grids. Pure and Applied Geophysics, pages
doi:10.1007/s00024–016–1431–8, 2016.
[66] T. Rabczuk, P.M.A. Areias, and T. Belytschko. A simplified mesh-free method for shear bands
with cohesive surfaces . Int. J. Num. Meth. Eng., 69:993–1021, 2007.
[67] J.N. Reddy. On penalty function methods in the finite element analysis of flow problems.
Int. J. Num. Meth. Fluids, 2:151–171, 1982.
[68] J. Revenaugh and B. Parsons. Dynamic topography and gravity anomalies for fluid layers whose
viscosity varies exponentially with depth. Geophysical Journal of the Royal Astronomical Society,
90(2):349–368, 1987.
[69] Y. Saad. Iterative methods for sparse linear systems. SIAM, 2003.
[70] R.L. Sani, P.M. Gresho, R.L. Lee, and D.F. Griffiths. The cause and cure (?) of the spurious
pressures generated by certain FEM solutions of the incompressible Navier-Stokes equations: part
1. Int. J. Num. Meth. Fluids, 1:17–43, 1981.
[71] R.L. Sani, P.M. Gresho, R.L. Lee, D.F. Griffiths, and M. Engelman. The cause and cure (?) of the
spurious pressures generated by certain fem solutions of the incompressible navier-stokes equations:
part 2. Int. J. Num. Meth. Fluids, 1:171–204, 1981.
[72] S.M. Schmalholz. A simple analytical solution for slab detachment. Earth Planet. Sci. Lett.,
304:45–54, 2011.
[73] H. Schmeling, A.Y. Babeyko, A. Enns, C. Faccenna, F. Funiciello, T. Gerya, G.J. Golabek,
S. Grigull, B.J.P. Kaus, G. Morra, S.M. Schmalholz, and J. van Hunen. A benchmark comparison of
spontaneous subduction models - Towards a free surface. Phys. Earth. Planet. Inter., 171:198–223,
2008.
[74] D.W. Schmid and Y.Y. Podlachikov. Analytical solutions for deformable elliptical inclusions in
general shear. Geophy. J. Int., 155:269–288, 2003.
[75] G. Schubert, D.L. Turcotte, and P. Olson. Mantle Convection in the Earth and Planets. Cambridge
University Press, 2001.
[76] M. Spiegelman, D.A. May, and C. Wilson. On the solvability of incompressible Stokes with vis-
coplastic rheologies in geodynamics. Geochem. Geophys. Geosyst., 17:2213–2238, 2016.
[77] J. Suckale, J.-C. Nave, and B.H. Hager. It takes three to tango: 1. Simulating buoyancy-driven
flow in the presence of large viscosity contrasts. J. Geophys. Res., 115(B07409), 2010.
130
[78] P. Tackley. Three-dimensional models of mantle convection: Influence of phase transitions and
temperature-dependent viscosity. PhD thesis, California Institute of Technology, 1994.
[79] E. Tan and M. Gurnis. Compressible thermochemical convection and application to lower mantle
structures. J. Geophys. Res., 112(B06304), 2007.
[80] Paul Tapponnier and Peter Molnar. Slip-line field theory and large-scale continental tectonics.
Nature, 264:319–324, November 1976.
[81] M. Thielmann, D.A. May, and B.J.P. Kaus. Discretization errors in the Hybrid Finite Element
Particle-In-Cell Method. Pure and Applied Geophysics, 2014.
[82] C. Thieulot. FANTOM: two- and three-dimensional numerical modelling of creeping flows for the
solution of geological problems. Phys. Earth. Planet. Inter., 188:47–68, 2011.
[83] C. Thieulot. GHOST: Geoscientific Hollow Sphere Tesselation. Solid Earth, 9(1–9), 2018.
[84] C. Thieulot, P. Fullsack, and J. Braun. Adaptive octree-based finite element analysis of two- and
three-dimensional indentation problems. J. Geophys. Res., 113:B12207, 2008.
[85] J.F. Thompson, B.K. Soni, and N.P. Weatherill. Handbook of grid generation. CRC press, 1998.
[86] R.A. Trompert and U. Hansen. On the Rayleigh number dependence of convection with a strongly
temperature-dependent viscosity. Physics of Fluids, 10(2):351–360, 1998.
[87] D.L. Turcotte and G. Schubert. Geodynamics, 2nd edition. Cambridge, 2012.
[88] P.E. van Keken, S.D. King, H. Schmeling, U.R. Christensen, D. Neumeister, and M.-P. Doin.
A comparison of methods for the modeling of thermochemical convection. J. Geophys. Res.,
102(B10):22,477–22,495, 1997.
[89] D.M. Whipp, C. Beaumont, and J. Braun. Feeding the aneurysm: Orogen-parallel mass
transport into Nanga Parbat and the western Himalayan syntaxis. J. Geophys. Res.,
119:doi:10.1002/2013JB010929, 2014.
[90] S.D. Willett. Dynamic and kinematic growth and change of a coulomb wedge. In K.R. McClay,
editor, Thrust Tectonics, pages 19–31. Chapman and Hall, 1992.
[91] H. Xing, W. Yu, and J. Zhang. In Advances in Geocomputing, Lecture Notes in Earth Sciences.
Springer-Verlag, Berlin Heidelberg, 2009.
[92] P. Yamato, L. Husson, J. Braun, C. Loiselet, and C. Thieulot. Influence of surrounding plates on
3D subduction dynamics. Geophys. Res. Lett., 36(L07303):doi:10.1029/2008GL036942, 2009.
[93] X. Yu and F. Tin-Loi. A simple mixed finite element for static limit analysis. Computers and
Structures, 84:1906–1917, 2006.
[94] S. Zhong. Analytic solutions for Stokes flow with lateral variations in viscosity. Geophys. J. Int.,
124:18–28, 1996.
[95] S. Zhong, M. Gurnis, and G. Hulbert. Accurate determination of surface normal stress in viscous
flow from a consistent boundary flux method. Phys. Earth. Planet. Inter., 78:1–8, 1993.
[96] S. Zhong, A. McNamara, E. Tan, L. Moresi, and M. Gurnis. A benchmark study on mantle
convection in a 3-D spherical shell using CITCOMS. Geochem. Geophys. Geosyst., 9(10), 2008.
[97] S.J. Zhong, D.A. Yuen, and L.N. Moresi. Treatise on Geophysics Volume 7 : Mantle Dynamics.
Elsevier B.V., 2007.
[98] O. Zienkiewicz and S. Nakazawa. The penalty function method and its application to the numerical
solution of boundary value problems. The American Society of Mechanical Engineers, 51, 1982.
131
[99] O.C. Zienkiewicz, M. Huang, and M. Pastor. Localization problems in plasticity using finite ele-
ments with adaptive remeshing. International Journal for Numerical and Analytical Methods in
Geomechanics, 19:127–148, 1995.
[100] O.C. Zienkiewicz, C. Humpheson, and R.W. Lewis. Associated and non-associated visco-plasticity
and plasticity in soil mechanics . G´eotechnique, 25(4):671–689, 1975.
132
Index
Pm×Pn, 12
Pm×P−n, 12
Q1×P0, 56, 63, 65, 71, 78, 82, 86, 88, 103, 110, 122,
124
Q1, 13, 17
Q2×Q1, 12, 89, 94
Q2, 13, 19
Q3×Q2, 97
Q3, 14, 20
Qm×P−n, 12
Qm×Qn, 12
Qm×Q−n, 12
analytical solution, 56, 65, 82, 86, 94, 97, 100, 103,
110
arithmetic mean, 78
basis functions, 17
Boussinesq, 8
bubble function, 12
bulk modulus, 105
bulk viscosity, 7
buoyancy-driven flow, 59
CG, 44
checkerboard, 40
cohesion, 39
Compressed Sparse Column, 32
Compressed Sparse Row, 32
compressibility, 105
compressible flow, 110
conforming element, 12
conjugate gradient, 44
connectivity array, 36
convex polygon, 35
CSC, 32
CSR, 32
divergence free, 22
Drucker-Prager, 39
dynamic viscosity, 7
Gauss quadrature, 10
geometric mean, 78
harmonic mean, 79
hyperbolic PDE, 50
incompressible flow, 65, 71, 78, 82, 86, 88, 94, 97,
100, 103, 122, 124
isoparametric, 51
isothermal, 56, 63, 65, 71, 78, 82, 86, 88, 94, 97,
100, 103, 122, 124
isoviscous, 56, 63, 82, 86, 94, 97, 103, 110
Legendre polynomial, 10
method of manufactured solutions, 28
midpoint rule, 9
mixed formulation, 82, 86, 88, 94, 97, 100, 103, 110,
122, 124
MMS, 28
Newton-Cotes, 10
non-conforming element, 12
non-isoviscous, 65, 71, 78, 88, 100
nonconforming Q1×P0, 100
nonlinear, 124
nonlinear rheology, 71
numerical benchmark, 122
particle-in-cell, 78
penalty formulation, 22, 56, 59, 63, 65, 71, 78
piecewise, 12
preconditioned conjugate gradient, 46
pressure normalisation, 90
pressure scaling, 42
pressure smoothing, 40, 82, 100, 103, 110
quadrature, 10
rectangle rule, 9
Schur complement, 44
Schur complement approach, 86, 88
second viscosity, 7
SPD, 44
static condensation, 27
Stokes sphere, 59, 88
strong form, 22
structured grid, 35
tensor invariant, 38
thermal expansion, 105
trapezoidal rule, 9
unstructured grid, 35
Viscosity Rescaling Method, 39
von Mises, 39
VRM, 39
weak form, 22, 23
work against gravity, 108
133

Notes
oinsertherefigure ............................................ 9
oinsertherefigure ............................................ 9
olist codes which use this approach . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
oadd more examples coming from geo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
oproduce drawing of node numbering . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
oinsert here the rederivation 2.1.1 of spmw16 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
oproducefiguretoexplainthis..................................... 41
olinktoprotopaper .......................................... 41
olink to least square and nodal derivatives . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
ohow to compute MfortheSchurcomplement?........................... 47
obuild S and have python compute its smallest and largest eigenvalues as a function of resolution? 86
134


