GROMACS Reference Manual 2018.3
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 270 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Introduction
- Definitions and Units
- Algorithms
- Introduction
- Periodic boundary conditions
- The group concept
- Molecular Dynamics
- Shell molecular dynamics
- Constraint algorithms
- Simulated Annealing
- Stochastic Dynamics
- Brownian Dynamics
- Energy Minimization
- Normal-Mode Analysis
- Free energy calculations
- Replica exchange
- Essential Dynamics sampling
- Expanded Ensemble
- Parallelization
- Domain decomposition
- Implicit solvation
- Interaction function and force fields
- Non-bonded interactions
- Bonded interactions
- Bond stretching
- Morse potential bond stretching
- Cubic bond stretching potential
- FENE bond stretching potential
- Harmonic angle potential
- Cosine based angle potential
- Restricted bending potential
- Urey-Bradley potential
- Bond-Bond cross term
- Bond-Angle cross term
- Quartic angle potential
- Improper dihedrals
- Proper dihedrals
- Tabulated bonded interaction functions
- Restraints
- Polarization
- Free energy interactions
- Methods
- Virtual interaction sites
- Long Range Electrostatics
- Long Range Van der Waals interactions
- Force field
- Topologies
- Special Topics
- Free energy implementation
- Potential of mean force
- Non-equilibrium pulling
- The pull code
- Adaptive biasing with AWH
- Enforced Rotation
- Electric fields
- Computational Electrophysiology
- Calculating a PMF using the free-energy code
- Removing fastest degrees of freedom
- Viscosity calculation
- Tabulated interaction functions
- Mixed Quantum-Classical simulation techniques
- Using VMD plug-ins for trajectory file I/O
- Interactive Molecular Dynamics
- Embedding proteins into the membranes
- Run parameters and Programs
- Analysis
- Using Groups
- Looking at your trajectory
- General properties
- Radial distribution functions
- Correlation functions
- Curve fitting in GROMACS
- Mean Square Displacement
- Bonds/distances, angles and dihedrals
- Radius of gyration and distances
- Root mean square deviations in structure
- Covariance analysis
- Dihedral principal component analysis
- Hydrogen bonds
- Protein-related items
- Interface-related items
- Some implementation details
- Averages and fluctuations
- Bibliography
- Index

GROMACS
Groningen Machine for Chemical Simulations
Reference Manual
Version 2018.3
GROMACS
Reference Manual
Version 2018.3
Contributions from
Emile Apol, Rossen Apostolov, Herman J.C. Berendsen,
Aldert van Buuren, Pär Bjelkmar, Rudi van Drunen,
Anton Feenstra, Sebastian Fritsch, Gerrit Groenhof,
Christoph Junghans, Jochen Hub, Peter Kasson,
Carsten Kutzner, Brad Lambeth, Per Larsson, Justin A. Lemkul,
Viveca Lindahl, Magnus Lundborg, Erik Marklund, Pieter Meulenhoff,
Teemu Murtola, Szilárd Páll, Sander Pronk,
Roland Schulz, Michael Shirts, Alfons Sijbers,
Peter Tieleman, Christian Wennberg and Maarten Wolf.
Mark Abraham, Berk Hess, David van der Spoel, and Erik
Lindahl.
c
1991–2000: Department of Biophysical Chemistry, University of Groningen.
Nijenborgh 4, 9747 AG Groningen, The Netherlands.
c
2001–2018: The GROMACS development teams at the Royal Institute of Technology and
Uppsala University, Sweden.
More information can be found on our website: www.gromacs.org.

iv
Preface & Disclaimer
This manual is not complete and has no pretention to be so due to lack of time of the contributors
– our first priority is to improve the software. It is worked on continuously, which in some cases
might mean the information is not entirely correct.
Comments on form and content are welcome, please send them to one of the mailing lists (see
www.gromacs.org), or open an issue at redmine.gromacs.org. Corrections can also be made in the
GROMACS git source repository and uploaded to gerrit.gromacs.org.
We release an updated version of the manual whenever we release a new version of the software,
so in general it is a good idea to use a manual with the same major and minor release number as
your GROMACS installation.
On-line Resources
You can find more documentation and other material at our homepage www.gromacs.org. Among
other things there is an on-line reference, several GROMACS mailing lists with archives and
contributed topologies/force fields.
Citation information
When citing this document in any scientific publication please refer to it as:
M.J. Abraham, D. van der Spoel, E. Lindahl, B. Hess, and the GROMACS
development team, GROMACS User Manual version 2018.3,www.gromacs.org
(2018)
However, we prefer that you cite (some of) the GROMACS papers [1,2,3,4,5,6,7,8] when
you publish your results. Any future development depends on academic research grants, since the
package is distributed as free software!
GROMACS is Free Software
The entire GROMACS package is available under the GNU Lesser General Public License (LGPL),
version 2.1. This means it’s free as in free speech, not just that you can use it without pay-
ing us money. You can redistribute GROMACS and/or modify it under the terms of the LGPL
as published by the Free Software Foundation; either version 2.1 of the License, or (at your
option) any later version. For details, check the COPYING file in the source code or consult
http://www.gnu.org/licenses/old-licenses/lgpl-2.1.html.
The GROMACS source code and and selected set of binary packages are available on our home-
page, www.gromacs.org. Have fun.
Contents
1 Introduction 1
1.1 Computational Chemistry and Molecular Modeling ................ 1
1.2 Molecular Dynamics Simulations .......................... 2
1.3 Energy Minimization and Search Methods ..................... 5
2 Definitions and Units 7
2.1 Notation ....................................... 7
2.2 MD units ...................................... 7
2.3 Reduced units .................................... 9
2.4 Mixed or Double precision ............................. 10
3 Algorithms 11
3.1 Introduction ..................................... 11
3.2 Periodic boundary conditions ............................ 11
3.2.1 Some useful box types ........................... 13
3.2.2 Cut-off restrictions ............................. 14
3.3 The group concept ................................. 14
3.4 Molecular Dynamics ................................ 15
3.4.1 Initial conditions .............................. 17
3.4.2 Neighbor searching ............................. 18
3.4.3 Compute forces ............................... 24
3.4.4 The leap-frog integrator .......................... 26
3.4.5 The velocity Verlet integrator ....................... 26
3.4.6 Understanding reversible integrators: The Trotter decomposition ..... 27
3.4.7 Multiple time stepping ........................... 29
3.4.8 Temperature coupling ........................... 29

vi Contents
3.4.9 Pressure coupling .............................. 35
3.4.10 The complete update algorithm ...................... 42
3.4.11 Output step ................................. 42
3.5 Shell molecular dynamics .............................. 44
3.5.1 Optimization of the shell positions ..................... 44
3.6 Constraint algorithms ................................ 45
3.6.1 SHAKE ................................... 45
3.6.2 LINCS ................................... 46
3.7 Simulated Annealing ................................ 48
3.8 Stochastic Dynamics ................................ 49
3.9 Brownian Dynamics ................................ 50
3.10 Energy Minimization ................................ 50
3.10.1 Steepest Descent .............................. 50
3.10.2 Conjugate Gradient ............................. 51
3.10.3 L-BFGS ................................... 51
3.11 Normal-Mode Analysis ............................... 51
3.12 Free energy calculations .............................. 52
3.12.1 Slow-growth methods ........................... 52
3.12.2 Thermodynamic integration ........................ 54
3.13 Replica exchange .................................. 55
3.14 Essential Dynamics sampling ............................ 56
3.15 Expanded Ensemble ................................. 57
3.16 Parallelization .................................... 57
3.17 Domain decomposition ............................... 57
3.17.1 Coordinate and force communication ................... 58
3.17.2 Dynamic load balancing .......................... 58
3.17.3 Constraints in parallel ........................... 60
3.17.4 Interaction ranges .............................. 60
3.17.5 Multiple-Program, Multiple-Data PME parallelization .......... 61
3.17.6 Domain decomposition flow chart ..................... 63
3.18 Implicit solvation .................................. 63
4 Interaction function and force fields 67
4.1 Non-bonded interactions .............................. 67

Contents vii
4.1.1 The Lennard-Jones interaction ....................... 68
4.1.2 Buckingham potential ........................... 69
4.1.3 Coulomb interaction ............................ 70
4.1.4 Coulomb interaction with reaction field .................. 70
4.1.5 Modified non-bonded interactions ..................... 71
4.1.6 Modified short-range interactions with Ewald summation ......... 73
4.2 Bonded interactions ................................. 73
4.2.1 Bond stretching ............................... 74
4.2.2 Morse potential bond stretching ...................... 75
4.2.3 Cubic bond stretching potential ...................... 75
4.2.4 FENE bond stretching potential ...................... 76
4.2.5 Harmonic angle potential .......................... 76
4.2.6 Cosine based angle potential ........................ 77
4.2.7 Restricted bending potential ........................ 78
4.2.8 Urey-Bradley potential ........................... 79
4.2.9 Bond-Bond cross term ........................... 79
4.2.10 Bond-Angle cross term ........................... 79
4.2.11 Quartic angle potential ........................... 79
4.2.12 Improper dihedrals ............................. 80
4.2.13 Proper dihedrals .............................. 81
4.2.14 Tabulated bonded interaction functions .................. 84
4.3 Restraints ...................................... 86
4.3.1 Position restraints .............................. 86
4.3.2 Flat-bottomed position restraints ...................... 87
4.3.3 Angle restraints ............................... 88
4.3.4 Dihedral restraints ............................. 88
4.3.5 Distance restraints ............................. 89
4.3.6 Orientation restraints ............................ 92
4.4 Polarization ..................................... 96
4.4.1 Simple polarization ............................. 96
4.4.2 Anharmonic polarization .......................... 96
4.4.3 Water polarization ............................. 97
4.4.4 Thole polarization ............................. 97
4.5 Free energy interactions ............................... 97

viii Contents
4.5.1 Soft-core interactions ............................ 100
4.6 Methods ....................................... 102
4.6.1 Exclusions and 1-4 Interactions. ...................... 102
4.6.2 Charge Groups ............................... 103
4.6.3 Treatment of Cut-offs in the group scheme ................ 103
4.7 Virtual interaction sites ............................... 104
4.8 Long Range Electrostatics ............................. 107
4.8.1 Ewald summation .............................. 107
4.8.2 PME .................................... 108
4.8.3 P3M-AD .................................. 109
4.8.4 Optimizing Fourier transforms and PME calculations ........... 110
4.9 Long Range Van der Waals interactions ...................... 110
4.9.1 Dispersion correction ............................ 110
4.9.2 Lennard-Jones PME ............................ 112
4.10 Force field ...................................... 115
4.10.1 GROMOS-96 ................................ 115
4.10.2 OPLS/AA .................................. 116
4.10.3 AMBER .................................. 116
4.10.4 CHARMM ................................. 117
4.10.5 Coarse-grained force fields ......................... 117
4.10.6 MARTINI .................................. 118
4.10.7 PLUM ................................... 118
5 Topologies 119
5.1 Introduction ..................................... 119
5.2 Particle type ..................................... 119
5.2.1 Atom types ................................. 120
5.2.2 Virtual sites ................................. 120
5.3 Parameter files ................................... 122
5.3.1 Atoms .................................... 122
5.3.2 Non-bonded parameters .......................... 122
5.3.3 Bonded parameters ............................. 123
5.4 Molecule definition ................................. 124
5.4.1 Moleculetype entries ............................ 124

Contents ix
5.4.2 Intermolecular interactions ......................... 125
5.4.3 Intramolecular pair interactions ...................... 125
5.4.4 Exclusions ................................. 126
5.5 Implicit solvation parameters ............................ 126
5.6 Constraint algorithms ................................ 127
5.7 pdb2gmx input files ................................. 128
5.7.1 Residue database .............................. 129
5.7.2 Residue to building block database ..................... 131
5.7.3 Atom renaming database .......................... 131
5.7.4 Hydrogen database ............................. 132
5.7.5 Termini database .............................. 133
5.7.6 Virtual site database ............................ 135
5.7.7 Special bonds ................................ 136
5.8 File formats ..................................... 137
5.8.1 Topology file ................................ 137
5.8.2 Molecule.itp file .............................. 146
5.8.3 Ifdef statements ............................... 147
5.8.4 Topologies for free energy calculations .................. 148
5.8.5 Constraint forces .............................. 150
5.8.6 Coordinate file ............................... 151
5.9 Force field organization .............................. 152
5.9.1 Force-field files ............................... 152
5.9.2 Changing force-field parameters ...................... 153
5.9.3 Adding atom types ............................. 153
6 Special Topics 155
6.1 Free energy implementation ............................ 155
6.2 Potential of mean force ............................... 156
6.3 Non-equilibrium pulling .............................. 157
6.4 The pull code .................................... 157
6.5 Adaptive biasing with AWH ............................ 161
6.5.1 Basics of the method ............................ 162
6.5.2 The initial stage ............................... 165
6.5.3 Choice of target distribution ........................ 166

x Contents
6.5.4 Multiple independent or sharing biases .................. 167
6.5.5 Reweighting and combining biased data .................. 168
6.5.6 The friction metric ............................. 169
6.5.7 Usage .................................... 169
6.6 Enforced Rotation .................................. 170
6.6.1 Fixed Axis Rotation ............................ 170
6.6.2 Flexible Axis Rotation ........................... 175
6.6.3 Usage .................................... 178
6.7 Electric fields .................................... 181
6.8 Computational Electrophysiology ......................... 182
6.8.1 Usage .................................... 183
6.9 Calculating a PMF using the free-energy code ................... 185
6.10 Removing fastest degrees of freedom ........................ 186
6.10.1 Hydrogen bond-angle vibrations ...................... 187
6.10.2 Out-of-plane vibrations in aromatic groups ................ 189
6.11 Viscosity calculation ................................ 189
6.12 Tabulated interaction functions ........................... 191
6.12.1 Cubic splines for potentials ......................... 191
6.12.2 User-specified potential functions ..................... 192
6.13 Mixed Quantum-Classical simulation techniques ................. 193
6.13.1 Overview .................................. 193
6.13.2 Usage .................................... 194
6.13.3 Output ................................... 196
6.13.4 Future developments ............................ 197
6.14 Using VMD plug-ins for trajectory file I/O ..................... 197
6.15 Interactive Molecular Dynamics .......................... 197
6.15.1 Simulation input preparation ........................ 197
6.15.2 Starting the simulation ........................... 198
6.15.3 Connecting from VMD ........................... 198
6.16 Embedding proteins into the membranes ...................... 198
7 Run parameters and Programs 201
7.1 Online documentation ................................ 201
7.2 File types ...................................... 201

Contents xi
7.3 Run Parameters ................................... 201
8 Analysis 203
8.1 Using Groups .................................... 203
8.1.1 Default Groups ............................... 204
8.1.2 Selections .................................. 206
8.2 Looking at your trajectory ............................. 207
8.3 General properties .................................. 207
8.4 Radial distribution functions ............................ 208
8.5 Correlation functions ................................ 210
8.5.1 Theory of correlation functions ...................... 210
8.5.2 Using FFT for computation of the ACF .................. 211
8.5.3 Special forms of the ACF .......................... 211
8.5.4 Some Applications ............................. 211
8.6 Curve fitting in GROMACS ............................ 212
8.6.1 Sum of exponential functions ....................... 212
8.6.2 Error estimation .............................. 212
8.6.3 Interphase boundary demarcation ..................... 213
8.6.4 Transverse current autocorrelation function ................ 213
8.6.5 Viscosity estimation from pressure autocorrelation function ....... 213
8.7 Mean Square Displacement ............................. 214
8.8 Bonds/distances, angles and dihedrals ....................... 214
8.9 Radius of gyration and distances .......................... 216
8.10 Root mean square deviations in structure ...................... 217
8.11 Covariance analysis ................................. 218
8.12 Dihedral principal component analysis ....................... 220
8.13 Hydrogen bonds ................................... 220
8.14 Protein-related items ................................ 222
8.15 Interface-related items ............................... 222
A Some implementation details 227
A.1 Single Sum Virial in GROMACS .......................... 227
A.1.1 Virial .................................... 227
A.1.2 Virial from non-bonded forces ....................... 228
A.1.3 The intra-molecular shift (mol-shift) .................... 229

xii Contents
A.1.4 Virial from Covalent Bonds ........................ 230
A.1.5 Virial from SHAKE ............................ 231
A.2 Optimizations .................................... 231
A.2.1 Inner Loops for Water ........................... 231
B Averages and fluctuations 233
B.1 Formulae for averaging ............................... 233
B.2 Implementation ................................... 234
B.2.1 Part of a Simulation ............................ 235
B.2.2 Combining two simulations ........................ 235
B.2.3 Summing energy terms ........................... 236
Bibliography 239
Index 253
Chapter 1
Introduction
1.1 Computational Chemistry and Molecular Modeling
GROMACS is an engine to perform molecular dynamics simulations and energy minimization.
These are two of the many techniques that belong to the realm of computational chemistry and
molecular modeling. Computational chemistry is just a name to indicate the use of computational
techniques in chemistry, ranging from quantum mechanics of molecules to dynamics of large
complex molecular aggregates. Molecular modeling indicates the general process of describing
complex chemical systems in terms of a realistic atomic model, with the goal being to under-
stand and predict macroscopic properties based on detailed knowledge on an atomic scale. Often,
molecular modeling is used to design new materials, for which the accurate prediction of physical
properties of realistic systems is required.
Macroscopic physical properties can be distinguished by (a)static equilibrium properties, such
as the binding constant of an inhibitor to an enzyme, the average potential energy of a system, or
the radial distribution function of a liquid, and (b)dynamic or non-equilibrium properties, such
as the viscosity of a liquid, diffusion processes in membranes, the dynamics of phase changes,
reaction kinetics, or the dynamics of defects in crystals. The choice of technique depends on the
question asked and on the feasibility of the method to yield reliable results at the present state of
the art. Ideally, the (relativistic) time-dependent Schrödinger equation describes the properties of
molecular systems with high accuracy, but anything more complex than the equilibrium state of a
few atoms cannot be handled at this ab initio level. Thus, approximations are necessary; the higher
the complexity of a system and the longer the time span of the processes of interest is, the more
severe the required approximations are. At a certain point (reached very much earlier than one
would wish), the ab initio approach must be augmented or replaced by empirical parameterization
of the model used. Where simulations based on physical principles of atomic interactions still
fail due to the complexity of the system, molecular modeling is based entirely on a similarity
analysis of known structural and chemical data. The QSAR methods (Quantitative Structure-
Activity Relations) and many homology-based protein structure predictions belong to the latter
category.
Macroscopic properties are always ensemble averages over a representative statistical ensemble

2 Chapter 1. Introduction
(either equilibrium or non-equilibrium) of molecular systems. For molecular modeling, this has
two important consequences:
•The knowledge of a single structure, even if it is the structure of the global energy min-
imum, is not sufficient. It is necessary to generate a representative ensemble at a given
temperature, in order to compute macroscopic properties. But this is not enough to compute
thermodynamic equilibrium properties that are based on free energies, such as phase equi-
libria, binding constants, solubilities, relative stability of molecular conformations, etc. The
computation of free energies and thermodynamic potentials requires special extensions of
molecular simulation techniques.
•While molecular simulations, in principle, provide atomic details of the structures and mo-
tions, such details are often not relevant for the macroscopic properties of interest. This
opens the way to simplify the description of interactions and average over irrelevant details.
The science of statistical mechanics provides the theoretical framework for such simpli-
fications. There is a hierarchy of methods ranging from considering groups of atoms as
one unit, describing motion in a reduced number of collective coordinates, averaging over
solvent molecules with potentials of mean force combined with stochastic dynamics [9],
to mesoscopic dynamics describing densities rather than atoms and fluxes as response to
thermodynamic gradients rather than velocities or accelerations as response to forces [10].
For the generation of a representative equilibrium ensemble two methods are available: (a)Monte
Carlo simulations and (b)Molecular Dynamics simulations. For the generation of non-equilibrium
ensembles and for the analysis of dynamic events, only the second method is appropriate. While
Monte Carlo simulations are more simple than MD (they do not require the computation of forces),
they do not yield significantly better statistics than MD in a given amount of computer time. There-
fore, MD is the more universal technique. If a starting configuration is very far from equilibrium,
the forces may be excessively large and the MD simulation may fail. In those cases, a robust en-
ergy minimization is required. Another reason to perform an energy minimization is the removal
of all kinetic energy from the system: if several “snapshots” from dynamic simulations must be
compared, energy minimization reduces the thermal noise in the structures and potential energies
so that they can be compared better.
1.2 Molecular Dynamics Simulations
MD simulations solve Newton’s equations of motion for a system of Ninteracting atoms:
mi
∂2ri
∂t2=Fi, i = 1 . . . N. (1.1)
The forces are the negative derivatives of a potential function V(r1,r2,...,rN):
Fi=−∂V
∂ri
(1.2)
The equations are solved simultaneously in small time steps. The system is followed for some
time, taking care that the temperature and pressure remain at the required values, and the coor-
dinates are written to an output file at regular intervals. The coordinates as a function of time

1.2. Molecular Dynamics Simulations 3
type of wavenumber
type of bond vibration (cm−1)
C-H, O-H, N-H stretch 3000–3500
C=C, C=O stretch 1700–2000
HOH bending 1600
C-C stretch 1400–1600
H2CX sciss, rock 1000–1500
CCC bending 800–1000
O-H···O libration 400– 700
O-H···O stretch 50– 200
Table 1.1: Typical vibrational frequencies (wavenumbers) in molecules and hydrogen-bonded liq-
uids. Compare kT/h = 200 cm−1at 300 K.
represent a trajectory of the system. After initial changes, the system will usually reach an equi-
librium state. By averaging over an equilibrium trajectory, many macroscopic properties can be
extracted from the output file.
It is useful at this point to consider the limitations of MD simulations. The user should be aware
of those limitations and always perform checks on known experimental properties to assess the
accuracy of the simulation. We list the approximations below.
The simulations are classical
Using Newton’s equation of motion automatically implies the use of classical mechanics to
describe the motion of atoms. This is all right for most atoms at normal temperatures, but
there are exceptions. Hydrogen atoms are quite light and the motion of protons is sometimes
of essential quantum mechanical character. For example, a proton may tunnel through a
potential barrier in the course of a transfer over a hydrogen bond. Such processes cannot be
properly treated by classical dynamics! Helium liquid at low temperature is another example
where classical mechanics breaks down. While helium may not deeply concern us, the high
frequency vibrations of covalent bonds should make us worry! The statistical mechanics of a
classical harmonic oscillator differs appreciably from that of a real quantum oscillator when
the resonance frequency νapproximates or exceeds kBT/h. Now at room temperature the
wavenumber σ= 1/λ =ν/c at which hν =kBTis approximately 200 cm−1. Thus, all
frequencies higher than, say, 100 cm−1may misbehave in classical simulations. This means
that practically all bond and bond-angle vibrations are suspect, and even hydrogen-bonded
motions as translational or librational H-bond vibrations are beyond the classical limit (see
Table 1.1). What can we do?
Well, apart from real quantum-dynamical simulations, we can do one of two things:
(a) If we perform MD simulations using harmonic oscillators for bonds, we should make
corrections to the total internal energy U=Ekin+Epot and specific heat CV(and to entropy
Sand free energy Aor Gif those are calculated). The corrections to the energy and specific
heat of a one-dimensional oscillator with frequency νare: [11]
UQM =Ucl +kT 1
2x−1 + x
ex−1(1.3)
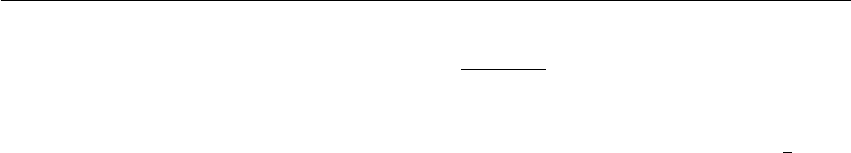
4 Chapter 1. Introduction
CQM
V=Ccl
V+k x2ex
(ex−1)2−1!,(1.4)
where x=hν/kT . The classical oscillator absorbs too much energy (kT ), while the high-
frequency quantum oscillator is in its ground state at the zero-point energy level of 1
2hν.
(b) We can treat the bonds (and bond angles) as constraints in the equations of motion. The
rationale behind this is that a quantum oscillator in its ground state resembles a constrained
bond more closely than a classical oscillator. A good practical reason for this choice is
that the algorithm can use larger time steps when the highest frequencies are removed. In
practice the time step can be made four times as large when bonds are constrained than
when they are oscillators [12]. GROMACS has this option for the bonds and bond angles.
The flexibility of the latter is rather essential to allow for the realistic motion and coverage
of configurational space [13].
Electrons are in the ground state
In MD we use a conservative force field that is a function of the positions of atoms only.
This means that the electronic motions are not considered: the electrons are supposed to
adjust their dynamics instantly when the atomic positions change (the Born-Oppenheimer
approximation), and remain in their ground state. This is really all right, almost always. But
of course, electron transfer processes and electronically excited states can not be treated.
Neither can chemical reactions be treated properly, but there are other reasons to shy away
from reactions for the time being.
Force fields are approximate
Force fields provide the forces. They are not really a part of the simulation method and
their parameters can be modified by the user as the need arises or knowledge improves.
But the form of the forces that can be used in a particular program is subject to limitations.
The force field that is incorporated in GROMACS is described in Chapter 4. In the present
version the force field is pair-additive (apart from long-range Coulomb forces), it cannot
incorporate polarizabilities, and it does not contain fine-tuning of bonded interactions. This
urges the inclusion of some limitations in this list below. For the rest it is quite useful and
fairly reliable for biologically-relevant macromolecules in aqueous solution!
The force field is pair-additive
This means that all non-bonded forces result from the sum of non-bonded pair interactions.
Non pair-additive interactions, the most important example of which is interaction through
atomic polarizability, are represented by effective pair potentials. Only average non pair-
additive contributions are incorporated. This also means that the pair interactions are not
pure, i.e., they are not valid for isolated pairs or for situations that differ appreciably from the
test systems on which the models were parameterized. In fact, the effective pair potentials
are not that bad in practice. But the omission of polarizability also means that electrons in
atoms do not provide a dielectric constant as they should. For example, real liquid alkanes
have a dielectric constant of slightly more than 2, which reduce the long-range electrostatic
interaction between (partial) charges. Thus, the simulations will exaggerate the long-range
Coulomb terms. Luckily, the next item compensates this effect a bit.
Long-range interactions are cut off
In this version, GROMACS always uses a cut-off radius for the Lennard-Jones interactions

1.3. Energy Minimization and Search Methods 5
and sometimes for the Coulomb interactions as well. The “minimum-image convention”
used by GROMACS requires that only one image of each particle in the periodic boundary
conditions is considered for a pair interaction, so the cut-off radius cannot exceed half the
box size. That is still pretty big for large systems, and trouble is only expected for systems
containing charged particles. But then truly bad things can happen, like accumulation of
charges at the cut-off boundary or very wrong energies! For such systems, you should
consider using one of the implemented long-range electrostatic algorithms, such as particle-
mesh Ewald [14,15].
Boundary conditions are unnatural
Since system size is small (even 10,000 particles is small), a cluster of particles will have a
lot of unwanted boundary with its environment (vacuum). We must avoid this condition if
we wish to simulate a bulk system. As such, we use periodic boundary conditions to avoid
real phase boundaries. Since liquids are not crystals, something unnatural remains. This
item is mentioned last because it is the least of the evils. For large systems, the errors are
small, but for small systems with a lot of internal spatial correlation, the periodic boundaries
may enhance internal correlation. In that case, beware of, and test, the influence of system
size. This is especially important when using lattice sums for long-range electrostatics, since
these are known to sometimes introduce extra ordering.
1.3 Energy Minimization and Search Methods
As mentioned in sec. 1.1, in many cases energy minimization is required. GROMACS provides a
number of methods for local energy minimization, as detailed in sec. 3.10.
The potential energy function of a (macro)molecular system is a very complex landscape (or hy-
persurface) in a large number of dimensions. It has one deepest point, the global minimum and
a very large number of local minima, where all derivatives of the potential energy function with
respect to the coordinates are zero and all second derivatives are non-negative. The matrix of
second derivatives, which is called the Hessian matrix, has non-negative eigenvalues; only the
collective coordinates that correspond to translation and rotation (for an isolated molecule) have
zero eigenvalues. In between the local minima there are saddle points, where the Hessian matrix
has only one negative eigenvalue. These points are the mountain passes through which the system
can migrate from one local minimum to another.
Knowledge of all local minima, including the global one, and of all saddle points would enable
us to describe the relevant structures and conformations and their free energies, as well as the
dynamics of structural transitions. Unfortunately, the dimensionality of the configurational space
and the number of local minima is so high that it is impossible to sample the space at a sufficient
number of points to obtain a complete survey. In particular, no minimization method exists that
guarantees the determination of the global minimum in any practical amount of time. Impractical
methods exist, some much faster than others [16]. However, given a starting configuration, it
is possible to find the nearest local minimum. “Nearest” in this context does not always imply
“nearest” in a geometrical sense (i.e., the least sum of square coordinate differences), but means the
minimum that can be reached by systematically moving down the steepest local gradient. Finding
this nearest local minimum is all that GROMACS can do for you, sorry! If you want to find other

6 Chapter 1. Introduction
minima and hope to discover the global minimum in the process, the best advice is to experiment
with temperature-coupled MD: run your system at a high temperature for a while and then quench
it slowly down to the required temperature; do this repeatedly! If something as a melting or glass
transition temperature exists, it is wise to stay for some time slightly below that temperature and
cool down slowly according to some clever scheme, a process called simulated annealing. Since
no physical truth is required, you can use your imagination to speed up this process. One trick
that often works is to make hydrogen atoms heavier (mass 10 or so): although that will slow
down the otherwise very rapid motions of hydrogen atoms, it will hardly influence the slower
motions in the system, while enabling you to increase the time step by a factor of 3 or 4. You can
also modify the potential energy function during the search procedure, e.g. by removing barriers
(remove dihedral angle functions or replace repulsive potentials by soft-core potentials [17]), but
always take care to restore the correct functions slowly. The best search method that allows rather
drastic structural changes is to allow excursions into four-dimensional space [18], but this requires
some extra programming beyond the standard capabilities of GROMACS.
Three possible energy minimization methods are:
•Those that require only function evaluations. Examples are the simplex method and its
variants. A step is made on the basis of the results of previous evaluations. If derivative
information is available, such methods are inferior to those that use this information.
•Those that use derivative information. Since the partial derivatives of the potential energy
with respect to all coordinates are known in MD programs (these are equal to minus the
forces) this class of methods is very suitable as modification of MD programs.
•Those that use second derivative information as well. These methods are superior in their
convergence properties near the minimum: a quadratic potential function is minimized in
one step! The problem is that for Nparticles a 3N×3Nmatrix must be computed, stored,
and inverted. Apart from the extra programming to obtain second derivatives, for most
systems of interest this is beyond the available capacity. There are intermediate methods
that build up the Hessian matrix on the fly, but they also suffer from excessive storage
requirements. So GROMACS will shy away from this class of methods.
The steepest descent method, available in GROMACS, is of the second class. It simply takes a
step in the direction of the negative gradient (hence in the direction of the force), without any
consideration of the history built up in previous steps. The step size is adjusted such that the
search is fast, but the motion is always downhill. This is a simple and sturdy, but somewhat
stupid, method: its convergence can be quite slow, especially in the vicinity of the local minimum!
The faster-converging conjugate gradient method (see e.g. [19]) uses gradient information from
previous steps. In general, steepest descents will bring you close to the nearest local minimum
very quickly, while conjugate gradients brings you very close to the local minimum, but performs
worse far away from the minimum. GROMACS also supports the L-BFGS minimizer, which is
mostly comparable to conjugate gradient method, but in some cases converges faster.

Chapter 2
Definitions and Units
2.1 Notation
The following conventions for mathematical typesetting are used throughout this document:
Item Notation Example
Vector Bold italic ri
Vector Length Italic ri
We define the lowercase subscripts i,j,kand lto denote particles: riis the position vector of
particle i, and using this notation:
rij =rj−ri(2.1)
rij =|rij|(2.2)
The force on particle iis denoted by Fiand
Fij =force on iexerted by j(2.3)
Please note that we changed notation as of version 2.0 to rij =rj−risince this is the notation
commonly used. If you encounter an error, let us know.
2.2 MD units
GROMACS uses a consistent set of units that produce values in the vicinity of unity for most
relevant molecular quantities. Let us call them MD units. The basic units in this system are nm,
ps, K, electron charge (e) and atomic mass unit (u), see Table 2.1. The values used in GROMACS
are taken from the CODATA Internationally recommended 2010 values of fundamental physical
constants (see http://nist.gov).
Consistent with these units are a set of derived units, given in Table 2.2.
The electric conversion factor f=1
4πεo= 138.935 458 kJ mol−1nm e−2. It relates the mechan-

8 Chapter 2. Definitions and Units
Quantity Symbol Unit
length r nm = 10−9m
mass m u (unified atomic mass unit) = 1.660 538 921 ×10−27 kg
time t ps = 10−12 s
charge q e=elementary charge = 1.602 176 565(×10−19 C
temperature T K
Table 2.1: Basic units used in GROMACS.
Quantity Symbol Unit
energy E, V kJ mol−1
Force FkJ mol−1nm−1
pressure pbar
velocity vnm ps−1= 1000 m s−1
dipole moment µenm
electric potential ΦkJ mol−1e−1= 0.010 364 269 19 Volt
electric field EkJ mol−1nm−1e−1= 1.036 426 919 ×107V m−1
Table 2.2: Derived units. Note that an additional conversion factor of 1028 a.m.u (≈16.6) is applied
to get bar instead of internal MD units in the energy and log files.
ical quantities to the electrical quantities as in
V=fq2
ror F=fq2
r2(2.4)
Electric potentials Φand electric fields Eare intermediate quantities in the calculation of energies
and forces. They do not occur inside GROMACS. If they are used in evaluations, there is a choice
of equations and related units. We strongly recommend following the usual practice of including
the factor fin expressions that evaluate Φand E:
Φ(r) = fX
j
qj
|r−rj|(2.5)
E(r) = fX
j
qj
(r−rj)
|r−rj|3(2.6)
With these definitions, qΦis an energy and qEis a force. The units are those given in Table 2.2:
about 10 mV for potential. Thus, the potential of an electronic charge at a distance of 1 nm equals
f≈140 units ≈1.4V. (exact value: 1.439 964 5 V)
Note that these units are mutually consistent; changing any of the units is likely to produce incon-
sistencies and is therefore strongly discouraged! In particular: if Å are used instead of nm, the unit
of time changes to 0.1 ps. If kcal mol−1(= 4.184 kJ mol−1) is used instead of kJ mol−1for energy,
the unit of time becomes 0.488882 ps and the unit of temperature changes to 4.184 K. But in both
cases all electrical energies go wrong, because they will still be computed in kJ mol−1, expecting
nm as the unit of length. Although careful rescaling of charges may still yield consistency, it is
clear that such confusions must be rigidly avoided.

2.3. Reduced units 9
Symbol Name Value
NAV Avogadro’s number 6.022 141 29 ×1023 mol−1
Rgas constant 8.314 462 1 ×10−3kJ mol−1K−1
kBBoltzmann’s constant idem
hPlanck’s constant 0.399 031 271 kJ mol−1ps
¯hDirac’s constant 0.063 507 799 3 kJ mol−1ps
cvelocity of light 299 792.458 nm ps−1
Table 2.3: Some Physical Constants
Quantity Symbol Relation to SI
Length r∗rσ−1
Mass m∗m M−1
Time t∗tσ−1p/M
Temperature T∗kBT−1
Energy E∗E−1
Force F∗Fσ −1
Pressure P∗Pσ3−1
Velocity v∗vpM/
Density ρ∗Nσ3V−1
Table 2.4: Reduced Lennard-Jones quantities
In terms of the MD units, the usual physical constants take on different values (see Table 2.3).
All quantities are per mol rather than per molecule. There is no distinction between Boltzmann’s
constant kand the gas constant R: their value is 0.008 314 462 1 kJ mol−1K−1.
2.3 Reduced units
When simulating Lennard-Jones (LJ) systems, it might be advantageous to use reduced units (i.e.,
setting ii =σii =mi=kB= 1 for one type of atoms). This is possible. When specifying
the input in reduced units, the output will also be in reduced units. The one exception is the
temperature, which is expressed in 0.008 314 462 1 reduced units. This is a consequence of using
Boltzmann’s constant in the evaluation of temperature in the code. Thus not T, but kBT, is the
reduced temperature. A GROMACS temperature T= 1 means a reduced temperature of 0.008 . . .
units; if a reduced temperature of 1 is required, the GROMACS temperature should be 120.272 36.
In Table 2.4 quantities are given for LJ potentials:
VLJ = 4"σ
r12
−σ
r6#(2.7)

10 Chapter 2. Definitions and Units
2.4 Mixed or Double precision
GROMACS can be compiled in either mixed or double precision. Documentation of previous
GROMACS versions referred to “single precision”, but the implementation has made selective
use of double precision for many years. Using single precision for all variables would lead to a
significant reduction in accuracy. Although in “mixed precision” all state vectors, i.e. particle
coordinates, velocities and forces, are stored in single precision, critical variables are double pre-
cision. A typical example of the latter is the virial, which is a sum over all forces in the system,
which have varying signs. In addition, in many parts of the code we managed to avoid double pre-
cision for arithmetic, by paying attention to summation order or reorganization of mathematical
expressions. The default configuration uses mixed precision, but it is easy to turn on double preci-
sion by adding the option -DGMX_DOUBLE=on to cmake. Double precision will be 20 to 100%
slower than mixed precision depending on the architecture you are running on. Double precision
will use somewhat more memory and run input, energy and full-precision trajectory files will be
almost twice as large.
The energies in mixed precision are accurate up to the last decimal, the last one or two decimals
of the forces are non-significant. The virial is less accurate than the forces, since the virial is only
one order of magnitude larger than the size of each element in the sum over all atoms (sec. A.1).
In most cases this is not really a problem, since the fluctuations in the virial can be two orders
of magnitude larger than the average. Using cut-offs for the Coulomb interactions cause large
errors in the energies, forces, and virial. Even when using a reaction-field or lattice sum method,
the errors are larger than, or comparable to, the errors due to the partial use of single precision.
Since MD is chaotic, trajectories with very similar starting conditions will diverge rapidly, the
divergence is faster in mixed precision than in double precision.
For most simulations, mixed precision is accurate enough. In some cases double precision is
required to get reasonable results:
•normal mode analysis, for the conjugate gradient or l-bfgs minimization and the calculation
and diagonalization of the Hessian
•long-term energy conservation, especially for large systems
Chapter 3
Algorithms
3.1 Introduction
In this chapter we first give describe some general concepts used in GROMACS: periodic bound-
ary conditions (sec. 3.2) and the group concept (sec. 3.3). The MD algorithm is described in
sec. 3.4: first a global form of the algorithm is given, which is refined in subsequent subsections.
The (simple) EM (Energy Minimization) algorithm is described in sec. 3.10. Some other algo-
rithms for special purpose dynamics are described after this.
A few issues are of general interest. In all cases the system must be defined, consisting of
molecules. Molecules again consist of particles with defined interaction functions. The detailed
description of the topology of the molecules and of the force field and the calculation of forces is
given in chapter 4. In the present chapter we describe other aspects of the algorithm, such as pair
list generation, update of velocities and positions, coupling to external temperature and pressure,
conservation of constraints. The analysis of the data generated by an MD simulation is treated in
chapter 8.
3.2 Periodic boundary conditions
The classical way to minimize edge effects in a finite system is to apply periodic boundary condi-
tions. The atoms of the system to be simulated are put into a space-filling box, which is surrounded
by translated copies of itself (Fig. 3.1). Thus there are no boundaries of the system; the artifact
caused by unwanted boundaries in an isolated cluster is now replaced by the artifact of periodic
conditions. If the system is crystalline, such boundary conditions are desired (although motions
are naturally restricted to periodic motions with wavelengths fitting into the box). If one wishes to
simulate non-periodic systems, such as liquids or solutions, the periodicity by itself causes errors.
The errors can be evaluated by comparing various system sizes; they are expected to be less severe
than the errors resulting from an unnatural boundary with vacuum.
There are several possible shapes for space-filling unit cells. Some, like the rhombic dodecahedron
and the truncated octahedron [20] are closer to being a sphere than a cube is, and are therefore
12 Chapter 3. Algorithms
j’ j’
i’ i’i’
i’
j’
i’ i’
y
x
y
x
j’ j’
i’
i’
i’i
j’
j’ j’j’
i’ii’
j’j’
j’
j
i’ i’i’
j’
i’ i’
j’
j’j’
j
Figure 3.1: Periodic boundary conditions in two dimensions.
better suited to the study of an approximately spherical macromolecule in solution, since fewer
solvent molecules are required to fill the box given a minimum distance between macromolecular
images. At the same time, rhombic dodecahedra and truncated octahedra are special cases of
triclinic unit cells; the most general space-filling unit cells that comprise all possible space-filling
shapes [21]. For this reason, GROMACS is based on the triclinic unit cell.
GROMACS uses periodic boundary conditions, combined with the minimum image convention:
only one – the nearest – image of each particle is considered for short-range non-bonded in-
teraction terms. For long-range electrostatic interactions this is not always accurate enough, and
GROMACS therefore also incorporates lattice sum methods such as Ewald Sum, PME and PPPM.
GROMACS supports triclinic boxes of any shape. The simulation box (unit cell) is defined by the
3 box vectors a,band c. The box vectors must satisfy the following conditions:
ay=az=bz= 0 (3.1)
ax>0, by>0, cz>0(3.2)
|bx| ≤ 1
2ax,|cx| ≤ 1
2ax,|cy| ≤ 1
2by(3.3)
Equations 3.1 can always be satisfied by rotating the box. Inequalities (3.2) and (3.3) can always
be satisfied by adding and subtracting box vectors.
Even when simulating using a triclinic box, GROMACS always keeps the particles in a brick-
shaped volume for efficiency, as illustrated in Fig. 3.1 for a 2-dimensional system. Therefore,
from the output trajectory it might seem that the simulation was done in a rectangular box. The
program trjconv can be used to convert the trajectory to a different unit-cell representation.
3.2. Periodic boundary conditions 13
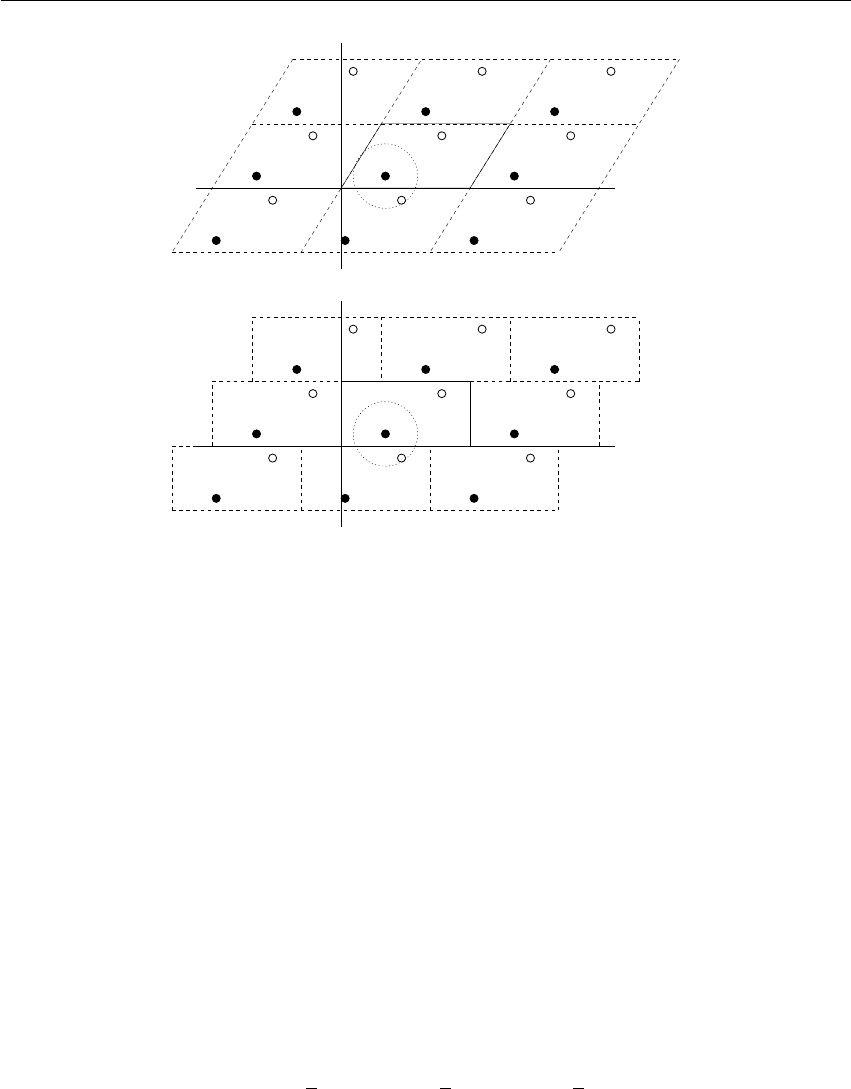
Figure 3.2: A rhombic dodecahedron and truncated octahedron (arbitrary orientations).
box type image box box vectors box vector angles
distance volume a b c 6bc 6ac 6ab
d0 0
cubic d d30d090◦90◦90◦
0 0 d
rhombic d01
2d
dodecahedron d1
2√2d30d1
2d60◦60◦90◦
(xy-square) 0.707 d30 0 1
2√2d
rhombic d1
2d1
2d
dodecahedron d1
2√2d301
2√3d1
6√3d60◦60◦60◦
(xy-hexagon) 0.707 d30 0 1
3√6d
truncated d1
3d−1
3d
octahedron d4
9√3d302
3√2d1
3√2d71.53◦109.47◦71.53◦
0.770 d30 0 1
3√6d
Table 3.1: The cubic box, the rhombic dodecahedron and the truncated octahedron.
It is also possible to simulate without periodic boundary conditions, but it is usually more efficient
to simulate an isolated cluster of molecules in a large periodic box, since fast grid searching can
only be used in a periodic system.
3.2.1 Some useful box types
The three most useful box types for simulations of solvated systems are described in Table 3.1.
The rhombic dodecahedron (Fig. 3.2) is the smallest and most regular space-filling unit cell. Each
of the 12 image cells is at the same distance. The volume is 71% of the volume of a cube having
the same image distance. This saves about 29% of CPU-time when simulating a spherical or
flexible molecule in solvent. There are two different orientations of a rhombic dodecahedron that
satisfy equations 3.1,3.2 and 3.3. The program editconf produces the orientation which has
a square intersection with the xy-plane. This orientation was chosen because the first two box
vectors coincide with the x and y-axis, which is easier to comprehend. The other orientation can

14 Chapter 3. Algorithms
be useful for simulations of membrane proteins. In this case the cross-section with the xy-plane is
a hexagon, which has an area which is 14% smaller than the area of a square with the same image
distance. The height of the box (cz) should be changed to obtain an optimal spacing. This box
shape not only saves CPU time, it also results in a more uniform arrangement of the proteins.
3.2.2 Cut-off restrictions
The minimum image convention implies that the cut-off radius used to truncate non-bonded inter-
actions may not exceed half the shortest box vector:
Rc<1
2min(kak,kbk,kck),(3.4)
because otherwise more than one image would be within the cut-off distance of the force. When a
macromolecule, such as a protein, is studied in solution, this restriction alone is not sufficient: in
principle, a single solvent molecule should not be able to ‘see’ both sides of the macromolecule.
This means that the length of each box vector must exceed the length of the macromolecule in the
direction of that edge plus two times the cut-off radius Rc. It is, however, common to compromise
in this respect, and make the solvent layer somewhat smaller in order to reduce the computational
cost. For efficiency reasons the cut-off with triclinic boxes is more restricted. For grid search the
extra restriction is weak:
Rc<min(ax, by, cz)(3.5)
For simple search the extra restriction is stronger:
Rc<1
2min(ax, by, cz)(3.6)
Each unit cell (cubic, rectangular or triclinic) is surrounded by 26 translated images. A particular
image can therefore always be identified by an index pointing to one of 27 translation vectors and
constructed by applying a translation with the indexed vector (see 3.4.3). Restriction (3.5) ensures
that only 26 images need to be considered.
3.3 The group concept
The GROMACS MD and analysis programs use user-defined groups of atoms to perform certain
actions on. The maximum number of groups is 256, but each atom can only belong to six different
groups, one each of the following:
temperature-coupling group The temperature coupling parameters (reference temperature, time
constant, number of degrees of freedom, see 3.4.4) can be defined for each T-coupling group
separately. For example, in a solvated macromolecule the solvent (that tends to generate
more heating by force and integration errors) can be coupled with a shorter time constant to
a bath than is a macromolecule, or a surface can be kept cooler than an adsorbing molecule.
Many different T-coupling groups may be defined. See also center of mass groups below.

3.4. Molecular Dynamics 15
freeze group Atoms that belong to a freeze group are kept stationary in the dynamics. This is
useful during equilibration, e.g. to avoid badly placed solvent molecules giving unreasonable
kicks to protein atoms, although the same effect can also be obtained by putting a restraining
potential on the atoms that must be protected. The freeze option can be used, if desired, on
just one or two coordinates of an atom, thereby freezing the atoms in a plane or on a line.
When an atom is partially frozen, constraints will still be able to move it, even in a frozen
direction. A fully frozen atom can not be moved by constraints. Many freeze groups can
be defined. Frozen coordinates are unaffected by pressure scaling; in some cases this can
produce unwanted results, particularly when constraints are also used (in this case you will
get very large pressures). Accordingly, it is recommended to avoid combining freeze groups
with constraints and pressure coupling. For the sake of equilibration it could suffice to
start with freezing in a constant volume simulation, and afterward use position restraints in
conjunction with constant pressure.
accelerate group On each atom in an “accelerate group” an acceleration agis imposed. This
is equivalent to an external force. This feature makes it possible to drive the system into
a non-equilibrium state and enables the performance of non-equilibrium MD and hence to
obtain transport properties.
energy-monitor group Mutual interactions between all energy-monitor groups are compiled dur-
ing the simulation. This is done separately for Lennard-Jones and Coulomb terms. In prin-
ciple up to 256 groups could be defined, but that would lead to 256×256 items! Better use
this concept sparingly.
All non-bonded interactions between pairs of energy-monitor groups can be excluded (see
details in the User Guide). Pairs of particles from excluded pairs of energy-monitor groups
are not put into the pair list. This can result in a significant speedup for simulations where
interactions within or between parts of the system are not required.
center of mass group In GROMACS the center of mass (COM) motion can be removed, for
either the complete system or for groups of atoms. The latter is useful, e.g. for systems
where there is limited friction (e.g. gas systems) to prevent center of mass motion to occur.
It makes sense to use the same groups for temperature coupling and center of mass motion
removal.
Compressed position output group In order to further reduce the size of the compressed tra-
jectory file (.xtc or .tng), it is possible to store only a subset of all particles. All x-
compression groups that are specified are saved, the rest are not. If no such groups are
specified, than all atoms are saved to the compressed trajectory file.
The use of groups in GROMACS tools is described in sec. 8.1.
3.4 Molecular Dynamics
A global flow scheme for MD is given in Fig. 3.3. Each MD or EM run requires as input a set of
initial coordinates and – optionally – initial velocities of all particles involved. This chapter does
not describe how these are obtained; for the setup of an actual MD run check the online manual at
www.gromacs.org.

16 Chapter 3. Algorithms
THE GLOBAL MD ALGORITHM
1. Input initial conditions
Potential interaction Vas a function of atom positions
Positions rof all atoms in the system
Velocities vof all atoms in the system
⇓
repeat 2,3,4 for the required number of steps:
2. Compute forces
The force on any atom
Fi=−∂V
∂ri
is computed by calculating the force between non-bonded atom
pairs:
Fi=PjFij
plus the forces due to bonded interactions (which may depend on 1,
2, 3, or 4 atoms), plus restraining and/or external forces.
The potential and kinetic energies and the pressure tensor may be
computed.
⇓
3. Update configuration
The movement of the atoms is simulated by numerically solving
Newton’s equations of motion
d2ri
dt2=Fi
mi
or
dri
dt=vi;dvi
dt=Fi
mi
⇓
4. if required: Output step
write positions, velocities, energies, temperature, pressure, etc.
Figure 3.3: The global MD algorithm
3.4. Molecular Dynamics 17
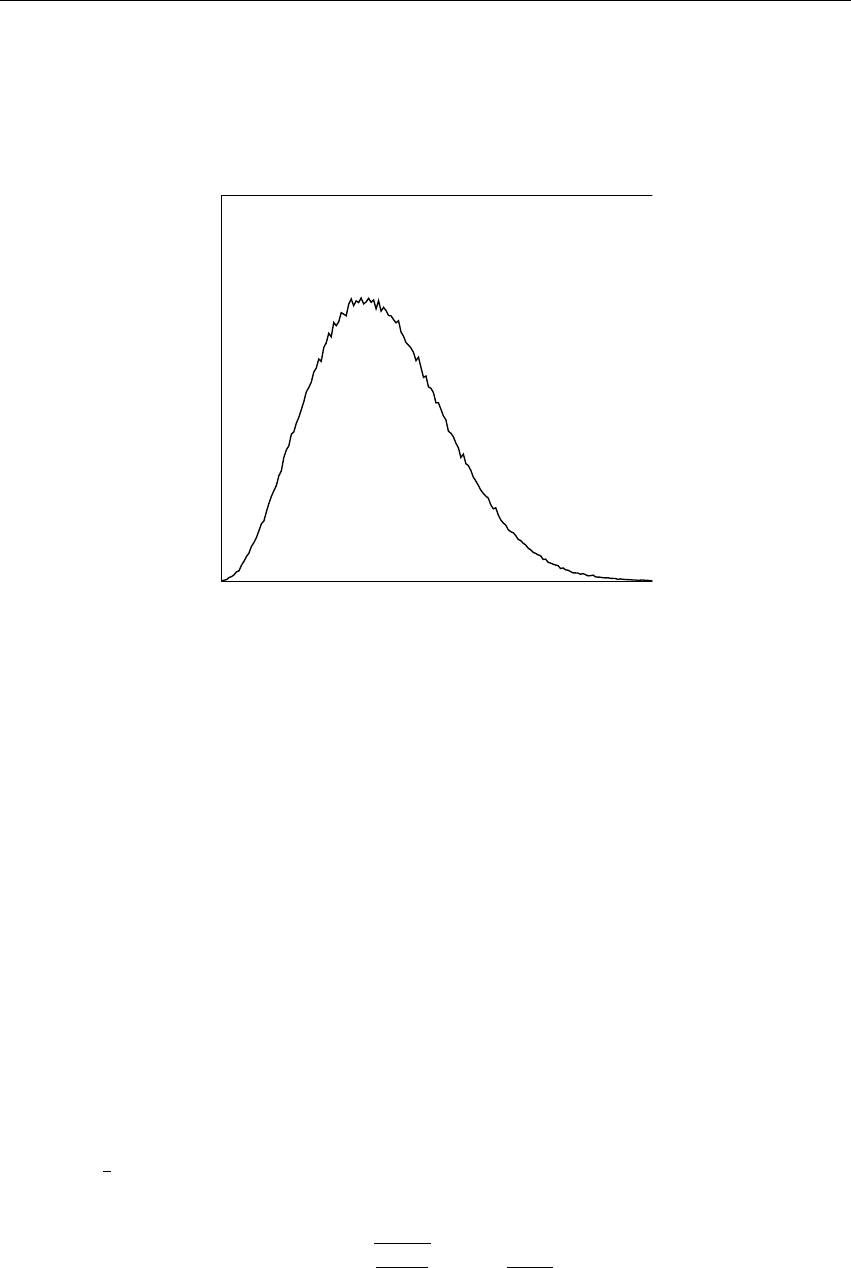
Velocity
Figure 3.4: A Maxwell-Boltzmann velocity distribution, generated from random numbers.
3.4.1 Initial conditions
Topology and force field
The system topology, including a description of the force field, must be read in. Force fields and
topologies are described in chapter 4and 5, respectively. All this information is static; it is never
modified during the run.
Coordinates and velocities
Then, before a run starts, the box size and the coordinates and velocities of all particles are re-
quired. The box size and shape is determined by three vectors (nine numbers) b1,b2,b3, which
represent the three basis vectors of the periodic box.
If the run starts at t=t0, the coordinates at t=t0must be known. The leap-frog algorithm, the
default algorithm used to update the time step with ∆t(see 3.4.4), also requires that the velocities
at t=t0−1
2∆tare known. If velocities are not available, the program can generate initial atomic
velocities vi, i = 1 . . . 3Nwith a (Fig. 3.4) at a given absolute temperature T:
p(vi) = rmi
2πkT exp −miv2
i
2kT !(3.7)

18 Chapter 3. Algorithms
where kis Boltzmann’s constant (see chapter 2). To accomplish this, normally distributed random
numbers are generated by adding twelve random numbers Rkin the range 0≤Rk<1and
subtracting 6.0 from their sum. The result is then multiplied by the standard deviation of the
velocity distribution pkT/mi. Since the resulting total energy will not correspond exactly to the
required temperature T, a correction is made: first the center-of-mass motion is removed and then
all velocities are scaled so that the total energy corresponds exactly to T(see eqn. 3.18).
Center-of-mass motion
The center-of-mass velocity is normally set to zero at every step; there is (usually) no net external
force acting on the system and the center-of-mass velocity should remain constant. In practice,
however, the update algorithm introduces a very slow change in the center-of-mass velocity, and
therefore in the total kinetic energy of the system – especially when temperature coupling is used.
If such changes are not quenched, an appreciable center-of-mass motion can develop in long runs,
and the temperature will be significantly misinterpreted. Something similar may happen due to
overall rotational motion, but only when an isolated cluster is simulated. In periodic systems with
filled boxes, the overall rotational motion is coupled to other degrees of freedom and does not
cause such problems.
3.4.2 Neighbor searching
As mentioned in chapter 4, internal forces are either generated from fixed (static) lists, or from
dynamic lists. The latter consist of non-bonded interactions between any pair of particles. When
calculating the non-bonded forces, it is convenient to have all particles in a rectangular box. As
shown in Fig. 3.1, it is possible to transform a triclinic box into a rectangular box. The output
coordinates are always in a rectangular box, even when a dodecahedron or triclinic box was used
for the simulation. Equation 3.1 ensures that we can reset particles in a rectangular box by first
shifting them with box vector c, then with band finally with a. Equations 3.3,3.4 and 3.5 ensure
that we can find the 14 nearest triclinic images within a linear combination that does not involve
multiples of box vectors.
Pair lists generation
The non-bonded pair forces need to be calculated only for those pairs i, j for which the distance
rij between iand the nearest image of jis less than a given cut-off radius Rc. Some of the particle
pairs that fulfill this criterion are excluded, when their interaction is already fully accounted for by
bonded interactions. GROMACS employs a pair list that contains those particle pairs for which
non-bonded forces must be calculated. The pair list contains particles i, a displacement vector for
particle i, and all particles jthat are within rlist of this particular image of particle i. The list
is updated every nstlist steps.
To make the neighbor list, all particles that are close (i.e. within the neighbor list cut-off) to a given
particle must be found. This searching, usually called neighbor search (NS) or pair search, involves
periodic boundary conditions and determining the image (see sec. 3.2). The search algorithm is
O(N), although a simpler O(N2)algorithm is still available under some conditions.

3.4. Molecular Dynamics 19
Cut-off schemes: group versus Verlet
From version 4.6, GROMACS supports two different cut-off scheme setups: the original one
based on particle groups and one using a Verlet buffer. There are some important differences
that affect results, performance and feature support. The group scheme can be made to work
(almost) like the Verlet scheme, but this will lead to a decrease in performance. The group scheme
is especially fast for water molecules, which are abundant in many simulations, but on the most
recent x86 processors, this advantage is negated by the better instruction-level parallelism available
in the Verlet-scheme implementation. The group scheme is deprecated in version 5.0, and will be
removed in a future version. For practical details of choosing and setting up cut-off schemes,
please see the User Guide.
In the group scheme, a neighbor list is generated consisting of pairs of groups of at least one
particle. These groups were originally charge groups (see sec. 3.4.2), but with a proper treatment
of long-range electrostatics, performance in unbuffered simulations is their only advantage. A
pair of groups is put into the neighbor list when their center of geometry is within the cut-off
distance. Interactions between all particle pairs (one from each charge group) are calculated for
a certain number of MD steps, until the neighbor list is updated. This setup is efficient, as the
neighbor search only checks distance between charge-group pair, not particle pairs (saves a factor
of 3×3=9with a three-particle water model) and the non-bonded force kernels can be optimized
for, say, a water molecule “group”. Without explicit buffering, this setup leads to energy drift as
some particle pairs which are within the cut-off don’t interact and some outside the cut-off do
interact. This can be caused by
•particles moving across the cut-off between neighbor search steps, and/or
•for charge groups consisting of more than one particle, particle pairs moving in/out of the
cut-off when their charge group center of geometry distance is outside/inside of the cut-off.
Explicitly adding a buffer to the neighbor list will remove such artifacts, but this comes at a high
computational cost. How severe the artifacts are depends on the system, the properties in which
you are interested, and the cut-off setup.
The Verlet cut-off scheme uses a buffered pair list by default. It also uses clusters of particles, but
these are not static as in the group scheme. Rather, the clusters are defined spatially and consist
of 4 or 8 particles, which is convenient for stream computing, using e.g. SSE, AVX or CUDA on
GPUs. At neighbor search steps, a pair list is created with a Verlet buffer, ie. the pair-list cut-off
is larger than the interaction cut-off. In the non-bonded kernels, interactions are only computed
when a particle pair is within the cut-off distance at that particular time step. This ensures that
as particles move between pair search steps, forces between nearly all particles within the cut-off
distance are calculated. We say nearly all particles, because GROMACS uses a fixed pair list
update frequency for efficiency. A particle-pair, whose distance was outside the cut-off, could
possibly move enough during this fixed number of steps that its distance is now within the cut-
off. This small chance results in a small energy drift, and the size of the chance depends on the
temperature. When temperature coupling is used, the buffer size can be determined automatically,
given a certain tolerance on the energy drift.
The Verlet cut-off scheme is implemented in a very efficient fashion based on clusters of particles.
The simplest example is a cluster size of 4 particles. The pair list is then constructed based on

20 Chapter 3. Algorithms
cluster pairs. The cluster-pair search is much faster searching based on particle pairs, because
4×4 = 16 particle pairs are put in the list at once. The non-bonded force calculation kernel can
then calculate many particle-pair interactions at once, which maps nicely to SIMD or SIMT units
on modern hardware, which can perform multiple floating operations at once. These non-bonded
kernels are much faster than the kernels used in the group scheme for most types of systems,
particularly on newer hardware.
Additionally, when the list buffer is determined automatically as described below, we also apply
dynamic pair list pruning. The pair list can be constructed infrequently, but that can lead to a lot
of pairs in the list that are outside the cut-off range for all or most of the life time of this pair
list. Such pairs can be pruned out by applying a cluster-pair kernel that only determines which
clusters are in range. Because of the way the non-bonded data is regularized in GROMACS, this
kernel is an order of magnitude faster than the search and the interaction kernel. On the GPU this
pruning is overlapped with the integration on the CPU, so it is free in most cases. Therefore we
can prune every 4-10 integration steps with little overhead and significantly reduce the number of
cluster pairs in the interaction kernel. This procedure is applied automatically, unless the user set
the pair-list buffer size manually.
Energy drift and pair-list buffering
For a canonical (NVT) ensemble, the average energy error caused by diffusion of jparticles from
outside the pair-list cut-off r`to inside the interaction cut-off rcover the lifetime of the list can
be determined from the atomic displacements and the shape of the potential at the cut-off. The
displacement distribution along one dimension for a freely moving particle with mass mover time
tat temperature Tis a Gaussian G(x)of zero mean and variance σ2=t2kBT /m. For the distance
between two particles, the variance changes to σ2=σ2
12 =t2kBT(1/m1+ 1/m2). Note that
in practice particles usually interact with (bump into) other particles over time tand therefore the
real displacement distribution is much narrower. Given a non-bonded interaction cut-off distance
of rcand a pair-list cut-off r`=rc+rbfor rbthe Verlet buffer size, we can then write the average
energy error after time tfor all missing pair interactions between a single iparticle of type 1
surrounded by all jparticles that are of type 2 with number density ρ2, when the inter-particle
distance changes from r0to rt, as:
h∆Vi=Zrc
0Z∞
r`
4πr2
0ρ2V(rt)Grt−r0
σdr0drt(3.8)
To evaluate this analytically, we need to make some approximations. First we replace V(rt)by
a Taylor expansion around rc, then we can move the lower bound of the integral over r0to −∞
which will simplify the result:
h∆Vi ≈ Zrc
−∞ Z∞
r`
4πr2
0ρ2hV0(rc)(rt−rc) +
V00(rc)1
2(rt−rc)2+
V000(rc)1
6(rt−rc)3+
O(rt−rc)4iGrt−r0
σdr0drt(3.9)
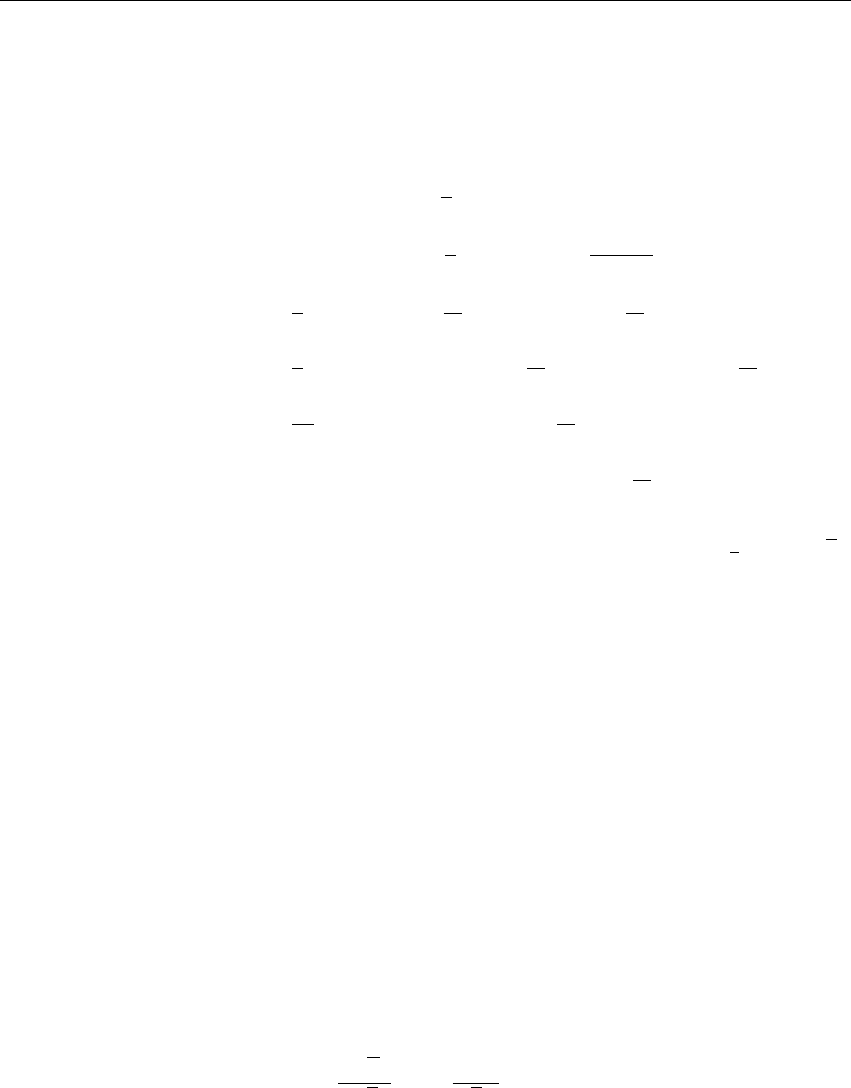
3.4. Molecular Dynamics 21
Replacing the factor r2
0by (r`+σ)2, which results in a slight overestimate, allows us to calculate
the integrals analytically:
h∆Vi ≈ 4π(r`+σ)2ρ2Zrc
−∞ Z∞
r`hV0(rc)(rt−rc) +
V00(rc)1
2(rt−rc)2+
V000(rc)1
6(rt−rc)3iGrt−r0
σdr0drt(3.10)
= 4π(r`+σ)2ρ21
2V0(rc)rbσGrb
σ−(r2
b+σ2)Erb
σ+
1
6V00(rc)σ(r2
b+ 2σ2)Grb
σ−rb(r2
b+ 3σ2)Erb
σ+
1
24V000(rc)rbσ(r2
b+ 5σ2)Grb
σ
−(r4
b+ 6r2
bσ2+ 3σ4)Erb
σ (3.11)
where G(x)is a Gaussian distribution with 0 mean and unit variance and E(x) = 1
2erfc(x/√2).
We always want to achieve small energy error, so σwill be small compared to both rcand r`,
thus the approximations in the equations above are good, since the Gaussian distribution decays
rapidly. The energy error needs to be averaged over all particle pair types and weighted with
the particle counts. In GROMACS we don’t allow cancellation of error between pair types, so
we average the absolute values. To obtain the average energy error per unit time, it needs to be
divided by the neighbor-list life time t= (nstlist −1) ×dt. The function can not be inverted
analytically, so we use bisection to obtain the buffer size rbfor a target drift. Again we note that in
practice the error we usually be much smaller than this estimate, as in the condensed phase particle
displacements will be much smaller than for freely moving particles, which is the assumption used
here.
When (bond) constraints are present, some particles will have fewer degrees of freedom. This will
reduce the energy errors. For simplicity, we only consider one constraint per particle, the heaviest
particle in case a particle is involved in multiple constraints. This simplification overestimates the
displacement. The motion of a constrained particle is a superposition of the 3D motion of the
center of mass of both particles and a 2D rotation around the center of mass. The displacement in
an arbitrary direction of a particle with 2 degrees of freedom is not Gaussian, but rather follows
the complementary error function:
√π
2√2σerfc |r|
√2σ(3.12)
where σ2is again t2kBT/m. This distribution can no longer be integrated analytically to obtain
the energy error. But we can generate a tight upper bound using a scaled and shifted Gaussian
distribution (not shown). This Gaussian distribution can then be used to calculate the energy error
as described above. The rotation displacement around the center of mass can not be more than the
length of the arm. To take this into account, we scale σin eqn. 3.12 (details not presented here) to
obtain an overestimate of the real displacement. This latter effect significantly reduces the buffer
22 Chapter 3. Algorithms
0 0.02 0.04 0.06 0.08 0.1
Verlet buffer (nm)
10−6
10−5
10−4
10−3
10−2
drift per atom (kJ/mol/ps)
estimate 1x1
estimate 4x4
double precision
mixed precision
Figure 3.5: Energy drift per atom for an SPC/E water system at 300K with a time step of 2 fs and
a pair-list update period of 10 steps (pair-list life time: 18 fs). PME was used with ewald-rtol
set to 10−5; this parameter affects the shape of the potential at the cut-off. Error estimates due to
finite Verlet buffer size are shown for a 1×1atom pair list and 4×4atom pair list without and
with (dashed line) cancellation of positive and negative errors. Real energy drift is shown for sim-
ulations using double- and mixed-precision settings. Rounding errors in the SETTLE constraint
algorithm from the use of single precision causes the drift to become negative at large buffer size.
Note that at zero buffer size, the real drift is small because positive (H-H) and negative (O-H)
energy errors cancel.
size for longer neighborlist lifetimes in e.g. water, as constrained hydrogens are by far the fastest
particles, but they can not move further than 0.1 nm from the heavy atom they are connected to.
There is one important implementation detail that reduces the energy errors caused by the finite
Verlet buffer list size. The derivation above assumes a particle pair-list. However, the GROMACS
implementation uses a cluster pair-list for efficiency. The pair list consists of pairs of clusters of
4 particles in most cases, also called a 4×4list, but the list can also be 4×8(GPU CUDA
kernels and AVX 256-bit single precision kernels) or 4×2(SSE double-precision kernels). This
means that the pair-list is effectively much larger than the corresponding 1×1list. Thus slightly
beyond the pair-list cut-off there will still be a large fraction of particle pairs present in the list.
This fraction can be determined in a simulation and accurately estimated under some reasonable
assumptions. The fraction decreases with increasing pair-list range, meaning that a smaller buffer
can be used. For typical all-atom simulations with a cut-off of 0.9 nm this fraction is around 0.9,
which gives a reduction in the energy errors of a factor of 10. This reduction is taken into account
during the automatic Verlet buffer calculation and results in a smaller buffer size.
In Fig. 3.5 one can see that for small buffer sizes the drift of the total energy is much smaller
than the pair energy error tolerance, due to cancellation of errors. For larger buffer size, the error
estimate is a factor of 6 higher than drift of the total energy, or alternatively the buffer estimate is
0.024 nm too large. This is because the protons don’t move freely over 18 fs, but rather vibrate.
3.4. Molecular Dynamics 23
j
i
i’
Figure 3.6: Grid search in two dimensions. The arrows are the box vectors.
Cut-off artifacts and switched interactions
With the Verlet scheme, the pair potentials are shifted to be zero at the cut-off, which makes the
potential the integral of the force. This is only possible in the group scheme if the shape of the
potential is such that its value is zero at the cut-off distance. However, there can still be energy
drift when the forces are non-zero at the cut-off. This effect is extremely small and often not
noticeable, as other integration errors (e.g. from constraints) may dominate. To completely avoid
cut-off artifacts, the non-bonded forces can be switched exactly to zero at some distance smaller
than the neighbor list cut-off (there are several ways to do this in GROMACS, see sec. 4.1.5). One
then has a buffer with the size equal to the neighbor list cut-off less the longest interaction cut-off.
Simple search
Due to eqns. 3.1 and 3.6, the vector rij connecting images within the cut-off Rccan be found by
constructing:
r000 =rj−ri(3.13)
r00 =r000 −c∗round(r000
z/cz)(3.14)
r0=r00 −b∗round(r00
y/by)(3.15)
rij =r0−a∗round(r0
x/ax)(3.16)
When distances between two particles in a triclinic box are needed that do not obey eqn. 3.1, many
shifts of combinations of box vectors need to be considered to find the nearest image.
Grid search
The grid search is schematically depicted in Fig. 3.6. All particles are put on the NS grid, with the
smallest spacing ≥Rc/2in each of the directions. In the direction of each box vector, a particle

24 Chapter 3. Algorithms
ihas three images. For each direction the image may be -1,0 or 1, corresponding to a translation
over -1, 0 or +1 box vector. We do not search the surrounding NS grid cells for neighbors of
iand then calculate the image, but rather construct the images first and then search neighbors
corresponding to that image of i. As Fig. 3.6 shows, some grid cells may be searched more than
once for different images of i. This is not a problem, since, due to the minimum image convention,
at most one image will “see” the j-particle. For every particle, fewer than 125 (53) neighboring
cells are searched. Therefore, the algorithm scales linearly with the number of particles. Although
the prefactor is large, the scaling behavior makes the algorithm far superior over the standard
O(N2)algorithm when there are more than a few hundred particles. The grid search is equally
fast for rectangular and triclinic boxes. Thus for most protein and peptide simulations the rhombic
dodecahedron will be the preferred box shape.
Charge groups
Charge groups were originally introduced to reduce cut-off artifacts of Coulomb interactions.
When a plain cut-off is used, significant jumps in the potential and forces arise when atoms with
(partial) charges move in and out of the cut-off radius. When all chemical moieties have a net
charge of zero, these jumps can be reduced by moving groups of atoms with net charge zero,
called charge groups, in and out of the neighbor list. This reduces the cut-off effects from the
charge-charge level to the dipole-dipole level, which decay much faster. With the advent of full
range electrostatics methods, such as particle-mesh Ewald (sec. 4.8.2), the use of charge groups
is no longer required for accuracy. It might even have a slight negative effect on the accuracy or
efficiency, depending on how the neighbor list is made and the interactions are calculated.
But there is still an important reason for using “charge groups”: efficiency with the group cut-off
scheme. Where applicable, neighbor searching is carried out on the basis of charge groups which
are defined in the molecular topology. If the nearest image distance between the geometrical
centers of the atoms of two charge groups is less than the cut-off radius, all atom pairs between
the charge groups are included in the pair list. The neighbor searching for a water system, for
instance, is 32= 9 times faster when each molecule is treated as a charge group. Also the highly
optimized water force loops (see sec. A.2.1) only work when all atoms in a water molecule form
a single charge group. Currently the name neighbor-search group would be more appropriate, but
the name charge group is retained for historical reasons. When developing a new force field, the
advice is to use charge groups of 3 to 4 atoms for optimal performance. For all-atom force fields
this is relatively easy, as one can simply put hydrogen atoms, and in some case oxygen atoms, in
the same charge group as the heavy atom they are connected to; for example: CH3, CH2, CH,
NH2, NH, OH, CO2, CO.
With the Verlet cut-off scheme, charge groups are ignored.
3.4.3 Compute forces
Potential energy
When forces are computed, the potential energy of each interaction term is computed as well. The
total potential energy is summed for various contributions, such as Lennard-Jones, Coulomb, and

3.4. Molecular Dynamics 25
bonded terms. It is also possible to compute these contributions for energy-monitor groups of
atoms that are separately defined (see sec. 3.3).
Kinetic energy and temperature
The temperature is given by the total kinetic energy of the N-particle system:
Ekin =1
2
N
X
i=1
miv2
i(3.17)
From this the absolute temperature Tcan be computed using:
1
2Ndf kT =Ekin (3.18)
where kis Boltzmann’s constant and Ndf is the number of degrees of freedom which can be
computed from:
Ndf = 3N−Nc−Ncom (3.19)
Here Ncis the number of constraints imposed on the system. When performing molecular dynam-
ics Ncom = 3 additional degrees of freedom must be removed, because the three center-of-mass
velocities are constants of the motion, which are usually set to zero. When simulating in vacuo,
the rotation around the center of mass can also be removed, in this case Ncom = 6. When more
than one temperature-coupling group is used, the number of degrees of freedom for group iis:
Ni
df = (3Ni−Ni
c)3N−Nc−Ncom
3N−Nc
(3.20)
The kinetic energy can also be written as a tensor, which is necessary for pressure calculation in a
triclinic system, or systems where shear forces are imposed:
Ekin =1
2
N
X
i
mivi⊗vi(3.21)
Pressure and virial
The pressure tensor Pis calculated from the difference between kinetic energy Ekin and the virial
Ξ:
P=2
V(Ekin −Ξ)(3.22)
where Vis the volume of the computational box. The scalar pressure P, which can be used for
pressure coupling in the case of isotropic systems, is computed as:
P= trace(P)/3(3.23)
The virial Ξtensor is defined as:
Ξ=−1
2X
i<j
rij ⊗Fij (3.24)
The GROMACS implementation of the virial computation is described in sec. A.1.

26 Chapter 3. Algorithms
1 20 t
x v x
Figure 3.7: The Leap-Frog integration method. The algorithm is called Leap-Frog because rand
vare leaping like frogs over each other’s backs.
3.4.4 The leap-frog integrator
The default MD integrator in GROMACS is the so-called leap-frog algorithm [22] for the inte-
gration of the equations of motion. When extremely accurate integration with temperature and/or
pressure coupling is required, the velocity Verlet integrators are also present and may be preferable
(see 3.4.5). The leap-frog algorithm uses positions rat time tand velocities vat time t−1
2∆t; it
updates positions and velocities using the forces F(t)determined by the positions at time tusing
these relations:
v(t+1
2∆t) = v(t−1
2∆t) + ∆t
mF(t)(3.25)
r(t+ ∆t) = r(t)+∆tv(t+1
2∆t)(3.26)
The algorithm is visualized in Fig. 3.7. It produces trajectories that are identical to the Verlet [23]
algorithm, whose position-update relation is
r(t+ ∆t)=2r(t)−r(t−∆t) + 1
mF(t)∆t2+O(∆t4)(3.27)
The algorithm is of third order in rand is time-reversible. See ref. [24] for the merits of this
algorithm and comparison with other time integration algorithms.
The equations of motion are modified for temperature coupling and pressure coupling, and ex-
tended to include the conservation of constraints, all of which are described below.
3.4.5 The velocity Verlet integrator
The velocity Verlet algorithm [25] is also implemented in GROMACS, though it is not yet fully
integrated with all sets of options. In velocity Verlet, positions rand velocities vat time tare used
to integrate the equations of motion; velocities at the previous half step are not required.
v(t+1
2∆t) = v(t) + ∆t
2mF(t)(3.28)
r(t+ ∆t) = r(t)+∆tv(t+1
2∆t)(3.29)
v(t+ ∆t) = v(t+1
2∆t) + ∆t
2mF(t+ ∆t)(3.30)

3.4. Molecular Dynamics 27
or, equivalently,
r(t+ ∆t) = r(t)+∆tv+∆t2
2mF(t)(3.31)
v(t+ ∆t) = v(t) + ∆t
2m[F(t) + F(t+ ∆t)] (3.32)
With no temperature or pressure coupling, and with corresponding starting points, leap-frog and
velocity Verlet will generate identical trajectories, as can easily be verified by hand from the equa-
tions above. Given a single starting file with the same starting point x(0) and v(0), leap-frog
and velocity Verlet will not give identical trajectories, as leap-frog will interpret the velocities as
corresponding to t=−1
2∆t, while velocity Verlet will interpret them as corresponding to the
timepoint t= 0.
3.4.6 Understanding reversible integrators: The Trotter decomposition
To further understand the relationship between velocity Verlet and leap-frog integration, we intro-
duce the reversible Trotter formulation of dynamics, which is also useful to understanding imple-
mentations of thermostats and barostats in GROMACS.
A system of coupled, first-order differential equations can be evolved from time t= 0 to time tby
applying the evolution operator
Γ(t) = exp(iLt)Γ(0)
iL =˙
Γ· ∇Γ,(3.33)
where Lis the Liouville operator, and Γis the multidimensional vector of independent variables
(positions and velocities). A short-time approximation to the true operator, accurate at time ∆t=
t/P , is applied Ptimes in succession to evolve the system as
Γ(t) =
P
Y
i=1
exp(iL∆t)Γ(0) (3.34)
For NVE dynamics, the Liouville operator is
iL =
N
X
i=1
vi· ∇ri+
N
X
i=1
1
mi
F(ri)· ∇vi.(3.35)
This can be split into two additive operators
iL1=
N
X
i=1
1
mi
F(ri)· ∇vi
iL2=
N
X
i=1
vi· ∇ri(3.36)
Then a short-time, symmetric, and thus reversible approximation of the true dynamics will be
exp(iL∆t) = exp(iL2
1
2∆t) exp(iL1∆t) exp(iL2
1
2∆t) + O(∆t3).(3.37)
28 Chapter 3. Algorithms
This corresponds to velocity Verlet integration. The first exponential term over 1
2∆tcorresponds
to a velocity half-step, the second exponential term over ∆tcorresponds to a full velocity step,
and the last exponential term over 1
2∆tis the final velocity half step. For future times t=n∆t,
this becomes
exp(iLn∆t)≈exp(iL2
1
2∆t) exp(iL1∆t) exp(iL2
1
2∆t)n
≈exp(iL2
1
2∆t)exp(iL1∆t) exp(iL2∆t)n−1
exp(iL1∆t) exp(iL2
1
2∆t)(3.38)
This formalism allows us to easily see the difference between the different flavors of Verlet inte-
grators. The leap-frog integrator can be seen as starting with Eq. 3.37 with the exp (iL1∆t)term,
instead of the half-step velocity term, yielding
exp(iLn∆t) = exp (iL1∆t) exp (iL2∆t) + O(∆t3).(3.39)
Here, the full step in velocity is between t−1
2∆tand t+1
2∆t, since it is a combination of the
velocity half steps in velocity Verlet. For future times t=n∆t, this becomes
exp(iLn∆t)≈exp (iL1∆t) exp (iL2∆t)n
.(3.40)
Although at first this does not appear symmetric, as long as the full velocity step is between t−1
2∆t
and t+1
2∆t, then this is simply a way of starting velocity Verlet at a different place in the cycle.
Even though the trajectory and thus potential energies are identical between leap-frog and velocity
Verlet, the kinetic energy and temperature will not necessarily be the same. Standard velocity
Verlet uses the velocities at the tto calculate the kinetic energy and thus the temperature only at
time t; the kinetic energy is then a sum over all particles
KEfull(t) = X
i1
2mi
vi(t)2
=X
i
1
2mi1
2vi(t−1
2∆t) + 1
2vi(t+1
2∆t)2
,(3.41)
with the square on the outside of the average. Standard leap-frog calculates the kinetic energy at
time tbased on the average kinetic energies at the timesteps t+1
2∆tand t−1
2∆t, or the sum over
all particles
KEaverage(t) = X
i
1
2mi1
2vi(t−1
2∆t)2+1
2vi(t+1
2∆t)2,(3.42)
where the square is inside the average.
A non-standard variant of velocity Verlet which averages the kinetic energies KE(t+1
2∆t)and
KE(t−1
2∆t), exactly like leap-frog, is also now implemented in GROMACS (as .mdp file
option md-vv-avek). Without temperature and pressure coupling, velocity Verlet with half-
step-averaged kinetic energies and leap-frog will be identical up to numerical precision. For

3.4. Molecular Dynamics 29
temperature- and pressure-control schemes, however, velocity Verlet with half-step-averaged ki-
netic energies and leap-frog will be different, as will be discussed in the section in thermostats and
barostats.
The half-step-averaged kinetic energy and temperature are slightly more accurate for a given step
size; the difference in average kinetic energies using the half-step-averaged kinetic energies (md
and md-vv-avek) will be closer to the kinetic energy obtained in the limit of small step size than
will the full-step kinetic energy (using md-vv). For NVE simulations, this difference is usually not
significant, since the positions and velocities of the particles are still identical; it makes a difference
in the way the the temperature of the simulations are interpreted, but not in the trajectories that
are produced. Although the kinetic energy is more accurate with the half-step-averaged method,
meaning that it changes less as the timestep gets large, it is also more noisy. The RMS deviation
of the total energy of the system (sum of kinetic plus potential) in the half-step-averaged kinetic
energy case will be higher (about twice as high in most cases) than the full-step kinetic energy.
The drift will still be the same, however, as again, the trajectories are identical.
For NVT simulations, however, there will be a difference, as discussed in the section on temper-
ature control, since the velocities of the particles are adjusted such that kinetic energies of the
simulations, which can be calculated either way, reach the distribution corresponding to the set
temperature. In this case, the three methods will not give identical results.
Because the velocity and position are both defined at the same time tthe velocity Verlet integrator
can be used for some methods, especially rigorously correct pressure control methods, that are not
actually possible with leap-frog. The integration itself takes negligibly more time than leap-frog,
but twice as many communication calls are currently required. In most cases, and especially for
large systems where communication speed is important for parallelization and differences between
thermodynamic ensembles vanish in the 1/N limit, and when only NVT ensembles are required,
leap-frog will likely be the preferred integrator. For pressure control simulations where the fine
details of the thermodynamics are important, only velocity Verlet allows the true ensemble to be
calculated. In either case, simulation with double precision may be required to get fine details of
thermodynamics correct.
3.4.7 Multiple time stepping
Several other simulation packages uses multiple time stepping for bonds and/or the PME mesh
forces. In GROMACS we have not implemented this (yet), since we use a different philosophy.
Bonds can be constrained (which is also a more sound approximation of a physical quantum
oscillator), which allows the smallest time step to be increased to the larger one. This not only
halves the number of force calculations, but also the update calculations. For even larger time
steps, angle vibrations involving hydrogen atoms can be removed using virtual interaction sites
(see sec. 6.10), which brings the shortest time step up to PME mesh update frequency of a multiple
time stepping scheme.
3.4.8 Temperature coupling
While direct use of molecular dynamics gives rise to the NVE (constant number, constant vol-
ume, constant energy ensemble), most quantities that we wish to calculate are actually from a

30 Chapter 3. Algorithms
constant temperature (NVT) ensemble, also called the canonical ensemble. GROMACS can use
the weak-coupling scheme of Berendsen [26], stochastic randomization through the Andersen
thermostat [27], the extended ensemble Nosé-Hoover scheme [28,29], or a velocity-rescaling
scheme [30] to simulate constant temperature, with advantages of each of the schemes laid out
below.
There are several other reasons why it might be necessary to control the temperature of the system
(drift during equilibration, drift as a result of force truncation and integration errors, heating due to
external or frictional forces), but this is not entirely correct to do from a thermodynamic standpoint,
and in some cases only masks the symptoms (increase in temperature of the system) rather than the
underlying problem (deviations from correct physics in the dynamics). For larger systems, errors
in ensemble averages and structural properties incurred by using temperature control to remove
slow drifts in temperature appear to be negligible, but no completely comprehensive comparisons
have been carried out, and some caution must be taking in interpreting the results.
When using temperature and/or pressure coupling the total energy is no longer conserved. In-
stead there is a conserved energy quantity the formula of which will depend on the combination or
temperature and pressure coupling algorithm used. For all coupling algorithms, except for Ander-
sen temperature coupling and Parrinello-Rahman pressure coupling combined with shear stress,
the conserved energy quantity is computed and stored in the energy and log file. Note that this
quantity will not be conserved when external forces are applied to the system, such as pulling on
group with a changing distance or an electric field. Furthermore, how well the energy is conserved
depends on the accuracy of all algorithms involved in the simulation. Usually the algorithms that
cause most drift are constraints and the pair-list buffer, depending on the parameters used.
Berendsen temperature coupling
The Berendsen algorithm mimics weak coupling with first-order kinetics to an external heat bath
with given temperature T0. See ref. [31] for a comparison with the Nosé-Hoover scheme. The
effect of this algorithm is that a deviation of the system temperature from T0is slowly corrected
according to:
dT
dt=T0−T
τ(3.43)
which means that a temperature deviation decays exponentially with a time constant τ. This
method of coupling has the advantage that the strength of the coupling can be varied and adapted
to the user requirement: for equilibration purposes the coupling time can be taken quite short (e.g.
0.01 ps), but for reliable equilibrium runs it can be taken much longer (e.g. 0.5 ps) in which case
it hardly influences the conservative dynamics.
The Berendsen thermostat suppresses the fluctuations of the kinetic energy. This means that one
does not generate a proper canonical ensemble, so rigorously, the sampling will be incorrect. This
error scales with 1/N , so for very large systems most ensemble averages will not be affected sig-
nificantly, except for the distribution of the kinetic energy itself. However, fluctuation properties,
such as the heat capacity, will be affected. A similar thermostat which does produce a correct
ensemble is the velocity rescaling thermostat [30] described below.
The heat flow into or out of the system is affected by scaling the velocities of each particle every

3.4. Molecular Dynamics 31
step, or every nTC steps, with a time-dependent factor λ, given by:
λ="1 + nTC∆t
τT(T0
T(t−1
2∆t)−1)#1/2
(3.44)
The parameter τTis close, but not exactly equal, to the time constant τof the temperature coupling
(eqn. 3.43):
τ= 2CVτT/Ndf k(3.45)
where CVis the total heat capacity of the system, kis Boltzmann’s constant, and Ndf is the
total number of degrees of freedom. The reason that τ6=τTis that the kinetic energy change
caused by scaling the velocities is partly redistributed between kinetic and potential energy and
hence the change in temperature is less than the scaling energy. In practice, the ratio τ /τTranges
from 1 (gas) to 2 (harmonic solid) to 3 (water). When we use the term “temperature coupling
time constant,” we mean the parameter τT.Note that in practice the scaling factor λis limited
to the range of 0.8 <=λ <=1.25, to avoid scaling by very large numbers which may crash the
simulation. In normal use, λwill always be much closer to 1.0.
The thermostat modifies the kinetic energy at each scaling step by:
∆Ek= (λ−1)2Ek(3.46)
The sum of these changes over the run needs to subtracted from the total energy to obtain the
conserved energy quantity.
Velocity-rescaling temperature coupling
The velocity-rescaling thermostat [30] is essentially a Berendsen thermostat (see above) with an
additional stochastic term that ensures a correct kinetic energy distribution by modifying it accord-
ing to
dK= (K0−K)dt
τT
+ 2sKK0
Nf
dW
√τT
,(3.47)
where Kis the kinetic energy, Nfthe number of degrees of freedom and dWa Wiener process.
There are no additional parameters, except for a random seed. This thermostat produces a correct
canonical ensemble and still has the advantage of the Berendsen thermostat: first order decay of
temperature deviations and no oscillations.
Andersen thermostat
One simple way to maintain a thermostatted ensemble is to take an NV E integrator and pe-
riodically re-select the velocities of the particles from a Maxwell-Boltzmann distribution. [27]
This can either be done by randomizing all the velocities simultaneously (massive collision) ev-
ery τT/∆tsteps (andersen-massive), or by randomizing every particle with some small
probability every timestep (andersen), equal to ∆t/τ , where in both cases ∆tis the timestep
and τTis a characteristic coupling time scale. Because of the way constraints operate, all par-
ticles in the same constraint group must be randomized simultaneously. Because of paralleliza-
tion issues, the andersen version cannot currently (5.0) be used in systems with constraints.

32 Chapter 3. Algorithms
andersen-massive can be used regardless of constraints. This thermostat is also currently
only possible with velocity Verlet algorithms, because it operates directly on the velocities at each
timestep.
This algorithm completely avoids some of the ergodicity issues of other thermostatting algorithms,
as energy cannot flow back and forth between energetically decoupled components of the system
as in velocity scaling motions. However, it can slow down the kinetics of system by randomizing
correlated motions of the system, including slowing sampling when τTis at moderate levels (less
than 10 ps). This algorithm should therefore generally not be used when examining kinetics or
transport properties of the system. [32]
Nosé-Hoover temperature coupling
The Berendsen weak-coupling algorithm is extremely efficient for relaxing a system to the target
temperature, but once the system has reached equilibrium it might be more important to probe a
correct canonical ensemble. This is unfortunately not the case for the weak-coupling scheme.
To enable canonical ensemble simulations, GROMACS also supports the extended-ensemble ap-
proach first proposed by Nosé [28] and later modified by Hoover [29]. The system Hamiltonian
is extended by introducing a thermal reservoir and a friction term in the equations of motion. The
friction force is proportional to the product of each particle’s velocity and a friction parameter, ξ.
This friction parameter (or “heat bath” variable) is a fully dynamic quantity with its own momen-
tum (pξ) and equation of motion; the time derivative is calculated from the difference between the
current kinetic energy and the reference temperature.
In this formulation, the particles’ equations of motion in Fig. 3.3 are replaced by:
d2ri
dt2=Fi
mi−pξ
Q
dri
dt,(3.48)
where the equation of motion for the heat bath parameter ξis:
dpξ
dt= (T−T0).(3.49)
The reference temperature is denoted T0, while Tis the current instantaneous temperature of the
system. The strength of the coupling is determined by the constant Q(usually called the “mass
parameter” of the reservoir) in combination with the reference temperature. 1
The conserved quantity for the Nosé-Hoover equations of motion is not the total energy, but rather
H=
N
X
i=1
pi
2mi
+U(r1,r2,...,rN) + p2
ξ
2Q+NfkT ξ, (3.50)
where Nfis the total number of degrees of freedom.
In our opinion, the mass parameter is a somewhat awkward way of describing coupling strength,
especially due to its dependence on reference temperature (and some implementations even in-
clude the number of degrees of freedom in your system when defining Q). To maintain the cou-
pling strength, one would have to change Qin proportion to the change in reference temperature.
1Note that some derivations, an alternative notation ξalt =vξ=pξ/Q is used.

3.4. Molecular Dynamics 33
For this reason, we prefer to let the GROMACS user work instead with the period τTof the oscil-
lations of kinetic energy between the system and the reservoir instead. It is directly related to Q
and T0via:
Q=τ2
TT0
4π2.(3.51)
This provides a much more intuitive way of selecting the Nosé-Hoover coupling strength (similar
to the weak-coupling relaxation), and in addition τTis independent of system size and reference
temperature.
It is however important to keep the difference between the weak-coupling scheme and the Nosé-
Hoover algorithm in mind: Using weak coupling you get a strongly damped exponential relax-
ation, while the Nosé-Hoover approach produces an oscillatory relaxation. The actual time it
takes to relax with Nosé-Hoover coupling is several times larger than the period of the oscillations
that you select. These oscillations (in contrast to exponential relaxation) also means that the time
constant normally should be 4–5 times larger than the relaxation time used with weak coupling,
but your mileage may vary.
Nosé-Hoover dynamics in simple systems such as collections of harmonic oscillators, can be non-
ergodic, meaning that only a subsection of phase space is ever sampled, even if the simulations
were to run for infinitely long. For this reason, the Nosé-Hoover chain approach was developed,
where each of the Nosé-Hoover thermostats has its own Nosé-Hoover thermostat controlling its
temperature. In the limit of an infinite chain of thermostats, the dynamics are guaranteed to be
ergodic. Using just a few chains can greatly improve the ergodicity, but recent research has shown
that the system will still be nonergodic, and it is still not entirely clear what the practical effect of
this [33]. Currently, the default number of chains is 10, but this can be controlled by the user. In the
case of chains, the equations are modified in the following way to include a chain of thermostatting
particles [34]:
d2ri
dt2=Fi
mi−pξ1
Q1
dri
dt
dpξ1
dt= (T−T0)−pξ1
pξ2
Q2
dpξi=2...N
dt= p2
ξi−1
Qi−1−kT !−pξi
pξi+1
Qi+1
dpξN
dt= p2
ξN−1
QN−1−kT !(3.52)
The conserved quantity for Nosé-Hoover chains is
H=
N
X
i=1
pi
2mi
+U(r1,r2,...,rN) +
M
X
k=1
p2
ξk
2Q0
k
+NfkT ξ1+kT
M
X
k=2
ξk(3.53)
The values and velocities of the Nosé-Hoover thermostat variables are generally not included in
the output, as they take up a fair amount of space and are generally not important for analysis
of simulations, but by setting an mdp option the values of all the positions and velocities of all

34 Chapter 3. Algorithms
Nosé-Hoover particles in the chain are written to the .edr file. Leap-frog simulations currently
can only have Nosé-Hoover chain lengths of 1, but this will likely be updated in later version.
As described in the integrator section, for temperature coupling, the temperature that the algorithm
attempts to match to the reference temperature is calculated differently in velocity Verlet and leap-
frog dynamics. Velocity Verlet (md-vv) uses the full-step kinetic energy, while leap-frog and
md-vv-avek use the half-step-averaged kinetic energy.
We can examine the Trotter decomposition again to better understand the differences between
these constant-temperature integrators. In the case of Nosé-Hoover dynamics (for simplicity, using
a chain with N= 1, with more details in Ref. [35]), we split the Liouville operator as
iL =iL1+iL2+iLNHC,(3.54)
where
iL1=
N
X
i=1 pi
mi·∂
∂ri
iL2=
N
X
i=1
Fi·∂
∂pi
iLNHC =
N
X
i=1 −pξ
Qvi· ∇vi+pξ
Q
∂
∂ξ + (T−T0)∂
∂pξ
(3.55)
For standard velocity Verlet with Nosé-Hoover temperature control, this becomes
exp(iL∆t) = exp (iLNHC∆t/2) exp (iL2∆t/2)
exp (iL1∆t) exp (iL2∆t/2) exp (iLNHC∆t/2) + O(∆t3).(3.56)
For half-step-averaged temperature control using md-vv-avek, this decomposition will not work,
since we do not have the full step temperature until after the second velocity step. However, we
can construct an alternate decomposition that is still reversible, by switching the place of the NHC
and velocity portions of the decomposition:
exp(iL∆t) = exp (iL2∆t/2) exp (iLNHC∆t/2) exp (iL1∆t)
exp (iLNHC∆t/2) exp (iL2∆t/2) + O(∆t3)(3.57)
This formalism allows us to easily see the difference between the different flavors of velocity
Verlet integrator. The leap-frog integrator can be seen as starting with Eq. 3.57 just before the
exp (iL1∆t)term, yielding:
exp(iL∆t) = exp (iL1∆t) exp (iLNHC∆t/2)
exp (iL2∆t) exp (iLNHC∆t/2) + O(∆t3)(3.58)
and then using some algebra tricks to solve for some quantities are required before they are actually
calculated [36].

3.4. Molecular Dynamics 35
Group temperature coupling
In GROMACS temperature coupling can be performed on groups of atoms, typically a protein and
solvent. The reason such algorithms were introduced is that energy exchange between different
components is not perfect, due to different effects including cut-offs etc. If now the whole system
is coupled to one heat bath, water (which experiences the largest cut-off noise) will tend to heat
up and the protein will cool down. Typically 100 K differences can be obtained. With the use of
proper electrostatic methods (PME) these difference are much smaller but still not negligible. The
parameters for temperature coupling in groups are given in the mdp file. Recent investigation has
shown that small temperature differences between protein and water may actually be an artifact
of the way temperature is calculated when there are finite timesteps, and very large differences in
temperature are likely a sign of something else seriously going wrong with the system, and should
be investigated carefully [37].
One special case should be mentioned: it is possible to temperature-couple only part of the system,
leaving other parts without temperature coupling. This is done by specifying −1for the time con-
stant τTfor the group that should not be thermostatted. If only part of the system is thermostatted,
the system will still eventually converge to an NVT system. In fact, one suggestion for minimiz-
ing errors in the temperature caused by discretized timesteps is that if constraints on the water
are used, then only the water degrees of freedom should be thermostatted, not protein degrees of
freedom, as the higher frequency modes in the protein can cause larger deviations from the “true”
temperature, the temperature obtained with small timesteps [37].
3.4.9 Pressure coupling
In the same spirit as the temperature coupling, the system can also be coupled to a “pressure
bath.” GROMACS supports both the Berendsen algorithm [26] that scales coordinates and box
vectors every step, the extended-ensemble Parrinello-Rahman approach [38,39], and for the ve-
locity Verlet variants, the Martyna-Tuckerman-Tobias-Klein (MTTK) implementation of pressure
control [35]. Parrinello-Rahman and Berendsen can be combined with any of the temperature
coupling methods above. MTTK can only be used with Nosé-Hoover temperature control. From
5.1 afterwards, it can only used when the system does not have constraints.
Berendsen pressure coupling
The Berendsen algorithm rescales the coordinates and box vectors every step, or every nPC steps,
with a matrix µ, which has the effect of a first-order kinetic relaxation of the pressure towards a
given reference pressure P0according to
dP
dt=P0−P
τp
.(3.59)
The scaling matrix µis given by
µij =δij −nPC∆t
3τp
βij{P0ij −Pij (t)}.(3.60)

36 Chapter 3. Algorithms
Here, βis the isothermal compressibility of the system. In most cases this will be a diagonal
matrix, with equal elements on the diagonal, the value of which is generally not known. It suffices
to take a rough estimate because the value of βonly influences the non-critical time constant of
the pressure relaxation without affecting the average pressure itself. For water at 1 atm and 300 K
β= 4.6×10−10 Pa−1= 4.6×10−5bar−1, which is 7.6×10−4MD units (see chapter 2). Most
other liquids have similar values. When scaling completely anisotropically, the system has to be
rotated in order to obey eqn. 3.1. This rotation is approximated in first order in the scaling, which
is usually less than 10−4. The actual scaling matrix µ0is
µ0=
µxx µxy +µyx µxz +µzx
0µyy µyz +µzy
0 0 µzz
.(3.61)
The velocities are neither scaled nor rotated. Since the equations of motion are modified by pres-
sure coupling, the conserved energy quantity also needs to be modified. For first order pressure
coupling, the work the barostat applies to the system every step needs to be subtracted from the
total energy to obtain the conserved energy quantity:
−X
i,j
(µij −δij)Pij V=X
i,j
2(µij −δij)Ξij (3.62)
where δij is the Kronecker delta and Ξis the virial. Note that the factor 2 originates from the
factor 1
2in the virial definition (eqn. 3.24).
In GROMACS, the Berendsen scaling can also be done isotropically, which means that instead
of Pa diagonal matrix with elements of size trace(P)/3is used. For systems with interfaces,
semi-isotropic scaling can be useful. In this case, the x/y-directions are scaled isotropically and
the zdirection is scaled independently. The compressibility in the x/y or z-direction can be set to
zero, to scale only in the other direction(s).
If you allow full anisotropic deformations and use constraints you might have to scale more slowly
or decrease your timestep to avoid errors from the constraint algorithms. It is important to note
that although the Berendsen pressure control algorithm yields a simulation with the correct average
pressure, it does not yield the exact NPT ensemble, and it is not yet clear exactly what errors this
approximation may yield.
Parrinello-Rahman pressure coupling
In cases where the fluctuations in pressure or volume are important per se (e.g. to calculate ther-
modynamic properties), especially for small systems, it may be a problem that the exact ensemble
is not well defined for the weak-coupling scheme, and that it does not simulate the true NPT
ensemble.
GROMACS also supports constant-pressure simulations using the Parrinello-Rahman approach [38,
39], which is similar to the Nosé-Hoover temperature coupling, and in theory gives the true NPT
ensemble. With the Parrinello-Rahman barostat, the box vectors as represented by the matrix b

3.4. Molecular Dynamics 37
obey the matrix equation of motion2
db2
dt2=VW−1b0−1(P−Pref ).(3.63)
The volume of the box is denoted V, and Wis a matrix parameter that determines the strength of
the coupling. The matrices Pand Pref are the current and reference pressures, respectively.
The equations of motion for the particles are also changed, just as for the Nosé-Hoover coupling.
In most cases you would combine the Parrinello-Rahman barostat with the Nosé-Hoover thermo-
stat, but to keep it simple we only show the Parrinello-Rahman modification here. The modified
Hamiltonian, which will be conserved, is:
Epot +Ekin +X
i
PiiV+X
i,j
1
2Wij dbij
dt2(3.64)
The equations of motion for the atoms, obtained from the Hamiltonian are:
d2ri
dt2=Fi
mi−Mdri
dt,(3.65)
M=b−1"bdb0
dt+db
dtb0#b0−1.(3.66)
This extra term has the appearance of a friction, but it should be noted that it is ficticious, and rather
an effect of the Parrinello-Rahman equations of motion being defined with all particle coordinates
represented relative to the box vectors, while GROMACS] uses normal Cartesian coordinates for
positions, velocities and forces. It is worth noting that the kinetic energy too should formally be
calculated based on velocities relative to the box vectors. This can have an effect e.g. for external
constant stress, but for now we only support coupling to constant external pressures, and for any
normal simulation the velocities of box vectors should be extremely small compared to particle
velocities. Gang Liu has done some work on deriving this for Cartesian coordinates[40] that we
will try to implement at some point in the future together with support for external stress.
The (inverse) mass parameter matrix W−1determines the strength of the coupling, and how the
box can be deformed. The box restriction (3.1) will be fulfilled automatically if the corresponding
elements of W−1are zero. Since the coupling strength also depends on the size of your box,
we prefer to calculate it automatically in GROMACS. You only have to provide the approximate
isothermal compressibilities βand the pressure time constant τpin the input file (Lis the largest
box matrix element):
W−1ij =4π2βij
3τ2
pL.(3.67)
Just as for the Nosé-Hoover thermostat, you should realize that the Parrinello-Rahman time con-
stant is not equivalent to the relaxation time used in the Berendsen pressure coupling algorithm.
In most cases you will need to use a 4–5 times larger time constant with Parrinello-Rahman cou-
pling. If your pressure is very far from equilibrium, the Parrinello-Rahman coupling may result in
very large box oscillations that could even crash your run. In that case you would have to increase
2The box matrix representation bin GROMACS corresponds to the transpose of the box matrix representation hin
the paper by Nosé and Klein. Because of this, some of our equations will look slightly different.
38 Chapter 3. Algorithms
the time constant, or (better) use the weak-coupling scheme to reach the target pressure, and then
switch to Parrinello-Rahman coupling once the system is in equilibrium. Additionally, using the
leap-frog algorithm, the pressure at time tis not available until after the time step has completed,
and so the pressure from the previous step must be used, which makes the algorithm not directly
reversible, and may not be appropriate for high precision thermodynamic calculations.
Surface-tension coupling
When a periodic system consists of more than one phase, separated by surfaces which are par-
allel to the xy-plane, the surface tension and the z-component of the pressure can be coupled to
a pressure bath. Presently, this only works with the Berendsen pressure coupling algorithm in
GROMACS. The average surface tension γ(t)can be calculated from the difference between the
normal and the lateral pressure
γ(t) = 1
nZLz
0Pzz(z, t)−Pxx(z, t) + Pyy(z, t)
2dz(3.68)
=Lz
nPzz(t)−Pxx(t) + Pyy(t)
2,(3.69)
where Lzis the height of the box and nis the number of surfaces. The pressure in the z-direction
is corrected by scaling the height of the box with µzz
∆Pzz =∆t
τp{P0zz −Pzz(t)}(3.70)
µzz = 1 + βzz ∆Pzz (3.71)
This is similar to normal pressure coupling, except that the factor of 1/3is missing. The pressure
correction in the z-direction is then used to get the correct convergence for the surface tension to
the reference value γ0. The correction factor for the box length in the x/y-direction is
µx/y = 1 + ∆t
2τp
βx/y nγ0
µzzLz−Pzz (t)+∆Pzz −Pxx(t) + Pyy(t)
2 (3.72)
The value of βzz is more critical than with normal pressure coupling. Normally an incorrect
compressibility will just scale τp, but with surface tension coupling it affects the convergence of
the surface tension. When βzz is set to zero (constant box height), ∆Pzz is also set to zero, which
is necessary for obtaining the correct surface tension.
MTTK pressure control algorithms
As mentioned in the previous section, one weakness of leap-frog integration is in constant pressure
simulations, since the pressure requires a calculation of both the virial and the kinetic energy at the
full time step; for leap-frog, this information is not available until after the full timestep. Velocity
Verlet does allow the calculation, at the cost of an extra round of global communication, and can
compute, mod any integration errors, the true NPT ensemble.
The full equations, combining both pressure coupling and temperature coupling, are taken from
Martyna et al. [35] and Tuckerman [41] and are referred to here as MTTK equations (Martyna-
Tuckerman-Tobias-Klein). We introduce for convenience = (1/3) ln(V/V0), where V0is a

3.4. Molecular Dynamics 39
reference volume. The momentum of is v=p/W = ˙=˙
V /3V, and define α= 1 + 3/Ndof
(see Ref [41])
The isobaric equations are
˙
ri=pi
mi
+p
Wri
˙
pi
mi
=1
mi
Fi−αp
W
pi
mi
˙=p
W
˙p
W=3V
W(Pint −P)+(α−1) N
X
n=1
p2
i
mi!,(3.73)
(3.74)
where
Pint =Pkin −Pvir =1
3V"N
X
i=1 p2
i
2mi−ri·Fi!#.(3.75)
The terms including αare required to make phase space incompressible [41]. The acceleration
term can be rewritten as
˙p
W=3V
W(αPkin −Pvir −P)(3.76)
In terms of velocities, these equations become
˙
ri=vi+vri
˙
vi=1
mi
Fi−αvvi
˙=v
˙v=3V
W(Pint −P)+(α−1) N
X
n=1
1
2miv2
i!
Pint =Pkin −Pvir =1
3V"N
X
i=1 1
2miv2
i−ri·Fi#(3.77)
For these equations, the conserved quantity is
H=
N
X
i=1
p2
i
2mi
+U(r1,r2,...,rN) + p
2W+P V (3.78)
The next step is to add temperature control. Adding Nosé-Hoover chains, including to the barostat
degree of freedom, where we use ηfor the barostat Nosé-Hoover variables, and Q0for the coupling
constants of the thermostats of the barostats, we get
˙
ri=pi
mi
+p
Wri

40 Chapter 3. Algorithms
˙
pi
mi
=1
mi
Fi−αp
W
pi
mi−pξ1
Q1
pi
mi
˙=p
W
˙p
W=3V
W(αPkin −Pvir −P)−pη1
Q0
1
p
˙
ξk=pξk
Qk
˙ηk=pηk
Q0
k
˙pξk=Gk−pξk+1
Qk+1
k= 1, . . . , M −1
˙pηk=G0
k−pηk+1
Q0
k+1
k= 1, . . . , M −1
˙pξM=GM
˙pηM=G0
M,
(3.79)
where
Pint =Pkin −Pvir =1
3V"N
X
i=1 p2
i
2mi−ri·Fi!#
G1=
N
X
i=1
p2
i
mi−NfkT
Gk=p2
ξk−1
2Qk−1−kT k = 2, . . . , M
G0
1=p2
2W−kT
G0
k=p2
ηk−1
2Q0
k−1−kT k = 2, . . . , M (3.80)
The conserved quantity is now
H=
N
X
i=1
pi
2mi
+U(r1,r2,...,rN) + p2
2W+P V +
M
X
k=1
p2
ξk
2Qk
+
M
X
k=1
p2
ηk
2Q0
k
+NfkT ξ1+kT
M
X
i=2
ξk+kT
M
X
k=1
ηk(3.81)
Returning to the Trotter decomposition formalism, for pressure control and temperature con-
trol [35] we get:
iL =iL1+iL2+iL,1+iL,2+iLNHC−baro +iLNHC (3.82)
where “NHC-baro” corresponds to the Nosè-Hoover chain of the barostat, and NHC corresponds
to the NHC of the particles,
iL1=
N
X
i=1 pi
mi
+p
Wri·∂
∂ri
(3.83)

3.4. Molecular Dynamics 41
iL2=
N
X
i=1
Fi−αp
Wpi·∂
∂pi
(3.84)
iL,1=p
W
∂
∂ (3.85)
iL,2=G
∂
∂p
(3.86)
and where
G= 3V(αPkin −Pvir −P)(3.87)
Using the Trotter decomposition, we get
exp(iL∆t) = exp (iLNHC−baro∆t/2) exp (iLNHC∆t/2)
exp (iL,2∆t/2) exp (iL2∆t/2)
exp (iL,1∆t) exp (iL1∆t)
exp (iL2∆t/2) exp (iL,2∆t/2)
exp (iLNHC∆t/2) exp (iLNHC−baro∆t/2) + O(∆t3)(3.88)
The action of exp (iL1∆t)comes from the solution of the the differential equation ˙
ri=vi+vri
with vi=pi/miand vconstant with initial condition ri(0), evaluate at t= ∆t. This yields the
evolution
ri(∆t) = ri(0)ev∆t+ ∆tvi(0)ev∆t/2sinh (v∆t/2)
v∆t/2.(3.89)
The action of exp (iL2∆t/2) comes from the solution of the differential equation ˙
vi=Fi
mi−
αvvi, yielding
vi(∆t/2) = vi(0)e−αv∆t/2+∆t
2mi
Fi(0)e−αv∆t/4sinh (αv∆t/4)
αv∆t/4.(3.90)
md-vv-avek uses the full step kinetic energies for determining the pressure with the pressure con-
trol, but the half-step-averaged kinetic energy for the temperatures, which can be written as a
Trotter decomposition as
exp(iL∆t) = exp (iLNHC−baro∆t/2) exp (iL,2∆t/2) exp (iL2∆t/2)
exp (iLNHC∆t/2) exp (iL,1∆t) exp (iL1∆t) exp (iLNHC∆t/2)
exp (iL2∆t/2) exp (iL,2∆t/2) exp (iLNHC−baro∆t/2) + O(∆t3)(3.91)
With constraints, the equations become significantly more complicated, in that each of these equa-
tions need to be solved iteratively for the constraint forces. Before GROMACS 5.1, these iterative
constraints were solved as described in [42]. From GROMACS 5.1 onward, MTTK with con-
straints has been removed because of numerical stability issues with the iterations.
Infrequent evaluation of temperature and pressure coupling
Temperature and pressure control require global communication to compute the kinetic energy and
virial, which can become costly if performed every step for large systems. We can rearrange the

42 Chapter 3. Algorithms
Trotter decomposition to give alternate symplectic, reversible integrator with the coupling steps
every nsteps instead of every steps. These new integrators will diverge if the coupling time step
is too large, as the auxiliary variable integrations will not converge. However, in most cases, long
coupling times are more appropriate, as they disturb the dynamics less [35].
Standard velocity Verlet with Nosé-Hoover temperature control has a Trotter expansion
exp(iL∆t)≈exp (iLNHC∆t/2) exp (iL2∆t/2)
exp (iL1∆t) exp (iL2∆t/2) exp (iLNHC∆t/2) .(3.92)
If the Nosé-Hoover chain is sufficiently slow with respect to the motions of the system, we can
write an alternate integrator over nsteps for velocity Verlet as
exp(iL∆t)≈(exp (iLNHC(n∆t/2)) [exp (iL2∆t/2)
exp (iL1∆t) exp (iL2∆t/2)]nexp (iLNHC(n∆t/2)) .(3.93)
For pressure control, this becomes
exp(iL∆t)≈exp (iLNHC−baro(n∆t/2)) exp (iLNHC(n∆t/2))
exp (iL,2(n∆t/2)) [exp (iL2∆t/2)
exp (iL,1∆t) exp (iL1∆t)
exp (iL2∆t/2)]nexp (iL,2(n∆t/2))
exp (iLNHC(n∆t/2)) exp (iLNHC−baro(n∆t/2)) ,(3.94)
where the box volume integration occurs every step, but the auxiliary variable integrations happen
every nsteps.
3.4.10 The complete update algorithm
The complete algorithm for the update of velocities and coordinates is given using leap-frog in
Fig. 3.8. The SHAKE algorithm of step 4 is explained below.
GROMACS has a provision to “freeze” (prevent motion of) selected particles, which must be
defined as a “freeze group.” This is implemented using a freeze factor fg, which is a vector, and
differs for each freeze group (see sec. 3.3). This vector contains only zero (freeze) or one (don’t
freeze). When we take this freeze factor and the external acceleration ahinto account the update
algorithm for the velocities becomes
v(t+∆t
2) = fg∗λ∗v(t−∆t
2) + F(t)
m∆t+ah∆t,(3.95)
where gand hare group indices which differ per atom.
3.4.11 Output step
The most important output of the MD run is the trajectory file, which contains particle coordi-
nates and (optionally) velocities at regular intervals. The trajectory file contains frames that could

3.4. Molecular Dynamics 43
THE UPDATE ALGORITHM
Given:
Positions rof all atoms at time t
Velocities vof all atoms at time t−1
2∆t
Accelerations F/m on all atoms at time t.
(Forces are computed disregarding any constraints)
Total kinetic energy and virial at t−∆t
⇓
1. Compute the scaling factors λand µ
according to eqns. 3.44 and 3.60
⇓
2. Update and scale velocities: v0=λ(v+a∆t)
⇓
3. Compute new unconstrained coordinates: r0=r+v0∆t
⇓
4. Apply constraint algorithm to coordinates: constrain(r0→r00;r)
⇓
5. Correct velocities for constraints: v= (r00 −r)/∆t
⇓
6. Scale coordinates and box: r=µr00;b=µb
Figure 3.8: The MD update algorithm with the leap-frog integrator

44 Chapter 3. Algorithms
include positions, velocities and/or forces, as well as information about the dimensions of the sim-
ulation volume, integration step, integration time, etc. The interpretation of the time varies with
the integrator chosen, as described above. For Velocity Verlet integrators, velocities labeled at
time tare for that time. For other integrators (e.g. leap-frog, stochastic dynamics), the velocities
labeled at time tare for time t−1
2∆t.
Since the trajectory files are lengthy, one should not save every step! To retain all information it
suffices to write a frame every 15 steps, since at least 30 steps are made per period of the highest
frequency in the system, and Shannon’s sampling theorem states that two samples per period of
the highest frequency in a band-limited signal contain all available information. But that still gives
very long files! So, if the highest frequencies are not of interest, 10 or 20 samples per ps may
suffice. Be aware of the distortion of high-frequency motions by the stroboscopic effect, called
aliasing: higher frequencies are mirrored with respect to the sampling frequency and appear as
lower frequencies.
GROMACS can also write reduced-precision coordinates for a subset of the simulation system to
a special compressed trajectory file format. All the other tools can read and write this format. See
the User Guide for details on how to set up your .mdp file to have mdrun use this feature.
3.5 Shell molecular dynamics
GROMACS can simulate polarizability using the shell model of Dick and Overhauser [43]. In
such models a shell particle representing the electronic degrees of freedom is attached to a nucleus
by a spring. The potential energy is minimized with respect to the shell position at every step
of the simulation (see below). Successful applications of shell models in GROMACS have been
published for N2[44] and water [45].
3.5.1 Optimization of the shell positions
The force FSon a shell particle Scan be decomposed into two components
FS=Fbond +Fnb (3.96)
where Fbond denotes the component representing the polarization energy, usually represented by
a harmonic potential and Fnb is the sum of Coulomb and van der Waals interactions. If we assume
that Fnb is almost constant we can analytically derive the optimal position of the shell, i.e. where
FS= 0. If we have the shell S connected to atom A we have
Fbond =kb(xS−xA).(3.97)
In an iterative solver, we have positions xS(n)where nis the iteration count. We now have at
iteration n
Fnb =FS−kb(xS(n)−xA)(3.98)
and the optimal position for the shells xS(n+ 1) thus follows from
FS−kb(xS(n)−xA) + kb(xS(n+ 1) −xA)=0 (3.99)

3.6. Constraint algorithms 45
if we write
∆xS=xS(n+ 1) −xS(n)(3.100)
we finally obtain
∆xS=FS/kb(3.101)
which then yields the algorithm to compute the next trial in the optimization of shell positions
xS(n+ 1) = xS(n) + FS/kb.(3.102)
3.6 Constraint algorithms
Constraints can be imposed in GROMACS using LINCS (default) or the traditional SHAKE
method.
3.6.1 SHAKE
The SHAKE [46] algorithm changes a set of unconstrained coordinates r0to a set of coordinates
r00 that fulfill a list of distance constraints, using a set rreference, as
SHAKE(r0→r00;r)(3.103)
This action is consistent with solving a set of Lagrange multipliers in the constrained equations
of motion. SHAKE needs a relative tolerance; it will continue until all constraints are satisfied
within that relative tolerance. An error message is given if SHAKE cannot reset the coordinates
because the deviation is too large, or if a given number of iterations is surpassed.
Assume the equations of motion must fulfill Kholonomic constraints, expressed as
σk(r1. . . rN) = 0; k= 1 . . . K. (3.104)
For example, (r1−r2)2−b2= 0. Then the forces are defined as
−∂
∂ri V+
K
X
k=1
λkσk!,(3.105)
where λkare Lagrange multipliers which must be solved to fulfill the constraint equations. The
second part of this sum determines the constraint forces Gi, defined by
Gi=−
K
X
k=1
λk
∂σk
∂ri
(3.106)
The displacement due to the constraint forces in the leap-frog or Verlet algorithm is equal to
(Gi/mi)(∆t)2. Solving the Lagrange multipliers (and hence the displacements) requires the so-
lution of a set of coupled equations of the second degree. These are solved iteratively by SHAKE.
For the special case of rigid water molecules, that often make up more than 80% of the simulation
system we have implemented the SETTLE algorithm [47] (sec. 5.6).
For velocity Verlet, an additional round of constraining must be done, to constrain the velocities of
the second velocity half step, removing any component of the velocity parallel to the bond vector.
This step is called RATTLE, and is covered in more detail in the original Andersen paper [48].
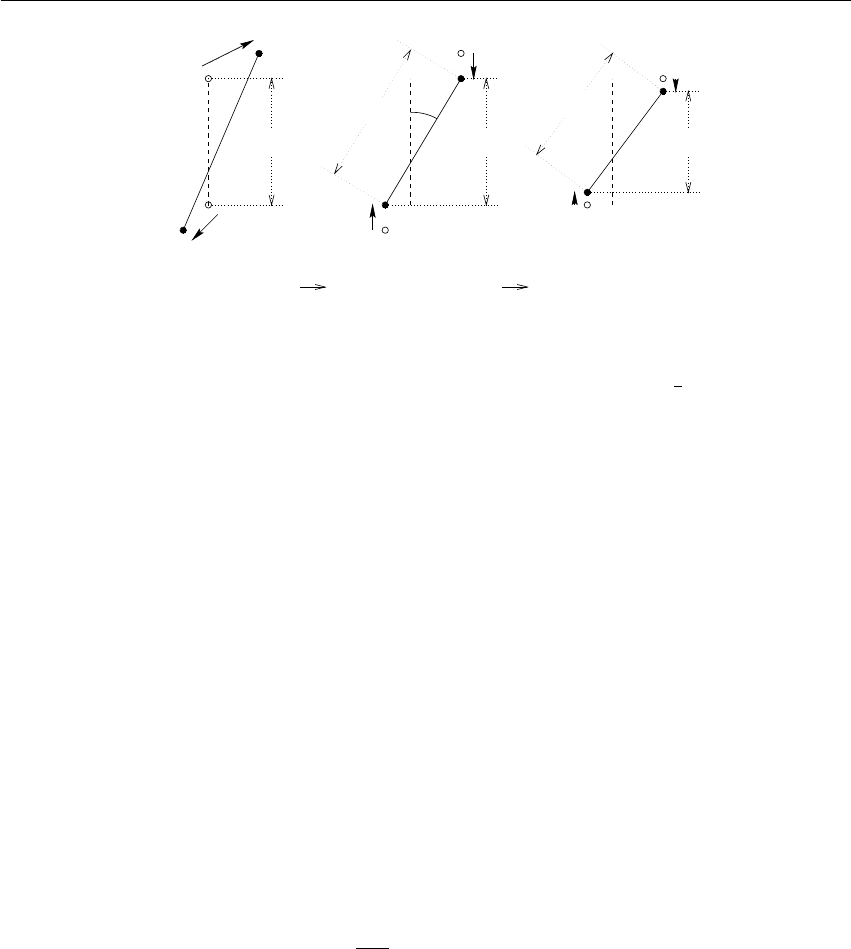
46 Chapter 3. Algorithms
unconstrained
update
correction for
rotational
lengthening
projecting out
forces working
along the bonds
θ
d
ld
p
d
Figure 3.9: The three position updates needed for one time step. The dashed line is the old bond
of length d, the solid lines are the new bonds. l=dcos θand p= (2d2−l2)1
2.
3.6.2 LINCS
The LINCS algorithm
LINCS is an algorithm that resets bonds to their correct lengths after an unconstrained update [49].
The method is non-iterative, as it always uses two steps. Although LINCS is based on matrices, no
matrix-matrix multiplications are needed. The method is more stable and faster than SHAKE, but
it can only be used with bond constraints and isolated angle constraints, such as the proton angle
in OH. Because of its stability, LINCS is especially useful for Brownian dynamics. LINCS has
two parameters, which are explained in the subsection parameters. The parallel version of LINCS,
P-LINCS, is described in subsection 3.17.3.
The LINCS formulas
We consider a system of Nparticles, with positions given by a 3Nvector r(t). For molecular
dynamics the equations of motion are given by Newton’s Law
d2r
dt2=M−1F,(3.107)
where Fis the 3Nforce vector and Mis a 3N×3Ndiagonal matrix, containing the masses of
the particles. The system is constrained by Ktime-independent constraint equations
gi(r) = |ri1−ri2| − di= 0 i= 1, . . . , K. (3.108)
In a numerical integration scheme, LINCS is applied after an unconstrained update, just like
SHAKE. The algorithm works in two steps (see figure Fig. 3.9). In the first step, the projec-
tions of the new bonds on the old bonds are set to zero. In the second step, a correction is applied
for the lengthening of the bonds due to rotation. The numerics for the first step and the second
step are very similar. A complete derivation of the algorithm can be found in [49]. Only a short
description of the first step is given here.

3.6. Constraint algorithms 47
A new notation is introduced for the gradient matrix of the constraint equations which appears on
the right hand side of this equation:
Bhi =∂gh
∂ri
(3.109)
Notice that Bis a K×3Nmatrix, it contains the directions of the constraints. The following equa-
tion shows how the new constrained coordinates rn+1 are related to the unconstrained coordinates
runc
n+1 by
rn+1 = (I−TnBn)runc
n+1 +Tnd=
runc
n+1 −M−1Bn(BnM−1BT
n)−1(Bnrunc
n+1 −d)(3.110)
where T=M−1BT(BM −1BT)−1. The derivation of this equation from eqns. 3.107 and 3.108
can be found in [49].
This first step does not set the real bond lengths to the prescribed lengths, but the projection of the
new bonds onto the old directions of the bonds. To correct for the rotation of bond i, the projection
of the bond, pi, on the old direction is set to
pi=q2d2
i−l2
i,(3.111)
where liis the bond length after the first projection. The corrected positions are
r∗
n+1 = (I−TnBn)rn+1 +Tnp.(3.112)
This correction for rotational effects is actually an iterative process, but during MD only one
iteration is applied. The relative constraint deviation after this procedure will be less than 0.0001
for every constraint. In energy minimization, this might not be accurate enough, so the number of
iterations is equal to the order of the expansion (see below).
Half of the CPU time goes to inverting the constraint coupling matrix BnM−1BT
n, which has to
be done every time step. This K×Kmatrix has 1/mi1+1/mi2on the diagonal. The off-diagonal
elements are only non-zero when two bonds are connected, then the element is cos φ/mc, where
mcis the mass of the atom connecting the two bonds and φis the angle between the bonds.
The matrix Tis inverted through a power expansion. A K×Kmatrix Sis introduced which is
the inverse square root of the diagonal of BnM−1BT
n. This matrix is used to convert the diagonal
elements of the coupling matrix to one:
(BnM−1BT
n)−1=SS−1(BnM−1BT
n)−1S−1S
=S(SBnM−1BT
nS)−1S=S(I−An)−1S(3.113)
The matrix Anis symmetric and sparse and has zeros on the diagonal. Thus a simple trick can be
used to calculate the inverse:
(I−An)−1=I+An+A2
n+A3
n+. . . (3.114)
This inversion method is only valid if the absolute values of all the eigenvalues of Anare smaller
than one. In molecules with only bond constraints, the connectivity is so low that this will always
be true, even if ring structures are present. Problems can arise in angle-constrained molecules. By

48 Chapter 3. Algorithms
constraining angles with additional distance constraints, multiple small ring structures are intro-
duced. This gives a high connectivity, leading to large eigenvalues. Therefore LINCS should NOT
be used with coupled angle-constraints.
For molecules with all bonds constrained the eigenvalues of Aare around 0.4. This means that
with each additional order in the expansion eqn. 3.114 the deviations decrease by a factor 0.4. But
for relatively isolated triangles of constraints the largest eigenvalue is around 0.7. Such triangles
can occur when removing hydrogen angle vibrations with an additional angle constraint in alcohol
groups or when constraining water molecules with LINCS, for instance with flexible constraints.
The constraints in such triangles converge twice as slow as the other constraints. Therefore, start-
ing with GROMACS 4, additional terms are added to the expansion for such triangles
(I−An)−1≈I+An+. . . +ANi
n+A∗
n+. . . +A∗
nNiANi
n(3.115)
where Niis the normal order of the expansion and A∗only contains the elements of Athat couple
constraints within rigid triangles, all other elements are zero. In this manner, the accuracy of angle
constraints comes close to that of the other constraints, while the series of matrix vector multi-
plications required for determining the expansion only needs to be extended for a few constraint
couplings. This procedure is described in the P-LINCS paper[50].
The LINCS Parameters
The accuracy of LINCS depends on the number of matrices used in the expansion eqn. 3.114.
For MD calculations a fourth order expansion is enough. For Brownian dynamics with large time
steps an eighth order expansion may be necessary. The order is a parameter in the *.mdp file.
The implementation of LINCS is done in such a way that the algorithm will never crash. Even
when it is impossible to to reset the constraints LINCS will generate a conformation which fulfills
the constraints as well as possible. However, LINCS will generate a warning when in one step a
bond rotates over more than a predefined angle. This angle is set by the user in the *.mdp file.
3.7 Simulated Annealing
The well known simulated annealing (SA) protocol is supported in GROMACS, and you can even
couple multiple groups of atoms separately with an arbitrary number of reference temperatures
that change during the simulation. The annealing is implemented by simply changing the current
reference temperature for each group in the temperature coupling, so the actual relaxation and
coupling properties depends on the type of thermostat you use and how hard you are coupling it.
Since we are changing the reference temperature it is important to remember that the system will
NOT instantaneously reach this value - you need to allow for the inherent relaxation time in the
coupling algorithm too. If you are changing the annealing reference temperature faster than the
temperature relaxation you will probably end up with a crash when the difference becomes too
large.
The annealing protocol is specified as a series of corresponding times and reference temperatures
for each group, and you can also choose whether you only want a single sequence (after which the
temperature will be coupled to the last reference value), or if the annealing should be periodic and

3.8. Stochastic Dynamics 49
restart at the first reference point once the sequence is completed. You can mix and match both
types of annealing and non-annealed groups in your simulation.
3.8 Stochastic Dynamics
Stochastic or velocity Langevin dynamics adds a friction and a noise term to Newton’s equations
of motion, as
mi
d2ri
dt2=−miγi
dri
dt+Fi(r)+ ◦
ri,(3.116)
where γiis the friction constant [1/ps]and ◦
ri(t)is a noise process with h◦
ri(t)◦
rj(t+s)i=
2miγikBT δ(s)δij . When 1/γiis large compared to the time scales present in the system, one
could see stochastic dynamics as molecular dynamics with stochastic temperature-coupling. But
any processes that take longer than 1/γi, e.g. hydrodynamics, will be dampened. Since each de-
gree of freedom is coupled independently to a heat bath, equilibration of fast modes occurs rapidly.
For simulating a system in vacuum there is the additional advantage that there is no accumulation
of errors for the overall translational and rotational degrees of freedom. When 1/γiis small com-
pared to the time scales present in the system, the dynamics will be completely different from MD,
but the sampling is still correct.
In GROMACS there is one simple and efficient implementation. Its accuracy is equivalent to the
normal MD leap-frog and Velocity Verlet integrator. It is nearly identical to the common way of
discretizing the Langevin equation, but the friction and velocity term are applied in an impulse
fashion [51]. It can be described as:
v0=v(t−1
2∆t) + 1
mF(t)∆t(3.117)
∆v=−αv0(t+1
2∆t) + skBT
m(1 −α2)rG
i(3.118)
r(t+ ∆t) = r(t) + v0+1
2∆v∆t(3.119)
v(t+1
2∆t) = v0+ ∆v(3.120)
α= 1 −e−γ∆t(3.121)
where rG
iis Gaussian distributed noise with µ= 0,σ= 1. The velocity is first updated a full time
step without friction and noise to get v0, identical to the normal update in leap-frog. The friction
and noise are then applied as an impulse at step t+ ∆t. The advantage of this scheme is that the
velocity-dependent terms act at the full time step, which makes the correct integration of forces that
depend on both coordinates and velocities, such as constraints and dissipative particle dynamics
(DPD, not implented yet), straightforward. With constraints, the coordinate update eqn. 3.119 is
split into a normal leap-frog update and a ∆v. After both of these updates the constraints are
applied to coordinates and velocities.
When using SD as a thermostat, an appropriate value for γis e.g. 0.5 ps−1, since this results in a
friction that is lower than the internal friction of water, while it still provides efficient thermostat-
ting.

50 Chapter 3. Algorithms
3.9 Brownian Dynamics
In the limit of high friction, stochastic dynamics reduces to Brownian dynamics, also called po-
sition Langevin dynamics. This applies to over-damped systems, i.e. systems in which the inertia
effects are negligible. The equation is
dri
dt=1
γi
Fi(r)+ ◦
ri(3.122)
where γiis the friction coefficient [amu/ps]and ◦
ri(t)is a noise process with h◦
ri(t)◦
rj(t+s)i=
2δ(s)δijkBT/γi. In GROMACS the equations are integrated with a simple, explicit scheme
ri(t+ ∆t) = ri(t) + ∆t
γi
Fi(r(t)) + s2kBT∆t
γi
rG
i,(3.123)
where rG
iis Gaussian distributed noise with µ= 0,σ= 1. The friction coefficients γican be
chosen the same for all particles or as γi=miγi, where the friction constants γican be different
for different groups of atoms. Because the system is assumed to be over-damped, large timesteps
can be used. LINCS should be used for the constraints since SHAKE will not converge for large
atomic displacements. BD is an option of the mdrun program.
3.10 Energy Minimization
Energy minimization in GROMACS can be done using steepest descent, conjugate gradients, or l-
bfgs (limited-memory Broyden-Fletcher-Goldfarb-Shanno quasi-Newtonian minimizer...we prefer
the abbreviation). EM is just an option of the mdrun program.
3.10.1 Steepest Descent
Although steepest descent is certainly not the most efficient algorithm for searching, it is robust
and easy to implement.
We define the vector ras the vector of all 3Ncoordinates. Initially a maximum displacement h0
(e.g. 0.01 nm) must be given.
First the forces Fand potential energy are calculated. New positions are calculated by
rn+1 =rn+Fn
max(|Fn|)hn,(3.124)
where hnis the maximum displacement and Fnis the force, or the negative gradient of the po-
tential V. The notation max(|Fn|)means the largest scalar force on any atom. The forces and
energy are again computed for the new positions
If (Vn+1 < Vn) the new positions are accepted and hn+1 = 1.2hn.
If (Vn+1 ≥Vn) the new positions are rejected and hn= 0.2hn.
The algorithm stops when either a user-specified number of force evaluations has been performed
(e.g. 100), or when the maximum of the absolute values of the force (gradient) components is

3.11. Normal-Mode Analysis 51
smaller than a specified value . Since force truncation produces some noise in the energy evalua-
tion, the stopping criterion should not be made too tight to avoid endless iterations. A reasonable
value for can be estimated from the root mean square force fa harmonic oscillator would exhibit
at a temperature T. This value is
f= 2πν√2mkT , (3.125)
where νis the oscillator frequency, mthe (reduced) mass, and kBoltzmann’s constant. For a
weak oscillator with a wave number of 100 cm−1and a mass of 10 atomic units, at a temperature
of 1 K, f= 7.7kJ mol−1nm−1. A value for between 1 and 10 is acceptable.
3.10.2 Conjugate Gradient
Conjugate gradient is slower than steepest descent in the early stages of the minimization, but
becomes more efficient closer to the energy minimum. The parameters and stop criterion are the
same as for steepest descent. In GROMACS conjugate gradient can not be used with constraints,
including the SETTLE algorithm for water [47], as this has not been implemented. If water is
present it must be of a flexible model, which can be specified in the *.mdp file by define =
-DFLEXIBLE.
This is not really a restriction, since the accuracy of conjugate gradient is only required for mini-
mization prior to a normal-mode analysis, which cannot be performed with constraints. For most
other purposes steepest descent is efficient enough.
3.10.3 L-BFGS
The original BFGS algorithm works by successively creating better approximations of the inverse
Hessian matrix, and moving the system to the currently estimated minimum. The memory re-
quirements for this are proportional to the square of the number of particles, so it is not practical
for large systems like biomolecules. Instead, we use the L-BFGS algorithm of Nocedal [52,53],
which approximates the inverse Hessian by a fixed number of corrections from previous steps.
This sliding-window technique is almost as efficient as the original method, but the memory re-
quirements are much lower - proportional to the number of particles multiplied with the correction
steps. In practice we have found it to converge faster than conjugate gradients, but due to the
correction steps it is not yet parallelized. It is also noteworthy that switched or shifted interactions
usually improve the convergence, since sharp cut-offs mean the potential function at the current
coordinates is slightly different from the previous steps used to build the inverse Hessian approxi-
mation.
3.11 Normal-Mode Analysis
Normal-mode analysis [54,55,56] can be performed using GROMACS, by diagonalization of the
mass-weighted Hessian H:
RTM−1/2HM−1/2R=diag(λ1, . . . , λ3N)(3.126)
λi= (2πωi)2(3.127)

52 Chapter 3. Algorithms
where Mcontains the atomic masses, Ris a matrix that contains the eigenvectors as columns, λi
are the eigenvalues and ωiare the corresponding frequencies.
First the Hessian matrix, which is a 3N×3Nmatrix where Nis the number of atoms, needs to
be calculated:
Hij =∂2V
∂xi∂xj
(3.128)
where xiand xjdenote the atomic x, y or z coordinates. In practice, this equation is not used, but
the Hessian is calculated numerically from the force as:
Hij =−fi(x+hej)−fi(x−hej)
2h(3.129)
fi=−∂V
∂xi
(3.130)
where ejis the unit vector in direction j. It should be noted that for a usual normal-mode cal-
culation, it is necessary to completely minimize the energy prior to computation of the Hessian.
The tolerance required depends on the type of system, but a rough indication is 0.001 kJ mol−1.
Minimization should be done with conjugate gradients or L-BFGS in double precision.
A number of GROMACS programs are involved in these calculations. First, the energy should
be minimized using mdrun. Then, mdrun computes the Hessian. Note that for generating the
run input file, one should use the minimized conformation from the full precision trajectory file,
as the structure file is not accurate enough. gmx nmeig does the diagonalization and the sorting
of the normal modes according to their frequencies. Both mdrun and gmx nmeig should be
run in double precision. The normal modes can be analyzed with the program gmx anaeig.
Ensembles of structures at any temperature and for any subset of normal modes can be generated
with gmx nmens. An overview of normal-mode analysis and the related principal component
analysis (see sec. 8.11) can be found in [57].
3.12 Free energy calculations
3.12.1 Slow-growth methods
Free energy calculations can be performed in GROMACS using a number of methods, including
“slow-growth.” An example problem might be calculating the difference in free energy of binding
of an inhibitor Ito an enzyme Eand to a mutated enzyme E0. It is not feasible with computer sim-
ulations to perform a docking calculation for such a large complex, or even releasing the inhibitor
from the enzyme in a reasonable amount of computer time with reasonable accuracy. However, if
we consider the free energy cycle in Fig. 3.10A we can write:
∆G1−∆G2= ∆G3−∆G4(3.131)
If we are interested in the left-hand term we can equally well compute the right-hand term.
If we want to compute the difference in free energy of binding of two inhibitors Iand I0to an
enzyme E(Fig. 3.10B) we can again use eqn. 3.131 to compute the desired property.
3.12. Free energy calculations 53
I
E’
E
I
EE’
G1∆ ∆G2
∆G4
∆G3
A
G1∆ ∆G2
∆G3
II’
E
I
E
I’
∆G4
B
Figure 3.10: Free energy cycles. A: to calculate ∆G12, the free energy difference between the
binding of inhibitor Ito enzymes Erespectively E0.B: to calculate ∆G12, the free energy differ-
ence for binding of inhibitors Irespectively I0to enzyme E.
Free energy differences between two molecular species can be calculated in GROMACS using
the “slow-growth” method. Such free energy differences between different molecular species
are physically meaningless, but they can be used to obtain meaningful quantities employing a
thermodynamic cycle. The method requires a simulation during which the Hamiltonian of the
system changes slowly from that describing one system (A) to that describing the other system
(B). The change must be so slow that the system remains in equilibrium during the process; if that
requirement is fulfilled, the change is reversible and a slow-growth simulation from B to A will
yield the same results (but with a different sign) as a slow-growth simulation from A to B. This is
a useful check, but the user should be aware of the danger that equality of forward and backward
growth results does not guarantee correctness of the results.
The required modification of the Hamiltonian His realized by making Ha function of a coupling
parameter λ:H=H(p, q;λ)in such a way that λ= 0 describes system A and λ= 1 describes
system B:
H(p, q; 0) = HA(p, q); H(p, q; 1) = HB(p, q).(3.132)
In GROMACS, the functional form of the λ-dependence is different for the various force-field
contributions and is described in section sec. 4.5.
The Helmholtz free energy Ais related to the partition function Qof an N, V, T ensemble, which
is assumed to be the equilibrium ensemble generated by a MD simulation at constant volume and
temperature. The generally more useful Gibbs free energy Gis related to the partition function
∆of an N, p, T ensemble, which is assumed to be the equilibrium ensemble generated by a MD
simulation at constant pressure and temperature:
A(λ) = −kBTln Q(3.133)
Q=cZZ exp[−βH(p, q;λ)] dp dq (3.134)
G(λ) = −kBTln ∆ (3.135)
∆ = cZZZexp[−βH(p, q;λ)−βpV ]dp dq dV (3.136)

54 Chapter 3. Algorithms
G=A+pV, (3.137)
where β= 1/(kBT)and c= (N!h3N)−1. These integrals over phase space cannot be evaluated
from a simulation, but it is possible to evaluate the derivative with respect to λas an ensemble
average:
dA
dλ =RR(∂H/∂λ) exp[−βH(p, q;λ)] dp dq
RRexp[−βH(p, q;λ)] dp dq =∂H
∂λ NV T ;λ
,(3.138)
with a similar relation for dG/dλ in the N, p, T ensemble. The difference in free energy between
A and B can be found by integrating the derivative over λ:
AB(V, T )−AA(V, T ) = Z1
0∂H
∂λ NV T ;λ
dλ (3.139)
GB(p, T )−GA(p, T ) = Z1
0∂H
∂λ NpT ;λ
dλ. (3.140)
If one wishes to evaluate GB(p, T )−GA(p, T ), the natural choice is a constant-pressure simu-
lation. However, this quantity can also be obtained from a slow-growth simulation at constant
volume, starting with system A at pressure pand volume Vand ending with system B at pressure
pB, by applying the following small (but, in principle, exact) correction:
GB(p)−GA(p) = AB(V)−AA(V)−ZpB
p
[VB(p0)−V]dp0(3.141)
Here we omitted the constant Tfrom the notation. This correction is roughly equal to −1
2(pB−
p)∆V= (∆V)2/(2κV ), where ∆Vis the volume change at pand κis the isothermal compress-
ibility. This is usually small; for example, the growth of a water molecule from nothing in a bath
of 1000 water molecules at constant volume would produce an additional pressure of as much as
22 bar, but a correction to the Helmholtz free energy of just -1 kJ mol−1.
In Cartesian coordinates, the kinetic energy term in the Hamiltonian depends only on the momenta,
and can be separately integrated and, in fact, removed from the equations. When masses do not
change, there is no contribution from the kinetic energy at all; otherwise the integrated contribution
to the free energy is −3
2kBTln(mB/mA).Note that this is only true in the absence of constraints.
3.12.2 Thermodynamic integration
GROMACS offers the possibility to integrate eq. 3.139 or eq. 3.140 in one simulation over the
full range from A to B. However, if the change is large and insufficient sampling can be expected,
the user may prefer to determine the value of hdG/dλiaccurately at a number of well-chosen
intermediate values of λ. This can easily be done by setting the stepsize delta_lambda to zero.
Each simulation can be equilibrated first, and a proper error estimate can be made for each value of
dG/dλ from the fluctuation of ∂H/∂λ. The total free energy change is then determined afterward
by an appropriate numerical integration procedure.
GROMACS now also supports the use of Bennett’s Acceptance Ratio [58] for calculating values of
∆G for transformations from state A to state B using the program gmx bar. The same data can
also be used to calculate free energies using MBAR [59], though the analysis currently requires
external tools from the external pymbar package, at https://SimTK.org/home/pymbar.
The λ-dependence for the force-field contributions is described in detail in section sec. 4.5.

3.13. Replica exchange 55
3.13 Replica exchange
Replica exchange molecular dynamics (REMD) is a method that can be used to speed up the sam-
pling of any type of simulation, especially if conformations are separated by relatively high energy
barriers. It involves simulating multiple replicas of the same system at different temperatures and
randomly exchanging the complete state of two replicas at regular intervals with the probability:
P(1 ↔2) = min 1,exp 1
kBT1−1
kBT2(U1−U2) (3.142)
where T1and T2are the reference temperatures and U1and U2are the instantaneous potential
energies of replicas 1 and 2 respectively. After exchange the velocities are scaled by (T1/T2)±0.5
and a neighbor search is performed the next step. This combines the fast sampling and frequent
barrier-crossing of the highest temperature with correct Boltzmann sampling at all the different
temperatures [60,61]. We only attempt exchanges for neighboring temperatures as the probability
decreases very rapidly with the temperature difference. One should not attempt exchanges for
all possible pairs in one step. If, for instance, replicas 1 and 2 would exchange, the chance of
exchange for replicas 2 and 3 not only depends on the energies of replicas 2 and 3, but also on the
energy of replica 1. In GROMACS this is solved by attempting exchange for all “odd” pairs on
“odd” attempts and for all “even” pairs on “even” attempts. If we have four replicas: 0, 1, 2 and 3,
ordered in temperature and we attempt exchange every 1000 steps, pairs 0-1 and 2-3 will be tried
at steps 1000, 3000 etc. and pair 1-2 at steps 2000, 4000 etc.
How should one choose the temperatures? The energy difference can be written as:
U1−U2=Ndf
c
2kB(T1−T2)(3.143)
where Ndf is the total number of degrees of freedom of one replica and cis 1 for harmonic poten-
tials and around 2 for protein/water systems. If T2= (1 + )T1the probability becomes:
P(1 ↔2) = exp −2c Ndf
2(1 + )!≈exp −2c
2Ndf (3.144)
Thus for a probability of e−2≈0.135 one obtains ≈2/pc Ndf . With all bonds constrained one
has Ndf ≈2Natoms and thus for c= 2 one should choose as 1/√Natoms. However there is one
problem when using pressure coupling. The density at higher temperatures will decrease, leading
to higher energy [62], which should be taken into account. The GROMACS website features a so-
called “REMD calculator,” that lets you type in the temperature range and the number of atoms,
and based on that proposes a set of temperatures.
An extension to the REMD for the isobaric-isothermal ensemble was proposed by Okabe et
al. [63]. In this work the exchange probability is modified to:
P(1 ↔2) = min 1,exp 1
kBT1−1
kBT2(U1−U2) + P1
kBT1−P2
kBT2(V1−V2)
(3.145)
where P1and P2are the respective reference pressures and V1and V2are the respective instanta-
neous volumes in the simulations. In most cases the differences in volume are so small that the
second term is negligible. It only plays a role when the difference between P1and P2is large or
in phase transitions.
56 Chapter 3. Algorithms
Hamiltonian replica exchange is also supported in GROMACS. In Hamiltonian replica exchange,
each replica has a different Hamiltonian, defined by the free energy pathway specified for the
simulation. The exchange probability to maintain the correct ensemble probabilities is:
P(1 ↔2) = min 1,exp 1
kBT−1
kBT((U1(x2)−U1(x1)) + (U2(x1)−U2(x2)))
(3.146)
The separate Hamiltonians are defined by the free energy functionality of GROMACS, with swaps
made between the different values of λdefined in the mdp file.
Hamiltonian and temperature replica exchange can also be performed simultaneously, using the
acceptance criteria:
P(1 ↔2) = min 1,exp 1
kBT−(U1(x2)−U1(x1)
kBT1
+U2(x1)−U2(x2)
kBT2
) (3.147)
Gibbs sampling replica exchange has also been implemented in GROMACS [64]. In Gibbs sam-
pling replica exchange, all possible pairs are tested for exchange, allowing swaps between replicas
that are not neighbors.
Gibbs sampling replica exchange requires no additional potential energy calculations. However
there is an additional communication cost in Gibbs sampling replica exchange, as for some permu-
tations, more than one round of swaps must take place. In some cases, this extra communication
cost might affect the efficiency.
All replica exchange variants are options of the mdrun program. It will only work when MPI is
installed, due to the inherent parallelism in the algorithm. For efficiency each replica can run on a
separate rank. See the manual page of mdrun on how to use these multinode features.
3.14 Essential Dynamics sampling
The results from Essential Dynamics (see sec. 8.11) of a protein can be used to guide MD sim-
ulations. The idea is that from an initial MD simulation (or from other sources) a definition of
the collective fluctuations with largest amplitude is obtained. The position along one or more of
these collective modes can be constrained in a (second) MD simulation in a number of ways for
several purposes. For example, the position along a certain mode may be kept fixed to monitor
the average force (free-energy gradient) on that coordinate in that position. Another application
is to enhance sampling efficiency with respect to usual MD [65,66]. In this case, the system is
encouraged to sample its available configuration space more systematically than in a diffusion-like
path that proteins usually take.
Another possibility to enhance sampling is flooding. Here a flooding potential is added to certain
(collective) degrees of freedom to expel the system out of a region of phase space [67].
The procedure for essential dynamics sampling or flooding is as follows. First, the eigenvectors
and eigenvalues need to be determined using covariance analysis (gmx covar) or normal-mode
analysis (gmx nmeig). Then, this information is fed into make_edi, which has many options
for selecting vectors and setting parameters, see gmx make_edi -h. The generated edi input
file is then passed to mdrun.

3.15. Expanded Ensemble 57
3.15 Expanded Ensemble
In an expanded ensemble simulation [68], both the coordinates and the thermodynamic ensemble
are treated as configuration variables that can be sampled over. The probability of any given state
can be written as:
P(~x, k)∝exp (−βkUk+gk),(3.148)
where βk=1
kBTkis the βcorresponding to the kth thermodynamic state, and gkis a user-specified
weight factor corresponding to the kth state. This space is therefore a mixed,generalized, or
expanded ensemble which samples from multiple thermodynamic ensembles simultaneously. gk
is chosen to give a specific weighting of each subensemble in the expanded ensemble, and can
either be fixed, or determined by an iterative procedure. The set of gkis frequently chosen to
give each thermodynamic ensemble equal probability, in which case gkis equal to the free energy
in non-dimensional units, but they can be set to arbitrary values as desired. Several different
algorithms can be used to equilibrate these weights, described in the mdp option listings.
In GROMACS, this space is sampled by alternating sampling in the kand ~x directions. Sampling
in the ~x direction is done by standard molecular dynamics sampling; sampling between the dif-
ferent thermodynamics states is done by Monte Carlo, with several different Monte Carlo moves
supported. The kstates can be defined by different temperatures, or choices of the free energy
λvariable, or both. Expanded ensemble simulations thus represent a serialization of the replica
exchange formalism, allowing a single simulation to explore many thermodynamic states.
3.16 Parallelization
The CPU time required for a simulation can be reduced by running the simulation in parallel over
more than one core. Ideally, one would want to have linear scaling: running on Ncores makes
the simulation Ntimes faster. In practice this can only be achieved for a small number of cores.
The scaling will depend a lot on the algorithms used. Also, different algorithms can have different
restrictions on the interaction ranges between atoms.
3.17 Domain decomposition
Since most interactions in molecular simulations are local, domain decomposition is a natural way
to decompose the system. In domain decomposition, a spatial domain is assigned to each rank,
which will then integrate the equations of motion for the particles that currently reside in its local
domain. With domain decomposition, there are two choices that have to be made: the division of
the unit cell into domains and the assignment of the forces to domains. Most molecular simulation
packages use the half-shell method for assigning the forces. But there are two methods that always
require less communication: the eighth shell [69] and the midpoint [70] method. GROMACS
currently uses the eighth shell method, but for certain systems or hardware architectures it might
be advantageous to use the midpoint method. Therefore, we might implement the midpoint method
in the future. Most of the details of the domain decomposition can be found in the GROMACS 4
paper [5].
58 Chapter 3. Algorithms
7
30
4c
r
1
6
5
Figure 3.11: A non-staggered domain decomposition grid of 3×2×2 cells. Coordinates in zones
1 to 7 are communicated to the corner cell that has its home particles in zone 0. rcis the cut-off
radius.
3.17.1 Coordinate and force communication
In the most general case of a triclinic unit cell, the space in divided with a 1-, 2-, or 3-D grid in
parallelepipeds that we call domain decomposition cells. Each cell is assigned to a particle-particle
rank. The system is partitioned over the ranks at the beginning of each MD step in which neighbor
searching is performed. Since the neighbor searching is based on charge groups, charge groups
are also the units for the domain decomposition. Charge groups are assigned to the cell where
their center of geometry resides. Before the forces can be calculated, the coordinates from some
neighboring cells need to be communicated, and after the forces are calculated, the forces need
to be communicated in the other direction. The communication and force assignment is based on
zones that can cover one or multiple cells. An example of a zone setup is shown in Fig. 3.11.
The coordinates are communicated by moving data along the “negative” direction in x,yor z
to the next neighbor. This can be done in one or multiple pulses. In Fig. 3.11 two pulses in x
are required, then one in yand then one in z. The forces are communicated by reversing this
procedure. See the GROMACS 4 paper [5] for details on determining which non-bonded and
bonded forces should be calculated on which rank.
3.17.2 Dynamic load balancing
When different ranks have a different computational load (load imbalance), all ranks will have to
wait for the one that takes the most time. One would like to avoid such a situation. Load imbalance
can occur due to four reasons:
•inhomogeneous particle distribution
•inhomogeneous interaction cost distribution (charged/uncharged, water/non-water due to
GROMACS water innerloops)
3.17. Domain decomposition 59
11
2
d
0
32
3’
rc
rb
2’
Figure 3.12: The zones to communicate to the rank of zone 0, see the text for details. rcand rb
are the non-bonded and bonded cut-off radii respectively, dis an example of a distance between
following, staggered boundaries of cells.
•statistical fluctuation (only with small particle numbers)
•differences in communication time, due to network topology and/or other jobs on the ma-
chine interfering with our communication
So we need a dynamic load balancing algorithm where the volume of each domain decomposition
cell can be adjusted independently. To achieve this, the 2- or 3-D domain decomposition grids
need to be staggered. Fig. 3.12 shows the most general case in 2-D. Due to the staggering, one
might require two distance checks for deciding if a charge group needs to be communicated: a
non-bonded distance and a bonded distance check.
By default, mdrun automatically turns on the dynamic load balancing during a simulation when
the total performance loss due to the force calculation imbalance is 2% or more. Note that the
reported force load imbalance numbers might be higher, since the force calculation is only part of
work that needs to be done during an integration step. The load imbalance is reported in the log
file at log output steps and when the -v option is used also on screen. The average load imbalance
and the total performance loss due to load imbalance are reported at the end of the log file.
There is one important parameter for the dynamic load balancing, which is the minimum allowed
scaling. By default, each dimension of the domain decomposition cell can scale down by at least
a factor of 0.8. For 3-D domain decomposition this allows cells to change their volume by about a
factor of 0.5, which should allow for compensation of a load imbalance of 100%. The minimum
allowed scaling can be changed with the -dds option of mdrun.
The load imbalance is measured by timing a single region of the MD step on each MPI rank. This
region can not include MPI communication, as timing of MPI calls does not allow separating wait
due to imbalance from actual communication. The domain volumes are then scaled, with under-
relaxation, inversely proportional with the measured time. This procedure will decrease the load
imbalance when the change in load in the measured region correlates with the change in domain
volume and the load outside the measured region does not depend strongly on the domain volume.
In CPU-only simulations, the load is measured between the coordinate and the force communica-
tion. In simulations with non-bonded work on GPUs, we overlap communication and work on the

60 Chapter 3. Algorithms
interaction range option default
non-bonded rc= max(rlist,rVdW,rCoul)mdp file
two-body bonded max(rmb,rc)mdrun -rdd starting conf. + 10%
multi-body bonded rmb mdrun -rdd starting conf. + 10%
constraints rcon mdrun -rcon est. from bond lengths
virtual sites rcon mdrun -rcon 0
Table 3.2: The interaction ranges with domain decomposition.
CPU with calculation on the GPU. Therefore we measure from the last communication before the
force calculation to when the CPU or GPU is finished, whichever is last. When not using PME
ranks, we subtract the time in PME from the CPU time, as this includes MPI calls and the PME
load is independent of domain size. This generally works well, unless the non-bonded load is
low and there is imbalance in the bonded interactions. Then two issues can arise. Dynamic load
balancing can increase the imbalance in update and constraints and with PME the coordinate and
force redistribution time can go up significantly. Although dynamic load balancing can signifi-
cantly improve performance in cases where there is imbalance in the bonded interactions on the
CPU, there are many situations in which some domains continue decreasing in size and the load
imbalance increases and/or PME coordinate and force redistribution cost increases significantly.
As of version 2016.1, mdrun disables the dynamic load balancing when measurement indicates
that it deteriorates performance. This means that in most cases the user will get good performance
with the default, automated dynamic load balancing setting.
3.17.3 Constraints in parallel
Since with domain decomposition parts of molecules can reside on different ranks, bond con-
straints can cross cell boundaries. Therefore a parallel constraint algorithm is required. GRO-
MACS uses the P-LINCS algorithm [50], which is the parallel version of the LINCS algorithm [49]
(see 3.6.2). The P-LINCS procedure is illustrated in Fig. 3.13. When molecules cross the cell
boundaries, atoms in such molecules up to (lincs_order + 1) bonds away are communi-
cated over the cell boundaries. Then, the normal LINCS algorithm can be applied to the local
bonds plus the communicated ones. After this procedure, the local bonds are correctly constrained,
even though the extra communicated ones are not. One coordinate communication step is required
for the initial LINCS step and one for each iteration. Forces do not need to be communicated.
3.17.4 Interaction ranges
Domain decomposition takes advantage of the locality of interactions. This means that there will
be limitations on the range of interactions. By default, mdrun tries to find the optimal balance
between interaction range and efficiency. But it can happen that a simulation stops with an error
message about missing interactions, or that a simulation might run slightly faster with shorter
interaction ranges. A list of interaction ranges and their default values is given in Table 3.2.
In most cases the defaults of mdrun should not cause the simulation to stop with an error message
of missing interactions. The range for the bonded interactions is determined from the distance be-
3.17. Domain decomposition 61
Figure 3.13: Example of the parallel setup of P-LINCS with one molecule split over three do-
main decomposition cells, using a matrix expansion order of 3. The top part shows which atom
coordinates need to be communicated to which cells. The bottom parts show the local constraints
(solid) and the non-local constraints (dashed) for each of the three cells.
tween bonded charge-groups in the starting configuration, with 10% added for headroom. For the
constraints, the value of rcon is determined by taking the maximum distance that (lincs_order
+ 1) bonds can cover when they all connect at angles of 120 degrees. The actual constraint com-
munication is not limited by rcon, but by the minimum cell size LC, which has the following lower
limit:
LC≥max(rmb, rcon)(3.149)
Without dynamic load balancing the system is actually allowed to scale beyond this limit when
pressure scaling is used. Note that for triclinic boxes, LCis not simply the box diagonal compo-
nent divided by the number of cells in that direction, rather it is the shortest distance between the
triclinic cells borders. For rhombic dodecahedra this is a factor of p3/2shorter along xand y.
When rmb > rc,mdrun employs a smart algorithm to reduce the communication. Simply
communicating all charge groups within rmb would increase the amount of communication enor-
mously. Therefore only charge-groups that are connected by bonded interactions to charge groups
which are not locally present are communicated. This leads to little extra communication, but also
to a slightly increased cost for the domain decomposition setup. In some cases, e.g. coarse-grained
simulations with a very short cut-off, one might want to set rmb by hand to reduce this cost.
3.17.5 Multiple-Program, Multiple-Data PME parallelization
Electrostatics interactions are long-range, therefore special algorithms are used to avoid summa-
tion over many atom pairs. In GROMACS this is usually PME (sec. 4.8.2). Since with PME all
62 Chapter 3. Algorithms
6 PP ranks 2 PME ranks
8 PP/PME ranks
Figure 3.14: Example of 8 ranks without (left) and with (right) MPMD. The PME communication
(red arrows) is much higher on the left than on the right. For MPMD additional PP - PME coordi-
nate and force communication (blue arrows) is required, but the total communication complexity
is lower.
particles interact with each other, global communication is required. This will usually be the lim-
iting factor for scaling with domain decomposition. To reduce the effect of this problem, we have
come up with a Multiple-Program, Multiple-Data approach [5]. Here, some ranks are selected to
do only the PME mesh calculation, while the other ranks, called particle-particle (PP) ranks, do
all the rest of the work. For rectangular boxes the optimal PP to PME rank ratio is usually 3:1,
for rhombic dodecahedra usually 2:1. When the number of PME ranks is reduced by a factor of
4, the number of communication calls is reduced by about a factor of 16. Or put differently, we
can now scale to 4 times more ranks. In addition, for modern 4 or 8 core machines in a network,
the effective network bandwidth for PME is quadrupled, since only a quarter of the cores will be
using the network connection on each machine during the PME calculations.
mdrun will by default interleave the PP and PME ranks. If the ranks are not number consecutively
inside the machines, one might want to use mdrun -ddorder pp_pme. For machines with a
real 3-D torus and proper communication software that assigns the ranks accordingly one should
use mdrun -ddorder cartesian.
To optimize the performance one should usually set up the cut-offs and the PME grid such that
the PME load is 25 to 33% of the total calculation load. grompp will print an estimate for this
load at the end and also mdrun calculates the same estimate to determine the optimal number
of PME ranks to use. For high parallelization it might be worthwhile to optimize the PME load
with the mdp settings and/or the number of PME ranks with the -npme option of mdrun. For
changing the electrostatics settings it is useful to know the accuracy of the electrostatics remains
nearly constant when the Coulomb cut-off and the PME grid spacing are scaled by the same factor.
Note that it is usually better to overestimate than to underestimate the number of PME ranks, since
the number of PME ranks is smaller than the number of PP ranks, which leads to less total waiting
time.
The PME domain decomposition can be 1-D or 2-D along the xand/or yaxis. 2-D decomposition
is also known as pencil decomposition because of the shape of the domains at high parallelization.
1-D decomposition along the yaxis can only be used when the PP decomposition has only 1 do-
main along x. 2-D PME decomposition has to have the number of domains along xequal to the
number of the PP decomposition. mdrun automatically chooses 1-D or 2-D PME decomposition
(when possible with the total given number of ranks), based on the minimum amount of commu-

3.18. Implicit solvation 63
nication for the coordinate redistribution in PME plus the communication for the grid overlap and
transposes. To avoid superfluous communication of coordinates and forces between the PP and
PME ranks, the number of DD cells in the xdirection should ideally be the same or a multiple of
the number of PME ranks. By default, mdrun takes care of this issue.
3.17.6 Domain decomposition flow chart
In Fig. 3.15 a flow chart is shown for domain decomposition with all possible communication for
different algorithms. For simpler simulations, the same flow chart applies, without the algorithms
and communication for the algorithms that are not used.
3.18 Implicit solvation
Implicit solvent models provide an efficient way of representing the electrostatic effects of solvent
molecules, while saving a large piece of the computations involved in an accurate, aqueous de-
scription of the surrounding water in molecular dynamics simulations. Implicit solvation models
offer several advantages compared with explicit solvation, including eliminating the need for the
equilibration of water around the solute, and the absence of viscosity, which allows the protein to
more quickly explore conformational space.
Implicit solvent calculations in GROMACS can be done using the generalized Born-formalism,
and the Still [71], HCT [72], and OBC [73] models are available for calculating the Born radii.
Here, the free energy Gsolv of solvation is the sum of three terms, a solvent-solvent cavity term
(Gcav), a solute-solvent van der Waals term (Gvdw), and finally a solvent-solute electrostatics
polarization term (Gpol).
The sum of Gcav and Gvdw corresponds to the (non-polar) free energy of solvation for a molecule
from which all charges have been removed, and is commonly called Gnp, calculated from the
total solvent accessible surface area multiplied with a surface tension. The total expression for the
solvation free energy then becomes:
Gsolv =Gnp +Gpol (3.150)
Under the generalized Born model, Gpol is calculated from the generalized Born equation [71]:
Gpol =1−1
n
X
i=1
n
X
j>i
qiqj
sr2
ij +bibjexp −r2
ij
4bibj(3.151)
In GROMACS, we have introduced the substitution [74]:
ci=1
√bi
(3.152)
which makes it possible to introduce a cheap transformation to a new variable xwhen evaluating
each interaction, such that:
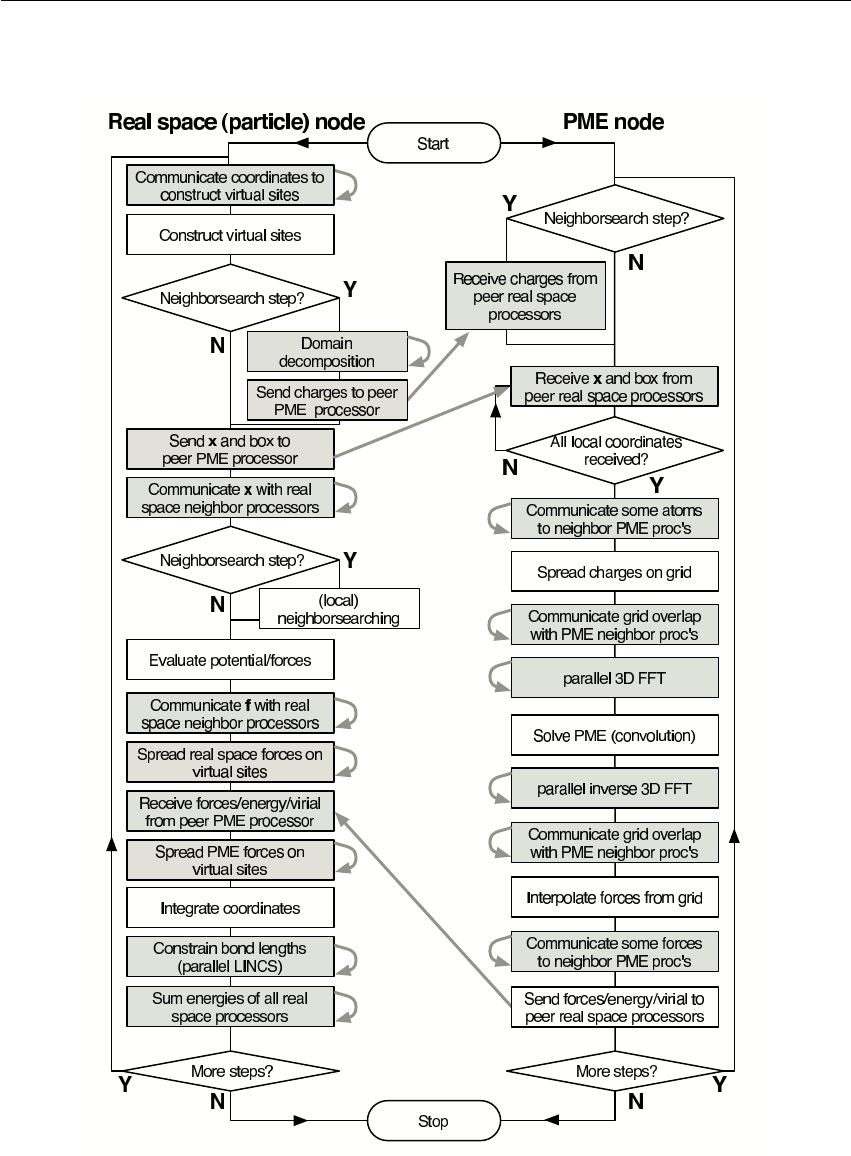
64 Chapter 3. Algorithms
Figure 3.15: Flow chart showing the algorithms and communication (arrows) for a standard MD
simulation with virtual sites, constraints and separate PME-mesh ranks.

3.18. Implicit solvation 65
x=rij
pbibj
=rijcicj(3.153)
In the end, the full re-formulation of 3.151 becomes:
Gpol =1−1
n
X
i=1
n
X
j>i
qiqj
pbibj
ξ(x) = 1−1
n
X
i=1
qici
n
X
j>i
qjcjξ(x)(3.154)
The non-polar part (Gnp) of Equation 3.150 is calculated directly from the Born radius of each
atom using a simple ACE type approximation by Schaefer et al. [75], including a simple loop
over all atoms. This requires only one extra solvation parameter, independent of atom type, but
differing slightly between the three Born radii models.

66 Chapter 3. Algorithms

Chapter 4
Interaction function and force
fields
To accommodate the potential functions used in some popular force fields (see 4.10), GROMACS
offers a choice of functions, both for non-bonded interaction and for dihedral interactions. They
are described in the appropriate subsections.
The potential functions can be subdivided into three parts
1. Non-bonded: Lennard-Jones or Buckingham, and Coulomb or modified Coulomb. The non-
bonded interactions are computed on the basis of a neighbor list (a list of non-bonded atoms
within a certain radius), in which exclusions are already removed.
2. Bonded: covalent bond-stretching, angle-bending, improper dihedrals, and proper dihedrals.
These are computed on the basis of fixed lists.
3. Restraints: position restraints, angle restraints, distance restraints, orientation restraints and
dihedral restraints, all based on fixed lists.
4. Applied Forces: externally applied forces, see chapter 6.
4.1 Non-bonded interactions
Non-bonded interactions in GROMACS are pair-additive:
V(r1, . . . rN) = X
i<j
Vij(rij ); (4.1)
Fi=−X
j
dVij(rij )
drij
rij
rij
(4.2)
Since the potential only depends on the scalar distance, interactions will be centro-symmetric,
i.e. the vectorial partial force on particle ifrom the pairwise interaction Vij(rij )has the opposite

68 Chapter 4. Interaction function and force fields
0.4 0.5 0.6 0.7 0.8
r (nm)
–0.2
0.0
0.2
0.4
V (kJ mole–1)
Figure 4.1: The Lennard-Jones interaction.
direction of the partial force on particle j. For efficiency reasons, interactions are calculated
by loops over interactions and updating both partial forces rather than summing one complete
nonbonded force at a time. The non-bonded interactions contain a repulsion term, a dispersion
term, and a Coulomb term. The repulsion and dispersion term are combined in either the Lennard-
Jones (or 6-12 interaction), or the Buckingham (or exp-6 potential). In addition, (partially) charged
atoms act through the Coulomb term.
4.1.1 The Lennard-Jones interaction
The Lennard-Jones potential VLJ between two atoms equals:
VLJ (rij) = C(12)
ij
r12
ij −C(6)
ij
r6
ij
(4.3)
See also Fig. 4.1 The parameters C(12)
ij and C(6)
ij depend on pairs of atom types; consequently they
are taken from a matrix of LJ-parameters. In the Verlet cut-off scheme, the potential is shifted by
a constant such that it is zero at the cut-off distance.
The force derived from this potential is:
Fi(rij) =
12 C(12)
ij
r13
ij −6C(6)
ij
r7
ij
rij
rij
(4.4)
The LJ potential may also be written in the following form:
VLJ (rij) = 4ij
σij
rij !12
− σij
rij !6
(4.5)
In constructing the parameter matrix for the non-bonded LJ-parameters, two types of combination
rules can be used within GROMACS, only geometric averages (type 1 in the input section of the

4.1. Non-bonded interactions 69
0.2 0.3 0.4 0.5 0.6 0.7 0.8
r (nm)
–0.5
0.0
0.5
1.0
1.5
V (kJ mole–1)
Figure 4.2: The Buckingham interaction.
force-field file):
C(6)
ij =C(6)
ii C(6)
jj 1/2
C(12)
ij =C(12)
ii C(12)
jj 1/2(4.6)
or, alternatively the Lorentz-Berthelot rules can be used. An arithmetic average is used to calculate
σij, while a geometric average is used to calculate ij (type 2):
σij =1
2(σii +σjj )
ij = (ii jj )1/2(4.7)
finally an geometric average for both parameters can be used (type 3):
σij = (σii σjj )1/2
ij = (ii jj )1/2(4.8)
This last rule is used by the OPLS force field.
4.1.2 Buckingham potential
The Buckingham potential has a more flexible and realistic repulsion term than the Lennard-Jones
interaction, but is also more expensive to compute. The potential form is:
Vbh(rij ) = Aij exp(−Bij rij)−Cij
r6
ij
(4.9)
See also Fig. 4.2. The force derived from this is:
Fi(rij) = "Aij Bij exp(−Bij rij )−6Cij
r7
ij #rij
rij
(4.10)
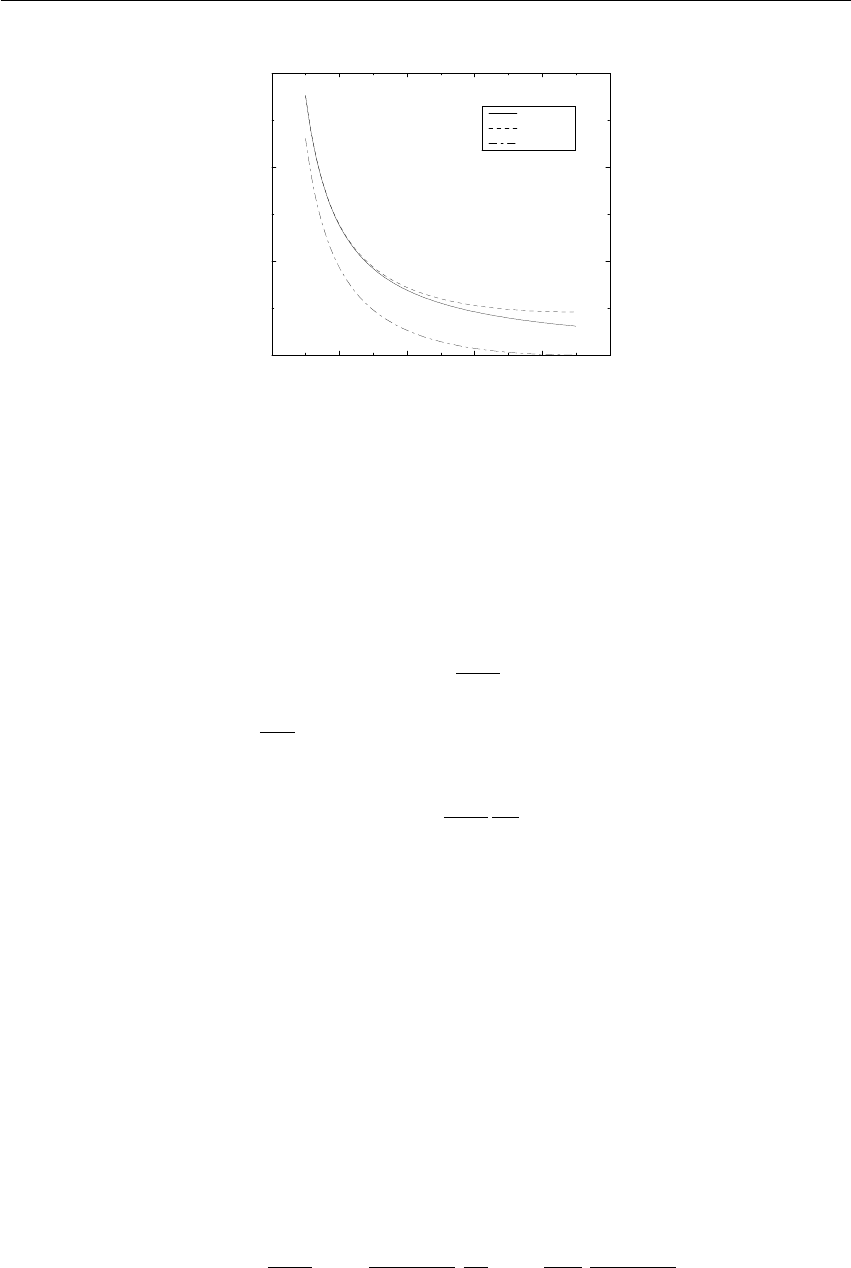
70 Chapter 4. Interaction function and force fields
0.0 0.2 0.4 0.6 0.8 1.0
r (nm)
0
500
1000
1500
V (kJ mol−1)
Coulomb
With RF
RF − C
Figure 4.3: The Coulomb interaction (for particles with equal signed charge) with and without
reaction field. In the latter case εrwas 1, εrf was 78, and rcwas 0.9 nm. The dot-dashed line is
the same as the dashed line, except for a constant.
4.1.3 Coulomb interaction
The Coulomb interaction between two charge particles is given by:
Vc(rij) = fqiqj
εrrij
(4.11)
See also Fig. 4.3, where f=1
4πε0= 138.935 458 (see chapter 2)
The force derived from this potential is:
Fi(rij) = fqiqj
εrr2
ij
rij
rij
(4.12)
A plain Coulomb interaction should only be used without cut-off or when all pairs fall within the
cut-off, since there is an abrupt, large change in the force at the cut-off. In case you do want to use
a cut-off, the potential can be shifted by a constant to make the potential the integral of the force.
With the group cut-off scheme, this shift is only applied to non-excluded pairs. With the Verlet
cut-off scheme, the shift is also applied to excluded pairs and self interactions, which makes the
potential equivalent to a reaction field with εrf = 1 (see below).
In GROMACS the relative dielectric constant εrmay be set in the in the input for grompp.
4.1.4 Coulomb interaction with reaction field
The Coulomb interaction can be modified for homogeneous systems by assuming a constant di-
electric environment beyond the cut-off rcwith a dielectric constant of εrf . The interaction then
reads:
Vcrf =fqiqj
εrrij "1 + εrf −εr
2εrf +εr
r3
ij
r3
c#−fqiqj
εrrc
3εrf
2εrf +εr
(4.13)
4.1. Non-bonded interactions 71
in which the constant expression on the right makes the potential zero at the cut-off rc. For charged
cut-off spheres this corresponds to neutralization with a homogeneous background charge. We can
rewrite eqn. 4.13 for simplicity as
Vcrf =fqiqj
εr"1
rij
+krf r2
ij −crf #(4.14)
with
krf =1
r3
c
εrf −εr
(2εrf +εr)(4.15)
crf =1
rc
+krf r2
c=1
rc
3εrf
(2εrf +εr)(4.16)
For large εrf the krf goes to r−3
c/2, while for εrf =εrthe correction vanishes. In Fig. 4.3 the
modified interaction is plotted, and it is clear that the derivative with respect to rij (= -force) goes
to zero at the cut-off distance. The force derived from this potential reads:
Fi(rij) = fqiqj
εr"1
r2
ij −2krf rij #rij
rij
(4.17)
The reaction-field correction should also be applied to all excluded atoms pairs, including self
pairs, in which case the normal Coulomb term in eqns. 4.13 and 4.17 is absent.
Tironi et al. have introduced a generalized reaction field in which the dielectric continuum beyond
the cut-off rcalso has an ionic strength I[76]. In this case we can rewrite the constants krf and
crf using the inverse Debye screening length κ:
κ2=2I F 2
ε0εrf RT =F2
ε0εrf RT
K
X
i=1
ciz2
i(4.18)
krf =1
r3
c
(εrf −εr)(1 + κrc) + 1
2εrf (κrc)2
(2εrf +εr)(1 + κrc) + εrf (κrc)2(4.19)
crf =1
rc
3εrf (1 + κrc+1
2(κrc)2)
(2εrf +εr)(1 + κrc) + εrf (κrc)2(4.20)
where Fis Faraday’s constant, Ris the ideal gas constant, Tthe absolute temperature, cithe
molar concentration for species iand zithe charge number of species iwhere we have Kdifferent
species. In the limit of zero ionic strength (κ= 0) eqns. 4.19 and 4.20 reduce to the simple forms
of eqns. 4.15 and 4.16 respectively.
4.1.5 Modified non-bonded interactions
In GROMACS, the non-bonded potentials can be modified by a shift function, also called a force-
switch function, since it switches the force to zero at the cut-off. The purpose of this is to replace
the truncated forces by forces that are continuous and have continuous derivatives at the cut-off
radius. With such forces the time integration produces smaller errors. But note that for Lennard-
Jones interactions these errors are usually smaller than other errors, such as integration errors at

72 Chapter 4. Interaction function and force fields
the repulsive part of the potential. For Coulomb interactions we advise against using a shifted
potential and for use of a reaction field or a proper long-range method such as PME.
There is no fundamental difference between a switch function (which multiplies the potential with
a function) and a shift function (which adds a function to the force or potential) [77]. The switch
function is a special case of the shift function, which we apply to the force function F(r), related
to the electrostatic or van der Waals force acting on particle iby particle jas:
Fi=c F (rij)rij
rij
(4.21)
For pure Coulomb or Lennard-Jones interactions F(r) = Fα(r) = α r−(α+1). The switched force
Fs(r)can generally be written as:
Fs(r) = Fα(r)r < r1
Fs(r) = Fα(r) + S(r)r1≤r < rc
Fs(r) = 0 rc≤r
(4.22)
When r1= 0 this is a traditional shift function, otherwise it acts as a switch function. The
corresponding shifted potential function then reads:
Vs(r) = Z∞
r
Fs(x)dx (4.23)
The GROMACS force switch function SF(r)should be smooth at the boundaries, therefore the
following boundary conditions are imposed on the switch function:
SF(r1)=0
S0
F(r1)=0
SF(rc) = −Fα(rc)
S0
F(rc) = −F0
α(rc)
(4.24)
A 3rd degree polynomial of the form
SF(r) = A(r−r1)2+B(r−r1)3(4.25)
fulfills these requirements. The constants A and B are given by the boundary condition at rc:
A=−α(α+ 4)rc−(α+ 1)r1
rα+2
c(rc−r1)2
B=α(α+ 3)rc−(α+ 1)r1
rα+2
c(rc−r1)3
(4.26)
Thus the total force function is:
Fs(r) = α
rα+1 +A(r−r1)2+B(r−r1)3(4.27)
and the potential function reads:
Vs(r) = 1
rα−A
3(r−r1)3−B
4(r−r1)4−C(4.28)

4.2. Bonded interactions 73
where
C=1
rα
c−A
3(rc−r1)3−B
4(rc−r1)4(4.29)
The GROMACS potential-switch function SV(r)scales the potential between r1and rc, and has
similar boundary conditions, intended to produce smoothly-varying potential and forces:
SV(r1)=1
S0
V(r1)=0
S00
V(r1)=0
SV(rc)=0
S0
V(rc)=0
S00
V(rc)=0
(4.30)
The fifth-degree polynomial that has these properties is
SV(r;r1, rc) = 1−10(r−r1)3(rc−r1)2+ 15(r−r1)4(rc−r1)−6(r−r1)
(rc−r1)5(4.31)
This implementation is found in several other simulation packages,[78,79,80] but differs from
that in CHARMM.[81] Switching the potential leads to artificially large forces in the switching
region, therefore it is not recommended to switch Coulomb interactions using this function,[77]
but switching Lennard-Jones interactions using this function produces acceptable results.
4.1.6 Modified short-range interactions with Ewald summation
When Ewald summation or particle-mesh Ewald is used to calculate the long-range interactions,
the short-range Coulomb potential must also be modified. Here the potential is switched to (nearly)
zero at the cut-off, instead of the force. In this case the short range potential is given by:
V(r) = ferfc(βrij )
rij
qiqj,(4.32)
where βis a parameter that determines the relative weight between the direct space sum and the
reciprocal space sum and erfc(x)is the complementary error function. For further details on long-
range electrostatics, see sec. 4.8.
4.2 Bonded interactions
Bonded interactions are based on a fixed list of atoms. They are not exclusively pair interac-
tions, but include 3- and 4-body interactions as well. There are bond stretching (2-body), bond
angle (3-body), and dihedral angle (4-body) interactions. A special type of dihedral interaction
(called improper dihedral) is used to force atoms to remain in a plane or to prevent transition to a
configuration of opposite chirality (a mirror image).
74 Chapter 4. Interaction function and force fields
b0
0.08 0.09 0.10 0.11
r (nm)
0
50
100
150
200
V (kJ mole–1)
Figure 4.4: Principle of bond stretching (left), and the bond stretching potential (right).
4.2.1 Bond stretching
Harmonic potential
The bond stretching between two covalently bonded atoms iand jis represented by a harmonic
potential:
Vb(rij) = 1
2kb
ij(rij −bij )2(4.33)
See also Fig. 4.4, with the force given by:
Fi(rij) = kb
ij(rij −bij )rij
rij
(4.34)
Fourth power potential
In the GROMOS-96 force field [82], the covalent bond potential is, for reasons of computational
efficiency, written as:
Vb(rij) = 1
4kb
ij r2
ij −b2
ij2(4.35)
The corresponding force is:
Fi(rij) = kb
ij(r2
ij −b2
ij)rij (4.36)
The force constants for this form of the potential are related to the usual harmonic force constant
kb,harm (sec. 4.2.1) as
2kbb2
ij =kb,harm (4.37)
The force constants are mostly derived from the harmonic ones used in GROMOS-87 [83]. Al-
though this form is computationally more efficient (because no square root has to be evaluated), it
is conceptually more complex. One particular disadvantage is that since the form is not harmonic,
the average energy of a single bond is not equal to 1
2kT as it is for the normal harmonic potential.

4.2. Bonded interactions 75
4.2.2 Morse potential bond stretching
For some systems that require an anharmonic bond stretching potential, the Morse potential [84]
between two atoms iand jis available in GROMACS. This potential differs from the harmonic
potential in that it has an asymmetric potential well and a zero force at infinite distance. The
functional form is:
Vmorse(rij ) = Dij [1 −exp(−βij (rij −bij))]2,(4.38)
See also Fig. 4.5, and the corresponding force is:
Fmorse(rij )=2Dij βij exp(−βij (rij −bij))∗
[1 −exp(−βij(rij −bij ))]rij
rij ,(4.39)
where Dij is the depth of the well in kJ/mol, βij defines the steepness of the well (in nm−1), and
bij is the equilibrium distance in nm. The steepness parameter βij can be expressed in terms of
the reduced mass of the atoms iand j, the fundamental vibration frequency ωij and the well depth
Dij:
βij =ωijsµij
2Dij
(4.40)
and because ω=qk/µ, one can rewrite βij in terms of the harmonic force constant kij :
βij =skij
2Dij
(4.41)
For small deviations (rij −bij), one can approximate the exp-term to first-order using a Taylor
expansion:
exp(−x)≈1−x(4.42)
and substituting eqn. 4.41 and eqn. 4.42 in the functional form:
Vmorse(rij ) = Dij [1 −exp(−βij (rij −bij))]2
=Dij[1 −(1 −rkij
2Dij (rij −bij))]2
=1
2kij(rij −bij ))2
(4.43)
we recover the harmonic bond stretching potential.
4.2.3 Cubic bond stretching potential
Another anharmonic bond stretching potential that is slightly simpler than the Morse potential
adds a cubic term in the distance to the simple harmonic form:
Vb(rij) = kb
ij(rij −bij )2+kb
ijkcub
ij (rij −bij)3(4.44)
A flexible water model (based on the SPC water model [85]) including a cubic bond stretching
potential for the O-H bond was developed by Ferguson [86]. This model was found to yield a
reasonable infrared spectrum. The Ferguson water model is available in the GROMACS library
76 Chapter 4. Interaction function and force fields
0.1 0.2 0.3 0.4 0.5 0.6
rij (nm)
0
100
200
300
400
Vij (kJ / mol)
Figure 4.5: The Morse potential well, with bond length 0.15 nm.
(flexwat-ferguson.itp). It should be noted that the potential is asymmetric: overstretching
leads to infinitely low energies. The integration timestep is therefore limited to 1 fs.
The force corresponding to this potential is:
Fi(rij)=2kb
ij(rij −bij )rij
rij
+ 3kb
ijkcub
ij (rij −bij)2rij
rij
(4.45)
4.2.4 FENE bond stretching potential
In coarse-grained polymer simulations the beads are often connected by a FENE (finitely extensi-
ble nonlinear elastic) potential [87]:
VFENE(rij ) = −1
2kb
ijb2
ij log 1−r2
ij
b2
ij !(4.46)
The potential looks complicated, but the expression for the force is simpler:
FFENE(rij ) = −kb
ij 1−r2
ij
b2
ij !−1
rij (4.47)
At short distances the potential asymptotically goes to a harmonic potential with force constant
kb, while it diverges at distance b.
4.2.5 Harmonic angle potential
The bond-angle vibration between a triplet of atoms i-j-kis also represented by a harmonic
potential on the angle θijk
Va(θijk) = 1
2kθ
ijk(θijk −θ0
ijk)2(4.48)
4.2. Bonded interactions 77
θ0
100 110 120 130 140
θ
0
10
20
30
40
50
Vθ (kJ mole-1)
Figure 4.6: Principle of angle vibration (left) and the bond angle potential (right).
As the bond-angle vibration is represented by a harmonic potential, the form is the same as the
bond stretching (Fig. 4.4).
The force equations are given by the chain rule:
Fi=−dVa(θijk)
dri
Fk=−dVa(θijk)
drk
Fj=−Fi−Fk
where θijk = arccos (rij ·rkj)
rijrkj
(4.49)
The numbering i, j, k is in sequence of covalently bonded atoms. Atom jis in the middle; atoms
iand kare at the ends (see Fig. 4.6). Note that in the input in topology files, angles are given in
degrees and force constants in kJ/mol/rad2.
4.2.6 Cosine based angle potential
In the GROMOS-96 force field a simplified function is used to represent angle vibrations:
Va(θijk) = 1
2kθ
ijk cos(θijk)−cos(θ0
ijk)2(4.50)
where
cos(θijk) = rij ·rkj
rijrkj
(4.51)
The corresponding force can be derived by partial differentiation with respect to the atomic posi-
tions. The force constants in this function are related to the force constants in the harmonic form
kθ,harm (4.2.5) by:
kθsin2(θ0
ijk) = kθ,harm (4.52)
In the GROMOS-96 manual there is a much more complicated conversion formula which is tem-
perature dependent. The formulas are equivalent at 0 K and the differences at 300 K are on the
order of 0.1 to 0.2%. Note that in the input in topology files, angles are given in degrees and force
constants in kJ/mol.
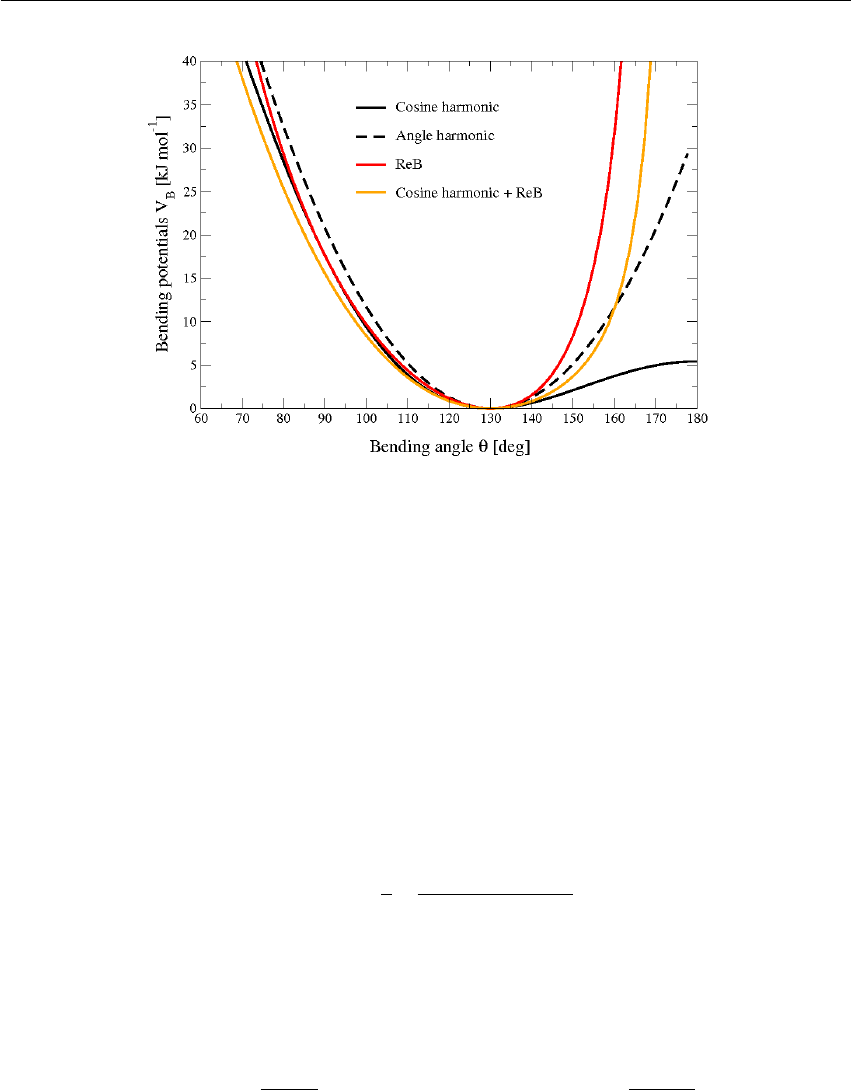
78 Chapter 4. Interaction function and force fields
Figure 4.7: Bending angle potentials: cosine harmonic (solid black line), angle harmonic (dashed
black line) and restricted bending (red) with the same bending constant kθ= 85 kJ mol−1and
equilibrium angle θ0= 130◦. The orange line represents the sum of a cosine harmonic (k= 50
kJ mol−1) with a restricted bending (k= 25 kJ mol−1) potential, both with θ0= 130◦.
4.2.7 Restricted bending potential
The restricted bending (ReB) potential [88] prevents the bending angle θfrom reaching the 180◦
value. In this way, the numerical instabilities due to the calculation of the torsion angle and
potential are eliminated when performing coarse-grained molecular dynamics simulations.
To systematically hinder the bending angles from reaching the 180◦value, the bending potential
4.50 is divided by a sin2θfactor:
VReB(θi) = 1
2kθ
(cos θi−cos θ0)2
sin2θi
.(4.53)
Figure Fig. 4.7 shows the comparison between the ReB potential, 4.53, and the standard one 4.50.
The wall of the ReB potential is very repulsive in the region close to 180◦and, as a result, the
bending angles are kept within a safe interval, far from instabilities. The power 2of sin θiin the
denominator has been chosen to guarantee this behavior and allows an elegant differentiation:
FReB(θi) = 2kθ
sin4θi
(cos θi−cos θ0)(1 −cos θicos θ0)∂cos θi
∂~rk
.(4.54)
Due to its construction, the restricted bending potential cannot be used for equilibrium θ0values
too close to 0◦or 180◦(from experience, at least 10◦difference is recommended). It is very
important that, in the starting configuration, all the bending angles have to be in the safe interval
to avoid initial instabilities. This bending potential can be used in combination with any form
of torsion potential. It will always prevent three consecutive particles from becoming collinear
and, as a result, any torsion potential will remain free of singularities. It can be also added to a

4.2. Bonded interactions 79
standard bending potential to affect the angle around 180◦, but to keep its original form around the
minimum (see the orange curve in Fig. 4.7).
4.2.8 Urey-Bradley potential
The Urey-Bradley bond-angle vibration between a triplet of atoms i-j-kis represented by a
harmonic potential on the angle θijk and a harmonic correction term on the distance between the
atoms iand k. Although this can be easily written as a simple sum of two terms, it is convenient
to have it as a single entry in the topology file and in the output as a separate energy term. It is
used mainly in the CHARMm force field [89]. The energy is given by:
Va(θijk) = 1
2kθ
ijk(θijk −θ0
ijk)2+1
2kUB
ijk (rik −r0
ik)2(4.55)
The force equations can be deduced from sections 4.2.1 and 4.2.5.
4.2.9 Bond-Bond cross term
The bond-bond cross term for three particles i, j, k forming bonds i−jand k−jis given by [90]:
Vrr0=krr0(|ri−rj| − r1e) (|rk−rj| − r2e)(4.56)
where krr0is the force constant, and r1eand r2eare the equilibrium bond lengths of the i−jand
k−jbonds respectively. The force associated with this potential on particle iis:
Fi=−krr0(|rk−rj| − r2e)ri−rj
|ri−rj|(4.57)
The force on atom kcan be obtained by swapping iand kin the above equation. Finally, the force
on atom jfollows from the fact that the sum of internal forces should be zero: Fj=−Fi−Fk.
4.2.10 Bond-Angle cross term
The bond-angle cross term for three particles i, j, k forming bonds i−jand k−jis given by [90]:
Vrθ =krθ (|ri−rk| − r3e) (|ri−rj| − r1e+|rk−rj| − r2e)(4.58)
where krθ is the force constant, r3eis the i−kdistance, and the other constants are the same as
in Equation 4.56. The force associated with the potential on atom iis:
Fi=−krθ "(|ri−rk| − r3e)ri−rj
|ri−rj|+ (|ri−rj| − r1e+|rk−rj| − r2e)ri−rk
|ri−rk|#
(4.59)
4.2.11 Quartic angle potential
For special purposes there is an angle potential that uses a fourth order polynomial:
Vq(θijk) =
5
X
n=0
Cn(θijk −θ0
ijk)n(4.60)
80 Chapter 4. Interaction function and force fields
k
li
j
i
kj
l
k
i
j
l
Figure 4.8: Principle of improper dihedral angles. Out of plane bending for rings (left), sub-
stituents of rings (middle), out of tetrahedral (right). The improper dihedral angle ξis defined as
the angle between planes (i,j,k) and (j,k,l) in all cases.
–20 –10 0 10 20
ξ
0
10
20
Vi (kJ mol–1)
(°)
Figure 4.9: Improper dihedral potential.
4.2.12 Improper dihedrals
Improper dihedrals are meant to keep planar groups (e.g. aromatic rings) planar, or to prevent
molecules from flipping over to their mirror images, see Fig. 4.8.
Improper dihedrals: harmonic type
The simplest improper dihedral potential is a harmonic potential; it is plotted in Fig. 4.9.
Vid(ξijkl) = 1
2kξ(ξijkl −ξ0)2(4.61)
Since the potential is harmonic it is discontinuous, but since the discontinuity is chosen at 180◦
distance from ξ0this will never cause problems. Note that in the input in topology files, angles are
given in degrees and force constants in kJ/mol/rad2.
4.2. Bonded interactions 81
j
k
l
i
0.0 90.0 180.0 270.0 360.0
φ
0.0
20.0
40.0
60.0
80.0
Vd (kJ mole–1)
Figure 4.10: Principle of proper dihedral angle (left, in trans form) and the dihedral angle potential
(right).
Improper dihedrals: periodic type
This potential is identical to the periodic proper dihedral (see below). There is a separate dihedral
type for this (type 4) only to be able to distinguish improper from proper dihedrals in the parameter
section and the output.
4.2.13 Proper dihedrals
For the normal dihedral interaction there is a choice of either the GROMOS periodic function or a
function based on expansion in powers of cos φ(the so-called Ryckaert-Bellemans potential). This
choice has consequences for the inclusion of special interactions between the first and the fourth
atom of the dihedral quadruple. With the periodic GROMOS potential a special 1-4 LJ-interaction
must be included; with the Ryckaert-Bellemans potential for alkanes the 1-4 interactions must be
excluded from the non-bonded list. Note: Ryckaert-Bellemans potentials are also used in e.g. the
OPLS force field in combination with 1-4 interactions. You should therefore not modify topologies
generated by pdb2gmx in this case.
Proper dihedrals: periodic type
Proper dihedral angles are defined according to the IUPAC/IUB convention, where φis the angle
between the ijk and the jkl planes, with zero corresponding to the cis configuration (iand lon
the same side). There are two dihedral function types in GROMACS topology files. There is the
standard type 1 which behaves like any other bonded interactions. For certain force fields, type 9 is
useful. Type 9 allows multiple potential functions to be applied automatically to a single dihedral
in the [ dihedral ] section when multiple parameters are defined for the same atomtypes in
the [ dihedraltypes ] section.
Vd(φijkl) = kφ(1 + cos(nφ −φs)) (4.62)
82 Chapter 4. Interaction function and force fields
C09.28 C2-13.12 C426.24
C112.16 C3-3.06 C5-31.5
Table 4.1: Constants for Ryckaert-Bellemans potential (kJ mol−1).
0.0 90.0 180.0 270.0 360.0
φ
0.0
10.0
20.0
30.0
40.0
50.0
Vd (kJ mole–1)
Figure 4.11: Ryckaert-Bellemans dihedral potential.
Proper dihedrals: Ryckaert-Bellemans function
For alkanes, the following proper dihedral potential is often used (see Fig. 4.11):
Vrb(φijkl) =
5
X
n=0
Cn(cos(ψ))n,(4.63)
where ψ=φ−180◦.
Note: A conversion from one convention to another can be achieved by multiplying every coeffi-
cient Cnby (−1)n.
An example of constants for Cis given in Table 4.1.
(Note: The use of this potential implies exclusion of LJ interactions between the first and the last
atom of the dihedral, and ψis defined according to the “polymer convention” (ψtrans = 0).)
The RB dihedral function can also be used to include Fourier dihedrals (see below):
Vrb(φijkl) = 1
2[F1(1 + cos(φ)) + F2(1 −cos(2φ)) + F3(1 + cos(3φ)) + F4(1 −cos(4φ))]
(4.64)
Because of the equalities cos(2φ) = 2 cos2(φ)−1,cos(3φ) = 4 cos3(φ)−3 cos(φ)and cos(4φ) =
8 cos4(φ)−8 cos2(φ)+1one can translate the OPLS parameters to Ryckaert-Bellemans param-
4.2. Bonded interactions 83
eters as follows:
C0=F2+1
2(F1+F3)
C1=1
2(−F1+ 3 F3)
C2=−F2+ 4 F4
C3=−2F3
C4=−4F4
C5= 0
(4.65)
with OPLS parameters in protein convention and RB parameters in polymer convention (this yields
a minus sign for the odd powers of cos(φ)).
Note: Mind the conversion from kcal mol−1for literature OPLS and RB parameters to kJ mol−1
in GROMACS.
Proper dihedrals: Fourier function
The OPLS potential function is given as the first three [91] or four [92] cosine terms of a Fourier
series. In GROMACS the four term function is implemented:
VF(φijkl) = 1
2[C1(1 + cos(φ)) + C2(1 −cos(2φ)) + C3(1 + cos(3φ)) + C4(1 −cos(4φ))] ,
(4.66)
Internally, GROMACS uses the Ryckaert-Bellemans code to compute Fourier dihedrals (see above),
because this is more efficient.
Note: Mind the conversion from kcal mol−1for literature OPLS parameters to kJ mol−1in GRO-
MACS.
Proper dihedrals: Restricted torsion potential
In a manner very similar to the restricted bending potential (see 4.2.7), a restricted torsion/dihedral
potential is introduced:
VReT(φi) = 1
2kφ
(cos φi−cos φ0)2
sin2φi
(4.67)
with the advantages of being a function of cos φ(no problems taking the derivative of sin φ) and
of keeping the torsion angle at only one minimum value. In this case, the factor sin2φdoes not
allow the dihedral angle to move from the [−180◦:0] to [0:180◦] interval, i.e. it cannot have
maxima both at −φ0and +φ0maxima, but only one of them. For this reason, all the dihedral
angles of the starting configuration should have their values in the desired angles interval and the
the equilibrium φ0value should not be too close to the interval limits (as for the restricted bending
potential, described in 4.2.7, at least 10◦difference is recommended).
Proper dihedrals: Combined bending-torsion potential
When the four particles forming the dihedral angle become collinear (this situation will never
happen in atomistic simulations, but it can occur in coarse-grained simulations) the calculation of

84 Chapter 4. Interaction function and force fields
the torsion angle and potential leads to numerical instabilities. One way to avoid this is to use the
restricted bending potential (see 4.2.7) that prevents the dihedral from reaching the 180◦value.
Another way is to disregard any effects of the dihedral becoming ill-defined, keeping the dihedral
force and potential calculation continuous in entire angle range by coupling the torsion potential
(in a cosine form) with the bending potentials of the adjacent bending angles in a unique expres-
sion:
VCBT(θi−1, θi, φi) = kφsin3θi−1sin3θi
4
X
n=0
ancosnφi.(4.68)
This combined bending-torsion (CBT) potential has been proposed by [93] for polymer melt sim-
ulations and is extensively described in [88].
This potential has two main advantages:
•it does not only depend on the dihedral angle φi(between the i−2,i−1,iand i+ 1
beads) but also on the bending angles θi−1and θidefined from three adjacent beads (i−2,
i−1and i, and i−1,iand i+ 1, respectively). The two sin3θpre-factors, tentatively
suggested by [94] and theoretically discussed by [95], cancel the torsion potential and force
when either of the two bending angles approaches the value of 180◦.
•its dependence on φiis expressed through a polynomial in cos φithat avoids the singularities
in φ= 0◦or 180◦in calculating the torsional force.
These two properties make the CBT potential well-behaved for MD simulations with weak con-
straints on the bending angles or even for steered / non-equilibrium MD in which the bending and
torsion angles suffer major modifications. When using the CBT potential, the bending potentials
for the adjacent θi−1and θimay have any form. It is also possible to leave out the two angle
bending terms (θi−1and θi) completely. Fig. 4.12 illustrates the difference between a torsion po-
tential with and without the sin3θfactors (blue and gray curves, respectively). Additionally, the
derivative of VCBT with respect to the Cartesian variables is straightforward:
∂VCBT(θi−1, θi, φi)
∂~rl
=∂VCBT
∂θi−1
∂θi−1
∂~rl
+∂VCBT
∂θi
∂θi
∂~rl
+∂VCBT
∂φi
∂φi
∂~rl
(4.69)
The CBT is based on a cosine form without multiplicity, so it can only be symmetrical around 0◦.
To obtain an asymmetrical dihedral angle distribution (e.g. only one maximum in [−180◦:180◦]
interval), a standard torsion potential such as harmonic angle or periodic cosine potentials should
be used instead of a CBT potential. However, these two forms have the inconveniences of the
force derivation (1/sin φ) and of the alignment of beads (θior θi−1= 0◦,180◦). Coupling such
non-cos φpotentials with sin3θfactors does not improve simulation stability since there are cases
in which θand φare simultaneously 180◦. The integration at this step would be possible (due to
the cancelling of the torsion potential) but the next step would be singular (θis not 180◦and φis
very close to 180◦).
4.2.14 Tabulated bonded interaction functions
For full flexibility, any functional shape can be used for bonds, angles and dihedrals through user-
supplied tabulated functions. The functional shapes are:
Vb(rij) = k fb
n(rij)(4.70)
4.2. Bonded interactions 85
-180 -90 0 90 180
0
30
60
90
120
150
180
0
5
10
15
20
25
30
35
40
45
VT [kJ mol-1]
CBT
RB
φ [deg]
θ [deg]
VT [kJ mol-1]
Figure 4.12: Blue: surface plot of the combined bending-torsion potential (4.68 with k= 10
kJ mol−1,a0= 2.41,a1=−2.95,a2= 0.36,a3= 1.33) when, for simplicity, the bending
angles behave the same (θ1=θ2=θ). Gray: the same torsion potential without the sin3θterms
(Ryckaert-Bellemans type). φis the dihedral angle.
Va(θijk) = k f a
n(θijk)(4.71)
Vd(φijkl) = k f d
n(φijkl)(4.72)
where kis a force constant in units of energy and fis a cubic spline function; for details see 6.12.1.
For each interaction, the force constant kand the table number nare specified in the topology.
There are two different types of bonds, one that generates exclusions (type 8) and one that does
not (type 9). For details see Table 5.5. The table files are supplied to the mdrun program. After
the table file name an underscore, the letter “b” for bonds, “a” for angles or “d” for dihedrals and
the table number must be appended. For example, a tabulated bond with n= 0 can be read from
the file table_b0.xvg. Multiple tables can be supplied simply by adding files with different
values of n, and are applied to the appropriate bonds, as specified in the topology (Table 5.5).
The format for the table files is three fixed-format columns of any suitable width. These columns
must contain x,f(x),−f0(x), and the values of xshould be uniformly spaced. Requirements for
entries in the topology are given in Table 5.5. The setup of the tables is as follows:
bonds:xis the distance in nm. For distances beyond the table length, mdrun will quit with an
error message.
angles:xis the angle in degrees. The table should go from 0 up to and including 180 degrees; the
derivative is taken in degrees.
dihedrals:xis the dihedral angle in degrees. The table should go from -180 up to and including
180 degrees; the IUPAC/IUB convention is used, i.e. zero is cis, the derivative is taken in degrees.

86 Chapter 4. Interaction function and force fields
0.00 0.02 0.04 0.06 0.08 0.10
r-R (nm)
0.0
2.0
4.0
6.0
8.0
10.0
Vposre (kJ mole–1)
Figure 4.13: Position restraint potential.
4.3 Restraints
Special potentials are used for imposing restraints on the motion of the system, either to avoid
disastrous deviations, or to include knowledge from experimental data. In either case they are not
really part of the force field and the reliability of the parameters is not important. The potential
forms, as implemented in GROMACS, are mentioned just for the sake of completeness. Restraints
and constraints refer to quite different algorithms in GROMACS.
4.3.1 Position restraints
These are used to restrain particles to fixed reference positions Ri. They can be used during
equilibration in order to avoid drastic rearrangements of critical parts (e.g. to restrain motion in a
protein that is subjected to large solvent forces when the solvent is not yet equilibrated). Another
application is the restraining of particles in a shell around a region that is simulated in detail, while
the shell is only approximated because it lacks proper interaction from missing particles outside
the shell. Restraining will then maintain the integrity of the inner part. For spherical shells, it is a
wise procedure to make the force constant depend on the radius, increasing from zero at the inner
boundary to a large value at the outer boundary. This feature has not, however, been implemented
in GROMACS.
The following form is used:
Vpr(ri) = 1
2kpr|ri−Ri|2(4.73)
The potential is plotted in Fig. 4.13.
The potential form can be rewritten without loss of generality as:
Vpr(ri) = 1
2hkx
pr(xi−Xi)2ˆ
x+ky
pr(yi−Yi)2ˆ
y+kz
pr(zi−Zi)2ˆ
zi(4.74)

4.3. Restraints 87
-1 -0.5 0 0.5 1
r [nm]
0
10
20
30
40
50
V(r) [kJ/mol]
-1 -0.5 0 0.5 1
r [nm]
0
10
20
30
40
50
2 rfb
AB
Figure 4.14: Flat-bottomed position restraint potential. (A) Not inverted, (B) inverted.
Now the forces are:
Fx
i=−kx
pr (xi−Xi)
Fy
i=−ky
pr (yi−Yi)
Fz
i=−kz
pr (zi−Zi)
(4.75)
Using three different force constants the position restraints can be turned on or off in each spatial
dimension; this means that atoms can be harmonically restrained to a plane or a line. Position
restraints are applied to a special fixed list of atoms. Such a list is usually generated by the
pdb2gmx program.
4.3.2 Flat-bottomed position restraints
Flat-bottomed position restraints can be used to restrain particles to part of the simulation volume.
No force acts on the restrained particle within the flat-bottomed region of the potential, however a
harmonic force acts to move the particle to the flat-bottomed region if it is outside it. It is possible
to apply normal and flat-bottomed position restraints on the same particle (however, only with the
same reference position Ri). The following general potential is used (Figure 4.14A):
Vfb(ri) = 1
2kfb[dg(ri;Ri)−rfb]2H[dg(ri;Ri)−rfb],(4.76)
where Riis the reference position, rfb is the distance from the center with a flat potential, kfb the
force constant, and His the Heaviside step function. The distance dg(ri;Ri)from the reference
position depends on the geometry gof the flat-bottomed potential.
The following geometries for the flat-bottomed potential are supported:
Sphere (g= 1): The particle is kept in a sphere of given radius. The force acts towards the center
of the sphere. The following distance calculation is used:
dg(ri;Ri) = |ri−Ri|(4.77)
Cylinder (g= 6,7,8): The particle is kept in a cylinder of given radius parallel to the x(g= 6),
y(g= 7), or z-axis (g= 8). For backwards compatibility, setting g= 2 is mapped to g= 8 in the
code so that old .tpr files and topologies work. The force from the flat-bottomed potential acts
towards the axis of the cylinder. The component of the force parallel to the cylinder axis is zero.
For a cylinder aligned along the z-axis:
dg(ri;Ri) = q(xi−Xi)2+ (yi−Yi)2(4.78)
88 Chapter 4. Interaction function and force fields
Layer (g= 3,4,5): The particle is kept in a layer defined by the thickness and the normal of the
layer. The layer normal can be parallel to the x,y, or z-axis. The force acts parallel to the layer
normal.
dg(ri;Ri) = |xi−Xi|,or dg(ri;Ri) = |yi−Yi|,or dg(ri;Ri) = |zi−Zi|.(4.79)
It is possible to apply multiple independent flat-bottomed position restraints of different geometry
on one particle. For example, applying a cylinder and a layer in zkeeps a particle within a disk.
Applying three layers in x,y, and zkeeps the particle within a cuboid.
In addition, it is possible to invert the restrained region with the unrestrained region, leading to
a potential that acts to keep the particle outside of the volume defined by Ri,g, and rfb. That
feature is switched on by defining a negative rfb in the topology. The following potential is used
(Figure 4.14B):
Vinv
fb (ri) = 1
2kfb[dg(ri;Ri)− |rfb|]2H[−(dg(ri;Ri)− |rfb|)].(4.80)
4.3.3 Angle restraints
These are used to restrain the angle between two pairs of particles or between one pair of particles
and the z-axis. The functional form is similar to that of a proper dihedral. For two pairs of atoms:
Var(ri,rj,rk,rl) = kar(1 −cos(n(θ−θ0))),where θ= arccos rj−ri
krj−rik·rl−rk
krl−rkk!
(4.81)
For one pair of atoms and the z-axis:
Var(ri,rj) = kar(1 −cos(n(θ−θ0))),where θ= arccos
rj−ri
krj−rik·
0
0
1
(4.82)
A multiplicity (n) of 2 is useful when you do not want to distinguish between parallel and anti-
parallel vectors. The equilibrium angle θshould be between 0 and 180 degrees for multiplicity 1
and between 0 and 90 degrees for multiplicity 2.
4.3.4 Dihedral restraints
These are used to restrain the dihedral angle φdefined by four particles as in an improper dihedral
(sec. 4.2.12) but with a slightly modified potential. Using:
φ0= (φ−φ0) MOD 2π(4.83)
where φ0is the reference angle, the potential is defined as:
Vdihr(φ0) =
1
2kdihr(φ0−φ0−∆φ)2for φ0>∆φ
0for φ0≤∆φ(4.84)
where ∆φis a user defined angle and kdihr is the force constant. Note that in the input in topology
files, angles are given in degrees and force constants in kJ/mol/rad2.
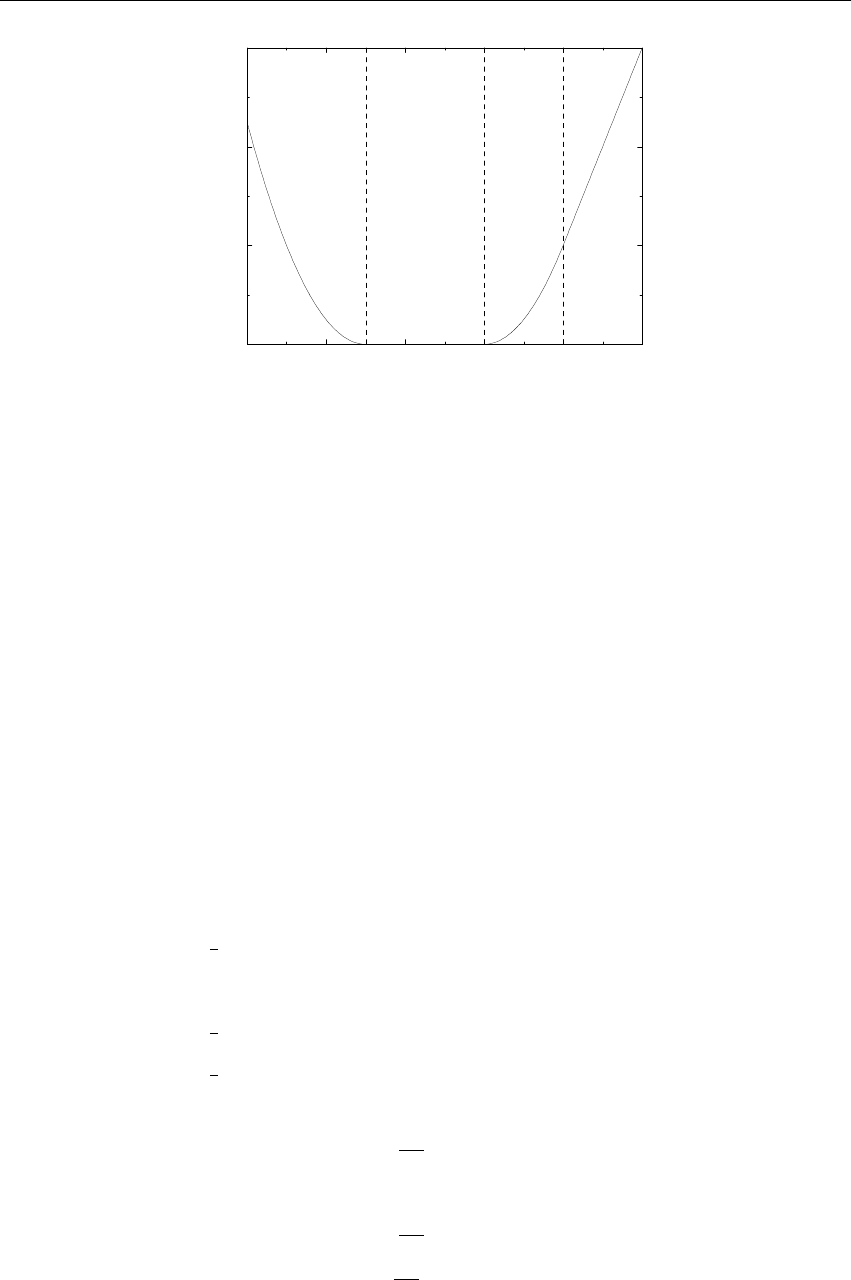
4.3. Restraints 89
0 0.1 0.2 0.3 0.4 0.5
r (nm)
0
5
10
15
Vdisre (kJ mol−1)
r0r1r2
Figure 4.15: Distance Restraint potential.
4.3.5 Distance restraints
Distance restraints add a penalty to the potential when the distance between specified pairs of
atoms exceeds a threshold value. They are normally used to impose experimental restraints from,
for instance, experiments in nuclear magnetic resonance (NMR), on the motion of the system.
Thus, MD can be used for structure refinement using NMR data. In GROMACS there are three
ways to impose restraints on pairs of atoms:
•Simple harmonic restraints: use [ bonds ] type 6 (see sec. 5.4.4).
•Piecewise linear/harmonic restraints: [ bonds ] type 10.
•Complex NMR distance restraints, optionally with pair, time and/or ensemble averaging.
The last two options will be detailed now.
The potential form for distance restraints is quadratic below a specified lower bound and between
two specified upper bounds, and linear beyond the largest bound (see Fig. 4.15).
Vdr(rij ) =
1
2kdr(rij −r0)2for rij < r0
0for r0≤rij < r1
1
2kdr(rij −r1)2for r1≤rij < r2
1
2kdr(r2−r1)(2rij −r2−r1)for r2≤rij
(4.85)
The forces are
Fi=
−kdr(rij −r0)rij
rij for rij < r0
0for r0≤rij < r1
−kdr(rij −r1)rij
rij for r1≤rij < r2
−kdr(r2−r1)rij
rij for r2≤rij
(4.86)
90 Chapter 4. Interaction function and force fields
For restraints not derived from NMR data, this functionality will usually suffice and a section of
[ bonds ] type 10 can be used to apply individual restraints between pairs of atoms, see 5.8.1.
For applying restraints derived from NMR measurements, more complex functionality might be re-
quired, which is provided through the [ distance_restraints ] section and is described
below.
Time averaging
Distance restraints based on instantaneous distances can potentially reduce the fluctuations in a
molecule significantly. This problem can be overcome by restraining to a time averaged dis-
tance [96]. The forces with time averaging are:
Fi=
−ka
dr(¯rij −r0)rij
rij for ¯rij < r0
0for r0≤¯rij < r1
−ka
dr(¯rij −r1)rij
rij for r1≤¯rij < r2
−ka
dr(r2−r1)rij
rij for r2≤¯rij
(4.87)
where ¯rij is given by an exponential running average with decay time τ:
¯rij =< r−3
ij >−1/3(4.88)
The force constant ka
dr is switched on slowly to compensate for the lack of history at the beginning
of the simulation:
ka
dr =kdr 1−exp −t
τ (4.89)
Because of the time averaging, we can no longer speak of a distance restraint potential.
This way an atom can satisfy two incompatible distance restraints on average by moving between
two positions. An example would be an amino acid side-chain that is rotating around its χdihedral
angle, thereby coming close to various other groups. Such a mobile side chain can give rise to
multiple NOEs that can not be fulfilled by a single structure.
The computation of the time averaged distance in the mdrun program is done in the following
fashion:
r−3ij(0) = rij (0)−3
r−3ij(t) = r−3ij (t−∆t) exp −∆t
τ+rij(t)−3h1−exp −∆t
τi (4.90)
When a pair is within the bounds, it can still feel a force because the time averaged distance can
still be beyond a bound. To prevent the protons from being pulled too close together, a mixed
approach can be used. In this approach, the penalty is zero when the instantaneous distance is
within the bounds, otherwise the violation is the square root of the product of the instantaneous
violation and the time averaged violation:
Fi=
ka
drq(rij −r0)(¯rij −r0)rij
rij for rij < r0and ¯rij < r0
−ka
dr min q(rij −r1)(¯rij −r1), r2−r1rij
rij for rij > r1and ¯rij > r1
0otherwise
(4.91)

4.3. Restraints 91
Averaging over multiple pairs
Sometimes it is unclear from experimental data which atom pair gives rise to a single NOE, in
other occasions it can be obvious that more than one pair contributes due to the symmetry of the
system, e.g. a methyl group with three protons. For such a group, it is not possible to distinguish
between the protons, therefore they should all be taken into account when calculating the distance
between this methyl group and another proton (or group of protons). Due to the physical nature of
magnetic resonance, the intensity of the NOE signal is inversely proportional to the sixth power
of the inter-atomic distance. Thus, when combining atom pairs, a fixed list of Nrestraints may be
taken together, where the apparent “distance” is given by:
rN(t) = "N
X
n=1
¯rn(t)−6#−1/6
(4.92)
where we use rij or eqn. 4.88 for the ¯rn. The rNof the instantaneous and time-averaged distances
can be combined to do a mixed restraining, as indicated above. As more pairs of protons contribute
to the same NOE signal, the intensity will increase, and the summed “distance” will be shorter than
any of its components due to the reciprocal summation.
There are two options for distributing the forces over the atom pairs. In the conservative option,
the force is defined as the derivative of the restraint potential with respect to the coordinates. This
results in a conservative potential when time averaging is not used. The force distribution over
the pairs is proportional to r−6. This means that a close pair feels a much larger force than a
distant pair, which might lead to a molecule that is “too rigid.” The other option is an equal
force distribution. In this case each pair feels 1/N of the derivative of the restraint potential with
respect to rN. The advantage of this method is that more conformations might be sampled, but the
non-conservative nature of the forces can lead to local heating of the protons.
It is also possible to use ensemble averaging using multiple (protein) molecules. In this case the
bounds should be lowered as in:
r1=r1∗M−1/6
r2=r2∗M−1/6(4.93)
where Mis the number of molecules. The GROMACS preprocessor grompp can do this auto-
matically when the appropriate option is given. The resulting “distance” is then used to calculate
the scalar force according to:
Fi=
0rN< r1
kdr(rN−r1)rij
rij r1≤rN< r2
kdr(r2−r1)rij
rij rN≥r2
(4.94)
where iand jdenote the atoms of all the pairs that contribute to the NOE signal.
Using distance restraints
A list of distance restrains based on NOE data can be added to a molecule definition in your
topology file, like in the following example:

92 Chapter 4. Interaction function and force fields
[ distance_restraints ]
; ai aj type index type’ low up1 up2 fac
10 16 1 0 1 0.0 0.3 0.4 1.0
10 28 1 1 1 0.0 0.3 0.4 1.0
10 46 1 1 1 0.0 0.3 0.4 1.0
16 22 1 2 1 0.0 0.3 0.4 2.5
16 34 1 3 1 0.0 0.5 0.6 1.0
In this example a number of features can be found. In columns ai and aj you find the atom
numbers of the particles to be restrained. The type column should always be 1. As explained
in 4.3.5, multiple distances can contribute to a single NOE signal. In the topology this can be
set using the index column. In our example, the restraints 10-28 and 10-46 both have index 1,
therefore they are treated simultaneously. An extra requirement for treating restraints together is
that the restraints must be on successive lines, without any other intervening restraint. The type’
column will usually be 1, but can be set to 2 to obtain a distance restraint that will never be time-
and ensemble-averaged; this can be useful for restraining hydrogen bonds. The columns low,
up1, and up2 hold the values of r0,r1, and r2from eqn. 4.85. In some cases it can be useful
to have different force constants for some restraints; this is controlled by the column fac. The
force constant in the parameter file is multiplied by the value in the column fac for each restraint.
Information for each restraint is stored in the energy file and can be processed and plotted with
gmx nmr.
4.3.6 Orientation restraints
This section describes how orientations between vectors, as measured in certain NMR experi-
ments, can be calculated and restrained in MD simulations. The presented refinement methodol-
ogy and a comparison of results with and without time and ensemble averaging have been pub-
lished [97].
Theory
In an NMR experiment, orientations of vectors can be measured when a molecule does not tum-
ble completely isotropically in the solvent. Two examples of such orientation measurements are
residual dipolar couplings (between two nuclei) or chemical shift anisotropies. An observable for
a vector rican be written as follows:
δi=2
3tr(SDi)(4.95)
where Sis the dimensionless order tensor of the molecule. The tensor Diis given by:
Di=ci
krikα
3xx −1 3xy 3xz
3xy 3yy −1 3yz
3xz 3yz 3zz −1
(4.96)
with: x=ri,x
krik, y =ri,y
krik, z =ri,z
krik(4.97)

4.3. Restraints 93
For a dipolar coupling riis the vector connecting the two nuclei, α= 3 and the constant ciis
given by:
ci=µ0
4πγi
1γi
2
¯h
4π(4.98)
where γi
1and γi
2are the gyromagnetic ratios of the two nuclei.
The order tensor is symmetric and has trace zero. Using a rotation matrix Tit can be transformed
into the following form:
TTST =s
−1
2(1 −η)00
0−1
2(1 + η) 0
0 0 1
(4.99)
where −1≤s≤1and 0≤η≤1.sis called the order parameter and ηthe asymmetry of
the order tensor S. When the molecule tumbles isotropically in the solvent, sis zero, and no
orientational effects can be observed because all δiare zero.
Calculating orientations in a simulation
For reasons which are explained below, the Dmatrices are calculated which respect to a reference
orientation of the molecule. The orientation is defined by a rotation matrix R, which is needed to
least-squares fit the current coordinates of a selected set of atoms onto a reference conformation.
The reference conformation is the starting conformation of the simulation. In case of ensemble av-
eraging, which will be treated later, the structure is taken from the first subsystem. The calculated
Dc
imatrix is given by:
Dc
i(t) = R(t)Di(t)RT(t)(4.100)
The calculated orientation for vector iis given by:
δc
i(t) = 2
3tr(S(t)Dc
i(t)) (4.101)
The order tensor S(t)is usually unknown. A reasonable choice for the order tensor is the tensor
which minimizes the (weighted) mean square difference between the calculated and the observed
orientations:
MSD(t) = N
X
i=1
wi!−1N
X
i=1
wi(δc
i(t)−δexp
i)2(4.102)
To properly combine different types of measurements, the unit of wishould be such that all terms
are dimensionless. This means the unit of wiis the unit of δito the power −2.Note that scaling
all wiwith a constant factor does not influence the order tensor.
Time averaging
Since the tensors Difluctuate rapidly in time, much faster than can be observed in an experiment,
they should be averaged over time in the simulation. However, in a simulation the time and the
number of copies of a molecule are limited. Usually one can not obtain a converged average of the
Ditensors over all orientations of the molecule. If one assumes that the average orientations of

94 Chapter 4. Interaction function and force fields
the rivectors within the molecule converge much faster than the tumbling time of the molecule,
the tensor can be averaged in an axis system that rotates with the molecule, as expressed by equa-
tion (4.100). The time-averaged tensors are calculated using an exponentially decaying memory
function:
Da
i(t) = Zt
u=t0
Dc
i(u) exp −t−u
τdu
Zt
u=t0
exp −t−u
τdu
(4.103)
Assuming that the order tensor Sfluctuates slower than the Di, the time-averaged orientation can
be calculated as:
δa
i(t) = 2
3tr(S(t)Da
i(t)) (4.104)
where the order tensor S(t)is calculated using expression (4.102) with δc
i(t)replaced by δa
i(t).
Restraining
The simulated structure can be restrained by applying a force proportional to the difference be-
tween the calculated and the experimental orientations. When no time averaging is applied, a
proper potential can be defined as:
V=1
2k
N
X
i=1
wi(δc
i(t)−δexp
i)2(4.105)
where the unit of kis the unit of energy. Thus the effective force constant for restraint iis kwi.
The forces are given by minus the gradient of V. The force Fiworking on vector riis:
Fi(t) = −dV
dri
=−kwi(δc
i(t)−δexp
i)dδi(t)
dri
=−kwi(δc
i(t)−δexp
i)2ci
krk2+α2RTSRri−2 + α
krk2tr(RTSRrirT
i)ri
Ensemble averaging
Ensemble averaging can be applied by simulating a system of Msubsystems that each contain
an identical set of orientation restraints. The systems only interact via the orientation restraint
potential which is defined as:
V=M1
2k
N
X
i=1
wihδc
i(t)−δexp
ii2(4.106)
The force on vector ri,m in subsystem mis given by:
Fi,m(t) = −dV
dri,m
=−kwihδc
i(t)−δexp
iidδc
i,m(t)
dri,m
(4.107)

4.3. Restraints 95
Time averaging
When using time averaging it is not possible to define a potential. We can still define a quantity
that gives a rough idea of the energy stored in the restraints:
V=M1
2ka
N
X
i=1
wihδa
i(t)−δexp
ii2(4.108)
The force constant kais switched on slowly to compensate for the lack of history at times close to
t0. It is exactly proportional to the amount of average that has been accumulated:
ka=k1
τZt
u=t0
exp −t−u
τdu(4.109)
What really matters is the definition of the force. It is chosen to be proportional to the square root
of the product of the time-averaged and the instantaneous deviation. Using only the time-averaged
deviation induces large oscillations. The force is given by:
Fi,m(t) =
0for a b ≤0
kawi
a
|a|√a b dδc
i,m(t)
dri,m
for a b > 0(4.110)
a=hδa
i(t)−δexp
ii
b=hδc
i(t)−δexp
ii
Using orientation restraints
Orientation restraints can be added to a molecule definition in the topology file in the section
[ orientation_restraints ]. Here we give an example section containing five N-H
residual dipolar coupling restraints:
[ orientation_restraints ]
; ai aj type exp. label alpha const. obs. weight
; Hz nm^3 Hz Hz^-2
31 32 1 1 3 3 6.083 -6.73 1.0
43 44 1 1 4 3 6.083 -7.87 1.0
55 56 1 1 5 3 6.083 -7.13 1.0
65 66 1 1 6 3 6.083 -2.57 1.0
73 74 1 1 7 3 6.083 -2.10 1.0
The unit of the observable is Hz, but one can choose any other unit. In columns ai and aj you
find the atom numbers of the particles to be restrained. The type column should always be 1. The
exp. column denotes the experiment number, starting at 1. For each experiment a separate order
tensor Sis optimized. The label should be a unique number larger than zero for each restraint. The
alpha column contains the power αthat is used in equation (4.96) to calculate the orientation.
The const. column contains the constant ciused in the same equation. The constant should

96 Chapter 4. Interaction function and force fields
have the unit of the observable times nmα. The column obs. contains the observable, in any unit
you like. The last column contains the weights wi; the unit should be the inverse of the square of
the unit of the observable.
Some parameters for orientation restraints can be specified in the grompp.mdp file, for a study
of the effect of different force constants and averaging times and ensemble averaging see [97].
Information for each restraint is stored in the energy file and can be processed and plotted with
gmx nmr.
4.4 Polarization
Polarization can be treated by GROMACS by attaching shell (Drude) particles to atoms and/or
virtual sites. The energy of the shell particle is then minimized at each time step in order to remain
on the Born-Oppenheimer surface.
4.4.1 Simple polarization
This is implemented as a harmonic potential with equilibrium distance 0. The input given in the
topology file is the polarizability α(in GROMACS units) as follows:
[ polarization ]
; Atom i j type alpha
1 2 1 0.001
in this case the polarizability volume is 0.001 nm3(or 1 Å3). In order to compute the harmonic
force constant kcs (where cs stands for core-shell), the following is used [45]:
kcs =q2
s
α(4.111)
where qsis the charge on the shell particle.
4.4.2 Anharmonic polarization
For the development of the Drude force field by Roux and McKerell [98] it was found that some
particles can overpolarize and this was fixed by introducing a higher order term in the polarization
energy:
Vpol =kcs
2r2
cs rcs ≤δ(4.112)
=kcs
2r2
cs +khyp(rcs −δ)4rcs > δ (4.113)
where δis a user-defined constant that is set to 0.02 nm for anions in the Drude force field [99].
Since this original introduction it has also been used in other atom types [98].
[ polarization ]
;Atom i j type alpha (nm^3) delta khyp
1 2 2 0.001786 0.02 16.736e8
The above force constant khyp corresponds to 4·108kcal/mol/nm4, hence the strange number.

4.5. Free energy interactions 97
4.4.3 Water polarization
A special potential for water that allows anisotropic polarization of a single shell particle [45].
4.4.4 Thole polarization
Based on early work by Thole [100], Roux and coworkers have implemented potentials for molecules
like ethanol [101,102,103]. Within such molecules, there are intra-molecular interactions be-
tween shell particles, however these must be screened because full Coulomb would be too strong.
The potential between two shell particles iand jis:
Vthole =qiqj
rij 1−1 + ¯rij
2exp−¯rij (4.114)
Note that there is a sign error in Equation 1 of Noskov et al. [103]:
¯rij =arij
(αiαj)1/6(4.115)
where ais a magic (dimensionless) constant, usually chosen to be 2.6 [103]; αiand αjare the
polarizabilities of the respective shell particles.
4.5 Free energy interactions
This section describes the λ-dependence of the potentials used for free energy calculations (see
sec. 3.12). All common types of potentials and constraints can be interpolated smoothly from state
A (λ= 0) to state B (λ= 1) and vice versa. All bonded interactions are interpolated by linear
interpolation of the interaction parameters. Non-bonded interactions can be interpolated linearly
or via soft-core interactions.
Starting in GROMACS 4.6, λis a vector, allowing different components of the free energy trans-
formation to be carried out at different rates. Coulomb, Lennard-Jones, bonded, and restraint terms
can all be controlled independently, as described in the .mdp options.
Harmonic potentials
The example given here is for the bond potential, which is harmonic in GROMACS. However,
these equations apply to the angle potential and the improper dihedral potential as well.
Vb=1
2h(1 −λ)kA
b+λkB
bihb−(1 −λ)bA
0−λbB
0i2(4.116)
∂Vb
∂λ =1
2(kB
b−kA
b)hb−(1 −λ)bA
0+λbB
0i2+
(bA
0−bB
0)hb−(1 −λ)bA
0−λbB
0ih(1 −λ)kA
b+λkB
bi(4.117)
98 Chapter 4. Interaction function and force fields
GROMOS-96 bonds and angles
Fourth-power bond stretching and cosine-based angle potentials are interpolated by linear interpo-
lation of the force constant and the equilibrium position. Formulas are not given here.
Proper dihedrals
For the proper dihedrals, the equations are somewhat more complicated:
Vd=h(1 −λ)kA
d+λkB
di1 + cos hnφφ−(1 −λ)φA
s−λφB
si (4.118)
∂Vd
∂λ = (kB
d−kA
d)1 + cos hnφφ−(1 −λ)φA
s−λφB
si+
(φB
s−φA
s)h(1 −λ)kA
d−λkB
disin hnφφ−(1 −λ)φA
s−λφB
si(4.119)
Note: that the multiplicity nφcan not be parameterized because the function should remain peri-
odic on the interval [0,2π].
Tabulated bonded interactions
For tabulated bonded interactions only the force constant can interpolated:
V= ((1 −λ)kA+λkB)f(4.120)
∂V
∂λ = (kB−kA)f(4.121)
Coulomb interaction
The Coulomb interaction between two particles of which the charge varies with λis:
Vc=f
εrf rij h(1 −λ)qA
iqA
j+λ qB
iqB
ji(4.122)
∂Vc
∂λ =f
εrf rij h−qA
iqA
j+qB
iqB
ji(4.123)
where f=1
4πε0= 138.935 458 (see chapter 2).
Coulomb interaction with reaction field
The Coulomb interaction including a reaction field, between two particles of which the charge
varies with λis:
Vc=f"1
rij
+krf r2
ij −crf #h(1 −λ)qA
iqA
j+λ qB
iqB
ji(4.124)
∂Vc
∂λ =f"1
rij
+krf r2
ij −crf #h−qA
iqA
j+qB
iqB
ji(4.125)
Note that the constants krf and crf are defined using the dielectric constant εrf of the medium
(see sec. 4.1.4).

4.5. Free energy interactions 99
Lennard-Jones interaction
For the Lennard-Jones interaction between two particles of which the atom type varies with λwe
can write:
VLJ =(1 −λ)CA
12 +λ CB
12
r12
ij −(1 −λ)CA
6+λ CB
6
r6
ij
(4.126)
∂VLJ
∂λ =CB
12 −CA
12
r12
ij −CB
6−CA
6
r6
ij
(4.127)
It should be noted that it is also possible to express a pathway from state A to state B using σand
(see eqn. 4.5). It may seem to make sense physically to vary the force field parameters σand
rather than the derived parameters C12 and C6. However, the difference between the pathways in
parameter space is not large, and the free energy itself does not depend on the pathway, so we use
the simple formulation presented above.
Kinetic Energy
When the mass of a particle changes, there is also a contribution of the kinetic energy to the free
energy (note that we can not write the momentum pas mv, since that would result in the sign of
∂Ek
∂λ being incorrect [104]):
Ek=1
2
p2
(1 −λ)mA+λmB(4.128)
∂Ek
∂λ =−1
2
p2(mB−mA)
((1 −λ)mA+λmB)2(4.129)
after taking the derivative, we can insert p= mv, such that:
∂Ek
∂λ =−1
2v2(mB−mA)(4.130)
Constraints
The constraints are formally part of the Hamiltonian, and therefore they give a contribution to the
free energy. In GROMACS this can be calculated using the LINCS or the SHAKE algorithm. If
we have k= 1 . . . K constraint equations gkfor LINCS, then
gk=|rk| − dk(4.131)
where rkis the displacement vector between two particles and dkis the constraint distance be-
tween the two particles. We can express the fact that the constraint distance has a λdependency
by
dk= (1 −λ)dA
k+λdB
k(4.132)
Thus the λ-dependent constraint equation is
gk=|rk| − (1 −λ)dA
k+λdB
k.(4.133)
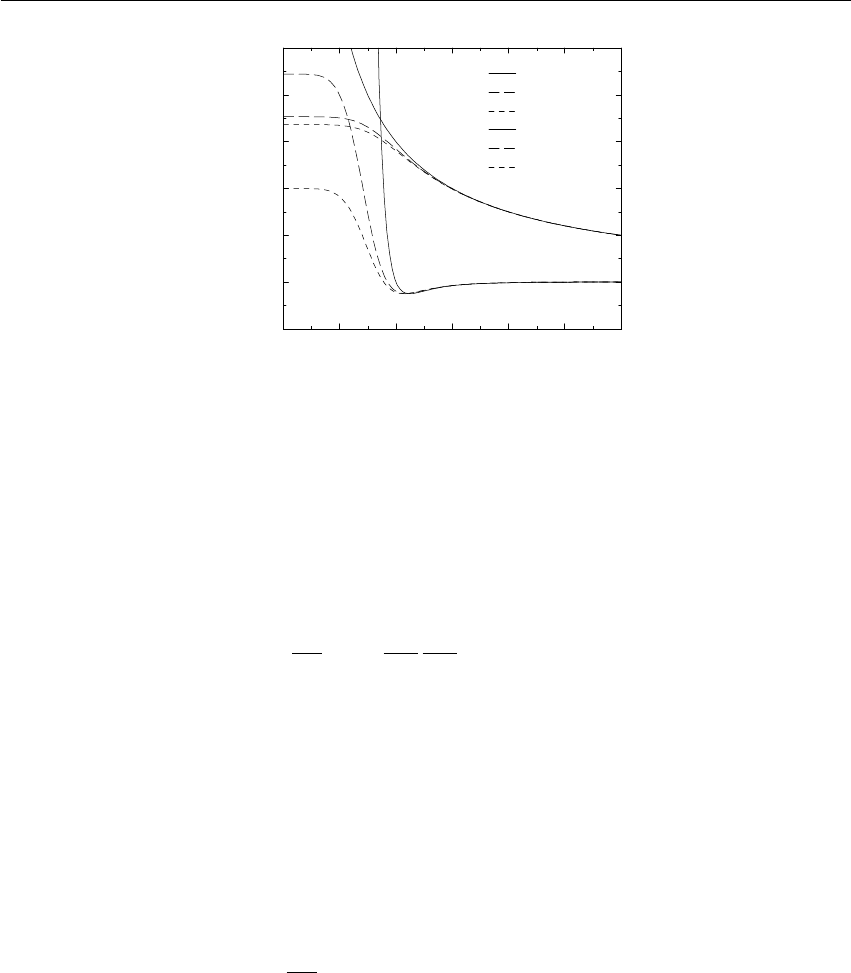
100 Chapter 4. Interaction function and force fields
0 0.5 1 1.5 2 2.5 3
r
−1
0
1
2
3
4
5
Vsc
LJ, α=0
LJ, α=1.5
LJ, α=2
3/r, α=0
3/r, α=1.5
3/r, α=2
Figure 4.16: Soft-core interactions at λ= 0.5, with p= 2 and CA
6=CA
12 =CB
6=CB
12 = 1.
The (zero) contribution Gto the Hamiltonian from the constraints (using Lagrange multipliers λk,
which are logically distinct from the free-energy λ) is
G=
K
X
k
λkgk(4.134)
∂G
∂λ =∂G
∂dk
∂dk
∂λ (4.135)
=−
K
X
k
λkdB
k−dA
k(4.136)
For SHAKE, the constraint equations are
gk=r2
k−d2
k(4.137)
with dkas before, so
∂G
∂λ =−2
K
X
k
λkdB
k−dA
k(4.138)
4.5.1 Soft-core interactions
In a free-energy calculation where particles grow out of nothing, or particles disappear, using the
the simple linear interpolation of the Lennard-Jones and Coulomb potentials as described in Equa-
tions 4.127 and 4.125 may lead to poor convergence. When the particles have nearly disappeared,
or are close to appearing (at λclose to 0 or 1), the interaction energy will be weak enough for
particles to get very close to each other, leading to large fluctuations in the measured values of
∂V/∂λ (which, because of the simple linear interpolation, depends on the potentials at both the
endpoints of λ).

4.5. Free energy interactions 101
To circumvent these problems, the singularities in the potentials need to be removed. This can be
done by modifying the regular Lennard-Jones and Coulomb potentials with “soft-core” potentials
that limit the energies and forces involved at λvalues between 0 and 1, but not at λ= 0 or 1.
In GROMACS the soft-core potentials Vsc are shifted versions of the regular potentials, so that the
singularity in the potential and its derivatives at r= 0 is never reached:
Vsc(r) = (1 −λ)VA(rA) + λV B(rB)(4.139)
rA=ασ6
Aλp+r61
6(4.140)
rB=ασ6
B(1 −λ)p+r61
6(4.141)
where VAand VBare the normal “hard core” Van der Waals or electrostatic potentials in state A
(λ= 0) and state B (λ= 1) respectively, αis the soft-core parameter (set with sc_alpha in
the .mdp file), pis the soft-core λpower (set with sc_power), σis the radius of the interaction,
which is (C12/C6)1/6or an input parameter (sc_sigma) when C6or C12 is zero.
For intermediate λ,rAand rBalter the interactions very little for r > α1/6σand quickly switch
the soft-core interaction to an almost constant value for smaller r(Fig. 4.16). The force is:
Fsc(r) = −∂Vsc(r)
∂r = (1 −λ)FA(rA)r
rA5
+λF B(rB)r
rB5(4.142)
where FAand FBare the “hard core” forces. The contribution to the derivative of the free energy
is:
∂Vsc(r)
∂λ =VB(rB)−VA(rA) + (1 −λ)∂V A(rA)
∂rA
∂rA
∂λ +λ∂V B(rB)
∂rB
∂rB
∂λ
=VB(rB)−VA(rA) +
pα
6hλF B(rB)r−5
Bσ6
B(1 −λ)p−1−(1 −λ)FA(rA)r−5
Aσ6
Aλp−1i(4.143)
The original GROMOS Lennard-Jones soft-core function [105] uses p= 2, but p= 1 gives a
smoother ∂H/∂λ curve.
Another issue that should be considered is the soft-core effect of hydrogens without Lennard-Jones
interaction. Their soft-core σis set with sc-sigma in the .mdp file. These hydrogens produce
peaks in ∂H/∂λ at λis 0 and/or 1 for p= 1 and close to 0 and/or 1 with p= 2. Lowering
sc-sigma will decrease this effect, but it will also increase the interactions with hydrogens
relative to the other interactions in the soft-core state.
When soft-core potentials are selected (by setting sc-alpha >0), and the Coulomb and Lennard-
Jones potentials are turned on or off sequentially, then the Coulombic interaction is turned off
linearly, rather than using soft-core interactions, which should be less statistically noisy in most
cases. This behavior can be overwritten by using the mdp option sc-coul to yes. Note that the
sc-coul is only taken into account when lambda states are used, not with couple-lambda0 /
couple-lambda1, and you can still turn off soft-core interactions by setting sc-alpha=0.
Additionally, the soft-core interaction potential is only applied when either the A or B state has
zero interaction potential. If both A and B states have nonzero interaction potential, default linear
scaling described above is used. When both Coulombic and Lennard-Jones interactions are turned
102 Chapter 4. Interaction function and force fields
i+1 i+3
i i+2 i+4
Figure 4.17: Atoms along an alkane chain.
off simultaneously, a soft-core potential is used, and a hydrogen is being introduced or deleted,
the sigma is set to sc-sigma-min, which itself defaults to sc-sigma-default.
Recently, a new formulation of the soft-core approach has been derived that in most cases gives
lower and more even statistical variance than the standard soft-core path described above. [106,
107] Specifically, we have:
Vsc(r) = (1 −λ)VA(rA) + λV B(rB)(4.144)
rA=ασ48
Aλp+r481
48 (4.145)
rB=ασ48
B(1 −λ)p+r481
48 (4.146)
This “1-1-48” path is also implemented in GROMACS. Note that for this path the soft core α
should satisfy 0.001 < α < 0.003, rather than α≈0.5.
4.6 Methods
4.6.1 Exclusions and 1-4 Interactions.
Atoms within a molecule that are close by in the chain, i.e. atoms that are covalently bonded,
or linked by one or two atoms are called first neighbors, second neighbors and third neighbors,
respectively (see Fig. 4.17). Since the interactions of atom iwith atoms i+1 and i+2 are mainly
quantum mechanical, they can not be modeled by a Lennard-Jones potential. Instead it is assumed
that these interactions are adequately modeled by a harmonic bond term or constraint (i, i+1) and
a harmonic angle term (i, i+2). The first and second neighbors (atoms i+1 and i+2) are therefore
excluded from the Lennard-Jones interaction list of atom i; atoms i+1 and i+2 are called exclusions
of atom i.
For third neighbors, the normal Lennard-Jones repulsion is sometimes still too strong, which
means that when applied to a molecule, the molecule would deform or break due to the internal
strain. This is especially the case for carbon-carbon interactions in a cis-conformation (e.g. cis-
butane). Therefore, for some of these interactions, the Lennard-Jones repulsion has been reduced
in the GROMOS force field, which is implemented by keeping a separate list of 1-4 and nor-
mal Lennard-Jones parameters. In other force fields, such as OPLS [108], the standard Lennard-
Jones parameters are reduced by a factor of two, but in that case also the dispersion (r−6) and the
Coulomb interaction are scaled. GROMACS can use either of these methods.

4.6. Methods 103
4.6.2 Charge Groups
In principle, the force calculation in MD is an O(N2)problem. Therefore, we apply a cut-off for
non-bonded force (NBF) calculations; only the particles within a certain distance of each other
are interacting. This reduces the cost to O(N)(typically 100Nto 200N) of the NBF. It also
introduces an error, which is, in most cases, acceptable, except when applying the cut-off implies
the creation of charges, in which case you should consider using the lattice sum methods provided
by GROMACS.
Consider a water molecule interacting with another atom. If we would apply a plain cut-off on an
atom-atom basis we might include the atom-oxygen interaction (with a charge of −0.82) without
the compensating charge of the protons, and as a result, induce a large dipole moment over the
system. Therefore, we have to keep groups of atoms with total charge 0 together. These groups are
called charge groups. Note that with a proper treatment of long-range electrostatics (e.g. particle-
mesh Ewald (sec. 4.8.2), keeping charge groups together is not required.
4.6.3 Treatment of Cut-offs in the group scheme
GROMACS is quite flexible in treating cut-offs, which implies there can be quite a number of
parameters to set. These parameters are set in the input file for grompp. There are two sort of
parameters that affect the cut-off interactions; you can select which type of interaction to use in
each case, and which cut-offs should be used in the neighbor searching.
For both Coulomb and van der Waals interactions there are interaction type selectors (termed
vdwtype and coulombtype) and two parameters, for a total of six non-bonded interaction
parameters. See the User Guide for a complete description of these parameters.
In the group cut-off scheme, all of the interaction functions in Table 4.2 require that neighbor
searching be done with a radius at least as large as the rcspecified for the functional form, because
of the use of charge groups. The extra radius is typically of the order of 0.25 nm (roughly the
largest distance between two atoms in a charge group plus the distance a charge group can diffuse
within neighbor list updates).
Type Parameters
Coulomb Plain cut-off rc,εr
Reaction field rc,εrf
Shift function r1,rc,εr
Switch function r1,rc,εr
VdW Plain cut-off rc
Shift function r1,rc
Switch function r1,rc
Table 4.2: Parameters for the different functional forms of the non-bonded interactions.

104 Chapter 4. Interaction function and force fields
| |
3fd
| |
| |
1-a a
b
a
1-a
a
2 3fad 3out 4fdn
c
b
3
θ
d
Figure 4.18: The six different types of virtual site construction in GROMACS. The constructing
atoms are shown as black circles, the virtual sites in gray.
4.7 Virtual interaction sites
Virtual interaction sites (called dummy atoms in GROMACS versions before 3.3) can be used in
GROMACS in a number of ways. We write the position of the virtual site rsas a function of the
positions of other particles ri:rs=f(r1..rn). The virtual site, which may carry charge or be
involved in other interactions, can now be used in the force calculation. The force acting on the
virtual site must be redistributed over the particles with mass in a consistent way. A good way to
do this can be found in ref. [109]. We can write the potential energy as:
V=V(rs,r1,...,rn) = V∗(r1,...,rn)(4.147)
The force on the particle iis then:
Fi=−∂V ∗
∂ri
=−∂V
∂ri−∂V
∂rs
∂rs
∂ri
=Fdirect
i+F0
i(4.148)
The first term is the normal force. The second term is the force on particle idue to the virtual site,
which can be written in tensor notation:
F0
i=
∂xs
∂xi
∂ys
∂xi
∂zs
∂xi
∂xs
∂yi
∂ys
∂yi
∂zs
∂yi
∂xs
∂zi
∂ys
∂zi
∂zs
∂zi
Fs(4.149)
where Fsis the force on the virtual site and xs,ysand zsare the coordinates of the virtual site. In
this way, the total force and the total torque are conserved [109].
The computation of the virial (eqn. 3.24) is non-trivial when virtual sites are used. Since the virial
involves a summation over all the atoms (rather than virtual sites), the forces must be redistributed
from the virtual sites to the atoms (using eqn. 4.149)before computation of the virial. In some
special cases where the forces on the atoms can be written as a linear combination of the forces on
the virtual sites (types 2 and 3 below) there is no difference between computing the virial before
and after the redistribution of forces. However, in the general case redistribution should be done
first.
There are six ways to construct virtual sites from surrounding atoms in GROMACS, which we
classify by the number of constructing atoms. Note that all site types mentioned can be constructed

4.7. Virtual interaction sites 105
from types 3fd (normalized, in-plane) and 3out (non-normalized, out of plane). However, the
amount of computation involved increases sharply along this list, so we strongly recommended
using the first adequate virtual site type that will be sufficient for a certain purpose. Fig. 4.18
depicts 6 of the available virtual site constructions. The conceptually simplest construction types
are linear combinations:
rs=
N
X
i=1
wiri(4.150)
The force is then redistributed using the same weights:
F0
i=wiFs(4.151)
The types of virtual sites supported in GROMACS are given in the list below. Constructing atoms
in virtual sites can be virtual sites themselves, but only if they are higher in the list, i.e. virtual
sites can be constructed from “particles” that are simpler virtual sites.
2. As a linear combination of two atoms (Fig. 4.18 2):
wi= 1 −a , wj=a(4.152)
In this case the virtual site is on the line through atoms iand j.
3. As a linear combination of three atoms (Fig. 4.18 3):
wi= 1 −a−b , wj=a , wk=b(4.153)
In this case the virtual site is in the plane of the other three particles.
3fd. In the plane of three atoms, with a fixed distance (Fig. 4.18 3fd):
rs=ri+brij +arjk
|rij +arjk|(4.154)
In this case the virtual site is in the plane of the other three particles at a distance of |b|from
i. The force on particles i,jand kdue to the force on the virtual site can be computed as:
F0
i=Fs−γ(Fs−p)
F0
j= (1 −a)γ(Fs−p)
F0
k=aγ(Fs−p)
where
γ=b
|rij +arjk|
p=ris ·Fs
ris ·ris
ris
(4.155)
3fad. In the plane of three atoms, with a fixed angle and distance (Fig. 4.18 3fad):
rs=ri+dcos θrij
|rij|+dsin θr⊥
|r⊥|where r⊥=rjk −rij ·rjk
rij ·rij
rij (4.156)
In this case the virtual site is in the plane of the other three particles at a distance of |d|from
iat an angle of αwith rij. Atom kdefines the plane and the direction of the angle. Note
that in this case band αmust be specified, instead of aand b(see also sec. 5.2.2). The force

106 Chapter 4. Interaction function and force fields
on particles i,jand kdue to the force on the virtual site can be computed as (with r⊥as
defined in eqn. 4.156):
F0
i=Fs−dcos θ
|rij|F1+dsin θ
|r⊥| rij ·rjk
rij ·rij
F2+F3!
F0
j=dcos θ
|rij|F1−dsin θ
|r⊥| F2+rij ·rjk
rij ·rij
F2+F3!
F0
k=dsin θ
|r⊥|F2
where F1=Fs−rij ·Fs
rij ·rij
rij ,F2=F1−r⊥·Fs
r⊥·r⊥
r⊥and F3=rij ·Fs
rij ·rij
r⊥
(4.157)
3out. As a non-linear combination of three atoms, out of plane (Fig. 4.18 3out):
rs=ri+arij +brik +c(rij ×rik)(4.158)
This enables the construction of virtual sites out of the plane of the other atoms. The force
on particles i, j and kdue to the force on the virtual site can be computed as:
F0
j=
a−c zik c yik
c zik a−c xik
−c yik c xik a
Fs
F0
k=
b c zij −c yij
−c zij b c xij
c yij −c xij b
Fs
F0
i=Fs−F0
j−F0
k
(4.159)
4fdn. From four atoms, with a fixed distance, see separate Fig. 4.19. This construction is a bit
complex, in particular since the previous type (4fd) could be unstable which forced us to
introduce a more elaborate construction:
rja =arik −rij =a(xk−xi)−(xj−xi)
rjb =bril −rij =b(xl−xi)−(xj−xi)
rm=rja ×rjb
xs=xi+crm
|rm|(4.160)
In this case the virtual site is at a distance of |c|from i, while aand bare parameters. Note
that the vectors rik and rij are not normalized to save floating-point operations. The force
on particles i,j,kand ldue to the force on the virtual site are computed through chain rule
derivatives of the construction expression. This is exact and conserves energy, but it does
4.8. Long Range Electrostatics 107
x
x
x
x
i
j
k
l
s
x
r
ja
jb
r
Figure 4.19: The new 4fdn virtual site construction, which is stable even when all constructing
atoms are in the same plane.
lead to relatively lengthy expressions that we do not include here (over 200 floating-point
operations). The interested reader can look at the source code in vsite.c. Fortunately,
this vsite type is normally only used for chiral centers such as Cαatoms in proteins.
The new 4fdn construct is identified with a ‘type’ value of 2 in the topology. The earlier
4fd type is still supported internally (‘type’ value 1), but it should not be used for new
simulations. All current GROMACS tools will automatically generate type 4fdn instead.
N. A linear combination of Natoms with relative weights ai. The weight for atom iis:
wi=ai
N
X
j=1
aj
−1
(4.161)
There are three options for setting the weights:
COG center of geometry: equal weights
COM center of mass: aiis the mass of atom i; when in free-energy simulations the mass of
the atom is changed, only the mass of the A-state is used for the weight
COW center of weights: aiis defined by the user
4.8 Long Range Electrostatics
4.8.1 Ewald summation
The total electrostatic energy of Nparticles and their periodic images is given by
V=f
2X
nxX
nyX
nz∗
N
X
i
N
X
j
qiqj
rij,n
.(4.162)
108 Chapter 4. Interaction function and force fields
(nx, ny, nz) = nis the box index vector, and the star indicates that terms with i=jshould be
omitted when (nx, ny, nz) = (0,0,0). The distance rij,nis the real distance between the charges
and not the minimum-image. This sum is conditionally convergent, but very slow.
Ewald summation was first introduced as a method to calculate long-range interactions of the peri-
odic images in crystals [110]. The idea is to convert the single slowly-converging sum eqn. 4.162
into two quickly-converging terms and a constant term:
V=Vdir +Vrec +V0(4.163)
Vdir =f
2
N
X
i,j X
nxX
nyX
nz∗
qiqj
erfc(βrij,n)
rij,n
(4.164)
Vrec =f
2πV
N
X
i,j
qiqjX
mxX
myX
mz∗
exp −(πm/β)2+ 2πim·(ri−rj)
m2(4.165)
V0=−fβ
√π
N
X
i
q2
i,(4.166)
where βis a parameter that determines the relative weight of the direct and reciprocal sums and
m= (mx, my, mz). In this way we can use a short cut-off (of the order of 1nm) in the direct
space sum and a short cut-off in the reciprocal space sum (e.g. 10 wave vectors in each direction).
Unfortunately, the computational cost of the reciprocal part of the sum increases as N2(or N3/2
with a slightly better algorithm) and it is therefore not realistic for use in large systems.
Using Ewald
Don’t use Ewald unless you are absolutely sure this is what you want - for almost all cases the PME
method below will perform much better. If you still want to employ classical Ewald summation
enter this in your .mdp file, if the side of your box is about 3nm:
coulombtype = Ewald
rvdw = 0.9
rlist = 0.9
rcoulomb = 0.9
fourierspacing = 0.6
ewald-rtol = 1e-5
The ratio of the box dimensions and the fourierspacing parameter determines the highest
magnitude of wave vectors mx, my, mzto use in each direction. With a 3-nm cubic box this ex-
ample would use 11 wave vectors (from −5to 5) in each direction. The ewald-rtol parameter
is the relative strength of the electrostatic interaction at the cut-off. Decreasing this gives you a
more accurate direct sum, but a less accurate reciprocal sum.
4.8.2 PME
Particle-mesh Ewald is a method proposed by Tom Darden [14] to improve the performance of
the reciprocal sum. Instead of directly summing wave vectors, the charges are assigned to a grid

4.8. Long Range Electrostatics 109
using interpolation. The implementation in GROMACS uses cardinal B-spline interpolation [15],
which is referred to as smooth PME (SPME). The grid is then Fourier transformed with a 3D FFT
algorithm and the reciprocal energy term obtained by a single sum over the grid in k-space.
The potential at the grid points is calculated by inverse transformation, and by using the interpo-
lation factors we get the forces on each atom.
The PME algorithm scales as Nlog(N), and is substantially faster than ordinary Ewald summa-
tion on medium to large systems. On very small systems it might still be better to use Ewald
to avoid the overhead in setting up grids and transforms. For the parallelization of PME see the
section on MPMD PME (3.17.5).
With the Verlet cut-off scheme, the PME direct space potential is shifted by a constant such that
the potential is zero at the cut-off. This shift is small and since the net system charge is close to
zero, the total shift is very small, unlike in the case of the Lennard-Jones potential where all shifts
add up. We apply the shift anyhow, such that the potential is the exact integral of the force.
Using PME
As an example for using Particle-mesh Ewald summation in GROMACS, specify the following
lines in your .mdp file:
coulombtype = PME
rvdw = 0.9
rlist = 0.9
rcoulomb = 0.9
fourierspacing = 0.12
pme-order = 4
ewald-rtol = 1e-5
In this case the fourierspacing parameter determines the maximum spacing for the FFT grid
(i.e. minimum number of grid points), and pme-order controls the interpolation order. Using
fourth-order (cubic) interpolation and this spacing should give electrostatic energies accurate to
about 5·10−3. Since the Lennard-Jones energies are not this accurate it might even be possible to
increase this spacing slightly.
Pressure scaling works with PME, but be aware of the fact that anisotropic scaling can introduce
artificial ordering in some systems.
4.8.3 P3M-AD
The Particle-Particle Particle-Mesh methods of Hockney & Eastwood can also be applied in GRO-
MACS for the treatment of long range electrostatic interactions [111]. Although the P3M method
was the first efficient long-range electrostatics method for molecular simulation, the smooth PME
(SPME) method has largely replaced P3M as the method of choice in atomistic simulations. One
performance disadvantage of the original P3M method was that it required 3 3D-FFT back trans-
forms to obtain the forces on the particles. But this is not required for P3M and the forces can be

110 Chapter 4. Interaction function and force fields
derived through analytical differentiation of the potential, as done in PME. The resulting method is
termed P3M-AD. The only remaining difference between P3M-AD and PME is the optimization
of the lattice Green influence function for error minimization that P3M uses. However, in 2012
it has been shown that the SPME influence function can be modified to obtain P3M [112]. This
means that the advantage of error minimization in P3M-AD can be used at the same computational
cost and with the same code as PME, just by adding a few lines to modify the influence function.
However, at optimal parameter setting the effect of error minimization in P3M-AD is less than
10%. P3M-AD does show large accuracy gains with interlaced (also known as staggered) grids,
but that is not supported in GROMACS (yet).
P3M is used in GROMACS with exactly the same options as used with PME by selecting the
electrostatics type:
coulombtype = P3M-AD
4.8.4 Optimizing Fourier transforms and PME calculations
It is recommended to optimize the parameters for calculation of electrostatic interaction such as
PME grid dimensions and cut-off radii. This is particularly relevant to do before launching long
production runs.
gmx mdrun will automatically do a lot of PME optimization, and GROMACS also includes a
special tool, gmx tune_pme, which automates the process of selecting the optimal number of
PME-only ranks.
4.9 Long Range Van der Waals interactions
4.9.1 Dispersion correction
In this section, we derive long-range corrections due to the use of a cut-off for Lennard-Jones
or Buckingham interactions. We assume that the cut-off is so long that the repulsion term can
safely be neglected, and therefore only the dispersion term is taken into account. Due to the
nature of the dispersion interaction (we are truncating a potential proportional to −r−6), energy
and pressure corrections are both negative. While the energy correction is usually small, it may be
important for free energy calculations where differences between two different Hamiltonians are
considered. In contrast, the pressure correction is very large and can not be neglected under any
circumstances where a correct pressure is required, especially for any NPT simulations. Although
it is, in principle, possible to parameterize a force field such that the pressure is close to the desired
experimental value without correction, such a method makes the parameterization dependent on
the cut-off and is therefore undesirable.
Energy
The long-range contribution of the dispersion interaction to the virial can be derived analytically, if
we assume a homogeneous system beyond the cut-off distance rc. The dispersion energy between

4.9. Long Range Van der Waals interactions 111
two particles is written as:
V(rij) = −C6r−6
ij (4.167)
and the corresponding force is:
Fij =−6C6r−8
ij rij (4.168)
In a periodic system it is not easy to calculate the full potentials, so usually a cut-off is applied,
which can be abrupt or smooth. We will call the potential and force with cut-off Vcand Fc. The
long-range contribution to the dispersion energy in a system with Nparticles and particle density
ρ=N/V is:
Vlr =1
2Nρ Z∞
0
4πr2g(r) (V(r)−Vc(r)) dr(4.169)
We will integrate this for the shift function, which is the most general form of van der Waals
interaction available in GROMACS. The shift function has a constant difference Sfrom 0 to r1
and is 0 beyond the cut-off distance rc. We can integrate eqn. 4.169, assuming that the density
in the sphere within r1is equal to the global density and the radial distribution function g(r)is 1
beyond r1:
Vlr =1
2NρZr1
0
4πr2g(r)C6Sdr+ρZrc
r1
4πr2(V(r)−Vc(r)) dr+ρZ∞
rc
4πr2V(r) dr
=1
2N4
3πρr3
1−1C6S+ρZrc
r1
4πr2(V(r)−Vc(r)) dr−4
3πNρ C6r−3
c(4.170)
where the term −1corrects for the self-interaction. For a plain cut-off we only need to assume
that g(r)is 1 beyond rcand the correction reduces to [113]:
Vlr =−2
3πNρ C6r−3
c(4.171)
If we consider, for example, a box of pure water, simulated with a cut-off of 0.9 nm and a density
of 1 g cm−3this correction is −0.75 kJ mol−1per molecule.
For a homogeneous mixture we need to define an average dispersion constant:
hC6i=2
N(N−1)
N
X
i
N
X
j>i
C6(i, j)(4.172)
In GROMACS, excluded pairs of atoms do not contribute to the average.
In the case of inhomogeneous simulation systems, e.g. a system with a lipid interface, the energy
correction can be applied if hC6ifor both components is comparable.
Virial and pressure
The scalar virial of the system due to the dispersion interaction between two particles iand jis
given by:
Ξ = −1
2rij ·Fij = 3 C6r−6
ij (4.173)
The pressure is given by:
P=2
3V(Ekin −Ξ) (4.174)

112 Chapter 4. Interaction function and force fields
The long-range correction to the virial is given by:
Ξlr =1
2Nρ Z∞
0
4πr2g(r)(Ξ −Ξc) dr(4.175)
We can again integrate the long-range contribution to the virial assuming g(r)is 1 beyond r1:
Ξlr =1
2Nρ Zrc
r1
4πr2(Ξ −Ξc) dr+Z∞
rc
4πr23C6r−6
ij dr
=1
2Nρ Zrc
r1
4πr2(Ξ −Ξc) dr+ 4πC6r−3
c(4.176)
For a plain cut-off the correction to the pressure is [113]:
Plr =−4
3πC6ρ2r−3
c(4.177)
Using the same example of a water box, the correction to the virial is 0.75 kJ mol−1per molecule,
the corresponding correction to the pressure for SPC water is approximately −280 bar.
For homogeneous mixtures, we can again use the average dispersion constant hC6i(eqn. 4.172):
Plr =−4
3πhC6iρ2r−3
c(4.178)
For inhomogeneous systems, eqn. 4.178 can be applied under the same restriction as holds for the
energy (see sec. 4.9.1).
4.9.2 Lennard-Jones PME
In order to treat systems, using Lennard-Jones potentials, that are non-homogeneous outside of the
cut-off distance, we can instead use the Particle-mesh Ewald method as discussed for electrostatics
above. In this case the modified Ewald equations become
V=Vdir +Vrec +V0(4.179)
Vdir =−1
2
N
X
i,j X
nxX
nyX
nz∗
Cij
6g(βrij,n)
rij,n6(4.180)
Vrec =π3
2β3
2VX
mxX
myX
mz∗
f(π|m|/β)×
N
X
i,j
Cij
6exp [−2πim·(ri−rj)] (4.181)
V0=−β6
12
N
X
i
Cii
6(4.182)
where m= (mx, my, mz),βis the parameter determining the weight between direct and recipro-
cal space, and Cij
6is the combined dispersion parameter for particle iand j. The star indicates that
terms with i=jshould be omitted when ((nx, ny, nz) = (0,0,0)), and rij,nis the real distance

4.9. Long Range Van der Waals interactions 113
between the particles. Following the derivation by Essmann [15], the functions fand gintroduced
above are defined as
f(x)=1/3h(1 −2x2)exp(−x2)+2x3√πerfc(x)i(4.183)
g(x) = exp(−x2)(1 + x2+x4
2).(4.184)
The above methodology works fine as long as the dispersion parameters can be combined geomet-
rically (eqn. 4.6) in the same way as the charges for electrostatics
Cij
6,geom =Cii
6Cjj
61/2(4.185)
For Lorentz-Berthelot combination rules (eqn. 4.7), the reciprocal part of this sum has to be cal-
culated seven times due to the splitting of the dispersion parameter according to
Cij
6,L−B= (σi+σj)6=
6
X
n=0
Pnσn
iσ(6−n)
j,(4.186)
for Pnthe Pascal triangle coefficients. This introduces a non-negligible cost to the reciprocal part,
requiring seven separate FFTs, and therefore this has been the limiting factor in previous attempts
to implement LJ-PME. A solution to this problem is to use geometrical combination rules in order
to calculate an approximate interaction parameter for the reciprocal part of the potential, yielding
a total interaction of
V(r < rc) = Cdir
6g(βr)r−6
| {z }
Direct space
+Crecip
6,geom[1 −g(βr)]r−6
| {z }
Reciprocal space
=Crecip
6,geomr−6+Cdir
6−Crecip
6,geomg(βr)r−6(4.187)
V(r > rc) = Crecip
6,geom[1 −g(βr)]r−6
|{z }
Reciprocal space
.(4.188)
This will preserve a well-defined Hamiltonian and significantly increase the performance of the
simulations. The approximation does introduce some errors, but since the difference is located in
the interactions calculated in reciprocal space, the effect will be very small compared to the total
interaction energy. In a simulation of a lipid bilayer, using a cut-off of 1.0 nm, the relative error
in total dispersion energy was below 0.5%. A more thorough discussion of this can be found in
[114].
In GROMACS we now perform the proper calculation of this interaction by subtracting, from the
direct-space interactions, the contribution made by the approximate potential that is used in the
reciprocal part
Vdir =Cdir
6r−6−Crecip
6[1 −g(βr)]r−6.(4.189)
This potential will reduce to the expression in eqn. 4.180 when Cdir
6=Crecip
6, and the total
interaction is given by
V(r < rc) = Cdir
6r−6−Crecip
6[1 −g(βr)]r−6
| {z }
Direct space
+Crecip
6[1 −g(βr)]r−6
| {z }
Reciprocal space
=Cdir
6r−6(4.190)
V(r > rc) = Crecip
6[1 −g(βr)]r−6.(4.191)

114 Chapter 4. Interaction function and force fields
For the case when Cdir
66=Crecip
6this will retain an unmodified LJ force up to the cut-off, and
the error is an order of magnitude smaller than in simulations where the direct-space interactions
do not account for the approximation used in reciprocal space. When using a VdW interaction
modifier of potential-shift, the constant
−Cdir
6+Crecip
6[1 −g(βrc)]r−6
c(4.192)
is added to eqn. 4.190 in order to ensure that the potential is continuous at the cutoff. Note
that, in the same way as eqn. 4.189, this degenerates into the expected −C6g(βrc)r−6
cwhen
Cdir
6=Crecip
6. In addition to this, a long-range dispersion correction can be applied to correct for
the approximation using a combination rule in reciprocal space. This correction assumes, as for
the cut-off LJ potential, a uniform particle distribution. But since the error of the combination rule
approximation is very small this long-range correction is not necessary in most cases. Also note
that this homogenous correction does not correct the surface tension, which is an inhomogeneous
property.
Using LJ-PME
As an example for using Particle-mesh Ewald summation for Lennard-Jones interactions in GRO-
MACS, specify the following lines in your .mdp file:
vdwtype = PME
rvdw = 0.9
vdw-modifier = Potential-Shift
rlist = 0.9
rcoulomb = 0.9
fourierspacing = 0.12
pme-order = 4
ewald-rtol-lj = 0.001
lj-pme-comb-rule = geometric
The same Fourier grid and interpolation order are used if both LJ-PME and electrostatic PME are
active, so the settings for fourierspacing and pme-order are common to both. ewald-rtol-lj
controls the splitting between direct and reciprocal space in the same way as ewald-rtol. In ad-
dition to this, the combination rule to be used in reciprocal space is determined by lj-pme-comb-rule.
If the current force field uses Lorentz-Berthelot combination rules, it is possible to set lj-pme-comb-rule
= geometric in order to gain a significant increase in performance for a small loss in accuracy.
The details of this approximation can be found in the section above.
Note that the use of a complete long-range dispersion correction means that as with Coulomb
PME, rvdw is now a free parameter in the method, rather than being necessarily restricted by the
force-field parameterization scheme. Thus it is now possible to optimize the cutoff, spacing, order
and tolerance terms for accuracy and best performance.
Naturally, the use of LJ-PME rather than LJ cut-off adds computation and communication done
for the reciprocal-space part, so for best performance in balancing the load of parallel simulations
using PME-only ranks, more such ranks should be used. It may be possible to improve upon the
automatic load-balancing used by mdrun.

4.10. Force field 115
4.10 Force field
A force field is built up from two distinct components:
•The set of equations (called the potential functions) used to generate the potential energies
and their derivatives, the forces. These are described in detail in the previous chapter.
•The parameters used in this set of equations. These are not given in this manual, but in the
data files corresponding to your GROMACS distribution.
Within one set of equations various sets of parameters can be used. Care must be taken that the
combination of equations and parameters form a consistent set. It is in general dangerous to make
ad hoc changes in a subset of parameters, because the various contributions to the total force are
usually interdependent. This means in principle that every change should be documented, verified
by comparison to experimental data and published in a peer-reviewed journal before it can be used.
GROMACS 2018.3 includes several force fields, and additional ones are available on the website.
If you do not know which one to select we recommend GROMOS-96 for united-atom setups and
OPLS-AA/L for all-atom parameters. That said, we describe the available options in some detail.
All-hydrogen force field
The GROMOS-87-based all-hydrogen force field is almost identical to the normal GROMOS-87
force field, since the extra hydrogens have no Lennard-Jones interaction and zero charge. The
only differences are in the bond angle and improper dihedral angle terms. This force field is only
useful when you need the exact hydrogen positions, for instance for distance restraints derived
from NMR measurements. When citing this force field please read the previous paragraph.
4.10.1 GROMOS-96
GROMACS supports the GROMOS-96 force fields [82]. All parameters for the 43A1, 43A2
(development, improved alkane dihedrals), 45A3, 53A5, and 53A6 parameter sets are included.
All standard building blocks are included and topologies can be built automatically by pdb2gmx.
The GROMOS-96 force field is a further development of the GROMOS-87 force field. It has
improvements over the GROMOS-87 force field for proteins and small molecules. Note that
the sugar parameters present in 53A6 do correspond to those published in 2004[115], which are
different from those present in 45A4, which is not included in GROMACS at this time. The 45A4
parameter set corresponds to a later revision of these parameters. The GROMOS-96 force field is
not, however, recommended for use with long alkanes and lipids. The GROMOS-96 force field
differs from the GROMOS-87 force field in a few respects:
•the force field parameters
•the parameters for the bonded interactions are not linked to atom types
•a fourth power bond stretching potential (4.2.1)

116 Chapter 4. Interaction function and force fields
•an angle potential based on the cosine of the angle (4.2.6)
There are two differences in implementation between GROMACS and GROMOS-96 which can
lead to slightly different results when simulating the same system with both packages:
•in GROMOS-96 neighbor searching for solvents is performed on the first atom of the solvent
molecule. This is not implemented in GROMACS, but the difference with searching by
centers of charge groups is very small
•the virial in GROMOS-96 is molecule-based. This is not implemented in GROMACS,
which uses atomic virials
The GROMOS-96 force field was parameterized with a Lennard-Jones cut-off of 1.4 nm, so be
sure to use a Lennard-Jones cut-off (rvdw) of at least 1.4. A larger cut-off is possible because the
Lennard-Jones potential and forces are almost zero beyond 1.4 nm.
GROMOS-96 files
GROMACS can read and write GROMOS-96 coordinate and trajectory files. These files should
have the extension .g96. Such a file can be a GROMOS-96 initial/final configuration file, a
coordinate trajectory file, or a combination of both. The file is fixed format; all floats are written
as 15.9, and as such, files can get huge. GROMACS supports the following data blocks in the
given order:
•Header block:
TITLE (mandatory)
•Frame blocks:
TIMESTEP (optional)
POSITION/POSITIONRED (mandatory)
VELOCITY/VELOCITYRED (optional)
BOX (optional)
See the GROMOS-96 manual [82] for a complete description of the blocks. Note that all GRO-
MACS programs can read compressed (.Z) or gzipped (.gz) files.
4.10.2 OPLS/AA
4.10.3 AMBER
GROMACS provides native support for the following AMBER force fields:
•AMBER94 [116]

4.10. Force field 117
•AMBER96 [117]
•AMBER99 [118]
•AMBER99SB [119]
•AMBER99SB-ILDN [120]
•AMBER03 [121]
•AMBERGS [122]
4.10.4 CHARMM
GROMACS supports the CHARMM force field for proteins [123,124], lipids [125] and nucleic
acids [126,127]. The protein parameters (and to some extent the lipid and nucleic acid parameters)
were thoroughly tested – both by comparing potential energies between the port and the standard
parameter set in the CHARMM molecular simulation package, as well by how the protein force
field behaves together with GROMACS-specific techniques such as virtual sites (enabling long
time steps) and a fast implicit solvent recently implemented [74] – and the details and results are
presented in the paper by Bjelkmar et al. [128]. The nucleic acid parameters, as well as the ones
for HEME, were converted and tested by Michel Cuendet.
When selecting the CHARMM force field in pdb2gmx the default option is to use CMAP (for
torsional correction map). To exclude CMAP, use -nocmap. The basic form of the CMAP term
implemented in GROMACS is a function of the φand ψbackbone torsion angles. This term is
defined in the .rtp file by a [ cmap ] statement at the end of each residue supporting CMAP.
The following five atom names define the two torsional angles. Atoms 1-4 define φ, and atoms
2-5 define ψ. The corresponding atom types are then matched to the correct CMAP type in the
cmap.itp file that contains the correction maps.
A port of the CHARMM36 force field for use with GROMACS is also available at http://
mackerell.umaryland.edu/charmm_ff.shtml#gromacs.
For branched polymers or other topologies not supported by pdb2gmx, it is possible to use Topo-
Tools [129] to generate a GROMACS top file.
4.10.5 Coarse-grained force fields
Coarse-graining is a systematic way of reducing the number of degrees of freedom representing
a system of interest. To achieve this, typically whole groups of atoms are represented by single
beads and the coarse-grained force fields describes their effective interactions. Depending on the
choice of parameterization, the functional form of such an interaction can be complicated and
often tabulated potentials are used.
Coarse-grained models are designed to reproduce certain properties of a reference system. This
can be either a full atomistic model or even experimental data. Depending on the properties to
reproduce there are different methods to derive such force fields. An incomplete list of methods is
given below:

118 Chapter 4. Interaction function and force fields
•Conserving free energies
–Simplex method
–MARTINI force field (see next section)
•Conserving distributions (like the radial distribution function), so-called structure-based
coarse-graining
–(iterative) Boltzmann inversion
–Inverse Monte Carlo
•Conversing forces
–Force matching
Note that coarse-grained potentials are state dependent (e.g. temperature, density,...) and should
be re-parametrized depending on the system of interest and the simulation conditions. This can
for example be done using the Versatile Object-oriented Toolkit for Coarse-Graining Applications
(VOTCA) [130]. The package was designed to assists in systematic coarse-graining, provides
implementations for most of the algorithms mentioned above and has a well tested interface to
GROMACS. It is available as open source and further information can be found at www.votca.org.
4.10.6 MARTINI
The MARTINI force field is a coarse-grain parameter set that allows for the construction of many
systems, including proteins and membranes.
4.10.7 PLUM
The PLUM force field [131] is an example of a solvent-free protein-membrane model for which
the membrane was derived from structure-based coarse-graining [132]. A GROMACS implemen-
tation can be found at code.google.com/p/plumx.
Chapter 5
Topologies
5.1 Introduction
GROMACS must know on which atoms and combinations of atoms the various contributions to
the potential functions (see chapter 4) must act. It must also know what parameters must be
applied to the various functions. All this is described in the topology file *.top, which lists the
constant attributes of each atom. There are many more atom types than elements, but only atom
types present in biological systems are parameterized in the force field, plus some metals, ions and
silicon. The bonded and special interactions are determined by fixed lists that are included in the
topology file. Certain non-bonded interactions must be excluded (first and second neighbors), as
these are already treated in bonded interactions. In addition, there are dynamic attributes of atoms
- their positions, velocities and forces. These do not strictly belong to the molecular topology,
and are stored in the coordinate file *.gro (positions and velocities), or trajectory file *.trr
(positions, velocities, forces).
This chapter describes the setup of the topology file, the *.top file and the database files: what
the parameters stand for and how/where to change them if needed. First, all file formats are
explained. Section 5.9.1 describes the organization of the files in each force field.
Note: if you construct your own topologies, we encourage you to upload them to our topology
archive at www.gromacs.org! Just imagine how thankful you’d have been if your topology had
been available there before you started. The same goes for new force fields or modified versions
of the standard force fields - contribute them to the force field archive!
5.2 Particle type
In GROMACS, there are three types of particles, see Table 5.1. Only regular atoms and virtual
interaction sites are used in GROMACS; shells are necessary for polarizable models like the Shell-
Water models [45].

120 Chapter 5. Topologies
Particle Symbol
atoms A
shells S
virtual interaction sites V (or D)
Table 5.1: Particle types in GROMACS
5.2.1 Atom types
Each force field defines a set of atom types, which have a characteristic name or number, and mass
(in a.m.u.). These listings are found in the atomtypes.atp file (.atp = atom type parameter
file). Therefore, it is in this file that you can begin to change and/or add an atom type. A sample
from the gromos43a1.ff force field is listed below.
O 15.99940 ; carbonyl oxygen (C=O)
OM 15.99940 ; carboxyl oxygen (CO-)
OA 15.99940 ; hydroxyl, sugar or ester oxygen
OW 15.99940 ; water oxygen
N 14.00670 ; peptide nitrogen (N or NH)
NT 14.00670 ; terminal nitrogen (NH2)
NL 14.00670 ; terminal nitrogen (NH3)
NR 14.00670 ; aromatic nitrogen
NZ 14.00670 ; Arg NH (NH2)
NE 14.00670 ; Arg NE (NH)
C 12.01100 ; bare carbon
CH1 13.01900 ; aliphatic or sugar CH-group
CH2 14.02700 ; aliphatic or sugar CH2-group
CH3 15.03500 ; aliphatic CH3-group
Note: GROMACS makes use of the atom types as a name, not as a number (as e.g. in GROMOS).
5.2.2 Virtual sites
Some force fields use virtual interaction sites (interaction sites that are constructed from other
particle positions) on which certain interactions are located (e.g. on benzene rings, to reproduce
the correct quadrupole). This is described in sec. 4.7.
To make virtual sites in your system, you should include a section [ virtual_sites? ] (for
backward compatibility the old name [ dummies? ] can also be used) in your topology file,
where the ‘?’ stands for the number constructing particles for the virtual site. This will be ‘2’ for
type 2, ‘3’ for types 3, 3fd, 3fad and 3out and ‘4’ for type 4fdn. The last of these replace an older
4fd type (with the ‘type’ value 1) that could occasionally be unstable; while it is still supported
internally in the code, the old 4fd type should not be used in new input files. The different types
are explained in sec. 4.7.
Parameters for type 2 should look like this:
[ virtual_sites2 ]

5.2. Particle type 121
; Site from funct a
5 1 2 1 0.7439756
for type 3 like this:
[ virtual_sites3 ]
; Site from funct a b
5 1 2 3 1 0.7439756 0.128012
for type 3fd like this:
[ virtual_sites3 ]
; Site from funct a d
5 1 2 3 2 0.5 -0.105
for type 3fad like this:
[ virtual_sites3 ]
; Site from funct theta d
5 1 2 3 3 120 0.5
for type 3out like this:
[ virtual_sites3 ]
; Site from funct a b c
5 1 2 3 4 -0.4 -0.4 6.9281
for type 4fdn like this:
[ virtual_sites4 ]
; Site from funct a b c
5 1 2 3 4 2 1.0 0.9 0.105
This will result in the construction of a virtual site, number 5 (first column ‘Site’), based on the
positions of the atoms whose indices are 1 and 2 or 1, 2 and 3 or 1, 2, 3 and 4 (next two, three
or four columns ‘from’) following the rules determined by the function number (next column
‘funct’) with the parameters specified (last one, two or three columns ‘a b . .’). Obviously,
the atom numbers (including virtual site number) depend on the molecule. It may be instructive
to study the topologies for TIP4P or TIP5P water models that are included with the GROMACS
distribution.
Note that if any constant bonded interactions are defined between virtual sites and/or normal
atoms, they will be removed by grompp (unless the option tt -normvsbds is used). This re-
moval of bonded interactions is done after generating exclusions, as the generation of exclusions
is based on “chemically” bonded interactions.
Virtual sites can be constructed in a more generic way using basic geometric parameters. The di-
rective that can be used is [ virtual_sitesn ]. Required parameters are listed in Table 5.5.
An example entry for defining a virtual site at the center of geometry of a given set of atoms might
be:
[ virtual_sitesn ]
; Site funct from
5 1 1 2 3 4

122 Chapter 5. Topologies
Property Symbol Unit
Type - -
Mass m a.m.u.
Charge q electron
epsilon kJ/mol
sigma σnm
Table 5.2: Static atom type properties in GROMACS
5.3 Parameter files
5.3.1 Atoms
The static properties (see Table 5.2 assigned to the atom types are assigned based on data in several
places. The mass is listed in atomtypes.atp (see 5.2.1), whereas the charge is listed in *.rtp
(.rtp = residue topology parameter file, see 5.7.1). This implies that the charges are only defined
in the building blocks of amino acids, nucleic acids or otherwise, as defined by the user. When
generating a topology (*.top) using the pdb2gmx program, the information from these files is
combined.
5.3.2 Non-bonded parameters
The non-bonded parameters consist of the van der Waals parameters V (c6 or σ, depending on the
combination rule) and W (c12 or ), as listed in the file ffnonbonded.itp, where ptype is
the particle type (see Table 5.1). As with the bonded parameters, entries in [*type ] directives
are applied to their counterparts in the topology file. Missing parameters generate warnings, except
as noted below in section 5.4.3.
[ atomtypes ]
;name at.num mass charge ptype V(c6) W(c12)
O 8 15.99940 0.000 A 0.22617E-02 0.74158E-06
OM 8 15.99940 0.000 A 0.22617E-02 0.74158E-06
.....
[ nonbond_params ]
; i j func V(c6) W(c12)
O O 1 0.22617E-02 0.74158E-06
O OA 1 0.22617E-02 0.13807E-05
.....
Note that most of the included force fields also include the at.num. column, but this same in-
formation is implied in the OPLS-AA bond_type column. The interpretation of the parameters
V and W depends on the combination rule that was chosen in the [ defaults ] section of the
topology file (see 5.8.1):
for combination rule 1 :Vii =C(6)
i= 4 iσ6
i[ kJ mol−1nm6]
Wii =C(12)
i= 4 iσ12
i[ kJ mol−1nm12 ](5.1)

5.3. Parameter files 123
for combination rules 2 and 3 :Vii =σi[ nm ]
Wii =i[ kJ mol−1](5.2)
Some or all combinations for different atom types can be given in the [ nonbond_params ]
section, again with parameters V and W as defined above. Any combination that is not given will
be computed from the parameters for the corresponding atom types, according to the combination
rule:
for combination rules 1 and 3 :C(6)
ij =C(6)
iC(6)
j1
2
C(12)
ij =C(12)
iC(12)
j1
2
(5.3)
for combination rule 2 :σij =1
2(σi+σj)
ij =√ij(5.4)
When σand need to be supplied (rules 2 and 3), it would seem it is impossible to have a non-zero
C12 combined with a zero C6parameter. However, providing a negative σwill do exactly that,
such that C6is set to zero and C12 is calculated normally. This situation represents a special case
in reading the value of σ, and nothing more.
There is only one set of combination rules for Buckingham potentials:
Aij = (Aii Ajj )1/2
Bij = 2/1
Bii +1
Bjj
Cij = (Cii Cjj )1/2
(5.5)
5.3.3 Bonded parameters
The bonded parameters (i.e. bonds, bond angles, improper and proper dihedrals) are listed in
ffbonded.itp. The entries in this database describe, respectively, the atom types in the in-
teractions, the type of the interaction, and the parameters associated with that interaction. These
parameters are then read by grompp when processing a topology and applied to the relevant
bonded parameters, i.e. bondtypes are applied to entries in the [ bonds ] directive, etc.
Any bonded parameter that is missing from the relevant [*type ] directive generates a fatal
error. The types of interactions are listed in Table 5.5. Example excerpts from such files follow:
[ bondtypes ]
; i j func b0 kb
C O 1 0.12300 502080.
C OM 1 0.12500 418400.
......
[ angletypes ]
; i j k func th0 cth
HO OA C 1 109.500 397.480
HO OA CH1 1 109.500 397.480
......
[ dihedraltypes ]

124 Chapter 5. Topologies
; i l func q0 cq
NR5*NR5 2 0.000 167.360
NR5*NR5*2 0.000 167.360
......
[ dihedraltypes ]
; j k func phi0 cp mult
C OA 1 180.000 16.736 2
C N 1 180.000 33.472 2
......
[ dihedraltypes ]
;
; Ryckaert-Bellemans Dihedrals
;
; aj ak funct
CP2 CP2 3 9.2789 12.156 -13.120 -3.0597 26.240 -31.495
In the ffbonded.itp file, you can add bonded parameters. If you want to include parameters
for new atom types, make sure you define them in atomtypes.atp as well.
For most interaction types, bonded parameters are searched and assigned using an exact match for
all type names and allowing only a single set of parameters. The exception to this rule are dihedral
parameters. For [ dihedraltypes ] wildcard atom type names can be specified with the
letter Xin one or more of the four positions. Thus one can for example assign proper dihedral
parameters based on the types of the middle two atoms. The parameters for the entry with the
most exact matches, i.e. the least wildcard matches, will be used. Note that GROMACS versions
older than 5.1.3 used the first match, which means that a full match would be ignored if it is
preceded by an entry that matches on wildcards. Thus it is suggested to put wildcard entries at the
end, in case someone might use a forcefield with older versions of GROMACS. In addition there
is a dihedral type 9 which adds the possibility of assigning multiple dihedral potentials, useful
for combining terms with different multiplicities. The different dihedral potential parameter sets
should be on directly adjacent lines in the [ dihedraltypes ] section.
5.4 Molecule definition
5.4.1 Moleculetype entries
An organizational structure that usually corresponds to molecules is the [ moleculetype ]
entry. This entry serves two main purposes. One is to give structure to the topology file(s), usu-
ally corresponding to real molecules. This makes the topology easier to read and writing it less
labor intensive. A second purpose is computational efficiency. The system definition that is kept
in memory is proportional in size of the moleculetype definitions. If a molecule is present
in 100000 copies, this saves a factor of 100000 in memory, which means the system usually fits
in cache, which can improve performance tremendously. Interactions that correspond to chemical
bonds, that generate exclusions, can only be defined between atoms within a moleculetype. It
is allowed to have multiple molecules which are not covalently bonded in one moleculetype

5.4. Molecule definition 125
definition. Molecules can be made infinitely long by connecting to themselves over periodic
boundaries. When such periodic molecules are present, an option in the mdp file needs to be
set to tell GROMACS not to attempt to make molecules that are broken over periodic boundaries
whole again.
5.4.2 Intermolecular interactions
In some cases, one would like atoms in different molecules to also interact with other interac-
tions than the usual non-bonded interactions. This is often the case in binding studies. When
the molecules are covalently bound, e.g. a ligand binding covalently to a protein, they are effec-
tively one molecule and they should be defined in one [ moleculetype ] entry. Note that
pdb2gmx has an option to put two or more molecules in one [ moleculetype ] entry. When
molecules are not covalently bound, it is much more convenient to use separate moleculetype
definitions and specify the intermolecular interactions in the [ intermolecular_interactions]
section. In this section, which is placed at the end of the topology (see Table 5.4), normal bonded
interactions can be specified using global atom indices. The only restrictions are that no interac-
tions can be used that generates exclusions and no constraints can be used.
5.4.3 Intramolecular pair interactions
Extra Lennard-Jones and electrostatic interactions between pairs of atoms in a molecule can be
added in the [ pairs ] section of a molecule definition. The parameters for these interactions
can be set independently from the non-bonded interaction parameters. In the GROMOS force
fields, pairs are only used to modify the 1-4 interactions (interactions of atoms separated by three
bonds). In these force fields the 1-4 interactions are excluded from the non-bonded interactions
(see sec. 5.4.4).
[ pairtypes ]
; i j func cs6 cs12 ; THESE ARE 1-4 INTERACTIONS
O O 1 0.22617E-02 0.74158E-06
O OM 1 0.22617E-02 0.74158E-06
.....
The pair interaction parameters for the atom types in ffnonbonded.itp are listed in the
[ pairtypes ] section. The GROMOS force fields list all these interaction parameters explic-
itly, but this section might be empty for force fields like OPLS that calculate the 1-4 interactions by
uniformly scaling the parameters. Pair parameters that are not present in the [ pairtypes ]
section are only generated when gen-pairs is set to “yes” in the [ defaults ] directive of
forcefield.itp (see 5.8.1). When gen-pairs is set to “no,” grompp will give a warning
for each pair type for which no parameters are given.
The normal pair interactions, intended for 1-4 interactions, have function type 1. Function type 2
and the [ pairs_nb ] are intended for free-energy simulations. When determining hydration
free energies, the solute needs to be decoupled from the solvent. This can be done by adding a
B-state topology (see sec. 3.12) that uses zero for all solute non-bonded parameters, i.e. charges

126 Chapter 5. Topologies
and LJ parameters. However, the free energy difference between the A and B states is not the total
hydration free energy. One has to add the free energy for reintroducing the internal Coulomb and
LJ interactions in the solute when in vacuum. This second step can be combined with the first step
when the Coulomb and LJ interactions within the solute are not modified. For this purpose, there is
a pairs function type 2, which is identical to function type 1, except that the B-state parameters are
always identical to the A-state parameters. For searching the parameters in the [ pairtypes ]
section, no distinction is made between function type 1 and 2. The pairs section [ pairs_nb ]
is intended to replace the non-bonded interaction. It uses the unscaled charges and the non-bonded
LJ parameters; it also only uses the A-state parameters. Note that one should add exclusions for
all atom pairs listed in [ pairs_nb ], otherwise such pairs will also end up in the normal
neighbor lists.
Alternatively, this same behavior can be achieved without ever touching the topology, by using
the couple-moltype,couple-lambda0,couple-lambda1, and couple-intramol
keywords. See sections sec. 3.12 and sec. 6.1 for more information.
All three pair types always use plain Coulomb interactions, even when Reaction-field, PME, Ewald
or shifted Coulomb interactions are selected for the non-bonded interactions. Energies for types
1 and 2 are written to the energy and log file in separate “LJ-14” and “Coulomb-14” entries per
energy group pair. Energies for [ pairs_nb ] are added to the “LJ-(SR)” and “Coulomb-
(SR)” terms.
5.4.4 Exclusions
The exclusions for non-bonded interactions are generated by grompp for neighboring atoms up
to a certain number of bonds away, as defined in the [ moleculetype ] section in the topol-
ogy file (see 5.8.1). Particles are considered bonded when they are connected by “chemical”
bonds ([ bonds ] types 1 to 5, 7 or 8) or constraints ([ constraints ] type 1). Type 5
[ bonds ] can be used to create a connection between two atoms without creating an interac-
tion. There is a harmonic interaction ([ bonds ] type 6) that does not connect the atoms by a
chemical bond. There is also a second constraint type ([ constraints ] type 2) that fixes
the distance, but does not connect the atoms by a chemical bond. For a complete list of all these
interactions, see Table 5.5.
Extra exclusions within a molecule can be added manually in a [ exclusions ] section. Each
line should start with one atom index, followed by one or more atom indices. All non-bonded
interactions between the first atom and the other atoms will be excluded.
When all non-bonded interactions within or between groups of atoms need to be excluded, is it
more convenient and much more efficient to use energy monitor group exclusions (see sec. 3.3).
5.5 Implicit solvation parameters
Starting with GROMACS 4.5, implicit solvent is supported. A section in the topology has been
introduced to list those parameters:
[ implicit_genborn_params ]

5.6. Constraint algorithms 127
; Atomtype sar st pi gbr hct
NH1 0.155 1 1.028 0.17063 0.79 ; N
N 0.155 1 1 0.155 0.79 ; Proline backbone N
H 0.1 1 1 0.115 0.85 ; H
CT1 0.180 1 1.276 0.190 0.72 ; C
In this example the atom type is listed first, followed by five numbers, and a comment (following
a semicolon).
Values in columns 1-3 are not currently used. They pertain to more elaborate surface area algo-
rithms, the one from Qiu et al. [71] in particular. Column 4 contains the atomic van der Waals
radii, which are used in computing the Born radii. The dielectric offset is specified in the *.mdp
file, and gets subtracted from the input van der Waals radii for the different Born radii methods, as
described by Onufriev et al. [73]. Column 5 is the scale factor for the HCT and OBC models. The
values are taken from the Tinker implementation of the HCT pairwise scaling method [72]. This
method has been modified such that the scaling factors have been adjusted to minimize differences
between analytical surface areas and GB using the HCT algorithm. The scaling is further modified
in that it is not applied pairwise as proposed by Hawkins et al. [72], but on a per-atom (rather than
a per-pair) basis.
5.6 Constraint algorithms
Constraints are defined in the [ constraints ] section. The format is two atom numbers
followed by the function type, which can be 1 or 2, and the constraint distance. The only differ-
ence between the two types is that type 1 is used for generating exclusions and type 2 is not (see
sec. 5.4.4). The distances are constrained using the LINCS or the SHAKE algorithm, which can
be selected in the *.mdp file. Both types of constraints can be perturbed in free-energy calcula-
tions by adding a second constraint distance (see 5.8.5). Several types of bonds and angles (see
Table 5.5) can be converted automatically to constraints by grompp. There are several options
for this in the *.mdp file.
We have also implemented the SETTLE algorithm [47], which is an analytical solution of SHAKE,
specifically for water. SETTLE can be selected in the topology file. See, for instance, the SPC
molecule definition:
[ moleculetype ]
; molname nrexcl
SOL 1
[ atoms ]
; nr at type res nr ren nm at nm cg nr charge
1 OW 1 SOL OW1 1 -0.82
2 HW 1 SOL HW2 1 0.41
3 HW 1 SOL HW3 1 0.41
[ settles ]
; OW funct doh dhh
1 1 0.1 0.16333

128 Chapter 5. Topologies
[ exclusions ]
123
213
312
The [ settles ] directive defines the first atom of the water molecule. The settle funct is
always 1, and the distance between O-H and H-H distances must be given. Note that the algorithm
can also be used for TIP3P and TIP4P [133]. TIP3P just has another geometry. TIP4P has a virtual
site, but since that is generated it does not need to be shaken (nor stirred).
5.7 pdb2gmx input files
The GROMACS program pdb2gmx generates a topology for the input coordinate file. Several
formats are supported for that coordinate file, but *.pdb is the most commonly-used format
(hence the name pdb2gmx). pdb2gmx searches for force fields in sub-directories of the GRO-
MACS share/top directory and your working directory. Force fields are recognized from the
file forcefield.itp in a directory with the extension .ff. The file forcefield.doc
may be present, and if so, its first line will be used by pdb2gmx to present a short description to
the user to help in choosing a force field. Otherwise, the user can choose a force field with the
-ff xxx command-line argument to pdb2gmx, which indicates that a force field in a xxx.ff
directory is desired. pdb2gmx will search first in the working directory, then in the GROMACS
share/top directory, and use the first matching xxx.ff directory found.
Two general files are read by pdb2gmx: an atom type file (extension .atp, see 5.2.1) from the
force-field directory, and a file called residuetypes.dat from either the working directory, or
the GROMACS share/top directory. residuetypes.dat determines which residue names
are considered protein, DNA, RNA, water, and ions.
pdb2gmx can read one or multiple databases with topological information for different types of
molecules. A set of files belonging to one database should have the same basename, preferably
telling something about the type of molecules (e.g. aminoacids, rna, dna). The possible files are:
•<basename>.rtp
•<basename>.r2b (optional)
•<basename>.arn (optional)
•<basename>.hdb (optional)
•<basename>.n.tdb (optional)
•<basename>.c.tdb (optional)
Only the .rtp file, which contains the topologies of the building blocks, is mandatory. Infor-
mation from other files will only be used for building blocks that come from an .rtp file with
the same base name. The user can add building blocks to a force field by having additional files

5.7. pdb2gmx input files 129
with the same base name in their working directory. By default, only extra building blocks can be
defined, but calling pdb2gmx with the -rtpo option will allow building blocks in a local file to
replace the default ones in the force field.
5.7.1 Residue database
The files holding the residue databases have the extension .rtp. Originally this file contained
building blocks (amino acids) for proteins, and is the GROMACS interpretation of the rt37c4.dat
file of GROMOS. So the residue database file contains information (bonds, charges, charge groups,
and improper dihedrals) for a frequently-used building block. It is better not to change this file
because it is standard input for pdb2gmx, but if changes are needed make them in the *.top file
(see 5.8.1), or in a .rtp file in the working directory as explained in sec. 5.7. Defining topologies
of new small molecules is probably easier by writing an include topology file *.itp directly.
This will be discussed in section 5.8.2. When adding a new protein residue to the database, don’t
forget to add the residue name to the residuetypes.dat file, so that grompp,make_ndx
and analysis tools can recognize the residue as a protein residue (see 8.1.1).
The .rtp files are only used by pdb2gmx. As mentioned before, the only extra information this
program needs from the .rtp database is bonds, charges of atoms, charge groups, and improper
dihedrals, because the rest is read from the coordinate input file. Some proteins contain residues
that are not standard, but are listed in the coordinate file. You have to construct a building block for
this “strange” residue, otherwise you will not obtain a *.top file. This also holds for molecules
in the coordinate file such as ligands, polyatomic ions, crystallization co-solvents, etc. The residue
database is constructed in the following way:
[ bondedtypes ] ; mandatory
; bonds angles dihedrals impropers
1 1 1 2 ; mandatory
[ GLY ] ; mandatory
[ atoms ] ; mandatory
; name type charge chargegroup
N N -0.280 0
H H 0.280 0
CA CH2 0.000 1
C C 0.380 2
O O -0.380 2
[ bonds ] ; optional
;atom1 atom2 b0 kb
N H
N CA
CA C
C O
-C N
[ exclusions ] ; optional
;atom1 atom2

130 Chapter 5. Topologies
[ angles ] ; optional
;atom1 atom2 atom3 th0 cth
[ dihedrals ] ; optional
;atom1 atom2 atom3 atom4 phi0 cp mult
[ impropers ] ; optional
;atom1 atom2 atom3 atom4 q0 cq
N -C CA H
-C -CA N -O
[ ZN ]
[ atoms ]
ZN ZN 2.000 0
The file is free format; the only restriction is that there can be at most one entry on a line. The first
field in the file is the [ bondedtypes ] field, which is followed by four numbers, indicating
the interaction type for bonds, angles, dihedrals, and improper dihedrals. The file contains residue
entries, which consist of atoms and (optionally) bonds, angles, dihedrals, and impropers. The
charge group codes denote the charge group numbers. Atoms in the same charge group should
always be ordered consecutively. When using the hydrogen database with pdb2gmx for adding
missing hydrogens (see 5.7.4), the atom names defined in the .rtp entry should correspond ex-
actly to the naming convention used in the hydrogen database. The atom names in the bonded
interaction can be preceded by a minus or a plus, indicating that the atom is in the preceding or
following residue respectively. Explicit parameters added to bonds, angles, dihedrals, and im-
propers override the standard parameters in the .itp files. This should only be used in special
cases. Instead of parameters, a string can be added for each bonded interaction. This is used in
GROMOS-96 .rtp files. These strings are copied to the topology file and can be replaced by
force-field parameters by the C-preprocessor in grompp using #define statements.
pdb2gmx automatically generates all angles. This means that for most force fields the [ angles ]
field is only useful for overriding .itp parameters. For the GROMOS-96 force field the interac-
tion number of all angles needs to be specified.
pdb2gmx automatically generates one proper dihedral for every rotatable bond, preferably on
heavy atoms. When the [ dihedrals ] field is used, no other dihedrals will be generated for
the bonds corresponding to the specified dihedrals. It is possible to put more than one dihedral
function on a rotatable bond. In the case of CHARMM27 FF pdb2gmx can add correction maps
to the dihedrals using the default -cmap option. Please refer to 4.10.4 for more information.
pdb2gmx sets the number of exclusions to 3, which means that interactions between atoms con-
nected by at most 3 bonds are excluded. Pair interactions are generated for all pairs of atoms
that are separated by 3 bonds (except pairs of hydrogens). When more interactions need to be
excluded, or some pair interactions should not be generated, an [ exclusions ] field can be
added, followed by pairs of atom names on separate lines. All non-bonded and pair interactions
between these atoms will be excluded.

5.7. pdb2gmx input files 131
ARG protonated arginine
ARGN neutral arginine
ASP negatively charged aspartic acid
ASPH neutral aspartic acid
CYS neutral cysteine
CYS2 cysteine with sulfur bound to another cysteine or a heme
GLU negatively charged glutamic acid
GLUH neutral glutamic acid
HISD neutral histidine with Nδprotonated
HISE neutral histidine with Nprotonated
HISH positive histidine with both Nδand Nprotonated
HIS1 histidine bound to a heme
LYSN neutral lysine
LYS protonated lysine
HEME heme
Table 5.3: Internal GROMACS residue naming convention.
5.7.2 Residue to building block database
Each force field has its own naming convention for residues. Most residues have consistent nam-
ing, but some, especially those with different protonation states, can have many different names.
The .r2b files are used to convert standard residue names to the force-field build block names. If
no .r2b is present in the force-field directory or a residue is not listed, the building block name is
assumed to be identical to the residue name. The .r2b can contain 2 or 5 columns. The 2-column
format has the residue name in the first column and the building block name in the second. The
5-column format has 3 additional columns with the building block for the residue occurring in
the N-terminus, C-terminus and both termini at the same time (single residue molecule). This is
useful for, for instance, the AMBER force fields. If one or more of the terminal versions are not
present, a dash should be entered in the corresponding column.
There is a GROMACS naming convention for residues which is only apparent (except for the
pdb2gmx code) through the .r2b file and specbond.dat files. This convention is only of
importance when you are adding residue types to an .rtp file. The convention is listed in Ta-
ble 5.3. For special bonds with, for instance, a heme group, the GROMACS naming convention
is introduced through specbond.dat (see 5.7.7), which can subsequently be translated by the
.r2b file, if required.
5.7.3 Atom renaming database
Force fields often use atom names that do not follow IUPAC or PDB convention. The .arn
database is used to translate the atom names in the coordinate file to the force-field names. Atoms
that are not listed keep their names. The file has three columns: the building block name, the
old atom name, and the new atom name, respectively. The residue name supports question-mark
wildcards that match a single character.

132 Chapter 5. Topologies
An additional general atom renaming file called xlateat.dat is present in the share/top
directory, which translates common non-standard atom names in the coordinate file to IUPAC/PDB
convention. Thus, when writing force-field files, you can assume standard atom names and no
further atom name translation is required, except for translating from standard atom names to the
force-field ones.
5.7.4 Hydrogen database
The hydrogen database is stored in .hdb files. It contains information for the pdb2gmx program
on how to connect hydrogen atoms to existing atoms. In versions of the database before GRO-
MACS 3.3, hydrogen atoms were named after the atom they are connected to: the first letter of
the atom name was replaced by an ‘H.’ In the versions from 3.3 onwards, the H atom has to be
listed explicitly, because the old behavior was protein-specific and hence could not be generalized
to other molecules. If more than one hydrogen atom is connected to the same atom, a number will
be added to the end of the hydrogen atom name. For example, adding two hydrogen atoms to ND2
(in asparagine), the hydrogen atoms will be named HD21 and HD22. This is important since atom
naming in the .rtp file (see 5.7.1) must be the same. The format of the hydrogen database is as
follows:
; res # additions
# H add type H i j k
ALA 1
1 1 H N -C CA
ARG 4
12HNCAC
1 1 HE NE CD CZ
2 3 HH1 NH1 CZ NE
2 3 HH2 NH2 CZ NE
On the first line we see the residue name (ALA or ARG) and the number of kinds of hydrogen
atoms that may be added to this residue by the hydrogen database. After that follows one line for
each addition, on which we see:
•The number of H atoms added
•The method for adding H atoms, which can be any of:
1one planar hydrogen, e.g. rings or peptide bond
One hydrogen atom (n) is generated, lying in the plane of atoms (i,j,k) on the plane
bisecting angle (j-i-k) at a distance of 0.1 nm from atom i, such that the angles (n-i-j)
and (n-i-k) are >90o.
2one single hydrogen, e.g. hydroxyl
One hydrogen atom (n) is generated at a distance of 0.1 nm from atom i, such that
angle (n-i-j)=109.5 degrees and dihedral (n-i-j-k)=trans.
3two planar hydrogens, e.g. ethylene -C=CH2, or amide -C(=O)NH2
Two hydrogens (n1,n2) are generated at a distance of 0.1 nm from atom i, such that

5.7. pdb2gmx input files 133
angle (n1-i-j)=(n2-i-j)=120 degrees and dihedral (n1-i-j-k)=cis and (n2-i-j-k)=trans,
such that names are according to IUPAC standards [134].
4two or three tetrahedral hydrogens, e.g. -CH3
Three (n1,n2,n3) or two (n1,n2) hydrogens are generated at a distance of 0.1 nm from
atom i, such that angle (n1-i-j)=(n2-i-j)=(n3-i-j)=109.47o, dihedral (n1-i-j-k)=trans,
(n2-i-j-k)=trans+120 and (n3-i-j-k)=trans+240o.
5one tetrahedral hydrogen, e.g. C3CH
One hydrogen atom (n0) is generated at a distance of 0.1 nm from atom i in tetrahedral
conformation such that angle (n0-i-j)=(n0-i-k)=(n0-i-l)=109.47o.
6two tetrahedral hydrogens, e.g. C-CH2-C
Two hydrogen atoms (n1,n2) are generated at a distance of 0.1 nm from atom i in
tetrahedral conformation on the plane bisecting angle j-i-k with angle (n1-i-n2)=(n1-i-
j)=(n1-i-k)=109.47o.
7two water hydrogens
Two hydrogens are generated around atom i according to SPC [85] water geometry.
The symmetry axis will alternate between three coordinate axes in both directions.
10 three water “hydrogens”
Two hydrogens are generated around atom i according to SPC [85] water geometry.
The symmetry axis will alternate between three coordinate axes in both directions.
In addition, an extra particle is generated on the position of the oxygen with the first
letter of the name replaced by ‘M’. This is for use with four-atom water models such
as TIP4P [133].
11 four water “hydrogens”
Same as above, except that two additional particles are generated on the position of
the oxygen, with names ‘LP1’ and ‘LP2.’ This is for use with five-atom water models
such as TIP5P [135].
•The name of the new H atom (or its prefix, e.g. HD2 for the asparagine example given
earlier).
•Three or four control atoms (i,j,k,l), where the first always is the atom to which the H atoms
are connected. The other two or three depend on the code selected. For water, there is only
one control atom.
Some more exotic cases can be approximately constructed from the above tools, and with suit-
able use of energy minimization are good enough for beginning MD simulations. For example
secondary amine hydrogen, nitrenyl hydrogen (C=NH) and even ethynyl hydrogen could be ap-
proximately constructed using method 2 above for hydroxyl hydrogen.
5.7.5 Termini database
The termini databases are stored in aminoacids.n.tdb and aminoacids.c.tdb for the N-
and C-termini respectively. They contain information for the pdb2gmx program on how to con-
nect new atoms to existing ones, which atoms should be removed or changed, and which bonded
interactions should be added. Their format is as follows (from gromos43a1.ff/aminoacids.c.tdb):

134 Chapter 5. Topologies
[ None ]
[ COO- ]
[ replace ]
C C C 12.011 0.27
O O1 OM 15.9994 -0.635
OXT O2 OM 15.9994 -0.635
[ add ]
28OCCAN
OM 15.9994 -0.635
[ bonds ]
C O1 gb_5
C O2 gb_5
[ angles ]
O1 C O2 ga_37
CA C O1 ga_21
CA C O2 ga_21
[ dihedrals ]
N CA C O2 gd_20
[ impropers ]
C CA O2 O1 gi_1
The file is organized in blocks, each with a header specifying the name of the block. These
blocks correspond to different types of termini that can be added to a molecule. In this example
[ COO- ] is the first block, corresponding to changing the terminal carbon atom into a depro-
tonated carboxyl group. [ None ] is the second terminus type, corresponding to a terminus
that leaves the molecule as it is. Block names cannot be any of the following: replace,add,
delete,bonds,angles,dihedrals,impropers. Doing so would interfere with the pa-
rameters of the block, and would probably also be very confusing to human readers.
For each block the following options are present:
•[ replace ]
Replace an existing atom by one with a different atom type, atom name, charge, and/or
mass. This entry can be used to replace an atom that is present both in the input coordinates
and in the .rtp database, but also to only rename an atom in the input coordinates such
that it matches the name in the force field. In the latter case, there should also be a corre-
sponding [ add ] section present that gives instructions to add the same atom, such that
the position in the sequence and the bonding is known. Such an atom can be present in the
input coordinates and kept, or not present and constructed by pdb2gmx. For each atom to
be replaced on line should be entered with the following fields:
–name of the atom to be replaced
–new atom name (optional)
–new atom type
–new mass
–new charge

5.7. pdb2gmx input files 135
•[ add ]
Add new atoms. For each (group of) added atom(s), a two-line entry is necessary. The
first line contains the same fields as an entry in the hydrogen database (name of the new
atom, number of atoms, type of addition, control atoms, see 5.7.4), but the possible types of
addition are extended by two more, specifically for C-terminal additions:
8two carboxyl oxygens, -COO−
Two oxygens (n1,n2) are generated according to rule 3, at a distance of 0.136 nm from
atom i and an angle (n1-i-j)=(n2-i-j)=117 degrees
9carboxyl oxygens and hydrogen, -COOH
Two oxygens (n1,n2) are generated according to rule 3, at distances of 0.123 nm and
0.125 nm from atom i for n1 and n2, respectively, and angles (n1-i-j)=121 and (n2-i-
j)=115 degrees. One hydrogen (n0) is generated around n2 according to rule 2, where
n-i-j and n-i-j-k should be read as n0-n2-i and n0-n2-i-j, respectively.
After this line, another line follows that specifies the details of the added atom(s), in the
same way as for replacing atoms, i.e.:
–atom type
–mass
–charge
–charge group (optional)
Like in the hydrogen database (see 5.7.1), when more than one atom is connected to an
existing one, a number will be appended to the end of the atom name. Note that, like in the
hydrogen database, the atom name is now on the same line as the control atoms, whereas it
was at the beginning of the second line prior to GROMACS version 3.3. When the charge
group field is left out, the added atom will have the same charge group number as the atom
that it is bonded to.
•[ delete ]
Delete existing atoms. One atom name per line.
•[ bonds ],[ angles ],[ dihedrals ] and [ impropers ]
Add additional bonded parameters. The format is identical to that used in the *.rtp file,
see 5.7.1.
5.7.6 Virtual site database
Since we cannot rely on the positions of hydrogens in input files, we need a special input file
to decide the geometries and parameters with which to add virtual site hydrogens. For more
complex virtual site constructs (e.g. when entire aromatic side chains are made rigid) we also need
information about the equilibrium bond lengths and angles for all atoms in the side chain. This
information is specified in the .vsd file for each force field. Just as for the termini, there is one
such file for each class of residues in the .rtp file.
The virtual site database is not really a very simple list of information. The first couple of sections
specify which mass centers (typically called MCH3/MNH3) to use for CH3, NH3, and NH2groups.

136 Chapter 5. Topologies
Depending on the equilibrium bond lengths and angles between the hydrogens and heavy atoms
we need to apply slightly different constraint distances between these mass centers. Note that we
do not have to specify the actual parameters (that is automatic), just the type of mass center to use.
To accomplish this, there are three sections names [ CH3 ],[ NH3 ], and [ NH2 ]. For each
of these we expect three columns. The first column is the atom type bound to the 2/3 hydrogens,
the second column is the next heavy atom type which this is bound, and the third column the type
of mass center to use. As a special case, in the [ NH2 ] section it is also possible to specify
planar in the second column, which will use a different construction without mass center. There
are currently different opinions in some force fields whether an NH2group should be planar or
not, but we try hard to stick to the default equilibrium parameters of the force field.
The second part of the virtual site database contains explicit equilibrium bond lengths and angles
for pairs/triplets of atoms in aromatic side chains. These entries are currently read by specific
routines in the virtual site generation code, so if you would like to extend it e.g. to nucleic acids
you would also need to write new code there. These sections are named after the short amino
acid names ([ PHE ],[ TYR ],[ TRP ],[ HID ],[ HIE ],[ HIP ]), and simply
contain 2 or 3 columns with atom names, followed by a number specifying the bond length (in
nm) or angle (in degrees). Note that these are approximations of the equilibrated geometry for the
entire molecule, which might not be identical to the equilibrium value for a single bond/angle if
the molecule is strained.
5.7.7 Special bonds
The primary mechanism used by pdb2gmx to generate inter-residue bonds relies on head-to-
tail linking of backbone atoms in different residues to build a macromolecule. In some cases
(e.g. disulfide bonds, a heme group, branched polymers), it is necessary to create inter-residue
bonds that do not lie on the backbone. The file specbond.dat takes care of this function.
It is necessary that the residues belong to the same [ moleculetype ]. The -merge and
-chainsep functions of pdb2gmx can be useful when managing special inter-residue bonds
between different chains.
The first line of specbond.dat indicates the number of entries that are in the file. If you
add a new entry, be sure to increment this number. The remaining lines in the file provide the
specifications for creating bonds. The format of the lines is as follows:
resA atomA nbondsA resB atomB nbondsB length newresA newresB
The columns indicate:
1. resA The name of residue A that participates in the bond.
2. atomA The name of the atom in residue A that forms the bond.
3. nbondsA The total number of bonds atomA can form.
4. resB The name of residue B that participates in the bond.
5. atomB The name of the atom in residue B that forms the bond.
6. nbondsB The total number of bonds atomB can form.

5.8. File formats 137
7. length The reference length for the bond. If atomA and atomB are not within length
±10% in the coordinate file supplied to pdb2gmx, no bond will be formed.
8. newresA The new name of residue A, if necessary. Some force fields use e.g. CYS2 for a
cysteine in a disulfide or heme linkage.
9. newresB The new name of residue B, likewise.
5.8 File formats
5.8.1 Topology file
The topology file is built following the GROMACS specification for a molecular topology. A
*.top file can be generated by pdb2gmx. All possible entries in the topology file are listed
in Tables 5.4 and 5.5. Also tabulated are: all the units of the parameters, which interactions
can be perturbed for free energy calculations, which bonded interactions are used by grompp for
generating exclusions, and which bonded interactions can be converted to constraints by grompp.

138 Chapter 5. Topologies
Parameters
interaction directive # f. parameters F. E.
type at. tp
mandatory defaults non-bonded function type;
combination rule(cr);
generate pairs (no/yes);
fudge LJ (); fudge QQ ()
mandatory atomtypes atom type; m (u); q (e); particle type;
V(cr); W(cr)
bondtypes (see Table 5.5, directive bonds)
pairtypes (see Table 5.5, directive pairs)
angletypes (see Table 5.5, directive angles)
dihedraltypes(∗)(see Table 5.5, directive dihedrals)
constrainttypes (see Table 5.5, directive constraints)
LJ nonbond_params 2 1 V(cr);W(cr)
Buckingham nonbond_params 2 2 a(kJ mol−1); b(nm−1);
c6(kJ mol−1nm6)
Molecule definition(s)
mandatory moleculetype molecule name; n(nrexcl)
ex
mandatory atoms 1 atom type; residue number; type
residue name; atom name;
charge group number; q(e); m(u) q, m
intra-molecular interaction and geometry definitions as described in Table 5.5
System
mandatory system system name
mandatory molecules molecule name; number of molecules
Inter-molecular interactions
optional intermolecular_interactions
one or more bonded interactions as described in Table 5.5, with two or more atoms,
no interactions that generate exclusions, no constraints, use global atom numbers
‘# at’ is the required number of atom type indices for this directive
‘f. tp’ is the value used to select this function type
‘F. E.’ indicates which of the parameters can be interpolated in free energy calculations
(cr)the combination rule determines the type of LJ parameters, see 5.3.2
(∗)for dihedraltypes one can specify 4 atoms or the inner (outer for improper) 2 atoms
(nrexcl)exclude neighbors nex bonds away for non-bonded interactions
For free energy calculations, type, qand mor no parameters should be added
for topology ‘B’ (λ= 1) on the same line, after the normal parameters.
Table 5.4: The topology (*.top) file.

5.8. File formats 139
Table 5.5: Details of [ moleculetype ] directives
Name of interaction Topology file directive num. func. Order of parameters and their units use in Cross-
atoms∗type†F.E.?‡references
bond bonds§,¶2 1 b0(nm); kb(kJ mol−1nm−2) all 4.2.1
G96 bond bonds§,¶2 2 b0(nm); kb(kJ mol−1nm−4) all 4.2.1
Morse bonds§,¶2 3 b0(nm); D(kJ mol−1); β(nm−1) all 4.2.2
cubic bond bonds§,¶2 4 b0(nm); Ci=2,3(kJ mol−1nm−i)4.2.3
connection bonds§2 5 5.4.4
harmonic potential bonds 2 6 b0(nm); kb(kJ mol−1nm−2) all 4.2.1,5.4.4
FENE bond bonds§2 7 bm(nm); kb(kJ mol−1nm−2)4.2.4
tabulated bond bonds§2 8 table number (≥0); k(kJ mol−1)k4.2.14
tabulated bondkbonds 2 9 table number (≥0); k(kJ mol−1)k4.2.14,5.4.4
restraint potential bonds 2 10 low, up1, up2(nm); kdr (kJ mol−1nm−2) all 4.3.5
extra LJ or Coulomb pairs 2 1 V∗∗;W∗∗ all 5.4.3
extra LJ or Coulomb pairs 2 2 fudge QQ (); qi,qj(e), V∗∗;W∗∗ 5.4.3
extra LJ or Coulomb pairs_nb 2 1 qi,qj(e); V∗∗;W∗∗ 5.4.3
angle angles¶3 1 θ0(deg); kθ(kJ mol−1rad−2) all 4.2.5
G96 angle angles¶3 2 θ0(deg); kθ(kJ mol−1) all 4.2.6
cross bond-bond angles 3 3 r1e,r2e(nm); krr0(kJ mol−1nm−2)4.2.9
cross bond-angle angles 3 4 r1e,r2er3e(nm); krθ (kJ mol−1nm−2)4.2.10
Urey-Bradley angles¶3 5 θ0(deg); kθ(kJ mol−1rad−2); r13 (nm);
kUB (kJ mol−1nm−2)
all 4.2.8
quartic angle angles¶3 6 θ0(deg); Ci=0,1,2,3,4(kJ mol−1rad−i)4.2.11
∗The required number of atom indices for this directive
†The index to use to select this function type
‡Indicates which of the parameters can be interpolated in free energy calculations
§This interaction type will be used by grompp for generating exclusions
¶This interaction type can be converted to constraints by grompp
∗∗The combination rule determines the type of LJ parameters, see 5.3.2
kNo connection, and so no exclusions, are generated for this interaction

140 Chapter 5. Topologies
Table 5.5: Details of [ moleculetype ] directives
Name of interaction Topology file directive num. func. Order of parameters and their units use in Cross-
atoms∗type†F.E.?‡references
tabulated angle angles 3 8 table number (≥0); k(kJ mol−1)k4.2.14
restricted bending potential angles 3 10 θ0(deg); kθ(kJ mol−1)4.2.7
proper dihedral dihedrals 4 1 φs(deg); kφ(kJ mol−1); multiplicity φ, k 4.2.13
improper dihedral dihedrals 4 2 ξ0(deg); kξ(kJ mol−1rad−2) all 4.2.12
Ryckaert-Bellemans dihedral dihedrals 4 3 C0,C1,C2,C3,C4,C5(kJ mol−1) all 4.2.13
periodic improper dihedral dihedrals 4 4 φs(deg); kφ(kJ mol−1); multiplicity φ, k 4.2.12
Fourier dihedral dihedrals 4 5 C1,C2,C3,C4(kJ mol−1) all 4.2.13
tabulated dihedral dihedrals 4 8 table number (≥0); k(kJ mol−1)k4.2.14
proper dihedral (multiple) dihedrals 4 9 φs(deg); kφ(kJ mol−1); multiplicity φ, k 4.2.13
restricted dihedral dihedrals 4 10 φ0(deg); kφ(kJ mol−1)4.2.13
combined bending-torsion
potential
dihedrals 4 11 a0,a1,a2,a3,a4(kJ mol−1)4.2.13
exclusions exclusions 1 one or more atom indices 5.4.4
constraint constraints§2 1 b0(nm) all 4.5,5.6
constraintkconstraints 2 2 b0(nm) all 4.5,5.6,5.4.4
SETTLE settles 1 1 dOH,dHH (nm) 3.6.1,5.6
2-body virtual site virtual_sites2 3 1 a() 4.7
3-body virtual site virtual_sites3 4 1 a,b() 4.7
3-body virtual site (fd) virtual_sites3 4 2 a(); d(nm) 4.7
3-body virtual site (fad) virtual_sites3 4 3 θ(deg); d(nm) 4.7
3-body virtual site (out) virtual_sites3 4 4 a,b(); c(nm−1)4.7
4-body virtual site (fdn) virtual_sites4 5 2 a,b(); c(nm) 4.7
N-body virtual site (COG) virtual_sitesn 1 1 one or more constructing atom indices 4.7
N-body virtual site (COM) virtual_sitesn 1 2 one or more constructing atom indices 4.7
N-body virtual site (COW) virtual_sitesn 1 3 one or more pairs consisting of
constructing atom index and weight
4.7
position restraint position_restraints 1 1 kx,ky,kz(kJ mol−1nm−2) all 4.3.1

5.8. File formats 141
Table 5.5: Details of [ moleculetype ] directives
Name of interaction Topology file directive num. func. Order of parameters and their units use in Cross-
atoms∗type†F.E.?‡references
flat-bottomed position re-
straint
position_restraints 1 2 g,r(nm), k(kJ mol−1nm−2)4.3.2
distance restraint distance_restraints 2 1 type; label; low, up1, up2(nm); weight () 4.3.5
dihedral restraint dihedral_restraints 4 1 φ0(deg); ∆φ(deg); kdihr
(kJ mol−1rad−2)
all 4.3.4
orientation restraint orientation_restraints 2 1 exp.; label; α;c(U nmα); obs. (U);
weight (U−1)
4.3.6
angle restraint angle_restraints 4 1 θ0(deg); kc(kJ mol−1); multiplicity θ, k 4.3.3
angle restraint (z) angle_restraints_z 2 1 θ0(deg); kc(kJ mol−1); multiplicity θ, k 4.3.3

142 Chapter 5. Topologies
Description of the file layout:
•Semicolon (;) and newline characters surround comments
•On a line ending with \the newline character is ignored.
•Directives are surrounded by [and ]
•The topology hierarchy (which must be followed) consists of three levels:
–the parameter level, which defines certain force-field specifications (see Table 5.4)
–the molecule level, which should contain one or more molecule definitions (see Ta-
ble 5.5)
–the system level, containing only system-specific information ([ system ] and
[ molecules ])
•Items should be separated by spaces or tabs, not commas
•Atoms in molecules should be numbered consecutively starting at 1
•Atoms in the same charge group must be listed consecutively
•The file is parsed only once, which implies that no forward references can be treated: items
must be defined before they can be used
•Exclusions can be generated from the bonds or overridden manually
•The bonded force types can be generated from the atom types or overridden per bond
•It is possible to apply multiple bonded interactions of the same type on the same atoms
•Descriptive comment lines and empty lines are highly recommended
•Starting with GROMACS version 3.1.3, all directives at the parameter level can be used
multiple times and there are no restrictions on the order, except that an atom type needs to
be defined before it can be used in other parameter definitions
•If parameters for a certain interaction are defined multiple times for the same combination
of atom types the last definition is used; starting with GROMACS version 3.1.3 grompp
generates a warning for parameter redefinitions with different values
•Using one of the [ atoms ],[ bonds ],[ pairs ],[ angles ], etc. without
having used [ moleculetype ] before is meaningless and generates a warning
•Using [ molecules ] without having used [ system ] before is meaningless and
generates a warning.
•After [ system ] the only allowed directive is [ molecules ]
•Using an unknown string in [ ] causes all the data until the next directive to be ignored
and generates a warning

5.8. File formats 143
Here is an example of a topology file, urea.top:
;
; Example topology file
;
; The force-field files to be included
#include "amber99.ff/forcefield.itp"
[ moleculetype ]
; name nrexcl
Urea 3
[ atoms ]
1 C 1 URE C 1 0.880229 12.01000 ; amber C type
2 O 1 URE O 2 -0.613359 16.00000 ; amber O type
3 N 1 URE N1 3 -0.923545 14.01000 ; amber N type
4 H 1 URE H11 4 0.395055 1.00800 ; amber H type
5 H 1 URE H12 5 0.395055 1.00800 ; amber H type
6 N 1 URE N2 6 -0.923545 14.01000 ; amber N type
7 H 1 URE H21 7 0.395055 1.00800 ; amber H type
8 H 1 URE H22 8 0.395055 1.00800 ; amber H type
[ bonds ]
1 2
1 3
1 6
3 4
3 5
6 7
6 8
[ dihedrals ]
; ai aj ak al funct definition
21349
21359
21679
21689
31679
31689
61349
61359
[ dihedrals ]
36124
14354
17684
[ position_restraints ]
; you wouldn’t normally use this for a molecule like Urea,
; but we include it here for didactic purposes
; ai funct fc
1 1 1000 1000 1000 ; Restrain to a point

144 Chapter 5. Topologies
2 1 1000 0 1000 ; Restrain to a line (Y-axis)
3 1 1000 0 0 ; Restrain to a plane (Y-Z-plane)
[ dihedral_restraints ]
; ai aj ak al type phi dphi fc
3 6 1 2 1 180 0 10
1 4 3 5 1 180 0 10
; Include TIP3P water topology
#include "amber99/tip3p.itp"
[ system ]
Urea in Water
[ molecules ]
;molecule name nr.
Urea 1
SOL 1000
Here follows the explanatory text.
#include "amber99.ff/forcefield.itp" :this includes the information for the force
field you are using, including bonded and non-bonded parameters. This example uses the AM-
BER99 force field, but your simulation may use a different force field. grompp will automatically
go and find this file and copy-and-paste its content. That content can be seen in
share/top/amber99.ff/forcefield.itp, and it is
#define _FF_AMBER
#define _FF_AMBER99
[ defaults ]
; nbfunc comb-rule gen-pairs fudgeLJ fudgeQQ
1 2 yes 0.5 0.8333
#include "ffnonbonded.itp"
#include "ffbonded.itp"
#include "gbsa.itp"
The two #define statements set up the conditions so that future parts of the topology can know
that the AMBER 99 force field is in use.
[ defaults ] :
•nbfunc is the non-bonded function type. Use 1 (Lennard-Jones) or 2 (Buckingham)
•comb-rule is the number of the combination rule (see 5.3.2).
•gen-pairs is for pair generation. The default is ‘no’, i.e. get 1-4 parameters from the
pairtypes list. When parameters are not present in the list, stop with a fatal error. Setting
‘yes’ generates 1-4 parameters that are not present in the pair list from normal Lennard-
Jones parameters using fudgeLJ

5.8. File formats 145
•fudgeLJ is the factor by which to multiply Lennard-Jones 1-4 interactions, default 1
•fudgeQQ is the factor by which to multiply electrostatic 1-4 interactions, default 1
•Nis the power for the repulsion term in a 6-Npotential (with nonbonded-type Lennard-
Jones only), starting with GROMACS version 4.5, mdrun also reads and applies N, for
values not equal to 12 tabulated interaction functions are used (in older version you would
have to use user tabulated interactions).
Note that gen-pairs,fudgeLJ,fudgeQQ, and Nare optional. fudgeLJ is only used when
generate pairs is set to ‘yes’, and fudgeQQ is always used. However, if you want to specify N
you need to give a value for the other parameters as well.
Then some other #include statements add in the large amount of data needed to describe the
rest of the force field. We will skip these and return to urea.top. There we will see
[ moleculetype ] :defines the name of your molecule in this *.top and nrexcl = 3 stands
for excluding non-bonded interactions between atoms that are no further than 3 bonds away.
[ atoms ] :defines the molecule, where nr and type are fixed, the rest is user defined. So
atom can be named as you like, cgnr made larger or smaller (if possible, the total charge of a
charge group should be zero), and charges can be changed here too.
[ bonds ] :no comment.
[ pairs ] :LJ and Coulomb 1-4 interactions
[ angles ] :no comment
[ dihedrals ] :in this case there are 9 proper dihedrals (funct = 1), 3 improper (funct =
4) and no Ryckaert-Bellemans type dihedrals. If you want to include Ryckaert-Bellemans type
dihedrals in a topology, do the following (in case of e.g. decane):
[ dihedrals ]
; ai aj ak al funct c0 c1 c2
12343
23453
In the original implementation of the potential for alkanes [136] no 1-4 interactions were used,
which means that in order to implement that particular force field you need to remove the 1-4
interactions from the [ pairs ] section of your topology. In most modern force fields, like
OPLS/AA or Amber the rules are different, and the Ryckaert-Bellemans potential is used as a
cosine series in combination with 1-4 interactions.
[ position_restraints ] :harmonically restrain the selected particles to reference posi-
tions (4.3.1). The reference positions are read from a separate coordinate file by grompp.
[ dihedral_restraints ] :restrain selected dihedrals to a reference value. The imple-
mentation of dihedral restraints is described in section 4.3.4 of the manual. The parameters speci-
fied in the [dihedral_restraints] directive are as follows:
•type has only one possible value which is 1
•phi is the value of φ0in eqn. 4.83 and eqn. 4.84 of the manual.

146 Chapter 5. Topologies
•dphi is the value of ∆φin eqn. 4.84 of the manual.
•fc is the force constant kdihr in eqn. 4.84 of the manual.
#include "tip3p.itp" :includes a topology file that was already constructed (see sec-
tion 5.8.2).
[ system ] :title of your system, user-defined
[ molecules ] :this defines the total number of (sub)molecules in your system that are de-
fined in this *.top. In this example file, it stands for 1 urea molecule dissolved in 1000 water
molecules. The molecule type SOL is defined in the tip3p.itp file. Each name here must
correspond to a name given with [ moleculetype ] earlier in the topology. The order of the
blocks of molecule types and the numbers of such molecules must match the coordinate file that
accompanies the topology when supplied to grompp. The blocks of molecules do not need to
be contiguous, but some tools (e.g. genion) may act only on the first or last such block of a
particular molecule type. Also, these blocks have nothing to do with the definition of groups (see
sec. 3.3 and sec. 8.1).
5.8.2 Molecule.itp file
If you construct a topology file you will use frequently (like the water molecule, tip3p.itp,
which is already constructed for you) it is good to make a molecule.itp file. This only lists
the information of one particular molecule and allows you to re-use the [ moleculetype ]
in multiple systems without re-invoking pdb2gmx or manually copying and pasting. An example
urea.itp follows:
[ moleculetype ]
; molname nrexcl
URE 3
[ atoms ]
1 C 1 URE C 1 0.880229 12.01000 ; amber C type
...
8 H 1 URE H22 8 0.395055 1.00800 ; amber H type
[ bonds ]
1 2
...
6 8
[ dihedrals ]
; ai aj ak al funct definition
21349
...
61359
[ dihedrals ]
36124
14354
17684

5.8. File formats 147
Using *.itp files results in a very short *.top file:
;
; Example topology file
;
; The force field files to be included
#include "amber99.ff/forcefield.itp"
#include "urea.itp"
; Include TIP3P water topology
#include "amber99/tip3p.itp"
[ system ]
Urea in Water
[ molecules ]
;molecule name nr.
Urea 1
SOL 1000
5.8.3 Ifdef statements
A very powerful feature in GROMACS is the use of #ifdef statements in your *.top file. By
making use of this statement, and associated #define statements like were seen in
amber99.ff/forcefield.itp earlier, different parameters for one molecule can be used
in the same *.top file. An example is given for TFE, where there is an option to use different
charges on the atoms: charges derived by De Loof et al. [137] or by Van Buuren and Berend-
sen [138]. In fact, you can use much of the functionality of the C preprocessor, cpp, because
grompp contains similar pre-processing functions to scan the file. The way to make use of the
#ifdef option is as follows:
•either use the option define = -DDeLoof in the *.mdp file (containing grompp input
parameters), or use the line #define DeLoof early in your *.top or *.itp file; and
•put the #ifdef statements in your *.top, as shown below:
...
[ atoms ]
; nr type resnr residu atom cgnr charge mass
#ifdef DeLoof
; Use Charges from DeLoof
1 C 1 TFE C 1 0.74
2 F 1 TFE F 1 -0.25
3 F 1 TFE F 1 -0.25
4 F 1 TFE F 1 -0.25

148 Chapter 5. Topologies
5 CH2 1 TFE CH2 1 0.25
6 OA 1 TFE OA 1 -0.65
7 HO 1 TFE HO 1 0.41
#else
; Use Charges from VanBuuren
1 C 1 TFE C 1 0.59
2 F 1 TFE F 1 -0.2
3 F 1 TFE F 1 -0.2
4 F 1 TFE F 1 -0.2
5 CH2 1 TFE CH2 1 0.26
6 OA 1 TFE OA 1 -0.55
7 HO 1 TFE HO 1 0.3
#endif
[ bonds ]
; ai aj funct c0 c1
6 7 1 1.000000e-01 3.138000e+05
1 2 1 1.360000e-01 4.184000e+05
1 3 1 1.360000e-01 4.184000e+05
1 4 1 1.360000e-01 4.184000e+05
1 5 1 1.530000e-01 3.347000e+05
5 6 1 1.430000e-01 3.347000e+05
...
This mechanism is used by pdb2gmx to implement optional position restraints (4.3.1) by #include-
ing an .itp file whose contents will be meaningful only if a particular #define is set (and
spelled correctly!)
5.8.4 Topologies for free energy calculations
Free energy differences between two systems, A and B, can be calculated as described in sec. 3.12.
Systems A and B are described by topologies consisting of the same number of molecules with
the same number of atoms. Masses and non-bonded interactions can be perturbed by adding B
parameters under the [ atoms ] directive. Bonded interactions can be perturbed by adding B
parameters to the bonded types or the bonded interactions. The parameters that can be perturbed
are listed in Tables 5.4 and 5.5. The λ-dependence of the interactions is described in section
sec. 4.5. The bonded parameters that are used (on the line of the bonded interaction definition, or
the ones looked up on atom types in the bonded type lists) is explained in Table 5.6. In most cases,
things should work intuitively. When the A and B atom types in a bonded interaction are not all
identical and parameters are not present for the B-state, either on the line or in the bonded types,
grompp uses the A-state parameters and issues a warning. For free energy calculations, all or no
parameters for topology B (λ= 1) should be added on the same line, after the normal parameters,
in the same order as the normal parameters. From GROMACS 4.6 onward, if λis treated as a
vector, then the bonded-lambdas component controls all bonded terms that are not explicitly
labeled as restraints. Restrain terms are controlled by the restraint-lambdas component.
Below is an example of a topology which changes from 200 propanols to 200 pentanes using the
GROMOS-96 force field.

5.8. File formats 149
B-state atom types parameters parameters in bonded types
all identical to on line A atom types B atom types message
A-state atom types A B A B A B
+AB −x x
+A +B x x
yes − − − − error
− − +AB −
− − +A +B
+AB −x x x x warning
+A +B x x x x
− − − − x x error
no − − +AB − − − warning
− − +A +B − − warning
− − +A x +B −
− − +A x + +B
Table 5.6: The bonded parameters that are used for free energy topologies, on the line of the
bonded interaction definition or looked up in the bond types section based on atom types. A and
B indicate the parameters used for state A and B respectively, + and −indicate the (non-)presence
of parameters in the topology, x indicates that the presence has no influence.
; Include force field parameters
#include "gromos43a1.ff/forcefield.itp"
[ moleculetype ]
; Name nrexcl
PropPent 3
[ atoms ]
; nr type resnr residue atom cgnr charge mass typeB chargeB massB
1 H 1 PROP PH 1 0.398 1.008 CH3 0.0 15.035
2 OA 1 PROP PO 1 -0.548 15.9994 CH2 0.0 14.027
3 CH2 1 PROP PC1 1 0.150 14.027 CH2 0.0 14.027
4 CH2 1 PROP PC2 2 0.000 14.027
5 CH3 1 PROP PC3 2 0.000 15.035
[ bonds ]
; ai aj funct par_A par_B
1 2 2 gb_1 gb_26
2 3 2 gb_17 gb_26
3 4 2 gb_26 gb_26
4 5 2 gb_26
[ pairs ]
; ai aj funct
141
251

150 Chapter 5. Topologies
[ angles ]
; ai aj ak funct par_A par_B
1 2 3 2 ga_11 ga_14
2 3 4 2 ga_14 ga_14
3 4 5 2 ga_14 ga_14
[ dihedrals ]
; ai aj ak al funct par_A par_B
1 2 3 4 1 gd_12 gd_17
2 3 4 5 1 gd_17 gd_17
[ system ]
; Name
Propanol to Pentane
[ molecules ]
; Compound #mols
PropPent 200
Atoms that are not perturbed, PC2 and PC3, do not need B-state parameter specifications, since the
B parameters will be copied from the A parameters. Bonded interactions between atoms that are
not perturbed do not need B parameter specifications, as is the case for the last bond in the example
topology. Topologies using the OPLS/AA force field need no bonded parameters at all, since both
the A and B parameters are determined by the atom types. Non-bonded interactions involving one
or two perturbed atoms use the free-energy perturbation functional forms. Non-bonded interac-
tions between two non-perturbed atoms use the normal functional forms. This means that when,
for instance, only the charge of a particle is perturbed, its Lennard-Jones interactions will also be
affected when lambda is not equal to zero or one.
Note that this topology uses the GROMOS-96 force field, in which the bonded interactions are not
determined by the atom types. The bonded interaction strings are converted by the C-preprocessor.
The force-field parameter files contain lines like:
#define gb_26 0.1530 7.1500e+06
#define gd_17 0.000 5.86 3
5.8.5 Constraint forces
The constraint force between two atoms in one molecule can be calculated with the free energy
perturbation code by adding a constraint between the two atoms, with a different length in the A
and B topology. When the B length is 1 nm longer than the A length and lambda is kept con-
stant at zero, the derivative of the Hamiltonian with respect to lambda is the constraint force. For
constraints between molecules, the pull code can be used, see sec. 6.4. Below is an example for
calculating the constraint force at 0.7 nm between two methanes in water, by combining the two
methanes into one “molecule.” Note that the definition of a “molecule” in GROMACS does not
necessarily correspond to the chemical definition of a molecule. In GROMACS, a “molecule” can

5.8. File formats 151
be defined as any group of atoms that one wishes to consider simultaneously. The added constraint
is of function type 2, which means that it is not used for generating exclusions (see sec. 5.4.4). Note
that the constraint free energy term is included in the derivative term, and is specifically included
in the bonded-lambdas component. However, the free energy for changing constraints is not
included in the potential energy differences used for BAR and MBAR, as this requires reevaluating
the energy at each of the constraint components. This functionality is planned for later versions.
; Include force-field parameters
#include "gromos43a1.ff/forcefield.itp"
[ moleculetype ]
; Name nrexcl
Methanes 1
[ atoms ]
; nr type resnr residu atom cgnr charge mass
1 CH4 1 CH4 C1 1 0 16.043
2 CH4 1 CH4 C2 2 0 16.043
[ constraints ]
; ai aj funct length_A length_B
1 2 2 0.7 1.7
#include "gromos43a1.ff/spc.itp"
[ system ]
; Name
Methanes in Water
[ molecules ]
; Compound #mols
Methanes 1
SOL 2002
5.8.6 Coordinate file
Files with the .gro file extension contain a molecular structure in GROMOS-87 format. A sample
piece is included below:
MD of 2 waters, reformat step, PA aug-91
6
1WATER OW1 1 0.126 1.624 1.679 0.1227 -0.0580 0.0434
1WATER HW2 2 0.190 1.661 1.747 0.8085 0.3191 -0.7791
1WATER HW3 3 0.177 1.568 1.613 -0.9045 -2.6469 1.3180
2WATER OW1 4 1.275 0.053 0.622 0.2519 0.3140 -0.1734
2WATER HW2 5 1.337 0.002 0.680 -1.0641 -1.1349 0.0257
2WATER HW3 6 1.326 0.120 0.568 1.9427 -0.8216 -0.0244
1.82060 1.82060 1.82060

152 Chapter 5. Topologies
This format is fixed, i.e. all columns are in a fixed position. If you want to read such a file in your
own program without using the GROMACS libraries you can use the following formats:
C-format: "%5i%5s%5s%5i%8.3f%8.3f%8.3f%8.4f%8.4f%8.4f"
Or to be more precise, with title etc. it looks like this:
"%s\n", Title
"%5d\n", natoms
for (i=0; (i<natoms); i++) {
"%5d%-5s%5s%5d%8.3f%8.3f%8.3f%8.4f%8.4f%8.4f\n",
residuenr,residuename,atomname,atomnr,x,y,z,vx,vy,vz
}
"%10.5f%10.5f%10.5f%10.5f%10.5f%10.5f%10.5f%10.5f%10.5f\n",
box[X][X],box[Y][Y],box[Z][Z],
box[X][Y],box[X][Z],box[Y][X],box[Y][Z],box[Z][X],box[Z][Y]
Fortran format: (i5,2a5,i5,3f8.3,3f8.4)
So confin.gro is the GROMACS coordinate file and is almost the same as the GROMOS-87
file (for GROMOS users: when used with ntx=7). The only difference is the box for which
GROMACS uses a tensor, not a vector.
5.9 Force field organization
5.9.1 Force-field files
Many force fields are available by default. Force fields are detected by the presence of <name>.ff
directories in the $GMXLIB/share/gromacs/top sub-directory and/or the working direc-
tory. The information regarding the location of the force field files is printed by pdb2gmx so
you can easily keep track of which version of a force field is being called, in case you have made
modifications in one location or another. The force fields included with GROMACS are:
•AMBER03 protein, nucleic AMBER94 (Duan et al., J. Comp. Chem. 24, 1999-2012, 2003)
•AMBER94 force field (Cornell et al., JACS 117, 5179-5197, 1995)
•AMBER96 protein, nucleic AMBER94 (Kollman et al., Acc. Chem. Res. 29, 461-469, 1996)
•AMBER99 protein, nucleic AMBER94 (Wang et al., J. Comp. Chem. 21, 1049-1074, 2000)
•AMBER99SB protein, nucleic AMBER94 (Hornak et al., Proteins 65, 712-725, 2006)
•AMBER99SB-ILDN protein, nucleic AMBER94 (Lindorff-Larsen et al., Proteins 78, 1950-58, 2010)
•AMBERGS force field (Garcia & Sanbonmatsu, PNAS 99, 2782-2787, 2002)
•CHARMM27 all-atom force field (CHARM22 plus CMAP for proteins)
•GROMOS96 43a1 force field
•GROMOS96 43a2 force field (improved alkane dihedrals)
•GROMOS96 45a3 force field (Schuler JCC 2001 22 1205)

5.9. Force field organization 153
•GROMOS96 53a5 force field (JCC 2004 vol 25 pag 1656)
•GROMOS96 53a6 force field (JCC 2004 vol 25 pag 1656)
•GROMOS96 54a7 force field (Eur. Biophys. J. (2011), 40„ 843-856, DOI: 10.1007/s00249-011-
0700-9)
•OPLS-AA/L all-atom force field (2001 aminoacid dihedrals)
A force field is included at the beginning of a topology file with an #include statement followed
by <name>.ff/forcefield.itp. This statement includes the force-field file, which, in turn,
may include other force-field files. All the force fields are organized in the same way. An example
of the amber99.ff/forcefield.itp was shown in 5.8.1.
For each force field, there several files which are only used by pdb2gmx. These are: residue
databases (.rtp, see 5.7.1) the hydrogen database (.hdb, see 5.7.4), two termini databases
(.n.tdb and .c.tdb, see 5.7.5) and the atom type database (.atp, see 5.2.1), which contains
only the masses. Other optional files are described in sec. 5.7.
5.9.2 Changing force-field parameters
If one wants to change the parameters of few bonded interactions in a molecule, this is most easily
accomplished by typing the parameters behind the definition of the bonded interaction directly in
the *.top file under the [ moleculetype ] section (see 5.8.1 for the format and units). If
one wants to change the parameters for all instances of a certain interaction one can change them
in the force-field file or add a new [ ???types ] section after including the force field. When
parameters for a certain interaction are defined multiple times, the last definition is used. As of
GROMACS version 3.1.3, a warning is generated when parameters are redefined with a different
value. Changing the Lennard-Jones parameters of an atom type is not recommended, because in
the GROMOS force fields the Lennard-Jones parameters for several combinations of atom types
are not generated according to the standard combination rules. Such combinations (and possibly
others that do follow the combination rules) are defined in the [ nonbond_params ] section,
and changing the Lennard-Jones parameters of an atom type has no effect on these combinations.
5.9.3 Adding atom types
As of GROMACS version 3.1.3, atom types can be added in an extra [ atomtypes ] section
after the the inclusion of the normal force field. After the definition of the new atom type(s), ad-
ditional non-bonded and pair parameters can be defined. In pre-3.1.3 versions of GROMACS, the
new atom types needed to be added in the [ atomtypes ] section of the force-field files, be-
cause all non-bonded parameters above the last [ atomtypes ] section would be overwritten
using the standard combination rules.

154 Chapter 5. Topologies
Chapter 6
Special Topics
6.1 Free energy implementation
For free energy calculations, there are two things that must be specified; the end states, and the
pathway connecting the end states. The end states can be specified in two ways. The most straight-
forward is through the specification of end states in the topology file. Most potential forms support
both an Astate and a Bstate. Whenever both states are specified, then the Astate corresponds to
the initial free energy state, and the Bstate corresponds to the final state.
In some cases, the end state can also be defined in some cases without altering the topology,
solely through the .mdp file, through the use of the couple-moltype,couple-lambda0,
couple-lambda1, and couple-intramol mdp keywords. Any molecule type selected in
couple-moltype will automatically have a Bstate implicitly constructed (and the Astate rede-
fined) according to the couple-lambda keywords. couple-lambda0 and couple-lambda1
define the non-bonded parameters that are present in the Astate (couple-lambda0) and the B
state (couple-lambda1). The choices are ’q’,’vdw’, and ’vdw-q’; these indicate the Coulom-
bic, van der Waals, or both parameters that are turned on in the respective state.
Once the end states are defined, then the path between the end states has to be defined. This path
is defined solely in the .mdp file. Starting in 4.6, λis a vector of components, with Coulombic,
van der Waals, bonded, restraint, and mass components all able to be adjusted independently. This
makes it possible to turn off the Coulombic term linearly, and then the van der Waals using soft
core, all in the same simulation. This is especially useful for replica exchange or expanded en-
semble simulations, where it is important to sample all the way from interacting to non-interacting
states in the same simulation to improve sampling.
fep-lambdas is the default array of λvalues ranging from 0 to 1. All of the other lambda arrays
use the values in this array if they are not specified. The previous behavior, where the pathway
is controlled by a single λvariable, can be preserved by using only fep-lambdas to define the
pathway.
For example, if you wanted to first to change the Coulombic terms, then the van der Waals terms,
changing bonded at the same time rate as the van der Waals, but changing the restraints throughout

156 Chapter 6. Special Topics
the first two-thirds of the simulation, then you could use this λvector:
coul-lambdas = 0.0 0.2 0.5 1.0 1.0 1.0 1.0 1.0 1.0 1.0
vdw-lambdas = 0.0 0.0 0.0 0.0 0.4 0.5 0.6 0.7 0.8 1.0
bonded-lambdas = 0.0 0.0 0.0 0.0 0.4 0.5 0.6 0.7 0.8 1.0
restraint-lambdas = 0.0 0.0 0.1 0.2 0.3 0.5 0.7 1.0 1.0 1.0
This is also equivalent to:
fep-lambdas = 0.0 0.0 0.0 0.0 0.4 0.5 0.6 0.7 0.8 1.0
coul-lambdas = 0.0 0.2 0.5 1.0 1.0 1.0 1.0 1.0 1.0 1.0
restraint-lambdas = 0.0 0.0 0.1 0.2 0.3 0.5 0.7 1.0 1.0 1.0
The fep-lambda array, in this case, is being used as the default to fill in the bonded and van
der Waals λarrays. Usually, it’s best to fill in all arrays explicitly, just to make sure things are
properly assigned.
If you want to turn on only restraints going from Ato B, then it would be:
restraint-lambdas = 0.0 0.1 0.2 0.4 0.6 1.0
and all of the other components of the λvector would be left in the Astate.
To compute free energies with a vector λusing thermodynamic integration, then the TI equation
becomes vector equation:
∆F=Zh∇Hi · d~
λ(6.1)
or for finite differences:
∆F≈ZXh∇Hi · ∆λ(6.2)
The external pymbar script downloaded from https://SimTK.org/home/pymbar can compute this
integral automatically from the GROMACS dhdl.xvg output.
6.2 Potential of mean force
A potential of mean force (PMF) is a potential that is obtained by integrating the mean force from
an ensemble of configurations. In GROMACS, there are several different methods to calculate the
mean force. Each method has its limitations, which are listed below.
•pull code: between the centers of mass of molecules or groups of molecules.
•AWH code: currently acts on coordinates provided by the pull code.
•free-energy code with harmonic bonds or constraints: between single atoms.
•free-energy code with position restraints: changing the conformation of a relatively im-
mobile group of atoms.

6.3. Non-equilibrium pulling 157
•pull code in limited cases: between groups of atoms that are part of a larger molecule for
which the bonds are constrained with SHAKE or LINCS. If the pull group if relatively large,
the pull code can be used.
The pull and free-energy code a described in more detail in the following two sections.
Entropic effects
When a distance between two atoms or the centers of mass of two groups is constrained or re-
strained, there will be a purely entropic contribution to the PMF due to the rotation of the two
groups [139]. For a system of two non-interacting masses the potential of mean force is:
Vpmf (r) = −(nc−1)kBTlog(r)(6.3)
where ncis the number of dimensions in which the constraint works (i.e. nc= 3 for a normal con-
straint and nc= 1 when only the z-direction is constrained). Whether one needs to correct for this
contribution depends on what the PMF should represent. When one wants to pull a substrate into a
protein, this entropic term indeed contributes to the work to get the substrate into the protein. But
when calculating a PMF between two solutes in a solvent, for the purpose of simulating without
solvent, the entropic contribution should be removed. Note that this term can be significant; when
at 300K the distance is halved, the contribution is 3.5 kJ mol−1.
6.3 Non-equilibrium pulling
When the distance between two groups is changed continuously, work is applied to the system,
which means that the system is no longer in equilibrium. Although in the limit of very slow pulling
the system is again in equilibrium, for many systems this limit is not reachable within reasonable
computational time. However, one can use the Jarzynski relation [140] to obtain the equilibrium
free-energy difference ∆Gbetween two distances from many non-equilibrium simulations:
∆GAB =−kBTlog De−βWAB EA(6.4)
where WAB is the work performed to force the system along one path from state A to B, the
angular bracket denotes averaging over a canonical ensemble of the initial state A and β= 1/kBT.
6.4 The pull code
The pull code applies forces or constraints between the centers of mass of one or more pairs of
groups of atoms. Each pull reaction coordinate is called a “coordinate” and it operates on usually
two, but sometimes more, pull groups. A pull group can be part of one or more pull coordinates.
Furthermore, a coordinate can also operate on a single group and an absolute reference position in
space. The distance between a pair of groups can be determined in 1, 2 or 3 dimensions, or can
be along a user-defined vector. The reference distance can be constant or can change linearly with
time. Normally all atoms are weighted by their mass, but an additional weighting factor can also
be used.
158 Chapter 6. Special Topics
V
z
zlink spring
rup
Figure 6.1: Schematic picture of pulling a lipid out of a lipid bilayer with umbrella pulling. Vrup
is the velocity at which the spring is retracted, Zlink is the atom to which the spring is attached
and Zspring is the location of the spring.
Several different pull types, i.e. ways to apply the pull force, are supported, and in all cases the
reference distance can be constant or linearly changing with time.
1. Umbrella pulling A harmonic potential is applied between the centers of mass of two
groups. Thus, the force is proportional to the displacement.
2. Constraint pulling The distance between the centers of mass of two groups is constrained.
The constraint force can be written to a file. This method uses the SHAKE algorithm but
only needs 1 iteration to be exact if only two groups are constrained.
3. Constant force pulling A constant force is applied between the centers of mass of two
groups. Thus, the potential is linear. In this case there is no reference distance of pull rate.
4. Flat bottom pulling Like umbrella pulling, but the potential and force are zero for coordi-
nate values below (pull-coord?-type = flat-bottom) or above (pull-coord?-type
= flat-bottom-high) a reference value. This is useful for restraining e.g. the distance
between two molecules to a certain region.
In addition, there are different types of reaction coordinates, so-called pull geometries. These are
set with the .mdp option pull-coord?-geometry.
Definition of the center of mass
In GROMACS, there are three ways to define the center of mass of a group. The standard way
is a “plain” center of mass, possibly with additional weighting factors. With periodic boundary
conditions it is no longer possible to uniquely define the center of mass of a group of atoms.
Therefore, a reference atom is used. For determining the center of mass, for all other atoms in the
group, the closest periodic image to the reference atom is used. This uniquely defines the center of
mass. By default, the middle (determined by the order in the topology) atom is used as a reference
atom, but the user can also select any other atom if it would be closer to center of the group.
6.4. The pull code 159
c
c
d
c
d
Figure 6.2: Comparison of a plain center of mass reference group versus a cylinder reference
group applied to interface systems. C is the reference group. The circles represent the center of
mass of two groups plus the reference group, dcis the reference distance.
For a layered system, for instance a lipid bilayer, it may be of interest to calculate the PMF of a
lipid as function of its distance from the whole bilayer. The whole bilayer can be taken as reference
group in that case, but it might also be of interest to define the reaction coordinate for the PMF
more locally. The .mdp option pull-coord?-geometry = cylinder does not use all
the atoms of the reference group, but instead dynamically only those within a cylinder with radius
pull-cylinder-r around the pull vector going through the pull group. This only works for
distances defined in one dimension, and the cylinder is oriented with its long axis along this one
dimension. To avoid jumps in the pull force, contributions of atoms are weighted as a function of
distance (in addition to the mass weighting):
w(r < rcyl)=1−2 r
rcyl !2
+ r
rcyl !4
(6.5)
w(r≥rcyl)=0 (6.6)
Note that the radial dependence on the weight causes a radial force on both cylinder group and
the other pull group. This is an undesirable, but unavoidable effect. To minimize this effect, the
cylinder radius should be chosen sufficiently large. The effective mass is 0.47 times that of a
cylinder with uniform weights and equal to the mass of uniform cylinder of 0.79 times the radius.
For a group of molecules in a periodic system, a plain reference group might not be well-defined.
An example is a water slab that is connected periodically in xand y, but has two liquid-vapor
interfaces along z. In such a setup, water molecules can evaporate from the liquid and they will
move through the vapor, through the periodic boundary, to the other interface. Such a system is
inherently periodic and there is no proper way of defining a “plain” center of mass along z. A
proper solution is to using a cosine shaped weighting profile for all atoms in the reference group.
The profile is a cosine with a single period in the unit cell. Its phase is optimized to give the
maximum sum of weights, including mass weighting. This provides a unique and continuous
reference position that is nearly identical to the plain center of mass position in case all atoms are

160 Chapter 6. Special Topics
all within a half of the unit-cell length. See ref [141] for details.
When relative weights wiare used during the calculations, either by supplying weights in the input
or due to cylinder geometry or due to cosine weighting, the weights need to be scaled to conserve
momentum:
w0
i=wi
N
X
j=1
wjmj,N
X
j=1
w2
jmj(6.7)
where mjis the mass of atom jof the group. The mass of the group, required for calculating the
constraint force, is:
M=
N
X
i=1
w0
imi(6.8)
The definition of the weighted center of mass is:
rcom =
N
X
i=1
w0
imiri,M(6.9)
From the centers of mass the AFM, constraint, or umbrella force Fcom on each group can be
calculated. The force on the center of mass of a group is redistributed to the atoms as follows:
Fi=w0
imi
MFcom (6.10)
Definition of the pull direction
The most common setup is to pull along the direction of the vector containing the two pull groups,
this is selected with pull-coord?-geometry = distance. You might want to pull along
a certain vector instead, which is selected with pull-coord?-geometry = direction.
But this can cause unwanted torque forces in the system, unless you pull against a reference group
with (nearly) fixed orientation, e.g. a membrane protein embedded in a membrane along x/y while
pulling along z. If your reference group does not have a fixed orientation, you should probably
use pull-coord?-geometry = direction-relative, see Fig. 6.3. Since the potential
now depends on the coordinates of two additional groups defining the orientation, the torque forces
will work on these two groups.
Definition of the angle and dihedral pull geometries
Four pull groups are required for pull-coord?-geometry = angle. In the same way
as for geometries with two groups, each consecutive pair of groups iand i+ 1 define a vector
connecting the COMs of groups iand i+ 1. The angle is defined as the angle between the two
resulting vectors. E.g., the .mdp option pull-coord?-groups = 1 2 2 4 defines the
angle between the vector from the COM of group 1 to the COM of group 2 and the vector from
the COM of group 2 to the COM of group 4. The angle takes values in the closed interval [0,
180] deg. For pull-coord?-geometry = angle-axis the angle is defined with respect
to a reference axis given by pull-coord?-vec and only two groups need to be given. The
dihedral geometry requires six pull groups. These pair up in the same way as described above and
6.5. Adaptive biasing with AWH 161
3
4
dp
2
1
Figure 6.3: The pull setup for geometry direction-relative. The “normal” pull groups
are 1 and 2. Groups 3 and 4 define the pull direction and thus the direction of the normal pull
forces (red). This leads to reaction forces (blue) on groups 3 and 4, which are perpendicular to the
pull direction. Their magnitude is given by the “normal” pull force times the ratio of dpand the
distance between groups 3 and 4.
so define three vectors. The dihedral angle is defined as the angle between the two planes spanned
by the two first and the two last vectors. Equivalently, the dihedral angle can be seen as the angle
between the first and the third vector when these vectors are projected onto a plane normal to the
second vector (the axis vector). As an example, consider a dihedral angle involving four groups:
1, 5, 8 and 9. Here, the .mdp option pull-coord?-groups = 8 1 1 5 5 9 specifies the
three vectors that define the dihedral angle: the first vector is the COM distance vector from group
8 to 1, the second vector is the COM distance vector from group 1 to 5, and the third vector is
the COM distance vector from group 5 to 9. The dihedral angle takes values in the interval (-180,
180] deg and has periodic boundaries.
Limitations
There is one theoretical limitation: strictly speaking, constraint forces can only be calculated
between groups that are not connected by constraints to the rest of the system. If a group contains
part of a molecule of which the bond lengths are constrained, the pull constraint and LINCS
or SHAKE bond constraint algorithms should be iterated simultaneously. This is not done in
GROMACS. This means that for simulations with constraints = all-bonds in the .mdp
file pulling is, strictly speaking, limited to whole molecules or groups of molecules. In some
cases this limitation can be avoided by using the free energy code, see sec. 6.9. In practice, the
errors caused by not iterating the two constraint algorithms can be negligible when the pull group
consists of a large amount of atoms and/or the pull force is small. In such cases, the constraint
correction displacement of the pull group is small compared to the bond lengths.
6.5 Adaptive biasing with AWH
The accelerated weight histogram method (AWH) [142] calculates the PMF along a reaction co-
ordinate by adding an adaptively determined biasing potential. AWH flattens free energy barriers
along the reaction coordinate by applying a history-dependent potential to the system that “fills
up” free energy minima. This is similar in spirit to other adaptive biasing potential methods, e.g.
the Wang-Landau [143], local elevation [144] and metadynamics [145] methods. The initial sam-
162 Chapter 6. Special Topics
pling stage of AWH makes the method robust against the choice of input parameters. Furthermore,
the target distribution along the reaction coordinate may be chosen freely.
6.5.1 Basics of the method
Rather than biasing the reaction coordinate ξ(x)directly, AWH acts on a reference coordinate λ.
The reaction coordinate ξ(x)is coupled to λwith a harmonic potential
Q(ξ, λ) = 1
2βk(ξ−λ)2,(6.11)
so that for large force constants k,ξ≈λ. Note the use of dimensionless energies for compatibility
with previously published work. Units of energy are obtained by multiplication with kBT= 1/β.
In the simulation, λsamples the user-defined sampling interval I. For a multidimensional reaction
coordinate ξ, the sampling interval is the Cartesian product I= ΠµIµ(a rectangular domain). The
connection between atom coordinates and λis established through the extended ensemble [68],
P(x, λ) = 1
Zeg(λ)−Q(ξ(x),λ)−V(x),(6.12)
where g(λ)is a bias function (a free variable) and V(x)is the unbiased potential energy of the
system. The distribution along λcan be tuned to be any predefined target distribution ρ(λ)(often
chosen to be flat) by choosing g(λ)wisely. This is evident from
P(λ) = ZP(x, λ)dx =1
Zeg(λ)Ze−Q(ξ(x),λ)−V(x)dx ≡1
Zeg(λ)−F(λ),(6.13)
where F(λ)is the free energy
F(λ) = −ln Ze−Q(ξ(x),λ)−V(x)dx. (6.14)
Being the convolution of the PMF with the Gaussian defined by the harmonic potential, F(λ)is
a smoothened version of the PMF. Eq. 6.13 shows that in order to obtain P(λ) = ρ(λ),F(λ)
needs to be determined accurately. Thus, AWH adaptively calculates F(λ)and simultaneously
converges P(λ)toward ρ(λ).
The free energy update
AWH is initialized with an estimate of the free energy F0(λ). At regular time intervals this estimate
is updated using data collected in between the updates. At update n, the applied bias gn(λ)is a
function of the current free energy estimate Fn(λ)and target distribution ρn(λ),
gn(λ) = ln ρn(λ) + Fn(λ),(6.15)
which is consistent with Eq. 6.13. Note that also the target distribution may be updated during the
simulation (see examples in section 6.5.3). Substituting this choice of g=gnback into Eq. 6.13
yields the simple free energy update
∆Fn(λ) = F(λ)−Fn(λ) = −ln Pn(λ)
ρn(λ),(6.16)

6.5. Adaptive biasing with AWH 163
which would yield a better estimate Fn+1 =Fn+ ∆Fn, assuming Pn(λ)can be measured accu-
rately. AWH estimates Pn(λ)by regularly calculating the conditional distribution
ωn(λ|x)≡Pn(λ|x) = egn(λ)−Q(ξ(x),λ)
Pλ0egn(λ0)−Q(ξ(x),λ0).(6.17)
Accumulating these probability weights yields Ptω(λ|x(t)) ∼Pn(λ), where RPn(λ|x)Pn(x)dx =
Pn(λ)has been used. The ωn(λ|x)weights are thus the samples of the AWH method. With the
limited amount of sampling one has in practice, update scheme 6.16 yields very noisy results.
AWH instead applies a free energy update that has the same form but which can be applied repeat-
edly with limited and localized sampling,
∆Fn=−ln Wn(λ) + Ptωn(λ|x(t))
Wn(λ) + Ptρn(λ)) .(6.18)
Here Wn(λ)is the reference weight histogram representing prior sampling. The update for W(λ),
disregarding the initial stage (see section 6.5.2), is
Wn+1(λ) = Wn(λ) + X
t
ρn(λ).(6.19)
Thus, the weight histogram equals the targeted, “ideal” history of samples. There are two impor-
tant things to note about the free energy update. First, sampling is driven away from oversampled,
currently local regions. For such λvalues, ωn(λ)> ρn(λ)and ∆Fn(λ)<0, which by Eq. 6.15
implies ∆gn(λ)<0(assuming ∆ρn≡0). Thus, the probability to sample λdecreases after the
update (see Eq. 6.13). Secondly, the normalization of the histogram Nn=PλWn(λ), determines
the update size |∆F(λ)|. For instance, for a single sample ω(λ|x), the shape of the update is
approximately a Gaussian function of width σ= 1/√βk and height ∝1/Nn[142],
|∆Fn(λ)| ∝ 1
Nn
e−1
2βk(ξ(x)−λ)2.(6.20)
Therefore, as samples accumulate in W(λ)and Nngrows, the updates get smaller, allowing for
the free energy to converge.
Note that quantity of interest to the user is not F(λ)but the PMF Φ(ξ).Φ(ξ)is extracted by
reweighting samples ξ(t)on the fly [142] (see also section 6.5.5) and will converge at the same
rate as F(λ), see Fig. 6.4. The PMF will be written to output (see section 6.5.7).
Applying the bias to the system
The bias potential can be applied to the system in two ways. Either by applying a harmonic
potential centered at λ(t), which is sampled using (rejection-free) Monte-Carlo sampling from
the conditional distribution ωn(λ|x(t)) = Pn(λ|x(t)), see Eq. 6.17. This is also called Gibbs
sampling or independence sampling. Alternatively, and by default in the code, the following
convolved bias potential can be applied,
Un(ξ) = −ln Zegn(λ)−Q(ξ,λ)dλ. (6.21)
These two approaches are equivalent in the sense that they give rise to the same biased probabilities
Pn(x)(cf. 6.12) while the dynamics are clearly different in the two cases. This choice does not
affect the internals of the AWH algorithm, only what force and potential AWH returns to the MD
engine.
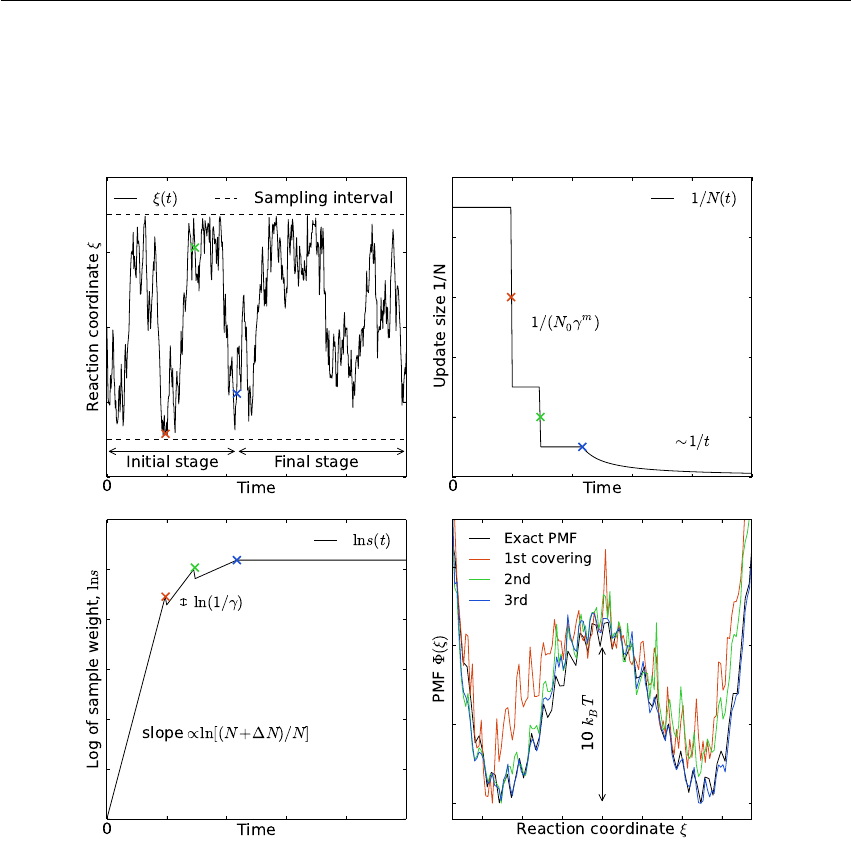
164 Chapter 6. Special Topics
Figure 6.4: AWH evolution in time for a Brownian particle in a double-well potential. The reaction
coordinate ξ(t)traverses the sampling interval multiple times in the initial stage before exiting
and entering the final stage (top left). In the final stage, the dynamics of ξbecomes increasingly
diffusive. The times of covering are shown as ×-markers of different colors. At these times
the free energy update size ∼1/N, where Nis the size of the weight histogram, is decreased by
scaling Nby a factor of γ= 3 (top right). In the final stage, Ngrows at the sampling rate and thus
1/N ∼1/t. The exit from the final stage is determined on the fly by ensuring that the effective
sample weight sof data collected in the final stage exceeds that of initial stage data (bottom left;
note that ln s(t)is plotted). An estimate of the PMF is also extracted from the simulation (bottom
right), which after exiting the initial stage should estimate global free energy differences fairly
accurately.

6.5. Adaptive biasing with AWH 165
6.5.2 The initial stage
Initially, when the bias potential is far from optimal, samples will be highly correlated. In such
cases, letting W(λ)accumulate samples as prescribed by Eq. 6.19, entails a too rapid decay of
the free energy update size. This motivates splitting the simulation into an initial stage where
the weight histogram grows according to a more restrictive and robust protocol, and a final stage
where the the weight histogram grows linearly at the sampling rate (Eq. 6.19). The AWH initial
stage takes inspiration from the well-known Wang-Landau algorithm [143], although there are
differences in the details.
In the initial stage the update size is kept constant (by keeping Nnconstant) until a transition
across the sampling interval has been detected, a “covering”. For the definition of a covering, see
Eq. 6.22 below. After a covering has occurred, Nnis scaled up by a constant “growth factor” γ,
chosen heuristically as γ= 3. Thus, in the initial stage Nnis set dynamically as Nn=γmN0,
where mis the number of coverings. Since the update size scales as 1/N ( Eq. 6.20) this leads to
a close to exponential decay of the update size in the initial stage, see Fig. 6.4.
The update size directly determines the rate of change of Fn(λ)and hence, from Eq. 6.15, also the
rate of change of the bias funcion gn(λ)Thus initially, when Nnis kept small and updates large,
the system will be driven along the reaction coordinate by the constantly fluctuating bias. If N0
is set small enough, the first transition will typically be fast because of the large update size and
will quickly give a first rough estimate of the free energy. The second transition, using N1=γN0
refines this estimate further. Thus, rather than very carefully filling free energy minima using a
small initial update size, the sampling interval is sweeped back-and-forth multiple times, using a
wide range of update sizes, see Fig. 6.4. This way, the initial stage also makes AWH robust against
the choice of N0.
The covering criterion
In the general case of a multidimensional reaction coordinate λ= (λµ), the sampling interval Iis
considered covered when all dimensions have been covered. A dimension dis covered if all points
λµin the one-dimensional sampling interval Iµhave been “visited”. Finally, a point λµ∈Iµ
has been visited if there is at least one point λ∗∈Iwith λ∗
µ=λµthat since the last covering
has accumulated probability weight corresponding to the peak of a multidimensional Gaussian
distribution
∆W(λ∗)≥wpeak ≡Y
µ
∆λµ
√2πσk
.(6.22)
Here, ∆λµis the point spacing of the discretized Iµand σk= 1/pβkµ(where kµis the force
constant) is the Gaussian width.
Exit from the initial stage
For longer times, when major free energy barriers have largely been flattened by the converging
bias potential, the histogram W(λ)should grow at the actual sampling rate and the initial stage
needs to be exited [146]. There are multiple reasonable (heuristic) ways of determining when
this transition should take place. One option is to postulate that the number of samples in the

166 Chapter 6. Special Topics
weight histogram Nnshould never exceed the actual number of collected samples, and exit the
initial stage when this condition breaks [142]. In the initial stage, Ngrows close to exponentially
while the collected number of samples grows linearly, so an exit will surely occur eventually. Here
we instead apply an exit criterion based on the observation that “artifically” keeping Nconstant
while continuing to collect samples corresponds to scaling down the relative weight of old samples
relative to new ones. Similarly, the subsequent scaling up of Nby a factor γcorresponds to scaling
up the weight of old data. Briefly, the exit criterion is devised such that the weight of a sample
collected after the initial stage is always larger or equal to the weight of a sample collected during
the initial stage, see Fig. 6.4. This is consistent with scaling down early, noisy data.
The initial stage exit criterion will now be described in detail. We start out at the beginning of a
covering stage, so that Nhas just been scaled by γand is now kept constant. Thus, the first sample
of this stage has the weight s= 1/γ relative to the last sample of the previous covering stage. We
assume that ∆Nsamples are collected and added to Wfor each update . To keep Nconstant, W
needs to be scaled down by a factor N/(N+ ∆N)after every update. Equivalently, this means
that new data is scaled up relative to old data by the inverse factor. Thus, after ∆nupdates a new
sample has the relative weight s= (1/γ)[(Nn+ ∆N)/Nn]∆n. Now assume covering occurs at
this time. To continue to the next covering stage, Nshould be scaled by γ, which corresponds
to again multiplying sby 1/γ. If at this point s≥γ, then after rescaling s≥1; i.e. overall the
relative weight of a new sample relative to an old sample is still growing fast. If on the contrary
s<γ, and this defines the exit from the initial stage, then the initial stage is over and from now N
simply grows at the sampling rate (see Eq. 6.19). To really ensure that s≥1holds before exiting,
so that samples after the exit have at least the sample weight of older samples, the last covering
stage is extended by a sufficient number of updates.
6.5.3 Choice of target distribution
The target distribution ρ(λ)is traditionally chosen to be uniform
ρconst(λ) = const.(6.23)
This choice exactly flattens F(λ)in user-defined sampling interval I. Generally, ρ(λ) = 0, λ /∈I.
In certain cases other choices may be preferable. For instance, in the multidimensional case the
rectangular sampling interval is likely to contain regions of very high free energy, e.g. where
atoms are clashing. To exclude such regions, ρ(λ)can specified by the following function of the
free energy
ρcut(λ)∝1
1 + eF(λ)−Fcut ,(6.24)
where Fcut is a free energy cutoff (relative to minλF(λ)). Thus, regions of the sampling interval
where F(λ)> Fcut will be exponentially suppressed (in a smooth fashion). Alternatively, very
high free energy regions could be avoided while still flattening more moderate free energy barriers
by targeting a Boltzmann distribution corresponding to scaling β= 1/kBTby a factor 0< sβ<
1,
ρBoltz(λ)∝e−sβF(λ),(6.25)
The parameter sβdetermines to what degree the free energy landscape is flattened; the lower sβ,
the flatter. Note that both ρcut(λ)and ρBoltz(λ)depend on F(λ), which needs to be substituted

6.5. Adaptive biasing with AWH 167
by the current best estimate Fn(λ). Thus, the target distribution is also updated (consistently with
Eq. 6.15).
There is in fact an alternative approach to obtaining ρBoltz(λ)as the limiting target distribution
in AWH, which is particular in the way the weight histogram W(λ)and the target distribution
ρare updated and coupled to each other. This yields an evolution of the bias potential which is
very similar to that of well-tempered metadynamics [147], see [142] for details. Because of the
popularity and success of well-tempered metadynamics, this is a special case worth considering.
In this case ρis a function of the reference weight histogram
ρBoltz,loc(λ)∝W(λ),(6.26)
and the update of the weight histogram is modified (cf. Eq. 6.19)
Wn+1(λ) = Wn(λ) + sβX
t
ω(λ|x(t)).(6.27)
Thus, here the weight histogram equals the real history of samples, but scaled by sβ. This target
distribution is called local Boltzmann since Wis only modified locally, where sampling has taken
place. We see that when sβ≈0the histogram essentially does not grow and the size of the
free energy update will stay at a constant value (as in the original formulation of metadynamics).
Thus, the free energy estimate will not converge, but continue to fluctuate around the correct value.
This illustrates the inherent coupling between the convergence and choice of target distribution for
this special choice of target. Furthermore note that when using ρ=ρBoltz,loc there is no initial
stage (section 6.5.2). The rescaling of the weight histogram applied in the initial stage is a global
operation, which is incompatible ρBoltz,loc only depending locally on the sampling history.
Lastly, the target distribution can be modulated by arbitrary probability weights
ρ(λ) = ρ0(λ)wuser(λ).(6.28)
where wuser(λ)is provided by user data and in principle ρ0(λ)can be any of the target distributions
mentioned above.
6.5.4 Multiple independent or sharing biases
Multiple independent bias potentials may be applied within one simulation. This only makes
sense if the biased coordinates ξ(1),ξ(2),. . . evolve essentially independently from one another.
A typical example of this would be when applying an independent bias to each monomer of a
protein. Furthermore, multiple AWH simulations can be launched in parallel, each with a (set of)
indepedendent biases.
If the defined sampling interval is large relative to the diffusion time of the reaction coordinate,
traversing the sampling interval multiple times as is required by the initial stage (section 6.5.2) may
take an infeasible mount of simulation time. In these cases it could be advantageous to parallelize
the work and have a group of multiple “walkers” ξ(i)(t)share a single bias potential. This can be
achieved by collecting samples from all ξ(i)of the same sharing group into a single histogram and
update a common free energy estimate. Samples can be shared between walkers within the simu-
lation and/or between multiple simulations. However, currently only sharing between simulations
is supported in the code while all biases within a simulation are independent.

168 Chapter 6. Special Topics
Note that when attempting to shorten the simulation time by using bias-sharing walkers, care
must be taken to ensure the simulations are still long enough to properly explore and equilibrate
all regions of the sampling interval. To begin, the walkers in a group should be decorrelated
and distributed approximately according to the target distribution before starting to refine the free
energy. This can be achieved e.g. by “equilibrating” the shared weight histogram before letting it
grow; for instance, W(λ)/N ≈ρ(λ)with some tolerance.
Furthermore, the “covering” or transition criterion of the initial stage should to be generalized to
detect when the sampling interval has been collectively traversed. One alternative is to just use
the same criterion as for a single walker (but now with more samples), see Eq. 6.22. However, in
contrast to the single walker case this does not ensure that any real transitions across the sampling
interval has taken place; in principle all walkers could be sampling only very locally and still
cover the whole interval. Just as with a standard umbrella sampling procedure, the free energy
may appear to be converged while in reality simulations sampling closeby λvalues are sampling
disconnected regions of phase space. A stricter criterion, which helps avoid such issues, is to
require that before a simulation marks a point λµalong dimension µas visited, and shares this
with the other walkers, also all points within a certain diameter Dcover should have been visited
(i.e.fulfill Eq. 6.22). Increasing Dcover increases robustness, but may slow down convergence. For
the maximum value of Dcover, equal to the length of the sampling interval, the sampling interval
is considered covered when at least one walker has independently traversed the sampling interval.
6.5.5 Reweighting and combining biased data
Often one may want to, post-simulation, calculate the unbiased PMF Φ(u)of another variable
u(x).Φ(u)can be estimated using ξ-biased data by reweighting (“unbiasing”) the trajectory using
the bias potential Un(t), see Eq. 6.21. Essentially, one bins the biased data along uand removes
the effect of Un(t)by dividing the weight of samples u(t)by e−Un(t)(ξ(t)),
ˆ
Φ(u) = −ln X
t
1u(u(t))eUn(t)(ξ(t)Zn(t).(6.29)
Here the indicator function 1udenotes the binning procedure: 1u(u0) = 1 if u0falls into the bin
labeled by uand 0otherwise. The normalization factor Zn=Re−Φ(ξ)−Un(ξ)dξ is the partition
function of the extended ensemble. As can be seen Zndepends on Φ(ξ), the PMF of the (biased)
reaction coordinate ξ(which is calculated and written to file by the AWH simulation). It is advis-
able to use only final stage data in the reweighting procedure due to the rapid change of the bias
potential during the initial stage. If one would include initial stage data, one should use the sample
weights that are inferred by the repeated rescaling of the histogram in the initial stage, for the sake
of consistency. Initial stage samples would then in any case be heavily scaled down relative to final
stage samples. Note that Eq. 6.29 can also be used to combine data from multiple simulations (by
adding another sum also over the trajectory set). Furthermore, when multiple independent AWH
biases have generated a set of PMF estimates {ˆ
Φ(i)(ξ)}, a combined best estimate ˆ
Φ(ξ)can be
obtained by applying self-consistent exponential averaging. More details on this procedure and a
derivation of Eq. 6.29 (using slightly different notation) can be found in [148].

6.5. Adaptive biasing with AWH 169
6.5.6 The friction metric
During the AWH simulation, the following time-integrated force correlation function is calcu-
lated,
ηµν (λ) = βZ∞
0hδFµ(x(t), λ)δFν(x(0), λ)ω(λ|x(t))ω(λ|x(0))i
hω2(λ|x)idt. (6.30)
Here Fµ(x, λ) = kµ(ξµ(x)−λµ)is the force along dimension µfrom an harmonic potential
centered at λand δFµ(x, λ) = Fµ(x, λ)− hFµ(x, λ)iis the deviation of the force. The fac-
tors ω(λ|x(t)), see Eq. 6.17, reweight the samples. ηµν (λ)is a friction tensor [149]. Its ma-
trix elements are inversely proportional to local diffusion coefficients. A measure of sampling
(in)efficiency at each λis given by
η1
2(λ) = qdet ηµν (λ).(6.31)
A large value of η1
2(λ)indicates slow dynamics and long correlation times, which may require
more sampling.
6.5.7 Usage
AWH stores data in the energy file (.edr) with a frequency set by the user. The data – the PMF,
the convolved bias, distributions of the λand ξcoordinates, etc. – can be extracted after the
simulation using the gmx awh tool. Furthermore, the trajectory of the reaction coordinate ξ(t)is
printed to the pull output file pullx.xvg. The log file (.log) also contains information; check
for messages starting with “awh”, they will tell you about covering and potential sampling issues.
Setting the initial update size
The initial value of the weight histogram size Nsets the initial update size (and the rate of change
of the bias). When Nis kept constant, like in the initial stage, the average variance of the free
energy scales as ε2∼1/(ND)[142], for a simple model system with constant diffusion Dalong
the reaction coordinate. This provides a ballpark estimate used by AWH to initialize Nin terms
of more meaningful quantities 1
N0
=1
N0(ε0, D)∼Dε2
0.(6.32)
Essentially, this tells us that a slower system (small D) requires more samples (larger N0) to
attain the same level of accuracy (ε0) at a given sampling rate. Conversely, for a system of given
diffusion, how to choose the initial biasing rate depends on how good the initial accuracy is. Both
the initial error ε0and the diffusion Donly need to be roughly estimated or guessed. In the typical
case, one would only tweak the Dparameter, and use a default value for ε0. For good convergence,
Dshould be chosen as large as possible (while maintaining a stable system) giving large initial
bias updates and fast initial transitions. Choosing Dtoo small can lead to slow initial convergence.
It may be a good idea to run a short trial simulation and after the first covering check the maximum
free energy difference of the PMF estimate. If this is much larger than the expected magnitude of
the free energy barriers that should be crossed, then the system is probably being pulled too hard
and Dshould be decreased. ε0on the other hand, would only be tweaked when starting an AWH
simulation using a fairly accurate guess of the PMF as input.

170 Chapter 6. Special Topics
Tips for efficient sampling
The force constant kshould be larger than the curvature of the PMF landscape. If this is not
the case, the distributions of the reaction coordinate ξand the reference coordinate λ, will differ
significantly and warnings will be printed in the log file. One can choose kas large as the time step
supports. This will neccessarily increase the number of points of the discretized sampling interval
I. In general however, it should not affect the performance of the simulation noticeably because
the AWH update is implemented such that only sampled points are accessed at free energy update
time.
As with any method, the choice of reaction coordinate(s) is critical. If a single reaction coordinate
does not suffice, identifying a second reaction coordinate and sampling the two-dimensional land-
scape may help. In this case, using a target distribution with a free energy cutoff (see Eq. 6.24)
might be required to avoid sampling uninteresting regions of very high free energy. Obtaining
accurate free energies for reaction coordinates of much higher dimensionality than 3 or possibly 4
is generally not feasible.
Monitoring the transition rate of ξ(t), across the sampling interval is also advisable. For reliable
statistics (e.g. when reweighting the trajectory as described in section 6.5.5), one would generally
want to observe at least a few transitions after having exited the initial stage. Furthermore, if
the dynamics of the reaction coordinate suddenly changes, this may be a sign of e.g. a reaction
coordinate problem.
Difficult regions of sampling may also be detected by calculating the friction tensor ηµν (λ)in
the sampling interval, see section 6.5.6.ηµν (λ)as well as the sampling efficiency measure η1
2(λ)
(Eq. 6.31) are written to the energy file and can be extracted with gmx awh. A high peak in η1
2(λ)
indicates that this region requires longer time to sample properly.
6.6 Enforced Rotation
This module can be used to enforce the rotation of a group of atoms, as e.g. a protein subunit.
There are a variety of rotation potentials, among them complex ones that allow flexible adaptations
of both the rotated subunit as well as the local rotation axis during the simulation. An example
application can be found in ref. [150].
6.6.1 Fixed Axis Rotation
Stationary Axis with an Isotropic Potential
In the fixed axis approach (see Fig. 6.5B), torque on a group of Natoms with positions xi(denoted
“rotation group”) is applied by rotating a reference set of atomic positions – usually their initial
positions y0
i– at a constant angular velocity ωaround an axis defined by a direction vector ˆ
vand
a pivot point u. To that aim, each atom with position xiis attracted by a “virtual spring” potential
to its moving reference position yi=Ω(t)(y0
i−u), where Ω(t)is a matrix that describes the
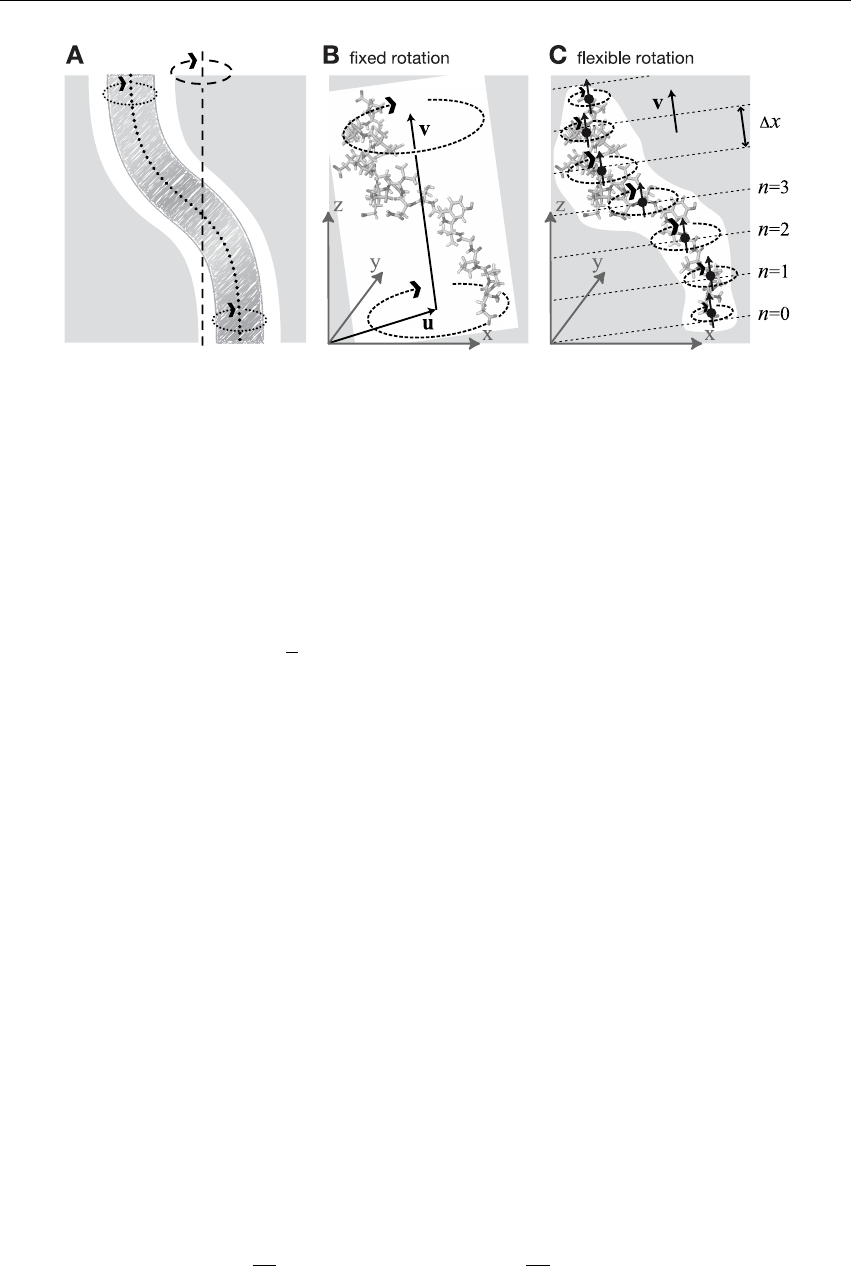
6.6. Enforced Rotation 171
Figure 6.5: Comparison of fixed and flexible axis rotation. A: Rotating the sketched shape inside
the white tubular cavity can create artifacts when a fixed rotation axis (dashed) is used. More
realistically, the shape would revolve like a flexible pipe-cleaner (dotted) inside the bearing (gray).
B: Fixed rotation around an axis vwith a pivot point specified by the vector u.C: Subdividing
the rotating fragment into slabs with separate rotation axes (↑) and pivot points (•) for each slab
allows for flexibility. The distance between two slabs with indices nand n+ 1 is ∆x.
rotation around the axis. In the simplest case, the “springs” are described by a harmonic potential,
Viso =k
2
N
X
i=1
wihΩ(t)(y0
i−u)−(xi−u)i2,(6.33)
with optional mass-weighted prefactors wi=N mi/M with total mass M=PN
i=1 mi. The
rotation matrix Ω(t)is
Ω(t) =
cos ωt +v2
xξ vxvyξ−vzsin ωt vxvzξ+vysin ωt
vxvyξ+vzsin ωt cos ωt +v2
yξ vyvzξ−vxsin ωt
vxvzξ−vysin ωt vyvzξ+vxsin ωt cos ωt +v2
zξ
,
where vx,vy, and vzare the components of the normalized rotation vector ˆ
v, and ξ:= 1−cos(ωt).
As illustrated in Fig. 6.6A for a single atom j, the rotation matrix Ω(t)operates on the initial
reference positions y0
j=xj(t0)of atom jat t=t0. At a later time t, the reference position has
rotated away from its initial place (along the blue dashed line), resulting in the force
Fiso
j=−∇jViso =k wjhΩ(t)(y0
j−u)−(xj−u)i,(6.34)
which is directed towards the reference position.
Pivot-Free Isotropic Potential
Instead of a fixed pivot vector uthis potential uses the center of mass xcof the rotation group as
pivot for the rotation axis,
xc=1
M
N
X
i=1
mixiand y0
c=1
M
N
X
i=1
miy0
i,(6.35)
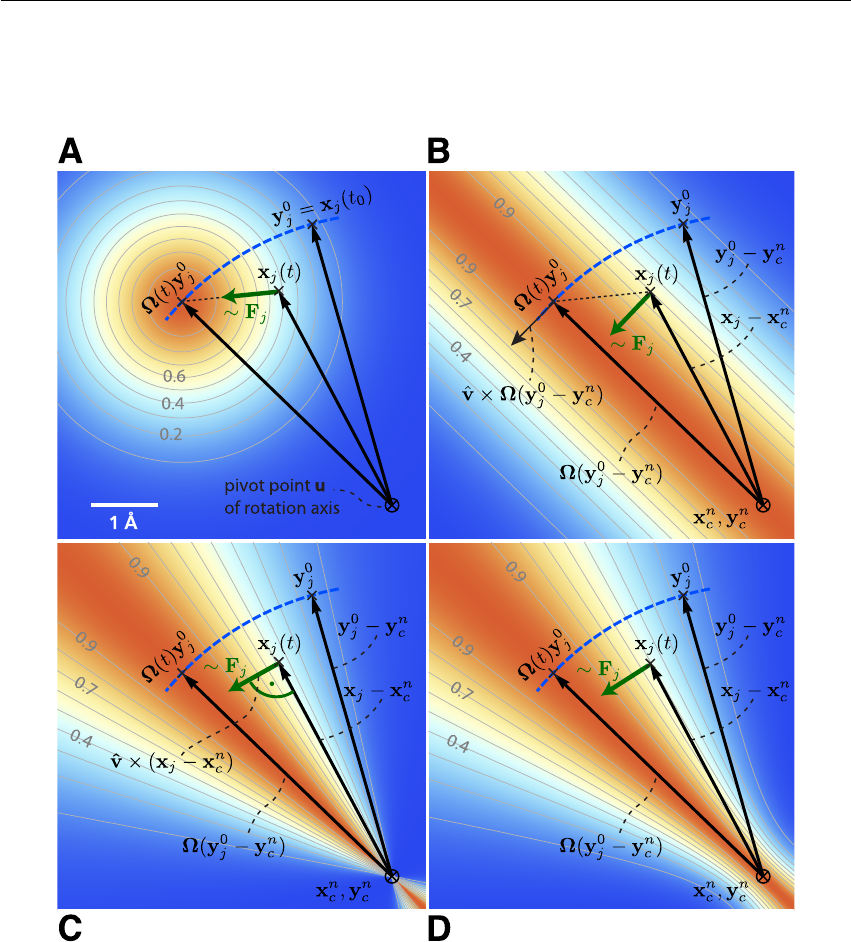
172 Chapter 6. Special Topics
Vrm,Vflex
V
iso
V
rm2,Vflex2 (=0.01 nm2
)
Vrm2,Vflex2 (= 0 nm2)
Figure 6.6: Selection of different rotation potentials and definition of notation. All four potentials
V(color coded) are shown for a single atom at position xj(t).A: Isotropic potential Viso,B:
radial motion potential Vrm and flexible potential Vflex,C–D: radial motion 2 potential Vrm2
and flexible 2 potential Vflex2 for 0= 0 nm2(C) and 0= 0.01 nm2(D). The rotation axis is
perpendicular to the plane and marked by ⊗. The light gray contours indicate Boltzmann factors
e−V/(kBT)in the xj-plane for T= 300 K and k= 200 kJ/(mol·nm2). The green arrow shows
the direction of the force Fjacting on atom j; the blue dashed line indicates the motion of the
reference position.

6.6. Enforced Rotation 173
which yields the “pivot-free” isotropic potential
Viso-pf =k
2
N
X
i=1
wihΩ(t)(y0
i−y0
c)−(xi−xc)i2,(6.36)
with forces
Fiso-pf
j=k wjhΩ(t)(y0
j−y0
c)−(xj−xc)i.(6.37)
Without mass-weighting, the pivot xcis the geometrical center of the group.
Parallel Motion Potential Variant
The forces generated by the isotropic potentials (eqns. 6.33 and 6.36) also contain components
parallel to the rotation axis and thereby restrain motions along the axis of either the whole ro-
tation group (in case of Viso) or within the rotation group (in case of Viso-pf ). For cases where
unrestrained motion along the axis is preferred, we have implemented a “parallel motion” variant
by eliminating all components parallel to the rotation axis for the potential. This is achieved by
projecting the distance vectors between reference and actual positions
ri=Ω(t)(y0
i−u)−(xi−u)(6.38)
onto the plane perpendicular to the rotation vector,
r⊥
i:= ri−(ri·ˆ
v)ˆ
v,(6.39)
yielding
Vpm =k
2
N
X
i=1
wi(r⊥
i)2
=k
2
N
X
i=1
winΩ(t)(y0
i−u)−(xi−u)
−nhΩ(t)(y0
i−u)−(xi−u)i·ˆ
voˆ
vo2,(6.40)
and similarly
Fpm
j=k wjr⊥
j.(6.41)
Pivot-Free Parallel Motion Potential
Replacing in eqn. 6.40 the fixed pivot uby the center of mass xcyields the pivot-free variant of
the parallel motion potential. With
si=Ω(t)(y0
i−y0
c)−(xi−xc)(6.42)
the respective potential and forces are
Vpm-pf =k
2
N
X
i=1
wi(s⊥
i)2,(6.43)
Fpm-pf
j=k wjs⊥
j.(6.44)

174 Chapter 6. Special Topics
Radial Motion Potential
In the above variants, the minimum of the rotation potential is either a single point at the reference
position yi(for the isotropic potentials) or a single line through yiparallel to the rotation axis (for
the parallel motion potentials). As a result, radial forces restrict radial motions of the atoms. The
two subsequent types of rotation potentials, Vrm and Vrm2, drastically reduce or even eliminate
this effect. The first variant, Vrm (Fig. 6.6B), eliminates all force components parallel to the vector
connecting the reference atom and the rotation axis,
Vrm =k
2
N
X
i=1
wi[pi·(xi−u)]2,(6.45)
with
pi:= ˆ
v×Ω(t)(y0
i−u)
kˆ
v×Ω(t)(y0
i−u)k.(6.46)
This variant depends only on the distance pi·(xi−u)of atom ifrom the plane spanned by ˆ
vand
Ω(t)(y0
i−u). The resulting force is
Frm
j=−k wjhpj·(xj−u)ipj.(6.47)
Pivot-Free Radial Motion Potential
Proceeding similar to the pivot-free isotropic potential yields a pivot-free version of the above
potential. With
qi:= ˆ
v×Ω(t)(y0
i−y0
c)
kˆ
v×Ω(t)(y0
i−y0
c)k,(6.48)
the potential and force for the pivot-free variant of the radial motion potential read
Vrm-pf =k
2
N
X
i=1
wi[qi·(xi−xc)]2,(6.49)
Frm-pf
j=−k wjhqj·(xj−xc)iqj+kmj
M
N
X
i=1
wi[qi·(xi−xc)] qi.(6.50)
Radial Motion 2 Alternative Potential
As seen in Fig. 6.6B, the force resulting from Vrm still contains a small, second-order radial
component. In most cases, this perturbation is tolerable; if not, the following alternative, Vrm2,
fully eliminates the radial contribution to the force, as depicted in Fig. 6.6C,
Vrm2 =k
2
N
X
i=1
wi(ˆ
v×(xi−u)) ·Ω(t)(y0
i−u)2
kˆ
v×(xi−u)k2+0,(6.51)
where a small parameter 0has been introduced to avoid singularities. For 0= 0 nm2, the equipo-
tential planes are spanned by xi−uand ˆ
v, yielding a force perpendicular to xi−u, thus not
contracting or expanding structural parts that moved away from or toward the rotation axis.

6.6. Enforced Rotation 175
Choosing a small positive 0(e.g.,0= 0.01 nm2, Fig. 6.6D) in the denominator of eqn. 6.51 yields
a well-defined potential and continuous forces also close to the rotation axis, which is not the case
for 0= 0 nm2(Fig. 6.6C). With
ri:= Ω(t)(y0
i−u)(6.52)
si:= ˆ
v×(xi−u)
kˆ
v×(xi−u)k≡Ψiˆ
v×(xi−u)(6.53)
Ψ∗
i:= 1
kˆ
v×(xi−u)k2+0(6.54)
the force on atom jreads
Frm2
j=−k(wj(sj·rj)"Ψ∗
j
Ψ
j
rj−Ψ∗2
j
Ψ3
j
(sj·rj)sj#)׈
v.(6.55)
Pivot-Free Radial Motion 2 Potential
The pivot-free variant of the above potential is
Vrm2-pf =k
2
N
X
i=1
wi(ˆ
v×(xi−xc)) ·Ω(t)(y0
i−yc)2
kˆ
v×(xi−xc)k2+0.(6.56)
With
ri:= Ω(t)(y0
i−yc)(6.57)
si:= ˆ
v×(xi−xc)
kˆ
v×(xi−xc)k≡Ψiˆ
v×(xi−xc)(6.58)
Ψ∗
i:= 1
kˆ
v×(xi−xc)k2+0(6.59)
the force on atom jreads
Frm2-pf
j=−k(wj(sj·rj)"Ψ∗
j
Ψ
j
rj−Ψ∗2
j
Ψ3
j
(sj·rj)sj#)׈
v
+kmj
M(N
X
i=1
wi(si·ri)"Ψ∗
i
Ψi
ri−Ψ∗2
i
Ψ3
i
(si·ri)si#)׈
v.(6.60)
6.6.2 Flexible Axis Rotation
As sketched in Fig. 6.5A–B, the rigid body behavior of the fixed axis rotation scheme is a drawback
for many applications. In particular, deformations of the rotation group are suppressed when the
equilibrium atom positions directly depend on the reference positions. To avoid this limitation,
eqns. 6.50 and 6.56 will now be generalized towards a “flexible axis” as sketched in Fig. 6.5C. This
will be achieved by subdividing the rotation group into a set of equidistant slabs perpendicular to
the rotation vector, and by applying a separate rotation potential to each of these slabs. Fig. 6.5C
shows the midplanes of the slabs as dotted straight lines and the centers as thick black dots.

176 Chapter 6. Special Topics
Figure 6.7: Gaussian functions gncentered at n∆xfor a slab distance ∆x= 1.5nm and n≥ −2.
Gaussian function g0is highlighted in bold; the dashed line depicts the sum of the shown Gaussian
functions.
To avoid discontinuities in the potential and in the forces, we define “soft slabs” by weighing the
contributions of each slab nto the total potential function Vflex by a Gaussian function
gn(xi)=Γexp −β2
n(xi)
2σ2!,(6.61)
centered at the midplane of the nth slab. Here σis the width of the Gaussian function, ∆xthe
distance between adjacent slabs, and
βn(xi) := xi·ˆ
v−n∆x . (6.62)
A most convenient choice is σ= 0.7∆xand
1/Γ = X
n∈Z
exp −(n−1
4)2
2·0.72!≈1.75464 ,
which yields a nearly constant sum, essentially independent of xi(dashed line in Fig. 6.7), i.e.,
X
n∈Z
gn(xi) = 1 + (xi),(6.63)
with |(xi)|<1.3·10−4. This choice also implies that the individual contributions to the force
from the slabs add up to unity such that no further normalization is required.
To each slab center xn
c, all atoms contribute by their Gaussian-weighted (optionally also mass-
weighted) position vectors gn(xi)xi. The instantaneous slab centers xn
care calculated from the
current positions xi,
xn
c=PN
i=1 gn(xi)mixi
PN
i=1 gn(xi)mi
,(6.64)
while the reference centers yn
care calculated from the reference positions y0
i,
yn
c=PN
i=1 gn(y0
i)miy0
i
PN
i=1 gn(y0
i)mi
.(6.65)
Due to the rapid decay of gn, each slab will essentially involve contributions from atoms located
within ≈3∆xfrom the slab center only.

6.6. Enforced Rotation 177
Flexible Axis Potential
We consider two flexible axis variants. For the first variant, the slab segmentation procedure with
Gaussian weighting is applied to the radial motion potential (eqn. 6.50 / Fig. 6.6B), yielding as the
contribution of slab n
Vn=k
2
N
X
i=1
wign(xi) [qn
i·(xi−xn
c)]2,
and a total potential function
Vflex =X
n
Vn.(6.66)
Note that the global center of mass xcused in eqn. 6.50 is now replaced by xn
c, the center of mass
of the slab. With
qn
i:= ˆ
v×Ω(t)(y0
i−yn
c)
kˆ
v×Ω(t)(y0
i−yn
c)k(6.67)
bn
i:= qn
i·(xi−xn
c),(6.68)
the resulting force on atom jreads
Fflex
j=−k wjX
n
gn(xj)bn
jqn
j−bn
j
βn(xj)
2σ2ˆ
v
+k mjX
n
gn(xj)
Phgn(xh)
N
X
i=1
wign(xi)bn
iqn
i−βn(xj)
σ2[qn
i·(xj−xn
c)] ˆ
v.(6.69)
Note that for Vflex, as defined, the slabs are fixed in space and so are the reference centers yn
c. If
during the simulation the rotation group moves too far in vdirection, it may enter a region where
– due to the lack of nearby reference positions – no reference slab centers are defined, rendering
the potential evaluation impossible. We therefore have included a slightly modified version of
this potential that avoids this problem by attaching the midplane of slab n= 0 to the center of
mass of the rotation group, yielding slabs that move with the rotation group. This is achieved by
subtracting the center of mass xcof the group from the positions,
˜
xi=xi−xc,and ˜
y0
i=y0
i−y0
c,(6.70)
such that
Vflex-t =k
2X
n
N
X
i=1
wign(˜
xi)"ˆ
v×Ω(t)(˜
y0
i−˜
yn
c)
kˆ
v×Ω(t)(˜
y0
i−˜
yn
c)k·(˜
xi−˜
xn
c)#2
.(6.71)
To simplify the force derivation, and for efficiency reasons, we here assume xcto be constant, and
thus ∂xc/∂x =∂xc/∂y =∂xc/∂z = 0. The resulting force error is small (of order O(1/N)or
O(mj/M)if mass-weighting is applied) and can therefore be tolerated. With this assumption, the
forces Fflex-t have the same form as eqn. 6.69.

178 Chapter 6. Special Topics
Flexible Axis 2 Alternative Potential
In this second variant, slab segmentation is applied to Vrm2 (eqn. 6.56), resulting in a flexible axis
potential without radial force contributions (Fig. 6.6C),
Vflex2 =k
2
N
X
i=1 X
n
wign(xi)(ˆ
v×(xi−xn
c)) ·Ω(t)(y0
i−yn
c)2
kˆ
v×(xi−xn
c)k2+0.(6.72)
With
rn
i:= Ω(t)(y0
i−yn
c)(6.73)
sn
i:= ˆ
v×(xi−xn
c)
kˆ
v×(xi−xn
c)k≡ψiˆ
v×(xi−xn
c)(6.74)
ψ∗
i:= 1
kˆ
v×(xi−xn
c)k2+0(6.75)
Wn
j:= gn(xj)mj
Phgn(xh)mh
(6.76)
Sn:=
N
X
i=1
wign(xi) (sn
i·rn
i)"ψ∗
i
ψi
rn
i−ψ∗2
i
ψ3
i
(sn
i·rn
i)sn
i#(6.77)
the force on atom jreads
Fflex2
j=−k(X
n
wjgn(xj) (sn
j·rn
j)"ψ∗
j
ψj
rn
j−ψ∗2
j
ψ3
j
(sn
j·rn
j)sn
j#)׈
v
+k(X
n
Wn
jSn)׈
v−k(X
n
Wn
j
βn(xj)
σ2
1
ψj
sn
j·Sn)ˆ
v
+k
2(X
n
wjgn(xj)βn(xj)
σ2
ψ∗
j
ψ2
j
(sn
j·rn
j)2)ˆ
v.(6.78)
Applying transformation (6.70) yields a “translation-tolerant” version of the flexible 2 potential,
Vflex2-t. Again, assuming that ∂xc/∂x,∂xc/∂y,∂xc/∂z are small, the resulting equations for
Vflex2-t and Fflex2-t are similar to those of Vflex2 and Fflex2.
6.6.3 Usage
To apply enforced rotation, the particles ithat are to be subjected to one of the rotation potentials
are defined via index groups rot-group0,rot-group1, etc., in the .mdp input file. The
reference positions y0
iare read from a special .trr file provided to grompp. If no such file is
found, xi(t= 0) are used as reference positions and written to .trr such that they can be used for
subsequent setups. All parameters of the potentials such as k,0, etc. (Table 6.1) are provided as
.mdp parameters; rot-type selects the type of the potential. The option rot-massw allows
to choose whether or not to use mass-weighted averaging. For the flexible potentials, a cutoff
value gmin
n(typically gmin
n= 0.001) makes shure that only significant contributions to Vand F
are evaluated, i.e. terms with gn(x)< gmin
nare omitted. Table 6.2 summarizes observables that
are written to additional output files and which are described below.

6.6. Enforced Rotation 179
Table 6.1: Parameters used by the various rotation potentials. x’s indicate which parameter is
actually used for a given potential.
parameter kˆ
v u ω 0∆x gmin
n
.mdp input variable name k vec pivot rate eps slab-dist min-gauss
unit kJ
mol·nm2- nm ◦/ps nm2nm -
fixed axis potentials: eqn.
isotropic Viso (6.33)x x x x - - -
— pivot-free Viso-pf (6.36)x x -x- - -
parallel motion Vpm (6.40)x x x x - - -
— pivot-free Vpm-pf (6.44)x x -x- - -
radial motion Vrm (6.45)x x x x - - -
— pivot-free Vrm-pf (6.50)x x -x- - -
radial motion 2 Vrm2 (6.51)x x x x x - -
— pivot-free Vrm2-pf (6.56)x x -x x - -
flexible axis potentials: eqn.
flexible Vflex (6.66)x x -x-x x
— transl. tol. Vflex-t (6.71)x x -x-x x
flexible 2 Vflex2 (6.72)x x -x x x x
— transl. tol. Vflex2-t -x x -x x x x
Table 6.2: Quantities recorded in output files during enforced rotation simulations. All slab-wise
data is written every nstsout steps, other rotation data every nstrout steps.
quantity unit equation output file fixed flexible
V(t)kJ/mol see 6.1 rotation x x
θref (t)degrees θref (t) = ωt rotation x x
θav(t)degrees (6.79)rotation x-
θfit(t),θfit(t, n)degrees (6.81)rotangles -x
y0(n),x0(t, n)nm (6.64,6.65)rotslabs -x
τ(t)kJ/mol (6.82)rotation x-
τ(t, n)kJ/mol (6.82)rottorque -x

180 Chapter 6. Special Topics
Angle of Rotation Groups: Fixed Axis
For fixed axis rotation, the average angle θav(t)of the group relative to the reference group is
determined via the distance-weighted angular deviation of all rotation group atoms from their
reference positions,
θav =
N
X
i=1
riθi,N
X
i=1
ri.(6.79)
Here, riis the distance of the reference position to the rotation axis, and the difference angles θi
are determined from the atomic positions, projected onto a plane perpendicular to the rotation axis
through pivot point u(see eqn. 6.39 for the definition of ⊥),
cos θi=(yi−u)⊥·(xi−u)⊥
k(yi−u)⊥·(xi−u)⊥k.(6.80)
The sign of θav is chosen such that θav >0if the actual structure rotates ahead of the reference.
Angle of Rotation Groups: Flexible Axis
For flexible axis rotation, two outputs are provided, the angle of the entire rotation group, and
separate angles for the segments in the slabs. The angle of the entire rotation group is determined
by an RMSD fit of xito the reference positions y0
iat t= 0, yielding θfit as the angle by which
the reference has to be rotated around ˆ
vfor the optimal fit,
RMSD(xi,Ω(θfit)y0
i)!
= min .(6.81)
To determine the local angle for each slab n, both reference and actual positions are weighted with
the Gaussian function of slab n, and θfit(t, n)is calculated as in eqn. 6.81) from the Gaussian-
weighted positions.
For all angles, the .mdp input option rot-fit-method controls whether a normal RMSD fit
is performed or whether for the fit each position xiis put at the same distance to the rotation axis
as its reference counterpart y0
i. In the latter case, the RMSD measures only angular differences,
not radial ones.
Angle Determination by Searching the Energy Minimum
Alternatively, for rot-fit-method = potential, the angle of the rotation group is deter-
mined as the angle for which the rotation potential energy is minimal. Therefore, the used rotation
potential is additionally evaluated for a set of angles around the current reference angle. In this
case, the rotangles.log output file contains the values of the rotation potential at the chosen
set of angles, while rotation.xvg lists the angle with minimal potential energy.
Torque
The torque τ(t)exerted by the rotation potential is calculated for fixed axis rotation via
τ(t) =
N
X
i=1
ri(t)×f⊥
i(t),(6.82)

6.7. Electric fields 181
where ri(t)is the distance vector from the rotation axis to xi(t)and f⊥
i(t)is the force component
perpendicular to ri(t)and ˆ
v. For flexible axis rotation, torques τnare calculated for each slab
using the local rotation axis of the slab and the Gaussian-weighted positions.
6.7 Electric fields
A pulsed and oscillating electric field can be applied according to:
E(t) = E0exp "−(t−t0)2
2σ2#cos [ω(t−t0)] (6.83)
where E0is the field strength, the angular frequency ω= 2πc/λ,t0is the time at of the peak in
the field strength and σis the with of the pulse. Special cases occur when σ= 0 (non-pulsed field)
and for ωis 0 (static field).
This simulated laser-pulse was applied to simulations of melting ice [151]. A pulsed electric field
may look ike Fig. 6.8. In the supporting information of that paper the impact of an applied electric
field on a system under periodic boundary conditions is analyzed. It is described that the effective
electric field under PBC is larger than the applied field, by a factor depending on the size of the box
and the dielectric properties of molecules in the box. For a system with static dielectric properties
this factor can be corrected for. But for a system where the dielectric varies over time, for example
a membrane protein with a pore that opens and closes during the simulatippn, this way of applying
an electric field is not useful. In such cases one can use the computational electrophysiology
protocol described in the next section (sec. 6.8).
0 0.5 1 1.5 2
Time (ps)
-2
-1
0
1
2
Electric field (V/nm)
Figure 6.8: A simulated laser pulse in GROMACS.
Electric fields are applied when the following options are specified in the grompp.mdp file. You
specify, in order, E0,ω,t0and σ:
electric-field-x = 0.04 0 0 0
yields a static field with E0= 0.04 V/nm in the X-direction. In contrast,

182 Chapter 6. Special Topics
electric-field-x = 2.0 150 5 0
yields an oscillating electric field with E0= 2 V/nm, ω= 150/ps and t0= 5 ps. Finally
electric-field-x = 2.0 150 5 1
yields an pulsed-oscillating electric field with E0= 2 V/nm, ω= 150/ps and t0= 5 ps and σ= 1 ps.
Read more in ref. [151]. Note that the input file format is changed from the undocumented older
version. A figure like Fig. 6.8 may be produced by passing the -field option to gmx mdrun.
6.8 Computational Electrophysiology
The Computational Electrophysiology (CompEL) protocol [152] allows the simulation of ion flux
through membrane channels, driven by transmembrane potentials or ion concentration gradients.
Just as in real cells, CompEL establishes transmembrane potentials by sustaining a small imbal-
ance of charges ∆qacross the membrane, which gives rise to a potential difference ∆Uaccording
to the membrane capacitance:
∆U= ∆q/Cmembrane (6.84)
The transmembrane electric field and concentration gradients are controlled by .mdp options,
which allow the user to set reference counts for the ions on either side of the membrane. If a dif-
ference between the actual and the reference numbers persists over a certain time span, specified
by the user, a number of ion/water pairs are exchanged between the compartments until the refer-
ence numbers are restored. Alongside the calculation of channel conductance and ion selectivity,
CompEL simulations also enable determination of the channel reversal potential, an important
characteristic obtained in electrophysiology experiments.
In a CompEL setup, the simulation system is divided into two compartments Aand Bwith inde-
pendent ion concentrations. This is best achieved by using double bilayer systems with a copy (or
copies) of the channel/pore of interest in each bilayer (Fig. 6.9 A, B). If the channel axes point in
the same direction, channel flux is observed simultaneously at positive and negative potentials in
this way, which is for instance important for studying channel rectification.
The potential difference ∆Uacross the membrane is easily calculated with the gmx potential
utility. By this, the potential drop along zor the pore axis is exactly known in each time interval
of the simulation (Fig. 6.9 C). Type and number of ions niof charge qi, traversing the channel in
the simulation, are written to the swapions.xvg output file, from which the average channel
conductance Gin each interval ∆tis determined by:
G=Piniqi
∆t∆U.(6.85)
The ion selectivity is calculated as the number flux ratio of different species. Best results are
obtained by averaging these values over several overlapping time intervals.
The calculation of reversal potentials is best achieved using a small set of simulations in which
a given transmembrane concentration gradient is complemented with small ion imbalances of
varying magnitude. For example, if one compartment contains 1 M salt and the other 0.1 M, and
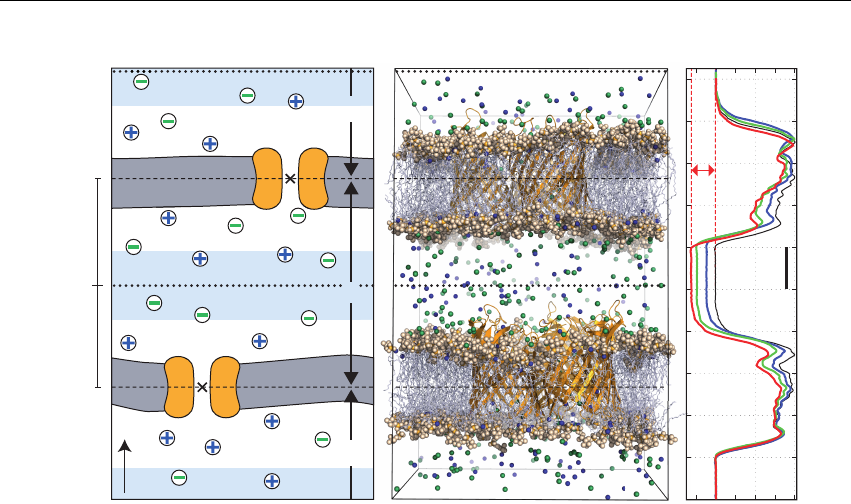
6.8. Computational Electrophysiology 183
B
B
A B C
U [V]
z
A
0 0.4 0.8
2 nm
qref
4 e
8 e
12 e
0 e
U
channel 1
channel 0
0
+1.0
-1.0
offset A
Figure 6.9: Typical double-membrane setup for CompEL simulations (A, B). Ion / water molecule
exchanges will be performed as needed between the two light blue volumes around the dotted
black lines (A). Plot (C) shows the potential difference ∆Uresulting from the selected charge
imbalance ∆qref between the compartments.
given charge neutrality otherwise, a set of simulations with ∆q= 0 e,∆q= 2 e,∆q= 4 ecould
be used. Fitting a straight line through the current-voltage relationship of all obtained I-Upairs
near zero current will then yield Urev .
6.8.1 Usage
The following .mdp options control the CompEL protocol:
swapcoords = Z ; Swap positions: no, X, Y, Z
swap-frequency = 100 ; Swap attempt frequency
Choose Zif your membrane is in the xy-plane (Fig. 6.9). Ions will be exchanged between com-
partments depending on their z-positions alone. swap-frequency determines how often a
swap attempt will be made. This step requires that the positions of the split groups, the ions, and
possibly the solvent molecules are communicated between the parallel processes, so if chosen too
small it can decrease the simulation performance. The Position swapping entry in the cycle
and time accounting table at the end of the md.log file summarizes the amount of runtime spent
in the swap module.
split-group0 = channel0 ; Defines compartment boundary
split-group1 = channel1 ; Defines other compartment boundary
massw-split0 = no ; use mass-weighted center?
massw-split1 = no

184 Chapter 6. Special Topics
split-group0 and split-group1 are two index groups that define the boundaries between
the two compartments, which are usually the centers of the channels. If massw-split0 or
massw-split1 are set to yes, the center of mass of each index group is used as boundary, here
in z-direction. Otherwise, the geometrical centers will be used (×in Fig. 6.9 A). If, such as here,
a membrane channel is selected as split group, the center of the channel will define the dividing
plane between the compartments (dashed horizontal lines). All index groups must be defined in
the index file.
If, to restore the requested ion counts, an ion from one compartment has to be exchanged with a
water molecule from the other compartment, then those molecules are swapped which have the
largest distance to the compartment-defining boundaries (dashed horizontal lines). Depending on
the ion concentration, this effectively results in exchanges of molecules between the light blue
volumes. If a channel is very asymmetric in z-direction and would extend into one of the swap
volumes, one can offset the swap exchange plane with the bulk-offset parameter. A value
of 0.0 means no offset b, values −1.0< b < 0move the swap exchange plane closer to the
lower, values 0<b<1.0closer to the upper membrane. Fig. 6.9 A (left) depicts that for the A
compartment.
solvent-group = SOL ; Group containing the solvent molecules
iontypes = 3 ; Number of different ion types to control
iontype0-name = NA ; Group name of the ion type
iontype0-in-A = 51 ; Reference count of ions of type 0 in A
iontype0-in-B = 35 ; Reference count of ions of type 0 in B
iontype1-name = K
iontype1-in-A = 10
iontype1-in-B = 38
iontype2-name = CL
iontype2-in-A = -1
iontype2-in-B = -1
The group name of solvent molecules acting as exchange partners for the ions has to be set with
solvent-group. The number of different ionic species under control of the CompEL protocol
is given by the iontypes parameter, while iontype0-name gives the name of the index
group containing the atoms of this ionic species. The reference number of ions of this type can
be set with the iontype0-in-A and iontype0-in-B options for compartments Aand B,
respectively. Obviously, the sum of iontype0-in-A and iontype0-in-B needs to equal
the number of ions in the group defined by iontype0-name. A reference number of -1 means:
use the number of ions as found at the beginning of the simulation as the reference value.
coupl-steps = 10 ; Average over these many swap steps
threshold = 1 ; Do not swap if < threshold
If coupl-steps is set to 1, then the momentary ion distribution determines whether ions are
exchanged. coupl-steps > 1 will use the time-average of ion distributions over the selected
number of attempt steps instead. This can be useful, for example, when ions diffuse near compart-
ment boundaries, which would lead to numerous unproductive ion exchanges. A threshold of
1 means that a swap is performed if the average ion count in a compartment differs by at least 1

6.9. Calculating a PMF using the free-energy code 185
from the requested values. Higher thresholds will lead to toleration of larger differences. Ions are
exchanged until the requested number ±the threshold is reached.
cyl0-r = 5.0 ; Split cylinder 0 radius (nm)
cyl0-up = 0.75 ; Split cylinder 0 upper extension (nm)
cyl0-down = 0.75 ; Split cylinder 0 lower extension (nm)
cyl1-r = 5.0 ; same for other channel
cyl1-up = 0.75
cyl1-down = 0.75
The cylinder options are used to define virtual geometric cylinders around the channel’s pore to
track how many ions of which type have passed each channel. Ions will be counted as having
traveled through a channel according to the definition of the channel’s cylinder radius, upper and
lower extension, relative to the location of the respective split group. This will not affect the
actual flux or exchange, but will provide you with the ion permeation numbers across each of the
channels. Note that an ion can only be counted as passing through a particular channel if it is
detected within the defined split cylinder in a swap step. If swap-frequency is chosen too
high, a particular ion may be detected in compartment Ain one swap step, and in compartment B
in the following swap step, so it will be unclear through which of the channels it has passed.
A double-layered system for CompEL simulations can be easily prepared by duplicating an exist-
ing membrane/channel MD system in the direction of the membrane normal (typically z) with gmx
editconf -translate 0 0 <l_z>, where l_z is the box length in that direction. If you
have already defined index groups for the channel for the single-layered system, gmx make_ndx
-n index.ndx -twin will provide you with the groups for the double-layered system.
To suppress large fluctuations of the membranes along the swap direction, it may be useful to
apply a harmonic potential (acting only in the swap dimension) between each of the two channel
and/or bilayer centers using umbrella pulling (see section 6.4).
Multimeric channels
If a split group consists of more than one molecule, the correct PBC image of all molecules with
respect to each other has to be chosen such that the channel center can be correctly determined.
GROMACS assumes that the starting structure in the .tpr file has the correct PBC representation.
Set the following environment variable to check whether that is the case:
•GMX_COMPELDUMP: output the starting structure after it has been made whole to .pdb
file.
6.9 Calculating a PMF using the free-energy code
The free-energy coupling-parameter approach (see sec. 3.12) provides several ways to calculate
potentials of mean force. A potential of mean force between two atoms can be calculated by
connecting them with a harmonic potential or a constraint. For this purpose there are special
potentials that avoid the generation of extra exclusions, see sec. 5.4.4. When the position of the

186 Chapter 6. Special Topics
minimum or the constraint length is 1 nm more in state B than in state A, the restraint or constraint
force is given by ∂H/∂λ. The distance between the atoms can be changed as a function of λand
time by setting delta-lambda in the .mdp file. The results should be identical (although not
numerically due to the different implementations) to the results of the pull code with umbrella
sampling and constraint pulling. Unlike the pull code, the free energy code can also handle atoms
that are connected by constraints.
Potentials of mean force can also be calculated using position restraints. With position restraints,
atoms can be linked to a position in space with a harmonic potential (see 4.3.1). These positions
can be made a function of the coupling parameter λ. The positions for the A and the B states are
supplied to grompp with the -r and -rb options, respectively. One could use this approach to
do targeted MD; note that we do not encourage the use of targeted MD for proteins. A protein
can be forced from one conformation to another by using these conformations as position restraint
coordinates for state A and B. One can then slowly change λfrom 0 to 1. The main drawback of
this approach is that the conformational freedom of the protein is severely limited by the position
restraints, independent of the change from state A to B. Also, the protein is forced from state A to
B in an almost straight line, whereas the real pathway might be very different. An example of a
more fruitful application is a solid system or a liquid confined between walls where one wants to
measure the force required to change the separation between the boundaries or walls. Because the
boundaries (or walls) already need to be fixed, the position restraints do not limit the system in its
sampling.
6.10 Removing fastest degrees of freedom
The maximum time step in MD simulations is limited by the smallest oscillation period that can
be found in the simulated system. Bond-stretching vibrations are in their quantum-mechanical
ground state and are therefore better represented by a constraint instead of a harmonic potential.
For the remaining degrees of freedom, the shortest oscillation period (as measured from a simu-
lation) is 13 fs for bond-angle vibrations involving hydrogen atoms. Taking as a guideline that
with a Verlet (leap-frog) integration scheme a minimum of 5 numerical integration steps should be
performed per period of a harmonic oscillation in order to integrate it with reasonable accuracy,
the maximum time step will be about 3 fs. Disregarding these very fast oscillations of period 13 fs,
the next shortest periods are around 20 fs, which will allow a maximum time step of about 4 fs.
Removing the bond-angle degrees of freedom from hydrogen atoms can best be done by defining
them as virtual interaction sites instead of normal atoms. Whereas a normal atom is connected
to the molecule with bonds, angles and dihedrals, a virtual site’s position is calculated from the
position of three nearby heavy atoms in a predefined manner (see also sec. 4.7). For the hydrogens
in water and in hydroxyl, sulfhydryl, or amine groups, no degrees of freedom can be removed,
because rotational freedom should be preserved. The only other option available to slow down
these motions is to increase the mass of the hydrogen atoms at the expense of the mass of the
connected heavy atom. This will increase the moment of inertia of the water molecules and the
hydroxyl, sulfhydryl, or amine groups, without affecting the equilibrium properties of the system
and without affecting the dynamical properties too much. These constructions will shortly be
described in sec. 6.10.1 and have previously been described in full detail [153].
6.10. Removing fastest degrees of freedom 187
D
d
α
d
BA C
Figure 6.10: The different types of virtual site constructions used for hydrogen atoms. The atoms
used in the construction of the virtual site(s) are depicted as black circles, virtual sites as gray
ones. Hydrogens are smaller than heavy atoms. A: fixed bond angle, note that here the hydrogen
is not a virtual site; B: in the plane of three atoms, with fixed distance; C: in the plane of three
atoms, with fixed angle and distance; D: construction for amine groups (-NH2or -NH+
3), see text
for details.
Using both virtual sites and modified masses, the next bottleneck is likely to be formed by the
improper dihedrals (which are used to preserve planarity or chirality of molecular groups) and the
peptide dihedrals. The peptide dihedral cannot be changed without affecting the physical behavior
of the protein. The improper dihedrals that preserve planarity mostly deal with aromatic residues.
Bonds, angles, and dihedrals in these residues can also be replaced with somewhat elaborate virtual
site constructions.
All modifications described in this section can be performed using the GROMACS topology build-
ing tool pdb2gmx. Separate options exist to increase hydrogen masses, virtualize all hydrogen
atoms, or also virtualize all aromatic residues. Note that when all hydrogen atoms are virtual-
ized, those inside the aromatic residues will be virtualized as well, i.e. hydrogens in the aromatic
residues are treated differently depending on the treatment of the aromatic residues.
Parameters for the virtual site constructions for the hydrogen atoms are inferred from the force-
field parameters (vis. bond lengths and angles) directly by grompp while processing the topology
file. The constructions for the aromatic residues are based on the bond lengths and angles for the
geometry as described in the force fields, but these parameters are hard-coded into pdb2gmx due
to the complex nature of the construction needed for a whole aromatic group.
6.10.1 Hydrogen bond-angle vibrations
Construction of virtual sites
The goal of defining hydrogen atoms as virtual sites is to remove all high-frequency degrees of
freedom from them. In some cases, not all degrees of freedom of a hydrogen atom should be
removed, e.g. in the case of hydroxyl or amine groups the rotational freedom of the hydrogen
atom(s) should be preserved. Care should be taken that no unwanted correlations are introduced
by the construction of virtual sites, e.g. bond-angle vibration between the constructing atoms could
translate into hydrogen bond-length vibration. Additionally, since virtual sites are by definition
massless, in order to preserve total system mass, the mass of each hydrogen atom that is treated as
virtual site should be added to the bonded heavy atom.
188 Chapter 6. Special Topics
ε
η
ζ
δ
ε
γ
ε
δ ε
δ
ε
δ
γ
ζ
ε
η
ε
δ
γ
Phe Tyr HisTrp
ζ
ε
ζ
ε
δ
γ
δδ
Figure 6.11: The different types of virtual site constructions used for aromatic residues. The atoms
used in the construction of the virtual site(s) are depicted as black circles, virtual sites as gray ones.
Hydrogens are smaller than heavy atoms. A: phenylalanine; B: tyrosine (note that the hydroxyl
hydrogen is not a virtual site); C: tryptophan; D: histidine.
Taking into account these considerations, the hydrogen atoms in a protein naturally fall into several
categories, each requiring a different approach (see also Fig. 6.10).
•hydroxyl (-OH) or sulfhydryl (-SH) hydrogen: The only internal degree of freedom in a
hydroxyl group that can be constrained is the bending of the C-O-H angle. This angle is
fixed by defining an additional bond of appropriate length, see Fig. 6.10A. Doing so removes
the high-frequency angle bending, but leaves the dihedral rotational freedom. The same goes
for a sulfhydryl group. Note that in these cases the hydrogen is not treated as a virtual site.
•single amine or amide (-NH-) and aromatic hydrogens (-CH-): The position of these hy-
drogens cannot be constructed from a linear combination of bond vectors, because of the
flexibility of the angle between the heavy atoms. Instead, the hydrogen atom is positioned
at a fixed distance from the bonded heavy atom on a line going through the bonded heavy
atom and a point on the line through both second bonded atoms, see Fig. 6.10B.
•planar amine (-NH2) hydrogens: The method used for the single amide hydrogen is not well
suited for planar amine groups, because no suitable two heavy atoms can be found to define
the direction of the hydrogen atoms. Instead, the hydrogen is constructed at a fixed distance
from the nitrogen atom, with a fixed angle to the carbon atom, in the plane defined by one
of the other heavy atoms, see Fig. 6.10C.
•amine group (umbrella -NH2or -NH+
3) hydrogens: Amine hydrogens with rotational free-
dom cannot be constructed as virtual sites from the heavy atoms they are connected to, since
this would result in loss of the rotational freedom of the amine group. To preserve the rota-
tional freedom while removing the hydrogen bond-angle degrees of freedom, two “dummy
masses” are constructed with the same total mass, moment of inertia (for rotation around
the C-N bond) and center of mass as the amine group. These dummy masses have no in-
teraction with any other atom, except for the fact that they are connected to the carbon and
to each other, resulting in a rigid triangle. From these three particles, the positions of the
nitrogen and hydrogen atoms are constructed as linear combinations of the two carbon-mass
vectors and their outer product, resulting in an amine group with rotational freedom intact,
but without other internal degrees of freedom. See Fig. 6.10D.

6.11. Viscosity calculation 189
6.10.2 Out-of-plane vibrations in aromatic groups
The planar arrangements in the side chains of the aromatic residues lends itself perfectly to a
virtual-site construction, giving a perfectly planar group without the inherently unstable con-
straints that are necessary to keep normal atoms in a plane. The basic approach is to define three
atoms or dummy masses with constraints between them to fix the geometry and create the rest of
the atoms as simple virtual sites type (see sec. 4.7) from these three. Each of the aromatic residues
require a different approach:
•Phenylalanine: Cγ,C1, and C2are kept as normal atoms, but with each a mass of one
third the total mass of the phenyl group. See Fig. 6.10A.
•Tyrosine: The ring is treated identically to the phenylalanine ring. Additionally, constraints
are defined between C1,C2, and Oη. The original improper dihedral angles will keep both
triangles (one for the ring and one with Oη) in a plane, but due to the larger moments of
inertia this construction will be much more stable. The bond-angle in the hydroxyl group
will be constrained by a constraint between Cγand Hη.Note that the hydrogen is not treated
as a virtual site. See Fig. 6.10B.
•Tryptophan: Cβis kept as a normal atom and two dummy masses are created at the center
of mass of each of the rings, each with a mass equal to the total mass of the respective ring
(Cδ2and C2are each counted half for each ring). This keeps the overall center of mass and
the moment of inertia almost (but not quite) equal to what it was. See Fig. 6.10C.
•Histidine: Cγ,C1and N2are kept as normal atoms, but with masses redistributed such
that the center of mass of the ring is preserved. See Fig. 6.10D.
6.11 Viscosity calculation
The shear viscosity is a property of liquids that can be determined easily by experiment. It is useful
for parameterizing a force field because it is a kinetic property, while most other properties which
are used for parameterization are thermodynamic. The viscosity is also an important property,
since it influences the rates of conformational changes of molecules solvated in the liquid.
The viscosity can be calculated from an equilibrium simulation using an Einstein relation:
η=1
2
V
kBTlim
t→∞
d
dt*Zt0+t
t0
Pxz(t0)dt02+t0
(6.86)
This can be done with gmx energy. This method converges very slowly [154], and as such a
nanosecond simulation might not be long enough for an accurate determination of the viscosity.
The result is very dependent on the treatment of the electrostatics. Using a (short) cut-off results
in large noise on the off-diagonal pressure elements, which can increase the calculated viscosity
by an order of magnitude.
GROMACS also has a non-equilibrium method for determining the viscosity [154]. This makes
use of the fact that energy, which is fed into system by external forces, is dissipated through viscous
190 Chapter 6. Special Topics
friction. The generated heat is removed by coupling to a heat bath. For a Newtonian liquid adding
a small force will result in a velocity gradient according to the following equation:
ax(z) + η
ρ
∂2vx(z)
∂z2= 0 (6.87)
Here we have applied an acceleration ax(z)in the x-direction, which is a function of the z-
coordinate. In GROMACS the acceleration profile is:
ax(z) = Acos 2πz
lz(6.88)
where lzis the height of the box. The generated velocity profile is:
vx(z) = Vcos 2πz
lz(6.89)
V=Aρ
ηlz
2π2(6.90)
The viscosity can be calculated from Aand V:
η=A
Vρlz
2π2(6.91)
In the simulation Vis defined as:
V=
N
X
i=1
mivi,x2 cos 2πz
lz
N
X
i=1
mi
(6.92)
The generated velocity profile is not coupled to the heat bath. Moreover, the velocity profile is
excluded from the kinetic energy. One would like Vto be as large as possible to get good statistics.
However, the shear rate should not be so high that the system gets too far from equilibrium. The
maximum shear rate occurs where the cosine is zero, the rate being:
shmax = max
z
∂vx(z)
∂z =Aρ
η
lz
2π(6.93)
For a simulation with: η= 10−3[kg m−1s−1], ρ= 103[kg m−3] and lz= 2π[nm], shmax =
1[ps nm−1]A. This shear rate should be smaller than one over the longest correlation time in
the system. For most liquids, this will be the rotation correlation time, which is around 10 ps. In
this case, Ashould be smaller than 0.1 [nm ps−2]. When the shear rate is too high, the observed
viscosity will be too low. Because Vis proportional to the square of the box height, the optimal
box is elongated in the z-direction. In general, a simulation length of 100 ps is enough to obtain
an accurate value for the viscosity.
The heat generated by the viscous friction is removed by coupling to a heat bath. Because this
coupling is not instantaneous the real temperature of the liquid will be slightly lower than the

6.12. Tabulated interaction functions 191
observed temperature. Berendsen derived this temperature shift [31], which can be written in
terms of the shear rate as:
Ts=η τ
2ρ Cv
sh2
max (6.94)
where τis the coupling time for the Berendsen thermostat and Cvis the heat capacity. Using
the values of the example above, τ= 10−13 [s] and Cv= 2 ·103[J kg−1K−1], we get: Ts=
25 [K ps−2] sh2
max. When we want the shear rate to be smaller than 1/10 [ps−1], Tsis smaller than
0.25 [K], which is negligible.
Note that the system has to build up the velocity profile when starting from an equilibrium state.
This build-up time is of the order of the correlation time of the liquid.
Two quantities are written to the energy file, along with their averages and fluctuations: Vand
1/η, as obtained from (6.91).
6.12 Tabulated interaction functions
6.12.1 Cubic splines for potentials
In some of the inner loops of GROMACS, look-up tables are used for computation of potential
and forces. The tables are interpolated using a cubic spline algorithm. There are separate tables
for electrostatic, dispersion, and repulsion interactions, but for the sake of caching performance
these have been combined into a single array. The cubic spline interpolation for xi≤x < xi+1
looks like this:
Vs(x) = A0+A1+A22+A33(6.95)
where the table spacing hand fraction are given by:
h=xi+1 −xi(6.96)
= (x−xi)/h (6.97)
so that 0≤ < 1. From this, we can calculate the derivative in order to determine the forces:
−V0
s(x) = −dVs(x)
d
d
dx=−(A1+ 2A2+ 3A32)/h (6.98)
The four coefficients are determined from the four conditions that Vsand −V0
sat both ends of each
interval should match the exact potential Vand force −V0. This results in the following errors for
each interval:
|Vs−V|max =V0000 h4
384 +O(h5)(6.99)
|V0
s−V0|max =V0000 h3
72√3+O(h4)(6.100)
|V00
s−V00|max =V0000 h2
12 +O(h3)(6.101)
V and V’ are continuous, while V” is the first discontinuous derivative. The number of points
per nanometer is 500 and 2000 for mixed- and double-precision versions of GROMACS, respec-
tively. This means that the errors in the potential and force will usually be smaller than the mixed
precision accuracy.

192 Chapter 6. Special Topics
GROMACS stores A0,A1,A2and A3. The force routines get a table with these four parameters
and a scaling factor sthat is equal to the number of points per nm. (Note that his s−1). The
algorithm goes a little something like this:
1. Calculate distance vector (rij) and distance rij
2. Multiply rij by sand truncate to an integer value n0to get a table index
3. Calculate fractional component (=srij −n0) and 2
4. Do the interpolation to calculate the potential Vand the scalar force f
5. Calculate the vector force Fby multiplying fwith rij
Note that table look-up is significantly slower than computation of the most simple Lennard-Jones
and Coulomb interaction. However, it is much faster than the shifted Coulomb function used in
conjunction with the PPPM method. Finally, it is much easier to modify a table for the potential
(and get a graphical representation of it) than to modify the inner loops of the MD program.
6.12.2 User-specified potential functions
You can also use your own potential functions without editing the GROMACS code. The potential
function should be according to the following equation
V(rij) = qiqj
4π0
f(rij) + C6g(rij ) + C12 h(rij )(6.102)
where f,g, and hare user defined functions. Note that if g(r)represents a normal dispersion
interaction, g(r)should be <0. C6, C12 and the charges are read from the topology. Also note
that combination rules are only supported for Lennard-Jones and Buckingham, and that your tables
should match the parameters in the binary topology.
When you add the following lines in your .mdp file:
rlist = 1.0
coulombtype = User
rcoulomb = 1.0
vdwtype = User
rvdw = 1.0
mdrun will read a single non-bonded table file, or multiple when energygrp-table is set (see
below). The name of the file(s) can be set with the mdrun option -table. The table file should
contain seven columns of table look-up data in the order: x,f(x),−f0(x),g(x),−g0(x),h(x),
−h0(x). The xshould run from 0 to rc+ 1 (the value of table_extension can be changed
in the .mdp file). You can choose the spacing you like; for the standard tables GROMACS uses a
spacing of 0.002 and 0.0005 nm when you run in mixed and double precision, respectively. In this
context, rcdenotes the maximum of the two cut-offs rvdw and rcoulomb (see above). These
variables need not be the same (and need not be 1.0 either). Some functions used for potentials
contain a singularity at x= 0, but since atoms are normally not closer to each other than 0.1 nm,

6.13. Mixed Quantum-Classical simulation techniques 193
the function value at x= 0 is not important. Finally, it is also possible to combine a standard
Coulomb with a modified LJ potential (or vice versa). One then specifies e.g. coulombtype =
Cut-off or coulombtype = PME, combined with vdwtype = User. The table file must
always contain the 7 columns however, and meaningful data (i.e. not zeroes) must be entered in
all columns. A number of pre-built table files can be found in the GMXLIB directory for 6-8, 6-9,
6-10, 6-11, and 6-12 Lennard-Jones potentials combined with a normal Coulomb.
If you want to have different functional forms between different groups of atoms, this can be
set through energy groups. Different tables can be used for non-bonded interactions between
different energy groups pairs through the .mdp option energygrp-table (see details in the
User Guide). Atoms that should interact with a different potential should be put into different
energy groups. Between group pairs which are not listed in energygrp-table, the normal
user tables will be used. This makes it easy to use a different functional form between a few types
of atoms.
6.13 Mixed Quantum-Classical simulation techniques
In a molecular mechanics (MM) force field, the influence of electrons is expressed by empirical
parameters that are assigned on the basis of experimental data, or on the basis of results from
high-level quantum chemistry calculations. These are valid for the ground state of a given covalent
structure, and the MM approximation is usually sufficiently accurate for ground-state processes
in which the overall connectivity between the atoms in the system remains unchanged. However,
for processes in which the connectivity does change, such as chemical reactions, or processes that
involve multiple electronic states, such as photochemical conversions, electrons can no longer be
ignored, and a quantum mechanical description is required for at least those parts of the system in
which the reaction takes place.
One approach to the simulation of chemical reactions in solution, or in enzymes, is to use a com-
bination of quantum mechanics (QM) and molecular mechanics (MM). The reacting parts of the
system are treated quantum mechanically, with the remainder being modeled using the force field.
The current version of GROMACS provides interfaces to several popular Quantum Chemistry
packages (MOPAC [155], GAMESS-UK [156], Gaussian [157] and CPMD [158]).
GROMACS interactions between the two subsystems are either handled as described by Field et
al. [159] or within the ONIOM approach by Morokuma and coworkers [160,161].
6.13.1 Overview
Two approaches for describing the interactions between the QM and MM subsystems are sup-
ported in this version:
1. Electronic Embedding The electrostatic interactions between the electrons of the QM re-
gion and the MM atoms and between the QM nuclei and the MM atoms are included in the
Hamiltonian for the QM subsystem:
HQM/MM =HQM
e−
n
X
i
M
X
J
e2QJ
4π0riJ
+
N
X
A
M
X
J
e2ZAQJ
eπ0RAJ
,(6.103)

194 Chapter 6. Special Topics
where nand Nare the number of electrons and nuclei in the QM region, respectively,
and Mis the number of charged MM atoms. The first term on the right hand side is the
original electronic Hamiltonian of an isolated QM system. The first of the double sums is
the total electrostatic interaction between the QM electrons and the MM atoms. The total
electrostatic interaction of the QM nuclei with the MM atoms is given by the second double
sum. Bonded interactions between QM and MM atoms are described at the MM level by the
appropriate force-field terms. Chemical bonds that connect the two subsystems are capped
by a hydrogen atom to complete the valence of the QM region. The force on this atom,
which is present in the QM region only, is distributed over the two atoms of the bond. The
cap atom is usually referred to as a link atom.
2. ONIOM In the ONIOM approach, the energy and gradients are first evaluated for the iso-
lated QM subsystem at the desired level of ab initio theory. Subsequently, the energy and
gradients of the total system, including the QM region, are computed using the molecular
mechanics force field and added to the energy and gradients calculated for the isolated QM
subsystem. Finally, in order to correct for counting the interactions inside the QM region
twice, a molecular mechanics calculation is performed on the isolated QM subsystem and
the energy and gradients are subtracted. This leads to the following expression for the total
QM/MM energy (and gradients likewise):
Etot =EQM
I+EMM
I+II −EMM
I,(6.104)
where the subscripts I and II refer to the QM and MM subsystems, respectively. The su-
perscripts indicate at what level of theory the energies are computed. The ONIOM scheme
has the advantage that it is not restricted to a two-layer QM/MM description, but can easily
handle more than two layers, with each layer described at a different level of theory.
6.13.2 Usage
To make use of the QM/MM functionality in GROMACS, one needs to:
1. introduce link atoms at the QM/MM boundary, if needed;
2. specify which atoms are to be treated at a QM level;
3. specify the QM level, basis set, type of QM/MM interface and so on.
Adding link atoms
At the bond that connects the QM and MM subsystems, a link atoms is introduced. In GROMACS
the link atom has special atomtype, called LA. This atomtype is treated as a hydrogen atom in the
QM calculation, and as a virtual site in the force-field calculation. The link atoms, if any, are part
of the system, but have no interaction with any other atom, except that the QM force working on
it is distributed over the two atoms of the bond. In the topology, the link atom (LA), therefore, is
defined as a virtual site atom:

6.13. Mixed Quantum-Classical simulation techniques 195
[ virtual_sites2 ]
LA QMatom MMatom 1 0.65
See sec. 5.2.2 for more details on how virtual sites are treated. The link atom is replaced at every
step of the simulation.
In addition, the bond itself is replaced by a constraint:
[ constraints ]
QMatom MMatom 2 0.153
Note that, because in our system the QM/MM bond is a carbon-carbon bond (0.153 nm), we use
a constraint length of 0.153 nm, and dummy position of 0.65. The latter is the ratio between the
ideal C-H bond length and the ideal C-C bond length. With this ratio, the link atom is always
0.1 nm away from the QMatom, consistent with the carbon-hydrogen bond length. If the QM and
MM subsystems are connected by a different kind of bond, a different constraint and a different
dummy position, appropriate for that bond type, are required.
Specifying the QM atoms
Atoms that should be treated at a QM level of theory, including the link atoms, are added to the
index file. In addition, the chemical bonds between the atoms in the QM region are to be defined
as connect bonds (bond type 5) in the topology file:
[ bonds ]
QMatom1 QMatom2 5
QMatom2 QMatom3 5
Specifying the QM/MM simulation parameters
In the .mdp file, the following parameters control a QM/MM simulation.
QMMM = no
If this is set to yes, a QM/MM simulation is requested. Several groups of atoms can be
described at different QM levels separately. These are specified in the QMMM-grps field
separated by spaces. The level of ab initio theory at which the groups are described is
specified by QMmethod and QMbasis Fields. Describing the groups at different levels of
theory is only possible with the ONIOM QM/MM scheme, specified by QMMMscheme.
QMMM-grps =
groups to be described at the QM level
QMMMscheme = normal
Options are normal and ONIOM. This selects the QM/MM interface. normal implies
that the QM subsystem is electronically embedded in the MM subsystem. There can only
be one QMMM-grps that is modeled at the QMmethod and QMbasis level of ab initio

196 Chapter 6. Special Topics
theory. The rest of the system is described at the MM level. The QM and MM subsystems
interact as follows: MM point charges are included in the QM one-electron Hamiltonian
and all Lennard-Jones interactions are described at the MM level. If ONIOM is selected, the
interaction between the subsystem is described using the ONIOM method by Morokuma
and co-workers. There can be more than one QMMM-grps each modeled at a different level
of QM theory (QMmethod and QMbasis).
QMmethod =
Method used to compute the energy and gradients on the QM atoms. Available meth-
ods are AM1, PM3, RHF, UHF, DFT, B3LYP, MP2, CASSCF, MMVB and CPMD. For
CASSCF, the number of electrons and orbitals included in the active space is specified by
CASelectrons and CASorbitals. For CPMD, the plane-wave cut-off is specified by
the planewavecutoff keyword.
QMbasis =
Gaussian basis set used to expand the electronic wave-function. Only Gaussian basis sets
are currently available, i.e. STO-3G, 3-21G, 3-21G*, 3-21+G*, 6-21G, 6-31G, 6-31G*,
6-31+G*, and 6-311G. For CPMD, which uses plane wave expansion rather than atom-
centered basis functions, the planewavecutoff keyword controls the plane wave ex-
pansion.
QMcharge =
The total charge in eof the QMMM-grps. In case there are more than one QMMM-grps, the
total charge of each ONIOM layer needs to be specified separately.
QMmult =
The multiplicity of the QMMM-grps. In case there are more than one QMMM-grps, the
multiplicity of each ONIOM layer needs to be specified separately.
CASorbitals =
The number of orbitals to be included in the active space when doing a CASSCF computa-
tion.
CASelectrons =
The number of electrons to be included in the active space when doing a CASSCF compu-
tation.
SH = no
If this is set to yes, a QM/MM MD simulation on the excited state-potential energy surface
and enforce a diabatic hop to the ground-state when the system hits the conical intersection
hyperline in the course the simulation. This option only works in combination with the
CASSCF method.
6.13.3 Output
The energies and gradients computed in the QM calculation are added to those computed by GRO-
MACS. In the .edr file there is a section for the total QM energy.

6.14. Using VMD plug-ins for trajectory file I/O 197
6.13.4 Future developments
Several features are currently under development to increase the accuracy of the QM/MM inter-
face. One useful feature is the use of delocalized MM charges in the QM computations. The most
important benefit of using such smeared-out charges is that the Coulombic potential has a finite
value at interatomic distances. In the point charge representation, the partially-charged MM atoms
close to the QM region tend to “over-polarize” the QM system, which leads to artifacts in the
calculation.
What is needed as well is a transition state optimizer.
6.14 Using VMD plug-ins for trajectory file I/O
GROMACS tools are able to use the plug-ins found in an existing installation of VMD in order
to read and write trajectory files in formats that are not native to GROMACS. You will be able to
supply an AMBER DCD-format trajectory filename directly to GROMACS tools, for example.
This requires a VMD installation not older than version 1.8, that your system provides the dlopen
function so that programs can determine at run time what plug-ins exist, and that you build shared
libraries when building GROMACS. CMake will find the vmd executable in your path, and from
it, or the environment variable VMDDIR at configuration or run time, locate the plug-ins. Alter-
natively, the VMD_PLUGIN_PATH can be used at run time to specify a path where these plug-ins
can be found. Note that these plug-ins are in a binary format, and that format must match the
architecture of the machine attempting to use them.
6.15 Interactive Molecular Dynamics
GROMACS supports the interactive molecular dynamics (IMD) protocol as implemented by VMD
to control a running simulation in NAMD. IMD allows to monitor a running GROMACS simu-
lation from a VMD client. In addition, the user can interact with the simulation by pulling on
atoms, residues or fragments with a mouse or a force-feedback device. Additional information
about the GROMACS implementation and an exemplary GROMACS IMD system can be found
on this homepage.
6.15.1 Simulation input preparation
The GROMACS implementation allows transmission and interaction with a part of the running
simulation only, e.g. in cases where no water molecules should be transmitted or pulled. The
group is specified via the .mdp option IMD-group. When IMD-group is empty, the IMD
protocol is disabled and cannot be enabled via the switches in mdrun. To interact with the entire
system, IMD-group can be set to System. When using grompp, a .gro file to be used as
VMD input is written out (-imd switch of grompp).

198 Chapter 6. Special Topics
6.15.2 Starting the simulation
Communication between VMD and GROMACS is achieved via TCP sockets and thus enables
controlling an mdrun running locally or on a remote cluster. The port for the connection can be
specified with the -imdport switch of mdrun, 8888 is the default. If a port number of 0 or
smaller is provided, GROMACS automatically assigns a free port to use with IMD.
Every Nsteps, the mdrun client receives the applied forces from VMD and sends the new posi-
tions to the client. VMD permits increasing or decreasing the communication frequency interac-
tively. By default, the simulation starts and runs even if no IMD client is connected. This behavior
is changed by the -imdwait switch of mdrun. After startup and whenever the client has dis-
connected, the integration stops until reconnection of the client. When the -imdterm switch is
used, the simulation can be terminated by pressing the stop button in VMD. This is disabled by
default. Finally, to allow interacting with the simulation (i.e. pulling from VMD) the -imdpull
switch has to be used. Therefore, a simulation can only be monitored but not influenced from the
VMD client when none of -imdwait,-imdterm or -imdpull are set. However, since the
IMD protocol requires no authentication, it is not advisable to run simulations on a host directly
reachable from an insecure environment. Secure shell forwarding of TCP can be used to connect
to running simulations not directly reachable from the interacting host. Note that the IMD com-
mand line switches of mdrun are hidden by default and show up in the help text only with gmx
mdrun -h -hidden.
6.15.3 Connecting from VMD
In VMD, first the structure corresponding to the IMD group has to be loaded (File →New
Molecule). Then the IMD connection window has to be used (Extensions →Simulation →IMD
Connect (NAMD)). In the IMD connection window, hostname and port have to be specified and
followed by pressing Connect.Detach Sim allows disconnecting without terminating the sim-
ulation, while Stop Sim ends the simulation on the next neighbor searching step (if allowed by
-imdterm).
The timestep transfer rate allows adjusting the communication frequency between simulation and
IMD client. Setting the keep rate loads every Nth frame into VMD instead of discarding them
when a new one is received. The displayed energies are in SI units in contrast to energies displayed
from NAMD simulations.
6.16 Embedding proteins into the membranes
GROMACS is capable of inserting the protein into pre-equilibrated lipid bilayers with mini-
mal perturbation of the lipids using the method, which was initially described as a ProtSqueeze
technique,[162] and later implemented as g_membed tool.[163] Currently the functionality of g_-
membed is available in mdrun as described in the user guide.
This method works by first artificially shrinking the protein in the xy-plane, then it removes lipids
that overlap with that much smaller core. Then the protein atoms are gradually resized back to
their initial configuration, using normal dynamics for the rest of the system, so the lipids adapt to

6.16. Embedding proteins into the membranes 199
the protein. Further lipids are removed as required.

200 Chapter 6. Special Topics
Chapter 7
Run parameters and
Programs
7.1 Online documentation
More documentation is available online from the GROMACS web site, http://manual.
gromacs.org/documentation.
In addition, we install standard UNIX man pages for all the programs. If you have sourced the
GMXRC script in the GROMACS binary directory for your host they should already be present in
your MANPATH environment variable, and you should be able to type e.g. man gmx-grompp.
You can also use the -h flag on the command line (e.g. gmx grompp -h) to see the same
information, as well as gmx help grompp. The list of all programs are available from gmx
help.
7.2 File types
Table 7.1 lists the file types used by GROMACS along with a short description, and you can find
a more detail description for each file in your HTML reference, or in our online version.
GROMACS files written in XDR format can be read on any architecture with GROMACS version
1.6 or later if the configuration script found the XDR libraries on your system. They should always
be present on UNIX since they are necessary for NFS support.
7.3 Run Parameters
The descriptions of .mdp parameters can be found at http://manual.gromacs.org/current/
mdp-options.html or in your installation at share/gromacs/html/mdp-options.html

202 Chapter 7. Run parameters and Programs
Default Default
Name Ext. Type Option Description
atomtp.atp Asc Atomtype file used by pdb2gmx
eiwit.brk Asc -f Brookhaven data bank file
state.cpt xdr Checkpoint file
nnnice.dat Asc Generic data file
user.dlg Asc Dialog Box data for ngmx
sam.edi Asc ED sampling input
sam.edo Asc ED sampling output
ener.edr Generic energy: edr ene
ener.edr xdr Energy file in portable xdr format
ener.ene Bin Energy file
eiwit.ent Asc -f Entry in the protein date bank
plot.eps Asc Encapsulated PostScript (tm) file
conf.esp Asc -c Coordinate file in ESPResSo format
conf.g96 Asc -c Coordinate file in Gromos-96 format
conf.gro Asc -c Coordinate file in Gromos-87 format
conf.gro -c Structure: gro g96 pdb esp tpr
out.gro -o Structure: gro g96 pdb esp
polar.hdb Asc Hydrogen data base
topinc.itp Asc Include file for topology
run.log Asc -l Log file
ps.m2p Asc Input file for mat2ps
ss.map Asc File that maps matrix data to colors
ss.mat Asc Matrix Data file
grompp.mdp Asc -f grompp input file with MD parameters
hessian.mtx Bin -m Hessian matrix
index.ndx Asc -n Index file
hello.out Asc -o Generic output file
eiwit.pdb Asc -f Protein data bank file
residue.rtp Asc Residue Type file used by pdb2gmx
doc.tex Asc -o LaTeX file
topol.top Asc -p Topology file
topol.tpr -s Generic run input: tpr
topol.tpr -s Structure+mass(db): tpr gro g96 pdb
topol.tpr xdr -s Portable xdr run input file
traj.trr Full precision trajectory: trr cpt
traj.trr xdr Trajectory in portable xdr format
root.xpm Asc X PixMap compatible matrix file
traj.xtc -f Trajec., input: xtc trr tng cpt gro g96 pdb
traj.xtc -f Trajectory, output: xtc trr tng gro g96 pdb
traj.xtc xdr Compressed trajectory (portable xdr format)
graph.xvg Asc -o xvgr/xmgr file
Table 7.1: The GROMACS file types.
Chapter 8
Analysis
In this chapter different ways of analyzing your trajectory are described. The names of the cor-
responding analysis programs are given. Specific information on the in- and output of these pro-
grams can be found in the online manual at www.gromacs.org. The output files are often produced
as finished Grace/Xmgr graphs.
First, in sec. 8.1, the group concept in analysis is explained. 8.1.2 explains a newer concept of
dynamic selections, which is currently supported by a few tools. Then, the different analysis tools
are presented.
8.1 Using Groups
gmx make_ndx, gmx mk_angndx, gmx select
In chapter 3, it was explained how groups of atoms can be used in mdrun (see sec. 3.3). In most
analysis programs, groups of atoms must also be chosen. Most programs can generate several
default index groups, but groups can always be read from an index file. Let’s consider the example
of a simulation of a binary mixture of components A and B. When we want to calculate the radial
distribution function (RDF) gAB(r)of A with respect to B, we have to calculate:
4πr2gAB(r) = V
NA
X
i∈A
NB
X
j∈B
P(r)(8.1)
where Vis the volume and P(r)is the probability of finding a B atom at distance rfrom an A
atom.
By having the user define the atom numbers for groups A and B in a simple file, we can calculate
this gAB in the most general way, without having to make any assumptions in the RDF program
about the type of particles.
Groups can therefore consist of a series of atom numbers, but in some cases also of molecule
numbers. It is also possible to specify a series of angles by triples of atom numbers, dihedrals
by quadruples of atom numbers and bonds or vectors (in a molecule) by pairs of atom numbers.

204 Chapter 8. Analysis
When appropriate the type of index file will be specified for the following analysis programs. To
help creating such index files (index.ndx), there are a couple of programs to generate them,
using either your input configuration or the topology. To generate an index file consisting of a
series of atom numbers (as in the example of gAB), use gmx make_ndx or gmx select. To
generate an index file with angles or dihedrals, use gmx mk_angndx. Of course you can also
make them by hand. The general format is presented here:
[ Oxygen ]
147
[ Hydrogen ]
2356
8 9
First, the group name is written between square brackets. The following atom numbers may be
spread out over as many lines as you like. The atom numbering starts at 1.
Each tool that can use groups will offer the available alternatives for the user to choose. That
choice can be made with the number of the group, or its name. In fact, the first few letters of the
group name will suffice if that will distinguish the group from all others. There are ways to use
Unix shell features to choose group names on the command line, rather than interactively. Consult
www.gromacs.org for suggestions.
8.1.1 Default Groups
When no index file is supplied to analysis tools or grompp, a number of default groups are
generated to choose from:
System
all atoms in the system
Protein
all protein atoms
Protein-H
protein atoms excluding hydrogens
C-alpha
Cαatoms
Backbone
protein backbone atoms; N, Cαand C
MainChain
protein main chain atoms: N, Cα, C and O, including oxygens in C-terminus
MainChain+Cb
protein main chain atoms including Cβ

8.1. Using Groups 205
MainChain+H
protein main chain atoms including backbone amide hydrogens and hydrogens on the N-
terminus
SideChain
protein side chain atoms; that is all atoms except N, Cα, C, O, backbone amide hydrogens,
oxygens in C-terminus and hydrogens on the N-terminus
SideChain-H
protein side chain atoms excluding all hydrogens
Prot-Masses
protein atoms excluding dummy masses (as used in virtual site constructions of NH3groups
and tryptophan side-chains), see also sec. 5.2.2; this group is only included when it differs
from the “Protein” group
Non-Protein
all non-protein atoms
DNA
all DNA atoms
RNA
all RNA atoms
Water
water molecules (names like SOL,WAT,HOH, etc.) See residuetypes.dat for a full
listing
non-Water
anything not covered by the Water group
Ion
any name matching an Ion entry in residuetypes.dat
Water_and_Ions
combination of the Water and Ions groups
molecule_name
for all residues/molecules which are not recognized as protein, DNA, or RNA; one group
per residue/molecule name is generated
Other
all atoms which are neither protein, DNA, nor RNA.
Empty groups will not be generated. Most of the groups only contain protein atoms. An atom is
considered a protein atom if its residue name is listed in the residuetypes.dat file and is
listed as a “Protein” entry. The process for determinding DNA, RNA, etc. is analogous. If you
need to modify these classifications, then you can copy the file from the library directory into your
working directory and edit the local copy.

206 Chapter 8. Analysis
8.1.2 Selections
gmx select
Currently, a few analysis tools support an extended concept of (dynamic) selections. There are
three main differences to traditional index groups:
•The selections are specified as text instead of reading fixed atom indices from a file, using
a syntax similar to VMD. The text can be entered interactively, provided on the command
line, or from a file.
•The selections are not restricted to atoms, but can also specify that the analysis is to be
performed on, e.g., center-of-mass positions of a group of atoms. Some tools may not
support selections that do not evaluate to single atoms, e.g., if they require information that
is available only for single atoms, like atom names or types.
•The selections can be dynamic, i.e., evaluate to different atoms for different trajectory
frames. This allows analyzing only a subset of the system that satisfies some geometric
criteria.
As an example of a simple selection, resname ABC and within 2 of resname DEF
selects all atoms in residues named ABC that are within 2 nm of any atom in a residue named
DEF.
Tools that accept selections can also use traditional index files similarly to older tools: it is possible
to give an .ndx file to the tool, and directly select a group from the index file as a selection, either
by group number or by group name. The index groups can also be used as a part of a more
complicated selection.
To get started, you can run gmx select with a single structure, and use the interactive prompt
to try out different selections. The tool provides, among others, output options -on and -ofpdb
to write out the selected atoms to an index file and to a .pdb file, respectively. This does not allow
testing selections that evaluate to center-of-mass positions, but other selections can be tested and
the result examined.
The detailed syntax and the individual keywords that can be used in selections can be accessed by
typing help in the interactive prompt of any selection-enabled tool, as well as with gmx help
selections. The help is divided into subtopics that can be accessed with, e.g., help syntax
/gmx help selections syntax. Some individual selection keywords have extended help
as well, which can be accessed with, e.g., help keywords within.
The interactive prompt does not currently provide much editing capabilities. If you need them,
you can run the program under rlwrap.
For tools that do not yet support the selection syntax, you can use gmx select -on to generate
static index groups to pass to the tool. However, this only allows for a small subset (only the first
bullet from the above list) of the flexibility that fully selection-aware tools offer.
It is also possible to write your own analysis tools to take advantage of the flexibility of these
selections: see the template.cpp file in the share/gromacs/template directory of your
installation for an example.

8.2. Looking at your trajectory 207
Figure 8.1: The window of gmx view showing a box of water.
8.2 Looking at your trajectory
gmx view
Before analyzing your trajectory it is often informative to look at your trajectory first. GROMACS
comes with a simple trajectory viewer gmx view; the advantage with this one is that it does not
require OpenGL, which usually isn’t present on e.g. supercomputers. It is also possible to generate
a hard-copy in Encapsulated Postscript format (see Fig. 8.1). If you want a faster and more fancy
viewer there are several programs that can read the GROMACS trajectory formats – have a look
at our homepage (www.gromacs.org) for updated links.
8.3 General properties
gmx energy, gmx traj
To analyze some or all energies and other properties, such as total pressure,pressure tensor,
density,box-volume and box-sizes, use the program gmx energy. A choice can be made from
a list a set of energies, like potential, kinetic or total energy, or individual contributions, like
Lennard-Jones or dihedral energies.
The center-of-mass velocity, defined as
vcom =1
M
N
X
i=1
mivi(8.2)
with M=PN
i=1 mithe total mass of the system, can be monitored in time by the program gmx
traj -com -ov. It is however recommended to remove the center-of-mass velocity every step
(see chapter 3)!

208 Chapter 8. Analysis
r
r+dr r+dr
r
θ+dθθ
e
A B
DC
Figure 8.2: Definition of slices in gmx rdf: A. gAB(r). B. gAB(r, θ). The slices are colored gray.
C. Normalization hρBilocal. D. Normalization hρBilocal, θ. Normalization volumes are colored
gray.
8.4 Radial distribution functions
gmx rdf
The radial distribution function (RDF) or pair correlation function gAB(r)between particles of
type Aand Bis defined in the following way:
gAB(r) = hρB(r)i
hρBilocal
=1
hρBilocal
1
NA
NA
X
i∈A
NB
X
j∈B
δ(rij −r)
4πr2
(8.3)
with hρB(r)ithe particle density of type Bat a distance raround particles A, and hρBilocal the
particle density of type Baveraged over all spheres around particles Awith radius rmax (see
Fig. 8.2C).
Usually the value of rmax is half of the box length. The averaging is also performed in time. In
practice the analysis program gmx rdf divides the system into spherical slices (from rto r+dr,
see Fig. 8.2A) and makes a histogram in stead of the δ-function. An example of the RDF of
oxygen-oxygen in SPC water [85] is given in Fig. 8.3.
With gmx rdf it is also possible to calculate an angle dependent rdf gAB (r, θ), where the angle
θis defined with respect to a certain laboratory axis e, see Fig. 8.2B.
gAB(r, θ) = 1
hρBilocal, θ
1
NA
NA
X
i∈A
NB
X
j∈B
δ(rij −r)δ(θij −θ)
2πr2sin(θ)(8.4)
cos(θij) = rij ·e
krijk kek(8.5)
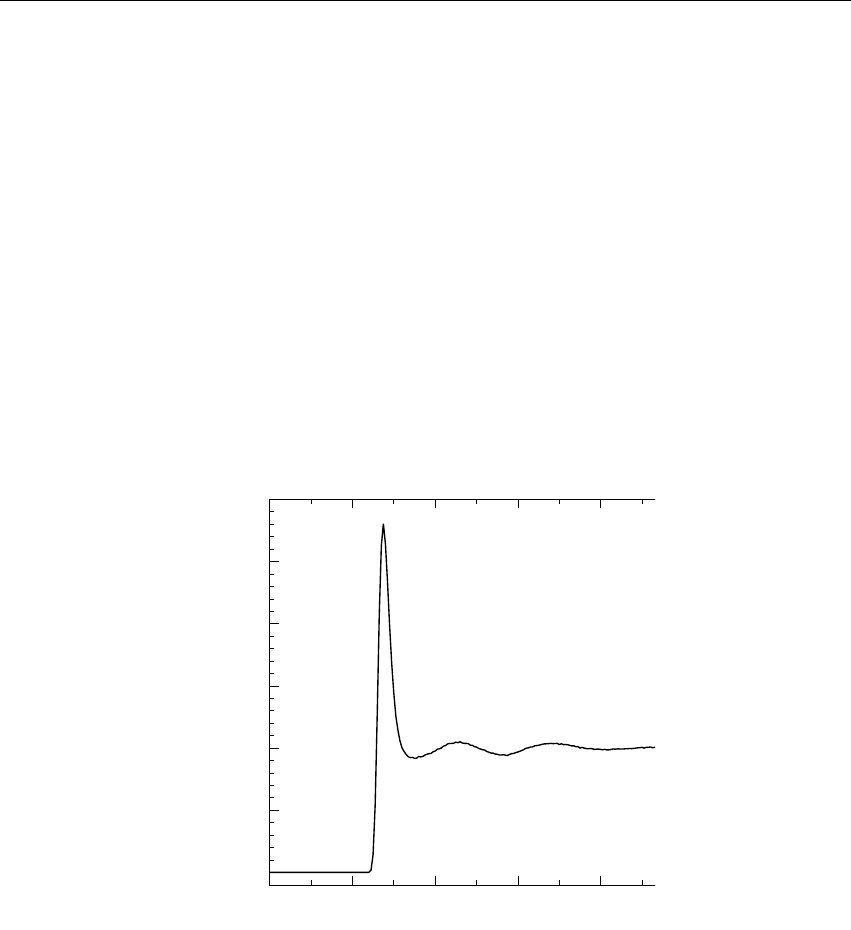
8.4. Radial distribution functions 209
0 0.2 0.4 0.6 0.8
r (nm)
0
0.5
1
1.5
2
2.5
3
g(r)
Figure 8.3: gOO(r)for Oxygen-Oxygen of SPC-water.

210 Chapter 8. Analysis
This gAB(r, θ)is useful for analyzing anisotropic systems. Note that in this case the normalization
hρBilocal, θ is the average density in all angle slices from θto θ+dθ up to rmax, so angle dependent,
see Fig. 8.2D.
8.5 Correlation functions
8.5.1 Theory of correlation functions
The theory of correlation functions is well established [113]. We describe here the implemen-
tation of the various correlation function flavors in the GROMACS code. The definition of the
autocorrelation function (ACF) Cf(t)for a property f(t)is:
Cf(t) = hf(ξ)f(ξ+t)iξ(8.6)
where the notation on the right hand side indicates averaging over ξ,i.e. over time origins. It is
also possible to compute cross-correlation function from two properties f(t)and g(t):
Cfg(t) = hf(ξ)g(ξ+t)iξ(8.7)
however, in GROMACS there is no standard mechanism to do this (note: you can use the xmgr
program to compute cross correlations). The integral of the correlation function over time is the
correlation time τf:
τf=Z∞
0
Cf(t)dt(8.8)
In practice, correlation functions are calculated based on data points with discrete time intervals
∆t, so that the ACF from an MD simulation is:
Cf(j∆t) = 1
N−j
N−1−j
X
i=0
f(i∆t)f((i+j)∆t)(8.9)
where Nis the number of available time frames for the calculation. The resulting ACF is obviously
only available at time points with the same interval ∆t. Since, for many applications, it is necessary
to know the short time behavior of the ACF (e.g. the first 10 ps) this often means that we have to
save the data with intervals much shorter than the time scale of interest. Another implication of
eqn. 8.9 is that in principle we can not compute all points of the ACF with the same accuracy, since
we have N−1data points for Cf(∆t)but only 1 for Cf((N−1)∆t). However, if we decide to
compute only an ACF of length M∆t, where M≤N/2we can compute all points with the same
statistical accuracy:
Cf(j∆t) = 1
M
N−1−M
X
i=0
f(i∆t)f((i+j)∆t)(8.10)
Here of course j < M .Mis sometimes referred to as the time lag of the correlation function.
When we decide to do this, we intentionally do not use all the available points for very short time
intervals (j << M), but it makes it easier to interpret the results. Another aspect that may not be
neglected when computing ACFs from simulation is that usually the time origins ξ(eqn. 8.6) are
not statistically independent, which may introduce a bias in the results. This can be tested using a

8.5. Correlation functions 211
block-averaging procedure, where only time origins with a spacing at least the length of the time
lag are included, e.g. using ktime origins with spacing of M∆t(where kM ≤N):
Cf(j∆t) = 1
k
k−1
X
i=0
f(iM∆t)f((iM +j)∆t)(8.11)
However, one needs very long simulations to get good accuracy this way, because there are many
fewer points that contribute to the ACF.
8.5.2 Using FFT for computation of the ACF
The computational cost for calculating an ACF according to eqn. 8.9 is proportional to N2, which
is considerable. However, this can be improved by using fast Fourier transforms to do the convo-
lution [113].
8.5.3 Special forms of the ACF
There are some important varieties on the ACF, e.g. the ACF of a vector p:
Cp(t) = Z∞
0
Pn(cos 6(p(ξ),p(ξ+t)) dξ(8.12)
where Pn(x)is the nth order Legendre polynomial 1. Such correlation times can actually be ob-
tained experimentally using e.g. NMR or other relaxation experiments. GROMACS can compute
correlations using the 1st and 2nd order Legendre polynomial (eqn. 8.12). This can also be used
for rotational autocorrelation (gmx rotacf) and dipole autocorrelation (gmx dipoles).
In order to study torsion angle dynamics, we define a dihedral autocorrelation function as [164]:
C(t) = hcos(θ(τ)−θ(τ+t))iτ(8.13)
Note that this is not a product of two functions as is generally used for correlation functions, but
it may be rewritten as the sum of two products:
C(t) = hcos(θ(τ)) cos(θ(τ+t)) + sin(θ(τ)) sin(θ(τ+t))iτ(8.14)
8.5.4 Some Applications
The program gmx velacc calculates the velocity autocorrelation function.
Cv(τ) = hvi(τ)·vi(0)ii∈A(8.15)
The self diffusion coefficient can be calculated using the Green-Kubo relation [113]:
DA=1
3Z∞
0hvi(t)·vi(0)ii∈Adt (8.16)
1P0(x) = 1,P1(x) = x,P2(x) = (3x2−1)/2

212 Chapter 8. Analysis
which is just the integral of the velocity autocorrelation function. There is a widely-held belief
that the velocity ACF converges faster than the mean square displacement (sec. 8.7), which can
also be used for the computation of diffusion constants. However, Allen & Tildesley [113] warn
us that the long-time contribution to the velocity ACF can not be ignored, so care must be taken.
Another important quantity is the dipole correlation time. The dipole correlation function for
particles of type Ais calculated as follows by gmx dipoles:
Cµ(τ) = hµi(τ)·µi(0)ii∈A(8.17)
with µi=Pj∈irjqj. The dipole correlation time can be computed using eqn. 8.8. For some
applications see [165].
The viscosity of a liquid can be related to the correlation time of the Pressure tensor P[166,167].
gmx energy can compute the viscosity, but this is not very accurate [154], and actually the
values do not converge.
8.6 Curve fitting in GROMACS
8.6.1 Sum of exponential functions
Sometimes it is useful to fit a curve to an analytical function, for example in the case of autocor-
relation functions with noisy tails. GROMACS is not a general purpose curve-fitting tool however
and therefore GROMACS only supports a limited number of functions. Table 8.1 lists the avail-
able options with the corresponding command-line options. The underlying routines for fitting use
the Levenberg-Marquardt algorithm as implemented in the lmfit package [168] (a bare-bones
version of which is included in GROMACS in which an option for error-weighted fitting was
implemented).
Table 8.1: Overview of fitting functions supported in (most) analysis tools that compute autocor-
relation functions. The “Note” column describes properties of the output parameters.
Command Functional form f(t)Note
line option
exp e−t/a0
aexp a1e−t/a0
exp_exp a1e−t/a0+ (1 −a1)e−t/a2a2≥a0≥0
exp5 a1e−t/a0+a3e−t/a2+a4a2≥a0≥0
exp7 a1e−t/a0+a3e−t/a2+a5e−t/a4+a6a4≥a2≥a0≥0
exp9 a1e−t/a0+a3e−t/a2+a5e−t/a4+a7e−t/a6+a8a6≥a4≥a2≥a0≥0
8.6.2 Error estimation
Under the hood GROMACS implements some more fitting functions, namely a function to esti-
mate the error in time-correlated data due to Hess [154]:
ε2(t) = ατ11 + τ1
te−t/τ1−1+ (1 −α)τ21 + τ2
te−t/τ2−1(8.18)

8.6. Curve fitting in GROMACS 213
where τ1and τ2are time constants (with τ2≥τ1) and αusually is close to 1 (in the fitting
procedure it is enforced that 0≤α≤1). This is used in gmx analyze for error estimation
using
lim
t→∞ ε(t) = σs2(ατ1+ (1 −α)τ2)
T(8.19)
where σis the standard deviation of the data set and Tis the total simulation time [154].
8.6.3 Interphase boundary demarcation
In order to determine the position and width of an interface, Steen-Sæthre et al. fitted a density
profile to the following function
f(x) = a0+a1
2−a0−a1
2erf x−a2
a2
3(8.20)
where a0and a1are densities of different phases, xis the coordinate normal to the interface, a2is
the position of the interface and a3is the width of the interface [169]. This is implemented in gmx
densorder.
8.6.4 Transverse current autocorrelation function
In order to establish the transverse current autocorrelation function (useful for computing viscos-
ity [170]) the following function is fitted:
f(x) = e−νcosh(ων) + sinh(ων)
ω(8.21)
with ν=x/(2a0)and ω=√1−a1. This is implemented in gmx tcaf.
8.6.5 Viscosity estimation from pressure autocorrelation function
The viscosity is a notoriously difficult property to extract from simulations [154,171]. It is in
principle possible to determine it by integrating the pressure autocorrelation function [166], how-
ever this is often hampered by the noisy tail of the ACF. A workaround to this is fitting the ACF
to the following function [172]:
f(t)/f(0) = (1 −C)cos(ωt)e−(t/τf)βf+Ce−(t/τs)βs(8.22)
where ωis the frequency of rapid pressure oscillations (mainly due to bonded forces in molecu-
lar simulations), τfand βfare the time constant and exponent of fast relaxation in a stretched-
exponential approximation, τsand βsare constants for slow relaxation and Cis the pre-factor that
determines the weight between fast and slow relaxation. After a fit, the integral of the function
f(t)is used to compute the viscosity:
η=V
kBTZ∞
0
f(t)dt (8.23)
This equation has been applied to computing the bulk and shear viscosity using different elements
from the pressure tensor [173]. This is implemented in gmx viscosity.
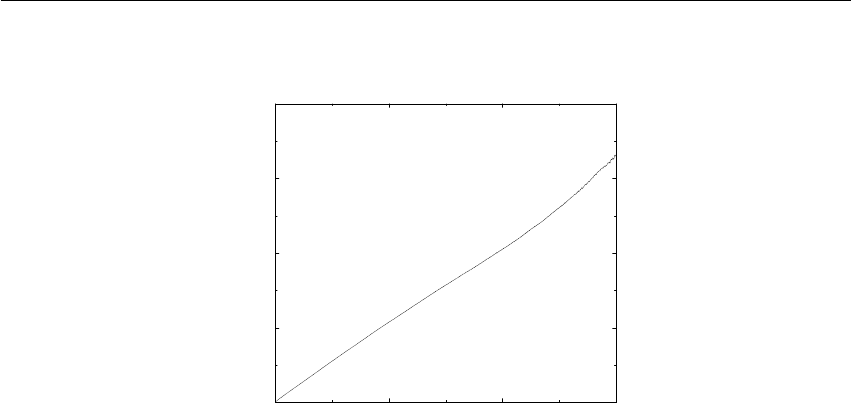
214 Chapter 8. Analysis
0.0 50.0 100.0 150.0
Time (ps)
0.0
1000.0
2000.0
3000.0
4000.0
MSD (10-5 cm2 s-1)
Mean Square Displacement
D = 3.5027 (10-5 cm2 s-1)
Figure 8.4: Mean Square Displacement of SPC-water.
8.7 Mean Square Displacement
gmx msd
To determine the self diffusion coefficient DAof particles of type A, one can use the Einstein
relation [113]:
lim
t→∞hkri(t)−ri(0)k2ii∈A= 6DAt(8.24)
This mean square displacement and DAare calculated by the program gmx msd. Normally
an index file containing atom numbers is used and the MSD is averaged over these atoms. For
molecules consisting of more than one atom, rican be taken as the center of mass positions of
the molecules. In that case, you should use an index file with molecule numbers. The results will
be nearly identical to averaging over atoms, however. The gmx msd program can also be used
for calculating diffusion in one or two dimensions. This is useful for studying lateral diffusion on
interfaces.
An example of the mean square displacement of SPC water is given in Fig. 8.4.
8.8 Bonds/distances, angles and dihedrals
gmx distance, gmx angle, gmx gangle
To monitor specific bonds in your modules, or more generally distances between points, the pro-
gram gmx distance can calculate distances as a function of time, as well as the distribution of
the distance. With a traditional index file, the groups should consist of pairs of atom numbers, for
example:
[ bonds_1 ]
1 2
3 4
8.8. Bonds/distances, angles and dihedrals 215
φ = 0φ = 0
A B
Figure 8.5: Dihedral conventions: A. “Biochemical convention”. B. “Polymer convention”.
9 10
[ bonds_2 ]
12 13
Selections are also supported, with first two positions defining the first distance, second pair of
positions defining the second distance and so on. You can calculate the distances between CA and
CB atoms in all your residues (assuming that every residue either has both atoms, or neither) using
a selection such as:
name CA CB
The selections also allow more generic distances to be computed. For example, to compute the
distances between centers of mass of two residues, you can use:
com of resname AAA plus com of resname BBB
The program gmx angle calculates the distribution of angles and dihedrals in time. It also gives
the average angle or dihedral. The index file consists of triplets or quadruples of atom numbers:
[ angles ]
123
234
345
[ dihedrals ]
1234
2355
For the dihedral angles you can use either the “biochemical convention” (φ= 0 ≡cis) or “poly-
mer convention” (φ= 0 ≡trans), see Fig. 8.5.
The program gmx gangle provides a selection-enabled version to compute angles. This tool can
also compute angles and dihedrals, but does not support all the options of gmx angle, such as
autocorrelation or other time series analyses. In addition, it supports angles between two vectors,
a vector and a plane, two planes (defined by 2 or 3 points, respectively), a vector/plane and the
216 Chapter 8. Analysis
A B C
z
D
Figure 8.6: Angle options of gmx gangle: A. Angle between two vectors. B. Angle between
two planes. C. Angle between a vector and the zaxis. D. Angle between a vector and the normal of
a sphere. Also other combinations are supported: planes and vectors can be used interchangeably.
zaxis, or a vector/plane and the normal of a sphere (determined by a single position). Also the
angle between a vector/plane compared to its position in the first frame is supported. For planes,
gmx gangle uses the normal vector perpendicular to the plane. See Fig. 8.6A, B, C) for the
definitions.
8.9 Radius of gyration and distances
gmx gyrate, gmx distance, gmx mindist, gmx mdmat, gmx pairdist, gmx
xpm2ps
To have a rough measure for the compactness of a structure, you can calculate the radius of gyra-
tion with the program gmx gyrate as follows:
Rg= Pikrik2mi
Pimi!1
2(8.25)
where miis the mass of atom iand rithe position of atom iwith respect to the center of mass of
the molecule. It is especially useful to characterize polymer solutions and proteins. The program
will also provide the radius of gyration around the coordinate axis (or, optionally, principal axes)
by only summing the radii components orthogonal to each axis, for instance
Rg,x =
Pir2
i,y +r2
i,zmi
Pimi
1
2
(8.26)
Sometimes it is interesting to plot the distance between two atoms, or the minimum distance be-
tween two groups of atoms (e.g.: protein side-chains in a salt bridge). To calculate these distances
between certain groups there are several possibilities:
•The distance between the geometrical centers of two groups can be calculated with the program
gmx distance, as explained in sec. 8.8.
•The minimum distance between two groups of atoms during time can be calculated with the
program gmx mindist. It also calculates the number of contacts between these groups
within a certain radius rmax.
8.10. Root mean square deviations in structure 217
21 30 40 50 60 70 80 90
21
30
40
50
60
70
80
90
t=0 ps
Residue Number
0 Distance (nm) 1.2
Figure 8.7: A minimum distance matrix for a peptide [174].
•gmx pairdist is a selection-enabled version of gmx mindist.
•To monitor the minimum distances between amino acid residues within a (protein) molecule,
you can use the program gmx mdmat. This minimum distance between two residues Ai
and Ajis defined as the smallest distance between any pair of atoms (i ∈Ai, j ∈Aj). The
output is a symmetrical matrix of smallest distances between all residues. To visualize this
matrix, you can use a program such as xv. If you want to view the axes and legend or if
you want to print the matrix, you can convert it with xpm2ps into a Postscript picture, see
Fig. 8.7.
Plotting these matrices for different time-frames, one can analyze changes in the structure,
and e.g. forming of salt bridges.
8.10 Root mean square deviations in structure
gmx rms, gmx rmsdist
The root mean square deviation (RMSD) of certain atoms in a molecule with respect to a refer-
ence structure can be calculated with the program gmx rms by least-square fitting the structure
to the reference structure (t2= 0) and subsequently calculating the RMSD (eqn. 8.27).
RMSD(t1, t2) = "1
M
N
X
i=1
mikri(t1)−ri(t2)k2#1
2
(8.27)
where M=PN
i=1 miand ri(t)is the position of atom iat time t.Note that fitting does not
have to use the same atoms as the calculation of the RM SD;e.g. a protein is usually fitted on

218 Chapter 8. Analysis
the backbone atoms (N,Cα,C), but the RMSD can be computed of the backbone or of the whole
protein.
Instead of comparing the structures to the initial structure at time t= 0 (so for example a crystal
structure), one can also calculate eqn. 8.27 with a structure at time t2=t1−τ. This gives some
insight in the mobility as a function of τ. A matrix can also be made with the RM SD as a function
of t1and t2, which gives a nice graphical interpretation of a trajectory. If there are transitions in a
trajectory, they will clearly show up in such a matrix.
Alternatively the RMSD can be computed using a fit-free method with the program gmx rmsdist:
RMSD(t) =
1
N2
N
X
i=1
N
X
j=1 krij(t)−rij (0)k2
1
2
(8.28)
where the distance rij between atoms at time tis compared with the distance between the same
atoms at time 0.
8.11 Covariance analysis
Covariance analysis, also called principal component analysis or essential dynamics [175], can
find correlated motions. It uses the covariance matrix Cof the atomic coordinates:
Cij =M
1
2
ii (xi− hxii)M
1
2
jj (xj− hxji)(8.29)
where Mis a diagonal matrix containing the masses of the atoms (mass-weighted analysis) or
the unit matrix (non-mass weighted analysis). Cis a symmetric 3N×3Nmatrix, which can be
diagonalized with an orthonormal transformation matrix R:
RTCR =diag(λ1, λ2, . . . , λ3N)where λ1≥λ2≥. . . ≥λ3N(8.30)
The columns of Rare the eigenvectors, also called principal or essential modes. Rdefines a
transformation to a new coordinate system. The trajectory can be projected on the principal modes
to give the principal components pi(t):
p(t) = RTM1
2(x(t)− hxi)(8.31)
The eigenvalue λiis the mean square fluctuation of principal component i. The first few principal
modes often describe collective, global motions in the system. The trajectory can be filtered along
one (or more) principal modes. For one principal mode ithis goes as follows:
xf(t) = hxi+M−1
2R∗ipi(t)(8.32)
When the analysis is performed on a macromolecule, one often wants to remove the overall rota-
tion and translation to look at the internal motion only. This can be achieved by least square fitting
to a reference structure. Care has to be taken that the reference structure is representative for the
ensemble, since the choice of reference structure influences the covariance matrix.

8.11. Covariance analysis 219
One should always check if the principal modes are well defined. If the first principal component
resembles a half cosine and the second resembles a full cosine, you might be filtering noise (see
below). A good way to check the relevance of the first few principal modes is to calculate the
overlap of the sampling between the first and second half of the simulation. Note that this can
only be done when the same reference structure is used for the two halves.
A good measure for the overlap has been defined in [176]. The elements of the covariance matrix
are proportional to the square of the displacement, so we need to take the square root of the matrix
to examine the extent of sampling. The square root can be calculated from the eigenvalues λiand
the eigenvectors, which are the columns of the rotation matrix R. For a symmetric and diagonally-
dominant matrix Aof size 3N×3Nthe square root can be calculated as:
A1
2=Rdiag(λ
1
2
1, λ
1
2
2, . . . , λ
1
2
3N)RT(8.33)
It can be verified easily that the product of this matrix with itself gives A. Now we can define a
difference dbetween covariance matrices Aand Bas follows:
d(A, B) = str A1
2−B1
22(8.34)
=rtr A+B−2A1
2B1
2(8.35)
=
N
X
i=1 λA
i+λB
i−2
N
X
i=1
N
X
j=1 qλA
iλB
jRA
i·RB
j2
1
2
(8.36)
where tr is the trace of a matrix. We can now define the overlap sas:
s(A, B) = 1 −d(A, B)
√trA+trB(8.37)
The overlap is 1 if and only if matrices Aand Bare identical. It is 0 when the sampled subspaces
are completely orthogonal.
A commonly-used measure is the subspace overlap of the first few eigenvectors of covariance
matrices. The overlap of the subspace spanned by morthonormal vectors w1,...,wmwith a
reference subspace spanned by northonormal vectors v1,...,vncan be quantified as follows:
overlap(v,w) = 1
n
n
X
i=1
m
X
j=1
(vi·wj)2(8.38)
The overlap will increase with increasing mand will be 1 when set vis a subspace of set w.
The disadvantage of this method is that it does not take the eigenvalues into account. All eigen-
vectors are weighted equally, and when degenerate subspaces are present (equal eigenvalues), the
calculated overlap will be too low.
Another useful check is the cosine content. It has been proven that the the principal components
of random diffusion are cosines with the number of periods equal to half the principal component
index [177,176]. The eigenvalues are proportional to the index to the power −2. The cosine
content is defined as:
2
T ZT
0
cos iπt
Tpi(t)dt!2 ZT
0
p2
i(t)dt!−1
(8.39)
220 Chapter 8. Analysis
D
H
α
A
r
Figure 8.8: Geometrical Hydrogen bond criterion.
When the cosine content of the first few principal components is close to 1, the largest fluctuations
are not connected with the potential, but with random diffusion.
The covariance matrix is built and diagonalized by gmx covar. The principal components and
overlap (and many more things) can be plotted and analyzed with gmx anaeig. The cosine
content can be calculated with gmx analyze.
8.12 Dihedral principal component analysis
gmx angle, gmx covar, gmx anaeig
Principal component analysis can be performed in dihedral space [178] using GROMACS. You
start by defining the dihedral angles of interest in an index file, either using gmx mk_angndx
or otherwise. Then you use the gmx angle program with the -or flag to produce a new .trr
file containing the cosine and sine of each dihedral angle in two coordinates, respectively. That
is, in the .trr file you will have a series of numbers corresponding to: cos(φ1), sin(φ1), cos(φ2),
sin(φ2), ..., cos(φn), sin(φn), and the array is padded with zeros, if necessary. Then you can use
this .trr file as input for the gmx covar program and perform principal component analysis
as usual. For this to work you will need to generate a reference file (.tpr,.gro,.pdb etc.)
containing the same number of “atoms” as the new .trr file, that is for ndihedrals you need
2n/3 atoms (rounded up if not an integer number). You should use the -nofit option for gmx
covar since the coordinates in the dummy reference file do not correspond in any way to the
information in the .trr file. Analysis of the results is done using gmx anaeig.
8.13 Hydrogen bonds
gmx hbond
The program gmx hbond analyzes the hydrogen bonds (H-bonds) between all possible donors
D and acceptors A. To determine if an H-bond exists, a geometrical criterion is used, see also
Fig. 8.8:
r≤rHB = 0.35 nm
α≤αHB = 30o(8.40)
The value of rHB = 0.35 nm corresponds to the first minimum of the RDF of SPC water (see also
Fig. 8.3).
The program gmx hbond analyzes all hydrogen bonds existing between two groups of atoms
(which must be either identical or non-overlapping) or in specified donor-hydrogen-acceptor triplets,
8.13. Hydrogen bonds 221
O
DA
H
H
H
(1) (2)
(2)
Figure 8.9: Insertion of water into an H-bond. (1) Normal H-bond between two residues. (2)
H-bonding bridge via a water molecule.
in the following ways:
•Donor-Acceptor distance (r) distribution of all H-bonds
•Hydrogen-Donor-Acceptor angle (α) distribution of all H-bonds
•The total number of H-bonds in each time frame
•The number of H-bonds in time between residues, divided into groups n-n+iwhere nand
n+istand for residue numbers and igoes from 0 to 6. The group for i= 6 also includes
all H-bonds for i > 6. These groups include the n-n+3,n-n+4and n-n+5H-bonds, which
provide a measure for the formation of α-helices or β-turns or strands.
•The lifetime of the H-bonds is calculated from the average over all autocorrelation functions
of the existence functions (either 0 or 1) of all H-bonds:
C(τ) = hsi(t)si(t+τ)i(8.41)
with si(t) = {0,1}for H-bond iat time t. The integral of C(τ)gives a rough estimate of
the average H-bond lifetime τHB:
τHB =Z∞
0
C(τ)dτ (8.42)
Both the integral and the complete autocorrelation function C(τ)will be output, so that more
sophisticated analysis (e.g. using multi-exponential fits) can be used to get better estimates
for τHB. A more complete analysis is given in ref. [179]; one of the more fancy option is
the Luzar and Chandler analysis of hydrogen bond kinetics [180,181].
•An H-bond existence map can be generated of dimensions # H-bonds×# frames. The order-
ing is identical to the index file (see below), but reversed, meaning that the last triplet in the
index file corresponds to the first row of the existence map.
•Index groups are output containing the analyzed groups, all donor-hydrogen atom pairs
and acceptor atoms in these groups, donor-hydrogen-acceptor triplets involved in hydrogen
bonds between the analyzed groups and all solvent atoms involved in insertion.

222 Chapter 8. Analysis
8.14 Protein-related items
gmx do_dssp, gmx rama, gmx wheel
To analyze structural changes of a protein, you can calculate the radius of gyration or the minimum
residue distances over time (see sec. 8.9), or calculate the RMSD (sec. 8.10).
You can also look at the changing of secondary structure elements during your run. For this,
you can use the program gmx do_dssp, which is an interface for the commercial program
DSSP [182]. For further information, see the DSSP manual. A typical output plot of gmx do_-
dssp is given in Fig. 8.10.
One other important analysis of proteins is the so-called Ramachandran plot. This is the projection
of the structure on the two dihedral angles φand ψof the protein backbone, see Fig. 8.11.
To evaluate this Ramachandran plot you can use the program gmx rama. A typical output is
given in Fig. 8.12.
When studying α-helices it is useful to have a helical wheel projection of your peptide, to see
whether a peptide is amphipathic. This can be done using the gmx wheel program. Two exam-
ples are plotted in Fig. 8.13.
8.15 Interface-related items
gmx order, gmx density, gmx potential, gmx traj
When simulating molecules with long carbon tails, it can be interesting to calculate their average
orientation. There are several flavors of order parameters, most of which are related. The program
gmx order can calculate order parameters using the equation:
Sz=3
2hcos2θzi − 1
2(8.43)
where θzis the angle between the z-axis of the simulation box and the molecular axis under
consideration. The latter is defined as the vector from Cn−1to Cn+1. The parameters Sxand Syare
defined in the same way. The brackets imply averaging over time and molecules. Order parameters
can vary between 1 (full order along the interface normal) and −1/2(full order perpendicular to
the normal), with a value of zero in the case of isotropic orientation.
The program can do two things for you. It can calculate the order parameter for each CH2segment
separately, for any of three axes, or it can divide the box in slices and calculate the average value
of the order parameter per segment in one slice. The first method gives an idea of the ordering of
a molecule from head to tail, the second method gives an idea of the ordering as function of the
box length.
The electrostatic potential (ψ) across the interface can be computed from a trajectory by evaluating
the double integral of the charge density (ρ(z)):
ψ(z)−ψ(−∞) = −Zz
−∞
dz0Zz0
−∞
ρ(z00)dz00/0(8.44)
where the position z=−∞ is far enough in the bulk phase such that the field is zero. With this
method, it is possible to “split” the total potential into separate contributions from lipid and water

8.15. Interface-related items 223
0 100 200 300 400 500 600 700 800 900 1000
1
5
10
15
Residue
Time (ps)
Coil Bend Turn A-Helix B-Bridge
Figure 8.10: Analysis of the secondary structure elements of a peptide in time.
C
O
N
C
H
R
C
O
α
N
H
H
ψ
φ
Figure 8.11: Definition of the dihedral angles φand ψof the protein backbone.

224 Chapter 8. Analysis
–180.0 –120.0 –60.0 0.0 60.0 120.0 180.0
Phi
–180.0
–120.0
–60.0
0.0
60.0
120.0
180.0
Psi
Ramachandran Plot
Figure 8.12: Ramachandran plot of a small protein.
HPr-A HIS-15+
THR-16
ARG-17+
PRO-18
ALA-19
ALA-20
GLN-21
PHE-22
VAL-23
LYS-24+
GLU-25-
ALA-26
LYS-27+
GLY-28
Figure 8.13: Helical wheel projection of the N-terminal helix of HPr.

8.15. Interface-related items 225
molecules. The program gmx potential divides the box in slices and sums all charges of the
atoms in each slice. It then integrates this charge density to give the electric field, which is in turn
integrated to give the potential. Charge density, electric field, and potential are written to xvgr
input files.
The program gmx traj is a very simple analysis program. All it does is print the coordinates,
velocities, or forces of selected atoms. It can also calculate the center of mass of one or more
molecules and print the coordinates of the center of mass to three files. By itself, this is probably
not a very useful analysis, but having the coordinates of selected molecules or atoms can be very
handy for further analysis, not only in interfacial systems.
The program gmx density calculates the mass density of groups and gives a plot of the density
against a box axis. This is useful for looking at the distribution of groups or atoms across the
interface.

226 Chapter 8. Analysis
Appendix A
Some implementation details
In this chapter we will present some implementation details. This is far from complete, but we
deemed it necessary to clarify some things that would otherwise be hard to understand.
A.1 Single Sum Virial in GROMACS
The virial Ξcan be written in full tensor form as:
Ξ = −1
2
N
X
i<j
rij ⊗Fij (A.1)
where ⊗denotes the direct product of two vectors.1When this is computed in the inner loop of
an MD program 9 multiplications and 9 additions are needed.2
Here it is shown how it is possible to extract the virial calculation from the inner loop [183].
A.1.1 Virial
In a system with periodic boundary conditions, the periodicity must be taken into account for the
virial:
Ξ = −1
2
N
X
i<j
rn
ij ⊗Fij (A.2)
where rn
ij denotes the distance vector of the nearest image of atom ifrom atom j. In this definition
we add a shift vector δito the position vector riof atom i. The difference vector rn
ij is thus equal
to:
rn
ij =ri+δi−rj(A.3)
or in shorthand:
rn
ij =rn
i−rj(A.4)
1(u⊗v)αβ =uαvβ
2The calculation of Lennard-Jones and Coulomb forces is about 50 floating point operations.
228 Appendix A. Some implementation details
In a triclinic system, there are 27 possible images of i; when a truncated octahedron is used, there
are 15 possible images.
A.1.2 Virial from non-bonded forces
Here the derivation for the single sum virial in the non-bonded force routine is given. There are a
couple of considerations that are special to GROMACS that we take into account:
•When calculating short-range interactions, we apply the minimum image convention and
only consider the closest image of each neighbor - and in particular we never allow inter-
actions between a particle and any of its periodic images. For all the equations below, this
means i6=j.
•In general, either the ior jparticle might be shifted to a neighbor cell to get the closest
interaction (shift δij). However, with minimum image convention there can be at most 27
different shifts for particles in the central cell, and for typical (very short-ranged) biomolec-
ular interactions there are typically only a few different shifts involved for each particle, not
to mention that each interaction can only be present for one shift.
•For the GROMACS nonbonded interactions we use this to split the neighborlist of each i
particle into multiple separate lists, where each list has a constant shift δifor the ipartlcle.
We can represent this as a sum over shifts (for which we use index s), with the constraint
that each particle interaction can only contribute to one of the terms in this sum, and the
shift is no longer dependent on the jparticles. For any sum that does not contain complex
dependence on s, this means the sum trivially reduces to just the sum over iand/or j.
•To simplify some of the sums, we replace sums over j < i with double sums over all
particles (remember, i6=j) and divide by 2.
Starting from the above definition of the virial, we then get
Ξ = −1
2
N
X
i<j
rn
ij ⊗Fij
=−1
2
N
X
i<j
(ri+δij −rj)⊗Fij
=−1
4
N
X
i=1
N
X
j=1
(ri+δij −rj)⊗Fij
=−1
4
N
X
i=1 X
s
N
X
j=1
(ri+δi,s −rj)⊗Fij,s
=−1
4
N
X
i=X
s
N
X
j=1
((ri+δi,s)⊗Fij,s −rj⊗Fij,s)
=−1
4
N
X
i=1 X
s
N
X
j=1
(ri+δi,s)⊗Fij,s +1
4
N
X
i=1 X
s
N
X
j=1
rj⊗Fij,s
A.1. Single Sum Virial in GROMACS 229
=−1
4
N
X
i=1 X
s
N
X
j=1
(ri+δi,s)⊗Fij,s +1
4
N
X
i=1
N
X
j=1
rj⊗Fij
=−1
4X
s
N
X
i=1
(ri+δi,s)⊗
N
X
j=1
Fij,s +1
4
N
X
j=1
rj⊗
N
X
i=1
Fij
=−1
4X
s
N
X
i=1
(ri+δi,s)⊗
N
X
j=1
Fij,s −1
4
N
X
j=1
rj⊗
N
X
i=1
Fji
=−1
4X
s
N
X
i=1
(ri+δi,s)⊗Fi,s −1
4
N
X
j=1
rj⊗Fj
=−1
4
N
X
i=1
ri⊗Fi+
N
X
j=1
rj⊗Fj
−1
4X
s
N
X
i=1
δi,s ⊗Fi,s
=−1
2
N
X
i=1
ri⊗Fi−1
4X
s
N
X
i=1
δi,s ⊗Fi,s
=−1
2
N
X
i=1
ri⊗Fi−1
4X
s
δs⊗Fs
= Ξ0+ Ξ1(A.5)
In the second-last stage, we have used the property that each shift vector itself does not depend
on the coordinates of particle i, so it is possible to sum up all forces corresponding to each shift
vector (in the nonbonded kernels), and then just use a sum over the different shift vectors outside
the kernels. We have also used
Fi=
N
X
j=1
Fij (A.6)
Fj=
N
X
i=1
Fji (A.7)
which is the total force on iwith respect to j. Because we use Newton’s Third Law:
Fij =−Fji (A.8)
we must, in the implementation, double the term containing the shift δi. Similarly, in a few places
we have summed the shift-dependent force over all shifts to come up with the total force per
interaction or particle.
This separates the total virial Ξinto a component Ξ0that is a single sum over particles, and a
second component Ξ1that describes the influence of the particle shifts, and that is only a sum over
the different shift vectors.
A.1.3 The intra-molecular shift (mol-shift)
For the bonded forces and SHAKE it is possible to make a mol-shift list, in which the periodicity
is stored. We simple have an array mshift in which for each atom an index in the shiftvec
array is stored.

230 Appendix A. Some implementation details
The algorithm to generate such a list can be derived from graph theory, considering each particle
in a molecule as a bead in a graph, the bonds as edges.
1 Represent the bonds and atoms as bidirectional graph
2 Make all atoms white
3 Make one of the white atoms black (atom i) and put it in the central box
4 Make all of the neighbors of ithat are currently white, gray
5 Pick one of the gray atoms (atom j), give it the correct periodicity with respect to any of its
black neighbors and make it black
6 Make all of the neighbors of jthat are currently white, gray
7 If any gray atom remains, go to [5]
8 If any white atom remains, go to [3]
Using this algorithm we can
•optimize the bonded force calculation as well as SHAKE
•calculate the virial from the bonded forces in the single sum method again
Find a representation of the bonds as a bidirectional graph.
A.1.4 Virial from Covalent Bonds
Since the covalent bond force gives a contribution to the virial, we have:
b=krn
ijk(A.9)
Vb=1
2kb(b−b0)2(A.10)
Fi=−∇Vb(A.11)
=kb(b−b0)rn
ij
b(A.12)
Fj=−Fi(A.13)
The virial contribution from the bonds then is:
Ξb=−1
2(rn
i⊗Fi+rj⊗Fj)(A.14)
=−1
2rn
ij ⊗Fi(A.15)
A.2. Optimizations 231
A.1.5 Virial from SHAKE
An important contribution to the virial comes from shake. Satisfying the constraints a force Gthat
is exerted on the particles “shaken.” If this force does not come out of the algorithm (as in standard
SHAKE) it can be calculated afterward (when using leap-frog) by:
∆ri=ri(t+ ∆t)−[ri(t) + vi(t−∆t
2)∆t+Fi
mi
∆t2](A.16)
Gi=mi∆ri
∆t2(A.17)
This does not help us in the general case. Only when no periodicity is needed (like in rigid water)
this can be used, otherwise we must add the virial calculation in the inner loop of SHAKE.
When it is applicable the virial can be calculated in the single sum way:
Ξ = −1
2
Nc
X
i
ri⊗Fi(A.18)
where Ncis the number of constrained atoms.
A.2 Optimizations
Here we describe some of the algorithmic optimizations used in GROMACS, apart from paral-
lelism.
A.2.1 Inner Loops for Water
GROMACS uses special inner loops to calculate non-bonded interactions for water molecules with
other atoms, and yet another set of loops for interactions between pairs of water molecules. There
highly optimized loops for two types of water models. For three site models similar to SPC [85],
i.e.:
1. There are three atoms in the molecule.
2. The whole molecule is a single charge group.
3. The first atom has Lennard-Jones (sec. 4.1.1) and Coulomb (sec. 4.1.3) interactions.
4. Atoms two and three have only Coulomb interactions, and equal charges.
These loops also works for the SPC/E [184] and TIP3P [133] water models. And for four site
water models similar to TIP4P [133]:
1. There are four atoms in the molecule.
2. The whole molecule is a single charge group.

232 Appendix A. Some implementation details
3. The first atom has only Lennard-Jones (sec. 4.1.1) interactions.
4. Atoms two and three have only Coulomb (sec. 4.1.3) interactions, and equal charges.
5. Atom four has only Coulomb interactions.
The benefit of these implementations is that there are more floating-point operations in a single
loop, which implies that some compilers can schedule the code better. However, it turns out that
even some of the most advanced compilers have problems with scheduling, implying that manual
tweaking is necessary to get optimum performance. This may include common-sub-expression
elimination, or moving code around.
Appendix B
Averages and fluctuations
B.1 Formulae for averaging
Note: this section was taken from ref [185].
When analyzing a MD trajectory averages hxiand fluctuations
D(∆x)2E1
2=D[x− hxi]2E1
2(B.1)
of a quantity xare to be computed. The variance σxof a series of Nxvalues, {xi}, can be computed
from
σx=
Nx
X
i=1
x2
i−1
Nx Nx
X
i=1
xi!2
(B.2)
Unfortunately this formula is numerically not very accurate, especially when σ
1
2
xis small compared
to the values of xi. The following (equivalent) expression is numerically more accurate
σx=
Nx
X
i=1
[xi− hxi]2(B.3)
with
hxi=1
Nx
Nx
X
i=1
xi(B.4)
Using eqns. B.2 and B.4 one has to go through the series of xivalues twice, once to determine
hxiand again to compute σx, whereas eqn. B.1 requires only one sequential scan of the series
{xi}. However, one may cast eqn. B.2 in another form, containing partial sums, which allows for
a sequential update algorithm. Define the partial sum
Xn,m =
m
X
i=n
xi(B.5)
234 Appendix B. Averages and fluctuations
and the partial variance
σn,m =
m
X
i=nxi−Xn,m
m−n+ 12(B.6)
It can be shown that
Xn,m+k=Xn,m +Xm+1,m+k(B.7)
and
σn,m+k=σn,m +σm+1,m+k+Xn,m
m−n+ 1 −Xn,m+k
m+k−n+ 1 2
∗
(m−n+ 1)(m+k−n+ 1)
k(B.8)
For n= 1 one finds
σ1,m+k=σ1,m +σm+1,m+k+X1,m
m−X1,m+k
m+k2m(m+k)
k(B.9)
and for n= 1 and k= 1 (eqn. B.8) becomes
σ1,m+1 =σ1,m +X1,m
m−X1,m+1
m+ 1 2
m(m+ 1) (B.10)
=σ1,m +[X1,m −mxm+1 ]2
m(m+ 1) (B.11)
where we have used the relation
X1,m+1 =X1,m +xm+1 (B.12)
Using formulae (eqn. B.11) and (eqn. B.12) the average
hxi=X1,Nx
Nx
(B.13)
and the fluctuation
D(∆x)2E1
2=σ1,Nx
Nx1
2(B.14)
can be obtained by one sweep through the data.
B.2 Implementation
In GROMACS the instantaneous energies E(m)are stored in the energy file, along with the values
of σ1,m and X1,m. Although the steps are counted from 0, for the energy and fluctuations steps are
counted from 1. This means that the equations presented here are the ones that are implemented.
We give somewhat lengthy derivations in this section to simplify checking of code and equations
later on.

B.2. Implementation 235
B.2.1 Part of a Simulation
It is not uncommon to perform a simulation where the first part, e.g. 100 ps, is taken as equili-
bration. However, the averages and fluctuations as printed in the log file are computed over the
whole simulation. The equilibration time, which is now part of the simulation, may in such a case
invalidate the averages and fluctuations, because these numbers are now dominated by the initial
drift towards equilibrium.
Using eqns. B.7 and B.8 the average and standard deviation over part of the trajectory can be
computed as:
Xm+1,m+k=X1,m+k−X1,m (B.15)
σm+1,m+k=σ1,m+k−σ1,m −X1,m
m−X1,m+k
m+k2m(m+k)
k(B.16)
or, more generally (with p≥1and q≥p):
Xp,q =X1,q −X1,p−1(B.17)
σp,q =σ1,q −σ1,p−1−X1,p−1
p−1−X1,q
q2(p−1)q
q−p+ 1 (B.18)
Note that implementation of this is not entirely trivial, since energies are not stored every time
step of the simulation. We therefore have to construct X1,p−1and σ1,p−1from the information at
time pusing eqns. B.11 and B.12:
X1,p−1=X1,p −xp(B.19)
σ1,p−1=σ1,p −[X1,p−1−(p−1)xp]2
(p−1)p(B.20)
B.2.2 Combining two simulations
Another frequently occurring problem is, that the fluctuations of two simulations must be com-
bined. Consider the following example: we have two simulations (A) of nand (B) of msteps, in
which the second simulation is a continuation of the first. However, the second simulation starts
numbering from 1 instead of from n+ 1. For the partial sum this is no problem, we have to add
XA
1,n from run A:
XAB
1,n+m=XA
1,n +XB
1,m (B.21)
When we want to compute the partial variance from the two components we have to make a
correction ∆σ:
σAB
1,n+m=σA
1,n +σB
1,m + ∆σ(B.22)
if we define xAB
ias the combined and renumbered set of data points we can write:
σAB
1,n+m=
n+m
X
i=1 "xAB
i−XAB
1,n+m
n+m#2
(B.23)

236 Appendix B. Averages and fluctuations
and thus
n+m
X
i=1 "xAB
i−XAB
1,n+m
n+m#2
=
n
X
i=1 "xA
i−XA
1,n
n#2
+
m
X
i=1 "xB
i−XB
1,m
m#2
+ ∆σ(B.24)
or
n+m
X
i=1
(xAB
i)2−2xAB
i
XAB
1,n+m
n+m+ XAB
1,n+m
n+m!2
−
n
X
i=1
(xA
i)2−2xA
i
XA
1,n
n+ XA
1,n
n!2
−
m
X
i=1
(xB
i)2−2xB
i
XB
1,m
m+ XB
1,m
m!2
= ∆σ(B.25)
all the x2
iterms drop out, and the terms independent of the summation counter ican be simplified:
XAB
1,n+m2
n+m−XA
1,n2
n−XB
1,m2
m−
2XAB
1,n+m
n+m
n+m
X
i=1
xAB
i+ 2 XA
1,n
n
n
X
i=1
xA
i+ 2 XB
1,m
m
m
X
i=1
xB
i= ∆σ(B.26)
we recognize the three partial sums on the second line and use eqn. B.21 to obtain:
∆σ=mXA
1,n −nXB
1,m2
nm(n+m)(B.27)
if we check this by inserting m= 1 we get back eqn. B.11
B.2.3 Summing energy terms
The gmx energy program can also sum energy terms into one, e.g. potential + kinetic = total.
For the partial averages this is again easy if we have Senergy components s:
XS
m,n =
n
X
i=m
S
X
s=1
xs
i=
S
X
s=1
n
X
i=m
xs
i=
S
X
s=1
Xs
m,n (B.28)
For the fluctuations it is less trivial again, considering for example that the fluctuation in potential
and kinetic energy should cancel. Nevertheless we can try the same approach as before by writing:
σS
m,n =
S
X
s=1
σs
m,n + ∆σ(B.29)
if we fill in eqn. B.6:
n
X
i=m" S
X
s=1
xs
i!−XS
m,n
m−n+ 1#2
=
S
X
s=1
n
X
i=m(xs
i)−Xs
m,n
m−n+ 12
+ ∆σ(B.30)
B.2. Implementation 237
which we can expand to:
n
X
i=m
S
X
s=1
(xs
i)2+ XS
m,n
m−n+ 1!2
−2
XS
m,n
m−n+ 1
S
X
s=1
xs
i+
S
X
s=1
S
X
s0=s+1
xs
ixs0
i
−
S
X
s=1
n
X
i=m"(xs
i)2−2Xs
m,n
m−n+ 1 xs
i+Xs
m,n
m−n+ 12#= ∆σ(B.31)
the terms with (xs
i)2cancel, so that we can simplify to:
XS
m,n2
m−n+ 1 −2XS
m,n
m−n+ 1
n
X
i=m
S
X
s=1
xs
i−2
n
X
i=m
S
X
s=1
S
X
s0=s+1
xs
ixs0
i−
S
X
s=1
n
X
i=m"−2Xs
m,n
m−n+ 1 xs
i+Xs
m,n
m−n+ 12#= ∆σ(B.32)
or
−XS
m,n2
m−n+ 1 −2
n
X
i=m
S
X
s=1
S
X
s0=s+1
xs
ixs0
i+
S
X
s=1 Xs
m,n2
m−n+ 1 = ∆σ(B.33)
If we now expand the first term using eqn. B.28 we obtain:
−PS
s=1 Xs
m,n2
m−n+ 1 −2
n
X
i=m
S
X
s=1
S
X
s0=s+1
xs
ixs0
i+
S
X
s=1 Xs
m,n2
m−n+ 1 = ∆σ(B.34)
which we can reformulate to:
−2
S
X
s=1
S
X
s0=s+1
Xs
m,nXs0
m,n +
n
X
i=m
S
X
s=1
S
X
s0=s+1
xs
ixs0
i
= ∆σ(B.35)
or
−2
S
X
s=1
Xs
m,n
S
X
s0=s+1
Xs0
m,n +
S
X
s=1
n
X
i=m
xs
i
S
X
s0=s+1
xs0
i
= ∆σ(B.36)
which gives
−2
S
X
s=1
Xs
m,n
S
X
s0=s+1
n
X
i=m
xs0
i+
n
X
i=m
xs
i
S
X
s0=s+1
xs0
i
= ∆σ(B.37)
Since we need all data points ito evaluate this, in general this is not possible. We can then make an
estimate of σS
m,n using only the data points that are available using the left hand side of eqn. B.30.
While the average can be computed using all time steps in the simulation, the accuracy of the
fluctuations is thus limited by the frequency with which energies are saved. Since this can be
easily done with a program such as xmgr this is not built-in in GROMACS.

238 Appendix B. Averages and fluctuations
Bibliography
[1] Bekker, H., Berendsen, H. J. C., Dijkstra, E. J., Achterop, S., van Drunen, R., van der
Spoel, D., Sijbers, A., Keegstra, H., Reitsma, B., Renardus, M. K. R. Gromacs: A parallel
computer for molecular dynamics simulations. In Physics Computing 92 (Singapore, 1993).
de Groot, R. A., Nadrchal, J., eds. . World Scientific.
[2] Berendsen, H. J. C., van der Spoel, D., van Drunen, R. GROMACS: A message-passing
parallel molecular dynamics implementation. Comp. Phys. Comm. 91:43–56, 1995.
[3] Lindahl, E., Hess, B., van der Spoel, D. GROMACS 3.0: A package for molecular simula-
tion and trajectory analysis. J. Mol. Mod. 7:306–317, 2001.
[4] van der Spoel, D., Lindahl, E., Hess, B., Groenhof, G., Mark, A. E., Berendsen, H. J. C.
GROMACS: Fast, Flexible and Free. J. Comp. Chem. 26:1701–1718, 2005.
[5] Hess, B., Kutzner, C., van der Spoel, D., Lindahl, E. GROMACS 4: Algorithms for Highly
Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput.
4(3):435–447, 2008.
[6] Pronk, S., Páll, S., Schulz, R., Larsson, P., Bjelkmar, P., Apostolov, R., Shirts, M. R., Smith,
J. C., Kasson, P. M., van der Spoel, D., Hess, B., Lindahl, E. GROMACS 4.5: a high-
throughput and highly parallel open source molecular simulation toolkit. Bioinformatics
29(7):845–854, 2013.
[7] Páll, S., Abraham, M. J., Kutzner, C., Hess, B., Lindahl, E. Tackling exascale software
challenges in molecular dynamics simulati ons with GROMACS. In: Solving Software
Challenges for Exascale. Vol. 8759. Markidis, S., Laure, E. eds. Vol. 8759. . Springer Inter-
national Publishing Switzerland London 2015 3–27.
[8] Abraham, M. J., Murtola, T., Schulz, R., Páll, S., Smith, J. C., Hess, B., Lindahl, E. GRO-
MACS: High performance molecular simulations through multi-level parallelism from lap-
tops to supercomputers. SoftwareX 1–2:19–25, 2015.
[9] van Gunsteren, W. F., Berendsen, H. J. C. Computer simulation of molecular dynamics:
Methodology, applications, and perspectives in chemistry. Angew. Chem. Int. Ed. Engl.
29:992–1023, 1990.
[10] Fraaije, J. G. E. M. Dynamic density functional theory for microphase separation kinetics
of block copolymer melts. J. Chem. Phys. 99:9202–9212, 1993.

240 Bibliography
[11] McQuarrie, D. A. Statistical Mechanics. New York: Harper & Row. 1976.
[12] van Gunsteren, W. F., Berendsen, H. J. C. Algorithms for macromolecular dynamics and
constraint dynamics. Mol. Phys. 34:1311–1327, 1977.
[13] van Gunsteren, W. F., Karplus, M. Effect of constraints on the dynamics of macromolecules.
Macromolecules 15:1528–1544, 1982.
[14] Darden, T., York, D., Pedersen, L. Particle mesh Ewald: An N•log(N) method for Ewald
sums in large systems. J. Chem. Phys. 98:10089–10092, 1993.
[15] Essmann, U., Perera, L., Berkowitz, M. L., Darden, T., Lee, H., Pedersen, L. G. A smooth
particle mesh ewald potential. J. Chem. Phys. 103:8577–8592, 1995.
[16] Geman, S., Geman, D. Stochastic relaxation, Gibbs distributions and the Bayesian restora-
tion of images. IEEE Trans. Patt. Anal. Mach. Int. 6:721, 1984.
[17] Nilges, M., Clore, G. M., Gronenborn, A. M. Determination of three-dimensional structures
of proteins from interproton distance data by dynamical simulated annealing from a random
array of atoms. FEBS Lett. 239:129–136, 1988.
[18] van Schaik, R. C., Berendsen, H. J. C., Torda, A. E., van Gunsteren, W. F. A structure
refinement method based on molecular dynamics in 4 spatial dimensions. J. Mol. Biol.
234:751–762, 1993.
[19] Zimmerman, K. All purpose molecular mechanics simulator and energy minimizer. J.
Comp. Chem. 12:310–319, 1991.
[20] Adams, D. J., Adams, E. M., Hills, G. J. The computer simulation of polar liquids. Mol.
Phys. 38:387–400, 1979.
[21] Bekker, H., Dijkstra, E. J., Renardus, M. K. R., Berendsen, H. J. C. An efficient, box shape
independent non-bonded force and virial algorithm for molecular dynamics. Mol. Sim.
14:137–152, 1995.
[22] Hockney, R. W., Goel, S. P., Eastwood, J. Quiet High Resolution Computer Models of a
Plasma. J. Comp. Phys. 14:148–158, 1974.
[23] Verlet., L. Computer experiments on classical fluids. I. Thermodynamical properties of
Lennard-Jones molecules. Phys. Rev. 159:98–103, 1967.
[24] Berendsen, H. J. C., van Gunsteren, W. F. Practical algorithms for dynamics simulations.
[25] Swope, W. C., Andersen, H. C., Berens, P. H., Wilson, K. R. A computer-simulation
method for the calculation of equilibrium-constants for the formation of physical clusters
of molecules: Application to small water clusters. J. Chem. Phys. 76:637–649, 1982.
[26] Berendsen, H. J. C., Postma, J. P. M., DiNola, A., Haak, J. R. Molecular dynamics with
coupling to an external bath. J. Chem. Phys. 81:3684–3690, 1984.
[27] Andersen, H. C. Molecular dynamics simulations at constant pressure and/or temperature.
J. Chem. Phys. 72:2384, 1980.

Bibliography 241
[28] Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol.
Phys. 52:255–268, 1984.
[29] Hoover, W. G. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A
31:1695–1697, 1985.
[30] Bussi, G., Donadio, D., Parrinello, M. Canonical sampling through velocity rescaling. J.
Chem. Phys. 126:014101, 2007.
[31] Berendsen, H. J. C. Transport properties computed by linear response through weak cou-
pling to a bath. In: Computer Simulations in Material Science. Meyer, M., Pontikis, V. eds.
. Kluwer 1991 139–155.
[32] Basconi, J. E., Shirts, M. R. Effects of temperature control algorithms on transport proper-
ties and kinetics in molecular dynamics simulations. J. Chem. Theory Comput. 9(7):2887–
2899, 2013.
[33] Cooke, B., Schmidler, S. J. Preserving the Boltzmann ensemble in replica-exchange molec-
ular dynamics. J. Chem. Phys. 129:164112, 2008.
[34] Martyna, G. J., Klein, M. L., Tuckerman, M. E. Nosé-Hoover chains: The canonical en-
semble via continuous dynamics. J. Chem. Phys. 97:2635–2643, 1992.
[35] Martyna, G. J., Tuckerman, M. E., Tobias, D. J., Klein, M. L. Explicit reversible integrators
for extended systems dynamics. Mol. Phys. 87:1117–1157, 1996.
[36] Holian, B. L., Voter, A. F., Ravelo, R. Thermostatted molecular dynamics: How to avoid
the Toda demon hidden in Nosé-Hoover dynamics. Phys. Rev. E 52(3):2338–2347, 1995.
[37] Eastwood, M. P., Stafford, K. A., Lippert, R. A., Jensen, M. O., Maragakis, P., Predescu, C.,
Dror, R. O., Shaw, D. E. Equipartition and the calculation of temperature in biomolecular
simulations. J. Chem. Theory Comput. ASAP:DOI: 10.1021/ct9002916, 2010.
[38] Parrinello, M., Rahman, A. Polymorphic transitions in single crystals: A new molecular
dynamics method. J. Appl. Phys. 52:7182–7190, 1981.
[39] Nosé, S., Klein, M. L. Constant pressure molecular dynamics for molecular systems. Mol.
Phys. 50:1055–1076, 1983.
[40] Liu, G. Dynamical equations for the period vectors in a periodic system under constant
external stress. Can. J. Phys. 93:974–978, 2015.
[41] Tuckerman, M. E., Alejandre, J., López-Rendón, R., Jochim, A. L., Martyna, G. J. A
Liouville-operator derived measure-preserving integrator for molecular dynamics simula-
tions in the isothermal-isobaric ensemble. J. Phys. A. 59:5629–5651, 2006.
[42] Yu, T.-Q., Alejandre, J., Lopez-Rendon, R., Martyna, G. J., Tuckerman, M. E. Measure-
preserving integrators for molecular dynamics in the isothermal-isobaric ensemble derived
from the liouville operator. Chem. Phys. 370:294–305, 2010.
[43] Dick, B. G., Overhauser, A. W. Theory of the dielectric constants of alkali halide crystals.
Phys. Rev. 112:90–103, 1958.

242 Bibliography
[44] Jordan, P. C., van Maaren, P. J., Mavri, J., van der Spoel, D., Berendsen, H. J. C. Towards
phase transferable potential functions: Methodology and application to nitrogen. J. Chem.
Phys. 103:2272–2285, 1995.
[45] van Maaren, P. J., van der Spoel, D. Molecular dynamics simulations of a water with a
novel shell-model potential. J. Phys. Chem. B. 105:2618–2626, 2001.
[46] Ryckaert, J. P., Ciccotti, G., Berendsen, H. J. C. Numerical integration of the cartesian
equations of motion of a system with constraints; molecular dynamics of n-alkanes. J.
Comp. Phys. 23:327–341, 1977.
[47] Miyamoto, S., Kollman, P. A. SETTLE: An analytical version of the SHAKE and RATTLE
algorithms for rigid water models. J. Comp. Chem. 13:952–962, 1992.
[48] Andersen, H. C. RATTLE: A “Velocity” version of the SHAKE algorithm for molecular
dynamics calculations. J. Comp. Phys. 52:24–34, 1983.
[49] Hess, B., Bekker, H., Berendsen, H. J. C., Fraaije, J. G. E. M. LINCS: A linear constraint
solver for molecular simulations. J. Comp. Chem. 18:1463–1472, 1997.
[50] Hess, B. P-LINCS: A parallel linear constraint solver for molecular simulation. J. Chem.
Theory Comput. 4:116–122, 2007.
[51] Goga, N., Rzepiela, A. J., de Vries, A. H., Marrink, S. J., Berendsen, H. J. C. Efficient
algorithms for Langevin and DPD dynamics. J. Chem. Theory Comput. 8:3637–3649,
2012.
[52] Byrd, R. H., Lu, P., Nocedal, J. A limited memory algorithm for bound constrained opti-
mization. SIAM J. Scientif. Statistic. Comput. 16:1190–1208, 1995.
[53] Zhu, C., Byrd, R. H., Nocedal, J. L-BFGS-B: Algorithm 778: L-BFGS-B, FORTRAN
routines for large scale bound constrained optimization. ACM Trans. Math. Softw. 23:550–
560, 1997.
[54] Levitt, M., Sander, C., Stern, P. S. The normal modes of a protein: Native bovine pancreatic
trypsin inhibitor. Int. J. Quant. Chem: Quant. Biol. Symp. 10:181–199, 1983.
[55] G¯o, N., Noguti, T., Nishikawa, T. Dynamics of a small globular protein in terms of low-
frequency vibrational modes. Proc. Natl. Acad. Sci. USA 80:3696–3700, 1983.
[56] Brooks, B., Karplus, M. Harmonic dynamics of proteins: Normal modes and fluctuations
in bovine pancreatic trypsin inhibitor. Proc. Natl. Acad. Sci. USA 80:6571–6575, 1983.
[57] Hayward, S., G¯o, N. Collective variable description of native protein dynamics. Annu. Rev.
Phys. Chem. 46:223–250, 1995.
[58] Bennett, C. H. Efficient Estimation of Free Energy Differences from Monte Carlo Data. J.
Comp. Phys. 22:245–268, 1976.
[59] Shirts, M. R., Chodera, J. D. Statistically optimal analysis of multiple equilibrium simula-
tions. J. Chem. Phys. 129:124105, 2008.

Bibliography 243
[60] Hukushima, K., Nemoto, K. Exchange Monte Carlo Method and Application to Spin Glass
Simulations. J. Phys. Soc. Jpn. 65:1604–1608, 1996.
[61] Sugita, Y., Okamoto, Y. Replica-exchange molecular dynamics method for protein folding.
Chem. Phys. Lett. 314:141–151, 1999.
[62] Seibert, M., Patriksson, A., Hess, B., van der Spoel, D. Reproducible polypeptide folding
and structure prediction using molecular dynamics simulations. J. Mol. Biol. 354:173–183,
2005.
[63] Okabe, T., Kawata, M., Okamoto, Y., Mikami, M. Replica-exchange Monte Carlo method
for the isobaric-isothermal ensemble. Chem. Phys. Lett. 335:435–439, 2001.
[64] Chodera, J. D., Shirts, M. R. Replica exchange and expanded ensemble simulations as
gibbs sampling: Simple improvements for enhanced mixing. J. Chem. Phys. 135:194110,
2011.
[65] de Groot, B. L., Amadei, A., van Aalten, D. M. F., Berendsen, H. J. C. Towards an ex-
haustive sampling of the configurational spaces of the two forms of the peptide hormone
guanylin. J. Biomol. Str. Dyn. 13(5):741–751, 1996.
[66] de Groot, B. L., Amadei, A., Scheek, R. M., van Nuland, N. A. J., Berendsen, H. J. C. An
extended sampling of the configurational space of HPr from E. coli. PROTEINS: Struct.
Funct. Gen. 26:314–322, 1996.
[67] Lange, O. E., Schafer, L. V., Grubmuller, H. Flooding in GROMACS: Accelerated barrier
crossings in molecular dynamics. J. Comp. Chem. 27:1693–1702, 2006.
[68] Lyubartsev, A. P., Martsinovski, A. A., Shevkunov, S. V., Vorontsov-Velyaminov, P. N. New
approach to Monte Carlo calculation of the free energy: Method of expanded ensembles. J.
Chem. Phys. 96:1776–1783, 1992.
[69] Liem, S. Y., Brown, D., Clarke, J. H. R. Molecular dynamics simulations on distributed
memory machines. Comput. Phys. Commun. 67(2):261–267, 1991.
[70] Bowers, K. J., Dror, R. O., Shaw, D. E. The midpoint method for parallelization of particle
simulations. J. Chem. Phys. 124(18):184109–184109, 2006.
[71] Qiu, D., Shenkin, P., Hollinger, F., Still, W. The GB/SA Continuum Model for Solvation.
A Fast Analytical Method for the Calculation of Approximate Born Radii. J. Phys. Chem.
A. 101:3005–3014, 1997.
[72] Hawkins, D., Cramer, C., Truhlar, D. Parametrized Models of Aqueous Free Energies
of Solvation Based on Pairwise Descreening of Solute Atomic Charges from a Dielectric
Medium. J. Phys. Chem. 100:19824–19839, 1996.
[73] Onufriev, A., Bashford, D., Case, D. Exploring protein native states and large-scale con-
formational changes with a modified Generalized Born model. PROTEINS: Struct. Funct.
Gen. 55(2):383–394, 2004.

244 Bibliography
[74] Larsson, P., Lindahl, E. A High-Performance Parallel-Generalized Born Implementation
Enabled by Tabulated Interaction Rescaling. J. Comp. Chem. 31(14):2593–2600, 2010.
[75] Schaefer, M., Bartels, C., Karplus, M. Solution conformations and thermodynamics of
structured peptides: molecular dynamics simulation with an implicit solvation model. J.
Mol. Biol. 284(3):835–848, 1998.
[76] Tironi, I. G., Sperb, R., Smith, P. E., van Gunsteren, W. F. A generalized reaction field
method for molecular dynamics simulations. J. Chem. Phys. 102:5451–5459, 1995.
[77] van der Spoel, D., van Maaren, P. J. The origin of layer structure artifacts in simulations of
liquid water. J. Chem. Theory Comput. 2:1–11, 2006.
[78] Ohmine, I., Tanaka, H., Wolynes, P. G. Large local energy fluctuations in water. II. Coop-
erative motions and fluctuations. J. Chem. Phys. 89:5852–5860, 1988.
[79] Kitchen, D. B., Hirata, F., Westbrook, J. D., Levy, R., Kofke, D., Yarmush, M. Conserving
energy during molecular dynamics simulations of water, proteins, and proteins in water. J.
Comp. Chem. 11:1169–1180, 1990.
[80] Guenot, J., Kollman, P. A. Conformational and energetic effects of truncating nonbonded
interactions in an aqueous protein dynamics simulation. J. Comp. Chem. 14:295–311, 1993.
[81] Steinbach, P. J., Brooks, B. R. New spherical-cutoff methods for long-range forces in
macromolecular simulation. J. Comp. Chem. 15:667–683, 1994.
[82] van Gunsteren, W. F., Billeter, S. R., Eising, A. A., Hünenberger, P. H., Krüger, P., Mark,
A. E., Scott, W. R. P., Tironi, I. G. Biomolecular Simulation: The GROMOS96 manual and
user guide. Zürich, Switzerland: Hochschulverlag AG an der ETH Zürich. 1996.
[83] van Gunsteren, W. F., Berendsen, H. J. C. Gromos-87 manual. Biomos BV Nijenborgh 4,
9747 AG Groningen, The Netherlands 1987.
[84] Morse, P. M. Diatomic molecules according to the wave mechanics. II. vibrational levels.
Phys. Rev. 34:57–64, 1929.
[85] Berendsen, H. J. C., Postma, J. P. M., van Gunsteren, W. F., Hermans, J. Interaction models
for water in relation to protein hydration. In: Intermolecular Forces. Pullman, B. ed. . D.
Reidel Publishing Company Dordrecht 1981 331–342.
[86] Ferguson, D. M. Parametrization and evaluation of a flexible water model. J. Comp. Chem.
16:501–511, 1995.
[87] Warner Jr., H. R. Kinetic theory and rheology of dilute suspensions of finitely extendible
dumbbells. Ind. Eng. Chem. Fundam. 11(3):379–387, 1972.
[88] Bulacu, M., Goga, N., Zhao, W., Rossi, G., Monticelli, L., Periole, X., Tieleman, D., Mar-
rink, S. Improved angle potentials for coarse-grained molecular dynamics simulations. J.
Chem. Phys. 123(11).

Bibliography 245
[89] Brooks, B. R., Bruccoleri, R. E., Olafson, B. D., States, D. J., Swaminathan, S., Karplus,
M. CHARMM: a program for macromolecular energy, minimization, and dynamics calcu-
lation. J. Comp. Chem. 4:187–217, 1983.
[90] Lawrence, C. P., Skinner, J. L. Flexible TIP4P model for molecular dynamics simulation of
liquid water. Chem. Phys. Lett. 372:842–847, 2003.
[91] Jorgensen, W. L., Maxwell, D. S., Tirado-Rives, J. Development and testing of the opls
all-atom force field on conformational energetics and properties of organic liquids. J. Am.
Chem. Soc. 118:11225–11236, 1996.
[92] Robertson, M. J., Tirado-Rives, J., Jorgensen, W. L. Improved peptide and protein torsional
energetics with the opls-aa force field. J. Chem. Theory Comput. 11:3499–3509, 2015.
[93] Bulacu, M., van der Giessen, E. Effect of bending and torsion rigidity on self-diffusion in
polymer melts: A molecular-dynamics study. JCTC 9(8):3282–3292, 2013.
[94] Scott, R. A., Scheraga, H. Conformational analysis of macromolecules. J. Chem. Phys.
44:3054–3069, 1966.
[95] Pauling, L. The nature of chemical bond. Ithaca and New York: Cornell University Press.
1960.
[96] Torda, A. E., Scheek, R. M., van Gunsteren, W. F. Time-dependent distance restraints in
molecular dynamics simulations. Chem. Phys. Lett. 157:289–294, 1989.
[97] Hess, B., Scheek, R. M. Orientation restraints in molecular dynamics simulations using
time and ensemble averaging. J. Magn. Reson. 164:19–27, 2003.
[98] Lopes, P. E. M., Huang, J., Shim, J., Luo, Y., Li, H., Roux, B., MacKerell, J. Alexander D.
Polarizable force field for peptides and proteins based on the classical drude oscillator. J.
Chem. Theory Comput 9:5430–5449, 2013.
[99] Yu, H., Whitfield, T. W., Harder, E., Lamoureux, G., Vorobyov, I., Anisimov, V. M., MacK-
erell, Jr., A. D., Roux, B. Simulating Monovalent and Divalent Ions in Aqueous Solution
Using a Drude Polarizable Force Field. J. Chem. Theory Comput. 6:774–786, 2010.
[100] Thole, B. T. Molecular polarizabilities with a modified dipole interaction. Chem. Phys.
59:341–345, 1981.
[101] Lamoureux, G., Roux, B. Modeling induced polarization with classical drude oscillators:
Theory and molecular dynamics simulation algorithm. J. Chem. Phys. 119:3025–3039,
2003.
[102] Lamoureux, G., MacKerell, A. D., Roux, B. A simple polarizable model of water based on
classical drude oscillators. J. Chem. Phys. 119:5185–5197, 2003.
[103] Noskov, S. Y., Lamoureux, G., Roux, B. Molecular dynamics study of hydration in ethanol-
water mixtures using a polarizable force field. J. Phys. Chem. B. 109:6705–6713, 2005.
[104] van Gunsteren, W. F., Mark, A. E. Validation of molecular dynamics simulations. J. Chem.
Phys. 108:6109–6116, 1998.

246 Bibliography
[105] Beutler, T. C., Mark, A. E., van Schaik, R. C., Greber, P. R., van Gunsteren, W. F. Avoid-
ing singularities and numerical instabilities in free energy calculations based on molecular
simulations. Chem. Phys. Lett. 222:529–539, 1994.
[106] Pham, T. T., Shirts, M. R. Identifying low variance pathways for free energy calculations
of molecular transformations in solution phase. J. Chem. Phys. 135:034114, 2011.
[107] Pham, T. T., Shirts, M. R. Optimal pairwise and non-pairwise alchemical pathways for
free energy calculations of molecular transformation in solution phase. J. Chem. Phys.
136:124120, 2012.
[108] Jorgensen, W. L., Tirado-Rives, J. The OPLS potential functions for proteins. energy mini-
mizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 110:1657–1666,
1988.
[109] Berendsen, H. J. C., van Gunsteren, W. F. Molecular dynamics simulations: Techniques and
approaches. In: Molecular Liquids-Dynamics and Interactions. et al., A. J. B. ed. NATO
ASI C 135. Reidel Dordrecht, The Netherlands 1984 475–500.
[110] Ewald, P. P. Die Berechnung optischer und elektrostatischer Gitterpotentiale. Ann. Phys.
64:253–287, 1921.
[111] Hockney, R. W., Eastwood, J. W. Computer simulation using particles. New York:
McGraw-Hill. 1981.
[112] Ballenegger, V., Cerdà, J. J., Holm, C. How to convert SPME to P3M: Influence functions
and error estimates. J. Chem. Theory Comput. 8(3):936—-947, 2012.
[113] Allen, M. P., Tildesley, D. J. Computer Simulations of Liquids. Oxford: Oxford Science
Publications. 1987.
[114] Wennberg, C. L., Murtola, T., Hess, B., Lindahl, E. Lennard-Jones Lattice Summation in
Bilayer Simulations Has Critical Effects on Surface Tension and Lipid Properties. J. Chem.
Theory Comput. 9:3527–3537, 2013.
[115] Oostenbrink, C., Villa, A., Mark, A. E., Van Gunsteren, W. F. A biomolecular force field
based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter
sets 53A5 and 53A6. Journal of Computational Chemistry 25(13):1656–1676, 2004.
[116] Cornell, W. D., Cieplak, P., Bayly, C. I., Gould, I. R., Merz, K. R. Jr., Ferguson, D. M.,
Spellmeyer, D. C., Fox, T., Caldwell, J. W., Kollman, P. A. A Second Generation Force
Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem.
Soc. 117(19):5179–5197, 1995.
[117] Kollman, P. A. Advances and Continuing Challenges in Achieving Realistic and Predic-
tive Simulations of the Properties of Organic and Biological Molecules. Acc. Chem. Res.
29(10):461–469, 1996.
[118] Wang, J., Cieplak, P., Kollman, P. A. How Well Does a Restrained Electrostatic Potential
(RESP) Model Perform in Calculating Conformational Energies of Organic and Biological
Molecules? J. Comp. Chem. 21(12):1049–1074, 2000.

Bibliography 247
[119] Hornak, V., Abel, R., Okur, A., Strockbine, B., Roitberg, A., Simmerling, C. Comparison of
Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters.
PROTEINS: Struct. Funct. Gen. 65:712–725, 2006.
[120] Lindorff-Larsen, K., Piana, S., Palmo, K., Maragakis, P., Klepeis, J. L., Dorr, R. O., Shaw,
D. E. Improved side-chain torsion potentials for the AMBER ff99SB protein force field.
PROTEINS: Struct. Funct. Gen. 78:1950–1958, 2010.
[121] Duan, Y., Wu, C., Chowdhury, S., Lee, M. C., Xiong, G., Zhang, W., Yang, R., Cieplak, P.,
Luo, R., Lee, T., Caldwell, J., Wang, J., Kollman, P. A Point-Charge Force Field for Molec-
ular Mechanics Simulations of Proteins Based on Condensed-Phase Quantum Mechanical
Calculations. J. Comp. Chem. 24(16):1999–2012, 2003.
[122] García, A. E., Sanbonmatsu, K. Y. α-Helical stabilization by side chain shielding of back-
bone hydrogen bonds. Proc. Natl. Acad. Sci. USA 99(5):2782–2787, 2002.
[123] MacKerell, J. A. D., Feig, M., Brooks III, C. L. Extending the treatment of backbone en-
ergetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing
protein conformational distributions in molecular dynamics simulations. J. Comp. Chem.
25(11):1400–15, 2004.
[124] MacKerell, A. D., Bashford, D., Bellott, Dunbrack, R. L., Evanseck, J. D., Field, M. J.,
Fischer, S., Gao, J., Guo, H., Ha, S., Joseph-McCarthy, D., Kuchnir, L., Kuczera, K., Lau,
F. T. K., Mattos, C., Michnick, S., Ngo, T., Nguyen, D. T., Prodhom, B., Reiher, W. E.,
Roux, B., Schlenkrich, M., Smith, J. C., Stote, R., Straub, J., Watanabe, M., Wiorkiewicz-
Kuczera, J., Yin, D., Karplus, M. All-atom empirical potential for molecular modeling and
dynamics studies of proteins. J. Phys. Chem. B. 102(18):3586–3616, 1998.
[125] Feller, S. E., MacKerell, A. D. An improved empirical potential energy function for molec-
ular simulations of phospholipids. J. Phys. Chem. B. 104(31):7510–7515, 2000.
[126] Foloppe, N., MacKerell, A. D. All-atom empirical force field for nucleic acids: I. Parameter
optimization based on small molecule and condensed phase macromolecular target data. J.
Comp. Chem. 21(2):86–104, 2000.
[127] MacKerell, A. D., Banavali, N. K. All-atom empirical force field for nucleic acids: II.
application to molecular dynamics simulations of DNA and RNA in solution. J. Comp.
Chem. 21(2):105–120, 2000.
[128] Bjelkmar, P., Larsson, P., Cuendet, M. A., Hess, B., Lindahl, E. Implementation of the
CHARMM force field in GROMACS: Analysis of protein stability effects from correction
maps, virtual interaction sites, and water models. J. Chem. Theory Comput. 6:459–466,
2010.
[129] Kohlmeyer, A., Vermaas, J. TopoTools: Release 1.6 with CHARMM export in topogro-
macs. Apr. 2016.
[130] Rühle, V., Junghans, C., Lukyanov, A., Kremer, K., Andrienko, D. Versatile Object-
Oriented toolkit for Coarse-Graining applications. J. Chem. Theory Comput. 5(12):3211–
3223, 2009.

248 Bibliography
[131] Bereau, T., Wang, Z.-J., Deserno, M. Solvent-free coarse-grained model for unbiased high-
resolution protein-lipid interactions. (submitted).
[132] Wang, Z.-J., Deserno, M. A systematically coarse-grained solvent-free model for quantita-
tive phospholipid bilayer simulations. J. Phys. Chem. B. 114(34):11207–11220, 2010.
[133] Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W., Klein, M. L. Comparison
of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935, 1983.
[134] IUPAC-IUB Commission on Biochemical Nomenclature. Abbreviations and Symbols for
the Description of the Conformation of Polypeptide Chains. Tentative Rules (1969). Bio-
chemistry 9:3471–3478, 1970.
[135] Mahoney, M. W., Jorgensen, W. L. A five-site model for liquid water and the reproduction of
the density anomaly by rigid, nonpolarizable potential functions. J. Chem. Phys. 112:8910–
8922, 2000.
[136] Ryckaert, J. P., Bellemans, A. Molecular dynamics of liquid alkanes. Far. Disc. Chem. Soc.
66:95–106, 1978.
[137] de Loof, H., Nilsson, L., Rigler, R. Molecular dynamics simulations of galanin in aqueous
and nonaqueous solution. J. Am. Chem. Soc. 114:4028–4035, 1992.
[138] van Buuren, A. R., Berendsen, H. J. C. Molecular Dynamics simulation of the stability of
a 22 residue alpha-helix in water and 30% trifluoroethanol. Biopolymers 33:1159–1166,
1993.
[139] Neumann, R. M. Entropic approach to Brownian Movement. Am. J. Phys. 48:354–357,
1980.
[140] Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett.
78(14):2690 – 2693, 1997.
[141] O. Engin, M. S. A. Villa, Hess, B. Driving forces for adsorption of amphiphilic peptides to
air-water interface. J. Phys. Chem. B.
[142] Lindahl, V., Lidmar, J., Hess, B. Accelerated weight histogram method for exploring free
energy landscapes. The Journal of chemical physics 141(4):044110, 2014.
[143] Wang, F., Landau, D. Efficient, multiple-range random walk algorithm to calculate the
density of states. Physical review letters 86(10):2050, 2001.
[144] Huber, T., Torda, A. E., van Gunsteren, W. F. Local elevation: a method for improving the
searching properties of molecular dynamics simulation. Journal of computer-aided molec-
ular design 8(6):695–708, 1994.
[145] Laio, A., Parrinello, M. Escaping free-energy minima. Proceedings of the National
Academy of Sciences 99(20):12562–12566, 2002.
[146] Belardinelli, R., Pereyra, V. Fast algorithm to calculate density of states. Physical Review
E 75(4):046701, 2007.

Bibliography 249
[147] Barducci, A., Bussi, G., Parrinello, M. Well-tempered metadynamics: a smoothly converg-
ing and tunable free-energy method. Physical review letters 100(2):020603, 2008.
[148] Lindahl, V., Villa, A., Hess, B. Sequence dependency of canonical base pair opening in the
dna double helix. PLoS computational biology 13(4):e1005463, 2017.
[149] Sivak, D. A., Crooks, G. E. Thermodynamic metrics and optimal paths. Physical review
letters 108(19):190602, 2012.
[150] Kutzner, C., Czub, J., Grubmüller, H. Keep it flexible: Driving macromolecular rotary
motions in atomistic simulations with GROMACS. J. Chem. Theory Comput. 7:1381–
1393, 2011.
[151] Caleman, C., van der Spoel, D. Picosecond Melting of Ice by an Infrared Laser Pulse - A
simulation study. Angew. Chem., Int. Ed. Engl. 47:1417–1420, 2008.
[152] Kutzner, C., Grubmüller, H., de Groot, B. L., Zachariae, U. Computational electrophysiol-
ogy: the molecular dynamics of ion channel permeation and selectivity in atomistic detail.
Biophys. J. 101:809–817, 2011.
[153] Feenstra, K. A., Hess, B., Berendsen, H. J. C. Improving efficiency of large time-scale
molecular dynamics simulations of hydrogen-rich systems. J. Comp. Chem. 20:786–798,
1999.
[154] Hess, B. Determining the shear viscosity of model liquids from molecular dynamics. J.
Chem. Phys. 116:209–217, 2002.
[155] Dewar, M. J. S. Development and status of MINDO/3 and MNDO. J. Mol. Struct. 100:41,
1983.
[156] Guest, M. F., Harrison, R. J., van Lenthe, J. H., van Corler, L. C. H. Computational chem-
istry on the FPS-X64 scientific computers - Experience on single- and multi-processor sys-
tems. Theor. Chim. Act. 71:117, 1987.
[157] Frisch, M. J., Trucks, G. W., Schlegel, H. B., Scuseria, G. E., Robb, M. A., Cheeseman,
J. R., Montgomery, J. A. Jr., Vreven, T., Kudin, K. N., Burant, J. C., Millam, J. M., Iyengar,
S. S., Tomasi, J., Barone, V., Mennucci, B., Cossi, M., Scalmani, G., Rega, N., Petersson,
G. A., Nakatsuji, H., Hada, M., Ehara, M., Toyota, K., Fukuda, R., Hasegawa, J., Ishida, M.,
Nakajima, T., Honda, Y., Kitao, O., Nakai, H., Klene, M., Li, X., Knox, J. E., Hratchian,
H. P., Cross, J. B., Bakken, V., Adamo, C., Jaramillo, J., Gomperts, R., Stratmann, R. E.,
Yazyev, O., Austin, A. J., Cammi, R., Pomelli, C., Ochterski, J. W., Ayala, P. Y., Morokuma,
K., Voth, G. A., Salvador, P., Dannenberg, J. J., Zakrzewski, V. G., Dapprich, S., Daniels,
A. D., Strain, M. C., Farkas, O., Malick, D. K., Rabuck, A. D., Raghavachari, K., Foresman,
J. B., Ortiz, J. V., Cui, Q., Baboul, A. G., Clifford, S., Cioslowski, J., Stefanov, B. B., Liu,
G., Liashenko, A., Piskorz, P., Komaromi, I., Martin, R. L., Fox, D. J., Keith, T., Al-Laham,
M. A., Peng, C. Y., Nanayakkara, A., Challacombe, M., Gill, P. M. W., Johnson, B., Chen,
W., Wong, M. W., Gonzalez, C., Pople, J. A. Gaussian 03, Revision C.02. Gaussian, Inc.,
Wallingford, CT, 2004.

250 Bibliography
[158] Car, R., Parrinello, M. Unified approach for molecular dynamics and density-functional
theory. Phys. Rev. Lett. 55:2471–2474, 1985.
[159] Field, M., Bash, P. A., Karplus, M. A combined quantum mechanical and molecular me-
chanical potential for molecular dynamics simulation. J. Comp. Chem. 11:700, 1990.
[160] Maseras, F., Morokuma, K. IMOMM: A New Ab Initio + Molecular Mechanics Geometry
Optimization Scheme of Equilibrium Structures and Transition States. J. Comp. Chem.
16:1170–1179, 1995.
[161] Svensson, M., Humbel, S., Froes, R. D. J., Matsubara, T., Sieber, S., Morokuma, K.
ONIOM a multilayered integrated MO + MM method for geometry optimizations and
single point energy predictions. a test for Diels-Alder reactions and Pt(P(t-Bu)3)2 + H2
oxidative addition. J. Phys. Chem. 100:19357, 1996.
[162] Yesylevskyy, S. ProtSqueeze: simple and effective automated tool for setting up membrane
protein simulations. J. Chem. Inf. Model. 47:1986–1994, 2007.
[163] Wolf, M., Hoefling, M., Aponte-Santamaría, C., Grubmüller, H., Groenhof, G. g_membed:
Efficient insertion of a membrane protein into an equilibrated lipid bilayer with minimal
perturbation. J. Comp. Chem. 31:2169–2174, 2010.
[164] van der Spoel, D., Berendsen, H. J. C. Molecular dynamics simulations of Leu-enkephalin
in water and DMSO. Biophys. J. 72:2032–2041, 1997.
[165] van der Spoel, D., van Maaren, P. J., Berendsen, H. J. C. A systematic study of water
models for molecular simulation. J. Chem. Phys. 108:10220–10230, 1998.
[166] Smith, P. E., van Gunsteren, W. F. The Viscosity of SPC and SPC/E Water. Chem. Phys.
Lett. 215:315–318, 1993.
[167] Balasubramanian, S., Mundy, C. J., Klein, M. L. Shear viscosity of polar fluids: Miolecular
dynamics calculations of water. J. Chem. Phys. 105:11190–11195, 1996.
[168] Wuttke, J. lmfit. http://apps.jcns.fz-juelich.de/doku/sc/lmfit. 2013.
[169] Steen-Sæthre, B., Hoffmann, A. C., van der Spoel, D. Order parameters and algorithmic ap-
proaches for detection and demarcation of interfaces in hydrate-fluid and ice-fluid systems.
J. Chem. Theor. Comput. 10:5606–5615, 2014.
[170] Palmer, B. J. Transverse-current autocorrelation-function calculations of the shear viscosity
for molecular liquids. Phys. Rev. E 49:359–366, 1994.
[171] Wensink, E. J. W., Hoffmann, A. C., van Maaren, P. J., van der Spoel, D. Dynamic proper-
ties of water/alcohol mixtures studied by computer simulation. J. Chem. Phys. 119:7308–
7317, 2003.
[172] Guo, G.-J., Zhang, Y.-G., Refson, K., Zhao, Y.-J. Viscosity and stress autocorrelation
function in supercooled water: a molecular dynamics study. Mol. Phys. 100:2617–2627,
2002.

Bibliography 251
[173] Fanourgakis, G. S., Medina, J. S., Prosmiti, R. Determining the bulk viscosity of rigid water
models. J. Phys. Chem. A 116:2564–2570, 2012.
[174] van der Spoel, D., Vogel, H. J., Berendsen, H. J. C. Molecular dynamics simulations of
N-terminal peptides from a nucleotide binding protein. PROTEINS: Struct. Funct. Gen.
24:450–466, 1996.
[175] Amadei, A., Linssen, A. B. M., Berendsen, H. J. C. Essential dynamics of proteins. PRO-
TEINS: Struct. Funct. Gen. 17:412–425, 1993.
[176] Hess, B. Convergence of sampling in protein simulations. Phys. Rev. E65:031910, 2002.
[177] Hess, B. Similarities between principal components of protein dynamics and random dif-
fusion. Phys. Rev. E62:8438–8448, 2000.
[178] Mu, Y., Nguyen, P. H., Stock, G. Energy landscape of a small peptide revelaed by dihedral
angle principal component analysis. PROTEINS: Struct. Funct. Gen. 58:45–52, 2005.
[179] van der Spoel, D., van Maaren, P. J., Larsson, P., Timneanu, N. Thermodynamics of hy-
drogen bonding in hydrophilic and hydrophobic media. J. Phys. Chem. B. 110:4393–4398,
2006.
[180] Luzar, A., Chandler, D. Hydrogen-bond kinetics in liquid water. Nature 379:55–57, 1996.
[181] Luzar, A. Resolving the hydrogen bond dynamics conundrum. J. Chem. Phys. 113:10663–
10675, 2000.
[182] Kabsch, W., Sander, C. Dictionary of protein secondary structure: Pattern recognition of
hydrogen-bonded and geometrical features. Biopolymers 22:2577–2637, 1983.
[183] Bekker, H., Berendsen, H. J. C., Dijkstra, E. J., Achterop, S., v. Drunen, R., v. d. Spoel,
D., Sijbers, A., Keegstra, H., Reitsma, B., Renardus, M. K. R. Gromacs Method of Virial
Calculation Using a Single Sum. In Physics Computing 92 (Singapore, 1993). de Groot,
R. A., Nadrchal, J., eds. . World Scientific.
[184] Berendsen, H. J. C., Grigera, J. R., Straatsma, T. P. The missing term in effective pair
potentials. J. Phys. Chem. 91:6269–6271, 1987.
[185] van Gunsteren, W. F., Berendsen, H. J. C. Molecular dynamics of simple systems.
Practicum Handleiding voor MD Practicum Nijenborgh 4, 9747 AG, Groningen, The
Netherlands 1994.

252 Bibliography
Index
τT31
εr70
1-4 interaction 81,125
A
accelerate group 15
adaptive biasing see AWH
adding atom types 153
AMBER force field 116
Andersen thermostat 31
angle
restraint 88
vibration 76
annealing, simulated
see simulated annealing
atom see particle
type 120
types, adding see adding atom types
autocorrelation function 210
average, ensemble see ensemble average
AWH 161
B
BAR 54
Bennett’s acceptance ratio 54
Berendsen pressure coupling
see pressure coupling, Berendsen
see temperature coupling, Berendsen
bond stretching 74
bonded parameter 123
Born-Oppenheimer 4
branched polymers 136
Brownian dynamics 50
Buckingham potential 69
building block 122
C
center of mass group 15
center-of-mass
pulling 157
velocity 18
charge group 19,24,103
CHARMM force field 117
chemistry, computational
see computational chemistry
choosing groups 204
citing iv
CMAP 117
combination rule 68,123,144
Compressed position output group 15
compressibility 36
computational chemistry 1
Computational Electrophysiology 182
conjugate gradient 51
connection 126
conserved energy quantity 30
constant, dielectric see dielectric constant
constraint 4
algorithms 45,127
force 150
pulling 158
constraints 25,60
correlation 210
Coulomb 70,98
covariance analysis 218
cut-off 4,71,103
Cut-off schemes 19
D
database
hydrogen ∼see hydrogen database
termini ∼see termini database
default groups 204
degrees of freedom 186
dielectric constant 70
diffusion coefficient 214

254 Index
dihedral 81,124
restraint 88
improper ∼see improper dihedral
proper ∼see proper dihedral
dipolar couplings 92
dispersion 68
correction 110
distance restraint 89
ensemble-averaged ∼
see ensemble-averaged distance restraint
time-averaged ∼
see time-averaged distance restraint
disulfide bonds 136
dodecahedron 13
domain decomposition 57
double precision see precision, double
Drude 96
dummy atoms see virtual interaction sites
dynamic load balancing 58
dynamics
Brownian ∼see Brownian dynamics
Langevin ∼see Langevin dynamics
mesoscopic ∼
see mesoscopic dynamics
stochastic ∼see stochastic dynamics,
see stochastic dynamics
E
Einstein relation 214
Electric fields 181
Embedding proteins into the membranes 198
energy
file 234
minimization 50
kinetic ∼see kinetic energy
potential ∼see potential energy
energy-monitor group 15
Enforced Rotation 170
ensemble average 1
ensemble-averaged distance restraint 91
equation, Schrödinger
see Schrödinger equation
equations of motion 2,26
equilibration 235
essential dynamics 56,
see covariance analysis
Ewald
sum 73,107
particle-mesh ∼73
exclusions 15,102,126
Expanded Ensemble 57
extended ensemble 32
F
FENE potential 76
file
type 201
energy ∼see energy file
index ∼see index file
log ∼see log file
topology ∼see topology file
trajectory ∼see trajectory file
files, GROMOS96 see GROMOS96 files
Flat-bottomed position restraint 87
flooding 56
force field 4,67,115,153
organization 152
force-field, coarse-grained 117
free energy
calculations 52,185
interactions 97
topologies 148
freedom, degrees of see degrees of freedom
freeze group 15,42
frozen atoms 15,42
G
Generalized Born methods 63
genion 146
gmx
anaeig 220
analyze 220
angle 215
bar 54
covar 220
density 225
dipoles 211,212
distance 214,216
do_dssp 222
energy 207,212,236
gangle 215,216
gyrate 216

Index 255
hbond 220
make_ndx 204
mdmat 217
mindist 216
mk_angndx 204
msd 214
nmeig 52
nmens 52
order 222
pairdist 217
potential 225
rama 222
rdf 208
rms 217
rmsdist 218
rotacf 211
select 204,206
traj 207,225
velacc 211
view 207
wheel 222
grid search 23
GROMOS96
files 116
force field 115
grompp 123,125,145,146,187
group 14
accelerate ∼see accelerate group
center of mass ∼
see center of mass group
charge ∼see charge group,
see charge group
Compressed position output ∼
see Compressed position output group
energy-monitor ∼
see energy-monitor group
freeze ∼see freeze group,
see freeze group
planar ∼see planar group
temperature-coupling ∼
see temperature-coupling group
groups 146,203
choosing ∼see choosing groups
default ∼see default groups
H
harmonic interaction 126
heme group 136
Hessian 51
hydrogen database 132
I
image, nearest see nearest image
implicit solvation 63
parameters 126
improper dihedral 80
index file 204
integration timestep 76
integrator
leap-frog ∼see leap-frog integrator
velocity Verlet ∼
see velocity Verlet integrator
interaction list 102
Interactive Molecular Dynamics 197
intermolecular interaction 125
intramolecular pair interaction 125
isothermal compressibility 36
K
kinetic energy 25
L
L-BFGS 51
Langevin dynamics 49
laser 181
leap-frog integrator 26
Lennard-Jones 68,99
limitations 3
LINCS 46,60,99
list, interaction see interaction list
LJ-PME 112
load balancing, dynamic
see dynamic load balancing
log file 235
M
Martini force field 118
mass, modified see modified mass
Maxwell-Boltzmann distribution 17
MD
units 7
non-equilibrium ∼
see non-equilibrium MD

256 Index
mechanics, statistical
see statistical mechanics
mesoscopic dynamics 2
mirror image
minimum image convention 12,14
80
mixed precision see precision, mixed
modeling, molecular
see molecular modeling
modified mass 187
molecular modeling 1
molecule definition 124
Morse potential 75
motion, equations of
see equations of motion, see equations of motion
N
nearest image 18
neighbor
list 18
searching 18
third ∼see third neighbor
NMA 51
nmr refinement 89
non-bonded parameter 122
non-equilibrium MD 15
normal-mode analysis 51
Nosé-Hoover temperature coupling
see temperature coupling, Nosé-Hoover
O
octahedron 13
online documentation 201
OPLS/AA force field 116
orientation restraint 92
P
P-LINCS 60
P3M-AD 109
parallelization 57
parameter 119
bonded ∼see bonded parameter
non-bonded ∼
see non-bonded parameter
run ∼see run parameter
Parrinello-Rahman pressure coupling
see pressure coupling, Parrinello-Rahman
particle 119
particle-mesh Ewald see PME
Particle-Particle Particle-Mesh see P3M
PCA see covariance analysis
pdb2gmx 81,87,117,122,128,136,187
pencil decomposition 62
performance 232
periodic boundary conditions 11,107,227
planar group 80
PLUM force field 118
PME 61,108
polarizability 44
position restraint 86
Flat-bottomed ∼
see Flat-bottomed position restraint
potential
energy 24
function 115,192
potentials of mean force 185
precision
double ∼10
mixed ∼10
pressure 25
pressure coupling 35
Berendsen ∼35
Parrinello-Rahman ∼36
surface-tension ∼38
principal component analysis 56,
see covariance analysis
proper dihedral 81
pulling
constraint ∼see constraint pulling
rotational ∼see enforced rotation
umbrella ∼see umbrella pulling
Q
QSAR 1
quadrupole 120
R
reaction field 70,98
reduced units 9
refinement,nmr 89
REMD 55
removing COM motion 15,18
replica exchange 55

Index 257
repulsion 68
residuetypes.dat 129,205
restraint
angle ∼see angle restraint
dihedral ∼see dihedral restraint
distance ∼see distance restraint
orientation ∼see orientation restraint
position ∼see position restraint
rhombic dodecahedron 11
rotational pulling see enforced rotation
run parameter 201
S
sampling 44
Schrödinger equation 1
search
grid ∼see grid search
simple ∼see simple search
searching, neighbor see neighbor searching
selections 206
SETTLE 45,127
SHAKE 45,99
shell 96,see particle
model 44
simple search 23
simulated annealing 48
slow-growth methods 52
soft-core interactions 100
specbond.dat 136
statistical mechanics 2
steepest descent 50
stochastic dynamics 2,49
stretching, bond see bond stretching
surface-tension pressure coupling
see pressure coupling, surface-tension
T
tabulated
bonded interaction function 84
interaction functions 191
targeted MD 186
temperature 25
temperature coupling 14,29
Nosé-Hoover 32
Berendsen ∼30
velocity-rescaling ∼31
temperature-coupling group 14,25,35
termini database 133
thermodynamic integration 54
third neighbor 102
Thole 97
time lag 210
time-averaged distance restraint 90
timestep, integration
see integration timestep
TNG 15
topology 119
topology file 137
42,197
triclinic unit cell 12
truncated octahedron 11
type
atom ∼see atom type
file ∼see file type
U
umbrella pulling 158
units 7
Urey-Bradley bond-angle vibration 79
V
velocity
Verlet integrator 26
center-of-mass ∼
see center-of-mass velocity
velocity-rescaling temperature coupling
see temperature coupling, velocity-rescaling
Versatile Object-oriented Toolkit for Coarse-
Graining Applications (VOTCA) 118
vibration
angle ∼see angle vibration
Urey-Bradley bond-angle ∼
see Urey-Bradley bond-angle vibration
virial 25,104,227
virtual interaction sites 104,120,186
viscosity 189,212
VMD plug-ins 197
W
water 75
weak coupling 30,35
X
