Manual SPECFEM3D GLOBE
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 102 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Contents
- 1 Introduction
- 2 Getting Started
- 2.1 Configuring and compiling the source code
- 2.2 Using the GPU version of the code
- 2.3 Compiling on an IBM BlueGene
- 2.4 Using a cross compiler
- 2.5 Adding OpenMP support in addition to MPI
- 2.6 Compiling on an Intel Xeon Phi (Knights Landing KNL)
- 2.7 Visualizing the subroutine calling tree of the source code
- 2.8 Becoming a developer of the code, or making small modifications in the source code
- 3 Running the Mesher xmeshfem3D
- 4 Running the Solver xspecfem3D
- 5 Regional Simulations
- 6 Adjoint Simulations
- 7 Doing tomography, i.e., updating the model based on the sensitivity kernels obtained
- 8 Noise Cross-correlation Simulations
- 9 Gravity integral calculations for the gravity field of the Earth
- 10 Graphics
- 11 Running through a Scheduler
- 12 Changing the Model
- 13 Post-Processing Scripts
- 14 Information for developers of the code, and for people who want to learn how the technique works
- Simulation features supported in SPECFEM3D_GLOBE
- Bug Reports and Suggestions for Improvements
- Notes and Acknowledgements
- Copyright
- Bibliography
- A Reference Frame Convention
- B Non-Dimensionalization Conventions
- C Benchmarks
- D SAC Headers
- E Channel Codes of Seismograms
- F Troubleshooting
- G License

User Manual
COMPUTATIONAL INFRASTRUCTURE FOR GEODYNAMICS (CIG)
Version 7.0
PRINCETON UNIVERSITY (USA)
CNRS and UNIVERSITY OF MARSEILLE (FRANCE)
ETH ZÜRICH (SWITZERLAND)
SPECFEM 3D
Globe
SPECFEM3D_GLOBE
User Manual
© Princeton University (USA) and CNRS / University of Marseille (France),
ETH Zürich (Switzerland),
Version 7.0
December 10, 2018
1
Authors
The SPECFEM3D package was first developed by Dimitri Komatitsch and Jean-Pierre Vilotte at Institut de Physique
du Globe (IPGP) in Paris, France from 1995 to 1997 and then by Dimitri Komatitsch and Jeroen Tromp at Harvard
University and Caltech, USA, starting in 1998. The story started on April 4, 1995, when Prof. Yvon Maday from
CNRS and University of Paris, France, gave a lecture to Dimitri Komatitsch and Jean-Pierre Vilotte at IPG about
the nice properties of the Legendre spectral-element method with diagonal mass matrix that he had used for other
equations. We are deeply indebted and thankful to him for that. That followed a visit by Dimitri Komatitsch to OGS
(Istituto Nazionale di Oceanografia e di Geofisica Sperimentale) in Trieste, Italy, in February 1995 to meet with Géza
Seriani and Enrico Priolo, who introduced him to their 2D Chebyshev version of the spectral-element method with a
non-diagonal mass matrix. We are deeply indebted and thankful to them for that.
Since then it has been developed and maintained by a development team: in alphabetical order, Michael Afanasiev,
Jean-Paul (Pablo) Ampuero, Kazuto Ando, Kangchen Bai, Piero Basini, Céline Blitz, Alexis Bottero, Ebru Bozda˘
g,
Emanuele Casarotti, Joseph Charles, Min Chen, Paul Cristini, Clément Durochat, Percy Galvez, Hom Nath Gharti,
Dominik Göddeke, Vala Hjörleifsdóttir, Sue Kientz, Dimitri Komatitsch, Jesús Labarta, Piero Lanucara, Nicolas Le
Goff, Pieyre Le Loher, Matthieu Lefebvre, Qinya Liu, Youshan Liu, David Luet, Yang Luo, Alessia Maggi, Federica
Magnoni, Roland Martin, René Matzen, Dennis McRitchie, Jean-François Méhaut, Matthias Meschede, Peter Mess-
mer, David Michéa, Takayuki Miyoshi, Vadim Monteiller, Surendra Nadh Somala, Tarje Nissen-Meyer, Daniel Peter,
Kevin Pouget, Max Rietmann, Vittorio Ruggiero, Elliott Sales de Andrade, Brian Savage, Bernhard Schuberth, Anne
Sieminski, James Smith, Leif Strand, Carl Tape, Jeroen Tromp, Seiji Tsuboi, Brice Videau, Jean-Pierre Vilotte, Zhinan
Xie, Chang-Hua Zhang, Hejun Zhu.
The cover graphic of the manual was created by Santiago Lombeyda from Caltech’s Center for Advanced Com-
puting Research (CACR), USA, with free satellite clipart pictures from http://www.4vector.com and http:
//www.clker.com added to it.
The code is released open-source under the GNU version 3 license, see the license at the end of this manual.

2
Current and past main participants or main sponsors of the SPECFEM project
(in no particular order)
Contents
Contents 3
1 Introduction 5
1.1 Citation .................................................. 7
1.2 Support .................................................. 8
2 Getting Started 9
2.1 Configuring and compiling the source code ............................... 9
2.2 Using the GPU version of the code .................................... 11
2.3 Compiling on an IBM BlueGene ..................................... 12
2.4 Using a cross compiler .......................................... 13
2.5 Adding OpenMP support in addition to MPI ............................... 13
2.6 Compiling on an Intel Xeon Phi (Knights Landing KNL) ........................ 14
2.7 Visualizing the subroutine calling tree of the source code ........................ 14
2.8 Becoming a developer of the code, or making small modifications in the source code ......... 14
3 Running the Mesher xmeshfem3D 15
3.1 Memory requirements ........................................... 26
4 Running the Solver xspecfem3D 27
4.1 Note on the simultaneous simulation of several earthquakes ....................... 32
5 Regional Simulations 34
5.1 One-Chunk Simulations .......................................... 34
6 Adjoint Simulations 38
6.1 Adjoint Simulations for Sources Only (not for the Model) ........................ 38
6.2 Adjoint Simulations for Finite-Frequency Kernels (Kernel Simulation) ................. 39
7 Doing tomography, i.e., updating the model based on the sensitivity kernels obtained 42
8 Noise Cross-correlation Simulations 43
8.1 New Requirements on ‘Old’ Input Parameter Files ............................ 43
8.2 Noise Simulations: Step by Step ..................................... 44
8.2.1 Pre-simulation .......................................... 44
8.2.2 Simulations ............................................ 45
8.2.3 Post-simulation .......................................... 46
8.3 Examples ................................................. 46
9 Gravity integral calculations for the gravity field of the Earth 47
3
CONTENTS 4
10 Graphics 48
10.1 Meshes .................................................. 48
10.2 Movies .................................................. 48
10.2.1 Movie Surface .......................................... 48
10.2.2 Movie Volume .......................................... 49
10.3 Finite-Frequency Kernels ......................................... 50
11 Running through a Scheduler 53
11.1 run_lsf.bash ............................................. 53
11.2 go_mesher_solver_lsf_globe.bash .............................. 54
11.3 run_lsf.kernel and go_mesher_solver_globe.kernel ................. 55
12 Changing the Model 56
12.1 Changing the Crustal Model ....................................... 56
12.2 Changing the Mantle Model ....................................... 57
12.2.1 Isotropic Models ......................................... 57
12.2.2 Anisotropic Models ........................................ 58
12.2.3 Point-Profile Models ....................................... 59
12.3 Anelastic Models ............................................. 60
13 Post-Processing Scripts 61
13.1 Clean Local Database ........................................... 61
13.2 Process Data and Synthetics ....................................... 61
13.2.1 process_data.pl ...................................... 62
13.2.2 process_syn.pl ....................................... 62
13.2.3 rotate.pl ........................................... 62
13.2.4 clean_sac_headers_after_crash.sh ......................... 62
13.3 Map Local Database ........................................... 63
14 Information for developers of the code, and for people who want to learn how the technique works 64
Simulation features supported in SPECFEM3D_GLOBE 65
Bug Reports and Suggestions for Improvements 66
Notes and Acknowledgements 67
Copyright 68
Bibliography 70
A Reference Frame Convention 78
B Non-Dimensionalization Conventions 79
C Benchmarks 80
D SAC Headers 86
E Channel Codes of Seismograms 88
F Troubleshooting 90
G License 92
Chapter 1
Introduction
ANNOUNCEMENT: SPECFEM3D_GLOBE can now perform gravity field cal-
culations in addition (or instead of) seismic wave propagation only. See flag
GRAVITY_INTEGRALS in file setup/constants.h.in. Please also refer
to http://komatitsch.free.fr/preprints/GJI_Martin_gravimetry_
2017.pdf. And yes, that is the reason why I added a gravity observation satellite
on the cover of the manual :-)
The software package SPECFEM3D_GLOBE simulates three-dimensional global and regional seismic wave prop-
agation and performs full waveform imaging (FWI) or adjoint tomography based upon the spectral-element method
(SEM). The SEM is a continuous Galerkin technique [Tromp et al.,2008,Peter et al.,2011], which can easily be made
discontinuous [Bernardi et al.,1994,Chaljub,2000,Kopriva et al.,2002,Chaljub et al.,2003,Legay et al.,2005,
Kopriva,2006,Wilcox et al.,2010,Acosta Minolia and Kopriva,2011]; it is then close to a particular case of the dis-
continuous Galerkin technique [Reed and Hill,1973,Lesaint and Raviart,1974,Arnold,1982,Johnson and Pitkäranta,
1986,Bourdel et al.,1991,Falk and Richter,1999,Hu et al.,1999,Cockburn et al.,2000,Giraldo et al.,2002,Riv-
ière and Wheeler,2003,Monk and Richter,2005,Grote et al.,2006,Ainsworth et al.,2006,Bernacki et al.,2006,
Dumbser and Käser,2006,De Basabe et al.,2008,de la Puente et al.,2009,Wilcox et al.,2010,De Basabe and Sen,
2010,Étienne et al.,2010], with optimized efficiency because of its tensorized basis functions [Wilcox et al.,2010,
Acosta Minolia and Kopriva,2011]. In particular, it can accurately handle very distorted mesh elements [Oliveira and
Seriani,2011].
It has very good accuracy and convergence properties [Maday and Patera,1989,Seriani and Priolo,1994,Deville
et al.,2002,Cohen,2002,De Basabe and Sen,2007,Seriani and Oliveira,2008,Ainsworth and Wajid,2009,2010,
Melvin et al.,2012]. The spectral element approach admits spectral rates of convergence and allows exploiting hp-
convergence schemes. It is also very well suited to parallel implementation on very large supercomputers [Komatitsch
et al.,2003,Tsuboi et al.,2003,Komatitsch et al.,2008,Carrington et al.,2008,Komatitsch et al.,2010b] as well as
on clusters of GPU accelerating graphics cards [Komatitsch,2011,Michéa and Komatitsch,2010,Komatitsch et al.,
2009,2010a]. Tensor products inside each element can be optimized to reach very high efficiency [Deville et al.,2002],
and mesh point and element numbering can be optimized to reduce processor cache misses and improve cache reuse
[Komatitsch et al.,2008]. The SEM can also handle triangular (in 2D) or tetrahedral (in 3D) elements [Wingate and
Boyd,1996,Taylor and Wingate,2000,Komatitsch et al.,2001,Cohen,2002,Mercerat et al.,2006] as well as mixed
meshes, although with increased cost and reduced accuracy in these elements, as in the discontinuous Galerkin method.
Note that in many geological models in the context of seismic wave propagation studies (except for instance for
fault dynamic rupture studies, in which very high frequencies or supershear rupture need to be modeled near the fault,
see e.g. Benjemaa et al. [2007,2009], de la Puente et al. [2009], Tago et al. [2010]) a continuous formulation is
sufficient because material property contrasts are not drastic and thus conforming mesh doubling bricks can efficiently
handle mesh size variations [Komatitsch and Tromp,2002a,Komatitsch et al.,2004,Lee et al.,2008,2009a,b]. This
is particularly true at the scale of the full Earth.
5
CHAPTER 1. INTRODUCTION 6
For a detailed introduction to the SEM as applied to global and regional seismic wave propagation, please consult
Tromp et al. [2008], Peter et al. [2011], Komatitsch and Vilotte [1998], Komatitsch and Tromp [1999], Chaljub [2000],
Komatitsch and Tromp [2002a,b], Komatitsch et al. [2002], Chaljub et al. [2003], Capdeville et al. [2003], Chaljub
and Valette [2004], Chaljub et al. [2007]. A detailed theoretical analysis of the dispersion and stability properties of
the SEM is available in Cohen [2002], De Basabe and Sen [2007], Seriani and Oliveira [2007], Seriani and Oliveira
[2008] and Melvin et al. [2012].
Effects due to lateral variations in compressional-wave speed, shear-wave speed, density, a 3D crustal model,
ellipticity, topography and bathymetry, the oceans, rotation, and self-gravitation are included. The package can ac-
commodate full 21-parameter anisotropy [Chen and Tromp,2007] as well as lateral variations in attenuation [Savage
et al.,2010]. Adjoint capabilities and finite-frequency kernel simulations are also included [Tromp et al.,2008,Peter
et al.,2011,Liu and Tromp,2006,2008,Fichtner et al.,2009,Virieux and Operto,2009].
The SEM was originally developed in computational fluid dynamics [Patera,1984,Maday and Patera,1989] and
has been successfully adapted to address problems in seismic wave propagation. Early seismic wave propagation ap-
plications of the SEM, utilizing Legendre basis functions and a perfectly diagonal mass matrix, include Cohen et al.
[1993], Komatitsch [1997], Faccioli et al. [1997], Casadei and Gabellini [1997], Komatitsch and Vilotte [1998] and
Komatitsch and Tromp [1999], whereas applications involving Chebyshev basis functions and a nondiagonal mass
matrix include Seriani and Priolo [1994], Priolo et al. [1994] and Seriani et al. [1995]. In the Legendre version that
we use in SPECFEM the mass matrix is purposely slightly inexact but diagonal (but can be made exact if needed, see
Teukolsky [2015]), while in the Chebyshev version it is exact but non diagonal.
Beware that, in a spectral-element method, some spurious modes (that have some similarities with classical so-
called "Hourglass modes" in finite-element techniques, although in the SEM they are not zero-energy modes) can
appear in some (but not all) cases in the spectral element in which the source is located. Fortunately, they do not
propagate away from the source element. However, this means that if you put a receiver in the same spectral element
as a source, the recorded signals may in some cases be wrong, typically exhibiting some spurious oscillations, which
are often even non causal. If that is the case, an easy option is to slightly change the mesh in the source region in order
to get rid of these Hourglass-like spurious modes, as explained in Duczek et al. [2014], in which this phenomenon is
described in details, and in which practical solutions to avoid it are suggested.
All SPECFEM3D_GLOBE software is written in Fortran2003 with full portability in mind, and conforms strictly
to the Fortran2003 standard. It uses no obsolete or obsolescent features of Fortran. The package uses parallel pro-
gramming based upon the Message Passing Interface (MPI) [Gropp et al.,1994,Pacheco,1997].
SPECFEM3D_GLOBE won the Gordon Bell award for best performance at the SuperComputing 2003 conference
in Phoenix, Arizona (USA) (see Komatitsch et al. [2003]). It was a finalist again in 2008 for a run at 0.16 petaflops
(sustained) on 149,784 processors of the ‘Jaguar’ Cray XT5 system at Oak Ridge National Laboratories (USA) [Car-
rington et al.,2008]. It also won the BULL Joseph Fourier supercomputing award in 2010.
It reached the sustained one petaflop performance level for the first time in February 2013 on the Blue Waters Cray
supercomputer at the National Center for Supercomputing Applications (NCSA), located at the University of Illinois
at Urbana-Champaign (USA).
The package includes support for GPU graphics card acceleration [Komatitsch,2011,Michéa and Komatitsch,
2010,Komatitsch et al.,2009,2010a] and also supports OpenCL.
The next release of the code will include support for Convolutional or Auxiliary Differential Equation Perfectly
Matched absorbing Layers (C-PML or ADE-PML) [Martin et al.,2008b,c,Martin and Komatitsch,2009,Martin et al.,
2010,Komatitsch and Martin,2007] for the case of single-chunk simulations in regional models.
CHAPTER 1. INTRODUCTION 7
1.1 Citation
You can find all the references below in BIBT
EXformat in file doc/USER_MANUAL/bibliography.bib.
If you use SPECFEM3D_GLOBE for your own research, please cite at least one of the following articles: Ko-
matitsch et al. [2016], Tromp et al. [2008], Peter et al. [2011], Vai et al. [1999], Lee et al. [2008,2009a,b], Komatitsch
et al. [2009,2010a], van Wijk et al. [2004], Komatitsch et al. [2004], Chaljub et al. [2007], Madec et al. [2009], Ko-
matitsch et al. [2010b], Carrington et al. [2008], Tromp et al. [2010a], Komatitsch et al. [2002], Komatitsch and Tromp
[2002a,b,1999]orKomatitsch and Vilotte [1998].
If you use the C-PML absorbing layer capabilities of the code, please cite at least one article written by the
developers of the package, for instance:
•Xie et al. [2014],
•Xie et al. [2016].
If you use the UNDO_ATTENUATION option of the code in order to produce full anelastic/viscoelastic sensitivity
kernels, please cite at least one article written by the developers of the package, for instance (and in particular):
•Komatitsch et al. [2016].
More generally, if you use the attenuation (anelastic/viscoelastic) capabilities of the code, please cite at least one article
written by the developers of the package, for instance:
•Komatitsch et al. [2016],
•Blanc et al. [2016].
If you use the kernel capabilities of the code, please cite at least one article written by the developers of the package,
for instance:
•Tromp et al. [2008],
•Peter et al. [2011],
•Liu and Tromp [2006],
•Morency et al. [2009].
If you use this new version, which has non blocking MPI for much better performance for medium or large runs,
please cite at least one of these five articles, in which results of 3D non blocking MPI runs are presented: Komatitsch
et al. [2010a,b], Komatitsch [2011], Peter et al. [2011], Carrington et al. [2008].
If you use GPU graphics card acceleration please cite e.g. Komatitsch [2011], Michéa and Komatitsch [2010],
Komatitsch et al. [2009], and/or Komatitsch et al. [2010a].
If you work on geophysical applications, you may be interested in citing some of these application articles as well,
among others: van Wijk et al. [2004], Ji et al. [2005], Krishnan et al. [2006a,b], Lee et al. [2008,2009a,b], Chevrot
et al. [2004], Favier et al. [2004], Ritsema et al. [2002], Godinho et al. [2009], Tromp and Komatitsch [2000], Savage
et al. [2010]. If you use 3D mantle model S20RTS, please cite Ritsema et al. [1999].
Domain decomposition is explained in detail in Martin et al. [2008a], and excellent scaling up to 150,000 processor
cores in shown for instance in Carrington et al. [2008], Komatitsch et al. [2008], Martin et al. [2008a], Komatitsch
et al. [2010a], Komatitsch [2011].
The corresponding BibT
EX entries may be found in file doc/USER_MANUAL/bibliography.bib.
CHAPTER 1. INTRODUCTION 8
1.2 Support
This material is based upon work supported by the U.S. National Science Foundation under Grants No. EAR-0406751
and EAR-0711177, by the French CNRS, French INRIA Sud-Ouest MAGIQUE-3D, French ANR NUMASIS under
Grant No. ANR-05-CIGC-002, and European FP6 Marie Curie International Reintegration Grant No. MIRG-CT-
2005-017461. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the
authors and do not necessarily reflect the views of the U.S. National Science Foundation, CNRS, INRIA, ANR or the
European Marie Curie program.
Chapter 2
Getting Started
2.1 Configuring and compiling the source code
To get the SPECFEM3D_GLOBE software package, type this:
git clone --recursive --branch devel https://github.com/geodynamics/specfem3d_globe.git
We recommend that you add ulimit -S -s unlimited to your .bash_profile file and/or limit
stacksize unlimited to your .cshrc file to suppress any potential limit to the size of the Unix stack.
Then, to configure the software for your system, run the configure shell script. This script will attempt to guess
the appropriate configuration values for your system. However, at a minimum, it is recommended that you explicitly
specify the appropriate command names for your Fortran compiler (another option is to define FC, CC and MPIF90 in
your .bash_profile or your .cshrc file):
./configure FC=gfortran CC=gcc MPIFC=mpif90
You can replace the GNU compilers above (gfortran and gcc) with other compilers if you want to; for instance for
Intel ifort and icc use FC=ifort CC=icc instead.
Before running the configure script, you should probably edit file flags.guess to make sure that it contains
the best compiler options for your system. Known issues or things to check are:
GCC gfortran compiler The code makes use of Fortran 2008 features, e.g., the contiguous array attribute.
We thus recommend using a gfortran version 4.6.0 or higher.
Intel ifort compiler See if you need to add -assume byterecl for your machine. In the case of that
compiler, we have noticed that initial release versions sometimes have bugs or issues that can lead to wrong
results when running the code, thus we strongly recommend using a version for which at least one service
pack or update has been installed. In particular, for version 17 of that compiler, users have reported problems
(making the code crash at run time) with the -assume buffered_io option; if you notice problems, remove
that option from file flags.guess or change it to -assume nobuffered_io and try again.
IBM compiler See if you need to add -qsave or -qnosave for your machine.
Mac OS You will probably need to install XCODE.
When compiling on an IBM machine with the xlf and xlc compilers, we suggest running the configure
script with the following options:
./configure FC=xlf90_r MPIFC=mpif90 CC=xlc_r CFLAGS="-O3 -q64" FCFLAGS="-O3 -q64"
If you have problems configuring the code on a Cray machine, i.e. for instance if you get an error message
from the configure script, try exporting these two variables: MPI_INC=$CRAY_MPICH2_DIR/include and
9
CHAPTER 2. GETTING STARTED 10
FCLIBS=" ", and for more details if needed you can refer to the utils/Cray_compiler_information di-
rectory. You can also have a look at the configure script called utils/Cray_compiler_information/configure_SPECFEM_for_Piz_Daint.bash.
On SGI systems, flags.guess automatically informs configure to insert “TRAP_FPE=OFF” into the gen-
erated Makefile in order to turn underflow trapping off.
If you run very large meshes on a relatively small number of processors, the static memory size needed on each pro-
cessor might become greater than 2 gigabytes, which is the upper limit for 32-bit addressing (dynamic memory alloca-
tion is always OK, even beyond the 2 GB limit; only static memory has a problem). In this case, on some compilers you
may need to add “-mcmodel=medium” (if you do not use the Intel ifort / icc compiler) or “-mcmodel=medium
-shared-intel” (if you use the Intel ifort / icc compiler) to the configure options of CFLAGS, FCFLAGS and
LDFLAGS otherwise the compiler will display an error message (for instance “relocation truncated to
fit: R_X86_64_PC32 against .bss” or something similar); on an IBM machine with the xlf and xlc
compilers, using -q64 is usually sufficient.
A summary of the most important configuration variables follows.
FC Fortran compiler command name. By default, configure will execute the command names of various well-
known Fortran compilers in succession, picking the first one it finds that works.
MPIFC MPI Fortran command name. The default is mpif90. This must correspond to the same underlying compiler
specified by FC; otherwise, you will encounter compilation or link errors when you attempt to build the code. If
you are unsure about this, it is usually safe to set both FC and MPIFC to the MPI compiler command for your
system:
./configure FC=mpif90 MPIFC=mpif90
FLAGS_CHECK Compiler flags.
LOCAL_PATH_IS_ALSO_GLOBAL If you want the parallel mesher to write a parallel (i.e., split) database for the
solver on the local disks of each of the compute nodes, set this flag to .false.. Some systems have no local
disks (e.g., BlueGene) and other systems have a fast parallel file system (LUSTRE, GPFS) that is easy and
reliable to use, in which case this variable should be set to .true.. Note that this flag is not used by the
mesher nor the solver; it is only used for some of the (optional) post-processing. If you do not know what is best
on your system, setting it to .true. is usually fine; or else, ask your system administrator.
In addition to reading configuration variables, configure accepts the following options:
--enable-double-precision The package can run either in single or in double precision mode. The de-
fault is single precision because for almost all calculations performed using the spectral-element method using
single precision is sufficient and gives the same results (i.e. the same seismograms); and the single precision
code is faster and requires exactly half as much memory. To specify double precision mode, simply provide
--enable-double-precision as a command-line argument to configure. On many current proces-
sors (e.g., Intel, AMD, IBM Power), single precision calculations are significantly faster; the difference can
typically be 10% to 25%. It is therefore better to use single precision. What you can do once for the physical
problem you want to study is run the same calculation in single precision and in double precision on your system
and compare the seismograms. If they are identical (and in most cases they will), you can select single precision
for your future runs.
--help Directs configure to print a usage screen which provides a short description of all configuration vari-
ables and options. Note that the options relating to installation directories (e.g., --prefix) do not apply to
SPECFEM3D_GLOBE.
The configure script runs a brief series of checks. Upon successful completion, it generates the files Makefile,
constants.h, and precision.h in the working directory.
Note: If the configure script fails, and you don’t know what went wrong, examine the log file config.log.
This file contains a detailed transcript of all the checks configure performed. Most importantly, it includes
the error output (if any) from your compiler.
CHAPTER 2. GETTING STARTED 11
The configure script automatically runs the script flags.guess. This helper script contains a number of sug-
gested flags for various compilers; e.g., Portland, Intel, Absoft, NAG, Lahey, NEC, IBM and SGI. The software has
run on a wide variety of compute platforms, e.g., various PC clusters and machines from Sun, SGI, IBM, Compaq, and
NEC. The flags.guess script attempts to guess which compiler you are using (based upon the compiler command
name) and choose the related optimization flags. The configure script then automatically inserts the suggested
flags into Makefile. Note that flags.guess may fail to identify your compiler; and in any event, the default
flags chosen by flags.guess are undoubtedly not optimal for your system. So, we encourage you to experiment
with these flags (by editing the generated Makefile by hand) and to solicit advice from your system administrator.
Selecting the right compiler and compiler flags can make a tremendous difference in terms of performance. We wel-
come feedback on your experience with various compilers and flags.
When using a slow or not too powerful shared disk system or when running extremely large simulations (on tens
of thousands of processor cores), one can add -DUSE_SERIAL_CASCADE_FOR_IOs to the compiler flags in file
flags.guess before running configure to make the mesher output mesh data to the disk for one MPI slice after
the other, and to make the solver do the same thing when reading the files back from disk. Do not use this option if
you do not need it because it will slow down the mesher and the beginning of the solver if your shared file system is
fast and reliable.
If you run scaling benchmarks of the code, for instance to measure its performance on a new machine, and are
not interested in the physical results (the seismograms) for these runs, you can set DO_BENCHMARK_RUN_ONLY to
.true. in file setup/constants.h.in before running the configure script.
If your compiler has problems with the use mpi statements that are used in the code, use the script called
replace_use_mpi_with_include_mpif_dot_h.pl in the root directory to replace all of them with include
’mpif.h’ automatically.
We recommend that you ask for exclusive use of the compute nodes when running on a cluster or a supercomputer,
i.e., make sure that no other users are running on the same nodes at the same time. Otherwise your run could run
out of memory if the memory of some nodes is used by other users, in particular when undoing attenuation using the
UNDO_ATTENUATION option in DATA/Par_file. To do so, ask your system administrator for the option to add to
your batch submission script; it is for instance #BSUB -x with SLURM and #$ -l exclusive=TRUE with Sun
Grid Engine (SGE).
2.2 Using the GPU version of the code
SPECFEM3D_GLOBE now supports OpenCL and NVIDIA CUDA GPU acceleration. OpenCL can be enabled with
the --with-opencl flag, and the compilation can be controlled through three variables: OCL_LIB=,OCL_INC=
and OCL_GPU_FLAGS=.
./configure --with-opencl OCL_LIB= OCL_INC= OCL_GPU_FLAGS=..
CUDA configuration can be enabled with --with-cuda flag and CUDA_FLAGS=,CUDA_LIB=,CUDA_INC=
and MPI_INC= variables.
./configure --with-cuda=cuda5 CUDA_FLAGS= CUDA_LIB= CUDA_INC= MPI_INC= ..
Both environments can be compiled simultaneously by merging these two lines. For the runtime configuration, the
GPU_MODE flag must be set to .true.. In addition, we use three parameters to select the environments and GPU:
GPU_RUNTIME = 0|1|2
GPU_PLATFORM = filter|*
GPU_DEVICE = filter|*
GPU_RUNTIME sets the runtime environments: 2for OpenCL, 1for CUDA and 0 for compile-time decision (hence,
SPECFEM should have been compiled with only one of --with-opencl or --with-cuda).
GPU_PLATFORM and GPU_DEVICE are both (case-insensitive) filters on the platform and device name in OpenCL,
device name only in CUDA. In multiprocessor (MPI)runs, each process will pick a GPU in this filtered subset,
in round-robin. The star filter (*) will match the first platform and all its devices.

CHAPTER 2. GETTING STARTED 12
GPU_RUNTIME,GPU_PLATFORM and GPU_DEVICE are not read if GPU_MODE is not activated. Regarding the
code, --with-opencl defines the macro-processor flag USE_OPENCL and --with-cuda defines USE_CUDA;
and GPU_RUNTIME set the global variable run_opencl or run_cuda. Texture support has not been validated in
OpenCL, but works as expected in CUDA.
Note about the OpenCL version: the OpenCL calculation kernels were created by Brice Videau and Kevin Pouget
from Grenoble, France, using their software package called BOAST [Videau et al.,2013].
2.3 Compiling on an IBM BlueGene
More recent installation instruction for IBM BlueGene, from October 2012:
Edit file flags.guess and put this for FLAGS_CHECK:
-g -qfullpath -O2 -qsave -qstrict -qtune=qp -qarch=qp -qcache=auto -qhalt=w \
-qfree=f90 -qsuffix=f=f90 -qlanglvl=95pure -Q -Q+rank,swap_all -Wl,-relax
The most relevant are the -qarch and -qtune flags, otherwise if these flags are set to “auto” then they are wrongly
assigned to the architecture of the frond-end node, which is different from that on the compute nodes. You will need
to set these flags to the right architecture for your BlueGene compute nodes, which is not necessarily “qp”; ask your
system administrator. On some machines if is necessary to use -O2 in these flags instead of -O3 due to a compiler bug
of the XLF version installed. We thus suggest to first try -O3, and then if the code does not compile or does not run
fine then switch back to -O2. The debug flags (-g, -qfullpath) do not influence performance but are useful to get at
least some insights in case of problems.
Before running configure, select the XL Fortran compiler by typing module load bgq-xl/1.0 or module
load bgq-xl (another, less efficient option is to load the GNU compilers using module load bgq-gnu/4.4.6
or similar).
Then, to configure the code, type this:
./configure FC=bgxlf90_r MPIFC=mpixlf90_r CC=bgxlc_r LOCAL_PATH_IS_ALSO_GLOBAL=true
Older installation instruction for IBM BlueGene, from 2011:
To compile the code on an IBM BlueGene, Laurent Léger from IDRIS, France, suggests the following: compile the
code with
FLAGS\_CHECK="-O3 -qsave -qstrict -qtune=auto -qarch=450d -qcache=auto \
-qfree=f90 -qsuffix=f=f90 -g -qlanglvl=95pure -qhalt=w -Q -Q+rank,swap_all -Wl,-relax"
Option "-Wl,-relax" must be added on many (but not all) BlueGene systems to be able to link the binaries xmeshfem3D
and xspecfem3D because the final link step is done by the GNU ld linker even if one uses FC=bgxlf90_r,
MPIFC=mpixlf90_r and CC=bgxlc_r to create all the object files. On the contrary, on some BlueGene systems
that use the native AIX linker option "-Wl,-relax" can lead to problems and must be suppressed from flags.guess.
One then just needs to pass the right commands to the configure script:
./configure --prefix=/path/to/SPECFEM3DG_SP --host=Babel --build=BGP \
FC=bgxlf90_r MPIFC=mpixlf90_r CC=bgxlc_r \
LOCAL_PATH_IS_ALSO_GLOBAL=false
This trick can be useful for all hosts on which one needs to cross-compile.
On BlueGene, one also needs to run the xcreate_header_file binary file manually rather than in the Makefile:
bgrun -np 1 -mode VN -exe ./bin/xcreate_header_file
CHAPTER 2. GETTING STARTED 13
2.4 Using a cross compiler
The “configure” script assumes that you will compile the code on the same kind of hardware as the machine on
which you will run it. On some systems (for instance IBM BlueGene, see also the previous section) this might not be
the case and you may compile the code using a cross compiler on a frontend computer that does not have the same
architecture. In such a case, typing “make all” on the frontend will fail, but you can use one of these two solutions:
1/ create a script that runs “make all” on a node instead of on the frontend, if the compiler is also installed on the
nodes
2/ after running the “configure” script, create two copies of the Makefiles:
TODO: this has not been tested out yet, any feedback is welcome
In src/create_header_file/Makefile put this instead of the current values:
FLAGS_CHECK = -O0
and replace
create_header_file: $O/create_header_file.o $(XCREATE_HEADER_OBJECTS)
${FCCOMPILE_CHECK} -o ${E}/xcreate_header_file $O/create_header_file.o $(XCREATE_HEADER_OBJECTS)
with
xcreate_header_file: $O/create_header_file.o $(XCREATE_HEADER_OBJECTS)
${MPIFCCOMPILE_CHECK} -o ${E}/xcreate_header_file $O/create_header_file.o $(XCREATE_HEADER_OBJECTS)
In src/specfem3D/Makefile comment out these last two lines:
#${OUTPUT}/values_from_mesher.h: reqheader
# (mkdir -p ${OUTPUT}; cd ${S_TOP}/; ./bin/xcreate_header_file)
Then:
make clean
make create_header_file
./bin/xcreate_header_file
make clean
make meshfem3D
make specfem3D
should work.
2.5 Adding OpenMP support in addition to MPI
OpenMP support can be enabled in addition to MPI. However, in many cases performance will not improve because
our pure MPI implementation is already heavily optimized and thus the resulting code will in fact be slightly slower.
A possible exception could be IBM BlueGene-type architectures.
To enable OpenMP, add the flag --enable-openmp to the configuration:
./configure --enable-openmp ..
This will add the corresponding OpenMP flag for the chosen Fortran compiler.
The DO-loop using OpenMP threads has a SCHEDULE property. The OMP_SCHEDULE environment variable
can set the scheduling policy of that DO-loop. Tests performed by Marcin Zielinski at SARA (The Netherlands)
showed that often the best scheduling policy is DYNAMIC with the size of the chunk equal to the number of OpenMP
threads, but most preferably being twice as the number of OpenMP threads (thus chunk size = 8 for 4 OpenMP threads
etc). If OMP_SCHEDULE is not set or is empty, the DO-loop will assume generic scheduling policy, which will slow
down the job quite a bit.
CHAPTER 2. GETTING STARTED 14
2.6 Compiling on an Intel Xeon Phi (Knights Landing KNL)
In case you want to run simulations on a KNL chip, the compilation doesn’t require much more effort than with any
other CPU system. All you could add is the flag -xMIC-AVX512 to your Fortran flags in the Makefile and use
--enable-openmp for configuration.
Since there are different memory types available with a KNL, make sure to use fast memory allocations, i.e.
MCDRAM, which has a higher memory bandwidth. Assuming you use a flat mode setup of the KNL chip, you could
use the Linux tool numactl to specify which memory node to bind to. For example, check with
numactl --hardware
which node contains CPU cores and which one only binds to MCDRAM (∼16GB). In flat mode setup, most likely
node 1 does. For a small example on a single KNL with 4 MPI processes and 16 OpenMP threads each, you would
run the solver with a command like
OMP_NUM_THREADS=16 mpirun -np 4 numactl --membind=1 ./bin/xspecfem3D
The ideal setup of MPI processes and OpenMP threads per KNL depends on your specific hardware and simulation
setup. We see good results when using a combination of both, with a total number of threads slightly less than the total
count of cores on the chip.
As a side remark for developers, another possibility would be to add following compiler directives in the source
code (in file src/specfem3D/specfem3D_par.F90):
real(kind=CUSTOM_REAL), dimension(:,:), allocatable :: &
displ_crust_mantle,veloc_crust_mantle,accel_crust_mantle
! FASTMEM attribute: note this attribute needs compiler flag -lmemkind to work...
!DEC$ ATTRIBUTES FASTMEM :: displ_crust_mantle,veloc_crust_mantle,accel_crust_mantle
These directives will work with Intel ifort compilers and will need the additional linker/compiler flag -lmemkind
to work properly. We omitted these directives for now to avoid confusion with other possible simulation setups.
2.7 Visualizing the subroutine calling tree of the source code
Packages such as doxywizard can be used to visualize the subroutine calling tree of the source code. Doxywizard
is a GUI front-end for configuring and running doxygen.
2.8 Becoming a developer of the code, or making small modifications in the
source code
If you want to develop new features in the code, and/or if you want to make small changes, improvements, or bug
fixes, you are very welcome to contribute. To do so, i.e. to access the development branch of the source code with
read/write access (in a safe way, no need to worry too much about breaking the package, there is a robot called
BuildBot that is in charge of checking and validating all new contributions and changes), please visit this Web page:
https://github.com/geodynamics/specfem3d/wiki.
To visualize the call tree (calling tree) of the source code, you can see the Doxygen tool available in directory
doc/call_trees_of_the_source_code.
Chapter 3
Running the Mesher xmeshfem3D
You are now ready to compile the mesher. In the directory with the source code, type ‘make meshfem3D’. If all
paths and flags have been set correctly, the mesher should now compile and produce the executable xmeshfem3D.
Note that all compiled executables are placed into the directory bin/. To run the executables, you must call them
from the root directory, for example type ‘mpirun -np 64 ./bin/meshfem3D‘ to run the mesher in parallel
on 64 CPUs. This will allow the executables to find the parameter file Par_file in the relative directory location
./DATA.
Input for the mesher (and the solver) is provided through the parameter file Par_file, which resides in the
subdirectory DATA. Before running the mesher, a number of parameters need to be set in the Par_file. This
requires a basic understanding of how the SEM is implemented, and we encourage you to read Komatitsch and Vilotte
[1998], Komatitsch and Tromp [1999], Chaljub [2000], Komatitsch and Tromp [2002a,b], Komatitsch et al. [2002],
Chaljub et al. [2003], Capdeville et al. [2003] and Chaljub and Valette [2004]. A detailed theoretical analysis of the
dispersion and stability properties of the SEM is available in Cohen [2002], De Basabe and Sen [2007] and Seriani
and Oliveira [2007].
In this chapter we will focus on simulations at the scale of the entire globe. Regional simulations will be addressed
in Chapter 5. The spectral-element mesh for a SPECFEM3D_GLOBE simulation is based upon a mapping from
the cube to the sphere called the cubed sphere [Sadourny,1972,Ronchi et al.,1996]. This cubed-sphere mapping
breaks the globe into 6 chunks, each of which is further subdivided in terms of n2mesh slices, where n≥1is a
positive integer, for a total of 6×n2slices (Figure 3.1). Thus the minimum number of processors required for a global
simulation is 6 (although it is theoretically possible to run more than one slice per processor).
To run the mesher for a global simulation, the following parameters need to be set in the Par_file (the list below
might be slightly obsolete or incomplete; for an up-to-date version, see comments in the default Par_file located
in directory DATA:
SIMULATION_TYPE is set to 1 for forward simulations, 2 for adjoint simulations for sources (see Section 6.1) and
3 for kernel simulations (see Section 10.3).
SAVE_FORWARD is only set to .true. for a forward simulation with the last frame of the simulation saved, as
part of the finite-frequency kernel calculations (see Section 10.3). For a regular forward simulation, leave
SIMULATION_TYPE and SAVE_FORWARD at their default values.
NCHUNKS must be set to 6 for global simulations.
ANGULAR_WIDTH_XI_IN_DEGREES Not needed for a global simulation. (See Chapter 5for regional simulations.)
ANGULAR_WIDTH_ETA_IN_DEGREES Not needed for a global simulation. (See Chapter 5for regional simula-
tions.)
CENTER_LATITUDE_IN_DEGREES Not needed for a global simulation. (See Chapter 5for regional simulations.)
CENTER_LONGITUDE_IN_DEGREES Not needed for a global simulation. (See Chapter 5for regional simulations.)
GAMMA_ROTATION_AZIMUTH Not needed for a global simulation. (See Chapter 5for regional simulations.)
15

CHAPTER 3. RUNNING THE MESHER XMESHFEM3D 16
Figure 3.1: Each of the 6 chunks that constitutes the cubed sphere is subdivided in terms of n2slices of elements,
where n≥1is a positive integer, for a total of 6×n2slices (and therefore processors). The figure on the left shows
a mesh that is divided in terms of 6×52= 150 slices as indicated by the various colors. In this cartoon, each slice
contains 5×5 = 25 spectral elements at the Earth’s surface. The figure on the right shows a mesh that is divided over
6×182= 1944 processors as indicated by the various colors. Regional simulations can be accommodated by using
only 1, 2 or 3 chunks of the cubed sphere. One-chunk simulations may involve a mesh with lateral dimensions smaller
than 90◦, thereby accommodating smaller-scale simulations.
NEX_XI The number of spectral elements along one side of a chunk in the cubed sphere (see Figure 3.1); this number
must be a multiple of 16 and 8 ×a multiple of NPROC_XI defined below. We do not recommend using NEX_XI
less than 64 because the curvature of the Earth cannot be honored if one uses too few elements, and distorted
elements can lead to inaccurate and unstable simulations, i.e., smaller values of NEX_XI are likely to result in
spectral elements with a negative Jacobian, in which case the mesher will exit with an error message. Table 3
summarizes various suitable choices for NEX_XI and the related values of NPROC_XI. Based upon benchmarks
against semi-analytical normal-mode synthetic seismograms, Komatitsch and Tromp [2002a,b] determined that
aNEX_XI = 256 run is accurate to a shortest period of roughly 17 s. Therefore, since accuracy is determined
by the number of grid points per shortest wavelength, for any particular value of NEX_XI the simulation will be
accurate to a shortest period determined approximately by
shortest period (s) '(256/NEX_XI)×17.(3.1)
The number of grid points in each orthogonal direction of the reference element, i.e., the number of Gauss-
Lobatto-Legendre points, is determined by NGLLX in the constants.h file. In the globe we use NGLLX = 5,
for a total of 53= 125 points per elements. We suggest not to change this value.
NEX_ETA For global simulations NEX_ETA must be set to the same value as NEX_XI.
NPROC_XI The number of processors or slices along one chunk of the cubed sphere (see Figure 3.1); we must have
NEX_XI = 8 ×c×NPROC_XI, where c≥1is a positive integer. See Table 3for various suitable choices.
NPROC_ETA For global simulations NPROC_ETA must be set to the same value as NPROC_XI.
MODEL Must be set to one of the following:
1D models with real structure:
CHAPTER 3. RUNNING THE MESHER XMESHFEM3D 17
1D_isotropic_prem Isotropic version of the spherically symmetric Preliminary Reference Earth Model
(PREM) [Dziewo´
nski and Anderson,1981].
1D_transversely_isotropic_prem Transversely isotropic version of PREM.
1D_iasp91 Spherically symmetric isotropic IASP91 model [Kennett and Engdahl,1991].
1D_1066a Spherically symmetric earth model 1066A [Gilbert and Dziewo´
nski,1975]. When ATTENTUATION
is on, it uses an unpublished 1D attenuation model from Scripps.
1D_ak135f_no_mud Spherically symmetric isotropic AK135 model [Kennett et al.,1995] modified to use
the density and Q attenuation models of Montagner and Kennett [1995]. That modified model is tradition-
ally called AK135-F, see http://rses.anu.edu.au/seismology/ak135/ak135f.html for
more details. As we do not want to use the 300 m-thick mud layer from that model nor the ocean layer,
above the d120 discontinuity we switch back to the classical AK135 model of Kennett et al. [1995], i.e.,
we use AK135-F below and AK135 above.
1D_ref A recent 1D Earth model developed by Kustowski et al. [2006]. This model is the 1D background
model for the 3D models s362ani, s362wmani, s362ani_prem, and s29ea.
For historical reasons and to provide benchmarks against normal-mode synthetics, the mesher accommodates versions
of various 1D models with a single crustal layer with the properties of the original upper crust. These ‘one-crust’
models are:
1D_isotropic_prem_onecrust
1D_transversely_isotropic_prem_onecrust
1D_iasp91_onecrust
1D_1066a_onecrust
1D_ak135f_no_mud_onecrust
Fully 3D models:
transversely_isotropic_prem_plus_3D_crust_2.0 This model has CRUST2.0 [Bassin et al.,
2000] on top of a transversely isotropic PREM. We first extrapolate PREM mantle velocity up to the
surface, then overwrite the model with CRUST2.0
s20rts By default, the code uses 3D mantle model S20RTS [Ritsema et al.,1999] and 3D crustal model
Crust2.0 [Bassin et al.,2000]. Note that S20RTS uses transversely isotropic PREM as a background
model, and that we use the PREM radial attenuation model when ATTENUATION is incorporated. See
Chapter 12 for a discussion on how to change 3D models.
s40rts A global 3D mantle model [Ritsema et al.,2011] succeeding S20RTS with a higher resolution.
S40RTS uses transversely isotropic PREM as a backgroun model and the 3D crustal model Crust2.0
[Bassin et al.,2000]. We use the PREM radial attenuation model when ATTENUATION is incorporated.
s362ani A global shear-wave speed model developed by Kustowski et al. [2006]. In this model, radial
anisotropy is confined to the uppermost mantle. The model (and the corresponding mesh) incorporate
tomography on the 650~km and 410~km discontinuities in the 1D reference model REF.
s362wmani A version of S362ANI with anisotropy allowed throughout the mantle.
s362ani_prem A version of S362ANI calculated using PREM as the 1D reference model.
s29ea A global model with higher resolution in the upper mantle beneath Eurasia calculated using REF as the
1D reference model.
3D_anisotropic See Chapter 12 for a discussion on how to specify your own 3D anisotropic model.
3D_attenuation See Chapter 12 for a discussion on how to specify your own 3D attenuation model.
PPM For a user-specified 3D model (Point-Profile-Model) given as ASCII-table, specifying Vs-perturbations
with respect to PREM. See Chapter 12 for a discussion on how to specify your own 3D model.
CHAPTER 3. RUNNING THE MESHER XMESHFEM3D 18
full_sh For a user-specified, transversely isotropic 3D model given in spherical harmonics. Coefficients for
the crustal model (up to degree 40) are stored in files named C**.dat and MOHO.dat, coefficients for
the mantle model (up to degree 20) are stored in files named M**.dat.
All model files reside in directory DATA/full_sphericalharmonic_model/. Note that to use the
crustal model, one has to set the crustal type value ITYPE_CRUSTAL_MODEL = ICRUST_CRUST_SH
in file setup/constants.h. This crustal model can be transversely isotropic as well.
sgloberani_iso Uses 3D mantle model SGLOBE-rani [Chang et al.,2015] with isotropic model perturba-
tions and 3D crustal model Crust2.0 [Bassin et al.,2000]. The model is parametrised horizontally in spher-
ical harmonics up to lmax=35 and with 21 depth splines for the radial direction. Note that SGLOBE-rani
uses transversely isotropic PREM as a background model, and that we use the PREM radial attenuation
model when ATTENUATION is incorporated.
sgloberani_aniso Uses 3D mantle model SGLOBE-rani [Chang et al.,2015] with anisotropic model
perturbations and 3D crustal model Crust2.0 [Bassin et al.,2000]. We take model perturbations from 50km
up to the surface. Note that SGLOBE-rani uses transversely isotropic PREM as a background model, and
that we use the PREM radial attenuation model when ATTENUATION is incorporated.
NOTE:
When a 3D mantle model is chosen in Par_file, the simulations are performed together with the 3D crustal
model Crust2.0. Alternatively, Crust2.0 can be combined with a higher resolution European crustal model
EUCrust07 [Tesauro et al.,2008]. This can be done by setting the crustal type to ICRUST_CRUSTMAPS
in the constant.h file. It is also possible to run simulations using a 3D mantle model with a 1D crustal
model on top. This can be done by setting the model in Par_file to <3D mantle>_1Dcrust, e.g.,
s20rts_1Dcrust, s362ani_1Dcrust, etc. In this case, the 1D crustal model will be the one that is
used in the 3D mantle model as a reference model (e.g., transversely isotropic PREM for s20rts, REF for
s362ani, etc.).
OCEANS Set to .true. if the effect of the oceans on seismic wave propagation should be incorporated based upon
the approximate treatment discussed in Komatitsch and Tromp [2002b]. This feature is inexpensive from a
numerical perspective, both in terms of memory requirements and CPU time. This approximation is accurate at
periods of roughly 20 s and longer. At shorter periods the effect of water phases/reverberations is not taken into
account, even when the flag is on.
ELLIPTICITY Set to .true. if the mesh should make the Earth model elliptical in shape according to Clairaut’s
equation [Dahlen and Tromp,1998]. This feature adds no cost to the simulation. After adding ellipticity,
the mesh becomes elliptical and thus geocentric and geodetic/geographic latitudes and colatitudes differ (lon-
gitudes are unchanged). From Dahlen and Tromp [1998]: "Spherically-symmetric Earth models all have the
same hydrostatic surface ellipticity 1/299.8. This is 0.5 percent smaller than observed flattening of best-
fitting ellipsoid 1/298.3. The discrepancy is referred to as the "excess equatorial bulge of the Earth", an
early discovery of artificial satellite geodesy." From Paul Melchior, IUGG General Assembly, Vienna, Aus-
tria, August 1991 Union lecture, available at www.agu.org/books: "It turns out that the spheroidal models
constructed on the basis of the spherically-symmetric models (PREM, 1066A) by using the Clairaut differ-
ential equation to calculate the flattening in function of the radius vector imply hydrostaticity. These have
surface ellipticity 1/299.8 and a corresponding dynamical flattening of .0033 (PREM). The actual ellipticty
of the Earth for a best-fitting ellipsoid is 1/298.3 with a corresponding dynamical flattening of .0034." Thus,
flattening f = 1/299.8 is what is used in SPECFEM3D_GLOBE, as it should. And thus eccentricity squared
e2= 1 −(1 −f)2= 1 −(1 −1/299.8)2= 0.00665998813529, and the correction factor used in the code
to convert geographic latitudes to geocentric is 1−e2= (1 −f)2= (1 −1/299.8)2= 0.9933400118647.
As a comparison, the classical World Geodetic System reference ellipsoid WGS 84 (see e.g. http://en.
wikipedia.org/wiki/World_Geodetic_System) has f= 1/298.2572236.
TOPOGRAPHY Set to .true. if topography and bathymetry should be incorporated based upon model ETOPO4
[NOAA,1988]. This feature adds no cost to the simulation. It you want to use other topographic models, use
the script download_the_whole_topography_database_if_you_want_other_topographic_models.bash provided
in the root directory of the code and change the name of the topographic model to use in file setup/constants.h.in
before configuring the code with the configure script.
CHAPTER 3. RUNNING THE MESHER XMESHFEM3D 19
GRAVITY Set to .true. if self-gravitation should be incorporated in the Cowling approximation [Komatitsch and
Tromp,2002b,Dahlen and Tromp,1998]. Turning this feature on is relatively inexpensive, both from the
perspective of memory requirements as well as in terms of computational speed.
ROTATION Set to .true. if the Coriolis effect should be incorporated. Turning this feature on is relatively cheap
numerically.
ATTENUATION Set to .true. if attenuation should be incorporated. Turning this feature on increases the memory
requirements significantly (roughly by a factor of 2), and is numerically fairly expensive. Of course for realistic
simulations this flag should be turned on. See Komatitsch and Tromp [1999,2002a] for a discussion on the
implementation of attenuation based upon standard linear solids.
ABSORBING_CONDITIONS Set to .false. for global simulations. See Chapter 5for regional simulations.
RECORD_LENGTH_IN_MINUTES Choose the desired record length of the synthetic seismograms (in minutes). This
controls the length of the numerical simulation, i.e., twice the record length requires twice as much CPU time.
This feature is not used at the time of meshing but is required for the solver, i.e., you may change this parameter
after running the mesher.
PARTIAL_PHYS_DISPERSION_ONLY or UNDO_ATTENUATION To undo attenuation for sensitivity kernel cal-
culations or forward runs with SAVE_FORWARD use one (and only one) of the two flags below. UNDO_ATTENUATION
is much better (it is exact) and is simpler to use but it requires a significant amount of disk space for temporary
storage. It has the advantage of requiring only two simulations for adjoint tomography instead of three in the
case of PARTIAL_PHYS_DISPERSION_ONLY, i.e. for adjoint tomography it is globally significantly less
expensive (each run is slightly more expensive, but only two runs are needed instead of three).
When using PARTIAL_PHYS_DISPERSION_ONLY, to make the approximation reasonably OK you need to
take the following steps:
1/ To calculate synthetic seismograms, do a forward simulation with full attenuation for the model of interest.
The goal is to get synthetics that match the data as closely as possible.
2a/ Make measurements and produce adjoint sources by comparing the resulting synthetics with the data. In the
simplest case of a cross-correlation traveltime measurement, use the time-reversed synthetic in the window of
interest as the adjoint source.
2b/ Do a second forward calculation with PARTIAL_PHYS_DISPERSION_ONLY = .true. and save the
last snapshot.
3/ Do an adjoint calculation using the adjoint source calculated in 1/, the forward wavefield reconstructed based
on 2b/, use PARTIAL_PHYS_DISPERSION_ONLY = .true. for the adjoint wavefield, and save the ker-
nel.
Thus the kernel calculation uses PARTIAL_PHYS_DISPERSION_ONLY = .true. for both the forward
and the adjoint wavefields. This is in the spirit of the banana-donut kernels. But the data that are assimilated are
based on the full 3D synthetic with attenuation.
Another, equivalent way of explaining it is:
1/ Calculate synthetics with full attenuation for the current model. Compare these to the data and measure
frequency-dependent traveltime anomalies ∆τ(ω), e.g.. based upon multi-tapering.
2/ Calculate synthetics with PARTIAL_PHYS_DISPERSION_ONLY = .true. and construct adjoint sources
by combining the seismograms from this run with the measurements from 1/. So in the expressions for the multi-
taper adjoint source you use the measurements from 1/, but synthetics calculated with PARTIAL_PHYS_DISPERSION_ONLY
= .true..
3/ Construct a kernel by calculating an adjoint wavefield based on the sources constructed in 2/ and convolving it
with a forward wavefield with PARTIAL_PHYS_DISPERSION_ONLY = .true.. Again, both the forward
and adjoint calculations use PARTIAL_PHYS_DISPERSION_ONLY = .true..
Note that if you replace multi-taper measurements with cross-correlation measurements you will measure a
cross-correlation traveltime anomaly in 1/, i.e., some delay time ∆T. Then you would calculate an adjoint
wavefield with PARTIAL_PHYS_DISPERSION_ONLY = .true. and use the resulting time-reversed seis-
mograms weighted by ∆Tas the adjoint source. This wavefield interacts with a forward wavefield calculated
with PARTIAL_PHYS_DISPERSION_ONLY = .true.. If ∆T= 1 one gets a banana-donut kernel, i.e., a
CHAPTER 3. RUNNING THE MESHER XMESHFEM3D 20
kernel for the case in which there are no observed seismograms (no data), as explained for instance on page 5 of
Zhou et al. [2011].
MOVIE_SURFACE Set to .false., unless you want to create a movie of seismic wave propagation on the Earth’s
surface. Turning this option on generates large output files. See Section 10.2 for a discussion on the generation
of movies. This feature is not used at the time of meshing but is relevant for the solver.
MOVIE_VOLUME Set to .false., unless you want to create a movie of seismic wave propagation in the Earth’s
interior. Turning this option on generates huge output files. See Section 10.2 for a discussion on the generation
of movies. This feature is not used at the time of meshing but is relevant for the solver.
NTSTEP_BETWEEN_FRAMES Determines the number of timesteps between movie frames. Typically you want to
save a snapshot every 100 timesteps. The smaller you make this number the more output will be generated! See
Section 10.2 for a discussion on the generation of movies. This feature is not used at the time of meshing but is
relevant for the solver.
HDUR_MOVIE determines the half duration of the source time function for the movie simulations. When this param-
eter is set to be 0, a default half duration that corresponds to the accuracy of the simulation is provided.
SAVE_MESH_FILES Set this flag to .true.to save AVS (http://www.avs.com), OpenDX (http://www.
opendx.org), or ParaView (http://www.paraview.org) mesh files for subsequent viewing. Turning
the flag on generates large (distributed) files in the LOCAL_PATH directory. See Section 10.1 for a discussion
of mesh viewing features.
NUMBER_OF_RUNS On machines with a run-time limit, for instance for a batch/queue system, a simulation may
need to be completed in stages. This option allows you to select the number of stages in which the simulation
will be completed (1, 2 or 3). Choose 1 for a run without restart files. This feature is not used at the time of
meshing but is required for the solver. At the end of the first or second stage of a multi-stage simulation, large
files are written to the file system to save the current state of the simulation. This state is read back from the
file system at the beginning of the next stage of the multi-stage run. Reading and writing the states can be very
time consuming depending on the nature of the network and the file system (in this case writing to the local file
system, i.e., the disk on a node, is preferable).
NUMBER_OF_THIS_RUN If you choose to perform the run in stages, you need to tell the solver what stage run to
perform. This feature is not used at the time of meshing but is required for the solver.
LOCAL_PATH Directory in which the databases generated by the mesher will be written. Generally one uses a
directory on the local disk of the compute nodes, although on some machines these databases are written on a
parallel (global) file system (see also the earlier discussion of the LOCAL_PATH_IS_ALSO_GLOBAL flag in
Chapter 2). The mesher generates the necessary databases in parallel, one set for each of the 6×NPROC_XI2
slices that constitutes the mesh (see Figure 3.1). After the mesher finishes, you can log in to one of the compute
nodes and view the contents of the LOCAL_PATH directory to see the (many) files generated by the mesher.
NTSTEP_BETWEEN_OUTPUT_INFO This parameter specifies the interval at which basic information about a run is
written to the file system (timestamp*files in the OUTPUT_FILES directory). If you have access to a fast
machine, set NTSTEP_BETWEEN_OUTPUT_INFO to a relatively high value (e.g., at least 100, or even 1000
or more) to avoid writing output text files too often. This feature is not used at the time of meshing. One can set
this parameter to a larger value than the number of time steps to avoid writing output during the run.
NTSTEP_BETWEEN_OUTPUT_SEISMOS This parameter specifies the interval at which synthetic seismograms are
written in the LOCAL_PATH directory. The seismograms can be created in three different formats by setting the
parameters OUTPUT_SEISMOS_ASCII_TEXT,OUTPUT_SEISMOS_SAC_ALPHANUM and OUTPUT_SEI-
SMOS_SAC_BINARY. One can choose any combination of these parameters (details on the formats follow in the
description of each parameter). SAC (http://www.iris.edu/software/sac/) is a signal-processing
software package. If a run crashes, you may still find usable (but shorter than requested) seismograms in this
directory. On a fast machine set NTSTEP_BETWEEN_OUTPUT_SEISMOS to a relatively high value to avoid
writing to the seismograms too often. This feature is not used at the time of meshing.
CHAPTER 3. RUNNING THE MESHER XMESHFEM3D 21
NTSTEP_BETWEEN_READ_ADJSRC The number of adjoint sources read in each time for an adjoint simulation.
USE_FORCE_POINT_SOURCE Turn this flag on to use a (tilted) FORCESOLUTION force point source instead of a
CMTSOLUTION moment-tensor source. When the force source does not fall exactly at a grid point, the solver
interpolates the force between grid points using Lagrange interpolants. This option can be useful for vertical
force, normal force, tilted force, impact force, etc. Note that in the FORCESOLUTION file, you will need to
edit the East, North and vertical components of an arbitrary (not necessarily unitary, the code will normalize it
automatically) direction vector of the force vector; thus refer to Appendix Afor the orientation of the reference
frame. This vector is made unitary internally in the solver and thus only its direction matters here; its norm is
ignored and the norm of the force used is the factor force source times the source time function.
OUTPUT_SEISMOS_ASCII_TEXT Set this flag to .true. if you want to have the synthetic seismograms written
in two-column ASCII format (the first column contains time in seconds and the second column the displacement
in meters of the recorded signal, no header information). Files will be named with extension .ascii, e.g.,
NT.STA.?X?.sem.ascii where NT and STA are the network and station codes given in STATIONS file,
and ?X? is the channel code (see Appendix E).
OUTPUT_SEISMOS_SAC_ALPHANUM Set this flag to .true. if you want to have the synthetic seismograms
written in alphanumeric (human readable) SAC format, which includes header information on the source and
receiver parameters (e.g., source/receiver coordinates, station name, etc., see Appendix D). For details on the
format, please check the SAC webpage (http://www.iris.edu/software/sac/). Files will be named
with extension .sacan.
OUTPUT_SEISMOS_SAC_BINARY Set this flag to .true. if you want to have the synthetic seismograms written
in binary SAC format. The header information included is the same as for the alphanumeric SAC format (see
Appendix D). Using this format requires the least disk space, which may be particulary important if you have
a large number of stations. For details on the binary format please also check the SAC webpage (http:
//www.iris.edu/software/sac/) and Appendix D. Files will be named with extension .sac.
ROTATE_SEISMOGRAMS_RT Set this flag to .true. if you want to have radial (R) and transverse (T) horizontal
components of the synthetic seismograms (default is .false. →East (E) and North (N) components).
WRITE_SEISMOGRAMS_BY_MASTER Set this flag to .true. if you want to have all the seismograms written by
the master (no need to collect them on the nodes after the run).
SAVE_ALL_SEISMOS_IN_ONE_FILE Set this flag to .true. if you want to have all the seismograms saved in
one large combined file instead of one file per seismogram to avoid overloading shared non-local file systems
such as GPFS for instance.
USE_BINARY_FOR_LARGE_FILE Set this flag to .true. if you want to use binary instead of ASCII for that
large file (not used if SAVE_ALL_SEISMOS_IN _ONE_FILE = .false.)
RECEIVERS_CAN_BE_BURIED This flag accommodates stations with instruments that are buried, i.e., the solver
will calculate seismograms at the burial depth specified in the STATIONS file. This feature is not used at the
time of meshing.
PRINT_SOURCE_TIME_FUNCTION Turn this flag on to print information about the source time function in the file
OUTPUT_FILES/plot_source_time_function.txt. This feature is not used at the time of meshing.
NUMBER_OF_SIMULTANEOUS_RUNS adds the ability to run several calculations (several earthquakes) in an embarrassingly-
parallel fashion from within the same run; this can be useful when using a very large supercomputer to com-
pute many earthquakes in a catalog, in which case it can be better from a batch job submission point of
view to start fewer and much larger jobs, each of them computing several earthquakes in parallel. To turn
that option on, set parameter NUMBER_OF_SIMULTANEOUS_RUNS to a value greater than 1. To imple-
ment that, we create NUMBER_OF_SIMULTANEOUS_RUNS MPI sub-communicators, each of them be-
ing labeled "my_local_mpi_comm_world", and we use them in all the routines in "src/shared/parallel.f90",
except in MPI_ABORT() because in that case we need to kill the entire run. When that option is on, of
CHAPTER 3. RUNNING THE MESHER XMESHFEM3D 22
course the number of processor cores used to start the code in the batch system must be a multiple of NUM-
BER_OF_SIMULTANEOUS_RUNS, all the individual runs must use the same number of processor cores,
which as usual is NPROC in the Par_file, and thus the total number of processor cores to request from the batch
system should be NUMBER_OF_SIMULTANEOUS_RUNS * NPROC. All the runs to perform must be placed
in directories called run0001, run0002, run0003 and so on (with exactly four digits).
Imagine you have 10 independent calculations to do, each of them on 100 cores; you have three options:
1/ submit 10 jobs to the batch system
2/ submit a single job on 1000 cores to the batch, and in that script create a sub-array of jobs to start 10 jobs,
each running on 100 cores (see e.g. http://www.schedmd.com/slurmdocs/job_array.html )
3/ submit a single job on 1000 cores to the batch, start SPECFEM3D on 1000 cores, create 10 sub-communicators,
cd into one of 10 subdirectories (called e.g. run0001, run0002,... run0010) depending on the sub-communicator
your MPI rank belongs to, and run normally on 100 cores using that sub-communicator.
The option NUMBER_OF_SIMULTANEOUS_RUNS implements 3/.
BROADCAST_SAME_MESH_AND_MODEL : if we perform simultaneous runs in parallel, if only the source and re-
ceivers vary between these runs but not the mesh nor the model (velocity and density) then we can also read the
mesh and model files from a single run in the beginning and broadcast them to all the others; for a large number
of simultaneous runs for instance when solving inverse problems iteratively this can DRASTICALLY reduce
I/Os to disk in the solver (by a factor equal to NUMBER_OF_SIMULTANEOUS_RUNS), and reducing I/Os is
crucial in the case of huge runs. Thus, always set this option to .true. if the mesh and the model are the same for
all simultaneous runs. In that case there is no need to duplicate the mesh and model file database (the content of
the DATABASES_MPI directories) in each of the run0001, run0002,... directories, it is sufficient to have one in
run0001 and the code will broadcast it to the others).
USE_FAILSAFE_MECHANISM : if one or a few of these simultaneous runs fail, kill all the runs or let the others
finish using a fail-safe mechanism (in most cases, should be set to true).
TODO / future work to do: currently the BROADCAST_SAME_MESH_AND_MODEL option assumes to
have the (master) mesh files in run0001/DATABASES_MPI or run0001/OUTPUT_FILES/DATABASES_MPI.
However, for adjoint runs you still need a DATABASES_MPI folder in each of the sub-runs directories, e.g.
run0002/DATABASES_MPI, etc. to store the forward wavefields, kernels etc. of each sub-run. This would not
be needed for forward simulations.
TODO / future work to do: the sensitivity kernel summing and smoothing tools in directory src/tomography are
currently not ported to this new option to do many runs simultaneously, only the solver (src/specfem3d) is. Thus
these tools should work, but in their current version will need to be run for each simulation result independently.
More precisely, the current kernel summing and smoothing routines work fine, with the exception that you need
to move out the mesh files (and also the parameters). This works because these routines consider multiple runs
by design. You simply have to provide them the directories where the kernels are.
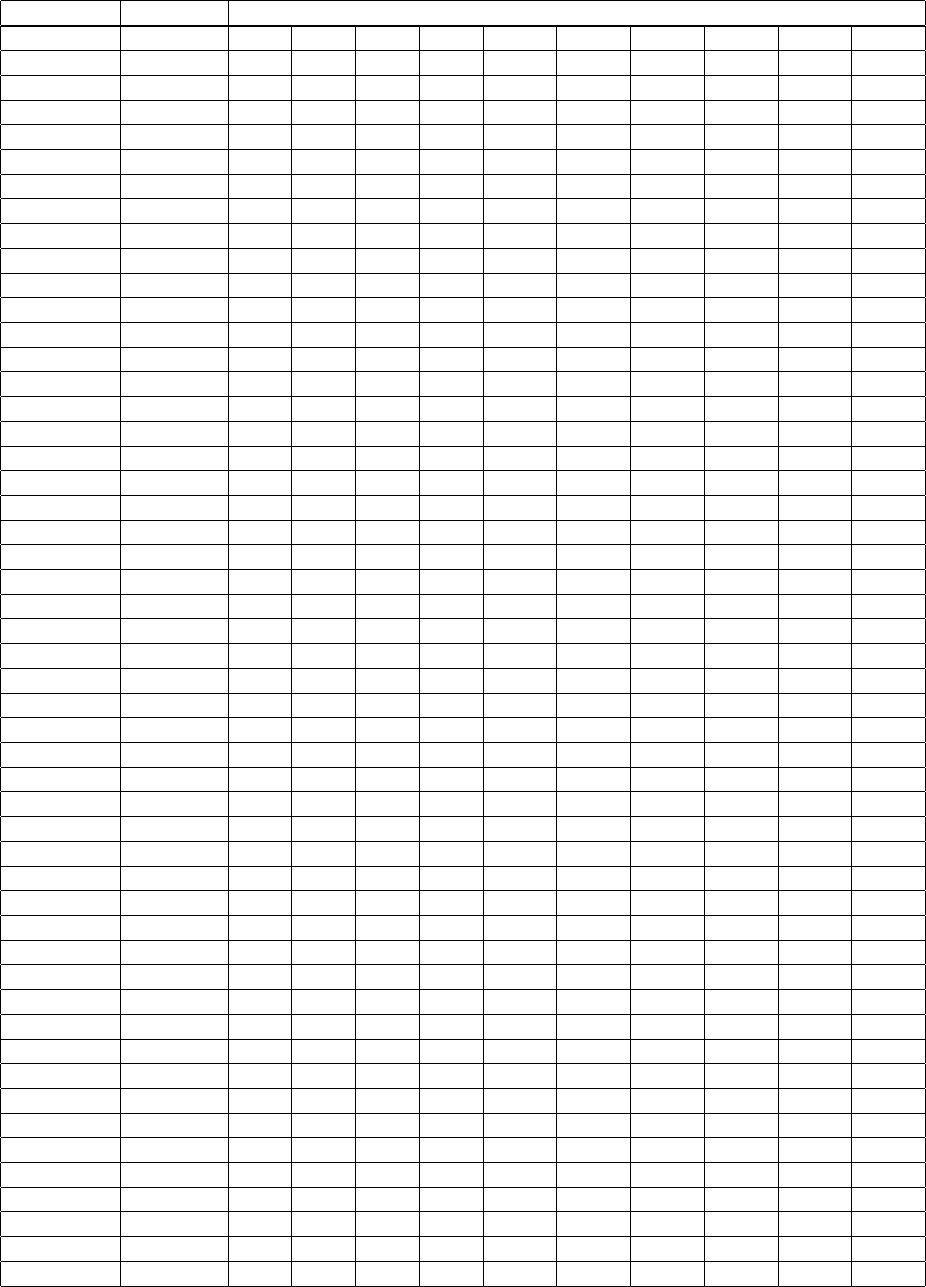
CHAPTER 3. RUNNING THE MESHER XMESHFEM3D 23
NPROC_XI processors NEX_XI
1 6 64 80 96 112 128 144 160 176 192 208
2 24 64 80 96 112 128 144 160 176 192 208
3 54 96 144 192 240 288 336 384 432 480 528
4 96 64 96 128 160 192 224 256 288 320 352
5 150 80 160 240 320 400 480 560 640 720 800
6 216 96 144 192 240 288 336 384 432 480 528
7 294 112 224 336 448 560 672 784 896 1008 1120
8 384 64 128 192 256 320 384 448 512 576 640
9 486 144 288 432 576 720 864 1008 1152 1296 1440
10 600 80 160 240 320 400 480 560 640 720 800
11 726 176 352 528 704 880 1056 1232 1408 1584 1760
12 864 96 192 288 384 480 576 672 768 864 960
13 1014 208 416 624 832 1040 1248 1456 1664 1872 2080
14 1176 112 224 336 448 560 672 784 896 1008 1120
15 1350 240 480 720 960 1200 1440 1680 1920 2160 2400
16 1536 128 256 384 512 640 768 896 1024 1152 1280
17 1734 272 544 816 1088 1360 1632 1904 2176 2448 2720
18 1944 144 288 432 576 720 864 1008 1152 1296 1440
19 2166 304 608 912 1216 1520 1824 2128 2432 2736 3040
20 2400 160 320 480 640 800 960 1120 1280 1440 1600
21 2646 336 672 1008 1344 1680 2016 2352 2688 3024 3360
22 2904 176 352 528 704 880 1056 1232 1408 1584 1760
23 3174 368 736 1104 1472 1840 2208 2576 2944 3312 3680
24 3456 192 384 576 768 960 1152 1344 1536 1728 1920
25 3750 400 800 1200 1600 2000 2400 2800 3200 3600 4000
26 4056 208 416 624 832 1040 1248 1456 1664 1872 2080
27 4374 432 864 1296 1728 2160 2592 3024 3456 3888 4320
28 4704 224 448 672 896 1120 1344 1568 1792 2016 2240
29 5046 464 928 1392 1856 2320 2784 3248 3712 4176 4640
30 5400 240 480 720 960 1200 1440 1680 1920 2160 2400
31 5766 496 992 1488 1984 2480 2976 3472 3968 4464 4960
32 6144 256 512 768 1024 1280 1536 1792 2048 2304 2560
33 6534 528 1056 1584 2112 2640 3168 3696 4224 4752 5280
34 6936 272 544 816 1088 1360 1632 1904 2176 2448 2720
35 7350 560 1120 1680 2240 2800 3360 3920 4480 5040 5600
36 7776 288 576 864 1152 1440 1728 2016 2304 2592 2880
37 8214 592 1184 1776 2368 2960 3552 4144 4736 5328 5920
38 8664 304 608 912 1216 1520 1824 2128 2432 2736 3040
39 9126 624 1248 1872 2496 3120 3744 4368 4992 5616 6240
40 9600 320 640 960 1280 1600 1920 2240 2560 2880 3200
41 10086 656 1312 1968 2624 3280 3936 4592 5248 5904 6560
42 10584 336 672 1008 1344 1680 2016 2352 2688 3024 3360
43 11094 688 1376 2064 2752 3440 4128 4816 5504 6192 6880
44 11616 352 704 1056 1408 1760 2112 2464 2816 3168 3520
45 12150 720 1440 2160 2880 3600 4320 5040 5760 6480 7200
46 12696 368 736 1104 1472 1840 2208 2576 2944 3312 3680
47 13254 752 1504 2256 3008 3760 4512 5264 6016 6768 7520
48 13824 384 768 1152 1536 1920 2304 2688 3072 3456 3840
49 14406 784 1568 2352 3136 3920 4704 5488 6272 7056 7840
50 15000 400 800 1200 1600 2000 2400 2800 3200 3600 4000
51 15606 816 1632 2448 3264 4080 4896 5712 6528 7344 8160
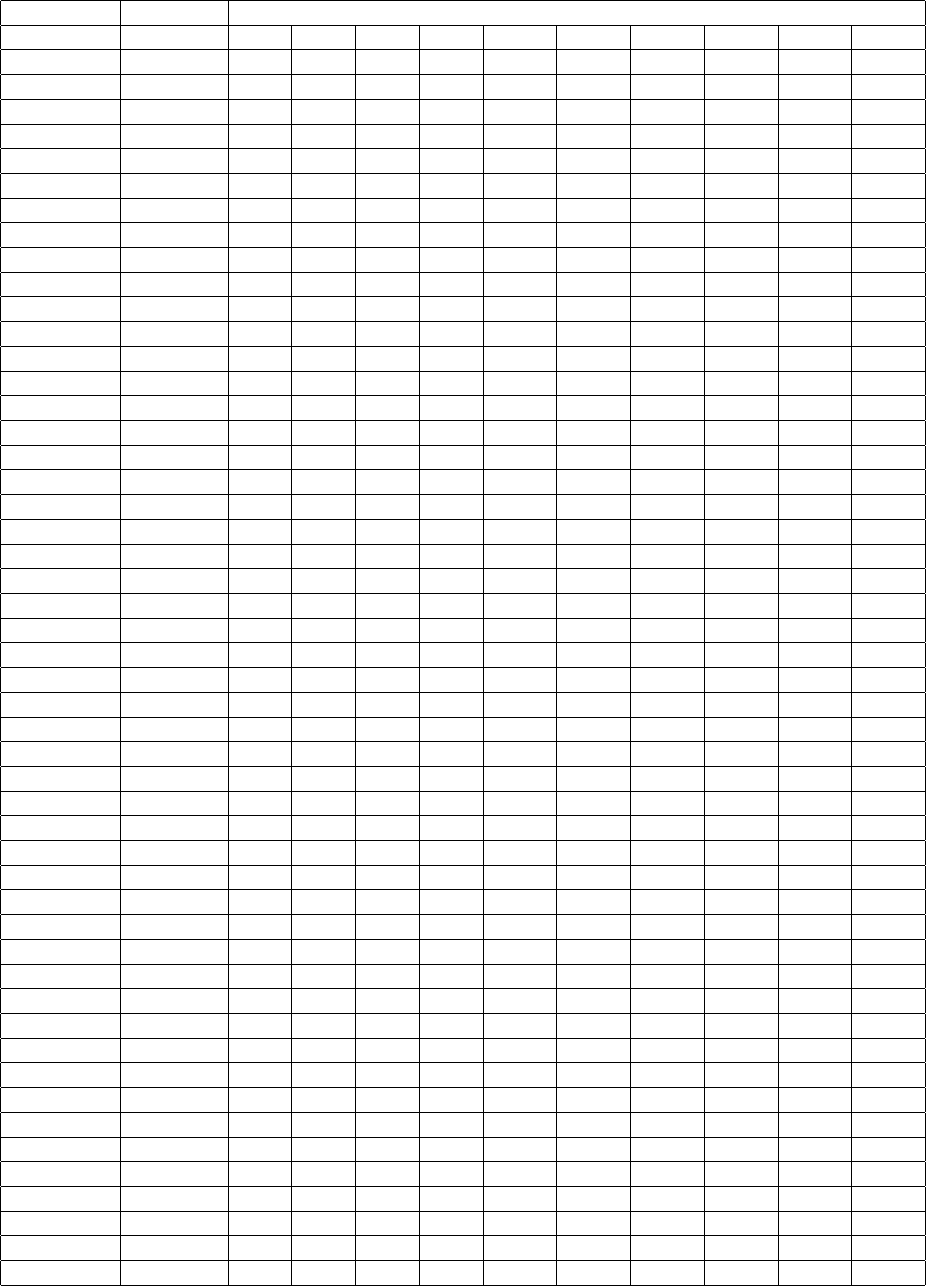
CHAPTER 3. RUNNING THE MESHER XMESHFEM3D 24
NPROC_XI processors NEX_XI
52 16224 416 832 1248 1664 2080 2496 2912 3328 3744 4160
53 16854 848 1696 2544 3392 4240 5088 5936 6784 7632 8480
54 17496 432 864 1296 1728 2160 2592 3024 3456 3888 4320
55 18150 880 1760 2640 3520 4400 5280 6160 7040 7920 8800
56 18816 448 896 1344 1792 2240 2688 3136 3584 4032 4480
57 19494 912 1824 2736 3648 4560 5472 6384 7296 8208 9120
58 20184 464 928 1392 1856 2320 2784 3248 3712 4176 4640
59 20886 944 1888 2832 3776 4720 5664 6608 7552 8496 9440
60 21600 480 960 1440 1920 2400 2880 3360 3840 4320 4800
61 22326 976 1952 2928 3904 4880 5856 6832 7808 8784 9760
62 23064 496 992 1488 1984 2480 2976 3472 3968 4464 4960
63 23814 1008 2016 3024 4032 5040 6048 7056 8064 9072 10080
64 24576 512 1024 1536 2048 2560 3072 3584 4096 4608 5120
65 25350 1040 2080 3120 4160 5200 6240 7280 8320 9360 10400
66 26136 528 1056 1584 2112 2640 3168 3696 4224 4752 5280
67 26934 1072 2144 3216 4288 5360 6432 7504 8576 9648 10720
68 27744 544 1088 1632 2176 2720 3264 3808 4352 4896 5440
69 28566 1104 2208 3312 4416 5520 6624 7728 8832 9936 11040
70 29400 560 1120 1680 2240 2800 3360 3920 4480 5040 5600
71 30246 1136 2272 3408 4544 5680 6816 7952 9088 10224 11360
72 31104 576 1152 1728 2304 2880 3456 4032 4608 5184 5760
73 31974 1168 2336 3504 4672 5840 7008 8176 9344 10512 11680
74 32856 592 1184 1776 2368 2960 3552 4144 4736 5328 5920
75 33750 1200 2400 3600 4800 6000 7200 8400 9600 10800 12000
76 34656 608 1216 1824 2432 3040 3648 4256 4864 5472 6080
77 35574 1232 2464 3696 4928 6160 7392 8624 9856 11088 12320
78 36504 624 1248 1872 2496 3120 3744 4368 4992 5616 6240
79 37446 1264 2528 3792 5056 6320 7584 8848 10112 11376 12640
80 38400 640 1280 1920 2560 3200 3840 4480 5120 5760 6400
81 39366 1296 2592 3888 5184 6480 7776 9072 10368 11664 12960
82 40344 656 1312 1968 2624 3280 3936 4592 5248 5904 6560
83 41334 1328 2656 3984 5312 6640 7968 9296 10624 11952 13280
84 42336 672 1344 2016 2688 3360 4032 4704 5376 6048 6720
85 43350 1360 2720 4080 5440 6800 8160 9520 10880 12240 13600
86 44376 688 1376 2064 2752 3440 4128 4816 5504 6192 6880
87 45414 1392 2784 4176 5568 6960 8352 9744 11136 12528 13920
88 46464 704 1408 2112 2816 3520 4224 4928 5632 6336 7040
89 47526 1424 2848 4272 5696 7120 8544 9968 11392 12816 14240
90 48600 720 1440 2160 2880 3600 4320 5040 5760 6480 7200
91 49686 1456 2912 4368 5824 7280 8736 10192 11648 13104 14560
92 50784 736 1472 2208 2944 3680 4416 5152 5888 6624 7360
93 51894 1488 2976 4464 5952 7440 8928 10416 11904 13392 14880
94 53016 752 1504 2256 3008 3760 4512 5264 6016 6768 7520
95 54150 1520 3040 4560 6080 7600 9120 10640 12160 13680 15200
96 55296 768 1536 2304 3072 3840 4608 5376 6144 6912 7680
97 56454 1552 3104 4656 6208 7760 9312 10864 12416 13968 15520
98 57624 784 1568 2352 3136 3920 4704 5488 6272 7056 7840
99 58806 1584 3168 4752 6336 7920 9504 11088 12672 14256 15840
100 60000 800 1600 2400 3200 4000 4800 5600 6400 7200 8000
101 61206 1616 3232 4848 6464 8080 9696 11312 12928 14544 16160
102 62424 816 1632 2448 3264 4080 4896 5712 6528 7344 8160
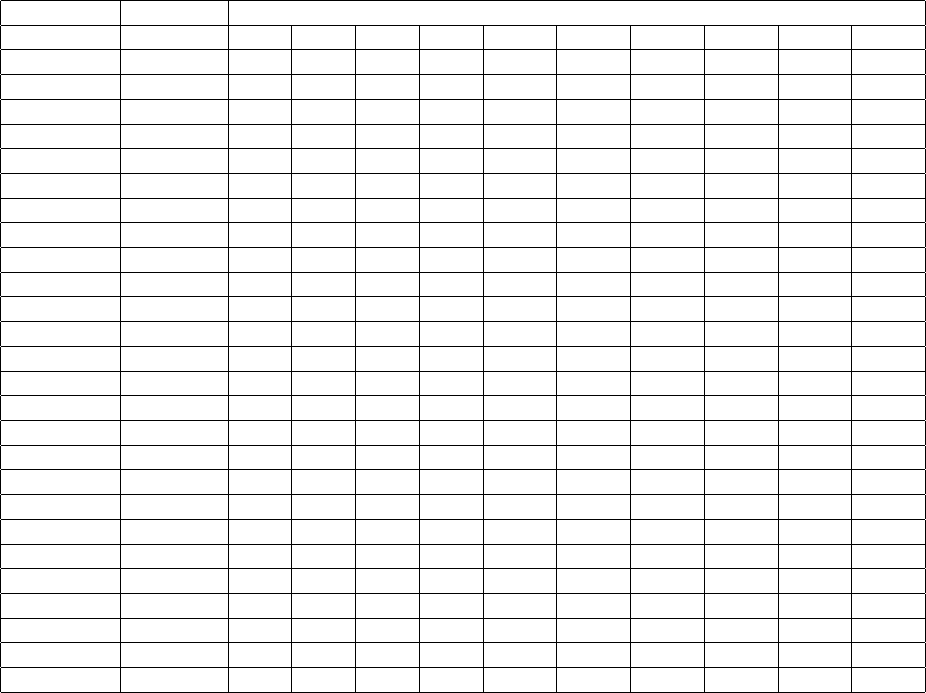
CHAPTER 3. RUNNING THE MESHER XMESHFEM3D 25
NPROC_XI processors NEX_XI
103 63654 1648 3296 4944 6592 8240 9888 11536 13184 14832 16480
104 64896 832 1664 2496 3328 4160 4992 5824 6656 7488 8320
105 66150 1680 3360 5040 6720 8400 10080 11760 13440 15120 16800
106 67416 848 1696 2544 3392 4240 5088 5936 6784 7632 8480
107 68694 1712 3424 5136 6848 8560 10272 11984 13696 15408 17120
108 69984 864 1728 2592 3456 4320 5184 6048 6912 7776 8640
109 71286 1744 3488 5232 6976 8720 10464 12208 13952 15696 17440
110 72600 880 1760 2640 3520 4400 5280 6160 7040 7920 8800
111 73926 1776 3552 5328 7104 8880 10656 12432 14208 15984 17760
112 75264 896 1792 2688 3584 4480 5376 6272 7168 8064 8960
113 76614 1808 3616 5424 7232 9040 10848 12656 14464 16272 18080
114 77976 912 1824 2736 3648 4560 5472 6384 7296 8208 9120
115 79350 1840 3680 5520 7360 9200 11040 12880 14720 16560 18400
116 80736 928 1856 2784 3712 4640 5568 6496 7424 8352 9280
117 82134 1872 3744 5616 7488 9360 11232 13104 14976 16848 18720
118 83544 944 1888 2832 3776 4720 5664 6608 7552 8496 9440
119 84966 1904 3808 5712 7616 9520 11424 13328 15232 17136 19040
120 86400 960 1920 2880 3840 4800 5760 6720 7680 8640 9600
121 87846 1936 3872 5808 7744 9680 11616 13552 15488 17424 19360
122 89304 976 1952 2928 3904 4880 5856 6832 7808 8784 9760
123 90774 1968 3936 5904 7872 9840 11808 13776 15744 17712 19680
124 92256 992 1984 2976 3968 4960 5952 6944 7936 8928 9920
125 93750 2000 4000 6000 8000 10000 12000 14000 16000 18000 20000
126 95256 1008 2016 3024 4032 5040 6048 7056 8064 9072 10080
127 96774 2032 4064 6096 8128 10160 12192 14224 16256 18288 20320
128 98304 1024 2048 3072 4096 5120 6144 7168 8192 9216 10240
129 99846 2064 4128 6192 8256 10320 12384 14448 16512 18576 20640
Table 3.2: Sample choices for NEX_XI given NPROC_XI based upon the relationship NEX_XI = 8×c×NPROC_XI,
where the integer c≥1. The number of MPI slices, i.e., the total number of required processors, is 6×NPROC_XI2,
as illustrated in Figure 3.1. The approximate shortest period at which the global simulation is accurate for a given
value of NEX_XI can be estimated by running the small serial program xcreate_header_file.
Finally, you need to provide a file that tells MPI what compute nodes to use for the simulations. The file must have
a number of entries (one entry per line) at least equal to the number of processors needed for the run. A sample file is
provided in the file mymachines. This file is not used by the mesher or solver, but is required by the go_mesher
and go_solver default job submission scripts. See Chapter 11 for information about running the code on a system
with a scheduler, e.g., LSF.
Now that you have set the appropriate parameters in the Par_file and have compiled the mesher, you are ready
to launch it! This is most easily accomplished based upon the go_mesher script. When you run on a PC cluster, the
script assumes that the nodes are named n001, n002, etc. If this is not the case, change the tr -d ‘n’ line in the
script. You may also need to edit the last command at the end of the script that invokes the mpirun command.
Mesher output is provided in the OUTPUT_FILES directory in output_mesher.txt; this file provides lots of
details about the mesh that was generated. Alternatively, output can be directed to the screen instead by uncommenting
a line in constants.h:
! uncomment this to write messages to the screen
! integer, parameter :: IMAIN = ISTANDARD_OUTPUT
Note that on very fast machines, writing to the screen may slow down the code.
CHAPTER 3. RUNNING THE MESHER XMESHFEM3D 26
Another file generated by the mesher is the header file OUTPUT_FILES/values_from_mesher.h. This file
specifies a number of constants and flags needed by the solver. These values are passed statically to the solver for
reasons of speed. Some useful statistics about the mesh are also provided in this file.
For a given model, set of nodes, and set of parameters in Par_file, one only needs to run the mesher once and
for all, even if one wants to run several simulations with different sources and/or receivers (the source and receiver
information is used in the solver only).
Please note that it is difficult to correctly sample S waves in the inner core of the Earth because S-wave velocity
is very small there. Therefore, correctly sampling S waves in the inner core would require a very dense mesh, which
in turn would drastically reduce the time step of the explicit time scheme because the P wave velocity is very high in
the inner core (Poisson’s ratio is roughly equal to 0.44). Because shear wave attenuation is very high in the inner core
(Qµis approximately equal to 85), we have therefore decided to design the inner core mesh such that P waves are
very well sampled but S waves are right at the sampling limit or even slightly below. This works fine because spurious
numerical oscillations due to S-wave subsampling are almost completely suppressed by attenuation. However, this
implies that one should not use SPECFEM3D_GLOBE with the regular mesh and period estimates of Table 3to study
the PKJKP phase very precisely. If one is interested in that phase, one should use typically 1.5 times to twice the
number of elements NEX indicated in the table.
Regarding fluid/solid coupling at the CMB and ICB, in SPECFEM3D_GLOBE we do not use the fluid-solid for-
mulation of Komatitsch and Tromp [2002a] and Komatitsch and Tromp [2002b] anymore, we now use a displacement
potential in the fluid (rather than a velocity potential as in Komatitsch and Tromp [2002a] and Komatitsch and Tromp
[2002b]). This leads to the simpler fluid-solid matching condition introduced by Chaljub and Valette [2004] with no
numerical iterations at the CMB and ICB.
For accuracy reasons, in the mesher the coordinates of the mesh points (arrays xstore, ystore and zstore) are always
created in double precision. If the solver is compiled in single precision mode, the mesh coordinates are converted to
single precision before being saved in the local mesh files.
3.1 Memory requirements
The SPECFEM3D_GLOBE memory requirements can be estimated before or after running the mesher using the
small serial program ./bin/xcreate_header_file, which reads the input file DATA/Par_file and displays the
total amount of memory that will be needed by the mesher and the solver to run it. This way, users can easily
modify the parameters and check that their simulation will fit in memory on their machine. The file created by
xcreate_header_file is called OUTPUT_FILES/values_from_mesher.h and contains even more details
about the future simulation.
Please note that running these codes is optional because no information needed by the solver is generated.
Chapter 4
Running the Solver xspecfem3D
Now that you have successfully run the mesher, you are ready to compile the solver. For reasons of speed, the solver
uses static memory allocation. Therefore it needs to be recompiled (type ‘make clean’ and ‘make specfem3D’)
every time one reruns the mesher with different parameters. To compile the solver one needs a file generated by the
mesher in the directory OUTPUT_FILES called values_from_mesher.h, which contains parameters describing
the static size of the arrays as well as the setting of certain flags.
The solver needs three input files in the DATA directory to run: the Par_file that was discussed in detail in
Chapter 3, the earthquake source parameter file CMTSOLUTION or the force source parameter file FORCESOLUTION,
and the stations file STATIONS. Most parameters in the Par_file should be set prior to running the mesher. Only
the following parameters may be changed after running the mesher:
• the simulation type control parameters: SIMULATION_TYPE and SAVE_FORWARD
• the record length RECORD_LENGTH_IN_MINUTES
• the movie control parameters MOVIE_SURFACE,MOVIE_VOLUME, and NTSTEPS_BETWEEN_FRAMES
• the multi-stage simulation parameters NUMBER_OF_RUNS and NUMBER_OF_THIS_RUN
• the output information parameters NTSTEP_BETWEEN_OUTPUT_INFO,NTSTEP_BETWEEN_OUTPUT_SEISMOS,
OUTPUT_SEISMOS_ASCII_TEXT,OUTPUT_SEISMOS_SAC_ALPHANUM,OUTPUT_SEISMOS_SAC_BINARY
and ROTATE_SEISMOGRAMS_RT
• the RECEIVERS_CAN_BE_BURIED and PRINT_SOURCE_TIME_FUNCTION flags
Any other change to the Par_file implies rerunning both the mesher and the solver.
For any particular earthquake, the CMTSOLUTION file that represents the point source may be obtained directly
from the Harvard Centroid-Moment Tensor (CMT) web page (http://www.globalcmt.org). It looks like this:
27

CHAPTER 4. RUNNING THE SOLVER XSPECFEM3D 28
PDE 2002 11 3 22 12 41.00 63.5200 -147.4400 4.9 7.0 8.5 CENTRAL ALASKA
event name: 110302J
time shift: 47.0000
half duration: 23.5000
latitude: 63.2300
longitude: -144.8900
depth: 15.0000
Mrr: 5.130000e+26
Mtt: -6.038000e+27
Mpp: 5.525000e+27
Mrt: 1.830000e+26
Mrp: 2.615000e+27
Mtp: -3.937000e+27
Harvard CMT solution
Preliminary Determination of Epicenter
year
month
day
hour
min
sec latitude longitude
body-wave magnitude
surface-wave magnitude
depth mb Ms PDE event name
Figure 4.1: CMTSOLUTION file obtained from the Harvard CMT catalog. The top line is the initial estimate of the
source, which is used as a starting point for the CMT solution. Mis the moment tensor, M0is the seismic moment,
and Mwis the moment magnitude.
The CMTSOLUTION should be edited in the following way:
• For point-source simulations (see finite sources, page 29) we recommend setting the source half-duration
parameter half duration equal to zero, which corresponds to simulating a step source-time function,
i.e., a moment-rate function that is a delta function. If half duration is not set to zero, the code will
use a Gaussian (i.e., a signal with a shape similar to a ‘smoothed triangle’, as explained in Komatitsch and
Tromp [2002a] and shown in Fig 4.2) source-time function with half-width half duration. We prefer
to run the solver with half duration set to zero and convolve the resulting synthetic seismograms in
post-processing after the run, because this way it is easy to use a variety of source-time functions (see Sec-
tion 13.2). Komatitsch and Tromp [2002a] determined that the noise generated in the simulation by using
a step source time function may be safely filtered out afterward based upon a convolution with the desired
source time function and/or low-pass filtering. Use the postprocessing script process_syn.pl (see Sec-
tion 13.2.2) with the -h flag, or the serial code convolve_source_timefunction.f90 and the script
utils/convolve_source_timefunction.csh for this purpose, or alternatively use signal-processing
software packages such as SAC (http://www.iris.edu/software/sac/). Type
make convolve_source_timefunction
to compile the code and then set the parameter hdur in utils/convolve_source_timefunction.csh
to the desired half-duration.
• The zero time of the simulation corresponds to the center of the triangle/Gaussian, or the centroid time of the
earthquake. The start time of the simulation is t=−1.5∗half duration (the 1.5 is to make sure the
moment rate function is very close to zero when starting the simulation). To convert to absolute time tabs, set
tabs =tpde +time shift +tsynthetic
where tpde is the time given in the first line of the CMTSOLUTION,time shift is the corresponding value
from the original CMTSOLUTION file and tsynthetic is the time in the first column of the output seismogram.
CHAPTER 4. RUNNING THE SOLVER XSPECFEM3D 29
half duration
source decay rate
half duration
-
-
tCMT
Figure 4.2: Comparison of the shape of a triangle and the Gaussian function actually used.
If you know the earthquake source in strike/dip/rake format rather than in CMTSOLUTION format, use the C code
utils/strike_dip_rake_to_CMTSOLUTION.c to convert it. The conversion formulas are given for instance
in Aki and Richards [1980]. Note that the Aki and Richards [1980] convention is slightly different from the Harvard
CMTSOLUTION convention (the sign of some components is different). The C code outputs both.
Centroid latitude and longitude should be provided in geographical coordinates. The code converts these coordi-
nates to geocentric coordinates [Dahlen and Tromp,1998]. Of course you may provide your own source representa-
tions by designing your own CMTSOLUTION file. Just make sure that the resulting file adheres to the Harvard CMT
conventions (see Appendix A). Note that the first line in the CMTSOLUTION file is the Preliminary Determination of
Earthquakes (PDE) solution performed by the USGS NEIC, which is used as a seed for the Harvard CMT inversion.
The PDE solution is based upon P waves and often gives the hypocenter of the earthquake, i.e., the rupture initiation
point, whereas the CMT solution gives the ‘centroid location’, which is the location with dominant moment release.
The PDE solution is not used by our software package but must be present anyway in the first line of the file.
In the current version of the code, the solver can run with a non-zero time shift in the CMTSOLUTION file.
Thus one does not need to set time shift to zero as it was the case for previous versions of the code. time
shift is only used for writing centroid time in the SAC headers (see Appendix D). CMT time is obtained by adding
time shift to the PDE time given in the first line in the CMTSOLUTION file. Therefore it is recommended not
to modify time shift to have the correct timing information in the SAC headers without any post-processing of
seismograms.
To simulate a kinematic rupture, i.e., a finite-source event, represented in terms of Nsources point sources, provide
aCMTSOLUTION file that has Nsources entries, one for each subevent (i.e., concatenate Nsources CMTSOLUTION
files to a single CMTSOLUTION file). At least one entry (not necessarily the first) must have a zero time shift,
and all the other entries must have non-negative time shift. If none of the entries has a zero time shift in
the CMTSOLUTION file, the smallest time shift is subtracted from all sources to initiate the simulation. Each
subevent can have its own half duration, latitude, longitude, depth, and moment tensor (effectively, the local moment-
density tensor).
Note that the zero in the synthetics does NOT represent the hypocentral time or centroid time in general, but the
timing of the center of the source triangle with zero time shift (Fig 4.3).
Although it is convenient to think of each source as a triangle, in the simulation they are actually Gaussians (as
they have better frequency characteristics). The relationship between the triangle and the Gaussian used is shown in
Fig 4.2. For finite fault simulations it is usually not advisable to use a zero half duration and convolve afterwards,
since the half duration is generally fixed by the finite fault model.
CHAPTER 4. RUNNING THE SOLVER XSPECFEM3D 30
The FORCESOLUTION file should be edited in the following way:
• The first line is only the header for the force solution, which can be used as the identifier for the force source.
•time shift: For a single force source, set this parameter equal to 0.0(The solver will not run otherwise!);
the time shift parameter would simply apply an overall time shift to the synthetics, something that can be done
in the post-processing (see Section 13.2).
•half duration: Set the half duration value (s) for Step source time function. In case that the solver uses
a (pseudo) Dirac delta source time function to represent a force point source, a very short duration of five time
steps is automatically set by default. For a Ricker source time function, set the dominant frequency value (Hz).
See the parameter source time function: below for source time functions.
•latitude: Set the latitude of the force source.
•longitude: Set the longitude of the force source.
•depth: Set the depth of the force source (km).
•source time function: Set the type of source time function. 0 = Step function, 1= Ricker function.
•factor force source: Set the magnitude of the force source.
•component dir vect source E: Set the East component of a direction vector for the force source.
Direction vector is not necessarily a unit vector.
•component dir vect source N: Set the North component of a direction vector for the force source.
•component dir vect source Z_up: Set the vertical component of a direction vector for the force
source. Sign convnetion follows the positive upward drection.
Where necessary, set a FORCESOLUTION file in the same way you configure a CMTSOLUTION file with Nsources
entries, one for each subevent (i.e., concatenate Nsources FORCESOLUTION files to a single FORCESOLUTION file).
At least one entry (not necessarily the first) must have a zero time shift, and all the other entries must have
non-negative time shift. Each subevent can have its own set of parameters latitude,longitude,depth:,
half duration, etc.
Figure 4.3: Example of timing for three sources. The center of the first source triangle is defined to be time zero. Note
that this is NOT in general the hypocentral time, or the start time of the source (marked as tstart). The parameter time
shift in the CMTSOLUTION file would be t1(=0), t2, t3 in this case, and the parameter half duration would
be hdur1, hdur2, hdur3 for the sources 1, 2, 3 respectively.
CHAPTER 4. RUNNING THE SOLVER XSPECFEM3D 31
Figure 4.4: Sample STATIONS file. Station latitude and longitude should be provided in geo-
graphical coordinates. The width of the station label should be no more than 32 characters (see
MAX_LENGTH_STATION_NAME in the constants.h file), and the network label should be no more than 8 char-
acters (see MAX_LENGTH_NETWORK_NAME in the constants.h file).
The solver can calculate seismograms at any number of stations for basically the same numerical cost, so the user
is encouraged to include as many stations as conceivably useful in the STATIONS file, which looks like this:
Each line represents one station in the following format:
Station Network Latitude(degrees) Longitude(degrees) Elevation(m) burial(m)
If you want to put a station on the ocean floor, just set elevation and burial depth in the STATIONS file to 0. Equiva-
lently you can also set elevation to a negative value equal to the ocean depth, and burial depth to 0.
Solver output is provided in the OUTPUT_FILES directory in the output_solver.txt file. Output can be
directed to the screen instead by uncommenting a line in constants.h:
! uncomment this to write messages to the screen
! integer, parameter :: IMAIN = ISTANDARD_OUTPUT
Note that on very fast machines, writing to the screen may slow down the code.
While the solver is running, its progress may be tracked by monitoring the ‘timestamp*’ files in the OUTPUT_FILES
directory. These tiny files look something like this:
Time step # 200
Time: 0.6956667 minutes
Elapsed time in seconds = 252.6748970000000
Elapsed time in hh:mm:ss = 0 h 04 m 12 s
Mean elapsed time per time step in seconds = 1.263374485000000
Max norm displacement vector U in solid in all slices (m) = 1.9325
Max non-dimensional potential Ufluid in fluid in all slices = 1.1058885E-22
The timestamp*files provide the Mean elapsed time per time step in seconds, which may
be used to assess performance on various machines (assuming you are the only user on a node), as well as the Max
norm displacement vector U in solid in all slices (m) and Max non-dimensional potential
Ufluid in fluid in all slices. If something is wrong with the model, the mesh, or the source, you will
see the code become unstable through exponentionally growing values of the displacement and/or fluid potential with
time, and ultimately the run will be terminated by the program when either of these values becomes greater than
STABILITY_THRESHOLD defined in constants.h. You can control the rate at which the timestamp files are
written based upon the parameter NTSTEP_BETWEEN_OUTPUT_INFO in the Par_file.
CHAPTER 4. RUNNING THE SOLVER XSPECFEM3D 32
Having set the Par_file parameters, and having provided the CMTSOLUTION and STATIONS files, you are
now ready to launch the solver! This is most easily accomplished based upon the go_solver script (see Chapter 11
for information about running the code through a scheduler, e.g., LSF). You may need to edit the last command at the
end of the script that invokes the mpirun command. Another option is to use the runall script, which compiles
and runs both mesher and solver in sequence. This is a safe approach that ensures using the correct combination of
mesher output and solver input.
It is important to realize that the CPU and memory requirements of the solver are closely tied to choices about
attenuation (ATTENUATION) and the nature of the model (i.e., isotropic models are cheaper than anisotropic models).
We encourage you to run a variety of simulations with various flags turned on or off to develop a sense for what is
involved.
For the same model, one can rerun the solver for different events by simply changing the CMTSOLUTION file,
and/or for different stations by changing the STATIONS file. There is no need to rerun the mesher. Of course it is best
to include as many stations as possible, since this does not add significantly to the cost of the simulation.
4.1 Note on the simultaneous simulation of several earthquakes
EXAMPLE ROOT DIR
bin
DATA
DATABASES MPI
OUTPUT FILES
run0001
DATA
DATABASES MPI
OUTPUT FILES
SEM
run0002
DATA
DATABASES MPI
OUTPUT FILES
SEM
run....
DATA
DATABASES MPI
OUTPUT FILES
SEM
Figure 4.5: Directory structure when simulating several earthquakes at once. To improve readability, only directories
have been drawn.
Figure 4.5 shows what the directory structure should looks like when simulating multiple earthquakes at ones.
• The simulation is launched within the root directory EXAMPLE_ROOT_DIR
(usually mpirun -np N ./bin/xspecfem3D).
•DATA should contain the Par_file parameter file with NUMBER_OF_SIMULTANEOUS_RUNS as explained
in Chapter 3.
CHAPTER 4. RUNNING THE SOLVER XSPECFEM3D 33
•DATABASES_MPI and OUTPUT_FILES directory may contain the mesher output but they are not required as
they are superseded by the ones in the runXXX directories.
•runXXXX directories must be created beforehand. There should be be as many as NUMBER_OF_SIMULTANEOUS_RUNS
and the numbering should be contiguous, starting from 0001. They all should have DATA,DATABASES_MPI
and OUTPUT_FILES directories. Additionally a SEM directory containing adjoint sources have to be created
to perform adjoint simulations.
•runXXXX/DATA directories must all contain a CMTSOLUTION file, a STATIONS file along with an eventual
STATIONS_ADJOINT file.
• If BROADCAST_SAME_MESH_AND_MODEL is set to .true. in DATA/Par_file, only run0001/OUTPUT_FILES
and run0001/DATABASES_MPI directories need to contain the files outputted by the mesher.
• If BROADCAST_SAME_MESH_AND_MODEL is set to .false. in DATA/Par_file, every runXXXX/OUTPUT_FILES
and runXXXX/DATABASES_MPI directories need to contain the files outputted by the mesher. Note that while
the meshes might have been created from different models and parameter sets, they should have been created
using the same number of MPI processes.
Chapter 5
Regional Simulations
The code has the option of running in one-chunk or six-chunk mode. The one-chunk options may be used for higher
resolution regional simulations. A one-chunk mesh may have lateral dimensions other than the customary 90◦per
chunk, which can further increase the resolution of the mesh, and thus reduce the shortest period in the synthetic
seismograms (but of course then also reducing the time step in order for the simulation to remain stable).
A disadvantage of regional simulations is that one needs to use approximate absorbing boundary conditions on the
side and bottom edges of the model (e.g., see Komatitsch and Tromp [1999] for a description of the paraxial boundary
conditions used). Figure 5.1 on the following page and Figure 5.2 on page 36 show an example of a one-chunk mesh
centered on the Japan subduction zone, applied in the Japan regional waveform simulation [Chen et al.,2007].
5.1 One-Chunk Simulations
For a one-chunk regional simulation the following parameters need to be set in the Par_file:
NCHUNKS Must be set to 1.
ANGULAR_WIDTH_XI_IN_DEGREES Denotes the width of one side of the chunk (90◦is a classical value, but you
can make it more or less if you want).
ANGULAR_WIDTH_ETA_IN_DEGREES Denotes the width of the second side of the chunk (90◦is a classical value,
but you can make it more or less if you want). Note that this value may be different from ANGULAR_WIDTH_XI_IN_DEGREES.
CENTER_LATITUDE_IN_DEGREES Defines the latitude of the center of the chunk (degrees).
CENTER_LONGITUDE_IN_DEGREES Defines the longitude of the center of the chunk (degrees).
GAMMA_ROTATION_AZIMUTH Defines the rotation angle of the chunk about its center measured counter clockwise
from due North (degrees). The corners of the mesh are output in OUTPUT_FILES/values_from_mesher.h.
The output corner progression in OUTPUT_FILES/values_from_mesher.h is bottom left, bottom right, top
left, top right. The rotation azimuth can be changed in the Par_file and the corners output (OUTPUT_FILES/
values_from_mesher.h)by using xcreate_header_file. It is important to note that the mesher or the
solver does not need to be run to determine the limits of a 1-chunk simulation.
NEX_XI The number of spectral elements along the ξside of the chunk. This number must be 8 ×a multiple of
NPROC_XI defined below. For a 90◦chunk, we do not recommend using NEX_XI less than 64 because the
curvature of the Earth cannot be honored if one uses too few elements, which results in inaccurate and unstable
simulations.
NEX_ETA The number of spectral elements along the ηside of the chunk. This number must be 8 ×a multiple of
NPROC_ETA defined below. Note that in order to get elements that are close to square on the Earth’s surface,
the following ratios should be similar:
34
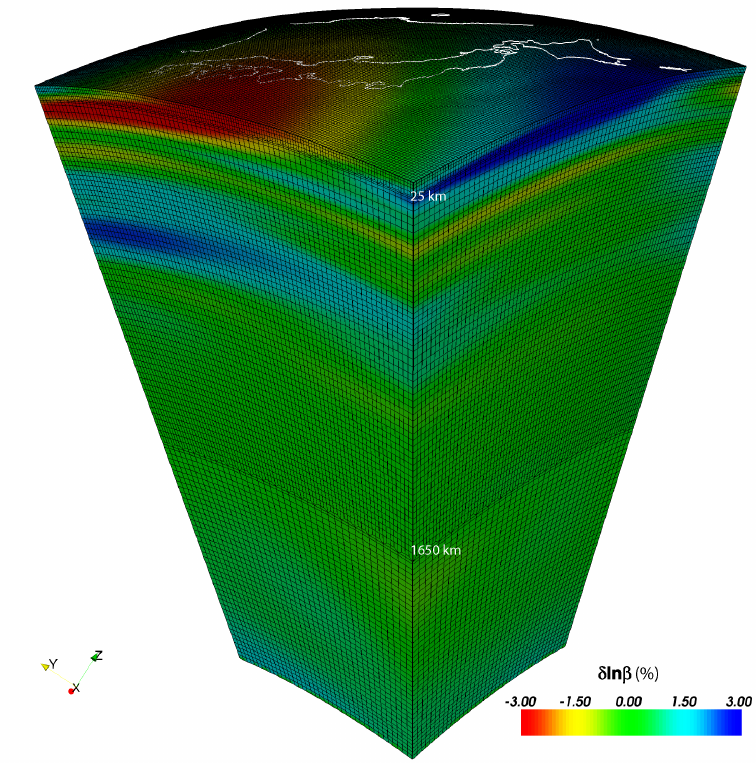
CHAPTER 5. REGIONAL SIMULATIONS 35
ANGULAR_WIDTH_XI_IN_DEGREES / NEX_XI
ANGULAR_WIDTH_ETA_IN_DEGREES / NEX_ETA
Because of the geometry of the cubed sphere, the option of having different values for NEX_XI and NEX_ETA
is available only for regional simulations when NCHUNKS = 1 (1/6th of the sphere).
NPROC_XI The number of processors or mesh slices along the ξside of the chunk. To accommodate the mesh
doubling layers, we must have NEX_XI = 8 ×c×NPROC_XI, where c≥1is a positive integer. See Table 3
for various suitable choices.
NPROC_ETA The number of processors or slices along the ηside of the chunk; we must have NEX_ETA = 8 ×c×
NPROC_ETA, where c≥1is a positive integer. NPROC_XI and NPROC_ETA must be equal when NCHUNKS =
6.
Figure 5.1: S-wave velocity anomalies from the global tomographic model s20rts [Ritsema and Van Heijst,2000] are
superimposed on the mesh. For parallel computing purposes, the one-chunk SEM simulation is subdivided in terms of
64 slices. The center of the chunk is at (38.5◦N, 137.5◦E), and the lateral dimensions are 30◦×30◦. Two doubling
layers are indicated at a depth of 25 km (PREM Moho depth) and a depth of about 1650 km. Shows full view of 25
neighboring slices; see Figure 5.2 for close-up of upper mantle mesh.

CHAPTER 5. REGIONAL SIMULATIONS 36
Figure 5.2: Close-up view of the upper mantle mesh shown in Figure 5.1. Note that the element size in the crust
(top layer) is 13 km ×13 km, and that the size of the spectral elements is doubled in the upper mantle. The velocity
variation is captured by NGLL = 5 grid points in each direction of the elements [Komatitsch and Tromp,2002a,b].
ABSORBING_CONDITIONS Set to .true. for regional simulations. For instance, see Komatitsch and Tromp
[1999] for a description of the paraxial boundary conditions used. Note that these conditions are never perfect,
and in particular surface waves may partially reflect off the artificial boundaries. Note also that certain arrivals,
e.g., PKIKPPKIKP, will be missing from the synthetics.
When the width of the chunk is different from 90◦(or the number of elements is greater than 1248), the radial
distribution of elements needs to be adjusted as well to maintain spectral elements that are as cube-like as possible.
The code attempts to do this, but be sure to view the mesh with your favorite graphics package to make sure that the
element are well behaved. Remember: a high-quality mesh is paramount for accurate simulations. In addition to a
reorganization of the radial distribution of elements, the time stepping and period range in which the attenuation is
applied is automatically determined. The minimum and maximum periods for attenuation are:
ωmax =ωmin ×10W3
where W3is the optimal width in frequency for 3 Standard Linear Solids, about 1.75. See read_compute_parameters.f90
for more details.
The time stepping is determined in a similar fashion as Equation (48) in Komatitsch and Tromp [2002a]:
dt = ScElement Width in km (r=ICB) / Velocity (r=ICB)
CHAPTER 5. REGIONAL SIMULATIONS 37
where Scis the stability condition (about 0.4). We use the radius at the inner core boundary because this is where the
maximum velocity/element width occurs. Again, see read_compute_parameters.f90 for all the details.
The approximate shortest period at which a regional simulation is accurate may be determined based upon the
relation
shortest period (s) '(256/NEX_XI)×(ANGULAR_WIDTH_XI_IN_DEGREES/90) ×17.(5.1)
Chapter 6
Adjoint Simulations
Adjoint simulations are generally performed for two distinct applications. First, they can be used for earthquake source
inversions, especially earthquakes with large ruptures such as the Sumatra-Andaman event [Lay et al.,2005,Ammon
et al.,2005,Park et al.,2005]. Second, they can be used to generate finite-frequency sensitivity kernels that are a
critical part of tomographic inversions based upon 3D reference models [Tromp et al.,2005,Liu and Tromp,2006,
Tromp et al.,2008,Liu and Tromp,2008]. In either case, source parameter or velocity structure updates are sought
to minimize a specific misfit function (e.g., waveform or traveltime differences), and the adjoint simulation provides a
means of computing the gradient of the misfit function and further reducing it in successive iterations. Applications and
procedures pertaining to source studies and finite-frequency kernels are discussed in Sections 6.1 and 6.2, respectively.
The two related parameters in the Par_file are SIMULATION_TYPE (1, 2 or 3) and SAVE_FORWARD (boolean).
6.1 Adjoint Simulations for Sources Only (not for the Model)
In the case where a specific misfit function is minimized to invert for the earthquake source parameters, the gradient
of the misfit function with respect to these source parameters can be computed by placing time-reversed seismograms
at the receivers and using them as sources in an adjoint simulation, and then the value of the gradient is obtained from
the adjoint seismograms recorded at the original earthquake location.
1. Prepare the adjoint sources
(a) First, run a regular forward simlation (SIMULATION_TYPE = 1 and SAVE_FORWARD = .false.).
You can automatically set these two variables using the utils/change_simulation_type.pl script:
utils/change_simulation_type.pl -f
and then collect the recorded seismograms at all the stations given in DATA/STATIONS.
(b) Then select the stations for which you want to compute the time-reversed adjoint sources and run the
adjoint simulation, and compile them into the DATA/STATIONS_ADJOINT file, which has the same
format as the regular DATA/STATIONS file.
• Depending on what type of misfit function is used for the source inversion, adjoint sources need to
be computed from the original recorded seismograms for the selected stations and saved in the SEM/
directory with the format NT.STA.?X?.adj, where STA,NT are the station name and network
code given in the DATA/STATIONS_ADJOINT file, and ?X? represents the channel name of a
particular adjoint seismogram where the first letter corresponds to the band code governed by the
resolution of simulations, for example, generally MX? for the current resolution of global simulations
(see Appendix Efor details). The last letter of channel names is the component name E/N/Z.
• The adjoint seismograms are in the same format as the original seismogram (NT.STA.?X?.sem?),
with the same start time, time interval and record length.
(c) Notice that even if you choose to time reverse only one component from one specific station, you still need
to supply all three components because the code is expecting them (you can set the other two components
to be zero).
38
CHAPTER 6. ADJOINT SIMULATIONS 39
(d) Also note that since time-reversal is done in the code itself, no explicit time-reversing is needed for the
preparation of the adjoint sources, i.e., the adjoint sources are in the same forward time sense as the original
recorded seismograms.
2. Set the related parameters and run the adjoint simulation
In the DATA/Par_file, set the two related parameters to be SIMULATION_TYPE = 2 and SAVE_FORWARD
= .false.. More conveniently, use the scripts utils/change_simulation_type.pl to modify the
Par_file automatically (change_simulation_type.pl -a). Then run the solver to launch the ad-
joint simulation.
3. Collect the seismograms at the original source location
After the adjoint simulation has completed successfully, get the seismograms from directory OUTPUT_FILES.
• These adjoint seismograms are recorded at the locations of the original earthquake sources given by the
DATA/CMTSOLUTION file, and have names of the form NT.S?????.S??.sem for the six-component
strain tensor (SNN,SEE,SZZ,SNE,SNZ,SEZ) at these locations, and NT.S?????.?X?.sem for the
three-component displacements (i.e., MXN,MXE,MXZ) recorded at these locations.
•S????? denotes the source number; for example, if the original CMTSOLUTION provides only a point
source, then the seismograms collected will start with S00001.
• These adjoint seismograms provide critical information for the computation of the gradient of the misfit
function.
6.2 Adjoint Simulations for Finite-Frequency Kernels (Kernel Simulation)
Finite-frequency sensitivity kernels are computed in two successive simulations (please refer to Liu and Tromp [2006]
and Tromp et al. [2008] for details).
1. Run a forward simulation with the state variables saved at the end of the simulation
Prepare the CMTSOLUTION and STATIONS files, set the parameters SIMULATION_TYPE = 1 and SAVE_FORWARD
= .true. in the Par_file (change_simulation_type -F), and run the solver.
• Notice that attenuation is not fully implemented yet for the computation of finite-frequency kernels; if
ATTENUATION = .true. is set in the Par_file, only effects on phase shift are accounted for but
not on amplitude of the signals. However, we suggest you use the same setting for ATTENUATION as for
your forward simulations.
• We also suggest you modify the half duration of the CMTSOLUTION to be similar to the accuracy of the
simulation (see Equation 3.1 or 5.1) to avoid too much high-frequency noise in the forward wavefield,
although theoretically the high-frequency noise should be eliminated when convolved with an adjoint
wavefield with the proper frequency content.
• This forward simulation differs from the regular simulations (SIMULATION_TYPE = 1 and SAVE_FORWARD
= .false.) described in the previous chapters in that the state variables for the last time step of the simula-
tion, including wavefields of the displacement, velocity, acceleration, etc., are saved to the LOCAL_PATH
to be used for the subsequent simulation.
• For regional simulations, the files recording the absorbing boundary contribution are also written to the
LOCAL_PATH when SAVE_FORWARD = .true..
2. Prepare the adjoint sources
The adjoint sources need to be prepared the same way as described in Section 6.1, item 1.
• In the case of traveltime finite-frequency kernel for one source-receiver pair, i.e., point source from the
CMTSOLUTION, and one station in the STATIONS_ADJOINT list, we supply a sample program in
utils/adjoint_sources/traveltime to cut a certain portion of the original displacement
seismograms and convert them into the proper adjoint source to compute the finite-frequency kernel.
CHAPTER 6. ADJOINT SIMULATIONS 40
xcreate_adjsrc_traveltime t1 t2 ifile[0-5] E/N/Z-ascii-files [baz]
where t1 and t2 are the start and end time of the portion you are interested in, ifile denotes the
component of the seismograms to be used (0 for all three components, 1 for east, 2 for north, and 3
for vertical, 4 for transverse, and 5 for radial component), E/N/Z-ascii-files indicate the three-
component displacement seismograms in the right order, and baz is the back-azimuth of the station from
the event location. Note that baz is only supplied when ifile = 4 or 5.
• Similarly, a sample program to compute adjoint sources for amplitude finite-frequency kernels may be
found in utils/adjoint_sources/amplitude and used in the same way as described for
traveltime measurements
xcreate_adjsrc_amplitude t1 t2 ifile[0-5] E/N/Z-ascii-files [baz].
For adjoint runs (SIMULATION_TYPE = 3), the adjoint sources need to be put in the "SEM" sub-directory in
the root directory of the code.
If your adjoint source have names of the following form for instance:
NET.STA00.MXZ.sem.ascii.adj NET.STA00.MXZ.sem.ascii.adj
you will need to rename them to:
NET.STA00.MXZ.adj NET.STA00.MXZ.adj
i.e. suppress ".sem.ascii".
You will also need to create a file called STATIONS_ADJOINT in the "DATA" directory in the root directory of
the code. That file can be identical to the DATA/STATIONS file if you had a single station in STATIONS.
3. Run the kernel simulation
With the successful forward simulation and the adjoint source ready in SEM/, set SIMULATION_TYPE =
3and SAVE_FORWARD = .false. in the Par_file(change_simulation_type.pl -b), and
rerun the solver.
• The adjoint simulation is launched together with the back reconstruction of the original forward wavefield
from the state variables saved from the previous forward simulation, and the finite-frequency kernels are
computed by the interaction of the reconstructed forward wavefield and the adjoint wavefield.
• The back-reconstructed seismograms at the original station locations are saved to the OUTPUT_FILES
directory at the end of the kernel simulations.
• These back-constructed seismograms can be compared with the time-reversed original seismograms to
assess the accuracy of the backward reconstruction, and they should match very well (in the time-reversed
sense).
• The files containing the density, P-wave speed and S-wave speed kernels are saved in the LOCAL_PATH
with the names of proc??????_reg_?_rho(alpha,beta)_kernel.bin, where proc??????
represents the processor number, and reg_? denotes the region these kernels are for, including mantle
(reg_1), outer core (reg_2), and inner core (reg_3). The output kernels are in the unit of s/km3.
• Note that if you set the flag APPROXIMATE_HESS_KL = .true. in the constants.h file and re-
compile the solver, the adjoint simulation also saves files proc??????_reg_1_hess_kernel.bin
which can be used as preconditioners in the crust-mantle region for iterative inverse optimization schemes.
4. Run the boundary kernel simulation
If you set the SAVE_BOUNDARY_MESH = .true. in the constants.h file before the simulations, i.e., at
the beginning of step 1, you will get not only the volumetric kernels as described in step 3, but also boundary ker-
nels for the Earth’s internal discontinuities, such as Moho, 410-km discontinuity, 670-km discontinuity, CMB
and ICB. These kernel files are also saved in the local scratch directory defined by LOCAL_PATH and have
names such as proc??????_reg_1(2)_Moho(d400,d670,CMB,ICB)_kernel.bin. For a theoret-
ical derivation of the boundary kernels, refer to Tromp et al. [2005], and for the visualization of the boundary
kernels, refer to Section 10.3.

CHAPTER 6. ADJOINT SIMULATIONS 41
5. Run the anisotropic kernel simulation
Instead of the kernels for the isotropic wave speeds, you can also compute the kernels for the 21 independent
components CIJ , I, J = 1, ..., 6(using Voigt’s notation) of the elastic tensor in the (spherical) geographi-
cal coordinate system. This is done by setting ANISOTROPIC_KL = .true. in constants.h before
step 3. The definition of the parameters CIJ in terms of the corresponding components cijkl, ijkl, i, j, k, l =
1,2,3of the elastic tensor in spherical coordinates follows Chen and Tromp [2007]. The computation of
the anisotropic kernels is only implemented in the crust and mantle regions. The 21 anisotropic kernels are
saved in the LOCAL_PATH in one file with the name of proc??????_reg1_cijkl_kernel.bin (with
proc?????? the processor number). The output kernels correspond to perturbation δCIJ of the elastic pa-
rameters and their unit is in s/GP a/km3. For consistency, the output density kernels with this option turned on
are for a perturbation δρ (and not δρ
ρ) and their unit is in s / (kg/m3) / km3. These ‘primary’ anisotropic kernels
can then be combined to obtain the kernels related to other descriptions of anisotropy. This can be done, for
example, when combining the kernel files from slices into one mesh file (see Section 10.3).
In general, the first three steps need to be run sequentially to ensure proper access to the necessary files at different
stages. If the simulations are run through some cluster scheduling system (e.g., LSF), and the forward simulation and
the subsequent kernel simulations cannot be assigned to the same set of computer nodes, the kernel simulation will
not be able to access the database files saved by the forward simulation. Solutions for this problem are provided in
Chapter 11. Visualization of the finite-frequency kernels is discussed in Section 10.3.
Chapter 7
Doing tomography, i.e., updating the model
based on the sensitivity kernels obtained
The process is described in the same chapter of the manual of SPECFEM3D. Please refer to it.
42
Chapter 8
Noise Cross-correlation Simulations
The new version of SPECFEM3D_GLOBE includes functionality for seismic noise tomography. Users are recom-
mended to familiarize themselves first with the procedures for running regular earthquake simulations (Chapters 3–5)
and adjoint simulations (Chapter 6). Also, make sure you read the paper ‘Noise cross-correlation sensitivity kernels’
[Tromp et al.,2010b] in order to understand noise simulations from a theoretical perspective.
8.1 New Requirements on ‘Old’ Input Parameter Files
As usual, the three main input files are crucial: DATA/Par_file,DATA/CMTSOLUTION and DATA/STATIONS.
DATA/CMTSOLUTION is required for all simulations. However, it may seem unexpected to have it listed here,
since the noise simulations should have nothing to do with the earthquake – hence the DATA/CMTSOLUTION. For
noise simulations, it is critical to have no earthquakes. In other words, the moment tensor specified in DATA/CMTSOLUTION
must be set to ZERO!
DATA/STATIONS remains the same as in previous earthquake simulations, except that the order of stations listed
in DATA/STATIONS is now important. The order will be used later to identify the ‘master’ receiver, i.e., the one
that simultaneously cross correlates with the others. Please be noted that the actual station file used in the simulation
is OUTPUT_FILES/STATIONS_FILTERED, which is generated when you run your simulations. (e.g., in regional
simulations we may have included stations out of the region of our interests in DATA/STATIONS, so we have to get
rid of them.)
DATA/Par_file also requires careful attention. New to this version of SPECFEM3D_GLOBE, a parameter
called NOISE_TOMOGRAPHY has been added that specifies the type of simulation to be run. NOISE_TOMOGRAPHY
is an integer with possible values 0, 1, 2 and 3. For example, when NOISE_TOMOGRAPHY equals 0, a regular earth-
quake simulation will be run. When NOISE_TOMOGRAPHY is equal to 1/2/3, you are about to run step 1/2/3 of the
noise simulations respectively. Should you be confused by the three steps, refer to Tromp et al. [2010b] for details.
Another change to DATA/Par_file involves the parameter RECORD_LENGTH_IN_MINUTES. While for reg-
ular earthquake simulations this parameter specifies the length of synthetic seismograms generated, for noise simula-
tions it specifies the length of the seismograms used to compute cross correlations. The actual cross correlations are
thus twice this length. The code automatically makes modification accordingly, if NOISE_TOMOGRAPHY is not zero.
There are other parameters in DATA/Par_file which should be given specific values. For instance, NUMBER_OF_RUNS
and NUMBER_OF_THIS_RUN must be 1; ROTATE_SEISMOGRAMS_RT,SAVE_ALL_SEISMOGRAMS_IN_ONE_FILES,
USE_BINARY_FOR_LARGE_FILE and MOVIE_COARSE should be .false.. Moreover, since the first two steps
for calculating noise cross-correlation kernels correspond to forward simulations, SIMULATION_TYPE must be 1
when NOISE_TOMOGRAPHY equals 1 or 2. Also, we have to reconstruct the ensemble forward wavefields in adjoint
simulations, therefore we need to set SAVE_FORWARD to .true. for the second step, i.e., when NOISE_TOMOGRAPHY
43
CHAPTER 8. NOISE CROSS-CORRELATION SIMULATIONS 44
equals 2. The third step is for kernel constructions. Hence SIMULATION_TYPE should be 3, whereas SAVE_FORWARD
must be .false..
8.2 Noise Simulations: Step by Step
Proper parameters in those ‘old’ input files are not enough for noise simulations to run. We have a lot more ‘new’ input
parameter files to specify: for example, the ensemble-averaged noise spectrum, the noise distribution etc. However,
since there are a few ‘new’ files, it is better to introduce them sequentially. Read through this section even if you don’t
understand some parts temporarily, since some examples you can go through are provided in this package.
8.2.1 Pre-simulation
• As usual, we first configure the software package using:
./configure FC=ifort MPIFC=mpif90
• Next, we need to compile the source code using:
make xmeshfem3D
make xspecfem3D
Before compilation, the DATA/Par_file must be specified correctly, e.g., NOISE_TOMOGRAPHY shouldn’t
be zero; RECORD_LENGTH_IN_MINUTES,NEX_XI and NEX_ETA must be what you want in your real sim-
ulations. Otherwise you may get wrong informations which will cause problems later. (it is good to always
re-complie the code before you run simulations)
• After compiling, you will find two important numbers besides the needed executables:
number of time steps = 31599
time_stepping of the solver will be: 0.19000
The first number will be denoted as NSTEP from now on, and the second one as dt. The two numbers are
essential to calculate the ensemble-averaged noise spectrum from either Peterson’s noise model or just a simple
flat power spectrum (corresponding to 1-bit preprocessing). Should you miss the two numbers, you can run
./xcreate_header_file to bring them up again (with correct DATA/Par_file!). FYI, NSTEP is
determined by RECORD_LENGTH_IN_MINUTES in DATA/Par_file, which is automatically doubled in
noise simulations; whereas dt is derived from NEX_XI and NEX_ETA, or in other words your element sizes.
• A Matlab script is provided to generate the ensemble-averaged noise spectrum.
EXAMPLES/noise_examples/NOISE_TOMOGRAPHY.m (main program)
EXAMPLES/noise_examples/PetersonNoiseModel.m
In Matlab, simply run:
NOISE_TOMOGRAPHY(NSTEP, dt, Tmin, Tmax, NOISE_MODEL)
NSTEP and dt have been given when compiling the specfem3D source code; Tmin and Tmax correspond to
the period range you are interested in; NOISE_MODEL denotes the noise model you will be using. Details can
be found in the Matlab script.
After running the Matlab script, you will be given the following information (plus a figure in Matlab):
CHAPTER 8. NOISE CROSS-CORRELATION SIMULATIONS 45
*************************************************************
the source time function has been saved in:
/data2/yangl/3D_NOISE/S_squared (note this path must be different)
S_squared should be put into directory:
./NOISE_TOMOGRAPHY/ in the SPECFEM3D_GLOBE package
In other words, the Matlab script creates a file called S_squared, which is the first ‘new’ input file we en-
counter for noise simulations.
One may choose a flat noise spectrum rather than Peterson’s noise model. This can be done easily by modifying
the Matlab script a little bit.
• Create a new directory in the SPECFEM3D_GLOBE package, name it as NOISE_TOMOGRAPHY. In fact, this
new directory should have been created already when checking out the package. We will add/replace some
information needed in this folder.
• Put the Matlab-generated-file S_squared in NOISE_TOMOGRAPHY.
That’s to say, you will have a file NOISE_TOMOGRAPHY/S_squared in the SPECFEM3D_GLOBE package.
• Create a file called NOISE_TOMOGRAPHY/irec_master_noise. Note that this file should be put in di-
rectory NOISE_TOMOGRAPHY as well. This file contains only one integer, which is the ID of the ‘master’
receiver. For example, if in this file shows 5, it means that the fifth receiver listed in DATA/STATIONS be-
comes the ‘master’. That’s why we mentioned previously that the order of receivers in DATA/STATIONS is
important.
Note that in regional (1- or 2-chunk) simulations, the DATA/STATIONS may contain receivers not within the
selected chunk(s). Therefore, the integer in NOISE_TOMOGRAPHY/irec_master_noise is actually the
ID in DATA/STATIONS_FILTERED (which is generated by xspecfem3D).
• Create a file called NOISE_TOMOGRAPHY/nu_master. This file holds three numbers, forming a (unit)
vector. It describes which component we are cross-correlating at the ‘master’ receiver, i.e., ˆναin Tromp et al.
[2010b]. The three numbers correspond to N/E/Z components respectively.
• Describe the noise direction and distributions in src/specfem3d/noise_tomography.f90. Search for
a subroutine called noise_distribution_direction in noise_tomography.f90. It is actually lo-
cated at the very beginning of noise_tomography.f90. The default assumes vertical noises and a uniform
distribution across the whole physical domain. It should be quite self-explanatory for modifications. Should you
modify this part, you have to re-compile the source code. (again, that’s why we recommend that you always
re-compile the code before you run simulations)
8.2.2 Simulations
As discussed in Tromp et al. [2010b], it takes three simulations to obtain one contribution of the ensemble sensitivity
kernels:
• Step 1: simulation for generating wavefield
SIMULATION_TYPE = 1
NOISE_TOMOGRAPHY = 1
SAVE_FORWARD not used, can be either .true. or .false.
• Step 2: simulation for ensemble forward wavefield
SIMULATION_TYPE = 1
NOISE_TOMOGRAPHY = 2
SAVE_FORWARD = .true.
• Step 3: simulation for ensemble adjoint wavefield and sensitivity kernels
CHAPTER 8. NOISE CROSS-CORRELATION SIMULATIONS 46
SIMULATION_TYPE = 3
NOISE_TOMOGRAPHY = 3
SAVE_FORWARD = .false.
Note Step 3 is an adjoint simulation, please refer to previous chapters on how to prepare adjoint sources and
other necessary files, as well as how adjoint simulations work.
It’s better to run the three steps continuously within the same job, otherwise you have to collect the saved surface
movies from the old nodes to the new nodes.
8.2.3 Post-simulation
After those simulations, you have all stuff you need, either in the OUTPUT_FILES or in the directory specified by
LOCAL_PATH in DATA/Par_file (most probably on local nodes). Collect whatever you want from the local nodes
to your workstation, and then visualize them. This process is the same as what you may have done for regular earth-
quake simulations. Refer Chapter 10 if you have problems.
Simply speaking, two outputs are the most interesting: the simulated ensemble cross correlations and one contri-
bution of the ensemble sensitivity kernels.
The simulated ensemble cross correlations are obtained after the second simulation (Step 2). Seismograms in
OUTPUT_FILES are actually the simulated ensemble cross correlations. Collect them immediately after Step 2, or the
Step 3 will overwrite them. Note that we have a ‘master’ receiver specified by NOISE_TOMOGRAPHY/irec_master_noise,
the seismogram at one station corresponds to the cross correlation between that station and the ‘master’. Since the
seismograms have three components, we may obtain cross correlations for different components as well, not necessar-
ily the cross correlations between vertical components.
One contribution of the ensemble cross-correlation sensitivity kernels are obtained after Step 3, stored in the
LOCAL_PATH on local nodes. The ensemble kernel files are named the same as regular earthquake kernels.
You need to run another three simulations to get the other contribution of the ensemble kernels, using different
forward and adjoint sources given in Tromp et al. [2010b].
8.3 Examples
In order to illustrate noise simulations in an easy way, three examples are provided in EXAMPLES/noise_examples/.
Note however that they are created for a specific cluster (SESAME@PRINCETON). You have to modify them to fit
your own cluster.
The three examples can be executed using (in directory EXAMPLES/noise_examples/):
./run_this_example.sh regional
./run_this_example.sh global_short
./run_this_example.sh global_long
Each corresponds to one example, but they are pretty similar.
Although the job submission only works on SESAME@PRINCETON, the procedure itself is universal. You may
review the whole process described in the last section by following commands in those examples.
Finally, note again that those examples show only one contribution of the ensemble kernels!
Chapter 9
Gravity integral calculations for the gravity
field of the Earth
SPECFEM can now compute the gravity field as well as its derivatives (i.e., gravity gradiometry) generated by any
given 3D Earth model at the height of an observation satellite, for instance GOCE
(see e.g. en.wikipedia.org/wiki/Gravity_Field_and_Steady-State_Ocean_Circulation_Explorer).
That feature is still experimental but should work just fine.
To see how it is implemented and to use it, type this in the root directory of the code:
grep -i GRAVITY_INTEGRALS src/*/*
All main gravity field computations can be found in file src/meshfem3d/gravity_integrals.F90. Please
make sure you compile the code with double-precision, i.e., use flag --enable-double-precision for the
configuration of the package.
47

Chapter 10
Graphics
10.1 Meshes
Use the serial code combine_AVS_DX.f90 (type ‘make combine_AVS_DX’ and then ‘xcombine_AVS_DX’)
to generate AVS (http://www.avs.com) output files (in AVS UCD format) or OpenDX (http://www.opendx.
org) output files showing the mesh, the MPI partition (slices), the NCHUNKS chunks, the source and receiver location,
etc. Use the AVS UCD files AVS_continent_boundaries.inp and AVS_plate_boundaries.inp or the
OpenDX files DX_continent_boundaries.dx and DX_plate_boundaries.dx (that can be created using
Perl scripts located in utils/Visualization/opendx_AVS) for reference.
10.2 Movies
To make a surface or volume movie of the simulation, set parameters MOVIE_SURFACE,MOVIE_VOLUME, and
NTSTEP_BETWEEN_FRAMES in the Par_file. Turning on the movie flags, in particular MOVIE_VOLUME, pro-
duces large output files. MOVIE_VOLUME files are saved in the LOCAL_PATH directory, whereas MOVIE_SURFACE
output files are saved in the OUTPUT_FILES directory. We save the velocity field. The look of a movie is determined
by the half-duration of the source. The half-duration should be large enough so that the movie does not contain fre-
quencies that are not resolved by the mesh, i.e., it should not contain numerical noise. This can be accomplished by
selecting a CMT HALF_DURATION > 1.1 ×smallest period (see figure 4.1). When MOVIE_SURFACE =.true. or
MOVIE_VOLUME = .true., the half duration of each source in the CMTSOLUTION file is replaced by
p(HALF_DURATION2+HDUR_MOVIE2)
NOTE: If HDUR_MOVIE is set to 0.0, the code will select the appropriate value of 1.1 ×smallest period.
As usual, for a point source one can set HALF_DURATION in the Par_file to be 0.0 and HDUR_MOVIE
= 0.0 to get the highest frequencies resolved by the simulation, but for a finite source one would keep all
the HALF_DURATIONs as prescribed by the finite source model and set HDUR_MOVIE = 0.0.
10.2.1 Movie Surface
When running xspecfem3D with the MOVIE_SURFACE flag turned on the code outputs moviedata??????
files in the OUTPUT_FILES directory. The files are in a fairly complicated binary format, but there are two programs
provided to convert the output into more user friendly formats. The first one, create_movie_AVS_DX.f90
outputs data in ASCII, OpenDX, AVS, or ParaView format. Run the code from the source directory (type ‘make
create_movie_AVS_DX’ first) to create an input file in your format of choice. The code will prompt the user for
input parameters. The second program create_movie_GMT_global.f90 outputs ASCII xyz files, convenient
for use with GMT. This codes uses significantly less memory than create_movie_AVS_DX.f90 and is therefore
useful for high resolution runs. A README file and sample Perl scripts to create movies using GMT are provided in
directory utils/Visualization/GMT.
48

CHAPTER 10. GRAPHICS 49
Figure 10.1: Snapshots from a global movie for the December 26, 2004, M=9.2 Sumatra-Andaman earthquake. Time
runs down successive columns.
10.2.2 Movie Volume
When running xspecfem3D with the MOVIE_VOLUME flag turned on, the code outputs several files in LOCAL_DIR. As
the files can be very large, there are several flags in the Par_file that control the region in space and time that is
saved. These are: MOVIE_TOP_KM,MOVIE_BOTTOM_KM,MOVIE_WEST_DEG,MOVIE_EAST_DEG,MOVIE_NORTH_DEG,
MOVIE_SOUTH_DEG,MOVIE_START and MOVIE_STOP. The code will save a given element if the center of the element
is in the prescribed volume.
The Top/Bottom: Depth below the surface in kilometers, use MOVIE_TOP = -100.0 to make sure the surface is
stored.
West/East: Longitude, degrees East [-180.0/180.0]
North/South: Latitute, degrees North [-90.0/90.0]
Start/Stop: Frames will be stored at MOVIE_START + i*NSTEP_BETWEEN_FRAMES, where i=(0,1,2..) while
i*NSTEP_BETWEEN_FRAMES <= MOVIE_STOP
The code saves several files, and the output is saved by each processor. The first is proc??????_movie3D_info.txt
which contains two numbers, first the number of points within the prescribed volume within this particular slice, and
CHAPTER 10. GRAPHICS 50
second the number of elements. The next files are proc??????_movie3D_x.bin,proc??????_movie3D_y.bin,
proc??????_movie3D_z.bin which store the locations of the points in the 3D mesh.
Finally the code stores the “value” at each of the points. Which value is determined by MOVIE_VOLUME_TYPE
in the Par_file. Choose 1 to save the strain, 2 to save the time integral of strain, and 3 to save µ*time integral of
strain in the subvolume. Choosing 4 causes the code to save the trace of the stress and the deviatoric stress in the
whole volume (not the subvolume in space), at the time steps specified. The name of the output file will depend on the
MOVIE_VOLUME_TYPE chosen.
Setting MOVIE_VOLUME_COARSE = .true. will make the code save only the corners of the elements, not all the
points within each element for MOVIE_VOLUME_TYPE = 1,2,3.
To make the code output your favorite “value” simply add a new MOVIE_VOLUME_TYPE, a new subroutine to
write_movie_volume.f90 and a subroutine call to specfem3D.F90.
A utility program to combine the files produced by MOVIE_VOLUME_TYPE = 1,2,3 is provided in combine_paraview
_strain_data.f90. Type xcombine_paraview_strain_data to get the usage statement. The program combine_vol
_data.f90 can be used for MOVIE_VOLUME_TYPE = 4.
10.3 Finite-Frequency Kernels
The finite-frequency kernels computed as explained in Section 6.2 are saved in the LOCAL_PATH at the end of the
simulation. Therefore, we first need to collect these files on the front end, combine them into one mesh file, and
visualize them with some auxilliary programs. Examples of kernel simulations may be found in the EXAMPLES
directory.
1. Create slice files
We will only discuss the case of one source-receiver pair, i.e., the so-called banana-doughnut kernels. Although
it is possible to collect the kernel files from all slices onto the front end, it usually takes up too much storage
space (at least tens of gigabytes). Since the sensitivity kernels are the strongest along the source-receiver great
circle path, it is sufficient to collect only the slices that are along or close to the great circle path.
A Perl script utils/Visualization/VTK_Paraview/global_slice_number.pl can help to fig-
ure out the slice numbers that lie along the great circle path (both the minor and major arcs), as well as the slice
numbers required to produce a full picture of the inner core if your kernel also illuminates the inner core.
(a) You need to first compile the utility programs provided in the utils/Visualization/VTK_Paraview/
global_slice_util directory. Then copy the CMTSOLUTION file, STATIONS_ADJOINT, and
Par_file, and run:
global_slice_number.pl CMTSOLUTION STATIONS_ADJOINT Par_file
In the case of visualization boundary kernels or spherical cross-sections of the volumetric kernels, it is
necessary to obtain the slice numbers that cover a belt along the source and receiver great circle path, and
you can use the hybrid version:
globe_slice_number2.pl CMTSOLUTION STATIONS _ADJOINT \
Par_file belt_width_in_degrees
A typical value for belt_width_in_degrees can be 20.
(b) For a full 6-chunk simulation, this script will generate the slice_minor,slice_major,slice_ic
files, but for a one-chunk simulation, this script only generates the slice_minor file.
(c) For cases with multiple sources and multiple receivers, you need to provide a slice file before proceeding
to the next step.
2. Collect the kernel files
After obtaining the slice files, you can collect the corresponding kernel files from the given slices.
(a) To accomplish this, you can use or modify the scripts in utils/collect_database directory:
copy_m(oc,ic)_globe_database.pl slice_file lsf_machine_file filename [jobid]
CHAPTER 10. GRAPHICS 51
for volumetric kernels, where lsf_machine_file is the machine file generated by the LSF scheduler,
filename is the kernel name (e.g., rho_kernel,alpha_kernel and beta_kernel), and the optional
jobid is the name of the subdirectory under LOCAL_PATH where all the kernel files are stored. For
boundary kernels, you need to use
copy_surf_globe_database.pl slice_file lsf_machine_file filename [jobid]
where the filename can be Moho_kernel,d400_kernel,d670_kernel,CMB_kernel and ICB_kernel.
(b) After executing this script, all the necessary mesh topology files as well as the kernel array files are col-
lected to the local directory on the front end.
3. Combine kernel files into one mesh file
We use an auxiliary program combine_vol_data.f90 to combine the volumetric kernel files from all slices
into one mesh file, and combine_surf_data.f90 to combine the surface kernel files.
(a) Compile it in the global code directory:
make combine_vol_data
./bin/xcombine_vol_data slice_list kernel_filename input_topo_dir \
input_file_dir output_dir low/high-resolution-flag-0-or-1 [region]
where input_dir is the directory where all the individual kernel files are stored, and output_dir is
where the mesh file will be written. Give 0 for low resolution and 1 for high resolution. If region is not
specified, all three regions (crust and mantle, outer core, inner core) will be collected, otherwise, only the
specified region will be.
Here is an example:
./xcombine_vol_data slices_major alpha_kernel input_topo_dir input_file_dir output_dir 1
For surface sensitivity kernels, use
./bin/xcombine_surf_data slice_list filename surfname input _dir output_dir low/high-resolution 2D/3D
where surfname should correspond to the specific kernel file name, and can be chosen from Moho,400,
670,CMB and ICB.
(b) Use 1 for a high-resolution mesh, outputting all the GLL points to the mesh file, or use 0 for low resolution,
outputting only the corner points of the elements to the mesh file. Use 0 for 2D surface kernel files and 1
for 3D volumetric kernel files.
(c) Use region = 1 for the mantle, region =2 for the outer core, region = 3 for the inner core, and region = 0
for all regions.
(d) The output mesh file will have the name reg_?_rho(alpha,beta)_kernel.mesh, or
reg_?_Moho(d400,d670,CMB,ICB)_kernel.surf.
4. Convert mesh files into .vtu files
(a) We next convert the .mesh file into the VTU (Unstructured grid file) format which can be viewed in
ParaView, for example:
mesh2vtu -i file.mesh -o file.vtu
(b) Notice that this program mesh2vtu, in the utils/Visualization/VTK_Paraview/mesh2vtu
directory, uses the VTK (http://www.vtk.org) run-time library for its execution. Therefore, make
sure you have it properly installed.
5. Copy over the source and receiver .vtk file
In the case of a single source and a single receiver, the simulation also generates the OUTPUT_FILES/sr.vtk
file to describe the source and receiver locations, which can be viewed in Paraview in the next step.
6. View the mesh in ParaView
Finally, we can view the mesh in ParaView (http://www.paraview.org).
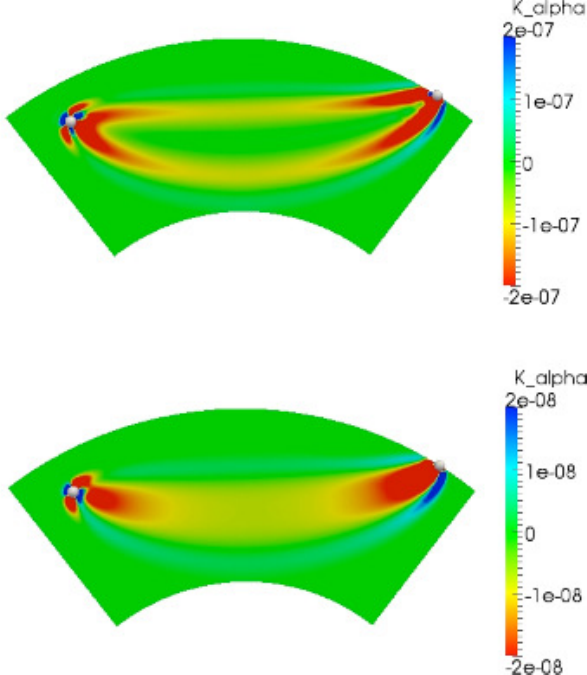
CHAPTER 10. GRAPHICS 52
(a) Open ParaView.
(b) From the top menu, File →Open data, select file.vtu, and click the Accept button.
• If the mesh file is of moderate size, it shows up on the screen; otherwise, only the outline is shown.
(c) Click Display Tab →Display Style →Representation and select wireframe of surface to display it.
(d) To create a cross-section of the volumetric mesh, choose Filter →cut, and under Parameters Tab, choose
Cut Function →plane.
(e) Fill in center and normal information given by the standard output from global_slice_number.pl
script.
(f) To change the color scale, go to Display Tab →Color →Edit Color Map and reselect lower and upper
limits, or change the color scheme.
(g) Now load in the source and receiver location file by File →Open data, select sr.vtk, and click the
Accept button. Choose Filter →Glyph, and represent the points by ‘spheres’.
(h) For more information about ParaView, see the ParaView Users Guide (http://www.paraview.org/
files/v1.6/ParaViewUsersGuide.PDF).
For illustration purposes, Figure 10.2 shows P-wave speed finite-frequency kernels from cross-correlation traveltime
and amplitude measurements for a P arrival recorded at an epicentral distance of 60◦for a deep event.
Figure 10.2: P-wave speed finite-frequency kernels from cross-correlation traveltime (top) and amplitude (bottom)
measurements for a P arrival recorded at an epicentral distance of 60◦. The kernels together with the associated files
and routines to reproduce them may be found in EXAMPLES/global_PREM_kernels/.
Chapter 11
Running through a Scheduler
The code is usually run on large parallel machines, often PC clusters, most of which use schedulers, i.e., queuing or
batch management systems to manage the running of jobs from a large number of users. The following considerations
need to be taken into account when running on a system that uses a scheduler:
• The processors/nodes to be used for each run are assigned dynamically by the scheduler, based on availability.
Therefore, in order for the mesher and the solver (or between successive runs of the solver) to have access to the
same database files (if they are stored on hard drives local to the nodes on which the code is run), they must be
launched in sequence as a single job.
• On some systems, the nodes to which running jobs are assigned are not configured for compilation. It may there-
fore be necessary to pre-compile both the mesher and the solver. A small program provided in the distribution
called create_header_file.f90 can be used to directly create OUTPUT_FILES/values_from_mesher.h
using the information in the DATA/Par_file without having to run the mesher (type ‘make create_header_
file’ to compile it and ‘./bin/xcreate_header_file’ to run it; refer to the sample scripts below). The
solver can now be compiled as explained above.
• One feature of schedulers/queuing systems is that they allow submission of multiple jobs in a “launch and
forget” mode. In order to take advantage of this property, care needs to be taken that output and intermediate
files from separate jobs do not overwrite each other, or otherwise interfere with other running jobs.
We describe here in some detail a job submission procedure for the Caltech 1024-node cluster, CITerra, under the
LSF scheduling system. We consider the submission of a regular forward simulation. The two main scripts are
run_lsf.bash, which compiles the Fortran code and submits the job to the scheduler, and go_mesher_solver_lsf
.bash, which contains the instructions that make up the job itself. These scripts can be found in utils/Cluster/lsf
directory and can straightforwardly be modified and adapted to meet more specific running needs.
11.1 run_lsf.bash
This script first sets the job queue to be ‘normal’. It then compiles the mesher and solver together, figures out the
number of processors required for this simulation from DATA/Par_file, and submits the LSF job.
#!/bin/bash
# use the normal queue unless otherwise directed queue="-q normal"
if [ $# -eq 1 ]; then
echo"Setting the queue to $1"
queue="-q $1"
fi
# compile the mesher and the solver
d=‘date‘
echo"Starting compilation $d"
53
CHAPTER 11. RUNNING THROUGH A SCHEDULER 54
make clean
make meshfem3D
make create_header_file
./bin/xcreate_header_file
make specfem3D
d=‘date‘
echo"Finished compilation $d"
# compute total number of nodes needed
NPROC_XI=‘grep ^NPROC_XI DATA/Par_file | cut -c 34- ‘
NPROC_ETA=‘grep ^NPROC_ETA DATA/Par_file | cut -c 34- ‘
NCHUNKS=‘grep ^NCHUNKS DATA/Par_file | cut -c 34- ‘
# total number of nodes is the product of the values read
numnodes=$(( $NCHUNKS *$NPROC_XI *$NPROC_ETA ))
echo "Submitting job"
bsub $queue -n $numnodes -W 60 -K <go_mesher_solver_lsf_globe.bash
11.2 go_mesher_solver_lsf_globe.bash
This script describes the job itself, including setup steps that can only be done once the scheduler has assigned a job-ID
and a set of compute nodes to the job, the run_lsf.bash commands used to run the mesher and the solver, and
calls to scripts that collect the output seismograms from the compute nodes and perform clean-up operations.
1. First the script directs the scheduler to save its own output and output from stdout into OUTPUT_FILES/%J.o,
where %J is short-hand for the job-ID; it also tells the scheduler what version of mpich to use (mpich_gm)
and how to name this job (go_mesher_solver_lsf).
2. The script then creates a list of the nodes allocated to this job by echoing the value of a dynamically set en-
vironment variable LSB_MCPU_HOSTS and parsing the output into a one-column list using the Perl script
utils/Cluster/lsf/remap_lsf_machines.pl. It then creates a set of scratch directories on these
nodes (/scratch/
$USER/DATABASES_MPI) to be used as the LOCAL_PATH for temporary storage of the database files. The
scratch directories are created using shmux, a shell multiplexor that can execute the same commands on many
hosts in parallel. shmux is available from Shmux (http://web.taranis.org/shmux/). Make sure that
the LOCAL_PATH parameter in DATA/Par_file is also set properly.
3. The next portion of the script launches the mesher and then the solver using run_lsf.bash.
4. The final portion of the script performs clean up on the nodes using the Perl script cleanmulti.pl
#!/bin/bash -v
#BSUB -o OUTPUT_FILES/%J.o
#BSUB -a mpich_gm
#BSUB -J go_mesher_solver_lsf
BASEMPIDIR=/scratch/$USER/DATABASES_MPI
echo "$LSB_MCPU_HOSTS" > OUTPUT_FILES/lsf_machines
echo "$LSB_JOBID" > OUTPUT_FILES/jobid
./remap_lsf_machines.pl OUTPUT_FILES/lsf_machines > OUTPUT_FILES/machines
# Modif : create a directory for this job
shmux -M50 -Sall \
CHAPTER 11. RUNNING THROUGH A SCHEDULER 55
-c "mkdir -p /scratch/$USER;mkdir -p $BASEMPIDIR.$LSB_JOBID" - < OUTPUT_FILES/machines >/dev/null
# Set the local path in Par_file
sed -e "s:^LOCAL_PATH .*:LOCAL_PATH = $BASEMPIDIR.$LSB_JOBID:" < DATA/Par_file > DATA/Par_file.tmp
mv DATA/Par_file.tmp DATA/Par_file
current_pwd=$PWD
mpirun.lsf --gm-no-shmem --gm-copy-env $current_pwd/bin/xmeshfem3D
mpirun.lsf --gm-no-shmem --gm-copy-env $current_pwd/bin/xspecfem3D
# clean up
cleanbase_jobid.pl OUTPUT_FILES/machines DATA/Par_file
11.3 run_lsf.kernel and go_mesher_solver_globe.kernel
For kernel simulations, you can use the sample run scripts run_lsf.kernel and go_mesher_solver_globe
.kernel provided in utils/Cluster directory, and modify the command-line arguments of xcreate_adjsrc_traveltime
in go_mesher_solver_globe.kernel according to the start and end time of the specific portion of the forward
seismograms you are interested in.
Chapter 12
Changing the Model
In this section we explain how to change the crustal, mantle, or inner core models. These changes involve contributing
specific subroutines that replace existing subroutines in the SPECFEM3D_GLOBE package.
12.1 Changing the Crustal Model
The 3D crustal model Crust2.0 [Bassin et al.,2000] is superimposed onto the mesh by the subroutine model_crust
.f90. To accomplish this, the flag CRUSTAL, set in the subroutine get_model_parameters.f90, is used to
indicate a 3D crustal model. When this flag is set to .true., the crust on top of the 1D reference model (PREM,
IASP91, or AK135F_NO_MUD) is removed and replaced by extending the mantle. The 3D crustal model is subse-
quently overprinted onto the crust-less 1D reference model. The call to the 3D crustal routine is of the form
call model_crust(lat,lon,r,vp,vs,rho,moho,foundcrust,CM_V,elem_in_crust)
Input to this routine consists of:
lat Latitude in degrees.
lon Longitude in degrees.
rNon-dimensionalized radius (0<r<1).
Output from the routine consists of:
vp Non-dimensionalized compressional wave speed at location (lat,lon,r).
vs Non-dimensionalized shear wave speed.
rho Non-dimensionalized density.
moho Non-dimensionalized Moho depth.
found_crust Logical that is set to .true. only if crust exists at location (lat,lon,r), i.e., .false. for
radii rin the mantle. This flags determines whether or not a particular location is in the crust and, if so, what
parameters to assign to the mesh at this location.
CM_V Fortran structure that contains the parameters, variables and arrays that describe the model.
elem_in_crust Logical that is used to force the routine to return crustal values, even if the location would be
below the crust.
All output needs to be non-dimensionalized according to the convention summarized in Appendix B. You can replace
this subroutine by your own routine provided you do not change the call structure of the routine, i.e., the new routine
should take exactly the same input and produce the required, properly non-dimensionalized output.
56
CHAPTER 12. CHANGING THE MODEL 57
Part of the file model_crust.f90 is the subroutine model_crust_broadcast. The call to this routine
takes argument CM_V and is used to once-and-for-all read in the databases related to Crust2.0 and broadcast the model
to all parallel processes. If you replace the file model_crust.f90 with your own implementation, you must provide
amodel_crust_broadcast routine, even if it does nothing. Model constants and variables read by the routine
model_crust_broadcast are passed to the subroutine read_crust_model through the structure CM_V. An
alternative crustal model could use the same construct. Please feel free to contribute subroutines for new models and
send them to us so that they can be included in future releases of the software.
NOTE: If you decide to create your own version of file model_crust.f90, you must add calls to
MPI_BCAST in the subroutine model_crust_broadcast after the call to the read_crust_model
subroutine that reads the isotropic mantle model once and for all in the mesher. This is done in order to
read the (potentially large) model data files on the master node (which is the processor of rank 0 in our
code) only and then send a copy to all the other nodes using an MPI broadcast, rather than using an im-
plementation in which all the nodes would read the same model data files from a remotely-mounted home
file system, which could create a bottleneck on the network in the case of a large number of nodes. For
example, in the current call to that routine from model_crust.f90, we write:
! the variables read are declared and stored in structure CM_V
if(myrank == 0) call read_crust_model(CM_V)
! broadcast the information read on the master to the nodes
call MPI_BCAST(CM_V%thlr,NKEYS_CRUST*NLAYERS_CRUST,MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(CM_V%velocp,NKEYS_CRUST*NLAYERS_CRUST,MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(CM_V%velocs,NKEYS_CRUST*NLAYERS_CRUST,MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(CM_V%dens,NKEYS_CRUST*NLAYERS_CRUST,MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(CM_V%abbreviation,NCAP_CRUST*NCAP_CRUST,MPI_CHARACTER,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(CM_V%code,2*NKEYS_CRUST,MPI_CHARACTER,0,MPI_COMM_WORLD,ier)
12.2 Changing the Mantle Model
This section discusses how to change isotropic and anisotropic 3D mantle models. Usually such changes go hand-in-
hand with changing the 3D crustal model.
12.2.1 Isotropic Models
The 3D mantle model S20RTS [Ritsema et al.,1999] is superimposed onto the mantle mesh by the subroutine
model_s20rts.f90. The call to this subroutine is of the form
call model_s20rts(radius,theta,phi,dvs,dvp,drho,D3MM_V)
Input to this routine consists of:
radius Non-dimensionalized radius (RCMB/R_ EARTH <r<RMOHO/R_ EARTH; for a given 1D reference
model, the constants RCMB and RMOHO are set in the get_model_parameters.f90 file). The code expects
the isotropic mantle model to be defined between the Moho (with radius RMOHO in m) and the core-mantle
boundary (CMB; radius RCMB in m) of a 1D reference model. When a 3D crustal model is superimposed, as
will usually be the case, the 3D mantle model is stretched to fill any potential gap between the radius of the
Moho in the 1D reference model and the Moho in the 3D crustal model. Thus, when the Moho in the 3D crustal
model is shallower than the Moho in the reference model, e.g., typically below the oceans, the mantle model is
extended to fill this gap.
theta Colatitude in radians.
phi Longitude in radians.
Output from the routine are the following non-dimensional perturbations:
dvs Relative shear-wave speed perturbations δβ/β at location (radius,theta,phi).
CHAPTER 12. CHANGING THE MODEL 58
dvp Relative compressional-wave speed perturbations δα/α.
drho Relative density perturbations δρ/ρ.
D3MM_V Fortran structure that contains the parameters, variables and arrays that describe the model.
You can replace the model_s20rts.f90 file with your own version provided you do not change the call structure
of the routine, i.e., the new routine should take exactly the same input and produce the required relative output.
Part of the file model_s20rts.f90 is the subroutine model_s20rts_broadcast. The call to this routine
takes argument D3MM_V and is used to once-and-for-all read in the databases related to S20RTS. If you replace the file
model_s20rts.f90 with your own implementation, you must provide a model_s20rts_broadcast routine,
even if it does nothing. Model constants and variables read by the routine model_s20rts_broadcast are passed
to the subroutine read_model_s20rts through the structure D3MM_V. An alternative mantle model should use
the same construct.
NOTE: If you decide to create your own version of file model_s20rts.f90, you must add calls to
MPI_BCAST in the subroutine model_s20rts_broadcast after the call to the read_model_s20rts
subroutine that reads the isotropic mantle model once and for all in the mesher. This is done in order to
read the (potentially large) model data files on the master node (which is the processor of rank 0 in our
code) only and then send a copy to all the other nodes using an MPI broadcast, rather than using an im-
plementation in which all the nodes would read the same model data files from a remotely-mounted home
file system, which could create a bottleneck on the network in the case of a large number of nodes. For
example, in the current call to that routine from model_s20rts.f90, we write:
! the variables read are declared and stored in structure D3MM_V
if(myrank == 0) call read_model_s20rts(D3MM_V)
! broadcast the information read on the master to the nodes
call MPI_BCAST(D3MM_V%dvs_a,(NK+1)*(NS+1)*(NS+1),MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(D3MM_V%dvs_b,(NK+1)*(NS+1)*(NS+1),MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(D3MM_V%dvp_a,(NK+1)*(NS+1)*(NS+1),MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(D3MM_V%dvp_b,(NK+1)*(NS+1)*(NS+1),MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(D3MM_V%spknt,NK+1,MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(D3MM_V%qq0,(NK+1)*(NK+1),MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(D3MM_V%qq,3*(NK+1)*(NK+1),MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
12.2.2 Anisotropic Models
Three-dimensional anisotropic mantle models may be superimposed on the mesh based upon the subroutine
model_aniso_mantle.f90
The call to this subroutine is of the form
call model_aniso_mantle(r,theta,phi,rho, &
c11,c12,c13,c14,c15,c16,c22,c23,c24,c25,c26, &
c33,c34,c35,c36,c44,c45,c46,c55,c56,c66,AMM_V)
Input to this routine consists of:
rNon-dimensionalized radius (RCMB/R_ EARTH <r<RMOHO/R_ EARTH; for a given 1D reference model,
the constants RCMB and RMOHO are set in the get_model_parameters.f90 file). The code expects the
anisotropic mantle model to be defined between the Moho and the core-mantle boundary (CMB). When a 3D
crustal model is superimposed, as will usually be the case, the 3D mantle model is stretched to fill any potential
gap between the radius of the Moho in the 1D reference model and the Moho in the 3D crustal model. Thus,
when the Moho in the 3D crustal model is shallower than the Moho in the reference model, e.g., typically below
the oceans, the mantle model is extended to fill this gap.
theta Colatitude in radians.
CHAPTER 12. CHANGING THE MODEL 59
phi Longitude in radians.
Output from the routine consists of the following non-dimensional model parameters:
rho Non-dimensionalized density ρ.
c11,···,c66 21 non-dimensionalized anisotropic elastic parameters.
AMM_V Fortran structure that contains the parameters, variables and arrays that describe the model.
You can replace the model_aniso_mantle.f90 file by your own version provided you do not change the call
structure of the routine, i.e., the new routine should take exactly the same input and produce the required relative
output. Part of the file model_aniso_mantle.f90 is the subroutine model_aniso_mantle_broadcast.
The call to this routine takes argument AMM_V and is used to once-and-for-all read in the static databases related to the
anisotropic model. When you choose to replace the file model_aniso_mantle.f90 with your own implemen-
tation you must provide a model_aniso_mantle_broadcast routine, even if it does nothing. Model constants
and variables read by the routine model_aniso_mantle_broadcast are passed through the structure AMM_V.
An alternative anisotropic mantle model should use the same construct.
NOTE: If you decide to create your own version of file model_aniso_mantle.f90, you must add
calls to MPI_BCAST in file model_aniso_mantle.f90 after the call to the read_aniso_mantle_model
subroutine that reads the anisotropic mantle model once and for all in the mesher. This is done in order
to read the (potentially large) model data files on the master node (which is the processor of rank 0 in
our code) only and then send a copy to all the other nodes using an MPI broadcast, rather than using an
implementation in which all the nodes would read the same model data files from a remotely-mounted
home file system, which could create a bottleneck on the network in the case of a large number of nodes.
For example, in the current call to that routine from model_aniso_mantle.f90, we write:
! the variables read are declared and stored in structure AMM_V
if(myrank == 0) call read_aniso_mantle_model(AMM_V)
! broadcast the information read on the master to the nodes
call MPI_BCAST(AMM_V%npar1,1,MPI_INTEGER,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(AMM_V%beta,14*34*37*73,MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
call MPI_BCAST(AMM_V%pro,47,MPI_DOUBLE_PRECISION,0,MPI_COMM_WORLD,ier)
Rotation of the anisotropic tensor elements from one coordinate system to another coordinate system may be
accomplished based upon the subroutine rotate_aniso_tensor. Use of this routine requires understanding the
coordinate system used in SPECFEM3D_GLOBE, as discussed in Appendix A.
12.2.3 Point-Profile Models
In order to facilitate the use of your own specific mantle model, you can choose PPM as model in the DATA/Par_file
file and supply your own model as an ASCII-table file. These generic models are given as depth profiles at a speci-
fied lon/lat location and a perturbation (in percentage) with respect to the shear-wave speed values from PREM. The
ASCII-file should have a format like:
#lon(deg), lat(deg), depth(km), Vs-perturbation wrt PREM(%), Vs-PREM (km/s)
-10.00000 31.00000 40.00000 -1.775005 4.400000
-10.00000 32.00000 40.00000 -1.056823 4.400000
...
where the first line is a comment line and all following ones are specifying the Vs-perturbation at a lon/lat location
and a given depth. The last entry on each line is specifying the absolute value of Vs (however this value is only
given as a supplementary information and not used any further). The background model is PREM with a transverse
isotropic layer between Moho and 220 km depth. The specified Vs-perturbations are added as isotropic perturbations.
Please see the file DATA/PPM/README for more informations how to setup the directory DATA/PPM to use your
own ASCII-file.
To change the code behavior of these PPM-routines, please have a look at the implementation in the source code
file model_ppm.f90 and set the flags and scaling factors as needed for your purposes. Perturbations in density and
Vp may be scaled to the given Vs-perturbations with constant scaling factors by setting the appropriate values in this
source code file. In case you want to change the format of the input ASCII-file, see more details in the Appendix F.
CHAPTER 12. CHANGING THE MODEL 60
12.3 Anelastic Models
Three-dimensional anelastic (attenuation) models may be superimposed onto the mesh based upon your subroutine .
model_atten3D.f90. The call to this routine would be as follows
call model_atten3D(radius, colatitude, longitude, Qmu, QRFSI12_Q, idoubling)
Input to this routine consists of:
radius scaled radius of the earth: 0 (center) <=r <= 1(surface)
latitude Colatitude in degrees: 0◦<=θ <= 180◦
longitude Longitude in degrees: −180◦<=φ <= 180◦
QRFSI12_Q Fortran structure that contains the parameters, variables and arrays that describe the model
idoubling value of the doubling index flag in each radial region of the mesh
Output to this routine consists of:
Qmu Shear wave quality factor: 0< Qµ<5000
A 3-D attenuation model QRFSI12 [Dalton et al.,2008] is provided, as well as 1-D models with a PREM and a 1DREF
attenuation structure. By default the PREM attenuation model is taken, using the routine model_attenuation_1D_PREM,
found in model_attenuation.f90.
To create your own three-dimensional attenuation model, you add your model using a routine like the
model_atten3D_QRFSI12 subroutine and the example routine above as a guide and replace the call in file
meshfem3D_models.f90 to your own subroutine.
Note that the resolution and maximum value of anelastic models are truncated. This speeds the construction of the
standard linear solids during the meshing stage. To change the resolution, currently at one significant figure following
the decimal, or the maximum value (5000), consult constants.h. In order to prevent unexpected results, quality
factors Qµshould never be equal to 0 outside of the inner core.
Chapter 13
Post-Processing Scripts
Several post-processing scripts/programs are provided in the utils/seis_process directory, most of which need
to be adjusted for different systems, for example, the path of the executable programs. Here we only list the available
scripts and provide a brief description, and you can either refer to the related sections for detailed usage or, in many
cases, type the script/program name without arguments to see its usage.
13.1 Clean Local Database
After all the simulations are done, you may need to clean the local scratch disks for the next simulation. This is
especially important in the case of 1- or 2-chunk kernel simulations, where very large files are generated for the
absorbing boundaries to help with the reconstruction of the regular forward wavefield. A sample script is provided in
utils/Cluster/lsf:
cleanbase.pl machines
13.2 Process Data and Synthetics
In many cases, the SEM synthetics are calculated and compared to observed seismograms recorded at seismic stations.
Since the SEM synthetics are accurate for a certain frequency range, both the original data and the synthetics need to
be processed before a comparison can be made. For such comparisons, the following steps are recommended:
1. Make sure that both synthetic and observed seismograms have the correct station/event and timing information.
2. Convolve synthetic seismograms with a source time function with the half duration specified in the CMTSOLUTION
file, provided, as recommended, you used a zero half duration in the SEM simulations.
3. Resample both observed and synthetic seismograms to a common sampling rate.
4. Cut the records using the same window.
5. Remove the trend and mean from the records and taper them.
6. Remove the instrument response from the observed seismograms (recommended) or convolve the synthetic
seismograms with the instrument response.
7. Make sure that you apply the same filters to both observed and synthetic seismograms. Preferably, avoid filtering
your records more than once.
8. Now, you are ready to compare your synthetic and observed seismograms.
We generally use the following scripts for processing:
61
CHAPTER 13. POST-PROCESSING SCRIPTS 62
13.2.1 process_data.pl
This script cuts a given portion of the original data, filters it, transfers the data into a displacement record, and picks
the first P and S arrivals. For more functionality, type ‘process_data.pl’ without any argument. An example of
the usage of the script:
process_data.pl -m CMTSOLUTION -s 1.0 -l 0/4000 -i -f -t 40/500 -p -x bp DATA/1999.330*.LH?.SAC
which has resampled the SAC files to a sampling rate of 1 seconds, cut them between 0 and 4000 seconds, transfered
them into displacement records and filtered them between 40 and 500 seconds, picked the first P and S arrivals, and
added suffix ‘bp’ to the file names.
Note that all of the scripts in this section actually use SAC, saclst and/or IASP91 to do the core operations; therefore
make sure that the SAC, saclst and IASP91 packages are installed on your system, and that all the environment
variables are set properly before running these scripts.
13.2.2 process_syn.pl
This script converts the synthetic output from the SEM code from ASCII to SAC format, and performs similar opera-
tions as ‘process_data.pl’. An example of the usage of the script:
process_syn.pl -m CMTSOLUTION -h -a STATIONS -s 1.0 -l 0/4000 -f -t 40/500 -p -x bp SEM/*.MX?.sem
which will convolve the synthetics with a triangular source-time function from the CMTSOLUTION file, convert the
synthetics into SAC format, add event and station information into the SAC headers, resample the SAC files with a
sampling rate of 1 seconds, cut them between 0 and 4000 seconds, filter them between 40 and 500 seconds with the
same filter used for the observed data, pick the first P and S arrivals, and add the suffix ‘bp’ to the file names.
More options are available for this script, such as adding a time shift to the origin time of the synthetics, convolving
the synthetics with a triangular source time function with a given half duration, etc. Type process_syn.pl without
any argument for detailed usage.
13.2.3 rotate.pl
To rotate the horizontal components of both the data and the synthetics (i.e., MXN and MXE) to the transverse and radial
directions (i.e., MXT and MXR), use rotate.pl:
data example:
rotate.pl -l 0 -L 4000 -d DATA/*.LHE.SAC.bp
synthetics example:
rotate.pl -l 0 -L 4000 SEM/*.MXE.sem.sac.bp
where the first command performs rotation on the SAC data obtained through IRIS (which may have timing informa-
tion written in the filename), while the second command rotates the processed synthetics.
For synthetics, another (simpler) option is to set flag ROTATE_SEISMOGRAMS_RT to .true. in the parameter
file DATA/Par_file.
13.2.4 clean_sac_headers_after_crash.sh
Note: You need to have the sismoutil-0.9b package installed on your computer if you want to run this script on
binary SAC files. The software is available via the ORFEUS web site (http://www.orfeus-eu.org).
In case the simulation crashes during run-time without computing and writing all time steps, the SAC files (if
flags OUTPUT_SEISMOS_SAC_ALPHANUM or OUTPUT_SEISMOS_SAC_BINARY have been set to .true.) are
corrupted and cannot be used in SAC. If the simulation ran long enough so that the synthetic data may still be of use,
you can run the script called clean_sac_headers_after_crash.sh (located in the utils/ directory) on
the SAC files to correct the header variable NPTS to the actually written number of time steps. The script must be
called from the SPECFEM3D main directory, and the input argument to this script is simply a list of SAC seismogram
files.
CHAPTER 13. POST-PROCESSING SCRIPTS 63
13.3 Map Local Database
A sample program remap_database is provided to map the local database from a set of machines to another set of
machines. This is especially useful when you want to run mesher and solver, or different types of solvers separately
through a scheduler (refer to Chapter 11).
run_lsf.bash --gm-no-shmem --gm-copy-env remap_database \
old_machines 150 [old_jobid new_jobid]
where old_machines is the LSF machine file used in the previous simulation, and 150 is the number of processors
in total. Note that you need to supply old_jobid and new_jobid(%J) which are the LSF job-IDs for the old and
new run if your databases are stored in a sub-directory named after the jobid on the scratch disk.
Chapter 14
Information for developers of the code, and
for people who want to learn how the
technique works
You can get a very simple 1D version of a demo code (there is one in Fortran and one in Python):
git clone --recursive https://github.com/geodynamics/specfem1d.git
We also have simple 3D demo source codes that implement the SEM in a single, small program, in directory
utils/small_SEM_solvers_in_Fortran_and_C_without_MPI_to_learn of the specfem3d package. They are useful to
learn how the spectral-element method works, and how to write or modify a code to implement it. Also useful to test
new ideas by modifying these simple codes to run some tests. We also have a similar, even simpler, demo source code
for the 2D case in directory
utils/small_SEM_solver_in_Fortran_without_MPI_to_learn of the specfem2d package.
For information on how to contribute to the code, i.e., for how to make your modifications, additions or improvements
part of the official package, see https://github.com/geodynamics/specfem3d/wiki .
64

Simulation features supported in
SPECFEM3D_GLOBE
The following lists all available features for a SPECFEM3D_GLOBE simulation, where CPU,CUDA and OpenCL
denote the code versions for CPU-only simulations, CUDA and OpenCL hardware support, respectively.
Feature CPU CUDA OpenCL
Physics Ocean load X X X
Ellipticity X X X
Topography X X X
Gravity X X X
Rotation X X X
Attenuation X X X
Simulation Setup Global (6-chunks) X X X
Regional (1,2-chunk) X X X
Restart/Checkpointing X X X
Simultaneous runs X X X
ADIOS file I/O X X X
Sensitivity kernels Partial physical dispersion X X X
Undoing of attenuation X X X
Anisotropic kernels X X X
Transversely isotropic kernels X X X
Isotropic kernels X X X
Approximate Hessian X X X
Time schemes Newmark X X X
LDDRK X - -
Visualization Surface movie X X X
Volumetric movie X X X
Seismogram formats Ascii X X X
SAC X X X
ASDF X X X
Binary X X X
65
Notes and Acknowledgements
In order to keep the software package thread-safe in case a multithreaded implementation of MPI is used, developers
should not add modules or common blocks to the source code but rather use regular subroutine arguments (which can
be grouped in “derived types” if needed for clarity).
The Gauss-Lobatto-Legendre subroutines in gll_library.f90 are based in part on software libraries from
the Massachusetts Institute of Technology, Department of Mechanical Engineering (Cambridge, Massachusetts, USA).
The non-structured global numbering software was provided by Paul F. Fischer (Brown University, Providence, Rhode
Island, USA, now at Argonne National Laboratory, USA).
OpenDX (http://www.opendx.org) is open-source based on IBM Data Explorer, AVS (http://www.
avs.com) is a trademark of Advanced Visualization Systems, and ParaView (http://www.paraview.org) is
an open-source visualization platform.
Please e-mail your feedback, questions, comments, and suggestions to the CIG Computational Seismology Mailing
List (cig-seismo@geodynamics.org).
67

Copyright
Main ‘historical’ authors: Dimitri Komatitsch and Jeroen Tromp (there are now many more!).
Princeton University, USA, and CNRS / University of Marseille, France.
© Princeton University, USA and CNRS / University of Marseille, France, April 2014
This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public
License as published by the Free Software Foundation (see Appendix G).
Please note that by contributing to this code, the developer understands and agrees that this project and contribution
are public and fall under the open source license mentioned above.
Evolution of the code:
v. 7.0, many developers, January 2015: simultaneous MPI runs, ADIOS file I/O support, ASDF seismograms,
new seismogram names, tomography tools, CUDA and OpenCL GPU support, CEM model support, updates AK135
model, binary topography files, fixes geocentric/geographic conversions, updates ellipticity and gravity factors, git
versioning system.
v. 6.0, Daniel Peter (ETH Zürich, Switzerland), Dimitri Komatitsch and Zhinan Xie (CNRS / University of Mar-
seille, France), Elliott Sales de Andrade (University of Toronto, Canada), and many others, in particular from Prince-
ton University, USA, April 2014: more flexible MPI implementation, GPU support, exact undoing of attenuation,
LDDRK4-6 higher-order time scheme, etc...
v. 5.1, Dimitri Komatitsch, University of Toulouse, France and Ebru Bozdag, Princeton University, USA, February
2011: non blocking MPI for much better scaling on large clusters; new convention for the name of seismograms, to
conform to the IRIS standard; new directory structure.
v. 5.0, many developers, February 2010: new Moho mesh stretching honoring crust2.0 Moho depths, new at-
tenuation assignment, new SAC headers, new general crustal models, faster performance due to Deville routines and
enhanced loop unrolling, slight changes in code structure (see also trivia at program start).
v. 4.0 David Michéa and Dimitri Komatitsch, University of Pau, France, February 2008: first port to GPUs using
CUDA, new doubling brick in the mesh, new perfectly load-balanced mesh, more flexible routines for mesh design,
new inflated central cube with optimized shape, far fewer mesh files saved by the mesher, global arrays sorted to speed
up the simulation, seismograms can be written by the master, one more doubling level at the bottom of the outer core
if needed (off by default).
v. 3.6 Many people, many affiliations, September 2006: adjoint and kernel calculations, fixed IASP91 model,
added AK135F_NO_MUD and 1066a, fixed topography/bathymetry routine, new attenuation routines, faster and bet-
ter I/Os on very large systems, many small improvements and bug fixes, new ‘configure’ script, new Pyre version, new
user’s manual etc..
v. 3.5 Dimitri Komatitsch, Brian Savage and Jeroen Tromp, Caltech, July 2004: any size of chunk, 3D attenuation,
case of two chunks, more precise topography/bathymetry model, new Par_file structure.
68
CHAPTER 14. INFORMATION FOR DEVELOPERS OF THE CODE, AND FOR PEOPLE WHO WANT TO LEARN HOW THE TECHNIQUE WORKS69
v. 3.4 Dimitri Komatitsch and Jeroen Tromp, Caltech, August 2003: merged global and regional codes, no itera-
tions in fluid, better movies.
v. 3.3 Dimitri Komatitsch, Caltech, September 2002: flexible mesh doubling in outer core, inlined code, OpenDX
support.
v. 3.2 Jeroen Tromp, Caltech, July 2002: multiple sources and flexible PREM reading.
v. 3.1 Dimitri Komatitsch, Caltech, June 2002: vectorized loops in solver and merged central cube.
v. 3.0 Dimitri Komatitsch and Jeroen Tromp, Caltech, May 2002: ported to SGI and Compaq, double precision
solver, more general anisotropy.
v. 2.3 Dimitri Komatitsch and Jeroen Tromp, Caltech, August 2001: gravity, rotation, oceans and 3-D models.
v. 2.2 Dimitri Komatitsch and Jeroen Tromp, Caltech, USA, March 2001: final MPI package.
v. 2.0 Dimitri Komatitsch, Harvard, USA, January 2000: MPI code for the globe.
v. 1.0 Dimitri Komatitsch, UNAM, Mexico, June 1999: first MPI code for a chunk.
Jeroen Tromp and Dimitri Komatitsch, Harvard, USA, July 1998: first chunk solver using OpenMP on a Sun ma-
chine.
Dimitri Komatitsch, IPG Paris, France, December 1996: first 3-D solver for the CM-5 Connection Machine, par-
allelized on 128 processors using Connection Machine Fortran.
Bibliography
C. A. Acosta Minolia and D. A. Kopriva. Discontinuous Galerkin spectral element approximations on moving meshes.
J. Comput. Phys., 230(5):1876–1902, 2011. doi: 10.1016/j.jcp.2010.11.038.
M. Ainsworth and H. Wajid. Dispersive and dissipative behavior of the spectral element method. SIAM Journal on
Numerical Analysis, 47(5):3910–3937, 2009. doi: 10.1137/080724976.
M. Ainsworth and H. Wajid. Optimally blended spectral-finite element scheme for wave propagation and nonstandard
reduced integration. SIAM Journal on Numerical Analysis, 48(1):346–371, 2010. doi: 10.1137/090754017.
M. Ainsworth, P. Monk, and W. Muniz. Dispersive and dissipative properties of discontinuous Galerkin finite element
methods for the second-order wave equation. Journal of Scientific Computing, 27(1):5–40, 2006. doi: 10.1007/
s10915-005-9044-x.
K. Aki and P. G. Richards. Quantitative seismology, theory and methods. W. H. Freeman, San Francisco, USA, 1980.
700 pages.
C. J. Ammon, C. Ji, H. K. Thio, D. Robinson, S. D. Ni, V. Hjörleifsdóttir, H. Kanamori, T. Lay, S. Das, D. Helmberger,
G. Ichinose, J. Polet, and D. Wald. Rupture process of the 2004 Sumatra-Andaman earthquake. Science, 3(5725):
1133–1139, 2005.
D. N. Arnold. An interior penalty finite element method with discontinuous elements. SIAM Journal on Numerical
Analysis, 19(4):742–760, 1982. doi: 10.1137/0719052.
C. Bassin, G. Laske, and G. Masters. The current limits of resolution for surface wave tomography in North America.
EOS, 81:F897, 2000.
M. Benjemaa, N. Glinsky-Olivier, V. M. Cruz-Atienza, J. Virieux, and S. Piperno. Dynamic non-planar crack rupture
by a finite volume method. Geophys. J. Int., 171(1):271–285, 2007. doi: 10.1111/j.1365-246X.2006.03500.x.
M. Benjemaa, N. Glinsky-Olivier, V. M. Cruz-Atienza, and J. Virieux. 3D dynamic rupture simulation by a finite
volume method. Geophys. J. Int., 178(1):541–560, 2009. doi: 10.1111/j.1365-246X.2009.04088.x.
M. Bernacki, S. Lanteri, and S. Piperno. Time-domain parallel simulation of heterogeneous wave propagation on
unstructured grids using explicit, nondiffusive, discontinuous Galerkin methods. J. Comput. Acoust., 14(1):57–81,
2006.
C. Bernardi, Y. Maday, and A. T. Patera. A new nonconforming approach to domain decomposition: the Mortar
element method. In H. Brezis and J. L. Lions, editors, Nonlinear partial differential equations and their applications,
Séminaires du Collège de France, pages 13–51, Paris, 1994. Pitman.
E. Blanc, D. Komatitsch, E. Chaljub, B. Lombard, and Z. Xie. Highly accurate stability-preserving optimization of
the Zener viscoelastic model, with application to wave propagation in the presence of strong attenuation. Geophys.
J. Int., 205(1):427–439, 2016. doi: 10.1093/gji/ggw024.
F. Bourdel, P.-A. Mazet, and P. Helluy. Resolution of the non-stationary or harmonic Maxwell equations by a discon-
tinuous finite element method: Application to an E.M.I. (electromagnetic impulse) case. In Proceedings of the 10th
international conference on computing methods in applied sciences and engineering, pages 405–422, Commack,
NY, USA, 1991. Nova Science Publishers.
70
BIBLIOGRAPHY 71
Y. Capdeville, E. Chaljub, J. P. Vilotte, and J. P. Montagner. Coupling the spectral element method with a modal
solution for elastic wave propagation in global Earth models. Geophys. J. Int., 152:34–67, 2003.
L. Carrington, D. Komatitsch, M. Laurenzano, M. Tikir, D. Michéa, N. Le Goff, A. Snavely, and J. Tromp. High-
frequency simulations of global seismic wave propagation using SPECFEM3D_GLOBE on 62 thousand processor
cores. In Proceedings of the SC’08 ACM/IEEE conference on Supercomputing, pages 60:1–60:11, Austin, Texas,
USA, Nov. 2008. IEEE Press. doi: 10.1145/1413370.1413432. Article #60, Gordon Bell Prize finalist article.
F. Casadei and E. Gabellini. Implementation of a 3D coupled Spectral Element solver for wave propagation and
soil-structure interaction simulations. Technical report, European Commission Joint Research Center Report
EUR17730EN, Ispra, Italy, 1997.
E. Chaljub. Modélisation numérique de la propagation d’ondes sismiques en géométrie sphérique : application à la
sismologie globale (Numerical modeling of the propagation of seismic waves in spherical geometry: application to
global seismology). PhD thesis, Université Paris VII Denis Diderot, Paris, France, 2000.
E. Chaljub and B. Valette. Spectral element modelling of three-dimensional wave propagation in a self-gravitating
Earth with an arbitrarily stratified outer core. Geophys. J. Int., 158:131–141, 2004.
E. Chaljub, Y. Capdeville, and J. P. Vilotte. Solving elastodynamics in a fluid-solid heterogeneous sphere: a parallel
spectral-element approximation on non-conforming grids. J. Comput. Phys., 187(2):457–491, 2003.
E. Chaljub, D. Komatitsch, J. P. Vilotte, Y. Capdeville, B. Valette, and G. Festa. Spectral element analysis in seismol-
ogy. In R.-S. Wu and V. Maupin, editors, Advances in wave propagation in heterogeneous media, volume 48 of
Advances in Geophysics, pages 365–419. Elsevier - Academic Press, London, UK, 2007.
S.-J. Chang, A. Ferreira, J. Ritsema, H. van Heijst, and J. Woodhouse. Joint inversion for global isotropic and radially
anisotropic mantle structure including crustal thickness perturbations. J. Geophys. Res., 120:4278–4300, 2015.
M. Chen and J. Tromp. Theoretical and numerical investigations of global and regional seismic wave propagation
in weakly anisotropic earth models. Geophys. J. Int., 168(3):1130–1152, 2007. doi: 10.1111/j.1365-246X.2006.
03218.x.
M. Chen, J. Tromp, D. Helmberger, and H. Kanamori. Waveform modeling of the slab beneath Japan. J. Geophys.
Res., 112:B02305, 2007. doi: 10.1029/2006JB004394.
S. Chevrot, N. Favier, and D. Komatitsch. Shear wave splitting in three-dimensional anisotropic media. Geophys. J.
Int., 159(2):711–720, 2004. doi: 10.1111/j.1365-246X.2004.02432.x.
B. Cockburn, G. E. Karniadakis, and C.-W. Shu. Discontinuous Galerkin Methods: Theory, Computation and Appli-
cations. Springer-Verlag, Heidelberg, Germany, 2000.
G. Cohen. Higher-order numerical methods for transient wave equations. Springer-Verlag, Berlin, Germany, 2002.
349 pages.
G. Cohen, P. Joly, and N. Tordjman. Construction and analysis of higher-order finite elements with mass lumping for
the wave equation. In R. Kleinman, editor, Proceedings of the second international conference on mathematical
and numerical aspects of wave propagation, pages 152–160. SIAM, Philadelphia, Pennsylvania, USA, 1993.
F. A. Dahlen and J. Tromp. Theoretical Global Seismology. Princeton University Press, Princeton, New-Jersey, USA,
1998. 944 pages.
C. A. Dalton, G. Ekström, and A. M. Dziewo´
nski. The global attenuation structure of the upper mantle. J. Geophys.
Res., 113:B05317, 2008. doi: 10.1029/2006JB004394.
J. D. De Basabe and M. K. Sen. Grid dispersion and stability criteria of some common finite-element methods for
acoustic and elastic wave equations. Geophysics, 72(6):T81–T95, 2007. doi: 10.1190/1.2785046.
J. D. De Basabe and M. K. Sen. Stability of the high-order finite elements for acoustic or elastic wave propagation
with high-order time stepping. Geophys. J. Int., 181(1):577–590, 2010. doi: 10.1111/j.1365-246X.2010.04536.x.
BIBLIOGRAPHY 72
J. D. De Basabe, M. K. Sen, and M. F. Wheeler. The interior penalty discontinuous Galerkin method for elastic wave
propagation: grid dispersion. Geophys. J. Int., 175(1):83–93, 2008. doi: 10.1111/j.1365-246X.2008.03915.x.
J. de la Puente, J. P. Ampuero, and M. Käser. Dynamic rupture modeling on unstructured meshes using a discontinuous
Galerkin method. J. Geophys. Res., 114:B10302, 2009. doi: 10.1029/2008JB006271.
M. O. Deville, P. F. Fischer, and E. H. Mund. High-Order Methods for Incompressible Fluid Flow. Cambridge
University Press, Cambridge, United Kingdom, 2002. 528 pages.
S. Duczek, S. Liefold, D. Schmicker, and U. Gabbert. Wave propagation analysis using high-order finite element
methods: Spurious oscillations excited by internal element eigenfrequencies. Technische Mechanik, 34:51–71,
2014.
M. Dumbser and M. Käser. An arbitrary high-order discontinuous Galerkin method for elastic waves on un-
structured meshes-II. The three-dimensional isotropic case. Geophys. J. Int., 167(1):319–336, 2006. doi:
10.1111/j.1365-246X.2006.03120.x.
A. M. Dziewo´
nski and D. L. Anderson. Preliminary reference Earth model. Phys. Earth planet. Inter., 25(4):297–356,
1981.
V. Étienne, E. Chaljub, J. Virieux, and N. Glinsky. An hp-adaptive discontinuous Galerkin finite-element method for
3-D elastic wave modelling. Geophys. J. Int., 183(2):941–962, 2010. doi: 10.1111/j.1365-246X.2010.04764.x.
E. Faccioli, F. Maggio, R. Paolucci, and A. Quarteroni. 2D and 3D elastic wave propagation by a pseudo-spectral
domain decomposition method. J. Seismol., 1:237–251, 1997.
R. S. Falk and G. R. Richter. Explicit finite element methods for symmetric hyperbolic equations. SIAM Journal on
Numerical Analysis, 36(3):935–952, 1999. doi: 10.1137/S0036142997329463.
N. Favier, S. Chevrot, and D. Komatitsch. Near-field influences on shear wave splitting and traveltime sensitivity
kernels. Geophys. J. Int., 156(3):467–482, 2004. doi: 10.1111/j.1365-246X.2004.02178.x.
A. Fichtner, H. Igel, H.-P. Bunge, and B. L. N. Kennett. Simulation and inversion of seismic wave propagation on
continental scales based on a spectral-element method. Journal of Numerical Analysis, Industrial and Applied
Mathematics, 4(1-2):11–22, 2009.
F. Gilbert and A. M. Dziewo´
nski. An application of normal mode theory to the retrieval of structural parameters and
source mechanisms from seismic spectra. Philos. Trans. R. Soc. London A, 278:187–269, 1975.
F. X. Giraldo, J. S. Hesthaven, and T. Warburton. Nodal high-order discontinuous Galerkin methods for the spherical
shallow water equations. J. Comput. Phys., 181(2):499–525, 2002. doi: 10.1006/jcph.2002.7139.
L. Godinho, P. A. Mendes, A. Tadeu, A. Cadena-Isaza, C. Smerzini, F. J. Sánchez-Sesma, R. Madec, and D. Ko-
matitsch. Numerical simulation of ground rotations along 2D topographical profiles under the incidence of elastic
plane waves. Bull. seism. Soc. Am., 99(2B):1147–1161, 2009. doi: 10.1785/0120080096.
W. Gropp, E. Lusk, and A. Skjellum. Using MPI, portable parallel programming with the Message-Passing Interface.
MIT Press, Cambridge, USA, 1994.
M. J. Grote, A. Schneebeli, and D. Schötzau. Discontinuous Galerkin finite element method for the wave equation.
SIAM Journal on Numerical Analysis, 44(6):2408–2431, 2006. doi: 10.1137/05063194X.
F. Q. Hu, M. Y. Hussaini, and P. Rasetarinera. An analysis of the discontinuous Galerkin method for wave propagation
problems. J. Comput. Phys., 151(2):921–946, 1999. doi: 10.1006/jcph.1999.6227.
C. Ji, S. Tsuboi, D. Komatitsch, and J. Tromp. Rayleigh-wave multipathing along the west coast of North America.
Bull. seism. Soc. Am., 95(6):2115–2124, 2005. doi: 10.1785/0120040180.
C. Johnson and J. Pitkäranta. An analysis of the discontinuous Galerkin method for a scalar hyperbolic equation.
Math. Comp., 46:1–26, 1986. doi: 10.1090/S0025-5718-1986-0815828-4.
BIBLIOGRAPHY 73
B. L. N. Kennett and E. R. Engdahl. Traveltimes for global earthquake location and phase identification. Geophys. J.
Int., 105:429–465, 1991.
B. L. N. Kennett, E. R. Engdahl, and R. Buland. Constraints on seismic velocities in the Earth from traveltimes.
Geophys. J. Int., 122:108–124, 1995.
D. Komatitsch. Méthodes spectrales et éléments spectraux pour l’équation de l’élastodynamique 2D et 3D en milieu
hétérogène (Spectral and spectral-element methods for the 2D and 3D elastodynamics equations in heterogeneous
media). PhD thesis, Institut de Physique du Globe, Paris, France, 1997. 187 pages.
D. Komatitsch. Fluid-solid coupling on a cluster of GPU graphics cards for seismic wave propagation. C. R. Acad.
Sci., Ser. IIb Mec., 339:125–135, 2011. doi: 10.1016/j.crme.2010.11.007.
D. Komatitsch and R. Martin. An unsplit convolutional Perfectly Matched Layer improved at grazing incidence for
the seismic wave equation. Geophysics, 72(5):SM155–SM167, 2007. doi: 10.1190/1.2757586.
D. Komatitsch and J. Tromp. Introduction to the spectral-element method for 3-D seismic wave propagation. Geophys.
J. Int., 139(3):806–822, 1999. doi: 10.1046/j.1365-246x.1999.00967.x.
D. Komatitsch and J. Tromp. Spectral-element simulations of global seismic wave propagation-I. Validation. Geophys.
J. Int., 149(2):390–412, 2002a. doi: 10.1046/j.1365-246X.2002.01653.x.
D. Komatitsch and J. Tromp. Spectral-element simulations of global seismic wave propagation-II. 3-D models, oceans,
rotation, and self-gravitation. Geophys. J. Int., 150(1):303–318, 2002b. doi: 10.1046/j.1365-246X.2002.01716.x.
D. Komatitsch and J. P. Vilotte. The spectral-element method: an efficient tool to simulate the seismic response of 2D
and 3D geological structures. Bull. seism. Soc. Am., 88(2):368–392, 1998.
D. Komatitsch, R. Martin, J. Tromp, M. A. Taylor, and B. A. Wingate. Wave propagation in 2-D elastic media
using a spectral element method with triangles and quadrangles. J. Comput. Acoust., 9(2):703–718, 2001. doi:
10.1142/S0218396X01000796.
D. Komatitsch, J. Ritsema, and J. Tromp. The spectral-element method, Beowulf computing, and global seismology.
Science, 298(5599):1737–1742, 2002. doi: 10.1126/science.1076024.
D. Komatitsch, S. Tsuboi, C. Ji, and J. Tromp. A 14.6 billion degrees of freedom, 5 teraflops, 2.5 terabyte earthquake
simulation on the Earth Simulator. In Proceedings of the SC’03 ACM/IEEE conference on Supercomputing, pages
4–11, Phoenix, Arizona, USA, Nov. 2003. ACM. doi: 10.1145/1048935.1050155. Gordon Bell Prize winner article.
D. Komatitsch, Q. Liu, J. Tromp, P. Süss, C. Stidham, and J. H. Shaw. Simulations of ground motion in the Los
Angeles basin based upon the spectral-element method. Bull. seism. Soc. Am., 94(1):187–206, 2004. doi: 10.1785/
0120030077.
D. Komatitsch, J. Labarta, and D. Michéa. A simulation of seismic wave propagation at high resolution in the inner
core of the Earth on 2166 processors of MareNostrum. Lecture Notes in Computer Science, 5336:364–377, 2008.
D. Komatitsch, D. Michéa, and G. Erlebacher. Porting a high-order finite-element earthquake modeling application to
NVIDIA graphics cards using CUDA. Journal of Parallel and Distributed Computing, 69(5):451–460, 2009. doi:
10.1016/j.jpdc.2009.01.006.
D. Komatitsch, G. Erlebacher, D. Göddeke, and D. Michéa. High-order finite-element seismic wave propagation
modeling with MPI on a large GPU cluster. J. Comput. Phys., 229(20):7692–7714, 2010a. doi: 10.1016/j.jcp.2010.
06.024.
D. Komatitsch, L. P. Vinnik, and S. Chevrot. SHdiff/SVdiff splitting in an isotropic Earth. J. Geophys. Res., 115(B7):
B07312, 2010b. doi: 10.1029/2009JB006795.
D. Komatitsch, Z. Xie, E. Bozda˘
g, E. Sales de Andrade, D. Peter, Q. Liu, and J. Tromp. Anelastic sensitivity kernels
with parsimonious storage for adjoint tomography and full waveform inversion. Geophys. J. Int., 206(3):1467–1478,
2016. doi: 10.1093/gji/ggw224.
BIBLIOGRAPHY 74
D. A. Kopriva. Metric identities and the discontinuous spectral element method on curvilinear meshes. Journal of
Scientific Computing, 26(3):301–327, 2006. doi: 10.1007/s10915-005-9070-8.
D. A. Kopriva, S. L. Woodruff, and M. Y. Hussaini. Computation of electromagnetic scattering with a non-conforming
discontinuous spectral element method. Int. J. Numer. Methods Eng., 53(1):105–122, 2002. doi: 10.1002/nme.394.
S. Krishnan, C. Ji, D. Komatitsch, and J. Tromp. Case studies of damage to tall steel moment-frame buildings in
Southern California during large San Andreas earthquakes. Bull. seism. Soc. Am., 96(4A):1523–1537, 2006a. doi:
10.1785/0120050145.
S. Krishnan, C. Ji, D. Komatitsch, and J. Tromp. Performance of two 18-story steel moment-frame buildings in
Southern California during two large simulated San Andreas earthquakes. Earthquake Spectra, 22(4):1035–1061,
2006b. doi: 10.1193/1.2360698.
B. Kustowski, A. M. Dziewo´
nski, and G. Ekstrom. Modeling the anisotropic shear-wave velocity structure in the
Earth’s mantle on global and regional scales. EOS, 87(52):Abstract S41E–02, 2006. Fall Meet. Suppl.
T. Lay, H. Kanamori, C. Ammon, M. Nettles, S. N. Ward, R. C. Aster, S. L. Beck, S. L. Bilek, M. R. Brudzinski,
R. Butler, H. R. DeShon, G. Ekstrom, K. Satake, and S. Sipkin. The great Sumatra-Andaman earthquake of 26
December 2004. Science, 3(5725):1127–1133, 2005.
S. J. Lee, H. W. Chen, Q. Liu, D. Komatitsch, B. S. Huang, and J. Tromp. Three-dimensional simulations of seismic
wave propagation in the Taipei basin with realistic topography based upon the spectral-element method. Bull. seism.
Soc. Am., 98(1):253–264, 2008. doi: 10.1785/0120070033.
S. J. Lee, Y. C. Chan, D. Komatitsch, B. S. Huang, and J. Tromp. Effects of realistic surface topography on seismic
ground motion in the Yangminshan region of Taiwan based upon the spectral-element method and LiDAR DTM.
Bull. seism. Soc. Am., 99(2A):681–693, 2009a. doi: 10.1785/0120080264.
S. J. Lee, D. Komatitsch, B. S. Huang, and J. Tromp. Effects of topography on seismic wave propagation: An example
from northern Taiwan. Bull. seism. Soc. Am., 99(1):314–325, 2009b. doi: 10.1785/0120080020.
A. Legay, H. W. Wang, and T. Belytschko. Strong and weak arbitrary discontinuities in spectral finite elements. Int. J.
Numer. Methods Eng., 64(8):991–1008, 2005. doi: 10.1002/nme.1388.
P. Lesaint and P. A. Raviart. On a finite-element method for solving the neutron transport equation (Proc. Symposium,
Mathematical Research Center). In U. of Wisconsin-Madison, editor, Mathematical aspects of finite elements in
partial differential equations, volume 33, pages 89–123, New York, USA, 1974. Academic Press.
Q. Liu and J. Tromp. Finite-frequency kernels based on adjoint methods. Bull. seism. Soc. Am., 96(6):2383–2397,
2006. doi: 10.1785/0120060041.
Q. Liu and J. Tromp. Finite-frequency sensitivity kernels for global seismic wave propagation based upon adjoint
methods. Geophys. J. Int., 174(1):265–286, 2008. doi: 10.1111/j.1365-246X.2008.03798.x.
Y. Maday and A. T. Patera. Spectral-element methods for the incompressible Navier-Stokes equations. In State of the
art survey in computational mechanics, pages 71–143, 1989. A. K. Noor and J. T. Oden editors.
R. Madec, D. Komatitsch, and J. Diaz. Energy-conserving local time stepping based on high-order finite elements for
seismic wave propagation across a fluid-solid interface. Comput. Model. Eng. Sci., 49(2):163–189, 2009.
R. Martin and D. Komatitsch. An unsplit convolutional perfectly matched layer technique improved at grazing inci-
dence for the viscoelastic wave equation. Geophys. J. Int., 179(1):333–344, 2009. doi: 10.1111/j.1365-246X.2009.
04278.x.
R. Martin, D. Komatitsch, C. Blitz, and N. Le Goff. Simulation of seismic wave propagation in an asteroid based upon
an unstructured MPI spectral-element method: blocking and non-blocking communication strategies. Lecture Notes
in Computer Science, 5336:350–363, 2008a.
BIBLIOGRAPHY 75
R. Martin, D. Komatitsch, and A. Ezziani. An unsplit convolutional perfectly matched layer improved at grazing
incidence for seismic wave equation in poroelastic media. Geophysics, 73(4):T51–T61, 2008b. doi: 10.1190/1.
2939484.
R. Martin, D. Komatitsch, and S. D. Gedney. A variational formulation of a stabilized unsplit convolutional perfectly
matched layer for the isotropic or anisotropic seismic wave equation. Comput. Model. Eng. Sci., 37(3):274–304,
2008c. doi: 10.3970/cmes.2008.037.274.
R. Martin, D. Komatitsch, S. D. Gedney, and E. Bruthiaux. A high-order time and space formulation of the unsplit
perfectly matched layer for the seismic wave equation using Auxiliary Differential Equations (ADE-PML). Comput.
Model. Eng. Sci., 56(1):17–42, 2010. doi: 10.3970/cmes.2010.056.017.
T. Melvin, A. Staniforth, and J. Thuburn. Dispersion analysis of the spectral-element method. Quarterly Journal of
the Royal Meteorological Society, 138(668):1934–1947, 2012. doi: 10.1002/qj.1906.
E. D. Mercerat, J. P. Vilotte, and F. J. Sánchez-Sesma. Triangular spectral-element simulation of two-dimensional
elastic wave propagation using unstructured triangular grids. Geophys. J. Int., 166(2):679–698, 2006.
D. Michéa and D. Komatitsch. Accelerating a 3D finite-difference wave propagation code using GPU graphics cards.
Geophys. J. Int., 182(1):389–402, 2010. doi: 10.1111/j.1365-246X.2010.04616.x.
P. Monk and G. R. Richter. A discontinuous Galerkin method for linear symmetric hyperbolic systems in inhomoge-
neous media. Journal of Scientific Computing, 22-23(1-3):443–477, 2005. doi: 10.1007/s10915-004-4132-5.
J. P. Montagner and B. L. N. Kennett. How to reconcile body-wave and normal-mode reference Earth models? Geo-
phys. J. Int., 122:229–248, 1995.
C. Morency, Y. Luo, and J. Tromp. Finite-frequency kernels for wave propagation in porous media based upon adjoint
methods. Geophys. J. Int., 179:1148–1168, 2009. doi: 10.1111/j.1365-246X.2009.04332.
NOAA. National Oceanic and Atmospheric Administration (NOAA) product information catalog - ETOPO5 Earth
Topography 5-minute digital model. Technical report, U.S. Department of Commerce, Washington D.C., USA,
1988. 171 pages.
S. P. Oliveira and G. Seriani. Effect of element distortion on the numerical dispersion of spectral-element methods.
Communications in Computational Physics, 9(4):937–958, 2011.
P. S. Pacheco. Parallel programming with MPI. Morgan Kaufmann Press, San Francisco, USA, 1997.
J. Park, T. R. A. Song, J. Tromp, E. Okal, S. Stein, G. Roult, E. Clevede, G. Laske, H. Kanamori, P. Davis, J. Berger,
C. Braitenberg, M. V. Camp, X. Lei, H. P. Sun, H. Z. Xu, and S. Rosat. Earth’s free oscillations excited by the 26
December 2004 Sumatra-Andaman earthquake. Science, 3(5725):1139–1144, 2005.
A. T. Patera. A spectral element method for fluid dynamics: Laminar flow in a channel expansion. J. Comput. Phys.,
54(3):468–488, 1984. doi: 10.1016/0021-9991(84)90128-1.
D. Peter, D. Komatitsch, Y. Luo, R. Martin, N. Le Goff, E. Casarotti, P. Le Loher, F. Magnoni, Q. Liu, C. Blitz,
T. Nissen-Meyer, P. Basini, and J. Tromp. Forward and adjoint simulations of seismic wave propagation on fully
unstructured hexahedral meshes. Geophys. J. Int., 186(2):721–739, 2011. doi: 10.1111/j.1365-246X.2011.05044.x.
E. Priolo, J. M. Carcione, and G. Seriani. Numerical simulation of interface waves by high-order spectral modeling
techniques. J. Acoust. Soc. Am., 95(2):681–693, 1994.
W. H. Reed and T. R. Hill. Triangular mesh methods for the neutron transport equation. Technical Report LA-UR-73-
479, Los Alamos Scientific Laboratory, Los Alamos, USA, 1973.
J. Ritsema and H. J. Van Heijst. Seismic imaging of structural heterogeneity in Earth’s mantle: Evidence for large-scale
mantle flow. Science Progress, 83:243–259, 2000.
J. Ritsema, H. J. Van Heijst, and J. H. Woodhouse. Complex shear velocity structure imaged beneath Africa and
Iceland. Science, 286:1925–1928, 1999.
BIBLIOGRAPHY 76
J. Ritsema, L. A. Rivera, D. Komatitsch, J. Tromp, and H. J. van Heijst. The effects of crust and mantle heterogeneity
on PP/P and SS/S amplitude ratios. Geophys. Res. Lett., 29(10):1430, 2002. doi: 10.1029/2001GL013831.
J. Ritsema, A. Deuss, H. J. Van Heijst, and J. H. Woodhouse. S40RTS: a degree-40 shear-velocity model for the man-
tle from new rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements.
Geophys. J. Int., 184(3):1223–1236, 2011. doi: 10.1111/j.1365-246X.2010.04884.x.
B. Rivière and M. F. Wheeler. Discontinuous finite element methods for acoustic and elastic wave problems. Contem-
porary Mathematics, 329:271–282, 2003.
C. Ronchi, R. Ianoco, and P. S. Paolucci. The “Cubed Sphere”: a new method for the solution of partial differential
equations in spherical geometry. J. Comput. Phys., 124:93–114, 1996.
R. Sadourny. Conservative finite-difference approximations of the primitive equations on quasi-uniform spherical
grids. Monthly Weather Review, 100:136–144, 1972.
B. Savage, D. Komatitsch, and J. Tromp. Effects of 3D attenuation on seismic wave amplitude and phase measure-
ments. Bull. seism. Soc. Am., 100(3):1241–1251, 2010. doi: 10.1785/0120090263.
G. Seriani and S. P. Oliveira. Optimal blended spectral-element operators for acoustic wave modeling. Geophysics,
72(5):SM95–SM106, 2007. doi: 10.1190/1.2750715.
G. Seriani and S. P. Oliveira. Dispersion analysis of spectral-element methods for elastic wave propagation. Wave
Motion, 45:729–744, 2008. doi: 10.1016/j.wavemoti.2007.11.007.
G. Seriani and E. Priolo. A spectral element method for acoustic wave simulation in heterogeneous media. Finite
Elements in Analysis and Design, 16:337–348, 1994.
G. Seriani, E. Priolo, and A. Pregarz. Modelling waves in anisotropic media by a spectral element method. In
G. Cohen, editor, Proceedings of the third international conference on mathematical and numerical aspects of wave
propagation, pages 289–298. SIAM, Philadephia, PA, 1995.
J. Tago, V. M. Cruz-Atienza, V. Étienne, J. Virieux, M. Benjemaa, and F. J. Sánchez-Sesma. 3D dynamic rupture with
anelastic wave propagation using an hp-adaptive Discontinuous Galerkin method. In Abstract S51A-1915 presented
at 2010 AGU Fall Meeting, San Francisco, California, USA, Dec. 2010.
M. A. Taylor and B. A. Wingate. A generalized diagonal mass matrix spectral element method for non-quadrilateral
elements. Appl. Num. Math., 33:259–265, 2000.
M. Tesauro, M. K. Kaban, and S. A. P. L. Cloetingh. Eucrust-07: A new reference model for the European crust.
Geophys. Res. Lett., 35:L05313, 2008. doi: 10.1029/2007GL032244.
S. A. Teukolsky. Short note on the mass matrix for Gauss-Lobatto grid points. J. Comput. Phys., 283:408–413, 2015.
doi: 10.1016/j.jcp.2014.12.012.
J. Tromp and D. Komatitsch. Spectral-element simulations of wave propagation in a laterally homogeneous Earth
model. In E. Boschi, G. Ekström, and A. Morelli, editors, Problems in Geophysics for the New Millennium, pages
351–372. INGV, Roma, Italy, 2000.
J. Tromp, C. Tape, and Q. Liu. Seismic tomography, adjoint methods, time reversal and banana-doughnut kernels.
Geophys. J. Int., 160(1):195–216, 2005. doi: 10.1111/j.1365-246X.2004.02453.x.
J. Tromp, D. Komatitsch, and Q. Liu. Spectral-element and adjoint methods in seismology. Communications in
Computational Physics, 3(1):1–32, 2008.
J. Tromp, D. Komatitsch, V. Hjörleifsdóttir, Q. Liu, H. Zhu, D. Peter, E. Bozda˘
g, D. McRitchie, P. Friberg, C. Trabant,
and A. Hutko. Near real-time simulations of global CMT earthquakes. Geophys. J. Int., 183(1):381–389, 2010a.
doi: 10.1111/j.1365-246X.2010.04734.x.
J. Tromp, Y. Luo, S. Hanasoge, and D. Peter. Noise cross-correlation sensitivity kernels. Geophys. J. Int., 183:
791–819, 2010b. doi: 10.1111/j.1365-246X.2010.04721.x.
BIBLIOGRAPHY 77
S. Tsuboi, D. Komatitsch, C. Ji, and J. Tromp. Broadband modeling of the 2002 Denali fault earthquake on the Earth
Simulator. Phys. Earth planet. Inter., 139(3-4):305–313, 2003. doi: 10.1016/j.pepi.2003.09.012.
R. Vai, J. M. Castillo-Covarrubias, F. J. Sánchez-Sesma, D. Komatitsch, and J. P. Vilotte. Elastic wave propagation
in an irregularly layered medium. Soil Dynamics and Earthquake Engineering, 18(1):11–18, 1999. doi: 10.1016/
S0267-7261(98)00027-X.
K. van Wijk, D. Komatitsch, J. A. Scales, and J. Tromp. Analysis of strong scattering at the micro-scale. J. Acoust.
Soc. Am., 115(3):1006–1011, 2004. doi: 10.1121/1.1647480.
B. Videau, V. Marangozova-Martin, and J. Cronsioe. BOAST: Bringing Optimization through Automatic Source-
to-Source Tranformations. In Proceedings of the 7th International Symposium on Embedded Multicore/Manycore
System-on-Chip (MCSoC), Tokyo, Japan, 2013.
J. Virieux and S. Operto. An overview of full-waveform inversion in exploration geophysics. Geophysics, 74(6):
WCC1–WCC26, 2009. doi: 10.1190/1.3238367.
L. C. Wilcox, G. Stadler, C. Burstedde, and O. Ghattas. A high-order discontinuous Galerkin method for wave
propagation through coupled elastic-acoustic media. J. Comput. Phys., 229(24):9373–9396, 2010. doi: 10.1016/j.
jcp.2010.09.008.
B. A. Wingate and J. P. Boyd. Spectral element methods on triangles for geophysical fluid dynamics problems. In
A. V. Ilin and L. R. Scott, editors, Proceedings of the Third International Conference on Spectral and High-order
Methods, pages 305–314, Houston, Texas, 1996. Houston J. Mathematics.
Z. Xie, D. Komatitsch, R. Martin, and R. Matzen. Improved forward wave propagation and adjoint-based sensitivity
kernel calculations using a numerically stable finite-element PML. Geophys. J. Int., 198(3):1714–1747, 2014. doi:
10.1093/gji/ggu219.
Z. Xie, R. Matzen, P. Cristini, D. Komatitsch, and R. Martin. A perfectly matched layer for fluid-solid problems:
Application to ocean-acoustics simulations with solid ocean bottoms. J. Acoust. Soc. Am., 140(1):165–175, 2016.
doi: 10.1121/1.4954736.
Y. Zhou, Q. Liu, and J. Tromp. Surface wave sensitivity: mode summation versus adjoint SEM. Geophys. J. Int., 187
(3):1560–1576, 2011. doi: 10.1111/j.1365-246X.2011.05212.x.
Appendix A
Reference Frame Convention
The code uses the following convention for the Cartesian reference frame:
• the xaxis points East
• the yaxis points North
• the zaxis points up
Note that this convention is different from both the Aki and Richards [1980] convention and the Harvard Centroid-
Moment Tensor (CMT) convention. The Aki & Richards convention is
• the xaxis points North
• the yaxis points East
• the zaxis points down
and the Harvard CMT convention is
• the xaxis points South
• the yaxis points East
• the zaxis points up
78
Appendix B
Non-Dimensionalization Conventions
All physical parameters used are non-dimensionalized internally in the code in order to work in a reference Earth of
radius 1. In Table B.1 in the right column are the values by which we divide the parameters of the left column internally to
perform the calculations. The values output and saved by the code (seismograms, sensitivity kernels...) are then scaled back to the
right physical dimensions before being saved.
quantity (units) divided internally by
distance (m) R_EARTH
time (s) 1/√PI ×GRAV ×RHOAV
density (kg/m3)RHOAV
Table B.1: Non-dimensionalization convention employed internally by the code. The constants R_EARTH (the radius
of the Earth), PI (the number π), GRAV (the universal gravitational constant), and RHOAV (the Earth’s average density)
are defined in the constants.h file.
79
Appendix C
Benchmarks
Komatitsch and Tromp [2002a,b] carefully benchmarked the spectral-element simulations of global seismic waves
against normal-mode seismograms. Version 4.0 of SPECFEM3D_GLOBE has been benchmarked again following the
same procedure.
In this appendix we present two tests: a ‘long-period’ (periods longer than 17 s) simulation of a shallow event
in isotropic PREM [Dziewo´
nski and Anderson,1981] without the ocean layer, without attenuation but including the
effects of self-gravitation (in the Cowling approximation) (Figures C.1 and C.2), and a ‘short-period’ (periods longer
than 9 s) simulation of a deep event in transversely isotropic PREM without the ocean layer and including the effects
of self-gravitation and attenuation (Figures C.3,C.4 and C.5).
The normal-mode synthetics are calculated with the code QmXD using mode catalogs with a shortest period of 8 s
generated by the code OBANI. No free-air, tilt, or gravitational potential corrections were applied [Dahlen and Tromp,
1998]. We also turned off the effect of the oceans in QmXD.
The normal-mode and SEM displacement seismograms are first calculated for a step source-time function, i.e.,
setting the parameter half duration in the CMTSOLUTION file to zero for the SEM simulations. Both sets of
seismograms are subsequently convolved with a triangular source-time function using the processing script
utils/seis_process/process_syn.pl. They are also band-pass filtered and the horizontal components are
rotated to the radial and transverse directions (with the script utils/seis_process/rotate.pl).
The match between the normal-mode and SEM seismograms is quite remarkable for the experiment with attenu-
ation, considering the very different implementations of attenuation in the two computations (e.g., frequency domain
versus time domain, constant Q versus absorption bands).
Further tests can be found in the EXAMPLES directory. It contains the normal-mode and SEM seismograms, and
the parameters (STATIONS,CMTSOLUTION and Par_file) for the SEM simulations.
Important remark: when comparing SEM results to normal mode results, one needs to convert source and receiver
coordinates from geographic to geocentric coordinates, because on the equator the geographic and geocentric latitude
are identical but not elsewhere. Even for spherically-symmetric simulations one must perform this conversion because
the source and receiver locations provided by globalCMT.org and IRIS involve geographic coordinates.
80
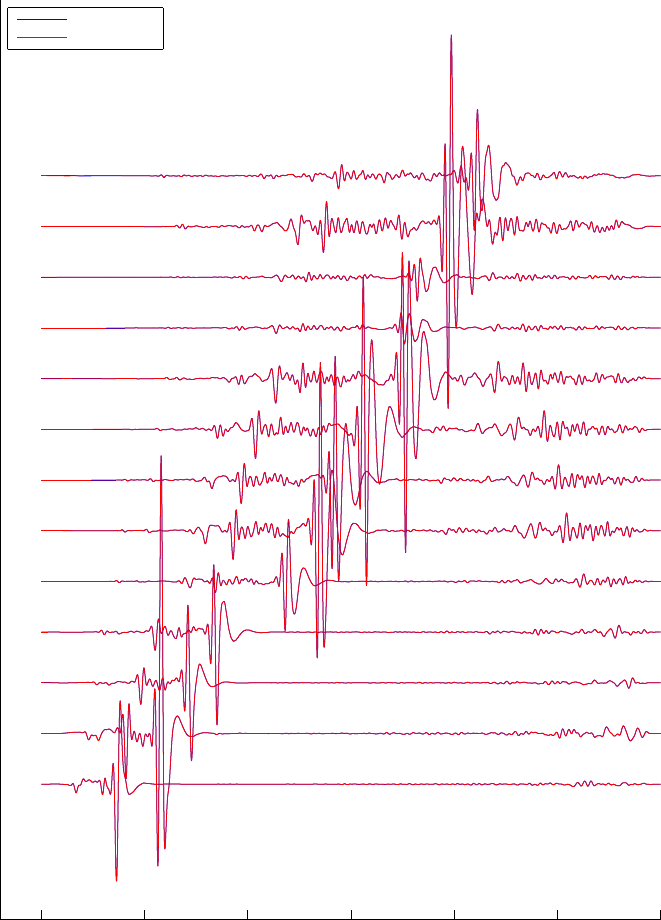
APPENDIX C. BENCHMARKS 81
0 1000 2000 3000 4000 5000 6000
CAN
PPT
KIP
INU
PAF
HYB
WUS
HDC
SAML
SFJD
TRIS
KOG
SSB
time [s]
vertical displacement
normal−mode
sem
Figure C.1: Normal-mode (blue) and SEM (red) vertical displacements in isotropic PREM considering the effects of
self-gravitation but not attenuation for 13 stations at increasing distance from the 1999 November 26th Vanuatu event
located at 15 km depth. The SEM computation is accurate for periods longer than 17 s. The seismograms have been
filtered between 50 s and 500 s. The station names are indicated on the left.
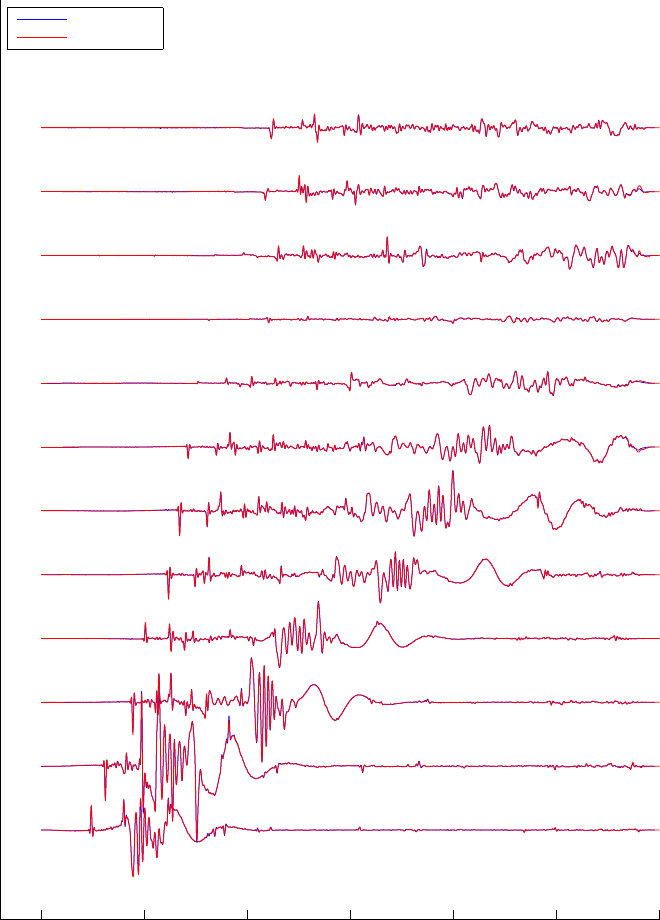
APPENDIX C. BENCHMARKS 83
0 500 1000 1500 2000 2500 3000
SPB
FDF
UNM
TRIS
SCZ
SFJD
ECH
RAO
ATD
AIS
WUS
INU
time [s]
vertical displacement
normal−mode
sem
Figure C.3: Normal-mode (blue) and SEM (red) vertical displacements in transversely isotropic PREM considering
the effects of self-gravitation and attenuation for 12 stations at increasing distance from the 1994 June 9th Bolivia
event located at 647 km depth. The SEM computation is accurate for periods longer than 9 s. The seismograms have
been filtered between 10 s and 500 s. The station names are indicated on the left.
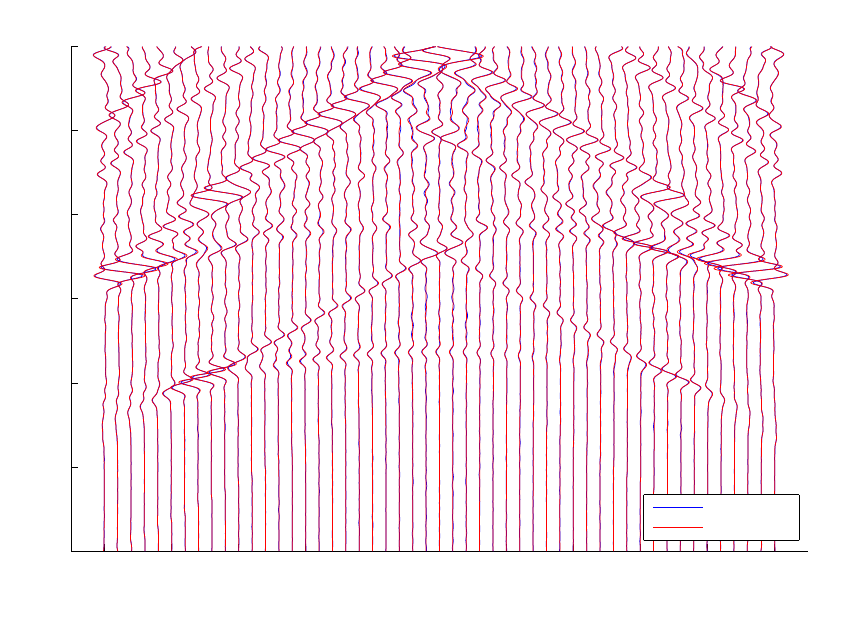
APPENDIX C. BENCHMARKS 85
130 140 150 160 170 180 190 200 210 220 230
900
1000
1100
1200
1300
1400
1500
time [s]
epicentral distance [degrees]
vertical displacement
normal−mode
sem
Figure C.5: Seismograms recorded between 130 degrees and 230 degrees, showing in particular the good agreement
for core phases such as PKP. This figure is similar to Figure 24 of Komatitsch and Tromp [2002a]. The results have
been filtered between 15 s and 500 s.
Appendix D
SAC Headers
Information about the simulation (i.e., event/station information, sampling rate, etc.) is written in the header of the
seismograms in SAC format. The list of values and related explanation are given in Figure D.1. Please check the SAC
webpages (http://www.iris.edu/software/sac/) for further information. Please note that the reference
time KZTIME is the centroid time (tCMT =tPDE +time shift) which corresponds to zero time in the synthetics.
For kinematic rupture simulations, KZTIME is equal to the CMT time of the source having the minimum time-shift in
the CMTSOLUTION file, and coordinates, depth and half-duration of the event are not provided in the headers.
86

APPENDIX D. SAC HEADERS 87
FILE: AAK.II.MXZ.sem.sac
NPTS = 37200
number of points per data component
B = -2.250000e+00
beginning value of time array
E = 6.005389e+03
end value of time array
IFTYPE = TIME SERIES FILE
type of file
LEVEN = TRUE
TRUE if data is evenly spaced
DELTA = 1.615000e-01
sampling rate (s)
IDEP = DISPLACEMENT (NM)
type of seismograms*
DEPMIN = -5.038710e-07
minimum displacement value
DEPMAX = 5.296865e-07
maximum displacement value
DEPMEN = -6.698920e-10
mean displacement value
OMARKER = 0
reference time in synthetics
KZDATE = FEB 04 (035), 2010
event date
KZTIME = 17:48:15.599
event origin time (centroid time)
IZTYPE = EVENT ORIGIN TIME
reference time
KSTNM = AAK
station name
CMPAZ = 0.000000e+00
component azimuth (degrees clockwise from north)
CMPINC = 0.000000e+00
component incident angle (degrees from vertical)
STLA = 4.263900e+01
station latitude (degrees, north positive)
STLO = 7.449400e+01
station longitude (degrees, east positive)
STEL = 1.645000e+03
station elevation (meters)
STDP = 3.000000e+01
station depth below surface (meters)
KEVNM = 201002041748A
event name
EVLA = -1.950000e+01
event CMT latitude (degrees, north positive)
EVLO = -1.732400e+02
event CMT longitude (degrees, east positive)
EVDP = 2.500000e+01
event CMT depth (km)
IEVTYP = EARTHQUAKE
event type
DIST = 1.326017e+04
great circle distance between event and station (km)
AZ = 3.085366e+02
event to station azimuth (degrees)
BAZ = 9.023685e+01
station to event azimuth (backazimuth, degrees)
GCARC = 1.191897e+02
great circle distance between event and station (degrees)
LOVROK = TRUE
TRUE if it is ok to write the file on disk
USER0 = 1.500000e+00
source half-duration (s)
USER1 = 1.700000e+01
shortest period at which simulations are accurate (s)
USER2 = 5.000000e+02
longest period at which simulations are accurate (s)
KUSER0 = SEM
method used to compute synthetic seismograms
KUSER1 = v5.1.0
version of the SEM code
KUSER2 = Tiger
version of the SEM code
NNVHDR = 6
header version number
SCALE = 1.000000e+09
scale factor to convert the unit of the synthetics
from meters to nanometers
LPSPOL = TRUE
TRUE if station components have positive polarity
LCALDA = TRUE
TRUE if DIST, AZ, BAZ and GCARC are
calculated from station and event coordinates
KCMPNM = MXZ
station component name
KNETWK = II
station network name
* the unit of synthetic seismograms is “meters”. Seismograms should be scaled by the header SCALE to
obtain units of nanometers.
Figure D.1: List of SAC headers and their explanations for a sample seismogram.
Appendix E
Channel Codes of Seismograms
Seismic networks, such as the Global Seismographic Network (GSN), generally involve various types of instruments
with different bandwidths, sampling properties and component configurations. There are standards to name channel
codes depending on instrument properties. IRIS (http://www.iris.edu) uses SEED/FDSN format for channel
codes, which are represented by three letters, such as LHN,BHZ, etc. In older versions of the SPECFEM package, a
common format was used for the channel codes of all seismograms, which was LHE/LHN/LHZ for three components.
To avoid confusion when comparisons are made to observed data, we are now using the FDSN convention for SEM
seismograms. In the following, we give a brief explanation of the FDSN convention and how it is adopted in SEM
seismograms. Please visit http://www.iris.edu/manuals/SEED_appA.htm for further information.
Band code: The first letter in the channel code denotes the band code of seismograms, which depends on the
response band and the sampling rate of instruments. The list of band codes used by IRIS is shown in Figure E.1.
The sampling rate of SEM synthetics is controlled by the resolution of simulations rather than instrument properties.
However, for consistency, we follow the FDSN convention for SEM seismograms governed by their sampling rate.
For SEM synthetics, we consider band codes for which dt ≤1s. The FDSN convention also considers the response
band of instruments. For instance, short-period and broad-band seismograms with the same sampling rate correspond
to different band codes, such as S and B, respectively. In such cases, we consider SEM seismograms as broad band,
ignoring the corner period (≥10 s) of the response band of instruments (note that at these resolutions, the minimum
period in the SEM synthetics will be less than 10 s). Accordingly, when you run a simulation the band code will be
chosen depending on the resolution of the synthetics, and channel codes of SEM seismograms will start with either L,
M,B,H,Cor F, shown by red color in the figure.
Instrument code: The second letter in the channel code corresponds to instrument codes, which specify the
family to which the sensor belongs. For instance, Hand Lare used for high-gain and low-gain seismometers, respec-
tively. The instrument code of SEM seismograms will always be X, as assigned by FDSN for synthetic seismograms.
Orientation code: The third letter in channel codes is an orientation code, which generally describes the phys-
ical configuration of the components of instrument packages. SPECFEM uses the traditional orientation code E/N/Z
(East-West, North-South, Vertical) for three components.
EXAMPLE: Depending on the resolution of your simulations, if the sampling rate is greater than 0.1s and less than 1s,
a seismogram recorded on the vertical component of station AAK will be named IU.AAK.MXZ.sem.sac, whereas
it will be IU.AAK.BXZ.sem.sac, if the sampling rate is greater than 0.0125 and less equal to 0.1 s.
88
APPENDIX E. CHANNEL CODES OF SEISMOGRAMS 89
Band
code
Band type
Sampling rate (sec)
Corner
period
(sec)
F
...
> 0.0002 to <= 0.001
≥ 10 sec
G
...
> 0.0002 to <= 0.001
< 10 sec
D
...
> 0.001 to <= 0.004
< 10 sec
C
...
> 0.001 to <= 0.004
≥ 10 sec
E
Extremely Short Period
<= 0.0125
< 10 sec
S
Short Period
<= 0.1 to > 0.0125
< 10 sec
H
High Broad Band
<= 0.0125
>= 10 sec
B
Broad Band
<= 0.1 to > 0.0125
>= 10 sec
M
Mid Period
< 1 to > 0.1
L
Long Period
1
V
Very Long Period
10
U
Ultra Long Period
100
R
Extremely Long Period
1000
P
On the order of 0.1 to 1 day
<= 100000 to > 10000
T
On the order of 1 to 10 days
<= 1000000 to > 100000
Q
Greater than 10 days
> 1000000
A
Administrative Instrument Channel
variable
NA
O
Opaque Instrument Channel
variable
NA
Figure E.1: The FDSN band code convention is based on the sampling rate and the response band of instruments.
Please visit http://www.iris.edu/manuals/SEED_appA.htm for further information. Grey rows show
the relative band-code range in SPECFEM, and the band codes used to name SEM seismograms are denoted in red.
Appendix F
Troubleshooting
FAQ
configuration fails: Examine the log file ’config.log’. It contains detailed informations. In many cases, the path’s to
these specific compiler commands F90, CC and MPIF90 won’t be correct if ‘./configure‘ fails.
Please make sure that you have a working installation of a Fortran compiler, a C compiler and an MPI imple-
mentation. You should be able to compile this little program code:
program main
include ’mpif.h’
integer, parameter :: CUSTOM_MPI_TYPE = MPI_REAL
integer ier
call MPI_INIT(ier)
call MPI_BARRIER(MPI_COMM_WORLD,ier)
call MPI_FINALIZE(ier)
end
compilation fails: In case a compilation error like the following occurs, stating
...
obj/meshfem3D.o: In function ‘MAIN__’:
meshfem3D.f90:(.text+0x14): undefined reference to ‘_gfortran_set_std’
...
make sure you’re pointing to the right ’mpif90’ wrapper command.
Normally, this message will appear when you are mixing two different Fortran compilers. That is, using e.g.
gfortran to compile non-MPI files and mpif90, wrapper provided for e.g. ifort, to compile MPI-files.
fix: e.g. specify
./configure FC=gfortran MPIF90=/usr/local/openmpi-gfortran/bin/mpif90
changing PPM model routines fails: In case you want to modify the PPM-routines in file model_ppm.f90, please
consider the following points:
1. Please check in file get_model_parameter.f90 that the entry for PPM models looks like:
...
else if(MODEL_ROOT == ’PPM’) then
! overimposed based on isotropic-prem
CASE_3D = .true.
CRUSTAL = .true.
ISOTROPIC_3D_MANTLE = .true.
ONE_CRUST = .true.
THREE_D_MODEL = THREE_D_MODEL_PPM
TRANSVERSE_ISOTROPY = .true. ! to use transverse-isotropic prem
...
90
APPENDIX F. TROUBLESHOOTING 91
You can set TRANSVERSE_ISOTROPY to .false. in case you want to use the isotropic PREM as 1D
background model.
2. Transverse isotropy would mean different values for horizontal and vertically polarized wave speeds, i.e.
different for vph and vpv, vsh and vsv, and it includes an additional parameter eta. By default, we take
these wave speeds from PREM and add your model perturbations to them. For the moment, your model
perturbations are added as isotropic perturbations, using the same dvp for vph and vpv, and dvs for vsh
and vsv, see in meshfem3D_models.f90:
...
case(THREE_D_MODEL_PPM )
! point profile model
call model_PPM(r_used,theta,phi,dvs,dvp,drho)
vpv=vpv*(1.0d0+dvp)
vph=vph*(1.0d0+dvp)
vsv=vsv*(1.0d0+dvs)
vsh=vsh*(1.0d0+dvs)
rho=rho*(1.0d0+drho)
...
You could modify this to add different perturbations for vph and vpv, resp. vsh and vsv. This would
basically mean that you add transverse isotropic perturbations. You can see how this is done with e.g. the
model s362ani, following the flag THREE_D_MODEL_S362ANI on how to modify accordingly the file
meshfem3D_models.f90.
In case you want to add more specific model routines, follow the code sections starting with:
!---
!
! ADD YOUR MODEL HERE
!
!---
to see code sections sensitive to model updates.
Appendix G
License
GNU GENERAL PUBLIC LICENSE
Version 3, 29 June 2007
Copyright © 2007 Free Software Foundation, Inc. http://fsf.org/
Everyone is permitted to copy and distribute verbatim copies of this
license document, but changing it is not allowed.
Preamble
The GNU General Public License is a free, copyleft license for software and other kinds of works.
The licenses for most software and other practical works are designed to take away your freedom to share and
change the works. By contrast, the GNU General Public License is intended to guarantee your freedom to share
and change all versions of a program–to make sure it remains free software for all its users. We, the Free Software
Foundation, use the GNU General Public License for most of our software; it applies also to any other work released
this way by its authors. You can apply it to your programs, too.
When we speak of free software, we are referring to freedom, not price. Our General Public Licenses are designed
to make sure that you have the freedom to distribute copies of free software (and charge for them if you wish), that
you receive source code or can get it if you want it, that you can change the software or use pieces of it in new free
programs, and that you know you can do these things.
To protect your rights, we need to prevent others from denying you these rights or asking you to surrender the rights.
Therefore, you have certain responsibilities if you distribute copies of the software, or if you modify it: responsibilities
to respect the freedom of others.
For example, if you distribute copies of such a program, whether gratis or for a fee, you must pass on to the
recipients the same freedoms that you received. You must make sure that they, too, receive or can get the source code.
And you must show them these terms so they know their rights.
Developers that use the GNU GPL protect your rights with two steps: (1) assert copyright on the software, and (2)
offer you this License giving you legal permission to copy, distribute and/or modify it.
For the developers’ and authors’ protection, the GPL clearly explains that there is no warranty for this free software.
For both users’ and authors’ sake, the GPL requires that modified versions be marked as changed, so that their problems
will not be attributed erroneously to authors of previous versions.
Some devices are designed to deny users access to install or run modified versions of the software inside them,
although the manufacturer can do so. This is fundamentally incompatible with the aim of protecting users’ freedom to
change the software. The systematic pattern of such abuse occurs in the area of products for individuals to use, which
is precisely where it is most unacceptable. Therefore, we have designed this version of the GPL to prohibit the practice
for those products. If such problems arise substantially in other domains, we stand ready to extend this provision to
those domains in future versions of the GPL, as needed to protect the freedom of users.
Finally, every program is threatened constantly by software patents. States should not allow patents to restrict
development and use of software on general-purpose computers, but in those that do, we wish to avoid the special
92
APPENDIX G. LICENSE 93
danger that patents applied to a free program could make it effectively proprietary. To prevent this, the GPL assures
that patents cannot be used to render the program non-free.
The precise terms and conditions for copying, distribution and modification follow.
TERMS AND CONDITIONS
0. Definitions.
“This License” refers to version 3 of the GNU General Public License.
“Copyright” also means copyright-like laws that apply to other kinds of works, such as semiconductor masks.
“The Program” refers to any copyrightable work licensed under this License. Each licensee is addressed as
“you”. “Licensees” and “recipients” may be individuals or organizations.
To “modify” a work means to copy from or adapt all or part of the work in a fashion requiring copyright
permission, other than the making of an exact copy. The resulting work is called a “modified version” of the
earlier work or a work “based on” the earlier work.
A “covered work” means either the unmodified Program or a work based on the Program.
To “propagate” a work means to do anything with it that, without permission, would make you directly or sec-
ondarily liable for infringement under applicable copyright law, except executing it on a computer or modifying
a private copy. Propagation includes copying, distribution (with or without modification), making available to
the public, and in some countries other activities as well.
To “convey” a work means any kind of propagation that enables other parties to make or receive copies. Mere
interaction with a user through a computer network, with no transfer of a copy, is not conveying.
An interactive user interface displays “Appropriate Legal Notices” to the extent that it includes a convenient and
prominently visible feature that (1) displays an appropriate copyright notice, and (2) tells the user that there is
no warranty for the work (except to the extent that warranties are provided), that licensees may convey the work
under this License, and how to view a copy of this License. If the interface presents a list of user commands or
options, such as a menu, a prominent item in the list meets this criterion.
1. Source Code.
The “source code” for a work means the preferred form of the work for making modifications to it. “Object
code” means any non-source form of a work.
A “Standard Interface” means an interface that either is an official standard defined by a recognized standards
body, or, in the case of interfaces specified for a particular programming language, one that is widely used
among developers working in that language.
The “System Libraries” of an executable work include anything, other than the work as a whole, that (a) is
included in the normal form of packaging a Major Component, but which is not part of that Major Component,
and (b) serves only to enable use of the work with that Major Component, or to implement a Standard Interface
for which an implementation is available to the public in source code form. A “Major Component”, in this
context, means a major essential component (kernel, window system, and so on) of the specific operating system
(if any) on which the executable work runs, or a compiler used to produce the work, or an object code interpreter
used to run it.
The “Corresponding Source” for a work in object code form means all the source code needed to generate,
install, and (for an executable work) run the object code and to modify the work, including scripts to control
those activities. However, it does not include the work’s System Libraries, or general-purpose tools or generally
available free programs which are used unmodified in performing those activities but which are not part of the
work. For example, Corresponding Source includes interface definition files associated with source files for the
work, and the source code for shared libraries and dynamically linked subprograms that the work is specifically
designed to require, such as by intimate data communication or control flow between those subprograms and
other parts of the work.
The Corresponding Source need not include anything that users can regenerate automatically from other parts
of the Corresponding Source.
The Corresponding Source for a work in source code form is that same work.
APPENDIX G. LICENSE 94
2. Basic Permissions.
All rights granted under this License are granted for the term of copyright on the Program, and are irrevocable
provided the stated conditions are met. This License explicitly affirms your unlimited permission to run the un-
modified Program. The output from running a covered work is covered by this License only if the output, given
its content, constitutes a covered work. This License acknowledges your rights of fair use or other equivalent,
as provided by copyright law.
You may make, run and propagate covered works that you do not convey, without conditions so long as your
license otherwise remains in force. You may convey covered works to others for the sole purpose of having
them make modifications exclusively for you, or provide you with facilities for running those works, provided
that you comply with the terms of this License in conveying all material for which you do not control copyright.
Those thus making or running the covered works for you must do so exclusively on your behalf, under your
direction and control, on terms that prohibit them from making any copies of your copyrighted material outside
their relationship with you.
Conveying under any other circumstances is permitted solely under the conditions stated below. Sublicensing is
not allowed; section 10 makes it unnecessary.
3. Protecting Users’ Legal Rights From Anti-Circumvention Law.
No covered work shall be deemed part of an effective technological measure under any applicable law fulfill-
ing obligations under article 11 of the WIPO copyright treaty adopted on 20 December 1996, or similar laws
prohibiting or restricting circumvention of such measures.
When you convey a covered work, you waive any legal power to forbid circumvention of technological measures
to the extent such circumvention is effected by exercising rights under this License with respect to the covered
work, and you disclaim any intention to limit operation or modification of the work as a means of enforcing,
against the work’s users, your or third parties’ legal rights to forbid circumvention of technological measures.
4. Conveying Verbatim Copies.
You may convey verbatim copies of the Program’s source code as you receive it, in any medium, provided
that you conspicuously and appropriately publish on each copy an appropriate copyright notice; keep intact all
notices stating that this License and any non-permissive terms added in accord with section 7 apply to the code;
keep intact all notices of the absence of any warranty; and give all recipients a copy of this License along with
the Program.
You may charge any price or no price for each copy that you convey, and you may offer support or warranty
protection for a fee.
5. Conveying Modified Source Versions.
You may convey a work based on the Program, or the modifications to produce it from the Program, in the form
of source code under the terms of section 4, provided that you also meet all of these conditions:
(a) The work must carry prominent notices stating that you modified it, and giving a relevant date.
(b) The work must carry prominent notices stating that it is released under this License and any conditions
added under section 7. This requirement modifies the requirement in section 4 to “keep intact all notices”.
(c) You must license the entire work, as a whole, under this License to anyone who comes into possession of a
copy. This License will therefore apply, along with any applicable section 7 additional terms, to the whole
of the work, and all its parts, regardless of how they are packaged. This License gives no permission to
license the work in any other way, but it does not invalidate such permission if you have separately received
it.
(d) If the work has interactive user interfaces, each must display Appropriate Legal Notices; however, if the
Program has interactive interfaces that do not display Appropriate Legal Notices, your work need not make
them do so.
A compilation of a covered work with other separate and independent works, which are not by their nature
extensions of the covered work, and which are not combined with it such as to form a larger program, in or
APPENDIX G. LICENSE 95
on a volume of a storage or distribution medium, is called an “aggregate” if the compilation and its resulting
copyright are not used to limit the access or legal rights of the compilation’s users beyond what the individual
works permit. Inclusion of a covered work in an aggregate does not cause this License to apply to the other parts
of the aggregate.
6. Conveying Non-Source Forms.
You may convey a covered work in object code form under the terms of sections 4 and 5, provided that you also
convey the machine-readable Corresponding Source under the terms of this License, in one of these ways:
(a) Convey the object code in, or embodied in, a physical product (including a physical distribution medium),
accompanied by the Corresponding Source fixed on a durable physical medium customarily used for soft-
ware interchange.
(b) Convey the object code in, or embodied in, a physical product (including a physical distribution medium),
accompanied by a written offer, valid for at least three years and valid for as long as you offer spare parts
or customer support for that product model, to give anyone who possesses the object code either (1) a copy
of the Corresponding Source for all the software in the product that is covered by this License, on a durable
physical medium customarily used for software interchange, for a price no more than your reasonable cost
of physically performing this conveying of source, or (2) access to copy the Corresponding Source from a
network server at no charge.
(c) Convey individual copies of the object code with a copy of the written offer to provide the Corresponding
Source. This alternative is allowed only occasionally and noncommercially, and only if you received the
object code with such an offer, in accord with subsection 6b.
(d) Convey the object code by offering access from a designated place (gratis or for a charge), and offer
equivalent access to the Corresponding Source in the same way through the same place at no further
charge. You need not require recipients to copy the Corresponding Source along with the object code. If
the place to copy the object code is a network server, the Corresponding Source may be on a different
server (operated by you or a third party) that supports equivalent copying facilities, provided you maintain
clear directions next to the object code saying where to find the Corresponding Source. Regardless of what
server hosts the Corresponding Source, you remain obligated to ensure that it is available for as long as
needed to satisfy these requirements.
(e) Convey the object code using peer-to-peer transmission, provided you inform other peers where the object
code and Corresponding Source of the work are being offered to the general public at no charge under
subsection 6d.
A separable portion of the object code, whose source code is excluded from the Corresponding Source as a
System Library, need not be included in conveying the object code work.
A “User Product” is either (1) a “consumer product”, which means any tangible personal property which is
normally used for personal, family, or household purposes, or (2) anything designed or sold for incorporation
into a dwelling. In determining whether a product is a consumer product, doubtful cases shall be resolved in
favor of coverage. For a particular product received by a particular user, “normally used” refers to a typical or
common use of that class of product, regardless of the status of the particular user or of the way in which the
particular user actually uses, or expects or is expected to use, the product. A product is a consumer product
regardless of whether the product has substantial commercial, industrial or non-consumer uses, unless such uses
represent the only significant mode of use of the product.
“Installation Information” for a User Product means any methods, procedures, authorization keys, or other
information required to install and execute modified versions of a covered work in that User Product from
a modified version of its Corresponding Source. The information must suffice to ensure that the continued
functioning of the modified object code is in no case prevented or interfered with solely because modification
has been made.
If you convey an object code work under this section in, or with, or specifically for use in, a User Product, and
the conveying occurs as part of a transaction in which the right of possession and use of the User Product is
transferred to the recipient in perpetuity or for a fixed term (regardless of how the transaction is characterized),
the Corresponding Source conveyed under this section must be accompanied by the Installation Information.
APPENDIX G. LICENSE 96
But this requirement does not apply if neither you nor any third party retains the ability to install modified
object code on the User Product (for example, the work has been installed in ROM).
The requirement to provide Installation Information does not include a requirement to continue to provide sup-
port service, warranty, or updates for a work that has been modified or installed by the recipient, or for the User
Product in which it has been modified or installed. Access to a network may be denied when the modifica-
tion itself materially and adversely affects the operation of the network or violates the rules and protocols for
communication across the network.
Corresponding Source conveyed, and Installation Information provided, in accord with this section must be in
a format that is publicly documented (and with an implementation available to the public in source code form),
and must require no special password or key for unpacking, reading or copying.
7. Additional Terms.
“Additional permissions” are terms that supplement the terms of this License by making exceptions from one
or more of its conditions. Additional permissions that are applicable to the entire Program shall be treated as
though they were included in this License, to the extent that they are valid under applicable law. If additional
permissions apply only to part of the Program, that part may be used separately under those permissions, but the
entire Program remains governed by this License without regard to the additional permissions.
When you convey a copy of a covered work, you may at your option remove any additional permissions from
that copy, or from any part of it. (Additional permissions may be written to require their own removal in certain
cases when you modify the work.) You may place additional permissions on material, added by you to a covered
work, for which you have or can give appropriate copyright permission.
Notwithstanding any other provision of this License, for material you add to a covered work, you may (if
authorized by the copyright holders of that material) supplement the terms of this License with terms:
(a) Disclaiming warranty or limiting liability differently from the terms of sections 15 and 16 of this License;
or
(b) Requiring preservation of specified reasonable legal notices or author attributions in that material or in the
Appropriate Legal Notices displayed by works containing it; or
(c) Prohibiting misrepresentation of the origin of that material, or requiring that modified versions of such
material be marked in reasonable ways as different from the original version; or
(d) Limiting the use for publicity purposes of names of licensors or authors of the material; or
(e) Declining to grant rights under trademark law for use of some trade names, trademarks, or service marks;
or
(f) Requiring indemnification of licensors and authors of that material by anyone who conveys the material
(or modified versions of it) with contractual assumptions of liability to the recipient, for any liability that
these contractual assumptions directly impose on those licensors and authors.
All other non-permissive additional terms are considered “further restrictions” within the meaning of section
10. If the Program as you received it, or any part of it, contains a notice stating that it is governed by this
License along with a term that is a further restriction, you may remove that term. If a license document contains
a further restriction but permits relicensing or conveying under this License, you may add to a covered work
material governed by the terms of that license document, provided that the further restriction does not survive
such relicensing or conveying.
If you add terms to a covered work in accord with this section, you must place, in the relevant source files, a
statement of the additional terms that apply to those files, or a notice indicating where to find the applicable
terms.
Additional terms, permissive or non-permissive, may be stated in the form of a separately written license, or
stated as exceptions; the above requirements apply either way.
8. Termination.
APPENDIX G. LICENSE 97
You may not propagate or modify a covered work except as expressly provided under this License. Any attempt
otherwise to propagate or modify it is void, and will automatically terminate your rights under this License
(including any patent licenses granted under the third paragraph of section 11).
However, if you cease all violation of this License, then your license from a particular copyright holder is
reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license,
and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior
to 60 days after the cessation.
Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder
notifies you of the violation by some reasonable means, this is the first time you have received notice of violation
of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your
receipt of the notice.
Termination of your rights under this section does not terminate the licenses of parties who have received copies
or rights from you under this License. If your rights have been terminated and not permanently reinstated, you
do not qualify to receive new licenses for the same material under section 10.
9. Acceptance Not Required for Having Copies.
You are not required to accept this License in order to receive or run a copy of the Program. Ancillary prop-
agation of a covered work occurring solely as a consequence of using peer-to-peer transmission to receive a
copy likewise does not require acceptance. However, nothing other than this License grants you permission
to propagate or modify any covered work. These actions infringe copyright if you do not accept this License.
Therefore, by modifying or propagating a covered work, you indicate your acceptance of this License to do so.
10. Automatic Licensing of Downstream Recipients.
Each time you convey a covered work, the recipient automatically receives a license from the original licensors,
to run, modify and propagate that work, subject to this License. You are not responsible for enforcing compliance
by third parties with this License.
An “entity transaction” is a transaction transferring control of an organization, or substantially all assets of one,
or subdividing an organization, or merging organizations. If propagation of a covered work results from an
entity transaction, each party to that transaction who receives a copy of the work also receives whatever licenses
to the work the party’s predecessor in interest had or could give under the previous paragraph, plus a right to
possession of the Corresponding Source of the work from the predecessor in interest, if the predecessor has it or
can get it with reasonable efforts.
You may not impose any further restrictions on the exercise of the rights granted or affirmed under this License.
For example, you may not impose a license fee, royalty, or other charge for exercise of rights granted under
this License, and you may not initiate litigation (including a cross-claim or counterclaim in a lawsuit) alleging
that any patent claim is infringed by making, using, selling, offering for sale, or importing the Program or any
portion of it.
11. Patents.
A “contributor” is a copyright holder who authorizes use under this License of the Program or a work on which
the Program is based. The work thus licensed is called the contributor’s “contributor version”.
A contributor’s “essential patent claims” are all patent claims owned or controlled by the contributor, whether
already acquired or hereafter acquired, that would be infringed by some manner, permitted by this License,
of making, using, or selling its contributor version, but do not include claims that would be infringed only
as a consequence of further modification of the contributor version. For purposes of this definition, “control”
includes the right to grant patent sublicenses in a manner consistent with the requirements of this License.
Each contributor grants you a non-exclusive, worldwide, royalty-free patent license under the contributor’s
essential patent claims, to make, use, sell, offer for sale, import and otherwise run, modify and propagate the
contents of its contributor version.
In the following three paragraphs, a “patent license” is any express agreement or commitment, however denomi-
nated, not to enforce a patent (such as an express permission to practice a patent or covenant not to sue for patent
APPENDIX G. LICENSE 98
infringement). To “grant” such a patent license to a party means to make such an agreement or commitment not
to enforce a patent against the party.
If you convey a covered work, knowingly relying on a patent license, and the Corresponding Source of the
work is not available for anyone to copy, free of charge and under the terms of this License, through a publicly
available network server or other readily accessible means, then you must either (1) cause the Corresponding
Source to be so available, or (2) arrange to deprive yourself of the benefit of the patent license for this particular
work, or (3) arrange, in a manner consistent with the requirements of this License, to extend the patent license to
downstream recipients. “Knowingly relying” means you have actual knowledge that, but for the patent license,
your conveying the covered work in a country, or your recipient’s use of the covered work in a country, would
infringe one or more identifiable patents in that country that you have reason to believe are valid.
If, pursuant to or in connection with a single transaction or arrangement, you convey, or propagate by procuring
conveyance of, a covered work, and grant a patent license to some of the parties receiving the covered work
authorizing them to use, propagate, modify or convey a specific copy of the covered work, then the patent
license you grant is automatically extended to all recipients of the covered work and works based on it.
A patent license is “discriminatory” if it does not include within the scope of its coverage, prohibits the exercise
of, or is conditioned on the non-exercise of one or more of the rights that are specifically granted under this
License. You may not convey a covered work if you are a party to an arrangement with a third party that is in
the business of distributing software, under which you make payment to the third party based on the extent of
your activity of conveying the work, and under which the third party grants, to any of the parties who would
receive the covered work from you, a discriminatory patent license (a) in connection with copies of the covered
work conveyed by you (or copies made from those copies), or (b) primarily for and in connection with specific
products or compilations that contain the covered work, unless you entered into that arrangement, or that patent
license was granted, prior to 28 March 2007.
Nothing in this License shall be construed as excluding or limiting any implied license or other defenses to
infringement that may otherwise be available to you under applicable patent law.
12. No Surrender of Others’ Freedom.
If conditions are imposed on you (whether by court order, agreement or otherwise) that contradict the conditions
of this License, they do not excuse you from the conditions of this License. If you cannot convey a covered work
so as to satisfy simultaneously your obligations under this License and any other pertinent obligations, then as
a consequence you may not convey it at all. For example, if you agree to terms that obligate you to collect a
royalty for further conveying from those to whom you convey the Program, the only way you could satisfy both
those terms and this License would be to refrain entirely from conveying the Program.
13. Use with the GNU Affero General Public License.
Notwithstanding any other provision of this License, you have permission to link or combine any covered work
with a work licensed under version 3 of the GNU Affero General Public License into a single combined work,
and to convey the resulting work. The terms of this License will continue to apply to the part which is the
covered work, but the special requirements of the GNU Affero General Public License, section 13, concerning
interaction through a network will apply to the combination as such.
14. Revised Versions of this License.
The Free Software Foundation may publish revised and/or new versions of the GNU General Public License
from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to
address new problems or concerns.
Each version is given a distinguishing version number. If the Program specifies that a certain numbered version
of the GNU General Public License “or any later version” applies to it, you have the option of following the
terms and conditions either of that numbered version or of any later version published by the Free Software
Foundation. If the Program does not specify a version number of the GNU General Public License, you may
choose any version ever published by the Free Software Foundation.
If the Program specifies that a proxy can decide which future versions of the GNU General Public License can
be used, that proxy’s public statement of acceptance of a version permanently authorizes you to choose that
version for the Program.
APPENDIX G. LICENSE 99
Later license versions may give you additional or different permissions. However, no additional obligations are
imposed on any author or copyright holder as a result of your choosing to follow a later version.
15. Disclaimer of Warranty.
THERE IS NO WARRANTY FOR THE PROGRAM, TO THE EXTENT PERMITTED BY APPLICABLE
LAW. EXCEPT WHEN OTHERWISE STATED IN WRITING THE COPYRIGHT HOLDERS AND/OR
OTHER PARTIES PROVIDE THE PROGRAM “AS IS” WITHOUT WARRANTY OF ANY KIND, EITHER
EXPRESSED OR IMPLIED, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF
MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE. THE ENTIRE RISK AS TO THE
QUALITY AND PERFORMANCE OF THE PROGRAM IS WITH YOU. SHOULD THE PROGRAM PROVE
DEFECTIVE, YOU ASSUME THE COST OF ALL NECESSARY SERVICING, REPAIR OR CORRECTION.
16. Limitation of Liability.
IN NO EVENT UNLESS REQUIRED BY APPLICABLE LAW OR AGREED TO IN WRITING WILL ANY
COPYRIGHT HOLDER, OR ANY OTHER PARTY WHO MODIFIES AND/OR CONVEYS THE PRO-
GRAM AS PERMITTED ABOVE, BE LIABLE TO YOU FOR DAMAGES, INCLUDING ANY GENERAL,
SPECIAL, INCIDENTAL OR CONSEQUENTIAL DAMAGES ARISING OUT OF THE USE OR INABIL-
ITY TO USE THE PROGRAM (INCLUDING BUT NOT LIMITED TO LOSS OF DATA OR DATA BEING
RENDERED INACCURATE OR LOSSES SUSTAINED BY YOU OR THIRD PARTIES OR A FAILURE OF
THE PROGRAM TO OPERATE WITH ANY OTHER PROGRAMS), EVEN IF SUCH HOLDER OR OTHER
PARTY HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAMAGES.
17. Interpretation of Sections 15 and 16.
If the disclaimer of warranty and limitation of liability provided above cannot be given local legal effect accord-
ing to their terms, reviewing courts shall apply local law that most closely approximates an absolute waiver of
all civil liability in connection with the Program, unless a warranty or assumption of liability accompanies a
copy of the Program in return for a fee.
END OF TERMS AND CONDITIONS
How to Apply These Terms to Your New Programs
If you develop a new program, and you want it to be of the greatest possible use to the public, the best way to
achieve this is to make it free software which everyone can redistribute and change under these terms.
To do so, attach the following notices to the program. It is safest to attach them to the start of each source file
to most effectively state the exclusion of warranty; and each file should have at least the “copyright” line and a
pointer to where the full notice is found.
<one line to give the program’s name and a brief idea of what it does.>
Copyright (C) <textyear> <name of author>
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program. If not, see <http://www.gnu.org/licenses/>.
Also add information on how to contact you by electronic and paper mail.
If the program does terminal interaction, make it output a short notice like this when it starts in an interactive
mode:
APPENDIX G. LICENSE 100
<program> Copyright (C) <year> <name of author>
This program comes with ABSOLUTELY NO WARRANTY; for details type ‘show w’.
This is free software, and you are welcome to redistribute it
under certain conditions; type ‘show c’ for details.
The hypothetical commands show w and show c should show the appropriate parts of the General Public
License. Of course, your program’s commands might be different; for a GUI interface, you would use an “about
box”.
You should also get your employer (if you work as a programmer) or school, if any, to sign a “copyright
disclaimer” for the program, if necessary. For more information on this, and how to apply and follow the GNU
GPL, see http://www.gnu.org/licenses/.
The GNU General Public License does not permit incorporating your program into proprietary programs. If
your program is a subroutine library, you may consider it more useful to permit linking proprietary applications
with the library. If this is what you want to do, use the GNU Lesser General Public License instead of this
License. But first, please read http://www.gnu.org/philosophy/why-not-lgpl.html.