Module Guide

User Manual:

Open the PDF directly: View PDF .
Page Count: 24

ﬂowPsi Module Guide

May 31, 2019

Contents

1 Introduction 1

1.1 Loci FVM Module Facilities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

1.2 ﬂowPsi facilitiesandvariables............................ 3

2 Custom Output 6

3 Custom Boundary Condition Input 8

4 Custom Initial Conditions 10

5 Surface Integration 11

6 Volume Integration 13

7 Adding a Volume Source 14

8 Scalar Transport 16

8.1 TracerVariableExample............................... 17

8.2 The Menter one equation turbulence model . . . . . . . . . . . . . . . . . . . . 17

8.2.1 Implementation................................ 18

1 Introduction

This module guide provides a set of tutorials for creating add on modules for the ﬂowPsi

solver. It is assumed that the reader has some basic understanding of the Loci programming

model. To gain that understanding please work through the tutorial provided with the Loci

framework. This document and examples will extend that tutorial to describe how to create

common types of extensions to the ﬂowPsi solver. In general modules are loaded into ﬂowPsi by

ﬁrst making sure that the directory that contains the module is either in the LD LIBRARY PATH

or the LOCI MODULE PATH environment variable. Then the modules can be loaded into your

ﬂowPsi case by adding a loadModule: followed by the module name at the top of the vars ﬁle.

The Makefile provided in these example directories are easy to use and can be copied for your

module development. The Makefile is designed such that all ﬁles that end in with the .loci

postﬁx will be compiled into a module. The ﬁle only needs to be edited to provide the module

name and the FLOWPSI BASE directory that points to where the ﬂowPsi solver is installed.

1.1 Loci FVM Module Facilities

Before we begin discussing building modules for ﬂowPsi lets review some of the basic facilities

that Loci provides for ﬁnite volume solvers that ﬂowPsi utilizes. First, ﬂowPsi uses the face

based data-structure that includes the face2node map that provides an ordered listing of the

nodes that form each face in the mesh as well as the cl and cr maps that provide the maps

from the face to the left and right cells. Faces on the boundary always have normals pointing

out of the domain and therefore the cl map points to the cell next to the boundary while the

cr cell may point to a ghost cell (in ﬂowPsi, ghost cells are only used to implement periodic

boundary conditions). The ci and ref maps are only deﬁned for boundary faces where ci

refers to the adjacent cell inside the mesh and ref refers to the reference surface that forms the

facets of that boundary. The pmap map associates the periodic boundary face with its periodic

pair. The cell to face maps upper,lower, and boundary map is used to form matrices that are

based on the face connectivity where upper refers to the faces that form the upper and lower

triangular matrix entries and the boundary map identiﬁes boundary faces of the cell.

In addition to these data structure elements, the Loci FVM module provides some generic

rules for computing grid metrics such as face areas and cell volumes. Additionally the module

provides some basic facilities for computing gradients and interpolating solutions from cells

to nodes for plot output. These facilities generally will need the cell center values and the

boundary face values. The boundary face values will have the naming convention of having a

fpostﬁx annotation denoting that it is a face value. A table that summarizes that facilities

provided by the FVM module are provided in table 1.

Table 1: Table of Loci FVM provided utilities

Supplied by Loci FVM facilities

Variable Type Description

Mesh Data Structures

ci map cell next to boundary face

cl map cell on left side of face

cr map cell on right side of face

ref map map from boundary faces to surface

face2node multiMap map from face to nodes

pmap map periodic matching face

upper multiMap map from cell to upper faces

lower multiMap map from cell to lower faces

boundary map multiMap map from cell to boundary faces

Mesh Metrics

pos vector node positions

cellcenter vector cell centroid location

facecenter vector face centroid location

area composite face area and normal

vol scalar cell volume

gridvol parameter total grid volume

Parametric Rules

grads(X) vector gradient of scalar variable X

gradv3d(X) tensor gradient of vector variable X

gradv(X) generic vector gradient of mixture vector X

grads f(X) vector face gradient of scalar X

gradv3d f(X) tensor face gradient of vector X

gradv f(X) generic vector gradient of mixture vector X

cell2node(X) scalar cell to node interpolation for scalar X

cell2node v3d(X) vector cell to node interpolation for vector X

cell2nodeMax(X) scalar nodal maximum of Xfor connected cells

cell2nodeMin(X) scalar nodal minimum of Xfor connected cells

L1Norm(X) parameter volume integrated L1norm of cell variable X

L2Norm(X) parameter volume integrated L2norm of cell variable X

LinfNorm(X) parameter volume integrated L∞norm of cell variable X

fileNumber(X) integer ﬁle numbering for variable X

Table 2: Table of ﬂowPsi Fluid Properties

ﬂowPsi ﬂuid properties variables

Variable Type Description

rho scalar ﬂuid density

rho f scalar ﬂuid density at face

temperature scalar ﬂuid temperature

temperature f scalar ﬂuid temperature at face

gagePressure scalar ﬂuid pressure reference to Pambient

gagePressure f scalar ﬂuid gage pressure at face

Pambient parameter reference pressure

pressure scalar ﬂuid pressure

uvector ﬂuid velocity in cell

u f vector ﬂuid velocity at face

divu scalar divergence of u

vort vector ﬂuid vorticity

vortMag scalar ﬂuid vorticity magnitude

strainRate scalar strain rate magnitude, S

tau symmetric tensor ﬂuid stress

mu scalar ﬂuid laminar viscosity

mu f scalar ﬂuid laminar viscosity at face

kconduct scalar ﬂuid laminar conductivity

kconduct f scalar ﬂuid laminar conductivity at face

us n scalar face grid velocity dot normal

us vector face grid velocity

Cp parameter ﬂuid Cp

gamma parameter ﬂuid isentropic index, γ

Rtilde parameter ﬂuid gas constant

tmu scalar turbulent viscosity

soundSpeed scalar local speed of sound

1.2 ﬂowPsi facilities and variables

When ﬂowPsi runs the only the conservative variables (and gage pressure) are carried from

time-step to time-step. All other variables that are derived from these conservative variables

are only computed during the Newton iteration. Thus most of the computations in ﬂowPsi

happen as part of the Newton iteration step. This section outlines some of the facilities that

are available during that step. Table 2 gives that generic ﬂuid properties that are available.

Solver speciﬁc variables that can be replaced through priority rules or used in control are shown

in table 3 while the parametric utilities are described in table 4. These tables are provided to

give a brief survey of the kinds of data that is available for interfacing to ﬂowPsi modules.

Table 3: Table of ﬂowPsi solver speciﬁc variables

ﬂowPsi solver speciﬁc variables

Variable Type Description

p0Ref scalar total pressure BC input

T0Ref scalar total temperature BC input

massFluxRef scalar mass ﬂux BC input

temperatureRef scalar temperature BC input

gagePressureRef scalar gagePressure BC input

uRef vector ﬂuid velocity BC input

Twall scalar viscous wall BC temperature

qwall scalar viscous wall BC heat ﬂux

wallVelocity vector viscous wall tangential velocity

src general vector source array for mass, momentum, and energy

iflux Array(5) inviscid ﬂux

vflux Array(4) viscous ﬂux

scalar mdot scalar mass ﬂux through face

srcJ matrix block diagonal jacobian term of src

fjp matrix block jacobian of ﬂux from left

fjm matrix block jacobian of ﬂux from right

min cell2noslip map Map from cell to closest viscous wall

dist noslip scalar distance from cell to nonslip wall

dt parameter timestep value in seconds

stime parameter simulation time in seconds

ncycle parameter simulation step

newtonFinished conditional Newton iteration complete

do restart conditional output restart ﬁles

do output conditional text output

do plot conditional plot ﬁle output

do boundary plot conditional boundary plot ﬁle output

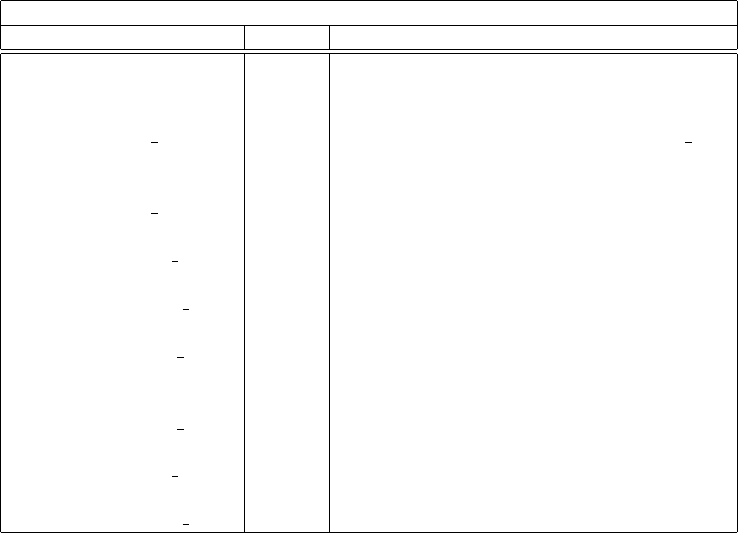
Table 4: Table of ﬂowPsi parametric variables

ﬂowPsi parametric variables

Variable Type Description

scalarTransport(X,C) generic build transport of scalar X, enabled by C

scalarTransportP(X,C) generic like above for positive scalar X

scalarMean(X) scalar time averaged cell value X

scalarMean f(X) scalar time averaged boundary face value X f

scalarVariance(X) scalar time variance of variable X

vect3dMean(X) vector time averaged vector mean

vect3dMean f(X) vector time averaged boundary vector mean

vect3dVariance(X) vector time variance of vector X

vect3dVariance f(X) vector time variance of boundary vector

vect3dCoVariance(X) vector co-variance of vector X

vect3dCoVariance f(X) vector co-variance of boundary vector x

scalarFavreMean(X) scalar Favre average of variable X

scalarFavreMean f(X) scalar Favre average of boundary variable

scalarFavreVar(X) scalar Favre weighted variance

vect3dFavreMean(X) vector vector Favre weighted mean

vect3dFavreMean f(X) vector vector Favre weighted boundary mean

vect3dFavreVar(X) vector vector Favre weighted variance

vect3dFavreVar f(X) vector vector Favre weighted variance boundary

vect3dFavreCoVar(X) vector vector Favre weighted co-variance

vect3dFavreCoVar f(X) vector vector Favre weighted co-variance boundary

2 Custom Output

One of the more common needs for add-on modules is the development of derived variable com-

putations. While it is possible to compute derived variables directly in post-processing software,

these computations can sometimes be misleading due to the fact that they are performed on

interpolated data which may introduce errors in the derived computations. So it is sometimes

useful to perform computations directly on the cell values before interpolation in order to get

more satisfactory results. For this example we will consider the output of a variable that can be

used for numerical schlieren imaging. This is done by computing the logarithm of the density

gradient. So in this example we will show how one goes about computing and outputting such

a variable in a module.

The ﬁrst step to this is to copy the Makeﬁle provided in the examples which will automatically

compile all .loci ﬁles in the directory. The only change that is needed is to set the MODULE NAME

variable in the Makeﬁle to the name that you wish to use in the loadModule line of the vars

ﬁle. In this case we will call the module schlieren, or

# What is the name of the module given to loadModule

MODULE_NAME = schlieren

At this point we can begin editing our Loci program which we will conveniently name schlieren.loci.

At the beginning of the ﬁle we need to include some ﬁles that will be needed to access the fa-

cilities we will be using. This is accomplished with the following includes:

// Include Loci system

#include <Loci.h>

// defines types used by flowPsi

#include "flowTypes.h"

// imports flowPsi IO functionality

#include "flowPsiIO.h"

// defines Loci types for flowPsi variables

$include "flowPsi.lh"

It is convenient but not necessary to add the code in the C++ namespace called flowPsi.

Alternatively, we can add the code in our own namespace but add code to tell C++ to use

variables from the flowPsi namespace such as:

namespace schlieren {

using namespace flowPsi ;

We now need to compute the variable that we are going to plot. Since ﬂowPsi computes

unknowns at cell centers this will be where we perform the computations. However, to improve

nodal interpolation accuracy we also need to compute the target variables for all boundary

faces as well. Since these variables are not part of the ﬂowPsi infrastructure we will need to

deﬁne their types ﬁrst:

// define types for cell and boundary face values

$type loggradrho store<double> ;

$type loggradrho_f store<double> ;

Then write rules to deﬁne how to compute these variables as well. These computations will use

the scalar gradient parametric rules provided by Loci’s FVM module. The rules will be deﬁned

as:

// To interpolate to the nodal values we need both cell values and boundary

// face values. Thus we have two rules to compute the value of interest

$rule pointwise(loggradrho<-grads(rho)) {

$loggradrho = log10(max(norm($grads(rho)),1e-4)) ;

}

$rule pointwise(loggradrho_f<-grads_f(rho)) {

$loggradrho_f = log10(max(norm($grads_f(rho)),1e-4)) ;

}

At this point we have deﬁned the variable that we wish to compute but as they are deﬁned

now they will not be computed because ﬂowPsi will never request these variables. Instead we

will want to tell ﬂowPsi that these variables are ones that we need plot ﬁles. For this, ﬂowPsi

provides a macro called OUTPUT SCALAR that interfaces with the ﬂowPsi plotting facilities. It

will allow this variable to be written out when requested by placing the given variable name in

the plot output variable in the vars ﬁle. This is accomplished with the line:

OUTPUT_SCALAR("cell2node(loggradrho)", schlieren) ;

This line tells the code to write out the variable cell2node(loggradrho) as a variable named

schlieren. Note that the variable that we wrote out is not the variable that we computed.

This is because volume data is plotted from nodal values and since ﬂowPsi computes its degrees

of freedom at the cells, an interpolation function is needed to compute the nodal values. The

cell2node parametric rules provided by the Loci FVM module performs this function. This

parametric rule will access the variables that we deﬁned earlier. Also this macro will enable

requesting this variable on cutting plane and isosurface output from ﬂowPsi as well.

In addition to volume data, we can also output boundary facet data. This is provided with the

macro OUTPUT BNDRY SCALAR. So if we wish to output the schlieren variable for the boundary

facets we can add the following line to or loci ﬁle:

OUTPUT_BNDRY_SCALAR("loggradrho_f",schlierenb,"ci") ;

The ﬁrst argument of this macro is the variable that we wish to plot, while the second is the

name of the variable (hear with a b appended to diﬀerentiate boundary facet data from the

nodal data). Finally, the last argument deﬁnes the set of boundaries that we wish to write this

data. Since all boundary faces have the attribute ci this will write out for all boundary faces.

Also not, for outputting 3D vector data replace the SCALAR with VECTOR in the above macros.

3 Custom Boundary Condition Input

Most of the boundary conditions provided by ﬂowPsi can be customized. Typically the inputs

for each boundary face are assigned to a Ref variables that can be overridden by modules to

change the basic behavior. For this example we will demonstrate this in a simple boundary

condition where the pressure is perturbed by a sinusoidal signal. In this particular case we will

override the deﬁnition of the gageP ressureRef variable so that instead of being the constant

deﬁned in the boundary condition, it will instead be a time varying value. Note, it is possible

to also change the boundary condition to be reactive to the solution itself. However, in these

cases the stability of the resulting boundary condition cannot be guaranteed.

To add this capability to an inﬂow boundary condition we want to be able to add a speciﬁcation

to each boundary where we want to add the perturbation that will give the amplitude and

frequency of the disturbance. By default the ﬂowPsi boundary condition checking code will

not allow these parameters to be added without generating error messages. Therefore it is

necessary to register these new boundary condition arguments with ﬂowPsi. This checker for

the boundary conditions are deﬁned in the read grid.h header ﬁle which will need to be

included. The checker for these two new variables is added through the following code:

// Here we create a checking class that inherits from BC_Check that is defined

// in readGrid.h

class pwave_check : public BC_Check {

string error_message ;

public:

// List which boundary conditions this checker is for

std::string boundaryConditions() { return "inflow,supersonicInflow,farfield" ; }

// List which variables this checker will verify

std::string variablesChecked() { return "amplitude,frequency" ; }

// Check for the existence of amplitude and frequency

// in our implementation these are optional, but if amplitude is

// given then frequency must also be given

bool checkOptions(const options_list& bc_options) {

error_message = "" ;

bool check = true ;

if(bc_options.optionExists("amplitude")) {

if(!check_scalar_units(bc_options,"amplitude","Pa")) {

error_message += "Pressure units needed for ’amplitude’ " ;

check = false ;

}

if(!bc_options.optionExists("frequency")) {

error_message += "’amplitude’ must also specify ’frequency’ " ;

check = false ;

}

return check ;

}

// Print out error messsage. Used if checker fails to generate error

// message to the user. Usually the error message is remembered from

// when the checker was run.

std::ostream &ErrorMessage(std::ostream &s) {

}

} ;

// The register_BC template registers this object in the boundary checker

// database. The names are not important only that we create the object

// so that it is registered.

register_BC<pwave_check> register_BC_pwave_check ;

Next we will need to extract the values for amplitude and pressure from the BC options variable

that is deﬁned for each boundary surface. For this we will use the constraint that is created

by the FVM grid reader that indicates what parameter are deﬁned in the BC options variable.

This will ensure that the variables will only be extracted for the boundary conditions where

these arguments are speciﬁed. The rules that extract these variables are as follows:

$type amplitude_BC store<real> ;

$rule pointwise(amplitude_BC<-BC_options),constraint(amplitude_BCoption) {

$BC_options.getOptionUnits("amplitude","Pa",$amplitude_BC) ;

}

$type frequency_BC store<real> ;

$rule pointwise(frequency_BC<-BC_options),constraint(frequency_BCoption) {

$BC_options.getOption("frequency",$frequency_BC) ;

}

We can now compute the time varying prescribed pressure and override the gagePressureRef

variable that will be used by the inﬂow boundary condition.

$type pgDelta_BC store<real> ;

$rule pointwise(pgDelta_BC<-stime,amplitude_BC,frequency_BC) {

$pgDelta_BC = $amplitude_BC*sin($stime*$frequency_BC*2.*M_PI) ;

}

// Override the reference condtions for the faces that adds in the

// perturbation. This will be used instead of the default settings

$rule pointwise(distrbance::gagePressureRef<-

ref->(gagePressureRef_BC,pgDelta_BC)) {

$gagePressureRef = $ref->$gagePressureRef_BC + $ref->$pgDelta_BC ;

}

Other variables can also be overridden using a similar process. For a complete list of the Ref

variables that can be overridden see table 3.

4 Custom Initial Conditions

// For the initial conditons we define temperature_ic, gagePressure_ic, and

// initial velocity (u_ic)

$rule pointwise(temperature_ic,gagePressure_ic,u_ic<-

Rtilde,cellcenter,Pambient),constraint(geom_cells) {

const double x = $cellcenter.x ;

const double y = $cellcenter.y ;

double coef = 3.5 ;

double u = -1.*coef*cos(x)*sin(y) ;

double v = coef*sin(x)*cos(y) ;

double Pref = $Pambient ;

if(Pref < 10)

Pref = 1e5 ;

double rho = 1.0 ;

double p0 = Pref-$Pambient ;

double pg = p0-rho*0.25*coef*coef*(cos(2.*x)+cos(2.*y)) ;

double P = pg+$Pambient ;

double T = P/($Rtilde*rho) ;

$gagePressure_ic = pg ;

$temperature_ic = T ;

$u_ic = vect3d(u,v,0.0) ; ;

}

5 Surface Integration

In this example we consider how to add a module that can integrate a function over the boundary

surfaces of the mesh. In this example we will compute the area averaged temperature over all of

the boundary surfaces of the mesh. In general, Loci is quite ﬂexible and will allow a wide range

of possible strategies for this. In eﬀect, an integration is simply a reduction with the summation

operator over some set of entities that deﬁnes the surface of interest. How does one identify

the set of interest? Actually one could identify the set of interest in many diﬀerent ways.

First, one could use the assigned boundary condition type. For example, one could integrate

over the set deﬁned by the constraint viscousWall BC which would include all boundaries

that were assigned the viscousWall boundary condition. Alternatively, the user could deﬁne

a new boundary condition argument that would allow a user to mark that boundary with a

special integrate ﬂag (say integrate) and then use a constraint of ref->integrate BCoption

to determine the set. In this example we use the parametric facility to integrate over each

boundary surface separately. To do this we use the fact that for each boundary a parametric

variable will be created in by the grid reader of the form boundaryName(X) where Xis replaced

by each boundary surface name. This is a string parameter which is deﬁned over the set of

faces that form that boundary surface. For our mean temperature we will use an area weighted

average, so at ﬁrst we will compute the total area for each boundary with the rule:

// This sets up the initial value of the boundary area before summing over

// faces. This needs to be set to zero as this is the indentity of the

// summation operator

$rule unit(boundaryArea_X<-boundaryName(X)),parametric(boundaryName(X)) {

$boundaryArea_X = 0 ;

}

// Add the areas from each face. In some cases, for example when

// running in axisymmetric mode the area might be zero, so the max

// function is there to keep that case from generating a divide by zero

// condition.

$rule apply(boundaryArea_X<-area,boundaryName(X))[Loci::Summation],

parametric(boundaryName(X)) {

// note, the area is the sada component of the area input, the n component

// is the normal vector

join($boundaryArea_X,max($area.sada,1e-13)) ;

}

In this set of parametric rules the boundaryArea X variable will be created for each boundary

condition with the Xreplaced by each boundary name. Now we can compute the weighted

temperature with the following rules:

// Now we will compute the area weighted average temperature

$type boundaryMeanTemp_X param<real> ;

// set the initial value for the mean temp

$rule unit(boundaryMeanTemp_X<-boundaryName(X)),parametric(boundaryName(X)) {

$boundaryMeanTemp_X = 0 ;

}

// Now compute the weighted sum of the of the temperature. The temperature

// at the boundary face is given by temperature_f

$rule apply(boundaryMeanTemp_X<-area,temperature_f,boundaryArea_X,boundaryName(X))[Loci::Summation],

parametric(boundaryName(X)) {

double weight = max($area.sada,1e-13)/$boundaryArea_X ;

join($boundaryMeanTemp_X,weight*$temperature_f) ;

}

Now we can output the integrated value. Note, that although this appears to be one rule, one

will be instantiated for each boundary surface. In the end this will generate output for each

boundary.

// Now output to stdout the average temperature. Do this output only

// when the code is outputting boundary plot files.

// Note, since this is only output once, we use the prelude and

// because we are in the prelude we must use the dereference operatpr

// ’*’ to access the computed parameters. The $[Once] tells Loci that

// you only want to output this once even when running in parallel where

// there would be multiple instances of execution

$rule pointwise(OUTPUT<-boundaryMeanTemp_X,boundaryName(X)),

conditional(do_boundary_plot),

parametric(boundaryName(X)), prelude {

$[Once] {

cout << "Boundary " << *$boundaryName(X) << " has mean temperature of "

<< *$boundaryMeanTemp_X << " Kelvin" << endl ;

}

} ;

//^ This semicolon is needed because we are not following the prelude

// section with a compute section.

6 Volume Integration

In this example we will show how to perform a volume integration over each named component

of the mesh. This will work similarly to the surface integration except that we will use the

volumeTag(X) parametric variable instead. For this example we will compute the integrated

ﬂuid kinetic energy by simply adding up the kinetic energy integrated over each cell. The basic

approach is as follows:

// KEComponent_X is the integrated kinetic energy for component X. This

// rule is parametric so one of these variables will be created for each

// component.

$type KEComponent_X param<double> ;

$rule unit(KEComponent_X),constraint(volumeTag(X)),

parametric(volumeTag(X)) {

$KEComponent_X = 0 ;

}

// Here we integrate the kinetic energy over each cell which by use

// of the midpoint rule is simply vol*rho*0.5*dot(u,u), then the sum

// is the total kinetic energy

$rule apply(KEComponent_X<-vol,rho,u)[Loci::Summation],

constraint(volumeTag(X)),parametric(volumeTag(X)) {

double kecell = 0.5*$vol*$rho*dot($u,$u) ;

join($KEComponent_X,kecell) ;

}

Then KEComponent X can be written out to the screen in a similar fashion as the previous

example.

7 Adding a Volume Source

Another common type of addition to the solver is to add a new source term to the equations.

In this example we add a body force to return momentum that is lost to viscous walls for

the purpose of computing channel ﬂow type of simulations. When using the implicit solver a

jacobian may need to also be computed depending on the stiﬀness of the source term. In ﬂowPsi

there are two diﬀerent possible jacobian types that will need to be supported to support all

implicit formulations. By default the code uses jacobians with respect to the primitive variables

density and gage pressure, but in modes using the local preconditioner it will use temperature

and gage pressure instead. If you want to support both modes of operation you will need to

deﬁne both types of jacobians.

For the channel ﬂow case we ﬁrst need to ﬁnd out how much momentum was lost through the

ﬂuid interaction with the viscous walls. For this we utilize a convenience variable (AllViscousBCs)

that contains all viscous boundary conditions including viscousWall and wallLaw. For the

integration of the momentum ﬂux we consider both the inviscid ﬂux, iflux, and the viscous

ﬂux vflux. Since these variables contain mass, momentum, and energy ﬂuxes, we need to

extract just the part that we are going to use. For the inviscid ﬂux we skip the ﬁrst item as

this is the mass ﬂux. For the viscous ﬂux the ﬁrst item is the momentum ﬂux as there is no

mass ﬂux in the variable vflux

$type viscousWallMomentumFlux param<vect3d> ;

$rule unit(viscousWallMomentumFlux),constraint(UNIVERSE) {

$viscousWallMomentumFlux = vect3d(0,0,0) ;

}

// Note viscous and inviscid flux have already been integrated over the

// boundary facet area. We just need to sum up their contributions

$rule apply(viscousWallMomentumFlux<-iflux)[Loci::Summation],

constraint(AllViscousBCs) {

const int mi = 1

// extract inviscid momentum flux

vect3d mflux($iflux[mi+0],$iflux[mi+1],$iflux[mi+2]) ;

join($viscousWallMomentumFlux,mflux) ;

}

$rule apply(viscousWallMomentumFlux<-vflux,qvi)[Loci::Summation],

constraint(AllViscousBCs) {

const int mi = 0 ;

// extract viscous momentum flux

vect3d mflux($vflux[mi+0],$vflux[mi+1],$vflux[mi+2]) ;

join($viscousWallMomentumFlux,mflux) ;

}

Now we can compute the total force that we need to add back into the system to restore the lost

momentum. To do this we also integrate the total mass in the volume using a similar unit/apply

rule combination to compute the variable massSum. The body force is then computed for each

cell based on the local density. We also add a term to the energy equation to account for

the energy added to the system due to this addition (since we do not wish this energy to be

deducted from the internal energy of the ﬂuid). Adding the resulting body force to the solver

then is implemented as:

//add friction loss to the source term

$rule apply(src<-dragAccel,rho,vol,cellcenter,u)[Loci::Summation] {

const int mi = 1 ;

const int mj = mi + 1 ;

const int mk = mi + 2 ;

const int ei = 4 ;

$src[mi] += $dragAccel.x*$rho*$vol ;

$src[mj] += $dragAccel.y*$rho*$vol ;

$src[mk] += $dragAccel.z*$rho*$vol ;

$src[ei] += $dragAccel.x*$u.x*$rho*$vol ;

}

The jacobians in ﬂowPsi are computed with respect to the primitive variables gage pressure,

temperature, and velocity. The jacobians for the diagonal blocks are stored in the variable

srcJ. For this simple source term the jacobians are straightforward to implement which is

shown below:

$rule apply(srcJ<-rho,gagePressure,temperature,Pambient,u,dragAccel,vol)[Loci::Summation],

constraint(vol) {

const int mi = 1 ;

const int mj = mi + 1 ;

const int mk = mi + 2 ;

const int ei = 4 ;

const real drdt = -$rho/$temperature ;

const real drdp = $rho/($gagePressure+$Pambient) ;

real coefP = drdp*$vol ;

real coefT = drdt*$vol ;

real rho_vol = $rho*$vol ;

$srcJ[mi][4] += $dragAccel.x*coefP ;

$srcJ[mj][4] += $dragAccel.y*coefP ;

$srcJ[mk][4] += $dragAccel.z*coefP ;

$srcJ[ei][4] += dot($dragAccel,$u)*coefP ;

$srcJ[mi][0] += $dragAccel.x*coefT ;

$srcJ[mj][0] += $dragAccel.y*coefT ;

$srcJ[mk][0] += $dragAccel.z*coefT ;

$srcJ[ei][0] += dot($dragAccel,$u)*coefT ;

$srcJ[ei][mi] += $dragAccel.x*rho_vol ;

$srcJ[ei][mj] += $dragAccel.y*rho_vol ;

$srcJ[ei][mk] += $dragAccel.z*rho_vol ;

}

8 Scalar Transport

The ﬂowPsi code provides an infrastructure that makes it simple to add new variables that

will be transported with the ﬂuid ﬂow. These variables makes it simple to add new models

to accompany the basic ﬂuid ﬂow. In this section we will discuss two examples. First the

development of a simple tracer variable that can inject spatially distributed sine waves that can

be convected with the ﬂow and a second which goes through the implementation of a simple

one equation turbulence model. One advantage of using the scalar transport facilities is that

these facilities include interfaces with the restart, overset, and time integration facilities of the

ﬂowPsi solver. Thus the scalar transport facilities gives a comprehensive way of adding new

variables to the ﬂow solver.

Before we begin, we will have a quick review of the implementation of the scalar transport

equations. The scalar transport equation in conservative form is written for a convected scalar,

φas ∂ρφ

∂t +∇ · (ρuφ) = ∇ · (λ∇φ) + Sφ,(1)

where ρis the ﬂuid density, uis the ﬂuid velocity vector, λis a diﬀusion coeﬃcient, and Sφ

is a prescribed source term. We note that by substituting φ= 1 into the above equation one

recovers the global continuity equation. We discretize the above equation in time and space to

arrive at the expression

∆t(1 + ψ)(φn+1ρn+1 −φnρn) + ψ(φnρn−φn−1ρn−1)= (2)

−Xφn+1

u˙mf+XDφf+Sφ,

where φuis an upwinded extrapolation of φbased on the sign of the face mass ﬂux ˙mand Dφf

is the numerical diﬀusion ﬂux for scalar φ. Note that the discrete continuity equation is given

∆t(1 + ψ)(ρn+1 −ρn) + ψ(ρn−ρn−1)=−X˙mf.(3)

To improve the diagonal dominance of the scheme we employ a trick where we recognize that

Eq. (3) is zero when the system of equation is solved, thus we multiply Eq. (3) by φn+1 and

subtract it from Eq. (3) to arrive at the following expression:

∆t(1 + ψ)φn+1 −φnρn+φnρn−φn−1ρn−1ψ−ρn−ρn−1φn+1ψ−(4)

hφn+1 X˙mf−Xφn+1

u˙mf+XDφf+Sφi=Lφ(φn+1)=0.

The above operator, Lφ, is solved using a Newton method concurrently with the ﬂuid equations.

These facilities can be enable to track the convection and diﬀusion of any arbitrary scalar. The

facility is provided by the parametric variables scalarTransport(X,C) or scalarTransportP(X,C)

where the ﬁrst version is for variables that can be of any sign while the second is for variables

that are always positive. The ﬁrst Xargument to the parameter is the name of the scalar to be

transported, while the second Cargument is a constraint that can be used to activate/deactivate

the scalar integration. Accessing this variable causes an entire iterative infrastructure to be

constructed that solves the scalar transport equations which can then be augmented with addi-

tional source terms to create a wide variety of models. An arbitrary number of scalar transport

equations can be constructed.

8.1 Tracer Variable Example

The ﬁrst example that we have is simply the convection of a tracer variable that will simply

be convected with the ﬂow. This will allow us to show how to set up the boundary and initial

conditions are setup. For this we will create the scalar transport for the variable tracer.

To setup ﬂowPsi to transport the variable we ﬁrst need to instantiate the scalar transport

equations. This is accomplished with the line:

$rule pointwise(OUTPUT<-scalarTransport(tracer,UNIVERSE)) { }

Note that this rule will never actually execute. Instead, the existence of this rule will cause the

parametric scalarTransport variable to be instantiated for the variable tracer. Setting the

second argument to UNIVERSE ensures that this scalar transport model will be always active.

To complete the scalar transport equations we need to provide the state of the tracer variable

at the boundaries. For this we deﬁne the boundary variable tracer bc. In general we will

deﬁne the variable for whatever our scalar name is followed by the bc postﬁx. In this case we

will use a spatially sinusoidal function for boundaries that we mark as having the tracer and set

the function to zero otherwise. By default the boundary condition will use simple upwinding

to determine the value of tracer f. To deﬁne this we simply use the rules:

$type tracer_bc store<real> ;

$rule pointwise(tracer_bc),constraint(ref->BC_options) {

$tracer_bc = 0 ;

}

$rule pointwise(marker::tracer_bc<-facecenter,tracerNormal,tracerPt,tracerInterval),constraint(ref->tracer_BCoption) {

real r = 2.*M_PI*dot($facecenter-$tracerPt,$tracerNormal)/$tracerInterval ;

$tracer_bc = cos(r) ;

}

Finally we need to output the tracer so that we can see where the tracer advected in the

simulation. This is accomplished with the line:

OUTPUT_SCALAR("cell2node(tracer)",tracer) ;

That is all that is needed to add the most basic type of scalar transport equation. Next we will

show how to develop a model with more comprehensive set of parts: a turbulence model.

8.2 The Menter one equation turbulence model

The Menter one equation turbulence model[1] is formally derived from the k−model after

eliminating kand from the equations by using the deﬁnition of the eddy viscosity and by

assuming that the turbulent shear stress is proportional to the turbulent kinetic energy. The

model solves the following single equation for the undamped eddy viscosity ˜νt:

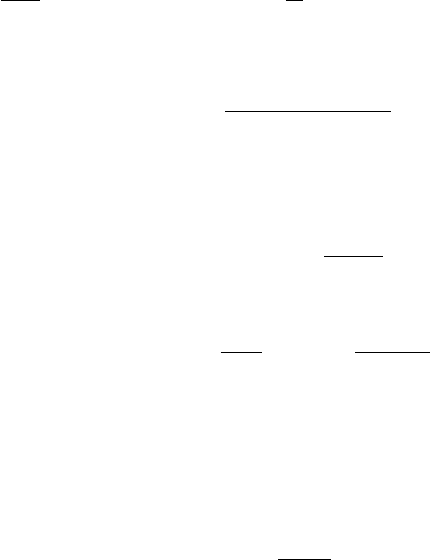
∂ρ˜νt

∂t +∇ · (ρ~u˜νt) = ∇ · ρν+˜νt

σ∇˜νt+ρc1D1˜νtS−ρc2E1e(5)

where Sis the strain rate deﬁned by:

S=q(∇~u)·(∇~u +∇~uT) (6)

The modiﬁed destruction term E1eis deﬁned as:

E1e=c3EBB tanh Ek−

c3EBB ,(7)

where

Ek−= ˜ν2

t1

LV K 2

= ˜ν2

t∇S· ∇S

S2(8)

involves the inverse of the von Karman length scale, and EBB is the Baldwin-Barth destruction

term:

EBB =∇˜νt· ∇˜νt.(9)

The damping terms D1and D2are deﬁned as:

D1=νt+ν

˜νt+ν(10)

D2= 1 −e−(˜νt/A+κν)2,(11)

and the model constants are:

c1= 0.144, c2= 1.86, c3= 7, κ = 0.41, σ = 1, A+= 13 .(12)

The damped eddy viscosity is obtained from:

νt=D2˜νt.(13)

The boundary conditions for ˜νtat a solid wall are ˜νt= 0. The initial and free-stream conditions

are ˜νt∞≤ν∞. The default initial and free-stream value for ˜νtis 5 x 10−9m2/s. Note that the

boundary conditions are given in terms of the undamped eddy viscosity (˜νt) rather than νt.

8.2.1 Implementation

Examining equation (5) we note that the scalar transport will implement the ﬁrst three terms.

We will need to deﬁne the diﬀusion coeﬃcient and the last two terms to implement the turbu-

lence model. First we invoke the scalar transport of the variable nuTM which represents the ˜νt

in the equations. This is accomplished with the following code:

$rule pointwise(OUTPUT<-scalarTransportP(nuTM,menter)) { }

Here we constraint the model by the variable menter which will be deﬁned as part of the model

as the set of constants that are used in the model. For the initial conditions we will extract

nu t from the initial conditions. This is extracted with the following rules:

$type nuTM_ic store<real> ;

$type icRegionInfo blackbox<ICparsedInitRegion> ;

$rule pointwise(nuTM_ic<-icRegionInfo,cellcenter),

constraint(geom_cells,menter) {

double nu_tm ;

$icRegionInfo.defaultState.get_nu_t(nu_tm) ;

$nuTM_ic = nu_tm ;

}

To complete the basic transport of nuTM we need to setup the boundary conditions for the

model For this we deﬁne:

$type nuTM_bcVal store<real> ;

// extract the boundary condition from BC_options

$rule pointwise(nuTM_bcVal<-BC_options) {

real nuTM = 5e-9 ;

if($BC_options.optionExists("nu_t"))

$BC_options.getOption("nu_t",nuTM) ;

$nuTM_bcVal = nuTM ;

}

// set boundary condition

$rule pointwise(nuTM_bc<- ref->nuTM_bcVal) {

$nuTM_bc = $ref->$nuTM_bcVal ;

}

This does not complete the boundary condition however, as the default is to use upwinding to

deﬁne the boundary face values. However for a boundary such as a viscous wall the boundary

value for nuTM f must be set explicitly. This is accomplished with the priority override rule

that will replace the upwind deﬁnition with this Dirichlet one:

$rule pointwise(noslip::nuTM_f),constraint(viscousWall_BC) {

$nuTM_f = 0.0 ;

}

Now we need to deﬁne the scalar diﬀusion term which is the third term in equation (5). This

will be deﬁned by a face value for the diﬀusion coeﬃcient which will have a name derived from

the scalar variable name by appending nu f. The diﬀusion term is thus implemented with the

following rules:

$type nuTM_nu_f store<real> ;

$rule pointwise(nuTM_nu_f<-rho_f,nuTM_f,mu_f,menter) {

const real sigma = $menter.sigma ;

$nuTM_nu_f = ($mu_f+$rho_f*$nuTM_f/sigma) ;

}

// The diffusion coefficient needs nuTM_f at all faces, but the

// infrastructure only defines them at the boundary.

// For interior faces we set the face value to be simply the

// reciprocal volume weighted average of the cell values

$rule pointwise(nuTM_f<-(cr,cl)->(vol,nuTM)) {

real vrvl = 1.0/($cr->$vol+$cl->$vol) ;

$nuTM_f = ($cr->$vol*$cl->$nuTM+$cl->$vol*$cr->$nuTM)*vrvl ;

}

Now we have completely deﬁned the ﬁrst three terms of equation (5). Now what remains is

to deﬁne the destruction and production terms. To add these terms we will use a unit rule

to combine them with the previous terms in the variable nuTM src. First lets consider the

production term which which can be added using the rules:

$type nuTM_prod store<real> ;

$rule pointwise(nuTM_prod<-nuTM,D1,rho,strainRate,vol,menter) {

const real c1 = $menter.c1 ;

const real P_k = $rho*c1*$D1*$nuTM*$strainRate ;

$nuTM_prod = P_k ;

}

//=======================================

// add integrated production term to rhs

//=======================================

$rule apply(nuTM_src<-nuTM_prod,vol)[Loci::Summation] {

$nuTM_src += $nuTM_prod*$vol ;

}

where strainRate is provide by the solver and D1 is the production damping function which

is deﬁned by the rule:

$type D1 store<real> ;

$rule pointwise(D1<-nuTM,tmu,mu,rho) {

const real nut = $tmu/$rho ;

const real nu = $mu/$rho ;

$D1 = (nut+nu)/($nuTM+nu) ;

}

Note, the turbulent viscosity (tmu) has not yet been deﬁned but will be shortly. The order

that rules appear in the ﬁle do not matter. Note, we have not considered the jacobian of the

production term. In general the sign of the production jacobian is destabilizing and as a general

rule it is desirable to leave this term out of an implicit implementation.

Next we will consider the last destruction term. This can be implemented using the following

rules:

$rule pointwise(nuTM_dest<-nuTM,strainRate,grads(nuTM),grads(strainRate),rho,menter) {

const real c3 = $menter.c3 ;

const real Ebb = dot($grads(nuTM),$grads(nuTM)) ;

const real Sdot = dot($grads(strainRate),$grads(strainRate)) ;

const real S2 = $strainRate*$strainRate ;

const real Eke = pow($nuTM,2)*Sdot/(S2+EPSILON) ;

real E1e = c3*Ebb*tanh(Eke/(c3*Ebb+EPSILON)) ;

const real c2 = $menter.c2 ;

$nuTM_dest = $rho*c2*E1e ;

}

//======================================

// Add integrated destruction term rhs

//======================================

$rule apply(nuTM_src<-nuTM_dest,vol)[Loci::Summation] {

join($nuTM_src, -$nuTM_dest*$vol) ;

}

One point to note on this is that we need the gradient of strainRate to implement this

term. For this implementation we are simply using the least squares gradient provided by the

FVM module to compute this. However, we will run into a problem here because the gradient

computation will require a value for strainRate at the face which is not provided by the solver.

For expediency we will assume that strainRate is relatively constant at the boundaries and

just copy from the cell to the face. This is accomplished with the rule

$rule pointwise(strainRate_f<-ci->strainRate) {

$strainRate_f = $ci->$strainRate ;

}

This implementation is OK in a pinch, but more sophisticated methods for computing this would

be suggested for a production level implementation. In particular the recursive application of

least squares gradients can be sensitive to numerical noise and the treatment of the boundary

values may lead to spurious results. For our limited tests this implementation seems to produce

satisfactory results.

For the destruction term it can be helpful to include a jacobian term. However, due to the

gradients of nuTM used in the destruction term, the exact jacobian can be expensive and tedious

to derive. For this reason we use a diagonalized approximation that can stabilize the solver

with a reasonable cost. The diagonal term of the jacobian is in the variable nuTM srcJ. Our

approximation is implemented using the following rule

//=================================================

// Apply an approximate destruction term jacobian

//=================================================

$type nuTM_srcJ store<real> ;

$rule apply(nuTM_srcJ<-nuTM_dest,vol,nuTM)[Loci::Summation] {

join($nuTM_srcJ, -$vol*2.*$nuTM*($nuTM_dest/pow($nuTM,2))) ;

}

Now all that remains is deﬁning the turbulent viscosity which is computed from the scalar

variable we are solving combined with a the damping term D2. This is deﬁned using the rules:

// nuTM damping function

$type D2 store<real> ;

$rule pointwise(D2<-nuTM,rho,mu,menter) {

const real aplus = $menter.aplus ;

const real kappa = $menter.kappa ;

const real nu = $mu/$rho ;

const real a1 = pow($nuTM/(aplus*kappa*nu),2) ;

$D2 = 1.-exp(-a1) ;

}

//=========================================================

// Define turbulent viscosity for mean flow solver to use

//=========================================================

$rule pointwise(menter::tmu<-nuTM,rho,D2) {

$tmu = $rho*$D2*$nuTM ;

}

And with this we complete the implementation of the turbulence model.

References

[1] F R. Menter. Eddy viscosity transport and equations and their relation to the k-model.

J. of Fluids Engineering, 119:876–884, 1997.

Module Guide

Navigation menu

Versions of this User Manual:

Views

Navigation