TBUF 100 Mt1 S11 Sol
User Manual: TBUF 100
Open the PDF directly: View PDF ![]() .
.
Page Count: 12
Midterm I Exam
15-122 Principles of Imperative Computation
Frank Pfenning
February 17, 2011
Name: Sample Solution Andrew ID: fp Section:
Instructions
•This exam is closed-book with one sheet of notes permitted.
•You have 80 minutes to complete the exam.
•There are 4 problems.
•Read each problem carefully before attempting to solve it.
•Do not spend too much time on any one problem.
•Consider if you might want to skip a problem on a first pass and return to it later.
Mod.arith. Search Stacks Queues
Prob 1 Prob 2 Prob 3 Prob 4 Total
Score 20 30 25 25 100
Max 20 30 25 25 100
Grader tc fp/jp kbn wjl/kbn
1

1 Modular Arithmetic (20 pts)
In C0, values of type int are defined to have 32 bits. In this problem we work with a version of
C0 called C8 where values of type int are defined to have only 8 bits. In other respects it is the
same as C0. All integer operations are still in two’s complement arithmetic, but now modulo 28.
All bitwise operations are still bitwise, except on only 8 bit words instead of 32 bit words.
Task 1 (10 pts). Fill in the missing quantities, in the specified notation.
a. The minimal negative integer, in decimal: -128
b. The maximal positive integer, in decimal: 127
c. −2, in hexadecimal: 0x FE
d. 19, in hexadecimal: 0x 13
e. 0x45, in decimal: 69
Task 2 (10 pts). Assume int x has been declared and initialized to an unknown value. For each
of the following, indicate if the expression always evaluates to true, or if it could sometimes be
false. In the latter case, indicate a counterexample in C8 by giving a value for xthat falsifies the
claim. You may use decimal or hexadecimal notation.
a. x+1 > x false, x = 127
b. (((x>>1)<<1) | (x&1)) == x true
c. (x ^ (~x)) == 0 false, x = 0 (or any other x)
d. x <= (1<<7)-1 true
e. x+x == 2*x true
2

2 Search Algorithms (30 pts)
We explore the application of ideas behind linear and binary search in a new context. We are given
an array of integers subject only to the requirement that the first integer in the array is negative
(A[0] <0) and the last integer in the array is nonnegative (A[n−1] ≥0). We cannot assume that
the array is sorted. We want to find an index iin the array such that A[i]<0and A[i+ 1] ≥0.
The following is a function to find such an index, searching through the array from left to right.
int find1(int[] A, int n)
//@requires 2 <= n && n <= \length(A);
//@requires A[0] < 0 && 0 <= A[n-1];
//@ensures 0 <= \result && \result < n-1;
//@ensures A[\result] < 0 && 0 <= A[\result+1];
{
for (int i = 0; i < n-1; i++)
//@loop_invariant 0 <= i && i <= n-1; /* answer line 1 */
//@loop_invariant A[i] < 0; /* answer line 2 */
{
if (0 <= A[i+1]) return i;
}
/* should never get here */
//@assert false;
return -1;
}
Task 1 (4 pts). Fill in loop invariants. Your loop invariants (together with the function precondi-
tions) should be strong enough to guarantee the postconditions.
Task 2 (1 pts). What is the worst-case asymptotic complexity of the find1 as a function of n, in
big-O notation? You do not need to justify your answer.
O(n)
Task 3 (2 pts). Show that your loop invariants hold initially.
Initially, i= 0, so 0≤iand i≤n−1since n≥2.
Also, A[i]<0since A[0] <0by precondition.
3

Task 4 (5 pts). Show that your loop invariants are preserved by one iteration of the loop.
For the first invariant, we assume the invariant 0≤i≤n−1. Also, i < n −1since the
loop condition is true. In the iteration we set i0=i+ 1. Then 0≤i0=i+ 1 since 0≤i. Also,
i0=i+ 1 ≤n−1since i<n−1.
For the second invariant, we only get back to the loop test if A[i+ 1] <0(otherwise we
return). But i0=i+ 1 so A[i0]<0.
Task 5 (5 pts). Show that your loop invariants (together with the function preconditions) imply the
postconditions. You may assume without proof that the statement after the loop is never reached,
so that the final return statement can never be executed.
The first postcondition holds because 0≤iby the loop invariant, and i<n−1by the loop
test, and we return i.
The second postcondition holds because A[i]<0by the loop invariant and 0≤A[i+ 1] by
the condition guarding the return, and we return i.
4

Task 6 (10 pts). Now apply the idea behind binary search to complete the following function to
satisfy the same pre- and post-condition. You do not need to prove this, but we suggest that you
reason it out to yourself to make sure your function and the invariants are correct.
int find2(int[] A, int n)
//@requires 2 <= n && n <= \length(A);
//@requires A[0] < 0 && A[n-1] >= 0;
//@ensures 0 <= \result && \result < n-1;
//@ensures A[\result] < 0 && 0 <= A[\result+1];
{ int lower = 0;
int upper = n-1;
while (upper-lower > 1)
//@loop_invariant 0 <= lower && lower < upper && upper < n;
//@loop_invariant A[lower] < 0 && 0 <= A[upper];
{ int mid = lower + (upper-lower)/2;
if (A[mid] < 0)
lower = mid;
else
upper = mid;
}
return lower;
}
Task 7 (2 pts). Does find2 always return the same answer as find1? Explain your answer in one
or two sentences.
No. find1 will always return the index of the first sign change, find2 might return another
one. For example, for the array {-1, 1, -1, 1, 2} find1 will return 0while find2 will
return 2.
Task 8 (1 pts). What is the worst-case asymptotic complexity of find2 as a function of n, in big-O
notation? You do not need to justify your answer.
O(log(n))
5
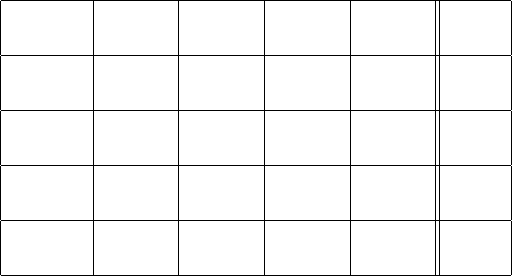
3 Stacks (25 pts)
In this problem we will implement a simple text buffer with some editing functions. A text buffer
consists of a sequence of characters with a distinguished position called the point. A buffer with
characters abcdef and the point between band cis written as
ab|cdef
The abstract interface has operations to create a new buffer, move point forward or backward, and
to insert or delete character at point. Each operation is explained in detail where you are asked to
implement it. All operations should be constant time (O(1)).
typedef struct tbuf* tbuf;
tbuf tbuf_new(); /* create new text buffer */
void insert_char(tbuf B, char c); /* insert character at point */
void delete_char(tbuf B); /* delete character before point */
void forward_char(tbuf B); /* move point forward one char */
void backward_char(tbuf B); /* move point backward one char */
// ... others elided
We are implementing a text buffer by two stacks, one with the characters before the point, and
one with the characters after the point. The text buffer
ab|cdef
above would be represented by the following two stacks:
!b!
!a!
!c!
!d!
!e!
!f!
before!
point!
a.er!
point!
The before stack has two elements, with bon top; the after stack has four elements with con top.
6
The implementation will use stacks of characters according to the following interface as devel-
oped in lecture.
typedef char elem;
typedef struct stack* stack;
bool stack_empty(stack S); /* O(1) */
stack stack_new(); /* O(1) */
void push(stack S, elem e); /* O(1) */
elem pop(stack S) /* O(1) */
//@requires !stack_empty(S);
;
As explained, a text buffer is represented by a struct containing two stacks, before and after.
struct tbuf {
stack before;
stack after;
};
The following function checks if Bis a valid text buffer. Your functions must preserve this prop-
erty.
bool is_tbuf(tbuf B) {
if (B == NULL) return false;
return (B->before != NULL && B->after != NULL);
}
Task 1 (5 pts). Write a function to create a new (empty) text buffer.
tbuf tbuf_new()
//@ensures is_tbuf(\result);
{
stack before = stack_new();
stack after = stack_new();
tbuf B = alloc(struct tbuf);
B->before = before;
B->after = after;
return B;
}
7

In response to the questions below, you do not need to write annotations, but you are free to
do so if you wish. You may assume that all function arguments of type tbuf are valid text buffers
(according to is_tbuf) and your functions should ensure that they remain valid.
Task 2 (5 pts). Write a function to insert a character into a text buffer before point. For example, if
a text buffer Bcontains
ab|cdef
then after insert_char(B, ’w’), it should have the form
abw|cdef
void insert_char(tbuf B, char c)
//@requires is_tbuf(B);
//@ensures is_tbuf(B);
{
push(B->before, c);
}
Task 3 (5 pts). Write a function to delete the character before point. If the point is at the left end of
the text buffer, the buffer should remain unchanged. For example, if a text buffer Bcontains
ab|cdef
then after delete_char(B), it should have the form
a|c d e f
void delete_char(tbuf B)
//@requires is_tbuf(B);
//@ensures is_tbuf(B);
{
if (!stack_empty(B->before))
pop(B->before);
}
8

Task 4 (5 pts). Write a function to move the point forward one character. If it is already at the right
end of the text buffer, it should remain unchanged.
void forward_char(tbuf B)
//@requires is_tbuf(B);
//@ensures is_tbuf(B);
{
if (!stack_empty(B->after))
push(B->before, pop(B->after));
}
Task 5 (5 pts). Write a function to move the point backward one character. If the point is already at
the left end of the text buffer, it should remain unchanged.
void backward_char(tbuf B)
//@requires is_tbuf(B);
//@ensures is_tbuf(B);
{
if (!stack_empty(B->before))
push(B->after, pop(B->before));
}
9
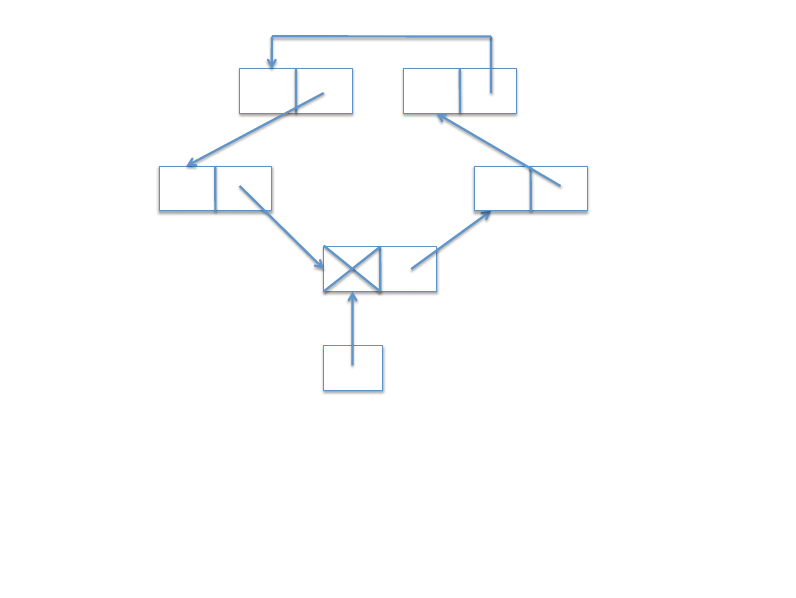
4 Queues and Linked Lists (25 pts)
Recall the definition of linked lists and the is_segment function that checks if a linked list begin-
ning at start eventually arrives at end.
struct list {
elem data;
struct list* next;
};
typedef struct list* list;
bool is_segment(list start, list end);
Ahoop represents a queue as a cyclic linked list with one extra node. For example, a queue with
items 1,2,3,4(in this order, 1at the front of the queue and 4at the back) would be represented as
the following hoop:
4"
2"3"
hoop"
data"
next"
1"
next"
queue"
data"
We define
struct queue {
list hoop;
};
typedef struct queue* queue;
10

As an example, here is a function that checks if the hoop is empty.
bool queue_empty(queue Q)
//@requires is_queue(Q);
{
return Q->hoop == Q->hoop->next;
}
Task 1 (5 pts). Write a function that checks if a given queue is valid. [Hint: Use is_segment, and
remember that pointers can be NULL.]
bool is_queue(queue Q) {
if (Q == NULL) return false;
if (Q->hoop == NULL) return false;
return is_segment(Q->hoop->next, Q->hoop);
}
Task 2 (10 pts). Write a function to dequeue an element from the front of the queue. Your function
should take constant time. [Hint: Draw a picture!]
elem deq(queue Q)
//@requires is_queue(Q);
//@requires !queue_empty(Q);
//@ensures is_queue(Q);
{
elem e = Q->hoop->next->data;
Q->hoop->next = Q->hoop->next->next;
return e;
}
11
Task 3 (10 pts). Write a function to enqueue an element at the end of the queue. Your function
should take constant time. [Hint: Draw a picture!]
void enq(queue Q, elem e)
//@requires is_queue(Q);
//@ensures is_queue(Q);
{
list h = alloc(struct list);
/* h->data is irrelevant */
h->next = Q->hoop->next;
Q->hoop->data = e;
Q->hoop->next = h;
Q->hoop = h;
return;
}
12