65 Rsd
User Manual: 65
Open the PDF directly: View PDF ![]() .
.
Page Count: 6

Title stata.com
sdtest — Variance-comparison tests
Syntax Menu Description Options
Remarks and examples Stored results Methods and formulas References
Also see
Syntax
One-sample variance-comparison test
sdtest varname == #if in , level(#)
Two-sample variance-comparison test using groups
sdtest varname if in , by(groupvar)level(#)
Two-sample variance-comparison test using variables
sdtest varname1== varname2if in , level(#)
Immediate form of one-sample variance-comparison test
sdtesti #obs #mean |.#sd #val , level(#)
Immediate form of two-sample variance-comparison test
sdtesti #obs,1#mean,1|.#sd,1#obs,2#mean,2|.#sd,2, level(#)
Robust tests for equality of variances
robvar varname if in , by(groupvar)
by is allowed with sdtest and robvar; see [D] by.
Menu
sdtest
Statistics >Summaries, tables, and tests >Classical tests of hypotheses >Variance-comparison test
sdtesti
Statistics >Summaries, tables, and tests >Classical tests of hypotheses >Variance-comparison test calculator
robvar
Statistics >Summaries, tables, and tests >Classical tests of hypotheses >Robust equal-variance test
1

2sdtest — Variance-comparison tests
Description
sdtest performs tests on the equality of standard deviations (variances). In the first form, sdtest
tests that the standard deviation of varname is #. In the second form, sdtest performs the same
test, using the standard deviations of the two groups defined by groupvar. In the third form, sdtest
tests that varname1and varname2have the same standard deviation.
sdtesti is the immediate form of sdtest; see [U] 19 Immediate commands.
Both the traditional Ftest for the homogeneity of variances and Bartlett’s generalization of this
test to Ksamples are sensitive to the assumption that the data are drawn from an underlying Gaussian
distribution. See, for example, the cautionary results discussed by Markowski and Markowski (1990).
Levene (1960) proposed a test statistic for equality of variance that was found to be robust under
nonnormality. Then Brown and Forsythe (1974) proposed alternative formulations of Levene’s test
statistic that use more robust estimators of central tendency in place of the mean. These reformulations
were demonstrated to be more robust than Levene’s test when dealing with skewed populations.
robvar reports Levene’s robust test statistic (W0) for the equality of variances between the groups
defined by groupvar and the two statistics proposed by Brown and Forsythe that replace the mean in
Levene’s formula with alternative location estimators. The first alternative (W50) replaces the mean
with the median. The second alternative replaces the mean with the 10% trimmed mean (W10).
Options
level(#)specifies the confidence level, as a percentage, for confidence intervals of the means. The
default is level(95) or as set by set level; see [U] 20.7 Specifying the width of confidence
intervals.
by(groupvar)specifies the groupvar that defines the groups to be compared. For sdtest, there
should be two groups, but for robvar there may be more than two groups. Do not confuse the
by() option with the by prefix; both may be specified.
Remarks and examples stata.com
Remarks are presented under the following headings:
Basic form
Immediate form
Robust test
Basic form
sdtest performs two different statistical tests: one testing equality of variances and the other
testing that the standard deviation is equal to a known constant. Which test it performs is determined
by whether you type a variable name or a number to the right of the equal sign.
Example 1: One-sample test of variance
We have a sample of 74 automobiles. For each automobile, we know the mileage rating. We wish
to test whether the overall standard deviation is 5 mpg:

sdtest — Variance-comparison tests 3
. use http://www.stata-press.com/data/r13/auto
(1978 Automobile Data)
. sdtest mpg == 5
One-sample test of variance
Variable Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
mpg 74 21.2973 .6725511 5.785503 19.9569 22.63769
sd = sd(mpg) c = chi2 = 97.7384
Ho: sd = 5 degrees of freedom = 73
Ha: sd < 5 Ha: sd != 5 Ha: sd > 5
Pr(C < c) = 0.9717 2*Pr(C > c) = 0.0565 Pr(C > c) = 0.0283
Example 2: Variance ratio test
We are testing the effectiveness of a new fuel additive. We run an experiment on 12 cars, running
each without and with the additive. The data can be found in [R]ttest. The results for each car are
stored in the variables mpg1 and mpg2:
. use http://www.stata-press.com/data/r13/fuel
. sdtest mpg1==mpg2
Variance ratio test
Variable Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
mpg1 12 21 .7881701 2.730301 19.26525 22.73475
mpg2 12 22.75 .9384465 3.250874 20.68449 24.81551
combined 24 21.875 .6264476 3.068954 20.57909 23.17091
ratio = sd(mpg1) / sd(mpg2) f = 0.7054
Ho: ratio = 1 degrees of freedom = 11, 11
Ha: ratio < 1 Ha: ratio != 1 Ha: ratio > 1
Pr(F < f) = 0.2862 2*Pr(F < f) = 0.5725 Pr(F > f) = 0.7138
We cannot reject the hypothesis that the standard deviations are the same.
In [R]ttest, we draw an important distinction between paired and unpaired data, which, in this
example, means whether there are 12 cars in a before-and-after experiment or 24 different cars. For
sdtest, on the other hand, there is no distinction. If the data had been unpaired and stored as
described in [R]ttest, we could have typed sdtest mpg, by(treated), and the results would have
been the same.
Immediate form
Example 3: sdtesti
Immediate commands are used not with data, but with reported summary statistics. For instance,
to test whether a variable on which we have 75 observations and a reported standard deviation of 6.5
comes from a population with underlying standard deviation 6, we would type

4sdtest — Variance-comparison tests
. sdtesti 75 . 6.5 6
One-sample test of variance
Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
x 75 . .7505553 6.5 . .
sd = sd(x) c = chi2 = 86.8472
Ho: sd = 6 degrees of freedom = 74
Ha: sd < 6 Ha: sd != 6 Ha: sd > 6
Pr(C < c) = 0.8542 2*Pr(C > c) = 0.2916 Pr(C > c) = 0.1458
The mean plays no role in the calculation, so it may be omitted.
To test whether the variable comes from a population with the same standard deviation as another
for which we have a calculated standard deviation of 7.5 over 65 observations, we would type
. sdtesti 75 . 6.5 65 . 7.5
Variance ratio test
Obs Mean Std. Err. Std. Dev. [95% Conf. Interval]
x 75 . .7505553 6.5 . .
y 65 . .9302605 7.5 . .
combined 140 . . . . .
ratio = sd(x) / sd(y) f = 0.7511
Ho: ratio = 1 degrees of freedom = 74, 64
Ha: ratio < 1 Ha: ratio != 1 Ha: ratio > 1
Pr(F < f) = 0.1172 2*Pr(F < f) = 0.2344 Pr(F > f) = 0.8828
Robust test
Example 4: robvar
We wish to test whether the standard deviation of the length of stay for patients hospitalized for a
given medical procedure differs by gender. Our data consist of observations on the length of hospital
stay for 1778 patients: 884 males and 894 females. Length of stay, lengthstay, is highly skewed
(skewness coefficient =4.912591) and thus violates Bartlett’s normality assumption. Therefore, we
use robvar to compare the variances.
. use http://www.stata-press.com/data/r13/stay
. robvar lengthstay, by(sex)
Summary of Length of stay in days
sex Mean Std. Dev. Freq.
male 9.0874434 9.7884747 884
female 8.800671 9.1081478 894
Total 8.9432508 9.4509466 1778
W0 = 0.55505315 df(1, 1776) Pr > F = 0.45635888
W50 = 0.42714734 df(1, 1776) Pr > F = 0.51347664
W10 = 0.44577674 df(1, 1776) Pr > F = 0.50443411

sdtest — Variance-comparison tests 5
For these data, we cannot reject the null hypothesis that the variances are equal. However, Bartlett’s
test yields a significance probability of 0.0319 because of the pronounced skewness of the data.
Technical note
robvar implements both the conventional Levene’s test centered at the mean and a median-centered
test. In a simulation study, Conover, Johnson, and Johnson (1981) compare the properties of the two
tests and recommend using the median test for asymmetric data, although for small sample sizes
the test is somewhat conservative. See Carroll and Schneider (1985) for an explanation of why both
mean- and median-centered tests have approximately the same level for symmetric distributions, but
for asymmetric distributions the median test is closer to the correct level.
Stored results
sdtest and sdtesti store the following in r():
Scalars
r(N) number of observations
r(p l) lower one-sided p-value
r(p u) upper one-sided p-value
r(p) two-sided p-value
r(F) Fstatistic
r(sd) standard deviation
r(sd 1) standard deviation for first variable
r(sd 2) standard deviation for second variable
r(df) degrees of freedom
r(df 1) numerator degrees of freedom
r(df 2) denominator degrees of freedom
r(chi2) χ2
robvar stores the following in r():
Scalars
r(N) number of observations
r(w50) Brown and Forsythe’s Fstatistic (median)
r(p w50) Brown and Forsythe’s p-value
r(w0) Levene’s Fstatistic
r(p w0) Levene’s p-value
r(w10) Brown and Forsythe’s Fstatistic (trimmed mean)
r(p w10) Brown and Forsythe’s p-value (trimmed mean)
r(df 1) numerator degrees of freedom
r(df 2) denominator degrees of freedom
Methods and formulas
See Armitage et al. (2002, 149 –153) or Bland (2000, 171–172) for an introduction and explanation
of the calculation of these tests.
The test for σ=σ0is given by
χ2=(n−1)s2
σ2
0
which is distributed as χ2with n−1 degrees of freedom.
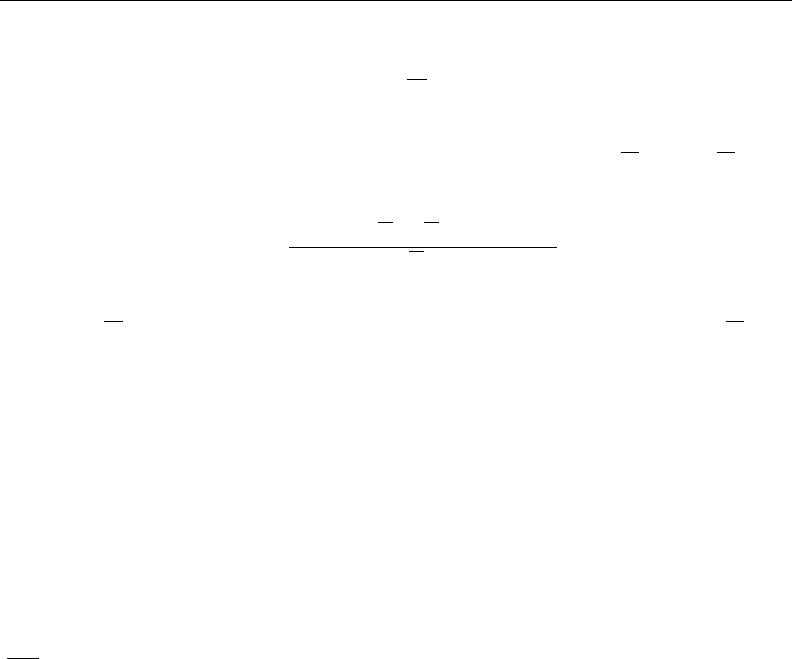
6sdtest — Variance-comparison tests
The test for σ2
x=σ2
yis given by
F=s2
x
s2
y
which is distributed as Fwith nx−1 and ny−1 degrees of freedom.
Let Xij be the jth observation of Xfor the ith group. Let Zij =|Xij −Xi|, where Xiis the
mean of Xin the ith group. Levene’s test statistic is
W0=Pini(Zi−Z)2/(g−1)
PiPj(Zij −Zi)2/Pi(ni−1)
where niis the number of observations in group iand gis the number of groups. W50 is obtained
by replacing Xiwith the ith group median of Xij , whereas W10 is obtained by replacing Xiwith
the 10% trimmed mean for group i.
References
Armitage, P., G. Berry, and J. N. S. Matthews. 2002. Statistical Methods in Medical Research. 4th ed. Oxford:
Blackwell.
Bland, M. 2000. An Introduction to Medical Statistics. 3rd ed. Oxford: Oxford University Press.
Brown, M. B., and A. B. Forsythe. 1974. Robust tests for the equality of variances. Journal of the American Statistical
Association 69: 364–367.
Carroll, R. J., and H. Schneider. 1985. A note on Levene’s tests for equality of variances. Statistics and Probability
Letters 3: 191–194.
Cleves, M. A. 1995. sg35: Robust tests for the equality of variances.Stata Technical Bulletin 25: 13–15. Reprinted
in Stata Technical Bulletin Reprints, vol. 5, pp. 91–93. College Station, TX: Stata Press.
. 2000. sg35.2: Robust tests for the equality of variances update to Stata 6.Stata Technical Bulletin 53: 17–18.
Reprinted in Stata Technical Bulletin Reprints, vol. 9, pp. 158–159. College Station, TX: Stata Press.
Conover, W. J., M. E. Johnson, and M. M. Johnson. 1981. A comparative study of tests for homogeneity of variances,
with applications to the outer continental shelf bidding data. Technometrics 23: 351–361.
Gastwirth, J. L., Y. R. Gel, and W. Miao. 2009. The impact of Levene’s test of equality of variances on statistical
theory and practice. Statistical Science 24: 343–360.
Levene, H. 1960. Robust tests for equality of variances. In Contributions to Probability and Statistics: Essays in Honor
of Harold Hotelling, ed. I. Olkin, S. G. Ghurye, W. Hoeffding, W. G. Madow, and H. B. Mann, 278–292. Menlo
Park, CA: Stanford University Press.
Markowski, C. A., and E. P. Markowski. 1990. Conditions for the effectiveness of a preliminary test of variance.
American Statistician 44: 322–326.
Seed, P. T. 2000. sbe33: Comparing several methods of measuring the same quantity.Stata Technical Bulletin 55:
2–9. Reprinted in Stata Technical Bulletin Reprints, vol. 10, pp. 73–82. College Station, TX: Stata Press.
Tob´
ıas, A. 1998. gr28: A graphical procedure to test equality of variances.Stata Technical Bulletin 42: 4–6. Reprinted
in Stata Technical Bulletin Reprints, vol. 7, pp. 68–70. College Station, TX: Stata Press.
Also see
[R]ttest —ttests (mean-comparison tests)