Snana Manual

User Manual:

Open the PDF directly: View PDF .
Page Count: 165 [warning: Documents this large are best viewed by clicking the View PDF Link!]

SNANA

User’s Manual:

Simulation, Lightcurve Fitters & Cosmology Fitters

Richard Kessler

University of Chicago

Kavli Institute for Cosmological Physics

Department of Astronomy & Astrophysics

April 19, 2019

Contents

1 Introduction 6

SNANA

Basics 6

2.1 Dr. Evil-ABORT-Face . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

2.2 Data Files . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

2.3 Citations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

3 The Calibration + K-Correction ﬁle 8

3.1 Changing the Mean Filter Wavelength . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

3.2 Deﬁning a

SPECTROGRAPH

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

4 The

SNANA

Simulation:

snlc_sim.exe

4.1 Overview of Model Magnitudes and Noise Calculation . . . . . . . . . . . . . . . . . . . 10

4.2 Getting Started Quickly . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

4.3 Synchronizing Random Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

4.4 Simulated TYPE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

4.5 The ‘

SIMLIB

’ Observing Conditions File . . . . . . . . . . . . . . . . . . . . . . . . . . 14

4.5.1

SIMLIB

Options in the Sim-Input File . . . . . . . . . . . . . . . . . . . . . . . . 17

4.5.2

SIMLIB SPECTROGRAPH

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

4.5.3

SIMLIB

Options for each LIBID . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

4.5.4 Saturation Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

4.5.5

APPEND

Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

4.5.6 SNR Monitor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

4.6 Simulating Fields . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

4.6.1 Overlapping Fields . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

4.6.2 Field Subset . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

4.7 Correlated Template Noise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

4.8 Simulating Multiple Instruments . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

4.9 Simulating Multiple Seasons . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

4.10 Simulating a Filter as a Sum of Components . . . . . . . . . . . . . . . . . . . . . . . . . 25

4.11 Noise Corrections: ˆ

SSNR and ˆ

σ0. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

4.11.1

FLUXERRMAP

Tables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

4.11.2 Suggested Strategy for Determining

FLUXERRMODEL

Tables . . . . . . . . . . . . 29

4.11.3 Extracting Information for

FLUXERRMAP

. . . . . . . . . . . . . . . . . . . . . . . 29

4.11.4 Legacy Noise Corrections . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

4.12 Example Noise Calculation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

4.13 K-corrections . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

4.14 Intrinsic Brightness Variations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

4.14.1 Supernova Brightness Variations . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

4.14.2 Galaxy Lensing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

4.15 Search Efﬁciency . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

4.15.1 Software-Pipeline Efﬁciency . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

4.15.2 Spectroscopic-Conﬁrmation Efﬁciency . . . . . . . . . . . . . . . . . . . . . . . 39

4.15.3 Unconﬁrmed Efﬁciency for Host-Galaxy Redshift . . . . . . . . . . . . . . . . . 42

4.15.4 Determining εspec . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

4.15.5 Time Above Detection and Number of Detections . . . . . . . . . . . . . . . . . . 45

4.16 Selection Cuts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

4.17 Varying the Exposure Time/Aperture/Efﬁciency . . . . . . . . . . . . . . . . . . . . . . . 48

4.18 Simulating Galactic Extinction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49

4.18.1 Some Details on Galactic Extinction Computations . . . . . . . . . . . . . . . . . 50

4.18.2 Correcting FLUXCAL for Galactic Extinction . . . . . . . . . . . . . . . . . . . 50

4.19 Simulating the Host Galaxy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51

4.20 Simulating Mis-Matched Host Galaxy . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58

4.21 Simulating Rate vs. Redshift: Volumetric and per Season . . . . . . . . . . . . . . . . . . 59

4.22 Simulating Rate vs. Galactic Coordinates . . . . . . . . . . . . . . . . . . . . . . . . . . 61

4.23 Simulating a

SPECTROGRAPH

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63

4.23.1 Spectral Time-Windows Relative to Peak Brightness . . . . . . . . . . . . . . . . 64

4.23.2 Calibration Warp vs. Wavelength . . . . . . . . . . . . . . . . . . . . . . . . . . 65

4.23.3

SPECTROGRAPH

Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65

4.23.4 Simulating a Single High-S/N Spectrum . . . . . . . . . . . . . . . . . . . . . . . 66

4.24 Simulating Rise-Time Variations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66

4.25 Altering Input SEDs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67

4.25.1 Simulating PEAKMJD or Time of Explosion . . . . . . . . . . . . . . . . . . . . 67

4.25.2 Extrapolating UV Flux . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67

4.26

NGEN

keys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68

4.27 “Perfect” Simulations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68

4.28 Generating Redshift (zhel,zcmb), Peculiar Velocity and Distance . . . . . . . . . . . . . . 69

4.29 Redshift-Dependent Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70

4.30 Generating Efﬁciency Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71

4.31 Light Curve Output Formats . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72

4.31.1 TEXT Light Curve Output (Default) . . . . . . . . . . . . . . . . . . . . . . . . 72

4.31.2 Model-Mag Light Curve Output . . . . . . . . . . . . . . . . . . . . . . . . . . . 73

4.31.3 Suppress

SIM_XXX

Info . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73

4.31.4 Random CID . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73

4.31.5 FITS Format . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74

4.31.6

PHOTFLAG

Mask . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74

4.31.7 Source of Each Redshift . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75

4.32 Simulation Dump Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76

4.32.1

SIMLIB_DUMP

Utility . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76

4.32.2 Cadence Figure of Merit Utility . . . . . . . . . . . . . . . . . . . . . . . . . . . 77

4.32.3

SIMGEN_DUMP

File . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77

4.32.4 Model Dump . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78

4.33 Including a Second Sim-Input File . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78

4.34 Multi-dimensional

GRID

Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79

4.35 TGRIDSTEP: Linear Interpolation of Model Flux . . . . . . . . . . . . . . . . . . . . . . 82

4.36 Marking Sub-Samples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82

4.37 Applying Systematic Errors (RANSYSTPAR) . . . . . . . . . . . . . . . . . . . . . . . 83

5 The

SNANA

Fitter:

snlc_fit.exe

5.1 Getting Started Quickly . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84

5.2 Discussion of Lightcurve Fits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84

5.3 Methods of Fit-Parameter Estimation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85

5.3.1 MINUIT Covariances . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86

5.4 Initial Fit-Parameter Estimation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87

5.5 Galactic Reddening . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88

5.6 Selecting Filters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

5.7 Fitting Priors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

5.8 Selecting an Efﬁciency Map for a Fitting Prior . . . . . . . . . . . . . . . . . . . . . . . . 90

5.9 Viewing Lightcurve Fits:

mkfitplots.pl

. . . . . . . . . . . . . . . . . . . . . . . . . 90

5.10 Tracking SN versus Cuts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91

5.11 PhotoZ Fits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92

5.11.1 Redshift-Dependent Selection in PhotoZ Fits . . . . . . . . . . . . . . . . . . . . 95

5.11.2 Initial Parameter Estimate . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96

5.11.3 Smooth Model Error Transition Across Filter Boundaries . . . . . . . . . . . . . . 97

5.11.4 Don’t Fool Yourself when PhotoZ-Fitting Simulations . . . . . . . . . . . . . . . 97

5.12 Including the log(σ) Term in the χ2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97

5.13 Optional Redshift Sources . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98

5.14 Excluding/Downweighting Filters and Epoch Ranges . . . . . . . . . . . . . . . . . . . . 99

5.15 Rest-Frame Wavelength Range . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100

5.16 Extracting Light Curve Shape from the Fit . . . . . . . . . . . . . . . . . . . . . . . . . . 101

5.17 Landolt ↔Bessell Color Transformations . . . . . . . . . . . . . . . . . . . . . . . . . . 101

5.18 Interpolating Fluxes and Magnitudes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102

5.19 Fitting Rest-Frame Peak-Magnitudes and Colors . . . . . . . . . . . . . . . . . . . . . . . 103

5.20 Peak-Mag Crosschecks:

FITMAGDIF

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

5.21 Selecting SNID(s), Field(s), and Telescope(s) . . . . . . . . . . . . . . . . . . . . . . . . 104

5.21.1 Selecting/Ignoring SNID . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104

5.21.2 Selecting Fields and Overlapping Fields . . . . . . . . . . . . . . . . . . . . . . . 105

5.21.3 Selecting Telescopes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105

5.21.4 Selecting MJD Ranges . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106

5.21.5 Quickly Analyzing a few SNe from a Large Sample . . . . . . . . . . . . . . . . . 106

5.22 Mag-Shifts in Zero Points and Primary Reference Star . . . . . . . . . . . . . . . . . . . 106

5.23 Fudging the

FLUXCAL

Offsets and Uncertainties . . . . . . . . . . . . . . . . . . . . . . . 107

5.24 Updating the Filter Transmission for each SN . . . . . . . . . . . . . . . . . . . . . . . . 107

5.25 Shifting the Mean Filter Transmission Wavelength . . . . . . . . . . . . . . . . . . . . . 108

5.26 Monitoring Fit-Jobs with “grep” . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108

5.27 User SN Tags . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109

5.28 Over-Riding Information in Data Files . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110

5.28.1 Over-Riding Header Information . . . . . . . . . . . . . . . . . . . . . . . . . . . 110

5.28.2 Over-Riding Light Curve Information . . . . . . . . . . . . . . . . . . . . . . . . 111

5.29 Peculiar Velocity Corrections . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111

5.30

SIMCHI2_CHEAT

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112

5.31 Cuts on true

SIM_XXX

Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112

5.32 IDEAL Fits with True Flux (Sim only) . . . . . . . . . . . . . . . . . . . . . . . . . . . 112

6 Private Options 113

6.1 Creating Your Private Code . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113

6.2 Private Sim Path:

PATH_SNDATA_SIM

. . . . . . . . . . . . . . . . . . . . . . . . . . . . 114

6.3 Private Data Path for Analysis:

PRIVATE_DATA_PATH

. . . . . . . . . . . . . . . . . . . . 114

6.4 Private Model-Path:

$SNANA_MODELPATH

. . . . . . . . . . . . . . . . . . . . . . . . . . 114

6.5 Private Variables in Data Files . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115

6.5.1 CUTWIN-selection on Private Variables . . . . . . . . . . . . . . . . . . . . . . . 115

6.5.2 Using a Private Redshift in the Analysis . . . . . . . . . . . . . . . . . . . . . . . 115

7 Adding a New Survey 116

7.1 Filter Names and Rules for K-corrections . . . . . . . . . . . . . . . . . . . . . . . . . . 117

7.2 Combining Surveys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118

8 Photometric Classiﬁcation 120

8.1

psnid.exe

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120

8.1.1 Preparing Photometric Templates for

psnid.exe

. . . . . . . . . . . . . . . . . . 121

8.1.2 Redshift Priors for

psnid.exe

. . . . . . . . . . . . . . . . . . . . . . . . . . . . 121

8.1.3 Rate Priors for

psnid.exe

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122

8.2 Nearest Neighbor Method . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123

9 Light Curve Models 125

9.1

MLCS2k2

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126

9.2 SALT-II . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127

9.3

SNooPy

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128

9.4

SIMSED

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129

9.5

NONIASED

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 132

9.5.1 Peculiar SNIa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133

9.6

NON1AGRID

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134

9.7

FIXMAG

and

RANMAG

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134

9.8

LCLIB

: Galactic Transients . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134

9.8.1 Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134

9.8.2 Deﬁning the Library . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135

9.8.3 Implementation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135

10 SALT-II Programs 138

10.1 Computing Distance Moduli from BBC Method:

SALT2mu.exe

..............138

10.2 SALT-II Training Scripts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138

11 Cosmology Fitters 139

11.1 Interpreting Redshift Variables in SNANA Tables . . . . . . . . . . . . . . . . . . . . . . 139

11.2 Peculiar Velocity Covariances . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140

12 Miscellaneous Tools and Features 141

12.1 Analysis-Output: Files, Tables, Variables . . . . . . . . . . . . . . . . . . . . . . . . . . 141

12.1.1 Combining Ascii “Fitres” Files:

combine_fitres.exe

...............143

12.1.2

SNTABLE

Dump Utility:

sntable_dump.pl

. . . . . . . . . . . . . . . . . . . . . 145

12.1.3 Extract Value from Fitres File:

get_fitresValue.pl

...............146

12.1.4 Working with IAUC names . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146

12.1.5

ovdatamc.py

: Plotting Utility for Data/MC Overlays . . . . . . . . . . . . . . . 147

12.2 General Misc. Tools . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147

12.2.1 Command-line Overrides . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147

12.2.2 Synchronizing/Updating Survey Files: survey_update.pl . . . . . . . . . . . . . . 148

12.2.3 Bug-Catcher: the

SNANA_tester

Script . . . . . . . . . . . . . . . . . . . . . . . 148

12.2.4 Data Backup/Archival:

backup_SNDATA_version.cmd

..............148

12.2.5 K-correction Dump Utility:

kcordump.exe

. . . . . . . . . . . . . . . . . . . . . 148

12.3 Misc. Simulation Tools . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 150

12.3.1 Simulate Ia/non-Ia mix:

sim_SNmix.pl

. . . . . . . . . . . . . . . . . . . . . . . 150

12.3.2 Co-Adding

SIMLIB

Observations on Same Night:

simlib_coadd.exe

. . . . . . 154

12.3.3 Creating a

SIMLIB

from Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154

12.3.4 Fudging Simulated Errors and Signal-to-Noise Ratio (S/N) . . . . . . . . . . . . 155

12.4 Misc. Fitting Tools . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156

12.4.1 Fit Multiple Samples with Multiple Fit-Options:

split_and_fit.pl

. . . . . . . 156

12.4.2 Analyzing Residuals from Lightcurve Fits . . . . . . . . . . . . . . . . . . . . . . 156

12.4.3 Extracting Light Curves into ASCII Formatted Files . . . . . . . . . . . . . . . . 156

12.4.4 Translating SNDATA ﬁles into SALT-II Format . . . . . . . . . . . . . . . . . . . 157

12.4.5 Translating TEXT data-ﬁles into FITS Format . . . . . . . . . . . . . . . . . . . . 157

12.4.6 Re-write Data FIles with Flux Fudges . . . . . . . . . . . . . . . . . . . . . . . . 158

12.4.7 Fudging Fitting Errors . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 158

12.4.8 1/Vmax Method: Post-Fit Calculations . . . . . . . . . . . . . . . . . . . . . . . 159

12.4.9 FILTER_REPLACE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 160

12.4.10 SNTABLE_FILTER_REMAP . . . . . . . . . . . . . . . . . . . . . . . . . . . . 160

12.4.11 Selecting Early Epochs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161

12.4.12 Selecting Epoch Ranges for Fast Transients (

REQUIRE_EPOCHS_STRING

) . . . . . 162

12.4.13 Miscellaneous

&SNLCINP

Options . . . . . . . . . . . . . . . . . . . . . . . . . . 162

12.5 Misc.

SIMSED

Utilities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162

12.5.1

SIMSED

Spectrum Extraction:

SIMSED_extractSpec.exe

.............162

12.5.2

SIMSED

Fudge Afterburner:

SIMSED_fudge.exe

. . . . . . . . . . . . . . . . . . 162

12.5.3

SIMSED

Preparation for SNANA:

SIMSED_prep.exe

................162

12.6 Reading gzip’ed Input Files . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163

12.7 Program Return Codes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163

SNANA

Updates 164

14 Reporting Problems 164

References 165

1 Introduction

This manual describes how to use the lightcurve simulation and ﬁtting programs in the

SNANA

product. This

code was originally developed for the SDSS-II Supernova Survey, and then it was modiﬁed to simulate

and ﬁt SN Ia lightcurves for an arbitrary survey. Current SN models include

MLCS2k2

[1], SALT-II [2],

SNooPy

[3], stretch [4], two-stretch[5], and Core Collapse[6].

The simulation is designed to be fast, generating ∼102-103lightcurves per second, and still provide

an accurate and realistic description of supernova lightcurves. In particular, the simulation accounts for

variations in noise, atmospheric transmission, and cadence. The reliability of the simulation is based on the

accuracy of the “observing conditions” in a “

SIMLIB

” ﬁle that describes the seeing, sky-noise, zeropoints,

and cadence. A

SIMLIB

ﬁle is easy to prepare post-survey; predicting the

SIMLIB

ﬁle before the survey

is crucial to making reliable predictions for the lightcurve quality. This simulation does not use pixels

or images directly, although it makes use of information generated from the images, such as scaling the

ﬂux-errors.

The underlying programs are binary executables based on a mix of fortran and C. Each program (ﬁtting

or simulation) requires an input ﬁle as an argument, plus optional command-line overrides (§12.2.1). The

command-line overrides allow making small perturbations so that a new input ﬁle is not needed for each

variation. For typical analyses that require many variations in both the ﬁtting and simulations, script

utilities are provided to launch job sequences on multiple cores using batch systems such as “qsub” or

“sbatch.” These utilities are

sim_SNmix.pl

for simulations (§12.3.1) and

split_and_fit.pl

for ﬁtting

(§12.4.1).

Finally, while the simulation is a stand-alone program with no user interface, the analysis programs

allow for user interaction in multuple ways using the private option (§6.1). The idea is to layer code on

top of the underlying

snana

code that reads data (real and sim) and applies basic selection cuts. This

architecture allows users to focus on writing new analysis features without worrying about the overhead of

reading data ﬁles. Three ways to use the private interface are 1) write an entire analysis or ﬁtting package

(e.g.,

snlc_fit

psnid

), 2) use existing code, but modify an underlying algorithm, and 3) add private

code in the user-interface routines (

USRINI,USRANA,USREND

), such as computing a new variable, writing

information in a speciﬁc format, etc.

SNANA

Basics

After installing

SNANA

(see install guide), make sure that the two main environment variables are deﬁned:

> echo $SNANA_DIR/

> echo $SNDATA_ROOT/

The environment variable $

SNANA_DIR

points to the software that is accessible to everyone, but write-

protected. The

SNANA

developers use a cvs repository to share code, and an updated version is “cut” (i.e,

released) on occasion to provide a stable software version for collaborators.

SNANA

is re-released as often

as necessary (§ 13), as bugs are ﬁxed and improvements are made. The main source codes for simulations

and ﬁtting are

> $SNANA_DIR/src/snlc_sim.c

> $SNANA_DIR/src/snlc_fit.car

> $SNANA_DIR/src/psnid.car

The environment variable $

SNDATA_ROOT

points to the group area, and contains general information

from surveys which have released data. In addition to public data, $

SNDATA_ROOT

contains information

needed as input to the

SNANA

codes: ﬁlter transmissions, CalSpec SEDs, SN models, Milky Way extinction

map, etc. Everyone has write privilege under $

SNDATA_ROOT

, so please be careful.

2.1 Dr. Evil-ABORT-Face

The

SNANA

simulation and ﬁtter programs have intensive error checking throughout the execution. If

anything looks ﬁshy, the program will abort with a message looking like

FATAL[get_user_input]: Cannot open input file :

’sim_BLABLA.input’

‘|‘‘‘‘‘‘‘|‘

<| o\ /o |>

|’;’|

| ___ | ABORT program on Fatal Error.

| |’ ’| |

| ‘---’ |

\_______/

While some of these aborts may at ﬁrst seem frustrating, they are crucial for catching bugs as early as

possible so that you don’t waste months (years) doing something silly.

2.2 Data Files

Data ﬁles can be written in TEXT (§4.31.1) or FITS (§4.31.5) format. Large data & sim samples should

use FITS format because it is much more compact and much faster to read. With TEXT format, each event

is written to a separate ASCII ﬁle. With FITS format, there are two FITS ﬁles: a summary HEAD ﬁle

with a one-row summary per event, and a PHOT ﬁle with the light curves. For fast reading, the HEAD ﬁle

includes pointers to the PHOT table, so do not catenate FITS ﬁles without updating these pointers.

2.3 Citations

While an

SNANA

citation is always appreciated ([7]), please make sure to reference any underlying work

that is used by

SNANA

. Referencing the appropriate light curve model (§1) is the most obvious example.

However, there may be other features to reference such as the source of spectra for the

SIMSED

model,

survey efﬁciencies, host-galaxy correlations, etc ... If you read a published article and suspect

SNANA

usage with a missing reference, please contact the lead author and one of the

SNANA

authors.

3 The Calibration + K-Correction ﬁle

Before running the simulation or light curve ﬁtting program, a “K-correction” ﬁle must be created. This

ﬁle contains

•ﬁlter transmissions.

•native mag for each ﬁlter.

•SED of the primary reference (i.e., AB, BD17, ...) and each SN epoch.

•zeropoint offsets (native −synthetic mags)

•Optional AB offsets (to apply to data)

•for rest-frame models requiring K-correction,

–K-correction tables vs. redshift, epoch, AV-warp.

–rest-frame magnitudes.

–Galactic extinction corrections.

The purpose of this ﬁle is two-fold: (1) collect the relevant information in one ﬁle that can be used for any

model such as SALT2 or mlcs2k2, and (2) for K-corrections, pre-compute quantities that vastly speeds up

the simulation and ﬁtting programs. The AV-warp parameter warps the SN SED to match a grid of colors,

and is used to quickly ﬁnd the warped SN SED that matches the observed colors. Example kcor-input ﬁles

are here:

$SNDATA_ROOT/sample_input_files/kcor

and the command to create a K-corr ﬁle is

kcor.exe myKcor.Input

The output ﬁle is speciﬁed by the kcor-input ﬁle key

OUTFILE: mySurvey.fits

3.1 Changing the Mean Filter Wavelength

The mean ﬁlter wavelength can be adjusted via the command-line argument

kcor.exe myKcor.Input FILTER_LAMSHIFT r 2.1 i 3.2

kcor.exe myKcor.Input FILTER_LAMSHIFT r 2.1 i 3.2 OUTFILE kcor_lamshift.fits

which shifts the mean r- and i-band wavelengths by 2.1 and 3.2 Å, respectively. These shifts can be

entered only via command-line arguments, and it is therefore recommended to also include a unique

OUTFILE

name as well, as shown in the 2nd example above. The LAMSHIFT info is written into the output

header. Note that to implement more complex wavelength variations requires a new set of transmission-

vs-λcurves.

§5.25 shows how to deﬁne a duplicate set of ﬁlters with a common wavelength shift, and how to select

the λ-shifted band(s) in the ﬁtting program.

3.2 Deﬁning a

SPECTROGRAPH

instrument is deﬁned as a list of SNR-vs-wavelength, SNR(λ), for two distinct magni-

tudes. SNR(λ)is deﬁned for two mag values so that in each λ-bin an effective zero point and skyNoise is

computed analytically, allowing SNR(λ)to computed for any mag. For each spectroscopic bin-center, the

zeropoint (ZP) and skyNoise (σsky) are given by

ZP =2.5log10 10−0.4m1−10−0.4m2

(10−0.4m1/SNR1)2−(10−0.4m2/SNR2)2(1)

σ2

sky = (F1/SNR1)2−F1;F1≡10−0.4(m1−ZP)(2)

where m1,2are the two mag-reference values, and SNR1,2are the corresponding SNR. To account for

exposure-time (Texpose) dependence, SNR(λ)can be deﬁned for multiple Texpose values. The

SPECTROGRAPH

is deﬁned in a separate text ﬁle with the following syntax:

INSTRUMENT: MYSPECDEVICE

MAGREF_LIST: 20 28 # used to define SNR1 and SNR2

TEXPOSE_LIST: 300 1000 2000 # seconds

# LAM LAM LAM

# MIN MAX RES SNR1 SNR2 SNR1 SNR2 SNR1 SNR2

SPECBIN: 4200 4210 12.4 11.39 0.017 24.78 0.063 50.72 0.168

SPECBIN: 4210 4222 14.5 12.39 0.018 24.94 0.066 50.82 0.172

etc ...

Each λ-bin (

SPECBIN

key) includes λmin and λmax (Å) to avoid confusion with non-uniform λbins. The

LAMRES

column speciﬁes the wavelength resolution in Å. Since there are three Texpose values in the example

above (see

TEXPOSE_LIST

key), three SNR pairs are given, where each SNR pair corresponds to the two

mag values following the

MAGREF_LIST

key. An abritrary number of Texpose values can be deﬁned, with

the corresponding number of SNR pairs. For the simulation, Texpose can be deﬁned in the

SIMLIB

ﬁle

(§4.5.2) or in the sim-input ﬁle (§4.23). SNR(Texpose)is interpolated based on the Texpose grid.

The above

SPECTROGRAPH

ﬁle is not read directly by the simulation, but instead it is ingested into a

kcor ﬁle along with the ﬁlters and calibration references. If the above ﬁle is named

MYSPECDEVICE.DAT

the following keys can be added to a kcor-input ﬁle, after a

FILTPATH

key:

SPECTROGRAPH: MYSPECDEVICE.DAT

# name minLam maxLam ABoff

SYN_FILTER: IFU-0 4200 4500 0.0

SYN_FILTER: IFU-1 6000 6600 0.0

SYN_FILTER: IFU-2 7200 7600 0.0

The

SPECTROGRAPH

key deﬁnes the ﬁle containing the noise properties. Optional

SYN_FILTER

keys deﬁne

IFU-like synthetic ﬁlters from the

SPECTROGRAPH

The

SPECTROGRAPH

λ-bins can be re-binned in the kcor ﬁle as follows,

SPECTROGRAPH: MYSPECDEVICE.DAT(rebin=3)

In this example, every three consecutive λ-bins are combined into one, and the SNR values are added in

quadrature. With 200 λ-bins in

MYSPECDEVICE.DAT

, the

rebin=3

option results in keeping 66 combined

bins. Since 3×66 =198 <200, the last two λ-bins are ignored.

4 The

SNANA

Simulation:

snlc_sim.exe

4.1 Overview of Model Magnitudes and Noise Calculation

The available lightcurve models are described in §9. For a rest-frame model of supernova, such as

MLCS2k2

SNooPy

, here is a brief overview of how the simulation generates observed ﬂuxes in CCD counts,

1. pick random shape parameter (e.g., ∆, DM15) and random extinction (AV) according to measured

distributions.

2. generate rest-frame light curve: U,B,V,R,Imag vs. time.

3. apply host-galaxy extinction to UBVRI mags.

4. add K-correction to transform UBVRI to observer-frame ﬁlters.

5. apply Galactic (MilkyWay) extinction.

6. apply zero-points to translate generated magnitude into CCD counts; this step account for atmo-

spheric transmission and telescope efﬁciency.

For an observer-frame mode such as SALT-II, steps 2-4 are replaced by a function that generates observer-

frame magnitudes.

The noise in the simulation is computed as follows,

σ2

SIM =F+ (A·b) + (F·ˆ

σZPT)2+ ( ˆ

σ0·100.4·ZPTpe)2+σ2

hostˆ

SNR (3)

where

•Fis the simulated ﬂux in photoelectrons (p.e.).

•Ais the noise-equivalent area given by [2πRPSF2(r,θ)rdr]−1.

•bis the background per unit area (includes sky + CCD readout + dark current).

•ˆ

σZPT is the zeropoint uncertainty.

•ˆ

σ0is a constant

FLUXCAL

uncertainty, and ZPTpe transforms ˆ

σ0into an uncertainty in p.e.

•ˆ

SSNR is an empirically determined scale that depends on the signal-to-nose ratio (SNR)

•σhost is from the underlying host galaxy.

The terms with hats (ˆ

σ0,ˆ

σZPT,ˆ

SSNR) may be difﬁcult to compute from ﬁrst principles, but these terms

can be determined empirically from ﬁts that match simulated uncertainties to those from the data. The

A,b,ˆ

σZPT terms are discussed in §4.5. The ˆ

σ0,ˆ

SSNR terms are discussed in §4.11. The host-galaxy noise

(σhost) is discussed in §4.19.

4.2 Getting Started Quickly

In this section, you should be able to start simulating lightcurves in a few minutes. There are many options

that may take some practice to use properly. The ﬁrst step is to copy a sample input ﬁle to your private

area,

> cp $SNDATA_ROOT/sample_input_files/mlcs2k2/sim_[SURVEY].input.

where

[SURVEY]

is one of the surveys for which a sample sim-input ﬁle is available. Edit the ﬁle and

change the

GENVERSION

name:

GENVERSION: CHANGE_ME

We recommend just adding your initials and/or project name so that you do not over-write somebody else’s

ﬁles. Now you can run the simulation, for example, with

> snlc_sim.exe sim_SDSS.input

which should generated ten lightcurves using the MLCS2k2 model. The next step is to modify the input

ﬁle to suit your needs. The input parameters are internally commented within the source code; for example,

to get more information about the

GENMAG_SMEAR

keyword,

> grep GENMAG_SMEAR $SNANA_DIR/src/snlc_sim.h

> grep GENMAG_SMEAR $SNANA_DIR/src/snlc_sim.c

will help you trace the meaning of this variable. All of the input options are deﬁned in a structure called

INPUTS

snlc_sim.h

. Please report variables that are not commented, or that have confusing comments.

Don’t hesitate contacting other people familiar with

snlc_sim.exe

. Some of the light curve parameters

are obscure (i.e, describing the distribution of extinction & ∆), and our best estimates of these parameters

can change. To reduce the burden of tracking all of these parameters, defaults for these obscure parameters

are stored in the ﬁle

$SNDATA_ROOT/models/snlc_sim.defaults .

If you simply ignore these obscure parameters in your input ﬁle, the “defaults” deﬁned above will be used

in the simulation. You can modify any parameter by deﬁning the parameter explicitly in your input ﬁle.

The simulated lightcurves are located in $

SNDATA_ROOT

SIM

. Do NOT try ‘ls’ !!! Instead, try ‘

ls -d

’ to see all versions. To avoid sifting through hundreds of versions from multiple users, I always use

‘

’ as a preﬁx for my versions, and therefore I can see my versions with ‘

ls -d RK*/

.’ Each simulated

version is located in a sub-directory named by your version. Recall that you have full write-privilege, so

use caution. Each version has an auto-generated README ﬁle. If your version is called ‘MYFIRSTSIM’,

then do

> more $SNDATA_ROOT/SIM/MYFIRSTSIM/MYFIRSTSIM.README

which contains a list of all your simulation options. The default format is FITS: one FITS ﬁle for the

header info with one row per SN, and a second FITS ﬁle with all of the light curves. Instead of FITS

format, you can generate a text ﬁle per SN with the option “

FORMAT_MASK: 2

” (§4.31). The

SNANA

ﬁtting

programs read both the FITS and TEXT formats. You can get a list of ﬁles with the commands

cd $SNDATA_ROOT/SIM/MYFIRSTSIM/

ls MYFIRSTSIM_SN*

more MYFIRSTSIM.LIST

4.3 Synchronizing Random Numbers

The simulation is designed to preserve the random number sequence when input parameters and options

are changed. This feature allows generating the exact same SNe (redshift, sky-coords, SN properties)

when making changes such as the

SIMLIB

, exposure time, mag-offsets, intrinsic smearing, and model

parameters. To ensure that different simulations are synchronized to the same random numbers, use the

same random seed (

RANSEED

key) and verify that the following output to the README ﬁle is identical:

Random Number Sync:

RANDOM SEED: 123459

FIRST/LAST Random Number (List=1): 0.181881 0.150452

FIRST/LAST Random Number (List=2): 0.196079 0.139981

The ﬁrst list is for the nominal generation, and the second list is for the intrinsic scatter models. The

optional sim-input key

RANLIST_START_GENSMEAR

can be used to pick different random numbers for the

intrinsic scatter without affecting the main random sequence. Note that this key value is an offset in a list

(not a SEED). Since each scatter model typically uses ∼10 randoms per SN,

RANLIST_START_GENSMEAR

should be set to multiples of about 10.

Selection cuts may result in a different number of generated SNe, and hence a different last random

number; in this case use the

SIMGEN_DUMP

option (§4.32.3) to verify the sync.

4.4 Simulated TYPE

The simulation produces an SNTYPE value for the data header, allowing speciﬁc sub-types to be ana-

lyzed.1There are two basic SNTYPEs assigned: SNTYPE for spec-conﬁrmed SNe (§4.15), and a different

SNTYPE for unconﬁrmed SNe; the latter correspond to a photometrically identiﬁed sample. By default,

the integer SNTYPE for unconﬁrmed SNe is 100 + the SNTYPE of spec-conﬁrmed SNe.

The SNIa-SNTYPE is determined with the sim-input key “

SNTYPE_Ia

” or “

SNTYPES_Ia

”. For exam-

ple, the SDSS–II code for type Ia is

SNTYPE_Ia: 120 # spec Ia -> type 120; photo-Ia -> type 220

SNTYPES_Ia: 120 106 # spec-Ia -> type 120; photo-Ia -> type 106

where the 2nd key allows specifying the photometric-id type to be different than 100 + spec-conﬁrmed

type. This integer code appears in the header of each output data ﬁle after the “

SNTYPE:

” key. For spec-

conﬁrmed SNIa, the default

SNTYPE_Ia

value is 1.

The SNTYPE values for

NON1ASED

and

NON1AGRID

models are given in the sim-input ﬁle as described

in §9.5. To specify TYPE for non-SN models, or over-ride the above, use

GENTYPE

as follows:

GENTYPE: 80 # specType=80, photoType=180

GENTYPES: 80 81 # specType=80, photoType=81

Beware of SNTYPE collisions ! The user must beware of SNTYPE collisions between SNIa and

Non-Ia. For example, consider the example above with “

SNTYPE_Ia: 120

” in the SNIa sim-input ﬁle,

and a separate Non-Ia input ﬁle in which SNTYPE=20 for one of the species. The unconﬁrmed Non-

Ia SNTYPE value will be 20 +100 =120, which conﬂicts with the SNIa-SNTYPE value. There is no

problem if the SNIa and Non-Ia samples are analyzed separately, but there could be a problem if the

samples are combined. There is no way for the simulation code to identify these conﬂicts because the Ia

and Non-Ia are generated separately; hence the user must check.

1See

&SNLCINP

namelist variable

SNTYPE_LIST

in the

snana.exe

and

snlc_fit.exe

programs.

4.5 The ‘

SIMLIB

’ Observing Conditions File

A user-generated ‘

SIMLIB

’ ﬁle2is needed to deﬁne the cadence, translate magnitudes into CCD counts,

and to compute the uncertainty as described in Eq. 3. As an example, the start of the

SIMLIB

ﬁle for the

SDSS-II 2005 survey is shown in Fig. 1. The public

SIMLIB

ﬁles are located in $

SNDATA_ROOT

simlib

and a

SIMLIB

ﬁle is speciﬁed in the sim-input ﬁle with the keyword

SIMLIB_FILE: SDSS2005_ugriz.SIMLIB

The simulation will ﬁrst check YOUR current working directory for this ﬁle; if it’s not there, then

snlc_sim.exe

will check the public directory $

SNDATA_ROOT

simlib

SIMLIB

ﬁle is created by someone with knowledge of the telescope and observation conditions.

There is a convenient utility,

SNANA_DIR

src/simlib_tools.c

, that you can use to create the

SIMLIB

ﬁle in the correct format. This utility has a lot of error checking to prevent you from accidentally writing

absurd values like a negative PSF. In principle, a

SIMLIB

ﬁle need be created only once per survey, although

systematic studies may require multiple

SIMLIB

s. If there are several exposures per ﬁlter per night, the

utility

simlib_coadd.exe

(§12.3.2) will re-make a

SIMLIB

with all exposures per ﬁlter combined into a

single effective exposure per night.

The

SIMLIB

ﬁle begins with a global header with the following keys:

# Required keys:

SURVEY: <SURVEY> # must find match in $SNDATA_ROOT/SURVEY.DEF

FILTERS: <filtList> # must find match in kcor/calib file

# Optional keys:

USER: <NAME> # user who created SIMLIB file

HOST: <NAME> # host computer where SIMLIB was created

SKYSIG_UNIT: ADU_PER_SQARCSEC # change SKYSIG unit from default per-pixel

PSF_UNIT: ARCSEC_FWHM # change PSF unit from default pixels

NPE_PIXEL_SATURATE: <VAL> # pixel-flux Saturation, photo-electrons

PHOTFLAG_SATURATE: <MASK> # saturation mask in output PHOTFLAG column

NLIBID: <VAL> # Number of obs-sequence (LIBIDs) in file

PIXSIZE: <VAL> # size of pixel, arcSec

COMMENT: <comment string>

For batch jobs submitted with

sim_SNmix.pl

script,

NLIBID

is used to assign a different starting

LIBID

(see below) for each batch core, ensuring uniform library sampling.

Following the global header is a list of observation sequences. Each sequence starts with a header as

follows:

# Required

LIBID: <ID> # integer id (does not have to be sequential)

NOBS: <VAL> # number of observations

RA: <VAL> # Right ascension, degrees

DEC: <VAL> # Declination, degrees

2“

SIMLIB

” is an abbreviation for

SIM

ulation

LIB

rary.

# Optional

MWEBV: <VAL> # MW E(B-V). If zero, use software options.

PIXSIZE: <VAL> # pixel size, arcSec

FIELD: <NAME> # name of FIELD

CCDNUM: <VAL> # CCD number (to locate on focal plane)

For a non-overlapping ﬁeld, the “

FIELD:

” header should appear only once per MJD-sequence. For over-

lapping ﬁelds, the

FIELD

key appears more than once as indicated in Fig. 1. You can repeatedly toggle

between two ﬁelds, or simply list all the MJDs for one ﬁeld (i.e, 82N) followed by all of the MJDs for

the other ﬁeld (i.e., 82S); the MJDs need not be chronological in the

SIMLIB

, as the simulation will sort

them internally. You can ignore the

FIELD

key in the

SIMLIB

as well, in which case the SNDATA ﬁles and

analysis lose track of the ﬁeld.

Following the

LIBID

header, below is a brief explanation for each column in the observation table,

along with references to terms in Eq. 3,

1. S: key starts a line with search-image info.

2. IDEXPT: arbitrary identiﬁer. You can set this to zero if you want. For SDSS, it glues together the

run and ﬁeld numbers.

3. FLT: single character to specify a ﬁlter for this observation.

4. CCD Gain: Number of photo-electrons per ADU or DN.

5. CCD Noise: CCD read noise in photo-electrons, per pixel. This term is usually much smaller than

the SKYSIG term below.

6. SKYSIG: Standard deviation of sky (including dark current), in ADU (or DN) per pixel. See §4.12

for noise calculation. You can optionally enter the skysig values per arcsec2by specifying the simlib

global header key

SKYSIG_UNIT: ADU_PER_SQARCSEC

The simulated README ﬁle includes the

SKYSIG_UNIT

value.

7. PSF1,2 and RATIO: The PSF is speciﬁed by a double-Gaussian with σ-widths (pixels) of σ1=

PSF1 and σ2=PSF2. RATIO refers to the ratio at the origin, PSF2(origin)/PSF1(origin). Note that

the default PSF unit is in pixels, not arcsec. You can optionally give the PSF values in the more

astronomy-friendly units of arcsec-FWHM by specifying the simlib header key

PSF_UNIT: ARCSEC_FWHM

The simulated README ﬁle includes the

PSF_UNIT

value. These PSF values are used to determine

a noise-equivalent area (Ain Eq. 3 and Eq. 10). If you have computed Afrom the measured PSF,

then you can simply deﬁne PSF1 =pA/4πand set PSF2=RATIO=0.

8. ZPTAVG: Zero point relating the source magnitude (m) to the CCD ﬂux measured in ADU:

Flux(ADU) = 10−0.4(m−ZPTAVG).

For example, if F20 is the ﬂux (in ADU) for a point source with mag=20, then ZPTAVG=20 +

2.5log10(F20). Note that ZPTAVG encodes information about the atmospheric transparency, tele-

scope aperture & efﬁciency, and the exposure time. For any given simlib ﬁle, the simulated ZPTAVG

can be changed globally or by ﬁlter as explained in §4.17. Note that the zeropoint in photoelectrons

is given by ZPTpe =ZPTAVG+2.5log10(GAIN).

9. ZPTSIG: See ˆ

σZPT term in Eq. 3.

A sequence of MJDs that span the survey constitutes one entry in the

SIMLIB

, and the index “LIBID”

labels each entry. A

SIMLIB

can have one LIBID, or hundreds. Large-area surveys, like SDSS-II, need

hundreds of LIBIDs to properly sample the sky. A small area survey, like DES, may need just one LIBID

per pointing, and per season.

SURVEY: SDSS FILTERS: gri

USER: rkessler HOST: sdssdp47.fnal.gov

COMMENT: ’Extract random RA,DECL,MJD from MYSQL: year=2005’

BEGIN LIBGEN Tue Apr 17 13:32:33 2007

# --------------------------------------------

LIBID: 1

RA: 26.430172 DECL: 0.844033 NOBS: 42 MWEBV: 0.026 PIXSIZE: 0.400

FIELD: 82N

# CCD CCD PSF1 PSF2 PSF2/1

# MJD IDEXPT FLT GAIN NOISE SKYSIG (pixels) RATIO ZPTAVG ZPTSIG

S: 53616.383 556600405 g 4.05 4.25 4.04 1.85 3.61 0.247 28.36 0.020

S: 53616.383 556600405 r 4.72 4.25 5.28 1.64 3.62 0.142 28.17 0.022

S: 53616.383 556600405 i 4.64 12.99 6.95 1.60 3.81 0.103 27.84 0.017

FIELD: 82S

S: 53622.395 558200552 g 4.03 5.45 4.09 1.58 3.31 0.107 28.45 0.018

S: 53622.395 558200552 r 4.89 4.65 5.00 1.46 3.55 0.065 28.15 0.028

S: 53622.395 558200552 i 4.76 10.71 6.43 1.53 3.65 0.075 27.85 0.029

S: 53626.359 560300625 g 4.05 4.25 4.40 1.83 3.50 0.282 28.24 0.020

etc ...

Figure 1: Header and part of ﬁrst entry of the

SIMLIB

ﬁle used for the SDSS-II survey.

4.5.1

SIMLIB

Options in the Sim-Input File

SIMLIB_MSKOPT: nnn # bit-mask of options (see below)

SIMLIB_IDSTART: nnn # start at LIBID nnn

SIMLIB_IDLOCK: nnn # use only LIBID nnn ; skip all others

SIMLIB_MAXRANSTART: nnn # start at random LIBID among first nnn entries

SIMLIB_NSKIPMJD: n # use every ’n+1’th observation

SIMLIB_IDSKIP: nn1 # ignore LIBID nn1

SIMLIB_IDSKIP: nn2 # ignore LIBID nn2 (add as many as you want)

SIMLIB_DUMP: 1 # dump summary of simlib

SIMLIB_NREPEAT: nn # repeat each LIBID nn times (for speed)

SIMLIB_FIELDLIST xyz # plus-separated list of field-substrings

SIMLIB_MINSEASON nn # remove seasons less than nn day duration

USE_SIMLIB_PEAKMJD: 1 # use peakMJD in header (if there)

USE_SIMLIB_REDSHIFT: 1 # use redshift in header (if there)

USE_SIMLIB_DISTANCE: 1 # use lumi-distance in header (invert to get zCMB)

More information about the

SIMLIB_DUMP

option is in §4.32.1. The

SIMLIB_MSKOPT

options are

•

MSKOPT

+= 2 : for each

LIBID

in the simlib, keep generating until an event is accepted. The number

generated for each

LIBID

is stored in the output tables(s) and SIMGEN-DUMP ﬁle as

NGEN_LIBID

To avoid inﬁnite loop, generation for a given LIBID stops when NGEN_LIBID >MXGEN_LIBID. To

preserve

NGEN_LIBID

information for no-accept LIBIDs, these events are forced to be accepted with

NOBS = NEPOCH = 0

to ensure that forced events fails all analysis cuts.

•

MSKOPT

+= 8 : debug option to replace correlated template noise (

TEMPLATE_XXX

keys below) with

random (uncorrelated) noise.

•

MSKOPT

+= 16 : ignore template noise in

SIMLIB

ﬁle.

•

MSKOPT

+= 32 : ignore

FLUXERR_COR

map in

SIMLIB

ﬁle.

•

MSKOPT

+= 128 : if any part of Trest range overlaps a season, include entire season in light curve.

Season deﬁned by gap ≥90 days.

•

MSKOPT

+= 256 : include every MJD in survey, regardless of Trest-range.

When the trigger efﬁciency is low, such as for

NON1A

models at high redshift, the simulation speed is

limited by reading the ascii

SIMLIB

ﬁle. The simulation speed can be improved by a factor of few using

‘

SIMLIB_NREPEAT: 10

’, where 10 is a suggested value. This option generates 10 SNe with each

SIMLIB

entry before reading the next

SIMLIB

entry, and thus reduces the amount of reading by a factor of 10.

Be careful to make sure that your

SIMLIB

is fully sampled. For example, if a

SIMLIB

has 1000 entries

and 1000 SNe are generated with

SIMLIB_NREPEAT=10

, then the ﬁrst 100

SIMLIB

entries are used and

the remaining 900 are ignored. In this situation at least 10,000 SNe should be generated to sample each

SIMLIB

entry.

SIMLIB_NREPEAT

BEWARE: this option results in non-uniform sampling of the SIMLIB, and it can

be corrected with

NGEN_LIBID

in the output table. However, if you are not sure how to correct with

NGEN_LIBID

then you should not be using this option.

Be careful with

SIMLIB_FIELDLIST

because it checks for substring matches, not an exact match.

For example, suppose we have 6

SIMLIB

ﬁelds named

MED1,MED2,MED3,DEEP1,DEEP2,DEEP3

. The

following will select all three of the

MED

ﬁelds:

SIMLIB_FIELDLIST: MED1+MED2+MED3

SIMLIB_FIELDLIST: MED # select all fields with MED in name

This sub-string select feature is convenient when there are many ﬁelds, but it can also lead to undesirable

behavior as illustrated in the following example. Consider ten

SIMLIB

ﬁelds

F1,F2,...F10

. Setting

“

SIMLIB_FIELDLIST: F1

” will select both

and

F10

since

is a sub-string of both. In this situation,

one should deﬁne the ten ﬁelds to be

F01,F02, ... F10

, and then selecting “

SIMLIB_FIELDLIST:

F01

” will select the correct ﬁeld.

SIMLIB_MAXRANSTART

is useful when using

sim_SNmix.pl

(§12.3.1) and each job generates fewer

events than the number of

SIMLIB

entries. For example, suppose a

SIMLIB

has 1000 entries, and a sim-job

generating 2000 events is distributed among 50 cores using

sim_SNmix

. The problem is that each of the

50 jobs generates 2000/50 =40 events, and each job samples only the ﬁrst 40

SIMLIB

entries, which does

not properly sample the

SIMLIB

. Using

SIMLIB_MAXRANSTART: 1000

each job will start at a random entry among the ﬁrst 1000

SIMLIB

entries, thereby assuring a proper

sampling of the full

SIMLIB

. If each of the 50 jobs has enough statistics to sample the full

SIMLIB

, there

is no need to use this feature. However, be careful when using

SIMLIB_NREPEAT

because the number of

sampled

SIMLIB

entries is reduced by this

NREPEAT

factor.

4.5.2

SIMLIB SPECTROGRAPH

SPECTROGRAPH

instrument is deﬁned in the kcor-input ﬁle as described in §3.2. The

SIMLIB

Search-

epoch key for a broadband ﬁlter is “S:” and the corresponding

SIMLIB

key for a spectrum is

SPECTROGRAPH: 54997.3 1840 # MJD & Texpose (seconds)

An arbitrary number of

SPECTROGRAPH

keys are allowed in a

SIMLIB

ﬁle. In addition to computing a

spectrum at the listed MJD, the optional synthetic magnitudes (

SYN_FILTERS

key in kcor-input ﬁlers) are

evaluated in the same way as any other broadband ﬁlter.

Correlated template noise in both the spectra and synthetic ﬁlters can be included by specifying the

template exposure time in the LIBID header as follows:

TEMPLATE_TEXPOSE_SPECTROGRAPH: 5010 # seconds

4.5.3

SIMLIB

Options for each LIBID

The following header options can follow each

LIBID

key in a

SIMLIB

ﬁle.

RA: xxx # right ascension, degrees

DECL: xxx # declination, degrees

NOBS: nnn # number of obs to follow (i.e., number of ’S:’ rows)

PIXSIZE: xxx # size of each pixel, arcsec

# optional

MWEBV: xxx # E(B-V) from Galactic extinction

FIELD: sss # name of field (optional)

REDSHIFT: xxx # force this redshift

PEAKMJD: xxx # force this peak-MJD

CUTWIN_REDSHIFT: xxx xxx # reject if zCMB is not in this range

REDSHIFT_RANGE: xxx xxx # idem with legacy key

GENRANGE_REDSHIFT: xxx xxx # regenerate zCMB in this range

GENRANGE_PEAKMJD: xxx xxx # regenerate PEAKMJD in this range

GENSIGMA_PEAKMJD: xxx # pick from Gaussian profile; otherwise flat

GENRANGE_SALT2x1: xxx xxx # regenerate SALT2x1 in this range

GENSIGMA_SALT2x1: xxx # pick from Gaussian profile; otherwise flat

GENRANGE_SALT2c: xxx xxx # regenerate SALT2c in this range

GENSIGMA_SALT2c: xxx # pick from Gaussian profile; otherwise flat

# correlated template noise

TEMPLATE_ZPT: <value for each filter> # ADU

TEMPLATE_SKYSIG: <value for each filter> # ADU/pix

TEMPLATE_CCDSIG: <value for each filter> # e-/pix

If any

GENRANGE_XXX

key appears without an associated

GENSIGMA_SIGMA

key, then the corresponding

value is re-generated from a ﬂat distribution. If the

GENSIGMA_SIGMA

is speciﬁed, then the new value is

re-generated from a Gaussian distribution whose peak value is at the center of the

GENRANGE_XXX

window.

For more info on the

TEMPLATE_XXX

keys, see §4.7. The

USE_SIMLIB_XXX

keys are speciﬁed in the

sim-input ﬁle (§4.5.1).

4.5.4 Saturation Option

Saturation is speciﬁed by two

SIMLIB

keys in the global header before the “

BEGIN LIBGEN

” key:

NPE_PIXEL_SATURATE: 65000 # Npe to saturate central pixel, per exposure

PHOTFLAG_SATURATE: 2048 # add this to PHOTFLAG for each epoch

The central PSF-pixel ﬂuxes are summed for source, galaxy and sky. If the resulting number of photoelec-

trons exceeds

NPE_PIXEL_SATURATE

, then this epoch is ﬂagged as saturated as follows:

•

PHOTFLAG = PHOTFLAG_SATURATE

•

MAG = -7

•

FLUXCAL

=0±108

Saturated epochs are not used to form trigger logic, and

SNANA

programs (snana.exe, snlc_ﬁt.exe) ignore

saturated epochs.

For co-added observations, the exposure-averaged ﬂux is compared with

NPE_PIXEL_SATURATE

. The

number of exposures in the co-add (

NEXPOSE

, default=1) can be optionally included with the IDEXPT

column as follows:

# PSF1 PSF1 PSF

# MJD ID*NEXPOSE FLT GAIN NOISE SKYSIG (pixels) RATIO ZPTAVG ZPTERR MAG

S: 59770.366 13819*6 r 1.00 1.12 138.55 1.45 0.00 0.000 34.89 0.005 99

etc ..

which corresponds to 6 exposures in the co-add. Note that

ID*NEXPOSE

is a single string with no blank

spaces between the characters. In this example, a saturated epoch is ﬂagged if

FLUX(central pixel)/6 > NPE_PIXEL_SATURATE

The fraction of ﬂux in the central pixel (fA) is computed analytically using a Talyor expansion of a Gaus-

sian:

fA=P2

2πσ21−P2

4πσ2

where Pis the pixel size and σrefers to the PSF. Beware that when P>σ, the analytic approximation

degrades. However, the computation of fAonly affects the saturation ﬂag, and is not used in determining

the broadband ﬂuxes.

Finally, the total number of saturated/unsaturated observations can be included in the

SIMGEN_DUMP

ﬁle (§4.32.3):

NOBS_SATURATE

and

NOBS_NOSATURATE

CUTWIN

options can be used to select based on the

number of [un]saturated observations per ﬁlter (§4.16).

4.5.5

APPEND

Option

The

SIMLIB-APPEND

feature prevents epochs from being MJD-sorted. This feature allows appending

SIMLIB

observations without changing the original light curve ﬂuxes and their Poisson ﬂuctuations. The

SIMLIB

syntax is shown below. Epochs after the

APPEND

key are not MJD-sorted, and thus won’t change

the random sync for epochs before the

APPEND

key. The integer argument after the

APPEND

key is a mask

that is added to the

PHOTMASK

column in the data ﬁle.

...

S: 53616.383 556600405 g 4.05 4.25 4.04 1.85 3.61 0.247 28.36 0.020

S: 53616.383 556600405 r 4.72 4.25 5.28 1.64 3.62 0.142 28.17 0.022

S: 53616.383 556600405 i 4.64 12.99 6.95 1.60 3.81 0.103 27.84 0.017

APPEND: 4

S: 53612.395 558200552 g 4.03 5.45 4.09 1.58 3.31 0.107 28.45 0.018

S: 53612.396 558200552 r 4.89 4.65 5.00 1.46 3.55 0.065 28.15 0.028

S: 53612.397 558200552 i 4.76 10.71 6.43 1.53 3.65 0.075 27.85 0.029

...

4.5.6 SNR Monitor

To monitor the quality of observing conditions at each epoch, the SNR for a ﬁxed magnitude can be

computed with the following sim-input:

MAGMONITOR_SNR: 20 # only integer mag allowed

which results in computing SNR for mag=20 at each MJD in the

SIMLIB

. The results are stored in the

data ﬁles under a photometry column labelled

SIM_SNRMAG20

. Beware that

SIM_SNRMAG20

depends on

the

SIMLIB

quantities (ZP,PSF,SKY) and does not depend on the light curve model. The argument of

MAGMONITOR_SNR

must be an integer in order to construct the variable name of the output photometry

column.

SIM_SNRMAG##

exists, it is automatically read by the analysis programs and included in output tables

with epoch columns: in particular, the tables

SNANA+EPOCHS

and

FITRES+RESIDUALS

4.6 Simulating Fields

4.6.1 Overlapping Fields

The simulation can handle overlapping ﬁelds, such as for the SDSS 82N/82S overlap, and the 20% overlap

of the LSST ﬁelds. Overlapping ﬁelds are speciﬁed in the

SIMLIB

ﬁle by specifying the

FIELD

keyword

as needed. Figure 1 above illustrates an overlap between the SDSS ﬁelds 82N and 82S. Note that over-

lapping ﬁelds make no sense if there is just one simlib entry per ﬁeld with the position selected at the

(non-overlapping) center of the ﬁeld. To generate light curves in overlapping ﬁelds, the

SIMLIB

should

include many LIBID entries per ﬁeld, where each LIBID is associated with a random RA & DEC. This

mechanism accounts for dithering as well as variations within a ﬁeld from Galactic extinction and observ-

ing conditions.

If the ﬁelds are small and non-overlapping (e.g., SNLS), then a single LIBID per ﬁeld, with the RA &

DEC at the center, may work reasonably well. However, this simlib will not probe variations in Galactic

extinction that can occur even on small angular scales.

The

&SNLCINP

namelist includes two FIELD-selection variables (§5.21) that work for both data and

simulations. First you can pick speciﬁc ﬁelds with

SNFIELD_LIST = ’field1’, ’field2’, ’field3’

By default all ﬁelds are analyzed when running the ﬁtting program. The second option is

CUTWIN_NFIELD

so that you can select SN that overlap more than 1 ﬁeld.

4.6.2 Field Subset

There are two distinct ways to simulate a subset of ﬁelds, and the difference is crucial for getting the right

normalization of generated events. The FIELD-subset options are illustrated with a hypothetical survey

with 10 ﬁelds: 8 of them are called SHALLOW and 2 of them are called DEEP. Assume that each ﬁeld has

the same area of 10 deg2, or 100 deg2total. Finally, consider a

SIMLIB

ﬁle with 200 DEEP-ﬁeld entries

and 800 SHALLOW-ﬁeld entries. If we select only DEEP ﬁelds, there are two different ways in which the

simulation can work: 1) count every SHALLOW and DEEP ﬁeld as part of NGENTOT_LC, or 2) ignore

SHALLOW ﬁelds as if they were not in the

SIMLIB

. For the ﬁrst option, only 20% of the events land on a

DEEP ﬁeld, and thus the efﬁciency will be less then 20%. For the 2nd option, all events are processed with

a DEEP ﬁeld

SIMLIB

entry, and thus the efﬁciency can be as high as 100%. For the 2nd option, one should

reduce the solid angle by a factor of 5 in order to get the same number of events as in the ﬁrst option.

These two

SIMLIB

-counting options are implemented in the sim-input ﬁle as follows:

SOLID_ANGLE: 0.03 # 100 deg^2

SIMLIB_FIELDLIST: DEEP1+DEEP2 # NGENTOT counts both SHALLOW and DEEP

SOLID_ANGLE(DEEP1+DEEP2): 0.006 # 20 deg^2 for DEEP only

Used with

sim_SNmix

, both of the above options result in the same number of output events (within

statistical errors), but 2nd efﬁciency will be ×5 larger than the ﬁrst to compensate the ﬁrst job generating

×5 more events.

Finally, there is a subtle issue using “

SOLID_ANGLE(DEEP)

” as a command line argument. Unix tries

to parse the parentheses, resulting in bad arguments passed to the simulation. To avoid this problem, use

single quotes or back-slashes:

snlc_sim.exe mySim.input ’SOLID_ANGLE(DEEP)’ 0.006

snlc_sim.exe mySim.input SOLID_ANGLE$DEEP$ 0.006

The

sim_SNmix

script automatically adds the backslashes, so there is no need to modify the

GENOPT

argument.

4.7 Correlated Template Noise

Coherent template noise is simulated with the following

SIMLIB

keys:

TEMPLATE_ZPT: <value for each filter> # ADU [required]

TEMPLATE_SKYSIG: <value for each filter> # ADU/pix [optional]

TEMPLATE_CCDSIG: <value for each filter> # e-/pix [optional]

where the list of ‘

NFILT

’ values corresponds to the list of

NFILT

ﬁlters following the

FILTERS

key in

the header. For example, if 6 ﬁlters are deﬁned by “

FILTERS: ugrizY

” then each

TEMPLATE_XXX

key

must be followed by 6 values, even for LIBIDs that use a subset of ﬁlters. The

TEMPLATE_XXX

keys can

appear before the ﬁrst LIBID to specify a global set of values for every generated SN. Alternatively, these

TEMPLATE_XXX

keys can appear after each LIBID (along with RA, DECL, etc ...) to specify an independent

template noise for each LIBID entry. Note that

TEMPLATE_ZPT

is required if one or both of the noise keys

(SKYSIG or CCDSIG) is speciﬁed. For each generated SN epoch, a ﬁlter-dependent random template

ﬂuctuation is normalized to the search image using the ZPT information, and the normalized ﬂuctuation

added to the ﬂux.

Internally the simulation adds two sets of ﬂuctuations: all errors excluding the template are used to pick

one ﬂuctuation and the template error is used for the other ﬂuctuation. The ﬁrst ﬂuctuation is independent

for all epochs; the 2nd ﬂuctuation is coherent among epochs in the same ﬁlter. The reported

FLUXCAL_ERR

combines these two sources in quadrature.

Off-diagonal errors coming soon ...

4.8 Simulating Multiple Instruments

SN photometric observations may come from more than one instrument, such as optical and infrared ob-

servations. To simulate all of the light curves together, each simlib entry can contain information from

multiple instruments. The only caveat is the that FIELD name and pixel size must be re-deﬁned as illus-

trated in Fig. 2.

Since the default units for the noise (CCD and SKY) and the PSF are both in pixels, the

PIXSIZE

value

has no practical effect. However, when using optional units of arcsec (§4.5), the correct

PIXSIZE

values

are important.

LIBID: 4

FIELD: F4 RA: 0.50 DECL: -43.0 MWEBV: 0.008

TELESCOPE: CTIO PIXSIZE: 0.270 asec

NOBS: 120

# CCD CCD PSF1 PSF2 PSF2/1

# MJD IDEXPT FLT GAIN NOISE SKYSIG (pixels) RATIO ZPTAVG ZPTSIG MAG

S: 56249.039 1002 g 1.00 10.00 91.90 1.93 0.00 0.000 33.02 0.020 99.

S: 56249.000 1003 r 1.00 10.00 151.40 1.49 0.00 0.000 33.29 0.020 99.

S: 56249.008 1004 i 1.00 10.00 275.66 1.62 0.00 0.000 33.42 0.020 99.

S: 56249.016 1005 z 1.00 10.00 442.18 1.40 0.00 0.000 34.31 0.020 99.

FIELD: V8 PIXSIZE: 0.339 # <== for different instrument

S: 56250.323 1006 Y 4.0 160.0 114.22 1.09 0.0 0.0 31.70 0.010 99.

S: 56256.033 1007 J 4.0 160.0 282.14 1.16 0.0 0.0 31.99 0.010 99.

Figure 2: Excerpt from

SIMLIB

with two instruments: DES optical (griz) and VIDEO infrared (YJ).

4.9 Simulating Multiple Seasons

Multiple seasons can be simulated with a separate

SIMLIB

ﬁle for each season, but this strategy requires

multiple generations and bookkeeping to generate a full multi-season sample. An alternative is to construct

a single

SIMLIB

ﬁle containing all seasons, either as separate LIBID entries for each season or as long

LIBID entries that each spans all of the seasons/years.

For the latter option using a single

SIMLIB

for multiple seasons, there are typically long MJD gaps

with no observations, leading to inefﬁcient generation. MJD masks can be speciﬁed in the

SIMLIB

header,

as illustrated here for the SDSS-II,

GENSKIP_PEAKMJD: 53710 53970 # skip the off-season

GENSKIP_PEAKMJD: 54070 54340 # idem

Each

GENSKIP_PEAKMJD

key must appear before the “

BEGIN LIBGEN

” key, and it speciﬁes an MJD-range

to ignore in the generation.

4.10 Simulating a Filter as a Sum of Components

OBSOLETE as of SNANA version v10_50m

There are some cases where the ﬂux in a ﬁlter should be simulated as a sum of components in order to

avoid ambiguities in the zeropoint. Examples are red-leakage in a UV ﬁlter, cross-correlation ﬁlters, or a

very broad ﬁlter. If the ﬁlter transmission for ’0’ is the sum of ﬁlter-transmissions 1+2+3+4, the following

SIMLIB entries are needed:

# CCD CCD PSF1 PSF2 PSF2/1

# MJD IDEXPT FLT GAIN NOISE SKYSIG (pixels) RATIO ZPTAVG ZPTSIG MAG

...

S: 56190.000 1000 0 1.00 10 100.00 2.00 0 0 1+2+3+4 0.020 99

S: 56190.000 1001 1 1.00 10 47.63 2.35 0 0 32.98 0.020 99

S: 56190.000 1002 2 1.00 10 98.63 2.35 0 0 32.33 0.020 99

S: 56190.000 1003 3 1.00 10 122.63 2.35 0 0 32.21 0.020 99

S: 56190.000 1004 4 1.00 10 147.63 2.35 0 0 32.16 0.020 99

...

The

ZPTAVG

value for ﬁlter-0 is assumed to be ambiguous because it depends on the magnitude of the

object (see below), and hence this entry is replaced by 1+2+3+4 to indicate that its ﬂux is a sum of ﬁlters

that have well-determined properties. Filters 01234 must all be deﬁned in the usual way in the kcor/calib

ﬁle, and the

GENFILTERS

key must include these ﬁve ﬁlters. The MJDs for 012345 must be exactly the

same; if not, the simulation will abort. The SIMLIB entries for 1234 must be accurately deﬁned, and any

reasonable values for ’0’ are sufﬁcient since the ﬁlter-0 ﬂux will get over-written with the sum of ﬂuxes

from 1+2+3+4. The zeropoint (Z0) for ﬁlter-0 is calculated to be

Z0=2.5×log10 "∑

10−0.4(mi−M0−Zi)#(4)

where miare the simulated magnitudes in ﬁlter components i=1,2,3,4, Ziare the user-determined ze-

ropoints in i=1,2,3,4, and M0is the simulated magnitude in ﬁlter-0. Note that for a coadd we have

mi=M0and recover the usual expression for the co-added zeropoint.

4.11 Noise Corrections: ˆ

SSNR and ˆ

σ0

From the noise calculation in Eq. 3 there are two quantities which the simuation cannot determine from

the

SIMLIB

ﬁle: 1) a global scale ˆ

SSNR, and 2) an offset ˆ

σ0. These quantities must be determined by the

survey team. §4.11.1 explains how to provide this information to the simulation via tables, and §4.11.2

suggests a general strategy on how to determine these corrections.

4.11.1

FLUXERRMAP

Tables

SSNR and ˆ

σ0are each deﬁned as an aribtrary multi-dimensional function of the following 8 variables:

MJD: Modified Julian date

PSF: FWHM, arcsec

SKYSIG: ADU/pixel

ZP: zero point, ADU

LOGSNR: log10(SNR)

SBMAG: surface-brightness mag, per arcsecond^2

GALAMG: total galaxy mag

SNSEP: SN-host separation, arcsec

The set of 8 observed values for each observation is refered to as ~

Oσ. Several 1D maps can be deﬁned, or

a single multi-dimensional map can be used to capture correlations. The 1D maps are illustrated for the

3-year SDSS sample in

$SNDATA_ROOT/simlib/SDSS/SDSS_fluxErrModel.DAT

The ﬁrst

NVAR-1

columns are input variables among the eight variables above. The last column is either

ERRSCALE

(=ˆ

SSNR) or

ERRADD

(=ˆ

σ0). The

BAND

key speciﬁes that each map corresponds only to that

band. There is also an optional

FIELD

key, but since the

FIELD

key is not used in this example, the map is

applied to all ﬁelds (82-N and 82-S). Similarly, leaving out the

BAND

key would apply the map to all ﬁlters.

The

MAPNAME

is chosen by the user, and only one of each

MAPNAME

can be used per observation. If

the simulation ﬁnds two valid maps with the sampe

MAPNAME

, the code will abort. Muliple maps can be

applied per observation, as long as each map has a different

MAPNAME

. In the SDSS example, two maps

are applied for each observation:

FLUXERR_ADD

and

FLUXERR_SCALE

. For a given ~

Oσ,ˆ

SSNR and ˆ

σ0are

computed from linear interpolation of the map. The map binning must be uniform, and the maps are not

extrapolated which means that the map range must cover all possible ~

Oσvalues from the survey: violating

either criteria results in an abort.

While the example ﬁle above (

SDSS_fluxErrModel.DAT

) illustrates 1D maps, Fig. 3 shows an explicit

example of a 2D map for the Dark Energy Survey (DES). This map has 3

bins and 5

PSF

bins; the total

map size is 3×5=15 bins. Fig. 3 illustrates an optional feature,

DEFINE_FIELDGROUP

, to associate a key

with a group of ﬁelds. The map corresponds to the

DEEP

ﬁelds, which is internally translated to

and

ﬁelds. The map applies to all four (griz) passbands.

The maps can be applied to simulations and to data. For simulations, the following sim-input command

will use the SDSS set of maps:

FLUXERRMODEL_FILE: SDSS_fluxErrModel.DAT

# option: suppress map(s) in reported errors for systematic tests:

FLUXERRMAP_IGNORE_DATAERR: FLUXERR_ADD

FLUXERRMAP_IGNORE_DATAERR: FLUXERR_SCALE

FLUXERRMAP_IGNORE_DATAERR: FLUXERR_ADD,FLUXERR_SCALE

# Option: re-write maps in FITRES format (for plotting,analysis, etc...)

# One output text file per MAPNAME

FLUXERRMODEL_OPTMASK: 256

The maps are always applied to the generated ﬂuxes to modify the true scatter on F−Ftrue. By default the

maps also modify the reported errors, but

FLUXERRMAP_IGNORE_DATAERR

allows suppressing some maps

from the reported errors in the data ﬁle to study the impact of under-estimated errors. The third

IGNORE

key suppresses both maps, which is equivalent to removing the

FLUXERRMODEL_FILE

key.

To modify data uncertainties in the analysis programs (

snana,exe,snlc_fit.exe,psnid.exe

&SNLCINP

FLUXERRMODEL_FILE = ’SDSS_fluxErrModel.DAT’ ! data only

FLUXERRMODEL_OPTMASK = 256 ! optional text dump of maps

SIM_FLUXERRMODEL_FILE = ’SDSS_fluxErrModel.DAT’ ! force on SIMs

By default, the

FLUXERRMODEL_FILE

key operates only on real data by adjusting the reported errors.

FLUXERRMODEL_FILE

is ignored for simulated samples because the simulated scatter and errors can be

altered during generation. To force simulated errors to be altered in the analysis stage, use the optional

key

SIM_FLUXERRMODEL_FILE

Finally, the

FLUXERRMODEL_OPTMASK=256

option (for simulation and analysis) writes out the maps in

the same TEXT format as the

FITRES

ﬁles, and writes one TEXT ﬁle per

MAPNAME

. This format may be

more useful for making plots and debugging.

DEFINE_FIELDGROUP: SHALLOW E1+E2+S1+S2+C1+C2+X1+X2

DEFINE_FIELDGROUP: DEEP C3+X3

MAPNAME: ERRSCALE_2D_ZPPSF

BAND: griz FIELD: DEEP

NVAR: 3

VARNAMES: ZP PSF ERRSCALE

ROW: 29 0.5 1.02

ROW: 29 1.5 1.25

ROW: 29 2.5 1.72

ROW: 29 3.5 2.06

ROW: 29 4.5 2.20

ROW: 32 0.5 1.0

ROW: 32 1.5 1.05

ROW: 32 2.5 1.12

ROW: 32 3.5 1.19

ROW: 32 4.5 1.30

ROW: 35 0.5 1.0

ROW: 35 1.5 1.05

ROW: 35 2.5 1.12

ROW: 35 3.5 1.19

ROW: 35 4.5 1.30

ENDMAP:

Figure 3: Illustration of 2D map to deﬁne ˆ

SSNR for DEEP ﬁelds in DES. While the bands and ﬁelds

correspond to DES, this map is made up for illustration and should not be used in any analysis.

4.11.2 Suggested Strategy for Determining

FLUXERRMODEL

Tables

For analyses requiring simulated bias corrections, here is a general strategy for determiming the

FLUXERRMODEL

maps from fake SN-like objects overlaid on images and processed through the same photometry pipeline

as the data. We do not make proposals for surveys without fakes.

Two

FLUXERRMODEL

maps are needed. The ﬁrst map corrects the simulated scatter to match the scatter

in the fake data. Correcting σSIM with ˆ

SSNR (Eq. 3) will correct both the true and reported uncertainties

in the simulations. The second map corrects the reported uncertainty in the fake data to reﬂect the true

scatter. This 2nd map is applied in the analysis stage via namelist parameter,

&SNLCINP

FLUXERRMODEL_FILE = ’DataCorMap.dat’

This map is applied to the fake data and the real data. It is not applied in the simulation because the

simulated true scatter corresponds to the reported uncertainty.

There are two reasons for using fakes: 1) the true ﬂux is known, and 2) the true model and rate are

known. The ﬁrst ˆ

SSNR map is created from both the fakes and the

SNANA

simulation:

SSNR(~

Oσ) = RMS[(Ftrue −F)/σSIM]fake

RMS[(Ftrue −F)/σSIM]sim (5)

where the ~

Oσ-dependence is also on the right-hand side, and RMS indicates root-mean-square in a bin

of ~

Oσ. The fakes and

SNANA

simulation must be generated with exactly the same light curve model

and redshift-dependent rate. Any bugs or features used to generate fakes should be reproduced in the

simulation. An example of such a feature is interpolating the fake ﬂux on a pre-computed grid in few-day

bins; this same interpolation should be used in the

SNANA

simulation. While Eq. 5 shows a general strategy,

each survey team must decide the appropriate subset of ~

Oσvariables to use, if the maps depend on band

and ﬁeld, and if there are sufﬁcient correlations to motivate multi-dimensional maps. Note that dividing

by σSIM (Eq. 3) is optional, but may be useful for debugging since each term should be near unity.

The second map is created soleley from the fakes,

SSNR(~

Oσ) = RMS[(Ftrue −F)/σSIM]fake

hσPhotPipe/σSIM ifake (6)

where σPhotPipe is the uncertainty from the photometry pipeline, and h i indicates an average in the ~

Oσ

bin. If there are ﬂux-outliers, it may be prudent to replace RMS with 1.48×median.

4.11.3 Extracting Information for

FLUXERRMAP

Here are some suggestions for extracting the 8 variables at the top of §4.11.1. The ﬁrst suggestion is to

simply parse the data ﬁle with your own script. The second method is to use the

FITRES+RESIDUALS

table

feature (§12.1) in the light curve ﬁtting program (

snlc_fitexe

). This feature produces information for

each observation in

ROOT

HBOOK

format. The epoch information can be extracted into

TEXT

format using

the

sntable_dump.pl

utulity (§12.1.2):

sntable_dump.pl myFile.root FITRES obs

A few of the output variables must be converted for the

FLUXERRMAP

SBMAG = 27.5 - 2.5*log10(SBFLUXCAL) [and protect SBFLUXCAL<0]

sigma_SIM = ERRTEST * FLUXCAL_DATA_ERR

PSF(arcSec) = PSF(sig,pixels) * 2.35 * PIXSIZE

4.11.4 Legacy Noise Corrections

Here is a legacy correction based on a table near the top of a

SIMLIB

ﬁle. These corrections are still

supported, but it is recommended to use the newer and more general ﬂux-error maps in §4.11. Note that if

the ﬂux-error maps are used, the

SIMLIB

noise terms below are ignored.

Global noise-terms ˆ

σ0and ˆ

SSNR (Eq. 3) can be speciﬁed in the simlib header. The ˆ

σ0term can be used

to account for additional noise from the SN-photometry. ˆ

SSNR is a global correction as a function of the

log of the signal-to-noise ratio, log10(SNR); this correction may be useful for PSF forms that are highly

non-Gaussian (e.g., in space), or as a global correction so that the simulated uncertainties better match the

those from the data.

FLUXERR_ADD: YJH 33 55 85 # sig_0 term for each filter

# Below is the S_SNR map,

# FILTs LOG10(SNR) ERROR/ERROR(SNANA)

FLUXERR_COR: YJH -5.00 1.0000 1.0000 1.0000

FLUXERR_COR: YJH -4.80 1.0000 1.0000 1.0000

FLUXERR_COR: YJH -4.60 1.0000 1.0000 1.0000

...

FLUXERR_COR: YJH 0.40 1.1387 1.1719 1.1775

FLUXERR_COR: YJH 0.60 1.1368 1.1704 1.1751

FLUXERR_COR: YJH 0.80 1.1295 1.1611 1.1654

FLUXERR_COR: YJH 1.00 1.1189 1.1470 1.1512

BEGIN LIBGEN

For SNR values outside the map-range, the correction at the min or max edge of the map is used. Thus for

the above map, SNR >10 results in corrections corresponding to the last

FLUXERR_COR

row.

To determine ˆ

σ0, plot the calibrated ﬂux-uncertainty “

FLUXCAL_ERRTOT

” (or

FLUXERR

in ntuple 7799)

for both data and simulation; adding the best-ﬁt ˆ

σ0in quadrature to the simulated uncertainty should match

the measured distribution. It is recommended to check the data-simulation comparison in PSF bins. There

is a utility in the SNANA ﬁtting program that calculates the noise analytically, allowing a more direct

comparison of the true uncertainty to the uncertainty that would be computed in a simulation. This feature

is automatically enabled for verbose-formatted data that includes the SKY, PSF and ZPTAVG for each

observation. See the SDSS data as an example of the verbose format. The quantity “

ERRTEST

,” the ratio

of calculated-to-true uncertainty, is included in ntuple 7799 for each observation.

To determine ˆ

SSNR, plot

ERRTEST

vs. log10(SNR)and the construct the

FLUXERR_COR

map from a

polynomial ﬁt or spline ﬁt.

Finally, note that there are no SNANA utilities to construct these maps.

4.12 Example Noise Calculation

Here is an example of how the simulation analytically computes the noise from the signal and sky-

background. The error on the signal (in photoelectrons) is simply pNpe. To get the error in observed

CCD counts (ADU), we start by relating the signal counts in ADU to the number of photoelectrons,

NADU =Npe ×G−1×SZP (7)

where Npe is the number of observed photoelectrons, Gis the number of photoelectrons per ADU (CCD

gain), and SZP is a scale factor applied to the signal so that the SN magnitude is referenced to the template

zeropoint. This factor is SZP =100.4(ZPt−ZPs), where ZPs,tare the zeropoints for the search and template

runs. In cloudy conditions, SZP >> 1 because the signal is much smaller than it would have been in the

template run. If no template is given, then SZP =1. The error on the signal (in ADU) is

σ2(NADU) = NADU ×G−1×SZP (8)

The sky-background error is computed from

σskytot =SZP ×qA×(σ2

skypix +¯

σ2

skypix)(9)

where σskypix is the search-run skynoise per pixel, ¯

σskypix is the template-run skynoise, Ais the noise-

equivalent area in square-pixels, and the units are ADU. There is a similar term for the CCD readout noise

per pixel (summed over the area), but it is left out here in this example.

Using double-Gaussian ﬁt parameters for the PSF, in which σ1,2are the PSF-sigma for the two Gaus-

sians, and h1,2are the heights at the origin3, the noise-equivalent area is

A=1

RPSF2(r,θ)rdrdθ=4π(σ2

1+σ2

1+4π2σ2

1σ2

2(h1+h2)2=4πσ2

1(1+R2

σ)(1+R2

σrh)2

σ(1+rh)2+ (1+R2

σrh)2,(10)

where in the second step Rσ≡σ2/σ1and rh≡h2/h1. For a single-Gaussian PSF, rh→0 for any value of

Rσ, and the area is just 4πσ2. For typical ground-based surveys A/(4πσ2

1)∼1.5.

The rest of this section will perform an explicit calculation of the noise, using an example from a DES

simulation. Here is the information for a random epoch on a random simulated lightcurve:

3A double-Gaussian PSF with normalization RPSF(r,θ)rdrdθ=1 has 2π(σ2

1h1+σ2

2h2) = 1

PASSBAND: g r i z Y

GAIN: 1.000 1.000 1.000 1.000 1.000 e/ADU

RDNOISE: 10.000 10.000 10.000 10.000 10.000 e-

SKY_SIG: 108.81 105.36 217.58 378.84 848.53 ADU

PSF_SIG1: 1.500 1.500 1.500 1.500 1.500 pixels

FLUX: 14707.89 12515.67 30756.55 28334.23 62748.97 ADU

FLUX_ERRTOT: 590.695 571.406 1170.485 2022.083 4518.783 ADU

FLUXCAL: 18.52 42.21 46.13 46.59 51.71 (x10^11)

FLUXCAL_ERRTOT: 0.986 2.403 2.385 3.683 4.141

MAG: 24.3311 23.4364 23.3402 23.3292 23.2160

MAG_ERRPLUS: 0.0569 0.0624 0.0565 0.0898 0.0892

MAG_ERRMINUS: 0.0569 0.0624 0.0565 0.0898 0.0892

ZEROPT: 34.7500 33.6800 34.5600 34.4600 35.2100

ZEROPT_SIG: 0.0350 0.0340 0.0350 0.0340 0.0350

For simplicity, note that the PSF is modeled as a single-Gaussian, and that the gain is unity. Now let’s

compute that ﬂux and noise for i-band.

The measured ﬂux (in ADU) and the calibrated ﬂux (for lightcurve ﬁts) are given in terms if the

magnitude (mi) and zeropoint (Zi),

FLUX =10−0.4(mi−Zi)=10−0.4(23.3402−34.56)=30755 ADU (11)

FLUXCAL =10−0.4mi×1011 =46.13 (12)

which agrees with the simulated values above. Since the gain is unity, 1 ADU = 1 photoelectron (p.e.),

and the noise from signal-photostatistics is σsig =pNpe =175.4p.e..

To include the sky-noise, we use the following information from the simulation library (see above

dump):

SKYSIG

=217.58 ADU/pixel, PSF(σ) = 1.50√pixels, and 1 pixel is 0.27′′ ×0.27′′. The ef-

fective aperture area is A=4π×PSF2=28.27 pixels. The total skynoise is thus σsky =SKYSIG ×

√A=1156.95 p.e.The total noise on the ﬂux is FLUX_ERRTOT =qσ2

sig +σ2

sky =√1156.942+175.42=

1170.2p.e=1170.2 ADU. The signal-to-noise ratio (SNR) is 30755/1170 ≃26.

4.13 K-corrections

For the stretch and

MLCS2k2

models, K-corrections are needed in both the simulation and the ﬁtter. K-

corrections are applied using a technique very similar to that used in [9, 1]. The basic idea is that for

each epoch and each pass-band, the spectral template is warped by applying the CCM89 extinction law

with a variable AV; “AV-warp” is the value of AVfor which the synthetic color matches the color of the

rest-frame lightcurve. The K-correction is then determined from this AV-warped spectral template. Note

that this method is model-independent and can therefore be applied to any lightcurve model.

The K-corrections and synthetic magnitudes are NOT computed internally because this would result

in slow code, especially for the ﬁtter. To speed up the calculations of these convolution-integrals, K-

corrections and synthetic mags are read from a lookup table generated with

SNANA_DIR/bin/kcor.exe

Before running the simulation or ﬁtter, the program

kcor.exe

must run, although it runs once and only

once until you need K-corrections that are not deﬁned. The

kcor

program reads a self-documented input

ﬁle such as

$SNDATA_ROOT/sample_input_files/kcor/kcor_[SURVEY].input

and then generates lookup tables as a function of redshift, epoch, and extinction parameter AV. A typical

table binning is 0.05 in redshift, 1 day in rest-frame epoch, and 0.25 in AV; this binning is used to store

every user-deﬁned Kxy, and to store synthetic lightcurves for every user-deﬁned ﬁlter.

A linear interpolation routine4determines a K-correction for arbitrary z,epoch,AV. A special function,

GET_AVWARP

, ﬁnds the magic AV-warp parameter such that the warped spectral template has the same

color as your lightcurve. The table format is

CERNLIB

’s

HBOOK

, and is stored in

$SNDATA_ROOT/kcor .

The subroutines that read and interpolate the

kcor

tables are written in fortran, and are stored in

snana.car

The

SNANA

product includes a fortran library

../lib/libsnana.a

, which allows C programs to use the

fortran utilities. The

extern

statements at the top of

snlc_sim.c

declare the fortran functions used to

lookup K-corrections.

4a double precision version of

CERNLIB

’s

FINT

is used for multi-dimensional linear interpolations.

4.14 Intrinsic Brightness Variations

4.14.1 Supernova Brightness Variations

There are six general methods to introduce intrinsic variations that result in anomalous scatter in the

Hubble diagram:

# method 1: coherent variation in all epochs & passbands

# note: colors are not varied.

GENMAG_SMEAR: 0.1 # coherent mag-smear in all measurements

# method 2: independent variation in each passband (coherent among epochs)

# that results in color variations

GENMODEL_ERRSCALE: 1.1 # scale MLCS peak-model error

GENMAG_SMEAR_FILTER: UBV 0.05 # and/or fixed smearing per filter

GENMAG_SMEAR_FILTER: RI 0.08 # and/or fixed smearing per filter

# method 3: Pick model name from specialized code in genSmear_models.c

GENMAG_SMEAR_MODELNAME: G10

GENMAG_SMEAR_SCALE: 1.0 # scale all magSmear values

GENMAG_SMEARPAR_OVERRIDE: BLA 1.234 # optional param override

GENMAG_SMEARPAR_OVERRIDE: BLALIST[3] 1.8 2.2 3.4 # idem

# method 4: vary RV with asymmetric Gaussian distribution

GENPEAK_RV: 1.6 # location of Gauss peak

GENSIGMA_RV: 0.1 0.9 # lower,upper Gaussian-sigmas

GENRANGE_RV: 1.3 4.5 # gen-range for RV

# method 5: apply intrinsic scatter matrix (SALT2 only)

COVMAT_SCATTER_SQRT[0][0]: 0.10 ! mB : sqrt(COV) = uncertainty

COVMAT_SCATTER_SQRT[1][1]: 0.22 ! x1 : sqrt(COV) = uncertainty

COVMAT_SCATTER_SQRT[2][2]: 0.05 ! color : sqrt(COV) = uncertainty

COVMAT_SCATTER_REDUCED[0][2]: 0.50 ! rho(mB,c) = COV/[sig(mB)*sig(c)]

# method 6: function of wavelength (SALT2 only); see text for details

GENMAG_SMEAR_USRFUN: <SIGCOH> <A5500> <LAMSEP> <LAMPHASE> <TAU_LAM> <TAU_DAY>

0. 0.

Note that methods 1&2 can be used together, as well as methods 1&3. However, methods 2&3 cannot be

used together. Methods 5-6 (scatter matrix) cannot be combined with any other method.

For rest-frame models, the argument of

GENMAG_SMEAR_FILTER

should be a list of rest-frame ﬁlters;

for observer-frame models, the argument is a list of observer-frame ﬁlters.

GENMAG_SMEAR_MODELNAME

allows the most ﬂexibility because this option allows for an arbitrarily

complex function to describe the smearing as a function of wavelength. These functions are in a separately

compiled module (

$SNANA_DIR/src/sntools_genSmear.c

) so that updates are relatively easy and so

that these functions can in principle be used in non-

SNANA

applications. The top of

sntools_genSmear.c

gives a list of model-name options. The models include a “PRIVATE” option so that anyone can quickly

implement a model of intrinsic smearing by adding code to the blank functions

init_genSmear_private

and

get_genSmear_private

. The “NONE” option can be used as a command-line override to turn off

this option.

GENMAG_SMEARPAR_OVERRIDE

allows overriding default smear-model parameters; a list of

allowed keys can be seen by grepping the source code,

grep GENMAG_SMEARPAR_OVERRIDE $SNANA_DIR/src/sntools_genSmear.c | grep KEY

While these smearing models are functions of rest-frame wavelength, there are two implementation

modes for the SNIa models. The mode is controlled by

FLAG_GENSMEAR

that is internally initialized in the

simulation. The ﬁrst mode is to properly include the wavelength dependence, and this mode is currently

set only for the SALT-II model. The second mode is an approximation in which the smearing value at

λobs/(1+z)is applied to the magnitude of the entire passband, where ¯

λobs is the central wavelength of

the passband. This mode is set for rest-frame models (i.e.,

SNooPy

MLCS2k2

). If/when the wavelength-

dependent smearing is upgraded to work for rest-frame models,

FLAG_GENSMEAR

will be modiﬁed accord-

ingly.

Each element of the intrinsic scatter matrix (method 5) can be entered as a covariance, as an uncertainty,

or as a reduced covariance. It is recommended to enter uncertainties for the diagonal elements, and to enter

reduced covariances (−1 to +1) for the off-diagonal terms. This model-smearing option currently works

only for SALT2, but can easily be extended to other models as needed.

The function for method 6 is as follows.

SIGCOH

is a coherent scatter term that is added independent

of the other parameters. The wavelength-dependent part is ﬁrst deﬁned at λ-nodes separated by

LAMSEP

with an initial phase of

LAMPHASE

Å. The 1σscatter magnitude (σmag) at each λ-node (λn) is

σmag =A5500 ×exp[−(λn−5500)/τλ]×exp[Trest/τday](13)

where τλ=

TAU_LAM

and τday =

TAU_DAY

. The last two zeros (7th and 8th params) are reserved for future

upgrades. After a Gaussian random scatter at each node is selected, a continuous function of λis made by

connecting the nodes with cosine functions that ensure that the derivative is zero at each node.

4.14.2 Galaxy Lensing

The effect of lensing is simulated using a pre-computed map of lensing probability as a function of redshift

and ∆µ≡ −2.5log(magniﬁcation). Maps are stored in $

SNDATA_ROOT

models/lensing

, and the lensing

effect is implemented with the following sim-input keys:

LENSING_PROBMAP_FILE: LENSING_PROBMAP_LogNormal+MICE.DAT

LENSING_DMUSCALE: 2.1 # default is 1.0

A MICE simulation [10] is used for z<1.4, and a log-normal approximation [11] is used for z>1.4.5The

magniﬁcation grid extends to about 4 (∆µ≃ −1.5), and thus does not include strong lensing, nor multiple

lenses. The distance-modulus (µ) scatter is about 0.04 ×z, about a factor of 2 smaller than the largest

scatter values found in the literature. Input key

LENSING_DMUSCALE

is used to increase or decrease the

scatter.

The randomly chosen

SIM_LENSDMU

is stored in the simulated data ﬁles, and also stored in the output

tables created by the analysis programs. Users should examine and validate the distribution of

SIM_LENSDMU

vs. redshift.

5We thanks Jacobo Asorey for creating this lensing library.

4.15 Search Efﬁciency

The simulation includes options to model the search efﬁciency of the survey. The search efﬁciency is

broken into three parts: (i) image subtraction pipelines characterized by efﬁciency vs. S/N or mag, (ii)

spectroscopic efﬁciency that describes visual scanning and spectroscopic targeting and selection, and (iii)

for spectroscopically-unconﬁrmed SNe, the “

zHOST

” efﬁciency for obtaining an accurate host-galaxy red-

shift. Some explicit examples of sim-input options will be given at the end of this section. To ensure that

your settings are correct, it is essential to always check that the simulated redshift distribution matches that

of the data, and to check separately for the spectroscopically-conﬁrmed and unconﬁrmed sub-samples.

Default efﬁciency ﬁles are stored in the directory

$SNDATA_ROOT/models/searcheff

, and the ﬁle-

name includes the name of the survey. However, you can specify an efﬁciency ﬁle in your private directory,

or ignore the efﬁciency ﬁle by specifying a ﬁle-name as

NULL

NONE

4.15.1 Software-Pipeline Efﬁciency

The image subtraction pipeline efﬁciency, εsubtr, is based on software algorithms and therefore in principle

this part of the efﬁciency can be rigorously determined. The simplest εsubtr requirement is a minimum

number of observations with the sim-input keyword “

MINOBS_SEARCH: <MINOBS>

” (default is 2). The

simulation also parametrizes εsubtr as a function of signal-to-noise (SNR) or magnitude in each ﬁlter. The

motivation is that fake SNe overlaid onto images during the survey can be used to measure the efﬁciency

curves. Examples of each type of efﬁciency curve (vs. SNR and vs. MAG) are in

$SNDATA_ROOT/models/searcheff/SEARCHEFF_PIPELINE_SDSS.DAT (vs SNR)

$SNDATA_ROOT/models/searcheff/SEARCHEFF_PIPELINE_HST.DAT (vs. MAG)

and one can add more ﬁles corresponding to different surveys. If no

SEARCHEFF_PIPELINE

ﬁle is found,

then εsubtr =1. Warning: do NOT deﬁne both the SNR-based and MAG-based efﬁciency for a survey. For

ground-based surveys we recommend using the SNR-based efﬁciency to properly account for variations

in observing conditions. The sim-input keyword

SEARCHEFF_PIPELINE_EFF_FILE: MY_PIPELINE.DAT

SEARCHEFF_PIPELINE_FILE: MY_PIPELINE.DAT

SEARCHEFF_PIPELINE_EFF_FILE: NONE # disable feature

overrides the default ﬁle or disables this feature. The simulation always checks ﬁrst if a ﬁle exists in your

private directory: if not there then the public directory above is checked. The

SEARCHEFF_PIPELINE_FILE

allows for two kinds of maps as shown in Fig. 4. These maps are very course for illustration, but much

ﬁner-grid maps can be used. The ﬁrst and more common map is the detection efﬁciency vs.

SNR

, or

MAG

ABS(SNR)

. The

ABS(SNR)

option is useful for galactic transients, which can have positive or negative sig-

nals in a subtracted image. The map must be contained betweem the keys “

MAPNAME_DETECT: <name>

”

and “

ENDMAP:

”. The example below shows one map valid for griz bands, but a separate map for each band

can be included.

The

PHOTFLAG_DETECT

key (Fig. 4) is a mask that is added to the

PHOTFLAG

column in the data ﬁle for

each detection. The

PHOTFLAG_TRIGGER

key speciﬁes the

PHOTFLAG

mask to add on the ﬁrst epoch satisfy-

ing the trigger logic (see

LOGIC

ﬁle below). In the analysis, setting

&SNLCINP

input

PHOTFLAG_DETECT=nnn

results in the following variables added to the SNANA & FITRES tables: NEPOCH_DETECT (number

of detections) and TLIVE_DETECT (time between ﬁrst and last detection).

The second type of optional map is used to specify a

PHOTPROB

value between zero and one. This

quantity is not used in the simulation, but is passed to the output data ﬁles so that cuts can be applied.

For example,

PHOTPROB

can represent a machine-learning score from difference-imaging, or from cuts

that reject ﬂux-outliers. The map consists of a

PHOTPROB

distribution in bins of

SNR

(or

LOGSNR

) and/or

SBMAG

(surface brightness). The

PHOTPROB_WGTLIST

is a histogram of events in each bin. The simulation

internally determines the cumulative distribution function (CDF) for each

SNR-SBMAG

bin, and interpolates

for each simulated epoch based on the generated

SNR

and

SBMAG

. The interpolated CDF is used to generate

a random

PHOTPROB

value for each observation. Finally, this example applies to all ﬁelds and bands, but

separate maps can be read for each band and/or each ﬁeld.

The optional

REQUIRE_DETECTION

ﬂag results in

PHOTPROB=0

when there is no detection, and

PHOTPROB>0

for detections. By default the

PHOTPROB

are independent for each observation. Optional

PHOTPROB

cor-

relations are introduced with the key “

REDUCED_CORR: <rho>

,” where

-1 < rho < +1.

The example

below introduces 50% correlations. If there is a separate map for each band, the correlation between

epochs in different bands is the geometric mean of each map-correlation, CORR12 =√CORR1 ·CORR2,

where

CORR1,CORR2

are the reduced correlations. Note that if either correlation is zero, CORR12 =0.

The correlation method for NPhotProb

PHOTPROB

values is as follows. First, the Cholesky decomposition

technique is used to determined NPhotProb correlated randoms from Gaussians with σ=1. Call these cor-

related Gaussian randoms Gi,i=1,NPhotProb. Each Giis converted to a uniform random between zero

and one, U[0,1], from the Gaussian distribution:

U[0,1]i= (2π)−1/2ZGi

−∞dx exp(−x2/2)(14)

where the explicit σterms are dropped since σ=1. The correlations between the Giare transferred to the

U[0,1]i. Finally, U[0,1]iand the

PHOTPROB

CDF are used to compute

PHOTPROB

U[0,1]i=ZPHOTPROBi

0dP CDF(P)(15)

Beware that while generating correlated Giis rigrous and robust, the

PHOTPROB

correlations are ad-hoc

and not rigorous. It is therefore recommended to check the correlations using the

NDUMP

option, which

produces a one-line per event dump to standard-out as follows:

777777 [SNID] [PHOTROB-1] [PHOTROB-2] . . . [PHOTROB-NDUMP]

The “777777” string allows using grep to extract the dump rows. The ﬁrst

NDUMP PHOTPROB>0

values per

event are included. If there are not enough

PHOTPROB

values for the dump, the dump is skipped for the

event.

Figure 4: Illustration of

SEARCHEFF_PIPELINE_FILE

# optional keys to set bit(s) in PHOTFLAG column of data files.

PHOTFLAG_DETECT: 4096 # set this bit for each detection

PHOTFLAG_TRIGGER: 2048 # set this bit on epoch when trigger forms

MAPNAME_DETECT: EFFDETECT_SNR-g

FILTER: griz

SNR: 0.0 0.0002

SNR: 2.0 0.22

SNR: 4.0 0.45

SNR: 6.0 0.75

SNR: 8.0 0.87

SNR: 10.0 0.98

SNR: 12.0 1.00

ENDMAP:

MAPNAME_PHOTPROB: MLSCORE_FAKES

BAND: griz FIELD: ALL # map applies to all fields and bands

REQUIRE_DETECTION: 1 # generate PHOTPROB only for detections, 0 otherwise

REDUCED_CORR: 0.5 # induce correlation among all PHOTROB per event

NDUMP: 3 # DEBUG: one-line dump of 3 PHOTPROB per event

NVAR: 6 # LOGSNR, SBMAG + 4 PHOTPRPB_WGTLIST bins

VARNAMES: LOGSNR SBMAG PHOTPROB_WGTLIST

ROW: 0.0 20 W11 W12 W13 N14

ROW: 1.0 20 W21 W22 W23 W24

ROW: 2.0 20 W31 W32 W33 W34

ROW: 0.0 22 W12 W12 W13 N14

ROW: 1.0 22 W22 W22 W23 W24

ROW: 2.0 22 W32 W32 W33 W34

ROW: 0.0 24 W13 W12 W13 N14

ROW: 1.0 24 W23 W22 W23 W24

ROW: 2.0 24 W33 W32 W33 W34

ENDMAP:

The above

SEARCHEFF

information gives the probability of a single-epoch detection in a particular

ﬁlter, but does not specify if the supernova would have been discovered. The discovery or trigger logic is

deﬁned for each survey in the ﬁle:

more $SNDATA_ROOT/models/searcheff/SEARCHEFF_PIPELINE_LOGIC.DAT

SDSS: 3 gr+ri+gi # require 3 epochs, each with detection in two bands.

DES 2 g+r+i+z # require 2 epochs, any band

HST: 1 6 # require 1 epoch with detection in filter ’6’ = F850LP_ACS

where the ﬁrst number is the minimum number of epochs required, and the string that follows deﬁnes the

logic for a detection. In the above examples, the SDSS discovery logic requires three epochs, where each

epoch has a detection in at least two of the three gri ﬁlters. The DES logic requires two single detections

in any band. The HST discovery logic requires a single detection in ﬁlter ’6’. As described above, a single

detection is deﬁned by the efﬁciency curves in

SEARCHEFF_PIPELINE_[SURVEY].DAT

. The ﬁnal caveat is

the epoch time-window used to count a detection. The sim-input key

NEWMJD_DIF: 0.4 # days

speciﬁes combining all observations within 0.4 days (i.e., one night) into a single detection. For the DES

logic, observations of all four griz bands in one night would count as one epoch and fail the trigger; an

additional observation on a different night is required to pass the trigger. If

NEWMJD_DIF

is reduced to

0.001 (1.4 minutes), then observations with any two of the four DES ﬁlters in one night would pass the

trigger.

The pipeline efﬁciency can be applied in the simulation, or the results can be stored in the data ﬁles for

future analysis: the user control ﬂag

APPLY_SEARCHEFF_OPT

is discussed below after the spectroscopic

efﬁciency is discussed.

The LOGIC ﬁle can be speciﬁed explicitly with sim-input key

SEARCHEFF_PIPELINE_LOGIC_FILE: $SNDATA_ROOT/models/searcheff/SEARCHEFF_PIPELINE_LOGIC.DAT

4.15.2 Spectroscopic-Conﬁrmation Efﬁciency

The human/spectroscopic efﬁciency (εspec) cannot be rigorously computed since it involves human de-

cision making during the survey. The

SNANA

simulation parametrizes εspec as an arbitrary function of

redshift, peak-mags, peak colors, and closest time to peak. §4.15.4 suggests how to determine this func-

tion from the data and simulations. Rather than using an analytical form for εspec, the simulated efﬁciency

is deﬁned on a multi-dimensional grid of redshift, peak-magnitudes and peak-colors. An example is shown

here,

SEARCHEFF_SPEC_FILE: $SNDATA_ROOT/models/searcheff/SEARCHEFF_SPEC_SDSS.DAT

SEARCHEFF_SPEC_SCALE: 0.8 # default=1.0

SEARCHEFF_SPEC_SCALE: ZERO # force EFF_SPEC=0 without map

If this ﬁle is not speciﬁed, then εspec =1. For each simulated SN, εspec is determined from multi-

dimensional (linear) interpolation. If more than one grid is given the logical OR among the efﬁciencies

is used; this feature may be useful in cases where different telescopes take spectra for SNe in different

magnitude ranges. It is important to note that εspec =0 outside the redshift/magnitude range given by the

grid. This feature allows using different telescopes to cover different magnitude ranges, but be careful that

very bright SNe can have εspec =0 if the magnitude range is not wide enough at the bright end. To avoid

mistakenly losing very bright SNe, we recommend adding an artiﬁcial grid with 100% efﬁciency for low

redshifts; this is the ﬁrst grid-map in Fig. 5.

Fig. 5 below illustrates a spectroscopic-efﬁciency grid with three tables. The ﬁrst table ensures 100%

efﬁciency for redshifts z<0.1. The second table describes the efﬁciency for r-band magnitudes below

22, and the last table deﬁnes the efﬁciency for iband magnitudes above 22. The second map depends

on the absolute peak r-band magnitude and the g−rcolor at peak. The 3rd map depends on the i-band

magnitude and redshift, and applies only for the ﬁeld named ’DEEPFIELD’: the ’FIELD:’ option allows

for ﬁeld-dependent maps. There essentially is no limit to the complexity: for example, one could deﬁne

“

NVAR: 7

” and “

VARNAMES: g r i g-r r-i REDSHIFT SPECEFF

” assuming that such a function could

be determined. A list of valid

VARNAMES

is shown in Fig. 6.

Figure 5: Illustration of spectroscopic efﬁciency format for the

SNANA

simulation.

# TABLE 1 -- ensure 100% eff at low redshift

NVAR: 2

VARNAMES: REDSHIFT SPECEFF

SPECEFF: 0.0 1.00

SPECEFF: 0.1 1.00

# TABLE 2 -- 4m telescope

NVAR: 3

VARNAMES: g-r r SPECEFF # can add comments here

SPECEFF: -0.5 18.0 1.0

SPECEFF: -0.5 20.0 0.6

SPECEFF: -0.5 22.0 0.3

SPECEFF: +0.5 18.0 0.2

SPECEFF: +0.5 20.0 0.08

SPECEFF: +0.5 22.0 0.02

# TABLE 3 -- 8m telescope

NVAR: 3

VARNAMES: REDSHIFT i SPECEFF

FIELD: DEEPFIELD

SPECEFF: 0.0 22.0 1.0

SPECEFF: 0.0 24.0 0.66

SPECEFF: 0.0 26.0 0.31 # can add comments here

SPECEFF: 0.5 22.0 0.22

SPECEFF: 0.5 24.0 0.14

SPECEFF: 0.5 26.0 0.022

In principle there is just one function of redshift and peak-magnitudes to describe the spectroscopic

efﬁciency. In practice, however, this efﬁciency can depend on the particular SN model for two reasons.

First, there is an overall magnitude offset between different SN models. Second, asymmetric (dim-side)

tails in the stretch and color distributions may not be properly modeled. To correct for the ﬁrst case there

is a sim-input parameter “

MAGSHIFT_SPECEFF: <shift>

” to shift the peak magnitude used to determine

εspec =0 from the grid-map. The second problem can be ﬁxed only by using distributions with appropriate

tails.

For each simulated SN, the search algorithm is evaluated separately for the image-subtraction and

spectroscopic efﬁciencies. Random numbers are compared against the efﬁciencies to determine which

epochs/SNe are selected. The results of these two search algorithms are stored in a bit-mask in each data

ﬁle, deﬁned as follows:

SIM_SEARCHEFF_MASK += 1 # detected by image-subtraction

SIM_SEARCHEFF_MASK += 2 # spectroscopically confirmed

SIM_SEARCHEFF_MASK += 4 # unconfirmed with host redshift (next section)

And here are some command examples,

SIM_SEARCHEFF_MASK = 1 # detected by image-subtr; spec-unconfirmed

SIM_SEARCHEFF_MASK = 2 # failed image-subtr, but spec-confirmed

SIM_SEARCHEFF_MASK = 3 # detected by image-subtr & spec confirmed

SIM_SEARCHEFF_MASK = 5 # detected by image-subtr, unconfirmed with zHOST

Note that

SIM_SEARCHEFF_MASK

=2 corresponds to an unphysical case since it is unlikely to get a spec-

trum of a SN that was not identiﬁed by the image-subtraction pipeline. Although the search efﬁciencies

are always evaluated, the user has the option to apply these efﬁciencies in the simulation, or to write out

all simulated SNe and use the

SIM_SEARCHEFF_MASK

for further investigation. The following sim-input

keys control trigger selection:

APPLY_SEARCHEFF_OPT: 0 # keep all SNe (default)

APPLY_SEARCHEFF_OPT: 1 # keep SN if software trigger passes

APPLY_SEARCHEFF_OPT: 3 # keep SN if software and spec triggers pass

APPLY_SEARCHEFF_OPT: 5 # keep SN if software trigger and zHOST

When “

APPLY_SEARCHEFF_OPT: 3

” is set, then

SIM_SEARCHEFF_MASK=3

for all SNe because those that

fail either of the search criteria are rejected. Setting “

APPLY_SEARCHEFF_OPT: 1

” results in SNe with

SIM_SEARCHEFF_MASK=1

and 3; i.e., SNe with and without spectroscopic conﬁrmation.

Finally,

SIM_SEARCHEFF_MASK

can be speciﬁed as a

SIMGEN_DUMP

variable (§4.32.3) and it appears in

the analysis tables (§12.1).

Figure 6: Valid

VARNAMES

to describe εspec.

* g r i # peak mag in any band

* PEAKMAG_[band] # idem for any [band]

* g-r # peak color

* g-i # another peak color

* REDSHIFT

* PEAKMJD

* DTPEAK # closest T-Tpeak; can be pos or negative

* HOSTMAG_[band] # mag of host galaxy

* SBMAG_[band] # surface brightness mag/arcsec^2

4.15.3 Unconﬁrmed Efﬁciency for Host-Galaxy Redshift

For the unconﬁrmed SNe, i.e., those with

SIM_SEARCHEFF_MASK=1

, the default redshift is assumed to have

the same precision as for the conﬁrmed SNe, presumably from a host-galaxy spectroscopic redshift. How-

ever, a redshift-dependent fraction of unconﬁrmed spectroscopic (host-galaxy) redshifts can be speciﬁed

with

SEARCHEFF_zHOST_FILE: <fileName>

SEARCHEFF_zHOST_FILE: NONE # Eff(zHOST) = 1.0

SEARCHEFF_zHOST_FILE: ZERO # Eff(zHOST) = 0.0

where the ﬁle contains an efﬁciency map. There are two kinds of maps: 1) legacy map which depends

only on true redshift, and 2) nominal map (starting with

v10_70

) deﬁning an arbitrary function of

HOSTLIB

parameters (see “

VARNAMES:

” key in Fig. 7).

Here we show an example of the redshift-dependent legacy map:

# LEGACY SEARCHEFF_zHOST map:

CUTWIN_SNRMAX: 5 1E8 # optional SNRMAX cut on source (not on host)

FIELDLIST: F1+F2 # optional

HOSTEFF: 0.0 1.0 # required: args are redshift & effic.

HOSTEFF: 0.50 0.8

HOSTEFF: 1.00 0.6

HOSTEFF: 1.50 0.2

FIELDLIST: F3+F4+F5

HOSTEFF: 0.0 1.0

HOSTEFF: 0.50 0.9

HOSTEFF: 1.00 0.8

HOSTEFF: 1.50 0.7

etc ...

The

FIELDLIST

arguments are optional, as leaving this out will apply the map to all ﬁelds.

HOSTEFF

keys

are required. In analogy with the spectroscopic efﬁciency, the default survey-dependent ﬁle is

$SNDATA_ROOT/models/searcheff/SEARCHEFF_zHOST_SDSS.DAT

and similary with ‘SDSS’ replaced by an arbitray survey name. This feature can be used even if there is

no host-galaxy simulation (§4.19).

Next, we given an example of a map with more complex function of

HOSTLIB

properties:

OPT_EXTRAP: 1 # 0=> abort, 1=>use value at edge of grid.

FIELDLIST: C3+X3

VARNAMES: g_obs i_obs HOSTEFF

HOSTEFF: 18 20 1.

HOSTEFF: 18 22 0.95

HOSTEFF: 18 24 0.55

HOSTEFF: 20 20 1.

HOSTEFF: 20 22 0.9

HOSTEFF: 20 24 0.5

HOSTEFF: 22 20 1.

HOSTEFF: 22 22 0.8

HOSTEFF: 22 24 0.4

HOSTEFF: 24 20 0.9

HOSTEFF: 24 22 0.7

HOSTEFF: 24 24 0.2

FIELDLIST: C1+C2+S1+S2+X1+X2+E1+E2

VARNAMES: g_obs i_obs HOSTEFF

HOSTEFF: 18 20 1.

HOSTEFF: 18 22 0.98

HOSTEFF: 18 24 0.58

HOSTEFF: 20 20 0.95

HOSTEFF: 20 22 0.85

HOSTEFF: 20 24 0.45

HOSTEFF: 22 20 0.95

HOSTEFF: 22 22 0.75

HOSTEFF: 22 24 0.34

HOSTEFF: 24 20 0.85

HOSTEFF: 24 22 0.65

HOSTEFF: 24 24 0.15

OPT_EXTRAP

is zero by default, which means that any parameter outside the map range results in an

abort.

OPT_EXTRAP=1

forces the map-edge value for parameters outside the map range.

FIELDLIST

optional for FIELD-dependent maps;

C3+X3

means that the map applies to both C3 and X3 ﬁelds. Sub-

string matching is used, and therefore “

FIELDLIST: X

” would apply to

X1, X2, X3

. Also note that

FIELDLIST

must come before the

VARNAMES

key. Finally, the ﬁrst N−1

VARNAMES

speciﬁes arbitrary

HOSTLIB

propertes from the

VARNAMES

key in Fig. 7. The last (Nth)

VARNAME

must be

HOSTEFF

For unconﬁrmed SNe that have no redshift information, the redshift and its error are set to −9; this

value ﬂags the photo-z ﬁtting option in

snlc_fit.exe

to ignore redshift-prior information (

OPT_PHOTOZ=2

(§5.11). When an accurate host-galaxy redshift is used, the 4-bit is set in

SIM_SEARCHEFF_MASK

. There is a

valid (i.e, positive) redshift when

SIM_SEARCHEFF_MASK

has either the 2-bit or 4-bit set.

SIM_SEARCHEFF_MASK=1

means that the SN is detected by the pipeline (§4.15.1) but that there is no valid redshift (

REDSHIFT_FINAL

= -9

). Finally, recall from §4.4 that the unconﬁrmed SNTYPE in the data header is 100 plus the spec-

conﬁrmed SNTYPE.

Specifying “NONE” for the zHOST ﬁlename results in a 100% zHOST efﬁciency. To specify zero

efﬁciency requires a zHOST ﬁle explcitly setting the efﬁciencies to zero: an example is here,

$SNDATA_ROOT/models/searcheff/SEARCHEFF_zHOST_ZERO.DAT

Below are a few examples of sim-input settings. First, to simulate a spectroscopically conﬁrmed

sample using private search-efﬁciency ﬁles,

APPLY_SEARCHEFF_OPT: 3 # apply PIPELINE+SPEC efficiencies

SEARCHEFF_PIPELINE_EFF_FILE: TESTEFF_PIPELINE.DAT # private file

SEARCHEFF_SPEC_FILE: TESTEFF_SPEC.DAT # private file

To simulate a mix of conﬁrmed and unconﬁrmed SN Ia:

APPLY_SEARCHEFF_OPT: 1 # apply only the software trigger

Events with

SIM_SEARCHEFF_MASK=3

or 5 have a spectroscopic redshift with uncertainty given by the

GENSIGMA_REDSHIFT

key. Events with

SIM_SEARCHEFF_MASK=1

(unconﬁrmed and no host spec-z) have

a host-galaxy photo-z if such information is availabe in the

HOSTLIB

; otherwise the redshift is set to -9.

To simulate and select events with spectroscopic host redshift,

APPLY_SEARCHEFF_OPT: 5 # apply software trigger & zHOST

SEARCHEFF_zHOST_FILE: SEARCHEFF_zHOST.DAT

Lastly we recommend putting measured efﬁciency ﬁles in the public area

$SNDATA_ROOT/models/searcheff

4.15.4 Determining εspec

Since there is no rigorous method to determine εspec, one must essentially start with a guess at the func-

tional form and ﬁt for parameters such as an exponential slope or power law. The spectroscopic efﬁciency

must have the form εspec(z,~m,~

E), where zis the redshift, ~mare the peak magnitudes and ~

Eare efﬁciency-

function parameters to be determined. Next generate a large simulated sample that includes the pipeline

efﬁciency (i.e,

APPLY_SEARCHEFF_OPT: 1

) and the same selection requirements that are applied to the

data. The last step is to ﬁt for ~

Eby minimizing

χ2=∑

[(NDATAi−NSIMi×E0εspec(z,~m,~

E))/σ2

i](16)

where E0is an overall scale such that the integrated data and simulation have the same statistics, iis an

index over bins, and σiis the statistical uncertainty on the data. The bins can be simply redshift bins, or

multi-dimensional bins of redshift and the peak magnitude(s). We suggest starting with the simple case of

redshift bins, and trying more complex binning only of the simple case is not adequate. After determining

Efrom the ﬁt, it is important to check data-simulation comparisons on distributions of other quantities,

namely the ﬁtted stretch and color parameters.

4.15.5 Time Above Detection and Number of Detections

In some analyses, it is useful to cut on the time above detection (e.g., looking for fast or long-live tran-

sients), and also the number of detections. This section explains how to access this information in the

SNANA

and

FITRES

tables via the following variables:

TLIVE_DETECT # MJD_DETECT(last) - MJD_DETECT(first)

NEPOCH_DETECT # Nobs with detection

The detection information must be stored as one of the bits in the

PHOTFLAG

column of the data ﬁles. For

real data, the survey team is responsible for setting this bit. For simulations, set the

PHOTFLAG_DETECT

mask as shown Fig. 4. To get

TLIVE_DETECT

and

NEPOCH_DETECT

in the analysis-output tables, set the

following analysis input:

&SNLCINP

PHOTFLAG_DETECT = nnn ! defines detection bt in PHOTFLAG

CUTWIN_PHOTPROB = xxx, yyy ! optional cut on PHOTPROB, each epoch

where nnn is the mask value (e.g., 4096). If

PHOTPROB

values are included in the data ﬁles,

CUTWIN_PHOTPROB

can be used to reject poor-quality observations. For simulations, default

PHOTPROB=1

, or a

PHOTPROB

map

can be deﬁned (Fig. 4).

4.16 Selection Cuts

Although selection cuts are usually applied with the ﬁtting program (§ 5) or some external program, the

simulation allows for some basic selection cuts. This feature is particularly useful, for example, to simplify

and speed up the generation of a large efﬁciency grid, and to estimate rates. The global ﬂag to implement

the “

CUTWIN_XXXX

” selection criteria is

APPLY_CUTWIN_OPT: 0 # => ignore selection cuts (default)

APPLY_CUTWIN_OPT: 1 # => implement selection cuts

APPLY_CUTWIN_OPT: 3 # => apply cuts to data files; NOT to SIMGEN_DUMP

For option 1 the selection cuts are applied to both the data ﬁles and to the entries in the

SIMGEN_DUMP

ﬁle (§4.32.3). The last option (3) is useful for keeping track of absolute efﬁciencies, along with the

SIMGEN_DUMPALL:

key.

A list of available cut-commands are as follows:

EPCUTWIN_LAMREST: 3000 9500 # cut-window for <lamobs>/(1+z)

EPCUTWIN_SNRMIN: +3 1E8 # min SNR for each observation

CUTWIN_TRESTMIN: -19 -5 # at least 1 epoch before -5 d (rest-frame)

CUTWIN_TRESTMAX: +30 +80 # at least 1 epoch past +30 d

CUTWIN_TGAPMAX: 0 20 # largest Trest gap (days)

CUTWIN_T0GAPMAX: 0 10 # largest Trest gap near peak (days)

CUTWIN_NOBSDIF: 6 999 # Number of obs passing MJDDIF cut

CUTWIN_MJDDIF: 0.4 999 # NOBSDIF++ if this much later than last MJD

CUTWIN_NEPOCH: 7 +5 # require 7 epochs with SNR>5

CUTWIN_SNRMAX: 10 griz 1 -20 60 # SNR>10 for at least 1 of griz filters

CUTWIN_SNRMAX: 5 griz 3 -20 60 # SNR>5 for at least 3 of griz filters

CUTWIN_SNRMAX: 5 griz 3 0 60 # idem, but after max

CUTWIN_SNRMAX: 5 ri 2 -20 60 # r & i must each have SNR > 5

CUTWIN_MWEBV: 0.0 0.1 # Galactic E(B-V)

CUTWIN_PEAKMAG: 10 27 # any filter-peakmag between 10 and 27

CUTWIN_PEAKMAG_ALL: 15 30 # ALL filter-peakmag between 15 and 30

CUTWIN_EPOCHS_SNRMIN: 5 20 iz # SNR(iz) > 5 for < 20 days

CUTWIN_NOBS_SATURATE: 0 3 griz # require <=3 saturations in each griz band

CUTWIN_NOBS_NOSATURATE: 5 500 griz # require >=5 unsaturated epochs each band

CUTWIN_REDSHIFT_TRUE: 0 1 # cut on true cmb redshift

CUTWIN_REDSHIFT_FINAL: 0 1 # cut on best redshift (zSpec or zPhot)

CUTWIN_HOST_ZPHOT: 0 1 # cut on host photo-z

Each cut-command can be speciﬁed in the sim-input ﬁle, or using the command-line override (§12.2.1)

without the colon. Any

CUTWIN_XXX

that is not speciﬁed results in no cut. The cuts beginning with

EPCUTWIN

apply to every epoch (observation), and only measurements passing these

EPCUTWIN_XXX

re-

quirements are used to evaluate cuts on global light curve properties.

CUTWIN_NEPOCH

includes its own

SNR requirement; thus you could set “

EPCUTWIN_SNRMIN: -5 1E8

” so that all measurements, regardless

of SNR, are used for cuts on

TRESTMIN

TRESTMAX

and

TGAPMAX

, while still requiring 7 observations to

have SNR>5.

Multiple

CUTWIN_SNRMAX

requirements can be speciﬁed. Note that this cut requires a certain number

of passbands to have a minimum SNR value, but does not specify which bands. For the example above,

“

CUTWIN_SNRMAX: 5 griz 3 -20 60

” is satisﬁed if the maximum SNR is >5 for either gri,grz,giz,

or riz. You can require SNR cuts for speciﬁc ﬁlters as illustrated above with “

CUTWIN_SNRMAX: 5 ri 2

-20 60

”; this requires both rand ito have a measurement with SNR>5.

The

TGAPMAX

requirement applies to observations between the lower-

TRESTMIN

and upper-

TRESTMAX

cuts; i.e., −19 to +80 days in the example above. The

T0GAPMAX

requirement applies to observations near

peak, meaning that the gap must overlap the range between the upper-

TRESTMIN

and lower-

TRESTMAX

cuts; i.e., −5 to +30 days. In this example, a gap deﬁned by −12 to −6 days is included in the evaluation

of the

TGAPMAX

cut, but not in the

T0GAPMAX

cut. Gaps of −6 to +2 and +20 to +35 days are included in

the evaluation of both cuts. A gap of +8.0 to +85 is ignored for both cuts.

Adding “

CUTMASK

to the

SIMGEN_DUMP

variable list shows which cuts pass/fail each generated event.

The

CUTMASK

bit-deﬁnitions are obtained by grepping the source-code,

grep CUTBIT $SNANA_DIR/src/snlc_sim.h | grep define

#define CUTBIT_TRESTMAX 0 // (1)

#define CUTBIT_TRESTMIN 1 // (2)

#define CUTBIT_SNRMAX 2 // (4) max SNR cut

#define CUTBIT_TGAPMAX 3 // (8) max Tgap

#define CUTBIT_T0GAPMAX 4 // (16) idem near peak

#define CUTBIT_NOBS_SNR 5 // (32) NOBS with special SNR cut

#define CUTBIT_NOBS_MJDDIF 6 // (64) NOBS with MJDDIF cut

#define CUTBIT_MWEBV 7 // (128) galactic extinction

#define CUTBIT_REDSHIFT 8 // (256) redshift

#define CUTBIT_PEAKMAG 9 // (512) peak mag

The generation and cut-selection statistics are printed at the end of the sim-

README

ﬁle (§ 4.2). Here

is an example when selection cuts are applied, while the search efﬁciency is not:

Generation Statistics:

Generated 250 simulated light curves.

Wrote 100 simulated light curves to SNDATA files.

Rejection Statistics:

1 rejected by GEN-RANGE cuts.

0 rejected by SEARCH-TRIGGER

149 rejected by CUTWIN-SELECTION

SEARCH+CUTS Efficiency: 0.402 +- 0.031

An efﬁciency grid can be quickly computed by looping over the variables of interest (redshift, SN bright-

ness, etc ) and using

grep “SEARCH+CUTS”

to extract the efﬁciencies.

The number of generated events is speciﬁed by the keyword “

NGEN_LC: 100

”, which instructs the sim-

ulation to generate 100 lightcurves that pass the SEARCH-TRIGGER & CUTWIN-SELECTION (§4.26).

4.17 Varying the Exposure Time/Aperture/Efﬁciency

For testing future (i.e, non-existent) surveys, the exposure times can be varied relative to that of the SIM-

LIB, and avoids the need to create a new SIMLIB for each sequence of exposure times. The sim-input

syntax is

EXPOSURE_TIME: 2.0 # global increase for all filters

EXPOSURE_TIME_FILTER: g 3.0 # x3.0 more exposure in g-band

EXPOSURE_TIME_FILTER: r 4.6 # x4.6 more exposure in r-band

EXPOSURE_TIME_FILTER izY 8.0 # x8 more exposure in izY bands

Since the global

EXPOSURE_TIME

multiples the ﬁlter-dependent exposure times, the net exposure-time

increase for the above example is 6 and 9.2 for gand r, respectively, and 16 for the izY ﬁlters. The default

exposure-time increase is one.

This option is equivalent running each exposure longer by the speciﬁed amount, or increasing the

aperture or efﬁciency. Technically, the simulation does the following for each ﬁlter:

ZPT(SIMLIB) -> ZPT + 2.5*LOG10(EXPOSURE_TIME)

SKYSIG -> SKYSIG * sqrt(EXPOSURE_TIME)

CCDNOISE -> CCDNOISE * sqrt(EXPOSURE_TIME)

The changes in the

ZPT

and

SKYSIG

are unambiguous for a given

EXPOSURE_TIME

, but the

CCDNOISE

should not change if the

EXPOSURE_TIME

is assumed to increase the efﬁciency without increasing the

number of times that the CCDs are read out. There is an option-mask to control which parameters to

modify,

EXPOSURE_TIME_MSKOPT: 7 # bits 1,2,3 => ZPT, SKYSIG, CCDNOIST

The default is to modify all three SIMLIB parameters. To modify

ZPT

and

SKYSIG

while leaving the

CCDNOISE

ﬁxed, set “

EXPOSURE_TIME_MSKOPT: 3

”

4.18 Simulating Galactic Extinction

The following sim-input parameters control MilkyWay (MW) Galactic extinction:

RV_MWCOLORLAW: 3.1 # default

OPT_MWCOLORLAW: 94 # default: CCM89+ODonnel94

OPT_MWEBV: 1 # default: MWEBV key in SIMLIB file

GENSIGMA_MWEBV_RATIO: 0.16 # default: smear by sig(MWEBV) = .16*MWEBV

# for systematic tests:

GENSIGMA_MWEBV: 0.0 # smear by fixed sig(MWEBV)

GENSHIFT_MWEBV: 0.0 # fixed shift relative to dust map

GENRANGE_MWEBV: xxx yyy # genrate flat distrib between xxx and yyy

The ﬁrst four keys control the RVvalue, color law, source of MWEBV=E(B−V), and the fractional uncer-

tainty on E(B−V). The remaining keys are intended for additional systematic tests. In

MWgaldust.c

, the

function ‘

GALextinct

’ applies the selected color law (based on

OPT_MWCOLORLAW

) to compute the extinc-

tion at arbitrary wavelengths, and ‘

modify_MWEBV_SFD

’ determines E(B−V)according to

OPT_MWEBV

To turn off Galactic extinction, set either

OPT_MWCOLORLAW

OPT_MWEBV

to zero. Analogous control keys

exist in the ﬁtting programs (§5.5), and thus systematic tests can be performed using both simulations and

ﬁtting.

Since options may change over time, a robust way to see the current options is to grep the deﬁnition

keys,

grep OPT_MWCOLORLAW $SNANA_DIR/src/MWgaldust.h

#define OPT_MWCOLORLAW_OFF 0 // No Extinction applied.

#define OPT_MWCOLORLAW_CCM89 89 // Clayton,Cardelli,Matheson, 1989

#define OPT_MWCOLORLAW_ODON94 94 // O’Donnel 1994 update

#define OPT_MWCOLORLAW_FITZ99 99 // Fitzpatrick 1999

grep OPT_MWEBV $SNANA_DIR/src/MWgaldust.h

#define OPT_MWEBV_OFF 0 // no extinction

#define OPT_MWEBV_FILE 1 // FILE value (simlib or data header)

#define OPT_MWEBV_SFD98 2 // use SFD98 value

#define OPT_MWEBV_Sch11_PS2013 3 // PS1-2013 implementation of Schlafly 2011

The default keys are indicated above, and these defaults are trivially implemented by running the simu-

lation without specifying any of the MWEBV keys in the sim-input ﬁle. With the default

OPT_MWEBV=1

the value of E(B−V)is taken from the simlib “

MWEBV: xxx

” key. If this key is missing, or the entry

value is zero, then

MWEBV

is calculated internally using the dust maps from [8], which is equivalent to

OPT_MWEBV=2

OPT_MWEBV>2

are intended for SFD98 recalibrations such as in Schlaﬂy 2011. For each

simulated SN, the nominal map-value of E(B−V)and its uncertainty are written to the header, and this

value is used in the ﬁtting programs (§5.5).

GENSIGMA_MWEBV_RATIO

controls the E(B−V)scatter relative

to the nominal map value, and the smeared values are used to redden the true magnitudes in the simulation.

If the smearing for a given SN results in negative extinction, the extinction is set to zero.

4.18.1 Some Details on Galactic Extinction Computations

The implementation of Galactic extinction is quite different for observer-frame and rest-frame models,

although the sim-input keys work the same for both. The discussion here is relevant for both the simulation

and ﬁtting programs.

For observer-frame models (e.g., SALT2, S11DM15) the extinction is computed exactly for each ﬁlter-

wavelength bin in the ﬂux integrals. For rest-frame models that require K-corrections (e.g., mlcs2k2,

snoopy) the Galactic extinctions are stored in the kcor/calib ﬁle; the resulting lookup improves CPU speed.

In the kcor/calib ﬁle, the extinction is computed and stored for E(B−V) = 0 and E(B−V) = 0.1 mag,

and interpolation is used to compute the extinction for arbitrary E(B−V). The treatment of

and

OPT_MWCOLORLAW

is more subtle. These two keys in the sim-input ﬁle are also used in the kcor-input ﬁle

to deﬁne the Galactic extinction values. If

and/or

OPT_MWCOLORLAW

are varied in the sim-input ﬁle or

in the ﬁt-input namelist (§5.5), i.e., are different than what was used to generate the kcor/calib ﬁle, an

extinction correction is computed at the central wavelength of the observer-frame ﬁlter.6The correction is

the extinction difference between using the sim-input (or ﬁt-input) parameters and those used to generate

the kcor/calib ﬁle. With this strategy, a new kcor/calib ﬁle is not required to use a different

value or color

law. However, for large variations it would be prudent to make an explicit crosscheck by re-generating

another kcor/calib ﬁle.

WARNING:

EXTINC_MILKYWAY

is obsolete and will cause the simulation to abort.

4.18.2 Correcting FLUXCAL for Galactic Extinction

By default, the reported

FLUXCAL

and uncertainties in the data ﬁles include the effect of Galactic extinction.

The analysis codes must therefore account for this effect. In some cases it is convenient to provide de-

reddened data ﬁles. Simulated

FLUXCAL

in the data ﬁles can be internally corrected by setting

OPT_MWEBV

to be negative: e.g., “

OPT_MWEBV: -2

” will apply a smeared SFD98 map to redden the observed ﬂuxes,

and then correct the observed ﬂuxes (

FLUXCAL

) using the SFD98 map value and central wavelength of each

ﬁlter. Although the ﬂuxes are MWEBV-corrected, the SNR is degraded from the reduced photo-statistics.

Because of MWEBV uncertainty, the true extinction differs from the map value and this true value is used

to correct

SIM_MAGOBS

(each epoch) and

SIM_PEAKMAG

6See function

GET_MWXT8

snana.car.

4.19 Simulating the Host Galaxy

Starting with

SNANA

v9_30G there is a host-galaxy package designed to simulate the following effects:

•select host galaxy based on arbitrary user-function of host properties; see

WGTMAP

•Generate SN propertes (e.g., stretch & color) correlated with host properties; see

VARNAMES list

•two methods to shift SN magnitudes (coherent for all epochs and wavelengths) based on host prop-

erties; add

SNMAGSHIFT

VARNAMES

list or use

WGTMAP

•host-galaxy photo-z to use as photo-z ﬁtting prior (§ 5.11); include

ZPHOT

ZPHOT_ERR

VARNAMES

list.

•select random SN location (near host galaxy) weighted by surface brightness; see Sersic params and

set

HOSTLIB_MSKOPT += 8

•host-galaxy contribution to [SN] Poisson noise at each epoch; set

HOSTLIB_MSKOPT += 2

The host-galaxy information is stored in a library, hereafter denoted “HOSTLIB”. An example HOSTLIB

is shown in Fig. 7. This self-documented ﬁle gives the number of variables describing each host (

NVAR

) and

a list of descriptive ”

VARNAMES

.” There are two mandatory variables:

GALID

and

ZTRUE

; the simulation will

abort if either variable is missing. The integer

GALID

must be the ﬁrst element, but

ZTRUE

can be anywhere

on the

VARNAMES

list. The library need not be sorted by

ZTRUE

since the simulation internally sorts the

library by redshift.

In principle a HOSTLIB needs to contain only

GALID

and

ZTRUE

, but such a library would not be useful

to simulate interesting effects. The remaining

VARNAMES

in Fig. 7 are optional, and control what kinds

of effects can be simulated. The

ZPHOT

and

ZPHOTERR

keys give the externally-computed photometric

redshift, and “[ﬁlt]_obs” are the observer-frame galaxy magnitudes needed to compute the noise. The

coordinate variable names can be

RA, RA_GAL or RA_HOST

, and similarly for

DEC

; one of the latter two

is recommended to avoid potential conﬂict with the RA,DEC of the SN in one of the output tables.

The galaxy shape is described by an arbitrary sum of Sersic proﬁles. The galaxy size is deﬁned by

VARNAMES

a0_Sersic - a9_Sersic

b0_Sersic - b9_Sersic ;

these are major- and minor-axis half-light sizes (arcseconds) for up to 10 Sersic components. There are

two options for deﬁning the the Sersic index

n0_Sersic - n9_Sersic

. First, the Sersic index can be

included as one of the

VARNAMES

as done with

n0_Sersic

in Fig. 7. This option allows a different Sersic

index for each host galaxy. The second option is to deﬁne a ﬁxed Sersic index after the

VARNAMES

list

as done with

n0_Sersic

in Fig. 7; this same value is used for each host galaxy. Commonly used Sersic

indices are n=0.5,1,4 for Gaussian, exponential and deVaucouleurs, respectively.

Finally, “

a_rot

” is the rotation angle (in degrees) of the major axis w.r.t. the +RA coordinate. If North

is up and East is to the right,

a_rot

is measured clockwise, from the East toward the South.

Figure 7: Example HOSTLIB for the

SNANA

simulation.

NVAR: 15 # obsolete key starting at SNANA version v10_70

VARNAMES: GALID RA_GAL DEC_GAL ZTRUE ZERR u_obs g_obs r_obs i_obs z_obs

n0_Sersic a0_Sersic b0_Sersic a_rot ZPHOTFLAG

n0_Sersic: 0.5 # optional: fix sersic index for each host

# Note that n0_Sersic can be defined only once;

# either among the VARNAMES or here.

NVAR_WGTMAP: 1 # obsolete key starting at SNANA version v10_70

VARNAMES_WGTMAP: r_obs WGT SNMAGSHIFT

WGT: -25.0 1.2 -0.05

WGT: -23.0 1.0 -0.05

WGT: -21.0 0.8 -0.05

WGT: -19.0 0.6 +0.05

WGT: -17.0 0.4 +0.05

WGT: -15.0 0.2 +0.05

GAL: 2940448741 52.67432 -27.17716 0.3964 0.0828 99

22.06580 20.99990 20.65600 20.33090 0.50 0.99290

0.73811 154.40625 1

GAL: 2940535300 52.67437 -28.42170 0.7860 0.0580 99

25.78030 23.14940 22.06930 21.49040 0.50 1.14660

0.51003 77.85583 1

etc ...

The next set of keys in Fig. 7 describes an optional weight map. In this example, galaxies are weighted

by the absolute r-band magnitude, and the SN brightness is also adjusted using the same map. Following

the

VARNAMES_WGTMAP

key, the ﬁrst “N−2” variables must be from the

VARNAMES

list in Fig. 7, which

describe an arbitrary dependence on host properties. The last two variables must be

WGT

and

SNMAGSHIFT

although any names can be used here. If no weight map is given the simulation will assign a weight of

unity to each host galaxy, with zero mag-shift. Starting with

SNANA

version v10_70, the “

NVAR:

” and

“

NVAR_WGTMAP:

" keys are obsolete, although leaving them in the

HOSTLIB

ﬁle will not cause any harm.

The host-galaxy selection starts by ﬁnding a “near-z” subset of host galaxies within ±0.01 of the SN

redshift. A random host among this near-zsubset is picked based on the weight map. A HOSTLIB should

have adequate statistics to densely cover the redshift range and parameter space used by the weight map.

The following HOSTLIB options can be set in the sim-input ﬁle (or via command-line override):

HOSTLIB_FILE: DES.HOSTLIB # required

# optional

HOSTLIB_WGTMAP_FILE: xxxx # default=none

HOSTLIB_ZPHOTEFF_FILE: xxxx # default=none

HOSTLIB_MAXREAD: 10000 # default=billion

HOSTLIB_MXINTFLUX_SNPOS: .999 # default=.99

HOSTLIB_MSKOPT: 8 # default=0

HOSTLIB_SBRADIUS: xxx # default=1.2 arcsec

HOSTLIB_GENRANGE_RA: xxx yyy # default= -999 to +999

HOSTLIB_GENRANGE_DECL: xxx yyy # default= -999 to +999)

HOSTLIB_STOREPAR: var1,var2,var3 # default = ’’

HOSTLIB_MINDAYSEP_SAMEGAL: xxx # default=9999999

HOSTLIB_DZTOL: a0 a1 a2 # default=0.002 0.040 0

HOSTLIB_GALID_PRIORITY: xxx yyy # default= 0 0

HOSTLIB_GENZPHOT_FUDGEPAR: a0 a1 a2 bprob b1 # default = all -9

HOSTLIB_GENZPHOT_BIAS: b0 b1 b2 b3 # 3rd order poly(ztrue)

HOSTLIB_SERSIC_SCALE: xxx # default= 1.0

# debug options

HOSTLIB_GALID_FORCE: #### # forced GALID

HOSTLIB_FIXRAN_RADIUS: #.## # fix radial random number (0-1)

HOSTLIB_FIXRAN_PHI: #.## # fix phi random number (0-1)

Only the

HOSTLIB_FILE

key is required, while the other keys are optional. Ideally all surveys would use

the same

HOSTLIB_FILE

, but in practice each survey will have its own HOSTLIB with a speciﬁc focus. Also

note that there is no standard method for creating a HOSTLIB. The optional

WGTMAP_FILE

overrides the de-

fault weight map embedded in the HOSTLIB ﬁle.

HOSTLIB_ZPHOTEFF_FILE

speciﬁes a 2-column ﬁle with

true redshift and efﬁciency of ﬁnding a host photo-z. For very large HOSTLIB ﬁles, the

MAXREAD

key may

be useful to reduce the initialization time or limit memory usage. The next option (

MXINTFLUX_SNPOS

) sets

the fraction of total galaxy ﬂux used to generate the SN position; this option truncates extreme galaxy-SN

separations.

HOSTLIB_STOREPAR

is a comma-separated list of parameters (case-insensitive, but no blank

spaces before or after each comma) to store in the data ﬁles; these “

STOREPAR

” paramaters are automati-

cally propagated into the SNTABLEs (ntuple or tree) and ascii ﬁtres ﬁle.

HOSTLIB_MINDAYSEP_SAMEGAL

speciﬁes the minimum

PEAKMJD

separation (in days) for re-using a galaxy. This option can be useful, for

example, in multi-year surveys with long seasonal gaps, and in very low-z simulations that have a limited

number of galaxies.

A redshift tolerance, dztol ≡max|zSN −zGAL|, sets a limit on the max difference between the SN

redshift and the redshift of the host galaxy picked from the

HOSTLIB

. This is needed because for each

generated SN redshift there is not a host with the exact same redshift. Requiring stricter z-tolerance

(and allowing only 1 SN per host) generally requires a larger

HOSTLIB

to avoid running out of hosts and

aborting. The input key

HOSTLIB_DZTOL

deﬁnes dztol as a 2nd order polynomial function of redshift:

a0+a1z+a2z2, where a0,1,2are three parameters following the

HOSTLIB_DZTOL

key. The default is

a0,1,2=0.002,0.040,0 so that dztol =0.002 at z=0 and increases to dztol =0.042 at z=1. To require

a ﬁxed 0.01 z-dif tolerance at all redshifts set “

HOSTLIB_DZTOL: 0.01 0 0

.” To monitor zSN −zGAL,

include

GALZDIF

in the

SIMGEN_DUMP

list (§4.32.3).

HOSTLIB_GALID_PRIORITY

allows giving priority to a subset speciﬁed by a GALID range. For exam-

ple, if there only a few real host galaxies with

GALID > 0

, and the majority are fake galaxies on random

sky with

GALID < 0

, then setting “

HOSTLIB_GALID_PRIORITY: 0 99999999

” will preferentially select

the real galaxies before picking the fake galaxies.

HOSTLIB_GENZPHOT_FUDGEPAR

speciﬁes an analytic description of the host photo-z proﬁle and its

error. This

FUDGEPAR

implemenation does not require

ZPHOT

and

ZPHOTERR

keys in the

HOSTLIB

; if these

keys exist in the

HOSTLIB

, their values are overwritten by the

FUDGEPAR

description. The

ZPHOT-ZTRUE

proﬁle is described by a sum of two Gaussian proﬁles. The ﬁrst Gaussian (G1) has a width described by

the ﬁrst 3

FUDGEPAR

parameters: σ1=a0+a1(1+z)+ a2(1+z)2. The second Gaussian (G2) is described

by the remaining two parameters: 1)

bprob

is the probability of selecting from G2, and

1-bprob

is the

prob of selecting from G1, and 2) σ2=b1(1+z)is the width of G2. G2 is intended to be broader than G1,

and to account for outliers and wrong-host matches. The reported

ZPHOTERR

is σ1, and thus G2 introduces

non-Gaussian outliers which are not described by the reported uncertainty.

To avoid negative photo-z with

FUDGEPAR

, the Gaussian distribution is internally modiﬁed to an asym-

metric Gaussian if the true redshift is less than 3σaway from 0.01. Deﬁning σ−and σ+to be bifurcated

Gaussian sigmas, and zpeak to be the redshift with max probability, these 3 quantities are constrained by

zpeak =0.01+3σ−(17)

ZTRUE =zpeak +h(σ−−σ+)p2/πi(18)

ZPHOTERR2=(σ++σ−)2+ (σ+−σ−)2(1−2/π)/4(variance)(19)

Although an exact solution exists for this quadratic equation, the solution for zpeak,σ−,σ+is found numer-

ically. If

ZPHOTERR/ZTRUE

ratio is too large, a solution cannot be found. In this case of no solution, the

mean

ZTRUE

is preserved while the variance will be smaller than the requested

ZPHOTERR

2. The reported

ZPHOTERR

reﬂects the calculated variance on the r.h.s of Eq. 19.

If b1≥10, the G2 distribution is ﬂat over the redshift range of the

HOSTLIB

. To specify a differ-

ent outlier photo-z range (e.g., 0.01 <Zphot <2.5), set the

(5th) element to the following string:

’FLAT(.01:2.5)’

HOSTLIB_GENZPHOT_BIAS

introduces a z-dependent bias on

ZPHOT

. The parmaeters

b0,b1,b2,b3

de-

scribe a 3rd order polynomial function of true redshift. This bias applies to

HOSTLIB_GENZPHOT_FUDGEPAR

or to the

ZPHOT[ERR]

columns in the

HOSTLIB

HOSTLIB_SERSIC_SCALE

scales the a0 and b0 half-light radii to make the galaxy sizes bigger or

smaller.

The

HOSTLIB_MSKOPT

options can be viewed with the grep-command

grep MSKOPT $SNANA_DIR/src/sntools_host.h

•

MSKOPT

+= 2 : compute the host-galaxy Poisson noise within an aperture of radius 2σPSF (added to

total error per epoch), and also compute the local surface brightness.7This option requires deﬁning

HOSTLIB header keys “f_obs” for each ﬁlter (see

VARNAMES

in Fig. 7), where ’f’ is the one-character

ﬁlter representation. These observer-frame

HOSTLIB

mags should be corrected for MW Galactic

extinction and correspond to the entire galaxy ﬂux.

•

MSKOPT

+= 4 : apply SN mag shift from WGTMAP. Does not control SNMAGSHIFT in VAR-

NAMES list.

•

MSKOPT

+= 8 : replace originally selected SN coordinates (i.e., randomly selected in ﬁeld or from

SIMLIB

) by SN coordinates near the host galaxy (i.e., randomly selected from the surface bright-

ness proﬁle). This option is useful to generate SNe for image simulations. SN-generated zcmb is

preserved; zhel is updated to account for new coordinates and generated vpec. Generated distance (µ)

is also updated.

•

MSKOPT

+= 16 : adjust the SN redshift, SN mags, and µto galaxy redshift,

ZTRUE

(useful for image

simulations). zhel =

ZTRUE

;zcmb and µare updated to account for new zhel and generated vpec.

•

MSKOPT

+= 32 : allow only one SN per host galaxy (results in abort if library is too small)

•

MSKOPT

+= 64 : use SN properties in hostlib to override default generation: examples are color (e..g,

c or AV), shape (e.g., x1 or Delta), RV, beta, alpha, and SNMAGSHIFT. Case-insensitive so that x1

or X1 will work. All available SN parameters are used; simulation aborts if no SN parameters are

found.

•

MSKOPT

+= 256 : increase verbosity to screen.

•

MSKOPT

+= 1024 : detailed screen dump for each selected host.

Options can be combined, such as

HOSTLIB_MSKOPT

=10 will transfer the SN redshift and coordinates to

that of the galaxy, and compute the galaxy noise.

7see “

HOSTGAL_SB_FLUXCAL

” key in data header: units are

FLUXCAL

per arcsec2.

Notes on CPU Resources:

The CPU generation time per host galaxy is dominated by the noise calculation that includes a convolution

of the galaxy ﬂux within a separate PSF-aperture for each epoch. The generation time is about 3 msec

per host for a single Sersic proﬁle, and 5 msec for a sum of 2 Sersic proﬁles. The main tool to minimize

the generation time is to pre-compute integral tables for 2-dimensional Gaussians, and for Sersic proﬁles.

Deﬁning a reduced radius ρ≡R/R1/2in terms of the half-light radius R1/2, the dimensionless Sersic

integrals

Sn(ρ) = 2πZρ

0exp[−Bn(x1/n−1)] xdx (20)

are tabulated and stored on a uniform grid as a function of 1/n(n=0.3−5) and as a function of log10(ρ)

(ρ=10−4to 100). The Bncoefﬁcients are chosen such that Sn(1)/Sn(∞) = 1/2. The galaxy ﬂux (F) at

local galaxy coordinates xgal and ygal is the sum over Sersic components,

F=∑

wnexp[−Bn(ρ1/n−1)]

anbnSn(∞)(21)

where wnis the Sersic weight such that ∑nwn=1, anand bnare the major and minor half-light axes,

respectively, and ρ2= (xgal/an)2+ (ygal/bn)2is the reduced radius.

Ensuring Host PhotoZ in Fitting Program:

To ensure that the light-curve ﬁtter cannot cheat when doing photoZ ﬁts on simulated SNe, there is an op-

tion to replace the output

REDSHIFT_FINAL

with the host-galaxy (photoZ) redshift so that the spectroscopic

redshift is not available in the data ﬁle; this option is invoked by setting

GENSIGMA_REDSHIFT

≥1. If there

is no host-galaxy photo-z,

GENSIGMA_REDSHIFT

≥1 results in undeﬁned

REDSHIFT_FINAL

=−9±−9.

HOSTLIB Variables for

SIMGEN_DUMP

ﬁle:

The

SIMGEN_DUMP

option is described in §4.32.3. Here is an example showing the HOSTLIB variables:

SIMGEN_DUMP: 7 CID Z GALZTRUE GALZPHOT GALSNDM GALWGT r_obs

The

GAL*

quantities can always be added, along with the subset of variables used to deﬁne the weight

map.

HOSTGAL vs. SIM_HOSTLIB variables in Data Files:

There are two sets of HOST-related parameters in the output. The ﬁrst set,

HOSTGAL_XXX

, corresponds

to observables which can appear in real data ﬁles. These obervables include

OBJID

ZPHOT

ZPHOT_ERR

and

LOGMASS

. Additional obervables may be added later. The second set,

SIM_HOSTLIB_XXX

, corresponds

to the user-selected parameters from the sim-input key

HOSTLIB_STOREPAR

. If this user-list includes an

observable such as

ZPHOT

, then

HOSTGAL_ZPHOT

and

SIM_HOSTLIB_ZPHOT

will both appear in the data

ﬁles and in the analysis output (SNTABLEs and ascii ﬁtres ﬁle).

HOSTLIB_ZPHOTEFF_FILE vs. SEARCHEFF_zHOST_FILE:

The former determines the probability (vs. redshift) for ﬁnding a host galaxy photo-z, and it has no

impact on setting

SIM_SEARCHEFF_MASK

. This option also requres

ZPHOT

in the

HOSTLIB

ﬁle. The latter

determines the probability (vs. redshift) for ﬁnding a spectroscopic galaxy redshift, and it sets the 4-bit of

SIM_SEARCHEFF_MASK

. This option does not depend on the

HOSTLIB

Visual Testing with HOSTLIB_FIXRAN :

To verify the “

a_rot

” convention, it is useful to ﬁx the radius and angle to known values and visually

inspect the location on a real image with the HOSTLIB galaxies. A relative galaxy position can be selected

with

•

HOSTLIB_FIXRAN_PHI

is a random number (0 <r<1) that ﬁxes the azimuthal angle to r×360:

r=0,0.5,1 correspond to the major axis (0◦,180◦,360◦); r=0.25 and 0.75 correspond to the

minor axis (90◦,270◦).

•

HOSTLIB_FIXRAN_RADIUS

is a random number (0 <r<1) where the reduced radius contains a

fraction ‘r’ of the total ﬂux.

Anomalous Flux-Scatter on Bright Galaxies :

The simulation supports a model of anomalous ﬂux-scatter related to subtractions near bright galaxies.

The true ﬂux uncertainty is increased as a function of surface brightness, while the nominal uncertainty is

reported in the data ﬁle. The sim-input key word is

HOSTNOISE_FILE: <fileName>

and the ﬁle syntax is

NOISEMODEL_NAME: SB_ERRSCALE

# SBMAG = mag/arcsec^2 in template at SN location

# = 27.5 - 2.5*log10(FLUXCAL_SB)

# ERRSCALE: fluxerr -> fluxerr x ERRSCALE

LIBID: 1

BAND: g FIELD: E1+E2+S1+S2+C1+C2+X1+X2

# SBMAG ERRSCALE

HOSTNOISE: 20.50 4.60

HOSTNOISE: 21.50 2.70

HOSTNOISE: 22.50 1.78

HOSTNOISE: 23.50 1.40

HOSTNOISE: 24.50 1.09

HOSTNOISE: 25.50 1.02

HOSTNOISE: 26.50 0.99

HOSTNOISE: 27.50 1.00

HOSTNOISE: 28.50 0.99

and repeat for each band and group of fields.

In the analysis, the data-ﬁle errors can be increased with the same model using

&SNLCINP

FUDGE_HOSTNOISE_FILE = ’<fileName>’

4.20 Simulating Mis-Matched Host Galaxy

For surveys that do not have SN spectroscopic conﬁrmation and instead rely on a host galaxy spectroscopic

redshift, there is the issue of matching each SN candidate to the correct host galaxy. This effect can be

simulated by specifying a “

WRONGHOST

” model with sim-input key

WRONGHOST_FILE: <file>

and the

WRONGHOST

model is deﬁned in the ﬁle with

# PROB_WRONGHOST_POLY: 0.065 0.015 -0.066 0.0544 [hard-code 3rd order]

# or

# PROB_WRONGHOST_POLY: 0.065,0.015,-0.066 [arbitrary order]

# ZTRUE ZMATCH

0.921 1.019

0.875 1.455

0.517 0.499

0.174 0.1674

0.995 0.7651

0.325 0.861

etc ...

The key

PROB_WRONGHOST_POLY

speciﬁes a 3rd order polynomial function of redshift to compute the

wrong-host probability; ﬁrst term is a constant, 2nd term is linear in redshift, etc. For incorrectly matched

host galaxies, the remainder of the ﬁle gives a list of the true SN redshift (

ZTRUE

) and the redshift of the

incorrectly matched galaxy (

ZMATCH

WRONGHOST

entries are rejected if either

ZTRUE

ZMATCH

is outside

the

HOSTLIB

redshift range.

For a given SN redshift (zSN), the

WRONGHOST

library is searched for nearby

ZTRUE

values within 0.01

of zSN; a random

ZTRUE

is selected among these nearby values. The host redshift is computed as

zhost =zSN + (ZMATCH −ZTRUE).

Note that the

WRONGHOST

model is created outside of the

SNANA

environment. Ideally, this model is

based on matching simulated SN locations to galaxies in a catalog generated from the survey.

There are two ways to identify mis-matched hosts from the data ﬁles. First is an explicit ﬂag,

SIM_ZFLAG=4

(see §?? for details). Second,

REDSHIFT_FINAL - SIM_REDSHIFT_CMB

should show a tail from wrong-

host matches. In the output tables (SNANA,FITRES) from snana-analysis, examine

zCMB-SIM_zCMB

, and

extract

SIM_ZFLAG

using the

APPEND_TABLE_TEXT

feature in

split_and_fit

4.21 Simulating Rate vs. Redshift: Volumetric and per Season

To simulate a constant volumetric rate at all redshifts, include the following in your sim-input ﬁle,

DNDZ: HUBBLE

and to simulate a redshift-dependent rate that depends on a power of 1+z,

DNDZ: POWERLAW 2.6E-5 1.5 # rate=2.6E-5*(1+z)^1.5 /yr/Mpc^3

Note that setting the second

POWERLAW

argument to zero is equivalent to the

HUBBLE

option of a constant

rate. Finally, to simulate multiple power laws in different redshift ranges,

# R0 Beta Zmin Zmax

DNDZ: POWERLAW2 2.2E-5 2.15 0.0 1.0 # rate = R0(1+z)^Beta

DNDZ: POWERLAW2 9.76E-5 0.0 1.0 2.0 # constant rate for z>1

where

is the rate (/yr/Mpc3) at z=0,

Beta

gives the z-dependence (

Beta=0

for constant rate), and

the last two entries give the min/max redshift range. The output

README

ﬁle includes a dump of the SN

volumetric rate in redshift bins of 0.1 (grep “

MODEL-RATE

”).

Highly distorted redshift distribution for special tests can be obtained with

DNDZ: FLAT # dN/dz = constant

DNDZ: ZPOLY <a0> <a1> <a2> <a3> # dN/dz = 3rd order polynom

DNDZ: CC_S15 # CC-Rate(z) from Strolger 2015 (Fig 6, green line)

DNDZ: CC_S15*.3 # 30% of S15 rate

DNDZ: MD14 Rate(z=0) # Rate(z) from Madau & Dickenson 2014

DNDZ_ZEXP_REWGT: -2.0 # dN/dz *= 1/z^2

DNDZ_ZPOLY_REWGT: 1.0 -0.2 0.003 -4E-6 # dN/dz *= [3rd prder polynom]

The “

FLAT

” command results in a ﬂat redshift distribution, and the

ZPOLY

option speciﬁes the redshift

distribution with a 3rd-order polynomial function of redshift.

CC_S15

is the HST-measured CC rate.

MD14

is the Star-formation rate, and there is one user-input parameter to deﬁne the rate (yr−1Mpc−3) at

z=0. The next two examples re-weight the distribution deﬁned by the

DNDZ

key above. The example

with “

DNDZ_ZEXP_REWGT: -2

” re-weights by z−2. The last option allows the user to multiply the “

DNDZ

”

redshift distribution by an arbitrary 3rd-order polynomial function of the redshift.

As a convenience, the absolute number of SN per season within your survey (Nseason) is written into

the output

README

ﬁle as follows:

Number of SN per season = 12345

This value does not depend on

NGEN_LC

NGENTOT_LC

,8and it is not used in the simulation. This

calculated value depends on the MJD range (

GENRANGE_PEAKMJD

), redshift range (

GENRANGE_REDSHIFT

DNDZ

option above, and coordinate ranges (

GENRANGE_RA

and

GENRANGE_DECL

). The sky area speciﬁed

by the RA and DECL ranges can be overwritten by explicitly deﬁning a solid angle in your sim-input ﬁle

using

NGEN_LC

is the number of SNe generated after trigger cuts and

NGENTOT_LC

is the total number generated regardless of the

trigger and cuts (§4.26).

SOLID_ANGLE: 0.0204 # solid angle (steridian) for SN/season estimate

The

SOLID_ANGLE

option is useful when the survey consists of several dis-connected patches of sky,

thereby requiring the RA and DECL ranges to represent a solid angle that is much larger than that of

the survey. Nseason can be used generate an arbitrary number of SN seasons. For example, to simulate 3

seasons set the following:

NGENTOT_LC: 37035 # 3*12345 = 3 seasons

NGEN_SEASON: 3.0

To scale the rates,

DNDZ_SCALE: xx yy # scales for Ia and NONIA

DNDZ_SCALE_NON1A: yy # scale NON1A rata (scaleIa=1.0)

DNDZ_ALLSCALE: xx # scale rate for any model

This option is also useful for

sim_SNmix

: e.g., to add a large Ia-biasCor sample, “

GENOPT: DNDZ_SCALE

10 1.0E-8

” scales the Ia sample by a factor of 10 while turning off the NON1A. Beware that the

NON1A

scales apply speciﬁcally to

NON1ASED

and

NON1AGRID

models.

SIMSED

models can be either Ia or NON1A,

and thus

DNDZ_ALLSCALE

applies to all models.

4.22 Simulating Rate vs. Galactic Coordinates

For the

LCLIB

model, the rate is deﬁned as a function of Galactic coordinates (land b). Current option is

DNDB: COSBPOLY: <b0> <b1> <b2> <b3> <b4> <b5>

DNDB: BPOLY: <b0> <b1> <b2> <b3> <b4> <b5>

# ------- example -------

DNDB: COSBPOLY: 1 0 0 0 0 0 # isotropic

which deﬁnes the b-dependence with a 5th-order polynomial function of cos(b)or b. The absolute number

of generated events is given by

NGENTOT_LC

. To reduce reading of the

SIMLIB

, and thus reduce processing

time, use the

SIMLIB_NREPEAT

feature (§4.5.1). While

SIMLIB_NREPEAT

is ﬁxed for isotropic rate models

that depend on redshift (§4.21), here it is multiplied by the relative rate:

SIMLIB_NREPEAT = max(SIMLIB_NREPEAT) * DNDB(b,l)/max[DNDB(b,l)]

The b-weight is thus implemented by how many times each

SIMLIB

entry is read. Since

SIMLIB_NREPEAT

is usually a ﬂoat, the ﬂoating remainder is compared with random number to determine whether to

use

NREPEAT=int(SIMLIB_NREPEAT)

int(SIMLIB_NREPEAT)+1

. If

NREPEAT=0

, the

SIMLIB

entry

is skipped.

The

DNDB

-rate feature speciﬁes a relative rate vs. b, but the simulation has no mechanism to normalize

separate simulations of different sky regions. Here we describe how to determine the relative normalization

using the

SIMLIB_DUMP

feature (§4.32.1). Consider three sky regions, S1, S2, S3, with solid angles

Ω1,Ω2,Ω3, and each with a separate

SIMLIB

-cadence ﬁle. Running the simulation with an

LCLIB model

and the

SIMLIB_DUMP

option results in a calculation and screen-dump of the average weight over the

SIMLIB

: ¯w1= [∑iDNDBi]/NLIBID1, and similarly for ¯w2and ¯w3. The sum over i=1,NLIBID runs over

each entry in the

SIMLIB

ﬁle. The

NGENTOT_LC

values to generate are

NGENTOT_LC =NΩ1¯w1(S1)

NGENTOT_LC =NΩ2¯w2(S2)

NGENTOT_LC =NΩ3¯w3(S3)

where Nis an arbitrary number setting the global normalization.

4.23 Simulating a

SPECTROGRAPH

As described in §3.2, a

SPECTROGRAPH

instrument can be deﬁned in a text ﬁle and then ingested into a kcor

ﬁle. While the photometric (broadband) ﬂuxes and SNR are computed from observational information

(ZP,PSF,SKY), spectral SNR-vs-λare stored in the kcor ﬁle and read by the simulation. Thus, users

must estimate spectral SNR properties with an external calculator. There are two methods for simulating

spectra. First, the

SPECTROGRAPH

can be included in the

SIMLIB

ﬁle as described in §4.5.2. This method

results in spectra at ﬁxed MJD values regardless of the explosion date. Since spectroscopic programs tend

to target SNe based on the time of peak brightness (t0), there is a second method to simulate spectra within

arbitrary time windows with respect to t0(§4.23.1).

Here are few warnings:

•works for the following models:

SALT2

NON1ASED

FIXMAG

BYOSED

(WARNING: does not work for SIMSED)

•if true ﬂux is negative, it is suppressed in the output. So beware of spectroscopic wavelength holes,

particularly at early epochs and the UV.

•there are no

SNANA

programs which read the simulated spectra.

•Units: dF/dλ, erg/s/cm2/Å.

For

TEXT

formatted data ﬁles (

FORMAT_MASK: 2

), the spectra are appended to the ascii ﬁle for each

SN; search for “

SPECTRUM_

” keys. For FITS format (

FORMAT_MASK: 32

), a separate

*SPEC.FITS

ﬁle is

created with three tables as follows:

TableName |Ncol| column names

--------------------------------------------------------------------

SPECTRO_LAMINDEX | 3 | LAMINDEX LAMMIN LAMMAX

SPECTRO_HEADER | 9 | SNID MJD Texpose SNR_COMPUTE LAMMIN_SNR LAMMAX_SNR

| | NBIN_LAM PTRSPEC_MIN PTRSPEC_MAX

SPECTRO_FLUX |4-5 | LAMINDEX FLAM FLAMERR 100*SIM_MAG 1000*SIM_WARP

The ﬁrst table (

SPECTRO_LAMINDEX

) is a map deﬁning short-integer “

LAMINDEX

” for each λbin, and

it is used in the large

SPECTRO_FLUX

table to easily identify λbins. The second

SPECTRO_HEADER

table provides a one-row summary for each spectrum: 1)

SNID

is the object ID, 2)

MJD

is the spec-

trum date, 3)

Texpose

is the exposure time (sec), 4)

SNR_COMPUTE

is computed SNR, or −9 if SNR-

option not used, 5,6)

LAMMIN_SNR,LAMMAX_SNR

is the observed λ-range whose ﬂux-sum corresponds to

SNR_COMPUTE

, 7)

NBIN_LAM

is the number of λbins (see comment above about suppressing negative

ﬂuxes), 8,9)

PTRSPEC_MIN,PTRSPEC_MAX

are pointers to extract the spectrum from the

SPECTRO_FLUX

table.

The

SPECTRO_FLUX

table contains information for every spectral bin for every SN: λbin

LAMINDEX

FLAM

(dF/dλ), its uncertainty

FLAMERR

, and the generated (true) mag,

SIM_MAG

. If a

WARP_SPECTRUM

key

is used, there is an extra

SIM_WARP

column. To save disk space,

SIM_MAG

is multplied by 100 and stored as

a short integer; similarly,

SIM_WARP

is multiplied by 1000 and stored as short int. After the last wavelength

bin of a spectrum in the

SPECTRO_FLUX

table, the next row is an end-of-spectrum marker containing “

777

-777 -777 0

”; this marker should be checked to ensure correct parsing.

The ﬁrst two tables are small, and should read quickly and stored in memory for quick access. The 3rd

(

SPECTRO_FLUX

) table can be very large (few GB), so beware of memory storage. To avoid memory issues,

each spectrum can be read quickly from

SPECTRO_FLUX

table using pointers in the

SPECTRO_HEADER

table.

4.23.1 Spectral Time-Windows Relative to Peak Brightness

In the sim-input ﬁle, spectroscopic exposure times can be assigned with

TAKE_SPECTRUM

keys as follows:

TAKE_SPECTRUM: TREST(-12:-10) TEXPOSE_ZPOLY(2000,500)

TAKE_SPECTRUM: TOBS(-7:7) TEXPOSE_ZPOLY(600,200,-3)

TAKE_SPECTRUM: TREST(0:2) TEXPOSE_ZPOLY(1000)

TAKE_SPECTRUM: TREST(10:12) TEXPOSE_ZPOLY(1500:2500,500)

Each

TREST

argument deﬁnes a 2-day rest-frame window from which to randomly select a spectroscopic

MJD. The

TOBS

argument deﬁnes a 2-week observer-frame window from which to randomly select a spec-

troscopic MJD. The

TEXPOSE_ZPOLY

key deﬁnes the exposure time (seconds) as a polynomial function of

redshift. The

TREST

exposure times are 2000 +500zsec (10-12 days before peak), 600 +200z−3z2sec

(7 days before peak), 1000 sec (near-peak), [1500 : 2500] + 500zsec (10-12 days after peak). The values

in parentheses can be ﬂoat or integer: e.g.,

TREST(-2.5:2.5)

. Beware that no blank spaces are allowed

inside the (). The colon separates a range, while commas separate a list; if you use the wrong punctuation,

the simulation will abort. A range for a polynomial coefﬁcient (4th example above) results in a randomly

selected coefﬁcient. Arbitrary polynomial orders are speciﬁed with comma-separated values; 1st value is

constant term, 2nd value is linear term, etc ...

The template exposure time is deﬁned in the

SIMLIB

ﬁle with the key

TEMPLATE_TEXPOSE_SPECTROGRAPH

Rather than pre-deﬁning exposure times, the exposure time can be computed from a requested SNR value:

# 1) rest-frame epoch, rest-frame SNR def

TAKE_SPECTRUM: TREST(-12:-10) SNR_ZPOLY(20,-5) SNR_LAMREST(5000:6000)

TAKE_SPECTRUM: TREST(0:2) SNR_ZPOLY(20) SNR_LAMREST(5000:6000)

TAKE_SPECTRUM: TREST(10:12) SNR_ZPOLY(20,-2) SNR_LAMREST(5000:6000)

# 2) obs-frame window, rest-frame SNR def

TAKE_SPECTRUM: TOBS(-7:7) SNR_ZPOLY(20) SNR_LAMREST(5000:6000)

# 3) rest-frame epoch, obs-frame SNR def

TAKE_SPECTRUM: TREST(-3:3) SNR_ZPOLY(20) SNR_LAMOBS(8000:10000)

TAKE_SPECTRUM: TREST(-3:3) SNR_ZPOLY(20) SNR_LAMOBS(13000:15000)

TAKE_SPECTRUM: TEMPLATE_TEXPOSE_SCALE(1.2)

The

TREST

and

TOBS

arguments are the same as in the previous example.

SNR_ZPOLY

speciﬁes the re-

quested SNR as a polynomial function of redshift. In the ﬁrst pre-peak example, SNR =20 −5z, allow-

ing the SNR to degrade with increasing redshift in order to reduce exposure time. The third argument,

SNR_LAMREST

, speciﬁes the rest-frame wavelength range for which SNR is deﬁned: for each event, the

observer wavelength range is 5000(1+z)Å to 6000(1+z)Å. The third block of arguments shows that

SNR can be deﬁned for observer-frame λ-ranges using

SNR_LAMOBS

When

SNR_ZPOLY

keys are deﬁned, the SNR and Texpose information is automatically added to the

SIMGEN_DUMP

ﬁle (§4.32.3). This allows checking Texpose vs. redshift, or vs any other quantity allowed in

the one-row-per-SN summary.

There are two methods to deﬁne the template exposure time. First is to deﬁned a ﬁxed exposure time

in the

SIMLIB

ﬁle with the key

TEMPLATE_TEXPOSE_SPECTROGRAPH

. The second option is deﬁned in the

example above with

TAKE_SPECTRUM: TEMPLATE_TEXPOSE_SCALE(1.2)

which sets the template exposure time to be 20% longer than that used at the epoch nearest peak brightness.

The template exposure time and noise are computed for each SN along with the search exposure times.

While the search exposure time varies with each epoch to acquire the speciﬁed SNR, the template exposure

time is the same for all epochs. This key overrides the

TEMPLATE_TEXPOSE_SPECTROGRAPH

key in the

SIMLIB

ﬁle.

WARNING: can use either the

TAKE_SPECTRUM

keys in sim-input ﬁle, or the

SPECTROGRAPH

keys in

the

SIMLIB

ﬁle; using both results in an abort.

4.23.2 Calibration Warp vs. Wavelength

Smooth spectral mis-calibration can be deﬁned as a polynominal function of wavelength using the sim-

input

WARP_SPECTRUM

key as follows:

WARP_SPECTRUM: LAMPOLY(1,1.0E-5)

TAKE_SPECTRUM: TREST(-12:-10) TEXPOSE_ZPOLY(2000,500,-20)

TAKE_SPECTRUM: TREST(0:5) SNR_ZPOLY(20:30,-5) SNR_LAMREST(5000:6000)

WARP_SPECTRUM: LAMPOLY(1,-1.0E-5:1.0E-5)

TAKE_SPECTRUM: TREST(10:12) TEXPOSE_ZPOLY(2000,500)

The ﬁrst

LAMPOLY

argument above is a multiplicative calibration warp of dF/dλ→dF/dλ×(1+10−5λ),

and it is applied to the ﬁrst two

TAKE_SPECTRUM

keys. The 2nd

LAMPOLY

argument speciﬁes a warp range

with a slope (dWARP/dλ) randomly selected between −10−5and +10−5; this random warp is applied to

the 3rd

TAKE_SPECTRUM

key. Analogous to the

TEXPOSE_ZPOLY

and

SNR_ZPOLY

arguments, the

LAMPOLY

argument can include an arbitrary polynomial order deﬁned with more comma-separated terms. The

warping is applied only to the measured dF/dλ(

FLAM

column in output); the true dF/dλis not warped

(

SIM_GENFLAM

4.23.3

SPECTROGRAPH

Options

The

SPECTROGRAPH_OPTMASK

key in the sim-input ﬁle can be used as follows:

SPECTROGRAPH_OPTMASK: 1 # turn off lambda smearing

SPECTROGRAPH_OPTMASK: 2 # double LAMSIGMA smearing

SPECTROGRAPH_OPTMASK: 4 # flux only in center lambda bin (delta function)

SPECTROGRAPH_OPTMASK: 8 # SNR -> SNR x 100

SPECTROGRAPH_OPTMASK: 16 # TREF -> TREF x 100 (template expose time)

SPECTROGRAPH_OPTMASK: 6 # flux only in center bin & LAMSIGMA*=2

SPECTROGRAPH_SCALE_TEXPOSE: 2.4 # scale exposure times by 2.4

Multiple options can be combined by adding values as illustrated by the last option above with

SPECTROGRAPH_OPTMASK=6

. The default is

SPECTROGRAPH_OPTMASK=0

, and the options above are in-

tended for testing and debugging.

The last option (

SCALE_TEXPOSE

) is a continuously tunable knob to scale the exposure times (for

search and template).

4.23.4 Simulating a Single High-S/N Spectrum

A single high-S/N spectrum (rest-frame) can be simulated at arbitrary redshift using the

NON1ASED

model

(§9.5), and deﬁning sim-input key

PATH_NON1ASED

to use a private NON1ASED directory. Instead of

deﬁning an SED time series covering a few-month range of epochs, the NON1ASED ﬁle can contain a

single spectrum at one epoch. The DAY column can have any value since internally the simulation will

shift the SED times such that DAY=0 at max ﬂux. Hence by deﬁnition, a single epoch will have DAY=0.

Recall that uniform wavelength binning is required.

To generate one spectrum, the sim-input key

GENRANGE_PEAKMJD

should be deﬁned as a δ-function

landing exactly on any

SPECTROGRAPH

MJD in the

SIMLIB

ﬁle. See §4.5.2 for how the

SPECTROGRAPH

deﬁned in the

SIMLIB

. It is also recommended to set “

GENRANGE_TREST: -1 1

” to remove photometry

output from epochs with an undeﬁned model. The simulated spectrum and photometry is artiﬁcially

deﬁned to appear at “peak,” but they really correspond to the epoch from which the input spectrum was

extracted. As a sanity check, the simulated mag should be compared with that from the input light curve.

Several spectra can be included in the NON1ASED model. For example, if there are 8 SEDs, then

setting “

NGENTOT_LC: 8

” will generate each spectrum once. If several spectra come from the same SN,

each spectrum should be deﬁned as a separate SED ﬁle.

4.24 Simulating Rise-Time Variations

The rise-time for any model can be adjusted using the following sim-input parameters:

GENPEAK_RISETIME_SHIFT: 2.3 # shift at -18 days

GENSIGMA_RISETIME_SHIFT: 0.6 0.6

GENRANGE_RISETIME_SHIFT: -4. 4.

In the above example, the rest-frame rise-time at each epoch is increased by 2.3×Trest/18 days with a

Gaussian sigma of 0.6 days, and shifts past ±4 days are excluded. The rise-time adjustments can be used,

for example, to generate a double-stretch model by simulating two separate samples, each with a different

rise-time shift.

4.25 Altering Input SEDs

The options in this section work for

NON1ASED

and

SIMSED

models.

4.25.1 Simulating PEAKMJD or Time of Explosion

For all models, the default light-curve time window is deﬁned by its time of peak brightnes, or

PEAKMJD

In particular, the sim-input key

GENRANGE_PEAKMJD: <MJDmin> <MJDmax>

speciﬁes an MJD window to randomly generate

PEAKMJD

For triggered events, such as from gravity waves (LIGO) or neutrinos (ICECUBE), it is more practical

to simulate sources based on time of explosion instead of

PEAKMJD

. For

NON1ASED

and

SIMSED

models, a

time of explosion can be speciﬁed with

MJD_EXPLODE: <MJD>

OPTMASK_T0SHIFT_EXPLODE: 0 # no shift: model T=0 at explosion (default)

OPTMASK_T0SHIFT_EXPLODE: 1 # T_explode at .01*FLUXMAX

OPTMASK_T0SHIFT_EXPLODE: 2 # T_explode at .001*FLUXMAX

Note that the time of explosion is not always observed, and thus can be ambiguous for for data-derived

template models. For models with well-deﬁned time of explosion at

DAY=0

, the default

OPTMASK=0

adds

no shift.

OPTMASK=1

computes explosion time to be the epoch when the rest-frame SED ﬂux, in any

wavelength bin, falls below 1% of the maximum ﬂux.

OPTMASK=2

requires less than 0.1% of max ﬂux.

Other options based on rise-time shape ﬁts may be added later.

4.25.2 Extrapolating UV Flux

At sufﬁciently high redshift, broadband ﬂuxes in UV ﬁlters are not deﬁned and thus not included in the

ouptut data ﬁles. For example, consider a UV ﬁlter spannng 3000-4000Å, and input SEDs starting at

2000 Å. For redshifts z>3000/2000−1=0.5, the UV ﬂux depends on the undeﬁned SED range below

2000 Å, and therefore this band is suppressed in the output. Missing UV bands are usually harmless,

but this artifact can potentially fool classiﬁers training on data, or provide un-intended clues in a data

challenge.

Since far-UV ﬂuxes are typically well below the sky noise, simply reporting a random sky noise would

be good enough. The simulation includes a somewhat better option, which is to extrapolate the UV ﬂux

down to arbitrary wavelength. The sim-input key is

UVLAM_EXTRAPFLUX: 500 # extrapolate SED flux down to 500 A.

Deﬁning Fλto be the ﬂux at a particular wavelength, F2000 is the edge-ﬂux at 2000Å. The

UVLAM

option

above will extrapolate the ﬂux to be linearly decreasing so that F500 =0. This option extends the valid

UV-ﬁlter redshift range from 0.5 to 3000/500 −1=5. Finally, users are cautioned to check that the UV

ﬂux is indeed negligible at high redshifts.

4.26

NGEN

keys

There are three “

NGEN

” keys to control the number of generated events:

NGEN_LC: 1000 ! default is zero

NGENTOT_LC: 1000 ! default is zero

NGEN_SCALE: 3 ! default is 1

The ﬁrst key,

NGEN_LC

, speciﬁes the number of SN generated and written out after trigger and selection

cuts. Thus if the simulated efﬁciency is 10% and

NGEN_LC = 1000

as shown in the example above, the

simulation will generate 10,000 SNe in order to get 1000 SN written out. In short, SNe are generated until

1000 are written out, regardless of the efﬁciency. The sim-input key

EFFERR_STOPGEN

prevents an inﬁnite

loop if the efﬁciency is near zero (§4.16).

The second key,

NGENTOT_LC

, speciﬁes the total number of SNe to generate regardless of the efﬁciency.

Thus in the example above with

NGENTOT_LC = 1000

and a 10% efﬁciency, only about 100 SNe are

written out. If the efﬁciency is very low, it is possible that zero events are written out. This option is

useful to generate statistics corresponding to a particular SN rate and survey length (§4.21). Only of of the

NGEN_LC

NGENTOT_LC

keys can be set; if both are set the simulation will abort.

Finally,

NGEN_SCALE

can be used to scale whichever

NGEN

key is set. This feature is useful, for exam-

ple, to change the statistics on several independent simulated samples while preserving the relative ratios

between samples.

4.27 “Perfect” Simulations

To make detailed numerical crosschecks, there is a “perfect” option to simulate light curves with ×104

nominal photostatistics, no galactic extinction (Milky Way and host), and no intrinsic mag-smearing.

The light curve ﬁtter should determine the shape and color parameters with very high precision, and the

cosmology ﬁtter should determine cosmological parameters that agree well with the input. This option is

invoked with

GENPERFECT: 1

and it automatically overrides the relevant parameters so that you need not change your sim-input ﬁle.

The top of the sim-

README

ﬁle summarizes the modiﬁed quantities. You can also unselect some of the

“PERFECT” options by specifying a bit-mask as the

GENPERFECT

argument. To see the bit-mask options,

snlc_sim.exe mysim.input GENPERFECT -1

will list the current bit-mask options and then quit without generating any SNe. You can then run, for

example,

snlc_sim.exe mysim.input GENPERFECT 6 # = 2+4 (bits 1 & 2)

which selects the ×104exposure-time option (bit 1) and turns off intrinsic mag-smearing (bit 2), but leaves

Galactic and host-galaxy extinction as deﬁned in your sim-input ﬁle.

4.28 Generating Redshift (zhel,zcmb), Peculiar Velocity and Distance

An overview of redshift-related inputs are as follows:

GENRANGE_REDSHIFT: 0.01 1.0 # ZCMB-gen range

GENSIGMA_REDSHIFT: 0.001 # Gaussian z-error (default=0)

GENBIAS_REDSHIFT: 1.0E-4 # global redshift bias (default=0)

GENSIGMA_VPEC: 300 # true sigma(v_pec), km/sec (default=0)

VPEC_ERR: 150 # measured error on VPEC (default=0)

VEL_CMBAPEX: 371 # CMB dipole, (default = 371 km/sec)

The CMB redshift is generated ﬁrst, and then the RA & DEC from the

SIMLIB

ﬁle is used to compute

zhel with ℓ=264.14 deg, b=48.26 deg, and default

VEL_CMBAPEX=371

. A Gaussian-random peculiar

velocity correction (vpec) is deﬁned by

GENSIGMA_VPEC

,9and corresponds to the true scatter.

VPEC_ERR

is the measured error on vpec (see §5.29).

VPEC

and

VPEC_ERR

are written to the data ﬁles. With true

peculiar-velocity value

SIM_VPEC

, the

VPEC

correction (vpec) in the data ﬁle is

VPEC = -SIM_VPEC + VPEC_ERR*GaussRan # VPEC_ERR < GENSIGMA_VPEC

VPEC = 0 # VPEC_ERR >= GENSIGMA_VPEC

For high-z samples that do not have a VPEC correction, set

VPEC_ERR

GENSIGMA_VPEC

as a ﬂag to apply

no correction.

To generate zhel =zcmb (sometimes useful for debugging), set

GENSIGMA_VPEC

and

VEL_CMBAPEX

zero in the sim-input ﬁle, or use the command-line override “

VEL_CMBAPEX 0 GENSIGMA_VPEC 0

”.

The simulated/true zcmb range is deﬁned by

GENRANGE_REDSHIFT

, and the probability vs. redshift

is deﬁned by the rate model (§4.21). The true zhel is transformed from zcmb using the sky coordinates

and a peculiar velocity (vpec) that is randomly drawn from a Gaussian with σvpec =

GENSIGMA_VPEC

. The

measured zhel (

REDSHIFT_HELIO

in data ﬁles) includes measurement noise drawn from a Gaussian with

σz=

GENSIGMA_REDSHIFT

. The measured zcmb (

REDSHIFT_CMB

in data ﬁles) is computed from the mea-

sured zhel using the sky coordinates. The true quanties (without measurement noise) are stored in the

data ﬁles as

SIM_REDSHIFT_CMB

and

SIM_REDSHIFT_HELIO

. Note that

SIM_REDSHIFT_HELIO

includes

the peculiar velocity, and therefore the

SIM_REDSHIFT_XXX

quantities will not transform under the usual

cmb↔heliocentric transformations unless vpec =0.

It is important to pay attention to redshift ranges in different parts of the analysis. While the sim-

ulation generates a zcmb range, the analysis programs (

snana.exe

and

snlc_fit.exe

) select a red-

shift range based on zhel because zhel is used for lightcurve ﬁtting (see &SNLCINP namelist parameter

CUTWIN_REDSHIFT

). Finally, the cosmology ﬁtting program is likely to apply cuts on the observed zcmb.

To be on the safe side, one should generate a slightly larger zcmb-redshift range compared to the anticipated

analysis cuts. The extended generation range should allow for vpec variations10 and measurement noise.

Finally, rather than simulating a z-bias with

GENBIAS_REDSHIFT

, a z-bias can be added in the analy-

sis/ﬁtting program (data or sim) with

&SNLCINP

parameter

REDSHIFT_FINAL_SHIFT = 0.0001

The simulated luminosity distance is computed as

DL= (1+zhel)r(zcmb),r(zcmb)≡(c/H0)Zzcmb

0dz/H(z).

For

SNANA

versions prior to v10_56, the DLprefactor was approximated as (1+zcmb).

SNANA

users would be grateful if somebody provides code to compute vpec based on RA, DEC, and zcmb.

10Beware that the maximum vpec-redshift variation is (1+z)371/cand not just 371/c.

4.29 Redshift-Dependent Parameters

Although the default simulation parameters are independent of redshift, you can specify an arbitrary z-

dependence for SN-related parameters such as dust parameters RV&τV,SALT-II parameters α&β, and

the population parameters for shape, color, etc ...

The z-dependence is speciﬁed as an additive shift. If the function is simple, you can specify a poly-

nomial function of redshift with arbitrary order. More complex functions can be speciﬁed in a ﬁle with a

z-dependent map. Examples for specifying both types of parameter-shift functions are given in this ﬁle,

$SNDATA_ROOT/sample_input_files/SALT2/SIM_ZVARIATION.PAR .

To get a complete list of parameters that can have a z-dependence, type the command

> snlc_sim.exe mysim.input ZVARIATION_FILE 0

Next, copy the

SIM_ZVARIATION.PAR

above to your working area, and modify as desired. Then add the

following keyword to your sim-input ﬁle,

ZVARIATION_FILE: SIM_ZVARIATION.PAR

or use the command-line override (§12.2.1). You can also change the name of the “

ZVARIATION

” ﬁle.

The polynomial option can be speciﬁed in the sim-input ﬁle (without a separate ﬁle) to deﬁne redshift-

dependent parameters with

ZVARIATION_POLY: GENPEAK_VARNAM1 a0,a1,a2 # 2nd order poly

ZVARIATION_POLY: GENPEAK_VARNAM2 a0,a1,a2,a3 # 3rd order

ZVARIATION_POLY: GENSIGMA[0]_VARNAM3 a0,a1 # lo-side sigma,linear

ZVARIATION_POLY: GENSIGMA[1]_VARNAM3 a0,a1 # hi-side sigma,linear

ZVARIATION_POLY: GENSKEW[0]_VARNAM3 a0,a1,a2,a3,a4

ZVARIATION_POLY: GENSKEW[1]_VARNAM3 a0,a1,a2

# hard-coded [LEGACY] 3rd order poly still supported:

ZVARIATION_POLY: GENPEAK_VARNAM1 a0 a1 a2 a3

ZVARIATION_POLY: GENPEAK_VARNAM2 a0 a1 a2 a3

etc ...

Note that either the

ZVARIATION_POLY

key or the

ZVARIATION_FILE

key is allowed; specifying both

results in an abort. Since populations are deﬁned by two

GENSIGMA

values and two

GENSKEW

values, the

redshift dependence is speciﬁed separately using the index in [] as shown above.

Beware that the function must give a shift of zero at z=0, otherwise the simulation will abort:

this ensures that the sim-input parameters are clearly deﬁned at z=0. For example, suppose we want

GENPEAK_SALT2c

to have the form −0.10 +0.01z. The following illustrates the incorrect and correct

sim-inputs:

GENPEAK_SALT2c: 0.0

ZVARIATION_POLY: GENPEAK_SALT2c -0.1,0.01 # ==> results in abort

GENPEAK_SALT2c: -0.1

ZVARIATION_POLY: GENPEAK_SALT2c 0.0,0.01 # ==> valid

4.30 Generating Efﬁciency Maps

An efﬁciency map as a function of SN parameters may be needed as part of a ﬁtting prior, or as part of

an MC-based correction such as correcting the SN rate for the selection efﬁciency. The simulation can be

used to generate an arbitrary efﬁciency map using the command

SIMEFF_MAPGEN.pl <SIMEFF input file>

and examples of the

SIMEFF

input ﬁle are in

$SNDATA_ROOT/sample_input_files/simeff_mapgen/

“

sntools.c

” contains functions read the generated efﬁciency map (

init_SIMEFFMAP

) and to evaluate

the efﬁciency for an arbitrary set of SN parameters (

get_SIMEFF

). The efﬁciency is determined by multi-

dimensional interpolation. Since the generation of a multi-dimensional efﬁciency map can be CPU inten-

sive, this script distributes jobs on several nodes deﬁned by the

NODELIST

key, and the simulation runs in

a mode where there are no output ﬁles, and hence no secondary

SNANA

jobs are needed. Your sim-input

ﬁle (speciﬁed inside the

SIMEFF

input ﬁle) must apply selection cuts as described in § 4.16. It is assumed

that the selection efﬁciency does not depend on the result of the light curve ﬁt.

The critical part of the

SIMEFF

input ﬁle is shown below,

# out

# sim-input key key NBIN MIN MAX

# --------------------------------------------------------

GENVAR: LIN GENRANGE_MWEBV MWEBV 2 0.0 0.3

GENVAR: LIN GENRANGE_REDSHIFT Z 23 0.05 1.15

GENVAR: LOG GENRANGE_AV AV 19 -3.0 0.6 (0.001 < AV < 4)

GENVAR: LIN GENRANGE_DELTA DELTA 14 -0.5 2.1

GENVAR: INV GENRANGE_RV RV 3 0.25 0.75 (4 > RV > 1.33)

Each

GENVAR

key speciﬁes one dimension of the multi-dimensional efﬁciency map. Following each

GENVAR

key is a key deﬁning whether that variable is stored linearly (LIN), logarithmically-base10 (LOG),

or as the inverse (INV). For example, the efﬁciency is quite linear as a function of 1/RVand hence fewer RV

bins are needed to describe the efﬁciency as a function of 1/RVcompared to using RV. The

GENRANGE_XXX

key is the simulation key used to specify that particular parameter. For example, a speciﬁc value of

DELTA

is simulated using

snlc_sim.exe <sim-input file> GENRANGE_DELTA -0.1 -0.1

All of the

GENRANGE_XXX

commands are catenated and given as input to the simulation. The output-key

is the name given in the output efﬁciency-map ﬁle. Any output key-name is valid, but to use this map

for a ﬁtting prior the key-names must correspond to one of the following: (i) any ﬁt-parameter name in

snlc_sim.exe

such as AV, DELTA, x1, c, (ii) REDSHIFT or Z, (iii) MWEBV.

The last three entries are the number of bins to deﬁne the efﬁciency map in each dimension (

NBIN

and the min/max range for each dimension. In the above example, 1/RVis generated for values 0.25, 0.50,

and 0.75 corresponding to RV=4,2,1.33, respectively. When the resulting efﬁciency map is used as part

of a ﬁtting prior, ﬁt-values outside the min/max range are pulled to the edge for evaluating the efﬁciency.

For example, if the ﬁtting program tries to evaluate the χ2for

DELTA

=2.4, the efﬁciency is evaluated at

the boundary

DELTA

=2.1.

Finally, one must be careful allocating appropriate resources since the computing time can be long. In

the above example the total number of bins in this efﬁciency map is 2×23 ×19×14×3=36708. If the

efﬁciency-uncertainty (see

SIMGEN_EFFERR

key) is set so that each simulation job takes 10 seconds, then

the total computing time needed for this map is 4.2 CPU-days, or about 10 wall-clock hours with 10 cores.

4.31 Light Curve Output Formats

Each simulated light curve is written to the directory

$SNDATA_ROOT/SIM/[GENVERSION]

where

GENVERSION

is the user-supplied version name. For the default FITS format two FITS ﬁles are

created: a “HEADER” ﬁle containing global information for each SN (SNID, redshift, RA, etc ...) and

a “PHOT” ﬁle containing all of the light curves. Pointers in the HEADER ﬁle are used to extract the

appropriate light curve from the PHOT ﬁle. These ﬁles can be visually examined with the product “fv.”

For text-output options each light curve is written to a separate ﬁle,

[GENVERSION]_SN######.DAT

, where

“######” is a six digit identiﬁer; the text-option is useful for testing small samples and debugging.

The output format is controlled by the sim-input keyword

FORMAT_MASK

, and the various options are

described below. Note that

FORMAT_MASK

is a bit-mask so that multiple format options can be included.

Note, however, that either TEXT or FITS format can be selected, but not both. Here is a quick summary

of the bit-mask format options,

FORMAT_MASK: 2 # TEXT format

FORMAT_MASK: 18 # 2(TEXT) + 16(RANDOM CID)

FORMAT_MASK: 26 # 2(TEXT) + 8(BLIND) + 16(RANDOM CID)

FORMAT_MASK: 32 # FITS format (default for version >= v9_82)

FORMAT_MASK: 48 # 32(FITS) + 16(RANDOM CID)

FORMAT_MASK: +64 # compact PHOT table

(remove GAIN,RDNOISE,SKYSIG_T,PSF_SIG2,PSF_RATIO,ZP_ERR)

FORMAT_MASK: 288 # 32(FITS) + 256(write filterTrans files)

and the sub-sections below give more details.

4.31.1 TEXT Light Curve Output (Default)

“FORMAT_MASK: 2” This option results in a simpliﬁed one-line-per-observation output for the light

curves. Header information includes RA, DECL, redshift, etc ... This output is recommended for analysis

with non-

SNANA

programs that need to parse data ﬁles generated by the SNANA simulation. Below is a

sample of the output.

# TEXT LIGHT CURVE OUTPUT:

NVAR: 9

VARLIST: MJD FLT FIELD FLUXCAL FLUXCALERR SNR MAG MAGERR SIM_MAG

OBS: 49562.316 Y 1694 -1.333e+03 5.891e+02 -2.26 128.000 0.000 27.313

OBS: 49572.430 z 1694 6.500e+01 1.708e+02 0.38 26.628 101.372 25.385

OBS: 49590.422 Y 1694 1.492e+02 1.635e+02 0.91 24.236 103.764 24.064

OBS: 49591.387 i 1694 3.733e+03 4.644e+02 8.04 23.970 0.144 24.198

OBS: 49591.414 z 1694 1.644e+03 3.271e+02 5.03 23.850 0.241 24.200

...

It is recommended to use the ﬂuxes instead of mags because the mags are not deﬁned for negative ﬂuxes,

and are ill-deﬁned for very small ﬂuxes. The

FIELD

is given for each measurement to properly label

overlapping ﬁelds,

SNR

is the signal-to-noise ratio (

FLUXCAL/FLUXCALERR

) and

SIM_MAG

is the exact mag-

nitude (without noise ﬂuctuations) computed from the SN model.

4.31.2 Model-Mag Light Curve Output

“FORMAT_MASK: 4” Dump out the model mag info. Set value to 6 to dump both the the nominal

output and the model-mag output. A sample output is as follows:

# MODEL MAG OUTPUT:

NVAR: 7

VARLIST: TOBS FLT MAGOBS MAGERR MAGREST KCOR(SYM,VAL)

OBS: -1.328 u 21.547 0.055 -19.810 K_Uu 1.379

OBS: -1.328 g 20.228 0.035 -19.396 K_Bg -0.205

OBS: -1.328 r 20.182 0.037 -19.421 K_Vr -0.157

etc ...

4.31.3 Suppress

SIM_XXX

Info

“FORMAT_MASK: 8” Suppress

SIM_XXX

header info. This option is useful for things like blind-testing

photometric classiﬁers.

4.31.4 Random CID

“FORMAT_MASK: 16” Generate random (integer) CID from 1-999,000 instead of the default sequential

generation. The purpose of this option is that mixing different SN samples (Ia,II,Ibc) cannot be sorted by

CID. Any random subset of the combined SN sample will contain similar fractions of each SN type.

Note that the keyword

CIDOFF

plays the role of selecting a unique set of random CIDs so that combined

SN samples will not have overlapping CIDs. For example, suppose you generate 1000 type Ia SNe with

CIDOFF: 0

. The CIDs will be the ﬁrst 1000 randomly selected (and non-repeating) integers between 1

and 999,000. Now suppose you generate 1000 type II with CIDOFF: 1000. The simulation will generate

2000 CIDs, but only use the last 1000 on the list (i.e., skip the ﬁrst 1000). When the type Ia and type II

SNe are combined (see

sim_SNmix.pl

), the CIDs will not overlap and the SN types (Ia and II) will be

perfectly mixed with no correlation between type and CID. It is up to the user to pick the correct

CIDOFF

value for each SN type, although

sim_SNmix.pl

will automatically assign the appropriate

CIDOFF

values.

After combining the SN samples, a useful unitarity check is to do

‘ls *.DAT | wc‘

and verify that the

total number of ﬁles matches the expected sum from the simulation jobs.

4.31.5 FITS Format

“FORMAT_MASK: 32” (default) uses the more compact binary-FITS format that is processed using the

cfitsio

library. The advantage of this format is that there are very few ﬁles to manage, reading is much

faster compared to the TEXT options, the compact binary ﬁles are portable to any computing platform,

and there are public ﬁts-viewing utilities such as “fv.”

Two ﬁts ﬁles are created by the simulation. First is a HEAD ﬁle with a one-row summary for each SN.

The summary info includes the SNID, sky coordinates, Galactic extinction, and many other quantities.

The HEAD ﬁle also contains the name of the second “PHOT” ﬁle which contains the photometric light

curves. All of the light curves are written sequentially into one PHOT-table, and pointers from the HEAD

ﬁle (see

PTROBS_MIN

and

PTROBS_MAX

) are used to select the appropriate rows from the PHOT table. For

a given SN-data version, the

[VERSION].LIST

ﬁle contains a list of HEAD ﬁts-ﬁles. Usually there is only

one such ﬁts-ﬁle, but several can be combined into one version, such as combining ﬁles from different

seasons.

The

PHOT

table columns are:

TTYPE1 = ’MJD ’ / MJD

TTYPE2 = ’FLT ’ / single-char band label

TTYPE3 = ’FIELD ’ / name of FIELD

TTYPE5 = ’PHOTFLAG’ / bit-mask from photometry pipeline

TTYPE6 = ’PHOTPROB’ / float FoM from photometry pipeline

TTYPE7 = ’FLUXCAL ’ / MAG = 27.5 - 2.5*LOG10(FLUXCAL)

TTYPE8 = ’FLUXCALERR’ / error on FLUXCAL

TTYPE12 = ’PSF_SIG1’ / central Gaussian PSF (sigma, pixels)

TTYPE12 = ’PSF_SIG2’ / 2nd Gaussian PSF (sigma, pixels)

TTYPE13 = ’PSF_RATIO’ / PSF2/PSF1 at origin

TTYPE14 = ’SKY_SIG ’ / Search image sky sigma (ADU/pixel)

TTYPE15 = ’SKY_SIG_T’ / Template sky sigma (ADU per pixel)

TTYPE16 = ’RDNOISE ’ / read noise (pe/pixel)

TTYPE17 = ’ZEROPT ’ / zero point (ADU)

TTYPE18 = ’ZEROPT_ERR’ / error on above

TTYPE19 = ’GAIN ’ / ADU per pe

4.31.6

PHOTFLAG

Mask

The

PHOTFLAG

data column is a 4-byte integer mask containing the following user-requested information:

# override mask(s) in SEARCHEFF_PIPELINE_EFF_FILE

PHOTFLAG_DETECT: <MASK> # set for each detection

PHOTFLAG_TRIGGER: <MASK> # set for epoch satisfying trigger

# overide mask(s) in SIMLIB global header

PHOTFLAG_SATURATE: <MASK> # saturation, see NPE_SATURATE in SIMLIB

PHOTFLAG_SNRMAX: <MASK> # set for epoch with max SNR

PHOTFLAG_NEARPEAK: <MASK> # set for epoch closest to peak

These

PHOTFLAG

masks can be speciﬁed in either an input table ﬁle, or the sim-input ﬁle; latter has pri-

ority if both are speciﬁed. Setting

PHOTFLAG

no impact on the simulation; it simply provides additional

information to the analysis programs.

4.31.7 Source of Each Redshift

The output data ﬁles include

REDSHIFT_FINAL

, the best redshift to use for Hubble diagrams. However,

the source of this best redshift can be from the SN, from a host-spectrum, from a host photo-z, or from a

wrong host. And integer ﬂag,

SIM_REDSHIFT_FLAG

, is written to the data ﬁles, and the intepretations can

be found with the following grep command:

grep REDSHIFT_FLAG $SNANA_DIR/src/snlc_sim.h | grep define

#define REDSHIFT_FLAG_NONE 0

#define REDSHIFT_FLAG_SNSPEC 1

#define REDSHIFT_FLAG_HOSTSPEC 2

#define REDSHIFT_FLAG_HOSTPHOT 3

#define REDSHIFT_FLAG_WRONGHOST 4

In the output tables (SNANA,FITRES), the ﬂag is called

SIM_ZFLAG

. This ﬂag is written to HBOOK

and ROOT ﬁles; to extract into TEXT tables, use the

APPEND_TABLE_TEXT

feature in

split_and_fit

4.32 Simulation Dump Options

4.32.1

SIMLIB_DUMP

Utility

To quickly check a

SIMLIB

, a screen-dump summary is obtained with the command:

> snlc_sim.exe mysim.input SIMLIB_DUMP 1

**************************************************

SIMLIB_DUMP

LIBID MJD-range NEPOCH(all,gri) GAPMAX(frac) <GAP>

-------------------------------------------------------------

001 53616-53705 126,42 42 42 11.0(0.12) 2.2

002 53622-53700 51,17 17 17 19.0(0.24) 4.9

003 53622-53705 69,23 23 23 10.1(0.12) 3.8

004 53622-53705 54,18 18 18 15.0(0.18) 4.9

...

050 53622-53705 57,19 19 19 15.0(0.18) 4.6

Done reading 496 SIMLIB entries.

LIBRARY AVERAGES PER FILTER:

<PSF>

<ZPT-pe> FWHM <SKYSIG> <SKYMAG> Cadence

FLT (mag) (asec) (ADU/pix) (asec^-2) <m5sig> <Nep> FoM

-----------------------------------------------------------------

u 30.86 0.866 9.0 22.65 19.99 2.86 0.036

g 34.31 0.828 117.8 20.75 19.99 29.71 0.123

r 35.04 0.820 173.5 20.50 19.99 29.71 0.130

i 34.81 0.829 216.2 19.74 19.99 31.43 0.128

z 34.18 0.823 205.7 19.20 19.99 32.14 0.135

Y 32.93 0.822 197.9 17.99 19.99 30.14 0.127

LIBRARY MIN-MAX RANGES:

RA: -59.994 to 58.766 deg

DECL: -1.253 to 1.257 deg

MJD: 53616.2 to 53705.4

CUT-WARNING: 46 SIMLIBS will fail user-cut on ’RA’

GAPMAX

and

<GAP>

are the maximum and average gaps (days) between epochs in the

SIMLIB

. The “

frac

”

after

GAPMAX

is the fraction of the MJD-range consumed by the largest gap. The

LIBRARY MIN-MAX

RANGES

show you the ranges needed to include all

SIMLIB

entries. The

CUT-WARNING

s shows how many

SIMLIB

entries are excluded by the selection ranges in your sim-input ﬁle.

CUT-WARNINGs

are checked for

RA, DECL and PEAKMJD.

In addition to the screen-dump, a one-line summary for each

LIBID

is written to

DUMP_LIBID-[simlib]

where

[simlib]

is the name of the

SIMLIB

ﬁle that you specify. This ﬁle is self-documented like the

“ﬁtres” ﬁles, and can be converted into an ntuple using the “

combine_fitres.exe

” program (§12.1.1).

A one-line dump per MJD, which includes ZP in photoelectrons, sky noise converted into mag/arcsec2,

and 5σlimiting mag calculation, can be obtained by setting the 2nd bit of the SIMLIB_DUMP mask,

snlc_sim.exe mysim.input SIMLIB_DUMP 2

and the corresponding output ﬁle is

DUMP_MJD-[simlib]

. To obtain both the LIBID and MJD dump-ﬁles,

set the

SIMLIB_DUMP

argument to 3.

4.32.2 Cadence Figure of Merit Utility

A ﬁgure of merit for the cadence can be determined in two ways. First, you can extract the function

“

SNcadenceFoM

” from

sntools.c

and pass the arguments from your own wrapper function. The second

method is to simply analyze any

SIMLIB

using the

SIMLIB_DUMP

option (§ 4.32.1). The FoM is appended

to each entry in the output

[simlib].DUMP

ﬁle. The FoM for each simlib entry is a function of the MJD

and the 5σlimiting magnitude for each observation.

4.32.3

SIMGEN_DUMP

File

To quickly analyze generated distributions, there is an option to dump generated quantities to a column-

formatted text ﬁle. For example, to check the generated redshift and SALT-II parameters, add the following

to your sim-input ﬁle:

# dump same SN that are written to data files

SIMGEN_DUMP: 5 CID ZCMB S2x0 S2x1 S2c

# dump all SN, even those rejected by trigger and cuts

SIMGEN_DUMPALL: 5 CID ZCMB S2x0 S2x1 S2c

# optional pre-scale (e.g., to limit output from DUMPALL)

SIMGEN_DUMP_PRESCALE: 10

PRESCALE_SIMGEN_DUMP: 10

SIMGEN_DUMP[ALL]

produces an auxiliary ﬁle

[VERSION].DUMP

in the same directory as the SNDATA

ﬁles. The self-documented dump-ﬁle looks like:

NVAR: 4

VARNAMES: ZCMB S2x0 S2x1 S2c

SN: 50001 1.3820e-01 3.8970e-04 1.0906e+00 -1.5431e-01

SN: 50002 3.1260e-01 1.0278e-04 1.8671e-01 -3.9044e-01

SN: 50003 2.4248e-01 1.9417e-04 8.8190e-01 -3.8711e-01

SN: 50004 2.5666e-01 8.3385e-05 -6.7122e-01 -1.5304e-01

A full list of allowed

SIMGEN_DUMP

variable names can be printed to the screen by specifying zero variables

as follows:

snlc_sim.exe mysim.input SIMGEN_DUMP 0

After printing the valid variable names, the program quits.

4.32.4 Model Dump

Model magnitudes can be dumped with the sim-input key

GENRANGE_DMPTREST: -20 60 # dump model for this Trest range, 1 day bins

This option will dump model magnitudes for a grid of

1. 1-day Trest bins

2. each observer-frame band

3. hard-wired range of shape-parameter values for the selected model

(e.g., x1for SALT2, dm15 for SNOOPY, etc ..).

4. color parameter (cor AV) is set to zero.

and the ﬁrst generated redshift is used for the dump. The

GENRANGE_DMPTREST

option results in an output

text ﬁle and then the simulation stops. The name of the output ﬁle is

DUMP_GENMAG_[MODELNAME].TEXT

and it contains the generated observer-frame model mag for a grid of {Trest,band,shapePar}.

Instead of generating model mags on a grid, a model mag can be generated for ﬁxed values of

{Filter,Trest,ShapePar,Redshift} with the following sim-input keys,

GENFILTERS: V # pick filter

GENRANGE_DMPTREST: 4.3 4.3 # pick Trest (this key flags the dumpFile)

GENRANGE_SALT2x1: 0.36 0.36 # pick SALT2x1

GENRANGE_REDSHIFT: 0.13 0.13 # pick redshift

The SALT2x1 parameter can be replaced with the appropriate model-dependent parameter. To dump

rest-frame mags, set the redshift to 2.335E-9 (10 pc).

4.33 Including a Second Sim-Input File

A sim-input ﬁle can be split into two ﬁles using the keyword

INPUT_FILE_INCLUDE: my2nd.input

which instructs the simulation to read and parse “

my2nd.input

” in exactly the same way as the original

sim-input ﬁle. To see why this might be useful, consider the

NONIASED

model that has many “

NON1ASED:

”

keywords. The

NON1ASED

keys can be stripped out into a separate ﬁle such as

NON1ASED_keys.input

, and

then included in many sim-input ﬁles. Thus a dozen sim-input ﬁles can each include

NON1ASED_keys.input

To modify or add a

NONIASED

key for all of the sim-input ﬁles, only one ﬁle needs to be modiﬁed.

4.34 Multi-dimensional

GRID

Option

Instead of generating random distributions in the variables describing each SN (redshift, shape parameter,

color, etc ..), the simulation can generate SNe on a well-deﬁned grid for each parameter using the following

sim-input options,

GENSOURCE: GRID # replaces RANDOM option

NGRID_LOGZ: 20 # log10(redshift)

NGRID_SHAPEPAR: 10 # x1, Delta, stretch,dm15 ...

NGRID_COLORPAR: 2 # AV or SALT2 color

NGRID_COLORLAW: 1 # RV or BETA

NGRID_TREST: 56 # rest-frame epoch

GRID_FORMAT: FITS # TEXT or FITS

GENRANGE_REDSHIFT: 0.01 1.2 # redshift range

GENRANGE_TREST: -20.0 90.0 # test epoch relative to peak (days)

GENFILTERS: griz

# ---------- Use one of the following models below ----------

# for mlcs2k2

GENRANGE_DELTA: -0.4 1.8 # delta-range (mlcs only)

GENRANGE_RV: 2.2 2.2 # range of CCM89-RV

GENRANGE_AV: 0.0 2.00 # AV range

# for SALT2

GENRANGE_SALT2x1: -3.0 3.0

GENRANGE_SALT2c: -0.3 0.5

GENRANGE_SALT2BETA: 3.2 3.2

# for SIMSED model

SIMSED_SHAPEPAR: DM15 # replace SIMSED_PARAM key to identify SHAPEPAR

GENRANGE_DM15: 0.6 1.59

SIMSED_COLORPAR: AV # replace SIMSED_PARAM key to identify COLORPAR

GENRANGE_AV: -1.0 2.8

SIMSED_COLORLAW: RV # replace SIMSED_PARAM key to identify COLORLAW

GENRANGE_RV: 2.2 2.2

and explicit examples of complete sim-input ﬁles are in

$SNDATA_ROOT/sample_input_files/GRID

Also see the

sim_SNgrid.pl

utility in §8.1.1. This GRID option allows external (non-

SNANA

) ﬁtting

programs to use the

SNANA

models. The original motivation is for the photometric SN id program (§8.1).

Each

NGRID_XXX

value divides the corresponding

GENRANGE_XXX

range into the speciﬁed number of bins

for the grid. The “

GRID_FORMAT: TEXT

” option produces a human-readable ﬁle intended only for visual

inspection. The “

GRID_FORMAT: FITS

” option produces a platform-independent ﬁle to be read by external

programs. To save memory for programs reading the FITS tables, the magnitudes and errors have been

multiplied by 1000 and stored as 16-bit (2-byte) integers. Magnitudes dimmer than 32 are written as

32000, and undeﬁned model magnitudes are stored as −9000 (i.e, mag=−9).

The GRID ﬁle is written in the same directory as the auxiliary ﬁles

$SNDATA_ROOT/SIM/MY_VERSION/MY_VERSION.GRID

where “

GENVERSION: MY_VERSION

” is speciﬁed in the sim-input ﬁle. Note that only the GRID ﬁle is

written; no light curve ﬁles are written out.

The FITS tables can be visually examined using a utility such as “

fdump

” or “

.”

SNANA

has a

“

fits_read_SNGRID

” utility to read in the generated GRID; to use this utility the following code-lines

must be included,

#define SNGRIDREAD // use only the read utilities in sngridtools.c

#ifdef SNGRIDREAD

#include "fitsio.h"

#include "sngridtools.h"

#include "sngridtools.c" // fits_read_SNGRID is in here

#endif

The read-back utility ﬁlls the following global arrays/structures in

sngridtools.h

GRIDGEN_INFO

GRIDGEN_SURVEY GRIDGEN_MODEL GRIDGEN_FILTERS

PTR_GRIDGEN_LC I2GRIDGEN_LCMAG I2GRIDGEN_LCERR

Also note that

genmag_snoopy.c

illustrated how to read and access the GRID.

Here is a brief description of the FITS tables and how to look up the correct magnitude and error

from a set of SN parameters. Technically only the ﬁrst (SNPAR-INFO) and last (I2LCMAG) tables are

needed; the intermediate tables provide additional information that you would otherwise have to compute

on your own. The SNPAR-INFO columns

NBIN

VALMIN

and

VALMAX

are simply copied from the sim-

input parameters. The

BINSIZE

is calculated from the previous parameters, and the

ILCOFF

are used to

determine the absolute light curve index (ILC) as a function of the SN parameters as follows:

ILC =1+

∑

i=1

ILCOFFi×(INDXi−1)(22)

The parameter index i=1,4 runs over (1) redshift, (2) color (AVor c), (3) color law (RVor β) and (4)

shape parameter. Each integer index INDXiruns from 1 to

NGRID

ifor parameter i. Do NOT extend

the summation to include the ﬁlter and epoch indices. While the physical grid-values corresponding to

each INDXican be computed from the SNPAR-INFO table, these grid values have been store in the

intermediate tables that have a

GRID

sufﬁx (and include FILTER-GRID and TREST-GRID).

Note that the ILCOFFiare ﬁxed, while the INDXidepend on the set of SN parameters. For example,

consider a redshift range of 0.01 to 1 and 200 bins; in logz space we have −2≤log10(z)≤0 and a logz

binsize of 0.01. For z=0.1, log10(z) = −1 and the GRID-index is INDX1=100.

Now we have an ILC index corresponding to a Supernova described by the four parameters above.

Each SN light curve is written out in all of the

GENFILTERS

, and all of the SNe are strung together in

the I2LCMAG table. This table contains one column of model magnitudes and another column of model

errors, each multiplied by 1000 to maintain millimag precision in 2-byte integer storage. The starting

location in the I2LCMAG table is given in a separate ’pointer table’ by

PTR_I2LCMAG(ILC)

. Note that

you could compute this pointer as

PTR_I2LCMAG[ILC] = 1 + ((NGRID_FILT * NGRID_TREST) + NWDPAD) * (ILC-1);

where

NGRID_FILT

is the number of “

GENFILTERS

” and

NWDPAD

=4 is the number of pad-words. Starting

at the speciﬁed pointer location for ILC, the ﬁrst word is a pad-word (−1111) and the second word is the

ﬁrst 8 bits of ILC; read-programs should verify these words to avoid getting lost. The next

NGRID_TREST

words are the magnitudes (×1000) for the ﬁrst ﬁlter (g), the next

NGRID_TREST

words are the magnitudes

for the second ﬁlter (r), etc.. Finally, after reading all of the light curve magnitudes there are two end-of-

lightcurve pad-words with values of −9999.

The I2LCMAG storage for a single SN light curve is illustrated below:

pad1 = -1111 <== start I2LCMAG address is PTR_I2LCMAG(ILC)

pad2 = first 8 bits of ILC

I2LCMAG(g,ep1) = mag * 1000

I2LCMAG(g,ep2)

I2LCMAG(g,ep3)

...

I2LCMAG(g,NGRID_TREST)

I2LCMAG(r,ep1)

...

I2LCMAG(r,NGRID_TREST)

...

I2LCMAG(z,NGRID_TREST)

pad3 = -9999

pad4 = -9999

While pointers are provided to compute ILC and to determine the starting I2LCMAG address from ILC,

you are on your own to ﬁnd the sub-index corresponding to the ﬁlter and epoch.

For the

NONIASED

GRID, there is no physically meaningful shape parameter; this parameter is therefore

used to store a sparse index that runs from 1 to the number of

NONIASED

templates that are speciﬁed with

the “

NON1ASED:

” keyword in the sim-input ﬁle. The FITS ﬁle includes an additional NONIA-INFO table

that gives the SNANA index, a character-string type (e.g., II, Ib, Ibc), and a character-string name of the

underlying SN used to create the template (e.g., ’SDSS-002744’).

4.35 TGRIDSTEP: Linear Interpolation of Model Flux

It is sometimes useful to simulate with linear interpolation between model points. An example is to repro-

duce fakes overlaid on images, where each fake model ﬂux is linearly interpolated from a pre-computed

model grid. The sim-input key is

TGRIDSTEP_MODEL_INTERP: 4

which will compute the model ﬂux on a 4-day grid, and then use linear interpolation to compute the ﬂux

at each MJD.

4.36 Marking Sub-Samples

Sometimes it is useful to generate many statistically independent samples. Rather than generating separate

versions, there is less bookkeeping to generate one large sample and mark subsamples with sim-input

NSUBSAMPLE_MARK: 20

which will mark 20 sub-samples with an integer index. This index is automatically included in the output

tables for all tables formats.

4.37 Applying Systematic Errors (RANSYSTPAR)

While systematic variations are typically done in the analysis stage, it may be useful to simulate a large

number of data-sized samples, each with a different random set of systematic errors applied. In principle

one can deﬁne each set of variations in a brute-force manner: e.g., picking random zero points offsets for

each simulated version, and specifying “

GENOPT: GENMAG_OFF_ZP <list>

” for each

GENVERSION

(see

§12.3.1).

Instead of the brute-force apporach, it is simpler to use the

RANSYSTPAR_XXX

input parameters so

that the user need only change

RANSEED

and the simulation picks random errors. Here are examples of

available options for the sim-input ﬁle:

GENFILTERS: griz

RANSYSTPAR_FUDGESCALE_FLUXERR: 1.02 # scale true & measured flux-errors

RANSYSTPAR_FUDGESCALE_FLUXERR2: 1.04 # scale measured flux-errors

RANSYSTPAR_FUDGESCALE_MWEBV: 1.05 # scale MWEBV

RANSYSTPAR_FUDGESHIFT_MWRV: 0.2 # shift RV

# filter-dependent variants:

RANSYSTPAR_FILTER_LAMSHIFT: 8 10 7 6 # filter shifts, Angstromgs

RANSYSTPAR_GENMAG_OFF_ZP: 0.014 0.013 0.022 0.012 # random ZP off

FUDGESCALE_XXX

parameters near 1 are interpreted as ﬁllows. A Gaussian sigma is deﬁned as σ=

FUDGESCALE_XX −1.0, and then a random Gaussian number, r, is picked. The

FUDGESCALE

used in the

simulation is 1+r.

•

RANSYSTPAR_FUDGESCALE_FLUXERR

applies a scale to the true and measured ﬂux-uncertainties to

either over- or under-estimate the uncertainties. The Gaussian σis obtained by subtracting one

(σ=1.02−1.0=0.02) and the random Gaussian number is added back to one.

•

RANSYSTPAR_FUDGESCALE_FLUXERR2

applies a scale to the measured ﬂux-uncertainties, but NOT

to the true uncertainty used to smear the ﬂuxes. The random scale is obtained in the same way as

RANSYSTPAR_FUDGESCALE_FLUXERR

above.

•

RANSYSTPAR_FUDGESCALE_MWEBV

applies a scale to Galactic extinction.

•

RANSYSTPAR_FUDGESHIFT_MWRV

applies a random shift to Galactice RV.

•

RANSYSTPAR_GENMAG_OFF_ZP

parameters are Gaussian sigmas, not ZP shifts.11 The simulation

uses these sigmas to select a random set of ZP offsets. Changing

RANSEED

results in a different

random set of ZP offsets, and there is no need for the user to pick random offsets.

•

RANSYSTPAR_FILTER_LAMSHIFT

applies a random shift to each ﬁlter.

GENMAG_OFF_ZP

key can be used to explicitly deﬁne ZP shifts.

5 The

SNANA

Fitter:

snlc_fit.exe

5.1 Getting Started Quickly

Here you will perform lightcurve ﬁts, hopefully in under a minute. To get started,

> cp $SNDATA_ROOT/sample_input_files/mlcs2k2/snfit_SDSS.nml .

> cp $SNDATA_ROOT/sample_input_files/SALT2/snfit_SDSS.nml .

(Edit .nml file and put in correct VERSION_PHOTOMETRY = ’xxx’)

> snlc_fit.exe snfit_SDSS.nml >! snfit_SDSS.log &

When the unix command “

” shows that the job has ﬁnished, congratulations ! You have ﬁt your

lightcurves with CERNLIB’s MINUIT program.12 To create a pdf ﬁle showing the light curve ﬁts (§5.9),

mkfitplots.pl --h snfit_SDSS.hbook

creates

snfit_SDSS_fits.pdf

. If you are shaking your head wondering what the heck you just did, that’s

a good sign.

5.2 Discussion of Lightcurve Fits

Before reading this section, make sure you have successfully run the commands described in §5.1. Let’s

start the discussion by checking the end of the log-ﬁle,

> tail snfit_SDSS.log

The very last line should be “

ENDING PROGRAM GRACEFULLY.

” If you do not see this, check that your

namelist variable

VERSION_PHOTOMETRY

is really pointing to an existing version in $

SNDATA_ROOT/SIM

If you still have trouble, contact an expert for help.

Inside the input ﬁle

snfit_SDSS.nml

, the namelist variable

FITRES_DMPFILE = ’snfit_SDSS.fitres’

results in a dump of the ﬁt parameters for each SN in a self-documented “ﬁtres” ﬁle. Go ahead and “

snfit_SDSS.fitres

” to see the results. The header keywords

NVAR

and

VARNAMES

specify the columns.

The

SNANA

library includes a utility called

RDFITRES

to read these ﬁles. You can “

cat

” multiple ﬁtres ﬁles

together and add comments, and still read them with the same parsing code.

To ﬁgure out what you did, you need to check the namelist options in

snfit_SDSS.nml

. There are

two separate namelists:

•

&SNLCINP:

deﬁnes selection of SNe and epochs by specifying criteria for the number of epochs,

earliest & latest times relative to peak, maximum signal-to-noise, etc ... All namelist options are

deﬁned and commented inside

SNANA_DIR/src/snana.car

•

&FITINP:

deﬁnes ﬁtting options such as priors, marginalization, and range of Trest in the second

ﬁt-iteration. All namelist options are deﬁned and commented inside

SNANA_DIR/src/snlc_fit.car

12http://wwwasdoc.web.cern.ch/wwwasdoc/minuit/minmain.html

In the sample namelist ﬁle, a prior on AVis used by setting

PRIOR_AVEXP = 0.40

, which translates

into a prior of the form exp(−AV/0.4). There is no marginalization so that your ﬁrst ﬁts run much faster.

To marginalize, set the number of integration bins per variable,

NGRID_PDF = 11

. Since the marginaliza-

tion is over four ﬁt variables (t0,AV,∆,µ), the CPU-time goes as the fourth power of

NGRID_PDF

; previous

studies indicate that 11 bins per ﬁt-variable is a good compromise between accuracy and CPU time.

5.3 Methods of Fit-Parameter Estimation

There are three methods that can be used to estimate light curve ﬁt-parameters:

1. MINIMIZATION based on CERNLIB’s MINUIT program13.

&SNLCINP

namelist parameter

NFIT_ITERATION

speciﬁes the number of iterations (2 or 3 recommended). You must always use

this option, even if you use the options below. For very high-SNR SNe the ﬁrst ﬁt-iteration can

simetimes fall into a false minimum, leading to pathological ﬁts on successive iterations. This

problem can be alleviated with

&FITINP

namelist variable

FUDGEALL_ITER1_MAXFRAC

(set to few

percent); on the ﬁrst ﬁt-iteration this option adds an extra error equal to its value ×the peak ﬂux,

thus reducing the chance of ﬁnding a false minumum. Consider using

FUDGEALL_ITER1_MAXFRAC

for ﬁnal ﬁts, or at least as a crosscheck, along with

NFIT_ITERATION=3

2. MARGINALIZATION using multi-dimensional integration in

SNANA

function

MARG_DRIVER

&FITINP

namelist parameter

NGRID_PDF

controls the number of grid-points per ﬁt-parameter (11 is recom-

mended). You must run the minimizer ﬁrst (

NFIT_ITERATION=2

) to get starting values and inte-

gration ranges. After marginalizing, the following crosschecks are performed: probability at the

boundaries and number of bins with zero probability; if either is too large, the integration ranges are

adjusted and the marginalization repeats.

3. Monte Carlo Markov Chain (MCMC): See &

MCMCINP

namelist parameters. WARNING: this

option has not been used for years, so it may be broken.

13http://wwwasdoc.web.cern.ch/wwwasdoc/minuit/minmain.html

5.3.1 MINUIT Covariances

As described in the MINUIT manual, each MINUIT ﬁt returns a covariance status,

MNSTAT_COV

, with one

of the following values:

MNSTAT_COV = 0 -> not calculated

MNSTAT_COV = 1 -> Diagonal approximation only, not accurate

MNSTAT_COV = 2 -> Full matrix, but forced positive-definite

MNSTAT_COV = 3 -> Full accurate covariance matrix (normal convergence)

After the last ﬁt iteration, if MNSTAT_COV <3 then the ﬁt is repeated to try getting a better evaluation of

the covariances. The ﬁnal

MNSTAT_COV

value is included in the

FITRES

table.

Roughly ∼1% of light curve ﬁts with the SALT2 model result in a covariance matrix, COV(mB,x1,c),

that is not invertible. The reason is subtle and related to how COV is determined. MINUIT-computed COV

is approximated from second derivatives, while the MINUIT errors are determined from better methods

(MIGRAD or MINOS). The COV diagonals are thus sometimes different than the error-squared. The

FITRES output includes errors and off-diagonal COV terms, and analysis codes must therefore reconstruct

COV diagonal terms using error-squared, which doesn’t alway correspond to the approximations used for

the off-diagonal terms.

There has long been a hack in the SALT2mu.exe program (which implements BBC method) to ﬁx non-

invertible matrices. To apply the same hack-ﬁx to the FITRES output of

snlc_fit.exe

, use the following

input:

&FITINP

OPT_COVAR_LCFIT = 1 ! fix non-invertible COV with old method

OPT_COVAR_LCFIT = 129 ! idem, with one-row summary per fix

OPT_COVAR_LCFIT = 385 ! idem, with full COV dump

OPT_COVAR_LCFIT = 2 ! newer COV fix using reduced corr.

Note that

OPT_COVAR_LCFIT

is a bit-mask; 1 ﬁxes non-invertible matrix, 128 gives one-row dump per

ﬁx, and 256 gives full COV dump per ﬁx. A newer option (

OPT_COVAR_LCFIT=2

) preserves the reduced

correlations (ρi j) from the MINUIT-computed COV, and uses the errors and ρi j to determine COV.

5.4 Initial Fit-Parameter Estimation

For MINUIT to converge, initial ﬁt-parameters must be chosen so that the initial model light curve roughly

overlaps the data. The color and shape parameter are ﬁxed to an average value, and the distance modulus

(or x0for SALT-II) is adjusted so that the model matches the data.

The estimate of the epoch of peak brightness (t0) is usually read from the data ﬁle from the keyword

SEARCH_PEAKMJD

. If this keyword is missing, then

SNANA

will try to estimate t0by ﬁtting a general function

of the form (see

SNANA

function

SET_PEAKMJD

)

f(t) = A[1+a1(t−¯

t) + a2(t−¯

t)2]×exp[−(t−¯

t)/Tfall]

1+exp[−(t−¯

t)/Trise],(23)

as suggested in the SNLS CC rate paper (Bazin et al, 2008). The ﬁtted parameters for each ﬁlter are

A,a1,a2,¯

t,Tfall,Trise. The time at peak is obtained by setting the derivative equal to zero: t0=¯

t+Trise ln(Tfall/Trise −

1). The initial ¯

tvalue is estimated to be the epoch with maximum ﬂux. Each ﬁlter is ﬁt independently

and the ﬁnal t0is the ﬁlter-weighted average. A ﬁlter’s t0is dropped from the average if: (1) its max-ﬂux

measurement has the smallest S/Nratio among ﬁlters and has S/N<10, or (2) its t0value is more than

30 days away from the average of the other ﬁlter-t0values (tested only if there are 3 or more ﬁlters). The

max-ﬂux epoch must have S/N>4 to make an estimate of t0.

Bit-mask options via &SNLCINP namelist variable

OPT_SETPKMJD

are:

OPT_SETPKMJD += 1 # fix a1 = a2 = 0 (no polynomial term)

OPT_SETPKMJD += 2 # float a1 & a2

OPT_SETPKMJD += 4 # do NOT abort when PKMJD cannot be found

OPT_SETPKMJD += 8 # PKMJD -> MJD at max-flux (no fit)

OPT_SETPKMJD += 16 # save fit-PKMJD params (each band) in SNANA table

OPT_SETPKMJD += 128 # DUMP info for each SN

Users should compare the initial t0(from above) to the ﬁnal t0from the light curve ﬁt and check for

outliers; outliers can be ﬁxed by visual inspection of the light curve and setting the

SEARCH_PEAKMJD

keyword in the data ﬁle. To avoid clogging up the standard log-ﬁle, the MINUIT output for these ﬁts is

dumped to a separate log-ﬁle speciﬁed by namelist variable

MNFIT_PKMJD_LOGFILE

: the default ﬁlename

MNFIT_PKMJD.LOG

WARNING (Jun 2010): The SN classiﬁer challenge has uncovered two serious problems with the

initial t0estimate for SNe Ia using Eq. 23. First, the ﬁlter-dependence of t0is not accounted for. Second,

Eq. 23 can sometimes be very nonIa-like (even for a perfectly good ﬁt), leading to t0estimates off by more

than a week. Will need to add an option to use a more Ia-like function.

5.5 Galactic Reddening

In the ﬁtting programs, Galactic extinction is applied to the model; i.e., the data are NOT de-reddened.

For

snlc_fit.exe

, the extinction is computed at each ﬁlter-wavelength bin in the ﬂux-integrals. In

psnid.exe

the Galactic extinction is approximated by the value at the central wavelength. The Galactic

extinction covariance is controlled with the

&FITINP

namelist option

OPT_COVAR_MWXTERR = 1 ! default: full covariance matrix

The reduced Nobs ×Nobs covariance matrix is 1 everywhere, and each diagonal element is the MWEBV

uncertainty at the central wavelength of the observer-frame passband. The covariance matrix is computed

and inverted between ﬁt iterations. For each SN the MWEBV value and uncertainty are read from the

header. For data, if MWEBV or its uncertainty are zero (or do not exist), then they are internally set to the

SFD98 value and 0.16 ×MWEBV, respectively. To allow for arbitrary tests in simulations, any value of

MWEBV and its uncertainty are accepted. For ﬁtting both data and simulations, Galactic extinction can

be disabled by setting either of the namelist parameters

OPT_MWCOLORAW

OPT_MWEBV

to zero.

Starting at snana version

v10_29n

, the Galactic reddening law and source of E(B−V)are determined

by the

&SNLCINP

namelist parameters

&SNLCINP

RV_MWCOLORLAW = 3.1 ! default

OPT_MWCOLORLAW = 94 ! default: CCM89+ODonnel94 (default)

OPT_MWEBV = 1 ! default: read E(B-V) from data header

MWEBV_SCALE = 1.0 ! default: scale all MWEBV values

MWEBV_SHIFT = 0.0 ! default: shift all MWEBV values

USE_MWCOR = F ! default: do NOT correct data, include in fit-model

A similar set of parameters controls reddening in the simulation, and additional option-values for these pa-

rameters is illustrated in §4.18. If no reddening law is speciﬁed (

OPT_MWCOLORLAW

), the default CCM89+ODonnel94

model is used in all programs with the exception of ﬁtting simulations; in this case the default reddening

model is that used in the simulation. Similarly, if

OPT_MWEBV

is not speciﬁed, the data-header values are

used for both data and simulation. In the ﬁtting programs (

snlc_fit.exe

and

psnid.exe

), specifying

OPT_MWCOLORLAW

OPT_MWEBV

explicitly in the

&SNLCINP

namelist will override the simulation default.

See §4.18.1 for a description of the Galactic extinction calculation for observer-frame models, and for

rest-frame models that require K-corrections.

Finally,

&SNLCINP

namelist parameter

USE_MWCOR

controls whether the data or ﬁt-model is corrected.

The default

USE_MWCOR=F

does not correct the data, and instead MW reddening vs. wavelength is in-

cluded in the ﬁt-model.

USE_MWCOR=T

corrects the data approximately, using the extinction at the central

wavelength of each ﬁlter band, and is then ignored in the ﬁtting model. We recommend using the default,

except for special cases such as building de-reddened templates.

5.6 Selecting Filters

By default the snana codes read and store epochs from all deﬁned ﬁlters. The ﬁtted ﬁlters must be speciﬁed

in the

&FITINP

namelist variable

FILTLIST_FIT = ’ugriz’

FILTLIST_DMPFUN = ’gri’ ! debug dump for SN model function

FILTLIST_DMPFCN = ’gri’ ! debug dump for chi2 function

The debug-dump options should be used only in special cases to debug a ﬁt problem, and only 1 or 2 SN

should be ﬁt to limit the size of the stdout.

The ﬁlters in

FILTLIST_FIT

must be deﬁned in the kcor/calib ﬁle and in the SURVEY ﬁlters deﬁned

in the data ﬁles. Any undeﬁned ﬁlter results in an ABORT. To estimate peak-mags in non-survey ﬁlters

(e.g., ’abc’), these extra ﬁlters must be deﬁned in the kcor/calib ﬁle; to prevent the ﬁtting program from

aborting, the non-survey ﬁlters must be explicitly deﬁned via the

&SNLCINP

namelist variable

NONSURVEY_FILTERS = ’abc’

Finally, ﬁlters can be selected based on the mean wavelength in the rest-frame (λrest =λobs/(1+z));

&SNLCINP

CUTWIN_RESTLAM = 4000, 8000.

CUTWIN_LAMREST = 4000, 8000. ! same as above

CUTWIN_LAMOBS = 4000, 8000. ! cut on <LAMOBS> instead of <LAMREST>

...

&FITINP

RESTLAMBDA_FITRANGE = 4000. , 8000.

...

Note that

RESTLAMBDA_FITRANGE

can be used only to reduce the λrest range of the SN model; i.e., you

cannot use this parameter to arbitrarily increase the wavelength range. If you really want to increase the

λrest range, then you must deﬁne your own model and modify the corresponding parameters in one of the

model-info ﬁles.

5.7 Fitting Priors

The ﬁtting prior options in

snlc_fit.exe

are mainly designed to prevent catastrophic ﬁts. There are also

options related to the host-galaxy extinction. Photo-zpriors are described in §5.11, and a brief description

of the other

&FITINP

namelist prior options are given below.

•PRIOR_MJDSIG: sigma on Gaussian prior for MJD at peak brightness. Default is 20 days.

•PRIOR_SHAPE_RANGE(2): range of ﬂat prior for shape parameter to prevent crazy values. Typ-

ical prior-range values are {−0.5,2.0} for the

MLCS2k2

parameter ∆, and {−5,+3} for SALT-II

parameter x1. Default range is {−9,+9}. The parameter below deﬁnes a smooth roll-off at the

edges.

•PRIOR_SHAPE_SIGMA: sigma of Gaussian roll-off at edge of ﬂat prior deﬁned above. Default

is 0.1.

•PRIOR_DELTA_PROFILE(4): Used only for

MLCS2k2

∆, the ﬁrst two elements are −σand +σ

for the asymmetric Gaussian prior, the 3rd element is the ∆value at the Gaussian peak, and the

4th element is the minimum ’ﬂat’ probability for all ∆values within

PRIOR_SHAPE_RANGE

. A ﬂat ∆

prior is obtained by simply setting the 4th element to 1.0. Setting the 4th element to ∼0.1 results

in a Gaussian prior with a ﬂat tail for large ∆values; this tail prevents the suppression of very fast

decliners (91bg-like).

•OPT_PRIOR: Default is 1 →use priors. Setting to zero turns off ALL priors regardless of their

values.

•OPT_PRIOR_AV: Used only for

MLCS2k2

model, default is 1 →use AVpriors. Setting to zero

turns off AV-related priors.

•PRIOR_AVEXP(2): For

MLCS2k2

only, deﬁnes up to two exponential slopes for AVprior.

•PRIOR_AVWGT(2): For

MLCS2k2

only, deﬁnes weight for the two AV-exponential terms.

•PRIOR_AVRES: Since the AVprior has a sharp boundary at AV=0 and therefore a discontinuity

in the ﬁtting function, this

PRIOR_AVRES

option allows a Gaussian smearing of the prior function

that results in a continuous function. Recommended values are .001 to 0.01.

5.8 Selecting an Efﬁciency Map for a Fitting Prior

The light curve ﬁtting prior includes an optional simulated efﬁciency as a function of redshift, Galactic

extinction (MWEBV) and model-dependent parameters that describe the SN brightness. For example,

the

MLCS2k2

model parameters are shape (∆), extinction (AV), and color law (RV). The ﬁtting prior and

efﬁciency map can be applied to other models too. An efﬁciency map can be generated using the

SNANA

script

SIMEFF_MAPGEN.pl

(§4.30), and a map is selected via the

&FITINP

namelist:

! Select file name explicitly. Will first check YOUR current working

! directory; if not there, then fitter checks public area

! $SNDATA_ROOT/models/simeff/mysimeff.dat

SIMEFF_FILE = ’mysimeff.dat’

The efﬁciency map is deﬁned on a multi-dimensional grid, and interpolation is used to determine the

efﬁciency for any set of SN model parameters. Note that these maps depend on the selection requirements

and are therefore analysis-speciﬁc; these maps should therefore not be considered as general purpose ﬁles

such as those describing K-corrections (§7) or search-efﬁciencies (§4.15).

5.9 Viewing Lightcurve Fits:

mkfitplots.pl

There is an after-burner script to prepare a pdf ﬁle showing each light curve (data + ﬁt) for each passband,

> mkfitplots.pl --h snlc_fit.hbook

The “

snlc_fit.hbook

” argument above is the name of the hbook ﬁle that was speciﬁed with the namelist

argument

HFILE_OUT

inside the

&SNLCINP

namelist. This script creates a ﬁle called

snlc_fit_fits.pdf

More generally, the pdf ﬁle name has the same preﬁx as the hbook ﬁle name. On each plot the black dots

are data (or simulated data) and the green curve is best-ﬁt model. There are many plotting options; see

instructions with

more \$SNANA_DIR/util/mkfitplots.pl

To view the light curves without doing any ﬁts, set

&SNLCINP

namelist variable

OPT_LCPLOT=1

, run

the

snana.exe

program, and then run the above

mkfitplots.pl

command.

For versions prior to

v10_17

you need to run a once-in-a-lifetime command

> paw_setup.cmd

For later versions there is no need to run this script, and there is no need to maintain a private

/kumacs

directory.

5.10 Tracking SN versus Cuts

Typically the ﬁnal number of processed SN is smaller than than the number read in, and thus it is often

useful to track the losses, particularly if there seem to be too few (e.g., zero) SNe. At the end of each

snana job, the stdout includes a statistics summary for each SN “Type” showing the number of SN vs.

incremental cut. An example is shown here,

Number of SN passing incremental cut for

CUT NAME ITYPE= 118 119 120

------------------------------------------------------------------------

CID 8 37 502

Trestmin 5 36 476

Trestmax 5 34 374

NFILT(SNRmax) 4 31 370

FIT + CUTS 4 30 369

The last row labeled ’FIT+CUTS’ is shown for the

snlc_fit.exe

job, and the previous rows are shown

for both the

snana.exe

and

snlc_fit.exe

jobs. Additional information is given by the following snana

table14 variables

CUTFLAG_SNANA = 0 -> failed snana cuts

CUTFLAG_SNANA bit0 -> passed snana cuts

CUTFLAG_SNANA bit1 -> passed fit & cuts

ERRFLAG_FIT = -9 -> no fit done (i.e., CUTFLAG_SNANA=0 or snana.exe job)

ERRFLAG_FIT = 0 -> no fitting errors

ERRFLAG_FIT > 0 -> see error codes with

grep ’ERRFLAG_’ \$SNANA_DIR/src/snlc_fit.car | grep ’&’

where this table is created with

LTUP_SNANA=T

(§12.1) and the variables can be extracted into text format

using the

sntable_dump.pl

utility (§12.1.2).

CUTFLAG_SNANA

=1 means that the snana cut-requirements

were satisﬁed, but the ﬁt either failed or was not attempted.

CUTFLAG_SNANA

=3 means that the SN

satisﬁed the snana cuts and has a valid ﬁt whose results are stored in the ﬁtres ﬁle and the ﬁtres ntuple.

ERRFLAG_FIT

is zero if the ﬁt is valid and the ﬁt-cuts are satisﬁed. A positive ﬂag indicates an error;

grep the source code for error deﬁnitions.

ERRFLAG_FIT

=−9 means that the ﬁt was not attempted; this

occurs if the snana cuts fail (

CUTFLAG_SNANA

=0) or when running

snana.exe

14The snana table id is 7100 for hbook or SNANA for root.

5.11 PhotoZ Fits

Here we describe light curve ﬁts that determine the SN Ia redshift (z) from photometry, called “SN-

photoZ” ﬁts. There are two fundamental methods to perform photoZ ﬁts. The ﬁrst method, called a

“constrained photoZ ﬁt,” is designed to identify SNe Ia that do not have a spectroscopic redshift: uses

include SN rates and targeting host-galaxy redshifts for unconﬁrmed SN Ia. For

MLCS2k2

photoZ ﬁts,

there are four ﬂoated parameters: z,t0,∆, and AV. For SALT-II photoZ ﬁts, the four ﬂoated parameters

are z,t0,x1, and c. The distance modulus is constrained (calculated) assuming a particular cosmology:

µ=µ(z,ΩM,ΩΛ,w)where zis ﬂoated in the ﬁt, and ΩM,ΩΛ,ware ﬁxed by the user. The cosmology can be

speciﬁed with &SNLCINP namelist parameters

H0_REF

OMAT_REF

, and

OLAM_REF

. For SALT-II photoZ

ﬁts, the distance modulus is converted into the x0parameter, and therefore

SALT2alpha

SALT2beta

must be speciﬁed as &FITINP namelist parameters.

The second method, called a “cosmology-photoZ” ﬁt, involves ﬂoating ﬁve parameters: µ,z,t0,∆, and

AVfor

MLCS2k2

, and x0,z,t0,x1, and cfor SALT-II. This method is designed to use large photometric

samples to measure distance moduli that can be used to measure cosmological parameters. One of the dif-

ﬁculties with the 5-parameter ﬁt is CPU time: the marginalization takes a few minutes per ﬁt, so studying

the bias on a sample of 104simulated SNe Ia requires about a CPU-month of resources.

In addition to the two main methods above, there are variations that involve using the host-galaxy

photoZ (host-photoZ) as a prior to help constrain the redshift. A distance-modulus prior can be applied

to the second method (5-parameter ﬁt); this is essentially a constrained-photoZ ﬁt, but the photoZ errors

will include uncertainties from the cosmological parameters. Needless to say, never run a cosmology ﬁt

on ouput where a distance-modulus prior is used !

There are ﬁve

&FITINP

namelist parameters that control photoZ ﬁts. The default values are set so that

photoZ ﬁts are turned off,

DOFIT_PHOTOZ = F

OPT_PHOTOZ = 0 ! 1=>hostgal photZ prior; 2=> specZ prior

INISTP_DLMAG = 0.1 ! 0=> constrain DLMAG; non-zero => float DLMAG

PRIOR_ZERRSCALE = 100.0 ! scale error on host-photoZ prior

PRIOR_MUERRSCALE = 100.0 ! scale error on distance modulus prior

Setting

DOFIT_PHOTOZ=T

and

INISTP_DLMAG=0.0

results in a 4-parameter constrained-photoZ ﬁt. Since

PRIOR_ZERRSCALE=100.0

by default, the host-photoZ errors are multiplied by 100 and therefore have no

impact on the ﬁts. Setting

PRIOR_ZERRSCALE = 1.0

results in using the host-photoZ prior described by

a Gaussian distribution15.

To switch from a constrained-photoZ ﬁt to a 5-parameter cosmology-photoZ ﬁt, set

INISTP_DLMAG

to any non-zero value such as 0.1. The use (or non-use) of the host-photoZ prior is controlled by the

value of

PRIOR_ZERRSCALE

. The parameter

OPT_PHOTOZ

controls the source of the redshift prior. When

you set

DOFIT_PHOTOZ=T

OPT_PHOTOZ

is automatically set to 1 so that the host-photoZ prior is used. If

you set

OPT_PHOTOZ=2

, the spectroscopic redshift is used as a prior: this option is designed solely as a

sanity check on the light curve ﬁtter, and is not meant to use for science. If you set

OPT_PHOTOZ

>0,

the

DOFIT_PHOTOZ

ﬂag is automatically set, and vice-versa: thus you can turn on the photoZ option with

either namelist variable.

PRIOR_MUERRSCALE

is 100 or larger (the default), then there is no prior applied to the distance

modulus (µ). Setting

PRIOR_MUERRSCALE = 2

will apply a µ-prior using a Gaussian proﬁle of width

σ=2σµ, where σµis calculated from the user-speciﬁed uncertainties in the cosmological parameters.

15Depending on user interest, non-Gaussian tails may be added later.

Note that

OMAT_REF

, and

W0_REF

are two-dimensional arrays that specify both the value and error. For

example,

OMAT_REF = 0.3, 0.03

W0_REF = -1.0, 0.1

would use σw=0.1 and σM=0.03 to calculate the µ-error for the photoZ at each ﬁt-iteration.

To get going quickly, some useful examples of setting the namelist options are given below in Fig. 8.

A few other photoZ-related issues are:

•To test the photoZ methods in simulated SN Ia samples, the simulation includes an option to include

host-galaxy photoZs based on an externally-supplied library (§ 4.19). To test SN-only photoZ ﬁts

(without host), increase

GENSIGMA_REDSHIFT

so that the initial redshift estimate is poor.

•To test the photoZ sensitivity to the initial redshift estimate, you can arbitrarily shift the redshifts

using &SNLCINP namelist parameter

REDSHIFT_FINAL_SHIFT

Figure 8: Examples of setting photoZ options within the

&FITINP

namelist.

! constrained photoZ fit, ignore host-galaxy photoZ:

DOFIT_PHOTOZ = T

PRIOR_ZERRSCALE = 100.0 ! inflate error on photoZ prior

INISTP_DLMAG = 0.0 ! fix MU = MU(zphot,cosmology)

! equivalent way to do the above

OPT_PHOTOZ = 1

PRIOR_ZERRSCALE = 100.0 ! inflate error on photoZ prior

INISTP_DLMAG = 0.0 ! fix MU = MU(zphot,cosmology)

! constrained photoZ fit using host-galaxy photoZ:

DOFIT_PHOTOZ = T

PRIOR_ZERRSCALE = 1.0

INISTP_DLMAG = 0.0 ! fix MU = MU(zphot,cosmology)

! constrained photoZ fit, host-galaxy photoZ errors inflated by 1.3

DOFIT_PHOTOZ = T

PRIOR_ZERRSCALE = 1.3

INISTP_DLMAG = 0.0 ! fix MU = MU(zphot,cosmology)

! cosmology photoZ fit, ignore host-galaxy photoZ:

DOFIT_PHOTOZ = T

PRIOR_ZERRSCALE = 100.0 ! inflate error on photoZ prior

INISTP_DLMAG = 0.1 ! float DLMAG

! cosmology photoZ fit using host-galaxy photoZ:

DOFIT_PHOTOZ = T

PRIOR_ZERRSCALE = 1.0

INISTP_DLMAG = 0.1 ! float DLMAG

! cosmology photoZ fit with priors on both distance & host-galaxy photoZ:

DOFIT_PHOTOZ = T

PRIOR_ZERRSCALE = 1.0 ! use host-galaxy photoZ errors

PRIOR_MUERRSCALE = 3.0 ! use x3 mu-error calculated from dw & dOM

INISTP_DLMAG = 0.1 ! float DLMAG

! spec-z fit or host photo-z fit, for mixed spec+photo-z sample

OPT_PHOTOZ = 2 ! use REDSHIFT_FINAL as prior

PRIOR_ZERRSCALE = 1.0 ! use REDSHIFT_FINAL_ERR in prior

INISTP_DLMAG = 0.1 ! float DLMAG

5.11.1 Redshift-Dependent Selection in PhotoZ Fits

There is a subtle ﬁtting issue concerning the usable observer-frame ﬁlters for which λobs/(1+z)is within

the valid λrest-range of the light curve model, and for which Trest =Tobs/(1+z)are valid. In addition,

requirements on quantities such as the min & max Trest are ambiguous before the photoZ ﬁt has ﬁnished,

yet it is useful to make such cuts before ﬁtting to prevent ﬁtting pathological light curves and to reduce

processing time. Here we discuss how to select ﬁlters and how to make cuts on Trest-dependent quantities.

For regular cosmology ﬁts using spectroscopic redshifts, a list of usable ﬁlters & the Trest-range is

made before the ﬁt starts. For a photoZ ﬁt, however, it is not clear which ﬁlters & epochs are valid until

the ﬁt has ﬁnished. For example, consider a gri photoZ ﬁt using SALT-II: when Zphot <0.072, i-band maps

to rest-frame wavelengths greater than the 7000 Å cutoff in SALT-II. Including i-band in the ﬁt results in

using an unphysical region of the model, while dropping i-band measurements results in a discontinuous

drop in the χ2. In the latter case, the minimizer is trapped in this low-χ2well, and quite often the minimum

occurs at the drop-out boundary Zphot =0.072. Another example is in DES & LSST, where g-band maps

below 3000 Å at redshifts above about 0.5.

To make initial Trest-dependent cuts before the photoZ ﬁt has started, the cuts are loosened by a factor

of “1+Zmax”, where Zmax =PHOTOZ_BOUND(2)is the maximum allowed redshift (speciﬁed in &

FITINP

The Trest-cuts are therefore loosened to be valid for any redshift in the range speciﬁed by

PHOTOZ_BOUND

For example, consider

PHOTOZ_BOUND = 0,1

and and a requirement that the min-Trest is before −4 days;

the initial cut would be a requirement of an epoch before −2 days using whatever

REDSHIFT_FINAL

is in

the data ﬁle, and the −4 day requirement is applied after the photoZ ﬁt has ﬁnished. Similarly, a max-Trest

requirement of 30-60 days is loosened to 15-120 days before the photoZ ﬁt. If a ﬁlter is dropped after the

ﬁrst ﬁt-iteration (see below), the loose Trest-cuts are re-applied before ﬁtting again.

To select observer-frame ﬁlters, the basic strategy is to perform the ﬁrst-iteration photoZ ﬁt with all

ﬁlters except for those in the UV with λ<4000 Å. A reasonable analytical extrapolation of the model

beyond the deﬁned wavelength range is required. This possibly biased photoZ is then used to determine

which ﬁlters to exclude (or add in case of UV ﬁlter) in the next iteration. Technically, when one more more

ﬁlters is excluded, the ﬁrst-iteration is repeated so that two complete ﬁt-iterations are performed with the

correct ﬁlters. The basic assumption in this strategy is that it does not matter if there is an unknown bias in

choosing the redshift to drop a ﬁlter ... as long as the ﬁt, with or without the ﬁlter in question, is unbiased.

As an example, consider photoZ ﬁts with griz ﬁlters. For z>0.49, g-band should be excluded. As a safety

margin, one might exclude g-band when the 1st-iteration photoZ value is above 0.43, or 0.44, or 0.45 ...

the cut does not matter as long as we are conﬁdent that when g-band is used, it is within the valid range of

the model.

The redshift safety margin is controlled by

&FITINP

namelist parameters

PHOTOZ_ITER1_LAMRANGE = 4000, 25000 ! 1st-iter obs-frame lambda range

PHOTOZ_BOUND = 1.0E-6, 1.4 ! hard MINUIT bound

PHOTODZ_REJECT = 0.05 ! dz cut

PHOTODZ1Z_REJECT = -99. ! dz/(1+z) cut; default is no cut

The default

PHOTOZ_ITER1_LAMRANGE

cut is set to exclude any UV ﬁlter on the ﬁrst iteration since this

ﬁlter is used only at the lowest redshifts. Note that the excluded UV ﬁlter can be added back after the

ﬁrst ﬁt-iteration if the photoZ value is low enough.

PHOTOZ_BOUND

is a hard MINUIT bound to prevent

crazy excursions during the minimization, and is also used to loosen the Trest-related cuts before the ﬁt has

started.

The next two cut-parameters deﬁne the redshift safety margin, and can be deﬁned as a cut on dz and/or

dz/(1+z). The

SNANA

default is to use only the cut on dz, so we use this for discussion, noting that the

other cut works in a similar manner. In principle it would be better to cut on the number of ﬁtted σz, but on

the ﬁrst iteration the MINUIT errors are sometimes pathological; it is therefore safer to make a ﬁxed cut.

The dz cut is illustrated here using g-band and the

MLCS2k2

model for which the valid wavelength

range is 3200-9500 Å. Since the mean ﬁlter wavelength is λg=4790 Å, the valid rest-frame redshifts

are given by Zmin =λg/9500 −1=−0.50 and Zmax =λg/3200 −1= +0.50. The g-band is excluded

if the 1st-iteration photoZ satisﬁes Zphot >Zmax −PHOTODZ_REJECT; in this example, Zphot >0.45. For

Y-band (λY=10095 Å), Zmin =0.062 and this ﬁlter is excluded if Zphot <Zmin +PHOTODZ_REJECT, or

Zphot <0.11. Note that

PHOTODZ_REJECT

is deﬁned to be positive when adding a safety margin, regardless

of whether a blue or red band is being tested. Setting

PHOTODZ_REJECT

to a large negative value (i.e, −99)

disables the cut. Finally, the

PHOTODZ_REJECT

cut is applied to all observer-frame ﬁlters, and often more

than one ﬁlter (i.e, ugr) is rejected.

A quick list of dropped ﬁlters can be viewed from the log-ﬁle with the following ’grep’ command:

grep "DROPPED" myjob.log

WARNING for SN 40002 : DROPPED obs-filter=g

WARNING for SN 40002 : DROPPED obs-filter=r

and similarly grepping for “

ADDED

” will ﬁnd any (UV) ﬁlters that were added.

To study ﬁlter dropouts in more detail, ﬁve variables are include in the ﬁtres-ntuple (ntid 7788):

•

NEARDROP

: index of ﬁlter that is closest to being dropped. Positive (negative) value indicates that

this ﬁlter was included (excluded) after the ﬁrst ﬁt-iteration.

•

DZMIN1:

redshift safety margin for ﬁlter

NEARDROP

after 1st iteration. Positive value always indi-

cates that it is within the valid region of the model; negative value indicates invalid region.

•

DZMIN2

: same as above, but after 2nd ﬁt-iteration.

•

DZ1ZMIN1 & DZ1ZMIN2

: same as above, but for dz/(1+z).

TRAINING & TUNING CUTS:

SNe with spectroscopic redshifts (Zspec) should be use to train the ﬁlter-selection cuts. For each ﬁlter

labeled by index “

IFILT

,” plot Zspec when

NEARDROP = IFILT

and check that there are no (or very few)

entries in the undeﬁned redshift-region of the model. Also plot Zspec when

NEARDROP = -IFILT

, and you

will see entries in the undeﬁned region, but this is OK since the ﬁlter was dropped. Zspec values in the

deﬁned region indicates that this dropped ﬁlter could have been safely used, but was rejected based on

its photoZ value from the ﬁrst ﬁt-iteration. Users will have to decide the trade off between including a

particular ﬁlter more often in the deﬁned region versus using that ﬁlter more often in the undeﬁned region.

5.11.2 Initial Parameter Estimate

To estimate initial parameters near the global-minimum χ2, a multi-dimensional grid-search is made over

redshift (0.025 bin-width), color (0.2 bin-width) and 3 bins in the shape parameter (x1, dm15, stretch ...).

The minimization over the distance parameter is done analytically as follows. For each grid point (photoZ,

color, shape) the model ﬂuxes are ﬁrst evaluated using the distance (SALT2- ¯x0or distance modulus ¯µ) cal-

culated from a reference set of cosmological parameters. To minimize the χ2w.r.t. the distance parameter,

a distance-scale is determined as

dscale =x0/¯x0or 100.4(µ−¯µ)=∑

(Fi

dataFi

model/σ2

i)/∑

(Fi

model/σi)2(24)

where σiis the quadrature sum of data and model errors and ’i’ is the epoch index.16 The resulting x0or

µvalue is used to re-evaluate the χ2at this grid-point. This approximation assumes that the model-error

does not depend on dscale. Also, prior to snana version

v9_93

the grid-search was over photoZ and color

only.

Cheater option:

OPT_PHOTOZ = 16

sets initial photoZ to spectroscopic redshift and skips the redshift

grid-search. This option is for debugging only.

5.11.3 Smooth Model Error Transition Across Filter Boundaries

For rest-frame models such as

MLCS2k2

, the model error changes abruptly when a photoZ variation results

in an observer-frame ﬁlter mapping into a different rest-frame ﬁlter. This abrupt change in the model error

causes a small kink in the χ2, and can cause ﬁtting pathologies. This pathology is treated by smoothly

transitioning the model error between ±200 Å of the transition wavelength (¯

λ). The 200 Å range can

be modiﬁed with the namelist parameter

LAMREST_MODEL_SMOOTH

. The transition weight-function is an

arc-tangent that is scaled to equal 0 at ¯

λ−200 and 1 at ¯

λ+200. (see function

RESTFILT_WGT

for more

info).

5.11.4 Don’t Fool Yourself when PhotoZ-Fitting Simulations

When studying photoZ ﬁts with simulations, avoid fooling yourself with simulations outside the valid

wavelength range. If you use the default light curve model in the simulation, measurements outside the

valid wavelength range are excluded, and therefore the ﬁtter has the same “initialization” advantage in

picking ﬁlters as using a spectroscopic redshift. For testing photoZ ﬁts, a “wavelength-extended” model

should be used as explained in §5.15. Even with a wavelength-extended model, you can fool yourself

because the same model is used in both the simulation and in the ﬁt; hence even if the extrapolated model

(i.e, below 3200 and above 9500 Å for

MLCS2k2

) is wrong in reality, it is by deﬁnition correct when ﬁtting

the simulation. This forced correctness of the extrapolated model means that the 1st ﬁt-iteration using all

of the ﬁlters is guaranteed to give good results. A better test is to ﬁt with a light curve model that deviates

from the simulated model in the extrapolated regions. The 1st ﬁt-iteration should then produce biased

photoZ estimates, and ideally the ﬁlter-exclusion cut will work well enough so that there is no bias after

the 2nd ﬁt-iteration.

5.12 Including the log(σ) Term in the χ2

The default ﬁts minimize the usual function χ2=∑i∆Fi/σ2

iwhere ∆Fiis the data-model ﬂux-difference

for observation i, and σ2

iis the quadrature-sum of the measurement plus model errors. If the model

error depends on one or more ﬁt parameters, there is a namelist option (

DOCHI2_SIGMA = T/F

) to add in

the extra term, 2ln(σi). To avoid adding or subtracting large values to the χ2, the actual term added is

∆χ2

σi=2ln(σi/σlast

i)where σlast

iis the uncertainty from the previous ﬁt-iteration. Typically ∆χ2

σiadds ∼1

to the total χ2, but sometimes ∆χ2

σican be very large (positive or negative) if a ﬁtted uncertainty undergoes

a signiﬁcant change between ﬁt iterations. Fits with a large ∆χ2

σivalue can be rejected using the

&FITINP

namelist variable

FITWIN_CHI2SIGMA

. Values of ∆χ2

σican be visually examined with

grep MINUIT fit.log | grep SIGMA | more

DOCHI2_SIGMA=F

by default for ﬁts with a ﬁxed redshift. Currently (snana v9_30) the only model

affected by setting

DOCHI2_SIGMA=T

is SALT-II because the model-error depends on the stretch/shape

16See

EP_FFSUM_XXX

variables in

snlc_fit.car

parameter. For the default ﬁts with

DOCHI2_SIGMA=F

, the stretch parameter in the error term is ﬁxed to the

value from the previous iteration; it is therefore recommended to set

NFIT_ITERATION=3

for SALT-II ﬁts.

For photoZ ﬁts

DOCHI2_SIGMA=T

is automatically set because the model errors change as the photoZ

sweeps through different rest-frame epochs and wavelengths for each observation. If a ﬁlter is added after

the ﬁrst ﬁt-iteration then σlast

iis undeﬁned and ∆χ2

σiis set to zero for this ﬁlter. In this case,

LREPEAT_ITER

is set to force a repeat ﬁt-iteration with the added ﬁlter; this logic ensures that ∆χ2

σiis deﬁned for each

ﬁlter in the last ﬁt-iteration.

5.13 Optional Redshift Sources

Some surveys may include more than one redshift source such as spectroscopic redshifts from an exter-

nal collaborator (e.g., BOSS redshifts for SDSS targets), or photometric redshifts obtained from different

methods. While the “

REDSHIFT_FINAL

” key speciﬁes the nominal redshift, optional redshifts and associ-

ated typings can be used with the namelist variable

&SNLCINP

ZEXTRA_SOURCE = ’ZZZ’

...

&END

where “

ZZZ

” is the name of the redshift source. The

SNANA

programs will then search each SN data ﬁle

for the optional keywords

[ZZZ]_TYPE: nnn # optional

[ZZZ]_REDSHIFT_HELIO: 0.04592 +- 0.0002 (Helio) # optional

[ZZZ]_REDSHIFT_CMB: 0.04500 +- 0.0002 (CMB) # optional

[ZZZ]_END: # mandatory key

where “

nnn

” is the SN type based on using the optional redshift. The ﬁrst three keys are optional, meaning

that they only need to be speciﬁed in data ﬁles where such information exists. The “

[ZZZ]_END:

” key is

required in every data ﬁle; if this key is missing, the program will abort. Several different sets of optional

redshifts can exist in each data ﬁle, but they must all go at the end of the header (just before the ﬁrst

observation).

These optional redshifts may be used only by a list of valid users speciﬁed in a global ﬁle called

more $SNDATA_ROOT/[SURVEY]/[ZZZ]_USERS.LIST

USER: <user1>

USER: <user2>

USER: <user3>

etc ...

This ﬁle-system is not a security system, but is only intended to prevent accidental mis-use.

5.14 Excluding/Downweighting Filters and Epoch Ranges

Here we discuss options to exclude or down-weight data in the light curve ﬁtter. The ﬁlter selection is

based on rest-frame wavelength so that a uniform cut can be applied to different ﬁlter systems. To globally

exclude the rest-frame ultraviolet (UV) region, for example, set

$SNLCINP

namelist variable

CUTWIN_RESTLAM = 3900. 20000.

which excludes ﬁlter(s) whose central wavelength satisﬁes ¯

λobs/(1+z)<3900 Å. This option excludes

data as if it were not part of the data ﬁle; hence the corresponding passband is not used for spectral warping,

Trest cuts, etc ...

One problem with the above option is that there is no way to extrapolate the model back to excluded

ﬁlter and check data-model ﬁt residuals. To visually monitor data-model residuals for the excluded region,

it is better to simply down-weight rather than exclude a particular range in wavelength or epoch. A set

FUDGE_FITERR_XXX

variables allow the user to down-weight arbitrary wavelength and epoch ranges.

These

&FITINP

namelist variables are illustrated in the following example:

FUDGE_FITERR_TREST = -20., 100. ! rest-frame range (days)

FUDGE_FITERR_RESTLAM = 1000., .3900. ! wavelength range (A)

FUDGE_FITERR_PASSBANDS = ’UBVRI’ ! observer filters

FUDGE_FITERR_MAXFRAC = 100. ! error -> 10*maxFlux

This example does essentially the same thing as the above example using “

CUTWIN_RESTLAM = 3900.,

20000.

” However, using the

FUDGE_FITERR_XXX

variables means that ﬁlters mapping onto the rest-frame

UV region are used in the spectral warping for K-corrections, and these ﬁlters are also used in the Trest

sampling requirements. In evaluating the lightcurve ﬁt-χ2, an additional uncertainty of 100×the maximum

ﬂux (

FUDGE_FITERR_MAXXFRAC=100

) is added in quadrature to each epoch-uncertainty that satisﬁes the

RESTLAM

and

TREST

windows, and hence such epochs are effectively excluded from the ﬁt. Note that

FUDGE_FITERR_PASSBANDS

speciﬁes the observer-frame ﬁlters for which the other criteria apply. If you

set the observer passbands to ’

’, then the

RESTLAM

and

TREST

criteria are applied only for observer-Uand

not the other ﬁlters. One can therefore choose to down-weight data based on ﬁlters or based on rest-frame

wavelength ranges.

Here is another example in which epochs before −5 days and after +50 days are excluded for all

ﬁlters:

FUDGE_FITERR_TREST = -99,-5.0, +50., 999.

FUDGE_FITERR_RESTLAM = 1000., 20000.

FUDGE_FITERR_PASSBANDS = ’UBVRI’

FUDGE_FITERR_MAXFRAC = 100

Two sets of “

RESTLAM

” windows can be deﬁned in the same that the two “

TREST

” window are deﬁned

above. To downweight all measurements more easily there are two global options,

FUDGEALL_MAXFRAC = 0.3 # all epoch, all fit-iterations

FUDGEALL_ITER1_MAXFRAC = 0.3 # all epochs, 1st fit-iter only

where the “

ITER1

” option inﬂates the errors only on the ﬁrst ﬁt-iteration. These options may be useful in

cases where the data uncertainties are smaller than the model errors, resulting in unstable ﬁts. Inﬂating

the errors generally results in more stable ﬁts. The “

ITER1

” option is intended to gives a reliable initial-

parameter estimate for the 2nd ﬁt-iteration that uses the nominal uncertainties.

5.15 Rest-Frame Wavelength Range

Each SN model includes a function that returns the valid rest-frame wavelength range (λrest-range) to the

ﬁtting program. There are two different ways to change the λrest-range, but note that you can only make

the λrest-range more restrictive; i.e, you cannot arbitrarily loosen the λrest-range for a SN model. The two

equivalent namelist options to change the λrest-range (Å) are

&SNLCINP

CUTWIN_RESTLAM = 2000 , 25000

&END

&FITINP

RESTLAMBDA_FITRANGE = 3500 , 9500

&END

The ﬁrst option rejects measurements as part of the pre-ﬁtting selection, and is useful if you want to apply

this requirement without running the ﬁt; i.e., using only the

snana.exe

program. The second option is

applied during the ﬁtting stage.

The λrest-ranges appear in your log-ﬁle as follows,

CUTWIN_RESTLAM = 2000. 25000.

SN-MODEL LAMBDA RANGE: 3200. - 9500.

USER-FIT LAMBDA RANGE: 3500. - 9500.

and again note that the most restrictive range is used. If you specify a wide open range such as 1000 to

30000, this simply tells the ﬁtting program to use the default range.

Finally, if you really insist on changing the default λrest-range for a particular SN model,17 you can

modify the default range by editing the ﬁle

$SNDATA_ROOT/models/[model-subdir]/RESTLAMBDA_RANGE.DAT

Such changes should be used with great caution because this change affects all users. Before making such

a change, consider creating a private model-version (i.e.,

mlcs2k2.LAM2800

17All maintenance warranties are null & void if you change the default λrest-range.

100

5.16 Extracting Light Curve Shape from the Fit

The light curve shape, deﬁned as the ﬂux-to-peakFlux ratio (F/F0) versus epoch, is determined after

each light curve ﬁt. In principle, this ratio is unity at the epoch of peak brightness. The residual-ntuple

variable is

FPKRAT

(ntuple id 7799) and the fortran variables are

EP_FPKRAT

and

EP_FPKRATERR

. See

fortran subroutine

FPKRAT

for example on how to access these arrays.

While the ﬂux values are from the data, the estimate of the peakFlux is based on the best-ﬁt model.

The peakFlux estimate can be signiﬁcantly off, particularly for multi-band light curves that ﬁt one of the

colors poorly. Such peakFlux errors are evident for light curves in which the the data points in a given

ﬁlter lie well above or below the best-ﬁt model. To get a better estimate of the peakFlux, one can correct

for the average data/model ratio in a particular epoch-range. This correction is implemented using the

$FITINP

namelist variable

TREST_PEAKRENORM = -10.0, +20. # rest-frame days

which speciﬁes the rest-frame range for which to include epochs in the data/model correction. The de-

fault values are 0,0 →no correction. A data/model weighted-average is taken over the epochs within

TREST_PEAKRENORM

. The weight (wi) at each epoch “i” is deﬁned to be

wi≡[σ2

i×(|Trest|+1)]−1,(25)

where σiis the data/model ﬂux-ratio uncertainty based on the data-ﬂux error (i.e., ignores the model error),

and “|Trest|+1” is an arbitrary factor (in days) used to downweight epochs away from peak.

To see the peakFlux estimates on the light curve ﬁt (§ 5.9), use the command

mkfitplots.pl --h <hisfile> PEAKFLUX

PAW > snana#fitres pkf=1

and a pink horizontal line is drawn through the peakFlux estimate for each ﬁlter and SN. The user is

encouraged to vary

TREST_PEAKRENORM

to check the sensitivity of the epoch range.

5.17 Landolt ↔Bessell Color Transformations

As explained in the ﬁrst-season SDSS–II results paper (Appendix B of arXiv:0908.4274), the nearby

SNe Ia magnitudes are reported in the Landolt system, but there are no UBVRI ﬁlter responses for this

system. We therefore deﬁne color transformations between the Landolt system and synthetic UBVRI

magnitudes using Bessell (1990) ﬁlter response functions (See Eqs. B1-B2 in above reference). These

color transformations can be implemented in the ﬁtter with the &

FITINP

namelist ﬂag

OPT_LANDOLT = 1 ! transform rest-frame Landolt model mags -> Bessell90

OPT_LANDOLT = 2 ! transform obs-frame Bessell90 mags -> Landolt

OPT_LANDOLT = 3 ! both of the above

For example, to analyze the JRK07 sample with MLCS2k2, set

OPT_LANDOLT=3

; to analyze with

SALT-II, set

OPT_LANDOLT=2

. To analyze ESSENCE data with MLCS2k2,

OPT_LANDOLT=1

. In the last

case, the ESSENCE RI ﬁlter response functions are well known, so there is no need to use Bessell90 ﬁlter

responses. Note that the 2nd bit should be used only when the UBVRI ﬁlter response is not known. Thus,

for example, do not set the 2nd bit for CFA3 & CFA4.

All of the above use BD17 as the primary reference. To use Vega, add 4 (3rd bit) to each

OPT_LANDOLT

value. You are also responsible for using the appropriate K-correction ﬁle with the matching primary

reference.

101

5.18 Interpolating Fluxes and Magnitudes

There are two methods for interpolating the SN ﬂux at a particular observation time (MJD). The ﬁrst

method is to use the generic ’any-LC’ function from §5.4, and the second method is to use an SN Ia light

curve model. For either method prepare a two-column ﬁle that lists each SNID and MJD to interpolate. To

interpolate all SN at a particular MJD replace the SNID with the keyword ’ALL’. In the following example

of a two-column input ﬁle,

1 53616.0

2 53610.0

2 53626.0

ALL 53640.0

one epoch is interpolated for SN 1, two epochs are interpolated for SN 2, and one epoch (53640) is

interpolated for all SNe. Specify input and output ﬁles with the following

&SNLCINP

namelist variables,

SNMJD_LIST_FILE = ’KECK-SDSS.LIST’

SNMJD_OUT_FILE = ’KECK-SDSS.OUT’

Errors on the interpolated ﬂuxes account for the errors and covariances among the ﬁtted parameters. The

interpolated results are dumped into a human-readable output ﬁle with keywords to simplify parsing. To

interpolate the ﬂux at peak brightness, specify MJD = 0 in the

SNMJD_LIST_FILE

The “any-LC” function is recommended in most cases since each ﬁlter is ﬁt separately and since a

more general class of light curve shapes can be accurately ﬁt. Note that you must run

snana.exe

instead

snlc_fit.exe

! The

&SNLCINP

namelist parameters are

OPT_SETPKMJD = 1 # fit with any-LC function

OPT_LCPLOT = 1 # make plots for PAW > snana#fitres .

Filters can be ignored, for example, setting

EPCUT_SNRMIN = ’g 99999 r 99999’

to skip the gand r

bands.

When ﬁtting with an SNIa model (2nd method) it is recommended to ﬁt a single passband by either

specifying one passband with the

&FITINP

namelist variable

FILTLIST_FIT

, or by downweighting the

other passbands using the

FUDGE_FITERR_XXX

options (§5.14). The latter is recommended because some

SNIa models return garbage if only one ﬁlter is included. Thus, to interpolate the ﬂux in each of the griz

passbands, four separate ﬁts should be done. The &

FITINP

namelist parameters to interpolate g-band by

downweighting the other bands are as follows:

FILTLIST_FIT = ’griz’

FUDGE_FITERR_TREST = -20. 80. 0. 0.

FUDGE_FITERR_PASSBANDS = ’riz’

FUDGE_FITERR_MAXFRAC = 100.

Note that you can use command-line arguments (§12.2.1) to write a wrapper that loops over the ﬁlters,

snlc_fit.exe myfit.nml FUDGE_FITERR_PASSBANDS riz SNMJD_OUT_FILE g.OUT

snlc_fit.exe myfit.nml FUDGE_FITERR_PASSBANDS giz SNMJD_OUT_FILE r.OUT

snlc_fit.exe myfit.nml FUDGE_FITERR_PASSBANDS grz SNMJD_OUT_FILE i.OUT

snlc_fit.exe myfit.nml FUDGE_FITERR_PASSBANDS gri SNMJD_OUT_FILE z.OUT

102

5.19 Fitting Rest-Frame Peak-Magnitudes and Colors

There are two ways to deﬁne rest-frame peak magnitudes (M⋆): 1) from the best-ﬁt model and 2) the true

mag. While the former is trivial to obtain after ﬁtting a light curve, the resulting rest-frame colors are

simply pegged to the SNIa model and may not reﬂect variations from intrinsic scatter. The true M⋆and

associated colors include intrinsic variations. This section focuses on obtaining the true M⋆and colors by

specifying the following

&FITINP

options for

snlc_fit.exe

FILTLIST_FITRESTMAG = ’UBV’

LAMEXTRAP_FITRESTMAG = 250 ! (A) allow this much rest-frame extrapolation

SHAPEFIX_FITRESTMAG = -0.2 ! => fix SHAPEPAR for PEAKMAG calc

The kcor/calibration ﬁle must include these extra (UBV) ﬁlters in addition to the observer-frame ﬁlters.

Each M⋆

U,B,Vis determined by ﬁtting only the two nearest observer-frame bands that bracket the rest-ﬁlter

in wavelength.

LAMEXTRAP_FITRESTMAG

allows wavelength slop in deﬁning the observer-frame ﬁlters,

and increases the redshift range for which all of the M⋆

U,B,Vcan be determined. For example, suppose that

the bluest observer-frame ﬁlter is gband with a central wavelength of λg=4800 Å, and the rest-frame

Uband has λU=3600 Å. If

LAMEXTRAP_FITRESTMAG

=0 (default) then the minimum redshift for which

M⋆

Ucan be determined is zmin =4800/3600−1=0.333; with

LAMEXTRAP_FITRESTMAG

=250 Å we have

zmin =4800/(3600+250)−1=0.247. Similar logic is applied to the reddest ﬁlter.

The ﬁtting for each SN proceeds as follows. The ﬁrst “

NFIT_ITERATION

” ﬁt-iterations are used to

determine the time-of-peak (t0) and stretch parameter (s0) from a ﬁt to all of the observer-frame bands.

One additional ﬁt-iteration is then performed for each M⋆using only the two nearest bands, holding t0and

s0ﬁxed from the global ﬁt. The ﬂoated color and distance parameters provide the ﬂexibility to ﬁt both

observer-frame bands. After each two-band ﬁt M⋆is computed as follows,

M⋆

X≡modelMag(TX,t0,s0,color,distance)−µz(26)

where TXis the ﬁlter-transmission for ﬁlter X=U,B,V, and s0is replaced by

SHAPEFIX_FITRESTMAG

this namelist parameter is set. The Galactic extinction

MWEBV

is set to zero for this rest-frame modelMag

calculation. µzis the calculated distance modulus using the known redshift and an assumed cosmology.

The subtraction of µzis done so that the M⋆

Xhave reasonable values (∼ −19), but it has no impact on the

rest-colors since the same µzis subtracted for each (UBV) ﬁlter. After all of the two-band ﬁts are done, a

ﬁnal ﬁt-iteration is performed using all of the ﬁlters so that the analysis variables (

Ndof

SNRMAX

FITPROB

etc ...) correspond to the global ﬁt.

The rest-mags are written to the ﬁtres-ﬁle as

M0_X

and

ERRM0_X

where X are the rest-ﬁlter character

names (e.g., U,B,V). For each ﬁlter in a 2-band ﬁt, the maximum S/N is required to satisfy the

&SNLCINP

namelist cut-variable

CUTWIN_SNRMAX2

. If both bands fail

CUTWIN_SNRMAX2

, the rest-mags are not evalu-

ated and

M0_X=999

5.20 Peak-Mag Crosschecks:

FITMAGDIF

To check the best-ﬁt model magnitudes there is an option to compute a given observer-frame magnitude

in two independent ways : 1) ﬁtting only the one band, and 2) ﬁtting the other bands and extrapolating the

model. An example of this

FITMAGDIF

option is as follows,

FILTER_FITMAGDIF = ’u’

FILTLIST_FIT = ’ugr’

103

The ﬁrst

NFIT_ITERATION

ﬁts are done with all of the

FILTLIST_FIT

(ugr) ﬁlters so that the time of peak

brightness (t0), stretch and color parameters are well determined and ﬁxed for the ﬁt-iterations that follow.

The next ﬁt-iteration is done only with ﬁlter “

FILTER_FITMAGDIF

” (u) in which the ﬂux-scale (x0or µ) is

the only ﬂoated parameter. The ﬁnal ﬁt-iteration is done with all of the

FILTLIST_FIT

(ugr) ﬁlters, but

with u-band deweighted so that it contributes nothing to the χ2and only the g & r bands are included in

the ﬁt. The quantity

MAGDIF_u

and its erros are computed as

MAGDIF_u = peakMag(u, extrapolate gr) - peakMag(u only)

= peakMag(predicted) - peakMag(measured)

The

MAGDIF

variable is in the ﬁtres table (ntuple 7788) and also in the ﬁtres-text outout.

5.21 Selecting SNID(s), Field(s), and Telescope(s)

All namelist variables discuss here are in

&SNLCINP

5.21.1 Selecting/Ignoring SNID

By default all candidate IDs (CID) are processed. Here are some example on how to select a range of

CIDs or a list of CIDs, and to ignore a list of CIDs:

CUTWIN_CID = 700, 2000 ! CID integer-range to process

SNCID_LIST = 5944, 10550 ! integer list of SN to process

SNCCID_LIST = ’5944’, ’10550’ ! same as above, using strings

CUTWIN_CID = 0,0 ! turn off range to process list

SNCID_LIST_FILE = ’myCIDs.list’ ! file with list of CIDs to process;

! separated by space or <CR>

SNCID_IGNORE = 4524, 8151, 7017 ! list of SN to ignore

SNCCID_IGNORE = ’4524’, ’8151’, ’7017’ ! same as above with strings

SNCID_IGNORE_FILE = ’reject.list’ ! list of CIDs to ignore;

! separate CIDs by space or <CR>

Internally all CIDs are strings. If the CIDs are integers then you can use

SNCID_LIST

and

SNCID_IGNORE

otherwise you must use the character-

CID

variables “

SNCCID_

” and put each CID in quotes. A zero or

blank acts as a terminator. For example,

SNCID_LIST = 5944, 0, 1032, 10550

would process SN

5944 and ignore the rest.

CUTWIN_CID

gives the integer range. For CIDs that are integers, you can specify the integer range

without worrying about the internal string conversions. For CIDs that are strings,

SNANA

internally assigns

integer CIDs that are sequential starting from 1. For example, consider the SNLS CIDs that are strings

(e.g., 04D1cc);

CUTWIN_CID = 1,10

would process the ﬁrst 10 SNe. However, for a survey using integer

CIDs that start at 1000,

CUTWIN_CID = 1,10

would discard all SNe.

Finally, note that the logical-OR is used for

CUTWIN_CID

and

SNCID_LIST

. Thus when using the LIST

option, make sure to set

CUTWIN_CID=0,0

to turn off the range-option.

104

5.21.2 Selecting Fields and Overlapping Fields

By default all ﬁelds and overlapping ﬁelds are used. Using SDSS 82N and 82S ﬁelds as an example, ﬁelds

are selected by

SNFIELD_LIST = ’82S’ ! select only 82S pointings (ignore 82N)

CUTWIN_NFIELD = 1, 1 ! select only SN with no 82N/82S overlap

CUTWIN_NFIELD = 2, 2 ! select only SN with 82N+82S overlap

SNFIELD_LIST

determine which ﬁeld-pointings to use for lightcurves; these ﬁelds must be speciﬁed in

SURVEY.DEF

, otherwise the code aborts. In the ﬁrst example above, only 82S pointings/epochs are used,

and overlap pointings on 82N are discarded. SNe that overlap 82S and 82N are used, but only the subset

of 82S pointings are selected. Similarly,

SNFIELD_LIST=’82N’

would select the epochs with an 82N

pointing.

CUTWIN_NFIELD=1,1

picks out SNe in which all observations are on the same pointing; i.e., no over-

laps.

CUTWIN_NFIELD=2,2

picks out only those SNe that overlap 82N and 82S.

Another example of selecting multiple ﬁelds is as follows:

SNFIELD_LIST = ’C1’, ’C2’, ’C3’

SNFIELD_LIST = ’C1+C2’, ’C3’

SNFIELD_LIST = ’C1+C2+C3’

SNFIELD_LIST = ’C1 C2 C3’

where the above three commands are equivalent. Either of the last two commands can be used as a

command-line override with an arbitrary number of ﬁelds.

Even if you don’t use the selection options above, there are table variables (§12.1) that can be used to

apply some of these selections after the ﬁtting:

NFIELD_OVP

is the number of overlapping ﬁelds for each

SN, and

FIELD

is the name of the ﬁeld(s). For SN on overlapping ﬁelds, such as 82N and 82S,

FIELD =

’82N+82S’

. The order of the overlapping ﬁelds in the

FIELD

string is the same as that in

SURVEY.DEF

. The

‘append’ option in the sntable-dump utility (§12.1.2) can be used to add

NFIELD_OVP

into the text-ﬁtres

ﬁle. Note that the

FIELD

string cannot be appended to the text-ﬁtres ﬁle (sorry!).

5.21.3 Selecting Telescopes

If lightcurves are constructed from multiple telescopes deﬁned in $

SNDATA_ROOT

SURVEY.DEF

, all epochs/telescopes

are used by default. To select a subset for analysis,

SNTEL_LIST = ’SDSS’ ! list of telescopes

would analyze lightcurves using SDSS epochs, and ignore observations from other hypothetical instru-

ments. The code aborts if an invalid telescope is selected; i.e., one that is not speciﬁed in the

SURVEY.DEF

ﬁle.

105

5.21.4 Selecting MJD Ranges

There are three

&SNLCINP CUTWIN

parameters to deﬁne MJD ranges:

CUTWIN_MJD = 53600, 53700 ! use obs only in this MJD range

CUTWIN_MJD_EXCLUDE = 53622, 53628 ! excluce obs in this MJD range

CUTWIN_MJD_INCLUDE = 53630, 53660 ! require at least 1 MJD in this range

The ﬁrst two

CUTWIN

parameters deﬁne epochs to select. The last cut (

CUTWIN_MJD_INCLUDE

) does not

pick epochs, but rejects the entire light curve if there is no observation in the deﬁned window.

5.21.5 Quickly Analyzing a few SNe from a Large Sample

This section is for the text-output option only (

FORMAT_MASK = 1 or 2

It is often useful to select a few SNe for ﬁtting and analysis, such as for debugging a particular problem.

From §5.21 above, the namelist variable

SNCID_LIST

can be used to select an arbitrary subset, but the

snana.exe

and

snlc_fit.exe

programs must read every SN data ﬁle up to the point where each SN in

the list has been found. The time to simply read these data ﬁles can be relatively slow (∼minute) if a large

number of data ﬁles must be screened. To read in the data ﬁles more quickly, a temporary

DEBUG_XXX

version can be created where

XXX

are your initials or some other identiﬁer. Just three ﬁles need to be

created:

$SNDATA_ROOT/lcmerge/DEBUG_XXX.README

$SNDATA_ROOT/lcmerge/DEBUG_XXX.IGNORE

$SNDATA_ROOT/lcmerge/DEBUG_XXX.LIST

and for simulations replace “

lcmerge

” with “

SIM

” and create a sub-directory

SIM_DEBUG_XXX

with the

appropriate ﬁles. The

IGNORE

and

README

ﬁles can be blank. The

LIST

ﬁle contains the name of each data

ﬁle to analyze. You can then analyze this debug version by specifying

$SNLCINP

namelist variables

VERSION_PHOTOMETRY = ’DEBUG_XXX’

CUTWIN_CID = 1, 100000

and there is no need to specify

SNCID_LIST

5.22 Mag-Shifts in Zero Points and Primary Reference Star

The

snlc_fit.exe

program provides an interface to modify zero-point offsets as well as the magnitudes

of the primary reference star. The primary magnitudes can be individually adjusted using the &

SNLCINP

namelist option

MAGOBS_SHIFT_PRIMARY = ’B .02 V .01’

MAGOBS_SHIFT_PRIMARY = ’B .01 V .01 R 0.01’

MAGOBS_SHIFT_PRIMARY = ’BVR 0.01’ # same as above

MAGREST_SHIFT_PRIMARY = ’B .02 V .01’

106

which shifts the primary mags by 0.02 and 0.01 for Band V, respectively, in the example above. Note

that separate strings are used for the observer-frame and rest-frame to allow for the same ﬁlter-character

to be used in each reference frame. This option is equivalent to re-generating the K-correction tables with

these shifts, but the

MAG[OBS,REST]_SHIFT_PRIMARY

option is much quicker since you can use the same

K-correction tables.

For the zero-points, there are two ways to introduce shifts. The ﬁrst method is to specify the offsets in

a ﬁle,

ZPOFF.DAT

, located in the

filters

sub-directory. For the SDSS AB-offsets, the ﬁle location is

> more $SNDATA_ROOT/filters/SDSS/ZPOFF.DAT

u -0.037 g 0.024 r 0.005 i 0.018 z 0.016

ZPOFF.DAT

does not exist, the shifts are zero. This method is used for standardized shifts.

The second option is designed to probe the uncertainty in the zero-point offsets; an arbitrary shift can

be speciﬁed with the &

SNLCINP

namelist string

MAGOBS_SHIFT_ZP = ’g .02 r .01 i .008’

MAGOBS_SHIFT_ZP = ’g .01 r .01 i .01’

MAGOBS_SHIFT_ZP = ’gri .01’ # same as above

Note that the shifts in

ZPOFF.DAT

and

MAGOBS_SHIFT_ZP

are added so that you make well-deﬁned shifts

relative to the standard shifts in

ZPOFF.DAT

Wavelength-dependent shifts can be applied with polynomial parameters in

&SNLCINP

MAGOBS_SHIFT_ZP_PARAMS = 0, 0.02, -0.01

MAGOBS_SHIFT_PRIMARY_PARAMS = 0, 0.01, 0

which applies a ZP shift of 0.02λobs −0.01λ2

obs, and a PRIMARY mag shift of 0.01λobs. Note that λobs

is the central wavelength in MICRONS, not Å, so that the

PARAMS

coefﬁents are about the size of the

mag-shift.

5.23 Fudging the

FLUXCAL

Offsets and Uncertainties

Filter-dependent offsets and errors can be added to the calibrated ﬂuxes and errors using the following

&SNLCINP

namelist variables,

FUDGE_FLUXCAL_OFFSET = ’u -0.6 g 0.4 r 1.2 i -3.7 z 2.2’

FUDGE_FLUXCAL_ERROR = ’u 24 g -12 r 44 i 19 z -22’

FUDGE_MAG_ERROR = ’u .01 g .011 r .009 i .01 z .018’

These fudges should be used for systematic studies only; permanent changes should be made in the data

ﬁles. The error fudges are added/subtracted in quadrature based on the sign of

FUDGE_FLUXCAL_ERROR

5.24 Updating the Filter Transmission for each SN

In 2009 the SNLS reported that their ﬁlter transmission depends on the focal plane position.18 While their

transmission function depends only on the radius from the center, in general the SN ﬁlter transmission

can be unique for each SN. Using the

SNANA

ﬁtting program, an SN-dependent ﬁlter transmission can be

speciﬁed, although it is assumed that each transmission function is the same for all epochs. This feature is

invoked by specifying an ’update’ directory from the

$SNLCINP

namelist as follows:

18Regnault et al., A&A 506 , 999 (2009).

107

FILTER_UPDATE_PATH = ’MYPATH’

MYPATH

can be a subdirectory under $

SNDATA_ROOT/filters

, or

MYPATH

can be the full directory name;

both directories are checked, with the former having priority. This directory must contain an instruction

ﬁle called ’

FILTER.INFO

’, along with a ﬁlter transmission text-ﬁle for each SN. Rather than giving an

explicit list of ﬁlter-transmission ﬁlenames, the INFO ﬁle speciﬁes the naming conventions for the ﬁlter-

transmission directories and ﬁles:

FILTER_SUBDIR: filters-{SNID}

FILETRANS_SN: SNtrans_*.dat

FILETRANS_REF: REFtrans_*.dat

The ﬁrst key speciﬁes the sub-directory name for each set of ﬁlter transmissions, and the directory name

depends on the name of each SN. The next two keys specify the transmission ﬁlenames residing within

each

FILTER_SUBDIR

. The star (*) represents the 1-letter representation for each ﬁlter. For example, the

SNLS ﬁlenames would be

SNtrans_g.dat

SNtrans_r.dat

, etc. The ﬁllter transmission can be different

for the SN and for the primary references (REF). However, if only one set of transmissions is speciﬁed

(either SN or REF), then these transmissions are used for both the SN and the primary reference.

WARNING: currently this ﬁlter-update feature works only for the SALT2 model; perhaps a future

SNANA

version will work for rest-frame models that use K-corrections.

5.25 Shifting the Mean Filter Transmission Wavelength

Each band can be indpendenlty shifted via

&SNLCINP

input

FILTER_LAMSHIFT = ’g -3.4 r 5.6 i 12.3’

5.26 Monitoring Fit-Jobs with “grep”

If you pipe the ﬁtter screen dump to a log ﬁle, the unix “

grep

” command can be used to quickly monitor

progress during the ﬁts, as well as after the ﬁts have completed. This is particularly useful when many

ﬁt-jobs are run in parallel so that you can monitor progress and catch aborts. Many screen outputs are

explicitly designed to help monitor the job status. Below are some examples of useful grep-commands

to run. A dagger ( †) indicates those commands that work only when the ﬁt-job has ﬁnished. Note that

adding “

| wc

” to the end of a grep command will count the number of entries.

•

grep GRACE fit*.log

†

lists the unique string

ENDING PROGRAM GRACEFULLY

to identify and count jobs that have ﬁnished.

•

grep " ABORT " fit*.log

†

identiﬁes jobs that have aborted. Note the blank space before and after

ABORT

to distinguish from

namelist variables that include

ABORT

as part of the name.

•

grep "after snana" fit*.log

†

shows the number of SN before and after

SNANA

cuts.

•

grep "after fit" fit*.log

†

shows the number of SN after ﬁtter cuts.

108

•

grep "PROCESS TIME" fit*.log

†

shows total processing time.

•

grep "PASSES FIT" fit*.log

lists each SN that passes ﬁt cuts.

•

grep "Cuts REJECT" fit*.log

lists each SN rejected by SNANA cuts.

•

grep "FAILED FIT" fit*.log

lists each SN rejected by ﬁtter cuts.

•

grep ":DLMAG" fit*.log | grep pdf

lists the marginalized distance-modulus for each ﬁtted light curve. Works for any ﬁt-parameter:

AV,

DELTA, PEAKKMJD, PHOTOZ

. Include the colon, or you will be overwhelmed by the screen dump.

•

grep ":x0" fit*.log | grep fitpar

lists the SALT2 amplitude for each ﬁtted light curve.

5.27 User SN Tags

User-deﬁned SN tags can be speciﬁed with the

&SNLCINP

namelist variable

&SNLCINP

USERTAGS_FILE = ’mytags.dat’

...

&END

more mytags.dat

SN: 1032 1

SN: 2033 1

SN: 2490 1

SN: 3088 2

etc ...

and these

USERTAG

indices will appear in the analysis ntuples. These tags may be useful, for example, to

label SNe conﬁrmed by a particular telescope.

109

5.28 Over-Riding Information in Data Files

5.28.1 Over-Riding Header Information

Here we describe how to over-ride header information in the data ﬁles without re-making the data ﬁles.

This feature can be useful, for example, for systematics or optimization studies The header information

includes host properties, peculiar velocities, redshifts, and Galactic extintion, all of which can be easily

modiﬁed for a particular study.

The input key for the analysis programs is

&SNLCINP

HEADER_OVERRIDE_FILE = ’myUpdates.dat’

more myUpdates.dat

NVAR: 5

VARNAMES: CID VPEC VPEC_ERR HOSTGAL_LOGMASS HOSTGAL_LOGMASS_ERR

SN: 1346137 78.4 150.0 10.87 0.21

SN: 1346387 -63.0 150.0 9.44 0.33

etc ...

In this example, four header values are updated: peculiar velocity correction, log of host mass, and the

error for each. For SNe missing from the update ﬁle, the original values in the data ﬁle header are used.

This feature does

NOT

work on epoch-dependent quantities.

110

5.28.2 Over-Riding Light Curve Information

Epoch-dependent mag-corrections can be applied via an external text ﬁle in order to avoid re-making data

ﬁles with each iteration of calibration offsets. These corrections are applied only to the

FLUXCAL

, and

not the

FLUXCAL_ERR

, and thus there is an implicit assumption that changes are small (∼1%). For large

changes, the data ﬁles should be re-made with the new errors as well. The syntax is

&SNLCINP

MAGCOR_FILE = ’magCor.dat’ ! data only (not for sims)

SIM_MAGCOR_FILE = ’magCor.dat’ ! force on sims (not data)

more magCor.dat

NVAR: 5

VARNAMES: ROW DUM1 MAGCOR DUM2 DUM3

ROW: 1346137-56542.271-g 23 0.0123 10.23 22.456

ROW: 1346137-56542.272-r 33 0.0094 10.12 24.679

ROW: 1346137-56542.274-i 67 -0.0025 11.98 21.023

etc ...

The SNID, MJD and BAND are glued together to form a unique

ROW

-string identifying the correction.

Only the

MAGCOR

column is used, and other optional columns (

DUM1,DUM2,DUM3

) are ignored. Each

FLUXCAL

is internally multipled by 10(−0.4·MAGCOR).

For public data releases, such corrections may be included in the data ﬁles. To avoid accidentally

applying these corrections twice, the

MAGCOR_FILE

should include the header key

VERSION_ADD: <VERSION>

for the data version that has the corrections included. The

SNANA

analysis codes will abort if

MAGCOR_FILE

is speciﬁed for a data version that already includes these mag-corrections. If mag-corrections have been

applied to data, the corrections can be removed with

&SNLCINP

MAGCOR_FILE = ’-magCor.dat’

where the minus sign in front is a command to subtract. This subtract option works only with the

VERSION_ADD

key.

5.29 Peculiar Velocity Corrections

By default, the CMB redshifts are used for the Hubble diagram analysis. Although

SNANA

has no explicit

code to compute peculiar-velocity corrections (vpec), such corrections can be made with external codes

and be included in the data ﬁles with

VPEC

and

VPEC_ERR

keys. The vpec values can also be read from

an external ﬁle as described in §5.28.1. The light curve ﬁtting program (

snlc_fit.exe

) reads vpec and

computes a corrected CMB redshift,

zHD = ZCMB + VPEC

which is written to the output tables and used by the

SNANA

program

SALT2mu.exe

111

5.30

SIMCHI2_CHEAT

For simulations, the χ2is automatically computed in which the ﬁtted parameters are replaced by the exact

simulated paarameter values. The resulting χ2variable is called

SIMCHI2_CHEAT

and it is stored in the

table output (ntuple for hbook, tree for root).

There is no ambguity for ﬁts with ﬁxed redshifts. For photo-z ﬁts, however, the deﬁned ﬁlter bands

based on the ﬁtted photo-z may be incorrect for the true redshift. For example, a ﬁtted photo-z of 0.4

would include the z-band ﬁlter for the SALT2 model, but if the true redshift is 0.1 then trying to evaluate

the z-band model-mag would result in an abort because it is too red for the SALT2 model in the rest-frame.

When undeﬁned ﬁlters are detected,

SIMCHI2_CHEAT

is set to −

NFILT_UNDEFINED

and the χ2calculation

is skipped to avoid the abort.

5.31 Cuts on true

SIM_XXX

Parameters

To apply cuts on generated (true) parameters,

&SNLCINP

SIMVAR_CUTWIN_STRING = ’SIM_c -0.1 0.1 SIM_REDSHIFT_CMB .1 .2’

! and/or

SIM_TEMPLATE_INDEX_LIST = 202,203

The ﬁrst option requires the true SALT2-color (for SALT2 model only) and true redshift (for any model)

to satisfy the above cut-windows. Also works on

SIM_x1

. The second option is for

NON1ASED

SIMSED

and

LCLIB

models; it selects a user-deﬁned list of template indices.

5.32 IDEAL Fits with True Flux (Sim only)

To determine the intrinsic scatter matrix from simulations (Σint), this section describes how to perform

“IDEAL” light curve ﬁts that use 1) true ﬂuxes instead of the reported ﬂuxes with Poisson ﬂuctuations, 2)

true Galactic extinction value for MWEBV, and 3) ﬁxes peak-MJD to its true value. The ﬂux uncertainties

are not modiﬁed with the options presented here. There are two methods for running IDEAL ﬁts:

&SNLCINP or &FITINP

USESIM_TRUEFLUX = T SIMFIT_IDEAL_PRESCALE = 4

The ﬁrst option (

USESIM_TRUEFLUX

) prepares IDEAL ﬁts and works with

psnid, snlc_fit

or any user

analysis. The second option (

PRESCALE

) works only with

snlc_fit

, but it performs both the IDEAL and

nominal ﬁt in the same job, thus simplifying higher-level pipelines. For example, ﬁtting with the SALT2

model results in the following ﬁt parameters store in the same

FITRES

table (TEXT,HBOOK,ROOT):

PKMJD c x1 x0 mB # Nominal

PKMJD_IDEAL c_IDEAL x1_IDEAL x0_IDEAL mB_IDEAL # IDEAL

The difference between IDEAL-ﬁtted parameters and the true generated parameters can be used to

compute Σint. For example, the mB-c element of Σint is compute with

FITRES

table elements as follows:

Σint(mB,c) = N−1∑[(mB_IDEAL−SIM_mB)(c_IDEAL −SIM_c)]

Since ﬁtting every event twice doubles the CPU time, this option is enabled with an explicit pre-scale

to allow reducing the CPU time if a smaller sample of IDEAL ﬁts is adequate. In the example above, 1/4

of the events are ﬁt twice (IDEAL plus nominal), thus increasing the CPU time by 25%. Events which do

not have an IDEAL ﬁt have their IDEAL parameter values set to 999.

112

6 Private Options

6.1 Creating Your Private Code

Here we describe how to create a private code version for the snana program (

snana.exe

) or the light

curve ﬁting program (

snlc_fit.exe

). This feature is useful to write your own analysis package without

the overhead of reading data ﬁles and applying selection cuts, and also to make small modiﬁcation to

the existing analysis codes. Modiﬁcations include writing out speciﬁc information to a ﬁle, calculating

a quantity that is not available, or testing variations on algorithms in the public code. This feature is

available for the fortran analysis codes, but is not available for the simulation.

There are two steps to creating your own private executable:

> cp $SNANA_DIR/src/snana_private.cra .

> snmake.pl snana_private

> cp $SNANA_DIR/src/snlc_fit_private.cra .

> snmake.pl snlc_fit_private

should result in a private executable ﬁle in your directory:

snana_private.exe

snlc_fit_private.exe

Now run your private version,

./snana_private.exe myinput.nml

./snlc_fit_private.exe myinput.nml

You can edit your private version of

snlc_fit_private.cra

and modify

USRINI

USRANA

and

USREND

The sample

USRANA

shows how to access ﬁt results, and how to access information for each epoch used

in the ﬁt. You can also re-name the code to any other name, such as ‘myﬁt.cra’, and then compile an

executable with the command “

snmake.pl myfit

” to produce the executable ﬁle

myfit.exe

In addition to adding private code into the

USR[INI,ANA,END]

routines, you can also modify the

ofﬁcial public code. Copy any subroutine from

$SNANA_DIR/src/snana.car

snlc_fit.car

, paste it

into your private

snlc_fit_private.cra

, and then make modiﬁcations. Once these changes are fully

tested, you can request that the modiﬁed routine(s) be installed into the next public release of

SNANA

. Your

changes may be included as the default, or they may be available to other users via input namelist ﬂags.

Note that modiﬁcations can also be made by checking out the entire

SNANA

product from CVS. You are

welcome to check code out of CVS (

cvs co

), but please do NOT check code in without contacting the

SNANA

manager. Working with

snlc_sim_private.cra

should be much easier than working with the

entire

SNANA

product.

WARNINGS:

•Do not trap yourself into an obsolete version of

SNANA

if you have lots of private code that is not

integrated into the public

SNANA

•If you ﬁnd yourself doing lots of cutting & pasting as part of your analysis, this is a bad sign: ask

for help!

•If you ﬁnd that you are doing lots of tedious/redundant operations, ask for help. Often adding just a

few lines of code into

SNANA

can greatly simplify your analysis procedure.

113

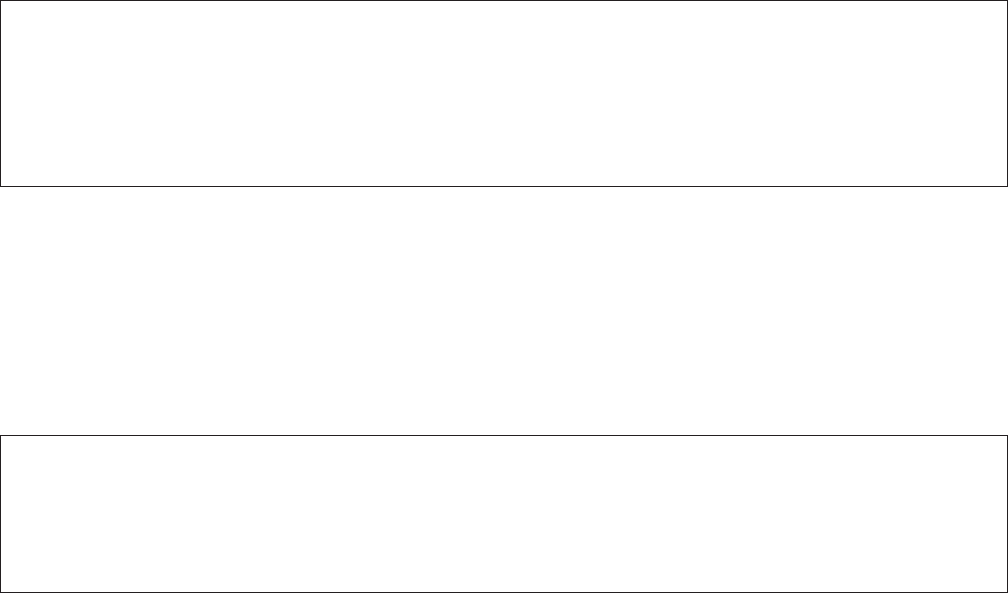
6.2 Private Sim Path:

PATH_SNDATA_SIM

By default, the simulation creates a “

GENVERSION

” sub-directory under

PATH_SNDATA_SIM = $SNDATA_ROOT/SIM

The simulated data ﬁles can be re-routed to a user-deﬁned path with sim-input key

PATH_SNDATA_SIM: <path>

This key works in the sim-input ﬁle with interactive

snlc_sim.exe

. To submit batch jobs with the

sim_SNmix.pl

script, (§12.3.1), this key must be in the sim-master-input ﬁle. This output re-route feature

is not recommended, except for special reasons such as insufﬁcient disk space under

$SNDATA_ROOT

The simulation automatically stores use user-deﬁned path names in

$SNDATA_ROOT/SIM/PATH_SNDATA_SIM.LIST

so that analysis programs (

snana.exe, snlc_sim.exe, psnid.exe

) know where to check for simulated

samples without user input. If a simulation needs to be moved out of

$SNDATA_ROOT/SIM

, the ﬁle above

(

PATH_SNDATA_SIM.LIST

) can be manually edited.

6.3 Private Data Path for Analysis:

PRIVATE_DATA_PATH

After creating or translating a new version of light curves, it is useful to run tests before copying these ﬁles

to the public/ofﬁcial area

$SNDATA_ROOT/lcmerge

SNANA

and ﬁtter jobs can read data (not simulations)

from a private directory as follows:

&SNLCINP

VERSION_PHOTOMETRY = ’myVersion’

PRIVATE_DATA_PATH = ’myDir’

&END

The version “

myVersion

” will be read from “

myDir

” in exactly the same way that it would have been

read from

$SNDATA_ROOT/lcmerge

. Users are cautioned to use this feature only for testing, and not as

long-term data storage for your analysis. For simulations,

PRIVATE_DATA_PATH

is ignored.

6.4 Private Model-Path:

$SNANA_MODELPATH

For a given SN model in the simulation (

GENVERSION

) or in the ﬁtter (

FITMODEL_NAME

), the model param-

eters are assumed to reside in

$SNDATA_ROOT/models/SALT2/*

$SNDATA_ROOT/models/mlcs2k2/*

$SNDATA_ROOT/models/snoopy/*

$SNDATA_ROOT/models/SIMSED/*

etc ...

While these public directories are intended for stable models, a private “

setenv SNANA_MODELPATH

”

directory can be deﬁned for testing models that are not suitable for public release. If this user-deﬁned

environment variable exists, then the model is assumed to be under this path. For example,

SALT2.Guy07

would be read from

$SNANA_MODELPATH/SALT2.Guy07

114

6.5 Private Variables in Data Files

Private variables can be included in data ﬁle headers as illustrated by the following example,

PRIVATE(HOST_PROPERTY): 43.22

PRIVATE(PHOTOFLAG): 439

PRIVATE(SEARCH_TYPE): 27

These ’PRIVATE’ keys must appear in the header before the light curve (MJD) observations. These

variables are included in the FITS-translated data ﬁles (§12.4.5). Using a private ﬁtter option (§6.1), the

value of any private variable can be accessed from the function

REAL*8 GET_PRIVATE_VALUE ! declare function

DVAL = GET_PRIVATE_VALUE(varName,0) ! do not abort on error

DVAL = GET_PRIVATE_VALUE(varName,1) ! abort on error

where

varName

is the name of any private variable. Note that

varName

can be simply

HOST_PROPERTY

it can be ’

PRIVATE(HOST_PROPERTY)’

6.5.1 CUTWIN-selection on Private Variables

Arbitrary cuts on private variables can be applied. Using the private variable example above, cuts are

deﬁned using the

&SNLCINP

namelist string

PRIVATE_CUTWIN_STRING = ’HOST_PROPERTY 20.4 100. PHOTOFLAG 1 600’

The current max string size is 100 characters.

6.5.2 Using a Private Redshift in the Analysis

A private redshift value can be used in the analysis and light curve ﬁtting. As an example, consider fake

SN overlaid onto an image, processed by a photometry pipeline, and private variable ‘

FAKE_z

’ is deﬁned

in the associated data ﬁles. This redshift can be used in the analysis with

&SNLCINP

namelist string

PRIVATE_REDSHIFT_CMB = ’FAKE_z’

The associated heliocentric redshift is computed internally.

115

7 Adding a New Survey

Starting with

SNANA v6_00

you can add a new survey without modiﬁcations to the software. Primary

SEDs, primary magnitudes and ﬁlter transmissions are deﬁned via K-correction ﬁles, even for models like

SALT-II that do not use K-corrections (but still use primary SEDs and magnitudes). A ﬁlter is deﬁned

by a single character to simplify the handling of a wide variety of output variable names that append the

ﬁlter string (i.e,

MAGT0_[filter]

), and to simplify output formatting. While the

SNANA

ﬁlter deﬁnition is

limited to the 1-character strings above, arbitrary ﬁlenames can be used to deﬁne the ﬁlter transmissions.

There are 62 allowed ﬁlter-characters: A-Z, a-z, and 0-9.

SNANA

versions prior to

v9_00

allowed only the

legacy ﬁlters ugriz,UBVRI,YJHK, along with 0-9. Additional ﬁlter-characters will be allowed when we

all switch to using Chinese keyboards. Here are the steps for adding a new survey:

1. Add your survey and telescope to the ﬁle $

SNDATA_ROOT/SURVEY.DEF

. Check if your survey and/or

telescope is already deﬁned before making changes.

2. Add new ﬁlters in $

SNDATA_ROOT/filters

. The wavelength spacings for the ﬁlter transmissions

must be uniform. If the wavelength spacings are large (several hundred Å) you should prepare a

ﬁner-binned ﬁlter set using an appropriate interpolation algorithm.

3. Generate K-correction tables using

kcor.exe

,19 and see §7.1 for rules about ﬁlter names. You can

leave your private K-correction table(s) in your directory where you run other jobs, or you can share

ofﬁcial K-correction tables in $

SNDATA_ROOT/kcor/

. For initial testing, use a very course grid so

that the tables are built quickly. Once the simulation and ﬁtter are working, you can generate the K-

correction tables with a ﬁner grid. The grid is controlled by

REDSHIFT_BINSIZE

and

AV_BINSIZE

WARNING: you must generate a K-correction ﬁle even if you plan to run an observer-frame ﬁt-

ter such as SALT-II that does not use K-corrections; in this case do “

kcor.exe mykcor.input

SKIPKCOR

” so that the K-corrections are skipped, but the ﬁlters and primary SED are included. Fi-

nally, for rest-frame models that use K-corrections, there is a limit of 10 rest-frame ﬁlters and 62

observer-frame ﬁlters. For observer-frame models such as SALT-II, the limit is 62 observer-frame

ﬁlters.

4. If you want to generate simulated samples, you need to prepare a simulation library. See examples

in $

SNDATA_ROOT/simlib

. This is usually the most difﬁcult part of setting up a new survey.

5. Check for an adequate rest-frame model to describe the supernova light curve.

6. If you plan to add new data ﬁles, use an existing data version as a template. To see existing ver-

sions do “

cd $SNDATA_ROOT/lcmerge ; ls *.README

”. The light-curve ﬁtter uses

FLUXCAL

10(11−0.4m). The scale-factor of 1011 is arbitrary; you can change it, but then your distance moduli

will all have a common offset, although the ﬁnal cosmological parameters are not affected by the

choice of scale-factor. Use a well-measured data point in each ﬁlter to get the

FLUXCAL/FLUX

ra-

tio, and then convert

FLUX

→

FLUXCAL

for each measurement. If you try to convert magnitudes to

FLUXCAL

, you will have problems for small & negative ﬂuxes.

7. To distribute survey-dependent

SNDATA_ROOT

ﬁles among collaborators working on different com-

puter systems, see §12.2.2.

8. Modify a sim-input and ﬁtter-input ﬁle by substituting your survey and ﬁlters. Good luck. And don’t

forget to send me a post-card about your experience.

19Sample kcor-input ﬁles are in $

SNDATA_ROOT/sample_input_files/kcor.

116

7.1 Filter Names and Rules for K-corrections

The ﬁlter names deﬁned in the K-correction input ﬁle can be anything, but only the last character (A-

Z,a-z,0-9) is propagated into the simulation and ﬁtting program. Thus, the following ﬁlter-names are all

translated into ’g’: SDSS-g, SDSSg, SDSS2.5m-g.

Filters are identiﬁed and stored separately for rest-frame and observer-frame. The reference frame is

implicitly deﬁned by KCOR entries such as

KCOR: Bessell-B SDSS-g K_Bg

which deﬁnes Bas a rest-frame ﬁlter and gas an observer-frame ﬁlter. If a ﬁlter is not used in a KCOR

entry (such as for the SALT-II model), then it is assumed to be an observer-frame ﬁlter.

Each rest-frame ﬁlter must have a unique last character, and each observer-frame ﬁlter must have a

unique last character; however, the same last character can be used in both the rest and observer frames.

For example, consider ﬁlter sets CSP-[ugri] and SDSS-[ugri]. These two sets cannot both be deﬁned

as observer-frame ﬁlters in the same K-correction ﬁle, but one set can be used for rest-frame ﬁlters that

describe a light curve model, and the other set can be used for the observer-frame. The K-corrections

deﬁned after the “

KCOR:

” keyword deﬁne which ﬁlters are used for rest/observer-frame.

Consider the following example that uses the same ﬁlter character ’B’.

MAGSYSTEM: VEGA (define mag system for filters below)

FILTSYSTEM: COUNT

FILTER: ACS_WFC_F435W-B ACS_WFC_F435W.dat

etc ...

MAGSYSTEM: VEGA

FILTSYSTEM: ENERGY (‘‘ENERGY’’ => Trans -> Trans/lambda)

FILTER: Bessell-B Bessell90_B.dat 0.021

etc ...

If no K-corrections are deﬁned, then Bis deﬁned twice as an observer-frame ﬁlter and the

snlc_fit.exe

ﬁtting program will abort because of the ambiguity. However, if a K-correction is deﬁned using Bessell-B

as a rest-frame ﬁlter, then

ACS_WFC_F435W-B

is the unambiguous observer-frame Bband ﬁlter.

117

7.2 Combining Surveys

For SNIa-cosmology analyses, there are many low-z samples consisting of different surveys, and different

ﬁlter systems within a survey. Because of duplicate ﬁlter names (e.g., UBVR appear in multiple samples),

SNANA

requires ﬁtting each low-z sample separately, which can complicate analysis pipelines. In addition,

low-z samples do not include meta-data (SKY,PSF,ZP) needed create

SIMLIB

ﬁles for simulations (§4.5).

To simplify analysis, and produce a

SIMLIB

ﬁle for simulations, data samples can be combined with the

following example based on hypothetical low-z samples:

combine_dataVersions.py myVersions.input

more myVersions.dat

VERSION: LOWZ_SET1 LOWZ/kcor_LOWZ_SET1.input # UBVRI

VERSION: LOWZ_SET2 LOWZ/kcor_LOWZ_SET2.input # UBVri

VERSION: LOWZ_SET3 LOWZ/kcor_LOWZ_SET3.input # uBVgri

SURVEY_OUT: LOWZ_COMBINED

The input ﬁle contains a list of data versions, and associated kcor-input ﬁle (§3) for each data version.

Note that kcor-INPUT ﬁles are speciﬁed, not the ﬁts ﬁles. The ﬁlters are listed in the comment ﬁeld, but

not required since the ﬁlters are read from the kcor-input ﬁles. Each kcor-input ﬁle is checked locally, and

under

$SNDATA_ROOT/kcor

. The script ‘

combine_dataVersions.py

’ performs the following tasks:

•merge all kcor-input ﬁles into a combined kcor-input ﬁle. Each original ﬁlter is mapped alphabeti-

cally to “abcde...xyzABCDE...XYZ01..89.” For the example data versions above, the ﬁlter remap-

ping is

LOWZ_SET1: UBVRI -> abcde

LOWZ_SET2: UBVri -> fghij

LOWZ_SET3: uBVgri -> klmnop

These 3 samples include 16 unique ﬁlter bands, which are mapped to 16 unique characters: “abcde-

fghijklmnop.” To help preserve the original ﬁlter name, the auto-generated combined kcor-input ﬁle

deﬁnes ﬁlters as follows,

FILTER: LOWZ_SET1-U/a LOWZ_SET1_U.dat 9.69

FILTER: LOWZ_SET1-B/b LOWZ_SET1_B.dat 9.82

FILTER: LOWZ_SET1-V/c LOWZ_SET1_V.dat 9.77

FILTER: LOWZ_SET1-R/d LOWZ_SET1_R.dat 9.44

FILTER: LOWZ_SET1-I/e LOWZ_SET1_I.dat 9.23

Thus we can still see the original ﬁlter name before the slash;

SNANA

only needs the last character in

the ﬁlter string, which is a,b,c,d,e for the above FILTER keys.

•produce combined data set with ﬁlter names replaced as indicated in the kcor-input ﬁles. The com-

bined survey name is speciﬁed by the

SURVEY_OUT

key in the

myVersions.dat

ﬁle above. Input

data versions must be in TEXT format.

•create

SIMLIB

ﬁle from data. For samples without meta-data (SKY,PSF,ZP), such as low-z, some

assumptions are needed. First, the PSF is ﬁxed to 1′′ FWHM. Second, SKYMAG vs. wavelength

is taken from an old LSST-DEEP simulation. For space-based surveys (HST,JWST,WFIRST), the

assumptions are modiﬁed: PSF is 0.2′′, and SKYMAG vs. wavelength is from WFIRST simulation.

The zeropoint (ZP) for each observation is computed in order to match the measured S/N in the data.

118

To run light-curve ﬁtting on the combined version, use the auto-generated kcor ﬁle and specify all bands

in the

&FITINP

name-list with

FILTLIST_FIT = ’abcdefghijklmnop’

Similarly, run the simulation using the same kcor ﬁle and sim-input key

GENFILTERS: abcdefghijklmnop

The SALT2-ﬁtted parameters to not depend on how the ﬁlters are named and neither does the cosmol-

ogy ﬁtting step. The main inconvenience with the remapped bands is deﬁning the spectroscopic selection

function for the simulation. For example, deﬁning εspec as a function of the original B-band is really a

function of the newly-deﬁned b,g,l- bands in the combined data ﬁle. There are a few

SNANA

featurs to

overcome this inconvenience:

1. For simulations, the εspec map can be deﬁned as a logical-or of bands,

NVAR: 2 # obsolete key starting v10_70

VARNAMES: b+g+l SPECEFF # peakMag for B band

SPECEFF: 12.10 1.0000

SPECEFF: 12.30 1.0000

SPECEFF: 12.50 1.0000

SPECEFF: 12.70 0.998

etc ...

which is equivalent to deﬁning 3 identical maps, each with a different band.

2. for the output SNANA and FITRES tables, the ﬁlter band names can be re-mapped back to their

original names using the following

&SNLCINP

namelist input:

SNTABLE_FILTER_REMAP =

’afk->U bgl->B chm->V n->g di->r ej->i’

This feature has no effect on ﬁtting, as the ﬁt still uses all 16 distinct bands. However, the output

tables are only a function of the re-mapped bands “UBVgri”. Thus instead of output peak-mag

table columns ‘

m0obs_b, m0obs_g, m0obs_l

,’ the REMAP feature results in just one column,

‘

m0obs_B

,’ to replace the original 3 bands.

3. While the combined data version has a new name (e.g., ‘

LOWZ_COMBINED

’), each original survey

name is stored as a

SUBSURVEY_NAME

. IDSURVEY in the output tables is based on the sub-survey

(

LOWZ_SET1, LOWZ_SET2, LOWZ_SET3

), allowing for studies to correlate with each input sample.

In principle, this script can be used to combine all data samples (e.g., low-z + SDSS + SNLS + PS1 +

DES + ...). The kcor-ﬁle and light-curve ﬁtting would be ﬁne. However, the auto-generated

SIMLIB

ﬁle is

based on rough guesses for missing meta-data. For surveys that provide the meta-data, it is better to use a

proper

SIMLIB

with random sky locations.

119

8 Photometric Classiﬁcation

8.1

psnid.exe

A separate program called “

psnid.exe

” (Photometric SN id) performs photometric classiﬁcation using

light curve templates. This program has the same

&SNLCINP

namelist as the

snana.exe

and

snlc_fit.exe

programs so that reading light curves and applying selection requirements is done the same way. Instead

of deﬁning a

&FITINP

namelist for the

snlc_fit.exe

program, there is a

&PSNIDINP

namelist with

declarations and deﬁnitions in

$SNANA_DIR/src/psnid.car

. The

psnid.exe

architecture allows for ar-

bitrary methods based on SNIa and CC templates. The templates are created with the simulation program

(

snlc_sim.exe

) as described in §4.34. The current

psnid.exe

method is based on [12], and is called

“Bayesian Evidence with Supernova Templates” (BEST); other methods can be added in

psnid.exe

using

either C or fortran functions. Example namelist ﬁles are in

$SNDATA_ROOT/sample_input_files/psnid

and the main namelist keys are as follows

&PSNIDINP

METHOD_NAME = ’BEST’

FILTLIST_FIT = ’griz’

OPT_ZPRIOR = 0 ! 0=flat, 1=Zspec, 2=Zphot(HOST)

FITRES_DMPFILE = ’PSNID_DES.fitres’ ! text-output (one row per SN)

PRIVATE_TEMPLATES_PATH = ’myDir’ ! optional private path for templates

TEMPLATES_SNIa = ’GRID_DES_SALT2.FITS’

TEMPLATES_NONIa = ’GRID_DES_NONIA.FITS’

FILTLIST_PEAKMAG_STORE = ’ri’ ! store peakmag for each model

etc ...

The default template location is “

$SNDATA_ROOT/models/psnid

” unless

PRIVATE_TEMPLATES_PATH

speciﬁed. In addition to these control keys, there are many variables (see

psnid.car

) to control the

detailed behavior of the classiﬁcation algorithm.

The multi-CPU distribution script (

split_and_fit.pl

; see §12.4.1) can be used in the same manner

as for

snlc_fit.exe

by simply specifying an additional key

JOBNAME_LCFIT: psnid.exe

at the top of the namelist ﬁle.

120

8.1.1 Preparing Photometric Templates for

psnid.exe

SN templates for both Ia and

NONIASED

are prepared with standard sim-input ﬁles. The script

$SNANA_DIR/util/sim_SNgrid.pl

is convenient for processing multiple sim-jobs and organizing the output. See top of script for usage

instructions.

The simulation input ﬁle (for

snlc_sim.exe

) is the same as for a normal simulation job, but with the

following additional keys:

GENSOURCE: GRID # make sure to remove RANDOM GENSOURCE

NGRID_LOGZ: 50 # logarithmic redshift bins

NGRID_SHAPEPAR: 10 # Delta or x1 or dm15 ...

NGRID_COLORPAR: 2 # AV or color

NGRID_COLORLAW: 1 # RV or Beta

NGRID_TREST: 56 # GENRANGE_TREST

GRID_FORMAT: FITS # TEXT or FITS

The standard

GENRANGE_XXX

keys give the range for each parameter.

8.1.2 Redshift Priors for

psnid.exe

There are three choices for a redshift prior in psnid using the

&PSNIDINP

namelist parameter

OPT_ZPRIOR

OPT_ZPRIOR data header

Value prior keyname

------------------------------------------------

0 flat/default ---

1 best/spectro REDSHIFT_FINAL

2 host photo-z HOSTGAL_PHOTOZ

where the above table shows which redshift key from the data header is used. Note that

REDSHIFT_FINAL

should correspond to the best available redshift, usually a spectroscopic redshift of either the SN or

the host. However, if only a host photo-z is available then

REDSHIFT_FINAL = HOSTGAL_PHOTOZ

and

OPT_ZPRIOR

values of 1 and 2 will give the same result. For

OPT_ZPRIOR=1

you can select the redshift

precision with namelist variable “

CUTWIN_ZERR= zmin,zmax

.”

The photo-z result implicitly assumes that the redshift prior information is independent of the SN light

curve. Thus beware when setting

REDSHIFT_FINAL

to the SN photo-z; in this case setting

OPT_ZPRIOR=1

results in a photo-z that is strongly correlated with the input [SN] redshift, and hence the photo-z error is

likely to be underestimated.

121

8.1.3 Rate Priors for

psnid.exe

By default there is a ﬂat rate prior such that the evidence is exp−χ2

i/2, where χ2

iis the best-ﬁt chi-squared

for the i’th template (SNIa or SNCC). A rate prior can be used to compute the evidence as Wi×exp−χ2

i/2,

where Wiis the relative rate. The rate prior options can be deﬁned in the

&PSNIDINP

namelist as

OPT_RATEPRIOR = 1 ! default is 0 (OFF)

ZRATEPRIOR_SNIA = 2.6E-5, 2.2, 1.0 ! alpha, beta, Zmax (default)

ZRATEPRIOR_NONIA = 6.8E-5, 3.6, 2.0 ! alpha, beta, Zmax (default)

where

ZRATEPRIOR_XXX

deﬁne the redshift-dependent rate model as

R(z) = α(1+z′)β(27)

with z′=zfor z<Zmax and z′=Zmax for z>Zmax. The Zmax option allows giving a ﬂat rate at high

redshift where the rate-uncertainty is large. In general one needs to specify only

OPT_RATEPRIOR=1

since

the default

ZRATEPRIOR_XXX

parameters are reasonable.

For SNIa, Wi=R(z). For SNCC we have Wi=R(z)×fi, where fiis the NONIA fraction (i.e., weight)

deﬁned in the sim-input ﬁle used to generate the GRID. The fiare internally renormalized so that ∑ifi=1.

122

8.2 Nearest Neighbor Method

This method follows that used in [13]. For this discussion we consider SN classiﬁcation based on nearest-

neighbor (NN) distances deﬁned by redshift (z), color (c) and shape (s), where cand sare ﬁtted parameters

from

snlc_fit.exe

. However, parameters from any light curve ﬁtting program (e.g.,

psnid.exe

) can be

used. The NN distance (di) between a SN from the data (real or mock) and the i’th SN in the simulated

training sample is

i=(z−zi)2

∆z2

max

+(c−ci)2

∆c2

max

+(s−si)2

∆s2

max

(28)

where ∆zmax,∆cmax,∆smax are parameters optimized in the NN-training process described below. We

count neighbors in the training set as the number of SN with di<1; hence the ∆max parameters are the

maximum allowed deviations to be included as a neighbor.

The simulation-based training procedure can be executed with

$SNANA_DIR/util/NEARNBR_pipeline.pl

and the input-ﬁle instructions are given at the top of this perl script. This script executes 5 serial stages:

1) simulate two large MC samples, REF and TRAIN, 2) ﬁt the MC-REF sample, 3) ﬁt and train us-

ing the MC-TRAIN sample, 4) determine optimal NN parameters (∆zmax,∆cmax,∆smax) to maximize

purity×efﬁciency. 5) apply training to data and simulation. While the

NEARNBR_pipeline.pl

script exe-

cutes all of these stages, it may be useful to run the steps manually at least once to better understand the

procedure. These ﬁve steps are described below in more detail:

1. Generate TWO large simulated samples, each including a mix of SNIa and SNCC. Use best esti-

mates of redshift-dependent rates to get the correct CC/Ia ratio. One simulation serves as the training

sample, while the other serves as a mock data sample. In principle one simulated sample could serve

both purposes, but using two independent samples avoids odd statistical artifacts.

2. Run ﬁtting program on the simulated training sample, and save the output asci/

FITRES

ﬁle. If using

split_and_fit

on multiple simulated versions, the key “COMBINE_ALL_FLAG: 1” is useful to

catenate all of the ascii/ﬁtres ﬁles.

3. Run ﬁtting program on simulated mock data sample with the following snana namelist,

&NNINP

NEARNBR_TRAINFILE_PATH = ’path’

NEARNBR_TRAINFILE_LIST = ’ascii/fitres file from previous step’

NEARNBR_SEPMAX_VARDEF =

’z .005 .14 .005 c .02 .30 .01 x1 .30 .80 .02’

NEARNBR_TRUETYPE_VARNAME = ’SIM_TYPE_INDEX’

!NEARNBR_SEPMAX_IGNORE = ’z x1’ ! optional disable list

&END

Note that

NEARNBR_SEPMAX_VARDEF

speciﬁes a 3-dimensional grid of ∆zmax,∆cmax,∆smax. For ex-

ample, ∆cmax runs from 0.02 to 0.30 with a bin-size of 0.01. The total number of bins in the

above example is 27 ×28 ×25 =18,900. Be careful not to deﬁne outrageously large grids that

cause memory problems. Either

HFILE_OUT

and/or

ROOTFILE_OUT

is required to deﬁne an out-

put hbook and/or root ﬁle. The

NNINP

namelist turns on special NN tables needed to optimize the

123

∆max parameters. See

sntools_nearnbr.c[h]

for more details. SEPMAX variables can be dis-

abled with

NEARNBR_SEPMAX_IGNORE

. This disable feature is convenient for using the batch script

split_and_fit

to run multiple trainings with different size

VARDEF

lists; specify the complete list

NEARNBR_SEPMAX_VARDEF

and then use the command-line override

NEARNBR_SEPMAX_IGNORE

to disable one or more variables. In the above example, z and x1 would be disabled leaving only 1

variable (c) for training. In addition to redshift, color and shape parameters, rest-frame peak-mags

(§5.19) can also be speciﬁed in

NEARNBR_SEPMAX_VARDEF

; e.g., ’

M0_B .3 0.8 0.05

’.

4. Use output tables from previous step to maximum the Figure-of-Merit deﬁned by

FoM =Efﬁciency×Purity =NIa−tag

true

NIa

all ×NIa−tag

true

NIa−tag

true +WfalseNfalse

(29)

where NIa−tag

true is the number of correctly classiﬁed SNIa, and Nfalse if the number of incorrectly

classiﬁed SNIa. This optimization is done with the snana program

nearnbr_maxFoM.exe <HFILE_OUT argument from previous stage>

nearnbr_maxFoM.exe <ROOTFILE_OUT argument from previous stage>

You will get a screen dump showing the optimzed ∆max values, each with a Wfalse grid of 1,3,5.

A classiﬁed SNIa from the mock data sample requires that a majority of nearest neighbors (with

di<1) in the training sample are true SNIa. To avoid statistical problems with few neighbors, the

SNIa-fraction must be 1σabove 50%. For example, 3 SNIa among a total of 5 neighbors has a

majority-signiﬁcance of (0.6−0.5)/(√3/5) = 0.3σ; this is below the 1σrequirement and is hence

ﬂagged as “unclassiﬁed.” Generating larger training samples reduces the number of unclassiﬁed

SNe.

5. To apply the trained ∆zmax,∆cmax,∆smax values on data, use the same

NNINP

namelist above, but

input the trained values as follows,

NEARNBR_SEPMAX_VARDEF = ’z .10 c 0.13 x1 0.62’

The output ntuple/tree will include the following variables:

NN_ITYPE ! best integer type (corresponding to SIM_ITYPE_INDEX)

NN_NCELL ! number or training SN in cell with d_i < 1

NN_PROB_IA ! Type Ia fraction in cell

NN_PROB_II ! Type II fraction in cell

NN_PROB_IBC ! Type Ibc fraction in cell

124

9 Light Curve Models

Here we discuss the available light curve models classes for the simulation and light-curve ﬁtting program.

This is brief a technical discussion on how to use the models in

SNANA

; a reference for each model is

provided for more details. While each model class described below can be used for simulations, only

the semi-analytic SNIa models can be used for light-curve ﬁtting with the

snlc_fit.exe

program; these

ﬁtting models (

MLCS2k2

,SALT-II,

SNooPy

) include

&FITINP

namelist information in addition to sim-input

keys. Simulated output data from any model class can be ﬁt with the

snlc_fit.exe

program.

GENMODEL

speciﬁcation is based on a directory path (class=SALT-II,

SIMSED

NONIASED

BYOSED

) or a

ﬁle (class=

NONIAGRID

LCLIB

). Examples are

# models based on directory: model class name is between slash and dot

GENMODEL: [PATH]/SALT2.JLA-B14 # this is a dir, not file name

GENMODEL: [PATH]/SIMSED.SNII-MOSFIT

GENMODEL: [PATH]/NONIASED.UV2IR

GENMODEL: [PATH]/BYOSED.TEST

GENMODEL: BYOSED [AnyPathName] # option without PATH name restriction

# models based on file; no restriction on PATH or fileName

GENMODEL: LCLIB [PATH]/fileName

GENMODEL: NONIAGRID [PATH]/fileName

An environement variable can be used as part of the

[PATH]

; e.g.,

GENMODEL: $DES_ROOT/models/SIMSED.TEST

Note that the model class must be speciﬁed between the last slash and a dot so that both class the path are

parsed from a single argument. The

BYOSED

class has an option to remove path-name restriction as shown

above.

Many model parameters are described by Gaussian or asymmetric Gaussian distributions. For param-

eter “XXX” the following input keys specify the distribution:

GENPEAK_XXX: <PEAK> (or legacy key GENMEAN_XXX)

GENRANGE_XXX: <MIN> <MAX>

GENSIGMA_XXX: <SIGNEG> <SIGPOS>

GENSKEW_XXX: <SKEW>

The

GENRANGE

values truncate the distribution. The

GENSIGMA

key has two values to specify an asymmetric

(or symmetric) Gaussian distribution.

GENSKEW

is used to deﬁne a value-dependent sigma, σ→σ×

|skew ×(x−Peak)|, where the sign of

GENSKEW

determine which side of the peak to add the longer tail.

GENSKEW

typically results in a larger tail compared with an asymmetric Gaussian.

125

9.1

MLCS2k2

Reference: Jha, Riess, Kirshner, AJ 659, 122 (2007).

Simulation input keys for

snlc_sim.exe

GENPEAK_DELTA: xxx # shape parameter

GENRANGE_DELTA: xxx xxx

GENSIGMA_DELTA: xxx xxx

GENPEAK_RV: xxx # CCM89 dust parameter

GENRANGE_RV: xxx xxx

GENSIGMA_RV: xxx xxx

GENRANGE_AV: xxx xxx # CCM89 V-band extinction

GENTAU_AV: xxx # dN/dAV = exp(-AV/xxx)

GENSIG_AV: xxx # += Guass(AV,sigma)

GENRATIO_AV0: xxx # Gauss/exp ratio at AV=0

FITINP

namelist variables for

snlc_fit.exe

OPT_SNXT = 1 ! Use CCM89 + ODonnel94 update

SCALE_COVAR = 4.1 ! scale cov matrix

OPT_LANDOLT = 1 ! 1=>transform Bessell90 <=> Landolt with color transf.

! 3=> same for mlcs model & nearby-Landolt mags

OPT_PRIOR_AV = 1 ! 0=> switch off AV prior

NGRID_PDF = 11 ! marginalize NGRID per variable (0 => fit min only)

NSIGMA_PDF = 4 ! initial guess at integration range: +- 4 sigma

OPT_SIMEFF = 1 ! use simulated eff as part of prior

PRIOR_AVEXP = 0.3 ! tau of exponential AV prior

PRIOR_AVRES = 0.005 ! smooth Gauss rolloff for AV<0.

PRIOR_MJDSIG = 10. ! Gauss prior on MJD at peak

INISTP_RV = xxx ! 0 => fix RV to INIVAL_RV

INIVAL_RV = 2.2 !

INISTP_AV = xxx ! 0 => fix AV = INIVAL_AV in fit; else float

INIVAL_AV = xxx

INISTP_SHAPE = xxx ! 0 => fix DELTA to INIVAL_SHAPE; else float

INIVAL_SHAPE = xxx

PRIOR_DELTA_PROFILE = xxx, xxx, xxx, xxx ! grep snlc_fit.car for details

126

9.2 SALT-II

Reference: J. Guy et al., A&A 466, 11 (2007).

Simulation input keys for

snlc_sim.exe

GENPEAK_SALT2x1: xxx ! peak PDF for shape parameter

GENSIGMA_SALT2x1: xxx xxx ! sigma-lo and sigma-hi

GENRANGE_SALT2x1: xxx xxx ! generation range

GENPROB2_SALT2x1: xxx ! optional PROB(2nd peak)/All

GENPEAK2_SALT2x1: xxx ! optional 2nd peak PDF

GENSIGMA2_SALT2x1: xxx xxx ! optional sigmas

GENPEAK_SALT2c: xxx ! peak PDF for color parameter

GENRANGE_SALT2c: xxx xxx

GENSIGMA_SALT2c: xxx xxx

# mag = mB* + alpha*x1 - beta*color

GENPEAK_SALT2BETA: 3.2 ! color coeff

GENSIGMA_SALT2BETA: 0 0 ! default is no beta smearing

GENRANGE_SALT2BETA: 0 5 ! restrict if SIGMA is non-zero

SALT2BETA_cPOLY: b0 b1 b2 ! 2nd order poly of c; overrides GENPEAK_SALT2BETA

GENPEAK_SALT2ALPHA: 0.14 ! x1 coeff

GENSIGMA_SALT2ALPHA: 0 0.0 ! default is no alpha smearing

GENRANGE_SALT2ALPHA: 0 0.3 ! restrict if SIGMA is non-zero

SALT2mu_FILE: XXX.FITRES ! use alpha,beta from this SALT2mu output

FITINP

namelist variables for

snlc_fit.exe

SALT2alpha = xxx ! used only to compute mu - muref

SALT2beta = xxx ! idem

INISTP_COLOR = xxx ! 0 => fix color to INIVAL_COLOR; else float

INIVAL_COLOR = xxx

INISTP_SHAPE = xxx ! 0 => fix x1 to INIVAL_SHAPE; else float

INIVAL_SHAPE = xxx

PRIOR_MJDSIG = xxx ! Gaussian prior on MJD at peak

PRIOR_SHAPE_RANGE = xxx, xxx ! flat prior on x1 (prevents crazy values)

PRIOR_SHAPE_SIGMA = xxx ! Gauss rolloff at edges of flat prior

SALT2_DICTFILE = ’xyz’ ! output formatted for original hubblefit

OPT_COVAR = 0 ! 0 => COV-diag only

! 1 => COV fixed during fit

! 2 => COV re-calculated for each chi2 in fit

127

Note that the

INISTP_XXX

and

INIVAL_XXX

parameters are speciﬁed only to ﬁx these parameters in the

ﬁt. If not speciﬁed, these parameters are ﬂoated in the ﬁt.

9.3

SNooPy

Reference: C. Burns et al., arXiv:1010.4040.

Simulation input keys for

snlc_sim.exe

GENPEAK_DM15: xxx # shape parameter

GENRANGE_DM15: xxx xxx

GENSIGMA_DM15: xxx xxx

GENPEAK_RV: xxx # CCM89 dust parameter

GENRANGE_RV: xxx xxx

GENSIGMA_RV: xxx xxx

GENRANGE_AV: xxx xxx # CCM89 V-band extinction

GENTAU_AV: xxx # dN/dAV = exp(-AV/xxx)

GENSIG_AV: xxx # += Guass(AV,sigma)

GENRATIO_AV0: xxx # Gauss/exp ratio at AV=0

FITINP

namelist variables for

snlc_fit.exe

OPT_PRIOR_AV = 1 ! 0=> switch off AV prior

NGRID_PDF = 11 ! marginalize NGRID per variable (0 => fit min only)

NSIGMA_PDF = 4 ! initial guess at integration range: +- 4 sigma

OPT_SIMEFF = 1 ! use simulated eff as part of prior

PRIOR_AVEXP = 0.3 ! tau of exponential AV prior

PRIOR_AVRES = 0.005 ! smooth Gauss rolloff for AV<0.

PRIOR_MJDSIG = 10. ! Gauss prior on MJD at peak

PRIOR_SHAPE_RANGE = 0.7, 2.0 ! constrain DM15 in this range

PRIOR_SHAPE_SIGMA = 0.7, 2.0 ! Gauss roll-off sigma for DM15 prior

INISTP_RV = xxx ! 0 => fix RV to INIVAL_RV

INIVAL_RV = 2.2 !

INISTP_AV = xxx ! 0 => fix AV = INIVAL_AV in fit; else float

INIVAL_AV = xxx

INISTP_SHAPE = xxx ! 0 => fix DELTA to INIVAL_SHAPE; else float

INIVAL_SHAPE = xxx

Without a tuned ATLAS library (for gsl), the

SNooPy

generator is very slow such that a single light curve

ﬁts takes several minutes. To speed up the generator, the

SNooPy

model can be parameterized on a three-

dimensional grid (ﬁlter, epoch, ∆M15) using the GRID option from §4.34. This grid is speciﬁed by the

GRIDFILE

keyword in the

SNooPY.INFO

ﬁle that resides in the same directory as the model templates; both

the simulation and ﬁtter interpolate the GRID for each set of parameters. Also note that

SNooPy

returns a

relative ﬂux normalized to one at peak; the conversion to absolute magnitude is given for each ﬁlter in the

SNooPY.INFO

ﬁle.

128

9.4

SIMSED

model is a ensemble of SED time series, where the ensemble spans an arbitrary set of parameters

characterizing the object.

SIMSED

models can be derived from specialized explosion-model codes (e.g.,

FLASH, Sedona, Pheonix), or determined from high-resolution spectroscopic data. Currently the

SIMSED

model is implemented only in the

SNANA

simulation. These simulated models can be ﬁt with

SNANA

ﬁtting codes (

snlc_fit.exe, psnid.exe

), but

SNANA

does not include programs to explicitly ﬁt with

the

SIMSED

model. A few examples in the pulic

SNDATA_ROOT

are here,

$SNDATA_ROOT/models/SIMSED/SIMSED.SNANA_tester # GCD explosion

$SNDATA_ROOT/models/SIMSED/SIMSED.KNovae_BarnesKasen2013 # theory KN

$SNDATA_ROOT/models/SIMSED/SIMSED.GW170817_AT2017gfo # GW170817 KN

Each directory above includes an “

SED.INFO

” ﬁle listing each SED and the corresponding parameters.

The only limit to the number of parameters (and SEDs) is the amount of memory on your computer. An

example of an

SED.INFO

ﬁle is as follows:

# optional keys:

FLUX_SCALE: 1.000 # global flux scale (e.g., to fix units)

RESTLAMBDA_RANGE: 2500 15000 # valid range of <lamObs>/(1+z)

OPTFLAG_T0SHIFT_PEAKMAG: 0 # do NOT time-shift PEAKMAG to DAY=0

# required keys

NPAR: 5

PARNAMES: MNI COSANGLE MBSED DM15SED TEXPL

SED: GCD2D_Ni0.47_Pre80_1.SED 0.47 -0.967 -18.350 0.571 -21.628

SED: GCD2D_Ni0.47_Pre80_8.SED 0.47 -0.500 -18.413 0.574 -20.977

SED: GCD2D_Ni0.47_Pre80_1.SED 0.47 -0.033 -18.426 0.654 -21.398

SED: GCD2D_Ni0.47_Pre80_2.SED 0.47 +0.500 -18.400 0.767 -21.385

etc ...

Users prepare the

SED.INFO

ﬁle, along with each SED time-series ﬁle with format

epoch(days) wavelength(A) flux(erg/cm^2/s/A) .

If the ﬂuxes have incorrect units, the

FLUX_SCALE

key can be used to make a global unit conversion. For

each SED, there is a default internal time-shift applied such that the bolometric ﬂux is maximum at T=0,

and this rest-frame epoch corresponds to

PEAKMJD

in the data header.

In cases where the explosion time is well deﬁned (e.g., triggered event from LIGO or ICECUBE), it

may be useful to leave the original T=0 deﬁnition in each SED ﬁle by specifying

OPTFLAG_T0SHIFT_PEAKMAG: 0 # do NOT shift PEAKMAG to T=0

in the

SED.INFO

ﬁle. With this option, beware that input

GENRANGE_PEAKMJD

and output

PEAKMJD

corre-

spond to the explosion time, not the time of maximum brightness.

The ﬁrst two parameters (

MNI

and

COSANGLE

) are the physical parameters for generation; the remaining

three baggage parameters (see below) depend on the ﬁrst two and they are inertly passed along to the

output tables, just as a small pebble in your food is passed through the digestive system.

129

To simulate a

SIMSED

model, the distribution for each physical parameter must be speciﬁed in the

sim-input ﬁle as follows,

SIMSED_PARAM: MNI # mass of Ni56

GENPEAK_MNI: 0.9 # mean of bifurcated Gaussian

GENRANGE_MNI: 0.47 1.26 # generation range

GENSIGMA_MNI: 0.4 0.25 # bifurcated Gaussian

SIMSED_GRIDONLY: COSANGLE # cosine of viewing angle

GENPEAK_COSANGLE: 0

GENRANGE_COSANGLE: -0.96 0.96

GENSIGMA_COSANGLE: 1.E7 1.E7 # large sigmas => flat distribution

SIMSED_REDCOR(MNI,COSANGLE): -0.26 # optional reduced covar; -1 to +1

SIMSED_COV(MNI,COSANGLE): -1.34 # optional covar

SIMSED_PATH_BINARY: <path for flux-table binary file>

Specify only those parameters that are used in the generation. For the

SIMSED_PARAM

keyword (

MNI

), the

simulation will interpolate magnitudes as a function of the explosion-model parameter, resulting in a con-

tinuous distribution of the speciﬁed bifurcated Gaussian. For the

SIMSED_GRIDONLY

keyword (

COSANGLE

only values at the grid nodes are generated, and the speciﬁed bi-Gaussian distribution is respected; each

randomly chosen parameter is ’snapped’ to the nearest grid value. This

GRIDONLY

option may be use-

ful in cases such as a ﬂag that speciﬁes a random ignition point, and therefore continuous interpolation

makes no sense. To simulate a ﬂat-random distribution, set the

GENSIGMA_XXX

values ≥107. Un-speciﬁed

parameters are treated as “baggage”parameters. These parameters are ignored in the generation, but the

interpolated values are computed and stored along with the other parameters.

A correlation between any pair of parameters can be introduced with either a reduced correlation key

(

SIMSED_REDCOR

) or a covariance key (

SIMSED_COV

). Default correlatios are all zero, and correlations

are allowed only for symmetric Gaussian proﬁles. If correlations between more than 2 parameters are

speciﬁed, the full off-diagonal correlation must be speciﬁed, noting that

GENSIGMA_XXX

deﬁne the diagonal

covariances. For example, correlations between 3 parameters require 3 correlation keys; correlations

between 4 parameters require 6 correlation keys.

To step through each grid-value sequentially,

SIMSED_GRIDONLY: SEQUENTIAL # sequential generation of grid values

and there is no need to specify parameter names or their distributions. The ﬁrst generated SN uses the ﬁrst

SED on the grid, the second SN uses the second value, etc. The number of generated SNe is internally set

to be the number of SEDs.

All SIMSED parameters (“baggage” and for generation) are automatically included in the output ta-

ble(s) and in the

SIMGEN_DUMP

list (§4.32.3). If you specify a SIMSED parameter in the

SIMGEN_DUMP

list

the simulation will abort because of a redundant parameter.

A binary ﬂux-table (see below) is created in your current directory by default. Since these binary ﬁles

can be quite large, a separate binary-table directory can be speciﬁed with the

SIMSED_PATH_BINARY

key

(see above).

130

There are two internal binary ﬁles to speed up the initialization. In principle this all works behind the

scenes, but it is explained here in case there are problems. The initialization takes about 1 second per

SED, and will be rather annoying if/when there are 100’s or 1000’s of SEDs to initialize. About half the

time is reading the SED text ﬁles, and the other half is spent doing all the ﬂux-integrals as a function of

passband, redshift, Trest, and SED surface. The ﬁrst time that a new

SIMSED

version is simulated, the

initialization will be slow, but two binary ﬁles are created to speed up future runs. The ﬁrst binary ﬁle

contains the SEDs (

SED.BINARY

), and it is stored in the same version (

VVV

) directory as the SED text ﬁles,

SNDATA_ROOT/models/SIMSED/VVV

. This

SED.BINARY

ﬁle will be automatically used by any

SNANA

user who speciﬁes the

VVV

version.

The second binary ﬁle is the ﬁlter-speciﬁc ﬂux-integral table, and this ﬁle is stored either in your lo-

cal directory (default) or the directory speciﬁed by

SIMSED_PATH_BINARY

. The reason for storing in a

user-speciﬁed directory is that the ﬂux integrals depend on the survey and ﬁlters, and therefore this ﬁle is

speciﬁc to your analysis. The validity of each binary ﬁle is veriﬁed internally; if there is an inconsistency

between the two binary ﬁles and/or the requested survey parameters, the simulation will abort and recom-

mend removing the old binary ﬁle(s) so that new ones can be created. A similar abort will occur if the

user’s binary ﬂux-integral table has a time-stamp that is earlier than the SIMSED model or earlier than the

K-cor ﬁle used to deﬁne the primary reference and ﬁlter transmissions.

If you are having problems with the binary ﬁles and just want to use the text ﬁles, the use of binary

ﬁles can be switched off with

snlc_sim.exe mysim.input SIMSED_USE_BINARY 0

131

9.5

NONIASED

While the Type Ia light curve models are based on a parametric equation or photometric templates, the

“

NONIASED

” models are based on smoothed light curves and spectral templates. A spectral template cor-

responds to a particular (well-observed) SN where a composite spectrum is warped to match the observed

photometry. In addition to non-Ia SNe, this feature can be used to simulate peculiar Ia, theoretical models,

AGN, or any transient object.

The observer-frame “

NONIASED

” model assumes that each rest-frame SED has been warped to match

the photometry of the underlying light curve. The observer-frame magnitudes are computed directly from

the SED the same way as for SALT2, and in fact using the same software tools. The

KCOR_FILE

key

is needed to read in the ﬁlters and primary reference. Optional host-galaxy extinction (from RVand

AV) is computed at ¯

λobs/(1+z), where ¯

λobs is the central wavelength of each ﬁlter; this approximation

is numerically accurate to about 0.01 mag. The distribution of RVand AVis controlled by the same

parameters as for

MLCS2k2

in §9.1.

A list of available

NONIASED

templates is given in

$SNDATA_ROOT/snsed/NON1A/NON1A.LIST

As explained below, the user selects

NONIASED

templates using the integer indices in the NON1A.LIST

ﬁle. As more

NONIASED

templates become available, the

NON1A.LIST

ﬁle will be updated by the relevant

experts. The

NONIASED

model is speciﬁed with the following sim-input keys,

NGENTOT_LC: 1000

GENMODEL: NON1ASED # or NON1A or NONIA or NONIASED

PATH_NON1ASED: <path> # optional: default is $SNDATA_ROOT/snsed/NON1A

GENMODEL: $PATH/NON1ASED.[XYZ]

NON1ASED_KEYS: 5 INDEX WGT MAGOFF MAGSMEAR SNTYPE

NON1ASED: 2 0.2 0.0 1.2 2

NON1ASED: 3 0.2 -0.2 0.8 2

NON1ASED: 4 0.4 -0.6 0.9 3

etc ...

GENRANGE_AV: xxx xxx # CCM89 V-band extinction

GENTAU_AV: xxx # dN/dAV = exp(-AV/xxx)

GENSIG_AV: xxx # += Guass(AV,sigma)

GENRATIO_AV0: xxx # Gauss/exp ratio at AV=0

There are two ways to specify model location. First is to specify a private

$PATH

and

GENMODEL

separately.

Second is to include path in the

GENMODEL

key. The latter option may be more convenient because it deﬁnes

path and model in one key, but the sub-directory name must be of the form “NON1ASED.[XYZ]” where

XYZ is an arbitrary sufﬁx.

Following the model speciﬁcation, each SED template gets an aribtrary weight (for rate), mag-offset

(

MAGOFF

), and Gaussian mag-smear (

MAGSMEAR

). The legacy keys “

NON1A

” and “

NON1A_KEYS

” have the

same meaning as

NON1ASED

and

NON1ASED_KEYS

,” respectively. Inside each generated light curve ﬁle,

the

NONIASED INDEX

is speciﬁed by “

SIM_TEMPLATE_INDEX: INDEX

”; the corresponding

SNANA

variable

132

SIM_TEMPLATE_INDEX

, and the ﬁtres-table variable is “

SIM_TEMPLATE_INDEX

.” The default

NONIASED

ﬁles are located in two locations

$SNDATA_ROOT/snsed/NON1A # older legacy path

$SNDATA_ROOT/models/NON1ASED/NON1ASED.* # current path

and it is recommended to use the current default paths. Each

NON1ASED.XYZ

directory contains a

NON1A.LIST

ﬁle, and also a default SIMGEN_INCLUDE_NON1A.INPUT ﬁle that lists each NON1ASED. You can

include this ﬁle as-is using the

INPUT_FILE_INCLUDE

key, or copy it locally and make modiﬁcations.

The

NON1ASED_KEYS

are used to specify additional parameters that depend on

NONIASED

type.

•INDEX is the index in the

NON1A.LIST

ﬁle.

•WGT are the relative rates. Since the weights are re-normalized to sum to unity, the ﬁrst 1/4 of the

generated SNe will use

INDEX

=2, the second 1/4 will use

INDEX

=3, and the latter 1/2 will use

INDEX

=4. The keyword

NGENTOT_LC

speciﬁes the total number to generate, which is different from

NGEN_LC

that speciﬁes the number passing trigger & cuts and that are written out to SNDATA ﬁles.

The relative

WGT

factors make physical sense only if

NGENTOT_LC

is used to specify the statistics.

•MAGOFF is a global magnitude offset applied to all passbands (i.e, equivalent to the

GENMAG_OFF_MODEL

keyword), and is used to adjust the average brightness of each

NONIASED

type.

For SEDs that are normalized to have a peak mag of zero (i.e., the Nugent templates) rather than to

physical units (erg/s/Å/cm2),

MAGOFF

must be used for the

NONIA

option to get meaningful results.

•MAGSMEAR is a Gaussian σfor global coherent magnitude ﬂuctuations (i.e, equivalent to

GENMAG_SMEAR

for SNIa), and is used to simulate intrinsic brightness variations. The generated

random value is stored in the data ﬁle (

SIM_MAGSMEAR_COH

key) and in the SNTABLEs.

•SNTYPE is a spec-conﬁrmed typing-index that appears after the

SNTYPE

keyword in the SNDATA

ﬁles (see §4.4 for SNTYPE details). In the above example,

NONIASED

indices 2 & 3 are both type

II SNe, so they both get

SNTYPE=2

NONIASED

index 3 is a different SN type, so it gets a different

SNTYPE

value.

SNe with the same

INDEX

are generated sequentially, and then the next

INDEX

is generated; i.e., the

NONIASED

indices are NOT randomly mixed. The sequential generation by

INDEX

is done for speed,

and avoids re-initializing templates multiple times. It is therefore crucial to analyze the entire simulated

sample in order to have the correct mixture of

NONIASED

types. While the

NONIASED

indices are processed

sequentially, random SNIDs can be assigned as described in §4.31. With random SNIDs, any subset of

the simulation is a truly random subset.

9.5.1 Peculiar SNIa

Peculiar SNIa (e.g., 91bg, 91T, Iax) are simulated the same way as NON1A, with an important caveat:

the rate-vs-redshift for peculiar Ia is different than for NON1A (core collapse). There are three input

modiﬁcations for peculiar Ia:

1. In the sim-input ﬁle, the ‘

NON1ASED:

’ keys are replaced with ‘

PEC1ASED:

’ (or ‘

PEC1A:

’)

2. In the

NON1A.LIST

ﬁle, the ‘

NON1A:

’ keys are replaced with ‘

PEC1A:

’ keys.

3. In the sim-input ﬁle, the rate-vs-redshift model for peculiar-Ia is deﬁned with the ‘

DNDZ_PEC1A:

’

key. The arguments following this key have the same meaning as the arguments following the

‘

DNDZ:

’ key (§4.21) which deﬁnes the NON1A rate model.

133

9.6

NON1AGRID

This is a model of pre-computed observer-frame magnitudes on a grid of redshift, rest-frame epoch, and

template index. Compared to the

NON1ASED

model, the advantages of the

NON1AGRID

model are 1) the

input grid can be created by non-

SNANA

codes using more sophisticated models, and 2) the

NON1A

index

is randonly picked for each event, instead of the sequential selection for

NON1ASED

. The syntax for this

model is

GENMODEL: NON1AGRID <GRIDFILENAME>

where

GRIDFILENAME

can reside either in your current working directory, include a full path, or reside

under

$SNDATA_ROOT/models/NON1AGRID

An input GRID ﬁle can be made from the

NON1ASED

model as described in §4.34; simply remove the SNIa

model keys and add the

NON1A

keys from §9.5. The

MAGOFF

values are included in the mag calculations,

but

MAGSMEAR

is not. When using the

NON1AGRID

model, the

MAGSMEAR

values are applied with a Gaussian

random number per event.

9.7

FIXMAG

and

RANMAG

These ﬂat-lightcurve models are not intended to reﬂect an astrophysical transient, but are instead intended

for debugging or generating fake magnitudes to overlay on images. Examples are as follows:

GENMODEL: FIXMAG 20

GENMODEL: FIXMAG 20:24

GENMODEL: RANMAG 20:24

In the ﬁrst case, all observer-frame magnitudes are 20. The 2nd and 3rd cases are identical. The observer-

frame mag for each event is randomly selected between 20 and 24; the same mag is used at all epochs,

but a different random mag is chosen for each event. The range of ﬁxed-mag epochs is determined by the

sim-input key

GENRANGE_TREST

9.8

LCLIB

: Galactic Transients

9.8.1 Overview

Galactic transient models include three general classes:

1. RECURRING-NONPERIODIC (e..g, AGN)

2. RECURRING-PERIDODIC (e.g., RRlyrae)

3. NON-RECURRING (e.g., micro-lens)

These models are simulated using a TEXT-ﬁle library and a list of template epochs speciﬁed in the sim-

input ﬁle as

GENMODEL: LCLIB MYMODEL.TEXT 1+2+3+4

LCLIB

(Light Curve LIBrary) is the generic model type in

SNANA

MYMODEL.TEXT

is the text-ﬁle library

(Fig 9) and

1+2+3+4

is a list of relative epochs to average for the template magnitude.

134

9.8.2 Deﬁning the Library

The TEXT library begins with a global header specifying the name of the SURVEY, and a list of broadband

FILTERS. Since there is no redshifting, these

LCLIB

models are deﬁned as pre-computed light curves

(broadband magnitudes vs. time), and not as an SED time series. The SURVEY & FILTERS in the header

are compared against the user-request to prevent accidental mixing (e..g, cannot use an LSST library

to simulate DES). The global header also includes a model name and list of model parameters names

(

MODEL_PARNAMES

), for which ﬂoating-point (or integer) values are given for each

LCLIB

event. These

model parameters are not used by the simulation, but they are written into the output data ﬁles to be used

in ofﬂine analyses. A series of comment ﬁelds should be used to provide model references and to deﬁne the

model parameters. An optional key

NEVENT

is used to re-use each event a total of

NUSE=NGENTOT/NEVENT

times in order to reduce read-time. Without the

NEVENT

key, the simulation would wrap around the library

NUSE

times, and waste time reading each event multiple times. Finally, the

RECUR_CLASS

key speciﬁes

which of the three Galactic transient classes.

After the global header there is a list of

LCLIB

“events,” where each event includes an event header

followed by a light curve in all ﬁlters. The event header contains the following information: 1) event ID

(for debugging), 2) number of rows for the light curve, including T+S (

NROW

), 3) parameter values after

PARVAL

key, 4) optional coordinate, either RA&DEC or l&b, 5) optional angle-matching radius if event

depends on Galactic coordinates.

Following the header, the light curve rows are deﬁned with the keys “T:" (Template) and “S:" (Search).

The

LCLIB

time steps can be non-uniform, and should be optimized to limit the library size. For example,

the time step should be small during periods of rapid variation, and then increase during periods of slow

change. Also note the recommended precision (%.3f for mags) to reduce ﬁle size.

For each of the three Galactic transient classes above, there are speciﬁc

LCLIB

features that must be

included as described below:

1. Recurring-NonPeriodic events require explicit template (T:) epochs prior to the search (S:) epochs.

The time-span of T-epochs should correspond to how templates are made in the survey, and the S-

range must be at least as long as the survey. If the S-range is longer than the survey time, a random

LCLIB

start-time used. For example, consider a 3 year survey and a 5 year S-range: the simulation

selects a random start-time within the ﬁrst two years of the

LCLIB

event.

2. Recurring-Periodic events require search (S:) epochs covering exactly one cycle. Explicit template

epochs are forbidden in the library because the simulation internally computes template epochs using

the periodicity. The ﬁrst and last S-epoch must have identical magnitudes, otherwise the simulation

aborts.

3. Non-Recurring events require a single template (T:) epoch since all previous epochs must have the

same quiescent magnitude. For the last S-epoch, the magnitudes should match the template epoch,

indicating that the light curve has ﬁnished.

9.8.3 Implementation

Here are a few details about how the simulation interprets the library deﬁned in §9.8.2. Note that "simu-

lated event" (or generated event) refers to the light curve generated on the survey cadence, while “

LCLIB

event" refers to the library events illustrated in Fig. 9.

For each simulated light curve with duration ∆Tsurvey, the corresponding range of the

LCLIB

event

is extracted and interpolation is used to compute the true mag at each simulated epoch. For recurring-

nonPeriodic, the

LCLIB

event duration must be greater than ∆Tsurvey (if not, sim aborts). For recurring-

135

periodic, the

LCLIB

event cycle is internally repeated until it spans ∆Tsurvey. For non-recurring events that

are shorter than ∆Tsurvey, the undeﬁned epochs are given template magnitudes.

LCLIB

Event Probabilities

Each recurring event is assumed to have the same probability. Non-Recurring events are fundamen-

tally different because any given event has an arbitrary start time. For example, an event with a 1,000

year duration can start any time within the previous 1,000 years and still leave a signal. To describe the

implementation we ﬁrst deﬁne ∆TTot ≡∆Tsurvey +∆Tevt (30)

where ∆Tevt is the

LCLIB

event duration. A key assumption for the library is that the rate per unit time

is the same for each

LCLIB

event, and thus an arbitrary rate of 1 per ∆Tsurvey is assigned. The mean

number of generated events is therefore hNgeni=∆TTot/∆Tsurvey. A Poisson generator picks Ngen and the

LCLIB

event is re-used Ngen times, each time with a different cadence and sky location. For a 3-year

survey (∆Tsurvey =3), a 1 month event (∆Tevt =0.083) results in hNgeni=1.028. For the same survey,

a century-long event (∆Tevt =100) results in hNgeni=34.33. Beware that including

LCLIB

events with

vastly different ∆Tevt values results in very large asymmetries in how many times each

LCLIB

event is

used.

Template Mags

A template magnitude is determined for each simulated event and each band. The last argument after

the

GENMODEL

key (§9.8.1) determines a list of user-requested template epochs to average, and the “T:"

rows in the

LCLIB

are used to interpolate mag values at the user-requested template epochs. Each template

mag is converted to ﬂux, the ﬂux values are averaged, and the average ﬂux is converted back into a

template mag to use for subtraction. Variations in observing conditions are NOT included in template-

mag computation.

For long-duration non-recurring events (∆Tevt ≫∆Tsurvey) that start well before the survey, the true

template mags are not observed. In this case, the event mags a few months prior to the survey are used to

compute the template mags. For short-duration non-recurring events (∆Tevt ≪∆Tsurvey), the true template

mag is used. For intermediate cases (∆Tevt ∼∆Tsurvey), the true template mag is used if the event starts after

the survey begins; otherwise the template is computed from light curve mags shortly before the survey.

Angle Matching

The optional

ANGLEMATCH

ANGLEMATCH_b

key in the event header speciﬁes how close the simu-

lated sky location must be to the

LCLIB

event. The simulation will keep reading

LCLIB

events until an

angle-match is found. This option allows Galactic event proﬁles to depend on sky location.

ANGLEMATCH

speciﬁes a radius (degrees), while

ANGLEMATCH_b

applies only to Galactic latitude (b), and ignores the

longitude coordinate.

To increase the efﬁciency for ﬁnding an

LCLIB

event satisfying

ANGLEMATCH_b

, a symmetry for events

at −band +bis used to require

where bSIM is for the simulated event and bLCLIB is for the

LCLIB

event.

Parameter Selection

To select a limited range of

PARVAL

values from the library, add the following key(s) to the sim-input

ﬁle:

LCLIB_CUTWIN: <PARNAME> <CUTMIN> <CUTMAX>

Note that this option does not reduce the number of generated events; rather it reduces the

LCLIB

size by

excluding

LCLIB

events.

136

# global header info

SURVEY: LSST

FILTERS: ugrizY

MODEL: MY_MODEL_NAME

MODEL_PARNAMES: PAR1,PAR2,PAR3 # comma-separated strings, no spaces

NEVENT: <NEVENT>

RECUR_CLASS: RECUR-NONPERIODIC (or RECUR-PERIODIC or NON-RECUR)

COMMENT: Created Sep 2017 by xyz, See arXiv:abcde

COMMENT: PAR1 is bla

COMMENT: PAR2 is bla-bla

COMMENT: PAR3 is bla-bla-bla

# info for 1st event

START_EVENT: <ID1> # internal integer ID

NROW: <NROW> RA: <RA> DEC: <DEC>

PARVAL: <VAL1>,<VAL2>,<VAL3> # comma-separated or space-separated

ANGLEMATCH: 10.0 # optional (deg) to match with cadence library

T: <DAY %7.4f> <mag_u %.3f> <mag_g> . . . . <mag_Y>

S: <DAY %7.4f> <mag_u %.3f> <mag_g> . . . . <mag_Y>

END_EVENT: <ID1>

# info for 2nd event

START_EVENT: <ID2> # internal integer ID

NROW: <NROW> RA: <RA> DEC: <DEC>

PARVAL: <VAL1>,<VAL2>,<VAL3> # comma-separated or space-separated

ANGLEMATCH: 10.0 # optional (deg) to match with cadence library

T: <DAY %7.4f> <mag_u %.3f> <mag_g> . . . . <mag_Y>

S: <DAY %7.4f> <mag_u %.3f> <mag_g> . . . . <mag_Y>

END_EVENT: <ID2>

etc É

Figure 9: TEXT-library format for

LCLIB

model type.

137

10 SALT-II Programs

10.1 Computing Distance Moduli from BBC Method:

SALT2mu.exe

The

SNANA

program

SALT2mu.exe

reads SALT-II ﬁtted parameters, performs a global ﬁt for αand β, and

computes distance moduli. The program also implements the “BEAMS with Bias Corrections” (BBC)

method in [14, 15], to produce bias-corrected distances in redshift bins. To include bias corrections,

SALT2mu

reads ﬁt parameters for the data and for a large simulation. A sample input ﬁle is in

$SNDATA_ROOT/sample_input_files/SALT2/SALT2mu.default

and a description of all input-ﬁle options are given at the top of the code in

$SNANA_DIR/src/SALT2mu.c

10.2 SALT-II Training Scripts

Scripts are

&SNANA_DIR/util/SALT2train_*

; more on this later after the paper is submitted.

138

11 Cosmology Fitters

There are currently two cosmology ﬁtters available. First is

wfit.exe

, which ﬁts for wand ΩMassuming

a ﬂat universe. Typing the

wfit.exe

command with no arguments lists the options. The BAO and CMB

priors are currently hard-wired, but a more ﬂexible method to specify priors may be added later. An

example command is as follows,

wfit.exe <fitresFile> -zmin .02 -zerr .001 -snrms .15 -bao -cmb

where the ﬁtres-ﬁle is output from the

SALT2mu.exe

program. The arguments specify using SNe with

z>0.02, adding a peculiar-velocity uncertainty of 300 km/s (i.e, the “

zerr

” arg is vpec/c), adding an

anomalous distance-uncertainty of 0.15 mag (“

snrms

” arg), and using the BAO & CMB priors. Peculiar-

velocity covariances can also be used as explained below in §11.2.

The second program,

sncosmo_mcmc.exe

, is a more general cosmology ﬁtter based on Monte Carlo

Markov chains. This ﬁtter handles more diverse cosmologies such as time-dependent wand non-zero

curvature. Sample inputs ﬁles are in

$SNDATA_ROOT/sample_input_files/sncosmo_mcmc/

Both of these cosmology ﬁtters read self-documented “ﬁtres” ﬁles (§12.1.1) that contain a redshift, dis-

tance modulus and survey index (other parameters in the ﬁtres ﬁle are ignored).

Beware that These cosmology ﬁtters are not state-of-the-art, and are thus useful for rapid testing or

systematics studies.

11.1 Interpreting Redshift Variables in SNANA Tables

The following redshift variables are included in the output tables from the ﬁtting programs

(

snlc_fit.exe, SALT2mu.exe

•

zHEL, zHELERR:

heliocentric redshift.

•

zCMB, zCMBERR:

redshift transformed to CMB

(ℓ=264.14 deg, b=48.26 deg, vapex =371 km/s)

•

VPEC, VPECERR:

peculiar-velocity correction.

If host galaxy is moving away from (toward) Earth, then

VPEC<0

(

VPEC>0

•

zHD, zHDERR

=(1+ZCMB)(1+VPEC)−1.

zHDERR

is the quadrature sum of

zCMBERR

and

(1+zCMB)*VPECERR

This corrected CMB redshift, or “Hubble-diagram” redshift, should be used to compute the lumi-

nosity distance (DL) in cosmology-ﬁtting programs.

To check that

VPEC

is used correctly with simulations, generate a large low-z sample, analyze with

snana.exe

snlc_fit.exe

program, and then verify the following from the

SNANA

FITRES

table:

1) zCMB - SIM_ZCMB distribution has RMS=GENSIGMA_VPEC and mean=0

2) zHD - SIM_ZCMB distribution has RMS=VPEC_ERR and mean=0

where

GENSIGMA_VPEC

and

VPEC_ERR

are sim-input keys deﬁned in §4.28.

139

11.2 Peculiar Velocity Covariances

The

wfit.exe

program has an option to account for peculiar velocity correlations (

SNANA v8_10

and

later). First prepare a ﬁle with the following syntax

COV: SN1 SN2 MUCOVAR(12)

COV: SN1 SN3 MUCOVAR(13)

COV: SN1 SN4 MUCOVAR(14)

etc ...

where

SN#

are the SN names used in the analysis (i.e, that appear in the ﬁtres ﬁle), and

MUCOVAR(ij)

are

the covariances between the distance moduli, with units of mag2. Only off-diagonal terms from this ﬁle

are used; diagonal terms are speciﬁed from the

-zerr

and

-snrms

options. The syntax is

wfit.exe <fitresFile> -mucovar <mucovarFile> <other options>

where “

mucovarFile

” is the name of the ﬁle specifying the off-diagonal covariances. The

wfit.exe

program will ﬁrst check your current directory for this ﬁle; if not there

wfit

will check the public area,

SNDATA_ROOT

models/mucovar/

. The covariances for the nearby sample have been computed by the

authors in [16], and these are available in

$SNDATA_ROOT/models/mucovar/Hui_LOWZ_mucovar.dat

The minimization function is given by χ2=∑i j[∆iV−1

i j ∆j]−B2/C,20 where ∆i≡µdata

i−µmodel

iis the

distance-modulus residual for the i’th SN, V−1

i j is the inverse of the covariance matrix, and the term B2/C

accounts for the analytic marginalization over H0as discussed in Appendix A of [17]. The Band C

parameters are

B=∑

(∆i/σ2

i)−→ ∑

i,j

(∆iV−1

i j )(32)

C=∑

1/σ2

i−→ ∑

i,j

V−1

i j ,(33)

where σiis the diagonal-uncertainty on the distance modulus. The expressions left of the arrows (Eqs. 32-

33) are from [17], while the expressions right of the arrows show the

wfit

implementation that accounts

for the off-diagonal covariance terms. The B2/Cterm is equivalent to re-minimizing with the weighted-

average distance-modulus residual subtracted from each distance-modulus residual; ∆i→∆i−<∆>.

20We leave out the constant term ln(C/2π).

140

12 Miscellaneous Tools and Features

12.1 Analysis-Output: Files, Tables, Variables

For each analysis program (

snana.exe, snlc_fit.exe, psnid.exe

) the output results are stored in

tables. The primary table-ﬁle formats are

ROOT

HBOOK

, which allow writing multiple structures in

parallel and include a plotting interface.

TEXT

-tables are also available for a subset of the variables, and

there is a separate utility (see

sntable_dump

, §12.1.2) to extract information from a

ROOT

HBOOK

ﬁle

and convert into text format. The available output tables are

•SNANA (ID=7100): general variables for all SN before ﬁtting

•FITRES (ID=7788): ﬁt results for SN passing ﬁt requirements. Fit residuals for each epoch can be

optionally included.

•SNLCPAK: used by

mkfitplots.pl

(§5.9) to make light curve plots for data and best-ﬁt model.

The SNANA and FITRES tables are intended to be accessed by users for continued analysis; the table

name is assigned to a “tree” in

ROOT

, while the the integer ID is assigned to an “ ntuple” in

HBOOK

. The

SNLCPAK table is for internal plotting scripts, and is not intended for general use. The user-selection of

format(s) and table(s) is described below.

COMPILATION FLAGS

The

SNANA

codes will compile with

HBOOK

if ENV

$CERN_DIR

is deﬁned, and will compile with

ROOT

if ENV

$ROOT_DIR

is deﬁned. To compile without

HBOOK

ROOT

, make sure that the associated ENV is

not deﬁned. Do not modify any ﬁles to adjust compilation with

HBOOK

ROOT

SELECTING TABLE FORMAT(S)

The output table format is deﬁned by the user in the

&SNLCINP

namelist,

HFILE_OUT = ’myout.hbook’

ROOTFILE_OUT = ’myout.root’

TEXTFILE_PREFIX = ’myout’

Multiple output formats can be speciﬁed, including all 3 as shown above. For the

ROOT

and

HBOOK

formats,

and all tables are written to the

ROOT

and

HBOOK

ﬁle. For the TEXT format, however, each table is written

to a separate ﬁle and thus a ﬁle preﬁx is speciﬁed rather than a ﬁle-name. The corresponding output-ﬁle

names are “

myout.[tableName].TEXT

” where the tableNames are

SNANA

FITRES

and

LCPLOT

.21

SELECTING TABLE(S)

The tables are selected by

&SNLCINP

namelist string

SNTABLE_LIST

with default value

SNTABLE_LIST = ’SNANA FITRES LCPLOT’

which selects all three tables by default. To protect memory and output ﬁle size for large jobs, the number

of light curve plots (

LCPLOT

) is limited by

&SNLCINP

namelist variable

MXLC_PLOT=100

: set to a higher

value to get more plotted light curves.

LCPLOT

corresponds to the

SNLCPAK

table.

141

If a

ROOT

ﬁle is speciﬁed via

&SNLCINP

namelist variable

ROOTFILE_OUT

, then all three tables are

created under the

ROOT

structure. Similarly, all three tables are created under the

HBOOK

structure if

HFILE_OUT

is deﬁned. For TEXT format with

TEXTFILE_PREFIX

, the defaut is different in that only the

ascii-FITRES table is produced for backward-compatibility. To generate text output for the other tables

requires additional speciﬁcations such as

SNTABLE_LIST = ’SNANA(text:key) FITRES(text:key) LCPLOT(text:col)’

SNTABLE_LIST = ’SNANA(text:key) FITRES LCPLOT(text:col)’

where the available text formats are

•key : key before each row, plus keyed header.

•csv : comma-separated with header.

•col : space-separated columns with no header.

The two

SNTABLE_LIST

strings above are equivalent because “

text:key

” is the default text format for

the FITRES table. Also note that the

SNTABLE_LIST

string is case-insensitive and thus the following are

equivalent,

SNTABLE_LIST = ’snana(text:csv) fitres(text:csv) lcplot(text:csv)’

SNTABLE_LIST = ’SNANA(text:csv) FITRES(text:csv) LCPLOT(text:csv)’

SNTABLE_LIST = ’SNANA(TEXT:CSV) FITRES(TEXT:CSV) LCPLOT(TEXT:CSV)’

For the FITRES table, data-ﬁt χ2-residuals can be included for each epoch using a feature of both

ROOT

and

HBOOK

that allows vector elements in tables columns. In addition to the data-ﬁt chi-squared,

the following are also included: PSF, sky-noise, zero point, best-ﬁt model ﬂux, etc ... Residuals can be

included with

SNTABLE_LIST = ’SNANA FITRES+RESIDUALS LCPLOT’

There is no text-format option for the residuals, but the

sntable_dump

utility (§12.1.2) has an “outlier” op-

tion to extract the residual information into text format. Finally, be aware that deﬁning

FITRES+RESIDUALS

results in a signiﬁcantly larger output ﬁle.

For the SNANA table, an optional cut-mask on

CUTFLAG_SNANA

can be deﬁned to select the following

subsets,

SNTABLE_LIST = ’SNANA(cutmask:0)’ ! write only events failing cuts

SNTABLE_LIST = ’SNANA(cutmask:1)’ ! write only events passing snana cuts

SNTABLE_LIST = ’SNANA(cutmask:2)’ ! write only events passing fit cuts

SNTABLE_LIST = ’SNANA(cutmask:3)’ ! default -> write all events

142

A few other miscellaneous table options are

SNTABLE_LIST = ’SNANA+EPOCHS’ # include epoch info in SNANA table

SNTABLE_LIST = ’SNANA+SIM_MAGOBS’ # idem, but only MJD,IFILT,SIM_MAGOBS

SNTABLE_LIST = ’SNANA FITRES NOSIMVAR’ # suppress SIM_xxx variables.

SNTABLE_LIST = ’SNANA FITRES SPECTRA’ # SALT2 model spectrum for each epoch

SNTABLE_LIST = ’SNANA(PS:10) FITRES’ # pre-scale SNANA table by 10

SNTABLE_LIST = ’FITRES NOZPHOT’ # suppress ZPHOT variables

•

SNANA+EPOCHS

and

SPECTRA

options work with

HBOOK

and

ROOT

format, but not with

TEXT

format.

•

SNANA+SIM_MAGOBS

is a compressed table to contain only the model light curves. EPOCH is deﬁned

on a grid w.r.t. Tpeak, and SIM_MAGOBS is interpolated at each grid-EPOCH so that model colors

can be easily examined.

•The

NOSIMVAR

option removes all simulated truth values, and is useful for blind challenges.

•The

SPECTRA

table works for SALT2 light-curve ﬁts only, and is ﬁlled for epochs (Trest) deﬁned by

the SALT2 model: includes scalars (CID,MJD,BAND,TOBS,etc) and a model spectrum (ﬂux vs.

wavelength). The

SPECTRA

table may be useful for calibration corrections that require an SED. To

save storage, each spectrum is stored within the wavelength range deﬁned by the passband.

•The pre-scale option (PS:10) reduces table output for large simulated samples.

•

NOZPHOT

suppresses photo-z output so that photo-z and spec-z (4-parameter) light curve ﬁts have

the same

FITRES

table columns and can therefore be combined. Note that

zHD

contains the relevant

redshift information so that

ZPHOT

is not needed. In addition,

NOZPHOT

results in adding

OPT_PHOTOZ

(

&FITINP

input) to the

FITRES

table, allowing analysis programs (e.g.,

SALT2mu

) to distinguish

spec-z and photo-z events. For spec-z ﬁts (i.e., NOT photo-z),

NOZPHOT

adds

OPT_PHOTOZ

to the

FITRES

table, but does not remove anything.

12.1.1 Combining Ascii “Fitres” Files:

combine_fitres.exe

As discussed in §5.2, the ﬁt results are written to a self-documented “ﬁtres” ﬁle. The simulation can also be

used to dump generated variables into a ﬁle with the same format (§4.32.3). The utility ‘

combine_fitres.exe

’

is useful to combine (merge) multiple ﬁtres ﬁles containing information about the same SNe. Note that

ﬁtres ﬁles with different SNe can be combined by simply using the unix “cat” command.

As an example, consider the following ﬁtres ﬁles generated from different light curve ﬁtters:

143

> more mlcs.fitres

NVAR: 2

VARNAMES: Z DLMAG

SN: 50001 0.1576 39.475

SN: 50002 0.2030 40.291

> more salt2.fitres

NVAR: 2

VARNAMES: x1 c

SN: 50001 -2.343 0.013

SN: 50002 0.893 0.235

> combine_fitres.exe mlcs.fitres salt2.fitres

> more combine_fitres.txt

NVAR: 5

VARNAMES: CID Z DLMAG x1 c

SN: 50001 0.157600001 39.4749985 -2.34299994 0.0130000003

SN: 50002 0.202999994 40.2910004 0.893000007 0.234999999

Although the SN candidate id (CID) is required after the “

SN:

” keyword, it is optional to specify

CID

the

VARNAMES

list.

Fitres ﬁles with the same variable names can also be combined. The second repeated variable gets a

“_2” appended to the variable name, the third repeated variable gets a “_3” appended, etc ... For example,

consider two

MLCS2k2

ﬁts with slightly different options,

> more mlcs.fitres

NVAR: 2

VARNAMES: Z DLMAG

SN: 50001 0.1576 39.475

SN: 50002 0.2030 40.291

> more mlcs_test.fitres

NVAR: 2

VARNAMES: Z DLMAG

SN: 50001 0.1576 39.829

SN: 50002 0.2030 40.443

> combine_fitres.exe mlcs.fitres mlcs_test.fitres

> more combine_fitres.txt

NVAR: 5

VARNAMES: CID Z DLMAG Z_2 DLMAG_2

SN: 50001 0.157600001 39.4749985 0.157600001 39.8289986

SN: 50002 0.202999994 40.2910004 0.202999994 40.4430008

144

Up to ten ﬁtres ﬁles can be merged together. If there are SNe in the second (3rd, 4th...) ﬁtres ﬁle that are

not in the ﬁrst ﬁtres ﬁle, then these extra SNe will be ignored. If there are SNe in the ﬁrst ﬁtres ﬁle that

are not in the other ﬁtres ﬁles, then values of −888 are stored for the missing SNe. In addition to creating

a merged ﬁtres ﬁle, a merged Table ﬁle (

combine_fitres.hbook/root

) is also created in hbook and/or

root format depending on the compile ﬂag(s) in

sntools_output.h

. This table can be analyzed with

PAW

ROOT

, or using the

sntable_dump.pl

utility (§12.1.2)

The default preﬁx for the output ﬁles is “

combine_fitres

.” This default can be changed using the

argument

-outprefix

> combine_fitres.exe mlcs.fitres mlcs_test.fitres -outprefix mlcs

which produces the ﬁles ’

mlcs.tup

’ and ’

mlcs.txt

.’

12.1.2

SNTABLE

Dump Utility:

sntable_dump.pl

The ﬁtres text-ﬁle output from the light curve ﬁtter contains a small fraction of the analysis variables. The

entire set of analysis variables is stored in a more compact “

SNTABLE

” structure using HBOOK and/or

ROOT based on the ⁀

&SNLCINP namelist inputs

HFILE_OUT = ’mjob.hbook’

ROOTFILE_OUT = ’mjob.root’

Additional

SNTABLE

formats (e.g., HDF5, Pickle) can be added within the existing architecture. There are

two primary

SNTABLEs

snlc_fit/psnid

snana fit results

--------------------------------------------

HBOOK TABLE ID 7100 7788 (column-wise ntuples)

ROOT TABLE ID SNANA FITRES (trees)

-----------------------------------------------

If you are ﬂuent in

PAW/HBOOK

ROOT

, then you can analyze these tables directly without using text ﬁles.

However, if you prefer a different analysis platform then

sntable_dump.pl

can be used to extract table

information into text format.

The script usage is explained at the top of

&SNANA_DIR/util/sntable_dump.pl

, and here we illus-

trate its three basic features:

1. Print list of

SNTABLE

variables:

sntable_dump.pl myjob.hbook 7100

sntable_dump.pl myjob.hbook 7788

sntable_dump.pl myjob.root SNANA

sntable_dump.pl myjob.root FITRES

2. For an arbitrary set of table variables, extract SN values into a ﬁtres-formatted text ﬁle:

sntable_dump.pl myjob.hbook 7100 --v RA DECL SNRMAX_r

sntable_dump.pl myjob.hbook 7788 --v m0obs_g m0obs_r

(and same for hbook/7100/7788 -> root/SNANA/FITRES)

145

3. Append an existing text ﬁle with variables from a

SNTABLE

sntable_dump.pl myjob.hbook 7100 --v RA DECL SNRMAX_r --a MYJOB.FITRES

sntable_dump.pl myjob.hbook 7788 --v m0obs_g m0obs_r --a MYJOB.FITRES

(and same for hbook/7100/7788 -> root/SNANA/FITRES)

4. Dump epoch-list of dataFlux-ﬁtFLux outliers:

sntable_dump.pl myjob.hbook 7788 --outlier 3 99

sntable_dump.pl myjob.root FITRES --outlier 3 99

sntable_dump.pl myjob.root FITRES --outlier 3 99 --v FITPROB SNRMAX3

(print epochs to ascii file with 3 < Nsigma < 99)

5. Dump epoch-list of dataFlux-simFLux outliers (sim only):

sntable_dump.pl myjob.hbook 7788 --outlier_sim 3 99

sntable_dump.pl myjob.root FITRES --outlier_sim 3 99

sntable_dump.pl myjob.root FITRES --outlier_Sim 3 99 --v FITPROB SNRMAX3

(print epochs to ascii file with 3 < Nsigma < 99)

6. Dump observations & variables needed to compute ﬂux-error maps in §4.11.1. Note that

ERRTEST

σSIM/σF, where σSIM is the calculated error and σFis the reported error.

sntable_dump.pl myjob.hbook FITRES obs

sntable_dump.pl myjob.root FITRES obs

Using the append option (#3 above with

a), a new text ﬁle is created containing the original variables

MYJOB.FITRES

plus the appended variables speciﬁed by the

v argument. The appended variables are

extracted from the

SNTABLE

(2nd argument of

sntable_dump.pl

To see pre-explosion epochs with the outlier option, optn the low-side of

&FITINP

namelist variable

FITWIN_TREST

, such as -100, +45.

12.1.3 Extract Value from Fitres File:

get_fitresValue.pl

See instructions at top of

$SNANA_DIR/util/get_fitresValue.pl

12.1.4 Working with IAUC names

Data ﬁles contain a required SNID and an optional IAUC name. By default, only the SNID is used and

propagated to the output tables as

CID

. However, using the IAUC name may sometimes be more practical.

For example, SNID could be an integer that keeps changing as data are reprocessed, while the IAUC name

remains ﬁxed.

On the input side,

&SNLCINP

namelist inputs that specify CID strings will work with either SNID or

IAUC names. These namelist inputs include

146

SNCCID_LIST

SNCCID_LIST_FILE

SNMJD_LIST_FILE

SNCCID_LIST

is an explicit list of SNIDs and/or IAUC names, and the list can contain a mix of SNID and

IAUC names. The next two

XXX_LIST_FILE

inputs point to a ﬁle containing a list of SN names, and these

can also be an arbitrary mix of SNID and IAUC names.

In the output tables, the CID column can be ﬁlled with the IAUC name by specifying an IAUC option

SNTABLE_LIST

SNTABLE_LIST = ’SNANA FITRES(iauc)’

SNTABLE_LIST = ’SNANA FITRES(text:key,iauc)’

SNTABLE_LIST = ’SNANA(iauc) FITRES(text:key)’

etc ...

If any one table has the IAUC speciﬁcation then all tables will have IAUC written into the CID column.

12.1.5

ovdatamc.py

: Plotting Utility for Data/MC Overlays

Once you have an ascii

FITRES

ﬁle from the data and MC simulation, the utility “

ovdatamc.py

” can be

used to plot a data/MC overlay for any variable, and with arbitrary cuts on any variable inside the FITRES

ﬁle. If the simulation includes core collapse SNe, then the Ia and CC contributions to the simulation

are overlaid separately and shown with different colors. To get a list of arguments and options, type

ovdatamc.py

with no arguments. Also read comments at top of

$SNANA_DIR/util/ovdatamc.py

12.2 General Misc. Tools

12.2.1 Command-line Overrides

The simulation and light curve ﬁtter described in the sections above are each driven by an input ﬁle that

speciﬁes instructions and parameters. For convenience, all input-ﬁle parameters can be speciﬁed on the

command line. For example, if you have

GENMODEL: mlcs2k2.v006

GENTAU_AV: 0.35

in your simulation-input ﬁle, you can override these options on the command-line without editing the input

ﬁle:

snlc_sim.exe mysim.input GENMODEL mlcs2k2.v007 GENTAU_AV 0.45

These command-line overrides are useful for quick testing, and for writing wrappers that do many analysis

variations without creating a new input ﬁle for each job. An invalid or unrecognized command-line option

results in an immediate abort. The command-line options are printed to stdout, and therefore if you pipe

your job to a log-ﬁle, you can rerun the same job as long as you have the original input ﬁle.

147

12.2.2 Synchronizing/Updating Survey Files: survey_update.pl

Collaborators within a survey who are working on different computer systems can keep ﬁles synchronized

using the script $

SNANA_DIR/util/survey_update.pl

. See usage instructions at the top of the script.

The basic idea is that a survey expert uses the script in “create tarball” mode to create a tarball containing

ﬁlter transmission ﬁles, K-correction tables and data version(s). This tarball is then distributed among

collaborators who use the same script in “install” mode.

12.2.3 Bug-Catcher: the

SNANA_tester

Script

To help verify that the

SNANA

code delivers the same results with each new version, there is a testing

utility,

SNANA_tester.cmd

(no arguments), that runs a pre-deﬁned list of jobs with two different versions

SNANA

, and reports discrepancies. Typically this script is run just before releasing a new

SNANA

version,

but users may want to run this script on other platforms. The goal is to catch and ﬁx unanticipated changes

(i.e, bugs) before releasing each new

SNANA

version. The top-level instruction ﬁle is here,

$SNDATA_ROOT/SNANA_TESTS/SNANA_TESTS.LIST

which speciﬁes a series of test-jobs, input ﬁles, and log-ﬁle parsing instructions to extract results to com-

pare between

SNANA

versions. The

SNANA_tester.cmd

script is written for the Fermilab ups product

system; on other platforms, script modiﬁcations will be needed to setup the correct versions of

SNANA

Users who use a particular feature of

SNANA

should check if the current test-jobs provide adequate protec-

tion; if not, you may request additional test-jobs.

12.2.4 Data Backup/Archival:

backup_SNDATA_version.cmd

A data version can be archived with

backup_SNDATA_version.cmd MYVERSION

which creates a tarball-backup in

$SNDATA_ROOT/lcmerge/archive/MYVERSION_[yyy]-[mm]-[dd].tar.gz

where

[yyyy]-[mm]-[dd]

is the year, month and day. This script is useful to backup a newly made data

version, archive a version used in a publication, or to send a data version to a collaborator. In general the

$SNDATA_ROOT

disk is not backup up, so to have a truly protected backup you need to either (1) backup

$SNDATA_ROOT

or (2) copy the tarball-backup to another storage device.

12.2.5 K-correction Dump Utility:

kcordump.exe

The K-correction tables are stored in

HBOOK

ﬁles, and accessing this information can be tricky even for

those familiar with

PAW

. The utility

kcordump.exe

can be used to check a K-correction value for speciﬁc

ﬁlter, epoch, and primary reference. If you type

kcordump.exe

with no arguments, the program will ask

you for all needed arguments. You can also use command-line arguments, as illustrated here for SNLS

KgU at peak at z=0.28:

> kcordump.exe KCOR_FILE Hsiao/kcor_SNLS_Bessell90_VEGA.fits \\

FILT_OBS g FILT_REST U Z .28 TREST 0.

148

The dump utility checks your current directory and $

SNDATA_ROOT

kcor

for the existence of the K-

correction ﬁle (argument of

KCOR_FILE

). All K-correction dumps are done with no spectral warping. To

see K-corrections with warping, generate simulated SNe Ia and scroll through the data ﬁles for symbols

containing “

KCOR

” and “

WARP

.” The slight disadvantage with using the simulation to check K-corrections

is that you cannot specify which K-corrections to check, but you can only compare to whatever the simu-

lation generates.

149

12.3 Misc. Simulation Tools

12.3.1 Simulate Ia/non-Ia mix:

sim_SNmix.pl

See instructions at top of $

SNDATA_ROOT/util/sim_SNmix.pl

. This script is used to simulate a mix of

Type Ia and non-Ia SNe, and to easily generate multiple sets of simulations with different sim-options. An

optional (recommended) list of computing nodes allows for parallel processing. The command syntax is

sim_SNmix.pl <name of master control file>

and a master-control ﬁle is illustrated in Fig. 10. This ﬁle gives batch instructions, and is NOT an input

ﬁle to the simulation program

snlc_sim.exe

. The keys are as follows.

•NODELIST, BATCH_INFO: deﬁnes CPU cores to distribute jobs.

NODELIST

is a simple list of

nodes, and you must be able to login without entering a password.

BATCH_INFO

speciﬁes a submit-

command, batch-template ﬁle, and number of cores (see ???). Recommended to deﬁne as many

cores (NCORE) as jobs (NJOB)22, although there is no harm in deﬁning too many or too few cores.

If NCORE <NJOB, some cores will run multiple jobs and hence take longer. Example 1: NJOB=10

and NCORE=5 →each core will simulate 2 jobs. Example 2: NJOB=5 and NCORE=10 →each

job is distributed to one core, and 5 other cores will do nothing.

•GENVERSION, GENOPT: An independent simulation job is done for each

GENVERSION

, and each

GENVERSION

can be analyzed by the

snana.exe

snlc_fit.exe

program. For each

GENVERSION

an optional

GENOPT

key applies command-line overrides. Note that multiple

GENOPT

keys can be

given, and multiple override commands can be given on one line.

•SNANA_LOGIN_SETUP: if your login script does not automatically setup

snana

23, this key is

needed. Everything on the line after this key is executed (prefably running a setup script), so don’t

append comments on the same line.

•GENOPT_GLOBAL: After the ‘

ENDLIST_GENVERSION:

’ key this is a ﬁnal (optional) global over-

ride key whose argument-list is applied to all of the simulations. Beware that that the

GENOPT

and

GENOPT_GLOBAL

options are applied to both the SNIa and NON-Ia simulations.24 Everything fol-

lowing this key is passed to the simulation, so don’t append comments at the end of this line.

•ZRANGE: optional redshift-range override, and is the same as

‘

GENOPT_GLOBAL: GENRANGE_REDSHIFT 0.1 1.2

.’

•SIMGEN_INFILE_Ia[NONIa]: A sim-input ﬁle is speciﬁed for the SNIa and/or SNCC sample;

one or both ﬁles can be speciﬁed.

•NGEN_UNIT: speciﬁes the number of “units” (e.g., seasons) to generate, and internally computes

the statistics appopriate for the speciﬁed redshift-range, peakMJD-range, solid angle, and SN rate

(based on

DNDZ

key). If the

NGEN_UNIT

key is left out, the simulated statistics is based on the

NGEN_LC

and

NGENTOT_LC

keys in the sim-input ﬁles.

•GENPREFIX: ﬁle preﬁx under the

GENVERSION

sub-directory. Note that the analysis points to

GENVERSION

, not

GENPREFIX

22NJOB = number of

GENVERSION

keys ×number or

RANSEED

keys.

23snana setup includes deﬁning

$SNDATA_ROOT

and adding

$SNANA_DIR/bin

to your path.

24There are som exceptions, such as

GENMAG_SMEARMODEL_NAME

that is ignored in the NON-Ia sims and applied only to the

Ia sim.

150

•FORMAT_MASK: 2-bit for ascii format and 32-bit for FITS format. The 16-bit results in random

CIDs so that any random subset contains a random mix of SNIa and SNCC.

•RANSEED: With one

RANSEED

key, each

GENVERSION

is generated once; multiple

RANSEED

keys

generate each version multiple times, each on a different CPU core. The left set of

RANSEED

keys

in Fig. 10 behaves in the obvious manner by generating three statistically independent simulations.

The generated versions are

DESY1_SNCC+SNIaSmearCOH-01

DESY1_SNCC+SNIaSmearCOH-02

DESY1_SNCC+SNIaSmearCOH-03

and similarly the other

GENVERSION

s have an index-sufﬁx. If using the random-CID option (16-bit

FORMAT_MASK

), the CIDs are unique within each version, but may be randomly duplicated among

different versions. The duplicate

RANSEED

keys on the right side of Fig. 10 also generate three

independent samples, but with two main differences compared to the

RANSEED

list on the left:

1. all CIDs are unique; the common

RANSEED

in each job is used to compute and reject all previ-

ous CIDs.

2. The three generated samples are combined to make one sample. This feature thus allows

distributing a large simulation job over multiple cores.

SIMLOGS

Before the simulation jobs are launched, a new directory is created under your current working direc-

tory,

SIMLOGS_[GENPREFIX]/

or ‘

SIMLOGS_DES/

’ for the control ﬁle in Fig. 10. All log-ﬁles are store here, and previous a directory

with the same name is clobbered without warning.25 A ﬁnal one-line per job summary is written to

SIMLOGS_[GENPREFIX]/SIMJOB_SUMMARY.LOG

. ALWAYS check the SUMMARY log-ﬁle to make sure

that the number of simulated events is reasoble (e.g., not zero) and that there are no aborted sim-jobs.

25More generally,

sim_SNmix.pl

overwrites all previously existing ﬁles and

GENVERSIONS

without warning.

151

Figure 10: Example of master-control ﬁle for

sim_SNmix.pl

# speficy nodes to run on, or batch system

NODELIST: des05 des06 des08 des09 des06 des10

#BATCH_INFO: sbatch SBATCH.TEMPLATE 5

#BATCH_INFO: qsub QSUB.TEMPLATE 5

SNANA_LOGIN_SETUP: <whatever command(s) to setup snana>

# specify version to generate, along with special options

GENVERSION: DESY1_SNCC+SNIaSmearCOH

GENOPT: GENMAG_SMEAR_MODELNAME COH

GENOPT: SMEARFLAG_ZEROPT 0 SMEARFLAG_FLUX 0

GENVERSION: DESY1_SNCC+SNIaSmearG10

GENOPT: GENMAG_SMEAR_MODELNAME G10

GENVERSION: DESY1_SNCC+SNIaSmearC11

GENOPT: GENMAG_SMEAR_MODELNAME C11

ENDLIST_GENVERSION:

# optional global-overrides

GENOPT_GLOBAL: EXPOSURE_TIME 1000 GENRANGE_PEAKMJD 56550 56720

ZRANGE: 0.1 1.2

# specify sim-input files for snlc_sim.exe

SIMGEN_INFILE_Ia: SIMGEN_DES_SALT2.input

SIMGEN_INFILE_NONIa: SIMGEN_DES_NONIA.input

NGEN_UNIT: 2 SEASON

RATESCALE_Ia: 1.0 # scale SNIa rate

RATESCALE_NONIa: 1.0 # scale all SNCC rates

# define required global items to ensure uniformity among all jobs

GENPREFIX: DES # prefix of all data filenames

FORMAT_MASK: 48 # 16=RanCID 32=FITS-FORMAT

152

Figure 11: Example of master-control ﬁle for

sim_SNmix.pl

: Continued

# 3 independent samples

RANSEED: 12349

RANSEED: 23287

RANSEED: 34308

# one large combined sample from 3 independent jobs

RANSEED: 12345

# The above can be implemented more compactly with

RANSEED_CHANGE: 3 12349 # equivalent to 3 different RANSEEDS

RANSEED_REPEAT: 3 12345 # equivalent to 3 identical RANSEEDs

153

12.3.2 Co-Adding

SIMLIB

Observations on Same Night:

simlib_coadd.exe

If a survey takes many exposures per ﬁlter in one night, the resulting

SIMLIB

can be quite large, and

there may be no beneﬁt to simulating each exposure within a night. Since one typically combines these

exposures into a single co-added exposure, there is a utility to translate a

SIMLIB

so that there is just one

effective co-added exposure per ﬁlter per night,

> simlib_coadd.exe MYSURVEY.SIMLIB

which produces an output

SIMLIB

called

MYSURVEY.SIMLIB.COADD

. By default, observations within 0.4

days are combined into a single co-added observation, and at least three observations are required to keep

a sequence of observations (i.e, a

LIBID

). The CCD noise, sky-noise and zeropoint are calculated to reﬂect

a single co-added exposure as follows,

ZPT(COADD) = 2.5log10 "∑

10(0.4·ZPTi)#NOISE(COADD) = r∑

NOISEi,(34)

where iis the exposure index. The co-added PSF is simply the average of the PSF values from the

individual exposures.

There are additional options to change the requirement on the minimum number of observations, to

change the time-separation for co-adding, and to determine the Milky Way Galactic extinction (MWEBV)

from [8],

> simlib_coadd.exe MYSURVEY.SIMLIB MWEBV --TDIF .2 --MINOBS 5

When the “MWEBV” option is used, observation sequences with MWEBV>2 are rejected. Read top of

SNANA_DIR

src/simlib_coadd.c

for additional options.

12.3.3 Creating a

SIMLIB

from Data

Ideally, a

SIMLIB

is created from a library of observations containing PSF, sky-noise and zero-point.

However, there may be cases where it is useful to create a

SIMLIB

directly from a data sample. The

snana.exe

program can create such a

SIMLIB

via the

&SNLCINP

input key

SIMLIB_OUT = ’mydata.simlib’

If the light curve data include meta data (PSF,SKY,ZP) for each epoch, these values are written out to the

SIMLIB

. If the meta data are not available (e.g., low-z samples), then two assumptions are used to compute

these values. First, the PSF(FWHM) is ﬁxed to 1′′. Second, the sky brightness (mag/asec2) vs wavelength

is taken from an old version of the LSST deep-drill cadence. For an arbitrary ﬁlter, the skyMag is in-

terpolated as a function of the central wavelenth of the ﬁlter. Fortran subroutine

COMPUTE_SIMLIB_INFO

computes the SKYSIG and ZP values using the above assumptions and the S/Nfrom the data.

If there are no meta-data, the default

ZPERR

is 0.01, which imposes an SNR ceiling of 100 in the

simulation. Arbitrary

ZPERR

values can be input via

&SNLCINP

as shown in the following example:

SIMLIB_ZPERR_LIST = ’u .02 gri .01 z 0.015’

Any band not listed above gets the default

ZPERR=0.01

The

SIMLIB

is updated for events passing cuts in the

&SNLCINP

namelist, and a

SIMLIB

row is written

for each epoch. The

SIMLIB

header for each event includes the redshift and peakMJD. When using this

SIMLIB

in the simulation, one can either generate random redshift & peakMJD values, or pick the data

values from the header using the following sim-input keys (§4.5.1):

USE_SIMLIB_PEAKMJD: 1 # use peakMJD in header (if there)

USE_SIMLIB_REDSHIFT: 1 # use redshift in header (if there)

154

12.3.4 Fudging Simulated Errors and Signal-to-Noise Ratio (S/N)

Errors and S/Ncan be fudged in the simulation as follows:

# 2. options to adjust exposure time (affects both SN flux and sky noise)

EXPOSURE_TIME: 20 # increase all exposure times by 20

EXPOSURE_TIME_FILTER: g 20 # increase g exposure by 20

FUDGESHIFT_ZPT: -3.0 # reduce ZPT by 3 mags

# 2. options to increase SKY-noise while leaving SN flux unchanged

FUDGESCALE_PSF: 2 # increase PSF

FUDGESCALE_SKYNOISE: 3 # increases SKYNOISE (note that SKY *= 3^2)

# 3. force nearest-peak S/N = 25 for all bands

FUDGE_SNRMAX: 25 # adjust exposure time

FUDGE2_SNRMAX: 25 # adjust sky-noise only (don’t change SN flux)

# 4. force nearest-peak S/N in r-band; use same EXPOSURE time in other bands

FUDGE_SNRMAX: r=25 # adjust exposure time for r-band

# 5. add magErr to all epochs

FUDGE_MAGERR: 0.03 # add .03 magErr to all epochs and bands

FUDGE_MAGERR_FILTER: g .01 # add .01 magErr to g-band

FUDGE_MAGERR_FILTER: riz .02 # add .02 magErr to riz bands

There are ﬁve classes of error-fudging: (1) adjust exposure time to change both the SN ﬂux and sky-noise,

(2) increase the sky-noise while leaving the SN ﬂux unchanged, (3) force nearest-peak S/Nto be the same

ﬁxed value in all bands, (4) force nearest-peak S/Nfor one band, then use computed,

EXPOSURE_TIME

in all bands. (5) add arbitrary mag-error at each epoch.

FUDGE2_SNRMAX

is useful for setting a nearly

ﬁxed error at all epochs, in contrast to a ﬁxed S/N, or mag-error. For both options to ﬁx the nearest-peak

S/Nratio, the simulation processes each SN twice. The ﬁrst iteration is done with nominal conditions

and the resulting

SNRMAX

26 is used to calculate the

EXPOSURE_TIME

for the second iteration. For option

3), the

EXPOSURE_TIME

is adjusted separately in each band to get the same ﬁxed S/N, while in option

4) the

EXPOSURE_TIME

is the same in each band to ﬁx S/Nin just one band. The

EXPOSURE_TIME

value

for each band is written to the header in each data ﬁle; see

SIM_EXPOSURE

key. Deﬁning SNRito be

the i’th-iteration S/Nwhere SNR2is the requested

FUDGE[2]_SNRMAX

value, and R≡SNR2/SNR1, the

zeropoint and sky-noise are modiﬁed for each passband in the second iteration as follows:

FUDGE_SNRMAX : EXPOSURE_TIME2=R2(35)

FUDGE_SNRMAX : ZPT2−ZPT1=5log(R)(36)

FUDGE_SNRMAX :σsky,2/σsky,1=R(37)

FUDGE2_SNRMAX : ZPT2−ZPT1=0 (38)

FUDGE2_SNRMAX :σsky,2/σsky,1=q[ (1/SNR2)2−1/ˆ

FSN ]/[ (1/SNR1)2−1/ˆ

FSN ](39)

where ˆ

FSN is the SN ﬂux (photoelectrons) at the epoch with the maximum S/N.

SNRMAX

is the maximum S/Nratio among all observations within a passband.

155

12.4 Misc. Fitting Tools

12.4.1 Fit Multiple Samples with Multiple Fit-Options:

split_and_fit.pl

See instructions at top of $

SNANA_DIR/util/split_and_fit.pl

. This script allows ﬁtting a matrix of

multiple versions and multiple ﬁt-options. A list of nodes or batch command allows for parallel processing.

The outputs of each split job are automatically merged when the ﬁtting jobs have ﬁnished.

Disk output from

split_and_fit.pl

can be reduced with the command

split_and_fit.pl CLEAN

split_and_fit.pl CLEANMASK <mask>

split_and_fit.pl CLEANMASK <mask> NOPROMPT

which removes unecessary ﬁles under every sub-directory from where the CLEAN command is launched.

It also gzips the ascii FITOPT* ﬁles. By default, explicit user-authorization is requested for each cleaning

stage; the

NOPROMPT

argument will clean without asking for authorization. Selective cleaning can be done

with the following

CLEANMASK

options:

CLEANMASK += 1 --> remove /SPLIT_JOBS_* /DEBUG S2mu*

CLEANMASK += 2 --> remove SIMGEN.DAT*

CLEANMASK += 4 --> gzip FITOPT*

CLEANMASK += 8 --> remove HBOOK and ROOT files

The default

CLEAN

argument sets

CLEANMASK=7

. “

CLEANMASK 15

” will run the default

CLEAN

, and also

remove the

HBOOK

and

ROOT

ﬁles.

12.4.2 Analyzing Residuals from Lightcurve Fits

There are two utilities to analyze residual from a lightcurve ﬁt:

mkfitplots.pl --h <hisFile> RESIDS

dump_lcfitOutliers.pl <hisFile> <Nsigma>

The ﬁrst command generates plots of the normalized residuals, ∆F/σwhere ∆F=Fdata −Fmodel, and also

plots ∆F/σvs. log10(SNR). Separate plots are made for each observer-frame passband. The second

command dumps out a text-ﬁle of outlier observations for which the data lie more than

Nsigma

σfrom

the best-ﬁt model. The format of the outlier text-ﬁle is such that entries can be pasted directly into the

IGNORE ﬁle for those observations that should be ignored in the analysis.

12.4.3 Extracting Light Curves into ASCII Formatted Files

For both the

snana.exe

and

snlc_fit.exe

programs, the ﬂuxes and best-ﬁt model can be dumped into

an ASCII text ﬁle with the &SNLCINP namelist option

LDMP_SNFLUX = T

This option creates a master ﬁle “

$SURVEY.LIST

” and a

FLUXFILE

for each ﬁlter for each SNID. The

master ﬁle contains the name of each SNID, its redshift and a list of

FLUXFILE

s. The format of the

FLUXFILE

Tobs FLUXCAL FLUXCAL_ERR DATAFLAG CFILT CHI2

156

where

Tobs

is the time relative to the epoch of peak brightness,

FLUXCAL

and

FLUXCAL_ERR

are the cali-

brated ﬂux and error,

DATAFLAG

is described below,

CFILT

is a one-character ﬁlter string, and

CHI2

is the

the data-model χ2from the ﬁt (0 if no ﬁt).

DATAFLAG

is +1 for data, −1 for data rejected by the ﬁt, and 0

for the best ﬁt (smooth) model.

12.4.4 Translating SNDATA ﬁles into SALT-II Format

The

snana.exe

program can convert

SNANA

-formatted data (or simulation) ﬁles into SALT-II format

needed to run the original (Guy07) SALT-II ﬁtter code and the SALT-II training code. A sample namelist is

as follows:

&SNLCINP

VERSION_PHOTOMETRY = ’SDSS_HOLTZ08’

OPT_REFORMAT_SALT2 = 2

REFORMAT_KEYS = ’@INSTRUMENT SLOAN @MAGSYS AB’

SNFIELD_LIST = ’82N’ , ’82S’

cutwin_cid = 0, 100000

&END

Note that

OPT_REFORMAT_SALT2=2

is for the newer SALT-II format with one ﬁle per SN (

snfit

version

2.3.0 and higher), while

OPT_REFORMAT_SALT2=1

is for the original format with one ﬁle per passband.

12.4.5 Translating TEXT data-ﬁles into FITS Format

For relatively large data samples, reading text ﬁles can be somewhat slow. A more efﬁcient storage mech-

anism uses FITS format. TEXT-formatted data ﬁles can be translated into FITS format using

snana.exe

and an input ﬁle with the following,

&SNLCINP

VERSION_PHOTOMETRY = ’MYSURVEY_TEXT’

VERSION_REFORMAT_FITS = ’MYSURVEY_FITS’

&END

or use NOFILE option with no input NML file:

snana.exe NOFILE \

VERSION_PHOTOMETRY MYSURVEY_TEXT \

VERSION_REFORMAT_FITS MYSURVEY_FITS

This translation should be used only for data since the simulation is written in FITS format by default.

In addition to translating the data into FITS format, the auxiliary ﬁles are also created:

MYSURVEY.LIST

MYSURVEY.IGNORE

MYSURVEY.README

. All of the output ﬁles are created in your current directory; to use

the for analysis, copy them into

$SNDATA_ROOT/lcmerge

157

12.4.6 Re-write Data FIles with Flux Fudges

There are options in the analysis programs to modify the ﬂuxes and ﬂux-errors read from the data ﬁles. To

re-write data ﬁles with these modiﬁcations,

&SNLCINP

VERSION_PHOTOMETRY = ’DES-SN3YR_DES’

MAGCOR_FILE = ’$DES_ROOT/lcmerge/DES3YR_DES_MAGCOR.DAT’

FLUXERRMODEL_FILE = ’$DES_ROOT/simlibs/DES3YR_FAKE_ERRORFUDGES.DAT’

OPT_REFORMAT_TEXT = 1 ! re-write data files in TEXT format

VERSION_REFORMAT_FITS = ’NEW_VERSION_NAME’ ! re-write in FITS format

&END

In this example,

MAGCOR_FILE

and

FLUXERRMODEL_FILE

are used to modify the ﬂuxes and their uncer-

tainties.

OPT_REFORMAT_TEXT

re-writes the data ﬁles in text format with the modiﬁed ﬂuxes so that future

analyses need not worry about using the

SNANA

ﬂux-modify options.

VERSION_REFORMAT_FITS

re-writes

in FITS format. This is particularly useful for data releases.

If the re-written data ﬁles include SNANA-computed ﬂux/ﬂuxErr fudges, a header variable in the data

ﬁles is included,

MASK_FLUXCOR_SNANA: <MASK>

where

MASK+=1

if the ﬂuxes include a correction, and

MASK+=2

if the ﬂux-errors have been correctd.

MASK=3

means that both the ﬂuxes and uncertainties have been corrected. When analyzing the re-written

data ﬁles,

MASK

is an instruction to ignore SNANA fudges, thus allowing the same input nameList ﬁle to

be used on original and re-written data ﬁles. When analyzing re-written data ﬁles that already include a

correction, an additional correction can be “FORCED” as follows,

MAGCOR_FILE = ’$DES_ROOT/lcmerge/DES3YR_DES_MAGCOR.DAT FORCE’

12.4.7 Fudging Fitting Errors

For the

snlc_fit.exe

ﬁtting program there are the

FUDGE_FITTER_XXX

parameters described in detail in

§5.14. The other fudge-option is the

&FITINP

namelist variable

FUDGE_MAGERR_MODEL = 0.1 # fix model mag-error in fitter

which replaces all model errors with 0.1 mag model-error at every epoch.

158

12.4.8 1/Vmax Method: Post-Fit Calculations

The 1/Vmax method can be used to compute Zmax and the associated volumne for each SN. These calcu-

lation are controlled with the following

&FITINP

namelist options,

MAGLIM_Vmax = ’r 21.5 i 21.0’

OPT_Vmax = 0 ! valid options: 0,1,2,3

MAGLIM_Vmax

deﬁnes a list of mag-limits and observer-frame ﬁlters to perform the 1/Vmax calculation.

Only one mag-limit per ﬁlter can be deﬁned, but a different mag-limit can be deﬁned for each ﬁlter.

OPT_Vmax

is a bit mask as follows.

•Bit0 controls how the SN magnitude is computed: OFF is for the brightest observed epoch (using

best-ﬁt mag) and ON is for the peak magnitude.

•Bit1 controls how Zmax is computed: OFF is for the brightest observed epoch (using best-ﬁt mag)

and ON is for the peak magnitude.

•Bit7 (128) turns on verbose mode to see Zmax at each iteration.

For example,

OPT_Vmax

=0 means that both the SN magnitude and Zmax are computed at Trest corresponding

to the brightest observed epoch. To avoid picking an epcoh with an upward ﬂuctuation, the best-ﬁt ﬂuxes

are used to determine the brightest observed epoch rather than the observed ﬂuxes.

OPT_Vmax

=3 means

that both the SN magnitude and Zmax are computed at the best-ﬁt epoch of peak brightness.

The following variables are automatically included in the ﬁtres-text ﬁle and the SNTABLE (ntuple or

Tree): Trest where mag is computed, mag, Zmax, volume.

159

12.4.9 FILTER_REPLACE

For ﬁlters that are very similar, such as multiple ﬁlters overlapping a patch of sky, it is sometimes conve-

nient to replace ﬁlter names. As an example, consider the SDSS ﬁlters ugrizUGRIZ, where the UGRIZ

ﬁlters are deﬁned for the small fraction of SN that land on overlapping CCD regions. To ﬁt with the usual

“

FILTLIST_FIT = ’ugriz’

” input, we can replace the upper-case ﬁlters with the following

&SNLCINP

namelist variable,

&SNLCINP

FILTER_REPLACE = ’UGRIZ -> ugriz’

This replacement is equivalent to modifying the data ﬁles with

U->u

G->g

, etc.

WARNING(v10_28l): When there are no UGRIZ bands, we expect that ﬁtting ugrizUGRIZ should

give the same result as ﬁtting ugriz with the

FILTER_REPLACE

command above. This test works perfectly

except when

OPT_COVAR

>0; hence something about using a model-error covariance matrix with off-

diagonal elements introduces a very small (few millimag) discrepancy. It is not yet clear if this discrepancy

is due to a bug, or if it is expected when using

OPT_COVAR

12.4.10 SNTABLE_FILTER_REMAP

This option is for a survey with many similar bands (e.g., low-z), and is used to remap the output bands.

For example, suppose we have the following bands: ab(U-like), cde(B-like), f ghi(V-like). The ’ fghi’

bands are all V-like, and correspond to very small changes in telescope transmission, such as from a ﬁlter

replacement. The output tables by default would include ﬁlter-dependent values for each band: abcde f ghi.

To simplify some analyses, it may be more convenient to work with UBV rather than with abcde f ghi. This

convenience is achieved in the output tables by remapping the ﬁlters with the command

&SNLCINP

SNTABLE_FILTER_REMAP = ’ab->U cde->B fghi->V’

This command only affects the output tables, and has no impact on selection cuts or ﬁtting: i.e., all 9 bands

(abcde f ghi) are still used in the light curve ﬁt.

160

12.4.11 Selecting Early Epochs

During a survey, light curves are ﬁt with only a few epochs for monitoring or spectroscopic target selection.

For testing on simulated data, however, the entire light curve exists because it is not practical to re-generate

simulations that stop at each successive night. The following

&SNLCNINP

inputs illustrate how to ﬁt light

curves (data or sim) using only a few epochs as if the latter epochs had not yet been observed:

&SNLCINP

EARLYLC_STRING = ’MAXOBS 4 FILTERS riz SNRMIN 4.5’ !1

EARLYLC_STRING = ’MAXOBS 4 FILTERS riz PHOTPROBMIN .5’ !2

EARLYLC_STRING = ’MAXOBS 4 FILTERS riz PHOTMASK 4096’ !3

EARLYLC_STRING = ’MAXNIGHT 2 FILTERS riz PHOTMASK 4096’ !4

EARLYLC_STRING = ’MAXNIGHT 2 PHOTMASK 4096 NDAYADD 20’ !5

EARLYLC_STRING = ’MAXNIGHT 2 PHOTMASK_START 4096’ !6a

EARLYLC_STRING = ’MAXOBS 3 SNR_START 5’ !6b

The

MAXOBS

key speciﬁes the maximum number of

EARLYC

observations to keep that satisfy the logical

AND of cuts on ﬁlters, signal-to-noise (

SNRMIN

), photometry-probability (

PHOTPROBMIN

) and photometry-

mask (

PHOTMASK

). The ﬁrst example above (!1) keeps epochs until there are 4 observations in r,i, or z that

have SNR above 4.5. In the second example (!2), the SNR requirement is replaced with the PHOTPRPOB-

MIN requirement. Third example (!3) requires four observations to have the 4096 bit of the photometry

mask (e.g., detection). Epochs satisfying the

EARLYLC

requirements may not occur until well after explo-

sion; thus all pre-

EARLYLC

(pre-explosion) epochs are kept. Once

MAXOBS=4 EARLYLC

epochs are found,

no additional epochs are kept.

The

MAXNIGHT

key (!4) includes all observations within a 12 hour period, or 1 night. For example,

consider a night with observations in the g,r,i,zbands, and they all satisfy the “

PHOTMASK & 4096

” re-

quirement. In the following night we have i,zobservations which pass

PHOTMASK

. While this counts as 6

observations toward

MAXOBS

, it counts as 2 nights towards

MAXNIGHT

. Once the

MAXNIGHT

requirement is

met with the ﬁrst i-observation in the 2nd night, all observations in the 2nd night are included.

NDAYADD

(!5) will add epochs for this many days after the last observation from the above keys.

Finally,

PHOTMASK_START

and

SNR_START

(!6a,6b) are requirements on when to start counting nights

(for

MAXNIGHT

) or observations (for

MAXOBS

). In 6a, a single observation satisfying “

PHOTMASK_START

& 4096

” starts the number-of-nights counter with no further requirements on successive observations.

Similarly in 6b, a single observation with

SNR>5

starts the number-of-observation counter. This feature is

useful for rapidly fading transients that may be detected on only 1 night, but still have useful observations

in successive nights.

The default cuts are wide open, except for the default

NDAYADD=0

. Not specifying

FILTERS

will count

all ﬁlters, not specifying

PHOTPROBMIN

will ignore

PHOTPROB

in counting early epochs, etc. Thus setting

EARLYLC_STRING=’MAXOBS 4’

will select the ﬁrst 4 observations in the data ﬁle, regardless of what is

measured.

To avoid mistakenly using the entire light curve in some part of an analysis, the removed epochs are

not stored in any arrays so that the internal arrays are ﬁlled as if the late epochs did not exist.

161

12.4.12 Selecting Epoch Ranges for Fast Transients (

REQUIRE_EPOCHS_STRING

)

To help select transients whose duration is faster than Supernova, the time above threshold is a useful

quantity that can be used with the following nameList input:

&SNLCINP

REQUIRE_EPOCHS_STRING ’FILTERS riz SNRMIN 5 TOBS_RANGES 14 20 25’

SNRMIN

deﬁnes the threshold. The three

TOBS_RANGES

values specify time-window 1) before threshold

is satisﬁed, 2) while SNR is above threshold, and 3) after SNR falls below threshold. More speciﬁcally,

events are selected whose time above SNRMIN is less than 20 days. To avoid getting fooled at the start or

end of a survey, an observation is required within 14 days prior to the ﬁrst epoch with

SNR>5

, and another

observation is required within 25 days after the last epoch with

SNR>5

. The pre- and post observation

ensure that an above-threshold epoch would have been seen, and was not hidden by a dormant survey.

12.4.13 Miscellaneous

&SNLCINP

Options

&SNLCINP

USESIM_SNCC = F ! ignore simulated CC (fit true Ia only)

USESIM_SNIA = F ! ignore simulated IA (fit true CC only)

SIM_PRESCALE = 4.0 ! fit 1/4 of sim sample, but still fit all data

12.5 Misc.

SIMSED

Utilities

12.5.1

SIMSED

Spectrum Extraction:

SIMSED_extractSpec.exe

For a

SIMSED

model, the program

SIMSED_extractSpec.exe

can be use to extract a single spectrum for

a particular

SIMSED

model version, epoch, and set of parameter values corresponding to the

PARNAMES

the

SED.INFO

ﬁle. The current program uses the parameter values on the

SED.INFO

grid that are closest to

the user-speciﬁed parameters; a future version may interpolate for better accuracy. See usage instructions

at top of

$SNANA_DIR/src/SIMSED_extractSpec.c

12.5.2

SIMSED

Fudge Afterburner:

SIMSED_fudge.exe

For a given

SIMSED

model (§9.4), an arbitrary color law can be applied to generate a new

SIMSED

version.

The program syntax is

SIMSED_fudge.exe <inFile>

where an example input ﬁle is here:

$SNDATA_ROOT/sample_input_files/SIMSED/colorFudge.input

12.5.3

SIMSED

Preparation for SNANA:

SIMSED_prep.exe

Translate native format of SED model into

SNANA

format.

162

12.6 Reading gzip’ed Input Files

To reduce disk usage and improve the speed in reading large input text ﬁles,

SNANA

will read any input

ﬁle that is compressed with

gzip

. Always specify the uncompressed name (e.g.,

mystuff.text

) and

SNANA

programs will check for both

mystuff.text

and

mystuff.text.gz

. If both the compressed and

uncompressed ﬁles exist, the code will abort. Reading compressed ﬁles is faster, with the cost of a little

added time (∼0.1 sec) opening the ﬁle with

popen

instead of

fopen

. Gzipped inputs include the

SIMLIB

ﬁle (§4.5),

HOSTLIB

ﬁle (§4.19),

SIMSED

model ﬁles (§9.4),

LCLIB

model ﬁles,

SALT2

model ﬁles, and

text-formatted data ﬁles.

Be aware that two of these input ﬁles (SIMLIB & LCLIB) are rewound each time the EOF is reached.

The “

popen

” command for gzipped ﬁles is not compatible with the “

rewind

” function, and thus rewinding

a gzipped ﬁle requires an explcit close and re-open. For small input ﬁles that are re-read many times, the

extra close-and-open overhead from a gzipped ﬁle may increase processing time. Thus it is recommended

to gzip only the large unput ﬁles, and leave the small input ﬁles unzipped.

12.7 Program Return Codes

Program return codes are useful for higher-level pipelines. Each C and fortran program returns 0 on

sucessfull completion. An abort or error results in the following error codes that can be examined with

unix command ‘echo $?’ :

Program return error code

------------------------------------------

kcor.exe 10

snlc_sim.exe 11

SALT2mu.exe 12

combine_fitres.exe 13

sntable_dump.exe 14

wfit.exe 15

merge_root.exe 16

merge_hbook.exe 17

snana.exe 21

snlc_fit.exe 22

psnid.exe 23

The batch-submission scripts

sim_SNmix.pl split_and_fit.pl SALT2mu_fit.pl

return an error code of 255.

163

SNANA

Updates

The

SNANA

software is released in incremental versions, reﬂecting improvements, new code, and bug ﬁxes.

Users should periodically check for updated versions. Details of each release can be found by doing

tail -100 $SNANA_DIR/doc/README_UPDATES

Users should develop an automated “download & setup” script to easily maintain the most current version

SNANA

, and to avoid getting trapped with an old or obsolete version. The

SNDATA_ROOT

tarball is updated

less frequently;

README_UPDATES

will indicate if and why a new

SNDATA_ROOT

is needed.

This manual ($

SNANA_DIR

doc/snana_manual.pdf

) is updated mostly in response to questions from

users. If you spot mistakes or obsolete information in the manual, please report it immediately !

14 Reporting Problems

Please don’t hesitate to report software problems or obsolete/incorrect information in the manual. If the

problem is related to an abort or crash, please include a tarball that contains the input ﬁle(s) and data ﬁle(s)

that reproduce the problem, as well as a log-ﬁle with the program’s screen-dump. Indicate which

SNANA

version was used, and try to isolate the problem in a single data ﬁle to avoid sending large numbers of data

ﬁles. WARNING: if you don’t provide enough information to reproduce the problem, we will not be

able to provide assistance.

164

References

[1] S. Jha, A. G. Riess, and R. P. Kirshner. Improved Distances to Type Ia Supernovae with Multicolor

Light Curve Shapes: MLCS2k2. AJ, 659:122, 2007.

[2] J. Guy et al. SALT2: Using Distant Supernovae to Improve the use of Type Ia Supernovae as Distance

Indicators. A&A, 466:11–21, 2007.

[3] C. R. Burns et al. The Carnegie Supernova Project: Light-curve Fitting with SNooPy. AJ, 141:19,

January 2011.

[4] G. Goldhaber et al. Timescale Stretch Parameterization of Type Ia Supernova B-band Light Curves.

Astrophys. J., 558:359–368, 2001.

[5] B. Hayden, P. Garnavich, and SDSS-SN Survey. The Rise and Fall of SDSS-II Supernovae. Bulletin

of the American Astronomical Society, 41:254, 2009.

[6] R. Kessler et al. Results from the Supernova Photometric Classiﬁcation Challenge. PASP, 122:1415–

1431, December 2010.

[7] R. Kessler et al.

SNANA

: A public software package for supernova analysis. PASP, 121:1028, 2009.

[8] D. J. Schlegel, D. P. Finkbeiner, and M. Davis. Maps of Dust Infrared Emission for Use in Estimation

of Reddening and Cosmic Microwave Background Radiation Foregrounds. Astrophys. J., 500:525,

June 1998.

[9] P. Nugent et al. K-Corrections and Extinction Corrections for Type Ia Supernovae. PASP, 114:803,

2002.

[10] J. Carretero et al. An algorithm to build mock galaxy catalogues using MICE simulations. mnras,

447:646–670, February 2015.

[11] V. Marra, M. Quartin, and L. Amendola. Accurate weak lensing of standard candles. I. Flexible

cosmological ﬁts. prd, 88(6):063004, September 2013.

[12] M. Sako et al. Photometric Type Ia Supernova Candidates from the Three-year SDSS-II SN Survey

Data. Astrophys. J., 738:162, September 2011.

[13] M. Sako et al. Data Release of the SDSS-II Supernova Survey. arXiv:1401.3317, 2014.

[14] J. Marriner et al. A More General Model for the Intrinsic Scatter in Type Ia Supernova Distance

Moduli. Astrophys. J., 740:72, October 2011.

[15] R. Kessler and D. Scolnic. Correcting Type Ia Supernova Distances for Selection Biases and Con-

tamination in Photometrically Identiﬁed Samples. apj, 836:56, February 2017.

[16] L. Hui and P. B. Greene. Correlated Fluctuations in Luminosity Distance and the Importance of

Peculiar Motion in Supernova Surveys. Phys. Rev., 73(12):123526, 2006.

[17] M. Goliath et al. Supernovae and the Nature of the Dark Energy. A&A, 380:6–18, 2001.

165

Snana Manual

Navigation menu

Versions of this User Manual:

Views

Navigation