Sonnet Users Guide
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 440 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Table of Contents
- Chapter 1 Introduction
- Chapter 2 What’s New in Sonnet Suites Release 16
- Chapter 3 Subsectioning
- Chapter 4 Metalization and Dielectric Layer Loss
- Chapter 5 Ports
- Chapter 6 De-embedding
- Chapter 7 Components
- Chapter 8 Adaptive Band Synthesis (ABS)
- Chapter 9 Parameterizing your Project
- Chapter 10 Parameter Sweep and Optimization Tutorial
- Chapter 11 Conformal Mesh
- Chapter 12 Netlist Project Analysis
- Chapter 13 Circuit Subdivision
- Chapter 14 Circuit Subdivision Tutorial
- Chapter 15 Vias
- Chapter 16 Thick Metal
- Chapter 17 Dielectric Bricks
- Chapter 18 Antennas and Radiation
- Chapter 19 Far Field Viewer Tutorial
- Creating an Antenna Pattern File
- Running the Far Field Viewer
- Calculating the Response
- Selecting the Response
- Zooming
- Probing the Plot
- Re-Normalizing the Plot
- Changing to a Polar Plot
- Turning Off the Legend
- Changing the Radius Axis
- Selecting a Frequency Plot
- Viewing a Surface Plot
- Saving the Far Field Viewer File
- Exiting the Far Field Viewer Program
- References
- Chapter 20 SPICE Model Synthesis
- Chapter 21 Box Resonances
- Chapter 22 Accuracy Benchmarking
- Appendix I Em and xgeom Command Line for Batch
- Appendix II Sonnet References
- Index


At Sonnet, we've been developing 3D planar high frequency EM
software since 1983, and our software has earned a solid
reputation as the world's most accurate commercial planar EM
analysis package for single and multi-layer planar circuits, packages
and antennas.
Sonnet Software Inc., founded by Dr. James C. Rautio, is a private
company, entirely dedicated to the development of commercial EM
software. We take great pride in providing quality technical
support for our products with timely response--which we believe to
be very important for high-end technical software products.
Sonnet is based in Syracuse, NY, USA with representatives across
the globe.

SONNET USER’S GUIDE
Published: May 2018
Release 16
Sonnet Software, Inc.
126 N. Salina Street
Syracuse, NY 13202
Phone: (315) 453-3096
Fax: (315) 451-1694
www.sonnetsoftware.com
Copyright 1989,1991,1993, 1995-2018 Sonnet Software, Inc. All Rights Reserved
Registration numbers: TX 2-723-907, TX 2-760-739
Rev 16.56

Copyright Notice
Reproduction of this document in whole or in part, without the prior express written authorization of
Sonnet Software, Inc. is prohibited. Documentation and all authorized copies of documentation must
remain solely in the possession of the customer at all times, and must remain at the software designated
site. The customer shall not, under any circumstances, provide the documentation to any third party
without prior written approval from Sonnet Software, Inc. This publication is subject to change at any
time and without notice. Any suggestions for improvements in this publication or in the software it
describes are welcome.
Trademarks
The program names, xgeom, emstatus, emvu, patvu, dxfgeo, ebridge, emgraph, gds, cvbridge,
emserver, emclient, sonntcds, and sonntawr, sonntawr64, Blink, Co-calibrated, Lite, LitePlus,
Level2 Basic, Level2 Silver, and Level3 Gold are trademarks of Sonnet Software, Inc.
Sonnet®, em®, and emCluster® are registered trademarks of Sonnet Software, Inc.
Windows XP, Windows Vista, Windows 7, Windows 8, Windows 10 and Internet Explorer® are U.S.
registered trademarks of Microsoft Corporation.
AutoCAD and Drawing Interchange file (DXF) are trademarks of Auto Desk, Inc.
Cadence® and Virtuoso® are registered trademarks of Cadence Design Systems, Inc.
GLOBALFOUNDRIES® is a registered trademark of GlobalFoundries, Inc.
Agilent, ADS, and Touchstone are trademarks of Keysight Technologies.
NI AWR and Microwave Office are registered trademarks and EM Socket is a trademark of National
Instruments, Inc.
HSPICE is a registered trademark of Synopsys, Inc.
GDSII is a trademark of Calma Company.
Flexera Software, Flexlm, FlexNet, InstallShield, are trademarks of Flexera Software, Inc. and/or
InstallShield Co.Inc. in the United States of America and/or other countries.
OSF/Motif is a trademark of the Open Software Foundation.
X Window System is a trademark of The Open Group
Linux® is a registered trademark of Linus Torvalds.
Red Hat® is a registered trademark of Red Hat, Inc.
SUSE®, openSUSE® and SLES® are registered trademarks of SUSE LLC.
OpenGL® is a registered trademark owned by Silicon Graphics, Inc.
MATLAB is a registered trademark of The MathWorks, Inc. in the United States and/or other countries.
Acrobat® is a registered trademark of Adobe Systems Incorporated.
Xpeedic® and IRIS® are registered trademarks of Xpeedic Technology.
ODB++® is a registered trademark of Mentor Graphics Corporation.
Modelithics® is a registered trademark of Modelithics, Inc.

Table of Contents
5
TABLE OF CONTENTS . . . . . . . . . . . . . . . . . . . . . . . . 5
1INTRODUCTION . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
The Sonnet Design Suite. . . . . . . . . . . . . . . . . . . . . . . . . 15
The Analysis Engine, em . . . . . . . . . . . . . . . . . . . . . . . . . 20
Em Origins. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2WHAT’S NEW IN SONNET SUITES RELEASE 16. . . . . . . . . . . . . 23
3S
UBSECTIONING . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
Metal Fill. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
Tips for Selecting A Good Cell Size . . . . . . . . . . . . . . . . . . 29
Viewing the Subsections. . . . . . . . . . . . . . . . . . . . . . . . . 31
Using the Speed/Memory Control. . . . . . . . . . . . . . . . . . . 32
Changing the Subsectioning of a Polygon . . . . . . . . . . . . . . 35
Default Subsectioning of a Polygon . . . . . . . . . . . . . . . 35
X Min and Y Min with Edge Mesh Off . . . . . . . . . . . . . . 37
X Min and Y Min with Edge Mesh On. . . . . . . . . . . . . . . 39
Using X Max and Y Max . . . . . . . . . . . . . . . . . . . . . . . 40
Setting the Maximum Subsection Size Parameter. . . . . . . . . 41
Defining the Subsectioning Frequency. . . . . . . . . . . . . . . . 41
Diagonal Fill Subsectioning . . . . . . . . . . . . . . . . . . . . . . . 42
Conformal Mesh Subsectioning. . . . . . . . . . . . . . . . . . . . . 43
Conformal Mesh Subsectioning Control. . . . . . . . . . . . . 45
4METALIZATION AND DIELECTRIC LAYER LOSS. . . . . . . . . . . . . . 47
Planar Metalization Loss. . . . . . . . . . . . . . . . . . . . . . . . . 48
Sonnet’s Loss Model for Planar Metalization . . . . . . . . . 48
Problems In Determining Planar Metal Loss. . . . . . . . . . 49
Determining Good Input Values . . . . . . . . . . . . . . . . . 50
Creating Planar Metal Types . . . . . . . . . . . . . . . . . . . 50
Via Metalization Loss . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
Creating Via Metal Types. . . . . . . . . . . . . . . . . . . . . . 59
Metal Libraries . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
Dielectric Layer Loss . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
TABLE OF CONTENTS

Sonnet User’s Guide
6
Dielectric Layer Parameters . . . . . . . . . . . . . . . . . . . 66
Frequency Dependent Loss . . . . . . . . . . . . . . . . . . . . 68
How to Create a New Dielectric Layer. . . . . . . . . . . . . 69
Dielectric Libraries . . . . . . . . . . . . . . . . . . . . . . . . . 69
5PORTS. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
Port Type Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
Port Normalizing Impedances . . . . . . . . . . . . . . . . . . . . . 73
Changing Port Impedance. . . . . . . . . . . . . . . . . . . . . 74
Special Port Numbering . . . . . . . . . . . . . . . . . . . . . . . . . 75
Ports with Duplicate Numbers . . . . . . . . . . . . . . . . . . 75
Ports with Negative Numbers . . . . . . . . . . . . . . . . . . 76
Using Port Number Zero for Ground Connections. . . . . . 77
Changing Port Numbering . . . . . . . . . . . . . . . . . . . . . 78
Renumbering All Ports . . . . . . . . . . . . . . . . . . . . . . . 79
Port Placement with Symmetry On . . . . . . . . . . . . . . . . . 79
Independent Reference Planes and Diagonal Ports . . . . . . . 80
Applying the Diagonal Port Feature to a Port . . . . . . . . 81
Diagonal Port Feature Limitations . . . . . . . . . . . . . . . 87
Standard Box-wall Port . . . . . . . . . . . . . . . . . . . . . . . . . 87
Adding Box-wall Ports . . . . . . . . . . . . . . . . . . . . . . . 88
Ref. Planes and Cal. Lengths for Box-wall Ports . . . . . . 88
Co-calibrated Internal Ports . . . . . . . . . . . . . . . . . . . . . . 89
Calibration Group Properties. . . . . . . . . . . . . . . . . . . 89
Adding Co-calibrated Ports . . . . . . . . . . . . . . . . . . . . 93
Rules for Co-Calibrated Ports . . . . . . . . . . . . . . . . . . 94
Ref. Planes and Cal. Lengths for Co-calibrated Ports . . . 97
Use in Components . . . . . . . . . . . . . . . . . . . . . . . . . 97
Via Ports. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
Adding Via Ports . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
Automatic-Grounded Ports. . . . . . . . . . . . . . . . . . . . . . . 99
Special Considerations for Auto-Grounded Ports . . . . . 100
Adding Auto-grounded Ports . . . . . . . . . . . . . . . . . . 101
Ref. Plane and Cal. Length for Autogrounded Ports . . . 101
Ungrounded Internal Ports . . . . . . . . . . . . . . . . . . . . . . 101
6DE-EMBEDDING . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

Table of Contents
7
Port Discontinuities . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
Shifting Reference Planes. . . . . . . . . . . . . . . . . . . . . . . 106
Single Feed Line . . . . . . . . . . . . . . . . . . . . . . . . . . 107
A Common Misconception . . . . . . . . . . . . . . . . . . . . 108
Rules for Reference Planes . . . . . . . . . . . . . . . . . . . . . . 109
Feed Lines Must Be Transmission Lines. . . . . . . . . . . . 109
De-embedding Without Reference Planes. . . . . . . . . . 110
Short Reference Planes for Boxwall Ports. . . . . . . . . . 110
Reference Planes Longer than the Feedline . . . . . . . . 112
Calibration Standards. . . . . . . . . . . . . . . . . . . . . . . . . . 114
Modifying Calibration Standard Lengths . . . . . . . . . . . 118
Coupled Transmission Lines. . . . . . . . . . . . . . . . . . . . . . 120
Shared reference planes . . . . . . . . . . . . . . . . . . . . . 121
Independent reference planes . . . . . . . . . . . . . . . . . 122
De-embedded Output Format . . . . . . . . . . . . . . . . . . . . 125
De-embedding Codes . . . . . . . . . . . . . . . . . . . . . . . 126
Plotting Z0 and Eeff. . . . . . . . . . . . . . . . . . . . . . . . . . . 126
Calculating Z0 and Eeff for Boxwall Ports . . . . . . . . . . 126
Lengths at Multiples of a Half-Wavelength . . . . . . . . . 129
Lengths Much Greater than One Wavelength. . . . . . . . 129
Single Transmission Line . . . . . . . . . . . . . . . . . . . . . 130
Coupled Transmission Lines . . . . . . . . . . . . . . . . . . . 134
7COMPONENTS. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 137
Component Assistant . . . . . . . . . . . . . . . . . . . . . . . . . . 138
Anatomy of a Component . . . . . . . . . . . . . . . . . . . . . . . 139
Component Types . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140
Data File . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140
Ideal Component . . . . . . . . . . . . . . . . . . . . . . . . . . 141
Ports Only . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 141
Sonnet Project . . . . . . . . . . . . . . . . . . . . . . . . . . . 142
User Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 142
Component Properties . . . . . . . . . . . . . . . . . . . . . . . . . 143
Ground Node Connection. . . . . . . . . . . . . . . . . . . . . 143
Terminal Width . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
Reference Planes. . . . . . . . . . . . . . . . . . . . . . . . . . 148

Sonnet User’s Guide
8
Calibration Lengths . . . . . . . . . . . . . . . . . . . . . . . . 148
Physical Size . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149
Rules for Using Components . . . . . . . . . . . . . . . . . . . . . 149
Analysis of a Component . . . . . . . . . . . . . . . . . . . . . . . 152
Data File Frequencies . . . . . . . . . . . . . . . . . . . . . . 152
Rerunning an Analysis . . . . . . . . . . . . . . . . . . . . . . 153
8ADAPTIVE BAND SYNTHESIS (ABS) . . . . . . . . . . . . . . . . . . 155
DC Point Extrapolation . . . . . . . . . . . . . . . . . . . . . . . . 156
ABS Resolution. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
Q-Factor Accuracy . . . . . . . . . . . . . . . . . . . . . . . . . . . 157
Enhanced Resonance Detection. . . . . . . . . . . . . . . . . . . 157
Running an Adaptive Sweep . . . . . . . . . . . . . . . . . . . . . 157
ABS Caching Level . . . . . . . . . . . . . . . . . . . . . . . . . . . 159
Multiple ABS Sweeps and Subsectioning. . . . . . . . . . . 159
Multi-Sweep Caching Scenarios . . . . . . . . . . . . . . . . 160
Find Minimum and Find Maximum . . . . . . . . . . . . . . . . . 162
Parameter Sweep. . . . . . . . . . . . . . . . . . . . . . . . . . . . 163
Analysis Issues . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165
Multiple Box Resonances . . . . . . . . . . . . . . . . . . . . 165
De-embedding . . . . . . . . . . . . . . . . . . . . . . . . . . . 165
Transmission Line Parameters . . . . . . . . . . . . . . . . . 166
Current Density Data . . . . . . . . . . . . . . . . . . . . . . . 166
Ripple in ABS S-Parameters. . . . . . . . . . . . . . . . . . . 166
Output Files. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166
Viewing the Adaptive Response. . . . . . . . . . . . . . . . . . . 167
ABS Preview. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 168
9PARAMETERIZING YOUR PROJECT . . . . . . . . . . . . . . . . . . . 171
Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172
How to Create a Variable . . . . . . . . . . . . . . . . . . . . 173
Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175
Dependent Variables . . . . . . . . . . . . . . . . . . . . . . . 176
Dimension Parameters. . . . . . . . . . . . . . . . . . . . . . . . . 177
Anchored Dimension Parameters . . . . . . . . . . . . . . . 179
Symmetrical Dimension Parameters . . . . . . . . . . . . . 180
Radial Dimension Parameters . . . . . . . . . . . . . . . . . 185
Reference Planes . . . . . . . . . . . . . . . . . . . . . . . . . 187

Table of Contents
9
Dependent Dimension Parameters. . . . . . . . . . . . . . . 187
Circular Dependencies in Parameters . . . . . . . . . . . . 188
Parameter Sweep . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189
Optimization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 192
10 PARAMETER SWEEP AND OPTIMIZATION TUTORIAL. . . . . . . . . . 197
Setting Up Dimension Parameters. . . . . . . . . . . . . . . . . . 198
Anchored Parameters . . . . . . . . . . . . . . . . . . . . . . . 198
Symmetric Parameters . . . . . . . . . . . . . . . . . . . . . . 203
Parameter Sweep . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206
Setting Up a Parameter Sweep. . . . . . . . . . . . . . . . . 207
Executing the Parameter Sweep. . . . . . . . . . . . . . . . 210
Observing the Parameter Sweep Data . . . . . . . . . . . . 210
Optimization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 213
Entering New Nominal Values. . . . . . . . . . . . . . . . . . 214
Setting Up an Optimization . . . . . . . . . . . . . . . . . . . 214
Running an Optimization. . . . . . . . . . . . . . . . . . . . . 219
Observing your Optimization Data. . . . . . . . . . . . . . . 220
Accepting the Optimized Values. . . . . . . . . . . . . . . . . . . 223
11 CONFORMAL MESH. . . . . . . . . . . . . . . . . . . . . . . . . . . . 227
Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 227
Use Conformal Meshing for Feed Lines, Not Patches. . . 229
Applying Conformal Meshing . . . . . . . . . . . . . . . . . . . . . 229
Conformal Meshing Rules . . . . . . . . . . . . . . . . . . . . . . . 231
Single Precision Option . . . . . . . . . . . . . . . . . . . . . . 233
Using Conformal Meshing Effectively. . . . . . . . . . . . . . . . 233
Use Conformal Meshing for Non-Manhattan Polygons . . 233
Boundaries Should Be Vertical or Horizontal . . . . . . . . 235
Cell Size and Processing Time . . . . . . . . . . . . . . . . . 235
Current Density Viewing. . . . . . . . . . . . . . . . . . . . . . . . 236
12 NETLIST PROJECT ANALYSIS . . . . . . . . . . . . . . . . . . . . . . 239
Networks. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 240
Example of Node Assignments in a Complex Circuit . . . 241
Creating a Netlist . . . . . . . . . . . . . . . . . . . . . . . . . . . . 244
Netlist Example Files . . . . . . . . . . . . . . . . . . . . . . . 244
Cascading S-, Y- and Z-Parameter Data Files . . . . . . . . . . 245

Sonnet User’s Guide
10
A Network File with Geometry Project . . . . . . . . . . . . . . 246
Inserting Modeled Elements into a Geometry. . . . . . . . . . 249
Using Ungrounded-Internal Ports . . . . . . . . . . . . . . . 252
13 CIRCUIT SUBDIVISION . . . . . . . . . . . . . . . . . . . . . . . . . . 255
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255
Circuit Subdivision in Sonnet . . . . . . . . . . . . . . . . . . . . 257
Choosing Subdivision Line Placement . . . . . . . . . . . . . . . 260
Good and Bad Placements of Subdivision Lines . . . . . . 261
Subdivision Line Orientation . . . . . . . . . . . . . . . . . . 265
Setting Up Circuit Properties . . . . . . . . . . . . . . . . . . . . 267
Setting Up the Coarse Step Size Frequency Sweep. . . . 268
Subdividing Your Circuit . . . . . . . . . . . . . . . . . . . . . . . 269
Analyzing Your Subdivided Circuit . . . . . . . . . . . . . . . . . 269
14 CIRCUIT SUBDIVISION TUTORIAL . . . . . . . . . . . . . . . . . . . . 271
Obtaining the Example File . . . . . . . . . . . . . . . . . . . . . 272
Adding the Subdivision Lines. . . . . . . . . . . . . . . . . . . . . 272
Setting Up Circuit Properties . . . . . . . . . . . . . . . . . . . . 275
Subdividing Your Circuit . . . . . . . . . . . . . . . . . . . . . . . 277
Analysis of the Network File. . . . . . . . . . . . . . . . . . . . . 280
Additional Improvements. . . . . . . . . . . . . . . . . . . . . . . 282
15 VIAS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 285
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 285
Creating Vias. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 286
Via Direction . . . . . . . . . . . . . . . . . . . . . . . . . . . . 287
Via Polygons . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 288
Via Subsections. . . . . . . . . . . . . . . . . . . . . . . . . . . 289
Meshing Fill for Vias . . . . . . . . . . . . . . . . . . . . . . . 290
Adding a Rectangular Via to Ground . . . . . . . . . . . . . 296
Via Loss. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 298
Via Pads . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 299
Via Ports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 299
Auto Height Vias. . . . . . . . . . . . . . . . . . . . . . . . . . 299
Edge Vias . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 300
Edge Via Loss . . . . . . . . . . . . . . . . . . . . . . . . . . . . 301
Simple Via Example . . . . . . . . . . . . . . . . . . . . . . . . . . 302

Table of Contents
11
16 THICK METAL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 303
Thick Metal Type . . . . . . . . . . . . . . . . . . . . . . . . . . . . 303
Creating a Thick Metal Polygon . . . . . . . . . . . . . . . . . . . 305
Viewing Thick Metal in the Project Editor . . . . . . . . . . . . 308
Stackup Manager . . . . . . . . . . . . . . . . . . . . . . . . . . 309
Modeling . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 310
Modeling Plated Metal . . . . . . . . . . . . . . . . . . . . . . . . . 311
Modeling Conductor-Via-Conductor Stackups . . . . . . . . . . 311
Bar Via Configuration . . . . . . . . . . . . . . . . . . . . . . . 312
Via Array Configuration. . . . . . . . . . . . . . . . . . . . . . 313
Modeling an Arbitrary Cross-Section . . . . . . . . . . . . . . . . 314
Thick Metal in the Current Density Viewer. . . . . . . . . . . . 315
17 DIELECTRIC BRICKS . . . . . . . . . . . . . . . . . . . . . . . . . . . 317
Applications of Dielectric Bricks. . . . . . . . . . . . . . . . . . . 319
Guidelines for Using Dielectric Bricks . . . . . . . . . . . . . . . 319
Subsectioning Dielectric Bricks. . . . . . . . . . . . . . . . . 319
Using Vias Inside a Dielectric Brick . . . . . . . . . . . . . . 319
Air Dielectric Bricks . . . . . . . . . . . . . . . . . . . . . . . . 320
Limitations of Dielectric Bricks . . . . . . . . . . . . . . . . . . . 320
Diagonal Fill . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 320
Antennas and Radiation . . . . . . . . . . . . . . . . . . . . . 320
Interfaces. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 320
Dielectric Brick Concepts . . . . . . . . . . . . . . . . . . . . . . . 321
Creating a Dielectric Brick. . . . . . . . . . . . . . . . . . . . 321
Viewing Dielectric Bricks. . . . . . . . . . . . . . . . . . . . . 321
Defining Dielectric Brick Materials . . . . . . . . . . . . . . 322
Changing Brick Materials . . . . . . . . . . . . . . . . . . . . . 324
Z-Partitioning . . . . . . . . . . . . . . . . . . . . . . . . . . . . 325
18 ANTENNAS AND RADIATION . . . . . . . . . . . . . . . . . . . . . . . 327
Background . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 328
Modeling Infinite Arrays . . . . . . . . . . . . . . . . . . . . . . . . 328
Modeling an Open Environment . . . . . . . . . . . . . . . . . . . 329
Validation Example . . . . . . . . . . . . . . . . . . . . . . . . . . . 333
Far Field Viewer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 334
Analysis Limitations . . . . . . . . . . . . . . . . . . . . . . . . 335

Sonnet User’s Guide
12
Spherical Coordinate System. . . . . . . . . . . . . . . . . . 336
Normalization . . . . . . . . . . . . . . . . . . . . . . . . . . . 339
Polarization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 340
References . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 340
19 FAR FIELD VIEWER TUTORIAL . . . . . . . . . . . . . . . . . . . . . 341
Creating an Antenna Pattern File . . . . . . . . . . . . . . . . . 342
Running the Far Field Viewer . . . . . . . . . . . . . . . . . . . . 343
Calculating the Response. . . . . . . . . . . . . . . . . . . . . . . 344
Selecting Phi Values . . . . . . . . . . . . . . . . . . . . . . . 345
Selecting Frequencies . . . . . . . . . . . . . . . . . . . . . . 345
Selecting the Response . . . . . . . . . . . . . . . . . . . . . . . . 346
Zooming . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 349
Probing the Plot. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 350
Re-Normalizing the Plot. . . . . . . . . . . . . . . . . . . . . . . . 351
Changing to a Polar Plot . . . . . . . . . . . . . . . . . . . . . . . 355
Turning Off the Legend . . . . . . . . . . . . . . . . . . . . . . . . 355
Changing the Radius Axis . . . . . . . . . . . . . . . . . . . . . . . 356
Selecting a Frequency Plot. . . . . . . . . . . . . . . . . . . . . . 358
Viewing a Surface Plot . . . . . . . . . . . . . . . . . . . . . . . . 361
Saving the Far Field Viewer File . . . . . . . . . . . . . . . . . . 361
Exiting the Far Field Viewer Program . . . . . . . . . . . . . . . 362
References . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 362
20 SPICE MODEL SYNTHESIS. . . . . . . . . . . . . . . . . . . . . . . . 363
PI Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 364
Using The PI Model Spice Option . . . . . . . . . . . . . . . 364
A Simple Microwave Example . . . . . . . . . . . . . . . . . 368
Topology Used for PI Model Output. . . . . . . . . . . . . . 368
N-Coupled Line Model . . . . . . . . . . . . . . . . . . . . . . . . . 369
Broadband SPICE Model . . . . . . . . . . . . . . . . . . . . . . . . 371
Class of Problems . . . . . . . . . . . . . . . . . . . . . . . . . 372
Creating a Broadband Spice Model . . . . . . . . . . . . . . 373
Checking the Accuracy of the Broadband Spice Model . 376
Improving the Accuracy of the Broadband Spice Model. 378
Broadband Spice Extractor Stability Factor . . . . . . . . 379
Inductor Model Extractor . . . . . . . . . . . . . . . . . . . . . . . 380
Model Topologies . . . . . . . . . . . . . . . . . . . . . . . . . 380

Table of Contents
13
Model Output. . . . . . . . . . . . . . . . . . . . . . . . . . . . 383
Using the Inductor Model Extractor (IME) . . . . . . . . . . 383
21 BOX RESONANCES . . . . . . . . . . . . . . . . . . . . . . . . . . . . 389
Introduction. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 389
Initial Indicators of a Box Resonance. . . . . . . . . . . . . . . . 390
Bandpass Filter Example with Resonances . . . . . . . . . . . . 391
Is It a Box Resonance? . . . . . . . . . . . . . . . . . . . . . . . . . 392
The Box Resonance Estimator . . . . . . . . . . . . . . . . . 392
Runtime Warning Messages . . . . . . . . . . . . . . . . . . . 394
Removing artificial box resonances. . . . . . . . . . . . . . . . . 396
Change box size. . . . . . . . . . . . . . . . . . . . . . . . . . . 397
Use a free space cover . . . . . . . . . . . . . . . . . . . . . . 397
Suppressing Real Resonances. . . . . . . . . . . . . . . . . . . . . 399
Changing the Box Size. . . . . . . . . . . . . . . . . . . . . . . 399
Adding Vias. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 399
Adding Absorbing Material. . . . . . . . . . . . . . . . . . . . 400
Using a Probe Circuit for a Quick Analysis . . . . . . . . . . . . 403
Viewing Electric Fields. . . . . . . . . . . . . . . . . . . . . . . . . 405
Summary. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 406
22 ACCURACY BENCHMARKING . . . . . . . . . . . . . . . . . . . . . . 407
An Exact Benchmark . . . . . . . . . . . . . . . . . . . . . . . . . . 407
Residual Error Evaluation . . . . . . . . . . . . . . . . . . . . . . . 409
Using the Error Estimates . . . . . . . . . . . . . . . . . . . . . . . 411
APPENDIX IEm AND XGEOM COMMAND LINE FOR BATCH . . . . . . . . . 413
em Command Line. . . . . . . . . . . . . . . . . . . . . . . . . . . . 413
Causal Dielectrics . . . . . . . . . . . . . . . . . . . . . . . . . 416
xgeom Command Line. . . . . . . . . . . . . . . . . . . . . . . . . . 417
Example of xgeom Command Line . . . . . . . . . . . . . . . 419
APPENDIX II SONNET REFERENCES . . . . . . . . . . . . . . . . . . . . . . 421
INDEX . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 429

Sonnet User’s Guide
14

Chapter 1 Introduction
15
Rev 16.56
Chapter 1 Introduction
The Sonnet User’s Guide is intended to provide in depth discussions of features
of Sonnet’s software. There is a short exposition of the theory behind Sonnet’s
analysis engine, em, followed by discussions of geometry elements and features
available in Sonnet. This manual also contains tutorials demonstrating how to use
some features in Sonnet. The tutorials follow chapters discussing that topic. Please
refer to the Table of Contents to see what tutorials are available.
For installation instructions and the basics of using Sonnet Suites, please refer to
the Getting Started manual. To learn about new features in this release, please
refer to Chapter 2, “What’s New in Sonnet Suites Release 16” on page 23.
The Sonnet Design Suite
The suite of Sonnet analysis tools is shown on page 19. Using these tools, Sonnet
provides an open environment to many other design and layout programs. The
following is a brief description of all of the Sonnet tools. Check with your system
administrator to find out if you are licensed for these products:

Sonnet User’s Guide
16
Rev 16.56
Project
Editor The project editor is a user-friendly graphical interface that enables you to input
your circuit geometry or circuit netlist for subsequent em analysis. If you have
purchased the DXF, GDSII and/or the Gerber translator, the translator interface is
found in the project editor. You also set up analysis controls for your project in the
project editor.
Program module: xgeom
Analysis
Engine Em is the electromagnetic analysis engine. It uses a modified method of moments
analysis based on Maxwell's equations to perform a true three dimensional current
analysis of predominantly planar structures. Em computes S, Y, or Z-parameters,
transmission line parameters (Z0, Eeff, VSWR, GMax, Zin, and the Loss Factor),
and SPICE equivalent lumped element networks. Additionally, it creates files for
further processing by the current density viewer and the far field viewer. Em’s
circuit netlist capability cascades the results of electromagnetic analyses with
lumped elements, ideal transmission line elements and external S-parameter data.
Program module: em
Analysis
Monitor The analysis monitor allows you to observe the on-going status of analyses being
run by em as well as creating and editing batch files to provide a queue for em
jobs.
Program module: emstatus
Response
Viewer The response viewer is the plotting tool. This program allows you to plot your
response data from em, as well as other simulation tools, as a Cartesian graph or
a Smith chart. You may also plot the results of an equation. In addition, the
response viewer may generate Spice lumped models.
Program module: emgraph
Current
Density
Viewer
The current density viewer is a visualization tool which acts as a post-processor to
em providing you with an immediate qualitative view of the electromagnetic
interactions occurring within your circuit. The currents may also be displayed in
3D.
Program module: emvu

Chapter 1 Introduction
17
Rev 16.56
Far Field
Viewer The far field viewer is the radiation pattern computation and display program. It
computes the far-field radiation pattern of radiating structures (such as patch
antennas) using the current density information from em and displays the far-field
radiation patterns in one of three formats: Cartesian plot, polar plot or surface plot.
Program module: patvu
GDSII
Translator The GDSII translator provides bidirectional translation of GDSII layout files to/
from the Sonnet project editor geometry format.
Program module: gds
DXF
Translator The DXF translator provides bidirectional translation of DXF layout files (such as
from AutoCAD) to/from the Sonnet project editor geometry format.
Program module: dxfgeo
Gerber
Translator The Gerber translator provides bidirectional translation of Gerber single layer and
multi-layer files to/from the Sonnet project editor geometry format.
Keysight
ADS
Interface
The Keysight ADS Interface provides a seamless translation capability between
Sonnet and Keysight’s ADS. From within ADS Layout package you can directly
create Sonnet geometry files. Em simulations can be invoked and the results
incorporated into your design without leaving the ADS environment.
Program module: ebridge
NI AWR
Microwave
Office
Interface
The NI AWR Microwave Office Interface provides a seamless incorporation of
Sonnet’s world class EM simulation engine, em, into the Microwave Office envi-
ronment using Microwave Office's EM Socket. You can take advantage of Son-
net’s accuracy without having to learn the Sonnet interface. Although, for
advanced users who wish to take advantage of powerful advanced features not
presently supported in the integrated environment, the partnership of AWR and
Sonnet has simplified the process of moving EM projects between Microwave Of-
fice and Sonnet.
Program Module: sonntawr
Cadence
Virtuoso
Interface
This Sonnet plug-in for the Cadence Virtuoso suite enables the RFIC designer to
configure and run the EM analysis from a layout cell, extract accurate electrical
models, and create a schematic symbol for Analog Artist and RFDE simulation.
Program Module: sonntcds
Broadband
Spice
Extractor
A Broadband Spice extraction module is available that provides high-order Spice
models. In order to create a Spice model which is valid across a broad band, the
Sonnet broadband SPICE Extractor feature finds a rational polynomial which
“fits” the S-Parameter data. This polynomial is used to generate the equivalent

Sonnet User’s Guide
18
Rev 16.56
lumped element circuits which may be used as an input to either PSpice or Spec-
tre. Since the S-Parameters are fitted over a wide frequency band, the generated
models can be used in circuit simulators for AC sweeps and transient simulations.

Chapter 1 Introduction
19
Rev 16.56
w

Sonnet User’s Guide
20
Rev 16.56
Em performs electromagnetic analysis [87, 88, 90] for arbitrary 3-D planar [62]
(e.g., microstrip, coplanar, stripline, etc.) geometries, maintaining full accuracy at
all frequencies. Em is a “full-wave” analysis in that it takes into account all pos-
sible coupling mechanisms. The analysis inherently includes dispersion, stray
coupling, discontinuities, surface waves, moding, metalization loss, dielectric loss
and radiation loss. In short, it is a complete electromagnetic analysis. Since em
uses a surface meshing technique, i.e. it meshes only the surface of the circuit met-
alization, em can analyze predominately planar circuits much faster than volume
meshing techniques.
The Analysis Engine, em
Em analyzes 3-D structures embedded in planar multilayered dielectric on an un-
derlying fixed grid. For this class of circuits, em can use the FFT (Fast Fourier
Transform) analysis technique to efficiently calculate the electromagnetic cou-
pling on and between each dielectric surface. This provides em with its several or-
ders of magnitude of speed increase over volume meshing and other non-FFT
based surface meshing techniques.
Em is a complete electromagnetic analysis; all electromagnetic effects, such as
dispersion, loss, stray coupling, etc., are included. There are only two approxima-
tions used by em. First, the finite numerical precision inherent in digital comput-
ers. Second, em subdivides the metalization into small subsections made up of
cells. A Simple Outline of the Theory

Chapter 1 Introduction
21
Rev 16.56
Em performs an electromagnetic analysis of a microstrip, stripline, coplanar
waveguide, or any other 3-D planar circuit by solving for the current distribution
on the circuit metalization using the Method of Moments. The metalization is
modeled as zero-thickness metal between dielectric layers.
Subsectioning the Circuit
Em evaluates the electric field everywhere due to the current in a single subsec-
tion. Em then repeats the calculation for every subsection in the circuit, one at a
time. In so doing, em effectively calculates the “coupling” between each possible
pair of subsections in the circuit.
Em analyzes planar structures inside a shielding box. Port
connections are usually made at the box sidewalls.
Metal Side Walls
Metal Box Top
Dielectric Layer
Zero-thickness metal
The picture on the left shows the circuit as viewed in the project editor.
On the right is shown the subsectioning used in analyzing the circuit.

Sonnet User’s Guide
22
Rev 16.56
Zero Voltage Across a Conductor
Each subsection generates an electric field everywhere on the surface of the sub-
strate, but we know that the total tangential electric field must be zero on the sur-
face of any lossless conductor. This is the boundary condition: no voltage is
allowed across a perfect conductor.
The problem is solved by assuming current on all subsections simultaneously. Em
adjusts these currents so that the total tangential electric field, which is the sum of
all the individual electric fields just calculated, goes to zero everywhere that there
is a conductor. The currents that do this form the current distribution on the met-
alization. Once we have the currents, the S-parameters (or Y- or Z-) follow imme-
diately.
If there is metalization loss, we modify the boundary condition. Rather than zero
tangential electric field (zero voltage), we make the tangential electric field (the
voltage on each subsection) proportional to the current in the subsection. Follow-
ing Ohm’s Law, the constant of proportionality is the metalization surface resis-
tivity (in Ohms/square).
Sonnet is designed to work with your existing CAE software. Since the output data
is in Touchstone or Compact format (at your discretion), em provides a seamless
interface to your CAE tool.
Em Origins
The technique used in em was developed at Syracuse University in 1986 by Rautio
and Harrington [87, 88, 90]. It was originally developed as an extension of an
analysis of planar waveguide probes [92]. The technique expresses the fields in-
side the box as a sum of waveguide modes and is thus closely related to the spec-
tral domain approach.
The complete theory has been published in detail in peer reviewed journals. A full
list of relevant papers is presented in Appendix II "Sonnet References" on page
421.

Chapter 2 What’s New in Sonnet Suites Release 16
23
Rev 16.56
Chapter 2 What’s New in Sonnet
Suites Release 16
Below is a summary of the major new features in release 16 of Sonnet Suites. For
a complete list of changes and bug fixes, please refer to the release notes, found at:
www.sonnetsoftware.com/release-notes
Custom User Model Components: You may now create a component which
allows you to add a model from a library that has been purchased, or developed
in-house, to your geometry. For more information, please see "User Model" on
page 142.
Modelithics Integration: You may use the User Model Component to add a
model from the Modelithics library to your circuit. For more information, please
see "User Model" on page 142.
Project Components: You may now create a component which represents an-
other Sonnet project. For more information, please see "Sonnet Project" on page
142.

Sonnet User’s Guide
24
Rev 16.56
Increase in Threads for High Performance Solver: The thread count for
the High Performance Solver has increased from 32 to 48 threads for release 16
improving processing time for larger circuits.
Thick Metal Extrusion: When using the thick or rough metal type models for
planar metal, you may now choose which direction from the metal layer, up or
down, that you wish the metal to extend. For more information, see the Planar
Metal Editor dialog box in Help.
Unified Ground Connections: This feature allows you to add an ideal short
circuit to your circuit in locations other than the analysis box sidewall, and is es-
pecially useful for grounding internal shields and ground planes. For more infor-
mation, please see "Using Port Number Zero for Ground Connections" on page 77
for more information.
ABS Preview: The ABS preview allows you to stop an adaptive sweep which
has not yet converged in order to evaluate the data and possibly determine a new
analysis band for your simulation. For more information, please see "ABS Pre-
view" on page 168.
DC Point Extrapolation in ABS Sweep: Starting an ABS sweep at 0.0 GHz
automatically generates data for a DC point by extrapolating from the ABS sweep
data. Please see "DC Point Extrapolation" on page 156 for more information.
Enhanced Resonance Detection: Automatic Adaptive Band Synthesis
(ABS) resolution adjustment to resolve extremely narrowband resonances as is
typical for superconductor applications. Please see "Enhanced Resonance Detec-
tion" on page 157 for more information.
New Boolean Editing Operations: There are four new commands for editing
the metal in your geometry available in the project editor: Union, Intersect, Trim
and Subtract. For more information see “Boolean operations” in the Index of Help.
Robust Loss Metals: Improved loss models for multiple metal layers stacked on
top of each other. See "Modeling Plated Metal" on page 311 and "Modeling Con-
ductor-Via-Conductor Stackups" on page 311.
ODB++ Translator: This release introduces an ODB++ translator allowing you
to import an ODB++ file archive or directory and translating the contents to a Son-
net project. For more details, please see the “Gerber/ODB++ Translator,” page 3.
Resistance Per Via: The Volume and Array Via metal loss models now support
a resistance per via definition for contact resistance dominated vias. For more in-
formation, please see "Via Metalization Loss" on page 58.

Chapter 2 What’s New in Sonnet Suites Release 16
25
Rev 16.56
Automatic Bar Vias: There is a new via metal fill model that models the bar vias
typically used in many RFIC processes in a more efficient manner. Bar vias may
be automatically identified during translation. For more information, please see
the “Via Simplification” appendix in any Interface or Translator manual.
Polygon Edge Checking Support for Technology Layers: In previous re-
leases, there was an option to have the analysis engine, em, consider adjacent
metal levels when computing the subsectioning. In this release, you may now con-
sider adjacent technology layers. For more information, please see “polygon
checking” in the Index of Help.
Via Simplification More Efficient for RFIC Circuits:Improvement in the
array simplification feature now makes it possible to efficiently analyze circuits
with 100,000+ microvias.
GDSII Translator 64-bit Support:The GDSII translator and via simplification
now provide 64-bit support.
Cadence Virtuoso Interface 64-bit Support: There are a number of new
features which have been incorporated into the Cadence Virtuoso Interface in-
cluding support for 64-bit. Also new with this release, Help is available in all di-
alog boxes in the Cadence Virtuoso Interface. For a detailed list of new features
in the Cadence Virtuoso Interface, please see What’s New in Sonnet Suite’s Ca-
dence Virtuoso Interface.
Keysight ADS Interface Enhancements: Supports the new advanced materi-
al settings in Release 16. There is also a new tutorial available for the Keysight
ADS Interface. Please see Chapter 2 "Keysight ADS Interface Tutorial" on page
17 of the Keysight ADS Interface manual.

Sonnet User’s Guide
26
Rev 16.56
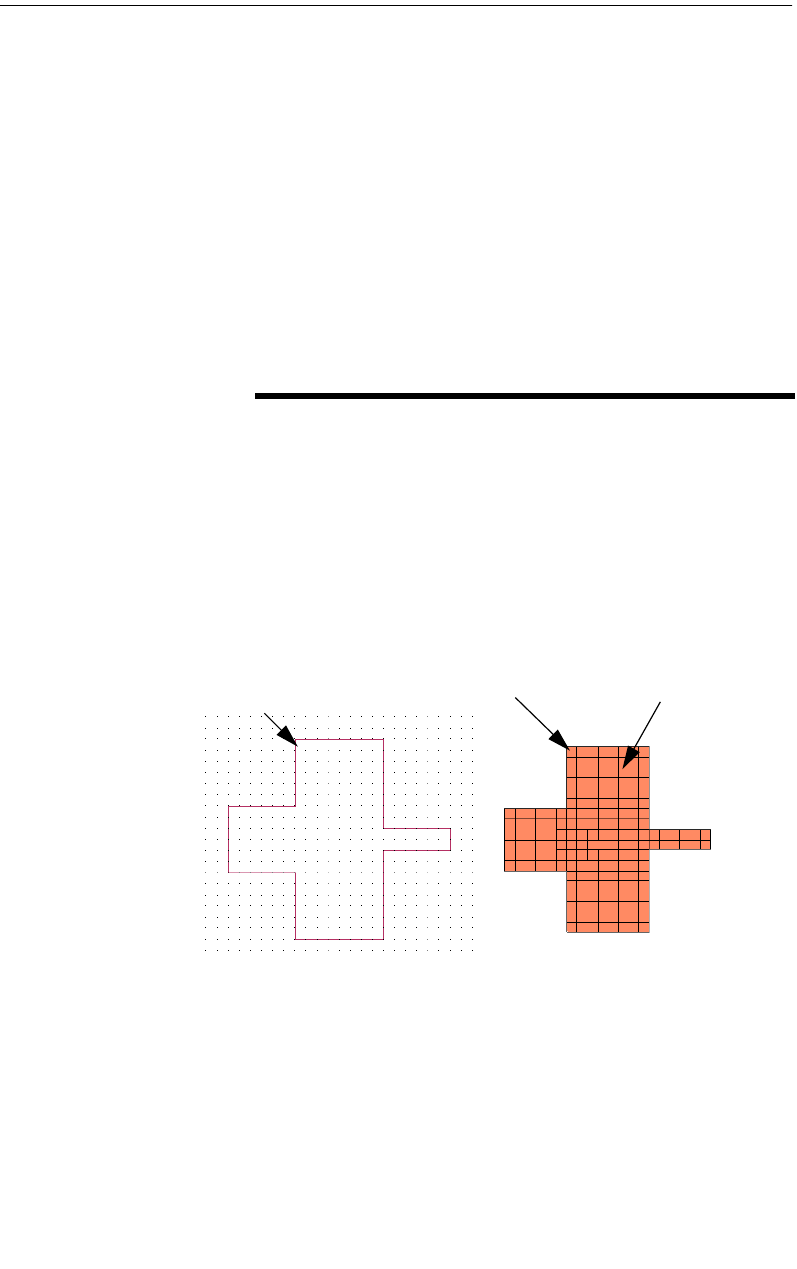
Chapter 3 Subsectioning
27
Rev 16.56
Chapter 3 Subsectioning
The Sonnet subsectioning is based on a uniform grid indicated by the small dots
in the project editor window. The small dots are placed at the corners of a “cell”.
One or more cells are automatically combined together to create subsections. Cells
may be square or rectangular (any aspect ratio), but must be the same over your
entire circuit.
A metal polygon with the cell grid is shown on the left. The
same metal polygon’s subsectioning is shown on the right.
Note that some subsections are comprised of only one cell,
while other subsections are made up of multiple cells.
Single Cell Single Cell Subsection Multiple Cell Subsection
Sonnet User’s Guide
28
Rev 16.56
The cell size is specified in the project editor in the Box Settings dialog box which
is opened by selecting CircuitBox. Since multiple cells are combined together
into a single subsection, the number of subsections is usually considerably smaller
than the number of cells. This is important because the analysis solves an N x N
matrix where N is the number of subsections. A small reduction in the value of N
results in a large reduction in analysis time and memory. All EM simulators have
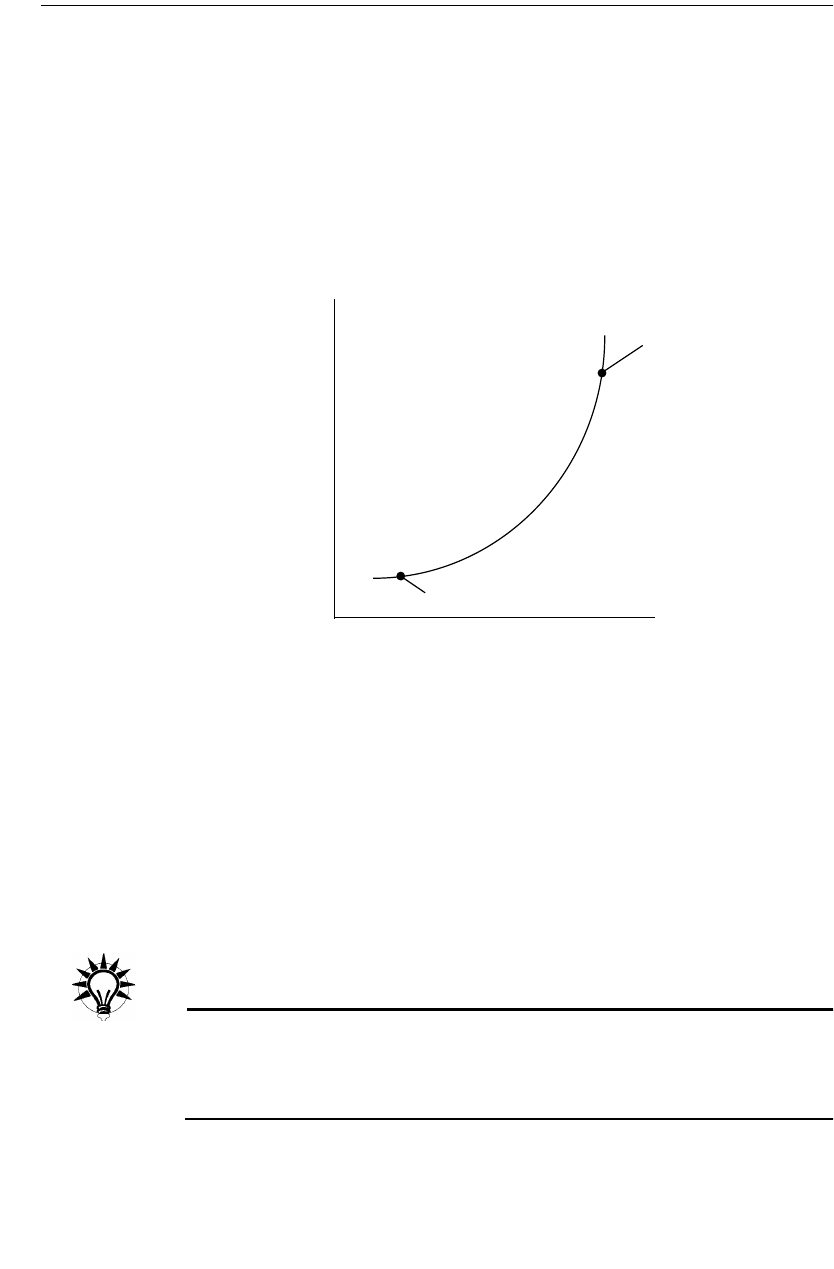
an inherent trade off between speed and accuracy. Decreasing the subsection size
typically increases the accuracy but also causes an increase in analysis time. The
figure below shows the typical trade off between analysis time and accuracy.
Em automatically places small subsections in critical areas where current density
is changing rapidly, but allows larger subsections in less critical areas, where cur-
rent density is smooth or changing slowly. However, in some cases you may wish
to modify the automatic algorithm because you want a faster, less accurate solu-
tion, or a slower, more accurate solution, than is provided by the automatic algo-
rithm.
This chapter explains how em combines cells into subsections and how you can
control this process to obtain an analysis time or the level of accuracy you require.
There is also a discussion of selecting the cell size and how that may affect the em
analysis.
TIP
For a discussion of efficient subsectioning practices with application examples,
please refer to the app note “Efficient Meshing in Sonnet” by Dr. Volker Mühl-
haus. This app note is available in help by looking under “subsectioning” in the
index.
Accuracy
Analysis
Time
Less subsections
More Subsections
Chapter 3 Subsectioning
29
Rev 16.56
Metal Fill
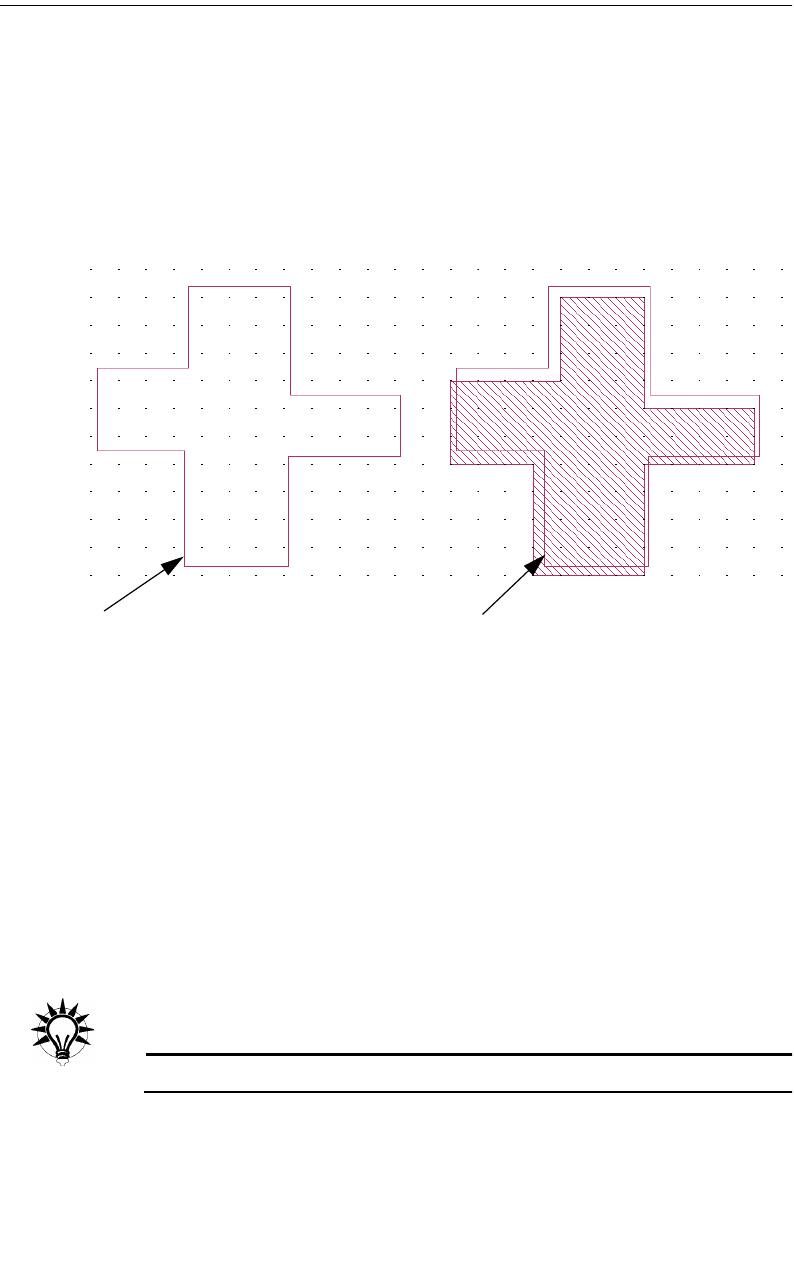
Metal polygons are represented with an outline and a cell fill pattern. The outline
represents exactly what you entered or imported. The cell fill represents the actual
metalization analyzed by em. Therefore, the actual metalization analyzed by em
may differ from that input by you as illustrated below.You turn the cell fill on and
off using the control-M key.
Tips for Selecting A Good Cell Size
As discussed above, em subdivides the circuit into subsections which are made up
of “cells,” the building block in the project editor. The following discussion de-
scribes how to select a cell size. To access the Cell Size calculator, click on the
Cell Size Calculator button in the Box Settings dialog box, which is invoked when
you select Circuit Box from the project editor menu.
TIP
Select a cell size that is smaller than 1/20 of a wavelength.
This shows the circuit with the cell fill
turned off. The outline shows the
polygon drawn by you. Notice that this
polygon is not “on” the grid.
This shows the circuit with the cell fill on.
The patterned area shows the actual metal
that is analyzed by the analysis engine, em.
Note that this metal is always “on” the grid.

Sonnet User’s Guide
30
Rev 16.56
Before calculating a cell size, it is important to calculate the wavelength at your
highest frequency of analysis. An exact number is not important. If you know the
approximate effective dielectric constant of your circuit, use this in the wave-
length calculation; otherwise, use the highest dielectric constant in your structure.
Most circuits require that your cell size be smaller than 1/20 of a wavelength.
Larger cell sizes usually result in unacceptable errors due to incorrect modeling of
the distributed effects across the circuit.
TIP
When possible, find a common factor for your most critical dimensions.
Since your circuit geometry is snapped to the nearest cell, you should set your cell
size to be a common factor of your most critical dimensions. For example, if your
circuit has dimensions of 30 microns, 40 microns and 60 microns, possible cell
sizes are 10 microns, 5 microns, 2.5 microns, 2 microns, etc. Large cell sizes result
in more efficient analyses, so choosing 10 microns is probably best.
Sonnet provides a cell size calculator utility which helps you find a good common
factor for your critical dimensions. Using the Cell Size Calculator is detailed in
Chapter 6, “Spiral Inductor” of the Getting Started manual.
TIP
After setting your initial cell size, visually inspect the metal fill (indicated by the
“hatched” pattern) for potential problems.
Once a common factor is found, some of your less critical dimensions may not be
a multiple of this factor. You should inspect your circuit for potential problems
caused by polygons which are not exact multiples of this cell size. An example is
shown below.
Notice that there is a
gap between the two
polygons as drawn by
the user, but the
actual on-grid metal
“shorts” the two
polygons together.

Chapter 3 Subsectioning
31
Rev 16.56
TIP
Calculate the X cell size and the Y cell size independently.
The X cell size and Y cell size do not have to be the same number. Calculate the
X cell size based on just your dimensions in the X direction, and your Y cell size
based on just your dimensions in the Y direction.
Viewing the Subsections
You can see the subsections used by Sonnet by following the instructions below.
Be aware that your dielectric layers and analysis frequencies must be defined and
at least one port must be added to your circuit before you may use the Estimate
Memory command.
To view the subsectioning, do the following:
1 From the project editor, select Analysis => Estimate Memory.
This calculates the amount of memory required for your analysis.
Sonnet User’s Guide
32
Rev 16.56
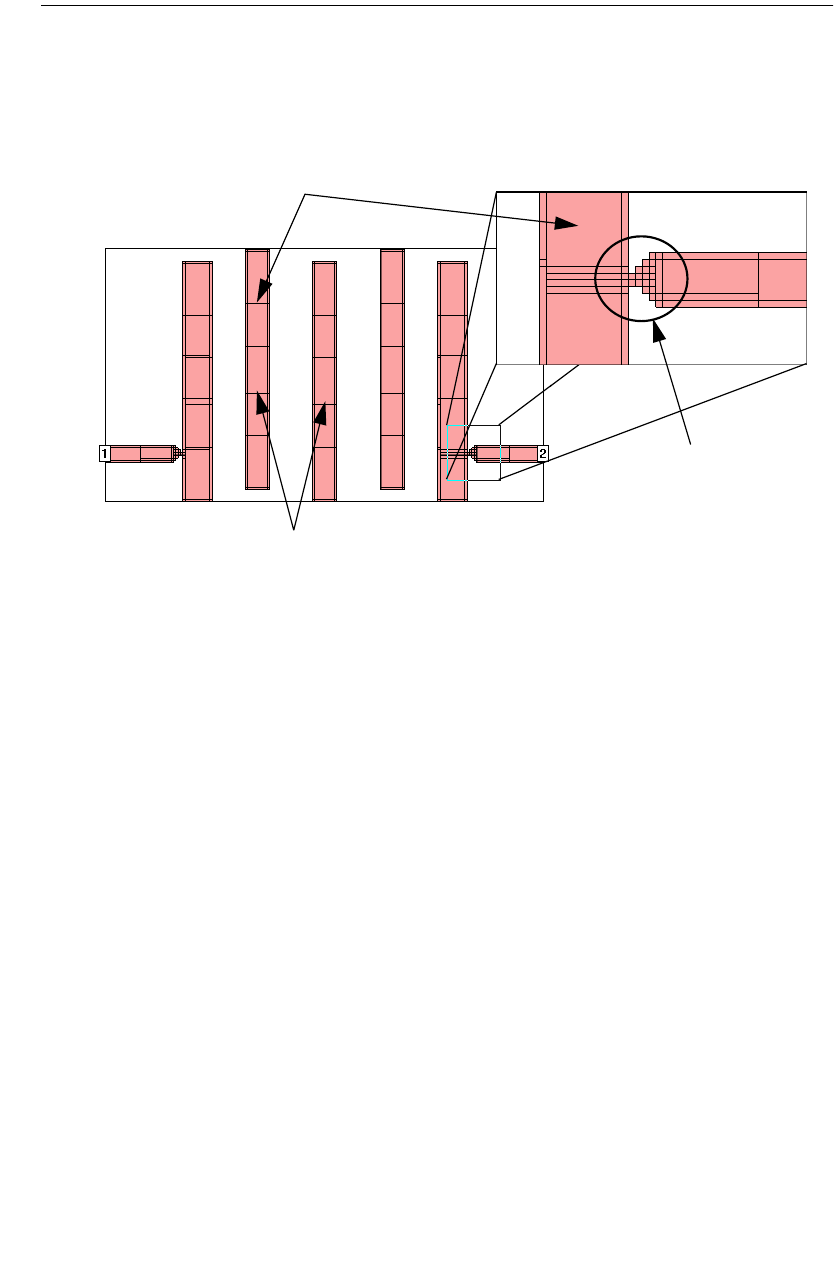
2 Click the View Subsections button.
A picture of your circuit will appear. The metal will show up as red, and the sub-
section borders will show up as black lines as shown in the illustration below:
Using the Speed/Memory Control
The Speed/Memory Control allows you to control the memory usage for an anal-
ysis by controlling the subsectioning of your circuit. The high memory settings
produce a more accurate answer and usually increase processing time. Converse-
ly, low memory settings run faster but do not yield as accurate an answer.
To access the Speed/Memory Control, follow the instructions below.
1 Select Analysis Setup from the project editor main menu.
Metalization
Note the use of smaller
subsections in an area
where current density
is changing rapidly.
Subsection Borders

Chapter 3 Subsectioning
33
Rev 16.56
2 In the Analysis Setup dialog box which appears, click on the Speed/Memory
button.
3 In the Analysis Speed/Memory Control dialog box which appears, select the
desired setting.
There are three settings for the Speed/Memory Control: Fine/Edge Meshing,
Coarse/Edge Meshing, Coarse/No Edge Meshing. Fine/Edge Meshing is the de-
fault setting and is described in “Default Subsectioning of a Polygon,” page 35.
An example is shown below. Again, note that this setting provides the most accu-
rate answer but demands the highest memory and processing time.
The second option is Coarse/Edge Meshing. This setting is often a good compro-
mise between speed and accuracy. Shown below is a typical circuit with this set-
ting. Notice the edges of the polygons have small subsections, but the inner
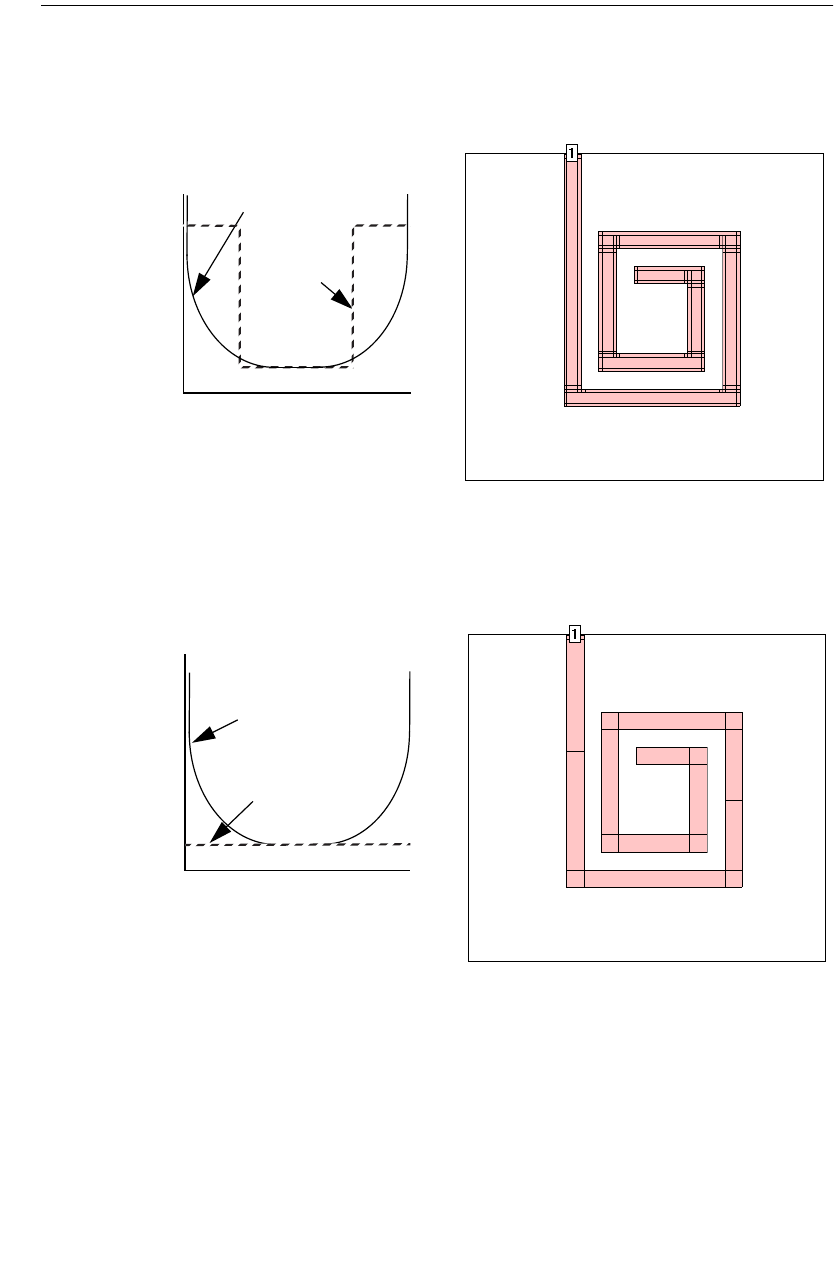
Sonnet User’s Guide
34
Rev 16.56
portions of the polygons have very large subsections This is a good compromise
between speed and accuracy because the currents on most RF traces change most
rapidly on the metal edge.
The last option is Coarse/No Edge Meshing. For this setting, all polygons are set
to use large subsections and edge mesh is set to “off.” This yields the fastest anal-
ysis, but is also the least accurate because the current across the width of the line
is constant. Shown below is the subsectioning of a typical circuit using this option.
Current
Distance across line width
Real Current
Modeled
Current
Current
plots
Current
Distance across line width
Real Current
Modeled
Current

Chapter 3 Subsectioning
35
Rev 16.56
Changing the Subsectioning of a Polygon
Sonnet allows you to control how cells are combined into subsections for each
polygon. This is done using the parameters “X Min”, “Y Min”, “X Max” and “Y
Max”. These parameters may be changed for each polygon, allowing you to have
coarser resolution for some polygons and finer resolution for others. You use the
Modify Metal Properties command to change these setting.
Please note that these controls are not used if conformal meshing is applied to the
metal polygon. There are separate controls when conformal mesh is applied to a
polygon. For more information about conformal meshing subsection control,
please refer to “Conformal Mesh Subsectioning Control,” page 45.
Before discussing how to make use of these parameters, we need to first under-
stand em’s automatic subsectioning for a polygon when the parameters are set to
their default settings.
Default Subsectioning of a Polygon
By default, Sonnet fills a polygon with “staircase” subsections. Other, more ad-
vanced fill types (diagonal and conformal) can be used. For diagonal subsections,
see "Diagonal Fill Subsectioning" on page 42. For conformal mesh, see "Confor-
mal Mesh Subsectioning" on page 43. This discussion applies to staircase fill.
This fill type is referred to as staircase because when using small rectangular sub-
sections to approximate a diagonal edge, the actual metalization takes on the ap-
pearance of a staircase, as in the example shown below.
The black outline represents
the polygon input by the user.
The patterned sections
represent the actual
metalization analyzed by em.
Staircase edge

Sonnet User’s Guide
36
Rev 16.56
The default values for the subsectioning parameters are X Min = 1, Y Min = 1,
X Max = 100 and Y Max = 100. These numbers specify the smallest and largest
allowed dimensions of the subsections in a polygon. With X Min = 1, the smallest
subsection in the X dimension is one cell. With X Max = 100, subsections are not
allowed to go over 100 cells in length.
The illustration below shows how these default subsectioning parameters are
used. Notice in the corner, the subsection size is just one cell. The current density
changes most rapidly here, thus, the smallest possible subsection size is used.
As we go away from the corner, along the edge, the subsections become longer.
For example, the next subsection is two cells long, the next one is four cells long,
etc. If the edge is long enough, the subsection length increases until it reaches X
Max (100) cells, or the maximum subsection size parameter, whichever comes
first, and then remains at that length until it gets close to another corner, disconti-
nuity, etc.
Subsection size is 1 cell by 1 cell on corner
Subsection size is 1 cell
Interior subsections are wide
Cell Size =
and long
wide along edge
A portion of circuit metal showing how em combines cells into
subsections. In this case the subsectioning parameters are set to their
default values: X Min = 1, Y Min = 1, X Max = 100 and Y Max = 100.

Chapter 3 Subsectioning
37
Rev 16.56
Notice, however, that no matter how long the edge subsection is, it is always one
cell wide. This is because the current density changes very rapidly as we move
from the edge toward the interior of the metal (this is called the edge singularity).
In order to allow an accurate representation of the very high edge current, the edge
subsections are allowed to be only one cell wide. (See the current plots on page
34.) However, the current density becomes smooth as we approach the interior of
the metal. Thus, wider subsections are allowed there. As before, the width goes
from one cell to two cells, then four, etc.
TIP
If two polygons butt up against each other or have a small overlap, the modeling
of the edge singularity will require a larger number of subsections at the boundary
between the two polygons. Using the Union command (Edit Boolean Opera-
tions Union) to join the two polygons into one will reduce the number of re-
quired subsections and speed up your analysis.
Conversely, if you have an area of your circuit at which you desire greater accu-
racy, using the Divide (Edit Divide Polygons) command at the point of interest
to create two polygons, forces the analysis to use smaller subsections in order to
model the edge singularities.
X Min and Y Min with Edge Mesh Off
On occasion, you may wish to change the default subsectioning for a given poly-
gon. You can do this using the subsectioning parameters X Min, Y Min, X Max
and Y Max.
Having the edge mesh option “on” is the default state for Sonnet projects; howev-
er, examining the case where edge mesh is “off” first makes understanding the
concept easier. This part of the discussion only applies to Manhattan polygons,
which is a polygon that has no diagonal edges. Turning edge mesh off for non-
manhattan polygons has no effect.
For Manhattan polygons with edge mesh off, X Min and Y Min set the size of the
edge subsections. By default, X Min and Y Min are 1. This means the edge sub-
sections are 1 cell wide. When X Min is set to 2, the subsections along vertical
edges are now 2 cells wide in the X direction (see the figure on page 38). This re-
duces the number of subsections and reduces the matrix size for a faster analysis.
However, accuracy may also be reduced due to the coarser modeling of the current
density near the structure edge or a discontinuity.

Sonnet User’s Guide
38
Rev 16.56
If X min or Y min are greater than your polygon size, em uses subsections as large
as possible to fill the polygon.
NOTE: The subsection parameters, X Min, Y Min, X Max and Y Max are
specified in cells (not mils, mm, microns, etc.). For example, X Min =
5 means that the minimum subsection size is 5 cells.
Although the X Min and Y Min parameters are very useful options, it is not a sub-
stitute for using a larger cell size. For example, a circuit with a cell size of 10 mi-
crons by 10 microns with X Min = 1 and Y Min =1 runs faster than the same circuit
with a cell size of 5 microns by 5 microns with X Min = 2 and Y Min = 2. Even
though the total number of subsections for each circuit may be the same, em must
spend extra time calculating the value for each subsection for the circuit with the
smaller cell size.
Cell Size =
{
2 Cells Wide
Y
X
{
1 Cell Wide
(Y Min = 1)
(X Min = 2) 4 Cells 8 Cells
4 Cells
2 Cells
A portion of circuit metal showing how em combines cells into subsections for
Manhattan polygons when X Min = 2 and Y Min = 1.

Chapter 3 Subsectioning
39
Rev 16.56
X Min and Y Min with Edge Mesh On
Having the edge mesh option “on” is the default state for Sonnet projects because
it provides a more accurate analysis. Having edge mesh “on” for a polygon chang-
es how the subsections on the very edge are handled. Starting from the left side of
the previous example with edge mesh off, the subsections were 2 cells, 4 cells and
8 cells wide. With edge mesh on, the subsections for the same polygon would be
1 cell, 4 cells, and 8 cells as shown in the illustration below. Notice only the out-
ermost edge is affected.
As mentioned in the previous section, the edge mesh setting only affects Manhat-
tan polygons (i.e. those with no diagonal or curved edges). Edge mesh is always
“on” for non-Manhattan polygons, regardless of the edge-mesh setting for that
polygon.
Cell Size =
Y
X
1 Cell by 1 Cell 4 Cells
on corner (2 * X Min)
A portion of circuit metal showing how em combines cells into subsections
for polygons with edge mesh on, with X Min = 2 and Y Min = 1. Edge mesh
polygons always have 1 cell wide edge subsections.

Sonnet User’s Guide
40
Rev 16.56
When used in conjunction with large X Min or Y Min values, the edge mesh op-
tion can be very useful in reducing the number of subsections but still maintaining
the edge singularity, as shown in a simple example below. This is very often a
good compromise between accuracy and speed.
In the case pictured above, X Min and Y Min are set to be very large, and the fre-
quency is low enough so that the Max. Subsection size parameter corresponds to
a subsection size that is larger than the polygon. This is exactly what is being done
when you set the Speed/Memory setting to “Coarse/Edge Meshing.”
Using X Max and Y Max
You may control the maximum subsection size of individual polygons by using
the X Max and Y Max parameters. For example, if X Max and Y Max are de-
creased to 1, then all subsections will be one cell. This results in a much larger
number of subsections and a very large matrix which are the cause of increased
analysis time. Thus, this should be done only on small circuits where extremely
high accuracy is required or you need a really smooth current density plot.
NOTE: If the maximum subsection size specified by X Max or Y Max is larger
than the size calculated by the Max. Subsection Size parameter, the
Max. Subsection Size parameter takes priority. The Max. Subsection
Size is discussed in "Setting the Maximum Subsection Size Parameter"
section which follows.

Chapter 3 Subsectioning
41
Rev 16.56
Setting the Maximum Subsection Size Parameter
The parameter Max. Subsection Size allows the specification of a maximum sub-
section size, in terms of subsections per wavelength, where the wavelength is ap-
proximated at the beginning of the analysis. By default, the highest analysis
frequency is used in the calculation of the wavelength. This value is a global set-
ting and is applied to the subsectioning of all polygons in your circuit.
The default of 20 subsections/- is fine for most work. This means that the maxi-
mum size of a subsection is 18 degrees at the highest frequency of analysis. In-
creasing this number decreases the maximum subsection size until the limit of 1
subsection = 1 cell is reached.
You might want to increase this parameter for a more accurate solution. For ex-
ample, changing it from 20 to 40 decreases the size of the largest subsections by
a factor of 2, resulting in a more accurate (but slower) solution. Keep in mind that
using smaller subsections in non-critical areas may have very little effect on the
accuracy of the analysis while increasing analysis time.
Another reason for using this parameter is when you require extremely smooth
current distributions for the current density viewer. With the default value of 20,
large interior subsections may make the current distribution look “choppy.” Set-
ting this value to a large number forces all subsections to be only 1 cell wide, pro-
viding smooth current distribution. Again, analysis time is impacted significantly.
The Max. Subsection Size parameter is specified in the Advanced Subsectioning
Controls which are opened by selecting Analysis Advanced Subsectioning from
the project editor main menu.
Defining the Subsectioning Frequency
The subsectioning parameter, Max. Subsection Size, applies to the subsectioning
of all polygons in your circuit, and is defined as subsections per wavelength. Nor-
mally, the highest analysis frequency is used to determine the wavelength. How-
ever, this may be changed by using the Subsectioning Frequency options in the
Advanced Subsectioning Control dialog box in the project editor. This dialog box
is opened by selecting Analysis Advanced Subsectioning from the project editor
main window. For details on what options are available to define the subsection-
ing frequency, click on the Help button in the Advanced Subsectioning Control di-
alog box.
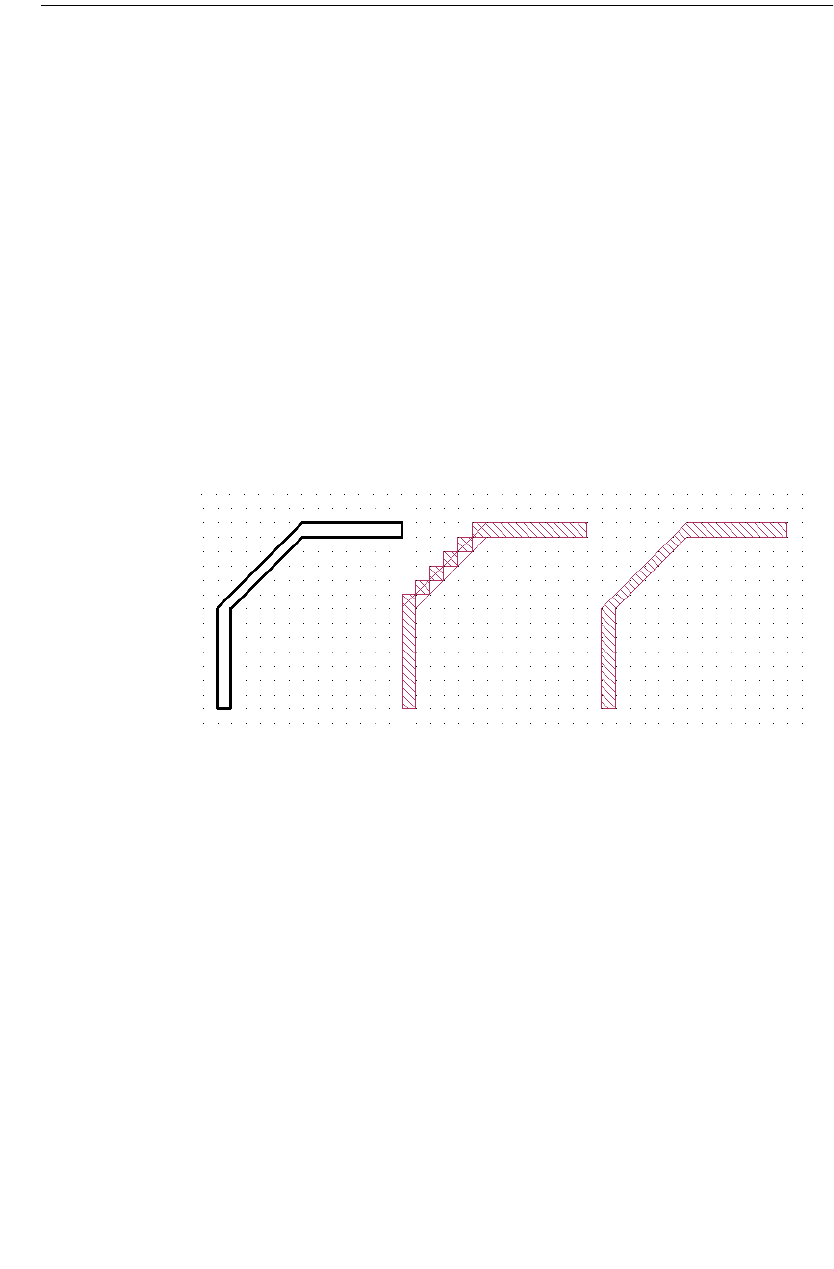
Sonnet User’s Guide
42
Rev 16.56
The frequency defined by the selected option is now used to determine the maxi-
mum subsection size instead of the highest frequency of analysis. Thus, the same
subsectioning can be used for several analyses which differ in the highest frequen-
cy being analyzed.
Diagonal Fill Subsectioning
Diagonal fill subsectioning is a technique which allows you to more accurately
model straight diagonal edges by using triangular subsection as well as rectangu-
lar. When modeling a circuit with one to two cell wide traces which contain a di-
agonal miter corner or a diagonal line, the metal fill using a staircase fill type
sometimes causes the actual metal being analyzed to have opens which do not
allow current to flow (see the graphic below). In these cases, applying the diagonal
fill type to a polygon creates a metal pattern which more accurately models the
polygon input by the user.
The first polygon on the left shows the polygon input by the user. The middle
polygon shows the metal fill pattern when the staircase fill type is used for the
polygon. Note that the metal fill is a series of polygons which only share a corner
hence not allowing any current to flow. The third polygon on the right shows the
metal fill pattern using the diagonal fill type. As you can see, the metal fill now
more closely matches the polygon input by the user and allows the current to flow.
Note that while diagonal fill yields more accurate answers, it increase processing
time and should only be used when necessary to correctly model your circuit.
Polygon input
by user. Metal fill using
staircase fill type. Metal fill using
diagonal fill type.
Chapter 3 Subsectioning
43
Rev 16.56
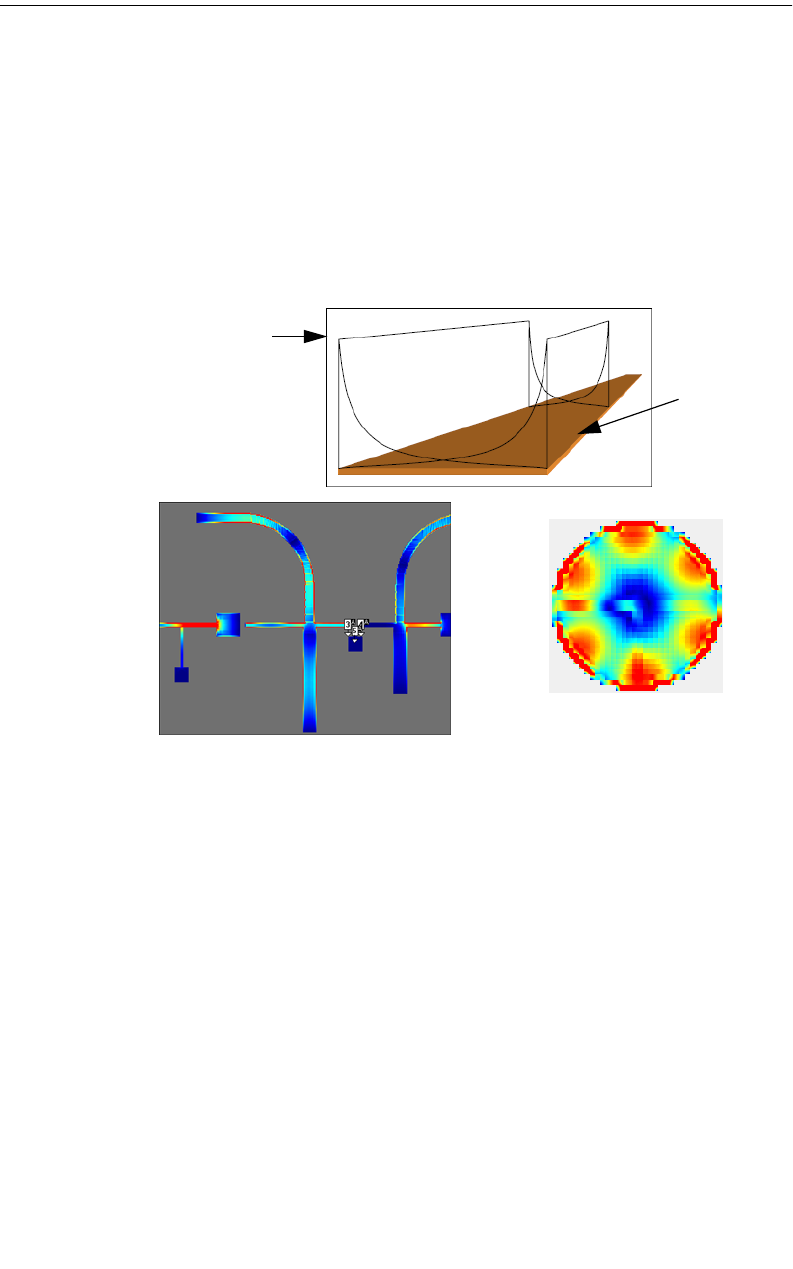
Conformal Mesh Subsectioning
Conformal meshing is a technique which can dramatically reduce the memory and
time required for analysis of a circuit with diagonal or curved polygon edges. For
a detailed discussion of conformal mesh and its rules of use, please refer to “Con-
formal Mesh,” page 227. Only the effect of conformal mesh on subsectioning is
discussed in this chapter. Conformal mesh assumes that most current flows on the
edges of circuit conductors, as shown below, and should only be applied when this
holds true.
This technique groups together strings of cells following diagonal and curved
metal contours to form long subsections along those contours. Whereas staircase
fill results in numerous small X- and Y-directed subsections, conformal mesh re-
Simplified
model of the
current density
basis function
for Conformal
Mesh
Transmission
Line
Conductor
Example of a good circuit for
conformal mesh (MMIC)
Example of a bad circuit for
conformal mesh (Patch
Antenna)
Sonnet User’s Guide
44
Rev 16.56
sults in a few long conformal subsections. The illustration below shows the actual
metalization of a conformal section in close up alongside the same section using
staircase fill.
Conformal sections, like standard subsections, are comprised of cells, so that the
actual metalization still shows a ''jagged'' edge when the polygon has a smooth
edge. However, the sections can be much larger due to conformal meshing. These
larger sections yield faster processing times with lower memory requirements for
your analysis.
Standard subsectioning requires a lot of subsections to model the correct current
distribution across the width of the line. Conformal subsections have this distribu-
tion built into the subsection. Sonnet conformal meshing automatically includes
the high edge current in each conformal section. This patented Sonnet capability
is unique. (U.S. Patent No. 6,163,762 issued December 19, 2000.)
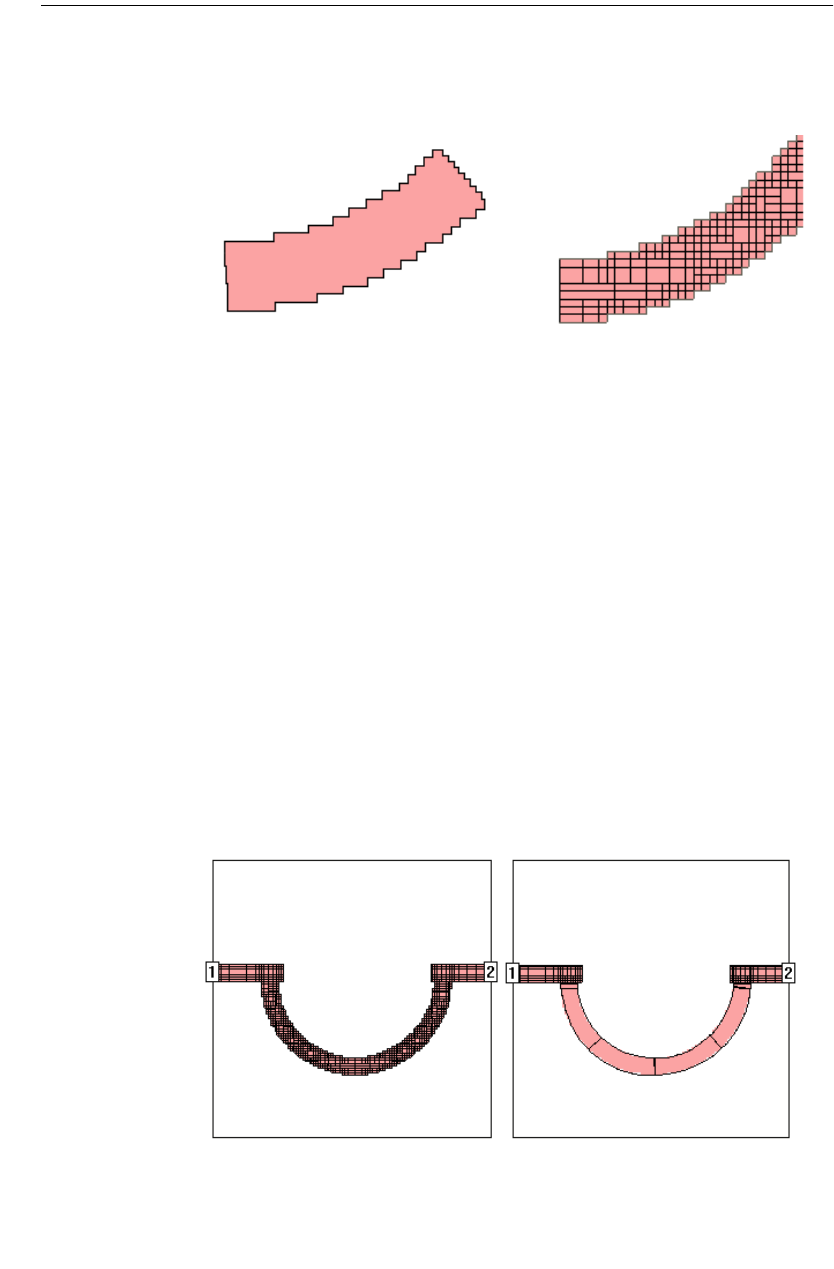
An example of a circuit using both standard subsectioning and conformal mesh is
shown below. The circuit shown at the left is displayed using standard subsection-
ing (staircase fill). Conformal meshing for the curved part of the circuit is shown
on the right. Note that for the curved part of the geometry, conformal mesh uses
substantially fewer subsections than the number used in the standard subsection-
ing.
Conformal section Staircase Fill
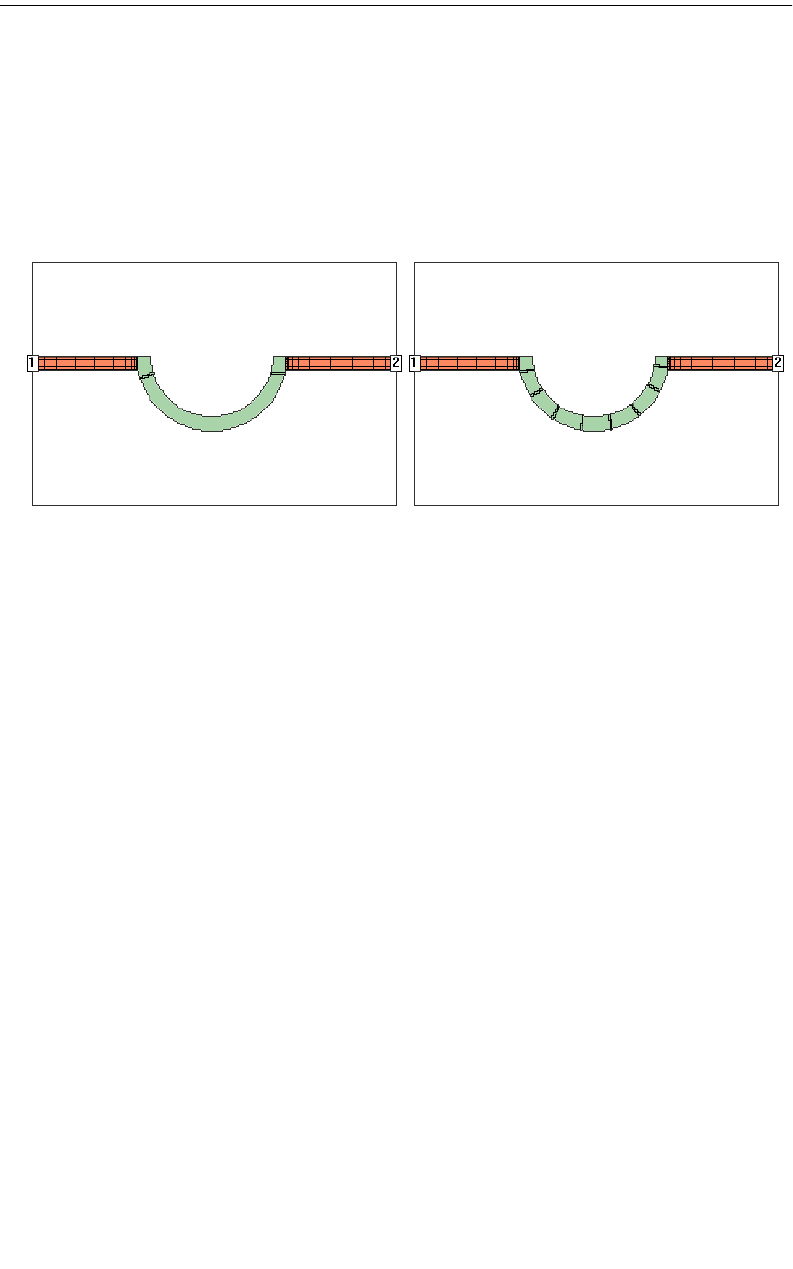
Chapter 3 Subsectioning
45
Rev 16.56
Conformal Mesh Subsectioning Control
When you apply conformal mesh to a polygon, it is possible to limit the maximum
length of a conformal section in order to provide a more accurate simulation. The
default length of a conformal section is 1/20 of the wavelength at the subsection-
ing frequency. For more information on the subsectioning frequency, see “Defin-
ing the Subsectioning Frequency,” page 41.
To set the maximum length for a conformal section, do the following:
1 Select the desired polygon(s).
The selected polygons are highlighted.
2 Select Modify Metal Properties
This opens the Metalization Properties dialog box.
3 Click on the Maximum Length checkbox in the Conformal Mesh
Subsectioning Controls section of the dialog box.
This will enable the Length text entry box to the right. Note that this checkbox is
only enabled when Conformal is chosen as the Fill Type.
4 Enter the desired Maximum Length in the text entry box.
Click on the OK button to close the dialog box and apply the changes.
For a more detailed discussion of Conformal Mesh, please refer to Chapter 11,
“Conformal Mesh” on page 227. There is also an application note on conformal
mesh available in Help; look up conformal mesh in the index.
Default Subsection Length Maximum Length = 20 mils
Setting the maximum length to 20 mils limits the length of the subsections. As you
can see pictured above, the default subsection length uses one subsection for most
of the curve. When the maximum length is set to 20 mils, multiple subsections are
used to model the same metal providing a more accurate answer.

Sonnet User’s Guide
46
Rev 16.56

Chapter 4 Metalization and Dielectric Layer Loss
47
Rev 16.56
Chapter 4 Metalization and
Dielectric Layer Loss
This chapter is composed of three parts: planar metalization loss, via metalization
loss and dielectric layer loss. For information on dielectric brick loss, see Chapter
17, “Dielectric Bricks” on page 317. Both the theoretical aspect of how Sonnet
models loss and the practical how to’s of assigning loss in your circuit are covered,
including the use of metal and dielectric material libraries. The discussion of met-
alization loss begins below. For the discussion of dielectric loss, see “Dielectric
Layer Loss,” page 66.
There is also a paper available by the president and founder of Sonnet Software,
Dr. James Rautio which contains a detailed discussion of metal losses; see refer-
ence [15] in Appendix II, “Sonnet References” for a detailed description. This
paper is also available on the Sonnet website.
There are two general metal types in Sonnet, planar metal types which are
assigned to metal polygons, and via metal types which are assigned to via
polygons. In metal polygons, the current flow is in the x and y direction, while in
via polygons, the current flows in the z direction between metal levels. The
underlying theory behind both types is the same, but the parameters you enter are
based on the physical properties of the object for which you will use the metal.
For example, a planar metal can be defined with a conductivity and a thickness,
while a via metal can be defined with a conductivity and solid cross-sectional
area. Planar metals are discussed first followed by via metals.

Sonnet User’s Guide
48
Rev 16.56
Planar Metalization Loss
Metalization loss is specified in the project editor in the Metal Types dialog box
which is opened by selecting CircuitMetal Types. You click on the Add Planar
button to add a planar metal. Planar metal types may be assigned to circuit metal,
top cover and ground plane. Sidewalls are always assumed to be perfect conduc-
tors.
A common misconception is that only one type of planar metalization is allowed
on any given level. In fact, different metalizations (i.e., different losses) can be
mixed together on any and all levels. For example, it is possible to have a thin film
resistor next to a gold trace on the same level.
Sonnet allows you to use pre-defined planar metals, such as gold and copper,
using the global library. The global library allows you to define your own metal
types as well. There is also a local metal library which can be created for an indi-
vidual or to share between users. There are both planar and via metals available in
the metal libraries.
Sonnet’s Loss Model for Planar Metalization
The Sonnet model of planar metal loss uses the concept of surface impedance,
measured in Ohms per square. This concept allows planar EM Simulators, such as
Sonnet em, to model real 3-dimensional metal in two dimensions.
If you are unfamiliar with this concept, please refer to any classic textbook such
as Fields and Waves in Communication Electronics by Simon Ramo, John R.
Whinnery and Theodore Van Duzer, John Wiley & Sons, New York, 1965.
It is important to note that this technique models the loss of the true 3-dimensional
metal fairly accurately, but does not model any change in field distribution due to
the metal thickness. This approximation is valid if the metal thickness is small
with respect to the width of the line, the separation between lines, and the thick-
ness of the dielectric. If the true 3-dimensional affect of the metal is important,
then you should consider using the Thick Metal Model metal type as discussed in
Chapter 16, “Thick Metal” on page 303.
Substrate
Real Metal Modeled Zero Thickness Metal

Chapter 4 Metalization and Dielectric Layer Loss
49
Rev 16.56
Some electromagnetic analyses use a “perturbational” approach for loss. This
means that they assume the current flowing everywhere is the same as the lossless
case. This approximation works for low loss metals (good conductors) at most RF
frequencies. However for thin film resistors and good conductors at low frequen-
cies, the lossless current is not the same as the lossy current and a perturbational
approach fails. Em's loss analysis is not perturbational. It works just as well for a
100 Ohms/square resistor as it does for a 0.004 Ohms/square good conductor. The
Sonnet loss analysis also properly models the transition between electrically thin
(low frequency) and electrically thick (high frequency) conductors. See reference
[26] in reference Appendix II listed on page 421 for a detailed description of the
theory used by Sonnet. See reference [93] listed on page 428 for the equations ac-
tually used in the Sonnet model.
Another aspect of loss is that the surface impedance of a good conductor has an
imaginary part which is equal to the real part. This reactive surface impedance is
physically due to the increased surface inductance caused by the current being
confined closer to the surface of the conductor. This surface reactance is included
in the Sonnet loss model. The effect is small, but potentially significant in certain
cases.
Keep in mind that a circuit running with lossless metal and dielectrics requires
about one-half the amount of memory and runs about twice as fast. Therefore, the
simplest approximation is to run a lossless simulation. This can be quite useful in
the initial design phase.
Problems In Determining Planar Metal Loss
Sonnet's planar metal loss model is very accurate if accurate values are used. In
practice, however, there are many aspects of metal loss that cannot easily be ac-
counted for. For example, surface roughness, metal purity, metal porosity, etc.
cannot easily be measured and included in an all-encompassing loss model. In ad-
dition, most software programs, Sonnet included, do not allow you to enter all of
the parameters that determine metal loss. Many users like to use the ideal values
as a starting point and add a little of their own “real-world” loss. But how much
should be added to the ideal models? This question is not easily answered, but is
addressed in the next section.
An additional loss problem exists with planar EM analysis tools such as Sonnet.
The problem stems from the fact that planar EM tools treat the planar metal con-
ductor as zero thickness. This means that there is no difference between the top of
the conductor and the bottom of the conductor. In some circuits, stripline for ex-

Sonnet User’s Guide
50
Rev 16.56
ample, the current is symmetrical with half of the current flowing on the top of the
conductor and half flowing on the bottom of the conductor. The zero thickness
model (Normal loss model) works well in these cases.
In other circuits, such as microstrip, the current can be unequally distributed, re-
sulting in higher loss than the equivalent stripline circuit. If you know the ratio be-
tween the top and the bottom currents, you can obtain a better loss model. All
planar solvers must either estimate this value in order to calculate metal loss, or
the information must be input by the user. For this class of circuits, it is difficult
for the user to know an exact value of the current ratio without obtaining measured
data on the circuit. For these cases, assuming all the current flows on one side of
the conductor gives a “worst case” loss result. This tends to compensate for the
“best case” loss caused by ignoring the other aspects of loss (metal porosity, etc.)
mentioned earlier.
Determining Good Input Values
The best method to determine proper loss values is to build and measure a simple
structure of the desired metalization. The structure should be sensitive enough to
loss so that measurement errors do not significantly affect the results. Then ana-
lyze the same structure in Sonnet and adjust the loss values until the calculated
loss matches the measured loss. This may take several iterations before success,
but then you can use these values for similar circuits. You are now effectively
using measured values for the loss parameters.
Creating Planar Metal Types
To assign loss to a polygon in Sonnet, you first define a planar metal type by in-
putting its loss parameters and then assign that planar metal type to the polygon
drawn in your circuit.
The Planar Metal Editor dialog box allows you to enter a loss definition for the
planar metal type. There are seven different methods for entering loss: Normal,
Resistor, Rdc/Rrf, General, Rough, Sense and Thick Metal Model. The different
planar loss models are discussed below followed with a procedure for entering
new planar metal types. The discussions assume simple, single conductor
microstrip and stripline geometries where mentioned.
You do not need to read the details of each loss model. Instead, you should make
yourself familiar with the loss models you are likely to use. Most users only need
concern themselves with “Normal.”

Chapter 4 Metalization and Dielectric Layer Loss
51
Rev 16.56
Conductivity, Resistivity, or Sheet Resistance at DC
Some of the loss models allow you to choose which parameter you wish to use to
calculate loss: Conductivity, Resistivity or Sheet Resistance at DC. The three pa-
rameters are defined as follows:
•Conductivity is the bulk conductivity of the metal. The default unit is S/
m.
•Resistivity = 1.0 / conductivity. Resistivity has a default unit of Ohm-
cm.
•Sheet Resistance at DC = 1.0 / (conductivity * thickness)
where “thickness” refers to the metal thickness in meters. Sheet resis-
tance at DC has a default unit of Ohms/square.
Normal
For the Normal planar metal type, you determine the loss using the metal thick-
ness, the current ratio and a third parameter. For the third parameter you may
choose bulk conductivity, resistivity or sheet resistance at DC.
NOTE: Metal thickness is used only in calculating loss; it does not change the
physical thickness of metalization in your circuit. The metalization in
your circuit is still modeled as zero-thickness.
Current Ratio: Normal metal models your circuit using zero thickness metal,
but your real circuit possesses a metal thickness. At higher frequencies current
flows in a thin skin around the edge of the metal, as pictured below. The current
ratio is the ratio of the current flowing on the top of the metal to the current flow-
ing on the bottom of the metal.
There are no sides in a zero thickness model; therefore when translating from
these parameters, the current which flows on the sides is ignored. In some cir-
cuits, stripline for example, the current is symmetrical with half of the current
~~~~~~~~~~~~~~~~~~~~~~~~~
~~~~~~~~~~~~~~~~~~~~~~~~~
Top
Bottom
Cross section of metalization
~~~ Current

Sonnet User’s Guide
52
Rev 16.56
flowing on the top of the metal and half flowing on the bottom of the metal. In
this instance, the current ratio is 1. If you had half as much current flowing on the
top as on the bottom, the current ratio is 0.5. This could occur for some
microstrip circuits, for example. It is difficult to know an exact value of the cur-
rent ratio without obtaining measured data on your circuit. All planar solvers not
using a thick metal model must estimate this value in order to calculate metal
loss; the Normal Metal model and Rough Metal model allow you to enter the
value. If you do not have access to measured data for your metal type, the default
values (0 for Normal Metal and 1 for Rough Metal) are reasonable for most
microstrip.
Thick Metal
For thick metal, you input four parameters: metal thickness, number of sheets, di-
rection and a fourth parameter. For the fourth parameter, you may choose bulk
conductivity, resistivity, or sheet resistance at DC. The loss is calculated in the
same manner as for the Normal metal type, except that the thickness in this case
represents a physical thickness which eliminates the need to enter the current ratio.
For more information about conductivity, resistivity, and sheet resistance at DC,
please see “Conductivity, Resistivity, or Sheet Resistance at DC,” page 51. The
direction setting determines if the thick metal extends upward into the dielectric
layer above, or down into the dielectric layer below. Up is the default.
For a detailed discussion of thick metal, see Chapter 16, “Thick Metal” on page
314.
Resistor
To define a planar metal which you wish to use as a resistor, enter the DC resis-
tance in Ohms/sq in the Rdc text entry box which appears when you select this
metal type. To use this loss model, the surface resistance should be constant over
the frequency range of interest.
Rdc/Rrf
This method allows you to enter two values: RDC and RRF. The first parameter,
RDC, determines loss at low frequency (where the conductor is much thinner than
the skin depth). Surprisingly, other electromagnetic analyses often predict zero
loss at low frequency because they assume RDC is zero.
The second parameter is the skin effect coefficient, RRF. Em multiplies this num-
ber by the square root of the frequency (in Hertz) to yield the Ohms/square value
at high frequency.
The equations for RDC and RRF are:

Chapter 4 Metalization and Dielectric Layer Loss
53
Rev 16.56
Typical values for RDC and RRF are 0.004 and 3e-7. If you start getting very
strange loss results, check RRF, paying special attention to the exponent.
TIP
Use this planar metal type if you wish to include the r effects in the metal type.
Sonnet allows you to do this by adjusting the RRF value.
Em also properly models the transition between electrically thin (low frequency)
and electrically thick (high frequency) conductors. The transition frequency from
RDC to RRF is the square of RDC/RRF. At this frequency, and a relatively narrow
band around it, both coefficients are important. If the skin effect coefficient (RRF)
is set to 0.0, then the value of RDC is used over all frequencies. This is the usual
case for resistors.
The above equation for RRF assumes that all of the current travels on just one side
of the conductor. This is a good approximation for some microstrip circuits. How-
ever, if the current really travels on both sides, this gives a pessimistic value for
the loss. The equation should be modified for other structures. Stripline, for exam-
ple, has current of equal amplitude on both the top and bottom of the conductor.
In this case, you should divide the RRF value by two, while maintaining RDC.
As an example, the conductivity (for copper is 5.8E+7 Siemens/m, giving RDC
= 0.006 Ohms/square (t = 3 m) and a microstrip RRF = 2.6E-7. In reality, the bulk
conductivity of copper, or any other given metal, may not equal the laboratory val-
ue, so the figures as calculated above are likely to be lower than actual results. The
table below provides calculated results of commonly used metals using the equa-
tions above.
RRF Skin effect coefficient ==
where
: Bulk conductivity in Siemens/meter
t: Metalization thickness in meters
* r
r = relative permeability of your metal, which is typically
1.0 for most metal materials. Magnetic materials, such as
nickel, have a r greater than 1 and therefore significantly
decrease the skin depth.
RDC 1t=

Sonnet User’s Guide
54
Rev 16.56
General
This loss model includes the metalization surface resistance described above in
Rdc/Rrf. It also includes the metalization reactance, composed of the surface re-
actance, Xdc and the surface inductance, Ls. Surface reactance, Xdc, is specified,
in Ohms/square and uses the same reactance at all frequencies. The surface induc-
tance, Ls, is specified in pH/square and models the reactance as being linearly pro-
portional to frequency.
A superconductive effect known as “kinetic inductance” slows the velocity of the
electrons with no loss of energy. This can be modeled as a surface inductance.
There are three recommended approaches to obtaining a value for Ls in supercon-
ductors. A first order approximation is to assume the metal is a perfect conductor.
This model works well for moderate frequencies (less then 150 GHz) and moder-
ate circuit dimensions which are much greater than the London depth of penetra-
tion.
Properties of Commonly Used Metals
Metal
(S/M)
RDC
(/sq)
t = 1 M
RDC
(/sq)
t = 1 mil
RRF
(Hz-1/2/sq)
“Skin Effect”
(microstrip)
Aluminum 3.72e7 0.027 1.1e-3 3.3e-7
Brass 1.57e7 0.070 2.5e-3 5.0e-7
Copper 5.80e7 0.017 6.8e-4 2.6e-7
Gold 4.09e7 0.024 9.6e-4 3.1e-7
Nichrome 1.00e6 1.000 3.9e-2 2.0e-6
Silver 6.17e7 0.016 6.4e-4 2.5e-7
Tantalum 6.45e6 0.155 6.1e-3 7.8e-7
Tin 8.70e6 0.115 4.5e-3 6.7e-7
Rrf 0=RDC 0= Ls0=XDC 0=

Chapter 4 Metalization and Dielectric Layer Loss
55
Rev 16.56
The second approach is a model which is still valid at moderate frequencies, but
includes effects due to kinetic inductance. The kinetic inductance is a function of
temperature and can be approximated in the following manner:
where
The third model should be used to account for high frequency effects or effects
due to small circuit dimensions. In these cases, the surface resistance’s proportion-
ality to 2 begins to dominate and the following model is suggested. The surface
resistance is a function of frequency-squared, so you should use the equation
below as the entry for RDC and use the FREQ function in the equation so that the
value is valid for all analysis frequencies. For more information about equation
syntax, please refer to Help. Use the following equations for this model:1
RDC 0= XDC 0= Ls0-LT=
Rrf 0=
0410 7–
=
-LT -
01TT
c
4
–=London depth of penetration at temp.
-0= London depth at T = 0 meters
Tc= Critical (Transition) Temperature in degrees Kelvin
H/m
Rrf 0=
RDC 1
2
---20
2-LT
3Nnns
+=
Ls0-LT=
XDC 0=

Sonnet User’s Guide
56
Rev 16.56
where
1Shen, Z. Y., “High-Temperature Superconducting Microwave Circuits,” Boston, 1994,
Artech House.
The Surface Impedance, Zs, is modeled using the following equation:
where RDC and Ls are defined in the superconductor models given above.
Rough Metal
Many circuit manufacturing processes produce planar metallization with rough
surfaces. Depending on how the metallization is formed, one, or both, of the trace
metal surfaces could be relatively rough. The Rough Metal type allows you to cap-
ture this surface roughness effect in your model.
At frequencies where the skin depth is comparable or smaller than the surface
roughness dimension, the current flow is forced into the surface roughness region
and this introduces excess resistance and excess inductance in your traces. This in
turn increases the insertion loss and insertion phase of your planar transmission
lines.
You do not necessarily need to use the Rough Metal type as you create models in
Sonnet. However, when you are working with circuits that are very sensitive to
these transmission line characteristics, it will improve your model accuracy. Gen-
erally, models with rough metal surfaces and narrow trace widths, that operate at
high frequency (above 5 GHz) are good candidates for the Rough Metal model.
The Sonnet Rough Metal Model is based on an extensive study of surface rough-
ness effects in printed circuit board conductors. See reference [1] in Appendix II,
“Sonnet References” for a detailed description.
It may be valid to apply Rough Metal to conductors from other manufacturing pro-
cesses, as long as the surface roughness effect that you are trying to capture is a
function of the trace top and bottom surfaces.
N= Conductivity of the superconductor in its normal state (Siemens/m
3
n= Normal state carrier density (1/m3)
s= Superconducting state carrier density (1/m3)
and -LT
0are as defined above
2f=radians/sec
ZsRDC jLs
+=

Chapter 4 Metalization and Dielectric Layer Loss
57
Rev 16.56
To define a Rough Metal type you must first obtain the metal trace top and bottom
surface roughness in RMS microns for the metal. Often circuit material suppliers
provide this information directly or you can ask the manufacturing group produc-
ing your physical parts.
TIP
Surface roughness can also exist on ground plane metal. If you are using a Sonnet
box cover to represent a ground plane, you can define a Rough Metal type and ap-
ply it to the cover. Rough Metal types assigned to a box cover are limited to a thin
cross section.
!WARNING
Care should be taken when using the results in a time domain simulation, as
the Rough Metal results are not guaranteed to be causal.
There are two variations of the Rough Metal: Thin and Thick. The Thin option
models the metal as a single “zero thickness” (2D sheet), like the Normal loss
model described on page 51 but with the surface roughness effect. With this op-
tion, the user must specify a Current Ratio.
Top Surface
Bottom Surface
Trace Cross Section with magnified views
of the top and bottom surfaces.
It is common for copper foils to
have one surface several times
rougher than the other surface.

Sonnet User’s Guide
58
Rev 16.56
The Thick option models the metal as two sheets of current; one for the top surface
and one for the bottom surface of the planar metal trace. This is very similar to the
Thick Metal loss model (with two sheets), with the surface roughness effect. See
Chapter 16 "Thick Metal" on page 303 for additional details on modeling metal
thickness.
For additional details about rough surface metal, please see “Rough metal model”
in the index of Help. You may access help by selecting Help Sonnet Help from
any Sonnet application.
Sense
Em solves for the current distribution; however, on occasion, you may want to
view the fields, not the current. You do this with what is called a “sense metal”.
The sense metal is a patch of conductor placed where you want to see the tangen-
tial electric field. (You cannot view the normal direction of the field with Sonnet.)
For further discussion of sense metal, see “View Tangential Electric Fields” under
Tips and App notes in Help.
How to Create a Planar Metal Type
For detailed instructions on creating a planar metal type, please refer to “metal
types” in the Index of Help. You may access help by selecting Help Sonnet
Help from the main menu of any Sonnet application or by clicking on the Help
button in any dialog box.
Via Metalization Loss
Via metalization loss is specified in the project editor in the Metal Types dialog
box which is opened by selecting CircuitMetal Types. You click on the Add
Via button to add a via metal type. Via metal types may be assigned to via poly-
gons only. Please note that edge vias are a special case which use the planar metal
type of the polygon to which they are attached. For a discussion of loss in edge
vias, please see "Edge Vias" on page 300.
Sonnet allows you to use pre-defined via metals, such as gold and copper, using
the global library. The global library allows you to define your own metal types
as well. There is also a local metal library which can be created for an individual
or to share between users.
Chapter 4 Metalization and Dielectric Layer Loss
59
Rev 16.56
Creating Via Metal Types
To assign loss to a via in Sonnet, you first define a via metal type by inputting its
loss parameters and then assign that via metal type to the via drawn in your circuit.
This section provides instructions for creating a via metal type and discusses the
loss models used in the Via Metal Editor dialog box.
The Via Metal Editor dialog box allows you to enter a loss definition for the via
metal type. There are three different loss models: Volume, Surface, and Array.
The different via loss models are discussed below.
You do not need to read the details of each loss model. Instead, you should make
yourself familiar with the loss models you are likely to use. Most users only need
concern themselves with “Volume.”
Volume Loss Model
The Volume via loss model is the most commonly used model because the values
you specify are directly related to the physical properties of the via. With the vol-
ume model, you enter a conductivity, resistivity, resistance per via, or sheet resis-
tance at DC and Volume Properties. An example using “Solid” Volume Properties
is shown below:
The Volume Properties section allows you to model both hollow and solid vias.
Examples are depicted below:
Sonnet User’s Guide
60
Rev 16.56
Hollow: If your vias are hollow, you enter the wall thickness of your vias. The
wall thickness and the shape of each via polygon are used to determine the cross-
sectional area used for the loss calculations. In the illustration below, a 3D view
of the via is shown on the left, with the cross sectional area shown on the right.
Solid: If your via is solid, you select the “Solid” radio button. The complete area
of the via polygon is used for the loss calculations. In the picture below, the cross
sectional area is the area of the circle.
NOTE: Note that defining your Volume Properties as either Wall Thickness or
Solid does not affect the subsectioning of the via or how the via
appears in the project editor.
Wall Thickness
Height
Cross Section of Via
3D Volume model of via with finite wall thickness (hollow via)
Wall Thicknes
s
Height
Cross Section of Via
3D Volume model of via with solid cross-sectional area

Chapter 4 Metalization and Dielectric Layer Loss
61
Rev 16.56
Loss Using Conductivity, Resistivity and Sheet Resistance at DC
If you specify your via loss using conductivity, resistivity, or sheet resistance at
DC, the Volume loss model is frequency-dependent with both a DC loss compo-
nent and an RF loss component. At DC, the vertical loss of a single via polygon is
a resistance given by the equation below:
Note that you may choose to use either the resistivity or sheet resistance at DC,
instead of the bulk conductivity as in the equation above to define your loss. If you
do so, this equation is modified based on the chosen parameter. For the relation-
ship between conductivity, resistivity, and sheet resistance at DC, please see
“Conductivity, Resistivity, or Sheet Resistance at DC,” page 51.
At RF, the equation is too complex to show here, but is the volumetric equivalent
of the surface impedance equation used by Sonnet for planar metal, and is de-
scribed in detail in reference [15] listed on page 422. This equation includes the
skin effect, resulting in a smooth transition from DC to high frequencies.
Loss Calculations for Volume Model Using Resistance Per Via
The loss may also be defined by using the Resistance per Via. Resistance per Via
for the volume model represents the total resistance in Ohms of the via polygon in
the vertical (Z) direction. This resistance is constant with frequency. If the via
polygon extends over more than one dielectric layer in the Z-direction, then the
total specified resistance is apportioned to each layer according to the thickness of
each layer. For example, if the specified RPV for a via polygon is 3.0 Ohms, and
if the via polygon extends from the top of dielectric layer 1 (10 um thick) to the
bottom of dielectric layer 2 (20 um thick), then 1 Ohm is apportioned to dielectric
layer 1 and 2 Ohms is apportioned to dielectric layer 2.
ZLoss 0() HA=
where
H: Height of via in meters.
: Conductivity of via metal in Siemens/meter.
A: Cross-sectional area of via based on wall thickness or solid setting.
(ohms)
Sonnet User’s Guide
62
Rev 16.56
Horizontal Loss for the Volume Model
When you are using the Volume Loss model (solid) for bar vias (mesh is set to
Bar), then the horizontal DC loss in ohms/square is calculated as follows:
The horizontal DC loss for other types of fill is geometry and meshing dependent
so it is not possible to provide an equation.
Surface Loss Model
The surface via loss model treats the via as an infinitely thin hollow tube giving it
a 2D surface as pictured below.
Loss Calculations for Surface Model
This method allows you to enter three values: RDC, RRF and XDC. The first param-
eter, RDC, determines loss at low frequency (where the conductor is much thinner
than the skin depth).
Zloss 0 1.0 H=
where
H: Height of via in meters.
: Conductivity of via metal in Siemens/meter.
Height
Perimeter of Via
Via as shown in the project editor 3D View of Surface Model of Via
2D Surface of Via
Height

Chapter 4 Metalization and Dielectric Layer Loss
63
Rev 16.56
The equation for RDC is:
The second parameter is the skin effect coefficient, RRF. At frequencies above
DC, em uses the same surface impedance equation used by Sonnet for planar
metal [15]. This equation includes the skin effect, resulting in a smooth transition
from DC to high frequencies. The equation for RRF is:
The third parameter is Xdc, the surface reactance, and is normally set to zero. This
parameter is provided for advanced users who want to customize the surface im-
pedance of the metal.
The horizontal loss at DC and RF for the Surface model is infinite.
Array Loss Model
The Array via loss model is used to represent an array of small solid vias by ap-
proximating the entire array as a single large via. This is usually done to reduce
the processing resources necessary to analyze the circuit, as having many small
vias is computationally expensive. The Array via loss model is most often used for
computing the loss of via arrays which have been simplified when translating a
circuit into a Sonnet project. In those cases, the Via metal type is automatically
created. You may also use this loss model to manually create a via metal type if
you wish to model a single via in the project editor that represents an array in your
final design.
NOTE: For a detailed discussion of array simplification, please see the Via
Array Simplification Appendix in any interface or translator manual.
RDC 1t=
where
: Conductivity of via metal in Siemens/meter.
t: Metalization thickness in meters
RRF Skin effect coefficient ==
where
: Bulk conductivity in Siemens/meter
* r
r = relative permeability of your metal, which is typically
1.0 for most metal materials. Magnetic materials, such as
nickel, have a r greater than 1 and therefore significantly
decrease the skin depth.
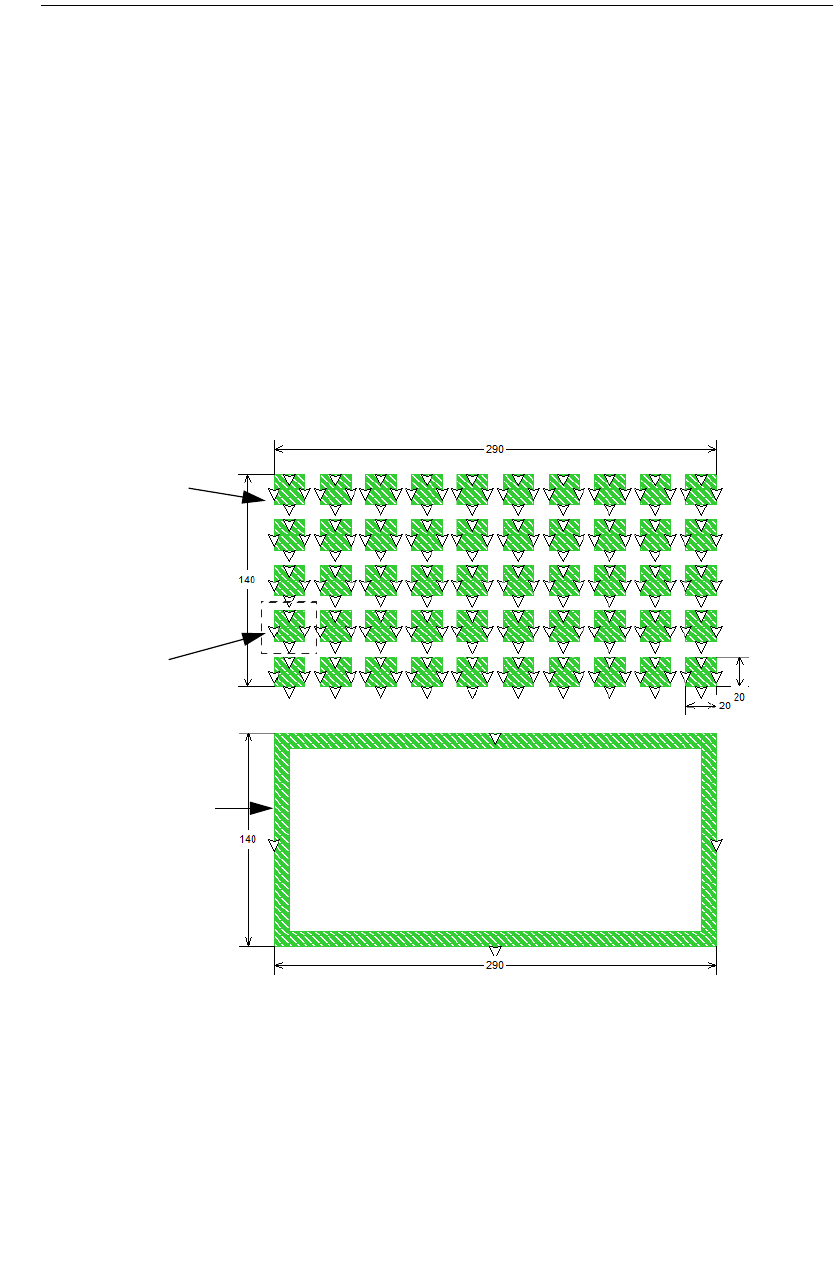
Sonnet User’s Guide
64
Rev 16.56
Like the Volume model defined above, it is a frequency-dependent model which
takes into account the 3D characteristics of the via array. The only difference be-
tween the Volume model and this model is the method by which the cross-section-
al area is computed. With the Volume model, the cross-sectional area is computed
based on the wall thickness or solid setting. For the Array model, the cross-sec-
tional area is computed using the Fill Factor or Density which is based on the orig-
inal via array.
The Fill Factor is a loss parameter when using conductivity or resistivity to define
the loss. The Fill Factor is a percentage indicating how much of the cross-sectional
area of the original via array is metal-filled. The Fill Factor is calculated by sum-
ming the areas of all the individual vias in the array and dividing that by the total
area of the array, defined as the bounding box which surrounds all the vias in the
array. The result is multiplied by 100 to convert to a percentage. An example of
an array and how to compute it’s fill factor is shown below.
The array, shown on top, consists of a 5 by10 array of 50 individual vias whose
cross section is a 20 micron by 20 micron square. Therefore the sum of the areas
of all the individual vias is 50 * 400 = 20,000 square microns. The total cross-sec-
tional area of this array is 40,600 square microns (290 microns * 140 microns).
This provides a Fill Factor of 49.3% ((20,000/40,600) * 100). The converted sim-
ple via modeled in Sonnet is shown on the bottom. Although the total cross sec-
Original Array
Individual via
Simplified Via
in translated
project

Chapter 4 Metalization and Dielectric Layer Loss
65
Rev 16.56
tional area of the simplified via is 40,600 microns, the Array loss model is set such
that the calculated DC loss for the via is based on the loss of the actual metal in
the array, (40,600 * 0.493 = 20,015.8) i.e., the 20,000 square microns.
NOTE: When translating circuits into Sonnet, if there are two or more arrays
which use the same metal but whose fill factors differ significantly,
two or more via metal types are created in the Sonnet project. For
example, there are two arrays, one with a fill factor of 50% and
another of 75% both using a metal named “viametal1.” The translated
project will contain two via metal types called “viametal1_1” and
“viametal1_2.”
The loss for the Array model may also be defined using the Resistance Per Via.
Resistance Per Via for the array model represents the vertical (Z) resistance in
Ohms of an individual via within the via array. As discussed above, the array of
vias is modeled as a single, merged via polygon, but the loss for that simplified
polygon is based on the actual metal present in the array.
The loss parameters of this simplified via polygon are Resistance Per Via
(Rper_via) in Ohms/via and Via Density (Dvia) in vias per square micron. The total
resistance in Ohms of the simplified via polygon is constant with frequency and is
computed as follows:
The horizontal loss at DC and RF for the Array model is infinite.
Metal Libraries
There are two types of metal libraries available in Sonnet: global and local. The
metal libraries contain standard definitions for metal types, both planar and via,
which may be used in your projects. There is no real difference between the global
and local library. The names refer to how they are used. The global library would
usually be used as a group wide library of standard metals for a group of designers.
Rsimplified via–
Rper via–
Dvia Avia
--------------------------------=
where Avia is the cross-sectional area of the simplified via
polygon in square microns.

Sonnet User’s Guide
66
Rev 16.56
There is a default global library supplied by Sonnet which contains definitions for
some common metals, both planar and via. The default location for the global li-
brary is in <Sonnet Data Directory>/data/libraries where <Sonnet Data Directo-
ry> is the directory in which your Sonnet software data is installed. You may
choose to use this location or can save this library in another location.
The local library would usually be used as the user's own library of metal defini-
tions. This library may be stored in a location of the user's choice. You use either
the Planar Metal Editor dialog box or the Via Metal Editor dialog box to add, edit
and delete entries to these libraries.
For instructions on adding planar and via metals to a metal library, editing metals
in a metal library or using metals defined in a metal library, please refer to Sonnet
Help available from the Help menu in any Sonnet application.
Dielectric Layer Loss
The dielectric layer loss calculations in Sonnet are virtually exact. Our web site
has a lossy conductivity benchmark you can perform on any electromagnetic solv-
er (or measurement system). See Benchmarking on the Products section of our
web site, www.sonnetsoftware.com/products/sonnet-suites/benchmarking.html.
The dielectric loss is calculated in Sonnet at the beginning stages of the analysis.
The method Sonnet uses starts with the calculation of a sum of waveguide modes.
The exact solution requires an infinite sum of modes, but Sonnet truncates this
sum to some reasonable value (the truncation has never been a source of error).
So, for each mode, if there is a lossy dielectric, the calculation involves complex
numbers instead of just real numbers. This is NOT a discretized function - it is a
continuous function. Therefore, the dielectric loss calculation can be thought of as
exact (only limited to the precision of the machine).
Dielectric Layer Parameters
You can set the dielectric constant and loss of a dielectric layer by changing the
following parameters in the project editor by selecting Circuits Dielectric Lay-
ers, then clicking on the Above, Below or Edit button in the Dielectric Layers di-
alog box. This opens the Dielectric Editor dialog box which allows you to edit the
parameters below.

Chapter 4 Metalization and Dielectric Layer Loss
67
Rev 16.56
• Erel: The relative dielectric constant (r). The ratio (/o), where is the real
part of the permittivity of the dielectric layer material, and o is the permittiv-
ity of free space. The ratio is dimensionless.
• Dielectric Loss Tan: The dielectric loss tangent. The ratio (’’/’), where
’ - j’’, and is the complex permittivity of the dielectric layer material.
The ratio is dimensionless.
• Conductivity: Dielectric conductivity, , where is the conductivity of the
dielectric. The default unit is S/m. You may define your dielectric loss using
conductivity or resistivity. To use conductivity, you should select “Conduc-
tivity” from the Specify Using drop list.
• Resistivity: Resistivity = 1.0 / conductivity. Resistivity has a default unit of
Ohm-cm.You may define your dielectric loss using conductivity or resistivi-
ty. To use resistivity, you should select “Resistivity” from the Specify Using
drop list.
• Mrel: The relative magnetic permeability (r) of the dielectric layer material.
• Magnetic Loss Tan: The magnetic loss tangent of the dielectric layer mate-
rial.
One last parameter that may be specified for a dielectric layer is the Z Partitioning.
This value may be changed in the Z Partitions dialog box which is opened when
you click on the Z Parts button in the Dielectric Layers dialog box.
• Z-Partitions: The z-partitioning parameter is the setting which controls the
number of partitions which the dielectric layer is divided into in the z direc-
tion. for the dielectric layer. While this parameter is specified in the dielectric
layer window, it only has an effect on the dielectric bricks on that layer.
Changing this value for a particular layer will have absolutely no affect on the
analysis if there are no bricks on the layer. If there are multiple bricks on the
layer, the Z subsectioning for all of those bricks will be identical.
The more partitions (better resolution) used in the Z-dimension, the more ac-
curate the analysis; however, analysis time and memory requirements also in-
crease dramatically.

Sonnet User’s Guide
68
Rev 16.56
Frequency Dependent Loss
Sonnet allows you to write your own frequency-dependent equations, or use a
lookup table for any of the parameters defining a dielectric. For example, you
could write a frequency-dependent equation for the conductivity of your dielec-
tric. For more information about using equations, please refer to the topic ‘Equa-
tion Syntax” in Help.
Most common dielectrics have either a fairly constant loss tangent or conductivity
as a function of frequency. Thus, it is normally not necessary to specify an equa-
tion for your dielectric loss. You can even enter both a loss tangent and a conduc-
tivity (or resistivity) for a dielectric and two values are combined to provide the
total loss for your analysis. The following equation can be used to calculate the
total effective tan used by em for this situation:
where, is the radian frequency ( = 2f, where f is frequency in hertz). Note that
tan has both a frequency-dependent term and a frequency-independent term
The above equation for tan can also be expressed in terms of conductivity as fol-
lows:
Both equations are equivalent. Each describes how em uses the input dielectric pa-
rameters to compute loss in the dielectric material.
NOTE: Note that if resistivity is input, instead of conductivity, the equation
used is altered accordingly.
See “Circuit Dielectric Layers” in the project editor’s Help for information on
setting these parameters.
tan Loss Tan
Diel Cond
Erel
o
-----------------------------+=
Total Effective Cond Loss TanErel
oDiel Cond+=

Chapter 4 Metalization and Dielectric Layer Loss
69
Rev 16.56
How to Create a New Dielectric Layer
For detailed instructions on creating a new dielectric layer, please refer to “dielec-
tric layers:adding” in the Index of Help. You may access help by selecting Help
Sonnet Help from the main menu of any Sonnet application or by clicking on
the Help button in any dialog box.
Dielectric Libraries
The dielectric libraries contain standard definitions of dielectric materials which
may be used for your dielectric layers. There are two types of dielectric libraries
available in Sonnet: global and local. There is no real difference between the two
libraries. The names refer to the way in which they are used.
NOTE: The Dielectric Libraries materials may not be used for dielectric
bricks but only for dielectric layers.
The global library would usually be used as a group wide library of standard di-
electrics for a group of designers.There is a default global library supplied by Son-
net which contains definitions for dielectric materials. The default location for
the global library is in <Sonnet Data Directory>/data/libraries where <Sonnet
Data Directory> is the directory in which your Sonnet software data is installed.
You may choose to use this location or can save this library in another location.
The local library would usually be used as the user's own library of dielectric ma-
terial definitions. This library may be stored in a location of the user's choice. You
use the Dielectric Editor dialog box to add, edit and delete entries to these librar-
ies.

Sonnet User’s Guide
70
Rev 16.56

Chapter 5 Ports
71
Rev 16.56
Chapter 5 Ports
This chapter describes the five different types of ports used in Sonnet, how they
are modeled and how to place or delete them in your circuit.
The five types of ports used in Sonnet are the standard box-wall port, the co-cali-
brated internal port, the via port, the auto-grounded port and the ungrounded in-
ternal port.
Port Type Overview
As mentioned above, the five types of ports available in Sonnet are the standard
box-wall, co-calibrated internal port, via port, autogrounded port and internal un-
grounded port. All ports in Sonnet are two-terminal devices. The box-wall and co-
calibrated port types are those used the majority of the time. Each type of port is
described below.
Box-wall:
•Most common type of port.
•Positive terminal is attached to a metal polygon and the negative
terminal is attached to the box-wall (ground).
•De-embedding is the most accurate for this type.
•Used for connections to the periphery of your geometry.

Sonnet User’s Guide
72
Rev 16.56
•Reference planes may be used.
For more information on box-wall ports, see “Standard Box-wall Port,” page 87.
Co-calibrated internal port:
•Used in the interior of a circuit.
•By default, automatically identified as part of a calibration group
with a common ground node connection. The ground node connec-
tion can be defined as floating or the Sonnet box. Please note that
you can use a single co-calibrated port if the ground node connec-
tion is set to the Sonnet box.
•When em performs the electromagnetic analysis, the co-calibrated
ports within a group are simultaneously de-embedded.
•Highly accurate de-embedding.
•Often used by a circuit simulation tool to connect some type of ele-
ment into your geometry at a later time outside the Sonnet environ-
ment.
•Reference planes may be used.
For more information on co-calibrated internal ports, see “Co-calibrated Internal
Ports,” page 89.
Via port:
•Used in the interior of a circuit.
•Negative terminal is connected to a polygon on a given level and
the positive terminal is connected to a second polygon on another
level above.
•Cannot be de-embedded.
•Most commonly used to attach a port between two adjacent levels
in your circuit or when you want a port to go up to the box cover
rather than down to ground.
•Reference planes cannot be used.
For more information on via ports, see “Via Ports,” page 98.
Auto-grounded port:
•Used in the interior of a circuit.
•The positive terminal is attached to the edge of a metal polygon and
the negative terminal is attached to the ground plane through all
intervening dielectric layers.
•Used in place of a co-calibrated port to reduce the de-embedding
processing time at the cost of less accuracy.
•Reference planes may be used.

Chapter 5 Ports
73
Rev 16.56
NOTE: When using auto-grounded ports, be aware that any coupling between
auto-grounded ports is not accounted for when performing the de-
embedding.
For more information on auto-grounded ports, see “Automatic-Grounded Ports,”
page 99.
Ungrounded Internal Ports:
•Used in the interior of a circuit.
•Each terminal is attached to one of two adjacent polygons.
•Used in place of a co-calibrated port when you do not want any
space between the two polygons.
•Will have a different ground reference from the other ports in the
circuit.
•Commonly used to add a series element in post em processing.
•Reference planes cannot be used.
For more information on ungrounded internal ports, see “Ungrounded Internal
Ports,” page 101.
Port Normalizing Impedances
The default normalizing impedance for a port is 50 ohms. This is done since 50
ohms is an industry standard; some analysis tools only accept the value of 50 ohms
as the normalizing impedance.
In rare cases, you may wish to have S-parameters normalized to some other im-
pedance. The normalizing impedance in Sonnet is represented by four numbers as
shown in the diagram below. First is the real part in ohms. Next comes the reactive
part in ohms. Third is the inductive part in nanohenries (nH). The last number is
Sonnet User’s Guide
74
Rev 16.56
the capacitive part in picofarads (pF). The inductive and capacitive parts modify
only the reactive portion of the load, they are included so you do not have to man-
ually re-calculate the reactive part at each frequency.
NOTE: The normalizing impedances are ignored if Y- or Z-parameters are
specified for output. Y- and Z-parameters are always normalized to
one ohm.
This capability should be used only by the most advanced user. This feature
should never be applied to data which is to be used in a standard circuit theory pro-
gram other than Sonnet’s. Many programs assume S-parameters normalized to ex-
actly 50 ohms; S-parameters normalized to another value would introduce error
into the analysis.
Changing Port Impedance
There are two methods for changing the impedance of a port. If you wish to
change the impedance of a given port, and do not need to see the impedance values
of other ports, take the following steps using the project editor:
1Select the desired port(s). This will enable the Modify menu option.
2Select Modify Port Properties to open the Port Properties dialog box.
3The impedance values can be changed by typing the desired values in
the Resistance, Reactance, Inductance and Capacitance text boxes in
the dialog box. This changes the parameters on all ports selected and all
ports with the same number as the ports selected.
V
R + jX L
C
Equivalent circuit of an em port.

Chapter 5 Ports
75
Rev 16.56
If you wish to change the impedance of a given port, and wish to see the imped-
ance values of other ports while doing so, proceed as follows:
1Select Circuit Ports from the main menu to open the Port Impedance
dialog box.
2The impedance values for any port can be changed by typing the desired
values in the Resistance, Reactance, Inductance and Capacitance fields
in the row labeled with the desired port number.
TIP
Note that the impedance of multiple ports may be changed at the same time
through the first method by selecting multiple ports before selecting Modify
Port Properties, and by the second method, by modifying all the desired port val-
ues while the Port Impedance dialog box is open.
Special Port Numbering
All ports are assigned a number at the time they are created in the project editor.
There is no limit on the number of ports and the number of ports has a minimal
impact on the analysis time needed for de-embedding. By default, the ports are
numbered by the order in which they are created (i.e. first port created is assigned
the number 1, second port created is assigned the number 2, etc.). With this default
method, all ports are positive and unique. However, there are some applications
that require the ports to have duplicate, and even negative, numbers. There is also
a special case of Port 0 which is used for a ground connection.
Ports with Duplicate Numbers
All ports with the same number, as pictured below, are electrically connected to-
gether. As many physical ports as desired may be given the same numeric label.
Such ports are common mode ports (sometimes referred to as “even-mode” or
Sonnet User’s Guide
76
Rev 16.56
“push-push” ports) and have many uses, including simulating the even-mode re-
sponse of a circuit. See “Modeling an Arbitrary Cross-Section,” page 314, for an
example of using common mode ports.
Ports with Negative Numbers
Ports may also have negative numbers as shown in the figure below. This feature
can be used to redefine ground. Strictly speaking, em sums the total current going
into all the positive ports with the same port number and sets that equal to the total
current going out of all the ports with that same negative port number. For exam-
ple, for a circuit with a +1 port and a -1 port, em sets current flowing into port +1
to be equal to the current flowing out of port -1. These are differential mode ports
(sometimes called “balanced”, “push-pull” or “odd-mode” ports). An example is
shown below.
Ports with identical
port numbers are
electrically
connected together.
The total current
going into port 1 is
equal to the total
current going out of
port -1.

Chapter 5 Ports
77
Rev 16.56
Coplanar lines can be represented with balanced ports. See below for an example
of differential ports.
Ports are required to be in sequential order with no numbers missing. If the ports
are not in sequential order, you will receive an error message when you attempt
an analysis. If you are editing your circuit in the project editor, you may renumber
all of the ports in your circuit to ensure that they are sequential in the Port Imped-
ance dialog box (Circuit Ports). The port order for the S, Y, or Z-parameters
will be listed in increasing numeric order. For the example of a two-port, the out-
put would be S11, S12, S21, and S22. For a four-port, it would be S11, S12, S13,
S14, S21, S22, etc.
For a discussion of using ports to model coplanar waveguides (CPW), please see
“Modeling Co-Planar Waveguide (CPW) in Sonnet” under Tips and App Notes in
Help. You can find this topic by selecting “CPW” in the help Index.
NOTE: When you are referred to Sonnet’s Help, you may access Help by
selecting Help Sonnet Help from the menu of any Sonnet
application or by clicking on the Help button in any dialog box.
Using Port Number Zero for Ground Connections
The Port 0 feature allows you to add connections to ground that are de-embedded
during the em simulation. Ports can be assigned a number “0” as shown in the
An example of a
coplanar waveguide
cross junction.

Sonnet User’s Guide
78
Rev 16.56
picture below.
This feature allows you to add an ideal short circuit to your circuit in locations
other than the analysis box sidewall. In the example above, a boxwall port with a
reference plane was used to create an ideal short circuit at the edge of a patterned
ground shield. Assigning the port number 0 sets the port to be an ideal short cir-
cuit, and the reference plane is used to shift the short circuit to the desired location.
All ports with the number “0” are treated as a normal port during the main part of
the EM simulation. These ports are de-embedded in exactly the same manner as
all other ports. When the simulation for a particular frequency is completed, em
then automatically shorts out all ports with the number 0. This means that the ef-
fects of the port are de-embedded without creating extra ports in your S-parameter
results.
All port types: box-wall, co-calibrated, auto-grounded and ungrounded-internal
can be set to 0. Multiple ports within a circuit can be set to number 0 just as mul-
tiple ports can use the same number as discussed in "Ports with Duplicate Num-
bers" on page 75.
Changing Port Numbering
You can change the port number of any port after it has been added to your circuit.
Any integer, zero, negative or positive, is valid. To change the number on a port
or ports, do the following:
1Select the port(s) whose number you wish to change.
2Select Modify Port Properties from the main menu to open the Port
Properties dialog box.
Ideal short circuit
Chapter 5 Ports
79
Rev 16.56
3The number for the selected port(s) can be changed by typing the
desired port number in the dialog box. Note that if multiple ports are
selected, all are set to the number input in the dialog box.
Renumbering All Ports
Ports in your circuit must be sequentially numbered prior to analysis. If you have
deleted some ports such that your ports are no longer sequentially numbered, you
may automatically renumber all of your ports. Duplicate port numbers can be
changed or kept. If you wish to renumber your ports, proceed as follows:
1Select Circuit Ports from the project editor’s main menu to open the
Port Impedance dialog box.
2Click on the Renumber button in the Port Impedance dialog box. If you
have ports with duplicate numbers, you will be asked if you wish to
keep the duplicates or renumber them. Ports numbered 0 are not affected
by this command, all other ports are renumbered.
Port Placement with Symmetry On
Symmetry can be used to considerably reduce the amount of memory and process-
ing time required to analyze a circuit which is symmetrical about the midline of
the substrate. When symmetry is turned on in the Box Settings dialog box (Circuit
Box), everything below the line of symmetry is ignored, and all metal above the
line of symmetry is “reflected” about the symmetry line. Special care should be
given to ports when using symmetry.
Normally, if you are using symmetry, ports are placed on the line of symmetry as
pictured below.
Line of Symmetry Ports are
placed on the
line of
symmetry

Sonnet User’s Guide
80
Rev 16.56
Ports can be placed off the line of symmetry, but the port placed above the line of
symmetry must have another port equidistant from and below the line of symme-
try. These two ports must also have the same port type, port number and proper-
ties. The basic premise of symmetry is that the voltage at any given point above
the line of symmetry must be equal to the voltage at the corresponding location
below the line of symmetry. Using the same port number, port type and properties
ensures that the voltage is the same at both required points since all ports with the
same number, as pictured below, are electrically connected together.
Independent Reference Planes and Diagonal
Ports
There are two types of reference planes: shared or independent. By default, all ref-
erence planes on a box side are shared and the same reference length is used for
all ports on that side. When independent reference planes are used, any coupling
between feed lines is not removed.
Line of Symmetry
Port Pair
Port Pair
This circuit has two
sets of ports placed
equidistant from the
line of symmetry.
Note that the
corresponding ports
above and below the
line of symmetry
have the same
number.
This circuit violates port
usage with symmetry. The
ports are equidistant from
the line of symmetry but
have different port
numbers so that the
voltage is not equal.
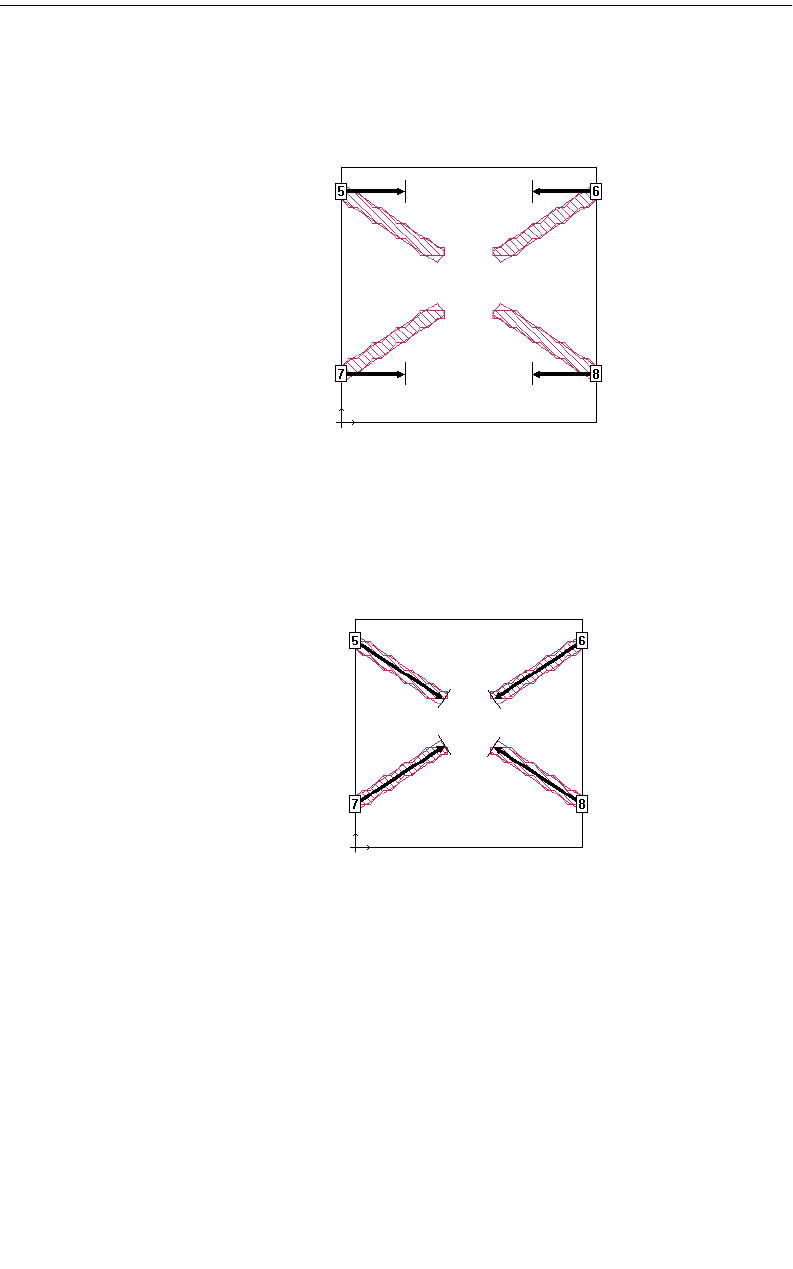
Chapter 5 Ports
81
Rev 16.56
For some designs, feed lines do not lie in either the x or y axis, but extend diago-
nally from the port. In this case, if the port is orthogonal, the reference plane does
not extend along the feed line, so that the feed line effects are not removed in the
de-embedding process. An example is shown below.
The solution to this problem is to apply the diagonal port feature to your port. A
reference plane must be defined as independent in order to use the diagonal fea-
ture. The diagonal feature may be applied to box-wall ports, co-calibrated ports
and components. This feature is not available for auto-grounded ports or via ports.
Once a port is designated as diagonal, the reference plane will extend along the
polygon to which the port is attached as shown below.
Applying the Diagonal Port Feature to a Port
In order to apply the diagonal feature to a port, you must first add the port to cir-
cuit. As mentioned earlier, the port defaults to being an orthogonal port. After the
port has been added, you may use the Port Properties dialog box to select the di-
agonal feature and specify the reference planes. Detailed instructions are provided
below.

Sonnet User’s Guide
82
Rev 16.56
1 Add the desired ports to your circuit.
For instructions on adding a port, please see the appropriate section later in this
chapter for the type of port you wish to add. This example uses standard box-wall
ports. For instructions on adding a box-wall port, see "Adding Box-wall Ports" on
page 88. An example circuit with four box-wall ports is shown below.
2 Double click on a port to open the Port Properties dialog box.
You can also select a port and then use the Modify Port Properties command
in the project editor’s main menu to open this dialog box.
Change
button
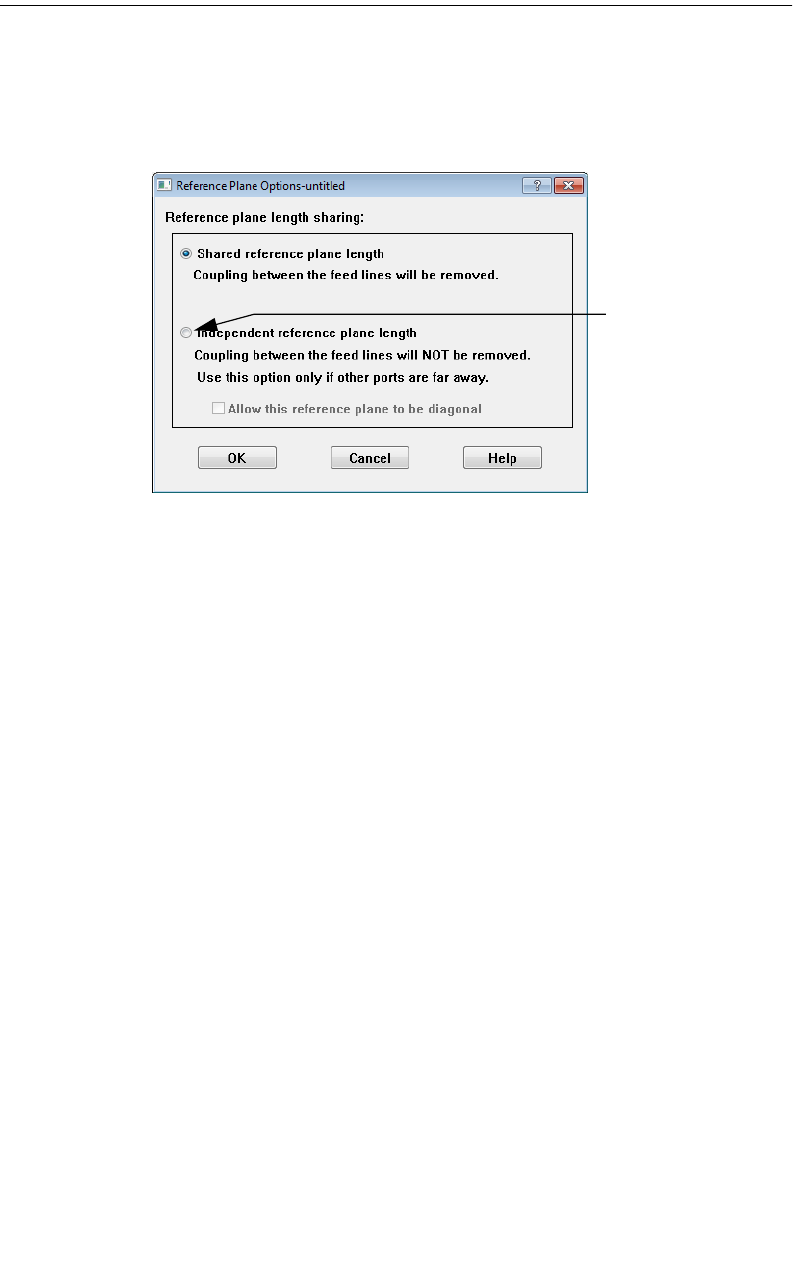
Chapter 5 Ports
83
Rev 16.56
3 Click on the Change button in the Advanced Options section of the dialog
box.
This opens the Reference Plane Options dialog box which allows you to specify
reference plane sharing and apply the diagonal feature.
4 Click on the “Independent reference plane lengths” radio button.
This option is used to make the reference plane for this port independent of other
reference planes for other ports. As mentioned previously, by default, all ports on
the same box-wall (or same side for components or co-calibrated port groups)
share the same reference plane length. This feature allows you to use a different
reference plane length for this port, regardless of reference plane lengths for other
ports, even ports which share a box-wall. A port cannot use the diagonal feature
unless it is using an independent reference plane. When you select this option, the
“Allow this reference plane to be diagonal” checkbox is enabled.
Independent
reference plane
length checkbox

Sonnet User’s Guide
84
Rev 16.56
5 Click on the “Allow this reference plane to be diagonal” checkbox.
This option allows your reference plane to occur at any angle in your circuit, in-
stead of being in x or y axis. The polygon to which the port is attached is used to
determine the direction of the reference plane instead of the box-wall.

Chapter 5 Ports
85
Rev 16.56
6 Click on the OK button to close the dialog box and apply the changes.
The Port Properties dialog box is updated and the Length field is updated to read
“Individual” and the Orientation field to read “Diagonal.” The options for the
reference plane have been reduced. For an independent port, you may only specify
a fixed length reference plane.
7 Click on the Mouse button to set the reference plane length for the port.
Clicking on the mouse icon allows you to click in your circuit to define the
reference plane. When you click on the icon, the dialog box disappears from your
display so that you may access the window.
8 Click at the desired location for the reference plane.
For this example, the reference plane is set at the end of the polygon to which the
port is attached so that the transmission line effects for the whole feed line are
removed during de-embedding. After clicking at the end of the polygon, the Port
Port
Orientation
Reference
Length Type
Mouse
Button

Sonnet User’s Guide
86
Rev 16.56
Properties dialog box reappears with a length entered in the Ref. Plane text entry
box. Note that you could have set the reference plane by entering a length into this
text entry box.
9 Click on the OK button to close the dialog box and apply the changes.
The reference plane is drawn, along the polygon, as shown below. This completes
applying the diagonal feature to your port. To complete this design, you would fol-
low the same procedure for the other three ports.
Reference
Plane
Length
Note that the reference
plane extends along the
feed line.

Chapter 5 Ports
87
Rev 16.56
Diagonal Port Feature Limitations
There are several limitations that the user should be aware of when applying the
diagonal port feature. Once you select a reference plane as an individual reference
plane any coupling between feed lines is no longer removed during the de-embed-
ding process. Therefore, when using the diagonal port feature, care should be
taken to place ports and their feedlines far enough apart that coupling effects are
not significant. An example of the feedlines being too close to use diagonal ports
is shown below.
In addition, the em analysis cannot calculate the transmission line parameters Eeff,
and Z0 for a diagonal port since the port is not separated from the feed lines when
de-embedded. However, the resulting response data is still accurate.
Standard Box-wall Port
A standard box-wall port is a grounded port, with one terminal attached to a poly-
gon edge coincident with a box-wall and the second terminal attached to ground.
The port, therefore, breaks the connection between the polygon and the wall and
is inserted in an “infinitesimal” gap between the polygon and the wall. The signal
(plus) portion of the port goes to the polygon, while the ground (negative) portion

Sonnet User’s Guide
88
Rev 16.56
of the port is attached to the box-wall (ground). An example of a standard box-
wall port is shown below. Standard box-wall ports can be de-embedded and can
also have reference planes. This type of port is the most commonly used.
Adding Box-wall Ports
You add a standard box-wall port to your circuit by selecting the command Tools
Add Ports and clicking on the polygon edge on the box-wall where you wish
to place the port. Ports are numbered automatically, in the order in which they are
added to your circuit, starting at the number one. You may change the properties
of a port after it has been added to the circuit by selecting the port and using the
Modify Port Properties command. For detailed instructions for these tasks,
please click on the Help button in the Modify Port Properties dialog box which ap-
pears when you select the command.
Ref. Planes and Cal. Lengths for Box-wall Ports
Reference planes and calibration lengths are both used during the de-embedding
process in which the analysis engine, em removes the port discontinuity and a de-
sired length of transmission line. For details of how these values are used during
the de-embedding process, please refer to Chapter 6, “De-embedding” on page
103.
portmode
lx wall
port on
page 46.
-+
V
Box-wall
Infinitesimal
Gap

Chapter 5 Ports
89
Rev 16.56
For a box-wall port, you may set either a reference plane or a calibration length;
both values cannot be set at the same time for box-wall ports. Ports can be shared
in which case all shared ports on the same box-wall use the same reference length
or calibration standard. If the port is set to individual, then a reference plane or cal-
ibration standard may be set that applies only to that port. Please note that if the
port is individual, then the coupling between ports is not de-embedded; coupling
is only removed between shared ports. To set either of these values for box-wall
ports, use the Modify Port Properties command. For details, please click on the
Help button in the Port Properties dialog box which appears when you select the
command.
Co-calibrated Internal Ports
Co-calibrated ports are used in the interior of a circuit. These ports are often used
by a circuit simulation tool to connect some type of element into your geometry at
a later time outside the Sonnet environment. Co-calibrated internal ports are iden-
tified as part of a calibration group with a common ground node connection. When
em performs the electromagnetic analysis, the co-calibrated ports within a group
are simultaneously de-embedded using a high accuracy de-embedding technique1;
thus, coupling between all the ports within a calibration group is removed during
de-embedding. This type of port is the most commonly used internal port.
Calibration Group Properties
A co-calibrated port is always associated with a calibration group. Co-calibrated
internal ports are automatically added to a calibration group made up of ports in
reasonable proximity who also share the same type of calibration group proper-
ties: ground node connection and terminal width. By default, a new co-calibrated
port uses the Sonnet Box as the ground node connection and the Feedline Width
as the terminal width. If these properties are subsequently changed, then this af-
fects the ports with which the modified port is grouped. If you wish to observe the
grouping determined by the software before running your analysis, you may select
the command View View Subsections from the project editor main menu.
It is also possible to manually define a calibration group which overrides the au-
tomatic settings. For more information, please refer to “calibration group” in
Help’s index.
1 ”Deembedding the Effect of a Local Ground Plane in Electromagnetic Analysis,” by James C. Rautio, presi-
dent and founder of Sonnet Software, Inc. The article is available in PDF format in the Support section of
our web site.
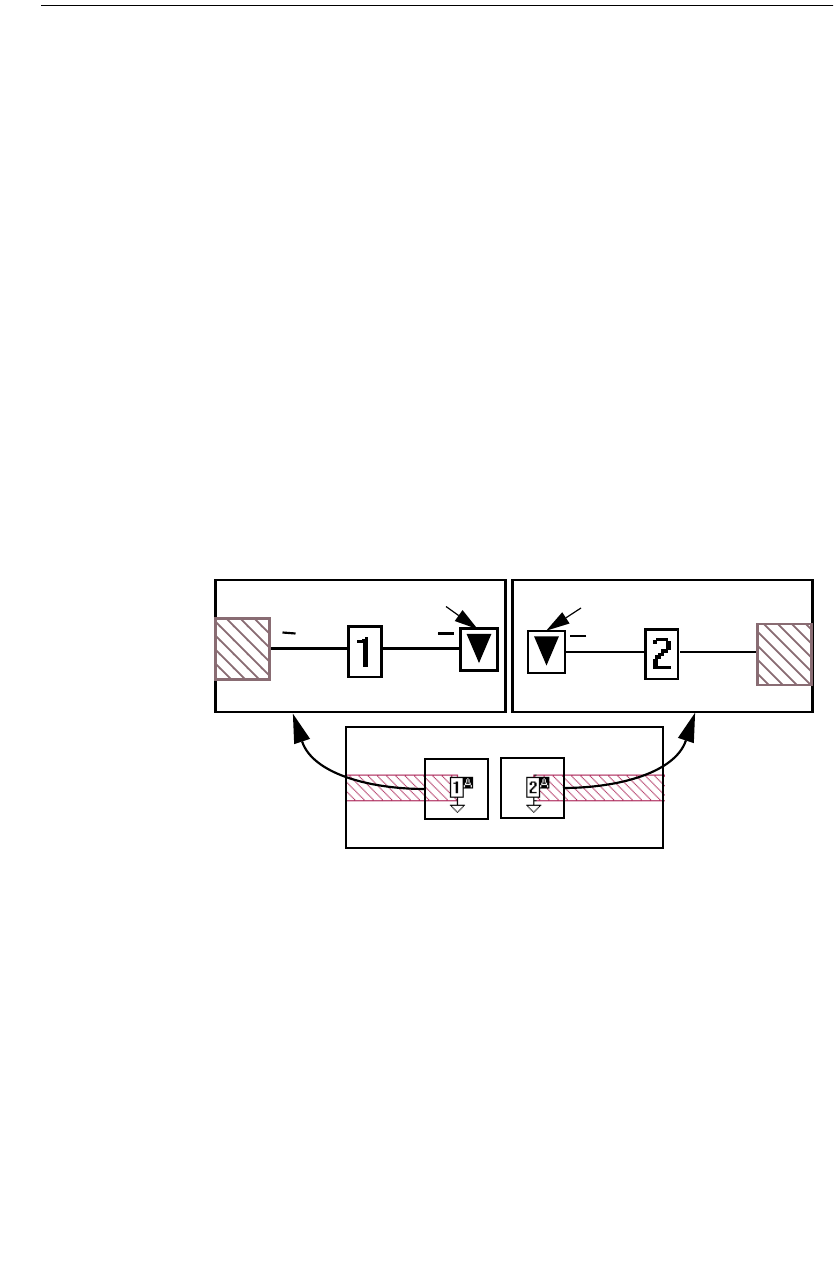
Sonnet User’s Guide
90
Rev 16.56
For a detailed explanation of the rules used in grouping co-calibrated ports, please
see "Rules for Co-Calibrated Ports" on page 94.
Ground Node Connection
You must define how the common ground of your calibration group is connected
to your circuit. There are two types of ground node connection: Sonnet Box and
Floating.
Sonnet Box: When the ground node connection is defined as the Sonnet box, all
co-calibrated ports in the group are globally grounded to the Sonnet box. To do
this, a via is automatically created which connects to the top or bottom of the Son-
net box. You should choose this option if the element model or measured data to
be connected to these ports includes shunt elements. Examples are:
•S-parameter data that includes pads or other coupling to ground.
•Transistor data that includes a via in the model/measurement.
This type of co-calibrated port is illustrated below. The positive terminal is at-
tached to a polygon edge of a feedline and the negative terminal is attached to a
via to ground which is removed during de-embedding.
When the Sonnet box is selected as the ground node connection, the analysis en-
gine automatically determines the most efficient direction the ground via extends
taking into consideration both the distance and the loss of the box top or bottom
box cover. When using this type of ground, you must make sure that there is a
clear path with no metal on other levels interfering with the path to the box top or
bottom.
Box-wall
port on
page 46.
+
Via to Ground +
Via to Ground

Chapter 5 Ports
91
Rev 16.56
In addition, either the box top or bottom must have loss less than 50 ohms/sq. For
example, you should not use “Free Space” for both your box top and bottom def-
inition. If the loss is too high on both the box top and bottom for a ground via from
the calibration group to be attached, the analysis engine will issue an error mes-
sage.
Floating: When the ground node connection is defined as Floating, all co-cali-
brated ports in the group are connected to a common ground but not to the Sonnet
box. Instead, the ground node is left unconnected to the rest of your circuit. You
should choose this option if the element model or measurement data that will be
connected to these ports does not have a ground reference, or does not have shunt
elements. Examples of this are:
•A series RL equivalent circuit
•S-Parameter data that was measured without any pads
This type of co-calibrated port is illustrated below. Sonnet automatically adds
extra metal which connects the co-calibrated ports in a calibration group. This
extra metal is defined as Generalized Local Ground (GLG) metal since it acts as
a local ground for the ports in the calibration group. This metal is removed during
the de-embedding process. The positive terminal of a co-calibrated port is attached
to a polygon edge of a feedline and the negative terminal is attached to GLG metal.
To observe the GLG metal for either type of ground node connection, you may se-
lect the View View Subsections command in the project editor. When the Sub-
section Viewer appears, select View GLG Metal from the subsection viewer’s
main menu. Views of two calibration groups, as viewed in the subsection viewer
GLG Metal
++
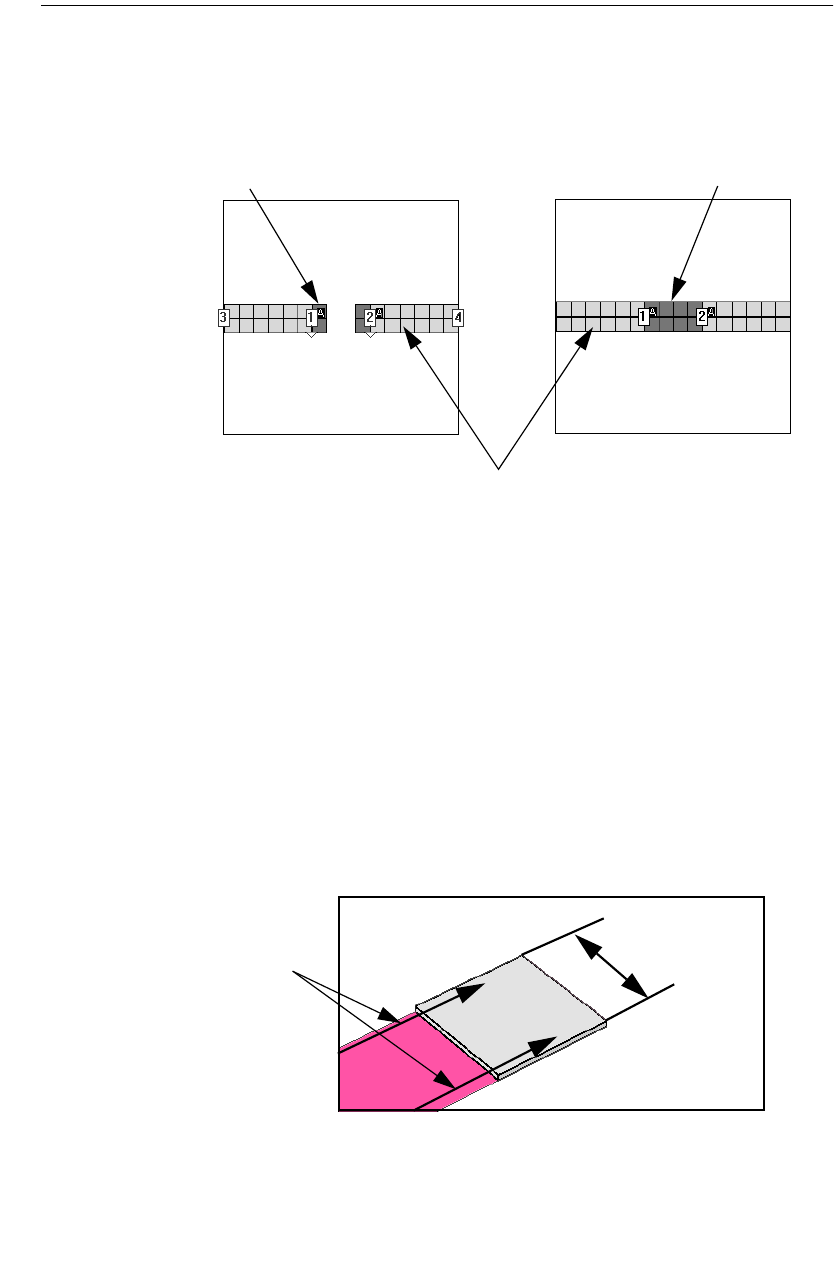
Sonnet User’s Guide
92
Rev 16.56
with the GLG metal displayed, are shown below. A calibration group which is
grounded to the Sonnet box is shown on the left and one with a floating ground is
shown on the right.
Terminal Width
You must also determine how you will define the terminal width for your calibra-
tion group. Terminal width is the electrical contact width of the component which
is to be attached. This allows the current flow from the circuit geometry into the
component to be accurately modeled. There are three settings for terminal width:
Feed Line Width, One Cell, and User Defined. Please note that the terminal width
is not shown in the project editor.
Feed Line Width: This defines the terminal width as equal to the feed line to
which the co-calibrated port is attached. This is illustrated below.
Circuit Metal
GLG Metal Via
Note that in the case of the Sonnet box ground node connection, the
GLG metal does not connect the two ports. Instead, there is a via
composed of GLG metal which extends to ground.
Sonnet Box Floating
GLG Metal Polygon
Current Flow Feed Line Width
Terminal Width
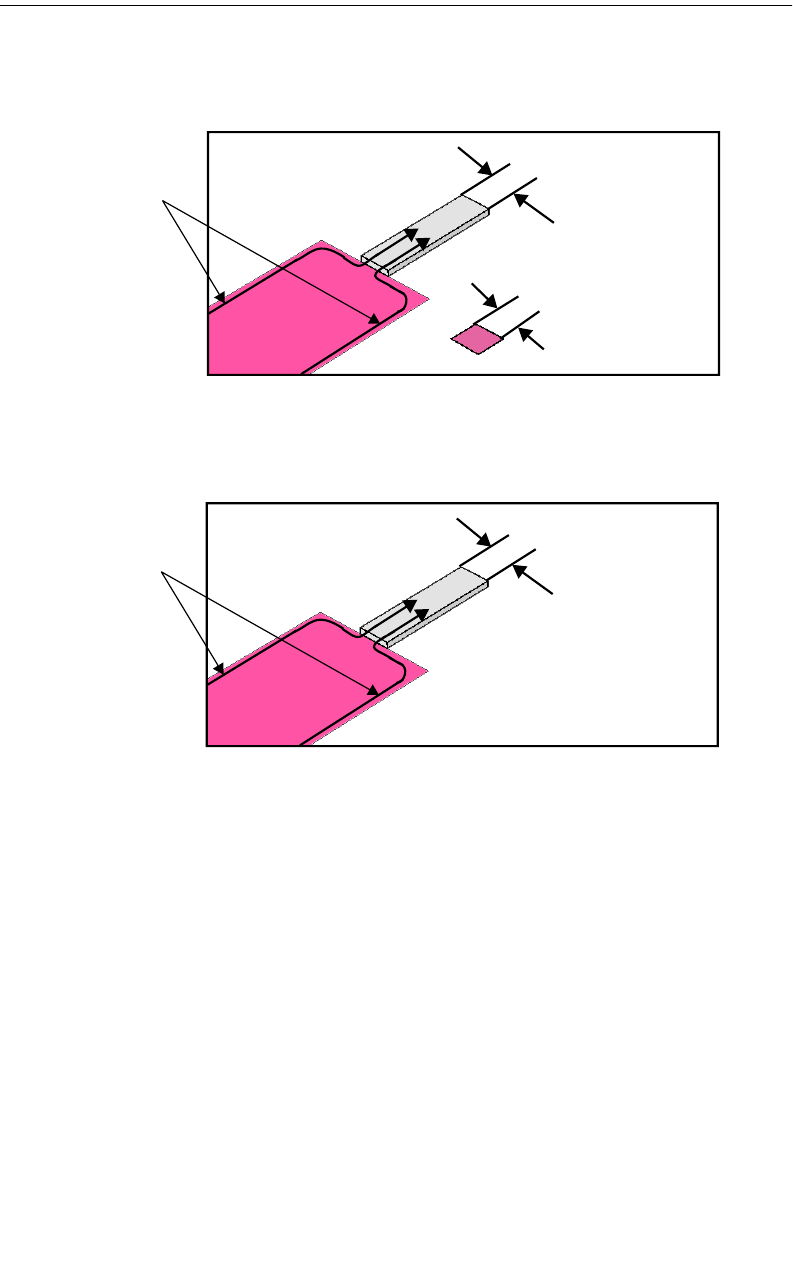
Chapter 5 Ports
93
Rev 16.56
One Cell: This defines the terminal width to the smallest possible size as pictured
below.
User Defined: This allows you to enter any value desired for the terminal width.
This type of Terminal Width is shown below.
Adding Co-calibrated Ports
You add co-calibrated ports to your circuit by selecting the command Tools Add
Ports and clicking on an open polygon edge where you wish to place the port.
Once the ports have been added to the circuit, you select the ports, then use the
Modify Port Properties command which allows you to select the co-calibrated
port type. For detailed instructions on this process, please refer to “co-calibrated
internal port” in Help’s index.
One Cell
Terminal Width
Current Flow
One Cell
User Defined
Terminal Width
Current Flow
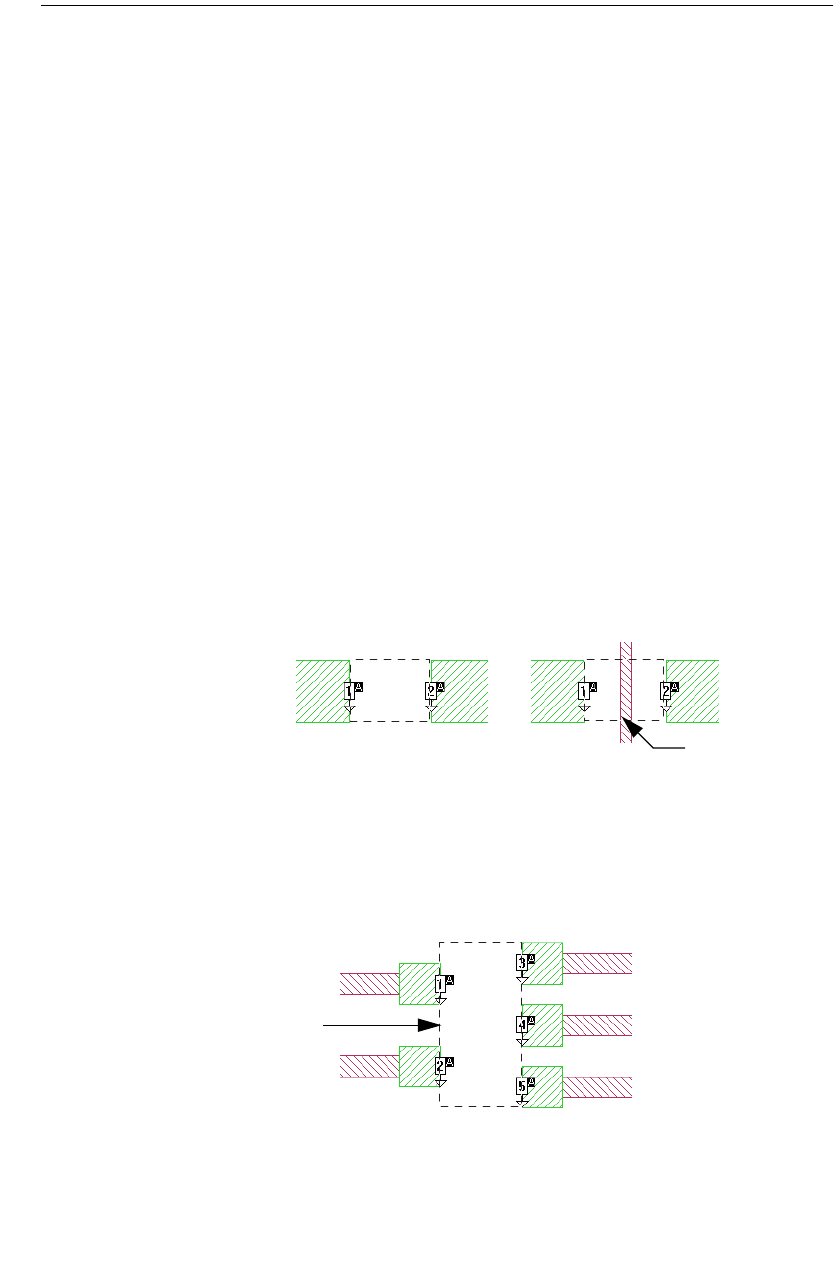
Sonnet User’s Guide
94
Rev 16.56
Rules for Co-Calibrated Ports
The set of criteria used by the software when autogrouping co-calibrated ports is
as follows:
•Proximity of the ports
•Calibration Group Properties: ground node connection and terminal
width (see "Calibration Group Properties" on page 89 for more details)
•Physical layout rules
The physical layout rules are detailed in this section. Note that these rules should
also be followed when manually defining a calibration group. For detailed instruc-
tions on manually creating a calibration group, please refer to “co-calibrated inter-
nal port” in Help’s index.
1. No objects may be placed within the “restricted space” in the
interior of the co-calibrated port group: Metal polygons, vias, or di-
electric bricks may not be present in the rectangular area defined by the
port locations and the terminal width, as illustrated below. The bottom
circuit shows the restricted area in a multiport Component. For the best
possible accuracy, no objects should be present on any layer in this re-
stricted space, even if the ports are not on these layers.
Right Wrong
The dashed boxes identify the “restricted space” for each co-
calibrated port group. On the circuit labeled “Wrong” a metal
polygon passes through the middle of the restricted space.
Illegal
Polygon
Restricted
Space
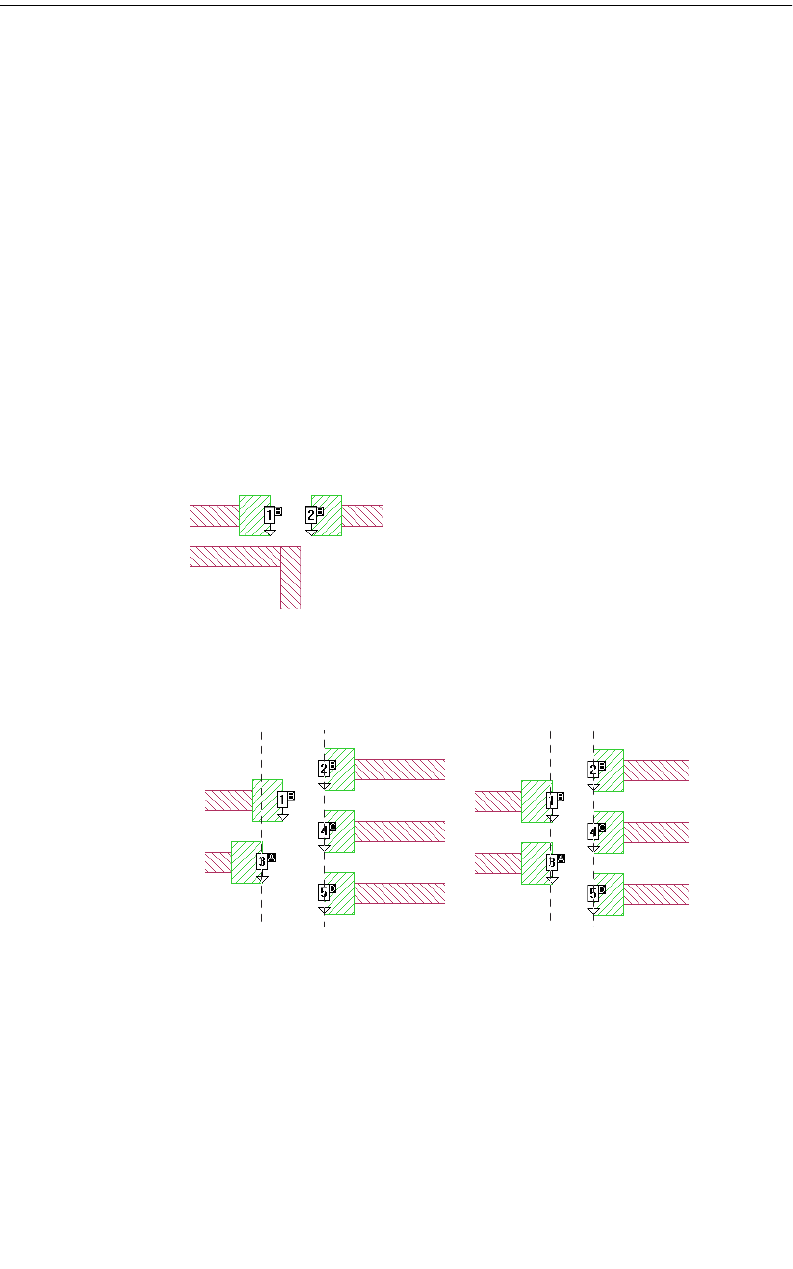
Chapter 5 Ports
95
Rev 16.56
2. Co-calibrated ports whose ground node connections are defined
as the Sonnet box require direct access to the Sonnet top or
bottom cover: The analysis engine determines the most efficient direction
the ground via extends taking into consideration both the distance and the
loss of the box top or bottom. When using this type of ground, you must
make sure that there is a clear path with no metal on other levels interfer-
ing with the path to either the box top or box bottom.
In addition, the box top or bottom should not have loss greater than 50
ohms/sq. If the loss is too high on both the box top or bottom for a ground
via from the co-calibrated ports to be attached, the analysis engine issues
an error message.
3. Nearby objects should be placed so that coupling between the
co-calibrated ports and the object does not occur: Metal polygons,
vias, or dielectric bricks which couple to the co-calibrated ports may de-
crease the accuracy of the analysis as shown below.
4. Multiple ports on the same side of the restricted area should be
aligned: In the illustration below, the co-calibrated ports on the left are
placed incorrectly and will produce an error during an analysis. The ports
on the right are placed correctly.
Wrong Correct
The dashed lines represent the alignment plane.

Sonnet User’s Guide
96
Rev 16.56
For multi-level co-calibrated ports, ports on different metal levels need to be
aligned in the x, y plane. In the illustrations below, the multi-level calibration
group on top is correct. The one on the bottom is incorrect since the ports on the
left side of metal level 0 are not aligned with the ports on the left side of metal
level 1
5. Reference planes for each side of a co-calibrated port group are
shared and therefore use the same reference plane length: How-
ever, reference planes can be set independently for each side of the “port
rectangle” as shown below. If a co-calibrated port is attached to a poly-
gon which does not lie in the x or y plane, then the port defaults to an in-
dependent, diagonal port and the reference plane is defined only for that
port. In the graphic below, ports 3 and 4 are shared orthogonal ports
which use the same reference plane length since they are on the same or-
thogonal side of the port group. Ports 1, 6, and 5 are all shared orthogonal
ports but may use different reference lengths since they are all on differ-
ent sides of the port group. If a port was added to the left side of the port
group, it would share a reference plane length with port 6. Both port 2

Chapter 5 Ports
97
Rev 16.56
and port 7 are independent diagonal ports whose reference lengths may
be different from each other and different from any of the shared ports on
an orthogonal side of the port group.
Ref. Planes and Cal. Lengths for Co-calibrated Ports
You may specify reference planes for ports in a co-calibrated port group as dis-
cussed in rule 5 above. Calibration lengths are automatically calculated by the
software. For a detailed discussion of how reference lengths and calibration
lengths are used during the de-embedding process, please refer to Chapter 6
"De-embedding" on page 103. For directions on how to set a reference plane and/
or calibration length for a co-calibrated port, please refer to “calibration group” in
the index of Help.
Use in Components
Co-calibrated ports are used to implement the Component feature. Many of the
considerations which apply to the setup of a Component also apply to the setup for
a calibration group. To gain a deeper understanding of the co-calibrated ports im-
plementation and uses, we highly recommend that you also read Chapter 6
"De-embedding" on page 103.

Sonnet User’s Guide
98
Rev 16.56
Via Ports
A via port has the negative terminal connected to a polygon on a given circuit level
and the positive terminal connected to a second polygon on another circuit level.
A via port can also have the negative terminal connected to the top or bottom of
the box. An example of this port type on an edge via is shown below.
Unlike co-calibrated ports, em cannot de-embed via ports. However, in a circuit
which contains a combination of via ports and other port types, the other port types
can still be de-embedded. Em will automatically identify all of the other ports
present in the circuit and de-embed them, but leave the via ports un-de-embedded.
The example file “stackedpatch” has an example of a via port used in a patch an-
tenna. This example file can be found in the Sonnet example files. You may access
the Sonnet Example Browser by selecting Help Browse Examples from the
menu of any Sonnet application. For instructions on using the Example Browser,
please click on the Help button in the Example Browser window.
In most cases where you need grounded ports, your first choice would be to use
co-calibrated ports (as discussed earlier), especially since it is possible to accurate-
ly de-embed co-calibrated ports. The most common case where a via port would
be used is when you wish to attach a port between two adjacent levels in your cir-
cuit. Another application is when you wish to connect a port to the interior of a
polygon, which is not allowed for co-calibrated ports which must be added to an
open polygon edge.
Level 0
+
-
1
Via Port
Upper Polygon
Lower Polygon
An example of a circuit with a standard via port. A side view of
the enclosed area on the circuit is shown in the middle.
Level 1

Chapter 5 Ports
99
Rev 16.56
You can not apply reference planes to via ports, since it is not possible for em to
de-embed them.
Adding Via Ports
To add a via port, you must first create a via. The via can be an edge-via or a via
polygon. For more details on how to create vias, see “vias” in Help’s index.
Once the via is in place, click on the Add a Port button in the tool box and click
on the via to add a port.
NOTE: The via port only appears in the project editor on the bottom level of
the via; if you are adding the port to any other level of the via, the
port is not displayed in the project editor. To see the port, go to the
metal level on which the bottom of the via is placed.
Automatic-Grounded Ports
An automatic-grounded port is a special type of port used in the interior of a circuit
similar to a co-calibrated internal port. This port type has the positive terminal at-
tached to the edge of a metal polygon located inside the box and the negative ter-
minal attached to the ground plane through all intervening dielectric layers. An
auto-grounded port with a reference plane is shown below. Auto-grounded ports
can be de-embedded by the analysis engine.
In most circuits, the addition of co-calibrated ports has little influence on the total
analysis time of the em job. However, for some circuits, co-calibrated ports may
require more time in the de-embedding phase of the analysis. In these cases, you
Auto-
grounded
port
picture.

Sonnet User’s Guide
100
Rev 16.56
may wish to use auto-grounded ports, which are more efficient but less accurate
than co-calibrated ports, since the de-embedding for auto-grounded ports does not
take into account the coupling between the auto-grounded ports.
Special Considerations for Auto-Grounded Ports
Metal Under Auto-Grounded Ports
Similar to co-calibrated ports which use the Sonnet box as the ground node con-
nection, you cannot have metal directly beneath an auto-grounded port in a multi-
layer circuit. Auto-grounded ports are two-terminal devices with the positive ter-
minal connected to an edge of a metal polygon and the negative terminal connect-
ed to the ground plane. When em detects the presence of an auto-grounded port,
it automatically connects the two terminals in this manner. This includes circuits
which have multiple dielectric layers between the polygon and the ground plane.
However, in order for em to accomplish this, there must be a direct path from the
edge of the metal polygon to the ground plane. When an auto-grounded port is
used in a circuit where there is more than one dielectric layer between the port and
the ground plane, em checks to make sure that there is no metal directly beneath
the auto-grounded port. If metal is found, em prints an error message and stops.
Edge of Metal Polygon is Lossless
Auto-grounded ports can attach to the edge of any metal polygon in the interior of
a circuit. There are no restrictions on the loss parameters of the metal used in the
polygon. However, along the edge of the metal polygon where the port is attached,
em does force the cells to be lossless. For most circuits, this should have little or
no effect on the results. If, however, the port is attached to a highly lossy metal
polygon, such as a thin-film resistor, the edge cell(s) of that polygon will be made
lossless, and the output results may be affected.
Using Negative Port Numbers with Autogrounded Ports
You are able to assign negative port numbers to autogrounded ports but should be
aware of some special considerations when doing so. The two autogrounded ports
(+n and -n), although associated by port number, are still de-embedded separately
so the coupling between the ports is not de-embedded which can affect the accu-
racy of your data. Because these ports are de-embedded separately, the port im-
pedance, Z0 only accounts for the impedance of the single line attached to the
autogrounded ports since the calibration standard does not include both lines of
the differential pair. Lastly, using reference planes in this case may also affect
your data, since reference planes are used to de-embed a single transmission line
while this configuration creates a differential transmission line.

Chapter 5 Ports
101
Rev 16.56
Adding Auto-grounded Ports
You add an auto-grounded port to your circuit by selecting the command Tools
Add Ports and clicking on the open polygon edge where you wish to place the port.
Once the port has been added to the circuit, you select the port, then Modify
Port Properties. In the Port Properties dialog box which appears, you select the
auto-grounded type. For detailed instructions on this process, please refer to
“auto-grounded ports” in Help’s index.
Ref. Plane and Cal. Length for Autogrounded Ports
To set a reference plane for an auto-grounded port, use the Modify Port Prop-
erties command. Calibration standards are automatically calculated by the soft-
ware. You enter the desired Reference Plane in the appropriate field. For detailed
instructions please refer to Help. Note that if you enter a reference plane, it applies
only to the selected port(s). For details on how reference planes and calibration
lengths are used in the de-embedding process, please refer to Chapter 6 "De-em-
bedding" on page 103.
TIP
Changing a port to an autoground type and setting up a reference plane for the port
can be accomplished at the same time in the Port Properties dialog box. It is also
possible to set reference planes for multiple auto-grounded ports by selecting the
desired ports, selecting Modify Port Properties and inputting a value in the Ref.
Plane text entry box in the Port Attributes dialog box.
Ungrounded Internal Ports
An ungrounded internal port is located in the interior of a circuit and has its two
terminals connected between abutted metal polygons. An ungrounded internal
port is illustrated below. Note that internal ports have their negative terminals on
the left or top side of the port depending on how the port is oriented. Ungrounded
internal ports can be de-embedded by em, however, you may not set a reference

Sonnet User’s Guide
102
Rev 16.56
plane or calibration length. Ungrounded internal ports are not as accurately de-em-
bedded as co-calibrated internal ports, but they do not require any space between
the two polygons as is required for a co-calibrated port.
Ungrounded internal ports are not allowed on the edge of a single polygon because
this would leave one terminal of the port unattached. Also, care should be taken
in interpreting the results for circuits which use these ports since the ports do not
all access a common ground.
You add an ungrounded-internal port in the same manner that you add a standard
box-wall port; for details, see “Adding Box-wall Ports,” page 88.
+
a) b)
1
-
+
1
-

Chapter 6 De-embedding
103
Rev 16.56
Chapter 6 De-embedding
Introduction
De-embedding is the process of calibrating the ports, similar to a calibration of an
RF measurement system with the probes or connectors used in the measurement.
Sonnet de-embedding is performed automatically, behind the scenes, and in most
cases, is not a concern for the user. However, just as in an RF measurement, un-
derstanding of the inner workings of the process can sometimes allow you to de-
sign your circuits in such a way as to produce more accurate results or analyze
your circuit more efficiently.
Each port in a circuit analyzed by em introduces a discontinuity into the analysis
results. In addition, any feed transmission lines that might be present introduce
phase shift, and possibly, impedance mismatch and loss. Depending upon the na-
ture of your analysis, this may or may not be desirable. De-embedding is the pro-
cess by which the port discontinuity and feed transmission lines are removed from
the analysis results.
The figure on page 104 illustrates the general layout of a circuit to be analyzed
with em. The device under test (DUT), shown as a box in the figure, is the circuitry
for which we wish to obtain analysis results. The DUT is located inside the metal
box and is connected to one or more ports. The ports may be located on box-walls,
as in the figure, or in the interior of the metal box (see Chapter 5 for a description
of port types available in em). Typically, feed lines are necessary to connect the
ports to the DUT.

Sonnet User’s Guide
104
Rev 16.56
When de-embedding is enabled, em performs the following sequence of steps:
1Calculates port discontinuities.
2Removes effects of port discontinuities from analysis results.
3Optionally shifts reference planes (negates effects of feed transmission
lines from analysis results).
4For most port types, calculates transmission line parameters Eeff, and Z0
for the feed transmission lines. For more information, please see "Plot-
ting Z0 and Eeff" on page 126.
Upon completion of the de-embedding process, em outputs de-embedded S-pa-
rameter results.
The de-embedding algorithm uses a Short Open Calibration (SOC) technique. For
an in-depth discussion of the calibration technique, please see reference [4] and
for a discussion of the de-embedding technique used for co-calibrated ports see
reference [6] in Appendix II, “Sonnet References.” Both of these articles are avail-
able in PDF format on the Sonnet web site.
Port
Port
Metal Box-walls
Device
Under
Test
(DUT)
Transmission Line
Transmission Line
General layout of a circuit to be analyzed with em.

Chapter 6 De-embedding
105
Rev 16.56
Port Discontinuities
The port discontinuity for box-wall ports is described in the section that follows.
The discontinuity for the other types of ports may be different, but the process out-
lined below is similar for all port types. Box-wall ports have one port terminal
connected to a polygon inside the metal box, and the second port terminal connect-
ed to ground (see the figure on page 88). The port discontinuity is modeled as a
series resistor, R, and capacitor, C, shunted to ground as shown below. If the cir-
cuit being analyzed is completely lossless, the resistor value, R, is zero. Even with
loss in the circuit, the capacitive reactance is normally very large compared to the
resistance.
When enabled, em’s de-embedding feature automatically calculates the values of
R and C for each box-wall port present in the circuit. The port discontinuities are
then removed by cascading a negative R and C as illustrated below.
R
C
S-parameters from em
without de-embedding
Device
Under
Test
Box-wall port
discontinuity
Port discontinuity associated with a box-wall port.
Sonnet User’s Guide
106
Rev 16.56
Shifting Reference Planes
Feed lines are required in many circuits to connect ports to the device under test
(DUT). If the length of a transmission line is more than a few degrees relative to
a wavelength, unwanted phase (and possibly loss) will be added to the results. If
the impedance of the transmission line differs from the normalizing impedance of
the S-parameters (usually 50 ohms), an additional error in the S-parameters re-
sults. Thus, if we are only interested in the behavior of the DUT, any “long” feed
lines connecting the ports to the DUT should be negated during de-embedding.
The process of negating lengths of transmission line during de-embedding is
known as “shifting reference planes”.
Reference planes may be specified in the project editor for box-wall, co-calibrat-
ed, and auto-grounded ports, but not ungrounded-internal and via ports. When
your circuit contains a reference plane, and de-embedding is enabled, em automat-
ically builds and analyzes the calibration standards necessary to de-embed the port
and shift the reference plane by the specified length.
R
C
S-parameters from em
without de-embedding
-R
-C
Device
Under
Test
Block cascaded to negate
box-wall port discontinuity Box-wall port
discontinuity
S-Parameters
from em with
de-embedding.
De-embedding automatically cancels the discontinuity associated with a box-wall port.
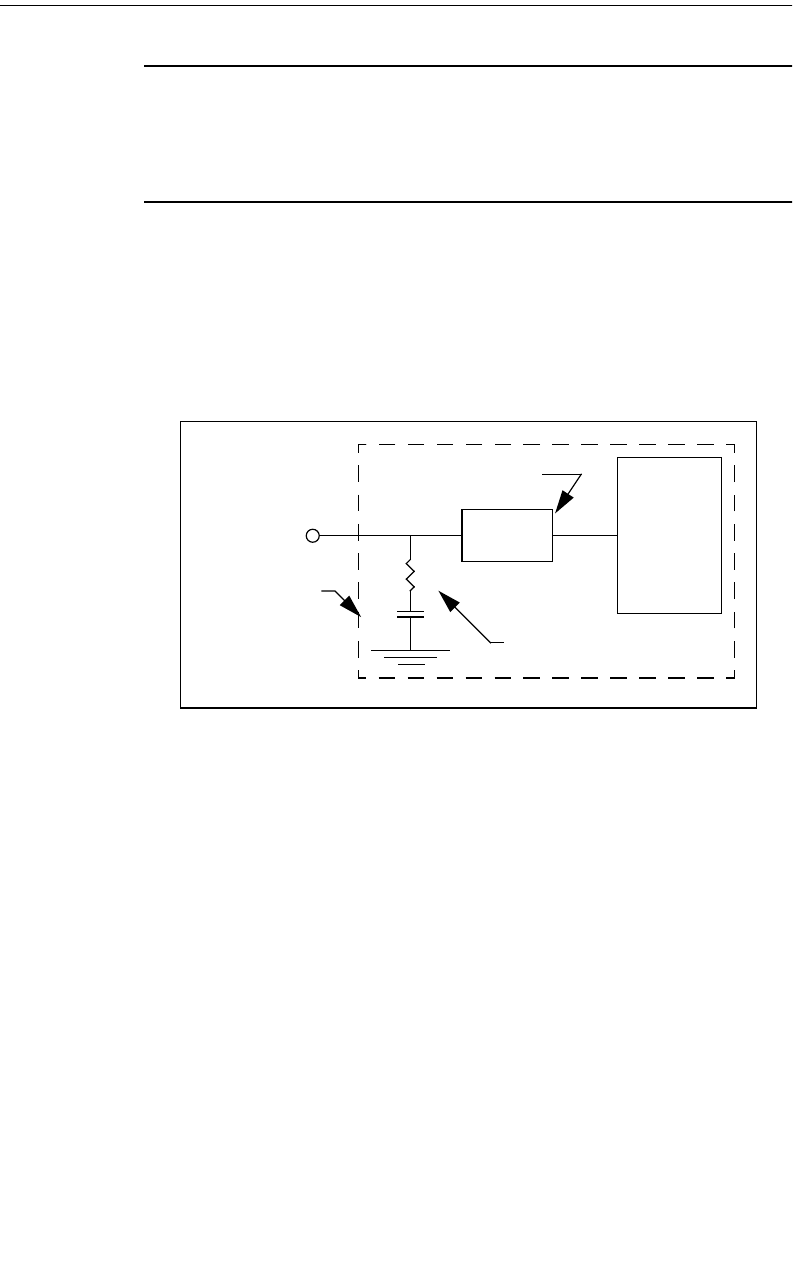
Chapter 6 De-embedding
107
Rev 16.56
NOTE: Reference planes are not necessary for de-embedding. If you do not
specify a reference plane in the project editor, the reference plane
length defaults to zero. This means that em will not shift the
reference plane for that port when de-embedding is enabled.
However, em will negate the discontinuity for that port.
Single Feed Line
Continuing with the box-wall port example, the figure below shows a circuit with a
length of transmission line, TRL, inserted between a box-wall port and the device
under test.
R
C
TRL
Box-wall port
discontinuity
Transmission line
Device
Under
Test
Results from em
without de-
embedding
Port discontinuity and transmission line
associated with a box-wall port.
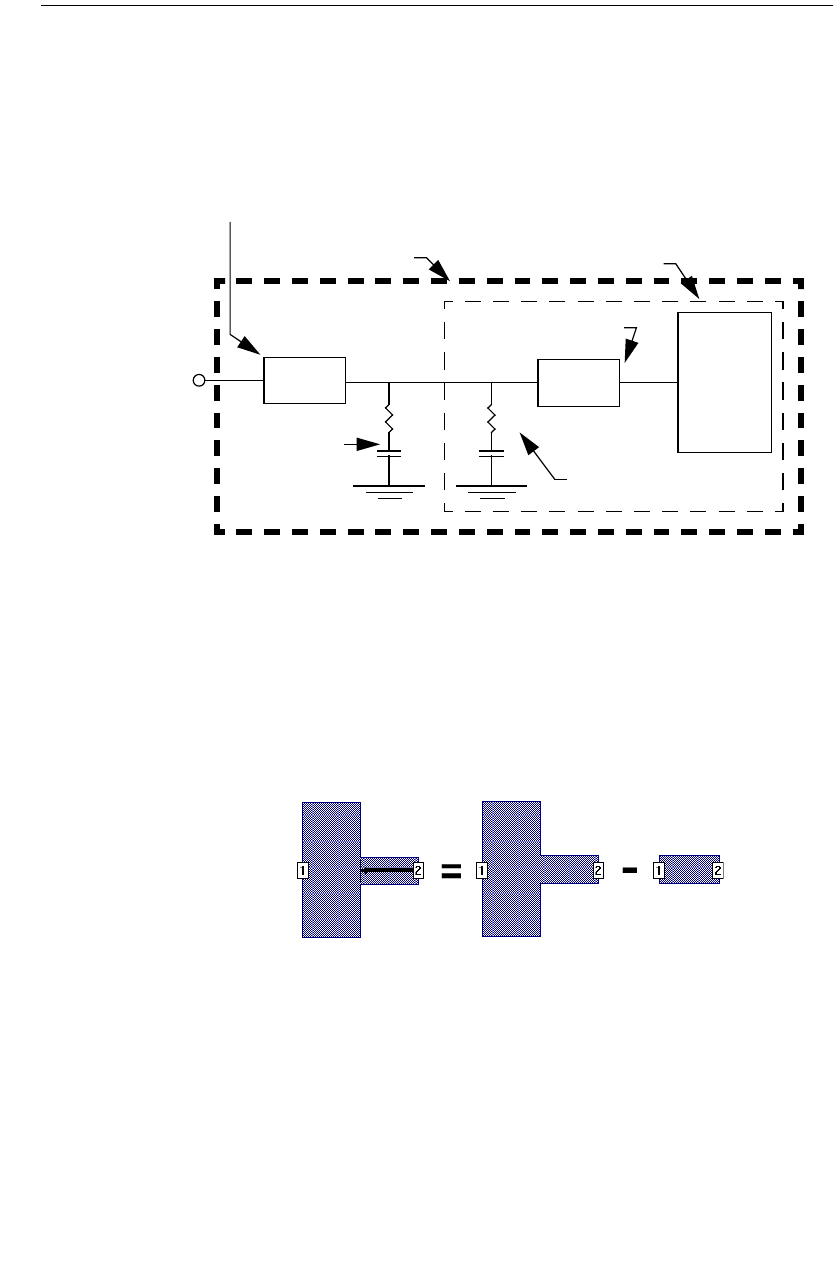
Sonnet User’s Guide
108
Rev 16.56
When the circuit has a reference plane, em negates the transmission line in a man-
ner similar to that used to remove the port discontinuity. Em calculates S-param-
eters for the line alone, and then cascades a “negative” line along with negative R
and C as illustrated in the next figure.
A Common Misconception
As explained above, a shifted reference plane negates the effects of one or more
transmission lines using circuit theory after the simulation of the entire circuit.
This concept is shown in the picture below:
R
C
Results from em
without de-embedding
TRL
Box-wall port
discontinuity
Transmission line
-R
-C
-TRL
Results from em
with de-embedding
Device
Under
Test
Block cascaded
to negate port
discontinuity
Block cascaded
to negate transmission line
Illustration of how de-embedding negates the port discontinuity
and transmission line associated with a box-wall port.
A Sonnet
structure with a
shifted
reference plane
The entire
Sonnet
structure
simulation
A uniform
transmission
line
-=
Chapter 6 De-embedding
109
Rev 16.56
Notice that reference planes do not remove the transmission line metal, but only
negate it. Shifting a reference plane is not the same as removing the metal from
the simulation:
A shifted reference plane does not remove the fringing fields due to the step in
width. This concept is illustrated below. Note that the fringing fields still exist in
the final Sonnet results after de-embedding.
Rules for Reference Planes
The Sonnet project editor places very few restrictions on the reference planes
which may be defined for a given circuit. This is done intentionally so as to pro-
vide maximum flexibility for all users. However, there are some basic guidelines
concerning reference planes that should almost always be followed. These guide-
lines are discussed below.
Feed Lines Must Be Transmission Lines
The first guideline is to ensure that your feed lines are true TEM or quasi-TEM
transmission lines. This means the following:
A Sonnet structure
with a shifted
reference plane
The same
structure with
no feed line
=
A Sonnet structure
with a shifted
reference plane
The same structure with
fringing from the feedline
which was negated
=

Sonnet User’s Guide
110
Rev 16.56
•Feed lines must be of uniform width across the entire distance which the
reference plane covers.
•Feed lines must not over-mode.
•The feed line(s) must not have an unusually high amount of loss. The
metal must be conductive enough to allow power to reach the other side
of the line. In addition, the dielectric must be resistive enough so the
power is not shorted to ground before it reaches the other side.
De-embedding Without Reference Planes
Reference planes are optional for co-calibrated, auto-grounded, and orthogonal
box-wall ports but are required for diagonal boxwall ports. If you do not specify a
reference plane for a particular port in the project editor, em will assume a zero-
length reference plane for that port. This means that de-embedding will remove
the discontinuity associated with that particular port, but will not shift the refer-
ence plane for it.
As discussed in the next section, em may generate bad de-embedded results if you
attempt to remove a very short (but greater than zero) reference plane for a box-
wall port. However, if you de-embed without a reference plane, em will not at-
tempt to negate any length of transmission line at all. As a result, de-embedding
without a reference plane does not lead to any error. Therefore, we recommend
that you de-embed without reference planes rather than specify very short, non-
zero, reference plane lengths for orthogonal boxwall ports.
Short Reference Planes for Boxwall Ports
While auto-grounded and co-calibrated ports do not have a minimum length for
their reference planes, short reference planes for boxwall ports, both orthogonal
and diagonal, can cause problems with your de-embedded results. If the reference
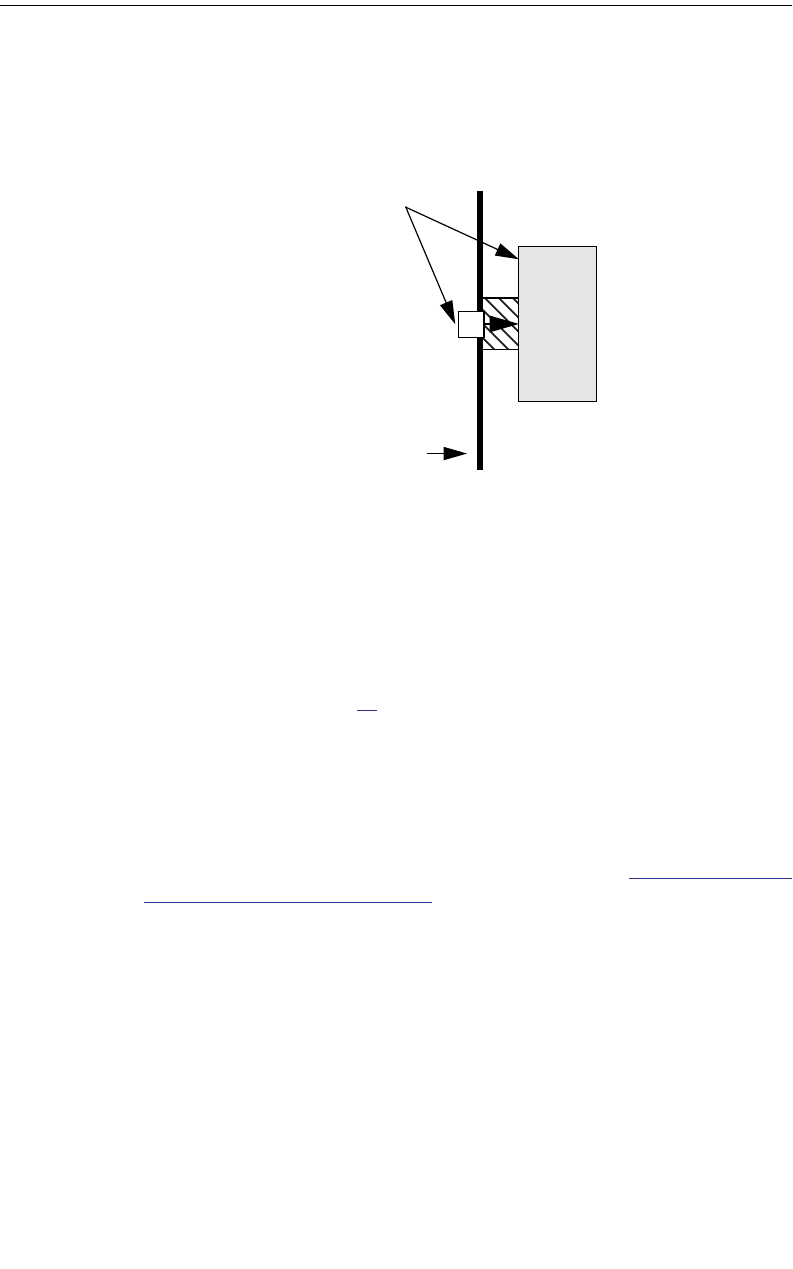
Chapter 6 De-embedding
111
Rev 16.56
plane for a boxwall port is very short relative to the substrate thickness or the
width of the transmission line, em may generate poor de-embedded results. This
is due to one or both of the reasons discussed below.
As shown above, the port is too close to the device under test (DUT). There are
fringing fields associated with the port and separate fringing fields associated with
the DUT. If the port and DUT are too close, the fringing fields interact. The de-
embedding algorithm (which is virtually identical to algorithms used in de-em-
bedding measured data) is based on circuit theory and cannot handle fringing field
interaction. See reference [68] in Appendix II, “Sonnet References” for a detailed
description of the problem.
The other possible problem is that the calibration standard is too short: The cali-
bration standard must be long enough such that the currents on the line(s) behave
like standard transmission line(s). Since the calibration standard length for a box-
wall port is based on the reference plane length, a short reference plane can result
in inaccurate results. For more details about this problem, see "Modifying Calibra-
tion Standard Lengths" on page 118.
There is no precise rule as to how long a boxwall port’s reference plane must be
made in order to prevent the above effects from corrupting the de-embedded re-
sults. The required length is dependent upon the circuit geometry and the nature
of the analysis. However, we recommend that you use reference planes equal to
or greater than several times the distance to the nearest ground metal. This is suf-
ficient for most types of analyses.
Poor de-embedding results may be obtained when very short (but
non-zero) reference plane lengths are used for boxwall ports.
DUT
1
Box-wall
Fringing fields from DUT
interact with fringing
fields from port.

Sonnet User’s Guide
112
Rev 16.56
Reference Planes Longer than the Feedline
Generally, reference planes should not be longer than the feed line(s) attached to
the port. This is because a reference plane is “negating” a transmission line. Thus
if your reference plane is longer than your feedline, you are effectively attempting
to negate a part of a transmission line which does not exist. Doing so may result
in non-physical S-parameters.
To illustrate this problem, consider the valid circuit shown below. In this circuit,
the reference planes are the same length as the feedlines. When de-embedding is
enabled, the port 1 discontinuity is negated along with a transmission line of width
W1 and length L1. Similarly, the port 2 discontinuity is negated along with a trans-
mission line of width W2 and length L2. The de-embedded result is a set of 2-port
S-parameters for the block in the middle of the circuit which is usually the desired
data.
Now, consider the figure on page 113. This circuit is identical to the circuit shown
above except that the length of the reference plane associated with Port 1 has been
increased. If em is run with de-embedding enabled on this circuit, it “negates” a
length of transmission line equal to the specified reference plane length. This oc-
curs even though the actual feed transmission line is shorter than the reference
W1 W2
L1
L2

Chapter 6 De-embedding
113
Rev 16.56
plane length. As a result, the de-embedded S-parameters may be non-physical
(i.e., the results may not obey the laws of physics by being non-passive or non-
causal).
A second de-embedding example leading to non-physical S-parameter results is
shown in the next figure. In this example, the circuit has two via pads on each side
of the port transmission line. The via pads are grounded to the box-wall.
Discontinuity
begins here
W1
L1
W2
L2
Example circuit for which non-physical results may
be obtained when em is run with de-embedding on.
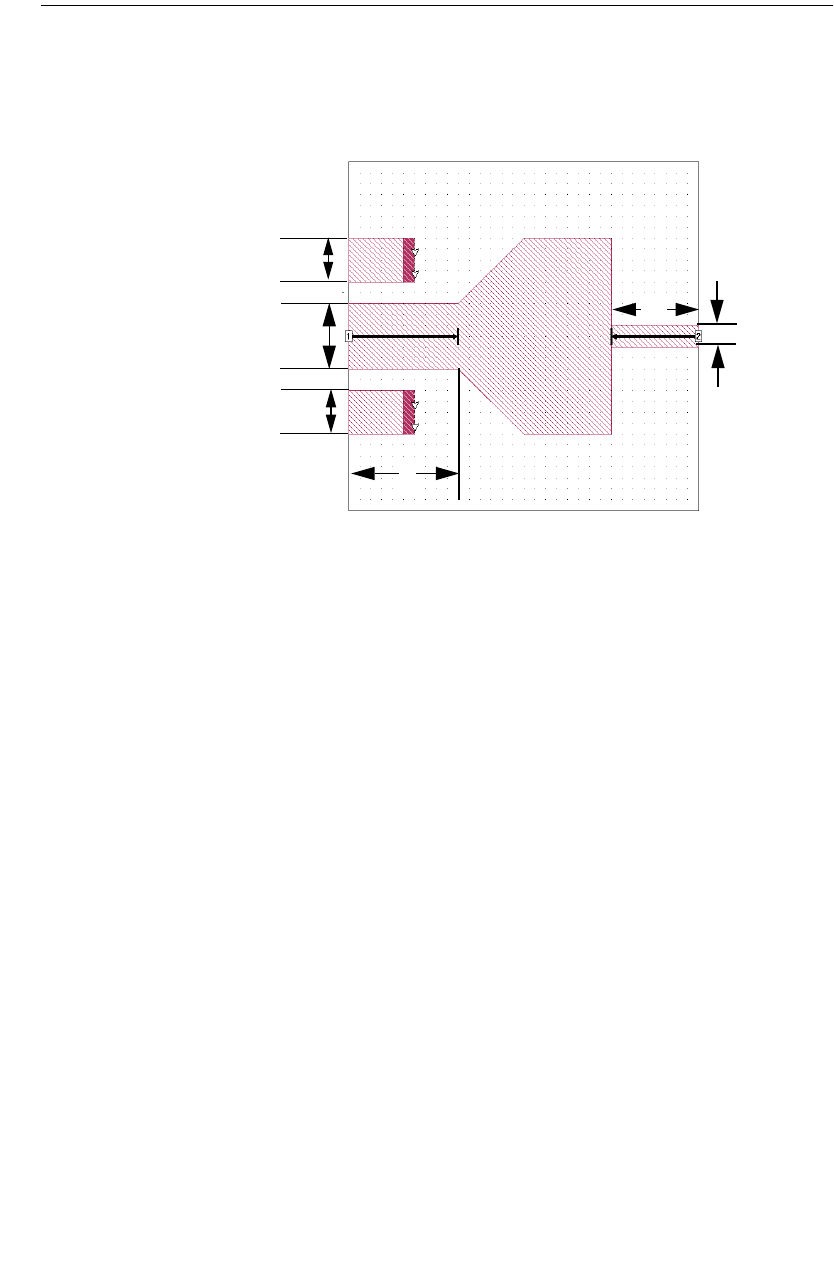
Sonnet User’s Guide
114
Rev 16.56
When em is run with de-embedding enabled on this circuit, it “negates” three cou-
pled feed lines with a length equal to the reference plane length. Since the refer-
ence plane extends from the box-wall beyond the vias, the de-embedded results
may be non-physical.
Calibration Standards
A user will rarely need to set their own calibration standard, normally using the
lengths automatically calculated by em. However, understanding calibration stan-
dards can help you simulate your circuit in the most efficient way while ensuring
the accuracy of your response data.
L
W1
W2
W3
W4
L2
Analyzing this may result in non-physical results because the
reference plane is longer than the coupled feedline.

Chapter 6 De-embedding
115
Rev 16.56
In order to de-embed a port discontinuity, Sonnet must electromagnetically ana-
lyze several calibration standards which include the same port discontinuity as is
in the primary circuit. For example, to de-embed port 2 in the circuit below, the
calibration standards contain a transmission line with the same line width as the
primary circuit.
For box-wall ports, Sonnet uses the Short Open Calibration (SOC) technique
which means a short and open standard must be analyzed. For orthogonal ports
(ports which are connected to transmission lines which are perpendicular to a Son-
net box-wall), the two calibration standards look like the picture below, where the
dashed line is replaced with an electric wall (for the short circuit) and a magnetic
wall (for the open circuit).
Cal 1: Electric Wall
Cal 2: Magnetic Wall

Sonnet User’s Guide
116
Rev 16.56
For box-wall ports, any object that touches the same wall as the port will be in-
cluded in the calibration standard. This rule applies to vias, dielectric bricks, and
metal on other levels as shown in the example below. This metal is included in the
calibration standard.
For diagonal ports, Sonnet uses the single three-port calibration standard shown
below, where the short and open data are generated by a single analysis, and by
short-circuiting and open-circuiting port 3.
Cal StandardCircuit
Diagonal Ports
Cal1: Port 3 short circuited
Cal2: Port 3 open circuited

Chapter 6 De-embedding
117
Rev 16.56
Shown below are some examples of the calibration standards used for various port
types. The calibration length for the boxwall ports is “L” and for all other ports the
calibration length is the same length as the reference plane.
For any of the pictures above which show a reference plane, em first analyzes the
structure without the reference planes, then simulates additional standards (not
shown) to remove the port discontinuity and shift the reference plane, just as it
would if this were your primary structure. For example, in the two-port co-cali-
brated port example above, Sonnet first analyzes the structure shown in the pic-
ture, and then analyzes the boxwall port calibration standards in order to de-embed
up to the co-calibrated ports.
Standard Boxwall Port Two shared boxwall ports Diagonal boxwall port
Group of two co-calibrated ports Group of four co-calibrated ports
Autogrounded port Internal Port
TW TW is the
terminal
width of the
co-cal port
as defined
by the user
on a box side

Sonnet User’s Guide
118
Rev 16.56
Modifying Calibration Standard Lengths
Sometime the calibration standard automatically determined by em is longer than
necessary, which can increase the analysis time. In most cases, de-embedding is
not a large part of the analysis, so the effect of a longer calibration standard is neg-
ligible. However, where the calibration standard is comprised of a significant
amount of metal, as for example, coplanar waveguide circuits, longer calibration
standards can impact analysis time.
There are also cases in which the automatically determined calibration standard is
too short. This can cause errors in your de-embedded results since the line must
be long enough to allow the currents flowing on the line to exhibit a traditional
TEM mode (see "Feed Lines Must Be Transmission Lines" on page 109). A box-
wall port with a calibration standard which is too short is illustrated below. Notice
the length of the calibration standard is even shorter than the width.
DUT
1
Box-wall
1
Box-wall
Circuit Calibration Standard

Chapter 6 De-embedding
119
Rev 16.56
In these cases, you may wish to override the automatically determined length. The
table below shows for which port types you may set the calibration length manu-
ally.
The second column shows how the default calibration length is determined. The
third column shows whether a manual setting is possible and if so, how to input
the desired length. For example, for standard boxwall ports which have a reference
plane, changing the reference plane length changes the calibration standard
Port Type Default Cal
Length Manual Setting of Cal
Length?
Standard Boxwall with
reference plane
Reference
plane length
Yes: Change reference plane
Standard Boxwall with-
out reference plane
Automatic Yes: Enter Cal Length in the
Port Properties dialog box
Diagonal Boxwall Reference
plane length
No
Co-calibrated Auto Yes: Enter Cal Length in the
Port Properties dialog box
Autogrounded Auto Yes: Enter Cal Length in the
Port Properties dialog box
Internal Ungrounded Auto No

Sonnet User’s Guide
120
Rev 16.56
length. For ports which allow you to change the calibration length, double-click
on the port and enter the desired value in the Cal Length text entry box as shown
below.
Coupled Transmission Lines
Sometimes, your circuit may contain multiple parallel feed lines as shown in the
circuits below:
There are two issues in the above examples:
1The ports are close to each other. When ports are close to each other,
their fringing fields can couple to each other. If the ports are not cali-
brated at the same time, this would result in errors. Fortunately, Sonnet
uses coupled lines for the calibration standards (by default), so all cou-
Cal Length
text entry box

Chapter 6 De-embedding
121
Rev 16.56
pling between the fringing fields of the ports is removed in the de-
embedding process (see the figure on page 122.)
2The feed lines are close to each other. When feed lines are close to each
other, they can couple to each other. If you are using reference planes,
this coupling should be removed. Since calibration standards are cou-
pled lines, this coupling is removed by default.
Both of these issues are resolved by using “shared” reference planes. When the
reference planes are set to “shared,” coupled lines are used for calibration stan-
dards, thus removing the coupling between the ports and the feed lines. The alter-
native to shared reference planes is “independent” reference planes. The table
below summarizes which types of reference planes, shared or independent, are
used for which type of ports:
The sections below discuss the implications of using shared or independent refer-
ence planes.
Shared reference planes
When ports have shared reference planes:
•The length of each reference plane is the same.
•Calibration standards are composed of multiple coupled lines as shown
below.
Port Type Reference Plane Type
Boxwall (orthogonal) with reference plane Shared or Independent
(Determined by user)
Boxwall (diagonal) Independent only
Co-calibrated (orthogonal using Sonnet Box
Ground)
Shared only
Co-calibrated (diagonal using Sonnet Box
Ground)
Independent only
Co-calibrated (Floating Ground) None
Auto-grounded Independent only
Internal Ungrounded None
Via Port None
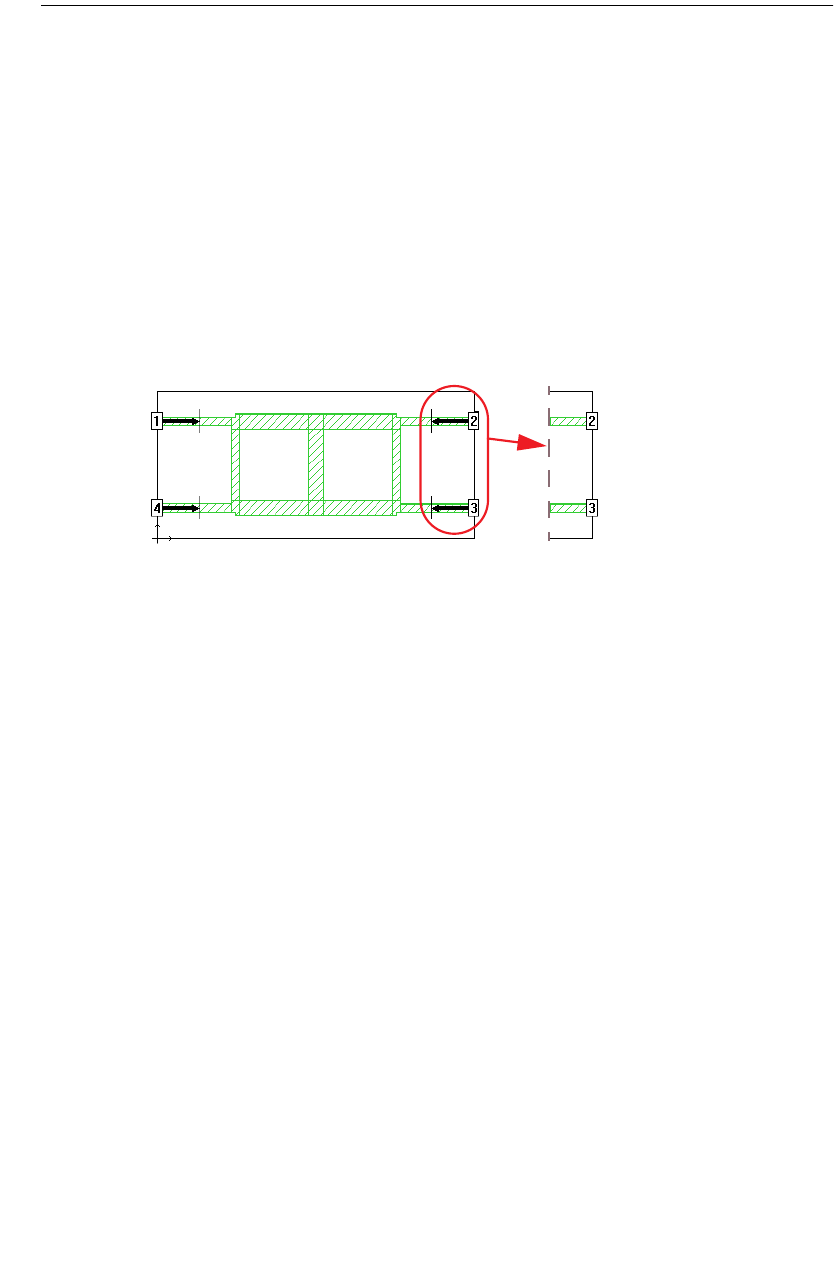
Sonnet User’s Guide
122
Rev 16.56
•Coupling between the fringing fields of the ports is removed to provide
a more accurate result.
•Coupling between feed lines is removed over the entire length of the
reference plane.
•Sonnet does not calculate a Z0 or Eeff. This is because the lines are
treated as coupled, and Z0 and Eeff are only valid for a single
transmission line. Two coupled lines, for example, have two modes, and
thus two Z0 and Eeff values. If you try to plot the Z0 or Eeff value of a
shared port, you will receive an error message. If you are looking at the
text output results, you will see “mp” de-embedding codes in place of
the Z0 and Eeff values.
The only ports which can have shared reference planes are orthogonal boxwall
ports and orthogonal co-calibrated ports with a Sonnet box ground node connec-
tion. For orthogonal boxwall ports, only ports on the same box-wall may be
shared. Orthogonal box-wall ports share reference planes by default. A user may
choose to make these reference planes independent. See the next section for de-
tails on changing the reference planes from shared to independent.
Independent reference planes
When ports have independent reference planes:
•The length of each reference plane may be set independently.
•Calibration standards are composed of single (uncoupled) lines as
shown below.
•Coupling between the fringing fields of the ports is not removed. Thus,
ports must be far apart to ensure an accurate result.
•Coupling between feed lines is not removed. Therefore, you should not
Cal 1: Magnetic Wall
Cal 2: Electric Wall
Calibration Standard for shared reference planes
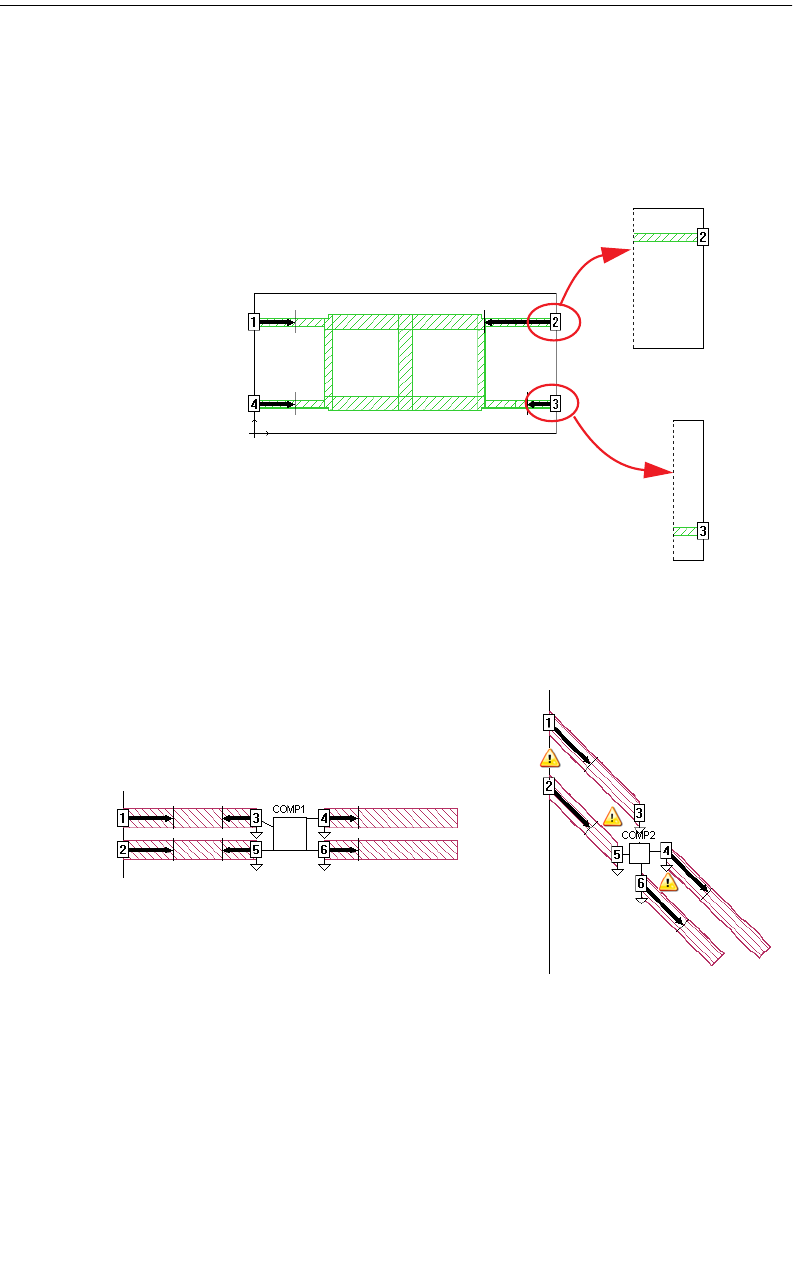
Chapter 6 De-embedding
123
Rev 16.56
use independent reference planes when the lines are close enough to
couple.
•Sonnet calculates a Z0 or Eeff for each feed line without the influence of
the nearby lines.
Auto-grounded ports, diagonal boxwall ports, and diagonal co-calibrated ports are
always independent. Thus, they should not be used if the ports or feed lines are
close to each other. This concept is shown below:
Cal Standards
Orthogonal ports can use shared reference planes, so being in close proximity is
allowed. However, Diagonal ports must use independent reference planes, so being in
close proximity is not allowed.
Orthogonal Ports Diagonal Ports

Sonnet User’s Guide
124
Rev 16.56
Orthogonal boxwall ports on a given box-wall may be set to independent or
shared. For instructions on how to change an orthogonal boxwall port from shared
to independent, please see "Applying the Diagonal Port Feature to a Port" on page
81.
Ports on different box-walls are always treated as independent from one another
as shown below.
Each port is calibrated independently because each port is
on a different box-wall.
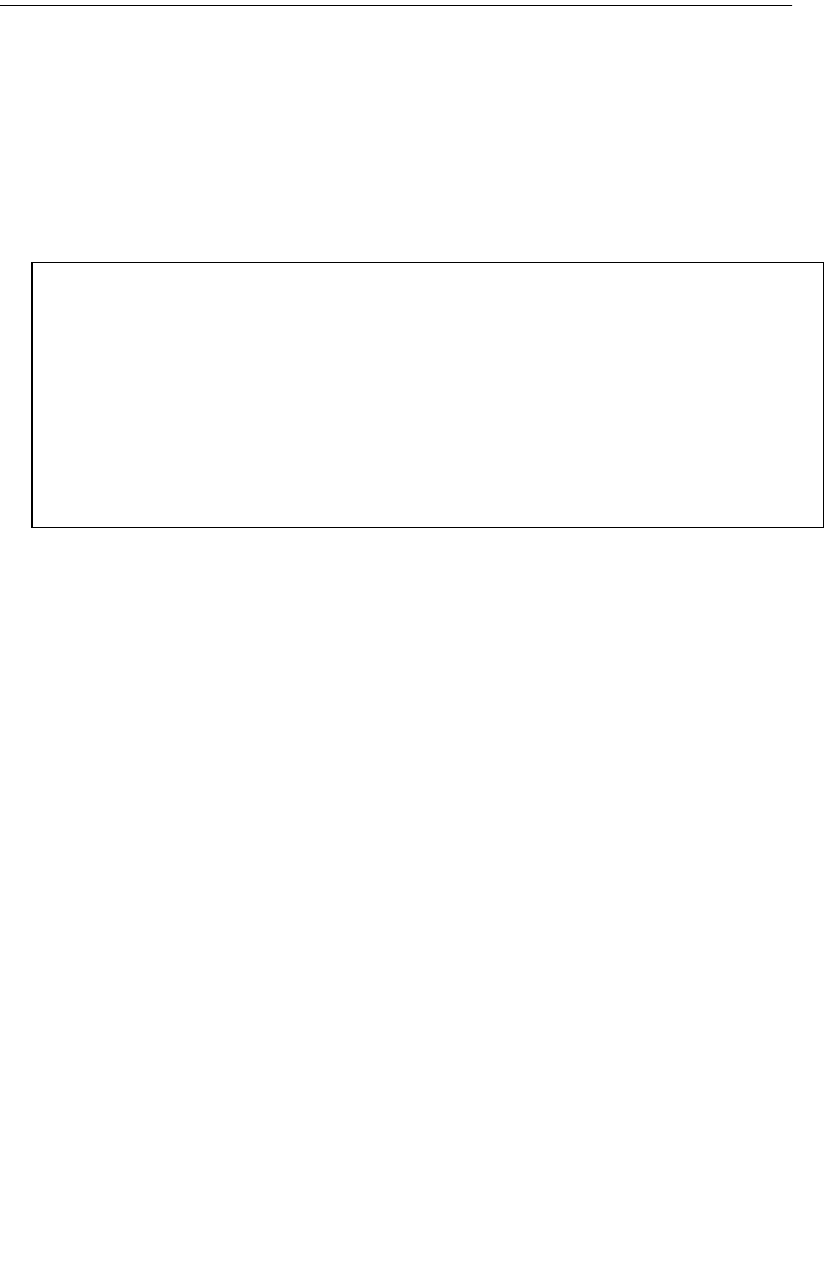
Chapter 6 De-embedding
125
Rev 16.56
De-embedded Output Format
The listing below shows an example of de-embedded results obtained from the
analysis of a filter circuit. This example illustrates the format of the de-embedded
data as output in the analysis monitor and saved as part of your project. This same
format is used in any output files generated by em as part of the analysis or by the
user when using the response viewer.
You should notice the following about the results in above:
•The two lines which start with “De-embedded” and “Magnitude/Angle”
are comment lines which describe the analysis results on the line below.
In this example, the results are de-embedded 50 ohm S-parameters in
Touchstone magnitude/angle format.
•The next line gives the analysis results.
•The remaining two lines give de-embedding information for each port in
the circuit. The various fields are defined as follows:
P#: Port number.
F: Frequency in units defined earlier in the results file.
Eeff: Effective dielectric constant of the transmission line connected to the port. Com-
plex value: [Real Imaginary].
Z0: Characteristic impedance of the transmission line connected to the port, in ohms.
Complex value: [Real Imaginary].
R: Equivalent series resistance of port discontinuity, in ohms.
C: Equivalent series capacitance of port discontinuity, in pF.
Run 1: Tue Jun 07 15:41:13 2011. sonnet9.aa.99999.
Em version 13.52 (32-bit Windows) on MENDOZA local.
Frequency: 8.975 GHZ
Frequency completed Tue Jun 07 15:41:16 2011.
De-embedded S-Parameters. 50.0 Ohm Port Terminations.
Magnitude/Angle. Touchstone Format. (S11 S21 S12 S22).
8.97500000 0.080414 143.59 0.996762 53.593 0.996762 53.593 0.080414 143.59
!< P1 F=8.975 Eeff=(6.65223738 0.0) Z0=(50.657578 0.0) R=0.0 C=0.07105378
!< P2 F=8.975 Eeff=(6.65223738 0.0) Z0=(50.657578 0.0) R=0.0 C=0.07105378
Analysis completed Tue Jun 07 15:41:23 2011.
Example showing format of results obtained when de-embedding is enabled in em.

Sonnet User’s Guide
126
Rev 16.56
NOTE: These values are not output for diagonal ports or ports with shared
reference planes.
De-embedding Codes
There are various conditions for which these values cannot be calculated and a de-
embedding code is shown instead. For example, if you have shared reference
planes (multiple ports on the same box-wall or multiple ports on the same side of
a component, for example), there are multiple values for each item. In order to
keep the output format concise, a de-embedding code is displayed in place of a
longer explanation. Please see “De-embedding Codes” in Help for explanations of
the code messages. To access Help, select Help Sonnet Help from any Sonnet
application.
Plotting Z0 and Eeff
When your circuit is de-embedded, the characteristic impedance, Z0, and the ef-
fective dielectric constant, Eeff, of the transmission line are calculated for each
port. These values are calculated for all port types except diagonal ports, ports
which share a reference plane and via ports.
NOTE: For ABS sweeps, Z0 and Eeff are calculated only for discrete
frequencies. These values are not calculated at adaptive data points.
Calculating Z0 and Eeff for Boxwall Ports
It is important to note that calculating the transmission line parameters is based on
the calibration standard. For boxwall ports, the calibration standard, as discussed
earlier in the chapter, is based on a cross section of any metalization touching the
box-wall, on all levels, that the port under consideration is on. This cross section
is extended the length of the calibration standard. Since the cross section is taken
at the box-wall, the interior of the circuit does not affect the basis of the calcula-
tion.
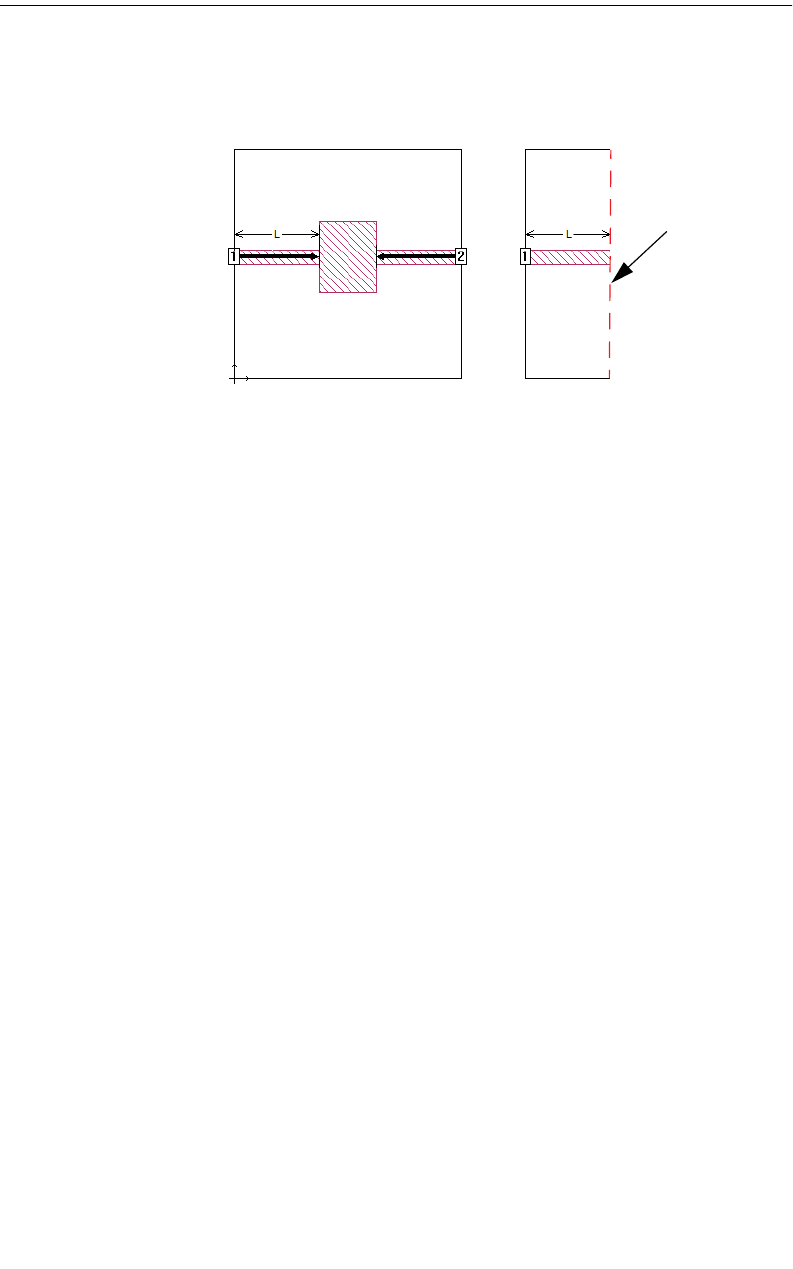
Chapter 6 De-embedding
127
Rev 16.56
In the first example shown below, there is a single feed line on the box-wall, with
no metal on another level. Therefore, the thru line upon which the calculation is
based is reasonable and the resulting values are accurate.
In the second example shown below, the circuit is more complex and the calibra-
tion standard thru line does not accurately reflect the actual circuit. Remember that
the thru line used for the calculation is based on the cross section at the box-wall
and is extended the length of the reference plane. In the actual circuit the metal on
the level below the port only extends from the box-wall for a length much shorter
than the calibration standard, but in the calibration thru line, this metal is extended
Original circuit Cal Standard
Electric/
Magnetic
Wall

Sonnet User’s Guide
128
Rev 16.56
for the whole length and the other metal polygons in the interior are completely
ignored. These transmission line parameters will not be as accurate as the first ex-
ample.
TIP
The RLGC parameters can be extracted from an EM simulation of a short section
of any periodic structure including the feed line of the actual circuit pictured
above. Please see "N-Coupled Line Model" on page 369 for more information.
Actual Circuit
Level 0 Level 1 3D View
Level 0 Level 1 3D View
Calibration Standard Thru Line

Chapter 6 De-embedding
129
Rev 16.56
Z0 and Eeff are also not as accurate for feed lines with non-uniform width. Because
the cross section is extended uniformly from the wall the length of the calibration
standard, a feed line with a varying width is not accurately modeled when calcu-
lating the transmission line parameters, as shown below.
Lengths at Multiples of a Half-Wavelength
Eeff and Z0 cannot be calculated when the length of the calibration standard is an
integral multiple of a half wavelength. At some point as the length of the calibra-
tion standard approaches a multiple of a half-wavelength, em is able to determine
that the calculated values of Eeff and Z0 are becoming corrupt. When this occurs,
em replaces the Eeff and Z0 data with the de-embedding code “undefined: nl” (see
“De-embedding Codes” in Help). Note, however, that while em is unable to deter-
mine Eeff and Z0, the de-embedded S-parameter results are still perfectly valid.
Lengths Much Greater than One Wavelength
If the length of the calibration standard is more than one wavelength, incorrect Eeff
results might be seen. However, the S-parameters are still completely valid.
Em’s calculation of Eeff is based on phase length. If the calibration standard is,
say, 365 degrees long, em first calculates Eeff based on a phase length of 5 degrees.
However, if a non-physical result is seen, em increases the calculated phase length
by 360 degrees at a time until physical (i.e., Eeff 1.0) results are obtained. This
usually corrects the problem.
Actual Circuit
Calibration Standard Thru Line

Sonnet User’s Guide
130
Rev 16.56
Thus, it takes a particularly long calibration standard before the Eeff calculation
fails. When it does fail, it suddenly jumps down to a value just above 1.0. Z0 and
the de-embedded S-parameter data still have full validity. This failure mode is
rarely seen.
Single Transmission Line
When you wish to determine the transmission line parameters, Z0 and Eeff, for a
single transmission line, you should use a standard box-wall port for the best re-
sults. It is not recommended that you use an ABS sweep, since the Z0 and Eeff data
is only calculated for the discrete data points, but not for any adaptive data; there-
fore an analysis will yield very few data points. If there are any problems in cal-
culating Z0 and Eeff, then em outputs a de-embedding code in place of a value. The
meaning of these codes may be found in Help under “De-embedding Codes.”
Creating the Plot
It is possible to plot Z0 or Eeff as a function of line width for a single transmission
line by using a dimension parameter for the width of the feedline. You then ana-
lyze the circuit using a parameter sweep varying the width of the line over the de-
sired range of values. Once you have the analysis results, you can use the response
viewer to create a plot of your data. A detailed example is provided below.
This example uses a simple stripline circuit show below.

Chapter 6 De-embedding
131
Rev 16.56
1 Add a dimension parameter to vary the line width.
A symmetric dimension parameter would work best with this circuit since it uses
symmetry. The circuit is shown below with a symmetric dimension parameter
“Width” added with its point sets highlighted. For more information about
symmetric parameters and how to add them to your circuit, please see
"Symmetrical Dimension Parameters" on page 180.
2 Set up a parameter sweep using the variable “Width.”
For this example, the circuit will be analyzed using a parameter sweep, varying
the width of the line from 2 mm to 6 mm in 0.25 mm increments at a single
frequency of 15 GHz. The Parameter Sweep Entry dialog box for the analysis is
shown below. For more information on setting up a parameter sweep, please see
"Parameter Sweep" on page 189.
Dimension
parameter
“Width”
Top Point Set
Bottom Point Set

Sonnet User’s Guide
132
Rev 16.56
3 Run the analysis, then open the response viewer.
The response viewer may be opened by clicking on the Response Viewer icon in
the analysis monitor (shown to the left) or selecting Project View Response
New Graph from the main menu of the project editor or analysis monitor once the
analysis has completed.
4 Select Graph Plot Over Parameter from the main menu of the
Response Viewer.
This will plot the selected data as a function of the value Width. If there were more
than one parameter in your circuit, you would have had to choose which to use but
since this circuit contains only one parameter, Width is automatically selected.
5 Select Curve Add Curve Group from the main menu of the response
viewer.
The Add Curve Group dialog box appears on your display as shown below.
Data Type

Chapter 6 De-embedding
133
Rev 16.56
6 Select “Port Z0” from the Data Type drop list.
This will plot the characteristic impedance of the feedline connected to the
selected port.
7 Double click on the desired port to move it to the Selected List.
For this example, we will plot Z0 for port 1, so MAG[PZ1] is moved to the select-
ed list.
8 Click on the Graph All Combinations checkbox in the Parameter
Combinations section of the dialog box.
There is only one frequency available, so selecting this checkbox will display that
frequency. If more than one frequency were available, you would plot all available
frequencies if the Graph All Combinations checkbox was selected. If you wished
to plot a particular frequency or set of frequencies, you would clear this checkbox,
then click on Select Combinations to choose the desired frequency(ies) to display.
The dialog box should appear similar to that shown below.

Sonnet User’s Guide
134
Rev 16.56
9 Click on the OK button to display the curve.
The plot show the magnitude of the characteristic impedance of Port 1 as a
function of line width. The characteristic impedance goes down as the line gets
wider. If you wished to plot the Eeff, you would have chosen “Port Eeff” from the
Data Type drop list.
Coupled Transmission Lines
If you have more than one port on a box-wall, Z0 and Eeff cannot be determined
as there is more than one mode for the transmission line. In this case, your output
data will use the “mp” de-embedding code indicating that there are multiple ports.
Even though Z0 and Eeff can not be determined, the S-parameter data is still valid.
However, Sonnet can be used to compute the common and differential mode Z0
and Eeff values for two symmetrical coupled lines. The common and differential
mode are very similar to the even mode and odd mode used by popular transmis-
sion line calculators (see "Interpreting Z0 and Eeff." on page 135 for details).

Chapter 6 De-embedding
135
Rev 16.56
To create a project which can be used to show the even and odd mode, start with
a four-port coupled line circuit like the one shown below:
Notice that the lines are placed precisely in the center of the box. This is not nec-
essary in many cases, but we suggest you do this to force the symmetry between
the two lines.
Next, renumber your ports as shown below. The left two ports (+1/-1) represent
the differential, or odd mode. The right two ports (+2/+2) represent the common,
or even mode:
To renumber a port, right-click on the port and select Port Properties. This opens
the Port Properties dialog box where you can change the port number.
Interpreting Z0 and Eeff.
There is a subtle difference between the even/odd mode and common/differential
mode Z0 1. Sonnet computes the common and differential mode Z0 values, but you
can easily calculate the even and odd mode Z0 values by either multiplying or di-
viding the sonnet results by two as shown in the equations below:
[1]Characterization of differential interconnects from time domain reflectometry measure-
ments by A. Tolescu and P. Svasta
Zeven 2ZCommon
=
Zodd Zdiff 2=

Sonnet User’s Guide
136
Rev 16.56
The Eeff values do not need to be modified. Shown below are plots of the differ-
ential mode (port 1) and common mode (port 2) Z0 and Eeff. Since the differential
mode Z0 is about 67 ohms, the odd mode Z0 is about 33.5 ohms. And since the
common mode Z0 is about 18 ohms, the even mode Z0 is about 36 ohms. As can
be seen by the plots, the Z0 and Eeff values are all a function of frequency.

Chapter 7 Components
137
Rev 16.56
Chapter 7 Components
Introduction
The Component feature is built upon the high accuracy de-embedding technique1
used for Sonnet co-calibrated internal ports technology. Using this technique, the
user can insert an ideal element, measurement of a physical component, a data file
created by another Sonnet project or another Sonnet project. In addition, using the
Component feature in conjunction with the Keysight ADS Interface, NI AWR Mi-
crowave Office Interface - 32-Bit, or the Cadence Virtuoso Interface provides a
powerful tool to model complex circuits.
The Components features allows for a high level of flexibility by using five dif-
ferent Component types:
• Data File type: If you would like to insert an S-parameter data file of
your component into your Sonnet model.
• Ideal type: If you would like to insert an ideal component (R, L, or C)
into your Sonnet model.
• Ports Only type: If you would like to use a separate circuit simulation
tool for the final, combined simulation, you may insert only ports within
the Sonnet model.
1”Deembedding the Effect of a Local Ground Plane in Electromagnetic Analysis,” by James C. Rautio, president
and founder of Sonnet Software, Inc. The article is available in PDF format in the Support section of our web
site.

Sonnet User’s Guide
138
Rev 16.56
• Sonnet Project: If you would like to insert another Sonnet project into
your Sonnet model.
• User Model: If you would like to insert a model from another source
into your Sonnet model.
In all cases except where the Ports Only component types are used, the Sonnet
solver uses a circuit simulation technique to produce the combined results. Since
this is a post EM analysis step, the user can change the ideal component value, or
associated S-parameter data file, Sonnet project or Modelithics model without re-
quiring a new EM analysis; only the circuit simulation part of the analysis is per-
formed by the analysis engine.
Please note that the coupling from the inside of the component to the rest of the
circuit is not considered in the Sonnet analysis. Only the coupling from the com-
ponent’s terminals is considered.
When connecting external parts to your EM structure, we highly recommend that
you use either the co-calibrated ports or the Component feature. This novel ap-
proach provides greatly enhanced accuracy for this application by perfectly de-
embedding the ports, thus completely removing all coupling between them. Auto-
grounded Ports have the limitation of not removing any port to port coupling.
Before proceeding to use the Component feature, it would be helpful to become
familiar with the related co-calibrated internal ports discussed in “Co-calibrated
Internal Ports,” page 89 in the Ports chapter.
Component Assistant
When you select any of the Add Component commands in the project editor, the
Component Assistant appears on your display. Whenever you select a control in
the Component Properties dialog box, the assistant provides a description of the
field, and often, an illustration of the principle, so that you may select the correct
setting and model your Component more accurately.
If the Component Assistant does not appear, you should select the “Use Compo-
nent/Calibration Group Assistant” checkbox on the Hints tab of the Preferences
dialog box in the project editor (File Preferences).
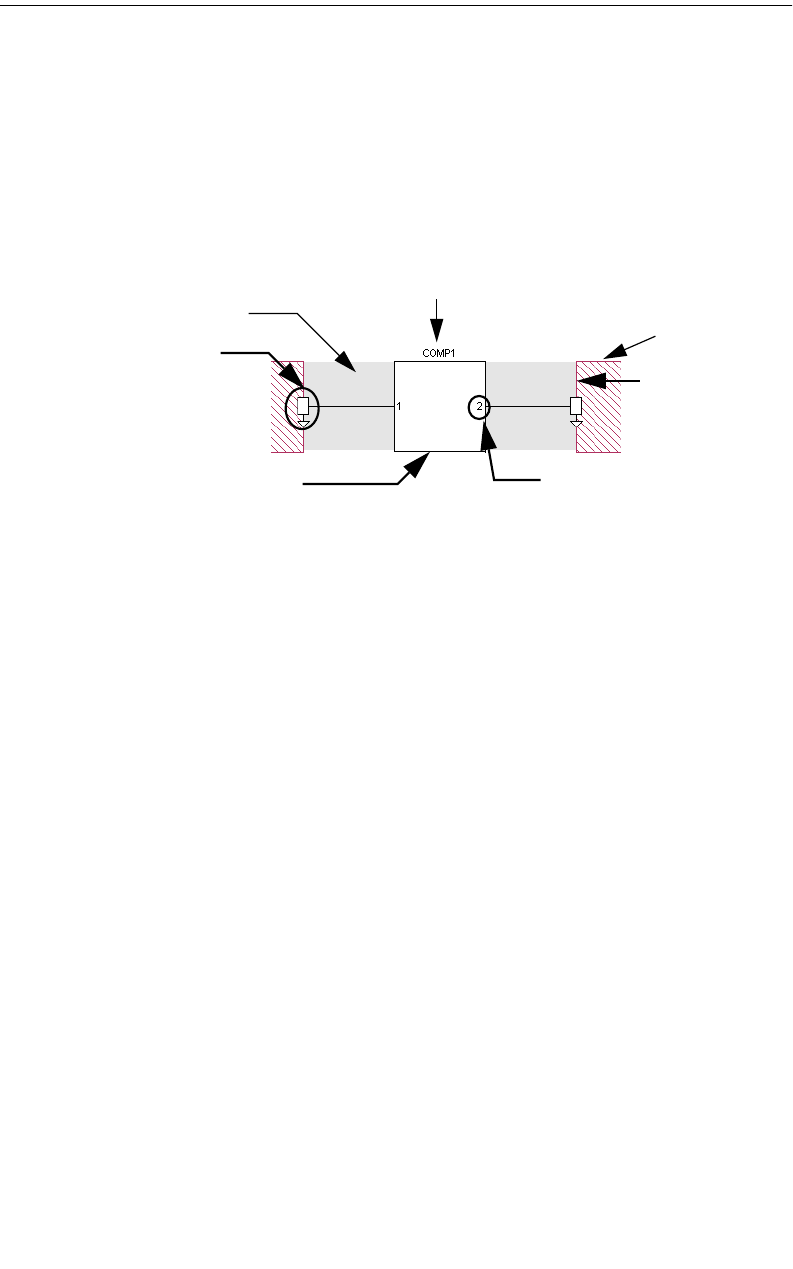
Chapter 7 Components
139
Rev 16.56
Anatomy of a Component
The Component is represented in your circuit by a component symbol. The label
of the Component appears above the component symbol and the terminal numbers
are identified there. Ports, indicating where the terminals of the Component are
connected to the metal in your circuit, are represented by a small rectangle. Com-
ponent ports are only numbered when the Component model type is Ports Only.
An example of a Component as it appears in the project editor is shown below.
Component
Symbol This is the symbol which represents your Component in your project.
Port The Component port defines the point at which the Component is connected to the
circuit metal and must be attached to an open polygon edge. This point also serves
as a reference plane for de-embedding the Component unless a reference plane is
added for the port. There is one Component port for each terminal on the Compo-
nent. Component ports are modeled using co-calibrated internal ports. For more
information on co-calibrated ports, please see “Co-calibrated Internal Ports,”
page 89. If the component type is a Sonnet project, the terminals correspond to the
ports in the Sonnet project.
Terminal
Numbers Terminal numbers identify the physical pin on your Component connected to the
corresponding Component port.
Components may have an unlimited number of terminals, with the exception of
those Components which use the Ideal Component model, since the available
ideal components are limited to two terminals. Terminals and/or ports are num-
bered in the order in which they are added to your circuit and may be modified
after the Component is added to your circuit.
Label The label is user-defined text which identifies the Component in your circuit. Each
Component label in a project must be unique.
Terminal Number
Component Symbol
Label
Port
Physical Size Metal Polygon
Open Polygon
Edge
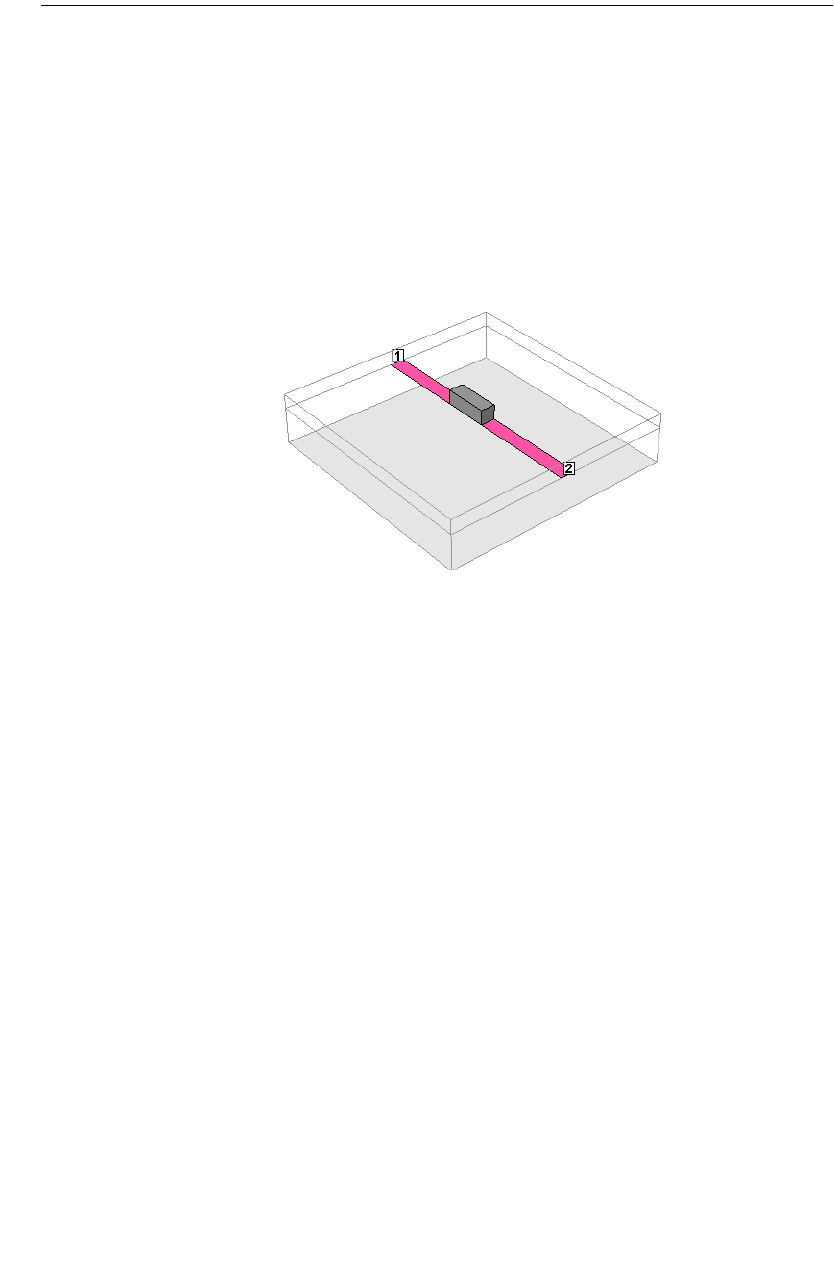
Sonnet User’s Guide
140
Rev 16.56
Open
Polygon
Edge
Component ports may be placed only on open polygon edges. You may use a ref-
erence plane to control how much, if any, of your circuit metal is also de-embed-
ded in addition to the Component. For more information, see “Reference Planes,”
page 148.
Physical
Size You may also optionally enter a physical package size for your Component. These
measurements (height, width, and length) are not used in the em simulation but are
there to provide a graphic in both the 2D and 3D view which represent the actual
size of the Component. This is especially useful for design presentations and re-
views. Shown below is a 3D view of the example Component pictured above:
Component Types
There are five types of Component model: Data File, Ideal, Ports Only, Sonnet
Project, and User Model. All five models are described below.
Data File
The Data File Component allows you to add a Component to your geometry that
is modeled with a user specified S, Y, or Z-Parameter file (Touchstone format).
The data file used for your Component can be the result of another simulation or
measured data from an actual component. There is no limit to the number of ports
you may use for a data file Component.
You add a data file type Component by selecting the command Tools Add Com-
ponent Data File. This command opens the Components Properties dialog box
as well as the Component Assistant.
Chapter 7 Components
141
Rev 16.56
Ideal Component
The Ideal component allows you to add a single 2-port ideal component. There are
three types of ideal components available: resistor, capacitor, or inductor. All ideal
components use a series element with two ports as shown below:
You add an Ideal component by selecting the command Tools Add Component
Ideal. This command opens the Components Properties dialog box as well as
the Component Assistant.
Ports Only
The Ports Only Component allows you to insert internal ports in your circuit
which may be used later in a circuit design program. All of the ports associated
with this Component have a common ground and are simultaneously de-embed-
ded during the electromagnetic analysis. There is no limit to the number of ports
your Component may have. This Component type is functionally equivalent to
using co-calibrated internal ports. For a detailed discussion of co-calibrated ports,
see “Co-calibrated Internal Ports,” page 89.
You add a Ports Only type Component by selecting the command Tools Add
Component Ports Only. This command opens the Components Properties dia-
log box as well as the Component Assistant.
Resistor
Capacitor
Inductor

Sonnet User’s Guide
142
Rev 16.56
Sonnet Project
The Sonnet Project Component allows you to add a Sonnet geometry or netlist
project to your geometry. If the Sonnet project used for the component does not
include analysis data, then em runs an analysis on the Component project as part
of the larger analysis. There is no limit to the number of ports you may use for a
Sonnet project Component.
If the Sonnet Project contains parameters, you may open the Model Parameters di-
alog box by clicking on the Parameters button in the Component Properties dialog
box. This dialog box allows you to define the values or link the parameters in the
Component project to parameters in the main project. You may also create a new
variable and assign it to a parameter value. Any change in the variables in the main
project also changes the value of the any parameters in the Component project that
are defined by that variable.
You add a Sonnet Project Component by selecting the command Tools Add
Component Sonnet Project. This command opens the Components Properties
dialog box as well as the Component Assistant.
User Model
The User Model Component allows you to add a model from a library that has
been purchased, or developed in-house, to your geometry. There is no limit to the
number of ports you may use for a User Model Component.
If the model contains parameters, you may open the Model Parameters dialog box
by clicking on the Parameters button in the Component Properties dialog box.
This dialog box allows you to define the values of the parameters in the User
Model Component. You may enter a fixed value or use a variable defined in the
main project as the value of the parameter(s). You may also create a new variable
and assign it to a parameter value. When a variable is assigned as a value, any
change in the variable in the main project also changes the value of the parameter
in the Component project.
You add a User Model Component by selecting the command Tools Add Com-
ponent User Model. This command opens the Components Properties dialog
box as well as the Component Assistant.
Modelithics models are presently the only supported vendor, although it is possi-
ble to create custom models. If you are interested in doing so, please contact your
Sonnet Software representative for details.

Chapter 7 Components
143
Rev 16.56
NOTE: Use of the Modelithics models requires a Modelithics license, which
must be purchased separately from Modelithics, Inc., in addition to
your Sonnet license.
Component Properties
An important part of modeling a Component in Sonnet is to consider the condi-
tions under which the measured data or model for your Component was obtained.
These conditions should be used to determine:
•The type of ground node connection
•The terminal width
•If reference planes are used for the Component ports and if so, of
what length
The em environment should be set up to use the Component in the same manner
that the component was measured. The correct setting of the Component proper-
ties is discussed in detail below.
Ground Node Connection
The ground node connection defines how the ground of your Component is con-
nected to your circuit. There are three types of ground node connections: Sonnet
Box, Floating, and Polygon Edge(s).
NOTE: The Ideal Component does not use a ground node connection by
definition. The ground node connection needs to be specified for all
other Component types.
Sonnet uses a common ground for all the Component ports associated with a given
Component. This common ground should model as closely as possible how your
component was measured or modeled. Vendors who supply components often
have measured S-parameters or a model which may be used to create S-parame-
ters. In either case, information about how these values were obtained should also
be available. Use this information to guide your choice of ground node connec-
tion. The three types of ground node connection are discussed below.

Sonnet User’s Guide
144
Rev 16.56
Floating
When your ground node connection is set to Floating, all the Component ports ref-
erence a common local ground as pictured below. This option should be used if
your Component does not have a ground reference, or if there are no shunt ele-
ments in your component model or measured data. Any shunt admittance is re-
moved by em.
Examples of this are:
•A series RL equivalent circuit
•S-Parameter data that was measured without pads
Sonnet Box
When your ground node connection is set to Sonnet box, all the Component ports
are globally grounded to the Sonnet box. To accomplish this, a via is automatically
created which connects to the top or bottom of the Sonnet box. This option should
be used if your component model, or measured data, includes shunt elements and
you want the Component’s ground reference to be connected to the Sonnet box.
Examples of this are:
•S-Parameter data that includes pads or other coupling to ground
•Transistor data that includes a via to ground in the model/measure-
ment
The analysis engine determines the most efficient direction the ground via extends
taking into consideration both the distance and the loss of the box top or bottom.
When using this type of ground, you must make sure that there is a clear path with
no metal on other levels interfering with the path to either the box top or bottom.
Floating - No ground reference
Sonnet Box
Ref

Chapter 7 Components
145
Rev 16.56
If you are using a Component whose ground node connection is to the Sonnet box,
either the box top or bottom must have loss less than 50 ohms/sq. For example,
you should not use “Free Space” as your box top and bottom definition. If the loss
is too high on both the box top and bottom for a ground via from the Component
to be attached, the analysis engine will issue an error message.
Polygon Edge(s)
When your ground node connection is set to Polygon Edge(s), the ground refer-
ence of your Component is connected to a polygon edge(s) selected by you when
adding the Component. You may specify as many ground terminals as you need.
Examples of this are:
•Transistor data without parasitics to ground, but with a ground path
included in the Sonnet structure
•A multi-pin module with one or more ground pins
NOTE: The Polygon Edge(s) ground node connection is only available for Data
File and Sonnet Project type Components.
Terminal Width
The terminal width is the electrical contact width of the Component. Entering a
terminal width allows you to accurately model the current flow from the circuit
geometry into the Component.
There are three types of terminal width: feedline, one cell and user defined. Each
type of terminal width is illustrated and explained below.
Ref
Circuit Metal

Sonnet User’s Guide
146
Rev 16.56
Feedline Width
Choosing Feedline Width sets your terminal width to match the length of the poly-
gon edge to which the Component is attached. This option should be used when
the polygon edge is about the same size as the width of the Component. An exam-
ple is pictured below.
One Cell
One Cell sets your terminal width to the smallest possible size of one cell wide as
pictured below.
User Defined
This option allows you to enter a known electrical contact width. An illustration
of a Component with User Defined terminal widths is shown below.

Chapter 7 Components
147
Rev 16.56
When you select user defined, your terminal width is defined based on the location
of the Component port. The point at which the port is placed on the polygon edge
becomes the center of the terminal width extending an equal distance on either
side.
This ability to limit the terminal width size is important in cases where more than
one Component port needs to connect to the same polygon edge or the polygon
edge is extremely large. The next two images demonstrate these concepts.
The component has two terminals connected to a single polygon edge.
The cell size is 2 mils and the user-defined terminal width is 8 mils as
shown.
Terminal Width
A coplanar waveguide that uses a two port component. To the
right is shown the entry in the Component Properties dialog box.

Sonnet User’s Guide
148
Rev 16.56
Reference Planes
Components require their ports to be on open polygon edges. Reference Planes
can be used to effectively move your port position away from the polygon edge.
To accomplish this, em uses circuit theory to cascade a negative length of the line
with the analysis results. If no reference plane is specified, then de-embedding the
Component removes none of the feedline metal but the port(s) are still de-embed-
ded. The use of reference planes is illustrated below.
NOTE: Reference planes may only be used when the ground node connection
is defined as the Sonnet box.
All the Component ports on a side of a Component use the same reference plane.
For a detailed discussion of reference planes and de-embedding, please see Chap-
ter 6, “De-embedding” on page 103.
The reference planes for Component ports are set in the Component Port Proper-
ties dialog box. This dialog box may be opened by double-clicking on a compo-
nent port or by selecting the component, then selecting the command Modify
Port Properties from the project editor main menu. For details on using this dialog
box, please click on the Help button.
As with all Sonnet reference planes, the Component reference planes are snapped
to the grid. It is important that you are working with a fine enough cell size to en-
sure the accurate placement of your reference planes. If the length is set to less
than one half the cell size, then the reference plane will not be displayed in the
project editor window.
Calibration Lengths
The analysis engine, em, will automatically determine appropriate lengths for the
calibration standards used in the de-embedding algorithm. Normally, the Auto set-
ting (default) produces efficient and highly accurate simulation results. In rare cas-

Chapter 7 Components
149
Rev 16.56
es, you may wish to manually override the automatic lengths. Before manually
overriding these settings, please be sure to read Chapter 6, “De-embedding” on
page 103.
The calibration lengths for Component ports are set in the Component Port Prop-
erties dialog box. This dialog box may be opened by double-clicking on a compo-
nent port or by selecting the component, then selecting the command Modify
Port Properties from the project editor main menu. For details on using this dialog
box, please click on the Help button.
Physical Size
You may enter a physical size for your Component for display purposes. The
physical dimensions length, width, and height, are not used in the simulation but
do affect how your Component is displayed in the project editor. You may enter
the precise dimensions or choose Auto to have the software choose approximate
dimensions based on your Component’s port placements. An example is shown
below.
Rules for Using Components
The following restrictions apply to the placement of Components in your circuit:
2D View 3D View
Physical Size of Component

Sonnet User’s Guide
150
Rev 16.56
1. No objects may be placed within the “restricted space” in the
interior of the Component: Metal polygons, vias, or dielectric bricks
may not be present in the rectangular area defined by the port locations
and the terminal width, as illustrated below. The bottom circuit shows the
restricted area in a multiport Component.
2. Components whose ground node connections are defined as the
Sonnet box require direct access to the Sonnet top or bottom
cover. The analysis engine determines the most efficient direction the
ground via extends taking into consideration both the distance and the
loss of the box top or bottom. When using this type of ground, you must
make sure that there is a clear path with no metal on other levels interfer-
ing with the path to either the box top or box bottom.
In addition, the box top or bottom should not have loss greater than 50
ohms/sq. If the loss is too high on both the box top or bottom for a ground
via from the Component to be attached, the analysis engine issues an er-
ror message.
Right Wrong
The dashed boxes identify the “restricted space” for each
Component. On the circuit labeled “Wrong” a metal polygon
passes through the middle of the restricted space.
Illegal
Polygon
Restricted
Space

Chapter 7 Components
151
Rev 16.56
3. Nearby objects should be placed so that coupling between the
Component and the object does not occur: Metal polygons, vias, or
dielectric bricks which couple to the Component ports may decrease the
accuracy of the analysis as shown below.
4. Multiple ports on the same side of a Component should be
aligned: In the illustration below, the ports on Comp1 are placed incorrectly
and will produce an error during an analysis. The ports on comp2 are
placed correctly.
5. Reference planes must be the same length for each side of a
Component: Note that the reference planes for ports 2 and 3 in the illustra-
tion below are the same length. It is important that these ports share a ref-
erence plane since the feedlines are close enough that coupling between
them becomes a factor and needs to be removed during de-embedding.
However, reference planes can be different lengths for each side of the
Wrong Correct
The dashed lines represent the alignment plane.

Sonnet User’s Guide
152
Rev 16.56
“component rectangle” as shown by ports 1, 4 and 5 below. Since these
ports are on different sides of the component, their reference planes are
independent from ports on other sides.
6. The angle between feed lines of diagonal components should be
at least 45 degrees: This means you should never have parallel diagonal
feed lines on a single side of a component.
Analysis of a Component
Data File Frequencies
When using a data file Component type, frequencies in your data file do not need
to precisely match the Sonnet analysis frequencies. The analysis engine will inter-
polate between data file frequencies if necessary, but it will not extrapolate outside
the frequency range of the data file.
45
Angle between feed lines is
at least 45 degrees Angle between feed lines
is zero

Chapter 7 Components
153
Rev 16.56
Rerunning an Analysis
When the analysis engine analyzes your circuit with a Component, it first per-
forms an electromagnetic analysis of the geometry, then uses circuit theory to con-
nect the Component to the geometry. If you change the data file used for a
Component or the value and/or type of an ideal component, in subsequent analy-
ses em only needs to perform the circuit theory part of the analysis, significantly
reducing processing time. Please note that any graphs of the response are not au-
tomatically updated. Instead, you need to select Graph Freshen Files to update
your graph in the response viewer.
The analysis engine, em runs an analysis on the Component project as part of the
analysis of the main project and stores analysis results for the component project.
The data resulting from the analysis of the Component project is then used in the
circuit theory part of the main analysis. This data will be reused as long as no
changes are made to the Component project.

Sonnet User’s Guide
154
Rev 16.56
Chapter 8 Adaptive Band Synthesis (ABS)
155
Rev 16.56
Chapter 8 Adaptive Band
Synthesis (ABS)
The Adaptive Band Synthesis (ABS) technique provides a fine resolution re-
sponse for a frequency band requiring only a small number of analysis points. Em
performs a full analysis at a few points and uses the resulting internal, or cache,
data to synthesize a fine resolution band.
TIP
This technique, in most cases, provides a considerable reduction in processing
time.
Using the input frequency band, em first performs a full analysis of the circuit at
the beginning and end frequencies. Em continues solving at discrete points, stor-
ing the full analysis data for each point. This process continues until enough inter-
nal, or cache, data is generated to synthesize a fine resolution response.
Once the frequency band response is synthesized, em outputs approximately 300
data points for the frequency band. These data points are a combination of the dis-
crete analysis points and synthesized points. This combined data is referred to as
adaptive data.

Sonnet User’s Guide
156
Rev 16.56
Em dedicates the bulk of the analysis time for an ABS analysis in calculating the
response data at the discrete data points. Once the adaptive band synthesis is com-
plete, calculating the adaptive data for the entire band uses a relatively small per-
centage of the processing time.
DC Point Extrapolation
If you enter a value of zero as the starting frequency for an ABS sweep, the data
for a DC Point is automatically calculated. Once the ABS sweep is complete and
has produced the adaptive data, em extrapolates the adaptive data to DC. If you
only need a DC Point and do not want to run an ABS sweep, you should use the
DC Frequency Sweep. For details, please see “DC Point” in the index of Help.
ABS Resolution
The ABS resolution is the value in frequency units between adaptive data points
in your response output from an adaptive sweep. Normally, the resolution in an
adaptive sweep is provided by em such that around 300 data points are output for
a frequency band. It is possible for you to override this setting and use a coarser
or finer resolution for your frequency band.
Entering a manual value to be used for ABS is done in the Advanced Options di-
alog box which is opened when you click on the Advanced button in the Analysis
Setup dialog box. The Analysis Setup dialog box is opened when you select Anal-
ysis Setup from the project editor menu. You enter the resolution by clicking
on the Manual radio button in the ABS Frequency Resolution Per Sweep section
of the Advanced Options dialog box and entering the desired resolution in the ad-
jacent text entry box. For details on these dialog boxes, please refer to Help for the
project editor.
There are several things to be aware of when using the manual setting for the ABS
resolution. Coarse resolution does not speed things up. Once a rational polynomial
is found to “fit” the solution, calculating the adaptive data uses very little process-
ing time. A really coarse resolution could produce bad results by not allowing the
ABS algorithm to analyze at the needed discrete frequencies. Fine resolution does
not slow down the analysis unless the number of frequency points in the band is
above approximately 1000 - 3000 points. A step size resulting in at least 50 points
and less than 2000 points is recommended.

Chapter 8 Adaptive Band Synthesis (ABS)
157
Rev 16.56
Q-Factor Accuracy
There is a Q-Factor analysis run option available in the Advanced Options dialog
box in the project editor (Select Analysis Setup, then click on the Advanced but-
ton in the Analysis Setup dialog box). Selecting this option forces a higher accu-
racy for ABS convergence by including the Q-factor of your analysis as a criterion
for convergence. This is done to insure high accuracy in the Q-Factor result when
ABS is used. The Q-Factor is defined as follows:
The result is higher accuracy from the ABS sweep, but. this accuracy comes at the
cost of requiring more discrete frequencies to be analyzed before convergence is
reached.
Enhanced Resonance Detection
There is an Enhanced Resonance Detection analysis run option available in the
Advanced Options dialog box in the project editor (Select Analysis Setup, then
click on the Advanced button in the Analysis Setup dialog box). This option is
useful when the circuit response includes one or more extremely narrowband res-
onances, a common occurrence with superconductor applications. When this op-
tion is enabled, ABS performs a full-wave discrete simulation at each detected
resonance to obtain the highest level of accuracy possible in terms of magnitude
and frequency. Be aware that this increased accuracy comes at the cost of in-
creased processing time since it requires analysis at more discrete frequency
points.
Running an Adaptive Sweep
To run an analysis using the Adaptive Band Synthesis technique, you do the fol-
lowing:
1 Open your project in the project editor.
Ynn
imagYnn
real

Sonnet User’s Guide
158
Rev 16.56
2 Select Analysis Setup from the main menu of the project editor.
The Analysis Setup dialog box appears on your display with an adaptive sweep
already selected since Adaptive Sweep is the default for analysis control.
3 Select Adaptive Sweep (ABS) from the Analysis Control drop list if
necessary.
This selects the ABS technique for the analysis.
4 Enter the desired frequency band in the Start and Stop text entry boxes.
This defines the frequency band on which you wish to perform the ABS analysis.
The step size is automatically set by em during the analysis. See page 156 for a
description of how the ABS resolution is determined.
5 Click on the OK button to close the dialog box and apply the changes.
6 Save the project by selecting File Save from the menu or by clicking on
the Save button on the tool bar.
You need to save the file before analyzing it.
7 Select Project Analyze from the menu or click on the Analyze button on
the tool bar.
Em performs an adaptive sweep on your project. The analysis monitor appears on
your display, and indicates the progress of the adaptive sweep.
The Adaptive Sweep is also available within the Frequency Sweep Combinations
analysis controls. This allows you to mix adaptive sweeps with other types of
sweeps. For more details, see the “Frequency Sweep Combinations” topic in Help
in the project editor.
Chapter 8 Adaptive Band Synthesis (ABS)
159
Rev 16.56
ABS Caching Level
There are three levels of ABS caching available: None, Stop/Restart, and Multi-
Sweep plus Stop/Restart. The options for ABS caching level are found in the Ad-
vanced Options dialog box. To access the Advanced Options dialog box, select
Analysis Setup from the project editor main menu, then click on the Advanced
button in the Analysis Setup dialog box which appears. The default is Stop/Re-
start.
Stop/Restart retains the cache data while the analysis is proceeding. Once the
adaptive data has been calculated, the cache data is deleted from the project. This
setting provides for the circumstance in which the analysis is stopped or interrupt-
ed before the adaptive data is synthesized; you will not lose the internal data pro-
duced so far.
Multi-Sweep with Stop/Restart retains all calculated cache data in your project for
every analysis job run. In addition, cache data is calculated and saved for even
non-ABS types of sweeps. This option can reduce processing time on subsequent
ABS analyses of your project but increases project size on non-ABS sweeps. In
order for the cache data to remain useful there are also subsectioning issues of
which you must be aware. For a detailed discussion of the Multi-Sweep cache op-
tion, please refer to “Multiple ABS Sweeps and Subsectioning,” page 159.
The third setting for ABS caching level is None. In this setting cache data is not
retained. This option should only be selected if you have constraints on disk space.
!WARNING
If you select None for the ABS caching level, and an ABS sweep is stopped
before the adaptive data has been calculated, you will have to start the
analysis over from the beginning. Any processing time invested in the
analysis is lost.
Multiple ABS Sweeps and Subsectioning
If you will need to run multiple ABS sweeps on a project, it is important to set your
ABS caching to Multi-sweep to avoid having to re-calculate your caching data
each time you analyze your circuit. But be aware that in order to maintain the va-
lidity of the caching data, the subsectioning of the circuit must remain the same.
To control the subsectioning you must use the Advanced Subsectioning Controls
which you open by selecting Analysis Advanced Subsectioning from the main
menu of the project editor.

Sonnet User’s Guide
160
Rev 16.56
TIP
The most efficient way to obtain response data for your circuit is to run a single
ABS sweep over the entire desired frequency band.
The analysis engine, em, uses the subsectioning frequency to calculate the wave-
length which is used in setting the Maximum subsection size. The default setting
used to determine the subsectioning frequency is to use the highest frequency from
the present analysis job. If you perform multiple sweeps over different frequency
bands then the cache data from one run will be invalid for the next, since the sub-
sectioning frequency would be different. In order to avoid this you should select
the Previous Analysis Only option which will use the highest frequency from all
previous analysis jobs run on the project. In this case, you should analyze the fre-
quency band with the highest upper limit first and take care to ensure that the sub-
sectioning frequency being used provides accurate subsectioning for your circuit.
For details on subsectioning, see Chapter 3 "Subsectioning" on page 27.
Another way to keep the subsectioning frequency consistent is to select the Fixed
Frequency option for the subsectioning frequency and enter the desired frequency.
This ensures that all analysis runs on the project will use the same subsectioning
frequency. Again, care should be taken that the subsectioning frequency entered
provides the desired accuracy.
Multi-Sweep Caching Scenarios
The analysis engine always attempts to use any existing data in the project which
is consistent with the present analysis. Described below are some common scenar-
ios describing ABS analyses when the ABS caching level is set to Multi-Sweep
with Stop/Restart and how data consistency is maintained.
Higher or Lower Resolution over the Same Frequency Band: You are running
an ABS analysis over the same band as a previous ABS analysis but with higher
or lower resolution; an example is shown below. In order for the caching data to
be valid for the second analysis, your Advanced Subsectioning controls must be
set such that the subsectioning frequency is the same for both runs. If the subsec-
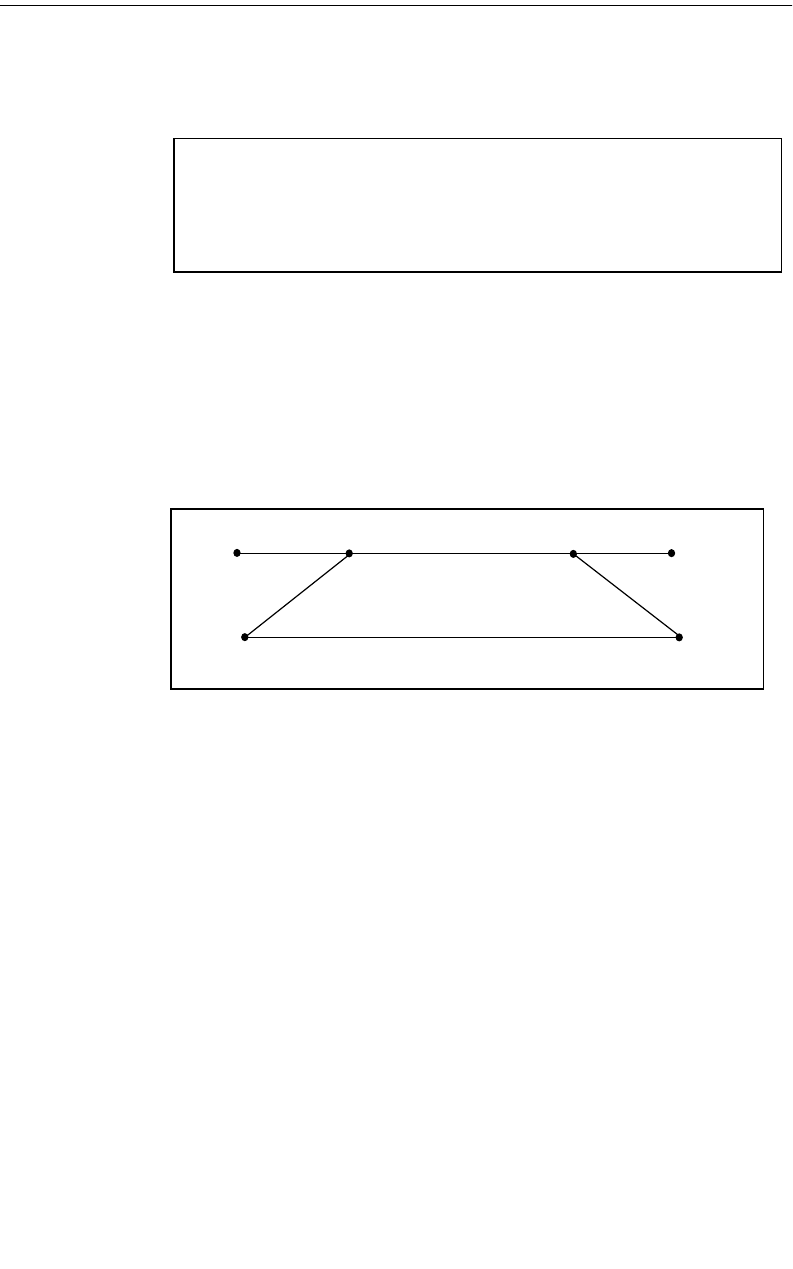
Chapter 8 Adaptive Band Synthesis (ABS)
161
Rev 16.56
tioning frequency remains the same, the second analysis will usually not require
any re-analysis and the results should be provided very quickly. The only excep-
tion would be if the difference between the resolutions is unusually high.
Zoom In: You are running an ABS analysis over a narrower band than the previ-
ous ABS analysis of the project, as shown in the diagram below. This provides
higher resolution over the narrower band since the ABS analysis defaults to ap-
proximately 300 data points. In order for the caching data to be valid for the sec-
ond analysis, your Advanced Subsectioning controls must be set such that the
subsectioning frequency is the same for both runs. If the subsectioning frequency
remains the same, the second analysis will not require any re-analysis and the re-
sults should be provided very quickly.
Extending the Band: You are running an ABS analysis which overlaps a previous
ABS analysis of the project, pictured in the diagram below. The caching data for
the overlap between the two analyses will be reused although some calculation
may need to be done in the extension of the frequency band where it does not over-
Frequency Band 10 - 40 GHz
1st ABS analysis: 10, 10.1, 10.2, 10. 3 ... 39.8, 39.9, 40
2nd ABS analysis: 10, 10.05, 10.1, 10.15, 10.2 ... 39.85, 39.9, 39.95, 40
10 GHz 30 GHz
25 GHz
15 GHz Frequency band of 2nd ABS analysis
Frequency band of 1st ABS analysis
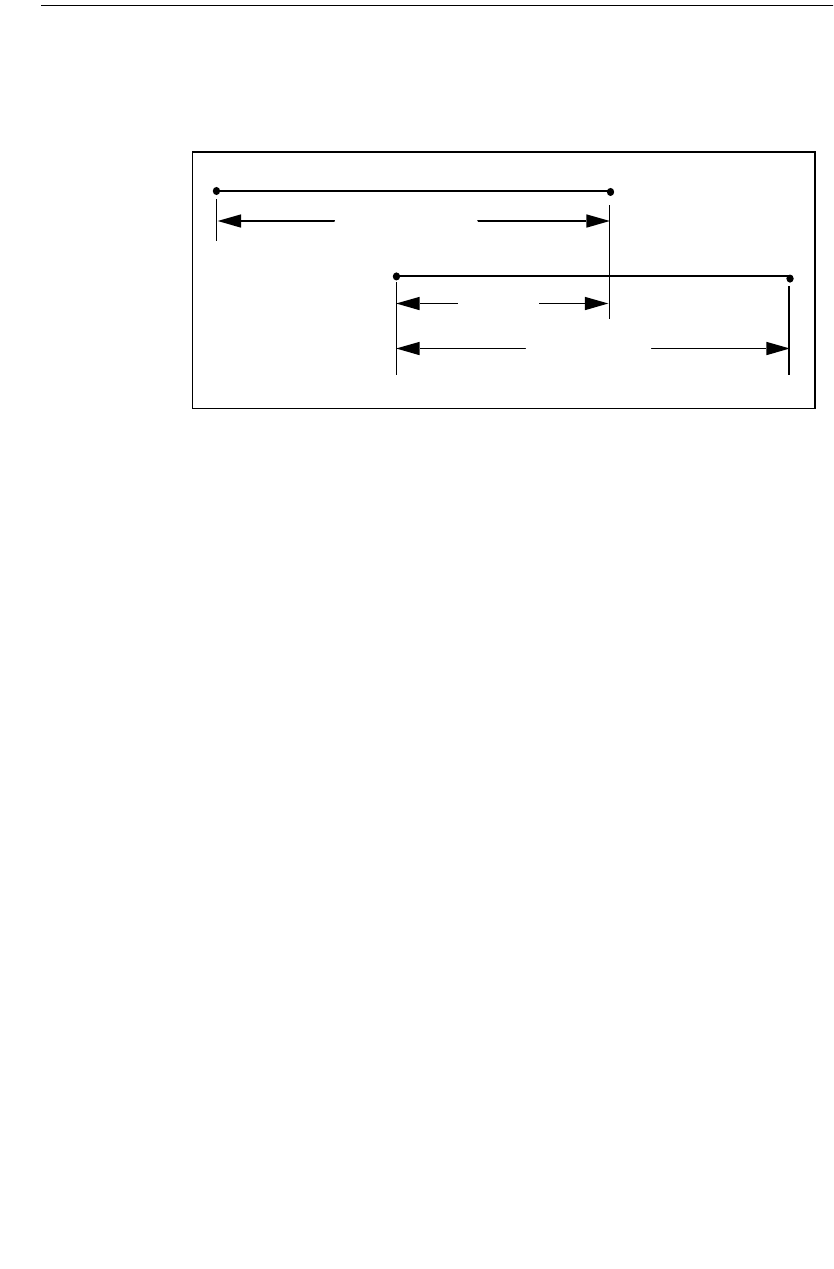
Sonnet User’s Guide
162
Rev 16.56
lap with a previous analysis. In order for the caching data to be valid for the second
analysis, your Advanced Subsectioning controls must be set such that the subsec-
tioning frequency is the same for both runs.
Accuracy Assurance: If you wish to check a particular data point in an ABS anal-
ysis and wish to ensure that a full calculation is done at a particular frequency
point, you should select a Linear Sweep. This analysis will calculate caching data
if Multi-sweep is selected for ABS caching data, but will not use the caching data
in producing analysis results.
Find Minimum and Find Maximum
Find Minimum determines the frequency where the circuit response reaches a
minimum. Find Maximum determines the frequency where the circuit response
reaches a maximum. You enter a starting and ending frequency in the Start and
Stop text entry boxes, respectively and select the parameter for which you wish
to determine the minimum or maximum value. Em performs an ABS analysis for
the frequency band, then uses the adaptive data to determine the frequency where
the response reaches a minimum or a maximum.
The Find Minimum and Find Maximum commands are both available in the Fre-
quency Sweep Combinations analysis controls. For more details, see the “Fre-
quency Sweep Combinations” topic in Help in the project editor.
30 - 50 GHz
Overlap
40 - 60 GHz
Frequency band of 1st ABS analysis
Frequency band of 2nd ABS analysis
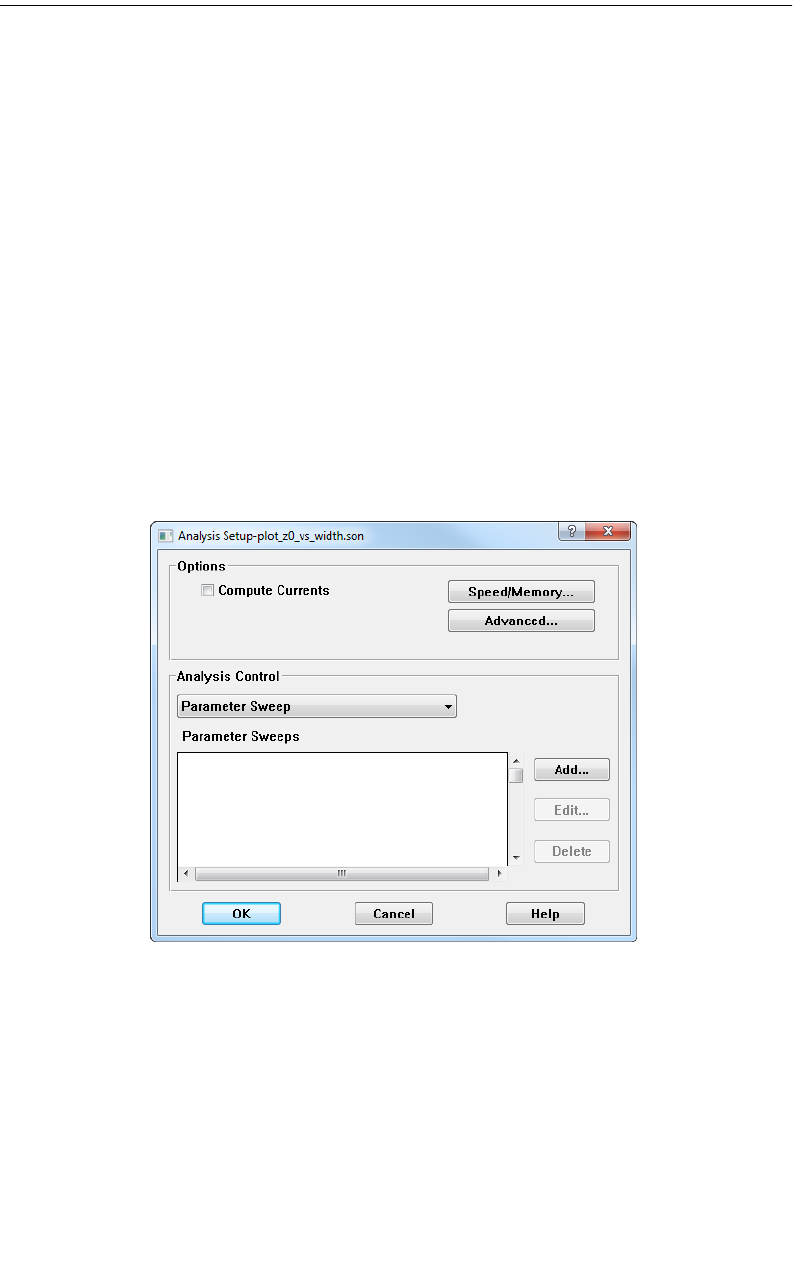
Chapter 8 Adaptive Band Synthesis (ABS)
163
Rev 16.56
Parameter Sweep
You may choose either a linear sweep or an adaptive sweep for a parameter sweep.
Selecting an adaptive sweep for a parameter sweep is done in the Parameter
Sweep Entry dialog box. For more information about parameter sweeps, please
see Chapter 9, “Parameterizing your Project” on page 171.
The following example assumes that you have already defined the parameter
“Width” in your circuit. For more information on inputting a parameter, please
refer to “Variables,” page 172.
To select ABS for a parameter sweep, do the following:
1 Select Analysis Setup from the project editor main menu.
The Analysis Setup dialog box appears on your display.
2 Select Parameter Sweep from the Analysis Control drop list.
The dialog box is updated to allow you to specify the parameter sweep.

Sonnet User’s Guide
164
Rev 16.56
3 Click on the Add button to the right of the Parameter Sweep list box.
The Parameter Sweep Entry dialog box appears on your display.
4 Select Adaptive Sweep (ABS) from the Sweep Type drop list to select an
adaptive frequency sweep.
The dialog box changes so that there are only Start and Stop text entry boxes.
5 Enter the frequency band for the ABS in the Start and Stop text entry boxes.
This completes setting up an ABS frequency sweep for the parameter sweep. You
would also need to select the parameters which you want to use in the parameter
sweep and enter their data ranges before closing this dialog box.

Chapter 8 Adaptive Band Synthesis (ABS)
165
Rev 16.56
Analysis Issues
There are several issues you should be aware of before using the ABS technique;
these are covered below.
Multiple Box Resonances
You should be aware that circuits with multiple box resonances make it difficult
for an ABS analysis to converge. The frequency band for an adaptive sweep
should not contain multiple box resonances. If multiple box resonances are pres-
ent, the number of discrete full analysis points goes up dramatically and synthesis
of the data becomes very difficult. If you do not know how to identify box reso-
nances, see Chapter 21, “Box Resonances” for a detailed discussion of box reso-
nances.
De-embedding
Adaptive data, resulting from an ABS analysis, is either de-embedded or non-de-
embedded. With other analysis types, when the de-embedding option is enabled
(default), then both de-embedded and non-de-embedded response data is calculat-
ed and available for display and output. This is not true for an adaptive sweep.
In an adaptive sweep, if you run with de-embedding enabled, de-embedded data
is available for the whole band. Non-de-embedded data is available only for the
discrete data points at which full analyses were performed while synthesizing the
response.
If you wish to have non-de-embedded data for the whole frequency band, you
must perform an adaptive sweep with the de-embed option disabled. Select Anal-
ysis Setup from the main menu to open the Analysis Setup dialog box, then
click on the Advanced button to open the Advanced Options dialog box. Click on
the De-embed checkbox to disable de-embedding. For details on these dialog box-
es, please refer to Help for the project editor.
For more information about de-embedding, see Chapter 6 "De-embedding" on
page 103.

Sonnet User’s Guide
166
Rev 16.56
Transmission Line Parameters
As part of the de-embedding process, em also calculates the transmission line pa-
rameters, Z0 and Eeff. You should be aware that when running an ABS analysis
these parameters are only calculated for the discrete data points at which a full
analysis is run. If you need the transmission line parameters at more data points,
analyze the circuit using a non-ABS analysis.
Current Density Data
Current density data is calculated for your circuit when the Compute Current Den-
sity option is enabled in the Analysis Setup dialog box. For non-ABS sweeps, cur-
rent density data is calculated for all the response data. For an adaptive sweep, the
current density data is only calculated for the discrete data points, therefore, your
plot in the current density viewer shows a coarse resolution of your frequency
band.
If you wish to calculate the current density data at more points in your band, run
a non-ABS sweep for the points in question with the Compute Current Density op-
tion enabled.
For more information about the Compute Current Density option, see the help
topic “Analysis Setup” in Help for the project editor.
Ripple in ABS S-Parameters
Please note that when the value of the S-parameters is close to 1 (0 dB) over the
entire band you may have small ripples or oscillations in the S-parameter values.
This is due to the rational fitting model having too many degrees of freedom when
trying to fit a straight line. If this is a problem, it is recommended that you analyze
the frequency band in which this occurs with another type of sweep.
Output Files
You specify additional output files in the Output Files dialog box which appears
on your display when you select Analysis Output Files from the project editor
menu. You click on the appropriate button to open the corresponding file entry di-
alog box. Each entry dialog box has an option pertinent to ABS.
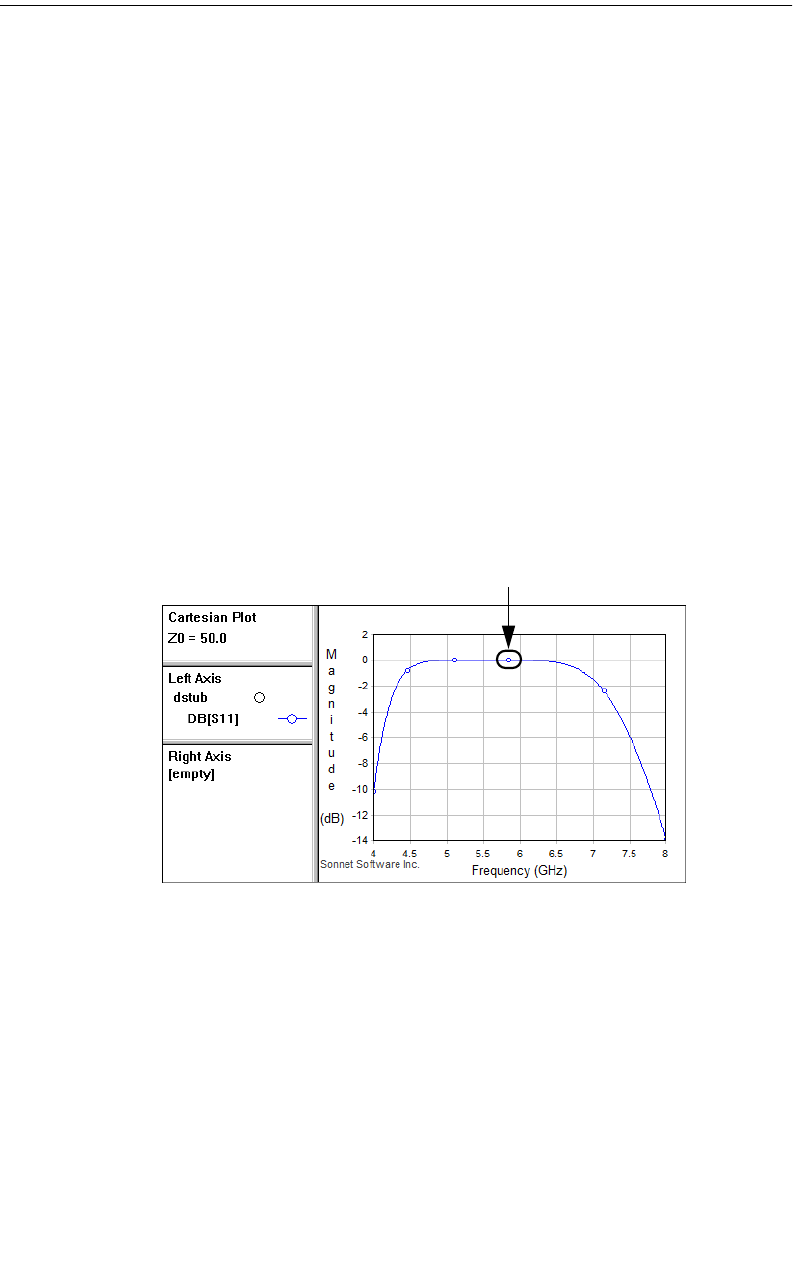
Chapter 8 Adaptive Band Synthesis (ABS)
167
Rev 16.56
Response File
When you specify an optional output file for your project, you may select which
type of data to output from an adaptive sweep. The data selection is controlled by
the Include Adaptive Data checkbox in the File Entry dialog box. If this checkbox
is selected, which is the default, then all the adaptive data from an ABS analysis
is included in the output file. If this checkbox is cleared, then only the data for the
discrete data points is included in the output file. We recommend leaving this box
checked.
Viewing the Adaptive Response
When viewing an adaptive response (ABS) in the response viewer, there are sev-
eral things of which you need to be aware. The adaptive data is plotted as a line.
A symbol indicating a data point only appears at the discrete frequencies at which
a full analysis was executed as shown in the picture below.
When exporting data, you may choose to output only the discrete frequencies or
the complete response data for the ABS analysis. To output only the discrete fre-
quency data, unselect the Include Adaptive Data checkbox in the Export Data di-
alog box in the response viewer. For details, see Help in the response viewer.
Discrete Data Point

Sonnet User’s Guide
168
Rev 16.56
ABS Preview
When running an adaptive sweep, discrete frequencies are computed until a ratio-
nal polynomial is found to “fit” the solution. When the fit meets the convergence
criteria, then the adaptive data is calculated and the analysis concludes. A majority
of circuits usually require around five to ten frequencies to converge. In some cas-
es, convergence may be more difficult to reach and more discrete frequencies may
be required while in some instances convergence cannot be reached. The ABS
preview allows you to stop an adaptive sweep which has not yet converged in
order to evaluate the data and possibly determine a new analysis band for your
simulation.
NOTE: The ABS Caching Level must be set to "Stop/Restart" in the Advanced
Options dialog box in order to use this command. See "ABS Caching
Level" on page 159.
If you stop an analysis running an adaptive sweep before it completes, any ABS
data which has been calculated is saved and may be examined in the response
viewer using the command View ABS Preview. Note that the an ABS preview
does not support the use of equations but all other data curves are available.
When you stop an analysis and open a plot, initially it will have a “jagged” appear-
ance since only the discrete frequencies that have been thus far calculated are dis-
played. When you select View ABS Preview, a new plot is created with ABS
data calculated before the analysis was stopped. A color bar at the bottom of the
window indicates the type of data as shown below. If you click in the color band,
the frequency you selected and its data status is displayed in the Status Bar at the
bottom of the response viewer window. In the case of the graph below, the con-
verged data starts at 3.4 GHz, so running the simulation and using 3.4 GHz as the
starting frequency will provide a completed ABS analysis.
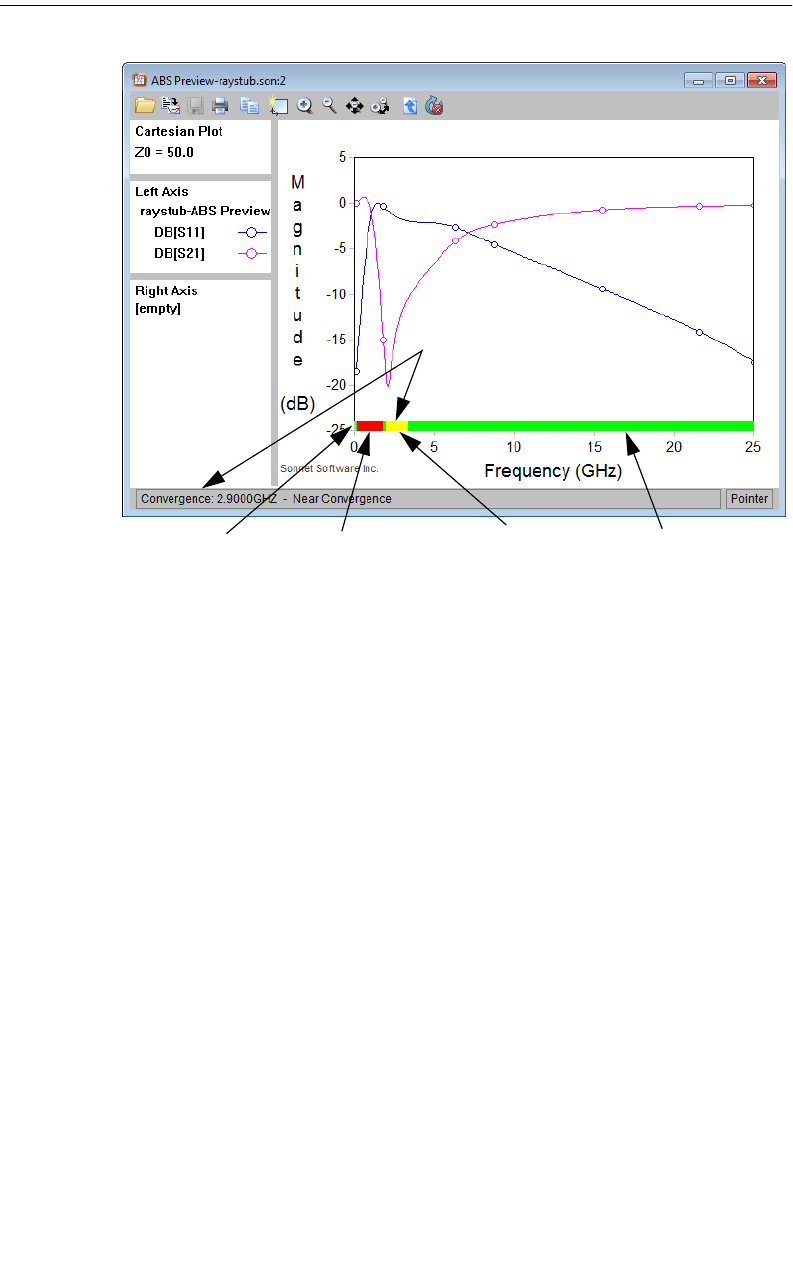
Chapter 8 Adaptive Band Synthesis (ABS)
169
Rev 16.56
Green - Good data
Convergence achieved
Yellow - Near
Convergence
Red - Bad Data
No Convergence
Gray - Outside of the
ABS analysis band
Frequency and
data status

Sonnet User’s Guide
170
Rev 16.56

Chapter 9 Parameterizing your Project
171
Rev 16.56
Chapter 9 Parameterizing your
Project
Sonnet allows you to assign variables and equations to many properties in order
to parameterize your project. Below are some of the reasons you might wish to pa-
rameterize your project:
•Avoid creating multiple projects
•Parameter Sweep of a project - allows you to vary a circuit property
during an analysis
•Optimization of a project
•Easier construction and maintenance of a project
•Using equations to establish relationships between circuit proper-
ties
Variables may be used for the following properties in your project:
•Geometry dimensions
•Metal Properties
•Dielectric Properties
•Ideal Component Values
•Layer Thicknesses
The value of a variable may be changed either by you or by the analysis engine
during a parameter sweep or optimization. During a parameter sweep, em sweeps
the variable values through a user defined range, therefore changing the properties
of your circuit. In an optimization, the analysis engine controls the variable value,

Sonnet User’s Guide
172
Rev 16.56
within a user defined range, in an attempt to reach a user defined goal. Both pa-
rameter sweeps and optimization of a project may be performed over a range of
analysis frequencies.
For a tutorial which details how to add variables to your circuit and perform an
optimization, please refer to Chapter 10, “Parameter Sweep and Optimization
Tutorial” on page 197.
For most circuit properties, you simply define a variable and enter that variable in
a property field. However, if you wish to vary the size of your geometry--for ex-
ample, changing the width of a feed line or the length of a polygon--you define a
dimension parameter which identifies the dimension you wish to change. Once the
dimension parameter is defined, you assign a variable to the dimension parameter.
The first step in performing a parameter sweep or optimization is defining the
variables and dimension parameters in the project editor.
Variables
Variables are user defined circuit attributes that allow the analysis engine, em, to
modify the circuit in order to perform parameter sweeps and optimization. Vari-
ables also provide a quick way for the user to change dimensions in the project
editor or multiple elements in a circuit. For example, the length of a transmission
line can be assigned the variable “L.” To change the length of the transmission
line, you edit the value for “L.” Another example would be a circuit which con-
tains 10 resistors, all of which have the same value. Entering a variable “R” for the
resistance of these ideal components allows you to change the value of all 10 re-
sistors by changing the value in only one place.
NOTE: Just because it is possible to use a variable in any given property field,
does NOT make it necessary to do so. You may enter a nominal value
for the field instead of a variable if you do not wish to change that
particular property during analysis.
A variable’s value may be defined using:
•A constant or nominal value
•Another variable
•An equation
Any of these definitions may be directly entered into a property field. For a more
detailed discussion of equations, please see "Equations" on page 175.

Chapter 9 Parameterizing your Project
173
Rev 16.56
How to Create a Variable
You may use two basic approaches to creating variables in your project. The first
approach is to define all the desired variables and then enter these variables as
property values. The second approach is to enter a variable in the desired property
field as needed. If the variable has not been previously defined, you are prompted
to enter a definition. Using the second approach allows you to define variables as
needed rather than defining them all ahead of time.
To define a variable do the following:
1 Open the Add/Edit Variable dialog box.
This dialog box may be opened one of four ways:
•By selecting Circuit Add Variable from the project editor main menu.
•Select Circuit Variable List from the project editor main menu, then
click on the Add or Edit button in the Variable List window which
appears.
•By entering an undefined variable in a property field in another dialog
box. When the dialog box is closed the Add/Edit Variable dialog box is
opened so you can define the variable.
•By selecting <Add Variable> from a drop list of a property field in
another dialog box.
Property field drop list

Sonnet User’s Guide
174
Rev 16.56
When you select <Add Variable> the Add/Edit dialog box is opened so
you can define the variable.
2 Enter the desired variable name in the Name text entry box.
If you opened this dialog box by entering an undefined variable in another dialog
box, this field will already contain that name.
3 Enter a constant value, another variable or an equation that defines the
value of the variable in the Value or Equation text entry box.
For information about the functions available and equation syntax, click on the
Equation Syntax Help button. If you wish to use another variable in the equation,
you may select it from the list of Available Variables and click on the Insert into
Eqn button. See the next section for more information on Equations. The variable
name will be entered at the present location of the cursor in the Value text entry
box.
4 Enter a brief description of the variable, if desired, in the Description text
entry box.
This description appears in the Variable list dialog box and allows you to identify
the purpose of the variable or which property it is being used to define. If the
variable is created when editing a dialog box (Dielectric Layers, Metal Types,
etc.) a default description is provided by the software. This may be changed by
entering a different description here. This field is not required.
5 Select the desired units for the variable from the Units drop list.
Available units are the length, frequency, resistance, capacitance and inductance
units presently set in your project. If none of these are suitable, then select Other
It is important to select the units for your variable so that if you change the units
used in your project, the value of the variable is converted correctly.
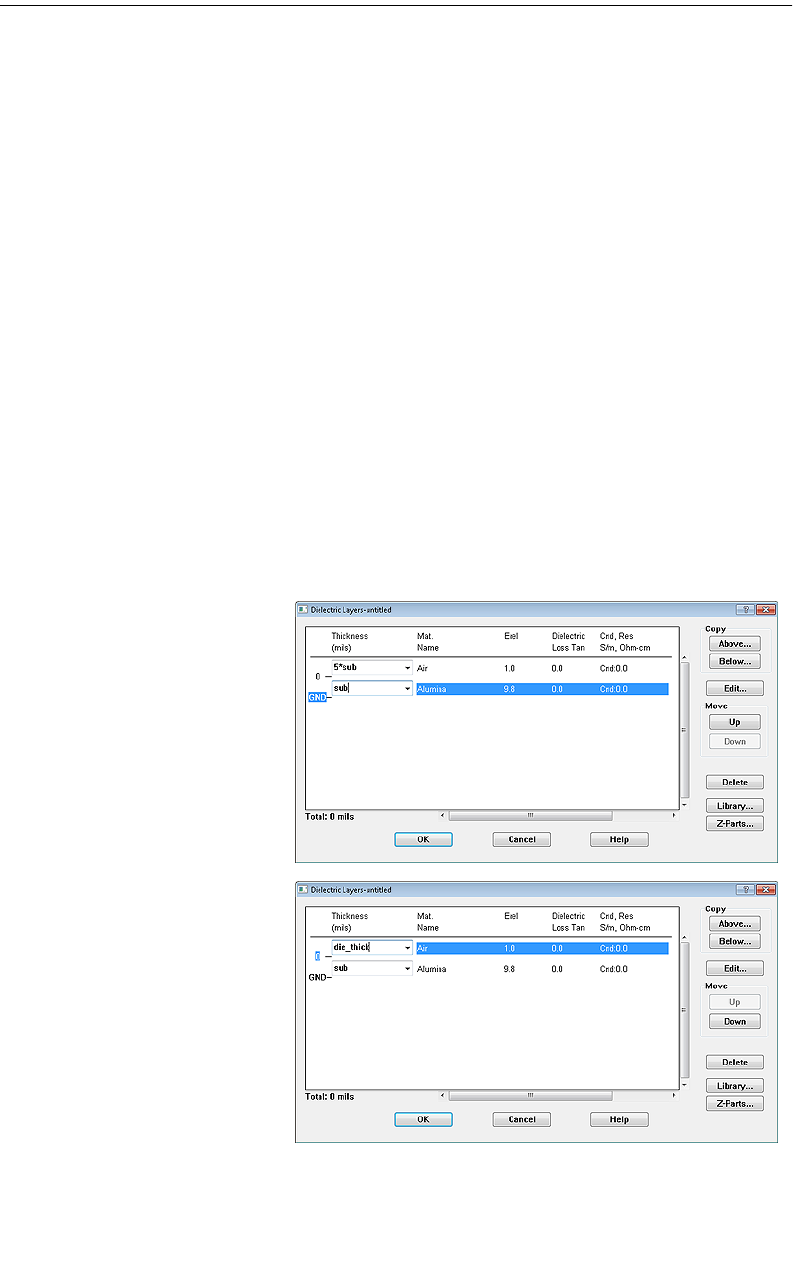
Chapter 9 Parameterizing your Project
175
Rev 16.56
Equations
As mentioned earlier, a variable may be defined by a constant, another variable or
an equation. An equation is composed of constants and/or variables. Below are
some examples of valid equations.
•3*3
•3*pi
•3*H
•sin(H)
•sqrt(H)
The last three equations are ones in which one variable is used to define another.
This allows you to relate properties in your circuit such that changing one effects
the other, maintaining a set relationship between them. For example, you wish to
define a dielectric layer which is always five times the thickness of your substrate.
To do so, you define a variable “sub” which you would enter as the thickness of
your substrate. Then you would enter “5*sub” as the value for the thickness of the
dielectric layer. There are two methods you may use to do this. The first is to de-
fine another variable “die_thick” which you define as “5*sub” and the second is
to simply enter the equation “5*sub” as the thickness of the dielectric layer. You
may enter an equation in any field in which you may enter a variable.
In this case, only one variable
“sub” is defined and the
equation “5*sub” is entered
directly in the Dielectric Layers
dialog box as the thickness of
the dielectric layer. The only
variable which appears in the
Variable List (opened using the
command Circuit Variable
List) is “sub.”
In this case, two variables are
defined: “sub” and “die_thick.”
The value entered for the
variable “die_thick” is the
equation “5*sub.” Both variables
appear in the Variable List.

Sonnet User’s Guide
176
Rev 16.56
Available functions for equations include:
•Operators such as addition, subtraction, multiplication, etc.
•Logarithmic functions
•Complex Math functions
•Trigonometric functions
•General Mathematical functions such as maximum or minimum
•Conversion functions for converting units
•Table function to use for data lookup
There are also constants available for equations including project constants such
as the cell size and box size and the frequency which is discussed more below.
For complete details on all the functions and constants available for equations and
their syntax, please refer to the equation syntax help topics in Help. You may ac-
cess these topics by clicking on the Equation Syntax Help button in the Add/Edit
Variable dialog box.
If you enter an equation which uses a variable as the definition of another variable,
then the variable defined by the equation is dependent on the variable used in the
equation. This is discussed later in the chapter, in "Dependent Variables" on page
176.
Frequency Dependency
There is a frequency constant, FREQ, available for use in Sonnet equations. This
allows you to model properties whose characteristics are frequency dependent
such as a dielectric. It is important to be aware that if a variable uses the FREQ
constant in its definition that the value of the variable changes during the analysis
even if the variable is NOT selected for the parameter sweep or optimization.
Dependent Variables
One variable is dependent upon another if the value of a variable is defined by an
equation that uses another variable. As the value of the variable in the equation is
changed, so is the dependent variable. If a variable is dependent, you may not di-
rectly edit its nominal value; instead, you change its value by changing the value
of the variable on which it is dependent. You may not delete a dependent variable.
If you wish to delete it, you must first remove the dependency by changing the def-
inition of the dependent variable.

Chapter 9 Parameterizing your Project
177
Rev 16.56
Variables which do not depend on another variable for their value are independent
variables. Only independent variables may be selected for a parameter sweep. To
vary a dependent variable in a parameter sweep, you must select the variable on
which it depends. For more details on parameter sweeps, see "Parameter Sweep"
on page 189.
Circular Dependencies in Variables
Care should be taken when adding dependent variables to your circuit that they do
not form a circular dependency. A circular dependency is formed when two vari-
ables are dependent on each other. This can happen for two variables or multiple
variables. In the case of multiple variables, the dependency extends from the first
variable through all the variables until the first variable is dependent upon the last.
An example of a circuit dependency would be the two equations A=2*B and
B=sin(A). For variables, if the project editor detects a circular dependency, an
error message appears and you are forced to correct the problem before proceed-
ing.You need to redefine one of the variables such that it is no longer dependent
on the other. A correction of the example would be A=2*B and B=sin(C).
Dimension Parameters
A dimension parameter allows you to identify dimensions in a geometry project
and assign a variable to the dimension, which allows you to vary those dimensions
within an analysis. The initial value of the dimension parameter is the length that
appears in your circuit. This is the nominal value of the variable assigned to the
dimension parameter. If you change the nominal value of the variable, then the cir-
cuit is redrawn with that length.
Anchored
Dimension
Parameter
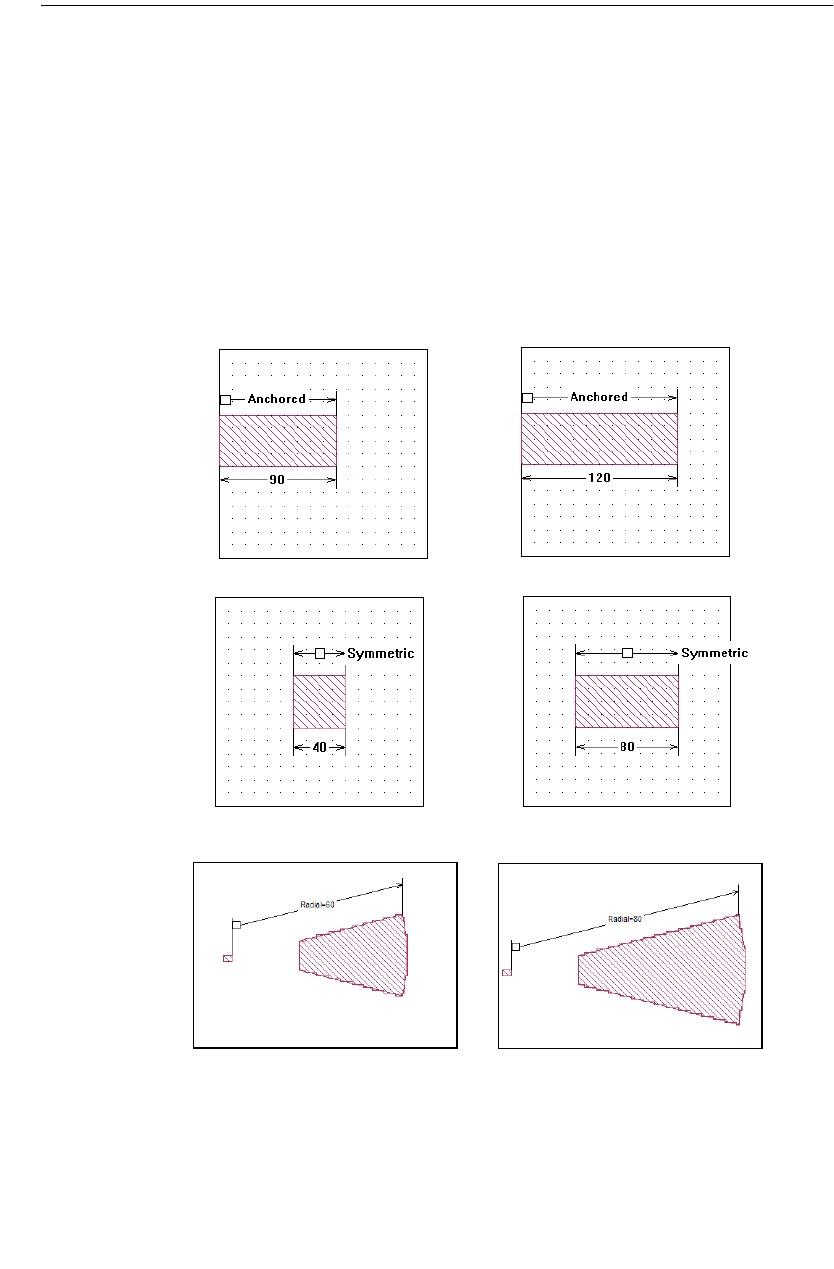
Sonnet User’s Guide
178
Rev 16.56
There are three types of dimension parameters: anchored, symmetric, and radial.
For brevity, we refer to anchored dimension parameters as anchored parameters,
symmetric dimension parameters as symmetric parameters, and radial dimension
parameters as radial parameters for the remainder of this discussion. An anchored
parameter allows you to fix one end of a parameter then vary its length extending
from that point. A symmetric parameter allows you to fix the center point of a di-
mension parameter and vary the distance it extends on each side. A radial param-
eter allows you to fix one end of a parameter then radiate out from that fixed point;
the direction is not restricted to the x or y direction, but may extend at an angle.
The three dimension parameter types are described in detail in the following sec-
tions.
Nominal Value = 90 mils Nominal Value = 120 mils
Nominal Value = 40 mils Nominal Value = 80 mils
Nominal Value = 60 mils Nominal Value = 80 mils

Chapter 9 Parameterizing your Project
179
Rev 16.56
Anchored Dimension Parameters
An anchored parameter defines a dimension using an anchor point, a reference
point and an adjustable point set. The nominal value of the parameter is defined
by the distance between the anchor point and the reference point. When the dimen-
sion is varied, each point moves relative to the anchor point. When defining your
dimension parameter, you perform the following steps:
•You select the anchor first. This is the fixed starting point for the
parameter.
•You select the reference point. The reference is the first point in the
adjustable point set, which is the set of points moved relative to the
anchor point when the value of the dimension parameter is changed.
The distance from the anchor point to the reference point is the value of
the dimension parameter. When the value of the dimension parameter is
changed, the anchor retains the same position, but the reference point,
moves to a new position.
•Third, you select any additional points in your circuit you wish to move
when the reference point moves; this is the adjustable point set. As the
value of the dimension parameter varies and the reference point is
moved, the positions of the points in the adjustable point set also move.
There is a setting associated with each dimension parameter that
determines how the adjustable point set is moved. With the default, and
simplest, option each point in the adjustable point set retains its relative
distance from the reference point. For a discussion of all the options
controlling moving the adjustable point set, see "Moving Adjustable
Point Sets" on page 183.
Note that the anchored parameter is always defined as the distance between the an-
chor and the reference point in either the X direction or the Y direction, never as
a diagonal distance between them.
Two examples of anchored parameters, each at two different nominal values, are
illustrated below. This example uses the default setting for how the adjustable
point set moves.
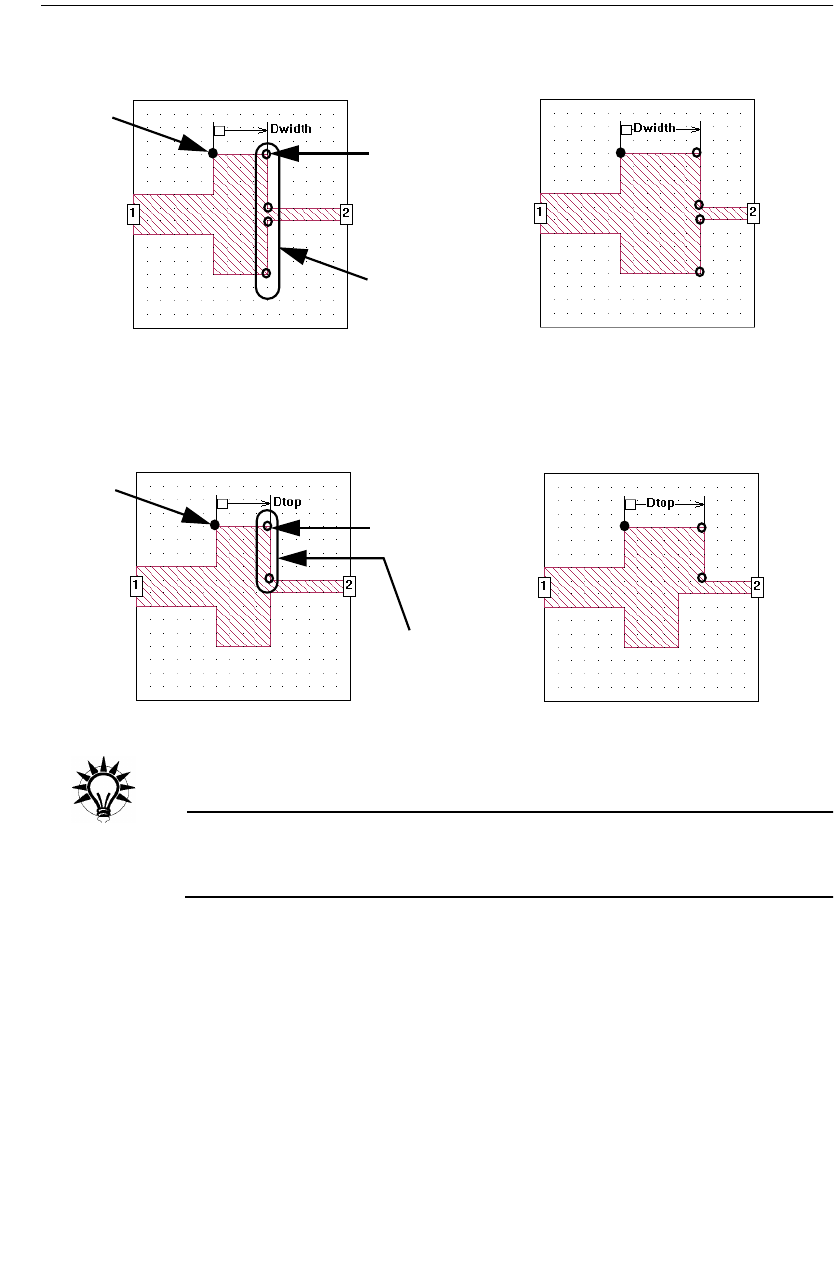
Sonnet User’s Guide
180
Rev 16.56
.
TIP
Once you have finished adding a dimension parameter, double-clicking on the
variable name and entering a new nominal value allows you to check whether the
dimension parameter was defined correctly.
Symmetrical Dimension Parameters
A symmetric parameter defines a dimension using two reference points and their
respective adjustable point sets. The nominal value of the parameter is the distance
between the two reference points. The anchor is defined as the midpoint between
Anchor
Point
Reference
Point
Adjustable
Point Set
Dwidth, nominal value = 60 mils
Anchor
Point
Reference
Point
Adjustable
Point Set
Dtop, nominal value = 40 mils Dtop, nominal value = 60 mils
Notice that although the top and bottom examples have identical anchor and reference
points and starting and ending nominal values, that the resulting polygon on the top differs
from that on the bottom due to a different adjustable point set (the point set is highlighted
by the oval).
Dwidth, nominal value = 40 mils

Chapter 9 Parameterizing your Project
181
Rev 16.56
the two reference points; the user does not define an anchor point for a symmetric
parameter. When the dimension is varied, each point moves relative to the anchor
point. When defining your dimension parameter, you perform the following steps:
•Select the first reference point.
•Select the adjustable point set that moves with the first reference point.
•Select the second reference point. The value of the parameter is the
distance between the two reference points.
•Select the adjustable point set that moves with the second reference
point.
There is a setting associated with each dimension parameter that determines how
the adjustable point sets are moved. With the default, and simplest, option each
point set moves one half the distance of the difference between the present value
and the previous value out from the middle point, maintaining its relative positive
to the reference point with which it is associated. For a discussion of all the options
controlling moving adjustable point sets, see "Moving Adjustable Point Sets" on
page 183.
Note that the symmetric parameter is always defined as the distance between the
reference points in either the X direction or the Y direction, never as a diagonal
distance between them.
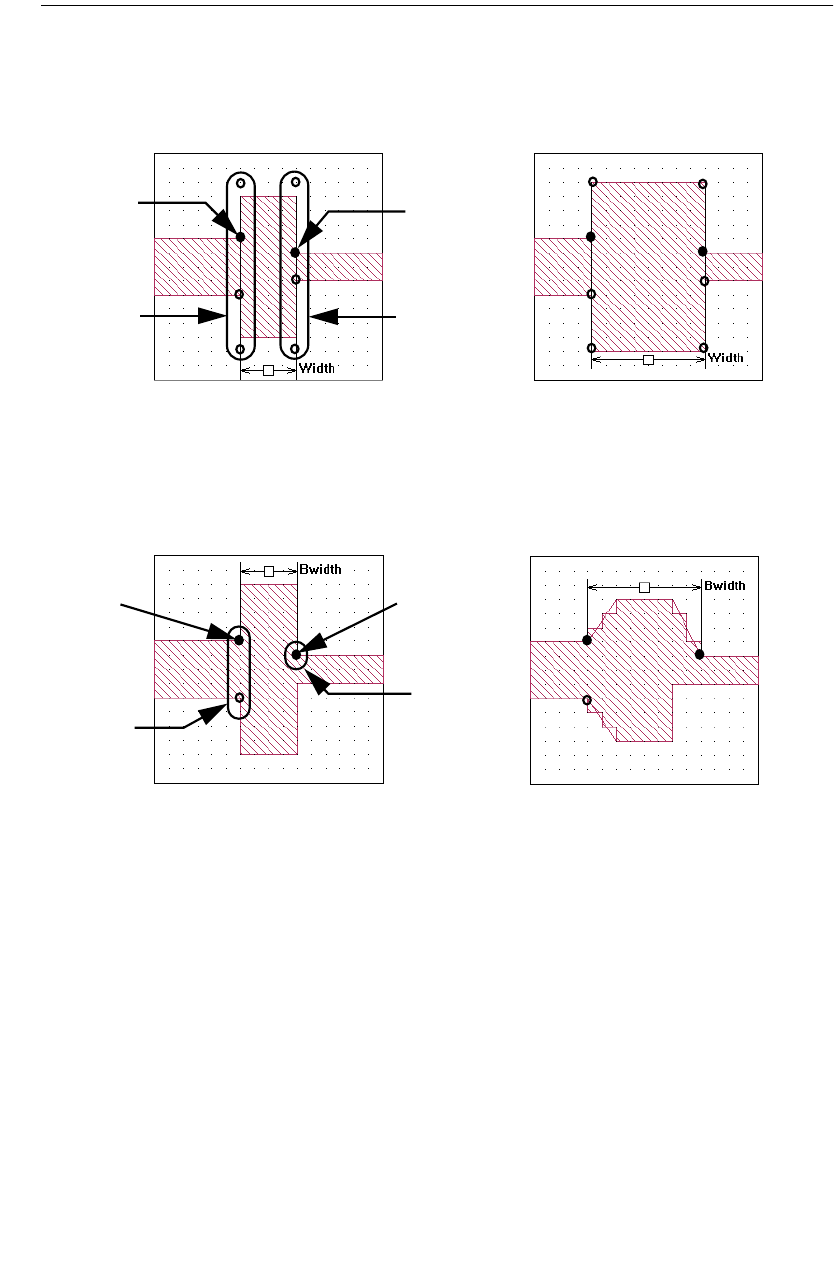
Sonnet User’s Guide
182
Rev 16.56
Two examples of symmetric parameters, each at two different nominal values, are
illustrated below. This example uses the default setting for how the adjustable
point set moves.
Adjustable
Point Set 1
Width, nominal value = 40 mils Width, nominal value = 80 mils
Bwidth, nominal value = 40 mils Bwidth, nominal value = 80 mils
Reference
Point 1 Reference
Point 2
Adjustable
Point Set 2
Reference
Point 1
Adjustable
Point Set 1
Reference
Point 2
Adjustable
Point Set 2
Notice that although the top and bottom examples have identical reference
points and starting and ending nominal values, that the resulting polygon on
the top differs from that on the bottom due to a different adjustable point set
(the point set is highlighted by the oval).
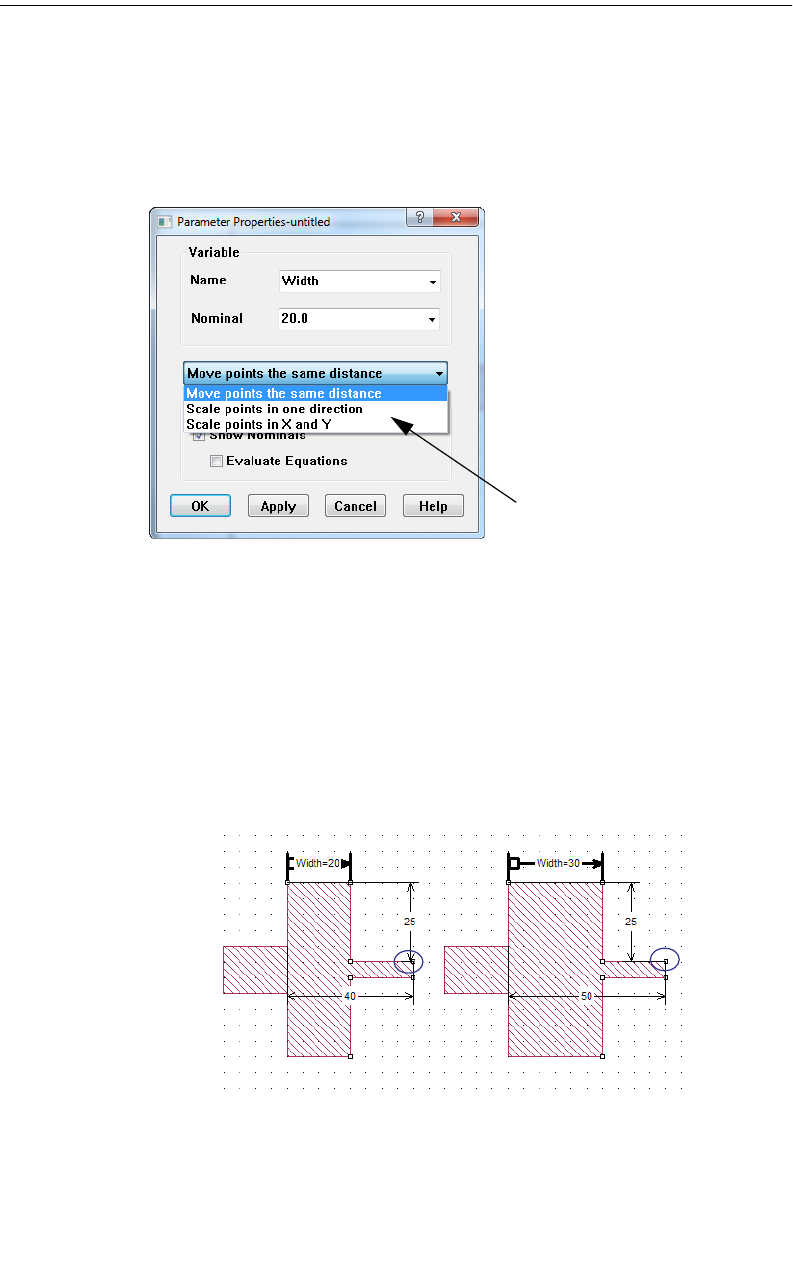
Chapter 9 Parameterizing your Project
183
Rev 16.56
Moving Adjustable Point Sets
Anchored and symmetric parameters have a setting which controls how the adjust-
able point sets are moved. There are three settings: Move points the same distance,
Scale points in one direction, and Scale points in X and Y. Each type is explained
below.
Move Points the Same Distance: This setting moves the adjustable point set
the same distance as the reference point is moved and all the points in the adjust-
able point set maintain their relative position. This is the default setting. An exam-
ple using an anchored dimension parameter is shown below. Note that the
adjustable point sets are highlighted.
The anchored dimension parameter is increased by 10 mils, so each point in the
adjustable point set is moved away from the anchor point by 10 mils. As shown in
the illustration, the original distance from the anchor to the circled point was 40
mils; when the value of the parameter is increased, the point was moved by 10 mils
so that it is now 50 mils away from the anchor point.
This is the Parameter
Properties dialog box in which
you select the moving option
from the drop list shown to the
left. This dialog box appears
when you are entering a
dimension parameter or when
you select the command Modify
Parameter Properties when
a dimension parameter is
selected.
Moving option drop list

Sonnet User’s Guide
184
Rev 16.56
Scale Points in one direction: When using this setting, the geometry con-
trolled by the parameter is scaled or stretched along either the x or y axis depend-
ing on the orientation of the parameter. Each point in the adjustable point set is
moved by an amount based on its relative distance from the anchor. Points closer
to the anchor are moved a smaller distance then points further away from the an-
chor. For symmetric parameters, the anchor is the center point between the two
reference points.
The scaling factor used is the ratio of the new nominal value to the present nomi-
nal value. Each point is moved by a delta calculated by multiplying its present dis-
tance from the anchor point by the scaling factor.
Scale Points in x and y: When using this setting, the geometry controlled by
the parameter is scaled or stretched along both the x and y axis keeping the pro-
portions of the geometry the same. Each point in the adjustable point set is moved
by an amount based on its relative distance from the anchor. Points closer to the
anchor are moved a smaller distance then points further away from the anchor. For
symmetric parameters, the anchor is the center point between the two reference
points.
The scaling factor used is the ratio of the new nominal value to the present nomi-
nal value. Each point is moved by a delta calculated by multiplying its present dis-
tance from the anchor point by the scaling factor.
An anchored dimension parameter being scaled in both directions is shown below.
The scaling factor is 1.5 since the new nominal value is 120 mils and the present
value is 80 mils. As shown in the illustration, the original distance from the anchor
of the circled point was 36.5 mils along the x axis and 43.5 mils along the y axis;
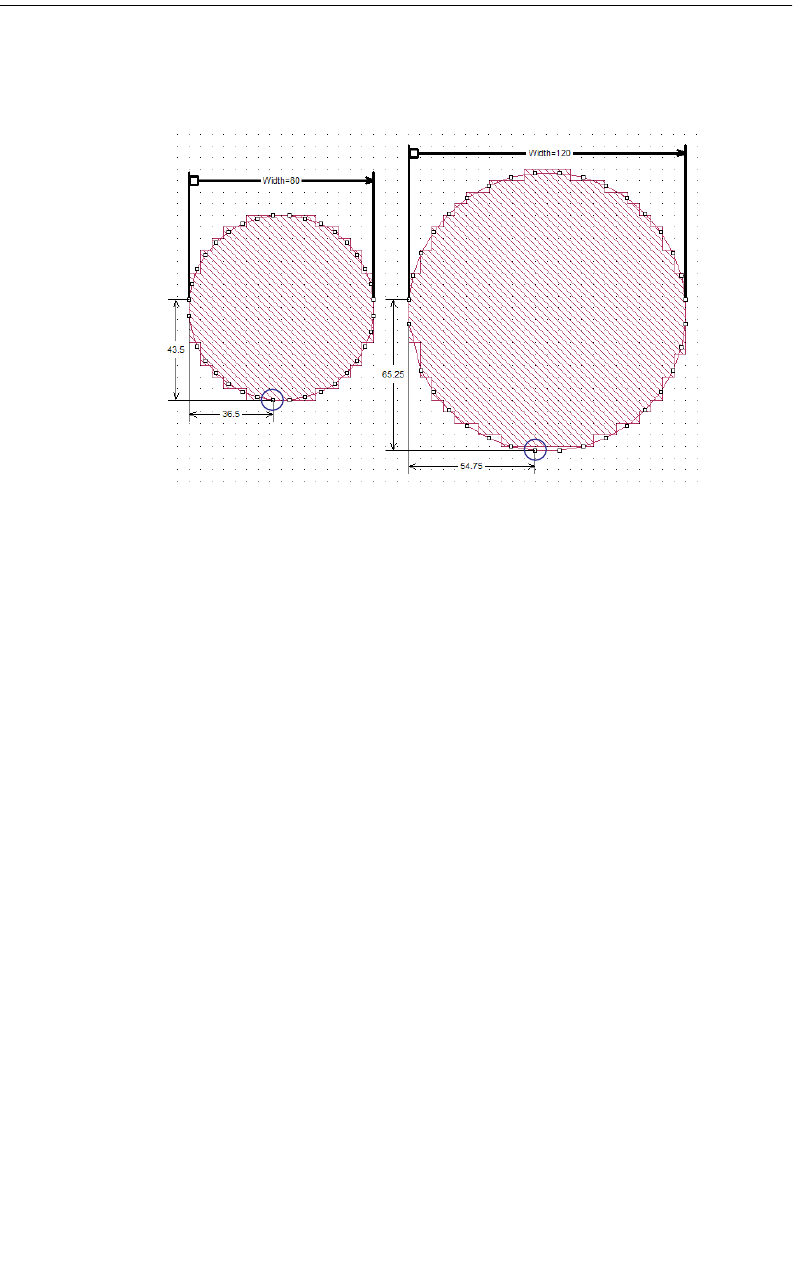
Chapter 9 Parameterizing your Project
185
Rev 16.56
when the value of the parameter is increased the point was moved to 54.75 mils
away from the anchor point along the x axis and 65.25 mils along the y axis; the
original distances multiplied by the scaling factor of 1.5.
Radial Dimension Parameters
A radial parameter defines a dimension using an anchor point, a reference point
and an adjustable point set. The nominal value of the parameter is defined by the
distance between the anchor point and the reference point. When the dimension is
varied, each point moves along a line extending from the anchor point through it’s
original position. Setting up a radial parameter is identical to setting up an an-
chored parameter. When defining your radial parameter, you perform the follow-
ing steps:
•You select the anchor first. This is the fixed starting point for the
parameter.
•You select the reference point. The reference is the first point in the
adjustable point set, which is the set of points moved relative to the
anchor point when the value of the radial parameter is changed. The
diagonal distance from the anchor point to the reference point is the
value of the dimension parameter. When the value of the dimension
parameter is changed, the anchor retains the same position, but the
reference point, along with the adjustable point set, moves to a new
position.
•Third, you select any additional points in your circuit you wish to move
when the reference point moves; this is the adjustable point set. As the
value of the dimension parameter is varied, the reference point, as well
as the rest of the adjustable point set, is moved accordingly. Each of the

Sonnet User’s Guide
186
Rev 16.56
points in the point set move the same distance along their radius from
the anchor point. An example is shown below.
Radial = 40 mils Radial = 80 mils
The view of Radial=40 mils is superimposed over the view of Radial=80
mils. As can be seen, each adjustable point moves the same distance
along its radius from the anchor point to its new position. Therefore line
segments AA’, BB’, CC’ and DD’ are all equal to 40 mils, the difference
between the two values of the dimension parameter Radial.

Chapter 9 Parameterizing your Project
187
Rev 16.56
Reference Planes
Linking your reference plane to a dimension parameter moves the reference plane
in response to a change in the dimension parameter helping to ensure correct
placement of your reference plane. In order to do this, link your reference plane to
a point in the adjustable point set for the desired dimension parameter as illustrat-
ed below.
Dependent Dimension Parameters
One dimension parameter is dependent upon another if the anchor point and/or the
reference point(s) for the second parameter are part of an adjustable point set for
the first parameter. This is allowed as long as a circular dependency is not formed;
see the following section. You need to be aware of dependent dimension parame-
ters so that you can take into consideration the complete impact on your circuit
when the value of the primary dimension parameter is changed. When the primary
dimension parameter is changed, a dependent parameter is adjusted, i.e., the an-
chor point or reference point is moved, along with the primary dimension param-
In the circuit shown at
the top, the reference
planes are a fixed
length. When the
dimension parameter
changes, the reference
plane lengths do not
change resulting in
incorrectly placed
reference planes.
On the bottom, the
reference planes are
linked to points in the
adjustable point set.
When the dimension
parameter is changed,
the reference planes
move with it keeping
the reference planes in
the correct place.
Link point for the
left reference plane
Link point for the
right reference plane
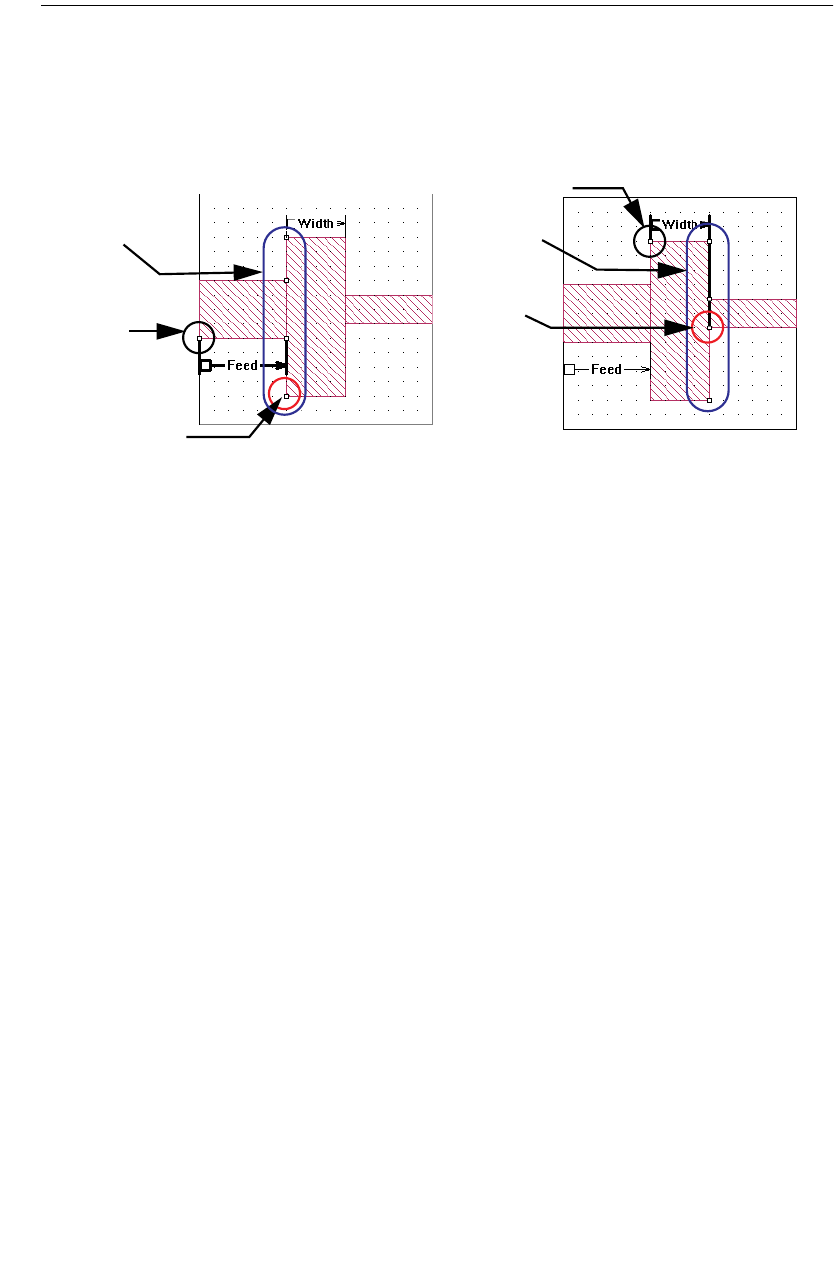
Sonnet User’s Guide
188
Rev 16.56
eter on which they depend. A picture of a dependent dimension parameter is
shown below with the Anchor and Reference points highlighted as well as the
point sets.
You may use the Select Dependents command in the project editor to determine
if there are any dependent dimension parameters. With the project open in the
project editor, do the following:
1 Right-click on a dimension parameter in your circuit.
The variable name and the dimension parameter point set is highlighted and a pop-
up menu appears on your display.
2 Select “Select Dependents” from the pop-up menu.
If any dependent dimension parameters are present in your geometry, the
dependent dimension parameter is highlighted.
Circular Dependencies in Parameters
Care should be taken when adding dimension parameters to your circuit that they
do not form a circular dependency. A circular dependency is formed when two di-
mension parameters are dependent on each other. This can happen for two dimen-
sion parameters or multiple dimension parameters. In the case of multiple
dimension parameters, the dependency extends from the first dimension parame-
ter through all the dimension parameters until the first dimension parameter is de-
pendent upon the last.
Feed Anchor
Point
Feed Ref. Pt.
Feed Adjustable
Pt. Set
Width Anchor
Point
Width
Ref. Pt.
Width Adjustable
Pt. Set
The dimension parameter “Width” is dependent on the dimension parameter “Feed”.
Note that the anchor point for the dimension parameter “Width”, shown on the right, is
part of the adjustable point set for the dimension parameter “Feed,” shown on the left.
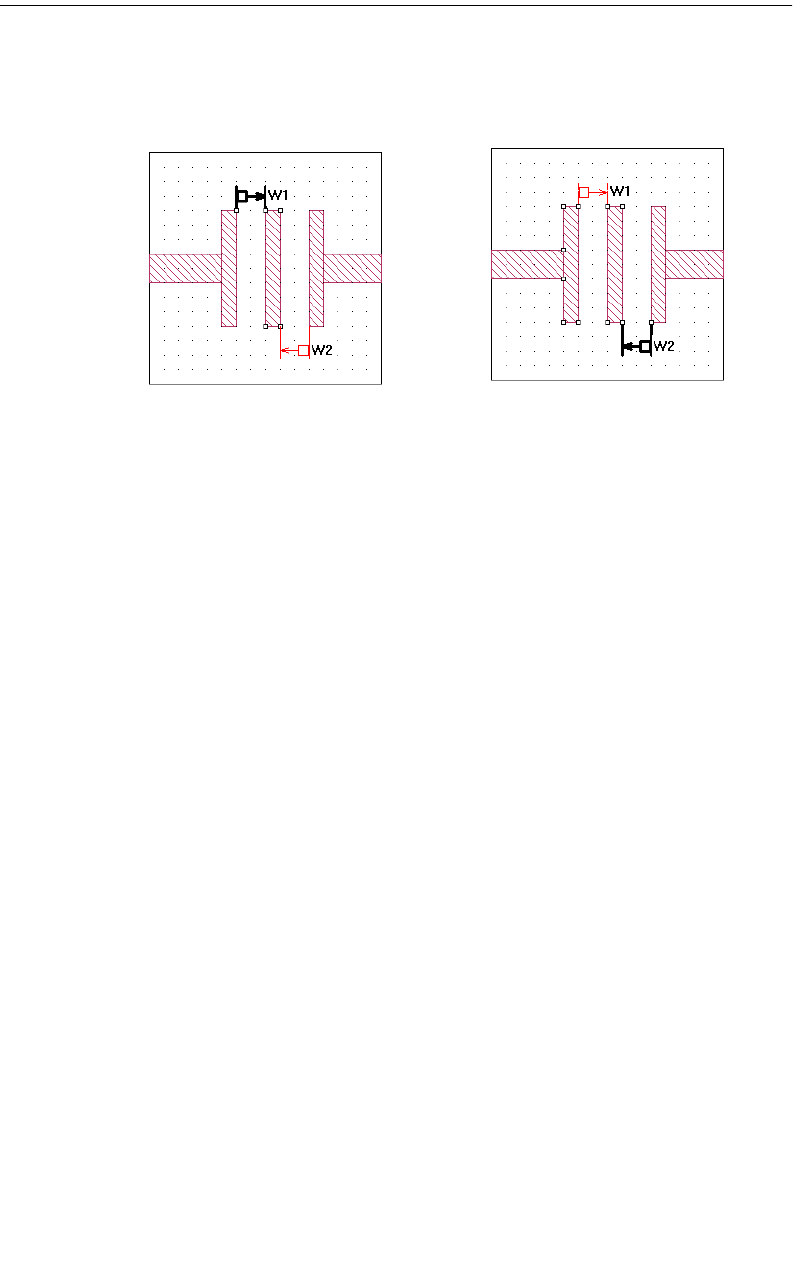
Chapter 9 Parameterizing your Project
189
Rev 16.56
If the project editor detects a circular dependency of dimension parameters, all the
involved dimension parameters are shown in red. An example of two dimension
parameters in a circular dependency is shown below.
A circular dependency is an error condition and must be corrected before you can
analyze your circuit. You need to redefine one of the dimension parameters such
that it is no longer dependent on the other.
Parameter Sweep
Once you have defined variables in your circuit, you may use the variables to per-
form a parameter sweep. A parameter sweep allows you to run through a set of
analyses, with different variable values, all in one step. This allows you to see how
changes in your circuit affect the response of your circuit.
You set up the parameter sweep in the Analysis Setup dialog box in the project
editor. To access this dialog box, select Analysis Setup from the main menu of
the project editor. In the dialog box which appears, select “Parameter Sweep”
from the Analysis Control drop list. For details on using this dialog box, please
refer to Help.
All frequency sweep types are available for a parameter sweep. You may allow
one or multiple variables to change when running a parameter sweep.
Sweep modes allow you to control what variable combinations are analyzed for a
parameter sweep. Sweep modes for a parameter sweep include Linear Sweep,
Corner Sweep, Sensitivity Sweep and Mixed Sweep Combinations.
•A linear sweep analyzes your circuit at every available combination of
variable values.
•A corner sweep allows you to analyze the “extremes” of your variables
by analyzing at all the combinations of the minimum and maximum

Sonnet User’s Guide
190
Rev 16.56
values of the variables as well as at the nominal values. This allows you
to see how your circuit varies over the data range of your variable. For a
corner sweep, the number of combinations which are analyzed is
where Nc is the number of combinations and Nv is the number of inde-
pendent variables selected for the parameter sweep.
•A Sensitivity Sweep allows you to see how “sensitive” your circuit is to
changes in any given variable. The nominal value of each variable is
combined with the maximum and minimum values of the other
variables as well as the nominal values. For a sensitivity sweep, the
number of combinations which are analyzed is
where Nc is the number of combinations and Nv is the number of inde-
pendent variables selected for the parameter sweep.
•Mixed Sweep Combinations allows you to define a range of values for
each variable, then perform an analysis at each possible combination of
variable values. There are four types of sweeps available: Fixed, Linear,
Linear (# steps), and Exponential.
Parameter Sweep Example
For example, the graphics below illustrate a linear parameter sweep of the circuit
“steps” with a single dimension parameter whose value is defined as the variable
“Width.” The parameter sweep starts with a value of 20 mils for the variable and
Nc2Nv1+=
Nc2Nv
1+=
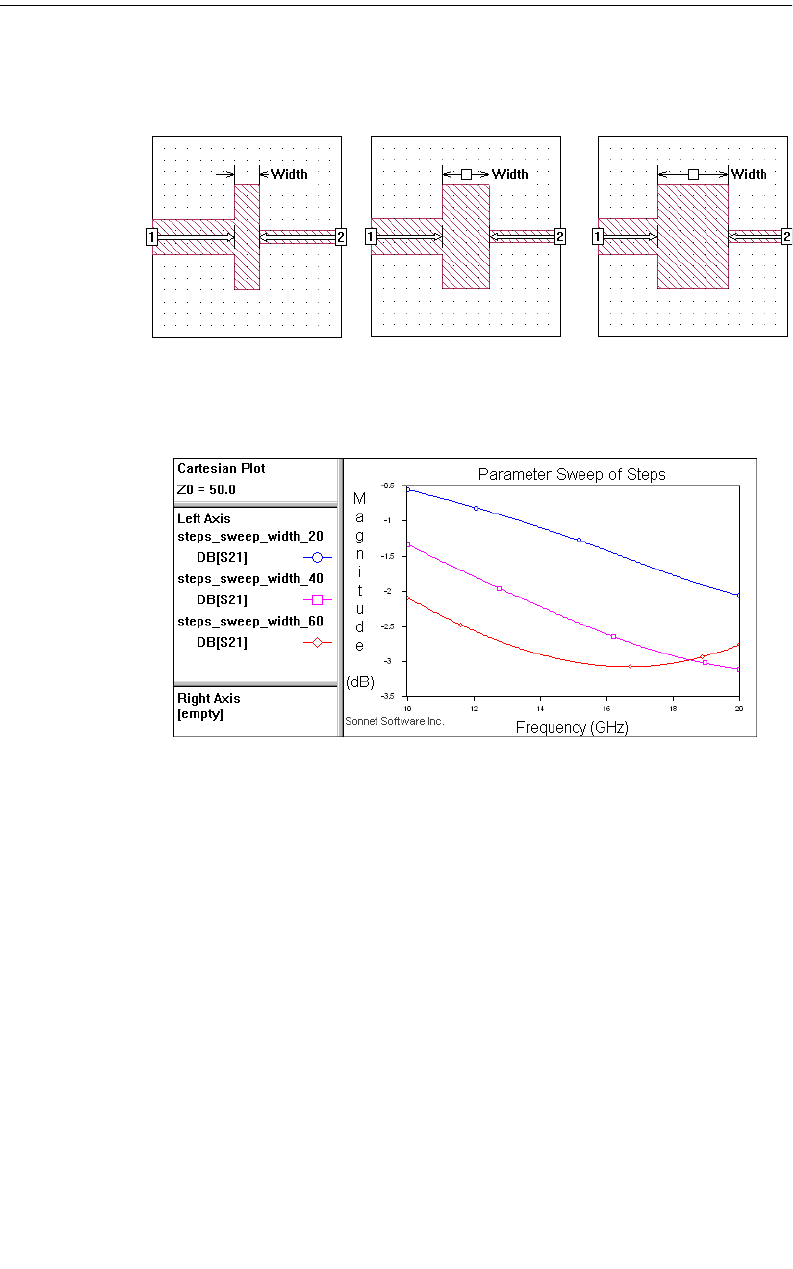
Chapter 9 Parameterizing your Project
191
Rev 16.56
increases in steps of 20 until the variable’s value is 60. Em automatically performs
an analysis at each specified frequency for each circuit shown below when the pa-
rameter sweep is executed.
In the case of this sweep, an ABS analysis from 10 - 20 GHz was performed. The
response data for the parameterization is shown in the graph below.
Width = 20 mils Width = 60 mils
Width = 40 mils
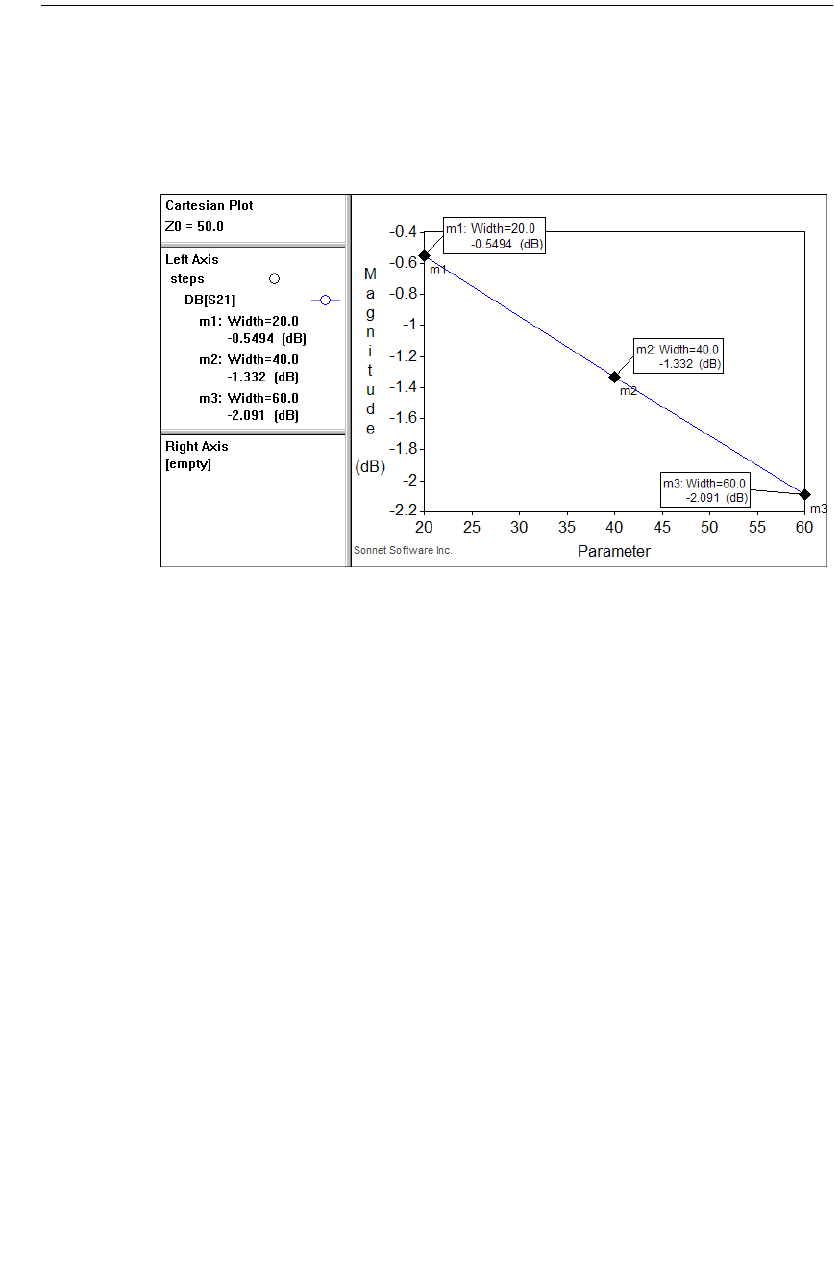
Sonnet User’s Guide
192
Rev 16.56
You may also plot your response data against the parameter values by selecting
the Graph Plot Over Parameter command in the response viewer. Shown
below is the plot of the magnitude in dB of S21 versus the variable Width at 10
Hz. Data markers have been added to the plot for clarity (Graph Marker Add
Data Marker).
Since an analysis of the circuit at each combination of variable values is executed
for each specified analysis frequency, care should be taken when choosing data
ranges. The higher the number of analysis frequencies and variable values, the
higher the number of analyses that must be computed by em. The number of com-
binations specified is displayed in the project editor.
Optimization
You may also use variables to perform an optimization on your circuit. An opti-
mization allows you to specify goals - the desired response of your circuit - and
the data range for the variables(s) over which you seek the response. The software,
using a conjugate gradient method, iterates through multiple variable values,
searching for the best set which meets your desired goals.
The conjugate gradient optimizer begins by analyzing the circuit at the nominal
variable values. It then perturbs each variable individually, while holding the oth-
ers fixed at their nominal values, to determine the gradient of the error function
for that variable. Once it has perturbed each variable, it then performs a line search
in the direction of decreasing error function for all variables. After some iterations
on the line search, the optimizer again calculates the gradients for all variables by

Chapter 9 Parameterizing your Project
193
Rev 16.56
perturbing them from their present “best” values. Following this, a new line search
is performed. This continues until one of three conditions are met: 1) the error
goes to zero 2) the error after the present line search is no better than the error from
the previous line search 3) the maximum number of iterations is reached. When
one of these three conditions is met, the optimizer halts.
The equations used to determine the optimization goal error are as follows:
Setting up an optimization consists of five parts:
•Specifying optimization frequencies
•Specifying your goals
•Choosing which variables to vary
•Specifying data ranges for the chosen variables
•Specifying the maximum number of iterations
EqualOperatorError Simulation f Tetfarg–
N
-----------------------------------------------------------------------------------=
where:
Target(f): Target value of measurement at frequency f.
Simulation(f): Simulated value of measurement at frequency f.
N: Number of frequencies in optimization goal.
GreaterThanOperatorError Tetfarg MIN Simulation fTetfarg[,]–
N
---------------------------------------------------------------------------------------------------------------------------------------=
where:
Target(f): Target value of measurement at frequency f.
Simulation(f): Simulated value of measurement at frequency f.
MIN[]: Determines minimum value of the specified arguments.
N: Number of frequencies in optimization goal.
LessThanOperatorError Simulation f MIN Simulation fTetfarg[,]–
N
------------------------------------------------------------------------------------------------------------------------------------------------
-
=
where:
Target(f): Target value of measurement at frequency f.
Simulation(f): Simulated value of measurement at frequency f.
MIN[]: Determines minimum value of the specified arguments.
N: Number of frequencies in optimization goal.
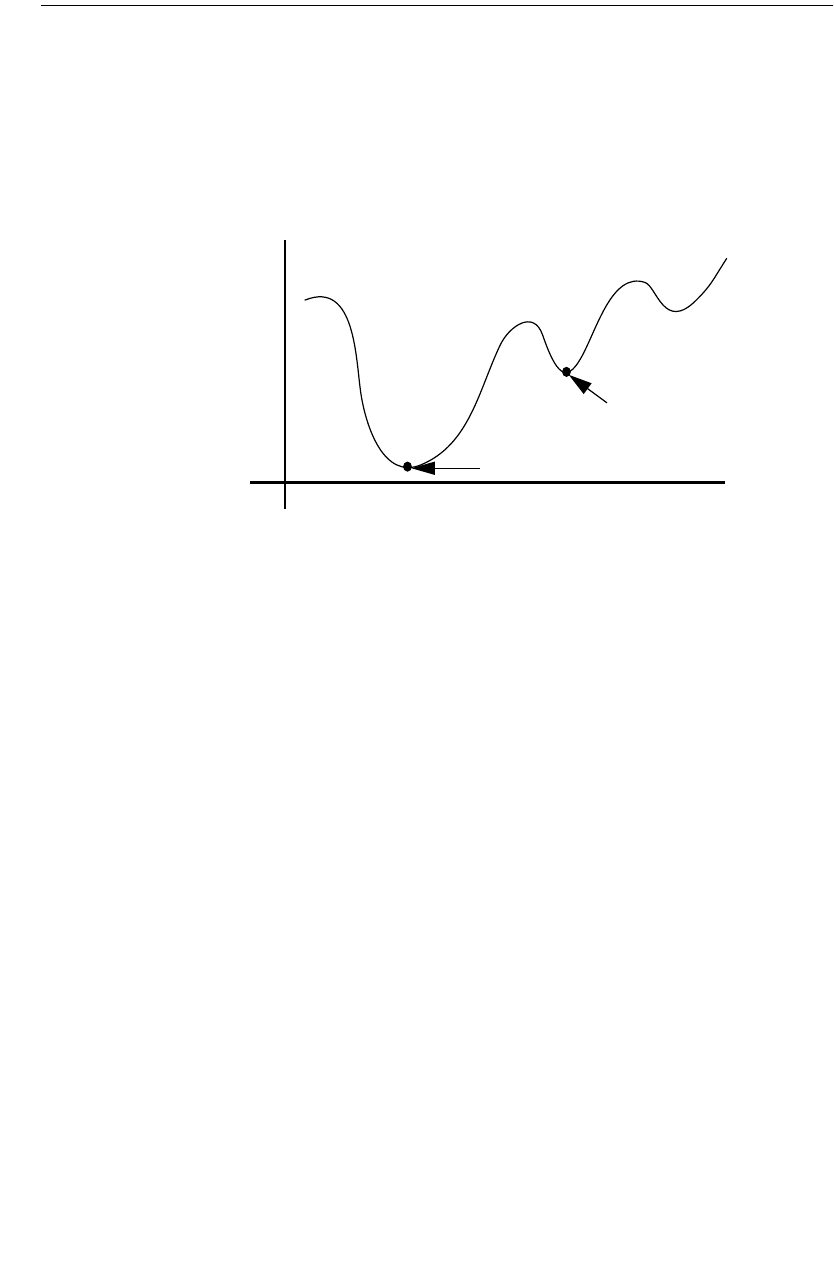
Sonnet User’s Guide
194
Rev 16.56
Care should be taken when setting the nominal values for the variables to be opti-
mized. The optimizer starts at the nominal values and converges to the minima
which is closest to those nominal values. Thus, it is highly recommended that you
perform some pre-analysis prior to doing the optimization to ensure that the nom-
inal values are in the right value range when the optimizer is started. Otherwise,
the optimizer may converge to a local minima for which the error is not the mini-
mum achievable value, as pictured below.
You specify a goal by identifying a particular measurement and what value you
desire it to be. For example S11 < -20 dB. Keep in mind that the goals you specify
may not be possible to satisfy. Em finds the solution with the least error.
You may also specify a goal by equating a measurement in one network to a mea-
surement in another network or file. For example, you may set S11 for network
“Model” equal to S11 for network “Measured.” Likewise, you may equate S11 for
network “Model” to S11 for data file “meas.s2p.”
You may select one or multiple variables to optimize. For each variable that you
select you must specify minimum and maximum bounds. The analysis limits the
variables to values within the specified bounds.
Variables that are used in an optimization have a granularity value assigned to
them; the granularity defines the finest resolution, the smallest interval between
values, of a variable for which em will do a full electromagnetic simulation during
optimization. For values which occur between those set by this resolution, em per-
forms an interpolation to produce the analysis data. By default, the software deter-
mines the granularity, but you may enter a value manually.
You specify the number of iterations. For each iteration, em selects a value for
each of the variables included in the optimization, then analyzes the circuit at each
frequency specified in the goals. Depending on the complexity of the circuit, the
number of analysis frequencies and the number of variable combinations, an op-
timization may take a significant amount of processing time. The number of iter-
Parameter Values
Error
Function
Local Minima
Actual Minimum

Chapter 9 Parameterizing your Project
195
Rev 16.56
ations provides a measure of control over the process. Note that the number of
iterations is a maximum. An optimization can stop after fewer iterations if the op-
timization goal is achieved or it finds a minima (finds no improvement in the error
in further iterations).
Once the optimization is complete, the user has a choice of accepting the optimal
values for the variables resulting from the em analysis. Note that for dimension
parameters, if the results of the optimization are accepted, the actual metalization
in the project editor is the closest approximation which fits the present grid set-
tings. As a matter of fact, em analyzes “snapped” circuits and interpolates to pro-
duce responses for circuits which do not exactly fit the grid. For more information
about the grid, see Chapter 3 "Subsectioning" on page 27.

Sonnet User’s Guide
196
Rev 16.56

Chapter 10 Parameter Sweep and Optimization Tutorial
197
Rev 16.56
Chapter 10 Parameter Sweep and
Optimization Tutorial
This tutorial shows you how to set up variables and dimension parameters in a cir-
cuit, set up and execute a parameter sweep, set up and execute an optimization and
view the results of both a parameter sweep and an optimization. For a detailed dis-
cussion of parameterization and optimization, please refer to Chapter 9.
This tutorial presumes that you are familiar with Sonnet Software, especially the
project editor and the analysis monitor. If you are new to Sonnet, please review
the tutorials in Chapter 4 and Chapter 5 of the Getting Started manual before per-
forming this tutorial.
This tutorial uses the Sonnet example Par_dstub. The example may be obtained
using the Sonnet Example browser.You may access the Sonnet Example browser
by selecting Help Browse Examples from the menu of any Sonnet application.
For instructions on using the Example Browser, please click on the Help button in
the Example Browser window. Save the example to your working directory.
This is an example of a microstrip interdigital bandstop filter. This circuit is used
to perform a parameter sweep and optimization. Most parameter sweeps and op-
timizations will present more of a challenge, but we have deliberately chosen a
simple example to more clearly demonstrate Sonnet’s methodology.
Our goal is to design the bandstop filter such that a stopband exists from 5 - 6 GHz
and the passbands are from 1 - 4 GHZ and 7-10 GHz.

Sonnet User’s Guide
198
Rev 16.56
1 Open the copy you made of the par_dstub example in the project editor.
Par_stub is displayed in the project editor.
Setting Up Dimension Parameters
Before executing either a parameter sweep or optimization, it is first necessary to
add your variables and dimension parameters. Variables should be used for the
properties most critical to the circuit’s response. Dimension parameters should be
added to those dimensions you deem critical to the circuit’s response. These prop-
erties and dimensions are the most likely to change as the design progresses.
For this example, you will enter three dimension parameters: two anchored di-
mension parameters which are linked and one symmetric dimension parameter.
Anchored dimension parameters are referred to as anchored parameters and sym-
metric dimension parameters are referred to as symmetric parameters for the rest
of the tutorial.
An anchored parameter is one in which one end of the dimension parameter is a
fixed point with a point set which moves in reference to that fixed, or anchored
point. A symmetric parameter is one with two reference points and two point sets
which move relative to the center point between the reference points.
Dimension parameters which appear in more than one place in a circuit but are of
the same length and assigned the same variable are linked. Changing the value of
the variable changes the length of both.
For a detailed discussion of variables and their definitions, please refer to "Vari-
ables" on page 172.
Anchored Parameters
The linked anchored parameters are input first, followed by the symmetric.
2 Select Tools Add Dimension Parameter Add Anchored from the project
editor’s main menu.
This places the project editor in Add an Anchored Parameter mode indicated by
the change in cursor. Note that the message “Click Mouse to Specify the Anchor
Point” appears in the status bar at the bottom of the project editor window. As you
add a parameter, directions for each step appear in the status bar.
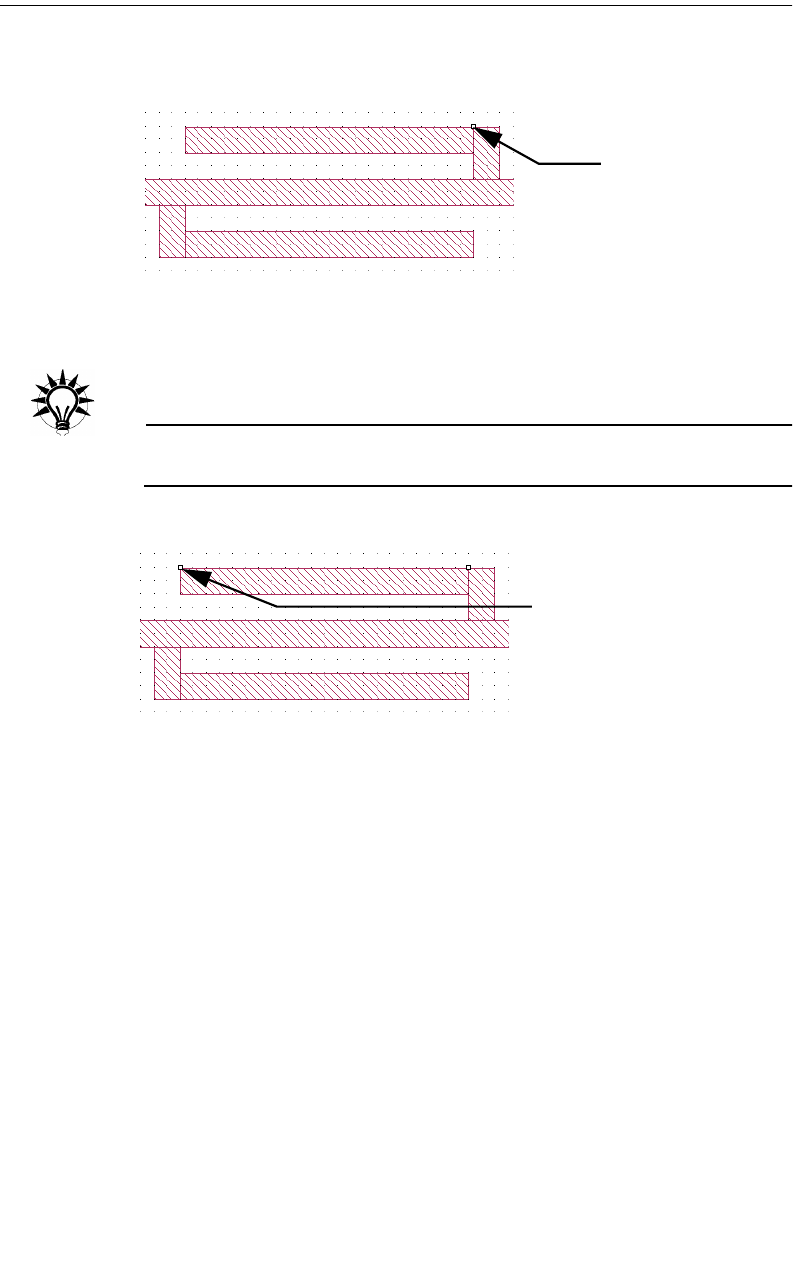
Chapter 10 Parameter Sweep and Optimization Tutorial
199
Rev 16.56
3 To specify the Anchor point for the parameter, click the mouse on the corner
of the upper stub, as shown in the picture below.
The anchor point is indicated by a small square which appears at the point you
clicked. The next step is to select the reference point.
TIP
If you select the wrong point for either the anchor or reference point, press the Es-
cape key to exit without adding a parameter. You may then start over.
4 Click on the top left end of the top stub to add the reference point.
The reference point is indicated by a small square which appears at the point you
clicked.
In the next step, you select the rest of the adjustable point set. Points may be se-
lected by clicking on individual points or by lassoing a set of points with your
mouse. You do not need to select the reference point since it is automatically in-
cluded in the adjustable point set.
Anchor Point
Reference Point
Sonnet User’s Guide
200
Rev 16.56
5 Drag the mouse until both points on the end of the stub are selected.
These points will be added to the adjustable point set. When the reference point
moves in response to a change in the parameter value, these points move relative
to the reference point.
6 Once all the desired points are selected, press Enter.
This completes the dimension parameter creation. The Parameter Properties
dialog box appears on your display.
7 Enter the variable “Lstub” in the Variable Name text entry box in the
Parameter Properties dialog box and click on the OK button.
This assigns the variable “Lstub” to the dimension parameter. When you click on
the OK button an arrow indicating the length and the name appear on your display.
8 Move the mouse until the name is positioned above the stub. When the name
is in the desired position, click on the mouse.
The dimension parameter should now appear as shown below.
Selected Points
Variable Name text
entry box
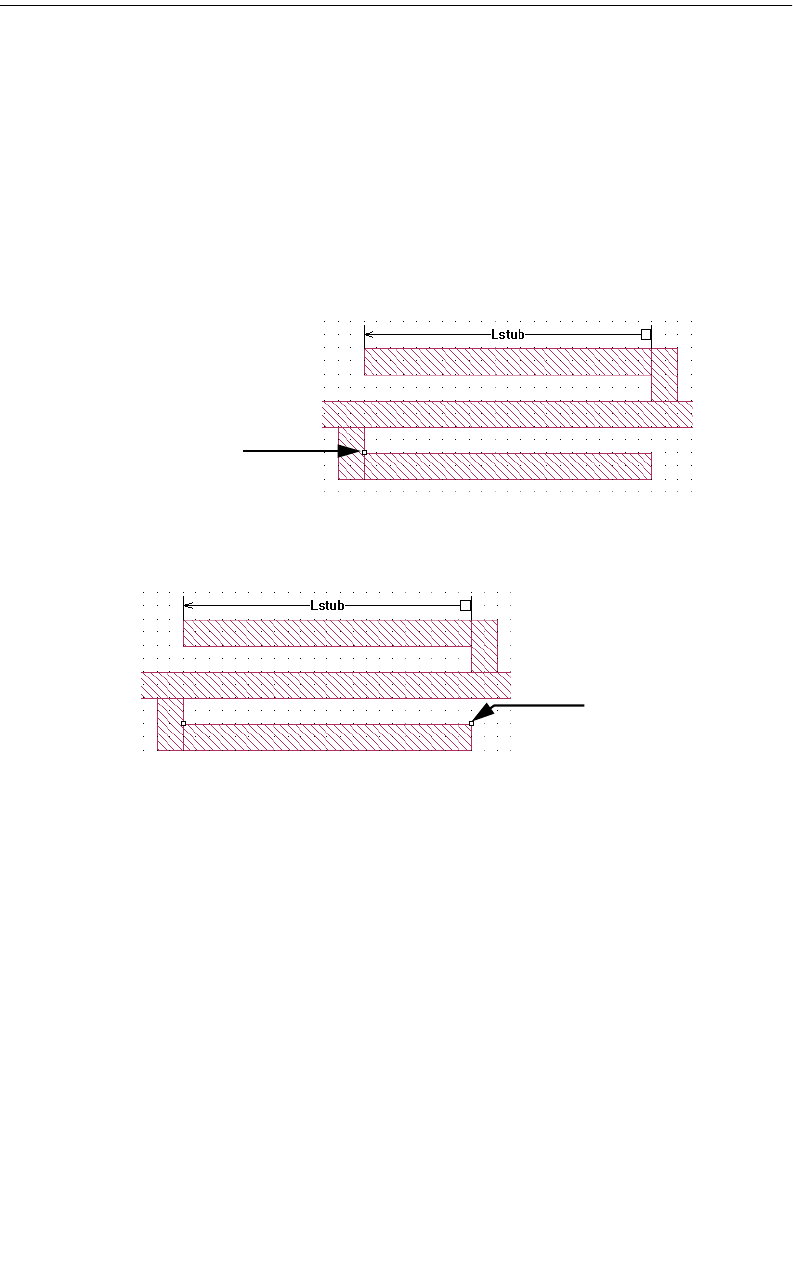
Chapter 10 Parameter Sweep and Optimization Tutorial
201
Rev 16.56
You will now enter the linked dimension parameter. A linked dimension parame-
ter is another dimension parameter identified in the circuit that has the same nom-
inal value and assigned variable.
9 Select Tools Add Dimension Parameter Add Anchored from the project
editor’s main menu.
This places the project editor in Add an Anchored Parameter mode indicated by
the change in cursor.
10 To specify the Anchor point for the parameter, click the mouse on the corner
of the lower stub, as shown in the picture below.
The anchor point is indicated by a small square which appears at the point you
clicked. The next step is to select the reference point.
11 Click on the top right end of the bottom stub to add the reference point.
The reference point is indicated by a small square which appears at the point you
clicked.
In the next step, you select the rest of the adjustable point set. Points may be se-
lected using the any of the edit commands available in the project editor.
Anchor Point
Reference Point

Sonnet User’s Guide
202
Rev 16.56
12 Drag the mouse until both points on the end of the stub are selected.
These points will be added to the adjustable point set. When the reference point
moves, these points move relative to the reference point.
13 Once all the desired points are selected, press Enter.
This completes the dimension parameter creation. The Parameter Properties
dialog box appears on your display.
14 Select the variable name “Lstub” from the drop list in the Variable Name
text entry box in the Properties dialog box and click on the OK button.
This assigns the variable “Lstub” to the dimension parameter. When you click on
the OK button an arrow indicating the length and the variable name appear on your
display. Use your mouse to move the label to the desired location, then click.
Since this dimension parameter’s nominal value is the same as the first parameter
you defined, the project editor allows you to assign the same variable to both di-
mension parameters. These dimension parameters are now linked. A change in
value of the variable changes both dimension parameters. If the dimension param-
eters had been of a different length, the variable name “Lstub” would not have ap-
peared in the list. Entering the variable name manually would invoke an error
message.
Selected Points
Since you have already
created the variable “Lstub”
and this dimension parameter
is the same length as the
dimension parameter to
which “Lstub” is already
assigned, the variable name is
available in the drop list.

Chapter 10 Parameter Sweep and Optimization Tutorial
203
Rev 16.56
Next, you define the last dimension parameter which is symmetric.
Symmetric Parameters
15 Select Tools Add Dimension Parameter Add Symmetric from the project
editor’s main menu.
This places the project editor in Add a Symmetric Parameter mode indicated by
the change in cursor. Note that the message “Click mouse to specify first reference
point” appears in the status bar at the bottom of the project editor window. As you
add a dimension parameter, directions for each step appear in the status bar and as
tool tips on your screen.
16 To specify the first reference point for the dimension parameter, click the
mouse on the intersection of the inside of the top stub to the transmission
line, as shown in the picture below.
The first reference point is indicated by a small square which appears at the point
you clicked. The next step is to select the point set you want attached to the first
reference point.
17 Drag the mouse until all points on the upper stub are selected.
These points will be added to the first adjustable point set. When the first reference
point moves, these points move in the same direction and distance as the reference
point.
First Reference
Point
Selected Points
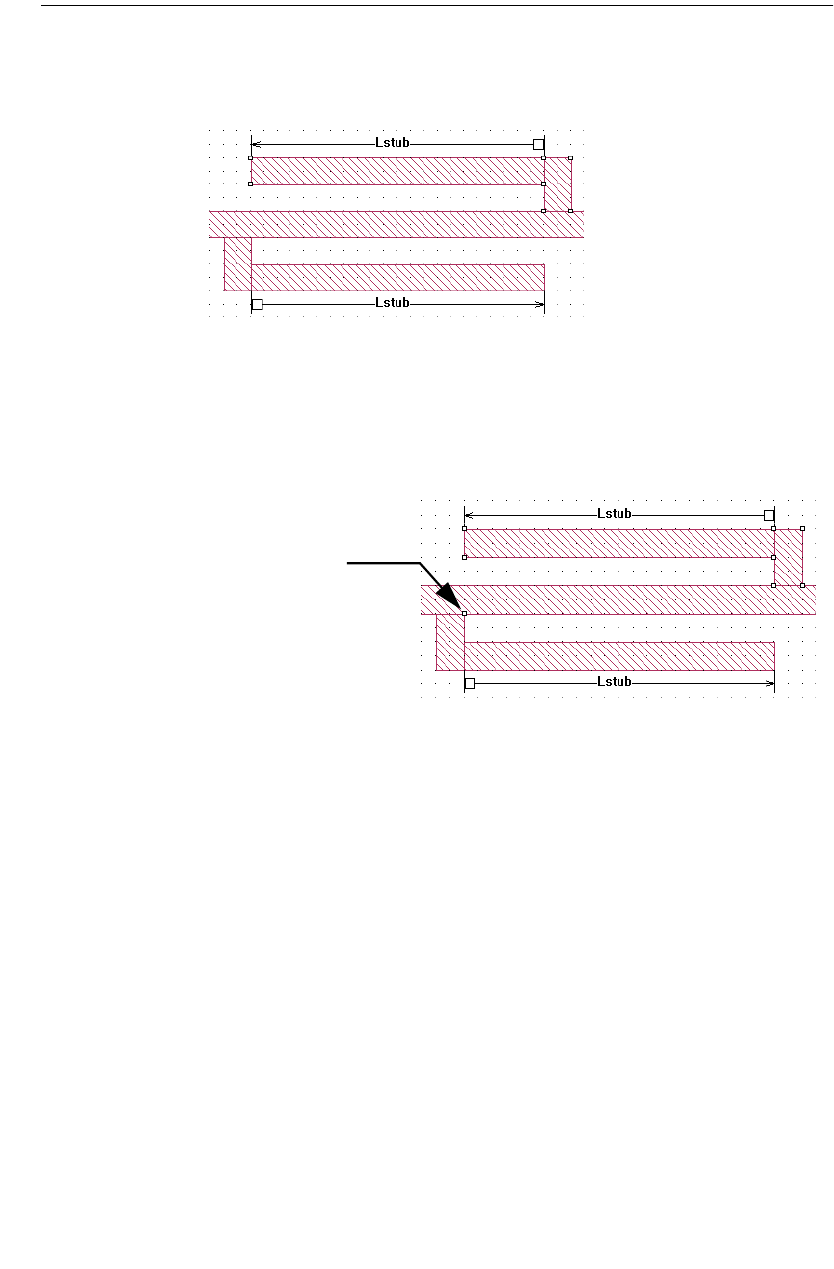
Sonnet User’s Guide
204
Rev 16.56
18 Once all the desired points are selected, press Enter.
This completes the first point set. Your circuit should look similar to this:
The message “Click Mouse to Specify Second Reference Point” appears on your
display. Next, you will specify the second reference point and its point set.
19 To specify the second reference point for the parameter, click the mouse on
the intersection of the inside of the bottom stub to the transmission line, as
shown in the picture below.
The second reference point is indicated by a small square which appears at the
point you clicked. Note that the first point set continues to be identified by small
squares on all its points. The next step is to select the point set you want attached
to the second reference point.
The first point set is
indicated by small open
squares on all the points
in the set.
Second Reference
Point

Chapter 10 Parameter Sweep and Optimization Tutorial
205
Rev 16.56
20 Drag the mouse until all points on the lower stub are selected.
These points will be added to the second adjustable point set. When the second
reference point moves, these points move in the same direction and distance as the
reference point.
21 Once all the desired points are selected, press Enter.
This completes the second point set and the symmetrical parameter. The
Parameter Properties dialog box appears on your display.
22 Enter the name “Sstub” in the Variable Name text entry box in the
Parameter Properties dialog box and click on the OK button.
This assigns the variable “Sstub” to the dimension parameter. When you click on
the OK button an arrow indicating the length and the variable name appear on your
display. Note that since there is a difference between the reference points in both
the x (horizontal) and y (vertical) direction, you may move the parameter name so
that the parameter is defined in either the x or y direction.
If you were to choose the y direction, moving the mouse to the left or right of both
reference points to define your parameter, it would appear like this:
However, for this example, you define the parameter in the x direction, moving
your mouse up or down, above or below both reference points.
Selected Points

Sonnet User’s Guide
206
Rev 16.56
23 Move the mouse until the name is positioned in the middle of the thru line.
When the name is in the desired position, click on the mouse.
This sets the dimension parameter in the x direction. The dimension parameter
should now appear as shown below.
This completes entering the dimension parameters. Note that Lstub is affected by
Sstub. As Sstub increases, although it does not directly affect the value of Lstub,
the two stubs do get further apart. The dimension parameter to which Lstub is as-
signed is dependent on the dimension parameter to which Sstub is assigned. How-
ever, the variable Lstub is NOT dependent on the variable Sstub so that both are
available to be selected for the parameter sweep and optimization covered later in
this tutorial. Only independent variables may be selected for parameter sweeps
and optimization.
24 Select File Save for the project editor main menu.
This saves the changes you have made to the circuit so that you can analyze it.
The next section of the tutorial teaches you how to setup and run a parameter
sweep on the circuit.
Parameter Sweep
The parameter sweep uses only the Lstub variable. You analyze the circuit at two
different lengths for Lstub over a frequency band of 2.0 GHz to 10.0 GHz. When
the sweep is complete, you view the response curves in the response viewer.
For a detailed discussion of a parameter sweep, please refer to “Parameter
Sweep,” page 189.
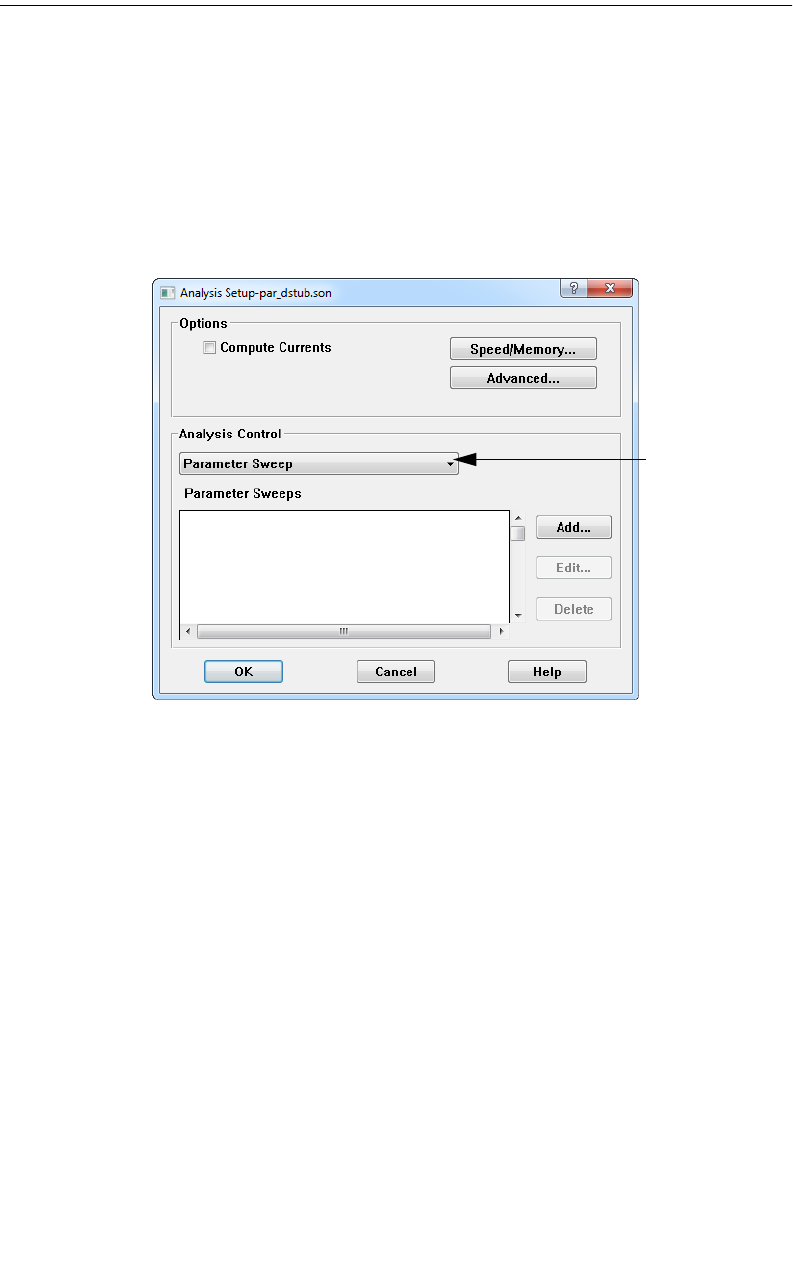
Chapter 10 Parameter Sweep and Optimization Tutorial
207
Rev 16.56
Setting Up a Parameter Sweep
1 Select Analysis Setup from the project editor’s main menu.
The Analysis Setup dialog box appears on your display.
2 Select Parameter Sweep from the Analysis Control drop list.
This selects a parameter sweep as the type of analysis. The dialog box’s
appearance changes to accommodate the input needed for a parameter sweep.
3 Click on the Add Button in the Analysis Control section of the dialog box.
The Parameter Sweep Entry dialog box appears. This dialog box allows you to add
a parameter sweep.
The first step is to specify the analysis frequencies you wish to use for the param-
eter sweep. For this example, you wish to perform an ABS sweep from 2.0 GHZ
to 10.0 GHz. Since Adaptive Sweep (ABS) is the default sweep type, you do not
need to take any action to select it.
4 Enter 2.0 in the Start text entry box in the Frequency Specification section of
the Parameter Sweep Entry dialog box.
This is the starting frequency.
5 Enter 10.0 in the Stop text entry box.
This is the highest frequency. This defines a band of 2 GHz to 10 GHz for the
adaptive sweep.
Next, you will select the variables you wish to sweep.
Analysis Control
drop list
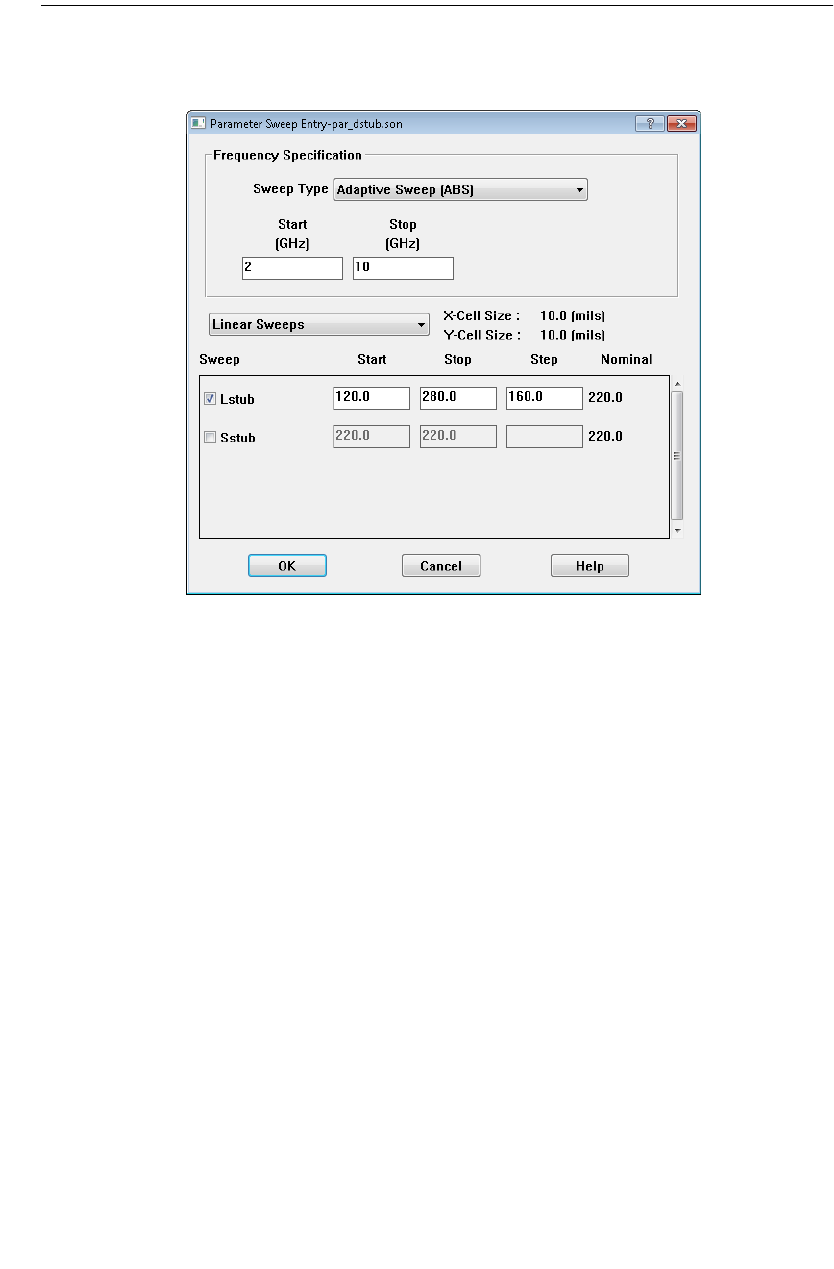
Sonnet User’s Guide
208
Rev 16.56
6 Click on the checkbox in the Sweep column of the entry for the Lstub
variable.
It is possible to select multiple variables for a parameter sweep; however, for this
example, only one variable is used. If you wished to deselect the variable, you
would simply click on the checkbox again. Unchecked variables are simulated at
their nominal value, so Sstub is a constant, fixed at 220 mils for the parameter
sweep.
The nominal value, that is the present value of the variable in the circuit, appears
in the Nominal column of the variable entry. In this case, the nominal value of
Lstub is 220 mils, so the project editor shows the length as 220 mils, even though
the start value for the variable is different.
7 Enter 120 in the Start text entry box in the Lstub row.
This sets 120 mils as the first variable value used for Lstub.
8 Enter 280 in the Stop text entry box in the Lstub row.
This sets 280 mils as the last variable value used for Lstub.
9 Enter 160 in the Step text entry box in the Lstub row.
The interval between variables is 160 mils; therefore, this parameter sweep
analyzes at two variable values, 120 and 280 mils.
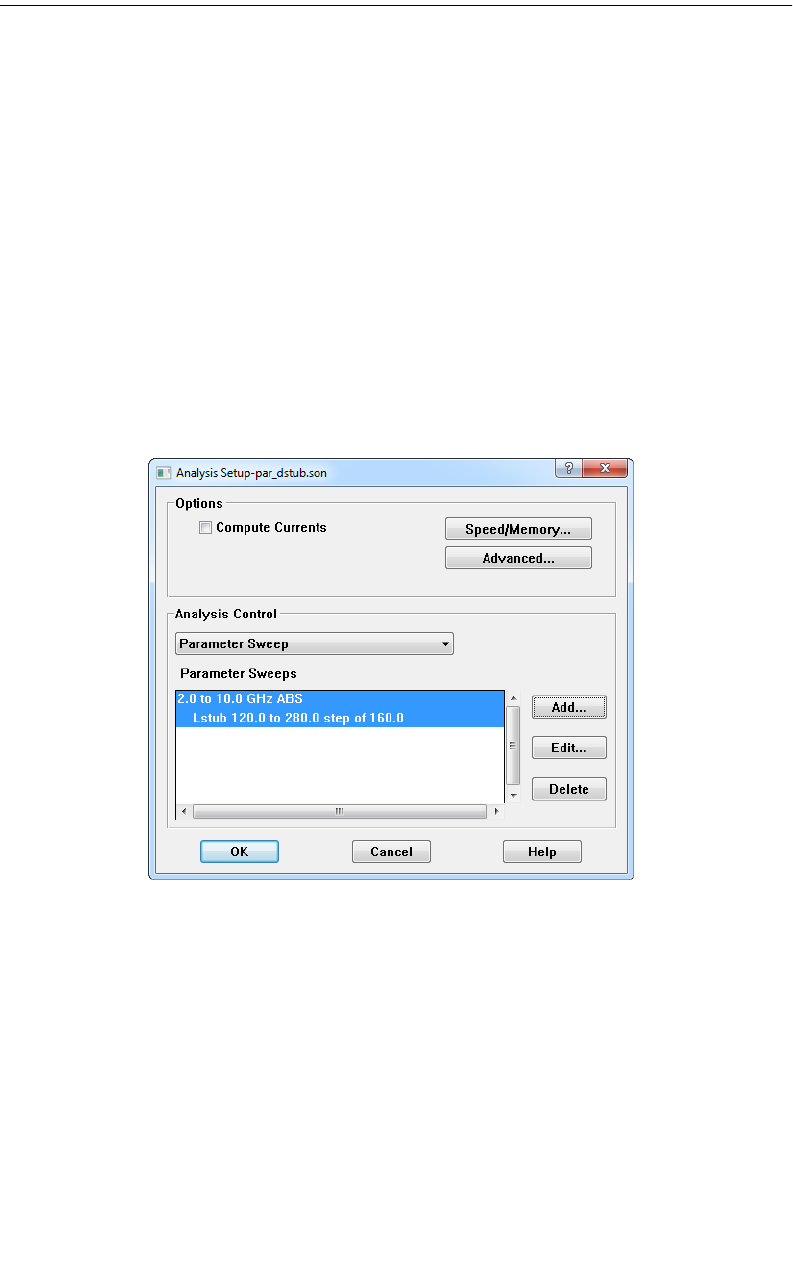
Chapter 10 Parameter Sweep and Optimization Tutorial
209
Rev 16.56
There is a drop list for the Sweep mode just above the entries for the variables. The
default mode of Linear Sweep is used for this example so there is no need to take
any action. For details on sweep modes, please refer to Help by clicking on the
Help button in this dialog box.
This completes the setup for the parameter sweep entry.
10 Click on the OK button to close the dialog box.
When the dialog box is closed, the Analysis Setup dialog box is updated with an
entry for the parameter sweep that you just defined. In this case, since there are
two values for a single variable, there are two parameter combinations. Each com-
bination is analyzed at each analysis frequency.
For example, you have two variables, the first has seven values and the second has
eleven values. In that case, there would be 77 variable combinations for the anal-
ysis.
11 Click on the OK button of the Analysis Setup dialog box.
This completes the entry of the parameter sweep.
Next, you run the analysis and use the analysis monitor to observe the progress.

Sonnet User’s Guide
210
Rev 16.56
Executing the Parameter Sweep
12 Select Project Analyze from the project editor’s main menu to invoke the
analysis engine, em, and start the analysis.
If you are prompted, save the file. The output window of the analysis monitor
appears on your display.
13 Click on the Response Data button in the analysis monitor output window.
This allows you to observe the analysis as it progresses. There is a progress bar at
the top of the window which shows what percentage of the total analysis is
complete with the number of frequencies analyzed appearing above it. The
response data is output in the bottom of the window.
The analysis could take a few minutes to run depending on your computer.
Once the analysis is complete, you open the response viewer to look at your
results.
Observing the Parameter Sweep Data
You want to see the data for the S21 response at Lstub = 120 mils and Lstub = 280
mils.
14 Select Project View Response New Graph from the main menu of the
analysis monitor output window.
The response viewer window appears on your display with S11 displayed.
15 Right click on par_dstub in the Curve Group legend.
A pop-up menu appears on your display.
16 Select Edit Curve Group from the pop-up menu.
The Edit Curve Group dialog box appears on your display.
17 Double click on DB[S11] in the Selected list.
This moves the S11 response to the Unselected list. It will no longer appear in your
plot.
18 Double click on DB[S21] in the Unselected list.
This moves the S21 response to the Selected list so that it appears in your plot.

Chapter 10 Parameter Sweep and Optimization Tutorial
211
Rev 16.56
19 Click on the Select Combinations button in the Edit Curve Group dialog
box.
The Select Parameters dialog box appears on your display. Note that by default
only variables which are varied during the parameter sweep are displayed, so only
Lstub appears. If you wish to also display variables which were not varied, in this
case Sstub, click on the Configure Columns button and select the “Static”
checkbox in the Configure Columns dialog box.
20 Click on the Select All button above the Selected Parameter Combinations
list.
There should be only one entry in this list; the Select All button was used to
demonstrate its function. This selects all the parameters in the Selected List.
21 Click on the Up Arrow button to move all the parameter combinations to the
Unselected list.
22 Double-click on Lstub = 120 mils in the Unselected List.
This moves this parameter combination to the selected list so that the data for this
combination appears in your plot.
23 Click on the OK button in the Select Parameters dialog box to apply the
changes and close the dialog box.
The entry “Lstub = 120.0 Sstub = 220.0” appears in the Parameter Combinations
section of the Edit Curve Group dialog box.
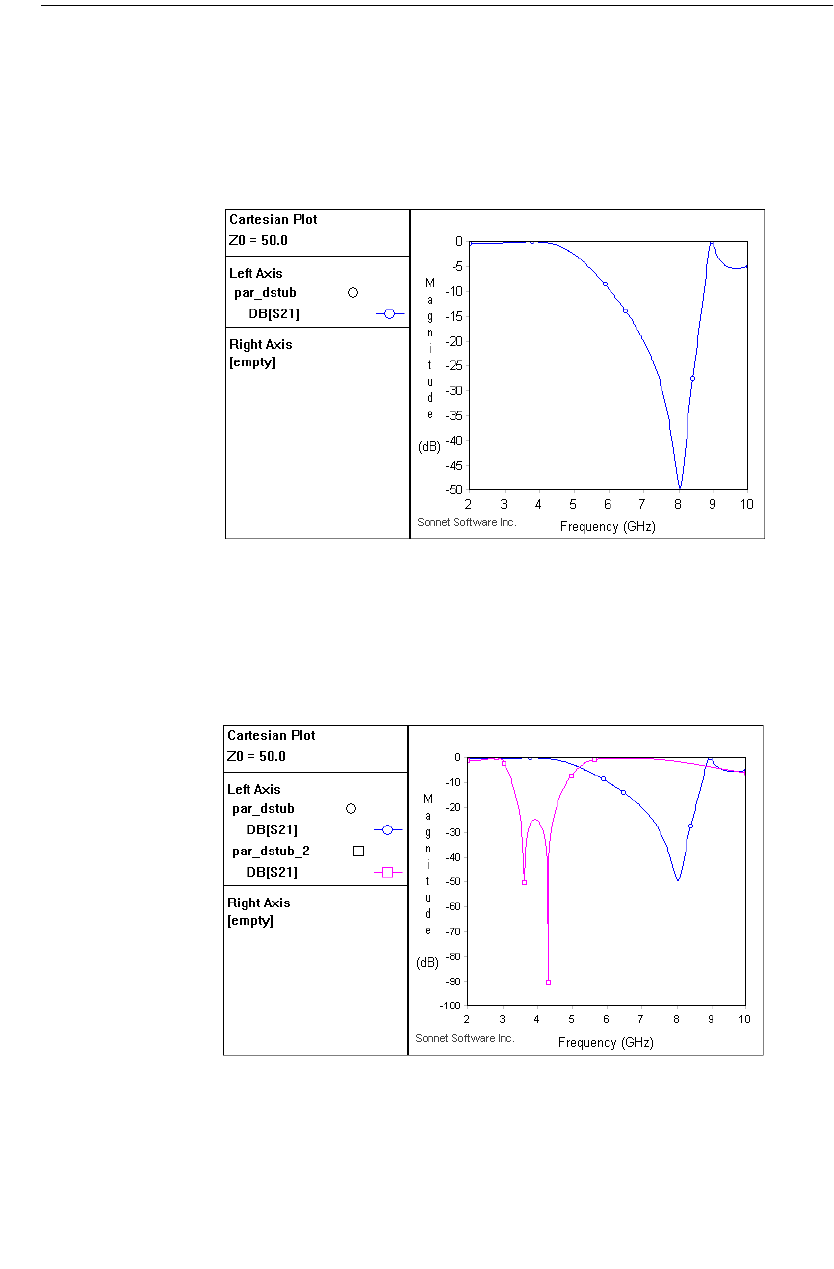
Sonnet User’s Guide
212
Rev 16.56
24 Click on the OK button in the Edit Curve Group dialog box to apply the
changes and close the dialog box.
The plot is updated with the S21 response for Sstub = 220 mils, Lstub = 120 mils.
The entry for the curve group, par_dstub appears in the Curve Group Legend. The
graph should be similar to the one shown below.
25 To add the response at Lstub = 280 mils, select Curve Add Curve Group
from the response viewer main menu.
The Add Curve Group dialog box appears. This curve group uses the default name
of par_dstub_2. Following the same steps you used for par_dstub above, set up
this curve group to display the S21 response for Lstub = 280 mils, Sstub = 220
mils. Your plot should now look like the one below.
You could also have right-clicked the curve group par_dstub in the Left Axis pane
of the legend and selected “Edit Curve Group” from the pop-up menu. Using the
Edit Curve group dialog box, you could have added this parameter combination to
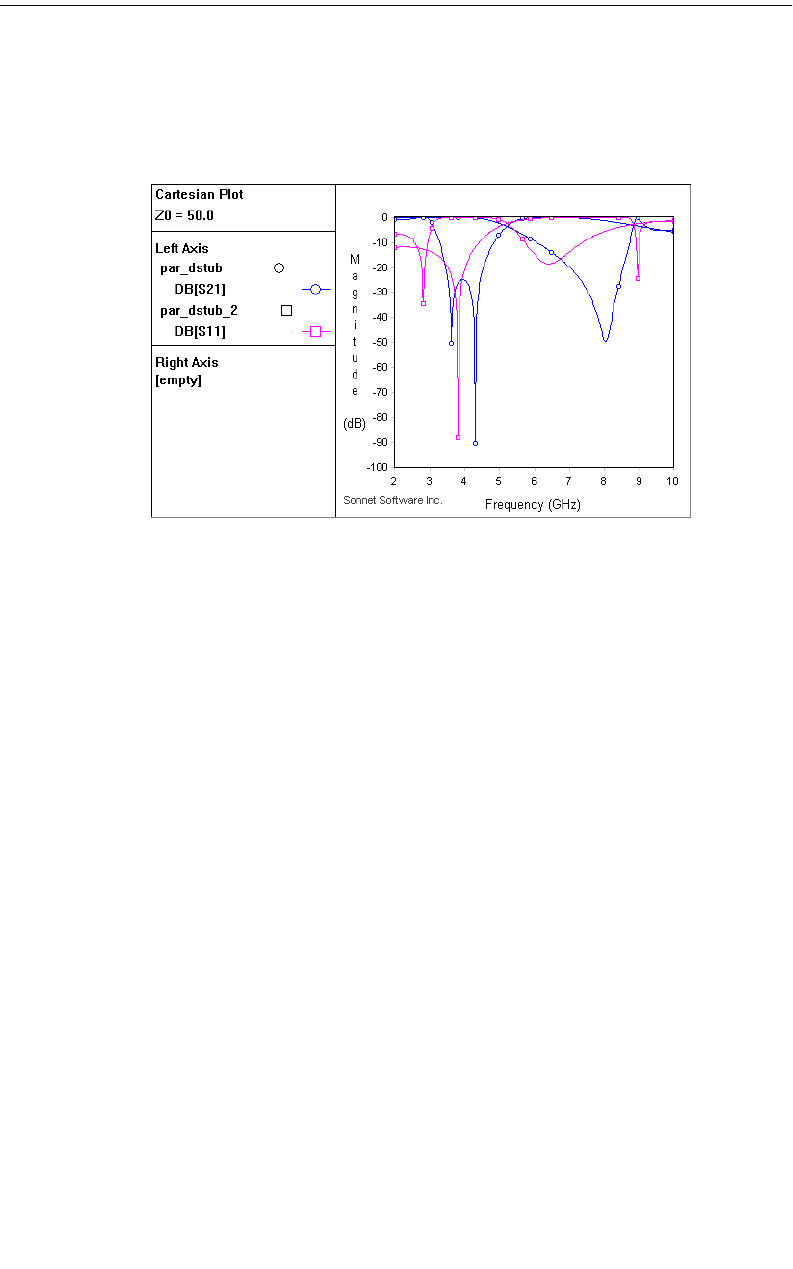
Chapter 10 Parameter Sweep and Optimization Tutorial
213
Rev 16.56
this curve group. This would result in one curve group with one symbol represent-
ing both parameter combinations. This is useful if you want multiple measure-
ments (S21 and S11 for example). Each measurement would use a different
symbol, but each parameter combination with a measurement would use the same
symbol. An example is pictured below.
In the beginning, the goal of the filter design was stated as a stopband between 5.0
and 6.0 GHz. By looking at the graph of Lstub=120 as compared to Lstub=280,
you can see that a filter with the required stopband would fall approximately in the
middle of the two curves. So a value of 220 mils is chosen for the nominal value
for Lstub for the optimization. A nominal value of 200 mils is chosen for Sstub.
Optimization
This next section of the tutorial shows how to set up and execute an optimization.
For a detailed discussion of optimization, please refer to "Optimization" on page
192.
If par_dstub.son is not still open in the project editor, open the file in the project
editor.
Sonnet User’s Guide
214
Rev 16.56
Entering New Nominal Values
Usually for this type of circuit, you would optimize using both of the defined pa-
rameters, Lstub and Sstub, but for the sake of processing time, the optimization
only uses one parameter, Lstub.
The nominal value used for Sstub will be 200 mils. This was arrived at by actually
executing the optimization using both parameters and using the closest value on
the grid of the optimized parameter.
26 Double-click on the parameter Sstub in the circuit.
The Parameter Properties dialog box for Sstub appears on your display.
27 Change the nominal value in the Nominal text entry box to 200.
28 Click on the OK button to close the dialog box and apply the new nominal
value.
The circuit is redrawn using the new nominal value for Sstub.
!WARNING
It is recommended that you change the nominal value of dimension
parameters by using the properties dialog box, since changing your nominal
value this way does not affect any previous response data in your project file.
If you change the nominal value of the dimension parameter by changing the
circuit through editing commands, such as a reshape, all previous response
data is deleted from the project file when you save.
Setting Up an Optimization
29 Select Analysis Setup from the main menu of the project editor.
The Analysis Setup dialog box appears on your display.
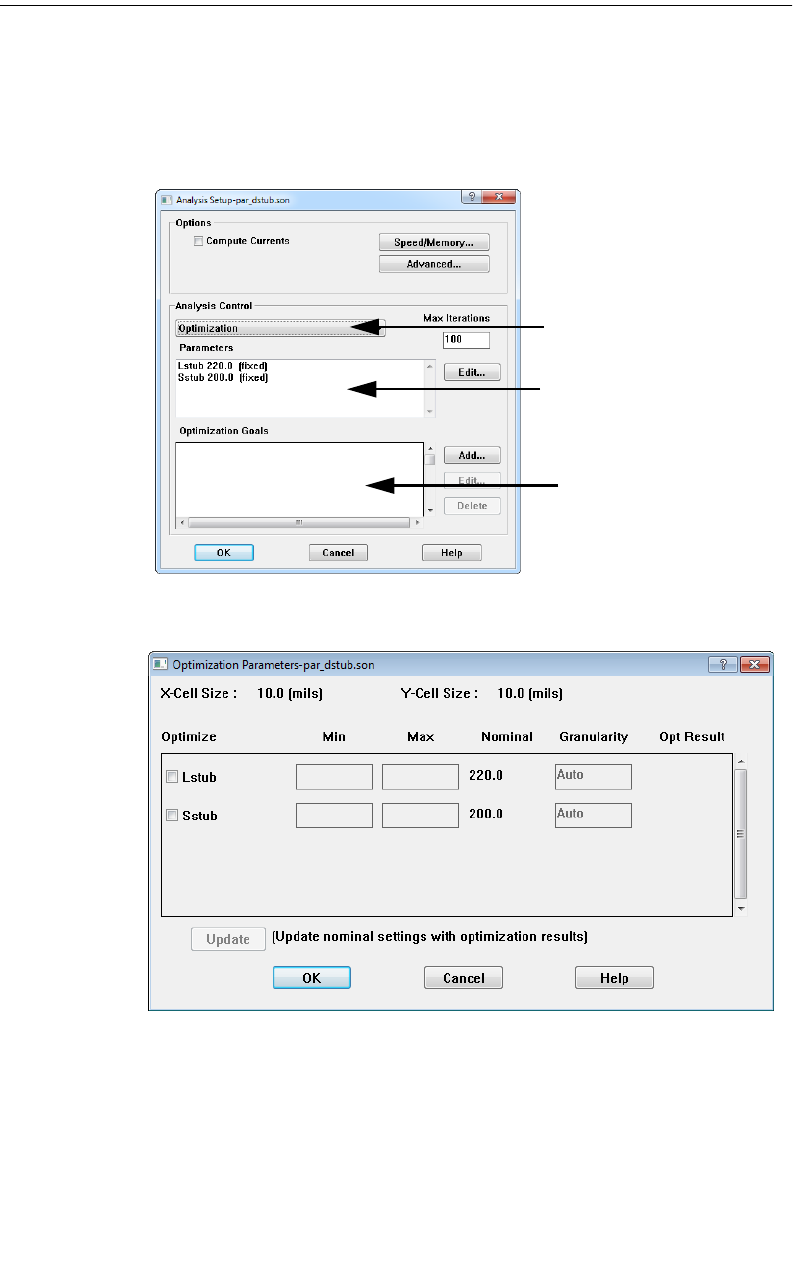
Chapter 10 Parameter Sweep and Optimization Tutorial
215
Rev 16.56
30 Select Optimization from the Analysis Control drop list.
This selects a optimization as the type of analysis. The dialog box’s appearance
changes to accommodate the input needed for an optimization. Note that initially
the nominal values are listed for the variables, since no range has yet been
specified.
31 Click on the Edit button on the right side of the Variables list.
The Optimization Parameters dialog box appears on your display.
Only one variable, Lstub, is used for this optimization. The range for Lstub is 100
mils to 300 mils.
Analysis Control
drop list
Variables list
Optimization Goals
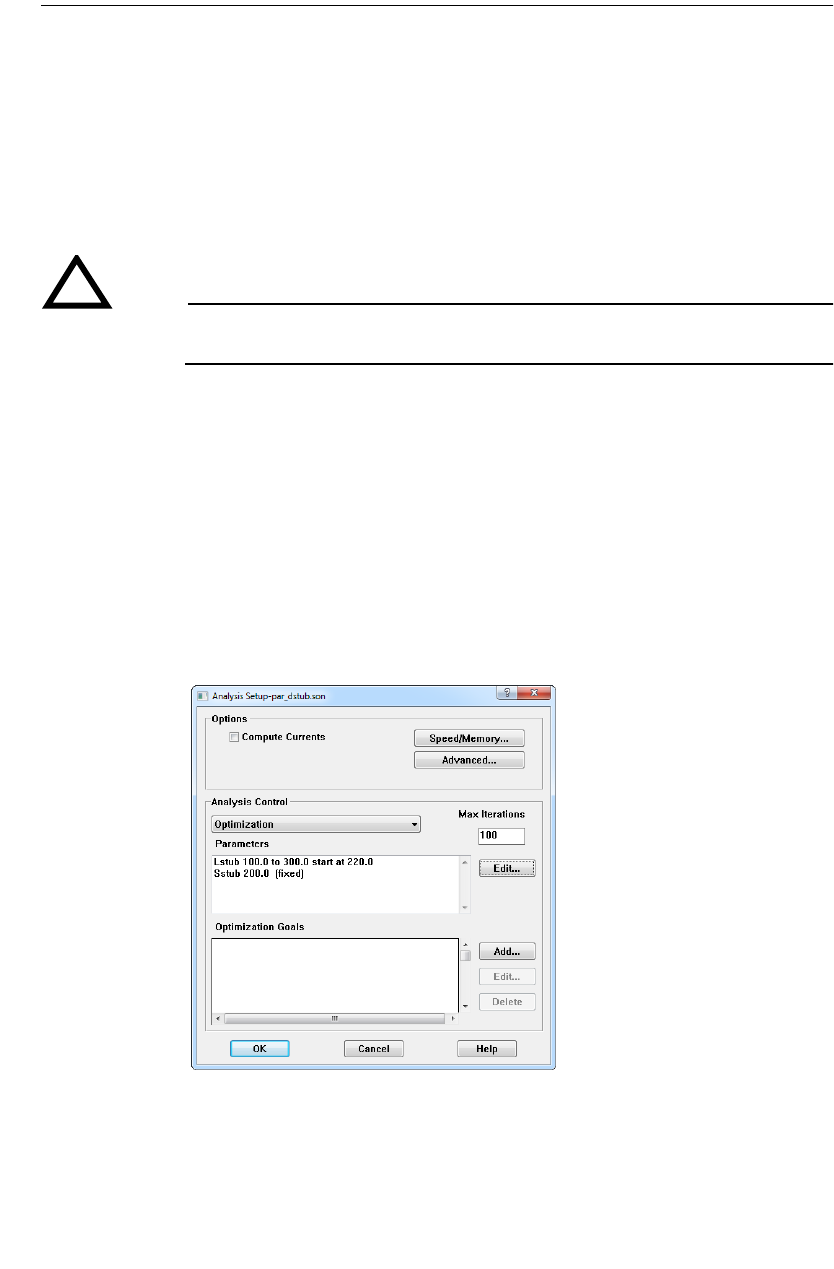
Sonnet User’s Guide
216
Rev 16.56
32 Click on the Optimize checkbox next to Lstub.
This selects the Lstub variable to be used in the optimization. Note that the
nominal value appears in the Nominal text entry box. If you wish to change the
nominal value, you may do so by entering a new value. The circuit will be redrawn
using the new nominal value. Since this is the first optimization run on this project
file the Min and Max entries are blank. If a previous optimization had been run,
the last entered values would remain.
!WARNING
Editing parameter settings or optimization goals causes any pre-existing
optimization iterations to be deleted from the project file.
33 Enter 100 in the Min text entry box in the Lstub row.
This sets the minimum value for the Lstub variable to 100 mils for the
optimization.
34 Enter 300 in the Max text entry box in the Lstub row.
This sets the maximum value for Lstub to 300 mils for the optimization.
35 Click on the OK button to apply the changes and close the dialog box.
When the dialog box is closed, the Analysis Setup dialog box is updated with an
entry for the optimization variables that you just defined.
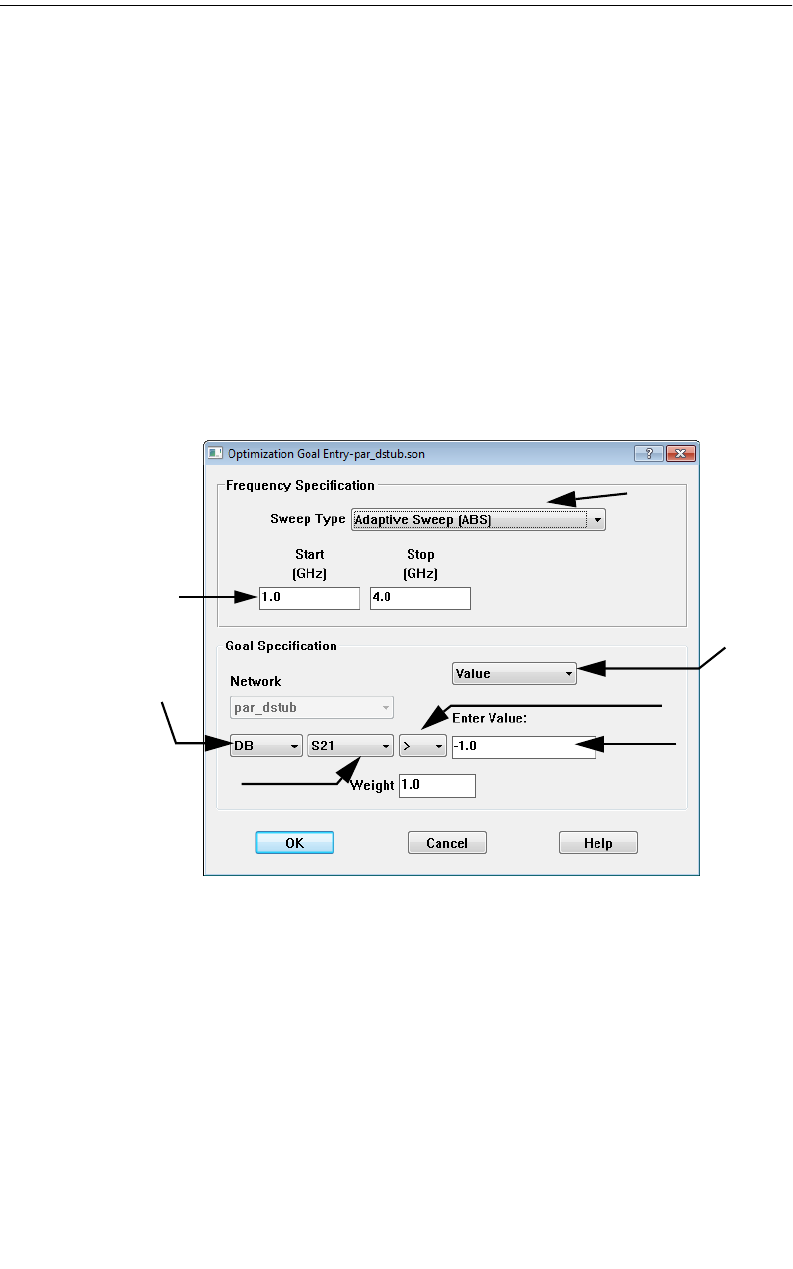
Chapter 10 Parameter Sweep and Optimization Tutorial
217
Rev 16.56
Now that you have identified which variable to vary and its range, you must spec-
ify the optimization goals. Since this is the first optimization for this project, there
are no previously defined optimization goals and the list is empty. Having no goals
present disables the Edit and Delete buttons. The Edit button allows you to modify
an existing goal, and the delete button removes the goal from the list.
As mentioned earlier in the example, our goal for the filter is to have passbands at
1-4 GHz and 7-10 GHz with a stopband at 5-6 GHz. The optimization goals are
set up accordingly. Since all three goals in this case are equally important, each
uses the default Weight of 1.0. In cases where one goal is more essential, assigning
it a higher weight than other goals tells em to concentrate more on reaching that
particular goal.
36 Click on the Add button to the right of the Optimization Goals list.
The Optimization Goal Entry dialog box appears on your display.
The first goal corresponds to the first passband; therefore, you need to set the ABS
frequency range to 1.0 GHz to 4.0 GHz. There are several different types of fre-
quency sweeps available; you will use the default ABS sweep for this optimiza-
tion.
37 Enter 1.0 in the Start text entry box in the Frequency Specification section of
the dialog box.
This sets the beginning of the frequency band for this optimization goal at 1.0
GHz.
Sweep
Type
Specification
Response Type
drop list
Response
drop list
Operand
Goal Type
Value text
entry box
Frequency
Controls

Sonnet User’s Guide
218
Rev 16.56
38 Enter 4.0 in the Stop text entry box in the Frequency Specification section of
the dialog box.
This sets the end of the frequency band for this optimization goal at 4.0 GHz. This
completes the specification of the frequency sweep for this optimization goal.
Since this is the first passband, your goal is to have DB[S21] be greater than -1.0
dB.
39 Select DB from the Response Type drop list on the left side of the equation.
This is the default, so DB may already be selected.
40 Select S21 from the Response drop list.
The display is updated with “S21.”
41 Select “>” from the Operand drop list.
The display is updated with “>.”
42 Select Value from the Goal Type drop list.
This choice allows you to put in a specific value. This is the default; you may also
specify another project file or another network in your project (if the project is a
Netlist project). In those cases, you may select a response for that circuit to which
you wish to match your selected response.
43 Enter -1.0 in the Value text entry box.
This sets your goal of DB[S21] > -1.0 dB.
44 Click on OK to apply the changes and close the dialog box.
The Analysis Setup dialog box is updated. An entry for this optimization goal now
appears in the Optimization Goals list.
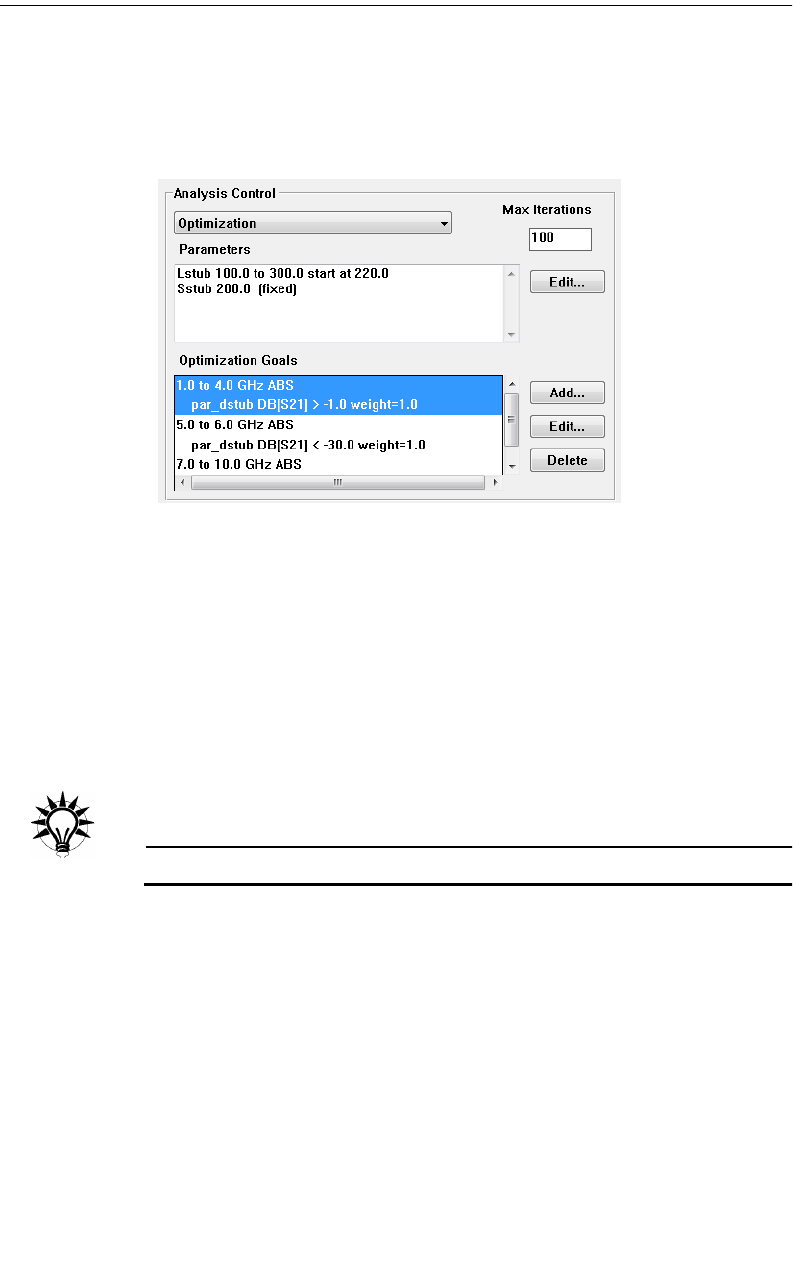
Chapter 10 Parameter Sweep and Optimization Tutorial
219
Rev 16.56
The other two goals should be entered in a similar manner. The second goal is a
adaptive sweep from 5.0 GHz to 6.0 GHz with a desired response of DB[S21] < -
30.0 dB. This is the stopband. The third goal is an adaptive sweep from 7.0 GHz
to 10.0 GHz with a desired response of DB[S21] > -1.0. When you have complet-
ed entering these goals, the Optimization Goals list should appear as shown below.
This completes the setup for the optimization.
Running an Optimization
This optimization took approximately 6.5 minutes on a 2 GHz Pentium 4.
45 Select Project Analyze from the main menu of the project editor.
The output window of the analysis monitor appears on your display.
TIP
You can also click on the Analyze button on the project editor tool bar.
46 Click on the Response Data button in the analysis monitor output window if
it is not already displaying the response data.
This allows you to observe the optimization as it progresses. The error for the first,
present and best iteration are displayed and updated as the optimization
progresses. The response data is output in the bottom of the window.

Sonnet User’s Guide
220
Rev 16.56
You may notice that some iterations complete more quickly than others. This is
because em can reuse portions of the response data calculated for previous itera-
tions.
Once the analysis is complete, you open the response viewer to look at your
results. Be aware that since this optimization took a number of iterations to
conclude, there may be small delays in opening the response viewer and the Edit
Curve Group dialog box.
TIP
You may use the response viewer to observe data produced by the optimization
while it is still running. The response viewer can chart any data which has been
generated. This allows you to stop the optimization and start it over using new
variable ranges or new goals, if the results are not desirable. If you wish to contin-
ue viewing data as the optimization runs, use the Freshen Files command in the
Response Viewer.
Observing your Optimization Data
Plotting the best iteration will allow you to judge whether or not to use the opti-
mized values of the parameters.
47 Select Project View Response New Graph from the main menu of the
analysis monitor.
The response viewer menu appears on your display with the DB[S11] response for
the nominal values parameter combination displayed. There may be some delay
while the project loads into the response viewer due to the amount of response data
now included.
The plot will display the last plot for par_dstu.son that you had open the last time
the response viewer was invoked for this project.
48 Click on a curve group in the legend to select it and select Curve Edit
Curve Group from the main menu of the response viewer.
The Edit Curve Group dialog box appears on your display.
49 Select Optimized from the Data Collection drop list in the Edit Curve Group
dialog box.
Notice that this drop list is now enabled since the project file now contains both
parameter sweep data and optimized data.

Chapter 10 Parameter Sweep and Optimization Tutorial
221
Rev 16.56
50 Move DB[S21] to the Selected list and all other responses to the Unselected
list.
Since your optimization goals were set in reference to the DB[S21] response, you
want to plot this response.
Notice that when you selected Optimized data that the parameter combination was
updated to read:
The best iteration is plotted by default when you select optimized data. If the op-
timization was still running, this provides a useful way of always plotting the best
iteration calculated thus far. Pressing the Freshen Files button on the tool bar of
the response viewer will always show the best iteration.
If you were to click on the Select Iterations button, the dialog box would appear
with all the variable values used in all 25 iterations available to plot. Since you
wish to see the response at the best iteration, you do not need to change the param-
eter value for this curve group.

Sonnet User’s Guide
222
Rev 16.56
51 Click on the OK button to close the dialog box and apply the changes.
The plot is updated showing DB[S21] for the best iteration. It should appear
similar to the plot pictured below.

Chapter 10 Parameter Sweep and Optimization Tutorial
223
Rev 16.56
As you can see, the optimized circuit is producing the desired response of a stop-
band from 5 - 6 GHz and the passbands from 1 - 4 GHZ and 7-10 GHz.
Accepting the Optimized Values
Since the desired responses have been achieved by the optimization, you return to
the project editor to update the nominal value of your parameters with the opti-
mized values.
If the project par_dstub is still open in the project editor, continue at step 54.
52 Click on the curve group, par_dstub in the Curve Group legend in the
response viewer.
This selects a project file and thereby enables the project menu.
53 Select Project Edit from the main menu of the response viewer.
The project editor appears on your display with par_dstub open.
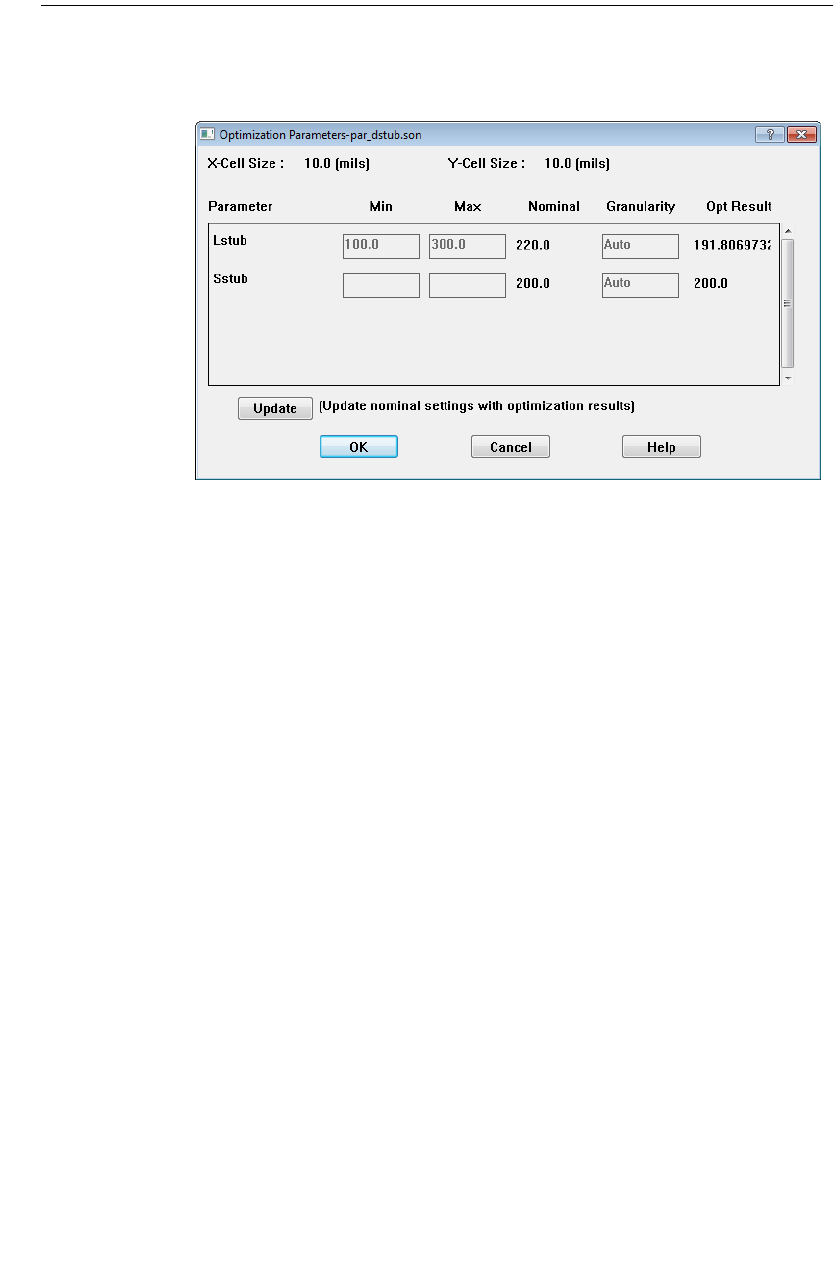
Sonnet User’s Guide
224
Rev 16.56
54 Select Analysis Optimization Results from project editor main menu.
The Optimization Parameters dialog box appears on your display.
Notice that the nominal value of both variables is still the value input at the begin-
ning of the optimization. But the optimization results for both variables are dis-
played in the last column. Since Sstub was not used in the optimization, its
optimization result is the same as the nominal value.
55 Click on the Update button to replace the present nominal values with the
optimization results.
Note that the entries in the Nominal text entry boxes are updated with the
optimized values.
56 Click on OK to close the dialog box and apply the changes.
Notice that the circuit has been redrawn with the new nominal values for the
dimension parameters. Since the parameter lengths are not integer multiples of the
cell size, the polygons are no longer exactly on the grid. You can see this by
pressing Ctrl-M to turn off the cell fill and looking at the actual polygons. The cell
fill represents the actual metal em analyzes.
The actual metalization analyzed by em is not the same as the optimized values.
Em actually interpolated from data created from analyzing “on grid” versions of
the circuit. If your optimization goals did not include a full frequency sweep, it is
a good idea to perform a full sweep across your frequency band to ensure that your
entire band shows reasonable results. Running a full frequency sweep is detailed
below.
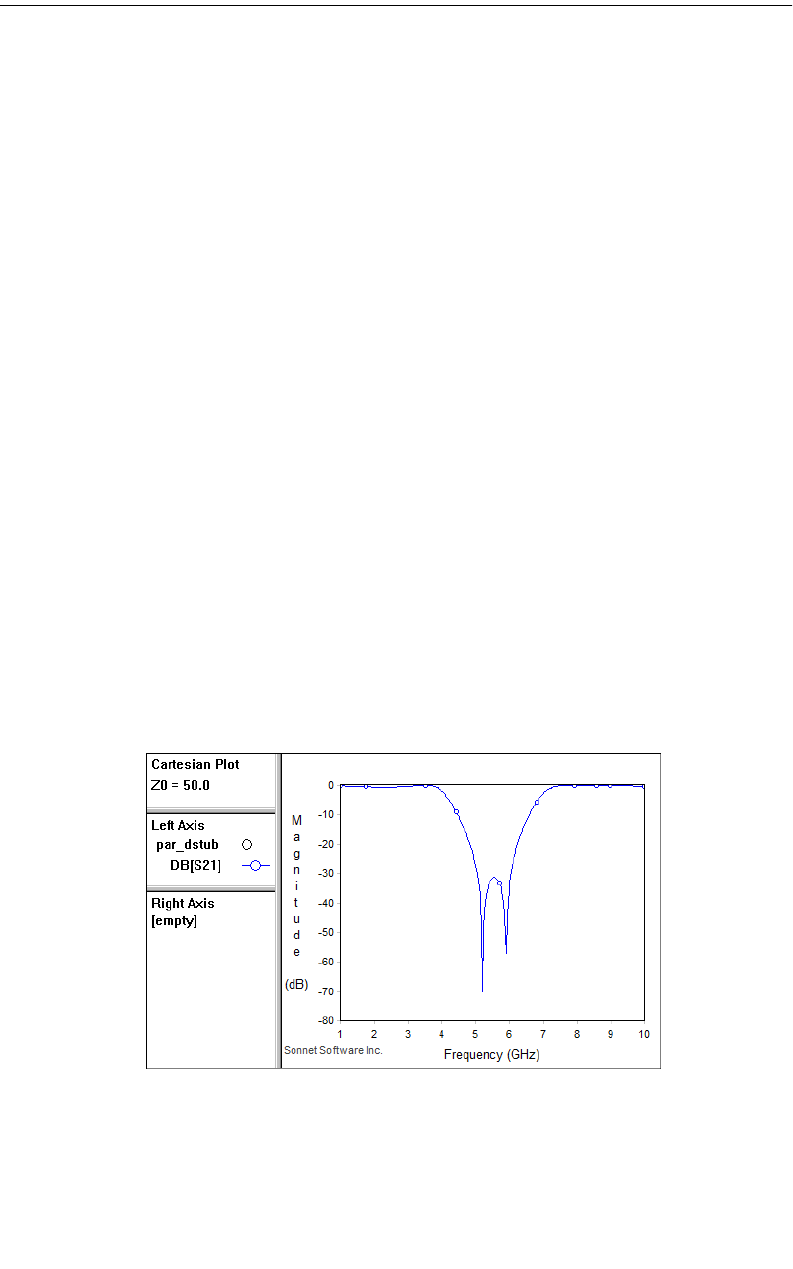
Chapter 10 Parameter Sweep and Optimization Tutorial
225
Rev 16.56
In order for em to use previously calculated response data, you should edit your
variable value(s) such that they are the closest “on grid” value to the optimization
result. For example, in this case the optimized value for Lstub is 191.6134. You
should edit the nominal value of Lstub to change it to 190 which, since the cell
size is 10, is on the grid.
57 Select Analysis Setup from the project editor main menu.
The Analysis Setup dialog box appears on your display.
58 Select Adaptive Sweep (ABS) from the Analysis Control drop list.
The appearance of the dialog box is changed to conform with an adaptive sweep.
Enter 1.0 GHz in the Start text entry box and 10 GHz in the Stop text entry box to
define a frequency band of 1 - 10 GHz for this analysis.
59 Click on OK to close the dialog box and apply the changes.
60 Click on the Analyze button to start the em analysis.
If prompted, save the circuit before analyzing.
61 When the analysis is complete, click on the View Response button on the
analysis monitor’s tool bar.
The response viewer appears on your display with the curve group, par_dstub,
from the last plot.
62 Right-click on the curve group, par_dstub, and select Edit Curve Group
from the pop-up menu which appears.
Select DB[S21] for display, the Nominal parameter combination, and close the
dialog box. Your plot should appear similar to that shown below.

Sonnet User’s Guide
226
Rev 16.56
The results conform closely enough to the design criteria that this optimization is
considered a success. As was stressed at the beginning of this tutorial, a simple ex-
ample was chosen in order to clearly demonstrate the optimization process.
You should be aware, however, that most optimization problems are much more
complicated and less straightforward. The designer needs to make decisions about
parameters, the parameter sweeps and optimization goals based on knowledge of
the circuit and design experience. Often, you must observe an optimization while
in progress, judge its viability and, as necessary, stop the optimization and start a
new one with new nominal values and data ranges.

Chapter 11 Conformal Mesh
227
Rev 16.56
Chapter 11 Conformal Mesh
Introduction
Analyzing circuits which have non-rectangular polygons can require extensive
memory and processing time since the number of subsections needed to model the
non-rectangular shapes is significantly higher than the number of subsections re-
quired for a rectangular polygon. Conformal meshing is a technique which can
dramatically reduce the memory and time required for analysis of a circuit with
diagonal or curved polygon edges.
This technique groups together strings of cells following diagonal and curved
metal contours. Whereas staircase fill results in numerous small X- and Y-directed
subsections, conformal mesh results in a few long conformal subsections. Fewer
subsections yields faster processing times with lower memory requirements for
your analysis.
In older meshing techniques, large non-rectangular subsections did not include the
high concentration of current on the edge of the lines required by Maxwell’s equa-
tions. The results could significantly under-estimate loss and inductance. In con-
trast, the Sonnet conformal meshing automatically includes the high edge current
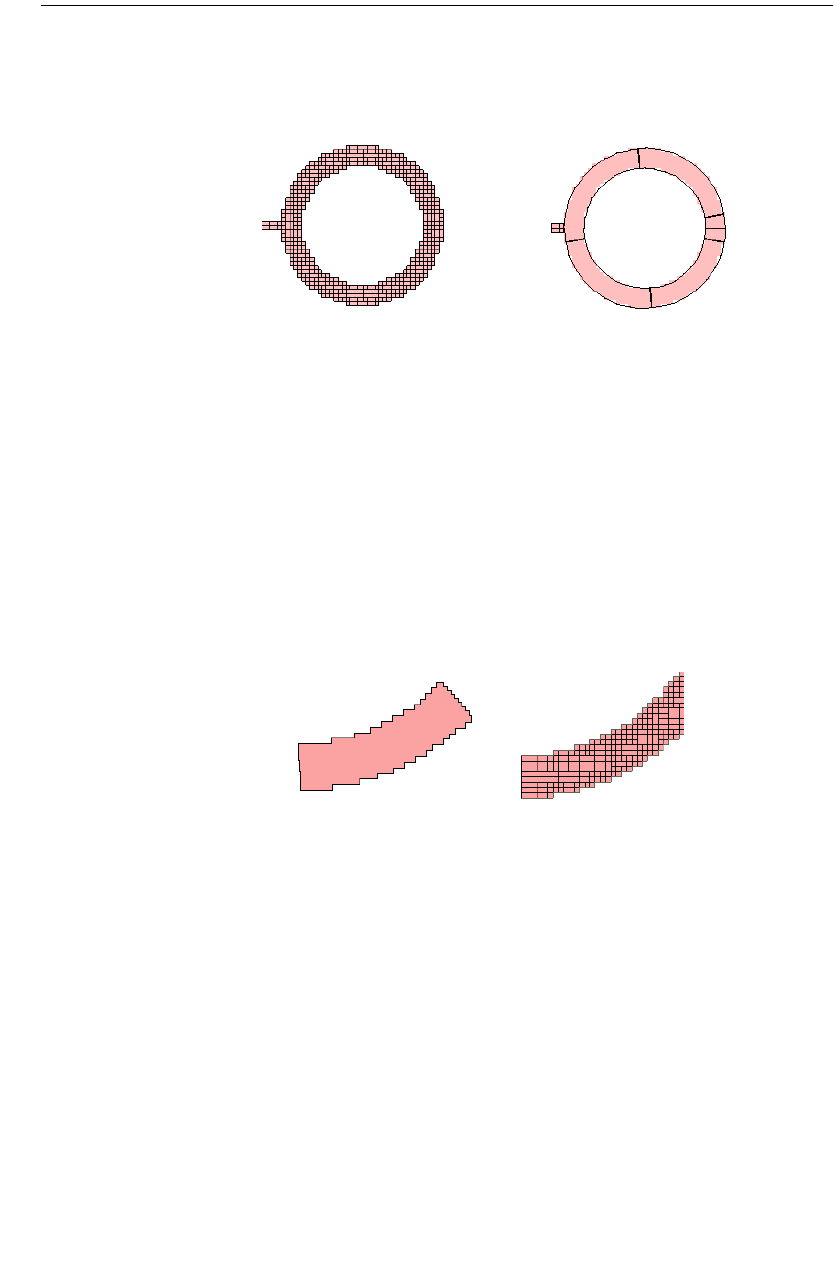
Sonnet User’s Guide
228
Rev 16.56
in each conformal section. In conformal meshing, Sonnet can achieve the speed of
using large subsections, and at the same time enjoy the accuracy of using small
cells. This patented1 Sonnet capability is unique.
Conformal sections, like standard subsections, are comprised of cells, so that the
actual metalization still shows a “jagged” edge when the polygon has a smooth
edge, as pictured below. However, the sections can be much larger due to confor-
mal meshing. You may now make the underlying grid sufficiently small to accu-
rately resolve challenging circuit dimensions without incurring excessive memory
and analysis time requirements.
Conformal meshing should be used in places where it will reduce subsection
count. For rectangular polygons with no diagonal or curved edges, it is more effi-
cient to use rectangular subsections (default). However, if a polygon contains a
curved edge, conformal meshing provides a quicker analysis.
For a discussion on subsectioning when using Conformal Mesh, see “Conformal
Mesh Subsectioning,” page 43.
1 U.S. Patent No. 6,163,762 issued December 19, 2000.
Pictured above is a typical circuit which would be appropriate for
Conformal Meshing. The left picture shows the rectangular
subsections created by using staircase fill. This results in
approximately 800 subsections (unknowns). The right picture
shows the conformal sections created by using conformal fill,
resulting in only about 130 subsections. Note that each conformal
section shown represents multiple subsections.

Chapter 11 Conformal Mesh
229
Rev 16.56
Use Conformal Meshing for Feed Lines, Not Patches
Conformal meshing assumes most of the current is flowing parallel to the edge of
the conformal subsection. This works well for feed lines. However, this is usually
not accurate for geometries like patch antennas. For large areas of metal in both x
and y directions, high current can flow parallel to the X axis edges, and parallel to
the Y-axis edges at the same time. Conformal meshing can include only one of
these currents. Thus, conformal meshing should only be used for transmission line
geometries, which have a “line width” that is small compared to wavelength.
Applying Conformal Meshing
Conformal Meshing is applied as a property of a metal polygon or a property of a
Metal Technology Layer. The following example shows how to set conformal
meshing in a project which does not have any Metal Technology Layers defined.
The process is very similar for a Technology Layer; you would edit the meshing
properties of the Technology Layer.
To use conformal meshing for a polygon, do the following:
1 Select the desired polygon(s) by clicking or lassoing.
The selected polygons are highlighted.

Sonnet User’s Guide
230
Rev 16.56
2 Select Modify Metal Properties from the main menu.
The Metal Properties dialog box appears on your display.
3 Select “Conformal” in the Fill Type drop list.
4 Click on the OK button to apply the changes and close the dialog box.
The polygon does not appear any different in the circuit. To see the difference, you
need to use the Analysis Estimate Memory command. When the Estimate
Memory dialog box appears, click on the View Subsections button. Shown below
is the subsectioning for the same spiral inductor. The circuit on the left uses
rectangular subsections and the one on the right uses conformal subsections. Note
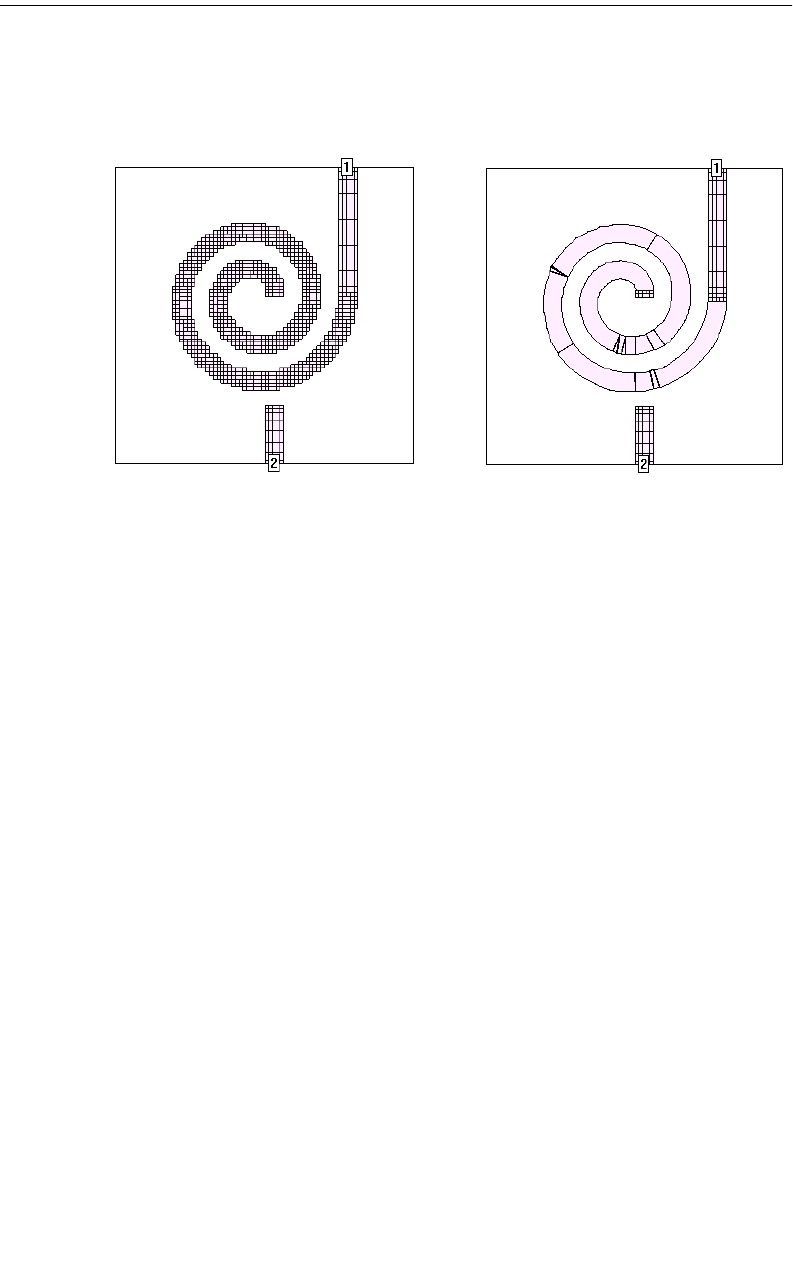
Chapter 11 Conformal Mesh
231
Rev 16.56
that the rectangular subsectioning uses a much higher number of subsections for
the spiral inductor than does the conformal meshing. Rectangular subsectioning
was used for the feed lines in both cases.
If you chose Conformal meshing, then the subsectioning controls in the Metaliza-
tion Properties dialog box - Xmin, Ymin, XMax, YMax and Edge Mesh - are dis-
abled and ignored.
Conformal Meshing Rules
Not all conditions which may affect accuracy or processing time are automatically
identified in the project editor. Below are some basic rules for using conformal
meshing you may follow to prevent causing an error in the analysis engine, em.
Spiral inductor with rectangular
subsections. (Default) Spiral inductor with conformal
subsections.
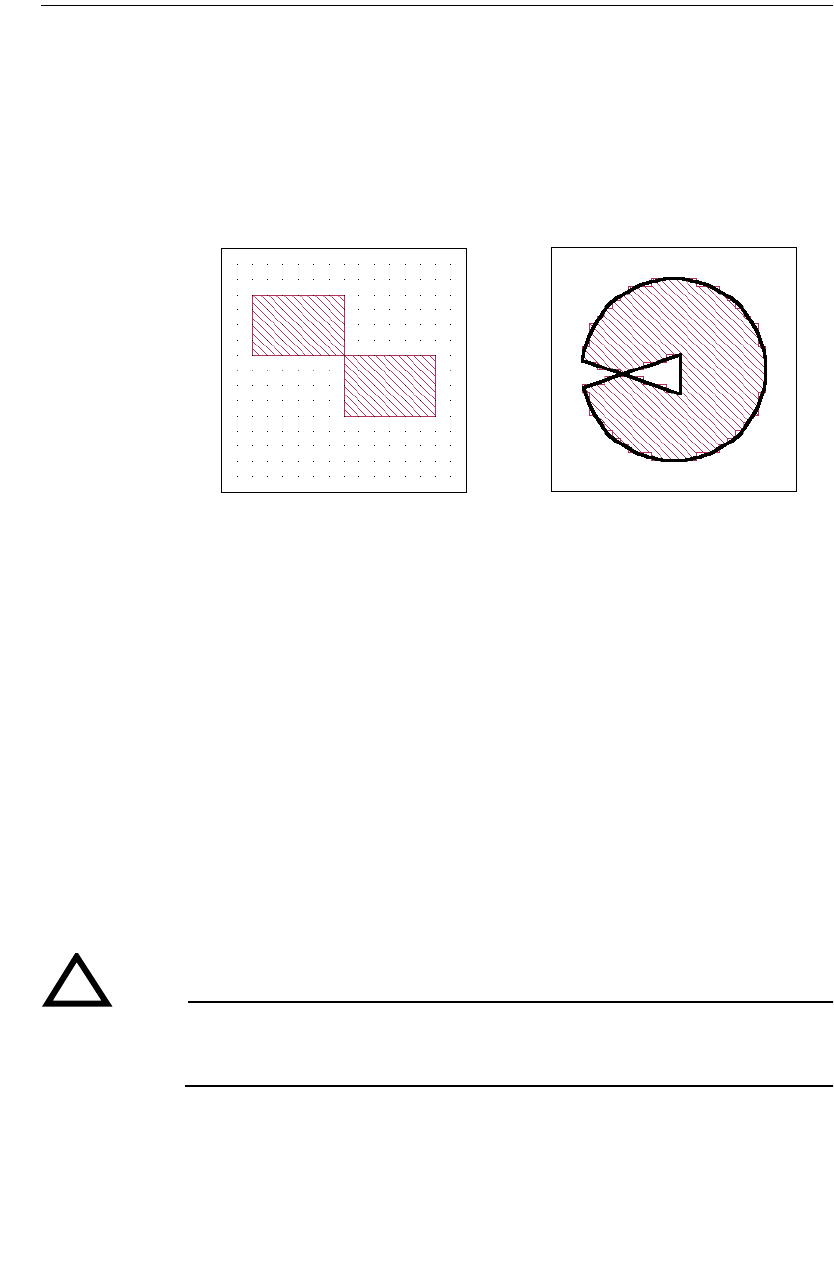
Sonnet User’s Guide
232
Rev 16.56
Rule 1: Figure Eight Polygons
A conformal mesh polygon should not wrap back around itself; in other words, its
vertices should not form a figure eight. This will result in an error message being
issued and em will stop the analysis job. Two examples of this type of polygon are
shown below. In the polygon shown on the left, the vertices have been labelled in
the order in which they were added.
Rule 2: Adjacent Polygons Should Have No Gap
Any polygon which is adjacent to another polygon using conformal meshing
should have its edges exactly touching with no gap existing between the two poly-
gons. Extremely tiny gaps are automatically removed, but should be avoided. Tiny
gaps can be easily avoided by using any of the following methods:
•Using a snap grid while drawing your circuit. (Tools Snap Setup)
•Creating a larger polygon, then dividing the polygon (Edit Divide
Polygons) and applying conformal meshing to one of the resulting
polygons. The resultant polygons are adjacent with no space in between.
•Adding a small polygon which bridges the gap and overlaps the two
polygons on either side of the gap.
•Snapping the existing polygons to the grid. (Modify Snap To
command using the Preserve shape and spacing option).
!WARNING
If you are snapping a circuit with curved edges, use the Preserve shape and
spacing option in the Snap Objects dialog box. Otherwise, curved edges can
become distorted and are difficult to restore in the project editor.
12
34
5
6
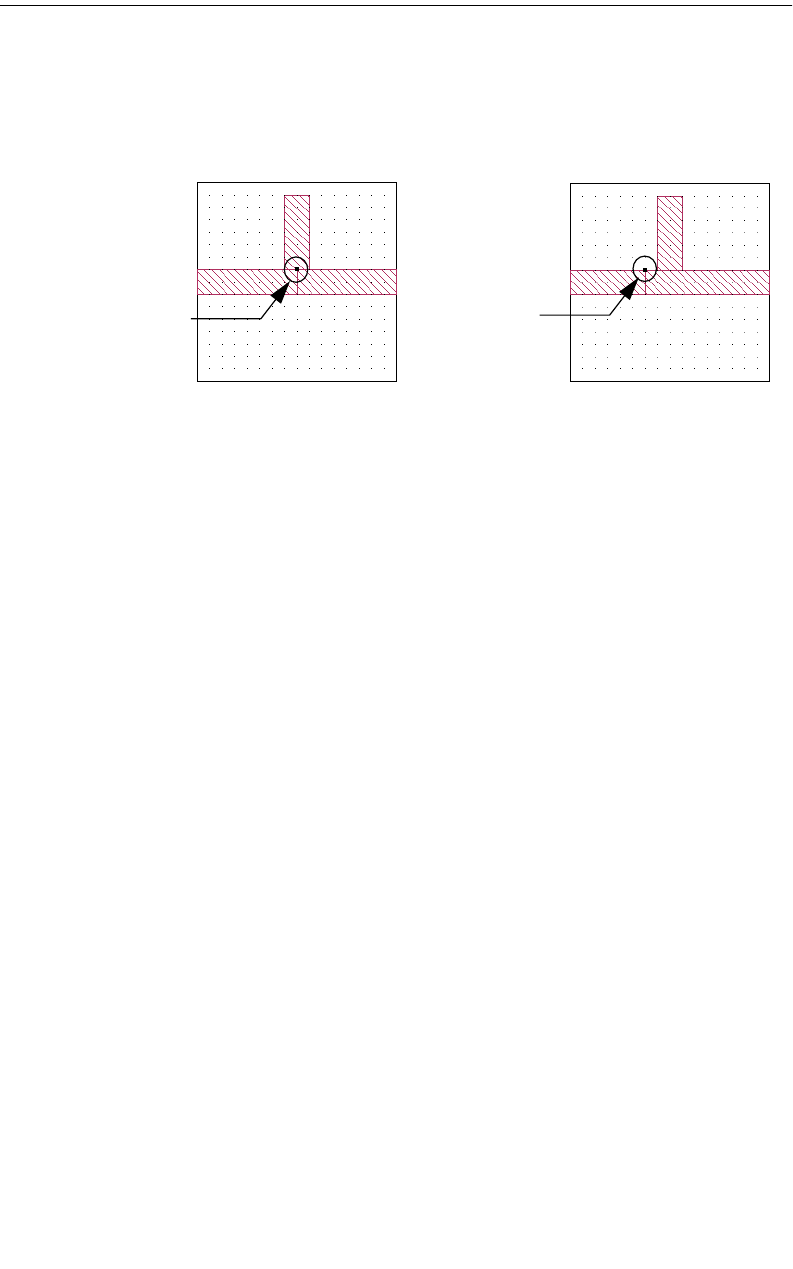
Chapter 11 Conformal Mesh
233
Rev 16.56
Rule 3: Adjacent Polygons Should Not Have an Interior Vertex
When three polygons are adjacent, a vertex where two polygons meet should not
occur between two vertices of the third polygon. See the illustration below.
Single Precision Option
It is recommended that single precision not be enabled when your circuit has poly-
gons using conformal mesh fill. This is because conformal mesh subsections are
sensitive to precision error. Since using the single precision option involves reduc-
ing the required memory at the expense of increasing precision error, its use may
lead to noisy S-parameter results for circuits with conformal mesh fill.
Using Conformal Meshing Effectively
This section discusses some guidelines to use in order to get the most improve-
ment in processing time and memory use and the most accurate results when using
conformal meshing. Following these guidelines will help you to use conformal
meshing in the most efficient manner.
Use Conformal Meshing for Non-Manhattan Polygons
Conformal meshing should be used for non-Manhattan polygons. Manhattan
polygons are polygons which only have vertical and horizontal edges, no diago-
nals or curves. For these types of polygons, rectangular subsections are more effi-
cient.
Error
Condition Correct
Placement

Sonnet User’s Guide
234
Rev 16.56
You should look at your geometry and, if necessary, divide it up into Manhattan
and non-Manhattan polygons using the Edit Divide Polygon. Then set the Man-
hattan polygons to staircase fill and the non-Manhattan polygons to Conformal
fill. For example, the spiral conductor shown below contains Manhattan sections
in the feed lines and non-Manhattan sections in the circular spiral. It should be di-
vided up such that the feedlines are represented by polygons set to staircase fill,
and the circular spiral is another polygon set to Conformal fill.
The exception to this rule is when relatively small Manhattan polygons are be-
tween conformal mesh polygons. In that case, the inefficiency of switching so fre-
quently between staircase and conformal mesh outweighs the gain of using
Manhattan polygons. In that case, conformal mesh should be applied to all the
polygons. An example is shown below.
.
Staircase Fill
Conformal
Fill
Normally, these polygons would use staircase fill, but because they are
relatively small areas and in between polygons on which you would use
conformal mesh, it is more efficient to apply conformal meshing to
these Manhattan polygons.
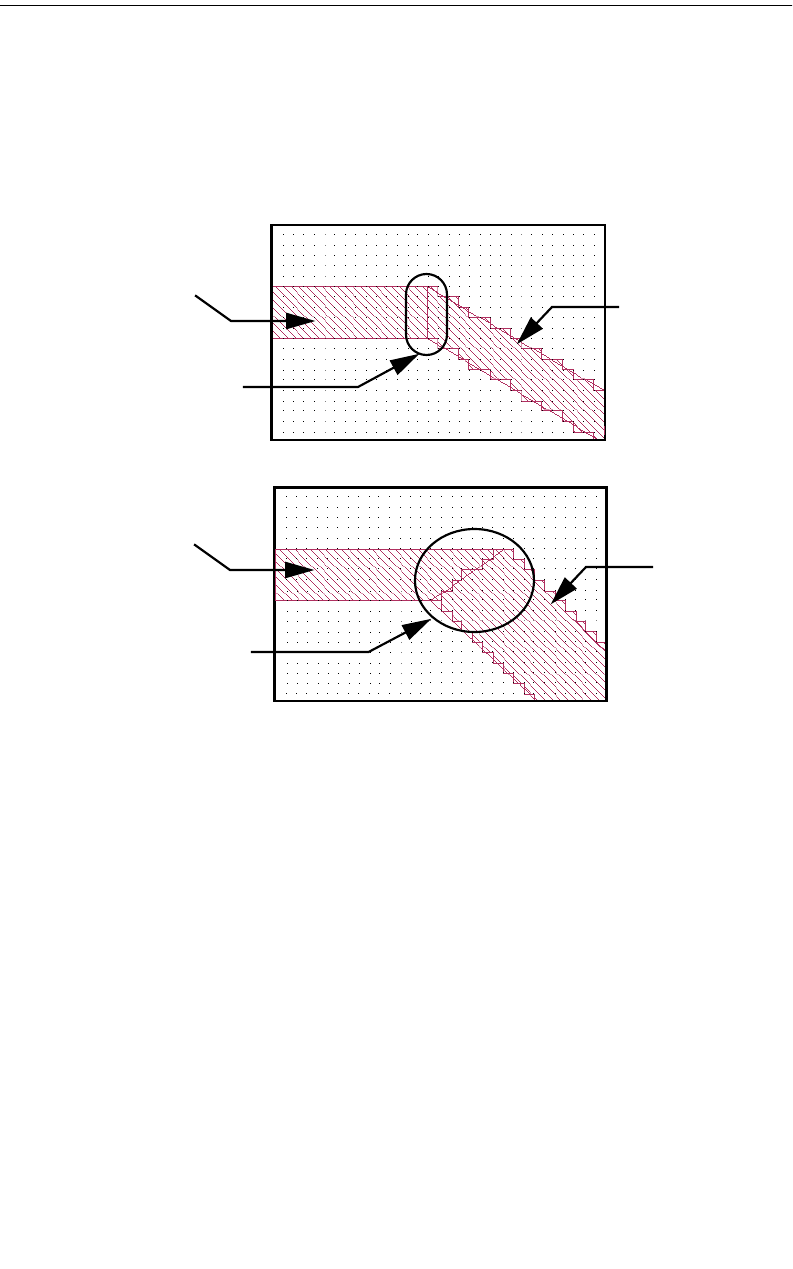
Chapter 11 Conformal Mesh
235
Rev 16.56
Boundaries Should Be Vertical or Horizontal
For the most efficient results, the boundaries between polygons using conformal
meshing and rectangular subsectioning should be vertical or horizontal as shown
in the first picture below. Diagonal boundaries, as shown in the second picture,
make the analysis less efficient.
Cell Size and Processing Time
Care should be taken when choosing your cell size when using conformal mesh.
Many users, especially experienced Sonnet users, will estimate processing time
based on the amount of memory required to analyze a circuit. The amount of
memory used for conformal mesh can be deceptive. Using a smaller cell size in a
circuit which uses conformal mesh may not increase the required memory but will
have a noticeable effect on processing time. The significant factor in determining
processing time with conformal meshing is the number of metalized cells needed
to construct a conformal section. The number of conformal mesh cells displayed
as the result of the Estimate Memory command may be more reliably used as a
guideline.
Polygon with
conformal
subsections.
Polygon
with
rectangular
Polygon with
conformal
subsections.
Polygon with
rectangular
subsections.
Vertical
Boundary
Diagonal
Boundary
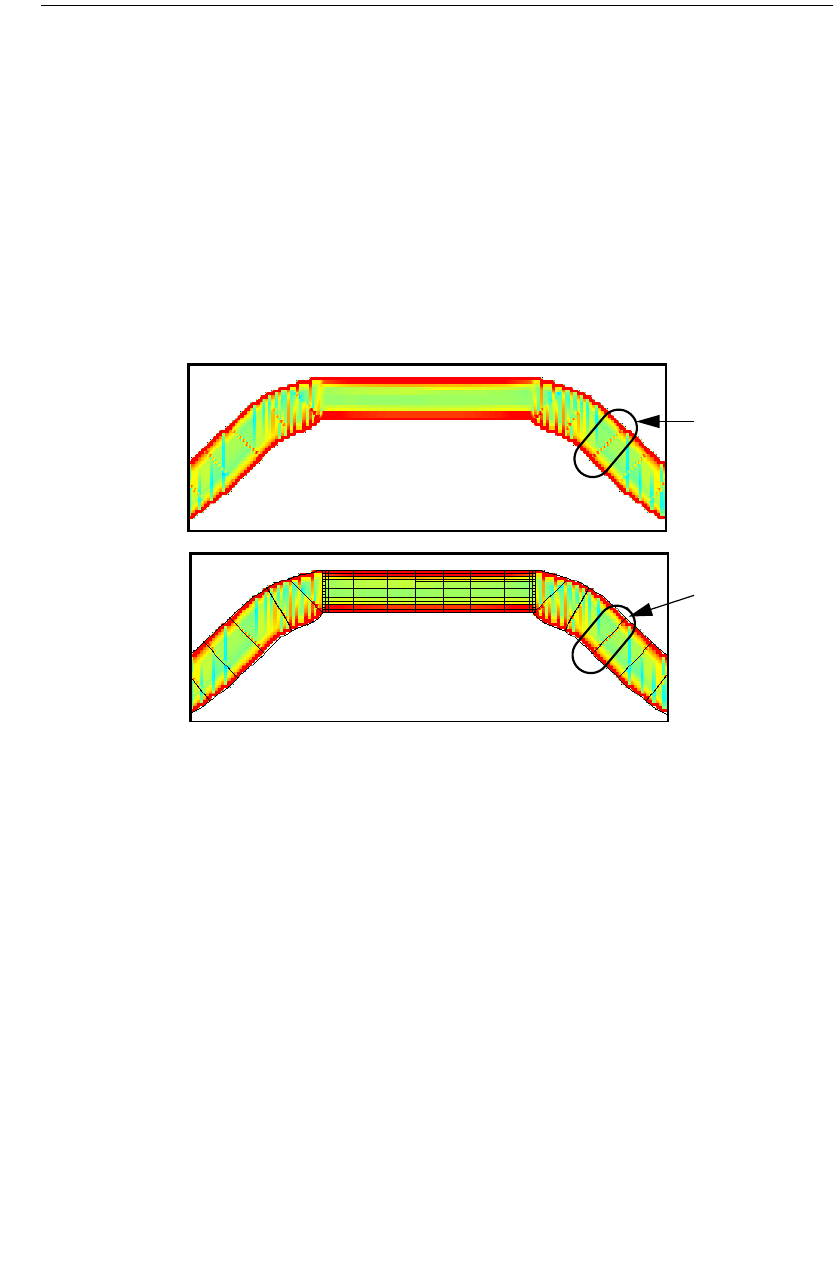
Sonnet User’s Guide
236
Rev 16.56
Current Density Viewing
You may view the current of circuits using conformal mesh just like any other cir-
cuit. However, the current density of conformal mesh polygons might show un-
usual “striping”. These stripes do not represent real current, but are a by product
of the conformal meshing algorithm.
There are two types of current striping:
1A single stripe of current can appear on the junction between two con-
formal sections as shown below.
2Horizontal or vertical stripes may appear within a curved conformal sec-
tion producing a “ripple” effect as shown below.
Current Stripe
Current stripe
with section
boundaries
shown.
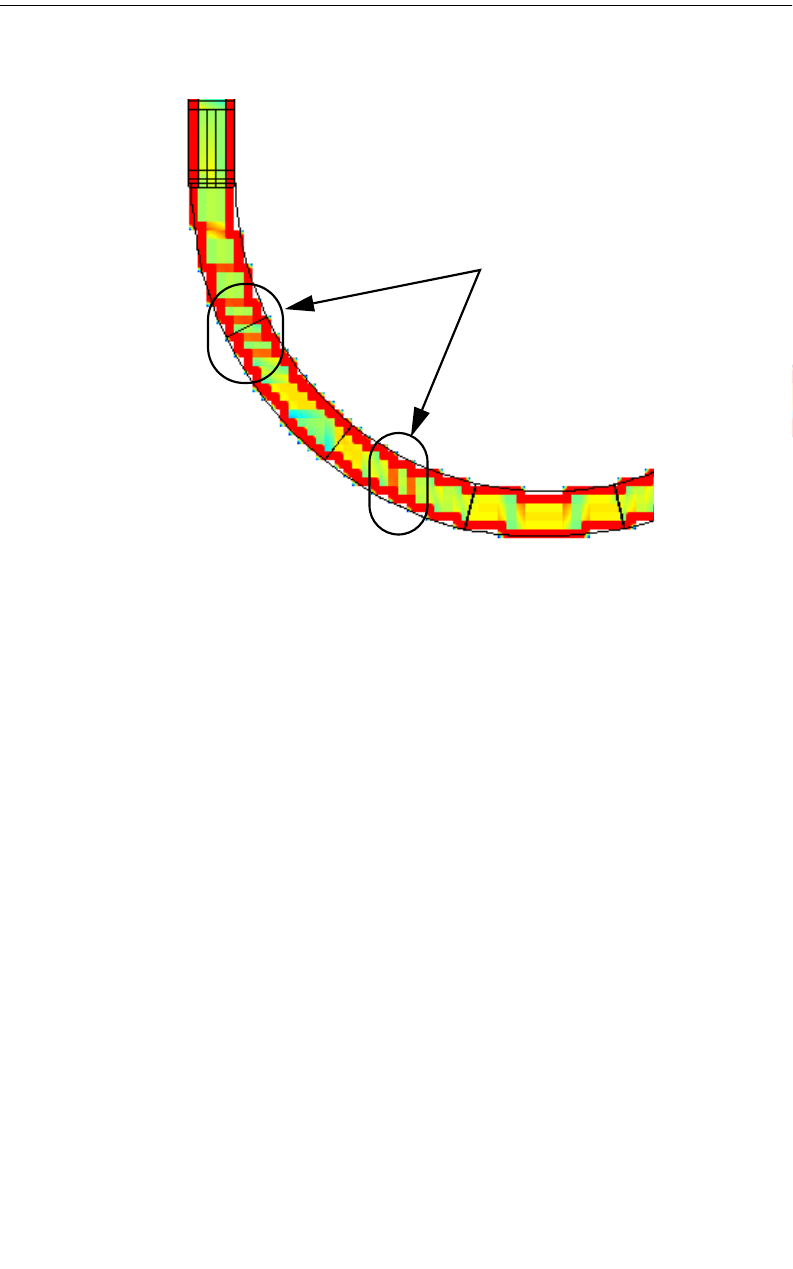
Chapter 11 Conformal Mesh
237
Rev 16.56
For a tutorial on using conformal meshing please see the “Conformal Mesh” topic
under Tips and App notes in Help. You may access Help by selecting Help Son-
net Help from the menu of any Sonnet application or by clicking on the Help but-
ton in any dialog box.
Current stripes

Sonnet User’s Guide
238
Rev 16.56

Chapter 12 Netlist Project Analysis
239
Rev 16.56
Chapter 12 Netlist Project
Analysis
Netlist projects provide you with a powerful circuit analysis tool. Examples of
ways in which the netlist may be used include:
• Cascading Sonnet projects: You can analyze and combine multiple proj-
ects using previously existing data for the subprojects if it is available. This
is particularly useful when analyzing large, complex circuits which require
circuit subdivision for an em analysis. When analyzing a netlist project, em
will automatically interpolate between frequencies if there are differences be-
tween the frequency sweeps used in the subprojects. It is also possible to im-
pose the same frequency sweep on all the subprojects in a netlist. For more
information about circuit subdivision, see Chapter 13, "Circuit Subdivision".
• Cascading S-, Y- and Z- parameter data files: You can read and com-
bine multiple sets of S-, Y- and Z-parameter data files. This is particular-
ly useful if you wish to combine results from another vendor’s software
for use in an analysis by em. When analyzing a netlist project, em will
automatically interpolate between frequencies if there are differences in
the frequencies between the data files.

Sonnet User’s Guide
240
Rev 16.56
• Inserting modeled elements into a circuit. Modeled elements, such as
resistors, capacitors, inductors and transmission lines, can be combined with
geometry subprojects and S-, Y- and Z-parameter data files.
Networks
A netlist project contains a netlist which consists of one or more networks with
elements connected together. The netlist provides a map in which the ports of in-
dividual elements in the netlist are connected to the ports of other elements by the
use of nodes. Nodes represent a connection between netlist elements. In other
words, you use ports in your circuits to define connections, but you use nodes in
a netlist. In order to connect a circuit in a netlist, you must assign its ports to nodes
in the netlist. This is done when you define the circuit as an element in a netlist.
The picture above shows the network represented by the netlist shown in the proj-
ect editor below it. The nodes are represented by the numbered black dots. The ge-
ometry project, steps.son, is connected between nodes 1 and 2 with node 1
corresponding to Port 1 in the geometry project and node 2 corresponding to Port
2. A resistor is connected between nodes 2 and 3. A capacitor is connected be-
tween node 3 and ground. The project steps.son is also connected between nodes
1234
GND
steps.son steps.son
example_net
12

Chapter 12 Netlist Project Analysis
241
Rev 16.56
3 and 4, with Port 1 corresponding to node 4 and Port 2 corresponding to node 3.
Port 1 of the network example_net corresponds to node 1 and port 2 of the network
corresponds to node 4.
A netlist project is simply a list of these elements, as you can see in the netlist pic-
tured above. Notice that the first number after the name of the element is the net-
work node which corresponds to port 1 of the element, the second number is the
network node which corresponds to port 2 of the element, and so on, for all the
ports in an element.
The sequence of steps for a netlist project analysis may be summarized as follows:
1You input the netlist using the project editor in netlist mode. The project
editor allows you to create and edit networks, network elements, project
elements, modeled elements, and data file elements in your netlist. You
also input the analysis controls which may include defining parameters
in the netlist.
2Em reads the netlist project which contains circuit and analysis control
information. This includes S-, Y- and Z-parameter data files, modeled
elements, geometry subprojects (project elements) and network ele-
ments.
3Em uses the analysis controls input as part of the netlist project to run
each electromagnetic analysis invoked by the network file. It is possible
to configure the analysis controls in such a way that geometry subproj-
ects are analyzed using their own analysis controls. Netlist subprojects
always inherit their analysis controls from the present netlist.
4Once the analysis of geometry subprojects is complete, em performs the
circuit analysis specified in the netlist.
5Em combines the electromagnetic results with the circuit results to
obtain the desired output results.
Note that the above sequence of steps is generalized for analyses which include
both electromagnetic and circuit analysis. In cases where the overall analysis is re-
stricted to either electromagnetic analysis or circuit analysis, some of the steps are
omitted.
Example of Node Assignments in a Complex Circuit
As discussed above, a node is used in a netlist to connect two elements. If an ele-
ment is a geometry project with multiple internal ports, as is the case with co-cal-
ibrated ports, nodes are assigned in the netlist to each port. In larger circuits, with
multiple co-calibrated ports, the netlist can be quite complex, so an example is

Sonnet User’s Guide
242
Rev 16.56
shown below of performing circuit subdivsion of a large circuit with co-calibrated
ports. The resulting netlist and subprojects will be examined to illustrate how the
ports in the geometry subprojects are assigned to nodes in the netlist which is cre-
ated when the circuit subdivision is performed. For a complete explanation of Cir-
cuit Subdivision, please refer to Chapter 13, “Circuit Subdivision” on page 255.
The full circuit, cocal_netlist.son, which contains 18 ports, is pictured below with
a subdivider. There are 16 co-calibrated ports, each group consisting of four ports
in the interior of the circuit. The subdivider is set so that the full circuit will be sub-
divided into two geometry projects, each containing half of the full circuit. When
the circuit is subdivided, a netlist is created which connects the two geometry proj-
ects together into a circuit equivalent to the full geometry project. When the netlist
is analyzed, each geometry subproject is analyzed and then those simulation re-
sults are used to simulate the response of the netlist circuit.
Once the subdivision is performed, three new projects are created. The netlist,
cocal_netlist_net.son, the S1 subproject, cocal_netlist_s1.son, and the S2 subproj-
ect, cocal_netlist_s2.son. The netlist is shown below. Note that the main network
has 18 ports, the same number as the original project before splitting it. For the
main network, the node number and port number are identical.
The second line of the netlist shows the Project Element which defines the inclu-
sion of the geometry subproject cocal_netlist_s2.son. Show below is the Edit El-
ement dialog box for the subproject displaying the correspondence of netlist nodes
to circuit ports. Also shown is a view of the subproject with both the correspond-
ing ports and nodes labeled. When you add an element to a netlist, each port de-
fined in the element is assigned to a node in the netlist. The Edit Element dialog
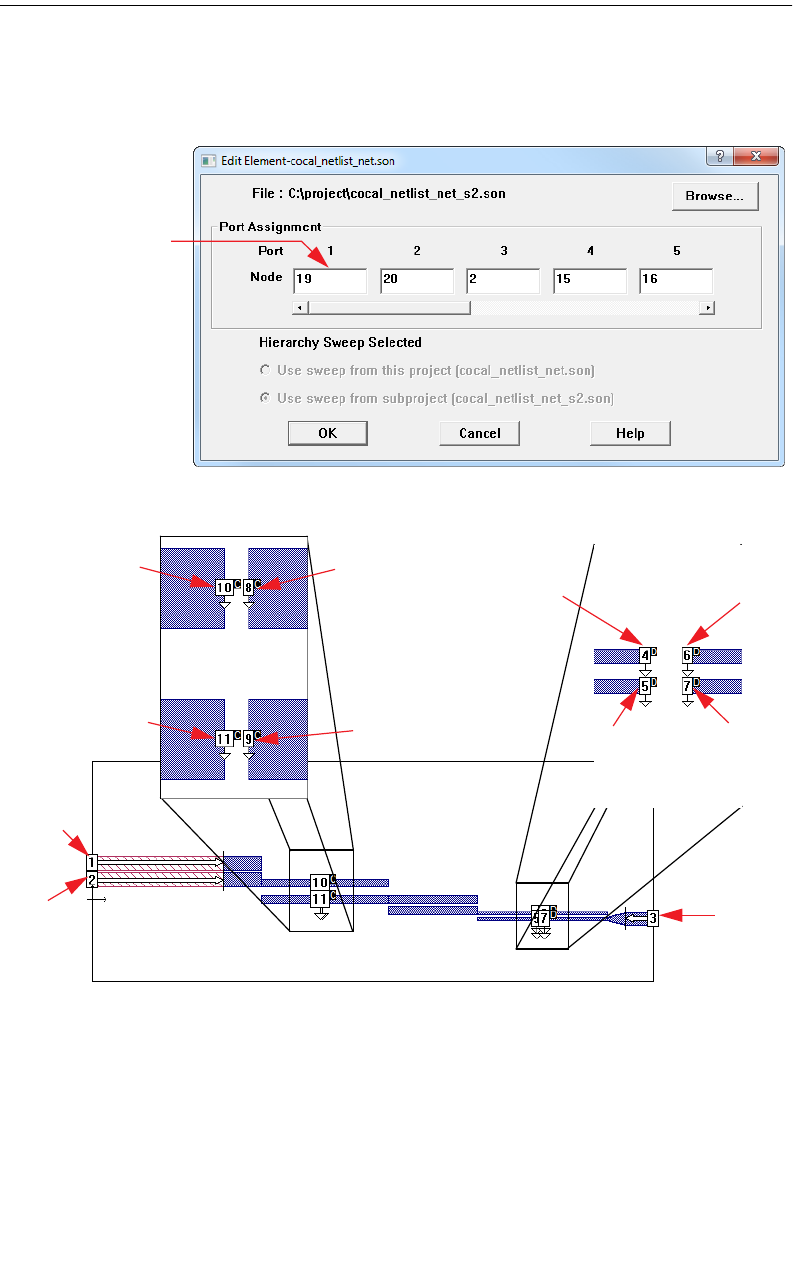
Chapter 12 Netlist Project Analysis
243
Rev 16.56
box will contain a text entry box for each port in the element. You enter the desired
node number for the port in that port’s text entry box. In the case of a circuit sub-
division, this assignment of nodes is done automatically by the software.
Note that there are two nodes, 19 and 20, which appear in the project elements, but
are not part of the main network which uses nodes 1 through 18. Nodes 19 and 20
are used to connect ports 2 and 3 of cocal_netlist_s1.son to ports 1 and 2 of
Node number
text entry for
Port 1
Node 19
Node 20
Node 14
Node 17
Node 15
Node 13
Node 11
Node 17
Node 16
Node 2
Node 12

Sonnet User’s Guide
244
Rev 16.56
cocal_netlist_s2.son. These were the ports added to the circuit when it was subdi-
vided. Connecting these ports by using the same netlist nodes makes the netlist cir-
cuit equivalent to the original circuit before subdivision.
Creating a Netlist
You create a netlist using the project editor. To create a new netlist, select File
New Netlist from the main menu of the project editor. The project editor tool bar
and menus change for the netlist editor, to allow you to add elements and networks
to your netlist.
The initial netlist file contains a default two-port network named Net. The last net-
work in the netlist is the main network. The main network is the network whose
solution you are solving for in this netlist. When you analyze the netlist, the re-
sponse data produced in the analysis is for the main network.
You can edit the name and attributes of this network including the number of ports
by double-clicking on the entry. This is true of all entries made in the netlist; you
must double-click on them to open the dialog box which allows you to edit the
entry or select the item, then select the Tools Modify command from the main
menu.
Netlist Example Files
All of the example files used in this chapter are available in the “Att” example in
the Sonnet examples. You should save the entire folder into your working direc-
tory if you wish to execute the examples.You may access the Sonnet Example
cocal_netlist_s1.son
Node 19
Node 20
Chapter 12 Netlist Project Analysis
245
Rev 16.56
Browser by selecting Help Browse Examples from the menu of any Sonnet ap-
plication. For instructions on using the Example Browser, please click on the Help
button in the Example Browser window.
Cascading S-, Y- and Z-Parameter Data Files
A particularly useful feature provided by a netlist project is the ability to cascade
multiple S-, Y- and Z-parameter data files. There are no restrictions on the file for-
mats which may be cascaded. For example, you can cascade em Z-parameter data
in Touchstone format with measured S-parameter data in Super-Compact format.
In addition, em can analyze at frequencies which are not included in the data files.
Em automatically interpolates if there are any differences between the requested
frequency points and those in the data files.
A good example of a cascading operation is the project att_cascade.son, which is
included in the Att example for this chapter. A schematic representation of the
two-port circuit is shown below. This circuit consists of two identical thin film re-
sistors connected in series. The S-parameters from the geometry project analysis
on the thin-film resistor are used as a data file element in the netlist. The desired
output network is the series combination of resistors. The S-Parameter data file,
att_res16.s2p, as well as the geometry project, att_res16.son, used to generate the
data file, are included in the examples for this chapter.
S-parameter
file“att_res16.s2p”
Node 2 Node 3Node 1
The two-port S-parameters contained in file “att_res16.s2p”
are cascaded to obtain an overall set of two-port S-parameters.
12
S-parameter
file“att_res16.s2p”

Sonnet User’s Guide
246
Rev 16.56
The netlist, att_cascade.son, for the circuit is pictured below.
The main network, Resnet, has two ports indicated by the “2” in DEF2P. Port 1
corresponds to node 1 in the network. Port 2 corresponds to node 3. There are two
data file elements in the network. The first entry is the response file att_res16.s2p
with 2 ports. Port 1 corresponds to node 1 of the network, which, as mentioned
above, is port 1 of the whole circuit. Port 2 for the data file corresponds to node 2
of the network. The other entry is also for the data file att_res16.s2p except that
port 1 of the data file goes to node 2 of the network which means that port 1 of the
second data file is connected to port 2 of the first data file. Port 2 of the second
data file corresponds to node 3 of the network. Node 3 of the network is Port 2 of
the network “RESNET”.
The S-Parameters for an analysis of the netlist are shown below.
A Network File with Geometry Project
The next example demonstrates a netlist project analysis which invokes a geome-
try project analysis in conjunction with using previously generated data.
Frequency: 200 MHz
50-Ohm S-Params. Mag/Ang. Touchstone Format. (S11 S21 S12 S22).
200.000000 0.250782 -5.309 0.748778 -6.263 0.748778 -6.263 0.250782 -5.309
Frequency: 300 MHz
50-Ohm S-Params. Mag/Ang. Touchstone Format. (S11 S21 S12 S22).
300.000000 0.250310 -7.963 0.748702 -9.395 0.748702 -9.395 0.250310 -7.963
Frequency: 400 MHz
50-Ohm S-Params. Mag/Ang. Touchstone Format. (S11 S21 S12 S22).
400.000000 0.249650 -10.62 0.748595 -12.53 0.748595 -12.53 0.249650 -10.62

Chapter 12 Netlist Project Analysis
247
Rev 16.56
To demonstrate a netlist with a geometry project, the two-port T-attenuator shown
below will be analyzed.
Pictured below is the geometry project “att_res67.son”, which is a 67 ohm thin-
film resistor. This project is read by em and analyzed during the netlist analysis.
The results of the project analysis are used to compute the results for the netlist.
S-parameter
file “att_res16.s2p”
12
geometry project
“att_res67.son”
Node 1 Node 2 Node 3
The two-port T-attenuator will be analyzed with em to demonstrate a
combined electromagnetic/circuit analysis.
S-parameter
file “att_res16.s2p”
Transmission
Line
Transmission
Line
67 ohm
Thin-Film
Resistor
Sonnet User’s Guide
248
Rev 16.56
The netlist project, att_combine.son is shown below. The project att_combine.son
is available as part of the Att example for this chapter.
The primary distinction between the netlist shown above and the previous netlist
is that this netlist contains an instruction to perform a project analysis. The PRJ
keyword instructs em to run an electromagnetic analysis on the project
“att_res67.son” using the analysis controls from the netlist. The analysis control
use is indicated by “Hierarchy Sweep” in the PRJ statement. When control is set
to “Hierarchy Sweep”, em automatically analyzes the subproject at the same fre-
quency sweep and run options as the netlist.
During the analysis, em performs the following steps:
1Reads S-parameter data from the file “att_res16.s2p”.
2Performs an electromagnetic analysis of the geometry project
“att_res67.son”, a 67 ohm thin-film resistor.
3Combines the S-parameter results from the electromagnetic analysis
with the S-parameter results from “att_res16.s2p” to obtain an overall
set of S-parameters for the T-attenuator.
TIP
Before executing a PRJ statement, em checks for the existence of data at the spec-
ified control frequencies. If the data already exists, and the project has not changed
since the data was generated, em does not execute an electromagnetic analysis, but
uses the available data.

Chapter 12 Netlist Project Analysis
249
Rev 16.56
The listing below shows the output of the netlist analysis, as it appears in the anal-
ysis monitor, which contains the overall set of S-parameters for the T-attenuator.
Inserting Modeled Elements into a Geometry
Another very useful feature of the netlist project is the ability to insert modeled
elements into a geometry project after an electromagnetic analysis has been per-
formed on that circuit. A modeled element is an ideal element such as a resistor,
inductor, capacitor or transmission line, which has a closed-form solution. No
electromagnetic analyses are performed on modeled elements.
To demonstrate the use of modeled elements, we will again analyze the T attenu-
ator. However, instead of the attenuator being the result of connecting the results
of electromagnetic analyses as shown previously in the chapter, in this case, the
geometry project, att_lgeo.son, has the full attenuator with cutouts where the mod-
eled elements need to be inserted. The three resistors will not be analyzed as part
of the geometry project, but will be inserted as modeled elements in the netlist.
The figure below shows the circuit layout with the modeled resistor elements. A
geometry project for the transmission line structures are created first. A netlist
project will then be used to insert the three resistors and calculate two-port S-pa-
rameters for the overall circuit.
To accomplish this task, it is necessary to create a geometry project with the trans-
mission line structure and three “holes” where modeled elements will eventually
be inserted. The figure on page 250 shows such a geometry project. Here, pairs of
co-calibrated ports have been placed on the edges of each modeled element
“hole”. Co-calibrated internal ports are identified as a calibration group with a
common ground node connection and a defined terminal width. When em per-
forms the electromagnetic analysis, the co-calibrated ports within the group are si-
multaneously de-embedded. When the modeled elements are inserted later on,
Frequency: 200 MHz
50-Ohm S-Params. Mag/Ang. Touchstone Format. (S11 S21 S12 S22).
200.000000 0.008924 67.700 0.500516 -5.758 0.500516 -5.758 0.008924 67.700
Frequency: 300 MHz
50-Ohm S-Params. Mag/Ang. Touchstone Format. (S11 S21 S12 S22).
300.000000 0.013072 68.918 0.501160 -8.647 0.501160 -8.647 0.013072 68.918
Frequency: 400 MHz
50-Ohm S-Params. Mag/Ang. Touchstone Format. (S11 S21 S12 S22).
400.000000 0.017177 67.763 0.502055 -11.54 0.502055 -11.54 0.017177 67.763

Sonnet User’s Guide
250
Rev 16.56
each is connected across the corresponding pair of co-calibrated ports. Note that
under certain conditions, ungrounded-internal ports can be used instead of co-cal-
ibrated ports. See “Using Ungrounded-Internal Ports,” page 252, for details.
2
1
16.77 16.77
67.11
Modeled Elements Modeled Element
Geometry Project
metalization
The two-port T attenuator will be re-analyzed to
demonstrate the use of modeled elements.
The geometry file “att_lgeo.son” contains three sets of co-
calibrated ports placed at locations where modeled elements
will eventually be inserted. This file is available as part of the
Att example used for this chapter.

Chapter 12 Netlist Project Analysis
251
Rev 16.56
Below is the netlist, att_lumped.son, that will be used for this example.
The netlist above instructs em to perform the following steps:
1Perform an electromagnetic analysis on the geometry file “att_lgeo.son”
using the Frequency sweep and run options defined for this netlist. Note
that according to the PRJ line, Ports 1-8 correspond to nodes 1-8 respec-
tively in the main network, atten. The node numbers are listed after the
PRJ keyword in the order of ports in the circuit.
2Insert a 16.77 ohm resistor between nodes 3 and 4 which is the equiva-
lent of inserting the resistor between autogrounded ports 3 and 4 in the
geometry project.
3Insert a 16.77 ohm resistor between nodes 5 and 6.
4Insert a 67.11 ohm resistor between nodes 7 and 8.
5Calculate an overall set of S-parameters for the T attenuator.
The two projects, att_lgeo.son and att_lumped.son are available in the Att exam-
ple for this chapter.

Sonnet User’s Guide
252
Rev 16.56
The listing below is the analysis output as it appears in the analysis monitor. Note
that these results are similar to the results given above for distributed elements.
Using Ungrounded-Internal Ports
In the example presented above, a pair of co-calibrated ports was placed at each
location in the em circuit layout where a modeled element would eventually be in-
serted. It is also possible to perform the same analysis using ungrounded-internal
ports, because each resistor in this example is a series modeled element without
access to ground. Any time access to ground is not required for a modeled ele-
ment, you can replace the pair of auto-grounded ports with a single ungrounded-
internal port.
Frequency: 200 MHz Frequency completed Tue May 03 14:28:44 2011.
S-Parameters. 50.0 Ohm Port Terminations.
Magnitude/Angle. Touchstone Format. (S11 S21 S12 S22).
200.000000 0.008537 67.966 0.500406 -5.009 0.500406 -5.009 0.008537 67.966
Frequency: 300 MHz Frequency completed Tue May 03 14:28:44 2011.
S-Parameters. 50.0 Ohm Port Terminations.
Magnitude/Angle. Touchstone Format. (S11 S21 S12 S22).
300.000000 0.012487 70.314 0.500823 -7.517 0.500823 -7.517 0.012487 70.314
Frequency: 400 MHz Frequency completed Tue May 03 14:28:45 2011.
S-Parameters. 50.0 Ohm Port Terminations.
Magnitude/Angle. Touchstone Format. (S11 S21 S12 S22).
400.000000 0.016447 70.118 0.501406 -10.03 0.501406 -10.03 0.016447 70.118
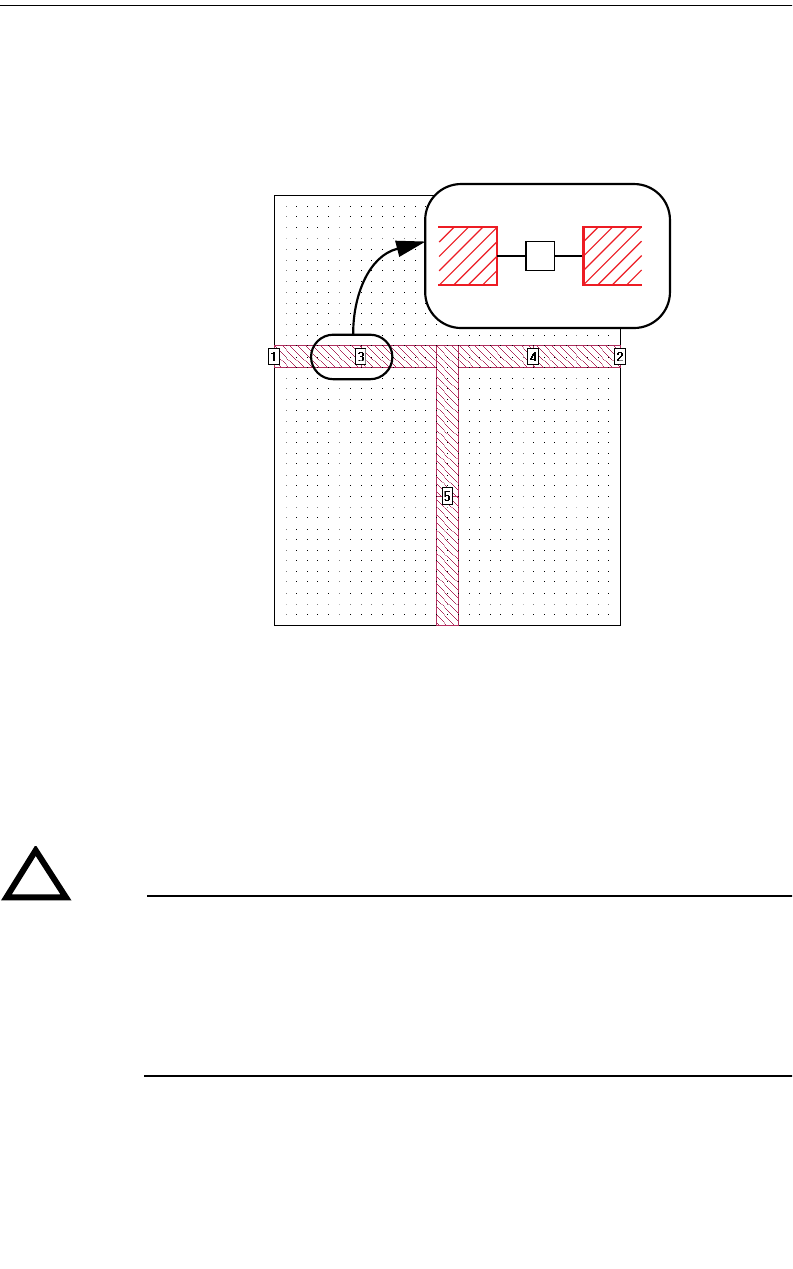
Chapter 12 Netlist Project Analysis
253
Rev 16.56
The figure below shows a geometry project for the T attenuator with ungrounded-
internal ports at each modeled element location. Note that the gaps between poly-
gons at these locations have been removed. This is because you must attach un-
grounded-internal ports between two abutted polygons. This slightly impacts the
overall performance of the attenuator.
The network file shown below connects the desired resistors across the unground-
ed-internal ports of the network shown on page 253. Since ungrounded-internal
ports do not have access to ground, only a single node is specified when connect-
ing an element across them.
!WARNING
Ungrounded-internal ports have one terminal connected to an edge of a
polygon and the second terminal connected to an abutted edge of a second
polygon. Ungrounded-internal ports do not have access to ground.
Therefore, only 1-port elements or 1-port networks may be connected across
ungrounded-internal ports. Resistors, capacitors, and inductors are
technically one-port elements and therefore, may be inserted in place of an
ungrounded-internal port in a netlist.
The geometry project “att_lgeo2.son” uses ungrounded-internal
ports at locations where modeled elements will eventually be
inserted.
Z3

Sonnet User’s Guide
254
Rev 16.56
The netlist for this circuit, att_lumped2.son, is shown below. Both the geometry
project, att_lgeo2.son, and this netlist are available in the Att example provided
for this chapter.
An important feature to notice in this netlist is the use of parameters. Three param-
eters, Z3, Z4 and Z5 have been defined in the netlist project and their values used
for the three resistor modeled elements. Parameters are defined in a netlist by se-
lecting Circuit Parameters from the main menu, then entering the parameter
name and nominal value in the Parameters dialog box which appears. Z3 and Z4
are equal to 16.77 and Z5 is equal to 67.11.
The listing below shows the S-parameter results obtained from the analysis with
ungrounded-internal ports. These results are very similar, but not identical, to the
results for co-calibrated ports. The differences are primarily due to the change in
the gap size between polygons at the points where lumped elements are inserted.
Frequency: 200 MHz
50-Ohm S-Params. Mag/Ang. Touchstone Format. (S11 S21 S12 S22).
200.000000 0.009217 68.496 0.500482 -5.785 0.500482 -5.785 0.009217 68.496
Frequency: 300 MHz
50-Ohm S-Params. Mag/Ang. Touchstone Format. (S11 S21 S12 S22).
300.000000 0.013510 70.114 0.500994 -8.683 0.500994 -8.683 0.013510 70.114
Frequency: 400 MHz
50-Ohm S-Params. Mag/Ang. Touchstone Format. (S11 S21 S12 S22).
400.000000 0.017788 69.364 0.501707 -11.59 0.501707 -11.59 0.017788 69.364

Chapter 13 Circuit Subdivision
255
Rev 16.56
Chapter 13 Circuit Subdivision
Introduction
Sonnet provides the capability to take a large circuit and split it into any number
of smaller projects, then connect the results in a netlist project to produce a re-
sponse for the whole circuit. This method can significantly reduce the required
processing time and memory necessary to analyze the circuit while still obtaining
an accurate answer.
The number of subsections in a circuit is one of the most important factors in de-
termining processing time since the matrix solve time is proportional to N3. To il-
lustrate how circuit subdivision reduces processing time, consider two subprojects
each with half as many subsections as the source project. The total matrix solve
time is now four times faster:
Circuit subdivision allows you to take advantage of this technique by breaking
your circuit into smaller parts with fewer subsections, hence, requiring less pro-
cessing time and memory to analyze. The trade off is that you introduce some
error into the analysis. However, by subdividing the circuit appropriately you can
minimize the error while still obtaining the reduction in processing time.
2N2
3N34=

Sonnet User’s Guide
256
Rev 16.56
The circuit should be split where there is no coupling across the subdivision line.
Areas where significant coupling occurs must be contained within a subproject. In
this way, all the significant coupling in the circuit is accounted for. If care is taken
when subdividing the circuit, the accuracy of the results is very high.
Circuit subdivision is not appropriate for every design, but in the cases of large
circuits (5-10 minutes processing time per frequency) where it is applicable, you
can obtain marked increases in processing efficiency.
Another advantage of circuit subdivision is the use of frequency interpolation in
the master netlist analysis. A netlist is used to connect the response data of the sub-
projects of the circuit to simulate the full circuit. If the subprojects are chosen in
such a way that their response data does not vary significantly over the frequency
band, very few frequency points need to be calculated for the subproject. So not
only do the smaller files require less time and memory because of their smaller
size, but you can also analyze these smaller circuits at fewer frequency points. In-
terpolating in the netlist file requires much less processing than calculating data
for a frequency point in a geometry project.
Shown below is an example showing the typical advantages of using this ap-
proach.
When the netlist analysis is performed, em will interpolate to provide simulation
data at frequencies not specified in the subprojects. Each subproject should be an-
alyzed at the same minimum and maximum frequency as the overall analysis and
at enough points in between to provide for reasonable interpolation of data at fre-
quencies which fall between these values. As you can see from the Smith chart be-
low, while you need many frequency points to obtain reasonable response data for
Large Circuit 30 minutes/frequency
X 25 frequencies = 750 minutes total
Netlist (Subdivided Large Circuit)
Small Circuit Small Circuit Small Circuit
4 mins/freq
X 5 freq
20 minutes
3 mins/freq
X 5 freq
15 minutes
4 mins/freq
X 5 freq
20 minutes
Netlist Total Analysis Time = 55 minutes - 14X faster
Chapter 13 Circuit Subdivision
257
Rev 16.56
the whole circuit, you need far fewer frequency points to obtain accurate data for
the smaller pieces of the whole circuit, whose response data does not vary appre-
ciably.
Be aware, however, that in some cases, you may need the added precision of ana-
lyzing all the pieces at the same resolution of the frequency band. Interpolation is
best used when the response of a subproject varies little over the frequency band
and the analysis time of the subproject is appreciable.
Circuit Subdivision in Sonnet
Circuit subdivision in Sonnet allows you to insert subdivision lines in your geom-
etry in the project editor. These subdivision lines create the sections from which
the subdivide command makes geometry subprojects. When you select the subdi-
Whole
Circuit
Circuit
Sections

Sonnet User’s Guide
258
Rev 16.56
vide command, the software creates a main netlist file and the geometry subproj-
ects. The main netlist connects the subprojects so that the response data for the
netlist may be substituted for the response data of the source project.
You should also be aware that if your main circuit contains any parameters or di-
mensions, they are removed during the subdivision process. After the subprojects
are created, you may enter parameters in any of the geometries. In fact, it is pos-
sible to run optimizations on the main netlist project using a parameter in one of
the subprojects.
Performing circuit subdivision as a method of analysis should, in general, be done
as follows:
1You should input as many of the circuit properties as possible before
subdividing. Dielectric layers, dielectric brick and metal types, grid size,
top cover height, etc. are inherited by the created geometry subprojects.
Source Circuit with Subdivision Lines Added
Generated Subprojects
s1 s2 s3
Generated Main Netlist

Chapter 13 Circuit Subdivision
259
Rev 16.56
2Decide where to subdivide your circuit. This step often requires exper-
tise and experience to avoid splitting the circuit at a junction where there
is coupling across the subdivision line.
3Create the subdivision lines in the project editor. These lines are used to
create the subprojects. A geometry project is created for each segment
of your circuit. These geometry projects contain significantly smaller
geometries that may be analyzed faster using less memory.
4If you plan to take advantage of the netlist interpolation feature, set up
the analysis frequency controls as a coarse resolution of the entire
desired frequency band in the project before subdividing. Both the
netlist and geometry subprojects all inherit these frequency specifica-
tions. Entering these frequency controls now in the Analysis Setup dia-
log box saves having to enter them in each individual subproject.
5Subdivide the circuit in the project editor to create the subprojects and
netlist project which connects the individual subprojects in a network
equivalent to the circuit as a whole. Ports and reference planes are added
to the subprojects as needed to connect to the larger circuit.
6Edit the subprojects to fine tune the geometries, if needed. Possible
adjustments would include the use of a binary box, adjusting the grid
size, setting z-partitions for bricks, changing the frequency sweep speci-
fication, and adding parameters.
TIP
If you add parameters to a subproject in a netlist, the parameters are not automat-
ically displayed in the netlist. You must save the main netlist and re-open it to dis-
play the parameters and make them available for editing.
7Set up the analysis controls in the netlist to use the complete set of
desired analysis frequencies if the subprojects are already set to analyze
the coarse frequency sweep. When the analysis is performed on the
master netlist project, em interpolates between the frequency points in
the subprojects, saving processing time.
You may also use a Hierarchy Sweep in which the frequency band set
up in the master netlist is imposed on the analyses of all the subprojects.
This is useful when additional accuracy is needed in the data and you do
not wish to use interpolation. This is accomplished by setting the Hier-
archy Sweep option in the Analysis Setup dialog box in the project edi-
tor.
8Analyze the netlist project. The data response for the netlist project pro-
vides analysis results that may be used for the whole circuit.

Sonnet User’s Guide
260
Rev 16.56
9It is often a good idea after analyses are complete on the resultant sub-
projects to check the response data to verify that data was calculated for
enough frequency points to provide accurate interpolated data.
Since it is possible for a netlist project to include a netlist subproject, it is possible
to use “double” subdivision. After subdividing your initial circuit, you then may
use subdivision on one of the resulting geometry subprojects. In this case, you
would need to change the name on the appropriate PRJ line from the old geometry
subproject to the new netlist subproject.
Choosing Subdivision Line Placement
As mentioned above, the difficult part in using circuit subdivision is to decide
where to place your subdivision lines to split the circuit. The subdivision lines
should be placed between polygons which have negligible coupling. Places on the
circuit where a high degree of coupling or rapidly varying currents are present
should be kept within an individual subproject.
The de-embedding of the port discontinuity in Sonnet is done by essentially mod-
eling infinitely long transmission lines at the port. This allows transmission lines
to be subdivided with very little loss of accuracy. This includes microstrip lines,
stripline, and coupled lines including coplanar. This point is illustrated below.
The circuit shown below, on the left, consists of a coupled transmission line. This
is too simple a circuit to require subdivision but is very useful in demonstrating
the principle. When subdivided, the circuit is split into two subprojects both of

Chapter 13 Circuit Subdivision
261
Rev 16.56
which would resemble the circuit shown on the right. Since the port discontinuity
is modeled as an infinite transmission line when the port is de-embedded the cou-
pling between points A and B is accounted for.
It is important to avoid areas where there is coupling across the subdivision line.
Subdivision lines should not split any diagonal polygon edges. Illustrated below
are good placements and bad placements of subdivision lines.
Good and Bad Placements of Subdivision Lines
This section contains a series of illustrations each showing the good placement of
a subdivision line in a circuit and its counterpart showing a bad (and in some cases
illegal) placement of a subdivision line. Setting a subdivision line perpendicular
to one or more transmission lines provides a good general guideline for line place-
ment.
The first example is a pair of coupled lines. As explained above, when you split
coupled lines as on the left, very little loss of accuracy results. However, on the
right, you have split the coupled pair along the axis where significant interaction
takes place. The subprojects have no way to account for this coupling and will pro-
duce bad data.
A
B
A
B
Infinite
Transmission
Line
Good Bad

Sonnet User’s Guide
262
Rev 16.56
The second example shows how to split a series of resonators. In this type of struc-
ture, there is strong coupling at the gaps between adjacent resonators. The exam-
ple on the left is good since the subdivision lines do not prevent this inter-
resonator coupling. The example on the right is incorrect since the resulting sub-
projects do not contain the inter-resonator coupling.
The third example shows a square spiral. The example on the left is a good place-
ment since the location where the spiral is divided is essentially a group of coupled
transmission lines and the subdivision line is perpendicular to those lines. Here,
the left side of the spiral is sufficiently far from the right side so that coupling is
negligible. The example on the right is bad because the lines on the left side of the
spiral do couple strongly with the lines on the right side.
Good Bad
Good Bad
Chapter 13 Circuit Subdivision
263
Rev 16.56
The meander line on the left is split in such a way that Sonnet provides an accurate
answer since the bends on the top are far enough away from the bends on the bot-
tom that coupling between them is negligible. The example on the right provides
an inaccurate result because the coupling between two close transmission lines is
eliminated by the subdivision.
The circuit shown below has coupled transmission lines on two different layers.
Once again, it is correct to place a subdivision line perpendicular to the transmis-
sions lines, but not parallel to them. Subdivision is valid for multi-layer structures
as long as the coupling across the subdivider is negligible.
In the double stub circuit shown on the left, the subdivision lines split the polygon
perpendicular to the direction of current flow and far from any discontinuities. The
circuit on the right however, shows the subdivision line splitting the bases of the
two stubs which may be coupled.
Good Bad
Good Bad
Good Bad

Sonnet User’s Guide
264
Rev 16.56
The subdivision line shown in the circuit on the right is wrong since the circuit is
split in the middle of a via between layers. In general, subdivision lines should
never be placed on top of discontinuities, such as vias. The subdivision line on the
left is the correct placement.
The subdivision line shown in the circuit on the right splits a polygon at the box-
wall which is an illegal placement for a subdivision line. It is illegal to subdivide
polygons grounded to the box-walls since such polygons do not behave like trans-
mission lines. Also, the new ports added during the subdivide would be shorted to
the box-wall. The circuit on the left is correct since there is no contact between the
top and bottom polygons with the top and bottom box-wall.
Good Bad
Good Bad

Chapter 13 Circuit Subdivision
265
Rev 16.56
Subdivision Line Orientation
Subdividers may split the circuit on a horizontal axis or a vertical axis, but you
may not mix orientation. Choosing the direction in which you split your circuit is
dependent upon the structure of your circuit. Shown below is a typical circuit in
which you would use the vertical orientation and another example in which you
would use the horizontal orientation.
You may use both orientations by using double subdivision mentioned earlier.
The first time you subdivide your main circuit you choose an orientation for your
subdivision lines. Then use circuit subdivision on the resulting geometry subproj-
ects, this time using the opposite orientation for your subdivision lines.
Example of Vertical Subdividers
Example of Horizontal Subdividers

Sonnet User’s Guide
266
Rev 16.56
Before adding subdividers to your geometry project, you should ensure that spec-
ification of your circuit is complete. Subprojects created when you execute the
subdivision inherit their properties from the source project. Such properties as cell
size, metal types, properties of the dielectric layers, dielectric bricks, metal levels,
etc. are all used in the resultant subprojects.
When you place a subdivider in your circuit, a line representing the subdivider
appears in the horizontal or vertical plane running through the point at which you
clicked. The resultant sections of the circuit are automatically labeled.
Subdivision sections are labeled from left to right, or top to bottom, depending
upon orientation. These labels are always sequential and are non-editable.
Once a subdivider has been added to your circuit, you may edit the subdivider as
you would any other object in your geometry. You may click on the subdivider
and move it. You may also control the display and selection of the subdivider lines
and labels in the Object Visibility dialog box and the Selection Filter dialog box.
The following are illegal conditions for subdivision lines:
•May not be off grid.
•Should not be placed where there is coupling across the subdivision
line.
•May not be colinear with polygon edges.
•May not split a diagonal polygon edge.
•May not split a port.
•May not be below the line of symmetry.
•May not split a polygon at a box-wall. See the picture below.
Chapter 13 Circuit Subdivision
267
Rev 16.56
Once you have completed adding all the desired subdividers to your circuit, you
must save the project before performing the subdivision.
Setting Up Circuit Properties
Since the geometry subprojects created by the subdivide inherit their properties
from the source project, you should complete entering all the desired attributes for
your circuit before performing the subdivide. This includes such things as defin-
ing the dielectric layers (which includes the height of the box top), top and bottom
box metals, metal and dielectric brick materials, cell size and box size. This saves
the effort of having to enter these values in each of the subprojects.
Legal
Illegal
Subdivision
Lines
Legal
Illegal
Subdivision
Lines

Sonnet User’s Guide
268
Rev 16.56
Setting Up the Coarse Step Size Frequency Sweep
If you plan to use interpolation to obtain response data when analyzing the master
netlist project, you should input the coarse frequency sweep at which you wish to
analyze the geometry subprojects before subdividing the circuit. These frequen-
cies should cover the same frequency range as the analysis frequencies for the
whole circuit but use a coarser step size. The subprojects should be analyzed at the
same minimum and maximum frequency as the overall analysis and at enough
points in between to provide for reasonable interpolation of the response.
By inputting the coarse frequency sweep prior to subdivision, the master netlist
and geometry subprojects created by the subdivide command will all inherit the
analysis setup. After subdividing, you will need to enter the desired finer frequen-
cy step size in the master netlist project before analyzing it. In addition, you will
need to turn off Hierarchy Sweep.
The figure below shows a Smith chart with a circuit analyzed at five frequency
points, next to the same circuit analyzed at only two points. As you can see, using
only two data points would result in more interpolating error than using five data
points. Whether or not two data points is acceptable depends upon the proximity
of points A and B. If A and B are very close, then two data points are sufficient.
If A and B are far away, then five or more data points should be used.
It is always a good idea to check the Smith chart for the response data of your sub-
projects to ensure that you have chosen enough frequency points at which to cal-
culate data so that any interpolated data is reasonably accurate.
A
B

Chapter 13 Circuit Subdivision
269
Rev 16.56
Subdividing Your Circuit
The actual subdividing of your circuit into separate geometry subprojects and a
master netlist project is performed by the software. You enter the desired names
for the master netlist and geometry subprojects. You may also automatically add
feedlines of lossless metal to any ports generated in the subprojects.
Feedlines should be added when discontinuities contained in sections of your
source circuit need to be moved away from the box-wall to prevent interaction be-
tween the box-walls and the discontinuity. The use of feedlines are optional; if you
choose to add a feedline, you may use the suggested length calculated by the soft-
ware or input your own value. By default, the software creates feedlines using the
suggested length.
When the subdivide is executed, Sonnet creates a geometry subproject for each
section of the circuit in which you placed the subdividers. It also creates a master
netlist that connects the geometry subprojects together to produce an equivalent
circuit for the original geometry project that you subdivided.
Each of the geometry subprojects uses the properties of the original circuit: cell
size, dielectric layers, dielectric and metal materials, analysis setup, etc. There-
fore, all the geometry subprojects contain the same analysis setup with the same
analysis frequencies specified.
Analyzing Your Subdivided Circuit
To obtain the desired response data, edit the analysis setup for the master netlist
so that all of the desired analysis frequencies are specified. Each of the geometry
subprojects are set up with the coarser resolution of analysis frequencies. When
the netlist is analyzed, em runs the geometry project analyses first to produce re-
sponse data for each part of the network. Then the analysis of the whole network
is executed. Em interpolates to produce data for frequency points in between those
available from the analysis of the geometry subprojects.
If properly subdivided, the results of the netlist analysis should provide an accu-
rate solution for your difficult to handle circuit using fewer resources. The use of
circuit subdivision is demonstrated in Chapter 14 "Circuit Subdivision Tutorial"
on page 271.

Sonnet User’s Guide
270
Rev 16.56
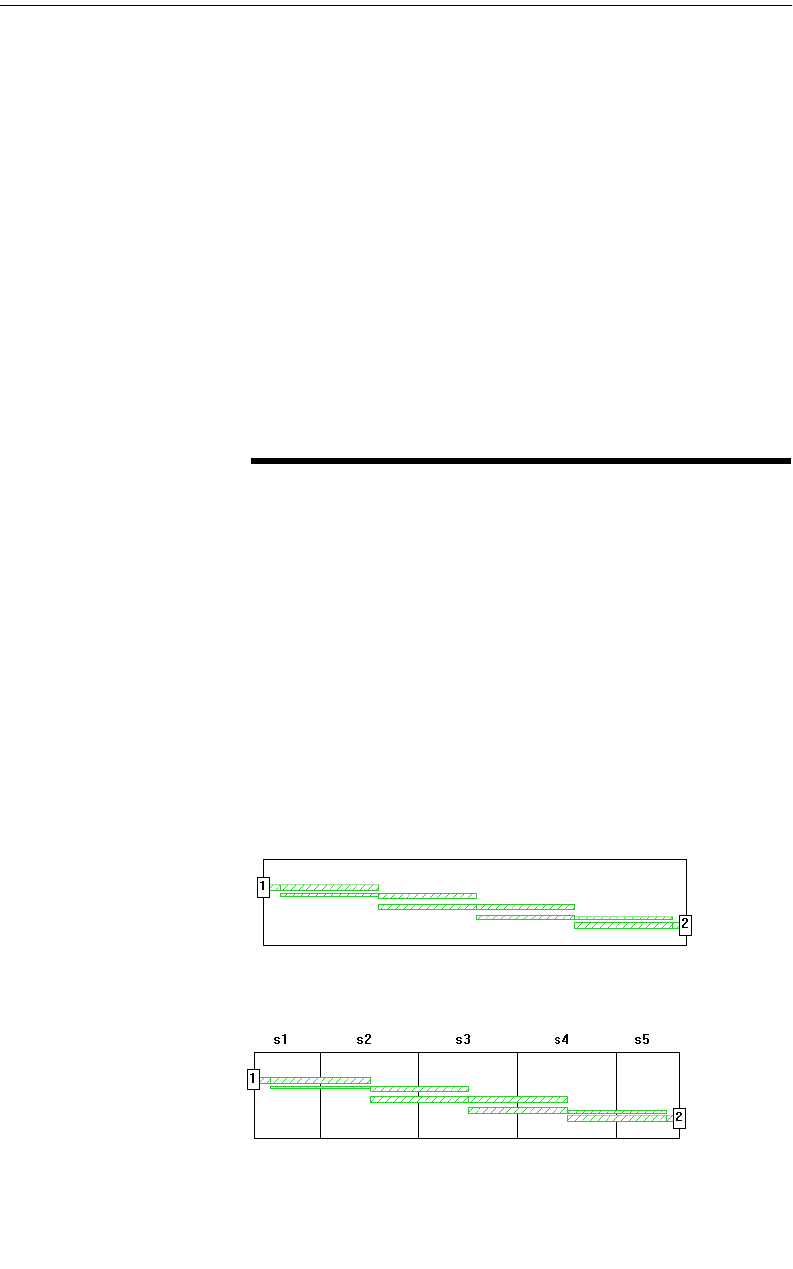
Chapter 14 Circuit Subdivision Tutorial
271
Rev 16.56
Chapter 14 Circuit Subdivision
Tutorial
This tutorial walks you through how to add subdivision lines, subdivide your cir-
cuit, and analyze the final netlist. The results of this subdivision are compared to
the analysis of the complete circuit in order to demonstrate the accuracy of the re-
sults of the subdivision and the savings in memory. For a detailed discussion of
circuit subdivision and the use of subdividers, please refer to Chapter 13.
The circuit, an edge-coupled microstrip bandpass filter, is a fairly simple example
of a circuit which you might decide to subdivide. In addition, it is not a very good
filter design. This circuit was chosen for the purposes of clarity in explaining cir-
cuit subdivision.
You will use four vertical subdivision lines to split the circuit into five sections as
shown below.
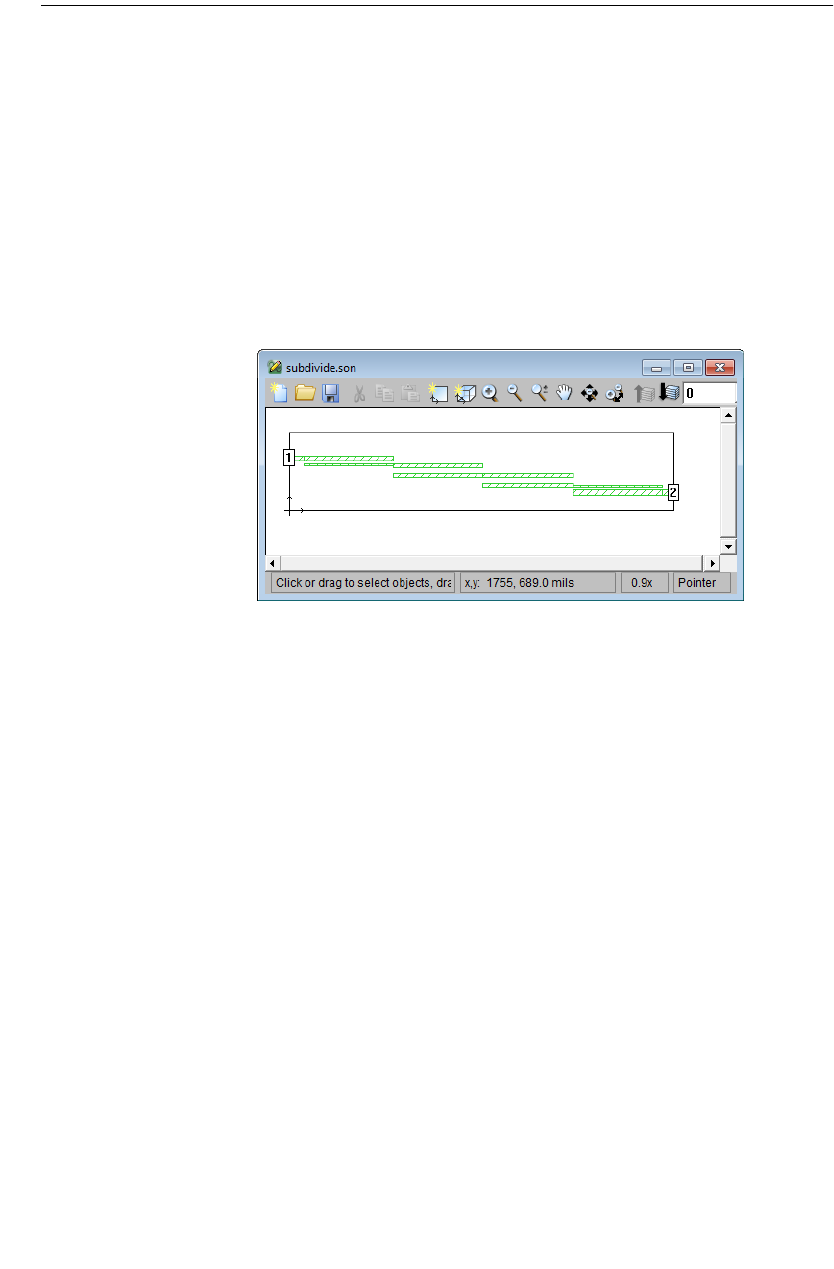
Sonnet User’s Guide
272
Rev 16.56
Obtaining the Example File
You use the example subdivision for this tutorial. The example may be obtained
using the Sonnet Example browser.You may access the Sonnet Example browser
by selecting Help Browse Examples from the menu of any Sonnet application.
For instructions on using the Example Browser, please click on the Help button in
the Example Browser window. Save the example to your working directory; there
are multiple files.
1 Open the project subdivide.son in the project editor.
The circuit appears as shown below.
Adding the Subdivision Lines
The first step in subdividing a circuit, as discussed in "Choosing Subdivision Line
Placement" on page 260, is to place the subdivision lines that indicate where you
wish to split your circuit. Subdivision lines should be placed in locations where
there is negligible coupling across the lines. The best place to put subdivision lines
in the example used here is at points in the circuit on the coupled lines as far from
the discontinuities as possible. Therefore, a vertical subdivision line will be placed
in the middle of each coupled pair of polygons.
Each coupled pair of polygons is 595 mils in the x direction. Subdivision lines
must be placed on the grid. The closest value to halfway which still remains on the
grid is 295 mils. For the first subdivider, you must take into account the feedline
polygon which is 100 mils in length. Therefore, the first subdivision line should
be placed at 100 mils + 295 mils = 395 mils from the left box-wall.

Chapter 14 Circuit Subdivision Tutorial
273
Rev 16.56
2 Select Tools Add Subdivider from the project editor menu while holding
down the shift key.
TIP
Holding down the shift key allows you to enter multiple subdivision lines without
having to select the command multiple times.
Since there were no subdivision lines in the circuit when you selected the Add
Subdivider command, the Subdivider Orientation dialog box appears on your dis-
play.
All subdividers in your circuit must have either a vertical (up-down) orientation
or a horizontal (left-right) orientation on the substrate.
3 Click on the vertical radio button to select the vertical orientation for your
subdividers.
This sets the orientation for all subdividers subsequently added to your circuit.
This dialog box does not appear again if you select Tools Add Subdivider. The
new subdivider assumes the same orientation. If all the subdividers are deleted
from a circuit, then when the Add Subdivider command is used again, this dialog
box appears.
4 Click on the OK button to apply your selections and close the dialog box.
The cursor changes to indicate that you are adding subdivision lines and a line
appears which moves with your cursor.
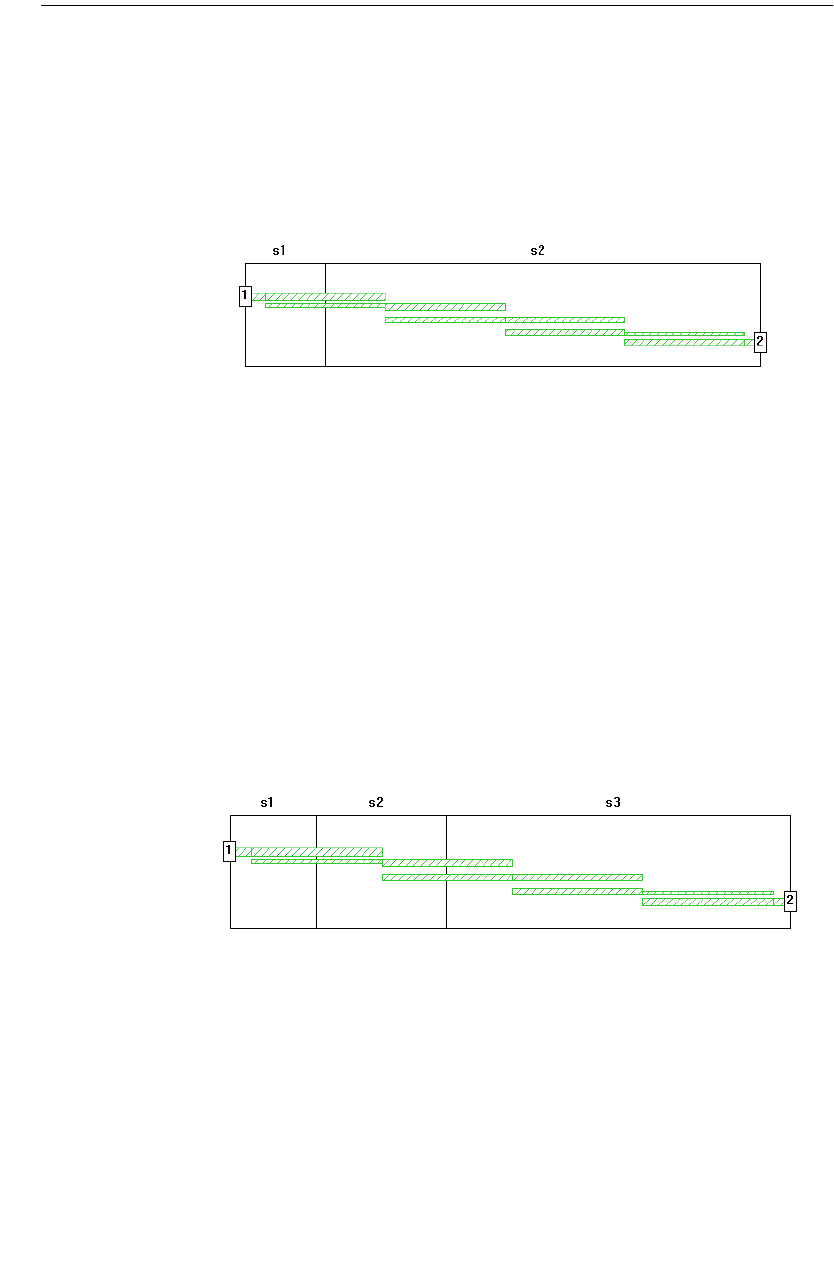
Sonnet User’s Guide
274
Rev 16.56
5 Move your cursor until the X coordinate of the cursor position in the status
bar is 395.0 and click.
A line representing the subdivider appears in the vertical plane running through
the point at which you clicked. The sections of the circuit are now labeled “s1”
and “s2”. Subdivision sections are labeled from left to right, or top to bottom,
depending upon orientation. These labels are always sequential and are non-
editable.
Subdivision lines are always snapped to the grid and may not be placed on top of
each other. Once a subdivider has been added to your circuit, you may edit the sub-
divider as you would any other object in your geometry. You may click on the sub-
divider and move it. You may also control the display of the subdivider lines and
labels in the Object Visibility dialog box, invoked by selecting View Object
Visibility from the project editor’s main menu.
Since each of the coupled line segments are 595 mils long and you wish to place
the subdivision lines at the halfway point, each subsequent subdivision line should
be placed 595 mils further to the right in the circuit. So the second subdivision line
should be placed at 990 mils from the left box-wall.
6 Move the cursor until the X coordinate is 990.0 in the status bar and click to
place the second subdivision line.
The subdivision line appears on your circuit and the sections are relabeled as
shown below.

Chapter 14 Circuit Subdivision Tutorial
275
Rev 16.56
7 Add subdividers at 1585 mils and 2180 mils from the left box-wall.
Once you have completed adding all the subdivision lines, press the Escape key
to return to pointer mode. Your circuit should now appear like this:
Setting Up Circuit Properties
For this example, the circuit properties such as box size, dielectric layers, metal
materials, etc. have already been input in the example circuit. It is important to
have the circuit properties input before performing the subdivide since these are
the properties used for all the subprojects created as the result of the subdivide. If
you do not enter all the desired properties, you will need to enter them individually
in each subproject or modify the original source project and execute the subdivide
again.
For this example, you will analyze the netlist using an adaptive sweep (ABS) with
Hierarchy Sweep turned on. When the Hierarchy Sweep option is used, the anal-
ysis control settings for the netlist are used to analyze all the subprojects in the
netlist. The desired frequency band for the circuit is 2.3 GHz to 2.5 GHz. An adap-
tive sweep provides approximately 300 data points. For more information on the
Adaptive Band Synthesis technique, see Chapter 9.
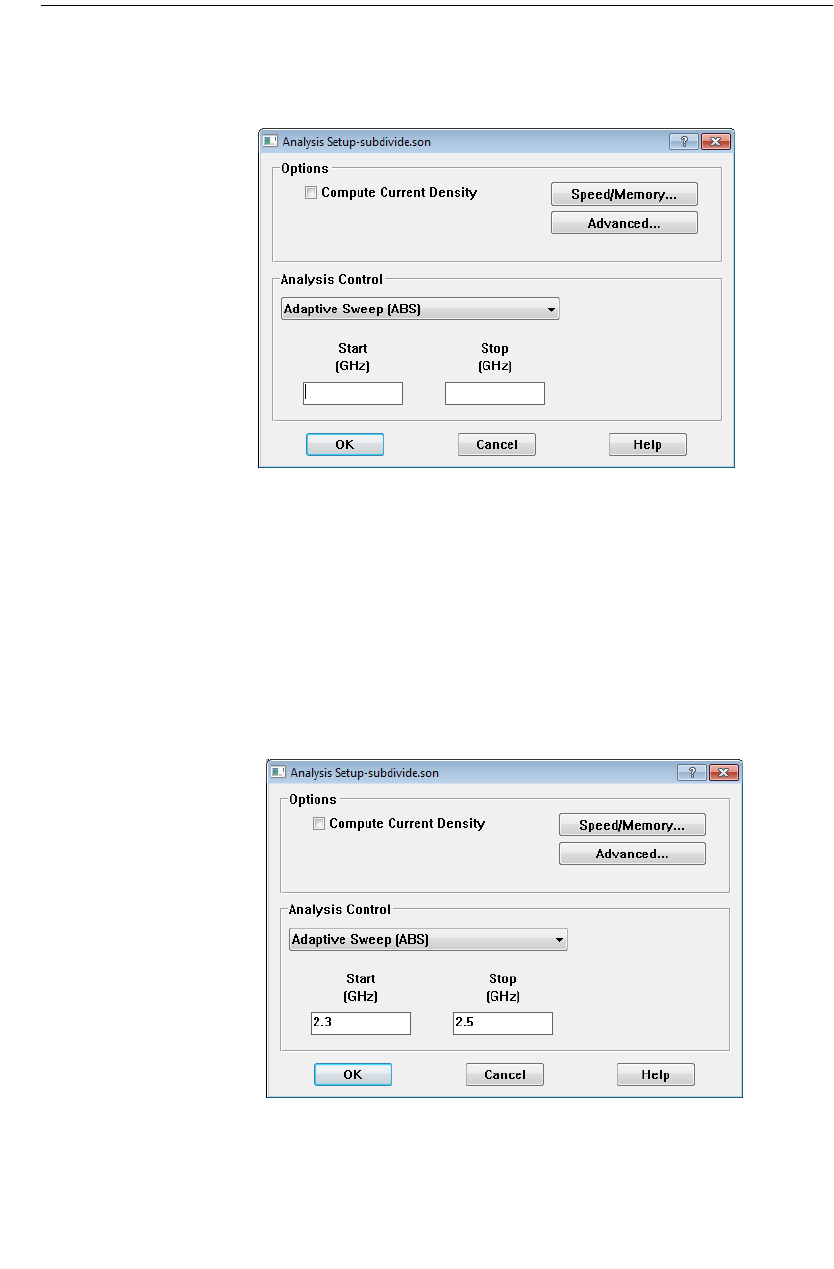
Sonnet User’s Guide
276
Rev 16.56
8 Select Analysis Setup from the main menu.
The Analysis Setup dialog box appears on your display.
9 Select “Adaptive Sweep (ABS)” from the Analysis Control drop list if it is
not already selected.
This selects the Adaptive Sweep as your type of analysis. The adaptive sweep
provides a fine resolution of response data over the given frequency band. Note
that the text entry boxes are updated to reflect your choice of analysis.
10 Enter 2.3 in the Start box and 2.5 in the Stop box.
This sets up the analysis frequency band. This analysis setup is duplicated in all
of the geometry subprojects when the subdivide is executed, as well as in the main
netlist. The Analysis Setup dialog box should appears as shown below.
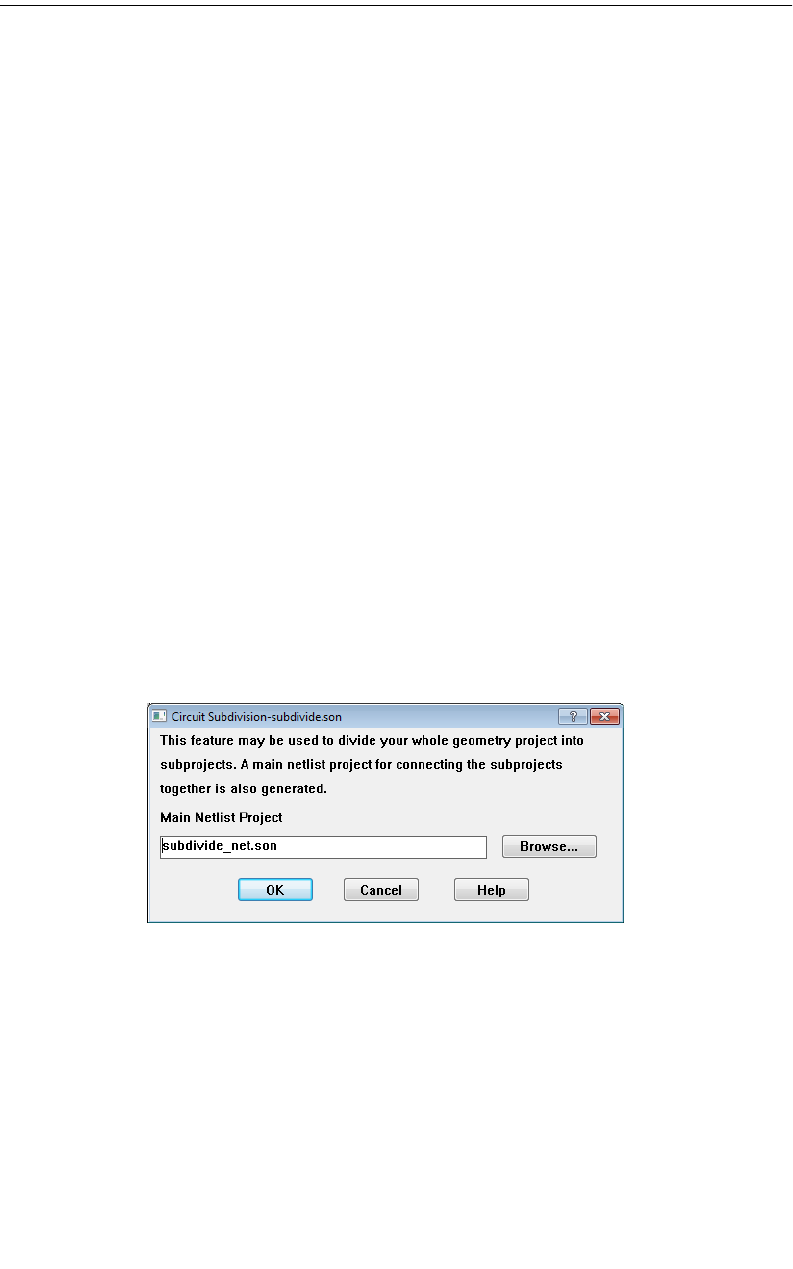
Chapter 14 Circuit Subdivision Tutorial
277
Rev 16.56
11 Click on the OK button to save the analysis setup and close the dialog box.
12 Select File Save from the main menu.
The file must be saved before executing the subdivide. The position of the
subdivision lines are saved as part of your source project.
Subdividing Your Circuit
The actual subdivision of the project is executed by the software but you must
enter names for the resulting main netlist file and subproject files produced as well
as, optionally, defining a feedline length to be added to the subprojects.
Feedlines should be added to the subprojects if you feel it necessary to move dis-
continuities in the various sections of the circuit further away from the box-walls
to prevent any interaction between the discontinuities and box-walls. This can
provide a more accurate analysis result for each section of the circuit. Any added
feedlines are of lossless metal, regardless of the metal type to which they are at-
tached.
Sonnet software provides a default recommended value for the feedline or you
may enter your own value.
13 Select Tools Subdivide Circuit from the project editor main menu.
The Circuit Subdivision dialog box appears on your display.
14 The name “subdivide_net.son” is provided by default in the Main Netlist
Project text entry box.
This name is used for the main netlist which connects the geometry projects
resulting from the subdivide. The default name is the basename of the source
project with a “_net” added on. You may use any project name you wish but it
must be different than the project name of the source file.

Sonnet User’s Guide
278
Rev 16.56
If you wish to change the directory in which the resulting files are created, click
on the Browse button to open a browse window. If you select an existing project
file, you are prompted if you wish to overwrite the existing file.
15 Click on OK to set the name and close the dialog box.
The Subproject Specifications dialog box appears on your display as shown
below. This dialog box allows you to enter names for each of the geometry
subprojects that result from performing the subdivide. Default names, consisting
of the main netlist project name with the section number added, are provided but
may be edited. For this example, use the default names.
The names for the subprojects must be unique and must be different from the
source project name and main netlist name.
The suggested length option is already selected for the feedline length. This feed-
line of lossless metal is added to ports generated when the subdivide is executed.
To enter your own feedline length, you would select the fixed length radio button
and enter the value in the corresponding text entry box. Select the None radio but-
ton if you do not wish to add a feedline.

Chapter 14 Circuit Subdivision Tutorial
279
Rev 16.56
16 Click on the Subdivide button to execute the subdivide.
The main netlist and subprojects are created using the names input by you. The
main netlist project is opened in the project editor.
The main network is defined as subdivide_net and has two ports. This corresponds
to the source circuit. There is a project (PRJ) entry line for each of the subprojects.
The project line includes the setting for the source of the analysis frequencies. A
Hierarchy sweep, in which the netlist frequency sweep is imposed on all the proj-
ect elements, is on by default. If you turn this off, the project default setting of
using its own sweep is displayed.
Pictured below are the geometries for the first two sections, subdivide_net_s1.son
and subdivide_net_s2.son. Note that in subdivide_net_s1.son, feedlines with a ref-
erence plane have only been added to ports 2 and 3, the ports created in the subdi-
vide, but not port 1 which is contained in the source project. All the ports in
subdivide_net_s2 have feedlines since all were created in the subdivide. Note that
the feedlines are all of lossless metal.
Added Feedlines
Original Port
subdivide_net_s1.son subdivide_net_s2.son

Sonnet User’s Guide
280
Rev 16.56
Analysis of the Network File
The last step to complete the analysis of the filter is to analyze the netlist project
created by the subdivide. The analysis controls you entered in the original project
are the ones you wish to use to analyze the netlist, so the analysis setup is already
complete. An adaptive sweep from 2.3 GHz to 2.5 GHz will be performed on the
netlist.
17 Click on the project editor window containing the netlist to make this the
active file.
This is indicated by the title bar on the netlist being highlighted.
TIP
You can switch the active file in the project editor by clicking on the title bar of
the project window or by selecting the project from the Windows menu on the
main menu.
18 Click on the Analyze button to launch the netlist analysis.
The analysis monitor appears on your display.
The project legend indicates that subdivide_net_s1.son is being analyzed. Em will
perform an adaptive sweep on each of the five subprojects and then use the result-
ing data to analyze the network. Status messages are output under the progress bar.

Chapter 14 Circuit Subdivision Tutorial
281
Rev 16.56
There are two results that are significant to observe. A comparison of the netlist
analysis data with the analysis data from the source circuit, and a comparison of
the amount of time and memory each analysis used. We have provided the source
project file including analysis data, subwhole.son, under the example subdivision
available in the Sonnet Examples.
The graph below shows the results of the netlist analysis versus the results of a full
analysis of the source project.
As you can see there is very good agreement between the two analysis results.
Both files were analyzed on the same computer. The time required for the netlist
was actually longer than the time required to analyze the circuit as a whole be-
cause this was a simple example chosen for clarity, and the benefits of circuit sub-
division are only seen for larger circuits.
Using circuit subdivision reduces your memory requirements for analysis of a
large circuit. Each of the subprojects requires less subsections to analyze than the
complete circuit. This improvement comes as a result of reducing the number of
subsections for any given analysis since both computation time and memory re-
quirements rise sharply as the subsections go up, as shown on the chart below. For
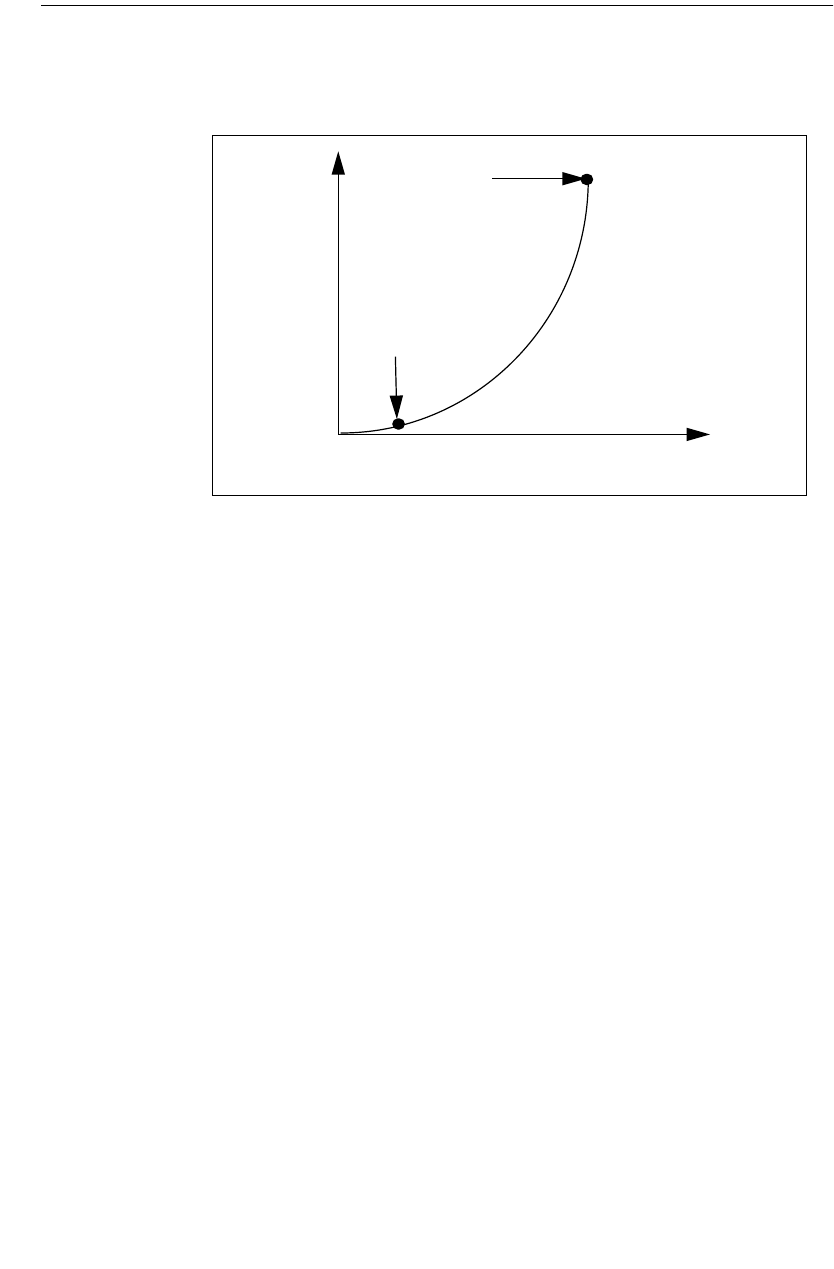
Sonnet User’s Guide
282
Rev 16.56
this example, the entire filter circuit used 2006 subsections while the largest indi-
vidual piece only required 1400 subsections and the smallest only required 854
subsections.
On many larger circuits the use of the automatic circuit subdivision features in
Sonnet can greatly improve the efficiency of your em usage.
Additional Improvements
There are two other ways this circuit could have been made even more efficient.
You could have refrained from adding the automatic feedlines and you could have
taken advantage of the fact that some of the subprojects were virtually identical.
For the purpose of illustration, this tutorial added feedlines to all ports generated
in the subdivide using the recommended length. Feedlines are added to a circuit
to move the discontinuities in the subprojects far enough from the box-walls to
prevent interaction. In the case of this example, either discontinuities were not
present or they were already far enough from the box-wall that additional feed-
lines were unnecessary.
If you leave the feedlines out by selecting None in the Subprojects Specifications
dialog box, the netlist analysis runs 1.5X faster than previously.
The last method that would allow you to decrease the processing time would be to
use fewer subprojects in the netlist to create the circuit. Observation of the circuit
geometry and response data shows that subdivide_net_s1.son and
subdivide_net_s5.son are virtually identical. The same is true for
Time &
Memory
Number of Subsections
Piece wise
Analysis
Full Filter

Chapter 14 Circuit Subdivision Tutorial
283
Rev 16.56
subdivide_net_s2.son and subdivide_net_s4.son. You could edit the main netlist,
subdivide_net.son so that you only use three files: subdivide_s1.son,
subidivide_net_s2.son and subdivide_net_s3.son to create the whole circuit. This
eliminates the need to calculate data for two out of five subprojects. This analysis
is 2X faster than the analysis using feedlines and all five subprojects.

Sonnet User’s Guide
284
Rev 16.56

Chapter 15 Vias
285
Rev 16.56
Chapter 15 Vias
Introduction
Sonnet vias can be used to connect metal on any level in a circuit to metal on any
other level. They are commonly used to model vias to ground, connections to air-
bridges, and can even be used to approximate wirebonds.
Sonnet vias use a uniform distribution of current along their height and thus are
not intended to be used to model electrically long vertical structures. Therefore,
the height of the via should be a small fraction of a wavelength. If you need to
make a connection through an electrically thick dielectric, you may need to divide
the dielectric into multiple layers to achieve an accurate analysis.
Sonnet User’s Guide
286
Rev 16.56
Creating Vias
Vias may be added to your circuit in a number of ways. Both the direction and type
of via is chosen in the Tools Add Via menu. You may also add vias to your
circuit by creating Via Technology Layers, then assigning via polygons to the
Technology Layer. For more information about Technology Layers, please see
“Technology Layers” in the index of Help. (Help Sonnet Help)
Via
Menu
Chapter 15 Vias
287
Rev 16.56
TIP
You may also use buttons in the Project Editor Tool Box, shown below, to add
vias and control the direction in which the via extends.
Via Direction
Vias connect metal from one level to metal on another level and can extend
through multiple layers; therefore, the connected metal levels do not need to be
adjacent. The initial direction of the via and the layers through which it extends
are based on your default settings when the via is added to your circuit or the set-
tings in the Via Technology Layer to which the via polygon is being added. How-
ever, the layers between which a via extends can be easily changed at any time.
The default may be set to go up one level, down one level, or down to ground,
through multiple layers if necessary. A via which goes down to ground extends
from the level of metalization to which it is added through all intervening levels
until it reaches the ground (bottom) of the box.
For vias not associated with a
Technology Layer, this button
controls the direction of the
via: up one level, down one
level or down to ground. Right-
click on the button to open a
popup menu of all the options.
This button controls the
type of via polygon:
Rectangular, circular or
edge via. Right-click on
the button to open a
popup menu of all the
options.
If you add a via to a Via
Technology Layer, it inherits
its properties from the Via
Technology Layer.

Sonnet User’s Guide
288
Rev 16.56
To change the direction of a via, or which metal levels it connects, you use the Via
Properties dialog box, shown below. You can use the Modify Via Properties
command, enabled when at least one via in your circuit is selected, to open this
dialog box. Double-clicking on a via also opens this dialog box.
Via Polygons
There are two types of vias: via polygons and edge vias. Via polygons provide the
most flexibility and are most commonly used by the majority of designers. Via
polygons are also the type of via created when you import a circuit using any of
Sonnet's translators. Edge vias provide a quick, convenient way to add a one cell
wide via. The rest of this section applies to via polygons. Edge vias are discussed
on page 300.
Via polygons can be rectangles, circles or any arbitrary shape and are added to
your circuit in much the same way that metal polygons are added to your circuit.
You may add rectangular or circular vias or draw an arbitrary polygon by placing
each vertex in its desired location.
An example of a via polygon is shown below. The shape drawn by the user ap-
pears in black and the subsections used by em are shown with the fill pattern as-
signed to the via metal. A 3D view of the via is shown on the right. The via is
modeled using the Ring meshing fill so that the middle of the via is hollow. (Note
that for clarity, these vias are shown with Via Pads turned off.) For more informa-
tion on via meshing fill, see "Meshing Fill for Vias" on page 290. The “up” via
symbol indicates that the via connects this level to the next level above. The vias
Level
and
Direction
Controls
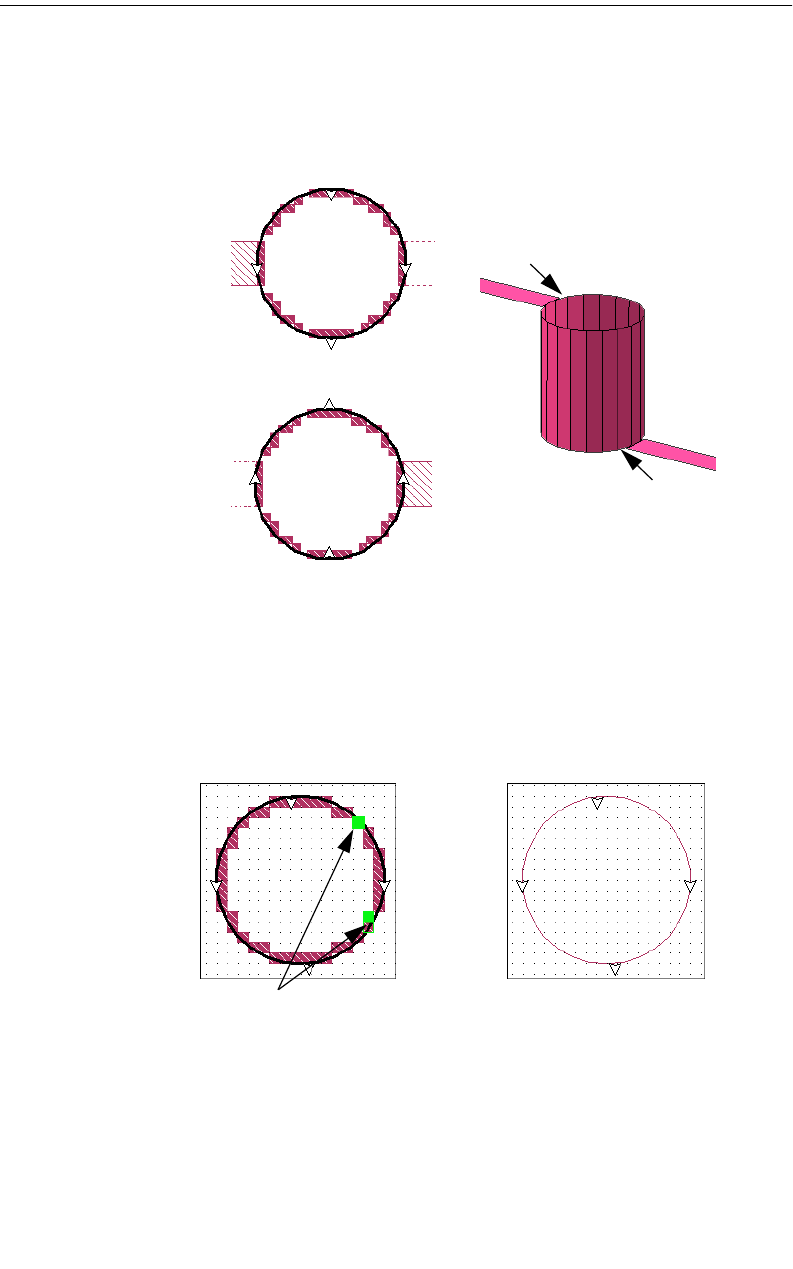
Chapter 15 Vias
289
Rev 16.56
on the upper level are shown with a “down” via symbol which is a “down” trian-
gle. Via symbols were automatically created on the destination level when the via
was added to the source level.
Via Subsections
With the metalization turned on (default setting), by setting ViewCell Fill to
“On”, the via subsections are also displayed using the pattern assigned to the via
metal type being used for the via.
Each via subsection is a rectangular cylinder of current, extending between the
present level to the next level above or below (depending on the direction of the
via). A via subsection has a horizontal cross-sectional area equal to one cell and a
Top of Vias - “down” via symbols
Bottom of Vias - “up” via symbols
Top of Via
Bottom of Via
Via subsections shown with the
“lossless” pattern. Two of the via
subsections are highlighted in green.
The via is indicated by only
triangles and an outline
when cell fill is off.

Sonnet User’s Guide
290
Rev 16.56
height equal to the thickness of the dielectric layer. If you change the cell size, then
the via is resubsectioned into via subsections using the new cell size. The place-
ment of via subsections is determined by the meshing fill chosen for the via.
Meshing Fill for Vias
There are five types of meshing fill for via polygons: Ring, Vertices, Center, Full
and Bar. The meshing fill provides the user with a way to control the trade off be-
tween accuracy and processing time.
You set the Meshing Fill for a via in the Via Meshing Fill dialog box, opened by
pressing the Change button in the Via Properties dialog box (Modify Via Prop-
erties) or clicking on the Edit button in the Meshing Properties section of the
Technology Layer dialog box, opened by double-clicking on a Via Technology
Layer in the Stackup Manager.

Chapter 15 Vias
291
Rev 16.56
NOTE: Note that for each mesh setting, the analysis engine adjusts the loss
of the individual via subsections to give the best possible overall DC
and RF loss corresponding to the loss model assigned to your via.
However, keep in mind that using less via subsections can change the
RF path of the current, thus changing the performance at RF.
Examples of via polygons using each type of meshing fill are shown below. Bar
meshing fill is not shown, since after the analysis engine simplifies bar via groups,
the resulting via is modeled using the Vertices fill. For more information, see
“Simplifying Bar Vias in the Analysis Engine,” page 292. The shape drawn by the
user appears in black. The actual via subsections are shown by the fill pattern
which was assigned to the via metal being used for the via.
Solid Ring Vertices Center

Sonnet User’s Guide
292
Rev 16.56
Ring: This is the default meshing fill for new vias and is the recommended mesh-
ing fill type for modeling both solid and hollow vias. The via is modeled as a one
cell wide wall of via subsections and is hollow in the middle, containing no metal.
This model provides a good compromise between speed and accuracy for both
solid and hollow vias. This meshing fill adequately models solid vias since at RF
most of the current travels along the perimeter of the via. Note that when used in
conjunction with the Volume loss model, both the DC and RF affects are accurate-
ly taken into account. For more information about the Volume loss model, please
see "Volume Loss Model" on page 59.
Vertices: This meshing fill models the via by placing a single cell wide via sub-
section at each vertex of the polygon. Notice that if you use this model, the current
may need to travel a longer path (i.e., longer than the real circuit) before it reaches
the via. Therefore, you should use this setting if you are not concerned about the
accuracy of the via but want a reasonable approximate model.
Center: A single cell wide via subsection is placed in the center of the via poly-
gon. Notice that if you use this model, the current may need to travel a longer path
(i.e., longer than the real circuit) before it reaches the via. Therefore, you should
use this option when you are not concerned about accuracy of the via but just want
to provide a connection from one level to another.
Full: This meshing fill models the via as solid metal. All subsections in the inte-
rior of the via are filled with metal extending the length of the via. This type of
meshing fill is the most costly in terms of processing time and memory. This
model should only be used if the via you are modeling is actually solid and you
require a high level of accuracy.
Bar: This meshing fill identifies the via as being a Bar via. Use this fill model for
vias within stacked multi-level conductors where the vias carry horizontal cur-
rents. During the analysis, multiple adjacent bar vias are merged into one wider
via to save memory and processing time. When the bar vias are grouped and sim-
plified by the analysis engine, they are meshed using a Vertices fill.
Simplifying Bar Vias in the Analysis Engine
Bar vias are vias whose length is significantly longer than their width. Bar vias are
identified in the project editor by assigning the Bar meshing fill to a via polygon
which uses the Volume loss model. This assignment may also be done automati-
cally, based on a length to width ratio, when using a translator or interface to Son-
net. For more information, please refer to the Via Simplification chapter in any
translator or interface manual.
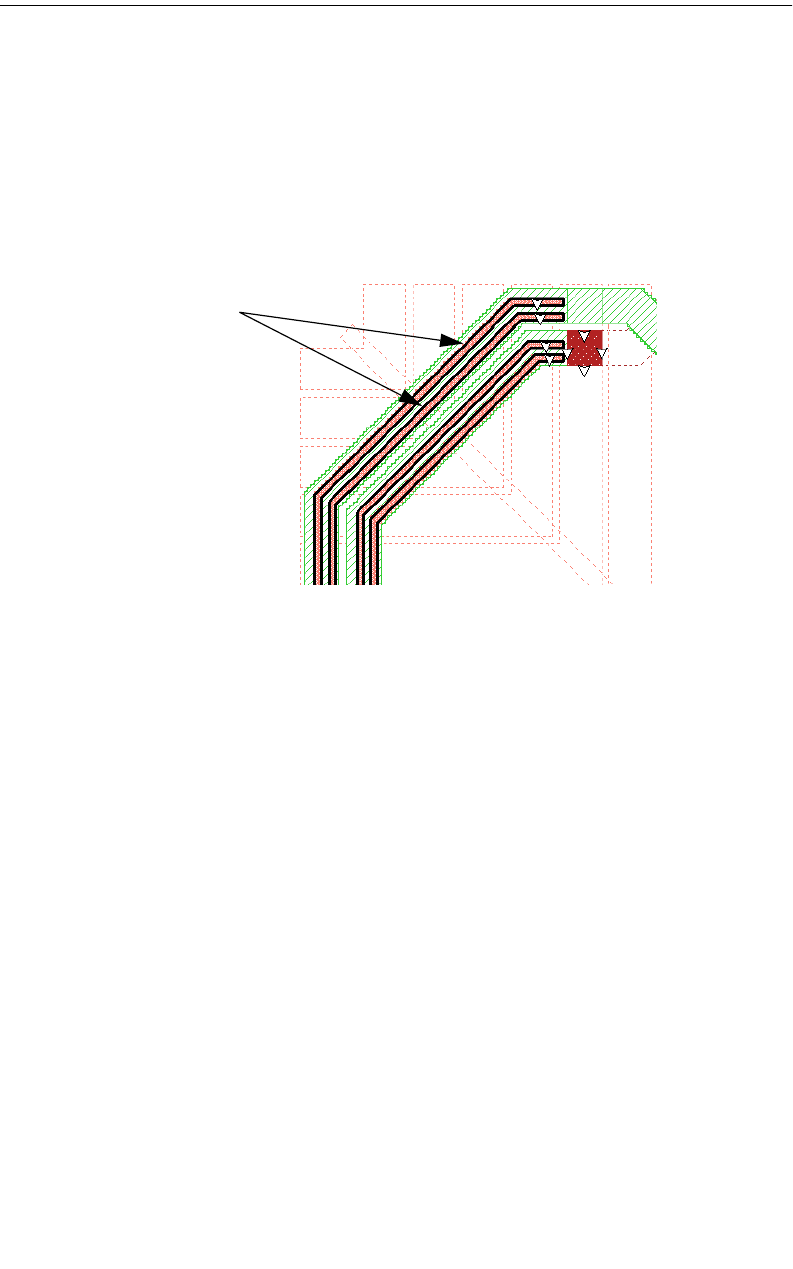
Chapter 15 Vias
293
Rev 16.56
Since bar vias are only identified in the project editor, the via polygon using the
Bar mesh fill is displayed as drawn by the user. The actual metal analyzed by em
is calculated during the analysis. Bar via groups are identified and combined, then
modeled using the Vertices mesh fill. An example is shown below.
The illustration below shows a section of an inductor which uses bar vias. The bar
via polygons are selected and highlighted with a black outline. Note that only part
of the via polygons is shown for clarity.
The Sonnet subsectioning automatically places more subsections in critical areas
where current density is changing rapidly, but allows larger subsections in less
critical areas, where current density is smooth or changing slowly. Therefore, if
these vias, placed on the interior of the traces, are not identified as bar vias, the
subsectioning requires a much finer resolution, which in turn dramatically increas-
es the memory and time needed for the analysis. The 2D view and 3D view of the
subsectioning of the inductor with the vias on the traces, which are not identified
as bar vias, is shown below. Planar metal using staircase fill is in orange, planar
metal using conformal mesh is green and via metal is blue. Note that even though
Bar vias

Sonnet User’s Guide
294
Rev 16.56
conformal mesh is applied to the traces, the placement of the vias on the traces
forces a staircase fill which is much less efficient for this circuit. The estimated
memory to analyze this circuit when not identifying bar vias is 55,994 MB.
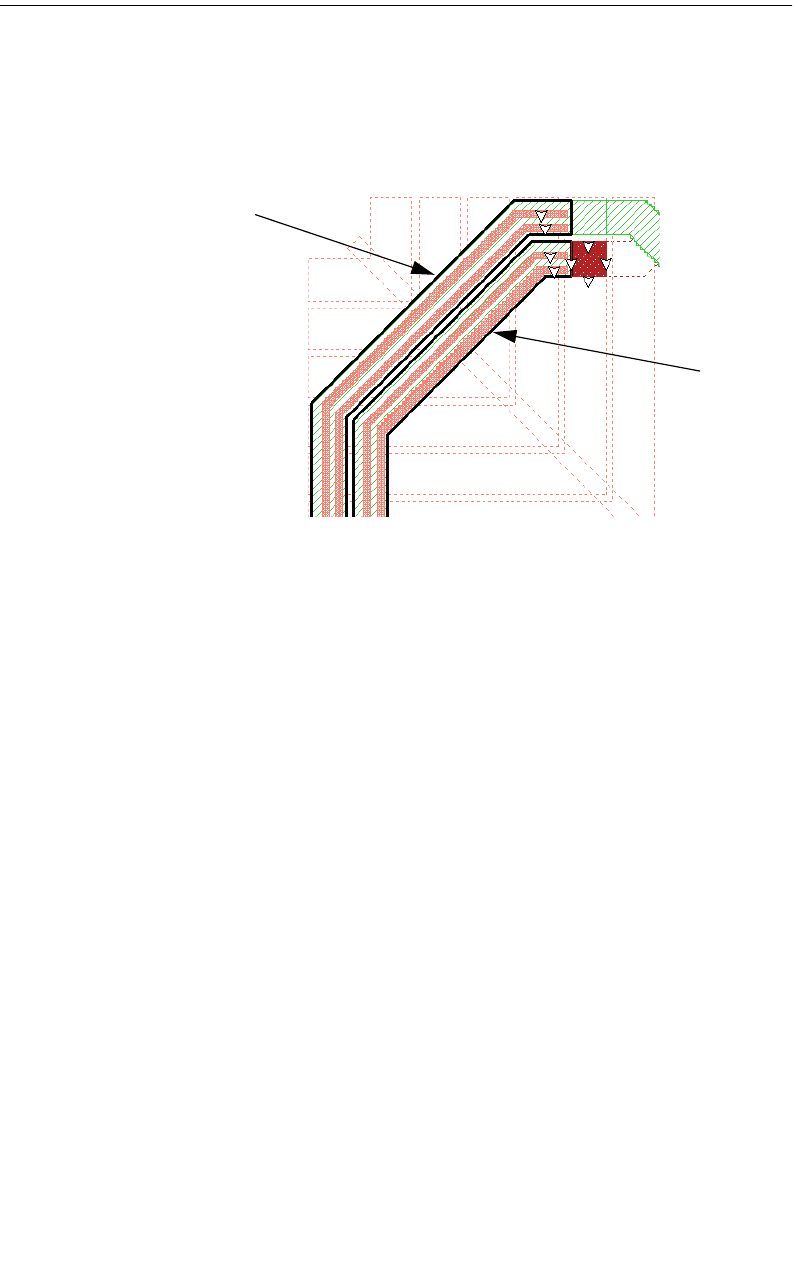
Chapter 15 Vias
295
Rev 16.56
Now we will look at the effect identifying the bar vias has on subsectioning and
memory requirements. When bar vias are identified, the analysis engine, em, sim-
plifies bar vias to reduce the required memory and processing time. Bar via groups
are first identified. In this example, the sets of two bar vias on the same trace make
up a bar via group.
Bar via groups are combined into one simplified via whose edges match the edge
of the trace, rather than being on the interior of the trace. This simplified via uses
the Vertices meshing fill. The subsectioning of the metal now matches that of trac-
es with no vias as pictured earlier. The 2D and 3D views of the subsectioning of
the circuit once the vias have been simplified is shown below; note that via metal
only appears at the vertices. In the 3D view, planar metal using staircase fill is de-
picted in orange, planar metal using conformal mesh is depicted in green and via
metal appears in blue. As you can see, the traces can now be modeled using con-
Bar via
group
Bar via
group

Sonnet User’s Guide
296
Rev 16.56
formal mesh in addition to the savings in metal from simplifying the bar vias. The
estimated memory when bar vias are identified is 794 MB, making this a much
more manageable analysis.
Adding a Rectangular Via to Ground
A via to ground can be added from any metalization level. This example shows a
rectangular via; the same steps would apply to a circular or polygon via; you
would just use the appropriate command for that shape of via. To add a via to
ground, go to the level from which you wish the via to extend downwards and per-
form the following:
1 Select Tools Add Via Down to Ground from the project editor menu.
Any vias subsequently added to your circuit will extend from the level to which
they are added down through all intervening levels to ground.
Via
Metal

Chapter 15 Vias
297
Rev 16.56
2 Select Tools Add Via Draw Rectangle to add the via.
This puts the project editor in Add via mode indicated by a change in the cursor.
3 Click and drag to draw the desired rectangle.
The via you input is drawn on the present level all the way down to the ground
level. An example of a via polygon going from level 0 to ground is pictured below.
The via polygon metalization is shown on Level 0. Note that the arrows are point-
ing down, indicating the direction of the via. Since this via uses the Ring meshing
fill, the center of the via does not contain metalization but is filled with the dielec-
tric of the dielectric layer. The ground level is completely metallized; however, the
subsectioning of the via is displayed on the ground level to indicate that there is a
via metalization in the layer above.
Ground Level Level 0
The lower figure depicts a via
going to ground. The same via is
shown in the top figures as it
appears in the project editor. The
rectangular via is subsectioned
into via subsections which are
rectangular cylinders of current,
extending between level 0 and the
ground plane.
Via Subsection
Planar
Via Polygon
Metalization
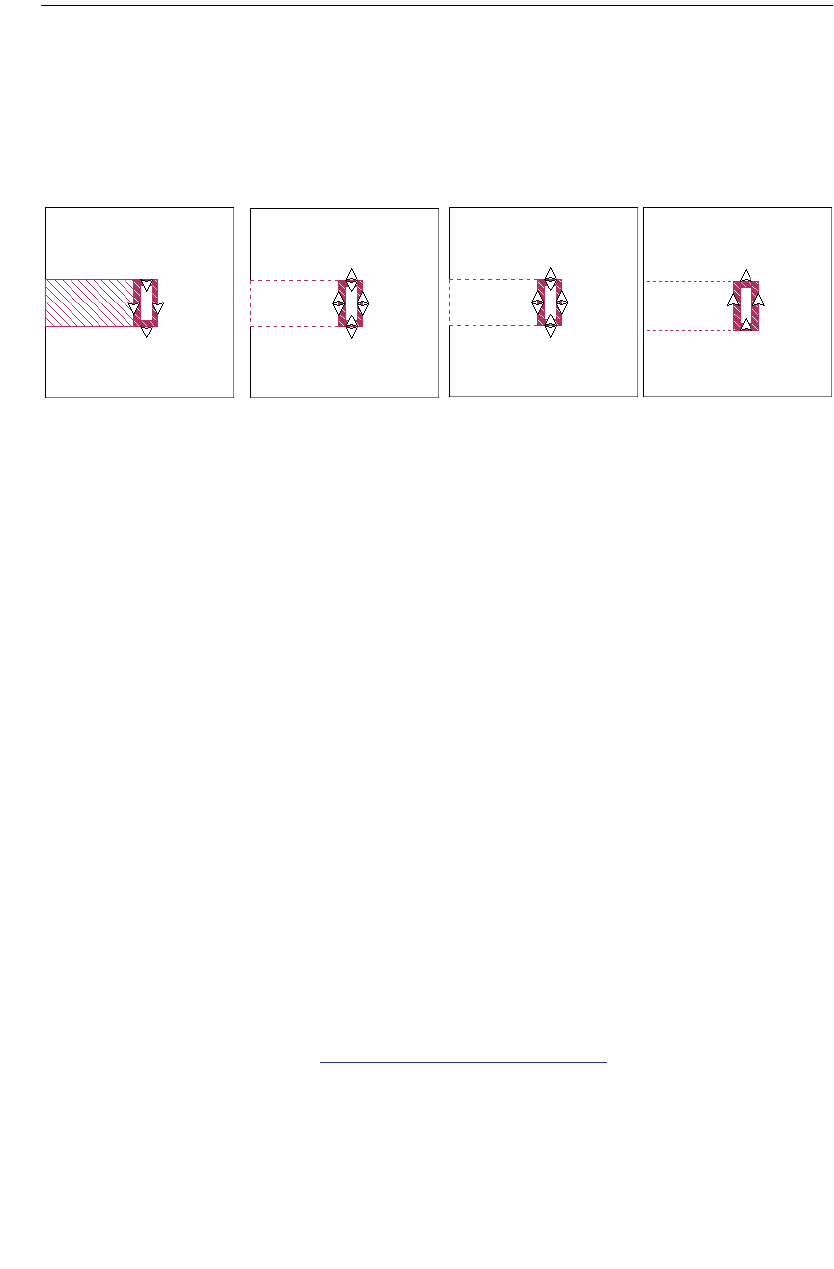
Sonnet User’s Guide
298
Rev 16.56
If the via to ground is added when there are multiple intervening metal levels be-
tween the present level and ground, the via polygon can be seen on each level. The
intervening levels have via arrows pointing in both directions to indicate that the
via extends both upward and downward. Below is shown a rectangular via poly-
gon extending from metal level 0 to ground in a three level circuit.
The via shown above extends from level 0, the highest metal level in the circuit
down to the ground level. The via arrows on the rectangular via on level 0 point
only in the downward direction. The via polygon appears on levels 1 and 2 in the
same position but with via arrows pointing in both the upward and downward po-
sition indicating that the via extends in both directions from these levels. The via
polygon is drawn on the ground plane to indicate its position with the via arrows
pointing upward indicating that the via extends upward. Since the complete
ground plane is metalization, the via polygon is drawn simply as a reference for
the user.
Via Loss
The loss of a via polygon is determined by the metal type it uses. When you draw
a via polygon, its metal type is set to the default metal used for new vias or the
metal type of a Via Technology Layer if it is being added to a Technology Layer.
The default metal type is controlled in the Metal Types dialog box accessed by se-
lecting Circuit Metal Types from the project editor’s menu. This metal type is
used for new independent vias or for new Via Technology Layers.
You may also change the metal type of the via polygon or Via Technology Layer
after it has been added to the circuit. You may use any via metal type defined in
your circuit for a via polygon. For a complete discussion of how loss is modeled
in via metal, see "Via Metalization Loss" on page 58.
Level 0 Level 2Level 1 Gnd
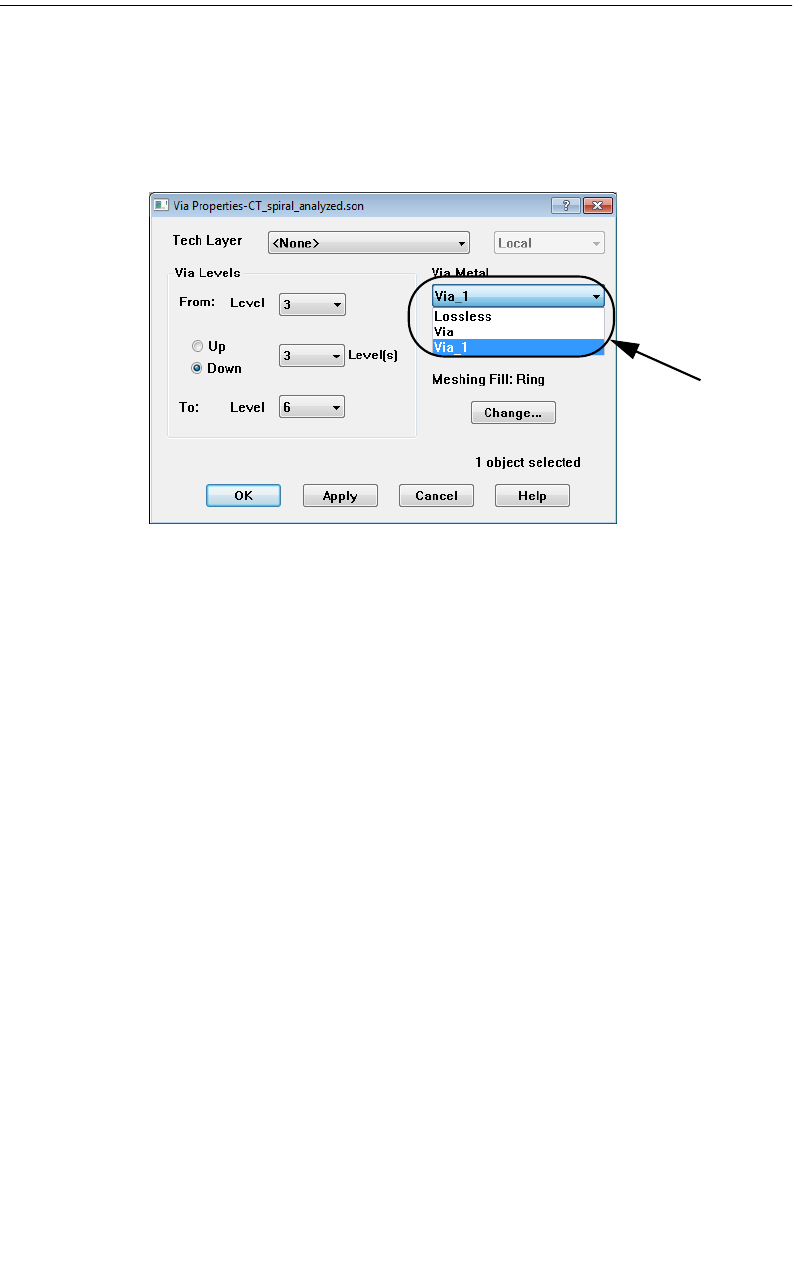
Chapter 15 Vias
299
Rev 16.56
1 Right-click on the via polygon and select Properties from the pop-up menu
which appears on your display.
The Via Properties dialog box appears on your display.
2 Select the desired metal type from the Via Metal drop list.
Via Pads
Vias have an option to add via pads. This feature is off by default for new vias but
may be turned on in the Via Properties dialog box. When this option is on, a via
pad is added to the top and bottom of the via which is the same size and shape as
the via polygon. The pad is modeled using a planar metal type with loss equivalent
to the loss of the via metal being used for the via polygon.
Via Ports
For a detailed discussion of via ports, please see "Via Ports" on page 98.
Auto Height Vias
Normally vias extend from the specified starting metal level to the specified end-
ing metal level. If the auto height vias option is selected, then a via will terminate
if its path, starting from the upper metal level and extending downward, contacts
planar metal. For example, if you define a via from metal level 3 to metal level 0
Via Metal
drop list
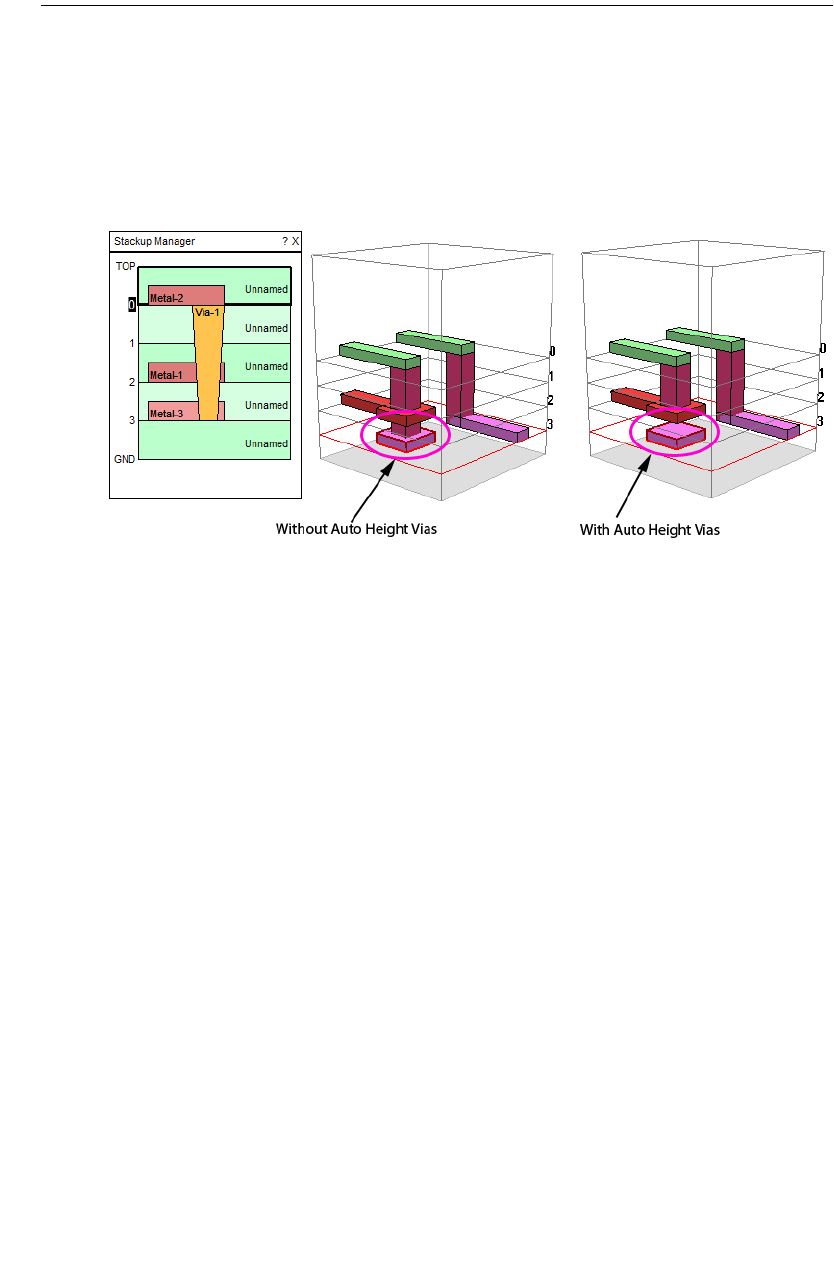
Sonnet User’s Guide
300
Rev 16.56
and there is a planar polygon in its path on level 2, then the via is terminated on
level 2 and therefore extends from level 0 to level 2. Note that the via is depicted
in both the 2D and 3D view as the actual metal which will be analyzed. However,
the associated Via Technology Layer still appears unchanged in the stackup since
other vias associated with the Technology Layer may still extend the fully defined
length as shown below.
Only polygons which completely cover the cross sectional area of the via are guar-
enteed to affect the height of the via. Note that planar metal that is on an interven-
ing metal level but does not intersect the path of the via does not affect the height
of the via.
This option may be set in the project editor in the Advanced Subsectioning Con-
trols dialog box (Analysis Advanced Subsectioning).
Edge Vias
Edge vias are vias that are attached to the edge of a metal polygon. As mentioned
earlier in the chapter, edge vias provide a quick, convenient way to add a one cell
wide via which extends for the length of the polygon edge. Edge vias are of the
same metal type as the polygon to which they are attached. The actual via metal
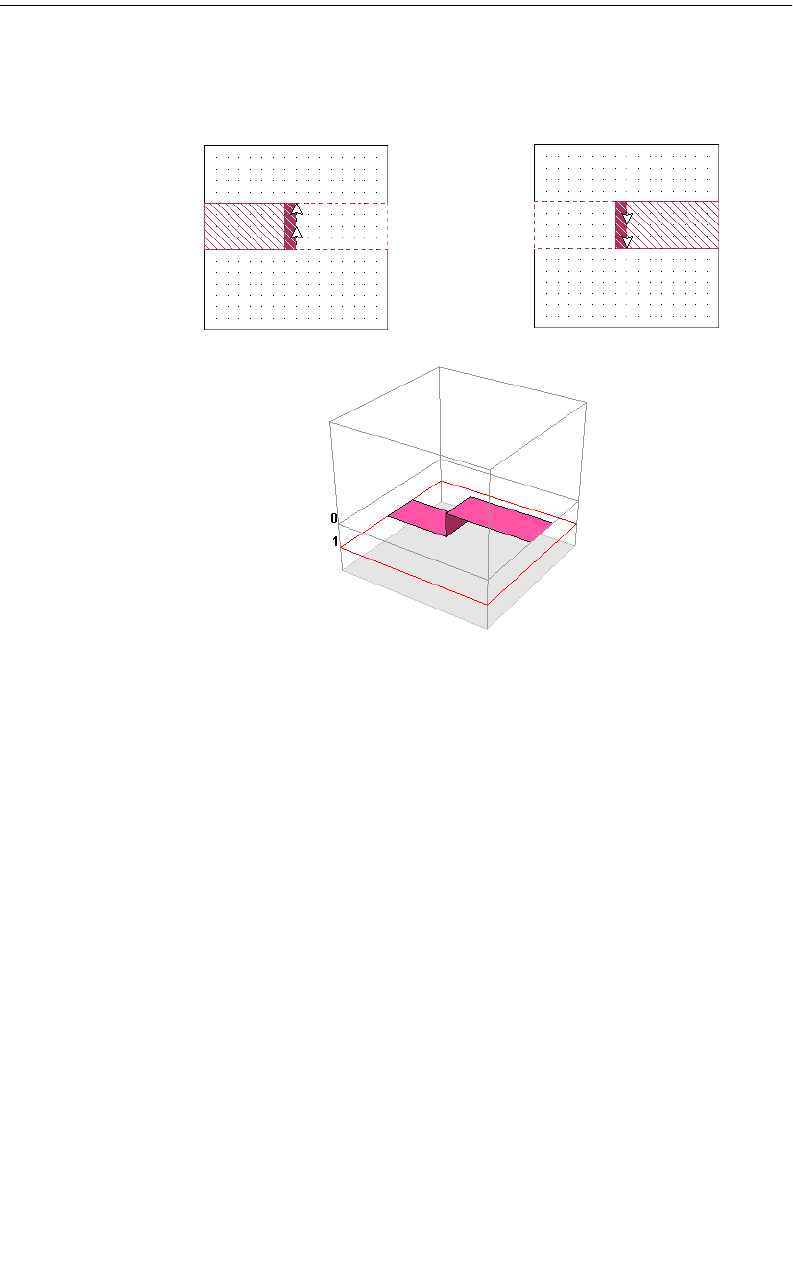
Chapter 15 Vias
301
Rev 16.56
is shown by the fill pattern which is the reverse video of the planar metal pattern.
The example shown below uses an edge via to connect two polygons on adjacent
levels.
Enough via subsections are placed to cover the entire length of the polygon edge.
If you change the cell size, then the via is resubsectioned into via subsections with
the new cell size.
Edge Via Loss
Loss in an edge via is modeled using the loss model of the planar metal type of the
polygon to which the edge via is attached. Edge via subsections are always one
cell wide, but be aware that the total DC loss of the edge via is independent of the
subsection size. For example, if your edge via is modeled using one micron thick
Gold, but your cell size is five microns, then the loss is based on the via being one
micron thick not five microns.
Lower Level - up triangles Upper Level - down triangles
3D View
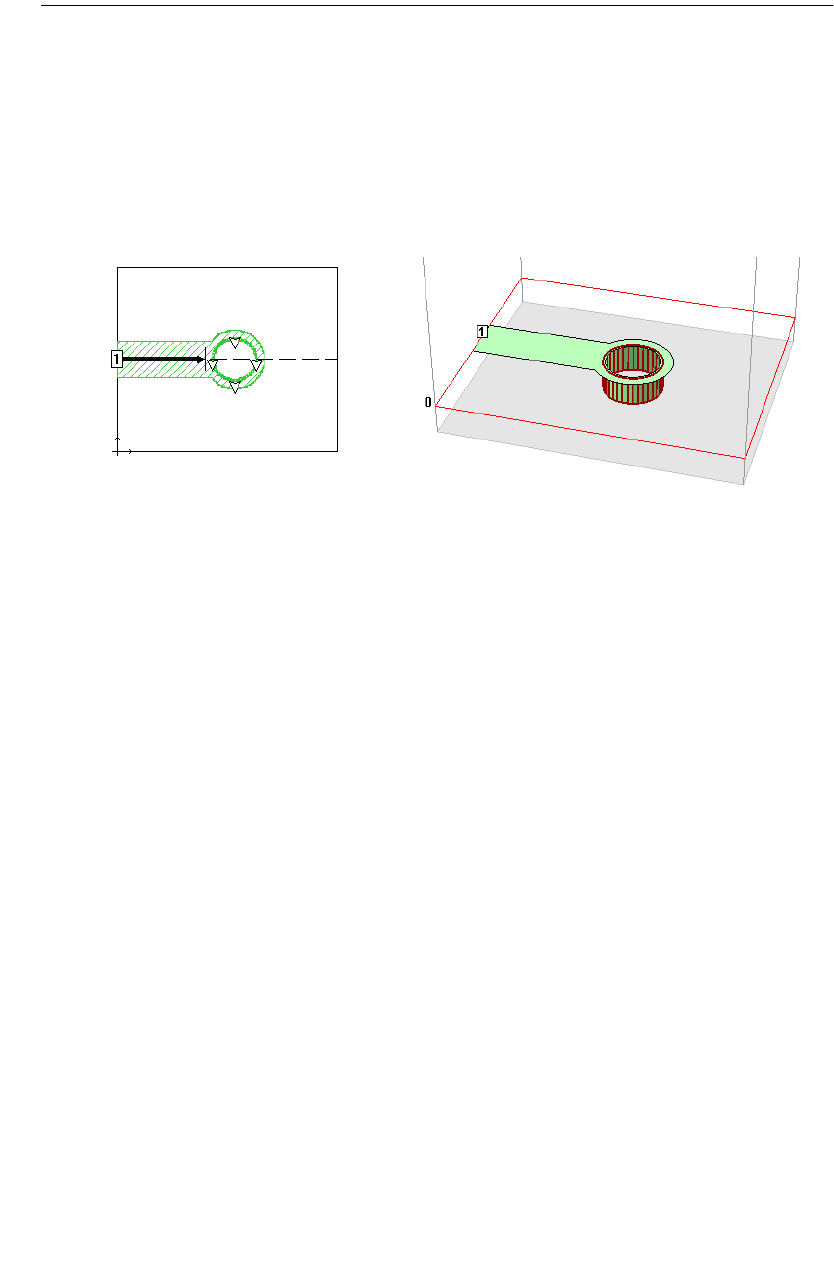
Sonnet User’s Guide
302
Rev 16.56
Simple Via Example
A simple via is stored in the example named “Via” and is shown below. To obtain
a copy of this example, open the Example Browser by selecting Help Browse
Examples from the menu of any Sonnet application. In the Search section of the
Example browser, select the “Name” radio button. Enter “Via” in the Search text
entry box, then click on the Search button. The via example is displayed.
A simple via to ground. On the left, as it would appear in the project
editor. On the right, a view in perspective.

Chapter 16 Thick Metal
303
Rev 16.56
Chapter 16 Thick Metal
Thick Metal Type
The Thick Metal metal type allows you to model physically thick metal. All other
metal types are modeled as having zero thickness where the entered thickness
value only affects the metal loss calculations. The Thick Metal type allows you to
more accurately model the true 3D characteristics of thick conductors. Using a
thick metal model not only allows for proper modeling of loss, but also includes
the EM effects of physically thick metal, such as coupling between closely spaced
conductors.
Since thick metal increases both your processing time and memory requirements,
it should only be used when necessary. Metal is considered to be thick metal when
its thickness is comparable to other dimensions in the circuit such as the width of
a conductor or gap between conductors.
When using thick metal, the structure is approximated by two or more infinitely
thin sheets of metal. The Number Of Sheets setting defines how many sheets of
horizontal metal are in the vertical stack that models the thick met.al. For the typ-
ical two sheet model, one sheet represents the top surface of the structure and a

Sonnet User’s Guide
304
Rev 16.56
second sheet represents the bottom surface of the structure. Vias are placed auto-
matically around the perimeter to allow current to flow between the sheets. An ex-
ample using two sheets is illustrated below.
For Number Of Sheets set to two sheets, the current travels on only the top and
bottom surface of the thick metal. Current on the sides of the thick conductor can
be approximated by using three or more sheets.
Bottom Sheet
Two Sheet (Default)
This is a cross section of
thick metal modeled using
two sheets; note that the
sidewalls are vias.
Top Sheet
Thick Metal
x
y
z
The two-sheet model: Current flows in the x-y plane
on the top and bottom of the thick metal polygon
shown here. Current is also allowed to flow between
the top and bottom sheets, but only in the z-direction.
No current flows in the zy or zx plane.

Chapter 16 Thick Metal
305
Rev 16.56
For most cases, using the default of two sheets provides a high accuracy solution.
However for very tightly coupled lines, where the gap between the lines is much
less than the metal thickness, the coupling between them may be underestimated.
In these cases, you may need to increase the number of sheets. However, increas-
ing the number of sheets increases the memory requirements and processing time.
Increasing the number of sheets adds more layers of infinitely thin metal between
the top and bottom metal sheet. A cross section of a four sheet model is shown be-
low.
Creating a Thick Metal Polygon
To create a thick metal polygon in your circuit, you must first define a metal type
using the Thick Metal model, then apply that metal type to the polygon in your
circuit. This creates a thick metal polygon which extends upwards (toward the box
top) from the metal level on which it is created. To do this, perform the following:
1 In the project editor, select Circuit Metal Types from the main menu.
The Metal Types dialog box appears on your display.
2 Click on the Add Planar button in the Metal Types dialog box.
The Planar Metal Editor dialog box appears on your display.
Four Sheet Thick Metal Top Metal
Bottom Metal
Interior Sheet
Interior Sheet
This is a cross section of thick metal modeled with
four sheets; note that the sidewalls are vias.
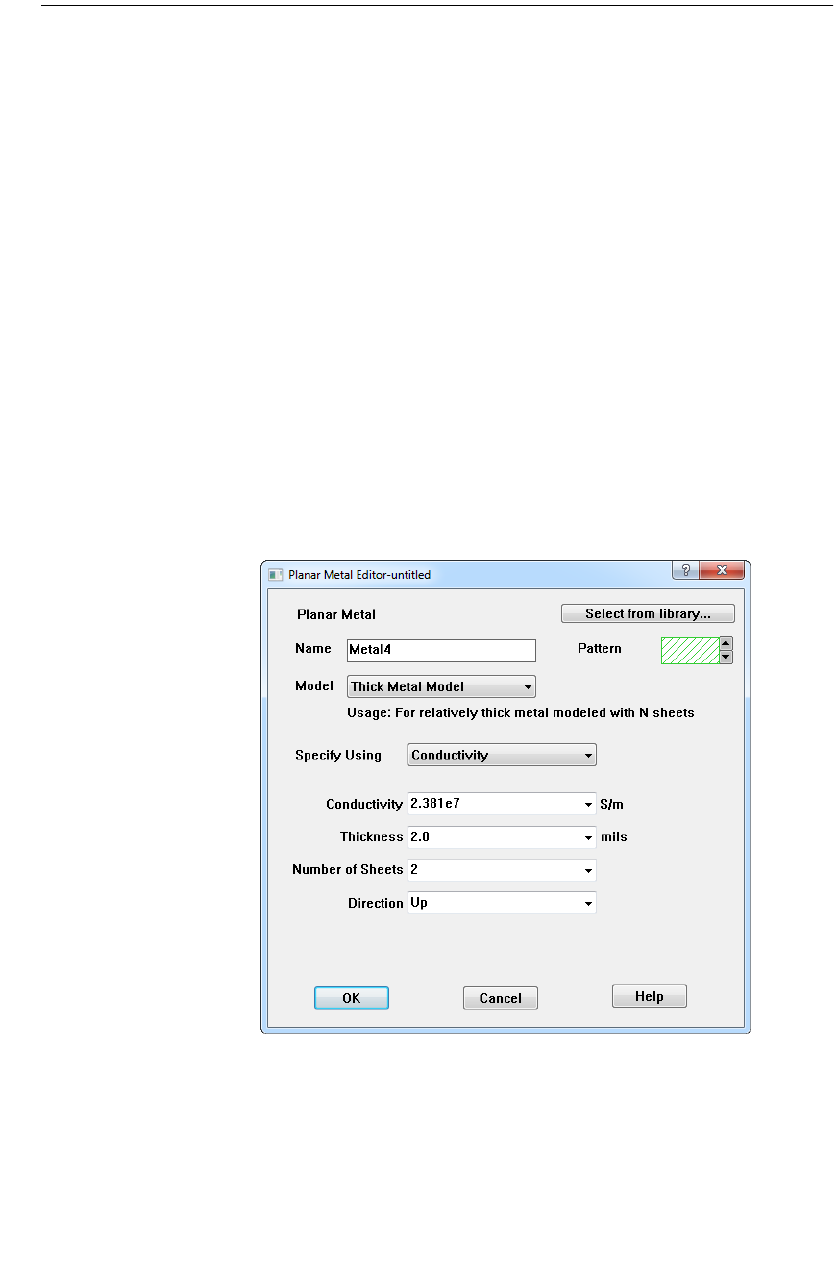
Sonnet User’s Guide
306
Rev 16.56
3 Select Thick Metal Model from the type drop list in the Metal Editor dialog
box.
This updates the dialog box with the text entry boxes for the four parameters
needed for the thick metal model: Thickness, Number of Sheets, Direction and a
fourth parameter which is set by selecting either Conductivity, Resistivity, or
Sheet Resistance at DC from the Specify Using drop list. The default is
Conductivity. The example below uses the Sheet Resistance at DC. Note that this
is the overall Sheet Resistance of the metal, and is not related to the number of
sheets being used. For more information on Conductivity, Resistivity, and Sheet
Resistance at DC, please see “Conductivity, Resistivity, or Sheet Resistance at
DC,” page 51.
The direction parameter defines whether the metal extends upward into the dielec-
tric layer above (the default setting) or extends downward into the dielectric layer
below.
4 Enter the four parameters in the appropriate text entry boxes.
5 If you do not wish to use the default metal name, enter the desired name for
the metal type in the Name text entry box.
The Metal Editor dialog box should appear similar to the picture below.

Chapter 16 Thick Metal
307
Rev 16.56
6 Click on the OK button to close the Planar Metal Editor dialog box and
apply the changes.
The Metal Types dialog box is updated with the new metal type.
7 Click on the OK button to close the Metal Types dialog box.
The thick metal is now available to use in your project.
8 Enter the desired polygon, then double-click on the polygon to open the
Metalization Properties dialog box.
9 Select the thick metal model metal type from the Metal drop list in the
Metalization Properties dialog box.
This will apply the metal type which uses thick metal to the selected polygon. In
this case, since the Direction selected was “Up,” the thick metal extends upwards
from the level on which the polygon was drawn. If you had selected “Down” for
the direction, the metal would have extended downward from the metal level.
10 Click on the OK button to close the Metalization Properties dialog box and
apply the changes.
The fill pattern of the polygon changes to the fill pattern used by the thick metal.
If the thick metal polygon is thicker than the dielectric layer(s) above it, the
polygon also appears on metal levels above.
You may also assign a thick metal model metal type to a Metal Technology Layer.

Sonnet User’s Guide
308
Rev 16.56
Viewing Thick Metal in the Project Editor
The thick metal can extend upward through the dielectric layer from the level on
which the polygon is drawn or downward into the dielectric layer below. If the
thick metal is not as thick as the dielectric layer, then the polygon only appears on
the level where it was drawn. If the thick metal is the same thickness or thicker
than the dielectric layer it appears on both the metal level where it was drawn and
on the next metal level. Note that the top of the thick metal may not appear in the
project editor if it is embedded in a dielectric layer. You will be able to view the
top sheet of metal in the current density viewer which is discussed later in the
chapter. Examples of both instances are shown below.
Level 2 Level 0
Level 1
A 3 mil thick metal polygon is drawn on level 2 below a 5 mil thick dielectric layer. The
polygon is visible on level 2 where it was drawn, but only the outline is visible on level
1 above since the thick metal does not pierce the dielectric.
A 5 mil thick metal polygon is drawn on level 2 below a 5 mil thick dielectric layer. The
polygon is visible on level 2 where it was drawn, and also on level 1 above since it is the
same thickness as the dielectric layer. Note that on level 1, the border of the polygon
is drawn with a dashed line to indicate that the origin of this polygon is not on this level.
Level 2 Level 0
Level 1
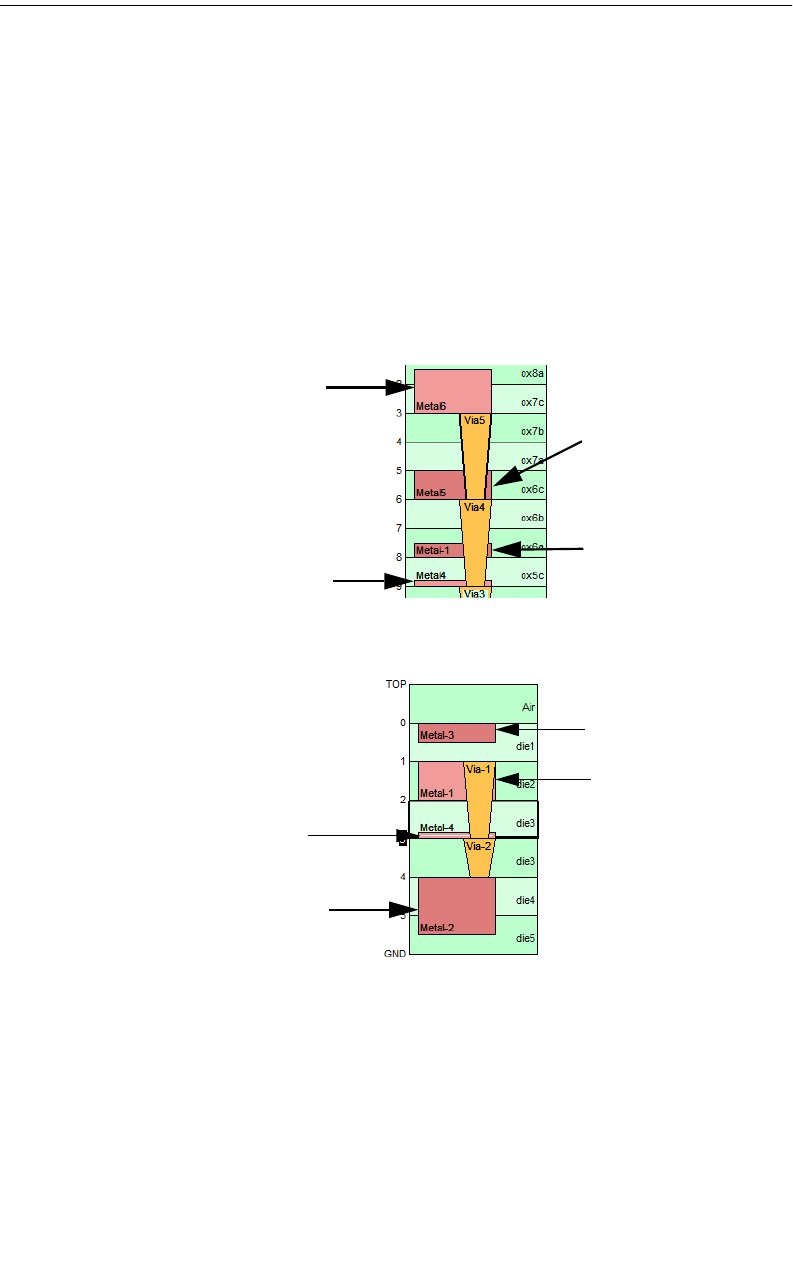
Chapter 16 Thick Metal
309
Rev 16.56
Stackup Manager
If a Metal Technology Layer is assigned a thick metal, then how it appears in the
stackup manger is based on its relationship to the dielectric layers. The thick metal
height is not drawn to scale in the stackup manager, but if its thickness is less than
that of the dielectric into which it extends, then the symbol covers half of the thick-
ness of the dielectric layer. If it is the same thickness as the dielectric layer then
the symbol is drawn the same height as the dielectric. If it is thicker than the di-
electric then it also extends half of the height of the next dielectric layer. Examples
of thick metal which extends upward and downward are shown below. Note that
all dielectric layers are represented as the same height in the stackup manager re-
gardless of their actual physical thickness.
Zero-thickness
metal
Less than
dielectric
height
Equal to
dielectric height
Greater than
dielectric height
Thick Metal- Up
Thick Metal- Down
Less than
dielectric
height
Equal to
dielectric height
Greater than
dielectric height
Zero-thickness
metal
Sonnet User’s Guide
310
Rev 16.56
Modeling
A side view of a circuit with three 50 mil dielectric layers (A, B, and C) and a 75
mil thick metal polygon on level 2 is shown below. Note that the top of the thick
metal only extends halfway through dielectric layer. The top of this thick metal is
not visible in the project editor.
Another important thing to note about the modeling of a thick metal which ends
in the interior of a dielectric layer is that even though you model the thick metal
with 2 sheets, the software actually uses three sheets. The bottom sheet is on level
2 where the polygon originates. The top sheet is in the interior of dielectric layer
A. The third sheet is on metal level 1. Whenever a thick metal polygon traverses
a metal level, a sheet is added on that level. This adds additional computational
time and should be kept in mind when using thick metals which encompass more
than one dielectric layer.
If Single Level select is enabled, then you may only select the thick metal polygon
on the level where it was drawn.
Thick metal polygons are connected to thin metal polygons by drawing the thin
metal polygon on the same level on which the thick metal was drawn and placing
the thin metal polygon adjacent to or overlapping the thick metal. This connects
the two structures electrically.
50 mils
100 mils
150 mils
75 mils
Dielectric Thick metal
Z-direction
A
B
C
Level 0
Level 1
Level 2

Chapter 16 Thick Metal
311
Rev 16.56
Modeling Plated Metal
Plated metal can be modeled in Sonnet by stacking two or more thick metal con-
ductors directly on top of each other as illustrated below with a stack of two dif-
ferent metals.
Independent properties can be defined for each individual layer of metal in the
stackup. The analysis engine, em, will precisely account for the unique properties
and thickness of each metal layer as it computes the loss of the combined stackup
of metals.
Modeling Conductor-Via-Conductor Stackups
Metal with conductor-via-conductor cross-sections, as is typical in RFIC applica-
tions, can be modeled in Sonnet by stacking thick metal conductors with vias con-
nected between them. There are two general configurations for these stackups,
characterized by the geometry of the vias: the bar via configuration and the via
array configuration.
Metal 1
Metal 2

Sonnet User’s Guide
312
Rev 16.56
Bar Via Configuration
With the bar via configuration, solid vias connect the thick metal conductors as
illustrated below. Because the vias are solid, these vias carry horizontal sidewall
currents in parallel to the currents carried by the thick metal conductors. These
sidewall currents have the effect of decreasing the loss of the overall metal stack-
up, and are accurately accounted for by the Sonnet analysis engine, em.
For more information on how bar vias are modeled in Sonnet, please see "Simpli-
fying Bar Vias in the Analysis Engine" on page 292.
Metal Conductor
Metal Conductor
Bar via

Chapter 16 Thick Metal
313
Rev 16.56
Via Array Configuration
In the case of the via array configuration, there is physical separation between
each of the individual vias making up the array. Thus, there is no horizontal side-
wall current on these vias. Only the thick metal conductors carry horizontal cur-
rent. This condition is accurately accounted for by the Sonnet analysis engine, em,
as is computes the loss of stackups with this type of cross-section.
For more information on how via arrays are modeled in Sonnet, please see Appen-
dix I “Via Simplification” in any translator or interface manual.
Metal Conductor
Metal Conductor
Via array
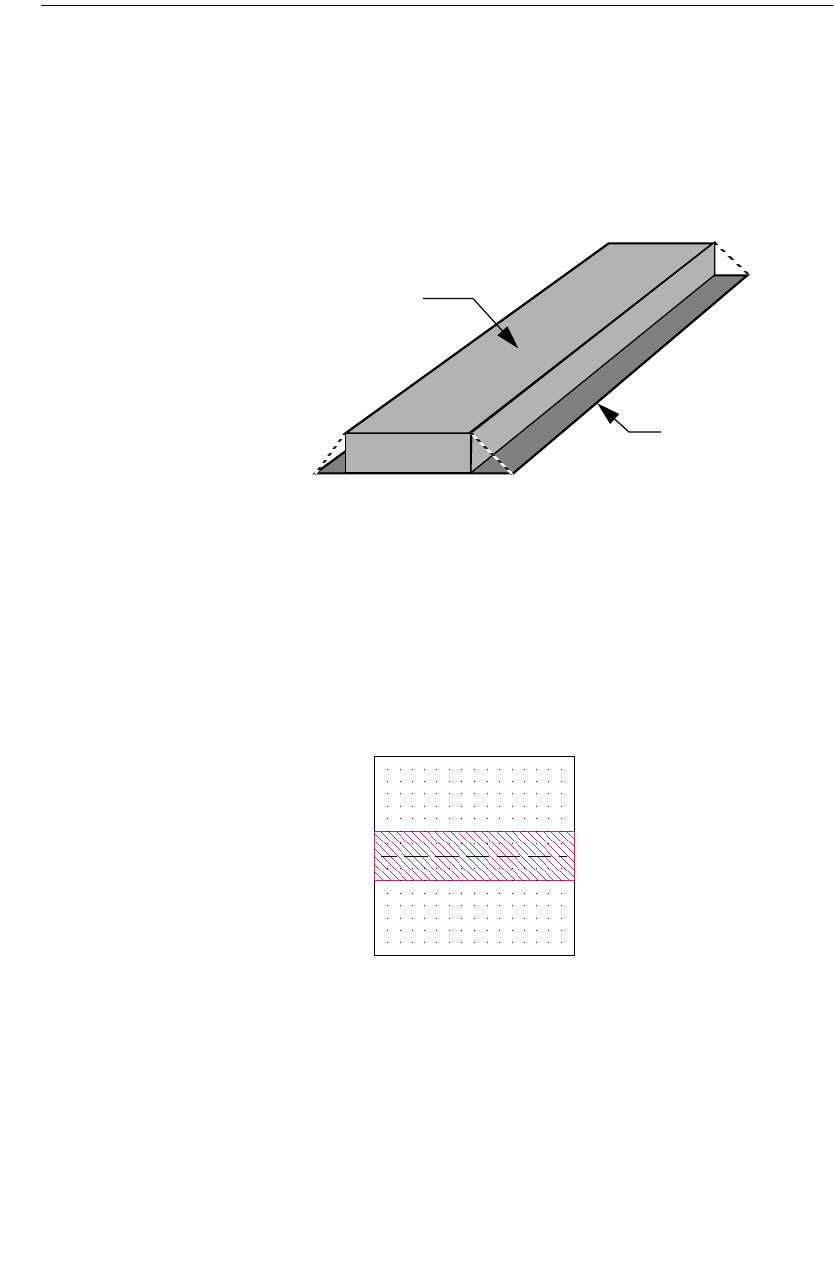
Sonnet User’s Guide
314
Rev 16.56
Modeling an Arbitrary Cross-Section
In this section, we use a combination of thick metal and Normal (zero thickness)
metal to approximate thick metal lines where the vertical cross-section has an ar-
bitrary geometry. To demonstrate this capability, we use a simple trapezoidal ge-
ometry, the cross section shown in the figure below.
To create the thick metal trapezoid, set up the dielectrics so that there is one layer
of dielectric with the same thickness as the thick metal. Then, place a polygon rep-
resenting the wider bottom side of the thick metal on the bottom side of that di-
electric layer. This polygon should use the Normal model for the metal type,
which is modeled as a zero-thickness metal.
A trapezoidal cross-section transmission line viewed in perspective. If the
line has no current going around the edge, it can be modeled, as shown,
as two infinitely thin sheets of current, one at the top and the other at the
bottom of the actual metal.
Zero thickness
polygon as the
wide bottom of
the trapezoid.
Thick metal
polygon placed on
top of zero
thickness
polygon.
The wide bottom of the trapezoidal line is made up of a polygon using
the Normal model for the metal type. This is a zero-thickness metal.
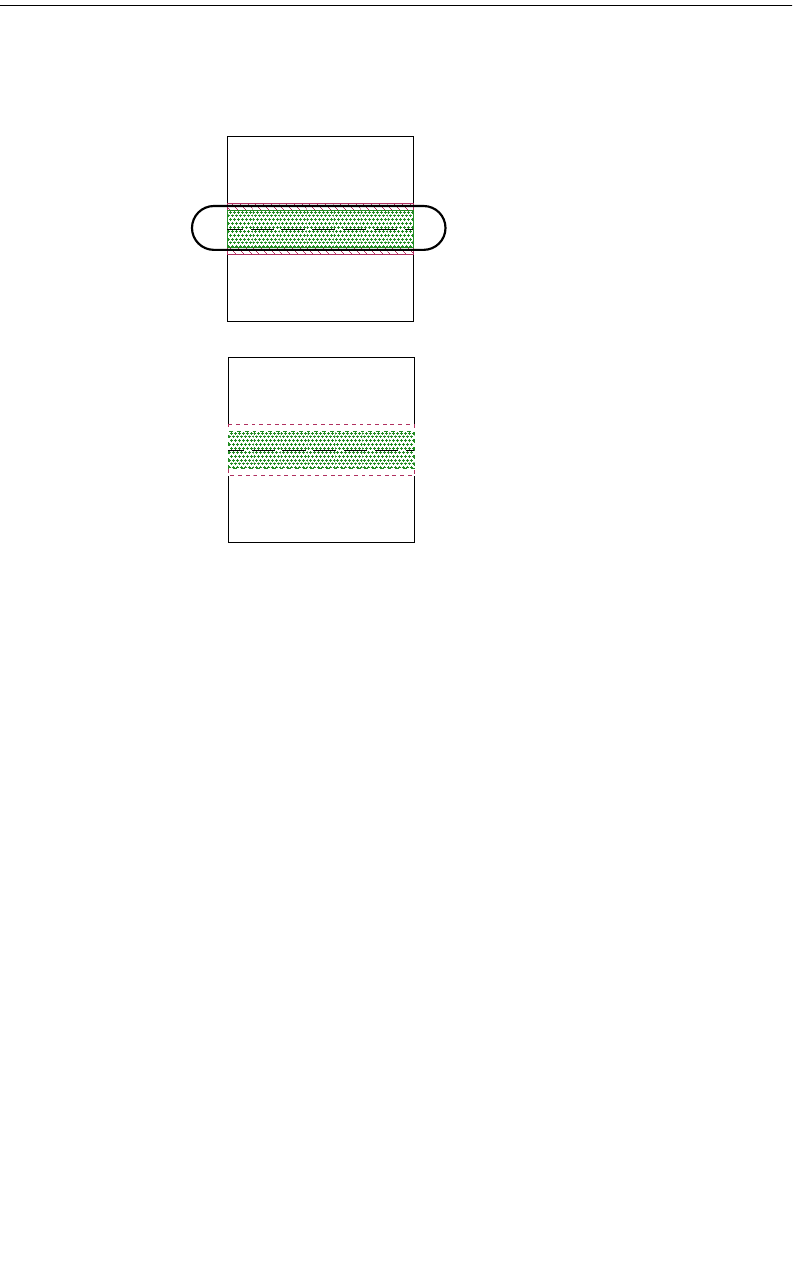
Chapter 16 Thick Metal
315
Rev 16.56
Then place a polygon representing the top side of the thick metal on the bottom
side of that dielectric layer using the Thick Metal metal type. Make this polygon
as thick as the dielectric layer.
Next, place any desired ports on the thick metal polygon, not on the thin metal
polygon. Since the thick metal polygon is placed on top of the zero-thickness poly-
gon, the two are connected electrically and the port is across both polygons.
Thick Metal in the Current Density Viewer
The current density viewer allows you to view the current density distribution in
your circuit. When you select the Compute Current Density option in the Analysis
Setup dialog box in the project editor, em calculates current density data for all the
metal levels in your circuit. When you have thick metal in your circuit which ends
in the interior of a dielectric layer, then the current density viewer creates “sublev-
els” of metal in order to display all the current density data.
For instance, you have a circuit with 3 mil thick metal using the default 2 sheets
placed on metal level #1 below a 25 mil dielectric layer as pictured below. The top
of the thick metal structure is placed in the interior of the dielectric layer. The cur-
Thick metal polygon on level 1
where it is drawn and placed on
top of the wider zero-thickness
polygon
The same polygon shown on level
0. Since the thick polygon is the
same thickness as the dielectric
layer, the metal also appears on
this level. Only the outline of the
zero-thickness metal is shown on
this level.
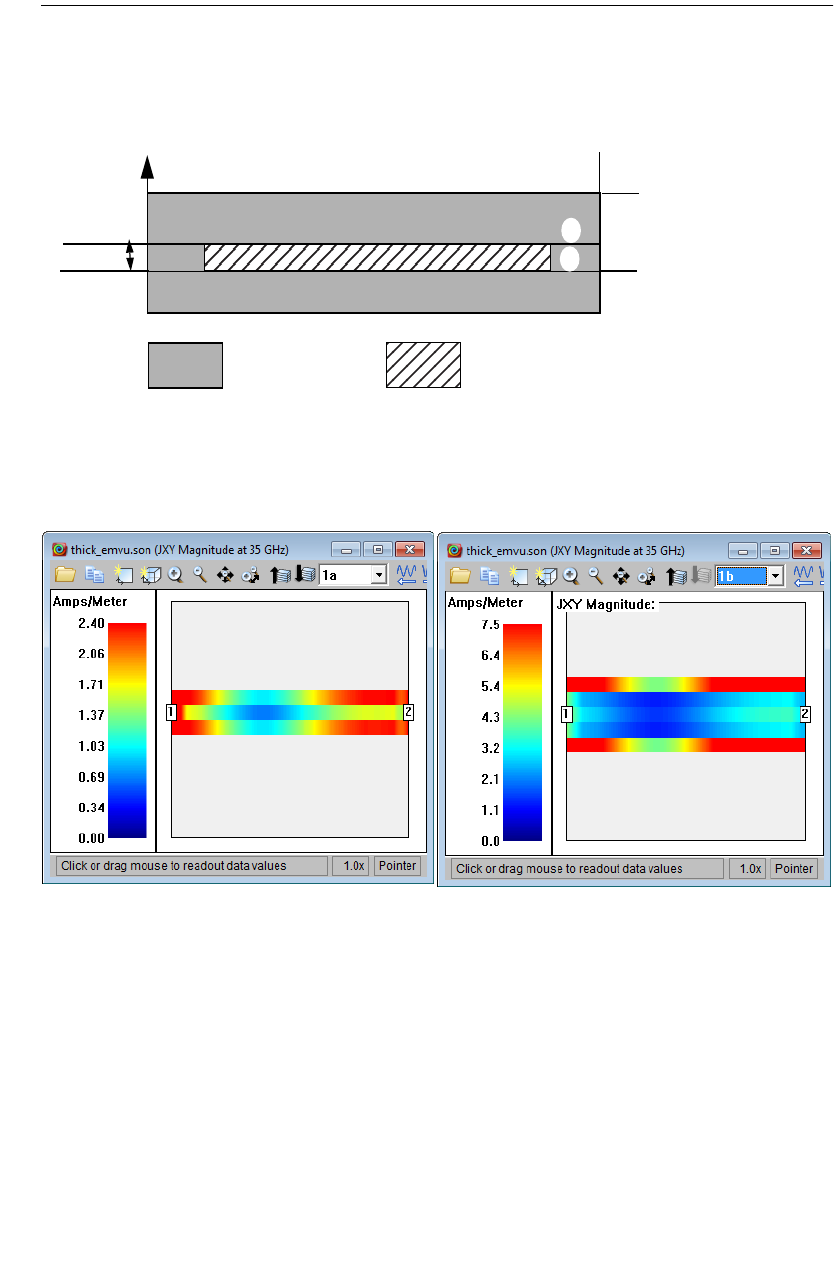
Sonnet User’s Guide
316
Rev 16.56
rent density viewer displays levels 1b and 1a, where 1b is the metal level on which
the thick metal was drawn and 1a is the top of the thick metal structure embedded
in the dielectric layer.
The current density viewer creates as many “sublevels” as are needed. A thick
metal which is defined as having 4 sheets placed on level 2 would appear in the
current density viewer as 2a, 2b, 2c and 2d with 2a being the top of the thick metal
structure and 2d being the bottom drawn on level 2.
50 mils
25 mils
3 mils
Dielectric Thick metal
Z-direction
A
B
Level 0
Level 1
Below are shown the views of level 1a and 1b in the current density viewer. Note that
1a is the top of the thick metal structure and is not visible in the project editor. 1b is
the bottom where the polygon was drawn and is visible in the project editor.
Chapter 17 Dielectric Bricks
317
Rev 16.56
Chapter 17 Dielectric Bricks
Although em is primarily a planar electromagnetic simulator, it also has the capa-
bility to add “dielectric brick” material anywhere in your circuit. A dielectric brick
is a solid volume of dielectric material embedded within a circuit layer. See the
illustration below. Dielectric bricks can be made from any dielectric material (in-
cluding air) and can be placed in circuit layers made from any other dielectric ma-
terial (including air). For example, dielectric bricks can be used to simulate
structures such as an embedded capacitor in an “air” circuit layer, or an “air hole”
in a dielectric substrate circuit layer.
!WARNING
Misuse of dielectric bricks can lead to significantly inaccurate results. It is
highly recommended that you read this entire chapter before attempting to
use dielectric bricks.
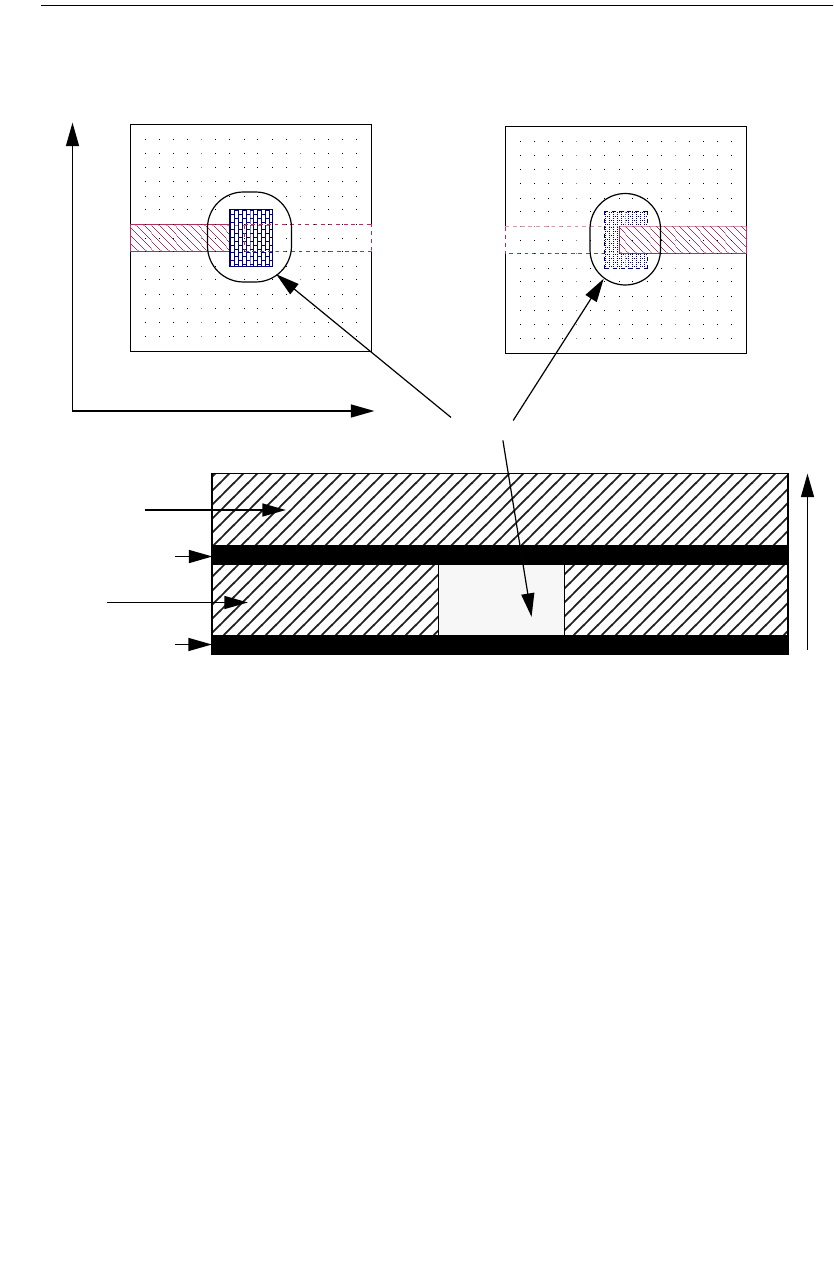
Sonnet User’s Guide
318
Rev 16.56
All realizable values for the dielectric constant, loss tangent and bulk conductivity
or resistivity can be used. Furthermore, it is possible to set these parameters inde-
pendently in each dimension to create anisotropic dielectric bricks.
Em is appropriate for simple structures using very localized dielectric bricks;
however, when your design requires large areas of brick material, you may need
a full 3-D electromagnetic analysis tool.
You should also be aware that the use of dielectric bricks can dramatically in-
crease the memory requirements, and thus the simulation time, for your circuit.
Bricks should only be used where strictly necessary for the accuracy of your sim-
ulation.
Care should be taken when using dielectric bricks, since improper modeling of
your dielectric brick can yield highly inaccurate data. We recommend that you run
a convergence test by doubling (or halving) the number of your Z-partitions, re-
Dielectric
Dielectric Brick
Layer
Side View of Circuit shown above.
Level 1 Metal
Level 0 Metal
Dielectric
Layer
Level 0
Level 1
Z
Y
X

Chapter 17 Dielectric Bricks
319
Rev 16.56
analyzing your circuit and comparing the two results to ensure that you are using
a sufficient number of Z-partitions. For more information on Z-partitioning, see
“Z-Partitioning,” page 325.
Applications of Dielectric Bricks
The use of dielectric bricks is appropriate for applications where the effects of di-
electric discontinuities or anisotropic dielectric materials are important. Examples
of such applications include dielectric resonators, dielectric overlays, airbridges,
microstrip-to-stripline transitions, dielectric bridges and crossovers, microslab
transmission lines, capacitors and module walls.
Guidelines for Using Dielectric Bricks
Subsectioning Dielectric Bricks
A dielectric brick simulates a volume of dielectric material. Because a brick sim-
ulates a volume, it must be subsectioned in the X, Y and Z dimensions. The more
subsections (finer resolution) used in each dimension, the more accurate the anal-
ysis.
X/Y subsectioning of dielectric bricks is identical to X/Y subsectioning of metal
polygons. You can control the X/Y subsectioning of both through your choice of
grid size, XMIN, YMIN, XMAX, YMAX and subsections-per-wavelength. See
Chapter 3, “Subsectioning,” for details.
Z subsectioning of dielectric bricks is controlled by the “number of Z-partitions”
parameter. This parameter specifies the number of Z subsections for all dielectric
bricks on a particular dielectric layer. See the “Z Partitions dialog box” topic in
the project editor’s Help for information on setting this parameter.
Using Vias Inside a Dielectric Brick
Vias through dielectric bricks are treated the same as vias through the standard di-
electric layers. Note that via ports inside dielectric bricks are not allowed.

Sonnet User’s Guide
320
Rev 16.56
Air Dielectric Bricks
Dielectric bricks can be made of any dielectric material and can be placed in any
circuit layer. This allows, for instance, “alumina” bricks to be created in an “air”
circuit layer. However, it is also possible to reverse this scenario. Dielectric bricks
made of “air” can also be created in alumina circuit layers. This is an important
consideration to remember. Depending upon the circuit geometry for a given ap-
plication, this ability to reverse the dielectric characteristics may simplify the cir-
cuit and make it faster to analyze.
Limitations of Dielectric Bricks
Diagonal Fill
Diagonal fill is not allowed for dielectric bricks. All dielectric bricks must use
“staircase fill”. Thus, dielectric bricks with curved or rounded edges must be stair
step approximated. Note that the error caused by such an approximation decreases
as the X and Y cell sizes are decreased. Thus, it is possible to make this error ar-
bitrarily small by choosing sufficiently small X and Y cell sizes.
Antennas and Radiation
The far field viewer does not support dielectric bricks. Circuits containing dielec-
tric bricks can be analyzed with the far field viewer, but the radiation effects of the
dielectric bricks are not accounted for in the analysis.
Interfaces
The Keysight ADS Interface, Cadence Virtuoso Interface and NI AWR MWOf-
fice Interface do not create dielectric bricks.

Chapter 17 Dielectric Bricks
321
Rev 16.56
Dielectric Brick Concepts
Creating a Dielectric Brick
To create a dielectric brick in the project editor, do the following:
1 Move to the circuit level where the base of the dielectric brick is to be
located.
The dielectric brick that is created will rest on this circuit level, and will extend
upward to the next level. Dielectric bricks can be placed on any level, including
the ground plane. If a brick is placed on the highest circuit level (level 0), it will
extend up to the top cover of the metal box.
2 Create a base polygon which defines the cross-section of the brick.
This is done by selecting either Tools Add Dielectric Brick Draw Rectangle
or Tools Add Dielectric Brick Draw Polygon from the project editor’s main
menu. The first option allows the vertices of arbitrarily shaped base polygons to
be entered on a point by point basis. This option is used to create dielectric bricks
with any cross-sectional shape. However, if the cross-section is rectangular in
shape, it is often quicker to create dielectric bricks using the second option.
Viewing Dielectric Bricks
Once a dielectric brick has been created in the project editor, it is possible to “see”
the brick from both the circuit layer where the base of the brick is located and the
circuit layer where the top of the brick is located. On both levels, you will see a
polygon which defines the cross-sectional shape of the dielectric brick. The
brightness of the polygon, however, will vary. When you are on the top level, you
will see a “dim” polygon; on the base level you will see a “bright” polygon.
Only the outline of the dielectric brick is visible from levels other than the origi-
nation and termination of the dielectric brick.
Note that while it is possible to “see” a brick from two different circuit levels, “se-
lecting” a brick, for cutting, copying, moving, changing attributes, etc., can only
be done from the circuit level where the base of the brick is located if you are in
Single layer edit mode. The polygon can be selected on either level if you are in
multilayer select.

Sonnet User’s Guide
322
Rev 16.56
Finally, it is possible to turn the display of dielectric bricks “on” or “off” in the
project editor. You select View Object Visibility from the main menu of the
project editor which opens the Object Visibility dialog box shown below.
Click on the Only Objects Checked Below radio button to enable the object choic-
es, then click on the Dielectric Bricks checkbox to turn off the display of the
bricks.
This will make any bricks present in the circuit invisible and unselectable, but
does not remove them from the circuit. The dielectric bricks can be turned back
“on” by once again selecting View Object Visibility and clicking the Dielectric
Bricks checkbox or the All Objects radio button.
Occasionally, when a circuit contains many layers, with overlapping metal poly-
gons and dielectric bricks, it may be somewhat difficult to distinguish the metal
polygons and dielectric bricks from one another. The ability to turn dielectric
bricks “off” usually makes it easier to view such circuits.
Defining Dielectric Brick Materials
Just as it is possible to define a variety of metal types, each with different proper-
ties, it is also possible to define a variety of dielectric brick materials. Dielectric
brick materials are defined using the parameters below:
• Erel: The relative dielectric constant (r). The ratio (/o), where is the real
part of the permittivity of the dielectric layer material, and o is the permittiv-
ity of free space. The ratio is dimensionless.
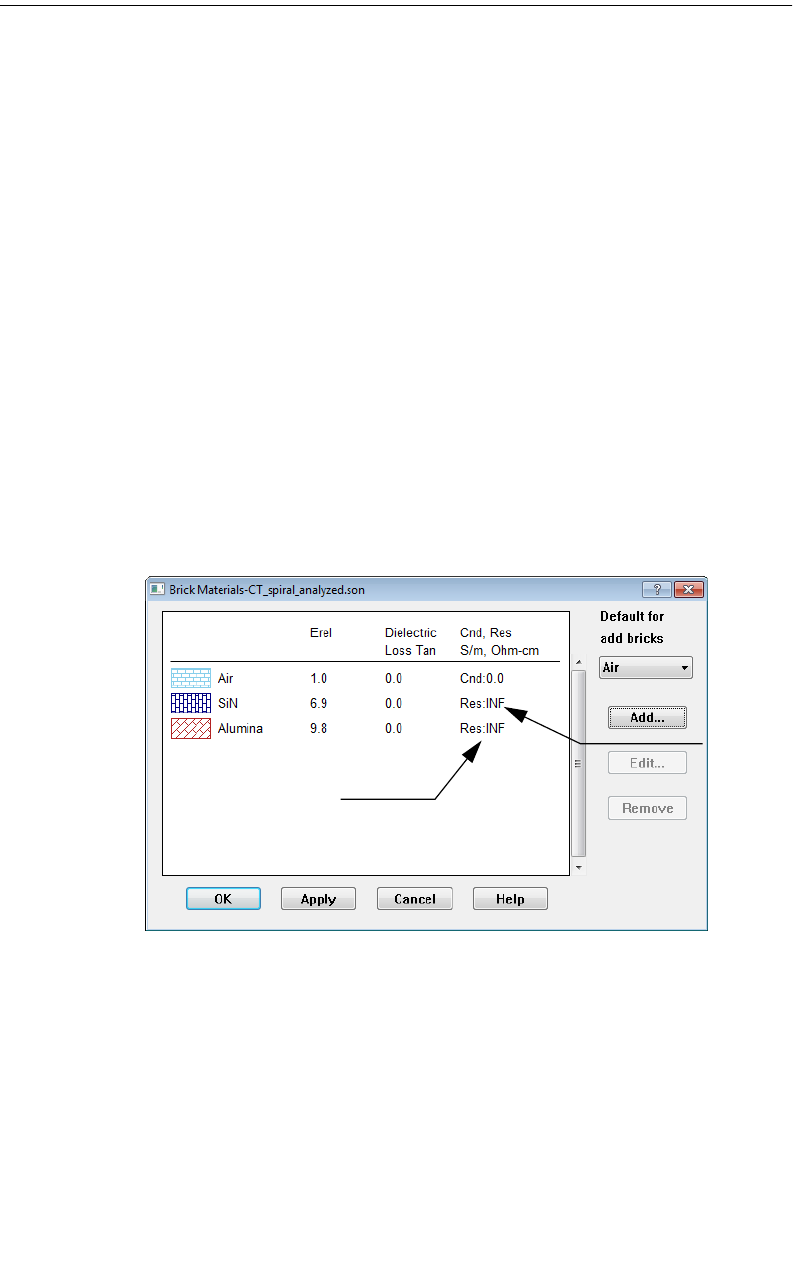
Chapter 17 Dielectric Bricks
323
Rev 16.56
• Dielectric Loss Tan: The dielectric loss tangent. The ratio (’’/’), where
’ - j’’, and is the complex permittivity of the dielectric layer material.
The ratio is dimensionless.
• Conductivity: Dielectric conductivity, , where is the conductivity of the
dielectric. The default unit is S/m. You may define your dielectric loss using
conductivity or resistivity. To use conductivity, you should select “Conduc-
tivity” from the Specify Using drop list.
• Resistivity: Resistivity = 1.0 / conductivity. Resistivity has a default unit of
Ohm-cm.You may define your dielectric loss using conductivity or resistivi-
ty. To use resistivity, you should select “Resistivity” from the Specify Using
drop list.
To define a new dielectric brick material, or to modify the characteristics of an ex-
isting material, you use the Brick Materials dialog box, which is opened by select-
ing Circuit Brick Materials from the main menu of the project editor.
The Brick Materials dialog box, shown on page 323, shows all the dielectric brick
materials previously defined, the color/fill pattern assigned to each brick material,
and whether the material is isotropic or anisotropic. To modify the settings for a
particular dielectric brick material, edit that materials text entry boxes.
If the brick type is isotropic only one set of parameters, X, will be set. Conversely,
if the brick material is set to anisotropic, each parameter is defined separately for
the X, Y, and Z dimensions. If you wish to make a brick material anisotropic, click
on the Ani checkbox.
The
brick
materi
als
dialog
box.
Defined using
Conductivity
Defined using
Resistivity

Sonnet User’s Guide
324
Rev 16.56
Note that Electrical Loss may be defined using Conductivity or Resistivity. Which
parameter is used is indicated by the prefix appearing before the value Conductiv-
ity/Resistivity column as pictured above.
The “default” material used when new dielectric bricks are created can also be set
in the Brick Materials dialog box. Select a brick type from the Default for add
bricks drop list. Once the default material has been set, all bricks created thereafter
will be made of that material.
Changing Brick Materials
The material type for bricks that already exist in a circuit can be changed by fol-
lowing the procedure given below:
1 Select the brick(s) by clicking on it or lassoing it.
The brick is highlighted.
2 Select Modify Brick Materials from the main menu of the project editor.
This will open the Dielectric Brick attributes dialog box, shown below.
3 Select the brick material you desire from the drop list labeled Brick.
This drop list contains all the types defined for dielectric bricks including the
default type, air.

Chapter 17 Dielectric Bricks
325
Rev 16.56
4 Click on the OK button to apply your selection and close the dialog box.
Z-Partitioning
A dielectric brick simulates a volume of dielectric material. Because a brick sim-
ulates a volume, it must be subsectioned in the X, Y, and Z dimensions. The more
subsections (finer resolution) used in each dimension, the more accurate the anal-
ysis.
X/Y subsectioning of dielectric bricks is identical to X/Y subsectioning of metal
polygons. You can control the X/Y subsectioning of both through your choice of
grid size, XMIN, YMIN, XMAX, YMAX, and subsections-per-lambda.
Z subsectioning of dielectric bricks is controlled by the Z Partitions dialog box
which is opened when you click on the Z Parts button in the Dielectric Layers di-
alog box (Circuit Dielectric Layers). You may enter a Z Parts value for each
dielectric layer in your circuit. This parameter specifies the number of Z partitions
for all dielectric bricks on a particular circuit layer.
The default for this parameter is zero so that you are forced to enter a value for this
field. If you use a dielectric brick in a layer, and do not set the z-partitions, em re-
ports an error and exits the analysis. You must enter a non-zero integer value for
this parameter in order to run an analysis. The value of this parameter is highly
dependent on your circuit design; therefore, Sonnet cannot determine a “reason-
able” value. This is the reason we suggest you run a convergence test, discussed
earlier in the chapter, on your circuit to determine the best value for the Z-parti-
tioning.
To set this parameter in the project editor, do the following:

Sonnet User’s Guide
326
Rev 16.56
1 Select Circuit Dielectric Layers from the project editor main menu.
The Dielectric Layers dialog box, shown below, is displayed.
2 Click on the Z-Parts button in the Dielectric Layers dialog box.
The Z Partitions dialog box appears on your display.
3 Enter the number of z partitions to be used for each dielectric layer in the
appropriate Z Parts text entry box.
Note that changing this value for a particular layer will have absolutely no affect
on the analysis if there are no bricks on the layer. If there are multiple bricks on
the layer, the Z subsectioning for all of those bricks will be identical. It is not pos-
sible to apply different Z partitions to brick polygons which appear on the same
layer.

Chapter 18 Antennas and Radiation
327
Rev 16.56
Chapter 18 Antennas and
Radiation
To this point, this manual has been focused on using Sonnet for the analysis of
high frequency circuits and transmission structures. However, there is a large class
of radiating structures for which Sonnet has proven very useful. This chapter de-
scribes how to use Sonnet to analyze 3-D planar radiating structures, such as mi-
crostrip patch arrays and microstrip discontinuities, using the “Open Waveguide
Simulator” technique. The underlying assumptions of this technique are described
in detail. Common modeling mistakes are also pointed out. Examples are provided
to illustrate the correct use of the modeling technique.
This chapter also discusses the far field viewer, an analysis and viewing tool
which calculates far field antenna patterns for arbitrary 3-D planar geometries.
The far field viewer uses the current distribution data in the project as input, and
creates a pattern. The pattern may be viewed as a cartesian, polar or surface plot.
NOTE: The far field viewer is only available if you have purchased a far field
viewer license from Sonnet. A far field viewer license is an optional
add-on to Sonnet Suites and must be purchased separately. It is only
available in the Sonnet Suites package and is not available in the Blink
package.

Sonnet User’s Guide
328
Rev 16.56
Background
Since em is an analysis of 3-D planar circuits in a completely enclosing,
shielding, rectangular box, the analysis of radiating structures is not an appli-
cation which immediately comes to mind.
However, em can be used to simulate infinite arrays using a waveguide simulator.
In this technique, as shown in on page 329, a portion of the array is placed within
a waveguide. The waveguide tube is vertical, connecting the radiating patches to
the termination, which is a matched load. The images formed by the waveguide
walls properly model the entire infinite array scanned to a specific angle.
The waveguide simulator inspired what we now call the Open Waveguide Simu-
lator Technique described in the next section.
Modeling Infinite Arrays
The sidewalls of the shielding box in the em analysis easily represent the sidewalls
of the waveguide in the infinite array waveguide simulator. A side view is shown
in the figure on page 329.
Providing a termination for the end of the waveguide requires a little more
thought. Any waveguide mode can be perfectly terminated by making the top
cover resistivity in em equal to the waveguide mode impedance. This can be done
in the project editor automatically at all frequencies and all modes by selecting
“WGLOAD” from the metals in the Top Metal drop list in the Box Settings dialog
box.

Chapter 18 Antennas and Radiation
329
Rev 16.56
In a phased array with the array scanned to a specific direction, a single waveguide
mode is generated. The em software can model the waveguide simulator of that
infinite array just by setting the top cover impedance to the impedance of the ex-
cited waveguide mode.
Modeling an Open Environment
If we can use a closed (i.e., terminated) waveguide to model an infinite array, we
can also model radiation from a finite array; although, it must be done under cer-
tain conditions. It is important to keep in mind that, unless the analysis is carefully
prepared, these conditions are easily violated, yielding incorrect results. When the
conditions are met, useful results can be obtained, as shall be demonstrated.
ZTE
1fc
f
------
2
–
----------------------------= ff
c
Z
TM 1fc
f
------
2
–= ff
c
fc
vc
2
------ m
A
-------
2n
B
------
2
+=
Waveguide
Termination
Substrate
Array
Patches
Waveguide
Walls
The waveguide simulator for infinite arrays inspired the technique described here. In this
side view, the waveguide walls form images of the array of microstrip patches, simulating
an infinite array. vc is the velocity of light in the medium filling the waveguide.

Sonnet User’s Guide
330
Rev 16.56
First Condition: Make both of the lateral substrate dimensions greater than one
or two wavelengths.
When using the Open Waveguide Simulator, we view the sidewalls of the shield-
ing box as forming a waveguide whose tube extends in the vertical direction, prop-
agating energy from the antenna toward the “Termination” as shown on page 329.
Radiation is then approximated as a sum of many waveguide modes. If the tube is
too small, there are few, if any, propagating modes, violating the First Condition.
There is an easily made mistake when modeling radiation from small discontinu-
ities. Discontinuities are usually small with respect to wavelength. For a disconti-
nuity analysis, the sidewalls are usually placed one or two substrate thicknesses
from the discontinuity. In this case, the substrate dimensions are unlikely to meet
the First Condition. If the sidewalls form below a cut-off waveguide, there is no
radiation.
Second Condition: Make sure the sidewalls are far enough from the radiating
structure that the sidewalls have no affect.
Another way to look at this condition is to consider the image of the structure (dis-
continuity or antenna) created by the sidewall. Position the sidewall so that the
image it forms has no significant coupling with the desired structure.
Usually two to three wavelengths from the sidewall is sufficient for discontinui-
ties. For single patch antennas, one to three wavelengths is suggested. Require-
ments for specific structures can easily be greater than these guidelines. If the First
Condition requires a larger substrate dimension than the Second Condition, it is
very important that the larger dimension is used.
If you are using the far field viewer, the larger the box the better. The far field
viewer assumes that S-parameters from em are from a perfect open environment.
If some of the power is reflected due to a box that is too small, the input power
calculated by the far field viewer will be slightly incorrect. The far field viewer
then calculates antenna efficiencies greater then 100%. If this occurs, the box size
should be increased.
Third Condition: Place the top cover outside the fringing fields (i.e., near field)
of the radiating structure, preferably a half wavelength.
If this condition is violated, the resistive top cover becomes involved in the reac-
tive fringing fields which form the near field of the radiator. This changes what
would have been reactive input impedance into resistive input impedance, overes-
timating the radiation loss.

Chapter 18 Antennas and Radiation
331
Rev 16.56
Do not place the top cover thousands of wavelengths away from the radiator. Ex-
treme aspect ratios of the box should be avoided. Empirical data for patch anten-
nas has shown that a distance of about 1/2 wavelength works best.
Fourth Condition: Set the top cover to Free Space.
This value is a compromise. As shown by the equations on the previous page, all
TE modes have a characteristic impedance larger than 377 ohms (), while all TM
modes are lower. Thus, while a 377 Ohms/square top cover does not perfectly ter-
minate any mode, it forms an excellent compromise termination for many modes.
This approximates removing the top cover of the box. If the box is large, it, in turn,
approximates radiation, as shall be demonstrated.
Fifth Condition: The radiating structure can not generate a significant surface
wave.
If there is a significant, compared to required accuracy, surface wave, it is reflect-
ed by the sidewalls of the box. Unless this is the actual situation, such antennas are
inappropriate for this technique. Actually, the Fifth Condition is a special case of
the Second Condition, since if there is significant surface wave, the Second Con-
dition cannot be met. This condition is stated explicitly because of its importance.
In general, any surface wave is both reflected and refracted when it encounters the
edge of the substrate. This boundary condition is different from either the conduct-
ing wall of Sonnet or the infinite substrate provided by a true open space analysis.
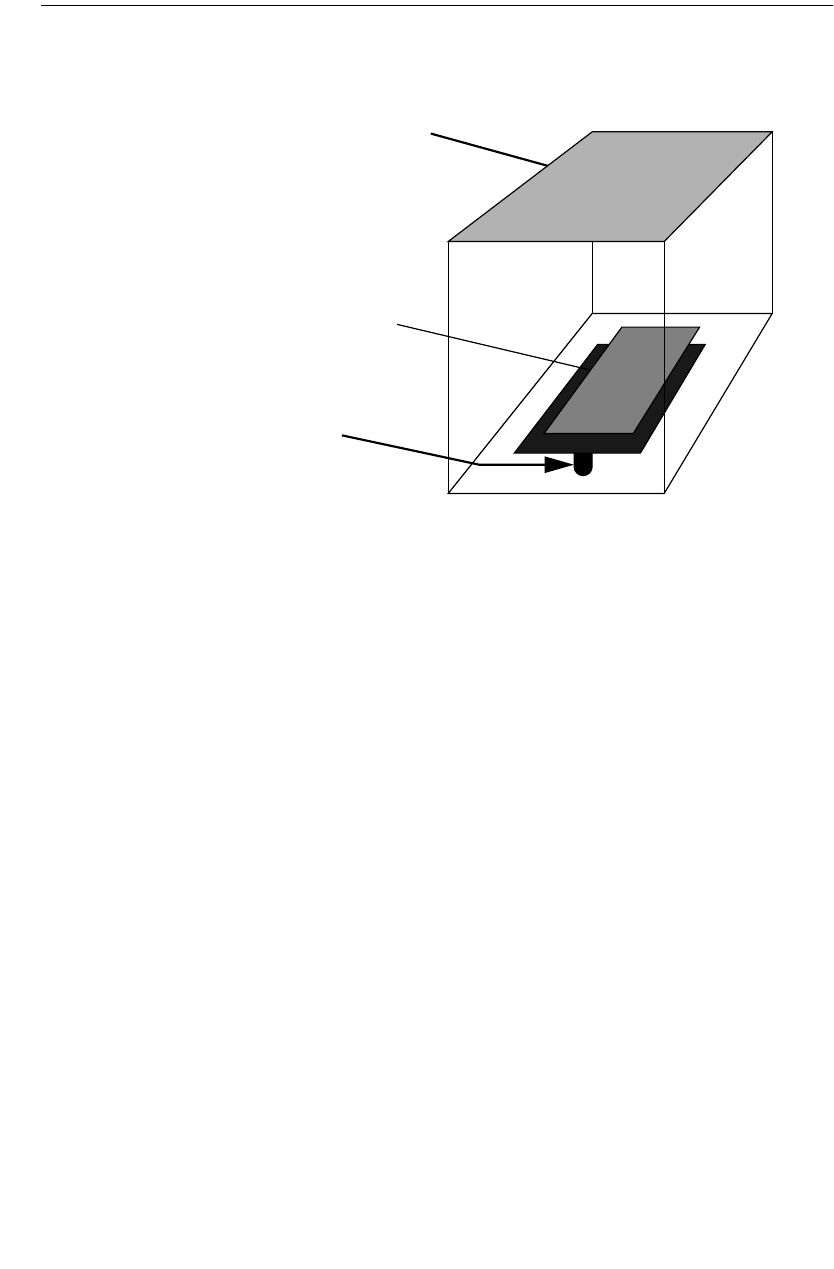
Sonnet User’s Guide
332
Rev 16.56
A dual patch antenna is illustrated conceptually below.
The feed point is created in the project editor by creating a via to ground at the
feed point. Then the ground end of that via is specified as a port, just as one would
specify a more typical port on the edge of the substrate at a box sidewall. A file
showing an antenna similar to this one is named “dual_patch.son” and is available
in the Sonnet examples.
Double Patch
Feed point
Free Space
Top Cover
Antenna
Radiation can be simulated by including a lossy top cover, a lossy
dielectric layer (optional) and by placing the sidewalls far from
the radiator (drawing not to scale). Place the top cover one half
wavelengths from the radiator.
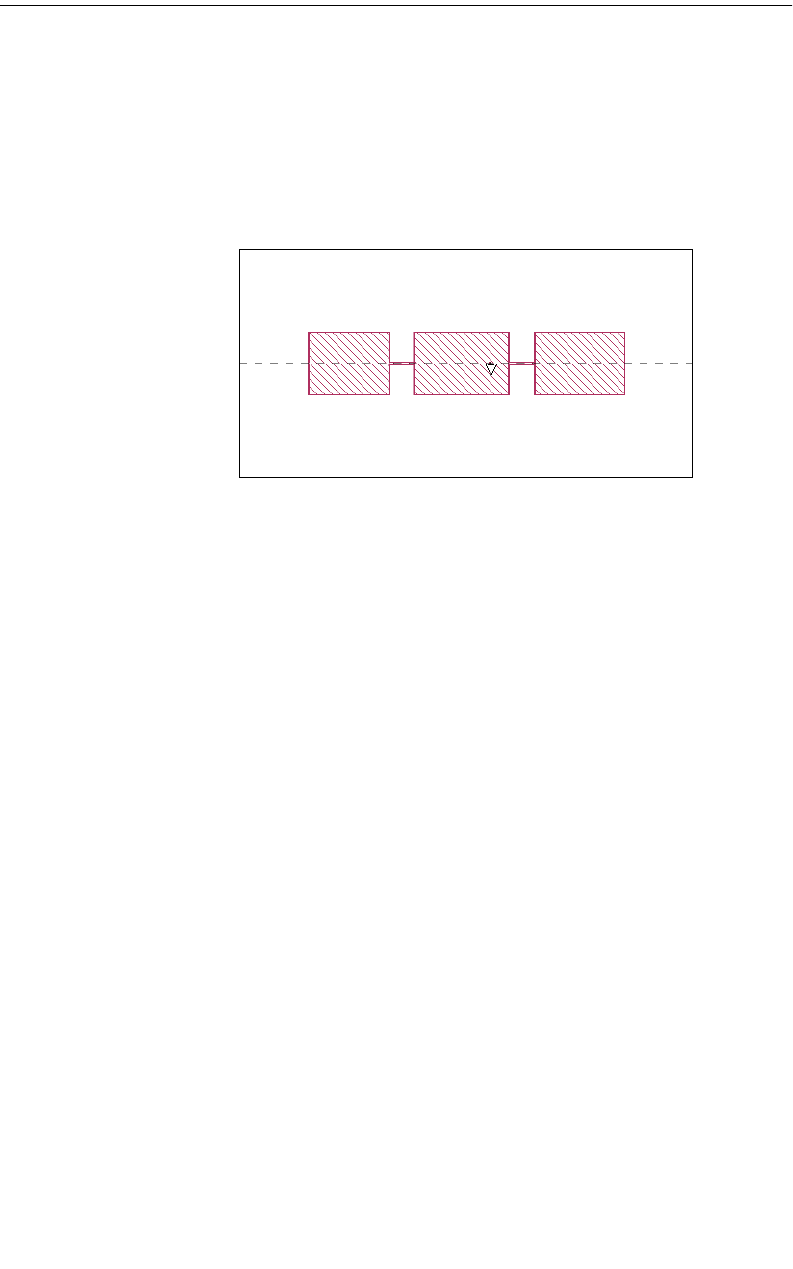
Chapter 18 Antennas and Radiation
333
Rev 16.56
Validation Example
For validation, we offer work performed by E. Ongareau of Matra Defense, An-
tennas & Stealthness Dept., France, as presented at the 1993 EEsof User’s Group
meeting at HYPER in Paris. (Reprinted with permission.) The antenna is a triple
patch structure, with a top view shown below. The antenna is a test realization in-
tended only for validation. It is not designed for optimum VSWR.
Good results are also regularly obtained on single microstrip patch antennas. We
cite this example as one of the more sophisticated antennas analyzed using the
Open Waveguide Simulator technique.
In this antenna, each patch has a slightly different resonant frequency, resulting in
an increased bandwidth. The antenna is fed from below with a coax probe attached
to the central patch. The feed point is indicated with a triangle.
The substrate is 3.04 mm thick with a dielectric constant of 2.94. The drawing is
to scale with substrate dimensions of 200 mm x 100 mm. The top cover is 200 mm
above the substrate surface. Cell size is 0.78125 mm square. A loss tangent of
0.001 is used in both air and substrate. The small air loss helps terminate the prop-
agating modes.
The antenna project, Tripat, is available in the Sonnet examples and may be ob-
tained using the Sonnet Example browser.You may access the Sonnet Example
browser by selecting Help Browse Examples from the menu of any Sonnet ap-
plication. For instructions on using the Example Browser, please click on the Help
button in the Example Browser window.
The chart below shows the result. We see that the low VSWR points of each patch
have differences between measured and calculated of about 1%. This is typical of
most analyses of patch antennas using this technique. The differences in resonant
Top view of a triple patch antenna (courtesy of Matra Defense). The
central patch is fed with a coaxial probe (indicated by a down pointing
triangle). Each patch is resonant at a different frequency to increase the
overall antenna bandwidth.

Sonnet User’s Guide
334
Rev 16.56
frequency (i.e., the reflection zeros) then determine the differences in the rest of
the plot. The degree to which these differences are due to analysis error, fabrica-
tion error and measurement error cannot be determined from this data.
If the typical differences between measured and calculated data shown above are
acceptable, given the specific requirements for a particular project, then the Open
Waveguide Simulator technique can provide useful results.
Far Field Viewer
The purpose of the far field viewer is to calculate the far field pattern of an antenna
for a given excitation and set of directions (for example, phi and theta ranges). The
far field viewer starts by reading the current density data generated by em for the
antenna at the desired frequencies. The far field viewer uses the current distribu-
tion information in the project and generates the desired far field antenna pattern
information. This pattern information is viewed in one of three ways: Cartesian,
polar, or surface plot. A default set of values for directions, port excitations and
terminations are used to calculate plots for the first frequency upon start-up of the
far field viewer. Thereafter, the user specifies the frequencies, directions for the
radiation pattern and the desired port excitations and terminations.
The measured and calculated data for the triple patch antenna were
obtained completely separately, so there was no chance to “tweak”
the model for agreement.

Chapter 18 Antennas and Radiation
335
Rev 16.56
Since the far field viewer uses the current density data generated by em, it can an-
alyze the same types of circuits as em. These include microstrip, coplanar struc-
tures, patch antennas, arrays of patches, and any other multi-layer circuit. As with
em, the far field viewer can analyze any number of ports, metal types, and fre-
quencies. The far field viewer cannot analyze circuits which radiate sideways,
structures with radiation due to vertical components, coaxial structures, wire an-
tennas, surface wave antennas, ferrite components, or structures that require mul-
tiple dielectric constants on a single layer.
Be aware that although the current data is calculated in em with a metal box, the
metal box is removed in the far field viewer calculations. The modeling consider-
ations discussed earlier in the chapter are important, however, for the accuracy of
the far field viewer data relies on the accuracy of the em simulation.
By default, the far field viewer analyzes the first frequency in the current density
data stored in the project at a default set of angles and port excitations when the
file is opened.
To obtain the antenna pattern for other than the first frequency, you must select
Graph Calculate from the far field viewer main menu. The Calculate dialog
box allows you to set up all the parameters for the data you desire to calculate. The
far field viewer calculates the fields radiated by the current that is stored in the
project. The analysis is performed in an open environment with a substrate of in-
finite extent. For details on the Calculate dialog box, please refer to the Help in the
far field viewer program.
Please refer to “Far Field Viewer Tutorial,” page 341 for a tutorial on using the far
field viewer.
Analysis Limitations
The analysis of the far field viewer has the following limitations:
•The plotted antenna patterns do not represent de-embedded data.
Therefore, the effect of the port discontinuity is still included even if
you specify de-embedding when running em.
•Radiation from triangular subsections (i.e., diagonal fill) is not included.
•The far field viewer patterns are for a substrate which extends to infinity
in the lateral dimensions.

Sonnet User’s Guide
336
Rev 16.56
Spherical Coordinate System
You view your antenna plot using the spherical coordinate system, which is de-
scribed below.
To view an antenna plot, the far field viewer uses the spherical coordinate system
shown below. The X, Y, and Z coordinates are those used in the analysis engine,
em, and the project editor. The XY plane is the plane of your project editor win-
dow, with the Z-axis pointing toward the top of the box. The spherical coordinate
system uses theta (and phi ( as shown in the figure below.
.
The far field viewer allows values for theta from 0 to 180 degrees. However, val-
ues of theta greater than 90 degrees are below the horizon and are only useful for
antennas without infinite ground planes. To view just the top hemisphere, sweep
theta from 0 to 90 degrees and sweep phi from -180 to + 180 degrees.
The X and Y axes in the figure above correspond to the X and Y axes in the project
editor. The origin is always in the lower left corner of the project editor window.
To look at an E-plane cut or an H-plane cut, set phi (to 0 or 90 degrees, and
sweep theta ( from 0 to 90 degrees. To view an azimuthal plot, set and sweep
.
Z
X
E
E
This edge is the top of the
project editor window.
This edge is the left
side of the project
editor window.
Toward Lossy Top
Cover

Chapter 18 Antennas and Radiation
337
Rev 16.56
NOTE: The far field viewer will allow the user to analyze the same space
twice with the user determining the appropriate angle ranges for each
analysis. For details, see “Graph - Select” in the far field viewer’s
help.
The far field viewer displays three plot types; cartesian, polar, and surface. All
three types of plots are shown below. The cartesian plot allows the magnitude (in
dB) to be plotted on a rectangular graph with your choice of theta (, phi (, or
frequency for the X-axis as shown in the figure below. The polar plot allows you
to select either theta or phi (for the angle axis. The surface plot shows all the
calculated values of theta and phi plotted against the gain for a single frequency.

Sonnet User’s Guide
338
Rev 16.56
theta (, phi (, or frequency
(a) Cartesian
(b) Polar
or
Magnitude (dB)
Radius
Axes
Angle
Axes
The far field viewer
allows you to sweep
theta (, phi (, or
frequency.

Chapter 18 Antennas and Radiation
339
Rev 16.56
Normalization
There are three types of normalization to chose from in the far field viewer. By
default, the far field viewer displays the power gain. The far field viewer can also
provide directive gain and absolute values. The three types of normalization are
discussed below.
The power gain is defined as the radiation intensity divided by the uniform radia-
tion intensity that would exist if the total power supplied to the antenna were ra-
diated isotropically[1].
Directive gain is defined as the radiation intensity from an antenna in a given di-
rection divided by the uniform radiation intensity for an isotropic radiator with the
same total radiation power.[2]
The Gain and Directive gain may be displayed relative to the isotropic antenna
(i.e. 0 dB), the maximum value of E for the antenna, or an arbitrary value.
Selecting Absolute for the normalization displays the radiated power in Watts/ste-
radian at a given angle.
You may change the normalization in the far field viewer using the Select Nor-
malization dialog box which is opened by selecting Graph Normalization from
the far field viewer main menu.
(c) Surface Plot

Sonnet User’s Guide
340
Rev 16.56
Polarization
The far field viewer displays the magnitude of the electric field vector for a given
direction. The magnitude may be represented as the vector sum of two polariza-
tion components, E-theta) and E-phi () as shown in the figure describing
spherical coordinates on page 336.
The far field viewer allows you to see the total magnitude or either component of
the magnitude. Other polarizations are also available in the far field viewer and
are discussed in “Graph - Polarization” in the far field viewer help.
References
[1] Simon Ramo, John R. Whinnery and Theodore Van Duzer, Fields and Waves in
Communication Electronics, John Wiley & Sons, Inc. 1994, pg. 601.
[2] Ibid, pg. 600.

Chapter 19 Far Field Viewer Tutorial
341
Rev 16.56
Chapter 19 Far Field Viewer
Tutorial
This tutorial describes an example of using the far field viewer to display plots.
The far field viewer displays far field radiation patterns using the current density
data created during an em analysis. In this example, we analyze an infinitesimal
dipole antenna above a ground plane, shown below, and compare the results to the
exact theoretical antenna pattern shown on page 358, as provided by reference 2.
NOTE: The far field viewer is only available if you have purchased a far field
viewer license from Sonnet. A far field viewer license is an optional
add-on to Sonnet Suites and must be purchased separately. Please see
you system administrator if you are unsure about the availability of
this program.
For more information about modeling antennas and using the far field viewer,
please refer to Chapter 18.
Although this example is not very practical, it is a good example to use for valida-
tion because of its simplicity. The infinitesimal electric dipole is placed one wave-
length (300 mm at 1 GHz) above the ground plane (an electric field reflection
boundary).

Sonnet User’s Guide
342
Rev 16.56
Creating an Antenna Pattern File
This tutorial uses an infinitesimal dipole one wavelength above the ground plane.
The project, Infpole, may be obtained using the Sonnet Example browser.You
may access the Sonnet Example browser by selecting Help Browse Examples
from the menu of any Sonnet application. For instructions on using the Example
Browser, please click on the Help button in the Example Browser window. Save
the file to your working directory.
1 Save a copy of “infpole.son” to your working directory.
The file “infpole.son” is the circuit geometry project file for the dipole antenna
which was created using the project editor. The dipole geometry can be viewed by
using the project editor.
It is important to remember that in order to produce data for input into the far field
viewer, the Compute Current Density option must be selected in the Analysis
Setup dialog box in the project editor.
Infpole was analyzed at a linear frequency sweep from 0.8 GHz to 1.2 GHz in in-
tervals of 0.1 GHz.
h = -
Ground Plane
h = -
Close-up of the project editor layout
Uniform Current Element
Image

Chapter 19 Far Field Viewer Tutorial
343
Rev 16.56
Running the Far Field Viewer
2 Click on the View Far Field button on the Sonnet task bar to invoke the far
field viewer.
A pop-up menu appears on your display.
3 Select “Browse for Project” from the pop-up menu.
A browse window appears on your display.
4 Using the browse window, select your saved copy of “inpole.son”.
The far field viewer window opens on the project file, “infpole.son”.
After the initial calculation is complete, a plot appears on your display as shown
below. When a new file is opened, the far field viewer performs an analysis on the
first frequency based on a default set of values for directions, port excitations and
terminations and displays the Gain (dB) versus theta for the first value of phi. The
calculation defaults are as follows:
•There are two values of phi: 0° and 90°
•Theta ranges from -90° to +90° in 5° intervals.
•Port 1 is set to a 1.0 V source magnitude with a 50.0 load.

Sonnet User’s Guide
344
Rev 16.56
The far field viewer display defaults to a cartesian plot with theta selected on the
X-axis. The polarization defaults to Theta/Phi. The Y-axis is set to display the
Gain (in dB) of the pattern response and is normalized to power gain of the ideal
isotropic antenna.
To change the calculation and display defaults, see File - Preferences in the far
field viewer’s help.
Calculating the Response
As mentioned above, when the far field viewer is invoked, the response data is cal-
culated for only the first frequency in the current response file. To calculate data
for the other frequencies at additional angles, perform the following:
5 Select Graph Calculate from the far field viewer main menu.
The Calculation Setup dialog box appears on your display with the Angles tab se-
lected as shown below.

Chapter 19 Far Field Viewer Tutorial
345
Rev 16.56
Selecting Phi Values
6 Enter 0 in Start text entry box, 90 in the Stop text entry box and 5 in the Step
text entry box of the Phi line.
This analyzes data points from phi = 0to in intervals of
Selecting Frequencies
7 Click on the Frequencies tab in the Calculation Setup dialog box.
The Frequencies tab is now displayed, as shown below.
8 Click on the Select All command button under the Available Frequencies.
All of the frequencies are highlighted.
9 Click on the Right Arrow button.
This moves all the selected frequencies to the Calculated Frequencies column.

Sonnet User’s Guide
346
Rev 16.56
10 Click on the Calculate command button.
There is a delay while the far field viewer calculates the requested data. The cal-
culations for each frequency are performed using the defaults cited above for phi,
theta, port excitation and exclusions, since none of these items were changed be-
fore selecting Calculate.
A status box appears on your display to provide updates on calculation progress.
The display is updated when the calculation is completed. Be aware that for larger,
more complicated circuits, this delay might be a considerable one.
Selecting the Response
The far field viewer allows you to select which data items you wish displayed at
any given time. In the next session, you display 1 GHz data at different phi’s.
11 Select Graph Select Frequencies from the far field viewer main menu.
The Select Frequencies dialog box appears on your display.
The Calculated column displays the frequencies for which data has been calculat-
ed, but is not presently displayed. The Plotted Column shows those frequencies
which are presently displayed. In this case, 0.8 GHz.
TIP
You may also open the Select Frequencies dialog box by right-clicking in the
Frequency area of the legend and selecting Select from the menu which appears
on your display.
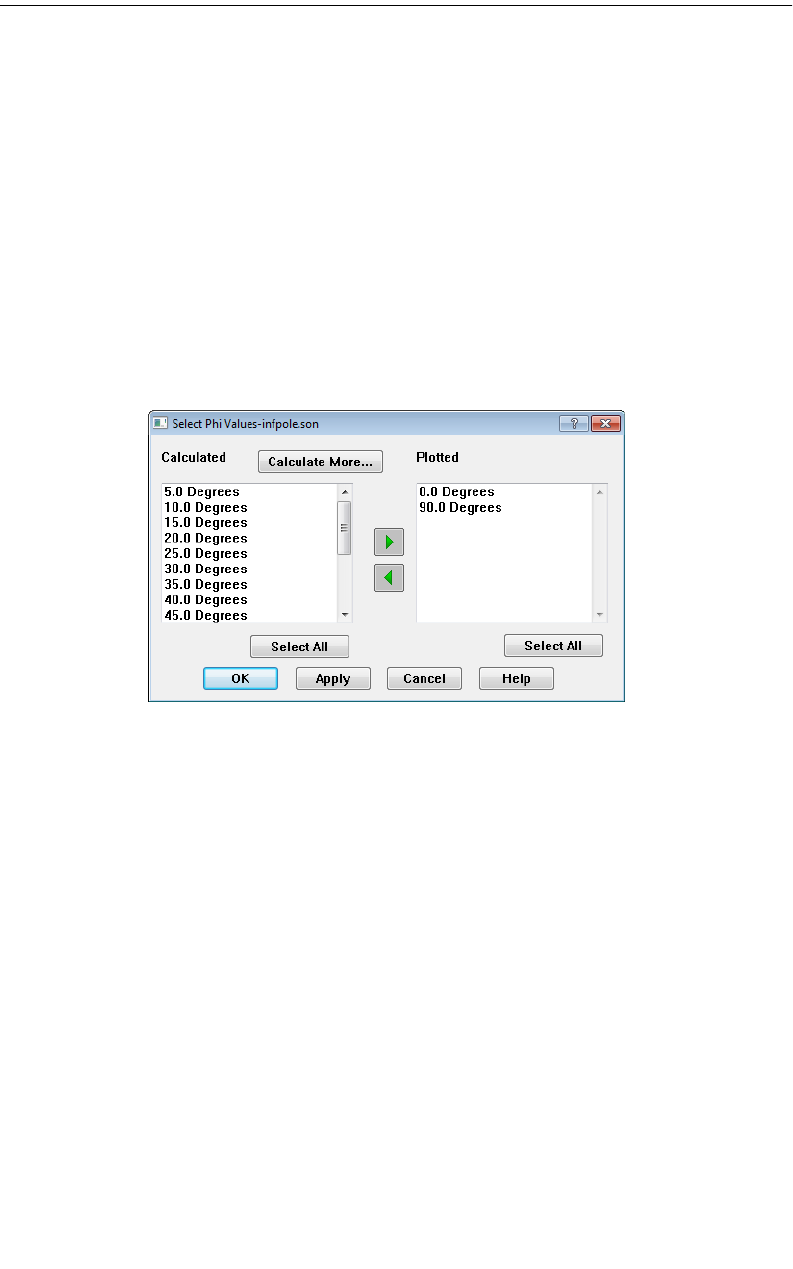
Chapter 19 Far Field Viewer Tutorial
347
Rev 16.56
12 Double-click on 0.8 in the Plotted column.
This moves 0.8 to the calculated column, i.e., this frequency is not displayed.
13 Double-click on 1.0 in the Calculated column.
This moves the value 1.0 to the Plotted column.
14 Click on the OK command button.
This closes the dialog box and updates the display with the data for 1.0 GHz at
Phi = 0°.
15 Select Graph Select Phi from the far field viewer main menu.
The Select Phi’s dialog box appears on your display.
16 Use the scroll bar on the Calculated Column to move down the list until 90.0
Degrees is displayed.
17 Double-click on 90.0 Degrees to move this value to the Plotted column.
Values in this column are displayed in the far field viewer.
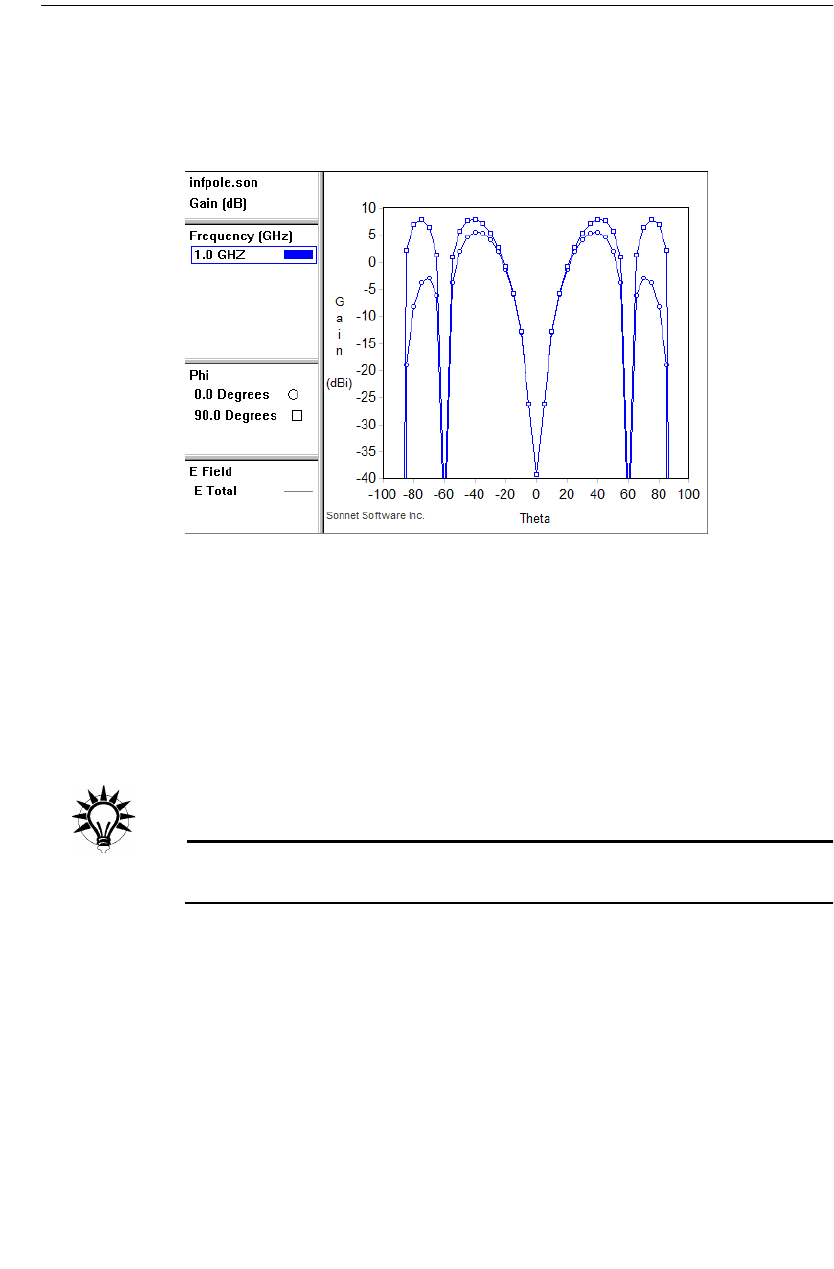
Sonnet User’s Guide
348
Rev 16.56
18 Click on the OK command button.
The dialog box disappears and the far field viewer display is updated. It should
appear similar to the figure below.
The plot is drawn showing two curves: Etotal at phi = 0 and 90 degrees. The upper
curve is the radiation pattern at phi = 90 degrees. The lower curve is the radiation
at phi = 0 degrees.
The far field viewer automatically selects an appropriate scale for the plot.
19 Select Graph Select Phi from the far field viewer main menu.
The Select Phi’s dialog box appears on your display.
TIP
You may also access the Select Phi’s dialog box by right-clicking in the Phi box
in the legend and selecting Select from the pop-up menu which appears.
20 Double-click on 90.0 degrees in the Plotted column to move it from the Plot-
ted column to the Calculated column.
This removes 90.0 degrees from the plot.
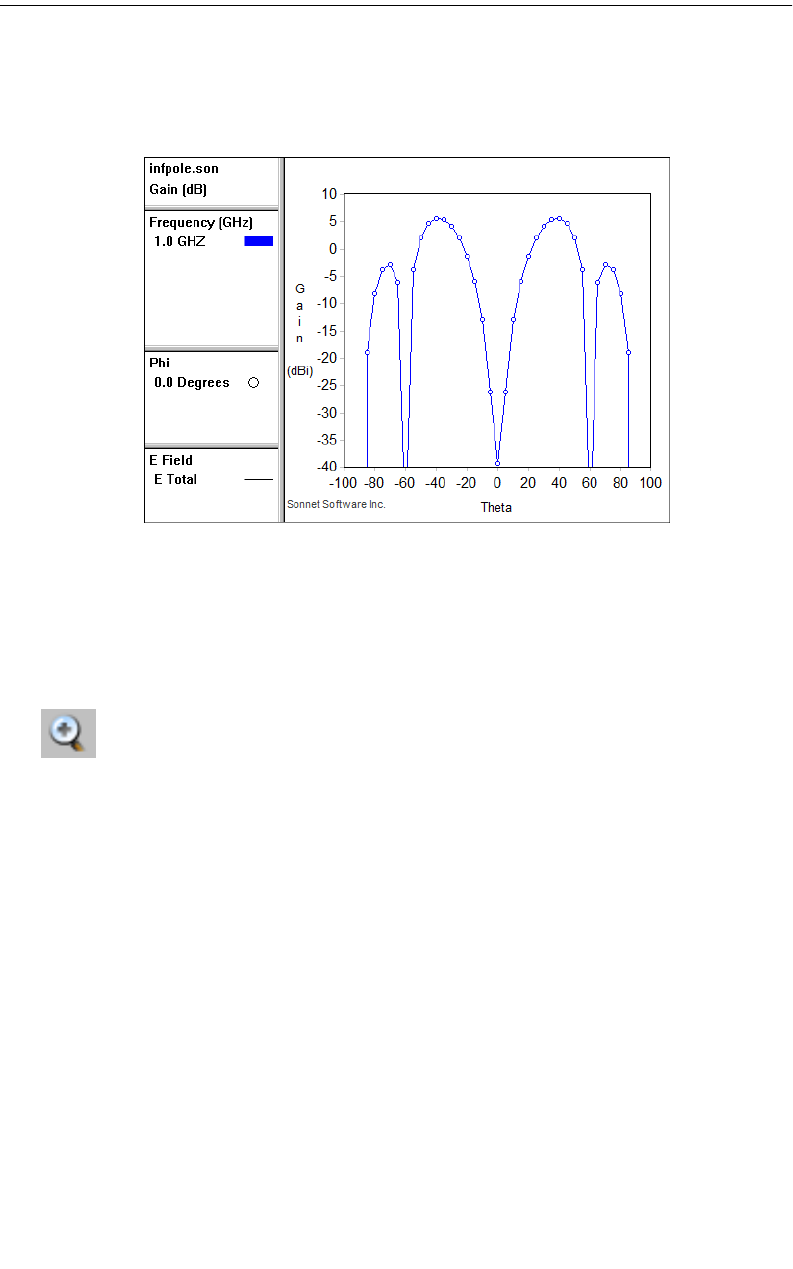
Chapter 19 Far Field Viewer Tutorial
349
Rev 16.56
21 Click on the OK command button.
The dialog box disappears and the far field viewer plot is updated. It should appear
as below.
Zooming
The zoom button, located on the tool bar, may be used to magnify a specific area
in the plot.
22 Click on the Zoom In button on the Tool bar.
For this example, zoom in on the area from 0 to 10 dB in Gain, where Theta ranges
from 20° to 50°.
You may also use ViewZoom In or the Space Bar for the zoom function.
23 Click on the point in the plot corresponding to 0 dB Gain and Theta = 20°,
then drag the mouse to the point in the plot corresponding to 10 dB Gain
and Theta = 50°
A rubber band surrounding the area to be magnified follows the mouse.
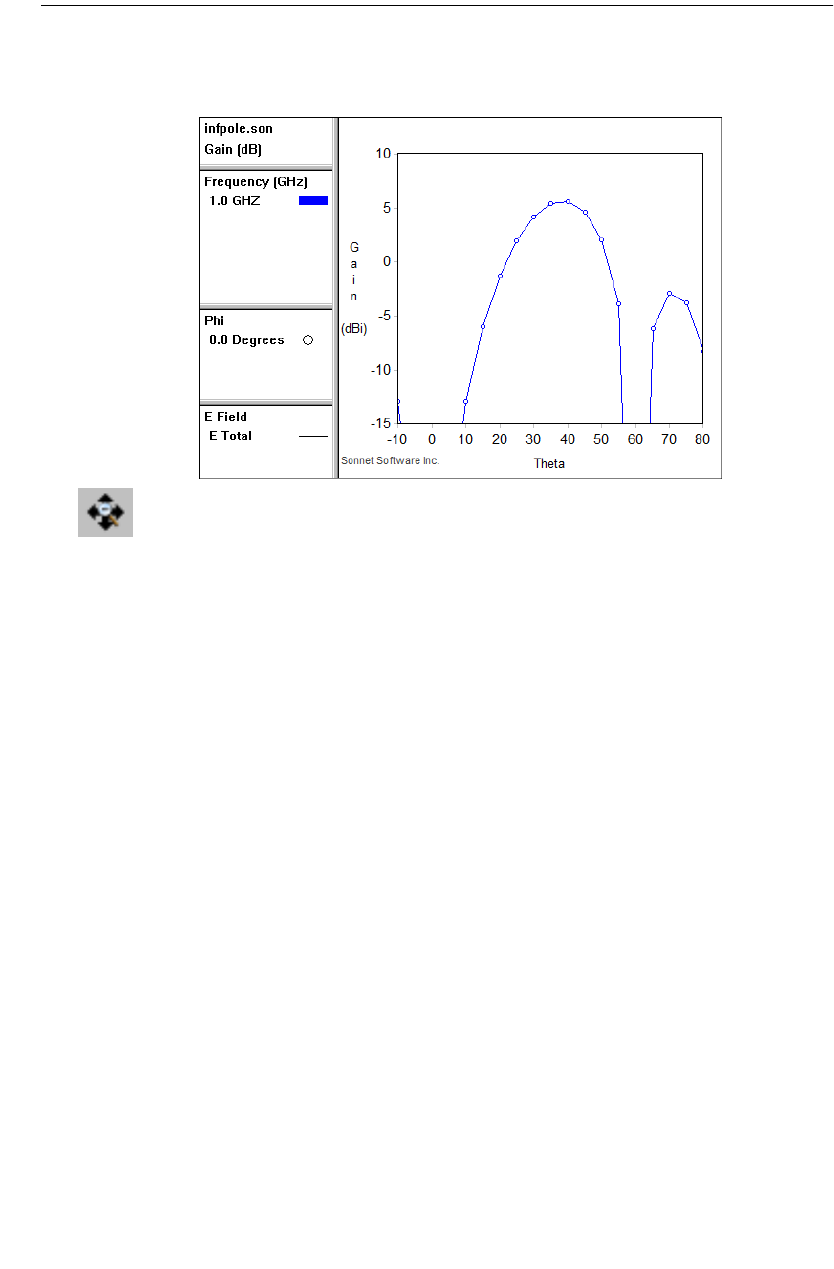
Sonnet User’s Guide
350
Rev 16.56
When the mouse is released, the plot is updated with a magnified view of the se-
lected area, as shown below.
24 Click on the Full View button on the Tool bar.
The full plot once again appears on your display.
Probing the Plot
To evaluate the pattern response at any location in your plot you simply click at
the desired location.
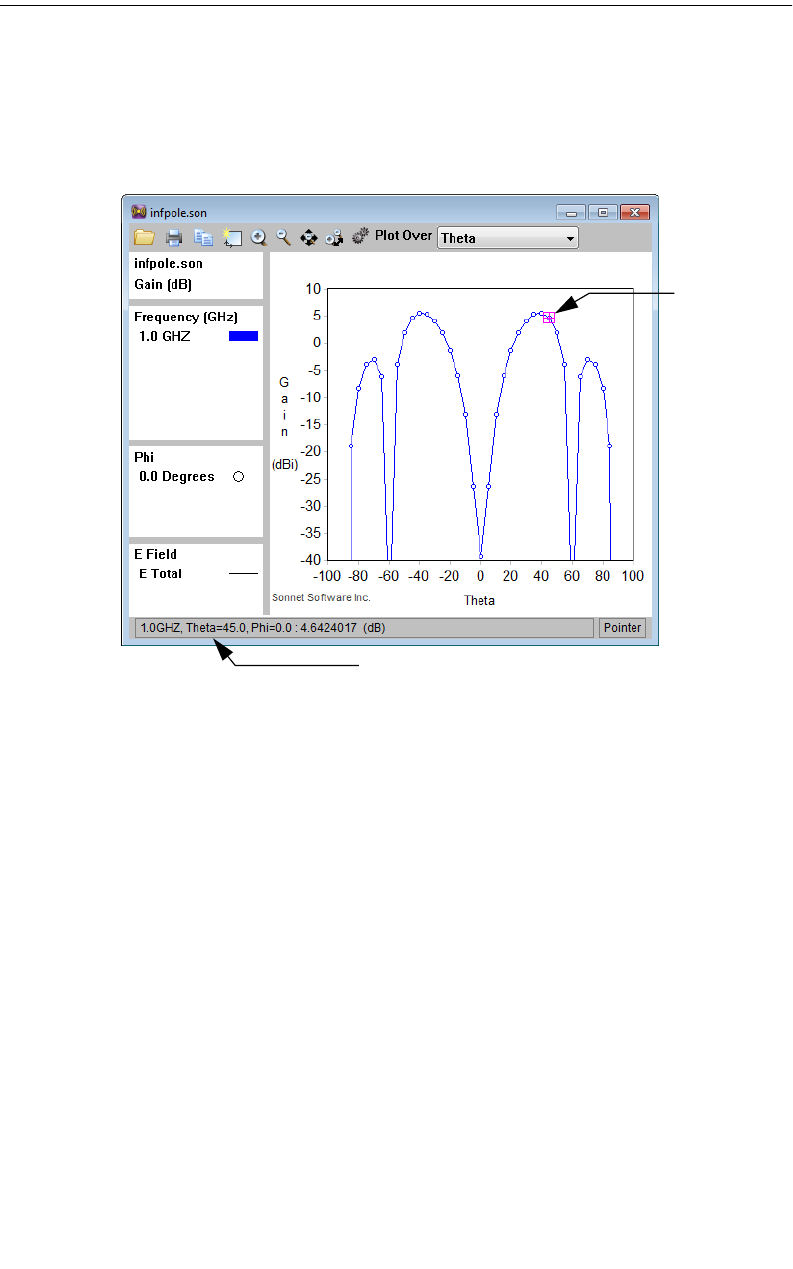
Chapter 19 Far Field Viewer Tutorial
351
Rev 16.56
25 Click on the theta = 45 point on the plot.
A square appears around the point, as shown below. The readout for the point in-
cluding the frequency, value of theta and phi, and the gain appear in the status bar
at the bottom of the far field viewer window.
26 Press the left arrow key, , to move to the theta = 40 point on the plot, or
alternately, click on that point.
The probe box now appears at that point and the data is updated in the status bar.
Note that if there is more than one data curve displayed, the up and down arrow
keys, and , would move the data probe between curves, while the left and right
arrow keys, and , move between data points on any given curve.
Re-Normalizing the Plot
By default, the far field viewer displays the power gain. The power gain is defined
as the radiation intensity divided by the uniform radiation intensity that would
exist if the total power supplied to the antenna were radiated isotropically[1].
We shall now normalize the plot to the maximum value.
Probe
Probe readout on status bar
Location

Sonnet User’s Guide
352
Rev 16.56
27 Select GraphNormalization to change the normalization.
The Select Normalization dialog box appears on your display.
28 If it is not already selected, click on the Directive Gain (dB) radio button.
The directive gain is defined at the radiation intensity from an antenna in a given
direction divided by the uniform radiation intensity for an isotropic radiator with
the same total radiation power.
The far field viewer calculates the directive gain based on the total power radiated
by your circuit. The far field viewer calculates the total power by using all the
theta and phi points to integrate over the entire surface. Therefore, the more theta
and phi points calculated, the more accurate the values provided for directive gain.
A Figure of Merit (F.O.M.) appears in the Gain section of the legend when direc-
tive gain is selected to provide you with an idea of how accurate is the data (100%
is perfect). If this figure is too low, try recalculating using more theta and phi data
points. If this figure is too high, that is an indication that the problem is over cal-
culated. i.e., angles are being analyzed twice. In this case, check for duplicate an-
gels such as theta = 180 and theta = -180.
29 Select Max from the Relative To drop list.
This selects the maximum value of radiation for the plot to be the 0 dB point of
the plot.

Chapter 19 Far Field Viewer Tutorial
353
Rev 16.56
30 Click on the OK command button.
The dialog box is closed and the display is updated with the data normalized to the
maximum value, which in this case is 8.44098 dB. Note that the FOM is only
47.76. As mentioned above, to increase this figure, you increase this by recalcu-
lating for more theta and phi angles.
31 Select Graph Calculate from the main menu.
The Calculation Setup dialog box appears on your display.

Sonnet User’s Guide
354
Rev 16.56
32 If it is not already selected, click on the “Angles” tab.
33 Enter “-90.0” in the Phi 1 Start text entry box.
This analyzes data points from phi = -90to in intervals of which doubles
the number of analysis points for phi.
34 Click on the Calculate button to close the dialog box and calculate new
values.
The plot is updated and now shows more data points. Note that the FOM has gone
up to 95.52%.
FOM
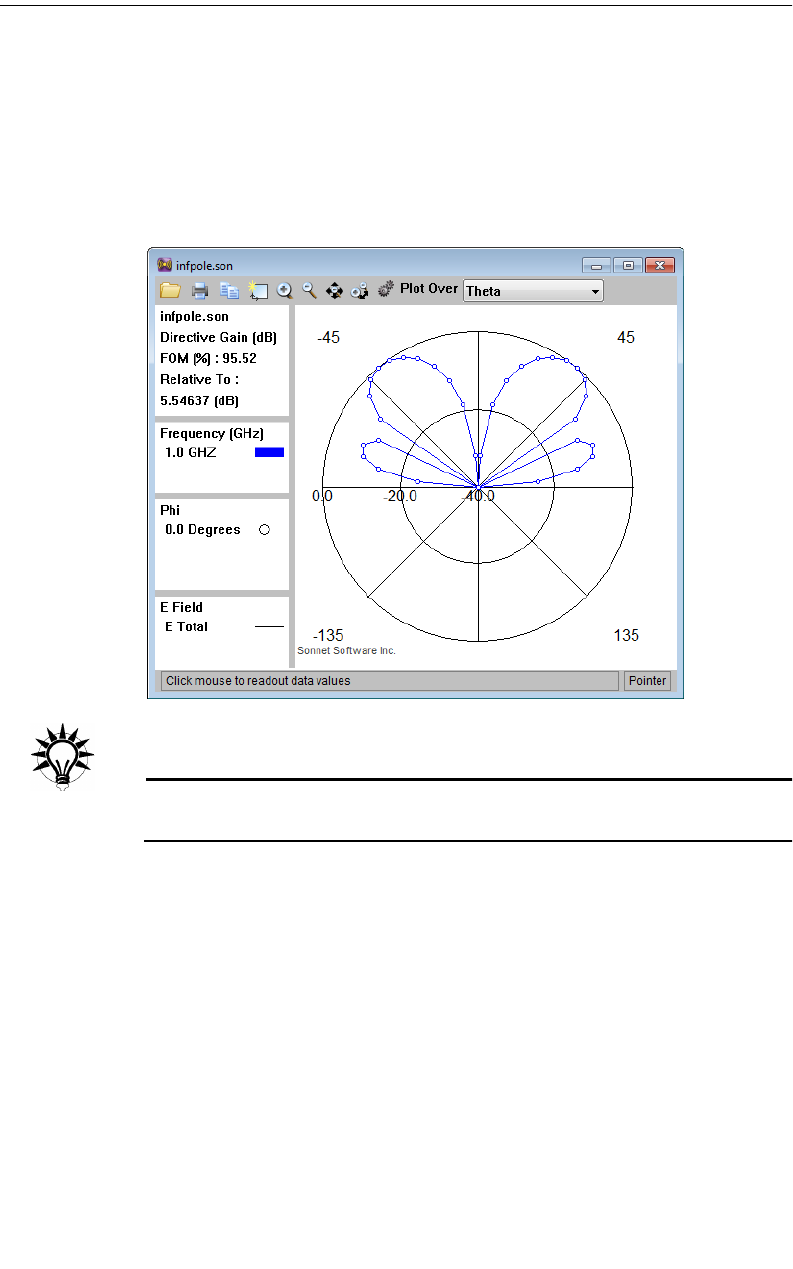
Chapter 19 Far Field Viewer Tutorial
355
Rev 16.56
Changingto a Polar Plot
35 Select Graph Type Polar to select a polar plot for the display.
A polar plot is chosen since the theoretical data for an infinitesimal dipole is
shown in a polar plot. The display is updated using the polar coordinate system.
Phi is held constant and theta is swept.
TIP
You may select another type of plot by right-clicking in the plot title area of the
far field viewer display and selecting Type from the pop-up menu which appears.
Turning Off the Legend
Since the legends take up a lot of space on the display, you may turn them off, al-
lowing the plot to fill the extra space.
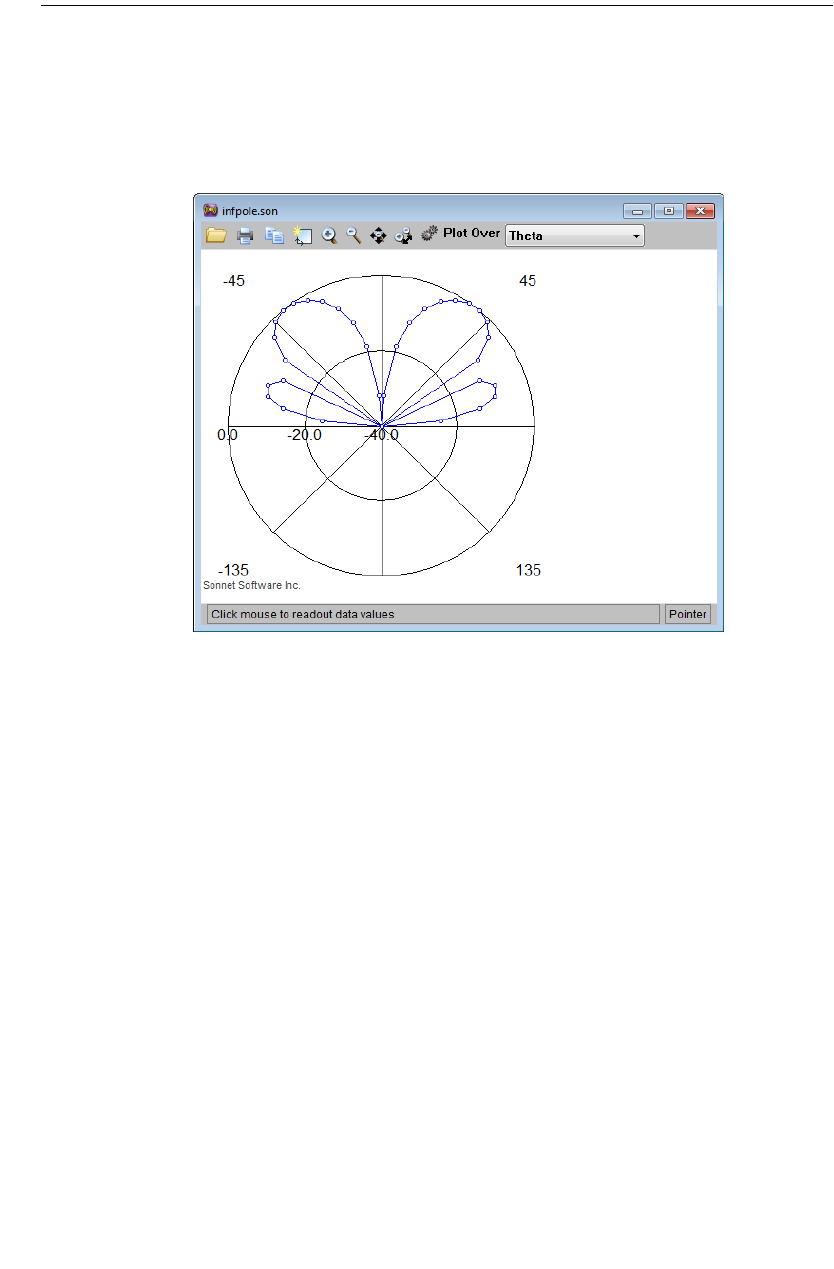
Sonnet User’s Guide
356
Rev 16.56
36 To turn off the legend, select View Legend.
This turns “off” the legend and the far field viewer redraws the plot without the
legends. The menu item toggles the display state of the legend, so that selecting
View Legend again displays the legend.
Changing the Radius Axis
You can change the radius axis limits of the plot to another value. For this exam-
ple, you will change the intervals from 20 dB to 10 dB.

Chapter 19 Far Field Viewer Tutorial
357
Rev 16.56
37 Select Graph Axes from the main the far field viewer menu.
The Axes Properties dialog box appears on your display.
38 Click on the AutoScale checkbox to turn it “off.”
This enables the Min and Max text entry boxes under Autoscale and the Interval
and Number text entry boxes under Tick Labels.
39 Enter “10” in the Interval text entry box.
This sets the intervals on the plot grid to 10 dB.
40 Click on the OK command button.
The dialog box disappears and the far field viewer display is updated with the new
interval value for the axes. Your display should be similar to the one shown below.

Sonnet User’s Guide
358
Rev 16.56
Shown above is the far field viewer calculated far field antenna pattern for the very
short dipole in the file infpole.son. The result should be compared with theoretical
result in the next figure.
Selecting a Frequency Plot
To see how the antenna pattern changes with frequency, you use a frequency plot.
Before you can select a frequency plot, you must return to a cartesian plot.
41 Select Graph Type Cartesian from the far field viewer main menu.
Your display is updated with a cartesian plot. Note that the autoscale is automati-
cally turned back on when you switch plot types.
42 Select View Legend from the far field viewer main menu.
The legend once again appears in your display.
Exact far field antenna pattern from reference [2] of an
infinitesimal dipole antenna one wavelength above a ground plane.

Chapter 19 Far Field Viewer Tutorial
359
Rev 16.56
43 Select Frequency from the Plot Over drop list on the far field viewer tool
bar.
44 Select Graph Select Theta from the far field viewer main menu.
The Select Theta’s dialog box appears on your display.
45 Double-click on -90.0 degrees in the Plotted list.
This value moves to the Calculated list which removes it from the display.
46 Double-click on 0.0 degrees in the Calculated list.
This value moves to the Plotted list which adds it to the display.
47 Click on the OK command button.
The display is updated with a frequency plot as shown below. Note that the gain
is now calculated relative to 7.65804 dB, since the Normalization is relative to
Max and this value is the maximum value of radiation for this plot.
Plot Over drop list

Sonnet User’s Guide
360
Rev 16.56
48 Select Graph Select Phi from the far field viewer main menu.
The Select Phi’s dialog box appears on your display.
TIP
You may also invoke the Select Phi’s dialog box by right-clicking on the Phi box
in legend and selecting Select from the pop-up window.
49 Double-click on 0.0 degrees in the Plotted list.
This value moves to the Calculated list which removes it from the display.
50 Double-click on 90.0 degrees in the Calculated list.
This value moves to the Plotted list which adds it to the display.
51 Click on the OK command button.
The dialog box disappears and the display window is updated.
52 Select Graph Select Theta from the far field viewer main menu.
The Select Theta’s dialog box appears on your display.
53 Double-click on 45.0 degrees and 90.0 degrees in the Calculated list.
These values move to the Plotted list which adds these values to the display.
54 Click on the OK command button.
The dialog box disappears and the display is updated as shown below.

Chapter 19 Far Field Viewer Tutorial
361
Rev 16.56
Notice that E-Total at Theta = 90 is shown in the legends, but does not appear on
the graph. This occurs because the magnitude is too small to show on the plot.
Viewing a Surface Plot
The surface plot shows all the calculated values of theta and phi plotted against
the gain for a single frequency.
55 Select Graph Type Surface from the main menu.
Your display is updated with a surface plot with the first frequency, 0.8 GHz, se-
lected for display.
Saving the Far Field Viewer File
56 Select File Save As from the far field viewer main menu.
The file is saved to the same filename with a “.pat” extension, i.e., “infpole.pat”.
This saves any data calculated during this the far field viewer session.

Sonnet User’s Guide
362
Rev 16.56
Exiting the Far Field Viewer Program
57 To stop the program, select FileExit.
The far field viewer window disappears from your display. This completes the tu-
torial.
References
[1] Simon Ramo, John R. Whinnery and Theodore Van Duzer, Fields and Waves in
Communication Electronics, John Wiley & Sons, Inc. 1994, pg. 601.
[2] Constantine A. Balanis, Antenna Theory Analysis and Design; New York;
Harper & Row, 1982, section 4.7.3

Chapter 20 SPICE Model Synthesis
363
Rev 16.56
Chapter 20 SPICE Model Synthesis
Sonnet’s analysis engine, em, provides a frequency domain solution in the form
of S- Y- and Z-parameters. Many time domain simulators, such as traditional
SPICE engines, do not have the capability to import frequency domain data, or
have problems with efficiency, stability, or accuracy when using frequency do-
main data.
To address these problems, Sonnet provides the capability to output your frequen-
cy domain data into a SPICE-compatible file. You may choose from four different
models, depending on your needs. A brief description of each is provided below,
and each model is discussed in detail in the sections following.
• PI Model: Appropriate for circuits that are electrically small (less than 1/20
wavelengths) and can be represented by a simple PI topology.
• N-Coupled Line Model: Appropriate for single or coupled transmission
lines. Generates an RLGC matrix which can be used in the Cadence Virtuoso
mtline element.
• Broadband Spice Model: Appropriate for most circuits. Generates a
lumped model based on a rational polynomial fit. Requires Broadband Spice
Extractor license.
• Inductor Model: Appropriate for spiral inductors. Generates a simple
lumped element model which is specific to spiral inductors. Requires Broad-
band Spice Extractor license.

Sonnet User’s Guide
364
Rev 16.56
PI Model
The PI Model may be used for circuits that are electrically small and can repre-
sented by a simple PI topology (see "Topology Used for PI Model Output" on
page 368). The results are generally valid only over a narrow frequency band. The
model may be saved in PSpice or Cadence Spectre format.
The PI model Spice generation capabilities are intended for any circuit which is
small with respect to the wavelength at the highest frequency of excitation. Typi-
cally, 1/20th wavelength is an appropriate limit. (If a circuit is too large, you can
often split it into two or more circuits and analyze each separately.) This limitation
is due to the circuit theory limitations of modeling a circuit with just a few lumped
elements. The Sonnet electromagnetic analysis is not intrinsically limited in this
fashion.
The model generated by the analysis includes any lumped elements (including
mutual inductors) between any ports of the circuit layout. Lumped elements from
any port to ground are also included. The synthesis capability does not allow in-
ternal nodes (nodes which are not connected to a port in the layout) with the single
exception of the internal node required to specify a resistor in series with an in-
ductor.
Any circuit which requires internal nodes for an accurate model should be split
into several parts so that the required points become nodes. Internal ports without
ground reference give incorrect results. Any internal ports should be carefully
specified and checked for reasonable results.
Using The PI Model Spice Option
The PI Model synthesis needs electromagnetic results for at least two frequencies
to accomplish its work. It is not possible to create a PI model if the circuit is ana-
lyzed at only one frequency. A PI model is created for pairs of frequencies. The
second frequency is determined by taking the first frequency and adding a percent-
age specified by the user. The second frequency then becomes the first frequency
for the next pair of frequencies for which a SPICE model is generated. The syn-
thesis continues in this way until all the frequencies have been used.
The default value for the separation percentage is 10%. In this case, a SPICE
model is generated using the first frequency and the next highest frequency which
provides a 10% gap. This continues until there are no more frequencies. For ex-

Chapter 20 SPICE Model Synthesis
365
Rev 16.56
ample, for a frequency sweep from 10 - 40 GHz with a 0.1 GHz resolution using
a separation of 10%, the first few frequencies used would be 10, 11, 12.1 and 13.3
GHz.
After completing the analysis, always do a “reality check” for reasonable values.
If you have bad data, the frequency may be too high or too low. If the frequency
is too low, the solution may have unity S-parameters, causing a strange SPICE
model. To be absolutely sure your results are good, select a different frequency
band and re-analyze the circuit. You should obtain similar results between the two
analyses.
You may obtain PI Model Spice data in two different ways. The first is to specify
an optional output file before executing your analysis. The second is to generate a
PI model from the response viewer. The second method has the advantage of al-
lowing you to perform the data check mentioned above before creating the SPICE
data file.
To specify a PI Model Spice output file from the response viewer, perform the fol-
lowing:
1 Analyze the circuit at the desired frequencies.
The analysis monitor appears on your display to show the progress of the analysis.
It is important to note that if your results contain more than two analysis frequen-
cies, then multiple Spice models, one for each pair of frequencies, will be created
in one file.
2 When the analysis is complete, click on the View Response button on the
analysis monitor’s tool bar.
The response viewer is invoked with a plot of your response data.
3 Click on the project name in the response viewer legend to select it.
An outline appears around the project name to indicate that it is presently selected.
If you have multiple projects open in the response viewer and have not selected a
project before using the extraction command, then a window appears which
allows you to select the desired project.
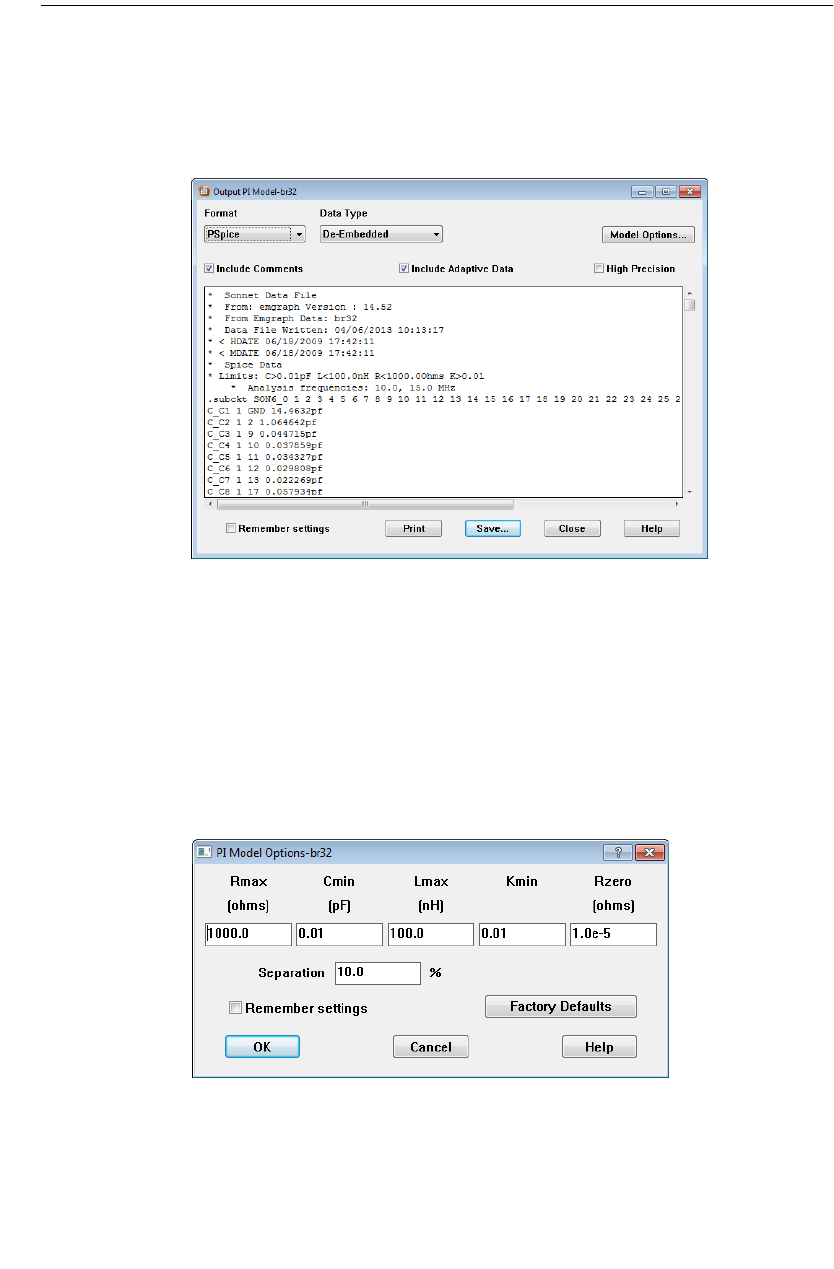
Sonnet User’s Guide
366
Rev 16.56
4 Select Output PI Model File from the response viewer main menu.
The Output PI Model dialog box appears on your display. The contents of the
output window in the Output PI Model dialog box displays the Spice data for the
PI Model in the PSpice format which is the default.
5 Select the desired file format from the Format drop list.
If you select Spectre as the Format (PSpice is the default), the contents of the
output window is updated.
6 To change the parameters for the SPICE data, click on the Model Options
button.
The PI Model Options dialog box appears on your display. To reduce the number
of lumped elements in the model, open circuit limits can be specified here as
shown below.
The values are defined as follows:

Chapter 20 SPICE Model Synthesis
367
Rev 16.56
RMAX: Maximum allowed resistance (ohms). The default value is 1000.0 ohms.
CMIN: Minimum allowed capacitance (pF). The default value is 0.01 pF.
LMAX: Maximum allowed inductance (nH). The default value is 100.0 nH.
KMIN: Minimum allowed mutual inductance (dimensionless ratio). The default
value is 0.01.
RZERO: Resistor to go in series with all lossless inductors (resistance in ohms).
Needed for some versions of SPICE. The default value is 0.0.
Separation: This is the calculation interval between the two frequencies used to
generate the SPICE model specified as a percentage. The second frequency is ob-
tained by adding the specified percentage of the first frequency to the second fre-
quency.
All calculated component values which fall outside the allowed range specified by
the user in the model options are excluded from the resulting lumped model. The
RZERO entry is provided for those versions of SPICE which need inductors to
have some small loss to avoid numerical difficulties. The default value of 0.0 dis-
ables this capability.
Enter the desired values for the parameters in the PI Model Options dialog box.
7 Click on the OK button in the PI Model Options dialog box to apply the
changes and close the dialog box.
8 Click on the Save button in the Output PI Model dialog box.
A browse window appears which allows you to save the data displayed in the
output window. The file extension depends on which type of SPICE format you
have selected.

Sonnet User’s Guide
368
Rev 16.56
A Simple Microwave Example
Shown below is a simple step discontinuity followed by the PI model produced
when you set up an optional PI Model Spice output file.
There are two capacitors to ground (node GND), one inductor connected between
node 1 and node 3, and one resistor connected between node 3 and node 2 in the
lumped element model.
Topology Used for PI Model Output
The topology of the lumped element model generated by em depends on the cir-
cuit being analyzed. In general, the model contains an inductor (in series with a
resistor if using loss), a capacitor and a resistor (when using loss) connected in
parallel from each port to ground. A similar parallel RLC network is also connect-
ed between each port. Therefore, a four-port circuit can contain more elements
than a two-port circuit. Each inductor may also have a mutual inductance to any
* Limits: C>0.01pF L<100.0nH R<1000.0Ohms K>0.01
* Analysis frequencies: 200.0, 220.0 MHz
.subckt spiral_0 1 2 GND
C_C1 1 GND 1.123431pf
C_C2 2 GND 1.316483pf
L_L1 1 3 30.66429nh
R_RL1 3 2 1.57292
.ends spiral_0

Chapter 20 SPICE Model Synthesis
369
Rev 16.56
other inductor in the network. The figure below shows the most complex equiva-
lent circuit possible for a two-port (mutual inductances not shown). Any values
that are outside of the open circuit limits are not included.
N-Coupled Line Model
Most circuit design programs provide models for single and multiple-coupled
transmission lines. However, it is often desirable to use EM simulated data in cir-
cuit design programs. These programs often provide transmission line models
which utilize RLGC parameters. R, L, G, and C are the resistance, inductance,
conductance and capacitance per meter of a transmission line. The RLGC param-
eters can be extracted from an EM simulation of a short section of the transmission
line. They can then be used to model any length of line having the same cross-sec-
tion.
Sonnet can export the RLGC parameters in a format compatible with the mtline
component in Cadence Virtuoso Spectre.
21
Equivalent circuit of a two-port structure using the PI Model. Mutual inductances
also exist between all inductors, but are not shown. Any component whose value is
outside of the open circuit limits are not printed in the SPICE output file.

Sonnet User’s Guide
370
Rev 16.56
Shown below is an example of a project composed of four transmission lines.
As in the circuit shown above, the input ports of your project must be numbered 1
through N and the output ports N+1 through 2N. The input of line M should be
port M and its output should be port M+N. The software does not check for this
condition, but issues a warning message if the number of ports is not an even num-
ber. The equivalent circuit is shown below for the four transmission lines shown
above.
You may generate RLGC parameters automatically by setting up an output file in
the project editor. To setup an output file in the project editor, select Analysis
Output Files from the project editor main menu, then click on the N-coupled Line
Model button in the Output Files dialog box which appears. You may also gener-

Chapter 20 SPICE Model Synthesis
371
Rev 16.56
ate an output file of RLGC parameters from previously generated response data in
the response viewer. To do so, open your project in the response viewer and select
Output N-coupled Line Model from the response viewer’s main menu. RLGC
parameters are generated for each analysis frequency.
Shown below are the RLGC parameters in Spectre format for a two-line project:
After the Sonnet header, the format of the RLGC data is provided. This is followed
by RLGC data and comments for each analysis frequency. Each comment line be-
gins with the “;” character. Though the comment lines can be ignored, they con-
tain useful modal information. Each value in the comment section has both a real
and imaginary part. Characteristic impedance (Z0), propagation constant (γ), and
the modal excitation vectors are provided for each mode.
Broadband SPICE Model
NOTE: The Broadband Spice Model is only available if you have purchased a
Broadband Spice Extractor license from Sonnet. Please see your
system administrator if you are unsure of the availability of this
feature.

Sonnet User’s Guide
372
Rev 16.56
In order to create a Spice model which is valid across a broad band, the Sonnet
broadband SPICE Extractor feature finds a rational polynomial which “fits” the S-
Parameter data. This polynomial is used to generate the equivalent lumped ele-
ment circuits in either PSpice or Spectre format. Since the S-Parameters are fitted
over a wide frequency band, the generated models can be used in circuit simula-
tors for AC sweeps and transient simulations.
To create a Broadband Spice file, you open your project in the response viewer
and select Output Broadband Model File from the main menu. (You may also
create a Broadband Model by using the Analysis Output Files command in the
project editor. See Help for Details) This opens the Output Broadband Model File
window which allows you to calculate a broadband SPICE file based on the anal-
ysis data for your project. You need a minimum of 50 frequency points in order to
generate a Broadband Spice file; therefore, we highly recommend that you use an
ABS sweep when analyzing your circuit to ensure the correct number of analysis
frequencies. If your circuit contains parameterization or optimization data and you
select more than one parameter or iteration combination, then you may choose to
create one file which contains all the Broadband Spice Models or multiple files,
one for each specified combination.
Class of Problems
Be aware that there are several types of responses for which an accurate Broad-
band Spice Model may not be produced:
•If your response data contains a data point which sharply deviates
from the data curve, such as you would see for a box resonance, or
a narrow band spike, the Broadband Spice model may not accu-
rately model that response.
•The Broadband Spice model is generally not accurate for response
data below -60 dB.
•A gentle curve may sometimes get fitted with a straight line.
•Broadband Spice Extractor has only been tested for passive circuits.
•Broadband Spice Extractor has only been tested using S-parameters
produced by em. However, you should be able to use S-parameters
produced by other sources such as other simulators or measured
data to create a Broadband Spice model.
If you are concerned with the accuracy of the model, you should visually inspect
the predicted S-Parameter data, produced by the same rational polynomial which
was used to create the Broadband model, to determine the usefulness of the Broad-
band Spice model.

Chapter 20 SPICE Model Synthesis
373
Rev 16.56
NOTE: Be aware that the processing time needed to create your models can
be significant. The processing time is proportional to the number of
analysis frequencies times the square of the number of ports in your
circuit.
Creating a Broadband Spice Model
You use the response data created as the result of an em analysis to create a Broad-
band Spice model. For the best results use an Adaptive sweep (ABS) to analyze
your circuit and produce response data spread evenly over the frequency band.
The following procedure demonstrates the method to be used in the response
viewer. For detailed instructions for setting up a Broadband Model file in the proj-
ect editor, please refer to Help.
Once you have completed the em analysis of your circuit, do the following to cre-
ate a Broadband Spice model:
1 Open your project in the response viewer.
2 Select Output Broadband Model File from the main menu of the response
viewer.
If you have more than one project open in the response viewer, and a project is not
presently selected, a window appears which allows you to select the desired proj-
ect. If there is only one project or one is presently selected, then the Output Broad-
band Model File dialog box is opened immediately.
3 Select the desired project from the project drop list.
You may only create a Broadband Spice Model for one project at a time.
4 Click on the OK button to select the project and close the dialog box.
The Output Broadband Model File dialog box appears on your display. You may
access Help by clicking on the Help button or use context sensitive help for an
explanation of a particular control or entry.
5 Select the file format of the Broadband Model: PSpice or Spectre from the
Format drop list.
PSpice and Spectre are the two formats of Spice file supported. A PSpice file uses
the extension “.lib” and a Spectre file uses the extension “.scs.” The PSpice file is
compatible for use with HSPICE.

Sonnet User’s Guide
374
Rev 16.56
6 Enter the desired name for the Spice model file in the Model File text entry
box.
A default filename is provided which places the Broadband Spice model file in the
same directory as your source project. If you have selected multiple parameter
combinations, a file is produced for each combination. If you wish to use another
name or save the file in another location you may edit the text entry box.
7 Enter the desired error threshold.
The lower the error threshold you set, the more processing time is required to
calculate the model. A lower threshold error also produces a more complex model,
which requires more time to process in the Spice simulator. The error threshold is
the error present between the source data and the fitted curve and is defined as
follows:
The calculation of the Broadband Spice model stops when this error threshold is
reached or when it proves impossible to improve the error. We recommend using
the default value of 1.0% initially and not setting the threshold below 0.1%.
8 Enter the desired stability factor.
For more information about the stability factor, please refer to "Broadband Spice
Extractor Stability Factor" on page 379.
9 Click on the Advanced button.
The Advanced Broadband Model options dialog box appears on your display.
10 Select the Write data file checkbox if it is not already selected.
This option is selected by default. When this option is selected, the Predicted S-
Parameter data upon which the model is based is also output to a file. The name
of the file appears below the checkbox and may not be changed. The file is created
Error
sf
Source sf
Fit
–
f1=
N
N
------------------------------------------------------------------------- 100=
where f = the number of the frequency point
N = the total number of frequency points
s(f)Source = the value of the S-parameter at the frequency
point f in the project source response
s(f)Fit = the value of the S-parameter at the frequency point f
in the fit curve data

Chapter 20 SPICE Model Synthesis
375
Rev 16.56
in the same directory in which your model file is created. Once the creation of the
model is completed, you may use the response viewer to compare your original
response data to the Predicted S-Parameter data to evaluate the accuracy of the
Broadband model.
By default, the predicted S-parameter data output from the model consists of the
original analysis band, plus a band from the highest frequency to three times the
highest frequency. This data is also used to check the stability of the model. You
may override this default by selecting the Override default additional frequencies
checkbox and entering the desired band.
11 Click on the OK button to close the Advanced Broadband Model Options
dialog box and apply the changes.
Please note that the predicted data band is set by default and the output file is
created by default, it is usually not necessary to open the Advanced Broadband
Model Options dialog box.
12 Click on the Extract button to create the Broadband Spice model.
A progress window appears on your display. Be aware that the processing time
needed to create your models can be significant. The processing time is
proportional to the number of analysis frequencies times the square of the number
of ports in your circuit. If you wish to stop the process before it is complete, click
on the Cancel button in the progress window.
13 Once the calculation is complete, the Broadband Spice details dialog box
appears on your display.
A log of the creation process appears in this dialog box. The log contains
information on the error for each parameter, which parameter had the greatest
error, and the filename of the predicted S-Parameter data. It will also indicate
whether the model achieved the error threshold. Use this information to determine
which parameters to examine in the response viewer. You should look at the S-
parameter with the greatest error as well as any critical S-parameters whose error
was greater than 0.1%.
For a detailed explanation of the log, see “Broadband Spice Extractor Log,”
page 377.
14 Click on the Plot button to open a plot of your response data versus the
predicted S-Parameter data.
The Predicted S-Parameter data is opened in the response viewer along with the
original response data. You should view the S-parameter with the greatest error
and any other critical response data whose error was greater than 0.1% to judge if
the ''fit'' or accuracy of the model is sufficient for your needs.

Sonnet User’s Guide
376
Rev 16.56
If the model is not accurate enough, see “Improving the Accuracy of the Broad-
band Spice Model,” page 378 for suggestions on improving your Broadband
Spice model.
Checking the Accuracy of the Broadband Spice Model
It is possible to save the predicted S-parameter data created while calculating your
Broadband Spice model so that you may visually check the accuracy of your
model when it is complete. To save the predicted S-parameter data, you should se-
lect the Write data file checkbox in the Advanced Broadband Model Options di-
alog box when you create your model. Note that this checkbox is selected by
default. The predicted S-parameter data file is created in the same directory as
your Broadband Spice model file.
Upon the completion of creating your Broadband model, you should open the
original project in the response viewer, then add the predicted S-parameter data
file to your graph and compare the two responses. If you are creating your Broad-
band Model in the response viewer, you may do this automatically by clicking on
the Plot button in the Broadband Spice Details dialog box which appears upon
completion of your model. Use the log information in the Details window, which
is detailed in the next section, to determine which parameter had the highest error
and any critical parameters whose error was greater than 0.1%. Check these pa-
rameters to see how much the curve fit data varies from your circuit response.
If your Broadband Spice Model is to be used for a transient analysis, be aware that
the frequency response of the model up to 1/T where T is the minimum time step
of the transient analysis is important. You should use the Advanced Broadband
Model options dialog box to specify additional predicted data up to 1/T. You ac-
cess this dialog box by clicking on the Advanced button in the Broadband Model
File entry dialog box in the project editor or in the Output Broadband Model dia-
log box in the response viewer. This allows you to view the frequency response of
your model at data points not included in your em analysis. You should look for
anomalies in the response that indicate a problem with the model, such as S-pa-
rameters greater than one or unexpected sharp resonances.
You may also use the stability factor in order to ensure a stable transient analysis.
Please see "Broadband Spice Extractor Stability Factor" on page 379.
If the model is not accurate enough, see “Improving the Accuracy of the Broad-
band Spice Model,” page 378 for suggestions on improving your Broadband
Spice model.

Chapter 20 SPICE Model Synthesis
377
Rev 16.56
Broadband Spice Extractor Log
The Broadband Spice Extractor log, displayed in the Broadband Spice details win-
dow, contains detailed information about the creation of your Spice model file.
You may view a summary of the log or the complete log. To view the summary
of the log, click on the Summary button at the bottom of the window. To return to
the full log, click on the Complete button. The information in the log file is also
included in the beginning of the output file.
You use the log to determine which parameters to examine in order to determine
if the Spice model is accurate enough for your use. Two log files are shown below,
the first log is for a model which achieved the error threshold and the second log
is one in which the error threshold was not achieved on all the S-Parameters. A
warning message is issued for all S-parameters whose error is greater than the
error threshold.
Generating files cocross.lib and cocross_predict.snp.
--Model Log for cocross--
Data set has 397 points and 4 ports
--Model Options--
Error threshold(%) = 1
Stability Factor: 0.001
Output predicted file: C:\project\cocross_predict.snp
S Parameter fitting enabled.
Max order target: 40
Using default predicted frequencies
--Model Results--
S11 Order = 2 Error(%) = 0.02663896
S12 Order = 2 Error(%) = 0.01073755
S13 Order = 2 Error(%) = 0.01566697
S14 Order = 2 Error(%) = 0.004835758
S22 Order = 2 Error(%) = 0.06025392
S23 Order = 2 Error(%) = 0.01543952
S24 Order = 2 Error(%) = 0.02405850
S33 Order = 2 Error(%) = 0.04248355
S34 Order = 2 Error(%) = 0.004751939
S44 Order = 2 Error(%) = 0.01848211
--Model Summary for cocross--
Maximum error was for S22, Error(%) = 0.0602539
Total model time: 0.158 seconds
Model cocross successful
Error Threshold
Error values for
S-parameters
S-parameter
with
greatest
error
Indicates that the Error Threshold
was achieved for all S-parameters
Curve Fit
Maximum Order
Stability Factor Data File
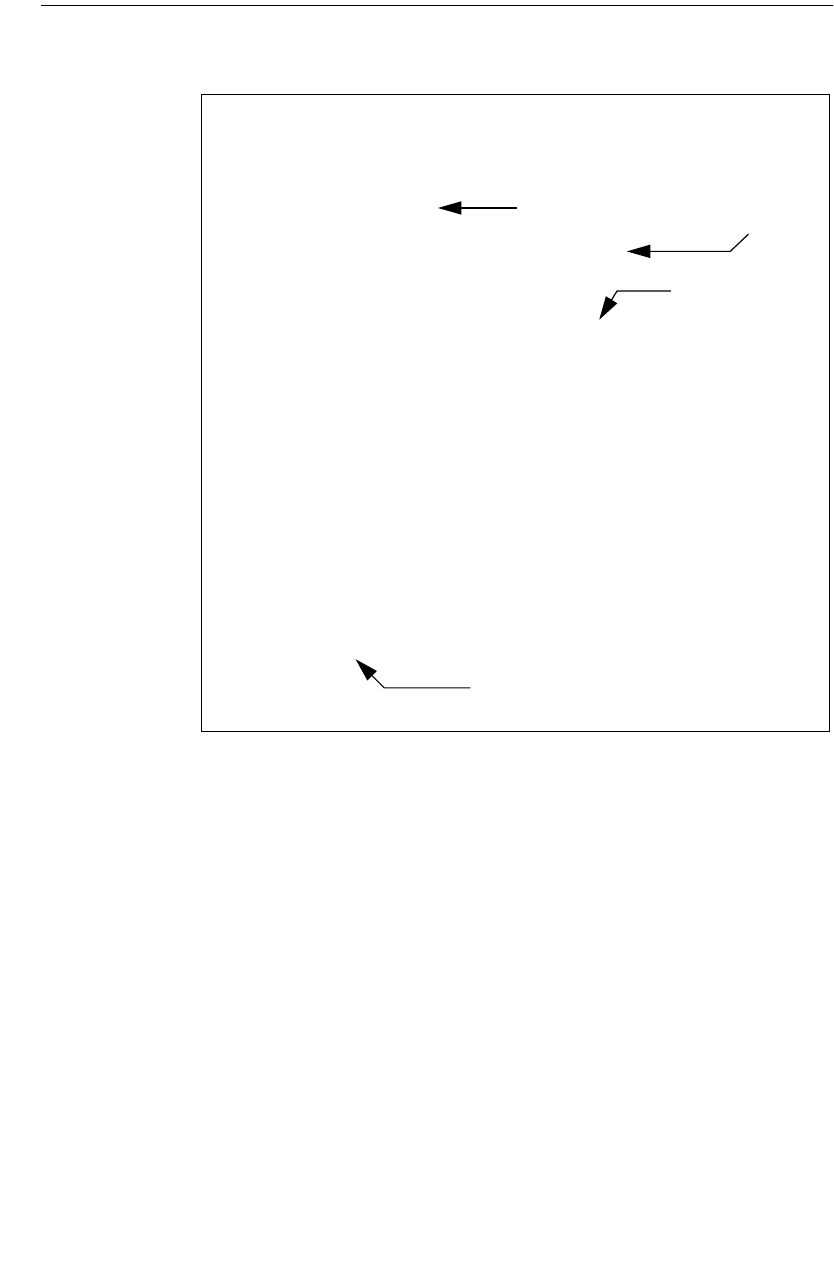
Sonnet User’s Guide
378
Rev 16.56
Improving the Accuracy of the Broadband Spice Model
If you need to increase the accuracy of your Broadband Spice model, there are
several strategies you may use.
•If the Broadband model met your error threshold criteria but is still not
acceptable, you may decrease the error threshold to increase the
accuracy of the model. Be aware, however, that the processing time may
be significantly increased by lowering the error threshold. Typically,
values below 0.1% result in unacceptably long analysis times.
•If there are more than 200 frequency points in your response data, try
decreasing the number of frequencies in your response data. To do so,
use the Analysis Clean Data command in the project editor to
remove the response data, then run another Adaptive sweep (ABS)
Generating files matchnet.lib and matchnet_predict.snp.
--Model Log for matchnet--
Data set has 1246 points and 2 ports
--Model Options--
Error threshold(%) = 0.5
Stability Factor: 0.001
Output predicted file: C:\Program Files\sonnet\proj-
ect\matchnet_predict.snp
Max order target: 200
--Model Results--
S11 Order = 203 Error(%) = 1.387911 WARNING: Error threshold
of 0.5 (%) not achieved
S12 Order = 208 Error(%) = 2.984112 WARNING: Error threshold
of 0.5 (%) not achieved
WARNING: Poor figure of merit on S12 parameter. Visual inspection
of predicted S12 recommended.
S22 Order = 214 Error(%) = 1.833756 WARNING: Error threshold
of 0.5 (%) not achieved
WARNING: Model prediction is not passive at 112 frequency points.
Error threshold may need to be decreased or input data may be non
passive.
--Model Summary for matchnet--
Maximum error was for S12, Error(%) = 2.98411
Total model time: 25 minutes 43 seconds
Model matchnet finished with no errors, 5 warnings
Error Threshold Curve Fit
Warning Messages
Indicates that a “fit” was found for all
S-parameters but for some the error
exceeded the error threshold.
Data File

Chapter 20 SPICE Model Synthesis
379
Rev 16.56
using a coarser resolution to produce less data points but still more than
50 data points. You may change the resolution of an adaptive sweep in
the Advanced Options dialog box in the project editor. Select Analysis
Setup, then click on the Advanced button in the Analysis Setup
dialog box which appears.
•Increase the number of data points in the critical frequency band in
which you are concerned and decrease the number of data points in
frequency ranges which are not as important.
•You may be able to increase the accuracy of your model by using the
Stability factor. Please see "Broadband Spice Extractor Stability Factor"
in the next section.
Broadband Spice Extractor Stability Factor
Although the extracted model may be a good fit to the S-parameters, a transient
analysis which uses the model may be unstable. To help with this problem, Sonnet
provides a control which pushes the poles away from the unstable region. Howev-
er, pushing the poles too far could result in a less accurate fit usually by causing a
decrease in the Q of the circuit. Therefore, you should only use this control if you
are having stability problems with the model.
The Broadband Spice stability factor allows you to control the amount by which
the model fitting forces the poles of your model away from the unstable region.
The factor represents a magnitude ratio for which the real part of a pole cannot be
less than the magnitude of the pole.
The higher the stability factor the greater the effect on the model. Reasonable val-
ues for the stability factor are between 1.0e-5 to 0.5; the default value is 1.0e-3. If
you are having stability problems, raising this value may result in a stable model.
The forcing done using the stability factor could result in a decrease in Q such that
strongly resonant structures need a lower value, but unstable structures need a
higher value to maintain their stability.
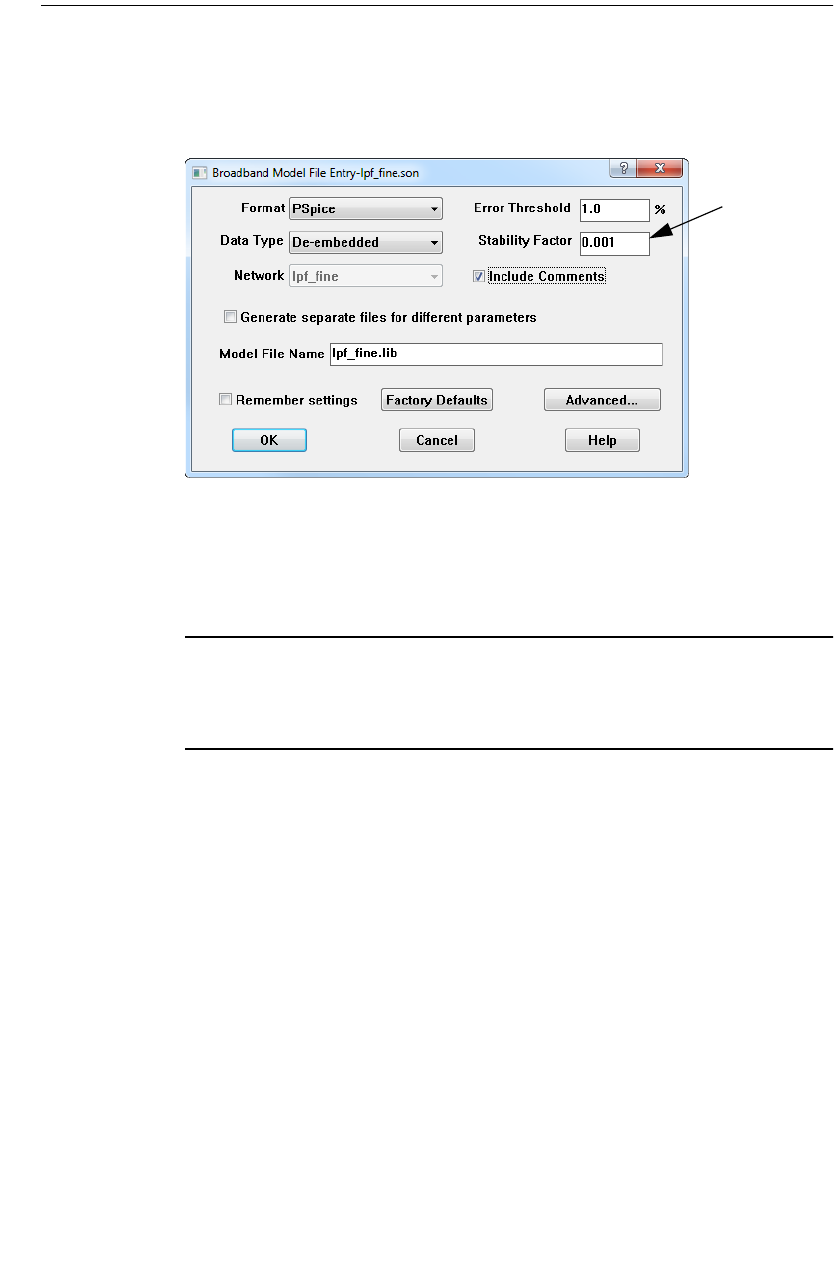
Sonnet User’s Guide
380
Rev 16.56
You input the stability factor in the Broadband Model File Entry dialog box,
opened when you set up a Broadband Spice output file in the project editor (Anal-
ysis Output Files) or response viewer (Output Broadband Model File). You
enter the stability factor in the Stability Factor text entry box as shown below.
Inductor Model Extractor
NOTE: The Inductor Model Extractor (IME) feature is only available if you
have purchased a Broadband Spice Extractor license from Sonnet.
Please see your system administrator if you are unsure of the
availability of this feature.
The Inductor Model Extractor (IME) feature allows you to extract an intuitive
equivalent circuit model from the EM analysis of a spiral inductor.
Model Topologies
There are two topologies available for the Inductor model: the “Untapped” model
and the “Center Tapped” model. Both topologies generate a simple, physical,
fixed-topology circuit model.
Stability
Factor
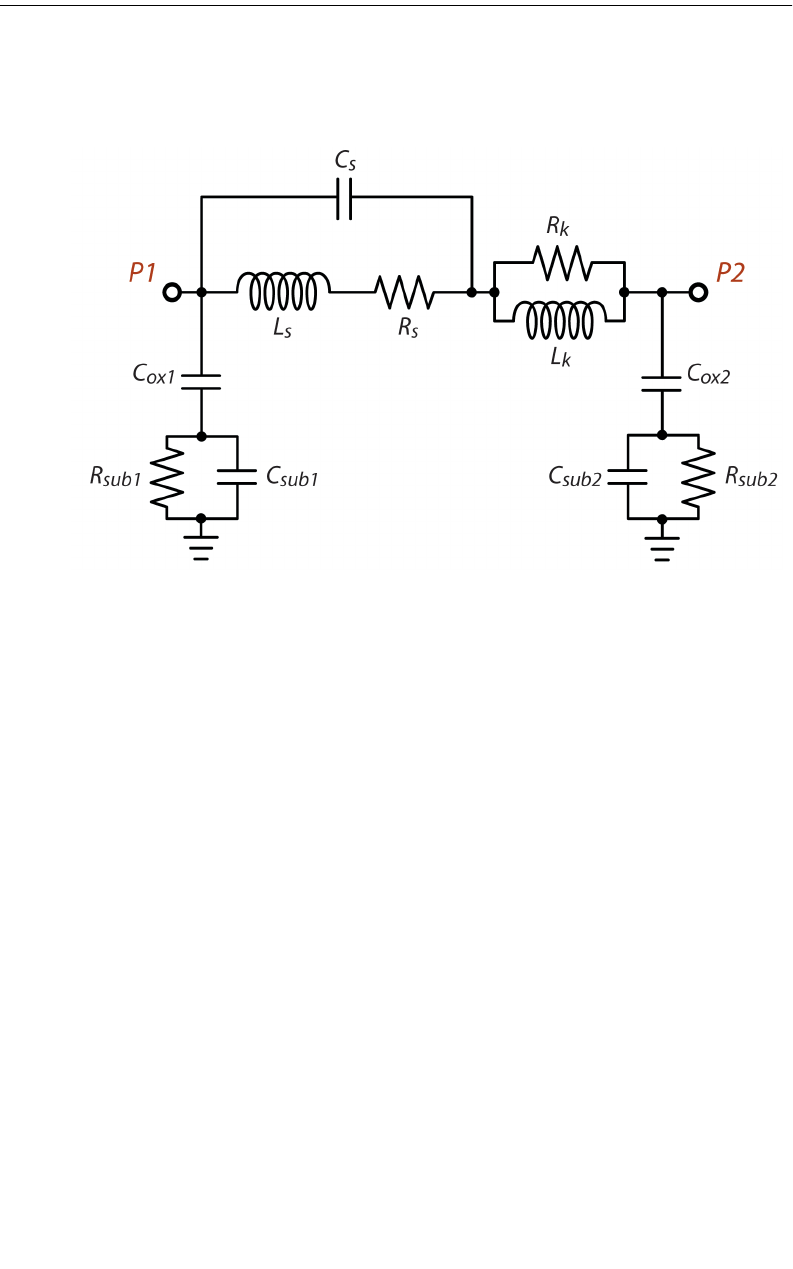
Chapter 20 SPICE Model Synthesis
381
Rev 16.56
Untapped Topology
Shown below is the schematic of the “Untapped” inductor model topology.
The Untapped model is appropriate under the following conditions:
•The inductor must have at least two ports. Ports 1 and 2 must be the
input/output ports of the inductor. If you include any additional ports,
the algorithm assumes that you will be connecting them to ground in
your circuit simulator. Thus, you may connect ports to a patterned
ground shield or ground ring if you wish.
•The analysis frequency band should extend from the frequency where Q
exceeds unity to approximately twice the frequency at which the
maximum Q-factor is found.
•This model extraction technique has proven most effective with spiral
inductors on a conductive substrate, such as those usually found in
RFIC processes involving lossy silicon substrates.

Sonnet User’s Guide
382
Rev 16.56
Center Tapped Topology
Shown below is the schematic of the “Center Tapped” inductor model topology.
The Center Tapped model is appropriate under the following conditions:
•The inductor must have at least three ports. Ports 1 and 2 must be the
input/output ports, and port 3 must be the center-tap port. If you include
any additional ports, the algorithm assumes that you will be connecting
them to ground in your circuit simulator. Thus, you may connect ports to
a patterned ground shield or ground ring if you wish.
•The analysis frequency band must include the frequency where Q is
maximum. In addition, it is recommended to do a wideband sweep to
improve the model performance. Since this topology is not meant to be
used above the self-resonance frequency, any data above the self-
resonance frequency is ignored by the extraction algorithm.
•This model extraction technique has proven most effective with spiral
inductors on a conductive substrate, such as those usually found in
RFIC processes involving lossy silicon substrates

Chapter 20 SPICE Model Synthesis
383
Rev 16.56
Model Output
When the model is extracted, a netlist with the specified topology is written. The
format of the netlist can be Spectre, PSpice, or Sonnet Netlist, and is specified
when setting up your output file. You also have the option of requesting a Touch-
stone file with the s-parameter response of the extracted model. For more details,
please see the following sections.
Using the Inductor Model Extractor (IME)
You have two options of when to create this model. You may specify an output
file in the project editor before your analysis, so that the inductor model output file
is created automatically at the end of your analysis. It is also possible to create the
output file after the analysis is complete when looking at your analysis response
data in the response viewer. Both methods are explained below.
Using the IME in the Project Editor
To setup your output file so that it is automatically generated as part of your EM
analysis, do the following:
1 Open the desired project in the project editor.

Sonnet User’s Guide
384
Rev 16.56
2 Select Analysis Output Files from the project editor main menu.
The Output Files dialog box appears on your display, as shown below.
3 Click on the Inductor Model button.
The Inductor Model File entry dialog box appears on your display. This dialog box
allows you to specify the desired topology and format of your output model file.
You may also choose to output the S-parameter data file for the inductor model.
This is useful if you wish to see how well the model output fits your original data.
For information about the controls in this dialog box, please click on the Help
button in the dialog box.
Inductor
Model
button

Chapter 20 SPICE Model Synthesis
385
Rev 16.56
4 Once you have finished selecting your format choices, click on the OK
button.
This closes the Inductor Model file dialog box and applies the changes. The
Output Files dialog box is updated and the file you just specified now appears in
the file list. An example is pictured below.
5 Click on the OK button in the Output Files dialog box.
This closes the dialog box and completes the specification of the model file. When
you run your analysis, this output file is created and written to the location
specified.
Using the IME in the Response Viewer
To extract an inductor model from your analysis results after the analysis is com-
plete, you may create the file using the response viewer. To create the file, do the
following:
1 Open the desired project in the response viewer.
Model File

Sonnet User’s Guide
386
Rev 16.56
2 Select Output Inductor Model File from the response viewer main menu.
The Inductor Model File dialog box appears on your display. This dialog box al-
lows you to specify the format of your output model file. You may also choose to
output the S-parameter data file for the inductor model. This is useful if you wish
to see how well the model output fits your original data. For information about the
controls in this dialog box, please click on the Help button in the dialog box.

Chapter 20 SPICE Model Synthesis
387
Rev 16.56
3 Once you have finished selecting your format choices, click on the Extract
button.
This closes the Inductor Model file dialog box and creates the output model file.
The Schematic window appears on your display with the schematic for your to-
pology displayed including the calculated values for your model. An example is
shown below. You may copy the schematic to use in presentations by clicking on
the Copy button (Windows only).
Calculated
values
Plot
button Details
button Copy
button

Sonnet User’s Guide
388
Rev 16.56
You may open the Details window by clicking on the Details button in the Sche-
matic window. The Details window displays a report on the model created. You
will need to use the scroll bar in the window to view the whole report. For details
on the information displayed and options available in this window, please click on
the Help button in the Details dialog box.
Clicking on the Plot button in the schematic window opens up a plot that shows
the inductance and Q factor of both the original response data and the data gener-
ated using the extracted model so that you may compare them.

Chapter 21 Box Resonances
389
Rev 16.56
Chapter 21 Box Resonances
Introduction
The Sonnet analysis engine, em, is not limited to a purely TEM or Quasi TEM
analysis. For a given structure, if a higher order mode (TE or TM) can propagate
or an evanescent mode can exist, it will be included in the Sonnet results. These
modes are sometimes called waveguide modes, cavity modes, or box modes. If the
cavity dimensions are large enough, these modes can resonate, causing spikes
(abrupt changes) in your measurements. Since em is a full-wave analysis engine,
these resonances will also be present in your Sonnet results. Thus, Sonnet can be
used to predict resonances inside rectangular packages and module housings.
In this chapter, we will outline several ways to detect and remove box resonances
within the Sonnet simulation. As you will see, this allows you to evaluate a pack-
age design early in the design cycle.
We will also discuss how to handle situations where your real circuit is not in a
metal box, but the Sonnet simulation shows resonances because of the em analysis
box which is not present in the real circuit. In other words, the simulation environ-
ment is introducing resonances which are not present in the real circuit.

Sonnet User’s Guide
390
Rev 16.56
Initial Indicators of a Box Resonance
There are several typical indicators of a box resonance:
1. Suspicious "spikes": A box resonance usually shows up as a spike (i.e., a
rapid change) in your response. Shown below are S-parameter plots of a cou-
pler with box resonances, but you may also notice spikes when plotting mag-
nitudes or phases of S,Y, Z-parameters, or equations, such as inductance,
capacitance and/or Q-factor.
2. Large number of discrete frequencies required for an ABS
sweep: Adaptive Band Synthesis (ABS) works best when your circuit does
not have box resonances. When your circuit contains box resonances, ABS
will still give accurate results, but may require a large number of points
around the resonance. If you find your analysis is requiring an unusually large
number of discrete points, then box resonances could be the cause.
3. Gain in your response: As mentioned in the de-embedding chapter of this
manual, de-embedding requires the analysis of calibration standards. If one
of these calibration standards has a box resonance, then the de-embedding re-
sults could be inaccurate at the resonant frequencies. Often, this shows up as
gain in the results, even though you are analyzing a passive circuit.
4. Two or more large box dimensions: A good rule of thumb for determin-
ing the lowest resonant frequency for a rectangular box is to calculate the fre-
quencies where the smallest two dimensions of your box are a half
wavelength. The lower of these two frequencies is often fairly close to the
lowest box resonance frequency. So, if your box has two dimensions larger
than a half wavelength, and you have not done anything to prevent box reso-
nances, box resonances will probably occur.

Chapter 21 Box Resonances
391
Rev 16.56
Bandpass Filter Example with Resonances
This chapter uses a bandpass filter as an example circuit which is suspected to
have box resonances, and shows how to determine if these resonances are caused
by the box. Various techniques are discussed to remove unwanted box resonances.
The bandpass filter and the variations mentioned in this chapter can be found in
the Sonnet example files under the name “box_resonance.” You may access the
Sonnet Example Browser by selecting Help Browse Examples from the menu
of any Sonnet application. For instructions on using the Example Browser, please
click on the Help button in the Example Browser window. Be aware that this ex-
ample contains multiple files.
The filter, “Filter_original.son,” is shown below. It is a microstrip edge coupled
filter which has been placed in a box which is large enough to support at least one
box resonance in the band of interest.

Sonnet User’s Guide
392
Rev 16.56
Is It a Box Resonance?
Below is an S21 plot for the example project “Filter_Original”, included in the box
resonance example set. Notice that there is a sharp change, or “spike”, in the data
at about 12.55 GHz.
But not every resonance in your response is necessarily a box resonance. For ex-
ample, it is possible that there could be resonances as part of the filter response.
The next section shows the simplest way to check your circuit for box resonances.
The Box Resonance Estimator
The quickest way to understand the box resonance situation within your circuit is
to use the Box Resonance Estimator tool before running an analysis. Routinely
using this tool before running a simulation can prevent a lot of wasted simulation
time. It is an extremely useful tool because it allows you to make modifications to
the box size and/or dielectric properties of your circuit and instantly gauge its im-
pact on box resonances. The Estimator can also be used after a simulation is com-
plete to help determine which characteristics of a complex data curve are related
to box resonances. The results of the tool are theoretical values based on lossless
materials, with the circuit metal removed. For most circuits, this is a good assump-
tion.

Chapter 21 Box Resonances
393
Rev 16.56
To access the Box Resonance Estimator, select Analysis Estimate Box Reso-
nances from the project editor main menu. The Box Resonances dialog box ap-
pears on your display. The result for our example circuit is shown below.
Notice the estimated frequency of the first box resonance is close to the frequency
of the resonance in the S-parameter response. Therefore, we can conclude that the
cause of the resonance is a strong box resonance which has induced coupling be-
tween the input and output ports at the resonant frequency.
The Box Resonance Estimator displays not only the resonant frequencies con-
tained in the simulation frequency range, but also tells the user the particular mode
type. It is sophisticated enough to realize that when Symmetry is enabled for a cir-
cuit that Even Y modes will not exist. For a complete description of propagation
modes, please refer to any classic field theory textbook.
The Box Resonance Estimator is nearly instantaneous because it ignores your cir-
cuit metal and only considers the dielectric stackup. In addition, it assumes the fol-
lowing:
• Lossless materials: All six walls of the analysis box are considered loss-
less. All dielectrics are lossless.
Sonnet User’s Guide
394
Rev 16.56
• Metal that creates a smaller box is ignored: As mentioned above,
the Estimator ignores circuit metal; therefore, even if you have a plane of met-
al that divides the box into two sections, it will be ignored. This could occur
in a Coplanar Waveguide (CPW) or slotline circuit where a large portion of
the layer is metalized.
• Vias ignored: Sometimes vias can be used to eliminate box resonances.
However, since circuit metal is ignored by the Estimator, the vias have no af-
fect on the estimated box resonances.
• De-embedding ignored: The Box Resonance Estimator only checks the
primary structure, not the de-embedding calibration standards. To determine
if a box resonance is caused by a de-embedding calibration standard, see the
section "Runtime Warning Messages" below.
Runtime Warning Messages
You may use the Box Resonance Info run option to estimate box resonances and
output warning messages in the analysis monitor during the simulation. To use
this option, do the following:
1 Select Analysis Setup from the project editor main menu.
The Analysis Setup dialog box appears on your display.
Advanced
button
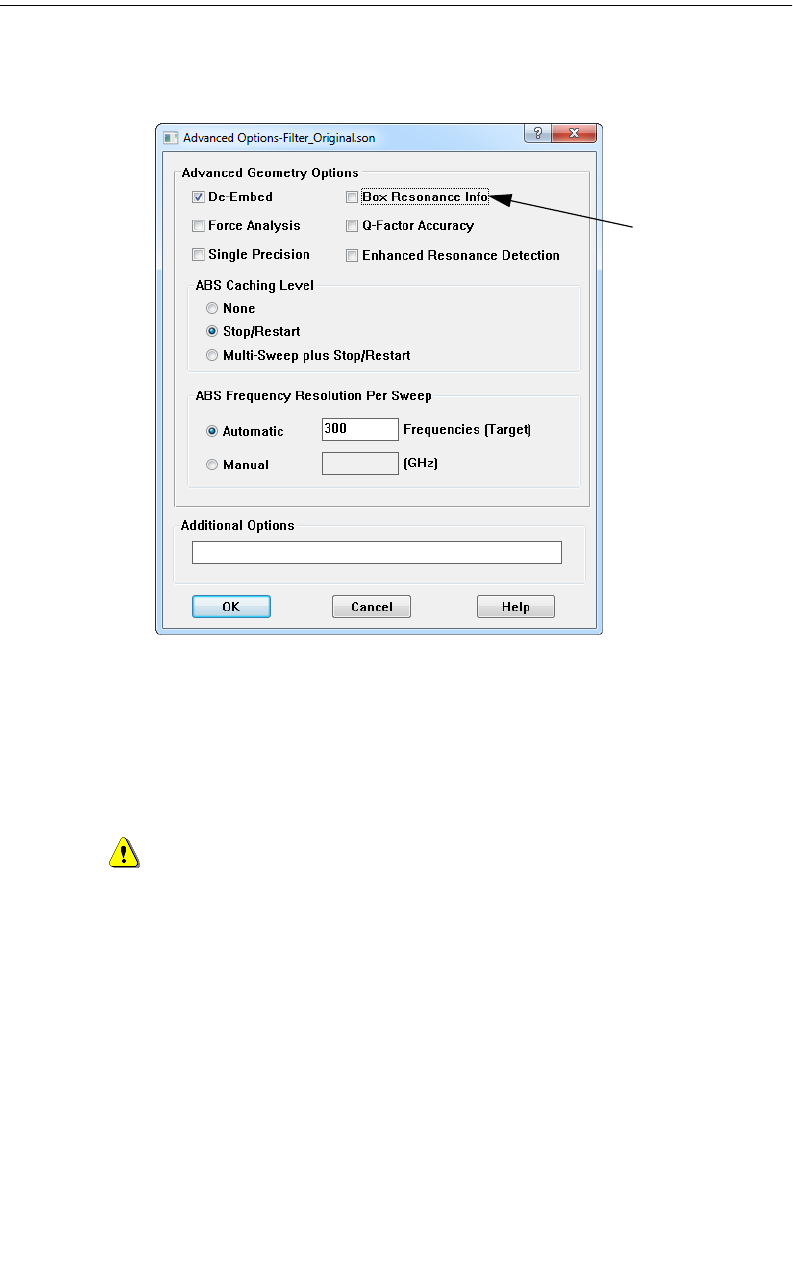
Chapter 21 Box Resonances
395
Rev 16.56
2 Click on the Advanced button in the Analysis Setup dialog box.
The Advanced Options dialog box appears on your display
3 Click on the Box Resonance Info check box in the Advanced Options dialog
box
4 Close both the Advanced Options dialog box and the Analysis Setup dialog
box by clicking on the OK button to close the dialog box and apply the
changes.
The warning symbol, shown to the left, appears in the analysis monitor when a box
resonance is detected. If you click on the Errors/Warning button in the analysis
monitor, you can view all of the warning messages associated with that particular
analysis.
Box Resonance
Info checkbox

Sonnet User’s Guide
396
Rev 16.56
Below is an example of the first type of box resonance warning message from an
analysis of the project. When this message appears there is a box resonance de-
tected in the primary structure.
Note that the warning message is describing box resonances which appear in the
primary structure. The term “primary” refers to the actual structure being analyzed
(as opposed to a de-embedding calibration standard). As with the Box Resonance
Estimator, the specified dielectric stackup is considered, but the effect of any cir-
cuit metallization and loss parameters are not.
Keep in mind that this option invokes the same algorithm as the Box Resonance
Estimator. However, it also checks for resonances in the de-embedding calibration
standards. If it detects a resonance in one of the calibration standards, a similar
warning message to the one above will appear except the “Circuit” line will name
the calibration standard. For example, if one of the calibration standards used to
de-embed ports on the left box wall is detected, the line will look something like
this:
For more information on the calibration standards used for de-embedding, please
refer to "Calibration Standards" on page 114.
Removing artificial box resonances
Sometimes you want to see the response of your circuit in an unshielded environ-
ment. In those cases, any resonances caused by the analysis box are considered an
artifact of the simulation and do not represent what you would measure. This sec-
tion shows several methods for removing, attenuating, or moving these artificial
resonances out of band.
Sonnet Warning EG2680:
Circuit has potential box resonances.
Circuit: primary structure
The estimated box resonance frequencies are listed below.
The calculations assume lossless materials, with a box filled with
only the specified dielectric stackup materials.
12.55 GHZ TM Mode 1,1,0
Only lowest order modes considered.
Circuit: left box wall SOC magnetic wall standard
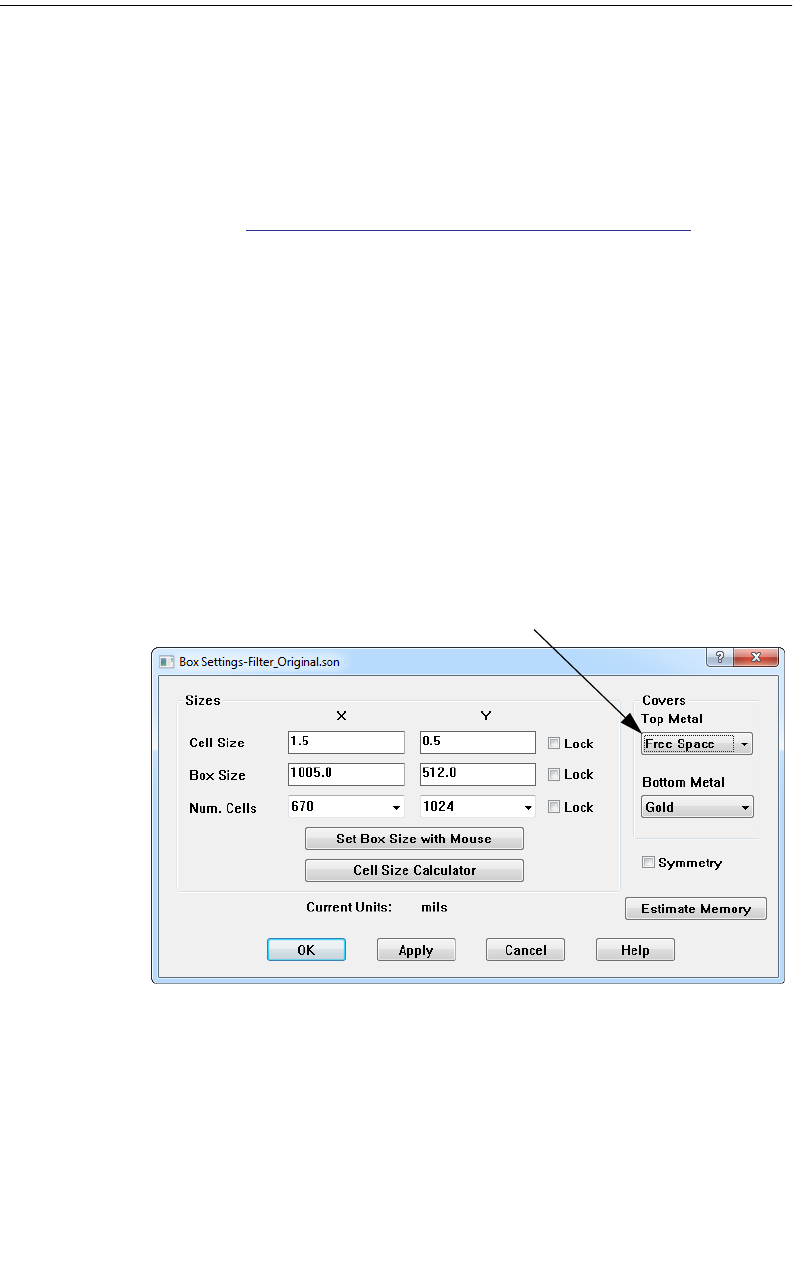
Chapter 21 Box Resonances
397
Rev 16.56
Change box size
One way to remove a box resonance is to change the size of the box - making it
either larger or smaller - to move the resonant frequency out of band. If the prob-
lem occurs in de-embedding, you may be able to change the length of the calibra-
tion standard in the project editor to move the box resonance out of the band of
interest. See "Modifying Calibration Standard Lengths" on page 118 for more in-
formation. The Box Resonance Estimator, discussed earlier, can be used to help
you find the proper dimensions which will move the resonances out of band.
Use a free space cover
Another simple way to remove, or at least attenuate, a box resonance is to remove
the top or bottom cover. We can create an approximation of this condition by set-
ting one of the covers to “Free Space” (a resistivity of 377 ohms/square). To do
this using Sonnet’s project editor, open the Box Settings dialog box (Circuit
Box) and change the top or bottom cover to “Free Space” by selecting “Free
Space” from the Top Metal or Bottom Metal drop list. If you are using an interface
to Sonnet, please refer to the manual for your interface for information on chang-
ing the top or bottom box metal.
This is an accurate approximation provided the cover is not so close that it inter-
acts with the evanescent fringing fields surrounding the circuit. Typically, the
cover should be separated from your circuit by a layer of air that is about a half-
wavelength thick. An example of this is shown in the example project,
Top Metal set to “Free Space”
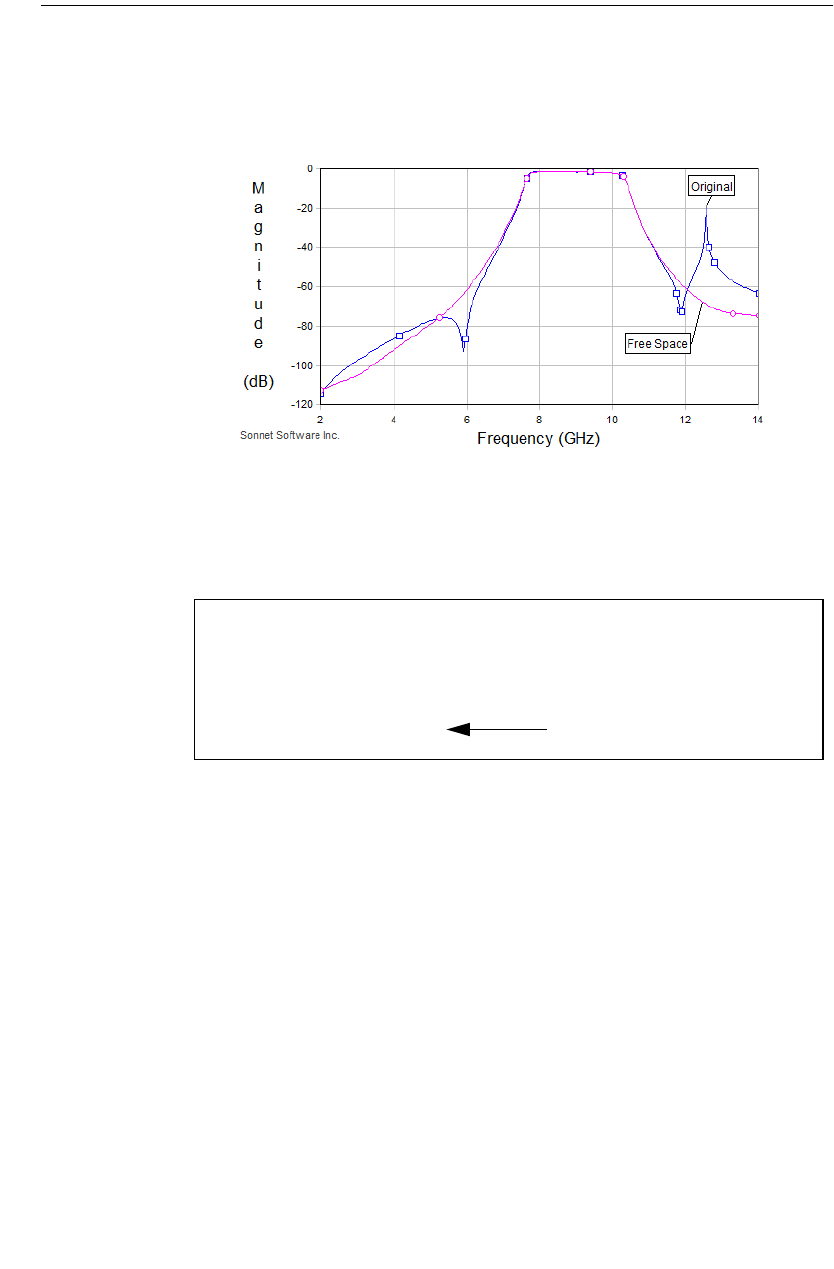
Sonnet User’s Guide
398
Rev 16.56
“Filter_FreeSpace.son.” Shown below is a plot of the original filter (blue) and the
filter with a free space top cover (magenta). Notice the resonance is no longer
present in the circuit with the free space top cover.
As discussed earlier, the Box Resonance Estimator calculates resonances based on
lossless covers. Therefore, when your circuit has a free space cover, the Box Res-
onance Estimator gives a warning message that the reported resonances may be
partially or entirely suppressed:
However, notice that below the warning message, the resonances based on loss-
less covers are still shown. These frequencies should typically be ignored, but are
listed so you know where the resonances would have been if the top cover was not
set to free space. Thus, you should not use the Estimator to determine if the cover
suppressed your box resonances. Instead, you should simulate your circuit, or use
the technique described in "Using a Probe Circuit for a Quick Analysis" on page
403.
***************************************************************
The circuit has a free space cover.
The resonant modes may be partially or entirely suppressed.
***************************************************************
12.55 GHZ TM Mode 1,1,0 Resonances based on
lossless covers

Chapter 21 Box Resonances
399
Rev 16.56
Suppressing Real Resonances
In the preceding section we mentioned some simple techniques for removing res-
onances that were an artifact of the simulation. But what if you need to put your
circuit in a large box that supports box resonances? In this case, if you do not fix
the problem, you will have unwanted resonances in your real circuit.
RF and microwave designers have developed many techniques for suppressing
unwanted resonances in their package. Sonnet can be an invaluable tool by allow-
ing you to test these techniques and evaluate the impact on box resonances. This
section describes just a few of those techniques and how to implement them in
Sonnet.
Changing the Box Size
As noted earlier, decreasing the box size usually moves the box resonances higher
in frequency and the Box Resonance Estimator may be used to determine if a sim-
ple change in one of the box dimensions will move the resonance out of band.
However, moving the box walls too close to the circuit could change the circuit
response. We recommend first changing the box dimensions, then checking the
new dimensions with the Box Resonance Estimator. Repeat these two steps until
an acceptable box size is found. Then, analyze the circuit with the new dimensions
to determine your new response.
Adding Vias
In many cases, ground vias or ground planes will help prevent box resonance
modes from forming. In simple terms, they have the effect of dividing the struc-
ture into smaller compartments, thus pushing the box resonances higher in fre-
quency. The use of a via fence or CPW type transmission line can help
“channelize” the circuit, preventing unwanted coupling between traces and reduc-
ing unwanted box resonance effects. All of these features can be included in the
Sonnet model.

Sonnet User’s Guide
400
Rev 16.56
Shown below is our example filter with vias connected from the top to the bottom
of the box (see example project “Filter_Vias.son”). The plot on the right shows the
response of the original filter (blue curve) and the new response with the vias (ma-
genta curve). Notice that the vias have eliminated the box resonance.
It should also be noted that the Box Resonance Estimator will still predict the box
resonance even though the circuit no longer has a resonance. This is because the
Estimator ignores the vias in the circuit. To determine the effect of the vias on box
resonances, you will need to simulate your circuit, or use the technique described
in the "Using a Probe Circuit for a Quick Analysis" on page 403.
Adding Absorbing Material
Another approach used by engineers to eliminate box resonances is to add an ab-
sorbing material in the housing cavity. The material is normally iron or carbon
loaded so it can provide a fairly high magnetic or electric loss tangent. It comes in
various forms such as liquid or sheet and is usually placed at a position such that
it has a minimal effect on the circuit performance and a large effect on the box res-
onance. If the material is placed across the entire XY plane, you can easily model
its effects in Sonnet by adding a dielectric layer to the stackup. For example, the

Chapter 21 Box Resonances
401
Rev 16.56
example file “Filter_Absorber.son” has an absorbing material attached under the
top lid of the box. To do this in Sonnet, simply add an extra dielectric layer which
has the properties of the absorbing material.
You will need to obtain the properties of the material from the supplier. If the val-
ues for the permittivity, dielectric Loss Tangent, permeability, or magnetic loss
tangent are a function of frequency, then you will either need to analyze over a
Absorption dielectric
layer

Sonnet User’s Guide
402
Rev 16.56
narrow band where the values do not vary much, or use a frequency-dependent
equation. The example project “Filter_Absorber.son” contains a frequency-de-
pendent equation for Mrel.
To learn more about using equations to represent dielectric properties, see the
“Equation Syntax” topic in Help (enter “Syntax” in the index tab).
Shown below is our example filter with the absorber material at the top of the box.
The plot shows the response of the original filter (blue curve) and the new re-
sponse with the absorber (magenta curve). Notice that the absorber has eliminated
the box resonance.
Frequency-Dependent Equation:
5.2-3.21E-11*(FREQ)

Chapter 21 Box Resonances
403
Rev 16.56
It should also be noted that the Box Resonance Estimator will still predict the box
resonance. This is because the Estimator ignores losses in the dielectrics. To de-
termine the effect of the absorber on box resonances, you will need to simulate
your circuit, or use the technique described in the "Using a Probe Circuit for a
Quick Analysis" section below.
Using a Probe Circuit for a Quick Analysis
The following section describes how to run a quick analysis of your box without
having to analyze the real circuit. This can be useful if you wish to quickly try out
different techniques for suppressing resonances (either real or artificial). To create
a project which does not require a lot of processing time, start with your original
circuit, keeping the box size and dielectric properties unchanged, but delete all of
the metal. Then set the cell size to be about 1/20 wavelength at your highest fre-
quency.
Once you have deleted your original circuit, you add two small “probes” to excite
and detect box resonances. The probes are just small (one or two cells long) short-
ed lines with a port on one end and a via on the other. The objective is to have
metal which has current in the X, Y, and Z directions, so it will excite and detect
all possible modes. Add a bend so you are creating both X and Y currents, and use
a via to create the Z-directed current. During a resonant situation, the coupling will
increase between the two probes.
Sweep the frequency in fine steps and look for resonances. We recommend using
a linear sweep because an ABS sweep could potentially miss a narrow band reso-
nance. You should run the analysis without de-embedding since de-embedding as-
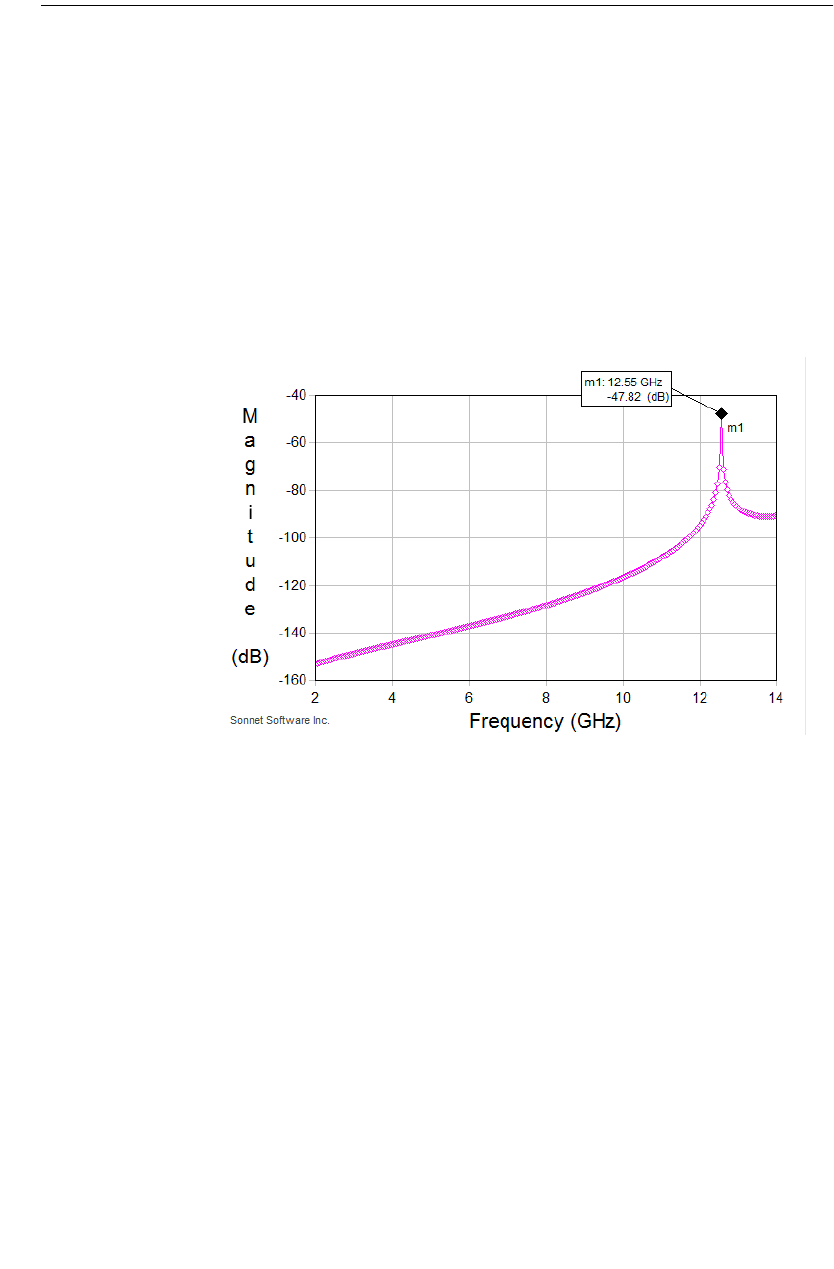
Sonnet User’s Guide
404
Rev 16.56
sumes there are no box resonances which can cause erroneous results. When the
box resonates, there should be stronger coupling between your two probes. This
can easily be seen by plotting the magnitude of S21.
Since there is no longer any circuit metal, except for the two small probes, any res-
onances in the results must be box resonances. Now that you have a simple circuit
which shows the box resonances, you can try different techniques, such as those
mentioned above, to see if any given technique will suppress the box resonance(s).
Shown below are the results of using the above technique on our filter example
(see example project “Probe_Original.son”). Notice the strong coupling at about
12.55 GHz, the frequency that was predicted to have box resonances:
There are two advantages of this approach:
•Since the circuit is so simple, you know that any resonance you see is a
box resonance.
•The analysis is fast, so you can quickly try many different variations.
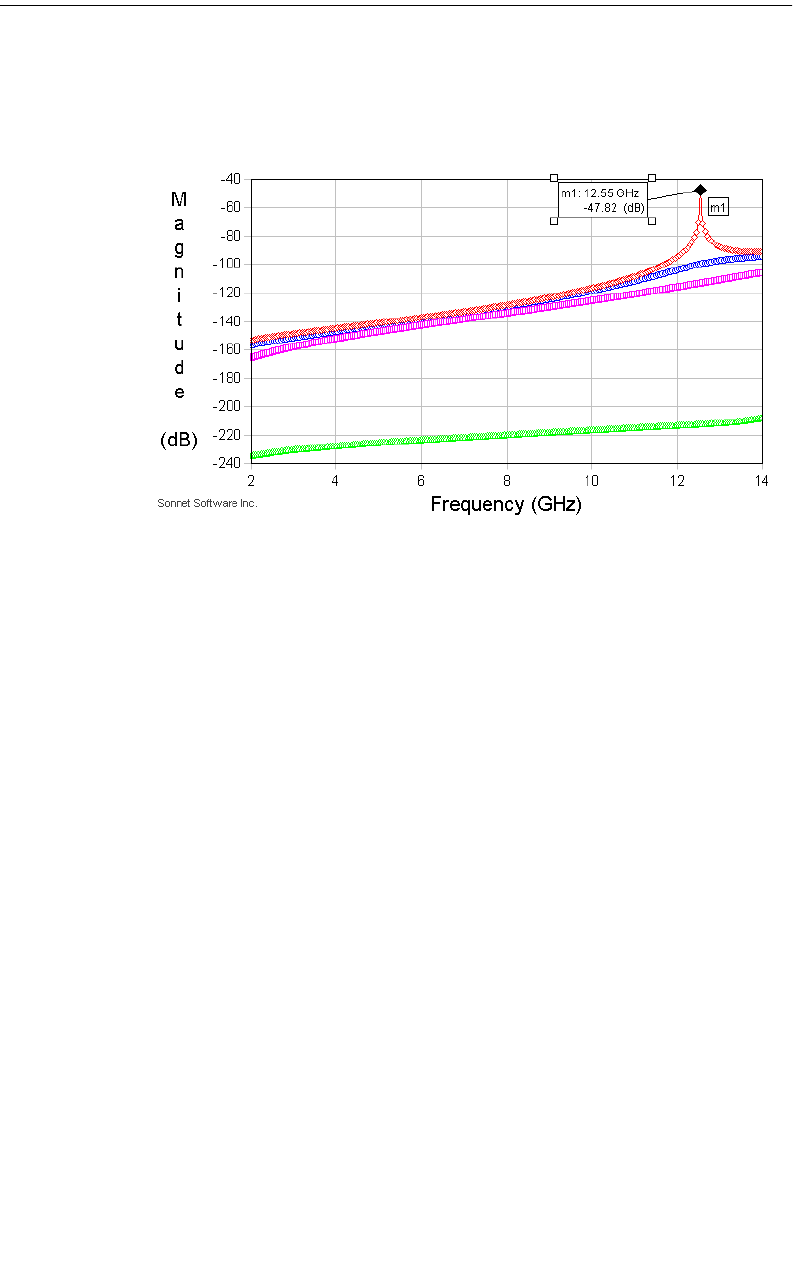
Chapter 21 Box Resonances
405
Rev 16.56
Shown below are the results of probe versions of all of the techniques discussed
above. The original probe circuit is also included for comparison purposes. Notice
that all of the techniques suppressed the box resonance.
The above technique assumes that you are investigating a resonance in the primary
structure. If you want to investigate a resonance in a calibration standard, you will
need to change the box length to be the same length as the calibration standard
length. The calibration standard length is reported in the log files and can be ac-
cessed by selecting Project View Log Timing Info.
Viewing Electric Fields
Viewing the fields in the box at the resonant frequency can often give you an in-
tuitive understanding of the resonance, helping you to find an appropriate method
to suppress the box resonance. Sonnet allows you to view the tangential electric

Sonnet User’s Guide
406
Rev 16.56
fields at any XY plane in your box. Below is a picture of the electric fields in an
XY plane which is 100 mils from the top of the box. This plot was generated by
adding a sense layer to the probe project (see “Probe_Sense.son”).
The frequency was chosen to be 12.55 GHz, which is the frequency where the Box
Resonance Estimator predicted a TM110 mode box resonance. For further infor-
mation on using a sense layer to view the tangential electric fields in your circuit,
see “View Tangential Electric Fields” under Tips and App notes in Help.
Summary
Indications that you may have a box resonance include:
•Seeing spikes in your response.
•Seeing gain in your response.
•An ABS sweep requires a large number of discrete frequencies.
•Any combination of the above items.
The techniques discussed in this chapter can be used to first determine if you have
a box resonance, and then to remove the box resonance from either your simula-
tion or your real measurement, or both.

Chapter 22 Accuracy Benchmarking
407
Rev 16.56
Chapter 22 Accuracy
Benchmarking
Electromagnetic analyses are often described as providing what is called “Good
Agreement Between Measured And Calculated” (GABMAC). However, in the
past, there has been little effort to decide just what “good” means. The more useful
result is the “Difference Between Measured And Calculated” (DMAC).
There is an example of a coupled stripline benchmark available in Help under Ap-
plications.
An Exact Benchmark
What we need to calculate DMAC is an exact benchmark. One source of an exact
benchmark is stripline. The characteristic impedance of a stripline has an exact
theoretical expression K(k) and is the complete elliptical integral of the first kind.

Sonnet User’s Guide
408
Rev 16.56
For evaluation on a computer, a polynomial for K(k) is available in Abramowitz
and Stegun, Handbook of Mathematical Functions, pp. 590 - 592. (Be sure to
note the errata, m1 = 1-m2, not 1-m.):
The expression for K(k) cited above provides an accuracy of about 1 x 10-8. When
programmed on a computer, the following values are obtained for three different
transmission line impedances (unity dielectric constant):
For a length of stripline, there are two parameters of interest: characteristic imped-
ance and propagation velocity. With the w/b given above, we know the exact an-
swer (to within 1 x 10-8) for Z0. With a dielectric constant of 1.0, we also know
the exact answer for the propagation velocity. It is the speed of light, known to
about 1 x 10-9. Any difference from these values is error, or, DMAC.
Table 1 Stripline Benchmark Dimensions
Z0 (ohms) w/b
25.0 3.3260319
50.0 1.4423896
100.0 0.50396767
b
w
Z0r
0
4
------Kk'
Kk
-------------=
k
2
---w
b
----
tanh= k'1k2
–=
0376.7303136=

Chapter 22 Accuracy Benchmarking
409
Rev 16.56
Each of the above three benchmarks is available in the Sonnet example
stripline_benchmarks. The example may be obtained using the Sonnet Example
browser.You may access the Sonnet Example browser by selecting Help
Browse Examples from the menu of any Sonnet application. For instructions on
using the Example Browser, please click on the Help button in the Example
Browser window. Save the file to your working directory.
The “b” dimension is exactly 1.0 mm, the “w” dimension is given by the above
table and the length of each line is 4.99654097 mm with a dielectric constant of
1.0. Each of these lines is precisely 0.25 wavelengths long at 15.0 GHz. The ge-
ometry projects have the subsectioning set so the lines are 16 cells wide and 128
cells long.
To evaluate DMAC, do an analysis of the line at 15 GHz, with de-embedding en-
abled. For the error in characteristic impedance, take the percent difference be-
tween the calculated value and the exact value, above. For the error in propagation
velocity, take the percent difference between the calculated S21 phase and -90 de-
grees. Total error, in percent, is the sum of the two errors.
Some types of analyses do not calculate characteristic impedance. A detailed error
analysis shows that, to first order for a 1/4 wavelength long 50 ohm line, the value
of |S11| is equal to the error in characteristic impedance. For example, an |S11| =
0.02 means that there is about 2% error in characteristic impedance. To use this
approximation for, say, a 25 ohm line, the S-parameters must be converted to 25
ohm S-parameters. This may be done by adding transformers in a circuit theory
program.
Residual Error Evaluation
We have performed a detailed analysis of the relationship between subsectioning
and residual error (DMAC). The simplest way to subsection a line is to use sub-
sections the same width as the line. In Sonnet, and in many other analyses, this re-
sults in a uniform current distribution across the width of the line. In reality, the
current distribution is singular at the edges of the line.
Since the current distribution is symmetrical about the center line, using either one
or two subsections across the width of the line gives the same amount of error.
We find that a one or two subsection wide line gives 5% to 6% error. If there is
not much stray coupling, circuit theory can often give a better result. When the line
is 16 cells wide, we see about 1% error, much more reasonable. We have found
(and you can verify) that convergence is very strong: Double the number of cells
per line width and the error is cut in half.

Sonnet User’s Guide
410
Rev 16.56
When we vary the number of cells per wavelength, along the length of the line, we
see an inverse square relationship. Double the number of cells per wavelength
along the length of the line and the percent error decreases by a factor of four.
An equation which expresses the error as a function of subsectioning is:
where
NW = Number of cells per line width,
NL = Number of cells per wavelength along line
length,
ET = Total Error (DMAC) (%).
This equation estimates subsectioning error only. For example, any de-embedding
errors are added to the above error. This error estimate should be valid for any
electromagnetic analysis which uses roof-top subsectioning.
Notice that the quantities used for the error estimate are in terms of cells, not sub-
sections. Cells are the smallest possible subsections size. In Sonnet, subsections
in the corners of polygons are one cell on a side. Subsections along the edge of
polygons are one cell wide and can be many cells long. Interior subsections can
be many cells in both dimensions.
We have found that, for most cases, the cell size is the important parameter in de-
termining error. Or in other words, the smallest subsection size is important. For
example, the stripline benchmark geometry projects, mentioned before, are set to
make the lines 16 cells wide, even though those 16 cells may be merged into only
4 or 5 subsections. It is the 16 cells which determine the level of error, not the 4
or 5 subsections.
In performing this error evaluation, we also found that the error in characteristic
impedance due to NW is always high, never low. Also, there is very little variation
in the error for different impedance lines. The above equation can be very accurate
in evaluating error. And, finally, for NL above about 40 cells per wavelength, all
the error is in the characteristic impedance. The error in velocity of propagation is
essentially zero.
The above equation can be very accurate in evaluating error. With this precise
knowledge of the error, we can now do something about it.
ET16
NW
--------- 2 16
NL
--------
2
+NW3NL16

Chapter 22 Accuracy Benchmarking
411
Rev 16.56
Using the Error Estimates
The above error estimate can be used to estimate the error for an overall circuit.
Let’s say that a cell size is used that makes some high impedance transmission
lines only 1 cell wide. Other, low impedance transmission lines, are, say, 30 cells
wide. The 1 cell wide lines give us about 5% error. The 30 cell wide lines give
about 0.5% error. In non-resonant situations, you can expect the total error to be
somewhere between 5% and 0.5%. If most of the circuit is the low impedance line,
the error is closer to 0.5%, etc.
However, let’s say that our circuit has resonant structures. Let’s say it is a low pass
filter. It is easy to verify by means of circuit theory that the low pass filter is very
sensitive to the high impedance lines. This means we can expect about 5% error,
even though the high impedance lines only make up half the filter.
Given this information, there are several courses of action. First, if 5% error is ac-
ceptable, no further effort is needed.
More likely, we wish to analyze the filter with less error. Since we now know the
error in the characteristic impedance is 5%, we can physically widen the line so
that the characteristic impedance is 5% lower to compensate for the known in-
crease in characteristic impedance due to subsectioning the line only one cell
wide. Very precise analyses are possible using this compensation technique.

Sonnet User’s Guide
412
Rev 16.56

Appendix I Em and xgeom Command Line for Batch
413
Appendix I Em and xgeom
Command Line for
Batch
em Command Line
If you wish to set up batch or script files to run your analyses overnight or at times
of the day when the processing load is lighter, it is possible to use command lines
to run em from a batch file. You should also be aware that it is possible to setup
batch files with start and stop times using the analysis monitor. For directions on
how to do so, please see How do I create a batch file to run multiple analysis
jobs? in online help.
You should be aware that running from the command line does not provide all of
the status information that is provided in the analysis monitor while running an
analysis.
The syntax of the command line is as follows:
em -[options] <project name> [external frequency file]
where:
Sonnet User’s Guide
414
<options> is one or more of the run options shown in the table below. If you use
multiple options they should be typed with no spaces in between after the minus
sign. Note that other run options may be set in the Analysis Setup dialog box for
your project and will be used during the analysis.
Option Meaning
-Dlicense Used for debugging em licensing problems. Displays all environment
information relevant to licensing.
-N Display number of subsections and estimated required memory. Em
then exits without running a full analysis.
-test Run em on a test circuit. Used to verify that em can get a license and
run successfully.
-v Display analysis information as the analysis is performed. The
analysis information is output to the command prompt window or
terminal from which the batch was executed.
-Lossless Perform simulation as if the entire circuit is completely lossless. All
metal polygons and vias, all dielectric layers, all dielectric bricks, and
the Sonnet top and bottom box covers are simulated as if they are
lossless.
-AbsCacheNone Disable ABS caching (overrides setting in project file).
-AbsCacheStopRestart Enable ABS stop-restart caching (overrides setting in project file).
-AbsCacheMultiSweep Enable ABS multi-sweep plus stop-restart caching (overrides project
file).
-AbsNoDiscrete Used when running ABS with pre-existing cache data. Tells the
analysis engine not to do any more discrete frequencies. If pre-
existing cache data is sufficient to get converged ABS solution, then
that solution is written to output. Otherwise, no processing is
performed.

Appendix I Em and xgeom Command Line for Batch
415
<project name> is the name of the project which you wish to analyze. If there is
no extension, then the extension “.son” is assumed. This field is required.
[external frequency file] is the name of an optional external frequency control
file whose extension is “.eff”. This extension must be included when specifying
the control file. You may create an external frequency control file in the project
editor. For details see Frequency Sweep Combinations in online help in the project
editor. The frequencies in this file override the frequencies in the project.
For example, if you wish to analyze the project steps.son in a batch file using the
-v option, the command line would be:
em -v steps.son
An example of a batch file which runs multiple analyses is shown below.
To execute a batch file on the PC, you should create a text file containing the
command lines with a “.bat” extension. Then open a DOS prompt window and
type the filename at the prompt and press return.
To execute a batch file on Linux, create a text file containing the command lines.
The filename does not need any extension. Then change the permissions mode of
the file to allow you to execute it. For example:
-SubFreqHz[value] where [value] is the subsectioning frequency in Hz. Note there is no
space before the value field.
This option allows subsectioning frequency to be specified on the
command line, thereby overriding the settings in the project file.
-ParamFile <filename> where <filename> is the name of a file which contains the value(s)
which you wish to use for parameter(s) in the circuit being analyzed.
These values override the value contained in the geometry project for
the analysis, but do not change the contents of the geometry project.
The syntax for the parameter file is <parname>=fnum where
<parname> is the name of the parameter and fnum is a floating point
number which defines the value of the parameter for the analysis.
Option Meaning
em -v steps.son
em -v filter.son filter.eff
em -v airbridge.son filter.eff
em -v airbridge.son

Sonnet User’s Guide
416
chmod a+x <filename>
where <filename> is the name of the batch file you wish to execute. Then, type the
name of the file at the Linux prompt and press return.
On Linux systems there are several additions to the command line which are
useful to know. Placing “nice” before the command runs it at lower priority.
Placing “&” at the end of the command runs it in background, so you get your
cursor back. Entering “nohup” before the command line allows you to log off
while the em job(s) keep running. If you are using the “&” or the “nohup”, you
might want to consider redirecting the output using “> outfile.” See your system
administrator for details on any of these options.
Causal Dielectrics
If you wish to export data from a Sonnet analysis to be used in a time domain tool,
you may wish to use causal dielectrics. Using a causal dielectric will vary the
properties of the dielectric layer - the relative dielectric constant, the dielectric loss
tangent, and the dielectric conductivity- slightly over a frequency band. The
variations are modeled using Debye functions based on a reference frequency1.
The reference frequency is the frequency at which the values entered for the
properties are known to be accurate based on obtained measurements or given by
the manufacturer. The options to use causal dielectrics are provided below.
1For a detailed technical discussion of Causal Dielectrics and the use of
Debye functions in modeling them, please see the following article:
Morgan, Chad, “Solutions for Causal Modeling and A Technique for
Measuring Causal, Broadband Dielectric Properties,” DesignCon
2008, February 4 - 7, 2008.
Option Meaning
-CausalDielectrics<freq> where <freq> is the reference frequency in Hz at which you know the
values for the dielectric properties are accurate. For example if your
reference frequency is 3.0e9 Hz than the option you enter would be -
CausalDielectrics3.0e9.
-CausalDielectrics Use this option if you do not know the reference frequency. In this
case, the analysis engine uses the average of the minimum and maxi-
mum analysis frequencies to obtain a reference frequency.

Appendix I Em and xgeom Command Line for Batch
417
xgeom Command Line
You may also run the project editor, xgeom, from a command line in order to
perform an export of a project file in DXF, GDSII or Gerber format.
The syntax of the command line is as follows:
xgeom <project> -Export <type> -RWOut <file> -ExpRegistry -ExpOptions <exfile>
<project> The name of the project which you wish to export. If there is no extension, then
the extension “.son” is assumed. This field is required.
<type> This identifies the format of the output file. Choices are DXF, GDS or GERBER
This field is required.
<file> For DXF and GDSII, this is the filename to which you wish to write your output
For Gerber, this is the folder to which you wish to write your output files. This
field is required. Use “.” as the folder name, if you wish to use the present folder.
-ExpRegistry This option instructs xgeom to use the export options from the registry. This field
is optional. If neither -Exp option is included then the default export options are
used. If both -Exp options are included in the command, the export options are
read first from the registry and then from the specified < exfile>. Any options set
in the file will override those in the registry. Any options in the registry overrides
the default setting. The export options in the registry are what was used the last
time you performed an export from the project editor.
-ExpOptions
<exfile> This option instructs xgeom to use the export options from the specified file
< exfile>. This field is optional. If neither -Exp option is included then the default
export options are used. This option is not applicable for a GDSII export. Any
options set in this file override any default options or options set in the registry.
Options which can be entered in the Export Options file < exfile> are in the
following table. The < boolean> field can use any of the following entries: yes, no,
true, false, on, off. Each option should be entered on a separate line. Not all
options need to be specified.
-New This option opens a new geometry project in xgeom.
-NewNET This option opens a net netlist project in xgeom.
-3D This option opens a 3D view of the project in xgeom.

Sonnet User’s Guide
418
Each entry corresponds to a control in the DXF or Gerber Export Options dialog
box. Each entry provides syntax and the control to which it corresponds. Please
refer to Help in the project editor for details about the control. You may access
Help by opening the appropriate Export Options dialog box and clicking on the
Help button in the dialog box.
Entry Definition
SepObj= <boolean> Separate By Object Types checkbox (DXF & Gerber)
SepMat= <boolean> Separate By Material Types checkbox (DXF & Gerber)
DivideMulti= <boolean> Divide Multi-layer Vias checkbox (DXF & Gerber)
Circles= <boolean> Convert Vias to Circles checkbox (DXF & Gerber)
CircleType= <type> <type> is inscribed or manual. Inscribed corresponds to the Auto
radio button. Manual corresponds to the Manual radio button.
This option may only be used when the Circles option is used.
CircleSize= <float> <float> is a floating string number. Manual text entry box. This
option is only used if CircleType is set to “manual.”
KeepMetals= <boolean> Metal Polygons checkbox (DXF & Gerber)
KeepVias= <boolean> Via Polygons checkbox (DXF & Gerber)
KeepBricks= <boolean> Brick Polygons checkbox (DXF & Gerber)
KeepEdgeVias= <boolean> Edge Vias convert to one cell wide vias checkbox (DXF &
Gerber)
KeepParent= <boolean> Output as Metal checkbox. This is only applicable if the
KeepEdgeVias option is on.
ConvertParent= <boolean> Convert to Vias checkbox. This is only applicable if the
KeepEdgeVias option is on.
GbrUnits=<unit> <unit> is either inch or mm (Gerber Only)
GbrWholeDigits=<num> <num> is an integer number from 2 to 6. Whole digits drop list
GbrDecimalDigits=<num> <num> is an integer number from 2 to 6. Decimal digits drop list
GbrFilenameType=<type> <type> is default, custom or project. Default corresponds to the
default radio button. Custom corresponds to the Custom Prefix
radio button. Project corresponds to the Project name radio
button. (Gerber Only)
Appendix I Em and xgeom Command Line for Batch
419
Example of xgeom Command Line
An example command line is shown below.
xgeom test.son -Export DXF -RWOut outfile.dxf -ExpRegistry -ExpOptions expopt.txt
The above command creates a DXF output file named outfile.dxf from the Sonnet
project test.son using the export options provided in the Export Options file
expopt.txt. this feature creates a DXF file called outfile.dxf. The programs closes
once the export is complete.
An example of an Export Options file is shown below:
SepObj=yes
SepMat=no
DivideMulti=no
Circles=yes
CircleType=inscribed
CircleSize=5.8
KeepMetals=yes
KeepVias=true
KeepBricks=no
KeepEdgeVias=off
KeepParent=TRUE
ConvertParent=OFF
GbrFilenamePrefix=<string> <string> is a character string of alphanumeric characters.
Custom Prefix text entry box. This is only applicable if the
GbrFilenameType option is set to custom. (Gerber Only)
GbrFilenameExt=<string> <string> is a character string of alphanumeric characters. ext.
text entry box. (Gerber Only)
GbrJobFilenameType=<type> <type> is custom or project. Custom corresponds to the Custom
Prefix radio button in the Netex-G Job Filename section of the
dialog box. Project corresponds to the Project Name radio
button. (Gerber Only)
GbrJobPrefix=<string> <string> is a character string of alphanumeric characters.
Custom Prefix text entry box. This is only applicable if the
GbrJobFilenameType option is set to custom. (Gerber Only)
Entry Definition

Sonnet User’s Guide
420
Appendix II Sonnet References
421
Appendix II Sonnet References
This appendix contains articles written by Sonnet authors or articles which
directly impacted the analysis theory used by Sonnet. An extensive list of articles
in which Sonnet was used as the analysis tool is available on Sonnet’s web site at
www.sonnetsoftware.com. Search for “References.”
[1] Allen F. Horn, John W. Reynolds, Patricia A. LaFrance, James C. Rautio, "Effect
of conductor profile on the insertion loss, phase constant, and dispersion in thin
high frequency transmission lines," DesignCon Best Paper Award, February
2010.
[2] James C. Rautio, "In Search of Maxwell," Microwave Journal, Vol. 49, No. 7,
July 2006, pp. 76-88.
[3] Heng-Tung Hsu, James C. Rautio, and San-Wen Chang, "Novel Planar
Wideband Omni-directional Quasi Log-Periodic Antenna," Asia-Pacific
Microwave Conference 2005, Suzhou, China, December 4-7, 2005.
[4] James C. Rautio and Vladimir I. Okhmatovski, "Unification of Double-Delay
and SOC Electromagnetic Deembedding," IEEE Transactions on Microwave
Theory and Techniques, Vol. 53, No. 9, September 2005, pp 2892 - 2898.
[5] James C. Rautio, "Applied numerical electromagnetic analysis for planar high-
frequency circuits," Encyclopedia of RF and Microwave Design, Wiley, New
York, Vol. 1, 2005, pp. 397-413.
[6] James C. Rautio, "Deembedding the Effect of a Local Ground Plane in
Electromagnetic Analysis," IEEE Transactions on Microwave Theory and
Techniques, Vol. 53, No. 2, February 2005, pp. 770 - 776.

Sonnet User’s Guide
422
[7] James C. Rautio, "Comments on "On Deembedding of Port Discontinuities in
Full-Wave CAD Models of Multiport Circuits"," IEEE Transactions on
Microwave Theory and Techniques - Letters, Vol. 52, No. 10, October 2004, pp.
2448 - 2449.
[8] James C. Rautio, "A Space-Mapped Model of Thick, Tightly Coupled
Conductors for Planar Electromagnetic Analysis," IEEE Microwave Magazine,
Vol. 5, No. 3, September 2004, pp. 62 - 72.James C. Rautio, “Accurate and
Efficient Analysis of Large Spiral Inductors with Thick Metal and Narrow Gaps
Using Space Mapping,” IEEE MTT-S International Microwave Symposium,
Workshop Notes & Short Courses - WFD-7, 6-11 June 2004.
[9] James C. Rautio, “In Defense of Uselessness,” IEEE Microwave Magazine, Vol.
5, No. 1, March 2004, pp. 100 - 102.
[10] James C. Rautio, “A Conformal Mesh for Efficient Planar Electromagnetic
Analysis,” IEEE Transactions on Microwave Theory and Techniques, Vol. 52,
No. 1, January 2004, pp. 257 - 264.
[11] David I. Sanderson, James C. Rautio, Robert A. Groves, and Sanjay Raman,
“Accurate Modeling of Monolithic Inductors Using Conformal Meshing for
Reduced Computation,” Microwave Magazine, Vol. 4, No. 4 December 2003, pp.
87 - 96.
[12] James C. Rautio, “Testing Limits of Algorithms Associated with High Frequency
Planar Electromagnetic Analysis,” European Microwave Conference Digest,
Munich, October 2003, pp. 463 - 466.
[13] Rautio, James C., “Generating Spectrally Rich Data Sets Using Adaptive Band
Synthesis Interpolation,” Workshop WFA, IEEE MTT Symposium Digest,
Philadelphia, June 8 - 13, 2003.
[14] James C. Rautio, “Conformal Subsections for Accurate EM Analysis,”
Microwave Journal, Vol. 46, No. 6, June 2003, pp. 116 - 120.
[15] James C. Rautio and Veysel Demir, “Microstrip Conductor Loss Models for
Electromagnetic Analysis,” IEEE Transactions on Microwave Theory and
Techniques, Vol. 51, No. 3, March 2003, pp. 915 - 921.
[16] James C. Rautio, “Electromagnetic Analysis Speeds RFID Design,” Microwaves
& RF, Vol. 42, No. 2, February 2003, pp. 55 - 62.
[17] James C. Rautio, “EM Approach Sets New Speed Records,” Microwaves & RF,
Vol. 41, No. 5, May 2002, pp. 81 - 96.
[18] James C. Rautio, Shawn Carpenter, et. al., “CAD/EDA virtual panel discussion,”
Microwave Engineering, May 2002, pp. 15 - 25.
[19] Shawn Carpenter, “Analysis and Optimization of a Compact CPW Filter Using
Planar EM Software,” MIcrowave Product Digest, October 2001, pp. 10-14, 28,
50.

Appendix II Sonnet References
423
[20] James C. Rautio, “Making Practical High Frequency Electromagnetic
Simulators-- Past, Present, and Future,” IEICE Transactions on Electronics, Vol.
E84-c, No. 7, July 2001, pp. 855-860.
[21] J. C. Rautio, “An Investigation of Microstrip Conductor Loss,” IEEE Microwave
Magazine, Volume 1, Number 4, December 2000, pp. 60-67.
[22] Shawn Carpenter, “Break and Interpolate Technique: A Strategy for Fast EM
Simulation of Planar Filters,” Microwave Project Digest, October 2000, pp. 18 -
27, 56 - 58.
[23] James C. Rautio, “The Impact on Education of Widely Available Commercial 3-
D Planar Electromagnetic Software,” Computer Applications in Engineering
Education, Vol. 8, No. 2, September 2000, pp. 51 - 60.
[24] G. L. Matthaei, J. C. Rautio, and B. A. Willemsen, “Concerning the influence of
housing dimensions on the response and design of microstrip filters with parallel-
line couplings,” IEEE MTT Transactions, Vol. 48, August 2000, pp. 1361 –1368.
[25] James C. Rautio, “Tips and Tricks for Using Sonnet Lite - Free EM software will
radically change the way you do high frequency design,” Microwave Product
Digest, November 1999, pp. 30 - 34, 67 - 70.
[26] James C. Rautio, “An Investigation of Microstrip Conductor Loss,” IEEE MTT
Magazine, December 2000, pp. 60-67. This article is available in the Support
Section of the Sonnet website, www.sonnetsoftware.com.
[27] Shawn Carpenter, “Break and Interpolate Technique: A Strategy for Fast EM
Simulation of Planar Filters,” Microwave Project Digest, October 2000, pp. 18 -
27, 56 - 58.
[28] James C. Rautio, “The Impact on Education of Widely Available Commercial 3-
D Planar Electromagnetic Software,” Computer Applications in Engineering
Education, Vol. 8, No. 2, September 2000, pp. 51 - 60.
[29] James C. Rautio, “Free EM Software Analyzes Spiral Inductor on Silicon,”
Microwaves & RF, September 1999, pp. 165 - 172.
[30] Takashi MIURA, Hideki NAKANO, Kohji KOSHIJI and Eimei SHU,
“Reduction of time required for electromagnetic analysis by dividing circuit,”
Faculty of Science and Technology, Science University of Tokyo, Japan Institute
of Electronics Packaging, pp.79-80, Mar. 1999. (Article in Japanese)
[31] James C. Rautio, “Tips and Tricks for Using Sonnet Lite - Free EM software will
radically change the way you do high frequency design,” Microwave Product
Digest, November 1999, pp. 30 - 34, 67 - 70.
[32] James C. Rautio, “EM Simulation,” 1999 IEEE MTT-S International Microwave
Symposium, Microwave and Millimeter-Wave Design Tool Applications
Workshop, Anaheim, CA, June 13, 1999.

Sonnet User’s Guide
424
[33] James C. Rautio, “Application of Electromagnetic Analysis Software to 3-D
Planar High Frequency Design”, International Multilayer Circuits Symposium
(IMCS), March 1999, pp. B2-1 - B2-17.
[34] Shigeki Nakamura, “Top Interview: Electromagnetic Analysis is not Difficult -
Big Rush to Install PC Version,” Electronic Products Digest, Vol. 16, No. 1,
January 1999, page 48. (Japanese Article)
[35] James C. Rautio, “Comments on ‘Revisiting Characteristic Impedance and Its
Definition of Microstrip Line with a Self-Calibrated 3-D MoM Scheme,’” IEEE
Transactions on Microwave Theory and Techniques, Vol. 47, No. 1, January
1999, pp. 115 - 117.
[36] James C. Rautio and George Matthaei, “Tracking Error Sources in HTS Filter
Simulations,” Microwaves and RF, Vol. 37, No. 13, December 1998, pp. 119 -
130.
[37] J.C. Rautio, “-Electromagnetic Analysis for Microwave Applications,”
Computational Electromagnetics and Its Applications, Vol. 5, Boston: Kluwer
Academic Publishers, 1997, pp. 80-96.
[38] Yasumasa Noguchi, Shin-ichi Nakao, Hideaki Fujimoto and Nobuo Okamoto,
“Characteristics of Shielded Coplanar Waveguides on Multilayer Substrates,”
Electronic Information and Communications Univerisity Meeting, Electronics
Society Conference, June 29, 1998. (Japanese Article)
[39] Erik H. Lenzing and James C. Rautio, “A Model for Discretization Error in
Electromagnetic Analysis of Capacitors,” IEEE Transactions on Microwave
Theory and Techniques, Vol. 46, No. 2, February 1998, pp. 162-166.
[40] J. C. Rautio, “Retracing Key Moments In the Life of Maxwell,” Microwaves &
RF,” Vol. 36, No. 11, November 1997, pp. 35-51.
[41] J. C. Rautio, “Electromagnetic Analysis for Microwave Applications,” NASA
CEM (Computational Electromagnetics) Workshop, Newport News, VA, May
1996.
[42] J. C. Rautio, “Seven Years Later,” Applied Microwave and Wireless, November/
December 1996, pp. 99-100.
[43] J. C. Rautio, “Questionable Reviews,” The Institute (IEEE newspaper), Jan.
1996, pg. 11.
[44] J. C. Rautio, “An Investigation of an Error Cancellation Mechanism with Respect
to Subsectional Electromagnetic Analysis Validation,” International Journal of
Microwave and Millimeter-Wave Computer-Aided Engineering, Vol. 6, No. 6,
November 1996, pp. 430-435.
[45] J. C. Rautio, “The Microwave Point of View on Software Validation,” IEEE
Antennas and Propagation Magazine, Vol. 38, No. 2, April 1996, pp. 68-71.

Appendix II Sonnet References
425
[46] J. C. Rautio and Hiroaki Kogure, “EMI Applications Of The Electromagnetic
Analysis By The Method Of Moments-Electromagnetic Analysis Applied To
Analog And Digital PCB Design,” JPCA Show 96 Text: Today and Tomorrow of
EMI Design, pp. 11-19.
[47] J. C. Rautio, “EM-Analysis Error Impacts Microwave Designs,” Microwaves and
RF, September 1996, pp. 134-144.
[48] James R. Willhite, “Turning Clean Theory into Reality,” Wireless Design and
Development, March 1996, Vol. 4, No. 3, pp. 19-20.
[49] J. C. Rautio, “Response #2. Comments on Zeland's Standard Stripline
Benchmark Results - MIC Simulation Column,” International Journal of
Microwave and Millimeter- Wave Computer-Aided Engineering, Vol. 5, No. 6,
November 1995, pp. 415-417.
[50] J. C. Rautio, “EMI Analysis from a Wireless Telecommunication and RF
Perspective,” Proceedings of the 1995 Nepcon West Conference, Anaheim, CA,
USA, pp. 749-755.
[51] J. C. Rautio and Hiroaki Kogure, “An Overview of the Sonnet Electromagnetic
Analysis,” Proceedings of the 1994 IEICE Fall Conference, Tokyo, pp. 325-326.
[52] J. C. Rautio, “An Ultra-High Precision Benchmark For Validation Of Planar
Electromagnetic Analyses,” IEEE Tran. Microwave Theory Tech., Vol. 42, No.
11, Nov. 1994, pp. 2046-2050.
[53] J. C. Rautio, “A Precise Benchmark for Numerical Validation,” IEEE
International Microwave Symposium, Workshop WSMK Digest, Atlanta, June
1993.
[54] “Comparison of Strategies for Analysis of Diagonal Structures,” Sonnet
Application Note 51-02.
[55] J. C. Rautio, “MIC Simulation Column - A Standard Stripline Benchmark,”
International Journal of Microwave & Millimeter-Wave Computer-Aided
Engineering, Vol. 4, No. 2, April 1994, pp. 209-212.
[56] J. C. Rautio, “Response #3. Standard Stripline Benchmark - MIC Simulation
Column,” International Journal of Microwave and Millimeter-Wave Computer-
Aided Engineering, Vol. 5, No. 5, September 1995, pp. 365-367.
[57] J. C. Rautio, “Some Comments on Approximating Radiation,” International
Journal of Microwave and Millimeter-Wave Computer-Aided Engineering, Vol.
4, No. 2, 1994, pp. 454-457.
[58] J. C. Rautio, “Synthesis of Lumped Models from N-Port Scattering Parameter
Data,” IEEE Tran. Microwave Theory Tech., Vol. 42, No. 3, March 1994, pp.
535-537.
[59] J. C. Rautio, “Educational Use of a Microwave Electromagnetic Analysis of 3-D
Planar Structures,” Computer Applications in Engineering Education, Vol. 1, No.
3, 1993, pp. 243-254.

Sonnet User’s Guide
426
[60] J. C. Rautio, “Characterization of Electromagnetic Software,” 42nd ARFTG
Conference Digest, San Jose, CA, Dec. 1993, pp. 81-86.
[61] J. C. Rautio, “Some Comments on Electromagnetic De-Embedding and
Microstrip Characteristic Impedance” International Journal of Microwave &
Millimeter-Wave Computer-Aided Engineering, Vol. 3, No. 2, April 1993, pp.
151-153.
[62] J. C. Rautio, “Some Comments on Electromagnetic Dimensionality,” IEEE
MTT-S Newsletter, Winter 1992, pg. 23.
[63] J. C. Rautio, “Sonnet Software Reveals Tangential Fields,” EEsof Wavelengths,
Vol. 9, No. 1, March 1993, pg. 12.
[64] J. C. Rautio, “Sonnet Introduces Antenna Pattern Visualization in New Release,”
EEsof Wavelengths, Vol. 9, No. 2, June 1993, pg. 21.
[65] J. C. Rautio, “EEsof Joins Forces With Sonnet Software,” EEsof Wavelengths,
Vol. 8, No. 3, Sept. 1992, pg. 14.
[66] J. C. Rautio, “Electromagnetic Design of Passive Structures - Emerging
Technology in Microwave CAD,” IEEE MTT-S Newsletter, Fall 1990, pp. 21-22.
[67] J. C. Rautio, “Electromagnetic Microwave Design,” RF/Microwave Applications
Conference, Santa Clara, CA, March 1992, pp. 105-109.
[68] J. C. Rautio, “Experimental Validation of Microwave Software,” IEEE
International Microwave Symposium, Panel Session PSB Digest, Albuquerque,
June 1992.
[69] J. C. Rautio, “Current Developments in 3-D Planar Microwave
Electromagnetics,” Microwave Hybrid Circuits Conference, Oct. 1991, Arizona.
[70] J. C. Rautio, “Current Developments in 3-D Planar Microwave
Electromagnetics,” Microwave Hybrid Circuits Conference, Oct. 1992, Arizona.
[71] J. C. Rautio, “Current Developments in 3-D Planar Microwave
Electromagnetics,” Microwave Hybrid Circuits Conference, Oct. 1993, Arizona.
[72] J. C. Rautio, “Current Developments in 3-D Planar Microwave
Electromagnetics,” Microwave Hybrid Circuits Conference, Oct. 1994, Arizona.
[73] J. C. Rautio, “Experimental Validation of Electromagnetic Software,”
International Journal of Microwave & Millimeter-Wave Computer-Aided
Engineering, Vol. 1, No. 4, Oct. 1991, pp. 379-385.
[74] J. C. Rautio, “Electromagnetic Microwave Analysis,” IEEE International
Microwave Symposium, Workshop WSA Digest, Albuquerque, June 1992.
[75] J. C. Rautio, “EM Visualization Assists Designers,” Microwaves and RF, Nov.
1991, pp. 102-106.
[76] J. C. Rautio, “Reviewing Available EM Simulation Tools,” Microwaves & RF,
June 1991, pp. 16A-20A.

Appendix II Sonnet References
427
[77] “Generating Spice Files Using the em Electromagnetic Analysis,” Sonnet
Application Note 104a, Dec. 1998.
[78] J. C. Rautio, “A New Definition of Characteristic Impedance,” MTT
International Symposium Digest, June 1991, Boston, pp. 761-764.
[79] J. C. Rautio, “A De-Embedding Algorithm for Electromagnetics,” International
Journal of Microwave & Millimeter-Wave Computer-Aided Engineering, Vol.1,
No. 3, July 1991, pp. 282-287.
[80] J. C. Rautio, “Triangle Cells in an Electromagnetic Analysis of Arbitrary
Microstrip Circuits,” MTT International Microwave Symposium Digest, Dallas,
June 1990, pp. 701-704.
[81] J. C. Rautio, “Experimental Validation of Microwave Software,” 35th ARFTG
Conference Digest, Dallas, May 1990, pp. 58-68. (Voted best paper at the
conference.)
[82] J. C. Rautio, “Preliminary Results of a Time-Harmonic Electromagnetic Analysis
of Shielded Microstrip Circuits,” 27th ARFTG Conference Digest, Dallas, Dec.
1986. (Voted best paper at the conference.)
[83] J. C. Rautio, “An Experimental Investigation of the Microstrip Step
Discontinuity,” IEEE Tran. Microwave Theory Tech., Vol. MTT-37, Nov. 1989,
pp. 1816-1818.
[84] J. C. Rautio, “A Possible Source of Error in On-Wafer Calibration,” 34th ARFTG
Conference, Ft. Lauderdale, FL, Dec. 1989, pp. 118-126.
[85] J. C. Rautio, “Microstrip Program Improves Accuracy of Circuit Models,”
Microwaves & RF, Vol. 27, No. 12, pp. 89-96, Nov. 1988.
[86] J. C. Rautio, “Reflection Coefficient Analysis of the Effect of Ground on
Antenna Patterns,” IEEE Antennas and Propagation Society Newsletter, Feb. 87,
pp. 5-11.
[87] J. C. Rautio and R. F. Harrington, “An Electromagnetic Time-Harmonic Analysis
of Shielded Microstrip Circuits,” IEEE Trans. Microwave Theory Tech., Vol.
MTT-35, pp. 726-730, Aug. 1987.
[88] J. C. Rautio and R. F. Harrington, “An Efficient Electromagnetic Analysis of
Arbitrary Microstrip Circuits,” MTT International Microwave Symposium
Digest, Las Vegas, June 1987, pp. 295-298.
[89] J. C. Rautio and R. F. Harrington, “Results and Experimental Verification of an
Electromagnetic Analysis of Microstrip Circuits,” Trans. of The Society for
Computer Simulation, Vol. 4, No. 2, pp. 125-156, Apr. 1987.
[90] J. C. Rautio, “A Time-Harmonic Electromagnetic Analysis of Shielded
Microstrip Circuits,” Ph. D. Dissertation, Syracuse University, Syracuse, NY,
1986.

Sonnet User’s Guide
428
[91] J. C. Rautio, “Preliminary Results of a Time-Harmonic Electromagnetic Analysis
of Shielded Microstrip Circuits,” ARFTG Conference Digest, Baltimore, pp.
121-134, June 1986. (Voted best paper at the conference.)
[92] J. C. Rautio, “Techniques for Correcting Scattering Parameter Data of an
Imperfectly Terminated Multiport When Measured with a Two-Port Network
Analyzer,” IEEE Trans. Microwave Theory Tech., Vol. MTT-31, May 1983, pp.
407-412.
[93] R. Horton, B. Easter, A. Gopinath, "Variation of Microstrip Losses with
Thickness of Strip", Electronics Letters, 26th August 1971, Vol. 7, No.17,
pp.490-481.
[94] R. F. Harrington, Time-Harmonic Electromagnetic Fields, New York:
McGraw-Hill, 1961, section 8-11, pg. 8.

Index
429
A
ABS caching level 159
subsectioning 159
ABS see adaptive band synthesis
absolute power 339
adaptive band synthesis 155–167
ABS caching level 159
analysis issues 165–167
current density data 166
de-embedding 165
multiple box resonances 165
optional files 166
ripple in S-Parameters 166
transmission line parameters 166
find maximum 162
find minimum 162
parameter sweep 163
resolution 156
running an adaptive sweep 157
viewing the response 167
adaptive sweep 157
addports
auto-grounded 101
standard 88
via ports 99
Add Subdivider 273
adjacent polygons 232, 233
adjustable point set 180, 181, 183
ADS interface 17
analysis
limitations 335
starting 210
analysis frequencies 207
analysis monitor 210
Analysis Setup dialog box 159, 207, 214
analyze 210
anchored dimension parameters 178, 179
adding 198
anchor point 179, 185
reference point 179, 185
Angle Axis 337
anisotropic dielectric bricks 318, 323
antennas 327–334
microstrip 333
pattern 342
surface wave 335
wire 335
array loss model 63
array model
horizontal loss 63, 65
att 244, 254
att_cascade.son 245
attenuator 250
auto height vias 299
auto-grounded ports 99, 100
autogrouping
viewing 89
autoscale 357
axes 357
axisZ 336
Axis Properties dialog box 357
B
balanced ports 76
bandpass filter 197
bar via
horizontal loss 62
Index

Sonnet User’s Guide
430
bar vias
simplifying in analysis engine 292
batch file 413
benchmark 407–411
residual error 409
best iteration 221
boundaries 235
box resonance 165
box-wall ports 87
bricks see dielectric bricks
broadband spice 371
checking accuracy of model 376
class of problems 372
creating a model 373
improving accuracy of model 378
stability factor 379
C
Cadence Virtuoso Interface 17
CAE software 22
calculate 335, 344
calculating the response 344
Calculation Setup dialog box 344
calculations
defaults 343
status of 346
Calculator
Cell Size 30
calibration group properties 89
ground node connection 90
terminal width 92
calibration lengths
for co-calibrated internal ports 97
for Components 148
capacitor 141
capacitors 240, 319
cartesian plot 327, 334, 337, 344, 358
cascading data files 239, 245
causal dielectrics 416
cell size 320
determining error 410
processing time 235
selecting 29–31
subsectioning 28, 38
wavelength 29
Cell Size Calculator 30
center tapped topology 382
circuit analyses 239, 241
circuit properties 267
circuit subdivision 255–269
additional improvements 281
analysis 269
coarse frequency sweep 268
comparison of results 281
executing 269, 277
feedlines 278
illegal conditions for subdivision lines
266
main netlist 258
placement of subdivision lines 260–264
procedure 258
reference planes 278
subdivision line orientation 265
subproject naming conventions 278
tutorial 271–283
using parameters 259
Circuit Subdivision dialog box 277
circular dependencies 177, 188
CKT 248
coarse frequency sweep 268
coaxial structures 335
co-calibrated internal ports 89–97
adding 93
calibration group properties 89
calibration lengths 97
de-embedding coupling 89
GLG metal 91
ground node connection 90
placement rules 94
reference planes 97
terminal width 92
use in Components 138, 139, 141
viewing autogrouping 89
combined circuit analyses 241
combining data files 239
command line 413
components 137
analysis 152
anatomy of 139
calibration lengths 148

Index
431
Component Assistant 138
component symbol 139
Data File type 140
defining physical size 149
definition 139
ground node connection 143
Ideal component 141
label 139
physical size 140
ports 139
Ports Only type 141
properties of 143
reference planes 96, 148, 151
restricted space 94, 150
restrictions 149
settings 143
terminal number 139
terminal width 145
types of 140
use rules 149
conductivity 51
conformal mesh 227–237
adjacent polygons 232
adjacent polygons with interior vertex
233
applying 229
cell size 235
current density viewer 236
current striping 236
figure-eight polygons 232
Manhattan polygons 233
polygon boundaries 235
processing time 235
rules of use 231
single precision 233
transmission lines 229
using effectively 233
conjugate gradient optimizer 192
convergence test
dielectric bricks 318
coordinate system
spherical 336
coplanar 76, 335
corner sweep 189
coupling 256, 261
current density data 166
current density file 335
current density viewer 16, 41
current striping 236
D
data blocks
CKT 248
Data File 140
data files 239
cascading 245
DC point 156
de-embedding 103–136, 335
box-wall ports 105, 107
components 89, 137
coupled transmission lines 109
enabling 105
port discontinuities 105
reference planes 106, 109
de-embedding codes 126
nl 129
dependent variable 176
design suite 15
diagonal fill 320
diagonal ports 80
dialog box
Parameter Properties 200
dialog boxes
Analysis Setup 159, 207, 214
Axis Properties 357
Calculation Setup 344
Circuit Subdivision 277
Dielectric Layers 66
Metal Editor 306
Metal Properties 230
Optimization Goal Entry 217
Optimization Parameters 215
Optimization Results 224
Parameter Sweep Entry 207
Port Impedance 75, 79
Select Frequencies 346

Sonnet User’s Guide
432
Select Normalization 352
Select Phi’s 347, 360
Subdivider Orientation 273
Subproject Specifications 278
dielectric 335
causal 416
multiple constants 335
dielectric bricks 317–326
air 320
anisotropic 323
applications 319
convergence test 318
far field viewer 320
limitations 320
materials 322, 324
subsectioning 319
vias 319
visibility 322
Z-partitions 325
dielectric layers
creating new 69
loss 47, 66
loss parameters 66
Dielectric Layers dialog box 66
dielectric library 69
dimension parameter
adjusting point set 183
anchored 178, 179
radial 178, 185
symmetric 178, 180
dipole
infinitesimal 341, 342, 358
directions 334
directive gain 339
dual_patch 332
DUT 103
DXF Translator 17
dxfgeo 17
E
E total 348
ebridge 17
edge mesh option 32
editing a circuit 16
Eeff 129, 166
electrically thick conductors 53
em batch file 413
command line 413
description 20
theory 21–22
emgraph 16
emstatus 16
emvu 16
E-plane 336
equivalent circuit 91
error function 192
error, residual 409
E-Total 361
example files
att 254
att_cascade.son 245
dual_patch 332
infpole 358
par_dstub 197
steps 240
sub_whole 281
Tripat 333
via example 302
examples
att 244
excitations 334
default values 343

Index
433
exit 362
exiting 362
extrapolation of a DC Point 156
F
far field 327, 334, 358
Far Field Viewer
exiting 362
saving a file 361
tool bar 359
tutorial 341
far field viewer 334–340
dielectric bricks 320
normalization 339
polarization 340
spherical coordinate system 336
feedlines 278
ferrite components 335
figure eight polygons 232
file exit 362
save 361
filter 197
Find Maximum 162
find maximum 162
Find Minimum 162
find minimum 162
FINDMAX 162
FINDMIN 162
first frequency 335
first reference point 181
floating ground 144
frequencies 338
default value 335
selecting to calculate 345
selecting to plot 346, 359
frequency
maximum 30
frequency interpolation 256
frequency plot 358
frequency specification 207
frequency sweep
coarse 268
full view button 350
G
GABMAC 407
gaindirective 339
power 339
relative to 339
max 352
gds 17
GDSII translator 16, 17
general metal type 54
Generalized Local Ground 91
geometry project 246
geometry subprojects 257
Gerber Translator 17
GLG metal 91
global ground 144
goal 194
goals 217
granularity 194
graph
axes 357
calculate 335, 344
normalization 339, 352
select
frequencies 346
phi 347, 348, 360
theta 359, 360
typecartesian 358
polar 355
surface 361
ground node connection 90, 143
floating 91, 144
polygon edge(s) 145
Sonnet box 90, 144

Sonnet User’s Guide
434
ground plane 341, 358
ground reference 144
ground terminals 145
H
highest frequency 30
horizontal loss
array model for via 63, 65
bar via 62
volume model for via 62
horizontal orientation 265
H-plane 336
I
ideal component 141
ideal element 137
impedance 74, 75, 78, 79
surface 56
importing
measurement data 137
independent reference planes 80
independent variable 177
inductor 141
inductor model extractor 380–388
center tapped topology 382
creating the model 383, 385
model topology 380
untapped topology 381
inductors 240
infinite array 328
infinitesimal dipole 341, 342, 358
infpole 358
interdigital 197
interface basics 23
interpolation 256
isotropic 339
iteration 221
iterations 194
selecting for display 221
K
Keysight ADS Interface 17
kinetic inductance 54
L
lateral dimensions 335
legend
selecting frequencies 346
selecting phi’s 348, 360
turning off 355
view 356, 358
libraries
metal 65
library
dielectric 69
metal 65
limitations 335
linear sweep 189
local ground de-embedding 89, 137
loss 22, 47–69
creating metal types 50, 59
dielectric layer 66
dielectric layer library 69
dielectric layer parameters 66
general metal type 54
low frequency 52, 62
metal libraries 65
microstrip 50, 52
normal metal type 51
planar metal types 48
problems in determining 49
properties of commonly used metals
54
Rdc/Rrf metal type 52
related to frequency 52, 63
resistor metal type 52
sense metal type 58
Sonnet model 48
thick metal type 52
vias 298
loss calculations
surface loss model 62
volume loss model 61

Index
435
lumped elements 249
capacitors 240
inductors 240
inserting 240
inserting in a geometry 249
resistors 240
transmission lines 240
M
magnetic permeability 53, 63, 67
main netlist 258
default name 277
Max 352
maximum frequency 30
maximum response 162
maximum subsection size 41
measurement data
importing 137
meshing fill
vias 290
metal
plated 311
stacked 311
Metal Editor dialog box 306
metal libraries 65
metal library 65
metal loss
normal loss model 51
Sonnet model 48
Metal Properties dialog box 230
metal type
creating 50, 59
general 54
instructions for creating. 58, 69
libraries 65
normal 51
properties of commonly used metals
54
Rdc/Rrf 52
resistor 52
sense 58
thick metal 52, 303
metalization
commonly used metals 54
loss 22, 47
metallization loss 48, 58
microstrip 197, 335
patch antennas 333
microstrip loss 50, 52
Microwave Office Interface 17
minima 195
minimum response 162
mixed sweep combinations 189
modeled elements 240
inserting 249
inserting in a geometry 249
modeling assumptions 335
modify
attributes
ports 74, 101
moving adjustable point set 183
mtline element 363
multi-sweep plus Stop/Restart caching
159
N
netlist
creating 244
invoking an analysis of a subproject
246
netlist editor 239
netlist project 239
analysis 241
network file
analysis 280
networks 240
newlink pimodel 369
NI AWR interface 17
nl de-embedding code 129
nominal value 177, 178
changing 214
nominal values
update with results 224
non-Manhattan polygons 233
normal loss model 51
normal metal type 51
normalization 339, 351
changing 339

Sonnet User’s Guide
436
default 339, 344
directive gain 339
power gain 339
number of iterations 194
O
open environment 335
opening a graph 210
optimization 171–195
best iteration 221
conjugate gradient method 192
data 220
data range for parameters 216
example 197, 213
executing 219
methodology 192
number of iterations 194
process 193
results 195, 223
selecting parameters for 216
setting up 214
specifying goals 194, 217
tutorial 197, 213
Optimization Goal Entry dialog box 217
Optimization Parameters dialog box 215
optimization results
update 224
Optimization Results dialog box 224
optimized values 223
optional files 166
orientation of subdivision lines 265
origin 336
output files
lumped.rsp 252
P
package resonances 389–??
par_dstub 197
Parameter Properties dialog box 200
parameter sweep 163, 189, 197
analysis frequencies 207
data 220
setting up 207
viewing the response 210
Parameter Sweep Entry dialog box 207
parameterization 171–195
tutorial 197
parameters
adding 198, 203
adjustable point set 179, 180, 181,
185
adjusting point set 183
anchor point 179, 185
anchored 178, 179
circular dependencies 177, 188
data range for optimization 216
example 197
first reference point 203
in a subproject 259
nominal value 177, 178, 214
ports 75, 78, 79
radial 178, 185
reference planes 187
reference point 179, 185
second reference point 204
select dependents 188
selecting for optimization 216
symmetric 178, 180
patch antenna 327
patch antennas 335
pattern 334, 342
pattern response 350
patvu 17
permeability 53, 63, 67
phased arrays 327
phi 336, 337
default values 343
selecting values to plot 347, 348, 360
specifying range for calculation 337,
345
physical size of Component 140
pin number 139
planar metal types
general loss model 54
loss 48
normal loss model 51
Rdc/Rrf loss model 52
resistor loss model 52
sense loss model 58

Index
437
thick metal loss model 52
plated metal 311
plotcartesian 327, 334, 337, 344, 358
frequency 358
polar 327, 334, 337, 355
probing 350
selecting type 355
surface 327, 334, 337, 361
title area 355
types 337
Plot Over drop list 359
polar 337, 355
polar plot 327, 334
polarization 340
default 344
polygon edges 261
Port Impedance dialog box 75, 79
ports 71–102
auto-grounded 99, 100, 101
balanced 76
box-wall 87, 105, 107
co-calibrated internal 89
component 139
diagonal 80
discontinuities 105
excitations 334, 343
impedance 74, 75, 78, 79
modify attributes 101
numbering 78, 88
push-pull 76
renumbering 75
standard 88
terminations 334, 343
ungrounded-internal 99, 250, 252
using with symmetry 79
via 99
via ports 99, 299
Ports Only Component 141
power gain 339
probe readout 351
probing the plot 350
processing time 235
Product Editor origin 336
Project Editor 342
project editor 16
netlist editor 239
project file
circuit geometry 342
properties
circuit 267
push-pull ports 76
R
radial dimension parameters 178, 185
radiation 327, 327–334
radius axis
changing 356
Rdc/Rrf metal type 52
reactive surface impedance 49
reference planes 106, 109
de-embedding without 110
for co-calibrated internal ports 97
for components 148
independent 80
parameters 187
short length 110
reference point 179, 185, 203, 204
first in symmetrical 181
second in symmetrical 181
references 340, 358, 362
reflection boundary 341
residual error 409
resistance 66
resistance per via 61
resistivity 51
resistor 141
resistor metal type 52
resistors 240
thin film 48, 245
response
maximum 162

Sonnet User’s Guide
438
minimum 162
response data
calculating 344
selecting 346
response viewer
invoking 210
results of optimization
accepting 223
right-click 188
right-clicking 346, 355, 360
ripple in S-parameters 166
Rrf 52, 53, 63
rules for co-calibrated ports 94
run options
edge mesh 32
S
saving a file 361
scroll bar 347
second reference point 181
sections 257
select
phi 348, 360
theta 359, 360
select dependents 188
Select Frequencies dialog box 346
Select Normalization dialog box 352
Select Phi’s dialog box 347, 360
selecting the response 346
sense metal type 58
sensitivity sweep 189
series RL equivalent circuit 91
sheet resistance at DC 51
shunt elements 91, 144
simplifying vias
bar vias 292
single precision
using with conformal mesh 233
skin effect coefficient 52, 53, 63
SMD 137
Sonnet
suite 15
space bar 349
S-parameter data
importing 137
S-Parameters
ripple in 166
Spectre 17
spherical coordinate system 336
stability factor 379
stacked metal 311
steps 240
steradian 339
Stop/Restart caching 159
stripline benchmark 407
sub_whole 281
Subdivide Circuit command 277
Subdivider Orientation dialog box 273
subdividing 269
subdivision 255–269
procedure 258
subdivision lines 257
adding 272
coupling across 256
illegal conditions 266
orientation 265, 273
placement 256, 260–267
placement examples 261
Subproject Specifications dialog box 278
subprojects 257
naming conventions 278
subs/lambda 41
subsectioning 20
ABS caching level 159
cell size 28, 38
frequency 160
vias 290
subsections 27, 41
of polygon 35
XMIN 39
YMIN 37
superconductor 54
surface impedance 56
surface impedance 56
surface loss model 62
loss calculations 62
surface plot 327, 334, 337, 361
selecting 361

Index
439
surface resistance 66
surface wave antennas 335
sweep
corner 189
linear 189
mixed combinations 189
sensitivity 189
symbol
component 139
symmetric dimension parameter 178, 180
adding 203
first reference point 181
second reference point 181
symmetry 266
port placement 79
T
T attenuator 247, 249
with ungrounded-internal ports 253
terminal number 139
terminal width 92
feedline width 92, 146
one cell 93, 146
user defined 93, 146
terminations 334
default values 343
theory 21–22
theta 336, 337
default values 343
selecting values to plot 359, 360
specifying range for calculation 337
thick metal 76, 303–316
arbitrary cross-section 314
creating a polygon 305
number of sheets 303
viewing in the current density viewer
315
viewing in the project editor 308
thick metal type 52, 303
thin film resistor 48, 245
two connected 245
tool bar 359
full view button 350
zoom in button 349
Tools
Add Subdivider 273
Subdivide Circuit 277
top cover
resistive 407
top hemisphere 336
translator 16
GDSII 17
Gerber 17
transmission line parameters 166
transmission lines 240
structures 249
triangular subsections 335
Tripat 333
tutorial 341
optimization 197
parameter sweep 197
two-port T attenuator 247
typecartesian 358
polar 355
surface 361
U
ungrounded-internal ports 250, 252
untapped topology 381
update nominal values 224
user interface 23
V
validation 341
variables 172
circular dependencies 177
dependent 176
independent 177
vertical components 335
vertical orientation 265
setting 273
via loss 58
array loss model 63
resistance per via 61
surface loss model 62
volume loss model 59

Sonnet User’s Guide
440
via metal types 58
array loss model 63
surface loss model 62
volume loss model 59
via ports 99, 299
vias 302
auto height 299
example 302
inside dielectric bricks 319
loss 298
meshing fill 290
subsections 289
symbol 288
to ground 296
view
legend 356, 358
zoom in 349
viewing the response 210
volume loss model 59
loss calculations 61
volume model
horizontal loss 62
W
warnings 253
waveguide simulator 328
wavelength 29
wire antennas 335
X
xgeom 16
XMAX 40
XMIN 37, 39
Y
YMAX 40
YMIN 37, 39
Z
Z0 129, 130, 166
Z-axis 336
zoom in 349
zoom in button 349
zooming 349
Z-partitioning 318, 319, 325–326