User Guide
User Manual:
Open the PDF directly: View PDF ![]() .
.
Page Count: 203 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Contents
- 1 Introduction
- 2 Installation
- 3 Theoretical background
- 4 Overview of rheoTool
- 4.1 The constitutiveEquations library
- 4.2 The EDFModels library
- 4.3 The BDmolecule library
- 4.4 The sparseMatrixSolvers library
- 4.4.1 Conditions to reuse the preconditioner/factorization
- 4.4.2 Residuals and tolerances
- 4.4.3 Generic parameters
- 4.4.4 OpenFOAM interface
- 4.4.5 Eigen interface
- 4.4.6 Hypre interface
- 4.4.7 Petsc interface
- 4.4.8 Coupled solvers
- 4.4.9 How to use sparseMatrixSolvers library in my own application?
- 4.4.10 Limitations
- 4.5 Solvers
- 4.6 Boundary conditions
- 4.7 Utilities
- 5 Tutorials
- 5.1 rheoFoam
- 5.1.1 General guidelines
- 5.1.2 A note on coded FunctionObjects
- 5.1.3 Case 1: flow between parallel plates
- 5.1.4 Case 2: lid-driven cavity flow
- 5.1.5 Case 3: flow in a 4:1 planar contraction
- 5.1.6 Case 4: flow around a confined cylinder
- 5.1.7 Case 5: bifurcation in a 2D cross-slot flow
- 5.1.8 Case 6: blood flow simulation in a real-model aneurysm
- 5.1.9 Case 7: viscous fluid damper (moving mesh)
- 5.2 rheoTestFoam
- 5.3 rheoInterFoam
- 5.4 rheoEFoam
- 5.4.1 General guidelines
- 5.4.2 Case I: EDF of power-law and PTT fluids in a microchannel
- 5.4.3 Case II: induced-charge electroosmosis around a cylinder
- 5.4.4 Case III: charge transport across an ion-selective membrane
- 5.4.5 Case IV: electrokinetic instabilities in a flow-focusing device
- 5.4.6 Case V: electrokinetic mixer
- 5.4.7 Case VI: electro-elastic instabilities in cross-shaped geometries
- 5.5 rheoBDFoam
- 5.1 rheoFoam
- 6 FAQs
- Appendix A Parameters and variables in rheoTool
- Bibliography

User Guide
Version 4.0
April 26, 2019

License
This document is licensed under
Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License
http://creativecommons.org/licenses/by-nc-nd/3.0/legalcode
Acknowledgments
The work leading to the preparation of this document has received funding from
the European Research Council under the European Union’s Seventh Framework
Programme (FP7/2007-2013)/ERC Grant agreement no307499. The
collaboration with Professor Fernando T. Pinho (University of Porto, Portugal),
Professor Paulo J. Oliveira (University of Beira Interior, Portugal) and Dr
Alexandre Afonso (University of Porto, Portugal) in the development of
numerical methods for computational rheology is also acknowledged.
Disclaimer
This offering is not approved or endorsed by OpenCFD Limited, producer and
distributor of the OpenFOAM software via www.openfoam.com, and owner of the
OPENFOAM R
and OpenCFD R
trade marks.
The recommendations expressed in this document are those of the authors and
are not necessarily the views of, or endorsement by, third parties named in this
document.
RheoTool, where this guide is included, is distributed in the hope that it will be
useful, but WITHOUT ANY WARRANTY. See the GNU General Public
License (http://www.gnu.org/licenses/) for more details.
Trademarks
Linux is a registered trademark of Linus Torvalds.
OpenFOAM is a registered trademark of of OpenCFD Limited.
Paraview is a registered trademark of Kitware.
Typeset in L
A
T
EX.
c
2016-2019 Francisco Pimenta, Manuel A. Alves
Contents
1 Introduction 1
1.1 Motivation................................ 1
1.2 Guideorganization ........................... 2
1.3 Changelog................................ 3
1.4 Citing rheoTool ............................. 7
1.5 Contacts................................. 7
1.6 Contributing............................... 7
2 Installation 8
2.1 Compatibility with OpenFOAM R
and foam-extend versions . . . . 8
2.2 Differences between versions . . . . . . . . . . . . . . . . . . . . . . 8
2.3 System requirements . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.4 Step-by-step instructions . . . . . . . . . . . . . . . . . . . . . . . . 9
2.4.1 Download/clone rheoTool ................... 9
2.4.2 Download Eigen library . . . . . . . . . . . . . . . . . . . . 10
2.4.3 Install Petsc library . . . . . . . . . . . . . . . . . . . . . . . 11
2.4.4 Compile rheoTool ........................ 13
3 Theoretical background 15
3.1 Governing equations of complex fluid flows . . . . . . . . . . . . . . 15
3.2 Stabilization of viscoelastic fluid flow simulations . . . . . . . . . . 16
3.2.1 The both-sides-diffusion (BSD) technique . . . . . . . . . . . 16
3.2.2 The log-conformation tensor approach . . . . . . . . . . . . 17
3.3 Coupling algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . 18
3.3.1 Pressure-velocity coupling . . . . . . . . . . . . . . . . . . . 18
3.3.2 Stress-velocity coupling . . . . . . . . . . . . . . . . . . . . . 19
3.4 High-resolution schemes . . . . . . . . . . . . . . . . . . . . . . . . 20
3.5 Movinggrids .............................. 21
3.6 Segregated vs coupled solvers . . . . . . . . . . . . . . . . . . . . . 22
3.7 Electrically-driven flow models . . . . . . . . . . . . . . . . . . . . . 22
3.7.1 Poisson-Nernst-Planck model . . . . . . . . . . . . . . . . . 23
3.7.2 Splitting the electric potential . . . . . . . . . . . . . . . . . 24
3.7.3 Poisson-Boltzmann model . . . . . . . . . . . . . . . . . . . 24
3.7.4 Debye-H¨uckel model . . . . . . . . . . . . . . . . . . . . . . 25
3.7.5 Slipmodel............................ 25
3.7.6 Ohmic (leaky dielectric) model . . . . . . . . . . . . . . . . 26
ii

CONTENTS iii
3.8 Brownian dynamics simulations . . . . . . . . . . . . . . . . . . . . 27
3.8.1 The bead-spring model . . . . . . . . . . . . . . . . . . . . . 27
3.8.2 Governing equations of beads motion . . . . . . . . . . . . . 30
3.8.3 Spring force models . . . . . . . . . . . . . . . . . . . . . . . 30
3.8.4 Time integration algorithm . . . . . . . . . . . . . . . . . . . 31
4 Overview of rheoTool 33
4.1 The constitutiveEquations library ................... 33
4.1.1 Available GNF and viscoelastic models . . . . . . . . . . . . 33
4.1.2 A note on FENE-type models . . . . . . . . . . . . . . . . . 41
4.1.3 Multi-mode modeling . . . . . . . . . . . . . . . . . . . . . . 43
4.1.4 Analysis of a code sample . . . . . . . . . . . . . . . . . . . 43
4.1.5 Advanced settings . . . . . . . . . . . . . . . . . . . . . . . . 49
4.1.6 Adding new viscoelastic or GNF models . . . . . . . . . . . 49
4.2 The EDFModels library ........................ 50
4.2.1 Available EDF models . . . . . . . . . . . . . . . . . . . . . 50
4.2.2 The potentials splitting approach and multi-species model-
ing in the PNP, PB and DH models . . . . . . . . . . . . . . 52
4.2.3 Electrokinetic coupling loop in the PNP model . . . . . . . . 52
4.2.4 Coupled PNP model . . . . . . . . . . . . . . . . . . . . . . 52
4.2.5 Analysis of a code sample . . . . . . . . . . . . . . . . . . . 53
4.2.6 Adding new EDF models . . . . . . . . . . . . . . . . . . . . 60
4.3 The BDmolecule library ........................ 61
4.3.1 Organization of variables . . . . . . . . . . . . . . . . . . . . 61
4.3.2 Solution sequence . . . . . . . . . . . . . . . . . . . . . . . . 62
4.3.3 External forcing type . . . . . . . . . . . . . . . . . . . . . . 65
4.3.4 External forcing interpolation . . . . . . . . . . . . . . . . . 65
4.3.5 Spring force and time-integration schemes . . . . . . . . . . 68
4.3.6 Tethering and fixing the molecules center of mass . . . . . . 70
4.3.7 Beadstracking ......................... 71
4.3.8 Data output for post-processing . . . . . . . . . . . . . . . . 71
4.3.9 Limitations ........................... 72
4.4 The sparseMatrixSolvers library.................... 73
4.4.1 Conditions to reuse the preconditioner/factorization . . . . . 73
4.4.2 Residuals and tolerances . . . . . . . . . . . . . . . . . . . . 74
4.4.3 Generic parameters . . . . . . . . . . . . . . . . . . . . . . . 74
4.4.4 OpenFOAM interface . . . . . . . . . . . . . . . . . . . . . . 76
4.4.5 Eigeninterface ......................... 76
4.4.6 Hypreinterface ......................... 77
4.4.7 Petscinterface.......................... 80
4.4.8 Coupledsolvers......................... 82
4.4.9 How to use sparseMatrixSolvers library in my own application? 84
4.4.10 Limitations ........................... 85
4.5 Solvers.................................. 86
4.5.1 rheoFoam ............................ 87
4.5.2 rheoTestFoam .......................... 95

CONTENTS iv
4.5.3 rheoInterFoam ......................... 97
4.5.4 rheoEFoam ........................... 98
4.5.5 rheoBDFoam .......................... 99
4.6 Boundary conditions . . . . . . . . . . . . . . . . . . . . . . . . . . 101
4.6.1 linearExtrapolation .......................101
4.6.2 navierSlip ............................101
4.6.3 zeroIonicFlux ..........................102
4.6.4 boltzmannEquilibrium ......................102
4.6.5 inducedPotential ........................103
4.6.6 slipSmoluchowski ........................103
4.6.7 slipSigmaDependent ......................103
4.6.8 A note on wall boundary conditions for pressure . . . . . . . 103
4.7 Utilities .................................105
4.7.1 GaussDefCmpw schemes for convective terms . . . . . . . . 105
4.7.2 Generic post-processing: ppUtil ................107
4.7.3 writeEfield ............................109
4.7.4 initMolecules ..........................110
4.7.5 averageMolcN ..........................114
4.7.6 averageMolcX ..........................114
5 Tutorials 116
5.1 rheoFoam ................................116
5.1.1 General guidelines . . . . . . . . . . . . . . . . . . . . . . . 116
5.1.2 A note on coded FunctionObjects ...............122
5.1.3 Case 1: flow between parallel plates . . . . . . . . . . . . . . 123
5.1.4 Case 2: lid-driven cavity flow . . . . . . . . . . . . . . . . . 125
5.1.5 Case 3: flow in a 4:1 planar contraction . . . . . . . . . . . . 126
5.1.6 Case 4: flow around a confined cylinder . . . . . . . . . . . . 129
5.1.7 Case 5: bifurcation in a 2D cross-slot flow . . . . . . . . . . 132
5.1.8 Case 6: blood flow simulation in a real-model aneurysm . . . 134
5.1.9 Case 7: viscous fluid damper (moving mesh) . . . . . . . . . 138
5.2 rheoTestFoam ..............................140
5.2.1 General guidelines . . . . . . . . . . . . . . . . . . . . . . . 140
5.2.2 Case I: Herschel-Bulkley model . . . . . . . . . . . . . . . . 143
5.2.3 Case II: FENE-CR model . . . . . . . . . . . . . . . . . . . 143
5.3 rheoInterFoam .............................147
5.3.1 General guidelines . . . . . . . . . . . . . . . . . . . . . . . 147
5.3.2 Case 1: impacting drop . . . . . . . . . . . . . . . . . . . . . 148
5.3.3 Case 2: planar die swell . . . . . . . . . . . . . . . . . . . . 150
5.4 rheoEFoam ...............................152
5.4.1 General guidelines . . . . . . . . . . . . . . . . . . . . . . . 152
5.4.2 Case I: EDF of power-law and PTT fluids in a microchannel 155
5.4.3 Case II: induced-charge electroosmosis around a cylinder . . 159
5.4.4 Case III: charge transport across an ion-selective membrane 161
5.4.5 Case IV: electrokinetic instabilities in a flow-focusing device 163
5.4.6 Case V: electrokinetic mixer . . . . . . . . . . . . . . . . . . 167

CONTENTS v
5.4.7 Case VI: electro-elastic instabilities in cross-shaped geometries169
5.5 rheoBDFoam ..............................171
5.5.1 General guidelines . . . . . . . . . . . . . . . . . . . . . . . 171
5.5.2 Molecules visualization with Paraview . . . . . . . . . . . . 176
5.5.3 Case 1: λ-DNA extension in a planar extensional flow . . . . 177
5.5.4 Case 2: 7λ-DNA extension in a flow-focusing device . . . . . 180
5.5.5 Case 3: λ-DNA dynamics in LAOE . . . . . . . . . . . . . . 183
6 FAQs 186
Appendix A Parameters and variables in rheoTool 188
Bibliography 193
Chapter 1
Introduction
1.1 Motivation
The open-source OpenFOAM R
toolbox can be used as a versatile finite-volume
solver for CFD simulations in general polyhedral grids. A number of constitutive
equations for Generalized Newtonian Fluids (GNF) are already available in the
toolbox for a long time. More recently, Favero et al. [1] created a library containing
a wide range of constitutive equations to model viscoelastic fluids, along with a
solver named viscoelasticFluidFoam which makes use of this library. However,
viscoelasticFluidFoam presents stability issues in certain conditions, such as, for
example, in the simulation of high Weissenberg number (Wi) flows or when there
is no solvent viscosity contribution (e.g. in the upper-convected Maxwell model).
In Ref. [2], we attempted to minimize those issues by modifying critical points
in the viscoelasticFluidFoam solver and in the handling of viscoelastic models. The
modified solver was tested in benchmark flows and second-order accuracy, both in
space and time, was observed, in addition to an enhanced stability [2]. The package
that we present in this document – rheoTool – implements the method described
in [2].
Afterwards, the capability to simulate electrically-driven flows was added to
rheoTool [3] and is available since version 2.0.
Recognizing the importance of modeling polymeric flows at different scales, a
Brownian dynamics solver has been implemented in rheoTool [4], which is available
since version 3.0.
In [5] we implemented coupled solvers for electrically-driven flows, which can
be also used for pressure-driven flows. Moreover, rheoTool was interfaced to ex-
ternal libraries (Petsc, Hypre, Eigen) that widen the range of available (direct and
iterative) sparse matrix solvers.
rheoTool is more than a collection of solvers and libraries. In addition to robust
solvers for the simulation of pressure- and electrically-driven flows of both GNF
and viscoelastic fluids, we provide also tutorials and utilities that can be useful for
the users starting to apply the OpenFOAM R
toolbox in the simulation of complex
fluid flows. In particular, some of the distinguishing features of rheoTool are:
•both GNF and viscoelastic models can be selected on run time and applied to
1

CHAPTER 1. Introduction 2
single-phase laminar flows. A solver for two-phase flows is also being devel-
oped and an experimental (but fully functional) version is already available.
•the log-conformation tensor methodology [6] is available for a wide range
of viscoelastic models. This minimizes the numerical instabilities frequently
observed for high Weissenberg number flows.
•a stress-velocity coupling term can be selected on run time in order to avoid
checkerboard fields under specific conditions, such as in the simulation of the
Upper-Convected Maxwell (UCM) model in strong extensional flows.
•high-resolution schemes for convective terms are available in a component-
wise and deferred correction approach, avoiding numerical instabilities (see
Ref. [2] for details). Additional schemes were added to the newly created
library, which are not available by default in the OpenFOAM R
toolbox.
•a solver (rheoTestFoam) is provided to compute the relevant material func-
tions of each GNF/viscoelastic model included in the library. The user can
select any canonical flow to be tested (shear flow, extensional flow, etc.).
•a number of models for electrically-driven flows is available and can be cou-
pled with any rheological model. Mixed pressure- and electrically-driven
flows are also allowed.
•transient flow solvers use the SIMPLEC algorithm for pressure-velocity cou-
pling, instead of the PISO implementation. Large time-steps can be used
without decoupling problems, and the use of under-relaxation is not required
(except for pressure in some problems using non-orthogonal grids).
•a solver is provided for Brownian dynamics simulations of polymer molecules
in generic meshes. Molecules can be linear or circular and they can also have
branches. The external forcing can be steady or transient.
•coupled and segregated solvers are available.
•rheoTool can use sparse matrix solvers from Petsc, Hypre and Eigen.
•the tool is provided with a user-guide (this document) and a selected set of
tutorials reproducing relevant benchmark or real-life flow problems.
•rheoTool is available for both 1OpenFOAM R
and 2foam-extend versions.
1.2 Guide organization
The remainder of this guide is organized as follows:
•Chapter 2describes the basic steps to install rheoTool.
1http://openfoam.org/
2http://www.extend-project.de/

CHAPTER 1. Introduction 3
•Chapter 3provides a succinct overview of the theory behind the governing
equations being solved. More details can be found in Refs. [2–4,7].
•Chapter 4presents an overview of the functionalities available in rheoTool,
and discusses technical details about the code implementation.
•Chapter 5contains several tutorials, guiding the reader into the use of
rheoTool.
The language and the content used in this guide assumes that the reader has a
basic knowledge on the use of the OpenFOAM R
toolbox and is familiar with the
finite-volume method applied to CFD problems. Thus, it is out the scope of this
document to serve as an introduction on those subjects.
Although rheoTool is available for different OpenFOAM R
and foam-extend
versions, for historical reasons Chapters 4and 5are still mainly based on
OpenFOAM R
version 2.2.2 to describe the contents (except the content related
with Brownian dynamics simulations, described for OpenFOAM R
version 5.x).
However, the small differences among different versions should not be an obstacle
to the readers using any other version.
The readers interested in the theory behind rheoTool are strongly encouraged
to first read Refs. [2], [3] and [4] before this guide.
1.3 Changelog
Version 4.0
Released on 04/04/2019.
Generic
•Add: added interfaces to Petsc, Hypre and Eigen libraries, allowing the use
of their (direct and iterative) sparse matrix solvers. All the interfaces can
be used in parallel, except the one for Eigen. Only for the OpenFOAM R
version.
•Add: rheoTool needs Petsc as an extra dependency. Added a script to install
this package. The instructions to install rheoTool have been updated (see
Chapter 2). Only for the OpenFOAM R
version.
•Add: added coupled solvers for both pressure- and electrically-driven flows.
Most viscoelastic models can be solved within a coupled solution method.
Only for the OpenFOAM R
version.
•Change: rheoTool version compatible with OpenFOAM R
v4.0/4.1 is discon-
tinued.
Electrically-driven flows

CHAPTER 1. Introduction 4
•Add: added coupled Poisson-Nernst-Planck model to EDF models (Type-
Name = NernstPlanckCoupled). Only for the OpenFOAM R
version.
Constitutive equations
•Change: the eXtended Pom-Pom model implementation has been changed in
order to allow using its thermodynamically consistent version [8]. Parameter
nhas been added (see Table 4.1) and should be adjusted by the user (n= 1
for thermodynamic consistency and n= 0 otherwise).
•Change: the code for the constitutive equations of viscoelastic models has
been modified to allow integration with coupled solvers. Only for the
OpenFOAM R
version.
Solvers
•Fix: fixed bug in rheoInterFoam for OpenFOAM R
version 6.0, which was
preventing post-processing (missing call to update()).
Tutorials
•Change: tutorial rheoFoam/Cavity now uses sparse matrix solvers from
Eigen library and is 1.6 times faster. Only for the OpenFOAMR
version.
•Change: tutorial rheoFoam/Cylinder is now solved coupled, being 30 times
faster. Only for the OpenFOAMR
version.
•Change: tutorial rheoEFoam/ICEO/NernstPlanck is now solved with the
coupled implementation of the PNP model and is 30 times faster. The name
of the tutorial was changed to rheoEFoam/ICEO/NernstPlanckCoupled.
Only for the OpenFOAM R
version.
•Change: tutorial rheoEFoam/selecMembrane/NernstPlanck/solution1D is
now solved with the coupled implementation of the PNP model and is twice
faster. Moreover, under-relaxation is not needed anymore to avoid numerical
divergence. Only for the OpenFOAMR
version.
•Fix: fixed bug related to the old flag for stabilization methods in several
tutorials, which was aborting the runs.
Version 3.0
Released on 18/09/2018.
Brownian dynamics solver
•Add: solvers, libraries, utilities and tutorials for Brownian dynamics simu-
lations of polymer molecules.
Generic

CHAPTER 1. Introduction 5
•Add: all solvers are now compatible with dynamic meshes. Due to this
change, and for convenience, momentum equation is the first to be solved,
followed by pressure equation and then the equations for the remaining vari-
ables (extra-stresses, passive scalar, etc.).
•Add: tutorial fluidDamper showing the use of rheoFoam with dynamic
meshes.
•Add: added an explicit Navier slip boundary condition for velocity.
•Change: Namespace encapsulation of several derived classes.
•Change: rheoTool version compatible with OpenFOAM R
v2.2.2 is discon-
tinued.
•Add: added rheoTool patch for OpenFOAM R
v6.0.
•Add: added note in the user-guide (Section 2.4.4) about parallel compilation
of rheoTool.
Constitutive equations
•Add: Papanastasiou regularization is now available for yield-stress GNF
models (Hershel-Bulkley/Bingham and Casson models).
•Add: Casson model has been added to the library of constitutive equations.
•Add: the Multi-Lambda Isotropic Kinematic Hardening (MLK-IKH) model
has been added to the library of constitutive equations.
•Add: the Vasquez-Cook-Mckinley (VCM) model has been added to the li-
brary of constitutive equations.
•Add: the Reactive Rod Model (RRM) model has been added to the library
of constitutive equations.
•Add: Saramito’s elastoviscoplastic model has been added to the library of
constitutive equations. Both stress and log-conformation versions are avail-
able.
•Add: the Bautista-Manero-Puig (BMP) model has been added to the library
of constitutive equations. Both stress and log-conformation versions are
available.
•Change: implemented functions tauTotal() and tauTotalMF() in base classes.
Solver rheoTestFoam and the utility retrieving the wall shear-stresses were
modified accordingly.
Version 2.0

CHAPTER 1. Introduction 6
Released on 09/02/2018.
Electrically-driven flows
•Add: solvers, libraries, utilities and tutorials for electrically-driven flows.
Constitutive equations
•Add: the Rolie-Poly viscoelastic model has been added to the library of
constitutive equations. Both the stress and log-conformation versions are
available.
•Add: the (single-equation) eXtended Pom-Pom viscoelastic model has been
added to the library of constitutive equations. Both the stress and log-
conformation versions are available.
•Change: sPTT models have been generalized to their full form by replacing
the upper-convected derivative by the Gordon-Schowalter derivative. It is
now possible to simulate PTT models with non-affine deformation, in both
the stress and log-conformation versions.
•Change: the stabilization method in viscoelastic simulations has been made
general and run time selectable: none,BSD or coupling.
•Change: a verification step has been added to the WhiteMetznerLog model
in order to prevent its incorrect use (see the note in the table displaying the
constitutive equations).
Post-Processing
•Add: class ppUtil for post-processing purposes has been added to the versions
for OpenFOAM R
and the one existing for foam-extend has been modified.
Enable the use of multiple ppUtil in simultaneous.
•Fix: sampling error was fixed for the tutorials of versions of40 and fe40.
Multiphase flows
•Change: (fvc::grad(U)&fvc::grad(etaS()*alpha)) has been replaced by
fvc::div(etaS()*alpha*dev2(T(fvc::grad(U)))) for the use in multi-
phase flows (constitutiveEq.C).
•Fix: call to constrainPressure() in rheoInterFoam, version of40, has been
corrected for the SIMPLEC algorithm (pEqn.H). Added a section in the user-
guide on how to use properly the fixedFluxPressure BC with rheoInterFoam
in versions of222 and fe40.
•Add: tutorials on the die swell problem.
Generic

CHAPTER 1. Introduction 7
•Change/Fix: code cleanup and bug fix (BC evaluation of the explicit fvc::
div(phi,X) operator) in class GaussDefCmpw.
•Change/Add: replace boundary condition extST by the Type-independent
linearExtrapolation boundary condition (no backward compatibility). Added
optional second-order regression.
•Change: major update of the user guide to include electrically-driven flows.
Other changes were made in its content and organization, and some typos
were corrected.
•Change: ensure compatibility with foam-extend 4.0 and OpenFOAMR
v4.1.
Version 1.0
Released on 6/12/2016.
Initial version.
1.4 Citing rheoTool
If you found rheoTool useful and want to cite it in your work, the following BibTex
entry can be used for that purpose:
@misc{rheoTool,
author = "F. Pimenta and M.A. Alves",
title = "rheoTool",
howpublished = "\url{https://github.com/fppimenta/rheoTool}",
year = "2016"}
Since the underlying theory of rheoTool has been mainly presented in technical
papers [2–5], these can also be used for citation purposes.
1.5 Contacts
rheoTool is under continuous development and new features and improvements
will be added in the future. If you have any suggestions, comments or doubts
regarding the tool, or if you found a bug or error, feel free to contact us:
RFrancisco Pimenta: fpimenta@fe.up.pt
RManuel A. Alves: mmalves@fe.up.pt
1.6 Contributing
In the open-source spirit, rheoTool is open to contributions from the community.
If you believe that your piece of code is worth to be incorporated in rheoTool’s
next version, feel free to contact us.
Chapter 2
Installation
2.1 Compatibility with OpenFOAM R
and foam-
extend versions
The development and testing of rheoTool is usually performed in the most re-
cent stable release of OpenFOAM R
. However, an effort has been made to keep
rheoTool also compatible with foam-extend, although not all features available for
the OpenFOAM R
version can be found there (see Section 2.2). Currently, we
provide versions of rheoTool for:
•OpenFOAM R
v6.0 (of60/).
•foam-extend 4.0 (fe40/).
The list above includes the versions which were effectively tested. This means
that a given version of rheoTool may be compatible with other OpenFOAM R
or
foam-extend versions not included in this list. The versions above were tested in
Ubuntu 16.04, but other operating systems running OpenFOAM R
can eventually
support some version of rheoTool. However, the installation is only described here
for a Linux OS.
2.2 Differences between versions
The complete version of rheoTool is the one available for OpenFOAMR
, since this
is the one used for development. There are two main components of this version
that are not available for the foam-extend version: the Brownian dynamics module
and the interfaces to external libraries (Petsc, Hypre and Eigen) providing access
to a wider range of sparse matrix solvers (including coupled solvers).
Besides those major differences, in order to make rheoTool compatible with
each OpenFOAM R
/foam-extend version, several modifications were required at
the programming level for each case. Still, the user-interface remained almost
unchanged among the different versions. The main exception is on the codedStream
FunctionObjects and coded boundary conditions, which are used in the tutorials
of Chapter 5. Indeed, while these functionalities are available in OpenFOAM R
,
8

CHAPTER 2. Installation 9
it is not the case for foam-extend. Thus, the coded boundary conditions and the
utilities implemented as codedStream FunctionObjects in OpenFOAM R
versions
had to be assembled and compiled in a library for the foam-extend version.
A second point to be taken into account is that rheoTool may perform differ-
ently in each OpenFOAM R
/foam-extend version, as it may happen with any other
default solver of OpenFOAM R
/foam-extend. This is naturally a consequence of
the evolution of the core machinery of OpenFOAM R
/foam-extend, transversal to
many solvers and libraries. Fortunately, in most of the cases the differences will
be small. The following issues were detected in the tests that we performed:
•in general, a tutorial of rheoTool for OpenFOAM R
versions may be run either
in serial or parallel while keeping the same numerical settings. However,
in the tests using the foam-extend version, it was observed that parallel
simulations are less stable than serial ones, usually requiring a smaller time-
step or some under-relaxation of the velocity (sometimes as low as 0.97).
2.3 System requirements
Only standard requirements are needed to install rheoTool:
•a compatible and functional version of OpenFOAM R
or foam-extend should
be already installed.
•the machine should be connected to the Internet.
OpenFOAM R
users might additionally need sudo privilege to install Petsc.
This is discussed in more detail in Section 2.4.3.
2.4 Step-by-step instructions
After ensuring that the prerequisites are fulfilled, the user is ready to start the
installation, which includes four (three) major steps:
1. Download/clone rheoTool (Section 2.4.1);
2. Download Eigen library (Section 2.4.2);
3. (Only for OpenFOAM R
users) Install Petsc library (Section 2.4.3);
4. Compile rheoTool (Section 2.4.4).
2.4.1 Download/clone rheoTool
This step is common to both OpenFOAM R
and foam-extend users.

CHAPTER 2. Installation 10
rheoTool is publicly available as a GitHub repository. There is a single branch
(master) in the repository, which always contains the most recent, stable version of
the code (there is no public dev branch or similar). Once a new version is pushed
to the master branch, the previous, old version is tagged as a release. Therefore,
releases are only checkpoints for older versions and should not be used to get the
most recent version of the code.
As explained in the Readme file of the repository, rheoTool can be either down-
loaded or cloned from GitHub. The structure of rheoTool (https://github.com
/fppimenta/rheoTool) is depicted in Fig. 2.1.
rheoTool ofxx
feyy
doc
src
tutorials
libs
solvers
(…) (…)
(…)
(…)
Figure 2.1: Directory organization of rheoTool.
The top-level directory of rheoTool contains the versions available for different
OpenFOAM R
(of ) and foam-extend (fe) versions. The folder doc/, containing the
user guide, is also in the top-level directory. Inside the folder for each version, there
are two directories: src/, where the source code can be found, and tutorials/,
containing several tutorial cases showing the use of rheoTool. The src/ directory
is further subdivided in a directory with the applications (solvers/) and another
one containing libraries (libs/).
After cloning/downloading rheoTool, the user is free to remove from the top-
level directory all the versions not needed and keep only the one(s) of interest.
2.4.2 Download Eigen library
This step is common to both OpenFOAM R
and foam-extend users.
In the directory corresponding to a given rheoTool version (e.g. of60, where
you will find file downloadEigen), open a terminal and check that file etc/bashrc
of your installed OpenFOAM R
or foam-extend version has been sourced. This is
particularly relevant if you have defined alias for different versions of OpenFOAMR
or foam-extend. If this is the case, be sure that the alias pointing to the desired
version has been typed. Shortly, you should only advance to the next step if a
command like ∼$icoFoam -help is recognized in the terminal. Note that in
this document we use the prepending ∼$ for any instruction to be typed in the

CHAPTER 2. Installation 11
command line (thus, ∼$icoFoam -help means that you only type icoFoam
-help). If this check is successful, run the script downloadEigen in that terminal:
∼$./downloadEigen
This script downloads Eigen version 3.2.9 (other versions close to that would
also work adequately) from the Internet (using wget), extracts it and moves it to
directory:
$WM PROJECT USER DIR/ThirdParty/Eigen3.2.9
Eigen is used in rheoTool for computation of eigenvalues and eigenvectors and
there is no need to install the library, since the inclusion of the required headers
is enough for our purposes.
However, its location in the system must defined and exported. This is achieved
by attributing to variable EIGEN_RHEO – the one used and recognized by rheoTool –
the actual path of Eigen. The command to do so has been displayed to the terminal
after running script downloadEigen (if everything was ok) and looks like:
∼$echo "export EIGEN_RHEO=/home/user/OpenFOAM/user-4.0/ThirdParty
/Eigen3.2.9">>/home/user/.bashrc
Do not copy this command, it is just an example of what is displayed to the
screen. Instead, copy-paste and run the command appearing in your terminal.
If, for some reason, the user wants to move Eigen to another directory (or
already has an Eigen version in another directory), then move Eigen to its final
location (if already not) and define variable EIGEN_RHEO accordingly. Note that
Eigen only needs to be installed once per system. Even if the user has
installed multiple versions of rheoTool in the same system, the above procedure
only needs to be run once (for the first version being installed), as long as the
directory containing Eigen since the first installation is not deleted, or renamed.
2.4.3 Install Petsc library
This step is only for OpenFOAM R
users.
Petsc [9–11] has been added to the dependencies used by rheoTool starting
from version 4.0. This library provides a number of efficient and scalable sparse
matrix solvers, that can be used in rheoTool with both segregated and coupled
solvers.
The script installPetsc is responsible for downloading Petsc and the de-
pendencies it needs, configuring Petsc, compiling the libraries and exporting the
variables needed to call and use Petsc from any location. While the script is run-
ning, the user will be prompted to insert its password (and Yes or No) to allow
the installation of some dependencies needed by Petsc:
libatlas-dev,libatlas-base-dev,libblas-dev,liblapack-dev,flex,bi
son,git,make,cmake,gfortran
Some of these dependencies might already exist in the system, and in those
cases nothing is done. Only the inexistent dependencies will be downloaded and

CHAPTER 2. Installation 12
installed. This is the only part of the script requiring sudo mode (password con-
firmation). If the user is sure that all these packages are already installed in
the system, then commenting section ## Install dependencies inside the script is
enough to avoid the need for sudo, which can be problematic for non-administrator
users.
The script has been tested on fresh installs of Ubuntu 18.04 and 16.04, after
installing OpenFOAM R
binaries. The system OpenMPI is being used by both
OpenFOAM R
and Petsc in such conditions. This is a point worth to emphasize:
both OpenFOAM R
and Petsc should be compiled with the same MPI software,
which, however, can be different from OpenMPI. At the beginning of script inst
allPetsc, the user can change the paths to the MPI library and wrappers upon
need.
Petsc library is configured with standard options, that the user can found and
modify under section ## Configure petsc. To check the full range of options
available, please consult Petsc references [9,10]. The configuration that we set as
default will download and install the following additional packages from within
Petsc:
hypre,parmetis,metis,ptscotch,mumps,scalapack
Note that Petsc could be also installed via apt-get (there are binaries available),
but this would not allow configuring and using the most recent versions of the
software.
For most of the users, the script to install Petsc can be run without any mod-
ification. In such cases, go the directory corresponding to one of the rheoTool
versions (where you will find file installPetsc), open a terminal and ensure that
file etc/bashrc of your installed OpenFOAM R
version was sourced (as for Eigen).
Then run the script installPetsc in that terminal:
∼$./installPetsc
Petsc library is saved and compiled to directory:
$WM PROJECT USER DIR/ThirdParty
which can be changed by the user inside the script (before running it).
Installing Petsc only needs to be performed once per system. For example,
if you have multiple versions of rheoTool in the same machine, only a single in-
stall of Petsc is needed (recommended). Note that script installPetsc modifies
your ~/.bashrc file by appending Petsc variables to it (see the code at the end
of the script). If you have multiple versions of Petsc installed, or if you change
the location or version of Petsc, do not forget to manage these variables. Run-
ning (until completion) installPetsc multiple times will duplicate these variables
and possibly cause conflicts of paths. After installing Petsc with success, it is
good idea to check your ~/.bashrc and verify if the three variables PETSC DIR,
PETSC ARCH and LD LIBRARY PATH appended at the end are correctly de-
fined and not duplicated.

CHAPTER 2. Installation 13
2.4.4 Compile rheoTool
This step is common to both OpenFOAM R
and foam-extend users.
It is recommended to save rheoTool in a location with write permission, other-
wise you will need to use sudo mode to run all the commands. A good location for
rheoTool is, for example, directory $WM PROJECT USER DIR, which is defined
by default when OpenFOAM R
or foam-extend is installed.
Note (only for OpenFOAM R
users): in some combinations of OpenFOAM R
patches/OS versions, it was observed that the linker is unable to locate
PETSc, whose path is absent in variable $LD LIBRARY PATH. Indeed, echo
$LD LIBRARY PATH will not include the path to PETSc libs in such situa-
tions. This is most frequently observed when there are aliases to different
OpenFOAM R
versions, since in these situations sourcing the etc/bashrc of
OpenFOAM R
cleans $LD LIBRARY PATH. When this happens, running the
Allwmake script as described below results in linking errors similar to:
/usr/bin/ld: warning: libpetsc.so.3.10, needed by /home/user/OpenFOAM/user-6/
platforms/linux64GccDPInt32Opt/lib/libconstitutiveEquations.so, not found (
try using -rpath or -rpath-link)
/home/user/OpenFOAM/user-6/platforms/linux64GccDPInt32Opt/lib/
libsparseMatrixSolvers.so: undefined reference to ‘VecSet’
...
To avoid this issue, the user needs to ensure that the path to PETSc library is
added to $LD LIBRARY PATH after sourcing the etc/bashrc of OpenFOAM R
,
such that it survives. Among the several possibilities, a simple one is to modify the
alias. For that, open your system ~/.bashrc in edit mode, for example running
gedit ∼/.bashrc, find your alias (typically at the bottom of the file) and
modify it appending command
export LD_LIBRARY_PATH=$PETSC_DIR/$PETSC_ARCH/lib:$LD_LIBRARY_PATH
at its end, with the two commands separated by a semicolon. Thus, an alias of
the form (this is just an example)
alias of60=’source /opt/openfoam6/etc/bashrc’
before the modification should look like this (single line)
alias of60=’source /opt/openfoam6/etc/bashrc; export LD_LIBRARY_PATH=$PETSC_DIR
/$PETSC_ARCH/lib:$LD_LIBRARY_PATH’
after the modification. Note that there are other ways that would lead to the
same result, as for example modifying the $LD LIBRARY PATH variable at the
end of the etc/bashrc file of OpenFOAM R
, creating symbolic links of PETSc
libraries inside one of the locations included by default by OpenFOAM R
in
$LD LIBRARY PATH, etc.
How do you know if the above procedure applies to your system? If you do not
have aliases for OpenFOAM R
versions, then you should not have this problem, as

CHAPTER 2. Installation 14
long as the command exporting $LD LIBRARY PATH is executed after sourcing
OpenFOAM R
’s bashrc. If you do have aliases, then this problem might happen
or not. It will happen if command echo $LD LIBRARY PATH does not include
the path to PETSc libs, which you can test before compiling rheoTool. Otherwise,
the compilation error similar to the one displayed above should be suggestive of
this issue.
After you move rheoTool to its final location, open a new terminal (to ensure
that your system ~/.bashrc is sourced and contains the path of Eigen and Petsc)
in the top-level directory of rheoTool (ensuring that the OpenFOAM R
or foam-
extend environment has been sourced, as previously) and enter the directory with
the version of rheoTool that is compatible with your OpenFOAM R
or foam-extend
version, and then go to directory src/. For example, for OpenFOAMR
v6.0, it
would be:
∼$cd of60/src
Now, run the script Allwmake to build the libraries and applications of
rheoTool. In order to speed up the compilation, several processors can be used, if
available. For OpenFOAM R
users, run
∼$./Allwmake -j N
for parallel compilation with Nprocessors. For example, ./Allwmake -j 3
will compile in parallel using 3 processors. If the number of processors is not
specified, all available processors are used. If option −jis not passed to the script,
the compilation will use WM NCOMPPROCS processors, where this variable is
usually defined in the etc/bashrc file of your OpenFOAM R
installation. For
foam-extend users, option −jis not recognized by the script, therefore simply run
∼$./Allwmake
The compilation in foam-extend will typically make use of all processors avail-
able in the system, since variable WM NCOMPPROCS is set by default in such
way.
Both the libraries and applications installed with rheoTool can be ”cleaned”
by running the script Allwclean.
Since the user will probably not need the remaining versions of rheoTool that
remain in the top-level directory, they can simply be deleted, if already not.
To check if the installation succeeded, the user should try running one of the
tutorials in Chapter 5.

Chapter 3
Theoretical background
The equations governing pressure- and electrically-driven flows of incompressible,
complex fluids are discussed in this Chapter, along with some important aspects
related with their discretization in the finite-volume framework. Since a thorough
discussion on this subject can be found in Refs. [2,3,5], some intermediate steps
are skipped and only the more relevant equations are presented.
The last Section of this Chapter is concerned with the theory of Brownian
dynamics simulations using coarse-grained models. Again, we will only present
the more relevant aspects for the scope of this user guide and more details can be
found in Ref. [4].
3.1 Governing equations of complex fluid flows
The basic equations governing isothermal, single-phase, transient flows, under lam-
inar conditions, for incompressible fluids, in static grids, establish mass conserva-
tion (Eq. 3.1) and momentum balance (Eq. 3.2),
∇·u= 0 (3.1)
ρ∂u
∂t +u·∇u=−∇p+∇·τ0+f(3.2)
where uis the velocity vector, tis the time, pis the pressure, τ0is the extra-stress
tensor and fis any external body-force, such as the electric force discussed in
Section 3.7. To simulate viscoelastic fluid flows, it is a common approach to split
the total extra-stress tensor in a solvent contribution (τs) and a polymeric contri-
bution (τ), τ0=τ+τs. In order to have a closed set of equations, a constitutive
equation is required for each tensor contribution, which can be generally written
as in Eqs. (3.3) and (3.4), for a wide range of models,
τs=ηs( ˙γ)(∇u+∇uT) (3.3)
f(τ)τ+λ( ˙γ)∇
τ+h(τ) = ηp( ˙γ)(∇u+∇uT) (3.4)
15

CHAPTER 3. Theoretical background 16
In Eqs. (3.3) and (3.4), ηsis the solvent viscosity, ηpis the polymeric viscosity
coefficient, λis the relaxation time, ˙γis the shear-rate, f(τ) is a general scalar
function depending on an invariant of τ,h(τ) is a tensor-valued function depend-
ing on τand ∇
τ=∂τ
∂t +u·∇τ−τ·∇u− ∇uT·τrepresents the upper-convected
time derivative, which renders the models frame-invariant. Some models use the
Gordon-Schowalter derivative (
τ=∇
τ+ζ(τ·D+D·τ), with D=1
2(∇u+∇uT))
instead of the upper-convected derivative, in order to take non-affine deformation
into account (controlled by parameter ζ). In rheoTool, this is the case of PTT-
type models. Other constitutive models exist, which can also make use of the
lower-convected time derivative, but those are not explored here. The constitu-
tive equation for a GNF is limited to Eq. (3.3), since elasticity is not considered
(τ0=τs). In Table 4.1 presented in the next Chapter, Eqs. (3.3) and (3.4) are
specified for several GNF and viscoelastic models.
Eqs. (3.1)–(3.4) represent the standard system of equations to be solved. How-
ever, due to numerical stability issues in viscoelastic fluid flow simulations, the
system is rarely solved in that form. Indeed, several techniques are available for
stabilization purposes (see, for instance, Ref. [12] for a comparison between the
most popular techniques) and the ones used in rheoTool are addressed next.
3.2 Stabilization of viscoelastic fluid flow simu-
lations
3.2.1 The both-sides-diffusion (BSD) technique
The both-sides-diffusion (BSD) is a technique already incorporated in the vis-
coelasticFluidFoam solver [1]. It consists in adding a diffusive term on both sides
of momentum equation (Eq. 3.2), with the difference that one of them (left-hand
side) is added implicitly, while the other one (right-hand side) is added explicitly.
Once steady-state is reached, both terms cancel each other exactly. Such method
increases the ellipticity of the momentum equation and, as such, has a stabiliz-
ing effect, mostly when there is no solvent contribution in the extra-stress tensor.
Incorporating the terms arising from the both-sides-diffusion in the momentum
equation, and making use of Eq. (3.3), then
ρ∂u
∂t +u·∇u− ∇·(ηs+ηp)∇u=−∇p− ∇·(ηp∇u) + ∇·τ+f(3.5)
Note that the added diffusive terms are scaled by the polymeric viscosity (ηp),
which is a common choice in the literature (e.g. Ref. [12]), although not mandatory.
In order to simplify the reading, the possible dependence of the viscosity and
relaxation time on the shear-rate will be dropped in the respective symbols, as
already done in Eq. (3.5), although this relation still holds to keep generality.

CHAPTER 3. Theoretical background 17
3.2.2 The log-conformation tensor approach
The log-conformation tensor approach consists in a change of variable when evolv-
ing in time the polymeric extra-stress and it was devised to tackle the numerical
instability faced at high Weissenberg number flows [6,13].
The polymeric extra-stress tensor is related with the conformation tensor (A).
For the Oldroyd-B model, for example, this relation is expressed as (see Table 4.1
for several viscoelastic models)
τ=ηp
λ(A−I) (3.6)
In the log-conformation tensor methodology, a new tensor (Θ) is defined as
the natural logarithm of the conformation tensor
Θ= ln(A) = Rln(Λ)RT(3.7)
In Eq. (3.7), the conformation tensor was diagonalized (A=RΛRT) because it
is positive definite, where Ris a matrix containing in its columns the eigenvectors
of Aand Λis a matrix whose diagonal elements are the respective eigenvalues
resulting from the decomposition of A. Eq. (3.4) written in terms of (Θ) becomes
[6]
∂Θ
∂t +u·∇Θ=ΩΘ −ΘΩ + 2B+1
λg(Θ) (3.8)
where g(Θ) is a model-specific tensorial function depending on Θ(see Table 4.1
for other viscoelastic models) and
B=R
mxx 0 0
0myy 0
0 0 mzz
RT(3.9)
Ω=R
0ωxy ωxz
−ωxy 0ωyz
−ωxz −ωyz 0
RT(3.10)
M=R∇uTRT=
mxx mxy mxz
myx myy myz
mzx mzy mzz
(3.11)
ωij =Λjmij +Λimji
Λj−Λi
(3.12)
After solving Eq. (3.8), Θis diagonalized in the form
Θ=RΛΘRT(3.13)
and the conformation tensor is recovered by the inverse relation of Eq. (3.7)
A= exp(Θ) = Rexp(ΛΘ)RT(3.14)

CHAPTER 3. Theoretical background 18
Finally, the polymeric extra-stress tensor can be computed from A(Eq. 3.6)
and used in the momentum equation.
Note that for PTT-type models, which may include non-affine deformation
through the Gordon-Schowalter derivative, the tensor M(Eq. 3.11) is computed
differently: M=R∇uT−ζDRT.
It is worth to mention that the log-conformation approach can be considered a
particular case of the kernel-conformation method [14]. However, from our expe-
rience, the log kernel is frequently the optimal kernel (in terms of robustness and
accuracy) for generic problems, so that only this one is widely used in rheoTool.
Nevertheless, for the Oldroyd-B model, the rootkkernel [14] and the square-root
transformation [15] are also included in rheoTool for demonstration purposes.
3.3 Coupling algorithms
3.3.1 Pressure-velocity coupling
Although the OpenFOAM R
toolbox is already able to solve linear systems of
equations in a coupled way, most of the solvers still rely on segregated solutions
(this is a rule for transient solvers). In segregated solvers, the equations for each
variable are solved sequentially. Even for a fully-implicit method, if the coupling
between variables is weak, then numerical divergence is prone to occur.
In the OpenFOAM R
toolbox, common algorithms for pressure-velocity cou-
pling are SIMPLE and SIMPLEC for steady-state solvers and either PISO or
PIMPLE (a combination of SIMPLE(C) and PISO) for transient solvers. From
the benchmark cases performed in Ref. [2], it was observed that SIMPLEC was
particularly suitable for transient viscoelastic fluid flows at low Reynolds numbers,
regarding stability and accuracy.
The continuity equation, implicit in the pressure variable, derived for SIM-
PLEC (a more detailed derivation is presented in Ref. [2]) leads to
∇·1
aP−H1
(∇p)P=∇·H
aP
+1
aP−H1−1
aP(∇p∗)P(3.15)
where aPare the diagonal coefficients from the momentum equation, H1=−P
nb
anb
is an operator representing the negative sum of the off-diagonal coefficients from
momentum equation, H=−P
nb
anbu∗
nb +bis an operator containing the off-
diagonal contributions, plus source terms (except the pressure gradient) of the
momentum equation and p∗is the pressure field known from the previous time-
step or iteration. Accordingly, the equation to correct the velocity after obtaining
the continuity-compliant pressure field from Eq. (3.15) is
u=H
aP
+1
aP−H1−1
aP(∇p∗)P−1
aP−H1
(∇p)P(3.16)
Importantly, in order to avoid the onset of checkerboard fields, the pressure
gradient terms involved in the computation of face velocities, i.e., in Eqs. (3.15)

CHAPTER 3. Theoretical background 19
and (3.16), are directly evaluated using the pressure on the cells straddling the face,
in a Rhie-Chow-like procedure (more details in Ref. [2]). Nonetheless, when Eq.
(3.16) is used to correct the cell-centered velocity field, the pressure gradient terms
are computed ”in the usual way”, for example using Green-Gauss integration.
Rhie-Chow methods used to avoid checkerboard fields, as the one described
in the previous paragraph, are known to be affected by the use of small time-
steps and they also present time-step dependency on steady-state results [16].
In OpenFOAM R
solvers, a common strategy to avoid such effects is to add a
corrective term to face-interpolated velocities, through functions ddtPhiCorr() or
ddtCorr(). Recently, in foam-extend the time-step dependency was solved in a
different way, by removing the transient term contribution from the aPcoefficients
of the momentum equation [17]. However, this approach may be problematic when
used with the SIMPLEC algorithm, since a division by zero is prone to happen.
In rheoTool, we keep using the added corrective term, although, as mentioned in
Ref. [2], this term can be improved in order to more efficiently avoid the small
time-step dependency of steady-state solutions.
3.3.2 Stress-velocity coupling
Stress-velocity decoupling problems can arise for similar reasons as those described
for pressure-velocity: the cell-centered velocity loses the influence of the forces
(either polymeric extra-stress or pressure gradient) of its direct neighborhood (cells
sharing a face in common). This usually happens in the interpolation from cell-
centered to face-centered fields. In the case of polymeric extra-stresses, it is the
divergence term (∇·τ) in the momentum equation, when τis linearly interpolated
from cell centers to face centers, which can be responsible for the decoupling.
In Ref. [2], we described a new stress-velocity coupling method, where the
polymeric extra-stresses at face centers are computed as
τf=τf+ηph∇u|f+(∇u)T|f−∇u|f+(∇u)T|fi (3.17)
where terms with an overbar are linearly interpolated from cell-centered values,
while the remaining velocity gradients are directly evaluated from the cell-centered
velocities straddling the face. When the definition of τfin Eq. (3.17) is inserted in
the momentum equation with the both-sides-diffusion terms already present (Eq.
3.5), then we obtain
ρ∂u
∂t +u·∇u− ∇·(ηs+ηp)∇u=−∇p− ∇·ηp∇u+∇·τ+f(3.18)
where the term ∇·ηp∇uis a ”special second-order derivative” (different from
the laplacian operator of OpenFOAM R
), defined as the divergence of the velocity
gradient, where the velocity gradient at the faces is obtained by linear interpolation
of the velocity gradient evaluated on the cell centers. More details are presented
in Ref. [2], where it is shown that with mesh refinement Eq. (3.17) approaches
τf=τfand the additional terms cancel out. Note that when inserting Eq. (3.17)

CHAPTER 3. Theoretical background 20
in the momentum equation (resulting in Eq. 3.18), we drop the transpose velocity
gradients for simplicity, since continuity imposes ∇·∇uT=0.
3.4 High-resolution schemes
The discretization of convective terms within the finite-volume framework leads to
ZV
(u·∇φ) dV=X
f
φf(uf·Sf) = X
f
φfFf(3.19)
where φis a generic variable being advected, Sfis the face-area vector and Ffis
the volumetric flux crossing face f. While fluxes are known at the faces from the
Rhie-Chow-like interpolation (Eq. 3.16), φat face centers need to be interpolated
from known values at cell centers. OpenFOAM R
offers a wide range of schemes to
perform such interpolation, from upwind – an unconditionally stable scheme, but
only first-order accurate –, to central differences – a conditionally stable, second-
order accurate scheme. A good compromise between both extremes is provided
by High-Resolution Schemes (HRSs). When represented in a Normalized Variable
Diagram (NVD), several HRSs are piecewise-linear functions and can be defined
using the Normalized Weighting Factor (NWF) approach [18]:
e
φf=αe
φC+β(3.20)
where the following definitions hold
e
φf=φf−φU
φD−φU
(3.21a)
e
φC=φC−φU
φD−φU
(3.21b)
In Eq. (3.20), αand βare scalars specific to each HRS and they can be functions
of e
φC. Subscripts in Eqs. (3.21a,b) have the following meaning: for a given face,
cell C is the cell from which the flux comes (upstream), cell D (downstream) is the
cell to which the flux goes and cell U (far-upstream) is the cell upstream to cell C.
In a general unstructured mesh, cell U cannot be identified unequivocally, and φU
in Eqs. (3.21a,b) can be evaluated as [19]
φU=φD−2(∇φ)C·dCD (3.22)
where dCD is the vector connecting the center of cells C and D. For a deferred
correction implementation of HRSs, the upwind part of the HRS is discretized
implicitly, while the remaining (difference between the HRS and the upwind differ-
encing scheme) is discretized explicitly (cf. Ref. [2]), which, using Eqs. (3.20-3.22),
results in
φf= [φC]implicit + [(α−1)φC+βφD+ (1 −α−β)(φD−2(∇φ)C·dCD)]explicit (3.23)
Handling the HRSs in a deferred correction approach avoids, in some cases,
numerical instabilities introduced by the central-differencing component of the

CHAPTER 3. Theoretical background 21
HRS. Additionally, in Ref. [2] it was observed that the usual methodology of
OpenFOAM R
to apply HRSs to non-scalar variables (tensors and vectors) can
locally introduce numerical instabilities in some viscoelastic flow problems. This
methodology consists in using a frame-invariant quantity for non-scalar variables,
such as the squared magnitude for vectors, or the trace (or double-dot product)
for tensors, to compute the αand βparameters in Eq. (3.23). It was observed
that such artificial instabilities can be significantly damped with a component-wise
handling of non-scalar variables [2], at the cost of losing frame-invariance, which
however is very weak and vanishes with grid refinement. Accordingly, non-scalar
variables are split into its components and Eq. (3.23) is applied independently to
each one of them. Note that this approach still generates one single matrix of co-
efficients for such variables, since the upwind differencing scheme coefficients are
common to all the components (they only depend on the flux). The differentiation
between components is only introduced in the explicit part of Eq. (3.23), generat-
ing a different source term for each individual tensor/vector component. This is
possible due to the use of a deferred correction approach.
3.5 Moving grids
Some CFD problems require the simulation of a moving entity interacting with a
fluid. There are several approaches than can be used to tackle such problems, and
the choice is usually made based on a case-by-case analysis. Consider for example
the flow induced inside a sphere due to its time-dependent rotation. Such case can
be easily handled by defining adequate boundary conditions for the flow variables
on the sphere surface, without further modifications of the usual solver setup. On
the other hand, if we consider the time-dependent simulation of the flow inside an
axisymmetric stirred tank reactor, such approach is no longer adequate. Instead,
we can use, for example, a (rotating) non-inertial reference frame, which allows
to keep the mesh steady and introduces some acceleration terms in the momen-
tum equation (OpenFOAM R
allows the use of such non-inertial reference frames).
However, if the tank is not axisymmetric, the non-inertial reference frame becomes
useless and a different approach is needed. An immersed boundary method can
be used for that purpose, avoiding the use of moving grids. However, we will turn
our attention to moving meshes, i.e. a computational mesh whose control volumes
move in space over time.
For moving control volumes, the equations governing the flow need to be
changed regarding convective terms, which should account for the grid motion [20],
ZS
φ(u−ub)·ndS=X
f
φf(uf−ub,f )·Sf(3.24)
where φis any generic variable being advected and ubis the velocity at which
surface Sis moving. Moreover, the space conservation law (SCL) needs to be
satisfied to ensure mass conservation [20],
d
dtZV
dV−ZS
ub·ndS= 0 (3.25)

CHAPTER 3. Theoretical background 22
If the SCL is ensured, the continuity equation remains unchanged and so does
the pressure equation. In practice, the SCL is imposed while computing RSub·ndS
in Eq. (3.24), which is the flux due to mesh motion. According to Eq. (3.25), the
form taken by this term involving the volume swept by the moving faces at different
times depends on the discretization scheme of time-derivatives. More details can
be found in [20].
In addition to changing the position of its control volumes, the mesh can also
change its topology if cells are removed or added. This is at the basis of auto-
matic mesh refinement (AMR), frequently used to locally (un)refine the mesh at
particular regions of interest (e.g. zones where the gradient of a given variable is
high). The introduction/removal of cells in the mesh requires defining the fields
and their fluxes in the newly generated cells/faces, which is based on a interpola-
tion procedure that uses the values in the neighboring cells.
3.6 Segregated vs coupled solvers
The governing equations in an implicit CFD code can be solved either segregated
or coupled. In a segregated solution method, the equations are solved sequentially,
one at a time (equations for multidimensional variables are further split into com-
ponents). This is the standard method used in OpenFOAM R
and in most CFD
codes based on finite-volumes. In a coupled solution method, all the governing
equations are solved simultaneously. There are also semi-coupled solvers, which
lie somewhere between segregated and coupled solvers. In a semi-coupled solver,
part of the equations are solved coupled and part are solved segregated.
The segregated solution method has been and continues being a popular strat-
egy for its low computational cost per time-step and low memory usage, compared
to the coupled solution method. Nonetheless, they are less stable than coupled
solvers, usually requiring lower time-steps and/or more under-relaxation in order
to avoid numerical divergence. Thus, the higher usage of resources by coupled
solvers is sometimes compensated by its enhanced stability, which translates in a
lower total time of computation. Moreover, due to its higher implicitness, coupled
solvers can be also more accurate in transient flow simulations [5].
In [5] we discussed the implementation of coupled and semi-coupled solvers in
rheoTool, in the context of electrically-driven flows. Semi-coupled solvers proved
to be faster and more accurate (time accuracy) than segregated solvers in a number
of situations. Similar advantages could be also observed in pressure-driven flows.
3.7 Electrically-driven flow models
Consider now that the fluid under analysis is a weak electrolyte subjected to an
electric field. In such conditions, the momentum equation (Eq. 3.2) should include
the contribution from an electric body-force,
f=fE=∇·εEE −kEk2
2I=ρEE−kEk2
2∇ε(3.26)

CHAPTER 3. Theoretical background 23
where Eis the electric field, ε=ε0εRis the electric permittivity and ρEis the
charge density (per unit volume). In order to close the system of equations for
electrically-driven flows (EDFs), additional relations must be provided to compute
the terms in Eq. (3.26). Some options, the ones available in rheoTool, are presented
next. Note that when referring generically to EDFs, we do not exclude the possi-
bility of having any other external forcing (for example due to an imposed pressure
difference), in addition to the electric forcing. When only an electric forcing exists,
we call this flow as pure EDF.
The second term of Eq. (3.26) is only non-zero for a system of two fluids, each
having a different electric permittivity.
3.7.1 Poisson-Nernst-Planck model
In the absence of magnetic effects, the electric potential (Ψ) can be computed by
Gauss’ law
∇·(ε∇Ψ) = −ρE(3.27)
where the electric field is E=−∇Ψin electrostatics. By definition, the charge
density is
ρE=F
N
X
i=1
zici(3.28)
where Fis Faraday’s constant, ziis the charge valence of specie iand ciis the
concentration of specie i(mol/m3). The sum is over the Ncharged species in
the electrolyte. The standard law governing the transport of charged species in a
weak electrolyte, under the action of an electric field and neglecting any reaction,
is embodied by the Nernst-Planck equation,
dci
dt +u·∇ci=∇·(Di∇ci) + ∇·
Di
ezi
kT ∇Ψ
| {z }
uM,i
ci
(3.29)
which closes the system of equations for an EDF. In Eq. (3.29), Dis the diffu-
sion coefficient, eis the elementary charge, kis Boltzmann’s constant and Tis
the absolute temperature. The last term of Eq. (3.29), representing the transport
of charged species due to an electric field, can be though as a standard convec-
tive term driven by an electromigration velocity (uM,i). However, it may also be
considered as the Laplacian operator applied to field Ψ, with a space and time
varying diffusion coefficient, Diezi
kT ci(this last approach is used in rheoTool for
discretization purposes).
The so-called Poisson-Nernst-Planck model (henceforth PNP model) is con-
stituted by Eqs. (3.27)-(3.29) and, coupled with the continuity and momentum
equations, is applicable to a wide range of EDFs. However, the coexistence of dif-
ferent scales of time and length in EDFs may originate a stiff system of equations
when the PNP model is used. As such, several simplified models can be derived to

CHAPTER 3. Theoretical background 24
mitigate these numerical issues, as described next. Note that the PNP model does
not take into account molecular crowding effects (e.g., the number of ions near a
surface may grow unbounded), so care must be taken when using it to simulate
electrolytes of mild to high ionic strength.
In the PNP model, the electric-related unknowns are ciand Ψ. Due to the
convective term in Eq. (3.29), there is a two-way coupling between the PNP and
the momentum equations.
3.7.2 Splitting the electric potential
Before proceeding to the derivation of other EDF models, we introduce here a
useful approach to simulate EDF problems. In the PNP model, a single electric
potential variable has been used, Ψ. However, in certain situations this can pose
some difficulties when defining the boundary conditions to solve the Poisson equa-
tion. A common approach to avoid such issues is the decomposition of the electric
potential in two variables: the externally imposed electric potential, φExt, and the
intrinsic electric potential, ψ, such that Ψ=φExt +ψ[3]. Following this approach,
Gauss’ law is also decomposed in two equations,
∇·(ε∇φExt) = 0 (3.30a)
∇·(ε∇ψ) = −ρE(3.30b)
An additional simplification which can be used simultaneously with the split-
ting approach is to consider fE=−ρE∇φExt in the momentum equation, i.e., the
intrinsic electric potential contribution is ignored in the electric field definition.
This can be justified by stating that this extra force not accounted for directly is
balanced by a pressure gradient, which mutually cancel each other in the momen-
tum equation [3], under the assumption that it would not affect the flow.
The splitting approach will be used in the derivation of the next two models.
3.7.3 Poisson-Boltzmann model
If we assume that the ions follow a Boltzmann equilibrium, then the PNP
model can be simplified to the so-called Poisson-Boltzmann model (henceforth
PB model), for which Gauss’ law reads
∇·(ε∇ψ) = −F
N
X
i=1
zici,0exp −ezi
kT (ψ−ψ0)(3.31)
with ci,0being a reference concentration of specie i, where the intrinsic poten-
tial is ψ0. Without loss of generality, we will assume that ci,0is the bulk ionic
concentration, where the intrinsic potential is ψ0= 0.
Note that the right hand side of Eq. (3.31) represents (minus) the charge density
for the PB model. Thus, Eq. (3.31) provides the definition of Eq. (3.30b) for the
PB model, under the splitting approach.

CHAPTER 3. Theoretical background 25
For this model, the only electric-related unknowns are the two electric poten-
tials, ψand φExt, computed from Eqs. (3.30a) and (3.31). Furthermore, as can
be seen from Eq. (3.31), there is no influence of flow variables in the PB model
(one-way coupling).
In order to increase the implicitness of Eq. (3.31), its source term can be lin-
earized by expansion in Taylor series up to the first-derivative, transforming the
equation into
∇·(ε∇ψ) + ψF
N
X
i=1
(aibi)∗=−F
N
X
i=1
(ai)∗+ψ∗F
N
X
i=1
(aibi)∗(3.32)
with bi=−ezi
kT and ai=zici,0exp (biψ). All the terms of Eq. (3.32) with a star are
evaluated explicitly.
3.7.4 Debye-H¨uckel model
Considering the PB model, if we further simplify Eq. (3.31) assuming low electric
potentials, ezi
kT ψ1 , then
∇·(ε∇ψ) = −F
N
X
i=1
zici,01−ezi
kT ψ(3.33)
which is the equation governing the electric potential distribution in the so-called
Debye-H¨uckel model (henceforth DH model).
As for the PB model, the only electric-related unknowns are the two electric
potentials, ψand φExt, computed from Eqs. (3.30a) and (3.33). Also, there is no
influence of flow variables in the DH model (one-way coupling).
3.7.5 Slip model
A common characteristic of electrokinetic problems is the spontaneous formation
of an electric double layer (EDL) near a charged surface, upon contact with an
electrolyte. The thickness of the EDL can be approximated by the Debye length
(λD), a physical parameter appearing when solving the Poisson equation for the
electric potential,
λD=v
u
u
u
t
εkT
F e
N
P
i=1
z2
ici,0
(3.34)
In several practical applications, the charge density is mainly located in the
EDL region, while the bulk electrolyte is neutral. If the Debye length is much
smaller than the characteristic dimension of the system (λD
W1) and assuming a
smooth, laminar flow inside the EDL, then it is possible to approximate the EDL
effect by a slip velocity at the surface, avoiding the need to solve the flow inside the
EDL. Such a case would be, for example, the pumping of a Newtonian electrolyte
(λD∼ O(10−9m)) in a microchannel of arbitrary shape (W∼ O(10−6m)), by

CHAPTER 3. Theoretical background 26
electroosmosis, at low voltage ( ez
kT ψ1) – the last conditions is usually relaxed.
The Helmholtz-Smoluchowski theory is frequently used to approximate the slip
velocity in such conditions,
uSch =µE(3.35)
where µ=−εζ
η0is the electroosmotic mobility (ζis usually the surface zeta-
potential). Thus, when Eq. (3.35) is used as a boundary condition for velocity
in the momentum equation, both the electroosmotic mobility and the electric field
at the surface must be known. The electroosmotic mobility is assumed to be known
a priori – it can be a fixed value over all the surface or have a known distribution.
On the other hand, the electric field on the surface must be computed, making use
of the initial assumption that no free charge exists in the bulk electrolyte, thus
Ψ=φExt +ψ=φExt, and
∇·(ε∇Ψ) = 0 (3.36)
When the slip model is used, the electric body-force is not included in the
momentum equation – electric effects contribute uniquely via the slip boundary
condition on the wall.
Note that slip models do not resolve any phenomena occurring in the EDL.
Thus, this approach is highly inaccurate for some flows, even though the condition
λD
W1 is satisfied. For example, this kind of model is unable to predict the high
values of shear-rate typically found in EDLs, which can trigger elastic instabilities
for complex fluid flows [21] – using a slip model would simply retrieve a smooth
flow in such cases.
3.7.6 Ohmic (leaky dielectric) model
The so-called Ohmic model [22] is particularly useful to simulate fluids of different
conductivities, although a generalized Ohmic model has been recently proposed
for different types of problems [23]. The model can be derived from the PNP
equations, rewritten in terms of the conductivity and free-charge density, and
assuming additionally instantaneous charge relaxation and electroneutrality [22].
The interested reader is directed to Ref. [22] for the full derivation of the Ohmic
model. Here, only the final equations are presented. Furthermore, and contrarily
to what was done for the previous models, we will restrict our analysis to a binary
electrolyte, i.e., an electrolyte composed of only one positive and one negative
species, with z+=−z−=z, but no restrictions in the relation between D+and
D−.
First, let’s start defining the conductivity (σ) and free-charge density (ρE) for
a binary electrolyte,
σ=F2z2
RT (D+c++D−c−) (3.37)
ρE=F z(c+−c−) (3.38)

CHAPTER 3. Theoretical background 27
where Ris the universal gas constant. Imposing the conservation of each variable
leads to (after the assumptions mentioned above; more details in Ref. [22])
∂σ
∂t +u·∇σ=Deff∇2σ(3.39)
∇·(σ∇Ψ) = 0 (3.40)
where the effective diffusivity is Deff =2D−D+
D−+D+. The conductivity is transported
through Eq. (3.39), while Eq. (3.40), derived from the conservation of charge-
density (then simplified on the basis of electroneutrallity), is actually used to
compute the distribution of electric potential. The electric force entering the mo-
mentum equation assumes its standard form, taking into account that the charge
density can be expressed as ρE=−∇·(ε∇Ψ) from Gauss’ law, then
fE=ρEE=∇·(ε∇Ψ)∇Ψ(3.41)
In order to close the Ohmic model, the EDL effect is commonly represented
by a slip velocity, which avoids detailing the flow inside the EDL using a very
fine mesh. Since the zeta-potential of a surface depends generally on the ionic
conductivity, a σ-dependent slip velocity is typically used [22], such as
uSch(σ) = µ0σ
σ0m
E(3.42)
where µ0=−εζ0
η0is a reference electroosmotic mobility, at a reference conduc-
tivity (σ0), and mis an exponent governing the power-law dependence of the
zeta-potential on the conductivity (m∈[−0.5,−0.3] is in agreement with several
works, e.g. [22]). Note that Ein Eq. (3.42) is the electric potential at the surface
where the slip velocity is computed.
3.8 Brownian dynamics simulations
In the previous Sections, polymeric fluid flows were addressed from a continuum
mechanics perspective. In this Section, we zoom-in the scale of analysis, such that
each polymer molecule is now modeled individually. We enter the kinetic the-
ory domain, which lays somewhere between continuum mechanics and atomistic
modeling. This means that even though each polymer molecule is simulated indi-
vidually, we ignore atomic-size events. Moreover, the models discussed here and
implemented in rheoTool neglect inter-molecular interactions, which is represen-
tative of dilute solutions. The interested reader is referred to [7] for a thorough
discussion on the kinetic theory of polymers.
3.8.1 The bead-spring model
The most commonly used coarse-grained models to simulate polymer molecules
are bead-spring and bead-rod models. Currently, only the bead-spring model
is available in rheoTool (Fig. 3.1). According to this model, the molecules are

CHAPTER 3. Theoretical background 28
represented by a set of Nbeads connected by NS= (N−1) springs, for open
chains, or NS=Nsprings for closed chains. Each ibead owns a group denoted
as githat contains the index of all the beads to which it is directly connected to
by springs. For chains without branches, gihas one (beads at the edges) or two
elements, but more elements can be present for branched polymers, such as the
ones depicted in Fig. 3.1. Note that each bead and spring in the chain aims to
represent a group of atoms, and not an individual atom. In this guide, we use
either |xij|=|rj−ri|, j ∈gi, or simply Rito denote the length of all the springs
associated with bead i.
Polymer molecules usually display a maximum contour length upon full-
extension (Lmax), which should be ideally reproduced by the numerical model.
Therefore, each spring also has a maximum length, l=Lmax/NS.
The minimum characteristic length featured in a spring is the so-called persis-
tence length (λP), below which the spring segments behave as rigid elements, with
fixed orientation. The Kuhn step size, defined as bk= 2λPis a measure commonly
used in coarse-grained models, especially in bead-rod models, where it represents
the fixed size of a single rod. For the physical representation of the springs to
remain valid, a minimum number of Kuhn steps should be used to represent a
(flexible) spring. The number of Kuhn steps per spring is denoted by Nk,s =l/bk
and is usually controlled by the choice of N.
In rheoTool, an individual molecule is represented by a set of beads and springs,
and a group of molecules is composed by an ensemble of molecules sharing the
same physical properties. Each simulation in rheoTool can handle simultaneously
several groups of molecules (Fig. 3.1).

CHAPTER 3. Theoretical background 29
Molecule
Group of Molecules
Group of Molecules
Group of Molecules
Bead
Spring
Branch
RheoTool simulation
Figure 3.1: Polymer molecules representation by a bead-spring model. The orga-
nization levels used in rheoTool are also represented: beads and springs, molecules
and groups of molecules.

CHAPTER 3. Theoretical background 30
3.8.2 Governing equations of beads motion
Consider a chain with an arbitrary topology, composed by Nbeads. The time
evolution of the position vector corresponding to each bead (ri) is governed by
[24,25]
∂ri
∂t =uf+
N
X
j=1
∂Dij
∂rj
+
N
X
j=1
DijFj
kT +6
∆t0.5i
X
j=1
σijnj(3.43)
where ufis a velocity imposed by an external forcing, Dij is the diffusion tensor,
kis Boltzmann’s constant, Tis the absolute temperature, Fjis the sum of spring
and exclusion volume (EV) forces (Fj=FS
j+FEV
j), ∆tis the discrete time-step, σ
is a tensor satisfying D=σσTand njis a vector whose 3 components are random
numbers uniformly distributed in the range [−1; 1].
Dand σare (N×N) symmetric tensors, whose ij elements are themselves
(3 ×3) tensors. The single model available in rheoTool to represent the diffusion
tensor is the Rotne–Prager–Yamakawa (RPY) model [4],
Dij =
kT
6πηaI=DI, i =j
3D
4
a
|xij |h1 + 2a2
3|xij |2I+1−2a2
|xij |2xij xij
|xij |2i, i 6=j∧ |xij | ≥ 2a
Dh1−9|xij |
32aI+3
32a
xij xij
|xij |i, i 6=j∧ |xij|<2a
(3.44)
where |xij|=|rj−ri|,ηis the fluid viscosity, ais the bead radius and Iis the unit
tensor (3 ×3). Note that in rheoTool,aand Dare defined independently by the
user and need not to be related. For the RPY tensor, ∂Dij
∂rj=0in Eq. (3.43). The
decomposition of D, a symmetric tensor, to obtain σis currently performed by a
Cholesky decomposition, whereby σresults in a lower triangular tensor (matrix).
The free-draining approach is sometimes assumed in bead-spring models, which
results from ignoring the beads disturbance in the continuum velocity field. In
such situations, hydrodynamic interactions are neglected and all the off-diagonal
tensor elements of tensor Dbecome zero. The diffusion becomes isotropic and
can simply be defined by coefficient D. The summations in Eq. (3.43) reduce to a
single element contribution (j=i), and σii =√DI.
The exclusion volume forces impose a repulsive potential between beads, which,
however, does not avoid any possible crossover between beads or springs (there is
also no collision between beads). The following exclusion volume force is used [25],
FEV
i=−9
2
kT
l
νEV
l33
4√π3
(2Nk,s)9/2
N
X
j=1
exp −9
2Nk,s |xij|2
l2xij
l(3.45)
where νEV is the exclusion volume parameter.
3.8.3 Spring force models
Several models can be used to express the spring force acting on each bead. Firstly,
one should distinguish between the models that limit the maximum spring length

CHAPTER 3. Theoretical background 31
and the models that do not impose any restriction on the spring length. Among
the mostly used models, the Marko-Siggia, Cohen Pad´e and FENE models fall into
the first category, while the Hookean model falls in the second one.
The Hookean model is arguably the simplest model representing a spring [24],
FS
i=
N
X
j∈gi
Hxij (3.46)
where H=3kT Nk,s
l2. As can be seen, the force is linearly proportional to the
spring extension and both are unlimited (here lis simply a parameter, and not
the effective limit of maximum spring extension). Although unphysical for high
deformations, the Hookean model is at the basis of the closed-form UCM and
Oldroyd-B constitutive equations used in continuum mechanics simulations, avail-
able in rheoTool. Some of the difficulties felt in the continuum simulations with
these two models arise precisely due to the unlimited stretch of Hookean springs,
which usually translate in unbounded stresses.
For the extension-limited models, we have [24]:
•Marko-Siggia model
FS
i=
N
X
j∈gi
2
3Hl "|xij|
l−1
4+1
4 (1 − |xij |/l)2#xij
|xij|(3.47)
•Cohen Pad´e model
FS
i=
N
X
j∈gi
H
33−(|xij|/l)2
1−(|xij|/l)2xij (3.48)
•FENE model (Warner spring law)
FS
i=
N
X
j∈gi
H1
1−(|xij|/l)2xij (3.49)
The relation between the spring force and the spring extension is non-linear in
these three models, and all are singular for |xij |=l, which represents an asymp-
tote for the springs extension. For low spring extension, the three models closely
approach the Hookean model. For high spring extension (close to the asymptote),
both FENE and Cohen Pad´e models present sharper gradients of force than the
Marko-Siggia model, which directly impacts the numerical stability of the time
integration algorithm.
3.8.4 Time integration algorithm
The integration over time of Eq. (3.43) can be performed with explicit, semi-
implicit or implicit methods, which differ essentially in numerical stability and

CHAPTER 3. Theoretical background 32
computational cost. Most of the methods suggested in the literature are first-order
accurate in time, using Euler schemes to discretize the time derivative (higher-order
methods are not effective due to the random nature of the Brownian term [26]).
The explicit first-order Euler method evolves the beads positions from the
previous time-step (t) to the new time-step (t+ ∆t) as,
rt+∆t
i=rt
i+ ∆tBt
i(3.50)
where Bt
irepresents the whole right hand side of Eq. (3.43) evaluated at the
previous time-step. This integration scheme only requires the explicit evaluation
of mathematical expressions, presenting a low computational cost per time-step.
However, the numerical stability of the scheme is highly dependent on ∆t, which
should be kept sufficiently small. The numerical stability is evaluated by the
capability of the method in respecting the constraint Ri≤l, when bounded spring
force models are used. In practice, the time-step that satisfies such constraint is
relatively small, leading to the need of a very high number of iterations (time-
steps) to simulate a given period of physical time. Therefore, the explicit time
integration is seldom used.
In the semi-implicit scheme described in [4], the explicit Euler scheme (Eq.
3.50) is used while Ri< αl, where 0 < α ≤1 is defined by the user, and is usually
close to 1. Once this condition is violated, a two-steps computation is used:
r∗
i=rt
i+ ∆t"uf+
N
X
j=1,j6=i
DijFS
j
kT +DiiFEV
i
kT +6
∆t0.5i
X
j=1
σijnj#t
(3.51)
rt+∆t
i=r∗
i+ ∆tDiiFs
i
kT t+∆t
(3.52)
In Eq. (3.51), the intermediate beads positions (r∗) are obtained explicitly from
the contribution of drag, Brownian and exclusion volume forces, and also from the
off-diagonal spring force terms. This results in a non-linear system of equations
that can be solved, for example, with the iterative Newton-Raphson method. As
discussed in [4], the Newton-Raphson method requires solving a linear system of
equations in each iteration (k),
Jk∆rk=−fk(3.53)
where fkis a vector function whose expression depends on the spring model, Jk
is the Jacobian of fkand ∆rkis a vector representing the difference in the beads
positions between the previous and the current iteration. Further details are given
in Ref. [4]. The linear system of equations (3.53) can be solved using different
methods.
Chapter 4
Overview of rheoTool
In the previous Chapter, the main theoretical points behind rheoTool were briefly
discussed. This Chapter focus on the numerical implementation of the governing
equations in the OpenFOAM R
environment, providing an overview of the func-
tionalities available in rheoTool.
4.1 The constitutiveEquations library
4.1.1 Available GNF and viscoelastic models
The constitutiveEquations library is a main component of rheoTool, since it con-
tains all the viscoelastic and GNF constitutive equations, which can be called from
the solvers. It was derived from the viscoelasticTransportModels library [1]. How-
ever, instead of restricting the library to viscoelastic models, we also extend it to
include GNF models, most of them already present in OpenFOAM R
. This was
done in order to allow accessing both classes of models from a single library, hence
from a single solver.
Most of the models available in the constitutiveEquations library are displayed
in Table 4.1, along with the respective expressions to be used in Eqs. (3.3), (3.4),
(3.6) and (3.8). However, some models falling in special categories as elastovis-
coplasticity and multispecies modeling, are presented in the text following the
table, in order to provide a more detailed discussion about them.
33

CHAPTER 4. Overview of rheoTool 34
Table 4.1: Available constitutive models in the constitutiveEquations library.
GNF models
Model 1TypeName ηs( ˙γ)
Newtonian Newtonian η
2(Bounded) Power-Law PowerLaw max ηmin,min ηmax, k ˙γn−1
Carreau-Yasuda CarreauYasuda η∞+ (η0−η∞)[1 + (k˙γ)a]n−1
a
2Herschel-Bulkley HerschelBulkley Bounded: min η0, τ0˙γ−1+k˙γn−1
3Papanastasiou reg.: min η0, τ0˙γ−1[1 −exp(−m˙γ)] + k˙γn−1
2Casson Casson
Bounded: max ηmin,min ηmax,√η∞+qτ0
˙γ2
Papanastasiou reg.: n√η∞+qτ0
˙γ1−exp −√m˙γo2
1Corresponds to the name entry identifying the model in the source code.
2Special care is taken in these models to avoid division by zero when ˙γis zero or very small and n−1<0. For ˙γ < VSMALL, the
value ˙γ=VSMALL is used in the computation of the shear viscosity (VSMALL = 10−300 for versions using double precision).
3The original Papanastasiou regularization does not include the artificial upper-bounding by η0. However, this bounding is needed
to avoid an infinite viscosity for ˙γ→0 (e.g. startup of flow) and n < 1. The original Papanastasiou regularization is recovered
for η0→ ∞. In practice, η0should be low enough to avoid an infinite viscosity in quiescent conditions and high enough to allow
Papanastasiou regularization to take control in the remaining situations.
Notes:
•˙γ=q˙
γ:˙
γ
2, with ˙
γ=∇u+∇uT.
•Iis the identity tensor and D
Dt(φ) = ∂φ
∂t +u·∇φrepresents the material derivative of the generic variable φ.
•∇
τ=∂τ
∂t +u·∇τ−τ·∇u− ∇uT·τis the upper-convected derivative of τ.
•
τ=∇
τ+ζ(τ·D+D·τ) is the Gordon-Schowalter derivative of τ, with D=1
2(∇u+∇uT).
34

CHAPTER 4. Overview of rheoTool 35
Continuation of Table 4.1
Viscoelastic models solved in the standard extra-stress or conformation tensor variables
Model TypeName ηs( ˙γ)ηp( ˙γ)λ( ˙γ) Constitutive Equation
Oldroyd-B Oldroyd-B ηsηpλτ+λ∇
τ=ηp(∇u+∇uT)
WhiteMetzner
(Carreau-Yasuda) WhiteMetznerCY ηsηp[1 + (K˙γ)a]n−1
aλ[1 + (L˙γ)b]m−1
bτ+λ( ˙γ)∇
τ=ηp( ˙γ)(∇u+∇uT)
Giesekus Giesekus ηsηpλτ+λ∇
τ+αλ
ηp(τ·τ) = ηp(∇u+∇uT)
PTT linear PTTlinear ηsηpλh1 + ελ
ηptr(τ)iτ+λ
τ=ηp(∇u+∇uT)
PTT exponential PTTexp ηsηpλe
ελ
ηptr(τ)τ+λ
τ=ηp(∇u+∇uT)
FENE-CR FENE-CR ηsηpλh1 + λD
Dt1
fiτ+λ
f∇
τ=ηp(∇u+∇uT)
where f=L2+λ
ηptr(τ)
L2−3
FENE-P FENE-P ηsηpλ
τ+λ
f∇
τ=aηp
f(∇u+∇uT)−D
Dt1
f[λτ+aηpI]
where f=L2+λ
aηptr(τ)
L2−3and a=L2
L2−3
3Rolie-Poly Rolie-Poly ηsηpλD
λD∇
A=−(A−I)−2kλD
λR1−p3/tr(A)A+βtr(A)
3δ(A−I)
where k=3−χ2
χ2
max 1−1
χ2
max
1−χ2
χ2
max 3−1
χ2
max and χ=qtr(A)
3
eXtended Pom-Pom XPomPom ηsηpλB
fτ+λB∇
τ+αλB
ηp(τ·τ) + ηp
λB(f−1) I=ηp(∇u+∇uT)
where f= 2λB
λSe2
q(Λ−1) 1−1
Λn+1 +1
Λ2h1−α
3
tr(τ·τ)
(ηP/λB)2iand Λ=q1 + tr(τ)
3ηP/λB
3See Ref. [27]. This model is exclusively solved in the conformation tensor variable, which is then converted to τusing, τ=ηp
λDk(A−I).
35

CHAPTER 4. Overview of rheoTool 36
Continuation of Table 4.1
‡Viscoelastic models solved with the log-conformation approach
Model TypeName Θ¸τ4,5Constitutive Equation
6Oldroyd-B Oldroyd-BLog τ=ηp
λ(eΘ−I)Υ=1
λe−Θ−I
7WhiteMetzner
(Carreau-Yasuda) WhiteMetznerCYLog τ=ηp
λ(eΘ−I)Υ=1
λ( ˙γ)e−Θ−I
Giesekus GiesekusLog τ=ηp
λ(eΘ−I)Υ=1
λhe−Θ−I−αeΘe−Θ−I2i
PTT linear PTTlinearLog τ=ηp
λ(1−ζ)(eΘ−I)Υ=1
λn1 + ε
1−ζtr(eΘ)−3o(e−Θ−I)
PTT exponential PTTexpLog τ=ηp
λ(1−ζ)(eΘ−I)Υ=1
λeε
1−ζ(tr(eΘ)−3)(e−Θ−I)
FENE-CR FENE-CRLog τ=ηpf
λ(eΘ−I)Υ=f
λe−Θ−I, where f=L2
L2−tr(eΘ)
FENE-P FENE-PLog τ=ηp
λ(feΘ−aI)Υ=1
λae−Θ−fI, where a=L2
L2−3and f=L2
L2−tr(eΘ)
8Rolie-Poly Rolie-PolyLog τ=ηp
λDk(eΘ−I)Υ=−1
λDe−Θ(eΘ−I)+2kλD
λR1−p3/tr(eΘ)eΘ+βtr(eΘ)
3δ(eΘ−I)
eXtended Pom-Pom XPomPomLog τ=ηp
λB(eΘ−I)
Υ=−1
λBe−Θ(f−2α)eΘ+αeΘeΘ+ (α−1)I
where f= 2λB
λSe2
q(Λ−1) 1−1
Λn+1 +1
Λ21−α−α
3tr(eΘ(eΘ−2I))and Λ=qtr(eΘ)
3
‡The solvent viscosity, the polymeric viscosity coefficient and the relaxation time for the models solved in variable Θare the same as those for the models solved in
variable τor A, in the previous page.
4For the shortness of notation, we have introduced the operator: Υ=∂Θ
∂t +u·∇Θ−(ΩΘ −ΘΩ)−2B.
5The following equivalences hold true: eΘ=A=RΛRTand e−Θ=A−1=RΛ−1RT.
6For this model, we also included the square-root conformation approach [15] (TypeName: Oldroyd-BSqrt) and the rootkkernel approach [14] (TypeName: Oldroyd-
BRootk), for demonstration purposes.
7This log-conformation tensor approach of the White-Metzner model is only applicable when ηp( ˙γ)
λ( ˙γ)=ηp
λis constant, i.e., for K=L,a=band n=m. The version
based on the extra-stress tensor variable is more general and does not have this restriction.
8The expression for kis the same as for the model solved in variable A, in the previous page, considering that A=eΘ.
36

CHAPTER 4. Overview of rheoTool 37
In a footnote of Table 4.1, the (invariant) shear-rate used to compute shear-rate
dependent variables was defined as
˙γ=r˙
γ:˙
γ
2=√2D:D,with ˙
γ=∇u+∇uTand D=1
2˙
γ(4.1)
In the code, the shear-rate is returned by function strainRate() as
strainRate() = sqrt(2.0)*mag(symm(fvc::grad(U())))
and it is equivalent to Eq. (4.1). Indeed,
symm(fvc::grad(U())) =1
2∇u+∇uT=1
2˙
γ=D
thus,
sqrt(2.0)*mag(symm(fvc::grad(U()))) =√2q1
2˙
γ:1
2˙
γ=q˙
γ:˙
γ
2=√2D:D
which is equal to Eq. (4.1) – the definitions of operators symm(),mag() and :
(double contraction) can be found in the OpenFOAM R
programmers’ guide. Note
that the invariant computed in Eq. (4.1) is actually the magnitude of the rate-of-
strain tensor, which is usually called shear rate or strain rate for shear-dominated
or extensional-dominated flows, respectively.
All the viscoelastic models presented in Table 4.1 can be solved in the standard
extra-stress tensor τ(Eq. 3.4) or using the log-conformation approach (Eq. 3.8).
The selection is made in dictionary constitutiveProperties, which should be
located inside the folder constant/ of the case (see more details in section 5.1.1).
For the Oldroyd-B model, we provide two additional methods for demonstration
purposes. One of them (TypeName: Oldroyd-BSqrt) consists in solving the con-
stitutive equation using the square-root of the conformation tensor, according to
Ref. [15]. The second approach (TypeName: Oldroyd-BRootk) allows to apply a
general rootkkernel, as described in Ref. [14]. Both can be used in 2D or 3D
simulations, as any other model in the library. Since both models are only illus-
trative, their implementation and theory are not described in this guide, although
both can be easily understood after a close inspection of the source code and tak-
ing as reference the literature cited for each one. Furthermore, tutorials for both
methodologies are included in rheoTool (see the tutorial of Section 5.1.7).
!Other models:
+VCM model (TypeName: VCM )
The Vasquez-Cook-McKinley (VCM) model [28] can be used to simulate worm-
like micellar solutions, being able to predict the shear-banding behavior typically
observed in these fluids. The model represents such fluids as a combination of
large (subscript A) and small chain (subscript B) species that can convert into
each other. A transport equation is solved for each species [28],
∂nA
∂t +u· ∇nA= 2DA∇2nA+1
2λA
cBn2
B−cAnA
λA
(4.2)
∂nB
∂t +u· ∇nB= 2DB∇2nB−cBn2
B
λA
+ 2cAnA
λA
(4.3)

CHAPTER 4. Overview of rheoTool 38
where nis the dimensionless number density of the specie, λis the relaxation time,
Dis the diffusivity coefficient and cAand cBare, respectively, the dimensionless
breakage and reformation rates, expressed as
cA=cAEq +χ
3˙
γ:A
nA(4.4)
cB=cBEq (4.5)
In Eqs. (4.2) and (4.3), the double contraction term originally presented in [28]
is not included, in order to simplify the definition of no-flux boundary conditions
for nAand nBat impermeable walls (which reduce to a zero-gradient condition).
The contribution of these omitted terms is typically negligible.
A constitutive equation is also solved for each species [28],
λA∇
A+A−nAI−λADA∇2A=cBnBB−cAA(4.6)
λA∇
B+B−nBI
2−λADB∇2B=−2cBnBB+ 2cAA(4.7)
where Aand Brepresent the conformation tensor of each species, and =λB
λA. The
contribution of each species to the polymeric extra-stress tensor is given by [28],
τ=G0[(A+ 2B)−(nA+nB)I] (4.8)
where G0is the elastic modulus. In the absence of flow, nA= 1, nB=q2cAEq
cBEq
,
A=I,B=nB
2Iand τ=0.
+RRM (TypeName: RRM )
Also in the context of modeling the flow of wormlike micellar solutions, Dutta
and Graham proposed recently the Reactive Rod Model (RRM), accounting for
the formation/destruction of flow-induced structures [29]. In this model, micelles
are approached by rods, whose orientation tensor, S, evolves according to [29],
dS
dt=−6DrS−I
3+∇uT·S+S· ∇u−2∇uT:<uuuu >(4.9)
where
Dr=Dr,0
L∗3ln L∗+m
m(4.10)
is a time-varying diffusion coefficient (units are s−1), L∗=L/L0is the time-varying
rod length normalized by its initial value and mis the initial aspect ratio of the
rods (see [29] for more details). In Eq. (4.9), the last term is approximated by [29]
∇uT:<uuuu >≈1
5[S·D+D·S−S·S·D−D·S·S+ 2S·D·S+ 3(S:D)S]
(4.11)

CHAPTER 4. Overview of rheoTool 39
and D=1
2∇u+∇uTis the rate of deformation tensor. The variation of the
normalized rod length is computed from [29]
dL∗
dt=λSDr,0
1−L∗
α+β/P e 2(1 −L∗) + kDr,0r3
2ˆ
S:ˆ
S(4.12)
where λS,α,βand kare parameters of the model, ˆ
S=S−I
3and P e is a P´eclet
number computed locally, P e =˙γ
Dr,0( ˙γis the strain-rate defined in Eq. 4.1). The
extra-stress due to the rods is accounted for as [29]
τ=G0
L∗3S−I
3+1
2Dr∇uT:<uuuu >(4.13)
where G0is the elastic modulus. Note that due to the generic strain-rate defi-
nition used in the P´eclet number, the strain-rate retrieved for a pure shear-flow
corresponds effectively to the local shear-rate, but for a pure extensional flow, the
strain-rate computed does not correspond to the extension rate (it differs by a con-
stant, that can be incorporated in parameter βof Eq. 4.12). Those considerations
are important when using rheoTestFoam. Other measures of the hydrodynamic
stresses can be used in the P´eclet number definition in order to generalize it for
any flow.
+Bautista-Manero-Puig model (TypeName: BMP and BMPLog)
The Bautista-Manero-Puig (BMP) model is still another option to simulate
worm-like micellar solutions [30]. This model can also predict thixotropy and it
results from the combination between the UCM model and Fredrickson’s kinetic
equation [30].
The polymeric extra-stress tensor is evolved according to
ϕG0τ+∇
τ=G0(∇u+∇uT) (4.14)
and Fredrickson’s kinetic equation governing the structure parameter (ϕ) is repre-
sented by
∂ϕ
∂t +u· ∇ϕ=ϕ0−ϕ
λ+k(ϕ∞−ϕ)τ:D(4.15)
In Eqs. (4.14) and (4.15), D=1
2(∇u+∇uT), G0is the instantaneous relaxation
modulus, ϕis the fluidity (≡η−1
P), ϕ0is the zero shear-rate fluidity, ϕ∞is the
infinite shear-rate fluidity, λis the structural relaxation time and kis a kinetic
constant for structure breaking down [30].
The model is also implemented within the log-conformation approach, taking
a form similar to the log-transformed Oldroyd-B equation presented in Table 4.1,
with λ−1replaced by ϕG0and ηPreplaced by ϕ−1.
+Saramito’s model (TypeName: Saramito and SaramitoLog)
Elastoviscoplastic fluids exhibit a solid-like behavior below the yield stress and
they flow as viscoelastic fluids when the yield stress is exceeded. The stress-strain
relation in each regime can assume several forms.

CHAPTER 4. Overview of rheoTool 40
The model proposed by Saramito [31] attempts to merge the Herschel–Bulkley
model for yield-stress fluids with the Oldroyd-B/PTT model for viscoelastic fluids.
Accordingly, the resulting constitutive relation is given by
f(τ)ηpmax 0,σ−τ0
kσn1
n
τ+λ
τ=ηp(∇u+∇uT) (4.16)
where τ0is the yield stress, f(τ) = 1 and σ=IIτD=pτD:τD
2is the second
invariant of the deviatoric stress tensor, τD=τ−tr(τ)
NI. An elastic modulus can
be defined, G=ηp
λ, which is often found in the literature in the description of
this model. We remember that
τrepresents the Gordon-Schowalter derivative
defined as,
τ=∇
τ+ζ(τ·D+D·τ), with D=1
2(∇u+∇uT), which reduces to the
upper-convected derivative for ζ= 0.
For n= 1 and k=ηp, Saramito’s model degenerates into a previous model pro-
posed by the same author [32], that merges the Bingham model with the Oldroyd-B
or PTT models, depending on the form taken by f(τ):
f(τ) =
1 , Oldroyd-B
1 + ελ
ηptr(τ) , linear PTT
eελ
ηptr(τ), exponential PTT
(4.17)
The four variants of the model are available in rheoTool, where both the Her-
schel–Bulkley and PTT variants can avoid the possible infinite Oldroyd-B elonga-
tional viscosity for W i ≥0.5 in extensional flows of Oldroyd-B fluids. In addition,
the four variants can also be solved with the log-conformation approach and the
governing equation becomes
∂Θ
∂t +u·∇Θ−(ΩΘ −ΘΩ)−2B=g(τ)
λe−Θ−I(4.18)
with
g(τ) =
ηpmax 0,σ−τ0
kσn1
n, Oldroyd-B–Herschel-Bulkley
max 0,σ−τ0
σ, Oldroyd-B–Bingham
max 0,σ−τ0
σn1 + ε
1−ζtr(eΘ)−3o, lin. PTT–Bingham
max 0,σ−τ0
σeε
1−ζ(tr(eΘ)−3) , exp. PTT–Bingham
(4.19)
and the polymeric extra-stress tensor is recovered using τ=ηp
λ(1−ζ)(eΘ−I).
+ML-IKH model (TypeName: ML-IKH )
Elastoviscoplastic models can be rendered more complex (and realistic) once
thixotropy is added to them. This is the case of the Multi-Lambda Isotropic Kine-
matic Hardening (MLK-IKH) model [33]. According to this model, the equation
governing the polymeric extra-stress tensor is given by [33]
max 0,1−λky
στeff +λλE∇
τ=ληp(∇u+∇uT) (4.20)

CHAPTER 4. Overview of rheoTool 41
where λEis the viscoelastic relaxation time, τeff =τ−κback, with κback =
khA+ 2A2, and σ=IIτD
eff =qτD
eff:τD
eff
2, where τD
eff =τeff −tr(τeff)
NI(Nis the
number of dimensions of the problem). Eq. (4.20) closely resembles the governing
equation for τin Saramito’s model (Eq. 4.16). Tensor Ais related with material
hardening and its evolution follows [33]
∂A
∂t +u· ∇A+Ω·A−A·Ω=Dp·A+A·Dp+Dp−qdpA(4.21)
where Ω=∇u− ∇uT/2 is the vorticity tensor, dp=qDp:Dp
2and
Dp=(0, if σ < λky
(σ−λky)
2ληp·τeff
σ, if σ≥λky
(4.22)
is the plastic component of the rate of deformation tensor. In the previous equa-
tions, λis a structure parameter regulating the thixotropic behavior and is ob-
tained from the multi-lambda model [33],
λ=
M
X
i=1
Ciλi(4.23)
where each of the Mmodes of λobeys
dλi
dt =Di−k1φaλn
i+k2φb(1 −λi) + k3(1 −λi)(4.24)
and φcan be computed in two ways [33],
φ=(max (0, σ −λky) , Stress-controlled form
2dp, Rate-controlled form (4.25)
The model implementation in rheoTool allows for arbitrary Mmodes, where
lists Cand D(size M) should be provided as input by the user. Thus, the complete
list of input parameters for this model is: ηp, C, D, a, n, b, k1, k2, k3, ky, kh, q and λE,
to which we should add the solvent viscosity (ηs) and the fluid density (ρ). If no
initial conditions are provided for each λi, the solvers assume λi,0= 1 by default.
As discussed in [33], the transformation of the ML-IKH model from its scalar
version to the above tensorial version assumes some simplifications, which impose
restrictions on the model applicability (see [33] for more details).
4.1.2 A note on FENE-type models
The Finitely Extensible Non-linear Elastic (FENE) models were originally devel-
oped based on the representation of polymer molecules by elastic dumbbells [7].
In such analysis, the end-to-end vector for each molecule is naturally related with
the conformation tensor, such that the constitutive equations for this family of
models is frequently written and handled as a function of the conformation tensor.
The polymeric contribution to the momentum equation is then accounted for by

CHAPTER 4. Overview of rheoTool 42
transforming the conformation tensor (A) in the extra-stress tensor (τ), using the
relations in Table 4.1 (for the models expressed in the log-conformation approach,
considering that eΘ=A). The same applies for the Roly-Polie model.
In order to write the constitutive equation for FENE-type models as a function
of τ, some terms arise, which may compromise the numerical stability. Further-
more, the computational cost to evaluate the resulting expression is higher than
for the original model. As such, some authors simplify the constitutive equation
by neglecting certain terms [34]. For the FENE-CR and FENE-P models, the
complete constitutive equation written as a function of Aand τand the modified
formulation in τare:
•FENE-CR
–Complete in A:
λ∇
A=−f(tr(A))(A−I), where f(tr(A)) = L2
L2−tr(A)
–Complete in τ(see Table 4.1):
h1 + λD
Dt1
fiτ+λ
f∇
τ=ηp(∇u+∇uT), where f=L2+λ
ηptr(τ)
L2−3
–Modified in τ(usually known as FENE-MCR):
τ+λ
f∇
τ=ηp(∇u+∇uT), where f=L2+λ
ηptr(τ)
L2−3
•FENE-P
–Complete in A:
λ∇
A=−[f(tr(A))A−aI], where f(tr(A)) = L2
L2−tr(A)and a=L2
L2−3
–Complete in τ(see Table 4.1):
τ+λ
f∇
τ=aηp
f(∇u+∇uT)−D
Dt1
f[λτ+aηpI], where f=L2+λ
aηptr(τ)
L2−3
and a=L2
L2−3
–Modified in τ:
τ+λ
f∇
τ=aηp
f(∇u+∇uT), where f=L2+λ
aηptr(τ)
L2−3and a=L2
L2−3
In rheoTool, all the formulations are available and can be used (see Section
5.1.1 to know how to select each one). The steady material functions evaluated
for canonical flows are the same for all the formulations. However, this is not true
when evaluating the transient material functions: the modified formulations have
a different behavior comparing with the complete ones, which are themselves simi-
lar. For a generic flow, the complete formulations, either in Aor τ, should provide
similar results, since they are mathematically equivalent. Due to discretization

CHAPTER 4. Overview of rheoTool 43
errors and stability issues, this may not be true. Regarding the modified formula-
tions, they are not expected to behave exactly as the complete ones, even in the
limit of highly refined grids.
From our experience, we strongly recommend using the formulations written
and solved as a function of Afor FENE-type models. Those are the most sta-
ble, the most accurate regarding the original theory presented in [7] and the ones
for which there is direct correspondence with the models solved with the log-
conformation approach, since those were derived from the constitutive equations
written as a function of the conformation tensor. Note that the FENE-CR and
FENE-P models available in the viscoelasticTransportModels library of viscoelas-
ticFluidFoam [1] are expressed in the modified form presented above.
4.1.3 Multi-mode modeling
Similarly to the viscoelasticTransportModels library [1], the constitutiveEquations
library also supports multi-mode modeling for viscoelastic models. In such cases,
the total extra-stress tensor is the sum of the extra-stress tensor resulting from
each kth mode
τ0=
N
X
k=1 τk+τk
s(4.26)
In practice, this is achieved by assembling and solving one constitutive equa-
tion for each kth mode, that is, Eq. (3.3) – solvent contribution – and Eq. (3.4)
or (3.8) – polymer contribution – are built and solved Ntimes each time-step. A
warning should be made at this point, since this approach is probably not the most
conventional. Indeed, τsin Eq. (4.26) is commonly placed outside the summation
symbol, since multiple modes are only assigned to the polymeric contribution. To
achieve this in rheoTool, and considering the expression for τsin Eq. (3.3), the
user must split the ”single-solvent viscosity” by the Nmodes consid-
ered, in any way, such that this ”single-solvent viscosity” is recovered summing
all these Nvalues in Eq. (4.26).
4.1.4 Analysis of a code sample
For the readers still initiating their journey in OpenFOAM R
, we will explore in this
section the implementation of the Oldroyd-B constitutive model, solved with the
log-conformation tensor approach. This example will establish the link between
part of the theory described in Chapter 3and its implementation in the source
code.
The source code displayed in Listing 4.1 is taken from file src/libs/constitut
iveEquations/constitutiveEqs/Oldroyd-B/Oldroyd-BLog/Oldroyd_BLog.C.
Let’s analyze the most important lines:
•lines 1-91: this section initializes the variables used in the constitutive model.
In terms of field variables, we have (lines 23-84): tau (τ), theta (Θ), eigVals
(Λ) and eigVecs (R). All those fields must be defined by the user when

CHAPTER 4. Overview of rheoTool 44
starting a simulation, except eigVals and eigVecs , which can be defined
or not. If defined (typical of a restart from a previous simulation), they are
used in the first time-step; otherwise, they are both initialized as the identity
tensor/matrix, corresponding to a null extra-stress tensor (τ). Afterwards,
the fluid properties are read from a dictionary (lines 85-88), along with the
stabilization method selected by the user (line 90): none, BSD or the stress-
velocity coupling described in Section 3.3.2.
•lines 94-151: this section implements the member function correct(), whose
purpose is to update the polymeric extra-stress field, by evolving Θaccord-
ing to the constitutive equation. From line 96 to 105, variables M,Ωand
B, defined in Eqs. (3.9)–(3.11), are computed. The function decomposeG-
radU() is a member function of the base class constitutiveEq (find it in the
file constitutiveEq.C), since it is used by all the models based on the
log-conformation tensor approach. Then, in lines 107-140, the constitutive
equation (Eq. 3.8) is built and solved, after which Θis diagonalized to com-
pute its eigenvectors/eigenvalues (line 144). The function doing this task
(calcEig()) is also a member function of the class constitutiveEq and the al-
gorithm being used by default for that purpose is the QR method provided
by the Eigen library [35]. Another method is also available, as discussed in
Section 4.1.5. Note that the eigenvalues retrieved by function (calcEig())
are already exponentiated, so that they correspond to Λ= exp(ΛΘ). Fi-
nally, with the currently computed eigenvectors/eigenvalues, the polymeric
extra-stress tensor (τ) is recovered from the conformation tensor (line 148),
according to the relation established in Eqs. (3.6) and (3.14) (check Table
4.1 for other models), and will be used in the divTau() function described
below.
•in the viscoelasticTransportModels library [1] each model was in charge to
define its own contribution to the momentum equation, i.e., the term (∇·τ0).
In the constitutiveEquations library there is a default definition of this term
in the base class. In fact, the function divTau() is now defined in class
constitutiveEq and can be found in file constitutiveEq.C, Listing 4.2. This
function starts by distinguishing between GNF and viscoelastic models in
line 7. For a GNF model (lines 8-14), the extra-stress contribution is ∇·τ0=
∇·η( ˙γ)∇u+∇u·∇η( ˙γ), divided by the density to be compliant with the
usual strategy of OpenFOAM R
for single-phase, incompressible fluid flows.
Note that the second term is included to account for a shear-rate dependent
viscosity coefficient. By definition, a GNF fluid has no elasticity, thus τ=0.
For a viscoelastic fluid (lines 17-49), the output depends on the stabilization
method selected (see function checkForStab() in constitutiveEq.C for the
correspondence between indexes and the method): if none, there is no added
stabilization and ∇·τ=∇·τ−∇·ηs∇u; if BSD, then the both-sides-diffusion
technique is used and ∇·τ=∇·τ− ∇·ηp∇u+∇·(ηs+ηp)∇u(Eq. 3.5);
otherwise (if coupling), the stress-velocity coupling technique of Eq. (3.17)
is used and ∇·τ=∇·τ− ∇·ηp∇u+∇·(ηs+ηp)∇u. Note that using the
coupling stabilization is the method recommended for most of the cases,

CHAPTER 4. Overview of rheoTool 45
being the one used by default if no information is provided by the user.
However, some cases may require the use of no stabilization, as for example
the simulation of multimode models with ηPηS– the amount of artificial
diffusion may mask the real phenomena in transient simulations. For the
cases using stabilization, the explicit behavior effects on transient results
can be minimized by performing inner iterations at each time-step, a subject
discussed later in this guide (see Section 4.5.1). In file consitutiveEq.C, a
function divTauS() is also included, which retrieves part of the extra-stress
contribution to the momentum equation, when solving two-phase flows (this
topic will be discussed later).
1#include "Oldroyd_BLog.H"
#include "addToRunTimeSelectionTable.H"
3
// **************Static Data Members ********
*****//
5
namespace Foam{
7namespace constitutiveEqs{
defineTypeNameAndDebug(Oldroyd_BLog, 0);
9addToRunTimeSelectionTable(constitutiveEq, Oldroyd_BLog,
dictionary);
}
11 }
// ****************Constructors *********
*****//
13
Foam::constitutiveEqs::Oldroyd_BLog::Oldroyd_BLog
15 (
const word& name,
17 const volVectorField& U,
const surfaceScalarField& phi,
19 const dictionary& dict
)
21 :
constitutiveEq(name, U, phi),
23 tau_
(
25 IOobject
(
27 "tau" + name,
U.time().timeName(),
29 U.mesh(),
IOobject::MUST_READ,
31 IOobject::AUTO_WRITE
),
33 U.mesh()
),
35 theta_
(
37 IOobject
(
39 "theta" + name,
U.time().timeName(),

CHAPTER 4. Overview of rheoTool 46
41 U.mesh(),
IOobject::MUST_READ,
43 IOobject::AUTO_WRITE
),
45 U.mesh()
),
47 eigVals_
(
49 IOobject
(
51 "eigVals" + name,
U.time().timeName(),
53 U.mesh(),
IOobject::READ_IF_PRESENT,
55 IOobject::AUTO_WRITE
),
57 U.mesh(),
dimensionedTensor
59 (
"I",
61 dimless,
pTraits<tensor>::I
63 ),
zeroGradientFvPatchField<tensor>::typeName
65 ),
eigVecs_
67 (
IOobject
69 (
"eigVecs" + name,
71 U.time().timeName(),
U.mesh(),
73 IOobject::READ_IF_PRESENT,
IOobject::AUTO_WRITE
75 ),
U.mesh(),
77 dimensionedTensor
(
79 "I",
dimless,
81 pTraits<tensor>::I
),
83 zeroGradientFvPatchField<tensor>::typeName
),
85 rho_(dict.lookup("rho")),
etaS_(dict.lookup("etaS")),
87 etaP_(dict.lookup("etaP")),
lambda_(dict.lookup("lambda")),
89 {
checkForStab(dict);
91 }
93 // ***************Member Functions ********
*****//
void Foam::constitutiveEqs::Oldroyd_BLog::correct()
95 {

CHAPTER 4. Overview of rheoTool 47
// Decompose grad(U).T()
97
volTensorField L = fvc::grad(U());
99
dimensionedScalar c1( "zero", dimensionSet(0, 0, -1, 0, 0, 0,
0), 0.);
101 volTensorField B = c1 *eigVecs_;
volTensorField omega = B;
103 volTensorField M = (eigVecs_.T() & L.T() & eigVecs_);
105 decomposeGradU(M, eigVals_, eigVecs_, omega, B);
107 // Solve the constitutive Eq in theta = log(c)
109 dimensionedTensor Itensor
(
111 "Identity",
dimensionSet(0, 0, 0, 0, 0, 0, 0),
113 tensor::I
);
115
fvSymmTensorMatrix thetaEqn
117 (
fvm::ddt(theta_)
119 + fvm::div(phi(), theta_)
==
121 symm
(
123 (omega&theta_)
- (theta_&omega)
125 + 2.0 *B
+ (1.0/lambda_)
127 *(
eigVecs_ &
129 (
inv(eigVals_)
131 - Itensor
)
133 & eigVecs_.T()
)
135 )
137 );
139 thetaEqn.relax();
thetaEqn.solve();
141
// Diagonalization of theta
143
calcEig(theta_, eigVals_, eigVecs_);
145
// Convert from theta to tau
147
tau_ = (etaP_/lambda_) *symm( (eigVecs_ & eigVals_ & eigVecs_
.T()) - Itensor);
149

CHAPTER 4. Overview of rheoTool 48
tau_.correctBoundaryConditions();
151 }
Listing 4.1: Source code for the Oldroyd-BLog constitutive model
(Oldroyd BLog.C)
1tmp<fvVectorMatrix> constitutiveEq::divTau
(
3const volVectorField& U
)const
5{
7if (isGNF())
{
9return
(
11 fvm::laplacian( eta()/rho(), U, "laplacian(eta,U)")
+ (fvc::grad(U) & fvc::grad(eta()/rho()))
13 );
}
15 else
{
17 if (stabMeth_ == 0) // none
{
19
return
21 (
fvc::div(tau()/rho(), "div(tau)")
23 + fvm::laplacian(etaS()/rho(), U, "laplacian(eta,U
)")
);
25
}
27 else if (stabMeth_ == 1) // BSD
{
29
return
31 (
fvc::div(tau()/rho(), "div(tau)")
33 - fvc::laplacian(etaP()/rho(), U, "laplacian(eta,U
)")
+ fvm::laplacian( (etaP()+ etaS())/rho(), U, "
laplacian(eta,U)")
35 );
37 }
else // coupling
39 {
41 return
(
43 fvc::div(tau()/rho(), "div(tau)")
- (etaP()/rho()) *fvc::div(fvc::grad(U))
45 + fvm::laplacian( (etaP() + etaS())/rho(), U, "
laplacian(eta,U)")
);

CHAPTER 4. Overview of rheoTool 49
47
}
49 }
}
Listing 4.2: Source code of the virtual function divTau() defined in file
constitutiveEq.C
4.1.5 Advanced settings
As aforementioned, the eigenvectors/eigenvalues used in the models based on the
log-conformation approach are computed, by default, using the QR algorithm pro-
vided by the Eigen library [35]. However, there is also the possibility to use an
iterative Jacobi method [36]. While both options offer good accuracy and stabil-
ity, the QR algorithm was seen to be slightly faster and this is the reason of being
the default option. Switching between either methods is not run time selectable,
but hard-coded, instead. This can be controlled in member function calcEig()
of class constitutiveEq, located in file constitutiveEq.C. The Jacobi method
can be selected by uncommenting the currently commented block (// Eigen de-
composition using the iterative jacobi algorithm) and commenting the block (//
Eigen decomposition using a QR algorithm of Eigen library), i.e., all the remain-
ing lines inside the function. The source code of jacobi() function is located in
utils/jacobi.H. Note that, independently of which method is used in func-
tion calcEig(), this function will return the eigenvectors of the input tensor, and
the exponential of the eigenvalues of the same tensor. After re-compiling the
library with those modifications, all the log-conformation-based models will be
affected by those changes.
4.1.6 Adding new viscoelastic or GNF models
For the users with minimal programming skills in OpenFOAM R
, adding new vis-
coelastic or GNF models should be a straightforward task. The main steps are:
•copy-paste the folder of an existing model (that we will call template
model) in directory src/libs/constitutiveEquations/constitut
iveEqs/ for viscoelastic models, or src/libs/constitutiveEquatio
ns/constitutiveEqs/GNF/ for GNF models. Rename the folder and
the files inside it (.C and .H files) with the new model’s name. Remove the
.dep file inside the folder, as well as the folder for the log-implementation (if
not needed), in case of viscoelastic models.
•inside the source .C and header .H files, find-replace the old model’s name
by the new one (e.g. Ctrl +Hin gedit). This is to change the name of the
class, which is usually equal to the name given to the respective source file.
However, it is a good idea to always check first the name given to the class
of the template model.

CHAPTER 4. Overview of rheoTool 50
•add the source code of the new model to the compilation list of the library.
For that, edit file src/libs/constitutiveEquations/Make/files
by adding the path for the source code (see the entries for the other models
already there).
•make a first compilation of the new model, by running the script Allwmake
in directory src/. Note that, until this point, the source code of the new
model is the one from the original template model, where only the name of
the class has been changed. Thus, the model should compile without errors.
If not, something wrong occurred in the previous steps.
•the last step is to change the source code of the model in order to implement
the desired constitutive equation. Typically, the changes will be in three
main places: (i) the header file, where the new variables and parameters
of the model have to be declared (delete the ones from the template model
that are not needed); (ii) the constructor in the source file, where those new
entries should be added and initialized (delete the ones not needed); (iii)
function correct(), which is aimed to either update the viscosity (GNF) or
the polymeric extra-stresses (viscoelastic model). Note that you may also
need to define functions divTau() and divTauS() for your new model, if the
ones defined and used by default in the base class (see constitutiveEq.C)
are not adequate. After all the changes on the code had been completed,
compile again by running script Allwmake.
If all the steps listed above were successfully executed, then the new model
is now available to all the solvers of rheoTool. In order to use library constitu-
tiveEquations in any solver other than the ones provided with rheoTool, the user
should:
•add the header #include ”constitutiveModel.H” to the main solver.
•create a constitutiveModel object by calling the constructor, with the correct
arguments, for example: constitutiveModel constEq(U, phi).
•add the library constitutiveEquations to the Make/options, and specify its
path (check the Make/options of the solvers in rheoTool for an example).
4.2 The EDFModels library
4.2.1 Available EDF models
The list of runtime selectable EDF models is presented in Table 4.2.

Table 4.2: Available models for electrically-driven flows in the EDFModels library. The last column indicates the section in the user guide where the model
has been described.
Model 1TypeName 2,3,4fE5Governing Equations Section
Poisson-Nernst-Planck
(PNP)
6NernstPlanck
6NernstPlanckCoupled −F
N
P
i=1
zici(∇Ψ−Ea)
∇·(ε∇φExt) = 0
∇·(ε∇ψ) = −F
N
P
i=1
zici
∂ci
∂t +u·∇ci=∇·(Di∇ci) + ∇·Diezi
kT ∇Ψci
Section 3.7.1
Poisson-Boltzmann
(PB) PoissonBoltzmann −F
N
P
i=1
zici,0exp −ezi
kT ψ(∇Ψ−Ea)
∇·(ε∇φExt) = 0
∇·(ε∇ψ) + ψF
N
P
i=1
(aibi)∗=−F
N
P
i=1
(ai)∗+ψ∗F
N
P
i=1
(aibi)∗
with bi=−ezi
kT and ai=zici,0exp (biψ)
Section 3.7.3
Debye-H¨uckel
(DH) DebyeHuckel −F
N
P
i=1
zici,01−ezi
kT ψ(∇Ψ−Ea)
∇·(ε∇φExt) = 0
∇·(ε∇ψ) = −F
N
P
i=1
zici,01−ezi
kT ψSection 3.7.4
Slip velocity slipSmoluchowski 0∇·(ε∇φExt) = 0 Section 3.7.5
Ohmic Ohmic [∇·(ε∇φExt)] (∇φExt −Ea)
∂σ
∂t +u·∇σ=Deff∇2σ
∇·(σ∇φExt) = 0
Section 3.7.6
1Corresponds to the name entry identifying the model in the source code.
2fEis the electric body-force entering the momentum equation.
3Eais an optional argument - a single vector - representing a uniform electric field.
4When the splitting of potentials approach is selected for the PNP, PB and DH models, the user may choose to use (∇φExt −Ea), instead of (∇Ψ−Ea). Recall that the splitting of
potentials is given by Ψ=φExt +ψ(cf. Section 3.7.2).
5For the PNP, PB and DH models, the equations are presented according to the splitting of potentials approach, which is optional. When a single electric potential is intended to be
used, then replace ψby Ψand ignore the equations in terms of φExt.
6Both models solve the PNP equations, but NernstPlanck uses a segregated solver, whereas NernstPlanckCoupled solves the PNP equations in a fully-coupled way, which can be
optionally coupled to the Navier-Stokes equations.
51

CHAPTER 4. Overview of rheoTool 52
4.2.2 The potentials splitting approach and multi-species
modeling in the PNP, PB and DH models
The possibility of splitting the electric potential into two variables, as described
in Section 3.7.2, is available for the PNP, PB and DH models. When used, one
Poisson equation for ψand one Laplace equation for φExt are solved, as shown in
Table 4.2. In practice, the choice between using one or two potentials is achieved
in the following way: if only one potential ( psi ⇔Ψ) is present in the starting-
time folder, then it is assumed than a unique potential is to be used, while if two
potentials (phiE ⇔φExt and psi ⇔ψ) are defined, then the splitting approach is
assumed. Under the splitting approach, the user still has the option to include or
not the contribution of the intrinsic potential in the electric field definition of the
body-force entering the momentum equation. The choice is through the variable
psiContrib, which should be defined in a dictionary, as explained later in Section
5.4.1.
All the PNP, PB and DH models support multi-species modeling, with an ar-
bitrary number of species, each having different properties (charge valence, and
diffusivity, when it applies). On the other hand, the Ohmic model is only imple-
mented for a binary, symmetric electrolyte, although the two species may have
different diffusion coefficients.
4.2.3 Electrokinetic coupling loop in the PNP model
The PNP model has a loop for the coupling between the Nernst-Planck equations
(ionic concentration) and the Poisson equation (electric potential). This loop was
seen to be required to keep the second-order accuracy in time of the PNP model
[3]. Furthermore, it also allows the use of higher time-steps, while ensuring the
conservation of ions. Although it is allowed to select one single iteration for this
loop, we recommend the use of at least two iterations in any generic case. Moreover,
two coupling iterations is the default behavior for this model if no information is
provided by the user.
4.2.4 Coupled PNP model
This feature is only available for OpenFOAM R
versions.
The PNP system of equations can be solved coupled instead of segregated. The
segregated solution method is implemented in the NernstPlanck model, whereas
the coupled solution method is implemented in the NernstPlanckCoupled model.
The coupled solver, which has been presented in [5], displays a higher numerical
stability, but consumes more computational resources (memory and CPU time) per
time-step. The PNP system of equations can not only be solved coupled alone, as
it can also be coupled with momentum and continuity equations.
The technical aspects related with the use of the NernstPlanckCoupled model
are discussed in Section 4.4.8.

CHAPTER 4. Overview of rheoTool 53
4.2.5 Analysis of a code sample
As previously done in Section 4.1.4 for the constitutiveEquations library, in this
Section we analyze a piece of code from the EDFModels library in order to illustrate
the connection between the code and the theory previously discussed. However,
we should note that the differences, at the code level, between the different models
of the EDFModels library are bigger than in the constitutiveEquations library, as
can be deduced from Table 4.2.
The piece of code selected for that purpose, Listing 4.3, represents the imple-
mentation of the PNP model and can be found in src/libs/EDFModels/mod
els/NernstPlanck/NernstPlanck.C. Let’s start the analysis to the most
important parts:
•lines 11-33: this is the constructor of a subclass (NPSpecie), nested in the
main class (NernstPlanck). Remember that the PNP, PB and DH models
were all presented in a multi-species formulation, which is the form avail-
able in the code. The NPSpecie subclass is exactly each specie of the PNP
model. For each new specie, we can see the initialization of the following
attributes (members): the concentration field (ci), the charge valence (zi)
and the diffusivity (Di). The NernstPlanck class may have Ninstances of
the NPSpecie subclass, as much as defined by the user.
•lines 35-107: this is the constructor of the main class, where the several
fields and variables are initialized. The call to function checkForPhiE() in
line 44, which is implemented in the base class (see EDFEquation.C), is
checking for the existence of field phiE in the folder corresponding to the
starting time. If it is found, the code will interpret that the electric potential
should be split into 2 variables (phiE ⇔φExt and psi ⇔ψ), otherwise, the
code will consider that only a single potential should be used (psi ⇔Ψ).
This is how we identify if the splitting of potentials approach should be used.
We also highlight lines 89-107, where each specie of the PNP model is being
constructed and saved in a P trList <>, named species .
•lines 110-156: as suggested by the function’s name (Fe), these lines im-
plement the function returning the electric body-force for the momentum
equation. The charge density (rhoE) is computed in lines 114-120 (compare
with Eq. 3.28), and multiplied by the electric field in lines 122-155 (compare
with Eq. 3.26 and Table 4.2). The computation of the electric field may
include, or not, the contribution from the intrinsic potential, as discussed in
Section 3.7.2 – this is a user selection. Furthermore, the vector extraE is
an extra, uniform electric field, which can be optionally defined by the user
(see Table 4.2 and its footnotes).
•lines 158-252: it is inside this function, named correct(), that the electric-
related equations are solved for. The function is generally prepared to use
the splitting approach, in which case three equations are solved: the Laplace
equation for the external potential (lines 172-186), the Poisson equation for
the intrinsic (or full, unique) potential (lines 188-218) and the Nernst-Planck

CHAPTER 4. Overview of rheoTool 54
transport equation for each ionic specie (220-250) – all these equations can
be seen in Table 4.2. Each equation is inserted in a while loop controlled by
the number of cycles and by the initial residual of the equation solved for.
This is to optionally converge the explicit terms inside each equation, for
each inner-iteration. In addition, and as discussed in Section 4.2.3, all the
equations are solved inside an electrokinetic coupling loop (lines 161-251),
whose number of iterations is controlled by variable nIterPNP , that is read
from dictionary fvSolution (line 86). If the variable is not specified by
the user, 2 iterations are carried out by default.
All the other EDF models also have the functions Fe() and correct() in their
structure, which are defined according to the given model. We believe that the
readers/users will easily understand those functions by reading the comments in-
cluded in the code, and by comparing the code with Table 4.2.

CHAPTER 4. Overview of rheoTool 55
#include "NernstPlanck.H"
2#include "addToRunTimeSelectionTable.H"
4// *********Static Data Members ********//
namespace Foam{
6namespace EDFEquations{
defineTypeNameAndDebug(NernstPlanck, 0);
8addToRunTimeSelectionTable(EDFEquation, NernstPlanck, dictionary);
}
10 }
// **********Constructors **********//
12 Foam::EDFEquations::NernstPlanck::NPSpecie::NPSpecie
(
14 const word& name,
const surfaceScalarField& phi,
16 const dictionary& dict
)
18 :
ci_
20 (
IOobject
22 (
name,
24 phi.time().timeName(),
phi.mesh(),
26 IOobject::MUST_READ,
IOobject::AUTO_WRITE
28 ),
phi.mesh()
30 ),
zi_(dict.lookup("z")),
32 Di_(dict.lookup("D"))
{}
34
// **********Constructors **********//
36 Foam::EDFEquations::NernstPlanck::NernstPlanck
(
38 const word& name,
const surfaceScalarField& phi,
40 const dictionary& dict
)
42 :
EDFEquation(name, phi),
44 solvePhiE_(checkForPhiE(name, phi)),
psi_
46 (
IOobject
48 (
"psi" + name,
50 phi.time().timeName(),
phi.mesh(),
52 IOobject::MUST_READ,
IOobject::AUTO_WRITE
54 ),
phi.mesh()
56 ),
phiE_

CHAPTER 4. Overview of rheoTool 56
58 (
IOobject
60 (
"phiE" + name,
62 phi.time().timeName(),
phi.mesh(),
64 IOobject::READ_IF_PRESENT,
solvePhiE_ == false ? (IOobject::NO_WRITE) : (IOobject::
AUTO_WRITE)
66 ),
phi.mesh(),
68 dimensionedScalar
(
70 "zero",
psi_.dimensions(),
72 pTraits<scalar>::zero
),
74 zeroGradientFvPatchField<scalar>::typeName
),
76 relPerm_(dict.lookup("relPerm")),
T_(dict.lookup("T")),
78 extraE_(dict.lookupOrDefault<dimensionedVector>("extraEField",
dimensionedVector("0", dimensionSet(1, 1, -3, 0, 0, -1, 0),
vector::zero))),
psiContrib_(dict.lookupOrDefault<bool>("psiContrib", true)),
80 phiEEqRes_(phi.mesh().solutionDict().subDict("electricControls").
subDict("phiEEqn").lookupOrDefault<scalar>("residuals", 1e-7)),
psiEqRes_(phi.mesh().solutionDict().subDict("electricControls").
subDict("psiEqn").lookupOrDefault<scalar>("residuals", 1e-7)),
82 ciEqRes_(phi.mesh().solutionDict().subDict("electricControls").
subDict("ciEqn").lookupOrDefault<scalar>("residuals", 1e-7)),
maxIterPhiE_(phi.mesh().solutionDict().subDict("electricControls").
subDict("phiEEqn").lookupOrDefault<scalar>("maxIter", 50)),
84 maxIterPsi_(phi.mesh().solutionDict().subDict("electricControls").
subDict("psiEqn").lookupOrDefault<scalar>("maxIter", 50)),
maxIterCi_(phi.mesh().solutionDict().subDict("electricControls").
subDict("ciEqn").lookupOrDefault<scalar>("maxIter", 50)),
86 nIterPNP_(phi.mesh().solutionDict().subDict("electricControls").
lookupOrDefault<int>("nIterPNP", 2)),
species_(),
88 nSpecies_(0)
{
90 PtrList<entry> specEntries(dict.lookup("species"));
nSpecies_ = specEntries.size();
92 species_.setSize(nSpecies_);
94 forAll (species_, specI)
{
96 species_.set
(
98 specI,
new NPSpecie
100 (
specEntries[specI].keyword(),
102 phi,
specEntries[specI].dict()
104 )

CHAPTER 4. Overview of rheoTool 57
);
106 }
}
108
// ******** Member Functions * *********//
110 Foam::tmp<Foam::volVectorField> Foam::EDFEquations::NernstPlanck::Fe()
const
{
112 volScalarField rhoE( psi_ *dimensionedScalar("norm", epsilonK_.
dimensions()/dimArea, 0.) );
114 forAll (species_, i)
{
116 rhoE
+= (
118 species_[i].zi()*species_[i].ci()*FK_
);
120 }
122 if (solvePhiE_)
{
124 if (psiContrib_)
{
126 return
(
128 -rhoE *( fvc::grad(phiE_+psi_) - extraE_)
);
130 }
else
132 {
return
134 (
-rhoE *( fvc::grad(phiE_) - extraE_)
136 );
}
138 }
else
140 {
if (psiContrib_)
142 {
return
144 (
-rhoE *( fvc::grad(psi_) - extraE_)
146 );
}
148 else
{
150 return
(
152 -rhoE *(-extraE_)
);
154 }
}
156 }
158 void Foam::EDFEquations::NernstPlanck::correct()
{

CHAPTER 4. Overview of rheoTool 58
160
// Electrokinetic coupling loop
162 for (int j=0; j<nIterPNP_; j++)
{
164
Info << "PNP Coupling iteration: " << j << endl;
166
scalar res=GREAT;
168 scalar iter=0;
170 //- Equation for the external potential (loop for the case
// of non-orthogonal grids)
172 if (solvePhiE_)
{
174 while (res > phiEEqRes_ && iter < maxIterPhiE_)
{
176 fvScalarMatrix phiEEqn
(
178 fvm::laplacian(phiE_)
);
180
phiEEqn.relax();
182 res=phiEEqn.solve().initialResidual();
184 iter++;
}
186 }
188 //- Equation for the intrinsic potential
190 res=GREAT;
iter=0;
192
volScalarField souE(psi_ *dimensionedScalar("norm1",dimless/dimArea
,0.));
194
forAll (species_, i)
196 {
souE +=
198 (
-species_[i].zi()*species_[i].ci()*FK_
200 /(relPerm_*epsilonK_)
);
202 }
204 while (res > psiEqRes_ && iter < maxIterPsi_)
{
206
fvScalarMatrix psiEqn
208 (
fvm::laplacian(psi_)
210 ==
souE
212 );
214 psiEqn.relax();
res=psiEqn.solve().initialResidual();

CHAPTER 4. Overview of rheoTool 59
216
iter++;
218 }
220 //- Nernst-Planck equation for each ionic specie
222 forAll (species_, i)
{
224 res=GREAT;
iter=0;
226
volScalarField& ci = species_[i].ci();
228
dimensionedScalar cf(species_[i].Di() *eK_ *species_[i].zi() / (kbK_
*T_) );
230
while (res > ciEqRes_ && iter < maxIterCi_)
232 {
234 fvScalarMatrix ciEqn
(
236 fvm::ddt(ci)
+fvm::div(phi(), ci, "div(phi,ci)")
238 ==
fvm::laplacian(species_[i].Di(), ci, "laplacian(D,ci)")
240 +fvc::laplacian(ci*cf, phiE_+psi_, "laplacian(elecM)")
);
242
ciEqn.relax(phi().mesh().equationRelaxationFactor("ci"));
244 res=ciEqn.solve(phi().mesh().solver("ci")).initialResidual();
246 ci = Foam::max( dimensionedScalar("lowerLimit",ci.dimensions(), 0.),
ci );
iter++;
248
}
250 }
}
252 }
Listing 4.3: Source code of the Poisson-Nernst-Planck model in file
NernstPlanck.C.

CHAPTER 4. Overview of rheoTool 60
4.2.6 Adding new EDF models
The steps required to add new EDF models are similar to the ones described
previously, in Section 4.1.6, for GNF and viscoelastic models. The main steps are:
•copy-paste the folder of an existing model (that we will call template model)
in directory src/libs/EDFModels/models/. Rename the folder and
the files inside it (.C and .H files) with the new model’s name. Remove the
.dep file inside the folder. We recommend to use model slipSmoluchowski as
template, since it is the simplest one and does not contain other sub-classes,
which would also need to be renamed in the next step.
•inside the source .C and header .H files, find-replace the old model’s name
by the new one (e.g. Ctrl +Hin gedit). This is to change the name of the
class, which is usually equal to the name given to the respective source file.
However, it is a good idea to always check first the name given to the class
of the template model.
•add the source code of the new model to the compilation list of the library.
For that, edit file src/libs/EDFModels/Make/files by adding the
path for the source code (see the entries for the other models already there).
•make a first compilation of the new model, by running the script Allwmake
in directory src/. Note that, until this point, the source code of the new
model is the one from the original template model, where only the name of
the class has been changed. Thus, the model should compile without errors.
If not, something wrong occurred in the previous steps.
•the last step is to change the source code of the model in order to implement
the desired EDF model. Depending on the characteristics of the new model,
several parts of the source and header files might need to be changed. Our
recommendation is to look to the closest model among the ones available.
After all the changes on the code had been completed, compile again by
running script Allwmake.
If all the steps listed above were successfully executed, then the new model is
now available to solver rheoEFoam (only). In order to use library EDFModels in
any solver other than rheoEFoam, the user should:
•add the header #include ”EDFModel.H” to the main solver.
•create an EDFModel object by calling the constructor with the correct ar-
guments, for example: EDFModel elecM(phi).
•add the library EDFModels to the Make/options, and specify its path
(check the Make/options of rheoEFoam for an example).

CHAPTER 4. Overview of rheoTool 61
4.3 The BDmolecule library
This library is only available for OpenFOAM R
versions.
Library BDmolecule contains the classes and routines implementing the Brownian
dynamics algorithm. The library is based on the solidParticle library provided
by OpenFOAM R
to perform the tracking of rigid particles. This library has been
copied and modified in order to allow the creation of molecules, which are simply
organized ensembles of beads. The interface of library BDmolecule is embodied
by class sPCloudInterface. The source code of the library can be found in src/
libs/brownianDynamics.
4.3.1 Organization of variables
The base class particle is commonly used in OpenFOAM R
to create a single La-
grangian entity that can be tracked. Several other classes are derived from this
one, adding new features to it. A Cloud is a template class representing a set
of particles, inheriting the properties of C++ doubly-linked lists. This type of
lists is not the most versatile one when we need to perform operations between
non-consecutive elements, as it happens when computing intra-molecular forces.
Thus, directly creating a molecule from a Cloud class seemed not to be the best
option, even more because this option would create 4Mfiles (Mbeing the number
of molecules) for each time-step saved, which would overburden any file trans-
fer operation, notwithstanding the small disk space used by each file. Therefore,
we decided to separate the particle tracking from the molecule-related tasks. As
such, we created a single (blind) Cloud object to contain all the particles (beads)
from all the molecules of the simulation and perform the tracking, and an addi-
tional structure establishing the link between each particle and the corresponding
molecule, that takes care of all the molecule-related tasks. We classified object
Cloud as blind, because it does not differentiate among the particles, ignoring the
molecules and groups to which they belong. This solves the two previous issues
related with indexing and the number of files generated, but requires the exchange
of information between structures and, consequently, some internal duplication of
data, which is not problematic in terms of performance, but hinders the efficient
parallelization of the code.
In the interface class (sPCloudInterface), object spc (a Cloud) is the one ded-
icated to the particle tracking. In addition, we can find a number of P trList <>
whose name starts with mand ends with an underscore (e.g. mx ,mSigma ,
mU , ...) which are used in the remaining operations. For example, mx is a
P trList < F ield < vector >> holding the beads positions (Cartesian coordi-
nates) for each molecule. The beads positions are also a member of spc , but the
difference comparing to mx is in the data organization. While we can use mx to
easily find the position of bead i, in molecule mof group g, this cannot be done
from inside spc .

CHAPTER 4. Overview of rheoTool 62
4.3.2 Solution sequence
For a proper understanding of the source code behind the Brownian dynamics
module of rheoTool, the user first needs to understand the interplay between the
local fields of sPCloudInterface and the particles fields inside spc , from solidPar-
ticle class. We believe that the comments left in the code will help in this task. It
would be unfeasible (and probably useless) to explain all the code details in this
guide, thus we decided to only explore the function controlling the main Brownian
dynamics loop. This function, named update(), a public member of sPCloudInter-
face, is charged of evolving the position and configuration of the molecules each
time-step. In what follows, we briefly discuss the structure of this function (Listing
4.4):
•line 3: the beads positions at the beginning of a time-step (mx ) are copied
to mx0 . The algorithm structure ensures that the beads positions in mx0
are such that all the springs of the active molecules are shorter than l, for
bounded models (Section 3.8.3).
•lines 5-6: if the user selects to account for hydrodynamic interactions, tensor
Dis computed from the RPY model (Eq. 3.44), and its Cholesky decompo-
sition results in tensor σ(Section 3.8.3). If hydrodynamic interactions are
suppressed, the diffusion is isotropic and can be represented by a scalar (D;
Eq. 3.44), which is used to compute each force acting on the beads (tensors
Dand σare not even computed in this case).
•line 8: this function computes the Brownian force contribution to the beads
velocity (last term of Eq. 3.43). The function is also defined inside sPClou
dInterface.C.
•lines 10-11: if exclusion volume forces are activated by the user, then their
contribution to the beads velocity is added through a call to function fEV(),
defined inside sPCloudInterface.C.
•line 13: function sendU() copies the beads velocity from the local mU
P trList <> to the particles field U. This function is defined inside sPClou
dInterface.C.
•line 16: function moveAndReceive() comprises two main steps. In the first
step, there is a call to the move() function of the solidParticleCloud object
spc . This executes the movement and tracking of all the beads, after adding
the drag force contribution to the particles velocity, which is done outside
class sPCloudInterface (see file solidParticle.C). In the second step,
the function updates mx with the final positions resulting from the particle
tracking. If for some reason a given particle (bead) is lost during the tracking
(e.g. if it exits the mesh through a patch), then the corresponding molecule
is labeled as non-active, and it is no more tracked. Up to this point, the
beads experienced all the forces, except the spring force.

CHAPTER 4. Overview of rheoTool 63
•line 19: the current beads positions are saved in mxStar . Since the spring
force still did not contributed to these positions, the computation of the
spring vectors from mxStar would result eventually in overstretched springs
(Ri> l).
•line 20: this call to a non-member function computes explicitly (Euler ex-
plicit) the spring force contribution to the beads velocity (mU ), using the
current beads positions (mxStar ). The local beads positions (mx ) are also
updated.
•line 23: based on the current beads positions (mx ), the spring vectors are
computed and a check is carried out for Ri< αl (see Section 3.8.4). For
each molecule, if any spring violates this condition mxStar is taken again
and the spring force contribution is now added implicitly, using the Newton-
Raphson method (Section 3.8.4). Of course, this is only done if the semi-
implicit method is selected (Euler-explicit is also available), and for any of
the bounded spring models. After the implicit call, the function checks if any
spring is overstretched. This can happen if the time-step is too large. Any
molecule having at least one spring overstretched is automatically deleted by
the algorithm and a warning message is printed to the terminal.
•lines 26-27: if the molecules are not tethered and if any of the components
of the push-back vector defined by the user is non-zero, the molecules center
of mass is pushed to its original position. This is equivalent to the transla-
tion of all the molecule’s beads by a fixed vector. In this case, we add the
corresponding velocity to mU , such that the translation can be effective in
the next particle tracking stage.
•line 29: see comment above for line 13.
•line 32: this is the second call to function moveAndReceive(), thus a second
call to the particle tracking engine. The operations carried out are the same
as described above for line 16, with the exception that, in this call, the beads
velocity does not receive the drag force contribution, since this was already
done in the first call (the distinction between calls is in the boolean argu-
ment passed to the function). At this point of the algorithm, the particles
positions and mx are synchronized and it can be ensured that none of the
active molecules has an overstretched spring. We do not care about the syn-
chronization of the beads’ velocity, because this field is not used in the next
time-step, contrarily to the beads’ positions.
•line 35: function writeM() ensures that the molecules’ data is written in the
case directory at each outputTime. It will create directories outputTime
/lagrangian/molecules/ and constant/runTimeInfo/outpuTi
me/, and write the molecules’ data therein. Both directories are needed on
restart of rheoBDFoam.
•lines 38-39: function writeStatistics() can be optionally activated by the
user, and will retrieve the molecules index/position/stretch over time.

CHAPTER 4. Overview of rheoTool 64
•lines 41-48: these lines enclose the conditional return value of function up-
date(). A value of true is returned as long as at least one molecule is still
active and under tracking. Otherwise, the function returns false and, as ex-
plained in Section 4.5.5, this will force rheoBDFoam to abort the run, even if
the endTime was still not reached (there is no interest in keeping the solver
running without any valid molecule).
While inspecting the source code, note that several intermediate operations
are carried out in a dimensionless form to reduce round-off errors, but final results
are always dimensional. Round-off errors can be an important source of numer-
ical error in Brownian dynamics simulations (the situation is worse in atomistic
simulations) if care is not taken with the different scales involved.
bool sPCloudInterface::update()
2{
mx0_ = mx_;
4
if (isHI_)
6computeDSigma();
8fBrownian();
10 if (isExclusionVolumeF_)
fEV();
12
sendU();
14
// Move particles: Drag + Brownian + Exclusion Volume
16 moveAndReceive(true);
18 // Compute Spring force term explicitly and update local mU and
mx.
mxStar_ = mx_;
20 spModel_->fSpring();
22 // Check for violations in spring lengths and add spring force
implicitly if needed
spModel_->checkSpringsLength(mxStar_, mx0_);
24
// Push back the molecules if not tethered and if pushback
vector is not negligible
26 if (!isTethered_ && mag(pBackV_)>SMALL)
pushToX0();
28
sendU();
30
// Move particles: spring force only
32 moveAndReceive(false);
34 // Write data (controlled by output time)
writeM();
36
// Write statistics (has its own control for output)
38 if (writeStats_)

CHAPTER 4. Overview of rheoTool 65
writeStatistics();
40
if (nMolc_>0)
42 {
return true;
44 }
else
46 {
return false;
48 }
}
Listing 4.4: Member function update() of class sPCloudInterface. The source
code can be found in file sPCloudInterface.C.
4.3.3 External forcing type
The external forcing (drag) acting on the beads is embodied by term ufin Eq.
(3.43). The forcing can be defined analytically or computed numerically.
In case it is defined analytically, tensor ∇u, provided by the user, defines the
gradient of the forcing (spatially homogeneous and constant over time, by default).
The computational mesh in those cases can (should) be simply a single cell. The
computational domain can be made large in all the directions if an unconfined flow
is intended, but a confined flow can also be imposed by shortening one or multiple
directions. Importantly, the boundaries used to impose confined flow conditions
must be of wall type (patch types will be crossed by the molecules, and remaining
types give undefined behavior).
In case it is computed numerically, then two types are still available in rheoTool:
hydrodynamic forcing, in which case ufis the fluid velocity; electric forcing for
polyelectrolytes immersed in an electric field, in which case uf=µEis the elec-
trophoretic velocity (µis the electrophoretic mobility and Eis the electric field).
Both types of forcing can coexist, and each one requires that the respective con-
tinuum field is available in the case directory.
Note that 2D meshes, and the corresponding continuum fields, are allowed in
Brownian dynamics simulations, but the motion equation of the beads (Eq. 3.43)
is always solved for the 3 Cartesian coordinates. This means, for example, that
the molecules will not feel the z-component effect of a planar velocity field solved
in the Oxy plane, but they still feel the Brownian force (and the remaining, except
drag) in that direction.
4.3.4 External forcing interpolation
Independently of the forcing nature, ufmust be interpolated to the current position
of the bead. Therefore, the question addressed in this section is how to compute
ufgiven a numerical field defined at cell centers (numerical forcing), or a forcing
gradient valid over all the domain (analytical forcing)? The following methods are
available in rheoTool:

CHAPTER 4. Overview of rheoTool 66
•Analytical: this scheme is the only available for analytical forcing and cannot
be used with a numerical forcing. The velocity is interpolated using uf=
∇uT·ri, where ∇uis user-defined.
•BarycentricWeights: this is the method that OpenFOAMR
uses by default
to compute the velocity of Lagrangian particles. Consider a generic cell
and its decomposition in tetrahedrons, where one vertex of the tetrahedron
is always the center of the cell, and the remaining vertices correspond to
vertices of one of the cell’s faces. For a rectangular cell, for example, one
would end-up with 12 non-unique tetrahedrons, two per face of the cell. It
is then possible to define a barycentric coordinate system for each tetrahe-
dron, such that any point inside it can be uniquely identified by a quadruplet
(b1b2b3b4), with
4
P
i=1
bi= 1. In addition to allow the spatial location of par-
ticles, these coordinates can also be used to weight the data at the vertexes
of the tetrahedron, acting as interpolants of the data at the tetrahedron’s
vertices, which is the method adopted when selecting BarycentricWeights.
Remember that the vertices of the tetrahedrons are either cell centers or
vertices of cells. Therefore, the numerical field computed at the cell-centers
(OpenFOAM R
uses co-located grids) also needs to be interpolated to ver-
tices, which is accomplished by simple inverse distance weighting.
•Gradient: in this approach, both the cell-centered field and its gradient are
used for the interpolation. Assuming that uCis the forcing known (com-
puted) at the cell center (located at xC) and that ∇uCis its gradient (com-
puted numerically), then the velocity at any point xPinside the cell can be
approximated by: uf=uC+ (xP−xC)·∇uC. The numerical scheme used
to compute the cell-centered gradient (∇uC) can be defined by the user un-
der keyword gradExternalForcing in dictionary fvSchemes. In general, we
recommend Gauss linear for hex-dominated grids and leastSquares in the
remaining cases.
Although the BarycentricWeights and Gradient methods display sub-cell reso-
lution, they both have some pitfalls, as illustrated in Fig. 4.1. The data/grid in this
figure corresponds to a fully-developed field in the x-direction, which displays a
maximum in the y-direction, for y= 0, and is symmetric about y= 0. The profile
in the y-direction can be a parabola, a piecewise linear function or any other func-
tion satisfying the aforementioned conditions of maximum and symmetry. This
could be the case, for example, of the velocity in a fully-developed Poiseuille flow
sampled at the centerline. The behavior of the two interpolation methods for this
case are plotted in the right of Fig. 4.1. For the case depicted, the interpolated
ufby the BarycentricWeights method is simply a field of quadrangular pyramids
(apex at cell centers), with the height of each vertex corresponding to the local
forcing value.
For a profile taken over y= 0, method Gradient approaches correctly the
theoretical function (constant over the x-direction), whereas method Barycen-
tricWeights retrieves a sawtooth profile. Consider now that the molecules’ center

CHAPTER 4. Overview of rheoTool 67
of mass is artificially fixed (see Section 4.3.6) somewhere between x=−1 and
x= 1 (keeping y= 0). For the Gradient method, the results will be independent
of the specific abscissa selected, as one would expected for a fully-developed field
in the x-direction. On the other hand, if the strain-rate in the sawtooth profile
retrieved by method BarycentricWeights is such that W i =λ˙γ >> 1, then the
results will strongly depend on the specific abscissa selected.
For a profile taken over x= 0, method Gradient is unable to capture any varia-
tion of the field in that direction for the central cell, since it predicts ∇uC= (0 0 0)
for all the cells at the centerline, which is only true exactly at the cell’s center. The
issue arises from the gradient computation method, and is akin to the checkerboard
problem that can happen for the U-pcoupling in the momentum equation. On
the other hand, method BarycentricWeights performs better this time, retrieving
a linear variation of ufover the y-direction (the interpolation is exact if the origi-
nal field displays a linear variation). If we consider a group of molecules traveling
over the x-axis, and only spanning the central layer of cells, then we can easily
conclude that they would not feel any forcing under the Gradient method, whereas
method BarycentricWeights would be able to approach the forcing gradient in the
y-direction (in addition to the artificial one in the x-direction).
3
33
1
1
1
1
1
1
2 2
2 2
y =1
y =3
y =-1
y =-3
x =-3 x =-1 x =1x =3
x
1
-1
uf3
Profile at
y = 0
y
1
-1
3
2
Profile at
x = 0
uf
2
Gradient
Barycentric
Weights
Gradient
Barycentric
Weights
Figure 4.1: Hypothetical 2D external forcing field (a scalar field to simplify) in a
co-located grid (values at cell centers), aiming to represent a fully-developed field
in the x-direction. The green values defined at vertices are obtained by inverse
distance weighting of the cell-centered data. On the right, the profiles of uftaken
at x= 0 and y= 0 are represented for two different interpolation methods.

CHAPTER 4. Overview of rheoTool 68
The previous case has shown that the numerical interpolation methods available
are prone to errors in certain conditions and care should be taken in their use. In
the specific case presented above, the issues with the two methods could have been
reduced by refining the grid in the y-direction, such that the molecules spanned
more than one cell in that direction, and by allowing the molecules to travel at least
one entire cell in the x-direction. Alternatively, the use of an unstructured grid
could possibly solve the issues in that particular case. The message that we want
to convey to the reader/user is to use refined meshes in BDS cases, even though
the interpolation methods have sub-cell resolution. Moreover, grid-dependency
studies are also advisable. In any generic situation, if Analytical interpolation can
be used, then this should always be the preferred method, since it is not prone to
such errors. If not possible, then method BarycentricWeights should be preferred
over Gradient.
4.3.5 Spring force and time-integration schemes
The spring force models available in library BDmolecule are presented in Table 4.3
and were briefly discussed in Section 3.8.3.

Table 4.3: Available spring force models for Brownian dynamics simulations.
Model (1)
TypeName (2)FS
i(3)fk
i(4,5)Jk
ij, a (j6=i, j∈gi)
Hookean Hookean H
N
P
j∈gi
xij – –
Marko-Siggia MarkoSiggia 2
3Hl
N
P
j∈gih|xij |
l−1
4+1
4(1−|xij |/l)2ixij
|xij |rk
i−r∗
i−∆tD
kT FS,k
i2
3
H0
dh 1
4(d−1)2+d−1
4δ2
d2−1−δ2
d1−1
2(d−1)3i
Cohen Pad´e CohenPade H
3
N
P
j∈gih3−(|xij |/l)2
1−(|xij |/l)2ixij rk
i−r∗
i−∆tD
kT FS,k
iH0
3
2δ2
(d2−1) hd2−3
d2−1−1−d2−3
2δ2i
FENE FENE H
N
P
j∈gi
1
1−(|xij |/l)2xij rk
i−r∗
i−∆tD
kT FS,k
iH0h1
d2−1−2δ2
(d2−1)2i
(1) Corresponds to the name entry identifying the model in the source code.
(2) H=3kT Nk,s
l2.
(3) Vectorial function used in the Newton-Raphson method (see Section 3.8.4). Superscript kdenotes the iteration index.
(4) The expressions in this column are for the off-diagonal ij (j6=i, j ∈gi) elements of the Jacobian matrix of the Cartesian component a=x, y, z of fk. All the
off-diagonal elements for which j /∈giare zero. The diagonal elements are obtained from the sum of the off-diagonal elements, Jk
ii,a = 1 −
N
P
m=1,m6=i
Jk
im,a. This
symmetric matrix is used in the Newton-Raphson method (see Section 3.8.4).
(5) H0=H∆tD
kT ,d=|xk
ij |/l =|rk
j−rk
i|/l,δ= (rk
j,a −rk
i,a)/l
69

CHAPTER 4. Overview of rheoTool 70
In general, the FENE and Cohen Pad´e models are stiffer to solve than the
Marko-Siggia model, thus requiring smaller time-steps.
An explicit time integration scheme (TypeName = explicit) is available for all
spring models. For the bounded spring models, the semi-implicit scheme (Type-
Name = semiImplicit) described in Section 3.8.4 is also available. The auxiliary
functions used in the semi-implicit scheme are specified in Table 4.3 for all bounded
models.
As mentioned in Section 3.8.4, several methods can be used to solve the lin-
ear system of equations (3.53). Four (direct) methods are available in library
BDmolecule:
TypeName –Description
QR – uses the Householder rank-revealing QR decomposition (function colPiv-
HouseholderQr()) of Eigen [35] to decompose matrix Jk
a. It can be used
in any situation, and it should be the default choice in case of doubt.
LLT – performs a standard Cholesky decomposition of matrix Jk
a, using the llt()
function of Eigen [35]. It should not be used for tethered molecules.
TDMA – implements Thomas algorithm for a tridiagonal matrix. It can be used for
open, linear (no branches), not tethered molecules. Better performance than
QR is achieved for a large number of beads per molecule (it only visits
elements i-1, i,i+1).
Gaussian – uses the Gaussian elimination method provided by OpenFOAMR
. Restric-
tions are the same as for TDMA method.
The reader may be questioning the need and utility of so many methods. The-
oretically, some methods should be faster than others, but possibly more stringent
in their application (only tridiagonal matrices, diagonal-dominant matrices, etc.).
In practice, we observe that the QR method is usually the best compromise. The
TDMA method presents a CPU time typically equal or smaller than QR, but has
restrictions in its application (see above). All the methods are implemented us-
ing full-matrices, notwithstanding the fact that most of the off-diagonal matrix
elements are zero. Sparse matrices and sparse matrix (iterative/direct) solvers
might be considered in a future version if memory overhead starts to be an issue
of concern (say >500 beads per molecule).
4.3.6 Tethering and fixing the molecules center of mass
rheoTool allows the simulation of tethered molecules, i.e., molecules with some
specific part of the chain fixed in space. The only restriction is that solely the
first bead of a given molecule (the one having index = 0 inside the chain) can be
fixed. The numerical procedure to simulate tethered molecules is similar to that
for generic molecules, with the exception that we impose a null resulting force
acting on the tethered bead.

CHAPTER 4. Overview of rheoTool 71
Fixing the center of mass of a molecule is different from tethering a molecule,
and the use of both in simultaneous is not allowed (would it make sense?). When
the option of fixing the molecules center of mass is selected, the molecules are
simulated in the usual way, but at the end of ntime-steps all the beads are
translated by a same vector, which restores the original center of mass (ntime-steps
before). This option is useful, for instance, when simulating molecules under an
analytical external forcing (homogeneous in space), or to equilibrate the molecules
in a local flow. The value of n, the number of consecutive time-steps in which
the molecules movement is unconstrained, is defined by the user. The existence of
this tunable parameter is mainly to avoid some of the inconsistencies previously
described in Section 4.3.4 for the BarycentricWeights interpolation method.
The reader should keep in mind that the molecules will always move in space
(over the mesh) according to the external forcing if none of these options is selected,
independently of the external forcing nature.
4.3.7 Beads tracking
The default particle tracking engine of OpenFOAM R
is used to move the beads
over the mesh. The algorithm has been greatly improved since OpenFOAMR
v5.0, where barycentric coordinates for the beads’ position have been general-
ized. It is out the scope of this user guide to explain the particle-tracking algo-
rithm. However, it is worth mentioning that the drag force (and only that one)
is re-interpolated inside the same time-step each time a particle (bead) crosses an
internal face of the mesh.
Once a bead hits a wall, it is repositioned at the location where the wall is
crossed or, optionally, at a given distance from that point, in the wall-normal di-
rection. This artificial repulsion aims to reproduce the finite size of the beads, that
would never let them to approach infinitely close to a surface in a real situation.
If a bead hits a patch, it will simply leave the mesh through such patch and
the corresponding molecule is deleted. If a 2D flow is simulated, we recommend to
make the empty direction long enough in order to avoid the unnecessary contact
of the empty boundaries with the beads. The contact of a bead with any other
boundary type will result in undefined behavior, although we expect the molecule
to be deleted in most of the cases. The corollary is to create meshes having only
patch,wall and empty boundary types for use in Brownian dynamics simulations.
Other types can be used as long as the beads do not enter the cells owning those
boundary faces.
It is well-known that the hydrodynamic interactions near a wall are different
than in the bulk. However, the current version of BDmolecule does not make any
correction at the walls. Therefore, care should be taken when simulating confined
problems, or when the molecule-wall contact is recurrent.
4.3.8 Data output for post-processing
The sPCloudInterface class can optionally save some information about the
molecules in runtime. When this option is active, a directory named rheoTo

CHAPTER 4. Overview of rheoTool 72
olPP/startTime/moleculesStates/groupName is created for each group
of molecules, and three files are written to this directory:
IDs.txt: contains three columns, where the first one is for the molecule name/ID,
the second is for the number of beads in the molecule and the third is for
the molecule’s group ID. This file includes such information for all molecules
starting the simulation, regardless of whether the molecule is deleted at some
time during the simulation (e.g. if one of the springs becomes overstretched).
Each row represents a molecule.
stretch.txt: the first column of this file is for the physical time and each of the remaining
columns represents the stretch of a molecule. There is a direct and sequential
one to one relation between the rows of IDs.txt and the columns of st
retch.txt (excluding the first column for time). We define stretch as
the maximum inter-bead distance in a molecule: stretch = max(|rj−ri|),
i, j ={1..N}. If a given molecule is deleted at some point of the simulation,
then the column corresponding to that molecule will be filled with zeros
starting from the row corresponding to that time. Since the length of a
molecule can never be zero, these entries can be used as flags to detect the
molecules that have been deleted during the simulation.
X.txt: the first column of this file is for the physical time and each of the following
triplets of columns represents the x-,y- and z-coordinates of the molecule
center of mass, xcm =1
N
N
P
i=1
ri. Again, there is a direct and sequential one
to one correspondence between the rows of IDs.txt and each triplet of
columns of X.txt (excluding the first column, for time).
4.3.9 Limitations
Some of the main limitations of the Brownian dynamics library have been pre-
viously described. However, to make them clear and to avoid any misuse of the
library, they are summarized below:
•only single-core runs are allowed.
•only patch,wall and empty boundary types can be present in a mesh.
•hydrodynamic interactions near surfaces are not corrected and the algorithm
for beads reflection at the walls is simplistic (accuracy in confined-flow con-
ditions can be compromised).
Of course, all these limitations can be seen as points to improve in future work.
Although the non-parallelization of the code is pointed out as an issue, we believe it
is not the most important one. Indeed, we expect the solver to be used essentially
with a steady external forcing. In such cases, if the code was parallelized we would
distribute the ensemble of Mmolecules by Pavailable processors (M/P molecules
per processor), in a single run (single mesh, single fields, etc.). Since this is not

CHAPTER 4. Overview of rheoTool 73
possible, we can prepare Pcases, with M/P molecules per case and run each one in
a processor. This is valid because all the molecules are similar objects and need not
to communicate between them. The two methods should perform closely in terms
of CPU time, although the non-parallel one consumes more memory (allocation
of the mesh Ptimes vs 1 time). For the cases with transient external forcing,
parallelization would be indisputably advantageous regarding CPU time.
4.4 The sparseMatrixSolvers library
This feature is only available for OpenFOAM R
versions.
rheoTool has interfaces to three external libraries: Eigen [35], Hypre [37] and
Petsc [9–11]. These interfaces allow solving ”externally” the linear systems of
equations built in OpenFOAM R
, thus increasing the availability of sparse matrix
solvers. Moreover, they also enable certain operations that would not be allowed
by OpenFOAM R
matrix solvers, as for example reusing the preconditioner. All
interfaces are parallelized with MPI, except Eigen’s interface, which can only be
used for serial runs. These features are incorporated in library sparseMatrixSolvers,
which also includes coupled solvers (Section 4.4.8).
The library is generic regarding the type of equations that can be handled
by the interfaces (scalar, vector, tensor, symmTensor and sphericalTensor). In
practice, we only use the library to solve the pressure and momentum equations
in segregated solvers, since those are usually the ones consuming more CPU time.
Note that the use of different sparse matrix solvers does not change the accuracy
of the algorithm. Indeed, as long as the system of equations is solved to a tight
tolerance, the solution retrieved by any solver should be the same. Speed is the
only factor involved when selecting the sparse matrix solver.
4.4.1 Conditions to reuse the preconditioner/factorization
In some situations, the discretized equations result in matrices with a large con-
dition number. For example, this happens often with the pressure equation. The
default sparse matrix solvers available in OpenFOAM R
might present convergence
issues in such cases, which is visible in the high number of iterations taken to con-
verge to the prescribed tolerance. The use of strong preconditioners can lower
the number of iterations, but this does not necessarily translates in a lower time
of computation, since computing and applying strong preconditioners is a costly
procedure. However, in some particular situations the matrix of coefficients does
not change over time, which allows computing the preconditioner only once. There
are also situations where the matrix of coefficients only changes slightly between
time-steps, such that a given preconditioner can be used more than once. Consid-
ering this range of situations, sparseMatrixSolvers library offers the possibility to
reuse the preconditioner.
Considering pressure and momentum equations, the respective matrix of coef-
ficients does not change over time when:

CHAPTER 4. Overview of rheoTool 74
•the time-step/under-relaxation factor is fixed;
•momentum convection is negligible (this term is removed from the equation,
see Section 4.7.1);
•the viscosity coefficient is constant over time;
•the density is constant over time.
These conditions are typically verified in inertialess microfluidic single-phase
flows. They allow computing the preconditioner (iterative solver) or factorization
(direct solver) once, at the first time-step, and reusing it in the remaining time-
steps. If some of these conditions are not verified, it might still be possible to reuse
the preconditioner/factorization in more than one time-step.
Note that using direct solvers or iterative solvers combined with strong pre-
conditioners typically increases the memory usage. Therefore, users should always
take this factor into consideration in order to prevent memory overflow.
4.4.2 Residuals and tolerances
The residuals are an indicator typically used in CFD to monitor convergence. The
definition of residuals is not consensual and each software package uses its own
definition. In OpenFOAM R
, the residuals of an equation are defined as
Residual = |Ax −b|1
|Ax −AxI|1+|b−AxI|1
(4.27)
where Ais the matrix of coefficients, bis the right hand-side vector, xis the
solution vector, Iis a vector of ones, xis the average value of xand ||1represents
the L1norm of a vector. For all the three interfaces, the residuals displayed to
the screen follow the definition of Eq. (4.27), independently of the sparse matrix
solver being used.
While solving a system of equations with an iterative solver, the iterative pro-
cess stops once a convergence criteria is satisfied. The most used criteria are
typically the absolute tolerance, the relative tolerance and an established maxi-
mum number of iterations. The formula used to define each tolerance is usually
software-dependent. For example, OpenFOAM R
solvers use the residuals to define
the tolerance. In the sparseMatrixSolvers library, the solvers belonging to each in-
terface use the tolerance definition imposed by the respective library. Therefore,
whereas OpenFOAM R
solvers present a direct relation between the absolute tol-
erance and the residuals, there is no such direct relation for the solvers from the
external libraries. This question does not arise with direct solvers, since they
always solve the equations to machine precision.
4.4.3 Generic parameters
The access to the sparse matrix solvers from the external libraries takes place in
dictionary fvSolution, under sub-dictionary solvers. There are four parameters
common to all interfaces:

CHAPTER 4. Overview of rheoTool 75
solverType– corresponds to the TypeName of the class of solvers to be used, one of
eigenSolver,hypreSolver,openFoamSolver or petscSolver. Each option cor-
responds to one of the external libraries, except openFoamSolver, which is
simply a wrapper to the default OpenFOAM R
solvers. If solverType is not
specified, then openFoamSolver is assumed by default, in order to keep back-
ward compatibility, and the remaining three parameters have no effect.
saveSystem– this bool indicates whether to reuse or not the elements needed to solve the
system of equations (matrix of coefficients, solver and preconditioner).
updatePrecond
Frequency – the frequency at which the preconditioner is updated. The counter is up-
dated each time the equation for the given field is assembled and solved.
If the matrix of coefficients is not changing and saveSystem = true, this
variable should be set to a high value (e.g. 105), such that, in practice, the
preconditioner is only computed at the beginning of the simulation. If the
matrix of coefficients is changing and saveSystem = true, this variable should
be carefully adjusted. If the matrix of coefficients changes quickly, the value
should be close to 1, whereas higher values can be selected otherwise. If this
parameter is set equal to -1, then an empiric algorithm [5] is employed to
automatically decide when to update the preconditioner. If a direct solver
is used, this parameter must be set equal to 1 (the factorization needs to be
computed each time-step) and an error message is retrieved if this condition
is not satisfied. If saveSystem = false, then this parameter has no meaning
and is not read.
update
MatrixCoeffs – this bool indicates whether to update or not the matrix of coefficients every
time the equation is solved. It should be set equal to true if the matrix
of coefficients changes over time and false otherwise. There is a (weak)
verification procedure at the beginning of a simulation to check if the matrix
of coefficients is changing. An error is retrieved if updateMatrixCoeffs is
inconsistent with the result from this verification. If saveSystem = false,
then this parameter has no meaning and is not read.
The set of options saveSystem = true, updatePrecondFrequency = 1 and up-
dateMatrixCoeffs = true results in a close, but not equal setup as saveSystem
= false. For the first set of options, some structures are reused, as for example
the sparsity pattern in the matrix of coefficients, whereas in the latter case all
structures are deleted after the equation is solved.
If the user is unsure about the possibility of reusing elements, then setting
saveSystem = false should be the first approach. The resulting setup might be
inefficient, but has unconstrained applicability (with the exceptions mentioned in
Section 4.4.10).
For programming reasons, when saveSystem = true, updatePrecondFrequency
= bigNumber and updateMatrixCoeffs = false, the factorization/preconditioner is
computed in the first two times the equation is solved, and not only in the
first time (that would be enough since the matrix is not changing from the first

CHAPTER 4. Overview of rheoTool 76
time it is assembled). These two solution times are expected to be significantly
slower than the following ones. Therefore, the user should not judge the speed
of the simulation based on these two initial time-steps.
The parameters specific to each interface are presented in the following sections.
4.4.4 OpenFOAM interface
This interface is selected by setting solverType = openFoamSolver and is simply a
wrapper to the default OpenFOAM R
sparse matrix solvers. Therefore, specifying
the solver, preconditioner and their corresponding parameters is as usual.
4.4.5 Eigen interface
Note: sparse matrix solvers from Eigen library can not be used in parallel runs.
The interface to Eigen library was built essentially due to the ease of use of
this library. This class of solvers is selected by setting solverType = eigenSolver.
The list of solvers available for this interface is presented in Table 4.4, and the list
of preconditioners in Table 4.5. Note that only part of the solvers/preconditioners
offered by Eigen is available through this interface. Moreover, the PCG solver
is restricted to symmetric matrices and SparseLU is the only direct solver made
available. The tolerance parameter owns Eigen’s definition. See Eigen’s documen-
tation [35] for more details about each solver/preconditioner and its parameters.
The preconditioner must be defined under a sub-dictionary named precondi-
tioner. It is not allowed using an iterative solver without preconditioner. In Listing
4.5 we present an example showing the use of a solver from Eigen library (an ILUT
preconditioned BiCGSTAB Krylov solver).
Table 4.4: Available sparse matrix solvers from Eigen interface. The values inside
brackets represent the default parameters used if they are not specified by the user.
Note that additional parameters might be available for each solver, but only those
listed in this Table can be changed through the interface (the ones not listed here
get default values defined by Eigen).
Solver Parameters Available preconditioners
BiCGSTAB maxIter (1000), tolerance (10−12) ILUT, Diagonal
GMRES maxIter (1000), tolerance (10−12) ILUT, Diagonal
PCG maxIter (1000), tolerance (10−12) ICC, Diagonal
SparseLU pivotThreshold (10−12) (Direct Solver)

CHAPTER 4. Overview of rheoTool 77
Table 4.5: Available preconditioners from Eigen interface. The values inside
brackets represent the default parameters used if they are not specified by the
user. Note that additional parameters might be available for each preconditioner,
but only those listed in this Table can be changed through the interface (the ones
not listed here get default values defined by Eigen).
Preconditioner Parameters
ILUT fillFactor (10), dropTol (10−12)
ICC –
Diagonal –
1solvers
{
3"(p|U)"
{
5solverType eigenSolver;
7saveSystem true;
updatePrecondFrequency 10000;
9updateMatrixCoeffs false;
11 solver BiCGSTAB;
tolerance 1e-12;
13 maxIter 1000;
15 preconditioner
{
17 preconditioner ILUT;
dropTol 0;
19 fillFactor 5;
}
21 }
}
Listing 4.5: Example of a solvers dictionary in fvSolution showing the use
of a sparse matrix solver from Eigen library to solve momentum and pressure
equations.
4.4.6 Hypre interface
The class of solvers in the Hypre interface is selected by setting solverType =
hypreSolver. The list of solvers available for this interface is presented in Table
4.6, and the list of preconditioners in Table 4.7. Note that only part of the solver-
s/preconditioners offered by Hypre is available through this interface. The PCG
solver is restricted to symmetric matrices and not all preconditioners can keep

CHAPTER 4. Overview of rheoTool 78
symmetry when used with this solver. The tolerance and relTol parameters own
Hypre’s definition. Some preconditioners can only be used in parallel runs and
preconditioner none is tantamount to not using any preconditioning method. See
Hypre’s documentation [37] for more details about each solver/preconditioner and
its parameters.
The preconditioner must be defined under a sub-dictionary named precondi-
tioner, even in the case it is none. In Listing 4.6 we present an example showing
the use of a solver from Hypre library (a BoomerAMG preconditioned GMRES
Krylov solver). Note that options updatePrecond and updateMatrixCoeffs are not
specified in this example because saveSystem = false (see Section 4.4.3).
Table 4.6: Available sparse matrix solvers from Hypre interface. The values
inside brackets represent the default parameters used if they are not specified by
the user. Note that additional parameters might be available for each solver, but
only those listed in this Table can be changed through the interface (the ones not
listed here get default values defined by Hypre).
Solver Parameters Available precondi-
tioners
BiCGSTAB maxIter (1000), relTol (0), tolerance
(10−8), printLevel (0), logging (0)
BoomerAMG, Euclid,
ParaSails, none
GMRES
maxIter (1000), relTol (0), tolerance
(10−8), KrylovSpaceDim (100), print-
Level (0), logging (0)
BoomerAMG, Euclid,
ParaSails, none
PCG
maxIter (1000), relTol (0), tolerance
(10−8), useTwoNorm (true), recom-
puteEndResidual (false), printLevel
(0), logging (0)
BoomerAMG, Euclid,
ParaSails, none
BoomerAMG
relTol (0), maxIter (1000), minIter (0),
convergenceType (0), relaxationType
(6), nSweeps (1), coarsenType (10),
restrictionType (0), cycleType (1),
AMGVariant (0), printLevel (0), relax-
Order (0), recoversOldDefault (true),
logging (0)
none

CHAPTER 4. Overview of rheoTool 79
Table 4.7: Available preconditioners from Hypre interface. The values inside
brackets represent the default parameters used if they are not specified by the
user. Note that additional parameters might be available for each preconditioner,
but only those listed in this Table can be changed through the interface (the ones
not listed here get default values defined by Hypre).
Preconditioner Parameters
Euclid ILUklevel (2), enableJacobiILU (false), en-
ableRowScaling (false), dropTol (0)
ParaSails printLevel (0), loadBalance (0)
BoomerAMG
relTol (0), maxIter (1000), minIter (0),
convergenceType (0), relaxationType (6),
nSweeps (1), coarsenType (10), restriction-
Type (0), cycleType (1), AMGVariant (0),
printLevel (0), relaxOrder (0), recoversOl-
dDefault (true), logging (0)
none —
solvers
2{
"(p|U)"
4{
solverType hypreSolver;
6
saveSystem false;
8
solver GMRES;
10 tolerance 0;
relTol 1e-8;
12 maxIter 1000;
14 preconditioner
{
16 preconditioner BoomerAMG;
maxIter 1;
18 }
}
20 }
Listing 4.6: Example of a solvers dictionary in fvSolution showing the use
of a sparse matrix solver from Hypre library to solve momentum and pressure
equations.

CHAPTER 4. Overview of rheoTool 80
4.4.7 Petsc interface
Petsc interface is the most complete among the three interfaces. This interface
is selected by setting solverType = petscSolver. In opposition to the other two
interfaces, no more parameters need to be specified under dictionary solvers of
fvSolution, other than the four general parameters discussed in Section 4.4.3, as
shown in the example of Listing 4.7. This is because all the parameters related with
the solvers and preconditioners are read from a different file, named petscDict,
that should be present in directory system of the case being solved. According to
Petsc terminology, this file is the options database and allows for a great flexibility.
solvers
2{
p
4{
solverType petscSolver;
6saveSystem true;
updatePrecondFrequency 100000;
8updateMatrixCoeffs false;
}
10
U
12 {
solverType petscSolver;
14 saveSystem true;
updatePrecondFrequency -1;
16 updateMatrixCoeffs true;
}
18 }
Listing 4.7: Example of a solvers dictionary in fvSolution showing the use
of a sparse matrix solver from Petsc library to solve momentum and pressure
equations.
Listing 4.8 shows an example of a petscDict database, which, in the case
illustrated, is used to control the solver options for momentum and pressure equa-
tions. The formating rules of this file are the same as for any Petsc database:
the lines starting with a ’#’ are ignored and every option should be prepended
with a ’-’. One additional rule must hold, which is specific from the interface: any
option related with the matrix/vector (Mat and Vec modules of Petsc) and solver
(ksp module of Petsc) contexts should be prepended with the name of the field
which is intended for, followed by an underscore. For example, option -ksp type
aims at specifying the sparse matrix solver of a ksp context, but if we want to
apply it to the pressure equation in particular, then this option should be written
as -p ksp type (Listing 4.8). The prefix is the way Petsc distinguishes between
options for different contexts (equations). Only the options which are generic, and
not bounded to a particular context, should not be prepended. This is the case,
for example, of option -help, which displays all the available options related with
Petsc in a given simulation (see Petsc’s documentation [9,10] for the meaning of
all options displayed). Note that the name of the prefixes should correspond to
the names used to identify the solvers in dictionary fvSolution (lines 3 and 11
of Listing 4.7).

CHAPTER 4. Overview of rheoTool 81
All the options that Petsc recognizes for the Mat,Vec and ksp modules can
be used in Petsc interface and selected in run-time through the options database.
Therefore, in opposition to the other two interfaces, there are no individual wrap-
pers to each solver/preconditioner offered by Petsc, such that, in theory, all can
be used. For the list of solvers/preconditioners available in Petsc, please consult
Petsc’s documentation [9,10], or start a simulation with option -help. Note that
some solvers/preconditioners are only available if additional packages are down-
loaded. This is the case, for example, of direct solvers from MUMPS. Moreover,
some solvers/preconditioners are only available for sequential runs, as specified in
Petsc’s documentation.
In the example of Listing 4.8, it can be shown that a Cholesky decomposition
(direct solver) is used to solve the pressure equation. Since saveSystem = true for
pin Listing 4.7 and the matrix is not changing (updateMatrixCoeffs = false), the
factorization is only computed once and reused in the remaining time-steps. For
the velocity, a BiCGStab iterative solver (bcgs) preconditioned with an incomplete
LU factorization (ilu) is employed. A number of options is further specified for this
preconditioner (lines 28-32). The solver-preconditioner are created/destroyed each
time the momentum equation is solved, as saveSystem = false in Listing 4.7. As
a matter of curiosity, this setup could not be used in a parallel run, since the two
preconditioners specified are not parallelized (see Petsc’s documentation [9,10]).
If the user followed the installation procedure of Chapter 2, in addition to the
default solvers/preconditioners from Petsc, there are also available solvers/precon-
ditioners from Hypre and MUMPS packages, which are downloaded via Petsc. It
should be noted that some of the solvers/preconditioners wrapped in the Hypre in-
terface (Section 4.4.6) can be also accessed from Petsc interface. However, they are
based on different implementations, since the solvers/preconditioners from Hypre
interface rely exclusively on Hypre’s environment, whereas those accessible from
Petsc’s interface are intermediated by and depend on Petsc environment.
###############################
2##----- Global settings -----##
###############################
4
#-help
6
##############################
8##----- Settings for p -----##
##############################
10 #--> KSP
-p_ksp_type preonly
12
#--> PC
14 -p_pc_type cholesky
-p_pc_factor_mat_solver_type petsc
16
##############################
18 ##----- Settings for U -----##
##############################
20 #--> KSP
-U_ksp_type bcgs
22 -U_ksp_max_it 1000

CHAPTER 4. Overview of rheoTool 82
-U_ksp_rtol 0
24 -U_ksp_atol 1e-12
-U_ksp_divtol 10
26
#--> PC
28 -U_pc_type ilu
-U_pc_factor_levels 10
30 -U_pc_factor_reuse_fill 1
-U_pc_factor_reuse_ordering 1
32 -U_pc_factor_mat_ordering_type rcm
Listing 4.8: Example of a petscDict options database showing the settings
to solve momentum and pressure equations.
4.4.8 Coupled solvers
Besides the three interfaces specified above for segregated solvers, library sparse-
MatrixSolvers also has a class for coupled solvers. Coupled solvers are implemented
based on Petsc, such that only the solvers/preconditioners available in Petsc can
be used with coupled solvers.
In rheoTool, the coupled solvers can be used in the following scenarios:
•solve p-ucoupled;
•solve p-u-τcoupled;
•solve the PNP system of equations coupled (restricted to the NernstPlanck-
Coupled model);
•solve the PNP system of equations coupled with p-u-τ(restricted to the
NernstPlanckCoupled model).
Coupled solvers are accessible from rheoFoam,rheoEFoam and rheoBDFoam
applications. In order to use a coupled solver, dictionary coupledSolvers should
be added to fvSolution. The options related with p-u-τshould be inserted
under sub-dictionary Uptau, whereas the options related with the PNP system of
equations (NernstPlanckCoupled model) should be inserted under sub-dictionary
ciPsi. This is exemplified in Listing 4.9 and the options available are:
Uptau sub-dictionary
solveCoupledUp– true to solve p-ucoupled and false to solve segregated.
solveCoupledTau– true to add τto the p-ucoupled system of equations and false to solve τseg-
regated. The variables p-u-τare only solved coupled if both solveCoupledUp
and solveCoupledTau are set to true.
saveSystem– see Section 4.4.3.
updatePrecond
Frequency – see Section 4.4.3.

CHAPTER 4. Overview of rheoTool 83
update
MatrixCoeffs – see Section 4.4.3.
robustSumCheck– this option is only enabled if saveSystem = true and controls the method
used to check if the matrix of coefficients is changing over time. If this option
is set to true, a robust method is employed, which, however, duplicates the
matrix of coefficients, thus increasing the memory usage. If the option is set
to true, the method used is the same as for segregated solvers and might fail
for coupled systems of equations. We recommend using the robust method.
If memory overflow is an issue of concern, simply run a few iterations in a
coarse mesh to detect any variation in the matrix of coefficients and once
the verification is done turn the option off and return to the fine mesh. Note
that the verification algorithm is only run at the beginning of a simulation.
ciPsi sub-dictionary
solveWithUptau– if true, the PNP system of equations is solved coupled with p-uand option-
ally τ. In that case, no other options are read from dictionary ciPsi (the
matrix controls are those of Uptau).
Remaining options are the same as for Uptau
coupledSolvers
2{
Uptau
4{
solveCoupledUp true;
6solveCoupledTau true;
8saveSystem true;
robustSumCheck true;
10 updatePrecondFrequency 1;
updateMatrixCoeffs true;
12 }
14 ciPsi
{
16 solveWithUptau false;
18 saveSystem true;
robustSumCheck true;
20 updatePrecondFrequency 1;
updateMatrixCoeffs true;
22 }
}
Listing 4.9: Example of a coupledSolvers dictionary in fvSolution.
Note that the conditions enumerated in Section 4.4.1 that allow reusing the
preconditioner/factorization still hold for the coupled p-usystem of equations.
However, if also τis solved coupled, the matrix of coefficients always changes over
time due to the convective term of the constitutive equation (Eq. 3.4). In that case,
saveSystem can sill be set to true, with a user-defined updatePrecondFrequency (-1

CHAPTER 4. Overview of rheoTool 84
for an automatic decision method), but updateMatrixCoeffs must be set equal to
true or an error will be retrieved otherwise (if the verification algorithm is working
correctly). For the coupled PNP system of equations, the matrix of coefficients
changes every time-step due to the implicit discretization of the electromigration
term.
Since coupled solvers are based on Petsc, the options database file (petscD
ict) controls the solution settings, as described in Section 4.4.7. The prefixes are
now ’Uptau ’ and ’ciPsi ’.
While solving a coupled system of equations, rheoTool will still output the
information for each sub-equation (solver name, residuals and number of iterations
to convergence). However, only the residual is different between sub-equations,
which are computed individually according to Eq. 4.27.
As shown in [5], semi-coupled solvers show a better performance than coupled
solvers in some cases, among other advantages. Therefore it is recommended to
first try semi-coupled solvers, before coupled solvers. A semi-coupled solver solves
part of the equations coupled and part segregated. For example, the set of op-
tions solveCoupledUp = true, solveWithUptau = true and solveCoupledTau = true
corresponds to a coupled solver, but if solveWithUptau = false or solveCoupledUp
=solveWithUptau = false, then a semi-coupled solver is obtained.
Coupled solvers in τcan be only used with viscoelastic fluid models solved
in τvariable, which excludes all the implementations based on transformation of
variables (conformation and log-conformation tensor). For GNF models, p-ucan
be solved coupled, but the viscosity is a fully-explicit function of the strain-rate.
4.4.9 How to use sparseMatrixSolvers library in my own
application?
!Segregated solvers
In order to use the interfaces from sparseMatrixSolvers library in a segregated
solver, follow these steps:
•include header sparseMatrixSolvers.H in your application. Note that this
header file should be ideally the first to be included, in order to avoid names-
pace conflict with Petsc;
•create an object autoP tr < sparseSolver < T ype >>, where Type can be
any of the valid OpenFOAMR
types. The constructor requires the field for
which the equation will be built and solved. See an example in createSo
lvers.H of solver rheoEFoam;
•call function solve(fvMatrix < T ype >) of the object created to solve the
equation. The Type of the matrix should be consistent with the Type used
in the constructor. See an example in pEqn.H of solver rheoEFoam;
•add the path of sparseMatrixSolvers library and its dependencies to the
Make/option file of your application. See, for example, the Make/option
file of solver rheoEFoam.

CHAPTER 4. Overview of rheoTool 85
!Coupled solvers
In order to use the interfaces from sparseMatrixSolvers library in a coupled
solver, follow these steps:
•include headers sparseMatrixSolvers.H and blockOperators.H in your appli-
cation. Note that header sparseMatrixSolvers.H should be ideally the first
to be included, in order to avoid namespace conflict with Petsc;
•create an object autoP tr < coupledSolver >;
•insert all the fields being solved in the object created, using function
insertF ield(volF ield < T ype >). Type is any valid OpenFOAM R
type.
Note that all fields must be already inserted before the first equation is in-
serted in the next step. You can lookup the autoP tr < coupledSolver >
object to add fields from other compilation units, since the class is object-
registered;
•insert all the equations in the autoP tr < coupledSolver > object with a
call to function insertEquation(word, word, eqT ype), where eqType is either
an fvMatrix < T ype > or a LMatrix < T ype >, with Type being any
valid OpenFOAM R
type. Note that class LMatrix < T ype > has been
created in rheoTool to handle special coupling terms that are discretized with
fvmb operators. The first and second arguments of function insertEquation()
correspond to the names of the field for which the equation is being written
and the field which is contributing to that equation, respectively. These are
technical details related with new classes added to OpenFOAM R
through
rheoTool. It is not expected that the reader (programmer) understand them
without having examined the code before;
•after all the equations and coupling terms have been inserted, solve the cou-
pled system of equations through a call to function solve(). Note that in a
coupled solution method all the governing equations are solved simultane-
ously;
•add the path of sparseMatrixSolvers and fvmb libraries and their dependen-
cies to the Make/option file of your application. See, for example, the
Make/option file of solver rheoEFoam.
The above explanation for coupled solvers might seem abstract if the code be-
hind was not analyzed before. Therefore, we strongly recommend programmers
to first take a look into directories fvmb and sparseMatrixSolvers and any
application using coupled solvers, as for example rheoEFoam and model Nernst-
PlanckCoupled.
4.4.10 Limitations
These are some known limitations of the sparseMatrixSolvers library:

CHAPTER 4. Overview of rheoTool 86
•the interfaces were not tested with cyclic-derived patches other than cyclic
itself. For example, cyclicAMI is untested.
•some preconditioners in Hypre (mostly) and Petsc interfaces do not work
correctly in serial runs.
•the residuals retrieved by coupled solvers in the first time the system of
equation is solved do not correspond to the reality for any non-zero initial
solution (field).
•Eigen interface can not be used in parallel.
•coupled solvers are not using the block matrix structures of Petsc, which is
probably deteriorating performance.
•the coupled PNP system of equations (NernstPlanckCoupled model) shows
some instability in non-orthogonal grids due to the electromigration term.
To mitigate this issue, use cellLimited gradient schemes for electric-related
variables.
•boundary condition fixedFluxExtrapolatedPressure for pressure can not be
used if p-uare solved coupled.
It is worth noting that the default OpenFOAM R
sparse matrix solvers display
the best performance in most of the times. The sparse matrix solvers from the
external libraries are only advantageous when OpenFOAM R
sparse matrix solvers
require a high number of iterations to converge. In those cases, it is typically
possible to setup a solver from an external library that outperforms the open-
FoamSolver interface. We simply want to alert that the default sparse matrix
solvers of OpenFOAM R
will continue being a good (the best) option in most of
the situations where a segregated solver is applied.
4.5 Solvers
The discussion presented in this Section assumes a segregated solution
method. However, a coupled solution method is also available for some
solvers in the OpenFOAM R
version.
The solvers available in rheoTool are summarized in Table 4.8. Each one is dis-
cussed in detail in the following sections.
Table 4.8: Brief description of the solvers available in rheoTool.
Name Description

CHAPTER 4. Overview of rheoTool 87
rheoFoam
Transient solver for pressure-driven, single-phase, lam-
inar, isothermal flows. Selection of rheology is general
among all the available GNF and viscoelastic models.
rheoInterFoam
Transient solver for pressure-driven, two-phase, lami-
nar, isothermal flows, using the volume-of-fluid (VOF)
approach. Selection of rheology for each phase is
general among all the available GNF and viscoelastic
models.
rheoTestFoam
Application to compute steady and transient material
properties for any of the available GNF and viscoelas-
tic models.
rheoEFoam
Transient solver for electrically-driven, single-phase,
laminar, isothermal flows. Mixed electric-/pressure-
driven flows are also allowed. Selection of rheology is
general among all the available GNF and viscoelastic
models.
rheoBDFoam
Solver for Brownian dynamics simulations. The exter-
nal forcing can be analytical or numerical (transient or
steady). The external numerical forcing can be elec-
trophoresis, electroosmosis, a pressure-driven flow or
a combination of them.
4.5.1 rheoFoam
Solver rheoFoam implements the transient, incompressible Navier-Stokes equations
for single-phase flows of GNF or viscoelastic fluids. Figure 4.2 displays the solving
sequence when the equations are solved segregated.
The solver has three main loops: L1, which is advancing the time; L2, which is
an inner-loop used to converge the solution at each time-step; and L3, a loop which
can be enabled for non-orthogonal grids, in order to update (inside each time-step
and each inner-iteration) the explicit correction of the pressure Laplacian, avoiding
stability problems and reducing the error in transient computations. More than
understanding each step identified in Fig. 4.2, we want to help the reader to identify
them in the source code and relate them with the theory presented in the previous
Chapter. With this purpose in mind, we will do a tour to the source code of
the solver and the most important points will be discussed, skipping the lines not
essential to understand the algorithm.
The solver rheoFoam is composed of one main file (rheoFoam.C) and other
associated header files, among which (createFields.H,createPPutil.H,
UEqn.H,pEqn.H,CEqn.H), that can be found in directory src/solvers/rh
eoFoam/. All the header files are included from the main .C file. We will start
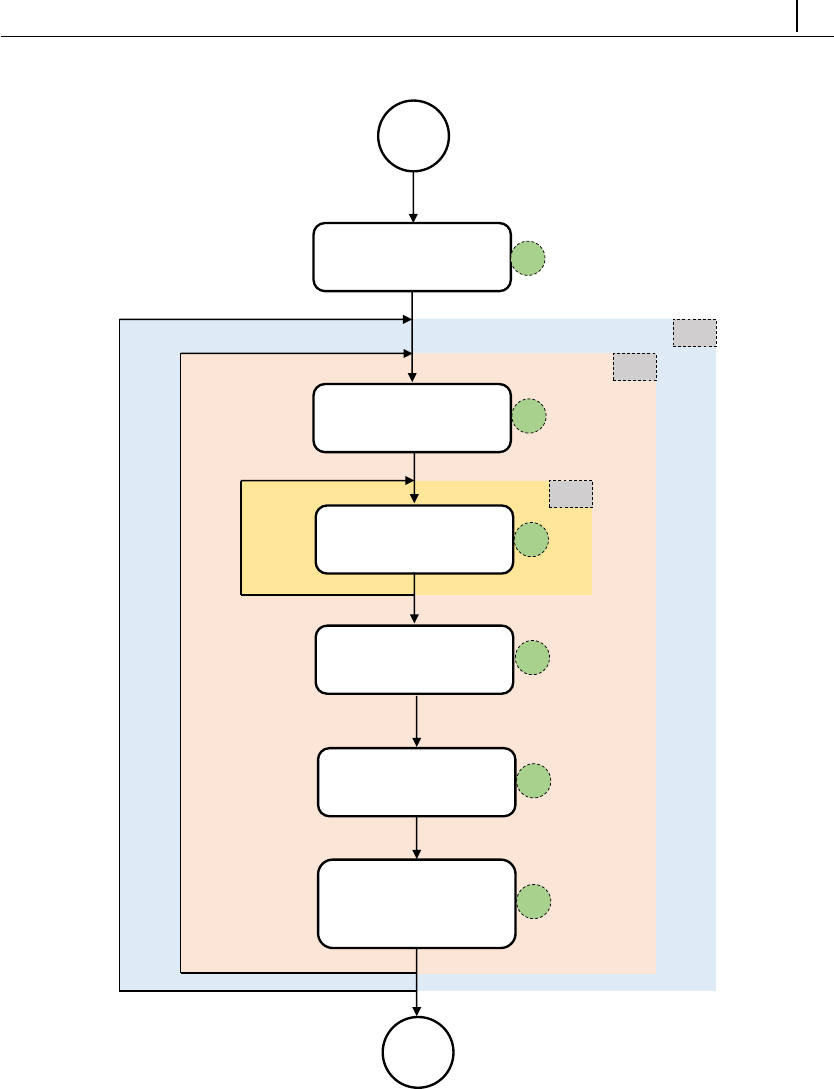
CHAPTER 4. Overview of rheoTool 88
Solve the constitutive
equation
Solve the momentum
equation
Solve the pressure
(continuity) equation
Correct cell velocities
and face fluxes
Initialize fields and
variables
End
Start
Inner loop: i = i + 1
Time loop: t = t + Δt
Non-orthogonality
corrector
loop
S5
S2
S3
S4
S1
L1
L2
L3
createField.H
rheoFoam.C
UEqn.H
pEqn.H
pEqn.H
Solve the transport
equation for a scalar
(optional)
S6
CEqn.H
Figure 4.2: Solving sequence of rheoFoam under a segregated solution method
(steps related with mesh motion are omitted for simplicity).
by digging into rheoFoam.C, whose source code is displayed in Listing 4.10.
•lines 1-9: those # include lines load classes used by OpenFOAM R
for stan-
dard tasks, transversal to most of the OpenFOAM R
solvers.
•line 11: this # include is providing access to a library of post-processing

CHAPTER 4. Overview of rheoTool 89
utilities, that we discuss later in Section 4.7.2.
•line 12: this # include allows the solver to access the models defined in the
constitutiveEquations library.
•lines 17-29: fields, variables, controls and the mesh are created (step S1 of
Fig. 4.2). Lines 23 and 27 point to the header files createFields.H and
createPPutil.H, respectively, located in the same directory as rheoFo
am.C. The later is responsible for the creation of post-processing utilities.
•lines 36-93: represents the time loop, i.e., L1 of Fig. 4.2. The solver will
keep running until the final specified time is reached or once the residuals of
the solved variables drop below some tolerance (this dual criterion is specific
of class simpleControl).
•lines 38-40: those # include allow automatic time-step adjustment, based
on the maximum Courant number specified by the user. This control can be
switched off by the user (more details in Section 5.1.1).
•lines 66-85: this is the inner loop, L2, of Fig. 4.2. Inside this loop, all
the conservation equations are solved nInIter times inside the same time-
step. This reduces the explicitness of the method, which exists, for example,
in the non-linear convective term of the momentum equation, in the both-
sides-diffusion technique and in several terms of the constitutive equation
(for a given equation, only the terms introduced through a fvm:: operator
are implicit). Furthermore, these iterations also strengthen the coupling
between velocity and pressure.
•lines 44: this function executes the mesh motion if the mesh is dynamic. For
a static mesh, this function has no practical effects.
•lines 46-63: these lines are only executed for dynamic meshes and include
an optional correction of fluxes (line 53). Note that the term ubof Eq. (3.24)
is subtracted from uin line 57.
•line 73: the momentum equation is solved. The header file UEqn.H (Listing
4.11) will be explored later.
•line 74: the pressure equation is solved. The header file pEqn.H (Listing
4.12) will be explored later.
•line 78: function correct() of the constitutive model is called. As seen before,
this function updates variable τby solving the constitutive equation(s).
•line 81-84: the equation for a passive scalar is optionally solved, depending
on a user-defined selection (more details in Section 5.1.1). The header file
CEqn.H (Listing 4.13) will be explored later.
•lines 87: this is where the post-processing utilities are evaluated, if any has
been selected by the user.
CHAPTER 4. Overview of rheoTool 90
1#include "fvCFD.H"
#include "IFstream.H"
3#include "OFstream.H"
#include "simpleControl.H"
5#include "fvOptions.H"
#include "extrapolatedCalculatedFvPatchField.H"
7#include "dynamicFvMesh.H"
#include "CorrectPhi.H"
9#include "adjustCorrPhi.H"
11 #include "ppUtilInterface.H"
#include "constitutiveModel.H"
13 // ********************************
*****//
15 int main(int argc, char *argv[])
{
17 #include "postProcess.H"
#include "setRootCase.H"
19 #include "createTime.H"
#include "createDynamicFvMeshDict.H"
21 #include "createDynamicFvMesh.H"
#include "initContinuityErrs.H"
23 #include "createFields.H"
#include "createControls.H"
25 #include "createUfIfNeeded.H"
#include "createFvOptions.H"
27 #include "createPPutil.H"
#include "CourantNo.H"
29 #include "setInitialDeltaT.H"
// ******************************
*****//
31
Info<< "\nStarting time loop\n" << endl;
33
// --- Time loop ---
35
while (simple.loop())
37 {
#include "readControls.H"
39 #include "CourantNo.H"
#include "setDeltaT.H"
41
Info<< "Time = " << runTime.timeName() << nl << endl;
43
mesh.update();
45
if (mesh.changing())
47 {
// Calculate absolute flux from the mapped surface
velocity
49 phi = mesh.Sf() & Uf();
51 if (correctPhi)
{
53 #include "correctPhi.H"

CHAPTER 4. Overview of rheoTool 91
}
55
// Make the flux relative to the mesh motion
57 fvc::makeRelative(phi, U);
59 if (checkMeshCourantNo)
{
61 #include "meshCourantNo.H"
}
63 }
65 // --- Inner loop iterations ---
for (int i=0; i<nInIter; i++)
67 {
Info << "Inner iteration: " << i << nl << endl;
69
// --- Pressure-velocity SIMPLEC corrector
71 {
// ---- Solve U and p ----
73 #include "UEqn.H"
#include "pEqn.H"
75 }
77 // ---- Solve constitutive equation ----
constEq.correct();
79
// --- Passive Scalar transport
81 if (sPS)
{
83 #include "CEqn.H"
}
85 }
87 postProc.update();
runTime.write();
89
Info<< "ExecutionTime = " << runTime.elapsedCpuTime() << "
s"
91 << " ClockTime = " << runTime.elapsedClockTime() << "
s"
<< nl << endl;
93 }
95 Info<< "End\n" << endl;
97 return 0;
}
Listing 4.10: Source code of rheoFoam.C.
The source code in file createFields.H will not be discussed, since it mainly
contains standard declaration/initialization of fields and variables. However, it is
worth mentioning the creation of a constitutiveModel object, named constEq, which
stores the data of the constitutive equation selected.
According to the SIMPLEC algorithm, the momentum equation is first solved

CHAPTER 4. Overview of rheoTool 92
to obtain an estimated velocity field, using the pressure field of the previous inner-
iteration or time-step. Then, we solve for the pressure field enforcing continuity.
Finally, using the correct pressure field, the previously estimated velocity is cor-
rected, both on faces and cell centers. This is what is being executed in UEqn.H
and pEqn.H. We follow the discussion by analyzing the content of UEqn.H, whose
code is displayed in Listing 4.11.
•lines 5-13: this is where the momentum equation is built. We can iden-
tify the transient term in line 7, an eventual acceleration term arising from
a non-inertial reference frame in line 8, the convective term in line 9, an
extra momentum source term in line 11 (term fin Eqs. 3.5 and 3.18) and
the extra-stress divergence in line 12 (∇·τ0), containing both the solvent
and the polymeric contributions (remember the output of divTau() function,
analyzed in Section 4.1.4).
•line 21: the momentum equation is solved considering the pressure gradi-
ent contribution, where the pressure field from the last time-step or inner-
iteration is used. This term was not added before in order for operator H
obtained from the momentum equation to be free of such contribution, as
discussed in Section 3.3.1. This is required to avoid the onset of checkerboard
fields, since a traditional Rhie-Chow interpolation is not used (cf. Ref. [2]).
// Momentum predictor
2
MRF.correctBoundaryVelocity(U);
4
tmp<fvVectorMatrix> tUEqn
6(
fvm::ddt(U)
8+ MRF.DDt(U)
+ fvm::div(phi, U)
10 ==
fvOptions(U)
12 + constEq.divTau(U)
);
14
fvVectorMatrix& UEqn = tUEqn.ref();
16
UEqn.relax();
18
fvOptions.constrain(UEqn);
20
solve(UEqn == -fvc::grad(p));
22
fvOptions.correct(U);
Listing 4.11: Source code of UEqn.H.
After having a guessed (non-conservative) velocity field, we will see how it is
used inside pEqn.H (Listing 4.12):
•lines 1-32: variables required to solve the pressure equation (Eq. 3.15) are
assembled. The sequence of steps can be easily understood, keeping in mind

CHAPTER 4. Overview of rheoTool 93
that UEqn().A() retrieves diagonal coefficients (aP) and that UEqn().H()
and UEqn().H1() stand for operators Hand H1, respectively. As previously
discussed in Section 3.3.1, pressure gradient terms entering the definition of
face fluxes (line 26) are directly evaluated on cell faces to avoid checkerboard
fields. Also, in line 8/11 there is the addition of the corrective term for
time-step dependency, described in Section 3.3.1.
•lines 35-50: this is the non-orthogonality corrector loop (L3 ) displayed in
Fig. 4.2. The goal is similar to the one of the inner loop: minimizing the
explicitness of the algorithm. At this point, the reader may be asking why
do this loop exists if the inner loop is already there doing a similar task?
To clarify this point, it should be noted that the non-orthogonality corrector
loop only makes sense to exist for non-orthogonal meshes. For those meshes,
the laplacian operator in line 39 is not completely handled in an implicit
way, but an explicit corrective term is added. For highly non-orthogonal
meshes, this term has an important contribution and, due to being explicit,
the pressure solution will not be continuity-compliant, which can afterwards
introduce continuity problems and lead the simulation to diverge. For this
reason, in such cases the implicitness of the Laplacian term is increased by
continuously solving that equation with the updated pressure-field, and the
fluxes are only corrected at the last iteration of this loop (lines 46-49). Is the
non-orthogonal corrector loop absolutely necessary when dealing with non-
orthogonal meshes? No, as long as the simulation does not diverge and if
only steady-state results are required. Otherwise, this loop should be active.
For a number of cases, doing 2-3 non-orthogonal iterations keeps the solver
stable, without the need of under-relaxing the pressure. Even if only one
non-orthogonal correction is performed, the Laplacian term should still be
discretized with the corrective term to keep the accuracy in non-orthogonal
meshes.
•lines 39,44: the pressure equation (Eq. 3.15) is assembled (line 39) and
solved (line 44).
•line 48: this is the equation which corrects the face fluxes (Eq. 3.16 interpo-
lated to the faces). Again, pressure gradient terms are directly evaluated on
cell faces: the snGrad() operator in line 26, when building phiHbyA, and the
one coming from the laplacian() operator in line 39, from which the flux()
operator is derived.
•line 57: this is the equation which corrects the cell-centered velocity field
(Eq. 3.16).
•line 69: the term ubof Eq. (3.24) is subtracted from u(the operation is on
face fluxes, variable phi).
1volScalarField rAU(1.0/UEqn.A());
volVectorField HbyA(constrainHbyA(rAU*UEqn.H(), U, p));
3surfaceScalarField phiHbyA
CHAPTER 4. Overview of rheoTool 94
(
5"phiHbyA",
mesh.changing() == true ?
7fvc::flux(HbyA)
+ fvc::interpolate(rAU)*fvc::ddtCorr(U, Uf())
9:
fvc::flux(HbyA)
11 + fvc::interpolate(rAU)*fvc::ddtCorr(U, phi)
);
13
MRF.makeRelative(phiHbyA);
15
if (p.needReference())
17 {
fvc::makeRelative(phiHbyA, U);
19 adjustCorrPhi(phiHbyA, U, p);
fvc::makeAbsolute(phiHbyA, U);
21 }
23 tmp<volScalarField> rAtU(rAU);
25 rAtU = 1.0/(1.0/rAU - UEqn.H1());
phiHbyA += fvc::interpolate(rAtU() - rAU)*fvc::snGrad(p)*mesh.
magSf();
27 HbyA -= (rAU - rAtU())*fvc::grad(p);
29 tUEqn.clear();
31 // Update the pressure BCs to ensure flux consistency
constrainPressure(p, U, phiHbyA, rAtU(), MRF);
33
// Non-orthogonal pressure corrector loop
35 while (simple.correctNonOrthogonal())
{
37 fvScalarMatrix pEqn
(
39 fvm::laplacian(rAtU(), p, "laplacian(p|(ap-H1))") ==
fvc::div(phiHbyA)
);
41
pEqn.setReference(pRefCell, pRefValue);
43
pEqn.solve();
45
if (simple.finalNonOrthogonalIter())
47 {
phi = phiHbyA - pEqn.flux();
49 }
}
51
#include "continuityErrs.H"
53
// Explicitly relax pressure for momentum corrector
55 p.relax();
57 U = HbyA - rAtU*fvc::grad(p);

CHAPTER 4. Overview of rheoTool 95
U.correctBoundaryConditions();
59 fvOptions.correct(U);
61 if (mesh.changing())
{
63 Uf() = fvc::interpolate(U);
surfaceVectorField n(mesh.Sf()/mesh.magSf());
65 Uf() += n*(phi/mesh.magSf() - (n & Uf()));
}
67
// Make the fluxes relative to the mesh motion
69 fvc::makeRelative(phi, U);
Listing 4.12: Source code of pEqn.H.
After pEqn.H is executed, both the pressure and the face fluxes are continuity-
compliant, but not the cell-centered velocity field. The conservative fluxes can now
be used to solve any transport equation. In rheoFoam, we offer the possibility to
solve a transport equation for a passive scalar. The governing equation, included
in file CEqn.H, is simply a convection-diffusion transport equation, as can be seen
in lines 5-11 of Listing 4.13.
1// Transport of passive scalar
3dimensionedScalar D_ = cttProperties.subDict("
passiveScalarProperties").lookup("D");
5fvScalarMatrix CEqn
(
7fvm::ddt(C)
+ fvm::div(phi, C)
9==
fvc::laplacian(D_,C)
11 );
13 CEqn.relax();
CEqn.solve();
15
if (U.time().outputTime())
17 {
C.write();
19 }
Listing 4.13: Source code of CEqn.H.
4.5.2 rheoTestFoam
The main purpose of solver rheoTestFoam is to evaluate the behavior of the con-
stitutive models for a user-defined ∇utensor. At the same time, it can also be
envisaged as a basic debugging tool to check for the correct implementation of the
constitutive models, since an analytical or semi-analytical solution usually exists,
which can be used for comparison.
Shortly, rheoTestFoam solves for the solvent and polymeric constitutive equa-
tions, Eqs. (3.3) and (3.4), respectively, for a prescribed ∇utensor, assuming
CHAPTER 4. Overview of rheoTool 96
homogeneous flow conditions (∇·τ=0;u·∇τ=0). Since there are no approx-
imations related with spatial discretization, the resulting steady-state solution
τ0=τ+τsis exact, and OpenFOAM R
is simply acting as a nonlinear matrix
solver. To obtain unsteady solutions, the temporal discretization introduces nu-
merical errors during the transient period, which can be reduced using a small
time-step.
The computational domain used with this solver is composed of a single cell: a
cube with unitary edge length (1 m). The boundary conditions for uare internally
manipulated inside the code, in order to get the tensor ∇udefined by the user,
Fig. 4.3. Thus, the default mesh and boundary conditions should not
be changed by the user when working with rheoTestFoam. We note that the
following definition holds in this guide (and in OpenFOAM R
, in general):
(∇u)ij =∂uj
∂xi
=
∂u
∂x
∂v
∂x
∂w
∂x
∂u
∂y
∂v
∂y
∂w
∂y
∂u
∂z
∂v
∂z
∂w
∂z
(4.28)
y
z
x
x+
x-
z+
z-
y-
y+
2
,
2
,
2321 y
y
u
y
y
u
y
y
uz
y
x
y
u
2
,
2
,
2321 x
x
u
x
x
u
x
x
uz
y
x
x
u
2
,
2
,
2321 z
z
u
z
z
u
z
z
uz
y
x
z
u
2
,
2
,
2321 y
y
u
y
y
u
y
y
uz
y
x
y
u
2
,
2
,
2321 x
x
u
x
x
u
x
x
uz
y
x
x
u
2
,
2
,
2321 z
z
u
z
z
u
z
z
uz
y
x
z
u
Figure 4.3: Boundary conditions manipulation in the single-cell mesh used with
rheoTestFoam. The constants currently used to represent the cell-centered velocity
are κ1=κ2=κ3= 0, although any other values could be used. The edge length
of the cubic cell is set to δx =δy =δz = 1m.
Two operation modes are available with this solver:
•ramp mode: the user defines a list of ∇utensors and the solver will retrieve
the steady solution for each entry. In this mode, the solver automatically
selects the ideal time-step value to be used and the steady-state is also auto-
matically detected (either the relative variation of the extra-stress magnitude

CHAPTER 4. Overview of rheoTool 97
drops below 10-8, or after a predefined number of time-steps has been ex-
ceeded – this last condition is used to avoid infinite loops).
•transient mode: the user defines one single ∇utensor and the solver will
return the evolution over time of the monitored variables. In this case,
both the time-step and the end time are controlled by the user. This mode
allows to determine the transient material functions of the constitutive model
selected.
As default behavior, rheoTestFoam writes a file named Report containing all
the components of the total extra-stress tensor, τ0(remember that τ0=τ+τsis
the total extra-stress tensor, including both solvent and polymeric contributions).
In ramp mode, also the status (Converged or Exceed Niter) is returned, along
with the relative error. The user can compute any relevant material function from
the tensor components retrieved. If for some reason the status Exceed Niter is
retrieved for any ∇uentry in ramp mode, we recommend to run rheoTestFoam in
transient mode for that same ∇u, using a small time-step – at convergence, the
steady material properties will be obtained. This may happens, for example, when
using a multimode model with very different modes, for which the automatic time-
stepping procedure fails to choose a stable time-step for the given ∇u. On the
other hand, some viscoelastic models are naturally unbounded under certain flow
conditions, such as the UCM and Oldroyd-B models for W i ≥0.5 in extensional
flow. Care should be taken for such situations, since the solver will most likely
retrieve a non-physical solution close to those limits and eventually diverge.
Note that rheoTestFoam is only adapted to work optimally in ramp mode
with the models implemented in the extra-stress tensor variable, which excludes
the models solved with the log-conformation approach or with the conformation
tensor (FENE-type). However, the material functions for a given model are the
same independently of the variable in which it is solved for, as long as all the terms
are accounted for. Thus, it is possible to extract the material functions of all the
models provided in rheoTool.
In a future release of rheoTool, we anticipate that the solver rheoTestFoam will
be able to fit the available constitutive models to experimental data input by the
user and return the best-fit model, along with the best-fit parameters (λ, η, ...).
This will allow to run simulations with a numerical model reproducing properly
the material functions of real fluids.
4.5.3 rheoInterFoam
Section 4.5.3 is under development.
The solver rheoInterFoam is a generalization of rheoFoam for two-phase flows, us-
ing the Volume of Fluid (VOF) method of OpenFOAM R
to represent the interface
between the two phases.
CHAPTER 4. Overview of rheoTool 98
Currently, rheoInterFoam solves a constitutive equation for each phase and the
extra-stress tensor contributing to the momentum equation is the weighted aver-
age of the extra-stress tensor for each phase, where the weighing is ensured by the
indicator function used in VOF. This approach allows to have phases represented
by different constitutive equations, although this is possibly not the most accurate
and stable way to do the computations. Additionally, the SIMPLEC algorithm
used for single-phase flows may need to be improved when used in rheoInterFoam.
Other aspects are still under test, which makes the current version of rheoInter-
Foam still experimental. Nonetheless, this version is fully functional.
4.5.4 rheoEFoam
The solver rheoEFoam is the extension of rheoFoam to electrically-driven flows –
note the additional Ein the solver name, which points to its Electric component.
Thus, with no surprise, both solvers share the same basic structure and only
minor differences exist between both at the code level. For this reason, we will
not discuss again the common parts. Instead, we refer the reader to Section
4.5.1 to eventually recall the structure of rheoFoam and in this Section we only
highlight the main differences introduced in rheoEFoam. Note that rheoEFoam
allows the combination of both electrically- and pressure-driven flows with no
restrictions. Pure pressure-driven flows can be also simulated with rheoEFoam, for
which the solver becomes functionally equivalent to rheoFoam, although directly
using rheoFoam is the more efficient option in these situations.
Starting by the file createFields.H, there is an extra line for the creation
of the electric model, as shown in Listing 4.14.
1// Create the electric model
EHDEKModel elecM(phi);
Listing 4.14: Line in the file createFields.H of rheoEFoam, where the
electric model is created.
In file rheoEFoam.C, the header # include ”EDFModel.H” has been added in
order to enable the use of the EDFModels library, whose path had also to be added
to file Make/options. The other change is in the inner-iteration loop, which now
includes solving the electric-related equations (line 21, Listing 4.15), calling the
function correct() of the electric model (recall an example of that function in lines
188-281 of Listing 4.3). The user may also choose not to solve the equations
governing the fluid flow (see the if condition in line 7 of Listing 4.15). This is
useful when only the electric component of the problem is of interest.
// --- Inner loop iterations ---
2for (int i=0; i<nInIter; i++)
{
4
Info << "Inner iteration: " << i << nl << endl;
6
if (solveFluid)
8{
// --- Pressure-velocity SIMPLEC corrector
10 {

CHAPTER 4. Overview of rheoTool 99
// ---- Solve U and p ----
12 #include "UEqn.H"
#include "pEqn.H"
14 }
16 // ---- Solve constitutive equation ----
constEq.correct();
18 }
20 // ---- Update electric terms ----
elecM.correct();
22
// --- Passive Scalar transport
24 if (sPS)
{
26 #include "CEqn.H"
}
28
}
Listing 4.15: Inner-iteration loop of rheoEFoam (source code:
rheoEFoam.C).
Finally, the last change at the code level is in file UEqn.H, containing the
momentum equation, which has been modified to include the electric body-force
(line 9, Listing 4.16) – it can be a null vector, depending on the EDF model
selected.
1tmp<fvVectorMatrix> tUEqn
(
3fvm::ddt(U)
+ MRF.DDt(U)
5+ fvm::div(phi, U)
==
7fvOptions(U)
+ constEq.divTau(U)
9+ elecM.Fe()/constEq.rho()
);
Listing 4.16: Momentum-balance equation in rheoEFoam (source code:
UEqn.H).
4.5.5 rheoBDFoam
Solver rheoBDFoam is intended for Brownian dynamics simulations in generic
meshes. In a glance, the source code of rheoBDFoam is simply the one of
rheoEFoam, to which we added an object of class sPCloudInterface, that is up-
dated over time. Therefore, we recommend the reader to first take a look at
Sections 4.3 and 4.5.4. The pieces of code specifically devoted to Brownian
dynamics are mainly contained in header files createLagrangianFields.H
and moleculesEqns.H. In createLagrangianFields.H, a sPCloudInter-
face object is created and named molecules. This header file is called once in
rheoBDSFoam.C, at the beginning of the simulation. On the other hand, header
CHAPTER 4. Overview of rheoTool 100
file moleculesEqns.H is included in rheoBDSFoam.C each iteration of the
main time loop. Let’s take a look on its source code (Listing 4.17):
•lines 8-14: these lines enclose a special loop, which first divides the Eulerian
time-step by nSubCycles, and then performs the operations inside it. The
old time is incremented by this new time-step in each iteration of the loop,
such that an entire original (Eulerian) time-step is elapsed upon completion
of the loop. This procedure allows to use the original Eulerian time-step
everywhere outside the loop (e.g. in solving continuum equations), while a
lower time-step can be used for the operations enclosed in the loop, as long
as nSubCycles > 1 (this variable should be a positive integer different from
0; line 1). The operation executed inside the loop is defined at line 10, which
basically consists in a call to function update() of object molecules. The tasks
carried out by this function have been discussed in Section 4.3.2 and result
essentially in the update of the molecules’ state. The return value of the
function is true if at least one valid molecule remains in the computational
mesh, otherwise it is false and forces an early exit from the loop (lines 12-13).
•lines 20-24: the main time loop of the solver is exited if no valid molecules
remain inside the mesh.
int nSubCycles = mesh.solutionDict().subDict("SIMPLE").
lookupOrDefault<int>("nSubCycles", 1);
2
Info<< "Moving molecules." << endl;
4
scalar t0(runTime.elapsedCpuTime());
6
bool cont;
8for (subCycleTime molcSubCycle(runTime, nSubCycles); !(++
molcSubCycle).end();)
{
10 cont = molecules.update();
// Exit subcycle
12 if (!cont)
break;
14 }
16 execTimeLagrang += (runTime.elapsedCpuTime() - t0);
Info<< "ExecutionTime Lagrangian = " << execTimeLagrang << " s"
<< endl;
18
// Exit simple loop
20 if (!cont)
{
22 Info << nl << "No more valid molecules inside the computational
domain." << nl << "Exiting time loop." << nl << endl;
break;
24 }
Listing 4.17: Source code of header file moleculesEqns.H used by solver
rheoBDFoam to update the molecules’ state.

CHAPTER 4. Overview of rheoTool 101
If an analytical external forcing is used, or if a numerical one is used but not
solved for (frozen flow), then rheoBDFoam is basically just updating the molecules
state. Otherwise, it also solves the continuum equations. Note that the algorithm
used for Brownian dynamics follows a one-way coupling approach: the continuum
fields affect the molecules motion, but not the opposite. Therefore, the momen-
tum equation, as well as any other equation related with the continuum, keeps
unchanged upon inclusion of molecules. Moreover, this also allows to decouple
continuum computations from Brownian dynamics computations, and, in prac-
tice, a steady-state continuum field previously computed can be simply used and
kept frozen over time to move the molecules. The sole exception is when we need to
study the molecules dynamics in a transient continuum field. Details on the sim-
ulation settings to run rheoBDFoam and to select between analytical/numerical,
steady/transient forcing, etc., are provided in Section 5.5.1.
4.6 Boundary conditions
4.6.1 linearExtrapolation
TypeName:linearExtrapolation
Type: fixed-value (any type field).
Formula:Tij, f =Tij, P + (∇Tij)P·dPf, where Tij is the ij component of the
generic field T(scalar, vector or tensor), indices f and P represent the boundary
face and the cell owning that face, respectively, and dPf is the vector connecting
their geometrical centers.
Description: linear extrapolation of each field component from boundary cells
to boundary faces. Shortly, this boundary condition starts by computing the gradi-
ent of each component at the center of the cell owning the boundary face (using the
previous iteration/time-step known values on the boundary face). Then, with both
the value and the gradient of each component at those locations, the components
at the boundary faces are estimated by linear extrapolation. The discretization
scheme to compute the gradients enrolled in the process is run time selectable
and can be adjusted in dictionary fvSchemes, through the entry linExtrapGrad
followed by the selected scheme, in the gradSchemes subDict. In general, using
linear extrapolation for the polymeric extra-stress tensor on walls should be pre-
ferred in relation to a zero-gradient boundary condition, which has a lower order
of accuracy [2].
Since version 2.0, an optional second-order accurate linear regression (see [38])
can be selected by adding the entry useRegression true to the dictionary defining
the BC, i.e., below keyword type, for example. If not present, the solver will execute
by default the linear extrapolation defined above.
4.6.2 navierSlip
TypeName:navierSlip
CHAPTER 4. Overview of rheoTool 102
Type: fixed-value (vector).
Formula:
ut+∆t
f= (1−URF)ut
f+URF
−knl τ0
w,fmτ0
w,f
|τ0
w,f|,model =nonLinearNavierSlip
−α1−β|τ0
w,f|τ0
w,f ,model =slipT T
where URF is the under-relaxation factor (0 < URF ≤1), ut
fis the boundary
velocity at the previous time-step, and knl, m, α and βare input model-dependent
parameters (the model name should be also defined). The wall stress vector is
tangent to the wall and is given by τ0
w,f =τ0
f·nf−τ0
f·nf·nfnfwith τ0
fcorre-
sponding to the total (solvent and polymeric) extra-stress tensor at the wall.
Description: fully-explicit implementation of slip models according to [39].
Supports both two-phase flows and moving meshes. In the latter case, the moving
wall velocity is added to the slip component computed as above. Lower values
of URF increase the numerical stability, but are not adequate for time-dependent
flows.
4.6.3 zeroIonicFlux
TypeName:zeroIonicFlux
Type: fixed-gradient (scalar).
Formula:∇ci|f·nf=−ci,f ezi
kT ∇Ψ|f·nf, with ci,f =ci,P exp −ezi
kT (ψf−ψP).
Indices f and P represent the boundary face and the cell owning that face (see the
definition of the other variables in Section 3.7.1).
Description: imposing a no-flux condition for an ionic specie, in the Poisson-
Nernst-Planck model. This boundary condition results from the balance of diffu-
sion and electromigration at the patch, assuming that a no-penetration condition
holds there. The expression being used has been derived from a Robin-type bound-
ary condition [3].
4.6.4 boltzmannEquilibrium
TypeName:boltzmannEquilibrium
Type: fixed-value (scalar).
Formula:ci,f =ci,0 exp ezi
kT (ψf−ψ0), where ci,0 is the reference concentration
(user-defined) at which the intrinsic electric potential is ψ0(user-defined; see the
definition of the other variables in Section 3.7.1). A common choice is to set ci,0
as the bulk concentration of ions and ψ0= 0.
Description: ionic concentration derived from the assumption of Boltzmann
equilibrium near the patch. This boundary condition is intended to be used when
the electric potential is split, in which case only the intrinsic potential is used
in the formula. This boundary condition does not guarantee the zero-flux of a
given specie in all the situations, and, in general, it is not accurate for transient
simulations.

CHAPTER 4. Overview of rheoTool 103
4.6.5 inducedPotential
TypeName:inducedPotential
Type: fixed-value (scalar).
Formula:ψf=−φExt,f +ψFix +
1
Nf
P
f=1 |Sf|
Nf
P
f=1
φExt,f|Sf|, where ψFix is the bias
voltage (user-defined) of the patch, i.e., the electric potential of the surface in the
absence of an external electric field.
Description: intrinsic potential induced in a conducting surface placed over
an electric field and having a bias voltage [40]. The last term in the formula
represents the area-averaged external electric potential over the surface. This
boundary condition can be used with the Poisson-Boltzmann and Debye-H¨uckel
models, under the potentials splitting approach.
4.6.6 slipSmoluchowski
TypeName:slipSmoluchowski
Type: fixed-value (vector).
Formula:uSch,f =µ(−∇φExt,f), where µis the electroosmotic mobility (user-
defined), as defined in Section 3.7.5.
Description: slip velocity derived from the Helmholtz-Smoluchowski theory
(Section 3.7.5). Although this boundary condition can be used with any EDF
model for which φExt is defined, it is primarily intended to be used with the slip
model.
4.6.7 slipSigmaDependent
TypeName:slipSigmaDependent
Type: fixed-value (vector).
Formula:uSch,f =µ0σf
σ0m(−∇φExt,f), as defined in Section 3.7.6. Parame-
ters µ0,σ0and mare user-defined.
Description: slip velocity derived from the Helmholtz-Smoluchowski theory
for a space-variable conductivity field (Section 3.7.6). This boundary condition
can be used with the Ohmic model.
4.6.8 A note on wall boundary conditions for pressure
In the simulation of incompressible flows, it is a common approach to assign a zero-
gradient boundary condition for the pressure at walls. This approach is efficient to
ensure no-penetration in the wall (continuity equation), but it results in a lower-
order approximation for the pressure gradient in the momentum equation and, in
some cases, it may significantly unbalance the remaining sources of momentum.

CHAPTER 4. Overview of rheoTool 104
A more general approach is to derive the pressure gradient at the boundary from
the continuity equation, by enforcing the no-penetration condition. Indeed, if Eq.
(3.16) is interpolated to the faces of a bounding wall, then setting the velocity, or
more correctly the flux, to zero (no-penetration condition) results in
uf·n= 0 ⇒(∇p)f·n= (aP−H1)Hf
aP
+1
aP−H1−1
aP(∇p∗)f·n(4.29)
Eq. (4.29) is generic since it does not depend on a specific form of the mo-
mentum equation. It can also be seen that if both sides of Eq. (4.29) are forced
to be zero – the zero-gradient approach –, the equality is still satisfied and the
no-penetration condition is still valid. The advantage in using Eq. (4.29) is that
the resulting normal pressure gradient is going to effectively balance the remaining
local forces in the momentum equation. In practice, the difference between using
Eq. (4.29) or the zero-gradient approximation is only noticeable when the stresses
at the wall are significant (high Hf
aP), as for example in EDFs, where a strong elec-
tric force normal to the wall may exists. In the tutorials provided with rheoTool,
the zero-gradient approximation is frequently used.
Since OpenFOAM R
version 4.0, the boundary equation embodied by Eq. (4.29)
is available by default under the name fixedFluxExtrapolatedPressure. However,
this boundary condition may not be usable in some cases, as for example in cases
with a zero velocity assigned to all boundaries. In such cases, there is a conflict
created by function adjustPhi() when it attempts to artificially adjust the fluxes.
This issue can be avoided by commenting the line where function adjustPhi() is
called in the code (typically inside file pEqn.H), provided the user is sure that
the set of boundary conditions under use verifies continuity. This limitation in the
boundary condition might be eventually solved in future releases of OpenFOAM R
.
Importantly, in multiphase flows with non-zero surface tension and/or gravity
effects, the zero-gradient condition for pressure is generally incorrect. Indeed, for
such flows it is usual to compute the fluxes in two steps in OpenFOAM R
, i.e., the
term Hf
aPin Eq. (4.29) is built in two steps. The last step adds the flux contribution
from surface-tension and gravity without enforcing a null contribution at the wall.
Thus, in general the right hand side of Eq. (4.29) is non-null in these cases and sim-
ply setting (∇p)f·n= 0 creates a local mass imbalance. The boundary conditions
fixedFluxPressure (available in OpenFOAM R
and foam-extend) and fixedFluxEx-
trapolatedPressure (only available in OpenFOAM R
starting from version 4.0) solve
this issue by equating the normal pressure gradient to this extra flux, and they
should be employed in such situations. In addition, for rheoTool versions run-
ning foam-extend, when the SIMPLEC algorithm is selected for pressure-velocity
coupling, the fixedFluxPressure BC requires that the entry Dp is defined and set
to ”rAtU ” (check the tutorials provided). This is not needed for the PIMPLE
coupling algorithm, or when using OpenFOAM R
v4.x.

CHAPTER 4. Overview of rheoTool 105
4.7 Utilities
4.7.1 GaussDefCmpw schemes for convective terms
The component-wise and deferred correction handling of HRSs, described in Sec-
tion 3.4, is included as a library in rheoTool. If the installation procedure pre-
sented in Chapter 2has been followed, this new class of schemes will only be
available when using the family of solvers provided with rheoTool. However, there
are several ways to make the schemes available to any solver of OpenFOAMR
.
One option (not requiring compilation) is to include this library (libgauss
DefCmpwConvectionSchemes.so) as a lib entry of controlDict in the
case directory. Another option is to compile the class inside library finiteVol-
ume, which is included by most OpenFOAMR
solvers. To access this class from
a specific solver, lgaussDefCmpwConvectionSchemes should be added to
the Make/options file of that solver, along with its path. We note that the
component-wise and deferred correction handling of HRSs improved significantly
the stability of viscoelastic fluid flow simulations [2], but its performance and ad-
vantage when used in other type of flows need to be tested (by no way we argue
that this is a magic bullet for all purposes).
The new group of HRSs is accessible from class GaussDefCmpw and its use
is similar to the standard HRSs of OpenFOAM R
. For example, the CUBISTA
scheme can be used by simply defining in dictionary fvSchemes:GaussDefCmpw
cubista; in front of the divergence term being discretized (remember that keywords
in OpenFOAM R
are case-sensitive). To obtain a list of all the schemes available,
simply type GaussDefCmpw; without any additional argument and you will ob-
tain all the possibilities, listed in Table 4.9. There is a scheme named none, which
corresponds to removing the convective term from the equation being discretized.
Note that all the limiters implemented in class GaussDefCmpw are totally inde-
pendent from the already existing limiters of OpenFOAM R
and all are defined
in file limiters.H. For example, you will have now GaussDefCmpw minmod
and Gauss Minmod, which are two different schemes, or, actually, two different
implementations of the same high-resolution scheme.
Details on the implementation of this class of schemes will not be pre-
sented in this guide, although the interested reader will easily find the anal-
ogy between the equations presented in Section 3.4 and the source code in files
gaussDefCmpwConvectionScheme.C and limiters.H. Nevertheless, for
documentation purposes, we summarize next the operations being executed by
each member function of class GaussDefCmpw:
•phifDefC(): depending on the boolean value of onlyDCphi, this function
returns either the interpolated variable on the faces – Eq. (3.23), with all the
terms explicitly evaluated –, or the deferred correction to the upwind scheme
– only the explicit term of Eq. (3.23).
•lims(): this function retrieves three variables: alpha, is a list containing αfor
each interval of the function defined in Eq. (3.20); beta is a list containing β
for each interval of the function defined in Eq. (3.20); bounds is a list of e
φC

CHAPTER 4. Overview of rheoTool 106
Table 4.9: Available High-Resolution schemes for convective terms in class gauss-
DefCmpw. The schemes are defined using the NWF approach (Eq. 3.20).
Scheme 1TypeName 2Equation
Upwind upwind [α, β] = [1,0]
CUBISTA cubista [α, β] =
[1,0] ˜
φC≤0∨˜
φC≥1
[7/4,0] 0 <˜
φC<3/8
[3/4,3/8] 3/8≤˜
φC≤3/4
[1/4,3/4] 3/4<˜
φC<1
MINMOD minmod [α, β] =
[1,0] ˜
φC≤0∨˜
φC≥1
[3/2,0] 0 <˜
φC<1/2
[1/2,1/2] 1/2≤˜
φC<1
SMART smart [α, β] =
[1,0] ˜
φC≤0∨˜
φC≥1
[3,0] 0 <˜
φC<1/6
[3/4,3/8] 1/6≤˜
φC≤5/6
[0,1] 5/6<˜
φC<1
WACEB waceb [α, β] =
[1,0] ˜
φC≤0∨˜
φC≥1
[2,0] 0 <˜
φC<3/10
[3/4,3/8] 3/10 ≤˜
φC≤5/6
[0,1] 5/6<˜
φC<1
SUPERBEE superbee [α, β] =
[1,0] ˜
φC≤0∨˜
φC≥1
[1/2,1/2] 0 <˜
φC<1/2
[3/2,0] 1/2≤˜
φC≤2/3
[0,1] 2/3<˜
φC<1
3no convection none –
1Corresponds to the name entry identifying the scheme in the source code.
2See Eq. (3.20).
3When this option is used, the convective term is deleted.
values, for which there is a change of branch in the function defined in Eq.
(3.20). Thus, function lims() defines Eq. (3.20) for the selected scheme.
•fvmDiv(): this function also exists for Gauss schemes and returns the matrix
of coefficients and the source term resulting from the discretization of the
implicit convective operator fvm::div(). Function phifDefC() is called from
here, whenever the selected scheme is different from upwind or none. Note
that both Gauss and GaussDefCmpw classes implement the upwind scheme
in the same way – it is the only scheme for which this happens.
•fvcDiv(): evaluates explicitly the operator fvc::div().
•interpolate(): returns face-interpolated values, by simpling calling

CHAPTER 4. Overview of rheoTool 107
phifDefC(), with the adequate boolean value.
•flux(): returns the field interpolated on face centers multiplied by the flux
on each face (phi).
The class GaussDefCmpw easily allows modifying or adding a new piecewise-
linear HRS, by simply adding a new instance or modifying an existing one in
function lims(), in file limiters.H. It is also possible to include HRSs not
defined as piecewise-linear functions, although this also requires modifying function
phifDefC().
4.7.2 Generic post-processing: ppUtil
In version 1.0 of rheoTool for OpenFOAM R
versions, the computation and writing
of quantities of interest after and/or during the simulations of the tutorial cases
was mainly exemplified by the use of coded FunctionObjects. The reader will easily
notice this throughout Chapter 5, where we even included a short Section devoted
to those utilities (Section 5.1.2). On the other hand, the same tasks accomplished
by such coded FunctionObjects were assembled in a library for the rheoTool version
running in foam-extend, since coded FunctionObjects are not available there. While
we recognize that coded FunctionObjects are a very useful tool, it is also true that
they do not allow the efficient execution of some advanced tasks. Therefore, since
rheoTool version 2.0 we generalized the post-processing dedicated library already
present for foam-extend versions to all rheoTool versions, while still keeping the
examples making use of coded FunctionObjects.
The post-processing library is named libpostProcessingRheoTool and it can
be found in directory src/libs/postProcessing/postProcUtils/. The
base class is named ppUtil and it is accessible from all the solvers included in
rheoTool through the ppUtilInterface class. Creating a new ppUtil is straightfor-
ward for a user with some knowledge on OpenFOAM R
programming:
•copy and paste the folder of an already existing ppUtil and give it a new
name of your choice. Delete the .dep file in that folder.
•find &replace the old name of the ppUtil by the name that you gave to the
folder. This should be done for both the .C and .H files (there are several
ways to do it automatically, for example, Ctrl +Hin gedit).
•modify the source code in order to do what you want.
•add the source file that was just created to the list of files for compilation in
the Make/file of the library.
•run the Allwmake script in src/ to compile, and it should be ready to use.
Several ppUtil can be used simultaneously in a given simulation. They should
be defined in subDict PostProcessing, located in dictionary fvSolution. Each
ppUtil should be provided as a different entry of group functions, as shown in
Listing 4.18. In this example, two ppUtil are selected and a name is given to each
one (ciMonitor and jMonitor; any name can be attributed).

CHAPTER 4. Overview of rheoTool 108
PostProcessing
2{
4functions
(
6
ciMonitor
8{
funcType calcBalance;
10 enabled true;
evaluateInterval 100;
12 }
14 jMonitor
{
16 funcType calcJpatch;
ListOfPatches
18 (
"cylinder"
20 );
enabled true;
22 evaluateInterval 100;
}
24
);
26
}
Listing 4.18: Example of a PostProcessing subDict.
For each ppUtil selected, at least three keywords must be defined:
•funcType: should specify the TypeName of the given ppUtil. To obtain a full
list of all the available utilities, simply insert any random letter.
•enabled: should be true or false and it determines whether the ppUtil is
active or not;
•evaluateInterval: should be any integer value >0 and corresponds to the
number of time-steps between consecutive calls to the given ppUtil. Cur-
rently, the execution interval can be only controlled by the number of time-
steps.
When a given ppUtil is active and programmed to write some quantity (or
several) of interest, a folder named rheoToolPP/startTimeName/ppUtilN
ame/ is created in the case directory and the output is forwarded to there.
The class ppUtil not only allows to create case-specific post-processing tools, as
it also offers the possibility to build generic post-processing applications. In Table
4.10 we present some generic ppUtil which are included in rheoTool and that can
be useful in a number of cases.

CHAPTER 4. Overview of rheoTool 109
Table 4.10: General-purpose ppUtil available in rheoTool.
TypeName Description
calcWSS
Computes the wall shear-stress magnitude for any con-
stitutive equation: W SSmag =|n·τ0−nn·τ0·n|
(Pa), where we remember that τ0represents
the total extra-stress tensor (see Section 3.1).
This ppUtil is used in the tutorial of Section 5.1.8.
calcJpatch
Computes the surface-averaged current density, for each
ionic specie, in the patches specified by the user:
Ji=ziF
|Spatch|
Nf
P
f=1 ci,fuf−Di∇ci,f −Diezi
kT ci,f∇Ψf·Sf(A/m2).
This ppUtil is only meaningful for the PNP model (an exam-
ple can be found in the tutorial of Section 5.4.4).
calcBalance
Computes the average concentration for each ionic specie:
ci=1
Vdomain
NC
P
j=1
ci,jVj(mol/m3). It also retrieves the net,
surface-averaged flux of each ionic specie through all the do-
main boundaries (equivalent to run calcJpatch for all the
boundaries, sum the fluxes and divide by ziF). This ppUtil is
only meaningful for the PNP model (an example can be found
in the tutorial of Section 5.4.3).
4.7.3 writeEfield
By default, the solver rheoEFoam does not write the electric field to the time
directories. The purpose of utility writeEfield is to read the electric potential
variable(s) and write the electric field, for each time directory. This means that
this utility can only be called after the simulation has been run. The utility sums
up all the electric potential variables available in the directories: Ψ(psi), φExt
(phiE) and/or ψ(psi).
The utility can be used by typing writeEfield in the terminal, without any
other requirements, except that at least one electric potential variable must exist
in the time directories. In addition, the time directories can not be decomposed
among processors (reconstruct the case if it is decomposed).
Note that the electric field can be also computed from the electric potential
in most of the visualization software, as for example Paraview, since a simple
differentiation operation is required.

CHAPTER 4. Overview of rheoTool 110
4.7.4 initMolecules
The purpose of utility initMolecules is to generate a set of files representing the
molecules that can be read by solver rheoBDFoam. The users can interpret this
utility as a sort of blockMesh application that generates molecules instead of a
computational mesh.
This utility reads its controls from dictionary initMoleculesDict, which
should be located inside folder constant/. An example of such dictionary is
presented in Listing 4.19. We will now analyze its entries. However, we should first
remember that solver rheoBDFoam can handle simultaneously multiple groups of
molecules with different physical properties. As such, both the physical properties
and the beads positions should be defined for each group. In the example of Listing
4.19, there are two groups of molecules defined inside dictionary groups, which were
arbitrarily named G1 (line 3) and G2 (line 27). The user can introduce and define
as many groups as needed (at least one should exist). For each group, the following
data must be present (we will only analyze group G1 in Listing 4.19):
•number of molecules (line 5): this is specified in entry nMolecules and should
be an integer ≥1. All the molecules generated inside a group will share the
same physical properties.
•physical properties (lines 7-12): these are the input parameters needed by
the physical model. We can find the diffusion coefficient (D), the beads
radius (a; only used if HI are active), the number of Kuhn steps per spring
(Nks), the exclusion volume parameter (nuEV ; only used if EV forces are
active) and the maximum length of a fully-stretched spring (Ls). See Section
3.8 for details about these parameters.
•spatial distribution and topology of the molecules (lines 15-24): these set-
tings should all be defined inside dictionary spatialDistributionCoeffs (lines
15-24). Currently, the molecules can be only distributed uniformly over a
straight line defined by its extreme points, p0 and p1. For a group with M
molecules, this means that the first bead of the first molecule will be at po-
sition p1 and the first bead of the remaining molecules will be spaced apart
consecutively by vector ∆s= (p1 −p0)/(M−1) (the first bead of the last
molecule will be at position p2 ). Note that p0 and p1 can be assigned the
same vector positions, in which case all the molecules have their first bead at
the same position. We remember that solver rheoBDFoam does not account
for inter-molecular interactions (for all the effects considered, each molecule
behaves as if it was alone in the surrounding fluid). The last entry of dictio-
nary spatialDistributionCoeffs, named branches() (lines 20-23), controls the
position of the remaining beads in each molecule. The molecules are built
branch-by-branch, thus each line of branches() should fully define a branch
according to a fixed syntax:
(A B C) (d0 d1 d2 ) (E F) (G H)
A - index of the master branch (integer).

CHAPTER 4. Overview of rheoTool 111
B - local index of the connecting bead in master branch (integer).
C - number of beads in the branch (integer).
(d0 d1 d2 ) - growth vector of the branch. Each component is expressed as a fraction
of Ls (vector of doubles).
E - is the branch growth random? Random (true) or not random (false)
(boolean).
F - does the last bead of the branch connects to any other branch? Yes
(true) or no (false) (boolean).
G - (optional) if F = true, then specify the local index of the connecting
bead in master branch (integer).
H - (optional)ifF=true, then specify the index of the master branch
(integer).
In order to simplify the understanding of this syntax, three examples are
provided in Fig. 4.4. Each line specified inside branches corresponds to a
branch of the molecule. The index automatically attributed to each branch
simply follows the order in which they are entered in the list. Importantly,
a given branch can only connect to a branch which has been already entered
in the list. All the examples provided have E = false, which means that
the current bead position is obtained from the previous bead position by
adding vector (d0 d1 d2 )Ls. In these cases, this vector is simply the spring
vector. However, when E = true, each component of the vector provided
is multiplied by a random number between -1 and 1. In either case, it is
user’s responsibility to ensure that the vector provided does not violate the
maximum spring length: d02+d12+d22<1
1groups
(
3G1
{
5nMolecules 1000;
7// Physical properties
D 0.065e-12;
9a .077e-6;
Nks 20;
11 nuEV 1.2e-21;
Ls 2.1e-6;
13
// Spatial distribution
15 spatialDistibutionCoeffs
{
17 p0 (0 0 0);
p1 (0 0.001 0);
19
branches
21 (
(0 0 11) ( 0.2 0 0) (true true)

CHAPTER 4. Overview of rheoTool 112
23 );
}
25 }
27 G2
{
29 nMolecules 700;
31 // Physical properties
D 0.15e-12;
33 a .053e-6;
Nks 15;
35 nuEV 4e-22;
Ls 2.1e-6;
37
// Spatial distribution
39 spatialDistibutionCoeffs
{
41 p0 (0 0 0);
p1 (0.005 0 0);
43
branches
45 (
(0 0 3) ( 0.1 -0.1 0 ) (false true)
47 (0 2 2) ( -0.1 -0.1 0 ) (false true)
(1 1 2) ( -0.1 0.1 0 ) (false true)
49 (111)(0.10.10)(false false) (0 0)
(213)(-0.100)(false true)
51 );
}
53 }
);
Listing 4.19: Example of a initMoleculesDict dictionary used to
generate molecules with utility initMolecules.
The execution of initMolecules generates a directory named lagrangian/m
olecules/ inside the startTime folder. The directory contains 5 files:
indices- field of triplets where the first value is the global bead index, the second is
the local bead index inside the molecule to which it belongs, and the third
is the index of the group to which the molecule belongs.
molcID- field of labels corresponding to the index of the molecule which contains the
given bead.
origID- field of labels corresponding to the global bead index. In most of the cases,
this field is equal to the first element of field indices. This field is kept to en-
sure compatibility with the generic particle-tracking engine of OpenFOAM R
.
origProcID- field of labels corresponding to the index of the processor containing the
bead. Since rheoBDFoam is still not able to run in parallel, this will be
always a field of zeros. Again, this field is kept to ensure compatibility with
the generic particle-tracking engine of OpenFOAM R
.
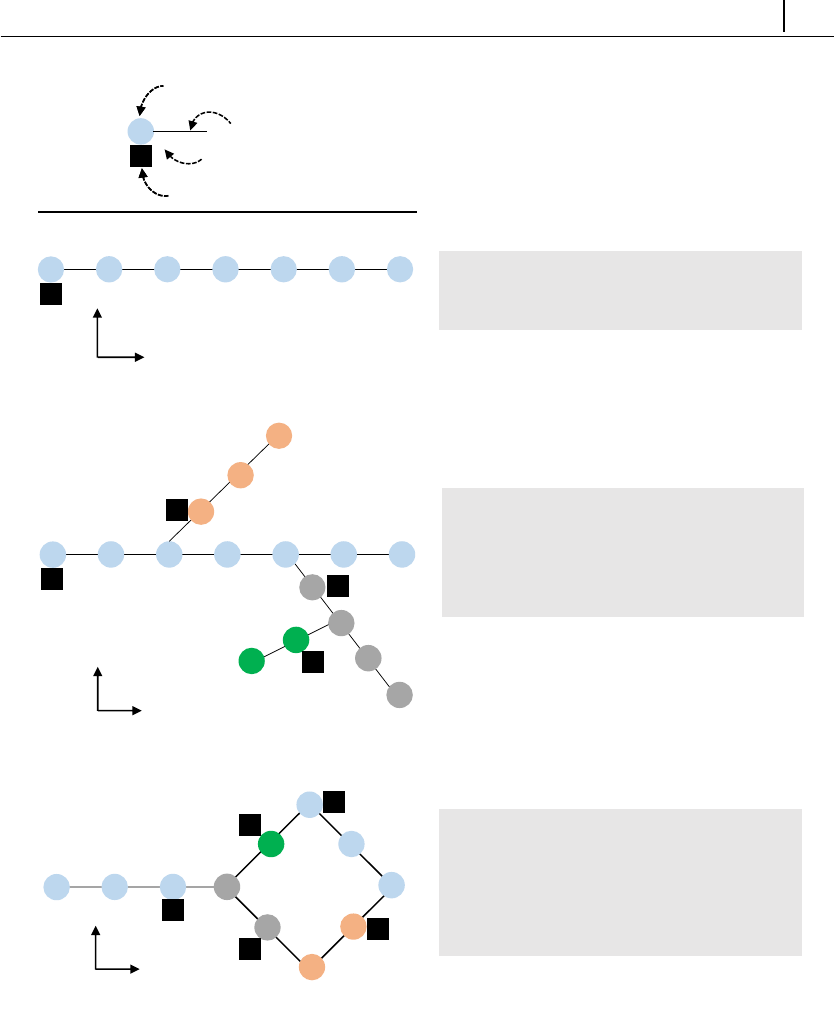
CHAPTER 4. Overview of rheoTool 113
01 2 3 4 5 6
0
01 2 3 4 5 6
0
x
y
0
1
2
1
0
1
2
3
1
0
2
3
x
y
0
1
2
0
1
0
1
0
21 0
x
y
0
1
2
3
4
branches
(
(0 0 7) ( 0.1 0 0 ) (false true)
);
branches
(
(0 0 7) ( 0.1 0 0 ) (false true)
(0 2 3) ( 0.1 0.1 0 ) (false true)
(0 4 4) ( 0.05 -0.05 0 ) (false true)
(2 1 2) ( -0.05 -0.05 0 ) (false true)
);
branches
(
(0 0 3) ( 0.1 -0.1 0 ) (false true)
(0 2 2) ( -0.1 -0.1 0 ) (false true)
(1 1 2) ( -0.1 0.1 0 ) (false true)
(2 1 1) ( 0.1 0.1 0 ) (false false) (0 0)
(2 1 3) ( -0.1 0 0 ) (false true)
);
01234 5 6
0123456
7
8
9
10
11
12
13
14
15
0
1
2
3
4
5
6
7
89
10
X
Y
Z
Legend: X–bead index inside the branch
Y–branch index
Z–bead index inside the molecule
Spring
Open linear chain
Open chain with branches
Closed chain with branches
Figure 4.4: Example of 3 molecules and corresponding branches settings to gen-
erate them with utility initMolecules.
positions- list of bead’s positions. This list has a special format defined by
OpenFOAM R
. Each entry is composed by the barycentric coordinates of
the bead (inside parentheses), the mesh cell index containing the bead,
the index of the face owning the tetrahedron containing the bead and the
point index defining that face. For more information, the user is advised to
check the source code of src/lagrangian/basic/particle/partic
le.H and src/lagrangian/basic/particle/particleIO.C pro-
vided with OpenFOAM R
(version 5.0 or newer).

CHAPTER 4. Overview of rheoTool 114
In addition to these files, initMolecules creates directory constant/runTi
meInfo/StartTime containing two files:
MoleculesInfo- holds information on the active molecules, as the physical properties of each
group of molecules. It also lists the index, number of beads and the group
that each active molecule belongs to.
springs- a list of triplets defining the springs of the active molecules (similarly to
faces in a mesh). The first element is the first-bead global index, the second
element is the second-bead global index and the third element is the molecule
index. A spring can be unequivocally defined with these elements.
The seven files described above are generated upon execution of initMolecules,
and they are automatically written by rheoBDFoam during a simulation, since they
are needed for an eventual restart. Note that all the information in dictionary in
itMoleculesDict is only read by utility initMolecules; changing this dictionary
after having run the utility or just before running solver rheoBDFoam will change
nothing. This is not a valid way to change the molecules’ physical properties
after having created the molecules. Such changes can be done manually in file
MoleculesInfo, although it is generally not recommended (it is preferable to
re-run initMolecules).
4.7.5 averageMolcN
The results obtained with solver rheoBDFoam usually require averaging over sev-
eral molecules due to the random nature of the Brownian term. Utility aver-
ageMolcN averages the molecular length over all the valid molecules registered
at a given time. This utility is mostly useful for homogeneous flows, where the
molecular extension does not depend on the spatial position.
The argument to this utility should be provided in the command line, following
this syntax:
∼$averageMolcN time
where time is the startTime.
The results for each group of molecules are written to file rheoToolPP/start
Time/moleculesStats/groupName/Stretch_Naverage.txt, where the
first column corresponds to time and the second column is the ensemble averaged
molecular length. Note that untracked/overstretched molecules are not accounted
in the average.
This utility requires (uses) the registry of the molecules’ position and stretch
over time, optionally written and saved by solver rheoBDFoam (see Section 4.3.8).
Therefore, this post-processing utility can only be called after a call to the solver.
4.7.6 averageMolcX
In some cases, it is useful to compute the average evolution of the molecules’ length
over space. Utility averageMolcX is intended for this purpose, since it retrieves the
average molecular length over a line defined by the user. This line can have any

CHAPTER 4. Overview of rheoTool 115
orientation and is divided in a finite number of bins. For example, consider line
connecting point (0,0,0) to point (10,0,0), that is divided in 10 bins. Then, all the
molecules whose center of mass, at a given instant, had its x-coordinate between
x= 0 and x= 1 will contribute to the average in the first bin. The second bin is
between x= 1 and x= 2, and so on for the remaining bins.
The arguments to this utility should be all provided in the command line,
following this syntax:
∼$averageMolcX time -biased bool -startPoint ”sP” -endPoint
”eP” -nBins nB
where time is the startTime,sP is the position of the first point of the line, eP
is the position of the second point of the line and nB is the number of bins. The
option -biased should receive a boolean and stands for the averaging method
used. The biased average (bool =true) takes all the hits in a given bin and
averages among all with equal weights per hit. This results, in general, in a biased
average, because the molecules with more hits in a given bin (for example the
ones with slower velocity) will have a higher representation in the results. The
unbiased average (bool =false; default option if none is specified) first computes
the average length of each molecule inside the bin, collecting all the hits of that
molecule in the bin, and then averages between all the molecules, attributing equal
weights to each one.
The results for each group of molecules are written to file rheoToolPP/start
Time/moleculesStats/groupName/Stretch_Xaverage.txt, where the
first three columns correspond to the x-,y- and z-coordinates of each bin’s center,
the fourth column contains the average molecular length in that bin and the fifth
column contains the number of values used in the average (number of molecules
for unbiased average, or total number of hits for biased average).
This utility requires (uses) the registry of the molecules’ position and stretch
over time, optionally written and saved by solver rheoBDFoam (see Section 4.3.8).
Therefore, this post-processing utility can only be called after a call to the solver.

Chapter 5
Tutorials
In this Chapter, we provide a step-by-step guide on how to use the solvers of
rheoTool. For each solver, general guidelines are first discussed, regarding the new
fields and dictionaries required by that application. Then, specific tutorials are
presented, which will illustrate the application of rheoTool to relevant problems.
These tutorials cover the full process to obtain results, from the mesh generation
to the post-processing stage.
The approach used in this Chapter assumes that the reader is familiar with
the typical folder organization of OpenFOAM R
cases and has basic knowledge on
how to run simulations in OpenFOAM R
.
The tutorials in this Chapter are mainly intended for learning purposes.
It is not our primary goal to obtain highly accurate results with such
examples, but solely to show how to run the solvers, preferably using
fast-running cases. Higher accuracy can be obtained in all the cases by
increasing the resolution in space and time.
5.1 rheoFoam
5.1.1 General guidelines
Before proceeding, we note that the sequence of operations required to prepare a
case in OpenFOAM R
does not need to be ordered as presented next (constant/
¸0/ ¸system/). This sequence was organized in such a way to be (hopefully)
logic and easy to follow and execute.
|constant/
Inside folder constant/ there are two main components of the simulation: the
mesh, in folder polyMesh/, and the dictionary constitutiveProperties,
which is a dictionary specific of rheoTool. Since the mesh is an element required
by almost all OpenFOAM R
solvers, it will not be discussed here and we assume
that a valid mesh already exists in folder polyMesh/.
116

CHAPTER 5. Tutorials 117
The dictionary constitutiveProperties used by rheoFoam includes in-
formation about the constitutive model and the passive scalar transport which can
optionally be activated in the simulation (Listing 5.1).
parameters
2{
type Oldroyd-BLog;
4
rho rho [1 -3 0 0 0 0 0] 1.;
6etaS etaS [1 -1 -1 0 0 0 0] 0.01;
etaP etaP [1 -1 -1 0 0 0 0] 0.99;
8lambda lambda [0 0 1 0 0 0 0] 1.;
10 stabilization coupling;
}
12
passiveScalarProperties
14 {
solvePassiveScalar off;
16 D D[02-10000]1e-9;
}
Listing 5.1: Example of a constitutiveProperties dictionary used
with rheoFoam.
The dictionary constitutiveProperties has two different sub-
dictionaries (subDict), which must necessarily exist: parameters, with information
on the constitutive model, and passiveScalarProperties, related with the scalar-
transport equation.
Regarding subDict parameters, in line 3 we define the TypeName of the consti-
tutive model to be used, which can be found in Table 4.1. In the example displayed
in Listing 5.1, we are using the Oldroyd-B model, solved with the log-conformation
approach (Oldroyd-B +Log). If we would like to use the same model without solv-
ing it with the log-conformation approach (solving the constitutive equation for
the extra-stress tensor), then the type would be simply Oldroyd-B – this naming
rule is valid for all viscoelastic models. Lines 5 to 8 specify the fluid properties
required by the constitutive model being solved. The density is a property com-
mon to all models (it is not related with the constitutive equation) and should
always be present, while the model-dependent properties can be checked in Table
4.1. Anyway, if some required parameter is not specified, the solver will retrieve
an error complaining for its absence.
The reader might be surprised with the unphysical parameters displayed in
Listing 5.1 (even just being an example), particularly the density of the fluid,
which is not realistic for any known viscoelastic liquid. The use of a unitary
density (ρ= 1 kg/m3) and many other unitary variables is simply to facilitate the
calculations. In the tutorials presented next, we frequently make use of this kind
of approach, since the computation of dimensionless parameters does not require
physically realistic quantities.
At line 10, the stabilization method is selected (recall that C++ is case-
sensitive): none for no stabilization; BSD to use the both-sides-diffusion technique;
coupling to use the stress-velocity coupling discussed in Section (3.3.2). Note that

CHAPTER 5. Tutorials 118
this option is only meaningful for viscoelastic models.
For multi-mode viscoelastic models, the TypeName is multimode and lines 3-
10 need to be included for each mode, enclosed in a dictionary identified with the
mode’s name. An example is provided in the tutorials (tutorials/rheoFoam
/OtherTests/).
For the FENE-type models not using the log-conformation approach, several
formulations are available, as discussed in Section 4.1.2. The selection between
them is also performed in subDict parameters. If nothing is specified, FENE mod-
els are evaluated using the (complete) formulation in A. In order to solve the
complete formulation in τ, the keyword solveInTau should be defined and set to
true. If the modified formulation in τis intended, both solveInTau and modified-
Form keywords should be defined and set to true. Some examples are provided in
the tutorials (tutorials/rheoFoam/OtherTests/). Note that the selection
between the available formulations of FENE-type models is not achieved by spec-
ifying different TypeNames for each one: the TypeName is the same for all the
formulations within the same model (FENE-CR or FENE-P) and the selection is
based on the keywords just described.
Focusing now on subDict passiveScalarProperties, only two entries are present.
In line 15, the user can select to solve (on, true or yes), or not (off, false or
no), the transport equation of a passive scalar. If the equation is solved, then
line 16 should specify the diffusion coefficient and field C(the name of the scalar
being transported) should be defined in the folder corresponding to the start-time.
Otherwise, none of these two actions is required. Importantly, if the option to solve
the transport equation is enabled, but field Cis not provided, then rheoFoam will
solve a transport equation (you can confirm it on the solver output) for a scalar not
present in the domain (its concentration will remain null over all the simulation
time), since this is how the field is internally initialized when there is no entry for
it in the start-time folder.
For a moving mesh, dictionary dynamicMeshDict is also required in direc-
tory constant/. This dictionary contains information on the mesh motion and
its entries depend on the type of motion specified. Since this is a generic topic of
OpenFOAM R
, we will not present further details. Starting from rheoTool v3.0,
dictionary dynamicMeshDict should always exist, even for static meshes. If not
defined by the user, the solver will create a dynamicMeshDict with the type set
to staticFvMesh, i.e., a static mesh. In that case, the solver for foam-extend and
OpenFOAM R
versions prior to v5.1 automatically add that dictionary to directory
constant/. Therefore, for simulations in static meshes, the user does not need
to take any action related with dictionary dynamicMeshDict.
|0/
At this point, both the mesh and the fluid are defined and some decisions have
been made about the numerical method. It is now time to create and define the
initial and boundary conditions for the variables used in the simulation, which will
depend on the constitutive equation selected. At least three scenarios are possible:
•GNF fluid: those cases only require defining pressure (divided by the den-
sity), p(in this guide represented by p
ρ), and velocity, U(in this guide rep-

CHAPTER 5. Tutorials 119
resented by u) fields. For all the GNF models, except for the Newtonian
case, the solver will automatically write the shear-rate dependent viscosity
at subsequent times.
•viscoelastic model using the standard extra-stress approach: those
cases require defining pressure (divided by the density), p, velocity, U, and
the polymeric extra-stress field, tau (in this guide represented by τ). The
novelty relative to the GNF cases is in variable tau, which is of type
symmTensor. All the three variables will be automatically written at fu-
ture times. When a multi-mode viscoelastic model is used, each mode owns
a variable tau, which should be present in folder 0/. The name given to
each variable should be consistent with the names attributed to each mode
in constitutiveProperties, i.e., this name should be appended at the
end of name tau. For example, having defined mode names M1 and M2,
then the names for the respective tau should be tauM1 and tauM2.
•viscoelastic model using the log-conformation approach: comparing
with the previous case, it requires defining the additional variable theta,
which represents the natural logarithm of the conformation tensor (in this
guide represented by Θ), which is also a symmTensor. In order to define
boundary conditions for theta, we suggest the reader to take a look at
Eqs. (3.6) and (3.7). For example, if the polymeric extra-stress (tau) is a
null tensor, then variable theta is also a null tensor. At subsequent times,
the solver will automatically write fields p,U,tau,theta and both the
eigenvectors, eigVecs (in this guide represented by R), and eigenvalues,
eigVals (in this guide represented by Λ), which are obtained from the di-
agonalization of the conformation tensor. Note that the fields eigVecs and
eigVals do not need to be present to start a simulation, although they are
read if they are present (for example, to restart a simulation from the exact
point where it finished). For a multi-mode model, the same considerations
previously described apply, including for variable theta.
When using FENE-type models solved in the conformation tensor, without
the logarithmic transformation (see Section 4.1.2), the conformation tensor field
(A) can be optionally defined in folder 0/, being read by the solver in that case.
However, if not defined, the solver automatically initializes the conformation tensor
field from τ, that should always be present. Independently of being or not present
in the starting time folder, field Awill be written to the case directory for the
remaining of the simulation.
For any of the previous cases, if the option to solve the transport equation of
a passive scalar has been enabled, then a field Cshould also be present in folder
0/. The utility setFields of OpenFOAM R
can be particularly helpful to initialize
this field, since it allows to assign different values of Cin different regions of the
domain.
If the simulation includes a moving mesh, depending on the type of mesh
motion, some fields may need to be defined inside folder 0/. For example, if the
mesh is being deformed by solving some equations, e.g. a Laplace equation, then

CHAPTER 5. Tutorials 120
boundary conditions need to be defined to solve such equations (see the tutorial
in Section 5.1.9). On the other hand, rigid-body like motions, for example, do
not need such procedure, since the whole mesh is simply transformed by some
geometric operation.
|system/
The last steps before starting the simulation are related with the dictionaries
located in folder system/, which mainly control the numerical method. In par-
ticular, we will focus our attention on the following dictionaries: controlDict,
fvSchemes and fvSolution. All the three dictionaries must be present for
the simulation to run, as required by most of the OpenFOAM R
solvers. Since
most of the entries in those dictionaries are transversal to both rheoFoam and any
OpenFOAM R
solver, we will limit our description to the new features introduced
by rheoFoam.
In controlDict dictionary, the options allowing to automatically control
the time-step by imposing a Courant number limit are available in rheoFoam and
can be used (following the same principles of other OpenFOAM R
solvers). Those
options are adjustTimeStep (on/off ), maxCo (the value of the limiting Courant
number) and maxDeltaT (the maximum admissible time-step). Furthermore, and
although not being a feature exclusive of rheoFoam,coded functionObjects can
be defined in controlDict and used with rheoFoam to extract and monitor
quantities of interest (this is not possible in foam-extend). This kind of functions
are frequently used in the tutorials of this Chapter.
Regarding dictionary fvSchemes, we remember that GaussDefCmpw schemes
(Section 4.7.1) are available for selection and can be used to discretize any con-
vective term with the generic form div(phi,variable), where variable is either
U,tau,theta or C. Still in the divSchemes subDict, the term div(grad(U))
is part of the stress-velocity coupling algorithm (see line 44 of Listing 4.2) and
should (always) be discretized using a central differencing scheme (Gauss linear),
if used. In the gradSchemes subDict, the entry linExtrapGrad is for the gradient of
the tensor components when using linear extrapolation of polymeric extra-stress
at a given boundary, as discussed in Section 4.6.1. Apart from this, the remaining
entries in fvSchemes should be familiar to the user and the selection of appropri-
ate discretization schemes for each one is essential to keep the numerical method
accurate and stable.
The dictionary fvSolution is the only remaining to be adjusted before run-
ning the simulation. In subDict solvers, the matrix solver for each equation being
solved should be specified (remember that there will be Nequations to solve for
theta/tau in a model using Nmodes; wildcard characters are useful in those
cases). If the user forgets to specify any, the solver will retrieve an error message
asking for it. Only the pressure equation results in a symmetric matrix of coeffi-
cients, while all the others generate non-symmetric matrices. The only exception
is the momentum equation without the convective term included, which also re-
sults in a symmetric matrix. This should be taken into account when selecting
the type of matrix solver, since some are specific for some type of matrices. If
a coupled solver or a sparse matrix solver from an external library is used, then
check the instructions provided in Section 4.4. In the SIMPLE subDict, there

CHAPTER 5. Tutorials 121
is a new entry specific of rheoFoam, which is nInIter. This variable was defined
in Section 4.5.1 and controls the number of inner-iterations (see Fig. 4.2). If not
defined, the solver will execute 1 inner-iteration as the default behavior. Still in
the SIMPLE subDict, the entry residualControl allows the solver to automatically
stop the simulation once the residuals for all the specified variables drop below
the prescribed value. This is mainly a characteristic of steady-state solvers of
OpenFOAM R
and it can be also used in rheoFoam. However, if the goal is to run
rheoFoam until the endTime specified in controlDict, simply leave this entry
empty. The last subDict in fvSolution is the relaxationFactors, that determines
the amount of explicit (fields) and implicit (equations) under-relaxation for each
field or equation. When using the SIMPLEC algorithm for pressure-velocity cou-
pling, as a rule of thumb, the pressure does not need to be explicitly under-relaxed
to correct the velocity (see Ref. [2]). The only exception occurs for non-orthogonal
grids, where a small amount of under-relaxation may eventually be needed for
pressure. The under-relaxation factor, ranging between 1 (no under-relaxation)
and 0 (total under-relaxation, pressure does not evolve in time), is case-specific
and should be as high as possible (it can be conditioned by stability issues). Re-
garding implicit under-relaxation (equations), it only makes sense to be used with
steady-state solvers, where the absence of a time-derivative term requires under-
relaxation for stability reasons. Since rheoFoam is by default a transient solver,
where time-derivatives are present in all the transport equations, implicit under-
relaxation is not needed. In practice, it is possible to run rheoFoam without those
time-derivatives by selecting a default steady-state discretization scheme in the
ddtSchemes subDict of fvSchemes and, by this way, rheoFoam will run as a
typical steady-state solver of OpenFOAM R
, requiring implicit under-relaxation.
However, in some situations (viscoelastic models solved with the log-conformation
approach) the user will probably face stability issues, due to the poor diagonal
dominance of the base matrix of coefficients. For this reason, unless the user is
experienced and knows what is doing, we strongly recommend to use rheoFoam in
transient mode. Note that, if it exists, the steady-state will be reached after some
time of a transient simulation (typically after several relaxation times, of the order
of 10 or above for higher Wi, for viscoelastic models). If the transient analysis is
not important, a high Courant number (1) can be defined to reach this state
faster, as long as the computations remain stable.
In all the tutorials presented next, a steady-state is reached for the range of
parameters used in the examples. However, in none of them we use the residuals
as the termination criteria. Indeed, we prefer to set a very long endTime and
monitor a relevant variable at sensitive points over time. It can be the extra-stress
near a singular point, the drag coefficient over a surface, a vortex length, or any
other relevant quantity for the problem at hand. This is usually achieved either
through a probe (when the variable exists within the solver) or a ppUtil or coded
FunctionObject (when the variable does not exist within the solver and needs to be
computed), in dictionary controlDict. The termination criteria is then based
on this variable. Of course, we have set the endTime in the tutorials based on
that analysis. The residuals displayed on the screen should not be used alone as
the termination criteria.

CHAPTER 5. Tutorials 122
As mentioned in Section 4.7.2, the PostProcessing subDict enabling the use of
the ppUtil class is also defined in dictionary fvSolution. A detailed discussion
on this subject can be found in Section 4.7.2.
5.1.2 A note on coded FunctionObjects
Most of the tutorials presented next use a coded FunctionObject. This is a run
time compilable code, executing run time functions coded by the user, which can
be defined in dictionary controlDict.
These functions allow to access almost all the data of the case, from field vari-
ables to information about the mesh. The frequency at which they are evaluated
can be controlled using the keywords outputControl and outputInterval. It is also
possible to disable these functions by setting the keyword enabled to off.
The coded FunctionObjects included in the tutorials are usually divided in
three sections: a section which reads data, a section which computes quantities of
interest from this data and a writing section. Usually, we create a dynamic list
to accommodate the data to be written, so that any extra quantity can be easily
added to the list. This also eases the writing step. The meaning of each column
of the data being written is usually displayed as a comment in the source code of
the coded FunctionObject, being of course dependent on the tutorial case.
Among the several possibilities to write the variables computed by coded Func-
tionObjects, we chose to use a .sh executable, named writeData. This executable
simply receives as arguments the name of the file to write to (the user can change
it in the codedStream functionObjects), along with the data to be written, both
provided by a system call from the coded FunctionObject. If the executable is not
present in the case directory, but it is being called by the FunctionObject, a warn-
ing is displayed in the terminal informing about this situation (it is also possible
to copy this script to a location loaded by default in each OpenFOAM R
session,
in order to avoid the need of having it in the case directory). Keep in mind that
this .sh executable only writes to a file the data it receives as argument, so that it
is unlikely that the user would need to change it.
One main advantage of coded FunctionObjects is that they are case-specific,
instead of solver-specific, which means that the code of the solver does not need
to be changed. They are probably also a good entry point to start programming
in OpenFOAM R
, since the compilation steps are automatically handled.
Note for foam-extend users: as mentioned in Section 2.2,coded objects
are not available in foam-extend. For these versions, functions executing the same
tasks as the coded objects are available in a dedicated post-processing library, as
discussed in Section 4.7.2.
The boundary conditions implemented in OpenFOAM R
versions as coded func-
tions were added to library libBCRheoTool.so in the foam-extend version.

CHAPTER 5. Tutorials 123
For most of the tutorials presented next, the commands required to
run them are specified. It is instructive for the less experienced users
to type each one in the command line, in order to exactly know what is
being done. However, in the directory for each tutorial we also provide a
script named Allrun that automatically runs all these commands. On
the other hand, the script Allclean also included cleans the directory,
deleting everything that has been created.
5.1.3 Case 1: flow between parallel plates
Itutorials/rheoFoam/Channel/Oldroyd-BLog/
!Overview
In this tutorial, the flow between two infinite parallel plates is simulated for
an Oldroyd-B fluid. Although apparently simple, this case can pose formidable
difficulties using the UCM and Oldroyd-B models at high Weissenberg number
flows [41]. This example also shows that the log-conformation approach is effective
in solving this stability issue, while retrieving the predicted analytical profiles.
Following Ref. [42], the Reynolds number for this problem is defined as Re =
ρUw
η0and the Weissenberg number as W i =λU
w(1 −β), where β=ηs
ηs+ηp=ηs
η0.
The case reproduced in the tutorial is for Re = 0 (the convective term in the
momentum equation is suppressed), W i = 0.99 and β= 0.01.
!Geometry & Mesh
The geometry is a planar channel (two parallel plates) with half-width w, Fig.
5.1. The mesh is composed of 50 cells in the x-direction and 60 cells in the y-
direction, uniformly distributed in both directions.
inlet
outlet
walls
y
x
2w
40w
walls
Figure 5.1: Planar channel geometry.
!Boundary conditions
This flow is 2D, being solved in the xy-plane. A uniform velocity profile (U)
is set at the inlet, along with zero-gradient for pressure and polymeric extra-
stress components. At the outlet, fully-developed flow conditions are assumed
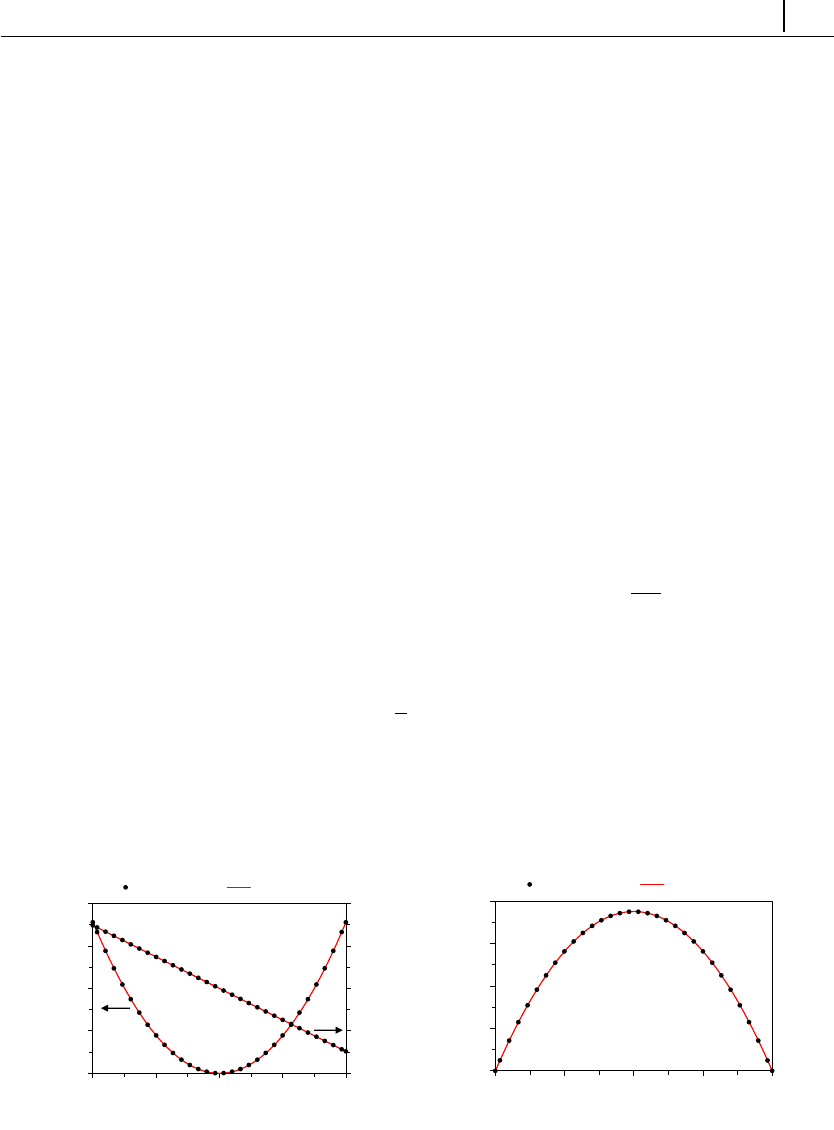
CHAPTER 5. Tutorials 124
(zero-gradient for all variables, except pressure, which is fixed to a constant value,
p= 0). A no-slip boundary condition is assigned at the walls (velocity is null,
polymeric extra-stress components are linearly extrapolated and a zero-gradient is
assumed for pressure in the normal direction to the wall).
!Command-line
1–Build the mesh:
∼$blockMesh
2–Run the solver:
∼$rheoFoam
3–Extract profiles for uand τalong line x= 35:
∼$sample
!Results
Figure 5.2 presents the fully-developed profiles at line x= 35. The variables
were normalized as follows: length is normalized with w, time with w/U, velocity
with Uand polymeric components of the extra-stress with η0U
w, as in Ref. [42].
A good agreement is observed between the numerical results and the analytical
solution written in dimensionless form [42]:
ux=3
21−y2
τxy =−3(1 −β)y
τxx = 18W i(1 −β)y2
-4
-2
0
2
4
0
5
10
15
20
-1 -0.5 0 0.5 1
τxy
τxx
y
Numerical Analytical
(a)
0.0
0.4
0.8
1.2
1.6
-1 -0.5 0 0.5 1
u
y
Numerical Analytical
(b)
Figure 5.2: (a) Polymeric extra-stress components and (b) velocity, at x= 35,
for Re = 0, W i = 0.99 and β= 0.01.
The user can test the solver with a UCM fluid (β= 0) and confirm that an
accurate solution is still achieved, without facing any numerical issue. However,
running the same cases without the log-conformation approach leads to numerical
divergence (try it!).
CHAPTER 5. Tutorials 125
This tutorial probes a point in the flow over time (to check for convergence),
which has been specified in controlDict dictionary. The data is written to a
directory named probes/, whose location in the case directory depends on the
OpenFOAM R
version.
5.1.4 Case 2: lid-driven cavity flow
Itutorials/rheoFoam/Cavity/Oldroyd-BLog/
!Overview
The flow in a lid-driven cavity is a common benchmark for numerical solvers,
for both Newtonian and viscoelastic fluids, being one of the mostly used geometries
for such purposes. One reason explaining the popularity is its simple geometry: a
square in 2D or a cube in 3D.
For viscoelastic fluids, stress boundary layers develop at the walls and, at high
Deborah numbers, the flow becomes time-dependent. A similar behavior is ob-
served with Newtonian fluids at high Reynold numbers.
The case reproduced in this tutorial is for an Oldroyd-B fluid with β=ηs
ηs+ηp=
0.5. The Deborah number is defined here as De =λU
L, while the Reynolds number
is Re =ρUL
η0. In this tutorial, we set De = 1 and Re = 0.01, so that the creeping
flow assumption is still adequate, notwithstanding the finite Re.
!Geometry & Mesh
The planar lid-driven cavity is simply a square, with side length L, Fig. 5.3.
The coordinate axis is located at the bottom-left corner. The mesh consists of one
single block with 127 cells uniformly distributed in both directions.
fixedWalls
fixedWalls
fixedWalls
movingLid
L
L
y
x
Figure 5.3: Geometry for the lid-driven cavity flow.
!Boundary conditions

CHAPTER 5. Tutorials 126
The flow is assumed to be 2D, being solved in the xy-plane. For the three
stationary walls, a no-slip boundary condition is assigned, with null velocity, lin-
early extrapolated polymeric extra-stresses and zero normal gradient for pressure.
At the moving lid wall, the same boundary conditions are used for pressure and
polymeric extra-stresses. Regarding the velocity, a time-space dependent condi-
tion is employed in order to impose a smooth start of the flow, and to avoid a local
singularity with infinite acceleration at the top-right and top-left corners [13]:
Ulid(x, t)=8U[1 + tanh {8(t−0.5)}]x2(1 −x)2(5.1)
Eq. (5.1) is directly implemented as a codedFixedValue boundary condition in
file 0/U. The variables were normalized as follows: length is normalized with L,
time with L/U, velocity with U, and polymeric extra-stresses with η0U
L.
!Command-line
1–Build the mesh:
∼$blockMesh
2–Run the solver:
∼$rheoFoam
3–Extract profiles for uand τalong lines x= 0.5 and y= 0.75:
∼$sample
!Results
Figure 5.4 presents spatial profiles for the x-component of the velocity and for
Θxy, along with the evolution over time of the volume-averaged ”kinetic energy”,
defined as
Ek=1
2VtZ|u|2dV=1
2Vt
N
X
k=1 |uk|2Vk=1
2N
N
X
k=1 |uk|2(5.2)
where Nis the number of cells of the mesh and Vt=NVkfor a uniform mesh.
A good agreement is observed between the results obtained by rheoFoam and the
reference data [13], which shows the good accuracy of the solver, both in space
and time. The contour maps for the components of Θare also provided in Fig.
5.5, together with the flow streamlines.
The ”kinetic energy” is written on run time to the case directory, using a coded
FunctionObject, defined in dictionary controlDict. The reader can check in
this function how Eq. (5.2) has been implemented.
5.1.5 Case 3: flow in a 4:1 planar contraction
Itutorials/rheoFoam/Contraction41/Oldroyd-BLog/
!Overview
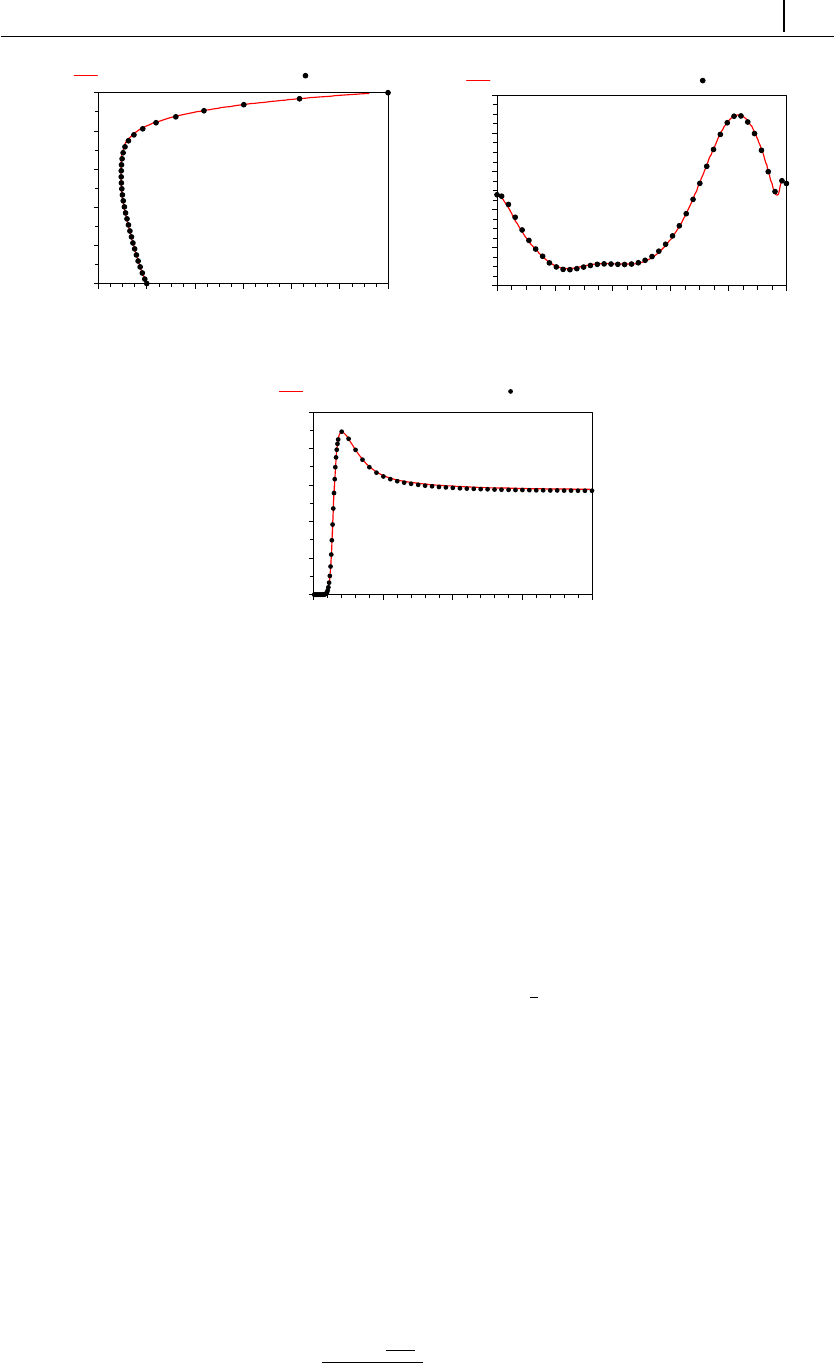
CHAPTER 5. Tutorials 127
0
0.2
0.4
0.6
0.8
1
-0.2 0 0.2 0.4 0.6 0.8 1
y
u (0.5, y)
Fattal & Kupferman (2005) rheoFoam
(a)
-0.4
0
0.4
0.8
1.2
1.6
0 0.2 0.4 0.6 0.8 1
ϴxy (x, 0.75)
x
Fattal & Kupferman (2005) rheoFoam
(b)
0
0.004
0.008
0.012
0.016
0.02
0 2 4 6 8
Ek
t
Fattal & Kupferman (2005) rheoFoam
(c)
Figure 5.4: (a) Velocity profile along line x= 0.5 (at t= 8), (b) Θxy profile along
line y= 0.5 (at t= 8) and (c) evolution of the average ”kinetic energy” over time.
All the results are for Re = 0.01, De = 1 and β= 0.5.
The 4:1 planar contraction is another traditional benchmark flow problem for
viscoelastic fluid flow solvers. The existence of singular points at the re-entrant
corners, where stresses grow exponentially as the corner is approached, make this
problem challenging from a numerical perspective.
This tutorial reproduces the work that we developed in Ref. [2] using an early
version of rheoFoam, where an Oldroyd-B fluid (β=1
9) was studied for De = 0−12.
The constitutiveProperties dictionary is adjusted to reproduce the case
for De = 1 and Re = 0.01.
!Geometry & Mesh
The geometry for this case is reproduced in Fig. 5.6. The mesh corresponds to
mesh M1 of Ref. [2].
!Boundary conditions
The boundary conditions used are described in Ref. [2]. It is worth mentioning
that the time-varying inlet velocity is implemented as a codedFixedValue boundary
condition in file 0/U. The function is implemented as
u(t) = (1−cos(πt
tlim )
fac dirN t≤tlim
Uav t > tlim
(5.3)
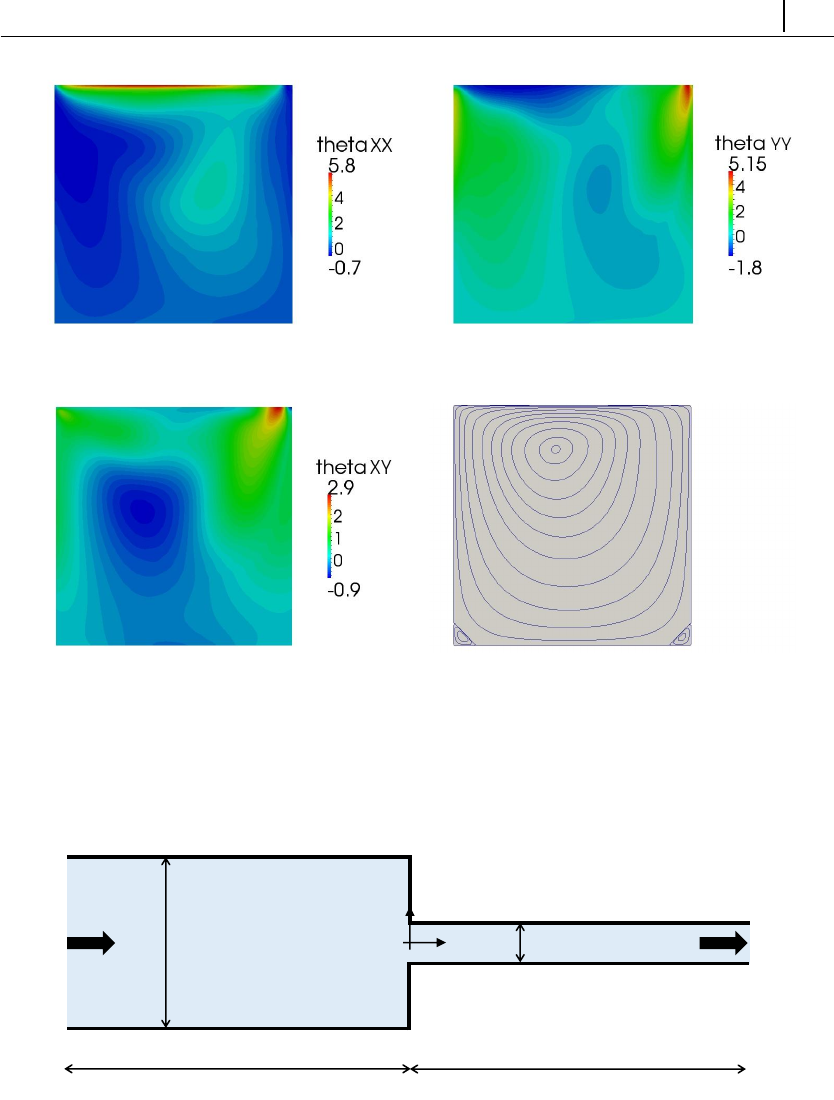
CHAPTER 5. Tutorials 128
(a) (b)
(c) (d)
Figure 5.5: Contours of (a) Θxx, (b) Θyy and (c) Θxy. In (d), the streamlines are
plotted. All the results are for Re = 0.01, De = 1, β= 0.5 and t= 8.
inlet
outlet
2H
100H
wall_vortdown
wall_vorttop
wall_liptop
wall_lipdown
walls
walls
100H
8H
y
x
Figure 5.6: Geometry for the 4:1 planar contraction.
where Uav and dirN are vectors, and fac and tlim are scalar parameters. For
Uav = (0.25,0,0), dirN = (1,0,0), fac = 8 and tlim = 1, this generates an inlet
velocity profile aligned with the x-axis and whose magnitude increases from 0, at
t= 0, to 0.25, at t= 1.
!Command-line
1–Build the mesh:

CHAPTER 5. Tutorials 129
∼$blockMesh
2–Run the solver:
∼$rheoFoam
3–Extract uand τat the cell centers immediately upstream and downstream of
vertical line x= 0:
∼$sample
!Results
The results obtained with mesh M1 can be found in Ref. [2].
Acoded FunctionObject returns the points where the wall-parallel velocity com-
ponent changes of sign (for both the walls near to the upper lip and corner vortices).
Those points are delimiting the lip and corner vortices (if present). The user can
easily add two extra coded FunctionObjects for the vortices in the lower-half of the
contraction.
5.1.6 Case 4: flow around a confined cylinder
Itutorials/rheoFoam/Cylinder/Oldroyd-BLog/
!Overview
The planar flow past a confined cylinder is another traditional benchmark prob-
lem in computational rheology. Since this flow has no singular points and because
extra-stresses can grow significantly in the wake of the cylinder, this problem is
particularly well-suited to test the accuracy and stability of numerical methods.
Furthermore, it is also a good problem to test the non-orthogonality handling by
the algorithms, both in terms of accuracy and stability, since the grids used for
this problem usually require some degree of non-orthogonality.
The Oldroyd-B model is used in this tutorial, since a reasonable amount of
data is available in the literature for comparison purposes. The Reynolds number
for this flow is defined as Re =ρUR
η0and the Weissenberg number as W i =λU
R. In
order to establish comparable conditions with Refs. [43,44], the solvent viscosity
ratio (β) is fixed at 0.59, the blockage ratio (diameter of cylinder/width of the
channel) is 50 % and Re = 0 (the convective term in the momentum equation is
removed). The case at W i = 0.7 is simulated in this tutorial.
!Geometry & Mesh
The geometry used in this case is composed of a channel with a cylinder of
radius Rvertically centered between its walls – spaced apart 4R–, and placed at
a distance of 20Rfrom the inlet, Fig. 5.7. The length of the channel downstream
of the cylinder is 60R. The mesh for this geometry is composed of 8 blocks (upper-
half), with a high cell-density near the wall of the cylinder. The minimum cell
length in the radial direction of the cylinder is 0.0049R, while in the tangential
direction it is 0.0053R.
!Boundary conditions
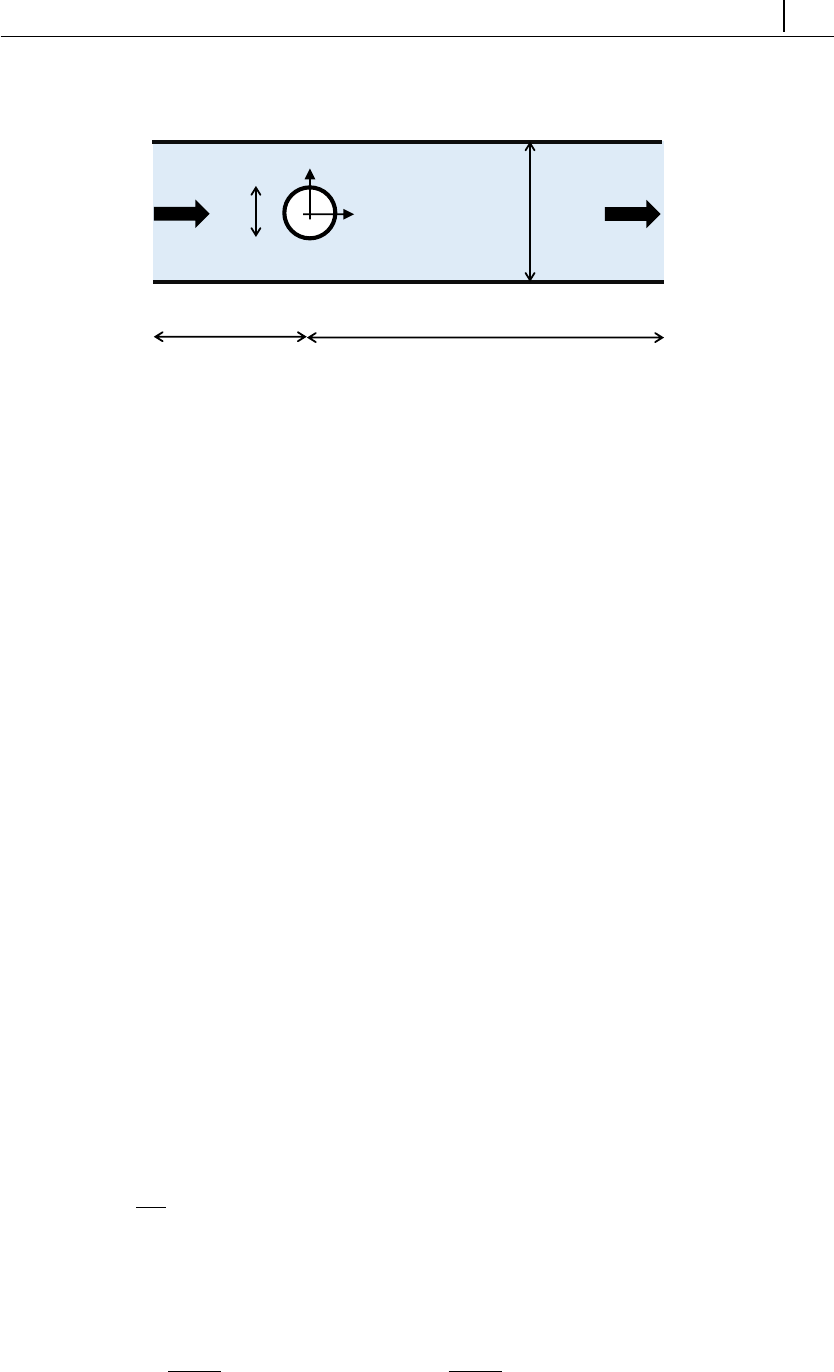
CHAPTER 5. Tutorials 130
walls
walls
inlet
outlet
cylinder
60R
4R
2R
y
x
20R
Figure 5.7: Cylinder vertically centered in a planar channel with 50 % blockage
ratio.
The flow is assumed to be 2D, being solved in the xy-plane. At the inlet, a
uniform velocity profile with magnitude Uis imposed, the polymeric extra-stresses
are null and zero-gradient is assigned to pressure. Channel and cylinder walls are
static (velocity is null, polymeric extra-stresses are linearly extrapolated to the
walls and a zero-gradient is imposed for pressure). At the outlet, fully-developed
conditions are assumed: zero-gradient for all variables, except pressure, which is
fixed to a constant value, p= 0.
!Command-line
1–Create half of the mesh:
∼$blockMesh
2–Reflect the half-mesh using plane xz as mirror, to obtain the full mesh:
∼$mirrorMesh -noFunctionObjects
3–Run the solver:
∼$rheoFoam
!Results
Figure 5.8 presents the contour plots for the first normal stress difference and
for the velocity magnitude (with superimposed streamlines), at Re = 0, W i = 0.7
and β= 0.59, using the Oldroyd-B model with the log-conformation approach.
Note that the velocity is normalized with U, time with R/Uand polymeric extra-
stresses with η0U
R. The drag coefficient obtained in such conditions is Cd= 117.357,
which is in reasonable agreement with Cd= 117.323 [44] and Cd= 117.315 [43].
Refining the mesh would further increase the accuracy of the numerical solution.
The drag coefficient was computed as
Cd=1
η0Uh Z
SpI+τ0·ˆ
i·dS=1
η0Uh
Nf
X
k=1
Sf·pfI+τ0
f·ˆ
i
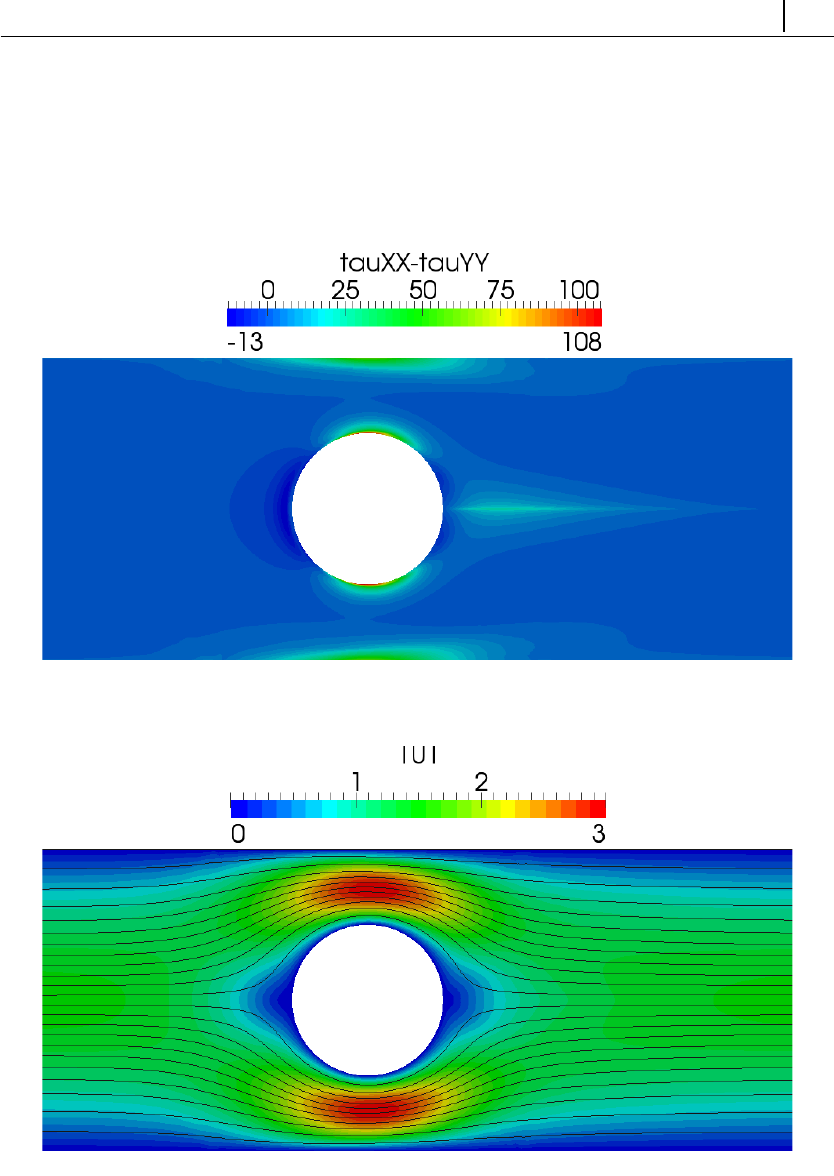
CHAPTER 5. Tutorials 131
where Sfis a vector normal to each face of the cylinder boundary, whose magnitude
is equal to the face’s area, his the depth of the cylinder in the neutral (empty)
direction and ˆ
iis a unitary vector aligned with the streamwise direction. The drag
coefficient is retrieved on run time by a coded FunctionObject, which can be found
in controlDict dictionary.
(a)
(b)
Figure 5.8: (a) First-normal stress difference and (b) velocity magnitude contours
with superimposed streamlines, at t= 15, for W i = 0.7, Re = 0 and β= 0.59.
Since version 4.0 of rheoTool, this tutorial is solved with a semi-coupled solver
(p-ucoupled and τsegregated) in OpenFOAM R
versions. Under this setup, a
higher time-step can be used, no pressure under-relaxation is needed and the

CHAPTER 5. Tutorials 132
non-orthogonality corrector loop is not used, notwithstanding the mesh non-
orthogonality. Overall, this allows a fast convergence to the final solution. Note,
however, that these conditions are not appropriate for a transient study.
5.1.7 Case 5: bifurcation in a 2D cross-slot flow
Itutorials/rheoFoam/CrossSlot/Oldroyd-BLog/
!Overview
While the previous tutorials were based on traditional benchmark flow prob-
lems, the case selected for this tutorial is a recent benchmark: the 2D cross-slot
flow [45]. For sufficiently high Deborah numbers, the flow in such geometry be-
comes asymmetric (steady or unsteady) [45]. At the stagnation point generated
by the two opposite-flowing streams, fluid elements can remain for a virtually in-
finite amount of time. Because the local strain-rate is non-zero, the accumulated
strain is high (theoretically infinite at the stagnation point), and this is especially
problematic for models based on springs with an infinite extension – the tensile
normal stress grows exponentially over time near that point. Thus, a singular
point exists in this case, although not being located at a wall, as commonly seen
in other geometries with singularities.
In directory tutorials/rheoFoam/CrossSlot/, there are four tutorials
for this case, each one using a different model or solution method. The tutorial
described here is the one solving the Oldroyd-B model with the log-conformation
approach (Oldroyd-BLog/). The remaining cases are: Oldroyd-BRootk/,
which solves the Oldroyd-B model using the rootkkernel, with k= 8; Oldroyd-B
Sqrt/, which solves the Oldroyd-B model using the square-root transformation
approach; and PTTlinearLog/, which solves the linear PTT model with the
log-conformation approach. All the tutorials with the Oldroyd-B model are for
the same conditions: De = 0.33, Re = 0 and β= 0 (UCM fluid). The tutorial
solving the linear PTT model is for De = 0.6, Re = 0, β= 1/9, ε= 0.02 and
ζ= 0 (simplified PTT). This group of tutorials also solves the transport equation
of a passive scalar, exemplifying how this extra-feature can be used.
The dimensionless numbers for this problem are defined as: Re =ρU W
η0,W i =
λU
W,β=ηs
η0and P e =W U
D. The P´eclet number (Pe) is only relevant for the scalar
transport equation and Dis the diffusion coefficient of the passive tracer. We set
P e = 500 in all the cases (representative, for example, of rhodamine-B in water
flowing in a 200 µm wide channel, at 1 mm/s).
!Geometry & Mesh
The cross-slot geometry for this tutorial is depicted in Fig. 5.9. It consists of
four identical arms (width W; length 10W), where the two vertically opposite arms
are inlets and the remaining are outlets. Each arm is meshed as a single block
with 60 cells in the streamwise direction (cells are compressed near the origin)
and 51 cells uniformly distributed in the transverse direction. As a consequence,
the central square block, (x, y)∈[−0.5W, 0.5W], has 51x51 uniformly spaced
cells. The use of an odd number of cells in both directions of the central square
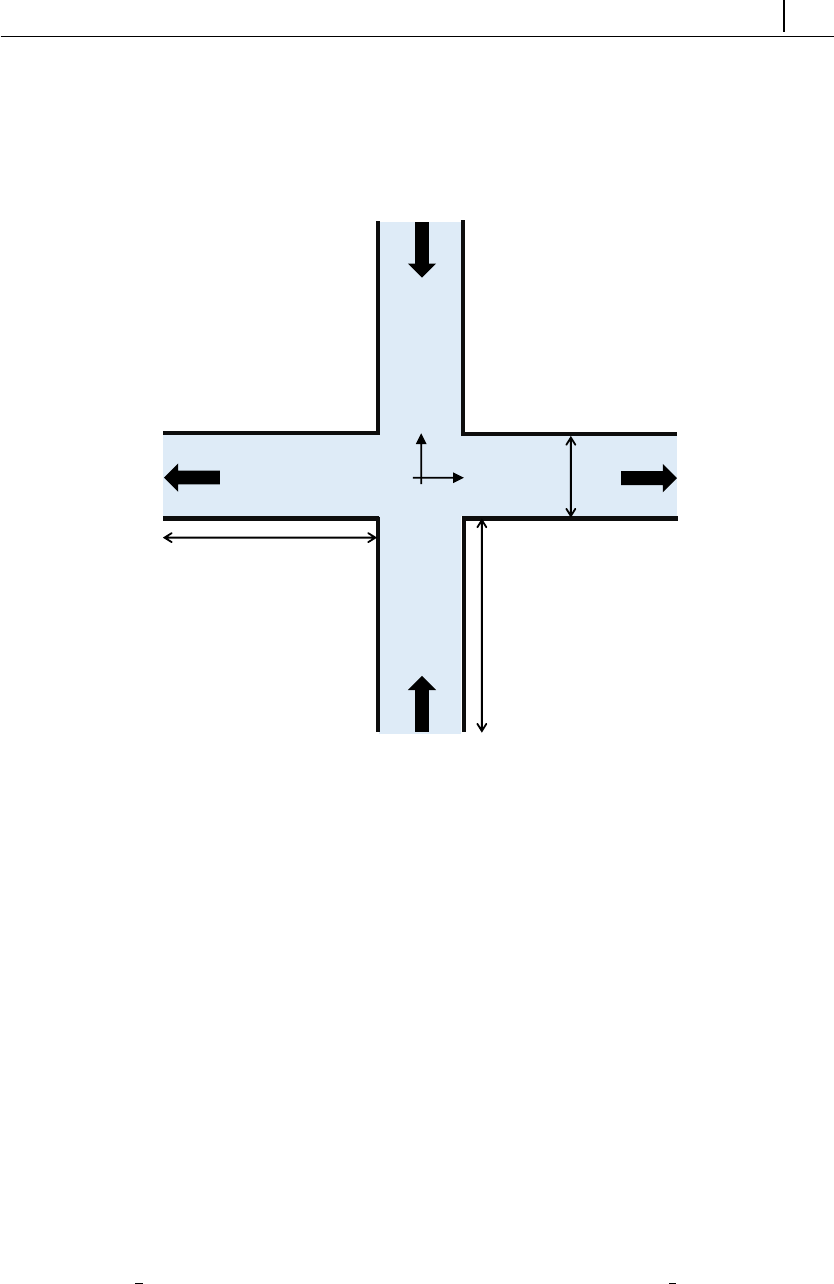
CHAPTER 5. Tutorials 133
generates a cell exactly centered at the stagnation point, which is advantageous
for the post-processing of quantities of interest at this location.
y
x
walls
walls
walls
walls
inlet_south
outlet_west
outlet_east
9.5W
inlet_north
9.5W
W
Figure 5.9: Cross-slot geometry composed of 4 arms with two balanced inlets
and two outlets.
!Boundary conditions
The flow is assumed to be 2D, being solved in the xy-plane. At both inlets, a
uniform velocity profile is specified, with magnitude Uand pointing to the origin,
so that those two streams are flowing in opposite directions. The polymeric extra-
stresses are null and for pressure a zero-gradient is used. The walls are stationary,
thus velocity is null, polymeric extra-stresses are linearly extrapolated and the
pressure is assumed to not change in the normal direction. Fully-developed flow
conditions are assigned at the outlets: null normal gradient for all variables, except
pressure, which is fixed at p= 0.
A passive scalar (tracer field C) is added to the problem, which requires the
assignment of initial and boundary conditions. We impose a continuous injection
of Cat inlet north (C= 1), while no tracer is injected at inlet south (C= 0).
In the remaining boundaries, we impose null normal gradient (meaning no flux of
Cacross the walls and fully-developed flow conditions at both outlets). At time
t= 0, when the simulation is started, the y-positive portion of the cross-slot is
filled with the tracer (C= 1, y > 0∧t= 0).

CHAPTER 5. Tutorials 134
!Command-line
1–Build the mesh:
∼$blockMesh
2–Create field Cby copying one already present, which is not initialized in the
interior domain:
∼$cp 0/C.org 0/C
3–Initialize field Cin the interior domain (C= 1, y > 0∧t= 0):
∼$setFields
4–Run the solver:
∼$rheoFoam
!Results
The contours for some important variables are displayed in Fig. 5.10, for Re =
0, W i = 0.33, β= 0 (UCM model) and P e = 500. The variables are normalized
with U(velocity), W/U (time) and η0U
W(stresses).
The local Weissenberg number at the origin, defined in Ref. [45] as the product
of the relaxation time by the velocity gradient magnitude at the stagnation point
streamlines, is W i0= 0.523, which is close to the benchmark value obtained in
a similar mesh, W i0= 0.509 (Ref. [45], for mesh M1). The local Weissenberg
number at the origin is retrieved by the solver to the case directory, through a
coded FunctionObject that can be found in dictionary controlDict.
The importance of stress-velocity coupling in this case can be evaluated by re-
running the tutorial with either BSD only or no stabilization method (stabilization
=none or BSD, in dictionary constitutiveProperties).
Checkerboard fields easily develop in such conditions (this is a critical case due to
the use of a UCM fluid).
Note that this tutorial makes use of a variable time-step, controlled by a maxi-
mum Courant number fixed at 0.4. This strategy is used because only steady-state
results are of interest. This is also the reason to use a high tolerance in the sparse
matrix solvers, in fvSolution dictionary – the steady asymmetry in the flow
develops faster with these conditions, since the transient numerical error is higher.
5.1.8 Case 6: blood flow simulation in a real-model
aneurysm
Itutorials/rheoFoam/Aneurysm/HerschelBulkley/
!Overview
The tutorial presented in this Section addresses the simulation of blood flow in
a real-model aneurysm. Contrarily to the previous tutorials, this case is based on
a 3D polyhedral (non-orthogonal) mesh and uses a GNF model. Furthermore, the
flow is simulated for a moderate Reynolds number, which will test the robustness
of the solver for such conditions, where inertia already plays an important role.
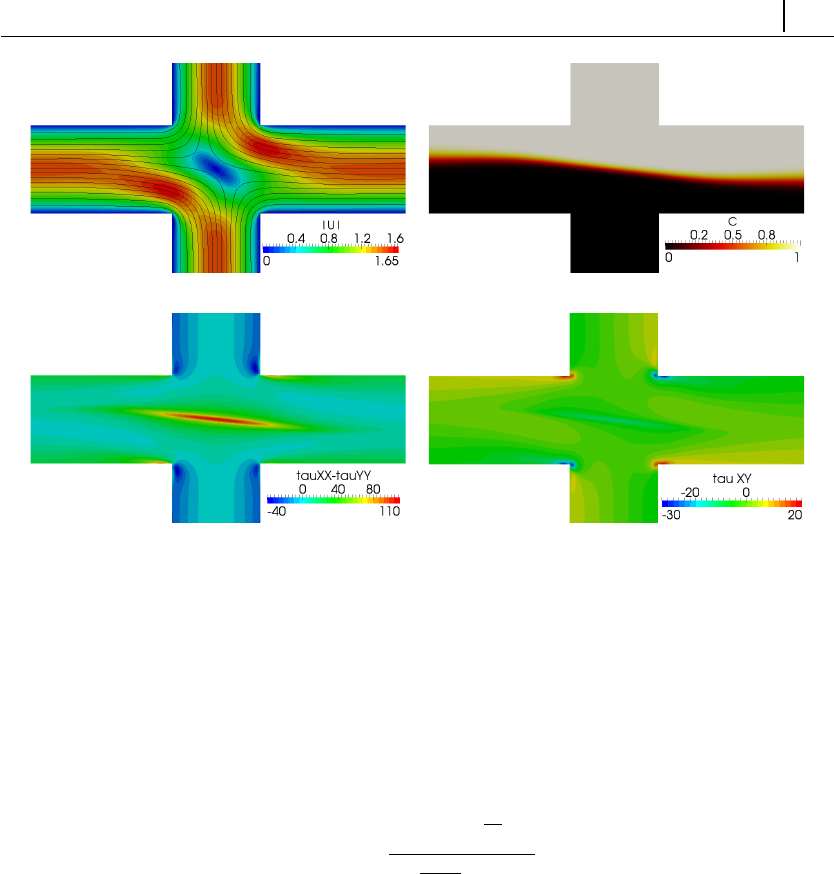
CHAPTER 5. Tutorials 135
(a) (b)
(c) (d)
Figure 5.10: (a) Velocity magnitude contours with superimposed streamlines, (b)
contours of C, (c) first-normal stress difference and (d) τxy contours, for Re = 0,
W i = 0.33, β= 0 and P e = 500.
The Herschel-Bulkley model was selected to simulate the blood rheology, fol-
lowing Ref. [46]. The generalized Reynolds number for this model, assuming τ0= 0
– the power-law limit –, is [46]:
ReGN =ρ(2Rin1)nU2−n
k3n+1
4nn8n−1
This tutorial simulates the flow at ReGN = 420.
!Geometry & Mesh
The STL file of the aneurysm surface was downloaded from a repository with
real-model aneurysms [47], extracted from 3D rotational angiographies of diseased
patients. From the list of available models, case ID C0005 was selected, which
refers to an aneurysm in the internal carotid artery (ICA).
The surface is composed of one main entry vessel (in1, the ICA), which bi-
furcates into two smaller vessels (out1 and out2 ), Fig. 5.11a. The aneurysm is
located near the bifurcation point. Due to the long extension of vessels upstream
and downstream of the aneurysm in the original STL file, all the vessels were
shortened and a cylindrical extension was connected to each one, in order to min-
imize entry/exit effects in the region near the aneurysm. The locations where
those connections were established are highlighted in Fig. 5.11a using red arrows.
The transition length between the tube connectors and the vessels is typically 10
% of the vessel radius and the radius of those tubes is equal to the equivalent
radius of the vessels at the connection point. The radius of each inlet/outlet is:
Rin1 = 1.66 mm, Rout1 = 1.17 mm and Rout2 = 0.95 mm.
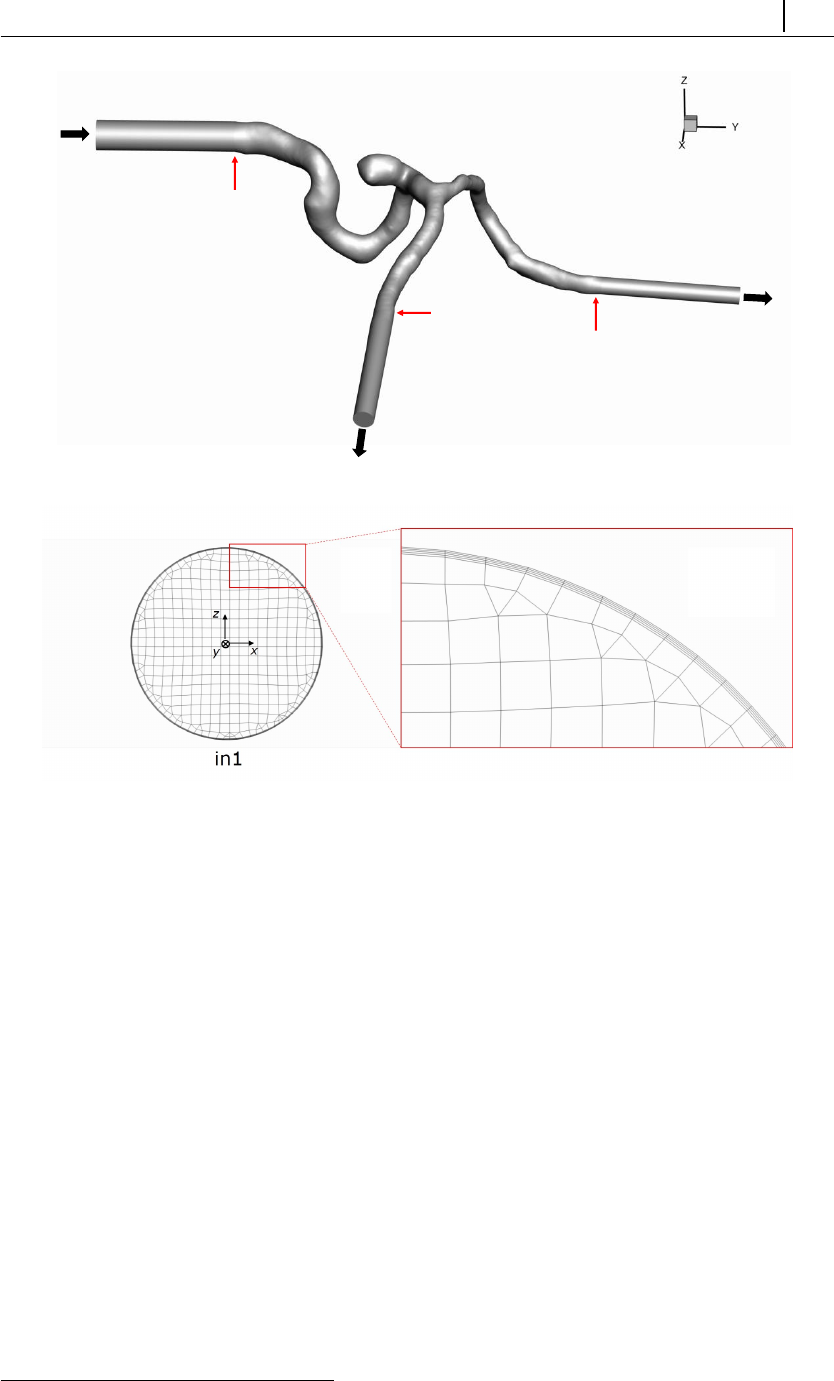
CHAPTER 5. Tutorials 136
in1
out2
walls
out1
(a)
(b)
Figure 5.11: (a) Geometry of the aneurysm considered in the tutorial. Red
arrows point to the transition regions between the aneurysm and the cylindrical
extensions. The radius of each inlet/outlet is: Rin1 = 1.66 mm, Rout1 = 1.17 mm
and Rout2 = 0.95 mm. (b) Detailed view of the mesh on patch in1, zooming the
cell layers near the wall. The reference axis for the geometry is centered on patch
in1, with the normal vector of the patch pointing in the negative direction of the
y-axis.
The mesh was built using 1cfMesh, a meshing tool available in foam-extend
since version 3.2. The maximum cell size was limited to 5 mm and boundary
cell layers were generated near to the vessel walls in order to accurately solve the
gradients developed there, Fig. 5.11b. The mesh provided with this tutorial has
around 280 kcells.
!Boundary conditions
The boundary conditions and fluid properties used in this tutorial are based in
Ref. [46], where also ICA aneurysms were studied. Accordingly, blood is modeled
with a Herschel-Bulkley model, with τ0= 0.0175 Pa, k= 8.9721 ×10−3Pa.sn,
1http://cfmesh.com/

CHAPTER 5. Tutorials 137
n= 0.8601 and η0= 0.15 Pa.s. Note that η0(see Table 4.1) is a parameter
characteristic of the model implementation in rheoTool, which limits the viscosity
for low strain-rate values – otherwise it would generate infinite values at points
with zero shear-rate. A relatively high value was attributed to η0in order to not
affect the results. Furthermore, a density of 1050 kg/m3is considered.
For this fluid model, a fully-developed velocity profile is imposed at the inlet
(in1 ), along with a null pressure gradient. For small τ0, we can use (approximately)
the fully-developed velocity profile for a power-law fluid:
U=U3n+ 1
n+ 1 1−r
Rn+1
n(5.4)
where Uis the mean velocity. In our case, Uis constant over time, thus steady
conditions are simulated, instead of the cardiac cycle (this is to shorten the simu-
lation time, since transient solutions would require a lower time-step, leading to a
higher computational time). Regarding the walls, a no-slip boundary condition is
imposed. At the outlets, the pressure is fixed to zero and the velocity is assumed
to be fully-developed (zero gradient for velocity). Since the Reynolds number used
in the tutorial is well below the critical value for transition to the turbulent regime,
no special conditions need to be defined regarding turbulence modeling.
!Command-line
The mesh is already built and can be found in folder polyMesh/.
1–Decompose the case among 2 processors to speed-up the computations (with
2 processors, it takes around 1h to reach convergence in a laptop with an Intel
i5-3210M processor, 2.5 GHz):
∼$decomposePar
2–Run the solver in parallel, using 2 processors:
∼$mpirun -np 2 rheoFoam -parallel
3–Reconstruct the last time-step of the case for post-processing:
∼$reconstructPar -latestTime
!Results
The results obtained at ReGN = 420 are displayed in Fig. 5.12, where both the
streamlines and the wall shear-stress magnitude (WSSmag) contours are shown.
The wall shear-stress magnitude is computed through a ppUtil (described in Sec-
tion 4.7.2), whose settings can be found in dictionary fvSolution, under subDict
PostProcessing.
This tutorial is defined to run with an adjustable time-step, controlled by a
maximum Courant number fixed at 50. The high Courant number is to quickly
achieve the steady-state, without the need to cancel the time-derivatives. The
non-orthogonality corrector loop was turned on, with 1 iteration per time-step
(the pressure is also under-relaxed with a factor of 0.9), in order to avoid possible
numerical issues due to non-orthogonality. The convergence can be monitored by
a probe located at one of the exit vessels, downstream of the aneurysm.
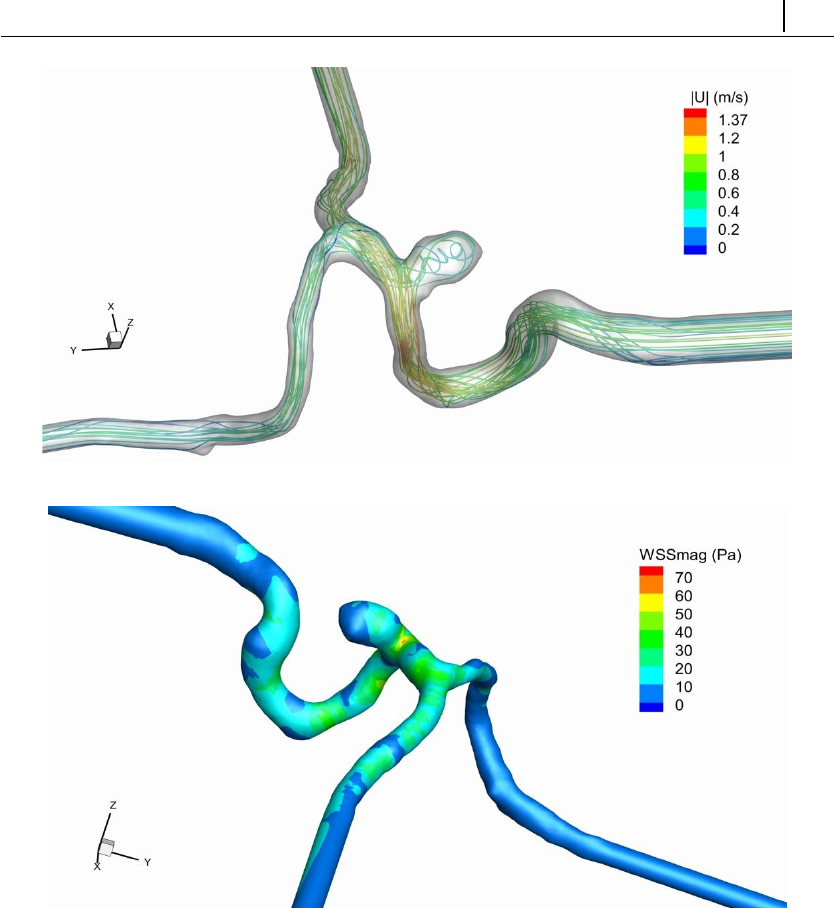
CHAPTER 5. Tutorials 138
(a)
(b)
Figure 5.12: (a) Streamlines (colored with the velocity magnitude) and (b) wall
shear-stress magnitude contours, at steady-state and for ReGN = 420.
5.1.9 Case 7: viscous fluid damper (moving mesh)
Itutorials/rheoFoam/fluidDamper/CarreauYasuda/
!Overview
Viscous fluid dampers react to applied loads with the generation of a back
pressure due to the high resistance experienced by a viscous fluid flowing through
narrow orifices. These mechanical elements are typically composed of a moving
piston enclosed inside a cage filled with a viscous fluid, with a narrow gap left
between the piston and the cage wall. The motion of the piston and the shaft
to which it is connected drive the fluid flow inside the cage. This tutorial aims
to simulate the fluid dynamics inside a damper subjected to an oscillatory load,
CHAPTER 5. Tutorials 139
whereby the piston and shaft motion are represented by a moving mesh.
The setup adopted in this tutorial aims to closely reproduce the conditions
presented by Syrakos et al. [48]. The case represented in this tutorial is for the
Careau-Yasuda fluid, named CY-100 in [48], at 32 Hz. Other conditions can be
easily tested by simple adjustment of the input parameters.
!Geometry & Mesh
The fluid damper geometry is depicted in Fig. 5.13. The geometry is equal
to that presented in [48], and the piston edges are rounded by the same radius
of curvature (Rcurv = 0.75 mm) as therein. The damper is axisymmetric, thus
only a slice of the total domain is simulated (Fig. 5.13). A Cartesian system of
coordinates is shown in Fig. 5.13 because that is the one used by OpenFOAM R
to
solve the problem, although keep in mind that symmetry around axis Oxholds.
The mesh is built using blockMesh and has a spatial resolution in the gap region
between patches top and piston, which is approximately half of mesh M1 in [48].
top
left
right
shaft
shaft
piston
y
x
z
z
y
x
wedge0
wedge1
top
45 mm
45 mm
20 mm
3 mm
17 mm
5 mm
Figure 5.13: Fluid damper geometry. The geometry is symmetric around axis Ox,
thus the computational domain corresponds to only a slice of the whole geometry.
!Boundary conditions
The Navier slip boundary condition is applied to the velocity field in all the
boundaries (except on wedges), in agreement with [48]. In addition, the velocity of
patches shaft and piston receive an extra contribution due to their own oscillatory
motion,
ushaft, piston =uNS +αωcos (ωt) (5.5)
where α= (α, 0,0) is the amplitude vector, α= 0.012 m and ω= 64πrad/s. Note
that Syrakos et al. [48] used a sine function for the motion, whereas a cosine is used
here for convenience (the two functions are offset by π/2 rad). A zero-gradient
condition is imposed for pressure.
Although physically both the shaft and piston move, in practice we only let
the piston patch to follow exactly the motion described by Eq. 5.5, while the
faces of patch shaft stretch or shrink according to the motion imposed by patch

CHAPTER 5. Tutorials 140
piston (slip boundary condition). The same happens for patch top, while the
remaining patches remain static. The mesh motion is obtained from the solution
of a Laplace equation with the previously described boundary conditions and a
variable diffusivity coefficient (see dynamicMeshDict dictionary). Note that
the boundary conditions presented in this paragraph are not related with the fluid
velocity field, whose boundary conditions were reported in the previous paragraph.
Still, such coupling can be obtained with boundary condition movingWallVelocity,
whereby the given patch velocity is used as boundary condition to the fluid velocity
(this can be used, for example, for patch piston, but not for patch shaft).
!Command-line
1–Build the mesh:
∼$blockMesh
2–Run the solver:
∼$rheoFoam
3–Check file Ffl generated by the solver.
!Results
The oscillatory piston motion can be directly observed in Paraview. In addition,
the solver writes in runtime the reaction force exerted by the fluid on the piston
and shaft (file Ffl),
Ffl=Z
S−pI+τ0·ˆ
i·dS=
Nf
X
k=1
Sf·−pfI+τ0
f·ˆ
i
where Sfis a vector normal to each face of the shaft/piston boundary, whose
magnitude is equal to the face’s area, and ˆ
iis a unitary vector aligned with the
Oxaxis. Since xpiston =αsin (ωt) is the known x-position of the piston midpoint
over time, then the force can be plotted against the displacement (Fig. 5.14). Note
that two periods of oscillation are simulated in the tutorial, and we can consider
that the first period is already in the steady regime. Moreover, in a plot such as
the one of Fig. 5.14 (considering the steady periodic regime), it is not relevant if
a sine or cosine function is used in Eq. (5.5).
5.2 rheoTestFoam
5.2.1 General guidelines
In Section 4.5.2,rheoTestFoam was presented as a testing application for the con-
stitutive models implemented in rheoTool, being not a general-purpose solver. For
this reason, some of the steps usually required to setup a generic simulation in
OpenFOAM R
are not necessary with rheoTestFoam, while, on the other hand,
extra-inputs need to be specified.
|constant/
CHAPTER 5. Tutorials 141
-3000
-2000
-1000
0
1000
2000
3000
-15 -10 -5 0 5 10 15
Ffl (N)
Displacement (mm)
rheoTool Syrakos et al. (2018)
Figure 5.14: Reaction force exerted by the Carreau-Yasuda fluid on the piston
and shaft over time, for f= 32 Hz. The results of Syrakos et al. [48] are also
plotted for reference.
One main difference of rheoTestFoam cases regarding, for example, rheoFoam
cases is in the mesh: the user should always use the same single-cell unitary mesh
when working with rheoTestFoam. Thus, changing the mesh from case to case is
unnecessary and not recommended.
The dictionary constitutiveProperties is composed of two subDict: pa-
rameters and rheoTestFoamParameters, as displayed in Listing 5.2. The entries in
parameters have exactly the same meaning as previously discussed for rheoFoam.
However, there are two entries which remain inactive in rheoTestFoam:rho and
stabilization. Remember from Section 4.5.2 that rheoTestFoam is only solving the
constitutive equations for a given ∇utensor, thus those two parameters related
with the momentum equation are useless. Nevertheless, they should be present
(with any assigned value) to avoid a run time error. rheoTestFoamParameters is
a subDict specific of rheoTestFoam, in the same way as passiveScalarProperties is
a particular subDict of rheoFoam. The keyword ramp stands for the operation
mode (see Section 4.5.2): ramp (true) or transient (false). The other two entries
define tensor ∇u, since we consider ∇u=gammaEpsilonDotL[i]·gradU, where
iis the index representing each entry of list gammaEpsilonDotL. If ramp =false,
the mode is transient and only one entry is expected in gammaEpsilonDotL – the
solver is testing the transient behavior of the constitutive model, for a (single)
given ∇u. On the other hand, in ramp mode (ramp =true), gammaEpsilonDotL
may have as many entries as defined by the user and steady-state variables will be
returned by the solver for each entry. Any combination of components is admissi-
ble for gradU, although only some correspond to canonical rheometric flows. The

CHAPTER 5. Tutorials 142
one displayed in Listing 5.2 is for a pure-shear flow: u= ( ˙γy, 0,0), where ˙γis the
gammaEpsilonDotL value.
1parameters
{
3type Oldroyd-B;
5etaS etaS [1 -1 -1 0 0 0 0] 1.;
etaP etaP [1 -1 -1 0 0 0 0] 1.;
7lambda lambda [0 0 1 0 0 0 0] 0.1;
9// Place-holder variables in rheoTestFoam
stabilization none;
11 rho rho [1 -3 0 0 0 0 0] 0.;
}
13
rheoTestFoamParameters
15 {
ramp false;
17
gradU (0. 0. 0.
19 1. 0 0.
0. 0. 0.);
21
gammaEpsilonDotL
23 (
1.
25 );
}
Listing 5.2: Example of a constitutiveProperties dictionary used
with rheoTestFoam.
|0/
When using rheoTestFoam, the same fields as for rheoFoam should be present
in folder 0/. However, any value can be assigned to their internal/boundary fields,
since the solver will internally manipulate those values (only for velocity) in order
to fulfill the specified ∇u(Fig. 4.3). Shortly, both the mesh and folder 0/
provided in the tutorials can be readily applied to any fluid, without
any change.
|system/
When running rheoTestFoam in ramp mode, the user does not have control
on deltaT (time-step), nor on the endTime. The time step is automatically set
based on the relaxation time and strain-rate values for viscoelastic fluids or is sim-
ply set to 1 s for GNF models (in this case, the value is not important since no
equation is solved implicitly). The endTime in ramp mode is not important, since
the stopping criteria is based on an hard-coded threshold for the residuals and for
the number of iterations. On the other hand, in transient mode, both variables
should be specified by the user in controlDict. Regarding the discretization
schemes (fvSchemes dictionary), only time-derivatives and grad(U) are used by
the solver. The discretization of grad(U) should be kept as Gauss linear, while

CHAPTER 5. Tutorials 143
any valid time-scheme can be selected (except steady-state), although in ramp
mode this should not make any difference, since we are looking for steady-state
solutions. In dictionary fvSolution, the matrix solvers required by the consti-
tutive equations must be defined and the number of inner-iterations may also be
controlled if running in transient mode. Note that since the mesh has only one
cell, a good time accuracy can be achieved by selecting a small time-step, without
compromising the CPU time (in general, simulations will be always fast). The use
of under-relaxation is not needed, as long as time-derivatives are not disabled in
fvSchemes (this is our recommendation).
5.2.2 Case I: Herschel-Bulkley model
Itutorials/rheoTestFoam/HerschelBulkley/
!Overview
This tutorial illustrates the behavior of the Herschel-Bulkley model used in
tutorial Case 6 to model the blood rheology (Section 5.1.8). A steady shear flow
is considered for this purpose.
!Geometry & Mesh
The geometry used with rheoTestFoam is always the same (see Sections 5.2.1
and 4.5.2). The mesh is already built (do not change it).
!Boundary conditions
The boundary conditions to be used with rheoTestFoam are always the same
(see Sections 5.2.1 and 4.5.2). Folder 0/ should not be changed.
!Command-line
1–Run the solver:
∼$rheoTestFoam
The file Report is created in the case directory, which contains the results.
!Results
For a GNF model, only the ramp mode of rheoTestFoam makes sense to be
used, since thixotropy is not considered in any of the GNF models implemented.
A steady shear flow is used, thus ∂u
∂y is the only non-zero component of tensor ∇u.
For the range of shear-rates between 0.01 s-1 and 10000 s-1, the Herschel-Bulkley
model behavior is displayed in Fig. 5.15. The model predicts a shear-thinning
behavior for ˙γ > ˙γ0, where ˙γ0is the critical strain-rate at which η=η0. For the
parameters defined in this example, ˙γ0= 0.13 s−1.
5.2.3 Case II: FENE-CR model
Itutorials/rheoTestFoam/FENE-CR/
!Overview
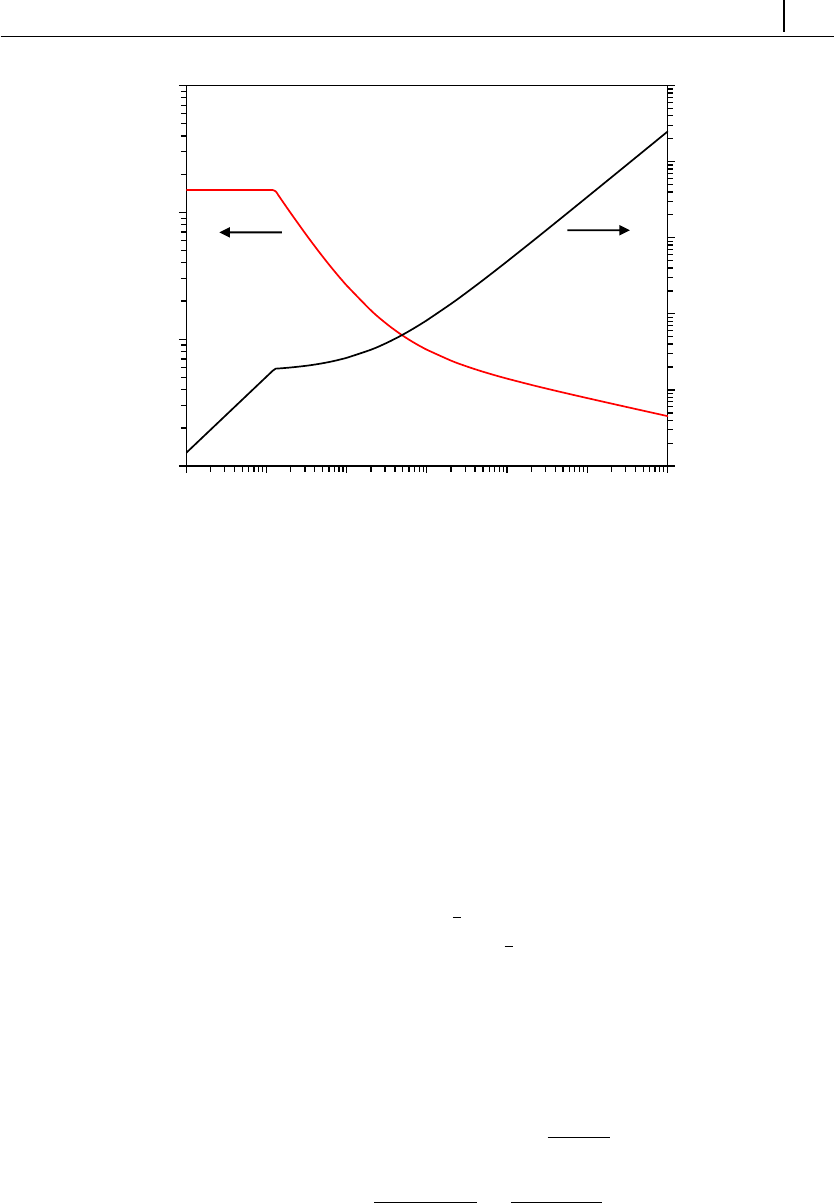
CHAPTER 5. Tutorials 144
0.001
0.01
0.1
1
10
100
0.001
0.01
0.1
1
0.01 0.1 1 10 100 1000 10000
τ'xy (Pa)
η(Pa.s)
Shear-rate (s-1)
Figure 5.15: Shear viscosity and τ0
xy (the only non-zero component of the sym-
metric extra-stress tensor) as a function of the shear-rate, in a steady shear
flow, for the Herschel-Bulkley model with parameters: τ0= 0.0175 Pa, k=
8.9721 ×10−3Pa.sn,n= 0.8601 and η0= 0.15 Pa.s.
This tutorial exemplifies the use of rheoTestFoam, both in transient and ramp
modes, with a constitutive equation for a viscoelastic fluid. The FENE-CR model
is selected and its behavior will be assessed for uniaxial extensional flow.
The uniaxial extensional flow may be described by the following velocity gra-
dient
∇u= ˙ε
1 0 0
0−1
20
0 0 −1
2
where ˙εis the extensional rate. The Weissenberg number, W i =λ˙ε, is the di-
mensionless group controlling the rate of stretch induced in the fluid and it was
varied between 0.01 and 100, by increasing the extensional rate from 0.01 to 100
s-1. The fluid properties used in the FENE-CR model are: ηs= 0.1 Pa.s, ηp= 0.9
Pa.s, λ= 1 s and different values of L2were tested (10, 100 and 1000). In such
conditions, the extensional viscosity, defined as ηE=τ0
xx−τ0
yy
˙ε, is given by [34]
ηE= 3ηs+ηp2
1−2λ˙ε/f +1
1 + λ˙ε/f (5.6)
where fis the solution of the cubic equation
(L2−3)f3−(λ˙ε)(L2−3) + L2f2
−2(λ˙ε)2(L2−3) −(λ˙ε)L2+ 6(λ˙ε)2f+ 2(λ˙ε)2L2= 0 (5.7)
!Geometry & Mesh

CHAPTER 5. Tutorials 145
The geometry used with rheoTestFoam is always the same (see Sections 5.2.1
and 4.5.2). The mesh is already built (do not change it).
!Boundary conditions
The boundary conditions to be used with rheoTestFoam are always the same
(see Sections 5.2.1 and 4.5.2). Folder 0/ should not be changed.
!Command-line
As it is, the tutorial will run in ramp mode.
1–Run the solver:
∼$rheoTestFoam
Take a look to file Report created in the case directory, which contains the results.
!Results
The results computed by rheoTestFoam, and displayed in Fig. 5.16a, show
that the FENE-CR model is correctly implemented, since the difference to the
analytical solution is negligible.
In addition to the ”steady” results in Fig. 5.16a, also the transient evolution
of the extensional viscosity (commonly denoted as η+
Ein the literature) can be
obtained with rheoTestFoam. For that purpose, simply switch the keyword ramp
(in constitutiveProperties) from true to false and define the desired ex-
tensional rate as the first entry of list gammaEpsilonDotL (the remaining entries
can be left, since they will not be read). The results obtained for Wi = 2, 5 and
10 are displayed in Fig. 5.16b.
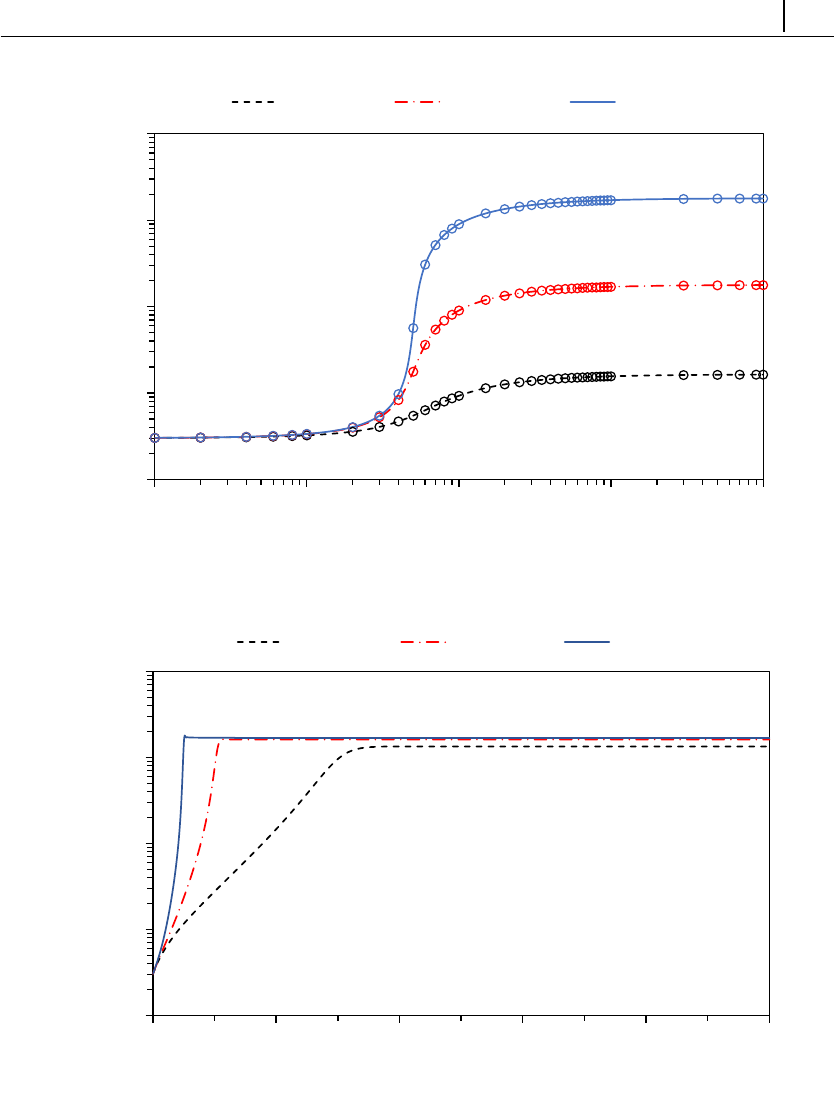
CHAPTER 5. Tutorials 146
1
10
100
1000
10000
0.01 0.1 1 10 100
ηE/η0
λε ̇
L2 = 10 L2 = 100 L2 = 1000
(a)
0.1
1
10
100
1000
0 1 2 3 4 5
ηE+/η0
t/λ
Wi = 2 Wi = 5 Wi = 10
(b)
Figure 5.16: (a) Steady extensional viscosity (ηE) as a function of W i =λ˙ε, for
different values of L2(points represent the numerical results of rheoTestFoam and
the lines correspond to the analytical solution of Eq. 5.6); (b) transient extensional
viscosity η+
Efor different Wi, at fixed L2= 100. The remaining parameters of the
FENE-CR model are ηs= 0.1 Pa.s and ηp= 0.9 Pa.s.

CHAPTER 5. Tutorials 147
5.3 rheoInterFoam
Section 5.3 is under development.
5.3.1 General guidelines
Since most of the steps required to set up a case for rheoInterFoam are the same
as for rheoFoam, only the major differences will be pointed out.
|constant/
The dictionary constitutiveProperties should contain the same infor-
mation as detailed for rheoFoam (Section 5.1.1), for each phase. The principle is
the same as for the default two-phase solvers of OpenFOAM R
(e.g. interFoam),
where each phase owns a dictionary defining its physical properties. Importantly,
subDict passiveScalarProperties, related with the transport of a passive
scalar, is general for the two phases and should only be defined once, outside each
phase. Finally, the surface tension between the two phases – parameter sigma –
should also be present.
Note that when using default names phase1 and phase2 for each phase, without
specifying the name of the phases in a wordList, then it is automatically assumed
that the phases are labeled 1and 2, respectively. Recent versions of OpenFOAM R
have a slightly different behavior regarding phases labeling.
|0/
In folder 0/, the internal and boundary field for the indicator (color) function
used by the VOF method should be defined. The indicator has a value of 1 for
one of the phases and 0 for the other phase. Ideally, and assuming that bound-
ary conditions were correctly assigned, the indicator should remain bounded in
this range. The name given to the file representing the indicator field should be
consistent with the naming in dictionary constitutiveProperties. If the
default names phase1 and phase2 were used, then the indicator function should
be named alpha1. If other name was used instead, then the indicator would be
named alpha suffixed with that name, without spaces in-between (recent versions of
OpenFOAM R
require a separation point). Although there are always two phases,
only one indicator field should be defined, since the indicator for the other phase
is computed from this one. In opposition to what is done in rheoFoam, the pres-
sure field used by rheoInterFoam is not divided by the density, thus retaining its
natural units (Pa.s).
Given that a constitutive equation is being defined and solved individually for
each phase, variables tau and theta should be labeled (suffixed) with the re-
spective phase name. Considering a viscoelastic model for each phase and default
naming of phases, we would have tau1,theta1 and tau2,theta2. If a mul-
timode mode model is assigned to a given phase, then the name of each mode
should also be appended.

CHAPTER 5. Tutorials 148
|system/
The main novelty comparing to rheoFoam is that when using rheoInterFoam
the user has the possibility to choose between PIMPLE and SIMPLEC for pressure-
velocity coupling. This is controled in dictionary fvSolution, in subDict PIM-
PLE, where the keyword SIMPLEC can be assigned to true or false. Independently
of the choice, the momentum equation is always solved. The variable nCorrectors
works in its usual way (looping the pressure equation) and the variable nInIter
assumes the same function as nOuterCorrectors. In a future release of rheoIn-
terFoam, this workflow will most likely change. There are currently these two
options because it is still not clear which one is more advantageous. Still in dictio-
nary fvSolution, other keywords must be assigned in subDict PIMPLE, which
are related with the VOF method and that the reader can found in the tutorials. If
a sparse matrix solver from an external library is used, then check the instructions
provided in Section 4.4
In dictionary fvSchemes, the discretization schemes for the two phases should
be defined, as well as the discretization schemes related with the VOF method,
which can also be found in the tutorials.
Besides the Courant number, the solvers using VOF, as rheoInterFoam, can
also restrict the time-step based on an interface Courant number, which should be
defined in dictionary controlDict.
The dictionary setFields, used to initialize parts of the domain with speci-
fied values, should also be present in folder system/ whenever used.
5.3.2 Case 1: impacting drop
Itutorials/rheoInterFoam/ImpactingDrop/Oldroyd-BLog/
!Overview
In this tutorial, a liquid drop composed of a viscoelastic fluid falls under gravity
and its shape (the drop width, more precisely) is monitored before and after the
drop impacts a rigid plate. Under such conditions, the drop width oscillates after
the impact. This problem has been used in the literature as a benchmark case for
viscoelastic two-phase flow solvers (e.g. [49,50]).
The configuration adopted in the tutorial reproduces the conditions in Ref.
[49], where an axisymmetric geometry has been used. The dimensionless numbers
governing the flow are: F r =U0
√gD ,Re =ρU0D
η0,W i =λU0
Dand β=ηs
ηs+ηp, where U0
is the initial velocity of the drop, gis the gravitational acceleration, Dis the drop
diameter, ρis the fluid density, η0is the total viscosity (polymer plus solvent) and
λis the relaxation time (all these fluid properties are for the drop phase). The
problem was simulated for F r = 2.26, Re = 5, W i = 1 and β= 0.1. Note that the
surface tension is set to zero and we assign low (but finite) density and viscosity
values to the fluid surrounding the drop.
!Geometry & Mesh
The geometry is composed by a plate on its bottom, while the other patches
simply act as open boundaries, representing the atmosphere. Axisymmetry is
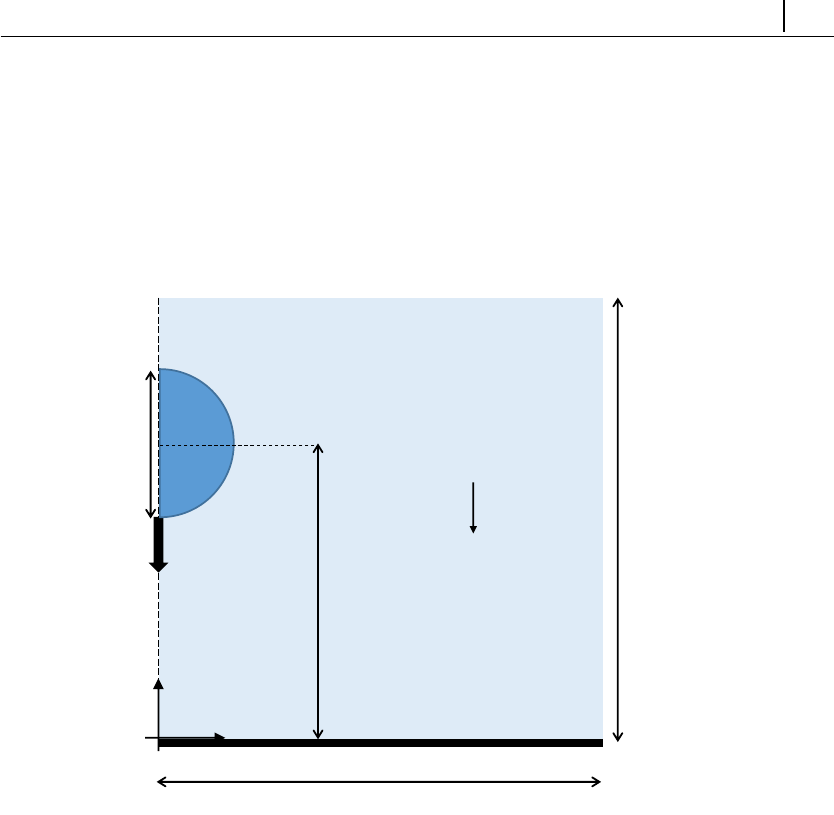
CHAPTER 5. Tutorials 149
considered around the y-axis. All the dimensions are expressed as a function of
the drop diameter, Fig. 5.17. The domain is big enough so that we can neglect
the influence of the open boundaries location in the results.
The domain is meshed uniformly with 120 cells in both the radial and axial
directions.
axis
atmosphere
y
r
D
3D
plate
3D
2D
atmosphere
phase 2
phase 1
U0
g
Figure 5.17: Geometry for the impacting drop problem.
!Boundary conditions
At the plate, no-slip boundary conditions are imposed with a null velocity,
linearly extrapolated polymeric extra-stress components and zero normal gradient
for the indicator field. We assign a fixedFluxPressure BC to the pressure, as
discussed in Section 4.6.8, for multiphase flows. The patches representing the
open boundaries (atmosphere) are assumed to not interfere with the dynamics of
the drop, so that zero-gradient is assumed for all variables, except the pressure,
which is fixed at p= 0.
Following Ref. [49], the drop has an initial velocity U0, in the vertical direction
(pointing downwards), and its center of mass is at a distance 2Dfrom the plate.
!Command-line
1–Build the mesh:
∼$blockMesh
2–Initialize the indicator and velocity fields in the drop region:
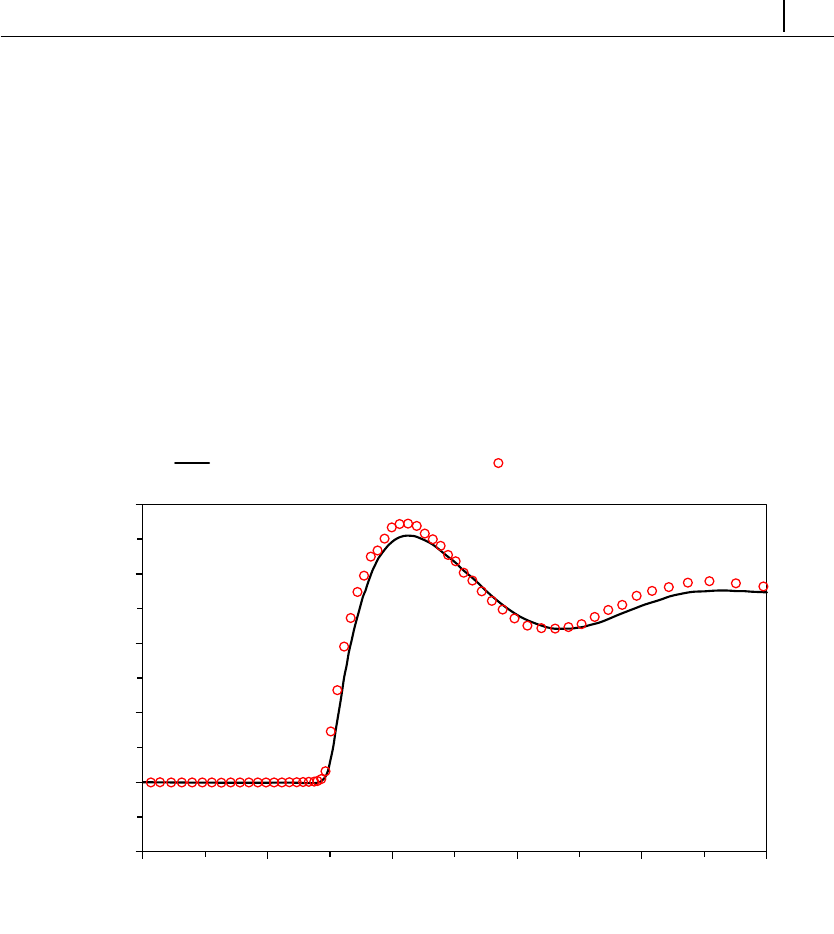
CHAPTER 5. Tutorials 150
∼$cp 0/alpha1.org 0/alpha1
∼$cp 0/U.org 0/U
∼$setFields
3–Run the solver:
∼$rheoInterFoam
!Results
The evolution of the drop width over time is plotted in Fig. 5.18. The width
is normalized with D(its initial diameter) and time with D/U0. The evolution of
the drop width over time is written to a file by a coded FunctionObject.
0.8
1
1.2
1.4
1.6
1.8
0 1 2 3 4 5
W
t
Figueiredo et al. (2016) rheoInterFoam
Figure 5.18: Evolution of the drop width over time for F r = 2.26, Re = 5,
W i = 1 and β= 0.1. The profile obtained with rheoInterFoam is compared with
the data of Figueiredo et al. [49].
5.3.3 Case 2: planar die swell
Itutorials/rheoInterFoam/DieSwell/
!Overview
A significant number of plastic objects that we use in our everyday life are pro-
duced by extrusion of molten polymers. In this process, the polymeric phase can
swell significantly at the exit of the die due to the development of normal stresses.
Predicting the amount of swell is important for the processing. Moreover, undesir-
able sharkskin defects in the extrudate surface can occur under certain conditions,
and the ability to predict such conditions can potentially reduce industrial wastes.
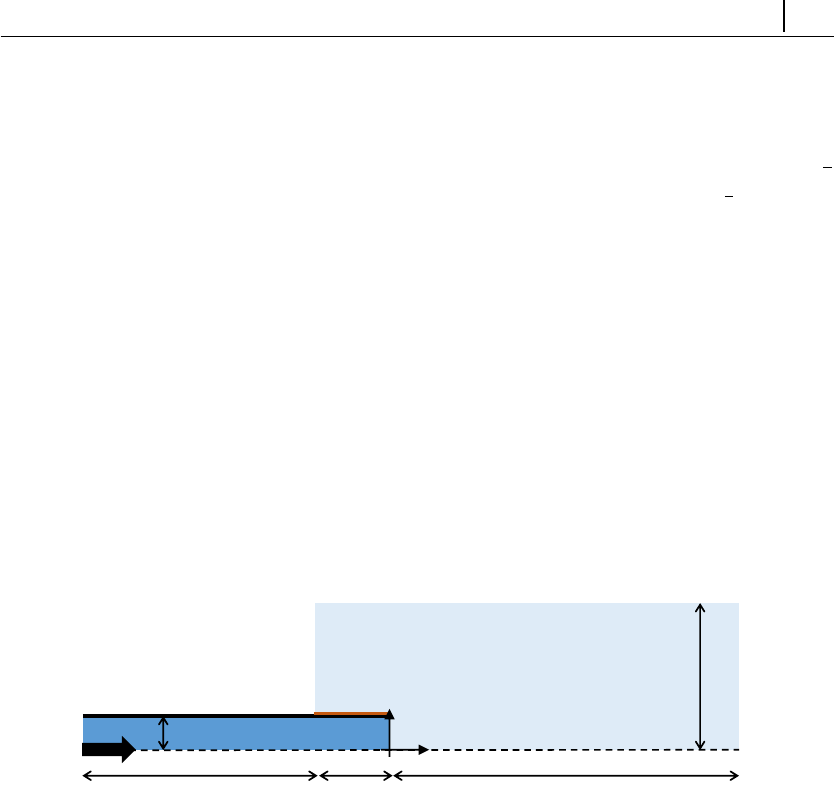
CHAPTER 5. Tutorials 151
This tutorial presents the swell of non-Newtonian fluids flowing through a pla-
nar rectangular die. The three cases provided reproduce the results obtained in
Ref. [51] using rheoTool, for mesh M1 and three different fluids: Carreau-Yasuda
fluid with n= 0.3 (directory CarreauYasuda/); Oldroyd-B fluid with β=1
9
and W i = 2 (directory Oldroyd-BLog/); Giesekus fluid with β=1
9,α= 0.5
and W i = 4 (directory GiesekusLog/). The viscoelastic fluid models are solved
with the log-conformation approach. Note that both gravity and surface-tension
effects are neglected in this tutorial. In addition, only the steady-state solution is
of interest.
!Geometry & Mesh
The geometry for this case is displayed in Fig. 5.19. The mesh corresponds to
mesh M1 of Ref. [51]. Note that this is a kind of stick-slip configuration, which
represents a die with negligible wall thickness. Accordingly, patch wallOut overlaps
part of the wallIn patch.
y
x
H
32.5H
40H
4H
2.5H
inlet
outlet
atmosphere
atmosphere
symmetry
phase 2
phase 1
wallIn
wallOut
Figure 5.19: Geometry for the planar die swell tutorial.
!Boundary conditions
The boundary conditions used are described in Ref. [51]. In order to avoid the
definition of an analytical solution at the inlet, a long entrance channel is used.
!Command-line
1–Build the mesh:
∼$blockMesh
2–Initialize the color function field:
∼$cp 0/alpha1.org 0/alpha1
∼$setFields
3–Run the solver:
∼$rheoInterFoam

CHAPTER 5. Tutorials 152
!Results
The results obtained with mesh M1 can be found in Ref. [51]. The users of
the foam-extend version (fe40 ) will notice an instability in the extrudate surface
close to the die exit, which eventually vanishes with time. Such instability is not
present in the OpenFOAM R
versions.
Several methods can be used to compute the amount of swell far from the die
exit. Assuming that the free-surface of the extrudate corresponds to α= 0.5, for
α∈[0,1], this isoline can be directly extracted with Paraview. Another option
is to extract the profile of the color function (α) over a vertical line far from
the die exit, using the sample utility of OpenFOAM R
. Then, the value α= 0.5
can be simply interpolated from the nearest values. A more complex, still more
versatile option is to code a ppUtil function (Section 4.7.2) retrieving in run time
the maximum free-surface position in a predefined region. This would also allow to
check for convergence of the free-surface position. Slight differences can be found
among the results from the different methods.
5.4 rheoEFoam
5.4.1 General guidelines
The first steps to set up a case for rheoEFoam are the same as for rheoFoam
(Section 5.1.1). After that, the hydrodynamic component of the problem will be
ready, and only the electric component will remain to be defined – this is the
subject of this section.
|constant/
The electricProperties dictionary should be added to folder constant
/. It contains most of the information about the EDF model to be used, as shown
in Listing 5.3, illustrating an example for the PNP model.
parameters
2{
type NernstPlanck;
4
T T[0001000]298;
6relPerm relPerm [ 0 0 0 0 0 0 0 ] 80.1;
8psiContrib true;
extraEField extraEField [ 1 1 -3 0 0 -1 0 ] (5000 0
0);
10
species
12 (
cCation
14 {
z z[0000000]1;
16 D D[02-10000]1e-9;
}
18
cAnion

CHAPTER 5. Tutorials 153
20 {
z z[0000000]-1;
22 D D[02-10000]1e-9;
}
24 );
}
Listing 5.3: Example of a electricProperties dictionary used with
rheoEFoam – the settings displayed are for the PNP model.
The electric properties in dictionary electricProperties are defined in-
side a subDict named parameters (line 1, Listing 5.3). The EDF model is selected
through keyword type, where the TypeName of any model in Table 4.2 can be used
(the user may type any random word to get the list of all available EDF models).
Apart from the type keyword, all the remaining entries are model-specific. In the
case of the PNP model in Listing 5.3,Tis the absolute temperature and relPerm
corresponds to the relative permittivity (dielectric constant) of the electrolyte, εR,
such that ε=εRε0, where ε0is the vacuum permittivity. In line 8, the entry
psiContrib set to true indicates that variable psi (either Ψor ψ) should con-
tribute to the electric field used in the definition of the electric body-force. The
default behavior, i.e., if the entry is not defined, is psiContrib = true. The next
line (line 9) is also optional and allows the user to define an additional uniform
electric field, extraEField (units are in SI, as always). This electric field will only
enter in the computation of the electric body-force in the momentum equation
(fE=ρE(E+extraEField); extraEField corresponds to vector Eain Table
4.2). Then, from line 11 to 24 each specie of the electrolyte is defined. In the
example, only two species are modeled: cCation and cAnion, each having its own
charge valence (z) and diffusivity (D). Note that the charge valence is a signed
integer: positive for cations and negative for anions. The user can add as many
species as desired to the list, for the model under analysis. The name given to
each specie is user-defined, but consistence must be kept when further defining the
respective fields, as explained next.
The example in Listing 5.3 should not be generalized to all the EDF models, as
stated before. The best way for the user to know how the electricProperties
dictionary should look like for a given EDF model is to analyze a tutorial provided
for that model (at least one tutorial is provided for each model).
|0/
In addition to the fields related with the hydrodynamics (pressure, velocity and
eventually extra-stress), when using rheoEFoam for EDFs, the fields specific to the
given EDF model should be specified in folder 0/ (or the equivalent starting time
folder when different from 0).
For the PNP model illustrated in Listing 5.3, we need to define 3 or 4 fields,
depending if we use one single electric potential or two, respectively. In the first
case, the fields would be psi (in this guide represented by Ψ), cCation and cAni
on (in this guide represented by ci). In the second case, field psi would be replaced
by psi (in this guide represented by ψ) and phiE (in this guide represented by
φExt). Note that although having the same name in both cases, field psi has
different meanings for each one: it is either the total, unique electric potential (Ψ),

CHAPTER 5. Tutorials 154
or the intrinsic electric potential (ψ) – in practice, the Poisson equation to be solved
is different in each case. The selection between both cases is made through variable
phiE: when present, psi is considered the intrinsic electric potential, ψ. It is
important to highlight that the fields representing the concentration of each specie
(in mol/m3) should keep the name defined in dictionary electricProperties,
in a one-to-one correspondence for each specie. These names are user-defined, in
opposition to the names for the electric potential variables, which are fixed: psi
and phiE.
The PNP model is the only to require the definition of fields for the concentra-
tion of each ionic specie. The other EDF models only require the electric potential
(one or two variables, depending on the model and on the user’s choice) to be
defined. The exception is the Ohmic model, which also requires a field for the
conductivity (sigma, in this guide represented by σ). Still for this model, only
one electric potential variable may exist and its name should be phiE. In case of
doubt, checking the tutorials is always a good starting point.
|system/
Since additional equations are solved for EDFs (comparing to pressure-driven
flows), the discretization schemes for the terms entering these equations need to
be defined, as well as the sparse matrix solvers and respective settings.
The discretization schemes are defined in dictionary fvSchemes. The new
entries to add to the dictionary are model-dependent and can be found in the
tutorials. If the discretization scheme for any term is missing, an error will be
retrieved complaining for it.
Regarding dictionary fvSolution, keep in mind when defining the matrix
solvers for the new fields that Poisson-type equations require, in general, a sym-
metric matrix solver, while generic transport equations (including advection) are
usually handled with an asymmetric matrix solver. If a coupled solver or a sparse
matrix solver from an external library is used, then check the instructions pro-
vided in Section 4.4. Regarding under-relaxation, our recommendations are the
same as the ones expressed for rheoFoam: by default, do not use under-relaxation,
except, eventually for pressure in non-orthogonal grids, if needed. Note that the
Nernst-Planck equations for each specie in the PNP model are collectively solved
under the name ci, instead of the name given to the specie (this should be taken
into account when defining the matrix solver and the under-relaxation factors).
Still in dictionary fvSolution, a new subDict needs to be defined for EDFs,
named electricControls, Listing 5.4. In the code sample analyzed in Section 4.2.5,
we have seen that each equation of a given EDF model is solved inside a while loop,
controlled by a maximum allowable number of iterations and the initial residual
of the equation being solved (the loop is exited when the first of the two criteria
is met). These loops are intended to converge explicit terms inside each equation,
since this can be critical for some EDFs. Thus, the controlling parameters of
these cycles – the maximum number of iterations and the threshold residual – are
defined in subDict electricControls. This needs to be done for each equation, or
default values are assumed otherwise (maxIter: 50; residuals: 10−7). For non-
stiff problems and when the mesh non-orthogonality is kept low, 1 iteration can
be enough. When the PNP model is used, the number of electrokinetic coupling

CHAPTER 5. Tutorials 155
iterations (see Section 4.2.3) can also be defined in this subDict, as shown in line 3
of Listing 5.4 (if not defined, nIterP NP = 2 is assumed by default). As mentioned
in Section 4.2.3, we recommend a minimum of 2 electrokinetic coupling iterations
for any generic case using this model.
1electricControls
{
3nIterPNP 2;
5phiEEqn
{
7residuals 1e-7;
maxIter 1;
9}
11 psiEqn
{
13 residuals 1e-7;
maxIter 1;
15 }
17 ciEqn
{
19 residuals 1e-7;
maxIter 1;
21 }
}
Listing 5.4: Example of an electricControls subDict in dictionary
fvSolution – the settings displayed are for the PNP model.
5.4.2 Case I: EDF of power-law and PTT fluids in a mi-
crochannel
Our first tutorial for rheoEFoam is aimed to predict the velocity profile for a purely
EDF of a power-law fluid (Part A) and for the mixed pressure-/electrically-driven
flow of a linear PTT fluid (Part B) in a slit microchannel. The numerical profiles
are compared with analytical solutions.
○Part A - Power-law fluid
Itutorials/rheoEFoam/channelEDF/PowerLaw/PoissonBoltzmann
!Overview
The analytical solution for the EDF of a power-law fluid in a slit microchannel
can be found in Ref. [52] for a generic flow behavior index (n) of the power-law
model, under the Debye-H¨uckel approximation. For fully-developed flow condi-
tions, the velocity profiles depend on nand on ˜κ=κH =H
λD=q2(zH)2ec0F
εkT ,
where λDis the Debye length for a binary, symmetric electrolyte, as defined in
Eq. (3.34), and His the channel half-width. Although we will only present results
for the PB model, we also provide the corresponding cases for the PNP and DH
CHAPTER 5. Tutorials 156
models – as you will see, the results are indistinguishable between the models, for
the conditions simulated.
!Geometry & Mesh
The geometry is a 2D (slit) microchannel with half-width H, Fig. 5.20. Due
to the periodic boundary conditions assumed on the inlet/outlet, the mesh has
one single cell in the x-direction and 300 non-uniformly distributed cells in the
y-direction, normal to the applied electric field.
inlet
outlet
walls
y
x
H
symmetry
E
Figure 5.20: Planar channel geometry.
!Boundary conditions
The flow is 2D in the xy-plane. At both the inlet and outlet, periodicity is
imposed. Thus, we assume from the beginning that this condition will retrieve the
fully developed profiles for an infinitely long microchannel. A symmetry condition
is imposed at y= 0. The walls are impermeable (u=0and zero-gradient for
pressure) and have a fixed intrinsic electric potential. Due to the simple geometry
of the channel, the flow is generated by imposing a uniform electric field through-
out the channel, parallel to the walls (E). Therefore, there is no need to solve
for the external electric potential variable (phiE ): the electric field is directly im-
posed through the extraEfield entry of dictionary electricProperties. These
boundary conditions hold for both the PB and DH models. In order to use the PNP
model, a boundary condition must be defined at the wall for the ionic species. Since
Boltzmann equilibrium holds and only the steady-solution is sought, the easiest
way is to simply compute the ionic concentration from the potential distribution
(check the boltzmannEquilibrium boundary condition described in Section 4.6.4).
The flow is initially at rest and the intrinsic electric potential is zero.
!Command-line
1–Build the mesh:
∼$blockMesh
2–Run the solver:
∼$rheoEFoam
3–Extract the profile of ualong the vertical direction:
∼$sample -latestTime
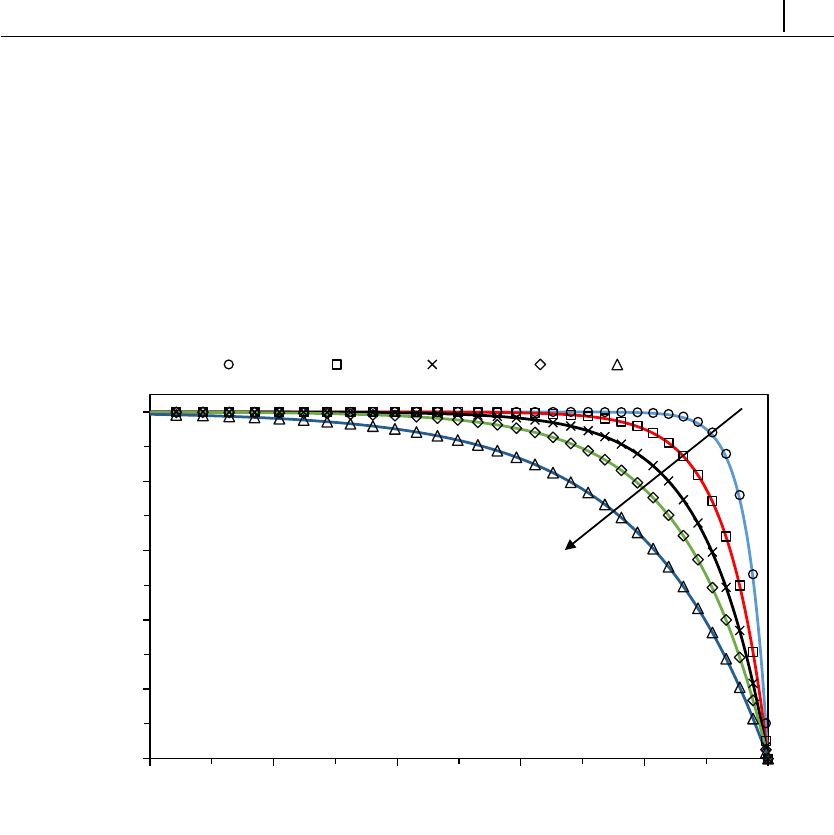
CHAPTER 5. Tutorials 157
!Results
The velocity profiles over the y-direction are depicted in Fig. 5.21 for varying n
= 0.25, 0.5, 0.75, 1 and 1.5, at fixed ˜κ= 15. The velocity profiles are normalized
by the velocity at the centerline of the channel, while the spatial coordinate is
normalized by the channel half-width. The numerical results reproduce accurately
the analytical solution [52] and show that shear-thinning fluids (n < 1) display an
apparently compressed EDL, while the opposite is observed for shear-thickening
fluids (n > 1).
0.0
0.2
0.4
0.6
0.8
1.0
0.5 0.6 0.7 0.8 0.9 1
|u|
y
n=0.25 n=0.5 n=0.75 n=1 n=1.5
n
Figure 5.21: Velocity magnitude over the direction transverse to the applied
electric field for a power-law fluid with different flow behavior index, at fixed
˜κ= 15. The points represent numerical values, while the lines are the analytical
solution [52]. Note that the x-scale has been truncated and only represents one-
quarter of the channel width (this is to have a zoomed view near the wall).
As aforementioned, the same results would be obtained with the PNP and DH
models and the user may confirm that from the cases provided. All the cases
are prepared for n= 0.75 (this can be easily changed in dictionary constitu
tiveProperties) and will converge in the total time of simulation defined in
controlDict. However, we should note that for low n, where n= 0.25 can be
included, the simulation will take a much longer time to reach the steady-state,
because of the low viscosity that develops near the wall, where the shear-rate
attains very high values (it becomes even worse for higher ˜κ). Furthermore, care
should be taken in defining the upper and lower bounds for the viscosity (check
the power-law model implementation in Table 4.1), since stringent bounds may
influence the numerical solution.
○Part B - linear PTT fluid

CHAPTER 5. Tutorials 158
Itutorials/rheoEFoam/channelEDF/PTTlinear/DebyeHuckel
!Overview
Afonso et al. [53] derived an analytical expression for the mixed pressure-
/electrically-driven flow of simplified (ζ= 0) linear PTT fluids in slit channels
with an homogeneous zeta-potential at the walls, under the Debye-H¨uckel approx-
imation. For creeping flow conditions (Re = 0), the velocity profiles depend on
Γ=−H2
ψ0|∇p|
|E|(ratio between pressure and electric forcing), ˜κ=κH =H
λD=
q2(zH)2ec0F
εkT and √εDe =√ελκU, where εis the extensibility parameter of the
PTT model, U=−ψ0|E|
η0is the Helmholtz–Smoluchowski velocity and ψ0is the
zeta-potential at the wall. Both ∇pand Eonly have a single non-zero component,
in our case, the x-component. Note that in this tutorial we use exceptionally to
represent the electric permittivity (instead of ε), in order to distinguish it from ε
that we use to represent the extensibility parameter of the PTT model.
In this tutorial, we analyze the effect of varying Γ, while keeping the remaining
dimensionless parameters fixed.
!Geometry & Mesh
The geometry is similar to the one used in Part A for the power-law fluid ex-
ample. However, the physical dimensions are different and, importantly, we do not
consider periodicity between the inlet and outlet. Instead, the flow is also solved
in the x-direction. We note that this is not mandatory and that cyclic conditions
would also provide the right solution. However, considering the full channel in the
x-direction eases the definition of the pressure gradient, at the expanse of having a
higher number of cells in the mesh. Several options would allow to keep the cyclic
patches and to impose directly the pressure gradient in the momentum equation,
as the fvOptions tool, but we consider them less straightforward than our choice
(at least for less experienced users).
!Boundary conditions
The boundary conditions are similar to the ones used in Part A, with some
modifications required by the use of a viscoelastic model and due to the different
conditions assigned to patches inlet and outlet. Since pressure gradients are al-
lowed, we fix the pressure at the outlet and adjust the inlet pressure as required
to get the desired Γ. Remember that in rheoEFoam field prepresents the pressure
divided by the density. A zero-gradient condition is imposed for the remaining
variables at those two patches. Regarding the wall, the polymeric extra-stresses
are linearly extrapolated.
!Command-line
1–Build the mesh:
∼$blockMesh
2–Run the solver:
∼$rheoEFoam
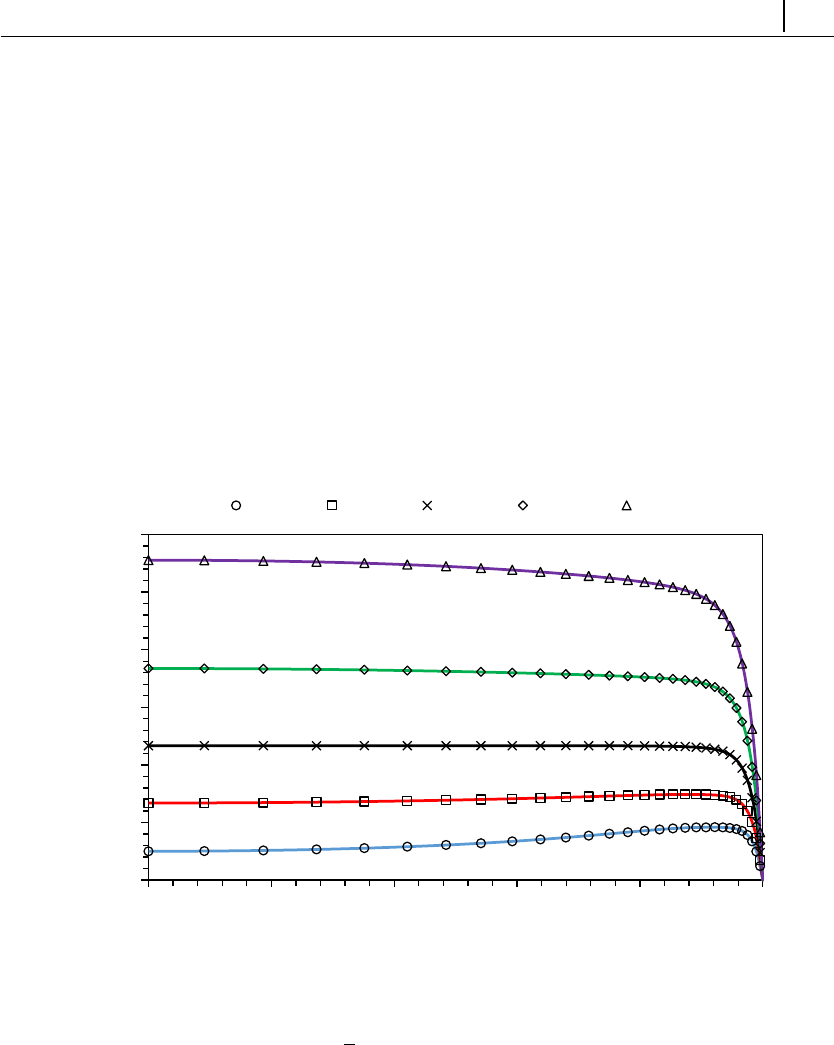
CHAPTER 5. Tutorials 159
3–Extract the profile of ualong the vertical direction for the latest time (the
x-position of the sampling line should not be important):
∼$sample -latestTime
!Results
Fig. 5.22 shows the velocity profiles under different forcing ratios. The velocity
is normalized by the Helmholtz–Smoluchowski velocity (U, defined above), while
the spatial coordinate is normalized by the channel half-width. Note that for a
Newtonian case and Γ= 0 (pure EDF), the (normalized) velocity profile at the
centerline would have a value very close to 1 (the higher ˜κ, the closer it is) and
we can see that this value is significantly higher for a linear PTT fluid due to
shear-thinning.
The parameters provided in the tutorial are for Γ= 4.
0
5
10
15
20
25
30
0 0.2 0.4 0.6 0.8 1
|u|
y
Γ=4
Γ=2
Γ=0
Γ=-2
Γ=-4
Figure 5.22: Velocity magnitude along the direction transverse to the applied
electric field and pressure gradient for a simplified linear PTT fluid, at different
forcing ratios Γ, for ˜κ= 20 and √εDe = 4. The points represent numerical values,
while the lines are the analytical solution [53].
5.4.3 Case II: induced-charge electroosmosis around a
cylinder
Itutorials/rheoEFoam/ICEO/NernstPlanckCoupled
!Overview
This tutorial analyzes the DC induced-charge electroosmosis (ICEO) around a
conducting cylinder. We have investigated this problem in Ref. [3] and we present
in this tutorial the setup used for ˜
V= 0.01 and ˜κ= 10, in mesh M1.
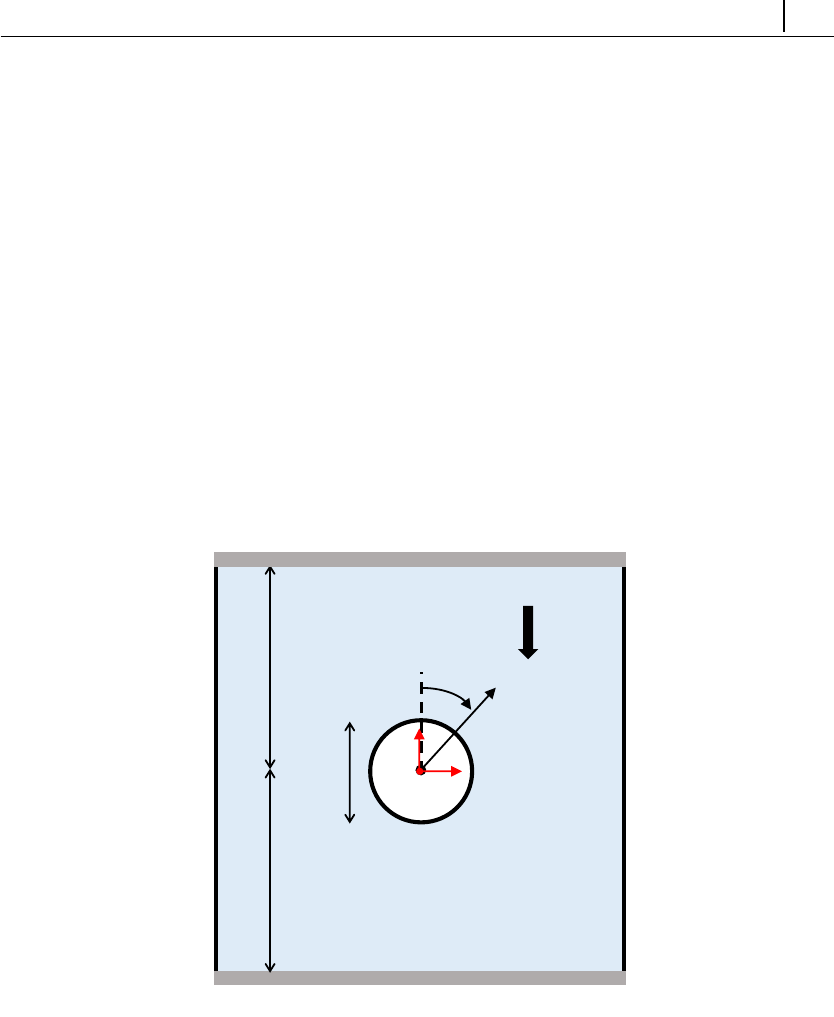
CHAPTER 5. Tutorials 160
In directory tutorials/rheoEFoam/ICEO/, the same case is available un-
der different EDF models (PNP, PB and DH). For the conditions aforementioned,
all give similar results in steady-state. The case for the PNP model uses one po-
tential (Ψ), while the remaining cases are solved under the splitting approach for
the electric potential (both φExt and ψare defined). For the last ones, you can
also see the use of the inducedPotential boundary condition described in Section
4.6.5.
The case for the PNP model (OpenFOAM R
versions only) uses a semi-coupled
solver, where the PNP system of equations is solved coupled, but separated from
continuity and momentum equations, which are themselves solved coupled.
!Geometry & Mesh
The geometry used in this tutorial is displayed in Fig. 5.23, being the same as
in Ref. [3]. The mesh corresponds to mesh M1 of that work, and more details on
the problem definition can be found therein.
elecNorth
wallWest
cylinder
50R
2R
θ
elecSouth
wallEast
50R
E
r
x
y
Figure 5.23: Metallic cylinder placed over an electric field. The surrounding
domain is square (edge size: 100R) and the cylinder lays on its center. The cylin-
drical coordinate system (r, θ) is plotted in black, while the Cartesian coordinate
system (x, y) is represented in red (remember that OpenFOAMR
uses the Carte-
sian system for computations).
!Boundary conditions
The boundary conditions are described in detail in Ref. [3]. The only difference
is on the boundary condition for pressure on the cylinder surface, which has been
changed to zero-gradient. This change is due to the use of a coupled solver.
!Command-line

CHAPTER 5. Tutorials 161
1–Build the mesh:
∼$blockMesh
2–Run the solver:
∼$rheoEFoam
3–Extract profiles of ualong the line θ= 45◦:
∼$sample -latestTime
!Results
You may find the following relation useful in converting the velocity from the
Cartesian base where it is computed, to the cylindrical base used in Ref. [3] to
display the results:
Ur
Uθ=sin(θ) cos(θ)
cos(θ)−sin(θ)Ux
Uy(5.8)
Note that two ppUtil (cf. Section 4.7.2) are used in this tutorial, returning
both the global balance of ions (calcBalance) and the current density through the
cylinder surface (calcJpatch). The latter allows to verify, in this specific case, that
the no-flux boundary conditions for the two ionic species is working as expected,
since a quasi-null current density is retrieved at the boundary where it is assigned.
5.4.4 Case III: charge transport across an ion-selective
membrane
Itutorials/rheoEFoam/selecMembrane/NernstPlanck
!Overview
This tutorial presents the charge transport across an ion-selective membrane
and will show the development of the so-called electroconvective instabilities (e.g.
[54]). We addressed this EDF in Ref. [3] and we present in this tutorial the setup
used for ˜
V= 120, in mesh M1. The case is adjusted to run until ˜
t= 0.01, but this
time can be easily increased in controlDict.
!Geometry & Mesh
The geometry for this tutorial is displayed in Fig. 5.24, being the same as in
Ref. [3]. The mesh corresponds to mesh M1 of that work, and more details on the
problem definition can be found therein.
!Boundary conditions
The boundary conditions were described in detail in Ref. [3]. For the users
of OpenFOAM R
v4.x, if the fixedFluxExtrapolatedPressure is intended to be used
at the membrane boundary – this is the most correct option –, then function
adjustPhi() must be disabled in solver rheoEFoam, as discussed in Section 4.6.8.
Since this would require a permanent change in the solver, we have chosen to use
azeroGradient BC in replacement.
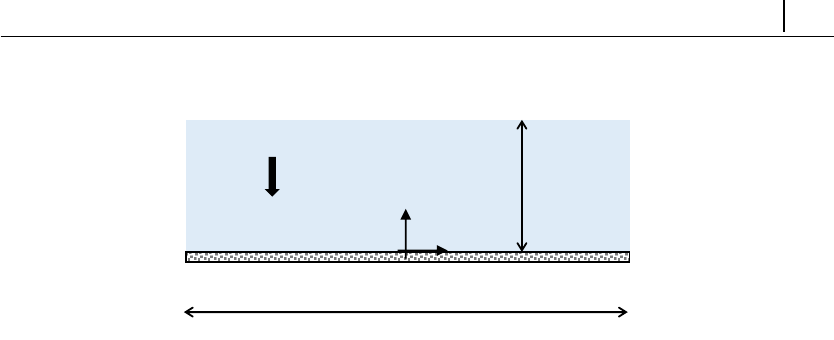
CHAPTER 5. Tutorials 162
cyc0
reservoir
H
membrane
cyc1
E
6H
y
x
Figure 5.24: Planar reservoir with an ion-selective membrane (only permeable
to cations) on its bottom.
!Command-line
This tutorial is slightly different from the previous ones regarding the
command-line sequence to run. This is because the problem is first solved in
a 1D configuration and the resulting solution is then disturbed and used as the
starting solution of the 2D configuration. Thus, we recommend to use directly the
Allrun script to run this tutorial, although we also explain next the main steps
accomplished by that script.
Firstly, in the directory of the main case you will find a folder named so
lution1D/. This is where the 1D problem is solved – script Allrun inside
this folder is the first call of the Allrun in the main directory. Computing the
1D solution is relatively straightforward in what respects the commands to be
executed, since it only requires building the mesh (blockMesh) and running the
solver (rheoEFoam). You may note that the hydrodynamic component of the
solver is switched off through the solveFluid keyword in dictionary fvSolution,
which is set to false. Thus, only the Poisson and Nernst-Planck equations are
being solved. The 1D solution is obtained by solving the PNP system of equations
coupled (see Sections 4.2.4 and 4.4.8). Under the current settings, the lower the
voltage on patch reservoir, the higher the time for the 1D solution to converge
(the endTime should be increased accordingly in these situations). Our criteria
for convergence relies in the monitor for the current density.
After the 1D solution is computed, the resulting fields are mapped to the
2D domain (also created with blockMesh beforehand), using the mapFields util-
ity available by default in OpenFOAM R
. Then, the fields for the cationic
and anionic concentration are locally disturbed by a 1 % random perturbation.
This is accomplished by a pre-processing utility named rndPerturbation, which
has been specifically created for this task and that can be found in directory
src/libs/preProcessing/rndPerturbation/. The case is ready to be
run with rheoEFoam, noticing that now solveFluid = true.
While the case is running, a ppUtil (cf. Section 4.7.2) is simultaneously being
executed (calcJpatch), which retrieves the surface-averaged current density over
time on both the reservoir and membrane patches (Fig. 5.24).

CHAPTER 5. Tutorials 163
!Results
The current density can be plotted over time and the contours of charge density
can be computed and visualized in Paraview (these are just some suggestions).
The electric field intensity can be controlled by changing the voltage in file
solution1D/0/psi, under the entry for patch reservoir. Note that any change
in the initial/boundary conditions of any field must be done in the files inside folder
solution1D due to the mapping procedure. By running the Allrun script in
the main folder, the 1D solution will be always computed first.
5.4.5 Case IV: electrokinetic instabilities in a flow-focusing
device
Itutorials/rheoEFoam/EKI/Ohmic
!Overview
This tutorial aims to reproduce qualitatively the electrokinetic instabilities aris-
ing in a flow-focusing device, when electrolytes of different conductivity join at the
converging region. The problem has been extensively studied in Ref. [55], both
experimentally and theoretically.
The use of the Ohmic model is illustrated in this tutorial, which also includes
the transport of a passive, neutral scalar.
As shown by Posner et al. [55], the dynamics of the problem is essentially
governed by three dimensionless numbers: the electric Rayleigh number, RaE=
εE2
ah2
ηD , the conductivity ratio γ=σW
σSand the voltage ratio β=VW
VS. The indices
refer to the north (N), south (S), west (W) and outlet (O) arms of the flow-focusing
device and h= 0.8His the channel depth. Furthermore, an apparent electric field
is computed as Ea=VN−VO
LN+LO, where the denominator of Earepresents the summed
distance of the north and east arms (distance between the ends of each arm, passing
by the center of the geometry: LN+LO= 24Hin this tutorial). The parameters
of the tutorial are chosen in order to simulate RaE= 839, γ= 10 and β= 1.05.
!Geometry & Mesh
The geometry is a 3D flow-focusing device (Fig. 5.25) composed of three con-
verging inlets and one outlet. The width and the depth of the channel are uniform
over all the geometry: 2Hand 0.8H, respectively. The inlet arms (west, south
and north) are all 8Hlong, while the outlet arm (east) is 16Hlong.
The geometry is divided into 12 blocks for meshing purposes. The dimen-
sions of the cells at the junction corners are approximately: (∆x, ∆y, ∆z)≈
(0.1,0.1,0.07)H.
!Boundary conditions
Since the Ohmic model is used in this simulation, we have to define boundary
conditions for pressure, velocity, electric potential and conductivity. We consider
that all the arms are open to the atmosphere, thus p= 0 and a zero-gradient is
assumed for the velocity. At inletNorth and inletSouth, the conductivity of the
fluid entering those arms is the same, but ten times lower than the conductivity of
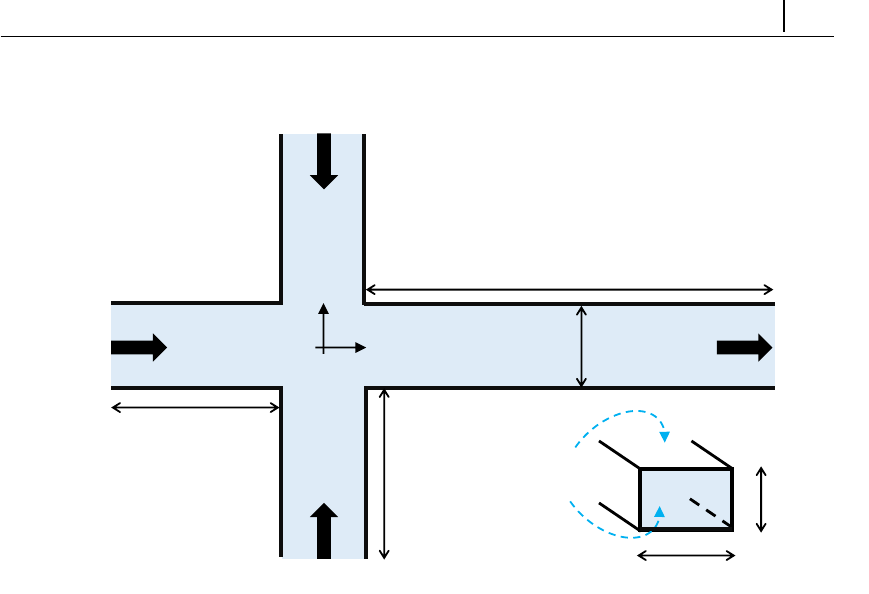
CHAPTER 5. Tutorials 164
y
x
walls
walls
walls
walls
inletSouth
intletWest
outlet
7H
inletNorth
7H
2H
15H
2H
0.8H
frontAndBack
Figure 5.25: Three-dimensional flow-focusing device.
the fluid entering inletWest (γ= 10). A passive scalar (neutral dye) is also entering
the geometry through inletWest, only. A zero-gradient condition is imposed for
both the conductivity and the passive-scalar concentration at the outlet. At the
walls we assume zero-gradient for all variables, except the velocity. As discussed
in Section 3.7.6, the Ohmic model is usually complemented with a conductivity-
dependent slip velocity (Eq. 3.42). In this tutorial, we use m=−0.3 for the
power-law index (see Section 4.6.7). Regarding the electric potential, the outlet
is grounded, while the potential at inletNorth and inletSouth are the same, being
adjusted in order to impose the desired RaE. The potential at inletWest is set
according to β.
Note that the passive-scalar (dye) has a diffusivity which is one order of magni-
tude lower than the diffusivity of the ions (conductivity), in agreement with typical
real conditions.
!Command-line
1–Build the mesh:
∼$blockMesh
2–Create fields Cand sigma by copying the ones already present, but which are
not initialized in the interior domain:
∼$cp 0/C.org 0/C
∼$cp 0/sigma.org 0/sigma
3–Initialize fields Cand sigma in the interior domain (C= 1 ∧σ=σWfor
x < −Hand t= 0):

CHAPTER 5. Tutorials 165
∼$setFields
4–Run the solver:
∼$rheoFoam
5–Post-process in Paraview (hint: slice the channel at the midplane in the z-
direction and plot the contours of C):
∼$paraFoam
!Results
The contours for the passive-scalar are displayed in Fig. 5.26 at the mid-plane
in z, for different RaE. The reader will probably note similarities between these
instabilities and von-K´arm´an vortex streets.
The patterns are qualitatively similar to those obtained in Ref. [55] (see Fig. 4
therein, although our RaEis defined differently from the one used in that work).
The periodicity or the chaotic behavior of the instabilities can be further evaluated
by looking to the probes of Cand U.
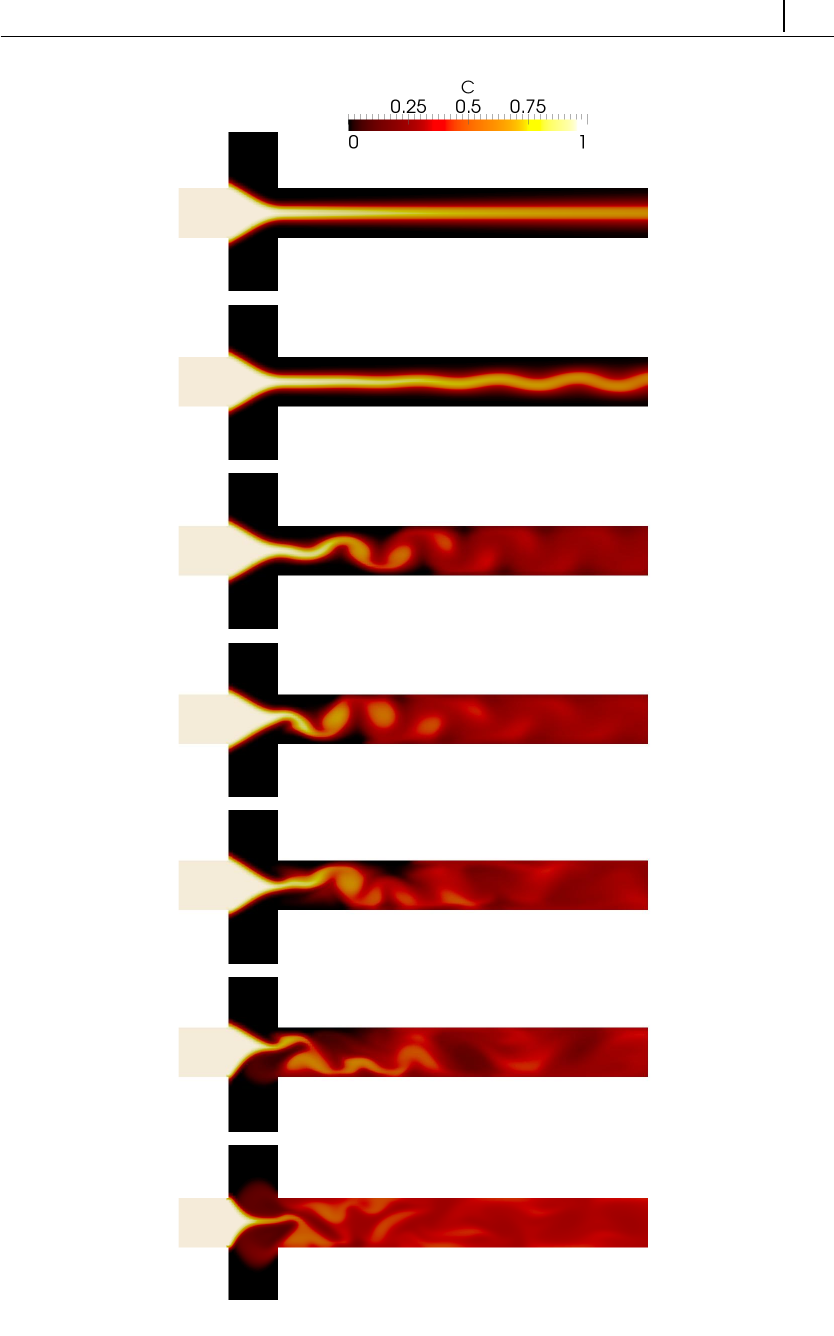
CHAPTER 5. Tutorials 166
RaE= 579
RaE= 481
RaE= 629
RaE= 839
RaE= 1424
RaE= 2164
RaE= 6239
Figure 5.26: Instantaneous contours of Cat the mid-plane in zfor different RaE
(γ= 10 and β= 1.05). The case provided in the tutorial is for RaE= 839 and
the remaining ones can be easily obtained by simply scaling the applied voltage
(phiE) at the inlets (see the definition of RaE).

CHAPTER 5. Tutorials 167
Note that we do not used exactly the same parameters as in Posner et al. [55],
since our purpose was solely to illustrate the qualitative behavior of electrokinetic
instabilities, through a fast-running case. The large time-step used (Courant-
controlled, with Co = 1.5) is also inadequate to capture accurately the transient
behavior of this case.
5.4.6 Case V: electrokinetic mixer
Itutorials/rheoEFoam/EKmixer/slipSmoluchowski
!Overview
The main purpose of this tutorial is to illustrate the use of the slipSmoluchowski
EDF model (see Section 3.7.5 and Table 4.2). Although simple, this model is very
useful to simulate Newtonian fluid flows in complex geometries, being accurate for
thin EDL and low intrinsic potentials. In addition, in this tutorial we also use AC
fields, combined with the transport of a passive-scalar.
The case that we propose is an electrokinetic-based micromixer, inspired on the
work of Coleman et al. [56]. In that work, the authors showed that a flow-focusing
geometry followed by an expansion can achieve a good degree of mixing between
two fluids, under AC-driven injection.
Note that this tutorial does not reproduce exactly the same geometrical dimen-
sions, nor the same operating conditions of Ref. [56].
!Geometry & Mesh
The 2D electrokinetic mixer is shown in Fig. 5.27 (the user can check the
dimensions by opening the mesh in Paraview or by inspecting the corresponding
blockMeshDict file). The device consists of a flow-focusing region where one
fluid is injected through inletWest and the other fluid is injected in inletNorth.
The geometry is made symmetric relative to the x-axis and an expansion region
exists downstream to the flow-focusing, which is where the mixing mainly occurs.
symmetry
walls
inletWest
inletNorth
outlet
y
x
Figure 5.27: Electrokinetic mixer similar to the device used by Coleman et
al. [56].
!Boundary conditions
We consider a purely EDF, thus p= 0 at both inlets and outlet boundaries, and
a zero-gradient condition is simultaneously assigned to the velocity. Regarding the

CHAPTER 5. Tutorials 168
externally applied potential, it is fixed at 0 V in the outlet and a custom sinusoidal
boundary condition is imposed at each inlet,
φExt(t) = φExt, DC +φExt, AC sin(2πft +θ) (5.9)
As long as φExt(t)>0 at each inlet, there is a unidirectional net flow of fluid
in the region x > 0, although the fluid can move both forward and backward in
the region x≤0, which constitutes the injecting mechanism of the mixer [56].
By changing φExt, DC, φExt, AC, f and/or θat each inlet, different degrees of mixing
can be achieved. At the wall, zero-gradient is considered for pressure and electric
potential and the Helmholtz-Smoluchowski equation (Eq. 3.35) is used for the slip
velocity.
A passive-scalar is injected at inletWest and the purpose of the mixer is pre-
cisely to achieve the perfect mixing of the passive-scalar stream (inletWest), with
the stream devoid of that scalar (inletNorth) – perfect mixing means C= 0.5 for
a passive-scalar in the range [0,1]. Note that, as stated in Ref. [56], the operating
conditions can be also tuned in order to obtain a pre-defined degree of mixture
different than a 0.5/0.5 stream at the outlet.
!Command-line
Since the list of commands to run is rather extensive, we recommend the user
to simply run the script Allrun. The commands executed by Allrun that might
seem new, regarding what has been done in the previous tutorials, are topoSet and
refineMesh. Those commands select the cells in the expansion region and perform
a refinement in the y-direction, respectively.
!Results
Fig. 5.28 shows the contours of the passive-scalar when either the stream devoid
of C, or rich in C, are injected. Both snapshots were taken after the system has
reached a periodic state. As can be seen, the conditions defined ensure a good
mixing between the streams, since C≈0.5 at the outlet.
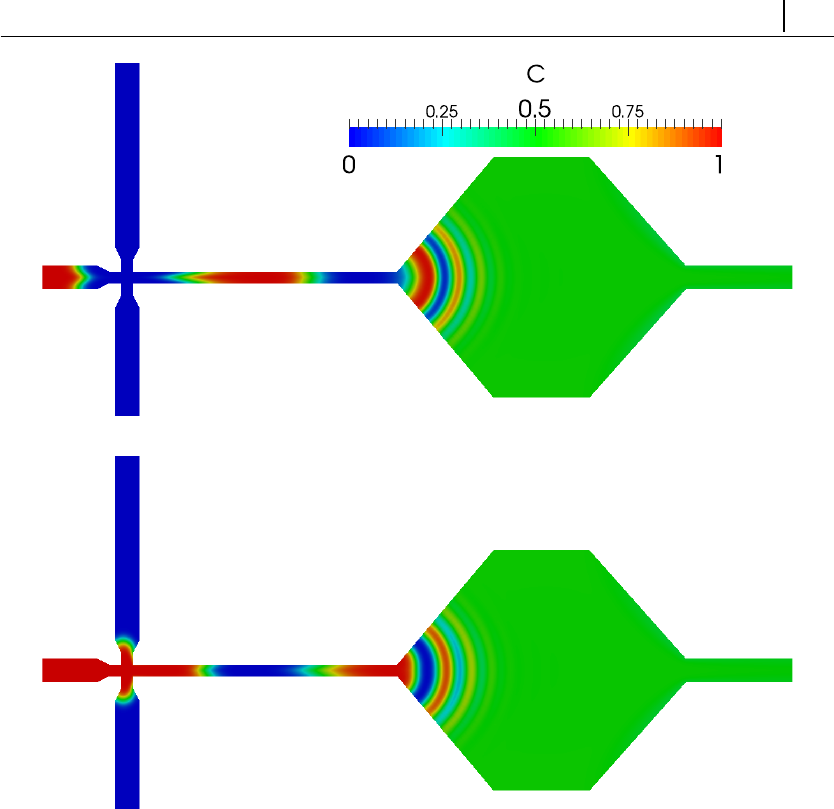
CHAPTER 5. Tutorials 169
(a)
(b)
Figure 5.28: Snapshots of the passive scalar concentration field at different in-
stants: (a) injecting the phase devoid of C(inletNorth) and (b) injecting the phase
rich in C(inletWest). Note that the geometry has been reflected relative to the x-
axis (in Paraview) for presentation purposes – only the upper-half of the geometry
is simulated.
The user can play with the several degrees of freedom of the electric potential
boundary conditions in order to achieve different degrees of mixing. Note that the
time-step used in the tutorial has been adjusted to obtain results in a reasonable
amount time, but it should be lowered to achieve higher accuracy in time. Such
a high time-step, as well as the ”coarse” mesh used, would not be possible to use
if, for instance, the full PNP model was used instead – the simulation would most
likely diverge due to stability issues.
5.4.7 Case VI: electro-elastic instabilities in cross-shaped
geometries
Itutorials/rheoEFoam/EEI/PoissonBoltzmann/
CHAPTER 5. Tutorials 170
!Overview
The electrically-driven flow of high-molecular weight polyacrylamide solutions
in cross-slot and flow-focusing devices was seen to become unstable after a thresh-
old electric potential is exceeded [57]. This tutorial addresses the numerical simula-
tion of such phenomena, as presented in Ref. [57]. This tutorial merges electrically-
driven flows with viscoelastic fluid models, where the electric charge distribution
is computed by the Poisson-Boltzmann model and the extra-stress tensor of the
viscoelastic fluid is evolved using the Oldroyd-B model (β= 0.4). The settings
of the tutorial reproduce the case with ∆V= 160 V, W iB= 2.06, W iκ= 103
(CrossSlot/) and ∆V= 160 V, W iB= 1.03, W iκ= 154 (FlowFocusing/)
of Ref. [57]. The physical time of the simulations is tf= 0.5 s = 10λ.
!Geometry & Mesh
The geometry for this case is displayed in Fig. 5.29. Both the geometry and
the mesh correspond to the ones used in Ref. [57]. The flow is assumed to be 2D,
being solved in the xy-plane. Note that the patch names for the cross-slot and
flow-focusing geometries differ in the west arm, which is either an outlet or an
inlet (Fig. 5.29).
y
x
walls
walls
walls
walls
49H
49H
2H
0.2H
outlet_east
inlet_south
inlet_north
outlet_west
inlet_west
Figure 5.29: Cross-slot and flow-focusing geometries. In the west arm, the black
arrow is for the cross-slot configuration (outlet west) and the purple arrow is for
the flow-focusing configuration (inlet west). In the tutorial, H= 5 ×10−5m.
!Boundary conditions

CHAPTER 5. Tutorials 171
The boundary conditions used are described in Ref. [57]. The tutorials also
include the transport of a passive tracer. Note that the pressure extrapolation
boundary condition at the wall is replaced by a zero-gradient condition in version
fe40, since it is not available therein.
!Command-line
Before presenting the command line sequence, it is worth to note that the
mesh for this case is built in a slightly different way. Indeed, the blockMesh
application only builds one-quarter of the geometry/mesh, the one in the first
quadrant (+,+). The remaining of the geometry/mesh is built by 2 sequential
mirroring operations (mirrorMesh): first using the Oyz plane and then using
the Oxz plane. Afterwards, patches should be renamed accordingly, which requires
selecting, spliting and removing faces of already existing patches (topoSet) and
creation of new ones (createPatch).
1–Build the mesh:
∼$blockMesh
∼$cp system/mirrorMeshDict0 system/mirrorMeshDict
∼$mirrorMesh
∼$cp system/mirrorMeshDict1 system/mirrorMeshDict
∼$mirrorMesh
∼$topoSet
∼$createPatch -overwrite
2–Initialize field Cin the interior domain:
∼$cp 0/C.org 0/C
∼$setFields
3–Run the solver:
∼$rheoEFoam
!Results
The dye patterns (field C) of the unstable flows can be visualized in Paraview.
5.5 rheoBDFoam
5.5.1 General guidelines
|constant/

CHAPTER 5. Tutorials 172
All the elements needed in directory constant/ for a simulation with
rheoEFoam (Section 5.4.1) should also be present in a simulation with rheoBD-
Foam. This includes a valid mesh and dictionaries electricProperties and
constitutiveProperties. If the simulation will not require the electric mod-
ule of rheoBDFoam, then simply set the electric model type to noModel inside
dictionary electricProperties (see the tutorial examples).
In addition to the above elements, the molecules’ structure and physical prop-
erties should also be present in subdirectory runTimeInfo. The easiest and
recommended way to generate this subdirectory and the files needed is running
utility initMolecules, as described in Section 4.7.4. The last element that must
be present in directory constant/ is dictionary moleculesControls. This
dictionary controls all the options specifically related with the Brownian dynam-
ics algorithm, discussed in Section 4.3. Listing 5.5 presents an example of a
moleculesControls dictionary, that we now analyze entry-by-entry:
•subDict externalFlow
writeFields – the continuum fields needed for the simulation must be present in the
startTime directory, but during the simulation it is possible to suppress
their write. This entry controls the writing of continuum fields during the
simulation. For example, when using a frozen field, there is no need to write
this constant field to the subsequent time directories (usually to save disk
space), unless we expect to restart the simulation from one of those times.
Even in the situation where a restart is expected, it is always possible to
keep the writeFields option disabled and later copy manually the continuum
fields to the new startTime directory. (boolean)
frozenFlow – as pointed out by the entry name, it should indicate if the flow (more gener-
ically all continuum fields) is frozen or not. A frozen flow does not change
over time. (boolean)
tethered – indicates whether the molecules are tethered or not. Remember that if this
option is enabled, all the molecules (of all groups) will be tethered by their
first bead (see Section 4.3.6). (boolean)
pushBackCmp – each component of this vector should be either 1, if the molecules’ center of
mass is fixed in that direction, or 0 otherwise (see Section 4.3.6). (vector of
0/1’s)
pushBackFreq – when the molecules’ center of mass is to be fixed in any direction, then
this entry corresponds to the frequency at which this is done (number of
time-steps between calls) (see Section 4.3.6). This entry is ignored if all
components of pushBackCmp are zero. (integer)
interpolation – the user should specify any valid interpolation method for the external forcing
(see Section 4.3.4). (string)
gradU – if interpolation = Analytical, then ∇ushould be defined in this entry. If any
other interpolation method is selected, this entry is not used (see Section
4.3.3). (tensor)

CHAPTER 5. Tutorials 173
•subDict outputOptions
writeStats – this option enables writing the index, position and stretch of all the molecules
over time (see Section 4.3.8). (boolean)
outputStats
Interval – number of time-steps between consecutive calls to the statistics writer. It
is independent from the writing of time directories. Only effective if the
previous option is enabled. (integer)
writeVTK – this option enables writing the molecules’ structure and properties in VTK
format, which should be readable by any version of Paraview. (boolean)
•subDict exclusionVolumeProperties
activeExclusion
Volume – this option allows to include or suppress exclusion volume forces between
beads (see Section 3.8.2). (boolean)
activeWall
Repulsion – this option enables to impose a minimum approximation distance of the
beads to the walls, upon collision. If not enabled, the beads are repositioned
at the collision point, inside the computational domain (see Section 4.3.7).
(boolean)
repulsiveDistance – if activeW allRepulsion =true, this entry defines the repositioning distance
of the beads in the wall-normal direction, starting from the collision point
on the wall (see Section 4.3.7). (double)
•subDict HIProperties
activeHI – this option allows to include or suppress hydrodynamic interactions, where
the latter corresponds to the free-draining approach (see Section 3.8.2).
(boolean)
•subDict electrophoresis
active – enabling this option adds an electrophoretic force (computed numerically)
acting on the beads center of mass. (boolean)
mobility – if active =true, this entry should correspond to the electrophoretic mobility
of each individual bead. (double)
•subDict springModelProperties
springModel – this entry should correspond to one of the available spring models (see Section
4.3.5). (string)
timeScheme – this entry should correspond to one of the available time integration schemes
(see Section 4.3.5). (string)
maxIter – maximum number of iterations of the Newton-Raphson method if a semi-
implicit time integration scheme is used. (integer)

CHAPTER 5. Tutorials 174
relTol – minimum normalized spring length variation below which the Newton-
Raphson method stops. (double)
tresholdF – fraction of the maximum spring length which triggers the algorithm to add
implicitly the diagonal spring force terms contribution. This is the αvariable
defined in Section 3.8.4, which should take values in the range ]0,1]. (double)
cutOffStretch – variable used to stabilize the Newton-Raphson method. In one given itera-
tion of the Newton-Raphson method, it may happen that a spring exceeds
its maximum admissible length (l). As such, when the springs length needs
to be used to compute fkand Jk(see Section 3.8.4), we replace its value
by min (Ri, cutOffStretch ×l). However, the resulting beads positions are
never corrected. In order to ensure that this stabilization method will not
affect the simulation results, this variable should always be higher than the
maximum expected fractional extension and ≤1. In most of the cases, a
value between 0.990 and 0.999 will be a good choice (FENE and Cohen Pad´e
models will typically require higher values, as 0.999 or even 1). (double)
solver – this entry should correspond to the name of one of the available matrix solvers
to be used in the Newton-Raphson method (see Section 4.3.5). (string)
externalFlow
2{
writeFields false;
4frozenFlow true;
6tethered false;
pushBackCmp (0 0 0);
8pushBackFreq 1;
10 interpolation BarycentricWeights;
gradU
12 (
000
14 000
000
16 );
}
18
outputOptions
20 {
writeStats true;
22 outputStatsInterval 10;
24 writeVTK true;
}
26
exclusionVolumeProperties
28 {
// bead-bead
30 activeExclusionVolume true;
32 // wall-bead

CHAPTER 5. Tutorials 175
activeWallRepulsion true;
34 repulsiveDistance 1e-7;
}
36
HIProperties
38 {
activeHI true;
40 }
42 electrophoresis
{
44 active false;
mobility 5.95767e-10;
46 }
48 springModelProperties
{
50 springModel MarkoSiggia;
52 timeScheme semiImplicit;
maxIter 20;
54 relTol 1e-6;
tresholdF 0.85;
56 cutOffStretch .99;
solver QR;
58 }
Listing 5.5: Example of a moleculesControls dictionary used with
rheoBDFoam.
|0/
As we have seen for directory constant/, a simulation with rheoBDFoam
requires all the elements that would be needed for a simulation with rheoEFoam
(Section 5.4.1). Therefore, continuum fields pand Umust always be present, and
phiE and/or psi should also be defined for an electrically-driven flow, or if molec-
ular electrophoresis is accounted for. Note that in case molecular electrophoresis
is considered, only the electric field represented by phiE (the externally applied
electric field) is used. Consider now three typical situations where rheoBDFoam is
likely to be used:
I- steady numerical external forcing. In this case, the continuum fields defined
in the startTime directory will be used and kept constant during the simu-
lation. The continuum is frozen in time. The usual procedure in this scenario
is to simulate the continuum flow elsewhere, in a separate simulation/case,
and then copy the steady-state continuum fields to the startTime directory
of the Brownian dynamics case.
II- transient numerical external forcing. In this situation, the continuum evolves
in time simultaneously with the molecules. Therefore the continuum fields
in the startTime directory should include initial and boundary conditions.
III- steady analytical external forcing. Although in this case the external forcing
is defined by an analytical expression, the continuum fields that would be

CHAPTER 5. Tutorials 176
needed for a numerical forcing should also be present. However, they are just
placeholders and are not used, such that their content is not important, but
needs to respect the expected syntax (have defined internal and boundary
fields compliant with the boundary types).
In addition to files for the continuum fields, the startTime directory still
needs to have a subdirectory lagrangian/molecules/ containing the fields
for the molecules. The easiest and recommended way to generate this subdirectory
and the files needed is running utility initMolecules, as described in Section 4.7.4.
Note that if any viscoelastic fluid model is used in the continuum flow, which
should probably be unusual, then also the corresponding variables should be de-
fined in the startTime directory (see Section 5.1.1). No additional files are
needed for a (non-elastic) generalized Newtonian fluid model.
|system/
Again, directory system/ for a rheoBDFoam case should have the same el-
ements as any rheoEFoam case. Moreover, most of the dictionaries do not re-
quire any change. The only modifications (additions) needed are in dictionary
fvSolution, in subDict SIMPLE:
solveFluid – this entry allows to switch on/off the resolution of the constitutive, momen-
tum and pressure equations. This option is typically set as false when the
external forcing is analytical, or when the external forcing is numerical but
frozen in time. (Switch)
solveElecM – this entry allows to switch on/off the resolution of the electric-related equa-
tions, independently of the option selected for solveFluid. (Switch)
nSubCycles – the Eulerian time-step – the one defined in controlDict – divided by
nSubCycles corresponds to the time-step used to solve the governing equa-
tions of beads motion (see Section 4.5.5). (integer)
5.5.2 Molecules visualization with Paraview
The purpose of this short Section is to briefly explain the procedure to visualize
the molecules in Paraview. There are at least two methods that can be used.
In the first method, open the case in Paraview in the usual way, for example,
running paraFoam in the terminal. In the Properties panel, on the left, under
Mesh Parts there is an entry named molecules-lagrangian. If not yet, check this
box. Then, scroll-down in the same panel and check the box for all Lagrangian
Fields. After clicking the Apply button, the molecules will be rendered in the
screen. However, this does not mean that you will immediately see them, because
the mesh is also represented and the molecules should lie inside the mesh. The
easiest way to solve this issue is to uncheck internalMesh in the Properties panel
(do not forget clicking the Apply button to update the changes). You should now
be able to see (very) small dots in the screen, where each dot is a bead. The size of
the dot is not related with the bead diameter (it is simply a setting of Paraview).
However, although you can now see the beads, you do not have a spatial reference.

CHAPTER 5. Tutorials 177
The ideal scenario would be to have both the mesh and the beads represented
together. Therefore, open (F ile →Open) again the same filename.OpenFOAM file
and select only the internalMesh under Mesh Parts. Depending on the geometry
of the case, you may be able to slice the mesh behind the position of the molecules,
ending with the representation of both. An alternative to the slice is to extract the
feature edges of the geometry, whereby you will obtain the external edges of the
geometry and be able to see the interior. The options are numerous. Nevertheless,
this method is not very fruitful in information, since the only ”interesting” field
associated to each bead is the molecule index (molcID) to which they belong.
The most one can do is to filter the beads by the molecule index, and isolate all
the beads of a given molecule. However, there is no information on the beads
connectivity, neither on the molecules’ group, which may be relevant variables.
There is still an additional issue: the position file associated to the Lagrangian
particles will not be read by old Paraview versions, thus the beads cannot be
visualized therein.
In order to solve these issues, rheoBDFoam can optionally output in runtime
the molecules data in VTK format. This option can be enabled in dictionary
moleculesControls, as seen in the previous Section, and it will create a di-
rectory named VTKMolecules, to which the molecules’ data is written for each
outputTime. When the molecules are visualized in VTK format, we recommend
also to convert the mesh and continuum fields to VTK format by running the
default OpenFOAM R
utility foamToVTK. Then, simply open the two stacks of
VTK files in Paraview. If using the paraFoam application, delete the object auto-
matically created in the Pipeline Browser and F ile →Open the two VTK stacks
(a stack contains the files generated for all the time-steps, under the same prefix
name). Note that the stack directly sent to directory VTK by OpenFOAM R
is the
one for the internal field data. If you open that one, then the slicing procedure
described above is also needed. The fields associated to each bead are globalID,
groupID,localID and molcID. Following a top-down approach, filters can be used
(Treshold in particular) to select a group of molecules (e.g. groupID = 0), a par-
ticular molecule of the group (e.g. molcID = 0) and finally the kth bead in that
molecule (localID =k). You can also color the beads of a given molecule by their
localID to see the connections. The Glyph filter may help to obtain nice images
(Fig. 5.30). In general, the VTK files will be read by any Paraview version.
Summarizing, we recommend using the fist method to routinely check a case
being prepared for simulation and to monitor the simulation. The second method
should be used to debug, to obtain good-quality images, or if an old Paraview
version is to be used.
5.5.3 Case 1: λ-DNA extension in a planar extensional
flow
Itutorials/rheoBDSFoam/planarExtensionalFlow
!Overview
This tutorial aims to illustrate the use of an analytical external forcing. The
CHAPTER 5. Tutorials 178
Figure 5.30: Screenshot of a molecule represented in Paraview, where the beads
are colored by the local index. Springs are represented by straight lines between
beads.
stretching of λ−DNA molecules in a planar extensional flow was selected for such
purpose, since this is a well-studied case. Before imposing the planar extensional
flow, the molecules are initialized in a stretched state and left to relax in no-flow
conditions. This allows one to estimate the relaxation time of the molecules and
also provides the starting molecular configurations for the planar extensional flow.
The λ−DNA molecules are modeled with the set of parameters provided in [25]:
N= 11 beads, D= 0.065 µm2/s, a= 0.077 µm, Nk,s = 19.81, νEV = 0.0012 µm3
and Lmax = 21 µm. The planar extensional flow is simulated for W i =λ˙= 2,
where ˙is the extensional-rate and λis the relaxation time of λ−DNA molecules
(λ≈4.1 s, as determined in the first part of the tutorial). The simulations are
run for an ensemble of 1000 molecules using the Marko-Siggia spring model.
!Geometry & Mesh
Since the forcing is analytical, a simple single-cell mesh can be used. The
dimensions are set large enough so that the molecules can be fully contained inside
the computational domain, even if fully-stretched. Furthermore, the molecules’
center of mass is held at a fixed position. The flow is unconfined.
!Boundary conditions
Due to the analytical nature of the forcing, any arbitrary, but consistent,
boundary condition can be attributed to the continuum fields (pressure and veloc-
ity); however, they will not be used. Consistent means here that if we assigned a
patch type to a given boundary while building the mesh, then we cannot assign,
for example, a symmetryPlane boundary condition to that boundary.
!Command-line
As aforementioned, in the first part of the tutorial the molecules are initialized
in a stretched configuration (L= 0.7Lmax) in order to study their relaxation to
equilibrium in no-flow conditions. This is carried out inside directory relaxati
on/:

CHAPTER 5. Tutorials 179
1–Build the mesh:
∼$blockMesh
2–Initialize the molecules:
∼$initMolecules
3–Run the solver:
∼$rheoBDFoam
4–Extract the ensemble average molecular length over time:
∼$averageMolcN 0
In the last time outputted by the solver (t= 50 s), the molecules display an
equilibrium configuration in no-flow conditions. These configurations are used in
the start of the planar extensional flow, thus they should be copied to the case
directory. The data needed is contained inside 50/lagrangian and constant
/runTimeInfo/50.
1–Build the mesh:
∼$blockMesh
2–Copy the equilibrium molecular configurations from directory relaxation/:
∼$cp -rf relaxation/50/lagrangian 0/
∼$mkdir -p constant/runTimeInfo/50
∼$cp -rf relaxation/constant/runTimeInfo/50/ constant/run
TimeInfo
∼$mv constant/runTimeInfo/50 constant/runTimeInfo/0
3–Run the solver:
∼$rheoBDFoam
4–Extract the ensemble average molecular length over time:
∼$averageMolcN 0
!Results
Firstly, we will estimate the relaxation time of the molecules. It can be ob-
tained from the ensemble average relaxation curve output to file relaxation
/rheoToolPP/0/moleculesStats/G1/Stretch_Naverage.txt by util-
ity averageMolcN. The molecular length should decay over time as [24],
L2(t) = L2
Iexp(−t/λ) + L2
0
where LIis the initial length of the molecules and L0is the equilibrium length for
t→ ∞. Therefore, when plotting ln(L2(t)−L2
0) as a function of t, the inverse of
the slope corresponds to −λ. The estimation is more accurate in the range of time
where Lis below 0.3Lmax [24]. The results obtained are presented in Fig. 5.31a,
where we can estimate λ=−1/−0.2429 ≈4.1 s.
CHAPTER 5. Tutorials 180
The evolution of the fractional molecular length over time, obtained in the
planar extensional flow at W i = 2 (second part of the tutorial), is plotted in Fig.
5.31b, along with the numerical results of [25].
Experimenting new Wi is as easy as changing the gradU entry in constant
/moleculesControls (the time-step may need adjustments). There is no need
to run again the initial molecules’ relaxation step. Also, the components of gradU
can easily be set to represent a shear flow.
(a) (b)
0
0.2
0.4
0.6
0.8
1
010 20 30
L/Lmax
t(s)
rheoTool Jendrejack et al. (2002)
y = -0.2429x - 22.945
R² = 0.999
-30
-28
-26
-24
-22
010 20 30
ln( L2 - L02 )
t(s)
Figure 5.31: (a) Decay of the molecular length over time during relaxation in
no-flow conditions. The red line represents a linear fit to the data for 5 ≤t≤13
s. (b) Fractional molecular length evolution over time in a planar extensional flow
at W i = 2. The symbols represent the numerical results from [25].
5.5.4 Case 2: 7λ-DNA extension in a flow-focusing device
Itutorials/rheoBDSFoam/flowFocusing
!Overview
This tutorial illustrates the application of rheoBDFoam in a case with a steady
numerical external forcing, where the forcing is either a pressure-driven flow (di-
rectory pressureDrivenFlow/) or electrophoresis (directory electrophore
sis/). The geometry used is a flow-focusing device, which imposes a non-
homogeneous extensional flow along its centerline.
The molecule selected for this tutorial is 7λ−DNA, which is modeled with the
following set of parameters [58]: N= 29 beads, D= 0.257 µm2/s, a= 0.101 µm,
Nk,s = 40, νEV = 0.0034 µm3and Lmax = 150 µm. According to [58], these
parameters give λ= 21 s in a 8.4 cP Newtonian buffer.
Considering a low Reynolds number flow (Re < 0.01), the relevant dimension-
less numbers are the velocity ratio (V R =UN/UW) and the centerline Weissenberg
number (W i =λ˙), where ˙=2.1UN
H, with factor 2.1 corresponding approximately

CHAPTER 5. Tutorials 181
to the ratio between the centerline velocity and the average velocity in the fully-
developed region of the north arm (valid for a pressure-driven laminar flow in
a straight channel with a square cross-section). Subscripts N and W point to
the North and West arms of the device. For the electrophoresis case, ˙=UN
Hand
U=µE is the relation between the electric field magnitude and the electrophoretic
velocity magnitude. Both µ(the electrophoretic mobility) and Ecan be adjusted
interchangeably to impose a given U. Note that a given electrophoretic VR can
not be obtained by an equal ratio of electric potentials (exception is for V R = 1).
The simulations are run for an ensemble of 1000 molecules, divided over two
groups of 500 molecules. The Marko-Siggia spring model is used.
!Geometry & Mesh
The 3D flow-focusing geometry used is similar to the one in the tutorial of
Section 5.4.5 (see Fig. 5.25). However, the height considered in this example is
equal to the width, h= 2H, and H= 100 µm.
!Boundary conditions
Pressure-driven flow
The velocity magnitude in the north and south inlets is equal, and 20×higher
than the velocity magnitude in the west arm (V R = 20). The velocities are selected
in order to have W i = 20. The pressure is fixed at zero at the outlet and no-slip
boundary conditions hold at the walls.
Electrophoresis
For the electrophoresis case, the sole purpose of the continuum simulation is to
obtain the electric potential distribution. Thus, we need to define field phiE and
select any model for electrically-driven flows that allows one to compute Laplace’s
equation. Note that we are not interested in solving for the electroosmotic flow; we
only need the electric potential distribution, but this requires selecting a complete
model. The slipSmoluchowski model (see Section 4.2.1) is the one displaying the
simplest electricProperties dictionary to define, thus this one has been
selected. The electric field is assumed to be tangential to the walls, and the
potential at the inlets is fixed in order to have an electric field (velocity) ratio
≈20 between the north (south) and west arms. Then, we select µin order to
match the Uvelocity corresponding to W i = 20 (we are not concerned with the
physical admissibility of µin the tutorial).
!Command-line
The sequence of commands to run these cases is somewhat long. Thus, we
recommend to use directly the Allrun scripts inside directories pressureDr
ivenFlow/ and electrophoresis/. Each of these scripts will first run the
solver to obtain the steady-state continuum fields (either rheoFoam or rheoEFoam),
and then they run the Brownian dynamics solver (rheoBDFoam, inside directory
BDS/). Regarding the Brownian dynamics simulations, the molecules are first left
to equilibrate in the local fully-developed flow of the west arm (x=−4H) for
around 20λ≈400s. This requires fixing the molecules center of mass (see Section
4.3.6). Then, this constraint is removed and the molecules flow freely until they
exit the geometry through the outlet patch. Both steps are carried out in the

CHAPTER 5. Tutorials 182
same directory (BDS/); the second simulation starts from the last time-step of the
first simulation. The second simulation stops when no molecule remains inside the
geometry. At the end of the simulation, we use utility averageMolcX (see Section
4.7.6) to extract the average molecular length over a line starting at x=−3Hand
ending at x= 15H, partitioned in 100 bins. You can see that the application is
called for time = 400 because this is the startTime of the second simulation.
The comments in the Allrun scripts should help to understand all the steps.
Nevertheless, we would like to highlight two points that may seem less clear.
Firstly, the commands
∼$foamDictionary -entry ...
simply use utility foamDictionary of OpenFOAM R
to automatically change a given
entry in a given dictionary from the command-line (or via scripting). More infor-
mation can be found in the OpenFOAM R
website. The second point is related
with the copy operations performed. For example, script pressureDrivenFl
ow/BDS/Allrun includes these lines,
∼$cp -rf ../flowSimulation/0.01/p*0/
∼$cp -rf ../flowSimulation/0.01/U*0/
which are simply intended to copy the steady-state (t= 0.01 s in this case) fields
Uand pfrom the continuum simulation directory, to directory BDS/. Some lines
below, you will find,
∼$cp -rf 0/p*400/
∼$cp -rf 0/U*400/
which have a related function. These lines of code are executed after the first
Brownian dynamics simulation (equilibrating the molecules in the local flow) has
been run, and we call them to copy again the continuum fields Uand pto the
startTime directory (in this case startTime = 400) of the next Brownian dy-
namics simulation, where they still do not exist, but are needed. The user may
be wondering why rheoBDFoam do not automatically wrote these fields during
the first run. This was because it was our option, by setting writeF ields =false
inside dictionary moleculesControls (see Section 5.5.1). This option was con-
sidered simply to save disk space (the advantage would be clearer if we would have
to save 1000 time-steps or if the mesh was much denser).
!Results
The fractional molecular length obtained for the pressure-driven flow and for
electrophoresis (V R =W i = 20) are plotted in Fig. 5.32. This data is the result
outputted by the call to averageMolcX. You can find it in rheoToolPP/400/
moleculesStats/G1/Stretch.txt and rheoToolPP/400/moleculesS
tats/G2/Stretch.txt for each of the two groups, and compute the average
between both groups. The pressure-driven flow seems to be slightly more effective
in stretching the molecules, eventually due to its higher flow heterogeneity over
the channel width. You can also visualize the molecules in Paraview using one of
the methods described in Section 5.5.1.
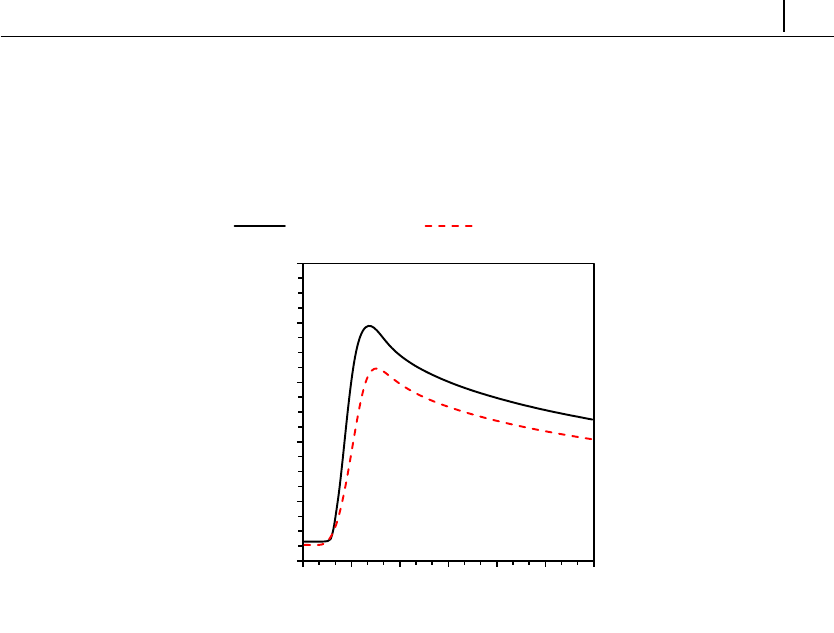
CHAPTER 5. Tutorials 183
It would be easy to run a case with the superposition of the two external
forcings, pressure-driven flow and electrophoresis. Moreover, we could even add
an electroosmotic flow. This exercise is left as a challenge.
0
0.2
0.4
0.6
0.8
1
-3 0 3 6 9 12 15
L/Lmax
x/H
Pressure-driven Electrophoresis
Figure 5.32: Fractional molecular length of 7λ-DNA in the flow-focusing geom-
etry, under two types of external forcing. Results are for V R =W i = 20.
5.5.5 Case 3: λ-DNA dynamics in LAOE
Itutorials/rheoBDSFoam/LAOE
!Overview
The previous tutorials used a steady external forcing, either analytical or nu-
merical. This tutorial exemplifies the use of rheoBDFoam in a case with a time-
varying numerical forcing. In such situations, both the continuum and Brownian
dynamics equations need to be evolved in time.
The case selected is the large-amplitude oscilatory extension (LAOE) of λ-DNA
molecules, as proposed in [59]. The working principle of LAOE is very similar to
LAOS (large-amplitude oscillatory shear), but the flow is extensionally-dominated
instead of shear-dominated [59]. This type of flow can be generated in the vicinity
of the stagnation point of a microfluidic cross-slot device with oscillatory inlet
streams.
This tutorial aims to reproduce one of the experiments presented in [59], for
W i =λ˙= 6.5 and De =λf = 0.45, where λis the molecules’ relaxation time, ˙
is the peak extensional-rate at the stagnation point of the cross-slot and fis the
oscillatory frequency of the inlet streams. The geometry used in [59] has a channel
width of 400 µm and the height is 90 µm. However, we use a 2D geometry (width =
400 µm) in this tutorial to reduce the computation time. Since 1/f is much higher
than the diffusion time-scale of the channel, the different diffusion time-scale of
the 2D geometry will not effect appreciably the results (momentum diffusion can

CHAPTER 5. Tutorials 184
still be considered ”instantaneous”). In addition, the z-component of the velocity
field is likely to have a negligible influence, as the molecules analyzed are all at
the channel mid-height. Hence, the 2D approximation seems to be reasonable a
priori. Remember that although the mesh and continuum fields are assumed 2D,
the three Cartesian components of the beads motion equation are solved for (see
Section 4.3.3).
The simulations are run for an ensemble of 500 molecules. The spring model
and physical parameters used to represent λ-DNA molecules are the same as those
presented in Section 5.5.3. We remember that those parameters give λ= 4.1 s
in a 43.3 cP buffer, which has a viscosity close to that of the buffer used in [59].
In [59], the molecules are immobilized at the stagnation point of the cross-slot
using a Stokes trap. Hence, in the tutorial we also fix the molecules center of mass
in the vicinity of the stagnation point. We remember that fixing the molecules
center of mass in rheoTool is not the same as tethering the molecules (see Section
4.3.6).
!Geometry & Mesh
The geometry of the 2D cross-slot device is similar (same boundary names) to
the one used in the tutorial of Section 5.1.7. For the scheme of Fig. 5.9,W=
400 µm and the four arms are 2 mm long.
!Boundary conditions
The y-component of the velocity in the inlet north boundary follows a sinu-
soidal profile,
vN(t) = −v0sin(2πft)
where v0is selected such that the maximum extensional-rate at the stagnation
point (computed numerically) is W i/λ. In the inlet south boundary, vS(t) =
−vN(t). These sinusoidal velocity profiles are imposed using a functionObject
(check file 0/U). No-slip boundary conditions are assigned at the walls.
!Command-line
The list of commands to be run is somewhat lengthy. Thus, we recommend
the user to directly run the Allrun script provided in the tutorial.
The tutorial performs two calls to rheoBDFoam. In the first call, the molecules
are equilibrated in no-flow conditions for approximately 10λ(40 s). In the second
call, starting from the equilibrium configurations (t= 40 s), the flow is switched-on
and the simulation runs up to t= 80 s.
!Results
The evolution of the fractional molecular length over time is plotted in Fig.
5.33. The data of this figure can be found in file rheoToolPP/40/molecule
sStats/G1/Stretch_Naverage.txt. The first cycles should be discarded,
since they are in the non-periodic regime (we need then to translate the curve in
time).
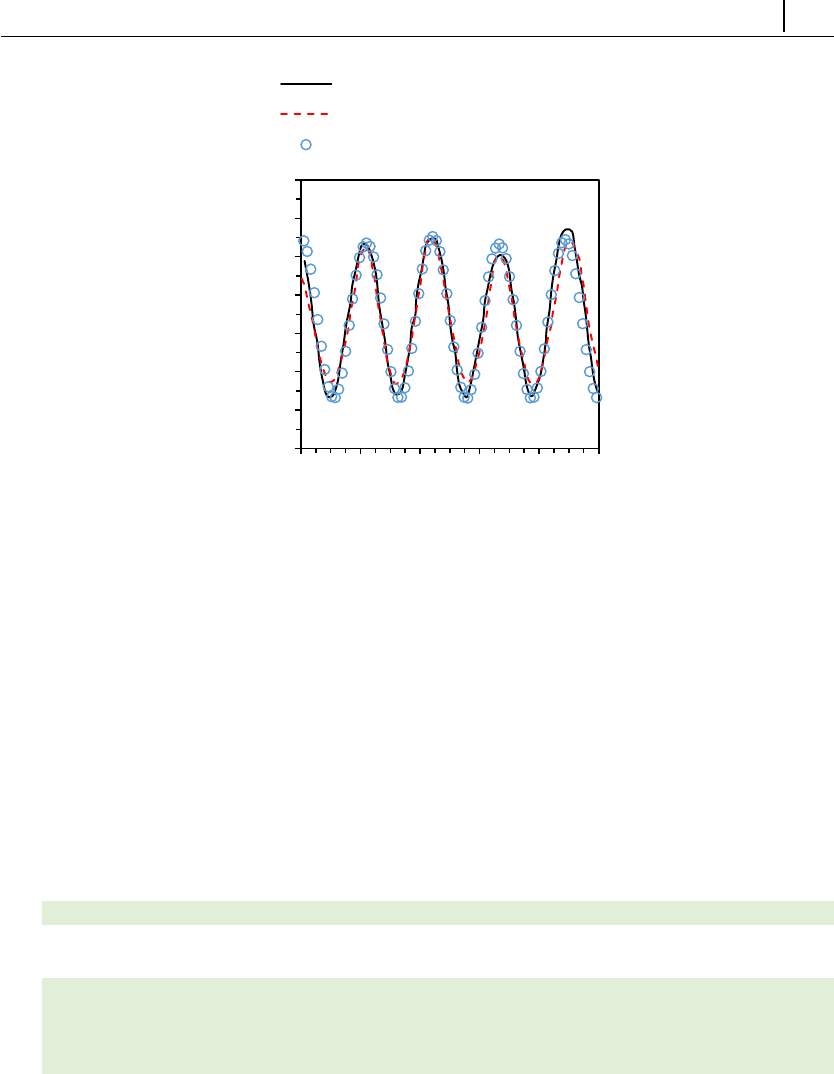
CHAPTER 5. Tutorials 185
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0 1 2 3 4 5
L/Lmax
t/λ
Zhou & Schroeder (2016) Num.
Zhou & Schroeder (2016) Exp.
rheoTool
Figure 5.33: Fractional molecular length of λ-DNA in LAOE, for W i = 6.5 and
De = 0.45. The lines are for the experimental (dashed) and numerical (solid)
results in [59], while the symbols represent the numerical results obtained with
rheoTool.
The reader may wonder if it would be possible to prescribe an analytical sinu-
soidal planar extensional flow, instead of simulating the full cross-slot flow, as it
was done in [59] (even if simulating the full flow is possibly more realistic). Shortly,
it is not possible to use a time-varying analytical flow in the form rheoTool is pro-
vided, but anyone with some programming experience can easily change the code
to do so. It would just require changing one line of code in AnalyticalI.H.
Indeed, line
return (gradU_.T() & sP.position());
should be replaced, for example, by
1scalar e0 = 1.5854 *Foam::sin(2*M_PI*mesh_.time().timeOutputValue
()*0.10976);
3return vector(-e0*sP.position().x(), e0*sP.position().y(), 0.);
The reader can easily try this, and check if the results are comparable, as
expected.

Chapter 6
FAQs
It is important for any new user of rheoTool to read this user-guide, if not entirely,
at least the Sections referring to the components that will be used. This will
prepare the user for any apparently unexpected behavior from the software. Since
the first version of rheoTool, we received some common questions about the code,
that we list below in the hope they can help future users.
While installing rheoTool the compilation fails with the error message:
fatal error: Eigen/Dense: No such file or directory. How to solve it?
This means that variable $EIGEN RHEO is not pointing to Eigen’s directory.
Either your ˜/.bashrc file was not sourced before compiling rheoTool and after
downloading Eigen (this is why it is important to compile rheoTool in a terminal
different from the one used to download Eigen), or the path is not valid any-
more (perhaps you moved Eigen to a different directory or you renamed it). In
the terminal where the error was retrieved, check the path with command echo
$EIGEN RHEO and be sure that Eigen is there, i.e. inside that directory you should
find folders bench,blas,cmake, etc. If an empty path is retrieved, then this
variable was not exported to your ˜/.bashrc. If nothing is inside the directory,
then the variable was wrongly assigned and should be exported again. See the
installation instructions in Chapter 2.
My simulation is running for Re >> 1but behaves as if it was laminar
(Re = 0). Is this a bug?
Check the convective scheme assigned to div(phi, U) in system/fvSchemes.
If it corresponds to GaussDefCmpw none then this means that momentum con-
vection is being ignored and that explains your results. Simply select a convective
scheme different from that one to fix the ’problem’ (see Section 4.7.1). This hap-
pens often when deriving a case from a tutorial running in inertialess conditions.
The results of my transient simulations with a viscoelastic fluid model
are very sensitive to the time-step. Is it normal?
When simulating a transient case, all the existing time-scales (momentum dif-
fusion, polymer relaxation, ion diffusion, etc.) should be taken into account and
the user should ensure that the time-step is low enough to resolve all of them.
In addition to this, care should be taken when using the coupling stabilization
method in cases where ηP>> ηS, since explicit stabilizing terms are introduced in
186

CHAPTER 6. FAQs 187
the momentum equation. To test if the stabilization method is the main reason for
exaggerated time-step sensitivity, simply disable it (set it equal to none). Note,
however, that the simulation will likely become more unstable and lower time-steps
might be needed. The BSD stabilizing option is less explicit than coupling and
could be also tried. The explicitness can be reduced by increasing the number of
inner iterations. Note that the explicitness of the coupling stabilization method
requires refinement in both time and space to disappear. See Sections 3.2 and
4.1.4 .
If your question is not in the list above and you can not find an answer for it
in this user-guide, then feel free to contact us (see contacts in Section 1.5).

Appendix A
Parameters and variables in
rheoTool
Table A.1: List of some relevant parameters and variables used by rheoTool
and correspondence with the nomenclature used in this guide. The list is not
exhaustive.
Name in
the guide
Name in
the code
Dimensions
[kg m s K mol A cd] Definition
αalpha [0 0 0 0 0 0 0]
Anisotropy parameter of
Giesekus and eXtended Pom-
Pom models (scalar)
αalpha [0 0 0 0 0 0 0] Parameter of the piecewise-linear
HRS functions (scalar)
αalpha [0 0 0 0 0 0 0] Indicator/Color function of the
VOF method (scalar)
AA[0 0 0 0 0 0 0] Conformation tensor (symmTen-
sor)
aa[0 0 0 0 0 0 0]
Dimensionless parameter of
Carreau-Yasuda and White-
Metzner models (scalar)
aa[0 0 0 0 0 0 0] Variable of FENE-P model
(scalar)
aa[0 1 0 0 0 0 0] Bead radius (scalar)
-AK [0 0 0 0 -1 0 0] Avogrado’s constant (scalar)
βbeta [0 0 0 0 0 0 0] Parameter of the piecewise-linear
HRS functions (scalar)
188

APPENDIX A. Parameters and variables in rheoTool 189
βbeta [0 0 0 0 0 0 0] CCR coefficient of Rolie-Poly
model (scalar)
bb[0 0 0 0 0 0 0] Dimensionless parameter of
White-Metzner model (scalar)
-b[0 0 0 0 0 0 0]
Square-root conformation tensor
of Ref. [15], for the Oldroyd-BSqrt
model (symmTensor)
χmax chiMax [0 0 0 0 0 0 0] Maximum stretch ratio in Rolie-
Poly model (scalar)
-C[0 0 0 0 0 0 0] Passive scalar (scalar)
ci-[0 -3 0 0 1 0 0] Concentration of specie iin
mol/m3(scalar)
c0c0 [0 -3 0 0 1 0 0] Reference ionic concentration
(scalar)
δdelta [0 0 0 0 0 0 0] Exponent of Rolie-Poly model
(scalar)
DD[0 2 -1 0 0 0 0]
Diffusion coefficient in the the
passive scalar transport equation
(scalar)
DD[0 2 -1 0 0 0 0] Isotropic diffusion coefficient of a
bead (scalar)
DiDi [0 2 -1 0 0 0 0] Diffusion coefficient of ionic
specie i(scalar)
µelecMobility [-1 0 2 0 0 1 0] Electroosmotic mobility (scalar)
µ0elecMobility0 [-1 0 2 0 0 1 0] Electroosmotic mobility at a ref-
erence conductivity (scalar)
εepsilon [0 0 0 0 0 0 0] Extensibility parameter of PTT-
type models (scalar)
ε–[-1 -3 4 0 0 2 0] Electric permittivity (scalar)
ε0epsilonK [-1 -3 4 0 0 2 0] Electric permittivity of vacuum
(scalar)
ηeta [1 -1 -1 0 0 0 0] Newtonian viscosity (scalar)
η( ˙γ)eta [1 -1 -1 0 0 0 0] Shear-rate dependent viscosity
from a GNF model (scalar)

APPENDIX A. Parameters and variables in rheoTool 190
η0eta0 [1 -1 -1 0 0 0 0] Zero shear-rate viscosity (scalar)
η0eta0 [1 -1 -1 0 0 0 0] Limiting viscosity in the
Herschel-Bulkley model (scalar)
η∞etaInf [1 -1 -1 0 0 0 0] Infinite shear-rate viscosity
(scalar)
ηmax etaMax [1 -1 -1 0 0 0 0] Upper bound for the viscosity in
the power-law model (scalar)
ηmin etaMin [1 -1 -1 0 0 0 0] Lower bound for the viscosity in
the power-law model (scalar)
ηpetaP [1 -1 -1 0 0 0 0] Polymeric viscosity coefficient
(scalar)
ηsetaS [1 -1 -1 0 0 0 0] Solvent viscosity (scalar)
ΛeigVals [0 0 0 0 0 0 0] Eigenvalues obtained in the diag-
onalization of A(tensor)
ReigVecs [0 0 0 0 0 0 0]
Eigenvectors obtained in the di-
agonalization of Θand A(ten-
sor)
eeK [0 0 1 0 0 1 0] Elementary charge (scalar)
EaextraEField [1 1 -3 0 0 -1 0] Constant and uniform extra elec-
tric field (vector)
ff[0 0 0 0 0 0 0] Variable of FENE-type models
(scalar)
FFK [0 0 1 0 -1 1 0] Faraday’s constant (scalar)
kk[1 -1 -1 0 0 0 0] Consistency index of power-law
model (scalar)
kk[0 0 1 0 0 0 0] Time-scale in the Carreau-
Yasuda model (scalar)
KK[0 0 1 0 0 0 0] Time-scale for ηpin the White-
Metzner model (scalar)
kkbK [1 2 -2 -1 0 0 0] Boltzmann’s constant (scalar)
λlambda [0 0 1 0 0 0 0] Relaxation time (scalar)
λBlambdaB [0 0 1 0 0 0 0] Relaxation time of the backbone
tube orientation (scalar)
λDlambdaD [0 0 1 0 0 0 0] Reptation time (scalar)

APPENDIX A. Parameters and variables in rheoTool 191
λRlambdaR [0 0 1 0 0 0 0] Rouse or stretch time (scalar)
λSlambdaS [0 0 1 0 0 0 0] Relaxation time for the tube
stretch (scalar)
LL[0 0 1 0 0 0 0] Time-scale for λin the White-
Metzner model (scalar)
L2L2 [0 0 0 0 0 0 0] Extensibility parameter of
FENE-type models (scalar)
lLs [0 1 0 0 0 0 0] Maximum length of a spring
(scalar)
mm[0 0 0 0 0 0 0] Dimensionless parameter of
White-Metzner model (scalar)
mm[0 0 0 0 0 0 0]
Power-law exponent for
the conductivity-dependent
Helmholtz-Smoluchowski veloc-
ity (scalar)
µmobility [-1 0 2 0 0 1 0] Electrophoretic mobility of a
bead (scalar)
νEV nuEV [0 3 0 0 0 0 0] Exclusion-volume parameter
(scalar)
nn[0 0 0 0 0 0 0]
Flow behavior index for shear-
rate dependent viscosity models
(scalar)
Nk,s Nks [0 0 0 0 0 0 0] Number of Kuhn steps lengths
per spring (scalar)
φExt phiE [1 2 -3 0 0 -1 0] Externally-applied electric po-
tential (scalar)
Ψpsi [1 2 -3 0 0 -1 0] Total electric potential (scalar)
ψpsi [1 2 -3 0 0 -1 0] Intrinsic electric potential
(scalar)
pp[1 -1 -2 0 0 0 0] Pressure, in rheoInterFoam
(scalar)
p
ρp[0 2 -2 0 0 0 0]
Pressure divided by the den-
sity, in rheoFoam and rheoEFoam
(scalar)
u·Sphi [0 3 -1 0 0 0 0] Face fluxes (scalar)

APPENDIX A. Parameters and variables in rheoTool 192
qq[0 0 0 0 0 0 0] Amount of arms at the end of the
polymer backbone (scalar)
ρrho [1 -3 0 0 0 0 0] Density (scalar)
ρE-[0 -3 1 0 0 1 0] Charge density (per unit volume)
(scalar)
εRrelPerm [0 0 0 0 0 0 0] Relative electric permittivity or
dielectric constant (scalar)
σsigma [-1 -3 3 0 0 2 0] Electric conductivity (scalar)
σ0sigma0 [-1 -3 3 0 0 2 0] Reference electric conductivity
(scalar)
˙γstrainRate() [0 0 -1 0 0 0 0] Shear-rate (scalar)
τtau [1 -1 -2 0 0 0 0] Polymeric extra-stress tensor
(symmTensor)
τ0tau0 [1 -1 -2 0 0 0 0] Yield stress (scalar)
-tauMF [1 -1 -2 0 0 0 0]
Polymeric extra-stress ten-
sor weighted by the indicator
function in rheoInterFoam
(symmTensor)
Θtheta [0 0 0 0 0 0 0] Natural logarithm of the confor-
mation tensor (symmTensor)
TT[0 0 0 1 0 0 0] Absolute temperature (scalar)
uU[0 1 -1 0 0 0 0] Velocity (vector)
ζzeta [0 0 0 0 0 0 0] Slip parameter of PTT-type
models (scalar)
zizi [0 0 0 0 0 0 0] Charge valence of specie i
(scalar)
Bibliography
[1] J. Favero, A. Secchi, N. Cardozo, and H. Jasak, “Viscoelastic fluid analysis
in internal and in free surface flows using the software OpenFOAM,” Com-
puters & Chemical Engineering, vol. 34, no. 12, pp. 1984 – 1993, 2010. 10th
International Symposium on Process Systems Engineering, Salvador, Bahia,
Brasil, 16-20 August 2009.
[2] F. Pimenta and M. Alves, “Stabilization of an open-source finite-volume
solver for viscoelastic fluid flows,” Journal of Non-Newtonian Fluid Mechan-
ics, vol. 239, pp. 85 – 104, 2017.
[3] F. Pimenta and M. Alves, “Simulation of electrically-driven flows using Open-
FOAM,” arXiv:1802.02843, 2018.
[4] F. Pimenta, R. G. Sousa, and M. A. Alves, “Optimization of flow-focusing
devices for homogeneous extensional flow,” Biomicrofluidics, vol. 12, no. 5,
p. 054103, 2018.
[5] F. Pimenta and M. Alves, “A coupled finite-volume solver for numerical sim-
ulation of electrically-driven flows,” arXiv:1904.02138, 2019.
[6] R. Fattal and R. Kupferman, “Constitutive laws for the matrix-logarithm
of the conformation tensor,” Journal of Non-Newtonian Fluid Mechanics,
vol. 123, no. 2–3, pp. 281 – 285, 2004.
[7] R. Bird and O. Hassager, Dynamics of Polymeric Liquids: Fluid mechanics,
vol. 1-2 of Dynamics of Polymeric Liquids. Wiley, 1987.
[8] M. G. Baltussen, W. M. Verbeeten, A. C. Bogaerds, M. A. Hulsen, and G. W.
Peters, “Anisotropy parameter restrictions for the extended pom-pom model,”
Journal of Non-Newtonian Fluid Mechanics, vol. 165, no. 19, pp. 1047 – 1054,
2010.
[9] S. Balay, S. Abhyankar, M. F. Adams, J. Brown, P. Brune, K. Buschelman,
L. Dalcin, A. Dener, V. Eijkhout, W. D. Gropp, D. Kaushik, M. G. Knepley,
D. A. May, L. C. McInnes, R. T. Mills, T. Munson, K. Rupp, P. Sanan,
B. F. Smith, S. Zampini, H. Zhang, and H. Zhang, “PETSc Web page.”
http://www.mcs.anl.gov/petsc, 2018.
[10] S. Balay, S. Abhyankar, M. F. Adams, J. Brown, P. Brune, K. Buschelman,
L. Dalcin, A. Dener, V. Eijkhout, W. D. Gropp, D. Kaushik, M. G. Knepley,
193

BIBLIOGRAPHY 194
D. A. May, L. C. McInnes, R. T. Mills, T. Munson, K. Rupp, P. Sanan, B. F.
Smith, S. Zampini, H. Zhang, and H. Zhang, “PETSc users manual,” Tech.
Rep. ANL-95/11 - Revision 3.10, Argonne National Laboratory, 2018.
[11] S. Balay, W. D. Gropp, L. C. McInnes, and B. F. Smith, “Efficient manage-
ment of parallelism in object oriented numerical software libraries,” in Modern
Software Tools in Scientific Computing (E. Arge, A. M. Bruaset, and H. P.
Langtangen, eds.), pp. 163–202, Birkh¨auser Press, 1997.
[12] X. Chen, H. Marschall, M. Sch¨afer, and D. Bothe, “A comparison of stabilisa-
tion approaches for finite-volume simulation of viscoelastic fluid flow,” Inter-
national Journal of Computational Fluid Dynamics, vol. 27, no. 6-7, pp. 229–
250, 2013.
[13] R. Fattal and R. Kupferman, “Time-dependent simulation of viscoelastic flows
at high weissenberg number using the log-conformation representation,” Jour-
nal of Non-Newtonian Fluid Mechanics, vol. 126, no. 1, pp. 23 – 37, 2005.
[14] A. Afonso, F. Pinho, and M. Alves, “The kernel-conformation constitutive
laws,” Journal of Non-Newtonian Fluid Mechanics, vol. 167–168, pp. 30 – 37,
2012.
[15] N. Balci, B. Thomases, M. Renardy, and C. R. Doering, “Symmetric fac-
torization of the conformation tensor in viscoelastic fluid models,” Journal of
Non-Newtonian Fluid Mechanics, vol. 166, no. 11, pp. 546 – 553, 2011. XVIth
International Workshop on Numerical Methods for Non-Newtonian Flows.
[16] ˇ
Z. Tukovi´c and H. Jasak, “A moving mesh finite volume interface tracking
method for surface tension dominated interfacial fluid flow,” Computers &
Fluids, vol. 55, pp. 70 – 84, 2012.
[17] H. Jasak, “Pressure-velocity coupling in FOAM, Consistent derivation for
steady and transient flow solvers.” OFW11, Guimar˜aes, Portugal, 2016.
[18] F. Moukalled, A. A. Aziz, and M. Darwish, “Performance comparison of the
NWF and DC methods for implementing high-resolution schemes in a fully
coupled incompressible flow solver,” Applied Mathematics and Computation,
vol. 217, no. 11, pp. 5041 – 5054, 2011.
[19] H. Jasak, H. Weller, and A. Gosman, “High resolution NVD differencing
scheme for arbitrarily unstructured meshes,” International Journal for Nu-
merical Methods in Fluids, vol. 31, no. 2, pp. 431 – 449, 1999.
[20] J. Ferziger and M. Peric, Computational Methods for Fluid Dynamics.
Springer Berlin Heidelberg, 2001.
[21] A. Afonso, F. Pinho, and M. Alves, “Electro-osmosis of viscoelastic fluids
and prediction of electro-elastic flow instabilities in a cross slot using a finite-
volume method,” Journal of Non-Newtonian Fluid Mechanics, vol. 179–180,
pp. 55 – 68, 2012.

BIBLIOGRAPHY 195
[22] C.-H. Chen, H. Lin, S. K. Lele, and J. G. Santiago, “Convective and abso-
lute electrokinetic instability with conductivity gradients,” Journal of Fluid
Mechanics, vol. 524, pp. 263–303, 2005.
[23] A. Persat and J. G. Santiago, “An ohmic model for electrokinetic flows of
binary asymmetric electrolytes,” Current Opinion in Colloid & Interface Sci-
ence, vol. 24, pp. 52 – 63, 2016.
[24] R. G. Larson, “The rheology of dilute solutions of flexible polymers: Progress
and problems,” Journal of Rheology, vol. 49, no. 1, pp. 1–70, 2005.
[25] R. M. Jendrejack, J. J. de Pablo, and M. D. Graham, “Stochastic simulations
of DNA in flow: Dynamics and the effects of hydrodynamic interactions,” The
Journal of Chemical Physics, vol. 116, no. 17, pp. 7752–7759, 2002.
[26] “Brownian dynamics simulations of bead-rod and bead-spring chains: numer-
ical algorithms and coarse-graining issues,” Journal of Non-Newtonian Fluid
Mechanics, vol. 108, no. 1, pp. 227 – 255, 2002.
[27] K. K. Kabanemi and J.-F. H´etu, “Nonequilibrium stretching dynamics of
dilute and entangled linear polymers in extensional flow,” Journal of Non-
Newtonian Fluid Mechanics, vol. 160, no. 2–3, pp. 113 – 121, 2009.
[28] P. A. Vasquez, G. H. McKinley, and L. P. Cook, “A network scission model
for wormlike micellar solutions: I. model formulation and viscometric flow
predictions,” Journal of Non-Newtonian Fluid Mechanics, vol. 144, no. 2,
pp. 122 – 139, 2007.
[29] S. Dutta and M. D. Graham, “Mechanistic constitutive model for wormlike
micelle solutions with flow-induced structure formation,” Journal of Non-
Newtonian Fluid Mechanics, vol. 251, pp. 97 – 106, 2018.
[30] F. Bautista, J. de Santos, J. Puig, and O. Manero, “Understanding thixotropic
and antithixotropic behavior of viscoelastic micellar solutions and liquid crys-
talline dispersions. i. the model,” Journal of Non-Newtonian Fluid Mechanics,
vol. 80, no. 2, pp. 93 – 113, 1999.
[31] P. Saramito, “A new elastoviscoplastic model based on the herschel–bulkley
viscoplastic model,” Journal of Non-Newtonian Fluid Mechanics, vol. 158,
no. 1, pp. 154 – 161, 2009. Visco-plastic fluids: From theory to application.
[32] P. Saramito, “A new constitutive equation for elastoviscoplastic fluid flows,”
Journal of Non-Newtonian Fluid Mechanics, vol. 145, no. 1, pp. 1 – 14, 2007.
[33] Y. Wei, M. J. Solomon, and R. G. Larson, “A multimode structural ki-
netics constitutive equation for the transient rheology of thixotropic elasto-
viscoplastic fluids,” Journal of Rheology, vol. 62, no. 1, pp. 321–342, 2018.
[34] P. J. Oliveira, “Asymmetric flows of viscoelastic fluids in symmetric planar
expansion geometries,” Journal of Non-Newtonian Fluid Mechanics, vol. 114,
no. 1, pp. 33 – 63, 2003.

BIBLIOGRAPHY 196
[35] G. Guennebaud, B. Jacob, et al., “Eigen v3.” http://eigen.tuxfamil
y.org, 2010.
[36] W. H. Press, B. P. Flannery, S. A. Teukolsky, and W. T. Vetterling, “Nu-
merical recipes (FORTRAN version),” Press Syndicate of the University of
Cambridge, Cambridge, UK, 1989.
[37] LLNL, “Hypre: High performance preconditioners.” http://www.llnl.g
ov/CASC/hypre, 2010.
[38] F. Habla, A. Woitalka, S. Neuner, and O. Hinrichsen, “Development of a
methodology for numerical simulation of non-isothermal viscoelastic fluid
flows with application to axisymmetric 4:1 contraction flows,” Chemical En-
gineering Journal, vol. 207, no. Supplement C, pp. 772 – 784, 2012. 22nd
International Symposium on Chemical Reaction Engineering (ISCRE 22).
[39] L. L. Ferr´as, A. M. Afonso, J. M. N´obrega, and F. T. Pinho, “A numerical and
theoretical study on viscoelastic fluid slip flows,” Physics of Fluids, vol. 29,
no. 5, p. 053102, 2017.
[40] Z. Wu and D. Li, “Mixing and flow regulating by induced-charge electrokinetic
flow in a microchannel with a pair of conducting triangle hurdles,” Microflu-
idics and Nanofluidics, vol. 5, no. 1, pp. 65–76, 2008.
[41] S. Xue and G. W. Barton, “An unstructured finite volume method for vis-
coelastic flow simulations with highly truncated domains,” Journal of Non-
Newtonian Fluid Mechanics, vol. 233, pp. 48 – 60, 2016. Papers presented at
the Rheology Symposium in honor of Prof. R. I. Tanner on the occasion of
his 82nd birthday, in Vathi, Samos, Greece.
[42] Y. Na and J. Y. Yoo, “A finite volume technique to simulate the flow of a
viscoelastic fluid,” Computational Mechanics, vol. 8, no. 1, pp. 43–55, 1991.
[43] M. A. Hulsen, R. Fattal, and R. Kupferman, “Flow of viscoelastic fluids past a
cylinder at high weissenberg number: Stabilized simulations using matrix log-
arithms,” Journal of Non-Newtonian Fluid Mechanics, vol. 127, no. 1, pp. 27
– 39, 2005.
[44] M. Alves, F. Pinho, and P. Oliveira, “The flow of viscoelastic fluids past a
cylinder: finite-volume high-resolution methods,” Journal of Non-Newtonian
Fluid Mechanics, vol. 97, no. 2–3, pp. 207 – 232, 2001.
[45] F. Cruz, R. Poole, A. Afonso, F. Pinho, P. Oliveira, and M. Alves, “A new
viscoelastic benchmark flow: Stationary bifurcation in a cross-slot,” Journal
of Non-Newtonian Fluid Mechanics, vol. 214, pp. 57 – 68, 2014.
[46] A. Valencia, A. Zarate, M. Galvez, and L. Badilla, “Non-newtonian blood
flow dynamics in a right internal carotid artery with a saccular aneurysm,”
International Journal for Numerical Methods in Fluids, vol. 50, no. 6, pp. 751–
764, 2006.

BIBLIOGRAPHY 197
[47] Aneurisk-Team, “AneuriskWeb project website, http://ecm2.mathcs.e
mory.edu/aneuriskweb.” Web Site, 2012.
[48] A. Syrakos, Y. Dimakopoulos, and J. Tsamopoulos, “Theoretical study of the
flow in a fluid damper containing high viscosity silicone oil: Effects of shear-
thinning and viscoelasticity,” Physics of Fluids, vol. 30, no. 3, p. 030708,
2018.
[49] R. Figueiredo, C. Oishi, A. Afonso, I. Tasso, and J. Cuminato, “A two-phase
solver for complex fluids: Studies of the weissenberg effect,” International
Journal of Multiphase Flow, vol. 84, pp. 98 – 115, 2016.
[50] C. Oishi, F. Martins, M. Tom´e, and M. Alves, “Numerical simulation of drop
impact and jet buckling problems using the extended pom–pom model,” Jour-
nal of Non-Newtonian Fluid Mechanics, vol. 169–170, pp. 91 – 103, 2012.
[51] R. Comminal, F. Pimenta, J. H. Hattel, M. A. Alves, and J. Spangenberg,
“Numerical simulation of the planar extrudate swell of pseudoplastic and vis-
coelastic fluids with the streamfunction and the VOF methods,” Journal of
Non-Newtonian Fluid Mechanics, vol. 252, pp. 1 – 18, 2018.
[52] C. Zhao and C. Yang, “An exact solution for electroosmosis of non-
newtonian fluids in microchannels,” Journal of Non-Newtonian Fluid Me-
chanics, vol. 166, no. 17–18, pp. 1076 – 1079, 2011.
[53] A. Afonso, M. Alves, and F. Pinho, “Analytical solution of mixed electro-
osmotic/pressure driven flows of viscoelastic fluids in microchannels,” Journal
of Non-Newtonian Fluid Mechanics, vol. 159, no. 1–3, pp. 50 – 63, 2009.
[54] C. L. Druzgalski, M. B. Andersen, and A. Mani, “Direct numerical simulation
of electroconvective instability and hydrodynamic chaos near an ion-selective
surface,” Physics of Fluids, vol. 25, no. 11, p. 110804, 2013.
[55] J. D. Posner and J. G. Santiago, “Convective instability of electrokinetic flows
in a cross-shaped microchannel,” Journal of Fluid Mechanics, vol. 555, pp. 1–
42, 05 2006.
[56] J. T. Coleman, J. McKechnie, and D. Sinton, “High-efficiency electrokinetic
micromixing through symmetric sequential injection and expansion,” Lab
Chip, vol. 6, pp. 1033–1039, 2006.
[57] F. Pimenta and M. Alves, “Electro-elastic instabilities in cross-shaped mi-
crochannels,” Journal of Non-Newtonian Fluid Mechanics, vol. 259, pp. 61 –
77, 2018.
[58] C. M. Schroeder, E. S. G. Shaqfeh, and S. Chu, “Effect of hydrodynamic
interactions on DNA dynamics in extensional flow: Simulation and single
molecule experiment,” Macromolecules, vol. 37, no. 24, pp. 9242–9256, 2004.
[59] Y. Zhou and C. M. Schroeder, “Single polymer dynamics under large ampli-
tude oscillatory extension,” Physical Review Fluids, vol. 1, p. 053301, 2016.