HP 12c_user's Guide_English_HDPMBF12E44 Guide_English_E_HDPMBF12E44 C00363319
If not then c00363319 Manual: ://h10032.www1.hp.com/ctg/Manual/c00363319
HP 12C Financial Calculator 0012C-90001 c00363319
User Manual: HP hp 12c_user's guide_English_E_HDPMBF12E44
Open the PDF directly: View PDF ![]() .
.
Page Count: 211 [warning: Documents this large are best viewed by clicking the View PDF Link!]

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 1 of 209
Printed Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
hp 12c financial calculator
user's guide
H
Edition 4
HP Part Number 0012C-90001

2
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 2 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Notice
REGISTER YOUR PRODUCT AT: www.register.hp.com
THIS MANUAL AND ANY EXAMPLES CONTAINED HEREIN ARE
PROVIDED “AS IS” AND ARE SUBJECT TO CHANGE WITHOUT NOTICE.
HEWLETT-PACKARD COMPANY MAKES NO WARRANTY OF ANY
KIND WITH REGARD TO THIS MANUAL, INCLUDING, BUT NOT
LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY,
NON-INFRINGEMENT AND FITNESS FOR A PARTICULAR PURPOSE.
HEWLETT-PACKARD CO. SHALL NOT BE LIABLE FOR ANY ERRORS OR
FOR INCIDENTAL OR CONSEQUENTIAL DAMAGES IN CONNECTION
WITH THE FURNISHING, PERFORMANCE, OR USE OF THIS MANUAL
OR THE EXAMPLES CONTAINED HEREIN.
© Copyright 1981, 2004 Hewlett-Packard Development Company, L.P.
Reproduction, adaptation, or translation of this manual is prohibited without prior
written permission of Hewlett-Packard Company, except as allowed under the
copyright laws.
Hewlett-Packard Company
4995 Murphy Canyon Rd,
Suite 301
San Diego, CA 92123
Printing History
Edition 4 August 2004

3
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 3 of 209
Printed Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Introduction
About This Handbook
This hp 12c user's guide is intended to help you get the most out of your
investment in your hp 12c Programmable Financial Calculator. Although the
excitement of acquiring this powerful financial tool may prompt you to set this
handbook aside and immediately begin “pressing buttons,” in the long run you’ll
profit by reading through this handbook and working through the examples it
contains.
Following this introduction is a brief section called Making Financial Calculations
Easy—which shows you that your hp 12c does just that! The remainder of this
handbook is organized basically into three parts:
z Part I (sections 1 through 7) describes how to use the various financial,
mathematics, statistics, and other functions (except for programming)
provided in the calculator:
z Section 1 is about Getting Started. It tells you how to use the keyboard,
how to do simple arithmetic calculations and chain calculations, and
how to use the storage registers (“memories”).
z Section 2 tells you how to use the percentage and calendar functions.
z Section 3 tells you how to use the simple interest, compound interest, and
amortization functions.
z Section 4 tells you how to do discounted cash flow analysis, bond, and
depreciation calculations.
z Section 5 tells you about miscellaneous operating features such as
Continuous Memory, the display, and special function keys.
z Sections 6 and 7 tell you how to use the statistics, mathematics, and
number-alteration functions.
z Part II (sections 8 through 11) describe how to use the powerful
programming capabilities of the hp 12c.
z Part III (sections 12 through 16) give you step-by-step solutions to specialized
problems in real estate, lending, savings, investment analysis, and bonds.
Some of these solutions can be done manually, while others involve running
a program. Since the programmed solutions are both self-contained and
step-by-step, you can easily employ them even if you don’t care to learn how
to create your own programs. But if you do start to create your own
programs, look over the programs used in the solutions: they contain
examples of good programming techniques and practices.

4 Introduction
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 4 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
z The various appendices describe additional details of calculator operation as
well as warranty and service information.
z The Function Key Index and Programming Key Index at the back of the
handbook can be used as a handy page reference to the comprehensive
information inside the manual
Financial Calculations in the United Kingdom
The calculations for most financial problems in the United Kingdom are identical to
the calculations for those problems in the United States — which are described in
this handbook. Certain problems, however, require different calculation methods in
the United Kingdom than in the United States. Refer to Appendix F for more
information.
For More Solutions to Financial Problems
In addition to the specialized solutions found in Sections 12 through 16 of this
handbook, many more are available in the optional hp 12c Solutions Handbook.
Included are solutions to problems in lending, forecasting, pricing, statistics,
savings, investment analysis, personal finance, securities, Canadian mortgages,
learning curves in manufacturing, and queuing theory. A Solutions Handbook is
available online (www.hp.com/calculators).

5
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 5 of 209
Printed Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Contents
Introduction.................................................................... 3
About This Handbook.....................................................................3
Financial Calculations in the United Kingdom.....................................4
For More Solutions to Financial Problems...........................................4
Part I. Problem Solving ......................................... 15
Section 1: Getting Started............................................. 16
Power On and Off........................................................................16
Low-Power Indication..............................................................16
The Keyboard ..............................................................................16
Keying in Numbers ................................................................17
Digit Separators ....................................................................17
Negative Numbers ................................................................17
Keying in Large Numbers .......................................................18
The CLEAR Keys ....................................................................18
Simple Arithmetic Calculations .......................................................19
Chain Calculations .......................................................................20
Storage Registers..........................................................................23
Storing and Recalling Numbers...............................................23
Clearing Storage Registers......................................................24
Storage Register Arithmetic .....................................................24
Section 2: Percentage and Calendar Functions................ 26
Percentage Functions.....................................................................26
Percentages ..........................................................................26
Net Amount..........................................................................27
Percent Difference..................................................................27
Percent of Total......................................................................28
Calendar Functions.......................................................................29
Date Format..........................................................................29
Future or Past Dates................................................................30
Number of Days Between Dates ..............................................31
Section 3: Basic Financial Functions............................... 32
The Financial Registers ..................................................................32
Storing Numbers Into the Financial Registers .............................32
Displaying Numbers in the Financial Registers...........................32

6 Contents
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 6 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Clearing the Financial Registers .............................................. 33
Simple Interest Calculations........................................................... 33
Financial Calculations and the Cash Flow Diagram.......................... 34
The Cash Flow Sign Convention.............................................. 36
The Payment Mode ............................................................... 37
Generalized Cash Flow Diagrams........................................... 37
Compound Interest Calculations..................................................... 39
Specifying the Number of Compounding Periods and the Periodic
Interest Rate ......................................................................... 39
Calculating the Number of Payments or Compounding Periods ... 39
Calculating the Periodic and Annual Interest Rates..................... 43
Calculating the Present Value ................................................. 44
Calculating the Payment Amount............................................. 46
Calculating the Future Value ................................................... 48
Odd-Period Calculations ........................................................ 50
Amortization ............................................................................... 54
Section 4: Additional Financial Functions ....................... 57
Discounted Cash Flow Analysis: NPV and IRR ................................. 57
Calculating Net Present Value (NPV) ....................................... 58
Calculating Internal Rate of Return (IRR) ................................... 63
Reviewing Cash Flow Entries................................................... 64
Changing Cash Flow Entries................................................... 65
Bond Calculations ....................................................................... 66
Bond Price ............................................................................67
Bond Yield ............................................................................67
Depreciation Calculations ............................................................. 68
Section 5: Additional Operating Features ....................... 70
Continuous Memory..................................................................... 70
The Display................................................................................. 71
Status Indicators ................................................................... 71
Number Display Formats ....................................................... 71
Scientific Notation Display Format........................................... 72
Special Displays ................................................................... 73
The key ..............................................................................74
The Key..............................................................................74
Arithmetic Calculations With Constants.................................... 75
Recovering From Errors in Digit Entry ....................................... 75

Contents 7
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 7 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 6: Statistics Functions........................................ 76
Accumulating Statistics..................................................................76
Correcting Accumulated Statistics ...................................................77
Mean .........................................................................................77
Standard Deviation.......................................................................79
Linear Estimation ..........................................................................80
Weighted Mean...........................................................................81
Section 7: Mathematics and Number-Alteration Functions 83
One-Number Functions .................................................................83
The Power Function.......................................................................85
Part II. Programming ............................................. 87
Section 8: Programming Basics ..................................... 88
Why Use Programs?.....................................................................88
Creating a Program......................................................................88
Running a Program.......................................................................89
Program Memory .........................................................................90
Identifying Instructions in Program Lines ....................................91
Displaying Program Lines........................................................92
The 00 Instruction and Program Line 00 ............................93
Expanding Program Memory ..................................................94
Setting the Calculator to a Particular Program Line .....................95
Executing a Program One Line at a Time.........................................96
Interrupting Program Execution.......................................................97
Pausing During Program Execution...........................................97
Stopping Program Execution .................................................101
Section 9: Branching and Looping ............................... 103
Simple Branching.......................................................................103
Looping ....................................................................................104
Conditional Branching ................................................................107
Section 10: Program Editing ......................................... 113
Changing the Instruction in a Program Line....................................113
Adding Instructions at the End of a Program ..................................114
Adding Instructions Within a Program...........................................115
Adding Instructions by Replacement.......................................115
Adding Instructions by Branching...........................................116

8 Contents
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 8 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 11: Multiple Programs ...................................... 120
Storing Another Program ............................................................ 120
Running Another Program........................................................... 122
Part III. Solutions .................................................. 123
Section 12: Real Estate and Lending .............................. 124
Annual Percentage Rate Calculations With Fees............................. 124
Price of a Mortgage Traded at a Discount or Premium.................... 126
Yield of a Mortgage Traded at a Discount or Premium ................... 128
The Rent or Buy Decision ............................................................ 130
Deferred Annuities ..................................................................... 134
Section 13: Investment Analysis .................................... 136
Partial-Year Depreciation............................................................. 136
Straight-Line Depreciation..................................................... 136
Declining-Balance Depreciation ............................................ 139
Sum-of-the-Years-Digits Depreciation ...................................... 141
Full- and Partial-Year Depreciation with Crossover .......................... 144
Excess Depreciation................................................................... 148
Modified Internal Rate of Return................................................... 148
Section 14: Leasing...................................................... 151
Advance Payments..................................................................... 151
Solving For Payment ............................................................ 151
Solving for Yield ................................................................. 154
Advance Payments With Residual ................................................ 156
Solving for Payment............................................................. 156
Solving For Yield................................................................. 158
Section 15: Savings...................................................... 160
Nominal Rate Converted to Effective Rate ..................................... 160
Effective Rate Converted to Nominal Rate ..................................... 161
Nominal Rate Converted to Continuous Effective Rate..................... 162
Section 16: Bonds ........................................................ 163
30/360 Day Basis Bonds........................................................... 163
Annual Coupon Bonds ............................................................... 166

Contents 9
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 9 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Appendixes ................................................................ 169
Appendix A: The Automatic Memory Stack ................... 170
Getting Numbers Into the Stack: The Key..............................171
Termination of Digit Entry .....................................................172
Stack Lift.............................................................................172
Rearranging Numbers in the Stack ...............................................172
The key .....................................................................172
The Key.......................................................................172
One-Number Functions and the Stack ...........................................173
Two-Number Functions and the Stack............................................173
Mathematics Functions .........................................................173
Percentage Functions............................................................ 174
Calendar and Financial Functions.................................................175
The LAST X Register and the Key .........................................176
Chain Calculations .....................................................................176
Arithmetic Calculations with Constants ..........................................177
Appendix B: More About L...................................... 179
Appendix C: Error Conditions ...................................... 181
Error 0: Mathematics ..................................................................181
Error 1: Storage Register Overflow ...............................................182
Error 2: Statistics ........................................................................182
Error 3: IRR................................................................................182
Error 4: Memory ........................................................................182
Error 5: Compound Interest..........................................................183
Error 6: Storage Registers............................................................183
Error 7: IRR................................................................................184
Error 8: Calendar.......................................................................184
Error 9: Service..........................................................................184
Pr Error .....................................................................................184
Appendix D: Formulas Used ........................................ 185
Percentage ................................................................................185
Interest ......................................................................................185
Simple Interest.....................................................................185
Compound Interest...............................................................186
Amortization..............................................................................186
Discounted Cash Flow Analysis ....................................................187
Net Present Value ................................................................187
Internal Rate of Return ..........................................................187
Calendar ..................................................................................187
Actual Day Basis .................................................................187

10 Contents
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 10 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
30/360 Day Basis.............................................................. 187
Bonds ...................................................................................... 188
Depreciation ............................................................................. 189
Straight-Line Depreciation..................................................... 189
Sum-of-the-Years-Digits Depreciation ...................................... 189
Declining-Balance Depreciation ............................................ 190
Modified Internal Rate of Return................................................... 190
Advance Payments..................................................................... 190
Interest Rate Conversions ............................................................ 191
Finite Compounding............................................................ 191
Continuous Compounding.................................................... 191
Statistics ................................................................................... 191
Mean................................................................................ 191
Weighted Mean ................................................................. 191
Linear Estimation................................................................. 191
Standard Deviation ............................................................. 192
Factorial ............................................................................ 192
The Rent or Buy Decision ............................................................ 192
Appendix E: Battery, Warranty, and Service Information 193
Battery ..................................................................................... 193
Low-Power Indication.................................................................. 193
Installing a New Battery ...................................................... 193
Verifying Proper Operation (Self-Tests) .......................................... 194
Warranty.................................................................................. 196
Service..................................................................................... 197
Regulatory Information ............................................................... 199
Temperature Specifications.......................................................... 199
Noise Declaration ..................................................................... 199
Disposal of Waste Equipment by Users in Private Household in the
European Union ........................................................................ 200
Appendix F: United Kingdom Calculations .................... 201
Mortgages................................................................................ 201
Annual Percentage Rate (APR) Calculations ................................... 202
Bond Calculations ..................................................................... 202
Function Key Index...................................................... 203
Programming Key Index .............................................. 206
Subject Index.............................................................. 208

11
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 11 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Making Financial
Calculations Easy
Before you begin to read through this handbook, let’s take a look at how easy
financial calculations can be with your hp 12c. While working through the
examples below, don’t be concerned about learning how to use the calculator;
we’ll cover that thoroughly beginning with Section 1.
Example 1: Suppose you want to ensure that you can finance your daughter’s
college education 14 years from today. You expect that the cost will be about
$6,000 a year ($500 a month) for 4 years. Assume she will withdraw $500 at the
beginning of each month from a savings account. How much would you have to
deposit into the account when she enters college if the account pays 6% annual
interest compounded monthly?
This is an example of a compound interest calculation. All such problems involve at
least three of the following quantities:
z n: the number of compounding periods.
z i: the interest rate per compounding period.
z PV: the present value of a compounded amount.
z PMT: the periodic payment amount.
z FV: the future value of a compounded amount.
In this particular example:
z n is 4 years × 12 periods per year = 48 periods.
z i is 6% per year ÷ 12 periods per year = 0.5% per period.
z PV is the quantity to be calculated — the present value when the financial
transaction begins.
z PMT is $500.
z FV is zero, since by the time your daughter graduates she (hopefully!) will
not need any more money.
To begin, turn the calculator on by pressing the ; key. Then, press the keys
shown in the Keystrokes column below.*
* If you are not familiar with the use of an hp calculator keyboard, refer to the description on
pages 16 and 17.

12 Making Financial Calculations Easy
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 12 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Note: A battery symbol (¼) shown in the lower-left corner of the display
when the calculator is on signifies that the available battery power is nearly
exhausted. To install new batteries, refer to Appendix E.
The calendar functions and nearly all of the financial functions take some
time to produce an answer. (This is typically just a few seconds, but the ¼,
!, L, and S functions could require a half-minute or more.) During
these calculations, the word running flashes in the display to let you know
that the calculator is running.
Keystrokes Display
fCLEARHf2 0.00 Clears previous data inside the
calculator and sets display to show
two decimal places.
4gA 48.00 Calculates and stores the number of
compounding periods.
6gC 0.50 Calculates and stores the periodic
interest rate.
500P 500.00 Stores periodic payment amount.
g× 500.00 Sets payment mode to Begin.
$ -21,396.61 Amount required to be deposited.*
Example 2: We now need to determine how to accumulate the required deposit
by the time your daughter enters college 14 years from now. Let’s say that she has
a paid-up $5,000 insurance policy that pays 5.35% annually, compounded
semiannually. How much would it be worth by the time she enters college?
In this example, we need to calculate FV, the future value.
Keystrokes Display
fCLEARG -21,396.61 Clears previous financial data inside
the calculator.
14\2µn 28.00 Calculates and stores the number of
compounding periods.
5.35\2z¼ 2.68 Calculates and stores the periodic
interest rate.
5000Þ$ -5,000.00 Stores the present value of the
policy.
M 10,470.85 Value of policy in 14 years.
* Don’t be concerned now about the minus sign in the display. That and other details will be
explained in Section 3.

Making Financial Calculations Easy 13
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 13 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 3: The preceding example showed that the insurance policy will
provide about half the required amount. An additional amount must be set aside to
provide the balance (21,396.61 – 10,470.85 = 10,925.76). Suppose you make
monthly payments, beginning at the end of next month, into an account that pays
6% annually, compounded monthly. What payment amount would be required in
order to accumulate $10,925.75 in the 14 years remaining?
Keystrokes Display
fCLEARG 10,470.85 Clears previous financial data
inside the calculator.
14gA 168.00 Calculates and stores the number of
compounding periods.
6gC 0.50 Calculates and stores the periodic
interest rate.
10925.76M 10.925.76 Stores the future value required.
g 10.925.76 Sets payment mode to End.
P –41.65 Monthly payment required.
Example 4: Suppose you cannot find a bank that currently offers an account
with 6% annual interest compounded monthly, but you can afford to make $45.00
monthly payments. What is the minimum interest rate that will enable you to
accumulate the required amount?
In this problem, we do not need to clear the previous financial data inside the
calculator, since most of it is unchanged from the preceding example.
Keystrokes Display
45ÞP –45.00 Stores payment amount.
¼ 0.42 Periodic interest rate.
12§ 5.01 Annual interest rate.
This is only a small sampling of the many financial calculations that can now be
done easily with your hp 12c. To begin learning about this powerful financial tool,
just turn the page.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 15 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Part I
Problem Solving
16
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 16 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 1
Getting Started
Power On and Off
To begin using your hp 12c, press the ; key*. Pressing ; again turns the
calculator off. If not manually turned off, the calculator will turn off automatically 8
to 17 minutes after it was last used.
Low-Power Indication
A battery symbol (¼) shown in the upper-left corner of the display when the
calculator is on signifies that the available battery power is nearly exhausted. To
replace the batteries, refer to Appendix E.
The Keyboard
Many keys on the hp 12c perform two or even three functions. The primary
function of a key is indicated by the characters printed in white on the upper face
of the key. The alternate function(s) of a key are indicated by the characters
printed in gold above the key and the characters printed in blue on the lower face
of the key. These alternate functions are specified by pressing the appropriate
prefix key before the function key:
z To specify the alternate function printed in
g
old
above a key, press the gold prefix key (f), then
press the function key.
z To specify the primary function printed on the uppe
r
face of a key, press the key alone.
z To specify the alternate function printed in blue on the
lower face of a key, press the blue prefix key (g),
then press the function key.
* Note that the ; key is lower than the other keys to help prevent its being pressed
inadvertently.

Section 1: Getting Started 17
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 17 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Throughout this handbook, references to the operation of an alternate function
appear as only the function name in a box (for example, “The L function …”).
References to the selection of an alternate function appear preceded by the
appropriate prefix key (for example, “Pressing fL …”). References to the
functions shown on the keyboard in gold under the bracket labeled “CLEAR”
appear throughout this handbook preceded by the word “CLEAR” (for example,
“The CLEARH function …” or “Pressing fCLEARH …”).
If you press the f or g prefix key mistakenly, you can cancel it by pressing
fCLEARX. This can also be pressed to cancel the ?, :, and i keys.
(These keys are “prefix” keys in the sense that other keys must be pressed after
them in order to execute the corresponding function.) Since the X key is also
used to display the mantissa (all 10 digits) of a displayed number, the mantissa of
the number in the display will appear for a moment after the X key is released.
Pressing the f or g prefix key turns on the corresponding status indicator — f
or g — in the display. Each indicator turns off when you press a function key
(executing an alternate function of that key), another prefix key, or fCLEARX.
Keying in Numbers
To key a number into the calculator, press the digit keys in sequence, just as if you
were writing the number on paper. A decimal point must be keyed in (using the
decimal point key) if it is part of the number unless it appears to the right of the last
digit.
Digit Separators
As a number is keyed in, each group of three digits to the left of the decimal point
is automatically separated in the display. When the calculator is first turned on
after coming from the factory — or after Continuous Memory is reset — the
decimal point in displayed numbers is a dot, and the separator between each
group of three digits is a comma. If you wish, you can set the calculator to display
a comma for the decimal point and a dot for the three-digit separator. To do so,
turn the calculator off, then press and hold down the . key while you press ;.
Doing so again sets the calculator to use the original digit separators in the
display.
Negative Numbers
To make a displayed number negative — either one that has just been keyed in or
one that has resulted from a calculation — simply press Þ (change sign) . When
the display shows a negative number — that is, the number is preceded by a
minus sign — pressing Þ removes the minus sign from the display, making the
number positive.

18 Section 1: Getting Started
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 18 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keying in Large Numbers
Since the display cannot show more than 10 digits of a number, numbers greater
than 9,999,999,999 cannot be entered into the display by keying in all the digits
in the number. However, such numbers can be easily entered into the display if the
number is expressed in a mathematical shorthand called “scientific notation.” To
convert a number into scientific notation, move the decimal point until there is only
one digit (a nonzero digit) to its left. The resulting number is called the “mantissa”
of the original number, and the number of decimal places you moved the decimal
point is called the “exponent” of the original number. If you moved the decimal
point to the left, the exponent is positive; if you moved the decimal point to the
right (this would occur for numbers less than one), the exponent is negative. To key
the number into the display, simply key in the mantissa, press Æ (enter exponent),
then key in the exponent. If the exponent is negative, press Þ after pressing
Æ.
For example, to key in $1,781,400,000,000, we move the decimal point 12
places to the left, giving a mantissa of 1.7814 and an exponent of 12:
Keystrokes Display
1.7814Æ12 1.7814 12 1,781,400,000,000 entered in
scientific notation.
Numbers entered in scientific notation can be used in calculations just like any
other number.
The CLEAR Keys
Clearing a register or the display replaces the number in it with zero. Clearing
program memory replaces the instructions there with gi00. There are several
clearing operations on the hp 12c, as shown in the table below:
Key(s) Clears:
O Display and X-register.
fCLEAR² Statistics registers (R1 through R6), stack registers, and
display.
fCLEARÎ Program memory (only when pressed in Program mode).
fCLEARG Financial registers.
fCLEARH Data storage registers, financial registers, stack and LAST X
registers, and display.

Section 1: Getting Started 19
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 19 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Simple Arithmetic Calculations
Any simple arithmetic calculation involves two numbers and an operation —
addition, subtraction, multiplication, or division. To do such a calculation on your
hp 12c, you first tell the calculator the two numbers, then tell the calculator the
operation to be performed. The answer is calculated when the operation key
(+,-,§, or z) is pressed.
The two numbers should be keyed into the calculator in the order they would
appear if the calculation were written down on paper left-to-right. After keying in
the first number, press the \ key to tell the calculator that you have completed
entering the number. Pressing \ separates the second number to be entered
from the first number already entered.
In summary, to perform an arithmetic operation:
1. Key in the first number.
2. Press \ to separate the second number from the first.
3. Key in the second number.
4. Press +,-,§, or z to perform the desired operation.
For example to calculate 13 ÷ 2, proceed as follows:
Keystrokes Display
13 13. Keys the first number into the
calculator.
\ 13.00 Pressing \ separates the second
number from the first.
2 2. Keys the second number into the
calculator.
z 6.50 Pressing the operation key calculates
the answer.
Notice that after you pressed \, two zeroes appeared following the decimal
point. This is nothing magical: the calculator’s display is currently set to show two
decimal places of every number that has been entered or calculated. Before you
pressed \, the calculator had no way of knowing that you had completed
entering the number, and so displayed only the digits you had keyed in. Pressing
\ tells the calculator that you have completed entering the number: it terminates
digit entry. You need not press \ after keying in the second number because
the +,-,§ and z keys also terminate digit entry. (In fact, all keys terminate
digit entry except for digit entry keys — digit keys, ., Þ, and Æ — and
prefix keys — f, g, ?, :, and (.)

20 Section 1: Getting Started
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 20 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Chain Calculations
Whenever the answer has just been calculated and is therefore in the display, you
can perform another operation with this number by simply keying in the second
number and then pressing the operation key: you need not press \ to separate
the second number from the first. This is because when a number is keyed in after
a function key (such as +,-,§, z, etc.) is pressed, the result of that prior
calculation is stored inside the calculator — just as when the \ key is pressed.
The only time you must press the \ key to separate two numbers is when you
are keying them both in, one immediately following the other.
The hp 12c is designed so that each time you press a function key in RPN mode,
the calculator performs the operation then — not later — so that you see the results
of all intermediate calculations, as well as the “bottom line.”
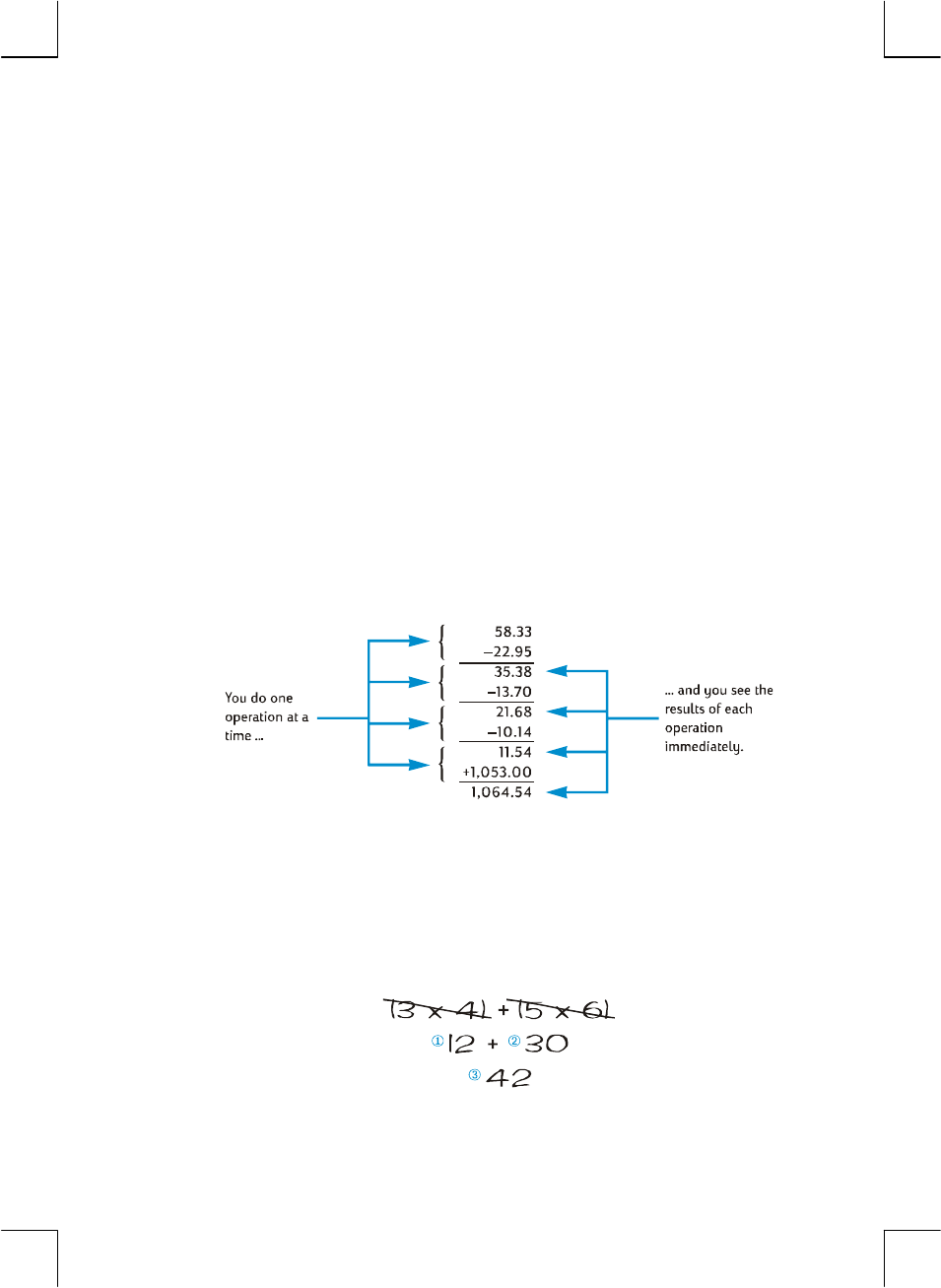
Example: Suppose you’ve written three checks without updating your checkbook,
and you’ve just deposited your paycheck for $1,053.00 into your checking
account. If your latest balance was $58.33 and the checks were written for
$22.95, $13.70, and $10.14, what is the new balance?
Solution: When written down on paper, this problem would read
58.33 – 22.95 – 13.70 – 10.14 + 1053
Keystrokes Display
58.33 58.33 Keys the first number.
\ 58.33 Pressing \ separates the second
number from the first.
22.95 22.95 Keys in the second number.
- 35.38 Pressing - subtracts the second
number from the first. The calculator
displays the result of this calculation,
which is the balance after subtracting
the first check.
13.70 13.70 Keys in the next number. Since a
calculation has just been performed,
do not press \; the next number
entered (13.70) is automatically
separated from the one previously in
the display (35.38).
Section 1: Getting Started 21
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 21 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
- 21.68 Pressing - subtracts the number just
entered from the number previously in
the display. The calculator displays the
result of this calculation, which is the
balance after subtracting the second
check.
10.14- 11.54 Keys in the next number and subtracts
it from the previous balance. The new
balance appears in the display. (It’s
getting rather low!)
1053+ 1,064.54 Keys in the next number — the
paycheck deposited — and adds it to
the previous balance. The new,
current balance appears in the
display.
The preceding example demonstrates how the hp 12c calculates just as you would
using pencil and paper (except a lot faster!):
Let’s see this happening in a different type of calculation — one that involves
multiplying groups of two numbers and then adding the results. (This is the type of
calculation that would be required to total up an invoice consisting of several items
with different quantities and different prices.)
For example, consider the calculation of (3 × 4) + (5 × 6). If you were doing this
on paper, you would first do the multiplication in the first parentheses, then the
multiplication in the second parentheses, and finally add the results of the two
multiplications:

22 Section 1: Getting Started
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 22 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Your hp 12c calculates the answer in just the same way:
Keystrokes Display
3\4§ 12.00 Step 1: Multiply the numbers in the
first parentheses.
5\6§ 30.00 Step 2: Multiply the numbers in the
second parentheses.
+ 42.00 Step 3: Add the results of the two
multiplications.
Notice that before doing step 2, you did not need to store or write down the result
of step 1: it was stored inside the calculator automatically. And after you keyed in
the 5 and the 6 in step 2, the calculator was holding two numbers (12 and 5)
inside for you, in addition to the 6 in the display. (The hp 12c can hold a total of
three numbers inside, in addition to the number in the display.) After step 2, the
calculator was still holding the 12 inside for you, in addition to the 30 in the
display. You can see that the calculator holds the number for you, just as you
would have them written on paper, and then calculates with them at the proper
time, just as you would yourself.* But with the hp 12c, you don’t need to write
down the results of an intermediate calculation, and you don’t even need to
manually store it and recall it later.
By the way, notice that in step 2 you needed to press \ again. This is simply
because you were again keying in two numbers immediately following each other,
without performing a calculation in between.
To check your understanding of how to calculate with your hp 12c, try the
following problems yourself. Although these problems are relatively simple, more
complicated problems can be solved using the same basic steps. If you have
difficulty obtaining the answers shown, review the last few pages.
00.77)65()43(
=
+
×
+
25.0
)3814(
)1427( =
+
−
13.0
21163
5=
++
* Although you don’t need to know just how these numbers are stored and brought back at just
the right time, if you’re interested you can read all about it in Appendix A. By gaining a more
complete understanding of the calculator’s operation, you’ll use it more efficiently and
confidently, yielding a better return on the investment in your hp 12c.

Section 1: Getting Started 23
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 23 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Storage Registers
Numbers (data) in the hp 12c are stored in memories called “storage registers” or
simply “registers.” (The singular term “ memory” is sometimes used in this
handbook to refer to the entire collection of storage registers.) Four special
registers are used for storing numbers during calculations (these “stack registers”
are described in Appendix A), and another (called the “LAST X” register) is used
for storing the number last in the display before an operation is performed. In
addition to these registers into which numbers are stored automatically, up to 20
“data storage” registers are available for manual storage of numbers. These data
storage registers are designated R0 through R9 and R.0 through R.9. Fewer registers
are available for data storage if a program has been stored in the calculator (since
the program is stored in some of those 20 registers), but a minimum of 7 registers
is always available. Still other storage registers — referred to as the “financial
registers” — are reserved for numbers used in financial calculations.
Storing and Recalling Numbers
To store the number from the display into a data storage register:
1. Press ? (store).
2. Key in the register number: 0 through 9 for registers R0 through R9, or .0
through .9 for registers R.0 through R.9.
Similarly, to recall a number from a storage register into the display, press :
(recall), then key in the register number. This copies the number from the storage
register into the display; the number remains unaltered in the storage register.
Furthermore, when this is done, the number previously in the display is
automatically held inside the calculator for a subsequent calculation, just as the
number in the display is held when you key in another number.
Example: Before you leave to call on a customer interested in your personal
computer, you store the cost of the computer ($3,250) and also the cost of a
printer ($2,500) in data storage registers. Later, the customer decides to buy six
computers and one printer. You recall the cost of the computer, multiply by the
quantity ordered, and then recall and add the cost of the printer to get the total
invoice.
Keystrokes Display
3250?1 3,250.00 Stores the cost of the computer in R1.
2500?2 2,500.00 Stores the cost of the printer in R2.
; Turns the calculator off.

24 Section 1: Getting Started
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 24 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Later that same day …
Keystrokes Display
; 2,500.00 Turns the calculator back on.
:1 3,250.00 Recalls the cost of the computer to the
display.
6§ 19,500.00 Multiplies the quantity ordered to get
the cost of the computers.
:2 2,500.00 Recalls the cost of the printer to the
display.
+ 22,000.00 Total invoice.
Clearing Storage Registers
To clear a single storage register — that is, to replace the number in it with
zero — merely store zero into it. You need not clear a storage register before
storing data into it; the storing operation automatically clears the register before
the data is stored.
To clear all storage registers at once — including the financial registers, the stack
registers, and the LAST X register — press fCLEARH.* This also clears the
display.
All storage registers are also cleared when Continuous Memory is reset (as
described on page 70).
Storage Register Arithmetic
Suppose you wanted to perform an arithmetic operation with the number in the
display and the number in a storage register, then store the result back into the
same register without altering the number in the display. The hp 12c enables you
to do all this in a single operation:
1. Press ?.
2. Press +, -, §, or z to specify the desired operation.
3. Key in the register number.
When storage register arithmetic is performed, the new number in the register is
determined according to the following rule:
* CLEARH is not programmable.

Section 1: Getting Started 25
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 25 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Storage register arithmetic is possible with only registers R0 through R4.
Example: In the example on page 20, we updated the balance in your
checkbook. Let’s suppose that because data is stored indefinitely in your
calculator’s Continuous Memory, you keep track of your checking account balance
in the calculator. You could use storage register arithmetic to quickly update the
balance after depositing or writing checks.
Keystrokes Display
58.33?0 58.33 Stores the current balance in register
R0.
22.95?-0 22.95 Subtracts the first check from the
balance in R0. Note that the display
continues to show the amount
subtracted; the answer is placed only
in R0.
13.70?-0 13.70 Subtracts the second check.
10.14?-0 10.14 Subtracts the third check.
1053?+0 1,053.00 Adds the deposit.
:0 1,064.54 Recalls the number in R0 to check the
new balance.

26
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 26 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 2
Percentage and Calendar
Functions
Percentage Functions
The hp 12c includes three keys for solving percentage problems: b, à, and Z.
You don’t need to convert percentages to their decimal equivalents; this is done
automatically when you press any of these keys. Thus, 4% need not be changed to
0.04; you key it in the way you see and say it: 4b.
Percentages
To find the amount corresponding to a percentage of a number:
1. Key in the base number.
2. Press \.
3. Key in the percentage.
4. Press b.
For example, to find 14% of $300:
Keystrokes Display
300 300. Keys in the base number.
\ 300.00 Pressing \ separates the next
number entered from the first number,
just as when an ordinary arithmetic
calculation is performed.
14 14. Keys in the percentage.
b 42.00 Calculates the amount.
If the base number is already in the display as a result of a previous calculation,
you should not press \ before keying in the percentage — just as in a chain
arithmetic calculation.

Section 2: Percentage and Calendar Functions 27
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 27 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Net Amount
A net amount — that is, the base amount plus or minus the percentage amount —
can be calculated easily with your hp 12c, since the calculator holds the base
amount inside after you calculate a percentage amount. To calculate a net amount,
simply calculate the percentage amount, then press = or -.
Example: You’re buying a new car that lists for $13,250. The dealer offers you
a discount of 8%, and the sales tax is 6%. Find the amount the dealer is charging
you, then find the total cost to you, including tax.
Keystrokes Display
13250\ 13,250.00 Keys in the base amount and
separates it from the percentage.
8b 1,060.00 Amount of discount.
- 12,190.00 Base amount less discount.
6b 731.40 Amount of tax (on $12,190).
= 12,921.40 Total cost: base amount less discount
plus tax.
Percent Difference
To find the percent difference between two numbers:
1. Key in the base number.
2. Press \ to separate the other number from the base number.
3. Key in the other number.
4. Press à.
If the other number is greater than the base number, the percent difference will be
positive. If the other number is less than the base number, the percent difference
will be negative. Therefore, a positive answer indicates an increase, while a
negative answer indicates a decrease.
If you are calculating a percent difference over time, the base number is typically
the amount occurring first.
Example: Yesterday your stock fell from 581/2 to 531/4 per share. What is the
percent change?
Keystrokes Display
58.5\ 58.50 Keys in the base number and
separates it from the other number.
53.25 53.25 Keys in the other number.
à –8.97 Nearly a 9% decrease.

28 Section 2: Percentage and Calendar Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 28 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The à key can be used for calculations of the percent difference between a
wholesale cost and a retail cost. If the base number entered is the wholesale cost,
the percent difference is called the markup; if the base number entered is the retail
cost, the percent difference is called the margin. Examples of markup and margin
calculations are included in the hp 12c Solutions Handbook.
Percent of Total
To calculate what percentage one number is of another:
1. Calculate the total amount by adding the individual amounts, just as in a
chain arithmetic calculation.
2. Key in the number whose percentage equivalent you wish to find.
3. Press Z.
Example: Last month, your company posted sales of $3.92 million in the U.S.,
$2.36 million in Europe, and $1.67 million in the rest of the world. What
percentage of the total sales occurred in Europe?
Keystrokes Display
3.92\ 3.92 Keys in the first number and separates
it from the second.
2.36+ 6.28 Adds the second number.
1.67+ 7.95 Adds the third number to get the total.
2.36 2.36 Keys in 2.36 to find what percentage
it is of the number in the display.
Z 29.69 Europe had nearly 30% of the total
sales.
The hp 12c holds the total amount inside after a percent of total is calculated.
Therefore, to calculate what percentage another amount is of the total:
1. Clear the display by pressing O.
2. Key in that amount.
3. Press Z again.
For example, to calculate what percent of the total sales in the preceding example
occurred in the U.S. and what percent occurred in the rest of the world:
Keystrokes Display
O3.92Z 49.31 The U.S. had about 49% of the total
sales.
O1.67 Z 21.01 The rest of the world had about 21%
of the total sales.

Section 2: Percentage and Calendar Functions 29
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 29 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
To find what percentage a number is of a total, when you already know the total
number:
1. Key in the total number.
2. Press \ to separate the other number from the total number.
3. Key in the number whose percentage equivalent you wish to find.
4. Press Z.
For example, if you already knew in the preceding example that the total sales
were $7.95 million and you wanted to find what percentage of that total occurred
in Europe:
Keystrokes Display
7.95\ 7.95 Keys in the total amount and separates
it from the next number.
2.36 2.36 Keys in 2.36 to find what percentage
it is of the number in the display.
Z 29.69 Europe had nearly 30% of the total
sales.
Calendar Functions
The calendar functions provided by the hp 12c — D and Ò — can handle
dates from October 15, 1582 through November 25, 4046.
Date Format
For each of the calendar functions — and also for bond calculations (E and
S) — the calculator uses one of two date formats. The date format is used to
interpret dates when they are keyed into the calculator as well as for displaying
dates.
Month-Day-Year. To set the date format to month-day-year, press gÕ. To
key in a date with this format in effect:
1. Key in the one or two digits of the month.
2. Press the decimal point key (.).
3. Key in the two digits of the day.
4. Key in the four digits of the year.
Dates are displayed in the same format.
For example, to key in April 7, 2004:
Keystrokes Display
4.072004 4.072004

30 Section 2: Percentage and Calendar Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 30 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Day-Month-Year. To set the date format to day-month-year, press gÔ. To
key in a date with this format in effect:
1. Key in the one or two digits of the day.
2. Press the decimal point key (.).
3. Key in the two digits of the month.
4. Key in the four digits of the year.
For example, to key in 7 April, 2004:
Keystrokes Display
7.042004 7.042004
When the date format is set to day-month-year, the D.MY status indicator in the
display is lit. If D.MY is not lit, the date format is set to month-day-year.
The date format remains set to what you last specified until you change it; it is not
reset each time the calculator is turned on. However, if Continuous Memory is reset,
the date format is set to month-day-year.
Future or Past Dates
To determine the date and day that is a given number of days from a given date:
1. Key in the given date and press \.
2. Key in the number of days.
3. If the other date is in the past, press Þ.
4. Press gD.
The answer calculated by the D function is displayed in a special format. The
numbers of the month, day, and year (or day, month, and year) are separated by
digit separators, and the digit at the right of the displayed answer indicates the
day of the week: 1 for Monday through 7 for Sunday.*
Example: If you purchased a 120-day option on a piece of land on 14 May
2004, what would be the expiration date? Assume that you normally express
dates in the day-month-year format.
Keystrokes Display
gÔ 7.04 Sets date format to day-month-year.
(Display shown assumes date
remains from preceding example.
The full date is not now displayed
because the display format is set to
show only two decimal places, as
described in Section 5.)
* The day of the week indicated by the D function may differ from that recorded in history
for dates when the Julian calendar was in use. The Julian calendar was standard in England
and its colonies until September 14, 1752, when they switched to the Gregorian calendar.
Other countries adopted the Gregorian calendar at various times.

Section 2: Percentage and Calendar Functions 31
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 31 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
14.052004\ 14.05 Keys in date and separates it from
number of days to be entered.
120gD 11,09,2004 6 The expiration date is 11 September
2004, a Saturday.
When D is executed as an instruction in a running program, the calculator
pauses for about 1 second to display the result, then resumes program execution.
Number of Days Between Dates
To calculate the number of days between two given dates:
1. Key in the earlier date and press \.
2. Key in the later date and press gÒ.
The answer shown in the display is the actual number of days between the two
dates, including leap days (the extra days occurring in leap years), if any. In
addition, the hp 12c also calculates the number of days between the two dates on
the basis of a 30-day month. This answer is held inside the calculator; to display it,
press ~. Pressing ~ again will return the original answer to the display.
Example: Simple interest calculations can be done using either the actual number
of days or the number of days counted on the basis of a 30-day month. What
would be the number of days counted each way, to be used in calculating the
simple interest accruing from June 3, 2004 to October 14, 2005? Assume that
you normally express dates in the month-day-year format.
Keystrokes Display
gÕ 11.09 Sets date format to month-day-year.
(Display shown assumes date remains
from preceding example.)
6.032004\ 6.03 Keys in earlier date and separates it
from the later date.
10.142005gÒ 498.00 Keys in later date. Display shows
actual number of days.
~ 491.00 Number of days counted on the basis
of a 30-day month.

32
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 32 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 3
Basic Financial Functions
The Financial Registers
In addition to the data storage registers discussed on page 23, the hp 12c has five
special registers in which numbers are stored for financial calculations. These
registers are designated n, i, PV, PMT, and FV. The first five keys on the top row of
the calculator are used to store a number from the display into the corresponding
register, to calculate the corresponding financial value and store the result into the
corresponding register, or to display the number stored in the corresponding
register.*
Storing Numbers Into the Financial Registers
To store a number into a financial register, key the number into the display, then
press the corresponding key (n, ¼, $, P, or M).
Displaying Numbers in the Financial Registers
To display a number stored in a financial register, press : followed by the
corresponding key.†
* Which operation is performed when one of these keys is pressed depends upon the last
preceding operation performed: If a number was just stored into a financial register (using
n, ¼, $, P, M, A, or C), pressing one of these five keys calculates the
corresponding value and stores it into the corresponding register; otherwise pressing one of
these five keys merely stores the number from the display into the corresponding register.
† It’s good practice to press the corresponding key twice after :, since often you may want
to calculate a financial value right after displaying another financial value. As indicated in
the preceding footnote, if you wanted to display FV and then calculate PV, for example, you
should press :MM$. If you didn’t press M the second time, pressing $ would
store FV in the PV register rather than calculating PV, and to calculate PV you would have to
press $ again.

Section 3: Basic Financial Functions 33
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 33 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Clearing the Financial Registers
Every financial function uses numbers stored in several of the financial registers.
Before beginning a new financial calculation, it is good practice to clear all of the
financial registers by pressing fCLEARG. Frequently, however, you may want
to repeat a calculation after changing a number in only one of the financial
registers. To do so, do not press fCLEARG; instead, simply store the new
number in the register. The numbers in the other financial registers remain
unchanged.
The financial registers are also cleared when you press fCLEARH and when
Continuous Memory is reset (as described on page 70).
Simple Interest Calculations
The hp 12c simultaneously calculates simple interest on both a 360-day basis and
a 365-day basis. You can display either one, as described below. Furthermore,
with the accrued interest in the display, you can calculate the total amount
(principal plus accrued interest) by pressing +.
1. Key in or calculate the number of days, then press n.
2. Key in the annual interest rate, then press ¼.
3. Key in the principal amount, then press Þ$.*
4. Press fÏ to calculate and display the interest accrued on a 360-day
basis.
5. If you want to display the interest accrued on a 365-day basis, press
d~.
6. Press + to calculate the total of the principal and the accrued interest now
in the display.
The quantities n, i, and PV can be entered in any order.
Example 1: Your good friend needs a loan to start his latest enterprise and has
requested that you lend him $450 for 60 days. You lend him the money at 7%
simple interest, to be calculated on a 360-day basis. What is the amount of
accrued interest he will owe you in 60 days, and what is the total amount owed?
Keystrokes Display
60n 60.00 Stores the number of days.
* Pressing the $ key stores the principal amount in the PV register, which then contains the
present value of the amount on which interest will accrue. The Þ key is pressed first to
change the sign of the principal amount before storing it in the PV register. This is required by
the cash flow sign convention, which is applicable primarily to compound interest
calculations.
34 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 34 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
7¼ 7.00 Stores the annual interest rate.
450Þ$ –450.00 Stores the principal.
fÏ 5.25 Accrued interest, 360-day basis.
+ 455.25 Total amount: principal plus accrued
interest.
Example 2: Your friend agrees to the 7% interest on the loan from the preceding
example, but asks that you compute it on a 365-day basis rather than a 360-day
basis. What is the amount of accrued interest he will owe you in 60 days, and
what is the total amount owed?
Keystrokes Display
60n
7¼
450Þ$
60.00
7.00
–450.00
If you have not altered the numbers in
the n, i, and PV registers since the
preceding example, you may skip
these keystrokes.
fÏd~ 5.18 Accrued interest, 365-day basis.
+ 455.18 Total amount: principal plus accrued
interest.
Financial Calculations and the Cash Flow Diagram
The concepts and examples presented in this section are representative of a wide
range of financial calculations. If your specific problem does not appear to be
illustrated in the pages that follow, don’t assume that the calculator is not capable
of solving it. Every financial calculation involves certain basic elements; but the
terminology used to refer to these elements typically differs among the various
segments of the business and financial communities. All you need to do is identify
the basic elements in your problem, and then structure the problem so that it will
be readily apparent what quantities you need to tell the calculator and what
quantity you want to solve for.
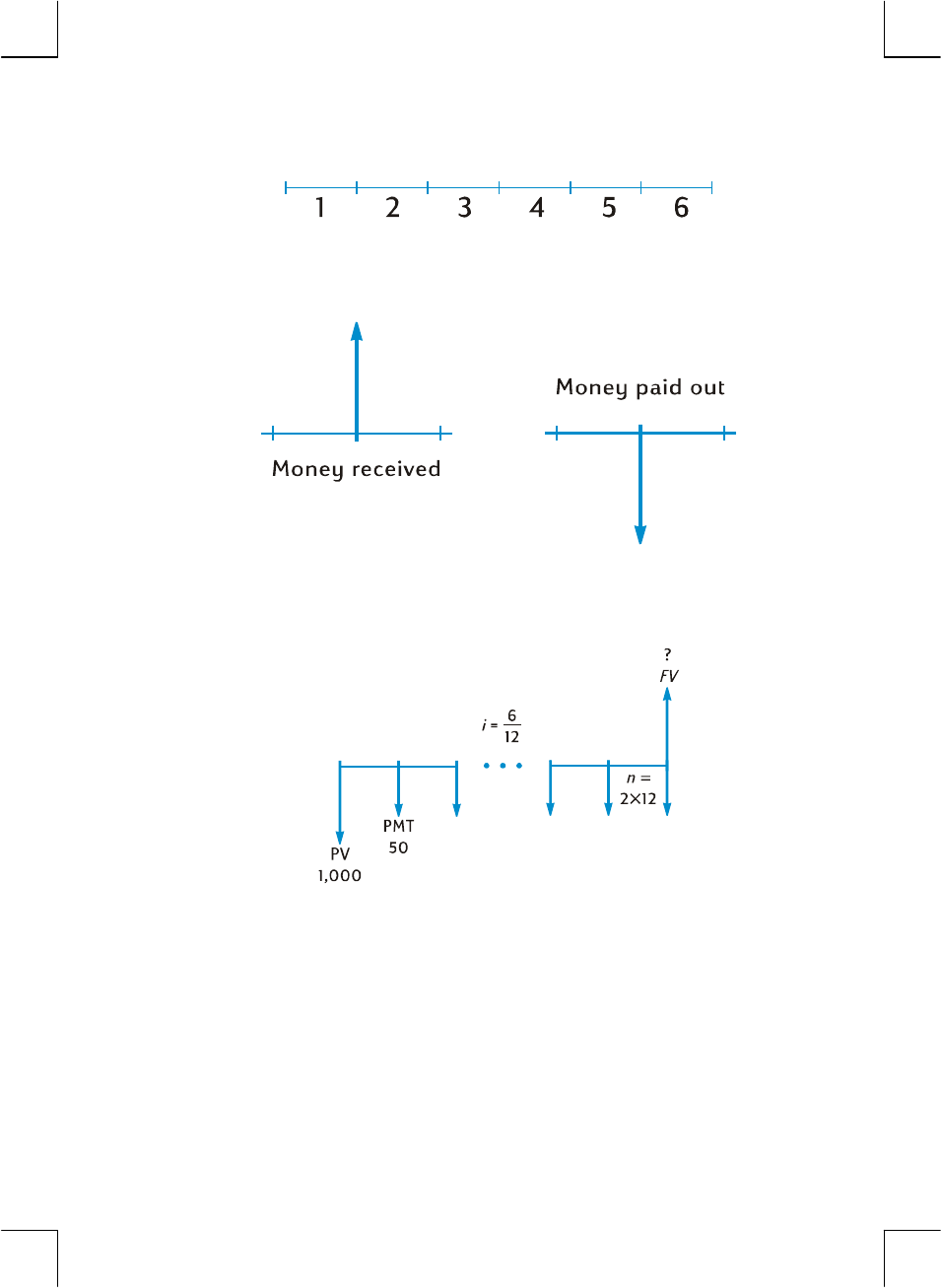
An invaluable aid for using your calculator in a financial calculation is the cash
flow diagram. This is simply a pictorial representation of the timing and direction
of financial transactions, labeled in terms that correspond to keys on the calculator.
The diagram begins with a horizontal line, called a time line. It represents the
duration of a financial problem, and is divided into compounding periods. For
example, a financial problem that transpires over 6 months with monthly
compounding would be diagrammed like this:
Section 3: Basic Financial Functions 35
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 35 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The exchange of money in a problem is depicted by vertical arrows. Money you
receive is represented by an arrow pointing up from the point in the time line when
the transaction occurs; money you pay out is represented by an arrow pointing
down.
Suppose you deposited (paid out) $1,000 into an account that pays 6% annual
interest and is compounded monthly, and you subsequently deposited an
additional $50 at the end of each month for the next 2 years. The cash flow
diagram describing the problem would look like this:
The arrow pointing up at the right of the diagram indicates that money is received
at the end of the transaction. Every completed cash flow diagram must include at
least one cash flow in each direction. Note that cash flows corresponding to the
accrual of interest are not represented by arrows in the cash flow diagram.
The quantities in the problem that correspond to the first five keys on the top row of
the keyboard are now readily apparent from the cash flow diagram.
z n is the number of compounding periods. This quantity can be expressed in
years, months, days, or any other time unit, as long as the interest rate is
expressed in terms of the same basic compounding period. In the problem
illustrated in the cash flow diagram above, n = 2 × 12.

36 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 36 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The form in which n is entered determines whether or not the calculator
performs financial calculations in Odd-Period mode (as described on pages
50 through 53). If n is a noninteger (that is, there is at least one nonzero
digit to the right of the decimal point), calculations of i, PV, PMT, and FV are
performed in Odd-Period mode.
z i is the interest rate per compounding period. The interest rate shown in the
cash flow diagram and entered into the calculator is determined by dividing
the annual interest rate by the number of compounding periods. In the
problem illustrated above, i = 6% ÷ 12.
z PV — the present value — is the initial cash flow or the present value of a
series of future cash flows. In the problem illustrated above, PV is the $1,000
initial deposit.
z PMT is the period payment. In the problem illustrated above PMT is the $50
deposited each month. When all payments are equal, they are referred to as
annuities. (Problems involving equal payments are described in this section
under Compound Interest Calculations; problems involving unequal
payments can be handled as described in under Discounted Cash Flow
Analysis: NPV and IRR. Procedures for calculating the balance in a savings
account after a series of irregular and/or unequal deposits are included in
the hp 12c Solutions Handbook.)
z FV — the future value — is the final cash flow or the compounded value of a
series of prior cash flows. In the particular problem illustrated above, FV is
unknown (but can be calculated).
Solving the problem is now basically a matter of keying in the quantities identified
in the cash flow diagram using the corresponding keys, and then calculating the
unknown quantity by pressing the corresponding key. In the particular problem
illustrated in the cash flow diagram above, FV is the unknown quantity; but in other
problems, as we shall see later, n, i, PV, or PMT could be the unknown quantity.
Likewise, in the particular problem illustrated above there are four known
quantities that must be entered into the calculator before solving for the unknown
quantity; but in other problems only three quantities may be known — which must
always include n or i.
The Cash Flow Sign Convention
When entering the PV, PMT, and FV cash flows, the quantities must be keyed into
the calculator with the proper sign, + (plus) or – (minus), in accordance with …
The Cash Flow Sign Convention: Money received (arrow pointing up)
is entered or displayed as a positive value (+). Money paid out (arrow
pointing down) is entered or displayed as a negative value (–).
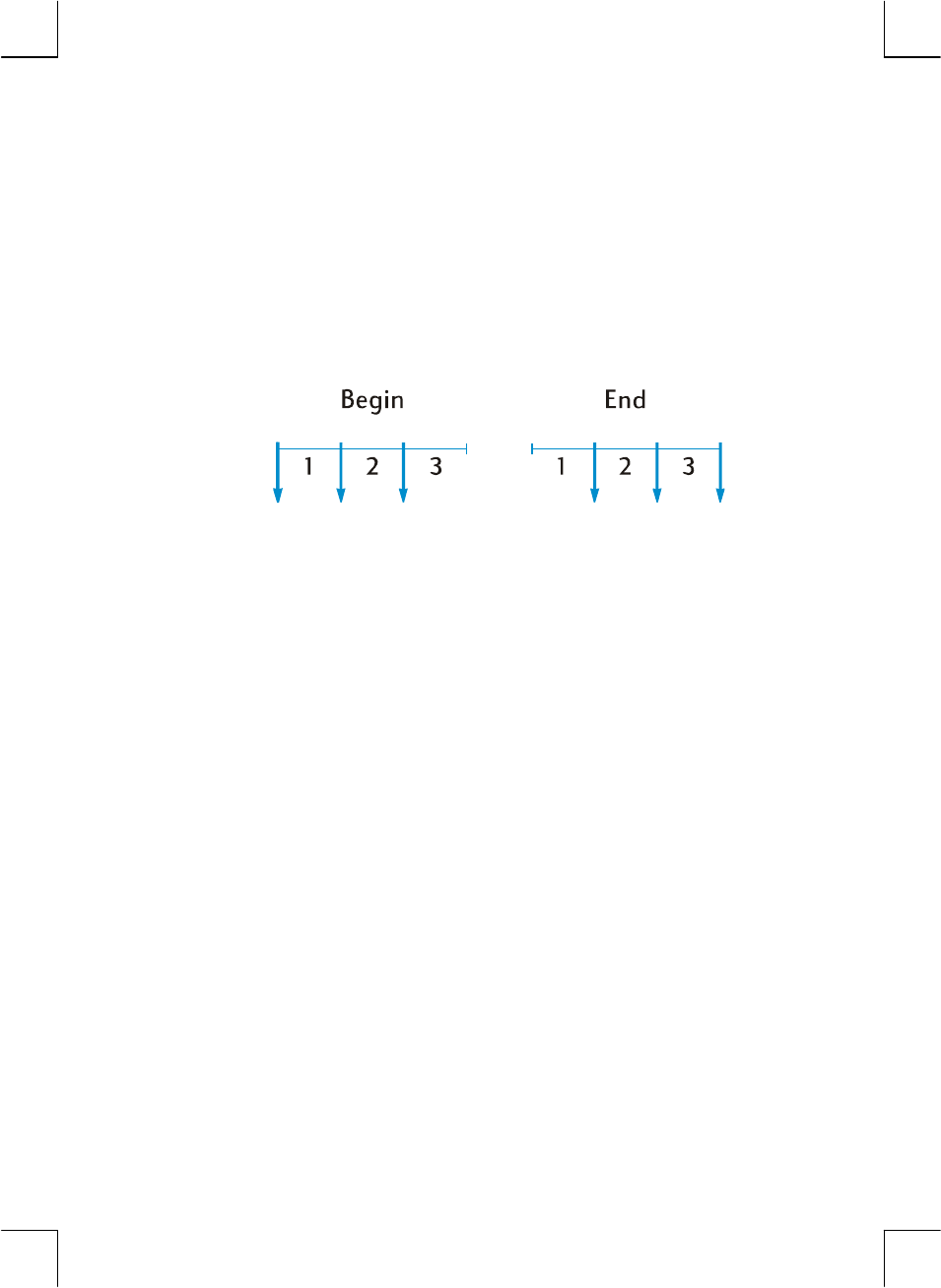
Section 3: Basic Financial Functions 37
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 37 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The Payment Mode
One more bit of information must be specified before you can solve a problem
involving periodic payments. Such payments can be made either at the beginning
of a compounding period (payments in advance, or annuities due) or at the end of
the period (payments in arrears, or ordinary annuities). Calculations involving
payments in advance yield different results than calculations involving payments in
arrears. Illustrated below are portions of cash flow diagrams showing payments in
advance (Begin) and payments in arrears (End). In the problem illustrated in the
cash flow diagram above, payments are made in arrears.
Regardless of whether payments are made in advance or in arrears, the number of
payments must be the same as the number of compounding periods.
To specify the payment mode:
z Press g× if payments are made at the beginning of the compounding
periods.
z Press g if payments are made at the end of the compounding periods.
The BEGIN status indicator is lit when the payment mode is set to Begin. If BEGIN
is not lit, the payment mode is set to End.
The payment mode remains set to what you last specified until you change it; it is
not reset each time the calculator is turned on. However, if Continuous Memory is
reset, the payment mode will be set to End.
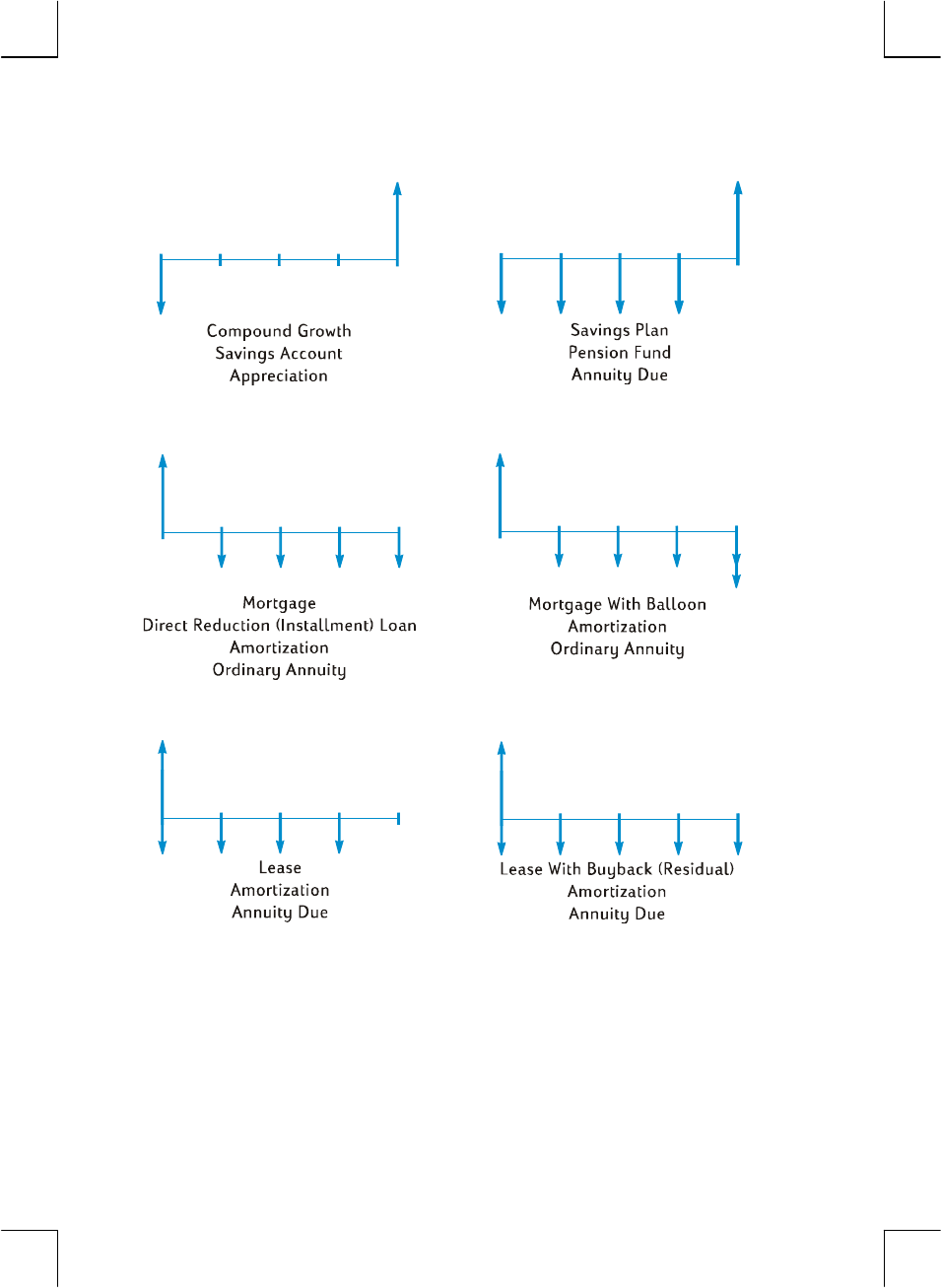
Generalized Cash Flow Diagrams
Examples of various kinds of financial calculations, together with the applicable
cash flow diagrams, appear under Compound Interest Calculations later in this
section. If your particular problem does not match any of those shown, you can
solve it nevertheless by first drawing a cash flow diagram, then keying the
quantities identified in the diagram into the corresponding registers. Remember
always to observe the sign convention when keying in PV, PMT, and FV.
The terminology used for describing financial problems varies among the different
segments of the business and financial communities. Nevertheless, most problems
involving compound interest can be solved by drawing a cash flow diagram in
one of the following basic forms. Listed below each form are some of the problems
to which that diagram applies.
38 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 38 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 39
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 39 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Compound Interest Calculations
Specifying the Number of Compounding Periods and the Periodic
Interest Rate
Interest rates are usually quoted at the annual rate (also called the nominal rate):
that is, the interest rate per year. However, in compound interest problems, the
interest rate entered into i must always be expressed in terms of the basic
compounding period, which may be years, months, days, or any other time unit.
For example, if a problem involves 6% annual interest compounded quarterly for 5
years, n — the number of quarters — would be 5 × 4 = 20 and i — the interest
rate per quarter — would be 6% ÷ 4 = 1.5%. If the interest were instead
compounded monthly, n would be 5 × 12 = 60 and i would be 6% ÷ 12 = 0.5%.
If you use the calculator to multiply the number of years by the number of
compounding periods per year, pressing n then stores the result into n. The same
is true for i. Values of n and i are calculated and stored like this in Example 2 on
page 47.
If interest is compounded monthly, you can use a shortcut provided on the
calculator to calculate and store n and i:
z To calculate and store n, key the number of years into the display, then press
gA.
z To calculate and store i, key the annual rate into the display, then press
gC.
Note that these keys not only multiply or divide the displayed number by 12; they
also automatically store the result in the corresponding register, so you need not
press the n or ¼ key next. The A and C keys are used in Example 1 on
page 46.
Calculating the Number of Payments or Compounding Periods
1. Press fCLEARG to clear the financial registers.
2. Enter the periodic interest rate, using ¼ or C.
3. Enter at least two of the following values:
z Present value, using $.
z Payment amount, using P.
z Future value, using M.
Note: Remember to observe
the cash flow sign convention.
4. If a PMT was entered, press g× or g to set the payment mode.
5. Press n to calculate the number of payments or periods.
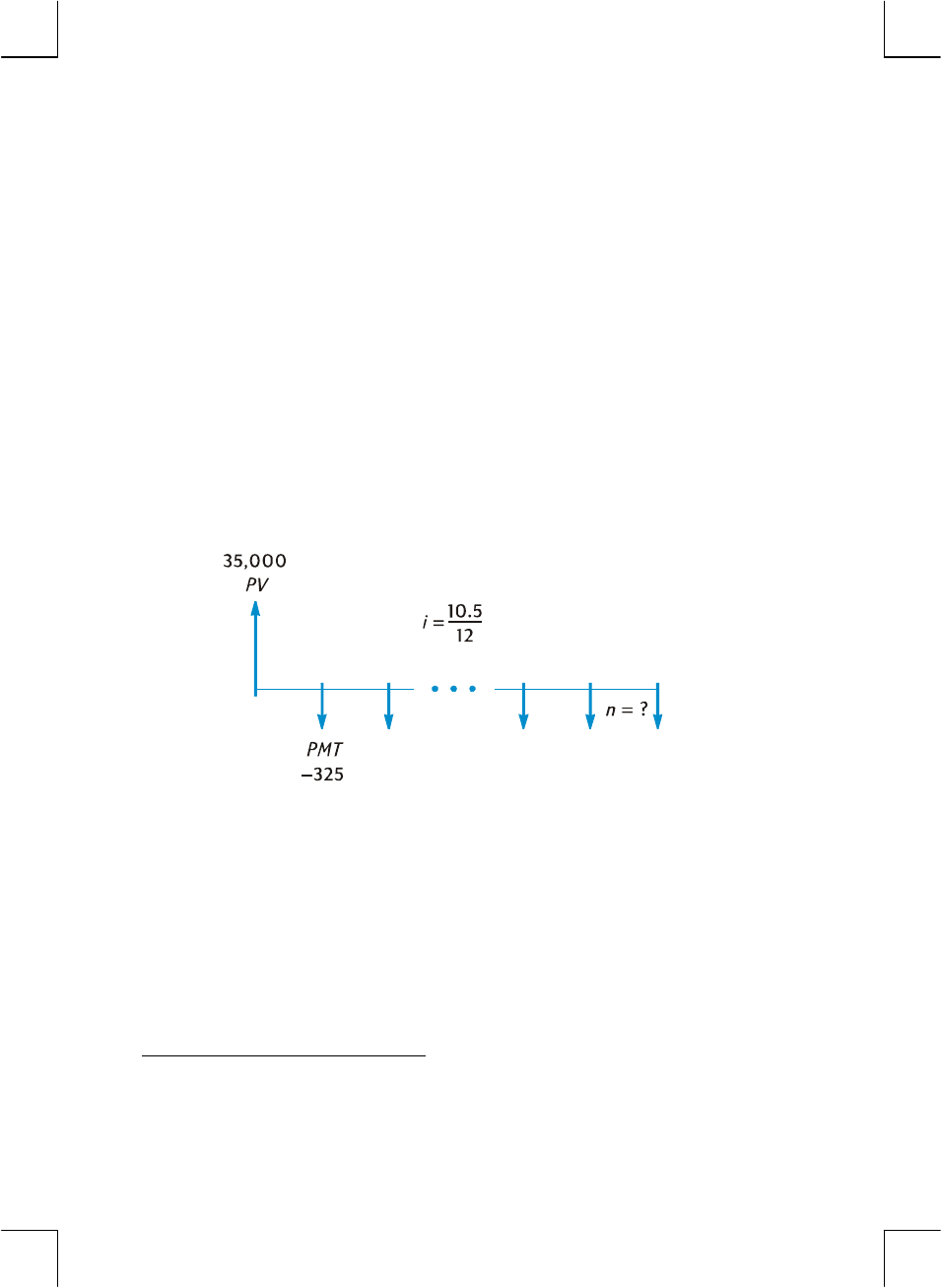
40 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 40 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
If the answer calculated is not an integer (that is, there would be nonzero digits to
the right of the decimal point), the calculator rounds the answer up to the next
higher integer before storing it in the n register and displaying it.* For example, if
n were calculated as 318.15, 319.00 would be the displayed answer.
n is rounded up by the calculator to show the total number of payments needed:
n–1 equal, full payments, and one final, smaller payment. The calculator does not
automatically adjust the values in the other financial registers to reflect n equal
payments; rather, it allows you to choose which, if any, of the values to adjust.†
Therefore, if you want to know the value of the final payment (with which you can
calculate a balloon payment) or desire to know the payment value for n equal
payments, you will need to press one of the other financial keys, as shown in the
following two examples.
Example 1: You’re planning to build a log cabin on your vacation property.
Your rich uncle offers you a $35,000 loan at 10.5% interest. If you make $325
payments at the end of each month, how many payments will be required to pay
off the loan, and how many years will this take?
Keystrokes Display
fCLEARG
10.5gC
0.88
Calculates and stores i.
35000$ 35,000.00 Stores PV.
325ÞP –325.00 Stores PMT (with minus sign for cash
paid out).
g –325.00 Sets the payment mode to End.
n 328.00 Number of payments required.
* The calculator will round n down to the next lower integer if the fractional portion of n is less
than 0.005.
† After calculating n, pressing ¼, $, P, or M will recalculate the value in the
corresponding financial register.

Section 3: Basic Financial Functions 41
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 41 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
12z 27.33 Twenty-seven years and four months.
Because the calculator rounds the calculated value of n up to the next higher
integer, in the preceding example it is likely that — while 328 payments will be
required to pay off the loan — only 327 full payments of $325 will be required,
the next and final payment being less than $325. You can calculate the final,
fractional, 328th payment as follows:
Keystrokes Display
328n 328.00 Stores total number of payments.*
M 181.89 Calculates FV — which equals the
overpayment if 328 full payments
were made.
:P –325.00 Recalls payment amount.
+ –143.11 Final, fractional payment.
Alternatively, you could make the fractional payment together with the 327th
payment. (Doing so will result in a somewhat smaller total of all payments, since
you will not have to pay interest during the 328th payment period.) You can
calculate this final, larger, 327th payment (essentially a balloon payment) as
follows:
Keystrokes Display
327n 327.00 Stores number of full payments.
M –141.87 Calculates FV — which is the balance
remaining after 327 full payments.
:P –325.00 Recalls payment amount.
+ –466.87 Final, balloon payment.
Instead of having a fractional (or balloon) payment at the end of the loan, you
might wish to make 327 or 328 equal payments. Refer to “Calculating the
Payment Amount” on page 46 for a complete description of this procedure.
* You could skip this step, since 328 is already stored in the n register. If you do so, however,
you will need to press M twice in the next step (for the reason discussed in the first footnote
on page 32; you would not have to press M twice if you had not pressed 12z after w in
the example above.) We choose to show this and the following example in a parallel format
so that the procedure is easy to remember: the number you key is the number of the final
payment — either the fractional payment or the balloon payment — whose amount is to be
calculated.
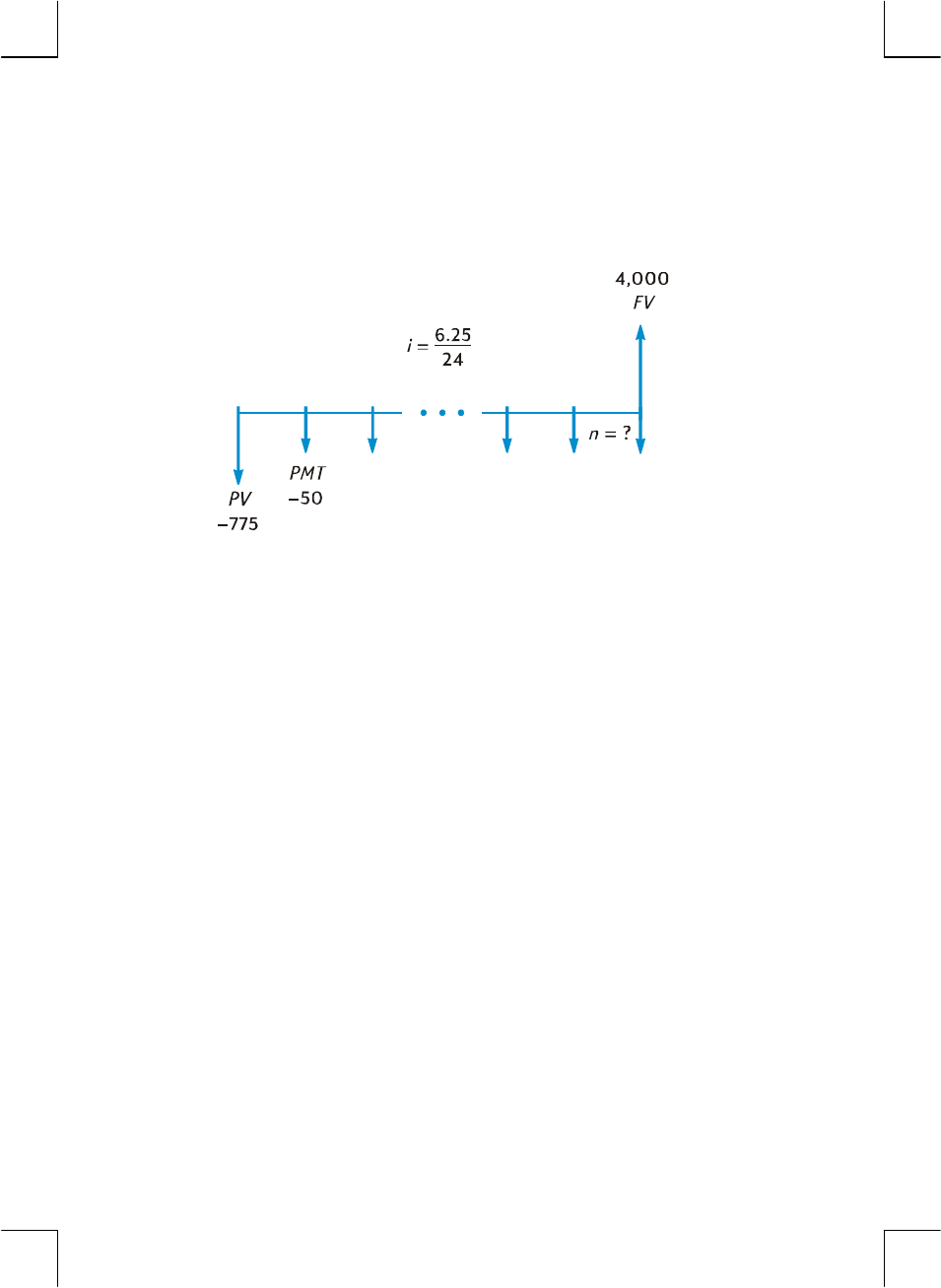
42 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 42 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 2: You’re opening a savings account today (the middle of the month)
with a $775 deposit. The account pays 61/4% interest compounded semimonthly.
If you make semimonthly deposits of $50 beginning next month, how long will it
take for your account to reach $4000?
Keystrokes Display
fCLEARG
6.25\24z¼
0.26
Calculates and stores i.
775Þ$ –775.00 Stores PV (with minus sign for cash
paid out).
50ÞP –50.00 Stores PMT (with minus sign for cash
paid out).
4000M 4,000.00 Stores FV.
g 4,000.00 Sets the payment mode to End.
n 58.00 Number of semimonthly deposits.
2z 29.00 Number of months.
As in Example 1, it is likely that only 57 full deposits will be required, the next and
final deposit being less than $50. You can calculate this final, fractional, 58th
deposit as in Example 1, except that for this example you must subtract the original
FV. (In Example 1, the original FV was zero.) The procedure is as follows:

Section 3: Basic Financial Functions 43
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 43 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
MM 4,027.27 Calculates FV – which equals the
balance in the account if 58 full
deposits were made.*
:P –50.00 Recalls amount of deposits.
+ 3,977.27 Calculates the balance in the account
if 57 full deposits were made and
interest accrued during the 58th
month.†
4000- –22.73 Calculates final, fractional, 58th
deposit required to reach $4,000.
Calculating the Periodic and Annual Interest Rates
1. Press fCLEARG to clear the financial registers.
2. Enter the number of payments or periods, using n or A.
3. Enter at least two of the following values:
z Present value, using $.
z Payment amount, using P.
z Future value, using M.
Note: Remember to
observe the cash flow si
g
n
convention.
4. If a PMT was entered, press g× or g to set the payment mode.
5. Press ¼ to calculate the periodic interest rate.
6. To calculate the annual interest rate, key in the number of periods per year,
then press §.
* In this example, M must be pressed twice, since the preceding key pressed was z. If we
had stored the number of deposits in n (as we did following Example 1), we would have to
press M only once here, since the preceding key pressed would have been w (as it was
following Example 1). Remember that it is not necessary to store the number of payments in n
before calculating the amount of the final, fractional payment. (Refer to the preceding
footnote.)
† You might think that we could calculate the balance in the account after 57 full deposits were
made simply by storing that number in n and then calculating FV, as we did using the second
method following Example 1. However, this balance would not include the interest accrued
during the 58th month.
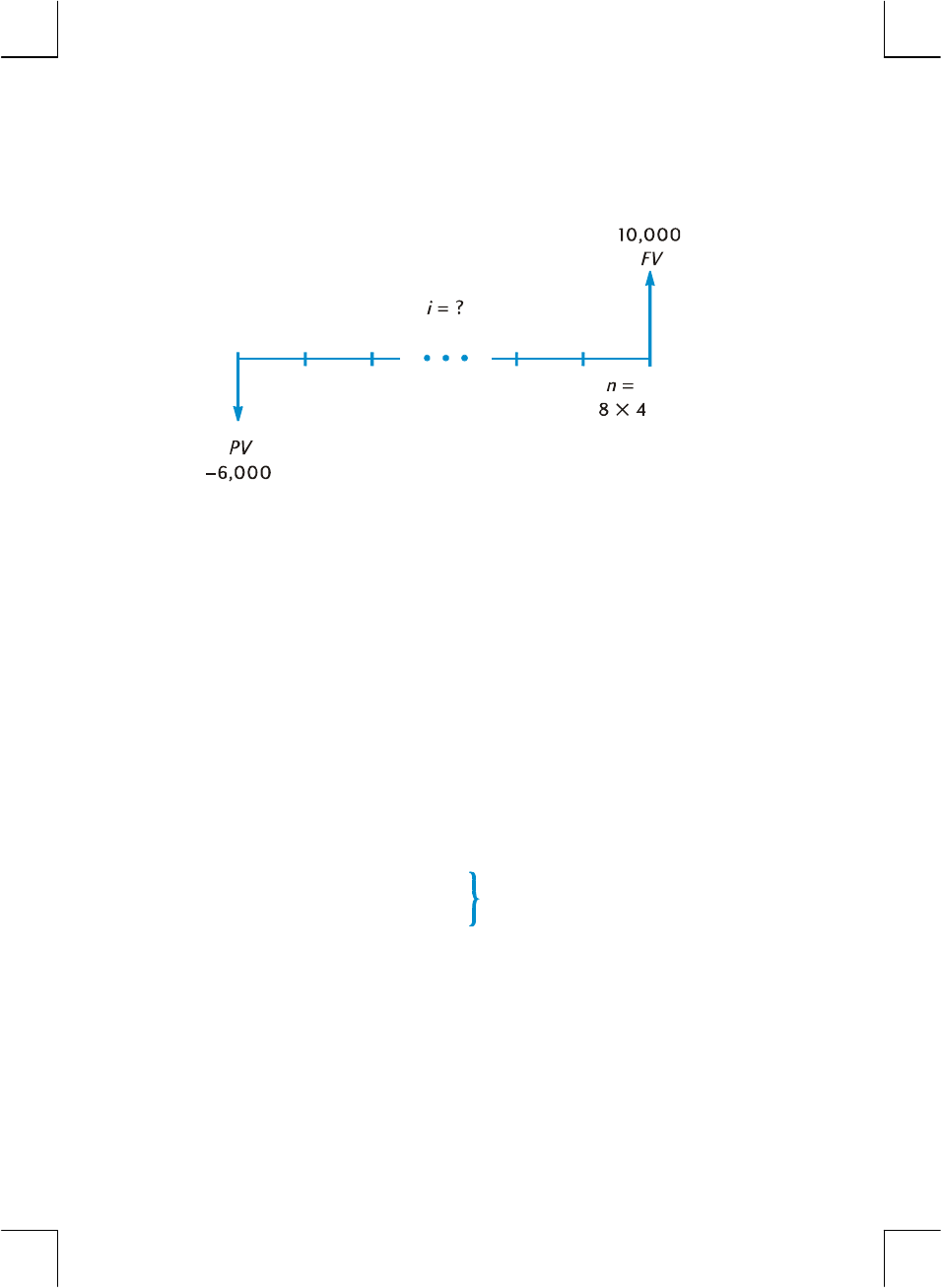
44 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 44 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example: What annual interest rate must be obtained to accumulate $10,000 in
8 years on an investment of $6,000 with quarterly compounding?
Keystrokes Display
fCLEARG
8\4§w
32.00
Calculates and stores n.
6000Þ$ –6,000.00 Stores PV (with minus sign for cash
paid out).
10000M 10,000.00 Stores FV.
¼ 1.61 Periodic (quarterly) interest rate.
4§ 6.44 Annual interest rate.
Calculating the Present Value
1. Press fCLEARG to clear the financial registers.
2. Enter the number of payments or periods, using n or A.
3. Enter the periodic interest rate, using ¼ or C.
4. Enter either or both of the following:
z Payment amount, using P.
z Future value, using M.
Note: Remember to
observe the cash flow si
g
n
convention.
5. If a PMT was entered, press g× or g to set the payment mode.
6. Press $ to calculate the present value.
Section 3: Basic Financial Functions 45
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 45 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 1: You’re financing a new car purchase with a loan from an institution
that requires 15% interest compounded monthly over the 4-year term of the loan. If
you can make payments of $150 at the end of each month and your down
payment will be $1,500, what is the maximum price you can pay for the car?
(Assume the purchase date is one month prior to the date of the first payment.)
Keystrokes Display
fCLEARG
4gA
48.00
Calculates and stores n.
15gC 1.25 Calculates and stores i.
150ÞP –150.00 Stores PMT (with minus sign for cash
paid out).
g –150.00 Sets payment mode to End.
$ 5,389.72 Maximum amount of loan.
1500+ 6,889.72 Maximum purchase price.
Example 2: A development company would like to purchase a group of
condominiums with an annual net cash flow of $17,500. The expected holding
period is 5 years, and the estimated selling price at that time is $540,000.
Calculate the maximum amount the company can pay for the condominiums in
order to realize at least a 12% annual yield.
46 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 46 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
fCLEARG
5n
5.00
Stores n.
12¼ 12.00 Stores i.
17500P 17,500.00 Stores PMT. Unlike in the previous
problem, here PMT is positive
since it represents cash received.
540000M 540,000.00 Stores FV.
g 540,000.00 Sets payment mode to End.
$ –369,494.09 The maximum purchase price to
provide a 12% annual yield. PV is
displayed with a minus sign since
it represents cash paid out.
Calculating the Payment Amount
1. Press fCLEARG to clear the financial registers.
2. Enter the number of payments or periods, using n or A.
3. Enter the periodic interest rate, using ¼ or C.
4. Enter either or both of the following:
z Present value, using $.
z Future value, using M.
Note: Remember to
observe the cash flow si
g
n
convention.
5. Press g× or g to set the payment mode.
6. Press P to calculate the payment amount.
Example 1: Calculate the payment amount on a 29-year, $43,400 mortgage at
141/4% annual interest.
Section 3: Basic Financial Functions 47
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 47 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
fCLEARG
29gA
348.00
Calculates and stores n.
14.25gC 1.19 Calculates and stores i.
43400$ 43,400.00 Stores PV.
g 43,400.00 Sets payment mode to End.
P –523.99 Monthly payment (with minus sign
for cash paid out).
Example 2: Looking forward to retirement, you wish to accumulate $60,000
after 15 years by making deposits in an account that pays 93/4% interest
compounded semiannually. You open the account with a deposit of $3,200 and
intend to make semiannual deposits, beginning six months later, from your
profit-sharing bonus paychecks. Calculate how much these deposits should be.
Keystrokes Display
fCLEARG
15\2µw
30.00
Calculates and stores n.
9.75\2z¼ 4.88 Calculates and stores i.
3200Þ$ –3200.00 Stores PV (with minus sign for cash
paid out).
60000M 60,000.00 Stores FV.
g 60,000.00 Sets payment mode to End.
P –717.44 Semiannual payment (with minus sign
for cash paid out).
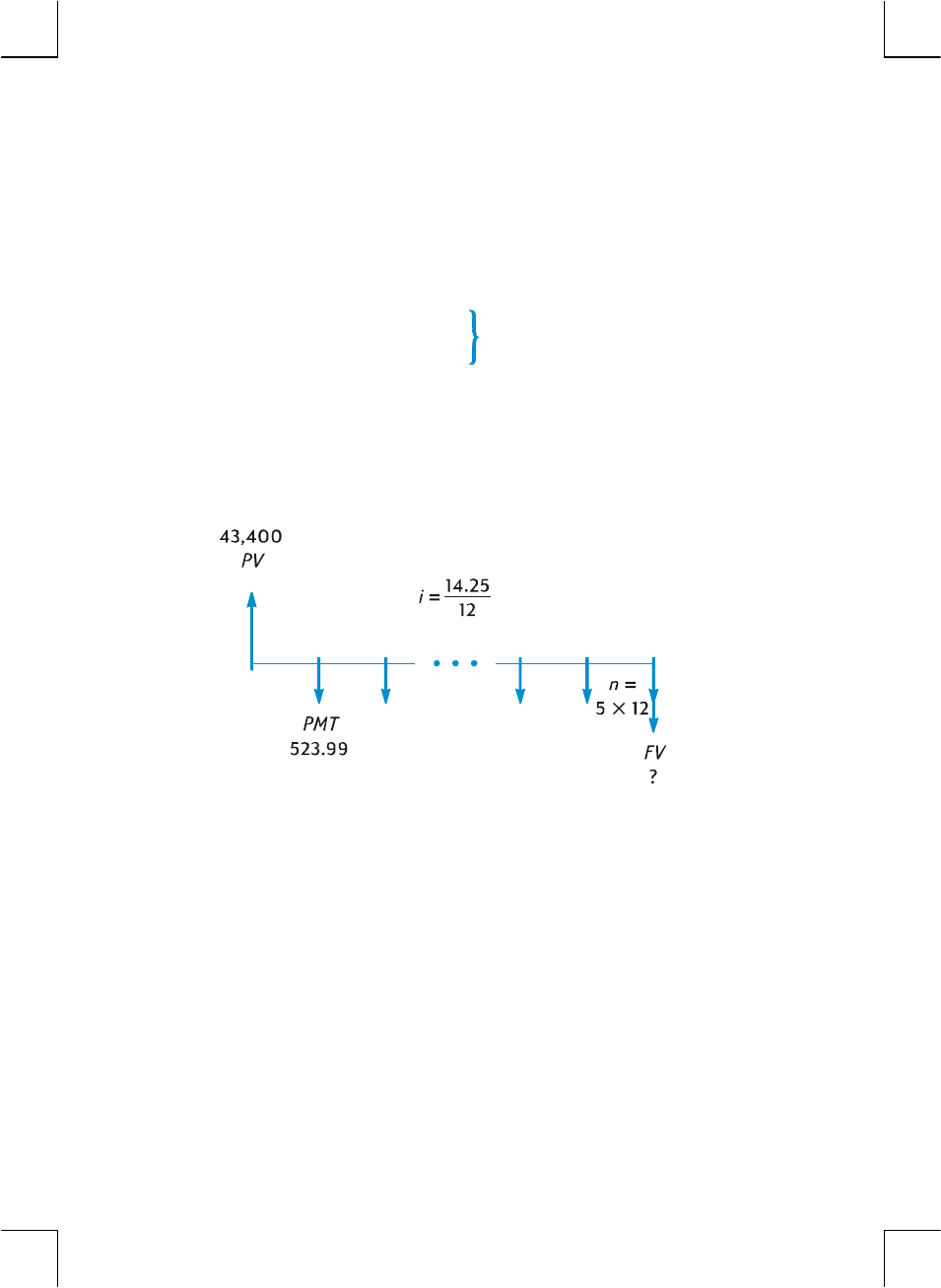
48 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 48 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Calculating the Future Value
1. Press fCLEARG to clear the financial registers.
2. Enter the number of payments or periods, using n or A.
3. Enter the periodic interest rate, using ¼ or C.
4. Enter either or both of the following:
z Present value, using $.
z Payment amount, using P.
Note: Remember to
observe the cash flow si
g
n
convention.
5. If a PMT was entered, press g× or g to set the payment mode.
6. Press M to calculate the future value.
Example 1: In Example 1 on page 46, we calculated that the payment amount
on a 29-year, $43,400 mortgage at 141/4% annual interest is $523.99. If the
seller requests a balloon payment at the end of 5 years, what would be the
amount of the balloon?
Keystrokes Display
fCLEARG
5gA
60.00
Calculates and stores n.
14.25gC 1.19 Calculates and stores i.
43400$ 43,400.00 Stores PV.
523.99ÞP –523.99 Stores PMT (with minus sign for cash
paid out).
g –523.99 Sets payment mode to End.
M –42,652.37 Amount of balloon payment.
Section 3: Basic Financial Functions 49
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 49 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 2: If you deposit $50 a month (at the beginning of each month) into a
new account that pays 61/4% annual interest compounded monthly, how much will
you have in the account after 2 years?
Keystrokes Display
fCLEARG
2gA
24.00
Calculates and stores n.
6.25gC 0.52 Calculates and stores i.
50ÞP –50.00 Stores PMT (with minus sign for cash
paid out).
g× –50.00 Sets payment mode to Begin.
M 1,281.34 Balance after 2 years.
Example 3: Property values in an unattractive area are depreciating at the rate
of 2% per year. Assuming this trend continues, calculate the value in 6 years of
property presently appraised at $32,000.
Keystrokes Display
fCLEARG
6n
6.00
Stores n.
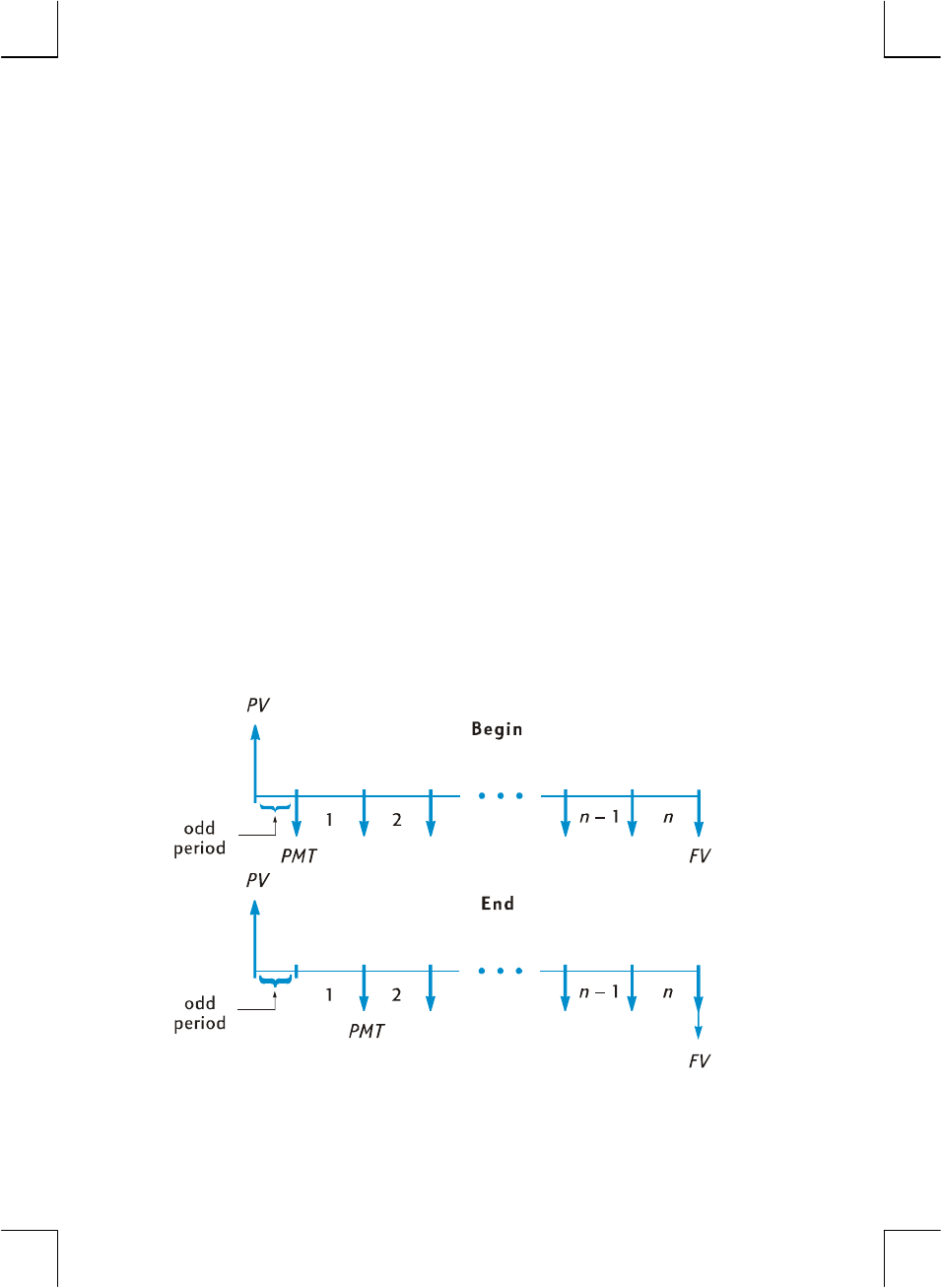
50 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 50 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
2Þ¼ –2.00 Stores i (with minus sign for a
“negative interest rate”).
32000Þ $ –32,000.00 Stores PV (with minus sign for cash
paid out).
M 28,346.96 Property value after 6 years.
Odd-Period Calculations
The cash flow diagrams and examples presented so far have dealt with financial
transactions in which interest begins to accrue at the beginning of the first regular
payment period. However, interest often begins to accrue prior to the beginning of
the first regular payment period. The period from the date interest begins accruing
to the date of the first payment, being not equal to the regular payment periods is
sometimes referred to as an “odd first period”. For simplicity, in using the hp 12c
we will always regard the first period as equal to the remaining periods, and we
will refer to the period between the date interest begins accruing and the
beginning of the first payment period as simply the “odd period” or the “odd
days”. (Note that the odd period is always assumed by the calculator to occur
before the first full payment period.) The following two cash flow diagrams
represent transactions including an odd period for payments in advance (Begin)
and for payments in arrears (End).

Section 3: Basic Financial Functions 51
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 51 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
You can calculate i, PV, PMT, and FV for transactions involving an odd period
simply by entering a noninteger n. (A noninteger is a number with at least one
nonzero digit to the right of the decimal point.) This places the calculator in
Odd-Period mode.* The integer part of n (the part to the left of the decimal point)
specifies the number of full payment periods, and the fractional part (the part to the
right of the decimal) specifies the length of the odd period as a fraction of a full
period. The odd period, therefore, cannot be greater than one full period.
The fractional part of n can be determined using either the actual number of odd
days or the number of odd days counted on the basis of a 30-day month.† The
Ò function can be used to calculate the number of odd days either way. The
fractional part of n is a fraction of a payment period, so the number of odd days
must be divided by the number of days in a period. If interest is compounded
monthly, for this number you can use either 30, 365/12, or (if the odd period falls
entirely within a single month) the actual number of days in that month. Usually, a
monthly period is taken to be 30 days long.
At your option, the calculations of i, PV, PMT, and FV can be performed with either
simple interest or compound interest accruing during the odd period. If the C status
indicator in the display is not lit, simple interest is used. To specify compound
interest, turn the C indicator on by pressing ?Æ.‡ Pressing ?Æ again
turns the C indicator off, and calculations will then be performed using simple
interest for the odd period.
* Calculations of i, PMT, and FV are performed using the present value at the end of the odd
period. This is equal to the number in the PV register plus the interest accrued during the odd
period. When calculating PV in Odd-Period mode, the calculator returns a value equal to the
present value at the beginning of the odd period and stores it in the PV register.
After calculating i, PV, PMT, or FV in Odd-Period mode, you should not try to calculate n. If
you do, the calculator will switch out of Odd-Period mode and compute n without taking the
odd period into account. The values in the other financial registers will correspond to the new
n, but the original assumptions for the problem will be changed.
† The two methods of counting odd days will yield slightly different answers. If you are
calculating i to determine the annual percentage rate (APR) for an odd-period transaction, the
lower APR will result if the calculation uses the greater number of odd days determined using
the two methods.
‡ ?Æ is not programmable.

52 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 52 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 1: A 36-month loan for $4,500 accrues interest at a 15% annual
percentage rate (APR), with the payments made at the end of each month. If
interest begins accruing on this loan on February 15, 2004 (so that the first period
begins on March 1, 2004), calculate the monthly payment, with the odd days
counted on the basis of a 30-day month and compound interest used for the odd
period.
Keystrokes Display
fCLEARG Clears financial registers.
gÕ Sets date format to month-day-year.
g Sets payment mode to End.
?Æ Turns on the
Cindicator in the display,
so that compound interest will be used
for the odd period.
2.152004\ 2.15 Keys in the date interest begins
accruing and separates it from the
next date entered.
3.012004 3.012004 Keys in the date of the beginning of
the first period.
gÒ 15.00 Actual number of odd days.
~ 16.00 Number of odd days counted on the
basis of a 30-day month.
30z 0.53 Divides by the length of a monthly
period to get the fractional part of n.
36+n 36.53 Adds the fractional part of n to the
number of complete payment periods,
then stores the result in n.
15gC 1.25 Calculates and stores i.
4500$ 4,500.00 Stores PV.
P –157.03 Monthly payment.

Section 3: Basic Financial Functions 53
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 53 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 2: A 42-month car loan for $3,950 began accruing interest on July 19,
2004, so that the first period began on August 1, 2004. Payments of $120 are
made at the end of each month. Calculate the annual percentage rate (APR), using
the actual number of odd days and simple interest for the odd period.
Keystrokes Display
fCLEARG Clears financial registers.
?Æ Turns off the Cindicator in the display,
so that simple interest will be used for
the odd period.
7.192004\ 7.19 Keys in the date interest begins
accruing and separates it from the
next date entered.
8.012004 8.012004 Keys in the date of the beginning of
the first period.
gÒ 13.00 Actual number of odd days.
30z 0.43 Divides by the length of a monthly
period to get the fractional part of n.
42+n 42.43 Adds the fractional part of n to the
number of complete payment periods,
then stores the result in n.
3950$ 3,950.00 Stores PV.
120ÞP –120.00 Stores PMT (with minus sign for cash
paid out).
¼ 1.16 Periodic (monthly) interest rate.
12§ 13.95 Annual percentage rate (APR).

54 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 54 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Amortization
The hp 12c enables you to calculate the amounts applied toward principal and
toward interest from a single loan payment or from several payments, and also
tells you the remaining balance of the loan after the payments are made.*
To obtain an amortization schedule:
1. Press fCLEARG to clear the financial registers.
2. Enter the periodic interest rate, using ¼ or C.
3. Enter the amount of the loan (the principal), using $.
4. Key in the periodic payment, then press ÞP (the sign of PMT must be
negative, in accordance with the cash flow sign convention).
5. Press g× or (for most direct reduction loans) g to set the payment
mode.
6. Key in the number of payments to be amortized.
7. Press
f! to display the amount from those payments applied toward
interest.
8. Press ~ to display the amount from those payments applied toward the
principal.
9. To display the number of payments just amortized, press dd.
10. To display the remaining balance of the loan, press :$.
11.To display the total number of payments amortized, press :n.
Example: For a house you’re about to buy, you can obtain a 25-year mortgage
for $50,000 at 131/4% annual interest. This requires payments of $573.35 (at the
end of each month). Find the amounts that would be applied to interest and to the
principal from the first year’s payments.
Keystrokes Display
fCLEARG
13.25gC
1.10
Enters i.
50000$ 50,000.00 Enters PV.
* All amounts calculated when f! is pressed are automatically rounded to the number of
decimal places specified by the display format. (The display format is described in Section 5.)
This rounding affects the number inside the calculator as well as how the number appears in
the display. The amounts calculated on your hp 12c may differ from those on the statements
of lending institutions by a few cents, since different rounding techniques are sometimes used.
To calculate answers rounded to a different number of decimal places, press f followed by
the number of decimal places desired before you press f!.

Section 3: Basic Financial Functions 55
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 55 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
573.35ÞP –573.35 Enters PMT (with minus sign for cash
paid out).
g –573.35 Sets payment mode to End.
12f! –6,608.89 Portion of first year’s payments (12
months) applied to interest.
~ –271.31 Portion of first year’s payments
applied to principal.
:$ 49,728.69 Balance remaining after 1 year.
:n 12.00 Total number of payments amortized.
The number of payments keyed in just before f! is pressed is taken to be the
payments following any that have already been amortized. Thus, if you now press
12f!, your hp 12c will calculate the amounts applied to interest and to the
principal from the second year’s payments (that is, the second 12 months):
Keystrokes Display
12f! –6,570.72 Portion of second year’s payments
applied to interest.
~ –309.48 Portion of second year’s payments
applied to principal.
dd 12.00 Number of payments just amortized.
:$ 49,419.21 Balance remaining after 2 years.
:n 24.00 Total number of payments amortized.
Pressing :$ or :n displays the number in the PV or n register. When you
did so after each of the last two calculations, you may have noticed that PV and n
had been changed from their original values. The calculator does this so that you
can easily check the remaining balance and the total number of payments
amortized. But because of this, if you want to generate a new amortization
schedule from the beginning, you must reset PV to its original value and reset n to
0.
For example, suppose you now wanted to generate an amortization schedule for
each of the first two months:
Keystrokes Display
50000$ 50,000.00 Resets PV to original value.
0n 0.00 Resets n to zero.

56 Section 3: Basic Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 56 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
1f! –552.08 Portion of first payment applied to
interest.
~ –21.27 Portion of first payment applied to
principal.
1f! –551.85 Portion of second payment applied to
interest.
~ –21.50 Portion of second payment applied to
principal.
:n 2.00 Total number of payments amortized.
If you want to generate an amortization schedule but do not already know the
monthly payment:
1. Calculate PMT as described on page 46.
2. Press 0n to reset n to zero.
3. Proceed with the amortization procedure listed on page 54 beginning with
step 6.
Example: Suppose you obtained a 30-year mortgage instead of a 25-year
mortgage for the same principal ($50,000) and at the same interest rate (131/4%)
as in the preceding example. Calculate the monthly payment, then calculate the
amounts applied to interest and to the principal from the first month’s payment.
Since the interest rate is not being changed, do not press fCLEARG; to
calculate PMT, just enter the new value for n, reset PV, then press P.
Keystrokes Display
30gA 360.00 Enters n.
50000$ 50,000.00 Enters PV.
P –562.89 Monthly payment.
0n 0.00 Resets n to zero.
1f! –552.08 Portion of first payment applied to
interest.
~ –10.81 Portion of first payment applied to
principal.
:$ 49,989.19 Remaining balance.
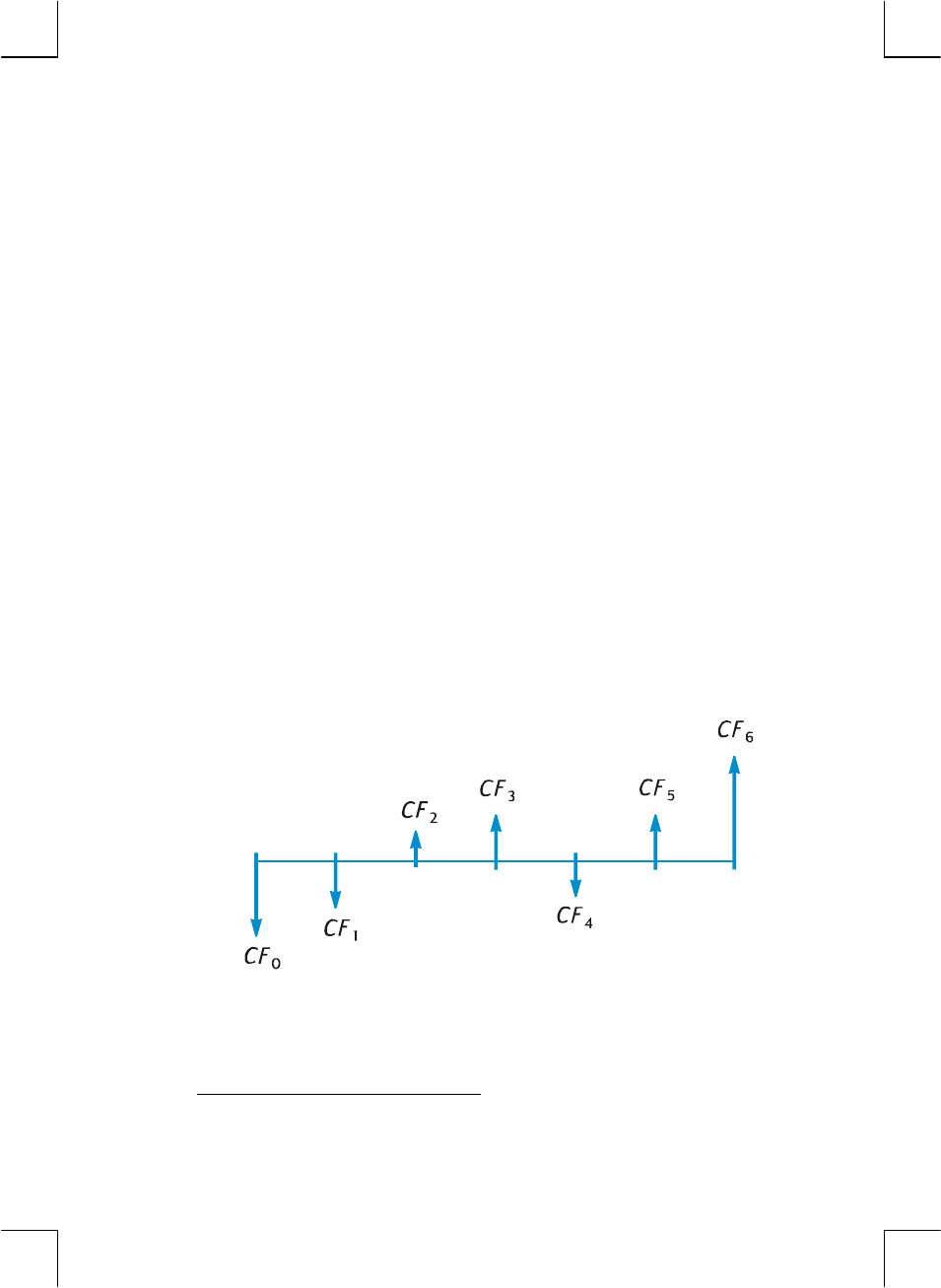
57
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 57 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 4
Additional Financial
Functions
Discounted Cash Flow Analysis: NPV and IRR
The hp 12c provides functions for the two most widely-used methods of discounted
cash flow analysis: l (net present value) and L (internal rate of return). These
functions enable you to analyze financial problems involving cash flows (money
paid out or received) occurring at regular intervals. As in compound interest
calculations, the interval between cash flows can be any time period; however, the
amounts of these cash flows need not be equal.
To understand how to use l and L, let’s consider the cash flow diagram for
an investment that requires an initial cash outlay (CF0) and generates a cash flow
(CF1) at the end of the first year, and so on up to the final cash flow (CF6) at the
end of the sixth year. In the following diagram, the initial investment is denoted by
CF0, and is depicted as an arrow pointing down from the time line since it is cash
paid out. Cash flows CF1 and CF4 also point down from the time line, because they
represent projected cash flow losses.
NPV is calculated by adding the initial investment (represented as a negative cash
flow) to the present value of the anticipated future cash flows. The interest rate, i,
will be referred to in this discussion of NPV and IRR as the rate of return.* The
value of NPV indicates the result of the investment:
* Other terms are sometimes used to refer to the rate of return. These include: required rate of
return, minimally acceptable rate of return, and cost of capital.

58 Section 4: Additional Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 58 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
z If NPV is positive, the financial value of the investor’s assets would be
increased: the investment is financially attractive.
z If NPV is zero, the financial value of the investor’s assets would not change:
the investor is indifferent toward the investment.
z If NPV is negative, the financial value of the investor’s assets would be
decreased: the investment is not financially attractive.
A comparison of the NPV’s of alternative investment possibilities indicates which of
them is most desirable: the greater the NPV, the greater the increase in the
financial value of the investor’s assets.
IRR is the rate of return at which the discounted future cash flows equal the initial
cash outlay: IRR is the discount rate at which NPV is zero. The value of IRR relative
to the present value discount rate also indicates the result of the investment:
z If IRR is greater than the desired rate of return, the investment is financially
attractive.
z If IRR is equal to the desired rate of return, the investor is indifferent toward
the investment.
z If IRR is less than the desired rate of return, the investment is not financially
attractive.
Calculating Net Present Value (NPV)
Calculating NPV for Ungrouped Cash Flows. If there are no equal
consecutive cash flows, use the procedure described (and then summarized) below.
With this procedure, NPV (and IRR) problems involving up to 20 cash flows (in
addition to the initial investment CF0) can be solved. If two or more consecutive
cash flows are equal — for example, if the cash flows in periods three and four
are both $8,500 — you can solve problems involving more than 20 cash flows, or
you can minimize the number of storage registers required for problems involving
less than 20 cash flows, by using the procedure described next (under Calculating
NPV for Grouped Cash Flows, page 61).
The amount of the initial investment (CF0) is entered into the calculator using the
J key. Pressing gJ stores CF0 in storage register R0 and also stores the
number 0 in the n register.

Section 4: Additional Financial Functions 59
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 59 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The amounts of the subsequent cash flows are stored – in the order they occur – in
the remaining storage registers: CF1 thru CF9 in R1 thru R9, and CF10 thru CF19 in R.0
thru R.9, respectively. If there is a CF20, that amount is stored in the FV register.*
Each cash flow (CF1, CF2, etc.) is designated CFj, where j takes on values from 1
up to the number of the final cash flow. The amount of a cash flow is entered using
the K key. Each time gK is pressed, the amount in the display is stored in
the next available storage register, and the number in the n register is increased
by 1. This register therefore counts how many cash flow amounts (in addition to
the initial investment CF0) have been entered.
Note: When entering cash flow amounts — including the initial investment
CF0 — remember to observe the cash flow sign convention by pressing Þ
after keying in a negative cash flow.
In summary, to enter the cash flow amounts:
1. Press fCLEARH to clear the financial and storage registers.
2. Key in the amount of the initial investment, press Þ if that cash flow is
negative, then press gJ. If there is no initial investment, press 0gJ.
3. Key in the amount of the next cash flow, press Þ if the cash flow is
negative, then press gK. If the cash flow amount is zero in the next
period, press 0 gK.
4. Repeat step 3 for each cash flow until all have been entered.
With the amounts of the cash flows stored in the calculator’s registers, you can
calculate NPV as follows:
1. Enter the interest rate, using ¼ or C.
2. Press fl.
The calculated value of NPV appears in the display and also is automatically
stored in the PV register.
* If you have stored a program in the calculator, the number of registers available for storing
cash flow amounts may be less than 21. (Storage registers are automatically allocated to
program lines beginning with R.9 and proceeding in reverse order to R7, as described on
pages 93 thru 95.) The maximum number of cash flow amounts (in addition to CF0) that can
be stored is the number that appears at the right of the display when gN is pressed. If the
maximum number of cash flow amounts is stored, the final cash flow amount is always stored
in the FV register. For example, if N displays P-08 r-20, the last cash flow amount that can
be stored – CF20 – will be stored in FV. Similarly, if N displays P-22 r-18, the last cash
flow amount that can be stored – CF18 – will be stored in FV.
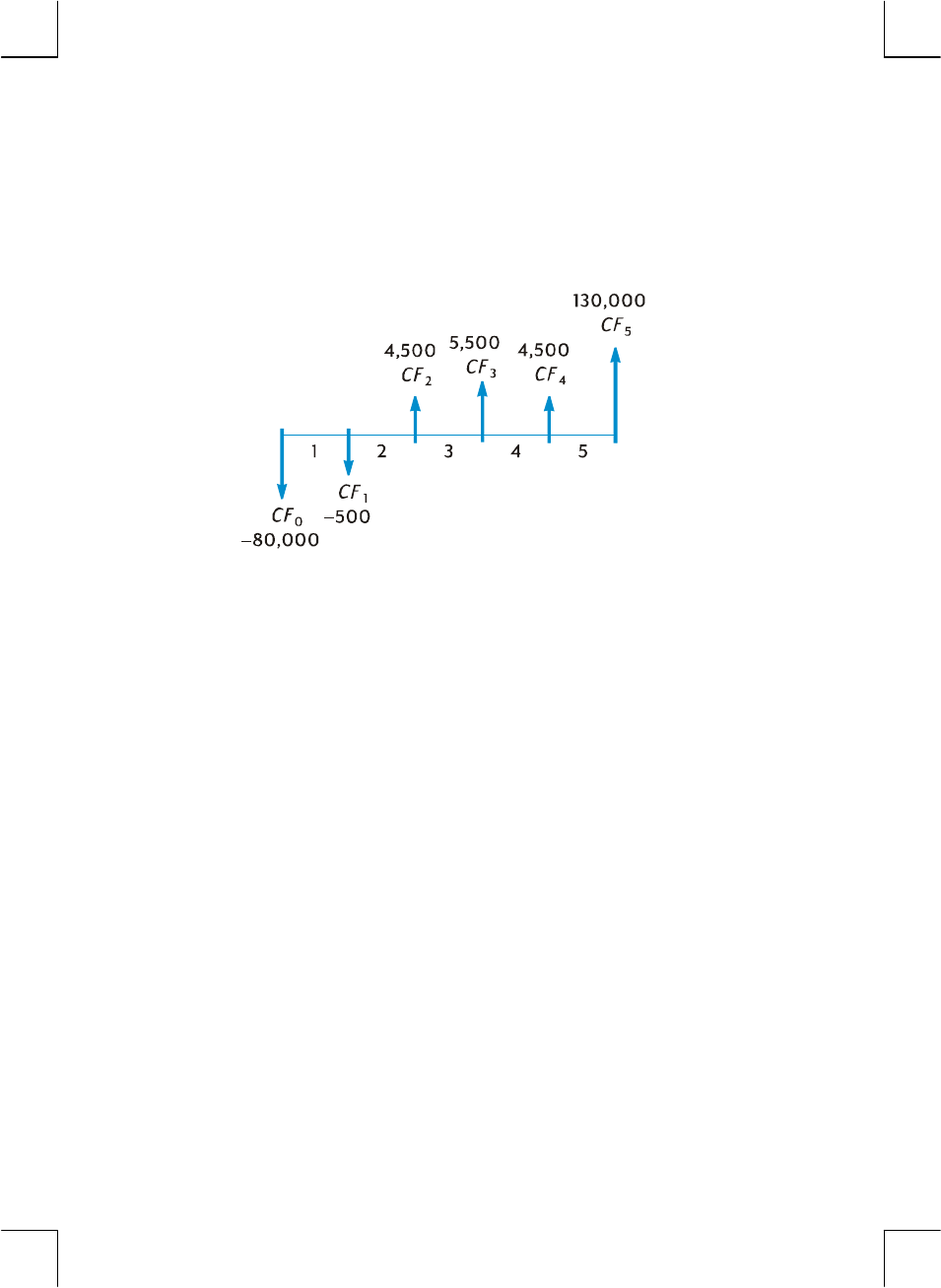
60 Section 4: Additional Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 60 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example: An investor has an opportunity to buy a duplex for $80,000 and
would like a return of at least 13%. He expects to keep the duplex 5 years and
then sell it for $130,000; and he anticipates the cash flows shown in the diagram
below. Calculate NPV to determine whether the investment would result in a return
or a loss.
Note that although a cash flow amount ($4,500) occurs twice, these cash flows
are not consecutive. Therefore, these cash flows must be entered using the method
described above.
Keystrokes Display
fCLEARH 0.00 Clears financial and storage registers.
80000ÞgJ –80,000.00 Stores CF0 (with minus sign for a
negative cash flow).
500ÞgK –500.00 Stores CF1 (with minus sign for a
negative cash flow).
4500gK 4,500.00 Stores CF2.
5500gK 5,500.00 Stores CF3.
4500gK 4,500.00 Stores CF4.
130000gK 130,000.00 Stores CF5.
:n 5.00 Checks number of cash flow amounts
entered (in addition to CF0 ).
13¼ 13.00 Stores i.
fl 212.18 NPV.
Since NPV is positive, the investment would increase the financial value of the
investor’s assets.

Section 4: Additional Financial Functions 61
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 61 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Calculating
NPV
for Grouped Cash Flows. A maximum of 20 cash flow
amounts (in addition to the initial investment CF0) can be stored in the hp 12c.*
However, problems involving more than 20 cash flows can be handled if among
the cash flows there are equal consecutive cash flows. For such problems, you
merely enter along with the amounts of the cash flows the number of times — up to
99 — each amount occurs consecutively. This number is designated Nj,
corresponding to cash flow amount CFj, and is entered using the a key. Each Nj
is stored in a special register inside the calculator.
This method can, of course, be used for problems involving fewer than 20 cash
flows — and it will require fewer storage registers than the method described
above under Calculating NPV for Ungrouped Cash Flows. Equal consecutive cash
flows can be entered using that method — provided there are enough storage
registers available to accommodate the total number of individual cash flows. The
facility of grouping equal consecutive cash flows is provided to minimize the
number of storage registers required.
Note: When entering cash flow amounts — including the initial investment
CF0 — remember to observe the cash flow sign convention by pressing Þ
after keying in the amount for a negative cash flow.
In summary, to enter the amounts of the cash flows and the number of times they
occur consecutively:
1. Press fCLEARH to clear the financial and storage registers.
2. Key in the amount of the initial investment, press Þ if that cash flow is
negative, then press gJ. If there is no initial investment, press 0gJ.
3. If the initial investment consists of more than one cash flow of the amount
entered in step 2, key in the number of those cash flows, then press ga. If
ga is not pressed, the calculator assumes that N0 is 1.
4. Key in the amount of the next cash flow, press Þ if that cash flow is
negative, then press gK. If the cash flow amount is zero in the next
period, press 0gK.
5. If the amount entered in step 4 occurs more than once consecutively, key in
the number of times that cash flow amount occurs consecutively, then press
ga. If ga is not pressed, the calculator assumes that Nj is 1 for the CFj
just entered.
6. Repeat steps 4 and 5 for each CFj and Nj until all cash flows have been
entered.
With the amounts of the cash flows and the number of times they occur
consecutively stored in the calculator, NPV can be calculated by entering the
interest rate and pressing fl, just as described earlier.
* If you have stored a program in the calculator, the number of registers available for storing
cash flow amounts may be less than 21.

62 Section 4: Additional Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 62 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example: An investor has an opportunity to purchase a piece of property for
$79,000; and he would like a 131/2% return. He expects to be able to sell it after
10 years for $100,000 and anticipates the yearly cash flows shown in the table
below:
Year Cash Flow Year Cash Flow
1
2
3
4
5
$14,000
$11,000
$10,000
$10,000
$10,000
6
7
8
9
10
$9,100
$9,000
$9,000
$4,500
$100,000
Since two cash flow amounts ($10,000 and $9,000) are repeated consecutively,
we can minimize the number of storage registers required by using the method just
described.
Keystrokes Display
fCLEARH 0.00 Clears financial and storage
registers.
79000ÞgJ –79,000.00 Initial investment (with minus si
g
n for
a negative cash flow).
14000gK 14,000.00 First cash flow amount.
11000gK 11,000.00 Next cash flow amount.
10000gK 10,000.00 Next cash flow amount.
3ga 3.00 Number of times this cash flow
amount occurs consecutively.
9100gK 9,100.00 Next cash flow amount.
9000gK 9,000.00 Next cash flow amount.
2ga 2.00 Number of times this cash flow
amount occurs consecutively.
4500gK 4,500.00 Next cash flow amount.
100000gK 100,000.00 Final cash flow amount.
:n 7.00 Seven different cash flow amounts
have been entered.
13.5¼ 13.50 Stores i.
fl 907.77 NPV.
Since NPV is positive, the investment would increase the financial value of the
investor’s assets by $907.77.

Section 4: Additional Financial Functions 63
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 63 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Calculating Internal Rate of Return (IRR)
1. Enter the cash flows using either of the methods described above under
Calculating Net Present Value.
2. Press fL.
The calculated value of IRR appears in the display and also is automatically stored
in the i register.
Note: Remember that the L function may take a significant amount of
time to produce an answer, during which the calculator displays running.
Example: The NPV calculated in the preceding example was positive, indicating
that the actual rate of return (that is, the IRR) was greater than the 131/2 used in the
calculation. Find the IRR.
Assuming the cash flows are still stored in the calculator, we need only press
fL:
Keystrokes Display
fL 13.72 IRR is 13.72%.
Note that the value calculated by L is the periodic rate of return. If the cash flow
periods are other than years (for example, months or quarters), you can calculate
the nominal annual rate of return by multiplying the periodic IRR by the number of
periods per year.
As noted above, the calculator may take several seconds or even minutes to
produce an answer for IRR. This is because the mathematical calculations for
finding IRR are extremely complex, involving a series of iterations — that is, a
series of successive calculations. In each iteration, the calculator uses an estimate
of IRR as the interest rate in a computation of NPV. The iterations are repeated
until the computed NPV reaches about zero.*
If you do not want to wait for the computation of IRR to be completed, press any
key. This halts the computation of IRR and displays the estimated value of IRR being
used in the current iteration.† You can then check how good this estimate is by
calculating NPV using this estimate: if the estimate is close to IRR, the NPV
calculated with it should be close to zero.* The values of IRR is put into the i
register at the end of each iteration. Therefore, to check how good an estimate of
IRR is after that estimate is in the display, just press fl.
* In practice, because the complex mathematical calculations inside the calculator are done
with numbers rounded to 10 digits, NPV may never reach exactly zero. Nevertheless, the
interest rate that results in a very small NPV is very close to the actual IRR.
† Provided the first iteration has been completed.

64 Section 4: Additional Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 64 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The complex mathematical characteristics of the IRR computation have an
additional ramification: Depending on the magnitudes and signs of the cash flows,
the computation of IRR may have a single answer, multiple answers, a negative
answer or no answer.*
For additional information regarding L, refer to Appendix B. For an alternative
method of calculating IRR, refer to Section 13.
Reviewing Cash Flow Entries
z To display a single cash flow amount, press :, then key in the number of
the register containing the cash flow amount to be displayed. Alternatively,
store the number of that cash flow amount (that is, the value of j for the CFj
desired) in the n register, then press :gK.
z To review all the cash flow amounts, press :g K repeatedly. This
displays the cash flow amounts in reverse order — that is, beginning with the
final cash flow and proceeding to CF0.
z To display the number of times a cash flow amount occurs consecutively —
that is, to display the Nj for a CFj — store the number of that cash flow
amount (that is, the value of j) in the n register, then press :ga.
z To review all the cash flow amounts together with the number of times each
cash flow amount occurs consecutively (that is, to review each CFj and Nj
pair), press :ga:gK repeatedly. This displays Nj followed by
CFj beginning with the final cash flow amount and proceeding to N0 and
CF0.
Note: Neither L nor l change the number in the n register. However,
each time :gK is pressed, the number in the n register is decreased
by 1. If this is done, or if you manually change the number in the n register
in order to display a single Nj and/or CFj, be sure to reset the number in the
n register to the total number of cash flow amounts originally entered (not
including the amount of the initial investment CF0). If this is not done, NPV
and IRR calculations will give incorrect results; also, a review of cash flow
entries would begin with Nn and CFn, where n is the number currently in the
n register.
For example, to display the fifth cash flow amount and the number of times that
amount occurs consecutively:
Keystrokes Display
:5 9,000.00 CF5
5n 5.00 Stores the value of j in the n register.
* In the case of multiple answers for IRR, the decision criteria listed on page 57 should be
modified accordingly.

Section 4: Additional Financial Functions 65
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 65 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
:ga 2.00 N5
7n 7.00 Resets the number in the n re
g
ister to
its original value.
To display all the cash flow amounts and the number of times they occur
consecutively:
Keystrokes Display
:ga 1.00 N7
:gK 100,000.00 CF7
:ga 1.00 N6
:gK 4,500.00 CF6
:ga 2.00 N5
:gK 9,000.00 CF5
.
.
.
.
.
.
.
.
.
:ga 1.00 N1
:gK 14,000.00 CF1
:ga 1.00 N0
:gK –79,000.00 CF0
7n 7.00 Resets the number in the n register
to its original value.
Changing Cash Flow Entries
z To change a cash flow amount:
1. Key the amount into the display.
2. Press ?.
3. Key in the number of the register containing the cash flow amount to be
changed.
z To change the number of times a cash flow amount occurs consecutively —
that is, to change the Nj for a CFj:
1. Store the number of that cash flow amount (that is, j) in the n register.
2. Key the number of times the cash flow amount occurs consecutively into
the display.
3. Press ga.

66 Section 4: Additional Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 66 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Note: If you change the number in the n register in order to change an Nj,
be sure to reset the number in the n register to the total number of cash flow
amounts originally entered (not including the amount of the initial investment
CF0). If this is not done, NPV and IRR calculations will give incorrect results.
Example 1: With the cash flows now stored in the calculator, change CF2 from
$11,000 to $9,000, then calculate the new NPV for a 131/2% return.
Keystrokes Display
9000?2 9,000.00 Stores the new CF2 in R2.
13.5¼ 13.50 Stores i.*
fl –644.75 The new NPV.
Since this NPV is negative, the investment would decrease the financial value of
the investor’s assets.
Example 2: Change N5 from 2 to 4, then calculate the new NPV.
Keystrokes Display
5n 5.00 Stores j in the n register.
4ga 4.00 Stores the new N5.
7n 7.00 Resets the number in the n register
to its original value.
fl –1,857.21 The new NPV.
Bond Calculations
The hp 12c enables you to solve for bond price (and the interest accrued since the
last interest date) and the yield to maturity.† The E and S calculations are
done assuming a semiannual coupon payment and using an actual/actual basis
(such as for U.S. Treasury bonds and U.S. Treasury notes). In accordance with
market convention, prices are based on a redemption (par) value of 100.
* This step is necessary in this example because we have calculated IRR since the first time we
calculated NPV. The IRR calculation replaced the 13.5 we keyed into i before calculating
NPV with the result for IRR – 13.72.
† All bond calculations are performed in accordance with. the Securities Industry Association’s
recommendations as contained in Spence, Graudenz, and Lynch, Standard Securities
Calculation Methods, Securities Industry Association, New York, 1973.

Section 4: Additional Financial Functions 67
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 67 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
To calculate bond price and yield for a 30/360 bond (that is, using the basis of a
30day month and a 360-day year — such as for municipal bonds, corporate
bonds, and state and local government bonds), and to calculate bond price for
bonds with an annual coupon payment, refer to Section 16: Bonds.
Bond Price
1. Enter the desired yield to maturity (as a percentage), using ¼.
2. Enter the annual coupon rate (as a percentage), using P.
3. Key in the settlement (purchase) date (as described on page 29), then press
\.
4. Key in the maturity (redemption) date.
5. Press fE.
The price is shown in the display and also is stored in the PV register. The interest
accrued since the last interest date is held inside the calculator: to display the
interest, press ~; to add the interest to the price, press +.
Example: What price should you pay on April 28, 2004 for a 63/4% U.S.
Treasury bond that matures on June 4, 2018, if you want a yield of 81/4%.
Assume that you normally express dates in the month-day-year format.
Keystrokes Display
8.25¼ 8.25 Enters yield to maturity.
6.75P 6.75 Enters coupon rate.
gÕ 6.75 Sets date format to month-day-year.
4.282004\ 4.28 Enters settlement (purchase) date.
6.042018 6.042018 Enters maturity (redemption) date.
fE 87.62 Bond price (as a percent of par).
+ 90.31 Total price, including accrued
interest.
Bond Yield
1. Enter the quoted price (as a percent of par), using $.
2. Enter the annual coupon rate (as a percentage), using P.
3. Key in the settlement (purchase) date, then press \.
4. Key in the maturity (redemption) date.
5. Press fS.
The yield to maturity is shown in the display and also is stored in the i register.
Note: Remember that the S function may take a significant amount of
time to produce an answer, during which the calculator displays running.

68 Section 4: Additional Financial Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 68 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example: The market is quoting 883/8% for the bond described in the preceding
example. What yield will that provide?
Keystrokes Display
3\8z 0.38 Calculates 3/8.
88+$ 88.38 Enters quoted price.
6.75P 6.75 Enters coupon rate.
4.282004\ 4.28 Enters settlement (purchase) date.
6.042018 6.042018 Enters maturity (redemption) date.
fS 8.15 Bond yield.
Depreciation Calculations
The hp 12c enables you to calculate depreciation and the remaining depreciable
value (book value minus salvage value) using the straight-line,
sum-of-the-years-digits, and declining-balance methods. To do so with any of these
methods:
1. Enter the original cost of the asset, using $.
2. Enter the salvage value of the asset, using M. If the salvage value is zero,
press 0M.
3. Enter the expected useful life of the asset (in years), using n.
4. If the declining-balance method is being used, enter the declining-balance
factor (as a percentage), using ¼. For example, 11/4 times the straight-line
rate — 125 percent declining-balance — would be entered as 125¼.
5. Key in the number of the year for which depreciation is to be calculated.
6. Press:
z fV for depreciation using the straight-line method.
z fÝ for depreciation using the sum-of-the-years digits method.
z f# for depreciation using the declining-balance method.
V, Ý, and #
each place the amount of depreciation in the display. To
display the remaining depreciable value (the book value less the salvage value)
after the depreciation has been calculated, press ~.

Section 4: Additional Financial Functions 69
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 69 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example: A metalworking machine, purchased for $10,000, is depreciated over
5 years. Its salvage value is estimated at $500. Find the depreciation and
remaining depreciable value for the first 3 years of the machine’s life using the
declining-balance method at double the straight-line rate (200 percent
declining-balance).
Keystrokes Display
10000$ 10,000.00 Enters original cost.
500M 500.00 Enters salvage value.
5n 5.00 Enters expected useful life.
200¼ 200.00 Enters declining-balance factor.
1f# 4,000.00 Depreciation in first year.
~ 5,500.00 Remaining depreciable value after
first year.
2f# 2,400.00 Depreciation in second year.
~ 3,100.00 Remaining depreciable value after
second year.
3f# 1,440.00 Depreciation in third year.
~ 1,660.00 Remaining depreciable value after
third year.
To calculate depreciation and the remaining depreciable value when the
acquisition date of the asset does not coincide with the beginning of the fiscal
accounting year, refer to the procedures in Section 13. That section also includes a
procedure for depreciation calculations when changing from the declining-balance
method to the straight-line method, and a procedure for calculating excess
depreciation.

70
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 70 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 5
Additional Operating
Features
Continuous Memory
The calculator’s Continuous Memory contains the data storage registers, the
financial registers, the stack and LAST X registers, program memory, and status
information such as display format, date format, and payment mode. All
information in Continuous Memory is preserved even while the calculator is turned
off. Furthermore, information in Continuous Memory is preserved for a short time
when the batteries are removed, so that you can change the batteries without
losing your data and programs.
Continuous Memory may be reset if the calculator is dropped or otherwise
traumatized, or if power is interrupted. You can also manually reset Continuous
Memory as follows:
1. Turn the calculator off.
2. Hold down the - key, and press ;.
When Continuous Memory is reset:
z All registers are cleared.
z Program memory consists of eight program lines, each containing the
instruction g(00.
z Display format is set to the standard format with two decimal places.
z Date format is set to month-day-year.
z Payment mode is set to End.
Whenever Continuous Memory has been reset, the display will show Pr Error.
Pressing any key will clear this message from the display.
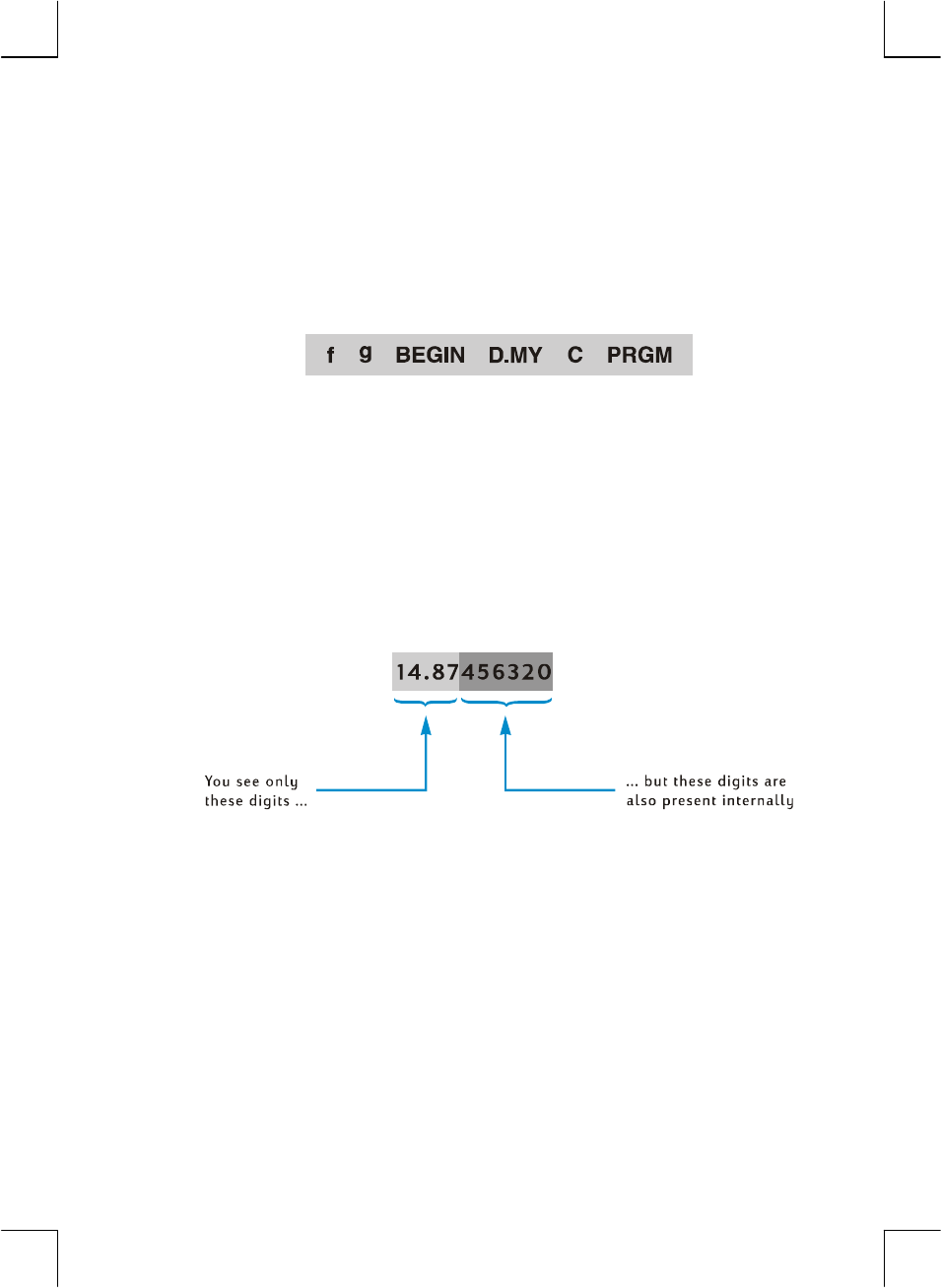
Section 5: Additional Operating Features 71
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 71 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The Display
Status Indicators
Six indicators that appear along the bottom of the display signify the status of the
calculator for certain operations. These status indicators are described elsewhere
in this handbook where the relevant operation is discussed.
Number Display Formats
When the calculator is first turned on after coming from the factory or after
Continuous Memory has been reset, answers are displayed with two decimal
places.
Keystrokes Display
19.8745632\ 19.87
5- 14.87
Although you see only two decimal places, all calculations in your hp 12c are
performed with full 10-digit numbers.
When only two decimal places are displayed, numbers are rounded to two
decimal places: if the third digit is 5 through 9, the second digit is increased by
one; if the third digit is 0 through 4, the second digit is not affected. Rounding
occurs regardless of how many decimal places are displayed.
Several options are provided for controlling how numbers appear in the display.
But regardless of which display format or how many displayed decimal places you
specify, the number inside the calculator — which appears altered in the
display — is not altered unless you use the B, !, V, Ý, or # functions.
Standard Display Format. The number 14.87 now in your calculator is
currently being displayed in the standard display format with two decimal places
shown. To display a different number of decimal places, press f followed by a
digit key (0 through 9) specifying the number of decimal places. In the following
examples, notice how the displayed form of the number inside the calculator —
14.87456320 — is rounded to the specified number of digits.
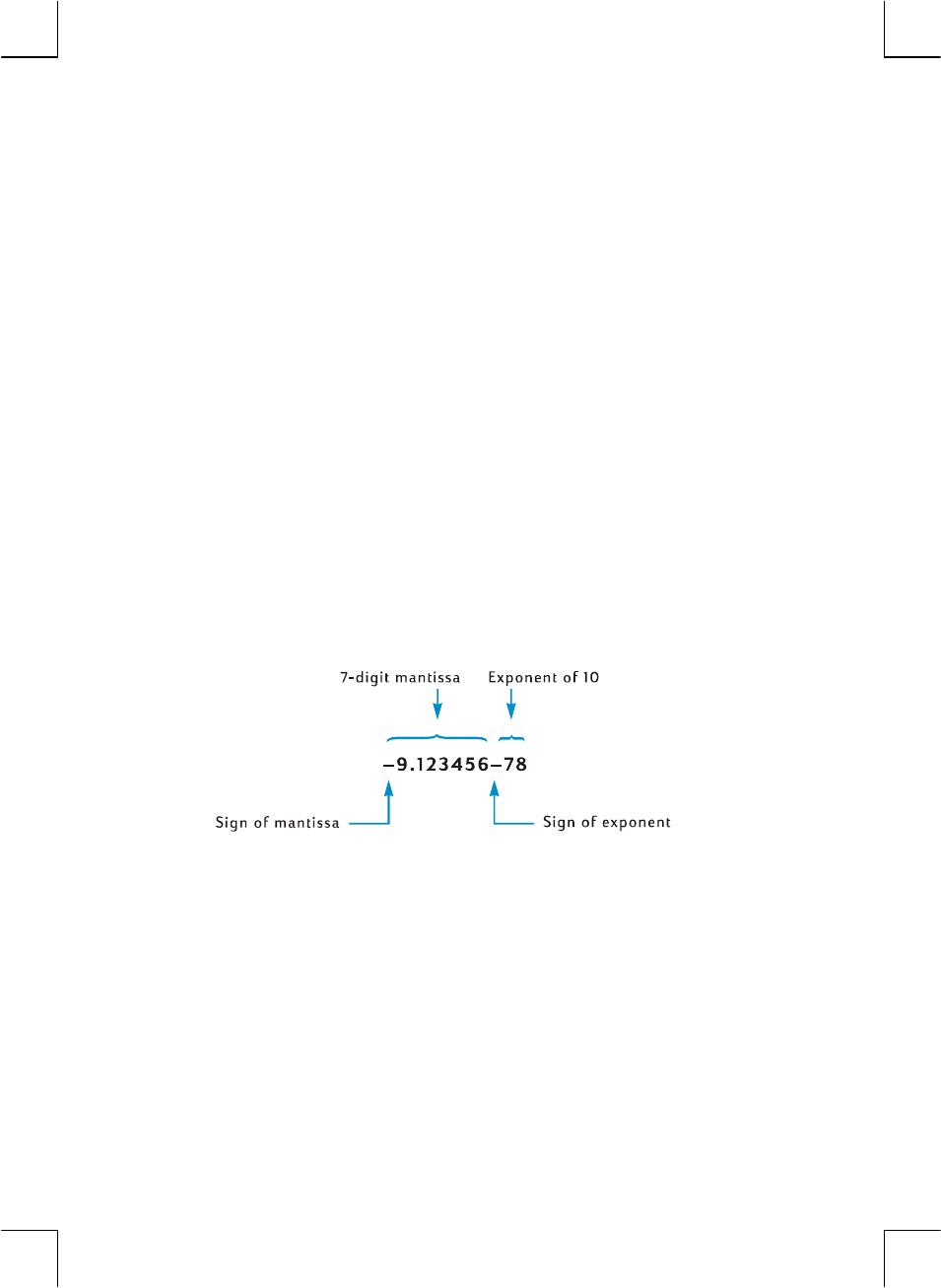
72 Section 5: Additional Operating Features
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 72 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
f4 14.8746
f1 14.9
f0 15.
f9 14.87456320 Although nine decimal places were
specified after f, only eight are
displayed since the display can
show a total of only 10 digits.
The standard display format, plus the specified number of decimal places, remain
in effect until you change them; they are not reset each time the calculator is turned
on. However, if Continuous Memory is reset, when the calculator is next turned on
numbers will be displayed in the standard display format with two decimal places
shown.
If a calculated answer is either too small or too large to be displayed in the
standard display format, the display format automatically switches to scientific
notation (described below). The display returns to the standard display format for
all numbers that can be displayed in that format.
Scientific Notation Display Format
In scientific notation, a number is displayed with its mantissa at the left and a
two-digit exponent at the right. The mantissa is simply the first seven digits in the
number, and has a single, nonzero digit to the left of the decimal point. The
exponent is simply how many decimal places you would move the decimal point in
the mantissa before writing down the number in standard format. If the exponent is
negative (that is, there is a minus sign between it and the mantissa), the decimal
point should be moved to the left; this occurs for any number less than 1. If the
exponent is positive (that is, there is a blank space between it and the mantissa),
the decimal point should be moved to the right; this occurs for any number greater
than or equal to 1.
To set the display format to scientific notation, press f.. For example (assuming
the display still shows 14.87456320 from the preceding example):

Section 5: Additional Operating Features 73
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 73 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
f. 1.487456 01
The exponent in this example indicates that the decimal point should be moved
one decimal place to the right, giving the number 14.87456, which is the first
seven digits of the number previously in the display.
To set the display back to standard display format, press f followed by the
desired number of decimal places. Scientific notation display format remains in
effect until you change to the standard display format; it is not reset each time the
calculator is turned on. However, if Continuous Memory is reset, when the
calculator is next turned on the standard display format, with two decimal places,
will be used.
Mantissa Display Format. Because both the standard display format and
scientific notation display format often show only a few digits of a number, you
may occasionally want to see all 10 digits — the full mantissa — of the number
inside the calculator. To do so, press fCLEARX and hold down the X key.
The display will show all 10 digits of the number as long as you hold down the
X key; after you release the key, the number will again be displayed in the
current display format. For instance, if the display still contains the result from the
preceding example:
Keystrokes Display
fCLEARX 1487456320 All 10 digits of the number inside
the calculator.
1.487456 01 Display returns to its former contents
when the X key is released.
f2 14.87 Returns display to standard format.
Special Displays
Running. Certain functions and many programs may take several seconds or
more to produce an answer. During these calculations, the word running flashes
in the display to let you know that the calculator is running.
Overflow and Underflow. If a calculation results in a number whose
magnitude is greater than 9.999999999 ×1099, the calculation is halted and the
calculator displays 9.999999 99 (if the number is positive) or –9.999999 99
(if the number is negative).
If a calculation results in a number whose magnitude is less than 10–99, the
calculation is not halted, but the value 0 is used for that number in subsequent
calculations.

74 Section 5: Additional Operating Features
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 74 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Errors. If you attempt an improper operation — such as division by zero — the
calculator will display the word Error followed by a digit (0 through 9). To clear
the Error display, press any key. This does not execute that key’s function, but
does restore the calculator to its condition before the improper operation was
attempted. Refer to Appendix C for a list of error conditions.
Pr Error. If power to the calculator is interrupted, the calculator will display Pr
Error when next turned on. This indicates that Continuous Memory — which
contains all data, program, and status information — has been reset.
The key
Suppose you need to subtract $25.83 from $144.25, and you (mistakenly) key in
25.83, press \, then key in 144.25. But then you realize that when written
down on paper, the desired calculation reads 144.25 – 25.83, so that you have
unfortunately keyed in the second number first. To correct this mistake, merely
exchange the first and second numbers by pressing ~, the exchange key.
Keystrokes Display
25.83\144.25 144.25 Oops! You mistakenly keyed in the
second number first.
~ 25.83 Exchanges the first and second
numbers. The first number keyed in is
now in the display.
- 118.42 The answer is obtained by pressing
the operation key.
The ~ key is also useful for checking the first number entered to make sure you
keyed it in correctly. Before pressing the operation key, however, you should press
~ again to return the second number entered to the display. Regardless of how
many times you press ~, the calculator considers the number in the display to
be the second number entered.
The Key
Occasionally you may want to recall to the display the number that was there
before an operation was performed. (This is useful for doing arithmetic calculations
with constants and for recovering from errors in keying in numbers.) To do so,
press gF (last x).

Section 5: Additional Operating Features 75
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 75 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Arithmetic Calculations With Constants
Example: At Permex Pipes a certain pipe fitting is packaged in quantities of 15,
75, and 250. If the cost per fitting is $4.38, calculate the cost of each package.
Keystrokes Display
15\ 15.00 Keys first quantity into calculator.
4.38 4.38 Keys unit cost into display.
§ 65.70 Cost of a package of 15.
75 75. Keys second quantity into display.
gF 4.38 Recalls unit cost — which was last
number in display before § was
pressed — into display.
§ 328.50 Cost of a package of 75.
250 250. Keys third quantity into display.
gF 4.38 Recalls unit cost into display again.
§ 1,095.00 Cost of a package of 250.
Another method for doing arithmetic calculations with constants is described on
page 177.
Recovering From Errors in Digit Entry
Example: Suppose you want to divide the total annual production for one of your
firm’s products (429,000) by the number of retail outlets (987) in order to
calculate the average number distributed by each outlet. Unfortunately, you
mistakenly key in the number of outlets as 9987 rather than as 987. It’s easy to
correct:
Keystrokes Display
429000\ 429,000.00
9987 9,987. You haven’t noticed your mistake
yet.
z 42.96 About 43 products per outlet — but
that seems too low!
gF 9,987.00 Recalls to the display the number
that was there before you press z.
You see that you keyed it in wrong.
429000\ 429,000.00 Begins the problem over.
987z 434.65 The correct answer.

76
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 76 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 6
Statistics Functions
Accumulating Statistics
The hp 12c can perform one- or two-variable statistical calculations. The data is
entered into the calculator using the _ key, which automatically calculates and
stores statistics of the data into storage registers R1, through R6. (These registers are
therefore referred to as the “statistics registers.”)
Before beginning to accumulate statistics for a new set of data, you should clear
the statistics registers by pressing fclear².*
In one-variable statistical calculations, to enter each data point — referred to as an
“x-value” — key the x-value into the display, then press _.
In two-variable statistical calculations, to enter each data pair — referred to as the
“x and y-values”:
1. Key the y-value into the display.
2. Press \.
3. Key the x-value into the display.
4. Press _.
Each time you press _, the calculator does the following:
z The number in R1 is increased by 1, and the result is copied into the display.
z The x-value is added to the number in R2.
z The square of the x-value is added to the number in R3.
z The y-value is added to the number in R4.
z The square of the y-value is added to the number in R5.
z The product of the x and y-values is added to the number in R6.
* This also clears the stack registers and the display.
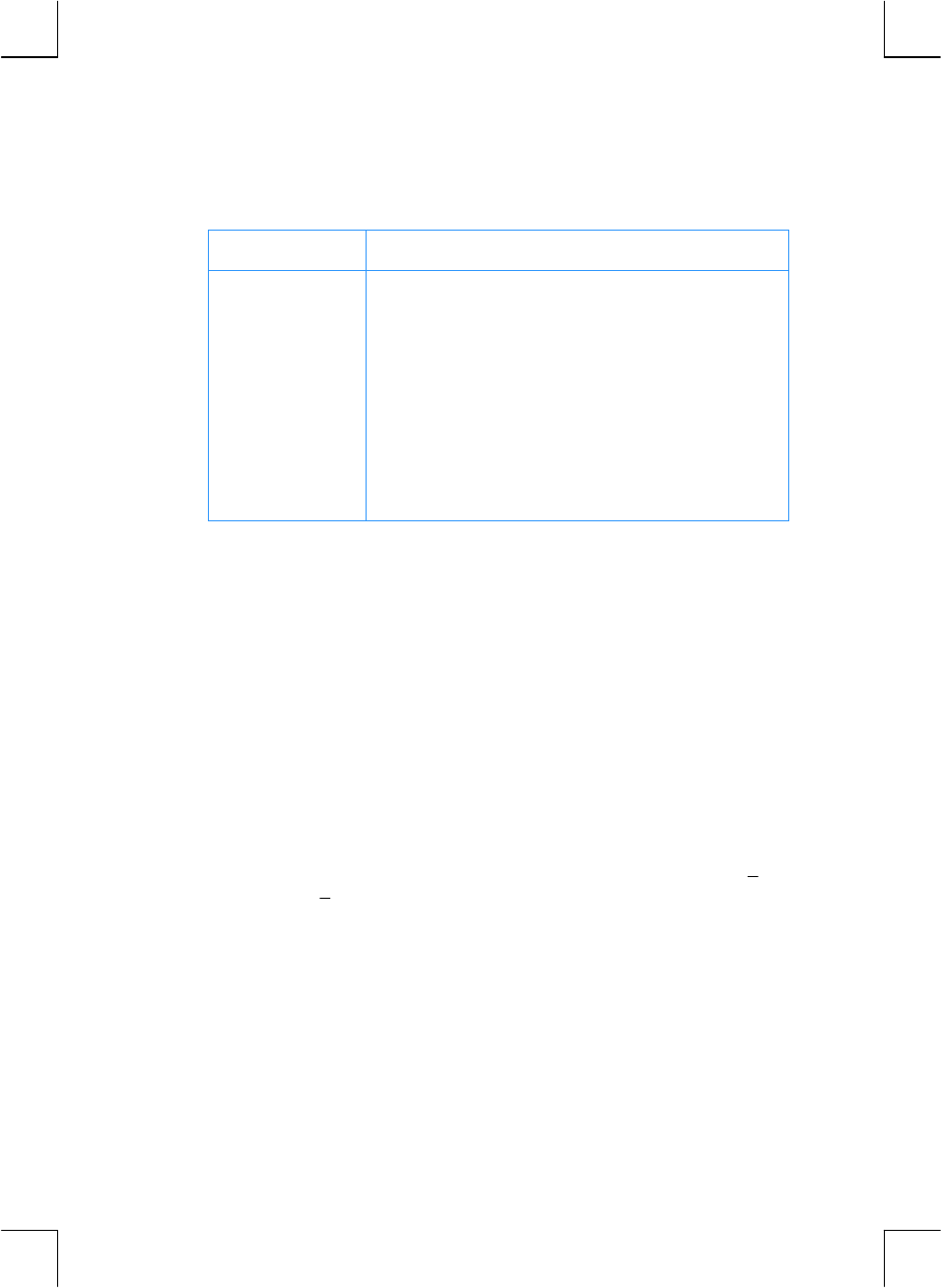
Section 6: Statistics Functions 77
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 77 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The table below shows where the accumulated statistics are stored.
Register Statistic
R1 (and display) n: number of data pairs accumulated.
R2 Σx: summation of x-values.
R3 Σx2: summation of squares of x-values.
R4 Σy: summation of y-values.
R5 Σy2 summation of squares of y-values.
R6 Σxy: summation of products of x-values and y-values.
Correcting Accumulated Statistics
If you discover you have entered data incorrectly, the accumulated statistics can
easily be corrected:
z If the incorrect data point or data pair has just been entered and _ has
been pressed, press gFg^.
z If the incorrect data point or data pair is not the most recent one entered, key
in the incorrect data point or data pair again as if it were new, but press
g^ instead of _.
These operations cancel the effect of the incorrect data point or data pair. You can
then enter the data correctly, using _, just as if it were new.
Mean
Pressing gÖ calculates the means (arithmetic averages) of the x-values ( x) and
of the y-values ( y). The mean of the x-values appears in the display after Ö is
pressed; to display the mean of the y-values, press ~.
Example: A survey of seven salespersons in your company reveals that they work
the following hours a week and sell the following dollar volumes each month. How
many hours does the average salesperson work each week? How much does the
average salesperson sell each month?

78 Section 6: Statistics Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 78 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Salesperson Hours/Week Hours/Week
1 32 $17,000
2 40 $25,000
3 45 $26,000
4 40 $20,000
5 38 $21,000
6 50 $28,000
7 35 $15,000
To find the average workweek and sales of this sample:
Keystrokes Display
fCLEAR² 0.00 Clears statistics registers.
32\
17000_
32.00
1.00
First entry.
40\
25000_
40.00
2.00
Second entry.
45\
26000_
45.00
3.00
Third entry.
40\
20000_
40.00
4.00
Fourth entry.
38\
21000_
38.00
5.00
Fifth entry.
50\
28000_
50.00
6.00
Sixth entry.
35\
15000_
35.00
7.00
Total number of entries in the
sample.
gÖ 21,714.29 Mean dollar sales per month ( x).
~ 40.00 Mean workweek in hours ( y).

Section 6: Statistics Functions 79
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 79 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Standard Deviation
Pressing gv calculates the standard deviation of the x-values (sx) and of the
y-values (sy). (The standard deviation of a set of data is a measure of the dispersion
around the mean.) The standard deviation of the x-values appears in the display
after v is pressed; to display the standard deviation of the y-values, press ~.
Example: To calculate the standard deviations of the x-values and of the y-values
from the preceding example:
Keystrokes Display
gv 4,820.59 Standard deviation of sales.
~ 6.03 Standard deviation of hours worked.
The formulas used in the hp 12c for calculating sx, and sy give best estimates of the
population standard deviation based on a sample of the population. Thus, current
statistical convention calls them sample standard deviations. So we have assumed
that the seven salespersons are a sample of the population of all salespersons, and
our formulas derive best estimates of the population from the sample.
What if the seven salespersons constituted the whole population of salespersons.
Then we wouldn’t need to estimate the population standard deviation. We can
find the true population standard deviation (σ) when the data set equals the total
population, using the following keystrokes.*
Keystrokes Display
gÖ 21,714.29 Mean (dollars)
_ 8.00 Number of entries + 1.
gv 4,463.00 σx
~ 5.58 σy
To continue summing data pairs, press gÖg^ before entering more data.
* It turns out that if you sum the mean of the population into the set itself and find the new s,
computed using the formulas on page 192, that s will be the population standard deviation,
σ, of the original set.

80 Section 6: Statistics Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 80 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Linear Estimation
With two-variable statistical data accumulated in the statistics registers, you can
estimate a new y-value ( y
ˆ) given a new x-value, and estimate a new x-value ( x
ˆ)
given a new y-value.
To calculate y
ˆ:
1. Key in a new x-value.
2. Press gR.
To calculate x
ˆ:
1. Key in a new y-value.
2. Press gQ.
Example: Using the accumulated statistics from the preceding problem, estimate
the amount of sales delivered by a new salesperson working 48 hours per week.
Keystrokes Display
48gQ 28,818.93 Estimated sales for a 48 hour
workweek.
The reliability of a linear estimate depends upon how closely the data pairs would,
if plotted on a graph, lie in a straight line. The usual measure of this reliability is
the correlation coefficient, r. This quantity is automatically calculated whenever y
ˆ
or x
ˆ is calculated; to display it, press ~. A correlation coefficient close to 1
or –1 indicates that the data pairs lie very close to a straight line. On the other
hand, a correlation coefficient close to 0 indicates that the data pairs do not lie
closely to a straight line; and a linear estimate using this data would not be very
reliable.
Example: Check the reliability of the linear estimate in the preceding example by
displaying the correlation coefficient.
Keystrokes Display
~ 0.90 The correlation coefficient is close to
1, so the sales calculated in the
preceding example is a good
estimate.
To graph the regression line, calculate the coefficients of the linear equation
y = A + Bx.
1. Press 0gR to compute the y-intercept (A).
2. Press 1gR~d~- to compute the slope of the line (B).

Section 6: Statistics Functions 81
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 81 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example: Compute the slope and intercept of the regression line in the preceding
example.
Keystrokes Display
0gR 15.55 y-intercept (A); projected value for x
= 0.
1 gR~d~- 0.001 Slope of the line (B); indicates the
change in the projected values
caused by an incremental chan
g
e in
the x value.
The equation that describes the regression line is:
y = 15.55 + 0.001x
Weighted Mean
You can compute the weighted mean of a set of numbers if you know the
corresponding weights of the items in question.
1. Press fCLEAR².
2. Key in the value of the item and press \, then key in its weight and press
_. Key in the second item’s value, press \, key in the second weight,
and press _. Continue until you have entered all the values of the items and
their corresponding weights. The rule for entering the data is “item \
weight _.”
3. Press g to calculate the weighted mean of the items.
Example: Suppose that you stop during a vacation drive to purchase gasoline at
four stations as follows: 15 gallons at $1.16 per gallon, 7 gallons at $1.24 per
gallon, 10 gallons at $1.20 per gallon, and 17 gallons at $1.18 per gallon. You
want to find the average cost per gallon of gasoline purchased. If you purchased
the same quantity at each station, you could determine the simple arithmetic
average or mean using the Ö key. But since you know the value of the item
(gasoline) and its corresponding weight (number of gallons purchased), use the
key to find the weighted mean:
Keystrokes Display
fCLEAR² 0.00 Clears statistics registers.
1.16\15_ 1.00 First item and weight.
1.24\7_ 2.00 Second item and weight.
1.20\10_ 3.00 Third item and weight.
1.18\17_ 4.00 Fourth item and weight.

82 Section 6: Statistics Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 82 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
g 1.19 Weighted mean cost per gallon.
A procedure for calculating the standard deviation and standard error (as well as
the mean) of weighted or grouped data is included in the hp 12c Solutions
Handbook.

83
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 83 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 7
Mathematics and
Number-Alteration Functions
The hp 12c provides several keys for mathematical functions and for altering,
numbers. These functions are useful for specialized financial calculations as well as
for general mathematics calculations.
One-Number Functions
Most of the mathematics functions require that only one number be in the
calculator (that is, the number in the display) before the function key is pressed.
Pressing the function key then replaces the number in the display by the result.
Reciprocal. Pressing y calculates the reciprocal of the number in the display —
that is, it divides 1 by the number in the display.
Square Root. Pressing gr calculates the square root of the number in the
display.
Logarithm. Pressing g° calculates the natural logarithm (that is, the
logarithm to the base e) of the number in the display. To calculate the common
logarithm (that is, the logarithm to the base 10) of the number in the display,
calculate the natural logarithm, then press 10g°z.
Exponential. Pressing g> calculates the exponential of the number in the
display — that is, it raises the base e to the number in the display.
Factorial. Pressing ge calculates the factorial of the number in the display —
that is, it calculates the product of the integers from 1 to n, where n is the number
in the display.
Round. The display format specifies to how many decimal places a number
inside the calculator is rounded when it appears in the display; but the display
format alone does not affect the number itself inside the calculator. Pressing
fB, however, changes the number inside the calculator to match its displayed
version. Thus, to round a number in the display to a given number of decimal
places, temporarily set the display format (as described on page 71) to show the
desired number of decimal places, then press fB.
Integer. Pressing gÑ replaces the number in the display by its integer
portion — that is, it replaces each digit to the right of the decimal point by 0. The
number is changed inside the calculator as well as in the display. The original
number can be recalled to the display by pressing gF.

84 Section 7: Mathematics and Number-Alteration Functions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 84 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Fractional. Pressing gT replaces the number in the display by its fractional
portion — that is, it replaces all digits to the left of the decimal point by 0. Like
Ñ, T changes the number inside the calculator as well as its displayed
version. The original number can be recalled to the display by pressing gF.
All of the above functions are used basically in the same way. For example, to find
the reciprocal of 0.258:
Keystrokes Display
.258 0.258 Keys the number into the display.
y 3.88 The reciprocal of 0.258, the ori
g
inal
number.
Any of the above functions can be done with a number in the display resulting
from a previous calculation, as well as with a number you have just keyed in.
Keystrokes Display
fCLEARX 3875968992 Displays all 10 digits of the number
inside the calculator.
3.88 Display returns to normal format
when X key is released.
fB 3.88 The number now in the display
appears the same as before, but …
fX 3880000000 Displaying all 10 digits of the
number inside the calculator shows
B has changed the number to
match its displayed version.
3.88 Display returns to normal format.
gÑ 3.00 The integer portion of the number
previously displayed.
gF 3.88 Recalls the original number to the
display.
gT 0.88 The fractional portion of the number
previously displayed.

Section 7: Mathematics and Number-Alteration Functions 85
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 85 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The Power Function
Pressing q calculates a power of a number — that is, yx. Like the arithmetic
function +, q requires two numbers:
1. Key in the base number (which is designated by the y on the key).
2. Press \ to separate the second number (the exponent) from the first (the
base).
3. Key in the exponent (which is designated by the x on the key).
4. Press q to calculate the power.
To Calculate Keystrokes Display
21.4 2\1.4q 2.64
2–1.4 2\1.4Þq 0.38
(–2)3 2Þ\3q –8.00
32or 21/3 2\3yq 1.26

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 87 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Part II
Programming

88
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 88 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 8
Programming Basics
Why Use Programs?
A program is simply a sequence of keystrokes that is stored in the calculator.
Whenever you have to calculate with the same sequence of keystrokes several
times, you can save a great deal of time by incorporating these keystrokes in a
program. Instead of pressing all the keys each time, you press just one key to start
the program: the calculator does the rest automatically!
Creating a Program
Creating a program consists simply of writing the program, then storing it:
1. Write down the sequence of keystrokes that you would use to calculate the
quantity or quantities desired.
2. Press fs to set the calculator to Program mode. When the calculator is
in Program mode, functions are not executed when they are keyed in, but
instead are stored inside the calculator. The PRGM status indicator in the
display is lit when the calculator is in Program mode.
3. Press fCLEARÎ to erase any previous programs that may be stored
inside the calculator. If you want to create a new program without erasing a
program already stored, skip this step and proceed as described in Section
11, Multiple Programs.
4. Key in the sequence of keystrokes that you wrote down in step 1. Skip the
beginning keystrokes that enter data, which would differ each time the
program is used.
Example: Your office supplies dealer is selling selected stock at 25% off. Create
a program that calculates the net cost of an item after the discount is subtracted
and the $5 handling charge is added.
First, we’ll manually calculate the net cost of an item listing for $200.
Keystrokes Display
200 200. Keys in cost of item.
\ 200.00 Separates cost of item from
percentage to be keyed in next.
25b 50.00 Amount of discount.

Section 8: Programming Basics 89
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 89 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
- 150.00 Price less discount.
5 5. Handling charge.
+ 155.00 Net cost (price less discount plus
handling charge).
Next, set the calculator to Program mode and erase any program(s) already
stored:
Keystrokes Display
fs 00- Sets calculator to Program mode.
fCLEARÎ 00- Clears program(s).
Finally, press the keys that we used above to solve the problem manually. Do not
key in 200; this number will vary each time the program is used. Don’t be
concerned right now about what appears in the display as you press the keys;
we’ll discuss that later in this section.
Keystrokes Display
\ 01- 36
2 02- 2
5 03- 5
b 04- 25
- 05- 30
5 06- 5
+ 07- 40
Running a Program
To run (sometimes called “execute”) a program:
1. Press fs to set the calculator back to Run mode. If the calculator is
already in Run mode (that is, the PRGM status indicator in the display is not
lit), skip this step.
2. Key any required data into the calculator, just as if you were calculating
manually. When a program is run, it uses the data already keyed into the
display and the registers inside the calculator.
3. Press t to begin program execution.

90 Section 8: Programming Basics
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 90 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example: Run the program created above to calculate the net cost of a typewriter
listing for $625 and an executive chair listing for $159.
Keystrokes Display
fs 155.00 Sets calculator to Run mode. Display
shows number previously calculated.
625 625. Keys in price of typewriter.
t 473.75 Net cost of typewriter.
159 159. Keys in list price of chair.
t 124.25 Net cost of chair.
That’s all there is to creating and running simple programs! But if you want to use
programs frequently, you’ll want to know more about programming — such as
how to check what keystrokes are stored in program memory, how many
keystrokes can be stored in program memory, how to correct or otherwise modify
programs, how to skip keystrokes when running a program, and so on. Before you
can understand these aspects of programming, we need to briefly discuss how
keystrokes are treated by the calculator when they are stored in Program mode
and when they are executed in Run mode.
Program Memory
Keystrokes entered into the calculator in Program mode are stored in program
memory. Each digit, decimal point, or function key is called an instruction and is
stored in one line of program memory — usually referred to simply as a program
line. Keystroke sequences beginning with the f, g, ?, :, and i prefix
keys are considered to comprise a complete instruction and are stored in only one
program line.
When a program is run, each instruction in program memory is executed — that is,
the keystroke in that program line is performed, just as if you were pressing the key
manually — beginning with the current line in program memory and proceeding
sequentially with the higher-numbered program lines.
Whenever the calculator is in Program mode (that is, whenever the PRGM status
indicator in the display is lit), the display shows information about the program line
to which the calculator is currently set. At the left of the display is the number of the
program line within program memory. The remaining digits in the display comprise
a code that indicates what instruction has been stored in that program line. No
code is shown for program line 00, since no regular instruction is stored there.

Section 8: Programming Basics 91
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 91 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Identifying Instructions in Program Lines
Each key on the hp 12c keyboard — except for the digit keys 0 through 9 — is
identified by a two-digit “keycode” that corresponds to the key’s position on the
keyboard. The first digit in the keycode is the number of the key row, counting
from row 1 at the top; the second digit is the number of the key in that row,
counting from 1 for the first key in the row through 9 for the ninth key in the row
and 0 for the tenth key in the row. The keycode for each digit key is simply the
digit on the key. Thus, when you keyed the instruction b into program memory,
the calculator displayed
04– 25
This indicates that the key for the instruction in program line 04 is in the second
row on the keyboard and is the fifth key in that row: the b key. When you keyed
the instruction + into program memory, the calculator displayed
07– 40
This indicates that the key for the instruction in program line 07 is in the fourth row
on the keyboard and is the tenth key in that row: the + key. When you keyed the
digit 5 into program memory, the keycode displayed was only the digit 5.
Since keystroke sequences beginning with f, g, ?, :, and i are stored
in only one program line, the display of that line would show the keycodes for all
the keys in the keystroke sequence.
Instruction Keycode
gÒ nn- 43 26
?=1 nn- 44 40 1
gi00 nn- 43,33 00

92 Section 8: Programming Basics
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 92 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Displaying Program Lines
Pressing fs to set the calculator from Run mode to Program mode displays the
line number and keycode for the program line to which the calculator is currently
set.
Occasionally you’ll want to check several or all of the instructions stored in
program memory. The hp 12c enables you to review program instructions either
forward or backward through program memory:
z Pressing Ê (single step) while the calculator is in Program mode advances
the calculator to the next line in program memory, then displays that line
number and the keycode of the instruction stored there.
z Pressing gÜ (back step) while the calculator is in Program mode sets the
calculator back to the previous line in program memory, then displays that
line number and the keycode of the instruction stored there.
For example, to display the first two lines of the program now stored in program
memory, set the calculator to Program mode and press Ê twice:
Keystrokes Display
fs 00- Sets calculator to Program mode
and displays current line of
program memory
Ê 01- 36
Program line 01: \
Ê 02- 2
Program line 02: digit 2.
Pressing gÜ does the reverse:
Keystrokes Display
gÜ 01- 36
Program line 01.
gÜ 00- Program line 00.
If either the Ê key or the Ü key is held down, the calculator displays all of the
lines in program memory. Press Ê again now, but this time hold it down until
program line 07 is displayed.
Keystrokes Display
Ê 01- 36
Program line 01
.
.
.
.
.
.
(Release Ê) 07- 40
Program line 07

Section 8: Programming Basics 93
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 93 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Program line 07 contains the last instruction you keyed into program memory.
However, if you press Ê again, you’ll see that this is not the last line stored in
program memory:
Keystrokes Display
Ê 08- 43, 33 00 Program line 08
As you should now be able to tell from the keycodes displayed, the instruction in
program line 08 is gi00.
The 00 Instruction and Program Line 00
Whenever you run the program now stored in program memory, the calculator
executes the instruction in line 08 after executing the seven instructions you keyed
in. This i00 instruction — as its name implies — tells the calculator to “go to”
program line 00 and execute the instruction in that line. Although line 00 does not
contain a regular instruction, it does contain a “hidden” instruction that tells the
calculator to halt program execution. Thus, after each time the program is run, the
calculator automatically goes to program line 00 and halts, ready for you to key in
new data and run the program again. (The calculator is also automatically set to
program line 00 when you press fs to set the calculator from Program mode
to Run mode.)
The i00 instruction was already stored in line 08 — in fact, in all program
lines — before you keyed in the program. If no instructions have been keyed into
program memory, if Continuous Memory is reset, or if fCLEARÎ is pressed (in
Program mode), the instruction i00 is automatically stored in program lines 01
through 08. As you key each instruction into program memory, it replaces the
i00 instruction in that program line.
If your program should consist of exactly eight instructions, there would be no
i00 instructions remaining at the end of program memory. Nevertheless, after
such a program is executed the calculator automatically returns to program line 00
and halts, just as if there were a i00 instruction following the program.
If you key in more than eight instructions, program memory automatically expands
to accommodate the additional instructions.
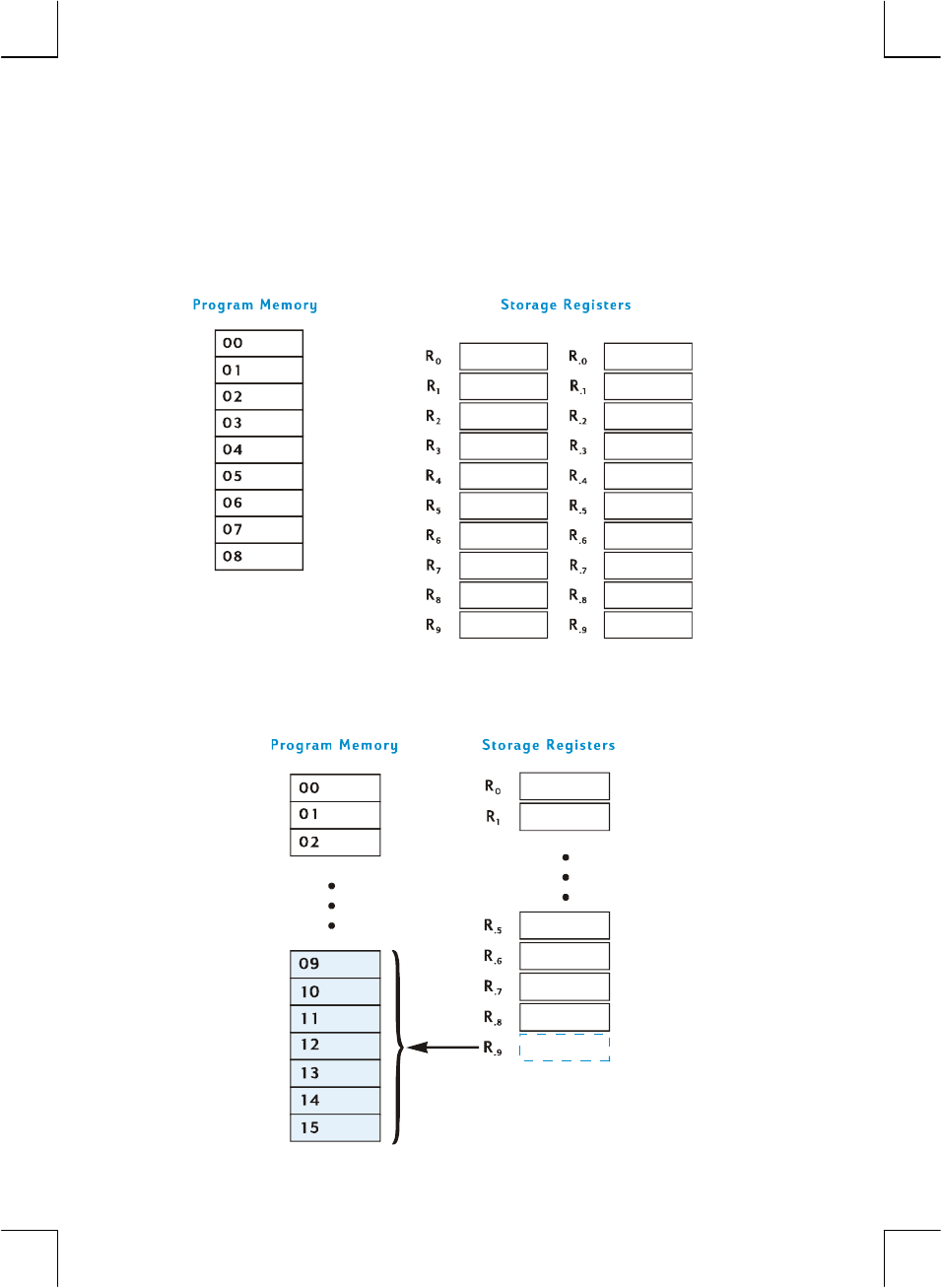
94 Section 8: Programming Basics
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 94 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Expanding Program Memory
If no instructions have been keyed into program memory, if Continuous Memory
has been reset, or if fCLEARÎ has been pressed (in Program mode), program
memory consists of 8 program lines, and there are 20 storage registers available
for storage of data.
As you key in a ninth instruction, storage register R.9 is automatically converted into
seven new lines of program memory. The instruction you key in is stored in
program line 09, and the instruction i00 is automatically stored in program
lines 10 through 15.
Section 8: Programming Basics 95
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 95 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Program memory is automatically expanded like this whenever another seven
instructions have been keyed into program memory — that is, when you key an
instruction into program line 16, 23, 30 etc. In each case, the additional program
lines made available are converted, seven lines at a time, from the last available
data storage register (whether or not data has been stored in that register; if it has,
it will be lost). Furthermore, the six new program lines (following the 16th, 23th
etc.) will each contain the instruction i00.
To determine at any time how many program lines (including those containing
i00) are currently in program memory and how many storage registers are
currently available for conversion to program lines or for data storage, press
gN (memory). The calculator will respond with a display like the following:
Up to 99 instructions can be stored in program memory. Doing so would require
the conversion of 13 data storage registers (because 99 = 8 + [13 × 7]), leaving
7 storage registers — R0 through R6 — available for data storage.
If you find yourself creating long programs, you should create your programs so
that they don’t use up program lines unnecessarily, since program memory is
limited to 99 program lines. One way to minimize program length is to replace
numbers consisting of more than just one digit — like the number 25 in lines 02
and 03 of the program keyed in above — by a : instruction, and then storing
the number in the designated storage register before running the program. In this
case, this would save one program line, since the : instruction requires only
one program line, not two as are required by the number 25. Of course, doing so
uses up data storage registers that you might want to save for other data. As in
many business and financial decisions, there is a trade off involved; here it is
between program lines and data storage registers.
Setting the Calculator to a Particular Program Line
There will be occasions when you’ll want to set the calculator directly to a
particular program line — such as when you’re storing a second program in
program memory or when you’re modifying an existing program. Although you
can set the calculator to any line by using Ç as described above, you can do so
more quickly as follows:
z With the calculator in Program mode, pressing gi. followed by two
digit keys sets the calculator to the program line specified by the digit keys,
and then displays that line number and the keycode of the instruction stored
there.

96 Section 8: Programming Basics
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 96 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
z With the calculator in Run mode, pressing gi followed by two digit keys
sets the calculator to the program line specified by the digit keys. Since the
calculator is not in Program mode, the line number and keycode are not
displayed.
The decimal point is not necessary if the calculator is in Run mode, but it is
necessary if the calculator is in Program mode.
For example, assuming the calculator is still in Program mode, you can set it to
program line 00 as follows:
Keystrokes Display
gi.00 00- Program line 00
Executing a Program One Line at a Time
Pressing Ç repeatedly with the calculator in Program mode (as described earlier)
enables you to verify that the program you have stored is identical to the program
you wrote — that is, to verify that you have keyed the instructions in correctly.
However, this does not ensure that the program you wrote calculates the desired
results correctly: even programs created by the most experienced programmers
often do not work correctly when they are first written.
To help you verify that your program works correctly, you can execute the program
one line at a time, using the Ç key. Pressing Ç while the calculator is in Run
mode advances the calculator to the next line in program memory, then displays
that line’s number and the keycode of the instruction stored there, just as in
Program mode. In Run mode, however, when the Ç key is released the
instruction in the program line just displayed is executed and the display then
shows the result of executing that line.
For example, to execute the program stored in the calculator one line at a time:
Keystrokes Display
fs 124.25 Sets calculator to Run mode and
to line 00 in program memory.
(Display shown assumes results
remain from previous
calculation.)
625 625. Keys in price of typewriter.
Ç 01- 36 Program line 01: \
625.00 Result of executin
g
pro
g
ram line
01.
Ç 02- 2 Program line 02: 2.

Section 8: Programming Basics 97
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 97 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
2. Result of executin
g
pro
g
ram line
02.
Ç 03- 5 Program line 03: 5.
25. Result of executin
g
pro
g
ram line
03.
Ç 04- 25 Program line 04: b
156.25 Result of executin
g
pro
g
ram line
04.
Ç 05- 30 Program line 05: -
468.75 Result of executin
g
pro
g
ram line
05.
Ç 06- 5 Program line 06: 5
5. Result of executin
g
pro
g
ram line
06.
Ç 07- 40 Program line 07: +
473.75 Result of executin
g
pro
g
ram line
07 (the last line of the program).
Pressing gÜ while the calculator is in Run mode sets the calculator to the
previous line in program memory, then displays that line’s number and the
keycode of the instruction stored there, just as in Program mode. In Run mode,
however, when the Ü key is released the display again shows the same number
as it did before gÜ was pressed: no instruction in program memory is
executed.
Interrupting Program Execution
Occasionally you’ll want a program to stop executing so that you can see an
intermediate result or enter new data. The hp 12c provides two functions for doing
so: u (pause) and t (run/stop).
Pausing During Program Execution
When a running program executes a u instruction, program execution halts for
about 1 second, then resumes. During the pause, the calculator displays the last
result calculated before the u instruction was executed.
If you press any key during a pause, program execution is halted indefinitely. To
resume program execution at the program line following that containing the u
instruction, press t.

98 Section 8: Programming Basics
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 98 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example: Create a program that calculates the entries in the AMOUNT, TAX,
and TOTAL columns for each item on the jewelry distributor’s invoice shown on the
next page, and also calculates the total in each of these columns for all items on
the invoice. Assume the sales tax is 63/4%.
To conserve lines of program memory, instead of keying in the tax rate before the
b instruction we’ll store it in register R0 and recall it before the b instruction.
Before storing the program in program memory, we’ll calculate the required
amounts for the first item on the invoice manually. The keystroke sequence will use
storage register arithmetic (described on page 24) in registers R1, R2, and R3 to
calculate the column sums. Since these registers are cleared when fCLEAR² is
pressed, we’ll press those keys before beginning the manual calculation — and
also later, before running the program — to ensure that the column sums are
“initialized” to zero. (Pressing fCLEARH would clear registers R1 through R3,
but would also clear R0, which will contain the tax rate.)

Section 8: Programming Basics 99
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 99 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Pressing the gu keys is not necessary when we do the calculations manually,
since in Run mode the result of every intermediate calculation is displayed
automatically; but we’ll include u instructions in the program so that the
intermediate results AMOUNT and TAX are automatically displayed when the
program is executed.
Keystrokes Display
6.75?0 6.75 Stores tax rate in R0.
fCLEAR² 0.00 Clears the registers in R1 throu
g
h
R6.
13 13. Keys in quantity of item.
\ 13.00 Separates quantity of item from
cost of item to be keyed in next.
68.5 68.5 Keys in cost of item.
§ 890.50 AMOUNT.
?+1 890.50 Adds AMOUNT to sum of
AMOUNT entries in register R1.
:0 6.75 Recalls tax rate to display.
b 60.11 TAX.
?+2 60.11 Adds TAX to sum of TAX entries
in register R2.
+ 950.61 TOTAL.
?+3 950.61 Adds TOTAL to sum of TOTAL
entries in register R3.
Now, we’ll store the program in program memory. Do not key in the quantity and
cost of each item; these numbers will vary each time the program is run.
Keystrokes Display
fs 00- Sets calculator to Program
mode.
fCLEARÎ 00- Clears program memory.
§ 01- 20
gu 02- 43 31 Pauses to display AMOUNT.
?+1 03- 44 40 1
:0 04- 45 0
b 05- 25

100 Section 8: Programming Basics
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 100 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
gu 06- 43 31 Pauses to display TAX.
?+2 07- 44 40 2
+ 08- 40
?+3 09- 44 40 3
Now, to run the program:
Keystrokes Display
fs 950.61 Sets calculator to Run mode.
fCLEAR² 0.00 Clears registers R1– R6.
6.75?0 Stores tax rate.
13\68.5 68.5 Enters quantity and price of first
item on invoice.
t 890.50 AMOUNT for first item.
60.11 TAX for first item.
950.61 TOTAL for first item.
18\72.9 72.9 Enters quantity and price of
second item on invoice.
t 1,312.20 AMOUNT for second item.
88.57 TAX for second item.
1,400.77 TOTAL for second item.
24\85 85. Enters quantity and price of third
item on invoice.
t 2,040.00 AMOUNT for third item.
137.70 TAX for third item.
2,177.70 TOTAL for third item.
5\345 345. Enters quantity and price of
fourth item on invoice.
t 1,725.00 AMOUNT for fourth item.
116.44 TAX for fourth item.
1,841.44 TOTAL for fourth item.
:1 5,967.70 Sum of AMOUNT column.
:2 402.82 Sum of TAX column.
:3 6,370.52 Sum of TOTAL column.

Section 8: Programming Basics 101
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 101 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
If the duration of the pause is not long enough to write down the number displayed,
you can prolong it by using more than one u instruction. Alternatively, you can
have the program automatically stop as described next.
Stopping Program Execution
Stopping Program Execution Automatically. Program execution is
automatically halted when the program executes a t instruction. To resume
executing the program from the program line at which execution was halted, press
t.
Example: Replace the program above by one containing t instructions
instead of u instructions.
Keystrokes Display
fs 00- Sets calculator to Program mode.
fCLEARÎ 00- Clears program memory.
§ 01- 20
t 02- 31 Stops program execution to display
AMOUNT.
?+1 03- 44 40 1
:0 04- 45 0
b 05- 25
t 06- 31 Stops program execution to display
TAX.
?+2 07- 44 40 2
+ 08- 40
?+3 09- 44 40 3
fs 6,370.52 Sets calculator to Run mode.
fCLEAR² 0.00 Clears registers R1 through R6.
13\68.5 68.5 First item.
t 890.50 AMOUNT for first item.
t 60.11 TAX for first item.
t 950.61 TOTAL for first item.
18\72.9 72.9 Second item.
t 1,312.20 AMOUNT for second item.
t 88.57 TAX for second item.
t 1,400.77 TOTAL for second item.

102 Section 8: Programming Basics
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 102 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
24\85 85. Third item.
t 2,040.00 AMOUNT for third item.
t 137.70 TAX for third item.
t 2,177.70 TOTAL for third item.
5\345 345. Fourth item.
t 1,725.00 AMOUNT for fourth item.
t 116.44 TAX for fourth item.
t 1,841.44 TOTAL for fourth item.
:1 5,967.70 Sum of AMOUNT column.
:2 402.82 Sum of TAX column.
:3 6,370.52 Sum of TOTAL column.
Program execution is also automatically halted when the calculator overflows (refer
to page 73) or attempts an improper operation that results in an Error display.
Either of these conditions signifies that the program itself probably contains an
error.
To determine at which program line execution has halted (in order to locate the
error), press any key to clear the Error display, then press fs to set the
calculator to Program mode and display that program line.
You may also want to display the current program line (by pressing fs) if
your program has halted at one of several t instructions in your program and
you want to determine which one that is. To continue executing the program
afterward:
1. Press fs to set the calculator back to Run mode.
2. If you want to resume execution from the program line at which execution
halted rather than from line 00, press gi followed by two digit keys that
specify the program line desired.
3. Press t to resume execution.
Stopping Program Execution Manually. Pressing any key while a program
is running halts program execution. You may want to do this if the calculated
results displayed by a running program appear to be incorrect (indicating that the
program itself is incorrect).
To halt program execution during a pause in a running program (that is, when
u is executed), press any key.
After stopping program execution manually, you can determine at which program
line execution has halted and/or resume program execution as described above.
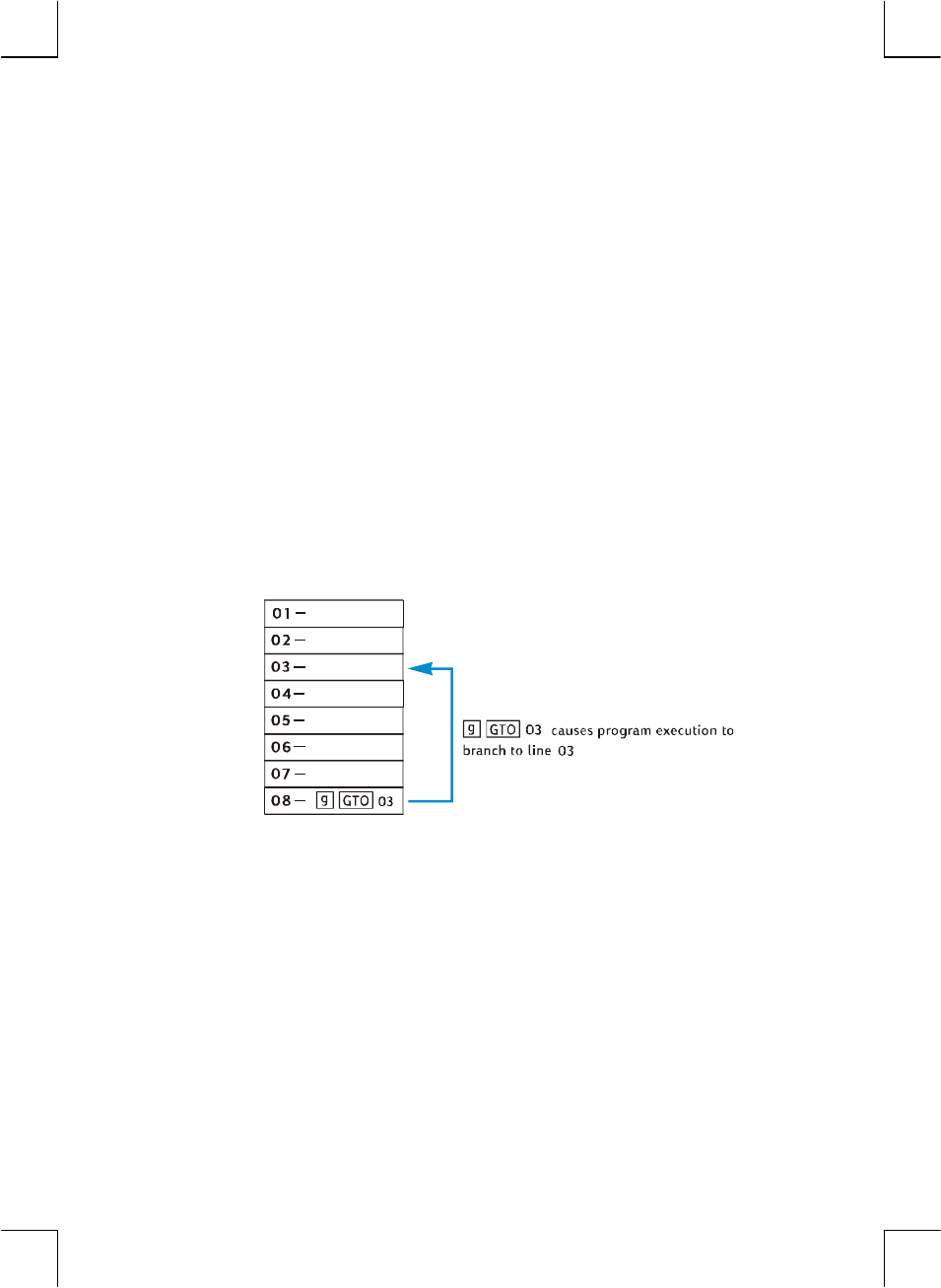
103
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 103 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 9
Branching and Looping
Although the instructions in a program normally are executed in order of their
program line numbers, in some situations it is desirable to have program execution
transfer or “branch” to a program line that is not the next line in program memory.
Branching also makes it possible to automatically execute portions of a program
more than once — a process called “looping.”
Simple Branching
The i (go to) instruction is used in a program to transfer execution to any
program line. The program line desired is specified by keying its two-digit line
number into the program line containing the i instruction. When the i
instruction is executed, program execution branches or “goes to” the program line
specified and then continues sequentially as usual.
You have already seen a common use of branching: the i00 instruction (that is
stored in program memory after the program you key in) transfers execution to
program line 00. A i instruction can be used to branch not only backward in
program memory — as in the case of i00 and as illustrated above — but also
forward in program memory. Backward branching is typically done to create
loops (as described next); forward branching is typically done in conjunction with
an o or m instruction for conditional branching (as described afterward).

104 Section 9: Branching and Looping
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 104 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Looping
If a i instruction specifies a lower-numbered line in program memory, the
instructions in the program lines between the specified line and the i instruction
will be executed repeatedly. As can be seen in the illustration above under Simple
Branching, once the program begins executing the “loop” it will execute it again
and again.
If you want to terminate the execution of a loop, you can include an o or m
instruction (described below) or an t instruction within the loop. You can also
terminate execution by pressing any key while the loop is being executed.
Example: The following program automatically amortizes the payments on a
home mortgage without requiring you to press f! for each payment. It will
amortize one month’s payments each time or one year’s payments each time the
loop is executed, depending on whether the number 1 or 12 is in the display
when you start running the program. Before running the program, we’ll “initialize”
it by storing the required data in the financial registers — just as we would do if
we were amortizing a single payment manually. We’ll run the program for a
$50,000 mortgage at 123/4% for 30 years, and we’ll key 1 into the display just
before running it in order to amortize monthly payments. For the first two “passes”
through the loop we’ll execute the program one line at a time, using Ç, so that
we can see the looping occurring; then we’ll use t to execute the entire loop a
third time before terminating execution.
Keystrokes Display
fs 00- Sets calculator to Program mode.
fCLEARÎ 00- Clears program memory
?0 01- 44 0 Stores the number from the display
into register R0. This number will be
the number of payments to be
amortized.

Section 9: Branching and Looping 105
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 105 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
:0 02- 45 0 Recalls the number of payments to
be amortized. This program line is
the one to which pro
g
ram execution
will later branch. It is included
because after the first time the loop
is executed, the number in the
“display”* is replaced by the result
of !.
f! 03- 42 11 Amortizes payment(s).
gu 04- 43 31 Pauses to display amount of
payment(s) applied to interest.
~ 05- 34 Brings amount of payment(s)
applied to principal into “display.”*
gu 06- 43 31 Pauses to display amount of
payment(s) applied to principal.
gi02 07- 43, 33 02 Transfers program execution to line
02, so that the number of payments
to be amortized can be recalled to
the display before the !
instruction in line 03 is executed.
fs 0.00 Sets calculator to Run mode.
(Display shown assumes no results
remain from previous calculations.)
fCLEARG 0.00 Clears financial registers.
30gA 360.00 Enters n.
12.75gC 1.06 Enters i.
50000$ 50,000.00 Enters PV.
g 50,000.00 Sets payment to End.
P –543.35 Calculates the monthly payment.
0n 0.00 Reset n to zero.
1 1. Keys 1 into the display to amortize
monthly payments.
Ê 01- 44 0 Line 01: ?0.
1.00
* More precisely, the number in the X-register.

106 Section 9: Branching and Looping
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 106 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
Ê 02- 45 0 Line 02: :0. This is the be
g
innin
g
of the first pass through the loop.
1.00
Ê 03- 42 11 Line 03: f!.
–531.25 Portion of first month’s payment
applied to interest.
Ê 04- 43 31 Line 04: gu.
–531.25
Ê 05- 34 Line 05: ~.
–12.10 Portion of first month’s payment
applied to principal.
Ê 06- 43 31 Line 06: gu.
–12.10
Ê 07- 43, 33 02 Line 07: gi02. This is the end
of the first pass through the loop.
–12.10
Ê 02- 45 0 Line 02: :0. Program execution
has branched to the beginning of
the loop for the second pass throu
g
h
it.
1.00
Ê 03- 42 11 Line 03: f!.
–531.12 Portion of second month’s payment
applied to interest.
Ê 04- 43 31 Line 04: gu.
–531.12
Ê 05- 34 Line 05: ~.
–12.23 Portion of second month’s payment
applied to principal.
Ê 06- 43 31 Line 06: gu.
–12.23

Section 9: Branching and Looping 107
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 107 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
Ê 07- 43, 33 02 Line 07: gi02.
This is the end of the second pass
through the loop.
–12.23
t –530.99 Portion of third month’s payment
applied to interest.
–12.36 Portion of third month’s payment
applied to principal.
t(or any key) –12.36 Halts program execution.
Conditional Branching
Often there are situations when it is desirable for a program to be able to branch
to different lines in program memory, depending on certain conditions. For
example, a program used by an accountant to calculate taxes might need to
branch to different program lines depending on the tax rate for the particular
income level.
The hp 12c provides two conditional test instructions that are used in programs for
conditional branching:
z o tests whether the number in the X-register (represented by the x in the
key symbol) is less than or equal to the number in the Y-register (represented
by the y in the key symbol). As discussed in Appendix A, the number in the
X-register is simply the number that would, if the calculator were in Run mode,
be currently in the display; and the number in the Y-register is the number
that would, if the calculator were in Run mode, have been in the display
when \ was pressed. For example, pressing 4\5 would place the
number 4 in the Y-register and the number 5 in the X-register.
z m tests whether the number in the X-register is equal to zero.
The possible results of executing either of these instructions are:
z If the condition tested for is true when the instruction is executed, program
execution continues sequentially with the instruction in the next line of
program memory.
z If the condition tested for is false when the instruction is executed, program
execution skips the instruction in the next line of program memory and
continues with the instruction in the following line.
These rules can be summarized as “DO if TRUE”.
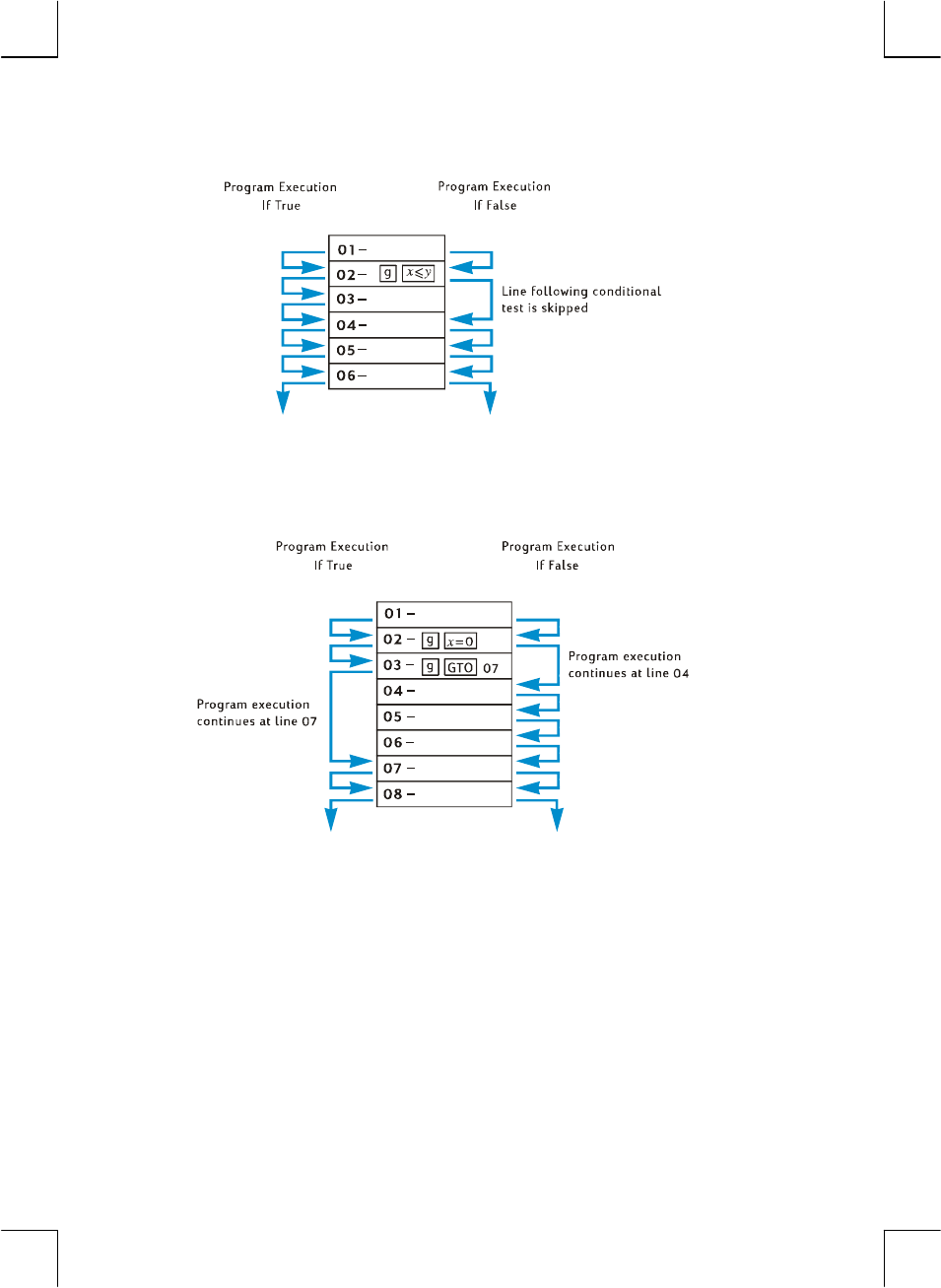
108 Section 9: Branching and Looping
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 108 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The program line immediately following that containing the conditional test
instruction can contain any instruction; however, the most commonly used
instruction there is i. If a i instruction follows a conditional test instruction,
program execution branches elsewhere in program memory if the condition is true
and continues with the next line in program memory if the condition is false.
Example: The following program calculates income tax at a rate of 20% on
incomes of $20,000 or less and 25% on incomes of more than $20,000. To
conserve program lines, the program assumes that the test value — 20,000 — has
been stored in register R0 and the tax rates — 20 and 25 — have been stored in
registers R1 and R2, respectively.
Note: If a program requires that certain numbers be in the X- and
Y-registers when instructions such as o are executed, it is extremely helpful
when writing the program to show the quantities in each register after each
instruction is executed, as in the following diagram.
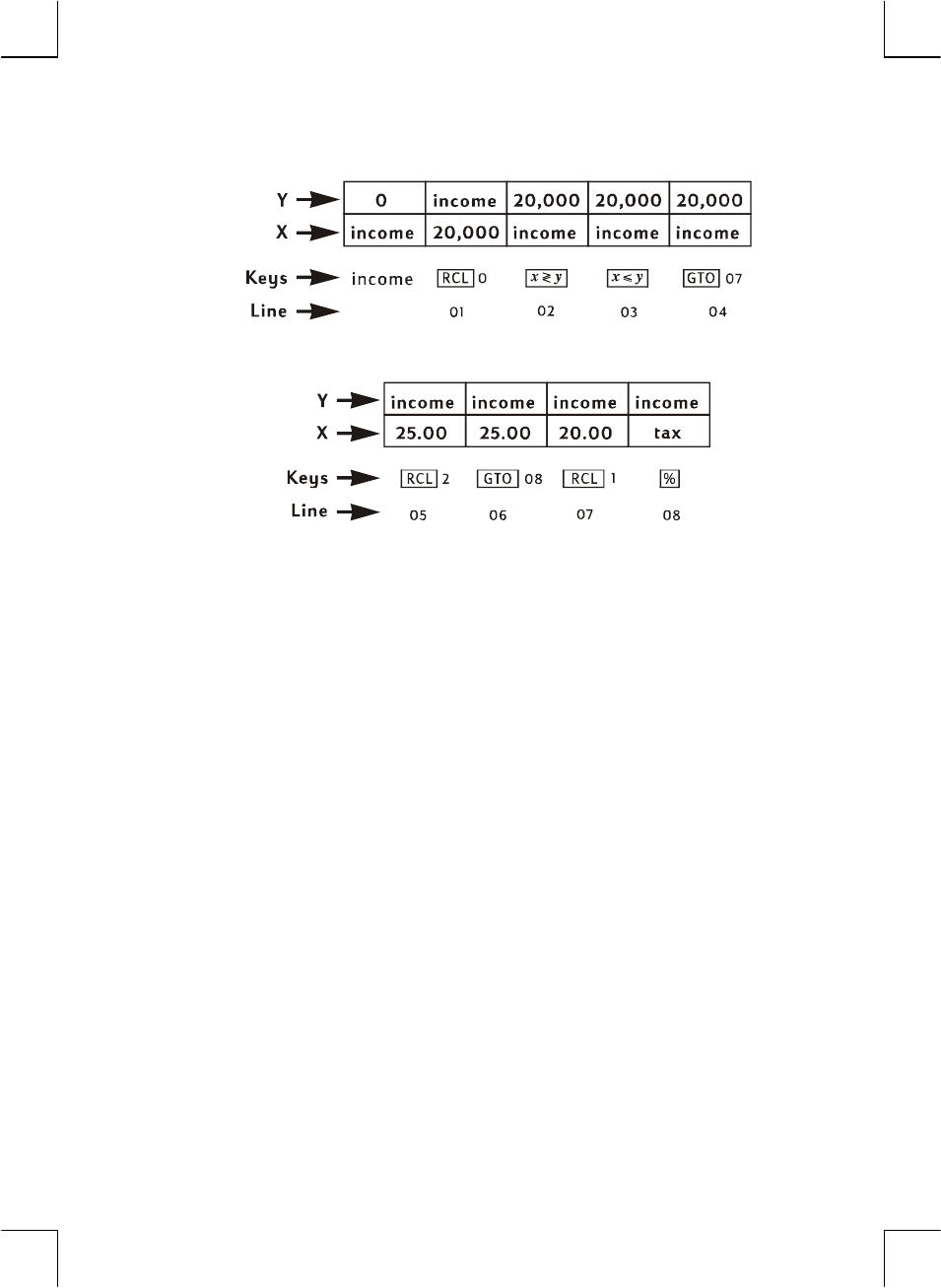
Section 9: Branching and Looping 109
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 109 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
We’ll key the income into the display before running the program so that it will be
in the X-register when the :0 instruction in program line 01 is executed. This
instruction will place the test value 20,000 in the X-register and (as explained in
Appendix A) move the income into the Y-register. The ~ instruction in program
line 02 will exchange the numbers in the X- and Y-registers (as also explained in
Appendix A): that is, it will place the income back into the X-register and place the
test value into the Y-register. This is necessary because when either the :2
instruction in line 05 or the :1 instruction in line 07 is executed, the number in
the X-register is moved into the Y-register; if the ~ instruction were not included,
the test value 20,000, rather than the income, would be in the Y-register when the
b instruction in line 08 is executed.
Keystrokes Display
fs 07- 43, 33 02 Sets calculator to Program mode.
(Display shows program line at
which execution was halted at end
of preceding example.)
fCLEARÎ 00- Clears program memory.
:0 01- 45 0 Recalls test value into X-register and
places income in Y-register.
~ 02- 34 Places income in X-register and test
value in Y-register.
go 03- 43 34 Tests whether number in X-register
(income) is less than or equal to
number in Y-register (20,000).

110 Section 9: Branching and Looping
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 110 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
gi07 04- 43, 33 07 If condition is true, branches to
program line 07.
:2 05- 45 2 If condition is false, recalls 25% tax
rate to X-register.
gi08 06- 43, 33 08 Branches to program line 08.
:1 07- 45 1 Recalls 20% tax rate to X-register.
b 08- 25 Calculates tax.
fs –12.36 Sets calculator to Run mode.
(Display shows results of running of
previous program.)
Now, we'll store the required numbers in registers R0, R1, and R2, then we’ll run the
program, using Ç so that we can check that the branching occurs properly. It’s
good practice with programs containing conditional test instructions to check that
the program branches correctly for all possible conditions: in this case, if the
income is less than, equal to, or greater than the test value.
Keystrokes Display
20000?0 20,000.00 Stores test value in register R0.
20?1 20.00 Stores 20% tax rate in register R1.
25?2 25.00 Stores 25% tax rate in register R2.
15000 15,000. Keys income less than test value into
display and X-register.
Ê 01- 45 0 Line 01: :0.
20,000.00 Test value has been recalled to
X-register, moving income to
Y-register.
Ê 02- 34 Line 02: ~
15,000.00 Income has been placed in
X-register and test value has been
placed in Y-register.
Ê 03- 43 34 Line 03: go
15,000.00
Ê 04- 43, 33 07 Condition tested by o was true,
so program execution continued
with line 04: gi07.

Section 9: Branching and Looping 111
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 111 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
15,000.00
Ê 07- 45 1 Line 07: :1.
20.00 20% tax rate has been recalled to
X-register, moving income to
Y-register.
Ê 08- 25 Line 08: b.
3,000.00 20% of 15,000 = 3,000.
20000 20,000. Keys income equal to test value into
display and X-register.
Ê 01- 45 0 Line 01: :0.
20,000.00 Test value has been recalled to
X-register, moving income to
Y-register.
Ê 02- 34 Line 02: ~.
20,000.00 Income has been placed in
X-register and test value has been
placed in Y-register.
Ê 03- 43 34 Line 03 go.
20,000.00
Ê 04- 43, 33 07 Condition tested by o was true,
so program execution continued
with line 04: gi07.
20,000.00
Ê 07- 45 1 Line 07: :1.
20.00 20% tax rate has been recalled to
X-register, moving income to
Y-register.
Ê 08- 25 Line 08: b.
4,000.00 20% of 20,000 = 4,000.
25000 25,000. Keys income greater than test value
into display and X-register.
Ê 01- 45 0 Line 01: :0.
20,000.00 Test value has been recalled to
X-register, moving income to
Y-register.

112 Section 9: Branching and Looping
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 112 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
Ê 02- 34 Line 02: ~.
25,000.00 Income has been placed in
X-register and test value has been
placed in Y-register.
Ê 03- 43 34 Line 03: go.
25,000.00
Ê 05- 45 2 Condition tested by o was false,
so program execution skipped the
next line and continued at line 05:
:2.
25.00 25% tax rate has been recalled to
X-register, moving income to
Y-register.
Ê 06- 43, 33 08 Line 06: gi08.
25.00
Ê 08- 25 Line 08: b.
6,250.00 25% of 25,000 = 6,250.

113
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 113 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 10
Program Editing
There are various reasons why you might want to modify a program you have
stored in Program memory: to correct a program that turns out to have errors; to
insert new instructions such as ? to store intermediate results or u to display
intermediate results; or to replace a u instruction by an t instruction.
Rather than clearing program memory and keying in the modified program, you
can modify the program already stored in the calculator. This is called program
editing.
Changing the Instruction in a Program Line
To change a single instruction in program memory:
1. Press fs to set the calculator to Program mode.
2. Use Ç, Ü, or i. to set the calculator to the program line preceding
the line containing the instruction to be changed.
3. Key in the new instruction.
For example, to change the instruction stored in program line 05, press
gi.04, then key in the new instruction that is to be stored in program line
05. The instruction previously stored in line 05 will be replaced; it is not
automatically “bumped” into line 06.
Example: With the last program from the preceding section still stored in the
calculator, suppose you wanted to use register R2 for some other purpose, and so
you needed to replace the :2 instruction in program line 05 with, say, :6.
You could change the instruction in line 05 as follows:
Keystrokes Display
fs 00- Sets calculator to Program mode.
gi.04 04- 43, 33 07 Sets calculator to program line
preceding that containing the instruction
to be changed.
:6 05- 45 6 Keys new instruction into program line
05, replacing the :2 instruction
previously there.
Ê 06- 43, 33 08 Shows that instruction in program line
06 has not been changed.

114 Section 10: Program Editing
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 114 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
fs 6,250.00 Sets calculator back to Run mode.
(Display shown assumes results remain
from last example in precedin
g
section.)
:2?6 25.00 Copies tax rate from R2 into R6.
Adding Instructions at the End of a Program
To add one or more instructions at the end of the last program stored in program
memory:
1. Press fs to set the calculator to Program mode.
2. Press gi. followed by two digits that specify the last line you keyed
into program memory (that is, the highest numbered line, not necessarily the
line most recently keyed in).
3. Key in the new instruction or instructions.
Note: To add one or more instructions at the end of a program that is not
the last program stored in program memory, use the procedure described
below under Adding Instructions Within a Program.
Example: With the last program from the preceding section stored in the
calculator, suppose you wanted to add a - instruction at the end in order to
calculate the net income after taxes. You could do so as follows:
Keystrokes Display
fs 00- Sets calculator to Program mode.
gi.08 08- 25 Sets calculator to last line keyed into
program memory.
- 09- 30 Keys new instruction into program
line 09.
fs 25.00 Sets calculator back to Run mode.
15000t 12,000.00 Net income after 20% tax is
subtracted from $15,000 income.

Section 10: Program Editing 115
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 115 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Adding Instructions Within a Program
If an instruction is to be added within a program, simply keying it in will replace
the instruction previously stored in that program line, as described above; the
contents of all higher-numbered program lines remain unchanged.
To add instructions within a program, you could simply key in the new instructions,
beginning at the proper program line, followed by the original instructions from
that program line through the end of the program. This method is described below
under Adding Instructions by Replacement. When instructions must be added in the
middle of a long program, however, using this method will require you to key in
numerous instructions — namely, the original instructions from the point at which
the new instructions are added through the end of program memory. Since keying
in these instructions may require a significant amount of time, in such situations you
may prefer to use the method described below under Adding Instructions by
Branching.
That method basically involves branching to the new instructions which are stored
at the end of program memory, then branching back to the program line
immediately following the line from which you branched out. Adding instructions
by branching is not so simple as adding instructions by replacement; however, it
generally will require fewer keystrokes whenever there are more than four program
lines between (and including) the first line to be executed after the new instruction(s)
and the last line you keyed into program memory. Furthermore, if program
memory includes branches to program lines following the point at which the new
instruction(s) are being added, adding instructions by branching will not require
that you change the line numbers specified in the i instructions, which may be
necessary when you add instructions by replacement.
Adding Instructions by Replacement
1. Press fs to set the calculator to Program mode.
2. Press gi. followed by two digits that specify the last program line to
be executed before the added instruction(s). This sets the calculator to the
proper program line for adding the new instruction(s) in the next step.
3. Key in the new instruction or instructions.
4. Key in the original instruction or instructions, beginning with the first
instruction to be executed after the added instruction(s), and continuing
through the last instruction you keyed into program memory.
Note: If program memory includes branches to program lines following that
at which the first new instruction is being added, remember to change the
line number(s) specified in the i instruction(s) — as described above
under Changing the Instruction in a Program Line — to the actual new line
number(s).

116 Section 10: Program Editing
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 116 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example: Assuming you have added a - instruction at the end of program
memory as in the preceding example, suppose you now wanted to insert an t
instruction before the - instruction so that the program will display the amount of
the tax before displaying the net income after tax. Since there is only one
instruction (-) following the point at which the new instruction is being added, it
is simplest to add the t instruction by replacement, as follows:
Keystrokes Display
fs 00- Sets calculator to Program mode.
gi.08 08- 25
Sets calculator to last pro
g
ram line
to be executed, which contains the
b instruction.
t 09- 31
Keys in new instruction.
- 10- 30
Keys in original instruction, which
was replaced by new instruction
added.
fs 12,000.00 Sets calculator back to Run mode.
15000t 3,000.00 Twenty percent tax on $15,000
income.
t 12,000.00 Net income after tax.
Adding Instructions by Branching
1. Press fs to set the calculator to Program mode.
2. Press gi. followed by two digits that specify the program line
immediately preceding the point at which the new instruction(s) are being
added — usually, the last program line to be executed before the added
instruction(s). This sets the calculator to the proper program line for inserting
a i instruction in the next step. This i instruction will replace whatever
instruction was already stored there, but that instruction will be keyed back
into program memory, to be executed just after the new instructions, in step
7.
3. Press gi followed by two digits that specify the second line after the last
line you keyed into program memory. (Branching to the second line rather
than to the first is necessary because the first line following the last program
in program memory must contain a i00 instruction. The i00
instruction ensures that program execution will branch to line 00 and halt
after the program is run.) For example, if the last line you keyed into
program memory was line 10, you would press gi12 at this step,
preserving the gi00 in line 11.
4. Press gi. followed by two digits that specify the last line you keyed
into program memory.

Section 10: Program Editing 117
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 117 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
5. Press gi00. This automatically converts a data storage register into
seven additional lines of program memory (if there was not already a
i00 instruction remaining at the end of program memory), and it ensures
that program execution will branch to line 00 after the program is run.
6. Key in the instruction(s) being added.
7. Key in the instruction that originally immediately followed the point at which
the new instruction(s) are being added — that is, the first instruction to be
executed after the added instruction(s). (This instruction was replaced by the
i instruction keyed in at step 3.)
8. Press gi followed by two digits that specify the second line following
the point at which the new instruction(s) are being added. This i
instruction will cause program execution to branch back to the proper line
within the original program.
Example: Continuing with the preceding example, suppose incomes less than or
equal to $7,500 were not to be taxed. You could modify the program to check for
this condition and stop at line 00, displaying the original income keyed in, by
storing 7,500 in register R3 and adding the following instructions between lines 00
and 01: :3~gogi00. Since there are more than four instructions
between (and including) the first line to be executed after the added instructions
(line 01) and the last line you keyed into program memory (line 10), it will require
fewer keystrokes to add the new instructions by branching than to add them by
replacement.
Keystrokes Display
fs 00- Sets calculator to Program mode.
gi.00 00- Sets calculator to program line
immediately preceding point at
which new instructions are being
added. (In this particular example,
this step could have been skipped
since calculator was already set at
the proper program line.)
gi12 01- 43, 33 12 Branches to program line 12, the
second line after last line of
program.
gi.10 10- 30
Sets calculator to last line of
program so that i00 instruction
keyed in next will be stored in first
line following program.
gi00 11- 43, 33 00 Ensures that i00 instruction
follows program.

118 Section 10: Program Editing
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 118 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
:3 12- 45 3
~ 13- 34
go 14- 43 34
gi00 15- 43, 33 00
Added instructions.
:0 16- 45 0
Keys in instruction immediately
following point at which new
instructions are being added. (This
instruction was replaced in line 01
by i12 instruction.)
gi02 17- 43, 33 02 Branches back to second line (line
02) following point at which new
instructions are being added.
fs 12,000.00 Sets calculator back to Run mode.
7500?3 7,500.00 Stores test value in register R3.
6500t 6,500.00 Runs program for income less than
$7,500. Display shows original
income keyed in, indicating that tax
is zero.
15000t 3,000.00 Tax on $15,000 income.
t 12,000.00 Net income after tax. This shows
program still works for an income
greater than $7,500 and less than
$20,000.
The following illustration of the edited program shows how program execution
branches to the instructions added at the end of program memory, then branches
back.
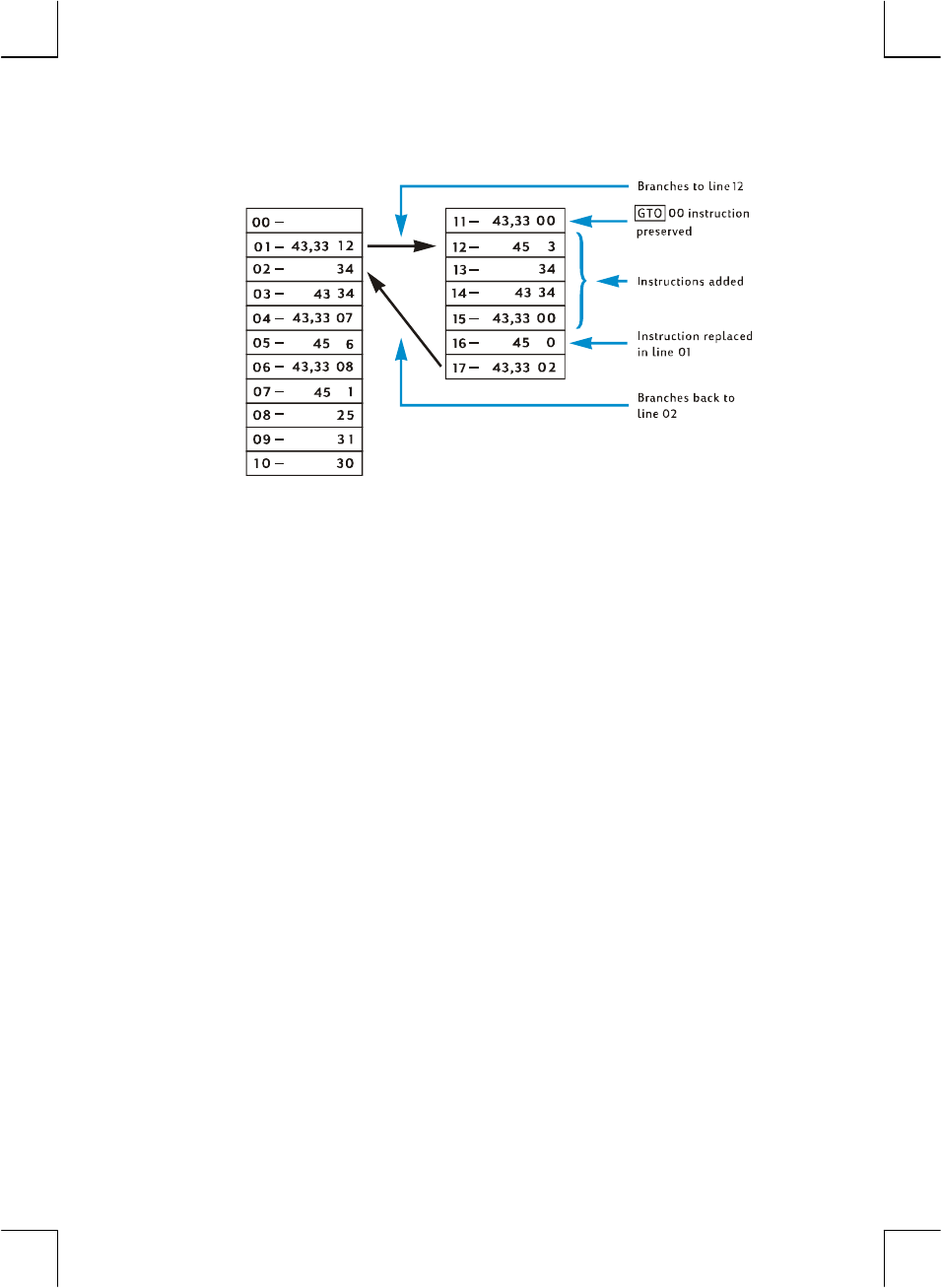
Section 10: Program Editing 119
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 119 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

120
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 120 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 11
Multiple Programs
You can store multiple programs in program memory, provided that you separate
them by instructions that will halt program execution after each program is run and
return to the beginning of the program if it is run again. You can run programs
after the first one stored in program memory by setting the calculator to the first
line of the program using i before pressing t.
Storing Another Program
To store a program after another program is already stored in program memory:
1. Press fs to set the calculator to Program mode. Do not clear program
memory.
2. Press gi. followed by two digits that specify the number of the last
line you keyed into program memory.
Note: If this is the second program to be stored in program memory, you
will need to ensure that a i00 instruction separates it from the first
program by doing step 3. If there are already two or more programs stored
in program memory, skip step 3 and proceed with step 4.
3. Press gi00. This automatically converts a data storage register into
seven additional lines of program memory (if there was not already a
i00 instruction remaining at the end of program memory), and it ensures
that program execution will branch to line 00 after the first program is run.
4. Key the program into program memory. If you are storing a program that
you originally had written to be stored at the beginning of program memory
and the program contains a i instruction, be sure to change the line
number specified in the instruction so that the program will branch to the
actual new line number.
Note: The next two steps are included so that program execution will halt
after this program is run and will return to the beginning of the program if it
is run again. If the program ends with a loop, you should skip steps 5 and 6
since the instructions in those steps would serve no purpose and never be
executed.
5. Press t. This halts program execution at the end of the program.
6. Press gi followed by two digit keys that specify the first line number of
your new program. This transfers program execution to the beginning of the
new program when the program is run again.

Section 11: Multiple Programs 121
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 121 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 1: Assuming that program memory still contains the last program from
the preceding section (which consisted of 17 program lines), store after that
program the office-supplies program from Section 8 (page 88). Since this is the
second program to be stored in program memory, we’ll ensure that a i00
instruction separates it from the first program by doing step 3 in the procedure
above. Furthermore, since this program does not end with a loop, we’ll do steps 5
and 6 too.
Keystrokes Display
fs 00- Sets calculator to Program mode.
gi.17 17- 43, 33 02 Sets calculator to last line keyed into
program memory.
gi00 18- 43, 33 00 Ensures that second program is
separated from first by i00.
\ 19- 36
2 20- 2
5 21- 5
b 22- 25
- 23- 30
5 24- 5
+ 25- 40
Keys in program.
t 26- 31
Halts program execution.
gi19 27- 43, 33 19 Branches to beginning of program.
fs 12,000.00 Sets calculator back to Run mode.
(Display shown assumes results
remain from running program in
previous example.)

122 Section 11: Multiple Programs
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 122 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 2: With the two programs now stored in program memory from the
preceding examples (occupying 27 program lines), store the amortization program
from Section 9(page 103). Since there are already two programs stored in
program memory, we’ll skip step 3 in the procedure above. Furthermore, since the
amortization program ends with a loop, we’ll skip steps 5 and 6. When the
amortization program was stored at the beginning of program memory, the i
instruction at the end of the program branched to the :0 instruction in line 02.
Since the :0 instruction is now in line 29, we’ll specify that line number with the
i instruction in line 34.
Keystrokes Display
fs 00- Sets calculator to Program
mode.
gi.27 27- 43, 33 19 Sets calculator to last line keyed
into program memory.
?0 28- 44 0
:0 29- 45 0
f! 30- 42 11
gu 31- 43 31
~ 32- 34
gu 33- 43 31
gi29 34- 43, 33 29
Keys in program
Running Another Program
To run a program that does not begin with program line 01:
1. Press fs to set the calculator to Run mode. If the calculator is already in
Run mode, skip this step.
2. Press gi followed by two digits that specify the first line of the program.
3. Press t.
Example: Run the office-supplies program, now stored in the calculator
beginning at program line 19, for the typewriter listing for $625.
Keystrokes Display
fs 12,000.00 Sets calculator to Program
mode.
gi19 12,000.00 Sets calculator to first line of
program to be executed.
625t 473.75 Net cost of typewriter.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 123 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Part III
Solutions

124
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 124 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 12
Real Estate and Lending
Annual Percentage Rate Calculations With Fees
Borrowers are usually charged fees in connection with the issuance of a mortgage,
which effectively raises the interest rate. The actual amount received by the
borrower (PV) is reduced, while the periodic payments remain the same. Given the
life or term of the mortgage, the interest rate, the mortgage amount, and the basis
of the fee charge (how the fee is calculated), the true Annual Percentage Rate (APR)
may be calculated. Information is entered as follows:
1. Press g and fCLEARG.
2. Calculate and enter the periodic payment amount of the loan.
a. Key in the total number of payment periods; press n.
b. Key in the periodic interest rate (as a percentage); press ¼.
c. Key in the mortgage amount; press $.*
d. To obtain the periodic payment amount, press P.*
3. Calculate and key in the actual net amount disbursed.*
z If fees are stated as a percentage of the mortgage amount (points), recall
the mortgage amount (:$) key in the fee (percentage) rate; press
b-$.
z If fees are stated as a flat charge, recall the mortgage amount (:$);
key in the fee amount (flat charge); press -$.
z If fees are stated as a percentage of the mortgage amount plus a flat
charge, recall the mortgage amount (:$); key in the fee
(percentage) rate, press b-; key in the fee amount (flat charge); press
-$.
4. Press ¼ to obtain the interest rate per compounding period.
5. To obtain the annual nominal percentage rate, key in the number of periods
per year, then press µ.
* Positive for cash received; negative for cash paid out.

Section 12: Real Estate and Lending 125
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 125 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 1: A borrower is charged 2 points for the issuance of his mortgage. If
the mortgage amount is $60,000 for 30 years and the interest rate is 111/2% per
year, with monthly payments, what true annual percentage rate is the borrower
paying? (One point is equal to 1% of the mortgage amount.)
Keystrokes Display
gÂ
fCLEARG
30gA 360.00 Months (into n)
11.5gC 0.96 Percent monthly interest rate (into i).
60000$ 60,000.00 Loan amount (into PV).
P –594.17 Monthly payment (calculated).
:$2b-$ 58,800.00 Actual amount received by borrower
(into PV).
¼ 0.98 Percent monthly interest rate
(calculated).
12§ 11.76 Annual percentage rate.
Example 2: Using the same information as given in example 1, calculate the
APR if the mortgage fee is $150 instead of a percentage.
Keystrokes Display
gÂ
fCLEARG
30gA 360.00 Months (into n)
11.5gC 0.96 Percent monthly interest rate (into i).
60000$ 60,000.00 Loan amount (into PV).
P –594.17 Monthly payment (calculated).
:$150-$ 59,850.00 Effective mortgage amount (into PV).
¼ 0.96 Monthly interest rate (calculated).
12§ 11.53 Annual percentage rate.

126 Section 12: Real Estate and Lending
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 126 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 3: Again using the information given in example 1, what is the APR if
the mortgage fee is stated as 2 points plus $150?
Keystrokes Display
gÂ
fCLEARG
30gA 360.00 Months (into n)
11.5gC 0.96 Percent monthly interest rate (into i).
60000$ 60,000.00 Loan amount (into PV).
P –594.17 Monthly payment (calculated).
:$2b- 58,800.00
150-$ 58,650.00 Effective mortgage amount (into PV).
¼ 0.98 Monthly interest rate (calculated).
12§ 11.80 Annual percentage rate.
Price of a Mortgage Traded at a Discount or Premium
Mortgages may be bought and/or sold at prices lower (discounted) or higher (at a
premium) than the remaining balance of the loan at the time of purchase. Given
the amount of the mortgage, the periodic payment, the timing and amount of the
balloon or prepayment, and the desired yield rate, the price of the mortgage may
be found. It should be noted that the balloon payment amount (if it exists) occurs
coincident with, and does not include, the last periodic payment amount.
Information is entered as follows:
1. Press g and fCLEARG.
2. Key in the total number of periods until the balloon payment or prepayment
occurs; press n. (If there is no balloon payment, key in total number of
payments and press n.)
3. Key in the desired periodic interest rate (yield) and press ¼.
4. Key in the periodic payment amount; press P.*
5. Key in the balloon payment amount and press M.* (If there is no balloon
payment, go to step 6.)
6. Press $ to obtain the purchase price of the mortgage.
* Positive for cash received; negative for cash paid out.

Section 12: Real Estate and Lending 127
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 127 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 1: A lender wishes to induce the borrower to prepay a low interest rate
loan. The interest rate is 5% with 72 payments remaining of $137.17 and a
balloon payment at the end of the sixth year of $2000. If the lender is willing to
discount the future payments at 9%, how much would the borrower need to prepay
the note?
Keystrokes Display
gÂ
fCLEARG
72n
72.00
Months (into n).
9gC 0.75 Discount rate (into i).
137.17P* 137.17 Monthly payments (into PMT).
2000M$ –8,777.61 Amount necessary to prepay the
note.
Example 2: A 91/2% mortgage with 26 years remaining and a remaining
balance of $49,350 is available for purchase. Determine the price to pay for this
mortgage if the desired yield is 12%. (Since the payment amount is not given, it
must be calculated.)
Keystrokes Display
gÂ
fCLEARG
26gA
312.00
Months (into n).
9.5gC 0.79 Percent monthly interest rate (into i).
49350Þ$P 427.17 Monthly payment to be received
(calculated).
12gC 1.00 Desired monthly interest rate (into i).
$ –40,801.57 Purchase price to achieve the
desired yield (calculated).
* Note that the payments are positive because this problem in seen from the viewpoint of the
lender who will be receiving payments. The negative PV indicates money that was lent out.

128 Section 12: Real Estate and Lending
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 128 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Yield of a Mortgage Traded at a Discount or Premium
The annual yield of a mortgage bought at a discount or premium can be
calculated given the original mortgage amount, interest rate, and periodic
payment, as well as the number of payment periods per year, the price paid for
the mortgage, and the balloon payment amount (if it exists).
Information is entered as follows:
1. Press g and fCLEARG.
2. Key in the total number of periods until the balloon payment occurs and
press n. (If there is no balloon payment, key in the total number of periods
and press n.)
3. Key in the periodic payment amount then press P.*
4. Key in the purchase price of the mortgage then press $.*
5. Key in the balloon payment amount then press M.* (If there is no balloon
payment, go to step 6.)
6. Press ¼ to obtain the yield per period.
7. Key in the number of periods per year and press § to obtain the nominal
annual yield.
Example 1: An investor wishes to purchase a $100,000 mortgage taken out at
9% for 21 years. Since the mortgage was issued, 42 monthly payments have been
made. What would be the annual yield if the purchase price of the mortgage is
$79,000? (Since PMT was not given, it must be calculated).
Keystrokes Display
gÂ
fCLEARG
21gA
252.00
Enter the number of periods (into
n).
9gC 0.75 Monthly interest rate (into i).
100000Þ$ –100,000.00 Mortgage amount (into PV;
negative to indicate money paid
out).
P 884.58 Payment received (calculated).
:n 252.00 Recall number of periods.
42-n 210.00 Number of periods left after
mortgage is bought (into n).
* Positive for cash received; negative for cash paid out.

Section 12: Real Estate and Lending 129
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 129 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
79000Þ$ –79,000.00 Input price of mortgage (into PV;
negative to indicate money paid
out).
¼ 0.97 Yield per month (calculated).
12§ 11.68 Percent annual yield.
Example 2: Using the same information given in example 1, calculate the annual
yield if the loan is to be paid in full at the end of the fifth year (from original
issuance). (In this case both the payment amount and the balloon must be
calculated since they are not given.)
Keystrokes Display
gÂ
fCLEARG
21gA
252.00
Input the number of periods (into
n).
9gC 0.75 Monthly interest rate (into PV).
100000Þ$ –100,000.00 Mortgage amount (into PV).
P 884.58 Payment (calculated).
Calculate the remaining balance of the loan after five years.
5gA 60.00 Number of periods to be
amortized.
M 89,849.34 Remaining balance of the loan
after five years.
:n 60.00
42-n 18.00 New life of loan.
79000Þ$¼ 1.77 Percent monthly yield. (calculated).
12§ 21.29 Percent annual yield.

130 Section 12: Real Estate and Lending
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 130 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The Rent or Buy Decision
The question of whether to rent or purchase a residence is not always easy to
answer, especially when the time period over which you would own or rent a
house is short. This program performs an analysis which could be helpful in
reaching a decision. Essentially, it calculates a yield or rate of return on the
proposed investment. This yield may be compared with the yield obtained by
renting a residence and investing the down payment and monthly payment
differences in a savings account or other investment opportunity. This program
takes into account the tax advantages obtained by a home owner on property
taxes and mortgage interest.
First the program computes the Net Cash Proceeds upon Resale (NCPR),* next the
yield on the investment in the house and then the value of the hypothetical savings
account at the end of the investment period. A comparison of the NCPR and the
final balance of the savings account and a comparison of the yields should aid in
determining whether to rent or buy.
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
fs M 33- 15
fCLEARÎ 00- t 34- 31
M 01- 15 d 35- 33
M† 02- 15 :n 36- 45 11
:7 03- 45 7 z 37- 10
b 04- 25 :4 38- 45 4
- 05- 30 - 39- 30
:n 06- 45 11 :.0 40-45 48 0
?0 07- 44 0 b 41- 25
:$ 08- 45 13 :P 42- 45 14
fCLEARG 09- 42 34 :4 43- 45 4
* The Net Cash Proceeds upon Resale (NCPR = sales price – commission – mortgage balance),
is the pre-tax proceeds. The program assumes that the buyer reinvests in like property and is
not subject to capital gains tax.
† FV is repeated in the program twice to ensure that it is computed and not stored.

Section 12: Real Estate and Lending 131
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 131 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
:1 10- 45 1 - 44- 30
- 11- 30 :5 45- 45 5
$ 12- 13 - 46- 30
:3 13- 45 3 :8 47- 45 8
gC 14- 43 12 + 48- 40
:2 15- 45 2 - 49- 30
gA 16- 43 11 Þ 50- 16
P 17- 14 P 51- 14
d 18- 33 :0 52- 45 0
d 19- 33 gA 53- 43 11
0 20- 0 :1 54- 45 1
n 21- 11 :6 55- 45 6
:0 22- 45 0 + 56- 40
1 23- 1 Þ 57- 16
2 24- 2 $ 58- 13
§ 25- 20 ¼ 59- 12
f! 26- 42 11 :gC 60-45 43 12
d 27- 33 t 61- 31
d 28- 33 :9 62- 45 9
d 29- 33 gC 63- 43 12
:$ 30- 45 13 M 64- 15
+ 31- 40 fs
Þ 32- 16

132 Section 12: Real Estate and Lending
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 132 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
REGISTERS
n: Period i: Apprec. PV: Price PMT: Used
FV: Used R0: Period R1: Dwn Pmt R2: Life
R3: i(Mtg)
R
4
: Taxes/Mo
R5: Improve.
R
6
: Closing C.
R7: % Comm. R8: Rent R9: Savings i R.0: Bracket
R.1: Unused.
1. Key in the program.
2. Key in the estimated down payment then press ?1.
3. Key in the life of the mortgage then press ?2.
4. Key in the annual mortgage interest rate then press ?3.
5. Key in the estimated monthly taxes then press ?4.
6. Key in the total amount estimated for monthly repairs, improvements,
incremental insurance, utility costs, and other expenses, then press ?5.
7. Key in the closing costs then press ?6.
8. Key in the selling cost as a percentage of the selling price. This should
include sales commission, escrow fees, etc. then press ?7.
9. Key in the monthly rent for the alternative housing then press ?8.
10. Key in the savings or alternative investment annual interest rate as a
percentage then press ?9.
11. Key in the combined State and Federal marginal tax rate* as a percentage
then press ?.0.
12. Press fCLEARG then key in the number of years involved in the
investment; press n.
13. Key in the estimated rate of yearly appreciation as a percentage then press
¼.
14. Key in the price of the house under consideration then press $.
15. Press t to compute the net proceeds from the sale of the house. (A
negative value indicates money lost.)
* The user should key in the total marginal income tax — Federal plus State — to obtain
calculations which reflect the tax advantages of home ownership. Because of the complexities
of tax laws and different financial and tax considerations for each individual, this program
should only serve as a guide in considering an investment of this type. For more specific,
detailed information, consult a tax accountant or qualified tax advisor.

Section 12: Real Estate and Lending 133
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 133 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
16. Press t to compute the yield on your investment in the house.*
17. Press t to compute the value of a savings account or other investment.
18. Compare the value of the hypothetical savings account to the net proceeds of
the sale of the house. Examine the sign and magnitude of the yield to arrive
at your decision.
19. To change data and repeat the calculations, store the changed values in the
appropriate registers and go to step 12.
Example: You are being transferred for 4 years to a distant city and are faced
with the decision of whether to rent or to buy a house. A quick survey of the
housing market indicates that you can purchase an acceptable house for $70,000
with a $7,000 down payment on a 30 year mortgage at 12% interest. The closing
costs would be about $1200. Selling costs include a 6% commission for resale
and miscellaneous other fees that amount to another 2% of the sale price. Housing
in the area is appreciating 10% per year. Property taxes would be about $110
per month, and you estimate that maintenance would cost an additional $65 per
month.
An alternative would be to rent a similar dwelling at $400 per month and to invest
the difference between the purchase cost and rent at 61/4% interest. Your personal
income tax rate (marginal) is 25% Federal and 5% State. Which alternative is
more financially attractive?
Keystrokes Display
fCLEARH 0.00
7000?1 7,000.00 Down payment.
30?2 30.00 Life of mortgage.
12?3 12.00 Interest rate.
110?4 110.00 Property taxes.
65?5 65.00 Monthly expenses.
1200?6 1,200.00 Closing costs.
8?7 8.00 Resale costs (as a percentage).
400?8 400.00 Rent.
6.25?9 6.25 Savings interest rate.
30?.0 30.00 Tax bracket.
fCLEARG 30.00 Clear financial registers.
* If the calculator displays a negative result or Error 5 when solving for yield then your
investment has resulted in a loss. The amount of interest earned on the alternative investment
is not taken into account in this calculation.

134 Section 12: Real Estate and Lending
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 134 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
4n 4.00 Years in investment.
10¼ 10.00 Yearly appreciation rate.
70000$ 70,000.00 House price.
t 32,391.87 NCPR (calculated).
t 19.56 Yield.
t 21,533.79 Balance in savings.
By purchasing a house, you would gain $10,858.08 (32,391.87 – 21,533.79)
over an alternate investment at 6.25% interest.
Deferred Annuities
Sometimes transactions are established where payments do not begin for a
specified number of periods; the payments are deferred. The technique for
calculating NPV may be applied assuming zero for the first cash flow. Refer to
pages 58 through 62.
Example 1: You have just inherited $20,000 and wish to put some of it aside for
your daughter’s college education. You estimate that when she is of college age, 9
years from now, she will need $7,000 at the beginning of each year for 4 years
for college tuition and expenses. You wish to establish a fund which earns 6%
annually. How much do you need to deposit in the fund today to meet your
daughter’s educational expenses?
Keystrokes Display
fCLEARH 0.00 Initialize.
0gJ 0.00 First cash flow.
0gK
8ga
0.00
8.00
Second through ninth cash flows.
7000gK
4ga
7,000.00
4.00
Tenth through thirteenth cash flows.
6¼ 6.00 Interest.
fl 15,218.35 NPV.
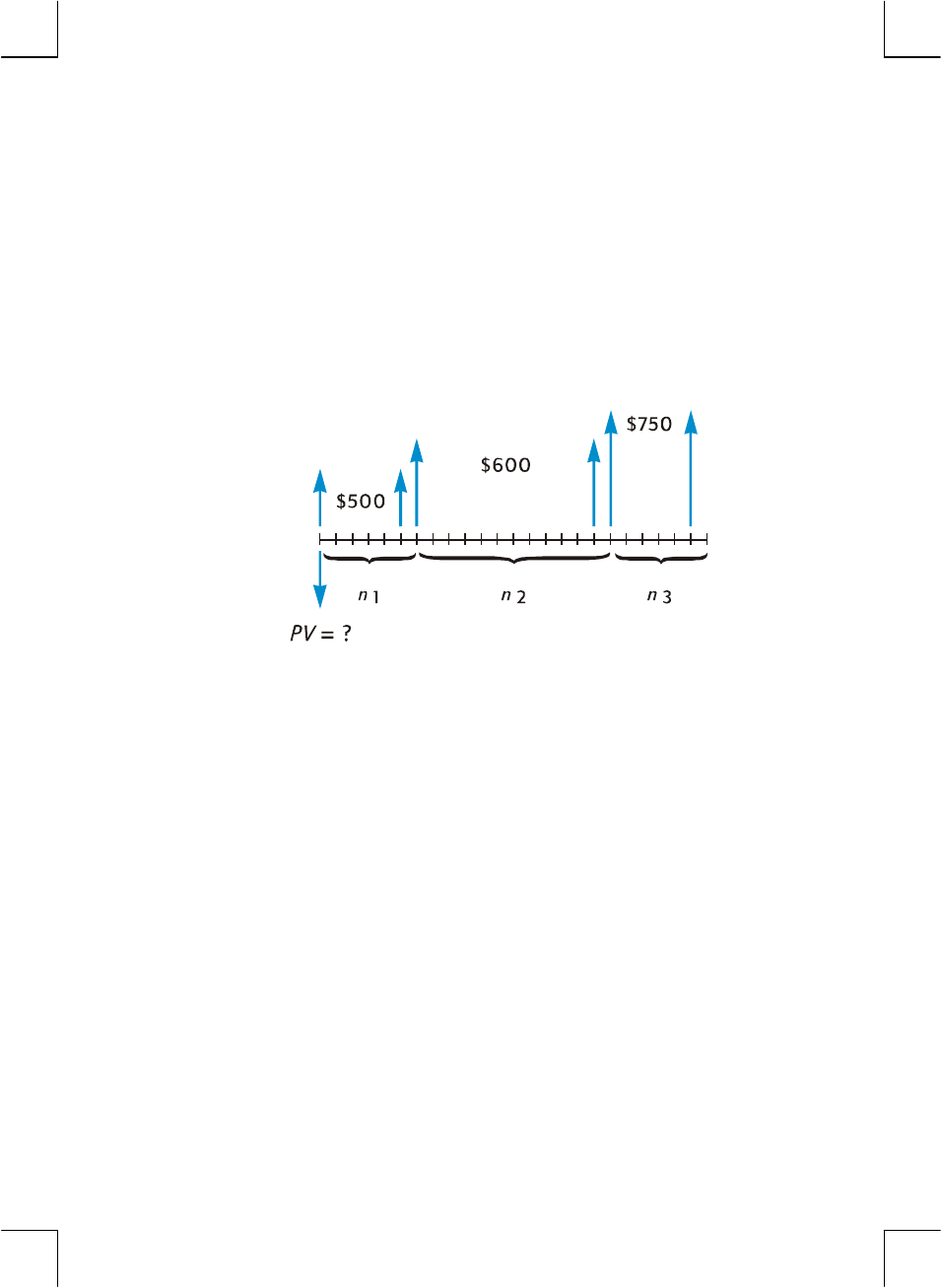
Section 12: Real Estate and Lending 135
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 135 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Leases often call for periodic contractual adjustments of rental payments. For
example, a 2-year lease calls for monthly payments (at the beginning of the month)
of $500 per month for the first 6 months, $600 per month for the next 12 months,
and $750 per month for the last 6 months. This situation illustrates what is called a
“step-up” lease. A “step-down” lease is similar, except that rental payments are
decreased periodically according to the lease contract. Lease payments are made
at the beginning of the period.
In the example cited, the rental payment stream for months 7 through 24 are
“deferred annuities,” as they start at some time in the future. The cash flow
diagram from the investor’s viewpoint looks like this:
To find today’s present value of the cash flows assuming a desired yield, the NPV
technique may be used. (Refer to pages 58 thru 62.)
Example 2: A 2-year lease calls for monthly payments (at the beginning of the
month) of $500 per month for the first 6 months, $600 per month for the next 12
months, and $750 per month for the last 6 months. If you wish to earn 13.5%
annually on these cash flows, how much should you invest (what is the present
value of the lease)?
Keystrokes Display
fCLEARH 0.00 Initialize.
500gJ 500.00 First cash flow.
gK
5ga
500.00
5.00
Second thru sixth cash flows.
600gK
12ga
600.00
12.00
Next twelve cash flows.
750gK
6ga
750.00
6.00
Last six cash flows.
13.5gC 1.13 Monthly interest rate.
fl 12,831.75 Amount to invest to achieve a
13.5% yield.

136
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 136 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 13
Investment Analysis
Partial-Year Depreciation
For both income tax purposes and financial analyses, it is valuable to calculate
depreciation based on a calendar or fiscal accounting year. When the acquisition
date of an asset does not coincide with the start of the year — which is the rule
rather than the exception — the amounts of depreciation in the first and last years
are computed as fractions of a full year’s depreciation.
Straight-Line Depreciation
The following hp 12c program calculates the straight-line depreciation for the year
desired with the acquisition date occurring at any time during the year.
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
fs - 21- 30
fCLEARÎ 00- n 22- 11
1 01- 1 :0 23- 45 0
2 02- 2 gm 24- 43 35
z 03- 10 gi35 25-43, 33 35
?1 04- 44 1 :2 26- 45 2
~ 05- 34 gu 27- 43 31
?2 06- 44 2 :0 28- 45 0
1 07- 1 fV 29- 42 23
- 08- 30 t 30- 31
?0 09- 44 0 1 31- 1
1 10- 1 ?=0 32-44 40 0
fV 11- 42 23 ?=2 33-44 40 2
:1 12- 45 1 gi26 34-43, 33 26
§ 13- 20 :2 35- 45 2
Section 13: Investment Analysis 137
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 137 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
?3 14- 44 3 gu 36- 43 31
:$ 15- 45 13 :$ 37- 45 13
~ 16- 34 :M 38- 45 15
- 17- 30 - 39- 30
$ 18- 13 :3 40- 45 3
:n 19- 45 11 gi30 41-43, 33 30
:1 20- 45 1 fs
REGISTERS
n: Life i: Unused PV: Dep. Value PMT: Unused
FV: Salvage R0: Used R1: #Mos./12 R2: Counter
R3: 1st Yr. Dep. R4–R.4: Unused
1. Key in the program.
2. Press fCLEARG.
3. Key in the book value then press $.
4. Key in the salvage value then press M.
5. Key in the life in years (an integer) then press n.
6. Key in the year desired then press \.
7. Key in the number of months in the first year and press t.* The display
will show the amount of depreciation for the desired year. If desired, press
~ to see the remaining depreciable value then press
:$:3=~-:M- to find the total depreciation from the
first year through the current year.
8. Press t for the amount of depreciation and remaining depreciable value
for the next year. Repeat this step for the following years.
9. For a new case, press gi00 and return to step 2.
* The display will pause showing the year number before showing the amount of depreciation
for that year.
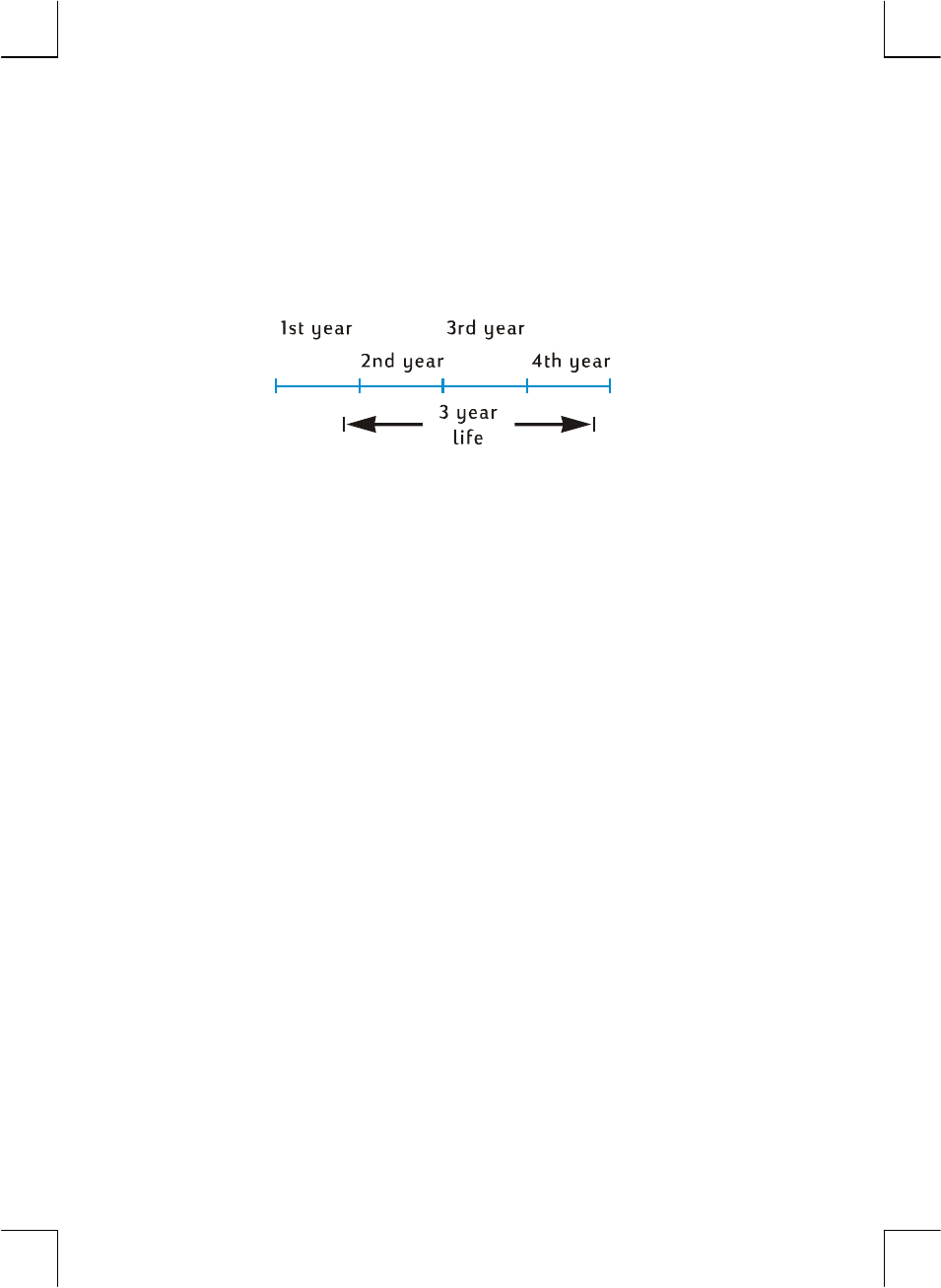
138 Section 13: Investment Analysis
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 138 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Note: If the number of months in the first calendar year is less than 12, the
amount of depreciation in the 1st year will be less than a full year’s
depreciation. The actual number of years that depreciation will occur is
equal to the life +1. For example, a drill has a life of 3 years and is
purchased 3 months before the year end. The following time diagram shows
that depreciation will occur over 4 calendar years.
Example 1: A property has just been purchased for $150,000. The purchase
price is allocated between $25,000 for land and $125,000 for improvements
(building). The remaining useful life of the building is agreed to be 25 years. There
is no salvage value forecasted at the end of the useful life of the building. Thus, the
depreciable value and book value is $125,000.
The building was acquired 4 months before the end of the year. Using straight-line
depreciation, find the amount of depreciation and remaining depreciable value for
the 1st, 2nd, 25th, and 26th years. What is the total depreciation after 3 years?
Keystrokes Display
fCLEARG Salvage value = 0 so FV = 0.
125000$ 125,000.00 Book value.
25n 25.00 Life.
1\ 1.00 Year desired.
4t
~
1.00
1,666.67
123,333.33
First year:
depreciation,
remaining depreciable value.
t
~
2.00
5,000.00
118,333.33
Second year:
depreciation,
remaining depreciable value.
t 3.00
5,000.00
Third year:
depreciation.
~:$:3
+~-
gi00
11,666.67
Total depreciation through third
year.
fCLEARG 11,666.67
125000$ 125,000.00 Book value.

Section 13: Investment Analysis 139
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 139 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
25n 25.00 Life.
25\ 25.00 Year desired.
4t
~
25.00
5,000.00
3,333.33
Twenty-fifth year:
depreciation,
remaining depreciable value.
t
~
26.00
3,333.33
0.00
Twenty-sixth year:
depreciation,
remaining depreciable value.
Example 2: A new car was purchased for $6,730 with 41/2 months remaining
in the year. If the expected life of the car is 5 years, what is the amount of
depreciation in the first year?
Keystrokes Display
gi00
fCLEARG
6730$ 6,730.00 Book value.
5n 5.00 Life.
1\ 1.00
4.5t 1.00
504.75
First year:
depreciation.
Declining-Balance Depreciation
The following hp 12c program calculates the declining-balance depreciation for
the year desired with the acquisition date occurring at any time during the year.
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
fs :0 19- 45 0
fCLEARÎ 00- gm 20- 43 35
1 01- 1 gi31 21-43, 33 31
2 02- 2 :2 22- 45 2
z 03- 10 gu 23- 43 31
?1 04- 44 1 :0 24- 45 0
~ 05- 34 f# 25- 42 25
?2 06- 44 2 t 26- 31

140 Section 13: Investment Analysis
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 140 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
1 07- 1 1 27- 1
- 08- 30 ?+0 28-44 40 0
?0 09- 44 0 ?+2 29-44 40 2
1 10- 1 gi22 30-43, 33 22
f# 11- 42 25 :2 31- 45 2
:1 12- 45 1 gu 32- 43 31
§ 13- 20 :$ 33- 45 13
?3 14- 44 3 :M 34- 45 15
:$ 15- 45 13 - 35- 30
~ 16- 34 :3 36- 45 3
- 17- 30 gi26 37-43, 33 26
$ 18- 13 fs
REGISTERS
n: Life i: Factor PV: Dep. Value PMT: Unused
FV: Salvage R0: Used R1: #Mos./12 R2: Counter
R3:1st Yr. Dep. R4–R.4: Unused
1. Key in the program.
2. Press fCLEARG.
3. Key in the book value then press $.
4. Key in the salvage value then press M.
5. Key in the declining-balance factor as a percentage then press ¼.
6. Key in the life in years (an integer) then press n.
7. Key in the year desired then press \.
8. Key in the number of months in first year* and press t.† The display will
show the amount of depreciation for the desired year. Press ~ to see the
* Refer to straight-line depreciation instruction note, page 137.
† The display will pause showing the year number before showing the amount of depreciation
for that year.

Section 13: Investment Analysis 141
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 141 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
remaining depreciable value. If desired, press
:$:3=~-:M- to find the total depreciation through the
current year.
9. Press t for the amount of depreciation then, if desired, press ~ for the
remaining depreciable value for the next year. Repeat this step for the
following years.
10. For a new case press gi00 and return to step 2.
Example: An electron beam welder which costs $50,000 is purchased 4 months
before the end of the accounting year. What will the depreciation be during the
first full accounting year (year 2) if the welder has a 6 year depreciable life, a
salvage value of $8,000 and is depreciated using the declining-balance
depreciation method? The declining-balance factor is 150%.
Keystrokes Display
fCLEARG
50000$ 50,000.00 Book value.
8000M 8,000.00 Salvage value.
150¼ 150.00 Declining-balance factor.
6n 6.00 Life.
2\ 2.00 Year desired.
4t 2.00
11,458.33
Second year:
depreciation.
Sum-of-the-Years-Digits Depreciation
The following hp 12c program calculates the sum-of-the-years-digits depreciation
for the year desired with the acquisition date occurring at any time during the
year.
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
fs - 21- 30
fCLEARÎ 00- n 22- 11
1 01- 1 :0 23- 45 0
2 02- 2 gm 24- 43 35
z 03- 10 gi35 25-43, 33 35
?1 04- 44 1 :2 26- 45 2
~ 05- 34 gu 27- 43 31

142 Section 13: Investment Analysis
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 142 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
?2 06- 44 2 :0 28- 45 0
1 07- 1 fÝ 29- 42 24
- 08- 30 t 30- 31
?0 09- 44 0 1 31- 1
1 10- 1 ?=0 32-44 40 0
fÝ 11- 42 24 ?=2 33-44 40 2
:1 12- 45 1 gi26 34-43, 33 26
§ 13- 20 :2 35- 45 2
?3 14- 44 3 gu 36- 43 31
:$ 15- 45 13 :$ 37- 45 13
~ 16- 34 :M 38- 45 15
- 17- 30 - 39- 30
$ 18- 13 :3 40- 45 3
:n 19- 45 11 gi30 41-43, 33 30
:1 20- 45 1 fs
REGISTERS
n: Life i: Unused PV: Dep. Value PMT: Unused
FV: Salvage R0: Used R1: #Mos./12 R2: Counter
R3: 1st Yr. Dep. R4–R.4: Unused
1. Key in the program.
2. Press fCLEARG.
3. Key in the book value then press $.
4. Key in the salvage value then press M.
5. Key in the life in years (an integer) then press n.
6. Key in the year desired then press \.

Section 13: Investment Analysis 143
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 143 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
7. Key in the number of months in first year* then press t.† The display will
show the amount of depreciation for the desired year. If desired, press ~
to see the remaining depreciable value, then press :$:3=
~-:M- to find the total depreciation through the current year.
8. Press t for the amount of depreciation then, if desired, press ~ for the
remaining depreciable value for the next year. Repeat this step for the
following years.
9. For a new case press gi00 and return to step 2.
Example: A commercial movie camera is purchased for $12,000. If maintained
properly, the camera has a useful life expectancy of 25 years with $500 salvage
value. Using the sum-of-the-years-digits method, what is the amount of depreciation
and the remaining depreciable value for the 4th and 5th years? Assume the first
depreciation year is 11 months long.
Keystrokes Display
fCLEARG
12000$ 12,000.00 Book value.
500M 500.00 Salvage value.
25n 25.00 Life.
4\ 4.00 Year desired.
11t
~
4.00
781.41
8,238.71
Fourth year:
depreciation,
remaining depreciable value.
t
~
5.00
746.02
7,492.69
Fifth year:
depreciation,
remaining depreciable value.
* Refer to straight-line depreciation instruction note, page 137.
† The display will pause showing the year number before showing the amount of depreciation
for that year.

144 Section 13: Investment Analysis
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 144 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Full- and Partial-Year Depreciation with Crossover
When calculating declining-balance depreciation it is often advantageous for tax
purposes to switch from declining balance to straight-line depreciation at some
point. This hp 12c program calculates the optimum crossover point and
automatically switches to straight-line depreciation at the appropriate time. The
crossover point is the end of the year in which the declining-balance depreciation
last exceeds or equals the amount of straight-line depreciation. The straight-line
depreciation is determined by dividing the remaining depreciable value by the
remaining useful life.
Given the desired year and the number of months in the first year, this program
calculates the depreciation for the desired year, the remaining depreciable value,
and the total depreciation through the current year.
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
fs :4 48- 45 4
fCLEARÎ 00- z 49- 10
1 01- 1 go 50- 43 34
2 02- 2 gi53 51-43, 33 53
z 03- 10 gi65 52-43, 33 65
?6 04- 44 6 d 53- 33
:n 05- 45 11 0 54- 0
~ 06- 34 :0 55- 45 0
- 07- 30 go 56- 43 34
?4 08- 44 4 gi86 57-43, 33 86
d 09- 33 :$ 58- 45 13
?0 10- 44 0 :5 59- 45 5
1 11- 1 - 60- 30
?-0 12-44 30 0 $ 61- 13
?2 13- 44 2 1 62- 1
?3 14- 44 3 ?-4 63-44 30 4
f# 15- 42 25 gi40 64-43, 33 40
:6 16- 45 6 :4 65- 45 4

Section 13: Investment Analysis 145
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 145 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
§ 17- 20 n 66- 11
?1 18- 44 1 0 67- 0
:$ 19- 45 13 ?6 68- 44 6
~ 20- 34 1 69- 1
- 21- 30 ?-2 70-44 30 2
$ 22- 13 ?=0 71-44 40 0
\ 23- 36 :5 72- 45 5
gF 24- 43 36 ?-1 73-44 30 1
~ 25- 34 :3 74- 45 3
:M 26- 45 15 fV 75- 42 23
- 27- 30 ?+1 76-44 40 1
~ 28- 34 1 77- 1
:0 29- 45 0 ?-0 78-44 30 0
1 30- 1 ?+2 79-44 40 2
go 31- 43 34 ?+3 80-44 40 3
gi39 32-43, 33 39 d 81- 33
d 33- 33 :0 82- 45 0
d 34- 33 1 83- 1
1 35- 1 go 84- 43 34
gu 36- 43 31 gi74 85-43, 33 74
d 37- 33 d 86- 33
t 38- 31 d 87- 33
1 39- 1 :2 88- 45 2
?+2 40-44 40 2 gu 89- 43 31
?-0 41-44 30 0 d 90- 33
f# 42- 42 25 t 91- 31

146 Section 13: Investment Analysis
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 146 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
?+1 43-44 40 1 :6 92- 45 6
?5 44- 44 5 gm 93- 43 35
:$ 45- 45 13 gi74 94-43, 33 74
:M 46- 45 15 gi58 95-43, 33 58
- 47- 30 fs
REGISTERS
n: Life i: Factor PV: Dep. Value PMT: Unused
FV: Salvage R0: Used R1: Dep. R2: Counter
R3: Used R4: Used R5: Used R6: Used
1. Key in the program.
2. Press fCLEARH.
3. Key in the book value then press $.
4. Key in the salvage value then press M.
5. Key in the life in years (an integer) then press n.
6. Key in the declining-balance factor as a percentage then press ¼.
7. Key in the desired year and press \.
8. Key in the number of months in the first year* then press t† to calculate
the amount of depreciation for the desired year.
9. If desired, press ~ to see the remaining depreciable value.
10. If desired, press :1 to see the total depreciation through the current year.
11. Continue pressing t* to find the amount of depreciation for the successive
years. Steps 9 and 10 may be repeated for each year.
12. For a new case press gi00 and return to step 2.
* Refer to straight-line depreciation note page 137.
† The display will pause with the year number before displaying the amount of depreciation for
that year.

Section 13: Investment Analysis 147
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 147 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example: An electronic instrument is purchased for $11,000, with 6 months
remaining in the current fiscal year. The instrument’s useful life is 8 years and the
salvage value is expected to be $500. Using a 200% declining-balance factor,
generate a depreciation schedule for the instrument’s complete life. What is the
remaining depreciable value after the first year? What is the total depreciation
after the 7th year?
Keystrokes Display
fCLEARH 0.00
11000$ 11,000.00 Book value.
500M 500.00 Salvage value.
8n 8.00 Life.
200¼ 200.00 Declining-balance factor.
1\ 1.00 First year depreciation desired.
6t
~
1.00
1,375.00
9,125.00
First year:
depreciation,
remaining depreciable value.
t 2.00
2,406.25
Second year:
depreciation.
t 3.00
1,804.69
Third year:
depreciation.
t 4.00
1,353.51
Fourth year:
depreciation.
t 5.00
1,015.14
Fifth year:
depreciation.
t 6.00
761.35
Sixth year:
depreciation.*
t 7.00
713.62
Seventh year:
depreciation.
:1 9,429.56 Total depreciation through the
seventh year.
t 8.00
713.63
Eight year:
depreciation
t 9.00
356.81
Ninth year:
depreciation.
* By observation the crossover was year 6. Years 7, 8, and 9 use straight-line depreciation.

148 Section 13: Investment Analysis
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 148 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Excess Depreciation
When accelerated depreciation is used, the difference between total depreciation
charged over a given period of time and the total amount that would have been
charged under straight-line depreciation is called excess depreciation. To obtain
excess depreciation:
1. Calculate the total depreciation then press \.
2. Key in the depreciable amount (cost less salvage) then press \. Key in the
useful life of the asset in years then press z. Key in the number of years in
the income projection period then press § to get the total straight-line
depreciation charge.
3. Press - to get the excess depreciation.
Example: What is the excess depreciation in the previous example over 7
calendar years? (Because of the partial first year, there are 61/2 years
depreciation in the first 7 calendar years.)
Keystrokes Display
9429.56\ 9,429.56 Total depreciation through seventh
year.
10500\ 10,500.00 Depreciable amount.
8z 1,312.50 Yearly straight-line depreciation.
6.5§ 8,531.25 Total straight-line depreciation.
- 898.31 Excess depreciation
Modified Internal Rate of Return
The traditional Internal Rate of Return (IRR) technique has several drawbacks which
hamper its usefulness in some investment applications. The technique implicitly
assumes that all cash flows are either reinvested or discounted at the computed
yield rate. This assumption is financially reasonable as long as the rate is within a
realistic borrowing and lending range (for example, 10% to 20%). When the IRR
becomes significantly greater or smaller, the assumption becomes less valid and
the resulting value less sound as an investment measure.
IRR also is limited by the number of times the sign of the cash flow changes
(positive to negative or vice versa). For every change of sign, the IRR solution has
the potential for an additional answer. The cash flow sequence in the example that
follows has three sign changes and hence up to three potential internal rates of
return. This particular example has three positive real answers: 1.86, 14.35, and
29. Although mathematically sound, multiple answers probably are meaningless
as an investment measure.

Section 13: Investment Analysis 149
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 149 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
This Modified Internal Rate of Return procedure (MIRR) is one of several IRR
alternatives which avoids the drawbacks of the traditional IRR technique. The
procedure eliminates the sign change problem and the reinvestment (or
discounting) assumption by utilizing user stipulated reinvestment and borrowing
rates.
Negative cash flows are discounted at a safe rate that reflects the return on an
investment in a liquid account. The figure generally used is a short-term security
(T-Bill) or bank passbook rate.
Positive cash flows are reinvested at a reinvestment rate which reflects the return on
an investment of comparable risk. An average return rate on recent market
investments might be used.
The steps in the procedure are:
1. Calculate the future value of the positive cash flows (NFV) at the reinvestment
rate.
2. Calculate the present value of the negative cash flows (NPV) at the safe rate.
3. Knowing n, PV, and FV, solve for i.
Example: An investor has the following unconventional investment opportunity.
The cash flows are:
Group # of Months Cash Flow ($)
0 1 –180,000
1 5 100,000
2 5 –100,000
3 9 0
4 1 200,000
Calculate the MIRR using a safe rate of 6% and a reinvestment (risk) rate of 10%.
Keystrokes Display
fCLEARH 0.00
0gJ 0.00 First cash flow.
100000gK
5ga 5.00 Second through sixth cash flows.
0gK5ga 5.00 Next five cash flows.
0gK9ga 9.00 Next nine cash flows.
200000gK 200,000.00 Last cash flow.

150 Section 13: Investment Analysis
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 150 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
10gCfl 657,152.37 NPV of positive cash flows.
Þ$
20nM 775,797.83 NFV of positive cash flows.
180000ÞgJ
0gK5ga
100000ÞK
5ga
6gCfl -660,454.55 NPV of negative cash flows.
20n¼ 0.81 Monthly MIRR
12§ 9.70 Annual MIRR.

151
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 151 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 14
Leasing
Advance Payments
Situations may exist where payments are made in advance (leasing is a good
example). These agreements call for extra payments to be made when the
transaction is closed.
This first procedure finds the periodic payment amount necessary to achieve a
desired yield when a number of payments are made in advance. And, given the
periodic payment, the second procedure calculates the periodic yield.
Solving For Payment
To calculate the payment, information is entered as follows:
1. Press g and fCLEARG.
2. Key in the total number of payments in the lease then press \.
3. Key in the total number of payments made in advance then press
?0-n.
4. Key in or calculate the periodic interest rate as a percentage then press ¼.
5. Press 1Þ$:0+.
6. Key in the initial loan amount then press ~z, to obtain the periodic
payment to be received by the lessor.
Example 1: Equipment worth $750 is leased for 12 months. The equipment is
assumed to have no salvage value at the end of the lease. The lessee has agreed
to make three payments at the time of closing. What monthly payment is necessary
to yield the lessor 10% annually?
Keystrokes Display
gÂ
fCLEARG
12\ 12.00 Duration of lease.
3?0-n 9.00 Number of periodic payments.
10gC 0.83
1ÞP –1.00
$:0+ 11.64
750~z 64.45 Monthly payment to be received.

152 Section 14: Leasing
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 152 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
If solving for the payment amount will be done repetitively, key in the following hp
12c program.
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
fs 1 09- 1
f
CLEAR
Î 00- Þ 10- 16
g 01- 43 8 P 11- 14
f
CLEAR
G 02- 42 34 $ 12- 13
:0 03- 45 0 :1 13- 45 1
:1 04- 45 1 + 14- 40
- 05- 30 :3 15- 45 3
n 06- 11 ~ 16- 34
:2 07- 45 2 z 17- 10
¼ 08- 12 fs
REGISTERS
n: n–#Adv. Pmt. i: i PV: Used PMT: –1
FV: 0 R0: n R1: #Adv. Pmt. R2: i
R3: Loan R4–R.7: Unused
1. Key in the program.
2. Key in the total number of payments in the lease then press ?0.
3. Key in the total number of payments made in advance then press ?1.
4. Key in the periodic interest rate as a percentage then press ?2.
5. Key in the loan amount and press ?3; then press t to obtain the
periodic payment to be received by the lessor.
6. For a new case, return to step 2. The values changed from the previous case
are the only values which need to be entered.

Section 14: Leasing 153
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 153 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 2: Using the preceding program, solve for the monthly payment using
the information given in example 1. Then change the yearly interest to 15% and
solve for the new payment amount.
Keystrokes Display
12?0 12.00 Duration of lease.
3?1 3.00 Number of advance payments.
10\12z
?2 0.83 Periodic interest rate.
750?3t 64.45 Monthly payment to be received.
15\12z
?2t 65.43 Monthly payment to achieve a 15%
yield.
Example 3: Using the information from example 1, what monthly payment is
necessary to yield the lessor 15% annually if one payment is due at the time of
closing?
Assuming that the previous example was just solved, the keystrokes are as follows:
Keystrokes Display
1?1t 66.86 Monthly payment to be received.
Since this problem is an annuity due situation (one payment at the beginning of the
period) the calculation could also be done as follows:
Keystrokes Display
g×
fCLEARG
12n15gC 1.25 Periodic interest rate (into i).
750Þ$P 66.86 Monthly payment to be received.

154 Section 14: Leasing
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 154 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Solving for Yield
To calculate the periodic yield, information is entered as follows:
1. Press g and fCLEARG.
2. Key in the total number of payments in the lease then press \.
3. Key in the total number of payments made in advance then press
?0-n.
4. Key in the periodic payment to be received then press P.
5. Key in the total amount of the loan then press Þ:0:P§+$.
6. Press ¼ to obtain the periodic yield.
Example 1: A lease has been written to run for 60 months. The leased
equipment has a value of $25,000 with a $600 monthly payment. The lessee has
agreed to make 3 payments at the time of closing ($1800). What is the annual
yield to the lessor?
Keystrokes Display
gÂ
fCLEARG
60\3
?0-n 57.00 Number of periodic payments.
600P
25000Þ:0 3.00 Number of advance payments.
:P§+$ -23,200.00 PV.
¼ 1.44 Monthly yield (calculated).
12§ 17.33 Annual yield (as a percentage).
Section 14: Leasing 155
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 155 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
If solving for yield will be done repetitively, key in the following hp 12c program:
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
fs :3 09- 45 3
fCLEARÎ 00- Þ 10- 16
g 01- 43 8 :1 11- 45 1
fCLEARG 02- 42 34 :P 12- 45 14
:0 03- 45 0 § 13- 20
:1 04- 45 1 + 14- 40
- 05- 30 $ 15- 13
n 06- 11 ¼ 16- 12
:2 07- 45 2 :gC 17-45, 43 12
P 08- 14 fs
REGISTERS
n: n–#Adv. Pmts. i: i PV: Used PMT: Pmt.
FV: 0 R0: n R1: Adv. Pmts. R2: Pmt.
R3: Loan R4–R.7: Unused
1. Key in the program.
2. Key in the total number of payments in the lease then press ?0.
3. Key in the total number of payments made in advance then press ?1.
4. Key in the periodic payment to be received then press ?2.
5. Key in the total amount of the loan, then press ?3; then press t to
obtain the periodic yield.
6. For a new case, return to step 2. The values changed from the previous case
are the only values which need to be re-entered.
Example 2: Using the program, solve for yield using the same information given
in example 1. Then change the payment to $625 and solve for the yield.
Keystrokes Display
60?0 60.00 Number of payments.
3?1 3.00 Number of advance payments.
600?2 600.00 Periodic payment.

156 Section 14: Leasing
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 156 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
25000?3t 17.33 Annual yield (as a percentage).
625?2t 19.48 Annual yield (as a percentage)
when PMT is increased $25.
Advance Payments With Residual
Situations may arise where a transaction has advance payments and a residual
value (salvage value) at the end of the normal term.
Solving for Payment
The following program solves for the periodic payment amount necessary to
achieve a desired yield.
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
fs M 14- 15
f
CLEAR
Î 00- :n 15- 45 11
g 01- 43 8 :4 16- 45 4
f
CLEAR
G 02- 42 34 - 17- 30
:0 03- 45 0 n 18- 11
n 04- 11 1 19- 1
:1 05- 45 1 Þ 20- 16
¼ 06- 12 P 21- 14
:3 07- 45 3 $ 22- 13
M 08- 15 :4 23- 45 4
$ 09- 13 + 24- 40
:2 10- 45 2 :5 25- 45 5
+ 11- 40 ~ 26- 34
?5 12- 44 5 z 27- 10
0 13- 0 fs
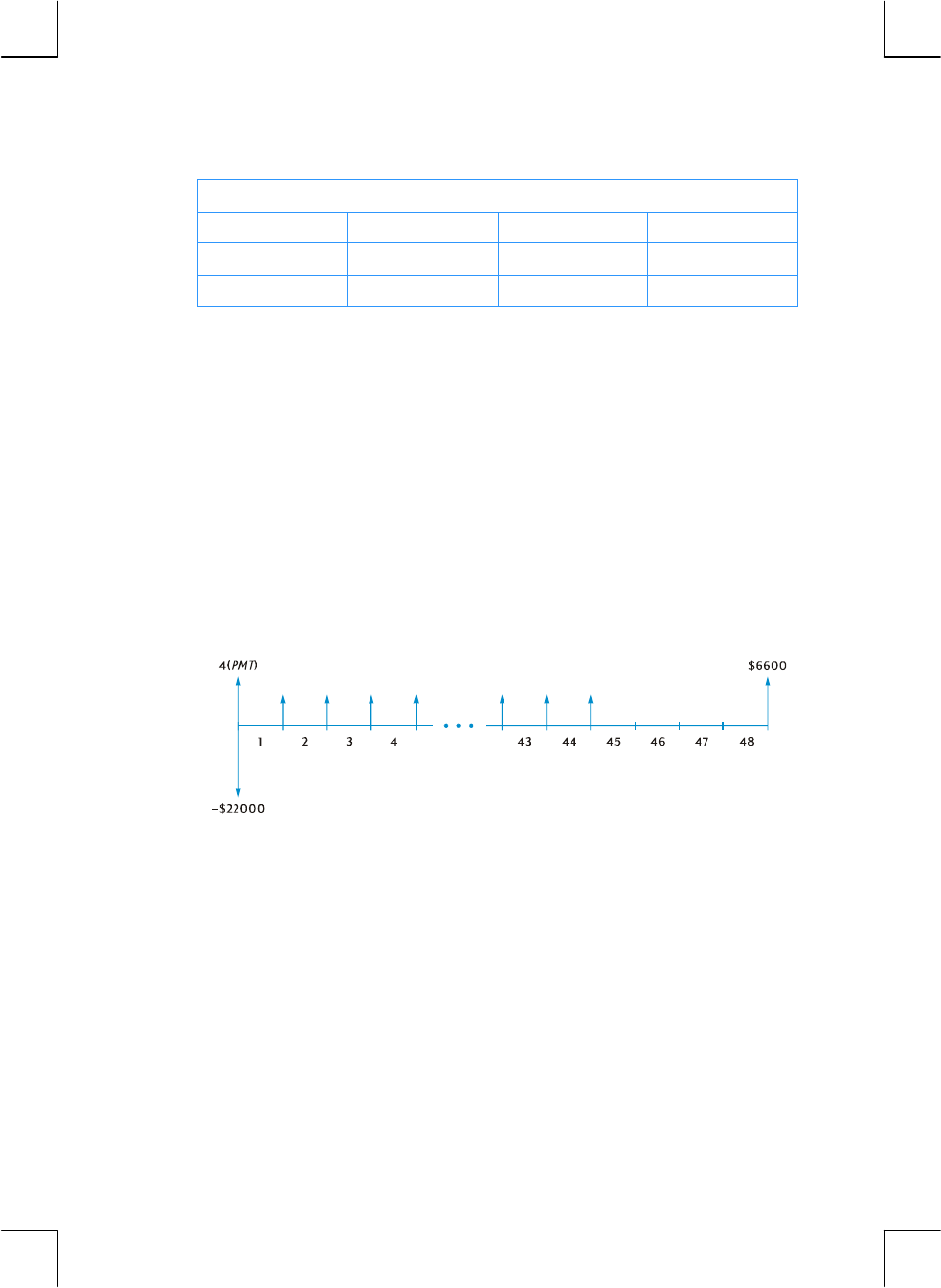
Section 14: Leasing 157
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 157 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
REGISTERS
n: Used. i: Interest PV: Used PMT: –1.
FV: Residual R0: # Pmts (n) R1: Interest. R2: Loan.
R3: Residual R4: # Adv. Pmt. R5: Used R6–R.6: Unused
1. Key in the program.
2. Key in the total number of payments then press ?0.
3. Key in or calculate the periodic interest rate then press ?1.
4. Key in the loan amount then press ?2.
5. Key in the residual value then press ?3.
6. Key in the total number of payments made in advance then press ?4.
Then press t to obtain the payment amount received by the lessor.
7. For a new case, return to step 2. The values changed from the previous case
are the only values which need to be re-entered.
Example 1: A copier worth $22,000 is to be leased for 48 months. The lessee
has agreed to make 4 payments in advance, with a purchase option at the end of
48 months enabling him to buy the copier for 30% of the purchase price. What
monthly payment is necessary to yield the lessor 15% annually:
Keystrokes Display
48?0
15\
12z?1 1.25 Monthly interest rate.
22000?2
30b?3
4?4t 487.29 Monthly payment received by lessor.
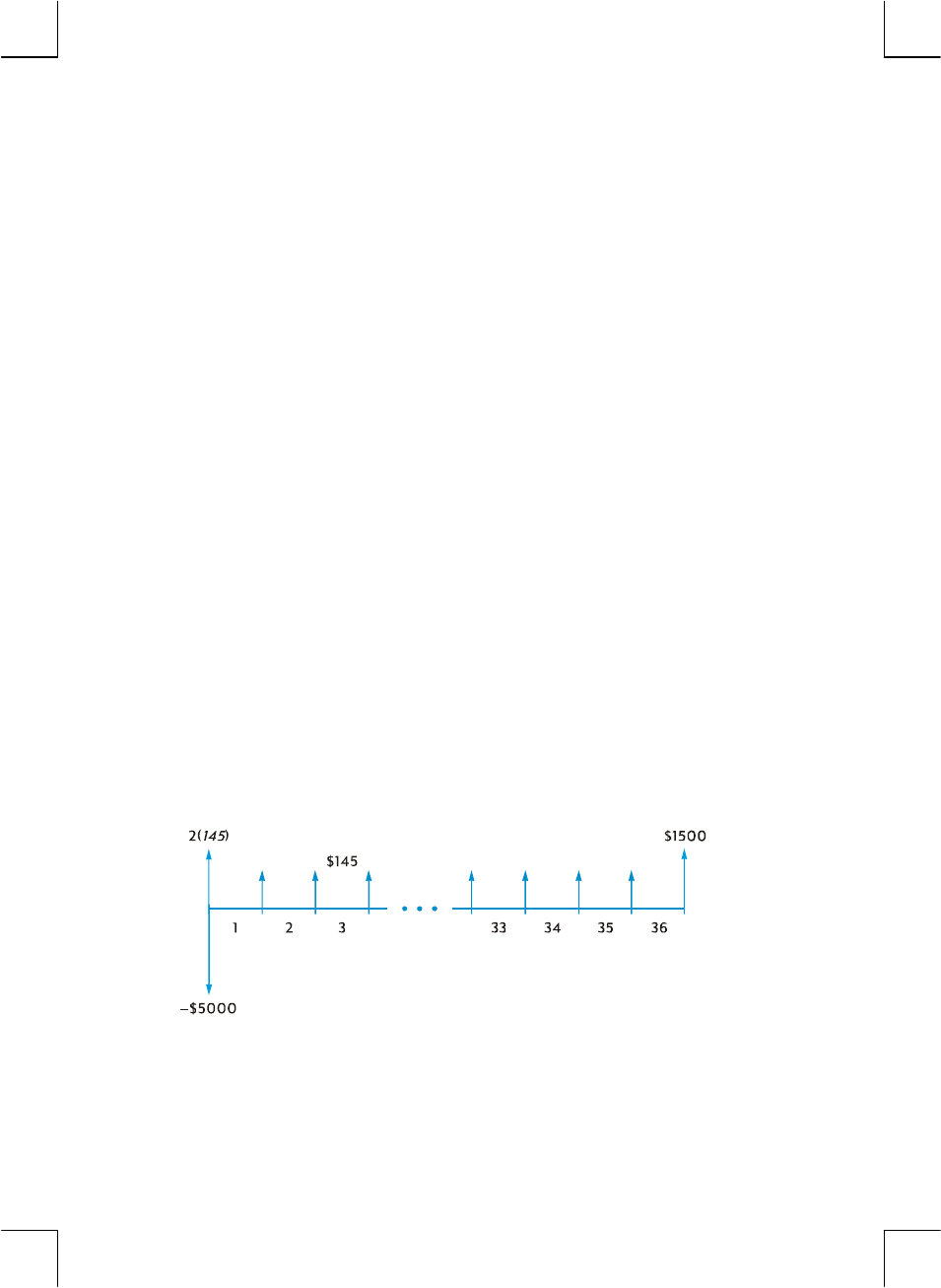
158 Section 14: Leasing
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 158 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Example 2: Using the information from example 1, what would the monthly
payments be if the lessor desired a yield of 18% annually?
Keystrokes Display
487.29 From previous example.
18\12z 1.50 Monthly interest rate.
?1t 520.81 Monthly payment received by lessor.
Solving For Yield
Solving for yield is essentially the same as solving for Internal Rate of Return (IRR).
The keystrokes are as follows:
1. Press fCLEARH.
2. Key in the amount of the first cash flow then press gJ. This initial amount
is the difference between the initial loan amount and any payments received
at closing time. Observe the sign convention: positive for cash received and
negative for cash paid out.
3. Key in the amount of the first cash flow then press gK. Then key in the
number of times that cash flow occurs then press ga.
4. Key in 0gK then the number of advance payments minus one. Then
press ga.
5. Key in the residual then press gK. Then press fL to solve for
periodic yield.
Example: Equipment worth $5000 is leased for 36 months at $145 per month.
The lessee has agreed to pay the first and last month’s payments in advance. At
the end of the lease, the equipment may be purchased for $1500. What is the
annual yield to the lessor if the equipment is purchased?
Keystrokes Display
fCLEARH
5000Þ\
145\2

Section 14: Leasing 159
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 159 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
§=gJ –4,710.00 Net amount of cash advanced.
145gK34ga 34.00 Thirty-four cash flows of $145.00.
0gK 0.00 Thirty-fifth cash flow.
1500gK 1,500.00 Thirty-sixth cash flow.
fL12§ 18.10 Annual yield to lessor.

160
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 160 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 15
Savings
Nominal Rate Converted to Effective Rate
Given a nominal interest rate and the number of compounding periods per year,
this keystroke procedure computes the effective annual interest rate.
1. Press g and fCLEARG.
2. Key in the annual nominal rate as a percentage, then press \.
3. Key in the number of compounding periods per year, then press nz¼.
4. Key in 100 then press Þ\$.
5. Press M+ to obtain the effective annual interest rate.
Example 1: What is the effective annual interest rate if the annual nominal rate
of 51/4% is compounded quarterly?
Keystrokes Display
gÂ
fCLEARG
5.25\ 5.25 Nominal rate.
4nz¼ 1.31 Percent quarterly interest rate.
100Þ\
$M+ 5.35 Percent effective interest rate.
For repeated calculations, the following hp 12c program can be used:
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
fs 0 07- 0
f
CLEAR
Î 00- 0 08- 0
g 01- 43 8 Þ 09- 16
f
CLEAR
G 02- 42 34 \ 10- 36
n 03- 11 $ 11- 13
z 04- 10 M 12- 15
¼ 05- 12 + 13- 40
1 06- 1 fs

Section 15: Savings 161
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 161 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
REGISTERS
n: # Periods. i: Nom. Rate/n PV: 0 PMT: Used.
FV: Eff. Rate R0–R.9: Unused
1. Key in the program.
2. Key in the annual nominal rate as a percentage then press \.
3. Key in the number of compounding periods per year then press t to
obtain the effective annual interest rate.
4. For a new case return to step 2.
Example 2: What is the effective annual rate of interest if the annual nominal
rate of 51/4% is compounded monthly?
Keystrokes Display
5.25\
12t 5.38 Percent effective interest rate.
Effective Rate Converted to Nominal Rate
Given an effective interest rate and the number of compounding periods per year,
this routine calculates the nominal interest rate.
1. Press fCLEARG.
2. Key in the number of periods per year then press n.
3. Key in 100 then press \$.
4. Key in the effective annual rate as a percentage then press +ÞM¼.
5. Press :n§ to obtain the annual nominal rate.
Example: Find the nominal rate if the effective annual rate is 5.35%
compounded quarterly.
Keystrokes Display
fCLEARG
4n100\$ 100.00
5.35+Þ –105.35
M¼ 1.31
:n§ 5.25 Percent nominal interest rate.

162 Section 15: Savings
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 162 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Nominal Rate Converted to Continuous Effective Rate
This procedure converts a nominal annual interest rate to the continuous effective
rate.
1. Press 1\.
2. Key in the nominal rate as a percentage then press b.
3. Press g>à.
Example: What is the effective rate resulting from a 51/4% passbook rate with
continuous compounding?
Keystrokes Display
1\5.25b
g> 1.05
à 5.39 Continuous rate.
163
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 163 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Section 16
Bonds
30/360 Day Basis Bonds
A bond is a contract to pay interest, usually semiannually, at a given rate (coupon)
and to pay the principal of the bond at some specified future date. A bond which
is calculated on a 30/360 day basis is one in which the day count basis is
computed using 30 days in a month and 360 days in a year.
The following program solves for the price given the yield or for the yield given the
price of a semiannual coupon bond which is calculated on a 30/360 day basis
and is held for more than six months.
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
fs :6 24- 45 6
fCLEARÎ 00- § 25- 20
fCLEARG 01- 42 34 :0 26- 45 0
g× 02- 43 7 gm 27- 43 35
:2 03- 45 2 gi39 28-43, 33 39
2 04- 2 2 29- 2
z 05- 10 z 30- 10
P 06- 14 ¼ 31- 12
?6 07- 44 6 $ 32- 13
:5 08- 45 5 Þ 33- 16
+ 09- 40 ~ 34- 34
M 10- 15 - 35- 30
:3 11- 45 3 gF 36- 43 36
:4 12- 45 4 ~ 37- 34
gÒ 13- 43 26 gi00 38-43, 33 00

164 Section 16: Bonds
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 164 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
d 14- 33 d 39- 33
1 15- 1 :1 40- 45 1
8 16- 8 + 41- 40
0 17- 0 Þ 42- 16
z 18- 10 $ 43- 13
n 19- 11 ¼ 44- 12
gT 20- 43 24 2 45- 2
1 21- 1 § 46- 20
~ 22- 34 fs
- 23- 30
REGISTERS
n: ∆ days/180 i: Yield/2 PV: Price PMT: Coupon/2.
FV: Red+Cpn./2 R0: Yield R1: Price. R2: Coupon
R3: Dset R
4: Dmat R
5: Redemption R6: Coupon/2.
R7–R.3: Unused
1. Key in the program.
2. If the C status indicator is not displayed, press ?É.
3. Key in the annual coupon interest rate as a percentage then press ?2.
4. Key in the settlement date (MM.DDYYYY)* then press ?3.
5. Key in the maturity date (MM.DDYYYY)* then press ?4.
6. Key in the redemption value as a percentage of par then press ?5.
7. If price is desired:
a. Key in the desired yield to maturity as a percentage then press ?0.
b. Press t to calculate price as a percentage of par value.
c. Press ~ to display accrued interest due the seller.
* For information about date format see pages 29 to 30.

Section 16: Bonds 165
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 165 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
For a new case return to step 3. Note that only those values which have been
changed need to be reentered and stored.
8. If yield is desired:
a. Press 0?0.
b. Key in the price as a percentage of par value and press ?1.
c. Press t to compute annual yield to maturity.
For a new case return to step 3. Note that only those values which have
been changed need to be reentered and stored.
Example 1: What price should you pay on August 28, 2004 for a 51/2% bond
(computed with a 30/360 basis) that matures on June 1, 2008, if you want a
yield of 73/4%? What price should you pay for a yield of 8%? This problem
assumes a redemption value of 100.
Keystrokes Display
?Æ Set compound interest mode if the C
indicator is not on.
5.5?2 5.50 Coupon into register 2.
8.282004?3 8.28 Settlement date into register 3.
6.012008?4 6.01 Maturity date into register 4.
100?5 100.00 Redemption value into register 5.
7.75?0 7.75 Yield into register 0.
t 92.77 Price (calculated).
~ 1.33 Accrued interest (calculated).
8?0 8.00 New yield into register 0.
t 92.01 Price to yield 8% (calculated).
~ 1.33 Accrued interest (calculated).
+ 93.34 Total price paid.
Example 2: The market is quoting 933/8% for the bond described in example 1.
What yield will that provide? What would be the yield to maturity if 92% were the
quoted price?
Keystrokes Display
93.34 From previous example.
0?0
3\8z
93+?1t 7.55 Yield at 933/8% (calculated).
92?1t 8.00 Yield at 92% (calculated).

166 Section 16: Bonds
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 166 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Annual Coupon Bonds
For bonds which have annual coupons, use the following hp 12c program to
evaluate price and accrued interest on an Actual/Actual day basis. This program
may be modified for annual coupon bonds to be calculated on a 30/360 day
basis.
KEYSTROKES DISPLAY KEYSTROKES DISPLAY
fs gÒ 19- 43 26
f
CLEAR
Î 00- ?7 20- 44 7
f
CLEAR
G 01- 42 34 :6 21- 45 6
g 02- 43 8 :4 22- 45 4
:0 03- 45 0 gÒ 23- 43 26
n 04- 11 :7 24- 45 7
:2 05- 45 2 z 25- 10
P 06- 14 n 26- 11
:1 07- 45 1 0 27- 0
¼ 08- 12 P 28- 14
:3 09- 45 3 M 29- 15
M 10- 15 Þ 30- 16
$ 11- 13 :n 31- 45 11
:5 12- 45 5 :2 32- 45 2
Æ 13- 26 Þ 33- 16
6 14- 6 § 34- 20
Þ 15- 16 t 35- 31
- 16- 30 - 36- 30
?6 17- 44 6 fs
:5 18- 45 5

Section 16: Bonds 167
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 167 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
REGISTERS
n: Used i: Yield PV: Used PMT: Cpn. or 0
FV: Used R0: # Periods (n) R1: Yield R2: Coupon
R3: Redemption R4: Settlement R5: Next Cpn. R6: Last Coupon
R7: Used R8–R.5: Unused
For annual coupon bonds calculated on a 30/360 day basis, insert d after
gÒ at steps 19 and 23 (making the program two steps longer).
1. Key in the program and press ?É if the C status indicator is not
displayed.
2. Key in the total number of coupons which are received and press ?0.
3. Key in the annual yield as a percentage then press ?1.
4. Key in the amount of the annual coupon then press ?2.*
5. Key in the redemption value then press ?3.*
6. Key in the settlement (purchase) date† then press ?4.
7. Key in the date of the next coupon then press ?5.
8. Press t to obtain the amount of accrued interest.
9. Press t to determine the priceof the bond.
10. For a new case, return to step 2.
Example: What is the price and accrued interest of a 20-year Eurobond with
annual coupons of 6.5% purchased on August 15, 2004 to yield 7%. The next
coupon is received on December 1, 2004.
Keystrokes Display
?Æ Set compound interest mode if the C
indicator is not on.
20?0 20.00 Total number of coupons.
7?1 7.00 Annual yield.
6.5?2 6.50 Annual coupon rate.
100?3 100.00 Redemption value.
8.152004?4 8.15 Settlement date.
12.012004?5 12.01 Next coupon date.
t –4.58 Accrued interest.
t –94.75 Purchase price.
* Positive for cash received; negative for cash paid out.
† For information about date format see pages 29 to 30.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 169 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Appendixes
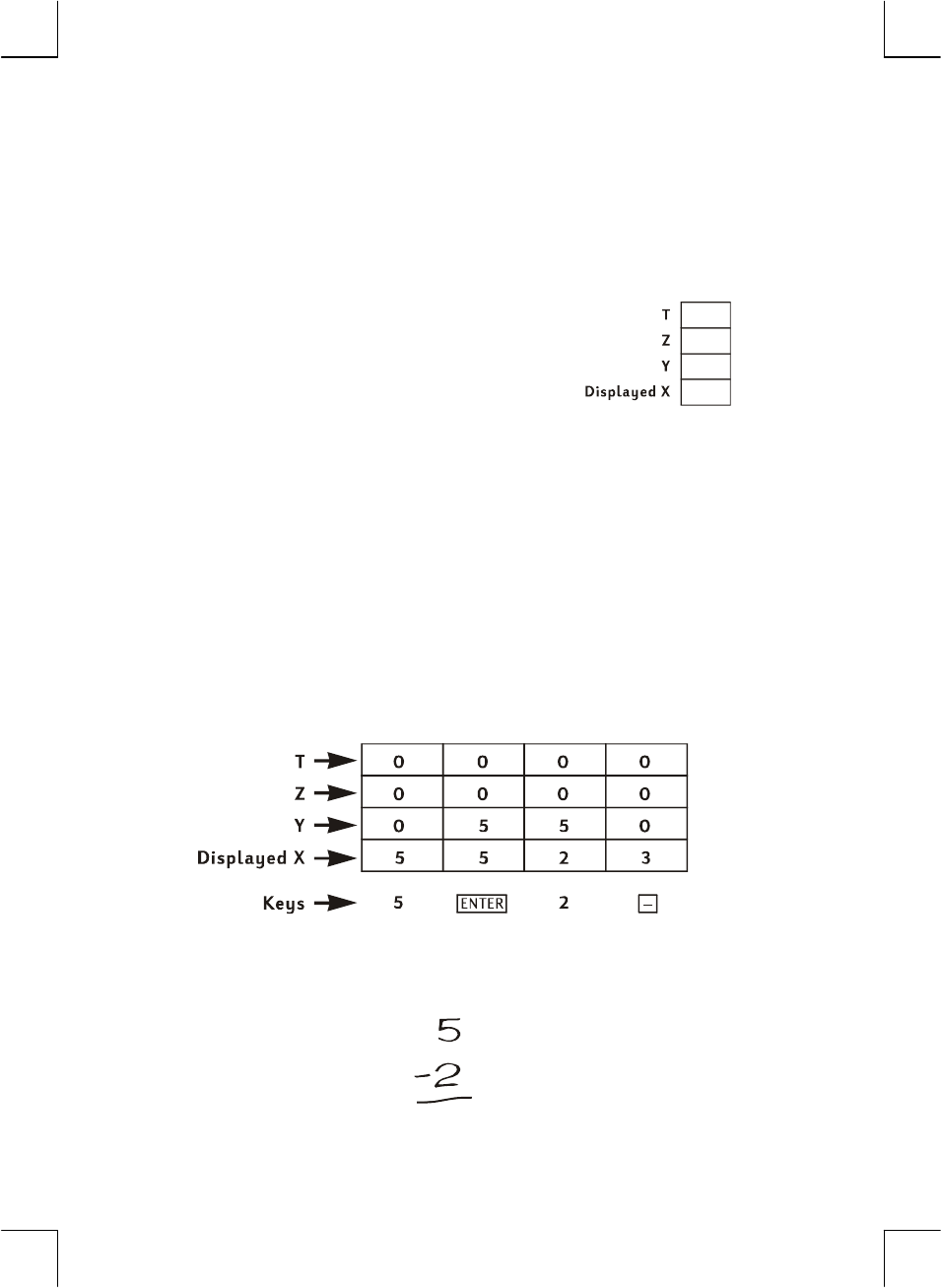
170
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 170 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Appendix A
The Automatic Memory Stack
Four special re
g
isters in the hp 12c are used for storin
g
numbers durin
g
calculations. To understand how these
re
g
isters are used, they should be visualized as stacked on
top of each other.
(For this reason, they are
g
enerally referred to as the “stack re
g
isters” or
collectively as “the stack.”) The stack registers are designated X, Y, Z, and T.
Unless the calculator is in Program mode, the number shown in the display is the
number in the X-register (modified according to the current display format).
The number in the X-register — and, for two-number functions, the number in the
Y-register — are the number(s) used in calculations. The Z- and T-registers are used
primarily for the automatic retention of intermediate results during chain
calculations, as described in section 1.
Before we discuss the details of the stack operation, let’s take a quick look at how
the stack is used in a simple arithmetic calculation and in a chain calculation. For
each key pressed in the keystroke sequence, the diagram illustrating the
calculation shows, above the key, the numbers in each of the stack registers after
that key is pressed.
First, let’s consider the calculation of 5 – 2:
The diagram shows why we said in section 1 that the \ key separates the
second number entered from the first number entered. Note also that this positions
the 5 in the Y-register above the 2 in the X-register — just like they would be
positioned if you wrote the calculation vertically on paper:
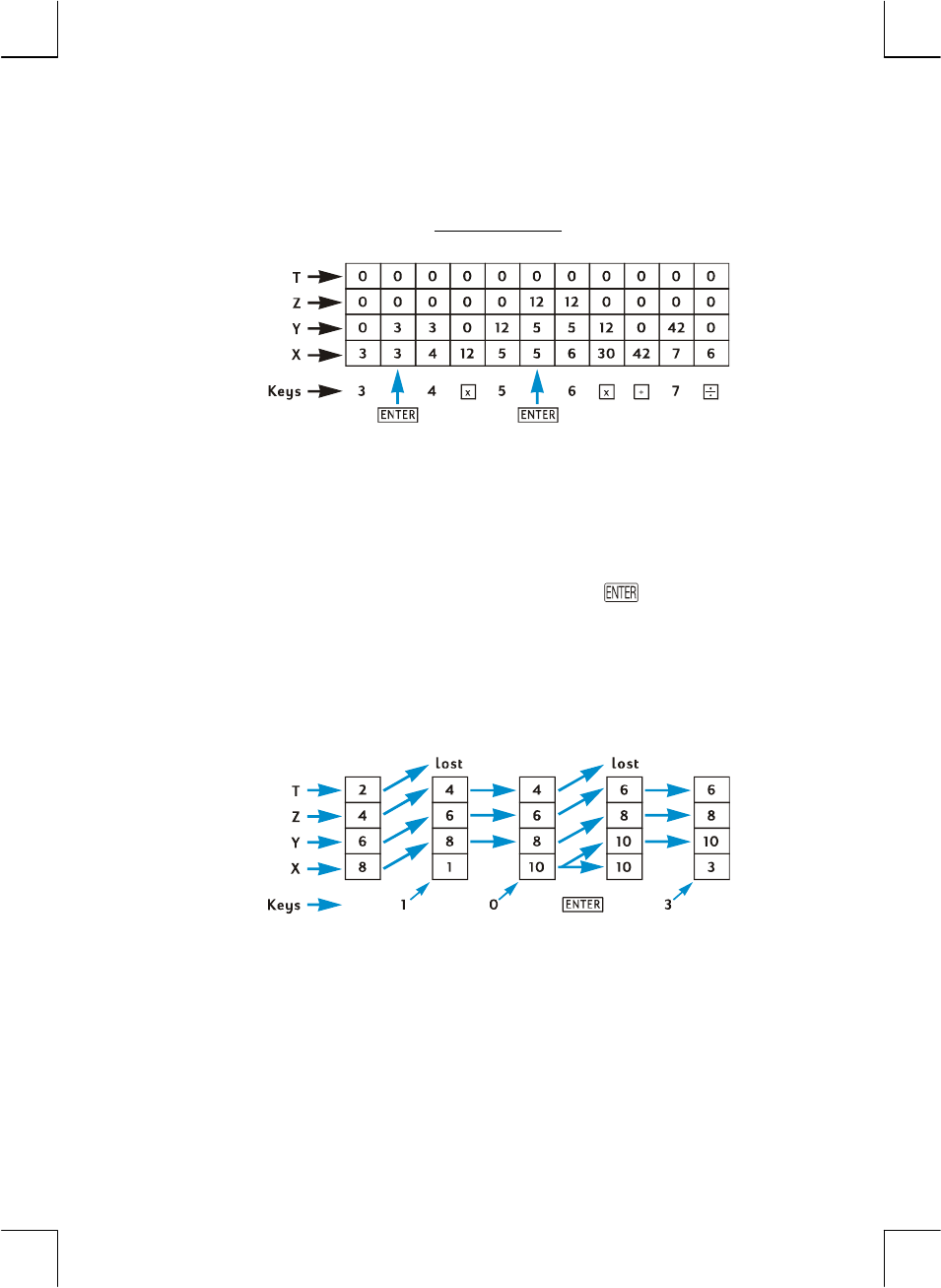
Appendix A: The Automatic Memory Stack 171
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 171 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Now let’s see what happens in the stack during a chain calculation:
7
)65()43(
×
+
×
See how the intermediate results are not only displayed when they are calculated,
but also automatically stored and available in the stack at just the right time!
That’s basically how the stack operates. In the rest of this appendix, we’ll take a
more detailed look at how numbers are entered into and rearranged within the
stack, and the effect of the various hp 12c functions on the numbers in the stack.
Getting Numbers Into the Stack: The Key
As discussed in earlier sections, if two numbers are being keyed in for a
two-number function — such as + — you press \ between the numbers to
separate them. The following diagram illustrates what happens in the stack when
you enter the numbers 10 and 3 (to calculate, for example, 10 ÷ 3). (Assume that
the stack registers have been already loaded with the numbers shown as the result
of previous calculations).
When a digit is keyed into the display, it is simultaneously entered into the
X-register. As additional digit keys are pressed, the corresponding digits are
appended (that is, added to the right of) those already in the displayed X-register
until \ is pressed. As shown in the preceding diagram, pressing \ does the
following:
1. It copies the number from the displayed X-register into the Y-register. This
process is part of the stack lift.
2. It tells the calculator that the number in the displayed X-register is complete:
that is, it terminates digit entry.
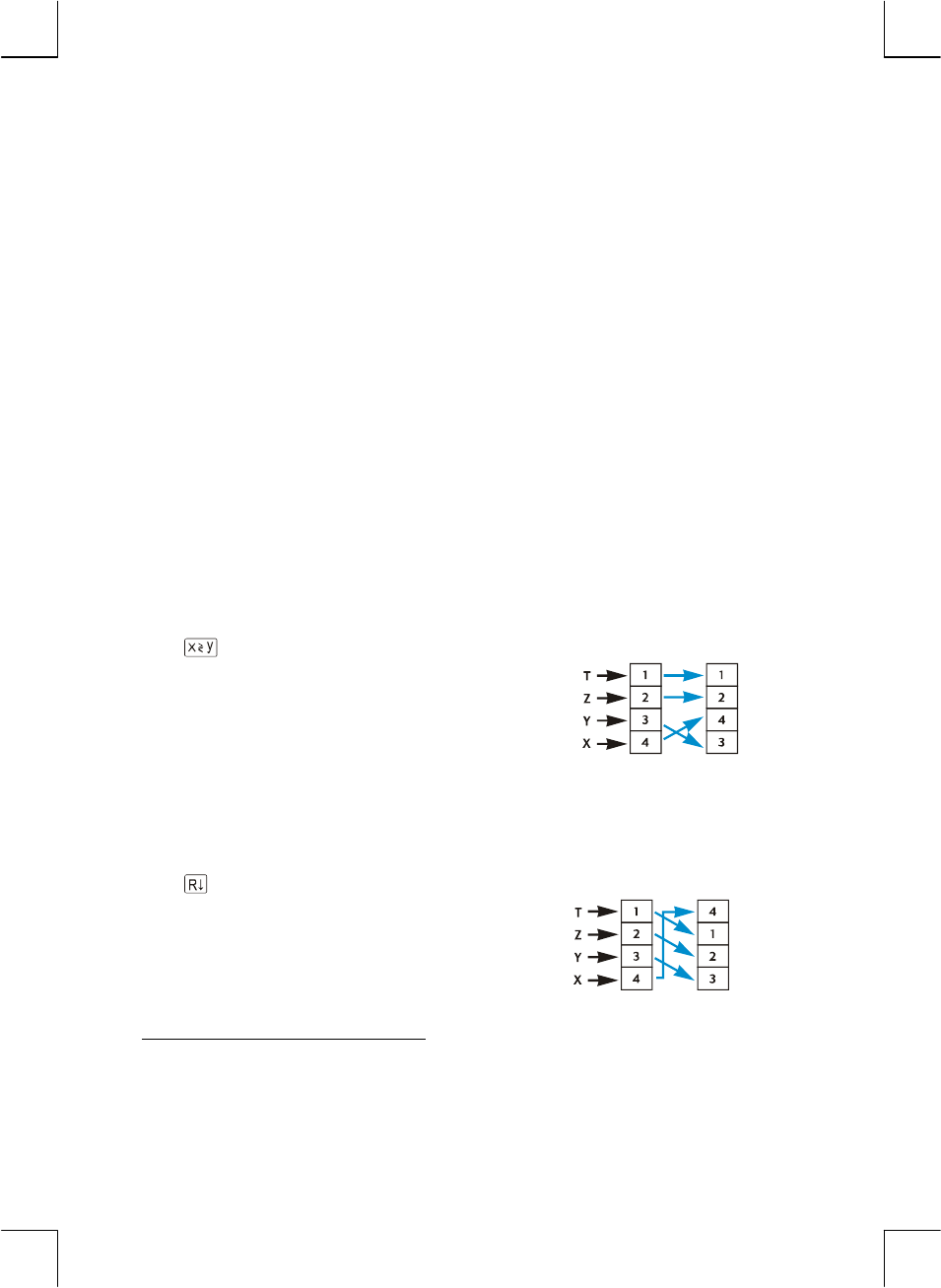
172 Appendix A: The Automatic Memory Stack
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 172 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Termination of Digit Entry
The first digit keyed in after digit entry has been terminated replaces the number
already in the displayed X-register. Digit entry is automatically terminated when
any key is pressed (except for digit entry keys — digit keys,., Þ, and É —
and prefix keys — f, g,?, :, and i).
Stack Lift
When the stack lifts, the number in each stack register is copied into the register
above, and the number formerly in the T-register is lost. The number formerly in the
X-register is then contained in both the X-register and the Y-register.
When a number is entered into the displayed X-register — either from the
keyboard, from a storage register (using :), or from the LAST X register (using
F) — the stack usually lifts first. The stack does not lift if the last key pressed
before a number is entered was one of the following: \, O, _, ^, A or
C.* If one of these keys was the last key pressed, the number in the displayed
X-register is replaced when a new number is entered.
Rearranging Numbers in the Stack
The key
Pressing ~ exchanges the numbers in the X- and
Y-registers.
Certain functions (Ò, Ï, !, E, V, Ý, #, Ö, v, R, and Q)
return answers to the Y-register as well as to the displayed X-register. The ~ key,
since it exchanges the number in the Y-register with that in the displayed X-register,
is used to display the second number calculated.
The Key
When d (roll down) is pressed the number in each
stack register is copied into the register below, and the
number formerly in the X-re
g
ister is copied into the
T-register.
* In addition, the stack does not lift when a number is entered if the last operation performed
was storing a number into a financial register. For example, the stack will not lift when a
number is entered following the sequence 100000$, but will lift when a number is entered
following the sequence 100000$M. Note also that although the stack lifts when \ is
pressed, it does not lift when a number is entered after \ is pressed.
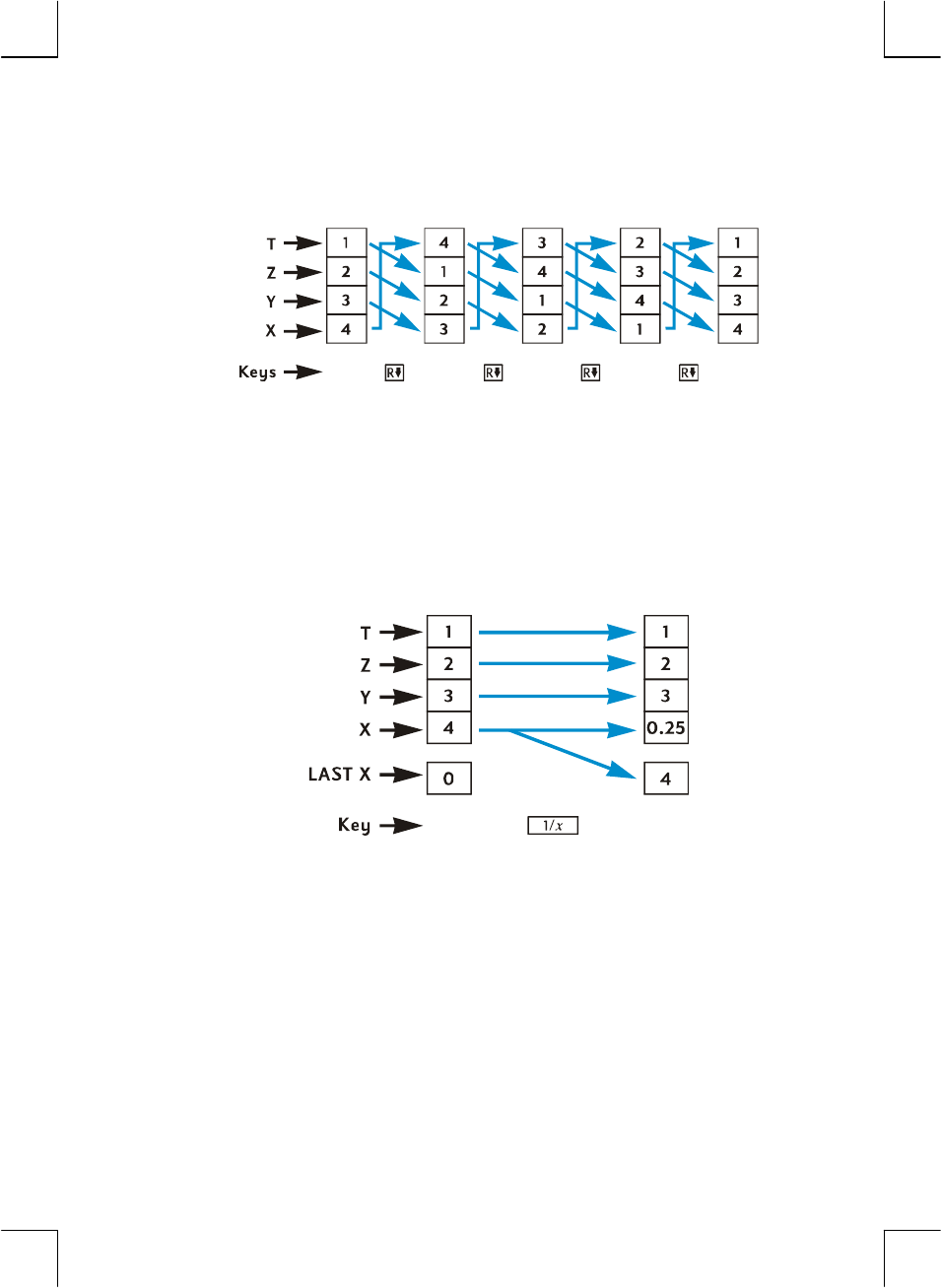
Appendix A: The Automatic Memory Stack 173
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 173 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Pressing d four times successively displays the numbers in the Y-, Z-, and
T-registers and returns the numbers to their original registers.
One-Number Functions and the Stack
One-number mathematics and number-alteration functions — y, r, °, >,
e, B, Ñ, and T — use only the number in the displayed X-register.
When the key is pressed, the function is performed upon the number in the
X-register, and the answer is then placed into the X-register. The stack does not lift,
so the number formerly in the X-register does not get copied into the Y-register; but
this number is copied into the LAST X register. The numbers in the Y-, Z-, and
T-registers are not affected when a one number function is performed.
Two-Number Functions and the Stack
Two-number functions — +, -, §, z, q, b, à, and Z — use the
numbers in both the X- and the Y-registers.
Mathematics Functions
To perform an arithmetic operation, the numbers are positioned in the X- and
Y-registers just as you would write them vertically on paper: the number you would
write on top goes in the Y-register, and the number you would write on the bottom
goes in the X-register. For example, to do each of the four arithmetic calculations
shown below, you would put the 8 in the Y-register (using \ and then key the 2
into the displayed X-register.)
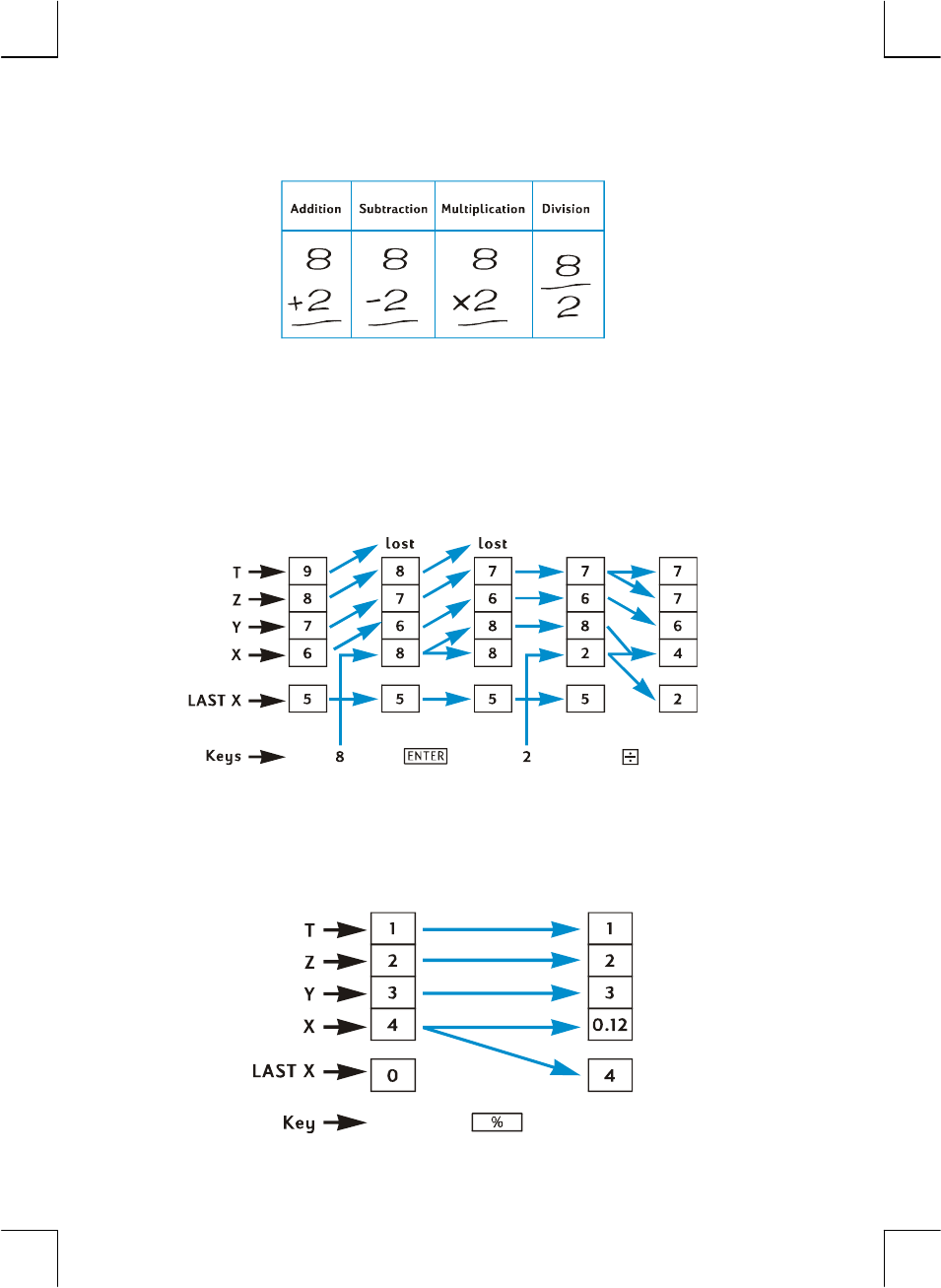
174 Appendix A: The Automatic Memory Stack
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 174 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
When an arithmetic operation or q is performed, the answer is placed in the
X-register, the number formerly in the X-register is copied into the LAST X register,
and the stack drops. When the stack drops, the number in the Z-register is copied
into the Y-register, and the number in the T-register is copied into the Z-register but
also remains in the T-register.
The diagram on the next page illustrates the stack operation when 8 ÷ 2 is
calculated. (Assume that the stack and LAST X registers have already been loaded
with the numbers shown as the result of previous calculations.)
Percentage Functions
When any of the three percentage functions is performed, the answer is placed in
the X-register, the number formerly in the X-register is copied into the LAST X
register, but the stack does not drop. The numbers in the Y-, Z-, and T-registers are
not changed when a percentage function is performed.

Appendix A: The Automatic Memory Stack 175
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 175 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Calendar and Financial Functions
The following table shows what quantity is in each stack register after the indicated
calendar or financial function key is pressed. The symbols x, y, z, and t represent
the number that was in the corresponding register (X, Y, Z, or T, respectively) at
the time the function key was pressed.
Register D Ò Ï
n, ¼, $,
P, M, l,
L*
!
T t t x t y
Z t z INT365 z
x (number of
payments)
Y z ∆DYS30-day
–PV y PMTPRIN
X DATE ∆DYSactual INT360 n, i, PV, PMT,
FV, NPV, IRR PMTINT
Register E S V, Ý, #
T y (settlement date) z y
Z x (maturity date) y (settlement date) x (number of year)
Y INT x (maturity date) RDV (remaining
depreciable value)
X PRICE YTM DEP
* For n, ¼, $, P, and M, the stack registers hold the quantities shown if the key is
pressed to calculate the corresponding quantity rather than to merely store a number in the
corresponding register.
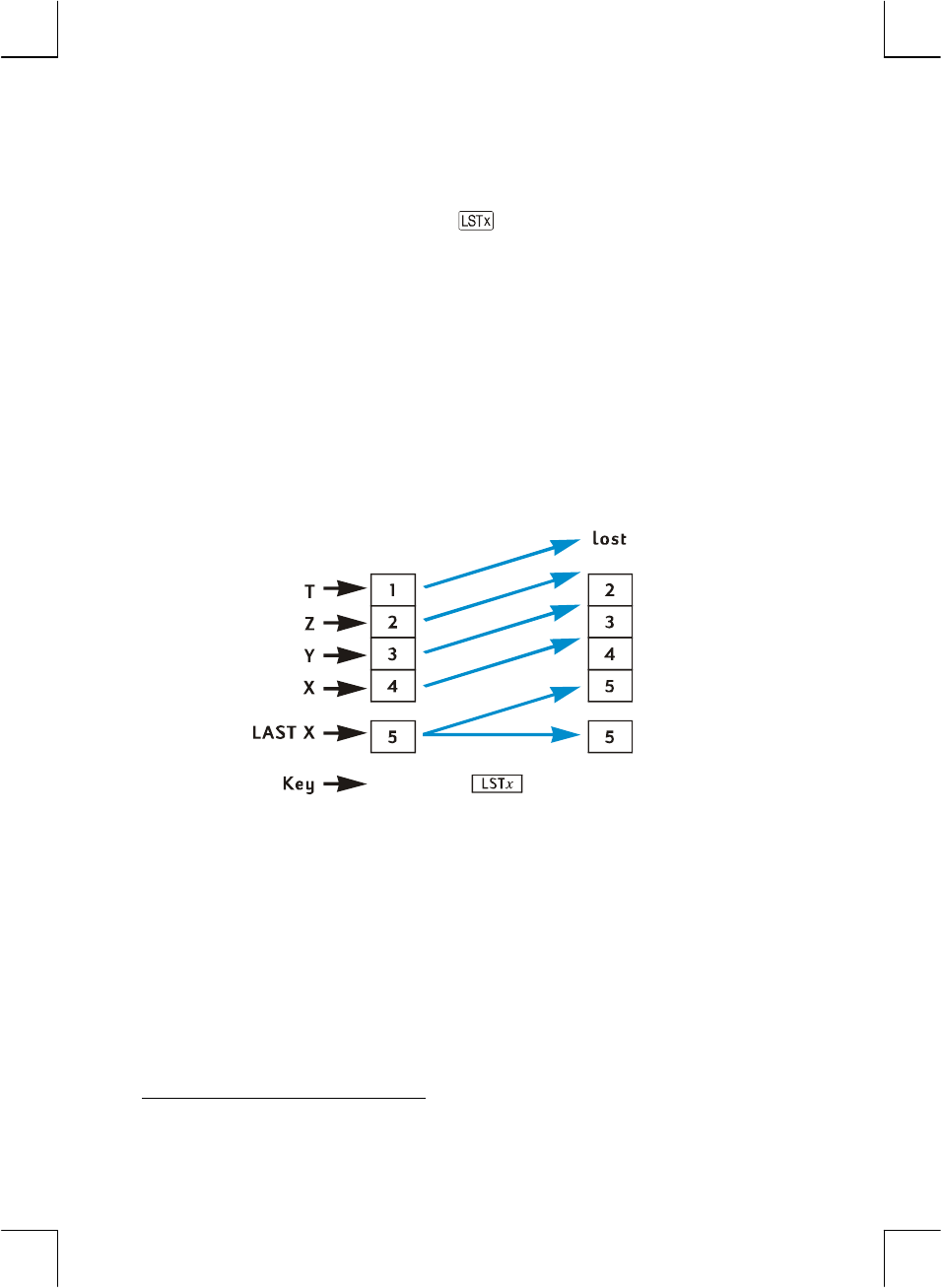
176 Appendix A: The Automatic Memory Stack
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 176 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The LAST X Register and the Key
The number in the displayed X-register is copied into the LAST X register
whenever any of the following function keys is pressed:
+ - § z y
q > ¿ r B
T Ñ _ ^ Q
R e b à Z
D Ò
Pressing gF lifts the stack (unless \, O, _, ^, A, or C was the
last key pressed, as described on page 172), then copies the number from the
LAST X register into the displayed X-register. The number remains also in the LAST
X register.
Chain Calculations
The automatic stack lift and stack drop make it possible to do chain calculations
without the necessity for keying in parentheses or storing intermediate results, as
are required on some other calculators. An intermediate result in the displayed
X-register is automatically copied into the Y-register when a number is keyed in
after a function key is pressed.* Therefore, when a two-number function key is
then pressed, that function is performed using the number keyed into the displayed
X-register and the intermediate result in the Y-register. The number then in the
Y-register, if remaining as an intermediate result from an earlier calculation, can
then be used with the intermediate result in the X-register for another calculation.
* Except for \, O, _, ^, A or C, and — under certain circumstances — n, ¼,
$, P, and M. For more information, refer to Stack Lift, page 172.

Appendix A: The Automatic Memory Stack 177
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 177 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
The diagram on page 171 illustrates how the automatic stack lift and stack drop
make chain calculations quick and error-free.
Virtually every chain calculation you are likely to encounter can be done using
only the four stack registers. However, to avoid having to store an intermediate
result in a storage register, you should begin every chain calculation at the
innermost number or pair of parentheses and then work outward — just as you
would if you were doing the calculation manually (that is, using pencil and paper).
For example, consider the calculation of
3 [4 + 5 (6 + 7)]
If this calculation were done from left to right — as were the (simpler) examples
under Chain Calculations on page 20 and page 22 — you would have to enter
five numbers into the calculator before doing the first operation possible (6 + 7).
But since the stack holds only four numbers, this calculation cannot be done
left-to-right. However, it can easily be done if you begin with the calculation in the
innermost pair of parentheses — again, (6 + 7).
Keystrokes Display
6\7+ 13.00 Intermediate result of (6+7).
5§ 65.00 Intermediate result of 5 (6+7).
4+ 69.00 Intermediate result of [4 + 5(6 + 7)].
3§ 207.00 Final result: 3 [4 + 5 (6 + 7)].
Arithmetic Calculations with Constants
Because the number in the T-register remains there when the stack drops, this
number can be used as a constant in arithmetic operations. To place the constant
into the T-register, key it into the display (that is, into the X-register), then press
\ three times. This also places the constant in the Y and Z-registers. Each time
an arithmetic operation is then performed — using the constant in the Y-register
and a number keyed into the displayed X-register — the constant will be
“dropped” back into the Y-register.
Example: The annual sales of solar engineering hardware your firm — currently
$84,000 — are projected to double each year for the next 3 years. Calculate the
annual sales for each of those years.
Keystrokes Display
2\\
\ 2.00 Enters constant into Y, Z, and
T-registers.

178 Appendix A: The Automatic Memory Stack
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 178 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Keystrokes Display
84000 84,000. Enters base amount into displayed
X-register.
§ 168,000.00 Annual sales after first year.
§ 336,000.00 Annual sales after second year.
§ 672,000.00 Annual sales after third year.
In the example above, the constant was repeatedly multiplied by the result of the
previous operation, which was already in the displayed X-register. In another class
of calculations with constants, the constant is multiplied by (or added to, etc.) a
new number keyed into the displayed X-register. For these calculations, you must
press O before keying in a new number after having pressed an operator key. If
this were not done, the stack would lift when you keyed in a new number after
pressing the operator key, and the Y-register would no longer contain the constant.
(Recall — from page 172 — that the stack does not lift when a number is keyed
into the displayed X-register after O is pressed.)
Example: At Permex Pipes a certain pipe fitting is packaged in quantities of 15,
75, and 250. If the cost per fitting is $4.38, calculate the cost of each package.*
Keystrokes Display
4.38\\
\ 4.38 Enters constant into Y-, Z-, and
T-registers.
15 15. Enters first quantity into displayed
X-register.
§ 65.70 Cost of a package of 15.
O75 75. Clears display and enters second
quantity into displayed X-register.
§ 328.50 Cost of a package of 75.
O250 250. Clears display and enters third
quantity into displayed X-register.
§ 1,095.00 Cost of a package of 250.
* You may want to compare this method of arithmetic calculations with constants to the method
using F described on page 74.

179
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 179 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Appendix B
More About L
Given a sequence of positive and negative cash flows, we hope that there is
enough information to determine whether an IRR answer exists, and what that
answer is. For the vast majority of cases, your hp 12c will find the unique IRR
answer if it exists. But the IRR computation is so complex that if the cash flow
sequence does not meet certain criteria, then sometimes the calculator is unable to
determine whether or not an answer or answers exist.
Let’s look at all of the possible outcomes of IRR as calculated by your hp 12c:
Case 1: A positive answer. If a positive answer is displayed, it is the only such
answer. One or more negative answers may also exist.
Case 2: A negative answer. If a negative answer is displayed, there may be
additional negative answers, and there may be a single positive answer. If
additional answers (negative or positive) exist, they can be calculated using the
procedure described below.
Case 3: The calculator displays Error 3. This indicates that the computation is
very complex, possibly involving multiple answers, and cannot be continued until
you give the calculator an estimate of IRR. The procedure for doing so is described
below.
Case 4: The calculator displays Error 7. This indicates that there is no answer to
the computation of IRR with the cash flow amounts you have entered. This situation
is probably the result of a mistake in entering the magnitudes or signs of the cash
flows or the number of times a cash flow amount occurs consecutively. Refer to
Reviewing Cash Flow Entries (page 64) and Changing Cash Flow Entries (page
65) to check and correct the entries. Error 7 will result if there is not at least one
positive cash flow and at least one negative cash flow.
Although the calculator will eventually reach one of the above outcomes, it may
take a long time to get there. You may wish to terminate the IRR iterative process,
by pressing any key, to see what interest rate the calculator has computed at that
point. If you stop the calculation, you may continue searching for IRR as described
below.
Searching for IRR. You can continue searching for IRR solutions, even after an
Error 3 indication, as follows:
1. Make a guess for the interest rate and key it in.
2. Press:gt.

180 Appendix B: More About L
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 180 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Your guess will aid the calculator in its search, and if it finds an IRR answer near
your guess, that answer will be displayed. Since the calculator cannot tell you the
number of solutions that exist when there is more than one mathematically correct
answer, you can continue to make guesses, pressing :gt after each one,
to search for IRR solutions.
You can hasten this process by using the l function to help you make a good
guess. Remember that a correct IRR solution will make the calculated NPV very
small. So continue to guess interest rates and solve for NPV until the answer you
obtain is reasonably close to zero. Then press :gt to calculate the IRR
answer near your guess.
How would this work in case 2 above? The calculator displays a negative answer
and you wish to check for a unique positive IRR. Key in successively larger guesses
for i (starting from 0) and solve for NPV until you reach a sign change in your NPV
outcomes. Then press :gt to find an IRR solution near the last interest rate
obtained using the l key.
If you stop the IRR iterative process, you can test the interest obtained using l,
and then restart the process by pressing :gt.

181
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 181 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Appendix C
Error Conditions
Some calculator operations cannot be performed under certain conditions (for
example, z when x = 0). If you attempt such an operation under these conditions,
the calculator will display the word Error followed by a digit, 0 through 9. Listed
below are operations that cannot be performed under the conditions specified. The
symbols x and y represent the number in the X- and Y-registers, respectively, when
the operation key is pressed.
Error 0: Mathematics
Operation Condition
z x = 0
y x = 0
r x < 0
° x ≤ 0
q y = 0 and x ≤ 0
y < 0 and x is noninteger.
à y = 0
Z y = 0
?z(0 through 4) x = 0
e x is noninteger
x < 0
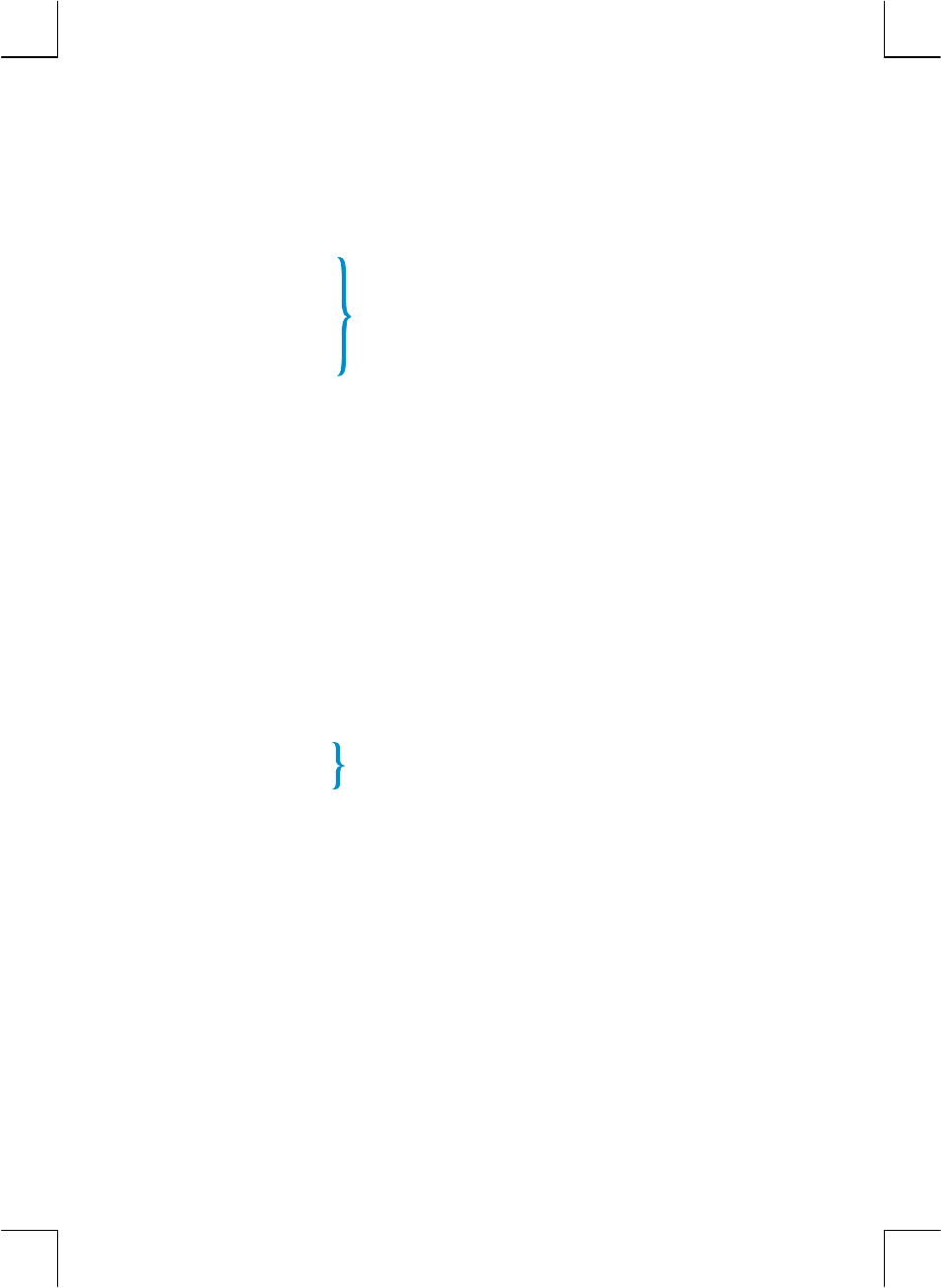
182 Appendix C: Error Conditions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 182 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Error 1: Storage Register Overflow
Operation Condition
?+(0 through 4)
?-(0 through 4)
?§(0 through 4)
?z(0 through 4)
A
Magnitude of result is greater than
9.999999999×1099.
Error 2: Statistics
Operation Condition
Ö n (number in R1) = 0
Σx = 0
v n = 0
n = 1
nΣx2 – (Σx)2< 0
nΣy2 – (Σy)2< 0
R n = 0
nΣx2 – (Σx)2 = 0
Q n = 0
nΣy2 – (Σy)2 = 0
R~
Q~ [nΣx2 – (Σx)2][nΣy2 – (Σy)2] ≤ 0
Error 3: IRR
Refer to Appendix B.
Error 4: Memory
z Attempting to enter more than 99 program lines.
z Attempting to i to a program line that does not exist.
z Attempting storage register arithmetic in R5 through R9 or R.0 through R.9.

Appendix C: Error Conditions 183
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 183 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Error 5: Compound Interest
Operation Condition
n PMT ≤ –PV × i
PMT = FV × i
i ≤ –100
The values in i, PV, and FV are such that no
solution exists for n.
¼ PMT = 0 and n < 0
Cash flows all have same sign.
$ i ≤ –100
P n = 0
i = 0
i ≤ –100
M i ≤ –100
! x ≤ 0
x is noninteger.
l i ≤ –100
V
Ý
#
n ≤ 0
n > 1010
x ≤ 0
x is noninteger
Error 6: Storage Registers
Operation Condition
?
:
Storage register specified does not exist or has
been converted to program lines.
K
a
n specifies a storage register that does not exist
or has been converted to program lines.
l
L
n > 20
n > r (as defined by N)
n < 0
n is noninteger
a x > 99
x < 0
x is noninteger
184 Appendix C: Error Conditions
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 184 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Error 7: IRR
Refer to Appendix B.
Error 8: Calendar
Operation Condition
Ò
D Improper date format or illegal date.
D Attempting to add days beyond calculator’s date
capacity.
E
S Improper date format or illegal date.
More than 500 years between settlement
(purchase) date and maturity (redemption) date.
Maturity date earlier than settlement date.
Maturity date has no corresponding coupon date
(6 months earlier).*
Error 9: Service
Refer to Appendix E.
Pr Error
z Continuous Memory has been reset. (Refer to Continuous Memory, page
70.)
z You have reset the calculator using the reset hole (see page 194).
* This is the case for the 31st of March, May, August, October, and December, plus August 29
(except in a leap year) and 30. For example, there is no September 31, so March 31 has no
corresponding coupon date 6 months earlier.
To correct this problem for all maturity dates except August 29 and 30, add one day to both
the settlement date and the maturity date in your calculations. For instance, if a bond were
purchased on June 1, 2004 (the settlement date) with a maturity date of December 31, 2005,
you should change the dates to June 2, 2004 and January 1, 2006 for your calculations.
For August 29 and 30, there is no calculator solution that gives the correct answer.

185
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 185 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Appendix D
Formulas Used
Percentage
100
)Rate()Base(
%xy ×
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−
=∆ )Base(
)Base()NewAmount(
100% y
yx
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=)Total(
)Amount(
100%T y
x
Interest
n = number of compounding periods.
i = periodic interest rate, expressed as a decimal.
PV = present value.
FV = future value or balance.
PMT = periodic payment.
S = payment mode factor (0 or 1) indicating treatment of PMT.
0 corresponds to End, 1 to Begin.
I = interest amount.
INTG (n) = integer portion of n.
FRAC (n) = fractional portion of n.
Simple Interest
iPV
n
I××= 360
360
iPV
n
I××= 365
365

186 Appendix D: Formulas Used
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 186 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Compound Interest
Without an odd period:
n
n
iFV
i
i
PMTiSPV −
−
++
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡+−
⋅⋅++= )1(
)1(1
)1(0
With simple interest used for an odd period:
)(INTG
)INTG(
)1(
)1(1
)1(])FRAC(1[0
n
n
iFV
i
i
PMTiSniPV
−
−
+
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡+−
+++=
With compound interest used for an odd period:
)(INTG
)INTG(
)FRAC(
)1(
)1(1
)1()1(0
n
n
n
iFV
i
i
PMTiSiPV
−
−
+
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡+−
+++=
Amortization
n= number of payment periods to be amortized.
INTj= amount of PMT applied to interest in period j.
PRNj= amount of PMT applied to principal in period j.
PVj= present value (balance) of loan after payment in period j.
j= period number.
INT1= {0 if n = 0 and payment mode is set to Begin.
|PV0 × i|RND (sign of PMT)
PRN1= PMT – INT1
PV1= PV0 + PRN1
INTj= |PVj –1 × i|RND × (sign of PMT) for j > 1.
PRNj= PMT – INTj
PVj= PVj –1 + PRNj
∑∑ =
+++== n
nj INTINTINTINTINT
1j 2
1...
∑∑ =
+++== n
nj PRNPRNPRNPRNPRN
1j 2
1...
∑
+= PRNPVPVn0

Appendix D: Formulas Used 187
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 187 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Discounted Cash Flow Analysis
Net Present Value
NPV = net present value of a discounted cash flow.
CFj = cash flow at period j.
n
n
i
CF
i
CF
i
CF
CFNPV )1(
...
)1(
)1( 2
2
1
1
0+
++
+
+
+
+=
Internal Rate of Return
n = number of cash flows
CFj = cash flow at period j.
IRR = Internal Rate of Return
0
1
)1(
)1(1
0CFIRR
IRR
IRR
CF jq
jnq
k
j
n
j+
⎥
⎦
⎤
⎢
⎣
⎡+⋅
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡+−
⋅= ∑
−
=
−
<
∑
Calendar
Actual Day Basis
∆DYS = f(DT2) – f(DT1)
where
f(DT) = 365 (yyyy) + 31 (mm – 1) + dd + INTG (z/4) – x
and
for mm ≤ 2
x = 0
z = (yyyy) – 1
for mm > 2
x = INTG (0.4mm + 2.3)
z = (yyyy)
INTG = Integer portion.
Note: Additional tests are performed in order to ensure that the century (but
not millennium) years are not considered leap years.
30/360 Day Basis
DAYS = f(DT2) – f(DT1)
f(DT) = 360 (yyyy) + 30mm + z
for f(DT1)
if dd1 = 31 then z = 30
if dd1 ≠ 31 then z = dd1
for f(DT2)
if dd2 = 31 and dd1 = 30 or 31 then z = 30
if dd2 = 31 and dd1 < 30 then z = dd2
if dd2 < 31 then z = dd2
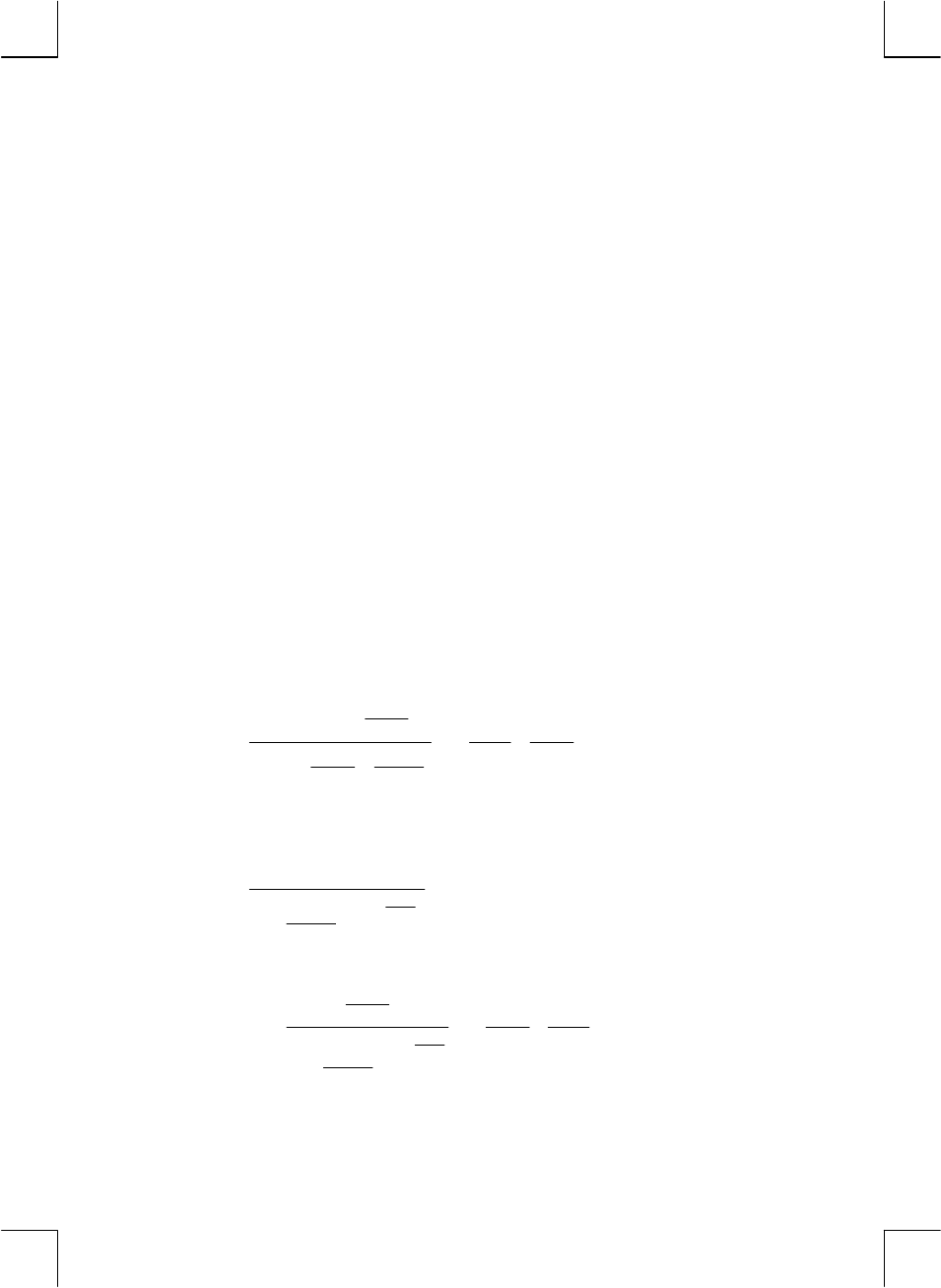
188 Appendix D: Formulas Used
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 188 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Bonds
Reference:
Spence, Graudenz, and Lynch, Standard Securities Calculation Methods,
Securities Industry Association, New York, 1973.
DIM = days between issue date and maturity date.
DSM = days between settlement date and maturity date.
DCS = days between beginning of current coupon period and
settlement date.
E= number of days in coupon period where settlement occurs.
DSC = E – DCS = days from settlement date to next 6–month coupon
date.
N= number of semiannual coupons payable between settlement
date and maturity date.
CPN = annual coupon rate (as a percentage).
YIELD = annual yield (as a percentage).
PRICE = dollar price per $100 par value.
RDV = redemption value.
For semiannual coupon with 6 months or less to maturity:
⎥
⎦
⎤
⎢
⎣
⎡×−
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
×+
+
=2
)
2
(100
)
2
(100 CPN
E
DCS
YIELD
E
DSM
CPN
RDV
PRICE
For semiannual coupon with more than 6 months to maturity:
⎥
⎦
⎤
⎢
⎣
⎡×−
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛+
+
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛+
=
∑
=+−
+−
E
DCSCPN
YIELD
CPN
YIELD
RDV
PRICE
N
KE
DSC
K
E
DSC
N
2
200
1
2
200
1
11
1
Appendix D: Formulas Used 189
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 189 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Depreciation
L = asset’s useful life expectancy.
SBV = starting book value.
SAL = salvage value.
FACT = declining-balance factor expressed as a percentage.
j = period number.
DPNj = depreciation expense during period j.
RDVj = remaining depreciable value at end of period j
= RDVj–1 – DPNj where RDV0 = SBV – SAL
RBVj = remaining book value = RBVj–1 – DPNj where RBV0 = SBV
Y1 = number of months in partial first year.
Straight-Line Depreciation
Keyboard function:
L
SALSBV
DPNJ
−
= for j = 1, 2, …, L
Program for partial first year:
12
1
1
Y
L
SALSBV
DPN ⋅
−
=
L
SALSBV
DPNJ
−
= for j = 2, 3, …, L
DPNL + 1 = RDVL
Sum-of-the-Years-Digits Depreciation
2
)2)(1(
F
W
W
SOYDk
+
+
=
where W = integer part of k
F = fractional part of k.
(i.e., for k = 12.25 years, W = 12 and F = 0.25).
Keyboard function:
)(
)1( SALSBV
SOYD
jL
DPN
L
J−⋅
+−
=
190 Appendix D: Formulas Used
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 190 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Program for partial year:
)(
12
1
1SALSBV
Y
SOYD
L
DPN −⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⎟
⎠
⎞
⎜
⎝
⎛
=
)(
2
1SALDSBV
SOYD
jLADJ
DPN
LADJ
j−−⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+−
= for j
≠ 1
where ⎟
⎠
⎞
⎜
⎝
⎛
−= 12
1
Y
LLADJ
Declining-Balance Depreciation
Keyboard function:
L
FACT
RBVDPN j
j100
1⋅= − for j = 1, 2, …, L
Program for partial first year:
12100
1
1
Y
L
FACT
SBVDPN ⋅⋅=
L
FACT
RBVDPN j
j100
1⋅= − for j
≠ 1
Modified Internal Rate of Return
n= number of compounding periods.
NFVP= Net future value of the positive cash flows.
NPVN= Net present value of the negative cash flows.
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=1100
1
n
N
P
NPV
NFV
MIRR
Advance Payments
A= number of payments made in advance.
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡+
+−
+−
=−−
−
A
i
i
iFVPV
PMT An
n
)(
)1(1
)1(

Appendix D: Formulas Used 191
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 191 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Interest Rate Conversions
C = number of compounding periods per year.
EFF = the effective annual interest rate as a decimal.
NOM = the nominal annual interest rate as a decimal.
Finite Compounding
11 −
⎟
⎠
⎞
⎜
⎝
⎛+=
C
C
NOM
EFF
Continuous Compounding
)1( −= NOM
eEFF
Statistics
Mean
n
x
x∑
= n
y
y∑
=
Weighted Mean
∑
∑
=w
w
x
xw
Linear Estimation
n = number of data pairs
B
x
A
y
+
=
ˆ
B
A
y
x−
=
ˆ
where
()
n
x
x
n
yx
xy
B2
2∑
∑
∑
∑
∑
−
⋅
−
=
x
B
y
A
−
=

192 Appendix D: Formulas Used
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 192 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
()
()
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡−⋅
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡−
⎥
⎦
⎤
⎢
⎣
⎡⋅
−
=
∑∑
∑∑
∑
∑
∑
n
y
y
n
x
x
n
yx
xy
r2
2
2
2
Standard Deviation
()
)1(
2
2
−
−
=∑∑
nn
xxn
sx
()
)1(
2
2
−
−
=∑∑
nn
yyn
sy
Factorial
0! = 1
For n > 1 where n is an integer:
∏
=
=n
i
in
1
!
The Rent or Buy Decision
Market Value = PRICE(1 + I)n
where:
I= appreciation per year (as decimal)
n= number of years
Net Cash Proceeds on Resale = Market Value – Mortgage Balance – Commission
The interest rate is obtained by solving the financial (compound interest) equation
for i using:
n = number of years house is owned
PV = down payment + closing costs
PMT = mortgage payment + taxes + maintenance –rent – (% tax)
(interest + taxes)
FV = net cash proceeds on resale
Annual interest rate = 12 × i

193
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 193 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Appendix E
Battery, Warranty, and
Service Information
Battery
The hp 12c is shipped with one 3 Volt CR2023 Lithium battery. Battery life
depends on how the calculator is used. If the calculator is being used to perform
operations other than running programs, it uses much less power.
Low-Power Indication
A battery symbol (¼) shown in the upper-left corner of the display when the
calculator is on signifies that the available battery power is running low. When the
battery symbol begins flashing, replace the battery as soon as possible to avoid
losing data.
Use only a fresh battery. Do not use rechargeable batteries.
Warning
There is the danger of explosion if the battery is
incorrectly replaced. Replace only with the same or
equivalent type recommended by the manufacturer.
Dispose of used batteries according to the
manufacturer’s instructions. Do not mutilate, puncture,
or dispose of batteries in fire. The batteries can burst or
explode, releasing hazardous chemicals. Replacement
battery is a Lithium 3V Coin Type CR2032.
Installing a New Battery
The contents of the calculator’s Continuous Memory are preserved for a short time
while the battery is out of the calculator (provided that you turn off the calculator
before removing the battery). This allows you ample time to replace the battery
without losing data or programs. If the battery is left out of the calculator for an
extended period, the contents of Continuous Memory may be lost.
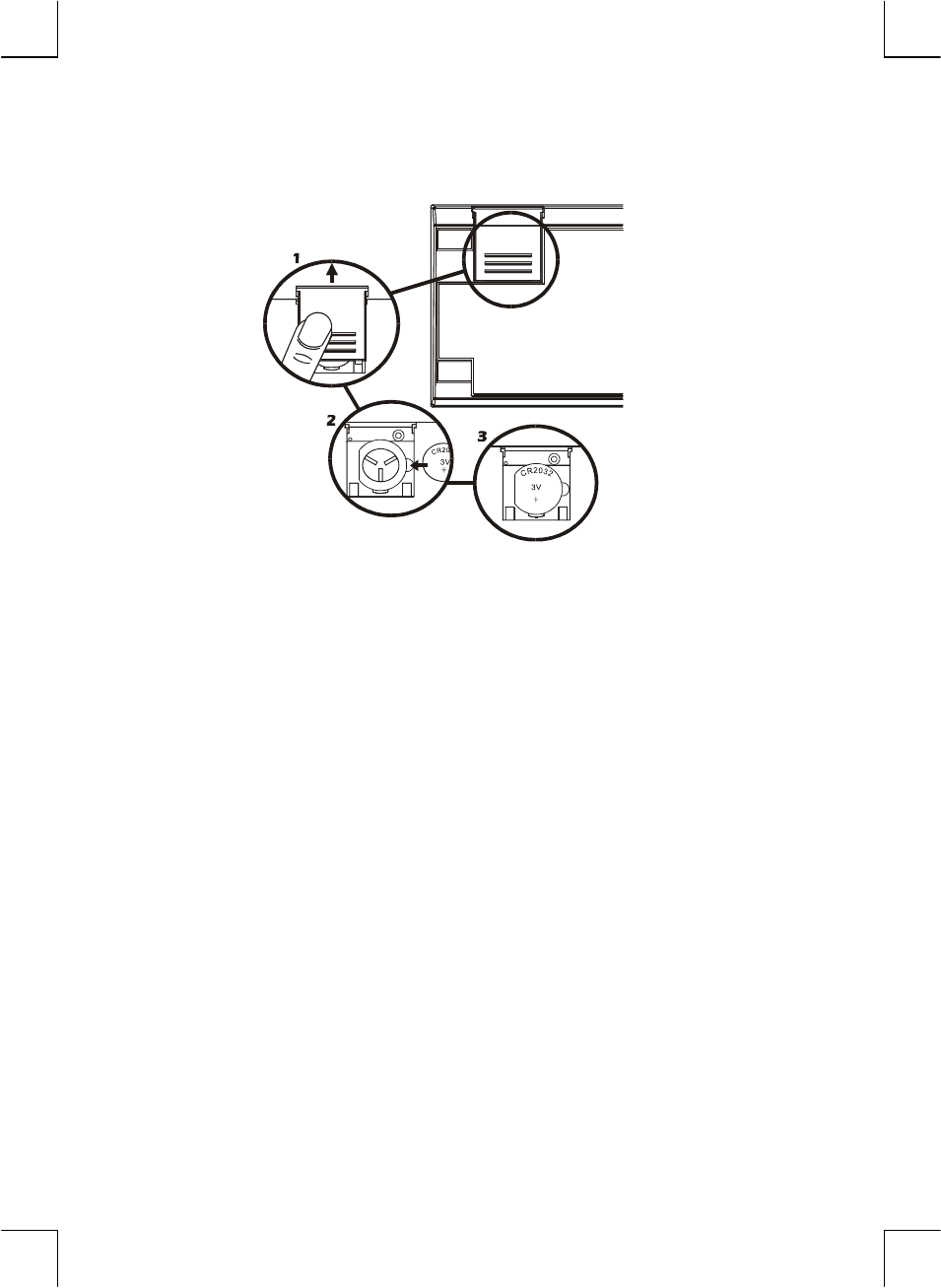
194 Appendix E: Battery, Warranty, and Service Information
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 194 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
To install a new battery, use the following procedure:
1. With the calculator turned off, slide the battery cover off.
2. Remove the old battery.
3. Insert a new battery, with positive polarity facing outward.
4. Replace the battery cover.
Note: Be careful not to press any keys while the battery is out of the calculator. If
you do so, the contents of Continuous Memory may be lost and keyboard control
may be lost (that is, the calculator may not respond to keystrokes).
5. Replace the battery compartment cover and press ; to turn on the power.
If for any reason Continuous Memory has been reset (that is, if its contents
have been lost), the display will show Pr Error. Pressing any key will clear
this message.
Verifying Proper Operation (Self-Tests)
If it appears that the calculator will not turn on or otherwise is not operating
properly, use one of the following procedures.
For a calculator that does respond to keystrokes:
1. With the calculator off, hold down the ; key and press §.
2. Release the ; key, then release the § key. This initiates a complete test of
the calculator’s electronic circuitry. If everything is working correctly, within
about 25 seconds (during which the word running flashes) the display
should show –8,8,8,8,8,8,8,8,8,8, and all of the status indicators (except

Appendix E: Battery, Warranty, and Service Information 195
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 195 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
the ¼ battery power indicator) should turn on.* If the display shows Error 9,
goes blank, or otherwise does not show the proper result, the calculator
requires service.†
Note: Tests of the calculator’s electronics are also performed if the = key
or the z key is held down when ; is released.‡ These tests are included
in the calculator to be used in verifying that it is operating properly during
manufacturing and service.
If you had suspected that the calculator was not working properly but the proper
display was obtained in step 2, it is likely that you made an error in operating the
calculator. We suggest you reread the section in this handbook applicable to your
calculation — including, if appropriate, appendix A. If you still experience
difficulty, write or telephone Hewlett-Packard at an address or phone number listed
under Service (Page 197).
* The status indicators turned on at the end of this test include some that normally are not
displayed on the hp 12c.
† If the calculator displays Error 9 as a result of the ;/µ test or the ;/+ test but you
wish to continue using your calculator, you should reset Continuous Memory as described on
page 70.
‡ The ;/= combination initiates a test that is similar to that described above, but continues
indefinitely. The test can be terminated by pressing any key, which will halt the test within 25
seconds. The ;/z combination initiates a test of the keyboard and the display. When the
; key is released, certain segments in the display will be lit. To run the test, the keys are
pressed in order from left to right along each row, from the top row to the bottom row. As
each key is pressed, different segments in the display are lit. If the calculator is operating
properly and all the keys are pressed in the proper order, the calculator will display 12 after
the last key is pressed. (The \ key should be pressed both with the third-row keys and with
the fourth-row keys.) If the calculator is not working properly, or if a key is pressed out of
order, the calculator will display Error 9. Note that if this error display results from an
incorrect key being pressed, this does not indicate that your calculator requires service. This
test can be terminated by pressing any key out of order (which will, of course, result in the
Error 9 display). Both the Error 9 display and the 12 display can be cleared by pressing
any key.

196 Appendix E: Battery, Warranty, and Service Information
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 196 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Warranty
hp 12c Financial Calculator; Warranty period: 12 months
1. HP warrants to you, the end-user customer, that HP hardware, accessories
and supplies will be free from defects in materials and workmanship after the
date of purchase, for the period specified above. If HP receives notice of
such defects during the warranty period, HP will, at its option, either repair
or replace products which prove to be defective. Replacement products may
be either new or like-new.
2. HP warrants to you that HP software will not fail to execute its programming
instructions after the date of purchase, for the period specified above, due to
defects in material and workmanship when properly installed and used. If HP
receives notice of such defects during the warranty period, HP will replace
software media which does not execute its programming instructions due to
such defects.
3. HP does not warrant that the operation of HP products will be uninterrupted
or error free. If HP is unable, within a reasonable time, to repair or replace
any product to a condition as warranted, you will be entitled to a refund of
the purchase price upon prompt return of the product.
4. HP products may contain remanufactured parts equivalent to new in
performance or may have been subject to incidental use.
5. Warranty does not apply to defects resulting from (a) improper or
inadequate maintenance or calibration, (b) software, interfacing, parts or
supplies not supplied by HP, (c) unauthorized modification or misuse, (d)
operation outside of the published environmental specifications for the
product, or (e) improper site preparation or maintenance.
6. HP MAKES NO OTHER EXPRESS WARRANTY OR CONDITION WHETHER
WRITTEN OR ORAL. TO THE EXTENT ALLOWED BY LOCAL LAW, ANY
IMPLIED WARRANTY OR CONDITION OF MERCHANTABILITY,
SATISFACTORY QUALITY, OR FITNESS FOR A PARTICULAR PURPOSE IS
LIMITED TO THE DURATION OF THE EXPRESS WARRANTY SET FORTH
ABOVE. Some countries, states or provinces do not allow limitations on the
duration of an implied warranty, so the above limitation or exclusion might
not apply to you. This warranty gives you specific legal rights and you might
also have other rights that vary from country to country, state to state, or
province to province.
7. TO THE EXTENT ALLOWED BY LOCAL LAW, THE REMEDIES IN THIS
WARRANTY STATEMENT ARE YOUR SOLE AND EXCLUSIVE REMEDIES.
EXCEPT AS INDICATED ABOVE, IN NO EVENT WILL HP OR ITS SUPPLIERS
BE LIABLE FOR LOSS OF DATA OR FOR DIRECT, SPECIAL, INCIDENTAL,
CONSEQUENTIAL (INCLUDING LOST PROFIT OR DATA), OR OTHER
DAMAGE, WHETHER BASED IN CONTRACT, TORT, OR OTHERWISE.
Appendix E: Battery, Warranty, and Service Information 197
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 197 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Some countries, States or provinces do not allow the exclusion or limitation
of incidental or consequential damages, so the above limitation or exclusion
may not apply to you.
8. The only warranties for HP products and services are set forth in the express
warranty statements accompanying such products and services. Nothing
herein should be construed as constituting an additional warranty. HP shall
not be liable for technical and editorial errors or omissions contained herein.
FOR CONSUMER TRANSACTIONS IN AUSTRALIA AND NEW ZEALAND: THE
WARRANTY TERMS CONTAINED IN THIS STATEMENT, EXCEPT TO THE
EXTENT LAWFULLY PERMITTED, DO NOT EXCLUDE, RESTRICT OR MODIFY
AND ARE IN ADDITION TO THE MANDATORY STATUTORY RIGHTS
APPLICABLE TO THE SALE OF THIS PRODUCT TO YOU.
Service
Europe Country : Telephone numbers
Austria +43-1-3602771203
Belgium +32-2-7126219
Denmark +45-8-2332844
Eastern Europe countries +420-5-41422523
Finland +35-89640009
France +33-1-49939006
Germany +49-69-95307103
Greece +420-5-41422523
Holland +31-2-06545301
Italy +39-02-75419782
Norway +47-63849309
Portugal +351-229570200
Spain +34-915-642095
Sweden +46-851992065
Switzerland +41-1-4395358 (German)
+41-22-8278780 (French)
+39-02-75419782 (Italian)
Turkey +420-5-41422523
UK +44-207-4580161
Czech Republic +420-5-41422523
South Africa +27-11-2376200
Luxembourg +32-2-7126219
Other European countries +420-5-41422523
198 Appendix E: Battery, Warranty, and Service Information
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 198 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Asia Pacific Country : Telephone numbers
Australia +61-3-9841-5211
Singapore +61-3-9841-5211
L.America Country : Telephone numbers
Argentina 0-810-555-5520
Brazil Sao Paulo 3747-7799; ROTC
0-800-157751
Mexico Mx City 5258-9922; ROTC
01-800-472-6684
Venezuela 0800-4746-8368
Chile 800-360999
Columbia 9-800-114726
Peru 0-800-10111
Central America &
Caribbean
1-800-711-2884
Guatemala 1-800-999-5105
Puerto Rico 1-877-232-0589
Costa Rica 0-800-011-0524
N.America Country : Telephone numbers
USA 1800-HP INVENT
Canada (905)206-4663 or
800-HP INVENT
ROTC = Rest of the country
Please logon to http://www.hp.com for the latest service and support information.

Appendix E: Battery, Warranty, and Service Information 199
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 199 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Regulatory Information
This section contains information that shows how the hp 12c financial calculator
complies with regulations in certain regions. Any modifications to the calculator
not expressly approved by Hewlett-Packard could void the authority to operate the
12c in these regions.
USA
This calculator generates, uses, and can radiate radio frequency energy and may
interfere with radio and television reception. The calculator complies with the limits
for a Class B digital device, pursuant to Part 15 of the FCC Rules. These limits are
designed to provide reasonable protection against harmful interference in a
residential installation.
However, there is no guarantee that interference will not occur in a particular
installation. In the unlikely event that there is interference to radio or television
reception(which can be determined by turning the calculator off and on), the user
is encouraged to try to correct the interference by one or more of the following
measures:
z Reorient or relocate the receiving antenna.
z Relocate the calculator, with respect to the receiver.
Canada
This Class B digital apparatus complies with Canadian ICES-003.
Cet appareil numerique de la classe B est conforme a la norme NMB-003 du
Canada.
Japan
この装置は、情報処理装置等電波障害自主規制協議会(VCCI)の基準
に基づく第二情報技術装置です。この装置は、家庭環境で使用することを目的とし
ていますが、この装置がラジオやテレビジョン受信機に近接して使用されると、受
信障害を引き起こすことがあります。
取扱説明書に従って正しい取り扱いをしてください。
Temperature Specifications
z Operating: 0º to 55º C (32º to 131º F)
z Storage: –40º to 65º C (–40º to 149º F)
Noise Declaration
In the operator position under normal operation (per ISO 7779): LpA < 70dB.

200 Appendix E: Battery, Warranty, and Service Information
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 200 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Disposal of Waste Equipment by Users in Private
Household in the European Union
This symbol on the product or on its packaging indicates that this
product must not be disposed of with your other household waste.
Instead, it is your responsibility to dispose of your waste
equipment by handing it over to a designated collection point for
the recycling of waste electrical and electronic equipment. The
separate collection and recycling of your waste equipment at the
time of disposal will help to conserve natural resources and ensure
that it is recycled in a manner that protects human health and the environment. For
more information about where you can drop off your waste equipment for
recycling, please contact your local city office, your household waste disposal
service or the shop where you purchased the product.

201
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 201 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Appendix F
United Kingdom Calculations
The calculations for most financial problems in the United Kingdom are identical to
the calculations for those problems in the United States — which are described
earlier in this handbook. Certain problems, however, require different calculation
methods in the United Kingdom than in the United States, even though the
terminology describing the problems may be similar. Therefore, it is recommended
that you ascertain the usual practice in the United Kingdom for the financial
problem you are solving.
The remainder of this appendix describes three types of financial calculations for
which the conventional practice differs significantly between the United Kingdom
and the United States.
Mortgages
The amount of the repayments on home loans and mortgages offered by banks in
the United Kingdom can usually be calculated as described under Calculating the
Payment Amount, page 46. Building Societies in the United Kingdom, however,
calculate the amount of these repayments differently. In general, the repayment
amount of a Building Society mortgage is calculated as follows: first, the annual
repayment amount is calculated using the annual interest rate; second, the periodic
repayment amount is calculated by dividing the annual repayment amount by the
number of repayment periods in one year.
Furthermore, the calculations used by Building Societies are rounded; therefore, to
match their scale repayment figures you would have to round your calculations
accordingly.

202 Appendix F: United Kingdom Calculations
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 202 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Annual Percentage Rate (APR) Calculations
In the United Kingdom, the calculation of the Annual Percentage Rate of Charge
(APR) in accordance with the United Kingdom Consumer Credit Act (1974) differs
from the calculation of the APR in the United States. Unlike the practice in the
United States, where the APR can be calculated by multiplying the periodic interest
rate by the number of periods per year, in the United Kingdom the APR is
calculated by converting the periodic interest rate to the “effective annual rate,”
then truncating the result to one decimal place. With the periodic interest rate in
the display and in the i register, the effective annual rate can be calculated by
keying in the number of compounding periods per year, pressing w, then
proceeding with step 4 of the procedure given on page 160 for converting a
nominal rate to an effective rate.
Bond Calculations
Solutions for the price and yield to maturity of United Kingdom bonds are not
included in this handbook. Actual practice differs according to the type of bond;
variations such as cumulative and ex-dividend pricing, simple or compound interest
discounting, etc., may be encountered.
Application Notes covering such situations may be available in the United
Kingdom; check with your local authorized Hewlett-Packard dealer.

203
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 203 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Function Key Index
General
; Power on /off key
(page 16).
f Shift key. Selects
alternate function in gold
above the function keys
(page 16). Also used in
display formatting
(page 71).
g Shift key. Selects
alternate function in blue
on the slanted face of the
function keys (page 16).
CLEARX after f, g,
?, : or i,
cancels that key
(page 18).
fCLEARX also
displays mantissa of
number in the displayed
X-register (page 73).
Digit Entry
\ Enters a copy of
number in displayed
X-register into Y-register.
Used to separate numbers
(pages 19 and 171).
Þ Changes sign of
number or exponent of
10 in X-register
(page 17).
É Enter exponent. After
pressing, next numbers
keyed in are exponents of
10 (page 18).
0 —9 digits. Used
for keying in numbers
(page 19) and display
formatting (page 71).
. Decimal point
(page 17). Also used
for display formatting
(page 71).
O Clears contents of
displayed X-register to
zero (page 18).
Arithmetic
+-§z} Arithm
etic operators
(page 19).
Storage Registers
? Store. Followed
by number key,
decimal point and
number key, or top row
financial key, stores
displayed number in
storage register
specified (page 23).
Also used to perform
storage register
arithmetic (page 24).
: Recall. Followed
by number key,
decimal point and
number key, or top-row
financial key, recalls
value from storage
register specified into
the displayed X-register
(page 23).
CLEAR H Clears
contents of stack (X,Y,Z
and T), all storage
registers, statistical
registers, and financial
registers (page 24).
Leaves program memory
untouched; not
programmable.
Percentage
b Computes x% of y
and retains the y-value in
the Y-register (page 26).
à Computes percent of
change between number
in Y-register and number
in displayed X-register
(page 27).
Z Computes percent
that x is of number in
Y-register (page 28).
Calendar
Ô Sets date format to
day-month-year
(page 30); not
programmable.
Õ Sets date format to
month-day-year
(page 29); not
programmable.
D Changes a date in
the Y-register by the
number of days in the
X-register and displays
day of week (page 30).
Ò Computes the
number of days between
two dates in the Y and
X-registers (page 31).

204 Function Key Index
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 204 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Financial
CLEAR G Clears
contents of financial
registers (page 33).
× Sets payment
mode to Begin for
compound interest
calculations involving
payments (page 37).
 Sets payment
mode to End for
compound interest
calculations involving
payments (page 37).
Ï Calculates simple
interest (page 33).
w Stores or computes
number of periods in
financial problem
(page 32).
A Multiplies a
number in displayed
X-register by 12 and
stores the resulting
value in the n-register
(page 39).
¼ Stores or computes
interest rate per
compounding period
(page 32).
C Divides number in
displayed X-register by
12 and stores the
resulting value in the
I-register (page 39).
$ Stores or computes
the present value (that
is, the initial cash flow)
of a financial problem
(page 32).
P Stores or
computes payment
amount (page 32).
M Stores or computes
future value (final cash
flow) of a financial
problem (page 32).
! Amortizes x
number of periods
using values stored in
PMT, i, PV, and the
display. Updates
values in PV and n
(page 54).
l Calculates the net
present value of up to
20 uneven cash flows
and initial investment
using values stored
with J, K, and
a (page 58).
L Calculates the
internal rate of return
(yield) for up to 20
uneven cash flows and
initial investment using
values stored with J,
K, and a
(page 63).
J Initial cash flow.
Stores contents of
displayed X-register in
R0, initializes n to zero,
sets N0 to 1. Used at
the beginning of a
discounted cash flow
problem (page 58).
K Cash flow j.
Stores the contents of
X-register in Rj ,
increments n by 1, and
sets Nj to 1. Used for
all cash flows except
the initial cash flow in
a discounted cash flow
problem (page 58).
V Calculates
depreciation using
straight-line method.
(page 68).
E Calculates bond
price, given desired
yield to maturity
(page 67).
S Calculates yield to
maturity, given bond
price (page 67).
a Stores the number
(from 1 to 99) of times
each cash flow occurs
as Nj. Assumes 1
unless otherwise
specified (page 61).
Ý Calculates
depreciation using
sum-of-the-years-digits
method (page 68).
# Calculates
depreciation using
declining-balance
method (page 68).
Statistics
CLEAR² Clears
statistical storage
registers R1 through R6
and stack registers
(page 76).
_ Accumulates
statistics using numbers
from X- and Y-registers
in storage registers R1
through R6 (page 76).
^ Cancels effect of
numbers from X- and
Y-registers in storage
registers R1 through R6
(page 77).

Function Key Index 205
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 205 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Ö Computes mean
(average) of x-values and
y-values using
accumulated statistics
(page 77).
Computes weighted
average of y-(item) and
x-(weight) values using
accumulated statistics
(page 81).
v Computes sample
standard deviations of x-
and y-values using
accumulated statistics
(page 79).
R Linear estimate
(X-register), correlation
coefficient (Y-register).
Fits a line to a set of (x,y)
data pairs entered using
_, then extrapolates this
line to estimate a y-value
for a given x-value. Also
computes strength of
linear relationship (r)
among that set of (x, y)
data pairs (page 80).
Q Linear estimate
(X-register), correlation
coefficient (Y-register).
Fits a line to a set of (x,
y) data pairs entered
using _, then
extra-polates this line to
estimate an x-value for a
given y-value. Also
computes strength of
linear relationship (r)
among that set of (x,y)
data pairs (page 80).
Mathematics
r Computes square root
of number in displayed
X-register (page 83).
q Raises number in
Y-register to power of
number in X-register
(page 85).
y Computes reciprocal
of number in displayed
X-register (page 83).
e Computes factorial
[n•(n–1)... 3•2•1] of
number in displayed
X-register (page 83).
> Natural antilogarithm.
Raises e (approximately
2.718281828) to power
of number in displayed
X-register (page 83).
¿ Computes natural
logarithm (base e) of
number in displayed
X-register (page 83).
Number Alteration
B Rounds mantissa of
10digit number in
X-register to match the
display (page 83).
Ñ Leaves only the
integer portion of
number in displayed
X-register by truncating
fractional portion
(page 83).
T Leaves only the
fractional portion of
number in displayed
X-register by truncating
integer portion
(page 84).
Stack Rearrangement
~ Exchanges contents
of X and Y-registers of
stack (pages 74 and
172).
d RolIs down contents
of stack for viewing in
displayed X-register
(page 172).
F Recalls number
displayed before the
previous operation back
into the displayed
X-register (pages 74
and 176).

206
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 206 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Programming Key Index
s Program/Run. Toggles into and out of Program mode. Automatically sets
program to line 00 when returning to Run mode (page 86).
N Memory map. Describes the current allocation of memory; the number of lines
allotted to program memory and the number of available data registers (page
93).
Program Mode Run Mode
In Program mode, function
keys are recorded in
program memory. Display
shows program memory
line number and the
keycode (keyboard row
and location in row) of the
function key.
In Run mode, function keys may be executed
as part of a recorded program or
individually by pressing from the keyboard.
Active Keys:
In Program mode only the
following keys are active;
they cannot be recorded in
program memory.
CLEARÎ
Clear program. Clears
program memory to all
i00 instructions and
resets calculator so
operations begin at line 00
of program memory. Resets
N to P08 r20
(page 95)
Pressed from
keyboard:
CLEARÎ
Resets calculator (in
Run mode) so
operations begin at
line 00 of program
memory. Does not
erase program
memory.
Executed as a
recorded program
instruction

Programming Key Index 207
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 207 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Program Mode Run Mode
Active Keys:
i Go to. Followed by a
decimal point and a
two-di
g
it number, positions
calculator to that line in
program memory. No
instructions are executed
(page 95)
Ç Single step. Displays
line number and contents
of next program memory
line. If held down,
displays line number and
contents of all program
memory lines, one at a
time (page 92).
Ü Back step. Displays
line number and contents
of previous program
memory line. When back
stepped from line 00,
goes to end of program
memory as defined by
gN. If held down,
displays line number and
contents of all program
memory lines, one at a
time (page 95).
Pressed from
keyboard:
t Run/Stop. Begins
execution of a stored
program. Stops
execution if program is
running (page 89).
iGo to. Followed by
a two-digit number,
positions calculator to
that line in program
memory. No instructions
are executed
(page 103).
Ç Single step.
Displays line number
and keycode of current
program memory line
when pressed; executes
instruction, displays
result, and moves to
next line when released
(page 96).
ÜBack step. Displays
line number and
keycode of previous
program memory line
when pressed; displays
original contents of
X-register when
released. No
instructions are
executed (page 97).
Any key. Pressing any
key on the keyboard
stops execution of a
program (page 102)
Executed as a
recorded program
instruction:
t Run/Stop. Stops
program execution
(page 101).
i Go to. Followed by
a two-digit number,
causes calculator to
branch to the specified
line number next, and
resumes program
execution from there
(page 103).
u Pause. Stops
program execution for
about 1 second and
displays contents of
X-register, then resumes
program execution
(page 97).
om Conditional.
o tests number in
X-register against that in
Y-register. m tests
number in X-register
against zero. If true,
calculator continues
execution at next
program memory line. If
false, calculator skips
next line before
resuming execution
(page 107)

208
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 208 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Subject Index
A
, 12, 54, 172
Adding instructions, 114–19
Advance payments, 151, 156
Amortization, 38, 54–56, 186
Annual interest rate, 39
Annual Percentage Rate, 52–53,
124–26, 202
Annuities, 36
Annuities, deferred, 134–35
Annuity due, 37–38
Appreciation, 38
APR. See Annual Percentage Rate
Arithmetic calculations with constants,
75, 177
Arithmetic calculations, chain,
20–22
Arithmetic calculations, simple, 19
Arithmetic operations and the stack,
173
Arithmetic, storage register, 24
Average. See Mean
Average See Mean, 77
B
, 37
, 92
Backstep, 92
Balloon payments, 40, 41
Battery, 193
Battery power, low, 12, 16, 193
Battery, installing, 193–94
BEGIN status indicator, 37
Bonds, 66–68, 163–67, 188, 202
Bonds, 30/360 day basis, 163–65
Bonds, annual coupon, 166
Bonds, corporate, 67
Bonds, municipal, 67
Bonds, state and local government,
67
Bonds, U.S. Treasury, 66
Branching, 103–12, 116
Branching, adding instructions by,
116–19
Branching, conditional, 107–8
Branching, simple, 103
C
, 61
, 59, 61, 64
, 17, 19, 33, 59
, 18, 28
, 172
, 172
C status indicator, 51
Calendar functions, 29–31, 187
Calendar functions and the stack,
175
Cash flow diagram, 34–38
Cash flow sign convention, 33, 36
Cash flows, changing, 65
Cash flows, reviewing, 64
Cash flows, storing for I and L, 58,
65
Chain calculations, 20–22, 176–77
Clearing display, 18
Clearing financial registers, 18
Clearing operations, 17, 18
Clearing prefix keys, 17
Clearing program memory, 18, 89
Clearing statistics registers, 18, 76
Clearing storage registers, 18, 24,
70
Clearing X-register, 18
Compound growth, 37, 39

Subject Index 209
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 209 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Compound interest, 39–53, 186
Compound interest calculation, 11
Compounding periods, 34, 39
Conditional branching, 107–8
Conditional test instructions, 107
Constants, arithmetic calculations
with, 177
Constants, arithmetic calculations
with, 75
Continuous compounding, 162, 191
Continuous effective rate, 162
Continuous memory, 70
Continuous memory, resetting of, 33,
37, 70, 72, 93, 94
D
, 29–31
, 68, 172
, 51, 172
D.MY status indicator, 30
Data storage registers, 23–25
Date format, 29, 70
Dates, days between, 31
Dates, future or past, 30
Days, between dates, 31
Decimal places, rounding, 71
Decimal point, changing, 17
Declining-balance depreciation, 139
Deferred annuities, 134–35
Depreciation, 68, 136–48, 189–90
Depreciation, declining-balance,
139
Depreciation, excess, 148
Depreciation, partial year, 136–48
Depreciation, sum-of-the-years-digits,
141
Depreciation, with crossover,
144–48
Digit entry, recovering from errors in,
75
Digit entry, termination of, 19, 171
Discounted cashflow analysis, 57
Display, 71
Display format, mantissa, 73
Display format, standard, 71
Display formats, number, 71
Display, scientific notation, 72
Displaying numbers, 32
Displays, special, 73
E
, 18
Editing a program, 113
Effective interest rate, converting,
161
Entry errors, 75
Error conditions, 74
Error, Pr, 74
Errors, 74
Errors, in digit entry, 75
Excess depreciation, 148
Exponent, 18, 85
Exponential, 83
F
Factorial, 83
Financial registers, 32
Financial registers, clearing, 33
Fractional, 84
Future value, 36
Future value, calculating, 48
FV, 36
G
, 93
I
, 12
, 172
, 12
Indicators, status, 71
Instructions in program lines, 91
Interest rate, annual, 43
Interest rate, periodic, 43

210 Subject Index
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 210 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Interest, simple, 33
Internal rate of return, 57
Internal rate of return, calculating,
63
Internal rate of return, modified, 148
Interrupting a program, 97
IRR, 57, 148
K
Keyboard, 16
L
, 74
LAST X register, 70
Leasing, 151
Linear estimation, 80
Logarithm, 83
Looping, 103
Low-power indicator, 16
M
, 172
Mantissa, 18, 73
Mantissa Display Format, 73
Mean, 77
Mean, weighted, 81
memory, 23
Memory, program, 94
Modified internal rate of return, 148
Mortgage, price of, 126
Mortgage, yield of, 128
Multiple programs, 120
N
Negative numbers, 17
Net amount, 27
Net present value, 57
Net present value, calculating, 58
Nominal interest rate, converting,
160
Nominal rate, 162
NPV, 57
Number display formats, 71
Numbers, keying in, 17
Numbers, large, 18
Numbers, negative, 17
Numbers, recalling, 23
Numbers, storing, 23
O
Odd-period calculations, 50
Odd-period mode, 36
One-number functions, 83
One-variable statistics, 76
Overflow, 73
P
, 97
, 172
Partial-year depreciation, 136
Payment, 36, 156
Payment amount, calculating, 46
Payment mode, 37
Payments, advance, 151, 156
Payments, number of, 39
Percent difference, 27
Percent of total, 28
Percentages, 26
PMT, 36
Populations, 79
Power function, 85
Pr error, 74
Prefix key, 16
Present value, 36
Present value, calculating, 44
PRGM status indicator, 88, 89
Program branching, 103
Program editing, 113
Program lines, displaying, 92
Program looping, 103
Program memory, 90, 94
Program mode, 88
Program, creating, 88
Program, interrupting, 97
Program, running, 89, 122

Subject Index 211
File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 211 of 209
Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm
Program, running one line at a time,
94
Program, stopping, 97, 101
Program, storing, 120
Programming, 88
Programs, multiple, 120
PV, 36
R
, 83
Reciprocal, 83
registers, 23
Registers, financial, 32
Registers, statistics, 76
Renting versus Buying, 130
Residual, 156
Round, 83
Rounding, 71
Running message, 12, 63
S
, 172
, 172
, 172
, 23
Samples, 79
Savings, 160
Scientific notation, 18, 72
Simple branching, 103
Simple interest, 33
Square Root, 83
Stack, 170
Standard deviation, 79
Statistics, 76
Status indicators, 71
Storage register arithmetic, 24
Storage registers, clearing, 24
Storing numbers, 32
Storing programs, 120
Straight-line depreciation, 136
Sum-of-the-years-digits depreciation,
141
T
Two-variable statistics, 76
U
Underflow, 73
W
Weighted mean, 81
X
, 74
Y
, 12
Yield, 154, 158