Hp 10Bii Financial Calculator Users Manual 10bII+_User Guide_English_EN_NW239 90001_Edition 1
HP 10bII+ Financial Calculator - User Manual c03066677
HP 10bII+ Financial Calculator - User Manual c02989763
10BII c02989763
2015-01-05
: Hp Hp-10Bii-Financial-Calculator-Users-Manual-152986 hp-10bii-financial-calculator-users-manual-152986 hp pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 187 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Legal Notice
- HP 10bII+ Financial Calculator
- Keyboard Map Legend
- Table of Contents
- At a Glance...
- Getting Started
- Power On and Off
- Manual Conventions and Examples
- Basics of Key Functions
- Shift Keys
- Boxed Key Functions
- Simple Arithmetic Calculations
- Understanding the Display and Keyboard
- Cursor
- Clearing the Calculator
- Annunciators
- Input Key
- Swap Key
- Statistics Keys
- Time Value of Money (TVM), Cash Flows, Bond, and Break-even Keys
- Math Functions
- Trigonometric and Hyperbolic Functions and Modes
- Pi
- Hyperbolic Functions
- Two-Number Functions
- In-line Functions
- Arithmetic with One-and Two-number Functions
- Last Answer
- Display Format of Numbers
- Scientific Notation
- Interchanging the Period and Comma
- Rounding Numbers
- Messages
- Business Percentages
- Number Storage and Storage Register Arithmetic
- Picturing Financial Problems
- Time Value of Money Calculations
- Depreciation
- Cash Flow Calculations
- Calendar Formats and Date Calculations
- Bonds
- Break-even
- Statistical Calculations
- Clearing Statistical Data
- Entering Statistical Data
- Viewing and Editing Statistical Data
- Summary of Statistical Calculations
- Mean, Standard Deviations, and Summation Statistics
- Linear Regression, Estimation, and Regression Modes
- Weighted Mean
- Regression Models and Variables
- Probability Calculations
- Factorial
- Permutations
- Combinations
- Random Number and Seed
- Advanced Probability Distributions
- Normal Lower Tail Probability
- Inverse of Normal Lower Tail Probability
- Student's T Probability Lower Tail
- Inverse of Student’s t Probability Lower Tail
- Conversions from Lower Tail
- Additional Examples
- Appendix A: Batteries and Answers to Common Questions
- Appendix B: More About Calculations
- Appendix C: Messages
- Warranty, Regulatory, and Contact Information
- Replacing the Batteries
- HP Limited Hardware Warranty and Customer Care
- Limited Hardware Warranty Period
- General Terms
- Exclusions
- Regulatory Information
- Federal Communications Commission Notice
- Modifications
- Declaration of Conformity for Products Marked with FCC Logo, United States Only
- Canadian Notice
- Avis Canadien
- European Union Regulatory Notice
- Japanese Notice
- Disposal of Waste Equipment by Users in Private Household in the European Union
- Perchlorate Material - special handling may apply
- Customer Care
- Contact Information
- Index

i
HP 10bII+ Financial Calculator
User’s Guide
HP Part Number: NW239-90001
Edition 1, May 2010
ii
Legal Notice
This manual and any examples contained herein are provided “as is” and are subject to
change without notice. Hewlett-Packard Company makes no warranty of any kind with
regard to this manual, including, but not limited to, the implied warranties of merchantability,
non-infringement and fitness for a particular purpose. In this regard, HP shall not be liable
for technical or editorial errors or omissions contained in the manual.
Hewlett-Packard Company shall not be liable for any errors or for incidental or consequential
damages in connection with the furnishing, performance, or use of this manual or the exam-
ples contained herein.
Copyright © 2010 Hewlett-Packard Development Company, L.P.
Reproduction, adaptation, or translation of this manual is prohibited without prior written
permission of Hewlett-Packard Company, except as allowed under the copyright laws.
Hewlett-Packard Company
Palo Alto, CA
94304
USA

iii
HP 10bII+ Financial Calculator

iv
Keyboard Map Legend
Number
(row of keys)
Primary Functions
(white)
SHIFT Down \
(orange functions on
key bevel)
SHIFT Up ]
(blue functions above
keys)
1 12 character, seven-
segment screen display
2 Time Value of Money
(TVM) Payments per year,
interest conversion,
amortization,
Bond calculations
3 Input key, markup, cost,
price and margin Date and change of
days, IRR per year, NPV,
beginning/end of
payment period
Calendar and coupon
payment schedules,
settlement and maturity
dates (bonds)
4 K memory register,
percent, cash flow
amount, statistics entry,
backspace
Swap, percent change,
cash flow count, delete
statistics, round
Break-even calculation
5 Change sign, recall
and memory Scientific notation, store,
clear statistics,
parentheses
Depreciation,
hyperbolic and
trigonometric functions
6 Shift (blue, up)
Shift (orange, down)
7 Numbered keys: 1, and
4-9 Statistics, weighted
mean and estimation Statistical functions and
regression modes
8 Clearing functions Clearing functions Clearing functions
9On Off Operating modes
10 Numbered keys: 0 and
2-3, decimal Common mathematical
functions Probability functions
11 Mathematical functions Common mathematical
functions, parentheses Trigonometric functions
12 Annun ciators
1
Table of Contents
Legal Notice...............................................................................................................ii
HP 10bII+ Financial Calculator....................................................................................iii
Keyboard Map Legend............................................................................................... iv
1 At a Glance........................................................................................................................ 1
Basics of Key Functions................................................................................................1
Shift Keys...................................................................................................................2
Boxed Key Functions ...................................................................................................2
Percentages ...............................................................................................................3
Memory Keys .............................................................................................................4
Time Value of Money (TVM) .........................................................................................6
TVM What if... ...........................................................................................................7
Amortization ..............................................................................................................8
Depreciation ..............................................................................................................9
Interest Rate Conversion.............................................................................................10
Cash Flows, IRR/YR, NPV, and NFV ...........................................................................11
Date and Calendar ...................................................................................................13
Bonds......................................................................................................................14
Break-even ...............................................................................................................16
Statistical Calculations...............................................................................................17
Probability ...............................................................................................................19
Trigonometric Functions .............................................................................................20
2 Getting Started................................................................................................................. 23
Power On and Off ....................................................................................................23
Manual Conventions and Examples.............................................................................23
Basics of Key Functions..............................................................................................24
Shift Keys.................................................................................................................25
Boxed Key Functions .................................................................................................25
Simple Arithmetic Calculations....................................................................................26
Understanding the Display and Keyboard....................................................................29
Cursor .....................................................................................................................29
Clearing the Calculator..............................................................................................29
Annunciators ............................................................................................................30
Input Key .................................................................................................................32
Swap Key ................................................................................................................32
Statistics Keys...........................................................................................................32
Time Value of Money (TVM), Cash Flows, Bond, and Break-even Keys ............................33
Math Functions .........................................................................................................33
Trigonometric and Hyperbolic Functions and Modes .....................................................35
Pi............................................................................................................................36
Hyperbolic Functions .................................................................................................36
Two-Number Functions ..............................................................................................37
In-line Functions ........................................................................................................37
2
Arithmetic with One-and Two-number Functions............................................................ 39
Last Answer ............................................................................................................. 41
Display Format of Numbers ....................................................................................... 41
Scientific Notation.................................................................................................... 43
Interchanging the Period and Comma ......................................................................... 43
Rounding Numbers................................................................................................... 43
Messages................................................................................................................ 44
3 Business Percentages.........................................................................................................45
The Business Percentage Keys .................................................................................... 45
Percent key.............................................................................................................. 45
Margin and Markup Calculations............................................................................... 47
4 Number Storage and Storage Register Arithmetic ...............................................................49
Using Stored Numbers in Calculations ........................................................................ 49
5 Picturing Financial Problems ..............................................................................................55
How to approach a Financial Problem ........................................................................ 55
Signs of Cash Flows ................................................................................................. 56
Periods and Cash Flows............................................................................................ 56
Simple and Compound Interest................................................................................... 56
Interest Rates............................................................................................................ 57
Two Types of Financial Problems................................................................................ 58
Recognizing a Cash Flow Problem ............................................................................. 59
6 Time Value of Money Calculations .....................................................................................61
Using the TVM Application ........................................................................................ 61
The TVM Keys.......................................................................................................... 61
Begin and End Modes............................................................................................... 62
Loan Calculations..................................................................................................... 62
Savings Calculations................................................................................................. 67
Lease Calculations.................................................................................................... 71
Amortization............................................................................................................ 74
Interest Rate Conversions........................................................................................... 79
Resetting the TVM Keys ............................................................................................. 82
7 Depreciation .....................................................................................................................83
The Depreciation Keys .............................................................................................. 83
Resetting the TVM Keys ............................................................................................. 86
3
8 Cash Flow Calculations..................................................................................................... 87
How to Use the Cash Flow Application........................................................................87
Clearing the Cash Flow Memory.................................................................................88
Calculating Internal Rate of Return...............................................................................90
NPV and IRR/YR: Discounting Cash Flows ...................................................................91
Organizing Cash Flows.............................................................................................91
Viewing and Editing Cash Flows.................................................................................93
Calculating Net Present Value and Net Future Value .....................................................95
Automatic Storage of IRR/YR and NPV........................................................................98
9 Calendar Formats and Date Calculations ........................................................................... 99
Calendar Format.......................................................................................................99
Date Format .............................................................................................................99
Date Calculations and Number of Days.....................................................................101
Number of Days .....................................................................................................102
10 Bonds .......................................................................................................................... 105
The Bond Keys........................................................................................................105
Resetting the bond keys ...........................................................................................108
11 Break-even .................................................................................................................. 109
The Break-even Keys................................................................................................109
Resetting the Break-even keys ...................................................................................112
12 Statistical Calculations .................................................................................................. 113
Clearing Statistical Data ..........................................................................................114
Entering Statistical Data ...........................................................................................114
Viewing and Editing Statistical Data..........................................................................116
Summary of Statistical Calculations ...........................................................................119
Mean, Standard Deviations, and Summation Statistics.................................................120
Linear Regression, Estimation, and Regression Modes..................................................121
Weighted Mean .....................................................................................................124
Regression Models and Variables .............................................................................125
Probability Calculations ...........................................................................................126
Factorial ................................................................................................................126
Permutations...........................................................................................................126
Combinations.........................................................................................................127
Random Number and Seed......................................................................................127
Advanced Probability Distributions ............................................................................128
Normal Lower Tail Probability ..................................................................................129
Inverse of Normal Lower Tail Probability....................................................................130
Student's T Probability Lower Tail ..............................................................................131
4
Inverse of Student’s t Probability Lower Tail................................................................ 132
Conversions from Lower Tail .................................................................................... 133
13 Additional Examples .....................................................................................................137
Business Applications.............................................................................................. 137
Loans and Mortgages ............................................................................................. 139
Savings................................................................................................................. 148
Cash Flow Examples............................................................................................... 152
14 Appendix A: Batteries and Answers to Common Questions ..................................................I
Power and Batteries..................................................................................................... I
Low Power Annunciator................................................................................................ I
Installing Batteries........................................................................................................ I
Determining if the Calculator Requires Service ................................................................II
Answers to Common Questions....................................................................................III
Environmental Limits................................................................................................... IV
15 Appendix B: More About Calculations.................................................................................I
IRR/YR Calculations..................................................................................................... I
Equations ................................................................................................................... I
16 Appendix C: Messages.......................................................................................................I
17 Warranty, Regulatory, and Contact Information .................................................................1
Replacing the Batteries................................................................................................ 1
HP Limited Hardware Warranty and Customer Care....................................................... 1
Limited Hardware Warranty Period .............................................................................. 1
General Terms ........................................................................................................... 2
Exclusions.................................................................................................................. 2
Regulatory Information ................................................................................................ 3
Federal Communications Commission Notice................................................................. 3
Modifications............................................................................................................. 3
Declaration of Conformity for Products Marked with FCC Logo, United States Only ............ 4
Canadian Notice ....................................................................................................... 4
Avis Canadien ........................................................................................................... 4
European Union Regulatory Notice............................................................................... 4
Japanese Notice ........................................................................................................ 5
Disposal of Waste Equipment by Users in Private Household in the European Union........... 5
Perchlorate Material - special handling may apply.......................................................... 6
Customer Care........................................................................................................... 6
Contact Information .................................................................................................... 6

At a Glance... 1
1 At a Glance...
This section is designed for you if you’re already familiar with calculator operation or financial
concepts. You can use it for quick reference. The rest of the manual is filled with explanations
and examples of the concepts presented in this section.
Basics of Key Functions
Table 1-1 Basics of key functions
Keys Display Description
=0.00 Turns calculator on.
] [blue]
0.00 Displays shift
annunciator .
\ [orange]
0.00 Displays shift
annunciator .
JGD| 12_ Erases last character.
M0.00 Clears display.
\t 0.00 Clears statistics
memory.
\N 12 P_ Y r (message flashes, then
disappears)
Clears all memory.
]Oj BOND CLR (message flashes,
then disappears)
Clears bond memory.
]OY BR EV CLR (message flashes,
then disappears)
Clears break-even
memory.
]OJ TVM CLR (message flashes, then
disappears)
Clears tvm registers.
]O: CFLO CLR (message flashes, then
disappears)
Clears cash flow
memory.
\> Turns calculator off.

At a Glance...2
Shift Keys
Most keys on the HP 10bII+ have three functions:
• a primary function printed in white on the key.
• a secondary function printed in orange on the bevel of the key.
• a tertiary function printed in blue above the key on the keyboard (see Figure 1).
Figure 1
As an example, the functions associated with the equals key, 4, are illustrated in the text
as follows:
• primary function (equals): 4
• secondary function (display): \5
• tertiary function (random): ]6
Boxed Key Functions
These special functions require subsequent key presses to operate. For example, the functions
associated with the clear key, M, include:
Table 1-2 Clearing functions
Keys Associated Function
MClear display.
\N Clear all memory.
]Oj Clears bond memory.

At a Glance... 3
For more information on the calculator’s keys and basic functions, refer to chapter 2, Getting
Started.
Percentages
Add 15% to 17.50.
Find the margin if the cost is 15.00 and selling price is 22.00.
]OY Clears break-even memory.
]OJ Clears TVM memory.
]O: Clears cash flow memory.
\t Clears statistics memory.
Table 1-2 Clearing functions
Keys Associated Function
Table 1-3 Keys for percentage calculations
Keys Description
§Percent
\¨ Percent change
ÀCost
¼Price
®Margin
ÃMarkup
Table 1-4 Calculating the price
Keys Display Description
Jj7V:1 17.50 Enters number.
JV§4 20.13 Adds 15%.

At a Glance...4
If the cost is 20.00 and the markup is 33%, what is the selling price?
For more information on percentages, refer to chapter 3, Business Percentages.
Memory Keys
Table 1-5 Finding the margin
Keys Display Description
JVÀ 15.0 0 E n te rs c o s t.
GG¼ 22.00 Enters price.
®31. 82 C a l cu l a t e s m a rg i n.
Table 1-6 Calculating the price
Keys Display Description
G:À 20.00 Enters cost.
DDÃ 33.00 Enters markup.
¼26.60 Calculates price.
Table 1-7 Memory keys
Keys Description
ªStores a constant operation.
sStores a value in the M register (memory location).
pRecalls a value from the M register.
mAdds a value to the number stored in the M register.
\w When followed by a number key, : to d, or 7 and : to d, stores a number in the
display into a numbered data storage register. There are 20 storage registers, designated 0-
19. Press \w7 followed by : through d to access registers 10-19.
vWhen followed by a number key, : to d, or 7 and : to d, recalls a number from
a storage register. Pressv7 followed by : through d to access registers 10-19.

At a Glance... 5
Multiply 17, 22, and 25 by 7, storing ‘× 7’ as a constant operation.
Store 519 in register 2, then recall it.
Store 1.25 into register 15, then add 3, and store the result in register 15.
For more information on number storage and storage register arithmetic, refer to chapter 4,
Number Storage and Storage Register Arithmetic.
Table 1-8 Storing ‘x 7’ as a constant
Keys Display Description
JjPjª 7.0 0 St ores ‘ × 7’ as a
constant operation.
4119.00 Multiplies 17 × 7.
GG4 154.00 Multiplies 22 × 7.
GV4 175.00 Multiplies 25 × 7.
Table 1-9 Storing and recalling
Keys Display Description
VJd\wG 519.00 Stores 519 in register 2.
M0.00 Clears display.
vG 519.0 0 Re c a l l s re g i s t e r 2.
Table 1-10 Storage register arithmetic
Keys Display Description
J7GV 1.25 I n p u t s 1. 25 i n t o t h e
display.
\w7V Stores 1.25 in register
15.
D\w17V 3.00 Adds 3 to 1.25 in
register 15 stores the
result in register 15.
M0.00 Clears the display.
v7V 4.25 Recalls register 15.

At a Glance...6
Time Value of Money (TVM)
Enter any four of the five values and solve for the fifth.
A negative sign in the display represents money paid out, and money received is positive.
If you borrow 14,000 (PV) for 360 months (N) at 10% interest (I/YR), what is the monthly
repayment?
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
Table 1-11 Keys for TVM calculations
Keys Description
]OJ Clears TVM memory and the current P_YR is
displayed.
ÙNumber of payments.
\Ú Multiplies a value by the number of payments
per year and stores as N.
ÒInterest per year.
ÏPresent value.
ÌPayment.
ÉFuture value.
\¯ Begin or End mode.
\Í Number of payments per year mode.
Table 1-12 Calculating the monthly payment
Keys Display Description
]OJ TVM CLR (message flashes, then
disappears)
Clears TVM memory and
displays the current P_YR.
JG\Í 12.00 Sets payments per year.
DS:Ù 360.00 Enters number of payments.
J:Ò 10.00 Enters interest per year.
JY:::Ï 14,000.00 Enters present value.
At a Glance... 7
TVM What if...
It is not necessary to reenter TVM values for each example. Using the values you just entered,
how much can you borrow if you want a payment of 100.00?
...how much can you borrow at a 9.5% interest rate?
For more information on TVM concepts and problems, refer to chapter 5, Picturing Financial
Problems, and chapter 6, Time Value of Money Calculations.
:É 0.00 Enters future value.
Ì-122.86 Calculates payment if paid
at end of period.
Table 1-12 Calculating the monthly payment
Keys Display Description
Table 1-13 Calculating a new payment
Keys Display Description
J::yÌ -100.00 Enters new payment
amount. (Money paid out is
negative).
Ï11,395.08 Calculates amount you can
borrow.
Table 1-14 Calculating a new interest rate
Keys Display Description
d7VÒ 9.50 Enters new interest rate.
Ï11,892.67 Calculates new present
value for 100.00 payment
and 9.5% interest.
J:Ò 10.00 Reenters original interest
rate.
JY:::Ï 14,000.00 Reenters original present
value.
Ì-122.86 Calculates original payment.

At a Glance...8
Amortization
After calculating a payment using Time Value of Money (TVM), input the periods to amortize
and press \Ê. Press \Ê once for periods 1-12, and once again for payments 13-
24. Press 4 to continually cycle through the principal, interest, and balance values (indicated
by the PRIN, INT, and BAL annunciators respectively). Using the previous TVM example,
amortize a single payment and then a range of payments.
Amortize the 20th payment of the loan.
Amortize the 1st through 24th loan payments.
Table 1-15 Amortizing the 20th payment of the loan
Keys Display Description
G:Æ 20.00 Enters period to amortize.
\Ê 20 – 20 Displays period to amortize.
4-7.25 Displays principal.
4-115.61 Displays interest. (Money
paid out is negative).
413,865.83 Displays the balance
amount.
Table 1-16 Amortization example
Keys Display Description
JÆJG 12_ Enters range of periods to
amortize.
\Ê 1 – 12 Displays range of periods
(payments).
4-77.82 Displays principal.
4-1,396.50 Displays interest. (Money
paid out is negative).
413,922.18 Displays the balance
amount.
\Ê 13 – 24 Displays range of periods.
4-85.96 Displays principal.

At a Glance... 9
For more information on amortization, refer to the section titled, Amortization in chapter 6,
Time Value of Money Calculations.
Depreciation
A metalworking machine, purchased for 10,000.00, is to be depreciated over five years. Its
salvage value is estimated at 500.00. Using the straight-line method, find the depreciation
and remaining depreciable value for each of the first two years of the machine's life.
4-1,388.36 Displays interest.
413,836.22 Displays the balance
amount.
Table 1-16 Amortization example
Keys Display Description
Table 1-17 Depreciation keys
Keys Description
ÙExpected useful life of the asset.
ÒDeclining balance factor entered as a
percentage.
ÏDepreciable cost of the asset at acquisition.
ÉSalvage value of the asset.
]{ Straight-line depreciation.
]x Sum-of-the-years’-digits depreciation.
]u Declining Balance depreciation.
Table 1-18 Calculating the depreciation
Keys Display Description
J::::Ï 10,000.00 Inputs cost of the item.
V::É 500.00 Inputs the salvage value of the
item.
VÙ 5.00 Inputs the useful life of the asset.
J]{ 1,900.00 Depreciation of the asset in year
one.

At a Glance...10
For more information on depreciation, refer to chapter 7, Depreciation.
Interest Rate Conversion
To convert between nominal and effective interest rates, enter the known rate and the number
of periods per year, then solve for the unknown rate.
Find the annual effective interest rate of 10% nominal interest compounded monthly.
For more information on interest rate conversions, refer to the section titled, Interest Rate
Conversions in chapter 6, Time Value of Money Calculations.
\« 7,600.00 Remaining depreciable value
after year one.
G]{ 1,900.00 Depreciation of the asset in year
two.
\« 5,700.00 Remaining depreciable value
after year two.
Table 1-18 Calculating the depreciation
Keys Display Description
Table 1-19 Keys for interest rate conversion
Keys Description
\Ó Nominal interest percent.
\Ð Effective interest percent.
\Í Periods per year.
Table 1-20 Calculating the interest rate
Keys Display Description
J:\Ó 10.00 Enters nominal rate.
JG\Í 12.00 Enters payments per year.
\Ð 10.47 Calculates annual effective
interest.

At a Glance... 11
Cash Flows, IRR/YR, NPV, and NFV
Table 1-21 Cash flows, IRR, NPV, and NFV keys
Keys Description
]O: Clears cash flow memory.
\Í Number of periods per year (default is
12). For annual cash flows, P/YR should
be set to 1; for monthly cash flows, use
the default setting, 12.
¤Cash flows, up to 45. “J” identifies the
cash flow number. When preceded by a
number, pressing ¤ enters a cash flow
amount.
number1 Æ number 2 ¤Enter a cash flow amount, followed by
Æ. Enter a number for the cash flow
count followed by ¤ to enter cash
flow amount and count simultaneously.
v¤ Opens editor for reviewing/editing
entered cash flows. Press 1 or A to
scroll through the cash flows.
\¥ Number of consecutive times cash flow
“J” occurs.
\Á Internal rate of return per year.
\½ Net present value.
\½\« Net future value.

At a Glance...12
If you have an initial cash outflow of 40,000, followed by monthly cash inflows of 4,700,
7,000, 7,000, and 23,000, what is the IRR/YR? What is the IRR per month?
What is the NPV and NFV if the discount rate is 10%?
Table 1-22 Calculating the IRR/YR and IRR per month
Keys Display Description
]O: CFLO CLR
(message flashes, then
disappears)
Clears cash flow memory.
JG\Í 12.00 Sets payments per year.
Y::::y¤ -40,000.00
(CF 0 flashes, then disappears)
Enters initial outflow.
Yj::¤ 4,700.00
(CF 1 flashes, then disappears)
Enters first cash flow.
j:::ÆG¤ 2.00
(CFn 2 flashes, then disappears)
Enters both the cash flow
amount (7000.00) and count
(2.00) simultaneously for second
cash flow.
GD:::¤ 23,000.00
(CF 3 flashes, then disappears)
Enters third cash flow.
v¤ 0 -40,000.00 Reviews entered cash flows
starting with the initial cash flow.
Press 1 to scroll through the
cash flow list to verify the cash
flow number, the amounts, and
count for each entry. Press M
to exit.
\Á 15 . 96 C a l c u l a t e s IRR/YR.
aJG4 1. 33 C a l c u l a t e s IRR per month.
Table 1-23 Calculating NPV and NFV
Keys Display Description
J:Ò 10.00 Enters I/YR.
\½ 622.85 Calculates NPV.

At a Glance... 13
For more information on cash flows, refer to chapter 8, Cash Flow Calculations in the HP
10bII+ Financial Calculator User’s Guide.
Date and Calendar
If the current date is February 28 2010, what is the date 52 days from now? Calculate the
date using the 365-day calendar (actual) and the M.DY settings.
If 360 is displayed, press ]Å. If D.MY is displayed, press ]È.
For more information on date and calendar functions, refer to chapter 9, Calendar Formats
and Date Calculations.
\½\« 643.88 Calculates NFV.
Table 1-23 Calculating NPV and NFV
Keys Display Description
Table 1-24 Keys used for dates and calendar functions
Keys Description
]È Enters dates in DD.MMYYYY or MM.DDYYYY formats. D.MY is the default.
Numbers at the far right of a calculated date indicate days of the week. 1
is for Monday; 7 is for Sunday.
]Å Toggles between 360-and 365-day (Actual) calendars.
\Ç Calculates the date and day, past or future, that is a given number of days
from a given date. Based on your current setting, returned result is
calculated using either 360-day or 365-day (Actual).
\Ä Calculates the number of days between two dates. Returned result is
always calculated based on the 365-day calendar (Actual).
Table 1-25 Calculating the date
Keys Display Description
G7GgG:J:
\Ç
2.28 Inputs the date in the
selected format.
VG4 4-21-2010 3 Inputs the number of days
and calculates the date
along with the day of the
week.

At a Glance...14
Bonds
Bond calculations, primarily calculating bond price and yield, are performed by two keys,
]Ñ and ]Ô. These keys permit you to input data or return results. Pressing ]Û
only calculates a result. The other keys used in bond calculations only permit you to input the
data required for the calculations.
What price should you pay on April 28, 2010 for a 6.75% U.S. Treasury bond maturing on
June 4, 2020, if you want a yield of 4.75%? Assume the bond is calculated on a semiannual
coupon payment on an actual/actual basis.
If SEMI is not displayed, press ]Â to select the semiannual coupon payment.
If D.MY is displayed, press ]È to select M.DY format.
Table 1-26 Bond calculation keys
Keys Description
]Oj Clears bond memory.
]Û Calculates accrued interest only.
]Ô Yield% to maturity or yield% to call date for
given price.
]Ñ Price per 100.00 face value for a given yield.
]Î Coupon rate stored as an annual %.
]Ë Call value. Default is set for a call price per
100.00 face value. A bond at maturity has a
call value of 100% of its face value.
]È Date format. Toggle between day-month-year
(dd.mmyyyy) or month-day-year (mm.ddyyyy).
]Å Day count calendar. Toggle between Actual
(365-day calendar) or 360 (30-day month/
360-day year calendar).
]Â Bond coupon (payment). Toggle between
semiannual and annual payment schedules.
]¾ Settlement date. Displays the current settlement
date.
]° Maturity date or call date. The call date must
coincide with a coupon date. Displays the
current maturity.
At a Glance... 15
For more information on bond calculations, refer to chapter 10, Bonds.
Table 1-27 Bond calculation
Keys Display Description
]Oj BOND CLR (message
flashes, then disappears)
Clears bond memory.
Y7GgG:J:
]¾
4-28-2010 3 Inputs the settlement date
(mm.ddyyyy format).
S7:YG:G:
]°
6-4-2020 4 Inputs the maturity date.
S7jV]Î 6.75 Inputs CPN%.
J::]Ë 100.00 Inputs call value. Optional,
as default is 100.
Y7jV]Ô 4.75 Inputs Yield%.
]Ñ 115.89 Calculates the price.
1]Û 2.69 Displays the current value
for accrued interest.
4118.59 Returns the result for total
price (value of price + value
of accrued interest). The net
price you should pay for the
bond is 118 . 5 9.
At a Glance...16
Break-even
The sale price of an item is 300.00, the cost 250.00, and fixed cost 150,000.00. For a profit
of 10,000.00, how many units would have to be sold?
For more information on break-even calculations, refer to chapter 11, Break-even.
Table 1-28 Break-even keys
Keys Description
]OY Clears break-even memory.
]¬ Stores the quantity of units required for a given
profit or calculates it.
]© Stores the sales price per unit or calculates it.
]¦ Stores variable cost per unit for manufacturing
or calculates it.
]£ Stores the fixed cost to develop and market or
calculates it.
]~ Stores the expected profit or calculates it.
Table 1-29 Calculating break-even
Keys Display Description
]OY BR EV CLR (message flashes,
then disappears)
Clears break-even memory.
JV::::]
£
150,000.00 Inputs fixed cost.
GV:]¦ 250.00 Inputs variable cost per unit.
D::]© 300.00 Inputs price.
J::::]~ 10,000.00 Inputs profit.
]¬ 3,200.00 Calculates the current value
for the unknown item,
UNITS.

At a Glance... 17
Statistical Calculations
Table 1-30 Statistics keys
Keys Description
\t Clear statistical registers.
x-data ¡
Enter one-variable statistical
data.
x-data \¢
Delete one-variable statistical
data.
x-data Æ y-data ¡
Enter two-variable statistical
data.
x-data Æ y-data \¢
Delete two-variable statistical
data.
v¡ Opens editor for reviewing/
editing entered statistical data.
\k \« Means of x and y.
\T \« Mean of x weighted by y. Also
calculates b, intercept.
\h \« Sample standard deviations of
x and y.
\e \« Population standard deviations
of x and y.
y-data \Z \«
Estimate of x and correlation
coefficient.
x-data \W \«
Estimate of y and slope.
]L Permits selection of six
regression models; linear is
default.

At a Glance...18
Using the following data, find the means of x and y, the sample standard deviations of x and
y, and the y-intercept and the slope of the linear regression forecast line. Then, use summation
statistics to find xy.
For more information on statistical calculations, refer to chapter 12, Statistical Calculations.
x-data 2 4 6
y-data 50 90 160
Table 1-31 Statistics example
Keys Display Description
\t 0.00 Clears statistics registers.
GÆV:¡ 1.00 Enters first x,y pair.
YÆd:¡ 2.00 Enters second x,y pair.
SÆJS:¡ 3.00 Enters third x,y pair.
v¡ 1 2.00 Reviews entered statistical
data, starting with the initial
x-value. Press 1 to scroll
through and verify the
entered statistical data.
Press M to exit.
\k 4.00 Displays mean of x.
\« 100.00 Displays mean of y.
\h 2.00 Displays sample standard
deviation of x.
\« 55.68 Displays sample standard
deviation of y.
\T\« -10.00 D isplays y-intercept of
regression line.
\W\« 27.50 Displays slope of regression
line.
]f 1,420.00 Displays xy, sum of the
products of x- and y-values.
Σ
Σ

At a Glance... 19
Probability
Enter .5 as a Z-value and calculate the cumulative probability of the Z-value and the Z-value
from a given cumulative probability.
For more information on probability, refer to the section titled, Probability in chapter 12,
Statistical Calculations.
Table 1-32 Probability keys
Keys Description
]F Calculates a cumulative normal probability
given a Z-value.
]o
F
Calculates a Z-value given a cumulative
normal probability.
]I Calculates the cumulative Student’s T
probability given degrees of freedom and a
T-value.
]o
I
Calculates a T-value given degrees of
freedom and the cumulative Student’s T
probability.
]< Calculates number of permutations of n items
taken r at a time.
]9 Calculates number of combinations of n taken
r at a time.
]E Calculates factorial of n (where -253 < n <
253).
Table 1-33 Calculating the probability
Keys Display Description
\5V 0.00000 Sets number display to five
digits to the right of the
decimal.
7V]F .69146 Calculates the cumulative
probability of the Z-value.
17GV4 .94146 Adds .25.
]oF 1.56717 Calculates the Z-value from
the cumulative probability.

At a Glance...20
Trigonometric Functions
Table 1-34 Trigonometry keys
Find Sin =.62 in degrees. If RAD is displayed, press ]3.
Keys Description
] c, R, or CCalculates sine, cosine, and tangent.
]o
c, R, or C
Calculates inverse sine, inverse cosine,
and inverse tangent.
]r
c, R, or C
Calculates hyperbolic sine, cosine and
tangent.
]ro
c, R, or C
Calculates inverse hyperbolic sine,
cosine, and tangent.
]3 Toggles between radians and degrees
modes. Degrees is the default setting.
Table 1-35 Trigonometry example
Keys Display Description
7SG .62 Enters value of sine for .
]oc 38.32 Calculates .
θ
θ
θ

At a Glance... 21
Convert the results to radians using Pi.
For more information on trigonometric functions, refer to chapter 2, Getting Started.
Table 1-36 Converting to radians
Keys Display Description
P\;aJg
:4
.67 Converts degrees to radians.
At a Glance...22

Getting Started 23
2 Getting Started
Power On and Off
To turn on your HP 10bII+, press =. To turn the calculator off, press the orange shift key,
\, then >. To change the brightness of the display, hold down = and then
simultaneously press 1 or A.
Since the calculator has continuous memory, turning it off does not affect the information you
have stored. To conserve energy, the calculator turns itself off after five minutes of inactivity.
The calculator uses two CR2032 coin batteries. If you see the low-battery symbol ( ) in
the display, replace the batteries. For more information, refer to the section titled, Installing
Batteries in Appendix A.
Manual Conventions and Examples
In this manual, key symbols are used to indicate the key presses used in the example prob-
lems. These symbols vary in appearance according to whether they indicate the primary,
secondary, or tertiary functions required for the problem. For example, the functions associ-
ated with the equals key, 4, are illustrated in the text as follows:
•primary function (equals): 4
•secondary function (display): \5
•tertiary function (random): ]6
Note the symbol for the primary function of the key, in this case, =, appears on each of the
key symbols depicted above. This repetition is intended to serve as a visual aid. By looking
for the symbol of the primary function on the key, you can quickly locate the keys used for the
secondary and tertiary functions on the calculator.
Displayed text
Text that appears in the display screen of the calculator is presented in BOLD CAPITAL letters
throughout the manual.
Examples
Example problems appear throughout the manual to help illustrate concepts and demonstrate
how applications work. Unless otherwise noted, these examples are calculated with CHAIN
set as the active operating mode. To view the current mode, press v]?. The
current mode, CHAIN or ALGEBRAIC, will flash, then disappear. To change the mode, press
] followed by ?.

Getting Started24
Basics of Key Functions
Table 2-1 Basics of key functions
Keys Display Description
= 0.00 Turns calculator on.
][blue]
0.00
Displays shift annunciator .
\[orange]
0.00
Displays shift annunciator .
JGD| 12_ Erases last character.
]3 RAD
(at the bottom of the display)
Toggles between radians and degrees.
The item before the / is the alternate; the
item after the / is the default setting.
Except for the operating mode,
annunciators in the display indicate
alternate settings are active.
M 0.00 Clears display.
\t 0.00 Clears statistics memory.
\N 12 P _ Y r (message flashes, then
disappears)
Clears all memory.
]Oj BOND CLR (message flashes,
then disappears)
Clears bond memory.
]OY BR EV CLR (message flashes,
then disappears)
Clears break-even memory.
]OJ TVM CLR (message flashes, then
disappears)
Clears tvm memory.
]O: CFLO CLR (message flashes, then
disappears)
Clears cash flow memory.
\> Turns calculator off.

Getting Started 25
Shift Keys
Most keys on the HP 10bII+ have three functions:
• a primary function printed in white on the key.
• a secondary function printed in orange on the bevel of the key.
• a tertiary function printed in blue above the key on the keyboard (see Figure 1).
Figure 1
When you press \ or ], a shift annunciator or is displayed to indicate that the
shifted functions are active. For example, press \ followed by 2 to multiply a num-
ber in the display by itself. To turn the shift annunciators off, press \ or ] again.
Boxed Key Functions
There are three shifted key functions on the calculator that are used to change the operation
of another key's function. These three tertiary functions, ]O, ]o and
]r, are bound by blue boxes to show that they operate differently. These special
functions require subsequent key presses to operate. For example, the functions associated
with the clear key, M, include:
Table 2-2 Clearing functions
Keys Associated Function
M Clear display.
\N Clear all memory.
\t Clear statistics memory.
]Oj Clears bond memory.

Getting Started26
Simple Arithmetic Calculations
Operating Modes
To change the operating mode, press the blue shift key, ] followed by ? to toggle
between Algebraic and Chain modes. A brief message is displayed indicating the selected
operating mode.
To view the current mode, press v]?. The current mode will flash, then disappear.
Arithmetic Operators
The following examples demonstrate using the arithmetic operators 1, A, P, and
a.
If you press more than one operator consecutively, for example 1, A, 1, P
1, all are ignored except the last one.
If you make a typing mistake while entering a number, press | to erase the incorrect digits.
When a calculation has been completed (by pressing 4), pressing a number key starts a
new calculation.
]OY Clears break-even memory.
]OJ Clears TVM memory.
]O: Clears cash flow memory.
Table 2-2 Clearing functions
Keys Associated Function
Table 2-3 Example displaying calculations using arithmetic operators
Keys Display Description
GY7jJ1SG7Yj4 87.18 Adds 24.71 and
62.47.
Table 2-4 Completing a calculation
Keys Display Description
JdPJG7Sg4 240.92 Calculates 19 × 12.68.

Getting Started 27
If you press an operator key after completing a calculation, the calculation is continued.
Calculations in Chain Mode
Calculations in Chain mode are interpreted in the order in which they are entered. For
example, entering the following numbers and operations as written from left to right,
J1GPD4, returns 9. If you press an operator key, 1,A,P, or
a, after 4, the calculation is continued using the currently displayed value.
You can do chain calculations without using 4 after each step.
Without clearing, now calculate 4 + 9 × 3.
In Chain mode, if you wish to override the left to right order of entry, use parentheses
\q and \n to prioritize operations.
Table 2-5 Continuing a calculation
Keys Display Description
1JJV7V4 356.42 Completes calculation of
240.92 + 115.5.
Table 2-6 Chain calculations
Keys Display Description
S7dPV7DVa 36.92 Pressing a displays
intermediate result (6.9 × 5.35).
7dJ4 40.57 Completes calculation.
Table 2-7 Chain calculations
Keys Display
Y1dP 13.00 Adds 4 and 9.
D4 39.00 Completes calculation.

Getting Started28
For example, to calculate 1 + (2 x 3), you may enter the problem as written from left to right,
with parentheses to prioritize the multiplication operation. When entered with parentheses,
this expression returns a result of 7.
Calculations in Algebraic Mode
In Algebraic mode, multiplication and division have a higher priority than addition and
subtraction. For example, in Algebraic mode, pressing J1GPD4 returns a
result of 7.00. In Chain mode, the same key presses return a result of 9.00.
In Algebraic mode, operations between two numbers have the following priority:
• Highest priority: combinations and permutations, T probability calculations, % change, and
date calculations
• Second priority: the power function ( )
• Third priority: multiplication and division
• Forth priority: addition and subtraction.
The calculator is limited to 12 pending operations. An operation is pending when it is waiting
for the input of a number or the result of an operation of higher priority.
Using Parentheses in Calculations
Use parentheses to postpone calculating an intermediate result until you’ve entered more
numbers. You can enter up to four open parentheses in each calculation. For example,
suppose you want to calculate:
If you enter D:agVA, the calculator displays the intermediate result, 0.35.
This is because calculations without parentheses are performed from left to right as you enter
them.
To delay the division until you’ve subtracted 12 from 85, use parentheses. Closing parentheses
at the end of the expression can be omitted. For example, entering 25 ÷ (3 × (9 + 12 = is
equivalent to 25 ÷ (3 × (9 + 12)) =.
If you type in a number, for example, 53, followed by the parenthesis symbol, the calculator
considers this implicit multiplication.
Example
yx
Table 2-8 Using parentheses in calculations
Keys Display Description
D:a\qgVA 85.00 No calculation yet.
JG\n 73.00 Calculates 85 - 12.
30
85 12–()
---------------------- 9×

Getting Started 29
Negative Numbers
Enter the number and press y to change the sign.
Calculate -75 ÷ 3.
Understanding the Display and Keyboard
Cursor
The blinking cursor ( _ ) is visible when you are entering a number.
Clearing the Calculator
Backspace
When the cursor is on, | erases the last digit you entered. Otherwise, | clears the
display and cancels the calculation.
Clear
M clears the current item on the display and replaces it with 0. If entry is in progress,
pressing M clears the current entry and replaces it with 0, but the current calculation
continues. Otherwise, M clears the display of its current contents and cancels the current
calculation.
Clear Memory
]O followed by j,Y,J,: clears a selected memory type (register). Other
memory is left intact.
P 0.41 Calculates 30 ÷ 73.
d4 3.70 Multiplies the result by 9.
Table 2-8 Using parentheses in calculations
Keys Display Description
Table 2-9 Changing the sign of numbers
Keys Display Description
jVy -75_ Changes the sign of 75.
aD4 –25.00 Calculates result.

Getting Started30
Clear All
\N all clears all memory in the calculator, with the exception of the payments per
year (P/Yr) setting. To clear all memory and reset calculator modes, press and hold down
=, then press and hold down both Ù and Ï. When you release all three, all
memory is cleared. The All Clear message is displayed.
Clearing Messages
When the HP 10bII+ is displaying an error message, |or M clears the message and
restores the original contents of the display.
Annunciators
Annunciators are symbols in the display that indicate the status of the calculator. For functions
that toggle between settings, annunciators indicate alternate settings are active. For the
defaults, no annunciators appear in the display. For example, when selecting a date format,
the default setting is month-day-year (M.DY). When day-month-year (D.MY) is active, the D.MY
in the display indicates it is the active setting. Table 2-11 lists all the annunciators that appear
in the display screen.
Table 2-10 Clear memory keys
Keys Description
]Oj Clears bond memory.
]OY Clears break-even memory.
]OJ Clears TVM memory.
]O: Clears cash flow memory.
\t Clears statistics memory.

Getting Started 31
Table 2-11 Annunciators and status
Annunciator Status
, A shift key has been pressed. When another key is pressed, the
functions labeled in orange or blue are executed.
INV Inverse mode is active for trigonometric or probability functions.
RAD Radians mode is active.
BEG Begin mode is active; payments are at the beginning of a
period.
D.MY Day-month-year date format (DD.MMYYYY) is active.
360 360-day calendar is active.
SEMI Semi-annual coupon payment schedule (bonds) is active.
PEND An operation is waiting for another operand.
INPUT The Æ key has been pressed and a number stored.
Battery power is low.
AMORT The amortization annunciator is lit, together with one of the
following four annunciators:
PER The range of periods for an amortization is displayed.
PRIN The principal of an amortization is displayed.
INT The interest of an amortization is displayed.
BAL The balance of an amortization is displayed.
CFLO The cash flow annunciator is lit, together with one of the
following two annunciators:
CF The cash flow number appears briefly, then the cash flow is
shown.
N The cash flow number appears briefly, then the number of
times the cash flow is repeated is shown.
STAT The statistics annunciator is lit, together with one of the following
two annunciators:
X The number of the data point, n, followed by an x-value is
shown, or, if STAT is not lit, indicates that the first of two
results is displayed.
Y The number of the data point, n, followed by a y-value is
shown, or, if STAT is not lit, indicates that the second of two
results is displayed.
ERROR The error annunciator is lit, together with one of the following
four annunciators:
TVM There is a TVM error (such as an invalid P/Yr), or, when
ERROR is not lit, a TVM calculation returned a second result.
FULL Available memory for cash flows or statistics is full, or the
pending operator memory is full.
STAT Incorrect data used in a statistics calculation or, when
ERROR is not lit, a statistical calculation has been performed.

Getting Started32
Input Key
The Æ key is used to separate two numbers when using two-number functions or two-
variable statistics. The Æ key can also be used to enter cash flows and cash flow counts,
ordered pairs, and evaluate any pending arithmetic operations, in which case the result is the
same as pressing 4.
Swap Key
Pressing \« exchanges the following:
• The last two numbers that you entered; for instance, to change the order of division or subtraction.
• The results of functions that return two values.
The « key toggles the item in the Æ register, or swaps the top two items in the
mathematical stack. This function is used to retrieve a secondary value returned during a
calculation, as well as to swap two items during a calculation.
Statistics Keys
The statistics keys are used to access summary statistics from the statistics memory registers.
When you press ] followed by a statistics key, you can recall one of six summary statistics
with the next keystroke.
For example, press ] followed by the X key to recall the sum of the x-values entered.
FUNC A math error has occurred (for example, division by zero).
Table 2-11 Annunciators and status
Annunciator Status
Table 2-12 Statistics keys
Keys Description
]l Sum of the squares of the x-
values.
]i Sum of the squares of the y-
values.
]f Sum of the products of the x- and
y-values.
][ Number of data points entered.

Getting Started 33
Time Value of Money (TVM), Cash Flows, Bond, and Break-even Keys
When entering data for TVM, cash flows, bond, depreciation and break-even calculations,
results are calculated based on data entered into specific memory registers. When pressed,
the keys used for these operations:
• store data.
• enter data for a variable that is used during calculations (input only).
• calculate unknown variables based on stored data.
For more information on how these keys function, refer to the specific chapters which cover
TVM problems, cash flows, and bond and break-even calculations.
Math Functions
One-Number Functions
Math functions involving one number use the number in the display. To execute one-number
functions, with a number displayed, press the key or key combination corresponding to the
operation you wish to execute. The result is displayed. See Table 2-14 for a list of one-number
functions.
Before doing any trigonometric calculations, check whether the angle mode is set for degrees
or radians (Rad). Degrees is the default setting. The RAD annunciator in the display indicates
radians is active. Press ]3 to toggle between the settings. You will need to change
the setting if the active mode is not what your problem requires.
Table 2-14 lists the one-number functions of the calculator.
]U Sum of the y-values.
]X Sum of the x-values.
Table 2-12 Statistics keys
Keys Description
Table 2-13 Example displaying one number functions
Keys Display Description
gd7GV\B 9.45 Calculates square root.
D7Vj1G7DS\b 0.42 1/2.36 is calculated
first.
4 3.99 Adds 3.57 and 1/2.36.

Getting Started34
The random function]6, and Pi \; are special operators. They insert values
for Pi, or a random number in the range 0 < x <1, into calculations.
Table 2-14 One-number functions
Keys Description
§ Divide a number by 100.
\} Rounds x to the number specified by the display format.
\b Calculates 1/x.
\B Calculates the square root of x.
\2 Calculates the square of x.
\K Calculates natural exponent to the power of x.
\H Calculates natural log.
\E Calculates factorial of n (where -253 < n < 253). The Gamma function is
used to calculate n! for non-integers or negative numbers.
]
c, R, or C
Calculates sine, cosine, or tangent.
]o
c, R, or C
Calculates inverse sine, cosine, or tangent.
]r
c, R, or C
Calculates hyperbolic sine, cosine, or tangent.
]ro
c, R, or C
Calculates inverse hyperbolic sine, cosine, or tangent.
]F Calculates a cumulative normal probability given a Z-value.
]oF Calculates a Z-value given a cumulative normal probability.

Getting Started 35
Trigonometric and Hyperbolic Functions and Modes
Selecting Angle Format
The trigonometric angle format determines how numbers are interpreted when using
trigonometry functions. The default format for angles on the 10bII+ is degrees. To change to
radians mode, press ]3. When radians mode is active, the RAD annunciator is
displayed.
Trigonometric Functions
Example
Perform the following trigonometric calculations. If RAD is lit in the display, press ]3.
Table 2-15 Trigonometric functions
Keys Description
]c Calculates sine, written as sin.
]R Calculates cosine, written as
cos.
]C Calculates tangent, written as
tan.
]oc Calculates inverse sine, also
written, arcsin, asin, or sin-1.
]oR Calculates inverse cosine, also
written, arccos, acos, or cos-1.
]oC Calculates inverse tangent, also
written, arctan, atan, or tan-1.
Table 2-16 Example using various trigonometric calculations
Keys Display Description
\5Y 0.0000 Set display to four decimal places.
JV]c 0.2588 Displays sine of 15o.
J1S:]C 1. 7321 Displays tangent of 60o.
4 2.7321 Calculates 1 + tangent of 60o.
7DV]oR 69.5127 Displays inverse cosine of 0.35.

Getting Started36
Pi
Pressing \; displays the value of . Although the displayed value is appears in the
current display format, the 12 digit value is actually used for calculations. is often used
during calculations in radians mode, as there are 2 radians in a circle.
Example
Find the surface area of a sphere with a radius of 4.5 centimeters. Use the formula:
Hyperbolic Functions
A7SG]oR 51.6839 D i sp l a ys i nve rse c o s in e o f 0 . 62.
4 17.8288 Calculates arccos 0.35 - arccos 0.62.
\5G 17.83 Return display to default format.
Table 2-16 Example using various trigonometric calculations
Keys Display Description
Table 2-17 Example using Pi
Keys Display Description
YP\; 3.14 Displays .
PY7V\2 20.25 Displays 4.52.
4 254.47 Calculates sphere surface area
in square centimeters.
π
π
π
A4πr2
=
π
Table 2-18 Hyperbolic and inverse hyperbolic functions
Keys Description
]rc Calculates hyperbolic sine, written as,
sinh.
]rR Calculates hyperbolic cosine, written
as, cosh.
]rC Calculates hyperbolic tangent, written
as, tanh.
]roc Calculates inverse hyperbolic sine,
written as, arcsinh, asinh, or, sinh-1.
]roR Calculates inverse hyperbolic sine, also
written, arccosh, acosh, or cosh-1.
]roC Calculates inverse hyperbolic tangent,
also written, arctanh, atanh, or tanh-1.

Getting Started 37
Example
Perform the following hyperbolic calculations.
Two-Number Functions
When a function requires two numbers, other than for addition, subtraction, multiplication,
division, and the power function, ( ), you may key in the numbers as follows: number1 Æ
number 2 followed by the operation. Pressing Æ evaluates the current expression and
displays the INPUT annunciator.
In-line Functions
For calculations involving \¨, \Ä, \Ç, ]9,
]<,]I, and ]oI, which require two numbers, you may also
key in the first number followed by the function keys, and then key in the second number
followed by 4 to return results. Throughout the manual, when examples are entered in this
manner without using Æ, they are referred to as in-line functions. For example, the
following keystrokes calculate the percent change between 17 and 29 using the \¨
keys as an in-line function:
Table 2-19 Example performing various hyperbolic calculations
Keys Display Description
\5Y 0.0000 Sets display to four decimal places.
J7GV]rc 1.6019 Display sinh 1.25.
17Vd]rC 0.5299 Displays tanh 0.59.
4 2.1318 Calculates sinh 1.25 + tanh 0.59.
]roR 1.3899 Ca l cu l a t e s a c os h 2.1318 .
\5G 1.39 Returns display to default format.
yx

Getting Started38
Press M, and now calculate the same example using the Æ key to store the first number,
then key in the second number and perform the operation.
Although the in-line function has fewer key strokes, performing this example using the Æ
key permits you to store a value and then perform other calculations following Æwithout
using parentheses.
Table 2-20 Example calculating percent change as an in-line function
Keys Display Description
Jj\¨ 17.00 E nt er s number1, displays the
PEND annunciator indicating the
calculator is awaiting
instructions.
Gd 29_ Enters number 2.
4 70.59 Calculates the percent change.
Table 2-21 Example calculating percent change using ‘INPUT’
Keys Display Description
JjÆ 17.00 E nt ers number1, and displays
the INPUT annunciator
indicating the number has been
stored.
Gd\¨ 70.59 Enters number 2 and calculates
the percent change.
Table 2-22 Example displaying two-number functions with chain calculation
Keys Display Description
JjÆ 17.0 0 E nt ers number1, and displays
the INPUT annunciator.
Gd1DD
1VYAgj
87_ Enters and performs the chain
calculation. Results are stored
and used in the next operation.
The PEND annunciator and the
blinking cursor indicate an
operation is pending as the
calculator awaits instructions.
\¨ 70.59 Calculates the percent change
between 17 and the result of the
chain operation (29).

Getting Started 39
The Table 2-23 below lists the two-number functions of the calculator.
Two-number functions may be performed in either CHAIN or ALGEBRAIC mode.
Arithmetic with One-and Two-number Functions
Math functions operate on the number in the display.
Example 1
Calculate 1/
4, then calculate + 47.2 + 1.12.
Table 2-23 Two-number functions
Keys Description
1APa Addition, subtraction,
multiplication, division.
\Q The power function.
\¨ % Change.
]9 Combinations.
]< Permutations.
\Ç The date and day, past or
future, that is a given number of
days from a given date.
\Ä The number of days between
two dates.
]I Calculates the cumulative
Student’s t probability given
degrees of freedom and a t-
value.
]oI Calculates a t-value given
degrees of freedom and the
cumulative Student’s t
probability.
Table 2-24 Calculating the expression
Keys Display Description
Y\b 0.25 Calculates the reciprocal of 4.
G:\B 4.47 Calculates .
20
20

Getting Started40
Example 2
Calculate natural logarithm (e2.5). Then calculate 790 + 4!
Example 3
The power operator, , raises the preceding number (y-value) to the power of the following
number (x-value).
Calculate 1253, then find the cube root of 125.
1Yj7G1 51. 67 Calculates + 47.20.
J7J\2 1. 21 Calculates 1.12.
4 52.88 Completes the calculation.
Table 2-25 Calculating the logarithm value
Keys Display Description
G7V\K 12.18 Calculates e2.5.
\H 2.50 Calculates natural logarithm of
the result.
jd:1Y\E 24.00 Calculates 4 factorial.
4 814.00 Completes calculation.
Table 2-26 Calculating the cube root
Keys Display Description
JGV\QD4 1,953,125.00 Calculates 1253.
JGV\QD\b4 5.00 Calculates the cube root of
125, or 1251/3
.
Table 2-24 Calculating the expression
Keys Display Description
20
yx

Getting Started 41
Last Answer
When a calculation is completed by pressing 4, or a calculation is completed during
another operation, the result is stored in a memory location that contains the last calculated
result. This enables the last result of a calculation to be used during the next calculation.
To access the last calculated answer, press v4. Unlike the other stored memory
registers however, this register is automatically updated when you complete a calculation.
Example 1
Example 2
Display Format of Numbers
When you turn on the HP 10bII+ for the first time, numbers are displayed with two decimal
places and a period as the decimal point. The display format controls how many digits
appear in the display.
If the result of a calculation is a number containing more significant digits than can be
displayed in the current display format, the number is rounded to fit the current display setting.
Table 2-27 Using last answer
Keys Display Description
VAJ7GV4 3.75 Calculate 5-1.25
D\Qv4 3.75 Recall last answer.
4 61.55 Calculate 33.75.
Table 2-28 Using last answer with ‘INPUT’
Keys Display Description
V:Æ 50.00 Store 50 in the INPUT register.
GG1JY\¨ -28.00 Calculate percent change.
S:Æ 60.00 Store 60 in the INPUT register.
v4 36.00 Recalls last calculation, 22+14.
\¨ -40.00 Calculate percent change.

Getting Started42
Regardless of the current display format, each number is stored internally as a signed, 12-digit
number with a signed, three-digit exponent.
Specifying Displayed Decimal Places
To specify the number of displayed decimal places:
1. P r e s s \5 followed by :–d for the desired decimal setting.
2. \5 followed by 7, v, or s changes the display mode. Pressing
\7 provides the best estimate and displays as many digits as required. v is
the value for 10, and s for 11.
When a number is too large or too small to be displayed in DISP format, it automatically
displays in scientific notation.
Displaying the Full Precision of Numbers
To set your calculator to display numbers as precisely as possible, press \57
(trailing zeros are not displayed.) To temporarily view all 12 digits of the number in the display
(regardless of the current display format setting), press \5 and hold 4. The number
is displayed as long as you continue holding 4. The decimal point is not shown.
Start with two decimal places \5G.
Table 2-29 Example displaying the number of decimal places
Keys Display Description
\M 0.00 Clears display.
\5D 0.000 Displays three decimal places.
YV7SP
7JGVS4
5.727
\5d 5.727360000 Displays nine decimal places.
\5G 5.73 Restores two decimal places.

Getting Started 43
Scientific Notation
Scientific notation is used to represent numbers that are too large or too small to fit in the
display. For example, if you enter the number 10,000,000 x 10,000,000 =, the result is
1.00E14, which means one times ten to the fourteenth power, or 1.00 with the decimal point
moved fourteen places to the right. You can enter this number by pressing J\
zJY. The E stands for exponent of ten.
Exponents can also be negative for very small numbers. The number 0.000000000004 is
displayed as 4.00E–12, which means four times ten to the negative twelfth power, or 4.0 with
the decimal point moved 12 places to the left. You can enter this number by pressing
Y\zyJG.
Interchanging the Period and Comma
To switch between the period and comma (United States and International display) used as
the decimal point and digit separator, press \8.
For example, one million can be displayed as 1,000,000.00 or 1.000.000,00.
Pressing \8, toggles between these options.
Rounding Numbers
The calculator stores and calculates using 12-digit numbers. When 12 digit accuracy is not
desirable, use \} to round the number to the displayed format before using it in a
calculation. Rounding numbers is useful when you want the actual (dollars and cents) monthly
payment.
Table 2-30 Example displaying all digits
Keys Display Description
Jaj4 1. 43 D i v id e s .
\54 142857142857 Displays all 12 digits.

Getting Started44
Messages
The HP 10bII+ displays messages about the status of the calculator or informs you that you
have attempted an incorrect operation. To clear a message from the display, press M or
|. For a complete list of error messages, refer to Appendix C.
Table 2-31 Example displaying rounding off numbers
Keys Display Description
d7gjSVYD
GJ
9.87654321_ Enters a number with more than
two nonzero decimal places.
\5G 9.88 Displays two decimal places.
\54
(while you press 4).
987654321000 Displays all digits without the
decimal.
\} 9.88 Rounds to two decimal places
(specified by pressing
\5G).
\54 988000000000 Shows rounded, stored number.

Business Percentages 45
3 Business Percentages
The Business Percentage Keys
When entering data for business percentage calculations, results are calculated based on
data entered into specific memory registers. When pressed, the keys used for these
operations:
• store data.
• enter known data for variables used during calculations.
• calculate unknown variables based on stored data.
You can use the 10bII+ to calculate simple percent, percent change, cost, price, margin, and
markup.
Percent key
The § key has two functions:
• Finding a percent
• Adding or subtracting a percent
Finding a Percent
The § key divides a number by 100 unless it is preceded by an addition or subtraction
sign.
Example
Find 25% of 200.
Adding or Subtracting a Percent
You can add or subtract a percent in one calculation.
Example 1
Decrease 200 by 25%.
Table 3-1 Finding a percent
Keys Display Description
G::P 200.00 Enters 200.
GV§ 0.25 Converts 25% to a decimal.
4 50.00 Multiplies 200 by 25%.

Business Percentages46
Example 2
You borrow 1,250 from a relative, and you agree to repay the loan in a year with 7% simple
interest. How much money will you owe?
Percent Change
Calculate the percent change between two numbers.
Example 1
Calculate the percent change between 291.7 and 316.8 using the in-line feature.
Example 2
Calculate the percent change between (12 × 5) and (65 + 18) using Æ.
For more information on in-line features, refer to chapter 2, Getting Started.
Table 3-2 Subtracting a percent in a calculation
Keys Display Description
G::A 200.00 Enters 200.
GV§ 50.00 Multiplies 200 by 0.25 and
subtracts 50 from 200.
4 150.00 Completes the calculation.
Table 3-3 Adding a percent in a calculation
Keys Display Description
JGV:1j§
4
1,337.50 Calculates loan interest, 87.50
and adds 87.50 and 1250.00 to
show the repayment amount.
Table 3-4 Calculating the percent change
Keys Display Description
GdJ7j\¨ 291.70 Enters number1.
DJS7g4 8.60 Calculates percent change.
Table 3-5 Calculating the percent change between two numbers
Keys Display Description
JGPVÆ 60.00 Calculates and enters number1.
Note the INPUT annunciator.
SV1Jg\¨ 38.33 Calculates percent change.

Business Percentages 47
Margin and Markup Calculations
The 10bII+ can calculate cost, selling price, margin, or markup.
To see any value used by the margin and markup application, press v and then the key
you wish to see. For example, to see the value stored as À, press vÀ.
Margin Calculations
Example
Kilowatt Electronics purchases televisions for 255. The televisions are sold for 300. What is
the margin?
Markup on Cost Calculations
Example
The standard markup on costume jewelry at Kleiner’s Kosmetique is 60%. They just received
a shipment of chokers costing 19.00 each. What is the retail price per choker?
Table 3-6 Keys for margin and markup
Application Keys Description
Margin À, ¼, ® Margin is markup expressed as a
percent of price.
Markup À, ¼, Ã Markup calculations are expressed
as a percent of cost.
Table 3-7 Calculating the margin
Keys Display Description
GVVÀ 255.00 Stores cost in CST.
D::¼ 300.00 Stores selling price in PRC.
® 15.0 0 Cal cu l a t es m argi n.
Table 3-8 Calculating the retail price
Keys Display Description
JdÀ 19.00 Stores cost.
S:Ã 60.00 Stores markup.
Business Percentages48
Using Margin and Markup Together
Example
A food cooperative buys cases of canned soup with an invoice cost of 9.60 per case. If the
co-op routinely uses a 15% markup, for what price should it sell a case of soup? What is the
margin?
¼ 30.40 Calculates retail price.
Table 3-8 Calculating the retail price
Keys Display Description
Table 3-9 Calculating the margin
Keys Display Description
d7SÀ 9.60 Stores invoice cost.
JVÃ 15.0 0 St o re s m a rku p.
¼ 11.04 Calculates the price on a case of
soup.
® 13. 0 4 C a l c u l a t e s margin.

Number Storage and Storage Register Arithmetic 49
4 Number Storage and Storage Register Arithmetic
Using Stored Numbers in Calculations
You can store numbers for reuse in several different ways:
•Use ª (Constant) to store a number and its operator for repetitive operations.
•Use 3 Key Memory (
s, p, and m) to store, recall, and sum numbers with a single
keystroke.
•Use
\w and v to store to, and recall from, the 20 numbered registers.
Using Constants
Use ª to store a number and arithmetic operator for repetitive calculations. Once the
constant operation is stored, enter a number and press 4. The stored operation is
performed on the number in the display.
Example 1
Calculate 5 + 2, 6 + 2, and 7 + 2.
Table 4-1 Storing ‘+2’ as constant
Keys Display Description
V1Gª 2.00 Stores + 2 as constant.
4 7.00 Adds 5 + 2.
S4 8.00 Adds 6 + 2.
j4 9.00 Adds 7 + 2.

Number Storage and Storage Register Arithmetic50
Example 2
Calculate 10 + 10%, 11 + 10%, and 25 + 10%.
Example 3
Calculate 23 and 43.
Table 4-2 Storing ‘+ 10%’ as a constant
Keys Display Description
J:1J:§ª 1. 0 0 S t o r e s + 10% as a constant.
4 11.00 Adds 10% to 10.
4 12.10 Ad ds 10 % t o 11.
GV4 27.50 Adds 10% to 25.
Table 4-3 Storing ‘y3’ as a constant
Keys Display Description
G\QDª 3.00 Stores y3 as constant.
4 8.00 Calculates 23.
Y4 64.00 Calculates 43.

Number Storage and Storage Register Arithmetic 51
Example 4
Calculate the percent change between 55 and 32 and store it as a constant. Then calculate
the percent change between 50 and 32, and 45 and 32.
All of the other two-number functions on the calculator may be used with ª in the same
manner as shown in example 4. For a complete list of two-number functions, refer to the
section titled, Two-Number Functions in chapter 2.
Using the M Register
The s, p, and m keys perform memory operations on a single storage register,
called the M register. In most cases, it is unnecessary to clear the M register, since s
replaces the previous contents. However, you can clear the M register by pressing :s.
To add a series of numbers to the M register, use s to store the first number and m to
add subsequent numbers. To subtract the displayed number from the number in the M register,
press y followed by m.
Table 4-4 Calculating percent change
Keys Display Description
VV\¨DGª 32.00 Stores % change 32 as constant.
4 -41.82 Calculates the % change
between 55 and 32.
V:4 -36.00 Calculates the % change
between 50 and 32.
YV4 -28.89 Calculates the % change
between 45 and 32.
Table 4-5 Keys for performing memory operations
Keys Description
s Stores displayed number in the M register.
p Recalls number from the M register.
m Adds displayed number to the M register.

Number Storage and Storage Register Arithmetic52
Example
Use the M register to add 17, 14.25, and 16.95. Then subtract 4.65 and recall the result.
Using Numbered Registers
The \w and v keys access the 20 user registers, designated 0-19. The
\w key is used to copy the displayed number to a designated register. The v key
is used to copy a number from a register to the display.
To store or recall a number in two steps:
•Press \w or v. To cancel this step, press | or M.
•Press
\w followed by a number key, : to d, or 7 and : to d, to store a
number in the display into a numbered data storage register. Press \w7 followed by
: through d to access registers 10-19.
•Press
v followed by a number key, : to d, or 7 and : to d, to recall a
number from a storage register. Press v7 followed by : through d to access registers
10-19.
Example
In the following example, two storage registers are used. Set the calculator for CHAIN mode
(]?) and calculate the following:
Table 4-6 Calculating basic arithmetic operations using M register
Keys Display Description
Jjs 17.00 Sto res 17 in M regist er.
JY7GVm 14. 25 Ad d s 14 . 25 t o M re g i s t er.
JS7dVm 16.95 Adds 16.95 to M register.
Y7SVym -4.65 Adds -4.65 to M register.
p 43.55 Recalls contents of the M
register.
475.6
39.15
---------------- and 560.1 475.6+
39.15
---------------------------------------

Number Storage and Storage Register Arithmetic 53
With the exception of the statistics registers, you can also use \w and v for
application registers. For example, \wÒ stores the number from the display in the
Ò register. vÒ copies the contents from Ò to the display.
In most cases, it is unnecessary to clear a storage register since storing a number replaces the
previous contents. However, you can clear a single register by storing 0 in it. To clear all the
registers at once, press \N.
Doing Arithmetic Inside Registers
You can do arithmetic inside storage registers R0 through R19. The result is stored in the
register.
Table 4-7 Calculating the expression using two storage registers
Keys Display Description
YjV7S
\w7Y
475.60 Stores 475.60 (displayed
number) in R14 .
aDd7JV
\wG
39.15 Stores 39.15 in R2.
4 12.15 Completes first calculation.
VS:7J1
v7Y
1,035.70 Recalls R14 .
NOTE: If the calculator is set for
Algebraic mode, press 4 at the
end of this step.
avG 39.15 Recalls R2.
4 26.45 Completes second calculation.
Table 4-8 Keys for performing arithmetic inside registers
Keys New Number in Register
\w1 register number Old contents + displayed number.
\wA register number Old contents - displayed number.
\wP register number Old contents × displayed number.

Number Storage and Storage Register Arithmetic54
Example 1
Store 45.7 in R3, multiply by 2.5, and store the result in R3.
Example 2
Store 1.25 into register 15, then add 3, and store the result in register 15.
\wa register number Old contents ÷ displayed number.
Table 4-9 Calculating and storing the result in the storage register
Keys Display Description
YV7j
\wD
45.70 Stores 45.7 in R3.
G7V
\wPD
2.50 Multiplies 45.7 in R3 by 2.5 and
stores result (114.25) in R3.
vD 114 . 2 5 D i s p l a y s R 3.
Table 4-10 Storage register arithmetic
Keys Display Description
J7GV 1. 25 In pu ts 1. 25 in to t h e d i s p l ay.
\w7V 1.25 St o re s 1. 25 i n R 15.
D\w17V 3.00 Adds 3 to 1.25 in R15 and
stores the result R15.
M 0.00 Clears the display.
v7V 4.25 Recalls R15.
Table 4-8 Keys for performing arithmetic inside registers
Keys New Number in Register
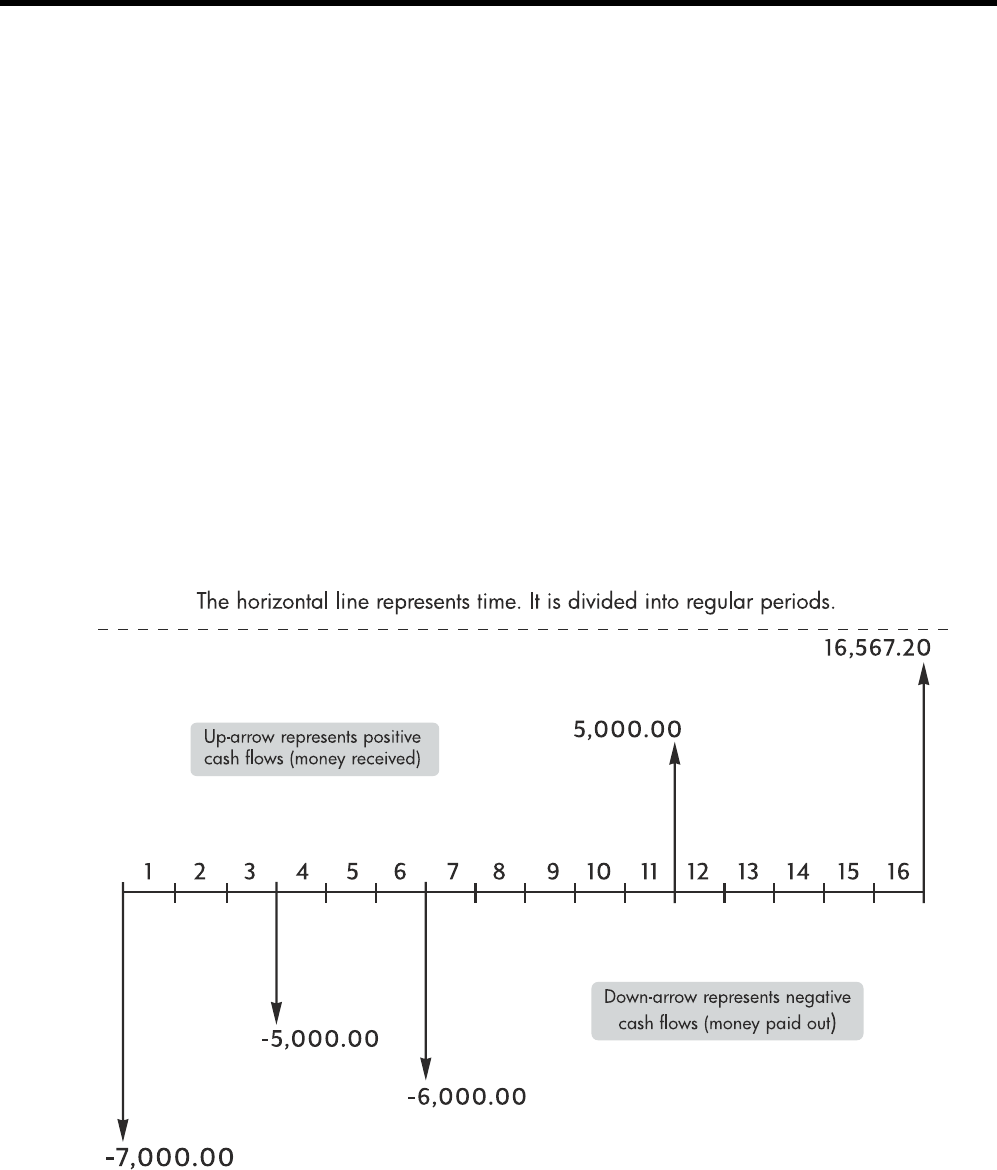
Picturing Financial Problems 55
5 Picturing Financial Problems
How to approach a Financial Problem
The financial vocabulary of the HP 10bII+ is simplified to apply to all financial fields. For
example, your profession may use the term balance, balloon payment, residual, maturity
value, or remaining amount to designate a value that the HP 10bII+ knows as É (future
value).
The simplified terminology of the HP 10bII+ is based on cash flow diagrams. Cash flow
diagrams are pictures of financial problems that show cash flows over time. Drawing a cash
flow diagram is the first step to solving a financial problem.
The following cash flow diagram represents investments in a mutual fund. The original
investment was 7,000.00, followed by investments of 5,000.00 and 6,000.00 at the end of
the third and sixth months. At the end of the 11th month, 5,000.00 was withdrawn. At the end
of the 16th month, 16,567.20 was withdrawn.
Figure 2 Cash flow diagram
Any cash flow example can be represented by a cash flow diagram. As you draw a cash flow
diagram, identify what is known and unknown about the transaction.
Time is represented by a horizontal line divided into regular time periods. Cash flows are
placed on the horizontal line when they occur. Where no arrows are drawn, no cash flows
occur.
Picturing Financial Problems56
Signs of Cash Flows
In cash flow diagrams, money invested is shown as negative and money withdrawn is shown
as positive. Cash flowing out is negative, cash flowing in is positive.
For example, from the lender’s perspective, cash flows to customers for loans are represented
as negative. Likewise, when a lender receives money from customers, cash flows are
represented as positive. In contrast, from the borrower’s perspective, cash borrowed is positive
while cash paid back is negative.
Periods and Cash Flows
In addition to the sign convention (cash flowing out is negative, cash flowing in is positive) on
cash flow diagrams, there are several more considerations:
• The time line is divided into equal time intervals. The most common period is a month, but days,
quarters, and annual periods are also common. The period is normally defined in a contract and
must be known before you can begin calculating.
• To solve a financial problem with the HP 10bII+, all cash flows must occur at either the beginning or
end of a period.
• If more than one cash flow occurs at the same place on the cash flow diagram, they are added
together or netted. For example, a negative cash flow of -250.00 and a positive cash flow of 750.00
occurring at the same time on the cash flow diagram are entered as a 500.00 cash flow (750 - 250
= 500).
• A valid financial transaction must have at least one positive and one negative cash flow.
Simple and Compound Interest
Financial calculations are based on the fact that money earns interest over time. There are two
types of interest:
• Simple interest
•Compound interest
The basis for Time Value of Money and cash flow calculations is compound interest.
Simple Interest
In simple-interest contracts, interest is a percent of the original principal. The interest and
principal are due at the end of the contract. For example, say you loan 500 to a friend for a
year, and you want to be repaid with 10% simple interest. At the end of the year, your friend
owes you 550.00 (50 is 10% of 500). Simple interest calculations are done using the §
key on your HP 10bII+. An example of a simple interest calculation can be found in chapter
6 under the section titled, Interest Rate Conversions.
Picturing Financial Problems 57
Compound Interest
A compound-interest contract is like a series of simple-interest contracts that are connected.
The length of each simple-interest contract is equal to one compounding period. At the end
of each period the interest earned on each simple-interest contract is added to the principal.
For example, if you deposit 1,000.00 in a savings account that pays 6% annual interest,
compounded monthly, your earnings for the first month look like a simple-interest contract
written for 1 month at 1
/
2% (6% ÷ 12). At the end of the first month the balance of the account
is 1,005.00 (5 is 1
/
2% of 1,000).
The second month, the same process takes place on the new balance of 1,005.00. The
amount of interest paid at the end of the second month is 1
/
2% of 1,005.00, or 5.03. The
compounding process continues for the third, fourth, and fifth months. The intermediate results
in this illustration are rounded to dollars and cents.
Figure 3 Annual interest compounded monthly
The word compound in compound interest comes from the idea that interest previously earned
or owed is added to the principal. Thus, it can earn more interest. The financial calculation
capabilities of the HP 10bII+ are based on compound interest.
Interest Rates
When you approach a financial problem, it is important to recognize that the interest rate or
rate of return can be described in at least three different ways:

Picturing Financial Problems58
• As a periodic rate. This is the rate that is applied to your money from period to period.
• As an annual nominal rate. This is the periodic rate multiplied by the number of periods in a year.
• As an annual effective rate. This is an annual rate that considers compounding.
In the previous example of a 1,000.00 savings account, the periodic rate is 1
/
2% (per month),
quoted as an annual nominal rate of 6% (1
/
2 × 12). This same periodic rate could be quoted
as an annual effective rate, which considers compounding. The balance after 12 months of
compounding is 1,061.68, which means the annual effective interest rate is 6.168%.
Examples of converting between nominal and annual effective rates can be found in the
section titled, Interest Rate Conversions in the next chapter.
Two Types of Financial Problems
The financial problems in this manual use compound interest unless specifically stated as
simple interest calculations. Financial problems are divided into two groups:
•TVM problems
• Cash flow problems
Recognizing a TVM Problem
If uniform cash flows occur between the first and last periods on the cash flow diagram, the
financial problem is a TVM (time value of money) problem. There are five main keys used to
solve a TVM problem.
You can calculate any value after entering the other four values. Cash flow diagrams for
loans, mortgages, leases, savings accounts, or any contract with regular cash flows of the
same amount are normally treated as TVM problems.
For example, following is a cash flow diagram, from the borrower’s perspective, for a 30-year,
150,000.00 mortgage, with a payment of 1,041.40, at 7.5% annual interest, with a 10,000
balloon payment.
Table 5-1 Keys for solving a TVM problem
Keys Description
Ù Number of periods or payments
Ò Annual percentage interest rate (usually the annual nominal
rate)
Ï Present value (the cash flow at the beginning of the time
line)
Ì Periodic payment
É Future value (the cash flow at the end of the cash flow
diagram, in addition to any regular periodic payment).
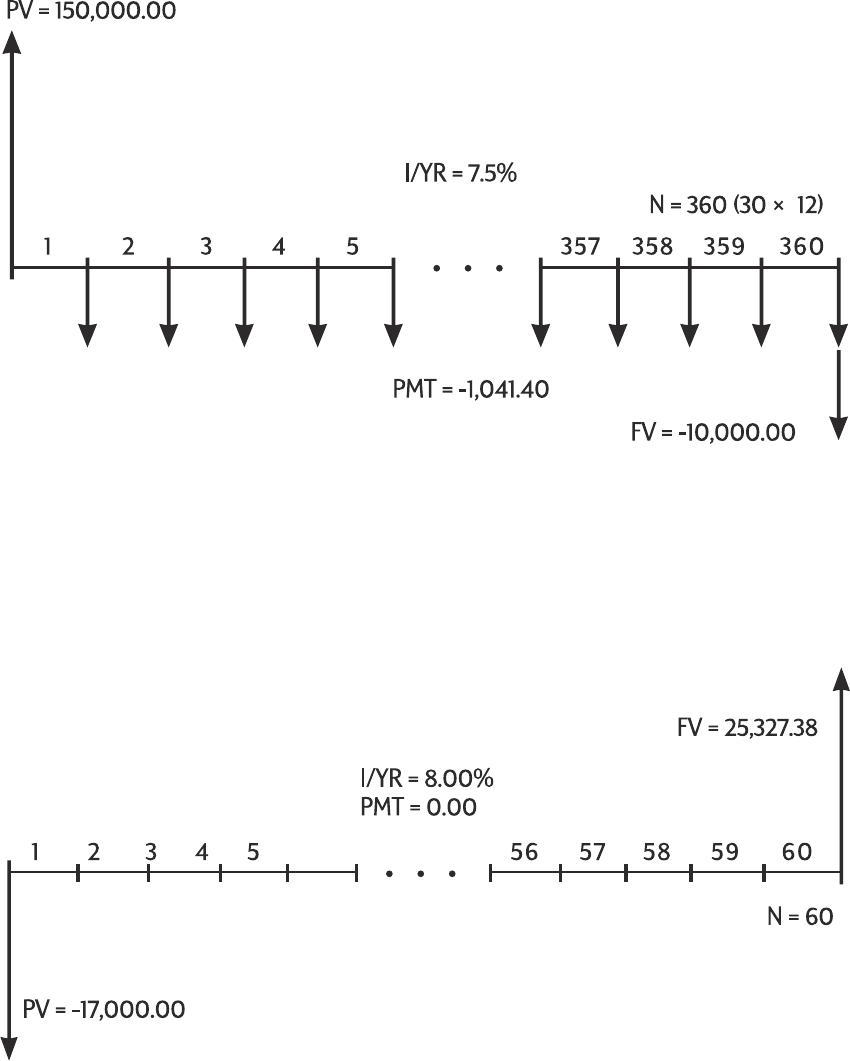
Picturing Financial Problems 59
Figure 4 Cash flow diagram (Borrower’s perspective)
One of the values for PV, PMT, FV can be zero. For example, following is a cash flow diagram
(from the saver’s perspective) for a savings account with a single deposit and a single
withdrawal five years later. Interest compounds monthly. In this example, PMT is zero.
Figure 5 Cash flow diagram (Saving perspective)
Time value of money calculations are described in the next chapter titled, Time Value of
Money Calculations.
Recognizing a Cash Flow Problem
A financial problem that does not have regular, uniform payments (sometimes called uneven
cash flows) is a cash flow problem rather than a TVM problem.
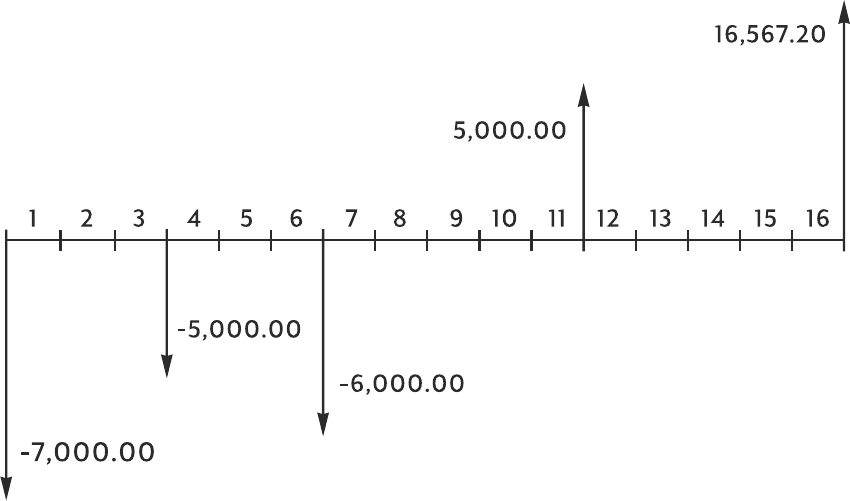
Picturing Financial Problems60
The following is a cash flow diagram for an investment in a mutual fund. This is an example
of a problem that is solved using either \½ (Net Present Value) or \Á
(Internal Rate of Return per Year).
Figure 6 Cash flow diagram (Investment in a mutual fund)
Cash flow problems are described in chapter 8 titled, Cash Flow Calculations.

Time Value of Money Calculations 61
6 Time Value of Money Calculations
Using the TVM Application
The time value of money (TVM) application is used for compound interest calculations that
involve regular, uniform cash flows – called payments. Once the values are entered you can
vary one value at a time, without entering all the values again.
To use TVM, several prerequisites must be met:
• The amount of each payment must be the same. If the payment amounts vary, use the procedures
described in chapter 8 titled, Cash Flow Calculations.
• Payments must occur at regular intervals.
• The payment period must coincide with the interest compounding period. If it does not, convert the
interest rate using the \Ó, \Ð, and \Í keys described below in the
section titled, Interest Rate Conversions.
• There must be at least one positive and one negative cash flow.
The TVM Keys
When entering data for TVM calculations, results are calculated based on data entered into
specific memory registers. When pressed, the keys used for these operations:
• store data.
• enter known data for variables used during calculations.
• calculate unknown variables based on stored data.
Table 6-1 Keys for performing TVM calculations
Keys Stores or Calculates
Ù Number of payments or compounding periods.
Ò Annual nominal interest rate.
Ï Present value of future cash flows. PV is usually an initial investment or
loan amount and always occurs at the beginning of the first period.
Ì Amount of periodic payments. All payments are equal, and none are
skipped; payments can occur at the beginning or end of each period.
É Future value. FV is either a final cash flow or compounded value of a
series of previous cash flows. FV occurs at the end of the last period.
\Í Stores the number of periods per year. The default is 12. Reset only
when you wish to change it.
\Ú Optional shortcut for storing N: number in display is multiplied by the
value in P/YR and the result is stored in N.

Time Value of Money Calculations62
To verify values, press vÙ, vÒ, vÏ, vÌ, and vÉ.
Pressing v\Ú recalls the total number of payments in years and v\Í
shows you the number of payments per year. Recalling these numbers does not change the
content of the registers.
Begin and End Modes
Before you start a TVM calculation, identify whether the first periodic payment occurs at the
beginning or end of the first period. If the first payment occurs at the end of the first period,
set your HP 10bII+ to End mode; if it occurs at the beginning of the first period, set your
calculator to Begin mode.
To switch between modes, press \¯. The BEGIN annunciator is displayed when your
calculator is in Begin mode. No annunciator is displayed when you are in End mode.
Mortgages and loans typically use End mode. Leases and savings plans typically use Begin
mode.
Loan Calculations
Example: A Car Loan
You are financing a new car with a three year loan at 10.5% annual nominal interest,
compounded monthly. The price of the car is 14,500. Your down payment is 1,500.
Part 1
What are your monthly payments at 10.5% interest? (Assume your payments start one month
after the purchase or at the end of the first period.)
\¯ Switches between Begin and End mode. In Begin mode, the BEGIN
annunciator is displayed.
\Ê Calculates an amortization table.
Table 6-1 Keys for performing TVM calculations
Keys Stores or Calculates
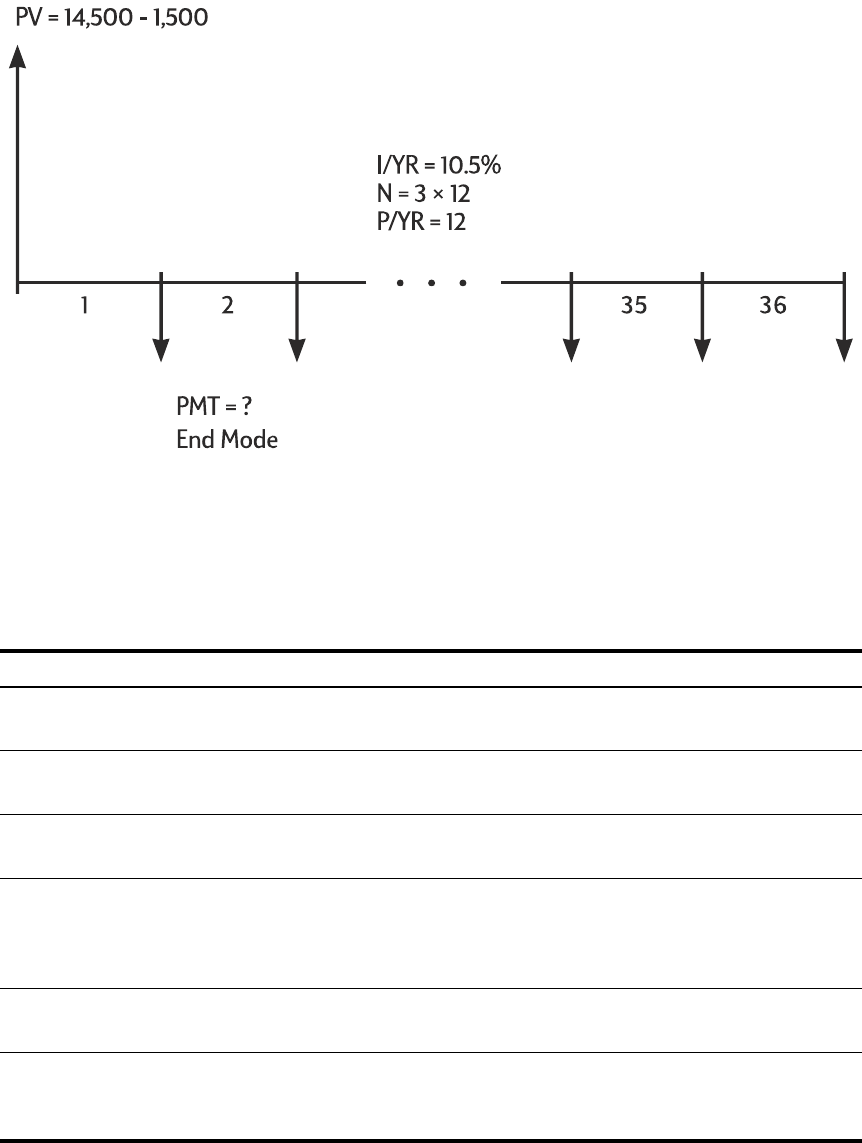
Time Value of Money Calculations 63
Figure 7 Cash flow diagram (Calculate PMT)
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
Part 2
At a price of 14,500, what interest rate is necessary to lower your payment by 50.00, to
372.53?
Table 6-2 Calculating the monthly payment
Keys Display Description
JG\Í 12.00 Sets periods per year (optional, as
12 is the default).
DPJGÙ 36.00 Stores number of periods in loan.
J:7VÒ 10.50 Stores annual nominal interest rate.
JYV::A
JV::Ï
13,000.00 Stores amount borrowed.
:É 0.00 Stores the amount left to pay after 3
years.
Ì -422.53 Calculates the monthly payment.
The negative sign indicates money
paid out.

Time Value of Money Calculations64
Part 3
If interest is 10.5%, what is the maximum you can spend on the car to lower your car payment
to 375.00?
Example: A Home Mortgage
You decide that the maximum monthly mortgage payment you can afford is 930.00. You can
make a 12,000 down payment, and annual interest rates are currently 7.5%. If you obtain a
30 year mortgage, what is the maximum purchase price you can afford?
Figure 8 Cash flow diagram (Calculate PV)
Table 6-3 Calculating the interest rate
Keys Display Description
1V:Ì -372.53 Decreases payment from 422.53.
Ò 2.03 Calculates annual interest rate for
the reduced payment.
Table 6-4 Calculating the amount
Keys Display Description
J:7VÒ 10.50 Stores original interest rate.
DjVyÌ -375.00 Stores desired payment.
Ï 11,537.59 Calculates amount of money to
finance.
1JV::4 13,037.59 Adds the down payment to the
amount financed for total price
of the car.

Time Value of Money Calculations 65
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
Example: A Mortgage With a Balloon Payment
You’ve obtained a 25 year, 172,500 mortgage at 8.8% annual interest. You anticipate that
you will own the house for four years and then sell it, repaying the loan with a balloon
payment. What will your balloon payment be?
Solve this problem using two steps:
1. Calculate the loan payment using a 25 year term.
2. Calculate the remaining balance after 4 years.
Step 1
First calculate the loan payment using a 25 year term.
Table 6-5 Calculating the maximum purchase price
Keys Display Description
JG\Í 12.00 Sets periods per year.
D:\Ú 360.00 Stores the length of the
mortgage (30 × 12).
:É 0.00 Pays mortgage off in 30 years.
j7VÒ 7.50 Stores interest rate.
dD:yÌ -930.00 Stores desired payment (money
paid out is negative).
Ï 133,006.39 Calculates the loan you can
afford with a 930 payment.
1JG:::4 145,006.39 Adds 12,000 down payment
for the total purchase price.
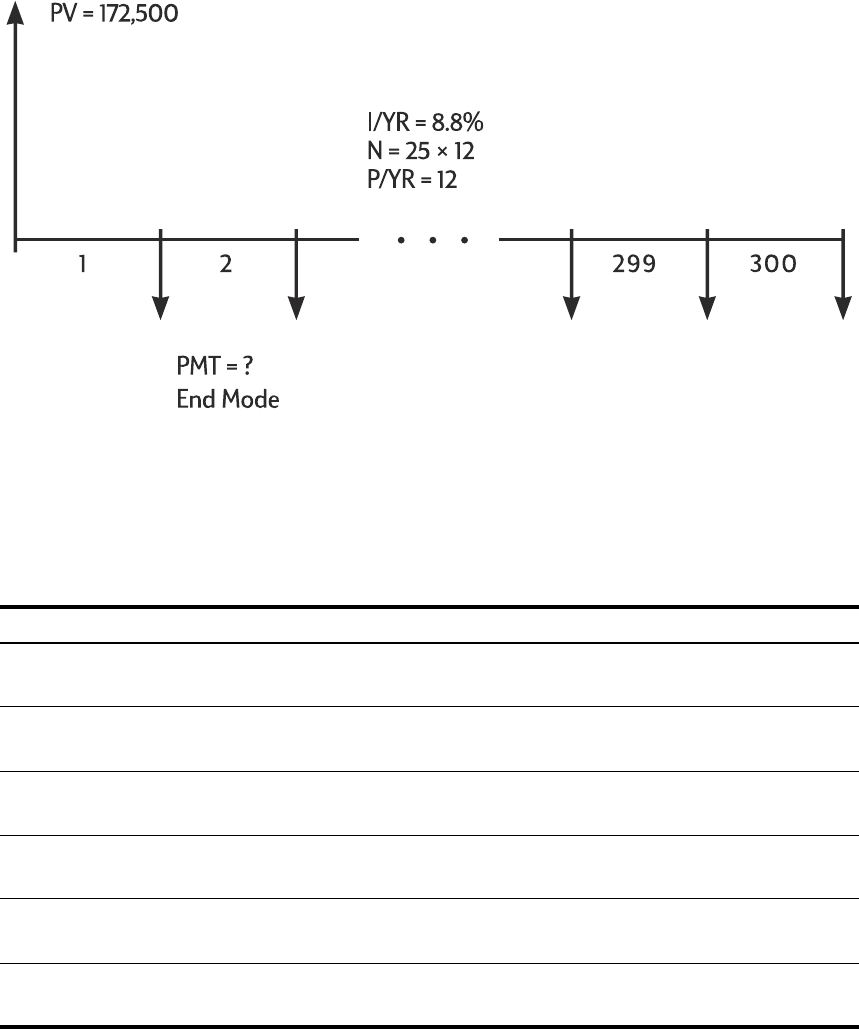
Time Value of Money Calculations66
Figure 9 Cash flow diagram (Calculate PMT)
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
Step 2
Since the payment is at the end of the month, the past payment and the balloon payment
occur at the same time. The final payment is the sum of PMT and FV.
Table 6-6 Calculating the monthly payment
Keys Display Description
JG\Í 12.00 Sets periods per year.
GV\Ú 300.00 Stores length of mortgage (25 ×
12 = 300 mont h s) .
:É 0.00 Stores loan balance after 25
years.
JjGV::Ï 172,500.00 Stores original loan balance.
g7gÒ 8.80 Stores annual interest rate.
Ì -1,424.06 Calculates the monthly payment.
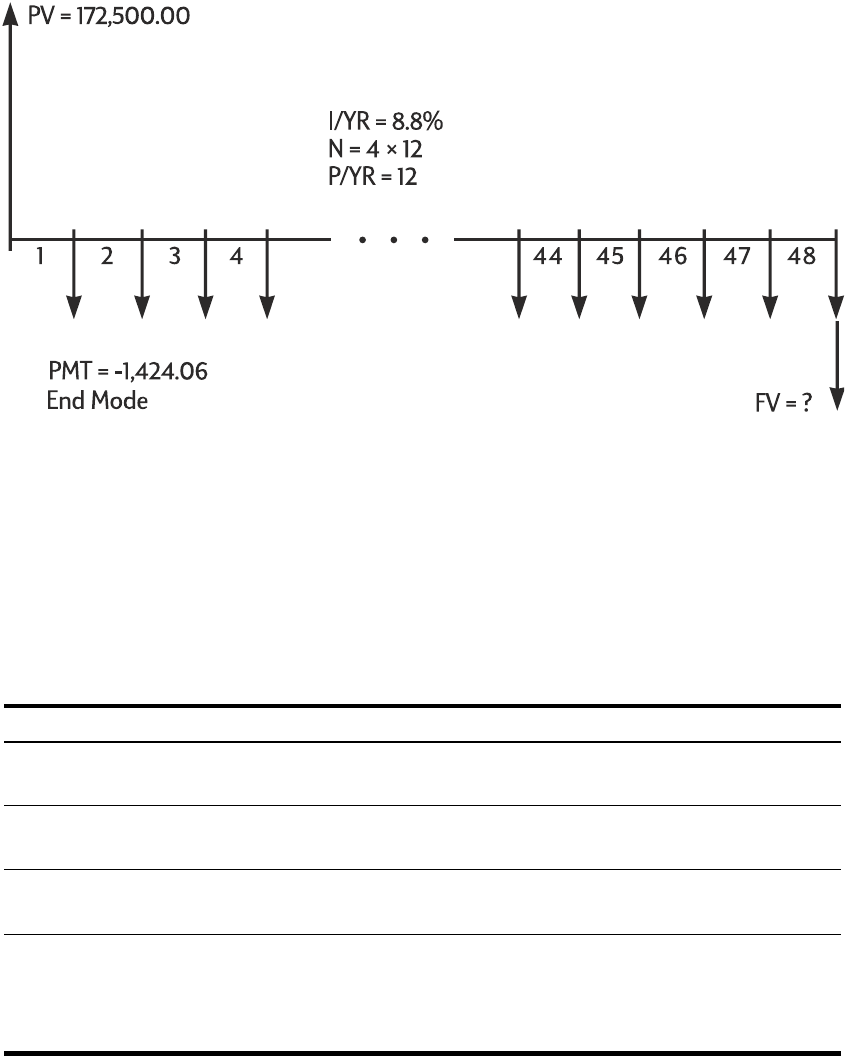
Time Value of Money Calculations 67
Figure 10 Cash flow diagram (Calculate FV)
The value in PMT should always be rounded to two decimal places when calculating FV or
PV to avoid small, accumulative discrepancies between non-rounded numbers and actual
(dollars and cents) payments. If the display is not set to two decimal places, press
\5G.
Savings Calculations
Example: A Savings Account
If you deposit 2,000 in a savings account that pays 7.2% annual interest compounded
annually, and make no other deposits to the account, how long will it take for the account to
grow to 3,000?
Table 6-7 Calculating the final amount
Keys Display Description
\}Ì -1,424.06 Rounds payment to two decimal
places, then stores.
YgÙ 48.00 Stores four year term (12 × 4)
that you expect to own house.
É -163,388.39 Calculates loan balance after
four years.
1vÌ4 -164,812.45 Calculates the total 48th
payment (PMT and FV) to pay
off the loan (money paid out is
negative).
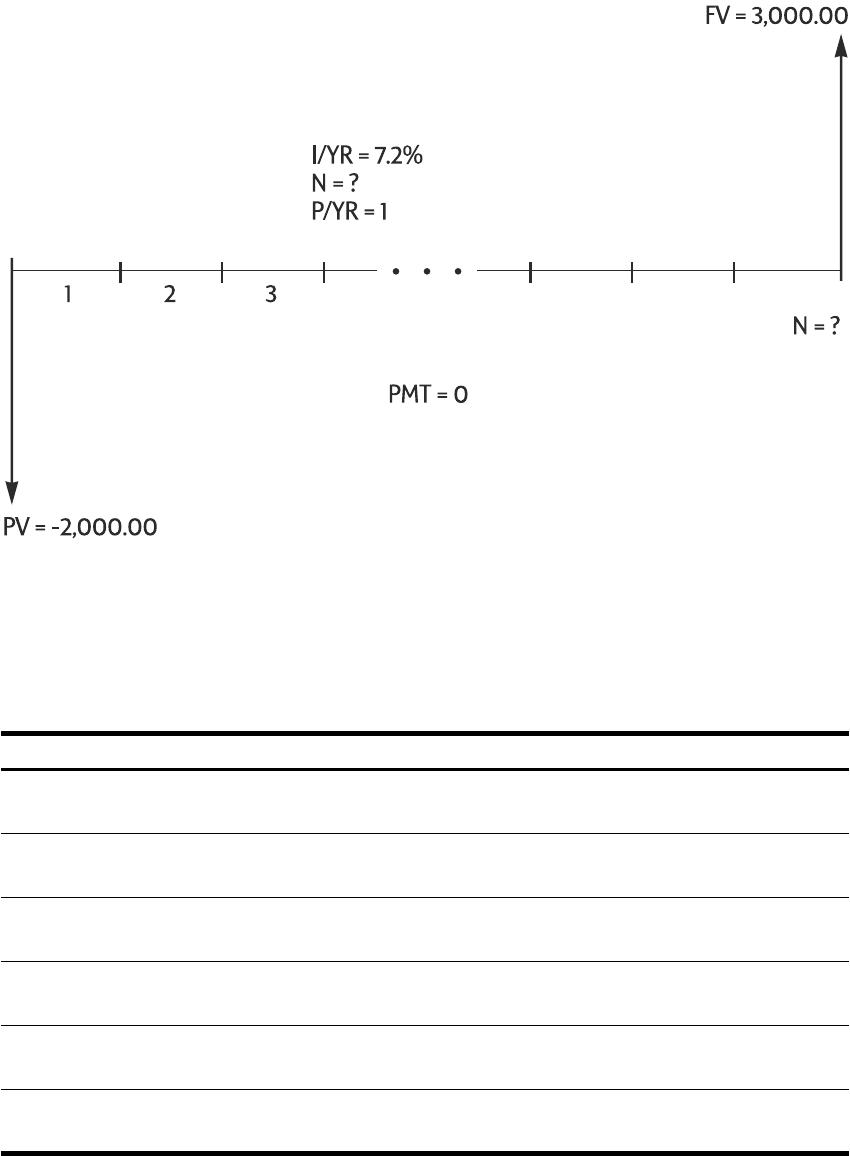
Time Value of Money Calculations68
Figure 11 Cash flow diagram (Calculate the number of years)
Since this account has no regular payments (PMT = 0), the payment mode (End or Begin) is
irrelevant.
Since the calculated value of N is between 5 and 6, it will take six years of annual
compounding to achieve a balance of at least 3,000. Calculate the actual balance at the end
of six years.
Table 6-8 Calculating the number of years
Keys Display Description
]OJ 0.00 Clears TVM memory.
J\Í 1. 0 0 S e t s P/YR to 1 since interest is
compounded annually.
G:::yÏ -2,000.00 Stores amount paid out for the
first deposit.
D:::É 3,000.00 Stores the amount you wish to
accumulate.
j7GÒ 7.20 Stores annual interest rate.
Ù 5.83 Calculates the number of years it
takes to reach 3,000.
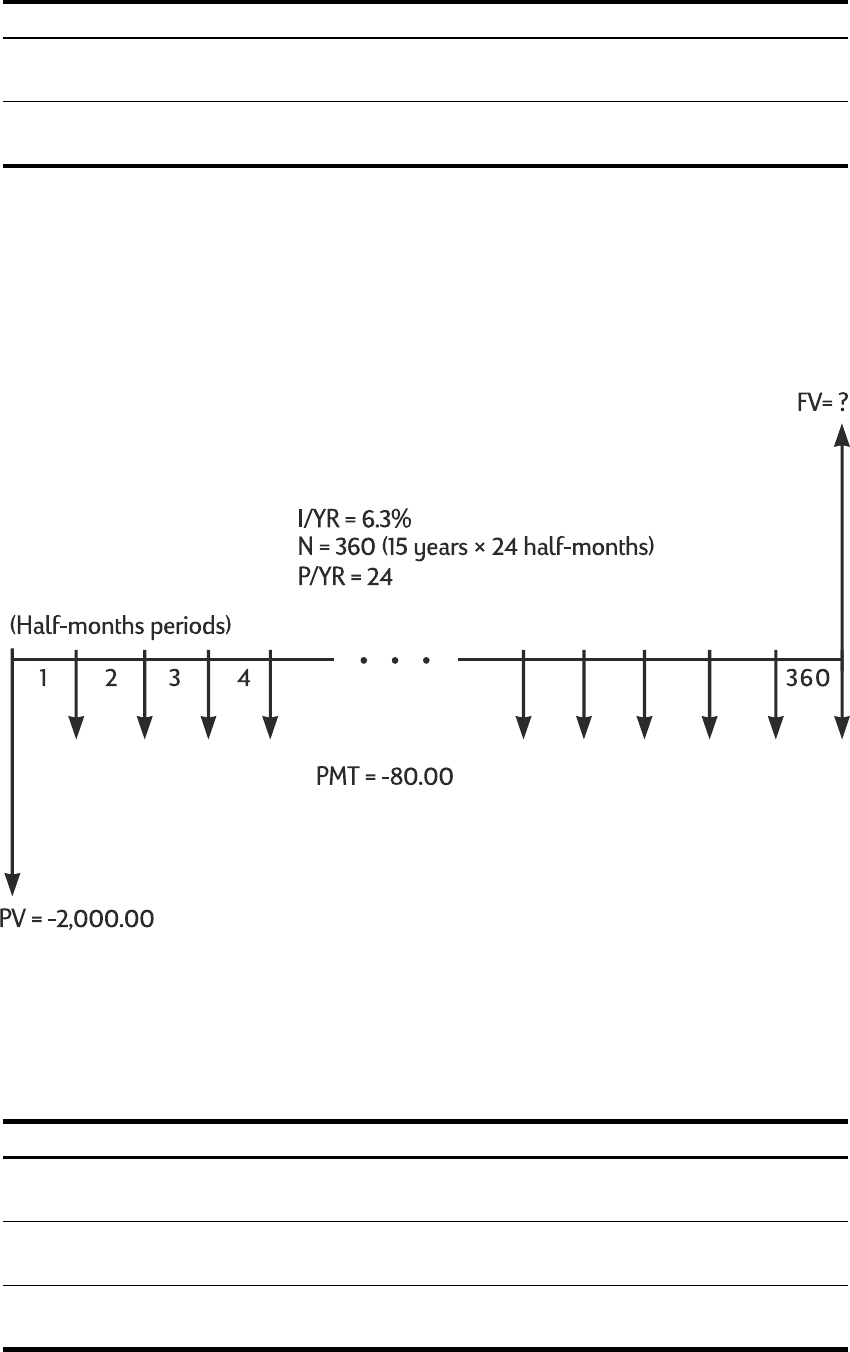
Time Value of Money Calculations 69
Example: An Individual Retirement Account
You opened an individual retirement account on April 14, 1995, with a deposit of 2,000.
80.00 is deducted from your paycheck and you are paid twice a month. The account pays
6.3% annual interest compounded semimonthly. How much will be in the account on
April 14, 2010?
Figure 12 Cash flow diagram (Calculate FV)
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
Table 6-9 Calculating the balance after six years
Keys Display Description
SÙ 6.00 Sets n to 6 years.
É 3,035.28 Calculates the amount you can
withdraw after six years.
Table 6-10 Calculating the balance amount
Keys Display Description
GY\Í 24.00 Sets number of periods per year.
G:::yÏ -2,000.00 Stores initial deposit.
g:yÌ -80.00 Stores regular semimonthly
deposits.
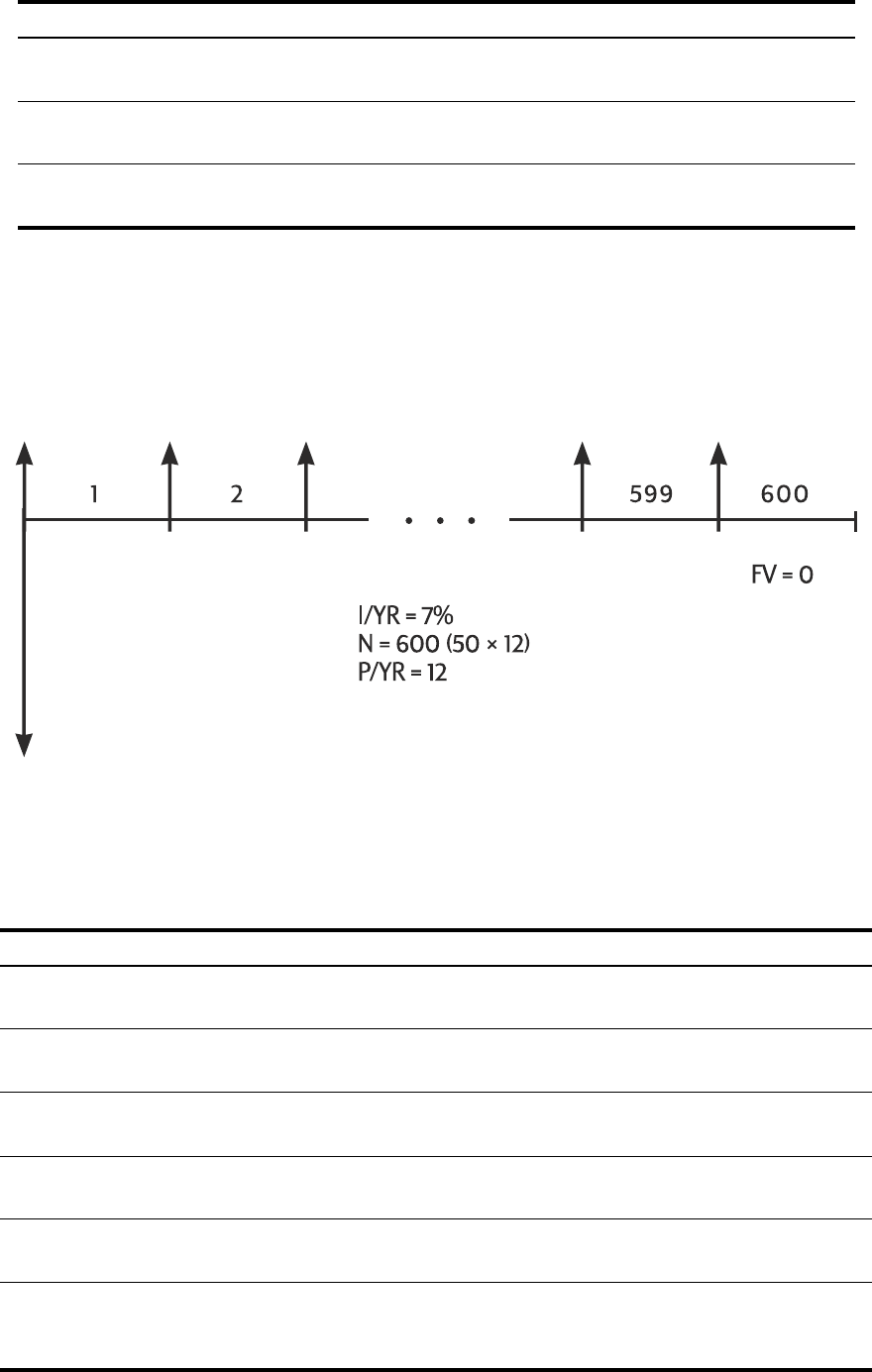
Time Value of Money Calculations70
Example: An Annuity Account
You opt for an early retirement after a successful business career. You have accumulated a
savings of 400,000 that earns an average of 7% annual interest, compounded monthly. What
annuity (repetitive, uniform, withdrawal of funds) will you receive at the beginning of each
month if you wish that savings account to support you for the next 50 years?
Figure 13 Cash flow diagram (Calculate the amount)
Set to Begin mode. Press \¯ if BEGIN annunciator is not displayed.
S7DÒ 6.30 Stores interest rate.
JV\Ú 360.00 Stores the number of deposits.
É 52,975.60 Calculates the balance amount.
Table 6-11 Calculating the amount at the beginning of each month
Keys Display Description
JG\Í 12.00 Sets payments per year.
Y:::::yÏ -400,000.00 Stores your nest egg as an
outgoing deposit.
jÒ 7.00 Stores annual interest rate you
expect to earn.
V:\Ú 600.00 Stores number of withdrawals.
:É 0.00 Stores balance of account after
50 years.
Ì 2,392.80 Calculates the amount that you
can withdraw at the beginning
of each month.
Table 6-10 Calculating the balance amount
Keys Display Description
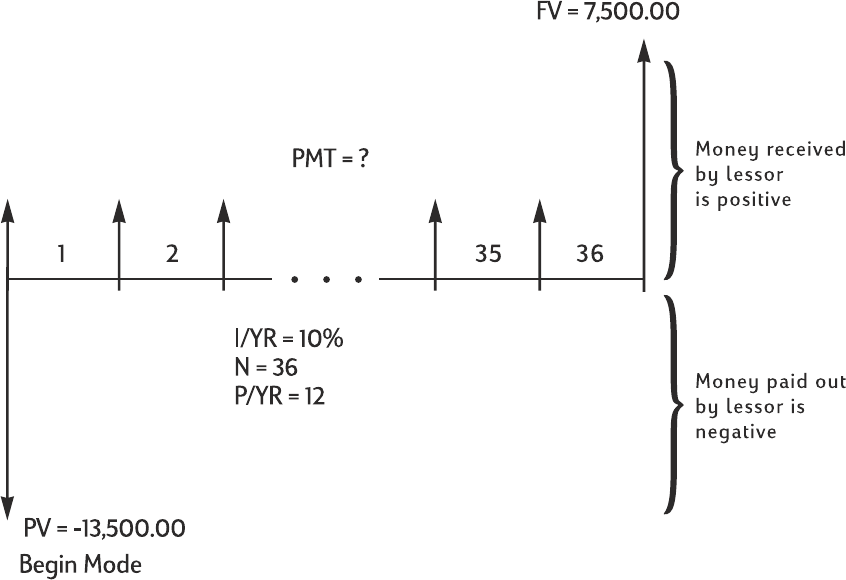
Time Value of Money Calculations 71
Lease Calculations
A lease is a loan of valuable property (like real estate, automobiles, or equipment) for a
specific amount of time, in exchange for regular payments. Some leases are written as
purchase agreements, with an option to buy at the end of the lease (sometimes for as little as
1.00). The defined future value (FV) of the property at the end of a lease is sometimes called
the residual value or buy out value.
All five TVM application keys can be used in lease calculations. There are two common lease
calculations.
• Finding the lease payment necessary to achieve a specified yield.
• Finding the present value (capitalized value) of a lease.
The first payment on a lease usually occurs at the beginning of the first period. Thus, most
lease calculations use Begin mode.
Example: Calculating a Lease Payment
A customer wishes to lease a 13,500 car for three years. The lease includes an option to buy
the car for 7,500 at the end of the lease. The first monthly payment is due the day the customer
drives the car off the lot. If you want to yield 10% annually, compounded monthly, what will
the payments be? Calculate the payments from your (the dealer’s) point of view.
Figure 14 Cash flow diagram (Calculate the monthly lease payment)
Set to Begin mode. Press \¯ if BEGIN annunciator is not displayed.

Time Value of Money Calculations72
Notice that even if the customer chooses not to buy the car, the lessor still includes a cash flow
coming in at the end of the lease equal to the residual value of the car. Whether the customer
buys the car or it is sold on the open market, the lessor expects to recover 7,500.
Example: Lease With Advance Payments
Your company, Quick-Kit Pole Barns, plans to lease a forklift for the warehouse. The lease is
written for a term of four years with monthly payments of 2,400. Payments are due at the
beginning of the month with the first and last payments due at the onset of the lease. You have
an option to buy the forklift for 15,000 at the end of the leasing period.
If the annual interest rate is 9%, what is the capitalized value of the lease?
Figure 15 Cash flow diagram (Calculate PV of the lease)
Table 6-12 Calculating the monthly lease payment
Keys Display Description
JG\Í 12.00 Sets payments per year.
J:Ò 10.00 Stores desired annual yield.
JDV::yÏ -13,500.00 Stores lease price.
jV::É 7,500.00 Stores residual (buy out value).
DSÙ 36.00 Stores length of lease, in months.
Ì 253.99 Calculates the monthly lease
payment.

Time Value of Money Calculations 73
This solution requires four steps:
1. Calculate the present value of the 47 monthly payments: (4 × 12) - 1 = 47.
2. Add the value of the additional advance payment.
3. Find the present value of the buy option.
4. Sum the values calculated in steps 2 and 3.
Step 1
Find the present value of the monthly payments.
Set to Begin mode. Press \¯ if BEGIN annunciator is not displayed.
Step 2
Add the additional advance payment to PV. Store the answer.
Step 3
Find the present value of the buy option.
Table 6-13 Calculating the present value
Keys Display Description
JG\Í 12.00 Sets payments per year.
YjÙ 47.00 Stores number of payments.
GY::yÌ -2,400.00 Stores monthly payment.
:É 0.00 Stores FV for Step 1.
dÒ 9.00 Stores interest rate.
Ï 95,477.55 Calculates the present value of
47 monthly payments.
Table 6-14 Adding the advance payment
Keys Display Description
1vÌy4 97,877.55 Adds additional advance.
payment
s 97,877.55 Stores result in M register.
Table 6-15 Calculating the present value of the last cash flow
Keys Display Description
YgÙ 48.00 Stores month when buy option
occurs.

Time Value of Money Calculations74
Step 4
Add the results of ’Step 2’ and ’Step 3’.
Amortization
Amortization is the process of dividing a payment into the amount that applies to interest and
the amount that applies to principal. Payments near the beginning of a loan contribute more
interest, and less principal, than payments near the end of a loan.
Figure 16 Graph
:Ì 0.00 Stores zero payment for this step
of solution.
JV:::yÉ -15,000.00 Stores value to discount.
Ï 10,479.21 Calculates the present value of
last cash flow.
Table 6-16 Calculating the present value of lease
Keys Display Description
1p4 108,356.77 Calculates the present (capitalized)
value of lease. (Rounding
discrepancies are explained on
page 67.)
Table 6-15 Calculating the present value of the last cash flow
Keys Display Description

Time Value of Money Calculations 75
The AMORT key on the HP 10bII+ allows you to calculate.
• The amount applied to interest in a range of payments.
• The amount applied to principal in a range of payments.
•The loan balance after a specified number of payments are made.
The \Ê function assumes you have just calculated a payment or you have stored the
appropriate amortization values in I/YR, PV, FV, PMT, and P/YR.
The numbers displayed for interest, principal, and balance are rounded to the current display
setting.
To Amortize
To amortize a single payment, enter the period number and press \Ê . The HP 10bII+
displays the annunciator PER followed by the starting and ending payments that will be
amortized.
Press 4 to see interest (INT). Press 4 again to see the principal (PRIN) and again to see
the balance (BAL). Continue pressing 4 to cycle through the same values again.
To amortize a range of payments, enter starting period number Æ ending period number,
then press \Ê. The HP 10bII+ displays the annunciator PER followed by the starting
and ending payments that will be amortized. Then press 4 repeatedly to cycle through
interest, principal, and balance.
Press \Ê again to move to the next set of periods. This auto-increment feature saves
you the keystrokes of entering the new starting and ending periods.
Table 6-17 Keys for storing the amortization values
Keys Description
Ò Annual nominal interest rate.
Ï Starting balance.
É Ending balance.
Ì Payment amount (rounded to the display format).
\Í Number of payments per year.

Time Value of Money Calculations76
If you store, recall, or perform any other calculations during amortization, pressing 4 will
no longer cycle through interest, principal, and balance. To resume amortization with the
same set of periods, press v\Ê.
Example: Amortizing a Range of Payments
Calculate the first two years of the annual amortization schedule for a 30 year, 180,000
mortgage, at 7.75% annual interest with monthly payments.
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
If you already know the mortgage payment, you can enter and store it just like you store the
other four values. Next, amortize the first year.
Table 6-18 Calculating the monthly payment
Keys Display Description
JG\Í 12.00 Sets payments per year.
D:\Ú 360.00 Stores total number of payments.
j7jVÒ 7. 75 St o re s i n te re s t p e r ye a r.
Jg::::Ï 180,000.00 Stores present value.
:É 0.00 Stores future value.
Ì -1,289.54 Calculates the monthly payment.
Table 6-19 Calculating the loan balance after a year
Keys Display Description
JÆJG 12_ Enters starting and ending
periods.
\Ê 1– 12 Displays the PER and AMORT
annunciators and range.
4 -1,579.84 Displays the PRIN annunciator
and the principal paid in the first
year.
4 -13,894.67 Displays the INT annunciator
and the interest paid in the first
year.
4 178,42 0 .16 Di s p lays th e BAL annunciator
and the loan balance after one
year.

Time Value of Money Calculations 77
The amount paid toward interest and principal (13,894.67 + 1,579.84 = 15,474.51) equals
the total of 12 monthly payments (12 × 1,289.54 = 15,474.51). The remaining balance equals
the initial mortgage, less the amount applied toward principal (180,000 - 1,579.84 =
178,420 .16 ) .
Amortize the second year:
The amount paid toward interest and principal (13,767.79 + 1,706.69 = 15,474.51) equals the
total of 12 monthly payments (12 × 1,289.54 = 15,474.51). The remaining balance equals the
initial mortgage less the amount applied toward principal (180,000 - 1,579.84 - 1,706.69 =
176,713.49). More money is applied to principal during the second year rather than the first
year. The succeeding years continue in the same fashion.
Example: Amortizing a Single Payment
Amortize the 1st, 25th, and 54th payments of a five year car lease. The lease amount is 14,250
and the interest rate is 11.5%. Payments are monthly and begin immediately.
Set to Begin mode. Press \¯ if BEGIN annunciator is not displayed.
Table 6-20 Calculating the remaining balance
Keys Display Description
JDÆGY
\Ê
13 – 24 Displays PER and the next range of
periods.
4 -1,70 6.69 Displays PRIN and the principal
paid in the second year.
4 -13,767.79 D ispl ays INT and the interest paid
in the second year.
4 176 ,713. 49 D i sp l ays BAL and the loan balance
after 24 payments.
Table 6-21 Calculating the monthly payment
Keys Display Description
JG\Í 12.00 Sets payments per year.
V\Ú 60.00 Stores number of payments.
JJ7VÒ 11.50 Stores interest per year.
JYGV:Ï 14,250.00 Stores present value.
:É 0.00 Stores future value.

Time Value of Money Calculations78
Amortize the 1st, 25th, and 54th payments
Ì -310.42 Calculates the monthly payment.
Table 6-22 Calculating the amount
Keys Display Description
JÆ 1.00 Enters first payment.
\Ê 1 – 1 Displays PER and the amortized payment
period.
4 -310.42 Displays PRIN and the first principal
payment.
4 0.00 Displays INT and the interest.
4 13 ,939. 58 D i s p l a y s BAL and the loan balance after
one payment.
GVÆ 25.00 Enters payment to amortize.
\Ê 25 – 25 Displays PER and the amortized payment
period.
4 -220.21 Displays PRIN and the principal paid on
the 25th payment.
4 -90.21 Displays INT and the interest paid on the
25th payment.
4 9,193.28 Displays BAL and the balance after the
25th payment.
VYÆ 54.00 Enters payment to amortize.
\Ê 54 – 54 Displays PER and the amortized payment
period.
4 -290.37 Displays PRIN and the principal paid on
the 54th payment.
4 -20.05 Displays INT and the interest paid on the
54th payment.
4 1,8 01.57 D i sp l ays BAL and the balance after the
54th payment.
Table 6-21 Calculating the monthly payment
Keys Display Description

Time Value of Money Calculations 79
Interest Rate Conversions
The Interest Conversion application uses three keys: \Ó, \Ð, and
\Í. They convert between nominal and annual effective interest rates.
If you know an annual nominal interest rate and you wish to solve for the corresponding
annual effective rate:
1. Enter the nominal rate and press \Ó.
2. Enter the number of compounding periods and press \Í.
3. Calculate the effective rate by pressing \Ð.
To calculate a nominal rate from a known effective rate:
1. Enter the effective rate and press \Ð.
2. Enter the number of compounding periods and press \Í.
3. Calculate the nominal rate by pressing \Ó.
In the TVM application, \Ó and Ò share the same memory.
Interest conversions are used primarily for two types of problems:
• Comparing investments with different compounding periods.
• Solving TVM problems where the payment period and the interest period differ.
Investments With Different Compounding Periods
Example: Comparing Investments
You are considering opening a savings account in one of three banks. Which bank has the
most favorable interest rate?
First Bank
First Bank 6.70% annual interest, compounded quarterly
Second Bank 6.65% annual interest, compounded monthly
Third Bank 6.63% annual interest, compounded 360 times per year
Table 6-23 Calculating the interest rate (First bank)
Keys Display Description
S7j\Ó 6.70 Stores nominal rate.
Y\Í 4.00 Stores quarterly compounding
periods.

Time Value of Money Calculations80
Second Bank
Third Bank
First Bank offers a slightly better deal since 6.87 is greater than 6.86 and 6.85.
Compounding and Payment Periods Differ
The TVM application assumes that the compounding periods and the payment periods are
the same. Some loan installments or savings deposits and withdrawals do not coincide with
the bank’s compounding periods. If the payment period differs from the compounding period,
adjust the interest rate to match the payment period before solving the problem.
To adjust an interest rate when the compounding period differs from the payment period
complete the following steps:
1. Enter the nominal rate and press \Ó. Enter the number of compounding periods
in a year and press \Í. Solve for the effective rate by pressing \Ð.
2. Enter the number of payment periods in a year and press \Í. Solve for the
adjusted nominal rate by pressing \Ó.
\Ð 6.87 Calculates the annual effective rate.
Table 6-24 Calculating the interest rate (Second bank)
Keys Display Description
S7SV\Ó 6.65 Stores nominal rate.
JG\Í 12.00 Stores monthly compounding
periods.
\Ð 6.86 Calculates the annual effective rate.
Table 6-25 Calculating the interest rate (Third bank)
Keys Display Description
S7SD\Ó 6.63 Stores nominal rate.
DS:\Í 360.00 Stores compounding periods.
\Ð 6.85 Calculates the annual effective rate.
Table 6-23 Calculating the interest rate (First bank)
Keys Display Description

Time Value of Money Calculations 81
Example: Monthly Payments, Daily Compounding
Starting today, you make monthly deposits of 25 to an account paying 5% interest,
compounded daily (using a 365 day year). What will the balance be in seven years?
Step 1
Calculate the equivalent rate with monthly compounding.
Since NOM% and I/YR share the same memory, this value is ready for use in the rest of the
problem.
Step 2
Calculate the future value.
Set to Begin mode. Press \¯ if BEGIN annunciator is not displayed.
Table 6-26 Calculating the equivalent nominal percentage rate
Keys Display Description
V\Ó 5.00 Stores nominal percentage rate.
DSV\Í 365.00 Stores bank’s compounding
periods per year.
\Ð 5.13 Calculates annual effective rate.
JG\Í 12.0 0 St o res mon t hly perio d s.
\Ó 5.01 Calculates the equivalent
nominal percentage rate for
monthly compounding.
Table 6-27 Calculating the future value
Keys Display Description
:Ï 0.00 Stores present value
GVyÌ -25.00 Stores payment
j\Ú 84.00 Stores total number of payments
É 2,519.61 Calculates the balance after 7
years.
Time Value of Money Calculations82
Resetting the TVM Keys
Press ]OJ to clear the TVM registers. This sets N, I/YR, PV, PMT, and FV to zero
and briefly displays TVM CLR, followed by
the current value in P/Yr.

Depreciation 83
7Depreciation
On the 10bII+, depreciation calculations are performed using the functions printed in blue on
the keyboard located under the blue bracket titled, DEPRECIATION. Depreciation calculations
are based on data entered into the Time Value of Money (TVM) keys: Ï, É, Ò, and
Ù.
The Depreciation Keys
When entering data for depreciation calculations, results are calculated based on data
entered into specific memory registers. When pressed, the keys used for these operations:
• store data.
• enter known data for variables used during calculations.
• calculate unknown variables based on stored data.
Table 7-1 Depreciation keys
TVM Key Description
]OJ Clear TVM memory. Since the TVM and depreciation applications
share the same memory, clearing TVM resets depreciation also.
Ù The expected useful life of the asset in years.
Ï The depreciable cost of the asset at acquisition.
É The salvage value of the asset at the end of its useful life.
]{ Straight line is a method of calculating depreciation presuming an
asset loses a certain percentage of its value annually at an amount
evenly distributed throughout its useful life.
]x Sum-of-the-years' digits is an accelerated depreciation method.
In SOYD, the depreciation in year y is (Life-y +1)/SOY of the asset,
where SOY is the sum-of-the-years for the asset, or, for an asset with a
5-year life, 5+4+3+2+1=15.
]u Declining balance is an accelerated depreciation method that
presumes an asset will lose the majority of its value during the first few
years of its useful life.
Ò The declining balance factor as a percentage. This is used for
declining balance method.
\« With the calculated depreciation displayed, press \« to
display the remaining depreciable value at the end of the given year.

Depreciation84
To perform a depreciation calculation:
1. Enter the original cost of the asset, using Ï.
2. Enter the salvage value of the asset, using FV. If the salvage value is zero, press
:É.
3. Enter the expected useful life of the asset (in years), followed by Ù.
4. If the declining-balance method is being used, enter the declining-balance factor (as a
percentage), followed by Ò. For example, 1-1/4 times the straight-line rate — 125
percent declining-balance — would be entered as 125.
5. Key in the number of the year for which depreciation is to be calculated followed by the
desired depreciation method:
•]{ for depreciation using the straight-line method.
•]u for depreciation using the sum-of-the-years digits method.
•]x for depreciation using the declining-balance method.
]{, ]u, and ]x each place the amount of depreciation in the display,
and the TVM and X annunciators are displayed. Press \« to display the remaining
depreciable value (the book value less the salvage value). After pressing \« to
display the remaining depreciable value, note the X annunciator changes to Y.
Example 1
A metalworking machine, purchased for 10,000.00, is to be depreciated over five years. Its
salvage value is estimated at 500.00. Using the straight-line method, find the depreciation
and remaining depreciable value for each of the first two years of the machine's life. See
Table 7-2.
Table 7-2 Depreciation example using SL
Keys Display Description
]OJ TVM CLR (message flashes
then disappears) Clears TVM registers.
J::::Ï 10,000.00 Enters 10,000.00 for the depreciable cost
of the item in the selected format.
V::É 500.00 Enters 500.00 for the salvage value of
the item in the selected format.

Depreciation 85
Example 2
A machine was purchased for 4,000 and is to be depreciated over four years with a 1,000
salvage value. Using the sum-of-the-year's digit method, what is the depreciation during the
machine's first year and third years? What is the remaining depreciable value?
VÙ 5.00 Inputs 5 for the expected useful life of the
asset in the selected format.
J]{ 1,900.00 Enters the year for which depreciation is
to be calculated and calculates the
depreciation of the asset in year one.
TVM and X are displayed.
\« 7,600.00 Displays remaining depreciable value
after year one. X changes to Y in the
display.
G]{ 1,900.00 Enters the year for which depreciation is
to be calculated and calculates the
depreciation of the asset in year two.
\« 5,700.00 Displays remaining depreciable value
after year two.
Table 7-2 Depreciation example using SL
Keys Display Description
Table 7-3 Depreciation example using SOYD
Keys Display Description
]OJ TVM CLR (message flashes
then disappears) Clears TVM registers.
Y:::Ï 4,000.00 Enters the depreciable cost of the asset at
acquisition.
YÙ 4.00 Enters the expected useful life of the asset.
J:::É 1,000.00 Enters the salvage value.
J]x 1,200.00 Calculates the depreciation for the first year.
D]x 600.00 Calculates the depreciation for the third year.
\« 300.00 Displays the remaining depreciable value.

Depreciation86
Example 3
A machine was purchased for 5,000 and is to be depreciated over seven years with no
salvage value. Using the double declining balance method, what is the depreciation for the
first three years of the machine's life? What is the remaining depreciable value?
Table 7-4 Depreciation example using Declining Balance
Resetting the TVM Keys
To clear the TVM registers and reset the TVM and depreciation functions to their default
values, press ]O, followed by J. The messages, TVM CLR and 12 P _yr appear
briefly to indicate the TVM registers have been reset.
Keys Display Description
]OJ TVM CLR (message flashes
then disappears) Clears TVM registers.
V:::Ï 5,000.00 Enters the depreciable cost of the asset at
acquisition.
jÙ 7.00 Enters the expected useful life of the asset.
G::Ò 200.00 Enters the double declining balance factor as a
percentage.
:É 0.00 Enters the salvage value.
J]u 1,428.57 Calculates the depreciation for the first year.
G]u 1,020.41 Calculates the depreciation for the second year.
D]u 728.86 Calculates the depreciation for the third year.
\« 1,822.16 Displays the remaining depreciable value.

Cash Flow Calculations 87
8 Cash Flow Calculations
How to Use the Cash Flow Application
The cash flow application is used to solve problems where cash flows occur over regular
intervals. Problems with regular, equal, periodic cash flows are handled more easily using the
TVM keys. To operate the cash flow system, cash flow amounts and repeat values are keyed
in either individually or together. In the following chapter, the term repeat value is used to
describe the number of times a cash flow occurs. Terms such as cash flow count, number of
occurrences, or cash flow group are also used to describe the repeat value.
If a new cash flow is entered, the calculator auto-increments the current cash flow count by 1.
A value of 1 is automatically entered for a repeat value. To enter a repeat value for the current
cash flow entry, enter a value using \¥. To enter the cash flow and a repeat value
together, enter the cash flow value followed by Æ, then enter the repeat value followed by
¤.
In general, use the following steps for cash flow calculations on the HP 10bII+:
1. Organize your cash flows on paper. A cash flow diagram is useful.
2. Clear the cash flow memory.
3. Enter the number of periods per year.
4. Enter the amount of the initial investment (CF0) using ¤ to enter the cash flow value.
The CF0 value may have a repeated value. To enter the cash flow amount and repeat
value simultaneously, enter a cash flow amount, followed by Æ, then enter a number
for the repeat value followed by ¤.
5. Unless the cash flow and repeat value have already been entered as described in step 4
using Æ and ¤, as an alternative, enter the repeat value using \¥.
6. Repeat steps 4 and 5 for each cash flow and repeat value.
7. To calculate net present value and net future value, you must first enter a value for the
annual interest rate and press Ò; then press \½. With NPV calculated, press
\«to display Net Future Value.
8. To calculate IRR, press \Á.

Cash Flow Calculations88
Clearing the Cash Flow Memory
It is always a good idea to clear the cash flow memory before beginning. To clear cash flows,
use ]O:. A brief message appears, CFLO CLR, to indicate the cash flow memory
has been reset.
On the 10bII+, there is always space reserved for up to 15 cash flows. In addition, up to 30
additional cash flows may be stored in memory shared with the statistics memory, as shown
in Figure 1 below.
Table 8-1 Cash Flow Keys
Key Description
]O: Clears cash flow memory.
\Í Number of periods per year (default is 12). For annual cash flows, P/YR should
be set to 1; for monthly cash flows, use the default setting, 12.
number1 ¤Cash flows, up to 45. J identifies the cash flow number. When preceded by a
number, pressing ¤ enters a cash flow amount.
number1 Æ
number 2 ¤
Enter a cash flow amount, followed by Æ. Enter a number for the repeat
value followed by ¤. This enters cash flow amount and repeat value
simultaneously.
number 2 \¥ An alternative for entering repeat value for cash flow J .
v¤ Opens editor for reviewing or editing entered cash flows. Press 1 or
A to scroll through the cash flow data.
\Á Internal rate of return per year.
\½ Net present value.
\½\« Net future value.
]X With cash flow editor open, displays total of cash flows.
]U With cash flow editor open, displays total number of cash flows.
Cash Flow Calculations 89
Figure 1
As illustrated in Figure 1, if no more than 15 data points are stored in the statistics memory,
you may store up to 45 cash flows with the shared memory space.
If more than 15 data points are stored in the statistics memory, the total memory available for
storing cash flows is reduced. For example, in Figure 2, there are 25 data points stored, and
the amount of available shared memory has therefore decreased by 10 slots.
Figure 2
If data storage in the calculator memory resembles Figure 2, and you have a cash flow
calculation requiring more than 35 data points, clearing unneeded statistical information will
free up more space for information. When available memory is reached (see Figure 3), the
FULL annunciator indicates there is not enough space to continue saving data. If you attempt
to enter another cash flow at this point, the ERROR annunciator is displayed. In this case, no
additional cash flow data can be entered until some data in the statistics memory is removed
and the shared memory is once again available.
Figure 3
Example 1: A Short Term Investment
The following cash flow diagram represents an investment in stock over three months.
Purchases were made at the beginning of each month, and the stock was sold at the end of
the third month. Calculate the annual internal rate of return and the monthly rate of return.
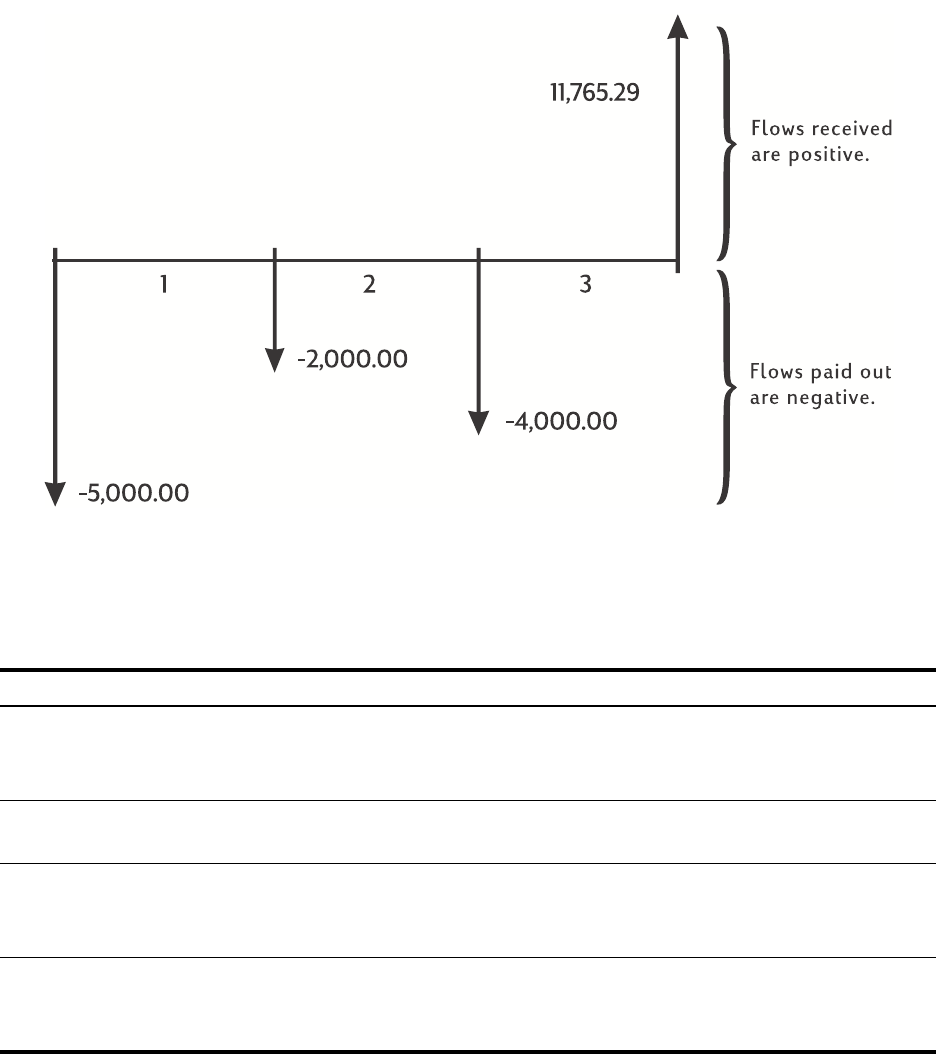
Cash Flow Calculations90
Calculating Internal Rate of Return
1. P r e s s ]O:, and store the desired number of periods per year in P/YR.
2. Enter the cash flows using Æ and ¤.
3. Press \Á.
Figure 4 Cash flow diagram (Investments in stock)
Table 8-2 Example 1: a short term investment
Keys Display Description
]O: CFLO CLR
(message flashes, then
disappears)
Clears cash flow memory.
JG\Í 12.00 Set payments per year.
V:::y¤ -5,000.00
(CF 0 flashes, then
disappears)
Enters initial cash flow. Note the
CFLO and CF annunciators.
G:::y¤ -2,000.00
(CF 1 flashes, then
disappears)
Enters first cash flow. Note the
CFLO and CF annunciators.

Cash Flow Calculations 91
NPV and IRR/YR: Discounting Cash Flows
Chapter 5 titled, Picturing Financial Problems demonstrates the use of cash flow diagrams to
clarify financial problems. This section describes discounted cash flows. The NPV, NFV and
IRR/YR functions are frequently referred to as discounted cash flow functions.
When a cash flow is discounted, you calculate its present value. When multiple cash flows
are discounted, you calculate the present values and add them together.
The net present value (NPV) function finds the present value of a series of cash flows. The
annual nominal interest rate must be known to calculate NPV.
The net future value (NFV) function finds the value of the cash flows at the time of the last cash
flow, discounting the earlier cash flows by the value set for the annual nominal interest rate.
The internal rate of return (IRR/YR) function calculates the annual nominal interest rate that is
required to give a net present value of zero.
The utility of these two financial tools becomes clear after working a few examples. The
next two sections describe organizing and entering your cash flows. Examples of NPV,
NFV, and IRR/YR calculations follow.
Organizing Cash Flows
The cash flow series is organized into an initial cash flow (CF0) and succeeding cash flow
groups (up to 44 cash flows). CF0 occurs at the beginning of the first period. A cash flow
group consists of a cash flow amount and the number of times it repeats.
For example, in the following cash flow diagram, the initial cash flow is -11,000. The next
group of cash flows consists of six flows of zero each, followed by a group of three 1,000
cash flows. The final group consists of one 10,000 cash flow.
Y:::y¤ -4,000.00
(CF 2 flashes, then
disappears)
Enters second cash flow. Note
the CFLO and CF annunciators.
JJjSV7Gd¤ 11, 7 6 5 . 2 9
(CF 3 flashes, then
disappears)
Enters third cash flow. Note the
CFLO and CF annunciators.
\Á 38.98 Calculates annual nominal yield.
aJG 3.25 Monthly yield.
Table 8-2 Example 1: a short term investment
Keys Display Description
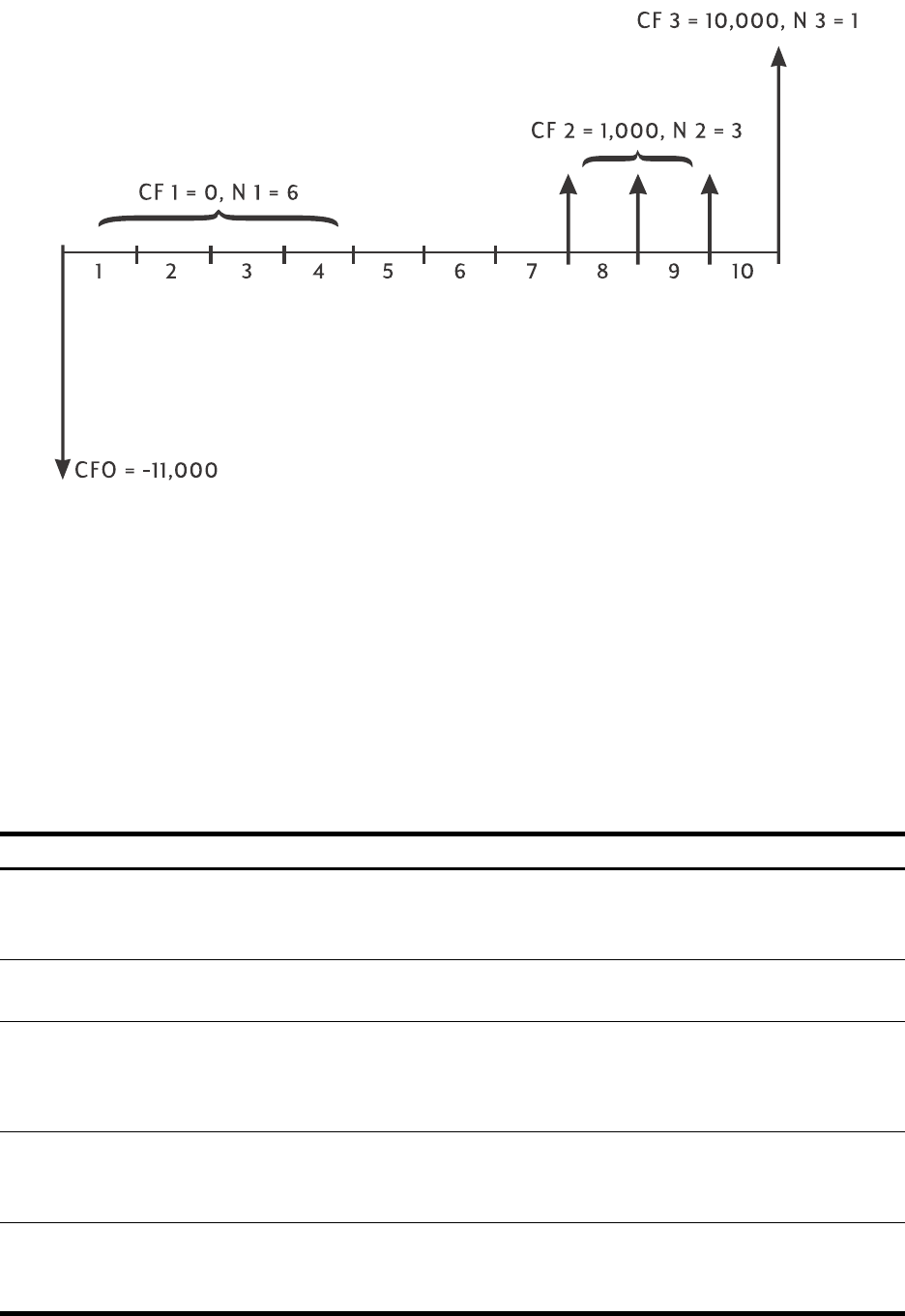
Cash Flow Calculations92
Figure 5 Initial cash flow and cash flow groups
Whenever you enter a series of cash flows, it is important to account for every period on the
cash flow diagram, even periods with cash flows of zero.
Example
Enter the cash flows from the preceding diagram and calculate the IRR/YR. Assume there are
12 periods per year.
Table 8-3 Example calculating IRR and effective interest rate
Keys Display Description
]O: CFLO CLR
(message flashes, then
disappears)
Clears cash flow memory.
JG\Í 12.00 Set payments per year.
JJ:::y¤ -11,000.00
(CF 0 flashes, then
disappears)
Enters initial cash flow. Displays
cash flow group number and
amount. Note the CFLO and CF
annunciators.
:¤ 0.00
(CF 1 flashes, then
disappears)
Enters first cash flow group
amount. Note the CF
annunciator.
S\¥ 6.00
(CFn 1 flashes, then
disappears)
Enters number of repetitions.
Note the CFLO and N
annunciators.

Cash Flow Calculations 93
Viewing and Editing Cash Flows
The cash flow editor application allows you to review entered data quickly to ensure accuracy.
In addition, you may edit, add, or delete cash flow data as needed.
1. P r e s s v¤ to open the editor. The current repeat value and the current cash flow
value are displayed. The CFLO annunciator appears, and either CF or N identifies which
value is being displayed.
2. Press 1 to move up through the current cash flow information. When you pass the
maximum of the data, an empty cash flow pair is displayed before wrapping around to
CF0, provided there is enough memory for another cash flow pair to be entered.
3. Press A to move down through the current cash flow information. At CF0 the display
wraps around to the maximum cash flow pair count.
4. At any time with the editor open, press ¤ to return to CF0. To jump to a specific cash
flow, type the desired whole number of the desired cash flow item, J, and press ¤.
The editor jumps to that position. If the number is higher than your maximum current
cash flow item count, it will place you at the highest cash flow value. If an invalid entry
is typed, such as a negative number or a non-whole number, the editor remains in its
current location.
5. To delete the current cash flow pair, press a. To add a new cash flow with a value of
0 and a repeat value of 1 before the currently displayed item, press P.
J:::¤ 1,000.00
(CF 2 flashes, then
disappears)
Enters second cash flow group
amount. Note the CFLO and CF
annunciators.
D\¥ 3.00
(CFn 2 flashes, then
disappears)
Enters number of repetitions.
Note the CFLO and N
annunciators.
J::::¤ 10,000.00
(CF 3 flashes, then
disappears)
Enters third cash flow. Note the
CFLO and CF annunciators.
\Á 21.22 Calculates the annual nominal
yield.
Table 8-3 Example calculating IRR and effective interest rate
Keys Display Description

Cash Flow Calculations94
6. To replace the currently displayed value, simply type a new number and press Æ.
Only valid entries are accepted. If you type an invalid entry, such as a value of 0 for the
count, the ERROR annunciator appears and the value is rejected.
7. To clear the current cash flow or repeat value without removing the entire pair, press
|. If the cash flow amount is displayed, it will be set to a value of 0. If the cash flow
repeat value is displayed, it will be set to a value of 1.
8. To view the current cash flow total, press ]X. To view the current total number of
cash flows, press ]U.
9. Press M to exit.
After completing the last example, open the cash flow list and modify the following cash flows
with the data in the table below. Calculate the new IRR/YR.
Table 8-4 Enter the new data
Cash Flow Group New Cash Flow Amount New Cash Flow Count
CF 0 -11,000.00 1
CF 1 0 3
CF 2 1,000.00 2
CF 3 7,500.00 2
CF 4 -1,200.00 2
Table 8-5 Editing cash flows
Keys Display Description
v¤ 0 -11,000.00 Open the cash flow list,
starting with the initial cash
flow CF0.
J¤1 1 6.00 Jumps to the group, CF1
,
and the repeat value, 6.00.
DÆ 1 3.00 Inputs new repeat value,
3.00, for CF1
.
11GÆ 2 2.00 Displays cash flow repeat
value and inputs new repeat
value for CF2.
D¤ 3 10,000.00 Displays the group, CF3,
and the cash flow amount,
10,000.00.

Cash Flow Calculations 95
Calculating Net Present Value and Net Future Value
The net present value (NPV) function is used to discount all cash flows to the front of the time
line using an annual nominal interest rate that you supply.
To calculate NPV or NFV:
1. P r e s s ]O: and store the desired number of periods per year in P/YR.
2. Enter the cash flow data.
3. Store the annual nominal interest rate in I/YR and press \½.
4. If you have just calculated NPV, press \« to calculate NFV.
Example: A Discounted Contract, Uneven Cash flows
You have an opportunity to purchase a contract with the following cash flows:
jV::Æ1GÆ 3 2.00 Inputs new cash flow
amount and repeat value.
Displays the new repeat
value, 2.00, for CF3.
1JG::yÆ1G
Æ
4 is displayed first, with
no value followed by
4 -1,200, then 4 2.00
Inputs new cash flow, CF4,
and repeat value.
]X 3,600.00 Displays total of the cash
flows.
M0.00 Exit the editor.
\Á 58.97 Calculate the new annual
yield.
Table 8-5 Editing cash flows
Keys Display Description
Table 8-6 Example of a contract with uneven cash flows
End of Month Amount
45,000.00
95,000.00
10 5,000.00
15 7,500.00
25 10,000.00
Cash Flow Calculations96
How much should you pay for the contract if you wish to yield a yearly rate of 15% on your
investment?
Figure 6 Cash flow diagram (Calculate the amount)
The following example uses the Æ and ¤ keys to enter the cash flow amount and repeat
value simultaneously. When the cash flow count is 1 for a given cash flow amount, the cash
flow amount may be entered simply by pressing the amount followed by ¤, as the default
for the count is 1. However, when using the Æ key to enter the cash flow amount, you must
then follow Æwith the repeat value followed by ¤, even if the repeat value is 1. This
process is shown here to demonstrate this application and for consistency with entering the
data for the example.
Table 8-7 Entering uneven cash flows
Keys Display Description
]O: CFLO CLR
(message flashes,
then disappears)
Clear cash flow memory.
JG\Í 12.00 Set payments per year.
:ÆY¤ 4.00
(CFn 0 flashes, then
disappears)
Input initial cash flow of zero and
the repeat value.
V:::ÆJ¤ 1. 0 0
(CFn 1 flashes, then
disappears)
Input second cash flow amount and
repeat value. Note the N
annunciator.
:ÆY¤ 4.00
(CFn 2 flashes, then
disappears)
Input third cash flow amount and
repeat value.
V:::ÆG¤ 2.00
(CFn 3 flashes, then
disappears)
Input fourth cash flow amount and
repeat value.

Cash Flow Calculations 97
The cash flows that describe your prospective investment are now in the calculator. Press
v¤. Press 1 or A to scroll through the list and verify the cash flows and the
repeat value is entered correctly. Press M to exit.
Now that you have entered the cash flows, store the interest rate and calculate the net present
value and net future value.
Table 8-8 Calculating NPV and NFV
This result shows that if you want a yield of 15% per year, you should pay 27,199.92 for the
contract. Notice that this amount is positive. The net present value is simply the summed (or
netted) value of a series of cash flows when they are discounted to the front of the time line.
:ÆY¤ 4.00
(CFn 4 flashes, then
disappears)
Input fifth cash flow amount and
repeat value.
jV::ÆJ¤ 1. 0 0
(CFn 5 flashes, then
disappears)
Input sixth cash flow amount and
repeat value.
:Æd¤ 9.00
(CFn 6 flashes, then
disappears)
Input seventh cash flow amount and
repeat value.
J::::ÆJ¤ 1. 0 0
(CFn 7 flashes, then
disappears)
Input eighth cash flow amount and
repeat value.
Keys Display Description
JVÒ 15.00 Store annual interest rate
\½ 27,199.92 Calculate net present value of
stored cash flows.
\« 37,105.94 Calculate NFV of stored cash
flows.
Keys Display Description
Cash Flow Calculations98
Figure 7 Cash flow diagram (Calculates NPV)
Automatic Storage of IRR/YR and NPV
When you calculate NPV, the result is stored in PV for your convenience. To recall that result,
press vÏ. If you haven’t changed the TVM values from the last example using NPV,
when you press vÏ the result is 27,199.92. When you calculate IRR/YR, the result is
stored in I/YR. Press vÒ to display the annualized yield. More examples of NPV, NFV
and IRR/YR calculations can be found in the chapter 13 titled, Additional Examples.

Calendar Formats and Date Calculations 99
9 Calendar Formats and Date Calculations
Calendar Format
The calendar options for bonds and date calculations are Actual (ACT) and 360. Press
]Å to toggle between these options. The default setting, Actual, is based on a 365-
day calendar. The alternate setting, 360, is based on a 360-day calendar. It is important to
note date and bond calculations return different values for each of these settings, so verify the
calendar mode is appropriate for your problem before you begin.
Table 9-1 Date and Calendar Keys
Date Format
The valid range of dates for the calendar functions of the HP 10bII+ is October 15, 1582
through December 31, 9999. For the date, the number of days between two dates, and bond
calculations, dates may be entered and displayed either in month-day-year (M.DY) or day-
month-year (D.MY) formats. In addition to a different display mode for the date and date
calculations, these functions also return different values based on the 365-day (ACT) and 360-
day (360) calendars.
Press ]È to toggle between the formats. The default setting is day-month-year
(dd.mmyyyy).
Press ]Å to toggle between the 360-and 365-day (actual) calendars.
To specify the number of displayed decimal places:
1. P r e s s \5.
Keys Description
]È Enters dates in DD.MMYYYY or MM.DDYYYY formats. D.MY is the default.
Numbers at the far right of a calculated date indicate days of the week. 1
is for Monday; 7 is for Sunday.
]Å Toggles between 360-and 365-day (Actual) calendars.
\Ç Calculates the date and day, past or future, that is a given number of days
from a given date. Note the returned result is
always
calculated on the
365-day calendar (Actual), regardless of the calendar setting.
\Ä Calculates the number of days between two dates. Based on your current
setting, returned result is calculated on either the 365-day (Actual) or the
360-day calendar.
Calendar Formats and Date Calculations100
2. Enter the number of digits : through d that you wish to appear after the decimal
point. To view the entire date, press S. For more information on changing the number
display, refer to the section titled, Specifying Displayed Decimal Places in chapter 2.
To key in a date in M.DY format:
1. Key in one or two digits for the month.
2. Press 7.
3. Key in two digits for the day.
4. Key in four digits for the year.
5. Press either \Ç or \Ä to display the date in the selected number
display format.
To key in a date in D.MY, press ]È until the D.MY annunciator appears.
1. Key in one or two digits for the day.
2. Press 7.
3. Key in two digits for the month.
4. Key in four digits for the year.
5. Press either \Ç or \Ä to display the date in the selected number
display format.
Using the INPUT key
You can also enter dates for date calculations and the number of days using Æ.
To enter a date in M.DY format using Æ:
1. Key in one or two digits for the month.
2. Press 7.
3. Key in two digits for the day.
4. Key in four digits for the year.
5. Press Æ.
For more information about using the data and number of days functions as in-line functions,
or with the Æ key, see the examples below and refer to the section titled, In-Line Functions
in chapter 2.
Calendar Formats and Date Calculations 101
Date Calculations and Number of Days
To calculate the date and day, past or future, that is a given number of days from a given date
as an in-line function:
1. Key in the given date and press \Ç.
2. Key in the number of days.
3. If the other date is in the past, press y.
4. Press 4 to display the date in the selected number display format.
To calculate the date and day, past or future, that is a given number of days from a given date
using Æ:
1. Key in the given date and press Æ.
2. Key in the number of days.
3. If the other date is in the past, press y.
4. Press \Ç to display the date in the selected number display format.
Regardless of the setting for displayed places after the decimal point, or whether you use
Æ or the in-line feature, the answer calculated by the \Ç function is displayed in
a special format. The numbers of the month, day, and year (or day, month, and year) are
separated by digit separators. The digit at the right of the displayed answer indicates the day
of the week: 1 is for Monday; 7 is for Sunday.
Date Calculation
Example 1
What is the date 100 days after December 18, 2011? Press ]È if the D.MY
annunciator is displayed. Calculate this example using the date feature as an in-line function
and with the Æ key.

Calendar Formats and Date Calculations102
To enter the data for this example using the Æ key:
Number of Days
Use the \Ä function to calculate the number of days between two dates.
1. Key in the earlier date and press \Ä.
2. Key in the later date and press \Ä to calculate the number of days between the
two dates in actual days.
Example 1
How many days remain in the 2010 fiscal year if today's date is June 4, 2010? Assume the
fiscal year ends on October 31st, and you wish to calculate the actual number of days (Actual)
using the D.MY format. Press ]Å if the 360 annunciator is displayed. Calculate the
example as an in-line function.
Table 9-2 Date calculation example as an in-line function
Keys Display Description
JG7JgG:JJ 12.182011_ Keys in the date in MM.DDYYYY
format.
\ÇJ::4 3-27-2012 2 Calculates the date.
Table 9-3 Date calculation example using the ‘INPUT’ key
Keys Display Description
JG7JgG:JJ 12.182011_ Keys in the date in MM.DDYYYY
format.
ÆJ::\Ç 3-27-2012 2 Returns the same results using the
Æ key.

Calendar Formats and Date Calculations 103
Example 2
How many days are there between October 17, 2012 and June 4, 2015? Use the M.DY setting
and compute the number of days in Actual (Act) mode. Press ]Å if the 360
annunciator is displayed; press ]È if the D.MY annunciator is displayed. Calculate
this example using the number of days feature as an in-line function and also with the Æ
key.
Table 9-4 Calculating the actual number of days as an in-line function
Keys Display Description
]È 0.00 Sets the desired date format.
Note the D.MY annunciator.
]Å 0.00 Sets the desired calendar
format, in this case, actual days
(optional if the 360 annunciator
is not displayed, as Actual is the
default).
\5S 0.000000 Sets the number of displayed
decimal places so the entire
date is displayed (optional).
Y7:SG:J:\Ä 4.062010 Inputs the starting date in the
selected format.
DJ7J:G:J: 4149.000000 Inputs the ending date in the
selected format and calculates
the number of actual days
between the starting and ending
dates.
\5G 149.00 Returns the number of displayed
decimal places to the default
(optional).
Table 9-5 Calculating the actual number of days as an in-line function
Keys Display Description
J:7JjG:JG 10.172012_ Keys in the date in
MM.DDYYYY format.
\ÄS7:YG:JV4 960.00 Calculates the days between
based on the 360-day
calendar.

Calendar Formats and Date Calculations104
Using the Æ key:
Table 9-6 Calculating the actual number of days using the ‘INPUT’ key
Keys Display Description
M0.00 Clear display.
J:7JjG:JGÆ 10.17 Keys in the date in MM.DDYYYY
format and displays digits in the
selected display format (2).
S7:YG:JV\Ä 960.00 Returns the same results.

Bonds 105
10 Bonds
The Bond Keys
On the 10bII+, bond calculations are based on data or settings stored in the ten keys which
make up the top two rows of the keyboard. The functions used in bond calculations are printed
in blue above the keys on the keyboard. To access the bond functions, press ] followed
by the desired function. See the table below for a description of the bond keys.
Bond calculations, primarily calculating bond price and yield, are performed by two keys,
]Ñ and ]Ô.
Table 10-1 Bond keys
Keys Description
]Oj Clears bond memory.
]Û Calculates accrued interest only.
]Ô Yield% to maturity or yield% to call date for given price.
]Ñ Price per 100.00 face value for a given yield.
]Î Coupon rate stored as an annual %.
]Ë Call value. Default is set for a call price per 100.00 face value. A bond at maturity
has a call value of 100% of its face value.
]È Date format. Toggle between day-month-year (dd.mmyyyy) or month-day-year
(mm.ddyyyy).
]Å Day count calendar. Toggle between Actual (365-day calendar) or 360 (30-day
month/360-day year calendar).
]Â Bond coupon (payment). Toggle between semiannual and annual payment
schedules.
]¾ Settlement date. Displays the current settlement date.
]° Maturity date or call date. The call date must coincide with a coupon date. Displays
the current maturity.

Bonds106
When entering data for bond calculations, results are calculated based on data entered into
specific memory registers. When pressed, the keys used for these operations:
• store data.
• enter data for variables used during calculations (input only).
• calculate unknown variables based on stored data.
Most of the other keys used in bond calculations allow you to enter data for a variable, but
you cannot solve for that variable. The exception is the ]Û key. This key permits you
to return results for accumulated interest, but you cannot enter data into this key.
Before you perform a bond calculation, be sure to verify the date format is set appropriately
for your problem. The default setting is mm.ddyyyy, but it can be set for dd.mmyyyy. For more
information about entering dates and date formats, see chapter 9, Calendar Formats and
Date Calculations. The range of acceptable dates is October 15, 1582 to December 31, 9999.
Verify that bond day counts (360/365) and annual or semiannual coupon payment schedules
are appropriate for your problem prior to inputting your data.
Example 1
What price should you pay on April 28, 2010 for a 6.75% U.S. Treasury bond maturing on
June 4, 2020, if you want a yield of 4.75%? Assume the bond is calculated on a semiannual
coupon payment on an actual/actual basis. If D.MY is displayed, press ]È before
beginning. See Table .
Table 10-2 Bond calculation example
Keys Display Description
]Oj BOND CLR
(message flashes, then
disappears)
Clears bond memory.
]Â 0.00 Selects semiannual coupon payment, as
required by the example. Note the
annunciator in the display.
Y7GgG:J:
]¾
4-28-2010 3 Inputs April 28, 2010 for the settlement
date (mm.ddyyyy format). Note: the 3 in
the far right of the display indicates the
day of the week. This number indicates
the day of the week corresponding to
that date. Monday
is 1, and Sunday is 7. April 4, 2010 is a
Wednesday.

Bonds 107
Example 2
A bond has a call provision at 104 and a coupon rate of 5.5%. If the bond matures on
October 15, 2020 and is presently selling at 101, what is the yield-to-call on April 15, 2012?
Assume the bond is calculated on a semiannual coupon payment on an actual/actual basis.
S7:YG:G:
]°
6-4-2020 4 Inputs June 4, 2020 for the maturity date.
S7jV]Î 6.75 Inputs 6.75% for the value for CPN%.
J::]Ë 100.00 Inputs call value. Optional, as default is
100. Note: if Call requires another value,
key in the number followed by
]Ë.
Y7jV]Ô 4.75 Inputs 4.75% for Yield%.
]Ñ 115.89 Calculates the price.
1]Û 2.69 Displays the current value for accrued
interest.
4118.58 Returns the result for total price (value of
price + value of accrued interest). The
net price you should pay for the bond is
118 . 5 8 .
Table 10-2 Bond calculation example
Keys Display Description
Table 10-3
Keys Display Description
]Oj BOND CLR
(message flashes, then
disappears)
Clears bond memory.
V7V]Î 5.50 Inputs coupon rate as an annual%.
J:Y]Ë 104.00 Inputs call value.
J:J]Ñ 101.00 Inputs price.
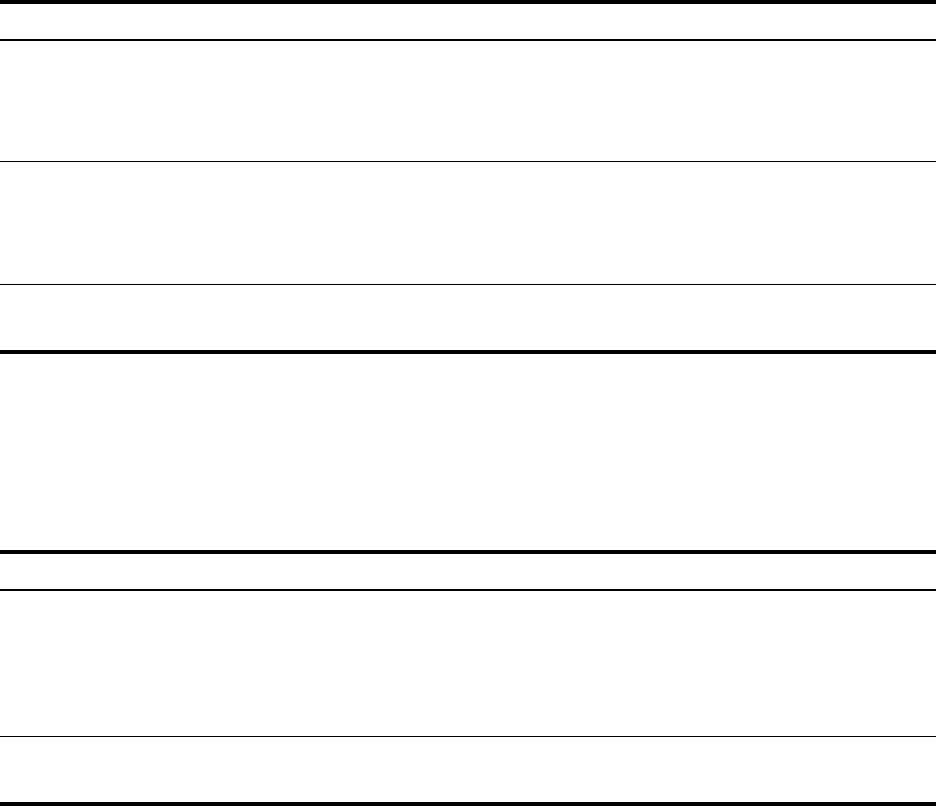
Bonds108
Continuing with the same bond problem, assume the bond will not be called. What is the
expected yield to maturity?
Resetting the bond keys
To reset the Bond keys to their default values, press ]Oj. The message, BOND CLR
flashes briefly on the screen to indicate the bond registers have been reset. To return to the
default calculator screen, press M.
J:7JVG:G:
]°
10-15-2020-4 Inputs October 15, 2020 for the
maturity date.
Y7JVG:JG
]¾
4-15-2012-7 Inputs April 15, 2012 for the
settlement date.
]Ô 5.72 Calculates yield as a %.
Table 10-4
Keys Display Description
J::]Ë 100.00 Inputs new call value. Since the
bond will not be called, the bond
at maturity has a call value of
100% of its face value.
]Ô 5.35 Calculates new yield%.
Table 10-3
Keys Display Description

Break-even 109
11 B r e a k - e v e n
The break-even function allows you to study problems involving a profit, when a quantity of
items, with a cost to manufacture and a fixed price to develop and market, is sold at a given
price. On the 10bII+, break-even calculations are performed using the functions printed in
blue on the keyboard located under the blue bracket titled, BREAKEVEN. Break-even
calculations are based on data entered into these keys, which are listed in the table below:
The Break-even Keys
When entering data for break-even calculations, results are calculated based on data entered
into specific memory registers. When pressed, the keys used for these operations:
• store data.
• enter known data for variables used during calculations.
• calculate unknown variables based on stored data.
Table 11-1 Break-even keys
Key Description
]OY Clears break-even memory.
]¬ Stores the quantity of units required for a given profit or calculates it.
]© Stores the sales price per unit or calculates it.
]¦ Stores variable cost per unit for manufacturing or calculates it.
]£ Stores the fixed cost to develop and market or calculates it.
]~ Stores the expected profit or calculates it.

Break-even110
Example 1
The sale price of an item is 300.00, the cost is 250.00, and the fixed cost is 150,000.00.
How many units would have to be sold to make a profit of 10,000.00?
Table 11-2 Break-even example
Keys Display Description
]OY BK EV CLR
(message flashes, then
disappears)
Clears break-even memory.
JV::::]£ 150,000.00 Inputs fixed cost.
GV:]¦ 250.00 Inputs variable cost per unit.
D::]© 300.00 Inputs price.
J::::]~ 10,000.00 Inputs profit.
]¬ 3,200.00 Calculates the current value for the
unknown item, UNITS.

Break-even 111
Example 2
What is the estimated maximum fixed cost you can afford to manufacture 10,000 water filters,
if your desired selling price is 45.00? Assume the cost per unit is 23.00. Since you want to
calculate the maximum fixed cost, your profit for the purpose of the example will be 0.00.
Table 11-3 Calculating the projected maximum fixed cost
Keys Display Description
]OY BK EV CLR
(message flashes, then
disappears)
Clears break-even memory.
J::::]¬ 10,000.00 Inputs the projected number of units.
YV]© 45.00 Inputs the projected selling price.
GD]¦ 23.00 Inputs the variable cost per unit.
:]~ 0.00 Inputs the profit, in this case, 0.
]£ 220,000.00 Calculates the maximum projected
fixed cost to develop and market the
water filter.
Break-even112
Resetting the Break-even keys
To reset the break-even keys to their default values, press ]OY. A brief message
flashes on the screen to indicate the break-even registers have been reset. To return to the
default calculator screen, press M.

Statistical Calculations 113
12 Statistical Calculations
The 10bII+ allows you to enter data for one- and two-variable statistics easily. Once data is
entered, you can use the statistical functions to calculate the following:
• Mean and standard deviation
• Regression statistics or a best fit
• Estimation and forecasting
• Weighted mean
• Summation statistics: n, x, x2, y, y2, and xy.
Table 12-1 Statistics keys
Keys Description
\t Clear statistics memory.
x-value ¡ Enter one-variable statistical data.
x-value \¢ Delete one-variable statistical data.
x-valueÆ y-value ¡ Enter two-variable statistical data.
x-value Æ y-value \¢ Delete two-variable statistical data.
v¡ Opens editor for reviewing or editing statistical data.
\k\« Means of x and y.
\T\« Mean of x weighted by y. Also calculates b coefficient.
\h\« Sample standard deviations of x and y.
\e\« Population standard deviations of x and y.
\Z\« Estimation of x. Also calculates r correlation coefficient.
\W\« Estimation of y. Also calculates slope and m coefficient.
]L Permits selection of six regression models or a best fit. Default is
linear.
Σ
Σ
Σ
Σ
Σ
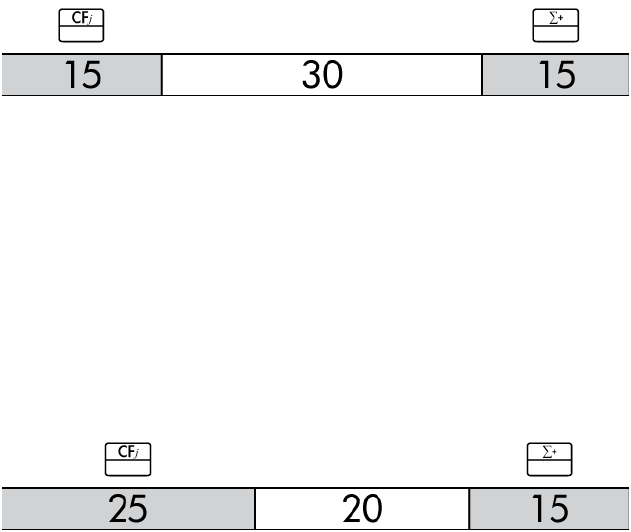
Statistical Calculations114
Clearing Statistical Data
Clear the statistical data before entering new data. If you don't clear the statistical data, new
information stored will be added to the current calculations. To clear all statistical data, press
\t. The message STAT CLR flashes briefly and the display is cleared. The regression
model is also reset to its default setting, LINEAR.
Entering Statistical Data
The 10bII+ uses a combination of list-based and register-based statistics when storing
statistical data. List-based statistics store every value and permit you to review and edit entered
data. Register-based statistics accumulate information, but you cannot easily edit or review
this information.
On the 10bII+, there is always space reserved for up to 15 data points. In addition, up to 30
additional data points may be stored in memory shared with the cash flow memory. See
Figure 1.
Figure 1
As illustrated in Figure 1, if no more than 15 cash flows are stored in the cash flow memory,
you may store up to 45 data points for statistical usage.
If more than 15 cash flows are stored in the cash flow memory, the total memory available for
storing statistical data is reduced. For example, in Figure 2, there are 25 cash flows stored,
and the amount of available shared memory has therefore decreased by 10 slots.
Figure 2
If data storage in the calculator memory resembles Figure 2, and you have a statistical
calculation requiring more than 35 data points, clearing unneeded cash flow information will
free up more space for information. If there are more data points than available memory, the
10bII+ automatically switches to register-based statistics to allow continued work. When
available memory is reached, the FULL annunciator indicates there is not enough space to
continue saving data. See Figure 3.

Statistical Calculations 115
Figure 3
When the calculator switches to register-based mode, some key points to consider:
• You may enter an unlimited number of data points.
• The statistics editor, accessed with v¡, is not available.
•While use of \¢ is allowed, viewing previously entered data is not possible.
• The only regression mode available is a linear regression.
One-Variable Statistics
To enter x-data for one-variable statistics complete the following steps:
1. Clear the statistical registers by pressing \t.
2. Enter the first value and press ¡. The HP 10bII+ displays n, the number of items
accumulated.
3. Continue accumulating values by entering the numbers and pressing ¡. The n-value
is increased with each entry.
Two-Variable Statistics and Weighted Mean
To enter x,y pairs of statistical data complete these steps:
1. Clear the statistical registers by pressing \t.
2. Enter the first x-value and press Æ. The HP 10bII+ displays the x-value.
3. Enter the corresponding y-value and press ¡. The HP 10bII+ displays n, the number
of pairs of items accumulated.
4. Continue entering x,y pairs. The n-value is increased with each entry.
To enter data for calculating the weighted mean, enter each data value as x, and its
corresponding weight as y in the statistics memory. Press \T to calculate the weighted
mean.

Statistical Calculations116
Viewing and Editing Statistical Data
1. P r e s s v¡to open the editor. The number of items accumulated, n, is displayed,
along with the current x-or y-value. The STAT annunciator appears, and the X or Y
identifies the displayed value.
2. Press 1to move up through the current statistical data. When you pass the maximum
of the data, an empty statistical pair displays before wrapping back to x1
, provided
there is enough memory for more data.
3. Press A to move down through the current statistical data. At x0, the display wraps
back to the maximum y-value.
4. At any time with the editor open, press ¡ to return to x1
. To jump to a specific data
pair, type the whole number which represents the pair’s n-value and press ¡. The
editor will jump to that data pair, unless your entered number is higher than your
maximum data pair, in which case it will jump to the highest x-value. If you type in an
invalid number, such as a negative number, or a non-whole number, the editor remains
in its current position.
5. To delete the currently displayed statistical data pair, press a. To add a new pair
with the x- and y-values equal to zero, press P.
6. To replace the currently displayed value, simply type in the new number and press
Æ.
7. To clear the currently displayed x-or y-value without removing the entire pair, press |
to set the value to 0.
8. Press M to exit the editor.
Example 1
A tropical beach resort has been having some very hot weather lately. A manager at the
beach resort has noticed an increase in the number of cold drinks sold during hot days and
wants to be able to predict how many employees are needed to sell drinks tomorrow. Each
employee can sell 200 drinks a day at most.
Table 12-2 Data
Past 3 Days
Temperature (Celsius) Cold Drinks Sold
32 415
35 515
38 725

Statistical Calculations 117
At what temperature would the manager predict to sell 800 drinks? How many employees
will be needed for tomorrow's predicted temperature of 43oC?
Continuing with this example, modify this data by adding more points: two additional days
of sales and their corresponding temperatures. The first day’s temperature of 43oC resulted in
the sale of 1,023 cold drinks. The next day’s temperature at 37oC resulted in the sale of 685
drinks.
Table 12-3 Example entering statistical data, opening the editor, and predicting
Keys Display Description
\t STAT CLR
(message flashes briefly,
then disappears)
Clears the statistics memory.
DGÆYJV¡ 1.00 Enters first ordered pair.
DVÆVJV¡ 2.00 Enters the second ordered pair.
DgÆjGV¡ 3.00 Enters the third ordered pair.
v¡ 1 32.00 Open the editor. Displays X
annunciator.
11111 3 725.00 Scroll and verify the data points,
starting with the x-value of the
first pair. The y-value of the third
pair is displayed.
M Exit the editor.
]LY 0.00 Set the regression model to
power. 4–POWER flashes briefly
after Y is pressed, then
disappears.
g::\Z 39.49 Predict the temperature.
\«\5d .988080878 Display the correlation
coefficient.
YD\W\5G 1,053.49 Predict the number of drinks sold
tomorrow.
aG::4 5.27 Manager should have at least 6
employees at work tomorrow to
cover the expected load.

Statistical Calculations118
After modifying the data, predict the next day’s activity at a record 45oC.
Table 12-4 Adding more data
Keys Display Description
YDÆJ:GD¡ 4.00 Enters fourth ordered pair.
DjÆSgV¡ 5.00 Enters fifth ordered pair.
Table 12-5 A new prediction
Keys Display Description
YV\W 1,204. 67 Predicts the drinks sold at 45oC.
But is this the best fit?
]L: 0.00 Sets regression mode to 0-BEST
FIT.
YV\W 1,128.12 All regressions are calculated
and LINEAR is selected as being
a better fit than POWER. The
result, 1128, is well within the
limit of six employees.

Statistical Calculations 119
Summary of Statistical Calculations
The STAT annunciator indicates that a statistical calculation was performed. Some functions
return two values. In this instance, the X annunciator is displayed along with STAT. Press
\« to see the second value. In this case, the X annunciator changes to a Y, indicating
the second value is being displayed.
Table 12-6 Statistical calculations that return two values
Keys Description
\«Displays:
\k Arithmetic mean (average) of the x-values. Mean (average) of the y-values if
you entered y-data.
\h Sample standard deviation of the x-values.
NOTE: The sample standard deviation
assumes that the data is a sampling of a
larger, complete set of data. The population
standard deviation assumes that the data
constitutes the entire population.
Sample standard deviation of the y-
values if you entered y-data.
NOTE: The sample standard
deviation assumes that the data is a
sampling of a larger, complete set of
data. The population standard
deviation assumes that the data
constitutes the entire population.
\e Population standard deviation of the x-values.
NOTE: The sample standard deviation
assumes that the data is a sampling of a
larger, complete set of data. The population
standard deviation assumes that the data
constitutes the entire population.
Population standard deviation of the
y-values if you entered y-data.
NOTE: The sample standard
deviation assumes that the data is a
sampling of a larger, complete set of
data. The population standard
deviation assumes that the data
constitutes the entire population.
y-value \Z Estimate of x for a given value of y. Correlation coefficient.
NOTE: The correlation coefficient is
a number in the range -1 through +1
that measures how closely the data
fits the calculated line. A value of +1
indicates a perfect positive
correlation, and -1 indicates a
perfect negative correlation. A value
close to zero indicates the line is a
poor fit.
x-value \W Estimate of y for a given value of x.Coefficient m of the current
regression.
\T Mean of the x-values weighted by the y-
values. Coefficient b of the current
regression.

Statistical Calculations120
Mean, Standard Deviations, and Summation Statistics
You can calculate the mean ( ), sample standard deviation (Sx), and population standard
deviation ( x), and summation statistics, n, x, and x2
of x-data. For x,y data, you can also
calculate the mean, sample standard deviation, and population standard deviation of the y-
data and the summation statistics y, y2
, and xy.
Example 2
A yacht captain wants to determine how long it takes to change a sail. She randomly chooses
six members of her crew, observes them as they carry out the sail change, and records the
numbers of minutes required: 4.5, 4, 2, 3.25, 3.5, 3.75. Calculate the mean and sample
standard deviation of the times. Also, calculate the root mean square, using the formula,
.
Table 12-7 Example calculating mean, standard deviation, and summation statistics
Keys Display Description
\t STAT CLR
(message flashes briefly,
then disappears)
Clears statistics memory.
Y7V¡ 1.00 Enters first time.
Y¡ 2.00 Enters second time.
G¡ 3.00 Enters third time.
D7GV¡ 4.00 Enters fourth time.
D7V¡ 5.00 Enters fifth time.
D7jV¡ 6.00 Enters sixth time
\k 3.50 Calculates the mean.
\h 0.85 Calculates the sample standard
deviation.
]l 77.13 Displays .
a][ 6.00 Displays n.
4\B 3.59 Calculates the root mean
square.
x
σ
Σ
Σ
Σ
Σ
Σ
x2n⁄
∑
Σx2
Statistical Calculations 121
The standard deviations calculated by \h and \h\« are the sample
standard deviations. They assume that the data is a sampling of a larger, complete set of data.
If the data constitutes the entire population, the true population standard deviations can be
calculated by pressing \e and \e\«.
Example 3
The coach has four new players on the team with heights of 193, 182, 177, and 185
centimeters and weights of 90, 81, 83, and 77 kilograms. Find the mean and population
standard deviation of both their heights and weights, then sum the y-data.
Linear Regression, Estimation, and Regression Modes
Linear regression is a statistical method for estimation and forecasting. It is used to find a
straight line that best fits a set of x,y data. There must be at least two different x,y pairs. The
straight line provides a relationship between the x- and y-variables: y = mx + b, where m is the
slope and b is the y-intercept.
Table 12-8 Example 3
Keys Display Description
\t STAT CLR
(message flashes briefly,
then disappears)
Clears statistics memory.
JdDÆd:¡ 1.00 Enters height and weight of
player 1.
JgGÆgJ¡ 2.00 Enters height and weight of
player 2.
JjjÆgD¡ 3.00 Enters height and weight of
player 3.
JgVÆjj¡ 4.00 Enters height and weight of
player 4.
\k 184.25 Calculates mean of heights (x).
\« 82.75 Displays mean of weights (y).
\e 5.80 Calculates population standard
deviation for heights (x).
\« 4.71 Displays population standard
deviation for weights (y).
]U 331.00 Displays the total of the y-values.

Statistical Calculations122
Linear Regression. Calculate r (the correlation coefficient), m, b, and as follows:
1. Clear the statistical registers by pressing \t.
2. Enter the first x-value and press Æ. The x-value is displayed.
3. Enter the corresponding y-value and press ¡. The HP 10bII+ displays n, the number
of pairs of items accumulated.
4. Continue entering x,y pairs. The n-value is increased with each entry.
5. To display r, the correlation coefficient, press \Z\«.
6. To display m, the slope, press \W\«.
7. To display b (the y-intercept), press \T\«.
Linear Estimation. The straight line calculated by linear regression can be used to estimate a
y-value for a given x-value, or vice versa:
1. E n t e r t h e x,y data.
2. Enter the known x-value or y-value.
• To estimate x for the given y, enter the y-value, then press \Z.
• To estimate y for the given x, enter the x-value, then press \W.
Example: 4
Ali’s Azaleas advertises on a local radio station. For the past six weeks, the manager has kept
records of the number of minutes of advertising that were purchased, and the sales for that
week.
What is the y-intercept, the slope, and the correlation coefficient?
Table 12-9 Recording the number of minutes of the advertisements and sales
Week Minutes of Advertising
(x-values)
Sales
(y-values)
121,400
21 920
33 1,100
452,265
552,890
642,200
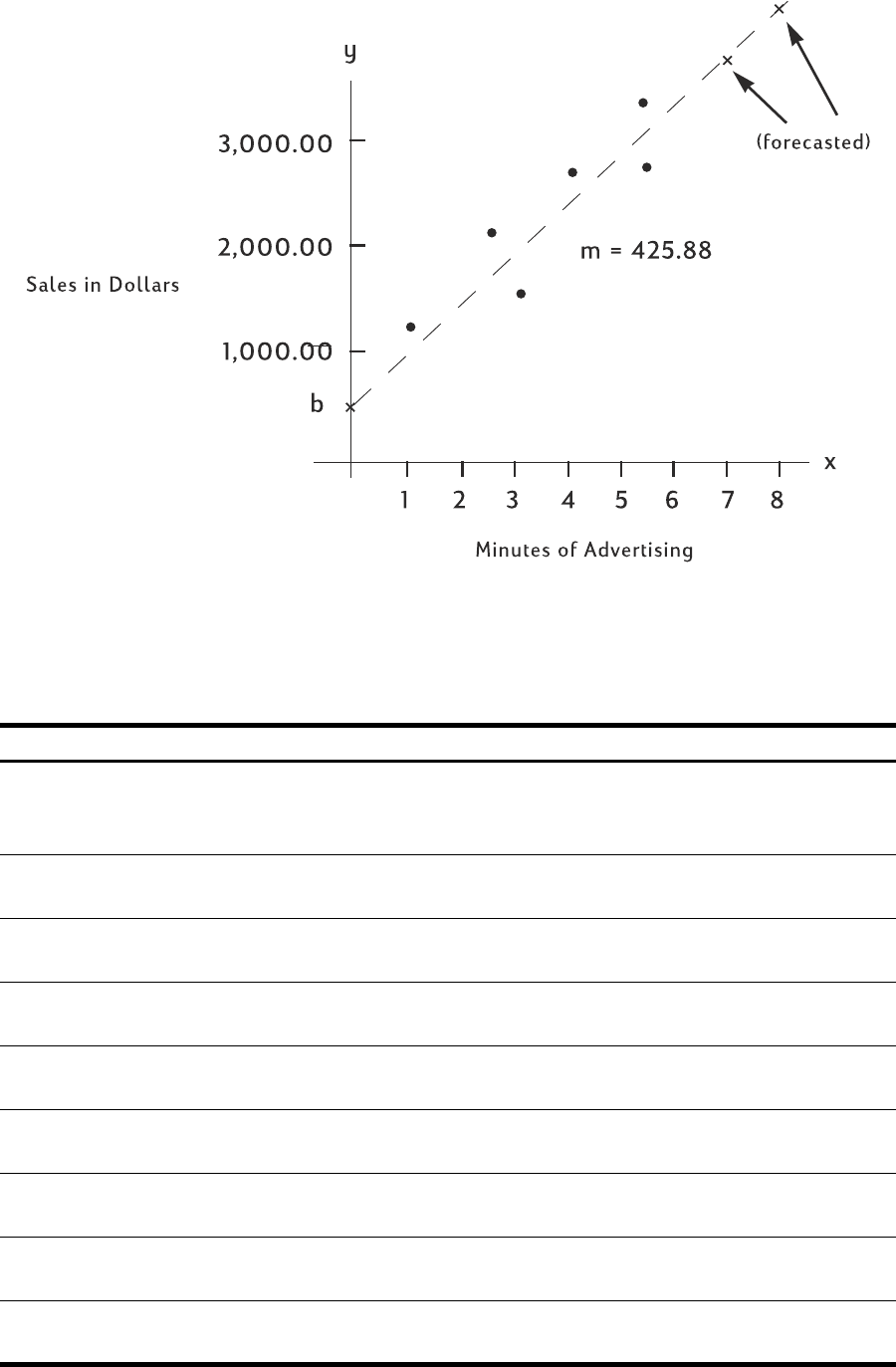
Statistical Calculations 123
Figure 4 Diagram on forecasting sales and minutes for advertising
Table 12-10 Example for forecasting
Keys Display Description
\t STAT CLR
(message flashes briefly,
then disappears)
Clears statistics memory.
GÆJY::¡ 1.00 Enters minutes and sales for
consecutive weeks.
JÆdG:¡ 2.00
DÆJJ::¡ 3.00
VÆGGSV¡ 4.00
VÆGgd:¡ 5.00
YÆGG::¡ 6.00
\T\« 376.25 Calculates y-intercept.
\W\« 425.88 Displays slope.
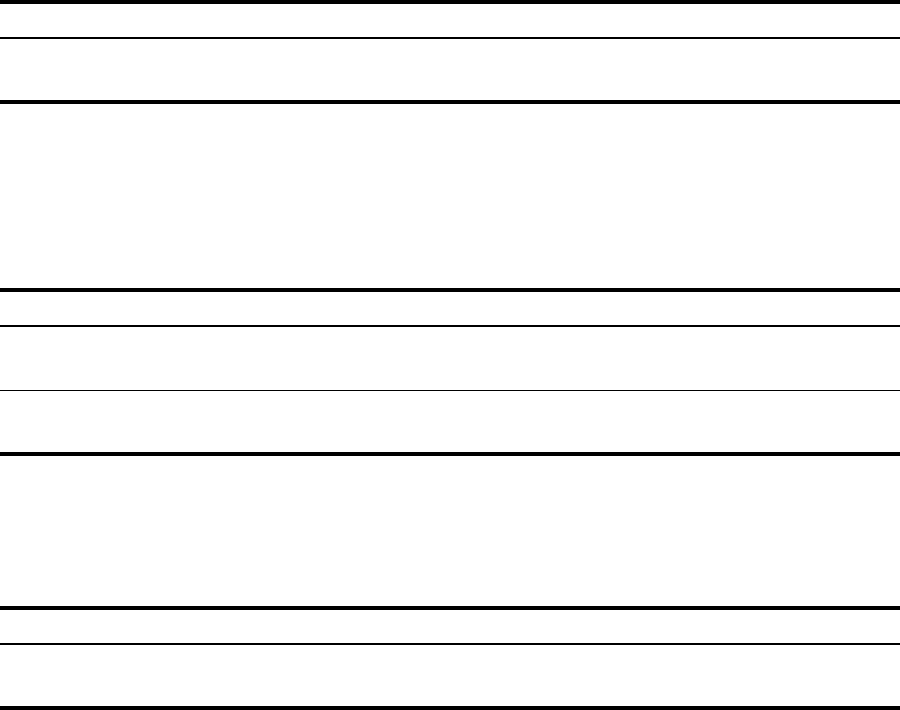
Statistical Calculations124
Estimate what the level of sales would be if the business purchased 7 or 8 minutes of
advertising.
How many minutes of advertising should Ali’s buy to attain sales of 3,000?
Weighted Mean
The following procedure calculates the weighted mean of data points x1
, x2, …, xn occurring
with weights y1
, y2, …, yn.
1. U s e Æ and ¡ to enter x,y pairs. The y-values are the weights of the x-values.
2. Press \T.
Example 5
A survey of 266 one-bedroom rental apartments reveals that 54 of them rent for 500 per
month, 32 for 505, 88 for 510, and 92 for 516. What is the average monthly rent?
\Z\« 0.90 Calculates correlation
coefficient.
Table 12-11 Estimating the level of sales
Keys Display Description
j\W 3,357.38 Estimates sales if 7 minutes of
advertising were purchased.
g\W 3,783.25 Estimates sales if 8 minutes were
purchased.
Table 12-12 Estimating the minutes of advertising for 3,000 sales
Keys Display Description
D:::\Z 6.16 Estimates minutes of advertising
required for 3,000 in sales.
Table 12-10 Example for forecasting
Keys Display Description

Statistical Calculations 125
Regression Models and Variables
The 10bII+ has six built-in regression models, as well as the ability to calculate which model
best fits the current data. These six regression modes are listed in the table below.
Press ]L to open the regression selection application. The initially displayed option is
the current setting. Press 1 or A to scroll through the available regressions. With the
desired model displayed, press Æ to select it. To exit without changing the current model,
press M. As an alternative to scrolling, and if you know the number of the desired model,
press ]L followed by the desired number of the fit option.
Table 12-13 Calculating the average monthly rent
Keys Display Description
\t STAT CLR
(message flashes briefly,
then disappears)
Clears statistics memory.
V::ÆVY¡ 1.00 Enters first rent and its weight.
V:VÆDG¡ 2.00 Enters second rent and its
weight.
VJ:Ægg¡ 3.00 Enters third rent and its weight.
VJSÆdG¡ 4.00 Enters fourth rent and its weight.
\T 509.44 Calculates the weighted mean.
Table 12-14 Regression models
Number and Mode Description
0-Best Fit Automatically selects fit
1-Linear m*x+b
2-Logarithm m*ln(x)+b
3-Exponential b*e(m*x)
4-Power b*xm
5-Exponent b*mx
6-Inverse m/x+b
Statistical Calculations126
If BEST FIT is selected, the 10bII+ calculates the best fit when \Z, \W, or
\T is pressed. When selected, BEST FIT flashes briefly, followed by the chosen fit. The
selected regression will remain set until a new one is selected, or the statistics memory is
cleared.
When the statistics memory is cleared using \t, the current regression model is set
back to LINEAR.
Probability Calculations
In many probability calculations, specific methods of counting possible outcomes are required
as part of a process to determine the likelihood of certain results. The three main operations
that allow this are:
Factorial
Factorial (!) is a mathematical operator that instructs you to multiply the current number by all
previous whole numbers. Writing out so many numbers can be cumbersome, so
mathematicians use !
to signify this process. For example:
5! is equivalent to 5 x 4 x 3 x 2 x 1 = 120.
On the 10bII+, the input value n must be within -253 < n < 253. The gamma function is used
to calculate n! for non-integer or negative values.
Permutations
The nPr function calculates the number of different arrangements, or permutations, of n items
taken r at a time. No item can occur more than once in a set of r items, and different orders
of the same r items are counted separately. This is calculated using the formula:
•!factorial
•nPr permutations
•nCrcombinations
PERMUTATIONS n!
nr–()!
------------------=

Statistical Calculations 127
Example
Using five books labeled A, B, C, D, and E, how many different ways can three books be
placed on a shelf?
Table 12-15 Example calculating permutations
Combinations
The nCr function calculates the number of different sets, or combinations, of n items taken r
at a time. No item can occur more than once in the set of r items, and different orders of the
same r items are not counted separately. This is calculated using the formula:
Example
Using five colored balls, how many different color combinations of three colors can be
chosen?
.
Random Number and Seed
The 10bII+ includes a random number generator function that generates a pseudo-random
number in the range 0 < x < 1. To store a seed value, type a positive number and press
\w]6. Storing a value of 0 will select a random number and store it as the
seed value.
Keys Display Description
V]<D4 60.00 Calculates permutations of n
items taken r at a time.
or, using Æ:
VÆD]< 60.00
COMBINATIONS n!
nr–()!r!
----------------------=
Table 12-16 Example calculating combinations
Keys Display Description
V]9D4 10.00 Calculates combinations of n
items taken r at a time.
or, using Æ:
VÆD]9 10.00

Statistical Calculations128
Example
Store a seed value of 42; set the number display to 9. Then generate three random numbers.
Advanced Probability Distributions
The 10bII+ allows easy calculation of the Z and Student's T probability distribution values. In
addition, it allows inverse calculations of both functions. The values are calculated using the
lower tail probability. This lower tail probability corresponds to the area under the curve to
the left of the input. If you need a value other than a lower tail, such as a two-sided value,
please see the conversion instructions at the end of this chapter.
Table 12-18 Advanced probability keys
These distribution functions replace the statistical tables found in the back of textbooks. Unlike
the textbook, the calculator can calculate any value, not just a limited selection found in the
table.
Table 12-17 Example storing a seed value and generating random numbers
Keys Display Description
YG\w]6 42.00 Stores 42 as the random number
generator seed.
\5d 42.000000000 Set display precision.
]6 .199873749 Generate first random number.
]6 .863046890 Generate second random
number.
]6 .504024868 Generate third random number.
\5G .50 Reset display to default setting.
Keys Description
]F Calculates a cumulative normal probability
given a Z-value.
]oF Calculates a Z-value given a cumulative
normal probability.
]I Calculates the cumulative Student’s T
probability given degrees of freedom and a
T-value.
]oI Calculates a T-value given degrees of
freedom and the cumulative Student’s T
probability.
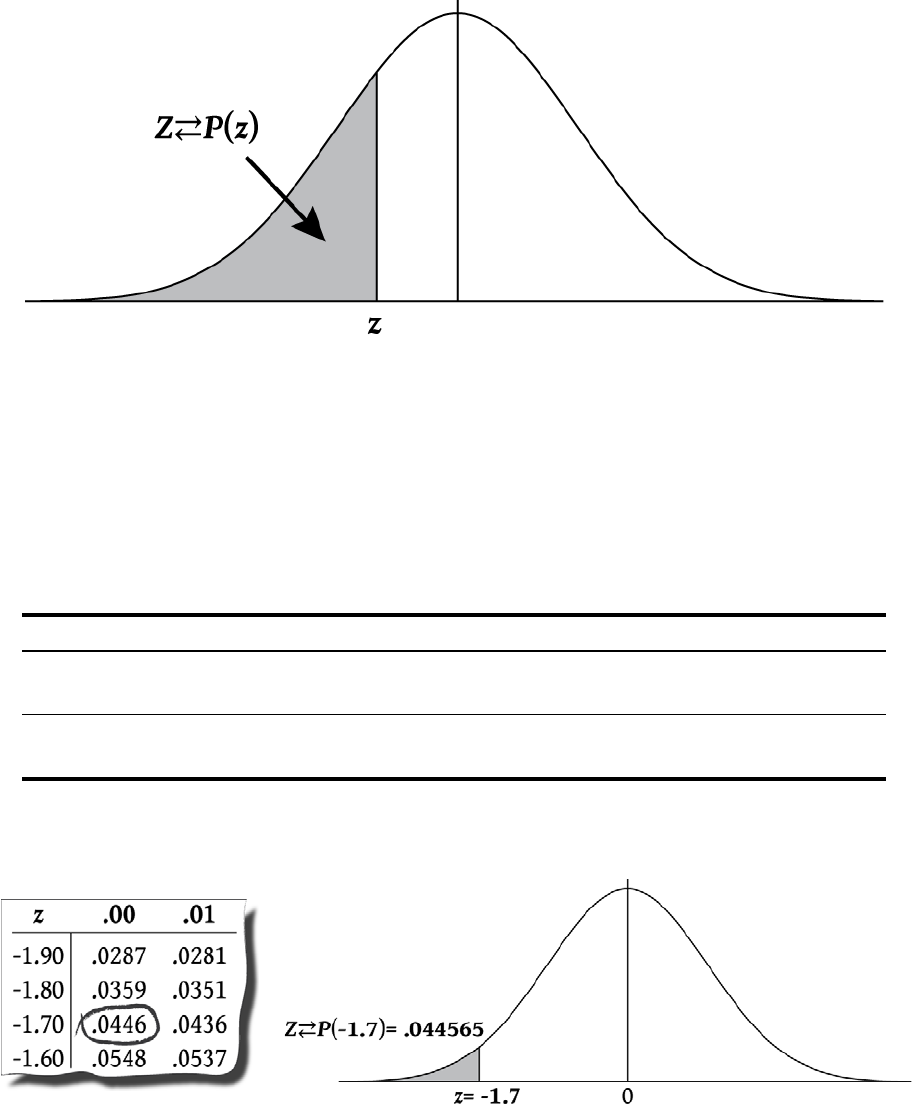
Statistical Calculations 129
Normal Lower Tail Probability
To calculate the area under the curve to the left of z (the lower tail probability), enter the z-
value and press ]F . This function calculates the probability that a standard normal
random variable, Z, is less than z.
Figure 5
Example
The variable Z is a standard normal random variable. What is the probability that Z is less
than -1. 7. ?
Table 12-19 Probability example
Keys Display Description
\5S .000000 Set display precision.
J7jy]F .044565 Calculate the probability.
Figure 6 Figure 7

Statistical Calculations130
Inverse of Normal Lower Tail Probability
Figure 8
What is the z-value corresponding to a lower tail cumulative probability of .025?
Table 12-20 Example calculating z-value (lower tail)
Keys Display Description
7:GV]oF -1.959964 Calculate the corresponding z-
value.
Figure 9 Figure 10
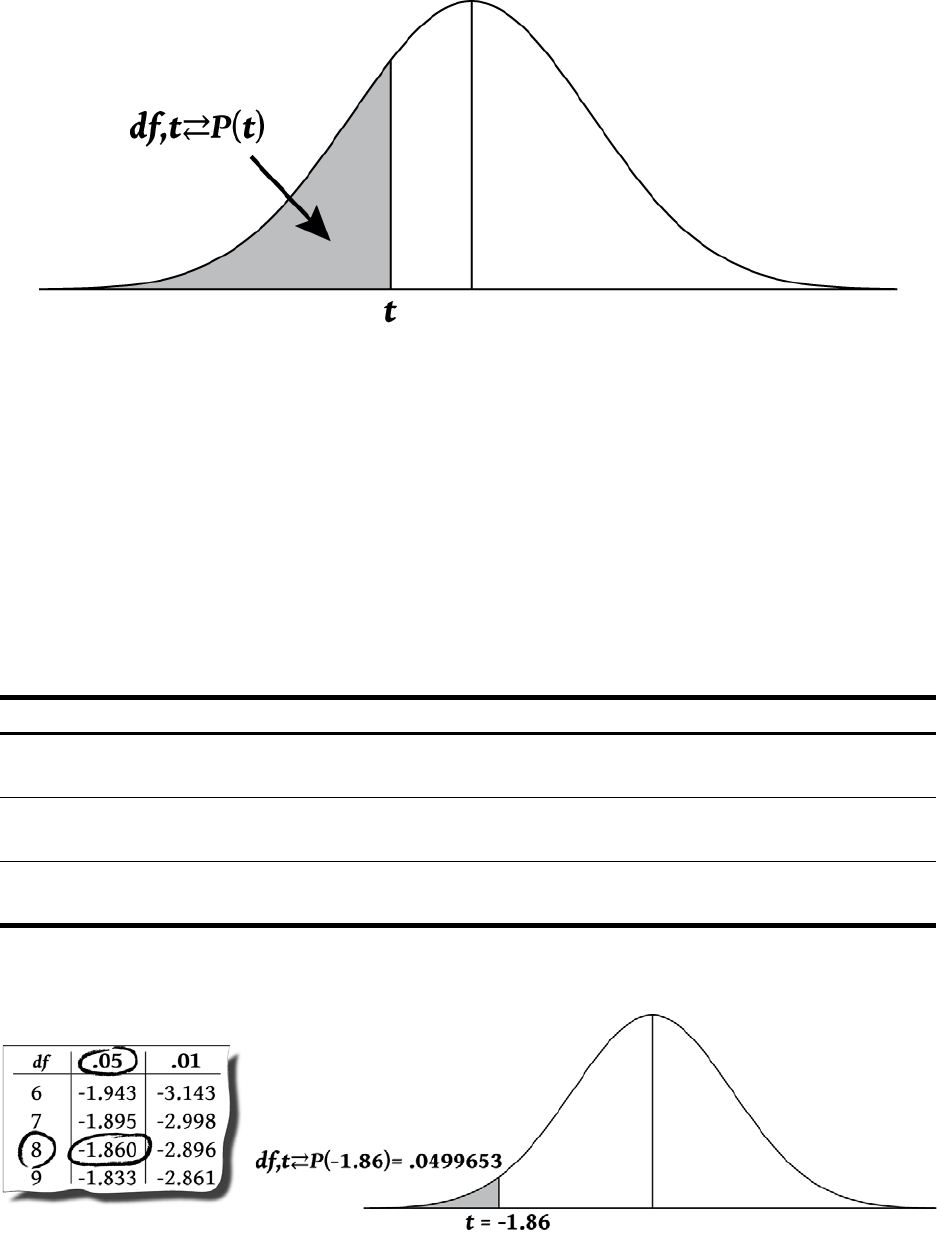
Statistical Calculations 131
Student's T Probability Lower Tail
Figure 11
To calculate the area under the Student's T Distribution curve, first enter the degrees of
freedom, followed by the t-value. It is a two-number function, so it may be entered as either
an in-line function, or by using Æ.
Example:
What is the lower tail probability associated with a Student’s T distribution with 8 degrees of
freedom (df1) with a t-value of -1. 86 ?
Table 12-21 Example of Student’s t (lower tail)
Keys Display Description
g]IJ7gSy4 .0499653 Calculates the lower tail
probability.
or, using Æ:
gÆJ7gSy]I Returns the same results.
Figure 12 Figure 13

Statistical Calculations132
Inverse of Student’s t Probability Lower Tail
If you know the lower tail probability, P, and you want to calculate t, enter the degrees of
freedom (df1), followed by Æ, then P. Press ]oIto calculate t.
Figure 14
Example
A hypothesis test requires a critical t-value from the Student’s T distribution with 26 degrees
of freedom. Find the t-value for a lower tail probability of .05.
Table 12-22 Example calculating the t-value (lower tail)
Keys Display Description
GS]oI7:V4 -1.705618 Enter degrees of freedom
and the probability, and
calculates the lower tail
t- value.
or, using Æ:
GSÆ7:V]oI Returns the same results.
Figure 15 Figure 16

Statistical Calculations 133
Conversions from Lower Tail
The distribution functions on the 10bII+ return values for the lower tail cumulative probability.
The lower tail probability corresponds to the area under the curve to the left of the given value.
Sometimes you will want to work with areas other than the lower tail. It is easy to convert from
lower tail to another area as long as you keep in mind that the total area under the curve is
equal to 1, and the Normal and the Student’s T distributions are symmetrical. In other words,
the portion of the curve to the left of zero is a mirror image of the portion of the curve to the
right of zero.
Example 1
The random variable Z is a standard normal random variable. What is the probability that z
is greater than -1.7?
Figure 17
The probability that z is greater than -1.7 is the area of the curve to the right of -1.7. You can
calculate the area to the left of -1.7 and subtract it from 1 (total area of the curve).
Table 12-23 Example converting from lower tail
Keys Display Description
J7jy]F .044565 Calculate the lower tail area.
Since the area is -1.7, ch an g e
the sign.
y1J4 .955435 Subtracts the lower tail from 1.
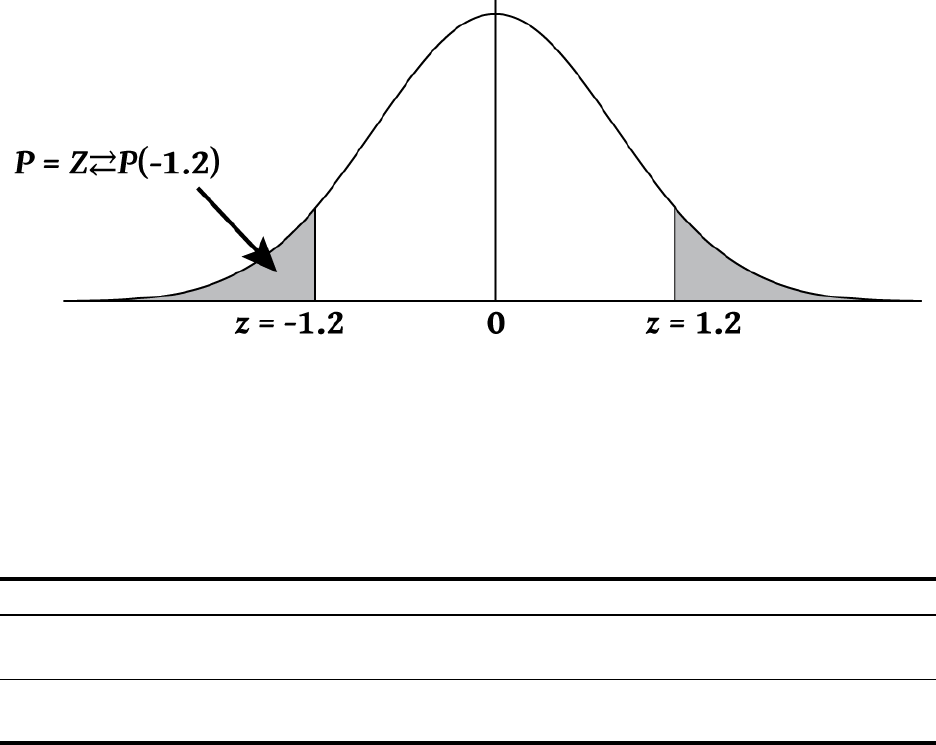
Statistical Calculations134
Example 2
The variable Z is a standard normal random variable. What is the probability that z is greater
than 1.2 or less than -1.2?
Figure 18
The desired area is to the right of 1.2 and to the left of -1.2. Since normal distributions are
symmetrical, and the areas are the same, you can calculate the lower tail area and simply
multiply by 2.
Table 12-24 Example converting from lower tail
Keys Display Description
J7Gy]F .115070 Calculate the lower tail area and
store the value.
PG4 .230139 Calculates the result.
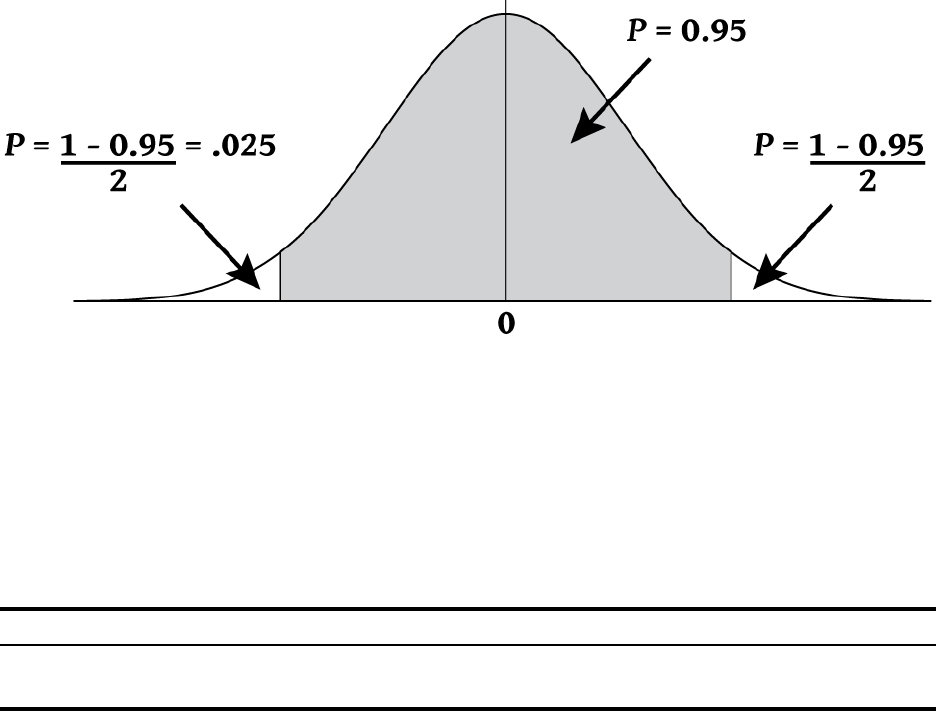
Statistical Calculations 135
Example 3
The variable Z is a standard normal random variable. Find z so that the probability that Z is
less than z and greater than -z is equal to 0.95.
Figure 19
The given area is 0.95. The area not included is 1-0.95/2 = 0.025. Since the normal
distribution is symmetrical, half of the desired area is in the lower tail, .05/2=.025. The
desired area corresponds to a lower tail probability of .025.
Table 12-25 Example converting from lower tail (the inner area)
Keys Display Description
7:GV]oF -1.959964 Returns desired value of z.
Statistical Calculations136

Additional Examples 137
13 Additional Examples
Business Applications
Setting a Sales Price
One method for setting the per unit sales price is to determine the cost of production per unit,
and then multiply by the desired rate of return. For this method to be accurate, you must
identify all costs associated with the product.
The following equation calculates unit price based on total cost and rate of return:
PRICE = TOTAL COST ÷ NUMBER OF UNITS × (1 + (%RTN ÷ 100))
Example
To produce 2,000 units, your cost is 40,000. You want a 20% rate of return. What price
should you charge per unit?
Forecasting Based on History
One method of forecasting sales, manufacturing rates, or expenses is reviewing historical
trends. Once you have historical data, the data are fit to a curve that has time on the x-axis
and quantity on the y-axis.
Example
Given the following sales data, what are the sales estimates for years six and seven?
Table 13-1 Calculating the price charged per unit
Keys Display Description
Y:::::a 40,000.00 Enters cost.
G:::P 20.00 Calculates unit cost.
\qJ1\q
G:aJ::4
24.00 Calculates the unit sales price.
Table 13-2 Sales data
Year Sales
110,000
211,210
313,060
416,075
5 20,590

Additional Examples138
Cost of Not Taking a Cash Discount
A cash discount gives a buyer a reduction in price if the payment is made within a specified
time period. For example, “2/10, NET/30” means that the buyer can deduct 2 percent if
payment is made within 10 days. If payment is not made within 10 days, the full amount must
be paid by the 30th day.
You can use the equation shown below to calculate the cost of failing to take the cash
discount. The cost is calculated as an annual interest rate charged for delaying payment.
DISC% is the discount percent if the payment is made early. TOTAL DAYS is the total number
of days until the bill must be paid. DISC DAYS is the number of days for which the discount is
available.
Example
You receive a bill with the credit terms 2/10, NET/30. What is the cost of not taking the cash
discount?
Table 13-3 Calculating the sales estimates for years six and seven
Keys Display Description
\t 0.00 Clears statistics registers.
JÆJ::::¡ 1.00 Enters first year and sales for
that year.
GÆJJGJ:¡ 2.00 Enters second year’s data.
DÆJD:S:¡ 3.00 Continues data entry.
YÆJS:jV¡ 4.00
VÆG:Vd:¡ 5.00
S\W 22,000.50 Estimates sales for year six.
j\W 24,605.00 Estimates sales for year seven.
COST%DISC%360×100×
100 DISC%–()TOTAL DAYS DISC DAYS–()×()
--------------------------------------------------------------------------------------------------------------------------------------------=

Additional Examples 139
Loans and Mortgages
Simple Annual Interest
Example
Your good friend needs a loan to start his latest enterprise and has asked you to lend him 450
for 60 days. You lend him the money at 10% simple annual interest, to be calculated on a
365-day basis. How much interest will he owe you in 60 days, and what is the total amount
owed?
This equation is used for calculating simple annual interest using a 365 day year:
Continuous Compounding
The equation for calculating an effective rate for continuous compounding is:
Table 13-4 Calculating the cost without the cash discount
Keys Display Description
GPDS:PJ
::a
72,000.00 Calculates numerator in
equation.
\q\qJ:
:AG\n
98.00 Parentheses force order of
calculation.
P\qD:A
J:4
36.73 Calculates, as an annual
percentage rate, cost of not
taking discount.
Table 13-5 Calculating the total amount owed
Keys Display Description
YV:sPJ:§ 0.10 Stores interest.
PS:aDSV4 7.4 0 C a l cu l a te s i n t e res t owe d.
1p4 457.40 Calculates the total amount
owed.
INTEREST LOAN AMOUNT INTEREST%×TERM OF LOAN IN DAYS()×
365
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------=
EFF%eNOM% 100÷()
1–()100×=

Additional Examples140
To solve a continuous compounding problem complete these steps:
1. Compute the annual effective rate using the above equation.
2. Either use this effective rate in your calculations with an annual period (P/YR = 1) or
convert this rate so that it applies to your payment period. In the following example,
P/YR = 12 so you have to calculate a new NOM% using the interest rate conversion
application with P/YR equal to 12.
Example
You currently have 4,572.80 in an account at Dream World Investments that earns 18%
annual interest compounded continuously. At the end of each month, you deposit 250.00 in
the account. What will the balance be after 15 years?
Set to End Mode. Press \¯ if BEGIN annunciator is displayed.
Table 13-6 Calculating the annual nominal rate
Keys Display Description
Jg§ 0.18 Divides nominal rate by 100.
\K 1. 2 0 R a i s e s e to 0.18 power.
AJPJ::4 19.72 Calculates annual effective rate.
\Ð 19.72 Stores effective rate.
JG\Í 12.00 Sets payments per year.
\Ó 18.14 Calculates the annual nominal
rate for a monthly payment
period.
Table 13-7 Calculating the balance amount after 15 years
Keys Display Description
JV\Ú 180.00 Stores number of months.
GV:yÌ -250.00 Stores regular payment.
YVjG7gy
Ï
-4,572.80 Stores current balance as a
negative value (like an initial
investment).
É 297,640.27 Calculates the account balance
after 15 years of payments with
18% int erest co m p o u n d e d
continuously.
Additional Examples 141
Yield of a Discounted (or Premium) Mortgage
The annual yield of a mortgage bought at a discount or premium can be calculated given the
original mortgage amount (PV), interest rate (I/YR), periodic payment (PMT), balloon payment
amount (FV), and the price paid for the mortgage (new PV).
Remember the cash flow sign convention: money paid out is negative; money received is
positive.
Example
An investor wishes to purchase a 100,000 mortgage taken out at 9% for 20 years. Since the
mortgage was issued, 42 monthly payments have been made. The loan is to be paid in full
(a balloon payment) at the end of its fifth year. What is the yield to the purchaser if the price
of the mortgage is 79,000?
Step 1
Calculate PMT. Make sure FV = 0.
Set to End Mode. Press \¯ if BEGIN annunciator is displayed.
Step 2
Enter the new value for N indicating when the balloon occurs, then find FV, the amount of the
balloon.
É
Table 13-8 Calculating the monthly payment
Keys Display Description
JG\Í 12.00 Sets payments per year.
dÒ 9.00 Stores interest rate.
G:\Ú 240.00 Stores number of months.
J:::::y
Ï
-100,000.00 Stores original amount of
mortgage.
:É 0.00 Enters amount left to pay after
20 years.
Ì 899.73 Calculates the regular payment.
Table 13-9 Calculating the balloon payment
Keys Display Description
\}Ì 899.73 Rounds payment to two decimal
places for accuracy.

Additional Examples142
Step 3
Enter actual, current values for N and PV; then find the new I/YR for the discounted mortgage
with balloon.
Annual Percentage Rate for a Loan With Fees
The Annual Percentage Rate, APR, incorporates fees usually charged when a mortgage is
issued, which effectively raises the interest rate. The actual amount received by the borrower
(the PV) is reduced, while the periodic payments remain the same. The APR can be calculated
given the term of the mortgage (N periods), the annual interest rate (I/PR), the mortgage
amount (new PV), and the amount of the fee.
Remember the cash flow sign convention: money paid out is negative; money received is
positive.
Example: APR for a Loan With Fees
A borrower is charged two points for the issuance of a mortgage. (One point is equal to 1%
of the mortgage amount.) If the mortgage amount is 160,000 for 30 years and the annual
interest rate is 8.5% with monthly payments, what APR is the borrower paying?
Set to End Mode. Press \¯ if BEGIN annunciator is displayed.
V\Ú 60.00 Stores number of payments until
balloon.
É 88,706.74 Calculates the balloon payment
(add to final payment).
Table 13-10
Keys Display Description
vÙAYGÙ 18.00 Stores remaining number of
payments.
jd:::yÏ -79,000.00 Stores price of mortgage.
Ò 20.72 Calculates the return on this
discounted mortgage.
Table 13-9 Calculating the balloon payment
Keys Display Description
Table 13-11 Calculating the annual percentage rate considering fees
Keys Display Description
JG\Í 12.00 Sets payments per year.
g7VÒ 8.50 Stores interest rate.

Additional Examples 143
Example: Interest-Only Loan With Fee
A 1,000,000, 10-year, 12% (annual interest) interest-only loan has an origination fee of three
points. What is the yield to the lender? Assume that monthly payments of interest are made.
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
D:\Ú 360.00 Stores length of mortgage.
JS::::Ï 160,000.00 Stores original amount of
mortgage.
:É 0.00 The loan will be completely paid
off in 30 years.
Ì -1,230.26 Calculates payment.
vÏ 160,000.00 Recalls loan amount.
-AG§Ï 156,800 Subtracts points.
Ò 8.72 Calculates APR, considering
fees.
Table 13-12 Calculating the annual percentage rate
Keys Display Description
JG\Í 12.00 Sets payments per year.
JGÒ 12.00 Stores interest rate.
J:\Ú 120.00 Stores length of mortgage.
J::::::
Ï
1,000,000.00 Stores original amount of
mortgage.
yÉ -1,000,000.00 Enters amount due at end of
term. Payments are interest only
so entire loan amount is due.
Ì -10,000.00 Calculates interest-only
payments.
vÏ 1,000,000.00 Recalls loan amount.
AD§Ï 970,000.00 Subtracts points.
Table 13-11 Calculating the annual percentage rate considering fees
Keys Display Description

Additional Examples144
Loan With a Partial (Odd) First Period
TVM calculations apply to financial transactions where each payment period is the same
length. However, situations exist where the first payment period is not the same length as the
remaining periods. This first period is sometimes called an odd or partial first period.
If interest is applied to an odd first period, it is usually calculated as simple interest. So using
the HP 10bII+ to do a payment calculation with an odd first period is a two step process:
1. Calculate the amount of simple interest that accrues during the fractional first period and
add it to the loan amount. This is the new PV. You must be able to calculate the length of
the odd first period as a fraction of the whole period. (For example, a 15-day odd first
period would be 0.5 periods assuming a whole period to be a 30-day month.)
2. Calculate the payment using the new PV, with N equal to the number of full periods. Use
Begin mode if the number of days until the first payment is less than 30; otherwise use
End mode.
Example
A 36-month loan for 4,500 has an annual rate of 15%. If the first monthly payment is made
in 46 days, what is the monthly payment amount assuming 30-day months?
The odd first period in this example is 16 days.
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
Ò12.53 Ca l cul a tes APR.
Table 13-12 Calculating the annual percentage rate
Keys Display Description
Table 13-13 Calculating the monthly payment amount
Keys Display Description
JG\Í 12.00 Sets payments per year.
JVÒ 15.00 Stores interest rate.
aJGP 1.25 Calculates periodic interest
rate.
JSaD:P 0.67 Multiplies by fraction of a
period.
YV::\Ǥ4 30.00 Calculates amount of simple
interest owed for odd
period.
1YV::Ï 4,530.00 Adds this simple interest to
present value.
DSÙ 36.00 Stores term of loan.

Additional Examples 145
Automobile Loan
Example
You are buying a new 14,000.00 sedan. Your down payment is 1,500 and you are going to
finance the remaining 12,500. The car dealer is offering two choices for financing:
• A 3-year loan with an annual interest rate of 3.5%.
• A 3-year loan with an annual interest rate of 9.5% and a 1,000.00 rebate.
With which choice do you pay less for the car?
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
Calculate the first option:
Calculate the second option:
:É 0.00 Enters amount left to pay
after 36 payments.
Ì -157.03 Calculates the payment
amount.
Table 13-13 Calculating the monthly payment amount
Keys Display Description
Table 13-14 Calculating the annual interest rate of 3.5%
Keys Display Description
JG\Í 12.00 Sets payments per year.
DSÙ 36.00 Stores known values.
JGV::Ï 12,500.00 Stores loan amount.
:É 0.00
D7VÒ 3.50 Stores first interest rate.
Ì -366.28 Calculates payment.
PvÙ4 -13,185.94 Calculates total interest and
principal.
Table 13-15 Calculating the annual interest rate of 9.5%
Keys Display Description
JJV::Ï 11,500.00 Stores loan amount with rebate.

Additional Examples146
The first option costs slightly less.
Canadian Mortgages
In Canadian mortgages, the compounding and payment periods are not the same. Interest is
compounded semi-annually while payments are made monthly. To use the TVM application
in the HP 10bII+, you need to calculate a Canadian mortgage factor (which is an adjusted
interest rate) to store in I/YR.
For additional information on interest rate conversions, see Interest Rate Conversions in Ch. 6.
Example
What is the monthly payment required to fully amortize a 30-year, 130,000 Canadian
mortgage if the annual interest rate is 12%?
d7VÒ 9.50 Stores second interest rate.
Ì -368.38 Calculates payment.
PvÙ4 -13,261.64 Calculates total interest and
principal.
Table 13-15 Calculating the annual interest rate of 9.5%
Keys Display Description
Table 13-16 Calculating the monthly payment for Canadian mortgage
Keys Display Description
JG\Ó 12.00 Stores known nominal percentage
and number of compounding
periods.
G\Í 2.00
\Ð 12.36 Calculates annual effective rate.
JG\Í 12.00 Sets payments per year.
\Ó 11 . 71 C a l c u l a t e s Canadian mortgage
factor (adjusted interest rate).
JD::::Ï 130,000 Stores other known values for
mortgage.
:ÉD:\Ú 360.00
Ì -1,308.30 Calculates monthly payment for
Canadian mortgage.

Additional Examples 147
What if … TVM Calculations
One of the most valuable aspects of the HP 10bII+’s TVM application is the ease with which
it handles the question “what if …” in financial calculations. For example, one of the most
popular “what if …” questions is, “What if the interest rate changes to …? How will that affect
my payment?” To answer this question, once you have calculated a payment based on one
interest rate, all you need to do is enter the new interest rate and recalculate PMT.
Some of the examples earlier in this manual have included some brief encounters with “what
if …” questions, but a more complete example follows.
Example
You are about to sign on the dotted line for a 30-year, 735,000 mortgage, on a vacation
home. The annual interest rate is 11. 2 % .
Part 1
What will your payments be at the end of the month?
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
Part 2
Your company’s regular payroll is generated every other Friday. The bank agrees to
automatically draw payments of 3,555.00 out of each paycheck (approximately half of what
a monthly payment would be) and adjust the payment period accordingly (26 compounding
periods per year). What would be the new term of the loan?
Table 13-17 Calculating the monthly payment
Keys Display Description
JG\Í 12.00 Sets payments per year.
jDV:::Ï 735,000.00 Stores known values.
JJ7GÒ 11. 2 0
D:\Ú 360.00
:É 0.00
Ì -7,110.88 Calculates payment.
Table 13-18 Calculating the number of years required to pay off the loan
Keys Display Description
DVVVyÌ -3,555.00 Enters new payment.

Additional Examples148
Part 3
What if you had monthly payments as in part 1, but chose a 15-year term? What would your
new payment be? What would be the total interest paid on the contract?
Savings
Saving for College Costs
Suppose you start saving now to accommodate a future series of cash outflows. An example
of this is saving money for college. To determine how much you need to save each period,
you must know when you’ll need the money, how much you’ll need, and at what interest rate
you can invest your deposits.
Example
Your oldest daughter will attend college in 12 years and you are starting a fund for her
education. She will need 15,000 at the beginning of each year for four years. The fund earns
9% annual interest, compounded monthly, and you plan to make monthly deposits, starting
at the end of the current month. The deposits cease when she begins college. How much do
you need to deposit each month?
This problem is solved in two steps. First calculate the amount you’ll need when she starts
college. Start with an interest rate conversion because of the monthly compounding.
GS\Í 26.00 Sets payments per year for every
two weeks.
Ù 514.82 Calculates number of biweekly
payments.
v\Ú 19.80 Displays years required to pay
off the loan.
Table 13-19 Calculating the total interest paid on the contract
Keys Display Description
JG\Í 12.00 Sets payments per year.
JV\Ú 180.00 Stores new term.
Ì -8,446.53 Calculates payment for shorter
term.
PvÙ1 -1,520,374.70 Calculates total paid.
vÏ4 -785,374.70 Displays the total interest paid
on the contract.
Table 13-18 Calculating the number of years required to pay off the loan
Keys Display Description

Additional Examples 149
Figure 20 Cash flow diagram
Set to Begin mode. Press \¯ if BEGIN annunciator is not displayed.
When compounding occurs only once per year, the effective rate and the nominal rate are
the same.
Set to Begin mode. Press \¯ if BEGIN annunciator is not displayed.
Table 13-20 Calculating the annual effective rate
Keys Display Description
d\Ó 9.00 Stores annual nominal rate.
JG\Í 12.0 0 St o res num b er of c o mpoun d ing
periods used with this nominal
rate.
\Ð 9.38 Calculates annual effective rate.
Ò 9.38 Stores effective rate as annual
rate.
Table 13-21 Calculating the amount required at the start
Keys Display Description
J\Í 1.00 Sets 1 payment per year.
JV:::
Ì
15,000.00 Stores annual withdrawal.
YÙ 4.00 Stores number of withdrawals.
:É 0.00 Stores balance at the end of four
years.
Ï -52,713.28 Calculates the amount required
when your daughter starts
college.
Additional Examples150
Then use that PV as the FV on the following cash flow diagram, and calculate the PMT.
Figure 21 Cash flow diagram (Calculate PMT)
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
Gains That Go Untaxed Until Withdrawal
You can use the TVM application to calculate the future value of a tax-free or tax-deferred
account. (Current tax laws and your income determine whether both interest and principal are
tax-free. You can solve for either case.)
The purchasing power of that future value depends upon the inflation rate and the duration
of the account.
Example
You are considering opening a tax-deferred account with a dividend rate of 8.175%. If you
invest 2,000 at the beginning of each year for 35 years, how much will be in the account at
retirement? How much will you have paid into the account? How much interest will you have
earned? If your post-retirement tax rate is 15%, what will the after tax future value of the
Table 13-22 Calculating the monthly deposit required
Keys Display Description
yÉ 52,713.28 Stores amount you need.
:Ï 0.00 Stores amount you are starting
with.
JG\Í 12.00 Sets payments per year.
JYYÙ 144.00 Stores number of deposits.
dÒ 9.00 Stores interest rate.
Ì -204.54 Calculates monthly deposit
required.

Additional Examples 151
account be? Assume that only the interest is taxed (assume the principal was taxed before
deposit). What is the purchasing power of that amount, in today’s dollars, assuming a 4%
inflation rate?
Set to Begin mode. Press \¯ if BEGIN annunciator is not displayed.
Value of a Taxable Retirement Account
This problem uses the TVM application to calculate the future value of a taxable retirement
account that receives regular, annual payments beginning today (Begin mode). The annual
tax on the interest is paid out of the account. (Assume the deposits have been taxed already.)
Table 13-23 Calculating the purchasing power of the amount
Keys Display Description
J\Í 1.00 Sets 1 payment per year.
DVÙ 35.00 Stores number of periods and
interest rate.
g7JjVÒ 8.18
:Ï 0.00 Stores amount you start with.
G:::yÌ -2,000.00 Stores amount of annual
payment.
É 387,640.45 Calculates amount in account at
retirement.
vÌPvÙ4 -70,000.00 Calculates amount you have
paid into account by retirement.
1vÉ4 317,640.45 Calculates interest account has
earned by retirement.
PJV§4 47,646.07 Calculates taxes at 15% of
interest.
y1vÉ4 339,994.39 Calculates after-tax FV.
É 339,994.39 Stores after-tax future value in
FV.
YÒ:ÌÏ -86,159.84 Calculates the present value
purchasing power of after-tax
FV, assuming a 4% inflation
rate.

Additional Examples152
Example
If you invest 3,000 each year for 35 years, with dividends taxed as ordinary income, how
much will you have in the account at retirement? Assume an annual dividend rate of 8.175%,
a tax rate of 28%, and that payments begin today. What is the purchasing power of that
amount in today’s dollars, assuming 4% inflation?
Set to Begin mode. Press \¯ if BEGIN annunciator is not displayed.
Cash Flow Examples
Wrap-Around Mortgages
A wrap-around mortgage is a combination of refinancing a mortgage and borrowing against
real estate equity. Usually the two unknown quantities in the wrapped mortgage are the new
payment and the rate of return to the lender. To arrive at a solution, you need to use both the
TVM and the cash flow applications.
Example
You have 82 monthly payments of 754 left on your 8% mortgage, leaving a remaining
balance of 47,510.22. You would like to wrap that mortgage and borrow an additional
35,000 for another investment. You find a lender who is willing to “wrap” an 82,510.22
mortgage at 9.5% for 15 years. What are your new payments and what return is the lender
getting on this wrap-around mortgage?
Table 13-24 Calculating the purchasing power, assuming 4% inflation rate
Keys Display Description
J\Í 1.00 Sets 1 payment per year.
DVÙ 35.00 Stores number of payment
periods until retirement.
g7JjVAGg
§4
5.89 Calculates interest rate
diminished by tax rate.
Ò 5.89 Stores adjusted interest rate.
:Ï 0.00 Stores amount you are starting
with.
D:::yÌ -3,000.00 Stores amount of annual
payment.
É 345,505.61 Calculates amount in account at
retirement.
YÒ:Ì Ï -87,556.47 Calculates present value
purchasing power of FV,
assuming a 4% inflation rate.

Additional Examples 153
The payment calculation is a straightforward TVM payment calculation using the new amount
as the PV.
Set to End mode. Press \¯ if BEGIN annunciator is displayed.
Then, to calculate the lender’s return, enter cash flows that represent the complete picture of
the wrap-around mortgage from the lender’s point of view:
Figure 22 Cash flow diagram (Wrap-around mortgage)
When you group the above cash flows, you’ll find that:
CF0 = 47,510.22 - 82,510.22 = -35,000
CF1 = 861.59 - 754.00 = 107.59
Table 13-25 Calculating the payment
Keys Display Description
]OJ 0.00 Clears TVM registers.
JG\Í 12.00 Sets payments per year.
gGVJ:7GG
Ï
82,510.22 Stores loan amount on which
your new payment is calculated.
d7VÒ 9.50 Stores interest rate.
:É 0.00 Stores final balance.
JV\Ú 180.00 Stores number of monthly
payments you will make.
Ì -861.59 Calculates your new payment.

Additional Examples154
N1 = 82
CF2 = 861.59
N2 = 180 - 82 = 98
Net Future Value
The net future value can be calculated by using the TVM keys to slide the net present value
(NPV) forward on the cash flow diagram.
Example: Value of a Fund
You have made the following deposits over the past two years into a money market fund
earning 8.8%. What is the current balance of the account?
Figure 23 Cash flow diagram
Table 13-26 Calculating the annual return
Keys Display Description
DV:::y¤ CF0
-35,000.00
Enters 35,000 for loan amount.
vÌyAjVY
¤
CF1
107.59
Enters net payment for first 82
months.
gG\¥ n1
82.00
Enters number of times payment
occurs.
vÌy¤ CF2
861.59
Enters net payment for next 98
months.
Jg:AgG\
¥
n2
98.00
Enters number of times payment
occurs.
\Á 10.16 Calculates annual return.

Appendix A: Batteries and Answers to Common Questions I
Appendix A: Batteries and Answers to Common Questions
Power and Batteries
The calculator is powered by two 3-volt lithium button-cell batteries, CR2032.
When changing batteries, use only fresh button-cell batteries. Both batteries must be changed
at the same time.
Do not use rechargeable batteries.
Low Power Annunciator
When the low battery-power annunciator ( ) comes on, you should replace the batteries
as soon as possible. If the battery annunciator is on and the display dims, you may lose data.
The All Clear message is displayed if data is lost due to low power.
Installing Batteries
Warning! There is a danger of explosion if batteries are incorrectly replaced.
Replace only with the same type of battery or with equivalent batteries (as recommended by
the manufacturer). Dispose of used batteries according to the manufacturer’s instructions.
• The calculator is powered by two 3-volt CR2032 coin batteries.
• When changing batteries, use only fresh coin-cell batteries. Do not use rechargeable batteries.
• Do not mutilate, puncture, or dispose of batteries in fire. The batteries can burst or explode, releasing
hazardous chemicals.
• Do not use new and old batteries together, and do not mix batteries of different types.
1. Have two fresh CR2032 batteries at hand. Only touch the batteries by their edges.
Wipe each battery with a lint-free cloth to remove dirt and oil.
2. Make sure the calculator is off. When changing the batteries, change the batteries one
at a time to avoid clearing the memory. As a back-up, write down any data that you
have stored and might need for later use.
3. Turn the calculator over and pry off the battery cover.
Accessing the battery compartment
4. Gently remove one battery.
5. Insert the new battery, making sure that the positive sign (+) battery is facing outward.
6. Gently remove the other battery.
Appendix A: Batteries and Answers to Common QuestionsII
7. I n s er t t h e o t h e r n ew b a t t e r y, making sure that the positive sign (+) battery is facing
outward.
8. Replace the battery-compartment lid.
9. Press =.
If the calculator does not turn on, follow the procedures below.
Determining if the Calculator Requires Service
Use these guidelines to determine if the calculator requires service. If these procedures confirm
that the calculator is not functioning properly, refer to the Warranty, Environmental, and
Contact Information located on the product CD.
The calculator won’t turn on:
This condition most likely indicates that the batteries have run out. Install new batteries.
If the calculator still does not turn on when you press O:
1. Reset the calculator (see below) and, if necessary,
2. Erase the memory (see below).
The All Clear message should now be displayed. If this is not the case, the calculator requires
service.
Resetting the calculator:
1. Turn the calculator over and remove the battery cover.
2. Insert the end of a paper clip into the small, round hole located between the batteries.
Insert the clip gently as far as it will go. Hold for one second and then remove the clip.
3. Press =.
4. If the calculator is still not responding, erase the memory (see below) and repeat steps 1
to 3 above one more time.
Erasing the calculator’s memory:
1. Press and hold down the = key.
2. Press and hold down the Ù and then the É key so all three keys are pressed
simultaneously.
3. Release all three keys.
Memory is cleared and All Clear should be displayed.
The calculator doesn’t respond to keystrokes:
1. Reset the calculator (see above) and, if necessary,
2. Erase the memory (see above).
The All Clear message should now be displayed. If this is not the case, the calculator requires
service.
Appendix A: Batteries and Answers to Common Questions III
The calculator responds to keystrokes, but you suspect that it is malfunctioning:
1. It is likely that you’ve made a mistake in operating the calculator. Try rereading portions
of the manual, and check Answers to Common Questions below.
2. Contact the Calculator Support department. The contact information is listed on the
product CD.
Answers to Common Questions
Hewlett-Packard is committed to providing you with ongoing support. For more information on
calculators and calculator learning products, visit www.hp.com/calculators. You also may
contact HP Customer Support. Contact information and phone numbers are available on the
product CD included in the package along with your calculator.
Please read Answers to Common Questions before contacting us. Our experience has shown
that many of our customers have similar questions about our products. If you don’t find an
answer to your question, you can contact us using the contact information and phone numbers
listed on the product CD.
Q: I’m not sure if the calculator is malfunctioning, or if I’m doing something incorrectly. How
can I determine if the calculator is operating properly?
A: See Determining If the Calculator Requires Service.
Q: My numbers contain commas instead of periods as decimal points. How do I restore the
periods?
A: Press \8 (Ch. 2 Getting Started).
Q: How do I change the number of decimal places that the HP 10bII+ displays?
A: Press \5 and the number of decimal places that you want (Ch. 2 Getting Started).
Q: What does an E in a number (for example, 2.51E–13) mean?
A: Exponent of ten. For example, 2.51 × 10–13 (Ch. 2 Getting Started).
Q: Why do I get a wrong answer or the No Solution message when using TVM?
A: Be sure to enter a value for four of the five TVM values before you solve for the fifth, even
if one of the values is zero. (Don’t forget to store a zero for É if you completely pay off a
loan.) Clearing all the TVM registers (]OJ) before entering your known values
accomplishes the same thing. Check to see that the calculator is in the appropriate payment
mode (Begin or End mode) and that P/YR is set correctly.
Appendix A: Batteries and Answers to Common QuestionsIV
Q: How can I change the sign of a number in a list of cash flows?
A: You must edit or replace the cash flow entry (Ch. 8 Cash Flow Calculations).
Q: What does PEND in the display mean?
A: An arithmetic operation is pending (in progress).
Q: What does INPUT in the display mean?
A:The Æ key has been pressed (Ch. 2 Getting Started).
Q: Why is IRR/YR larger than I expected?
A: This is IRR per year. To see a periodic IRR, divide IRR/YR by P/YR.
Environmental Limits
To maintain product reliability, you should avoid getting the calculator wet and observe the
following temperature and humidity limits:
• Operating temperature: 0° to 40°C (32° to 104°F).
• Storage temperature: -20° to 65°C (-4° to 149°F).
• Operating and storage humidity: 90% relative humidity at 40°C (104°F) maximum.

Appendix B: More About Calculations I
Appendix B: More About Calculations
IRR/YR Calculations
The calculator determines IRR/YR for a set of cash flows using mathematical formulas that
search for the answer. The process finds a solution by estimating an answer and then using
that estimate to do another calculation. This is called an iterative process.
In most cases, the calculator finds the desired answer, since there is usually only one solution
to the calculation. However, calculating IRR/YR for certain sets of cash flows is more complex.
There may be more than one (or no) mathematical solution to the problem.
Possible Outcomes of Calculating IRR/YR
These are the possible outcomes of an IRR/YR calculation:
•Case 1. The calculator displays a positive answer. This is the only positive answer. However, one or
more negative answers may exist.
•Case 2. The calculator displays a negative answer and no message.This is the only answer.
•Case 3. The calculator displays: No Solution. There is no answer. This situation might be the result of
an error, such as a mistake in keying in the cash flows. A common mistake that results in this message
is putting the wrong sign on a cash flow. A valid cash-flow series for an IRR/YR calculation must have
at least one positive and one negative cash flow.
Range of Numbers
The largest positive and negative numbers available on the calculator are ± 9.99999999999
× 10499; the smallest positive and negative numbers available are ±1 × 10–499
. Underflow
briefly displays UFLO and then displays zero. Refer to the messages OFLO and UFLO in
Appendix C.
Equations
Business Percentages and Break-even Calculations
%CHG = PROFIT = (SP-VC) x UNITS - FC
Probability
MAR PRC COST–
PRC
----------------------------------
⎝⎠
⎛⎞
100×=
MU PRC COST–
COST
----------------------------------
⎝⎠
⎛⎞
100×=
NEW OLD–
OLD
--------------------------------
⎝⎠
⎛⎞
100×
Pn!
nr–()!
------------------=
Cn!
nr–()!r!
----------------------
=
Appendix B: More About CalculationsII
Time Value of Money (TVM)
Payment Mode Factor: S = 0 for End mode; 1 for Begin mode.
Amortization
BAL is initially PV rounded to the current display setting.
PMT is initially PMT rounded to the current display setting.
For each payment amortized:
Interest Rate Conversions
i%I/YR
P/YR
-------------
=
0PV 1i%S×
100
---------------+
⎝⎠
⎛⎞
+PMT
11
i%
100
--------+
⎝⎠
⎛⎞
N–
–
i%
100
--------
--------------------------------------
⎝⎠
⎜⎟
⎜⎟
⎜⎟
⎛⎞
××
FV+1i%
100
--------+
⎝⎠
⎛⎞
N–
×
=
ΣINT = accumulated interest
ΣPRN = accumulated principal
i= periodic interest rate
INT' =BAL × i (INT' is rounded to the current display setting;
INT’ = 0 for period 0 in Begin mode.)
INT =INT' (with sign of PMT)
PRN =PMT + INT'
BALnew =BALold + PRN
ΣINTnew =ΣINTold + INT
ΣPRNnew =ΣPRNold + PRN
iIYR
⁄
PYR 100×⁄
-----------------------------=
EFF%1NOM%
100 PYR⁄×
-----------------------------+
⎝⎠
⎛⎞
PYR⁄
1–
⎝⎠
⎛⎞
100×=
Appendix B: More About Calculations III
Cash-Flow Calculations
When NPV = 0, the solution for i% is the periodic internal rate of return.
NFV = NPV x SPFV(i % : N) where N =
TOTAL =
COUNT =
i% = periodic interest rate.
j= the group number of the cash flow.
CFj= amount of the cash flow for group j.
nj= number of times the cash flow occurs for group j.
k= the group number of the last group of cash flows.
Nj = = total number of cash flows prior to group j.
nl
1lj<≤
∑
NPV CF0CFj
j1=
k
∑
+=
11
i%
100
--------+
⎝⎠
⎛⎞
nj
–
–
i%
100
--------
--------------------------------------
⎝⎠
⎜⎟
⎜⎟
⎜⎟
⎛⎞
×1i%
100
--------+
⎝⎠
⎛⎞
nj
–
×
nj
j1=
k
∑
njCFj
×()
j0=
k
∑
nj
j0=
k
∑
Appendix B: More About CalculationsIV
Bonds
Reference: Lynch, John J. Jr. and Jan Mayle, Stanford Securities Calculation Methods,
Securities Industry Association, New York, 1986.
A = accrued days, the number of days from beginning of coupon period to settlement date.
E = number of days in coupon bracketing settlement date. By convention, E is 180 (or 360) if
calendar basis is 30/360.
DSC = number of days from settlement date to next coupon date. (DSC= E - A).
M = coupon periods per year (1 = annual, 2 = semiannual).
N = number of coupon periods between settlement and redemption dates. If N has a
fractional part (settlement not on coupon date), then round it to the next higher whole number.
Y = annual yield as a decimal fraction, YLD% / 100.
For one or fewer coupon period to redemption:
Note: coupon (CPN) is a percentage (CPN%) in both cases.
For more than one coupon period to redemption:
The end of month convention is used to determine coupon dates in the following exceptional
situations. This affects calculations for YLD%, PRICE, and ACCRU.
• If the maturity date falls on the last day of the month, then the coupon payments will also fall on the
last day of the month. For example, a semiannual bond that matures on September 30 will have
coupon payment dates on March 31 and September 30.
• If the maturity date of a semiannual bond falls on August 29 or 30, then the February coupon
payment dates will fall on the last day of February (28, or 29 in leap years).
PRICE
CALL CPN
M
------------+
1DSC
E
------------Y
Y
---
×
⎝⎠
⎛⎞
+
-------------------------------------A
E
--- CPN
M
------------
×
⎝⎠
⎛⎞
–=
CALL
1Y
Y
---+
⎝⎠
⎛⎞
N1–DSC
E
------------+
----------------------------------------
CPN
M
------------
1Y
M
-----+
⎝⎠
⎛⎞
K1–DSC
E
------------+
------------------------------------------
N
∑A
E
--- CPN
M
------------
×
⎝⎠
⎛⎞
–+
Appendix B: More About Calculations V
Depreciation
For the given year number (YR) and with Factor (FACT) as a percentage:
For the last year of depreciation, DB equals the remaining depreciable value for the prior year.
Statistics
, ,
SL BASIS SALV–
LIFE
-------------------------------------=
SOYD BASIS SALV–
LIFE LIFE 1+()
2
---------------------------
×
------------------------------------------------LIFE YR–1+()×=
DB
BASIS FACT
100
---------------
×
LIFE
---------------------------------------1
FACT
100
---------------
⎝⎠
⎛⎞
LIFE
---------------------–
⎝⎠
⎜⎟
⎜⎟
⎜⎟
⎛⎞
YR 1–()
×=
xx
∑
n
---------=
yy
∑
n
---------=
xw
xy
∑
y
∑
-----------=
Sx
x2
∑x
∑
()
2
n
----------------–
n1–
----------------------------------=
Sy
y2
∑y
∑
()
2
n
----------------–
n1–
----------------------------------=
σx
x2
∑x
∑
()
2
n
----------------–
n
----------------------------------=
σy
y2
∑y
∑
()
2
n
----------------–
n
----------------------------------=
r
xy
∑x
∑y
∑
n
------------------–
x2
∑x
∑
()
2
n
----------------–
⎝⎠
⎜⎟
⎛⎞
y2
∑y
∑
()
2
n
----------------–
⎝⎠
⎜⎟
⎛⎞
------------------------------------------------------------------------------------=
m
xy
∑x
∑y
∑
n
------------------–
x2
∑x
∑
()
2
n
----------------–
-------------------------------------=
bymx–=
x
ˆyb–
m
-----------=
y
ˆmx b+=

Appendix B: More About CalculationsVI
Forecasting
Name Fit
Best Fit Automatically selects fit
Linear m*x+b
Logarithm m*ln(x)+b
Exponential b*e(m*x)
Power b*xm
Exponent b*mx
Inverse m/x+b

Appendix C: Messages I
Appendix C: Messages
Clear Messages
Press M or | to clear a message from the display.
Table C-1 Messages
Message Displayed Description
ALL CLEAR Memory has been erased (Ch. 2).
COPR HP 2010 Copyright message.
Oflo (Overflow). The magnitude of a result is too large for the
calculator to handle. Message is displayed for a moment, then
the overflow result is returned (±9.99999999999E499). The
overflow message is also displayed if an intermediate TVM or
cashflow calculation results in an overflow condition.
Uflo (Underflow). An intermediate result in TVM is too small for the
HP 10bII+ to process. This message is also briefly displayed if
any calculation underflows. In this case, it is followed by zero.
no Solution No solution exists for values entered (Appendix B).
not Found A solution for IRR/YR or I/YR may or may not exist. If you are
attempting to solve I/YR, you may be able to perform the
calculation using IRR/YR. If you are attempting an IRR/YR
calculation, refer to (Appendix B).
Error I_Yr Invalid value in I/Yr register or error solving for I/Yr.
Error P_Yr Invalid value in P/Yr register or error solving for P/Yr.
Error N Invalid value in N register or error solving for N.
Error LN An invalid number was entered for the LN function.
Error 0 / 0 An attempt was made to divide 0 by 0.
Error / 0 An attempt was made to divide by 0.
Algebraic Algebraic calculation mode is active.
Chain Chain calculation mode is active.
Error days An invalid date or range was attempted with the ]È
function.
Error ddays An invalid date or range was attempted with the \Ä
function.
CFLOW CLR cashflow memory was cleared.
TVM CLR tvm registers were cleared.
BR EV CLR breakeven registers were cleared.

Appendix C: MessagesII
BOND CLR bond registers were cleared.
STAT CLR statistical memory and registers were cleared.
Best Fit The calculator selected the best fit regression which is
subsequently flashed for 1 second.
running Displays if a calculation takes longer than .25 seconds.
User Stop An IRR/YR, I/YR, or amortization calculation was interrupted
by pressing M.
Table C-1 Messages
Message Displayed Description

Warranty, Regulatory, and Contact Information 1
17 Warranty, Regulatory, and Contact Information
Replacing the Batteries
Warning! There is a danger of explosion if batteries are incorrectly replaced. Replace only
with the same type of battery or with equivalent batteries (as recommended by the manufac-
turer). Dispose of used batteries according to the manufacturer’s instructions. Do not mutilate,
puncture, or dispose of batteries in fire. The batteries can burst or explode, releasing hazard-
ous chemicals.
•The calculator is powered by two 3-volt CR2032 coin batteries.
•When changing batteries, use only fresh coin-cell batteries. Do not use rechargeable
batteries.
•Do not mutilate, puncture, or dispose of batteries in fire. The batteries can burst or
explode, releasing hazardous chemicals.
•Do not use new and old batteries together, and do not mix batteries of different types.
1. Have two fresh CR2032 batteries at hand. Only touch the batteries by their edges.
Wipe each battery with a lint-free cloth to remove dirt and oil.
2. Make sure the calculator is off. When changing the batteries, change the batteries one
at a time to avoid clearing the memory. As a back-up, write down any data that you
have stored and might need for later use.
3. Turn the calculator over and pry off the battery cover.
4. Gently remove one battery.
5. Insert the new battery, making sure that the positive sign (+) battery is facing outward.
6. Gently remove the other battery.
7. Insert the other new battery, making sure that the positive sign (+) battery is facing
outward.
8. Replace the battery-compartment lid.
9. Press =.
10. If the calculator does not turn on, follow the procedures in the section titled, Determining
if the Calculator Requires Service in Appendix A of the HP 10bII+ Financial Calculator
User’s Guide.
HP Limited Hardware Warranty and Customer Care
This HP Limited Warranty gives you, the end-user customer, express limited warranty rights
from HP, the manufacturer. Please refer to HP's Web site for an extensive description of your
limited warranty entitlements. In addition, you may also have other legal rights under appli-
cable local law or special written agreement with HP.
Limited Hardware Warranty Period
Duration: 12 months total (may vary by region, please visit www.hp.com/support for latest
information).
Warranty, Regulatory, and Contact Information2
General Terms
EXCEPT FOR THE WARRANTIES SPECIFICALLY PROVIDED FOR IN SUBSEQUENT PARA-
GRAPHS OF THIS SECTION, HP MAKES NO OTHER EXPRESS WARRANTY OR CONDITION
WHETHER WRITTEN OR ORAL. TO THE EXTENT ALLOWED BY LOCAL LAW, ANY IMPLIED
WARRANTY OR CONDITION OF MERCHANTABILITY, SATISFACTORY QUALITY, OR FITNESS
FOR A PARTICULAR PURPOSE IS LIMITED TO THE DURATION OF THE EXPRESS WARRANTY
SET FORTH IN THE SUBSEQUENT PARAGRAPHS OF THIS SECTION. Some countries, states or
provinces do not allow limitations on the duration of an implied warranty, so the above limi-
tation or exclusion might not apply to you. This warranty gives you specific legal rights and
you might also have other rights that vary from country to country, state to state, or province
to province. TO THE EXTENT ALLOWED BY LOCAL LAW, THE REMEDIES IN THIS WARRANTY
STATEMENT ARE YOUR SOLE AND EXCLUSIVE REMEDIES. EXCEPT AS INDICATED ABOVE, IN
NO EVENT WILL HP OR ITS SUPPLIERS BE LIABLE FOR LOSS OF DATA OR FOR DIRECT, SPE-
CIAL, INCIDENTAL, CONSEQUENTIAL (INCLUDING LOST PROFIT OR DATA), OR OTHER DAM-
AGE, WHETHER BASED IN CONTRACT, TORT, OR OTHERWISE. Some countries, States or
provinces do not allow the exclusion or limitation of incidental or consequential damages, so
the above limitation or exclusion may not apply to you. FOR CONSUMER TRANSACTIONS IN
AUSTRALIA AND NEW ZEALAND: THE WARRANTY TERMS CONTAINED IN THIS STATEMENT,
EXCEPT TO THE EXTENT LAWFULLY PERMITTED, DO NOT EXCLUDE, RESTRICT OR MODIFY
AND ARE IN ADDITION TO THE MANDATORY STATUTORY RIGHTS APPLICABLE TO THE SALE
OF THIS PRODUCT TO YOU. Notwithstanding the above disclaimers, HP expressly warrants
to you, the end-user customer, that HP hardware, accessories and supplies will be free from
defects in materials and workmanship after the date of purchase, for the period specified
above. If HP receives notice of such defects during the warranty period, HP will, at its option,
either repair or replace products which prove to be defective. Replacement products may be
either new or like-new. HP also expressly warrants to you that HP software will not fail to exe-
cute its programming instructions after the date of purchase, for the period specified above,
due to defects in material and workmanship when properly installed and used. If HP receives
notice of such defects during the warranty period, HP will replace software media which
does not execute its programming instructions due to such defects.
Exclusions
HP does not warrant that the operation of HP products will be uninterrupted or error free. If
HP is unable, within a reasonable time, to repair or replace any product to a condition as
warranted, you will be entitled to a refund of the purchase price upon prompt return of the
product with proof of purchase. HP products may contain remanufactured parts equivalent to
new in performance or may have been subject to incidental use. Warranty does not apply to
defects resulting from (a) improper or inadequate maintenance or calibration, (b) software,
interfacing, parts or supplies not supplied by HP, (c) unauthorized modification or misuse, (d)
operation outside of the published environmental specifications for the product, or (e)
improper site preparation or maintenance. HP MAKES NO OTHER EXPRESS WARRANTY
Warranty, Regulatory, and Contact Information 3
OR CONDITION WHETHER WRITTEN OR ORAL. TO THE EXTENT ALLOWED BY LOCAL
LAW, ANY IMPLIED WARRANTY OR CONDITION OF MERCHANTABILITY, SATISFACTORY
QUALITY, OR FITNESS FOR A PARTICULAR PURPOSE IS LIMITED TO THE DURATION OF
THE EXPRESS WARRANTY SET FORTH ABOVE. Some countries, states or provinces do not
allow limitations on the duration of an implied warranty, so the above limitation or exclusion
might not apply to you. This warranty gives you specific legal rights and you might also have
other rights that vary from country to country, state to state, or province to province. TO THE
EXTENT ALLOWED BY LOCAL LAW, THE REMEDIES IN THIS WARRANTY STATEMENT ARE
YOUR SOLE AND EXCLUSIVE REMEDIES. EXCEPT AS INDICATED ABOVE, IN NO EVENT
WILL HP OR ITS SUPPLIERS BE LIABLE FOR LOSS OF DATA OR FOR DIRECT, SPECIAL, INCI-
DENTAL, CONSEQUENTIAL (INCLUDING LOST PROFIT OR DATA), OR OTHER DAMAGE,
WHETHER BASED IN CONTRACT, TORT, OR OTHERWISE. Some countries, States or prov-
inces do not allow the exclusion or limitation of incidental or consequential damages, so the
above limitation or exclusion may not apply to you. The only warranties for HP products and
services are set forth in the express warranty statements accompanying such products and
services. HP shall not be liable for technical or editorial errors or omissions contained herein.
FOR CONSUMER TRANSACTIONS IN AUSTRALIA AND NEW ZEALAND: THE WAR-
RANTY TERMS CONTAINED IN THIS STATEMENT, EXCEPT TO THE EXTENT LAWFULLY
PERMITTED, DO NOT EXCLUDE, RESTRICT OR MODIFY AND ARE IN ADDITION TO THE
MANDATORY STATUTORY RIGHTS APPLICABLE TO THE SALE OF THIS PRODUCT TO YOU.
Regulatory Information
Federal Communications Commission Notice
This equipment has been tested and found to comply with the limits for a Class B digital
device, pursuant to Part 15 of the FCC Rules. These limits are designed to provide reasonable
protection against harmful interference in a residential installation. This equipment generates,
uses, and can radiate radio frequency energy and, if not installed and used in accordance
with the instructions, may cause harmful interference to radio communications. However, there
is no guarantee that interference will not occur in a particular installation. If this equipment
does cause harmful interference to radio or television reception, which can be determined by
turning the equipment off and on, the user is encouraged to try to correct the interference by
one or more of the following measures:
• Reorient or relocate the receiving antenna.
• Increase the separation between the equipment and the receiver.
• Connect the equipment into an outlet on a circuit different from that to which the receiver is
connected.
• Consult the dealer or an experienced radio or television technician for help.
Modifications
The FCC requires the user to be notified that any changes or modifications made to this device
that are not expressly approved by Hewlett-Packard Company may void the user's authority
to operate the equipment.
Warranty, Regulatory, and Contact Information4
Declaration of Conformity for Products Marked with FCC Logo, United
States Only
This device complies with Part 15 of the FCC Rules. Operation is subject to the following two
conditions:
1. This device may not cause harmful interference
2. This device must accept any interference received, including interference that may cause
undesired operation.
If you have questions about the product that are not related to this declaration, write to:
Hewlett-Packard Company
P. O. Box 692000, Mail Stop 530113
Houston, TX 77269-2000
For questions regarding this FCC declaration, write to:
Hewlett-Packard Company
P. O. Box 692000, Mail Stop 510101
Houston, TX 77269-2000
or call HP at 281-514-3333
To identify your product, refer to the part, series, or model number located on the product.
Canadian Notice
This Class B digital apparatus meets all requirements of the Canadian Interference-Causing
Equipment Regulations.
Avis Canadien
Cet appareil numérique de la classe B respecte toutes les exigences du Règlement sur le
matériel brouilleur du Canada.
European Union Regulatory Notice
Products bearing the CE marking comply with the following EU Directives:
• Low Voltage Directive 2006/95/EC
• EMC Directive 2004/108/EC
• Ecodesign Directive 2009/125/EC, where applicable
CE compliance of this product is valid if powered with the correct CE-marked AC adapter
provided by HP. Compliance with these directives implies conformity to applicable
harmonized European standards (European Norms) that are listed in the EU Declaration of
Conformity issued by HP for this product or product family and available (in English only)
either within the product documentation or at the following web site: www.hp.eu/certificates
(type the product number in the search field). The compliance is indicated by one of the
following conformity markings placed on the product:

Warranty, Regulatory, and Contact Information 5
Please refer to the regulatory label provided on the product. The point of contact for regulatory
matters is:
Hewlett-Packard GmbH, Dept./MS: HQ-TRE, Herrenberger Strasse 140, 71034 Boeblingen,
GERMANY.
Japanese Notice
Disposal of Waste Equipment by Users in Private Household in the
European Union
This symbol on the product or on its packaging indicates that this
product must not be disposed of with your other household waste.
Instead, it is your responsibility to dispose of your waste equipment by
handing it over to a designated collection point for the recycling of
waste electrical and electronic equipment. The separate collection
and recycling of your waste equipment at the time of disposal will help
to conserve natural resources and ensure that it is recycled in a
manner that protects human health and the environment. For more
information about where you can drop off your waste equipment for recycling, please contact
your local city office, your household waste disposal service or the shop where you purchased
the product.
For non-telecommunications products and for EU
harmonized telecommunications products, such as
Bluetooth® within power class below10mW.
For EU non-harmonized telecommunications
products (If applicable, a 4-digit notified body
number is inserted between CE and !).

Warranty, Regulatory, and Contact Information6
Perchlorate Material - special handling may apply
This calculator's Memory Backup battery may contain perchlorate and may require special
handling when recycled or disposed in California.
Customer Care
In addition to the one year hardware warranty, your HP calculator also comes with one year
of technical support. If you need assistance with warranty, please refer to the warranty infor-
mation on the product CD. HP customer care can be reached by either email or telephone.
Before calling please locate the call center nearest you from the list provided. Have your
proof of purchase and calculator serial number ready when you call. Telephone numbers are
subject to change, and local and national telephone rates may apply. A complete list is
available on the web at: www.hp.com/support.
Contact Information
Table 17-1 Contact Information
Country/
Region Contact Country/
Region Contact
Algeria www.hp.com/support Anguila 1-800-711-2884
Antigua 1-800-711-2884 Argentina 0-800-555-5000
Aruba 800-8000;
800-711-2884 Austria
Österreich 01 360 277 1203
Bahamas 1-800-711-2884 Barbados 1-800-711-2884
Belgique
(Français) 02 620 00 85 Belgium
(English) 02 620 00 86
Bermuda 1-800-711-2884 Bolivia 800-100-193
Botswana www.hp.com/support Brazil Brasil 0-800-709-7751
British Virgin
Islands 1-80 0 -711-2884 Bul garia w ww.hp. com/suppor t
Canada 800-HP-INVENT Cayman
Island 1-80 0 -711-2884
Chile 800-360-999 China
中国
800-820-9669
Costa Rica 0-800-011-0524 Croatia www.hp.com/support
Curacao 001-800-872-2881
+ 800 -711-2884 Czech
Republic
Česká
republikaik
296 335 612
Denmark 82 33 28 44 Dominica 1-800-711-2884
Dominican
Republic 1-80 0 -711-2884 Egypt w ww.h p.com /sup port

Warranty, Regulatory, and Contact Information 7
El Salvador 800-6160 Equador 1-999-119;
800-711-2884 (Andinatel)
1-800-225-528;
800-711-2884 (Pacifitel)
Estonia www.hp.com/support Finland
Suomi 09 8171 0281
France 01 4993 9006 French
Antilles 0-800-990-011;
800-711-2884
French
Guiana 0-800-990-011;
800-711-2884 Germany
Deutschland 069 9530 7103
Ghana www.hp.com/support Greece
Ελλάδα 210 969 6421
Grenada 1-800-711-2884 Guadelupe 0-800-990-011;
800-711-2884
Guatemala 1-800-999-5105 Guyana 159; 800-711-2884
Haiti 183; 800-711-2884 Honduras 800-0-123; 800-711-2884
Hong Kong
香港特別行
政區
800-933011Hungarywww.hp.com/support
India 1-800-1147 72 I n d o n e s i a ( 21) 35 0 - 3 40 8
Ireland 01 605 0356 Italy Italia 02 754 19 782
Jamaica 1-800-711-2884 Japan
日本
00531-86-0011
Kazakhstan www.hp.com/support Latvia www.hp.com/support
Lebanon www.hp.com/support Lithuania www.hp.com/support
Luxembourg 2730 2146 Malaysia 1800-88-8588
Martinica 0-800-990-011;
877-219-8671 Mauritius www.hp.com/support
Mexico
México 01-800-474-68368
(800 HP INVENT) Montenegro www.hp.com/support
Montserra t 1-800 -711-2884 Morocco w ww.hp.com /s upport
Namibia www.hp.com/support Netherlands 020 654 5301
Netherland
Antilles 001-800-872-2881;
800-711-2884 New
Zealand 0800-551-664
Nicaragua 1-800-0164;
800-711-2884 Norway
Norwegen 23500027
Panama
Panamá 001-800-711-2884 Paraguay (009) 800-541-0006
Country/
Region Contact Country/
Region Contact

Warranty, Regulatory, and Contact Information8
Peru
Perú 0-800-10111 Philippines (2)-867-3351
Poland
Polska www.hp.com/support Portugal 021 318 0093
Puerto Rico 1-877 232 0589 Romania www.hp.com/support
Russia
Россия 495-228-3050 Saudi
Arabia www.hp.com/support
Serbia www.hp.com/support Singapore 6272-5300
Slovakia www.hp.com/support South Africa 0800980410
South Korea
한국
00798-862-0305 Spain
España 913753382
St Kitts &
Nevis 1-800 -711-2884 St Lucia 1-800 - 478- 4602
St Marteen 1-800-711-2884 St Vincent 01-800-711-2884
Suriname 156; 800-711-2884 Swaziland www.hp.com/support
Sweden
Sverige 08 5199 2065 Switzerland 022 827 8780
Switzerland
(Suisse
Français)
022 827 8780 Switzerland
(Schweiz
Deutsch)
01 439 5358
Switzerland
(Svizzeera
Italiano)
022 567 5308 Taiwan
臺灣
00801-86-1047
Thailand
ไทย
(2)-353-9000 Trinidad &
Tobago 1-800 -711-2884
Tunisia www.hp.com/support Turkey
Türkiye www.hp.com/support
Turks &
Caicos 01-800 -711-2884 UAE www.hp.com/suppor t
United
Kingdom 0207 458 0161 Uruguay 0004-054-177
US Virgin
Islands 1-800 -711-2884 United
States 800-HP INVENT
Venezuela 0-800-474-68368
(0-800 HP INVENT) Vietnam
Viêt Nam +65-6272-5300
Zambia www.hp.com/support
Country/
Region Contact Country/
Region Contact
Warranty, Regulatory, and Contact Information 9
Warranty, Regulatory, and Contact Information10
1
A
Advance payments 72
Algebraic mode
calculations 28
Amortization 74
equations II
range of payments 76
single payment 77
TVM keys used 75
Angle format
selecting 35
Annuity account 70
Annunciators 30
Arithmetic operators 26
At a Glance
quick reference guide 1
B
Balloon payment 65
Batteries I
installing I
Battery
replacing the batteries 1, 6
Bonds 105
clear memory 105
example 106
keys used 105
resetting bond keys 108
Break-even 109
example 16, 110
keys used 109
resetting keys 112
C
Calendar 99
Calendar format 99
Calendar keys 99
Cash flow
equations III
Cash flows
application 87
calculating NPV and NFV 95
clearing memory 88
discounting 91
keys used 88
organizing 91
periods 56
recognizing one 59
signs of 56
storage of 89
storing IRR and NPV 98
viewing and editing 93
Chain mode
calculations 27
Clearing
backspace 29
messages in the display 30
Comma
interchanging with period 43
Comma separator III
Constants
using 49
Cursor 29
Customer care and contact information 6
D
Date calculations 101
Date format 99
bonds 106
Date keys 99
Decimal
specifying display of decimal places 42
Depreciation 83
resetting TVM keys 86
TVM keys used 83
Display
full precision 42
Display format 41
E
Environmental limits IV
Equations
amortization II
bonds IV
cash-flow calculations III
depreciation V
forecasting V
interest rate conversions II
margins and markups I
statistical V
TVM II
Error messages I
F
Factorial 126
FAQ I, III
Frequently Asked Questions I, III
H
Home mortgage 64
Hyperbolic functions 35
I
Individual retirement account 69
2
In-line functions 37
Interest
compound interest 57
interest rates 57
simple interest 56
Interest rate conversions 79
Investments
different compounding periods 79
IRR calculating IRR 90
IRR/YR I
IRR/YR calculations
possible outcomes I
K
Keyboard iv
map legend iv
Keys
360/ACT 99
Accint (bonds) 105
advanced probability distributions 128
Alg/Chain 26
Amort 62
backspace 29
basic functions 24
Beg/End 62
boxed key functions 25
business percentages 45
C STAT 113
call (bonds) 105
CFj 87
clear 29
clear all 30
clear memory 29
clearing functions 25
CPN% (bonds) 105
CST (cost business) 47
date 99
DB (declining balance) 83
DISP 42
DMY/MDY 99
E 43
eff% 79
estimation of x 113
estimation of y 113
FC (break-even) 109
FV 61
I/YR 61
input 32
K 49
M 51
MAR (margin) 47
matdate (bonds) 105
mean of x weighted by y 113
means of x and y 113
MU (markup) 47
N 61
NFV 88
Nj 87
nom% 79
NPV 88
number of days 99
off 23
on 23
one-number functions 33
P/YR 61
parentheses 28
percent 45
period/comma 43
plus, minus, multiply, divide 26
PMT 61
population standard deviation 113
PRC (price business) 47
price (bonds) 105
profit (break-even) 109
PV 61
RAND 127
regression models 113
RND 43
sample standard deviation 113
semi/ann (bonds) 105
setdate (bonds) 105
shift keys 25
SL (straight line) 83
SOYD 83
SP (break-even) 109
statistics 32
STO (store) 52
swap 32
two-number functions 39
units (break-even) 109
VC (break-even) 109
xP/YR 61
YTM (bonds) 105
L
Last answer 41
Lease calculations 71
Legal notice ii
Loan calculations 62
M
Manual conventions 23
Margin 47
Markup 47
Memory
3
clearing II
Messages I
calculator status 44
list of I
Modes
TVM begin and end 62
N
Negative numbers 29
Net future value 95
Net present value 95
Number of days 101
Number storage 49
Numbers
display format 41
range of I
O
One-number functions 33
arithmetic with 39
Operating conditions IV
Operating modes 26
P
Parentheses
use in calculations 28
Percent
dividing by 100 45
percent change 46
Percentages
business 45
Period
interchanging with comma 43
Pi 36
Probability
advanced distributions 128
combinations 126
conversions from lower tail 133
inverse normal lower tail 130
inverse Student’s T lower tail 132
keys used 128
normal lower tail 129
permutations 126
Student’s T and inverse 128
Student’s T lower tail 131
Z and inverse 128
Q
Questions I, III
R
Random number and seed 127
Registers
M register 51
using numbered registers 51
Regulatory Information 3
Reset II
Rounding numbers 43
S
Savings calculations 67
Scientific notation 43
Screen display iv
Service II
Statistics
calculations that return two values 119
clearing data 114
entering data 114
keys used 113
linear regression, estimation, and regression
modes 121
mean, standard deviation and summation 120
memory and storage 114
one-variable 115
regression models and variables 125
summary of calculations 119
two-variable 115
viewing and editing data 116
weighted mean 115, 124
Storage registers
arithmetic with 49
T
Trigonometric functions 35
Troubleshooting II
TVM
equations II
keys 61
recognizing one 58
TVM keys
resetting 82
Two number functions 37
Two-number functions
arithmetic with 39
W
Warranty 1