JBL Engineering Mathematics Made Easy With TI 36X Pro (All India Syllabus) – A Guidebook Illustrative Examples TI36PRO EN
User Manual: JBL Engineering Mathematics Made Easy with TI-36X Pro (All India Syllabus) – A guidebook with illustrative examples TI-36X Pro Guidebook - Engineering Mathematics Made Easy with TI-36X Pro (All India Syllabus) – A guidebook with illustrative examples
Open the PDF directly: View PDF ![]() .
.
Page Count: 148 [warning: Documents this large are best viewed by clicking the View PDF Link!]

Engineering Mathematics
Made Easy with TI-36X Pro
(All India Syllabus)
By PROF. AJOY K RAY

Page 2 of 148
Engineering Mathematics Made Easy with TI-36X Pro (All India Syllabus)
Published by Statworks India Private Limited (“Statworks”)
Copyright ©2012 by Statworks India Private Limited (“Statworks”)
All rights reserved. No part of this publication maybe reproduced or distributed in
any form or by any means or stored in a database or retrieval system or
transmitted in any form or by any means, electronic, mechanical, photocopying or
otherwise, without the prior written permission of the publisher.
Trademark and Copyright of Texas Instruments Inc. (“TI”) : TI-36XPRO
Disclaimer:
The guidebook Engineering Mathematics Made Easy with TI-36X Pro (All India
Syllabus) is solely the written work of Statworks and its consultants and Statworks
acknowledges that Texas Instruments (TI) has no liability or claims whatsoever in
respect of this guidebook and its content.

Page 3 of 148
FOREWORD
To all Academicians and Students
Are you expecting to solve Engineering Mathematics easily and quickly using the
latest and leading Scientific Calculator in the market right now? If your answer is a
resounding YES, then you are on the right path purchasing my book:
ENGINEERING MATHEMATICS MADE EASY WITH TI-36XPRO (All India
Syllabus).
This book is an interesting combo package – It is designed to be used in
conjunction with Engineering Mathematics Textbooks. The calculator selected for
this workbook is the Texas Instruments Scientific Calculator – TI-36XPRO.
Each section in this workbook shows how to use the calculator to work out solutions
to problems similar to those found in Engineering Mathematics textbooks. Most
types of problems are covered. Emphasis is on the use of the scientific functions of
the calculator. The only assumption is that students have the identical calculator. If
another model of calculator is used, it is possible, or even likely, that other
keystroke sequences will be needed to achieve correct results. Some calculators will
not be able to do all the types of problems demonstrated in this workbook. This
guidebook will enable students and academicians to be in a better position to assist
others on the usage of the scientific calculator to solve Engineering Mathematics
problems.
The students will find this book useful in assisting them to improve their skills on
how to use the Scientific Calculator TI-36XPRO to efficiently solve their problems.
The ENGINEERING MATHEMATICS MADE EASY WITH TI-36XPRO (All India
Syllabus) provides the Engineering Mathematics examples, answers and step to be
followed with the calculator to solve these mathematics problems. A student could
either refer to the answer before following the steps or the student could follow the
steps and check whether their methods and answers are correct in solving the
problems. It is a way for the students to assess themselves with the help of the
book.
Texas Instruments TI 36X Pro is the leading Advanced Scientific Calculator (non-
programmable) which is widely used in US, Europe and other Asian Countries. It is
fast gaining acceptance in India due to its unique features and ease of use. This
guidebook helps academicians and students to learn to use TI-36XPRO thoroughly
which in turn help students to save time in solving mathematical problems during
their examinations.

Page 4 of 148
ABOUT THE AUTHOR
The Author, Prof. Ajoy Kumar Ray is the Vice Chancellor of the Bengal Engineering
and Science University, Shibpur. Previously, he was a Professor of Electronics and
Electrical Communication Engineering and Head, School of Medical Science and
Technology at IIT Kharagpur. He has co-authored about 90 research papers well as
has authored five books published by International Publishing Houses, such as John
Wiley, Tata McGraw Hill, Prentice Hall of India etc. He is an expert in engineering
mathematics and is experienced in using various types of calculators whereby which
he has selected the TI-36XPRO Scientific Calculator and has written a Guidebook to
assist students and academicians in solving Engineering Mathematics problems
easily.

Page 5 of 148
TABLE OF CONTENTS
Basic Algebra
Arithmetic ................................................................................................... 7
Fractions, Decimals and Percentages ........................................................ 12
Indices, Standard Form and Engineering Notation .................................... 16
Calculations and Evaluation of Formulae................................................... 20
Computer Numbering Systems .................................................................. 24
Algebra ..................................................................................................... 28
Logarithms ................................................................................................ 32
Number Sequences ................................................................................... 38
Complex Number
Complex Number ...................................................................................... 43
Theory of Equation
Simple Equations ...................................................................................... 46
Simultaneous Equation ............................................................................. 51
Matrices and Vector
Determinants and Matrices ....................................................................... 56
Vector ....................................................................................................... 61

Page 6 of 148
Geometry and Trigonometry
Introduction to Trigonometry ................................................................... 66
Cartesian and polar co-ordinates .............................................................. 71
Geometry and Triangles ............................................................................ 74
Adding of Waveforms ................................................................................ 86
Analytical Solid Geometry
Areas of Plane Figures .............................................................................. 94
The Circle ................................................................................................ 100
Volumes of common solids ...................................................................... 103
Calculus
Integration ............................................................................................. 108
Differentiation ........................................................................................ 112
Statistics and Probability
Correlation and Regression ..................................................................... 117
Measures of Central Tendency and Dispersion ........................................ 128
Distributions ........................................................................................... 134
Probability .............................................................................................. 140
Sampling and Inference .......................................................................... 143

Topic:
Basic Arithmetic
Math Concepts:
Arithmetic Sequence, Arithmetic Progressions, Arithmetic
Series.
Page 7 of 148
Arithmetic
Overview / Introduction / Terminology:
Arithmetic is the study of numerical quantities. At least a basic understanding of arithmetic is
fundamental in the study of algebra and all other mathematical studies. This book assumes that the
reader already understands some mathematics but wishes to relearn it in a more formal manner.
Arithmetic Sequence
Arithmetic sequence is a sequence of numbers that has a constant difference between every two
consecutive terms.
In other words, arithmetic sequence is a sequence of numbers in which each term except the first term
is the result of adding the same number, called the common difference, to the preceding term. Example:
The sequence . . . is an arithmetic sequence; because the same number (i.e. the
common difference) is added to each term of the sequence to get the succeeding term.
Arithmetic Progressions
By an arithmetic progression of m terms, we mean a finite sequence of the form
The real number is called the first term of the arithmetic progression, and the real number d is called
the difference of the arithmetic progression.
Arithmetic Series
A series such as which has a constant
difference between terms. The first term is , the common difference is and the number of terms is
. The sum of an arithmetic series is found by multiplying the number of terms times the average of the
first and last terms. Formula:
Keystrokes:
,,

Topic:
Basic Arithmetic
Math Concepts:
Arithmetic Sequence, Arithmetic Progressions, Arithmetic
Series.
Page 8 of 148
Example:
1. Fine the value of the following summation:
From the formula ("") for the n-th term, each term will be two units larger than the previous
term. (Plug in values for n if you're not sure about this.) So this is indeed an arithmetical sum. But this
summation starts at , not at , and the summation formula applies to sums starting at
. So how can it work with this summation?
The quickest way to find the value of this sum is to find the and partial sums, and then
subtract the from the . By doing this subtraction, it be left with the value of the sum of the
through terms. The first term is . The other necessary terms are
and .
Subtracting:

Topic:
Basic Arithmetic
Math Concepts:
Arithmetic Sequence, Arithmetic Progressions, Arithmetic
Series.
Page 9 of 148
No
Keystrokes
Screenshots
1
Assume
Firstly press button, or 5:sum(,
2
Insert value in the formulae,
The answer = .
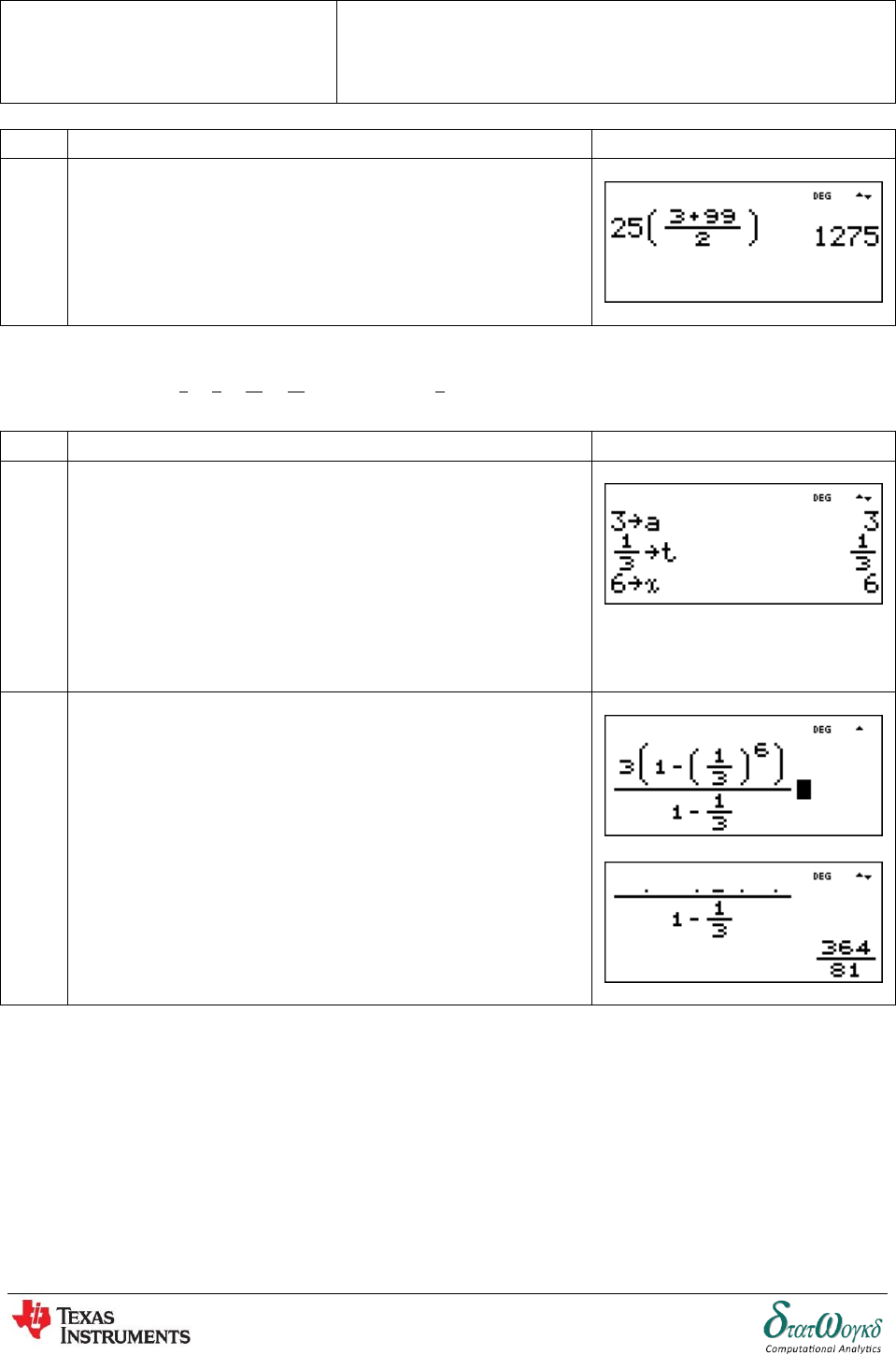
2. has and To find use the explicit formula for an
arithmetic sequence.
No
Keystrokes
Screenshots
1
Firstly solve value for n, press ,
Then insert value
2
Assume and press
Press to go to the home screen.
Topic:
Basic Arithmetic
Math Concepts:
Arithmetic Sequence, Arithmetic Progressions, Arithmetic
Series.
Page 10 of 148
No
Keystrokes
Screenshots
3
And then, insert in the formula and press
.
The answer is .
3. Solve,
has
and
No
Keystrokes
Screenshots
1
Store the value in the variable Press
,
and
.
And press (home screen).
2
Then, insert value in the formula, press
.
Exercise:
1. Holes are drilled mm apart in a metal plate. If a row of holes is drilled, determine the
distance, in centimeters, between the centers of the first and last holes.
2. Determine the HCF and LCM of the numbers given:
a)
b)
c)
Topic:
Basic Arithmetic
Math Concepts:
Arithmetic Sequence, Arithmetic Progressions, Arithmetic
Series.
Page 11 of 148
3. Simplify the expressions given in below:
a)
b)
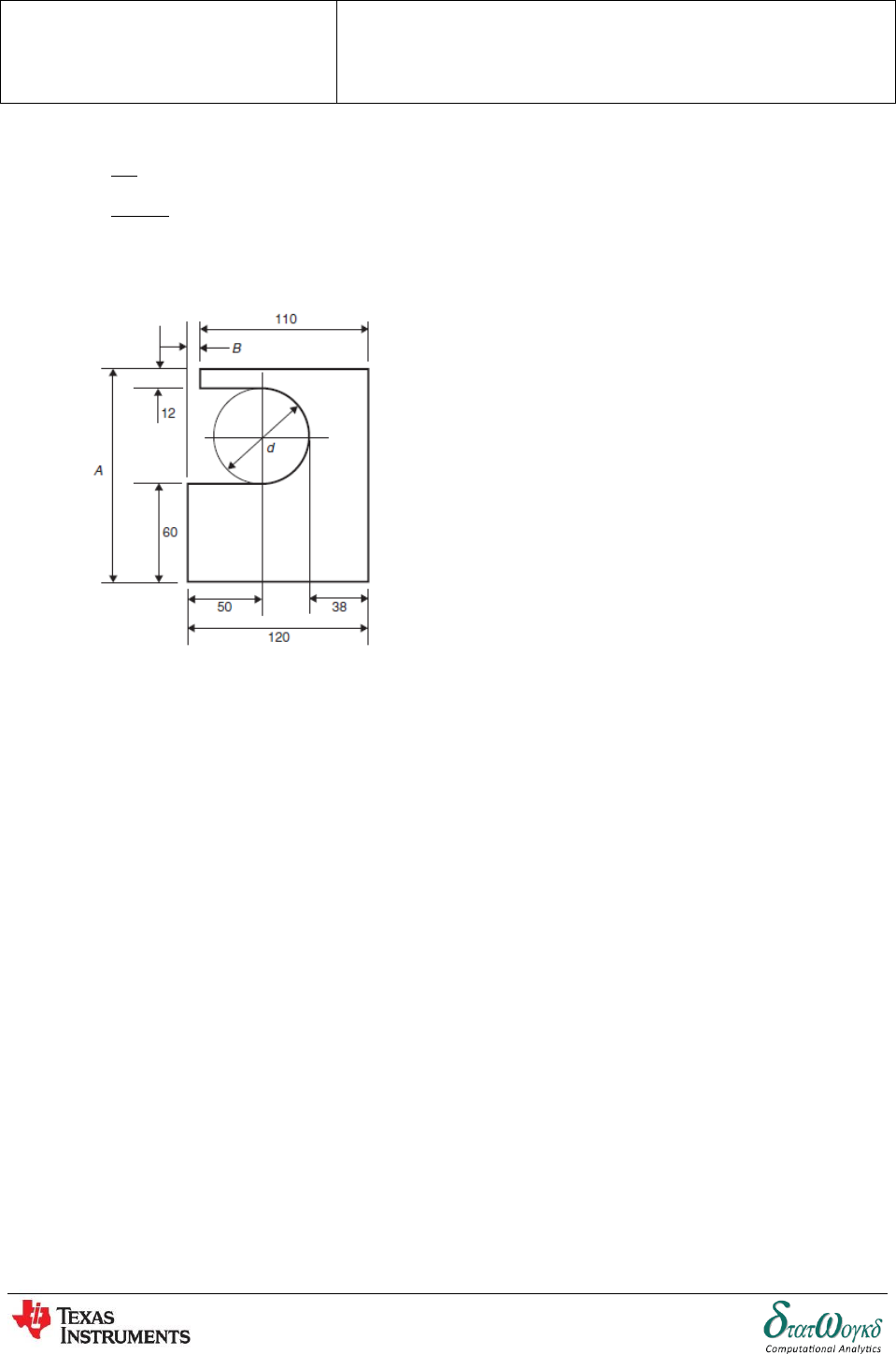
4. Calculate the diameter and dimensions and for the template shown in the figure below.
All dimensions are in the millimeters.
5. Expand the following series and find the sum :
Answer:
1.
2. a) ,
b) ,
c) ,
3. a)
b)
4.
5.
Topic:
Fractions, Decimals and Percentages
Math Concepts:
Fractions, Decimals, Percentages and Converter.
Page 12 of 148
Fractions, Decimals and Percentages
Overview / Introduction / Terminology:
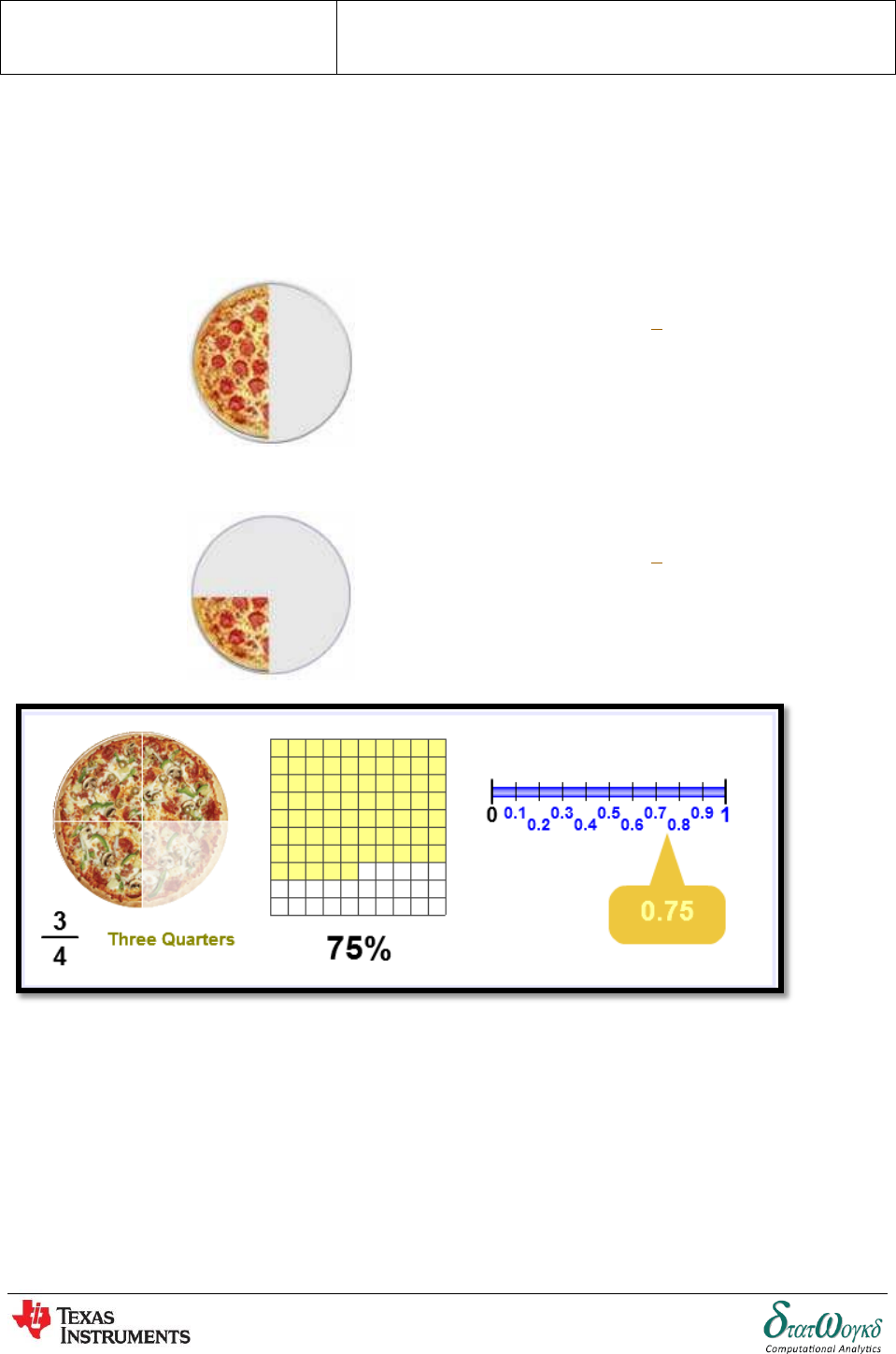
Decimals, Fractions and Percentages are just different ways of showing the same value:
A Half can be written...
As a fraction:
As a decimal:
As a percentage:
A Quarter can be written...
As a fraction:
As a decimal:
As a percentage:
Keystrokes:
, , (DEC), ,

Topic:
Fractions, Decimals and Percentages
Math Concepts:
Fractions, Decimals, Percentages and Converter.
Page 13 of 148
Example:
1. Find the value of
No
Keystrokes
Screenshots
1
To view a value as a mathprint mode, Press:
.
Go to a home screen with press .
2
Press to enter a mixed number. Insert value with
press,
3
To chance the proper fractions to the mixed fraction, press
1: .
4
Press to continue,
The answer is
2. A mining company extracts tons of ore with a concentration of metal of and tons
with a concentration of On the basis of these two extraction figures, what is the total quantity
of metal obtained?
If one ton of metal is worth dollars, what is the total value of the metal extracted?

Topic:
Fractions, Decimals and Percentages
Math Concepts:
Fractions, Decimals, Percentages and Converter.
Page 14 of 148
No
Keystrokes
Screenshots
1
Press
Then press
2
After get a value, Press
The two extractions represent a total of tons of metal
for a total value of dollars.
3. Express as decimal fraction:
No
Keystrokes
Screenshots
1
Press to get the template for mixed fraction
Then insert
2
To change the answer as decimal, press
Thus,
Topic:
Fractions, Decimals and Percentages
Math Concepts:
Fractions, Decimals, Percentages and Converter.
Page 15 of 148
Exercise:
1.
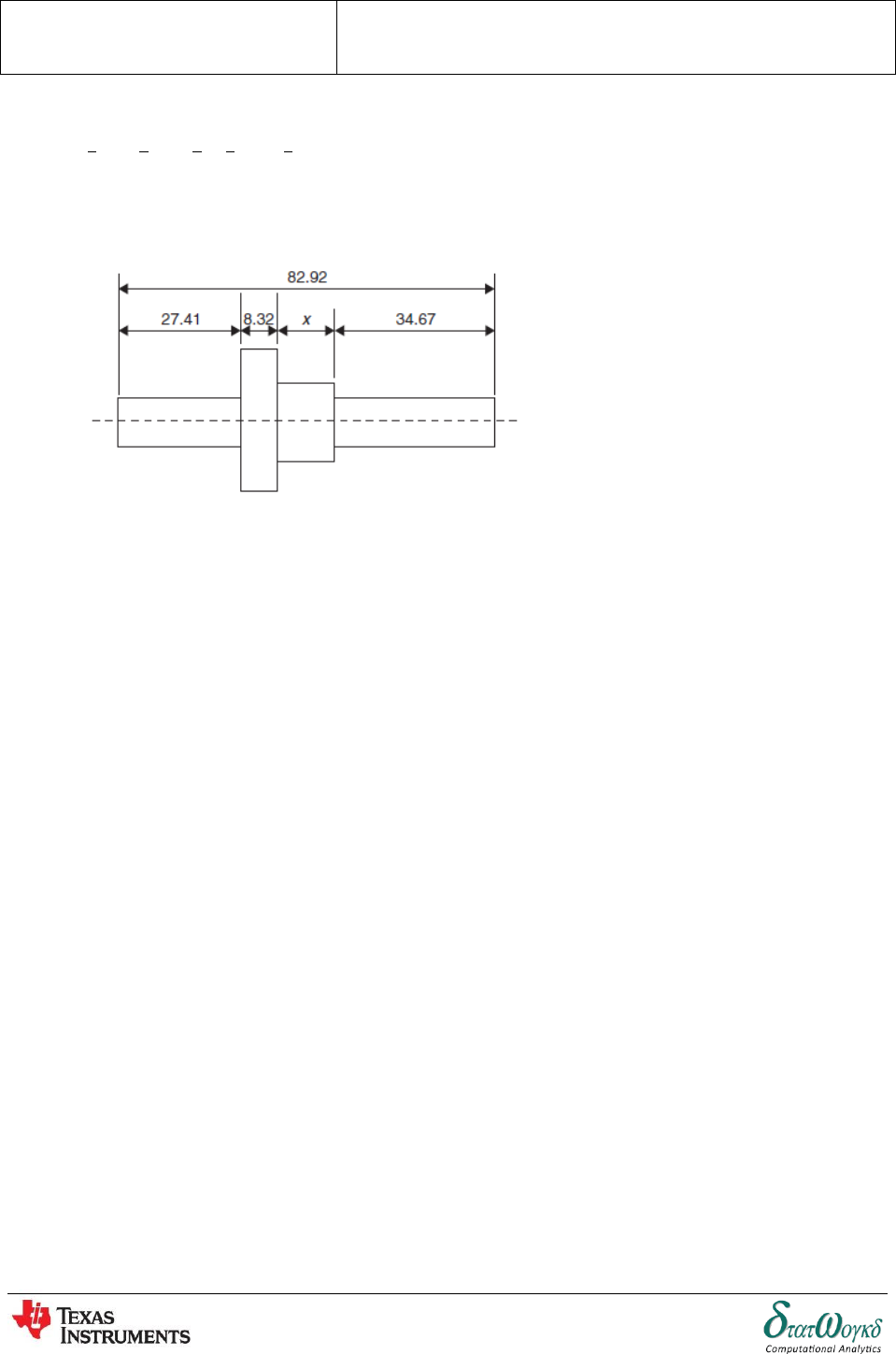
2. Determine the dimension marked x in the length of shaft shown in Figure below. The dimentions
are in millimeters.
3. A concrete mixture contain seven parts by volume of ballast, four parts by volume of sand and
two parts by volume of cement. Determine the percentage of each of these three constituents
correct to the nearest and the mass of cement in a two tonne dry mix, correct to
significant figure.
4. Convert to percentages:
a)
b)
c)
5. In a sample of iron ore, 18% is iron. How much more is needed to produce kg of iron?
Answer:
1.
2.
3.
4. (a)
(b)
(c)
5.

Topic:
Calculations and Evaluation of
Formulae
Math Concepts:
Calculations and Evaluation of Formulae
Page 16 of 148
Indices, Standard Form and Engineering Notation
Overview / Introduction / Terminology:
General use of decimal notation for whole numbers and decimal fractions dates from 1585 when
Simon Stevin (15481620) published his book, Die Thiende. Stevin used powers of 10 to introduce place
value and showed how the algebra of powers (the index laws) led to relatively simple ways of doing
arithmetic. We write a number such as: Three hundred and sixteen and a quarter in terms of powers of
as and shorten this to
Here, (n times) when
.
When we multiply by we use the index law, e (and the distributive law) to
obtain the quick answer .
The two basic index laws: and can be easily checked from the
definitions when a and b are positive integers. A little more thought is needed when a and/or b are
negative integers (or fractions!).
The definitions of and
and later of
, are chosen to ensure that the
basic index laws
The index laws allow us to write very large numbers in a compact and manageable form. For Example,
the number of atoms in the universe is frighteningly large but elementary arguments show that this
number is approximately . Scientific notation provides an agreed way of giving in standard form
the approximate value of very large numbers which occur in science, e.g.
Writing numbers in this form makes it easy to do rough calculators. For example,
Keystrokes:
[MATH][NUM],[SCI][ENG],
Topic:
Calculations and Evaluation of
Formulae
Math Concepts:
Calculations and Evaluation of Formulae
Page 17 of 148
Example:
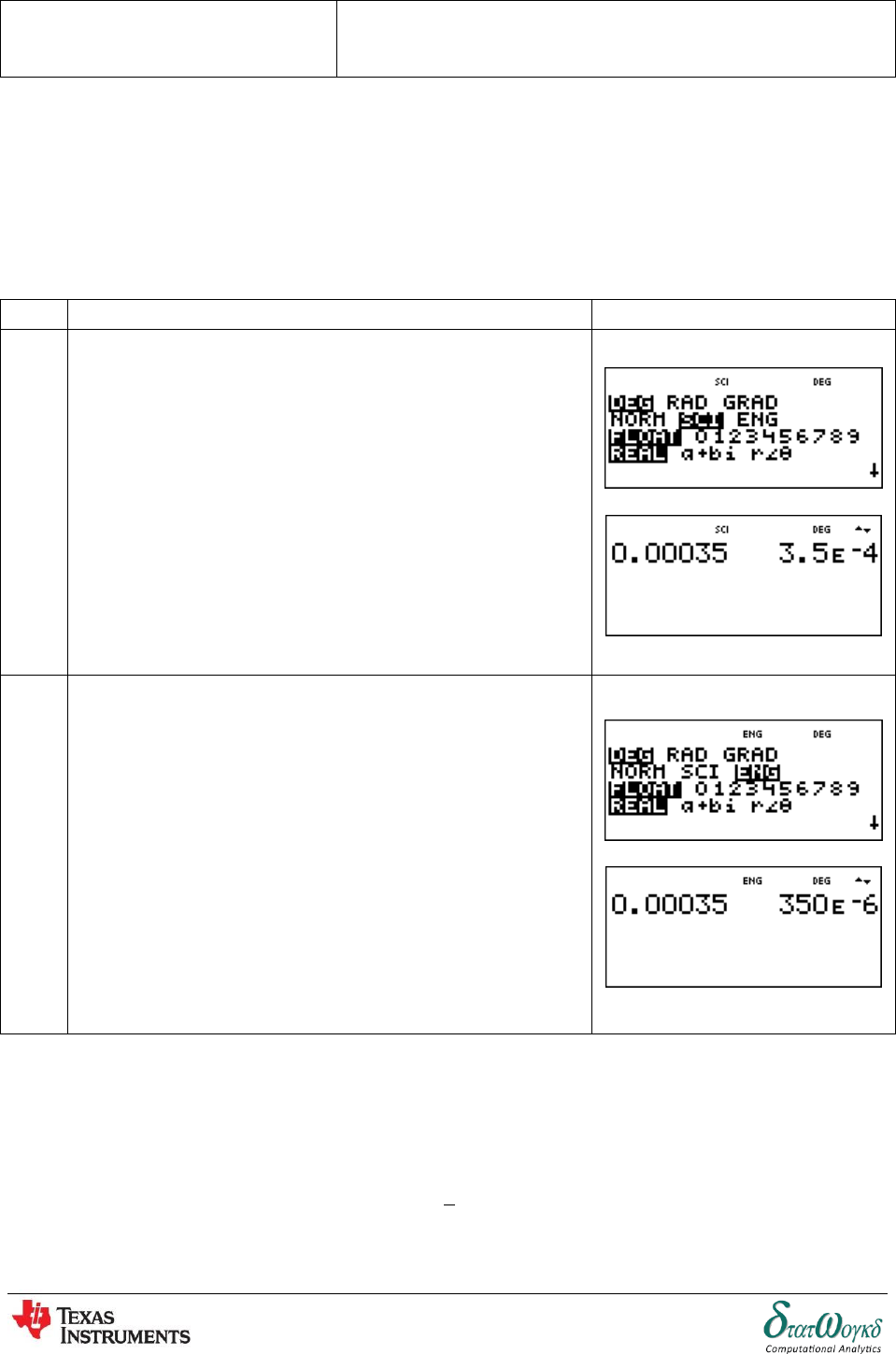
1. Engineering notation is similar to scientific notation except that the power of ten is always a
multiple of . For example,
in scientific notation,
in engineering notation.
No
Keystrokes
Screenshots
1
In scientific notation, press ,
.
2
In engineering notation, press
,.
Thus, in scientific notation =
and in engineering notation =
2. Find the value of on the following equation:

Topic:
Calculations and Evaluation of
Formulae
Math Concepts:
Calculations and Evaluation of Formulae
Page 18 of 148
No
Keystrokes
Screenshots
1
To find the value of press ,
2
Insert equation in the formulae. Press
.
Then press .
3
Assume that and press
4
So, value of .
Press to back to home screen.
3. Evaluate . Expressing answer is standard form.
No
Keystrokes
Screenshots
1
Firstly, Change mode calculator to the scientific mode with
press, .

Topic:
Calculations and Evaluation of
Formulae
Math Concepts:
Calculations and Evaluation of Formulae
Page 19 of 148
No
Keystrokes
Screenshots
2
Press to get the absolute value.
3
Then, press
So the answer is
Exercise:
1. In problems (a) to (e), simplify the expressions given, expressing the answers in index form and
with positive indices:
a)
b)
c)
2. Expressing the answers in standard form.
3. Use a calculator to evaluate the following in engineering notation:
a)
b)
4. Find the intercepts for this equation
5. Find the value of
Answer:
1. a)
b)
c)
2.
3. a)
b)
4.
5.

Topic:
Calculations and Evaluation of
Formulae
Math Concepts:
Calculations and Evaluation of Formulae
Page 20 of 148
Calculations and Evaluation of Formulae
Overview / Introduction / Terminology:
One commonly distinguishes between the relative error and the absolute error. The absolute
error is the magnitude of the difference between the exact value and the approximation. The relative
error is the absolute error divided by the magnitude of the exact value. The percent error is the relative
error expressed in terms of per .
As an example, if the exact value is 50 and the approximation is 49.9, then the absolute error is
and the relative error is . The relative error is often used to compare
approximations of numbers of widely differing size; for example, approximating the number with
an absolute error of 3 is, in most applications, much worse than approximating the number
with an absolute error of ; in the first case the relative error is and in the second it is
only .
Another example would be if you measured a beaker and read . The correct reading would
have been . This means that your error (Approximate error) would be error.
Given some value and its approximation the absolute error is
where the vertical bars denote the absolute value. If the relative error is
and the percent error is
These definitions can be extended to the case when and are n-dimensional vectors, by
replacing the absolute value with an n-norm.
Keystrokes:
,,,

Topic:
Calculations and Evaluation of
Formulae
Math Concepts:
Calculations and Evaluation of Formulae
Page 21 of 148
Example:
1. The area of a triangle is given by
The base when measures is found to be ,
and the perpendicular height is . Determine the area of the triangle.
No
Keystrokes
Screenshots
1
Firstly, insert value in the variable using STO button.
First variable
Second variable
2
After that, calculate
with press button
.
Thus,
=
2. Calculate
.
No
Keystrokes
Screenshots
1
Firstly, press .
2
Insert the calculation. Press
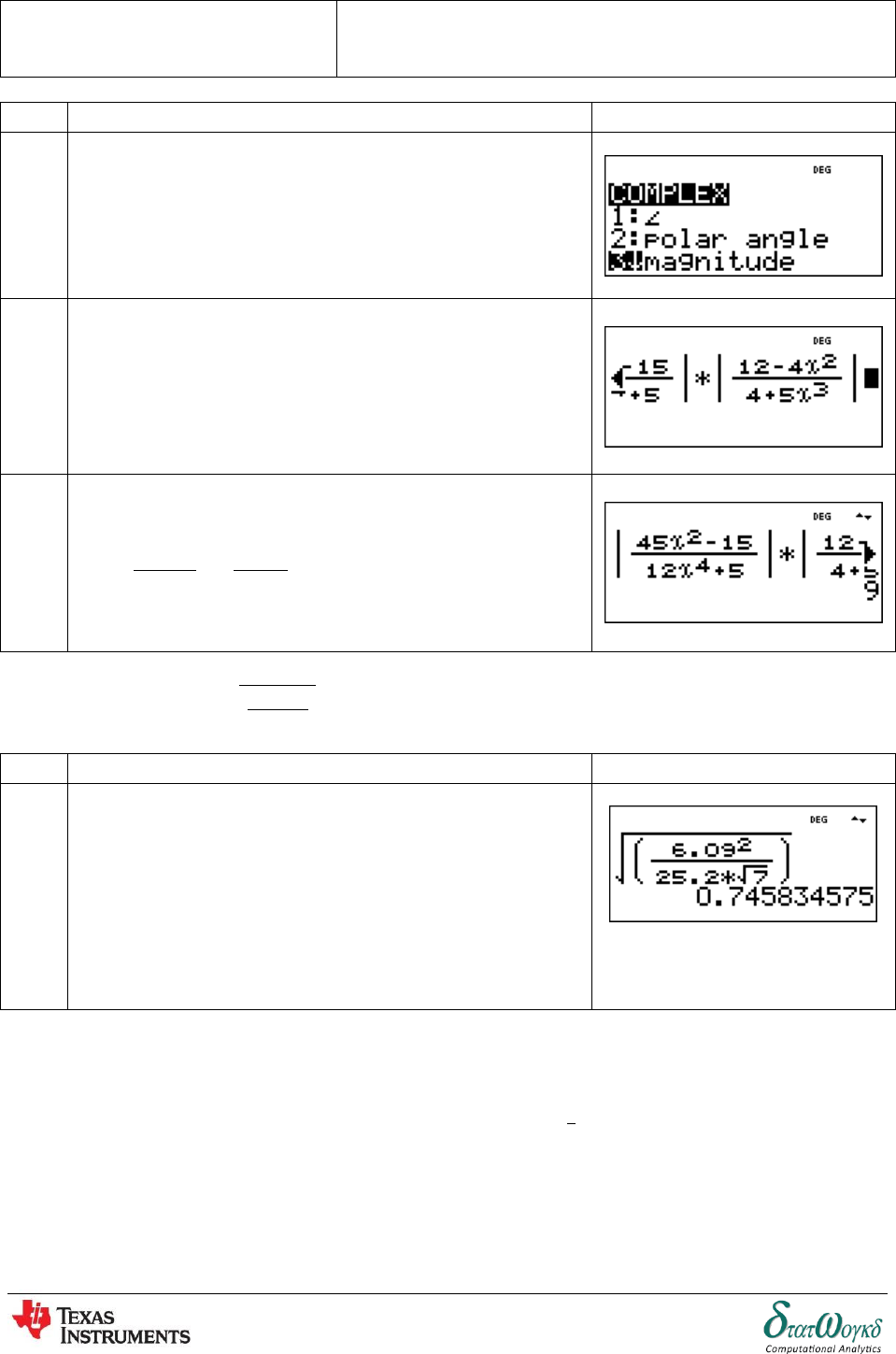
Topic:
Calculations and Evaluation of
Formulae
Math Concepts:
Calculations and Evaluation of Formulae
Page 22 of 148
No
Keystrokes
Screenshots
3
Then press
4
Continue with the calculation. Press
5
Press .
Thus,
3. Evaluate the value of
No
Keystrokes
Screenshots
1
Using the square root button
Press
.
So, the answer is
4. The volume of a right circular cone is given by
. Given that and
find the volume.

Topic:
Calculations and Evaluation of
Formulae
Math Concepts:
Calculations and Evaluation of Formulae
Page 23 of 148
No
Keystrokes
Screenshots
1
Insert a value in the variable
Press ,
4 times to get
variable .
2
Calculate
with press
.
Hence volume,
Exercise:
1. For a gas When pressure.
2. Use a calculator to evaluate correct to 4 significant figures:
a)
b)
3. Resistance is given by Find , correct to 4 significant figures, when
4. The area, of a circle is given by Determine the area correct to 2 decimal place, given
radius .
5. The time of swing seconds of a simple pendulum is given by
. Determine the time,
correct to 3 decimal place, given that
Answer:
1. Measured value, hence.
2. a)
b)
3.
4. Hence area, , correct to 2 decimal place.
5. Hence time seconds, correct to 3 decimal place.

Topic:
Computer Numbering Systems
Math Concepts:
Binary, Decimal, Octal and Hexadecimal.
Page 24 of 148
Computer Numbering Systems
Overview / Introduction / Terminology:
All computers do the amazing things that they do by simply manipulating ones and zeros. Computers
can only do binary (base 2) arithmetic. It is able to use the binary number system in order to appreciate
how the computer works. Since the computer works with the binary number system and since it is
relatively easy to convert hexadecimal (base 16) and octal numbers (base 8) into binary, computer
scientists need to be familiar with the octal and hexadecimal number systems.
I. Numbering Systems
1. Decimal System
o base
o valid digits
2. Binary System
o base
o valid digits
3. Octal System
o base
o valid digits
4. Hexadecimal System
o base
o valid digits
o A refers to decimal , B refers to decimal , etc.
II. To convert a number in a base other than to the base
1. Easy way: To convert (base 8) to decimal, it would be label the three columns as the
and columns from right to left. Then, multiply the digits by these column labels
and compute the sum of the products. Since a is in the column, multiply to obtain .
Since is in the 8's column, multiply to get . Then add to the from the step
before to get a running total of . Finally, since a 5 is in the 1's column, multiply 1 x 5 to get
the product of and add it to the running toal of to get . That final value,, is the
decimal equivalent to the original number .
2. Formal way: Expand the number into expanded form. Expanded form is written as
III. To convert a decimal number into a base other than 10

Topic:
Computer Numbering Systems
Math Concepts:
Binary, Decimal, Octal and Hexadecimal.
Page 25 of 148
1. Write out the powers in the other base starting at the power of 0 until you reach a number
higher than the given number.
2. Divide the highest power of the base that can divided at least once into the given number.
3. Put the quotient of that division into a column that will eventually be the leftmost digit of the
final answer.
4. Continue steps 2 & 3 using the remainder of the previous division but add each successive
quotient to the right of previous quotients in the final answer.
Keystrokes:
Example:
1. Convert into decimal number.
No
Keystrokes
Screenshots
1
Firstly, change the calculator mode to engineering mode.
Press and press to back to home
screen.
2
Press in the calculator.
After that, press , to get the b=binary.
3
Then, to change to the decimal, press
[Dec].
4
Thus, to decimal

Topic:
Computer Numbering Systems
Math Concepts:
Binary, Decimal, Octal and Hexadecimal.
Page 26 of 148
2. Convert into decimal
No
Keystrokes
Screenshots
1
Firstly, press , in the calculator.
2
And followed by , to find the o =
octal
3
Then, to convert to decimal, press
.
4
into decimal
3. Convert into hexadecimal number
No
Keystrokes
Screenshots
1
Press in the calculator.

Topic:
Computer Numbering Systems
Math Concepts:
Binary, Decimal, Octal and Hexadecimal.
Page 27 of 148
No
Keystrokes
Screenshots
2
Press [:d]to find the d=decimal and press
,
3
To change the decimal to hexadecimal number, Press
.
4
Thus into
Exercise:
1. Convert binary numbers given to decimal numbers:
a)
b)
2. Convert the decimal numbers to the octal numbers:
a)
b)
3. Convert octal numbers to their hexadecimal equations.
a)
b)
4. Convert the following hexadecimal numbers into their binary equivalents.
a)
b)
5. Convert binary to hexadecimal for .
Answer:
1. a) b) 450
2. a) b)
3. a) b)
4. a) b)
5.

Topic:
Algebra
Math Concepts:
Basic Algebra, Laws of Indices, Formula and Literal Equations.
Page 28 of 148
Algebra
Overview / Introduction / Terminology:
Algebra is the branch of mathematics that uses letters in place of some unknown numbers. You've been
using algebra since your early schooling, when you learned formulas like the area of a rectangle, with
width w, height h:
We used letters to stand for numbers. Once we knew the width and height, we could substitute them
into the formula and find our area. Another one you may have seen is the area of a square, with sides s:
As soon as we know the length of the sides, we can find the area.
Literal numbers (the letters used in algebra) can either stand for variables (the value of the letter can
change, like in the examples of the area of a rectangle and the area of a square) or constants (where the
value does not change), for example e (which has a constant value of ).
Keystrokes:
,,

Topic:
Algebra
Math Concepts:
Basic Algebra, Laws of Indices, Formula and Literal Equations.
Page 29 of 148
Example:
1. Simplify
and evaluate when , taking positive roots only.
No
Keystrokes
Screenshots
1
Firstly you need to store a value into a variable
Insert value
Press
Press ,
Press .
2
Calculate the equation. Press ,
,
,
,
,
2. What is the area of circle if the radius is ?
Reminder:
No
Keystrokes
Screenshots
1
Press . The area of the circle is
square cm.

Topic:
Algebra
Math Concepts:
Basic Algebra, Laws of Indices, Formula and Literal Equations.
Page 30 of 148
No
Keystrokes
Screenshots
2
Then press . The area of the circle is approximately
square cm when rounded to one decimal place.
3. is directly proportional to strain within the elastic limit of a
material. When, for mild steel, the stress is pascals, the strain is . Determine:
a) The coefficient of proportionality
b) The value of strain when the stress is pascals.
No
Keystrokes
Screenshots
1
a) , i.e. , from which . Hence the
coefficient of proportionality
Firstly, change mode calculator in the engineering mode
with press,
2
Then press
.
So or
3
b) After that, change the calculator to the normal mode
with press .
4
Since . Hence when
Then press
.
So

Topic:
Algebra
Math Concepts:
Basic Algebra, Laws of Indices, Formula and Literal Equations.
Page 31 of 148
Exercise:
1. Subtract
2. Simplify
and evaluate when
and
3.
4. If is inversely proportional to and when , determine:
a) The coefficient of proportionality
b) The value of when is
c) The value of when is
5.
inversely proportional to its absolute pressure. If a gas occupies a volume of at a pressure
of pascals, determine
a) The constant od proportionality
b) The volume when the pressure is pascals
c) The pressure when the volume is .
Answer:
1.
2. ,
3.
4. a)
b)
c)
5. a)
b)
c)

Topic:
Number Sequences
Math Concepts:
Simple Sequence, Arithmetic Sequence, Geometric Sequence.
Page 32 of 148
Logarithms
Overview / Introduction / Terminology:
If a number y can be written in the form , then the index x is called the ogarithm of y to the
base
of
a
If , then . Thus, since , then
Types of logarithms:
(a) Logarithms having a base of 10 are called common logarithms and log10 is usually abbreviated to
lg.
For example:
(b)
2.7183) are called hyperbolic, Napierian or natural logarithms, and loge or usually abbreviated as
ln.
For example:
Laws of logarithms
(i) To multiply two numbers :
(ii) To divide to numbers :
(iii) To raise a number to the power :
A logarithmic scale is a scale of measurement that displays the value of a physical quantity using
intervals corresponding to orders of magnitude, rather than a standard linear scale.
An exponential function is one which contains , e being a constant called the exponent
and having an approximate value of . The exponent arises from the natural laws of growth and
decay and is used as a base for natural or Napierian logarithms.
For example: ,
,
The Laws of Growth and Decay
The laws of exponential growth and decay are of the form and
, where and are constants.
Keystrokes:

Topic:
Number Sequences
Math Concepts:
Simple Sequence, Arithmetic Sequence, Geometric Sequence.
Page 33 of 148
Example:
1. The power dissipated by a resistor was measured for varying values of current flowing in the
resistor and the results are as shown:
Current, I amperes
Power, P watts
Prove that the law relating current and power is of the form , where R and n are
constants, and determine the law. Hence calculate the power when the current is amperes
and the current when the power is .
No
Keystrokes
Screenshots
1
To key in, the data, press and key in the values.
2
To key in the data values in the table, press
3
To key in the data values in second table, press and press
4
To calculate the value of x and y, press

Topic:
Number Sequences
Math Concepts:
Simple Sequence, Arithmetic Sequence, Geometric Sequence.
Page 34 of 148
No
Keystrokes
Screenshots
5
Press to choose Power Regression
.
6
Press to get the answer.
Thus, value for
7
To round the answer, press to choose
rounded to 0.
8
To get the answer, press to go back
to the table.
9
Thus, the answer is rounded to O.
So, the equation is 2
Topic:
Number Sequences
Math Concepts:
Simple Sequence, Arithmetic Sequence, Geometric Sequence.
Page 35 of 148
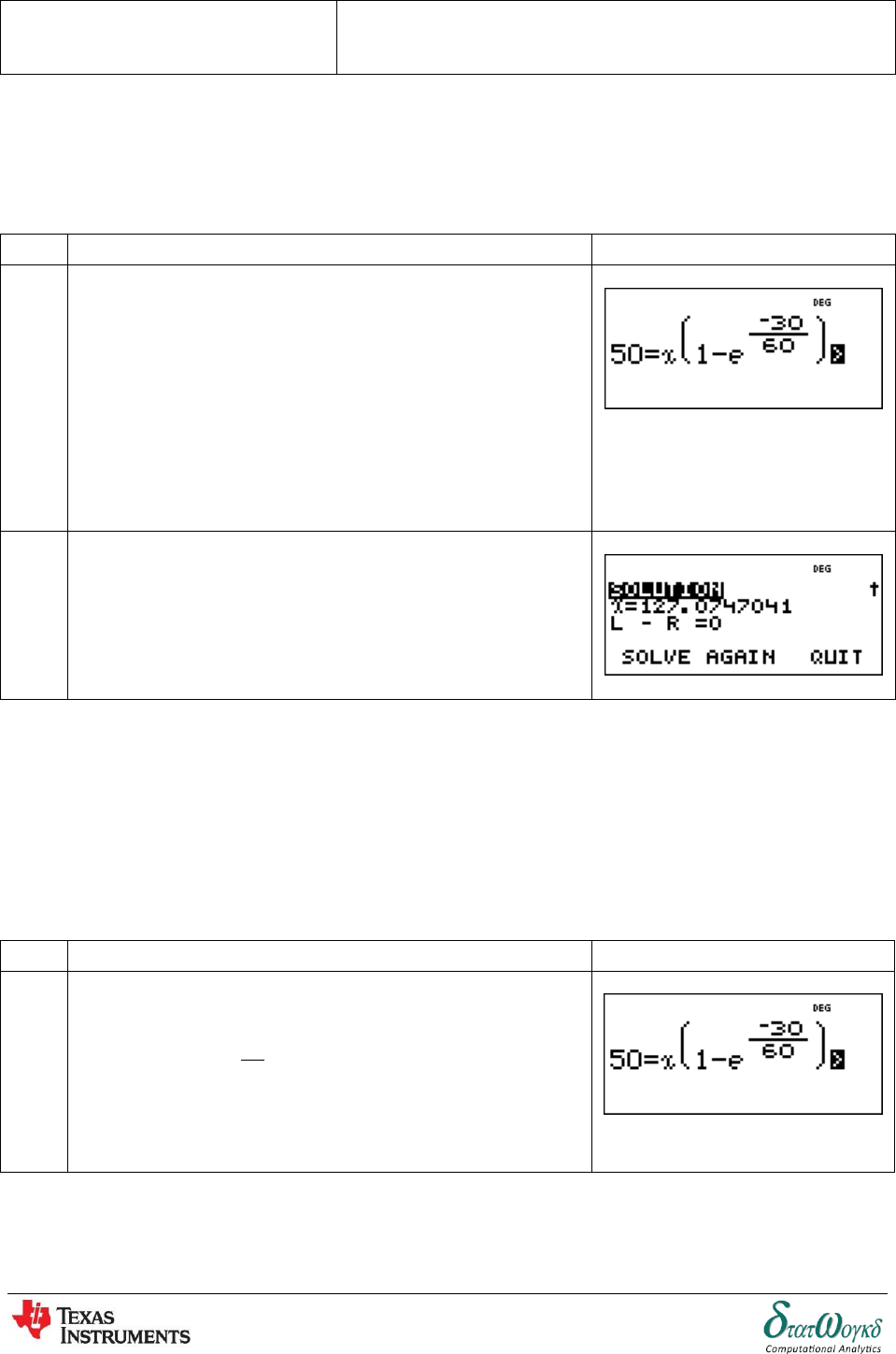
2. The temperature 2 of a winding which is being heated electrically at time is given by:
where 1 is the temperature (in degrees Celsius) at time = 0 and
is a constant. Calculate the value of 1 , correct to the nearest degree, when 2 is , is
and is .
No
Keystrokes
Screenshots
1
Based on the question,
To enter the equation and values, press
2
To get the answer, press
Thus,
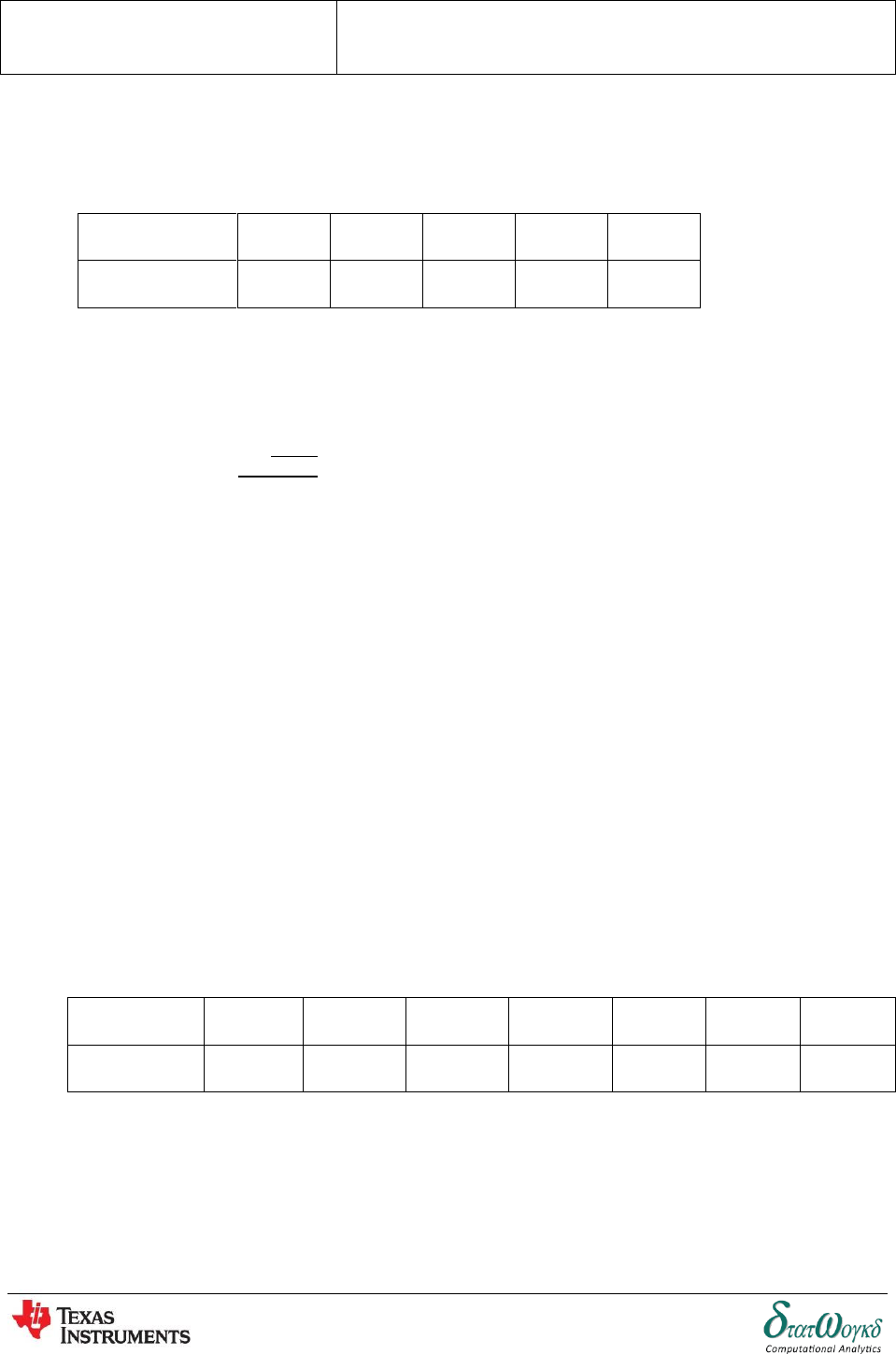
3. The temperature 2 of a winding which is being heated electrically at time is given by
where is the temperature (in degrees Celsius) at time 0 and
is a constant. Calculate:
(a) , correct to the nearest degree, when is , is 30s and is .
(b) The time correct to 1 decimal place, for to be half the value of .
No
Keystrokes
Screenshots
1
To enter the values in the equation, press
)

Topic:
Number Sequences
Math Concepts:
Simple Sequence, Arithmetic Sequence, Geometric Sequence.
Page 36 of 148
No
Keystrokes
Screenshots
2
To get the answer, press
Thus,
3
Quit the previous calculation by press .
Before do the calculation, set the decimal place to 1.
Press
Press to exit from the mode screen.
4
Since
, thus
From equation, let
)
To enter the new values in the equation, press
to go back to the previous equation.
Enter the new values in the equation, press
5
To get the answer, press
Thus,
Topic:
Number Sequences
Math Concepts:
Simple Sequence, Arithmetic Sequence, Geometric Sequence.
Page 37 of 148
Exercise:
1. Atmospheric pressure p is measured at varying altitudes h and the results are as shown below:
Show that the quantities are related by the , where a and k are constants.
Determine the values of a and k and state the law. Find also the atmospheric pressure at
2. When a chain of length 2L is suspended from two points, 2D metres apart, on the same
horizontal level
Evaluate when = 75m and = 180 m.
3. Choose = 10 in the expression and calculate using your calculator for
.
4. The amount of product (in mol/cm3 ) found in a chemical reaction starting with 2.5 mol/cm3 of
reactant is given by where is the time, in minutes, to form product
Plot a graph at 30 second intervals up to 2.5 minutes and determine after 1 minute.
5. The amount after years of a sum invested is given by the compound interest law:
when the per unit interest rate is added continuously. Determine, correct
to the nearest pounds, the amount after 8 years for a sum of invested if the interest rate
is per annum.
Answer:
, , = 76 ,
2.
3.
4.
5.

Topic:
Number Sequences
Math Concepts:
Simple Sequence, Arithmetic Sequence, Geometric Sequence.
Page 38 of 148
Number Sequences
Overview / Introduction / Terminology:
Number sequences can be used as a tool to practice and improve any numerical reasoning skills. By
activities like loan calculations, groceries or during job applications in assessments.
Simple Sequence
If the sequence is simple enough one can look at the first few terms and guess the general rule for
computing the nth term. For instance:
The graph of a sequence will look like a collection of dots whose x-coordinates are spaced one apart.
Some examples of graphs of sequences are shown in Figure below.
Arithmetic Sequence
An arithmetic sequence is a mathematical sequence consisting of a sequence in which the next term
originates by adding a constant to its predecessor. When the first term x1 and the difference of the
sequence d is known, the whole sequence is fixed, or in formula:
An example of this type of number sequence could be the following:
This common difference is -. The pattern is continued by subtracting 2 each time.
Geometric Sequence
A Geometric sequence is a mathematical sequence consisting of a sequence in which the next term
originates by multiplying the predecessor with a constant, better known as the common ratio. When the
first term x1 and the common ratio are known, the whole sequence is fixed, or in formula:
An example of this type of number sequence could be the following:
This sequence has a factor of 3 between each number, however as can be seen the sequence can work
both by increasing as well as decreasing the value of numbers. The pattern is continued by dividing the
last number by 3 each time.
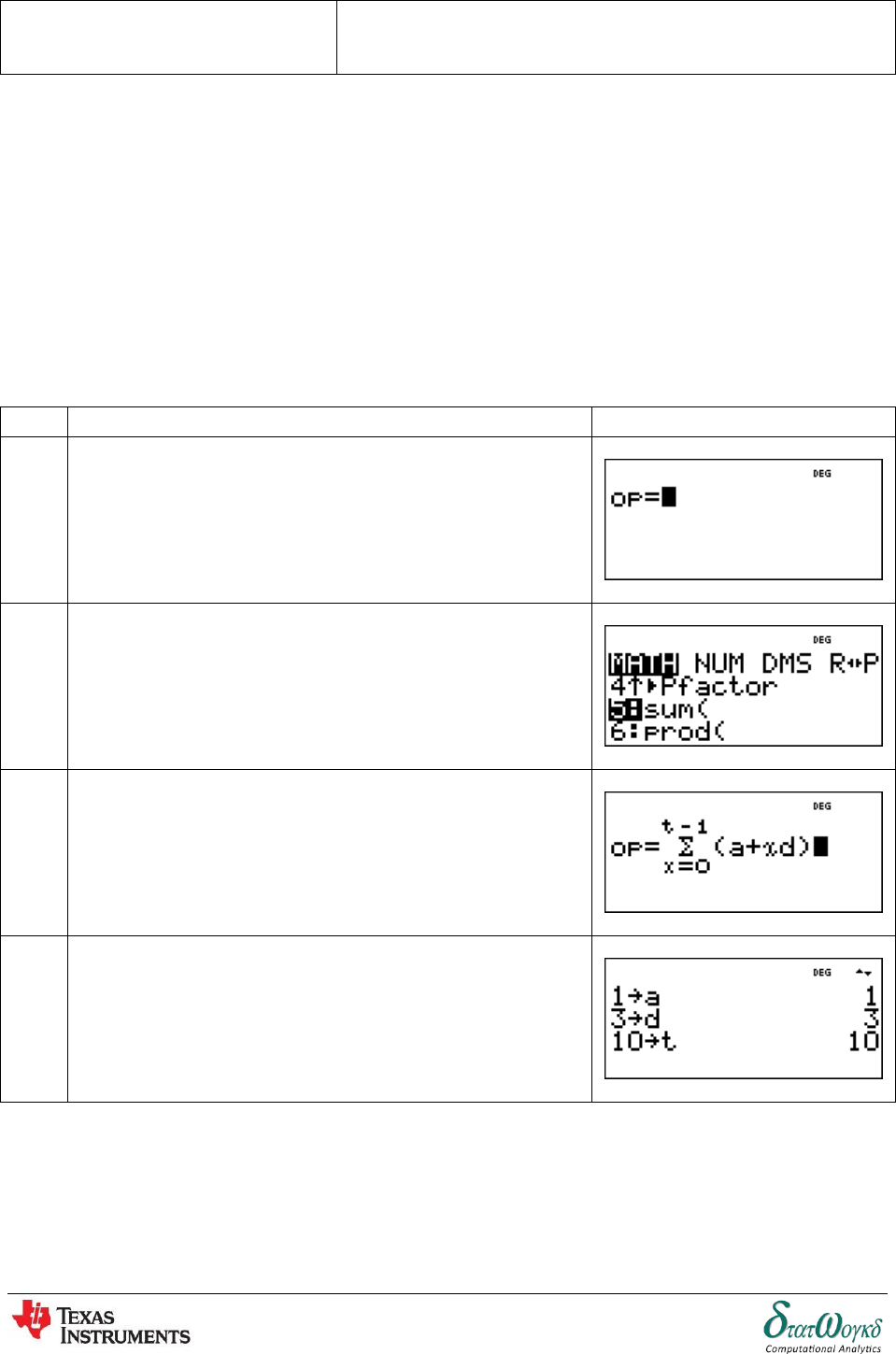
Topic:
Number Sequences
Math Concepts:
Simple Sequence, Arithmetic Sequence, Geometric Sequence.
Page 39 of 148
Keystrokes:
,,,[sum(].
Example:
1. Add up the first 10 terms of the arithmetic sequence:
The value of
No
Keystrokes
Screenshots
1
Set operation with press ,
2
Then, press button [sum(].
3
Insert value,
.
4
Insert value for variable,
,
, and
.

Topic:
Number Sequences
Math Concepts:
Simple Sequence, Arithmetic Sequence, Geometric Sequence.
Page 40 of 148
No
Keystrokes
Screenshots
5
Recall the operation with press
So, the answer is .
2. Find the 10th term of the geometric sequence for This sequence has a
factor of 3 between each number.
The value of (first term) and (common ratio)
No
Keystrokes
Screenshots
1
Firstly, set the operation with press button.
Insert value,
.
2
After that, store value in the variable,
,
,
.
3
After finish, recall the operation, press
And the answer is
3. Sum the first terms of This sequence has a factor of 3 between each
number.
The value of are:

Topic:
Number Sequences
Math Concepts:
Simple Sequence, Arithmetic Sequence, Geometric Sequence.
Page 41 of 148
No
Keystrokes
Screenshots
1
Set the operation in the calculation, press .
2
Then press [sum(],
3
Insert value and press
.
4
After that, insert value in variable,
.
5
Press to get the answer.
The answer is
4.
No
Keystrokes
Screenshots
1
For the common ratio,
Press

Topic:
Number Sequences
Math Concepts:
Simple Sequence, Arithmetic Sequence, Geometric Sequence.
Page 42 of 148
No
Keystrokes
Screenshots
2
For the sum of 0 terms =
Press
.
The answer is
Exercise:
1. The seventh term of a series is and the eleventh term is. Determine the sixteenth term.
2. The sum of terms of an arithmetic progression is 202.5 and the common difference is 2. Find
the term of the series.
3. Which term of the series ?
4. The first, twelfth and last term of an arithmetic progression are
and
respectively.
Determine,
a) The number of terms in the series
b) The sum of all the terms
c)
5. In a geometric progression the 5th term is 9 times the 3th term and the sum of the 6th and 7th
terms is . Determine,
a) The common ratio,
b) The first term,
c) The sum of the to terms inclusive.
Answer:
1.
2.
3.
4. (a)
(b)
(c)
5. (a)
(b)
(c)
Topic:
Complex Number
Math Concepts:
Complex Conjugate, magnitude, Polar form of complex number
and distance between 2 complex numbers
Page 43 of 148
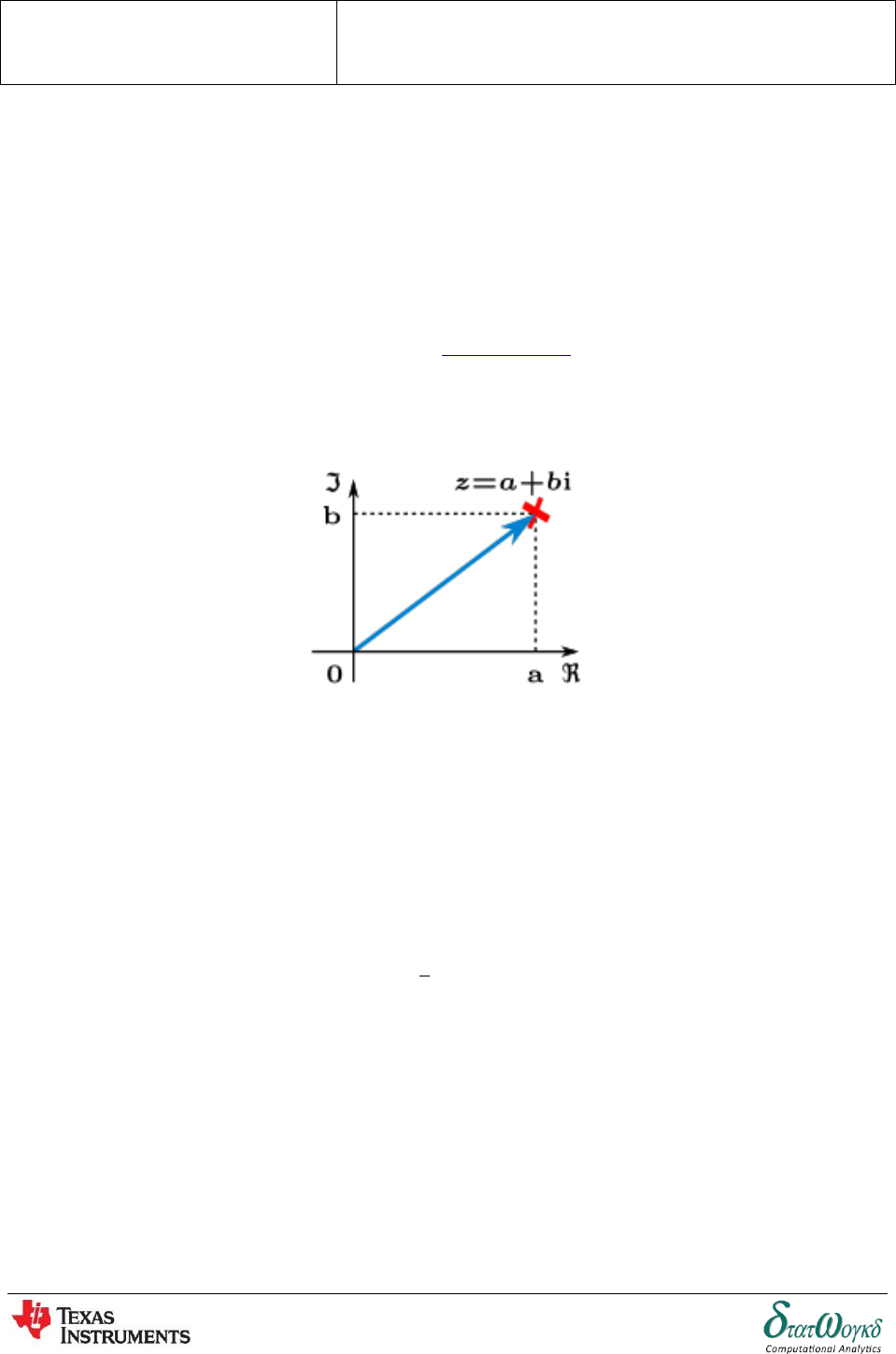
Complex Number
Overview / Introduction / Terminology:
A complex number is a number that can be expressed in the form
where a and b are real numbers and i is the imaginary unit, satisfying . For example,
is a complex number. It is common to write a for and for Moreover,
when the imaginary part is negative, it is common to write a with instead of
for example instead of
Complex Conjugates are a pair of complex numbers, both having the same real part, but
with imaginary parts of equal magnitude and opposite signs. For example, and are
complex conjugates.
The conjugate of the complex number
where and are real numbers, is
Keystrokes:
Topic:
Complex Number
Math Concepts:
Complex Conjugate, magnitude, Polar form of complex number
and distance between 2 complex numbers
Page 44 of 148
Example:
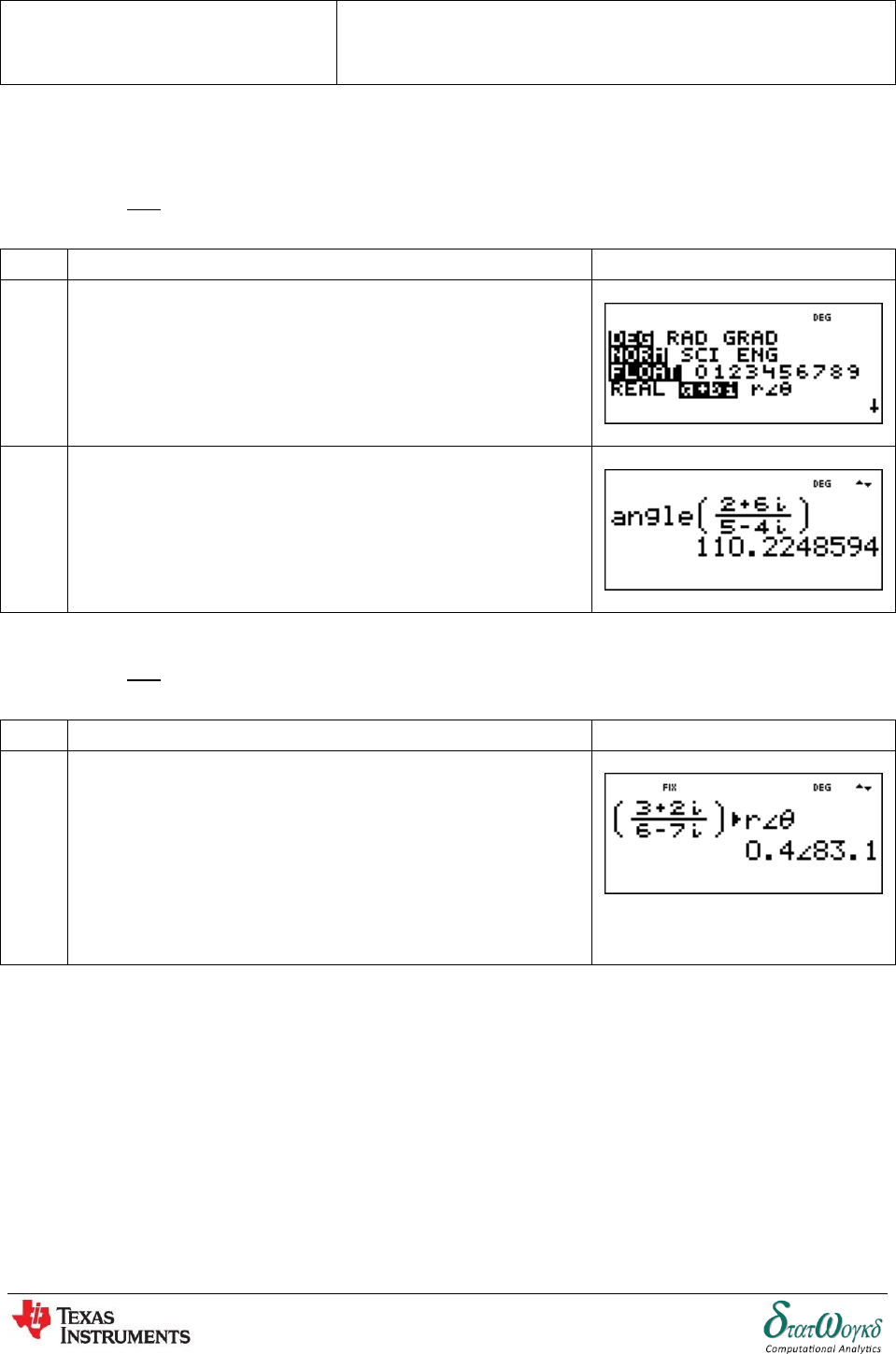
1. Solve
in polar form
No
Keystrokes
Screenshots
1
Change REAL mode to COMPLEX mode
Press
2
Press
2. Solve
in
No
Keystrokes
Screenshots
1
Press

Topic:
Complex Number
Math Concepts:
Complex Conjugate, magnitude, Polar form of complex number
and distance between 2 complex numbers
Page 45 of 148
3. Solve
, answer must in the form of
No
Keystrokes
Screenshots
1
Press
Exercise:
1. Solve magnitude of
2. Solve
in
3. Solve in polar form
4. Solve
5. Solve magnitude of
Answer:
1.
2.
3.
4.
5.

Topic:
Simple Equations
Math Concepts:
Linear, Absolute Value, Quadratic Equations.
Page 46 of 148
Simple Equations
Overview / Introduction / Terminology:
A mathematical equation is a formula containing an equals sign ( = ) with a mathematical expression on
each side of it. The equals sign says that both sides are exactly the same.
There are two kinds of mathematical equations:
The kind of equation that is either true or false; these are also called identities
Example:
The kind of equation that lets you calculates the value of one or several variables. The equation is
only true if the variable(s) have that value.
Example:
The second kind is often used to solve problems in which you have to know the value of some
variables. For example, if
The second kind of equation is used in algebra. For example, to solve the equation by
finding x you would follow an algebraic rule. Then you can work out that
An equation is like a weighing scale - both sides should always be perfectly balanced. To solve the
equation you need to find the value of missing numbers and perform the same operation to each side.
For example, suppose you are trying to find out how many sweets are in the bag shown here.
By subtracting three sweets from each side, the scales remain balanced. You can now see that one bag is
equivalent to two sweets. Written algebraically, this is:
Subtract 3 from both sides, to give:
Keystrokes:
, NUM,

Topic:
Simple Equations
Math Concepts:
Linear, Absolute Value, Quadratic Equations.
Page 47 of 148
Example:
1. Find value for
No
Keystrokes
Screenshots
1
Firstly, press [NUM]
2
Insert value in the equation,
3
Thus,
2. In the equation , is the coefficient of the term, is the coefficient of the
term, and is the constant. Substitute 9 for, -86 for, and 6 for in the quadratic formula and
simplify.
The quadratic formula is:
No
Keystrokes
Screenshots
1
If you have already defined variables, the solver will assume
those values.
To solve this equation, press

Topic:
Simple Equations
Math Concepts:
Linear, Absolute Value, Quadratic Equations.
Page 48 of 148
No
Keystrokes
Screenshots
2
Then, insert value with press
.
3
Press , ,,,(YES)
So, and
Topic:
Simple Equations
Math Concepts:
Linear, Absolute Value, Quadratic Equations.
Page 49 of 148
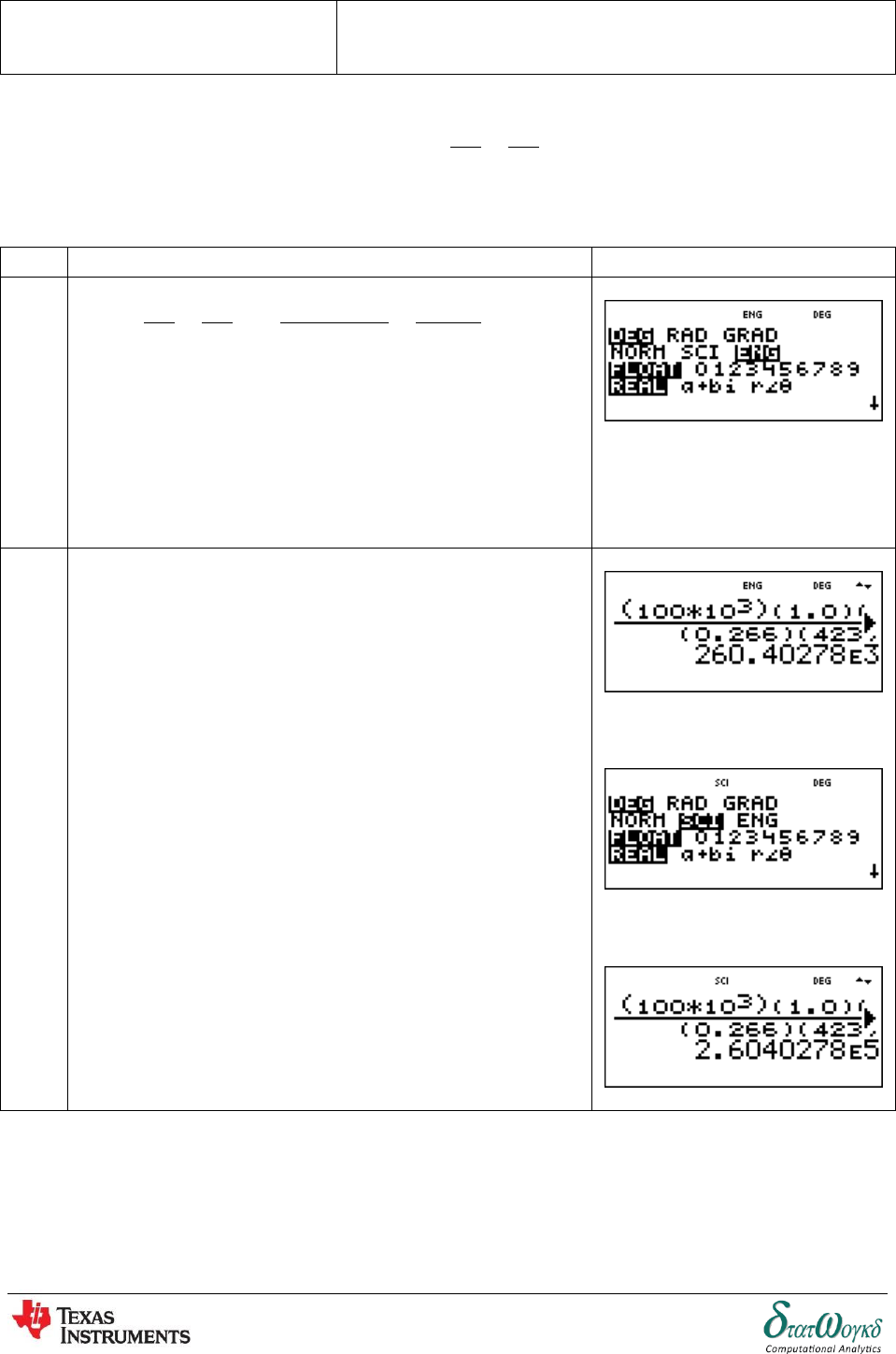
3. A formula relating initial and final states of pressures, and , , volumes , and , and absolute
temperatures, , and , , of an ideal gas is
. Find the value of given
.
No
Keystrokes
Screenshots
1
Since is
then
-
Firstly, press to change to engineering
mode. Then press to go to home screen.
2
After that, insert the equation, press
.
Then press
Try change to the scientific mode with press
.
Press to select the last equation and press to get
the new answer.
Hence

Topic:
Simple Equations
Math Concepts:
Linear, Absolute Value, Quadratic Equations.
Page 50 of 148
Exercise:
1. Solve
2. Solve this equation
3. A rectangle has a length of 20 cm and width cm. When its width is reduced by 4 cm its area
becomes . Find the original width and area of the rectangle.
4. If , find the value of given
5. The extension m of an aluminum tie bar of length m and cross-sectional area when
carrying a load of newton is given by the modulus of elasticity Find the extension
of the tie bar (in mm) if
Answer:
1.
2.
3.
4.
5.

Topic:
Simultaneous Equation
Math Concepts:
Transposition of Formulae, Simultaneous Equation, Quadratic
Equation, Cubic Equation
Page 51 of 148
Simultaneous Equation
Overview / Introduction / Terminology:
The terms simultaneous equations and systems of equations refer to conditions where two or more
unknown variables are related to each other through an equal number of equations. Consider the
following example:
The intersection point has been defined at point () which is and
Three methods of solving simultaneous equations analytically are:
(a) by substitution, and
(b) by elimination.
(c) using formula,
Quadratic equation is the equation contains power 2 in general form:
Ex: with two roots which is
There are four methods of solving quadratic equations.
These are: (i) by factorization (where possible)
(ii) by
(iv) graphically
The cubic equation which have the equation up to power 3 in general form:
Ex: - 27 + = 0 with three roots which are
Keystrokes:
Topic:
Simultaneous Equation
Math Concepts:
Transposition of Formulae, Simultaneous Equation, Quadratic
Equation, Cubic Equation
Page 52 of 148
Example:
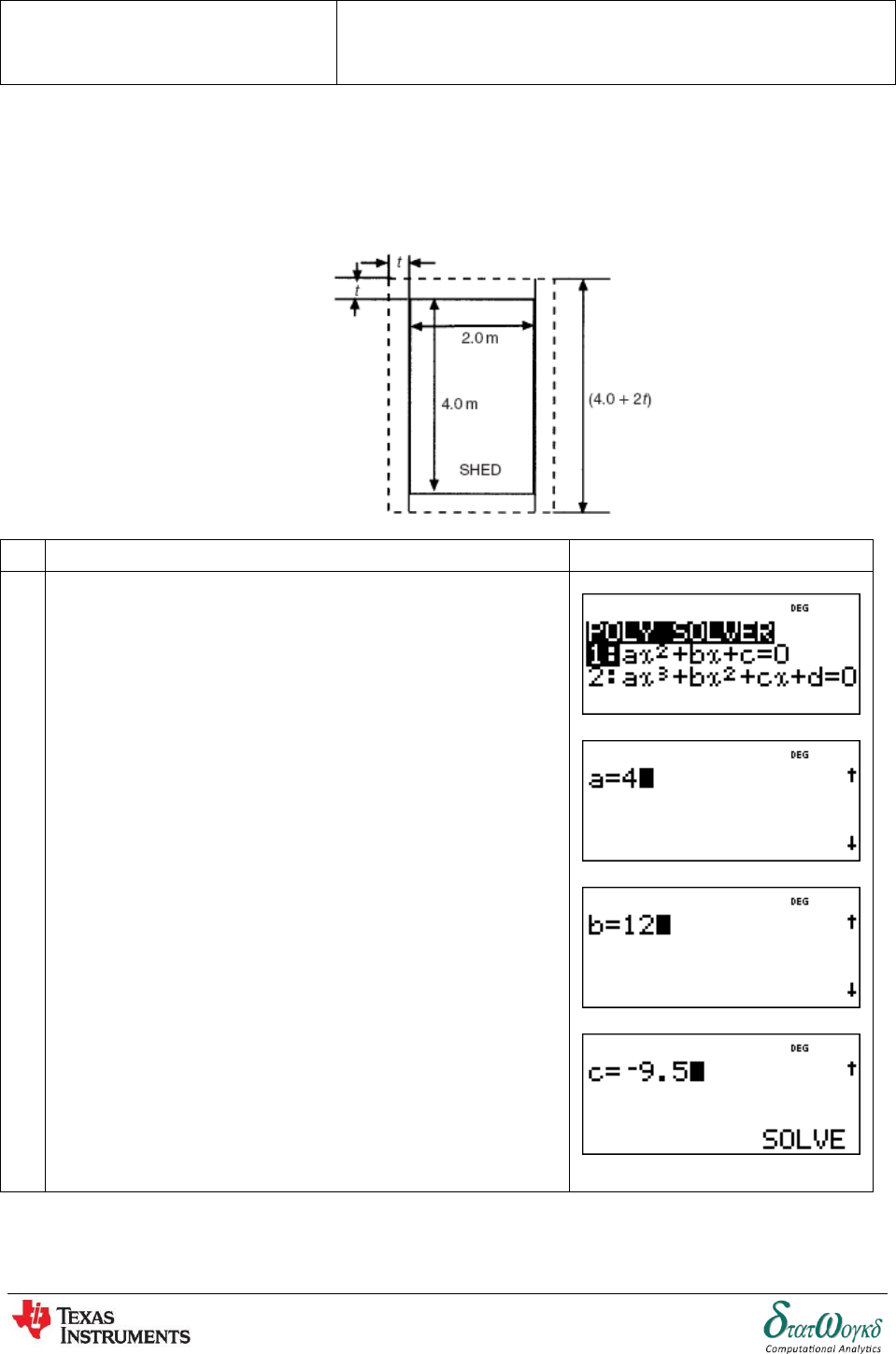
1. A shed is 4.0 m long and 2.0 m wide. A concrete path of constant width is laid all the way around
the shed. If the area of the path is 9.50 m2 , calculate its width.
No
Keystrokes
Screenshots
1
From the above figure, it shows a plan view of the shed with
its surrounding path of width t metres.
Or
We can rearrange the equation:
Therefore; a = 4 , b = 12 , c = -9.5
To enter the quadratic equation solver, press :
choose no 1 and then press
To enter coefficient of a:
To enter coefficient for b :
To enter coefficient for c :
Topic:
Simultaneous Equation
Math Concepts:
Transposition of Formulae, Simultaneous Equation, Quadratic
Equation, Cubic Equation
Page 53 of 148
No
Keystrokes
Screenshots
2
To find the answer. Root 1:
3
To find Root 2:
Thus,
1 = 0.6505813168 m
1 = - 3.650581317 m
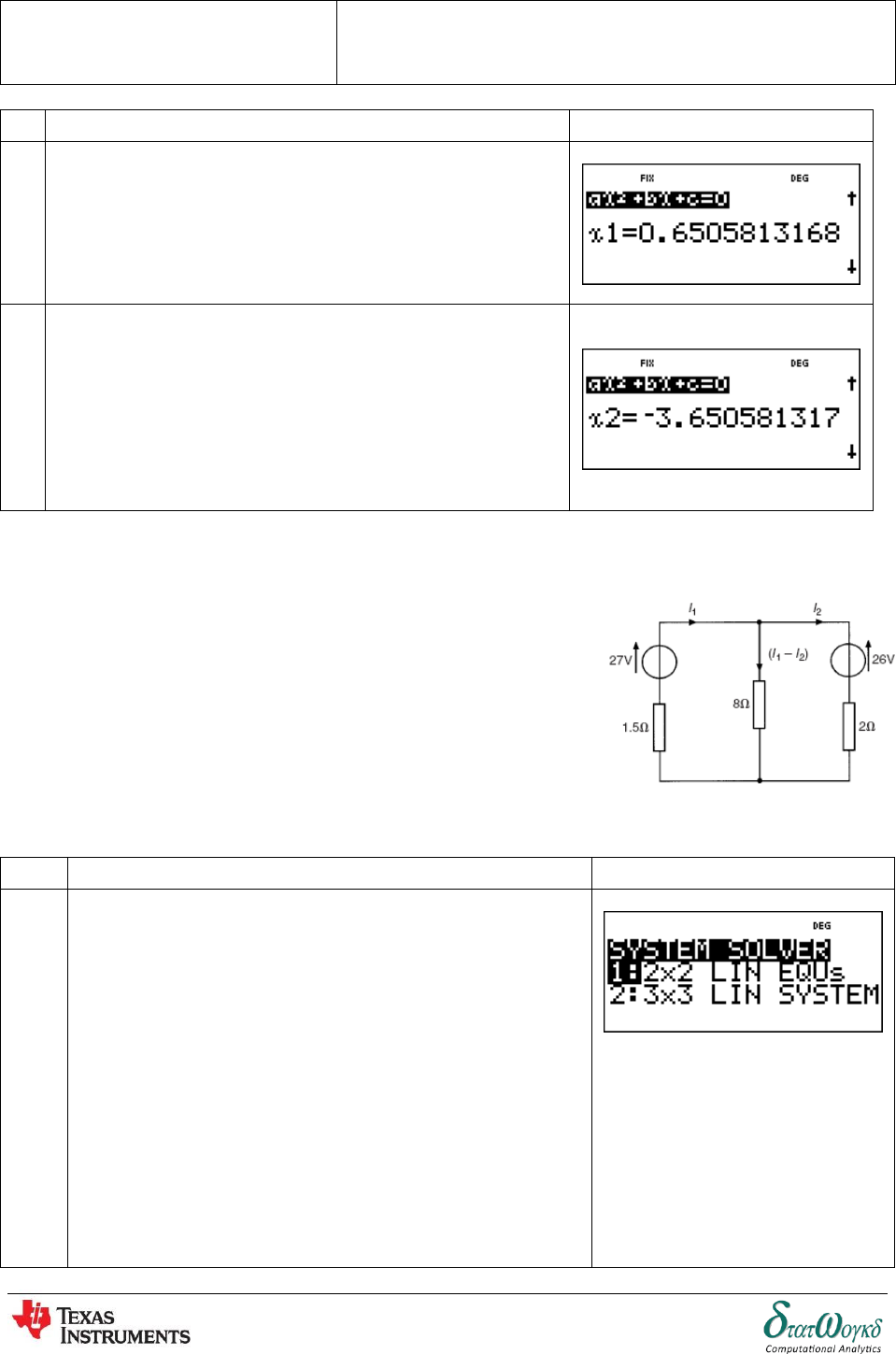
2. When
Kirchhoff
s laws are
applied
to
the
electrical circuit shown in Figure 9.1 the currents
I
1
and
I
2
are connected by the equations:
-------------- (
1)
------------- (2)
Solve the equations to find the values of currents I1 and I2.
No
Keystrokes
Screenshots
1
From the equation,
-------------- (
1)
-------------- (2)
To enter to system solver for simultaneous equation,
Press and choose 1, .

Topic:
Simultaneous Equation
Math Concepts:
Transposition of Formulae, Simultaneous Equation, Quadratic
Equation, Cubic Equation
Page 54 of 148
No
Keystrokes
Screenshots
2
Assume l1 , l2
To enter the values in first equation,
3
To enter the values in second equation,
4
To get the answer, press
Thus,
3. If one of the roots of the equation + 11 6 = 0 is 2, then the other two roots are:
No
Keystrokes
Screenshots
1
To enter to equation solver, press
2
To enter the values in the equation,
To get the answers, press

Topic:
Simultaneous Equation
Math Concepts:
Transposition of Formulae, Simultaneous Equation, Quadratic
Equation, Cubic Equation
Page 55 of 148
Thus the answers are:
Exercise:
1. In an electrical alternating current circuit the impedance is given by:
.
Transpose the formula to make C the subject and hence evaluate C when ,
.
2. An approximate relationship between the number of teeth, , on a milling cutter, the diameter
of cutter, , and the depth of cut, , is given by: =
Determine the value of when
= and = .
3. A rectangular building is long by wide. A concrete
path
of
constant width
is
laid
all
the
way around the building. If the area of the path is , calculate its width correct to the
nearest millimeter.
4. The resistance of copper wire at
t
C
is given by
where R0 is the
resistance at
0
C
and α is the temperature
coefficient
of resistance. If at
and
at
,
find α and
R
0
.
5. One real root of the equation lies in the interval?
Answer:
1.
, x
2.
3.
4. ,
5.

Topic:
Determinants and Matrices
Math Concepts:
Basic Algebra, Matrices
Page 56 of 148
Determinants and Matrices
Overview / Introduction / Terminology:
The expression is called a determinant of the second order a1b2 – a2b1’. It contains 4
number a1 , b1 , a2 , b2 (called elements) which are arranged along two horizontal lines (called rows) and
two vertical lines (called columns).
A =
A system of numbers arranged in a rectangular formation along rows and columns and bounded
by the brackets [ ] is called an by matrix; which is written x matrix.
A =
Matrix Operations
1. Equality of Matrices
Two matrices A and B are said to equal if and only if
(i) They are of the same order
(ii) Each element of A is equal to the corresponding element of B
2. Addition and Subtraction of matrices :
+
=
3. Multiplication of matrix by a scalar : k
=
4. Multiplication of matrices :
x
=
Types of matrices:
1. Transpose of a matrix : A = A’
A =
A’ =
2. Adjoint of a square matrix : Adjoint of the matrix A = Adj. A
3. Inverse of a matrix : A = A-1 =
Keystrokes:

Topic:
Determinants and Matrices
Math Concepts:
Basic Algebra, Matrices
Page 57 of 148
Example:
1. If
and
, verify that , where is the transpose
of .=
No
Keystrokes
Screenshots
1
To enter to matrices screen, press .
Press to choose first matrix, A.
Press to enter the matrix screen.
2
To enter the values, key in the values in matrix A.
3
To enter the values in matrix B, press
.
Press to enter the matrix screen
4
To enter the values, key in the values in matrix B.
5

Topic:
Determinants and Matrices
Math Concepts:
Basic Algebra, Matrices
Page 58 of 148
6
Thus, is proved.
3. Verify that the following matrix is orthogonal.
No
Keystrokes
Screenshots
1
To enter to matrices screen, press .
Press to choose first matrix, A.
Press to enter the matrix screen.
2
To enter the values,

Topic:
Determinants and Matrices
Math Concepts:
Basic Algebra, Matrices
Page 59 of 148
No
Keystrokes
Screenshots
3
To define the matrix is orthogonal. Press, to quit
from the matrix template.
To do calculation, press
4
To get the answer, press .
Thus, the matrix is orthogonal.
4. If
, find the value of , where is a unit matrix of second order.
No
Keystrokes
Screenshots
1
To enter to matrices screen, press .
Press to choose first matrix, A.
Press to enter the matrix screen.
2
To enter the values,
3
Press to quit from the matrix form.
To get the answer, key in the equation, .

Topic:
Determinants and Matrices
Math Concepts:
Basic Algebra, Matrices
Page 60 of 148
No
Keystrokes
Screenshots
4
To get the answer, press .
Thus, the answer is .
Exercise:
1. If
,
, and
, verify that and
2. If
, and I is the unit matrix of order 3, evaluate
3. If
, compute adj and . Also find such that
4. If
find A-1. Also find two non-singular matrices P and Q such that
Where I is the unit matrix and verify that A-1 = QP.
5. Find the inverse of the following matrix.
Answer:
1. Proved.
2.
3.
4.
5.
Topic:
Vector
Math Concepts:
Basic Algebra, Vector Algebra
Page 61 of 148
Vector
Overview / Introduction / Terminology:
Some physical quantities are entirely defined by a numerical value and are called scalar
quantities or scalars. Other physical quantities are defined by both a numerical value and a direction in
space and these are called vector quantities or vectors.
There are many types of symbol for vector such as
, , , , and in column matric
.
Vector Addition
Vector Subtraction
Figure (b) shows the resultant of vector addition is
:
.
Figure (a) shows the resultant of vector addition is
.
Figure (b) shows vectors that is,
and the vector equation is
Resolution of Vectors
A vector can be resolved into two component parts such that the vector addition of the component
parts is equal to the original vector.
For the vector 1 and 2 shown in the figure, the horizontal
component of vector addition is:
And the vertical component of vector addition is:

Topic:
Vector
Math Concepts:
Basic Algebra, Vector Algebra
Page 62 of 148
Relative velocity
In any vector equation, only the start and
finish points affect the resultant vector of a system.
Two different systems are shown in figure below,
but in each of the systems, the resultant vector is
.
Keystrokes:
Example:
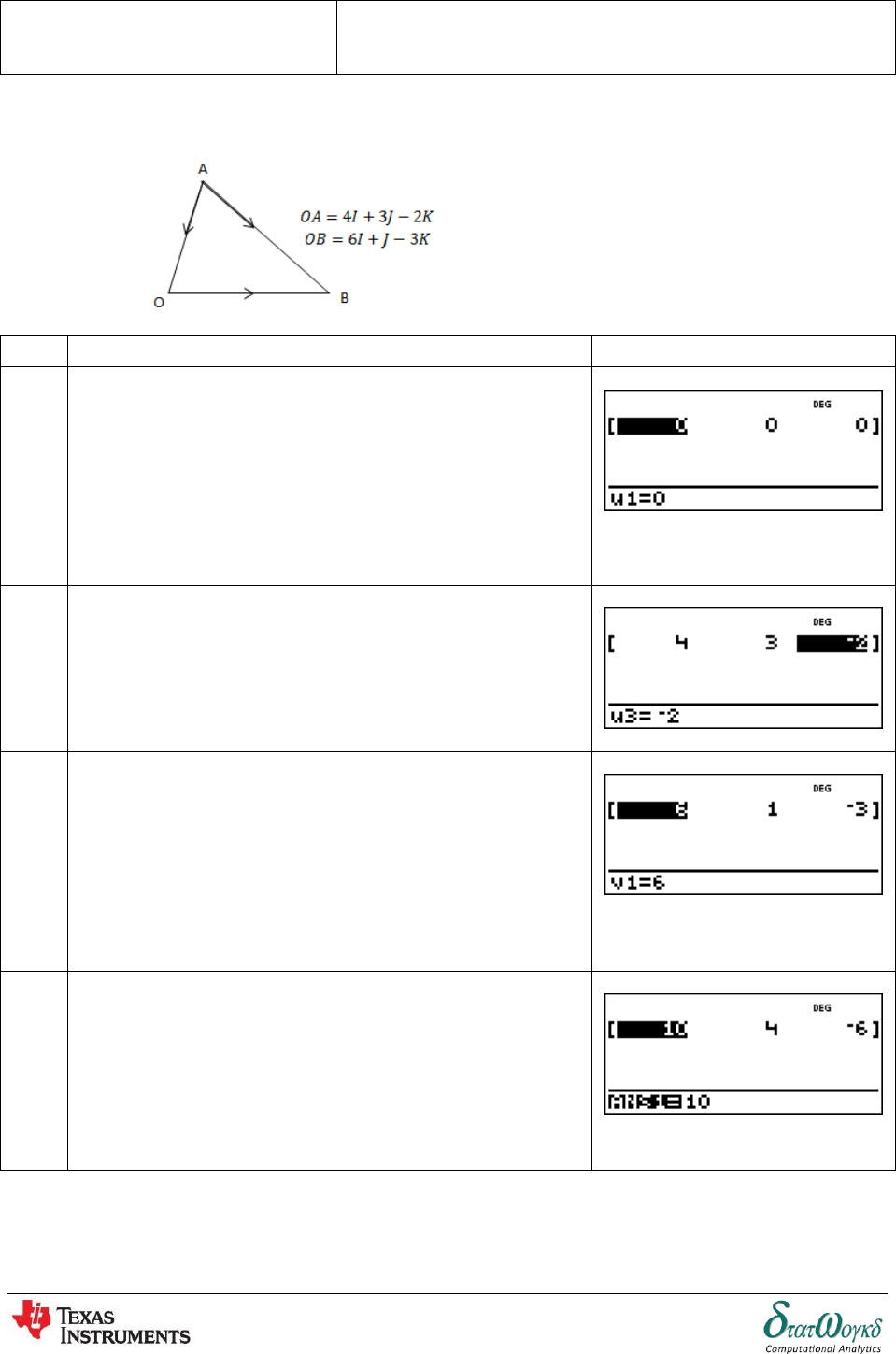
1. If the equation Find the dot product for
No
Keystrokes
Screenshots
1
To enter to vector screen, press
2
Key in the values,
3
To key in the values in vector B, press
And key in the values,
4
To do calculation, A.B press
Thus, the answer is .
Topic:
Vector
Math Concepts:
Basic Algebra, Vector Algebra
Page 63 of 148
2. Find the AB.
No
Keystrokes
Screenshots
1
To enter to vector screen, press
2
Key in the values,
3
key in the values in vector B, press
And key in the values,
4
To do calculation,
Topic:
Vector
Math Concepts:
Basic Algebra, Vector Algebra
Page 64 of 148
3. Find the norm magnitude for vector and
No
Keystrokes
Screenshots
1
To enter to vector screen, press
2
Key in the values,
3
Key in the values in vector B, press
And key in the values,
4
Press to quit from the vector template.
To do calculation,
5
To calculate norm magnitude for B, press
Thus, norm magnitude for
Topic:
Vector
Math Concepts:
Basic Algebra, Vector Algebra
Page 65 of 148
Exercise:
1. If find:
(i) (ii) (
2. Find the moment about a line through the origin having direction of due to a
force acting at a point in the direction of .
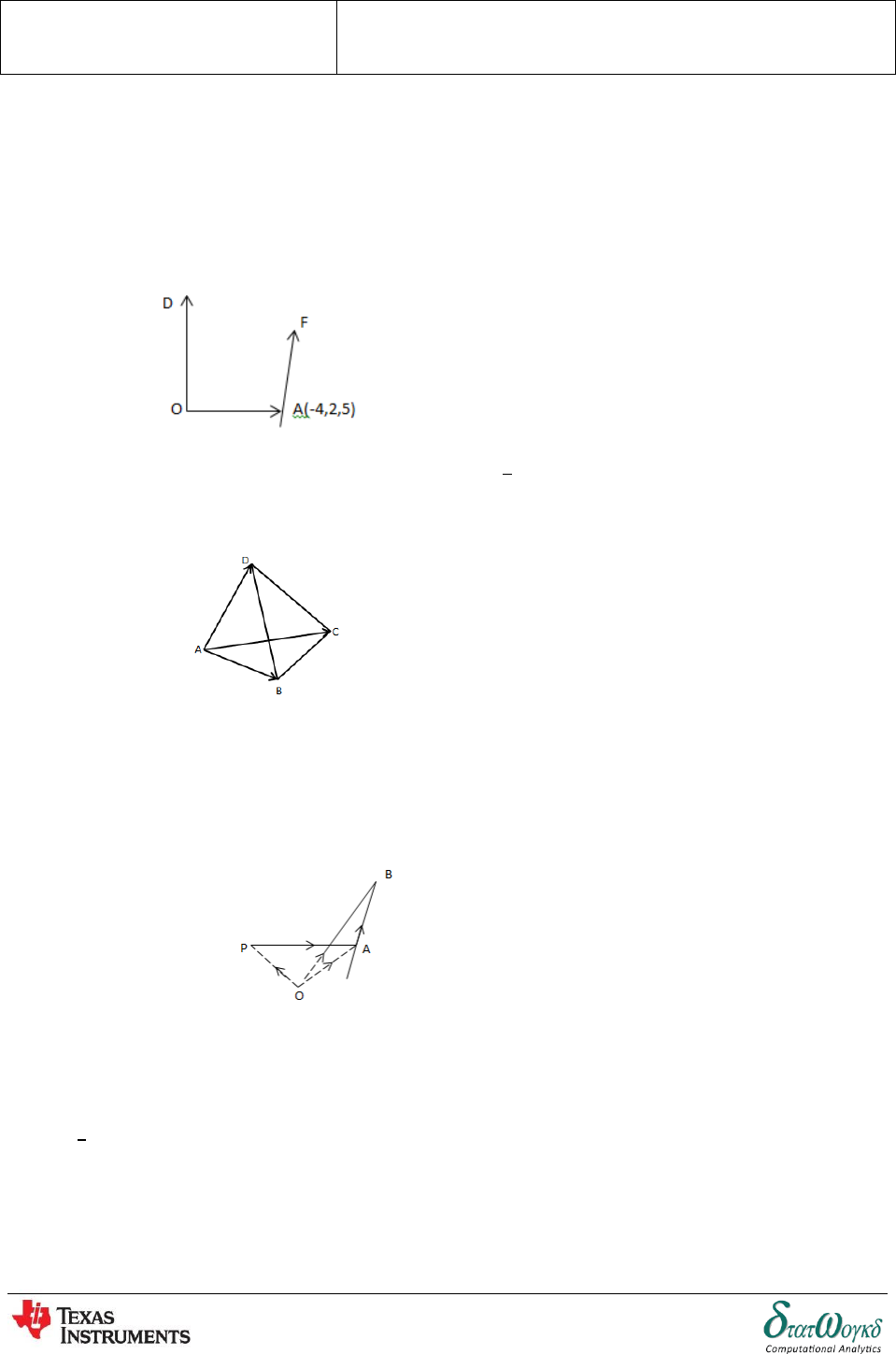
3. Show that the volume of the tetrahedron is
[
,
].
Hence find the volume of the tetrahedron formed by the points and
.
4. Show that the points and are
coplanar.
5. Find the torque about the point of a force represented by acting through the
point .
Answer:
1. (i) (ii)
2.
3.
4. [
,
] . Thus, A,B,C,D are coplanar.
5. Magnitude of the moment
Topic:
Introduction to Trigonometry
Math Concepts:
sin, cos, tan, angle, Pythagorean theorem, trigonometric ratios
Page 66 of 148
Introduction to Trigonometry
Overview / Introduction / Terminology:
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides
and the angles between these sides.
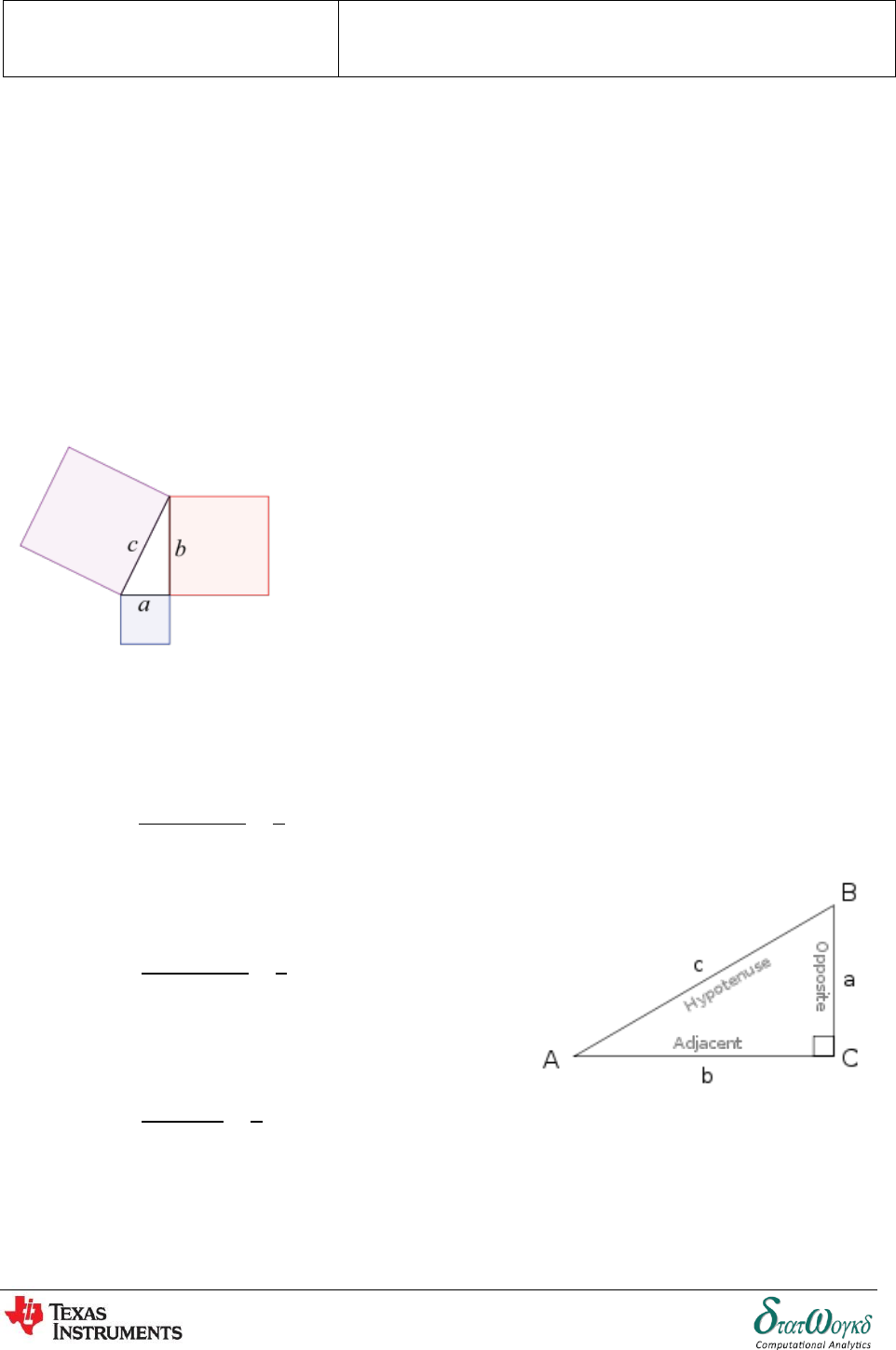
Pythagorean theorem:
The theorem can be written as an equation relating the lengths of the sides a, b and c, often called the
Pythagorean equation:
where c represents the length of the hypotenuse, and a and b
represent the lengths of the other two sides.
Trigonometric ratios are given by the following trigonometric functions of the known angle A, where a, b
and c refer to the lengths of the sides in the accompanying figure:
Sine function (sin), defined as the ratio of the side opposite the angle to the hypotenuse.
Cosine function (cos), defined as the ratio of the adjacent leg
to the hypotenuse.
Tangent function (tan), defined as the ratio of the opposite
leg to the adjacent leg.
Topic:
Introduction to Trigonometry
Math Concepts:
sin, cos, tan, angle, Pythagorean theorem, trigonometric ratios
Page 67 of 148
Keystrokes:
Example:
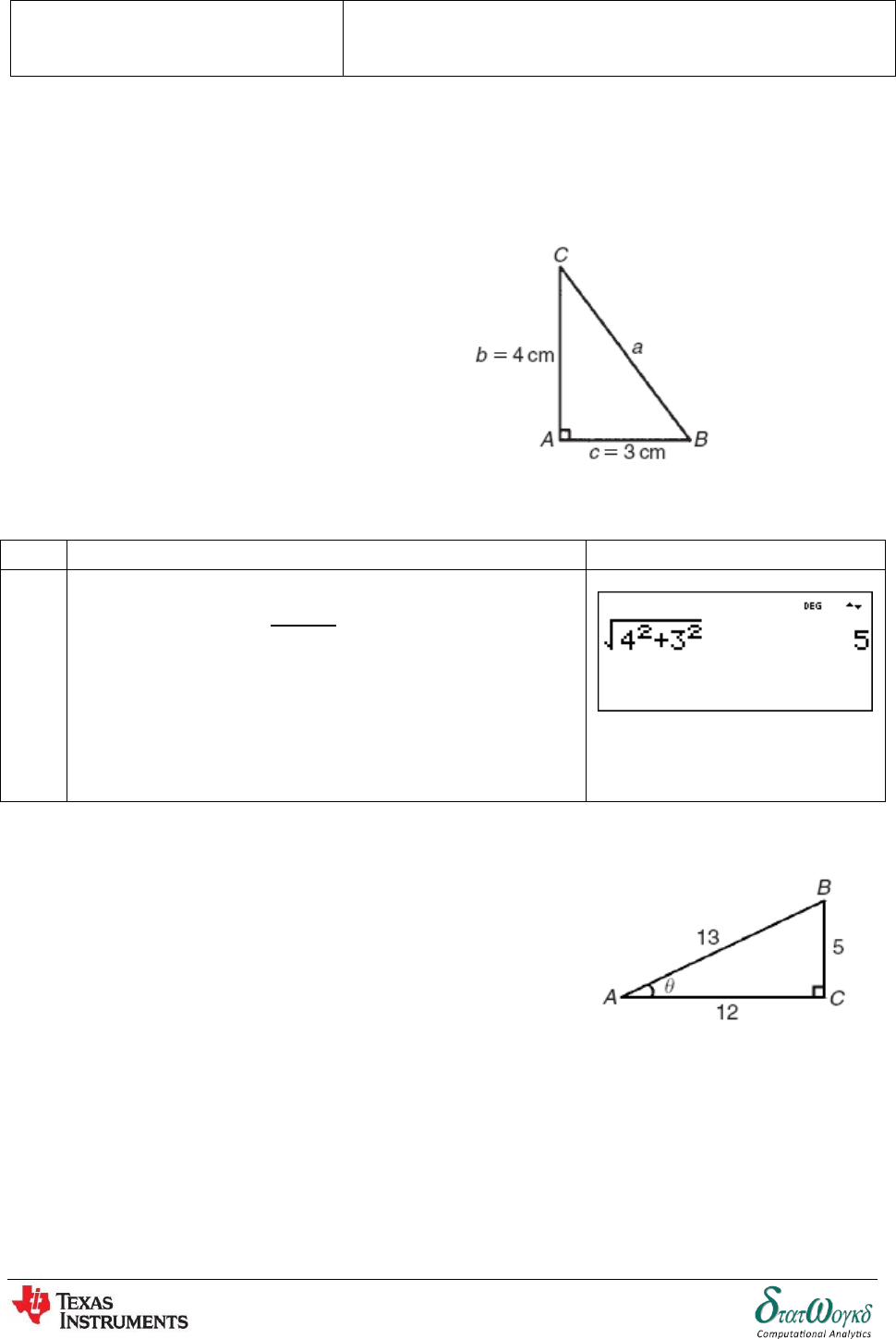
1. Find the length of BC
No
Instructions / Keystrokes
Screenshots
1
. We can rearrange
the equation as . From the figure we know
that and .
Key-in:
Thus
2. Determine the values of , and for the right-
angled triangle ABC

Topic:
Introduction to Trigonometry
Math Concepts:
sin, cos, tan, angle, Pythagorean theorem, trigonometric ratios
Page 68 of 148
No
Instructions / Keystrokes
Screenshots
1
By definition:
,
and
Key-in:
for
for
for
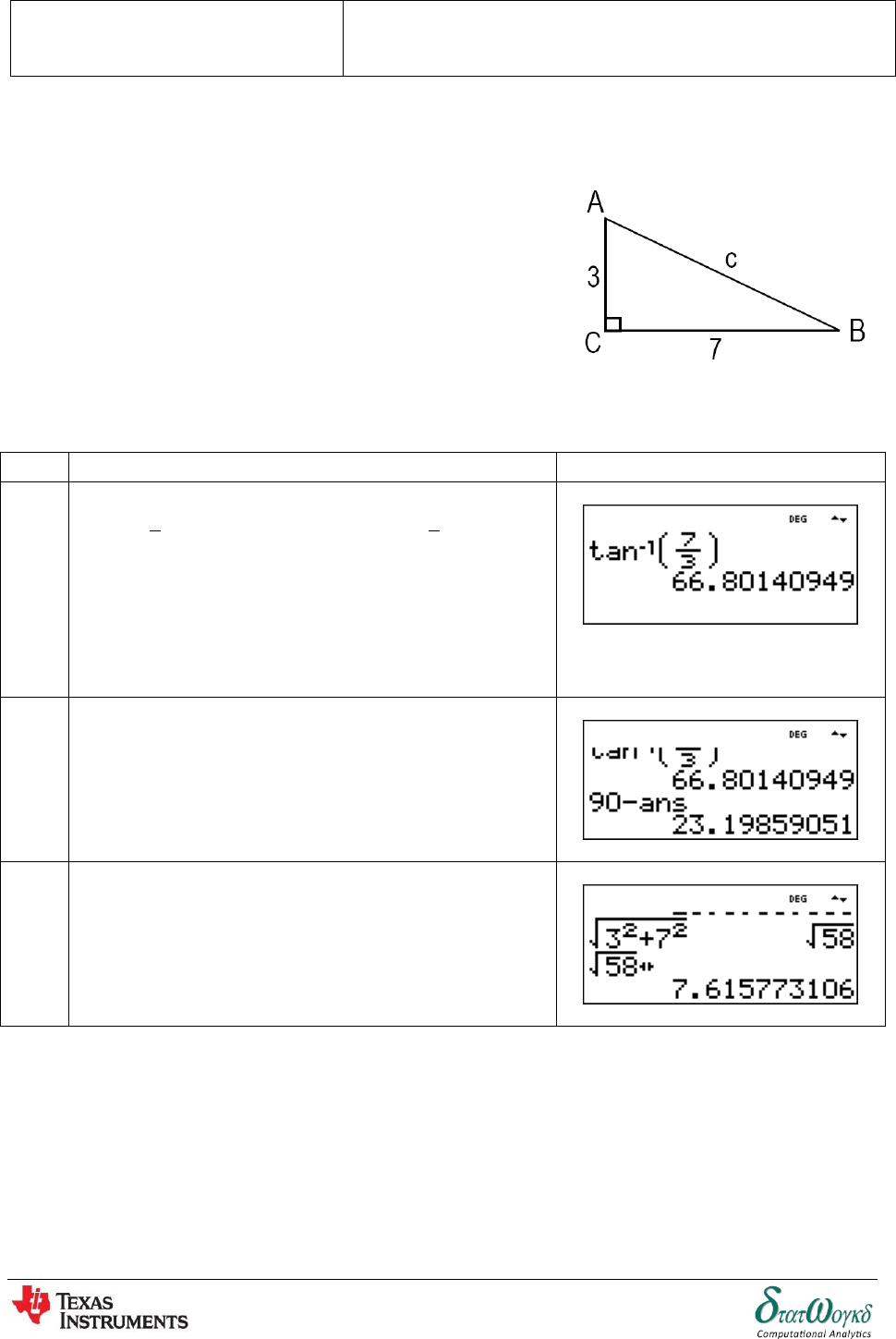
Topic:
Introduction to Trigonometry
Math Concepts:
sin, cos, tan, angle, Pythagorean theorem, trigonometric ratios
Page 69 of 148
3. Find angle A of the right triangle below. Then calculate angle
B and the length of the hypotenuse c. Lengths are in meters.
No
Instructions / Keystrokes
Screenshots
1
To get the answer, press
2
Key-in to calculate the value of
angle B
3
For length of hypotenuse c, press
Press to convert the answer in decimal mode.

Topic:
Introduction to Trigonometry
Math Concepts:
sin, cos, tan, angle, Pythagorean theorem, trigonometric ratios
Page 70 of 148
Exercises:
1. When driving, a steep hill is typically only 12°. What is the cosine of this angle?
2. The angle that waves hit a shoreline is 75°. What is the tangent of this angle?
3. The angle of repose is the steepest angle at which dry,
unconsolidated sediment is stable. You create a conical pile of
sand that is as steep as you can make it. The pile is cm high and
has a radius of cm. What is the angle of repose of this sand?
4. You are walking up a meter high hill. The trail has an incline of degrees. How far will you
walk to get to the top?
5. You note that a bed coal is tilted at degrees and comes to the surface kilometers from your
property. How deep will you have to dig to get to the coal bed on your property?
Answers:
1.
2.
3. , the angle of repose for this sand.
4. The trail up the hill is
5. the depth of the coal bed, is , or .
Topic:
Cartesian and polar co-ordinates
Math Concepts:
Radius, Angle, Cartesian coordinates, Polar coordinates
Page 71 of 148
Cartesian and polar co-ordinates
Overview / Introduction / Terminology:
Type of coordinates
Cartesian Coordinates
Using Cartesian Coordinates you mark a point
by how far along and how far up it is:
Polar Coordinates
Using Polar Coordinates you mark a point by how
far away, and what angle it is:
Converting
To convert from one to the other, you need to solve the triangle:
To convert from Cartesian to Polar
The Cartesian coordinates (also called Rectangular coordinates) and can be converted to polar
coordinates and with and in the interval by:
To convert from Polar to Cartesian
The two polar coordinates and can be converted to the two Cartesian coordinates and by using
the trigonometric functions sine and cosine:
Keystrokes: > RP

Topic:
Cartesian and polar co-ordinates
Math Concepts:
Radius, Angle, Cartesian coordinates, Polar coordinates
Page 72 of 148
Example:
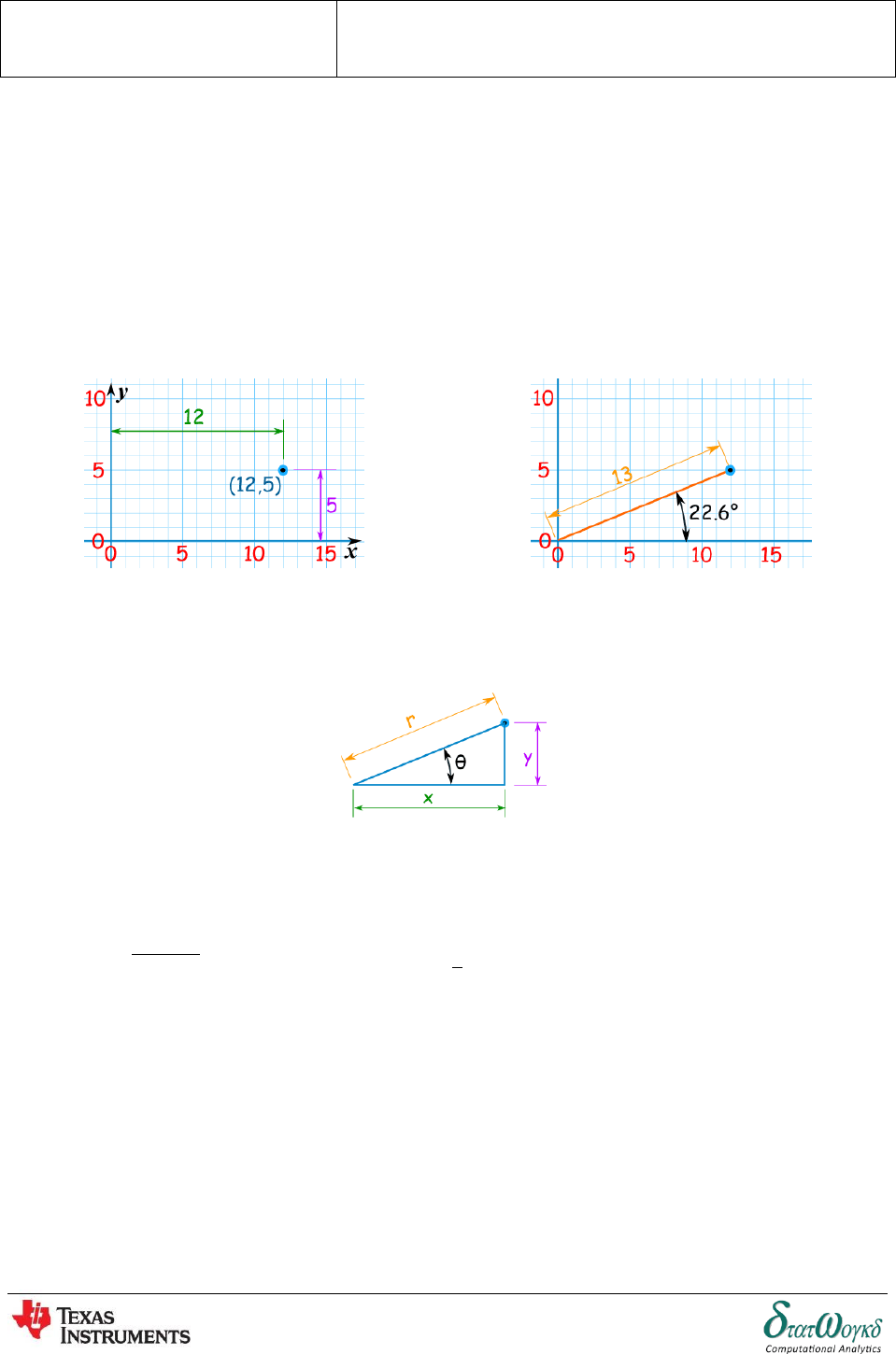
1. Convert polar coordinates into rectangular coordinates. Then convert
rectangular coordinates into polar coordinates. Round the results to one decimal
place.
No
Instructions / Keystrokes
Screenshots
1
To set mode to one decimal place, press
. Then press to go back to
home screen.
2
Press and using tight cursor, choose RP.
3
To convert to polar coordinates and display choose 1.
P Rx( . Press or . Key-in this value in your
calculator:
4
To convert to polar coordinates and display choose 2.
R Py( . Press or . Key-in this value in your
calculator:
Converting gives
5
To convert to polar coordinates and display choose 3.
R Pr( . Press or . Key-in this value in your
calculator:

Topic:
Cartesian and polar co-ordinates
Math Concepts:
Radius, Angle, Cartesian coordinates, Polar coordinates
Page 73 of 148
No
Instructions / Keystrokes
Screenshots
6
To convert to polar coordinates and display choose 4. R
P( . Press or . Key-in this value in your
calculator:
Converting gives
Exercises:
1. Change the Cartesian co-ordinates into polar co-ordinates.
a.
b.
c.
d.
2. Change the polar co-ordinates into Cartesian co-ordinates.
a. ()
b. ()
c. ()
Answers:
1. Question 1:
a. () or ()
b. () or ()
c. () or ()
d. () or ()
2. Question 2
a. ()
b. ()
c. ()
Topic:
Geometry and Triangles
Math Concepts:
Basic Algebra, Triangle, Degree, Radian,
Page 74 of 148
Geometry and Triangles
Overview / Introduction / Terminology:
Geometry is a part of mathematics in which the properties of points, lines, surfaces and solids are
investigated.
An angle is the amount of rotation between two straight lines. Angles may be measured in either
degrees ( 0)or radians.
1 revolution = degrees, thus 1 degree =
th of one revolution.
1 minute =
th of a degree is written as 1’
1 second =
th of a minute is written as 1’’
Properties of triangles
A triangle is a figure enclosed by three straight lines. The sum of the three angles of a triangle is equal to
.
Congruent triangles : Two triangles are said to be congruent if they are equal in all respects.
Similar triangles : Two triangles are said to be similar if the angles of one triangle are equal to the
angles of the other triangle.
Topic:
Geometry and Triangles
Math Concepts:
Basic Algebra, Triangle, Degree, Radian,
Page 75 of 148
Keystrokes:
Example:
1. In the below figure, find the length of side
No
Keystrokes
Screenshots
1
Based on the figure, it shows the similar triangle.
.
To get the answer, calculation will be:
,
To enter the equation, press
2
Key in the values,
3
To get the answer, press .
Thus, the answer is
Topic:
Geometry and Triangles
Math Concepts:
Basic Algebra, Triangle, Degree, Radian,
Page 76 of 148
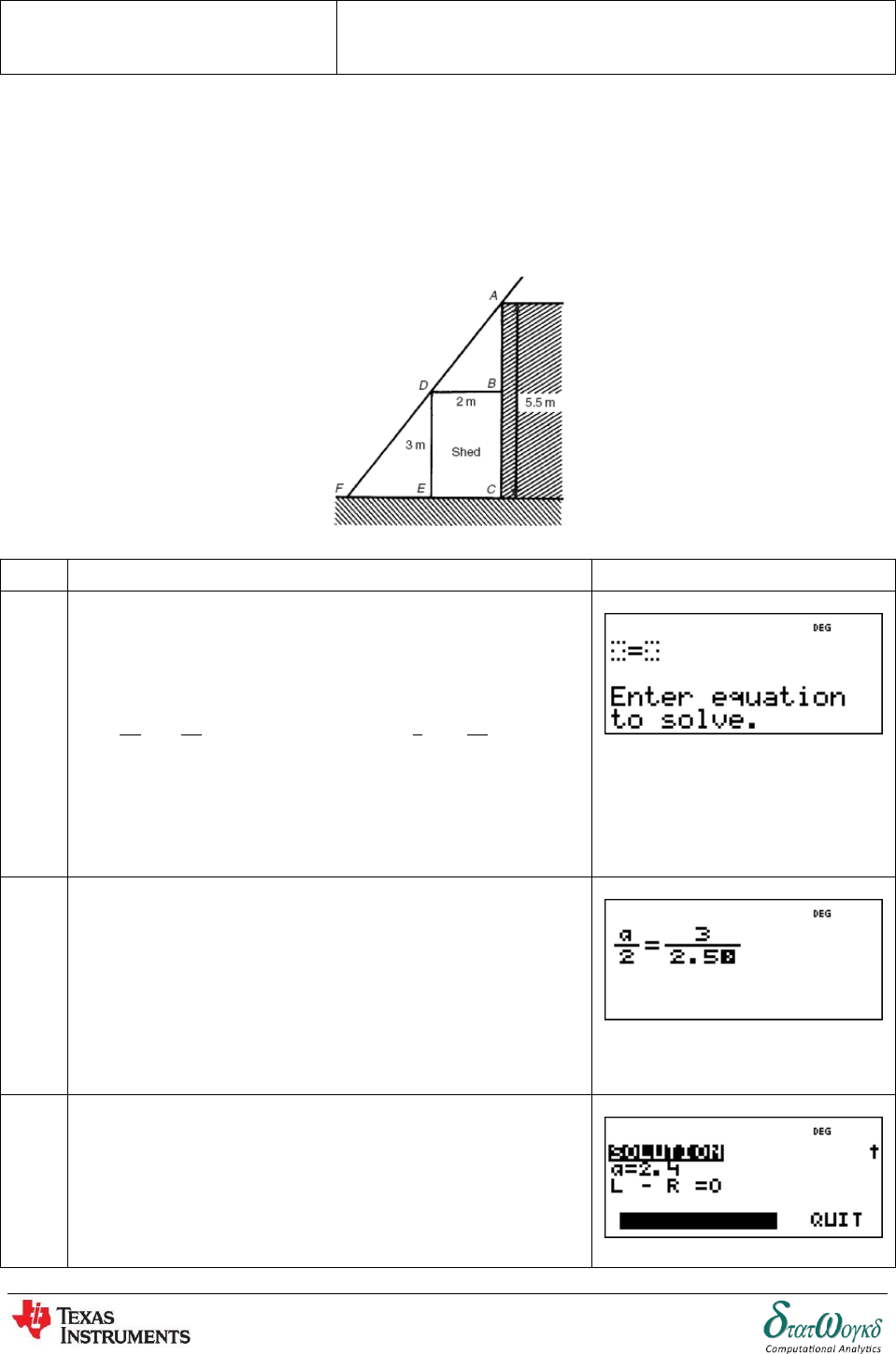
2. A rectangular shed 2m wide and 3m high stands against a perpendicular building of height
. A ladder is used to gain access to the roof of the building. Determine the minimum
distance between the bottom of the ladder and the shed.
No
Keystrokes
Screenshots
1
Based on the figure, value .
So, the equation for calculation will be:
, assume = , so,
To enter the equation, press
2
Key in the values,
3
To get the answer, press .
Thus, the answer is @
Topic:
Geometry and Triangles
Math Concepts:
Basic Algebra, Triangle, Degree, Radian,
Page 77 of 148
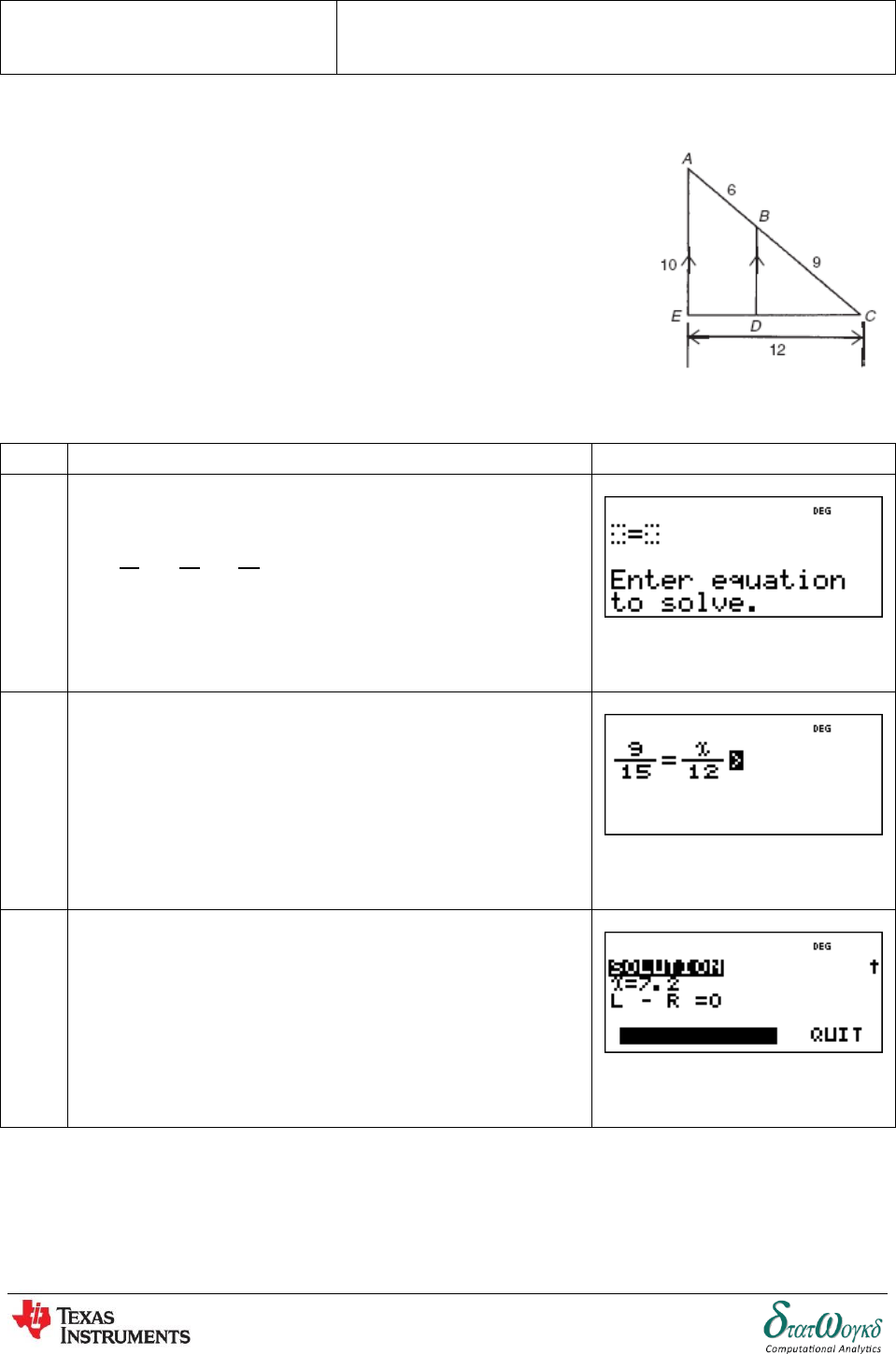
3. In figure at the right, show the triangles and are similar
and hence find the length of and
No
Keystrokes
Screenshots
1
Based on the figure, the proportion will be:
To enter the equation, press
2
To enter the values, press
3
To get the answer, press
Thus, length of
Topic:
Geometry and Triangles
Math Concepts:
Basic Algebra, Triangle, Degree, Radian,
Page 78 of 148
No
Keystrokes
Screenshots
4
To get the answer for length of BD,
To change the value, press again, and change
the value. Press
5
To get the answer, press
Thus,
Exercise:
1. Add together the angles : , and
2. Convert the following angles to degrees and decimals of a degree, correct to 3 decimal
places:
(a) (b) (c) (d)
3. Find the lengths x and y.
4. PQR is an equilateral triangle of side . When PQ and PR are produced to S and T,
respectively, ST is found to be parallel with QR. If PS is 9 cm, find the length of ST. X is a
point on ST between S and T such that the line PX is the bisector of SPT. Find the length of
PX .
Topic:
Geometry and Triangles
Math Concepts:
Basic Algebra, Triangle, Degree, Radian,
Page 79 of 148
5. Find (a) the length of BC when and (b) the length of
when and
Answer:
1.
2. (a) (b) (c) (d)
3. ,
4. ,
5. (a) (b)
Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 80 of 148
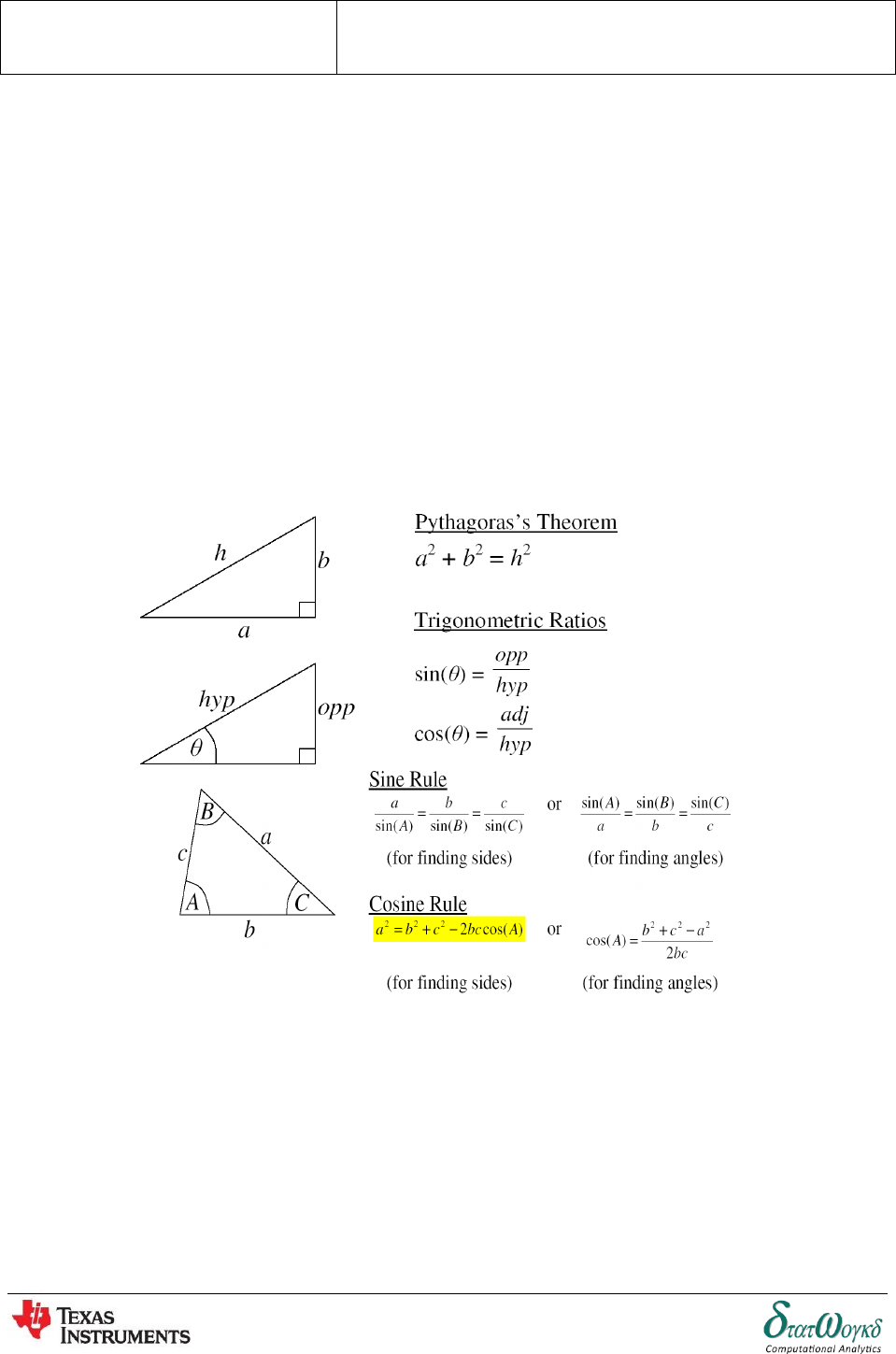
Triangles and some practical applications
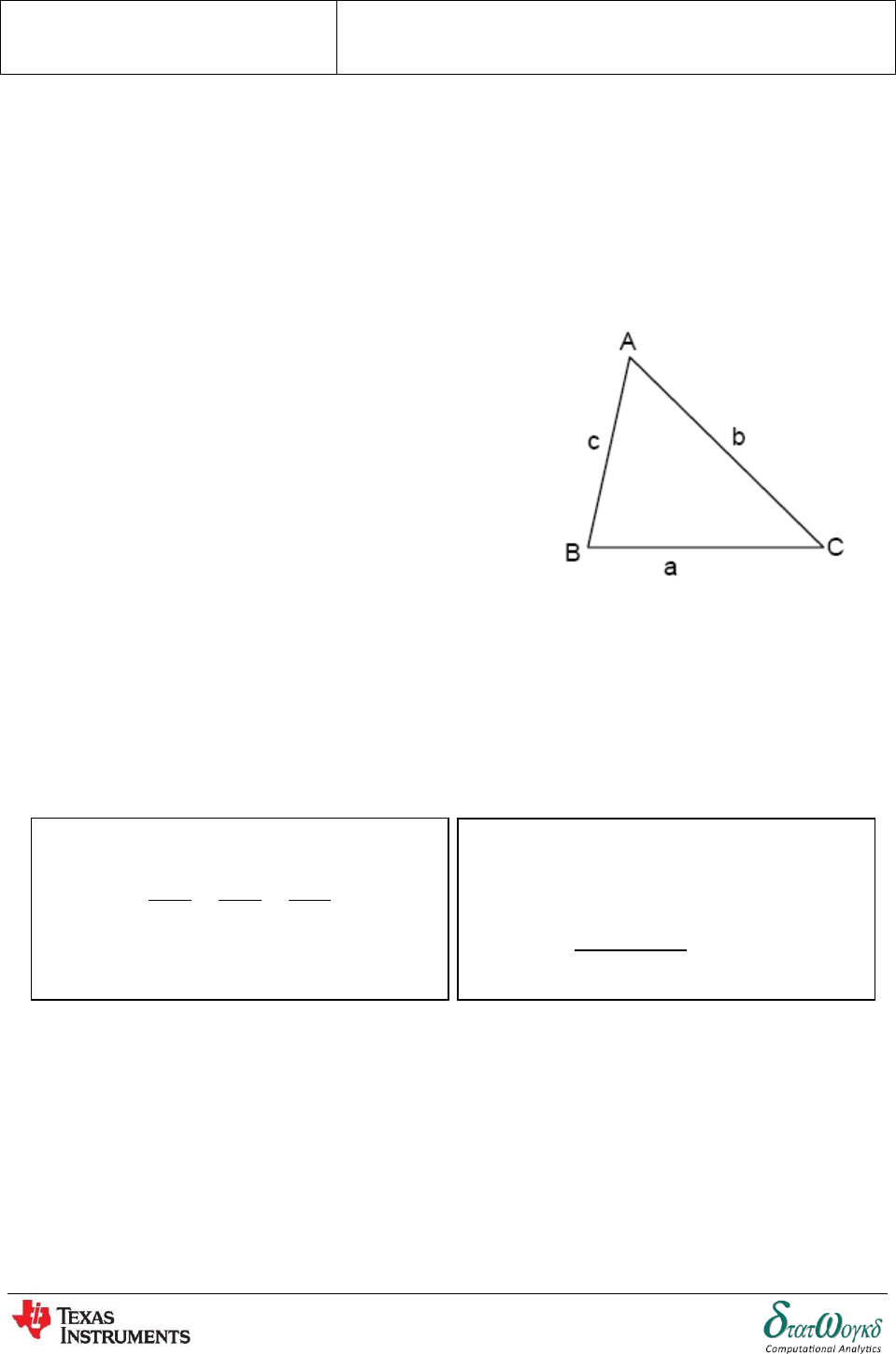
Overview / Introduction / Terminology:
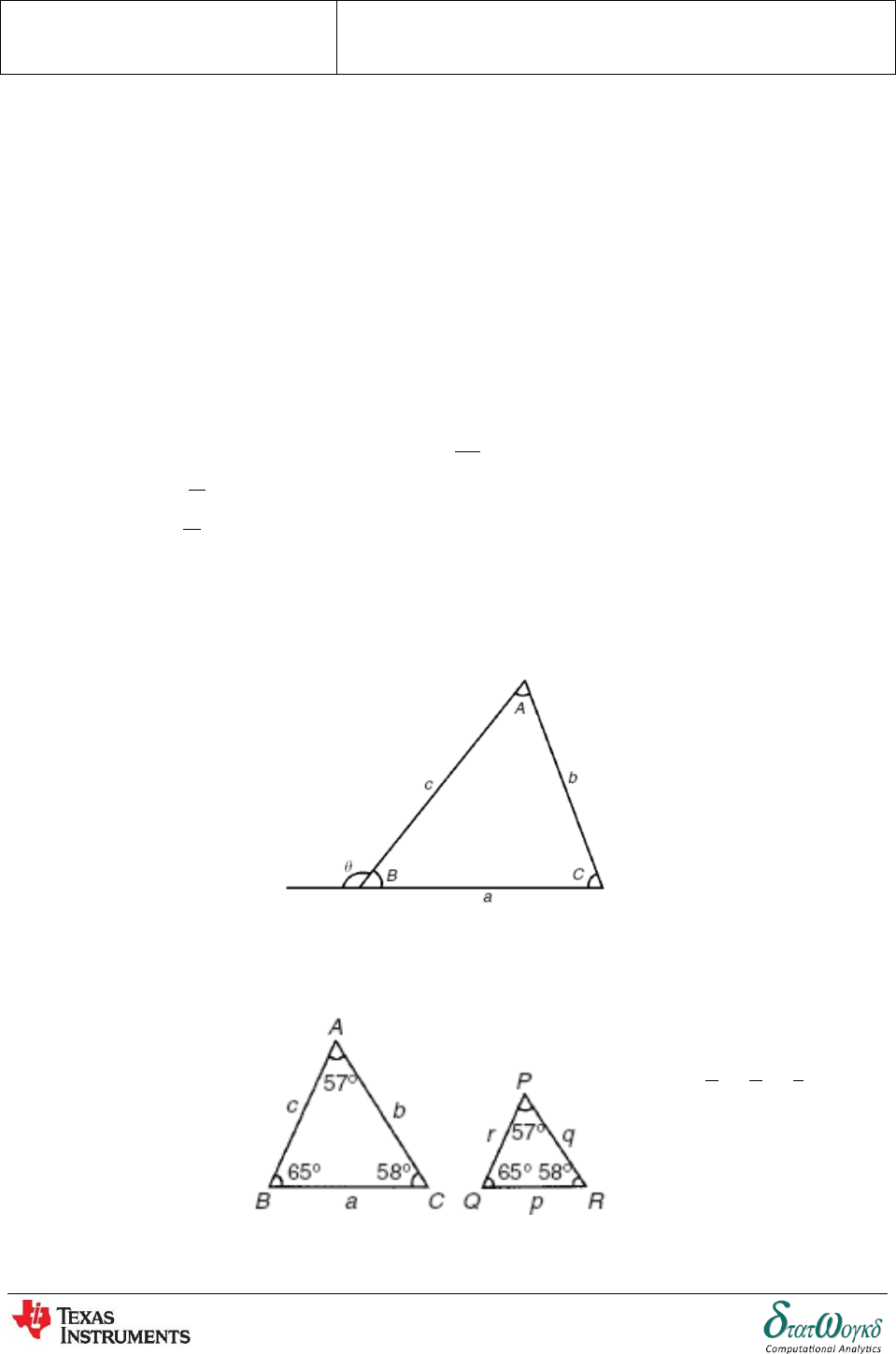
Sine and Cosine Rules:
For triangles which are not right-angled we use the sine and
cosine rules. The triangle on the right has the conventional
notation of small letters for the lengths of sides and capital
letters for the angles opposite. To find lengths and angles,
use:
The sine rule may be used only when:
1 side and any 2 angles are initially given, or
2 sides and an angle (not the included angle) are
initially given.
The cosine rule may be used only when:
2 sides and the included angle are initially given, or
3 sides are initially given.
ame for each pair
of sides and angles. And in the cosine rule, ensure that the side on the LHS of the equation matches the
angle on the RHS.
Area of a non-right angled triangle:
If you know two sides of a triangle, and the size of the angle between the two sides, then the area of the
triangle can be found using:
SINE RULE
COSINE RULE
Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 81 of 148
Keystrokes
basic operational keys
Example
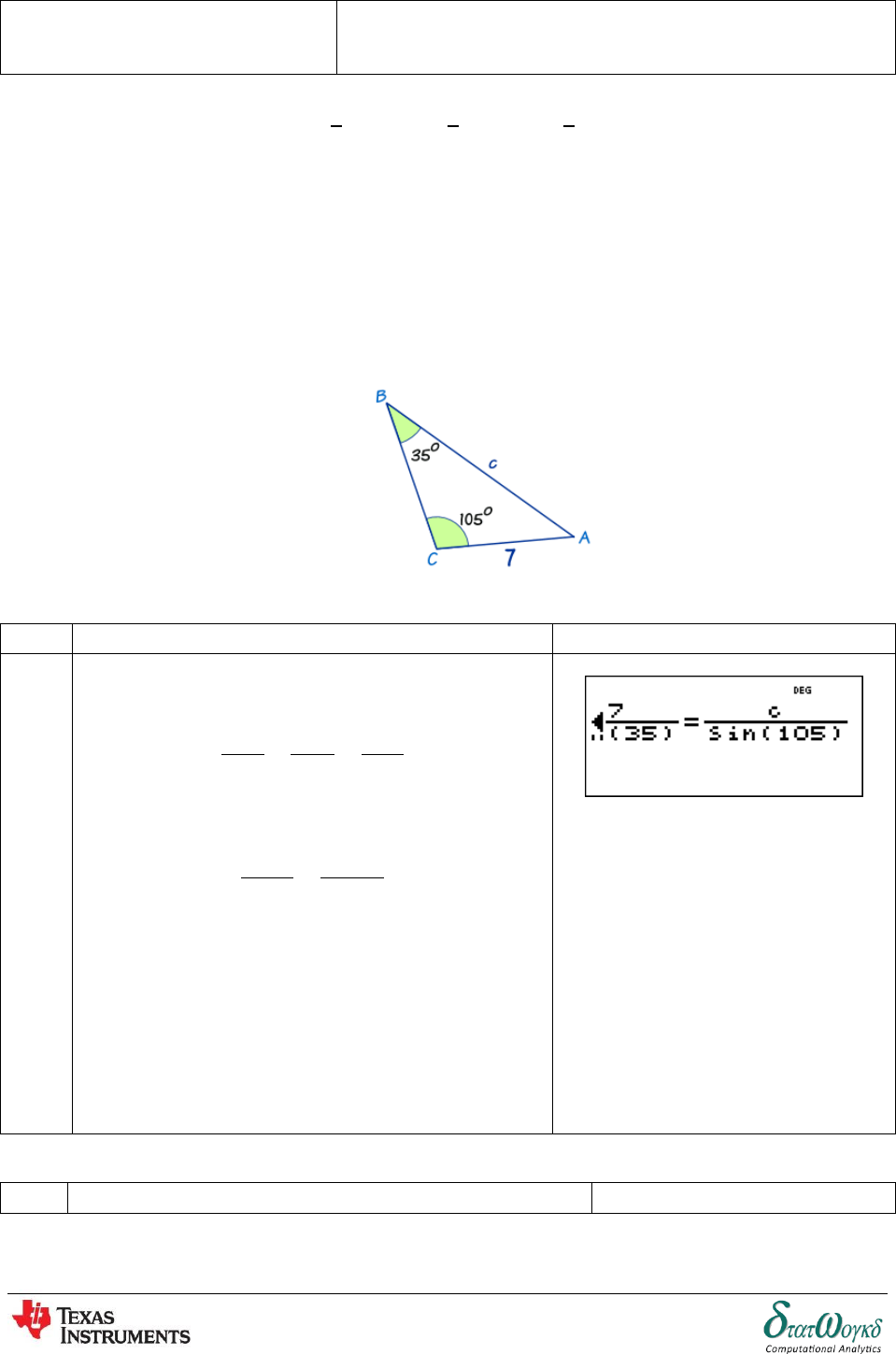
1. Calculate side C
No
Instructions / Keystrokes
Screenshots
1
Law of sine:
We can only find angle C at the moment, by using:
We can use numerical solver from scientific calculator.
No
Keystrokes
Screenshots
Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 82 of 148
2
Bring you cursor to C and press to get the answer.
Thus, side C is equal to
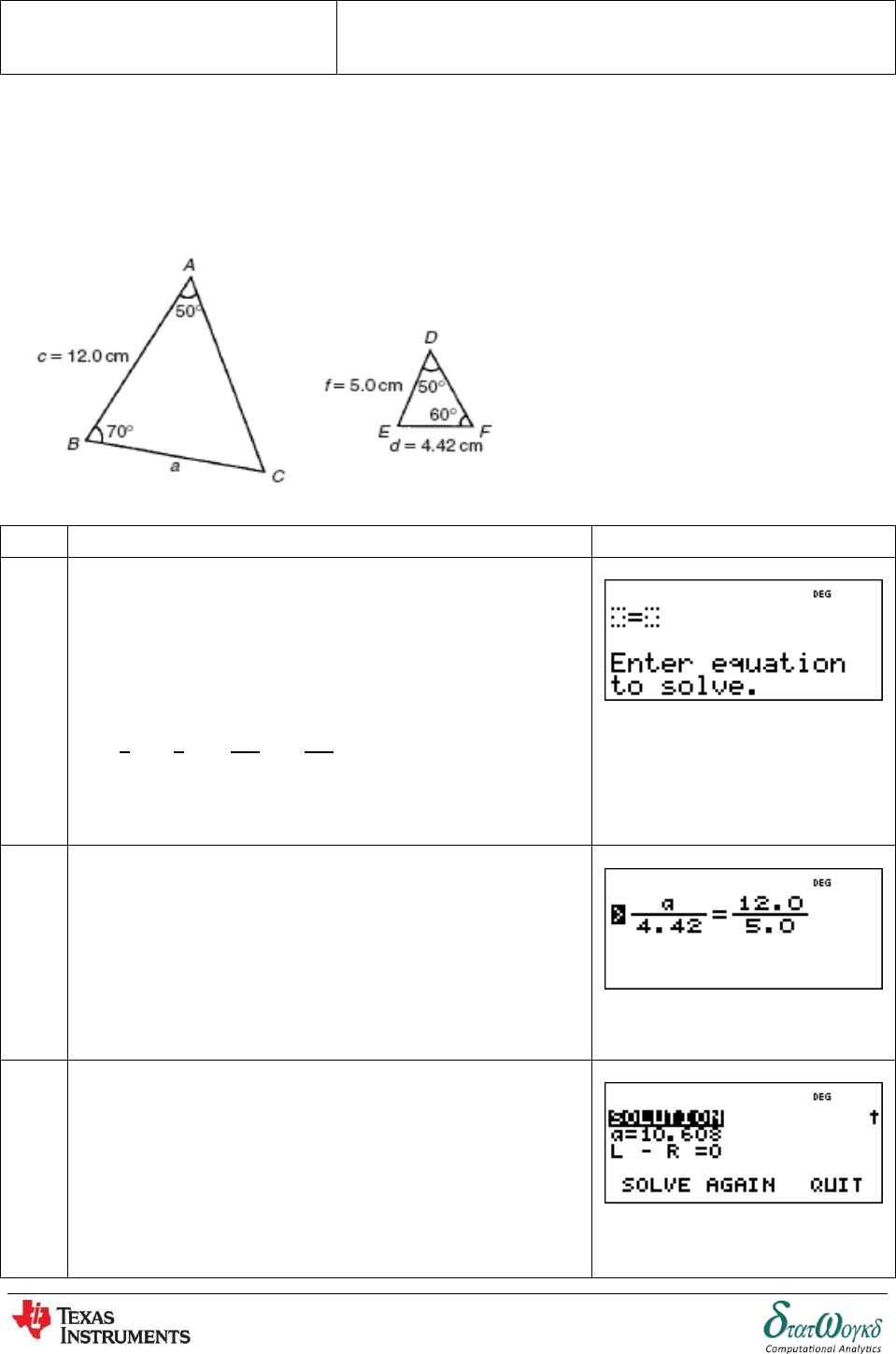
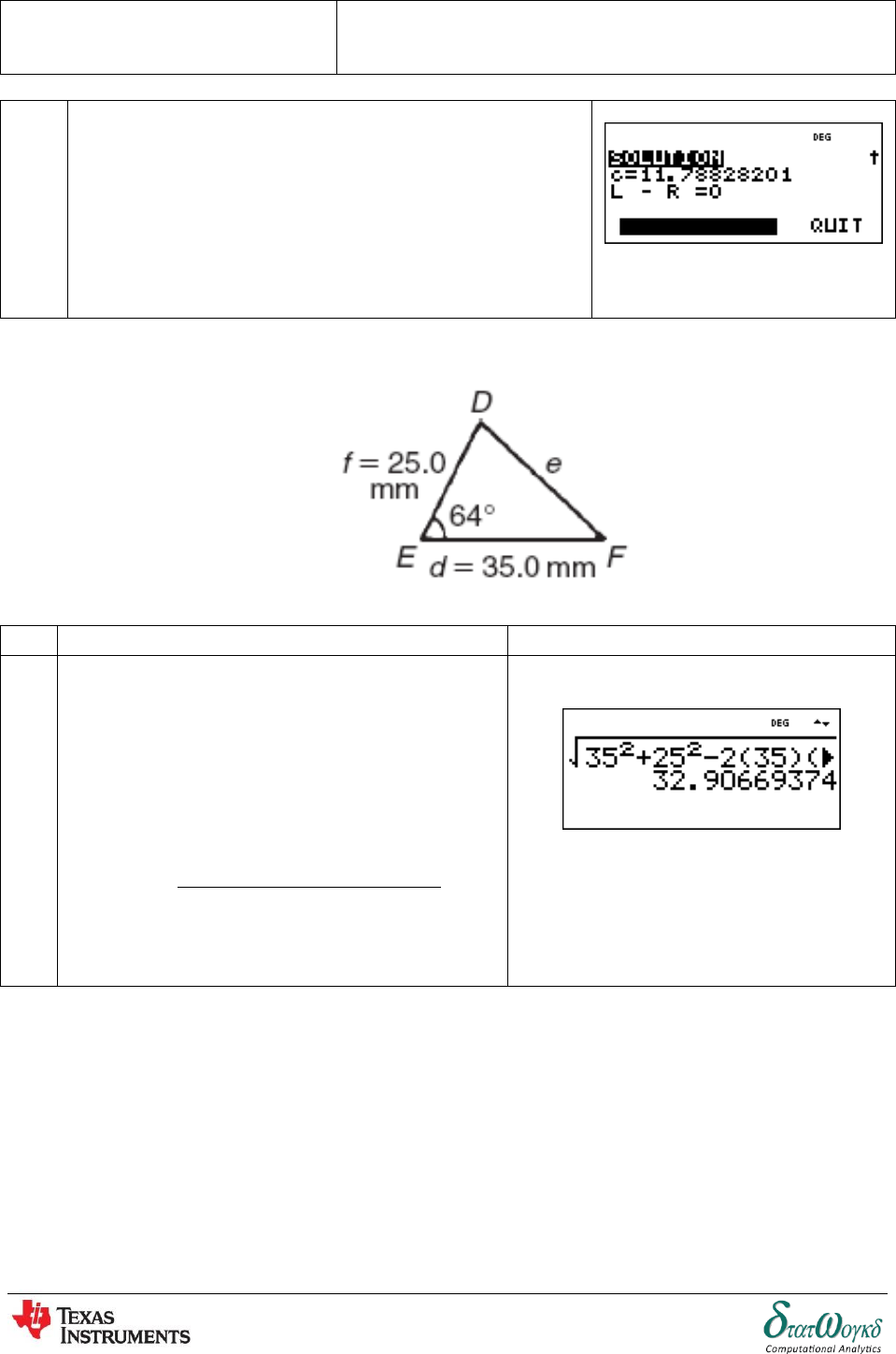
2. Solve triangle DEF and find its area given that EF =35.0 mm, DE =25.0mm and E =64
No
Instructions / Keystrokes
Screenshots
1
Applying the cosine rule
In your calculator, key-in this equation:
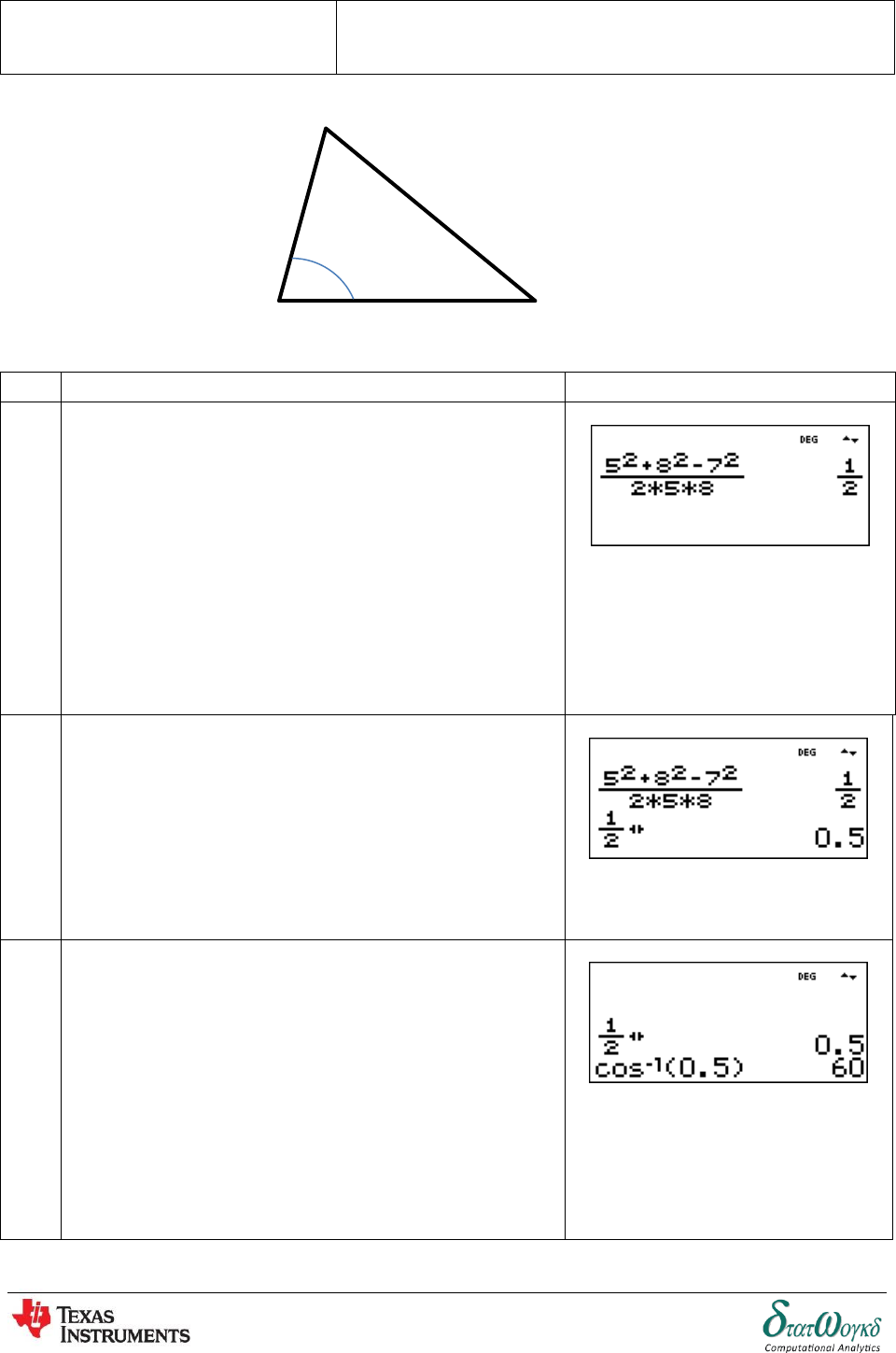
3. The diagram shows a triangle with sides 5, 7 and 8. Find the size of the smallest angle.
Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 83 of 148
No
Instructions / Keystrokes
Screenshots
1
The smallest angle is opposite the smallest side, 5. Using
cosine rule, fill in the values you know, and the unknown
length. Press:
2
Press to convert the answer in decimal mode.
Thus,
3
Evaluate the right-hand-side and then use inverse-cosine
to find the angle
So, the angle is
P
5
7
8
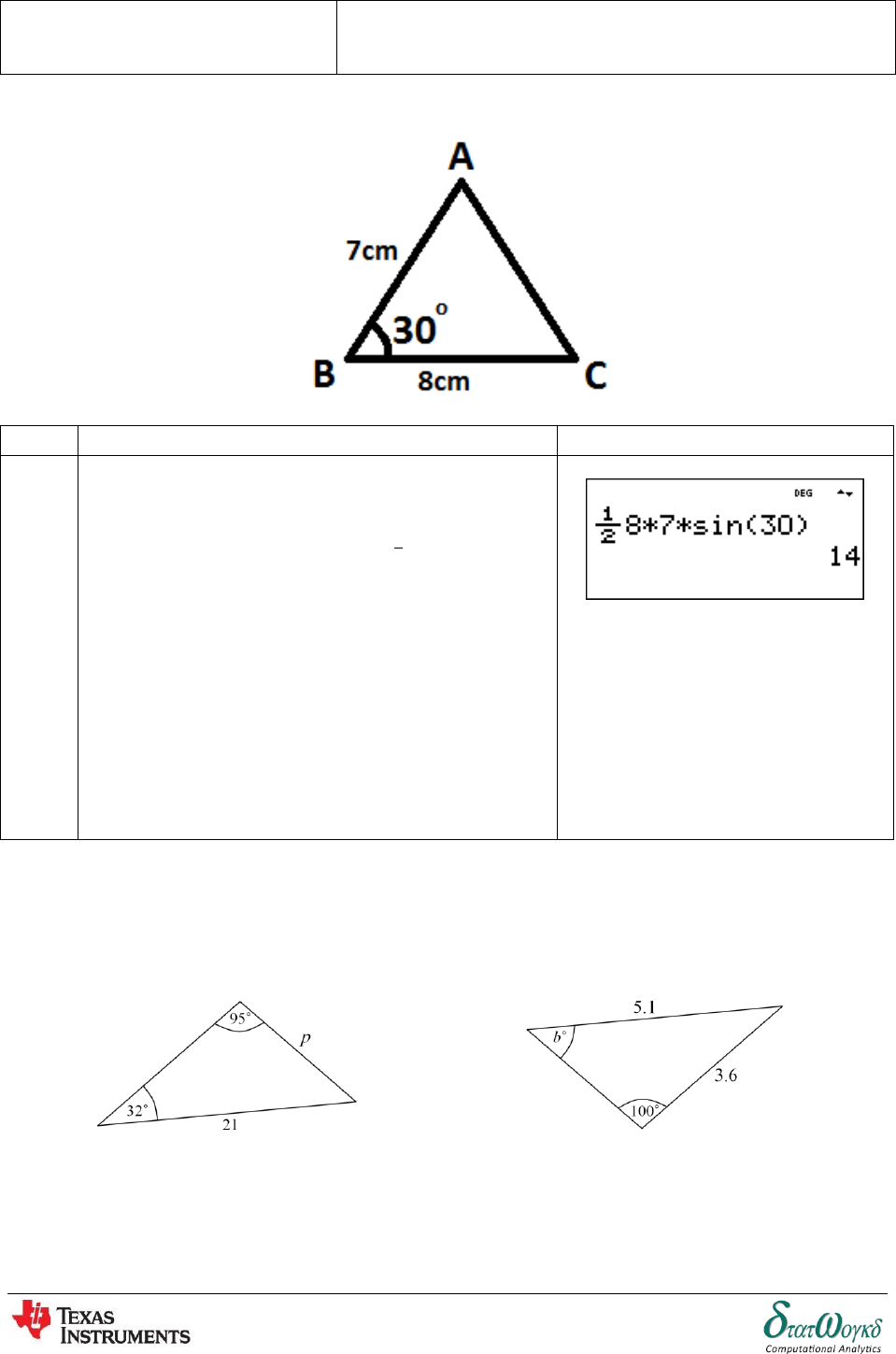
Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 84 of 148
4. Find the area for below triangle:
No
Instructions / Keystrokes
Screenshots
1
Given that .
Using the formula for area,
key in
Thus, the area of triangle is
Exercises
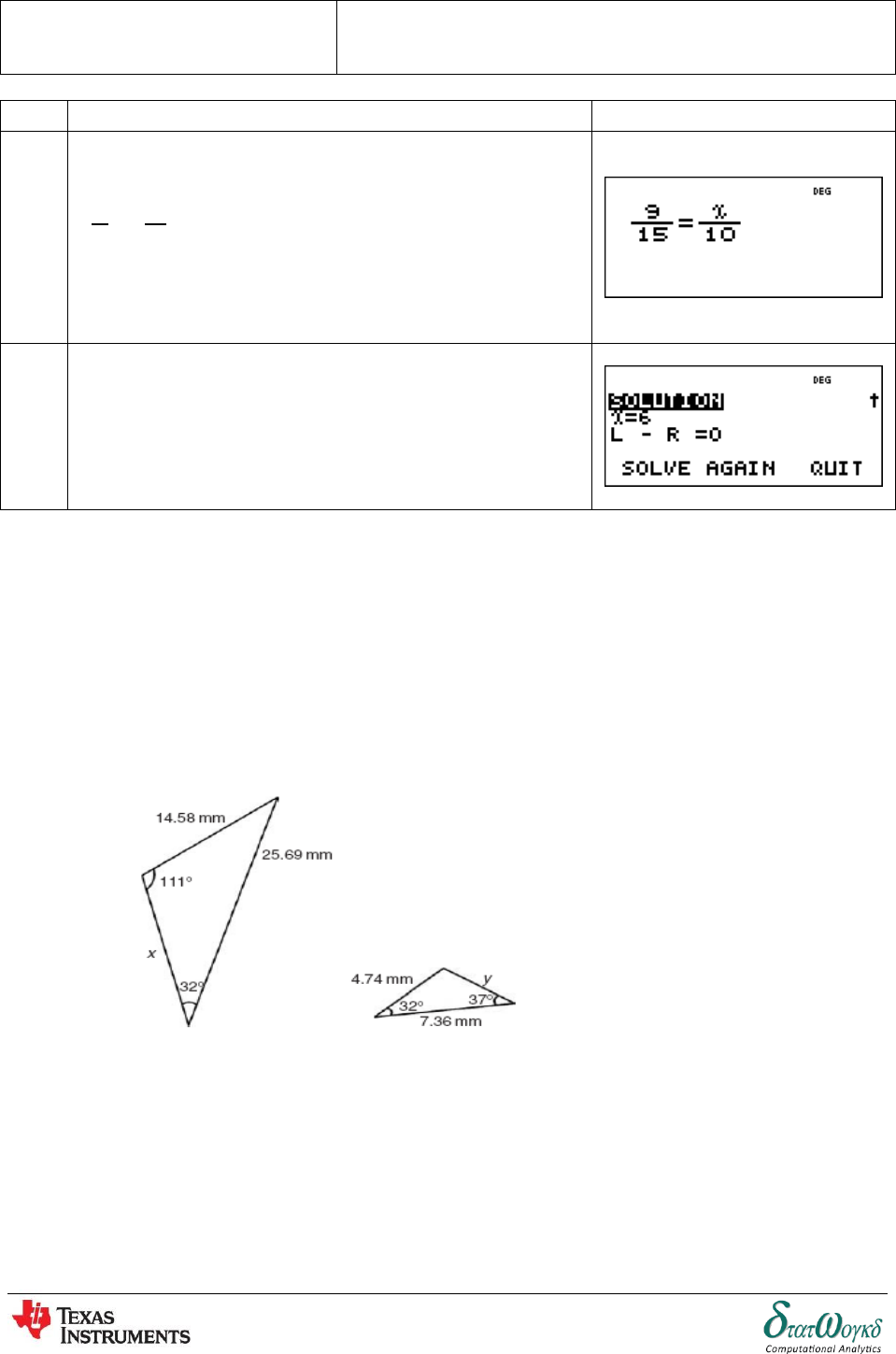
Find the unknown side or angle in each of the following diagrams. Round the answer to 3 significant
features:
1.
2.
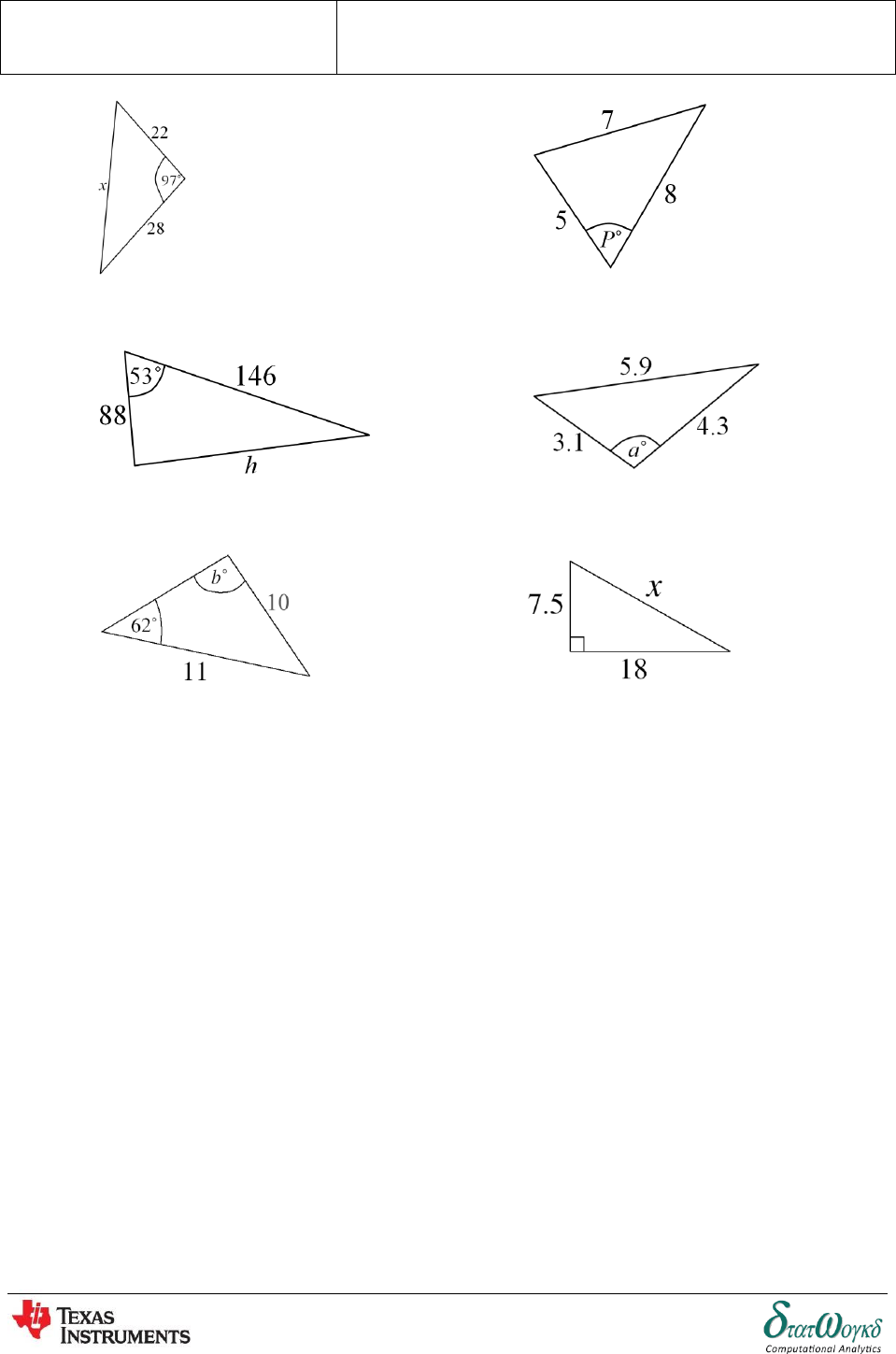
Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 85 of 148
3.
4.
5.
6.
7.
8.
9. Farmer Jones owns a triangular piece of land. The length of fence AB is . The length of the
fence BC is . The angle between fence AB and fence BC is 0. How much land does
Farmer Jones own?
Answers
1.
2.
3.
4.
5.
6.
7.
8.
9. Farmer Jones has of land
Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 86 of 148
Adding of Waveforms
Overview / Introduction / Terminology:
Determining Resultant Phasors by Calculation
This section will cover how to:
Use the Sine Rule to find unknown sides and angles
Use the Cosine Rule to find unknown sides and angles
Combine trigonometry skills to solve problems
Each topic is introduced with a theory section including examples and then some practice questions. At
the end of the page there is an exercise where you can test your understanding of all the topics covered
in this page. You should already know each of the following formulae:
Keystrokes:
,,,,
Formulae
for right-
angled
triangles.
Formulae
for all
triangles.
Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 87 of 148
Example:
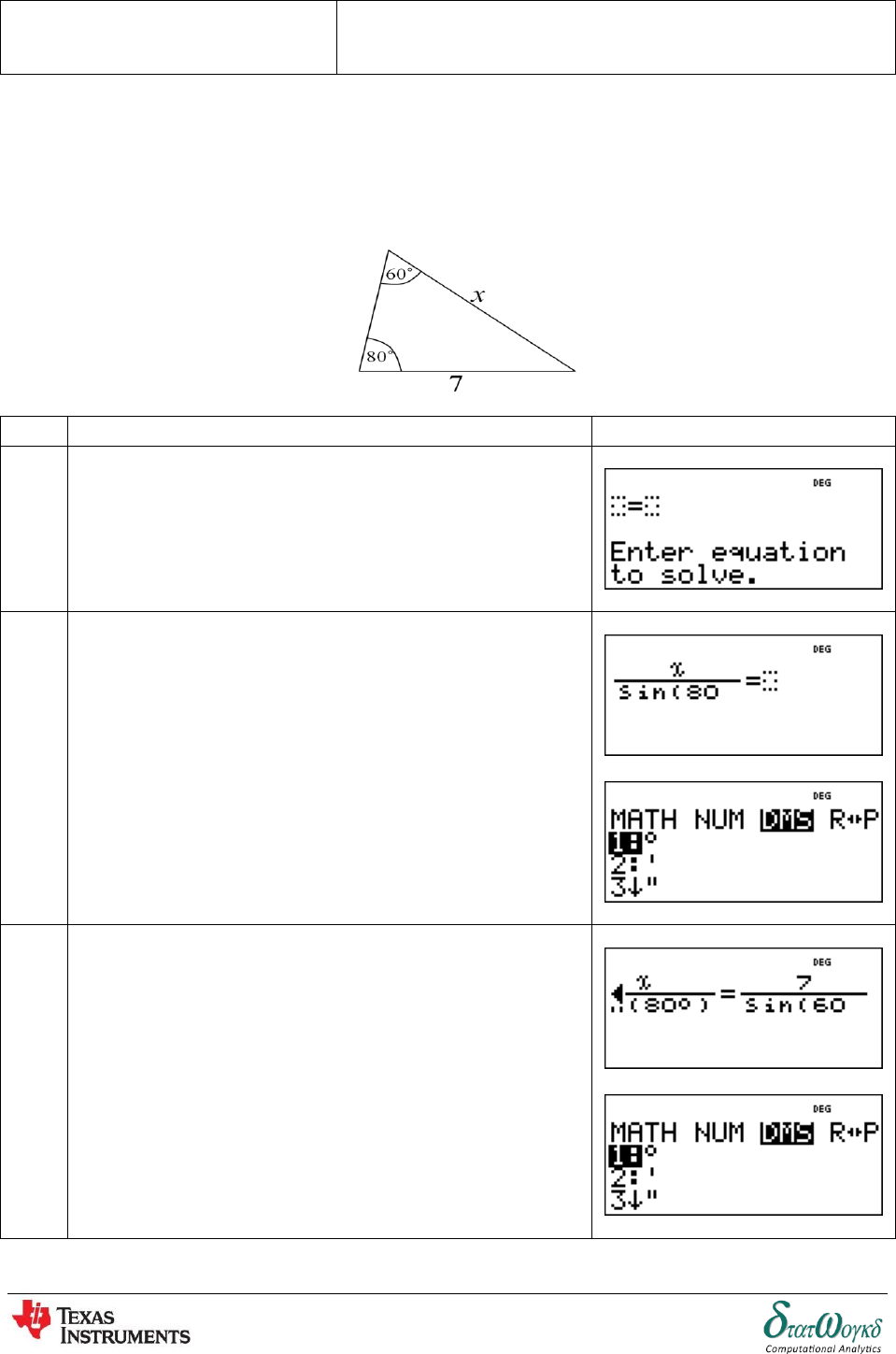
1. The Sine Rule can be used in any triangle (not just right-angled triangles) where a side and its
opposite angle are known.
Finding Sides: Work out the length of in the diagram below,
No
Keystrokes
Screenshots
1
Press ,
2
Insert equation in the number solving, press
.
3
Then press
.
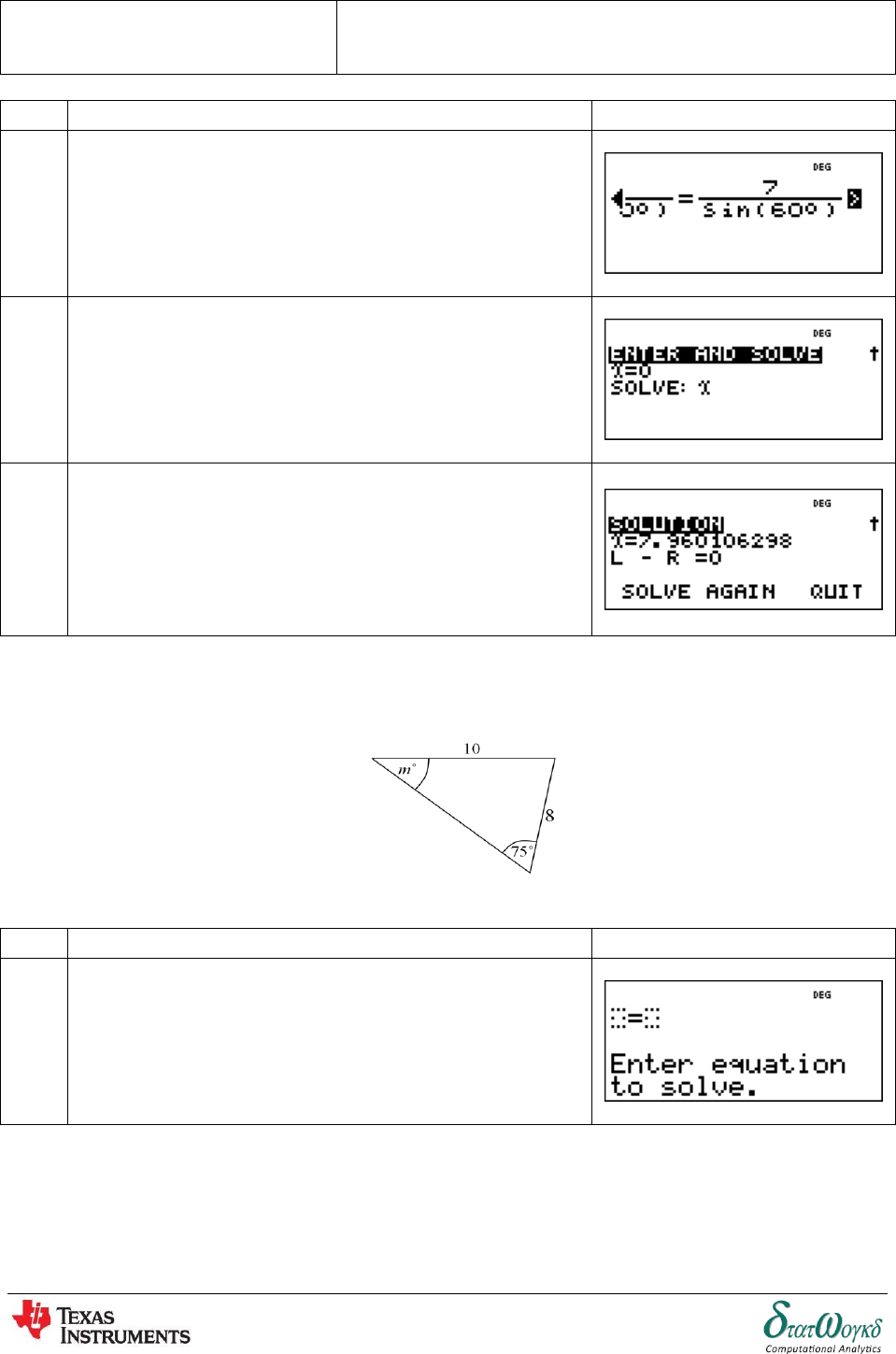
Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 88 of 148
No
Keystrokes
Screenshots
4
to solve the equation.
5
Assume that ,
6
Press
The answer is (accurate to 3 significant
figures)
2. Finding Angles: Work out angle in the diagram below: (Note, Change to .)
No
Keystrokes
Screenshots
1
Press ,

Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 89 of 148
No
Keystrokes
Screenshots
2
Insert equation in the number solving, press
.
3
Then press
.
4
to solve the equation.
5
Assume that ,
Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 90 of 148
No
Keystrokes
Screenshots
6
Press
The answer is (accurate to 3 significant figures)
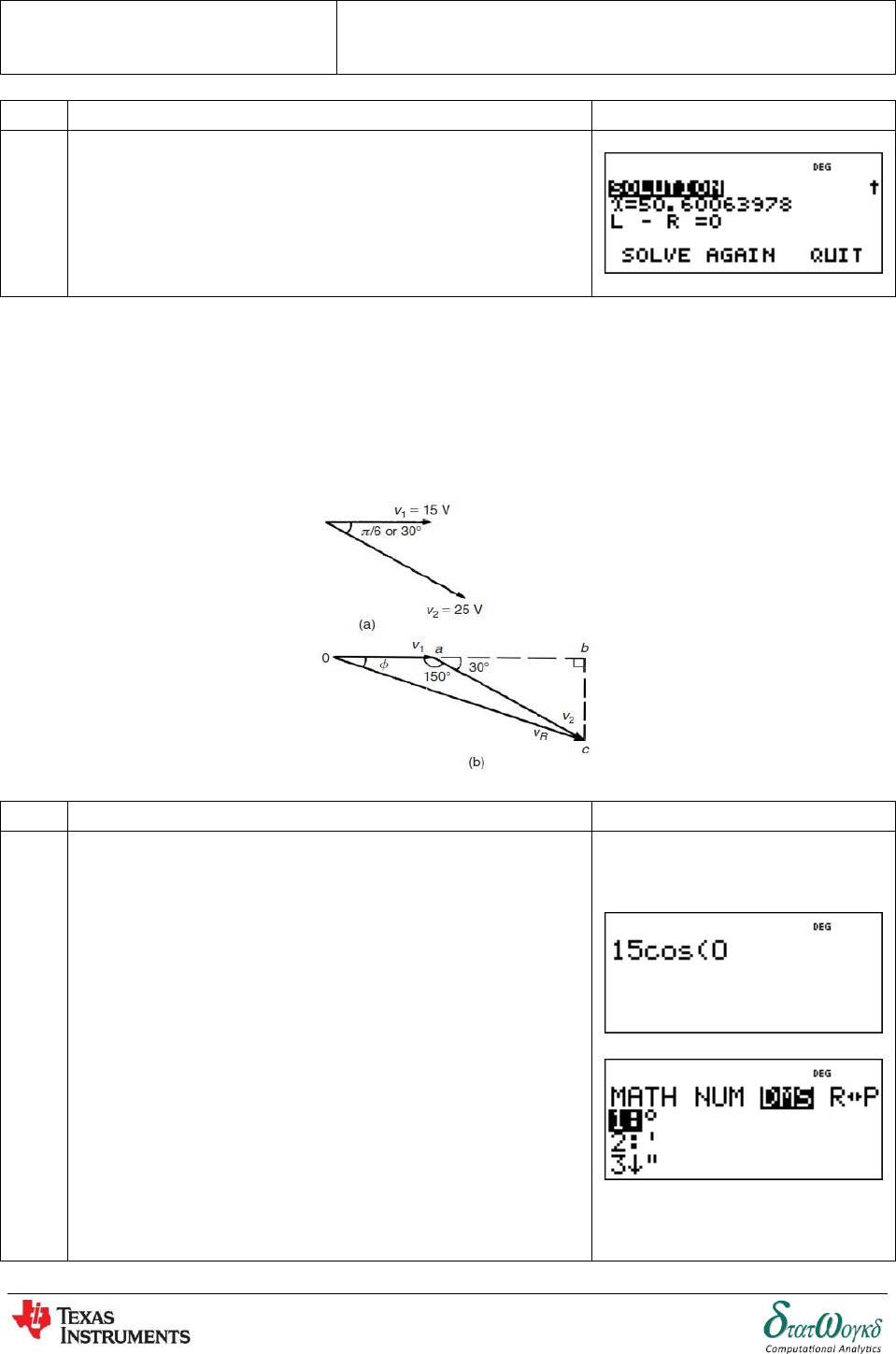
3. Two alternating voltages are given by volts and volts.
Determine a sinusoidal expression for the resultant by finding horizontal and vertical
components.
a) The relative positions of and at time
b) The phasor diagram
No
Keystrokes
Screenshots
1
Firstly, for the horizontal component of ,
Press ,
Then press
Then continue press
.

Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 91 of 148
Change to the decimal, press .
2
For the vertical component of ,
Press
Then press
Then continue press
.
Change to the decimal, press

Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 92 of 148
No
Keystrokes
Screenshots
3
Press
Hence volts
4
Press
5
Press ,
Change to Radians mode. Press
Recall or select the last equation. Press
Hence
Topic:
Adding of Waveforms
Math Concepts:
Determining Resultant Phasors by Calculation
Page 93 of 148
Exercise:
1. Find the missing side in the diagram below: (Use Sine Rule)
2. Find the missing angle in the diagram below: (Use Cosine Rule)
3. Work out the value of for each of the diagram below. The diagrams are not to scale.
Try and use the most efficient method you can and give your answer to 3 significant figures.
a) b)
4. Express the combination of periodic functions
in the form
.
5. Express the combination of periodic functions
in the
form .
Answer:
1. (accurate to 3 significant figures)
2. (accurate to 3 significant figures)
3. (a) (b)
4.
5.
Topic:
Areas of plane figures
Math Concepts:
area, width, height, square, rectangle, parallelogram, triangle,
trapezium
Page 94 of 148
Areas of Plane Figures
Overview / Introduction / Terminology:
Area is the measurement of the amount of space occupied by a closed flat surface and is measured
in square units. Every unit of length has a corresponding unit of area, namely the area of a square with
the given side length. Thus areas can be measured in square meters (), square centimeters (),
square millimeters (), square kilometers (), square feet (), square yards (), square
miles ( ), and so forth. Algebraically, these units can be thought of as the squares of the
corresponding length units. The SI unit of area is the square meter, which is considered an SI derived
unit.
A plane is a flat or level surface in two dimensions. Figures such as circles or squares have all of their
parts lying on a plane and thus, are examples of plane figures.
Triangle
Square
Rectangle
Parallelogram
Trapezium
Circle
Ellipse
Sector
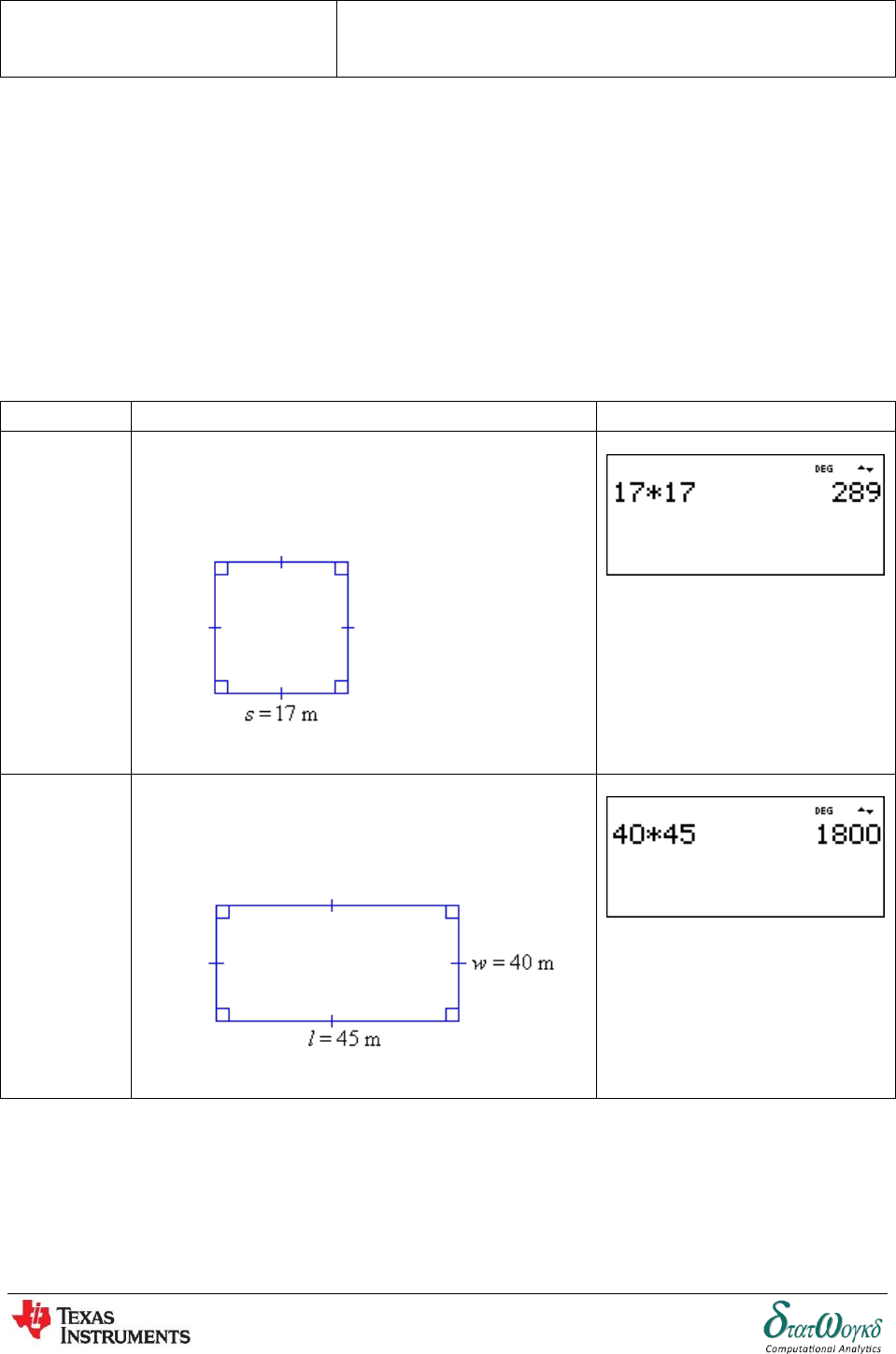
Topic:
Areas of plane figures
Math Concepts:
area, width, height, square, rectangle, parallelogram, triangle,
trapezium
Page 95 of 148
Keystrokes: Numbers and basic operational keys
Example:
1. Find the area of:
a. A square flower-bed of side
b. A rectangular field 45 m long and wide
c. A triangle of base length and height
No
Instructions / Keystrokes
Screenshots
1
Key in:
2
Key in:
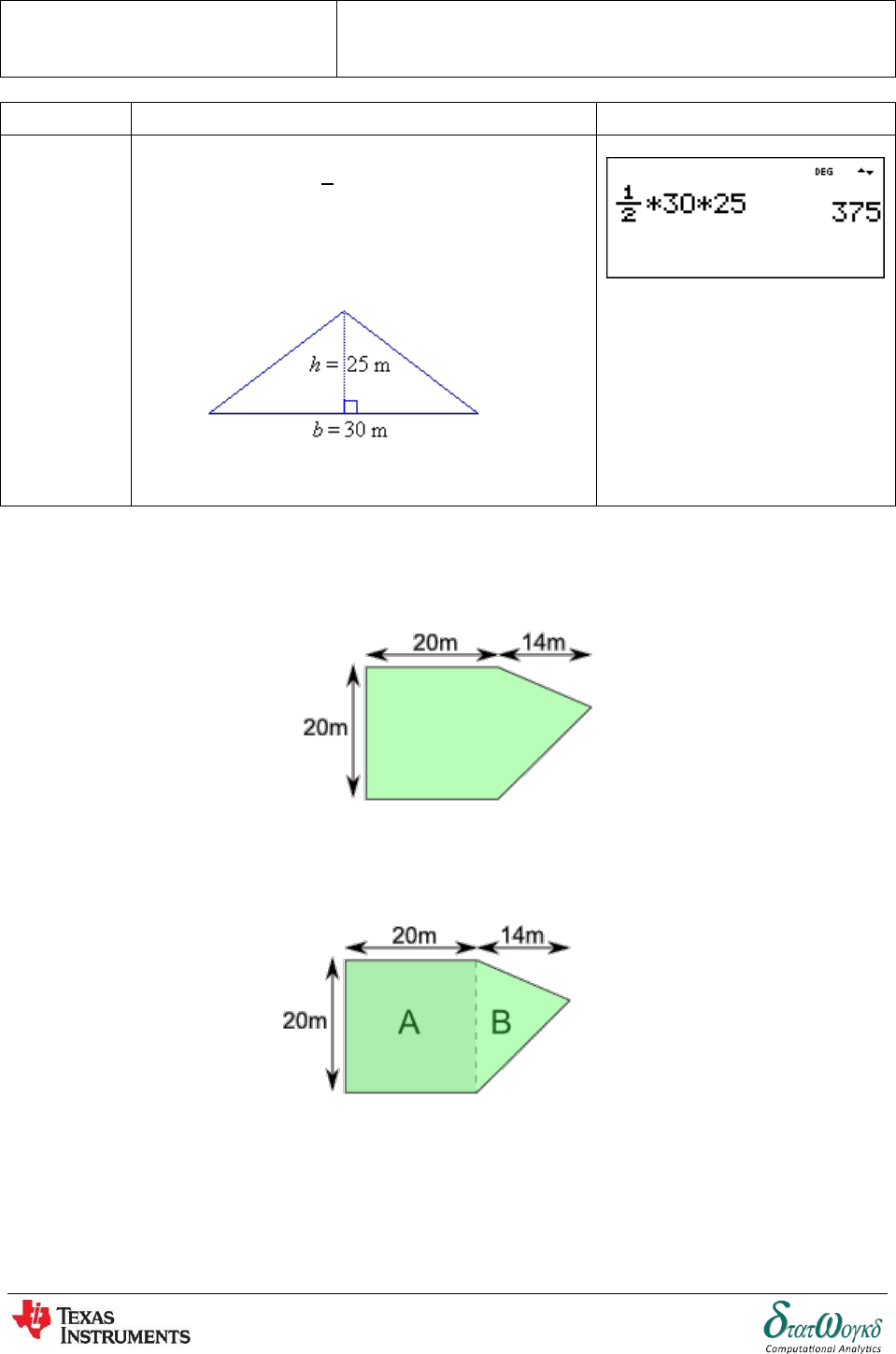
Topic:
Areas of plane figures
Math Concepts:
area, width, height, square, rectangle, parallelogram, triangle,
trapezium
Page 96 of 148
No
Instructions / Keystrokes
Screenshots
3
Key in:
2. Sam cuts grass at RM0.10 per square meter. How much does Sam earn cutting this area:

Topic:
Areas of plane figures
Math Concepts:
area, width, height, square, rectangle, parallelogram, triangle,
trapezium
Page 97 of 148
No
Instructions / Keystrokes
Screenshots
1
Part A is a square
Area of A = =
2
Part B is a triangle. Viewed sideways it has a base of
and a height of
Area of B =
3
So total area is:
To calculate the total area:
Copy answer Area A by pressing
Enter plus sign, and copy answer Area B by
pressing
Press to get the total area
4
Sam earns RM per square meter
For , Sam earns =

Topic:
Areas of plane figures
Math Concepts:
area, width, height, square, rectangle, parallelogram, triangle,
trapezium
Page 98 of 148
3. The area of a trapezium is and the bases are and . Find
the .
No
Instructions / Keystrokes
Screenshots
1
Area of trapezium =
To solve this problem we can use numeric equation solver
(num-solv) function. Press
2
Key-in the equation by pressing:
( )
( )
( )
( )
3
Insert known value for and and press . Leave
blank for value t.

Topic:
Areas of plane figures
Math Concepts:
area, width, height, square, rectangle, parallelogram, triangle,
trapezium
Page 99 of 148
No
Instructions / Keystrokes
Screenshots
1
Press to go to next page. Bring your cursor to variable
by pressing right arrow.
2
Press get the answer.
Thus, the height of trapezium is .
Exercises:
1. The height of a parallelogram is more units than the base. What is the area of the
parallelogram if the base is ?
2. Find the area of a trapezium with bases of and , and a height of .
3. The area of a trapezoid is 52 square inches and the bases are 11 inches and 15 inches. Find the
height.
4. A triangular-shaped piece of paper has an area of 36 square centimeters and a base of .
Find the height.
5. The perimeter of a square-shaped rug is . Find the area.
Answers:
1.
2.
3.
4.
5.
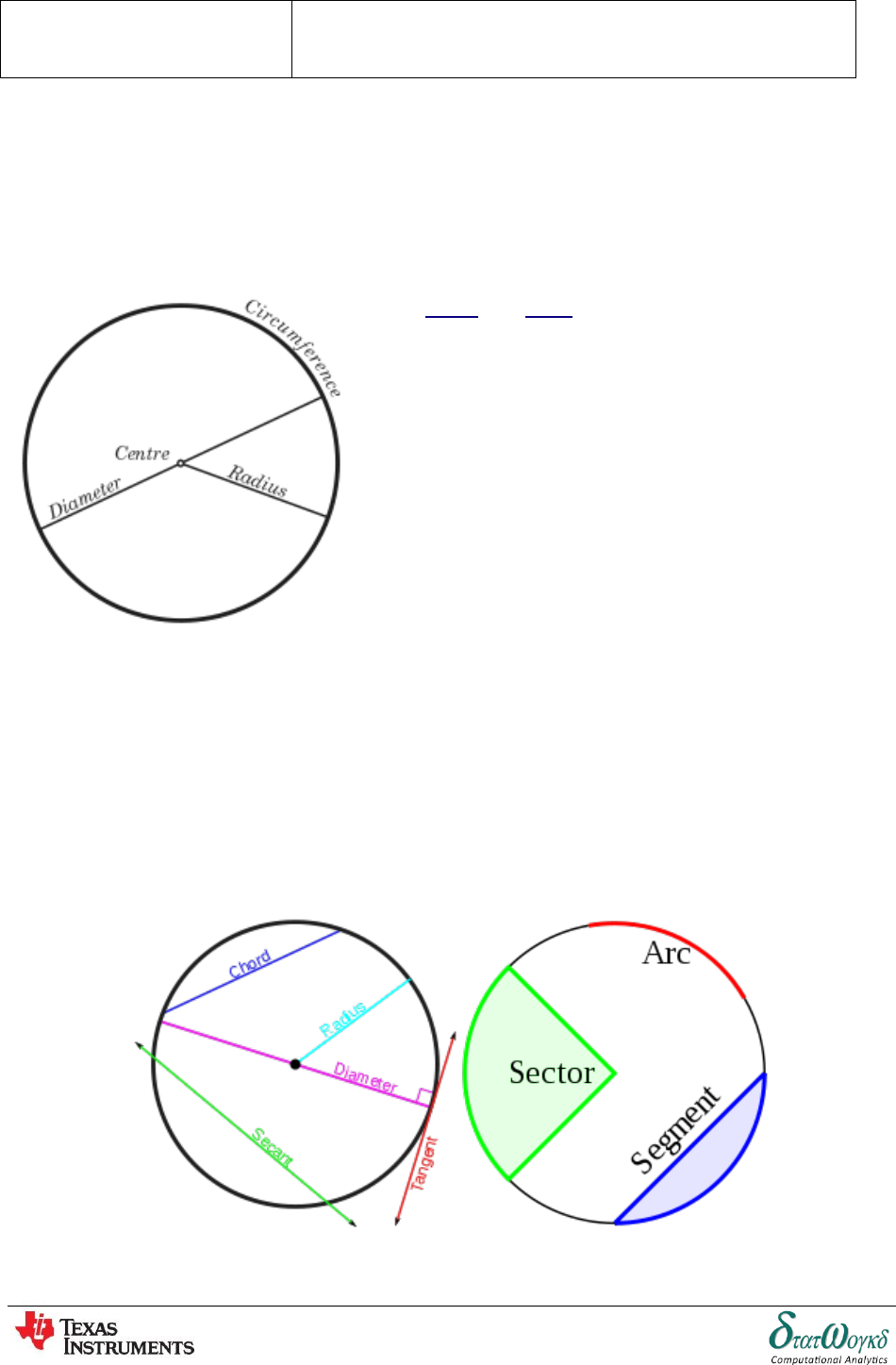
Topic:
The circle
Math Concepts:
circle, radius, circumference, diameter, semicircle, quadrant,
tangent, sector, chord, segment, arc, angle, equation of a circle
Page 100 of 148
The Circle
Overview / Introduction / Terminology:
A circle is a simple shape of Euclidean geometry consisting of
those points in a plane that are equidistant from a given
point, the centre. The distance between any of the points
and the centre is called the radius.
A circle's diameter is the length of a line segment
whose endpoints lie on the circle and which passes through
the centre. This is the largest distance between any two
points on the circle. The diameter of a circle is twice
the radius, or distance from the centre to the circle's
boundary. The term "diameter" and "radius" also refer to the
line segment which fit these descriptions.
The circumference is the distance around the outside of a
circle.
A chord is a line segment whose endpoints lie on the circle. A diameter is the longest chord in a circle.
A tangent to a circle is a straight line that touches the circle at a single point, while a secant is an
extended chord: a straight line cutting the circle at two points.
An arc of a circle is any connected part of the circle's circumference. A sector is a region bounded by two
radii and an arc lying between the radii, and a segment is a region bounded by a chord and an arc lying
between the chord's endpoints.
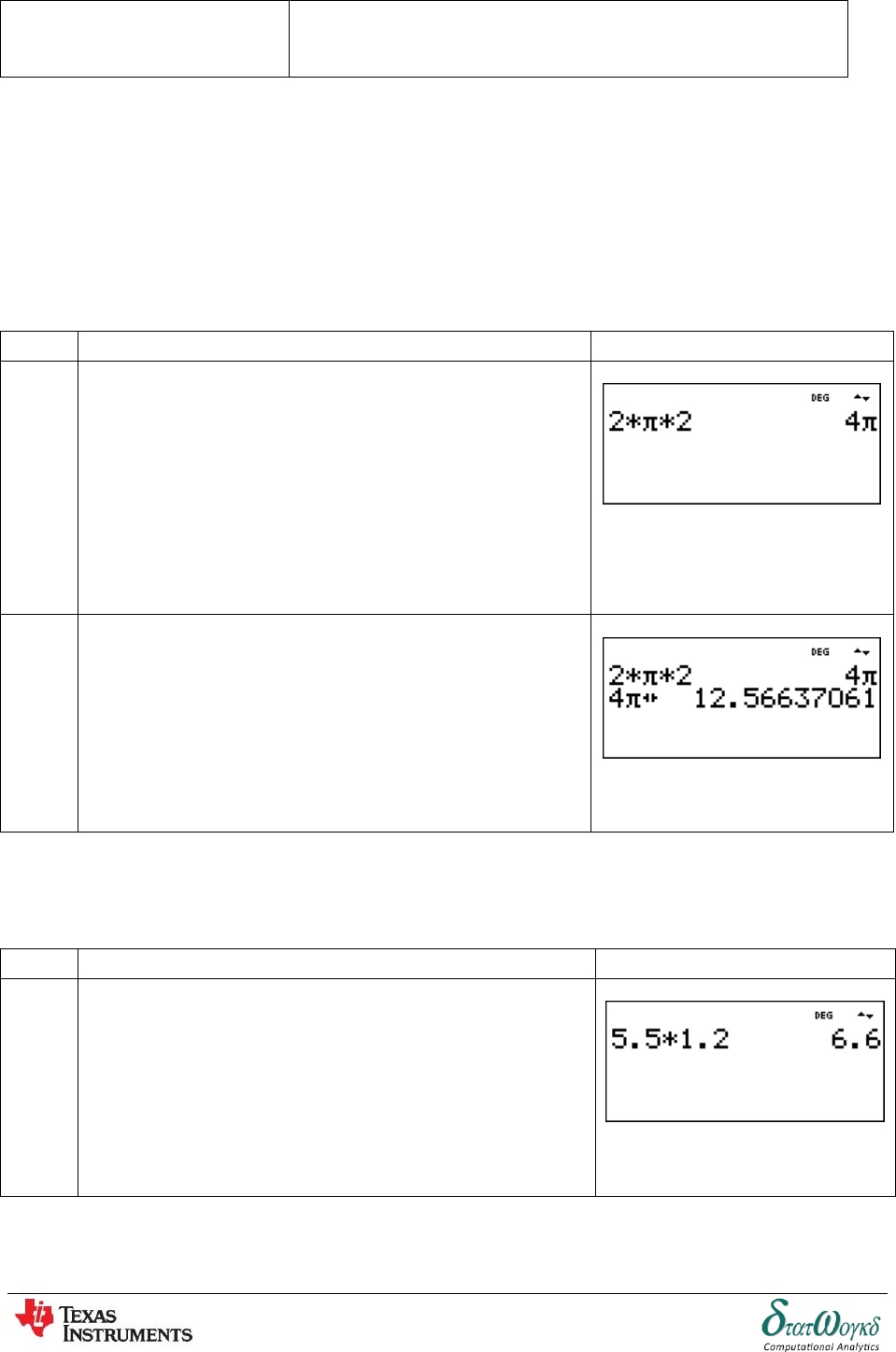
Topic:
The circle
Math Concepts:
circle, radius, circumference, diameter, semicircle, quadrant,
tangent, sector, chord, segment, arc, angle, equation of a circle
Page 101 of 148
Keystrokes:
Numbers and basic operational keys
Example:
1. If a circle has a diameter of , find the circumference of a circle.
No
Instructions / Keystrokes
Screenshots
1
Formula of circumference,
We already know that , so . Substitute the
value in the formula.
Key-in
2
To get the answer in decimal mode, press
Thus, the answer is
2. Find the length of arc of a circle of radius 5.5 cm when the angle subtended at the centre is1.20
radians.
No
Instructions / Keystrokes
Screenshots
1
Formula length of arc, , where is in radians
Press
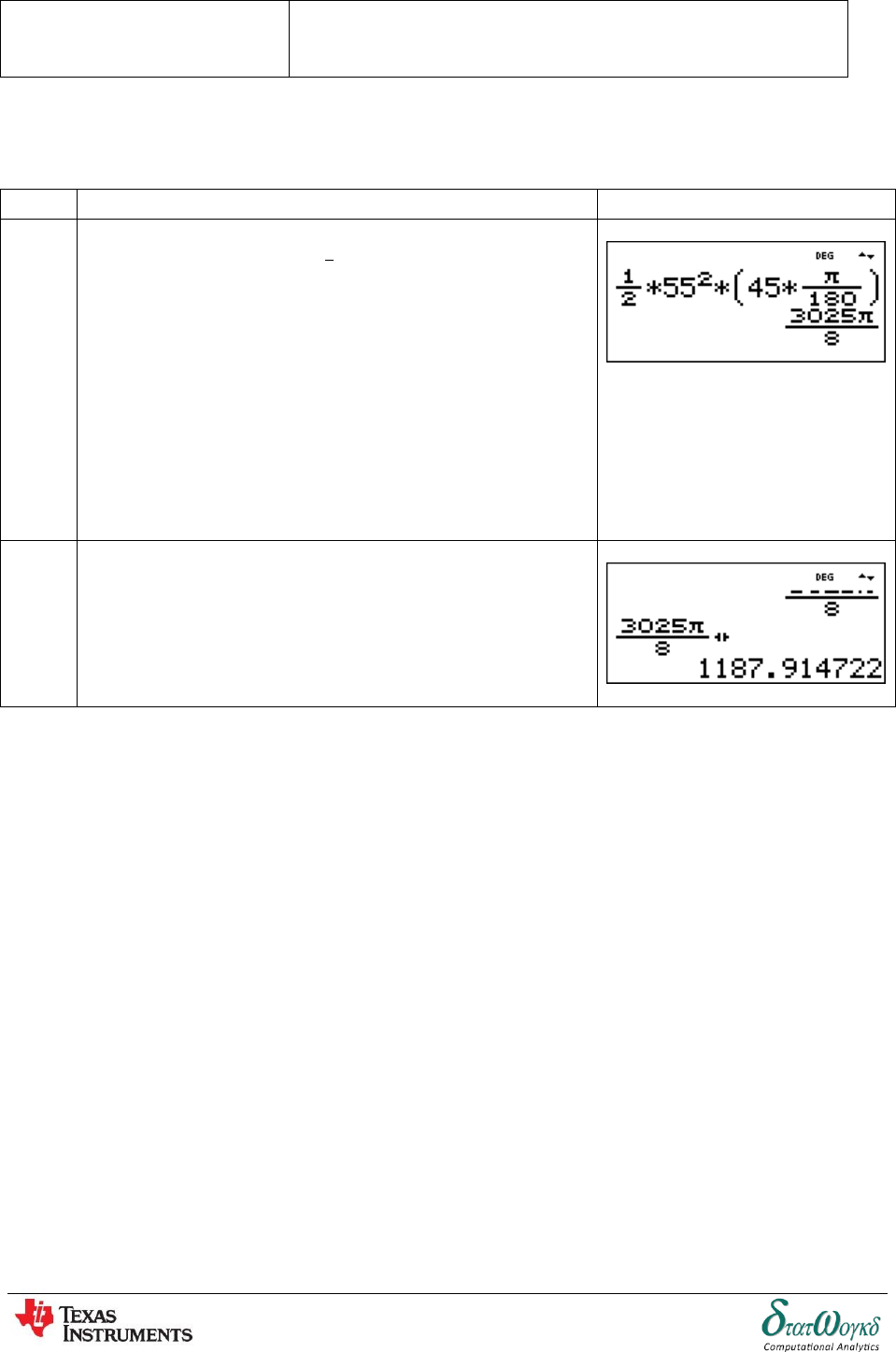
Topic:
The circle
Math Concepts:
circle, radius, circumference, diameter, semicircle, quadrant,
tangent, sector, chord, segment, arc, angle, equation of a circle
Page 102 of 148
3. A football stadium floodlight can spread its illumination over an angle of 45 to a distance of
. Determine the maximum area that is floodlit.
No
Instructions / Keystrokes
Screenshots
1
Formula for area of sector =
Press:
2
Press to get the answer in decimal mode.
Thus, the answer is
Exercises:
1. If the diameter of a circle is , find its circumference.
2. Determine the radius of a circle if its perimeter is .
3. Find the circumference of a circle of radius .
4. Determine the diameter and circumference of a circle if an arc of length subtends an
angle of .
5. An automatic garden sprays produces a spray to a distance of and revolves through an angle
α which may be varied. If the desired spray catchment area is to be , to what should angle
α be set, correct to the nearest degree.
Answers:
1.
2.
3.
4.
5.
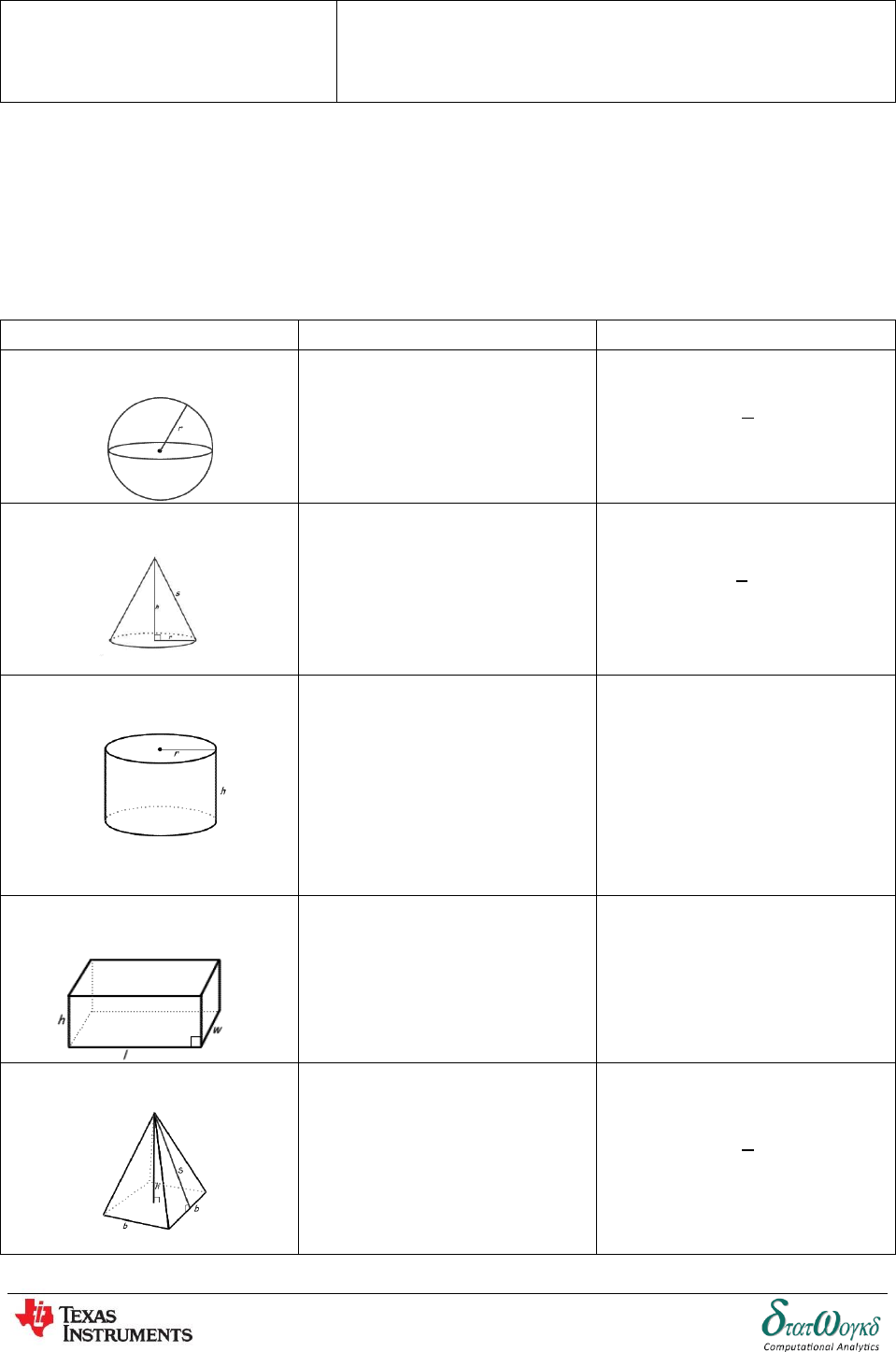
Topic:
Volumes of common solids
Math Concepts:
Solid figures, area, volume, height, base, sphere, cone, cylinder,
cuboid, pyramid
Page 103 of 148
Volumes of common solids
Overview / Introduction / Terminology:
The volume is a measure of the amount of space inside the figure. Different figures lead to different
computation. Common figures where the volume is calculated are shown below
Regular Solids
Surface Area
Volume
Sphere
Cone
Area of the cone is
Area of the base is
Therefore the formula is
Cylinder
Area of the top is
Area of the base is
Area of the side is
Therefore the formula is
Rectangular Prism (Cuboid)
Square Based Pyramid

Topic:
Volumes of common solids
Math Concepts:
Solid figures, area, volume, height, base, sphere, cone, cylinder,
cuboid, pyramid
Page 104 of 148
Keystrokes:
Numbers and basic operational keys
Example:
1. What is the surface area of a cylinder with a height of 8 m and a base with a radius of ?
(Leave your answer in terms of .)
No
Instructions / Keystrokes
Screenshots
1
Substitute the values into formula. Key-in
Press to get the answer.
2. What is the surface area of a sphere with a radius of ? Leave your answer in terms of .
No
Instructions / Keystrokes
Screenshots
1
Substitute the values into formula. Key-in
Press to get the answer.
3. What is the surface area of a rectangular prism with a length of , a height of , and a
width of ?
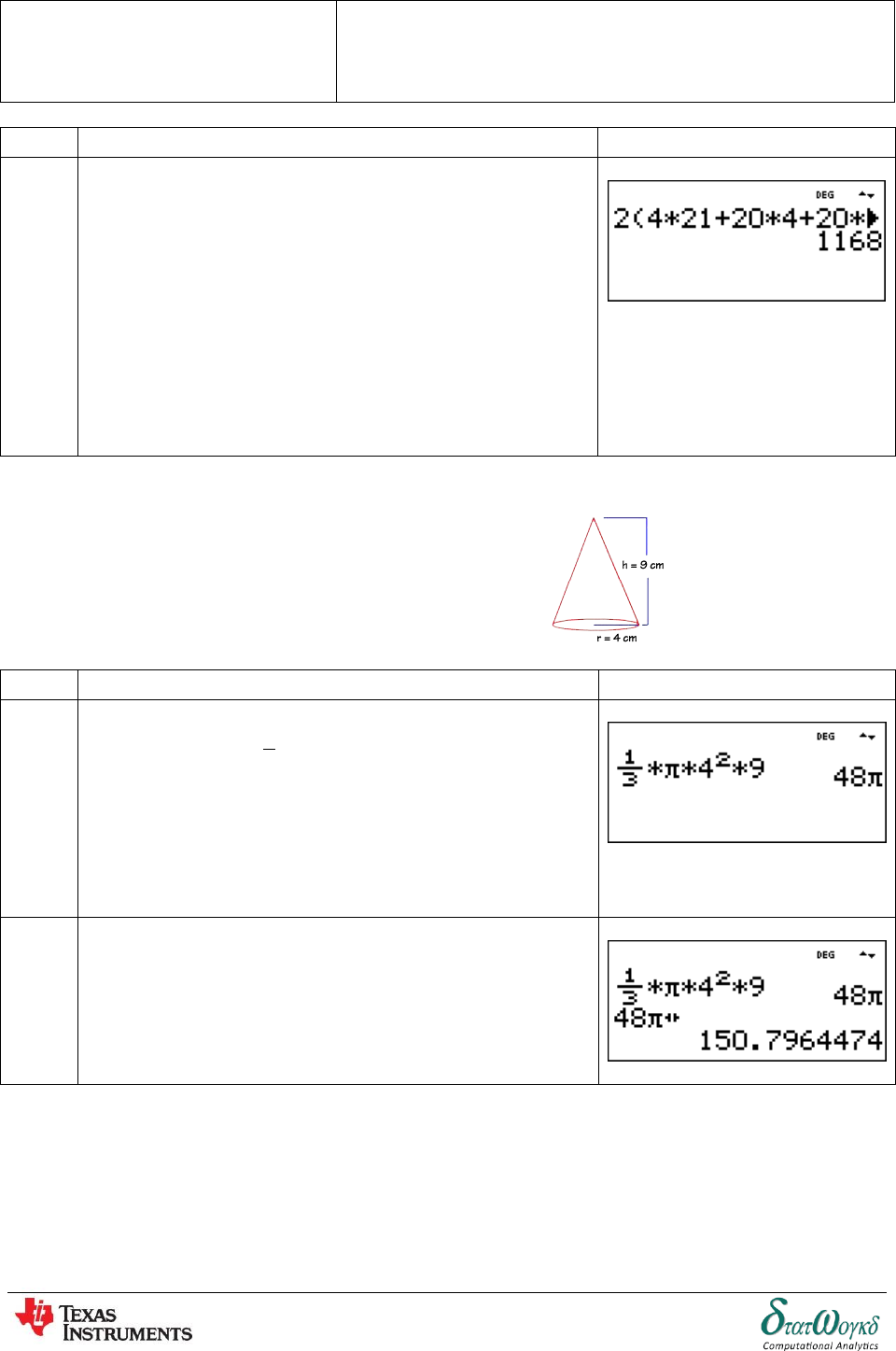
Topic:
Volumes of common solids
Math Concepts:
Solid figures, area, volume, height, base, sphere, cone, cylinder,
cuboid, pyramid
Page 105 of 148
No
Instructions / Keystrokes
Screenshots
1
Substitute the values into formula. Key-in
Press to get the answer.
Thus the answer is
4.
We can substitute the values into the volume formula.
No
Instructions / Keystrokes
Screenshots
1
Substitute the values into the volume formula. Key-in
2
Press to get the answer in decimal mode.
When we perform the calculations, we find that the volume
is .
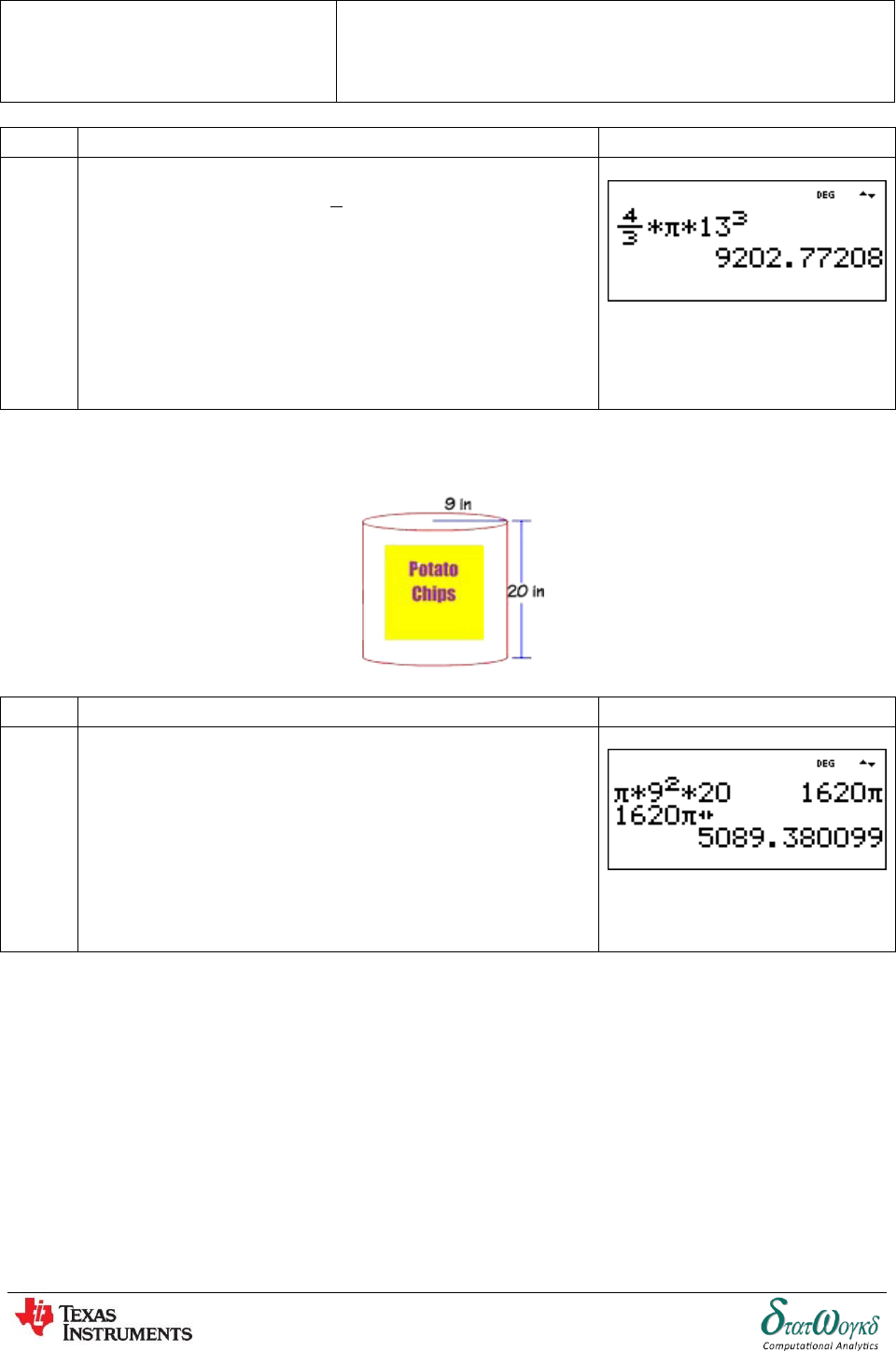
Topic:
Volumes of common solids
Math Concepts:
Solid figures, area, volume, height, base, sphere, cone, cylinder,
cuboid, pyramid
Page 106 of 148
No
Instructions / Keystrokes
Screenshots
1
Substitute the values into the volume formula. Key-
in
Thus, the answer is .
5. Find the volume of this can of potato chips.
No
Instructions / Keystrokes
Screenshots
1
To find the volume of cylinder, here is the formula:
Substitute the values into the formula. Key-in
Press to get the answer in decimal mode.
Exercises:
1. What is the surface area of a cylinder with a height of and a base radius of ? (Leave your
answer in terms of.).=
2. What is the surface area of a cylinder with a base area of . and a height of .? (Leave
your answer in terms of .)==
3. What is the surface area of a sphere with a radius of

Topic:
Volumes of common solids
Math Concepts:
Solid figures, area, volume, height, base, sphere, cone, cylinder,
cuboid, pyramid
Page 107 of 148
4. What is the measure of the radius of a sphere with a total surface area of ?
5. What is the volume of a pyramid with a square base with sides of , and a height of ?
6. Find the volume of a sphere with a diameter of 5 in. us for and round your answer to the
nearest inch.
7. Find the volume of a rectangular prism that has a base measuring 6 in by 4 in and a height of 8 in.
Answers:
1.
2.
3. The radius is
4.
5.
6.

Topic:
Integration
Math Concepts:
Integration
Page 108 of 148
Integration
Overview / Introduction / Terminology:
The process of integration reverses the process of differentiation. In differentiation, if
then. Thus the integral of 4x is 2x2, i.e. integration is the process of moving from ) to
. B similar reasoning, the integral of is .
The general solution of integrals of the form where a and n are constants is given by:
Definite integrals are those in which limits are applied. If an expression is written as b
a
change a function into a form which can be integrated by using either:
a) an algebraic substitution
b) trigonometric substitutions
c) integration by parts
Keystrokes:

Topic:
Integration
Math Concepts:
Integration
Page 109 of 148
Example:
1. Evaluate
No
Instructions / Keystrokes
Screenshots
1
Press
Thus,
2. Find x when
No
Instructions / Keystrokes
Screenshots
1
At the left hand side,
Press
2
At the right hand side,
Press
3
Press
4
Thus,

Topic:
Integration
Math Concepts:
Integration
Page 110 of 148
3. The average value of a complex voltage waveform is given by the following. Evaluate V correct to 2
decimal places
No
Instructions / Keystrokes
Screenshots
1
Change Angle to Degree
2
Change Float to 2 decimal places
3
Press
4. Evaluate the following
No
Instructions / Keystrokes
Screenshots
1
Press

Topic:
Integration
Math Concepts:
Integration
Page 111 of 148
5. Evaluate the following
No
Instructions / Keystrokes
Screenshots
1
Press
Exercise:
1. Determine the area enclosed by , the x-axis and coordinates at and
2. Find x when the equation is given,
3. Evaluate the following definite integral, correct to 4 significant figures
Answer:
1.
2.
3.
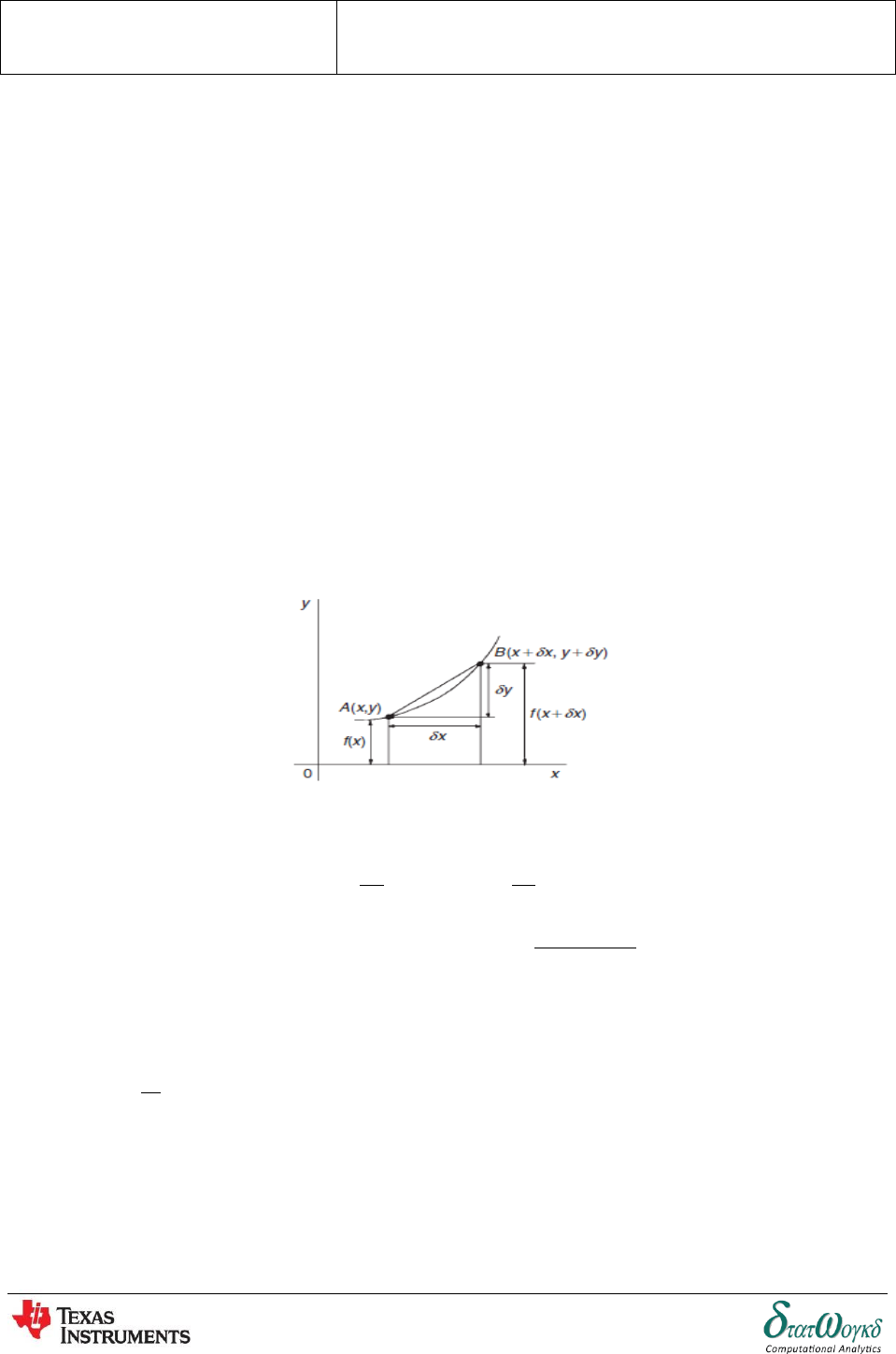
Topic:
Differentiation
Math Concepts:
Differentiation
Page 112 of 148
Differentiation
Overview / Introduction / Terminology:
Calculus is a branch of mathematics involving or leading to calculations dealing with continuously
varying functions. Calculus is a subject that falls into two parts:
a) differential calculus (or differentiation) and
b) integral calculus (or integration).
Differentiation is used in calculations involving velocity and acceleration, rates of change and maximum
and minimum values of curves.
A and B are two points very close together on a curve, δx (delta x) and δy (delta y) representing small
increments in the x and y directions, respectively.
Summarizing the differential coefficient:
=
From differentiation by first principles, a general rule for differentiating axn emerges where a and n are
any constants. This rule is:
, then
Keystrokes:

Topic:
Differentiation
Math Concepts:
Differentiation
Page 113 of 148
Example:
1. If find:
a.
b.
No
Instructions / Keystrokes
Screenshots
1
Press . Select option No 2: Edit Function Press
2
Key in
Press
3
Key in table setup:
Start: Press
Step: Press
Press
4
Press . Select option No 1: f(
Press
Press
Press

Topic:
Differentiation
Math Concepts:
Differentiation
Page 114 of 148
2. Find the differential coefficient of
when
No
Instructions / Keystrokes
Screenshots
1
Press
Thus,
3. Determine the derivative of the following and determine the gradient of the curve at
No
Instructions / Keystrokes
Screenshots
1
Press
4. Determine the rate of change of voltage given the following when
No
Instructions / Keystrokes
Screenshots
1
Press
Replace variable t as x
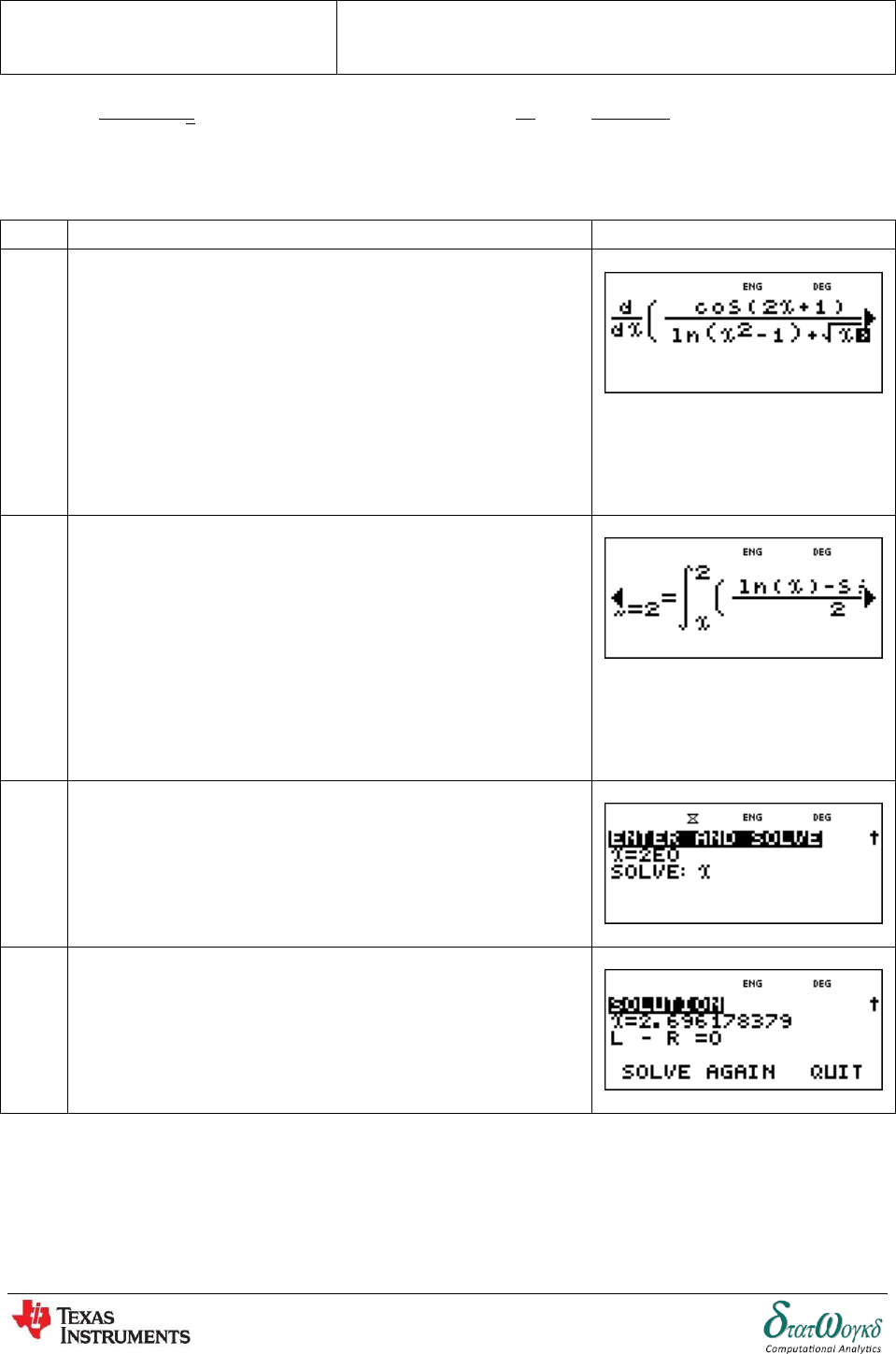
Topic:
Differentiation
Math Concepts:
Differentiation
Page 115 of 148
5. If
, find dy/dx and solve the equality for
No
Instructions / Keystrokes
Screenshots
1
At left hand side,
Press
2
At right hand side,
Press
3
Press
4
Thus,

Topic:
Differentiation
Math Concepts:
Differentiation
Page 116 of 148
Exercise:
1. Differentiate when , given
. Give the answer correct to 3 significant
figures.
2. Find the gradient of the curve at the points () and ()
3. An alternating current, i amperes, is given by , where is the frequency in hertz and
the time in seconds. Determine the rate of change of current when , given that
.
4. The distance x metres moved by a carin a time t seconds is given by: .
Determine the velocity and acceleration when
Answer:
1.
2.
3.
4.
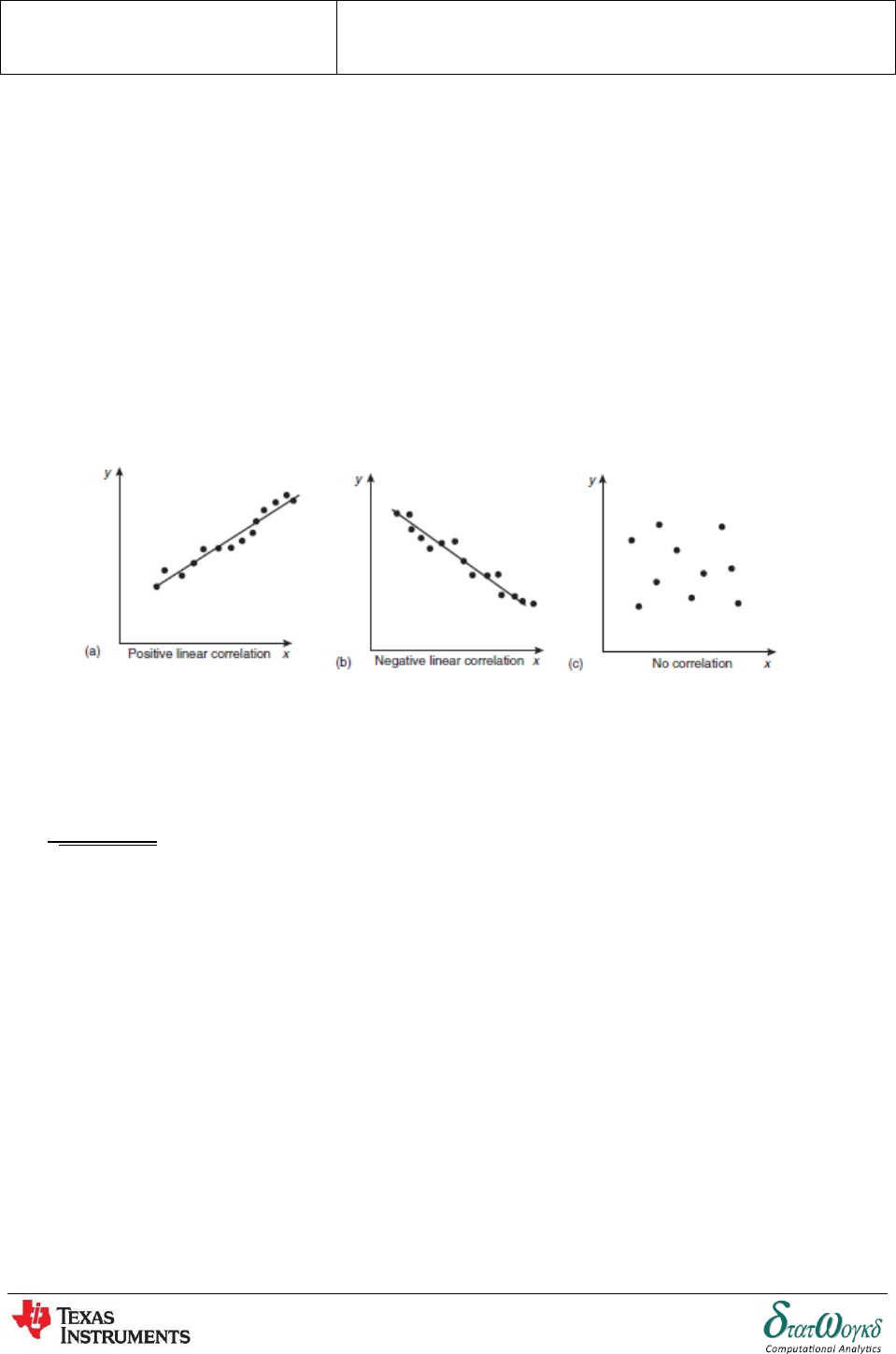
Topic:
Correlation and Regression
Math Concepts:
Correlation and Regression
Page 117 of 148
Correlation and Regression
Overview / Introduction / Terminology:
Correlation is a measure of the amount of association existing between two variables. For linear
correlation, if points are plotted on a graph and all the points lie on a straight line, then perfect linear
correlation is said to exist. When a straight line having a positive gradient can reasonably be drawn
through points on a graph positive or direct linear correlation exists, similarly, when a straight line
having a negative gradient can reasonably be drawn through points on a graph, negative or inverse
linear correlation exists
The amount of linear correlation between two variablesis expressed by a coefficient of correlation,
given the symbol r. This is defined in terms of the derivations of the co-ordinates of two variables from
their mean values and is given by the product-moment formula which states:
The results of this determination give values of r
Between these values, the smaller the value of r, the less is the amount of correlation which exists.
Generally, values of r in the ranges and 1 and show that a fair amount of correlation
exists.
Regression analysis, usually termed regression, is used -ordinates
on a graph. The techniques used enable a mathematical equation of the straight line form
to be deduced for a given set of co-ordinate values, the line being such that the sum of the deviations of
the co-ordinate values from the line is a minimum, i.e. it is the line

Topic:
Correlation and Regression
Math Concepts:
Correlation and Regression
Page 118 of 148
analysis is made, it is possible to obtain two lines of best fit, depending on which variable is selected as
the dependent variable and which variable is the independent variable.
The equation of the least-squares regression line is usually written as , where a0 is the Y-
axis intercept value and a1 is the gradient of the line (analogous to c and m in the equation y=mx +c).
The regression line of Y onX is used to estimate values of Y for given value
ofX. By using the regression line of X on Y, values of X corresponding to given values of Y may be found
byeither interpolation or extrapolation.
The equation of the regression line is of the form: X =b0 +b1Y and the normal equations become:
The regression line of X on Y is used to estimated values of X for given values of Y. The regression line of
Y on X is used to determine any value of Y corresponding to a given value of X. If the value of Y lies
within the range of Y-values of the extreme co-ordinates, the process of finding the corresponding value
of X is called linear interpolation. If it lies outside of the range of Y-values of the extreme co-ordinates
than the process is called linear extrapolation and the assumption must be made that the line of best fit
extends.
Keystrokes:

Topic:
Correlation and Regression
Math Concepts:
Correlation and Regression
Page 119 of 148
Example:
1. In an experiment to determine the relationship between force on a wire and the resulting extension,
the following data is obtained:
Determine the linear coefficient of correlation for this data.
No
Instructions / Keystrokes
Screenshots
1
Press .Key in the data in list L1and L2
2
Select Press
Select option No 3: 2-Var Stats by using Press
3
Select default option :
xData: L1
yData: L2
Frq: One
4
Use to move to CALC
Press .
Scroll using to access the r statistics which shows the
linear correlation

Topic:
Correlation and Regression
Math Concepts:
Correlation and Regression
Page 120 of 148
2. Find the coefficient of correlation between the values X and Y
No
Instructions / Keystrokes
Screenshots
1
Press twice to clear list L1 by selecting the option
to clear L1.
Press Press again and scroll using to select list
L2 to clear. Press
Key in the new data in list L1and L2
2
Select Press
Select option No 3: 2-Var Stats by using
Press
3
Select default option :
xData: L1, yData: L2
Frq: One
4
Use to move to CALC
Press .
Scroll using to access the r statistics which shows the
linear correlation

Topic:
Correlation and Regression
Math Concepts:
Correlation and Regression
Page 121 of 148
3. In an experiment to determine the relationship between frequency and the inductive reactance of
an electrical circuit, the following results were obtained: Determine the equation of the regression
line of inductive reactance on frequency, assuming a linear relationship.
No
Instructions / Keystrokes
Screenshots
1
Press twice to clear list L1 by selecting the option
to clear L1. Press Press again and scroll using to
select list L2 to clear. Press
Key in the new data in list L1and L2
2
Select Press
Select option No 4: LinReg by using
Press
3
Select default option :
xData: L1
yData: L2
Frq: One
RegEQ :Use to move to Yes. Press
4
Use to move to CALC
Press .
Scroll using to access the regression equation
coefficients and r statistics
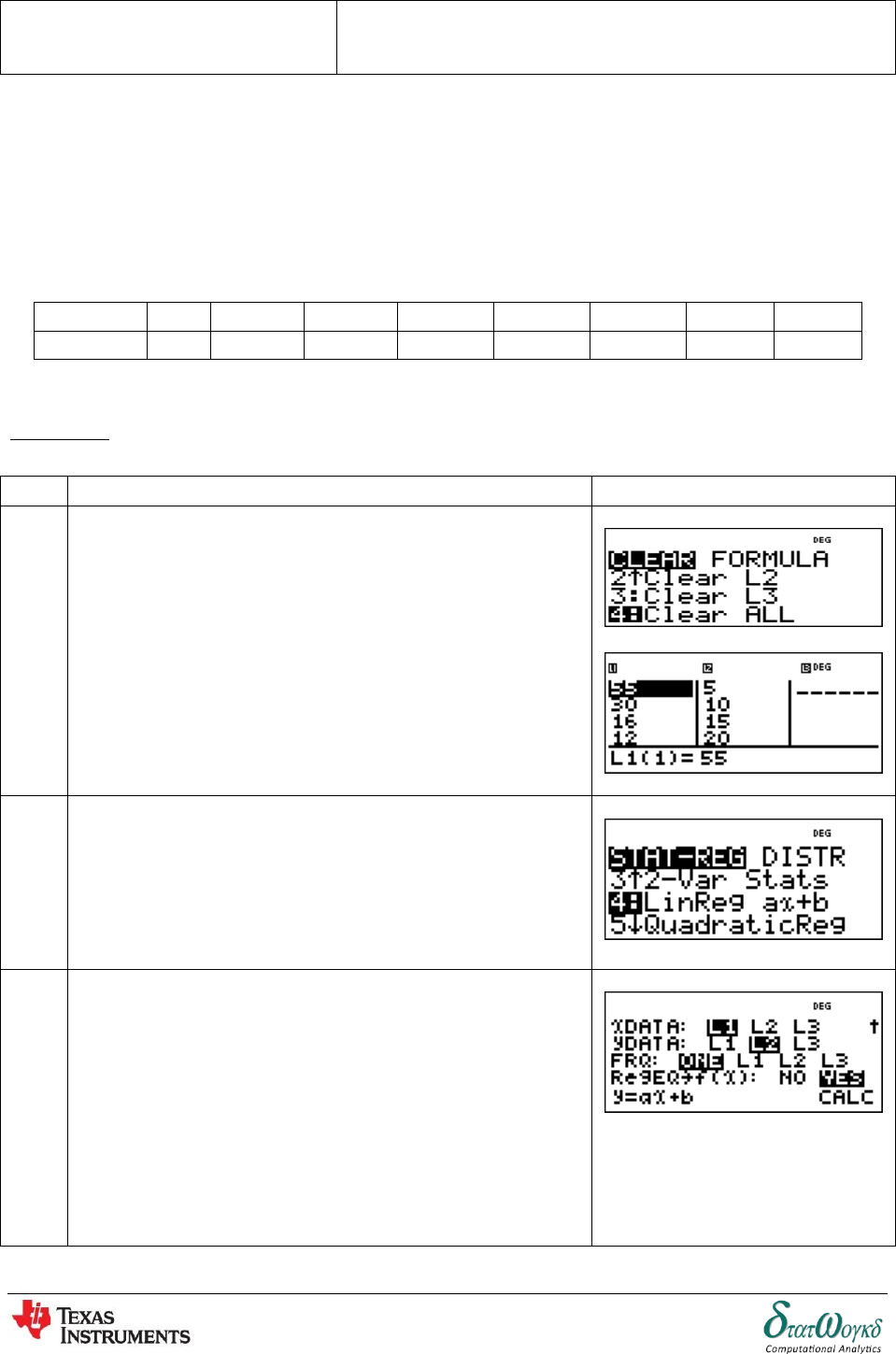
Topic:
Correlation and Regression
Math Concepts:
Correlation and Regression
Page 122 of 148
4. The experimental values relating centripetal force and radius, for a mass travelling at constant
velocity in a circle, are as shown: Determine the equations of
a) the regression line of force on radius and
b) calculate the force at a radius of
c) the regression line of radius on force.
d) calculate the radius corresponding to a force of
Solve 4a& b
No
Instructions / Keystrokes
Screenshots
1
Press twice to clear all lists by selecting the option
to clear All. Press
Key in the new data in list L1and L2
2
Select Press
Select option No 4: LinReg by using
Press
3
Select default option :
xData: L1, yData: L2
Frq: One
RegEQ : Use to move to Yes
Press

Topic:
Correlation and Regression
Math Concepts:
Correlation and Regression
Page 123 of 148
No
Instructions / Keystrokes
Screenshots
4
Use to move to CALCPress .
Scroll using to access the regression equation
coefficients and r statistics
5
Select Press
Select option No 1: StatsVar
Press
6
Scroll using to access the function variable force when
Press
7
Key in 40 and Press)
Press .
Solve 4c& d
No
Instructions / Keystrokes
Screenshots
1
Press twice to clear all lists by selecting the option
to clear All. Press
Key in the new data in list L1and L2
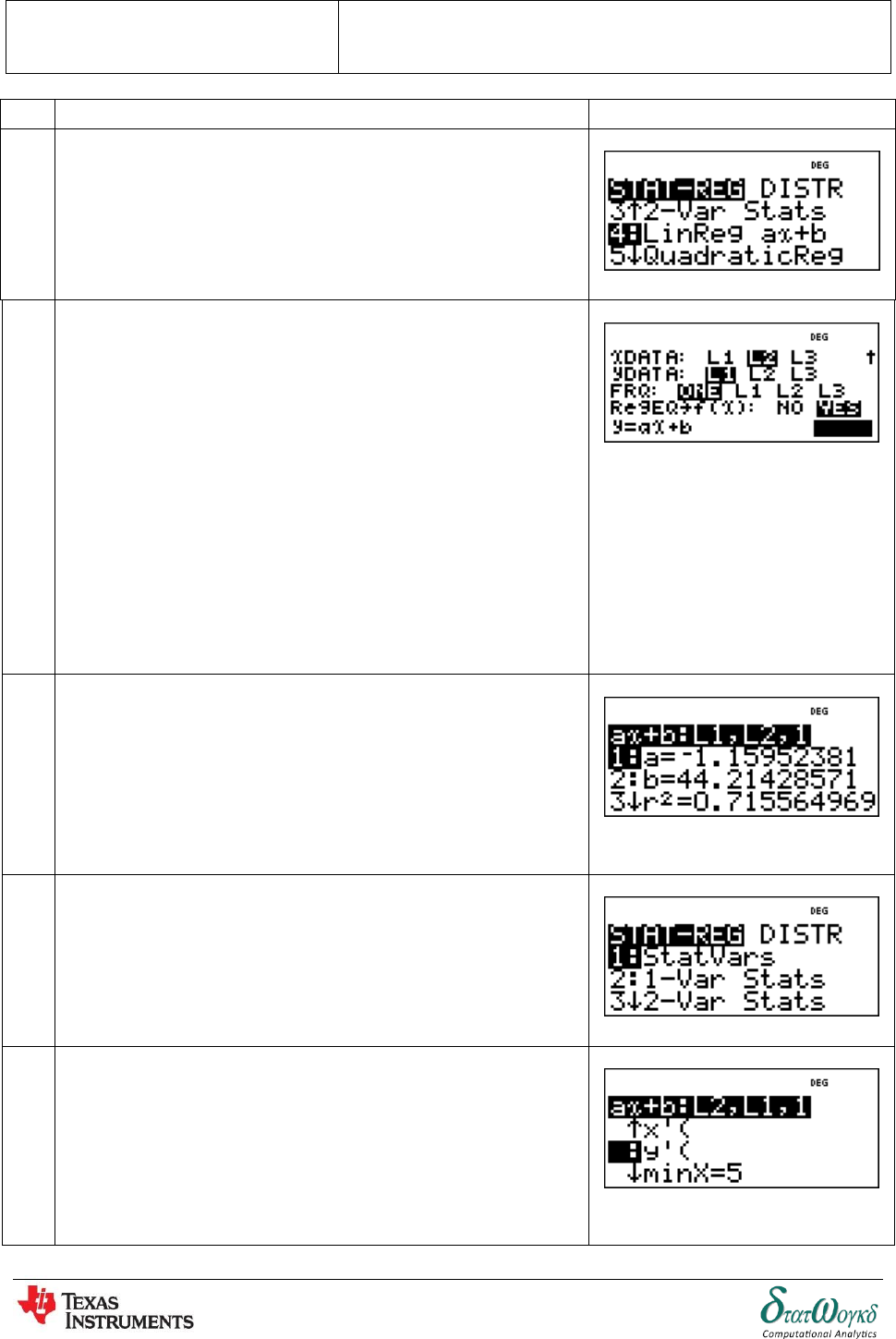
Topic:
Correlation and Regression
Math Concepts:
Correlation and Regression
Page 124 of 148
No
Instructions / Keystrokes
Screenshots
2
Select Press
Select option No 4: LinReg by using
Press
3
Select default option :
xData: L2
yData: L1
Frq: One
RegEQ : Use to move to Yes
Press
4
Use to move to CALC
Press .
Scroll using to access the regression equation coefficients
and r statistics
5
Select Press
Select option No 1: StatsVar
Press
6
Scroll using to access the function variable radius when
Press
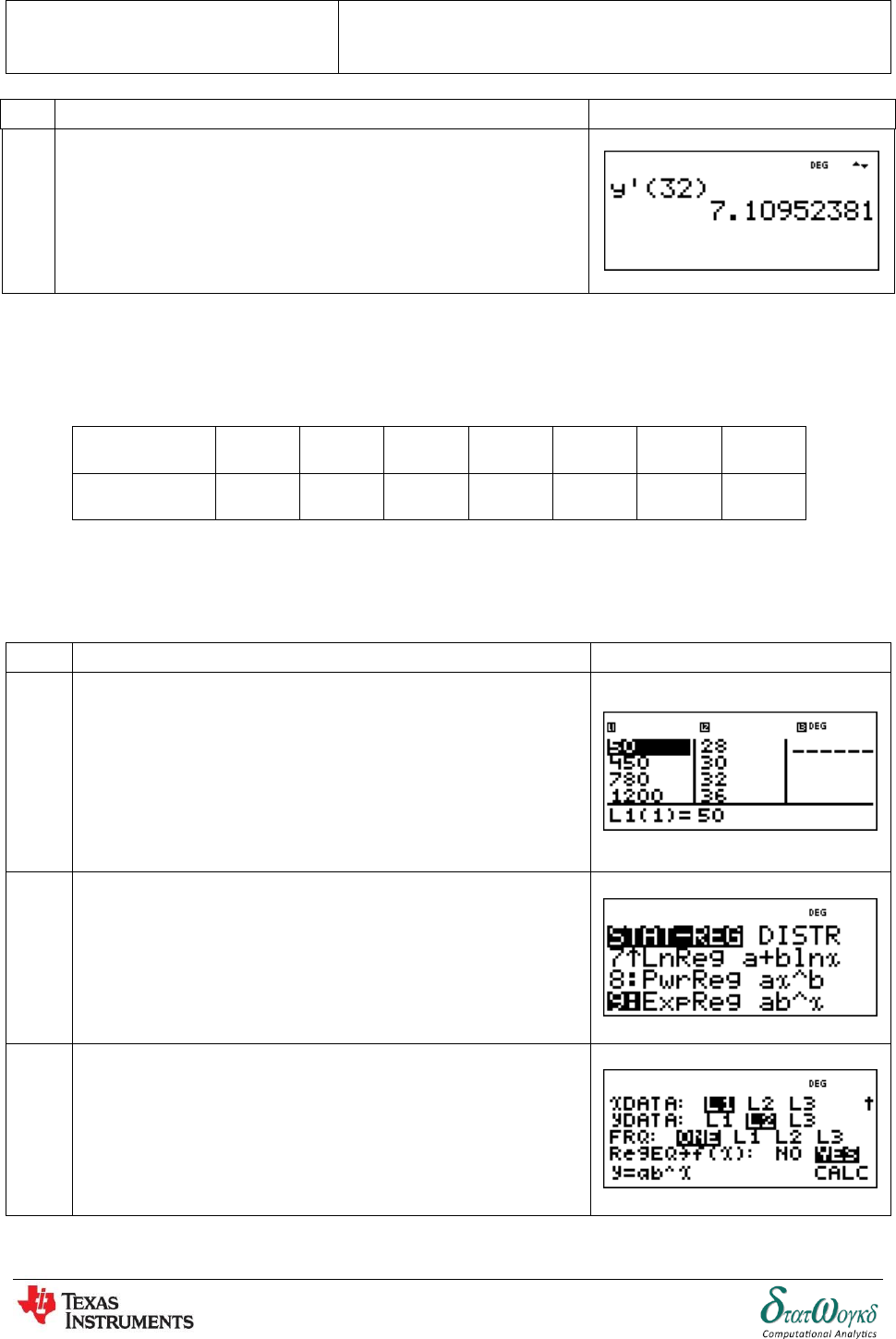
Topic:
Correlation and Regression
Math Concepts:
Correlation and Regression
Page 125 of 148
No
Instructions / Keystrokes
Screenshots
7
Key in 32 and Press)
Press .
5. Predict the mean radiation dose at an altitude of by fitting an exponential curve to the given
data
Let be the exponential curve. Then
No
Instructions / Keystrokes
Screenshots
1
Press twice to clear all lists. Scroll using to
select all Lists to clear. Press
Key in the new data in list L1and L2
2
Select Press
Select option No 9: ExpReg by using
Press
3
Select default option :
xData: L1
yData: L2

Topic:
Correlation and Regression
Math Concepts:
Correlation and Regression
Page 126 of 148
Frq: One
RegEQ :Use to move to Yes. Press
4
Use to move to CALC
Press .
Scroll using to access the regression equation
coefficients and r statistics
5
To get the the value of the radiation dose at an altitude of
.
Press to access the exponential function. Scroll to
select Edit Function. Press
Press
6
Key in 3000 at Start.
Use to move to CALC
Press .
7
Therefore at an altitude of , the radiation dose is at

Topic:
Correlation and Regression
Math Concepts:
Correlation and Regression
Page 127 of 148
Exercise:
1. In an experiment to determine the relationship between the current flowing in an electrical circuit
and the applied voltage, the results obtained are:
Find the coefficient of correlation for these results.
2. The data shown below refers to the number of times machine tools had to be taken out of service,
in equal time periods, due to faults occurring and the number of hours worked by maintenance
teams.
Calculate the coefficientof correlation for this data.
3. Calculate the coeffiecient of the regression equation
Answer:
1. Correlation
2. Correlation
3. Regression :
Topic:
Measures of Central Tendency and
Dispersion
Math Concepts:
Measures of Central Tendency and Dispersion
Page 128 of 148
Measures of Central Tendency and Dispersion
Overview / Introduction / Terminology:
Statistics is the area of science that deals with collection, organization, analysis, and interpretation of
data. It also deals with methods and techniques that can be used to draw conclusions about the
characteristics of a large number of data points--commonly called a population. If the data set is based
on a sample of a larger population, then the analyst can extend inferences onto the population based on
the statistical results from the sample. Some statistical measures include regression analysis, mean,
kurtosis, skewness, analysis of variance and variance.
Data are obtained largely by two methods:
by countingfor example, the number of engines sold in equal periods of time, and
by measurement for example, the heights of a group of people.
A quantitative variable has a value or numerical measurement for which operations such as addition or
averaging make sense. A qualitative variable describes and individual by placing the individual into a
category or group such as male or female
T h e r e are two types of data:
Attribute data are countable data or data that can be put into categories
Variable data are measurement data, based on some continuous scale

Topic:
Measures of Central Tendency and
Dispersion
Math Concepts:
Measures of Central Tendency and Dispersion
Page 129 of 148
Descriptive statistics enable us to understand data through summary values and graphical
presentations. Summary values not only include the average, but also the spread, median, mode, range,
interquartiles range, standard deviation and variances.
Arithmetic Mean
Median – The number that is located in the middle of a set of numbers when that set is ordered
sequentially from the smallest to the largest.
Range
Interquartiles
Standard Deviation
Variances
Keystrokes:
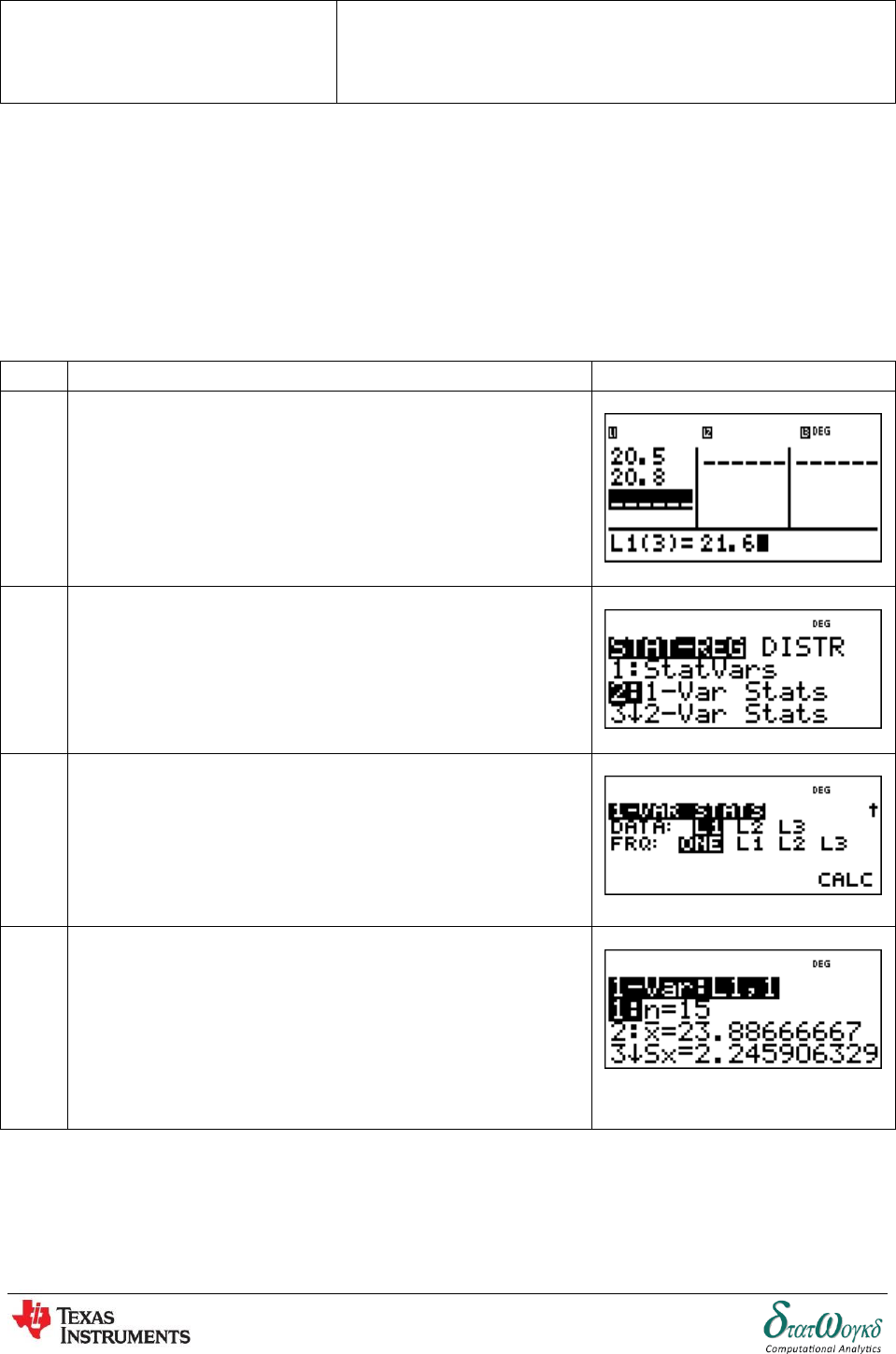
Topic:
Measures of Central Tendency and
Dispersion
Math Concepts:
Measures of Central Tendency and Dispersion
Page 130 of 148
Example:
1. The frequency distribution for the value of resistance in ohms of 48 resistors is as shown. Determine
the mean, median, range and standard deviation value of resistance.
No
Instructions / Keystrokes
Screenshots
1
Press.Key in the data in list L1
2
Select Press
Select option No 2: 1-Var Stats. Press
3
Select default option :
Data: L1
Frq: One
4
Use to move to CALC
Press .
Scroll using to access all parameters like mean, sample
standard deviation etc
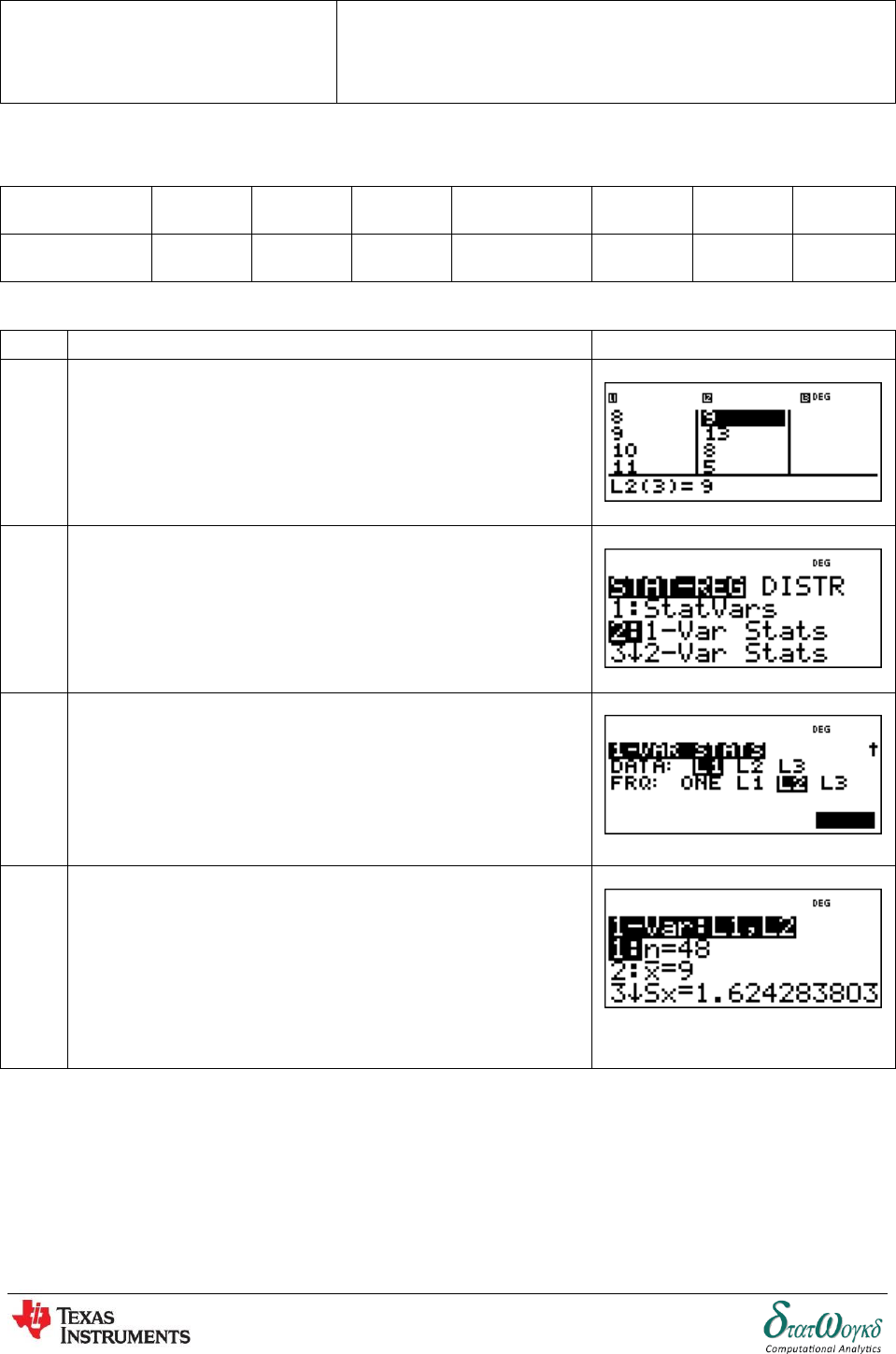
Topic:
Measures of Central Tendency and
Dispersion
Math Concepts:
Measures of Central Tendency and Dispersion
Page 131 of 148
2. Calculate the mean, median, interquartile range, standard deviation and variance for the following:
No
Keystrokes
Screenshots
1
Press to clear all previous entries.
Press . Key in the data in list L1 and list L2
2
Select Press
Select option No 2: 1-Var Stats. Press
3
Select option :
Data: L1. Use to move down
Frq: Use to select L2 :
4
Useto move to CALC
Press .
Scroll using to access all parameters like mean, median,
sample standard deviation etc
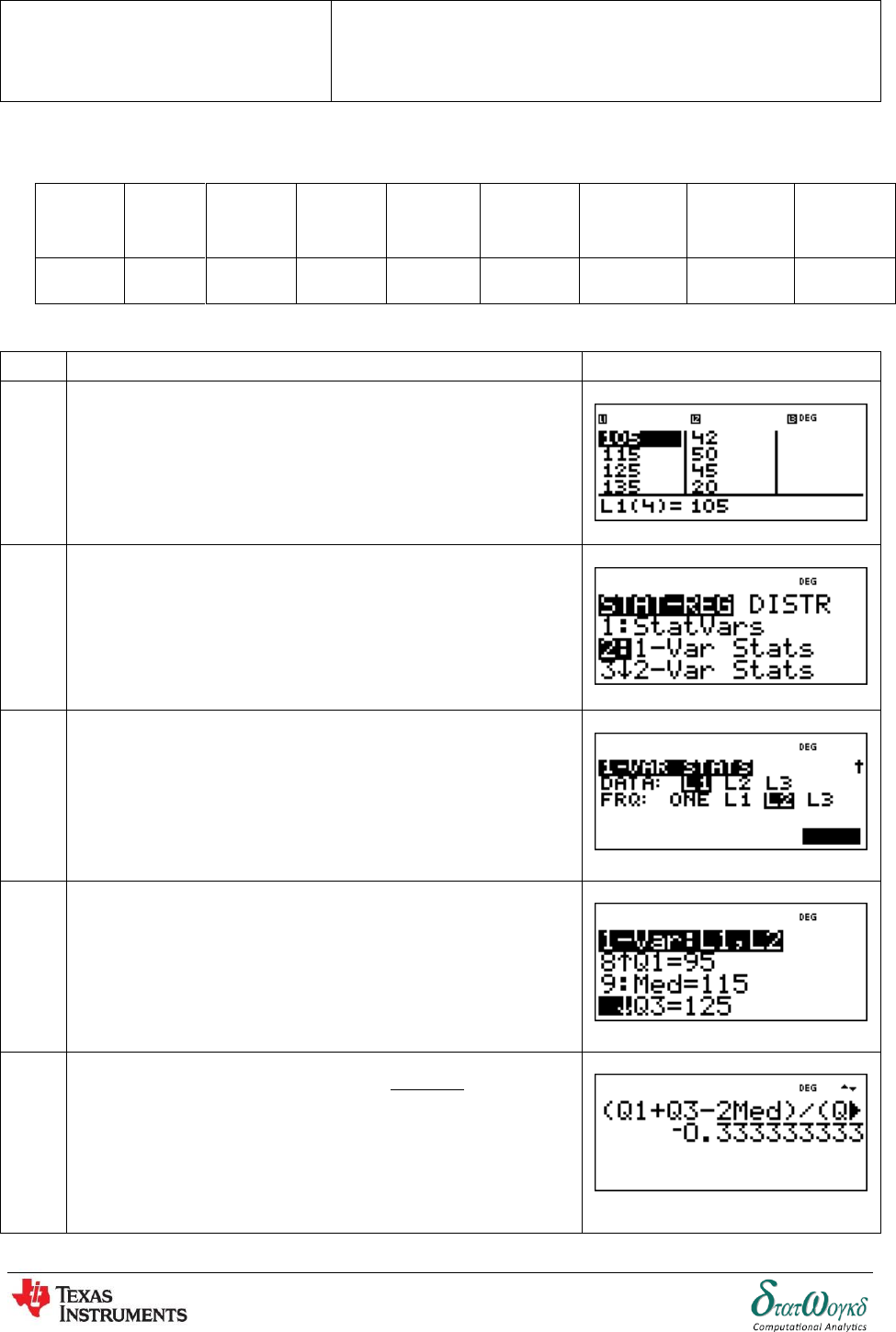
Topic:
Measures of Central Tendency and
Dispersion
Math Concepts:
Measures of Central Tendency and Dispersion
Page 132 of 148
3. Calculate the mean, median, quartiles and the quartile coefficient of skewness for the following:
No
Instructions / Keystrokes
Screenshots
1
Press to clear all previous entries.
Press . Key in the data in list L1 (take the midpoint
example : (70+80)/2 = 75 and list L2
2
Select Press
Select option No 2: 1-Var Stats. Press
3
Select option :
Data: L1. Use to move down
Frq: Use to select L2 :
4
Useto move to CALC
Press .
Scroll using to access all parameters
5
The quartile coefficient of skewness =
Press (. Press . Select 1: StatVars. Scroll
to access Q1. Press . Repeat the steps to acess Q3 and
Q2
Topic:
Measures of Central Tendency and
Dispersion
Math Concepts:
Measures of Central Tendency and Dispersion
Page 133 of 148
Exercise:
1. The scores of two golfers for 7 rounds each are
A
58
59
60
54
65
66
52
B
69
52
84
56
92
65
86
Who may be regarded as the more consistent player?
2. Given below are the marks obtained by a batch of 20 students in a certain class test in statistics and
mathematics. In which subject is the level of knowledge of students higher?
Answer:
1. Golfer A
2. Statistics

Topic:
Distribution
Math Concepts:
Distribution
Page 134 of 148
Distributions
Overview / Introduction / Terminology:
The binomial distribution is a discrete probability distribution which is used when there are exactly two
mutually exclusive outcomes of trials. These outcomes are appropriately labeled success and failure.
This is used to obtain the probability of observing x successes in n trials, with the probability of success
on a single trial denoted by p.
Binomial Formula. Suppose a binomial experiment consists of n trials and results in x successes. If the
probability of success on an individual trial is P, then the binomial probability is:
A Poisson distribution is the probability distribution that results from a Poisson experiment that results
in in outcomes that can be classified as successes or failures. Note that the specified region could take
many forms. For instance, it could be a length, an area, a volume, a period of time, etc.
Poisson Formula. Suppose we conduct a Poisson experiment, in which the average number of successes
If n is large and p is small, and the product npis less than 5, a very good approximation to a binomial
distribution is given by the corresponding Poisson distribution
The normal distribution refers to a family of continuous probability distributions described by the
normal equation
Normal equation. The value of the random variable Y is:
where is a normal random variable, is the mean, is the standard deviation, is approximately
, and e is approximately .
The graph of the normal distribution depends on two factors - the mean and the standard deviation. The
mean of the distribution determines the location of the center of the graph, and the standard deviation
determines the height and width of the graph. When the standard deviation is large, the curve is short
and wide; when the standard deviation is small, the curve is tall and narrow. All normal distributions
look like a symmetric, bell-shaped curve.
Topic:
Distribution
Math Concepts:
Distribution
Page 135 of 148
When a normal distribution curve has been standardized, the normal curve is called a standardized
normal curve or a normal probability curve, and any normally distributed data may be represented by
the same normal probability curve. The area under part of a normal probability curve is directly
proportional to probability and the value of the shaded area.
Keystrokes:

Topic:
Distribution
Math Concepts:
Distribution
Page 136 of 148
Example:
1. 10% of screws produced in a certain factory turn out to be defective. Find the probability that in a
sample of 10 screws chosen at random, exactly two will be defective.
No
Instructions / Keystrokes
Screenshots
1
Press . Pressto select
distributions option. Then press to scroll to option 4:
Binomialpdf. Press
2
Press to select thex: single option
3
Key in the following:
n = . Use to go to the next option
p = . Use to go to the next option
x = . Use to go to CALC
Press
2. If 3% of the gearwheels produced by a company are defective, determine the probabilities that in a
sample of 80 gearwheels
a. (a) two and
b. more than two will be defective.
The solution is to determine that
= np = 80 x 0.03 = 2.4< 5 therefore use Poisson distribution

Topic:
Distribution
Math Concepts:
Distribution
Page 137 of 148
No
Instructions / Keystrokes
Screenshots
1
Press . Pressto select
distributions option. Then keep press again and again to
scroll to option 6: Poissonpdf. Press
No
Instructions / Keystrokes
Screenshots
2
Press to select thex: single option
3
Key in the following:
mu = . Use to go to the next option
x = . Use to go to CALC
Press
4
The probability of having more than 2 defective is 1(the
sum of the probabilities of having 0, 1, and 2 defective
gearwheels), i.e.
1 (0.0907 + 0.2177 + 0.2613)
Key in the following:
Use to go to Solve Again
mu = . Use to go to the next option
x = . Use to go to CALC
Press

Topic:
Distribution
Math Concepts:
Distribution
Page 138 of 148
Use to go to Solve Again
mu = . Use to go to the next option
x = . Use to go to CALC
Press
3. A component is classed as defective if it has a diameter of less than 69 mm. In a batch of 350
components, the mean diameter is 75mm and the standard deviation is 2.8 mm.Determinehow
many are likely to be classed as defective
No
Instructions / Keystrokes
Screenshots
1
Press . Pressto select
distributions option. Then press to scroll to option 2:
Normalcdf. Press
2
Press to enter for mean
Press to enter for sigma
Press
Press
3
Key in the following:
Use to go to the variable a under STORE
Use to Qui

Topic:
Distribution
Math Concepts:
Distribution
Page 139 of 148
No
Instructions / Keystrokes
Screenshots
4
Press
Use to scroll to variable a
Press
The number of components that will be classified as
defective is 6.
Exercise:
1. 2 percent of the electric bulbs produced by a company are defective. Find the probability that in a
sample of 200 bulbs
a. less than bulbs are defective and
b. more than 3 bulbs are defective.
2. An average light bulb manufactured by the Acme Corporation lasts 300 days with a standard
deviation of 50 days. Assuming that bulb life is normally distributed, what is the probability that an
Acme light bulb will last at most 365 days
Answer:
1.
2.

Topic:
Probability
Math Concepts:
Probability
Page 140 of 148
Probability
Overview / Introduction / Terminology:
Probabilities, permutations and combinations are used daily in many different fields that range from
gambling and games, to mechanical or structural failure rates, to rates of detection in medical screening.
The probability of something happening is the likelihood or chance of it happening. Values of probability
lie between 0 and 1, where 0 represents an absolute impossibility and 1 represents an absolute
certainty. The probability of an event happening usually lies somewhere between these two extreme
values and is expressed either as a proper or decimal fraction
P(A) =
The Number Of Ways Event A Can Occur
The total number Of Possible Outcomes
Permutation: Use the equation to calculate the number of permutations of a given set of data, where n
is the total number of elements in the data set, and k is the number of elements selected at one time.
Notice that the definition of a permutation states that the ordering of the element selection does
matter.
Combination: Use the equation to calculate the number of combinations of a given set of data, where n
is the total number of elements in the data set, and k is the number of elements selected at one time.
Notice that the definition of a combination states that the ordering of the element selection does not
matter.
Keystrokes:

Topic:
Probability
Math Concepts:
Probability
Page 141 of 148
Example:
1. Calculate the number of permutations there are of
a. 5 distinct objects taken 2 at a time
b. 4 distinct objects taken2 at a time
No
Instructions / Keystrokes
Screenshots
1
Press
2
Press
2. A class has 24 students. 4 can represent the class at an exam board. How many combinations are
possible when choosing this group?
No
Instructions / Keystrokes
Screenshots
1
Press
3. There are 4 Engineers and 3 Managers in a firm. 3 of them are put on duty at a time. What is the
probability that there are 2 Engineers and 1 Manager?
No
Instructions / Keystrokes
Screenshots
1
Total no of people = 7
Total number of combinations of taking 3 out of 7 is 7
The combination of 2 Engineers and 1 Manager is

Topic:
Probability
Math Concepts:
Probability
Page 142 of 148
Probability
Press
Exercise:
1. In how many ways can a team of six be picked from ten possible players?
2. boxes can each hold one object. In how many ways can identical objects be placedin the
boxes?
Answer:
1.
2.
Topic:
Sampling and Inference
Math Concepts:
Sampling and Inference
Page 143 of 148
Sampling and Inference
Overview / Introduction / Terminology:
The sampling of attributes maybe regarded as the selection of samples from a population whose
members possess the attributes K or not K. The presence of K maybe called a success and its absence a
failure.
Suppose we draw a simple sample of n items. Clearly it is same as a series of n independent trials with
the same probability p of success. The probabilities of successes are the terms in the
binomial expansion of where
If consider the proportion of successes, then:
1. Mean proposrtion of successes = = p
2. Standard error of the proposrtion of successes =
=
3. Precision of the proportion of successes =
Tests of significance:
1) Large samples :
, if ---it is significant
2) Small samples :
, if ---it is significant
Keystrokes:
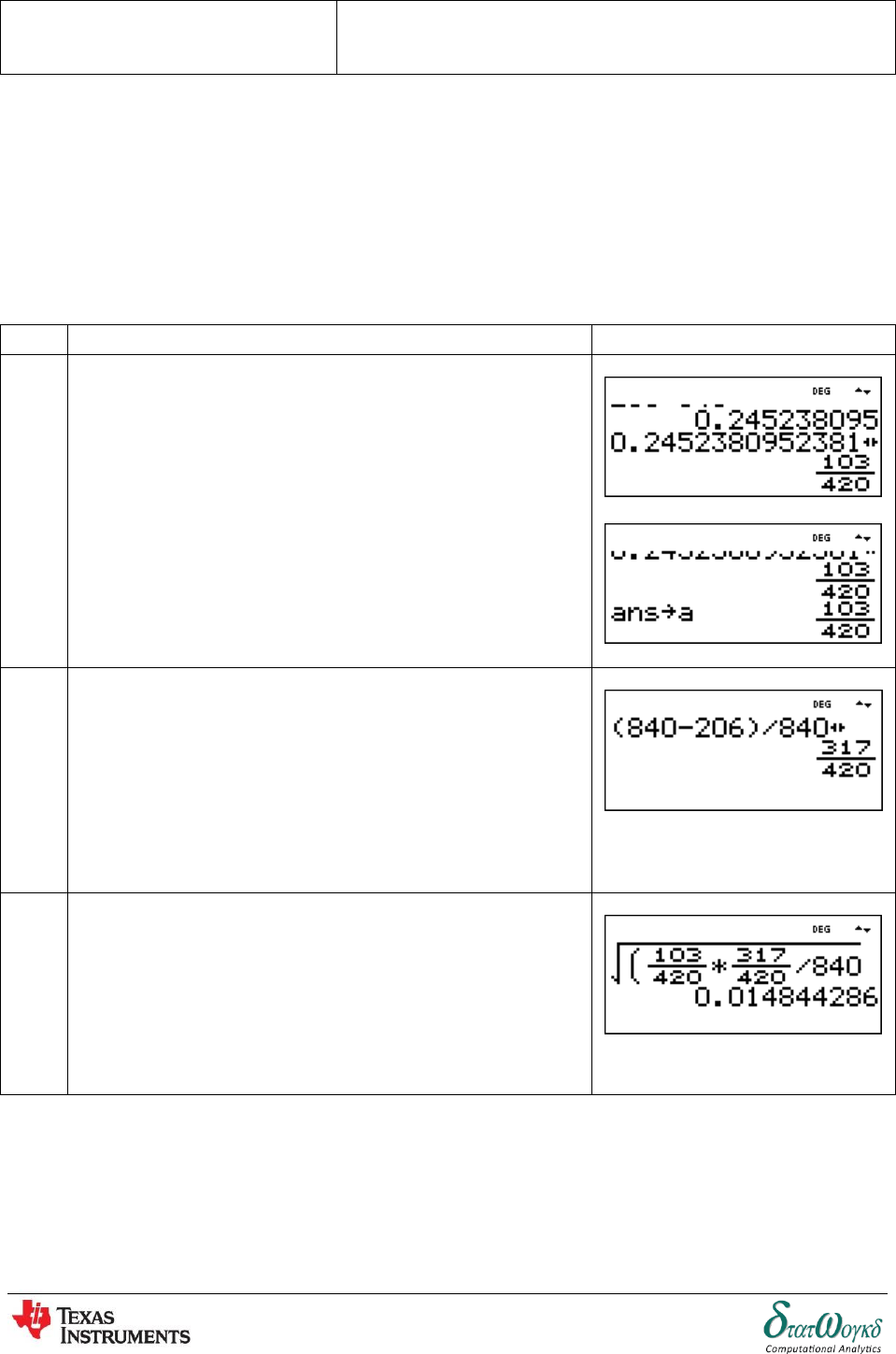
Topic:
Sampling and Inference
Math Concepts:
Sampling and Inference
Page 144 of 148
Example:
1. In a locality containing families, a sample of families was selected at random. Of these
families, families were found to have a monthly income of or less. It is desired to
estimate how many out of families have a monthly income of or less. Within what
limits would you place your estimate?
No
Instructions / Keystrokes
Screenshots
1
Define a.
Press . Press
Press to convert to fraction. Press
2
Define b.
Press . Press
Press to convert to fraction.
Press
3
Standard error of population:
Press Scroll until a Press Press
Scroll until b
Hence taking or to be the estimate of families having a monthly income of
or less in the locality, the limits are () which is and respectively.
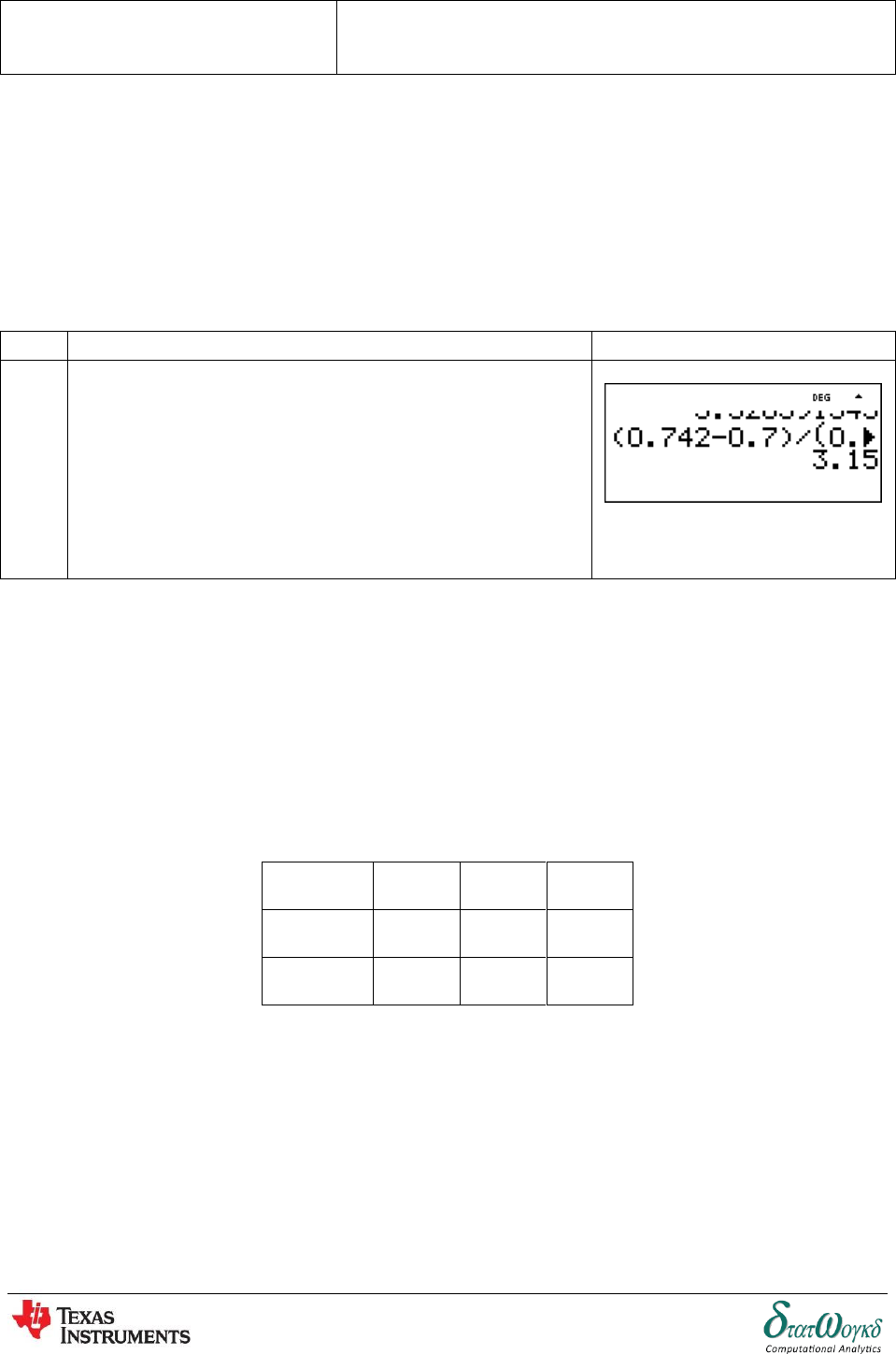
Topic:
Sampling and Inference
Math Concepts:
Sampling and Inference
Page 145 of 148
2. A machinist is making engine parts with axle diameter of . A random sample of 10 parts
shows mean diameter with a standard deviation of . On the basis of this
sample, would you say that work is inferior?
Taking the hypothesis that the product is not inferior, there is no significant differences between the
means
No
Keystrokes
Screenshots
1
Press
The value of t 0.05 = 2.262. Therefore t = 3.15 > 2.262, the value of t is significant. This implies that
sample mean differs significantly from and the hypothesis is rejected. Hence the work is inferior.
Exercise:
1. 2 A group of boys and girls were given an intelligence test. The mean score, standard deviation and
numbers in each group are as follows:
Is the mean score of boys significantly different from the girls?
Answer:
1. No

NOTES
Page 146 of 148

NOTES
Page 147 of 148

NOTES
Page 148 of 148