JBL TI84Plus_OS255MP TI 84 Plus / Silver Edition Guidebook (English) TI84Plus EN
User Manual: JBL TI-84 Plus / TI-84 Plus Silver Edition guidebook (English) TI-84 Plus / TI-84 Plus Silver Edition Guidebook
Open the PDF directly: View PDF ![]() .
.
Page Count: 422 [warning: Documents this large are best viewed by clicking the View PDF Link!]
- Important Information
- Chapter 1: Operating the TI-84 Plus Silver Edition
- Documentation Conventions
- TI-84 Plus Keyboard
- Turning On and Turning Off the TI-84 Plus
- Setting the Display Contrast
- The Display
- Interchangeable Faceplates
- Using the Clock
- Entering Expressions and Instructions
- Setting Modes
- Using TI-84 Plus Variable Names
- Storing Variable Values
- Recalling Variable Values
- Scrolling Through Previous Entries on the Home Screen
- ENTRY (Last Entry) Storage Area
- TI-84 Plus Menus
- VARS and VARS Y-VARS Menus
- Equation Operating System (EOS™)
- Special Features of the TI-84 Plus
- Other TI-84 Plus Features
- Error Conditions
- Chapter 2: Math, Angle, and Test Operations
- Chapter 3: Function Graphing
- Getting Started: Graphing a Circle
- Defining Graphs
- Setting the Graph Modes
- Defining Functions
- Selecting and Deselecting Functions
- Setting Graph Styles for Functions
- Setting the Viewing Window Variables
- Setting the Graph Format
- Displaying Graphs
- Exploring Graphs with the Free-Moving Cursor
- Exploring Graphs with TRACE
- Exploring Graphs with the ZOOM Instructions
- Using ZOOM MEMORY
- Using the CALC (Calculate) Operations
- Chapter 4: Parametric Graphing
- Chapter 5: Polar Graphing
- Chapter 6: Sequence Graphing
- Getting Started: Forest and Trees
- Defining and Displaying Sequence Graphs
- Selecting Axes Combinations
- Exploring Sequence Graphs
- Graphing Web Plots
- Using Web Plots to Illustrate Convergence
- Graphing Phase Plots
- Comparing TI-84 Plus and TI-82 Sequence Variables
- Keystroke Differences Between TI-84 Plus and TI-82
- Chapter 7: Tables
- Chapter 8: Draw Instructions
- Getting Started: Drawing a Tangent Line
- Using the DRAW Menu
- Clearing Drawings
- Drawing Line Segments
- Drawing Horizontal and Vertical Lines
- Drawing Tangent Lines
- Drawing Functions and Inverses
- Shading Areas on a Graph
- Drawing Circles
- Placing Text on a Graph
- Using Pen to Draw on a Graph
- Drawing Points on a Graph
- Drawing Pixels
- Storing Graph Pictures (Pic)
- Recalling Graph Pictures (Pic)
- Storing Graph Databases (GDB)
- Recalling Graph Databases (GDB)
- Chapter 9: Split Screen
- Chapter 10: Matrices
- Chapter 11: Lists
- Chapter 12: Statistics
- Getting Started: Pendulum Lengths and Periods
- Setting Up Statistical Analyses
- Using the Stat List Editor
- Attaching Formulas to List Names
- Detaching Formulas from List Names
- Switching Stat List Editor Contexts
- Stat List Editor Contexts
- STAT EDIT Menu
- Regression Model Features
- STAT CALC Menu
- Statistical Variables
- Statistical Analysis in a Program
- Statistical Plotting
- Statistical Plotting in a Program
- Chapter 13: Inferential Statistics and Distributions
- Chapter 14: Applications
- The Applications Menu
- Getting Started: Financing a Car
- Getting Started: Computing Compound Interest
- Using the TVM Solver
- Using the Financial Functions
- Calculating Time Value of Money (TVM)
- Calculating Cash Flows
- Calculating Amortization
- Calculating Interest Conversion
- Finding Days between Dates/Defining Payment Method
- Using the TVM Variables
- The EasyData™ Application
- Chapter 15: CATALOG, Strings, Hyperbolic Functions
- Chapter 16: Programming
- Chapter 17: Activities
- The Quadratic Formula
- Box with Lid
- Comparing Test Results Using Box Plots
- Graphing Piecewise Functions
- Graphing Inequalities
- Solving a System of Nonlinear Equations
- Using a Program to Create the Sierpinski Triangle
- Graphing Cobweb Attractors
- Using a Program to Guess the Coefficients
- Graphing the Unit Circle and Trigonometric Curves
- Finding the Area between Curves
- Using Parametric Equations: Ferris Wheel Problem
- Demonstrating the Fundamental Theorem of Calculus
- Computing Areas of Regular N-Sided Polygons
- Computing and Graphing Mortgage Payments
- Chapter 18: Memory and Variable Management
- Chapter 19: Communication Link
- Appendix A: Functions and Instructions
- Appendix B: Reference Information
- Appendix C: Service and Warranty Information

TI-84 Plus and
TI-84 Plus Silver Edition
Guidebook
Note: This guidebook for the TI-84 Plus or TI-84 Plus Silver Edition with operating system (OS)
version 2.55MP. If your calculator has a previous OS version, your screens may look different
and some features may not be available. You can download the latest OS
education.ti.com/guides.

ii
Important Information
Texas Instruments makes no warranty, either express or implied, including but not limited to
any implied warranties of merchantability and fitness for a particular purpose, regarding any
programs or book materials and makes such materials available solely on an "as-is" basis. In
no event shall Texas Instruments be liable to anyone for special, collateral, incidental, or
consequential damages in connection with or arising out of the purchase or use of these
materials, and the sole and exclusive liability of Texas Instruments, regardless of the form of
action, shall not exceed the purchase price of this product. Moreover, Texas Instruments shall
not be liable for any claim of any kind whatsoever against the use of these materials by any
other party.
© 2004–2010 Texas Instruments Incorporated
Vernier EasyData, Vernier LabPro, and Vernier Go! Motion are a trademarks of Vernier
Software & Technology.

Contents
iii
Important Information .................................................................................................................... ii
Chapter 1:
Operating the TI-84 Plus Silver Edition .................................................................... 1
Documentation Conventions .......................................................................................................... 1
TI-84 Plus Keyboard ......................................................................................................................... 1
Turning On and Turning Off the TI-84 Plus .................................................................................... 3
Setting the Display Contrast ........................................................................................................... 4
The Display ....................................................................................................................................... 5
Interchangeable Faceplates ............................................................................................................ 8
Using the Clock ................................................................................................................................ 9
Entering Expressions and Instructions ..........................................................................................11
Setting Modes ................................................................................................................................ 14
Using TI-84 Plus Variable Names ................................................................................................... 19
Storing Variable Values ................................................................................................................. 20
Recalling Variable Values .............................................................................................................. 21
Scrolling Through Previous Entries on the Home Screen ............................................................ 22
ENTRY (Last Entry) Storage Area .................................................................................................. 22
TI-84 Plus Menus ............................................................................................................................ 25
VARS and VARS Y-VARS Menus .....................................................................................................27
Equation Operating System (EOS™) ............................................................................................. 29
Special Features of the TI-84 Plus ................................................................................................. 30
Other TI-84 Plus Features .............................................................................................................. 31
Error Conditions ............................................................................................................................. 33
Chapter 2:
Math, Angle, and Test Operations ......................................................................... 35
Getting Started: Coin Flip ............................................................................................................. 35
Keyboard Math Operations .......................................................................................................... 36
MATH Operations .......................................................................................................................... 38
Using the Equation Solver ............................................................................................................. 42
MATH NUM (Number) Operations ................................................................................................ 45
Entering and Using Complex Numbers ........................................................................................ 50
MATH CPX (Complex) Operations ................................................................................................ 54
MATH PRB (Probability) Operations ............................................................................................. 56
ANGLE Operations ......................................................................................................................... 59
TEST (Relational) Operations ........................................................................................................ 62
TEST LOGIC (Boolean) Operations ................................................................................................63
Chapter 3:
Function Graphing .................................................................................................. 65
Getting Started: Graphing a Circle ............................................................................................... 65
Defining Graphs ............................................................................................................................. 66
Setting the Graph Modes .............................................................................................................. 67
Defining Functions ........................................................................................................................ 68
Selecting and Deselecting Functions ............................................................................................69
Setting Graph Styles for Functions ............................................................................................... 71
Setting the Viewing Window Variables ....................................................................................... 73
Setting the Graph Format ............................................................................................................. 74
Displaying Graphs .......................................................................................................................... 76
Exploring Graphs with the Free-Moving Cursor .......................................................................... 78
Exploring Graphs with TRACE ....................................................................................................... 78
Exploring Graphs with the ZOOM Instructions ............................................................................ 80
Using ZOOM MEMORY .................................................................................................................. 85
Using the CALC (Calculate) Operations ........................................................................................ 87

iv
Chapter 4:
Parametric Graphing .............................................................................................. 91
Getting Started: Path of a Ball ...................................................................................................... 91
Defining and Displaying Parametric Graphs ................................................................................ 93
Exploring Parametric Graphs ........................................................................................................ 95
Chapter 5:
Polar Graphing ........................................................................................................ 97
Getting Started: Polar Rose ........................................................................................................... 97
Defining and Displaying Polar Graphs ......................................................................................... 98
Exploring Polar Graphs ................................................................................................................ 100
Chapter 6:
Sequence Graphing ............................................................................................... 102
Getting Started: Forest and Trees ............................................................................................... 102
Defining and Displaying Sequence Graphs ................................................................................ 103
Selecting Axes Combinations ...................................................................................................... 107
Exploring Sequence Graphs ........................................................................................................ 107
Graphing Web Plots ..................................................................................................................... 109
Using Web Plots to Illustrate Convergence ................................................................................ 110
Graphing Phase Plots ................................................................................................................... 111
Comparing TI-84 Plus and TI-82 Sequence Variables ................................................................. 113
Keystroke Differences Between TI-84 Plus
and TI-82 ................................................................................................................................. 114
Chapter 7:
Tables ..................................................................................................................... 115
Getting Started: Roots of a Function .......................................................................................... 115
Setting Up the Table .................................................................................................................... 116
Defining the Dependent Variables ............................................................................................. 117
Displaying the Table .................................................................................................................... 118
Chapter 8:
Draw Instructions ................................................................................................. 121
Getting Started: Drawing a Tangent Line .................................................................................. 121
Using the DRAW Menu ............................................................................................................... 122
Clearing Drawings ....................................................................................................................... 123
Drawing Line Segments .............................................................................................................. 124
Drawing Horizontal and Vertical Lines ...................................................................................... 125
Drawing Tangent Lines ................................................................................................................ 126
Drawing Functions and Inverses .................................................................................................127
Shading Areas on a Graph .......................................................................................................... 128
Drawing Circles ............................................................................................................................ 128
Placing Text on a Graph .............................................................................................................. 129
Using Pen to Draw on a Graph ...................................................................................................130
Drawing Points on a Graph ......................................................................................................... 131
Drawing Pixels ............................................................................................................................. 132
Storing Graph Pictures (Pic) ......................................................................................................... 134
Recalling Graph Pictures (Pic) ...................................................................................................... 135
Storing Graph Databases (GDB) ..................................................................................................135
Recalling Graph Databases (GDB) ............................................................................................... 136
Chapter 9:
Split Screen ........................................................................................................... 137
Getting Started: Exploring the Unit Circle ................................................................................. 137
Using Split Screen ........................................................................................................................ 138

v
Horiz (Horizontal) Split Screen .................................................................................................... 139
G-T (Graph-Table) Split Screen .................................................................................................... 140
TI-84 Plus Pixels in Horiz and G-T Modes .................................................................................... 141
Chapter 10:
Matrices ................................................................................................................. 143
Getting Started: Using the MTRX Shortcut Menu ..................................................................... 143
Getting Started: Systems of Linear Equations ............................................................................ 144
Defining a Matrix ........................................................................................................................ 145
Viewing and Editing Matrix Elements ........................................................................................ 146
Using Matrices with Expressions ................................................................................................. 148
Displaying and Copying Matrices ............................................................................................... 149
Using Math Functions with Matrices .......................................................................................... 151
Using the MATRX MATH Operations .......................................................................................... 154
Chapter 11:
Lists ........................................................................................................................ 161
Getting Started: Generating a Sequence ................................................................................... 161
Naming Lists ................................................................................................................................. 162
Storing and Displaying Lists ........................................................................................................ 163
Entering List Names ..................................................................................................................... 164
Attaching Formulas to List Names .............................................................................................. 165
Using Lists in Expressions ............................................................................................................ 167
LIST OPS Menu ............................................................................................................................. 168
LIST MATH Menu ......................................................................................................................... 175
Chapter 12:
Statistics ................................................................................................................ 178
Getting Started: Pendulum Lengths and Periods ...................................................................... 178
Setting Up Statistical Analyses .................................................................................................... 184
Using the Stat List Editor ............................................................................................................. 185
Attaching Formulas to List Names .............................................................................................. 188
Detaching Formulas from List Names ......................................................................................... 190
Switching Stat List Editor Contexts ............................................................................................. 190
Stat List Editor Contexts .............................................................................................................. 192
STAT EDIT Menu ........................................................................................................................... 193
Regression Model Features ......................................................................................................... 195
STAT CALC Menu .......................................................................................................................... 198
Statistical Variables ...................................................................................................................... 206
Statistical Analysis in a Program ................................................................................................. 207
Statistical Plotting ........................................................................................................................ 208
Statistical Plotting in a Program ................................................................................................. 212
Chapter 13:
Inferential Statistics and Distributions ............................................................... 215
Getting Started: Mean Height of a Population ......................................................................... 215
Inferential Stat Editors ................................................................................................................ 218
STAT TESTS Menu ......................................................................................................................... 221
Inferential Statistics Input Descriptions ......................................................................................239
Test and Interval Output Variables .............................................................................................240
Distribution Functions ................................................................................................................. 241
Distribution Shading ................................................................................................................... 248
Chapter 14:
Applications .......................................................................................................... 251
The Applications Menu ............................................................................................................... 251

vi
Getting Started: Financing a Car ................................................................................................ 252
Getting Started: Computing Compound Interest ...................................................................... 253
Using the TVM Solver ................................................................................................................. 253
Using the Financial Functions ..................................................................................................... 254
Calculating Time Value of Money (TVM) ................................................................................... 255
Calculating Cash Flows ................................................................................................................ 257
Calculating Amortization ............................................................................................................ 258
Calculating Interest Conversion .................................................................................................. 261
Finding Days between Dates/Defining Payment Method ......................................................... 261
Using the TVM Variables ............................................................................................................. 262
The EasyData™ Application ........................................................................................................ 263
Chapter 15:
CATALOG, Strings, Hyperbolic Functions ............................................................ 266
Browsing the TI-84 Plus CATALOG .............................................................................................. 266
Entering and Using Strings ......................................................................................................... 267
Storing Strings to String Variables .............................................................................................. 268
String Functions and Instructions in the CATALOG ................................................................... 269
Hyperbolic Functions in the CATALOG ....................................................................................... 273
Chapter 16:
Programming ........................................................................................................ 275
Getting Started: Volume of a Cylinder ....................................................................................... 275
Creating and Deleting Programs ................................................................................................ 276
Entering Command Lines and Executing Programs ................................................................... 278
Editing Programs ......................................................................................................................... 279
Copying and Renaming Programs .............................................................................................. 280
PRGM CTL (Control) Instructions ................................................................................................. 281
PRGM I/O (Input/Output) Instructions ........................................................................................ 288
Calling Other Programs as Subroutines ...................................................................................... 293
Running an Assembly Language Program ................................................................................. 294
Chapter 17:
Activities ............................................................................................................... 296
The Quadratic Formula ............................................................................................................... 296
Box with Lid ................................................................................................................................. 299
Comparing Test Results Using Box Plots ..................................................................................... 306
Graphing Piecewise Functions .................................................................................................... 308
Graphing Inequalities .................................................................................................................. 309
Solving a System of Nonlinear Equations ................................................................................... 310
Using a Program to Create the Sierpinski Triangle .................................................................... 311
Graphing Cobweb Attractors ...................................................................................................... 312
Using a Program to Guess the Coefficients ................................................................................ 313
Graphing the Unit Circle and Trigonometric Curves ................................................................. 315
Finding the Area between Curves .............................................................................................. 316
Using Parametric Equations: Ferris Wheel Problem .................................................................. 317
Demonstrating the Fundamental Theorem of Calculus ............................................................ 319
Computing Areas of Regular N-Sided Polygons ........................................................................ 321
Computing and Graphing Mortgage Payments ........................................................................ 323
Chapter 18:
Memory and Variable Management .................................................................... 326
Checking Available Memory ....................................................................................................... 326
Deleting Items from Memory .....................................................................................................329
Clearing Entries and List Elements .............................................................................................329
Archiving and UnArchiving Variables ......................................................................................... 330

vii
Resetting the TI-84 Plus ............................................................................................................... 333
Grouping and Ungrouping Variables ......................................................................................... 336
Garbage Collection ...................................................................................................................... 339
ERR:ARCHIVE FULL Message .......................................................................................................343
Chapter 19:
Communication Link ............................................................................................. 344
Getting Started: Sending Variables ............................................................................................ 344
TI-84 Plus LINK ............................................................................................................................. 345
Selecting Items to Send ............................................................................................................... 347
Receiving Items ............................................................................................................................ 350
Backing Up RAM Memory ........................................................................................................... 351
Error Conditions ........................................................................................................................... 352
Appendix A:
Functions and Instructions ................................................................................... 354
Appendix B:
Reference Information ......................................................................................... 383
Variables ....................................................................................................................................... 383
Statistics Formulas ....................................................................................................................... 384
Financial Formulas ....................................................................................................................... 387
Important Things You Need to Know About Your TI-84 Plus ................................................... 391
Error Conditions ........................................................................................................................... 394
Accuracy Information .................................................................................................................. 398
Appendix C:
Service and Warranty Information ...................................................................... 400
Texas Instruments Support and Service ...................................................................................... 400
Battery Information ..................................................................................................................... 400
In Case of Difficulty ..................................................................................................................... 402

Chapter 1: Operating the TI-84 Plus Silver Edition 1
Chapter 1:
Operating the TI-84 Plus Silver Edition
Documentation Conventions
In the body of this guidebook, TI-84 Plus refers to the TI-84 Plus Silver Edition, but all of the
instructions, examples, and functions in this guidebook also work for the TI-84 Plus. The two
graphing calculators differ only in available RAM memory, interchangeable faceplates, and Flash
application ROM memory. Sometimes, as in Chapter 19, the full name TI-84 Plus Silver Edition is
used to distinguish it from the TI-84 Plus.
Screen shots were taken using OS version 2.53MP and higher in either MathPrint™ or Classic
mode. All features are available in both modes; however, screens make look slightly different
depending on the mode setting. Many examples highlight features that are not available in
previous OS versions. If your calculator does not have the latest OS, features may not be available
and your screens may look different. You can download the latest OS from education.ti.com.
A new MODE menu item, STAT WIZARDS is available with OS version 2.55MP for syntax entry
help for commands and functions in the STAT CALC menu, DISTR DISTR menu, DISTR DRAW
menu and the seq( function (sequence) in the LIST OPS menu. When selecting a supported
statistics command, regression or distribution with the STAT WIZARDS setting ON: (the default
setting) a syntax help (wizard) screen is displayed. The wizard allows the entry of required and
optional arguments. The function or command will paste with the entered arguments to the Home
Screen history or in most other locations where the cursor is available for input. If a command or
function is accessed from N the command or function will paste without wizard support. Run
the Catalog Help application (Œ) for more syntax help when needed. APPS
TI-84 Plus Keyboard
Generally, the keyboard is divided into these zones: graphing keys, editing keys, advanced
function keys, and scientific calculator keys.
Keyboard Zones
Graphing — Graphing keys access the interactive graphing features. The third function of these
keys (t ^-a) displays the shortcut menus, which include templates for fractions, n/d, quick
matrix entry, and some of the functions found on the MATH and VARS menus.
Editing — Editing keys allow you to edit expressions and values.
Advanced — Advanced function keys display menus that access the advanced functions.
Scientific — Scientific calculator keys access the capabilities of a standard scientific calculator.
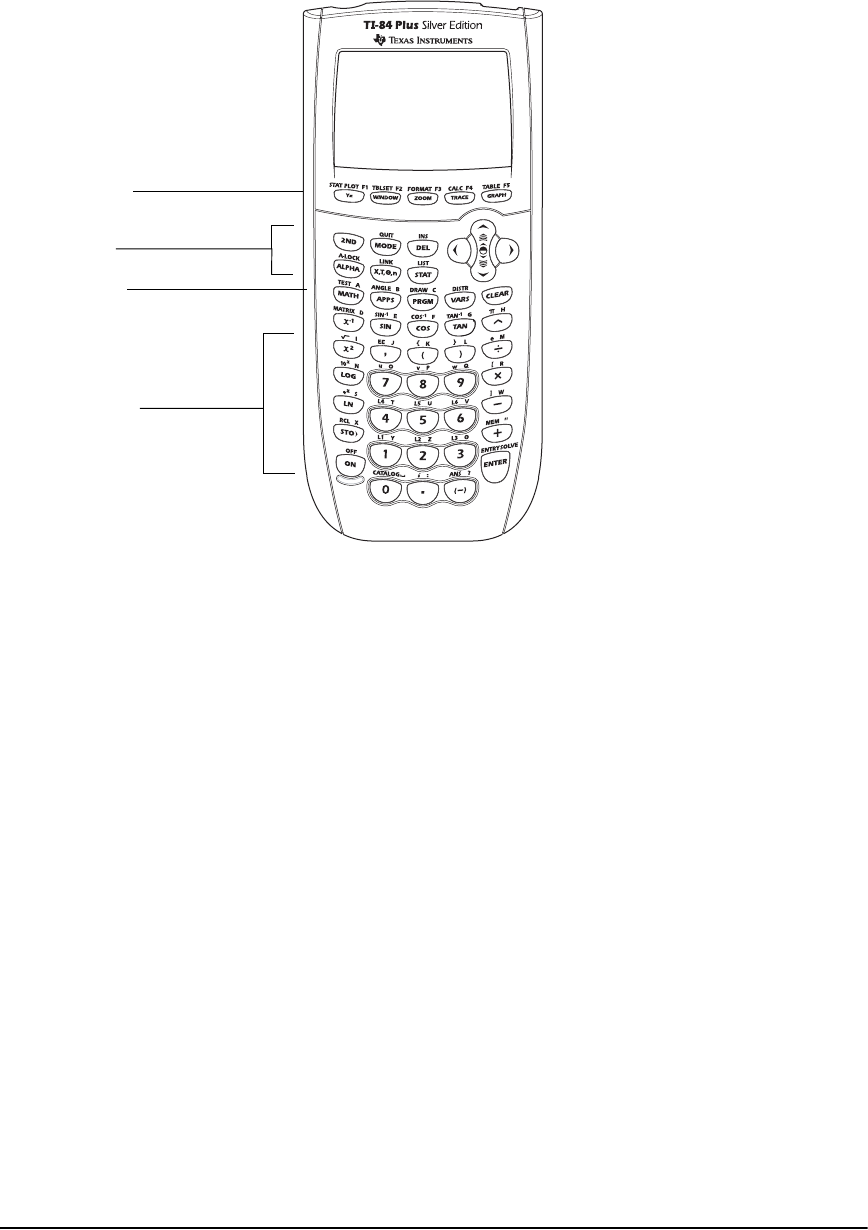
G
raphing Keys
Editing Keys
Advanced
Function Keys
Scientific
Calculator Keys
Chapter 1: Operating the TI-84 Plus Silver Edition 2
TI-84 Plus Silver Edition
Using the Color.Coded Keyboard
The keys on the TI-84 Plus are color-coded to help you easily locate the key you need.
The light colored keys are the number keys. The keys along the right side of the keyboard are the
common math functions. The keys across the top set up and display graphs. The Πkey provides
access to applications such as the Inequality Graphing, Transformation Graphing, Conic Graphing,
Polynomial Root Finder and Simultaneous Equation Solver, and Catalog Help.
The primary function of each key is printed on the keys. For example, when you press , the
MATH menu is displayed.
Using the y and ƒ Keys
The secondary function of each key is printed above the key. When you press the y key, the
character, abbreviation, or word printed above the other keys becomes active for the next
keystroke. For example, when you press y and then , the TEST menu is displayed. This
guidebook describes this keystroke combination as y :.
Many keys also have a third function. These functions are printed above the keys in the same
color as the ƒ key. The third functions enter alphabetic characters and special symbols as
well as access SOLVE and shortcut menus. For example, when you press ƒ and then ,
the letter A is entered. This guidebook describes this keystroke combination as ƒ [A].
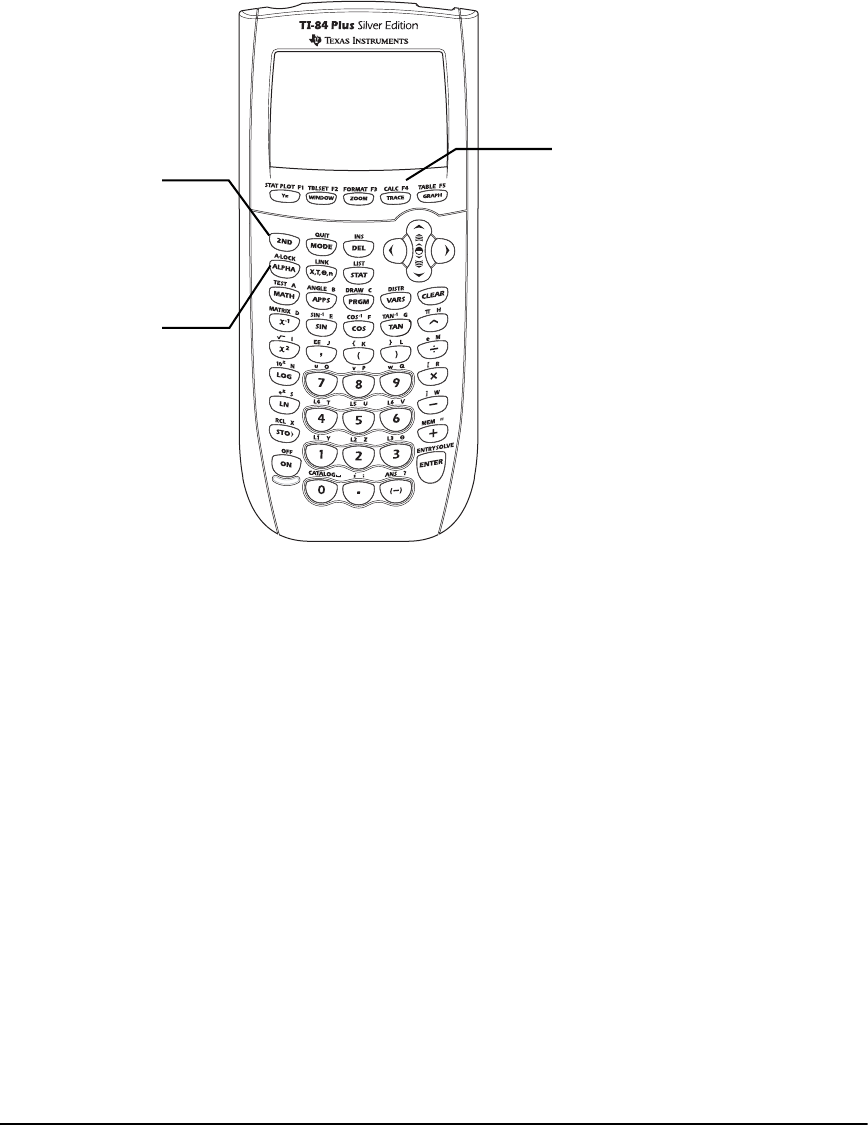
y
Accesses the
second function
printed above each
key.
ƒ
Accesses the third
function printed
above each key.
ƒ ^ - a
Access shortcut
menus for
functionality
including templates
for fractions, n/d,
and other
functions.
Chapter 1: Operating the TI-84 Plus Silver Edition 3
If you want to enter several alphabetic characters in a row, you can press y 7 to lock the
alpha key in the On position and avoid having to press ƒ multiple times. Press ƒ a
second time to unlock it.
Note: The flashing cursor changes to Ø when you press ƒ, even if you are accessing a
function or a menu.
Turning On and Turning Off the TI-84 Plus
Turning On the Graphing Calculator
To turn on the TI-84 Plus, press É. An information screen displays reminding you that you can
press t ^ - a to display the shortcut menus. This message also displays when you reset
RAM.
fTo continue but not see this information screen again, press 1.
fTo continue and see this information screen again the next time you turn on the TI-84 Plus,
press 2.
• If you previously had turned off the graphing calculator by pressing y M, the TI-84 Plus
displays the home screen as it was when you last used it and clears any error. (The
information screen displays first, unless you chose not to see it again.) If the home screen is
blank, press } to scroll through the history of previous calculations.
• If Automatic Power Down™ (APD™) had previously turned off the graphing calculator, the
TI-84 Plus will return exactly as you left it, including the display, cursor, and any error.

Chapter 1: Operating the TI-84 Plus Silver Edition 4
• If the TI-84 Plus is turned off and connected to another graphing calculator or personal
computer, any communication activity will “wake up” the TI-84 Plus.
To prolong the life of the batteries, APD™ turns off the TI-84 Plus automatically after about five
minutes without any activity.
Turning Off the Graphing Calculator
To turn off the TI-84 Plus manually, press y M.
• All settings and memory contents are retained by the Constant Memory™ function.
• Any error condition is cleared.
Batteries
The TI-84 Plus uses five batteries: four AAA alkaline batteries and one button cell backup battery.
The backup battery provides auxiliary power to retain memory while you replace the AAA
batteries. To replace batteries without losing any information stored in memory, follow the steps in
Appendix C.
Setting the Display Contrast
Adjusting the Display Contrast
You can adjust the display contrast to suit your viewing angle and lighting conditions. As you change
the contrast setting, a number from 0 (lightest) to 9 (darkest) in the top-right corner indicates the
current level. You may not be able to see the number if contrast is too light or too dark.
Note: The TI-84 Plus has 40 contrast settings, so each number 0 through 9 represents four
settings.
The TI-84 Plus retains the contrast setting in memory when it is turned off.
To adjust the contrast, follow these steps.
fPress y } to darken the screen one level at a time.
fPress y † to lighten the screen one level at a time.
Note: If you adjust the contrast setting to 0, the display may become completely blank. To restore
the screen, press y } until the display reappears.
When to Replace Batteries
When the batteries are low, a low-battery message is displayed when you turn on the graphing
calculator.
To replace the batteries without losing any information in memory, follow the steps in Appendix C.

Chapter 1: Operating the TI-84 Plus Silver Edition 5
Generally, the graphing calculator will continue to operate for one or two weeks after the low-
battery message is first displayed. After this period, the TI-84 Plus will turn off automatically and
the unit will not operate. Batteries must be replaced. All memory should be retained.
Note:
• The operating period following the first low-battery message could be longer than two weeks if
you use the graphing calculator infrequently.
• Always replace batteries before attempting to install a new operating system.
The Display
Types of Displays
The TI-84 Plus displays both text and graphs. Chapter 3 describes graphs. Chapter 9 describes
how the TI-84 Plus can display a horizontally or vertically split screen to show graphs and text
simultaneously.
Home Screen
The home screen is the primary screen of the TI-84 Plus. On this screen, enter instructions to
execute and expressions to evaluate. The answers are displayed on the same screen. Most
calculations are stored in the history on the home screen. You can press } and † to scroll through
the history of entries on the home screen and you can paste the entries or answers to the current
entry line.
Displaying Entries and Answers
• When text is displayed, the TI-84 Plus screen can display a maximum of 8 lines with a
maximum of 16 characters per line in Classic mode. In MathPrint™ mode, fewer lines and
fewer characters per line may be displayed.
• If all lines of the display are full, text scrolls off the top of the display.
- To view previous entries and answers, press }.
- To copy a previous entry or answer and paste it to the current entry line, move the cursor
to the entry or answer you want to copy and press Í.
Note: List and matrix outputs cannot be copied. If you try to copy and paste a list or matrix
output, the cursor returns to the input line.
• If an expression on the home screen, the Y= editor (Chapter 3), or the program editor
(Chapter 16) is longer than one line, it wraps to the beginning of the next line in Classic mode.
In MathPrint™ mode, an expression on the home screen or Y= editor that is longer than one
line scrolls off the screen to the right. An arrow on the right side of the screen indicates that
you can scroll right to see more of the expression. In numeric editors such as the window
screen (Chapter 3), a long expression scrolls to the right and left in both Classic and
MathPrint™ modes. Press y ~ to move the cursor to the end of the line. Press y | to
move the cursor to the beginning of the line.
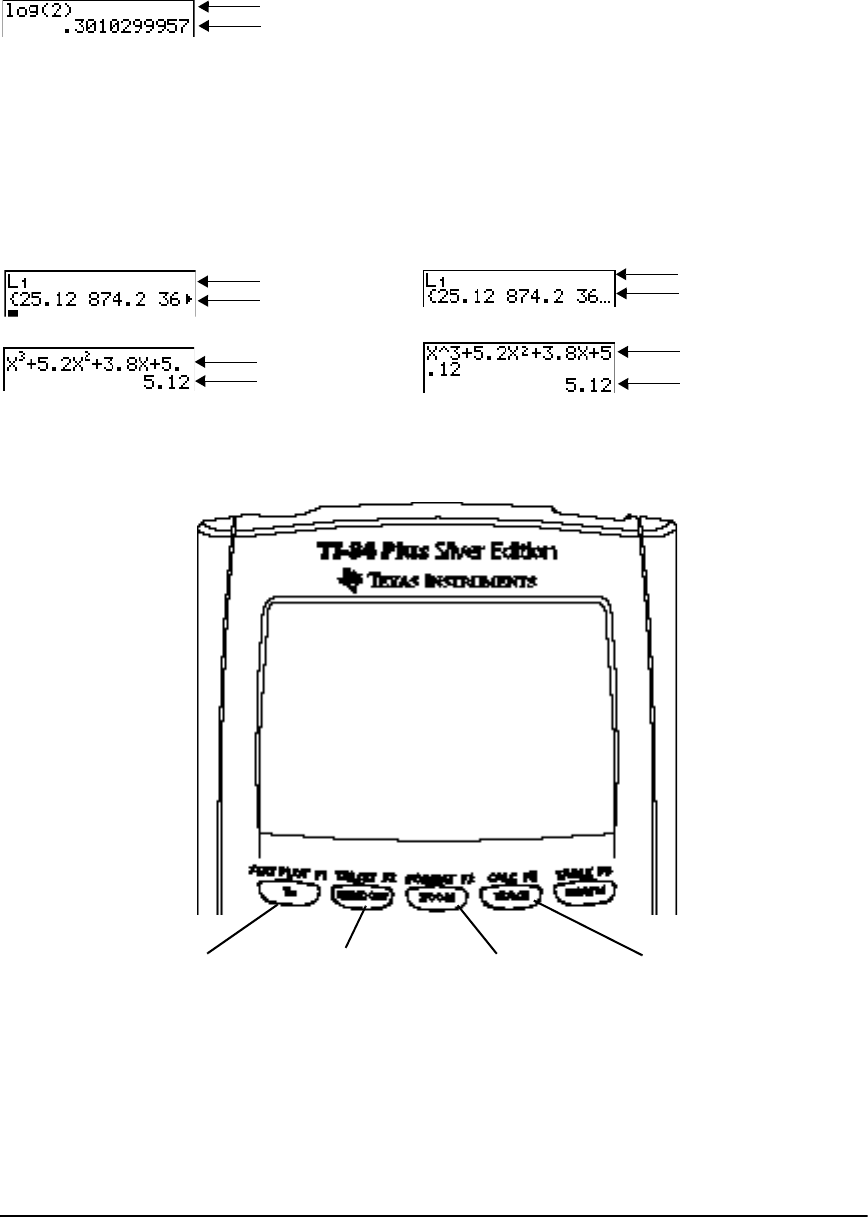
Entry
Answer
t ^
Opens FRAC
menu.
t _
Opens FUNC
menu.
t `
Opens MTRX
menu.
t a
Opens YVAR
menu.
Chapter 1: Operating the TI-84 Plus Silver Edition 6
When an entry is executed on the home screen, the answer is displayed on the right side of the
next line.
The mode settings control the way the TI-84 Plus interprets expressions and displays answers.
If an answer, such as a list or matrix, is too long to display entirely on one line, an arrow
(MathPrint™) or an ellipsis (Classic) is displayed to the right or left. Press ~ and | to display the
answer.
Using Shortcut Menus
Shortcut menus allow quick access to the following:
Answer
Entry
MathPrint™
Answer
Entry
Classic
Answer
Entry
Answer
Entry
Chapter 1: Operating the TI-84 Plus Silver Edition 7
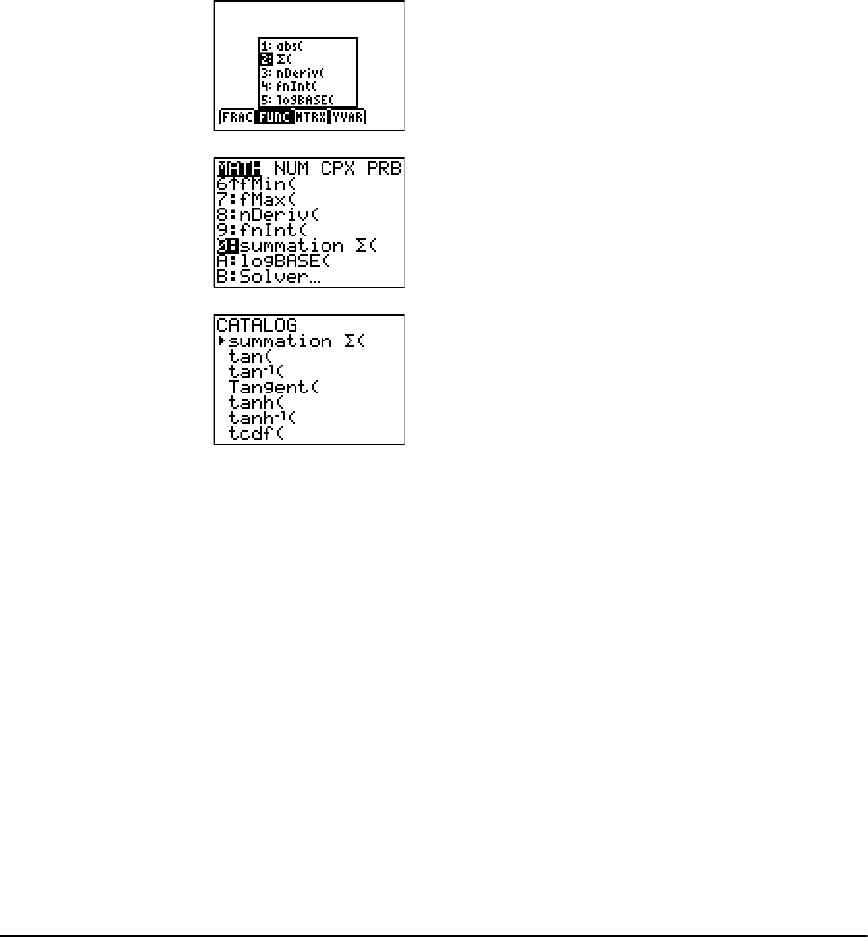
• Templates to enter fractions and selected functions from the MATH MATH and MATH NUM
menus as you would see them in a textbook. Functions include absolute value, summation,
numeric differentiation, numeric integration, and log base n.
• Matrix entry.
• Names of function variables from the VARS Y-VARS menu.
Initially, the menus are hidden. To open a menu, press t plus the F-key that corresponds to
the menu, that is, ^ for FRAC, _ for FUNC, ` for MTRX, or a for YVAR. To select a menu
item, either press the number corresponding to the item, or use the arrow keys to move the cursor
to the appropriate line and then press Í.
All shortcut menu items except matrix templates can also be selected using standard menus. For
example, you can choose the summation template from three places:
The shortcut menus are available to use where input is allowed. If the calculator is in Classic
mode, or if a screen is displayed that does not support MathPrint™ display, entries will be
displayed in Classic display. The MTRX menu is only available in MathPrint™ mode on the home
screen and in the Y= editor.
Note: Shortcut menus may not be available if t plus F-key combinations are used by an
application that is running, such as Inequality Graphing or Transformation Graphing.
Returning to the Home Screen
To return to the home screen from any other screen, press y 5.
FUNC shortcut menu
MATH MATH menu
Catalog

Chapter 1: Operating the TI-84 Plus Silver Edition 8
Busy Indicator
When the TI-84 Plus is calculating or graphing, a vertical moving line is displayed as a busy
indicator in the top-right corner of the screen. When you pause a graph or a program, the busy
indicator becomes a vertical moving dotted line.
Display Cursors
In most cases, the appearance of the cursor indicates what will happen when you press the next
key or select the next menu item to be pasted as a character.
If you press ƒ during an insertion, the cursor becomes an underlined A (A). If you press y
during an insertion, the underlined cursors becomes an underlined # (#).
Note: If you highlight a small character such as a colon or a comma and then press ƒ or y,
the cursor does not change because the cursor width is too narrow.
Graphs and editors sometimes display additional cursors, which are described in other chapters.
Interchangeable Faceplates
The TI-84 Plus Silver Edition has interchangeable faceplates that let you customize the
appearance of your unit. To purchase additional faceplates, refer to the TI Online Store at
education.ti.com.
Cursor Appearance Effect of Next Keystroke
Entry Solid rectangle
$
A character is entered at the cursor; any existing
character is overwritten
Insert Underline
__
A character is inserted in front of the cursor
location
Second Reverse arrow
Þ
A 2nd character is entered or a 2nd operation is
executed
Alpha Reverse A
Ø
An alpha character is entered, SOLVE is
executed, or shortcut menus are displayed.
Full Checkerboard rectangle
#
No entry; the maximum characters are entered at
a prompt or memory is full
MathPrint™ Right arrow The cursor moves to either the next part of the
template or out of the template.
Chapter 1: Operating the TI-84 Plus Silver Edition 9
Removing a Faceplate
1. Lift the tab at the bottom edge of
the faceplate away from the TI-84
Plus Silver Edition case.
2. Carefully lift the faceplate away
from the unit until it releases. Be
careful not to damage the
faceplate or the keyboard.
Installing New Faceplates
1. Align the top of the faceplate in the
corresponding grooves of the TI-84
Plus Silver Edition case.
2. Gently click the faceplate into
place. Do not force.
3. Make sure you gently press each
of the grooves to ensure the
faceplate is installed properly. See
the diagram for proper groove
placement.
Using the Clock
Use the clock to set the time and date, select the clock display format, and turn the clock on and
off. The clock is turned on by default and is accessed from the mode screen.
Displaying the Clock Settings
1. Press z.
2. Press the † to move the cursor to SET CLOCK.
3. Press Í.

Chapter 1: Operating the TI-84 Plus Silver Edition 10
Changing the Clock Settings
1. Press the ~ or | to highlight the date format you
want. Press Í.
2. Press † to highlight YEAR. Press ‘ and type
the year.
3. Press † to highlight MONTH. Press ‘ and
type the number of the month (1-12).
4. Press † to highlight DAY. Press ‘ and type
the date.
5. Press † to highlight TIME. Press ~ or | to
highlight the time format you want. Press Í.
6. Press † to highlight HOUR. Press ‘ and type
the hour (a number from 1-12 or 0-23).
7. Press † to highlight MINUTE. Press ‘ and
type the minutes (a number from 0-59).
8. Press † to highlight AM/PM. Press ~ or | to
highlight the format. Press Í.
9. To save changes, press † to highlight SAVE.
Press Í.
Error Messages
Turning the Clock On
There are two options to turn the clock on. One option is through the MODE screen, the other is
through the Catalog.
If you type the wrong date for the month, for example,
June 31 (June does not have 31 days), you will
receive an error message with two choices:
• To quit the clock application and return to the
home screen, select 1: Quit.
— or —
• To return to the clock application and correct the
error, select 2: Goto.

Chapter 1: Operating the TI-84 Plus Silver Edition 11
Using the Mode Screen to turn the clock on
1. If the clock is turned off, Press † to highlight TURN
CLOCK ON.
2. Press Í Í.
Using the Catalog to turn the clock on
1. If the clock is turned off, Press y N
2. Press † or } to scroll the CATALOG until the
selection cursor points to ClockOn.
3. Press Í Í.
Turning the Clock Off
1. Press y N.
2. Press † or } to scroll the CATALOG until the
selection cursor points to ClockOff.
3. Press Í Í.
Entering Expressions and Instructions
What Is an Expression?
An expression is a group of numbers, variables, functions and their arguments, or a combination of
these elements. An expression evaluates to a single answer. On the TI-84 Plus, you enter an
expression in the same order as you would write it on paper. For example, pR2 is an expression.
You can use an expression on the home screen to calculate an answer. In most places where a
value is required, you can use an expression to enter a value.
Chapter 1: Operating the TI-84 Plus Silver Edition 12
Entering an Expression
To create an expression, you enter numbers, variables, and functions using the keyboard and
menus. An expression is completed when you press Í, regardless of the cursor location. The
entire expression is evaluated according to Equation Operating System (EOS™) rules, and the
answer is displayed according to the mode setting for Answer.
Most TI-84 Plus functions and operations are symbols comprising several characters. You must
enter the symbol from the keyboard or a menu; do not spell it out. For example, to calculate the log
of 45, you must press « 45. Do not enter the letters L, O, and G. If you enter LOG, the TI-84 Plus
interprets the entry as implied multiplication of the variables L, O, and G.
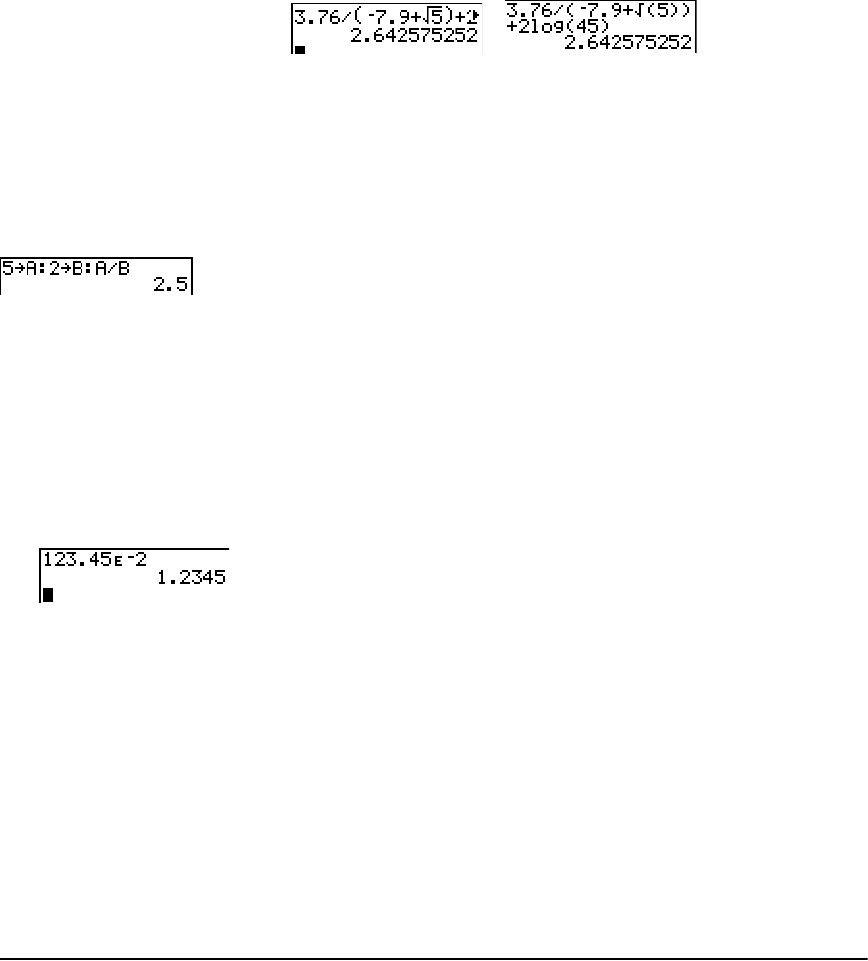
Calculate 3.76 P (L7.9 + ‡5) + 2 log 45.
Multiple Entries on a Line
To enter two or more expressions or instructions on a line, separate them with colons (ƒ [:]).
All instructions are stored together in last entry (ENTRY).
Entering a Number in Scientific Notation
1. Enter the part of the number that precedes the exponent. This value can be an expression.
2. Press y D. â is pasted to the cursor location.
3. Enter the exponent, which can be one or two digits.
Note: If the exponent is negative, press Ì, and then enter the exponent.
When you enter a number in scientific notation, the TI-84 Plus does not automatically display
answers in scientific or engineering notation. The mode settings and the size of the number
determine the display format.
Functions
A function returns a value. For example, ÷, L, +, ‡, and log( are the functions in the example on the
previous page. In general, the first letter of each function is lowercase on the TI-84 Plus. Most
functions take at least one argument, as indicated by an open parenthesis following the name. For
example, sin( requires one argument, sin(value).
3 Ë 76 ¥ £ Ì 7 Ë 9 Ã
y C 5 ¤ ¤ Ã 2 « 45 ¤
Í
MathPrint™
Classic

Chapter 1: Operating the TI-84 Plus Silver Edition 13
Note: The Catalog Help App contains syntax information for most of the functions in the catalog.
Instructions
An instruction initiates an action. For example, ClrDraw is an instruction that clears any drawn
elements from a graph. Instructions cannot be used in expressions. In general, the first letter of
each instruction name is uppercase. Some instructions take more than one argument, as indicated
by an open parenthesis at the end of the name. For example, Circle( requires three arguments,
Circle(X,Y,radius).
Interrupting a Calculation
To interrupt a calculation or graph in progress, which is indicated by the busy indicator, press É.
When you interrupt a calculation, a menu is displayed.
• To return to the home screen, select 1:Quit.
• To go to the location of the interruption, select 2:Goto.
When you interrupt a graph, a partial graph is displayed.
• To return to the home screen, press ‘ or any non-graphing key.
• To restart graphing, press a graphing key or select a graphing instruction.
TI-84 Plus Edit Keys
Keystrokes Result
~ or |Moves the cursor within an expression; these keys repeat.
} or †Moves the cursor from line to line within an expression that occupies
more than one line; these keys repeat.
Moves the cursor from term to term within an expression in MathPrint™
mode; these keys repeat.
On the home screen, scrolls through the history of entries and answers.
y | Moves the cursor to the beginning of an expression.
y ~ Moves the cursor to the end of an expression.
y }On the home screen, moves the cursor out of a MathPrint™ expression.
In the Y=editor, moves the cursor from a MathPrint™ expression to the
previous Y-var.
y †In the Y=editor, moves the cursor from a MathPrint ™ expression to the
next Y-var.
ÍEvaluates an expression or executes an instruction.
‘On a line with text on the home screen, clears the current line.
On a blank line on the home screen, clears everything on the home
screen.
In an editor, clears the expression or value where the cursor is located; it
does not store a zero.

Chapter 1: Operating the TI-84 Plus Silver Edition 14
Setting Modes
Checking Mode Settings
Mode settings control how the TI-84 Plus displays and interprets numbers and graphs. Mode
settings are retained by the Constant ‘Memory™ feature when the TI-84 Plus is turned off. All
numbers, including elements of matrices and lists, are displayed according to the current mode
settings.
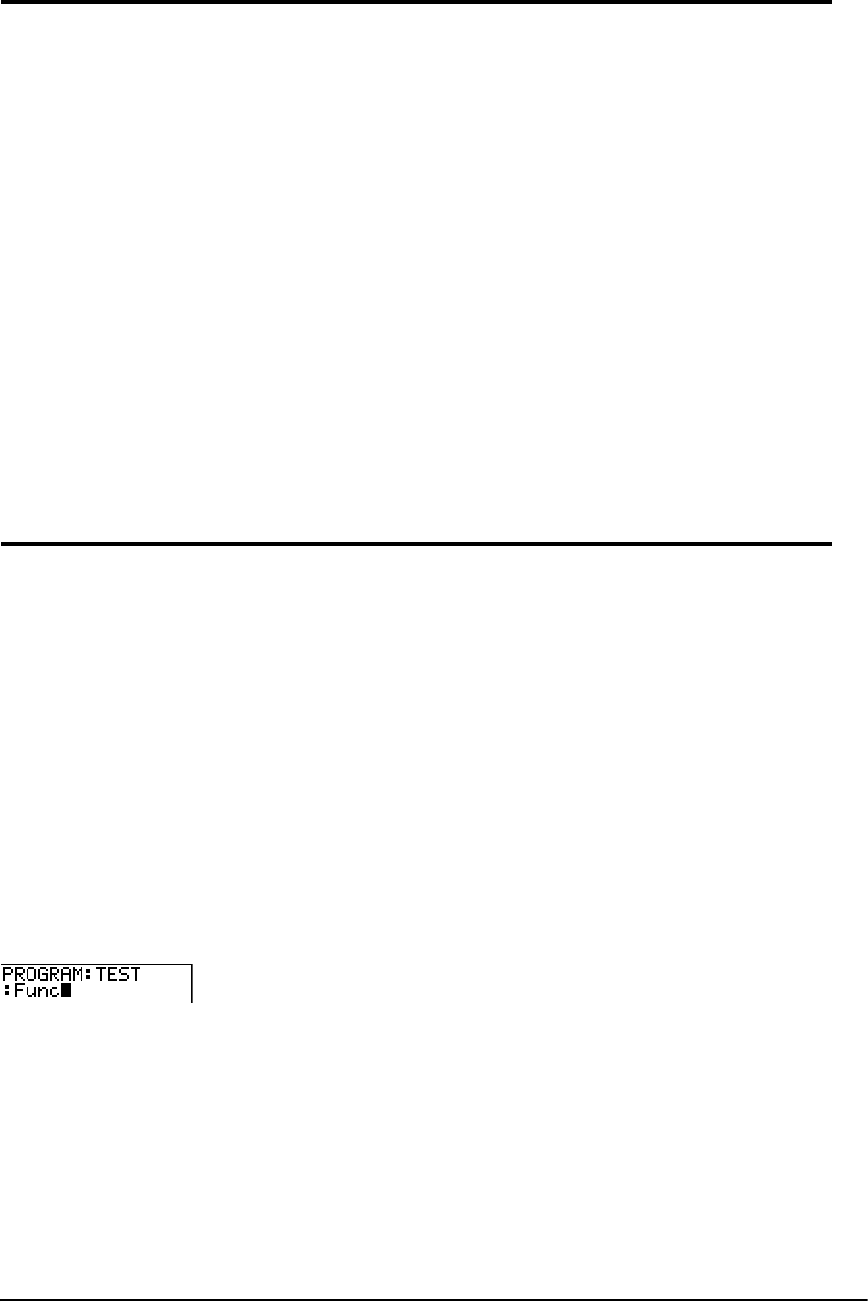
To display the mode settings, press z. The current settings are highlighted. Defaults are
highlighted below. The following pages describe the mode settings in detail.
{Deletes a character at the cursor; this key repeats.
y 6 Changes the cursor to an underline (__); inserts characters in front of the
underline cursor; to end insertion, press y 6 or press |, }, ~, or
†.
yChanges the cursor to Þ; the next keystroke performs a 2nd function
(displayed above a key and to the left); to cancel 2nd, press y again.
ƒChanges the cursor to Ø; the next keystroke performs a third function of
that key (displayed above a key and to the right), executes SOLVE
(Chapters 10 and 11), or accesses a shortcut menu; to cancel ƒ,
press ƒ or press |, }, ~, or †.
y 7 Changes the cursor to Ø; sets alpha-lock; subsequent keystrokes
access the third functions of the keys pressed; to cancel alpha-lock,
press ƒ. If you are prompted to enter a name such as for a group or
a program, alpha-lock is set automatically.
„Pastes an X in Func mode, a T in Par mode, a q in Pol mode, or an n in
Seq mode with one keystroke.
Normal Sci Eng Numeric notation
Float 0123456789 Number of decimal places in answers
Radian Degree Unit of angle measure
Func Par Pol Seq Type of graphing
Connected Dot Whether to connect graph points
Sequential Simul Whether to plot simultaneously
Real a+bi re^qiReal, rectangular complex, or polar complex
Full Horiz G-T Full screen, two split-screen modes
MathPrint Classic Controls whether inputs and outputs on the home screen and in
the Y= editor are displayed as they are in textbooks
n/d Un/d Displays results as simple fractions or mixed fractions
Answers: Auto Dec Frac Controls the format of the answers
Keystrokes Result
Chapter 1: Operating the TI-84 Plus Silver Edition 15
Changing Mode Settings
To change mode settings, follow these steps.
1. Press † or } to move the cursor to the line of the setting that you want to change.
2. Press ~ or | to move the cursor to the setting you want.
3. Press Í.
Setting a Mode from a Program
You can set a mode from a program by entering the name of the mode as an instruction; for
example, Func or Float. From a blank program command line, select the mode setting from the
mode screen; the instruction is pasted to the cursor location.
Normal, Sci, Eng
Notation modes only affect the way an answer is displayed on the home screen. Numeric answers
can be displayed with up to 10 digits and a two-digit exponent and as fractions. You can enter a
number in any format.
Normal notation mode is the usual way we express numbers, with digits to the left and right of the
decimal, as in 12345.67.
GoTo Format Graph: No Yes Shortcut to the Format Graph screen (y .)
StatDiagnostics: Off On Determines which information is displayed in a statistical
regression calculation
StatWizards: On Off Determines if syntax help prompts are provided for optional and
required arguments for many statistical, regression and
distribution commands and functions.
On: Selection of menu items in STAT CALC, DISTR
DISTR, DISTR DRAW and seq( in LIST OPS displays a
screen which provides syntax help (wizard) for the entry
of required and optional arguments into the command or
function. The function or command will paste the entered
arguments to the Home Screen history or to most other
locations where the cursor is available for input. Some
calculations will compute directly from the wizard. If a
command or function is accessed from N the
command or function will paste without wizard support.
Run the Catalog Help application (Œ) for more syntax
help when needed.
Off: The function or command will paste to the cursor
location with no syntax help (wizard).
Set Clock Sets the time and date

Chapter 1: Operating the TI-84 Plus Silver Edition 16
Sci (scientific) notation mode expresses numbers in two parts. The significant digits display with
one digit to the left of the decimal. The appropriate power of 10 displays to the right of å, as in
1.234567â4.
Eng (engineering) notation mode is similar to scientific notation. However, the number can have
one, two, or three digits before the decimal; and the power-of-10 exponent is a multiple of three, as
in 12.34567â3.
Note: If you select Normal notation, but the answer cannot display in 10 digits (or the absolute
value is less than .001), the TI-84 Plus expresses the answer in scientific notation.
Float, 0123456789
Float (floating) decimal mode displays up to 10 digits, plus the sign and decimal.
0123456789 (fixed) decimal mode specifies the number of digits (0 through 9) to display to the right
of the decimal for decimal answers.
The decimal setting applies to Normal, Sci, and Eng notation modes.
The decimal setting applies to these numbers, with respect to the Answer mode setting:
• An answer displayed on the home screen
• Coordinates on a graph (Chapters 3, 4, 5, and 6)
•The
Tangent( DRAW instruction equation of the line, x, and dy/dx values (Chapter 8)
• Results of CALCULATE operations (Chapters 3, 4, 5, and 6)
• The regression equation stored after the execution of a regression model (Chapter 12)
Radian, Degree
Angle modes control how the TI-84 Plus interprets angle values in trigonometric functions and
polar/rectangular conversions.
Radian mode interprets angle values as radians. Answers display in radians.
Degree mode interprets angle values as degrees. Answers display in degrees.
Func, Par, Pol, Seq
Graphing modes define the graphing parameters. Chapters 3, 4, 5, and 6 describe these modes in
detail.
Func (function) graphing mode plots functions, where Y is a function of X (Chapter 3).
Par (parametric) graphing mode plots relations, where X and Y are functions of T (Chapter 4).
Pol (polar) graphing mode plots functions, where r is a function of q (Chapter 5).
Chapter 1: Operating the TI-84 Plus Silver Edition 17
Seq (sequence) graphing mode plots sequences (Chapter 6).
Connected, Dot
Connected plotting mode draws a line connecting each point calculated for the selected functions.
Dot plotting mode plots only the calculated points of the selected functions.
Sequential, Simul
Sequential graphing-order mode evaluates and plots one function completely before the next
function is evaluated and plotted.
Simul (simultaneous) graphing-order mode evaluates and plots all selected functions for a single
value of X and then evaluates and plots them for the next value of X.
Note: Regardless of which graphing mode is selected, the TI-84 Plus will sequentially graph all stat
plots before it graphs any functions.
Real, a+bi, re^qi
Real mode does not display complex results unless complex numbers are entered as input.
Two complex modes display complex results.
•a+bi (rectangular complex mode) displays complex numbers in the form a+bi.
•re^qi (polar complex mode) displays complex numbers in the form re^qi.
Note: When you use the n/d template, both n and d must be real numbers. For example, you can
enter (the answer is displayed as a decimal value) but if you enter , a data type error
displays. To perform division with a complex number in the numerator or denominator, use regular
division instead of the n/d template.
Full, Horiz, G-T
Full screen mode uses the entire screen to display a graph or edit screen.
Each split-screen mode displays two screens simultaneously.

Chapter 1: Operating the TI-84 Plus Silver Edition 18
•Horiz (horizontal) mode displays the current graph on the top half of the screen; it displays the
home screen or an editor on the bottom half (Chapter 9).
•G-T (graph-table) mode displays the current graph on the left half of the screen; it displays the
table screen on the right half (Chapter 9).
MathPrint™, Classic
MathPrint™ mode displays most inputs and outputs the way they are shown in textbooks, such as
and .
Classic mode displays expressions and answers as if written on one line, such as 1/2 + 3/4.
Note: If you switch between these modes, most entries will be preserved; however matrix
calculations will not be preserved.
n/d, Un/d
n/d displays results as a simple fraction. Fractions may contain a maximum of six digits in the
numerator; the value of the denominator may not exceed 9999.
Un/d displays results as a mixed number, if applicable. U, n, and d must be all be integers. If U is a
non-integer, the result may be converted U … n/d. If n or d is a non-integer, a syntax error is
displayed. The whole number, numerator, and denominator may each contain a maximum of three
digits.
Answers: Auto, Dec, Frac
Auto displays answers in a similar format as the input. For example, if a fraction is entered in an
expression, the answer will be in fraction form, if possible. If a decimal appears in the expression,
the output will be a decimal number.
Dec displays answers as integers or decimal numbers.
Frac displays answers as fractions, if possible.
Note: The Answers mode setting also affects how values in sequences, lists, and tables are
displayed. Choose Dec or Frac to ensure that values are displayed in either decimal or fraction
form. You can also convert values from decimal to fraction or fraction to decimal using the FRAC
shortcut menu or the MATH menu.
GoTo Format Graph: No, Yes
No does not display the FORMAT graph screen, but can always be accessed by pressing
y ..
1
2
---3
4
---+ x2xd
1
2
∫

Chapter 1: Operating the TI-84 Plus Silver Edition 19
Yes leaves the mode screen and displays the FORMAT graph screen when you press Í so
that you can change the graph format settings. To return to the mode screen, press z.
Stat Diagnostics: Off, On
Off displays a statistical regression calculation without the correlation coefficient (r) or the
coefficient of determination (r2).
On displays a statistical regression calculation with the correlation coefficient (r), and the
coefficient of determination (r2), as appropriate.
Stat Wizards: On, Off
On: Selection of menu items in STAT CALC, DISTR DISTR, DISTR DRAW and seq( in LIST OPS
displays a screen which provides syntax help (wizard) for the entry of required and optional
arguments into the command or function. The function or command will paste the entered
arguments to the Home Screen history or to most other locations where the cursor is available for
input. Some calculations will compute directly from the wizard. If a command or function is
accessed from N the command or function will paste without wizard support. Run the
Catalog Help application (Œ) for more syntax help when needed.
Off: The function or command will paste to the cursor location with no syntax help (wizard)
Set Clock
Use the clock to set the time, date, and clock display formats.
Using TI-84 Plus Variable Names
Variables and Defined Items
On the TI-84 Plus you can enter and use several types of data, including real and complex
numbers, matrices, lists, functions, stat plots, graph databases, graph pictures, and strings.
The TI-84 Plus uses assigned names for variables and other items saved in memory. For lists, you
also can create your own five-character names.
Variable Type Names
Real numbers (including
fractions)
A, B, ... , Z, q
Complex numbers A, B, ... , Z, q
Matrices ãAä, ãBä, ãCä, ... , ãJä
Lists L1, L2, L3, L4, L5, L6, and user-defined names
Functions Y1, Y2, ... , Y9, Y0
Parametric equations X1T and Y1T, ... , X6T and Y6T

Chapter 1: Operating the TI-84 Plus Silver Edition 20
Notes about Variables
• You can create as many list names as memory will allow (Chapter 11).
• Programs have user-defined names and share memory with variables (Chapter 16).
• From the home screen or from a program, you can store to matrices (Chapter 10), lists
(Chapter 11), strings (Chapter 15), system variables such as Xmax (Chapter 1), TblStart
(Chapter 7), and all Y= functions (Chapters 3, 4, 5, and 6).
• From an editor, you can store to matrices, lists, and Y= functions (Chapter 3).
• From the home screen, a program, or an editor, you can store a value to a matrix element or a
list element.
• You can use DRAW STO menu items to store and recall graph databases and pictures
(Chapter 8).
• Although most variables can be archived, system variables including r, T, X, Y, and q cannot be
archived (Chapter 18)
•Apps are independent applications.which are stored in Flash ROM. AppVars is a variable
holder used to store variables created by independent applications. You cannot edit or change
variables in AppVars unless you do so through the application which created them.
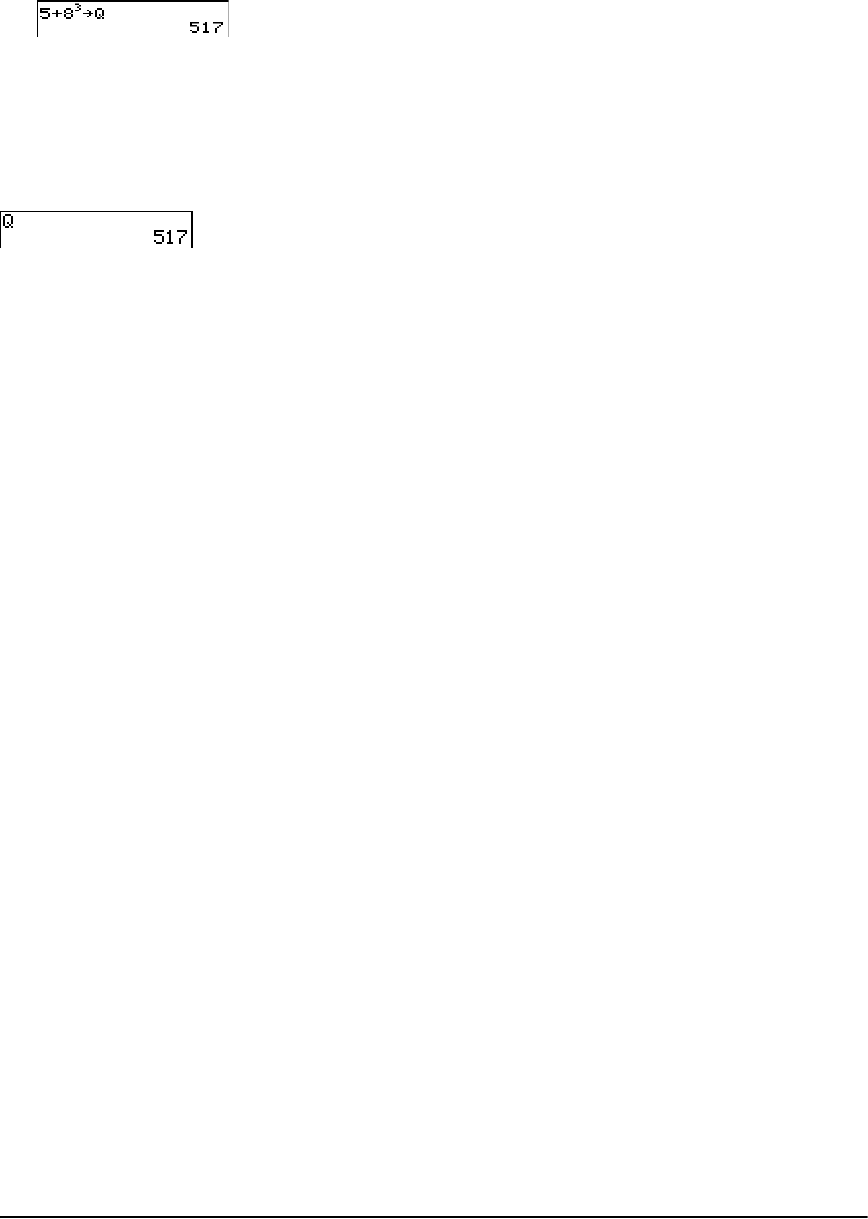
Storing Variable Values
Storing Values in a Variable
Values are stored to and recalled from memory using variable names. When an expression
containing the name of a variable is evaluated, the value of the variable at that time is used.
To store a value to a variable from the home screen or a program using the ¿ key, begin on a
blank line and follow these steps.
1. Enter the value you want to store. The value can be an expression.
2. Press ¿. ! is copied to the cursor location.
Polar functions r1, r2, r3, r4, r5, r6
Sequence functions u, v, w
Stat plots Plot1, Plot2, Plot3
Graph databases GDB1, GDB2, ... , GDB9, GDB0
Graph pictures Pic1, Pic2, ... , Pic9, Pic0
Strings Str1, Str2, ... , Str9, Str0
Apps Applications
AppVars Application variables
Groups Grouped variables
System variables Xmin, Xmax, and others
Variable Type Names
Chapter 1: Operating the TI-84 Plus Silver Edition 21
3. Press ƒ and then the letter of the variable to which you want to store the value.
4. Press Í. If you entered an expression, it is evaluated. The value is stored to the variable.
Displaying a Variable Value
To display the value of a variable, enter the name on a blank line on the home screen, and then
press Í.
Archiving Variables (Archive, Unarchive)
You can archive data, programs, or other variables in a section of memory called user data archive
where they cannot be edited or deleted inadvertently. Archived variables are indicated by asterisks
(ä) to the left of the variable names. Archived variables cannot be edited or executed. They can
only be seen and unarchived. For example, if you archive list L1, you will see that L1 exists in
memory but if you select it and paste the name L1 to the home screen, you won’t be able to see its
contents or edit it until it is unarchived.
Recalling Variable Values
Using Recall (RCL)
To recall and copy variable contents to the current cursor location, follow these steps. To leave
RCL, press ‘.
1. Press y K. RCL and the edit cursor are displayed on the bottom line of the screen.
2. Enter the name of the variable in one of five ways.
• Press ƒ and then the letter of the variable.
• Press y 9, and then select the name of the list, or press y [Ln].
• Press y >, and then select the name of the matrix.
• Press to display the VARS menu or ~ to display the VARS Y-VARS menu; then
select the type and then the name of the variable or function.
• Press t a to display the YVAR shortcut menu, then select the name of the function.
• Press |, and then select the name of the program (in the program editor only).
The variable name you selected is displayed on the bottom line and the cursor disappears.

Chapter 1: Operating the TI-84 Plus Silver Edition 22
3. Press Í. The variable contents are inserted where the cursor was located before you
began these steps.
Note: You can edit the characters pasted to the expression without affecting the value in
memory.
Scrolling Through Previous Entries on the Home Screen
You can scroll up through previous entries and answers on the home screen, even if you have
cleared the screen. When you find an entry or answer that you want to use, you can select it and
paste it on the current entry line.
Note: List and matrix answers cannot be copied and pasted to the new entry line. However, you
can copy the list or matrix command to the new entry line and execute the command again to
display the answer.
fPress } or † to move the cursor to the entry or answer you want to copy and then press
Í. TThe entry or answer that you copied is automatically pasted on the current input line at
the cursor location.
Note: If the cursor is in a MathPrint™ expression, press y } to move the cursor out of the
expression and then move the cursor to the entry or answer you want to copy.
fPress u or { to delete an entry/answer pair. After an entry/answer pair has been
deleted, it cannot be displayed or recalled again.
ENTRY (Last Entry) Storage Area
Using ENTRY (Last Entry)
When you press Í on the home screen to evaluate an expression or execute an instruction,
the expression or instruction is placed in a storage area called ENTRY (last entry). When you turn
off the TI-84 Plus, ENTRY is retained in memory.
To recall ENTRY, press y [. The last entry is pasted to the current cursor location, where
you can edit and execute it. On the home screen or in an editor, the current line is cleared and the
last entry is pasted to the line.

Chapter 1: Operating the TI-84 Plus Silver Edition 23
Because the TI-84 Plus updates ENTRY only when you press Í, you can recall the previous
entry even if you have begun to enter the next expression.
Accessing a Previous Entry
The TI-84 Plus retains as many previous entries as possible in ENTRY, up to a capacity of 128
bytes. To scroll those entries, press y [ repeatedly. If a single entry is more than 128 bytes,
it is retained for ENTRY, but it cannot be placed in the ENTRY storage area.
If you press y [ after displaying the oldest stored entry, the newest stored entry is displayed
again, then the next-newest entry, and so on.
Executing the Previous Entry Again
After you have pasted the last entry to the home screen and edited it (if you chose to edit it), you
can execute the entry. To execute the last entry, press Í.
To execute the displayed entry again, press Í again. Each subsequent execution displays the
entry and the new answer.
Multiple Entry Values on a Line
To store to ENTRY two or more expressions or instructions, separate each expression or
instruction with a colon, then press Í. All expressions and instructions separated by colons
are stored in ENTRY.
5 Ã 7
Í
y [
1 ¿ ƒ A
Í
2 ¿ ƒ B
Í
y [
y [
0 ¿ ƒ N
Í
ƒ N Ã 1 ¿ ƒ N
ƒ ã:䊃ÄN ¡ Í
Í
Í
Chapter 1: Operating the TI-84 Plus Silver Edition 24
When you press y [, all the expressions and instructions separated by colons are pasted to
the current cursor location. You can edit any of the entries, and then execute all of them when you
press Í.
Example: For the equation A=pr2, use trial and error to find the radius of a circle that covers 200
square centimeters. Use 8 as your first guess.
Continue until the answer is as accurate as you want.
Clearing ENTRY
Clear Entries (Chapter 18) clears all data that the TI-84 Plus is holding in the ENTRY storage area.
Using Ans in an Expression
When an expression is evaluated successfully from the home screen or from a program, the TI-84
Plus stores the answer to a storage area called Ans (last answer). Ans may be a real or complex
number, a list, a matrix, or a string. When you turn off the TI-84 Plus, the value in Ans is retained in
memory.
You can use the variable Ans to represent the last answer in most places. Press y Z to copy the
variable name Ans to the cursor location. When the expression is evaluated, the TI-84 Plus uses the
value of Ans in the calculation.
Calculate the area of a garden plot 1.7 meters by 4.2 meters. Then calculate the yield per square
meter if the plot produces a total of 147 tomatoes.
8 ¿ ƒ R ƒ ã:ä
y B ƒ R ¡ Í
y [
y | 7 y 6 Ë 95
Í
1 Ë 7 ¯ 4 Ë 2
Í
147 ¥ y Z
Í

Chapter 1: Operating the TI-84 Plus Silver Edition 25
Continuing an Expression
You can use Ans as the first entry in the next expression without entering the value again or
pressing y Z. On a blank line on the home screen, enter the function. The TI-84 Plus pastes
the variable name Ans to the screen, then the function.
Storing Answers
To store an answer, store Ans to a variable before you evaluate another expression.
Calculate the area of a circle of radius 5 meters. Next, calculate the volume of a cylinder of radius
5 meters and height 3.3 meters, and then store the result in the variable V.
TI-84 Plus Menus
Using a TI-84 Plus Menu
You can access most TI-84 Plus operations using menus. When you press a key or key
combination to display a menu, one or more menu names appear on the top line of the screen.
• The menu name on the left side of the top line is highlighted. Up to seven items in that menu
are displayed, beginning with item 1, which also is highlighted.
• A number or letter identifies each menu item’s place in the menu. The order is 1 through 9,
then 0, then A, B, C, and so on. The LIST NAMES, PRGM EXEC, and PRGM EDIT menus only
label items 1 through 9 and 0.
• When the menu continues beyond the displayed items, a down arrow ($) replaces the colon
next to the last displayed item.
• When a menu item ends in an ellipsis (...), the item displays a secondary menu or editor when
you select it.
• When an asterisk (ä) appears to the left of a menu item, that item is stored in user data archive
(Chapter 18).
5 ¥ 2
Í
¯ 9 Ë 9
Í
y B 5 ¡
Í
¯ 3 Ë 3
Í
¿ ƒ V
Í

Chapter 1: Operating the TI-84 Plus Silver Edition 26
Displaying a Menu
Moving from One Menu to Another
Note: FRAC shortcut menu items are also found on the
MATH NUM menu. FUNC shortcut menu items are
also found on the MATH MATH menu.
Scrolling a Menu
To scroll down the menu items, press †. To scroll up the menu items, press }.
To page down six menu items at a time, press ƒ †. To page up six menu items at a time,
press ƒ }.
To go to the last menu item directly from the first menu item, press }. To go to the first menu item
directly from the last menu item, press †.
While using your TI-84 Plus, you often will need to
access items from its menus.
When you press a key that displays a menu, that
menu temporarily replaces the screen where you are
working. For example, when you press , the
MATH menu is displayed as a full screen.
After you select an item from a menu, the screen
where you are working usually is displayed again.
Some keys access more than one menu. When you
press such a key, the names of all accessible menus
are displayed on the top line. When you highlight a
menu name, the items in that menu are displayed.
Press ~ and | to highlight each menu name.

Chapter 1: Operating the TI-84 Plus Silver Edition 27
Selecting an Item from a Menu
You can select an item from a menu in either of two ways.
Note: On the LIST NAMES, PRGM EXEC, and PRGM EDIT menus, only items 1 through 9 and 0 are
labeled in such a way that you can select them by pressing the appropriate number key. To move
the cursor to the first item beginning with any alpha character or q, press the key combination for
that alpha character or q. If no items begin with that character, the cursor moves beyond it to the
next item.
Example: Calculate 3‡27.
Leaving a Menu without Making a Selection
You can leave a menu without making a selection in any of four ways.
• Press y 5 to return to the home screen.
• Press ‘ to return to the previous screen.
• Press a key or key combination for a different menu, such as or y 9.
• Press a key or key combination for a different screen, such as o or y 0.
VARS and VARS Y-VARS Menus
VARS Menu
You can enter the names of functions and system variables in an expression or store to them
directly.
• Press the number or letter of the item you want to
select. The cursor can be anywhere on the menu,
and the item you select need not be displayed on
the screen.
• Press † or } to move the cursor to the item you
want, and then press Í.
After you select an item from a menu, the TI-84 Plus
typically displays the previous screen.
† † † Í
27 Í

Chapter 1: Operating the TI-84 Plus Silver Edition 28
To display the VARS menu, press . All VARS menu items display secondary menus, which
show the names of the system variables. 1:Window, 2:Zoom, and 5:Statistics each access more
than one secondary menu.
Selecting a Variable from the VARS Menu or VARS Y-VARS Menu
To display the VARS Y-VARS menu, press ~. 1:Function, 2:Parametric, and 3:Polar display
secondary menus of the Y= function variables.
Note:
• The sequence variables (u, v, w) are located on the keyboard as the second functions of ¬,
−, and ®.
• These Y= function variables are also on the YVAR shortcut menu.
To select a variable from the VARS or VARS Y-VARS menu, follow these steps.
1. Display the VARS or VARS Y-VARS menu.
• Press to display the VARS menu.
• Press ~ to display the VARS Y-VARS menu.
2. Select the type of variable, such as 2:Zoom from the VARS menu or 3:Polar from the
VARS Y-VARS menu. A secondary menu is displayed.
3. If you selected 1:Window, 2:Zoom, or 5:Statistics from the VARS menu, you can press ~ or |
to display other secondary menus.
4. Select a variable name from the menu. It is pasted to the cursor location.
VARS Y-VARS
1: Window... X/Y, T/q, and U/V/W variables
2: Zoom... ZX/ZY, ZT/Zq, and ZU variables
3: GDB... Graph database variables
4: Picture... Picture variables
5: Statistics... XY, G, EQ, TEST, and PTS variables
6: Table... TABLE variables
7: String... String variables
VARS Y-VARS
1: Function... Yn functions
2: Parametric... XnT, YnT functions, also found on the YVARS shortcut
menu
3: Polar... rn functions, also found on the YVARS shortcut menu
4: On/Off... Lets you select/deselect functions

Chapter 1: Operating the TI-84 Plus Silver Edition 29
Equation Operating System (EOS™)
Order of Evaluation
The Equation Operating System (EOS™) defines the order in which functions in expressions are
entered and evaluated on the TI-84 Plus. EOS™ lets you enter numbers and functions in a simple,
straightforward sequence.
EOS™ evaluates the functions in an expression in this order.
Note: Within a priority level, EOS™ evaluates functions from left to right. Calculations within
parentheses are evaluated first.
Implied Multiplication
The TI-84 Plus recognizes implied multiplication, so you need not press ¯ to express
multiplication in all cases. For example, the TI-84 Plus interprets 2p, 4sin(46), 5(1+2), and (2…5)7 as
implied multiplication.
Note: TI-84 Plus implied multiplication rules, although like the TI-83, differ from those of the TI-82.
For example, the TI-84 Plus evaluates 1à2X as (1à2)…X, while the TI-82 evaluates 1à2X as 1à(2…X)
(Chapter 2).
Parentheses
All calculations inside a pair of parentheses are completed first. For example, in the expression
4(1+2), EOS first evaluates the portion inside the parentheses, 1+2, and then multiplies the answer,
3, by 4.
Order Number Function
1Functions that precede the argument, such as ‡, sin(, or log(
2Functions that are entered after the argument, such as 2, M1, !, ¡, r, and
conversions
3Powers and roots, such as 25 or
4 Permutations (nPr) and combinations (nCr)
5 Multiplication, implied multiplication, and division
6 Addition and subtraction
7Relational functions, such as > or
8 Logic operator and
9 Logic operators or and xor
5x32

Chapter 1: Operating the TI-84 Plus Silver Edition 30
Negation
To enter a negative number, use the negation key. Press Ì and then enter the number. On the
TI-84 Plus, negation is in the third level in the EOS™ hierarchy. Functions in the first level, such as
squaring, are evaluated before negation.
Example: MX2, evaluates to a negative number (or 0). Use parentheses to square a negative
number.
Note: Use the ¹ key for subtraction and the Ì key for negation. If you press ¹ to enter a negative
number, as in 9 ¯ ¹ 7, or if you press Ì to indicate subtraction, as in 9 Ì 7, an error occurs. If
you press ƒ A Ì ƒ B, it is interpreted as implied multiplication (A…MB).
Special Features of the TI-84 Plus
Flash – Electronic Upgradability
The TI-84 Plus uses Flash technology, which lets you upgrade to future software versions without
buying a new graphing calculator.
As new functionality becomes available, you can electronically upgrade your TI-84 Plus from the
Internet. Future software versions include maintenance upgrades that will be released free of
charge, as well as new applications and major software upgrades that will be available for
purchase from the TI Web site: education.ti.com. For details, refer to Chapter 19.
1.5 Megabytes of Available Memory
1.5 MB of available memory are built into the TI-84 Plus Silver Edition, and 0.5 MB for the
TI-84 Plus. About 24 kilobytes (K) of RAM (random access memory) are available for you to
compute and store functions, programs, and data.
About 1.5 M of user data archive allow you to store data, programs, applications, or any other
variables to a safe location where they cannot be edited or deleted inadvertently. You can also free
up RAM by archiving variables to user data. For details, refer to Chapter 18.
Applications
Many applications are preloaded on your TI-84 Plus and others can be installed to customize the
TI-84 Plus to your needs. The 1.5 MB archive space lets you store up to 94 applications at one
time on the TI-84 Plus Silver Edition. Applications can also be stored on a computer for later use or
linked unit-to-unit. There are 30 App slots for the TI-84 Plus. For details, refer to Chapter 18.

Chapter 1: Operating the TI-84 Plus Silver Edition 31
Archiving
You can store variables in the TI-84 Plus user data archive, a protected area of memory separate
from RAM. The user data archive lets you:
• Store data, programs, applications or any other variables to a safe location where they cannot
be edited or deleted inadvertently.
• Create additional free RAM by archiving variables.
By archiving variables that do not need to be edited frequently, you can free up RAM for
applications that may require additional memory. For details, refer to: Chapter 18.
Other TI-84 Plus Features
The TI-84 Plus guidebook that is included with your graphing calculator has introduced you to
basic TI-84 Plus operations. This guidebook covers the other features and capabilities of the TI-84
Plus in greater detail.
Graphing
You can store, graph, and analyze up to 10 functions, up to six parametric functions, up to six polar
functions, and up to three sequences. You can use DRAW instructions to annotate graphs.
The graphing chapters appear in this order: Function, Parametric, Polar, Sequence, and DRAW.
For graphing details, refer to Chapters 3, 4, 5, 6, 8.
Sequences
You can generate sequences and graph them over time. Or, you can graph them as web plots or
as phase plots. For details, refer to Chapter 6.
Tables
You can create function evaluation tables to analyze many functions simultaneously. For details,
refer to Chapter 7.
Split Screen
You can split the screen horizontally to display both a graph and a related editor (such as the Y=
editor), the table, the stat list editor, or the home screen. Also, you can split the screen vertically to
display a graph and its table simultaneously. For details, refer to Chapter 9.
Matrices
You can enter and save up to 10 matrices and perform standard matrix operations on them. For
details, refer to Chapter 10.

Chapter 1: Operating the TI-84 Plus Silver Edition 32
Lists
You can enter and save as many lists as memory allows for use in statistical analyses. You can
attach formulas to lists for automatic computation. You can use lists to evaluate expressions at
multiple values simultaneously and to graph a family of curves. For details, refer to:Chapter 11.
Statistics
You can perform one- and two-variable, list-based statistical analyses, including logistic and sine
regression analysis. You can plot the data as a histogram, xyLine, scatter plot, modified or regular
box-and-whisker plot, or normal probability plot. You can define and store up to three stat plot
definitions. For details, refer to Chapter 12.
Inferential Statistics
You can perform 16 hypothesis tests and confidence intervals and 15 distribution functions. You
can display hypothesis test results graphically or numerically. For details, refer to Chapter 13.
Applications
Press Πto see the complete list of applications that came with your graphing calculator.
Visit education.ti.com/guides for additional Flash application guidebooks. For details, refer to
Chapter 14.
CATALOG
The CATALOG is a convenient, alphabetical list of all functions and instructions on the TI-84 Plus.
You can paste any function or instruction from the CATALOG to the current cursor location. For
details, refer to Chapter 15.
Programming
You can enter and store programs that include extensive control and input/output instructions. For
details, refer to Chapter 16.

Chapter 1: Operating the TI-84 Plus Silver Edition 33
Archiving
Archiving allows you to store data, programs, or other variables to user data archive where they
cannot be edited or deleted inadvertently. Archiving also allows you to free up RAM for variables
that may require additional memory.
For details, refer to Chapter 16.
Communication Link
The TI-84 Plus has a USB port using a USB unit-to-unit cable to connect and communicate with
another TI-84 Plus or TI-84 Plus Silver Edition. The TI-84 Plus also has an I/O port using an I/O
unit-to-unit cable to communicate with a TI-84 Plus Silver Edition, a TI-84 Plus, a TI-83 Plus Silver
Edition, a TI-83 Plus, a TI-83, a TI-82, a TI-73, CBL 2™, or a CBR™ System.
With TI Connect™ software and a USB computer cable, you can also link the TI-84 Plus to a
personal computer.
As future software upgrades become available on the TI Web site, you can download the software
to your PC and then use the TI Connect™ software and a USB computer cable to upgrade your
TI-84 Plus.
For details, refer to: Chapter 19
Error Conditions
Diagnosing an Error
The TI-84 Plus detects errors while performing these tasks.
• Evaluating an expression
• Executing an instruction
• Plotting a graph
• Storing a value
When the TI-84 Plus detects an error, it returns an error message as a menu title, such as
ERR:SYNTAX or ERR:DOMAIN. Appendix B describes each error type and possible reasons for the
error.
Archived variables are indicated by asterisks (ä) to the
left of the variable names.

Chapter 1: Operating the TI-84 Plus Silver Edition 34
• If you select 1:Quit (or press y 5 or ‘), then the home screen is displayed.
• If you select 2:Goto, then the previous screen is displayed with the cursor at or near the error
location.
Note: If a syntax error occurs in the contents of a Y= function during program execution, then the
Goto option returns to the Y= editor, not to the program.
Correcting an Error
To correct an error, follow these steps.
1. Note the error type (ERR:error type).
2. Select 2:Goto, if it is available. The previous screen is displayed with the cursor at or near the
error location.
3. Determine the error. If you cannot recognize the error, refer to Appendix B.
4. Correct the expression.
Chapter 2: Math, Angle, and Test Operations 35
Chapter 2:
Math, Angle, and Test Operations
Getting Started: Coin Flip
Getting Started is a fast-paced introduction. Read the chapter for details. For more probability
simulations, try the Probability Simulations App for the TI-84 Plus. You can download this App
from education.ti.com.
Suppose you want to model flipping a fair coin 10 times. You want to track how many of those 10
coin flips result in heads. You want to perform this simulation 40 times. With a fair coin, the
probability of a coin flip resulting in heads is 0.5 and the probability of a coin flip resulting in tails is
0.5.
1. Begin on the home screen. Press | to
display the MATH PRB menu. Press 7 to select
7:randBin( (random Binomial). randBin( is pasted
to the home screen. Press 10 to enter the number
of coin flips. Press ¢. Press Ë 5 to enter the
probability of heads. Press ¢. Press 40 to enter
the number of simulations. Press ¤.
2. Press Í to evaluate the expression.
A list of 40 elements is generated with the first 7
displayed. The list contains the count of heads
resulting from each set of 10 coin flips. The list has
40 elements because this simulation was
performed 40 times. In this example, the coin
came up heads five times in the first set of 10 coin
flips, five times in the second set of 10 coin flips,
and so on.
3. Press ~ or | to view the additional counts in the
list. An arrow (MathPrint™ mode) or an ellipses
(Classic mode) indicate that the list continues
beyond the screen.
4. Press ¿ y d Í to store the data to the
list name L1. You then can use the data for
another activity, such as plotting a histogram
(Chapter 12).
Note: Since randBin( generates random numbers, your
list elements may differ from those in the example.
MathPrint™
Classic

Chapter 2: Math, Angle, and Test Operations 36
Keyboard Math Operations
Using Lists with Math Operations
Math operations that are valid for lists return a list calculated element by element. If you use two
lists in the same expression, they must be the same length.
Addition, Subtraction, Multiplication, Division
You can use + (addition, Ã), N (subtraction, ¹), … (multiplication, ¯), and à (division, ¥) with real
and complex numbers, expressions, lists, and matrices. You cannot use à with matrices. If you
need to input A/2, enter this as A †1/2 or A †.5.
Trigonometric Functions
You can use the trigonometric (trig) functions (sine, ˜; cosine, ™; and tangent, š) with real
numbers, expressions, and lists. The current angle mode setting affects interpretation. For
example, sin(30) in radian mode returns L.9880316241; in degree mode it returns .5.
You can use the inverse trig functions (arcsine, y ?; arccosine, y @; and arctangent,
y A) with real numbers, expressions, and lists. The current angle mode setting affects
interpretation.
Note: The trig functions do not operate on complex numbers.
Power, Square, Square Root
You can use ^ (power, ›), 2 (square, ¡), and ‡( (square root, y C) with real and complex
numbers, expressions, lists, and matrices. You cannot use ‡( with matrices.
valueA+valueB
valueA…valueB
valueA N valueB
valueA à valueB
sin(value)cos(value)tan(value)
sinL1(value)cos
L1(value)tan
L1(value)
MathPrint™: valuepower
Classic: value^power È
value2‡(value) È
Chapter 2: Math, Angle, and Test Operations 37
Inverse
You can use L1 (inverse, œ) with real and complex numbers, expressions, lists, and matrices. The
multiplicative inverse is equivalent to the reciprocal, 1àx.
value-1
log(, 10^(, ln(
You can use log( (logarithm, «), 10^( (power of 10, y G), and ln( (natural log, μ) with real
or complex numbers, expressions, and lists.
Exponential
e^( (exponential, y J) returns the constant e raised to a power. You can use e^( with real or
complex numbers, expressions, and lists.
Constant
e (constant, y [e]) is stored as a constant on the TI-84 Plus. Press y [e] to copy e to the cursor
location. In calculations, the TI-84 Plus uses 2.718281828459 for e.
Negation
M (negation, Ì) returns the negative of value. You can use M with real or complex numbers,
expressions, lists, and matrices.
log(value)MathPrint™: 10power
Classic: 10^(power)
ln(value)
MathPrint™: epower
Classic: e^(power)
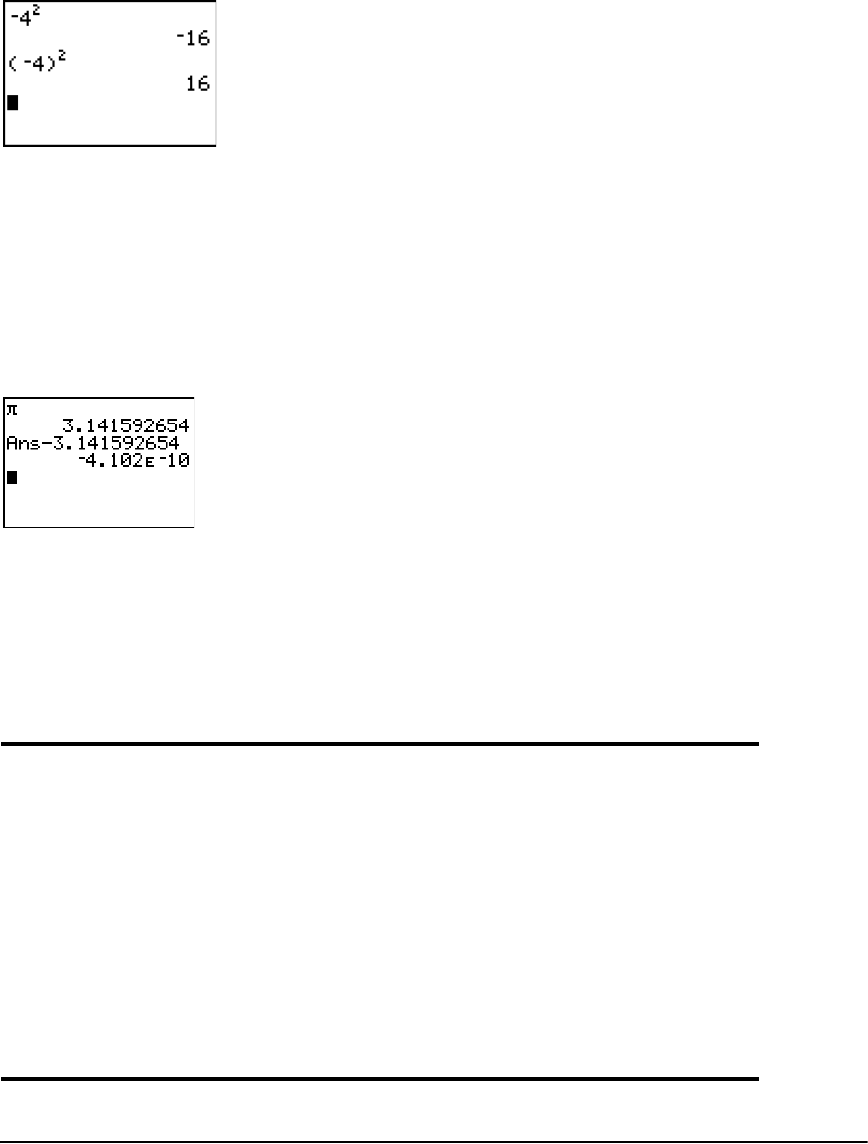
Chapter 2: Math, Angle, and Test Operations 38
Mvalue
EOS™ rules (Chapter 1) determine when negation is evaluated. For example, L42 returns a
negative number, because squaring is evaluated before negation. Use parentheses to square a
negated number, as in (L4)2.
Note: On the TI-84 Plus, the negation symbol (M) is shorter and higher than the subtraction sign (N),
which is displayed when you press ¹.
Pi
p (Pi, y B) is stored as a constant in the TI-84 Plus. In calculations, the TI-84 Plus uses
3.1415926535898 for p.
MATH Operations
MATH Menu
To display the MATH menu, press .
MATH NUM CPX PRB
1: 4Frac Displays the answer as a fraction.
2: 4Dec Displays the answer as a decimal.
3: 3Calculates the cube.
4: 3‡(Calculates the cube root.
5: x‡Calculates the xth root.
6: fMin( Finds the minimum of a function.
7: fMax( Finds the maximum of a function.
8: nDeriv( Computes the numerical derivative.

Chapter 2: Math, Angle, and Test Operations 39
4Frac, 4Dec
4Frac (display as a fraction) displays an answer as its rational equivalent. You can use 4Frac with
real or complex numbers, expressions, lists, and matrices. If the answer cannot be simplified or
the resulting denominator is more than three digits, the decimal equivalent is returned. You can
only use 4Frac following value.
value 4Frac
4Dec (display as a decimal) displays an answer in decimal form. You can use 4Dec with real or
complex numbers, expressions, lists, and matrices. You can only use 4Dec following value.
value 4Dec
Note: You can quickly convert from one number type to the other by using the FRAC shortcut
menu. Press t ^ 4:4F3 4D to convert a value.
Cube, Cube Root
3 (cube) returns the cube of value. You can use 3 with real or complex numbers, expressions, lists,
and square matrices.
value3
3‡( (cube root) returns the cube root of value. You can use 3‡( with real or complex numbers,
expressions, and lists.
3‡(value)
9: fnInt( Computes the function integral.
0: summation )(Returns the sum of elements of list from start to end, where
start <= end.
A: logBASE( Returns the logarithm of a specifed value determined from a
specified base: logBASE(value, base).
B: Solver... Displays the equation solver.
MATH NUM CPX PRB

Chapter 2: Math, Angle, and Test Operations 40
x‡ (Root)
x‡ (xth root) returns the xth root of value. You can use x‡ with real or complex numbers, expressions,
and lists.
xthrootx‡value
fMin(, fMax(
fMin( (function minimum) and fMax( (function maximum) return the value at which the local
minimum or local maximum value of expression with respect to variable occurs, between lower and
upper values for variable. fMin( and fMax( are not valid in expression. The accuracy is controlled by
tolerance (if not specified, the default is 1âL5).
fMin(expression,variable,lower,upper[,tolerance])
fMax(expression,variable,lower,upper[,tolerance])
Note: In this guidebook, optional arguments and the commas that accompany them are enclosed
in brackets ([ ]).
MathPrint™
Classic
nDeriv(
nDeriv( (numerical derivative) returns an approximate derivative of expression with respect to
variable, given the value at which to calculate the derivative and H (if not specified, the default is
1âL3). nDeriv( is valid only for real numbers.

f
′x() fx ε+()fx ε–()–
2ε
------------------------------------------=
Chapter 2: Math, Angle, and Test Operations 41
MathPrint™:
Classic: nDeriv(expression,variable,value[,H])
nDeriv( uses the symmetric difference quotient method, which approximates the numerical
derivative value as the slope of the secant line through these points.
As H becomes smaller, the approximation usually becomes more accurate. In MathPrint™ mode,
the default H is 1EM3. You can switch to Classic mode to change H for investigations.
You can use nDeriv( once in expression. Because of the method used to calculate nDeriv(, the TI-84
Plus can return a false derivative value at a nondifferentiable point.
fnInt(
fnInt( (function integral) returns the numerical integral (Gauss-Kronrod method) of expression with
respect to variable, given lower limit, upper limit, and a tolerance (if not specified, the default is 1âL5).
fnInt( is valid only for real numbers.
In MathPrint™ mode, the default H is 1EM3. You can switch to Classic mode to change H for
investigations.
MathPrint™
Classic
MathPrint™:
Classic: fnInt(expression,variable,lower,upper[,tolerance])

Chapter 2: Math, Angle, and Test Operations 42
Note: To speed the drawing of integration graphs (when fnInt( is used in a Y= equation), increase
the value of the Xres window variable before you press s.
Using the Equation Solver
Solver
Solver displays the equation solver, in which you can solve for any variable in an equation. The
equation is assumed to be equal to zero. Solver is valid only for real numbers.
When you select Solver, one of two screens is displayed.
• The equation editor (see step 1 picture below) is displayed when the equation variable eqn is
empty.
• The interactive solver editor is displayed when an equation is stored in eqn.
Entering an Expression in the Equation Solver
To enter an expression in the equation solver, assuming that the variable eqn is empty, follow
these steps.
1. Select B:Solver from the MATH menu to display the equation editor.
2. Enter the expression in any of three ways.
• Enter the expression directly into the equation solver.
• Paste a Y= variable name from the YVARS shortcut menu (t a) to the equation
solver.
• Press y K, paste a Y= variable name from the YVARS shortcut menu, and press
Í. The expression is pasted to the equation solver.
The expression is stored to the variable eqn as you enter it.
3. Press Í or †. The interactive solver editor is displayed.
• The equation stored in eqn is set equal to zero and displayed on the top line.
• Variables in the equation are listed in the order in which they appear in the equation. Any
values stored to the listed variables also are displayed.

Chapter 2: Math, Angle, and Test Operations 43
• The default lower and upper bounds appear in the last line of the editor
(bound={L1â99,1â99}).
•A $ is displayed in the first column of the bottom line if the editor continues beyond the
screen.
Note: To use the solver to solve an equation such as K=.5MV2, enter eqn:0=KN.5MV2 in the
equation editor.
Entering and Editing Variable Values
When you enter or edit a value for a variable in the interactive solver editor, the new value is stored
in memory to that variable.
You can enter an expression for a variable value. It is evaluated when you move to the next
variable. Expressions must resolve to real numbers at each step during the iteration.
You can store equations to any VARS Y-VARS variables, such as Y1 or r6, and then reference the
variables in the equation. The interactive solver editor displays all variables of all Y= functions
recalled in the equation.
Solving for a Variable in the Equation Solver
To solve for a variable using the equation solver after an equation has been stored to eqn, follow
these steps.
1. Select B:Solver from the MATH menu to display the interactive solver editor, if not already
displayed.
2. Enter or edit the value of each known variable. All variables, except the unknown variable,
must contain a value. To move the cursor to the next variable, press Í or †.

Chapter 2: Math, Angle, and Test Operations 44
3. Enter an initial guess for the variable for which you are solving. This is optional, but it may help
find the solution more quickly. Also, for equations with multiple roots, the TI-84 Plus will
attempt to display the solution that is closest to your guess.
The default guess is calculated as .
4. Edit bound={lower,upper}. lower and upper are the bounds between which the TI-84 Plus searches
for a solution. This is optional, but it may help find the solution more quickly. The default is
bound={L1â99,1â99}.
5. Move the cursor to the variable for which you want to solve and press ƒ \.
• The solution is displayed next to the variable for which you solved. A solid square in the
first column marks the variable for which you solved and indicates that the equation is
balanced. An ellipsis shows that the value continues beyond the screen.
Note: When a number continues beyond the screen, be sure to press ~ to scroll to the
end of the number to see whether it ends with a negative or positive exponent. A very
small number may appear to be a large number until you scroll right to see the exponent.
• The values of the variables are updated in memory.
•leftNrt=diff is displayed in the last line of the editor. diff is the difference between the left
and right sides of the equation when evaluated at the calculated solution. A solid square in
the first column next to leftNrt indicates that the equation has been evaluated at the new
value of the variable for which you solved.
Editing an Equation Stored to eqn
To edit or replace an equation stored to eqn when the interactive equation solver is displayed,
press } until the equation editor is displayed. Then edit the equation.
Equations with Multiple Roots
Some equations have more than one solution. You can enter a new initial guess or new bounds to
look for additional solutions.
Further Solutions
After you solve for a variable, you can continue to explore solutions from the interactive solver
editor. Edit the values of one or more variables. When you edit any variable value, the solid
upper lower+()
2
-----------------------------------------

Chapter 2: Math, Angle, and Test Operations 45
squares next to the previous solution and leftNrt=diff disappear. Move the cursor to the variable for
which you now want to solve and press ƒ \.
Controlling the Solution for Solver or solve(
The TI-84 Plus solves equations through an iterative process. To control that process, enter
bounds that are relatively close to the solution and enter an initial guess within those bounds. This
will help to find a solution more quickly. Also, it will define which solution you want for equations
with multiple solutions.
Using solve( on the Home Screen or from a Program
The function solve( is available only from CATALOG or from within a program. It returns a solution
(root) of expression for variable, given an initial guess, and lower and upper bounds within which the
solution is sought. The default for lower is L1â99. The default for upper is L1â99. solve( is valid only
for real numbers.
solve(expression,variable,guess[,{lower,upper}])
expression is assumed equal to zero. The value of variable will not be updated in memory. guess may
be a value or a list of two values. Values must be stored for every variable in expression, except
variable, before expression is evaluated. lower and upper must be entered in list format.
MATH NUM (Number) Operations
MATH NUM Menu
To display the MATH NUM menu, press ~.
MathPrint™
Classic
MATH NUM CPX PRB
1: abs( Absolute value
2: round( Round
3: iPart( Integer part
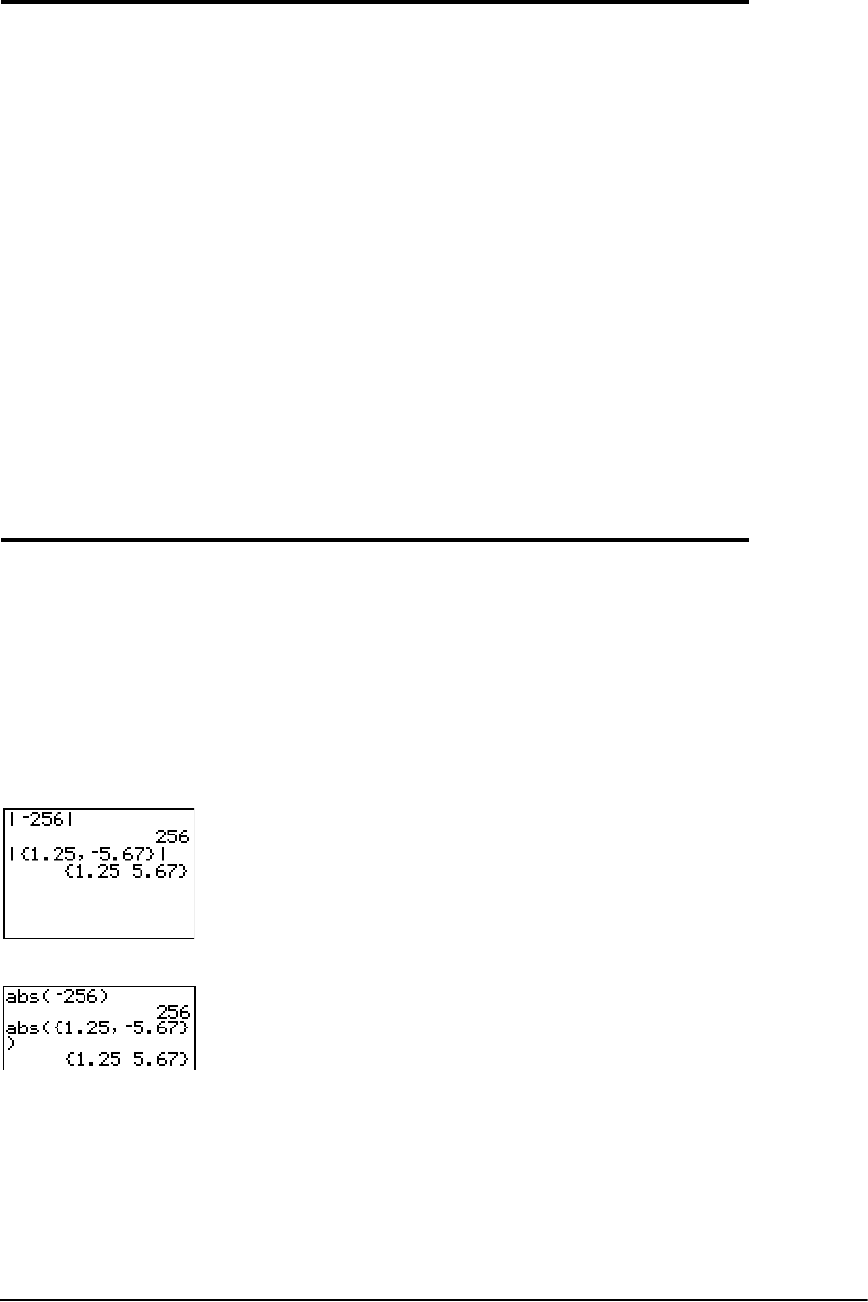
Chapter 2: Math, Angle, and Test Operations 46
abs(
abs( (absolute value) returns the absolute value of real or complex (modulus) numbers,
expressions, lists, and matrices.
Note: abs( is also found on the FUNC shortcut menu (t _ 1).
abs(value)
MathPrint™
Classic
Note: abs( is also available on the MATH CPX menu.
4: fPart( Fractional part
5: int( Greatest integer
6: min( Minimum value
7: max( Maximum value
8: lcm( Least common multiple
9: gcd( Greatest common divisor
0: remainder( Reports the remainder as a whole number from a division of two
whole numbers where the divisor is not zero.
A: 4n/d3 4Un/d Converts an improper fraction to a mixed number or a mixed number
to an improper fraction.
B: 4F3 4DConverts a decimal to a fraction or a fraction to a decimal.
C: Un/d Displays the mixed number template in MathPrint™ mode. In Classic
mode, displays a small u between the whole number and fraction.
D: n/d Displays the fraction template in MathPrint™ mode. In Classic mode,
displays a thick fraction bar between the numerator and the
denominator.
MATH NUM CPX PRB

Chapter 2: Math, Angle, and Test Operations 47
round(
round( returns a number, expression, list, or matrix rounded to #decimals (9). If #decimals is omitted,
value is rounded to the digits that are displayed, up to 10 digits.
round(value[,#decimals])
iPart(, fPart(
iPart( (integer part) returns the integer part or parts of real or complex numbers, expressions, lists,
and matrices.
iPart(value)
fPart( (fractional part) returns the fractional part or parts of real or complex numbers, expressions,
lists, and matrices.
fPart(value)
Note: The way the fractional result is displayed depends on the Answers mode setting. To convert from one
format to another, use 4F3 4D on the FRAC shortcut menu (t ^ 4).
int(
int( (greatest integer) returns the largest integer real or complex numbers, expressions, lists, and
matrices.
int(value)

Chapter 2: Math, Angle, and Test Operations 48
Note: For a given value, the result of int( is the same as the result of iPart( for nonnegative numbers
and negative integers, but one integer less than the result of iPart( for negative noninteger
numbers.
min(, max(
min( (minimum value) returns the smaller of valueA and valueB or the smallest element in list. If listA
and listB are compared, min( returns a list of the smaller of each pair of elements. If list and value
are compared, min( compares each element in list with value.
max( (maximum value) returns the larger of valueA and valueB or the largest element in list. If listA
and listB are compared, max( returns a list of the larger of each pair of elements. If list and value are
compared, max( compares each element in list with value.
Note: min( and max( also are available on the LIST MATH menu.
lcm(, gcd(
lcm( returns the least common multiple of valueA and valueB, both of which must be nonnegative
integers. When listA and listB are specified, lcm( returns a list of the least common multiple of each
pair of elements. If list and value are specified, lcm( finds the least common multiple of each
element in list and value.
gcd( returns the greatest common divisor of valueA and valueB, both of which must be nonnegative
integers. When listA and listB are specified, gcd( returns a list of the greatest common divisor of
each pair of elements. If list and value are specified, gcd( finds the greatest common divisor of each
element in list and value.
min(valueA,valueB)
min(list)
min(listA,listB)
min(list,value)
max(valueA,valueB)
max(list)
max(listA,listB)
max(list,value)
lcm(valueA,valueB)
lcm(listA,listB)
lcm(list,value)
gcd(valueA,valueB)
gcd(listA,listB)
gcd(list,value)

Chapter 2: Math, Angle, and Test Operations 49
remainder(
remainder( returns the remainder resulting from the division of two positive whole numbers, dividend
and divisor, each of which can be a list. The divisor cannot be zero. If both arguments are lists, they
must have the same number of elements. If one argument is a list and the other a non-list, the non-
list is paired with each element of the list, and a list is returned.
4n/d3 4Un/d
4n/d3 4Un/d converts an improper fraction to a mixed number or a mixed number to an improper
fraction. You can also access 4n/d3 4Un/d from the FRAC shortcut menu (t ^ 3).
remainder(dividend, divisor)
remainder(list, divisor)
remainder(dividend, list)
remainder(list, list)
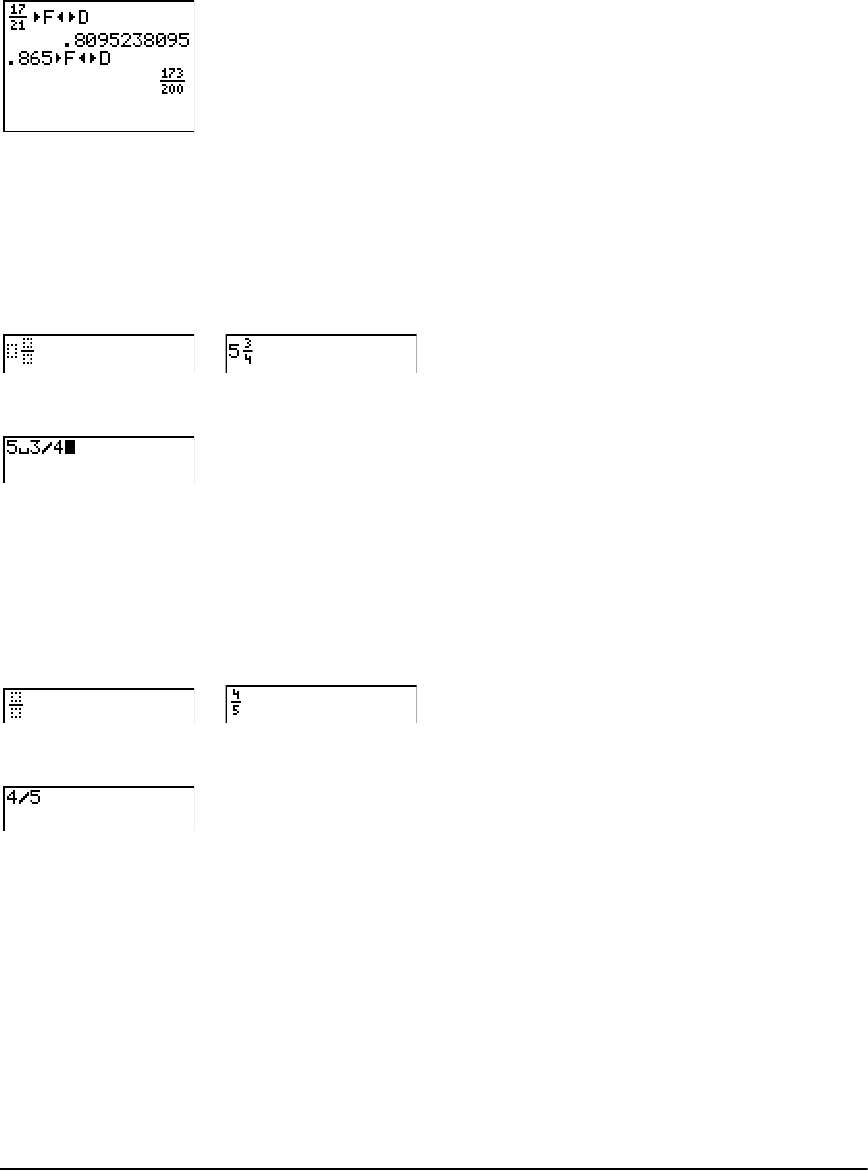
Chapter 2: Math, Angle, and Test Operations 50
4F3 4D
4F3 4D converts a fraction to a decimal or a decimal to a fraction. You can also access 4F3 4D from
the FRAC shortcut menu (t ^ 4).
Un/d
Un/d displays the mixed number template. You can also access Un/d from the FRAC shortcut
menu (t ^ 2). In the fraction, n and d must be non-negative integers.
MathPrint™
"
Classic
n/d
n/d displays the mixed number template. You can also access n/d from the FRAC shortcut menu
(t ^ 1). n and d can be real numbers or expressions but may not contain complex numbers.
MathPrint™
"
Classic
Entering and Using Complex Numbers
Complex-Number Modes
The TI-84 Plus displays complex numbers in rectangular form and polar form. To select a
complex-number mode, press z, and then select either of the two modes.
•a+bi (rectangular-complex mode)
•re^qi (polar-complex mode)
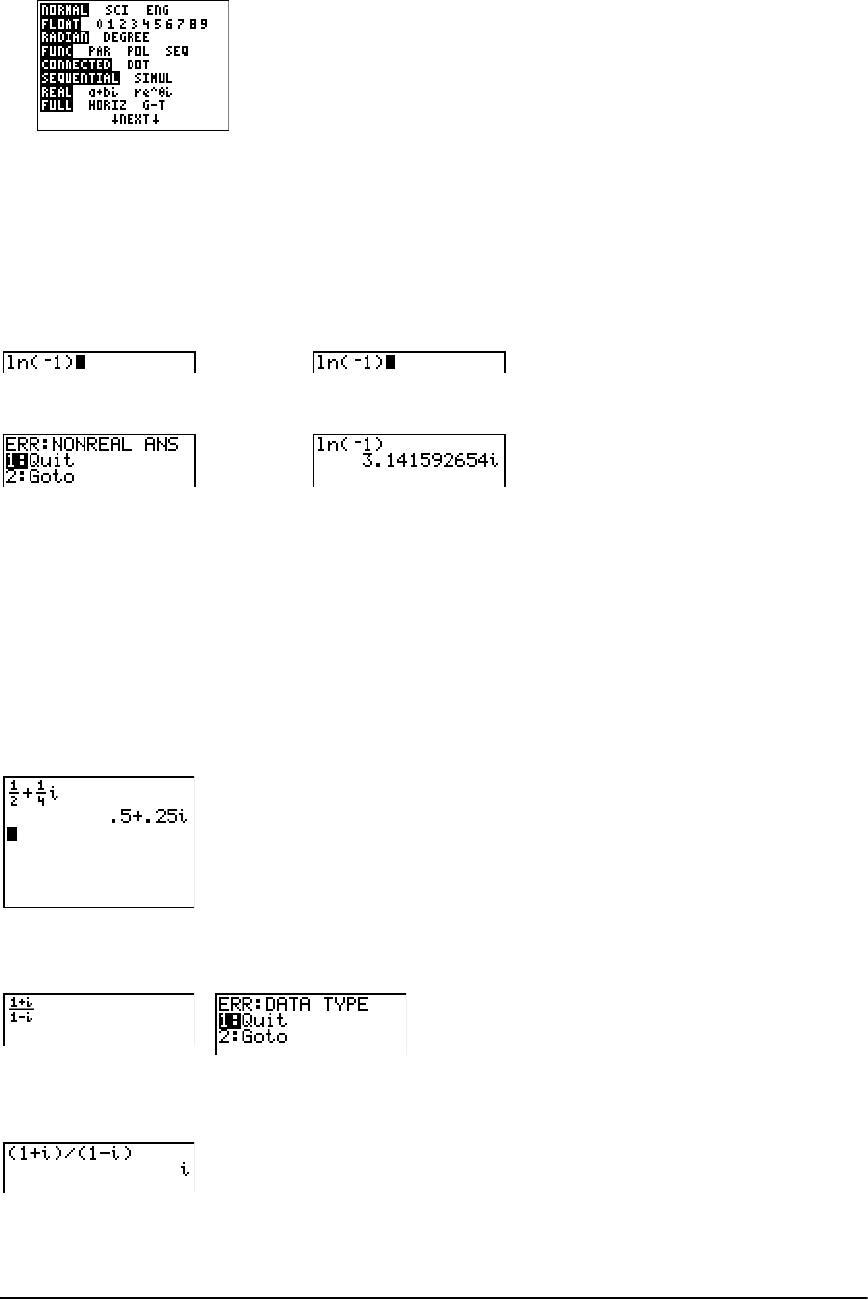
Chapter 2: Math, Angle, and Test Operations 51
On the TI-84 Plus, complex numbers can be stored to variables. Also, complex numbers are valid
list elements.
In Real mode, complex-number results return an error, unless you entered a complex number as
input. For example, in Real mode ln(L1) returns an error; in a+bi mode ln(L1) returns an answer.
Entering Complex Numbers
Complex numbers are stored in rectangular form, but you can enter a complex number in
rectangular form or polar form, regardless of the mode setting. The components of complex
numbers can be real numbers or expressions that evaluate to real numbers; expressions are
evaluated when the command is executed.
You can enter fractions in complex numbers, but the output will always be a decimal value.
When you use the n/d template, a fraction cannot contain a complex number.
"
You can use division to compute the answer:
Real mode a+bi mode
$$

Chapter 2: Math, Angle, and Test Operations 52
Note about Radian Versus Degree Mode
Radian mode is recommended for complex number calculations. Internally, the TI-84 Plus
converts all entered trigonometric values to radians, but it does not convert values for exponential,
logarithmic, or hyperbolic functions.
In degree mode, complex identities such as e^(iq) = cos(q) + i sin(q) are not generally true
because the values for cos and sin are converted to radians, while those for e^() are not. For
example, e^(i45) = cos(45) + i sin(45) is treated internally as e^(i45) = cos(p/4) + i sin(p/4).
Complex identities are always true in radian mode.
Interpreting Complex Results
Complex numbers in results, including list elements, are displayed in either rectangular or polar
form, as specified by the mode setting or by a display conversion instruction. In the example
below, polar-complex (re^qi) and Radian modes are set.
Rectangular-Complex Mode
Rectangular-complex mode recognizes and displays a complex number in the form a+bi, where a is
the real component, b is the imaginary component, and i is a constant equal to .
To enter a complex number in rectangular form, enter the value of a (real component), press à or ¹,
enter the value of b (imaginary component), and press y V (constant).
real component(+ or N)imaginary component i
Polar-Complex Mode
Polar-complex mode recognizes and displays a complex number in the form re^qi, where r is the
magnitude, e is the base of the natural log, q is the angle, and i is a constant equal to .
MathPrint™:
Classic:
1–
1–

Chapter 2: Math, Angle, and Test Operations 53
To enter a complex number in polar form, enter the value of r (magnitude), press y J
(exponential function), enter the value of q (angle), press y V (constant), and then press ¤.
magnitudee^(anglei)
MathPrint™
Classic
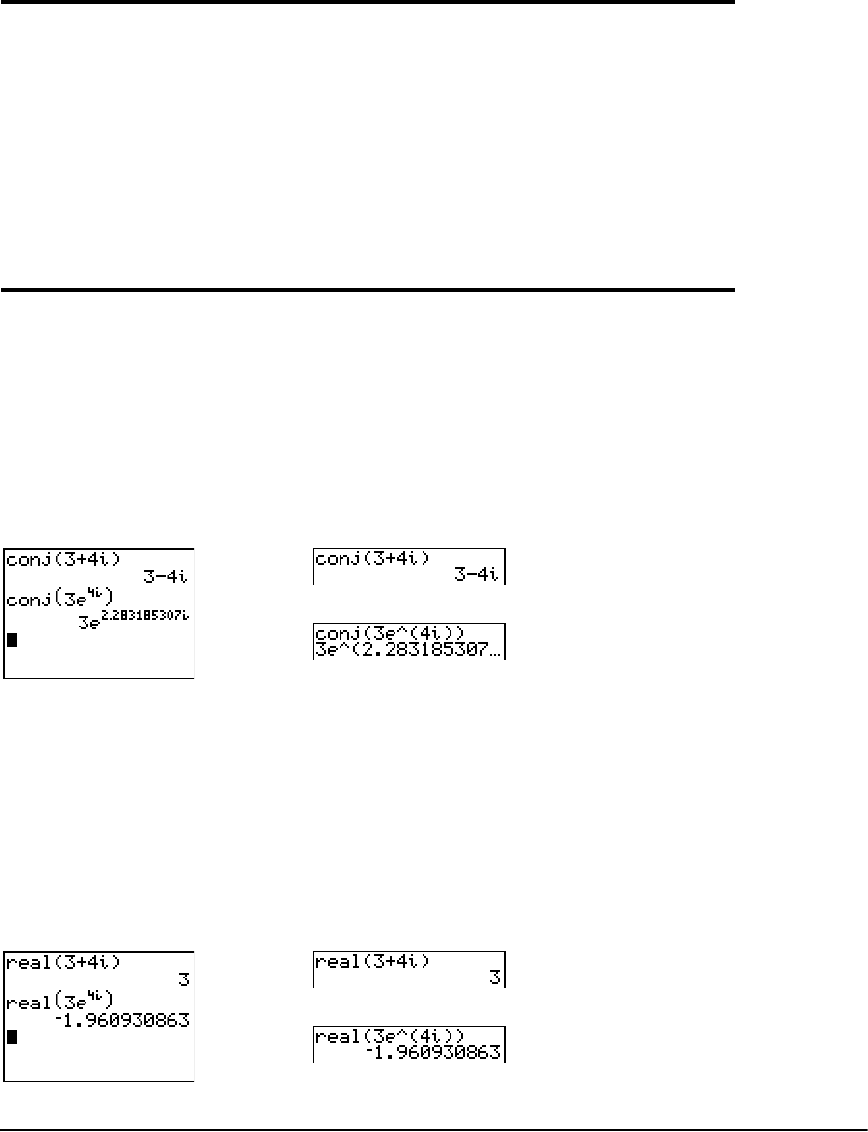
Chapter 2: Math, Angle, and Test Operations 54
MATH CPX (Complex) Operations
MATH CPX Menu
To display the MATH CPX menu, press ~ ~.
conj(
conj( (conjugate) returns the complex conjugate of a complex number or list of complex numbers.
conj(a+bi) returns aNbi in a+bi mode.
conj(re^(qi)) returns re^(Lqi) in re^qi mode.
MathPrint™ Classic
real(
real( (real part) returns the real part of a complex number or list of complex numbers.
real(a+bi) returns a.
real(re^(qi)) returns r†cos(q).
MathPrint™ Classic
MATH NUM CPX PRB
1: conj( Returns the complex conjugate.
2: real( Returns the real part.
3: imag( Returns the imaginary part.
4: angle( Returns the polar angle.
5: abs( Returns the magnitude (modulus).
6: 4Rect Displays the result in rectangular form.
7: 4Polar Displays the result in polar form.
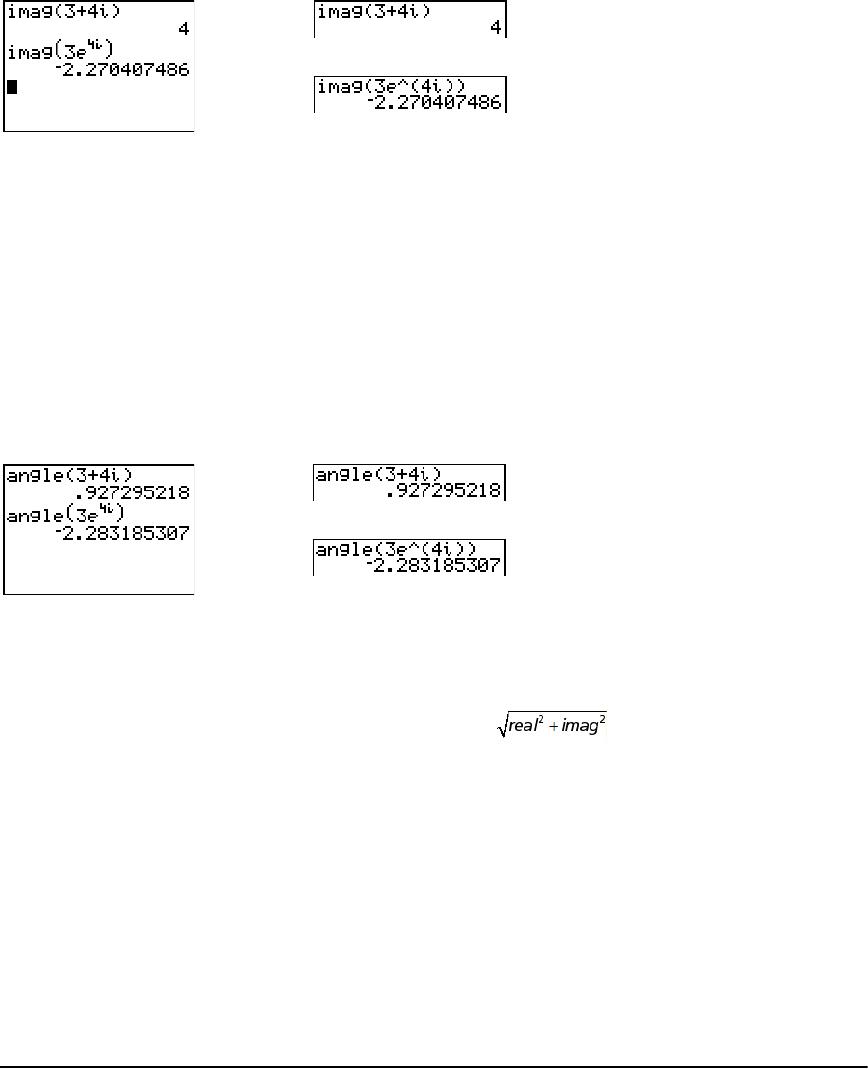
Chapter 2: Math, Angle, and Test Operations 55
imag(
imag( (imaginary part) returns the imaginary (nonreal) part of a complex number or list of complex
numbers.
imag(a+bi) returns b.
imag(re^(qi)) returns r†sin(q).
MathPrint™ Classic
angle(
angle( returns the polar angle of a complex number or list of complex numbers, calculated as tanL1
(b/a), where b is the imaginary part and a is the real part. The calculation is adjusted by +p in the
second quadrant or Np in the third quadrant.
angle(a+bi) returns tanL1(b/a).
angle(re^(qi)) returns q, where Lp<q<p.
MathPrint™ Classic
abs(
abs( (absolute value) returns the magnitude (modulus), , of a complex number or list
of complex numbers. You can also access abs( from the FUNC shortcut menu (t _ 1).
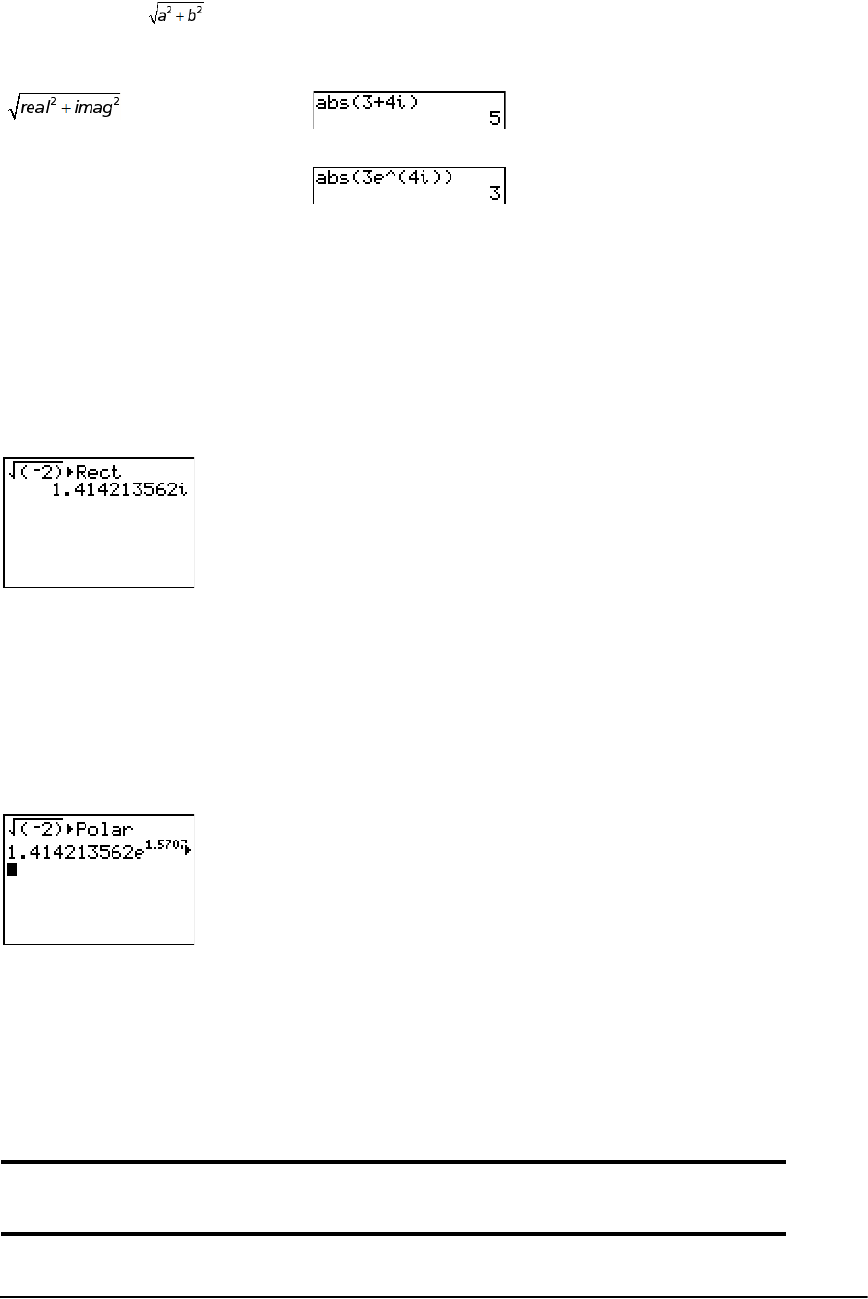
Chapter 2: Math, Angle, and Test Operations 56
abs(a+bi) returns .
abs(re^(qi)) returns r (magnitude).
4Rect
4Rect (display as rectangular) displays a complex result in rectangular form. It is valid only at the
end of an expression. It is not valid if the result is real.
complex result8Rect returns a+bi.
4Polar
4Polar (display as polar) displays a complex result in polar form. It is valid only at the end of an
expression. It is not valid if the result is real.
complex result8Polar returns re^(qi).
MATH PRB (Probability) Operations
MATH PRB Menu
To display the MATH PRB menu, press |.
MATH NUM CPX PRB
1: rand Random-number generator

Chapter 2: Math, Angle, and Test Operations 57
rand
rand (random number) generates and returns one or more random numbers > 0 and < 1. To
generate a list of random-numbers, specify an integer > 1 for numtrials (number of trials). The
default for numtrials is 1.
rand[(numtrials)]
Note: To generate random numbers beyond the range of 0 to 1, you can include rand in an
expression. For example, rand5 generates a random number > 0 and < 5.
With each rand execution, the TI-84 Plus generates the same random-number sequence for a
given seed value. The TI-84 Plus factory-set seed value for rand is 0. To generate a different
random-number sequence, store any nonzero seed value to rand. To restore the factory-set seed
value, store 0 to rand or reset the defaults (Chapter 18).
Note: The seed value also affects randInt(, randNorm(, and randBin( instructions.
nPr, nCr
nPr (number of permutations) returns the number of permutations of items taken number at a time.
items and number must be nonnegative integers. Both items and number can be lists.
items nPr number
nCr (number of combinations) returns the number of combinations of items taken number at a time.
items and number must be nonnegative integers. Both items and number can be lists.
items nCr number
2: nPr Number of permutations
3: nCr Number of combinations
4: ! Factorial
5: randInt( Random-integer generator
6: randNorm( Random # from Normal distribution
7: randBin( Random # from Binomial distribution
8: randIntNoRep( Random ordered list of integers in a range
MATH NUM CPX PRB
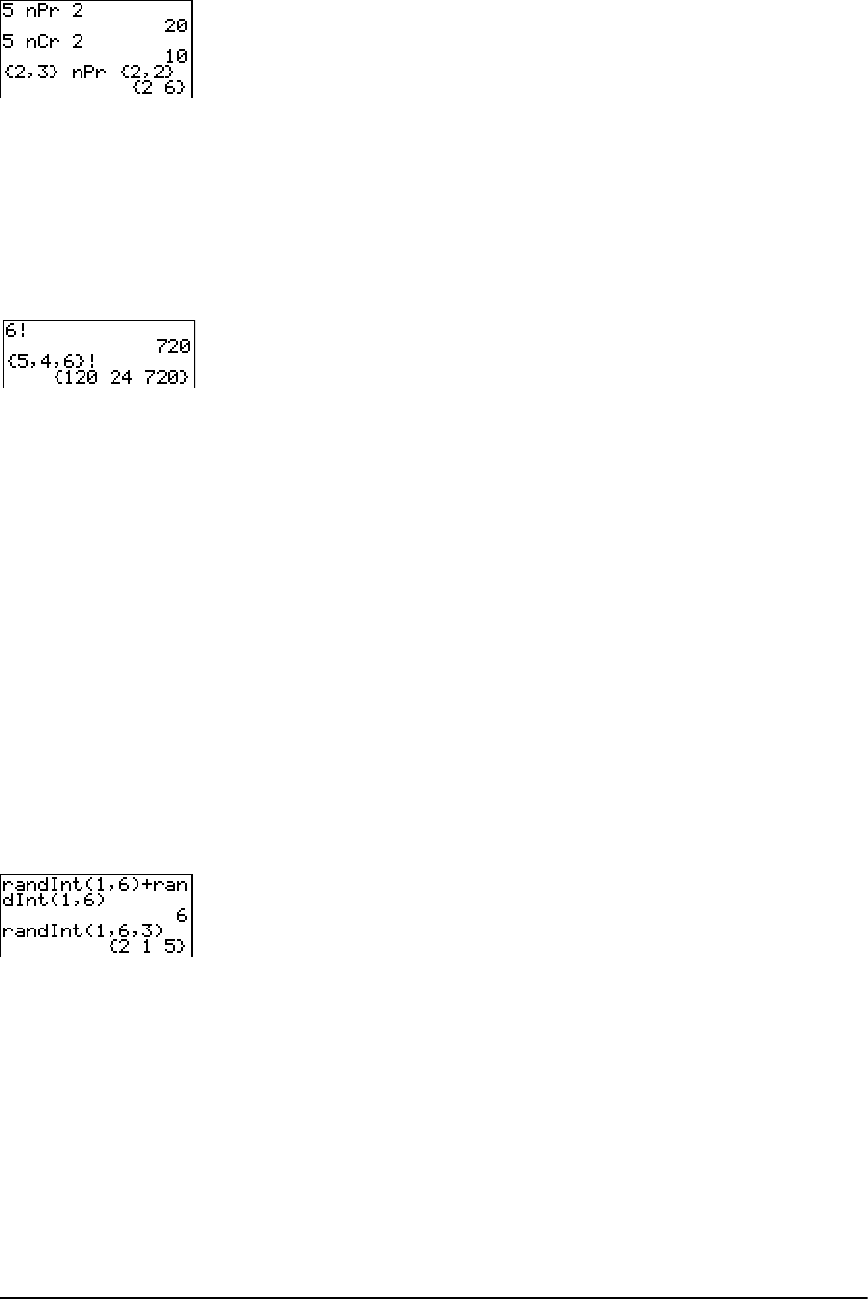
Chapter 2: Math, Angle, and Test Operations 58
Factorial
! (factorial) returns the factorial of either an integer or a multiple of .5. For a list, it returns factorials
for each integer or multiple of .5. value must be ‚ L.5 and 69.
value!
Note: The factorial is computed recursively using the relationship (n+1)! = n…n!, until n is reduced
to either 0 or L1/2. At that point, the definition 0!=1 or the definition (L1à2)!=‡p is used to complete
the calculation. Hence:
n!=n…(nN1)…(nN2)… ... …2…1, if n is an integer ‚ 0
n!= n…(nN1)…(nN2)… ... …1à2…‡p, if n+1à2 is an integer ‚ 0
n! is an error, if neither n nor n+1à2 is an integer ‚ 0.
(The variable n equals value in the syntax description above.)
randInt(
randInt( (random integer) generates and displays a random integer within a range specified by
lower and upper integer bounds. To generate a list of random numbers, specify an integer > 1 for
numtrials (number of trials); if not specified, the default is 1.
randInt(lower,upper[,numtrials])
randNorm(
randNorm( (random Normal) generates and displays a random real number from a specified
Normal distribution. Each generated value could be any real number, but most will be within the
interval [mN3(s), m+3(s)]. To generate a list of random numbers, specify an integer > 1 for numtrials
(number of trials); if not specified, the default is 1.
randNorm(m,s[,numtrials])

Chapter 2: Math, Angle, and Test Operations 59
randBin(
randBin( (random Binomial) generates and displays a random integer from a specified Binomial
distribution. numtrials (number of trials) must be ‚ 1. prob (probability of success) must be ‚ 0 and
1. To generate a list of random numbers, specify an integer > 1 for numsimulations (number of
simulations); if not specified, the default is 1.
randBin(numtrials,prob[,numsimulations])
Note: The seed value stored to rand also affects randInt(, randNorm(, and randBin( instructions.
randIntNoRep(
randIntNoRep( returns a random ordered list of integers from a lower integer to an upper integer.
The list of integers may include the lower integer and the upper integer.
randIntNoRep(lowerint, upperint)
MathPrint™
Classic
ANGLE Operations
ANGLE Menu
To display the ANGLE menu, press y ;. The ANGLE menu displays angle indicators and
instructions. The Radian/Degree mode setting affects the TI-84 Plus’s interpretation of ANGLE
menu entries.
ANGLE
1: ¡Degree notation
2: ' DMS minute notation

Chapter 2: Math, Angle, and Test Operations 60
Entry Notation
DMS (degrees/minutes/seconds) entry notation comprises the degree symbol (¡), the minute
symbol ('), and the second symbol ("). degrees must be a real number; minutes and seconds must be
real numbers ‚ 0.
Note: DMS entry notation does not support fractions in minutes or seconds.
degrees¡minutes'seconds"
For example, we know that 30 degrees is the same as p/6 radians, and we can verify that by
looking at the values in degree and radian modes. If the angle mode is not set to Degree, you must
use ¡ so that the TI-84 Plus can interpret the argument as degrees, minutes, and seconds.
Degree
¡ (degree) designates an angle or list of angles as degrees, regardless of the current angle mode
setting. In Radian mode, you can use ¡ to convert degrees to radians.
value¡
{value1,value2,value3,value4,...,value n}¡
¡ also designates degrees (D) in DMS format.
' (minutes) designates minutes (M) in DMS format.
" (seconds) designates seconds (S) in DMS format.
Note: " is not on the ANGLE menu. To enter ", press ƒ [ã].
3: r Radian notation
4: 8DMS Displays as degree/minute/second
5: R8Pr( Returns r, given X and Y
6: R8Pq(Returns q, given X and Y
7: P8Rx( Returns x, given R and q
8: P8Ry( Returns y, given R and q
Degree mode Radian mode
ANGLE
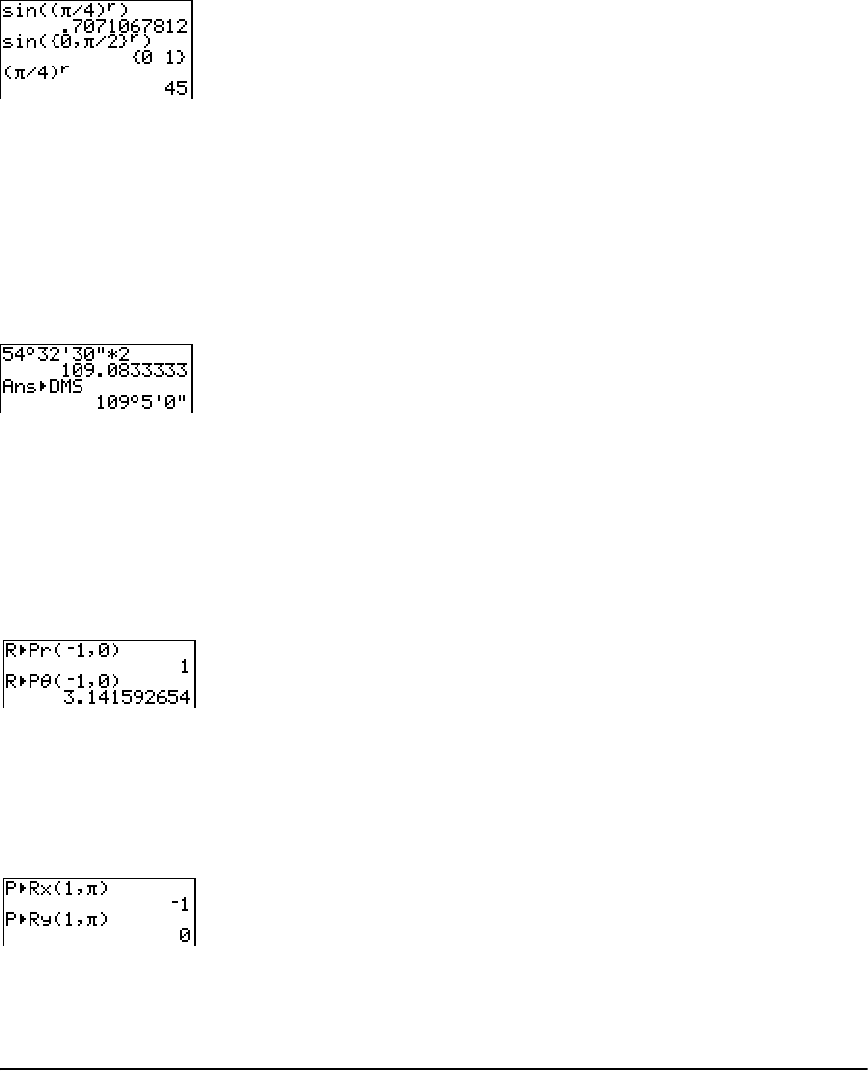
Chapter 2: Math, Angle, and Test Operations 61
Radians
r (radians) designates an angle or list of angles as radians, regardless of the current angle mode
setting. In Degree mode, you can use r to convert radians to degrees.
valuer
Degree mode
8DMS
8DMS (degree/minute/second) displays answer in DMS format. The mode setting must be Degree
for answer to be interpreted as degrees, minutes, and seconds. 8DMS is valid only at the end of a
line.
answer8DMS
R8Pr (, R8Pq(, P8Rx(, P8Ry(
R8Pr( converts rectangular coordinates to polar coordinates and returns r. R8Pq( converts
rectangular coordinates to polar coordinates and returns q. x and y can be lists.
R8Pr(x,y), R8Pq(x,y)
P8Rx( converts polar coordinates to rectangular coordinates and returns x. P8Ry( converts polar
coordinates to rectangular coordinates and returns y. r and q can be lists.
P8Rx(r,q), P8Ry(r,q)
Note: Radian mode is set.
Note: Radian mode is set.

Chapter 2: Math, Angle, and Test Operations 62
TEST (Relational) Operations
TEST Menu
To display the TEST menu, press y :.
Ä=, ƒ, >, ‚, <,
Relational operators compare valueA and valueB and return 1 if the test is true or 0 if the test is false.
valueA and valueB can be real numbers, expressions, or lists. For = and ƒ only, valueA and valueB also
can be matrices or complex numbers. If valueA and valueB are matrices, both must have the same
dimensions.
Relational operators are often used in programs to control program flow and in graphing to control
the graph of a function over specific values.
Using Tests
Relational operators are evaluated after mathematical functions according to EOS rules
(Chapter 1).
• The expression 2+2=2+3 returns 0. The TI-84 Plus performs the addition first because of EOS
rules, and then it compares 4 to 5.
• The expression 2+(2=2)+3 returns 6. The TI-84 Plus performs the relational test first because it
is in parentheses, and then it adds 2, 1, and 3.
This operator... Returns 1 (true) if...
TEST LOGIC
1: = Equal
2: ƒNot equal to
3: > Greater than
4: ‚Greater than or equal to
5: < Less than
6: Less than or equal to
valueA=valueB
valueA>valueB
valueA<valueB
valueAƒvalueB
valueA‚valueB
valueAvalueB

Chapter 2: Math, Angle, and Test Operations 63
TEST LOGIC (Boolean) Operations
TEST LOGIC Menu
To display the TEST LOGIC menu, press y : ~.
Boolean Operators
Boolean operators are often used in programs to control program flow and in graphing to control
the graph of the function over specific values. Values are interpreted as zero (false) or nonzero
(true).
and, or, xor
and, or, and xor (exclusive or) return a value of 1 if an expression is true or 0 if an expression is
false, according to the table below. valueA and valueB can be real numbers, expressions, or lists.
valueA and valueB
valueA or valueB
valueA xor valueB
valueA valueB and or xor
ƒ0ƒ0returns 110
ƒ00returns 011
0ƒ0returns 011
0 0 returns 000
not(
not( returns 1 if value (which can be an expression) is 0.
not(value)
Using Boolean Operations
This operator... Returns a 1 (true) if...
TEST LOGIC
1: and Both values are nonzero (true).
2: or At least one value is nonzero (true).
3: xor Only one value is zero (false).
4: not( The value is zero (false).

Chapter 2: Math, Angle, and Test Operations 64
Boolean logic is often used with relational tests. In the following program, the instructions store 4
into C.
Chapter 3: Function Graphing 65
Chapter 3:
Function Graphing
Getting Started: Graphing a Circle
Getting Started is a fast-paced introduction. Read the chapter for details.
Graph a circle of radius 10, centered on the origin in the standard viewing window. To graph this
circle, you must enter separate formulas for the upper and lower portions of the circle. Then use
ZSquare (zoom square) to adjust the display and make the functions appear as a circle.
1. In Func mode, press o to display the Y= editor.
Press y C £ 100 ¹ „ ¡ ¤ Í to
enter the expression Y=‡(100NX2), which defines
the top half of the circle.
The expression Y=L‡(100NX2) defines the bottom
half of the circle. On the TI-84 Plus, you can define
one function in terms of another. To define Y2=LY1,
press Ì to enter the negation sign. Press t
a to display the Y-VARS shortcut menu, and then
press Í to select Y1.
2. Press q 6 to select 6:ZStandard. This is a
quick way to reset the window variables to the
standard values. It also graphs the functions; you
do not need to press s.
Notice that the functions appear as an ellipse in
the standard viewing window. This is due to the
range of values that ZStandard defines for the
X-axis and Y-axis.
3. To adjust the display so that each pixel represents
an equal width and height, press q 5 to select
5:ZSquare. The functions are replotted and now
appear as a circle on the display.

Chapter 3: Function Graphing 66
Defining Graphs
TI-84 Plus—Graphing Mode Similarities
Chapter 3 specifically describes function graphing, but the steps shown here are similar for each
TI-84 Plus graphing mode. Chapters 4, 5, and 6 describe aspects that are unique to parametric
graphing, polar graphing, and sequence graphing.
Defining a Graph
To define a graph in any graphing mode, follow these steps. Some steps are not always
necessary.
1. Press z and set the appropriate graph mode.
2. Press o and enter, edit, or select one or more functions in the Y= editor.
3. Deselect stat plots, if necessary.
4. Set the graph style for each function.
5. Press p and define the viewing window variables.
6. Press y . and select the graph format settings.
Displaying and Exploring a Graph
After you have defined a graph, press s to display it. Explore the behavior of the function or
functions using the TI-84 Plus tools described in this chapter.
Saving a Graph for Later Use
You can store the elements that define the current graph to any of 10 graph database variables
(GDB1 through GDB9, and GDB0; Chapter 8). To recreate the current graph later, simply recall the
graph database to which you stored the original graph.
These types of information are stored in a GDB.
•Y= functions
• Graph style settings
• Window settings
• Format settings
4. To see the ZSquare window variables, press
p and notice the new values for Xmin, Xmax,
Ymin, and Ymax.

Chapter 3: Function Graphing 67
You can store a picture of the current graph display to any of 10 graph picture variables (Pic1
through Pic9, and Pic0; Chapter 8). Then you can superimpose one or more stored pictures onto
the current graph.
Setting the Graph Modes
Checking and Changing the Graphing Mode
To display the mode screen, press z. The default settings are highlighted below. To graph
functions, you must select Func mode before you enter values for the window variables and before
you enter the functions.
The TI-84 Plus has four graphing modes.
•Func (function graphing)
•Par (parametric graphing; Chapter 4)
•Pol (polar graphing; Chapter 5)
•Seq (sequence graphing; Chapter 6)
Other mode settings affect graphing results. Chapter 1 describes each mode setting.
•Float or 0123456789 (fixed) decimal mode affects displayed graph coordinates.
•Radian or Degree angle mode affects interpretation of some functions.
•Connected or Dot plotting mode affects plotting of selected functions.
•Sequential or Simul graphing-order mode affects function plotting when more than one function
is selected.
Setting Modes from a Program
To set the graphing mode and other modes from a program, begin on a blank line in the program
editor and follow these steps.
1. Press z to display the mode settings.
2. Press †, ~, |, and } to place the cursor on the mode that you want to select.
3. Press Í to paste the mode name to the cursor location.
The mode is changed when the program is executed.

Chapter 3: Function Graphing 68
Defining Functions
Displaying Functions in the Y= Editor
To display the Y= editor, press o. You can store up to 10 functions to the function variables Y1
through Y9, and Y0. You can graph one or more defined functions at once. In this example,
functions Y1 and Y2 are defined and selected.
Defining or Editing a Function
To define or edit a function, follow these steps.
1. Press o to display the Y= editor.
2. Press † to move the cursor to the function you want to define or edit. To erase a function,
press ‘.
3. Enter or edit the expression to define the function.
• You may use functions and variables (including matrices and lists) in the expression.
When the expression evaluates to a nonreal number, the value is not plotted; no error is
returned.
• You can access the shortcut menus by pressing ƒ ^ - a.
• The independent variable in the function is X. Func mode defines „ as X. To enter X,
press „ or press ƒ [X].
• When you enter the first character, the = is highlighted, indicating that the function is
selected.
As you enter the expression, it is stored to the variable Yn as a user-defined function in the
Y= editor.
4. Press Í or † to move the cursor to the next function.
Defining a Function from the Home Screen or a Program
To define a function from the home screen or a program, begin on a blank line and follow these
steps.
1. Press ƒ [ã], enter the expression, and then press ƒ [ã] again.
2. Press ¿.

Chapter 3: Function Graphing 69
3. Press ƒ a to display the YVAR shortcut menu, move the cursor to the function name,
and then press Í.
"expression"!Yn
When the instruction is executed, the TI-84 Plus stores the expression to the designated variable
Yn, selects the function, and displays the message Done.
Evaluating Y= Functions in Expressions
You can calculate the value of a Y= function Yn at a specified value of X. A list of values returns a list.
Yn(value)
Yn({value1,value2,value3, . . .,value n})
Selecting and Deselecting Functions
Selecting and Deselecting a Function
You can select and deselect (turn on and turn off) a function in the Y= editor. A function is selected
when the = sign is highlighted. The TI-84 Plus graphs only the selected functions. You can select
any or all functions Y1 through Y9, and Y0.
To select or deselect a function in the Y= editor, follow these steps.
1. Press o to display the Y= editor.
2. Move the cursor to the function you want to select or deselect.
3. Press | to place the cursor on the function’s = sign.
4. Press Í to change the selection status.
When you enter or edit a function, it is selected automatically. When you clear a function, it is
deselected.

Plot1 is turned on.
Plot2 and Plot3 are turned off.
Chapter 3: Function Graphing 70
Turning On or Turning Off a Stat Plot in the Y= Editor
To view and change the on/off status of a stat plot in the Y= editor, use Plot1 Plot2 Plot3 (the top
line of the Y= editor). When a plot is on, its name is highlighted on this line.
To change the on/off status of a stat plot from the Y= editor, press } and ~ to place the cursor on
Plot1, Plot2, or Plot3, and then press Í.
Selecting and Deselecting Functions from the Home Screen or a Program
To select or deselect a function from the home screen or a program, begin on a blank line and
follow these steps.
1. Press ~ to display the VARS Y-VARS menu.
2. Select 4:On/Off to display the ON/OFF secondary menu.
3. Select 1:FnOn to turn on one or more functions or 2:FnOff to turn off one or more functions.
The instruction you select is copied to the cursor location.
4. Enter the number (1 through 9, or 0; not the variable Yn) of each function you want to turn on
or turn off.
• If you enter two or more numbers, separate them with commas.
• To turn on or turn off all functions, do not enter a number after FnOn or FnOff.
FnOn[function#,function#, . . .,function n]
FnOff[function#,function#, . . .,function n]
5. Press Í. When the instruction is executed, the status of each function in the current mode
is set and Done is displayed.
For example, in Func mode, FnOff :FnOn 1,3 turns off all functions in the Y= editor, and then turns
on Y1 and Y3.
Chapter 3: Function Graphing 71
Setting Graph Styles for Functions
MATH Graph Style Icons in the Y= Editor
This table describes the graph styles available for function graphing. Use the styles to visually
differentiate functions to be graphed together. For example, you can set Y1 as a solid line, Y2 as a
dotted line, and Y3 as a thick line.
Note: Some graph styles are not available in all graphing modes. Chapters 4, 5, and 6 list the
styles for Par, Pol, and Seq modes.
Setting the Graph Style
To set the graph style for a function, follow these steps.
1. Press o to display the Y= editor.
2. Press † and } to move the cursor to the function.
3. Press | | to move the cursor left, past the = sign, to the graph style icon in the first column.
The insert cursor is displayed. (Steps 2 and 3 are interchangeable.)
4. Press Í repeatedly to rotate through the graph styles. The seven styles rotate in the same
order in which they are listed in the table above.
5. Press ~, }, or † when you have selected a style.
Icon Style Description
çLine A solid line connects plotted points; this is the default in
Connected mode
èThick A thick solid line connects plotted points
éAbove Shading covers the area above the graph
êBelow Shading covers the area below the graph
ëPath A circular cursor traces the leading edge of the graph and draws
a path
ìAnimate A circular cursor traces the leading edge of the graph without
drawing a path
íDot A small dot represents each plotted point; this is the default in Dot
mode
Chapter 3: Function Graphing 72
Shading Above and Below
When you select é or ê for two or more functions, the TI-84 Plus rotates through four shading
patterns.
• Vertical lines shade the first function with a é or ê graph style.
• Horizontal lines shade the second.
• Negatively sloping diagonal lines shade the third.
• Positively sloping diagonal lines shade the fourth.
• The rotation returns to vertical lines for the fifth é or ê function, repeating the order described
above.
When shaded areas intersect, the patterns overlap.
Note: When é or ê is selected for a Y= function that graphs a family of curves, such as Y1={1,2,3}X,
the four shading patterns rotate for each member of the family of curves.
Setting a Graph Style from a Program
To set the graph style from a program, select H:GraphStyle( from the PRGM CTL menu. To display
this menu, press while in the program editor. function# is the number of the Y= function name
in the current graphing mode. graphstyle# is an integer from 1 to 7 that corresponds to the graph
style, as shown below.
GraphStyle(function#,graphstyle#)
For example, when this program is executed in Func mode, GraphStyle(1,3) sets Y1 to é (above).
1 = ç (line)
2 = è (thick)
3 = é (above)
4 = ê (below)
5 = ë (path)
6 = ì (animate)
7 = í (dot)
Chapter 3: Function Graphing 73
Setting the Viewing Window Variables
The TI-84 Plus Viewing Window
The viewing window is the portion of the coordinate plane defined by Xmin, Xmax, Ymin, and Ymax.
Xscl (X scale) defines the distance between tick marks on the x-axis. Yscl (Y scale) defines the
distance between tick marks on the y-axis. To turn off tick marks, set Xscl=0 and Yscl=0.
Displaying the Window Variables
To display the current window variable values, press p. The window editor above and to the
right shows the default values in Func graphing mode and Radian angle mode. The window
variables differ from one graphing mode to another.
Xres sets pixel resolution (1 through 8) for function graphs only. The default is 1.
•At
Xres=1, functions are evaluated and graphed at each pixel on the x-axis.
•At
Xres=8, functions are evaluated and graphed at every eighth pixel along the x-axis.
Note: Small Xres values improve graph resolution but may cause the TI-84 Plus to draw graphs
more slowly.
Changing a Window Variable Value
To change a window variable value from the window editor, follow these steps.
1. Press † or } to move the cursor to the window variable you want to change.
2. Edit the value, which can be an expression.
• Enter a new value, which clears the original value.
• Move the cursor to a specific digit, and then edit it.
3. Press Í, †, or }. If you entered an expression, the TI-84 Plus evaluates it. The new
value is stored.
Note: Xmin<Xmax and Ymin<Ymax must be true in order to graph.
Storing to a Window Variable from the Home Screen or a Program
To store a value, which can be an expression, to a window variable, begin on a blank line and
follow these steps.

Chapter 3: Function Graphing 74
1. Enter the value you want to store.
2. Press ¿.
3. Press to display the VARS menu.
4. Select 1:Window to display the Func window variables (X/Y secondary menu).
• Press ~ to display the Par and Pol window variables (T/q secondary menu).
• Press ~ ~ to display the Seq window variables (U/V/W secondary menu).
5. Select the window variable to which you want to store a value. The name of the variable is
pasted to the current cursor location.
6. Press Í to complete the instruction.
When the instruction is executed, the TI-84 Plus stores the value to the window variable and
displays the value.
@X and @Y
ΔXXmax Xmin–()
94
---------------------------------------=
The variables @X and @Y (items 8 and 9 on the VARS (1:Window) X/Y secondary menu; @X is also
on the Window screen) define the distance from the center of one pixel to the center of any
adjacent pixel on a graph (graphing accuracy). @X and @Y are calculated from Xmin, Xmax, Ymin,
and Ymax when you display a graph.
ΔYYmax Ymin–()
62
---------------------------------------=
You can store values to @X and @Y. If you do, Xmax and Ymax are calculated from @X, Xmin, @Y,
and Ymin.
Note: The ZFrac ZOOM settings (Zfrac1/2, ZFrac1/3, ZFrac1/4, ZFrac1/5, ZFrac1/8, ZFrac1/10)
change @X and @Y to fractional values. If fractions are not needed for your problem, you can adjust
@X and @Y to suit your needs.
Setting the Graph Format
Displaying the Format Settings
To display the format settings, press y .. The default settings are highlighted below.
Note: You can also go to the Format Graph screen from the Mode screen by selecting YES at the
GoTo Format Graph prompt. After you make changes, press z to return to the Mode screen.
RectGC PolarGC Sets cursor coordinates.
CoordOn CoordOff Sets coordinates display on or off.
GridOff GridOn Sets grid off or on.

Chapter 3: Function Graphing 75
Format settings define a graph’s appearance on the display. Format settings apply to all graphing
modes. Seq graphing mode has an additional mode setting (Chapter 6).
Changing a Format Setting
To change a format setting, follow these steps.
1. Press †, ~, }, and | as necessary to move the cursor to the setting you want to select.
2. Press Í to select the highlighted setting.
RectGC, PolarGC
RectGC (rectangular graphing coordinates) displays the cursor location as rectangular coordinates
X and Y.
PolarGC (polar graphing coordinates) displays the cursor location as polar coordinates R and q.
The RectGC/PolarGC setting determines which variables are updated when you plot the graph,
move the free-moving cursor, or trace.
•RectGC updates X and Y; if CoordOn format is selected, X and Y are displayed.
•PolarGC updates X, Y, R, and q; if CoordOn format is selected, R and q are displayed.
CoordOn, CoordOff
CoordOn (coordinates on) displays the cursor coordinates at the bottom of the graph. If ExprOff
format is selected, the function number is displayed in the top-right corner.
CoordOff (coordinates off) does not display the function number or coordinates.
GridOff, GridOn
Grid points cover the viewing window in rows that correspond to the tick marks on each axis.
GridOff does not display grid points.
GridOn displays grid points.
AxesOn, AxesOff
AxesOn displays the axes.
AxesOn AxesOff Sets axes on or off.
LabelOff LabelOn Sets axes label off or on.
ExprOn ExprOff Sets expression display on or off.

Chapter 3: Function Graphing 76
AxesOff does not display the axes.
This overrides the LabelOff/LabelOn format setting.
LabelOff, LabelOn
LabelOff and LabelOn determine whether to display labels for the axes (X and Y), if AxesOn format
is also selected.
ExprOn, ExprOff
ExprOn and ExprOff determine whether to display the Y= expression when the trace cursor is
active. This format setting also applies to stat plots.
When ExprOn is selected, the expression is displayed in the top-left corner of the graph screen.
When ExprOff and CoordOn both are selected, the number in the top-right corner specifies which
function is being traced.
Displaying Graphs
Displaying a New Graph
To display the graph of the selected function or functions, press s. TRACE, ZOOM
instructions, and CALC operations display the graph automatically. As the TI-84 Plus plots the
graph, the busy indicator is on. As the graph is plotted, X and Y are updated.
Pausing or Stopping a Graph
While plotting a graph, you can pause or stop graphing.
• Press Í to pause; then press Í to resume.
• Press É to stop; then press s to redraw.
Smart Graph
Smart Graph is a TI-84 Plus feature that redisplays the last graph immediately when you press
s, but only if all graphing factors that would cause replotting have remained the same since
the graph was last displayed.
If you performed any of the following actions since the graph was last displayed, the TI-84 Plus will
replot the graph based on new values when you press s.
• Changed a mode setting that affects graphs
• Changed a function in the current picture
• Selected or deselected a function or stat plot
Chapter 3: Function Graphing 77
• Changed the value of a variable in a selected function
• Changed a window variable or graph format setting
• Cleared drawings by selecting ClrDraw
• Changed a stat plot definition
Overlaying Functions on a Graph
On the TI-84 Plus, you can graph one or more new functions without replotting existing functions.
For example, store sin(X) to Y1 in the Y= editor and press s. Then store cos(X) to Y2 and
press s again. The function Y2 is graphed on top of Y1, the original function.
Graphing a Family of Curves
If you enter a list (Chapter 11) as an element in an expression, the TI-84 Plus plots the function for
each value in the list, thereby graphing a family of curves. In Simul graphing-order mode, it graphs
all functions sequentially for the first element in each list, and then for the second, and so on.
{2,4,6}sin(X) graphs three functions: 2 sin(X), 4 sin(X), and 6 sin(X).
{2,4,6}sin({1,2,3}X) graphs 2 sin(X), 4 sin(2X), and 6 sin(3X) .
Note: When using more than one list, the lists must have the same dimensions.
Free- moving cursor
appears to be on the curve
Chapter 3: Function Graphing 78
Exploring Graphs with the Free-Moving Cursor
Free-Moving Cursor
When a graph is displayed, press |, ~, }, or † to move the cursor around the graph. When you
first display the graph, no cursor is visible. When you press |, ~, }, or †, the cursor moves from
the center of the viewing window.
As you move the cursor around the graph, the coordinate values of the cursor location are
displayed at the bottom of the screen if CoordOn format is selected. The Float/Fix decimal mode
setting determines the number of decimal digits displayed for the coordinate values.
To display the graph with no cursor and no coordinate values, press ‘ or Í. When you
press |, ~, }, or †, the cursor moves from the same position.
Graphing Accuracy
The free-moving cursor moves from pixel to pixel on the screen. When you move the cursor to a
pixel that appears to be on the function, the cursor may be near, but not actually on, the function.
The coordinate value displayed at the bottom of the screen actually may not be a point on the
function. To move the cursor along a function, use r.
The coordinate values displayed as you move the cursor approximate actual math coordinates,
accurate to within the width and height of the pixel. As Xmin, Xmax, Ymin, and Ymax get closer
together (as in a Zoom In) graphing accuracy increases, and the coordinate values more closely
approximate the math coordinates.
Exploring Graphs with TRACE
Beginning a Trace
Use TRACE to move the cursor from one plotted point to the next along a function. To begin a
trace, press r. If the graph is not displayed already, press r to display it. The trace cursor
is on the first selected function in the Y= editor, at the middle X value on the screen. The cursor
coordinates are displayed at the bottom of the screen if CoordOn format is selected. The
Y= expression is displayed in the top-left corner of the screen, if ExprOn format is selected.
Chapter 3: Function Graphing 79
Moving the Trace Cursor
To move the TRACE cursor do this:
To the previous or next plotted point, press | or ~.
Five plotted points on a function (Xres
affects this),
press y | or y ~.
To any valid X value on a function, enter a value, and then press Í.
From one function to another, press } or †.
When the trace cursor moves along a function, the Y value is calculated from the X value; that is,
Y=Yn(X). If the function is undefined at an X value, the Y value is blank.
Trace cursor on the curve
If you move the trace cursor beyond the top or bottom of the screen, the coordinate values at the
bottom of the screen continue to change appropriately.
Moving the Trace Cursor from Function to Function
To move the trace cursor from function to function, press † and }. The cursor follows the order of
the selected functions in the Y= editor. The trace cursor moves to each function at the same X
value. If ExprOn format is selected, the expression is updated.
Moving the Trace Cursor to Any Valid X Value
To move the trace cursor to any valid X value on the current function, enter the value. When you
enter the first digit, an X= prompt and the number you entered are displayed in the bottom-left
corner of the screen. You can enter an expression at the X= prompt. The value must be valid for
the current viewing window. When you have completed the entry, press Í to move the cursor.
Note: This feature does not apply to stat plots.

Chapter 3: Function Graphing 80
Panning to the Left or Right
If you trace a function beyond the left or right side of the screen, the viewing window automatically
pans to the left or right. Xmin and Xmax are updated to correspond to the new viewing window.
Quick Zoom
While tracing, you can press Í to adjust the viewing window so that the cursor location
becomes the center of the new viewing window, even if the cursor is above or below the display.
This allows panning up and down. After Quick Zoom, the cursor remains in TRACE.
Leaving and Returning to TRACE
When you leave and return to TRACE, the trace cursor is displayed in the same location it was in
when you left TRACE, unless Smart Graph has replotted the graph.
Using TRACE in a Program
On a blank line in the program editor, press r. The instruction Trace is pasted to the cursor
location. When the instruction is encountered during program execution, the graph is displayed
with the trace cursor on the first selected function. As you trace, the cursor coordinate values are
updated. When you finish tracing the functions, press Í to resume program execution.
Exploring Graphs with the ZOOM Instructions
ZOOM Menu
To display the ZOOM menu, press q. You can adjust the viewing window of the graph quickly
in several ways. All ZOOM instructions are accessible from programs.
ZOOM MEMORY
1: ZBox Draws a box to define the viewing window.
2: Zoom In Magnifies the graph around the cursor.
3: Zoom Out Views more of a graph around the cursor.
4: ZDecimal Sets @X and @Y to 0.1.
5: ZSquare Sets equal-size pixels on the X and Y axes.
6: ZStandard Sets the standard window variables.
7: ZTrig Sets the built-in trig window variables.
8: ZInteger Sets integer values on the X and Y axes.
9: ZoomStat Sets the values for current stat lists.
0: ZoomFit Fits YMin and YMax between XMin and XMax.
A: ZQuadrant1 Displays the portion of the graph that is in quadrant 1
Chapter 3: Function Graphing 81
Note: You can adjust all window variables from the VARS menu by pressing 1:Window and
then selecting the variable from the X/Y, T/q, or U/V/W menu.
Zoom Cursor
When you select 1:ZBox, 2:Zoom In, or 3:Zoom Out, the cursor on the graph becomes the zoom
cursor (+), a smaller version of the free-moving cursor (+).
ZBox
To define a new viewing window using ZBox, follow these steps.
1. Select 1:ZBox from the ZOOM menu. The zoom cursor is displayed at the center of the screen.
2. Move the zoom cursor to any spot you want to define as a corner of the box, and then press
Í. When you move the cursor away from the first defined corner, a small, square dot
indicates the spot.
3. Press |, }, ~, or †. As you move the cursor, the sides of the box lengthen or shorten
proportionately on the screen.
Note: To cancel ZBox before you press Í, press ‘.
4. When you have defined the box, press Í to replot the graph.
B: ZFrac1/2 Sets the window variables so that you can trace in increments of
, if possible. Sets @X and @Y to .
C: ZFrac1/3 Sets the window variables so that you can trace in increments of
, if possible. Sets @X and @Y to .
D: ZFrac1/4 Sets the window variables so that you can trace in increments of
, if possible. Sets @X and @Y to .
E: ZFrac1/5 Sets the window variables so that you can trace in increments of
, if possible. Sets @X and @Y to .
F: ZFrac1/8 Sets the window variables so that you can trace in increments of
, if possible. Sets @X and @Y to .
G: ZFrac1/10 Sets the window variables so that you can trace in increments of
, if possible. Sets @X and @Y to .
ZOOM MEMORY

Chapter 3: Function Graphing 82
To use ZBox to define another box within the new graph, repeat steps 2 through 4. To cancel
ZBox, press ‘.
Zoom In, Zoom Out
Zoom In magnifies the part of the graph that surrounds the cursor location. Zoom Out displays a
greater portion of the graph, centered on the cursor location. The XFact and YFact settings
determine the extent of the zoom.
To zoom in on a graph, follow these steps.
1. Check XFact and YFact; change as needed.
2. Select 2:Zoom In from the ZOOM menu. The zoom cursor is displayed.
3. Move the zoom cursor to the point that is to be the center of the new viewing window.
4. Press Í. The TI-83 Plus adjusts the viewing window by XFact and YFact; updates the
window variables; and replots the selected functions, centered on the cursor location.
5. Zoom in on the graph again in either of two ways.
• To zoom in at the same point, press Í.
• To zoom in at a new point, move the cursor to the point that you want as the center of the
new viewing window, and then press Í.
To zoom out on a graph, select 3:Zoom Out and repeat steps 3 through 5.
To cancel Zoom In or Zoom Out, press ‘.
ZDecimal
ZDecimal replots the functions immediately. It updates the window variables to preset values, as
shown below. These values set @X and @Y equal to 0.1 and set the X and Y value of each pixel to
one decimal place.
ZSquare
ZSquare replots the functions immediately. It redefines the viewing window based on the current
values of the window variables. It adjusts in only one direction so that @X=@Y, which makes the
graph of a circle look like a circle. Xscl and Yscl remain unchanged. The midpoint of the current
graph (not the intersection of the axes) becomes the midpoint of the new graph.
Xmin=L4.7
Xmax=4.7
Xscl=1
Ymin=L3.1
Ymax=3.1
Yscl=1

Chapter 3: Function Graphing 83
ZStandard
ZStandard replots the functions immediately. It updates the window variables to the standard
values shown below.
ZTrig
ZTrig replots the functions immediately. It updates the window variables to preset values that are
appropriate for plotting trig functions. Those preset values in Radian mode are shown below.
ZInteger
ZInteger redefines the viewing window to the dimensions shown below. To use ZInteger, move the
cursor to the point that you want to be the center of the new window, and then press Í;
ZInteger replots the functions.
ZoomStat
ZoomStat redefines the viewing window so that all statistical data points are displayed. For regular
and modified box plots, only Xmin and Xmax are adjusted.
ZoomFit
ZoomFit replots the functions immediately. ZoomFit recalculates YMin and YMax to include the
minimum and maximum Y values of the selected functions between the current XMin and XMax.
XMin and XMax are not changed.
ZQuadrant1
ZQuandrant1 replots the function immediately. It redefines the window settings so that only
quadrant 1 is displayed.
Xmin=L10
Xmax=10
Xscl=1
Ymin=L10
Ymax=10
Yscl=1
Xres=1
Xmin=L(47à24)p (decimal equivalent)
Xmax=(47à24)p (decimal equivalent)
Xscl=p/2 (decimal equivalent)
Ymin=L4
Ymax=4
Yscl=1
@X=1
@Y=1
Xscl=10
Yscl=10

Chapter 3: Function Graphing 84
ZFrac1/2
ZFrac1/2 replots the functions immediately. It updates the window variables to preset values, as
shown below. These values set @X and @Y equal to 1/2 and set the X and Y value of each pixel to
one decimal place.
ZFrac1/3
ZFrac1/3 replots the functions immediately. It updates the window variables to preset values, as
shown below. These values set @X and @Y equal to 1/3 and set the X and Y value of each pixel to
one decimal place.
ZFrac1/4
ZFrac1/4 replots the functions immediately. It updates the window variables to preset values, as
shown below. These values set @X and @Y equal to 1/4 and set the X and Y value of each pixel to
one decimal place.
ZFrac1/5
ZFrac1/5 replots the functions immediately. It updates the window variables to preset values, as
shown below. These values set @X and @Y equal to 1/5 and set the X and Y value of each pixel to
one decimal place.
Xmin=L47/2
Xmax=47/2
Xscl=1
Ymin=L31/2
Ymax=31/2
Yscl=1
Xmin=L47/3
Xmax=47/3
Xscl=1
Ymin=L31/3
Ymax=31/3
Yscl=1
Xmin=L47/4
Xmax=47/4
Xscl=1
Ymin=L31/4
Ymax=31/4
Yscl=1
Xmin=L47/5
Xmax=47/5
Xscl=1
Ymin=L31/5
Ymax=31/5
Yscl=1

Chapter 3: Function Graphing 85
ZFrac1/8
ZDecimal replots the functions immediately. It updates the window variables to preset values, as
shown below. These values set @X and @Y equal to 1/8 and set the X and Y value of each pixel to
one decimal place.
ZFrac1/10
ZFrac1/10 replots the functions immediately. It updates the window variables to preset values, as
shown below. These values set @X and @Y equal to 1/10 and set the X and Y value of each pixel to
one decimal place.
Using ZOOM MEMORY
ZOOM MEMORY Menu
To display the ZOOM MEMORY menu, press q ~.
ZPrevious
ZPrevious replots the graph using the window variables of the graph that was displayed before you
executed the last ZOOM instruction.
ZoomSto
ZoomSto immediately stores the current viewing window. The graph is displayed, and the values of
the current window variables are stored in the user-defined ZOOM variables ZXmin, ZXmax, ZXscl,
ZYmin, ZYmax, ZYscl, and ZXres.
These variables apply to all graphing modes. For example, changing the value of ZXmin in Func
mode also changes it in Par mode.
Xmin=L47/8
Xmax=47/8
Xscl=1
Ymin=L31/8
Ymax=31/8
Yscl=1
Xmin=L47/10
Xmax=47/10
Xscl=1
Ymin=L31/10
Ymax=31/10
Yscl=1
ZOOM MEMORY
1: ZPrevious Uses the previous viewing window.
2: ZoomSto Stores the user-defined window.
3: ZoomRcl Recalls the user-defined window.
4: SetFactors... Changes Zoom In and Zoom Out factors.

Chapter 3: Function Graphing 86
ZoomRcl
ZoomRcl graphs the selected functions in a user-defined viewing window. The user-defined
viewing window is determined by the values stored with the ZoomSto instruction. The window
variables are updated with the user-defined values, and the graph is plotted.
ZOOM FACTORS
The zoom factors, XFact and YFact, are positive numbers (not necessarily integers) greater than or
equal to 1. They define the magnification or reduction factor used to Zoom In or Zoom Out around a
point.
Checking XFact and YFact
To display the ZOOM FACTORS screen, where you can review the current values for XFact and
YFact, select 4:SetFactors from the ZOOM MEMORY menu. The values shown are the defaults.
Changing XFact and YFact
You can change XFact and YFact in either of two ways.
• Enter a new value. The original value is cleared automatically when you enter the first digit.
• Place the cursor on the digit you want to change, and then enter a value or press { to delete
it.
Using ZOOM MEMORY Menu Items from the Home Screen or a Program
From the home screen or a program, you can store directly to any of the user-defined ZOOM
variables.
From a program, you can select the ZoomSto and ZoomRcl instructions from the ZOOM MEMORY
menu.
Chapter 3: Function Graphing 87
Using the CALC (Calculate) Operations
CALCULATE Menu
To display the CALCULATE menu, press y /. Use the items on this menu to analyze the
current graph functions.
value
value evaluates one or more currently selected functions for a specified value of X.
Note: When a value is displayed for X, press ‘ to clear the value. When no value is displayed,
press ‘ to cancel the value operation.
To evaluate a selected function at X, follow these steps.
1. Select 1:value from the CALCULATE menu. The graph is displayed with X= in the bottom-left
corner.
2. Enter a real value, which can be an expression, for X between Xmin and Xmax.
3. Press Í.
The cursor is on the first selected function in the Y= editor at the X value you entered, and the
coordinates are displayed, even if CoordOff format is selected.
To move the cursor from function to function at the entered X value, press } or †. To restore the
free-moving cursor, press | or ~.
CALCULATE
1: value Calculates a function Y value for a given X.
2: zero Finds a zero (x-intercept) of a function.
3: minimum Finds a minimum of a function.
4: maximum Finds a maximum of a function.
5: intersect Finds an intersection of two functions.
6: dy/dx Finds a numeric derivative of a function.
7: ‰f(x)dx Finds a numeric integral of a function.
Chapter 3: Function Graphing 88
zero
zero finds a zero (x-intercept or root) of a function using solve(. Functions can have more than one
x-intercept value; zero finds the zero closest to your guess.
The time zero spends to find the correct zero value depends on the accuracy of the values you
specify for the left and right bounds and the accuracy of your guess.
To find a zero of a function, follow these steps.
1. Select 2:zero from the CALCULATE menu. The current graph is displayed with Left Bound? in
the bottom-left corner.
2. Press } or † to move the cursor onto the function for which you want to find a zero.
3. Press | or ~ (or enter a value) to select the x-value for the left bound of the interval, and then
press Í. A 4 indicator on the graph screen shows the left bound. Right Bound? is
displayed in the bottom-left corner. Press | or ~ (or enter a value) to select the x-value for
the right bound, and then press Í. A 3 indicator on the graph screen shows the right
bound. Guess? is then displayed in the bottom-left corner.
4. Press | or ~ (or enter a value) to select a point near the zero of the function, between the
bounds, and then press Í.
The cursor is on the solution and the coordinates are displayed, even if CoordOff format is
selected. To move to the same x-value for other selected functions, press } or †. To restore the
free-moving cursor, press | or ~.
minimum, maximum
minimum and maximum find a minimum or maximum of a function within a specified interval to a
tolerance of 1âL5.
To find a minimum or maximum, follow these steps.
1. Select 3:minimum or 4:maximum from the CALCULATE menu. The current graph is displayed.
2. Select the function and set left bound, right bound, and guess as described for zero.
Chapter 3: Function Graphing 89
The cursor is on the solution, and the coordinates are displayed, even if you have selected
CoordOff format; Minimum or Maximum is displayed in the bottom-left corner.
To move to the same x-value for other selected functions, press } or †. To restore the free-
moving cursor, press | or ~.
intersect
intersect finds the coordinates of a point at which two or more functions intersect using solve(. The
intersection must appear on the display to use intersect.
To find an intersection, follow these steps.
1. Select 5:intersect from the CALCULATE menu. The current graph is displayed with
First curve? in the bottom-left corner.
2. Press † or }, if necessary, to move the cursor to the first function, and then press Í.
Second curve? is displayed in the bottom-left corner.
3. Press † or }, if necessary, to move the cursor to the second function, and then press Í.
4. Press ~ or | to move the cursor to the point that is your guess as to location of the
intersection, and then press Í.
The cursor is on the solution and the coordinates are displayed, even if CoordOff format is
selected. Intersection is displayed in the bottom-left corner. To restore the free-moving cursor,
press |, }, ~, or †.
dy/dx
dy/dx (numerical derivative) finds the numerical derivative (slope) of a function at a point, with
H=1âL3.
To find a function’s slope at a point, follow these steps.
1. Select 6:dy/dx from the CALCULATE menu. The current graph is displayed.
2. Press } or † to select the function for which you want to find the numerical derivative.
3. Press | or ~ (or enter a value) to select the X value at which to calculate the derivative, and
then press Í.
The cursor is on the solution and the numerical derivative is displayed.
To move to the same x-value for other selected functions, press } or †. To restore the free-
moving cursor, press | or ~.
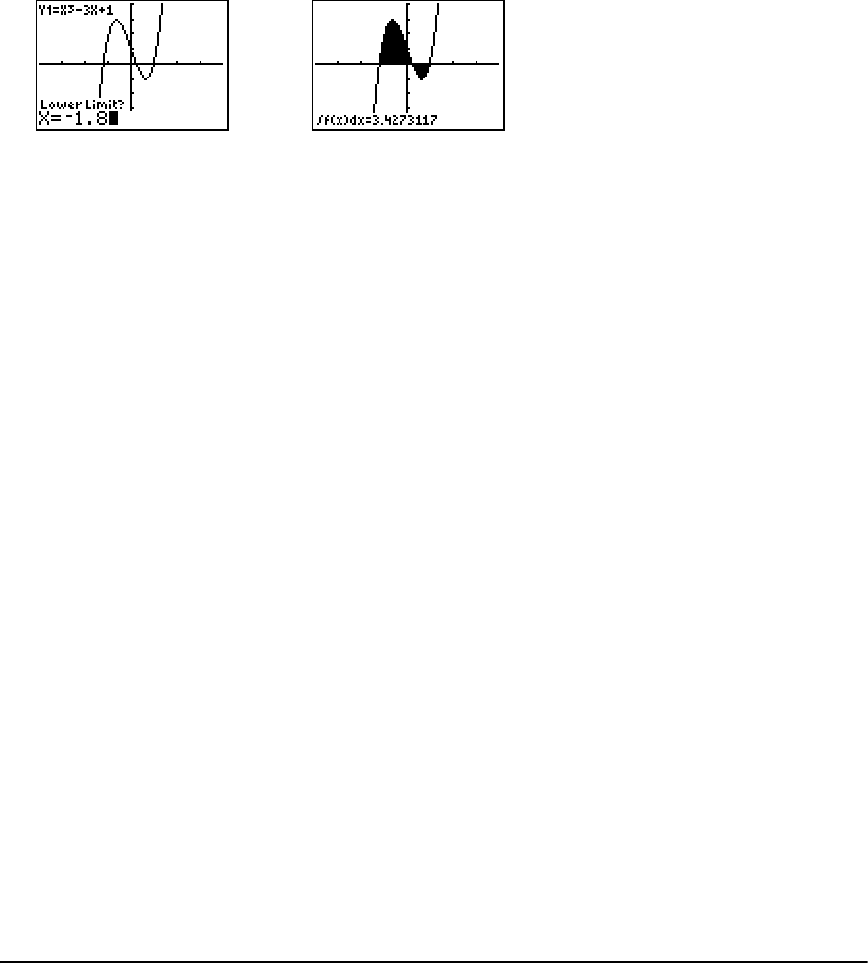
Chapter 3: Function Graphing 90
‰f(x)dx
‰f(x)dx (numerical integral) finds the numerical integral of a function in a specified interval. It uses
the fnInt( function, with a tolerance of H=1âL3.
To find the numerical integral of a function, follow these steps.
1. Select 7:‰f(x)dx from the CALCULATE menu. The current graph is displayed with
Lower Limit? in the bottom-left corner.
2. Press } or † to move the cursor to the function for which you want to calculate the integral.
3. Set lower and upper limits as you would set left and right bounds for zero. The integral value is
displayed, and the integrated area is shaded.
Note: The shaded area is a drawing. Use ClrDraw (Chapter 8) or any action that invokes Smart
Graph to clear the shaded area.

Chapter 4: Parametric Graphing 91
Chapter 4:
Parametric Graphing
Getting Started: Path of a Ball
Getting Started is a fast-paced introduction. Read the chapter for details.
Graph the parametric equation that describes the path of a ball hit at an initial speed of 30 meters
per second, at an initial angle of 25 degrees with the horizontal from ground level. How far does
the ball travel? When does it hit the ground? How high does it go? Ignore all forces except gravity.
For initial velocity vo and angle q, the position of the ball as a function of time has horizontal and
vertical components.
Horizontal: X1(t)=tv0cos(q) Vertical: Y1(t)=tv0sin(q)N gt2
The vertical and horizontal vectors of the ball’s motion also will be graphed.
Vertical vector:
Horizontal vector:
Gravity constant:
X2(t)=0
X3(t)=X1(t)
g=9.8 m/sec2
Y2(t)=Y1(t)
Y3(t)=0
1. Press z. Press † † † ~ Í to select Par
mode. Press † † ~ Í to select Simul for
simultaneous graphing of all three parametric
equations in this example.
2. Press † † †† † † ~ Í to go to the Format
Graph screen. Press † † † ~ Í to select
AxesOff, which turns off the axes.
1
2
---

Chapter 4: Parametric Graphing 92
3. Press o. Press 30 „ ™ 25 y ; 1 (to
select ¡) ¤ Í to define X1T in terms of T.
4. Press 30 „ ˜ 25 y ; 1 ¤ ¹ t
^ 1 (to select n/d) 9.8 ~ 2 ~ „ ¡ Í to
define Y1T.
The vertical component vector is defined by X2T
and Y2T.
5. Press 0 Í to define X2T.
6. Press t a † Í Í to define Y2T.
The horizontal component vector is defined by X3T
and Y3T.
7. Press t a Í Í to define X3T.
8. Press 0 Í to define Y3T.
9. Press | | } Í to change the graph style to
è for X3T and Y3T. Press } Í Í to
change the graph style to ë for X2T and Y2T. Press
} Í Í to change the graph style to ë for
X1T and Y1T. (These keystrokes assume that all
graph styles were set to ç originally.)
10. Press p. Enter these values for the window
variables.
Tmin=0 Xmin=L10 Ymin=L5
Tmax=5 Xmax=100 Ymax=15
Tstep=.1 Xscl=50 Yscl=10
Note: You can check all WINDOW variables,
including @X and @Y by pressing 1:Window.
11. Press s. The plotting action simultaneously
shows the ball in flight and the vertical and
horizontal component vectors of the motion.
Note: To simulate the ball flying through the air, set
graph style to ì (animate) for X1T and Y1T.
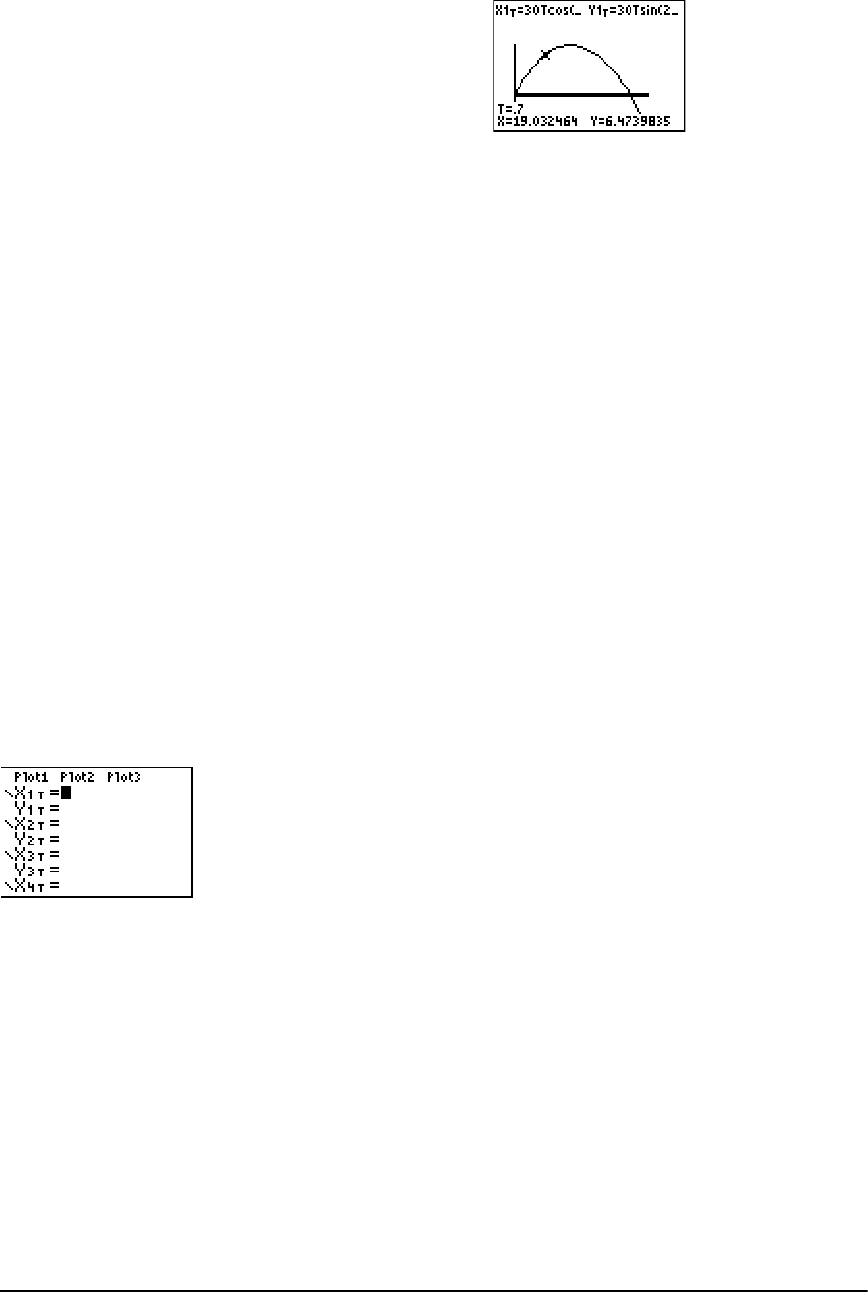
Chapter 4: Parametric Graphing 93
Defining and Displaying Parametric Graphs
TI-84 Plus Graphing Mode Similarities
The steps for defining a parametric graph are similar to the steps for defining a function graph.
Chapter 4 assumes that you are familiar with Chapter 3: Function Graphing. Chapter 4 details
aspects of parametric graphing that differ from function graphing.
Setting Parametric Graphing Mode
To display the mode screen, press z. To graph parametric equations, you must select
parametric graphing mode before you enter window variables and before you enter the
components of parametric equations.
Displaying the Parametric Y= Editor
After selecting parametric graphing mode, press o to display the parametric Y= editor.
In this editor, you can display and enter both the X and Y components of up to six equations, X1T
and Y1T through X6T and Y6T. Each is defined in terms of the independent variable T. A common
application of parametric graphs is graphing equations over time.
Selecting a Graph Style
The icons to the left of X1T through X6T represent the graph style of each parametric equation. The
default in parametric mode is ç (line), which connects plotted points. Line, è (thick), ë (path),
ì (animate), and í (dot) styles are available for parametric graphing.
12. Press r to obtain numerical results and
answer the questions at the beginning of this
section.
Tracing begins at Tmin on the first parametric
equation (X1T and Y1T). As you press ~ to trace
the curve, the cursor follows the path of the ball
over time. The values for X (distance), Y (height),
and T (time) are displayed at the bottom of the
screen.

Chapter 4: Parametric Graphing 94
Defining and Editing Parametric Equations
To define or edit a parametric equation, follow the steps in Chapter 3 for defining a function or
editing a function. The independent variable in a parametric equation is T. In parametric graphing
mode, you can enter the parametric variable T in either of two ways.
• Press „.
• Press ƒ [T].
Two components, X and Y, define a single parametric equation. You must define both of them.
Selecting and Deselecting Parametric Equations
The TI-84 Plus graphs only the selected parametric equations. In the Y= editor, a parametric
equation is selected when the = signs of both the X and Y components are highlighted. You may
select any or all of the equations X1T and Y1T through X6T and Y6T.
To change the selection status, move the cursor onto the = sign of either the X or Y component
and press Í. The status of both the X and Y components is changed.
Setting Window Variables
To display the window variable values, press p. These variables define the viewing window.
The values below are defaults for parametric graphing in Radian angle mode.
Note: To ensure that sufficient points are plotted, you may want to change the T window variables.
Setting the Graph Format
To display the current graph format settings, press y .. Chapter 3 describes the format
settings in detail. The other graphing modes share these format settings; Seq graphing mode has
an additional axes format setting.
Tmin=0 Smallest T value to evaluate
Tmax=6.2831853... Largest T value to evaluate (2p)
Tstep=.1308996... T value increment (pà24)
Xmin=L10 Smallest X value to be displayed
Xmax=10 Largest X value to be displayed
Xscl=1 Spacing between the X tick marks
Ymin=L10 Smallest Y value to be displayed
Ymax=10 Largest Y value to be displayed
Yscl=1 Spacing between the Y tick marks
Chapter 4: Parametric Graphing 95
Displaying a Graph
When you press s, the TI-84 Plus plots the selected parametric equations. It evaluates the X
and Y components for each value of T (from Tmin to Tmax in intervals of Tstep), and then plots
each point defined by X and Y. The window variables define the viewing window.
As the graph is plotted, X, Y, and T are updated.
Smart Graph applies to parametric graphs.
Window Variables and Y.VARS Menus
You can perform these actions from the home screen or a program.
• Access functions by using the name of the X or Y component of the equation as a variable.
• Store parametric equations.
• Select or deselect parametric equations.
• Store values directly to window variables.
Exploring Parametric Graphs
Free-Moving Cursor
The free-moving cursor in parametric graphing works the same as in Func graphing.
In RectGC format, moving the cursor updates the values of X and Y; if CoordOn format is selected,
X and Y are displayed.
In PolarGC format, X, Y, R, and q are updated; if CoordOn format is selected, R and q are
displayed.
Chapter 4: Parametric Graphing 96
TRACE
To activate TRACE, press r. When TRACE is active, you can move the trace cursor along
the graph of the equation one Tstep at a time. When you begin a trace, the trace cursor is on the
first selected function at Tmin. If ExprOn is selected, then the function is displayed.
In RectGC format, TRACE updates and displays the values of X, Y, and T if CoordOn format is on.
In PolarGC format, X, Y, R, q and T are updated; if CoordOn format is selected, R, q, and T are
displayed. The X and Y (or R and q) values are calculated from T.
To move five plotted points at a time on a function, press y | or y ~. If you move the cursor
beyond the top or bottom of the screen, the coordinate values at the bottom of the screen continue
to change appropriately.
Quick Zoom is available in parametric graphing; panning is not.
Moving the Trace Cursor to Any Valid T Value
To move the trace cursor to any valid T value on the current function, enter the number. When you
enter the first digit, a T= prompt and the number you entered are displayed in the bottom-left
corner of the screen. You can enter an expression at the T= prompt. The value must be valid for
the current viewing window. When you have completed the entry, press Í to move the cursor.
ZOOM
ZOOM operations in parametric graphing work the same as in Func graphing. Only the X (Xmin,
Xmax, and Xscl) and Y (Ymin, Ymax, and Yscl) window variables are affected.
The T window variables (Tmin, Tmax, and Tstep) are only affected when you select ZStandard. The
VARS ZOOM secondary menu ZT/Zq items 1:ZTmin, 2:ZTmax, and 3:ZTstep are the zoom memory
variables for parametric graphing.
CALC
CALC operations in parametric graphing work the same as in Func graphing. The CALCULATE
menu items available in parametric graphing are 1:value, 2:dy/dx, 3:dy/dt, and 4:dx/dt.
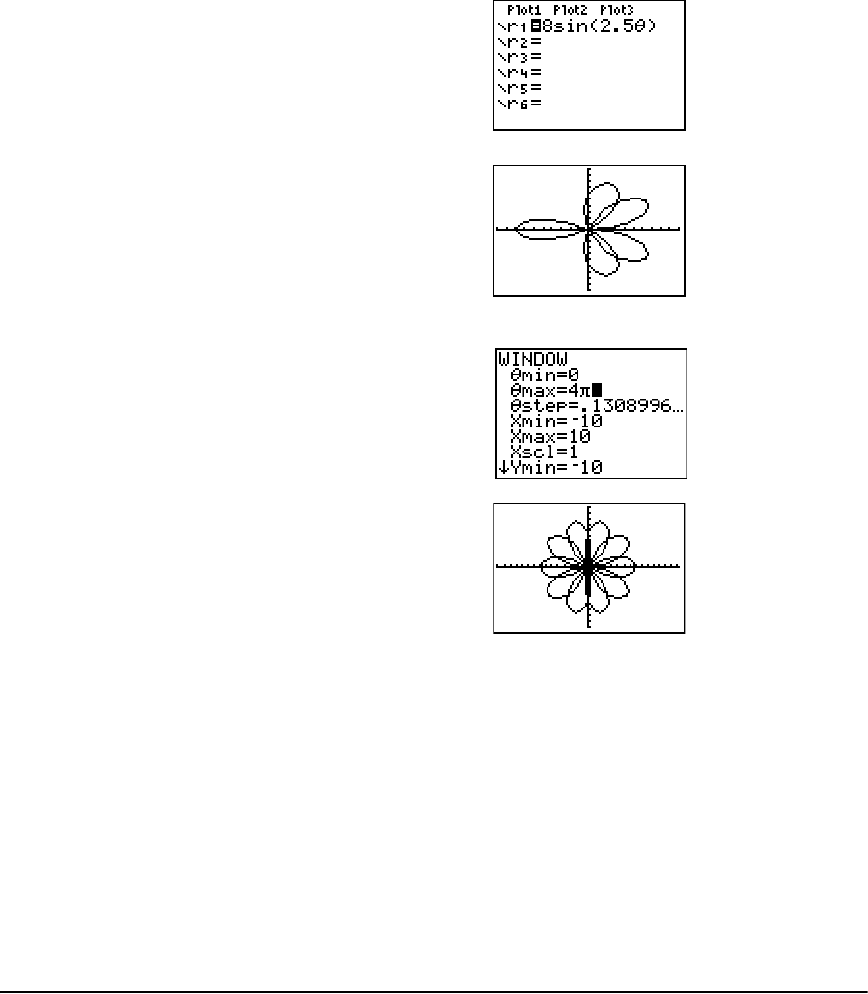
Chapter 5: Polar Graphing 97
Chapter 5:
Polar Graphing
Getting Started: Polar Rose
Getting Started is a fast-paced introduction. Read the chapter for details.
The polar equation R=Asin(Bq) graphs a rose. Graph the rose for A=8 and B=2.5, and then
explore the appearance of the rose for other values of A and B.
1. Press z to display the MODE screen. Press †
† † ~ ~ Í to select Pol graphing mode.
Select the defaults (the options on the left) for the
other mode settings.
2. Press o to display the polar Y= editor. Press 8
˜ 2.5 „ ¤ Í to define r1.
3. Press q 6 to select 6:ZStandard and graph the
equation in the standard viewing window. The
graph shows only five petals of the rose, and the
rose does not appear to be symmetrical. This is
because the standard window sets qmax=2p and
defines the window, rather than the pixels, as
square.
4. Press p to display the window variables.
Press † 4 y B to increase the value of qmax to
4p.
5. Press q 5 to select 5:ZSquare and plot the
graph.
6. Repeat steps 2 through 5 with new values for the
variables A and B in the polar equation
r1=Asin(Bq). Observe how the new values affect
the graph.

Chapter 5: Polar Graphing 98
Defining and Displaying Polar Graphs
TI-84 Plus Graphing Mode Similarities
The steps for defining a polar graph are similar to the steps for defining a function graph. Chapter
5 assumes that you are familiar with Chapter 3: Function Graphing. Chapter 5 details aspects of
polar graphing that differ from function graphing.
Setting Polar Graphing Mode
To display the mode screen, press z. To graph polar equations, you must select Pol graphing
mode before you enter values for the window variables and before you enter polar equations.
Displaying the Polar Y= Editor
After selecting Pol graphing mode, press o to display the polar Y= editor.
In this editor, you can enter and display up to six polar equations, r1 through r6. Each is defined in
terms of the independent variable q.
Selecting Graph Styles
The icons to the left of r1 through r6 represent the graph style of each polar equation. The default
in Pol graphing mode is ç (line), which connects plotted points. Line, è (thick), ë (path), ì (animate),
and í (dot) styles are available for polar graphing.
Defining and Editing Polar Equations
To define or edit a polar equation, follow the steps in Chapter 3 for defining a function or editing a
function. The independent variable in a polar equation is q. In Pol graphing mode, you can enter
the polar variable q in either of two ways.
• Press „.
• Press ƒ [q].
Selecting and Deselecting Polar Equations
The TI-84 Plus graphs only the selected polar equations. In the Y= editor, a polar equation is
selected when the = sign is highlighted. You may select any or all of the equations.

Chapter 5: Polar Graphing 99
To change the selection status, move the cursor onto the = sign, and then press Í.
Setting Window Variables
To display the window variable values, press p. These variables define the viewing window.
The values below are defaults for Pol graphing in Radian angle mode.
Note: To ensure that sufficient points are plotted, you may want to change the q window variables.
Setting the Graph Format
To display the current graph format settings, press y .. Chapter 3 describes the format
settings in detail. The other graphing modes share these format settings.
Displaying a Graph
When you press s, the TI-84 Plus plots the selected polar equations. It evaluates R for each
value of q (from qmin to qmax in intervals of qstep) and then plots each point. The window
variables define the viewing window.
As the graph is plotted, X, Y, R, and q are updated.
Smart Graph applies to polar graphs.
Window Variables and Y.VARS Menus
You can perform these actions from the home screen or a program.
• Access functions by using the name of the equation as a variable. These function names are
available on the YVARS shortcut menu (t a).
qmin=0 Smallest q value to evaluate
qmax=6.2831853... Largest q value to evaluate (2p)
qstep=.1308996... Increment between q values (pà24)
Xmin=L10 Smallest X value to be displayed
Xmax=10 Largest X value to be displayed
Xscl=1 Spacing between the X tick marks
Ymin=L10 Smallest Y value to be displayed
Ymax=10 Largest Y value to be displayed
Yscl=1 Spacing between the Y tick marks
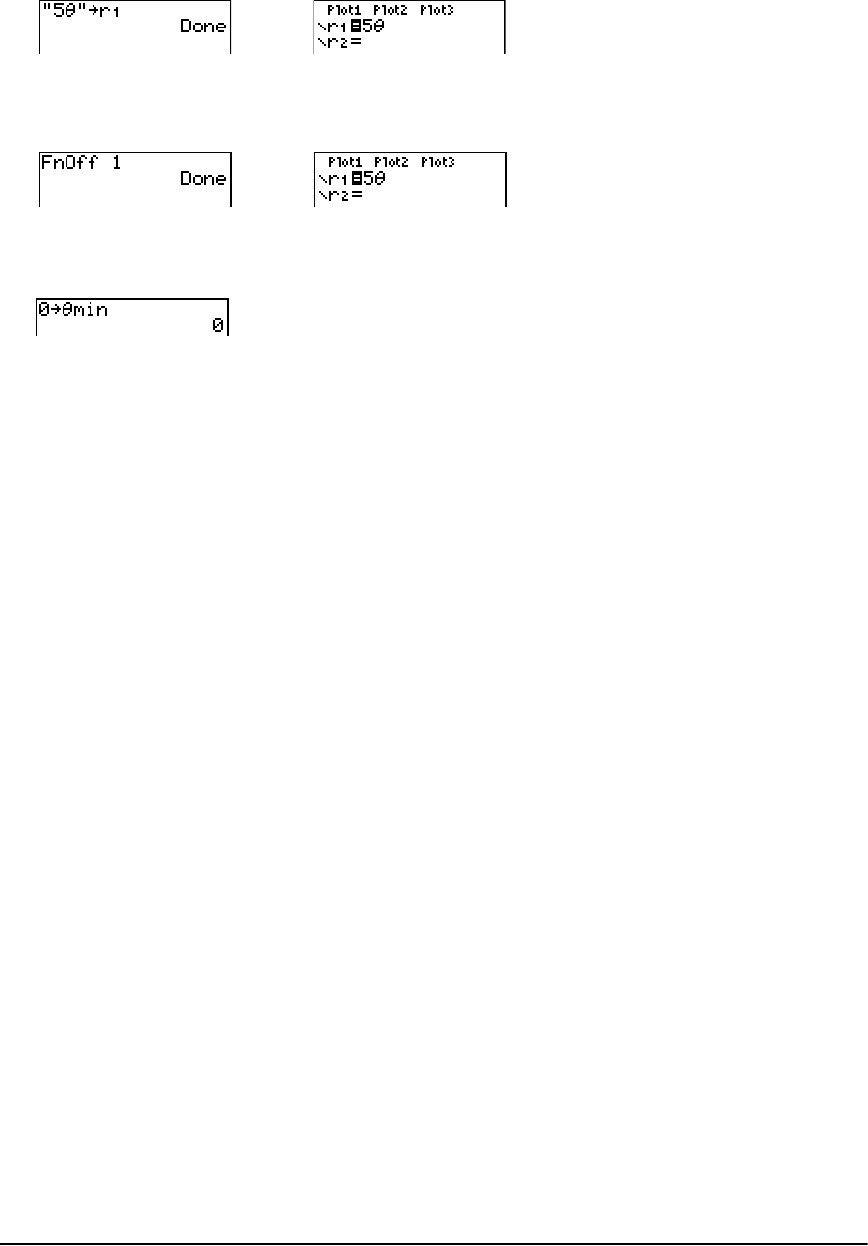
Chapter 5: Polar Graphing 100
• Store polar equations.
• Select or deselect polar equations.
• Store values directly to window variables.
Exploring Polar Graphs
Free-Moving Cursor
The free-moving cursor in Pol graphing works the same as in Func graphing. In RectGC format,
moving the cursor updates the values of X and Y; if CoordOn format is selected, X and Y are
displayed. In PolarGC format, X, Y, R, and q are updated; if CoordOn format is selected, R and q
are displayed.
TRACE
To activate TRACE, press r. When TRACE is active, you can move the trace cursor along
the graph of the equation one qstep at a time. When you begin a trace, the trace cursor is on the
first selected function at qmin. If ExprOn format is selected, then the equation is displayed.
In RectGC format, TRACE updates the values of X, Y, and q; if CoordOn format is selected, X, Y,
and q are displayed. In PolarGC format, TRACE updates X, Y, R, and q; if CoordOn format is
selected, R and q are displayed.
To move five plotted points at a time on a function, press y | or y ~. If you move the trace
cursor beyond the top or bottom of the screen, the coordinate values at the bottom of the screen
continue to change appropriately.
Quick Zoom is available in Pol graphing mode; panning is not.
Moving the Trace Cursor to Any Valid Theta Value
To move the trace cursor to any valid q value on the current function, enter the number. When you
enter the first digit, a q= prompt and the number you entered are displayed in the bottom-left corner
of the screen. You can enter an expression at the q= prompt. The value must be valid for the
current viewing window. When you complete the entry, press Í to move the cursor.

Chapter 5: Polar Graphing 101
ZOOM
ZOOM operations in Pol graphing work the same as in Func graphing. Only the X (Xmin, Xmax, and
Xscl) and Y (Ymin, Ymax, and Yscl) window variables are affected.
The q window variables (qmin, qmax, and qstep) are not affected, except when you select
ZStandard. The VARS ZOOM secondary menu ZT/Zq items 4:Zqmin, 5:Zqmax, and 6:Zqstep are
zoom memory variables for Pol graphing.
CALC
CALC operations in Pol graphing work the same as in Func graphing. The CALCULATE menu
items available in Pol graphing are 1:value, 2:dy/dx, and 3:dr/dq.

Chapter 6: Sequence Graphing 102
Chapter 6:
Sequence Graphing
Getting Started: Forest and Trees
Note: Getting Started is a fast-paced introduction. Read the chapter for details.
A small forest of 4,000 trees is under a new forestry plan. Each year 20 percent of the trees will be
harvested and 1,000 new trees will be planted. Will the forest eventually disappear? Will the forest
size stabilize? If so, in how many years and with how many trees?
1. Press z. Press † † † ~ ~ ~ Í to select
Seq graphing mode.
2. Press y . and select Time axes format
and ExprOn format if necessary.
3. Press o. If the graph-style icon is not ç (dot),
press | |, press Í until ç is displayed, and
then press ~ ~.
4. Press ~ 3 to select iPart( (integer part)
because only whole trees are harvested. After
each annual harvest, 80 percent (.80) of the trees
remain.
Press Ë 8 y [u] £ „ ¹ 1 ¤ to define the
number of trees after each harvest. Press à 1000
¤ to define the new trees. Press † 4000 to define
the number of trees at the beginning of the
program.
Note: Be sure to press y [u], not t [U]. [u] is
the second function of the ¬ key.
5. Press p 0 to set nMin=0. Press † 50 to set
nMax=50. nMin and nMax evaluate forest size over
50 years. Set the other window variables.
PlotStart=1 Xmin=0 Ymin=0
PlotStep=1 Xmax=50 Ymax=6000
Xscl=10 Yscl=1000

Chapter 6: Sequence Graphing 103
Defining and Displaying Sequence Graphs
TI-84 Plus Graphing Mode Similarities
The steps for defining a sequence graph are similar to the steps for defining a function graph.
Chapter 6 assumes that you are familiar with Chapter 3: Function Graphing. Chapter 6 details
aspects of sequence graphing that differ from function graphing.
Setting Sequence Graphing Mode
To display the mode screen, press z. To graph sequence functions, you must select Seq
graphing mode before you enter window variables and before you enter sequence functions.
Sequence graphs automatically plot in Simul mode, regardless of the current plotting-order mode
setting.
TI-84 Plus Sequence Functions u, v, and w
The TI-84 Plus has three sequence functions that you can enter from the keyboard: u, v, and w.
They are second functions of the ¬, −, and ® keys. Press y [u] to enter u, for example.
You can define sequence functions in terms of:
• The independent variable n
• The previous term in the sequence function, such as u(nN1)
• The term that precedes the previous term in the sequence function, such as u(nN2)
• The previous term or the term that precedes the previous term in another sequence function,
such as u(nN1) or u(nN2) referenced in the sequence v(n).
Note: Statements in this chapter about u(n) are also true for v(n) and w(n); statements about u(nN1)
are also true for v(nN1) and w(nN1); statements about u(nN2) are also true for v(nN2) and w(nN2).
Displaying the Sequence Y= Editor
After selecting Seq mode, press o to display the sequence Y= editor.
6. Press r. Tracing begins at nMin (the start of
the forestry plan). Press ~ to trace the sequence
year by year. The sequence is displayed at the top
of the screen. The values for n (number of years),
X (X=n, because n is plotted on the x-axis), and Y
(tree count) are displayed at the bottom. When will
the forest stabilize? With how many trees?

Chapter 6: Sequence Graphing 104
In this editor, you can display and enter sequences for u(n), v(n), and w(n). Also, you can edit the
value for nMin, which is the sequence window variable that defines the minimum n value to
evaluate.
The sequence Y= editor displays the nMin value because of its relevance to u(nMin), v(nMin), and
w(nMin), which are the initial values for the sequence equations u(n), v(n), and w(n), respectively.
nMin in the Y= editor is the same as nMin in the window editor. If you enter a new value for nMin in
one editor, the new value for nMin is updated in both editors.
Note: Use u(nMin), v(nMin), or w(nMin) only with a recursive sequence, which requires an initial
value.
Selecting Graph Styles
The icons to the left of u(n), v(n), and w(n) represent the graph style of each sequence (Chapter 3).
The default in Seq mode is í (dot), which shows discrete values. Dot, ç (line), and è (thick) styles
are available for sequence graphing. Graph styles are ignored in Web format.
Selecting and Deselecting Sequence Functions
The TI-84 Plus graphs only the selected sequence functions. In the Y= editor, a sequence function
is selected when the = signs of both u(n)= and u(nMin)= are highlighted.
To change the selection status of a sequence function, move the cursor onto the = sign of the
function name, and then press Í. The status is changed for both the sequence function u(n)
and its initial value u(nMin).
Defining and Editing a Sequence Function
To define or edit a sequence function, follow the steps in Chapter 3 for defining a function. The
independent variable in a sequence is n.
In Seq graphing mode, you can enter the sequence variable in either of two ways.
• Press „.
• Press y N [N].
You can enter the function name from the keyboard (y [u], y [v], y [w]).
Generally, sequences are either nonrecursive or recursive. Sequences are evaluated only at
consecutive integer values. n is always a series of consecutive integers, starting at zero or any
positive integer.

Chapter 6: Sequence Graphing 105
Nonrecursive Sequences
In a nonrecursive sequence, the nth term is a function of the independent variable n. Each term is
independent of all other terms.
For example, in the nonrecursive sequence below, you can calculate u(5) directly, without first
calculating u(1) or any previous term.
The sequence equation above returns the sequence 2, 4, 6, 8, 10, … for n = 1, 2, 3, 4, 5, … .
Note: You may leave blank the initial value u(nMin) when calculating nonrecursive sequences.
Recursive Sequences
In a recursive sequence, the nth term in the sequence is defined in relation to the previous term or
the term that precedes the previous term, represented by u(nN1) and u(nN2). A recursive sequence
may also be defined in relation to n, as in u(n)=u(nN1)+n.
For example, in the sequence below you cannot calculate u(5) without first calculating u(1), u(2),
u(3), and u(4).
Using an initial value u(nMin) = 1, the sequence above returns 1, 2, 4, 8, 16, ... .
Note: On the TI-84 Plus, you must type each character of the terms. For example, to enter u(nN1),
press y [u] £ „ ¹ À ¤.
Recursive sequences require an initial value or values, since they reference undefined terms.
• If each term in the sequence is defined in relation to the previous term, as in u(nN1), you must
specify an initial value for the first term.

Chapter 6: Sequence Graphing 106
• If each term in the sequence is defined in relation to the term that precedes the previous term,
as in u(nN2), you must specify initial values for the first two terms. Enter the initial values as a
list enclosed in brackets { } with commas separating the values.
The value of the first term is 0 and the value of the second term is 1 for the sequence u(n).
Setting Window Variables
To display the window variables, press p. These variables define the viewing window. The
values below are defaults for Seq graphing in both Radian and Degree angle modes.
nMin must be an integer | 0. nMax, PlotStart, and PlotStep must be integers | 1.
nMin is the smallest n value to evaluate. nMin also is displayed in the sequence Y= editor. nMax is
the largest n value to evaluate. Sequences are evaluated at u(nMin), u(nMin+1), u(nMin+2), ... ,
u(nMax).
PlotStart is the first term to be plotted. PlotStart=1 begins plotting on the first term in the sequence.
If you want plotting to begin with the fifth term in a sequence, for example, set PlotStart=5. The first
four terms are evaluated but are not plotted on the graph.
PlotStep is the incremental n value for graphing only. PlotStep does not affect sequence
evaluation; it only designates which points are plotted on the graph. If you specify PlotStep=2, the
sequence is evaluated at each consecutive integer, but it is plotted on the graph only at every
other integer.
nMin=1 Smallest n value to evaluate
nMax=10 Largest n value to evaluate
PlotStart=1First term number to be plotted
PlotStep=1Incremental n value (for graphing only)
Xmin=L10 Smallest X value to be displayed
Xmax=10 Largest X value to be displayed
Xscl=1Spacing between the X tick marks
Ymin=L10 Smallest Y value to be displayed
Ymax=10 Largest Y value to be displayed
Yscl=1Spacing between the Y tick marks

Chapter 6: Sequence Graphing 107
Selecting Axes Combinations
Setting the Graph Format
To display the current graph format settings, press y .. Chapter 3 describes the format
settings in detail. The other graphing modes share these format settings. The axes setting on the
top line of the screen is available only in Seq mode.
Setting Axes Format
For sequence graphing, you can select from five axes formats. The table below shows the values
that are plotted on the x-axis and y-axis for each axes setting.
Displaying a Sequence Graph
To plot the selected sequence functions, press s. As a graph is plotted, the TI-84 Plus
updates X, Y, and n.
Smart Graph applies to sequence graphs (Chapter 3).
Exploring Sequence Graphs
Free-Moving Cursor
The free-moving cursor in Seq graphing works the same as in Func graphing. In RectGC format,
moving the cursor updates the values of X and Y; if CoordOn format is selected, X and Y are
Time Web uv vw uw Type of sequence plot (axes)
RectGC Polar GC Rectangular or polar output
CoordOn CoordOff Cursor coordinate display on/off
GridOff GridOn Grid display off or on
AxesOn AxesOff Axes display on or off
LableOff LabelOn Axes label display off or on
ExprOn ExprOff Expression display on or off
Axes Setting x-axis y-axis
Time nu(n), v(n), w(n)
Web u(nN1), v(nN1), w(nN1) u(n), v(n), w(n)
uv u(n)v(n)
vw v(n)w(n)
uw u(n)w(n)
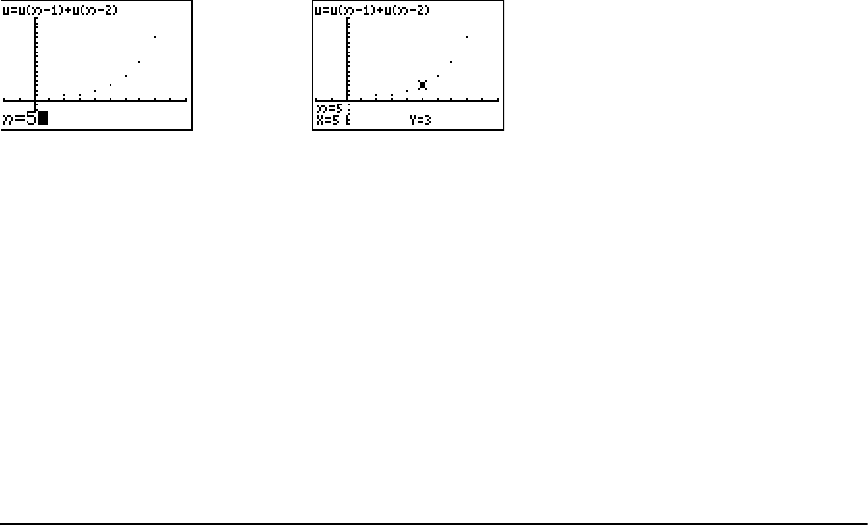
Chapter 6: Sequence Graphing 108
displayed. In PolarGC format, X, Y, R, and q are updated; if CoordOn format is selected, R and q
are displayed.
TRACE
The axes format setting affects TRACE.
When Time, uv, vw, or uw axes format is selected, TRACE moves the cursor along the sequence
one PlotStep increment at a time. To move five plotted points at once, press y ~ or y |.
• When you begin a trace, the trace cursor is on the first selected sequence at the term number
specified by PlotStart, even if it is outside the viewing window.
• Quick Zoom applies to all directions. To center the viewing window on the current cursor
location after you have moved the trace cursor, pressÍÍ. The trace cursor returns to nMin.
In Web format, the trail of the cursor helps identify points with attracting and repelling behavior in
the sequence. When you begin a trace, the cursor is on the x-axis at the initial value of the first
selected function.
Note: To move the cursor to a specified n during a trace, enter a value for n, and press Í. For
example, to quickly return the cursor to the beginning of the sequence, paste nMin to the n= prompt
and press Í.
Moving the Trace Cursor to Any Valid n Value
To move the trace cursor to any valid n value on the current function, enter the number. When you
enter the first digit, an n= prompt and the number you entered are displayed in the bottom-left
corner of the screen. You can enter an expression at the n= prompt. The value must be valid for
the current viewing window. When you have completed the entry, press Í to move the cursor.
ZOOM
ZOOM operations in Seq graphing work the same as in Func graphing. Only the X (Xmin, Xmax,
and Xscl) and Y (Ymin, Ymax, and Yscl) window variables are affected.
PlotStart, PlotStep, nMin, and nMax are only affected when you select ZStandard. The VARS Zoom
secondary menu ZU items 1 through 7 are the ZOOM MEMORY variables for Seq graphing.
CALC
The only CALC operation available in Seq graphing is value.
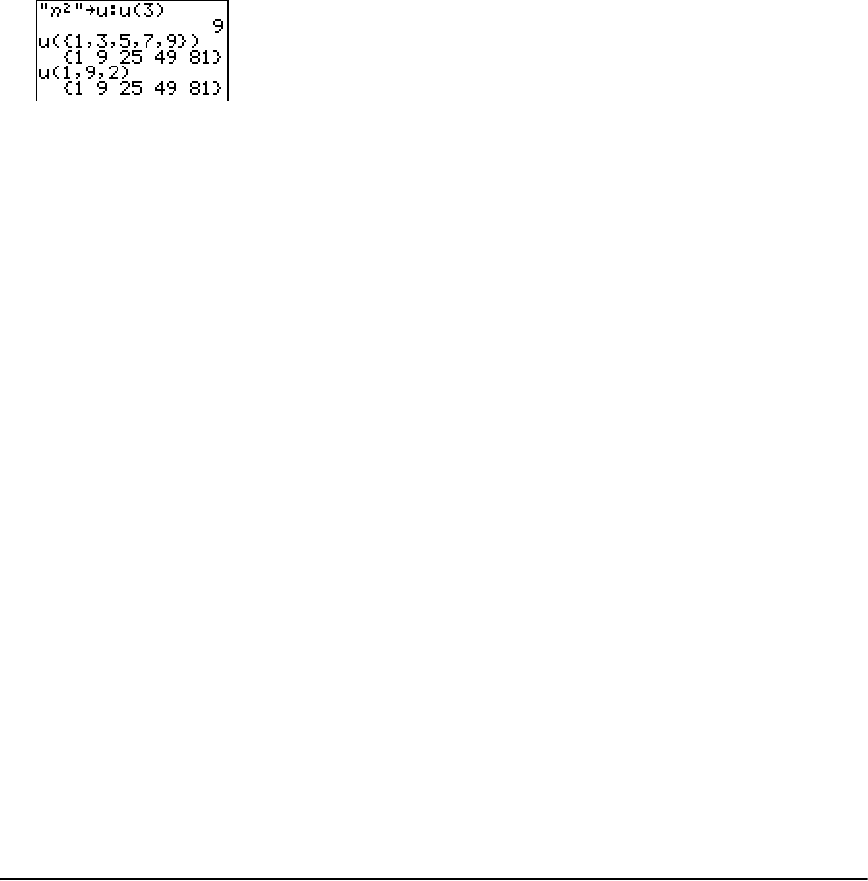
Chapter 6: Sequence Graphing 109
• When Time axes format is selected, value displays Y (the u(n) value) for a specified n value.
• When Web axes format is selected, value draws the web and displays Y (the u(n) value) for a
specified n value.
• When uv, vw, or uw axes format is selected, value displays X and Y according to the axes
format setting. For example, for uv axes format, X represents u(n) and Y represents v(n).
Evaluating u, v, and w
To enter the sequence names u, v, or w, press y [u], y [v], or y [w]. You can evaluate these
names in any of three ways.
• Calculate the nth value in a sequence.
• Calculate a list of values in a sequence.
• Generate a sequence with u(nstart,nstop[,nstep]). nstep is optional; default is 1.
Graphing Web Plots
Graphing a Web Plot
To select Web axes format, press y . ~ Í. A web plot graphs u(n) versus u(nN1),
which you can use to study long-term behavior (convergence, divergence, or oscillation) of a
recursive sequence. You can see how the sequence may change behavior as its initial value
changes.
Valid Functions for Web Plots
When Web axes format is selected, a sequence will not graph properly or will generate an error.
• It must be recursive with only one recursion level (u(nN1) but not u(nN2)).
• It cannot reference n directly.
• It cannot reference any defined sequence except itself.
Displaying the Graph Screen
In Web format, press s to display the graph screen. The TI-84 Plus:
•Draws a y=x reference line in AxesOn format.
• Plots the selected sequences with u(nN1) as the independent variable.
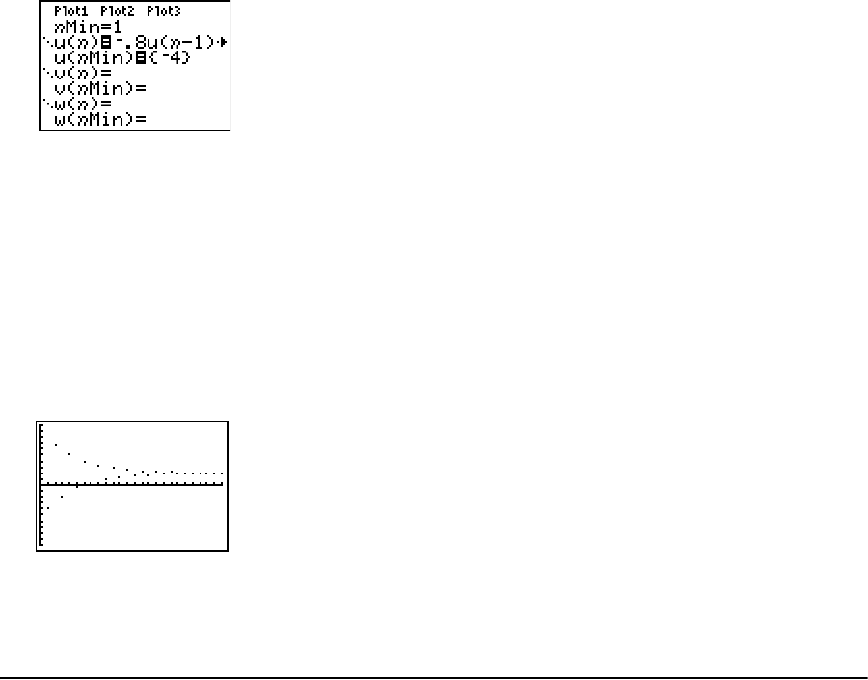
Chapter 6: Sequence Graphing 110
Note: A potential convergence point occurs whenever a sequence intersects the y=x reference
line. However, the sequence may or may not actually converge at that point, depending on the
sequence’s initial value.
Drawing the Web
To activate the trace cursor, press r. The screen displays the sequence and the current n, X,
and Y values (X represents u(nN1) and Y represents u(n)). Press ~ repeatedly to draw the web
step by step, starting at nMin. In Web format, the trace cursor follows this course.
1. It starts on the x-axis at the initial value u(nMin) (when PlotStart=1).
2. It moves vertically (up or down) to the sequence.
3. It moves horizontally to the y=x reference line.
4. It repeats this vertical and horizontal movement as you continue to press ~.
Using Web Plots to Illustrate Convergence
Example: Convergence
1. Press o in Seq mode to display the sequence Y= editor. Make sure the graph style is set to
í (dot), and then define nMin, u(n) and u(nMin) as u(n) = -.8u(n-1) + 3.6.
2. Press y . Í to set Time axes format.
3. Press p and set the variables as shown below.
4. Press s to graph the sequence.
5. Press y . and select the Web axes setting.
nMin=1
nMax=25
PlotStart=1
PlotStep=1
Xmin=0
Xmax=25
Xscl=1
Ymin=L10
Ymax=10
Yscl=1

Chapter 6: Sequence Graphing 111
6. Press p and change the variables below.
7. Press s to graph the sequence.
8. Press r, and then press ~ to draw the web. The displayed cursor coordinates n, X (u(nN1)),
and Y (u(n)) change accordingly. When you press ~, a new n value is displayed, and the trace
cursor is on the sequence. When you press ~ again, the n value remains the same, and the
cursor moves to the y=x reference line. This pattern repeats as you trace the web.
Graphing Phase Plots
Graphing with uv, vw, and uw
The phase-plot axes settings uv, vw, and uw show relationships between two sequences. To
select a phase-plot axes setting, press y ., press ~ until the cursor is on uv, vw, or uw,
and then press Í.
Example: Predator-Prey Model
Use the predator-prey model to determine the regional populations of a predator and its prey that
would maintain population equilibrium for the two species.
This example uses the model to determine the equilibrium populations of foxes and rabbits, with
initial populations of 200 rabbits (u(nMin)) and 50 foxes (v(nMin)).
These are the variables (given values are in parentheses):
Xmin=L10 Xmax=10
Axes Setting x-axis y-axis
uv u(n)v(n)
vw v(n)w(n)
uw u(n)w(n)
R = number of rabbits
M = rabbit population growth rate without foxes (.05)
K = rabbit population death rate with foxes (.001)
W = number of foxes
G = fox population growth rate with rabbits (.0002)
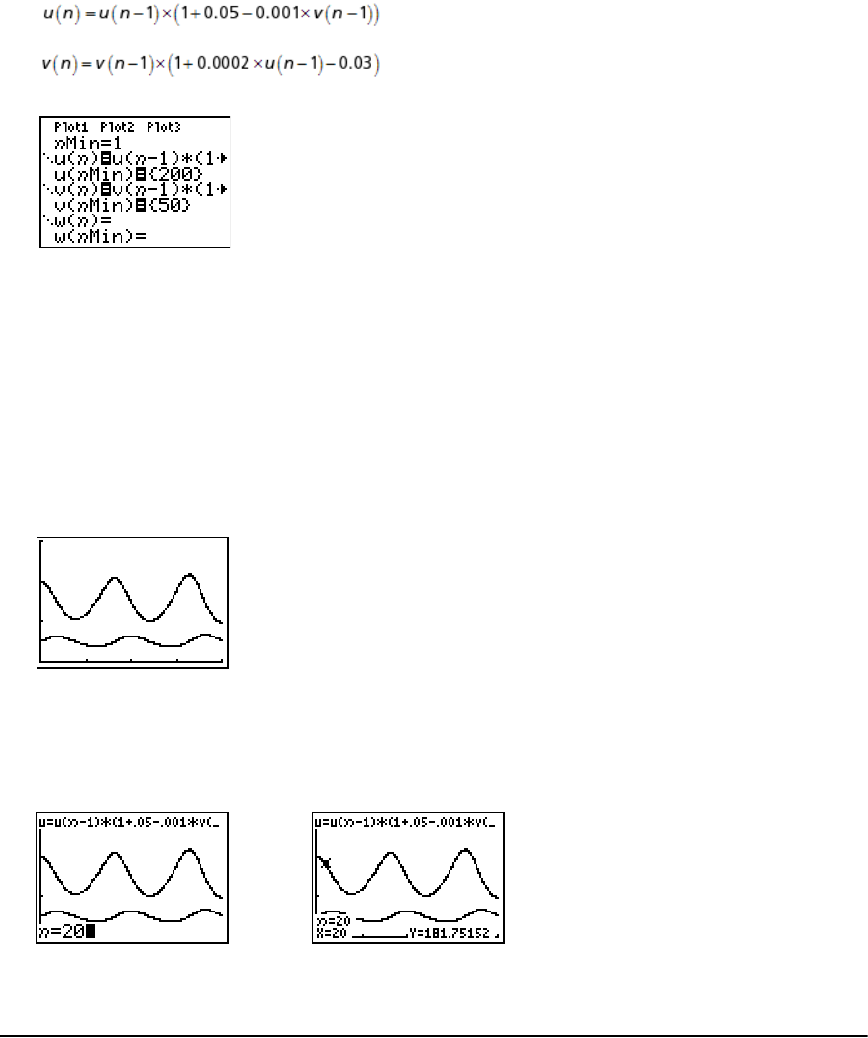
Chapter 6: Sequence Graphing 112
1. Press o in Seq mode to display the sequence Y= editor. Define the sequences and initial
values for Rn and Wn as shown below. Enter the sequence Rn as u(n) and enter the sequence
Wn as v(n).
2. Press y . Í to select Time axes format.
3. Press p and set the variables as shown below.
4. Press s to graph the sequence.
5. Press r ~ to individually trace the number of rabbits (u(n)) and foxes (v(n)) over time (n).
Note: Press a number, and then press Í to jump to a specific n value (month) while in
TRACE.
D = fox population death rate without rabbits (.03)
n= time (in months)
Rn=RnN1(1+MNKWnN1)
Wn=WnN1(1+GRnN1ND)
nMin=0
nMax=400
PlotStart=1
PlotStep=1
Xmin=0
Xmax=400
Xscl=100
Ymin=0
Ymax=300
Yscl=100

Chapter 6: Sequence Graphing 113
6. Press y . ~ ~ Í to select uv axes format.
7. Press p and change these variables as shown below.
8. Press r. Trace both the number of rabbits (X) and the number of foxes (Y) through 400
generations.
Note: When you press r, the equation for u
is displayed in the
top-left corner. Press } or † to
see the equation for v.
Comparing TI-84 Plus and TI-82 Sequence Variables
Sequences and Window Variables
Refer to the table if you are familiar with the TI-82. It shows TI-84 Plus sequences and sequence
window variables, as well as their TI-82 counterparts.
Xmin=84
Xmax=237
Xscl=50
Ymin=25
Ymax=75
Yscl=10
TI-84 Plus TI-82
In the Y= editor:
u(n)Un
u(nMin) UnStart (window variable)
v(n)Vn
v(nMin) VnStart (window variable)
w(n)not available
w(nMin) not available
In the window editor:
nMin nStart
nMax nMax
PlotStart nMin
PlotStep not available

Chapter 6: Sequence Graphing 114
Keystroke Differences Between TI-84 Plus
and TI-82
Sequence Keystroke Changes
Refer to the table if you are familiar with the TI-82. It compares TI-84 Plus sequence-name syntax
and variable syntax with TI-82 sequence-name syntax and variable syntax.
TI-84 Plus / TI-82 On TI-84 Plus, press: On TI-82, press:
n / n„y ô
u(n) / Uny [u]
£ „ ¤
y ó ¶¦À
v(n) / Vny [v]
£ „ ¤
y ó ¶¦Á
w(n)y [w]
£ „ ¤
not available
u(nN1) / UnN1y [u]
£ „ ¹ À ¤
y õ
v(nN1) / VnN1y [v]
£ „ ¹ À ¤
y ö
w(nN1) y [w]
£ „ ¹ À ¤
not available
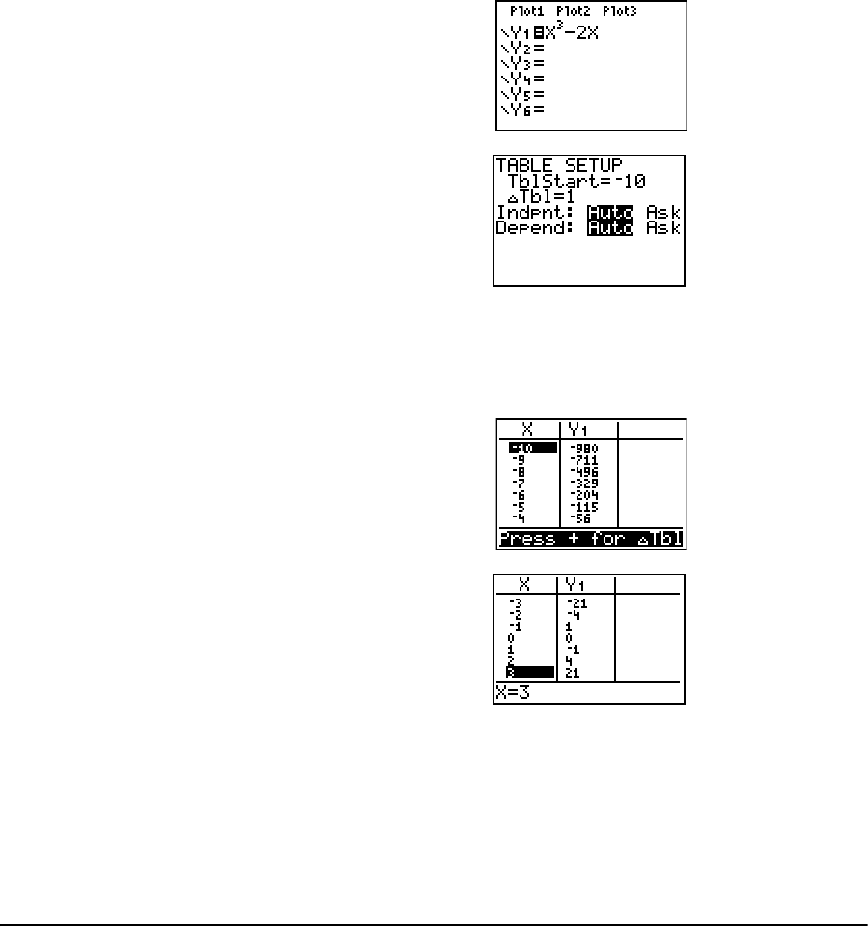
Chapter 7: Tables 115
Chapter 7:
Tables
Getting Started: Roots of a Function
Getting Started is a fast-paced introduction. Read the chapter for details.
Evaluate the function Y = X3 N 2X at each integer between L10 and 10. How many sign changes
occur, and at what X values?
1. Press z † † † Í to set Func graphing
mode.
2. Press o. Press „ 3 to select 3. Then
press ¹ 2 „ to enter the function Y1=X3N2X.
3. Press y - to display the TABLE SETUP
screen. Press Ì 10 Í to set TblStart=L10.
Press 1 Í to set @Tbl=1.
Press Í to select Indpnt: Auto (automatically
generated independent values). Press † Í to
select Depend: Auto (automatically generated
dependent values).
4. Press y 0 to display the table screen.
Note: The message on the entry line, “Press + for
@Tbl” is a reminder that you can change @Tbl from
this table view. The entry line is cleared when you
press any key.
5. Press †until you see the sign changes in the
value of Y1. How many sign changes occur, and at
what X values?
In this case, you can also see the roots of the
function by finding when Y1=0. You can explore
changes in X by pressing à to display the @TTbl
prompt, entering a new value, and searching for
your answer.

Chapter 7: Tables 116
Setting Up the Table
TABLE SETUP Screen
To display the TABLE SETUP screen, press y -.
TblStart, @Tbl
TblStart (table start) defines the initial value for the independent variable. TblStart applies only
when the independent variable is generated automatically (when Indpnt: Auto is selected).
@Tbl (table step) defines the increment for the independent variable.
Indpnt: Auto, Indpnt: Ask, Depend: Auto, Depend: Ask
Selections Table Characteristics
Indpnt: Auto
Depend: Auto
Values are displayed automatically in both the independent-
variable column and in all dependent-variable columns.
Indpnt: Ask
Depend: Auto
The table is empty. When you enter a value for the independent
variable, all corresponding dependent-variable values are
calculated and displayed automatically.
Indpnt: Auto
Depend: Ask
Values are displayed automatically for the independent variable.
To generate a value for a dependent variable, move the cursor to
that cell and press Í.
Indpnt: Ask
Depend: Ask
The table is empty; enter values for the independent variable. To
generate a value for a dependent variable, move the cursor to
that cell and press Í.
Setting Up the Table from the Home Screen or a Program
To store a value to TblStart, @Tbl, or Tbl[nput from the home screen or a program, select the
variable name from the VARS TABLE secondary menu. TblZnput is a list of independent-variable
values in the current table.
When you press y - in the program editor, you can select IndpntAuto, IndpntAsk,
DependAuto, and DependAsk.
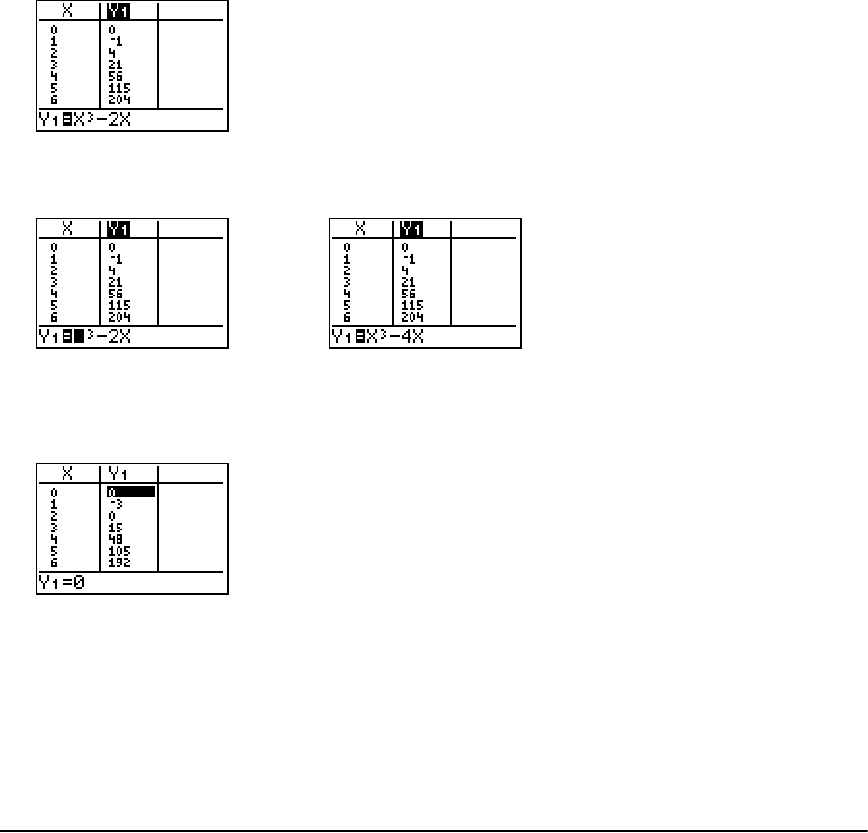
Chapter 7: Tables 117
Defining the Dependent Variables
Defining Dependent Variables from the Y= Editor
In the Y= editor, enter the functions that define the dependent variables. Only functions that are
selected in the Y= editor are displayed in the table. The current graphing mode is used. In
parametric mode, you must define both components of each parametric equation (Chapter 4).
Editing Dependent Variables from the Table Editor
To edit a selected Y= function from the table editor, follow these steps.
1. Press y 0 to display the table, then press ~ or | to move the cursor to a dependent-
variable column.
2. Press } until the cursor is on the function name at the top of the column. The function is
displayed on the bottom line.
3. Press Í. The cursor moves to the bottom line. Edit the function.
4. Press Í or †. The new values are calculated. The table and the Y= function are updated
automatically.
Note: You also can use this feature to view the function that defines a dependent variable
without having to leave the table.

Chapter 7: Tables 118
Displaying the Table
The Table
To display the table, press y 0.
Note: The table abbreviates the values, if necessary.
Current cell
Current cell’s full value
Dependent-variable
values in the second
and third columns
Independent-variable
values in the first
column
Note: When the table first displays, the message “Press + for @Tbl” is on the entry line. This
message reminds you that you can press à to change @Tbl at any time. When you press any key,
the message disappears.
Independent and Dependent Variables
The current graphing mode determines which independent and dependent variables are displayed
in the table (Chapter 1). In the table above, for example, the independent variable X and the
dependent variables Y1 and Y2 are displayed because Func graphing mode is set.
Clearing the Table from the Home Screen or a Program
From the home screen, select the ClrTable instruction from the CATALOG. To clear the table,
press Í.
From a program, select 9:ClrTable from the PRGM I/O menu or from the CATALOG. The table is
cleared upon execution. If IndpntAsk is selected, all independent and dependent variable values
on the table are cleared. If DependAsk is selected, all dependent variable values on the table are
cleared.
Graphing Mode
Independent Variable
Dependent Variable
Func (function) X Y1 through Y9, and Y0
Par (parametric) T X1T/Y1T through X6T/Y6T
Pol (polar) qr1 through r6
Seq (sequence) nu(n), v(n), and w(n)
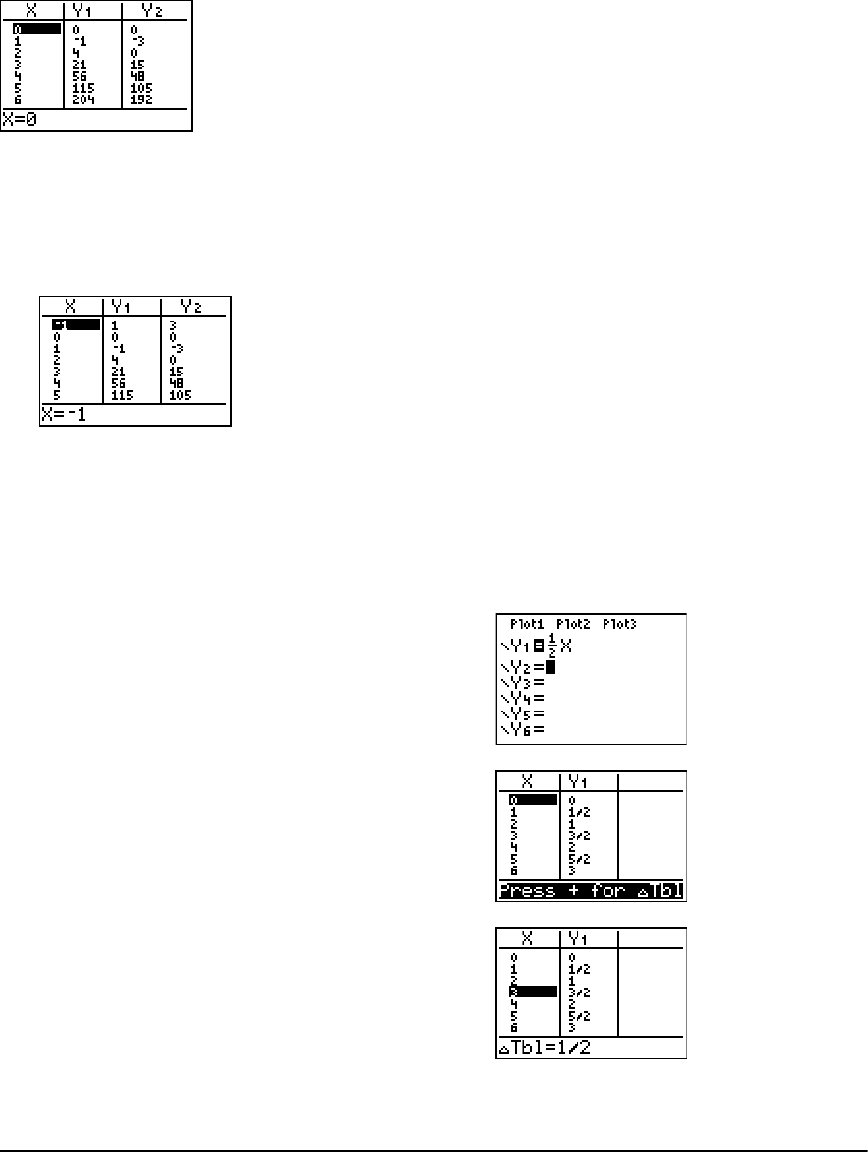
Chapter 7: Tables 119
Scrolling Independent-Variable Values
If Indpnt: Auto is selected, you can press } and † in the independent-variable column to display
more values. As you scroll the column, the corresponding dependent-variable values also are
displayed. All dependent-variable values may not be displayed if Depend: Ask is selected.
Note: You can scroll back from the value entered for TblStart. As you scroll, TblStart is updated
automatically to the value shown on the top line of the table. In the example above, TblStart=0 and
@Tbl=1 generates and displays values of X=0, …, 6; but you can press } to scroll back and display
the table for X=M1, …, 5.
Changing Table Settings from the Table View
You can change table settings from the table view by highlighting a value in the table, pressing Ã,
and entering a new @ value.
1. Press o and then press 1 t ^ 1 2 ~ „
to enter the function Y1=1/2x.
2. Press y 0.
3. Press † † † to move the cursor to highlight 3,
and then press Ã.
4. Press 1 t ^ 1 2 to change the table settings
to view changes in X in increments of 1/2.
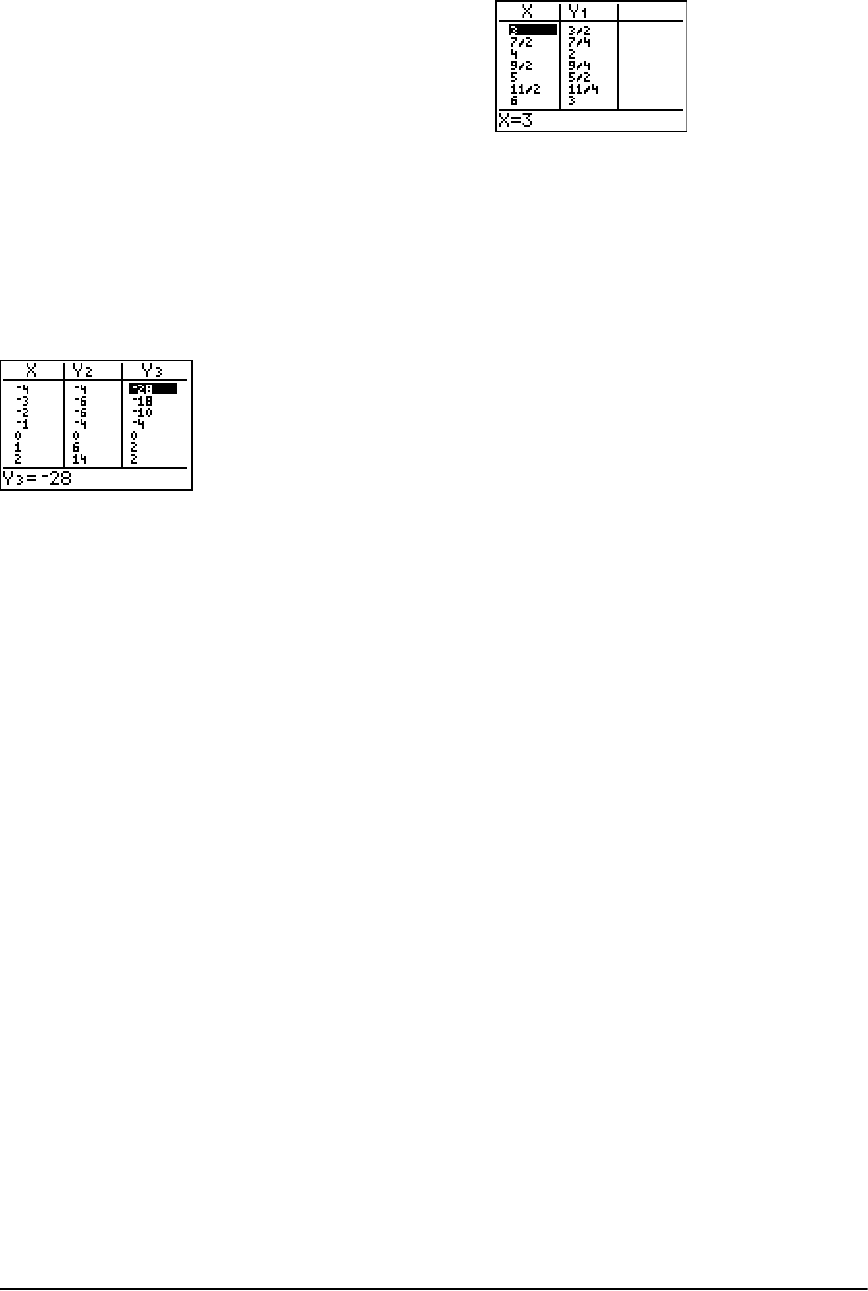
Chapter 7: Tables 120
Displaying Other Dependent Variables
If you have defined more than two dependent variables, the first two selected Y= functions are
displayed initially. Press ~ or | to display dependent variables defined by other selected Y=
functions. The independent variable always remains in the left column, except during a trace with
parametric graphing mode and G-T split-screen mode set.
Note: To simultaneously display two dependent variables on the table that are not defined as
consecutive Y= functions, go to the Y= editor and deselect the Y= functions between the two you
want to display. For example, to simultaneously display Y4 and Y7 on the table, go to the Y= editor
and deselect Y5 and Y6.
5. Press Í.
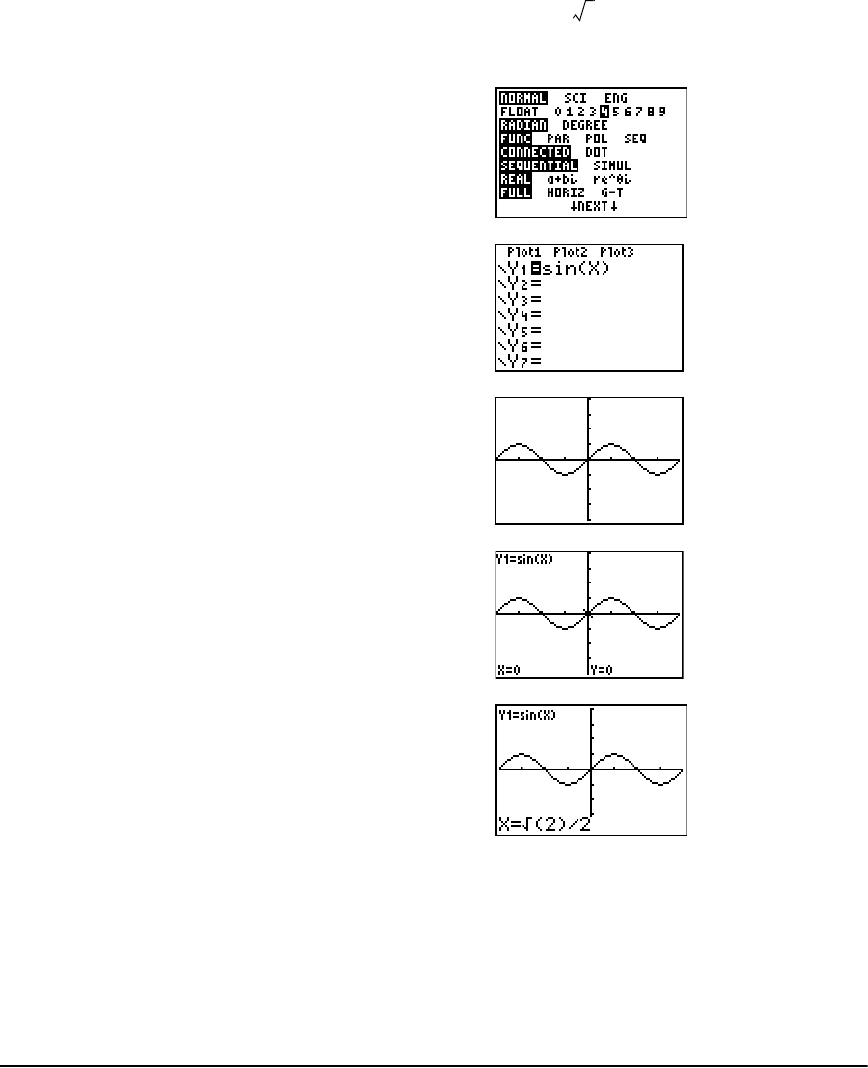
Chapter 8: Draw Instructions 121
Chapter 8:
Draw Instructions
Getting Started: Drawing a Tangent Line
Getting Started is a fast-paced introduction. Read the chapter for details.
Suppose you want to find the equation of the tangent line at X = for the function Y=sin(X).
1. Before you begin, press z and select 4, Radian
and Func, if necessary.
2. Press o to display the Y= editor. Press
˜ „ ¤ to store sin(X) in Y1.
3. Press q 7 to select 7:ZTrig, which graphs the
equation in the Zoom Trig window.
4. Press y < 5 to select 5:Tangent(. The
tangent instruction is initiated.
5. Press y C 2 ¤ ¥ 2.
2
2
-------
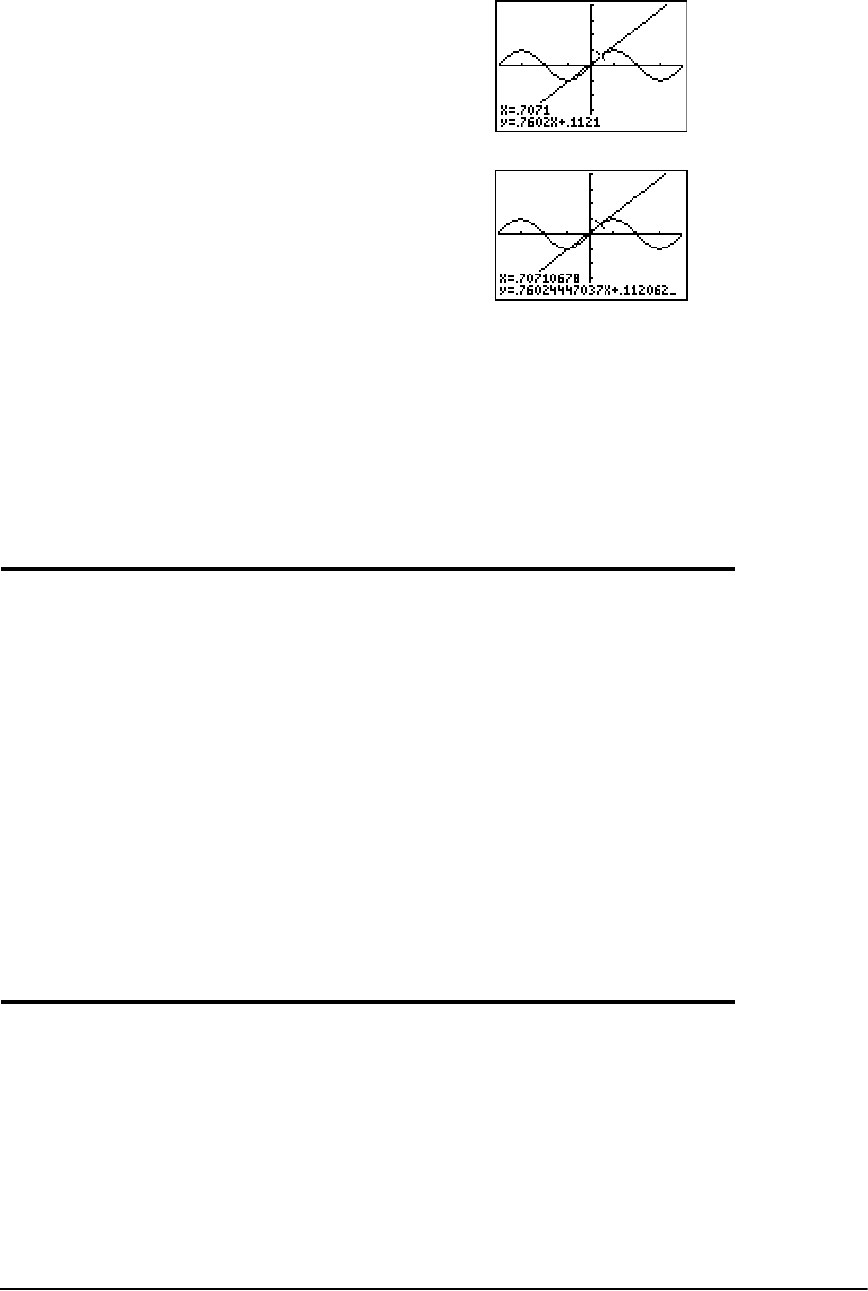
Chapter 8: Draw Instructions 122
Using the DRAW Menu
DRAW Menu
To display the DRAW menu, press y <. The TI-84 Plus’s interpretation of these instructions
depends on whether you accessed the menu from the home screen or the program editor or
directly from a graph.
Before Drawing on a Graph
The DRAW instructions draw on top of graphs. Therefore, before you use the DRAW instructions,
consider whether you want to perform one or more of the following actions.
• Change the mode settings on the mode screen.
• Change the format settings on the format screen. You can press y . or use the
shortcut on the mode screen to go to the format graph screen.
6. Press Í. The tangent line is drawn; the X
value and the tangent-line equation are displayed
on the graph.
Consider repeating this activity with the mode set to
the number of decimal places desired. The first screen
shows four decimal places. The second screen shows
the decimal setting at Float.
DRAW POINTS STO
1: ClrDraw Clears all drawn elements.
2: Line( Draws a line segment between 2 points.
3: Horizontal Draws a horizontal line.
4: Vertical Draws a vertical line.
5: Tangent( Draws a line segment tangent to a function.
6: DrawF Draws a function.
7: Shade( Shades an area between two functions.
8: DrawInv Draws the inverse of a function.
9: Circle( Draws a circle.
0: Text( Draws text on a graph screen.
A: Pen Activates the free-form drawing tool.

Chapter 8: Draw Instructions 123
• Enter or edit functions in the Y= editor.
• Select or deselect functions in the Y= editor.
• Change the window variable values.
• Turn stat plots on or off.
• Clear existing drawings with ClrDraw.
Note: If you draw on a graph and then perform any of the actions listed above, the graph is
replotted without the drawings when you display the graph again. Before you clear drawings, you
can store them with StorePic.
Drawing on a Graph
You can use any DRAW menu instructions except DrawInv to draw on Func, Par, Pol, and Seq
graphs. DrawInv is valid only in Func graphing. The coordinates for all DRAW instructions are the
display’s x-coordinate and y-coordinate values.
You can use most DRAW menu and DRAW POINTS menu instructions to draw directly on a graph,
using the cursor to identify the coordinates. You also can execute these instructions from the
home screen or from within a program. If a graph is not displayed when you select a DRAW menu
instruction, the home screen is displayed.
Clearing Drawings
Clearing Drawings When a Graph Is Displayed
All points, lines, and shading drawn on a graph with DRAW instructions are temporary.
To clear drawings from the currently displayed graph, select 1:ClrDraw from the DRAW menu. The
current graph is replotted and displayed with no drawn elements.
Clearing Drawings from the Home Screen or a Program
To clear drawings on a graph from the home screen or a program, begin on a blank line on the
home screen or in the program editor. Select 1:ClrDraw from the DRAW menu. The instruction is
copied to the cursor location. Press Í.
When ClrDraw is executed, it clears all drawings from the current graph and displays the message
Done. When you display the graph again, all drawn points, lines, circles, and shaded areas will be
gone.
Note: Before you clear drawings, you can store them with StorePic.
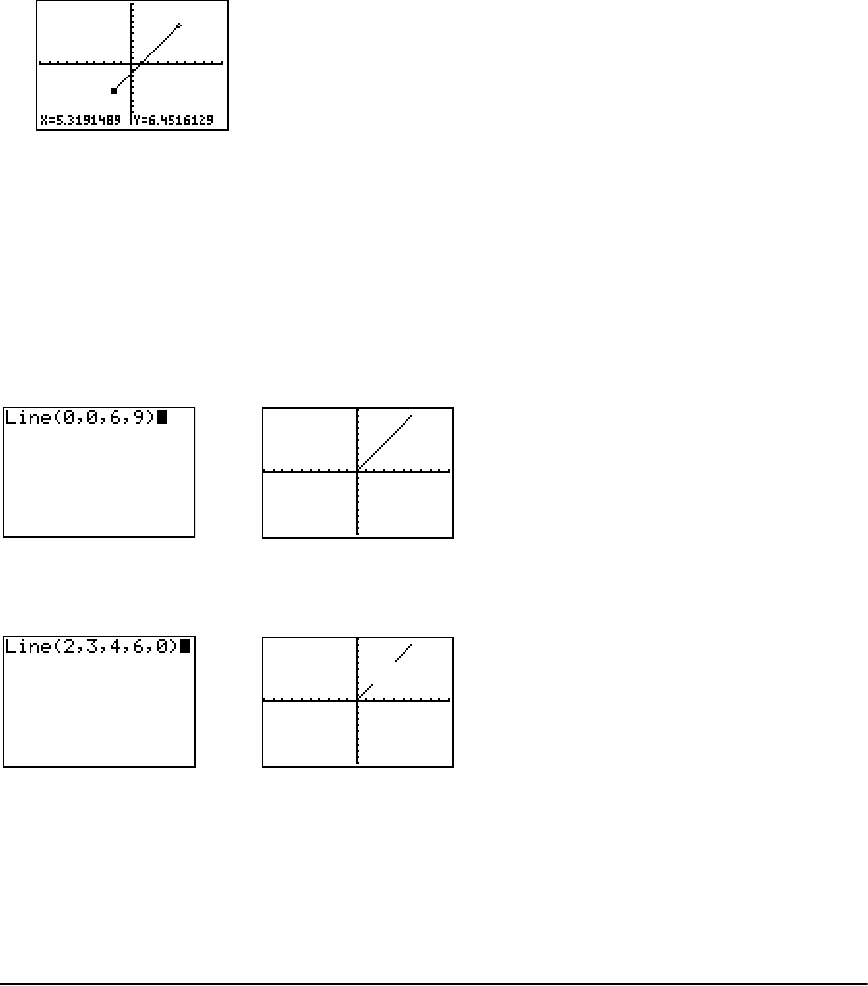
Chapter 8: Draw Instructions 124
Drawing Line Segments
Drawing a Line Segment Directly on a Graph
To draw a line segment when a graph is displayed, follow these steps.
1. Select 2:Line( from the DRAW menu.
2. Place the cursor on the point where you want the line segment to begin, and then press Í.
3. Move the cursor to the point where you want the line segment to end. The line is displayed as
you move the cursor. Press Í.
To continue drawing line segments, repeat steps 2 and 3. To cancel Line(, press ‘.
Drawing a Line Segment from the Home Screen or a Program
Line( also draws a line segment between the coordinates (X1,Y1) and (X2,Y2). The values may be
entered as expressions.
Line(X1,Y1,X2,Y2)
To erase a line segment, enter Line(X1,Y1,X2,Y2,0)
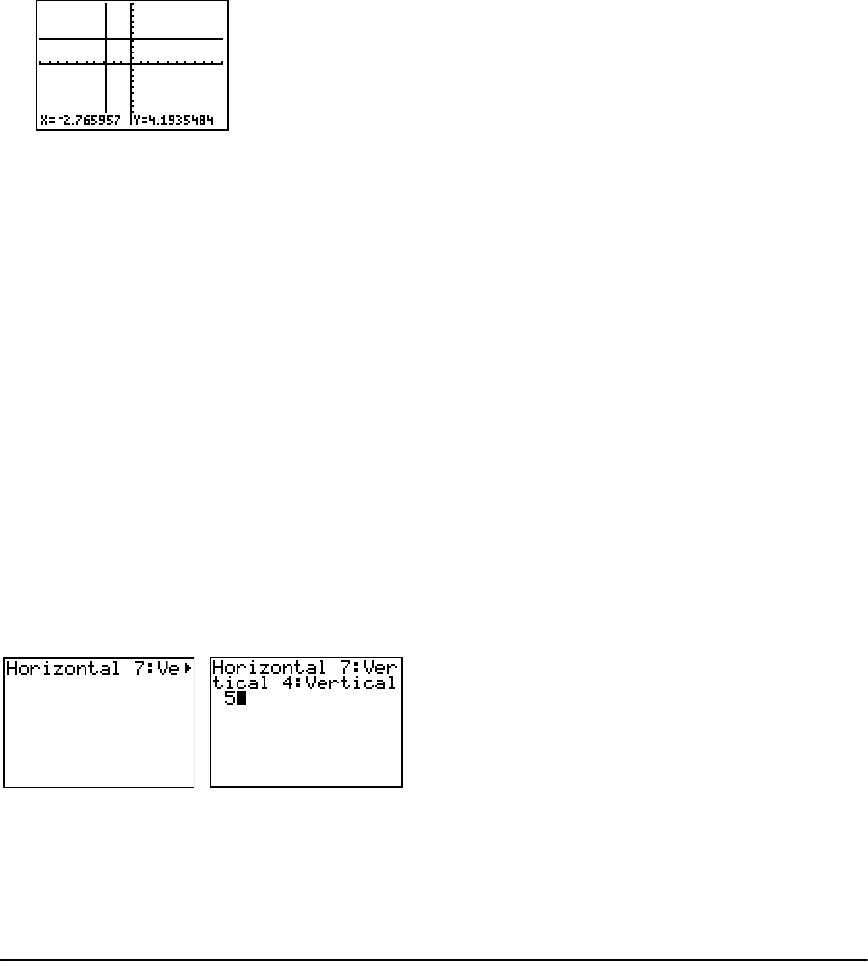
Chapter 8: Draw Instructions 125
Drawing Horizontal and Vertical Lines
Drawing a Line Directly on a Graph
To draw a horizontal or vertical line when a graph is displayed, follow these steps.
1. Select 3:Horizontal or 4:Vertical from the DRAW menu. A line is displayed that moves as you
move the cursor.
2. Place the cursor on the y-coordinate (for horizontal lines) or x-coordinate (for vertical lines)
through which you want the drawn line to pass.
3. Press Í to draw the line on the graph.
To continue drawing lines, repeat steps 2 and 3.
To cancel Horizontal or Vertical, press ‘.
Drawing a Line from the Home Screen or a Program
Horizontal (horizontal line) draws a horizontal line at Y=y. y, which can be an expression but not a
list.
Horizontal y
Vertical (vertical line) draws a vertical line at X=x. x, which can be an expression but not a list.
Vertical x
To instruct the TI-84 Plus to draw more than one horizontal or vertical line, separate each
instruction with a colon ( : ).
MathPrint™ Classic

Chapter 8: Draw Instructions 126
Drawing Tangent Lines
Drawing a Tangent Line Directly on a Graph
To draw a tangent line when a graph is displayed, follow these steps.
1. Select 5:Tangent( from the DRAW menu.
2. Press † and } to move the cursor to the function for which you want to draw the tangent line.
The current graph’s Y= function is displayed in the top-left corner, if ExprOn is selected.
3. Press ~ and | or enter a number to select the point on the function at which you want to draw
the tangent line.
4. Press Í. In Func mode, the X value at which the tangent line was drawn is displayed on
the bottom of the screen, along with the equation of the tangent line. In all other modes, the
dy/dx value is displayed.
5. Change the fixed decimal setting on the mode screen if you want to see fewer digits displayed
for X and the equation for Y.
Drawing a Tangent Line from the Home Screen or a Program
Tangent( (tangent line) draws a line tangent to expression in terms of X, such as Y1 or X2, at point
X=value. X can be an expression. expression is interpreted as being in Func mode.
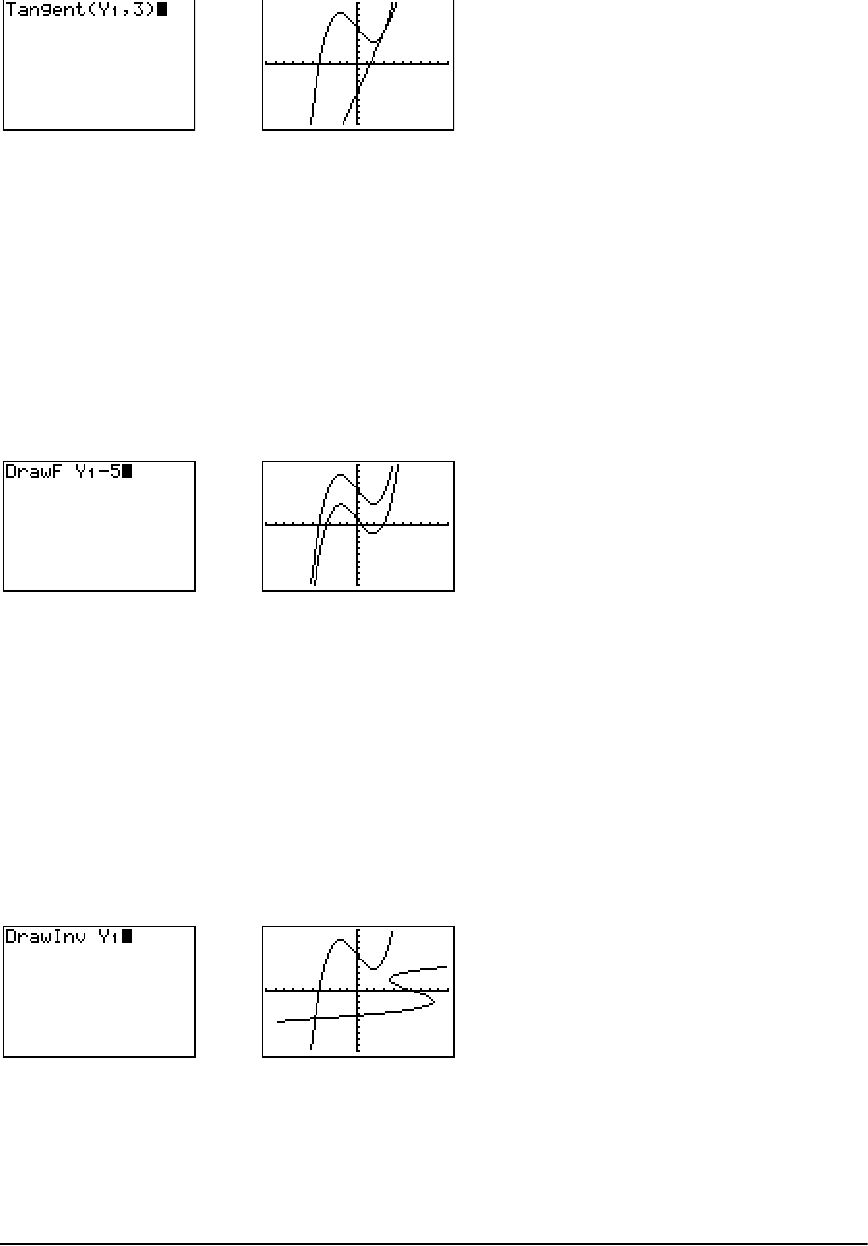
Chapter 8: Draw Instructions 127
Tangent(expression,value)
Drawing Functions and Inverses
Drawing a Function
DrawF (draw function) draws expression as a function in terms of X on the current graph. When you
select 6:DrawF from the DRAW menu, the TI-84 Plus returns to the home screen or the program
editor. DrawF is not interactive.
DrawF expression
Note: You cannot use a list in expression to draw a family of curves.
Drawing an Inverse of a Function
DrawInv (draw inverse) draws the inverse of expression by plotting X values on the y-axis and Y
values on the x-axis. When you select 8:DrawInv from the DRAW menu, the TI-84 Plus returns to
the home screen or the program editor. DrawInv is not interactive. DrawInv works in Func mode
only.
DrawInv expression
Note: You cannot use a list of expressions with DrawInv.

Chapter 8: Draw Instructions 128
Shading Areas on a Graph
Shading a Graph
To shade an area on a graph, select 7:Shade( from the DRAW menu. The instruction is pasted to
the home screen or to the program editor.
Shade(lowerfunc,upperfunc[,Xleft,Xright,pattern,patres])
Shade( draws lowerfunc and upperfunc in terms of X on the current graph and shades the area that is
specifically above lowerfunc and below upperfunc. Only the areas where lowerfunc < upperfunc are
shaded.
Xleft and Xright, if included, specify left and right boundaries for the shading. Xleft and Xright must be
numbers between Xmin and Xmax, which are the defaults.
pattern specifies one of four shading patterns.
patres specifies one of eight shading resolutions.
Drawing Circles
Drawing a Circle Directly on a Graph
To draw a circle directly on a displayed graph using the cursor, follow these steps.
1. Select 9:Circle( from the DRAW menu.
MathPrint™
Classic
pattern=1
pattern=2
pattern=3
pattern=4
vertical (default)
horizontal
negative—slope 45¡
positive—slope 45¡
patres=1
patres=2
patres=3
patres=4
patres=5
patres=6
patres=7
patres=8
shades every pixel (default)
shades every second pixel
shades every third pixel
shades every fourth pixel
shades every fifth pixel
shades every sixth pixel
shades every seventh pixel
shades every eighth pixel
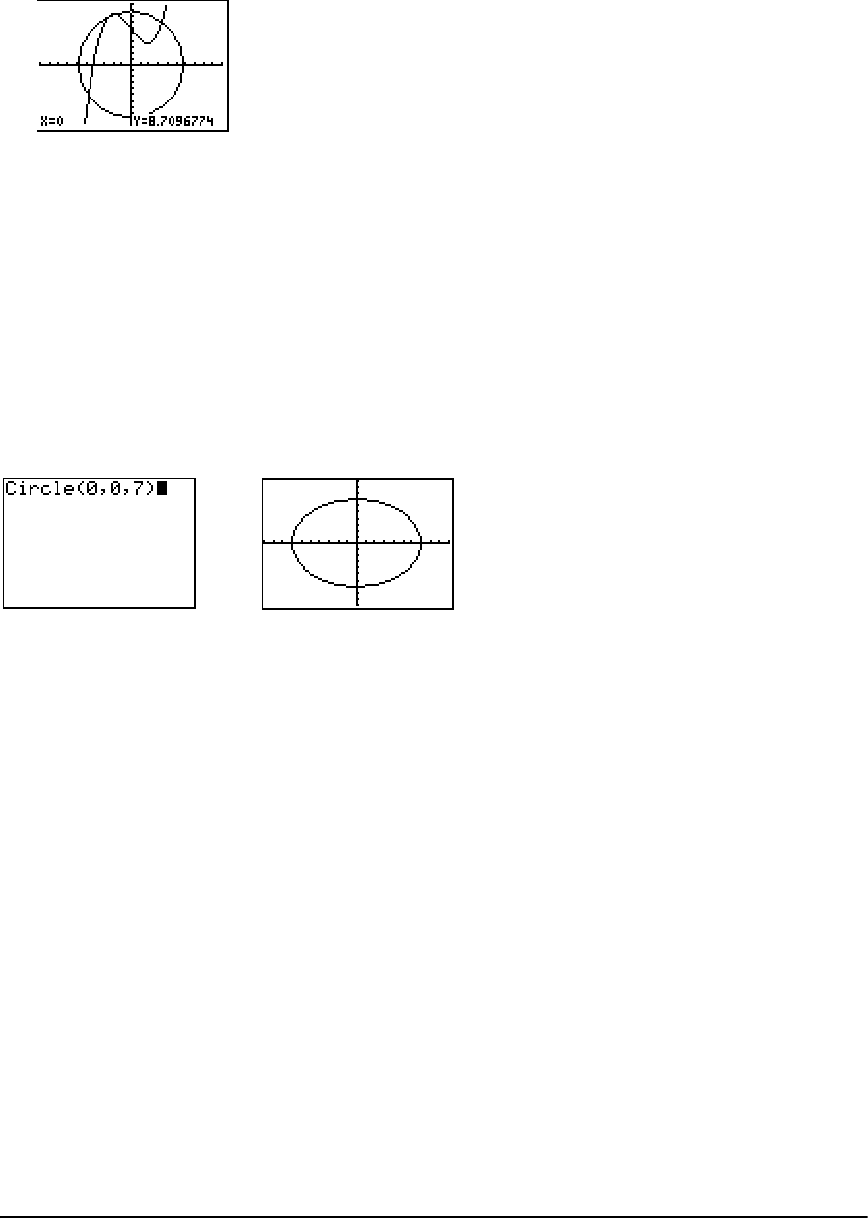
Chapter 8: Draw Instructions 129
2. Place the cursor at the center of the circle you want to draw. Press Í.
3. Move the cursor to a point on the circumference. Press Í to draw the circle on the graph.
Note: This circle is displayed as circular, regardless of the window variable values, because you
drew it directly on the display. When you use the Circle( instruction from the home screen or a
program, the current window variables may distort the shape.
To continue drawing circles, repeat steps 2 and 3. To cancel Circle(, press ‘.
Drawing a Circle from the Home Screen or a Program
Circle( draws a circle with center (X,Y) and radius. These values can be expressions.
Circle(X,Y,radius)
Note: When you use Circle( on the home screen or from a program, the current window values
may distort the drawn circle. Use ZSquare (Chapter 3) before drawing the circle to adjust the
window variables and make the circle circular.
Placing Text on a Graph
Placing Text Directly on a Graph
To place text on a graph when the graph is displayed, follow these steps.
1. Select 0:Text( from the DRAW menu.
2. Place the cursor where you want the text to begin.
3. Enter the characters. Press ƒ or y 7 to enter letters and q. You may enter TI-84
Plus functions, variables, and instructions. The font is proportional, so the exact number of
characters you can place on the graph varies. As you type, the characters are placed on top of
the graph.
To cancel Text(, press ‘.
Chapter 8: Draw Instructions 130
Placing Text on a Graph from the Home Screen or a Program
Text( places on the current graph the characters comprising value, which can include TI-84 Plus
functions and instructions. The top-left corner of the first character is at pixel (row,column), where
row is an integer between 0 and 57 and column is an integer between 0 and 94. Both row and column
can be expressions.
Text(row,column,value,value…)
value can be text enclosed in quotation marks ( " ), or it can be an expression. The TI-84 Plus will
evaluate an expression and display the result with up to 10 characters.
Split Screen
On a Horiz split screen, the maximum value for row is 25. On a G-T split screen, the maximum
value for row is 45, and the maximum value for column is 46.
Using Pen to Draw on a Graph
Using Pen to Draw on a Graph
Pen draws directly on a graph only. You cannot execute Pen from the home screen or a program.
You can capture the image you created using TI-Connect™ software and save it to your computer
for homework or teaching material or store it as a picture file on your TI-84 Plus (see Storing
Graph Pictures below).
To draw on a displayed graph, follow these steps.
1. Select A:Pen from the DRAW menu.
2. Place the cursor on the point where you want to begin drawing. Press Í to turn on the
pen.
3. Move the cursor. As you move the cursor, you draw on the graph, shading one pixel at a time.
4. Press Í to turn off the pen.
Classic
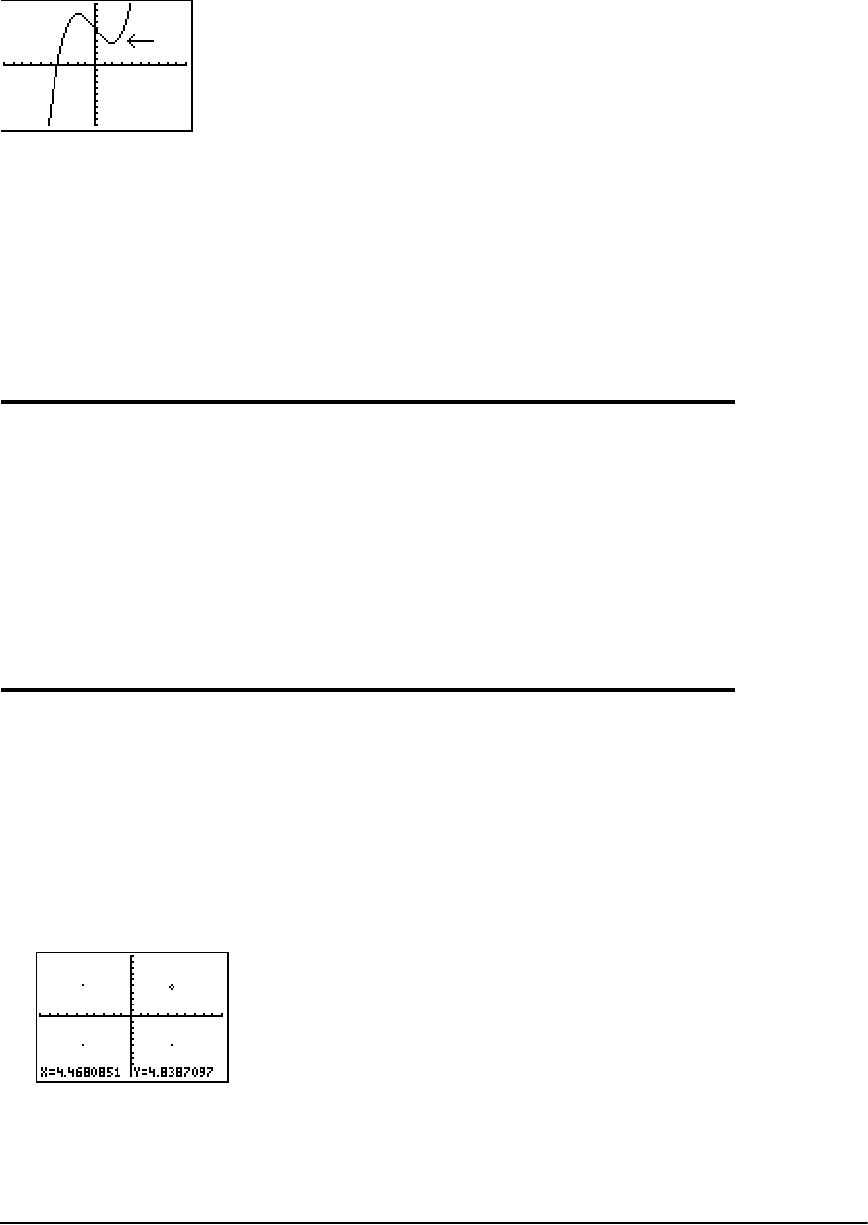
Chapter 8: Draw Instructions 131
For example, Pen was used to create the arrow pointing to the local minimum of the selected
function.
Drawing Points on a Graph
DRAW POINTS Menu
To display the DRAW POINTS menu, press y < ~. The TI-84 Plus’s interpretation of these
instructions depends on whether you accessed this menu from the home screen or the program
editor or directly from a graph.
Drawing Points Directly on a Graph with Pt-On(
To draw a point on a graph, follow these steps.
1. Select 1:Pt-On( from the DRAW POINTS menu.
2. Move the cursor to the position where you want to draw the point.
3. Press Í to draw the point.
To continue drawing points, repeat steps 2 and 3. To cancel Pt-On(, press ‘.
Note: To continue drawing on the graph, move the
cursor to a new position where you want to begin
drawing again, and then repeat steps 2, 3, and 4. To
cancel Pen, press ‘.
DRAW POINTS STO
1: Pt-On( Turns on a point.
2: Pt-Off( Turns off a point.
3: Pt-Change( Toggles a point on or off.
4: Pxl-On( Turns on a pixel.
5: Pxl-Off( Turns off a pixel.
6: Pxl-Change( Toggles a pixel on or off.
7: pxl-Test( Returns 1 if pixel on, 0 if pixel off.
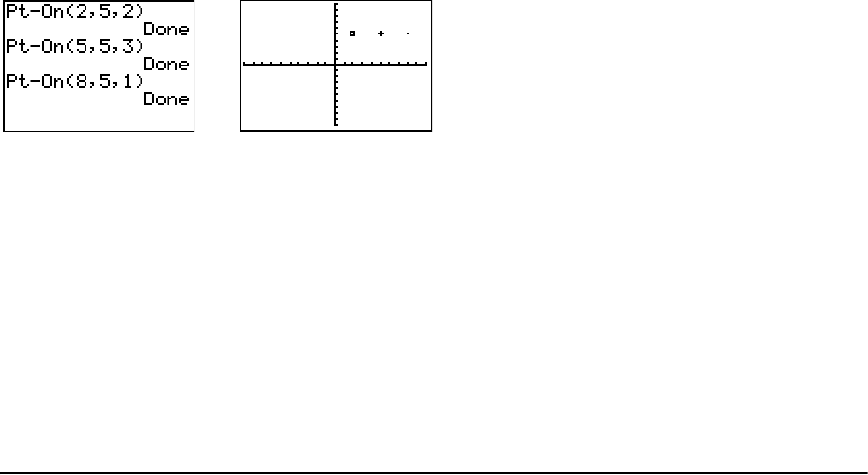
Chapter 8: Draw Instructions 132
Erasing Points with Pt-Off(
To erase (turn off) a drawn point on a graph, follow these steps.
1. Select 2:Pt-Off( (point off) from the DRAW POINTS menu.
2. Move the cursor to the point you want to erase.
3. Press Í to erase the point.
To continue erasing points, repeat steps 2 and 3. To cancel Pt-Off(, press ‘.
Changing Points with Pt-Change(
To change (toggle on or off) a point on a graph, follow these steps.
1. Select 3:Pt-Change( (point change) from the DRAW POINTS menu.
2. Move the cursor to the point you want to change.
3. Press Í to change the point’s on/off status.
To continue changing points, repeat steps 2 and 3. To cancel Pt-Change(, press ‘.
Drawing Points from the Home Screen or a Program
Pt-On( (point on) turns on the point at (X=x,Y=y). Pt-Off( turns the point off. Pt-Change( toggles the
point on or off. mark is optional; it determines the point’s appearance; specify 1, 2, or 3, where:
1 = ¦ (dot; default) 2 = › (box) 3 = + (cross)
Pt-On(x,y[,mark])
Pt-Off(x,y[,mark])
Pt-Change(x,y)
Note: If you specified mark to turn on a point with Pt-On(, you must specify mark when you turn off
the point with Pt-Off(. Pt-Change( does not have the mark option.
Drawing Pixels
TI-84 Plus Pixels
A pixel is a square dot on the TI-84 Plus display. The Pxl- (pixel) instructions let you turn on, turn
off, or reverse a pixel (dot) on the graph using the cursor. When you select a pixel instruction from

Chapter 8: Draw Instructions 133
the DRAW POINTS menu, the TI-84 Plus returns to the home screen or the program editor. The
pixel instructions are not interactive.
Turning On and Off Pixels with Pxl-On( and Pxl-Off(
Pxl-On( (pixel on) turns on the pixel at (row,column), where row is an integer between 0 and 62 and
column is an integer between 0 and 94.
Pxl-Off( turns the pixel off. Pxl-Change( toggles the pixel on and off.
Pxl-On(row,column)
Pxl-Off(row,column)
Pxl-Change(row,column)
Using pxl-Test(
pxl-Test( (pixel test) returns 1 if the pixel at (row,column) is turned on or 0 if the pixel is turned off on
the current graph. row must be an integer between 0 and 62. column must be an integer between 0
and 94.
pxl-Test(row,column)
Split Screen
On a Horiz split screen, the maximum value for row is 30 for Pxl-On(, Pxl-Off(, Pxl-Change(, and
pxl-Test(.
On a G-T split screen, the maximum value for row is 50 and the maximum value for column is 46 for
Pxl-On(, Pxl-Off(, Pxl-Change(, and pxl-Test(.

Chapter 8: Draw Instructions 134
Storing Graph Pictures (Pic)
DRAW STO Menu
To display the DRAW STO menu, press y < |. When you select an instruction from the
DRAW STO menu, the TI-84 Plus returns to the home screen or the program editor. The picture
and graph database instructions are not interactive.
Storing a Graph Picture
You can store up to 10 graph pictures, each of which is an image of the current graph display, in
picture variables Pic1 through Pic9, or Pic0. Later, you can superimpose the stored picture onto a
displayed graph from the home screen or a program.
A picture includes drawn elements, plotted functions, axes, and tick marks. The picture does not
include axes labels, lower and upper bound indicators, prompts, or cursor coordinates. Any parts
of the display hidden by these items are stored with the picture.
To store a graph picture, follow these steps.
1. Select 1:StorePic from the DRAW STO menu. StorePic is pasted to the current cursor location.
2. Enter the number (from 1 to 9, or 0) of the picture variable to which you want to store the
picture. For example, if you enter 3, the TI-84 Plus will store the picture to Pic3.
Note: You also can select a variable from the PICTURE secondary menu ( 4). The
variable is pasted next to StorePic.
3. Press Í to display the current graph and store the picture.
DRAW POINTS STO
1: StorePic Stores the current picture.
2: RecallPic Recalls a saved picture.
3: StoreGDB Stores the current graph database.
4: RecallGDB Recalls a saved graph database.

Chapter 8: Draw Instructions 135
Recalling Graph Pictures (Pic)
Recalling a Graph Picture
To recall a graph picture, follow these steps.
1. Select 2:RecallPic from the DRAW STO menu. RecallPic is pasted to the current cursor
location.
2. Enter the number (from 1 to 9, or 0) of the picture variable from which you want to recall a
picture. For example, if you enter 3, the TI-84 Plus will recall the picture stored to Pic3.
Note: You also can select a variable from the PICTURE secondary menu ( 4). The
variable is pasted next to RecallPic.
3. Press Í to display the current graph with the picture superimposed on it.
Note: Pictures are drawings. You cannot trace a curve that is part of a picture.
Deleting a Graph Picture
To delete graph pictures from memory, use the MEMORY MANAGEMENT/DELETE secondary menu
(Chapter 18).
Storing Graph Databases (GDB)
What Is a Graph Database?
A graph database (GDB) contains the set of elements that defines a particular graph. You can
recreate the graph from these elements. You can store up to 10 GDBs in variables GDB1 through
GDB9, or GDB0 and recall them to recreate graphs.
A GDB stores five elements of a graph.
• Graphing mode
• Window variables
• Format settings
• All functions in the Y= editor and the selection status of each
• Graph style for each Y= function
GDBs do not contain drawn items or stat plot definitions.
Storing a Graph Database
To store a graph database, follow these steps.
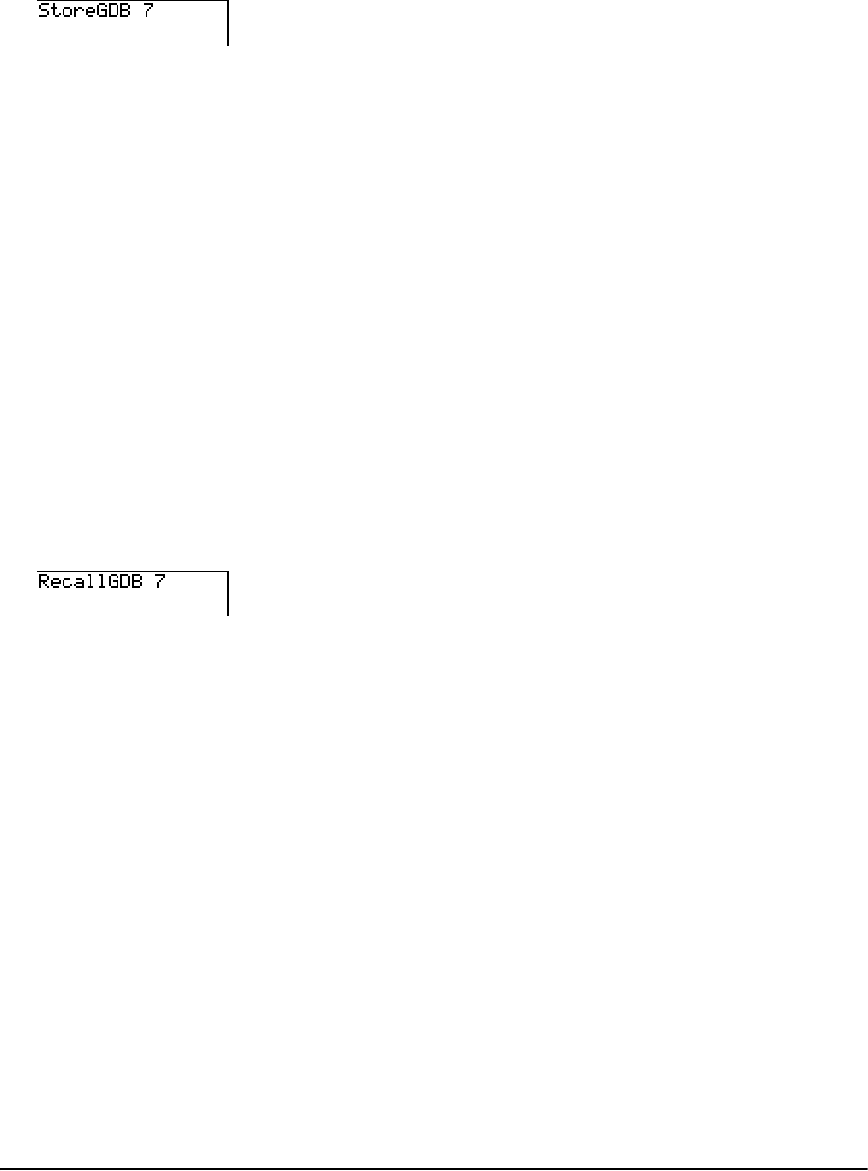
Chapter 8: Draw Instructions 136
1. Select 3:StoreGDB from the DRAW STO menu. StoreGDB is pasted to the current cursor
location.
2. Enter the number (from 1 to 9, or 0) of the GDB variable to which you want to store the graph
database. For example, if you enter 7, the TI-84 Plus will store the GDB to GDB7.
Note: You also can select a variable from the GDB secondary menu ( 3). The variable is
pasted next to StoreGDB.
3. Press Í to store the current database to the specified GDB variable.
Recalling Graph Databases (GDB)
Recalling a Graph Database
CAUTION: When you recall a GDB, it replaces all existing Y= functions. Consider storing the
current Y= functions to another database before recalling a stored GDB.
To recall a graph database, follow these steps.
1. Select 4:RecallGDB from the DRAW STO menu. RecallGDB is pasted to the current cursor
location.
2. Enter the number (from 1 to 9, or 0) of the GDB variable from which you want to recall a GDB.
For example, if you enter 7, the TI-84 Plus will recall the GDB stored to GDB7.
Note: You also can select a variable from the GDB secondary menu ( 3). The variable is
pasted next to RecallGDB.
3. Press Í to replace the current GDB with the recalled GDB. The new graph is not plotted.
The TI-84 Plus changes the graphing mode automatically, if necessary.
Deleting a Graph Database
To delete a GDB from memory, use the MEMORY MANAGEMENT/DELETE secondary menu
(Chapter 18).
Chapter 9: Split Screen 137
Chapter 9:
Split Screen
Getting Started: Exploring the Unit Circle
Getting Started is a fast-paced introduction. Read the chapter for details.
Use G-T (graph-table) split-screen mode to explore the unit circle and its relationship to the
numeric values for the commonly used trigonometric angles of 0¡ 30¡, 45¡, 60¡, 90¡, and so on.
1. Press z to display the mode screen. Press †
† ~ Í to select Degree mode. Press † ~
Í to select Par (parametric) graphing mode.
Press † † † † ~ ~ Í to select G-T (graph-
table) split-screen mode.
2. Press † † † † ~ Í to display the format
screen. Press † † † † † ~ Í to select
ExprOff.
3. Press o to display the Y= editor for Par graphing
mode. Press ™ „ ¤ Í to store cos(T)
to X1T. Press ÷ ˜ „ ¤ Í to store sin(T)
to Y1T.
4. Press p to display the window editor. Enter
these values for the window variables.
Tmin=0 Xmin=L2.3 Ymin=L2.5
Tmax=360 Xmax=2.3 Ymax=2.5
Tstep=15 Xscl=1 Yscl=1
5. Press r. On the left, the unit circle is graphed
parametrically in Degree mode and the trace
cursor is activated. When T=0 (from the graph
trace coordinates), you can see from the table on
the right that the value of X1T (cos(T)) is 1 and Y1T
(sin(T)) is 0. Press ~ to move the cursor to the
next 15¡ angle increment. As you trace around the
circle in steps of 15¡, an approximation of the
standard value for each angle is highlighted in the
table.
6. Press y - and change Indpnt to Ask.
Chapter 9: Split Screen 138
Using Split Screen
Setting a Split-Screen Mode
To set a split-screen mode, press z, and then move the cursor to Horiz or G-T and press Í.
•Select
Horiz (horizontal) to display the graph screen and another screen split horizontally.
•Select
G-T (graph-table) to display the graph screen and table screen split vertically.
The split screen is activated when you press any key that applies to either half of the split screen.
If stat plots are turned on, the plots are shown along with the x-y plots in graphs. Press y 0
to make the table portion of the split screen active and to display the list data. Press † or } to
highlight a value you want to edit, and then enter a new value directly in the table to overwrite the
previous value. Press ~ repeatedly to display each column of data (both table and list data).
7. Press y 0 to make the table portion of the
split screen active.
$$
Chapter 9: Split Screen 139
Split-screen display with both x-y plots and stat plots
Some screens are never displayed as split screens. For example, if you press z in Horiz or G-T
mode, the mode screen is displayed as a full screen. If you then press a key that displays either
half of a split screen, such as r, the split screen returns.
When you press a key or key combination in either Horiz or G-T mode, the cursor is placed in the
half of the display to which that key applies. For example, if you press r, the cursor is placed
in the half where the graph is displayed. If you press y 0, the cursor is placed in the half
where the table is displayed.
The TI-84 Plus will remain in split-screen mode until you change back to Full screen mode.
Horiz (Horizontal) Split Screen
Horiz Mode
In Horiz (horizontal) split-screen mode, a horizontal line splits the screen into top and bottom
halves.
The top half displays the graph.
The bottom half displays any of these screens.
• Home screen (four lines)
• Y= editor (four lines)
• Stat list editor (two rows)
• Window editor (three settings)
• Table editor (two rows)
Moving from Half to Half in Horiz Mode
To use the top half of the split screen:

Chapter 9: Split Screen 140
• Press s or r.
• Select a ZOOM or CALC operation.
To use the bottom half of the split screen:
• Press any key or key combination that displays the home screen.
• Press o (Y= editor).
• Press … Í (stat list editor).
• Press p (window editor).
• Press y 0 (table editor).
Full Screens in Horiz Mode
All other screens are displayed as full screens in Horiz split-screen mode.
To return to the Horiz split screen from a full screen when in Horiz mode, press any key or key
combination that displays the graph, home screen, Y= editor, stat list editor, window editor, or
table editor.
G-T (Graph-Table) Split Screen
G-T Mode
In G-T (graph-table) split-screen mode, a vertical line splits the screen into left and right halves.
The left half displays all active graphs and plots.
The right half displays either table data corresponding to the graph at the left or list data
corresponding to the plot at the left.
Moving from Half to Half in G-T Mode
To use the left half of the split screen:
• Press s or r.
• Select a ZOOM or CALC operation.
To use the right half of the split screen, press y 0. If the values on the right are list data,
these values can be edited similarly to using the Stat List Editor.
Chapter 9: Split Screen 141
Using TRACE in G-T Mode
As you press | or ~ to move the trace cursor along a graph in the split screen’s left half in G-T
mode, the table on the right half automatically scrolls to match the current cursor values. If more
than one graph or plot is active, you can press } or † to select a different graph or plot.
Note: When you trace in Par graphing mode, both components of an equation (XnT and YnT) are
displayed in the two columns of the table. As you trace, the current value of the independent
variable T is displayed on the graph.
Full Screens in G-T Mode
All screens other than the graph and the table are displayed as full screens in G-T split-screen
mode.
To return to the G-T split screen from a full screen when in G-T mode, press any key or key
combination that displays the graph or the table.
TI-84 Plus Pixels in Horiz and G-T Modes
TI-84 Plus Pixels in Horiz and G-T Modes
Note: Each set of numbers in parentheses above represents the row and column of a corner pixel,
which is turned on.
DRAW POINTS Menu Pixel Instructions
For Pxl-On(, Pxl-Off(, Pxl-Change(, and pxl-Test(:
•In
Horiz mode, row must be {30; column must be {94.
•In
G-T mode, row must be {50; column must be {46.
Pxl-On(row,column)

Chapter 9: Split Screen 142
DRAW Menu Text( Instruction
For the Text( instruction:
•In
Horiz mode, row must be {25; column must be {94.
•In
G-T mode, row must be {45; column must be {46.
Text(row,column,"text")
PRGM I/O Menu Output( Instruction
For the Output( instruction:
•In
Horiz mode, row must be {4; column must be {16.
•In
G-T mode, row must be {8; column must be {16.
Output(row,column,"text")
Note: The Output( instruction can only be used within a program.
Setting a Split-Screen Mode from the Home Screen or a Program
To set Horiz or G-T from a program, follow these steps.
1. Press z while the cursor is on a blank line in the program editor.
2. Select Horiz or G-T.
The instruction is pasted to the cursor location. The mode is set when the instruction is
encountered during program execution. It remains in effect after execution.
Note: You also can paste Horiz or G-T to the home screen or program editor from the CATALOG
(Chapter 15).
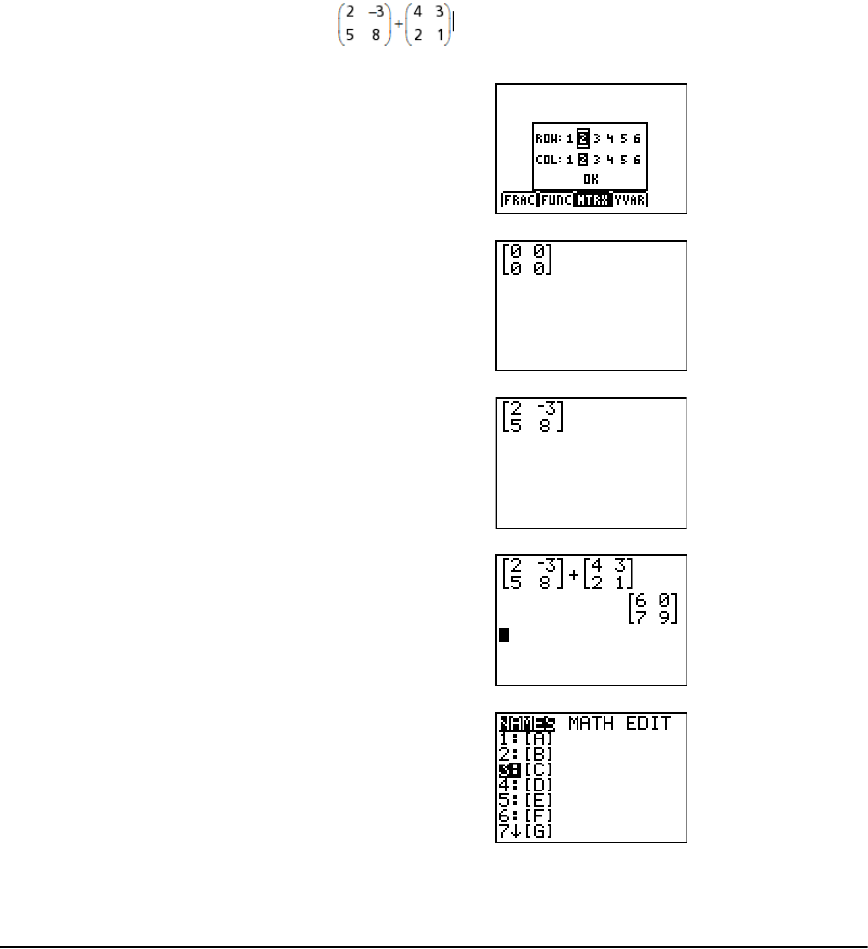
Chapter 10: Matrices 143
Chapter 10:
Matrices
Getting Started: Using the MTRX Shortcut Menu
Getting Started is a fast-paced introduction. Read the chapter for details.
You can use the MTRX shortcut menu (t `) to enter a quick matrix calculation on the home
screen or in the Y= editor.
Note: To input a fraction in a matrix, delete the pre-populated zero first.
Example: Add the following matrices: and store the result to matrix C.
1. Press t ` to display the quick matrix editor.
The default size of the matrix is two rows by two
columns.
2. Press † † to highlight OK and then press Í.
3. Press 2 ~ k 3 ~ 5 ~ 8 ~ to create the first
matrix.
4. Press à t ` † † Í 4 ~ 3 ~ 2 ~ 1 ~
Í to create the second matrix and perform the
calculation.
5. Press v y Q and select 3:[C].
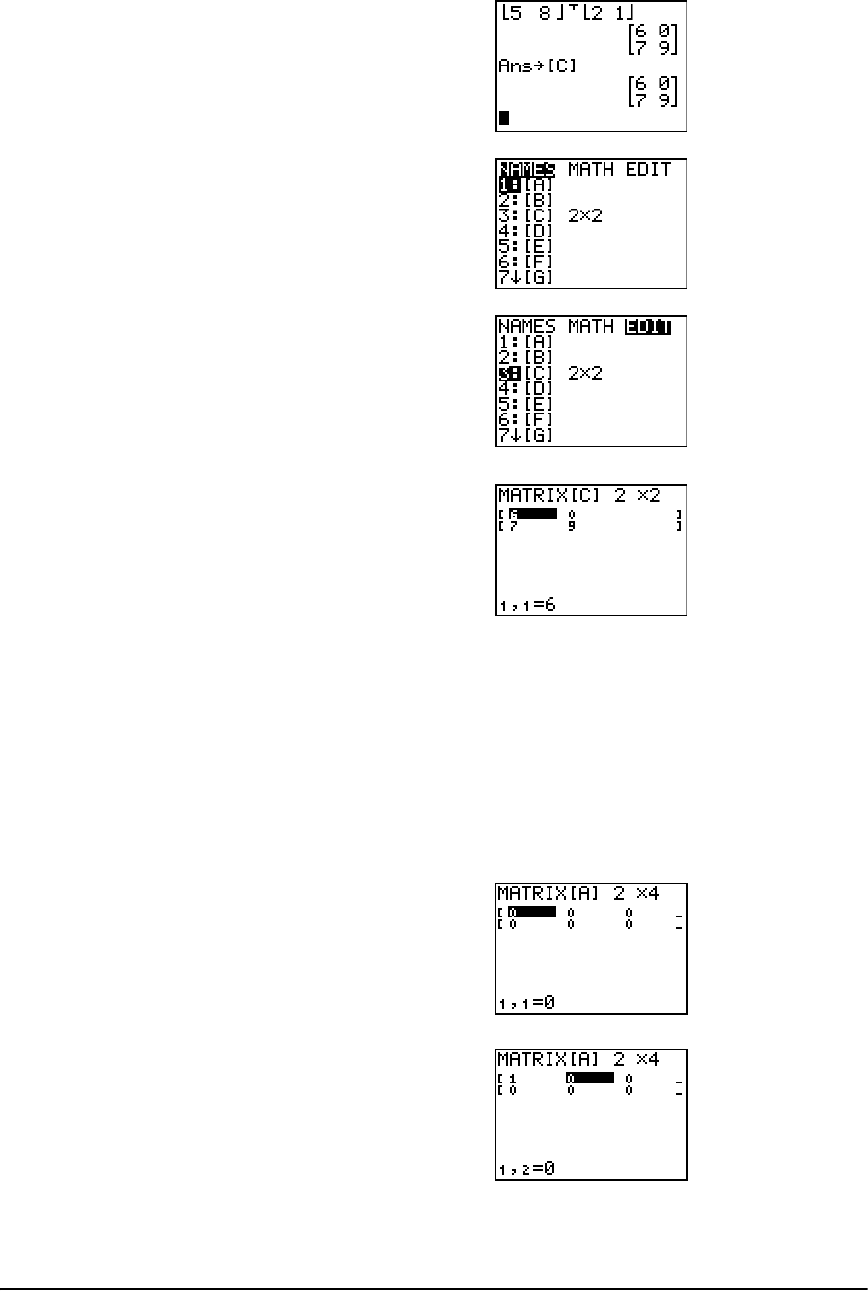
Chapter 10: Matrices 144
Getting Started: Systems of Linear Equations
Getting Started is a fast-paced introduction. Read the chapter for details.
Find the solution of X + 2Y + 3Z = 3 and 2X + 3Y + 4Z = 3. On the TI-84 Plus, you can solve a
system of linear equations by entering the coefficients as elements in a matrix, and then using rref(
to obtain the reduced row-echelon form.
6. Press Í to store the matrix to [C].
In the matrix editor (y Q), you can see that
matrix [C] has dimension 2x2.
You can press ~ ~ to display the EDIT screen and
then select [C] to edit it.
1. Press y . Press ~ ~ to display the
MATRX EDIT menu. Press 1 to select 1: [A].
2. Press 2 Í 4 Í to define a 2×4 matrix. The
rectangular cursor indicates the current element.
Ellipses (...) indicate additional columns beyond
the screen.
3. Press 1 Í to enter the first element. The
rectangular cursor moves to the second column of
the first row.

Chapter 10: Matrices 145
Defining a Matrix
What Is a Matrix?
A matrix is a two-dimensional array. You can display, define, or edit a matrix in the matrix editor.
You can also define a matrix using the MTRX shortcut menu (t `).The TI-84 Plus has 10
matrix variables, [A] through [J]. You can define a matrix directly in an expression. A matrix,
depending on available memory, may have up to 99 rows or columns. You can store only real
numbers in TI-84 Plus matrices. Fractions are stored as real numbers and can be used in
matrices.
Selecting a Matrix
Before you can define or display a matrix in the editor, you first must select the matrix name. To do
so, follow these steps.
1. Press y | to display the MATRX EDIT menu. The dimensions of any previously
defined matrices are displayed.
2. Select the matrix you want to define. The MATRX EDIT screen is displayed.
4. Press 2 Í 3 Í 3 Í to complete the first
row for X + 2Y + 3Z = 3.
5. Press 2 Í 3 Í 4 Í 3 Í to enter the
second row for 2X + 3Y + 4Z = 3.
6. Press y 5 to return to the home screen. If
necessary, press ‘ to clear the home screen.
Press y ~ to display the MATRX MATH
menu. Press } to wrap to the end of the menu.
Select B:rref( to copy rref( to the home screen.
7. Press y 1 to select 1: [A] from the
MATRX NAMES menu. Press ¤ Í. The
reduced row-echelon form of the matrix is
displayed and stored in Ans.
1X N 1Z = L3 therefore X = L3 + Z
1Y + 2Z = 3 therefore Y = 3 N 2Z

Chapter 10: Matrices 146
Accepting or Changing Matrix Dimensions
The dimensions of the matrix (row × column) are displayed on the top line. The dimensions of a new
matrix are 1 × 1. You must accept or change the dimensions each time you edit a matrix. When
you select a matrix to define, the cursor highlights the row dimension.
• To accept the row dimension, press Í.
• To change the row dimension, enter the number of rows (up to 99), and then press Í.
The cursor moves to the column dimension, which you must accept or change the same way you
accepted or changed the row dimension. When you press Í, the rectangular cursor moves to
the first matrix element.
Viewing and Editing Matrix Elements
Displaying Matrix Elements
After you have set the dimensions of the matrix, you can view the matrix and enter values for the
matrix elements. In a new matrix, all values are zero.
Select the matrix from the MATRX EDIT menu and enter or accept the dimensions. The center
portion of the matrix editor displays up to seven rows and three columns of a matrix, showing the
values of the elements in abbreviated form if necessary. The full value of the current element,
which is indicated by the rectangular cursor, is displayed on the bottom line.
This is an 8 × 4 matrix. Ellipses in the left or right column indicate additional columns. # or $ in the
right column indicate additional rows.
Deleting a Matrix
To delete matrices from memory, use the MEMORY MANAGEMENT/DELETE secondary menu
(Chapter 18).
Viewing a Matrix
The matrix editor has two contexts, viewing and editing. In viewing context, you can use the cursor
keys to move quickly from one matrix element to the next. The full value of the highlighted element
is displayed on the edit line.

Chapter 10: Matrices 147
Select the matrix from the MATRX EDIT menu, and then enter or accept the dimensions.
Using Viewing-Context Keys
Key Function
| or ~Moves the cursor within the current row
† or }Moves the cursor within the current column; on the top row, }
moves the cursor to the column dimension; on the column
dimension, } moves the cursor to the row dimension
ÍSwitches to editing context; activates the edit cursor on the bottom
line
‘Switches to editing context; clears the value on the bottom line
Any entry character Switches to editing context; clears the value on the bottom line;
copies the character to the bottom line
y 6 Nothing
{Nothing
Editing a Matrix Element
In editing context, an edit cursor is active on the bottom line. To edit a matrix element value, follow
these steps.
1. Select the matrix from the MATRX EDIT menu, and then enter or accept the dimensions.
2. Press |, }, ~, and † to move the cursor to the matrix element you want to change.
3. Switch to editing context by pressing Í, ‘, or an entry key.
4. Change the value of the matrix element using the editing-context keys described below. You
may enter an expression, which is evaluated when you leave editing context.
Note: You can press ‘ Í to restore the value at the cursor if you make a mistake.
5. Press Í, }, or † to move to another element.

Chapter 10: Matrices 148
Using Editing-Context Keys
Key Function
| or ~Moves the edit cursor within the value
† or }Stores the value displayed on the edit line to the matrix element;
switches to viewing context and moves the cursor within the
column
ÍStores the value displayed on the edit line to the matrix element;
switches to viewing context and moves the cursor to the next row
element
‘Clears the value on the bottom line
Any entry character Copies the character to the location of the edit cursor on the
bottom line
y 6 Activates the insert cursor
{Deletes the character under the edit cursor on the bottom line
Using Matrices with Expressions
To use a matrix in an expression, you can do any of the following.
• Copy the name from the MATRX NAMES menu.
• Recall the contents of the matrix into the expression with y K (Chapter 1).
• Enter the matrix directly (see below).
Entering a Matrix in an Expression
You can enter, edit, and store a matrix in the matrix editor. You also can enter a matrix directly in
an expression.
To enter a matrix in an expression, follow these steps.
1. Press y [ [ ] to indicate the beginning of the matrix.
2. Press y [ [ ] to indicate the beginning of a row.
3. Enter a value, which can be an expression, for each element in the row. Separate the values
with commas.
4. Press y [ ] ] to indicate the end of a row.
5. Repeat steps 2 through 4 to enter all of the rows.
6. Press y [ ] ] to indicate the end of the matrix.
The resulting matrix is displayed in the form:
[[element1,1,...,element1,n],...,[elementm,1,...,elementm,n]]
Any expressions are evaluated when the entry is executed.
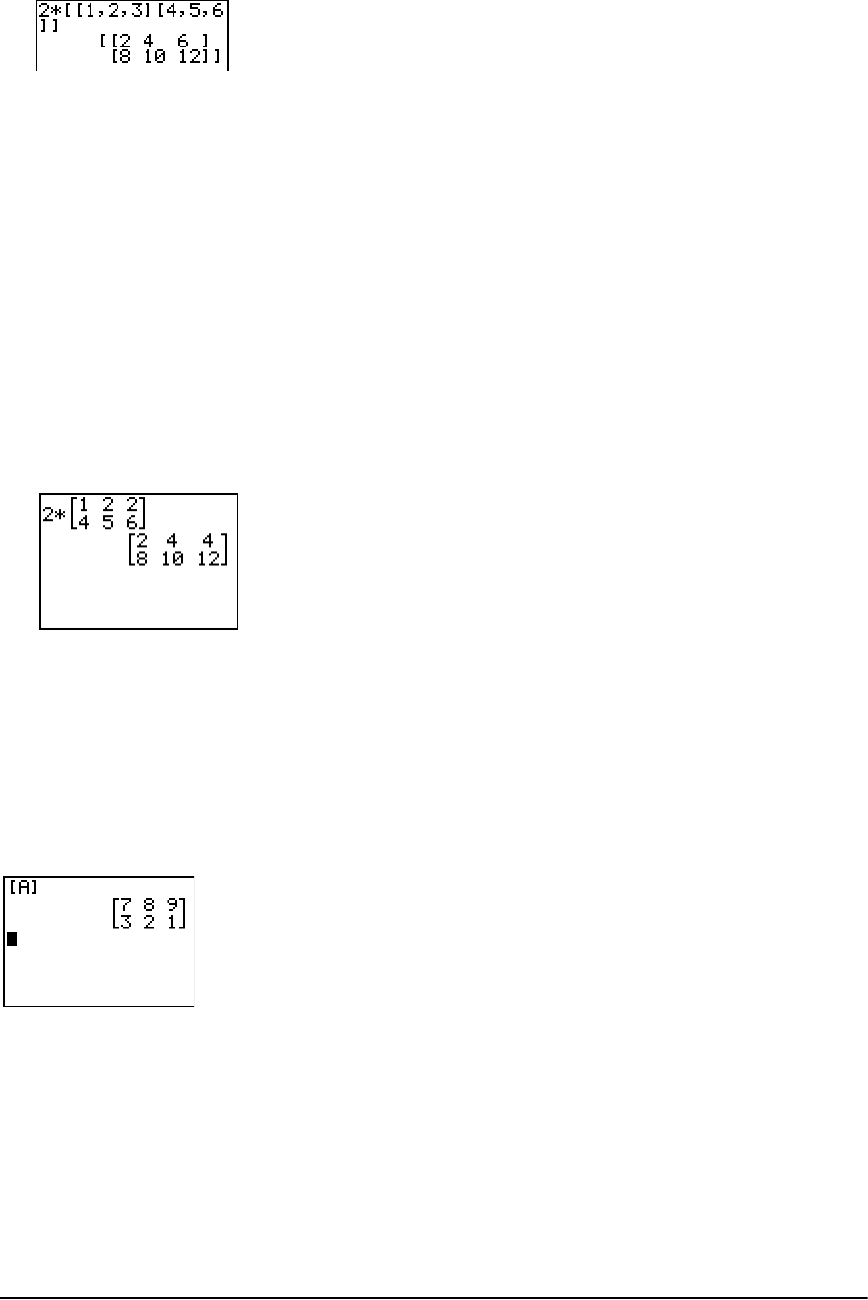
Chapter 10: Matrices 149
Note:
• The commas that you must enter to separate elements are not displayed on output.
• Closing brackets are required when you enter a matrix directly on the home screen or in
an expression.
• When you define a matrix using the matrix editor, it is automatically stored. However,
when you enter a matrix directly on the home screen or in an expression, it is not
automatically stored, but you can store it.
In MathPrint™ mode, you could also use the MTRX shortcut menu to enter this kind of matrix:
1. Press t ` † ~ ~ Í † Í to define the matrix dimension.
2. Press 1 ~ 2 ~ 2 ~ 4 ~ 5 ~ 6 ~ to define the matrix.
3. Press Í to perform the calculation.
Displaying and Copying Matrices
Displaying a Matrix
To display the contents of a matrix on the home screen, select the matrix from the MATRX NAMES
menu, and then press Í.
In MathPrint™ mode:
• An arrow at the left or right indicates additional columns.
• An arrow at the top or bottom indicates additional rows.
In Classic mode:
• Ellipses in the left or right column indicate additional columns.

Chapter 10: Matrices 150
•# or $ in the right column indicate additional rows.
In either mode, press ~, |, †, and } to scroll the matrix. You can scroll the matrix after you
press Í to calculate the matrix. If you cannot scroll the matrix, press } Í Í to repeat
the calculation.
Note:
• You cannot copy a matrix output from the history.
• Matrix calculations are not saved when you change from MathPrint™ mode to Classic mode
or vice-versa.
Copying One Matrix to Another
To copy a matrix, follow these steps.
1. Press y > to display the MATRX NAMES menu.
2. Select the name of the matrix you want to copy.
3. Press ¿.
4. Press y > again and select the name of the new matrix to which you want to copy the
existing matrix.
5. Press Í to copy the matrix to the new matrix name.
Accessing a Matrix Element
On the home screen or from within a program, you can store a value to, or recall a value from, a
matrix element. The element must be within the currently defined matrix dimensions. Select matrix
from the MATRX NAMES menu.
[matrix](row,column)
MathPrint™
Classic
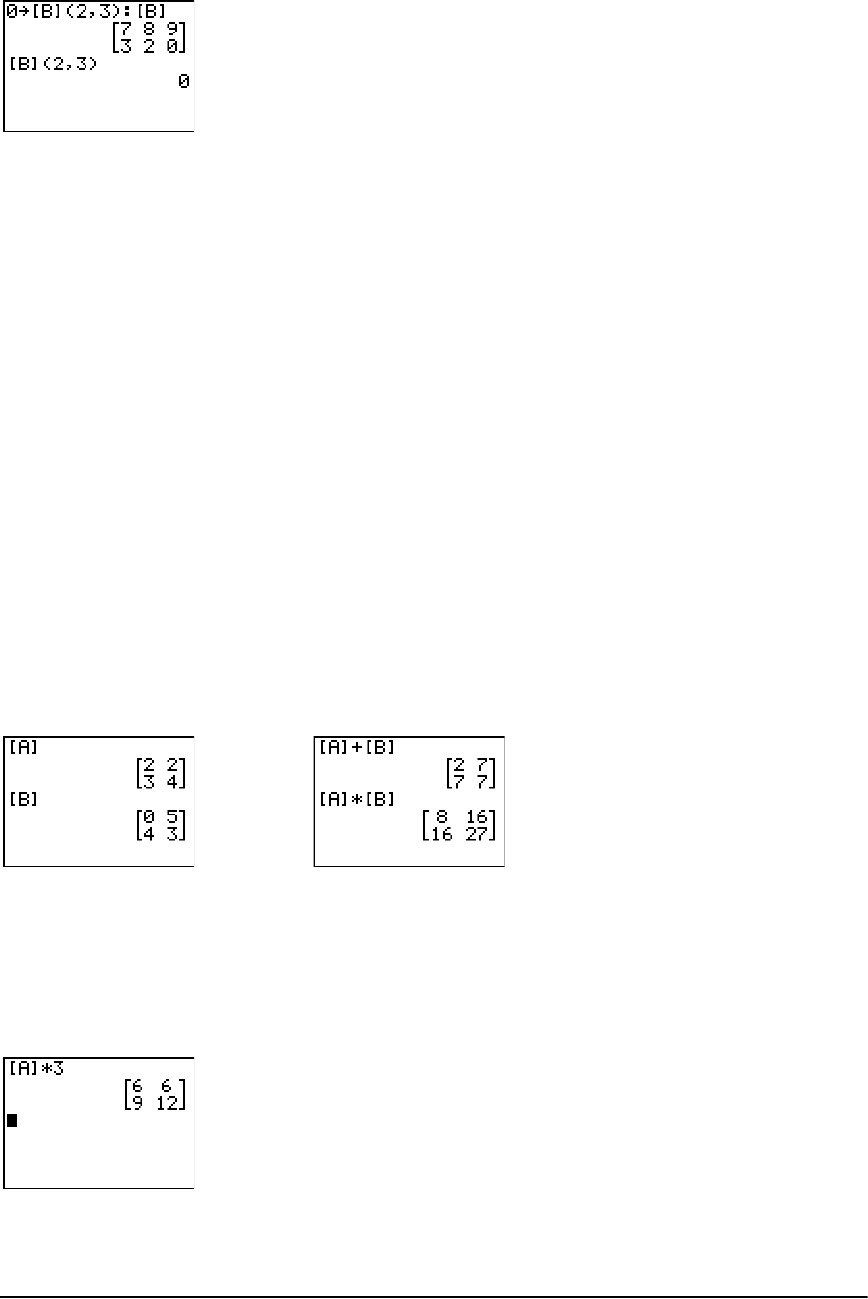
Chapter 10: Matrices 151
Using Math Functions with Matrices
Using Math Functions with Matrices
You can use many of the math functions on the TI-84 Plus keypad, the MATH menu, the MATH NUM
menu, and the MATH TEST menu with matrices. However, the dimensions must be appropriate.
Each of the functions below creates a new matrix; the original matrix remains the same.
Addition, Subtraction, Multiplication
To add or subtract matrices, the dimensions must be the same. The answer is a matrix in which
the elements are the sum or difference of the individual corresponding elements.
matrixA+matrixB
matrixANmatrixB
To multiply two matrices together, the column dimension of matrixA must match the row dimension
of matrixB.
matrixA…matrixB
Multiplying a matrix by a value or a value by a matrix returns a matrix in which each element of matrix
is multiplied by value.
matrix…value
value…matrix
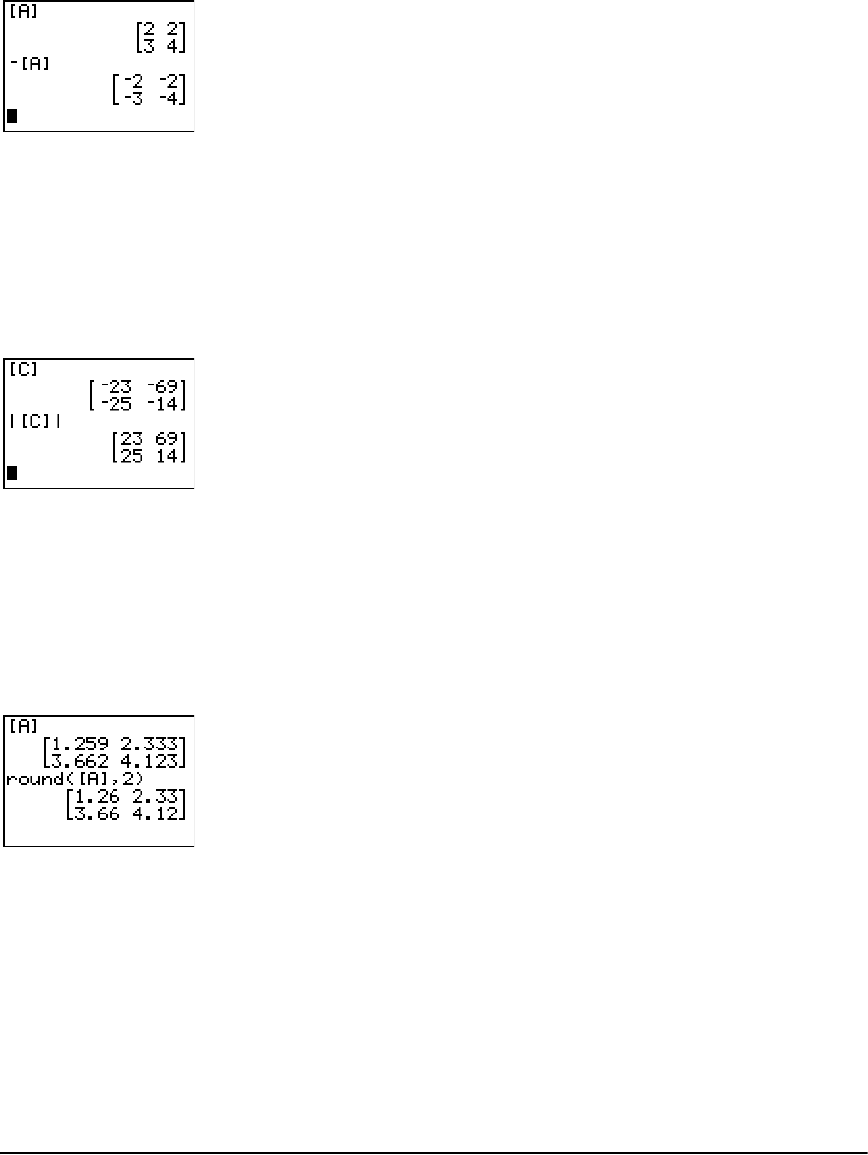
Chapter 10: Matrices 152
Negation
Negating a matrix returns a matrix in which the sign of every element is changed.
Lmatrix
abs(
abs( (absolute value, MATH NUM menu) returns a matrix containing the absolute value of each
element of matrix.
abs(matrix)
round(
round( (MATH NUM menu) returns a matrix. It rounds every element in matrix to #decimals ( 9). If
#decimals is omitted, the elements are rounded to 10 digits.
round(matrix[,#decimals])
Inverse
Use the L1 function (œ) or › L1 to invert a matrix. matrice must be square. The determinant cannot
equal zero.
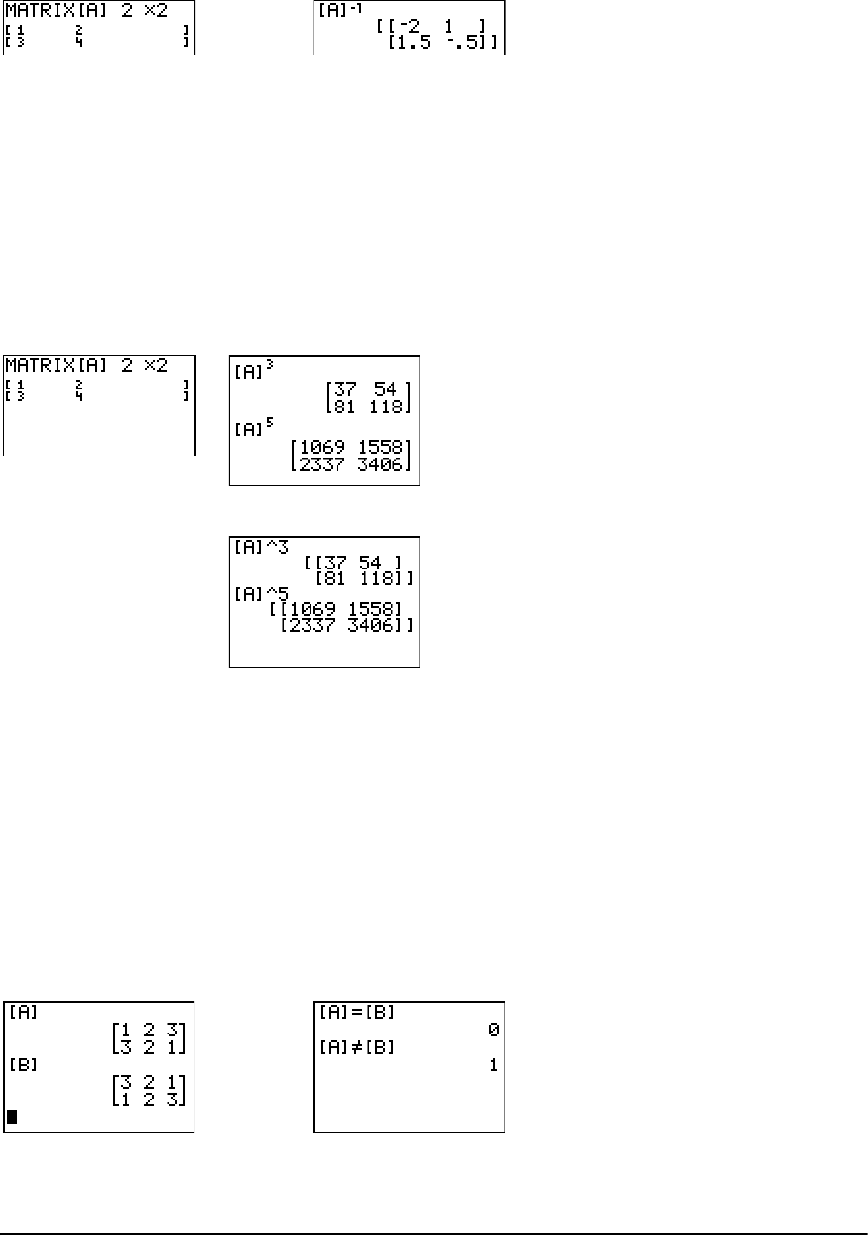
Chapter 10: Matrices 153
matrixL1
Powers
To raise a matrix to a power, matrix must be square. You can use 2 (¡), 3 (MATH menu), or ^power
(›) for integer power between 0 and 255.
matrix2
matrix3
matrix^power
Relational Operations
To compare two matrices using the relational operations = and ƒ (TEST menu), they must have the
same dimensions. = and ƒ compare matrixA and matrixB on an element-by-element basis. The other
relational operations are not valid with matrices.
matrixA=matrixB returns 1 if every comparison is true; it returns 0 if any comparison is false.
matrixAƒmatrixB returns 1 if at least one comparison is false; it returns 0 if no comparison is false.
MathPrint™
Classic
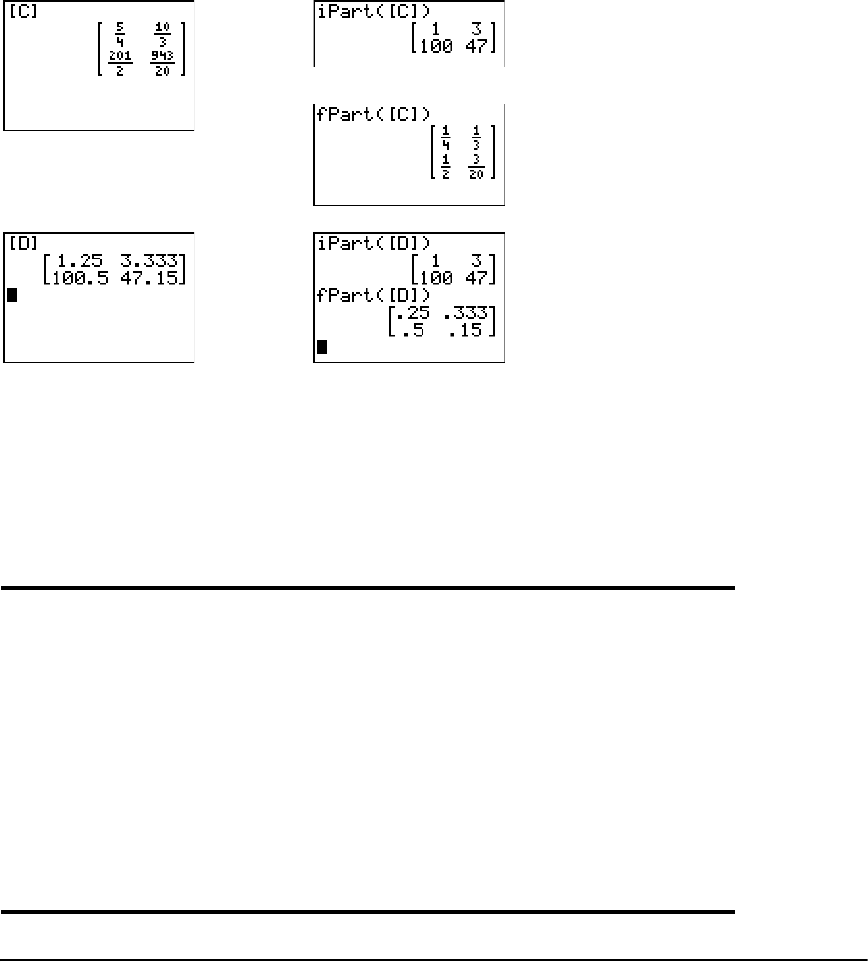
Chapter 10: Matrices 154
iPart(, fPart(, int(
iPart( (integer part), fPart( (fractional part), and int( (greatest integer) are on the MATH NUM menu.
iPart( returns a matrix containing the integer part of each element of matrix.
fPart( returns a matrix containing the fractional part of each element of matrix.
int( returns a matrix containing the greatest integer of each element of matrix.
iPart(matrix)
fPart(matrix)
int(matrix)
Using the MATRX MATH Operations
MATRX MATH Menu
To display the MATRX MATH menu, press y ~.
NAMES MATH EDIT
1: det( Calculates the determinant.
2: TTransposes the matrix.
3: dim( Returns the matrix dimensions.
4: Fill( Fills all elements with a constant.
5: identity( Returns the identity matrix.
6: randM( Returns a random matrix.
7: augment( Appends two matrices.
8: Matr4list( Stores a matrix to a list.
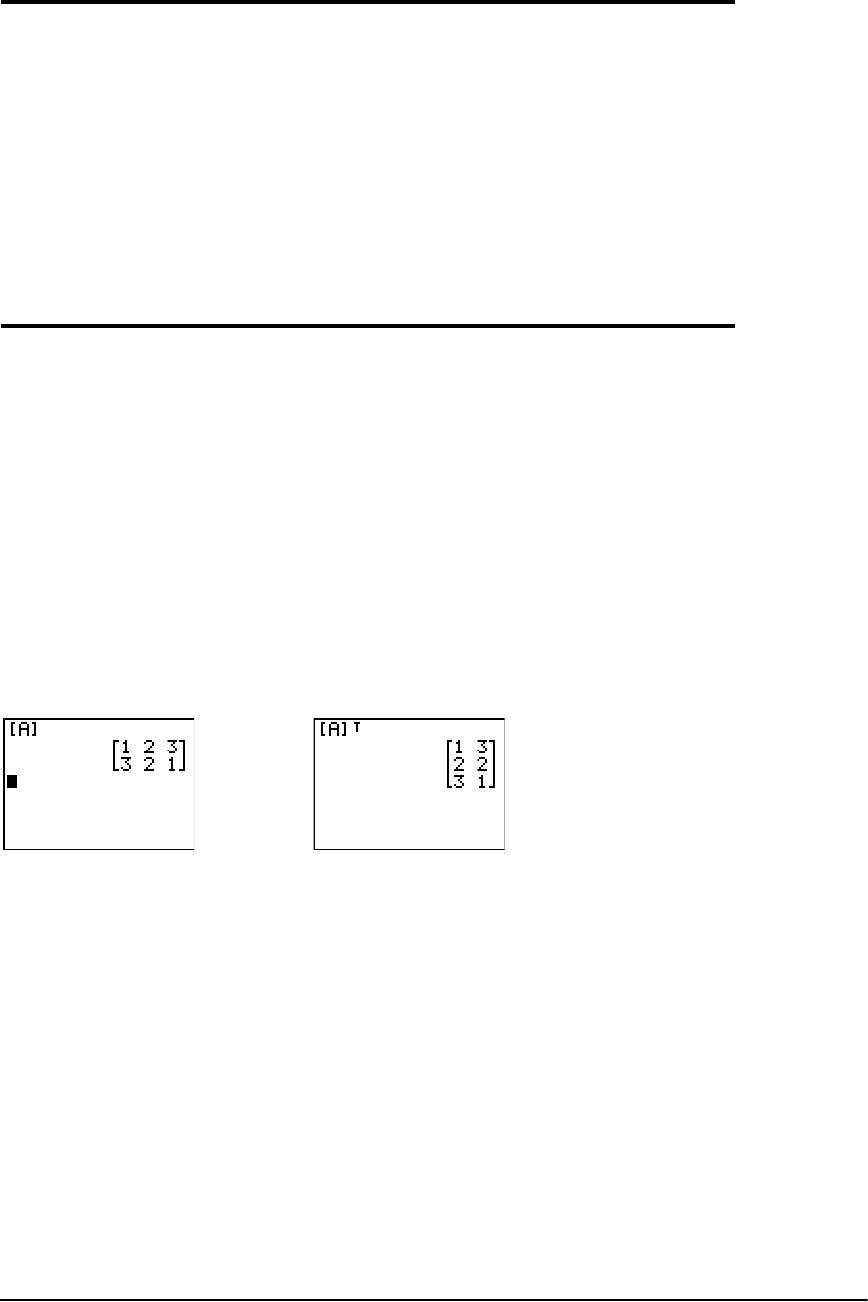
Chapter 10: Matrices 155
det(
det( (determinant) returns the determinant (a real number) of a square matrix.
det(matrix)
Transpose
T (transpose) returns a matrix in which each element (row, column) is swapped with the
corresponding element (column, row) of matrix.
matrixT
Accessing Matrix Dimensions with dim(
dim( (dimension) returns a list containing the dimensions ({rows columns}) of matrix.
dim(matrix)
9: List4matr( Stores a list to a matrix.
0: cumSum( Returns the cumulative sums of a matrix.
A: ref( Returns the row-echelon form of a matrix.
B: rref( Returns the reduced row-echelon form.
C: rowSwap( Swaps two rows of a matrix.
D: row+( Adds two rows; stores in the second row.
E: …row( Multiplies the row by a number.
F: …row+( Multiplies the row, adds to the second row.
NAMES MATH EDIT

Chapter 10: Matrices 156
Note: dim(matrix)"Ln:Ln(1) returns the number of rows. dim(matrix)"Ln:Ln(2) returns the number of
columns.
Creating a Matrix with dim(
Use dim( with ¿ to create a new matrixname of dimensions rows × columns with 0 as each element.
{rows,columns}"dim(matrixname)
Redimensioning a Matrix with dim(
Use dim( with ¿ to redimension an existing matrixname to dimensions rows × columns. The
elements in the old matrixname that are within the new dimensions are not changed. Additional
created elements are zeros. Matrix elements that are outside the new dimensions are deleted.
{rows,columns}"dim(matrixname)
Fill(
Fill( stores value to every element in matrixname.
Fill(value,matrixname)
identity(
identity( returns the identity matrix of dimension rows × dimension columns.
identity(dimension)
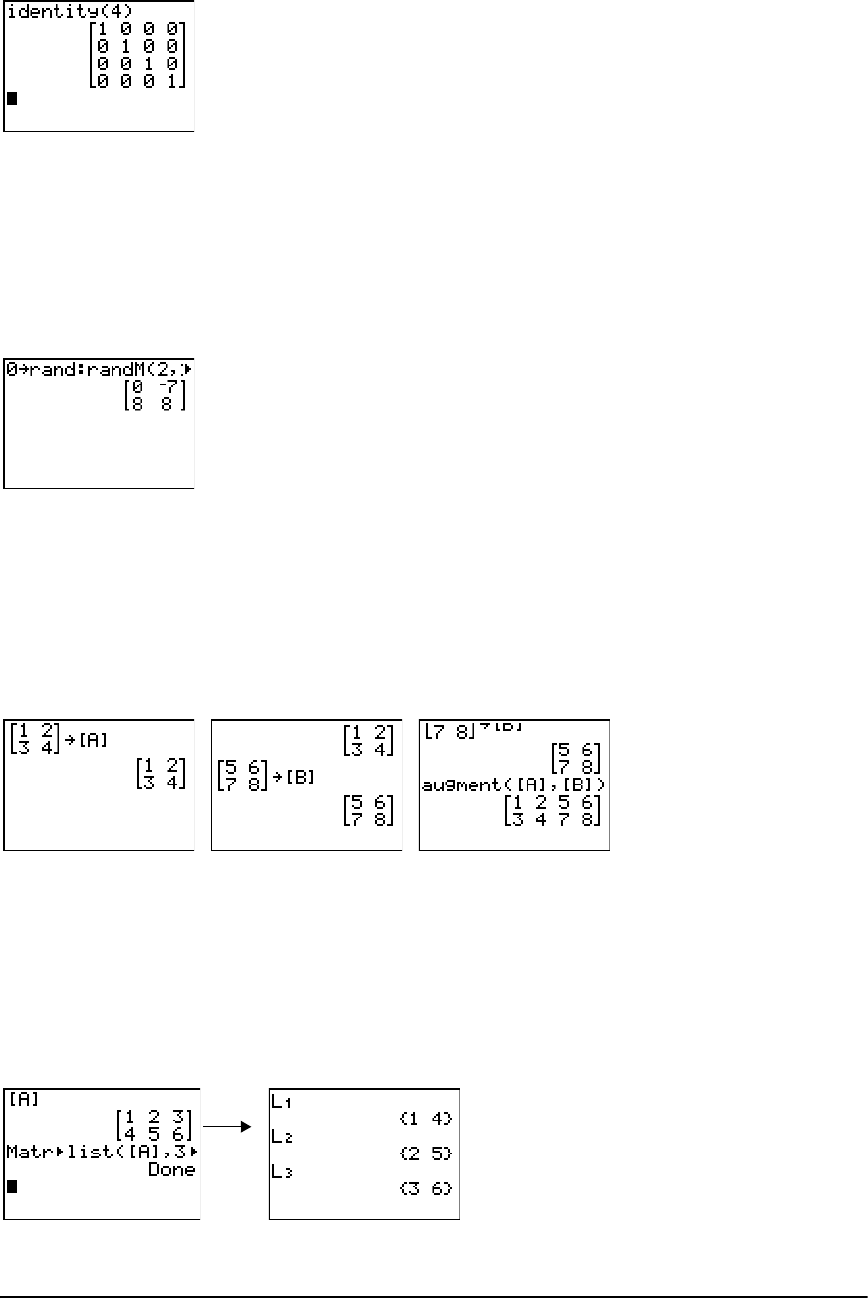
Chapter 10: Matrices 157
randM(
randM( (create random matrix) returns a rows × columns random matrix of integers ‚ L9 and 9. The
seed value stored to the rand function controls the values (Chapter 2).
randM(rows,columns)
augment(
augment( appends matrixA to matrixB as new columns. matrixA and matrixB both must have the same
number of rows.
augment(matrixA,matrixB)
Matr4list(
Matr4list( (matrix stored to list) fills each listname with elements from each column in matrix. Matr4list(
ignores extra listname arguments. Likewise, Matr4list( ignores extra matrix columns.
Matr4list(matrix,listnameA,...,listname n)
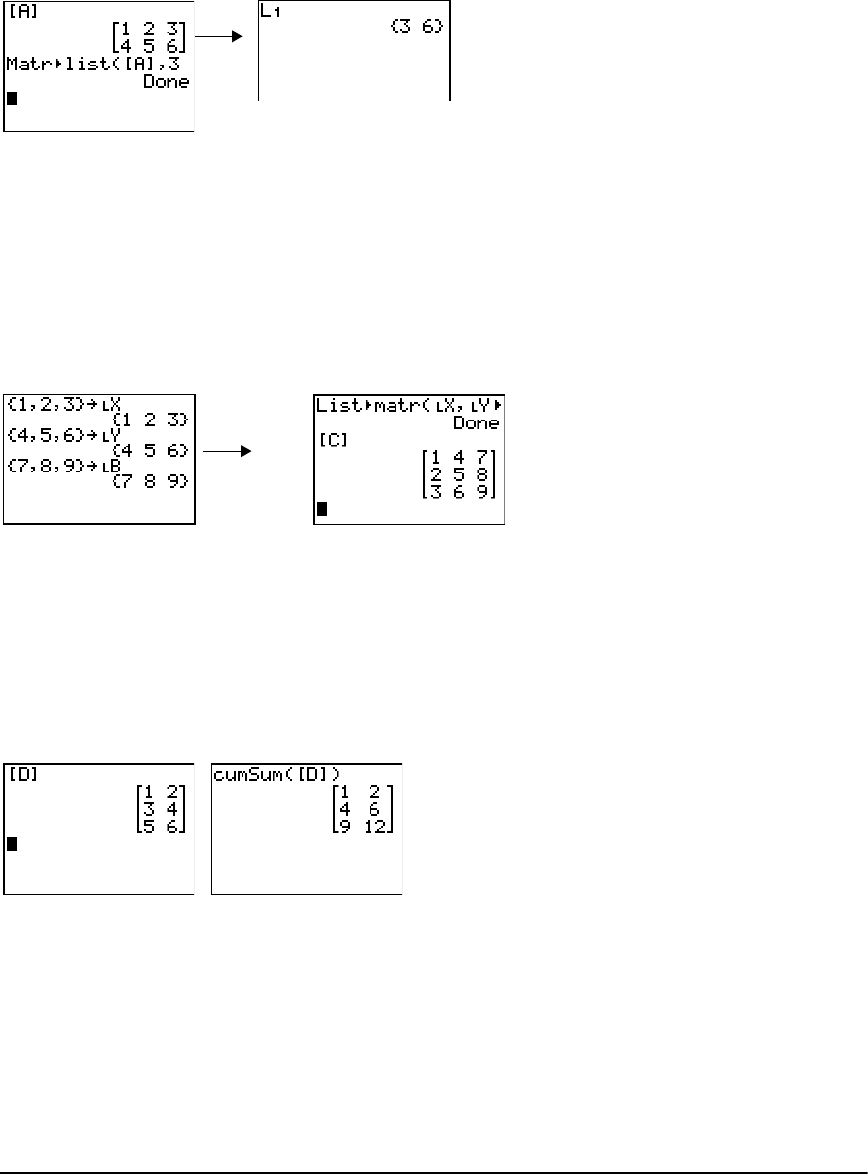
Chapter 10: Matrices 158
Matr4list( also fills a listname with elements from a specified column# in matrix. To fill a list with a specific
column from matrix, you must enter column# after matrix.
Matr4list(matrix,column#,listname)
List4matr(
List4matr( (lists stored to matrix) fills matrixname column by column with the elements from each list. If
dimensions of all lists are not equal, List4matr( fills each extra matrixname row with 0. Complex lists are
not valid.
List4matr(listA,...,list n,matrixname)
cumSum(
cumSum( returns cumulative sums of the elements in matrix, starting with the first element. Each
element is the cumulative sum of the column from top to bottom.
cumSum(matrix)
Row Operations
MATRX MATH menu items A through F are row operations. You can use a row operation in an
expression. Row operations do not change matrix in memory. You can enter all row numbers and
values as expressions. You can select the matrix from the MATRX NAMES menu.
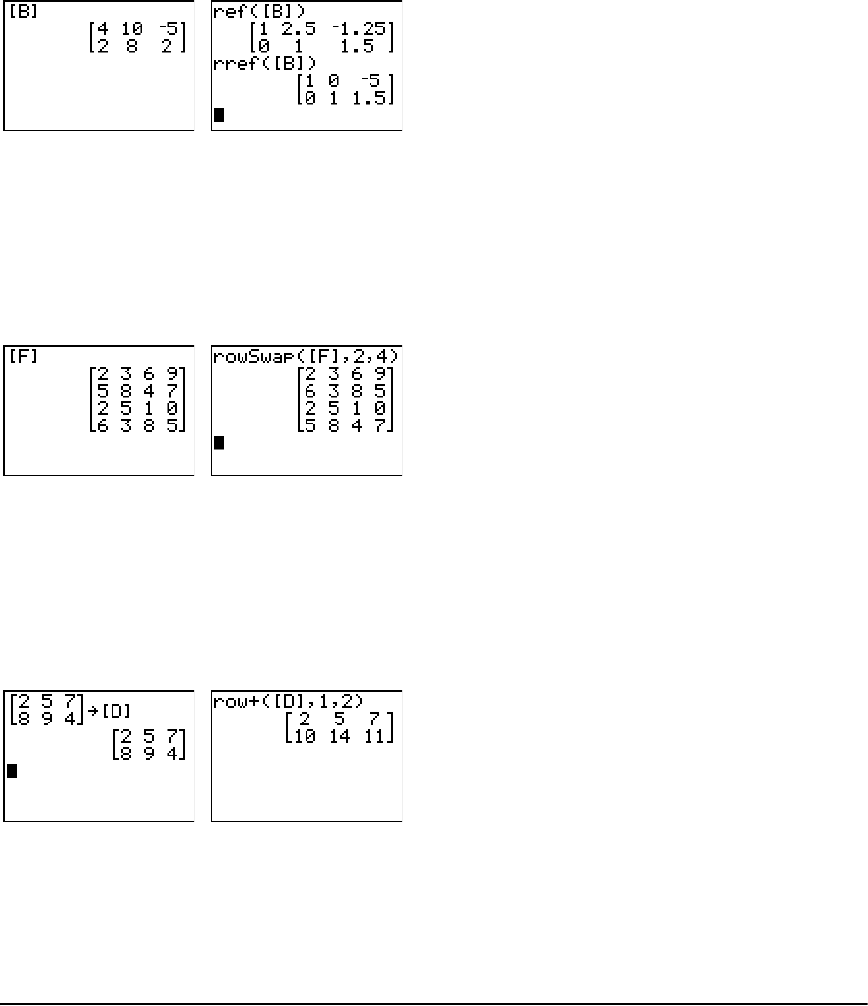
Chapter 10: Matrices 159
ref(, rref(
ref( (row-echelon form) returns the row-echelon form of a real matrix. The number of columns must
be greater than or equal to the number of rows.
ref(matrix)
rref( (reduced row-echelon form) returns the reduced row-echelon form of a real matrix. The number
of columns must be greater than or equal to the number of rows.
rref(matrix)
rowSwap(
rowSwap( returns a matrix. It swaps rowA and rowB of matrix.
rowSwap(matrix,rowA,rowB)
row+(
row+( (row addition) returns a matrix. It adds rowA and rowB of matrix and stores the results in rowB.
row+(matrix,rowA,rowB)

Chapter 10: Matrices 160
…row(
…row( (row multiplication) returns a matrix. It multiplies row of matrix by value and stores the results in
row.
…row(value,matrix,row)
…row+(
…row+( (row multiplication and addition) returns a matrix. It multiplies rowA of matrix by value, adds it
to rowB, and stores the results in rowB.
…row+(value,matrix,rowA,rowB)

Chapter 11: Lists 161
Chapter 11:
Lists
Getting Started: Generating a Sequence
Getting Started is a fast-paced introduction. Read the chapter for details.
Calculate the first eight terms of the sequence 1/A2. Store the results to a user-created list. Then
display the results in fraction form. Begin this example on a blank line on the home screen.
1. Press y 9 ~ to display the LIST OPS menu.
2. Press 5 to select 5:seq(, which opens a wizard to
assist in the entry of the syntax.
3. Press 1 t ^ Í ƒ [A] ¡ † ƒ [A]
† 1 † 8 † 1 to enter the sequence.
Press †, to select Paste, and press Í to paste
the seq( to the current cursor location.
4. Press ¿, and then press y 7 to turn on
alpha-lock. Press [S] [E] [Q], and then press ƒ
to turn off alpha-lock. Press 1 to complete the list
name.
Note: Since the seq( command creates a list, you
can name give the list a name up to five
characters long.
5. Press Í to generate the list and store it in
SEQ1. The list is displayed on the home screen.
An ellipsis (...) indicates that the list continues
beyond the viewing window. Press ~ repeatedly
(or press and hold ~) to scroll the list and view all
the list elements.

Chapter 11: Lists 162
Naming Lists
Using TI-84 Plus List Names L1 through L6
The TI-84 Plus has six list names in memory: L1, L2, L3, L4, L5, and L6. The list names L1 through
L6 are the second functions of À through ¸. To paste one of these names to a valid screen, press
y, and then press the appropriate key. L1 through L6 are stored in stat list editor columns 1
through 6 when you reset memory.
Creating a List Name on the Home Screen
To create a list name on the home screen, follow these steps.
1. Press y E, enter one or more list elements, and then press y F. Separate list elements
with commas. List elements can be real numbers, complex numbers, or expressions.
2. Press ¿.
3. Press ƒ [letter from A to Z or q] to enter the first letter of the name.
4. Enter zero to four letters, q, or numbers to complete the name.
5. Press Í. The list is displayed on the next line. The list name and its elements are stored in
memory. The list name becomes an item on the LIST NAMES menu.
Note: If you want to view a user-created list in the stat list editor, you must retrieve the list in
the stat list editor (Chapter 12).
6. Press y 9 to display the LIST NAMES menu.
Press 7 to select 7:SEQ1 to paste ÙSEQ1 to the
current cursor location. (If SEQ1 is not item 7 on
your LIST NAMES menu, move the cursor to SEQ1
before you press Í.)
7. Press to display the MATH menu. Press 2 to
select 2:4Dec, which pastes 4Dec to the current
cursor location.
8. Press Í to show the sequence in decimal
form. Press ~ repeatedly (or press and hold ~) to
scroll the list and view all the list elements.
Chapter 11: Lists 163
You also can create a list name in these four places.
• At the Name= prompt in the stat list editor
•At an Xlist:, Ylist:, or Data List: prompt in the stat plot editor
•At a List:, List1:, List2:, Freq:, Freq1:, Freq2:, XList:, or YList: prompt in the inferential stat
editors
• On the home screen using SetUpEditor
You can create as many list names as your TI-84 Plus memory has space to store.
Storing and Displaying Lists
Storing Elements to a List
You can store list elements in either of two ways.
• Use brackets and ¿ on the home screen.
• Use the stat list editor (Chapter 12).
The maximum dimension of a list is 999 elements.
Note: When you store a complex number to a list, the entire list is converted to a list of complex
numbers. To convert the list to a list of real numbers, display the home screen, and then enter
real(listname)!listname.
Displaying a List on the Home Screen
To display the elements of a list on the home screen, enter the name of the list (preceded by Ù, if
necessary), and then press Í. An ellipsis indicates that the list continues beyond the viewing
window. Press ~ repeatedly (or press and hold ~) to scroll the list and view all the list elements.
Copying One List to Another
To copy a list, store it to another list.

Chapter 11: Lists 164
Accessing a List Element
You can store a value to or recall a value from a specific list element. You can store to any element
within the current list dimension or one element beyond.
listname(element)
Deleting a List from Memory
To delete lists from memory, including L1 through L6, use the MEMORY MANAGEMENT/DELETE
secondary menu (Chapter 18). Resetting memory restores L1 through L6. Removing a list from the
stat list editor does not delete it from memory.
Using Lists in Graphing
To graph a family of curves, you can use lists (Chapter 3) or the Transformation Graphing App.
Entering List Names
Using the LIST NAMES Menu
To display the LIST NAMES menu, press y 9. Each item is a user-created list name except for
L1 through L6. LIST NAMES menu items are sorted automatically in alphanumerical order. Only the
first 10 items are labeled, using 1 through 9, then 0. To jump to the first list name that begins with a
particular alpha character or q, press ƒ [letter from A to Z or q].
Note: From the top of a menu, press } to move to the bottom. From the bottom, press † to move
to the top.
When you select a list name from the LIST NAMES menu, the list name is pasted to the current
cursor location.
• The list name symbol Ù precedes a list name when the name is pasted where non-list name
data also is valid, such as the home screen.

Chapter 11: Lists 165
•The Ù symbol does not precede a list name when the name is pasted where a list name is the
only valid input, such as the stat list editor’s Name= prompt or the stat plot editor’s XList: and
YList: prompts.
Entering a User-Created List Name Directly
To enter an existing list name directly, follow these steps.
1. Press y 9 ~ to display the LIST OPS menu.
2. Select B:Ù, which pastes Ù to the current cursor location. Ù is not always necessary.
Note: You also can paste Ù to the current cursor
location from the CATALOG.
3. Enter the characters that comprise the list name.
Attaching Formulas to List Names
Attaching a Formula to a List Name
You can attach a formula to a list name so that each list element is a result of the formula. When
executed, the attached formula must resolve to a list.
When anything in the attached formula changes, the list to which the formula is attached is
updated automatically.
• When you edit an element of a list that is referenced in the formula, the corresponding element
in the list to which the formula is attached is updated.
• When you edit the formula itself, all elements in the list to which the formula is attached are
updated.
For example, the first screen below shows that elements are stored to L3, and the formula L3+10 is
attached to the list name ÙADD10. The quotation marks designate the formula to be attached to
ÙADD10. Each element of ÙADD10 is the sum of an element in L3 and 10.
The next screen shows another list, L4. The elements of L4 are the sum of the same formula that
is attached to L3. However, quotation marks are not entered, so the formula is not attached to L4.
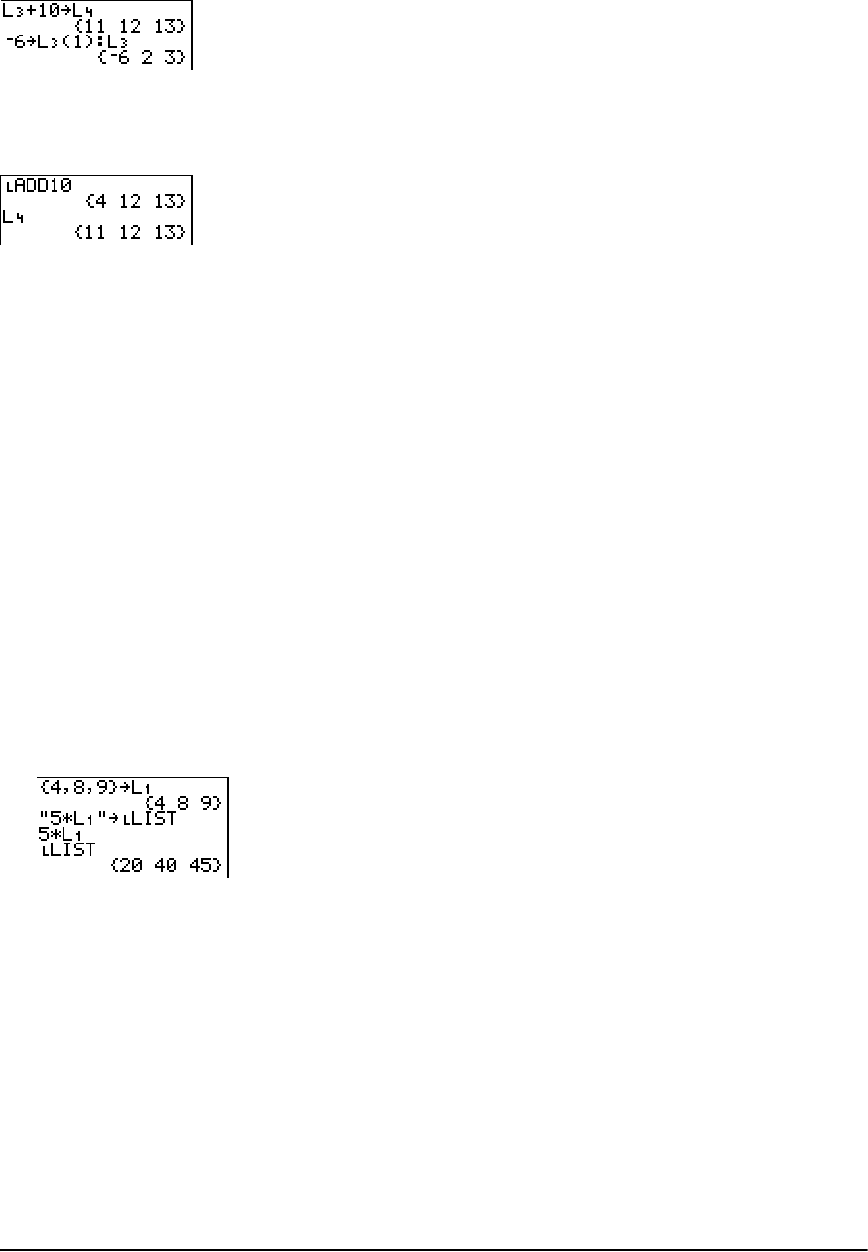
Chapter 11: Lists 166
On the next line, L6!L3(1):L3 changes the first element in L3 to L6, and then redisplays L3.
The last screen shows that editing L3 updated ÙADD10, but did not change L4. This is because the
formula L3+10 is attached to ÙADD10, but it is not attached to L4.
Note: To view a formula that is attached to a list name, use the stat list editor (Chapter 12).
Attaching a Formula to a List on the Home Screen or in a Program
To attach a formula to a list name from a blank line on the home screen or from a program, follow
these steps.
1. Press ƒ [ã], enter the formula (which must resolve to a list), and press ƒ [ã] again.
Note: When you include more than one list name in a formula, each list must have the same
dimension.
2. Press ¿.
3. Enter the name of the list to which you want to attach the formula.
• Press y, and then enter a TI-84 Plus list name L1 through L6.
• Press y 9 and select a user.created list name from the LIST NAMES menu.
• Enter a user.created list name directly using Ù.
4. Press Í.
Note: The stat list editor displays a formula-lock symbol next to each list name that has an
attached formula. Chapter 12 describes how to use the stat list editor to attach formulas to lists,
edit attached formulas, and detach formulas from lists.
Detaching a Formula from a List
You can detach (clear) an attached formula from a list in several ways.
For example:
•Enter ã ã !listname on the home screen.
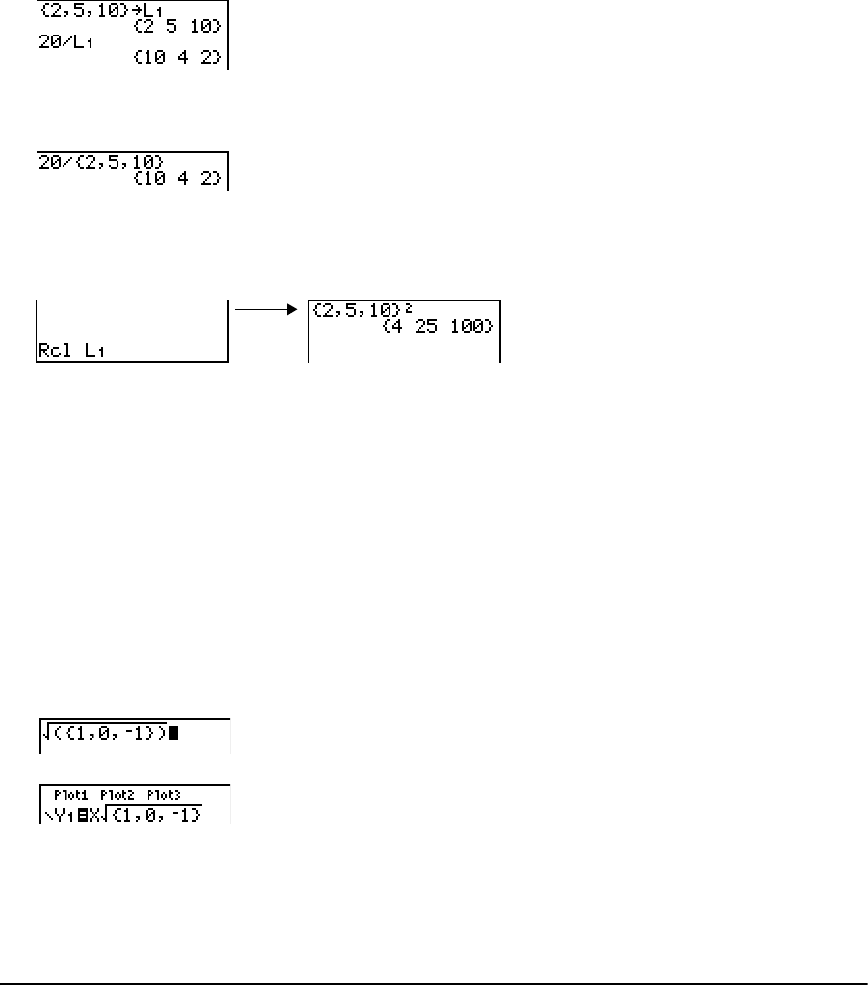
Chapter 11: Lists 167
• Edit any element of a list to which a formula is attached.
• Use the stat list editor (Chapter 12).
• Use ClrList or ClrAllList to detach a formula from a list (Chapter 18).
Using Lists in Expressions
You can use lists in an expression in any of three ways. When you press Í, any expression is
evaluated for each list element, and a list is displayed.
•Use
L1–L6 or any user-created list name in an expression.
• Enter the list elements directly.
• Use y K to recall the contents of the list into an expression at the cursor location
(Chapter 1).
Note: You must paste user-created list names to the Rcl prompt by selecting them from the
LIST NAMES menu. You cannot enter them directly using Ù.
Using Lists with Math Functions
You can use a list to input several values for some math functions. See Appendix A specify for
information about where a list is valid. The function is evaluated for each list element, and a list is
displayed.
• When you use a list with a function, the function must be valid for every element in the list. In
graphing, an invalid element, such as L1 in ‡({1,0,L1}), is ignored.
• When you use two lists with a two-argument function, the dimension of each list must be the
same. The function is evaluated for corresponding elements.
This returns an error.
This graphs X…‡(1) and X…‡(0), but skips
X…‡(L1).

Chapter 11: Lists 168
• When you use a list and a value with a two-argument function, the value is used with each
element in the list.
LIST OPS Menu
LIST OPS Menu
To display the LIST OPS menu, press y 9 ~.
SortA(, SortD(
SortA( (sort ascending) sorts list elements from low to high values. SortD( (sort descending) sorts
list elements from high to low values. Complex lists are sorted based on magnitude (modulus).
With one list, SortA( and SortD( sort the elements of listname and update the list in memory.
NAMES OPS MATH
1: SortA( Sorts lists in ascending order.
2: SortD( Sorts lists in descending order.
3: dim( Sets the list dimension.
4: Fill( Fills all elements with a constant.
5: seq( Creates a sequence.
6: cumSum( Returns a list of cumulative sums.
7: @List( Returns difference of successive elements.
8: Select( Selects specific data points.
9: augment( Concatenates two lists.
0: List4matr( Stores a list to a matrix.
A: Matr4list( Stores a matrix to a list.
B: ÙDesignates the list-name data type.
SortA(listname)SortD(listname)
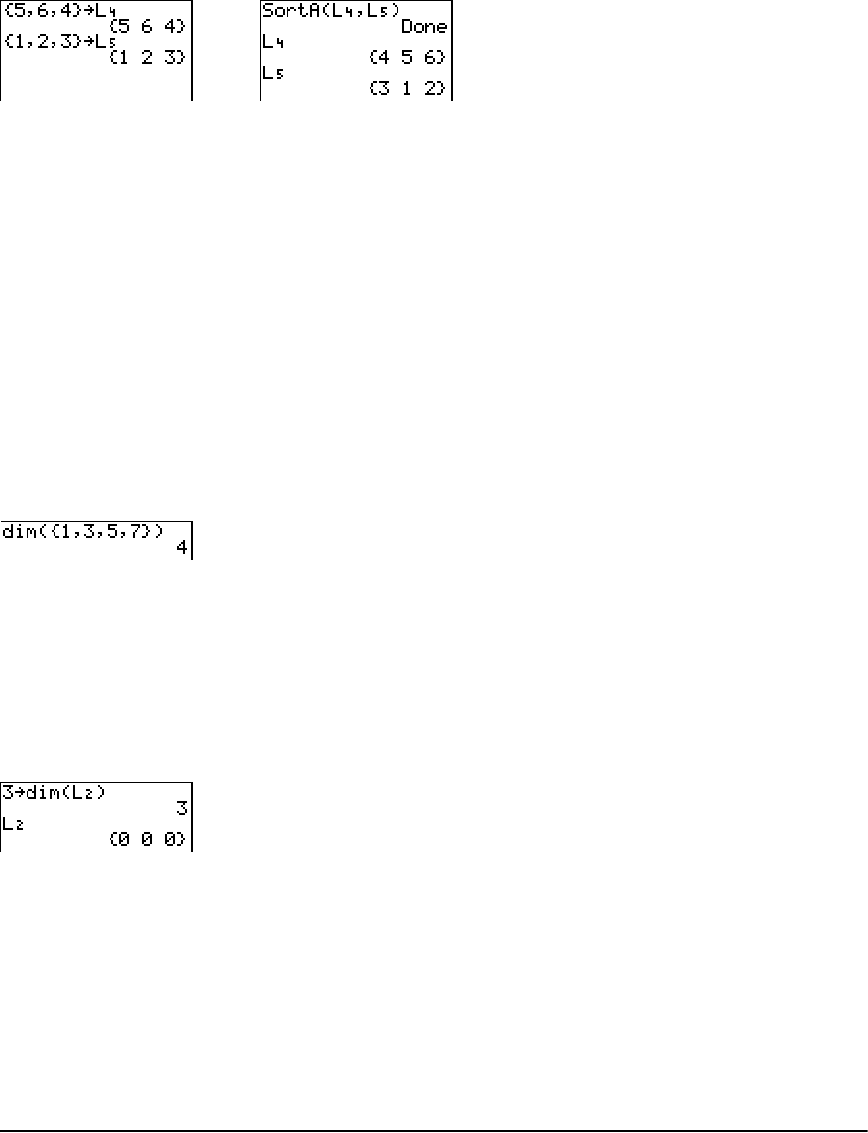
Chapter 11: Lists 169
With two or more lists, SortA( and SortD( sort keylistname, and then sort each dependlist by placing its
elements in the same order as the corresponding elements in keylistname. All lists must have the
same dimension.
SortA(keylistname,dependlist1[,dependlist2,...,dependlist n])
SortD(keylistname,dependlist1[,dependlist2,...,dependlist n])
Note:
• In the example, 5 is the first element in L4, and 1 is the first element in L5. After SortA(L4,L5), 5
becomes the second element of L4, and likewise, 1 becomes the second element of L5.
•SortA( and SortD( are the same as SortA( and SortD( on the STAT EDIT menu (Chapter 12).
• You cannot sort a locked list.
Using dim( to Find List Dimensions
dim( (dimension) returns the length (number of elements) of list.
dim(list)
Using dim( to Create a List
You can use dim( with ¿ to create a new listname with dimension length from 1 to 999. The
elements are zeros.
length!dim(listname)
Using dim( to Redimension a List
You can use dim with ¿ to redimension an existing listname to dimension length from 1 to 999.
• The elements in the old listname that are within the new dimension are not changed.
• Extra list elements are filled by 0.
• Elements in the old list that are outside the new dimension are deleted.
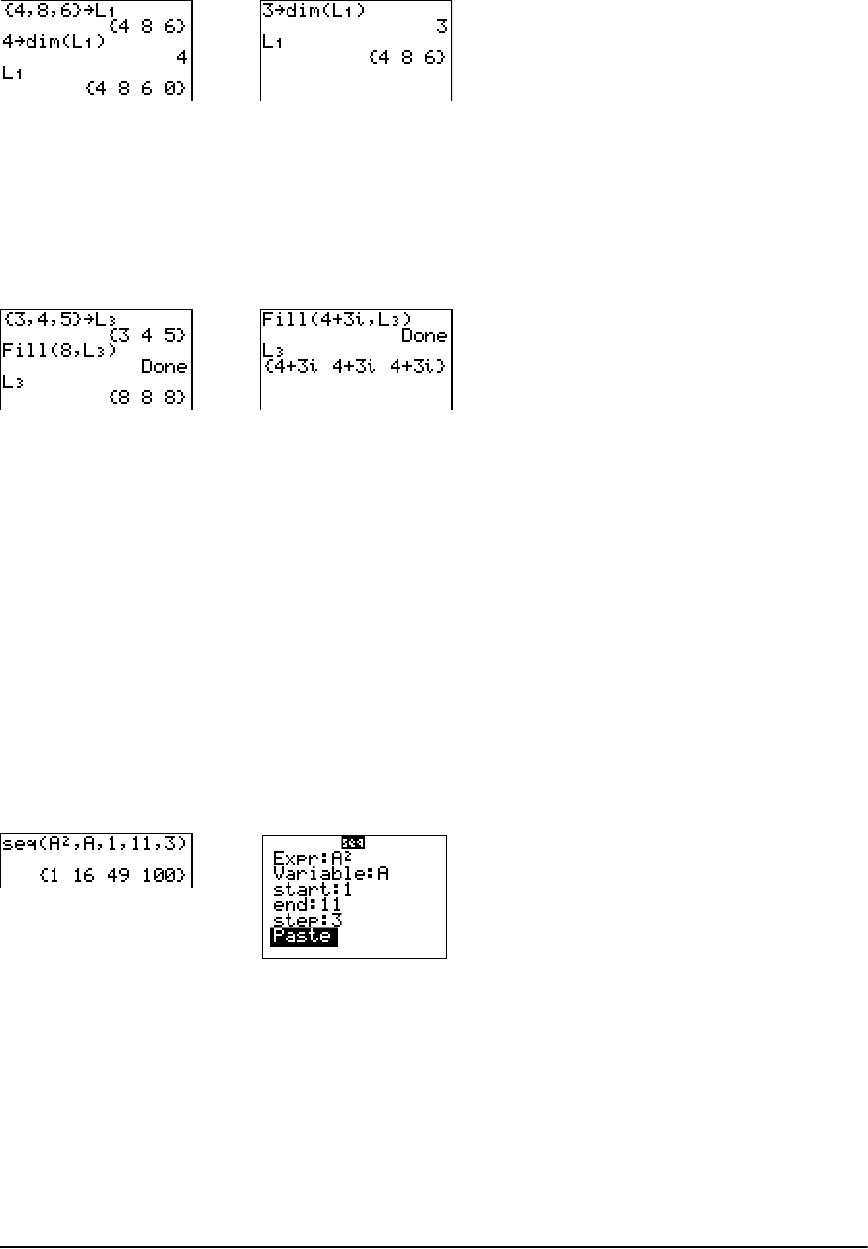
Chapter 11: Lists 170
length!dim(listname)
Fill(
Fill( replaces each element in listname with value.
Fill(value,listname)
Note: dim( and Fill( are the same as dim( and Fill( on the MATRX MATH menu (Chapter 10).
seq(
seq( (sequence) returns a list in which each element is the result of the evaluation of expression with
regard to variable for the values ranging from begin to end at steps of increment. variable need not be
defined in memory. increment can be negative; the default value for increment is 1. seq( is not valid
within expression. Complex lists are not valid.
A wizard will open to assist the entry of the syntax.
Note: seq( is the only function in LIST OPS that has a wizard.
seq(expression,variable,begin,end[,increment])
cumSum(
cumSum( (cumulative sum) returns the cumulative sums of the elements in list, starting with the
first element. list elements can be real or complex numbers.
cumSum(list)

Chapter 11: Lists 171
@List(
@List( returns a list containing the differences between consecutive elements in list. @List subtracts
the first element in list from the second element, subtracts the second element from the third, and
so on. The list of differences is always one element shorter than the original list. list elements can
be a real or complex numbers.
@List(list)
Select(
Select( selects one or more specific data points from a scatter plot or xyLine plot (only), and then
stores the selected data points to two new lists, xlistname and ylistname. For example, you can use
Select( to select and then analyze a portion of plotted CBL 2™/CBL™ or CBR™ data.
Select(xlistname,ylistname)
Note: Before you use Select(, you must have selected (turned on) a scatter plot or xyLine plot.
Also, the plot must be displayed in the current viewing window.
Before Using Select(
Before using Select(, follow these steps.
1. Create two list names and enter the data.
2. Turn on a stat plot, select " (scatter plot) or Ó (xyLine), and enter the two list names for Xlist:
and Ylist: (Chapter 12).
3. Use ZoomStat to plot the data (Chapter 3).
MathPrint™
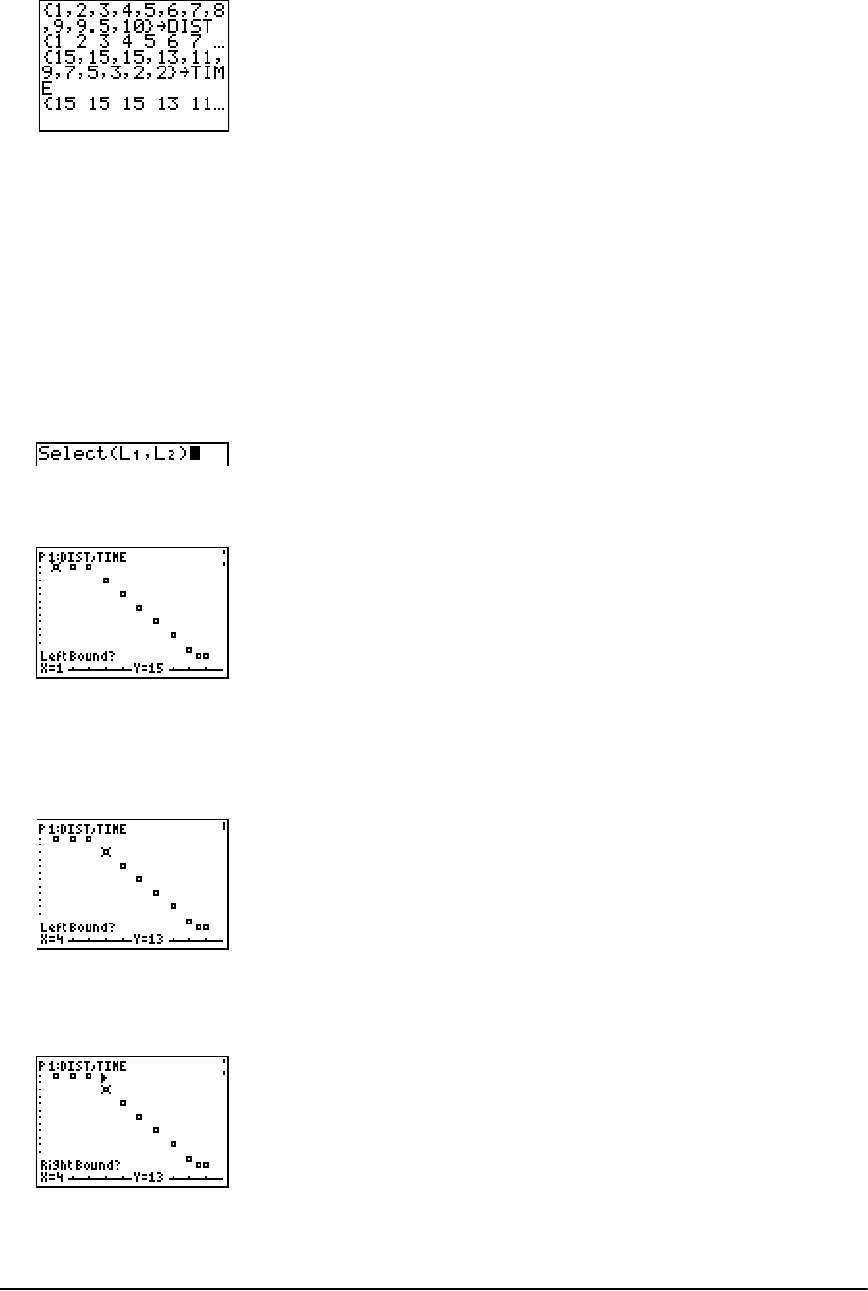
Chapter 11: Lists 172
Using Select( to Select Data Points from a Plot
To select data points from a scatter plot or xyLine plot, follow these steps.
1. Press y 9 ~ 8 to select 8:Select( from the LIST OPS menu. Select( is pasted to the home
screen.
2. Enter xlistname, press ¢, enter ylistname, and then press ¤ to designate list names into which
you want the selected data to be stored.
3. Press Í. The graph screen is displayed with Left Bound? in the bottom-left corner.
4. Press } or † (if more than one stat plot is selected) to move the cursor onto the stat plot from
which you want to select data points.
5. Press | and ~ to move the cursor to the stat plot data point that you want as the left bound.
6. Press Í. A 4 indicator on the graph screen shows the left bound. Right Bound? is
displayed in the bottom-left corner.
Classic

Chapter 11: Lists 173
7. Press | or ~ to move the cursor to the stat plot point that you want for the right bound, and
then press Í.
The x-values and y-values of the selected points are stored in xlistname and ylistname. A new stat
plot of xlistname and ylistname replaces the stat plot from which you selected data points. The list
names are updated in the stat plot editor.
Note: The two new lists (xlistname and ylistname) will include the points you select as left bound and
right bound. Also, left-bound x-value { right-bound x-value must be true.
augment(
augment( concatenates the elements of listA and listB. The list elements can be real or complex
numbers.
augment(listA,listB)
List4matr(
List4matr( (lists stored to matrix) fills matrixname column by column with the elements from each list.
If the dimensions of all lists are not equal, then List4matr( fills each extra matrixname row with 0.
Complex lists are not valid.
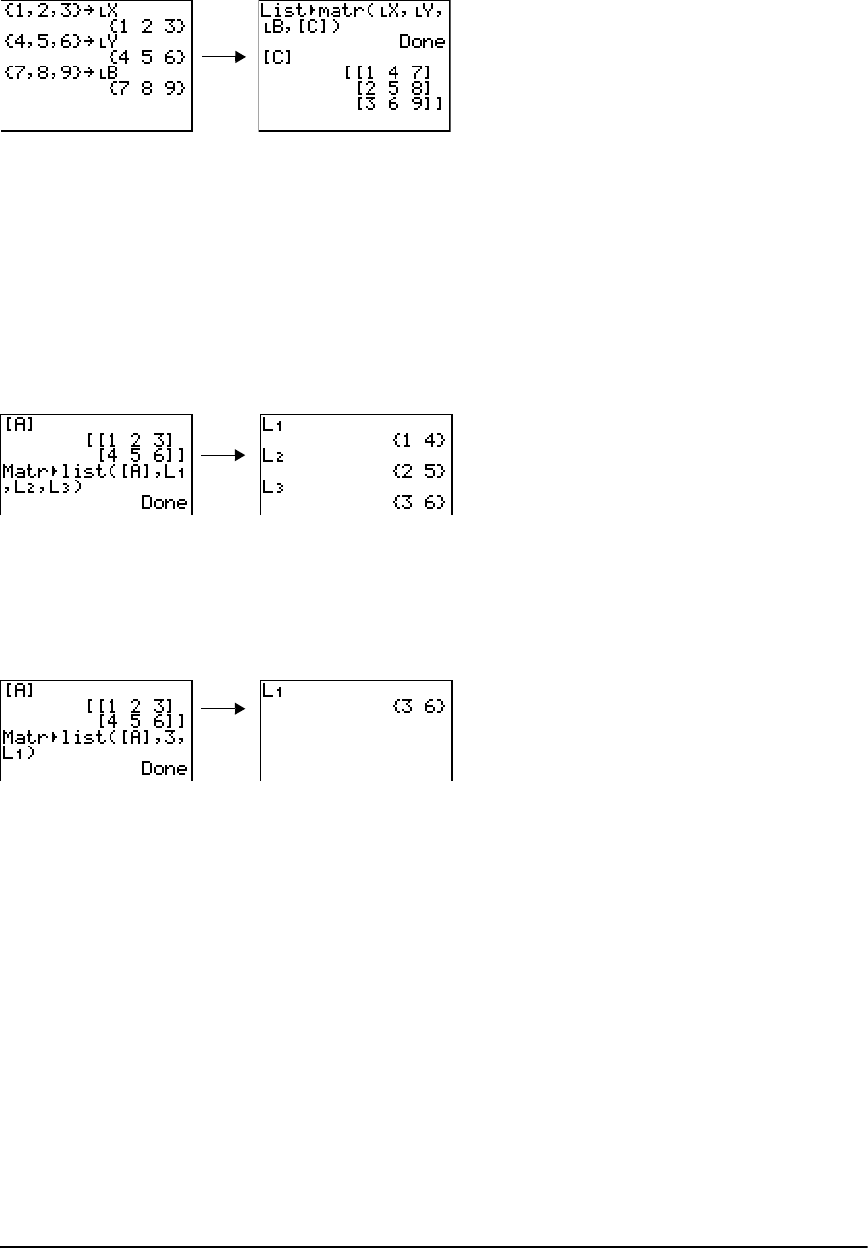
Chapter 11: Lists 174
List4matr(list1,list2, ... ,list n,matrixname)
Matr4list(
Matr4list( (matrix stored to lists) fills each listname with elements from each column in matrix. If the
number of listname arguments exceeds the number of columns in matrix, then Matr4list( ignores
extra listname arguments. Likewise, if the number of columns in matrix exceeds the number of
listname arguments, then Matr4list( ignores extra matrix columns.
Matr4list(matrix,listname1,listname2, . . . ,listname n)
Matr4list( also fills a listname with elements from a specified column# in matrix. To fill a list with a
specific column from matrix, you must enter a column# after matrix.
Matr4list(matrix,column#,listname)
Ù preceding one to five characters identifies those characters as a user-created listname. listname
may comprise letters, q, and numbers, but it must begin with a letter from A to Z or q.
Ùlistname
Generally, Ù must precede a user-created list name when you enter a user-created list name
where other input is valid, for example, on the home screen. Without the Ù, the TI-84 Plus may
misinterpret a user-created list name as implied multiplication of two or more characters.
Ù need not precede a user-created list name where a list name is the only valid input, for example,
at the Name= prompt in the stat list editor or the Xlist: and Ylist: prompts in the stat plot editor. If
you enter Ù where it is not necessary, the TI-84 Plus will ignore the entry.

Chapter 11: Lists 175
LIST MATH Menu
LIST MATH Menu
To display the LIST MATH menu, press y 9 |.
min(, max(
min( (minimum) and max( (maximum) return the smallest or largest element of listA. If two lists are
compared, it returns a list of the smaller or larger of each pair of elements in listA and listB. For a
complex list, the element with smallest or largest magnitude (modulus) is returned.
min(listA[,listB])
max(listA[,listB])
MathPrint™
Classic
Note: min( and max( are the same as min( and max( on the MATH NUM menu.
mean(, median(
mean( returns the mean value of list. median( returns the median value of list. The default value for
freqlist is 1. Each freqlist element counts the number of consecutive occurrences of the
corresponding element in list. Complex lists are not valid.
NAMES OPS MATH
1: min( Returns minimum element of a list.
2: max( Returns maximum element of a list.
3: mean( Returns mean of a list.
4: median( Returns median of a list.
5: sum( Returns sum of elements in a list.
6: prod( Returns product of elements in list.
7: stdDev( Returns standard deviation of a list.
8: variance( Returns the variance of a list.
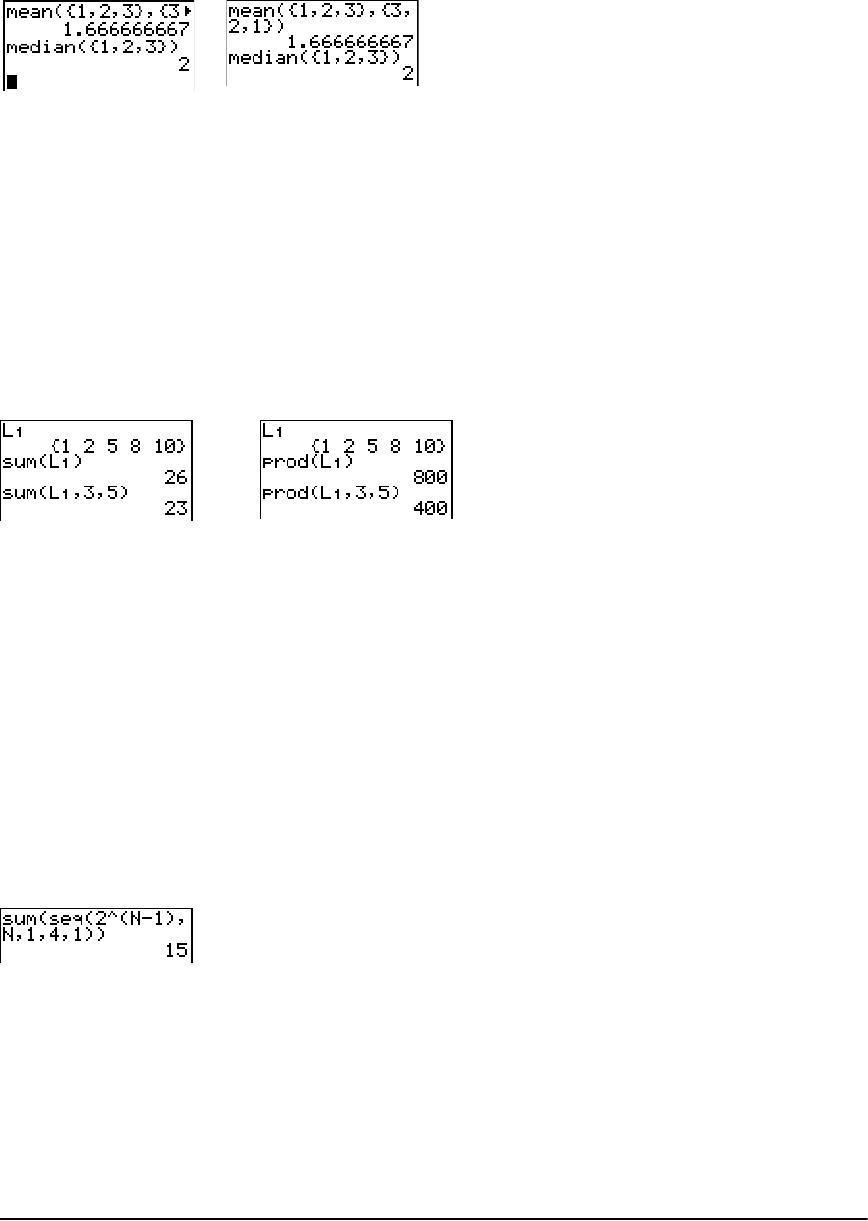
Chapter 11: Lists 176
mean(list[,freqlist])
median(list[,freqlist])
MathPrint™
Classic
sum(, prod(
sum( (summation) returns the sum of the elements in list. start and end are optional; they specify a
range of elements. list elements can be real or complex numbers.
prod( returns the product of all elements of list. start and end elements are optional; they specify a
range of list elements. list elements can be real or complex numbers.
Sums and Products of Numeric Sequences
You can combine sum( or prod( with seq( to obtain:
To evaluate G 2(N–1) from N=1 to 4:
stdDev(, variance(
stdDev( returns the standard deviation of the elements in list. The default value for freqlist is 1. Each
freqlist element counts the number of consecutive occurrences of the corresponding element in list.
Complex lists are not valid.
sum(list[,start,end])prod(list[,start,end])
upper
G expression(x)
x=lower
upper
∏ expression(x)
x=lower
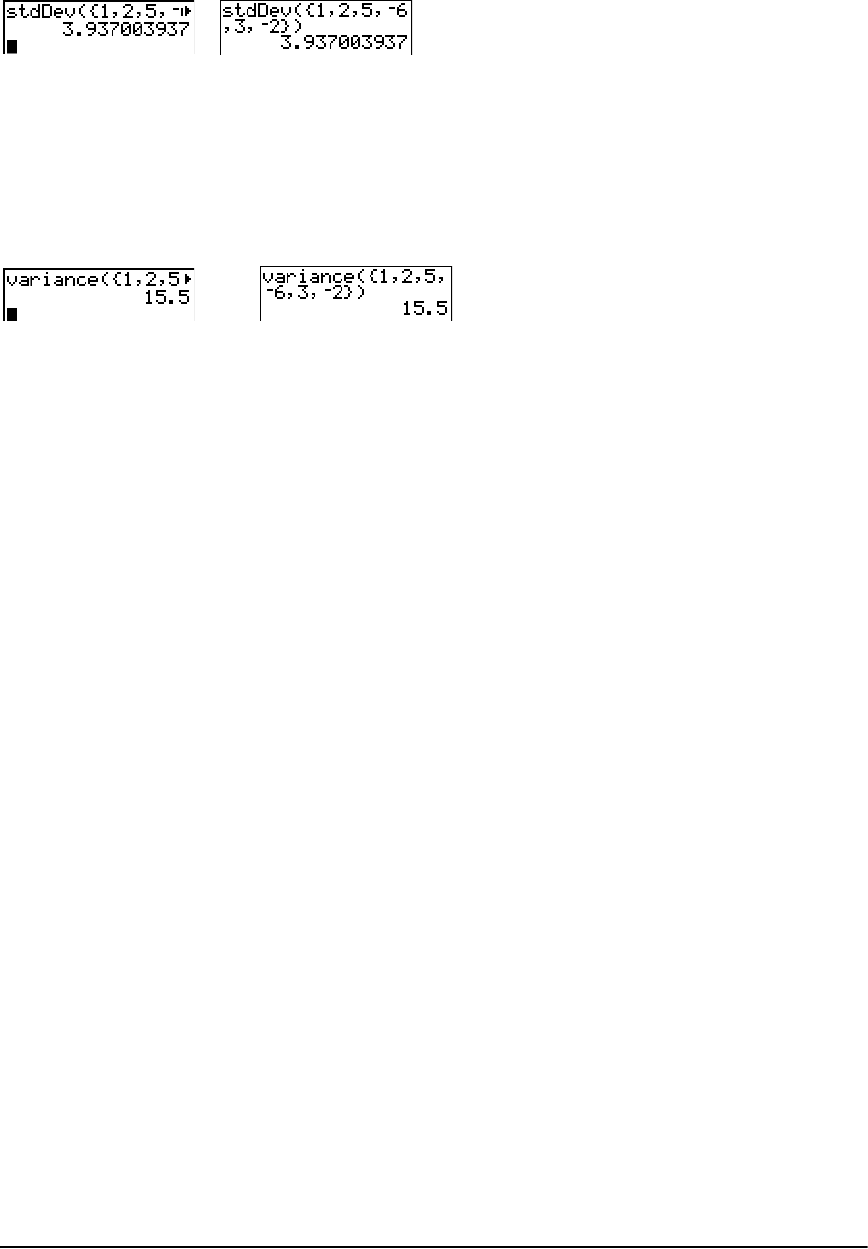
Chapter 11: Lists 177
stdDev(list[,freqlist])
MathPrint™
Classic
variance( returns the variance of the elements in list. The default value for freqlist is 1. Each freqlist
element counts the number of consecutive occurrences of the corresponding element in list.
Complex lists are not valid.
variance(list[,freqlist])
MathPrint™
Classic
Chapter 12: Statistics 178
Chapter 12:
Statistics
Getting Started: Pendulum Lengths and Periods
Getting Started is a fast-paced introduction. Read the chapter for details.
A group of students is attempting to determine the mathematical relationship between the length of
a pendulum and its period (one complete swing of a pendulum). The group makes a simple
pendulum from string and washers and then suspends it from the ceiling. They record the
pendulum’s period for each of 12 string lengths.*
*This example is quoted and adapted from Contemporary Precalculus Through Applications, by the North
Carolina School of Science and Mathematics, by permission of Janson Publications, Inc., Dedham, MA. 1-
800-322-MATH. © 1992. All rights reserved.
Length (cm) Time (sec) Length (cm) Time (sec)
6.50.5124.41.01
11.0 0.68 26.6 1.08
13.2 0.73 30.5 1.13
15.0 0.79 34.3 1.26
18.0 0.88 37.6 1.28
23.1 0.99 41.5 1.32
1. Press z † † † Í to set Func graphing
mode.
2. Press … 5 to select 5:SetUpEditor. SetUpEditor
is pasted to the home screen.
Press Í. This removes lists from stat list editor
columns 1 through 20, and then stores lists L1
through L6 in columns 1 through 6.
Note: Removing lists from the stat list editor does
not delete them from memory.
3. Press … 1 to select 1:Edit from the STAT EDIT
menu. The stat list editor is displayed. If elements
are stored in L1 and L2, press } to move the
cursor onto L1, and then press ‘ Í ~ }
‘ Í to clear both lists. Press | to move
the rectangular cursor back to the first row in L1.
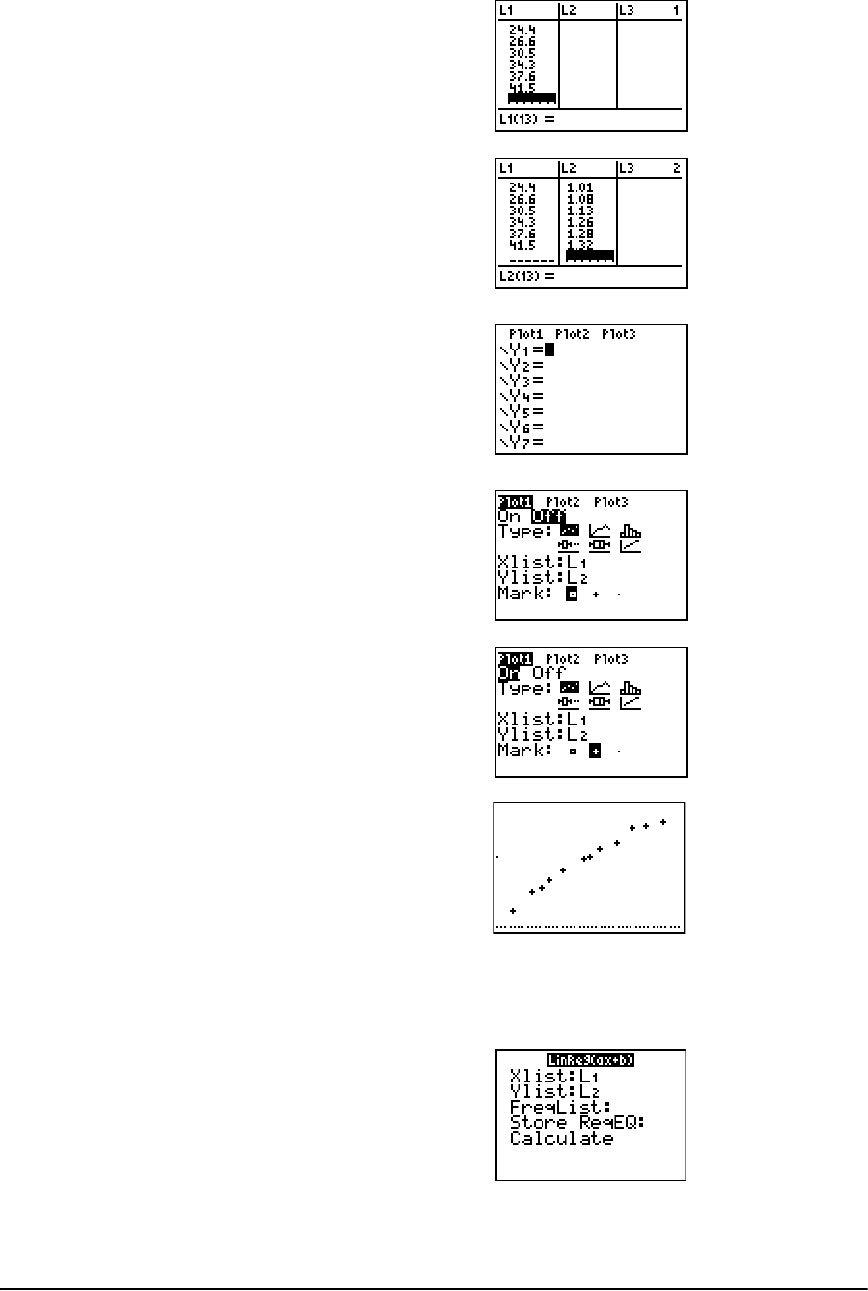
Chapter 12: Statistics 179
Since the scatter plot of time-versus-length data appears to be approximately linear, fit a line to the
data.
4. Press 6 Ë 5 Í to store the first pendulum
string length (6.5 cm) in L1. The rectangular cursor
moves to the next row. Repeat this step to enter
each of the 12 string length values in the table.
5. Press ~ to move the rectangular cursor to the first
row in L2.
Press Ë 51 Í to store the first time
measurement (.51 sec) in L2. The rectangular
cursor moves to the next row. Repeat this step to
enter each of the 12 time values in the table.
6. Press o to display the Y= editor.
If necessary, press ‘ to clear the function Y1.
As necessary, press }, Í, and ~ to turn off
Plot1, Plot2, and Plot3 from the top line of the
Y= editor (Chapter 3). As necessary, press †, |,
and Í to deselect functions.
7. Press y , 1 to select 1:Plot1 from the
STAT PLOTS menu. The stat plot editor is
displayed for plot 1.
8. Press Í to select On, which turns on plot 1.
Press † Í to select " (scatter plot). Press
† y d to specify Xlist:L1 for plot 1. Press
† y e to specify Ylist:L2 for plot 1. Press
† ~ Í to select + as the Mark for each data
point on the scatter plot.
9. Press q 9 to select 9:ZoomStat from the ZOOM
menu. The window variables are adjusted
automatically, and plot 1 is displayed. This is a
scatter plot of the time-versus-length data.
10. Press … ~ 4 to select 4:LinReg(ax+b) (linear
regression model) from the STAT CALC menu.

Chapter 12: Statistics 180
The regression line appears to fit the central portion of the scatter plot well. However, a residual
plot may provide more information about this fit.
11. Fill in each argument in the stat wizard displayed.
Press y d (for Xlist:), and † y e (for Ylist:),
Press † † (to Store ReqEQ:)and then press
t a Í to paste Y1. Press † (to select
Calculate).
12. Press Í to execute LinReg(ax+b). The linear
regression for the data in L1 and L2 is calculated.
Values for a and b are displayed in a temporary
result screen. The linear regression equation is
stored in Y1. Residuals are calculated and stored
automatically in the list name RESID, which
becomes an item on the LIST NAMES menu.
Note:
- You can control the number of decimal places
displayed by changing the decimal mode setting.
- The statistics reported are not stored in the history on
the home screen.
-Press
5 ~ ~ ~ to access the statistical
variables.
- Press ‘ to return to the home screen.
13. The stat wizard pastes the populated command in
the home screen history for repeated use, if
needed (press ‘ } } to view the home
screen history as show in the screen).
14. Press s. The regression line and the scatter
plot are displayed.
15. Press … 1 to select 1:Edit. The stat list editor is
displayed.
Press ~ and } to move the cursor onto L3.
Press y 6. An unnamed column is displayed
in column 3; L3, L4, L5, and L6 shift right one
column. The Name= prompt is displayed in the
entry line, and alpha-lock is on.
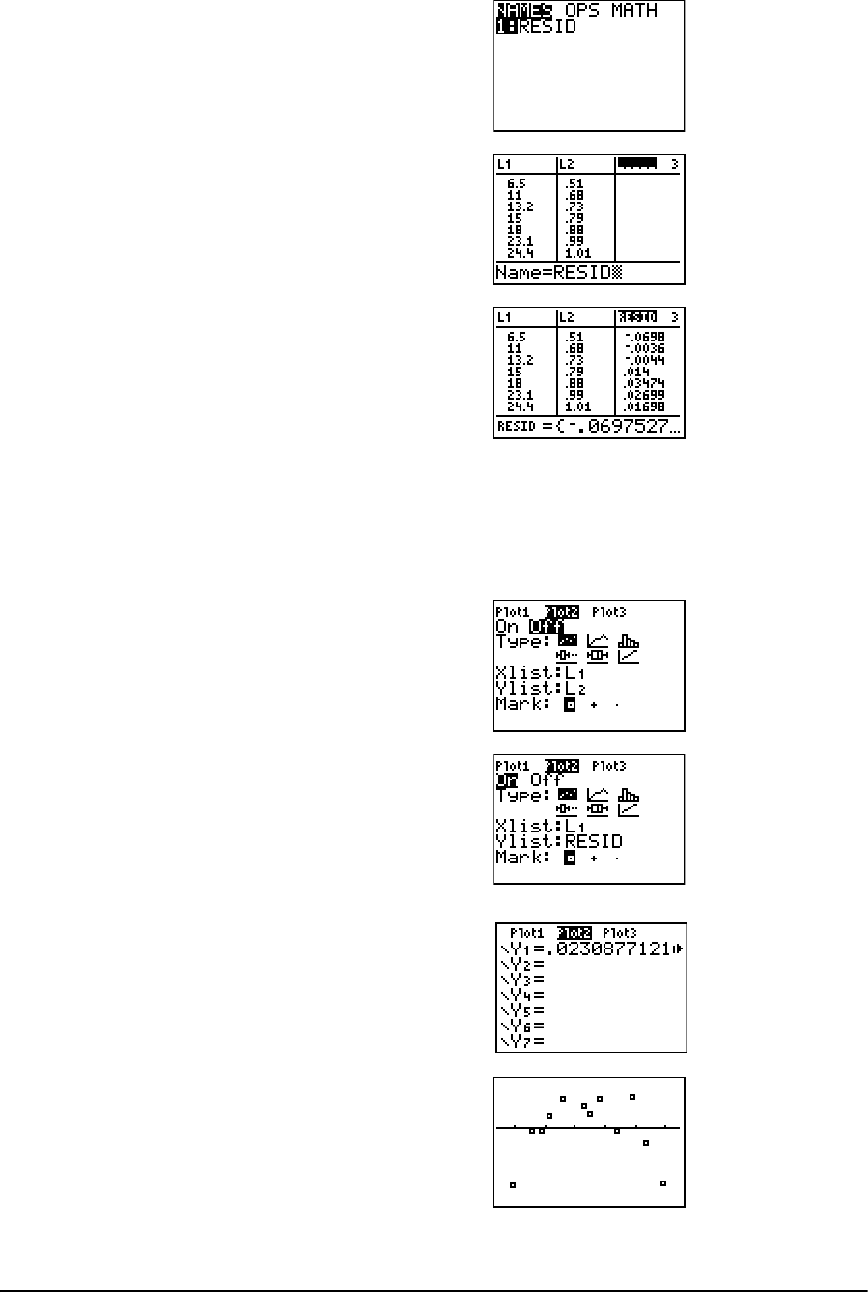
Chapter 12: Statistics 181
Notice that the first three residuals are negative. They correspond to the shortest pendulum string
lengths in L1. The next five residuals are positive, and three of the last four are negative. The latter
correspond to the longer string lengths in L1. Plotting the residuals will show this pattern more
clearly.
16. Press y 9 to display the LIST NAMES menu.
If necessary, press † to move the cursor onto the
list name RESID.
17. Press Í to select RESID and paste it to the
stat list editor’s Name= prompt.
18. Press Í. RESID is stored in column 3 of the
stat list editor.
Press † repeatedly to examine the residuals.
19. Press y , 2 to select 2:Plot2 from the
STAT PLOTS menu. The stat plot editor is
displayed for plot 2.
20. Press Í to select On, which turns on plot 2.
Press † Í to select " (scatter plot). Press
† y d to specify Xlist:L1 for plot 2. Press † ãRä
ãEä ãSä ãIä ãDä (alpha-lock is on) to specify
Ylist:RESID for plot 2. Press † Í to select ›
as the mark for each data point on the scatter plot.
21. Press o to display the Y= editor.
Press | to move the cursor onto the = sign, and
then press Í to deselect Y1. Press } Í to
turn off plot 1.
22. Press q 9 to select 9:ZoomStat from the ZOOM
menu. The window variables are adjusted
automatically, and plot 2 is displayed. This is a
scatter plot of the residuals.
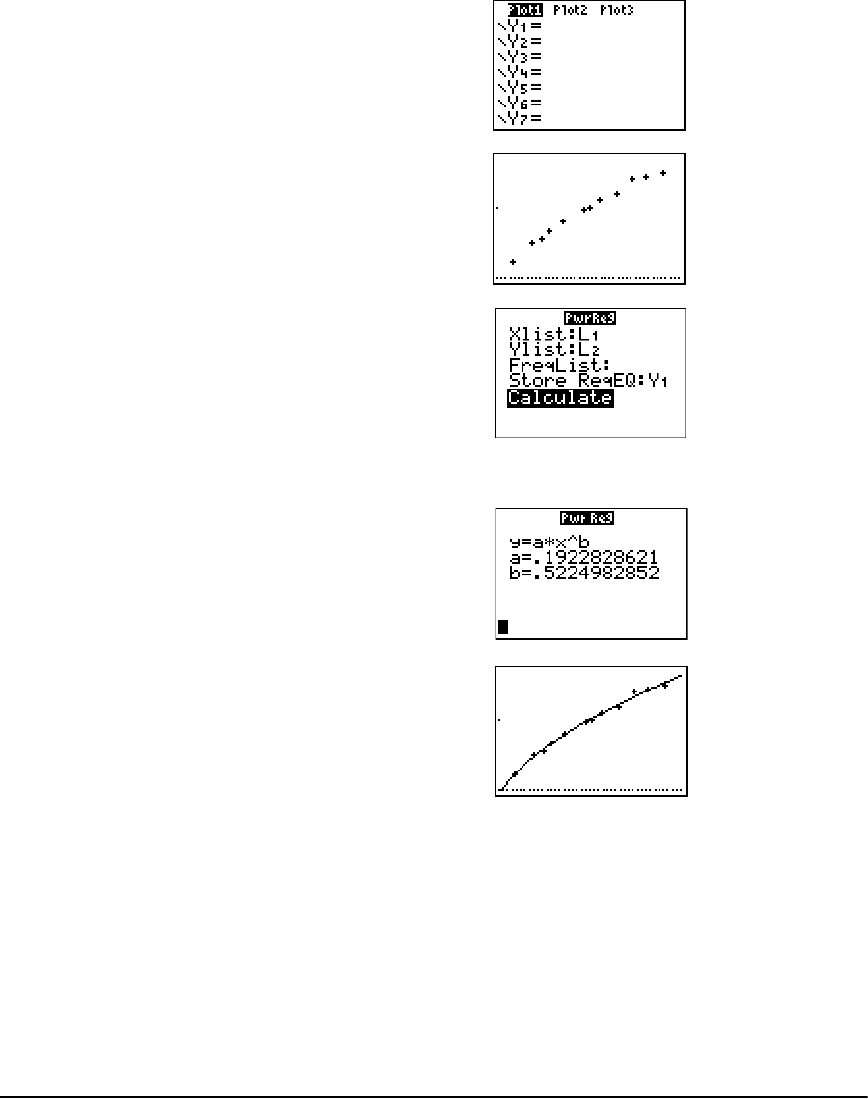
Chapter 12: Statistics 182
Notice the pattern of the residuals: a group of negative residuals, then a group of positive
residuals, and then another group of negative residuals.
The residual pattern indicates a curvature associated with this data set for which the linear model
did not account. The residual plot emphasizes a downward curvature, so a model that curves
down with the data would be more accurate. Perhaps a function such as square root would fit. Try
a power regression to fit a function of the form y = a … xb.
23. Press o to display the Y= editor.
Press ‘ to clear the linear regression
equation from Y1. Press } Í to turn on plot 1.
Press ~ Í to turn off plot 2.
24. Press q 9 to select 9:ZoomStat from the ZOOM
menu. The window variables are adjusted
automatically, and the original scatter plot of time-
versus-length data (plot 1) is displayed.
25. Press … ~ ƒ ãAä to select A:PwrReg from
the STAT CALC menu. PwrReg is pasted to the
home screen.
Press y d † y e † † t a Í † to
highlight Calculate.
Note: You can also use the VARS Y-VARS
FUNCTION menu, ~ 1 to select Y1.
26. Press Í to calculate the power regression.
Values for a and b are displayed on the home
screen. The power regression equation is stored
in Y1. Residuals are calculated and stored
automatically in the list name RESID.
27. Press s. The regression line and the scatter
plot are displayed.
Chapter 12: Statistics 183
The new function y=.192x.522 appears to fit the data well. To get more information, examine a
residual plot.
The new residual plot shows that the residuals are random in sign, with the residuals increasing in
magnitude as the string length increases.
To see the magnitudes of the residuals, continue with these steps.
Now that you have a good model for the relationship between length and period, you can use the
model to predict the period for a given string length. To predict the periods for a pendulum with
string lengths of 20 cm and 50 cm, continue with these steps.
28. Press o to display the Y= editor.
Press | Í to deselect Y1.
Press } Í to turn off plot 1. Press ~ Í to
turn on plot 2.
Note: Step 19 defined plot 2 to plot residuals
(RESID) versus string length (L1).
29. Press q 9 to select 9:ZoomStat from the ZOOM
menu. The window variables are adjusted
automatically, and plot 2 is displayed. This is a
scatter plot of the residuals.
30. Press r.
Press ~ and | to trace the data. Observe the
values for Y at each point.
With this model, the largest positive residual is
about 0.041 and the smallest negative residual is
about L0.027. All other residuals are less than 0.02
in magnitude.
31. Press ~ 1 to display the VARS Y-VARS
FUNCTION secondary menu, and then press 1 to
select 1:Y1. Y1 is pasted to the home screen.
Note: You can also use the YVARS (t a)
shortcut menu to select Y1.
32. Press £ 20 ¤ to enter a string length of 20 cm.
Press Í to calculate the predicted time of
about 0.92 seconds.
Based on the residual analysis, we would expect
the prediction of about 0.92 seconds to be within
about 0.02 seconds of the actual value.

Chapter 12: Statistics 184
Setting Up Statistical Analyses
Using Lists to Store Data
Data for statistical analyses is stored in lists, which you can create and edit using the stat list
editor. The TI-84 Plus has six list variables in memory, L1 through L6, to which you can store data
for statistical calculations. Also, you can store data to list names that you create (Chapter 11).
Setting Up a Statistical Analysis
To set up a statistical analysis, follow these steps. Read the chapter for details.
1. Enter the statistical data into one or more lists.
2. Plot the data.
3. Calculate the statistical variables or fit a model to the data.
4. Graph the regression equation for the plotted data.
5. Graph the residuals list for the given regression model.
Displaying the Stat List Editor
The stat list editor is a table where you can store, edit, and view up to 20 lists that are in memory.
Also, you can create list names from the stat list editor.
To display the stat list editor, press …, and then select 1:Edit from the STAT EDIT menu.
33. Press y [ to recall the Last Entry.
Press | | | 5 to change the string length to 50
cm.
34. Press Í to calculate the predicted time of
about 1.48 seconds.
Since a string length of 50 cm exceeds the lengths
in the data set, and since residuals appear to be
increasing as string length increases, we would
expect more error with this estimate.
Note: You also can make predictions using the
table with the TABLE SETUP settings Indpnt:Ask
and Depend:Auto (Chapter 7).
Chapter 12: Statistics 185
The top line displays list names. L1 through L6 are stored in columns 1 through 6 after a memory
reset. The number of the current column is displayed in the top-right corner.
The bottom line is the entry line. All data entry occurs on this line. The characteristics of this line
change according to the current context.
The center area displays up to seven elements of up to three lists; it abbreviates values when
necessary. The entry line displays the full value of the current element.
Using the Stat List Editor
Entering a List Name in the Stat List Editor
To enter a list name in the stat list editor, follow these steps.
1. Display the Name= prompt in the entry line in either of two ways.
• Move the cursor onto the list name in the column where you want to insert a list, and then
press y 6. An unnamed column is displayed and the remaining lists shift right one
column.
• Press } until the cursor is on the top line, and then press ~ until you reach the unnamed
column.
Note: If list names are stored to all 20 columns, you must remove a list name to make room for
an unnamed column.
The Name= prompt is displayed and alpha-lock is on.
2. Enter a valid list name in any of four ways.
• Select a name from the LIST NAMES menu (Chapter 11).
•Enter L1, L2, L3, L4, L5, or L6 from the keyboard.
• Enter an existing user-created list name directly from the keyboard.
• Enter a new user-created list name.
3. Press Í or † to store the list name and its elements, if any, in the current column of the
stat list editor.

Chapter 12: Statistics 186
To begin entering, scrolling, or editing list elements, press †. The rectangular cursor is
displayed.
Note: If the list name you entered in step 2 already was stored in another stat list editor
column, then the list and its elements, if any, move to the current column from the previous
column. Remaining list names shift accordingly.
Creating a Name in the Stat List Editor
To create a name in the stat list editor, follow these steps.
1. Display the Name= prompt.
2. Press [letter from A to Z or q] to enter the first letter of the name. The first character cannot be a
number.
3. Enter zero to four letters, q, or numbers to complete the new user-created list name. List
names can be one to five characters long.
4. Press Í or † to store the list name in the current column of the stat list editor. The list
name becomes an item on the LIST NAMES menu (Chapter 11).
Removing a List from the Stat List Editor
To remove a list from the stat list editor, move the cursor onto the list name and then press {. The
list is not deleted from memory; it is only removed from the stat list editor.
Notes:
• To delete a list name from memory, use the MEMORY MANAGEMENT/DELETE secondary
menu (Chapter 18).
• If you archive a list, it will be removed from the stat list editor.
Removing All Lists and Restoring L1 through L6
You can remove all user-created lists from the stat list editor and restore list names L1 through L6
to columns 1 through 6 in either of two ways.
• Use SetUpEditor with no arguments.
• Reset all memory (Chapter 18).

Chapter 12: Statistics 187
Clearing All Elements from a List
You can clear all elements from a list in any of five ways.
• Use ClrList to clear specified lists.
• In the stat list editor, press } to move the cursor onto a list name, and then press
‘ Í.
• In the stat list editor, move the cursor onto each element, and then press { one by one.
• On the home screen or in the program editor, enter 0!dim(listname) to set the dimension of
listname to 0 (Chapter 11).
•Use
ClrAllLists to clear all lists in memory (Chapter 18).
Editing a List Element
To edit a list element, follow these steps.
1. Move the cursor onto the element you want to edit.
2. Press Í to move the cursor to the entry line.
Note: If you want to replace the current value, you can enter a new value without first pressing
Í. When you enter the first character, the current value is cleared automatically.
3. Edit the element in the entry line.
• Press one or more keys to enter the new value. When you enter the first character, the
current value is cleared automatically.
You can use the shortcut menus to enter values. When you use n/d to enter a fraction, it is
not displayed as a stacked fraction in the list. Instead, the fraction has a thick bar
separating the numerator and denominator.
Thick-bar fraction on the list editor entry line:
Thin-bar fraction on the home screen (regular division):
Note: Order of operations applies to fractions. For example, evaluates to
because the order of operations dictates that division is performed before addition. To
evaluate , enter with parentheses around the numerator.
• Press ~ to move the cursor to the character before which you want to insert, press y 6,
and then enter one or more characters.
• Press ~ to move the cursor to a character you want to delete, and then press { to delete
the character.
To cancel any editing and restore the original element at the rectangular cursor, press
‘ Í.
Chapter 12: Statistics 188
Note: You can enter expressions and variables for elements.
4. Press Í, }, or † to update the list. If you entered an expression, it is evaluated. If you
entered only a variable, the stored value is displayed as a list element.
When you edit a list element in the stat list editor, the list is updated in memory immediately.
Attaching Formulas to List Names
Attaching a Formula to a List Name in Stat List Editor
You can attach a formula to a list name in the stat list editor, and then display and edit the
calculated list elements. When executed, the attached formula must resolve to a list. Chapter 11
describes in detail the concept of attaching formulas to list names.
To attach a formula to a list name that is stored in the stat list editor, follow these steps.
1. Press … Í to display the stat list editor.
2. Press } to move the cursor to the top line.
3. Press | or ~, if necessary, to move the cursor onto the list name to which you want to attach
the formula.
Note: If a formula in quotation marks is displayed on the entry line, then a formula is already
attached to the list name. To edit the formula, press Í, and then edit the formula.
4. Press ƒ ããä, enter the formula, and press ƒ ããä.
Note: If you do not use quotation marks, the TI-84 Plus calculates and displays the same initial
list of answers, but does not attach the formula for future calculations.
Note: Any user-created list name referenced in a formula must be preceded by an Ù symbol
(Chapter 11).
Chapter 12: Statistics 189
5. Press Í. The TI-84 Plus calculates each list element and stores it to the list name to which
the formula is attached. A lock symbol is displayed in the stat list editor, next to the list name to
which the formula is attached.
lock symbol
Using the Stat List Editor When Formula-Generated Lists Are Displayed
When you edit an element of a list referenced in an attached formula, the TI-84 Plus updates the
corresponding element in the list to which the formula is attached (Chapter 11).
When a list with a formula attached is displayed in the stat list editor and you edit or enter elements
of another displayed list, then the TI-84 Plus takes slightly longer to accept each edit or entry than
when no lists with formulas attached are in view.
Note: To speed editing time, scroll horizontally until no lists with formulas are displayed, or
rearrange the stat list editor so that no lists with formulas are displayed.
Handling Errors Resulting from Attached Formulas
On the home screen, you can attach to a list a formula that references another list with dimension
0 (Chapter 11). However, you cannot display the formula-generated list in the stat list editor or on
the home screen until you enter at least one element to the list that the formula references.
All elements of a list referenced by an attached formula must be valid for the attached formula. For
example, if Real number mode is set and the attached formula is log(L1), then each element of L1
must be greater than 0, since the logarithm of a negative number returns a complex result.
When you use the shortcut menus, all values must be valid for use in the templates. For example,
if you use the n/d template, both the numerator and denominator must be integers.
Notes:
• If an error menu is returned when you attempt to display a formula-generated list in the stat list
editor, you can select 2:Goto, write down the formula that is attached to the list, and then press
‘ Í to detach (clear) the formula. You then can use the stat list editor to find the

Chapter 12: Statistics 190
source of the error. After making the appropriate changes, you can reattach the formula to a
list.
• If you do not want to clear the formula, you can select 1:Quit, display the referenced list on the
home screen, and find and edit the source of the error. To edit an element of a list on the home
screen, store the new value to listname(element#) (Chapter 11).
Detaching Formulas from List Names
Detaching a Formula from a List Name
You can detach (clear) a formula from a list name in several ways.
For example:
• In the stat list editor, move the cursor onto the name of the list to which a formula is attached.
Press Í ‘ Í. All list elements remain, but the formula is detached and the lock
symbol disappears.
• In the stat list editor, move the cursor onto an element of the list to which a formula is attached.
Press Í, edit the element, and then press Í. The element changes, the formula is
detached, and the lock symbol disappears. All other list elements remain.
•Use
ClrList. All elements of one or more specified lists are cleared, each formula is detached,
and each lock symbol disappears. All list names remain.
• Use ClrAllLists (Chapter 18). All elements of all lists in memory are cleared, all formulas are
detached from all list names, and all lock symbols disappear. All list names remain.
Editing an Element of a Formula-Generated List
As described above, one way to detach a formula from a list name is to edit an element of the list
to which the formula is attached. The TI-84 Plus protects against inadvertently detaching the
formula from the list name by editing an element of the formula-generated list.
Because of the protection feature, you must press Í before you can edit an element of a
formula-generated list.
The protection feature does not allow you to delete an element of a list to which a formula is
attached. To delete an element of a list to which a formula is attached, you must first detach the
formula in any of the ways described above.
Switching Stat List Editor Contexts
Stat List Editor Contexts
The stat list editor has four contexts.
• View-elements context
• View-names context
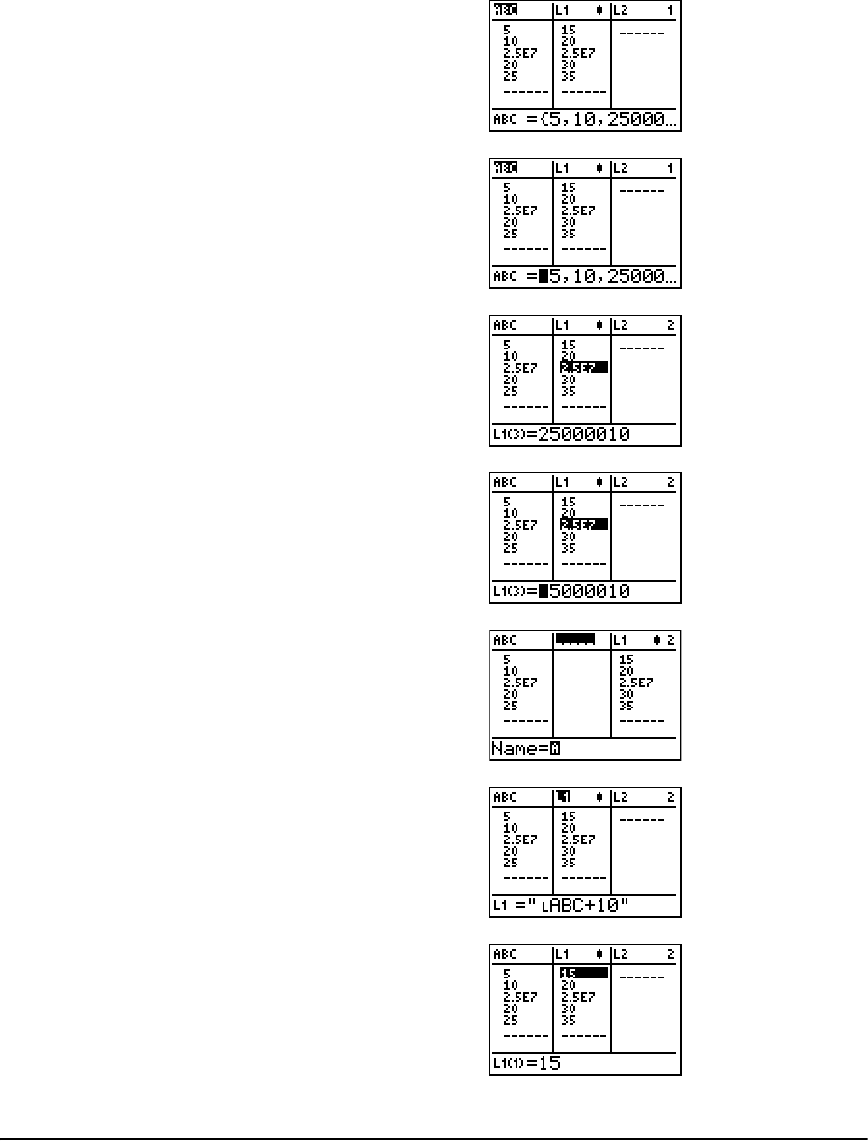
Chapter 12: Statistics 191
• Edit-elements context
• Enter-name context
The stat list editor is first displayed in view-elements context. To switch through the four contexts,
select 1:Edit from the STAT EDIT menu and follow these steps.
1. Press } to move the cursor onto a list name and
switch to view-names context. Press ~ and | to
view list names stored in other stat list editor
columns.
2. Press Í to switch to edit-elements context.
You may edit any element in a list. All elements of
the current list are displayed in braces ( { } ) in the
entry line. Press ~ and | to view more list
elements.
3. Press Í again to switch to view-elements
context. Press ~, |, †, and } to view other list
elements. The current element’s full value is
displayed in the entry line.
4. Press Í again to switch back to edit-elements
context. You may edit the current element in the
entry line.
5. Press } until the cursor is on a list name, then
press y 6 to switch to enter-name context.
6. Press ‘ to switch to view-names context.
7. Press † to switch back to view-elements context.
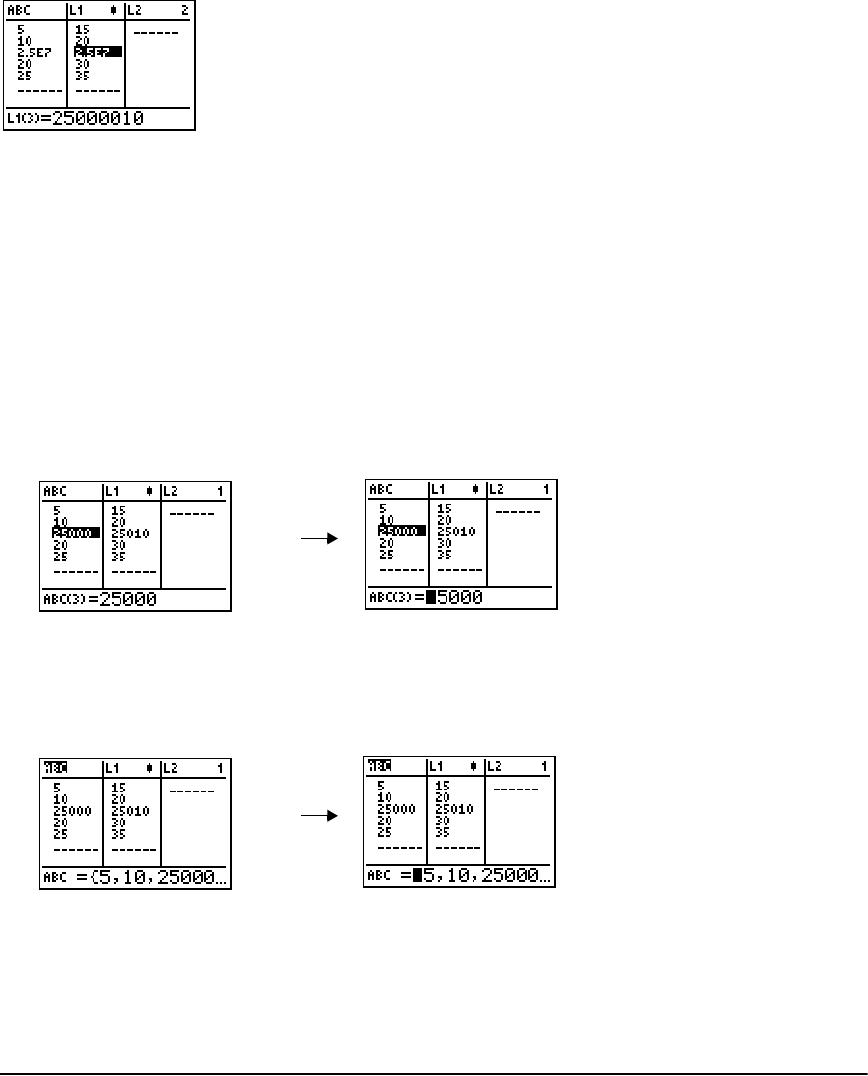
Chapter 12: Statistics 192
Stat List Editor Contexts
View-Elements Context
In view-elements context, the entry line displays the list name, the current element’s place in that
list, and the full value of the current element, up to 12 characters at a time. An ellipsis (...) indicates
that the element continues beyond 12 characters.
To page down the list six elements, press ƒ †. To page up six elements, press ƒ }. To
delete a list element, press {. Remaining elements shift up one row. To insert a new element,
press y 6. 0 is the default value for a new element.
Edit-Elements Context
In edit-elements context, the data displayed in the entry line depends on the previous context.
• When you switch to edit-elements context from view-elements context, the full value of the
current element is displayed. You can edit the value of this element, and then press † and }
to edit other list elements.
• When you switch to edit-elements context from view-names context, the full values of all
elements in the list are displayed. An ellipsis indicates that list elements continue beyond the
screen. You can press ~ and | to edit any element in the list.
Note: In edit-elements context, you can attach a formula to a list name only if you switched to it
from view-names context.
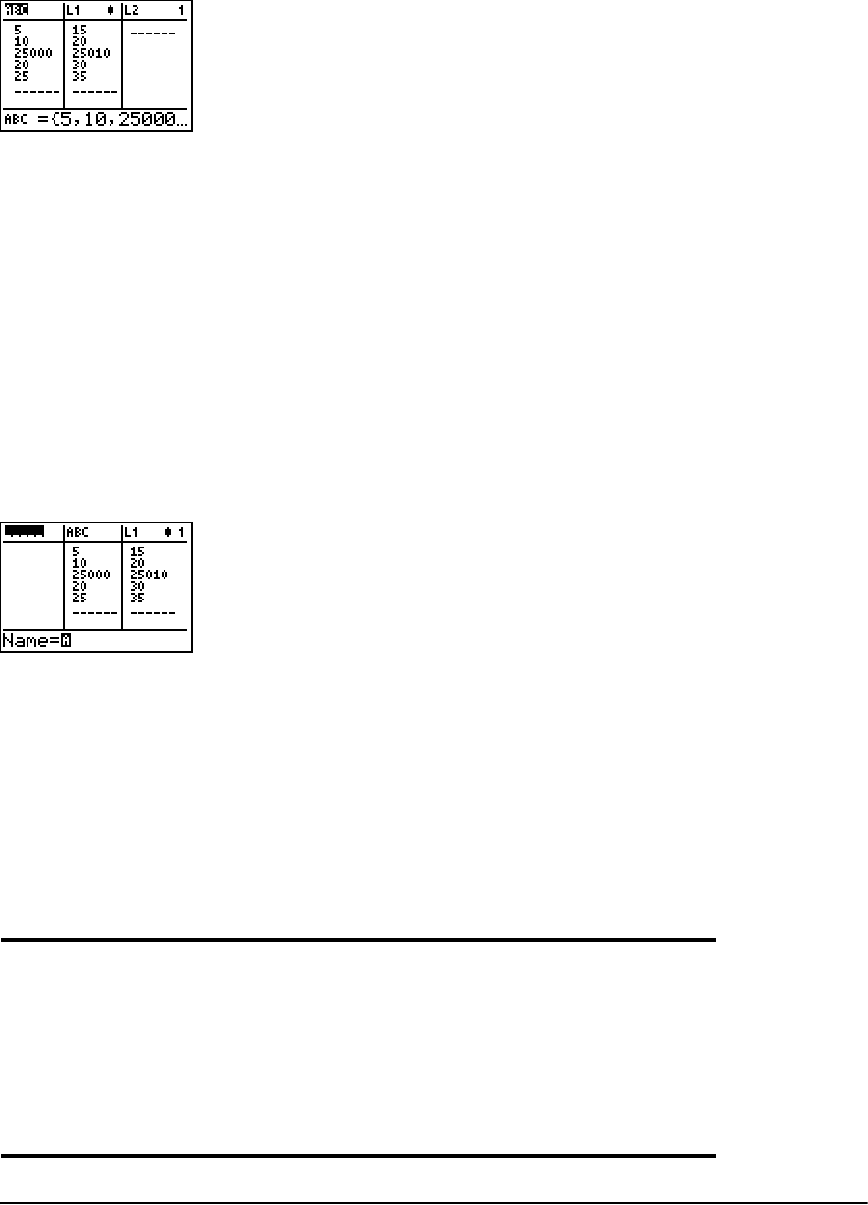
Chapter 12: Statistics 193
View-Names Context
In view-names context, the entry line displays the list name and the list elements.
To remove a list from the stat list editor, press {. Remaining lists shift to the left one column.
The list is not deleted from memory.
To insert a name in the current column, press y 6. Remaining columns shift to the right one
column.
Enter-Name Context
In enter-name context, the Name= prompt is displayed in the entry line, and alpha-lock is on.
At the Name= prompt, you can create a new list name, paste a list name from L1 to L6 from the
keyboard, or paste an existing list name from the LIST NAMES menu (Chapter 11). The Ù symbol is
not required at the Name= prompt.
To leave enter-name context without entering a list name, press ‘. The stat list editor
switches to view-names context.
STAT EDIT Menu
STAT EDIT Menu
To display the STAT EDIT menu, press ….
EDIT CALC TESTS
1: Edit... Displays the stat list editor.
2: SortA( Sorts a list in ascending order.
3: SortD( Sorts a list in descending order.
4: ClrList Deletes all elements of a list.
5: SetUpEditor Stores specified lists in the stat list editor.
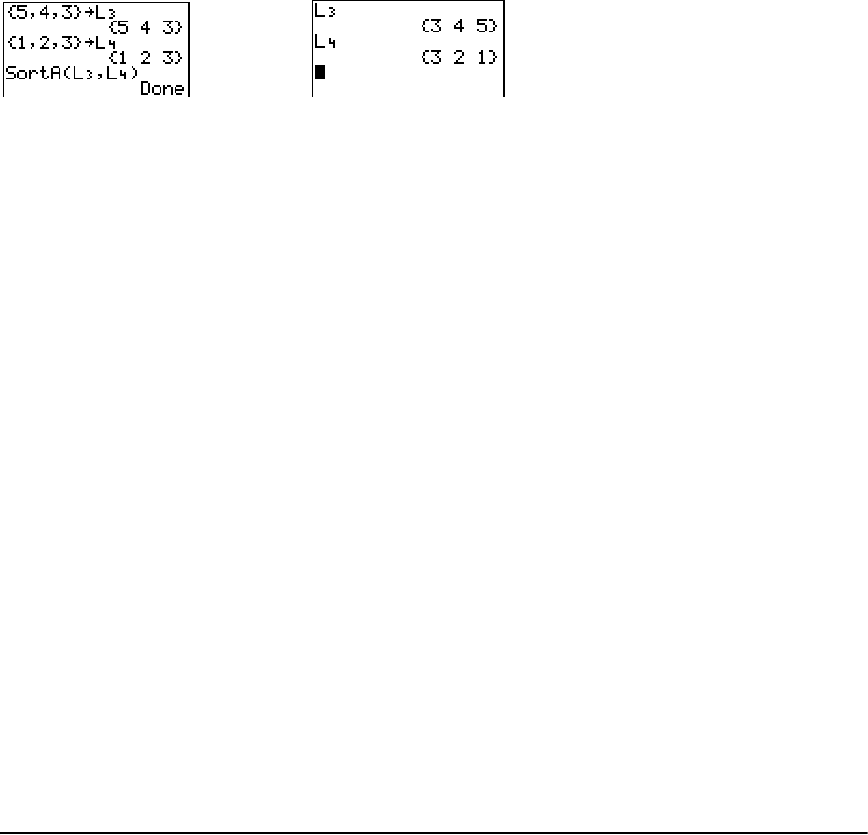
Chapter 12: Statistics 194
SortA(, SortD(
SortA( (sort ascending) sorts list elements from low to high values. SortD( (sort descending) sorts
list elements from high to low values. Complex lists are sorted based on magnitude (modulus).
SortA( and SortD( each can sort in either of two ways.
• With one listname, SortA( and SortD( sort the elements in listname and update the list in memory.
• With two or more lists, SortA( and SortD( sort keylistname, and then sort each dependlist by
placing its elements in the same order as the corresponding elements in keylistname. This lets
you sort two-variable data on X and keep the data pairs together. All lists must have the same
dimension.
The sorted lists are updated in memory.
SortA(listname)
SortD(listname)
SortA(keylistname,dependlist1[,dependlist2,...,dependlist n])
SortD(keylistname,dependlist1[,dependlist2,...,dependlist n])
Note: SortA( and SortD( are the same as SortA( and SortD( on the LIST OPS menu.
ClrList
ClrList clears (deletes) from memory the elements of one or more listnames. ClrList also detaches
any formula attached to a listname.
ClrList listname1,listname2,...,listname n
Note: To clear from memory all elements of all list names, use ClrAllLists (Chapter 18).
SetUpEditor
With SetUpEditor you can set up the stat list editor to display one or more listnames in the order that
you specify. You can specify zero to 20 listnames.
Additionally, if you want to use listnames which happen to be archived, the SetUp Editor will
automatically unarchive the listnames and place them in the stat list editor at the same time.
SetUpEditor [listname1,listname2,...,listname n]
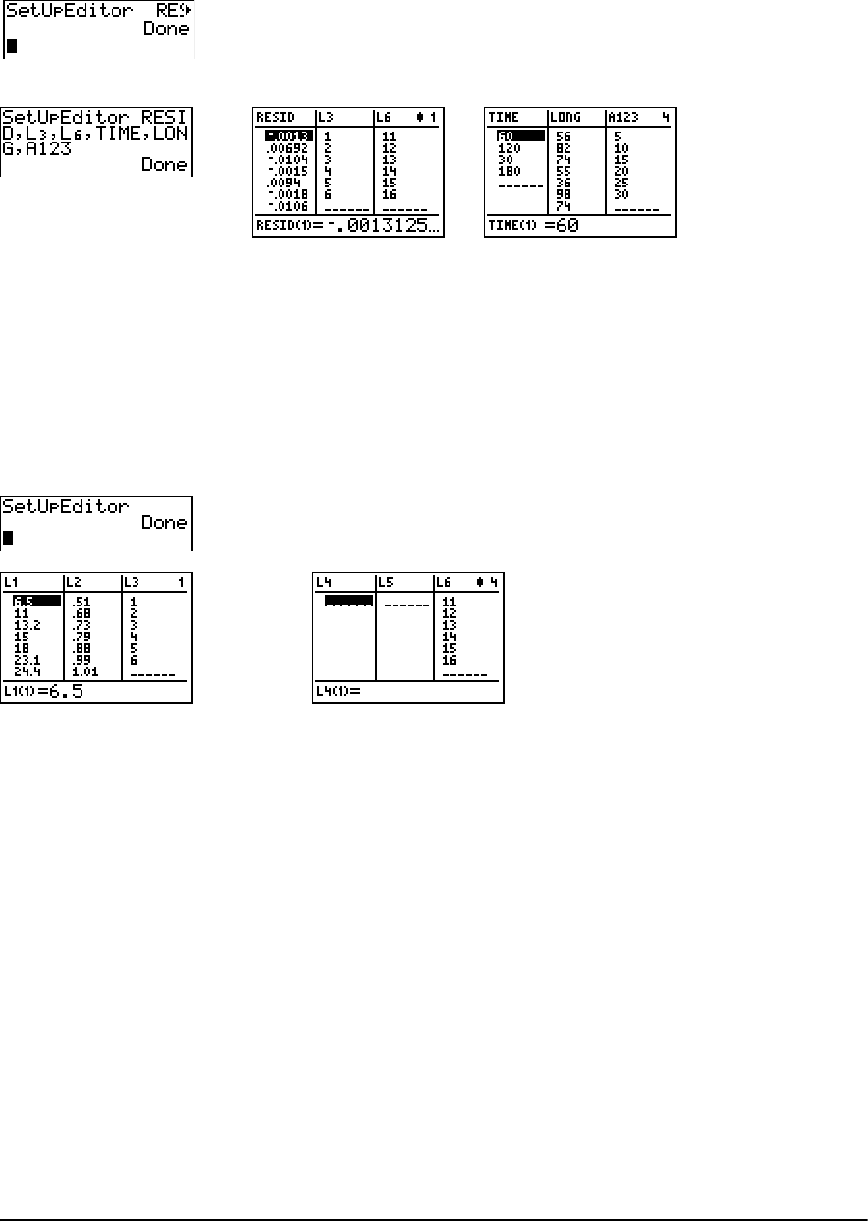
Chapter 12: Statistics 195
SetUpEditor removes all list names from the stat list editor and then stores listnames in the stat list
editor columns in the specified order, beginning in column 1.
If you enter a listname that is not stored in memory already, then listname is created and stored in
memory; it becomes an item on the LIST NAMES menu.
Restoring L1 through L6 to the Stat List Editor
SetUpEditor with no listnames removes all list names from the stat list editor and restores list names
L1 through L6 in the stat list editor columns 1 through 6.
Regression Model Features
Regression Model Features
STAT CALC menu items 3 through C are regression models. The automatic residual list and
automatic regression equation features apply to all regression models. Diagnostics display mode
applies to some regression models.
Automatic Residual List
When you execute a regression model, the automatic residual list feature computes and stores the
residuals to the list name RESID. RESID becomes an item on the LIST NAMES menu
(Chapter 11).
MathPrint™
Classic
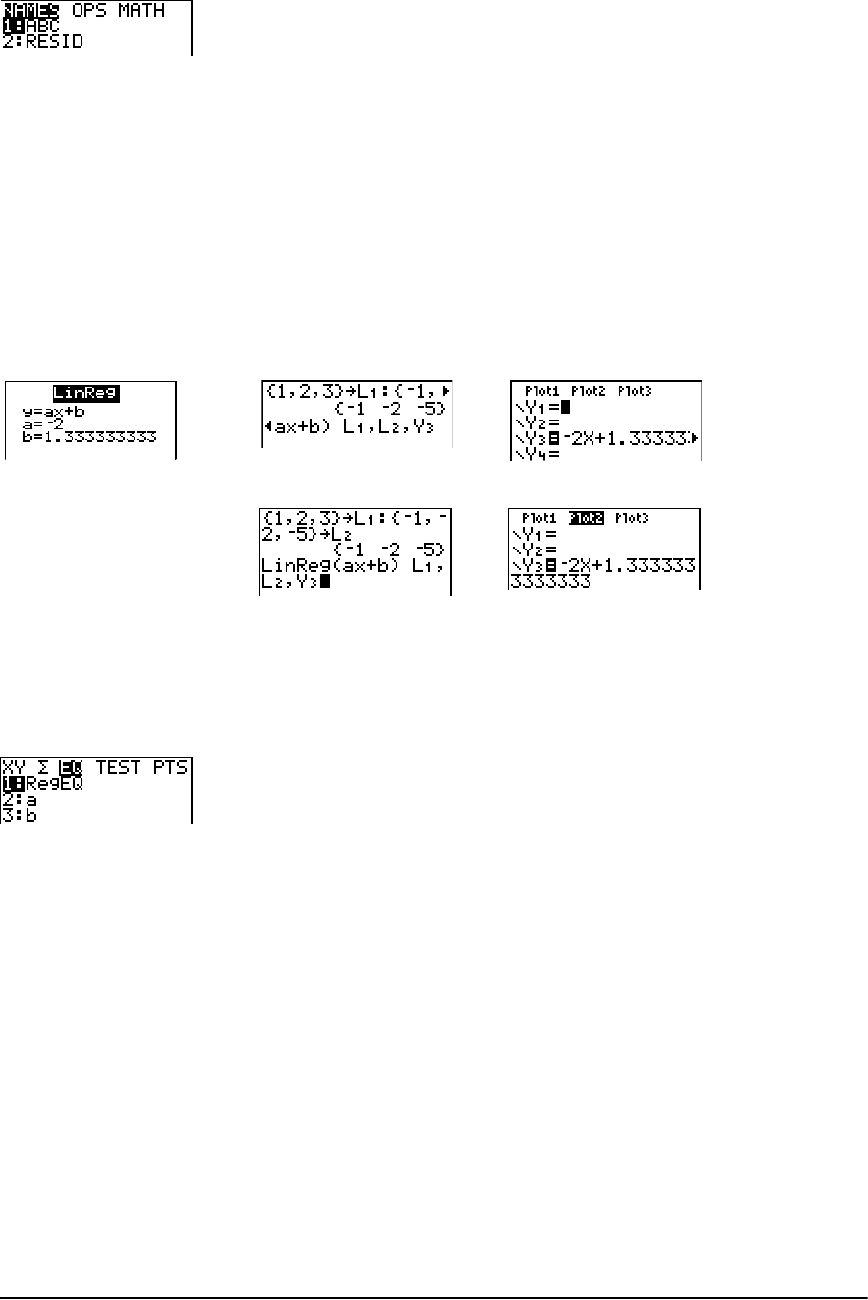
Chapter 12: Statistics 196
The TI-84 Plus uses the formula below to compute RESID list elements. The next section
describes the variable RegEQ.
RESID = Ylistname N RegEQ(Xlistname)
Automatic Regression Equation
Each regression model has an optional argument, regequ, for which you can specify a Y= variable
such as Y1. Upon execution, the regression equation is stored automatically to the specified Y=
variable and the Y= function is selected.
Regardless of whether you specify a Y= variable for regequ, the regression equation always is
stored to the TI-84 Plus variable RegEQ, which is item 1 on the VARS Statistics EQ secondary
menu.
Note: For the regression equation, you can use the fixed-decimal mode setting to control the
number of digits stored after the decimal point (Chapter 1). However, limiting the number of digits
to a small number could affect the accuracy of the fit.
Diagnostics Display Mode
When you execute some regression models, the TI-84 Plus computes and stores diagnostics
values for r (correlation coefficient) and r2 (coefficient of determination) or for R2 (coefficient of
determination). You can control whether these values are displayed by turning StatDiagnostics on
or off on the mode screen.
r and r2 are computed and stored for these regression models.
MathPrint™
MathPrint™
MathPrint™
Classic
Classic
LinReg(ax+b)
LinReg(a+bx)
LnReg
ExpReg
PwrReg
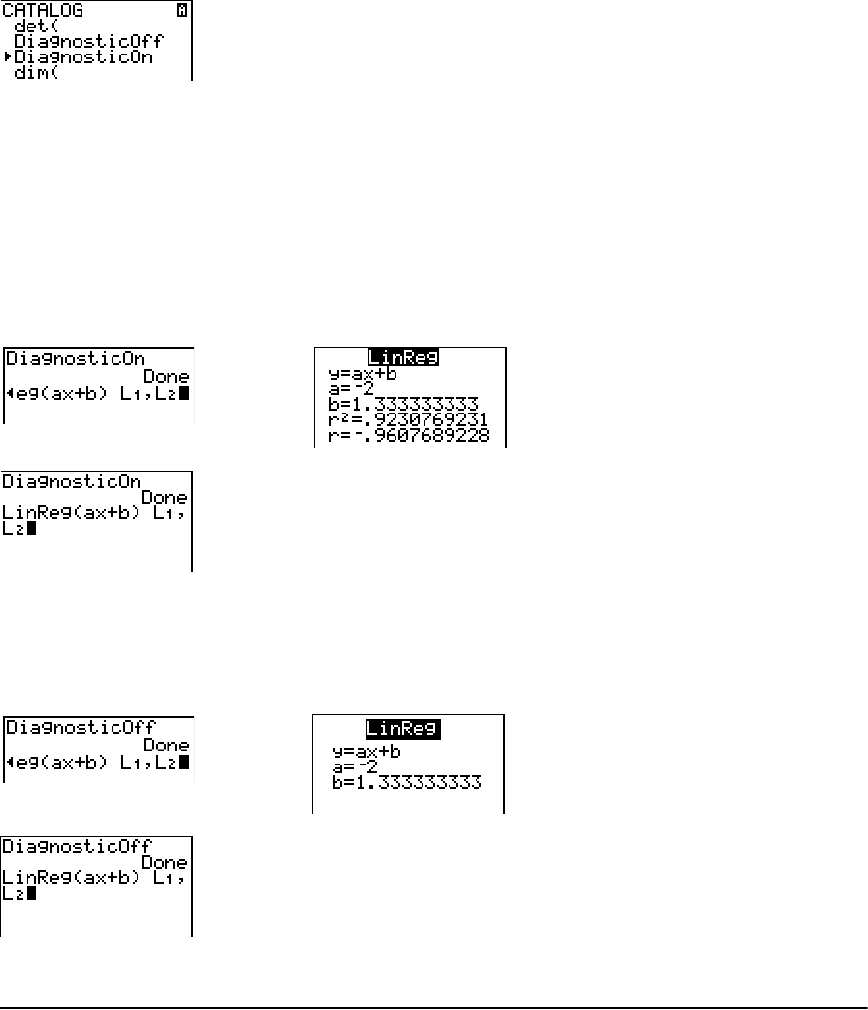
Chapter 12: Statistics 197
R2 is computed and stored for these regression models.
The r and r2 that are computed for LnReg, ExpReg, and PwrReg are based on the linearly
transformed data. For example, for ExpReg (y=ab^x), r and r2 are computed on ln y=ln a+x(ln b).
By default, these values are not displayed with the results of a regression model when you
execute it. However, you can set the diagnostics display mode by executing the DiagnosticOn or
DiagnosticOff instruction. Each instruction is in the CATALOG (Chapter 15).
• To turn diagnostics on or off from the mode screen, select On or Off for StatDiagnostics. The
default is Off.
•To set DiagnosticOn or DiagnosticOff from the home screen, press y N, and then
select the instruction for the mode you want. The instruction is pasted to the home screen.
Press Í to set the mode.
When DiagnosticOn is set, diagnostics are displayed with the results when you execute a
regression model.
When DiagnosticOff is set, diagnostics are not displayed with the results when you execute a
regression model.
QuadReg CubicReg QuartReg
MathPrint™
Classic
MathPrint™
Classic

Chapter 12: Statistics 198
STAT CALC Menu
STAT CALC Menu
To display the STAT CALC menu, press … ~.
For each STAT CALC menu item, if neither Xlistname nor Ylistname is specified, then the default list
names are L1 and L2. If you do not specify freqlist, then the default is 1 occurrence of each list
element.
STAT WIZARDS in STAT CALC
When STAT WIZARDS is set to ON in MODE, a wizard will open by default. The wizard will
prompt for required and optional arguments. In STAT CALC, select Calculate to paste the popu-
lated command to home screen and display the results to a temporary view.
Note: After a calculation, statistical variables are available in the VARS menu.
EDIT CALC TESTS
1: 1-Var Stats Calculates 1-variable statistics.
2: 2-Var Stats Calculates 2-variable statistics.
3: Med-Med Calculates a median-median line.
4: LinReg(ax+b) Fits a linear model to data.
5: QuadReg Fits a quadratic model to data.
6: CubicReg Fits a cubic model to data.
7: QuartReg Fits a quartic model to data.
8: LinReg(a+bx) Fits a linear model to data.
9: LnReg Fits a logarithmic model to data.
0: ExpReg Fits an exponential model to data.
A: PwrReg Fits a power model to data.
B: Logistic Fits a logistic model to data.
C: SinReg Fits a sinusoidal model to data.
D: Manual Linear Fit Fits a linear equation interactively to a scatter plot.
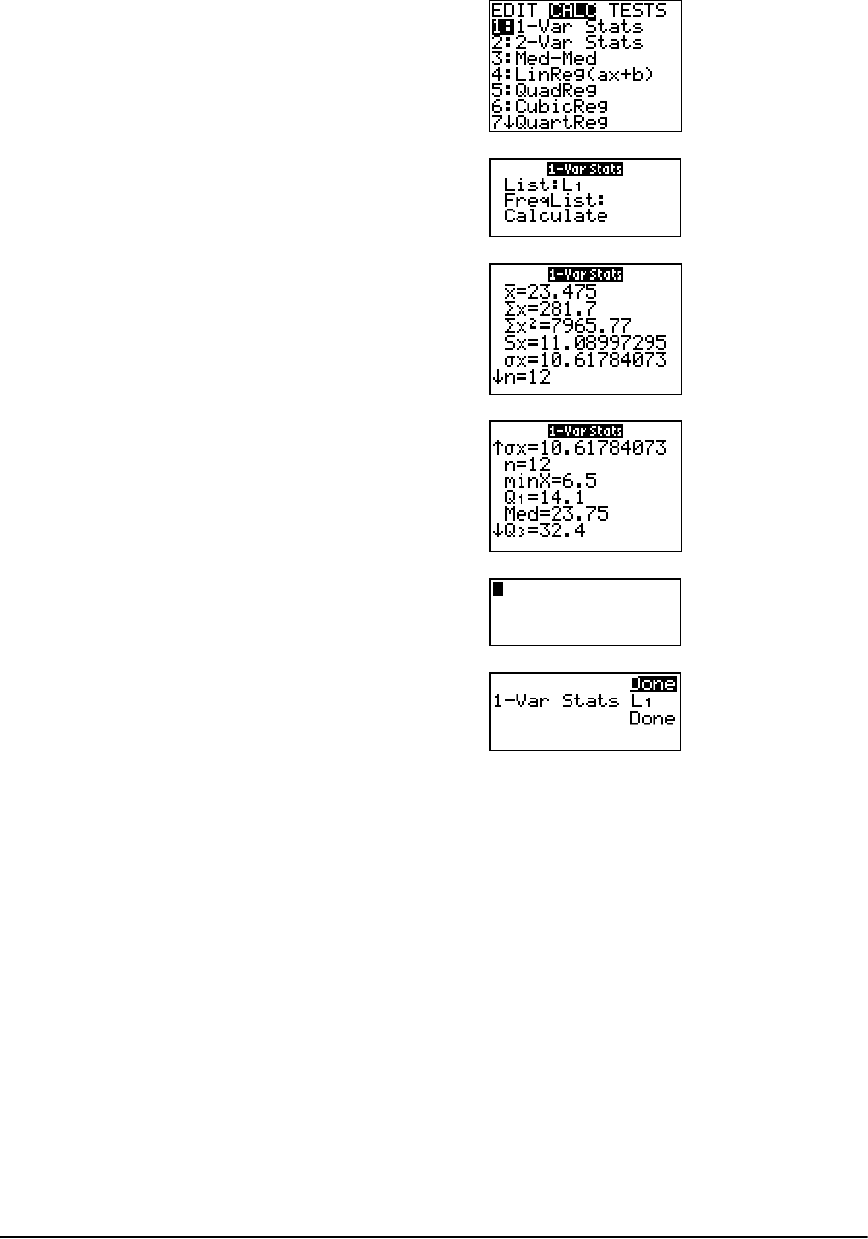
Chapter 12: Statistics 199
The following screens demonstrate the STAT WIZARDS flow for a STAT CALC menu command.
If the STAT WIZARD mode option if OFF, for each STAT CALC menu item, if neither Xlistname nor
Ylistname is specified, then the default list names are L1 and L2. If you do not specify freqlist, then
the default is 1 occurrence of each list element.
Frequency of Occurrence for Data Points
For most STAT CALC menu items, you can specify a list of data occurrences, or frequencies
(freqlist).
Each element in freqlist indicates how many times the corresponding data point or data pair occurs
in the data set you are analyzing.
For example, if L1={15,12,9,14} and ÙFREQ={1,4,1,3}, then the TI-84 Plus interprets the instruction
1-Var Stats L1, ÙFREQ to mean that 15 occurs once, 12 occurs four times, 9 occurs once, and 14
occurs three times.
1. Press press … ~ to select the STAT CALC
menu. Select 1 Í to select the 1 -Var Stats
menu.
Note: In this example, data has been entered in
L1.
2. The 1 -Var Stats wizard opens. Enter the values in the
wizard. Scroll down to Calculate and press Í.
Note: FreqList is an optional argument.
3. The STAT CALC results are displayed.
4. Press † to scroll down through the data.
Note: This is a temporary view. Press 5 to
view the statistic variables after clearing the
temporary result screen.
5. Press ‘ to clear the data from the screen.
6. Press } to view the populated command pasted.

Chapter 12: Statistics 200
Each element in freqlist must be ‚ 0, and at least one element must be > 0.
Noninteger freqlist elements are valid. This is useful when entering frequencies expressed as
percentages or parts that add up to 1. However, if freqlist contains noninteger frequencies, Sx and
Sy are undefined; values are not displayed for Sx and Sy in the statistical results.
1-Var Stats
1-Var Stats (one-variable statistics) analyzes data with one measured variable. Each element in
freqlist is the frequency of occurrence for each corresponding data point in Xlistname. freqlist
elements must be real numbers > 0.
1-Var Stats [Xlistname,freqlist]
2-Var Stats
2-Var Stats (two-variable statistics) analyzes paired data. Xlistname is the independent variable.
Ylistname is the dependent variable. Each element in freqlist is the frequency of occurrence for each
data pair (Xlistname,Ylistname).
2-Var Stats [Xlistname,Ylistname,freqlist]
Med-Med (ax+b)
Med-Med (median-median) fits the model equation y=ax+b to the data using the median-median
line (resistant line) technique, calculating the summary points x1, y1, x2, y2, x3, and y3. Med-Med
displays values for a (slope) and b (y-intercept).
Med-Med [Xlistname,Ylistname,freqlist,regequ]
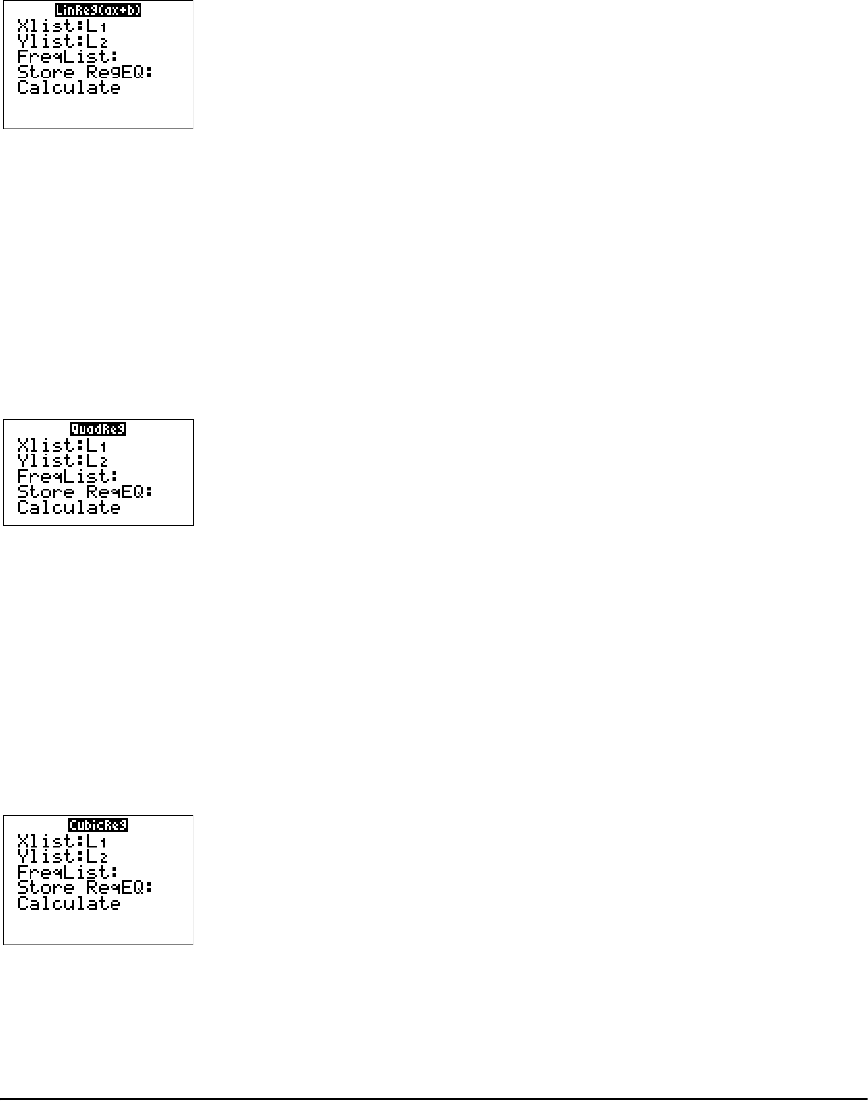
Chapter 12: Statistics 201
LinReg (ax+b)
LinReg(ax+b) (linear regression) fits the model equation y=ax+b to the data using a least-squares fit.
It displays values for a (slope) and b (y-intercept); when DiagnosticOn is set, it also displays values
for r2 and r.
LinReg(ax+b) [Xlistname,Ylistname,freqlist,regequ]
QuadReg (ax2+bx+c)
QuadReg (quadratic regression) fits the second-degree polynomial y=ax2+bx+c to the data. It
displays values for a, b, and c; when DiagnosticOn is set, it also displays a value for R2. For three
data points, the equation is a polynomial fit; for four or more, it is a polynomial regression. At least
three data points are required.
QuadReg [Xlistname,Ylistname,freqlist,regequ]
CubicReg—(ax3+bx2+cx+d)
CubicReg (cubic regression) fits the third-degree polynomial y=ax3+bx2+cx+d to the data. It
displays values for a, b, c, and d; when DiagnosticOn is set, it also displays a value for R2. For four
points, the equation is a polynomial fit; for five or more, it is a polynomial regression. At least four
points are required.
CubicReg [Xlistname,Ylistname,freqlist,regequ]

Chapter 12: Statistics 202
QuartReg—(ax4+bx3+cx2+ dx+e)
QuartReg (quartic regression) fits the fourth-degree polynomial y=ax4+bx3+cx2+dx+e to the data. It
displays values for a, b, c, d, and e; when DiagnosticOn is set, it also displays a value for R2. For
five points, the equation is a polynomial fit; for six or more, it is a polynomial regression. At least
five points are required.
QuartReg [Xlistname,Ylistname,freqlist,regequ]
LinReg—(a+bx)
LinReg(a+bx) (linear regression) fits the model equation y=a+bx to the data using a least-squares fit.
It displays values for a (y-intercept) and b (slope); when DiagnosticOn is set, it also displays values
for r2 and r.
LinReg(a+bx) [Xlistname,Ylistname,freqlist,regequ]
LnReg—(a+b ln(x))
LnReg (logarithmic regression) fits the model equation y=a+b ln(x) to the data using a least-
squares fit and transformed values ln(x) and y. It displays values for a and b; when DiagnosticOn is
set, it also displays values for r2 and r.
LnReg [Xlistname,Ylistname,freqlist,regequ]
ExpReg—(abx)
ExpReg (exponential regression) fits the model equation y=abx to the data using a least-squares fit
and transformed values x and ln(y). It displays values for a and b; when DiagnosticOn is set, it also
displays values for r2 and r.

Chapter 12: Statistics 203
ExpReg [Xlistname,Ylistname,freqlist,regequ]
PwrReg—(axb)
PwrReg (power regression) fits the model equation y=axb to the data using a least-squares fit and
transformed values ln(x) and ln(y). It displays values for a and b; when DiagnosticOn is set, it also
displays values for r2 and r.
PwrReg [Xlistname,Ylistname,freqlist,regequ]
Logistic—c/(1+a…e-bx)
Logistic fits the model equation y=c/(1+a…eLbx) to the data using an iterative least-squares fit. It
displays values for a, b, and c.
Logistic [Xlistname,Ylistname,freqlist,regequ]
SinReg—a sin(bx+c)+d
SinReg (sinusoidal regression) fits the model equation y=a sin(bx+c)+d to the data using an
iterative least-squares fit. It displays values for a, b, c, and d. At least four data points are required.
At least two data points per cycle are required in order to avoid aliased frequency estimates.
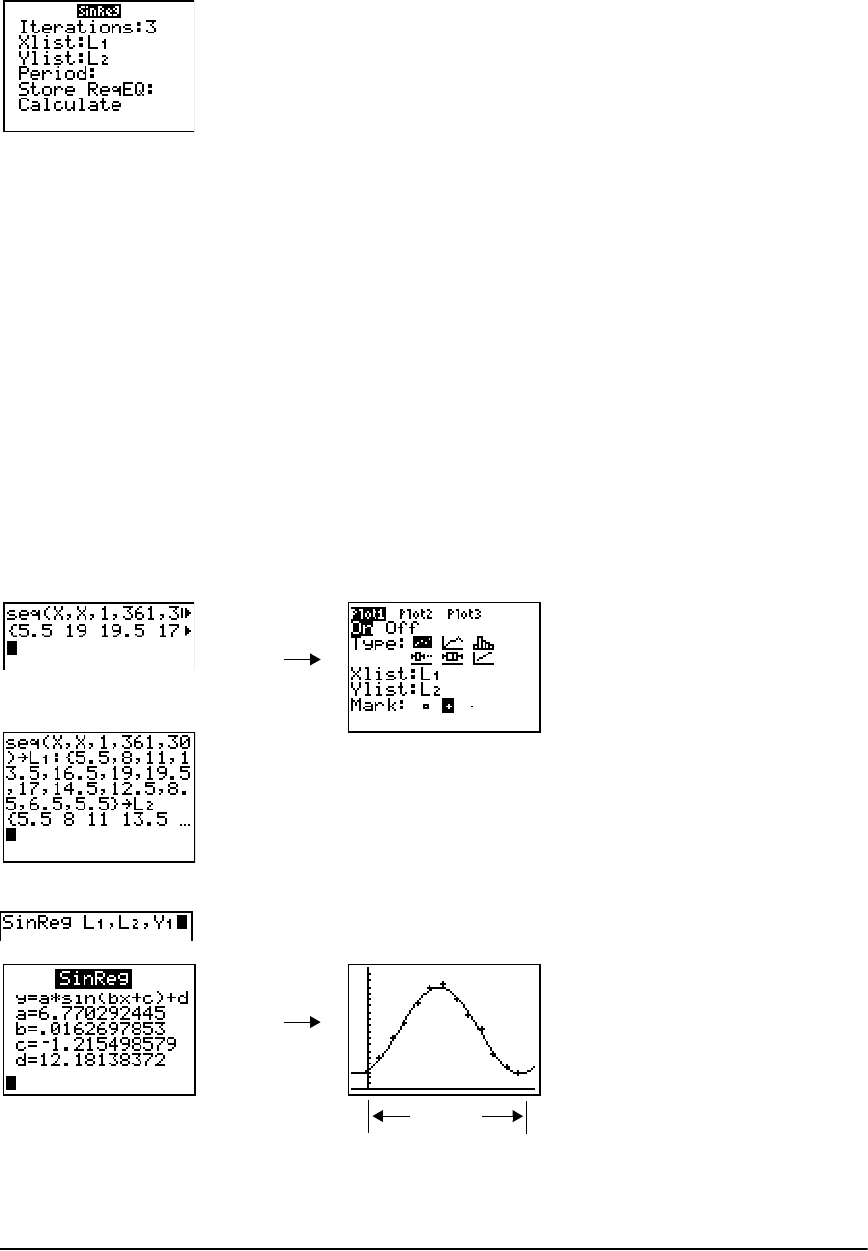
Chapter 12: Statistics 204
SinReg [iterations,Xlistname,Ylistname,period,regequ]
iterations is the maximum number of times the algorithm will iterate to find a solution. The value for
iterations can be an integer ‚ 1 and 16; if not specified, the default is 3. The algorithm may find a
solution before iterations is reached. Typically, larger values for iterations result in longer execution
times and better accuracy for SinReg, and vice versa.
A period guess is optional. If you do not specify period, the difference between time values in
Xlistname must be equal and the time values must be ordered in ascending sequential order. If you
specify period, the algorithm may find a solution more quickly, or it may find a solution when it
would not have found one if you had omitted a value for period. If you specify period, the differences
between time values in Xlistname can be unequal.
Note: The output of SinReg is always in radians, regardless of the Radian/Degree mode setting.
SinReg Example: Daylight Hours in Alaska for One Year
Compute the regression model for the number of hours of daylight in Alaska during one year.
With noisy data, you will achieve better convergence results when you specify an accurate
estimate for period. You can obtain a period guess in either of two ways.
MathPrint™
Classic
1 period
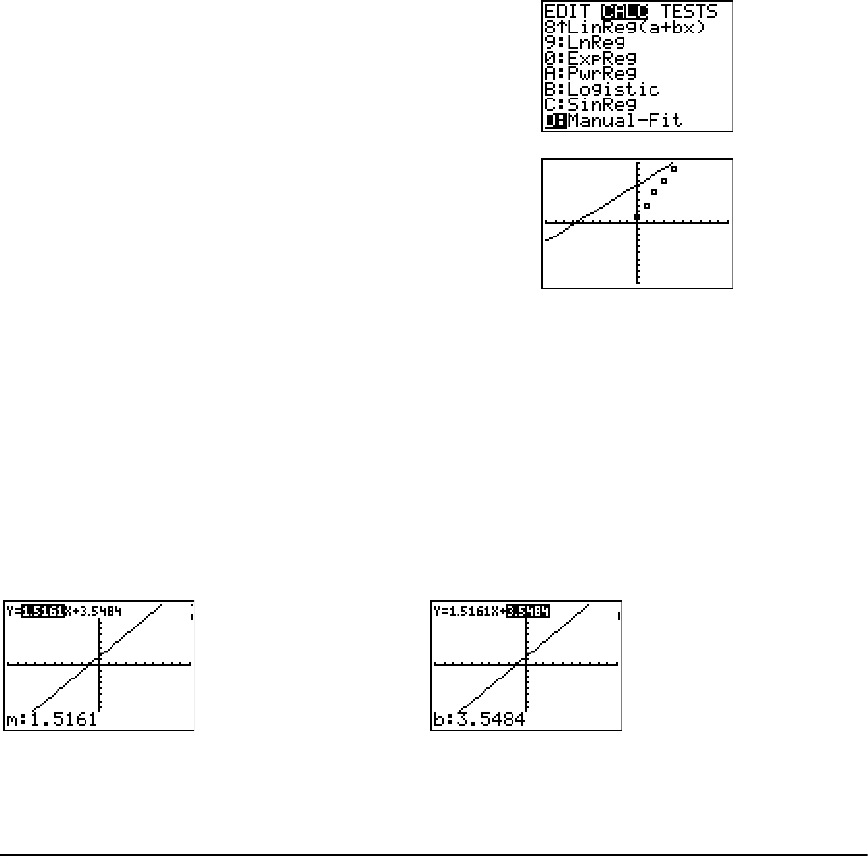
Chapter 12: Statistics 205
• Plot the data and trace to determine the x-distance between the beginning and end of one
complete period, or cycle. The illustration above and to the right graphically depicts a complete
period, or cycle.
• Plot the data and trace to determine the x-distance between the beginning and end of N
complete periods, or cycles. Then divide the total distance by N.
After your first attempt to use SinReg and the default value for iterations to fit the data, you may find
the fit to be approximately correct, but not optimal. For an optimal fit, execute
SinReg 16,Xlistname,Ylistname,2p/b where b is the value obtained from the previous SinReg execution.
Manual Linear Fit
Manual Linear Fit allows you to visually fit a linear function to a scatter plot. Manual Linear Fit is an
option in the … / menu.
After entering List data and viewing the StatPlot, select the Manual-Fit function.
The linear function is displayed. The Manual-Fit Line equation displays in the form of Y=mX+b.
The current value of the first parameter (m) is highlighted in the symbolic expression.
Modify parameter values
Press the cursor navigation keys ( | ~ ) to move from the first parameter (m) or (b) the second
parameter. You can press Í and type a new parameter value. Press Í to display the new
parameter value. When you edit the value of the selected parameter, the edit can include insert,
delete, type over, or mathematical expression.
The screen dynamically displays the revised parameter value. Press Í to complete the
modification of the selected parameter, save the value, and refresh the displayed graph. The
1. Press … to display the Stat menu. Press ~ to select
CALC. Press † several times to scroll down to select
D:Manual-Fit. Press Í. This displays a free-floating
cursor at the center of the display screen.
2. Press the cursor navigation keys (} † | ~ ) to move
the cursor to the desired location. Press Í to select
the first point.
3. Press the cursor navigation keys (} † | ~ ) to move
the cursor to the second location. Press Í. This
displays a line containing the two points selected.

Chapter 12: Statistics 206
system displays the revised parameter value in the symbolic expression Y=mX+B, and refreshes
the graph with the updated Manual-Fit Line.
Select y 5 to finish the Manual Fit function. The calculator stores the current mX+b
expression into Y1 and makes that function active for graphing. You can also select Manual-Fit
while on the Home screen. You can then enter a different Y-Var such as Y4 and then press Í.
This takes you to the Graph screen and then pastes the Manual-Fit equation in the specified Y-Var.
In this example, Y4.
Statistical Variables
The statistical variables are calculated and stored as indicated below. To access these variables
for use in expressions, press , and select 5:Statistics. Then select the VARS menu shown in
the column below under VARS menu. If you edit a list or change the type of analysis, all statistical
variables are cleared.
Variables
1-Var
Stats
2-Var
Stats Other
VARS
menu
mean of x values vv XY
sum of x values GxGxG
sum of x2 values Gx2Gx2G
sample standard deviation of x Sx Sx XY
population standard deviation of x sxsxXY
number of data points n n XY
mean of y values wXY
sum of y values GyG
sum of y2 values Gy2G
sample standard deviation of y Sy XY
population standard deviation of y syXY
sum of x … y Gxy G
minimum of x values minX minX XY
maximum of x values maxX maxX XY
minimum of y values minY XY
maximum of y values maxY XY
1st quartile Q1 PTS
median Med PTS
3rd quartile Q3 PTS
regression/fit coefficients a, b EQ
polynomial, Logistic, and SinReg
coefficients
a, b, c,
d, e
EQ

Chapter 12: Statistics 207
Q1 and Q3
The first quartile (Q1) is the median of points between minX and Med (median). The third quartile
(Q3) is the median of points between Med and maxX.
Statistical Analysis in a Program
Entering Stat Data
You can enter statistical data, calculate statistical results, and fit models to data from a program.
You can enter statistical data into lists directly within the program (Chapter 11).
Statistical Calculations
To perform a statistical calculation from a program, follow these steps.
1. On a blank line in the program editor, select the type of calculation from the STAT CALC menu.
2. Enter the names of the lists to use in the calculation. Separate the list names with a comma.
3. Enter a comma and then the name of a Y= variable, if you want to store the regression equation
to a Y= variable.
correlation coefficient r EQ
coefficient of determination r2, R2EQ
regression equation RegEQ EQ
summary points (Med-Med only) x1, y1, x2,
y2, x3, y3
PTS
Variables
1-Var
Stats
2-Var
Stats Other
VARS
menu
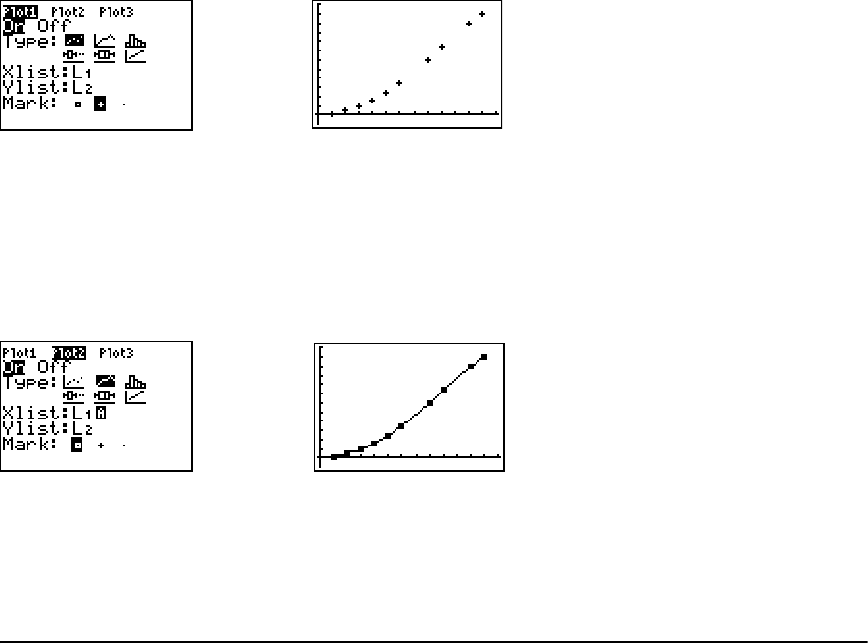
Chapter 12: Statistics 208
Statistical Plotting
Steps for Plotting Statistical Data in Lists
You can plot statistical data that is stored in lists. The six types of plots available are scatter plot,
xyLine, histogram, modified box plot, regular box plot, and normal probability plot. You can define
up to three plots.
To plot statistical data in lists, follow these steps.
1. Store the stat data in one or more lists.
2. Select or deselect Y= functions as appropriate.
3. Define the stat plot.
4. Turn on the plots you want to display.
5. Define the viewing window.
6. Display and explore the graph.
Scatter
Scatter (")plots plot the data points from Xlist and Ylist as coordinate pairs, showing each point as
a box ( › ), cross ( + ), or dot ( ¦ ). Xlist and Ylist must be the same length. You can use the same
list for Xlist and Ylist.
xyLine
xyLine (Ó)is a scatter plot in which the data points are plotted and connected in order of
appearance in Xlist and Ylist. You may want to use SortA( or SortD( to sort the lists before you plot
them.
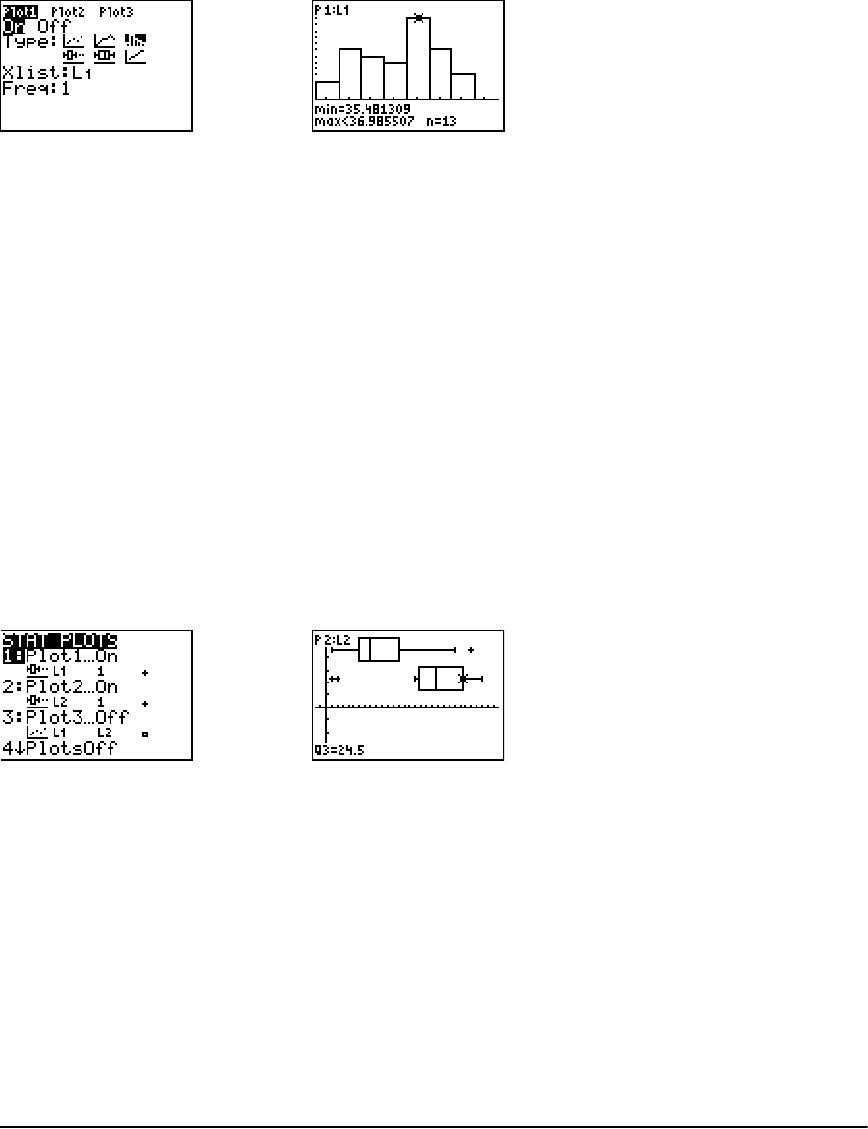
Chapter 12: Statistics 209
Histogram
Histogram (Ò) plots one-variable data. The Xscl window variable value determines the width of
each bar, beginning at Xmin. ZoomStat adjusts Xmin, Xmax, Ymin, and Ymax to include all values,
and also adjusts Xscl. The inequality (Xmax N Xmin) à Xscl 47 must be true. A value that occurs on
the edge of a bar is counted in the bar to the right.
ModBoxplot
ModBoxplot (Õ) (modified box plot) plots one-variable data, like the regular box plot, except
points that are 1.5 … Interquartile Range beyond the quartiles. (The Interquartile Range is defined
as the difference between the third quartile Q3 and the first quartile Q1.) These points are plotted
individually beyond the whisker, using the Mark (› or + or ¦) you select. You can trace these points,
which are called outliers.
The prompt for outlier points is x=, except when the outlier is the maximum point (maxX) or the
minimum point (minX). When outliers exist, the end of each whisker will display x=. When no
outliers exist, minX and maxX are the prompts for the end of each whisker. Q1, Med (median), and
Q3 define the box.
Box plots are plotted with respect to Xmin and Xmax, but ignore Ymin and Ymax. When two box
plots are plotted, the first one plots at the top of the screen and the second plots in the middle.
When three are plotted, the first one plots at the top, the second in the middle, and the third at the
bottom.
Boxplot
Boxplot (Ö)(regular box plot) plots one-variable data. The whiskers on the plot extend from the
minimum data point in the set (minX) to the first quartile (Q1) and from the third quartile (Q3) to the
maximum point (maxX). The box is defined by Q1, Med (median), and Q3.
Box plots are plotted with respect to Xmin and Xmax, but ignore Ymin and Ymax. When two box
plots are plotted, the first one plots at the top of the screen and the second plots in the middle.

Chapter 12: Statistics 210
When three are plotted, the first one plots at the top, the second in the middle, and the third at the
bottom.
NormProbPlot
NormProbPlot (Ô) (normal probability plot) plots each observation X in Data List versus the
corresponding quantile z of the standard normal distribution. If the plotted points lie close to a
straight line, then the plot indicates that the data are normal.
Enter a valid list name in the Data List field. Select X or Y for the Data Axis setting.
• If you select X, the TI-84 Plus plots the data on the x-axis and the z-values on the y-axis.
• If you select Y, the TI-84 Plus plots the data on the y-axis and the z-values on the x-axis.
Defining the Plots
To define a plot, follow these steps.
1. Press y ,. The STAT PLOTS menu is displayed with the current plot definitions.
2. Select the plot you want to use. The stat plot editor is displayed for the plot you selected.

Chapter 12: Statistics 211
3. Press Í to select On if you want to plot the statistical data immediately. The definition is
stored whether you select On or Off.
4. Select the type of plot. Each type prompts for the options checked in this table.
Plot Type XList YList Mark Freq
Data
List
Data
Axis
" Scatter _ _ _ œœœ
Ó xyLine _ _ _ œœœ
Ò Histogram _ œ œ _ œ œ
Õ ModBoxplot _ œ_ _ œ œ
Ö Boxplot _ œ œ _ œ œ
Ô NormProbPlot œ œ _ œ_ _
5. Enter list names or select options for the plot type.
•Xlist (list name containing independent data)
•Ylist (list name containing dependent data)
•Mark (› or + or ¦)
•Freq (frequency list for Xlist elements; default is 1)
•Data List (list name for NormProbPlot)
•Data Axis (axis on which to plot Data List)
Displaying Other Stat Plot Editors
Each stat plot has a unique stat plot editor. The name of the current stat plot (Plot1, Plot2, or Plot3)
is highlighted in the top line of the stat plot editor. To display the stat plot editor for a different plot,
press } and ~ to move the cursor onto the name in the top line, and then press Í. The stat
plot editor for the selected plot is displayed, and the selected name remains highlighted.

Chapter 12: Statistics 212
Turning On and Turning Off Stat Plots
PlotsOn and PlotsOff allow you to turn on or turn off stat plots from the home screen or a program.
With no plot number, PlotsOn turns on all plots and PlotsOff turns off all plots. With one or more
plot numbers (1, 2, and 3), PlotsOn turns on specified plots, and PlotsOff turns off specified plots.
PlotsOff [1,2,3]
PlotsOn [1,2,3]
Note: You also can turn on and turn off stat plots in the top line of the Y= editor (Chapter 3).
Defining the Viewing Window
Stat plots are displayed on the current graph. To define the viewing window, press p and
enter values for the window variables. ZoomStat redefines the viewing window to display all
statistical data points.
Tracing a Stat Plot
When you trace a scatter plot or xyLine, tracing begins at the first element in the lists.
When you trace a histogram, the cursor moves from the top center of one column to the top center
of the next, starting at the first column.
When you trace a box plot, tracing begins at Med (the median). Press | to trace to Q1 and minX.
Press ~ to trace to Q3 and maxX.
When you press } or † to move to another plot or to another Y= function, tracing moves to the
current or beginning point on that plot (not the nearest pixel).
The ExprOn/ExprOff format setting applies to stat plots (Chapter 3). When ExprOn is selected, the
plot number and plotted data lists are displayed in the top-left corner.
Statistical Plotting in a Program
Defining a Stat Plot in a Program
To display a stat plot from a program, define the plot, and then display the graph.
To define a stat plot from a program, begin on a blank line in the program editor and enter data into
one or more lists; then, follow these steps.

Chapter 12: Statistics 213
1. Press y , to display the STAT PLOTS menu.
2. Select the plot to define, which pastes Plot1(, Plot2(, or Plot3( to the cursor location.
3. Press y , ~ to display the STAT TYPE menu.
4. Select the type of plot, which pastes the name of the plot type to the cursor location.
5. Press ¢. Enter the list names, separated by commas.
6. Press ¢ y , | to display the STAT PLOT MARK menu. (This step is not necessary if
you selected 3:Histogram or 5:Boxplot in step 4.)
Select the type of mark (› or + or ¦) for each data point. The selected mark symbol is pasted to
the cursor location.
7. Press ¤ Í to complete the command line.

Chapter 12: Statistics 214
Displaying a Stat Plot from a Program
To display a plot from a program, use the DispGraph instruction (Chapter 16) or any of the ZOOM
instructions (Chapter 3).
Chapter 13: Inferential Statistics and Distributions 215
Chapter 13:
Inferential Statistics and Distributions
Getting Started: Mean Height of a Population
Getting Started is a fast-paced introduction. Read the chapter for details.
Suppose you want to estimate the mean height of a population of women given the random
sample below. Because heights among a biological population tend to be normally distributed, a t
distribution confidence interval can be used when estimating the mean. The 10 height values
below are the first 10 of 90 values, randomly generated from a normally distributed population with
an assumed mean of 165.1 centimeters and a standard deviation of 6.35 centimeters
(randNorm(165.1,6.35,90) with a seed of 789).
Height (in centimeters) of Each of 10 Women
169.43 168.33 159.55 169.97 159.79 181.42 171.17 162.04 167.15 159.53
1. Press … Í to display the stat list editor.
Press } to move the cursor onto L1, and then
press y 6 to insert a new list. The Name=
prompt is displayed on the bottom line. The Ø
cursor indicates that alpha-lock is on. The existing
list name columns shift to the right.
Note: Your stat editor may not look like the one
pictured here, depending on the lists you have
already stored.
2. Enter [H] [G] [H] [T] at the Name= prompt, and then
press Í to create the list to store the women’s
height data.
Press † to move the cursor into the first row of the
list. HGHT(1)= is displayed on the bottom line.
Press Í.
3. Press 169 Ë 43 to enter the first height value. As
you enter it, it is displayed on the bottom line.
Press Í. The value is displayed in the first
row, and the rectangular cursor moves to the next
row.
Enter the other nine height values the same way.
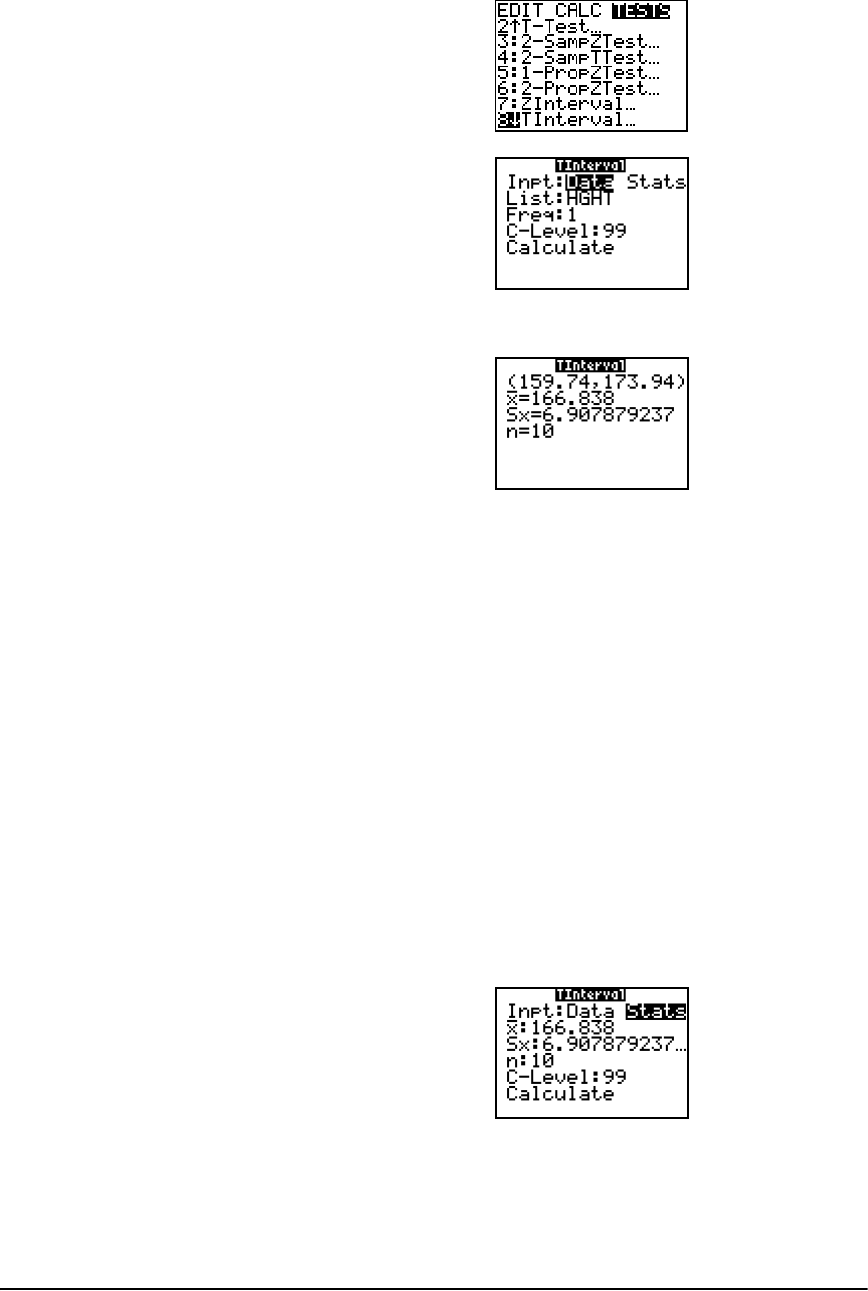
Chapter 13: Inferential Statistics and Distributions 216
Interpreting the results
The first line, (159.74,173.94), shows that the 99 percent confidence interval for the population
mean is between about 159.74 centimeters and 173.94 centimeters. This is about a 14.2
centimeters spread.
The .99 confidence level indicates that in a very large number of samples, we expect 99 percent of
the intervals calculated to contain the population mean. The actual mean of the population
sampled is 165.1 centimeters, which is in the calculated interval.
The second line gives the mean height of the sample v used to compute this interval. The third line
gives the sample standard deviation Sx. The bottom line gives the sample size n.
To obtain a more precise bound on the population mean m of women’s heights, increase the
sample size to 90. Use a sample mean v of 163.8 and sample standard deviation Sx of 7.1
calculated from the larger random sample. This time, use the Stats (summary statistics) input
option.
4. Press … | to display the STAT TESTS menu,
and then press † until 8:TInterval is highlighted.
5. Press Í to select 8:TInterval. The inferential
stat editor for TInterval is displayed. If Data is not
selected for Inpt:, press | Í to select Data.
Press † y 9 and press † until HGHT is
highlighted and then press Í.
Press † † Ë 99 to enter a 99 percent confidence
level at the C-Level: prompt.
6. Press † to move the cursor onto Calculate, and
then press Í. The confidence interval is
calculated, and the TInterval results are displayed
on the home screen.
1. Press … | 8 to display the inferential stat
editor for TInterval.
Press ~ Í to select Inpt:Stats. The editor
changes so that you can enter summary statistics
as input.

Chapter 13: Inferential Statistics and Distributions 217
If the height distribution among a population of women is normally distributed with a mean m of
165.1 centimeters and a standard deviation s of 6.35 centimeters, what height is exceeded by only
5 percent of the women (the 95th percentile)?
The result is displayed on the home screen; it shows that five percent of the women are taller than
175.5 centimeters.
Now graph and shade the top 5 percent of the population.
2. Press † 163 Ë 8 Í to store 163.8 to v.
Press 7 Ë 1 Í to store 7.1 to Sx.
Press 90 Í to store 90 to n.
3. Press † to move the cursor onto Calculate, and
then press Í to calculate the new 99 percent
confidence interval. The results are displayed on
the home screen.
4. Press ‘ to clear the home screen.
Press y = to display the DISTR
(distributions) menu.
5. Press 3 to open the invNorm( wizard. Enter the
information as follows:
Press Ë 95 †165 Ë 1 † 6 Ë 35 † (95 is the
area, 165.1 is m, and 6.35 is s).
6. Press Í to paste the function and Í again
to calculate the result.
7. Press p and set the window variables to
these values.
Xmin=145 Ymin=L.02 Xres=1
Xmax=185 Ymax=.08
Xscl=5 Yscl=0
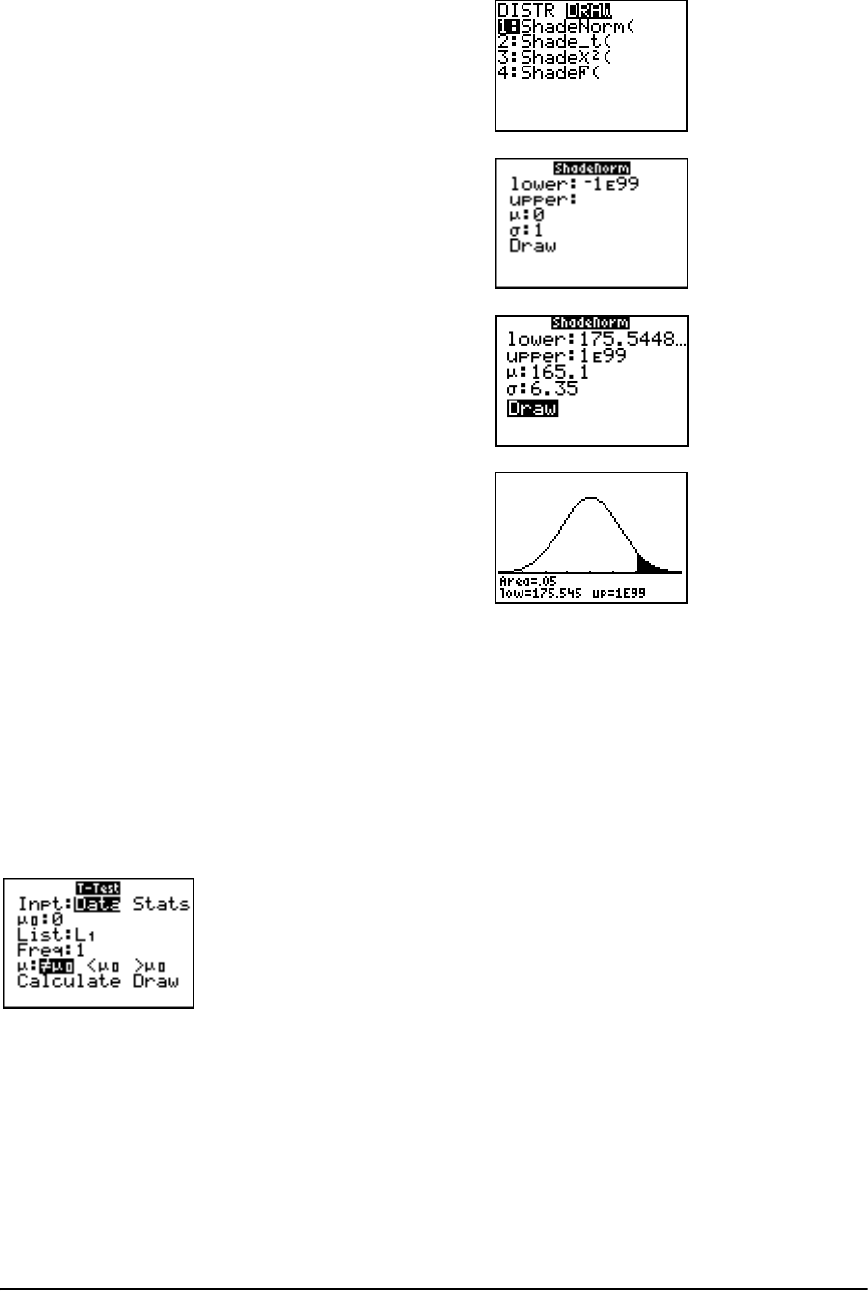
Chapter 13: Inferential Statistics and Distributions 218
Inferential Stat Editors
Displaying the Inferential Stat Editors
When you select a hypothesis test or confidence interval instruction from the home screen, the
appropriate inferential statistics editor is displayed. The editors vary according to each test or
interval’s input requirements. Below is the inferential stat editor for T-Test.
Note: When you select the ANOVA( instruction, it is pasted to the home screen. ANOVA( does not
have an editor screen.
Using an Inferential Stat Editor
To use an inferential stat editor, follow these steps.
8. Press y = ~ to display the DISTR DRAW
menu.
9. Press Í to open a wizard for the input of the
ShadeNorm( parameters.
10. Enter 175 Ë 5448205 for the lower bound and
press †. Enter 1 y D 99 for the upper bound
and press †. Enter the mean m of 165 Ë 1 for the
normal curve and press †. Enter a standard
deviation s of 6 Ë 35.
11. Press † to select Draw and then press Í to
plot and shade the normal curve.
Area is the area above the 95th percentile. low is
the lower bound. up is the upper bound.

Chapter 13: Inferential Statistics and Distributions 219
1. Select a hypothesis test or confidence interval from the STAT TESTS menu. The appropriate
editor is displayed.
2. Select Data or Stats input, if the selection is available. The appropriate editor is displayed.
3. Enter real numbers, list names, or expressions for each argument in the editor.
4. Select the alternative hypothesis (Ā, <, or >) against which to test, if the selection is available.
5. Select No or Yes for the Pooled option, if the selection is available.
6. Select Calculate or Draw (when Draw is available) to execute the instruction.
• When you select Calculate, the results are displayed on the home screen.
• When you select Draw, the results are displayed in a graph.
Select Data or
Stats input
Select an
alternative
hypothesis
Enter values
for arguments Select
Calculate or
Draw output
This chapter describes the selections in the above steps for each hypothesis test and confidence
interval instruction.
Selecting Data or Stats
Most inferential stat editors prompt you to select one of two types of input. (1-PropZInt and
2-PropZTest, 1-PropZInt and 2-PropZInt, c2-Test, c2GOF-Test, LinRegTInt, and LinRegTTest do not.)
•Select
Data to enter the data lists as input.
•Select
Stats to enter summary statistics, such as v, Sx, and n, as input.
To select Data or Stats, move the cursor to either Data or Stats, and then press Í.
Entering the Values for Arguments
Inferential stat editors require a value for every argument. If you do not know what a particular
argument symbol represents, see the Inferential Statistics Input Descriptions tables.
When you enter values in any inferential stat editor, the TI-84 Plus stores them in memory so that
you can run many tests or intervals without having to reenter every value.
Selecting an Alternative Hypothesis (ă < >)
Most of the inferential stat editors for the hypothesis tests prompt you to select one of three
alternative hypotheses.
• The first is a ƒ alternative hypothesis, such as mƒm0 for the Z-Test.
• The second is a < alternative hypothesis, such as m1<m2 for the 2-SampTTest.

Chapter 13: Inferential Statistics and Distributions 220
• The third is a > alternative hypothesis, such as p1>p2 for the 2-PropZTest.
To select an alternative hypothesis, move the cursor to the appropriate alternative, and then press
Í.
Selecting the Pooled Option
Pooled (2-SampTTest and 2-SampTInt only) specifies whether the variances are to be pooled for
the calculation.
•Select
No if you do not want the variances pooled. Population variances can be unequal.
•Select
Yes if you want the variances pooled. Population variances are assumed to be equal.
To select the Pooled option, move the cursor to Yes, and then press Í.
Selecting Calculate or Draw for a Hypothesis Test
After you have entered all arguments in an inferential stat editor for a hypothesis test, you must
select whether you want to see the calculated results on the home screen (Calculate) or on the
graph screen (Draw).
•Calculate calculates the test results and displays the outputs on the home screen.
•Draw draws a graph of the test results and displays the test statistic and p-value with the
graph. The window variables are adjusted automatically to fit the graph.
To select Calculate or Draw, move the cursor to either Calculate or Draw, and then press Í.
The instruction is immediately executed.
Selecting Calculate for a Confidence Interval
After you have entered all arguments in an inferential stat editor for a confidence interval, select
Calculate to display the results. The Draw option is not available.
When you press Í, Calculate calculates the confidence interval results and displays the
outputs on the home screen.
Bypassing the Inferential Stat Editors
To paste a hypothesis test or confidence interval instruction to the home screen without displaying
the corresponding inferential stat editor, select the instruction you want from the CATALOG menu.
Appendix A describes the input syntax for each hypothesis test and confidence interval instruction.
Note: You can paste a hypothesis test or confidence interval instruction to a command line in a
program. From within the program editor, select the instruction from either the CATALOG
(Chapter 15) or the STAT TESTS menu.

Chapter 13: Inferential Statistics and Distributions 221
STAT TESTS Menu
STAT TESTS Menu
To display the STAT TESTS menu, press … |. When you select an inferential statistics
instruction, the appropriate inferential stat editor is displayed.
Most STAT TESTS instructions store some output variables to memory. For a list of these variables,
see the Test and Interval Output Variables table.
Note: When a new test or interval is computed, all previous output variables are invalidated.
Inferential Stat Editors for the STAT TESTS Instructions
In this chapter, the description of each STAT TESTS instruction shows the unique inferential stat
editor for that instruction with example arguments.
• Descriptions of instructions that offer the Data/Stats input choice show both types of input
screens.
EDIT CALC TESTS
1: Z-Test... Tes t f o r 1 m, known s
2: T-Test... Tes t f o r 1 m, unknown s
3: 2-SampZTest... Test comparing 2 m’s, known s’s
4: 2-SampTTest... Test comparing 2 m’s, unknown s’s
5: 1-PropZTest... Test for 1 proportion
6: 2-PropZTest... Test comparing 2 proportions
7: ZInterval... Confidence interval for 1 m, known s
8: TInterval... Confidence interval for 1 m, unknown s
9: 2-SampZInt... Confidence interval for difference of 2 m’s, known s’s
0: 2-SampTInt... Confidence interval for difference of 2 m’s, unknown s’s
A: 1-PropZInt... Confidence interval for 1 proportion
B: 2-PropZInt... Confidence interval for difference of 2 proportions
C: c2-Test... Chi-square test for 2-way tables
D: c2-GOF Test... Chi-square Goodness of Fit test
E: 2-SampÛTest... Test comparing 2 s’s
F: LinRegTTest... t test for regression slope and r
G: LinRegTInt... Confidence interval for linear regression slope coefficient b
H: ANOVA( One-way analysis of variance

Chapter 13: Inferential Statistics and Distributions 222
• Descriptions of instructions that do not offer the Data/Stats input choice show only one input
screen.
The description then shows the unique output screen for that instruction with the example results.
• Descriptions of instructions that offer the Calculate/Draw output choice show both types of
screens: calculated and graphic results.
• Descriptions of instructions that offer only the Calculate output choice show the calculated
results on the home screen.
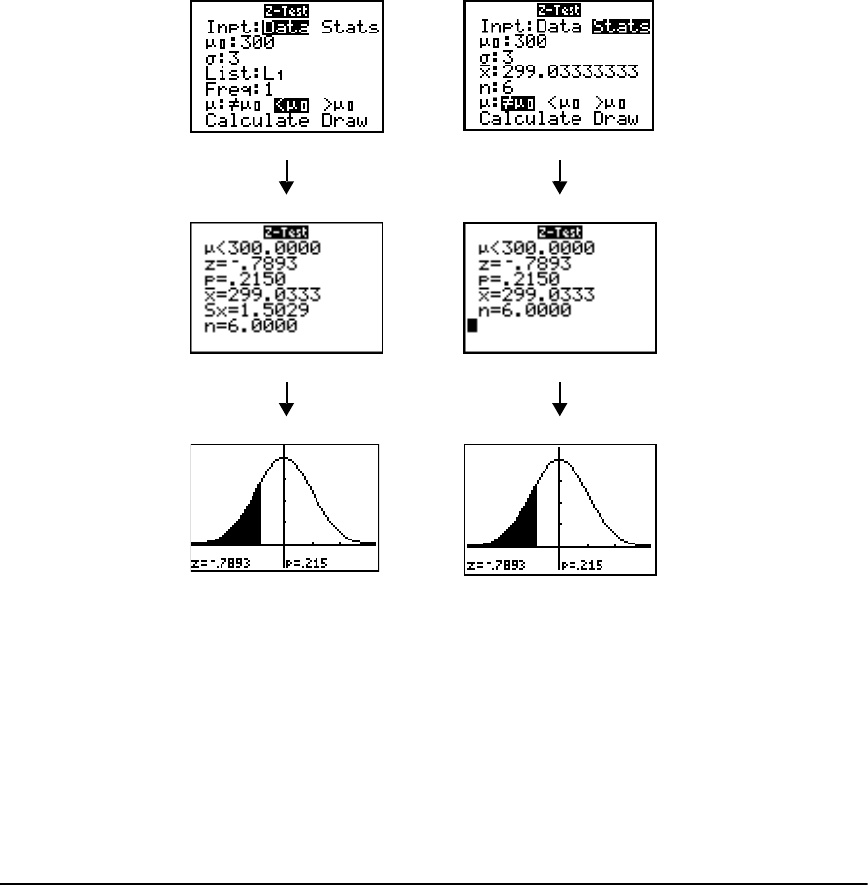
Chapter 13: Inferential Statistics and Distributions 223
Z-Test
Z-Test (one-sample z test; item 1) performs a hypothesis test for a single unknown population
mean m when the population standard deviation s is known. It tests the null hypothesis H0: m=m0
against one of the alternatives below.
•H
a: mƒm0 (m:ƒm0)
•H
a: m<m0 (m:<m0)
•H
a: m>m0 (m:>m0)
In the example:
L1={299.4, 297.7, 301, 298.9, 300.2, 297}
Note: All STAT TESTS examples assume a fixed-decimal mode setting of 4 (Chapter 1). If you set
the decimal mode to Float or a different fixed-decimal setting, your output may differ from the
output in the examples.
Data Stats
Input:
Calculated
results:
Drawn
results:
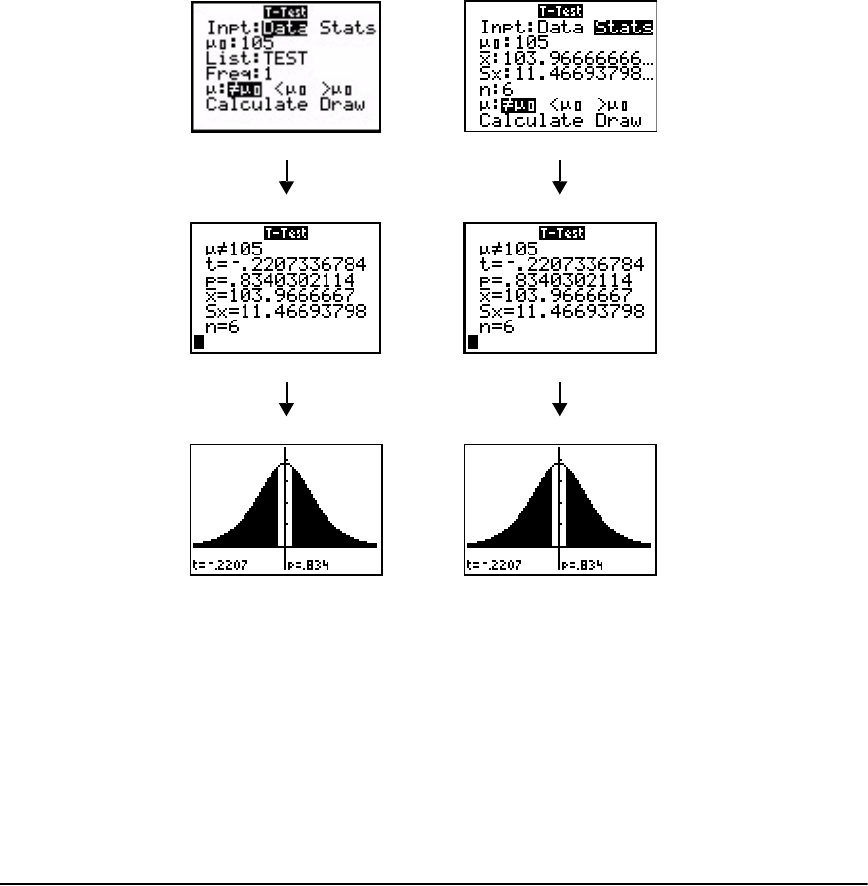
Chapter 13: Inferential Statistics and Distributions 224
T-Test
T-Test (one-sample t test; item 2) performs a hypothesis test for a single unknown population mean
m when the population standard deviation s is unknown. It tests the null hypothesis H0: m=m0
against one of the alternatives below.
•H
a: mƒm0 (m:ƒm0)
•H
a: m<m0 (m:<m0)
•H
a: m>m0 (m:>m0)
In the example:
TEST={91.9, 97.8, 111.4, 122.3, 105.4, 95}
Data Stats
Input:
Calculated
results:
Drawn
results:
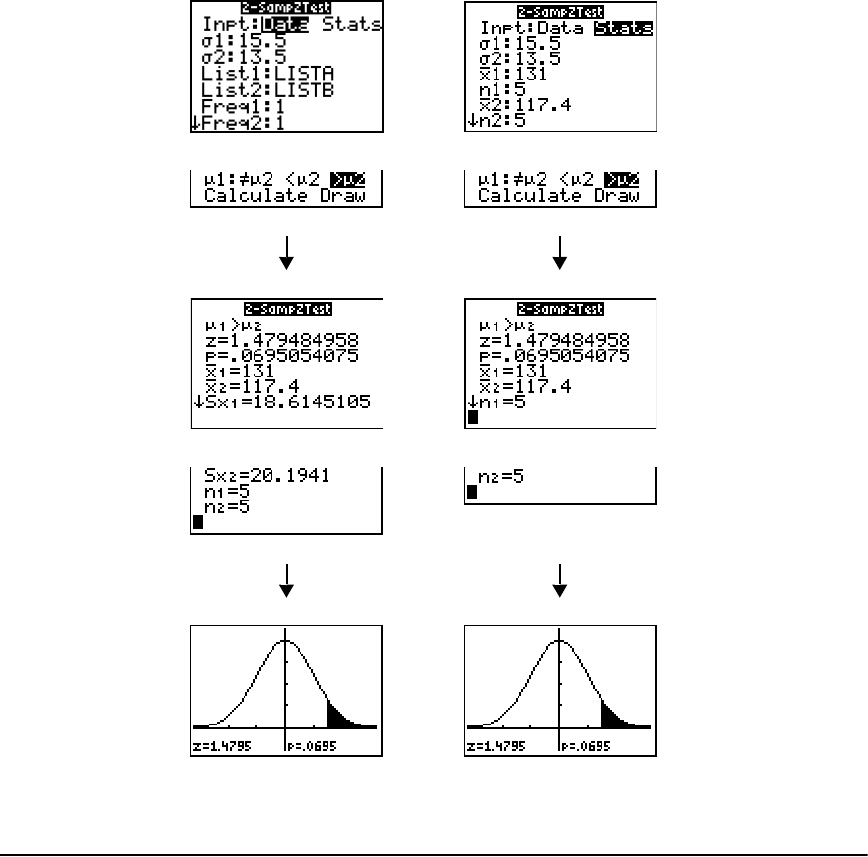
Chapter 13: Inferential Statistics and Distributions 225
2-SampZTest
2-SampZTest (two-sample z test; item 3) tests the equality of the means of two populations (m1 and
m2) based on independent samples when both population standard deviations (s1 and s2) are
known. The null hypothesis H0: m1=m2 is tested against one of the alternatives below.
•H
a: m1ƒm2 (m1:ƒm2)
•H
a: m1<m2 (m1:<m2)
•H
a: m1>m2 (m1:>m2)
In the example:
LISTA={154, 109, 137, 115, 140}
LISTB={108, 115, 126, 92, 146}
Data Stats
Input:
Calculated
results:
Drawn
results:
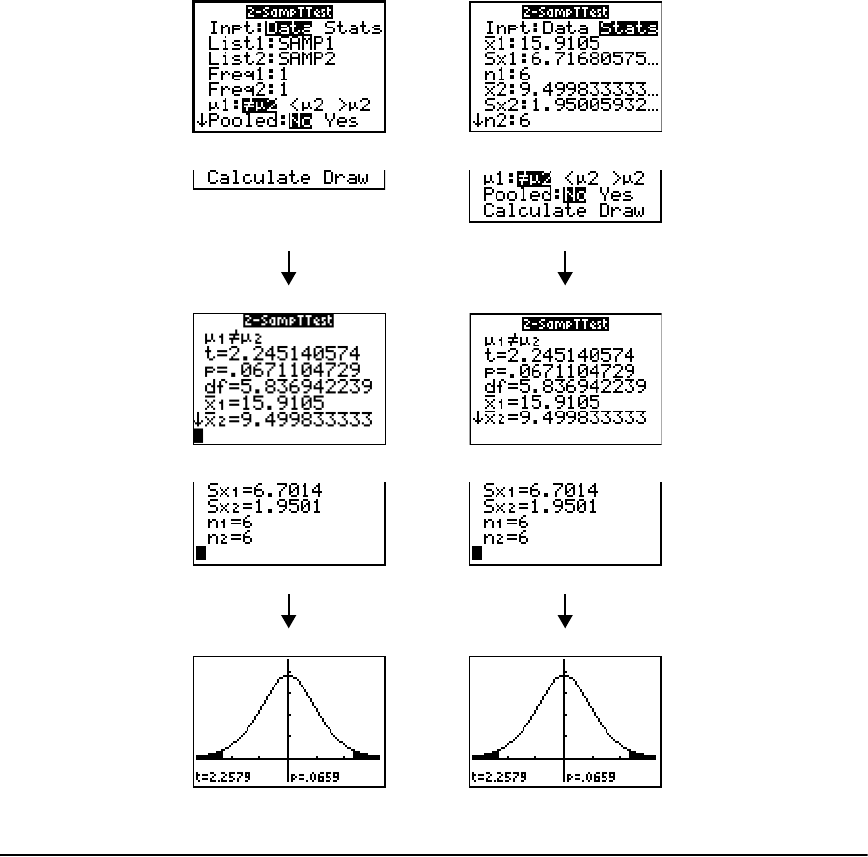
Chapter 13: Inferential Statistics and Distributions 226
2-SampTTest
2-SampTTest (two-sample t test; item 4) tests the equality of the means of two populations (m1 and
m2) based on independent samples when neither population standard deviation (s1 or s2) is
known. The null hypothesis H0: m1=m2 is tested against one of the alternatives below.
•H
a: m1ƒm2 (m1:ƒm2)
•H
a: m1<m2 (m1:<m2)
•H
a: m1>m2 (m1:>m2)
In the example:
SAMP1={12.207, 16.869, 25.05, 22.429, 8.456, 10.589}
SAMP2={11.074, 9.686, 12.064, 9.351, 8.182, 6.642}
Data Stats
Input:
Calculated
results:
Drawn
results:
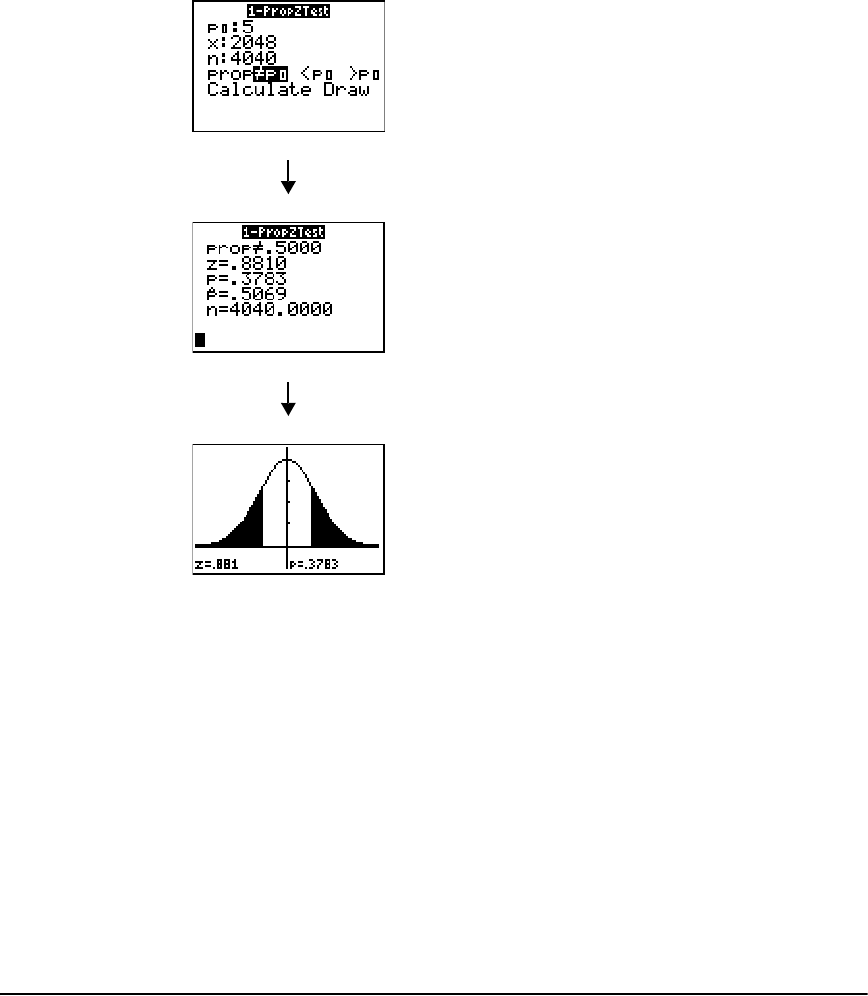
Chapter 13: Inferential Statistics and Distributions 227
1-PropZTest
1-PropZTest (one-proportion z test; item 5) computes a test for an unknown proportion of
successes (prop). It takes as input the count of successes in the sample x and the count of
observations in the sample n. 1-PropZTest tests the null hypothesis H0: prop=p0 against one of the
alternatives below.
•H
a: propƒp0 (prop:ƒp0)
•H
a: prop<p0 (prop:<p0)
•H
a: prop>p0 (prop:>p0)
Input:
Calculated
results:
Drawn
results:
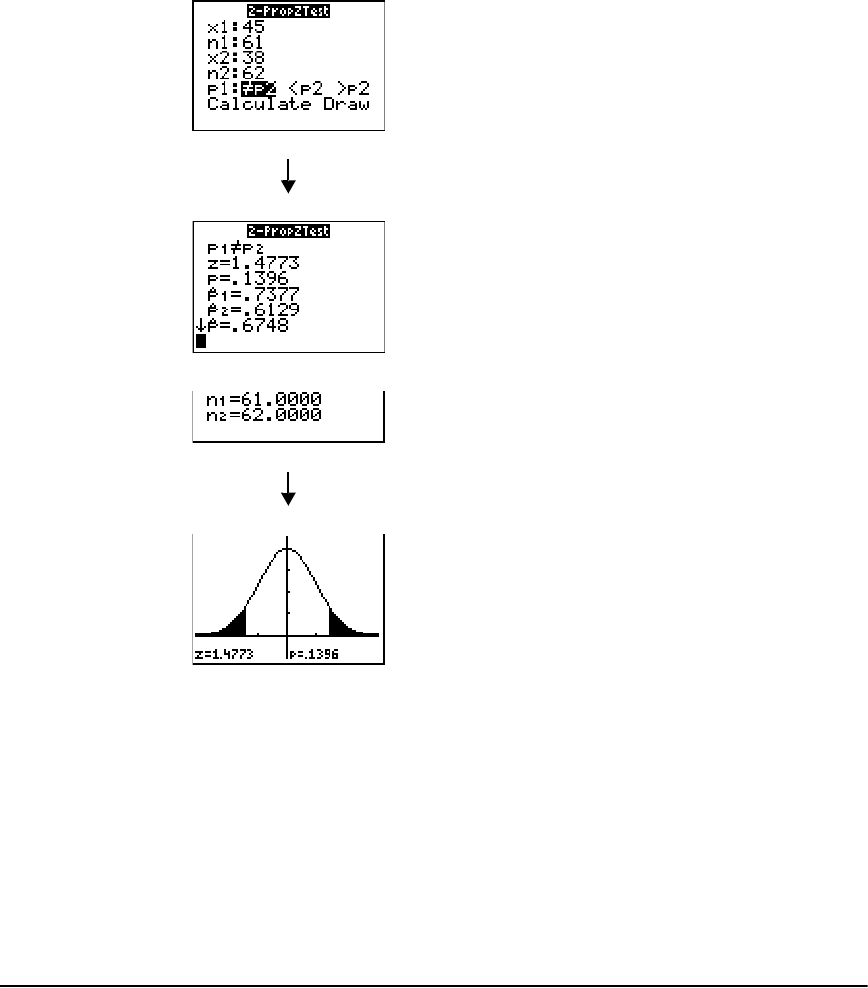
Chapter 13: Inferential Statistics and Distributions 228
2-PropZTest
2-PropZTest (two-proportion z test; item 6) computes a test to compare the proportion of successes
(p1 and p2) from two populations. It takes as input the count of successes in each sample (x1 and
x2) and the count of observations in each sample (n1 and n2). 2-PropZTest tests the null hypothesis
H0: p1=p2 (using the pooled sample proportion Ç) against one of the alternatives below.
•H
a: p1ƒp2 (p1:ƒp2)
•H
a: p1<p2 (p1:<p2)
•H
a: p1>p2 (p1:>p2)
Input:
Calculated
results:
Drawn
results:
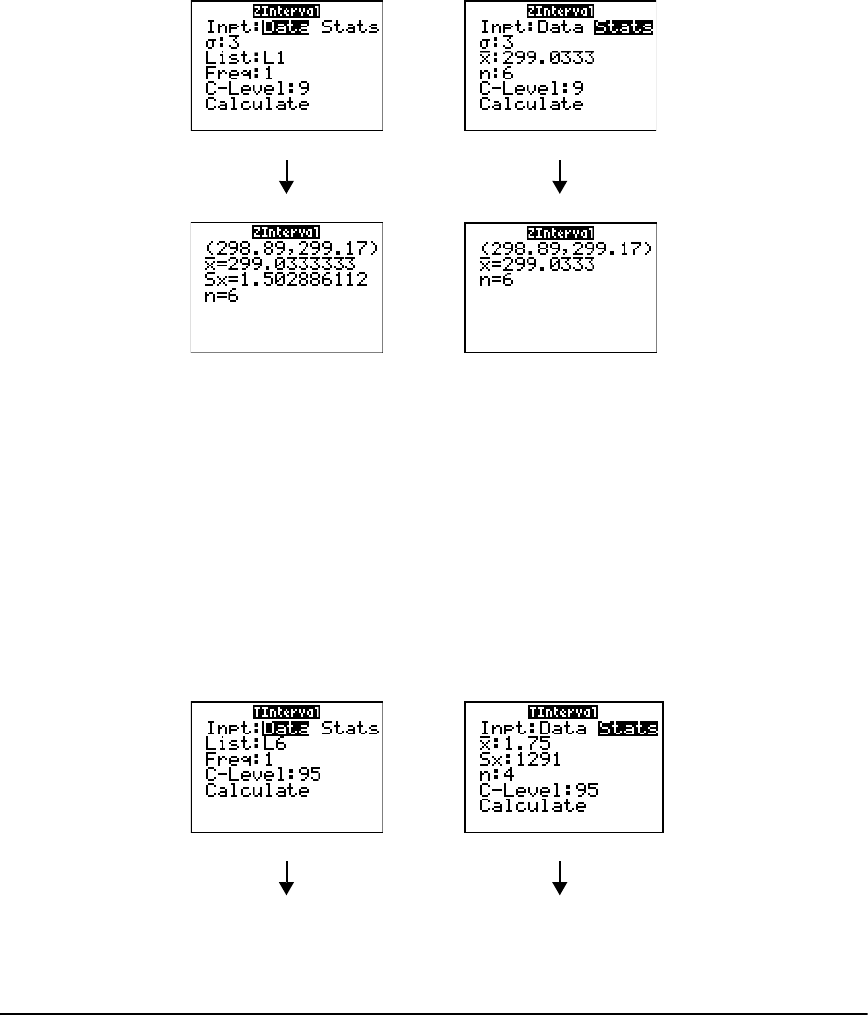
Chapter 13: Inferential Statistics and Distributions 229
ZInterval
ZInterval (one-sample z confidence interval; item 7) computes a confidence interval for an unknown
population mean m when the population standard deviation s is known. The computed confidence
interval depends on the user-specified confidence level.
In the example:
L1={299.4, 297.7, 301, 298.9, 300.2, 297}
TInterval
TInterval (one-sample t confidence interval; item 8) computes a confidence interval for an unknown
population mean m when the population standard deviation s is unknown. The computed
confidence interval depends on the user-specified confidence level.
In the example:
L6={1.6, 1.7, 1.8, 1.9}
Data Stats
Input:
Calculated
results:
Data Stats
Input:
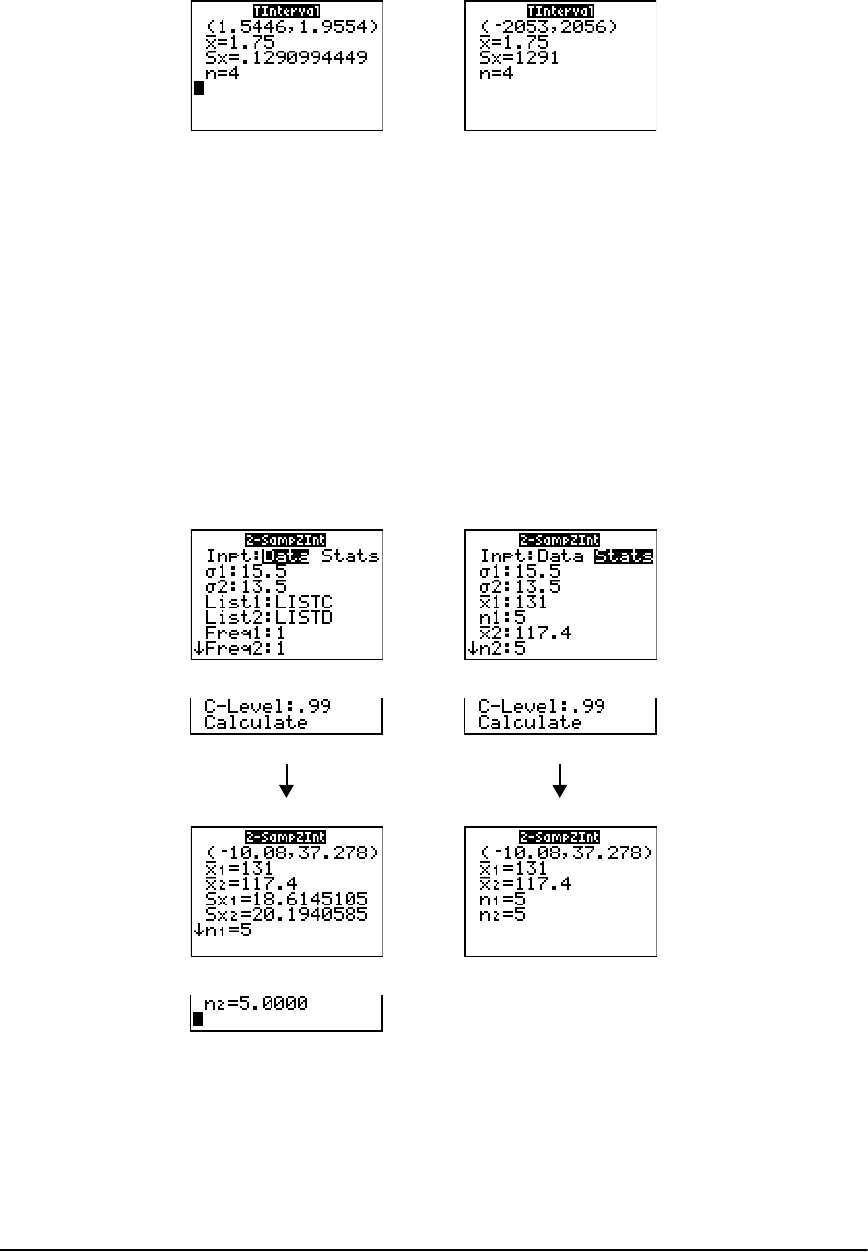
Chapter 13: Inferential Statistics and Distributions 230
2-SampZInt
2-SampZInt (two-sample z confidence interval; item 9) computes a confidence interval for the
difference between two population means (m1Nm2) when both population standard deviations (s1
and s2) are known. The computed confidence interval depends on the user-specified confidence
level.
In the example:
LISTC={154, 109, 137, 115, 140}
LISTD={108, 115, 126, 92, 146}
Calculated
results:
Data Stats
Input:
Calculated
results:
Data Stats
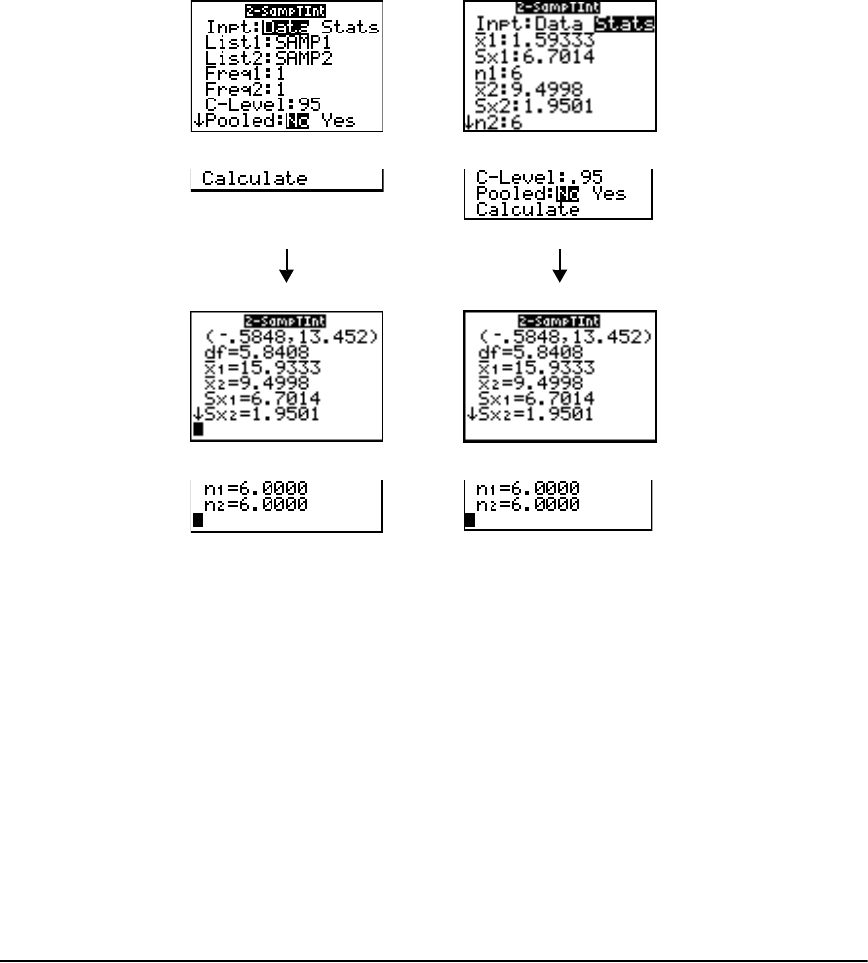
Chapter 13: Inferential Statistics and Distributions 231
2-SampTInt
2-SampTInt (two-sample t confidence interval; item 0) computes a confidence interval for the
difference between two population means (m1Nm2) when both population standard deviations (s1
and s2) are unknown. The computed confidence interval depends on the user-specified
confidence level.
In the example:
SAMP1={12.207, 16.869, 25.05, 22.429, 8.456, 10.589}
SAMP2={11.074, 9.686, 12.064, 9.351, 8.182, 6.642}
Data Stats
Input:
Calculated
results:
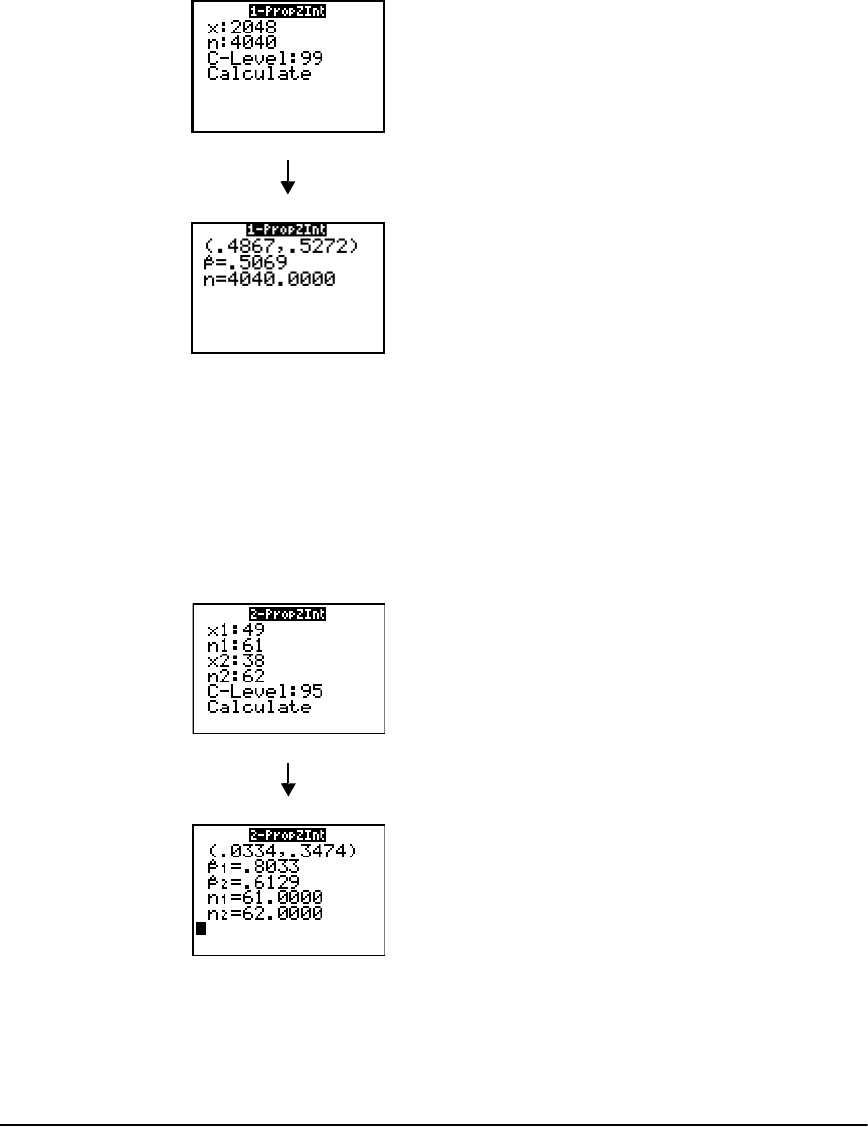
Chapter 13: Inferential Statistics and Distributions 232
1-PropZInt
1-PropZInt (one-proportion z confidence interval; item A) computes a confidence interval for an
unknown proportion of successes. It takes as input the count of successes in the sample x and the
count of observations in the sample n. The computed confidence interval depends on the user-
specified confidence level.
2-PropZInt
2-PropZInt (two-proportion z confidence interval; item B) computes a confidence interval for the
difference between the proportion of successes in two populations (p1Np2). It takes as input the
count of successes in each sample (x1 and x2) and the count of observations in each sample
(n1 and n2). The computed confidence interval depends on the user-specified confidence level.
Input:
Calculated
results:
Input:
Calculated
results:
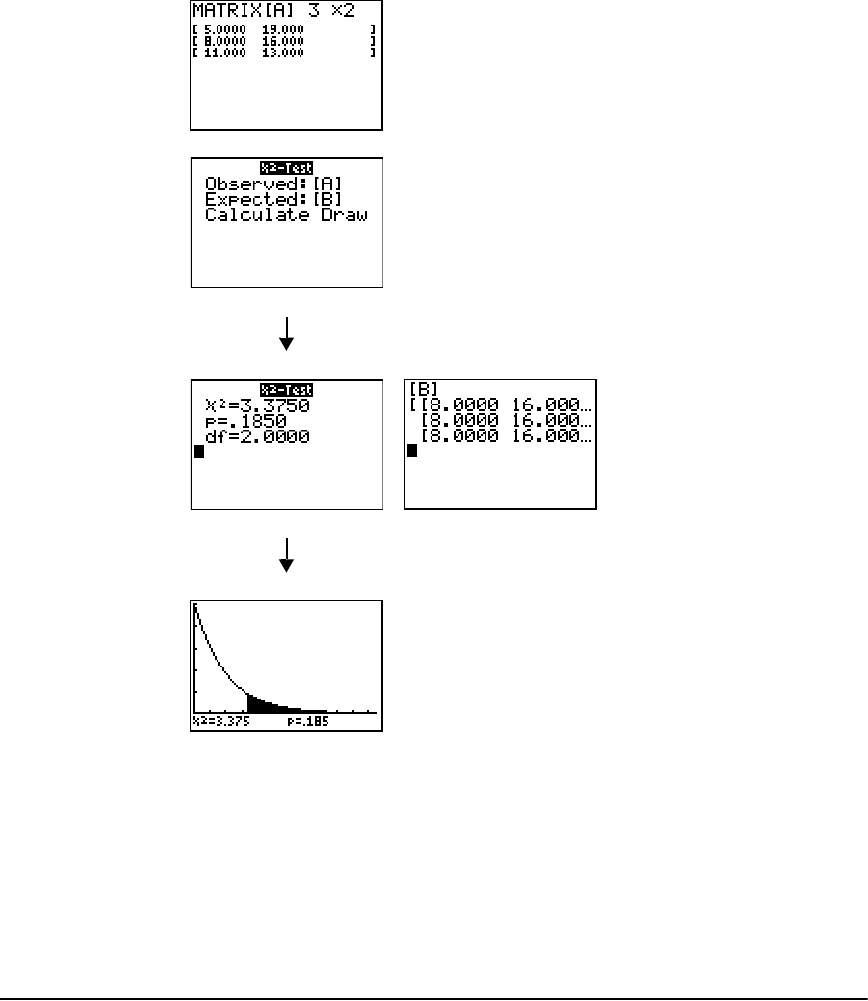
Chapter 13: Inferential Statistics and Distributions 233
c2-Test
c2-Test (chi-square test; item C) computes a chi-square test for association on the two-way table of
counts in the specified Observed matrix. The null hypothesis H0 for a two-way table is: no
association exists between row variables and column variables. The alternative hypothesis is: the
variables are related.
Before computing a c2-Test, enter the observed counts in a matrix. Enter that matrix variable
name at the Observed: prompt in the c2.Test editor; default=[A]. At the Expected: prompt, enter the
matrix variable name to which you want the computed expected counts to be stored; default=[B].
Matrix
editor:
Note: Press y ú ~ ~ 1 to
select 1:[A] from the MATRX EDIT
menu.
Input:
Note: Press y ú †] Í to
display matrix [B].
Calculated
results:
Drawn results:
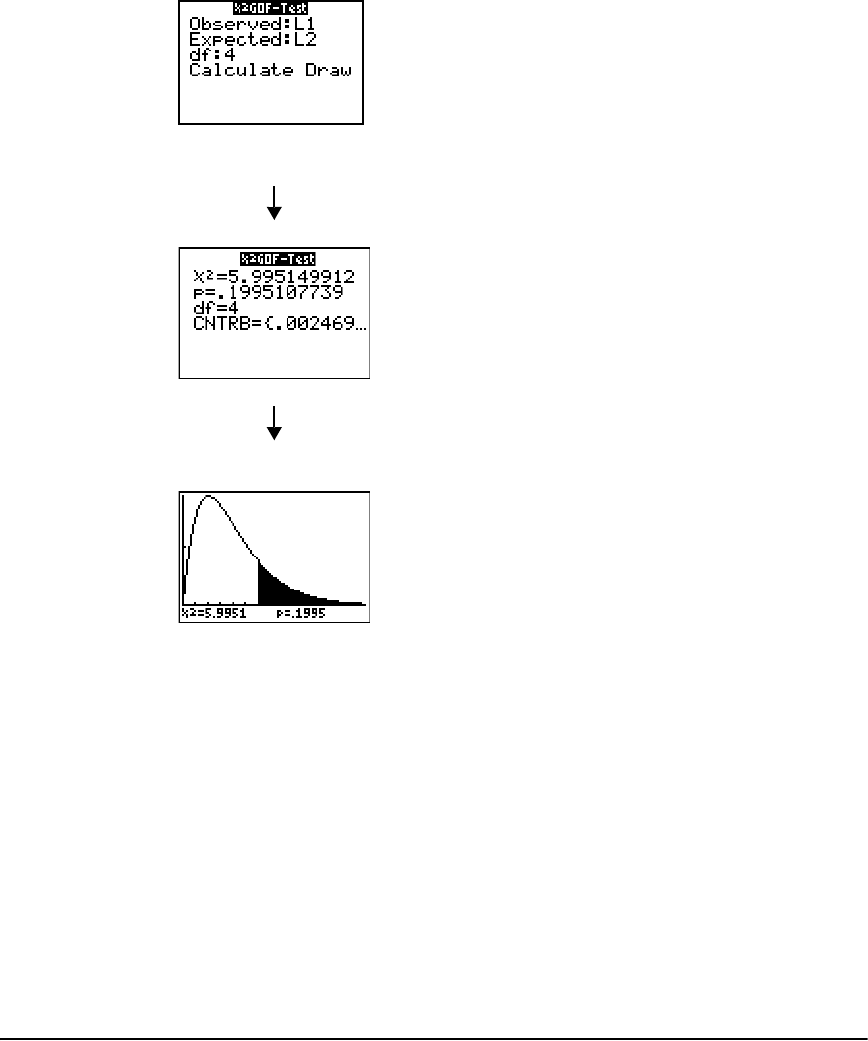
Chapter 13: Inferential Statistics and Distributions 234
c2GOF-Test
c2GOF-Test (Chi Square Goodness of Fit; item D) performs a test to confirm that sample data is
from a population that conforms to a specified distribution. For example, c2 GOF can confirm that
the sample data came from a normal distribution.
In the example:
list 1={16, 25, 22, 8, 10}
list 2={16.2, 21.6, 16.2, 14.4, 12.6}
The Chi-square
Goodness of Fit
input screen:
Note: Press … ~ ~ to
select TESTS. Press †
several times to select
D:X2GOF-Test... Press
Í. To enter data for
df (degree of freedom),
press † † †. Type 4.
Calculated
results:
Drawn results:
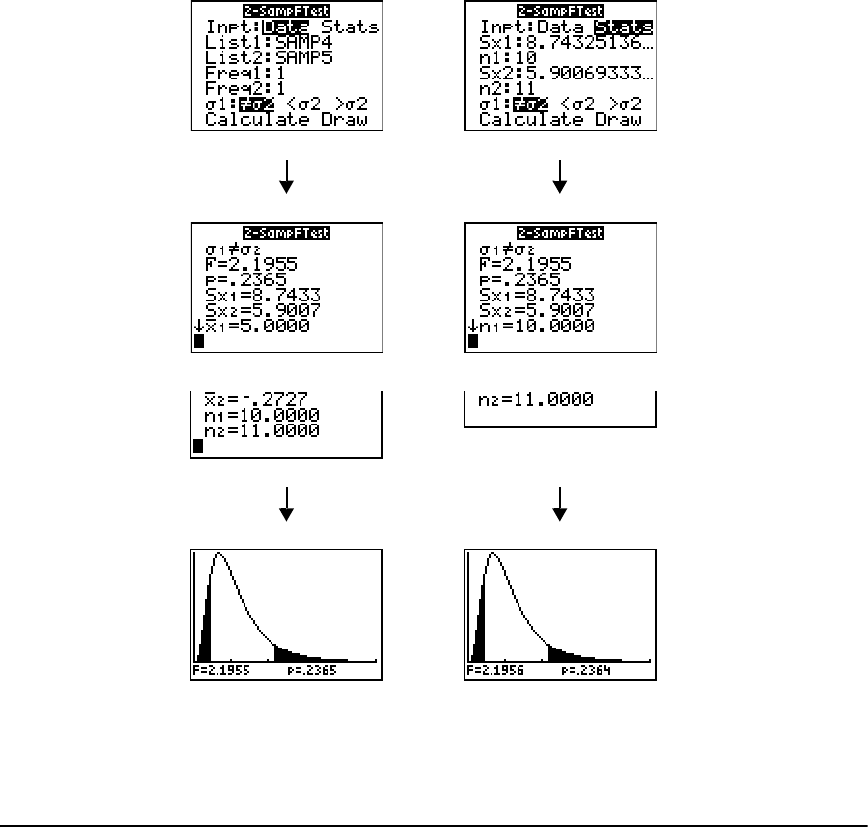
Chapter 13: Inferential Statistics and Distributions 235
2-SampFTest
2-SampÜTest (two-sample Ü-test; item E) computes an Ü-test to compare two normal population
standard deviations (s1 and s2). The population means and standard deviations are all unknown.
2-SampÜTest, which uses the ratio of sample variances Sx12/Sx22, tests the null hypothesis
H0: s1=s2 against one of the alternatives below.
•H
a: s1ƒs2 (s1:ƒs2)
•H
a: s1<s2 (s1:<s2)
•H
a: s1>s2 (s1:>s2)
In the example:
SAMP4={7,L4, 18, 17, L3, L5, 1, 10, 11, L2}
SAMP5={L1, 12, L1, L3, 3, L5, 5, 2, L11, L1, L3}
Data Stats
Input:
Calculated
results:
Drawn results:
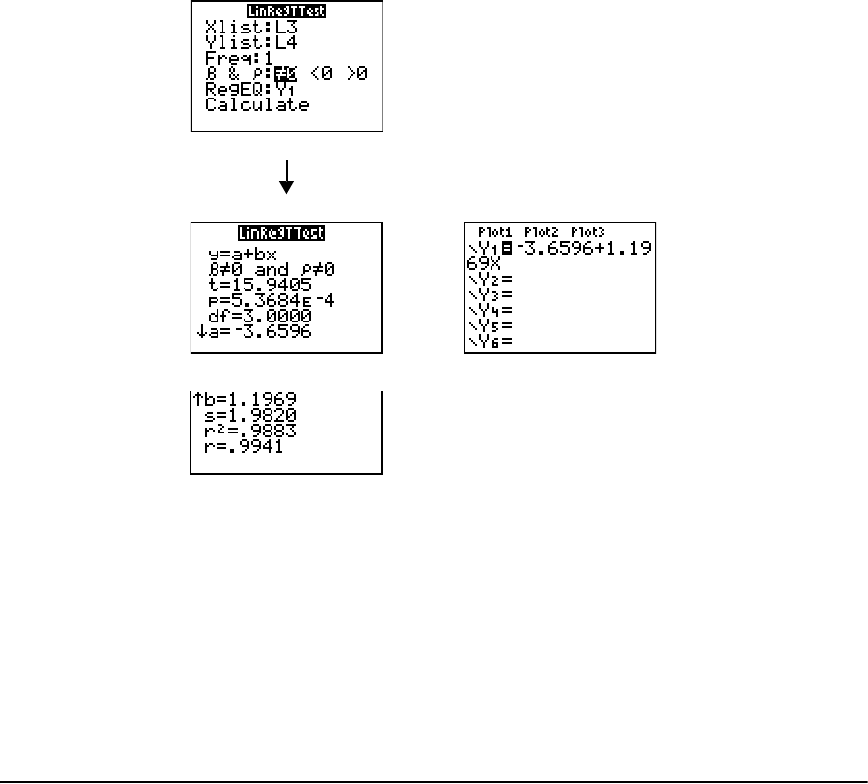
Chapter 13: Inferential Statistics and Distributions 236
LinRegTTest
LinRegTTest (linear regression t test; item F) computes a linear regression on the given data and a
t test on the value of slope b and the correlation coefficient r for the equation y=a+bx. It tests the
null hypothesis H0: b=0 (equivalently, r=0) against one of the alternatives below.
•H
a: bƒ0 and rƒ0 (b & r:ă0)
•H
a: b<0 and r<0 (b & r:<0)
•H
a: b>0 and r>0 (b & r:>0)
The regression equation is automatically stored to RegEQ (VARS Statistics EQ secondary menu). If
you enter a Y= variable name at the RegEQ: prompt, the calculated regression equation is
automatically stored to the specified Y= equation. In the example below, the regression equation is
stored to Y1, which is then selected (turned on).
In the example:
L3={38, 56, 59, 64, 74}
L4={41, 63, 70, 72, 84}
When LinRegTTest is executed, the list of residuals is created and stored to the list name RESID
automatically. RESID is placed on the LIST NAMES menu.
Note: For the regression equation, you can use the fix-decimal mode setting to control the number
of digits stored after the decimal point (Chapter 1). However, limiting the number of digits to a
small number could affect the accuracy of the fit.
Input:
Calculated
results:

Chapter 13: Inferential Statistics and Distributions 237
LinRegTInt
LinRegTInt computes a linear regression T confidence interval for the slope coefficient b. If the
confidence interval contains 0, this is insufficient evidence to indicate that the data exhibits a linear
relationship.
In the example:
list 1={4, 5, 6, 7, 8}
list 2={1, 2, 3, 3.5, 4.5}
Xlist, Ylist is the list of independent and dependent variables. The list containing the Freq
(frequency) values for the data is stored in List. The default is 1. All elements must be real
numbers. Each element in the Freq list is the frequency of occurrence for each corresponding data
point in the input list specified in the List fields. RegEQ (optional) is the designated Yn variable for
storing the regression equation. StoreRegEqn (optional) is the designated variable for storing the
regression equation. The C level is the Confidence level probability with default = .95.
LinRegTInt input
screen:
Note: Press … ~ ~ to
select TESTS. Press †
several times to select
G:LinRegTint... Press
Í. Press † several
times to select Calculate.
Press Í.
Calculated
results:
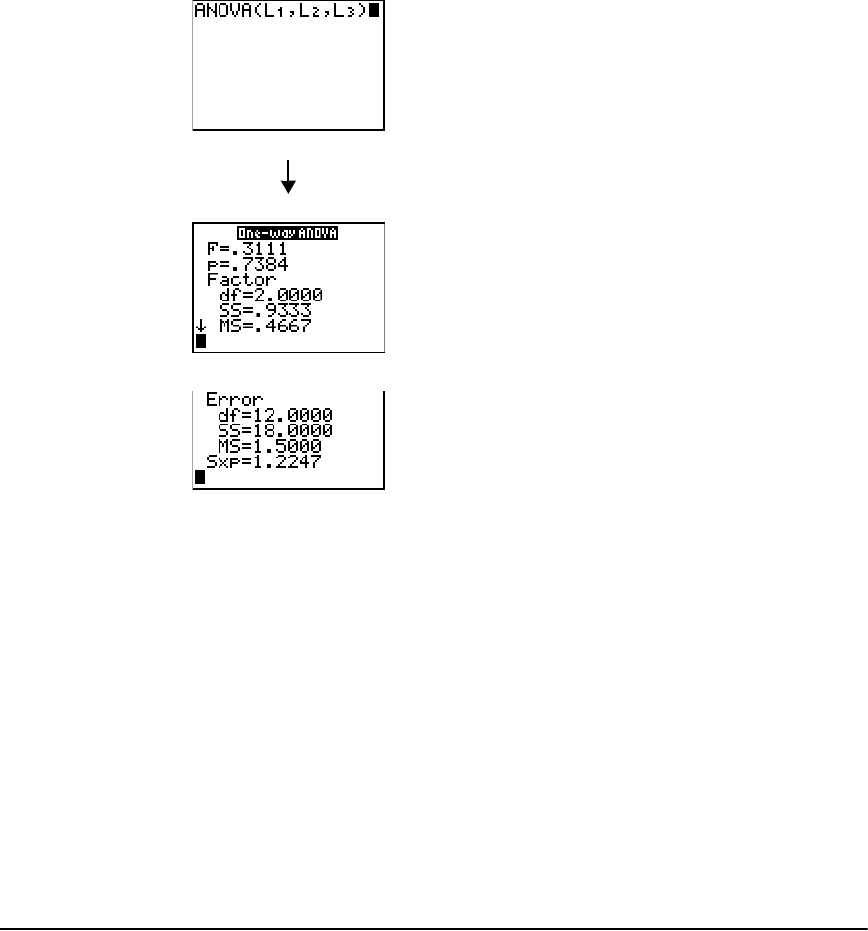
Chapter 13: Inferential Statistics and Distributions 238
ANOVA(
ANOVA( (one-way analysis of variance; item H) computes a one-way analysis of variance for
comparing the means of two to 20 populations. The ANOVA procedure for comparing these means
involves analysis of the variation in the sample data. The null hypothesis H0: m1=m2=...=mk is
tested against the alternative Ha: not all m1...mk are equal.
ANOVA(list1,list2[,...,list20])
In the example:
L1={7 4 6 6 5}
L2={6 5 5 8 7}
L3={4 7 6 7 6}
Note: SS is sum of squares and MS is mean square.
Input:
Calculated
results:

Chapter 13: Inferential Statistics and Distributions 239
Inferential Statistics Input Descriptions
The tables in this section describe the inferential statistics inputs discussed in this chapter. You
enter values for these inputs in the inferential stat editors. The tables present the inputs in the
same order that they appear in this chapter.
Input Description
m0 Hypothesized value of the population mean that you are testing.
sThe known population standard deviation; must be a real number
> 0.
List The name of the list containing the data you are testing.
Freq The name of the list containing the frequency values for the data
in List. Default=1. All elements must be integers | 0.
Calculate/Draw Determines the type of output to generate for tests and intervals.
Calculate displays the output on the home screen. In tests, Draw
draws a graph of the results.
v, Sx, nSummary statistics (mean, standard deviation, and sample size)
for the one-sample tests and intervals.
s1The known population standard deviation from the first population
for the two-sample tests and intervals. Must be a real number > 0.
s2The known population standard deviation from the second
population for the two-sample tests and intervals. Must be a real
number > 0.
List1, List2 The names of the lists containing the data you are testing for the
two-sample tests and intervals. Defaults are L1 and L2,
respectively.
Freq1, Freq2 The names of the lists containing the frequencies for the data in
List1 and List2 for the two-sample tests and intervals.
Defaults=1. All elements must be integers | 0.
v1, Sx1, n1, v2, Sx2, n2Summary statistics (mean, standard deviation, and sample size)
for sample one and sample two in the two-sample tests and
intervals.
Pooled Specifies whether variances are to be pooled for 2-SampTTest
and 2-SampTInt. No instructs the TI-84 Plus not to pool the
variances. Yes instructs the TI-84 Plus to pool the variances.
p0 The expected sample proportion for 1-PropZTest. Must be a real
number, such that 0 < p0 < 1.
xThe count of successes in the sample for the 1-PropZTest and
1-PropZInt. Must be an integer | 0.
nThe count of observations in the sample for the 1-PropZTest and
1-PropZInt. Must be an integer > 0.
x1 The count of successes from sample one for the 2-PropZTest
and 2-PropZInt. Must be an integer | 0.
x2 The count of successes from sample two for the 2-PropZTest
and 2-PropZInt. Must be an integer | 0.

Chapter 13: Inferential Statistics and Distributions 240
Test and Interval Output Variables
The inferential statistics variables are calculated as indicated below. To access these variables for
use in expressions, press 5 (5:Statistics), and then select the VARS menu listed in the last
column below.
n1 The count of observations in sample one for the 2-PropZTest
and 2-PropZInt. Must be an integer > 0.
n2 The count of observations in sample two for the 2-PropZTest and
2-PropZInt. Must be an integer > 0.
C-Level The confidence level for the interval instructions. Must be ‚ 0 and
< 100. If it is ‚ 1, it is assumed to be given as a percent and is
divided by 100. Default=0.95.
Observed (Matrix) The matrix name that represents the columns and rows for the
observed values of a two-way table of counts for the c2-Test and
c2GOF-Test. Observed must contain all integers | 0. Matrix
dimensions must be at least 2×2.
Expected (Matrix) The matrix name that specifies where the expected values should
be stored. Expected is created upon successful completion of
the c2-Test and c2GOF-Test.
df df (degree of freedom) represents (number of sample categories)
- (number of estimated parameters for the selected distribution +
1).
Xlist, Ylist The names of the lists containing the data for LinRegTTest and
LinRegTInt. Defaults are L1 and L2, respectively. The
dimensions of Xlist and Ylist must be the same.
RegEQ The prompt for the name of the Y= variable where the calculated
regression equation is to be stored. If a Y= variable is specified,
that equation is automatically selected (turned on). The default is
to store the regression equation to the RegEQ variable only.
Variables Tests Intervals
LinRegTTest,
ANOVA
VARS
Menu
p-value ppTEST
test statistics z, t, c2, Üt, ÜTEST
degrees of freedom df df df TEST
sample mean of x values for
sample 1 and sample 2
v1, v2v1, v2TEST
sample standard deviation of x for
sample 1 and sample 2
Sx1,
Sx2
Sx1,
Sx2
TEST
number of data points for sample 1
and sample 2
n1, n2 n1, n2 TEST
pooled standard deviation SxP SxP SxP TEST
Input Description

Chapter 13: Inferential Statistics and Distributions 241
Note: The variables listed above cannot be archived.
Distribution Functions
DISTR menu
Note: Selection of any of the DISTR functions will take the user to a wizard screen for that function.
To display the DISTR menu, press y =.
estimated sample proportion ‚Ç ‚Ç TEST
estimated sample proportion for
population 1
‚Ç1‚Ç1TEST
estimated sample proportion for
population 2
‚Ç2‚Ç2TEST
confidence interval pair lower,
upper
TEST
mean of x values vv XY
sample standard deviation of x Sx Sx XY
number of data points nn XY
standard error about the line sTEST
regression/fit coefficients a, b EQ
correlation coefficient rEQ
coefficient of determination r2 EQ
regression equation RegEQ EQ
DISTR DRAW
1: normalpdf( nn probability density function
2: normalcdf( nn cumulative distribution function
3: invNorm( Inverse cumulative normal distribution
4: invT( Inverse cumulative Student-t distribution
5: tpdf( Student-t probability density
6: tcdf( Student-t distribution probability
7: c2pdf( Chi-square probability density
8: c2cdf Chi-square distribution probability
9: Üpdf( wÜprobability density
0: Ücdf( wÜdistribution probability
Variables Tests Intervals
LinRegTTest,
ANOVA
VARS
Menu
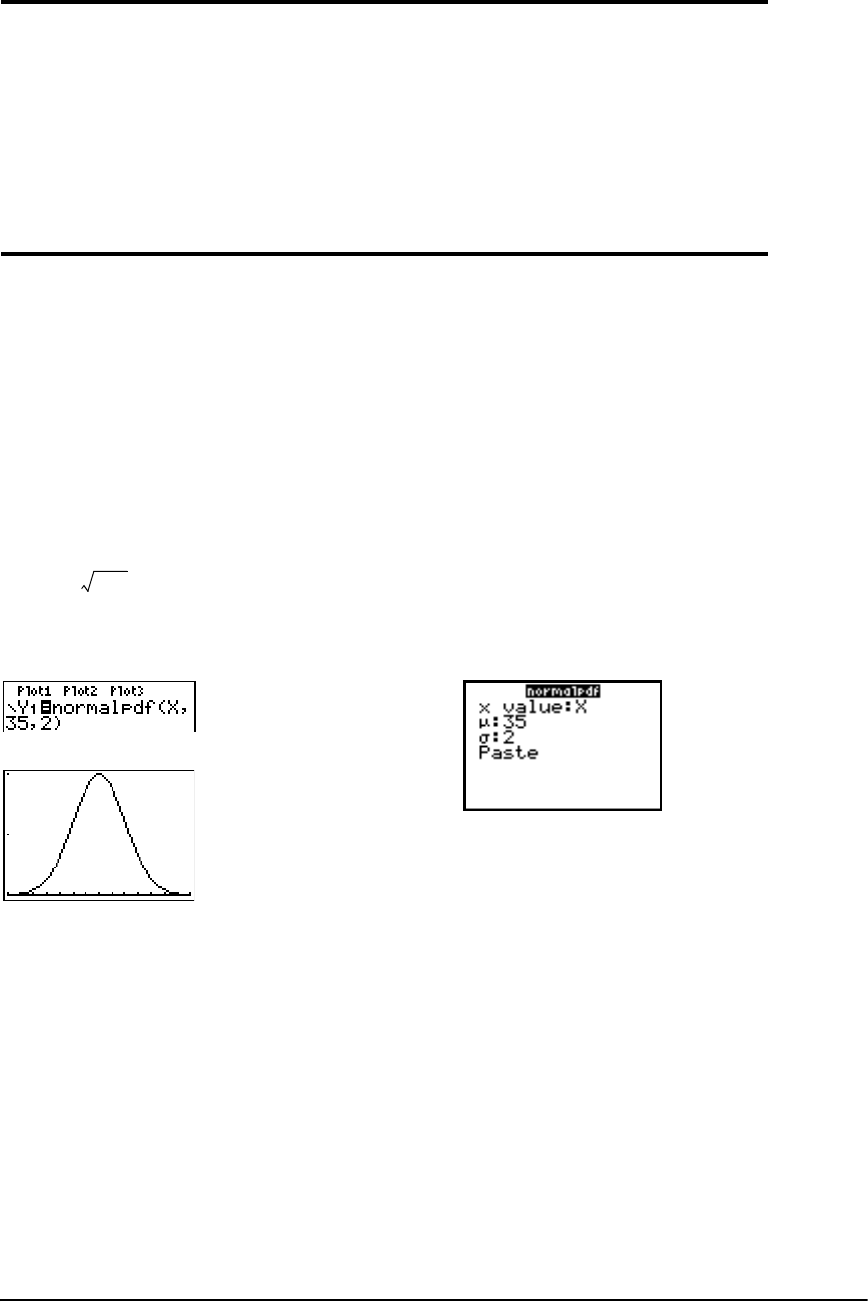
Chapter 13: Inferential Statistics and Distributions 242
Note: L1â99 and 1â99 specify infinity. If you want to view the area left of upperbound, for example,
specify lowerbound= L1â99.
fx() 1
2πσ
-------------- e
xμ–()
2
2σ2
-------------------–
–
σ0>,=
normalpdf(
normalpdf( computes the probability density function (pdf) for the normal distribution at a specified
x value. The defaults are mean m=0 and standard deviation s=1. To plot the normal distribution,
paste normalpdf( to the Y= editor. The probability density function (pdf) is:
normalpdf(x[,m,s])
Note: For plotting the normal distribution, you can set window variables Xmin and Xmax so that the
mean m falls between them, and then select 0:ZoomFit from the ZOOM menu.
normalcdf(
normalcdf( computes the normal distribution probability between lowerbound and upperbound for the
specified mean m and standard deviation s. The defaults are m=0 and s=1.
A: binompdf( Binomial probability
B: binomcdf( Binomial cumulative density
C: poissonpdf( Poisson probability
D: poissoncdf( Poisson cumulative density
E: geometpdf( Geometric probability
F: geometcdf( Geometric cumulative density
Note: For this example,
Xmin = 28
Xmax = 42
Xscl = 1
Ymin = 0
Ymax = .2
Yscl = .1
DISTR DRAW
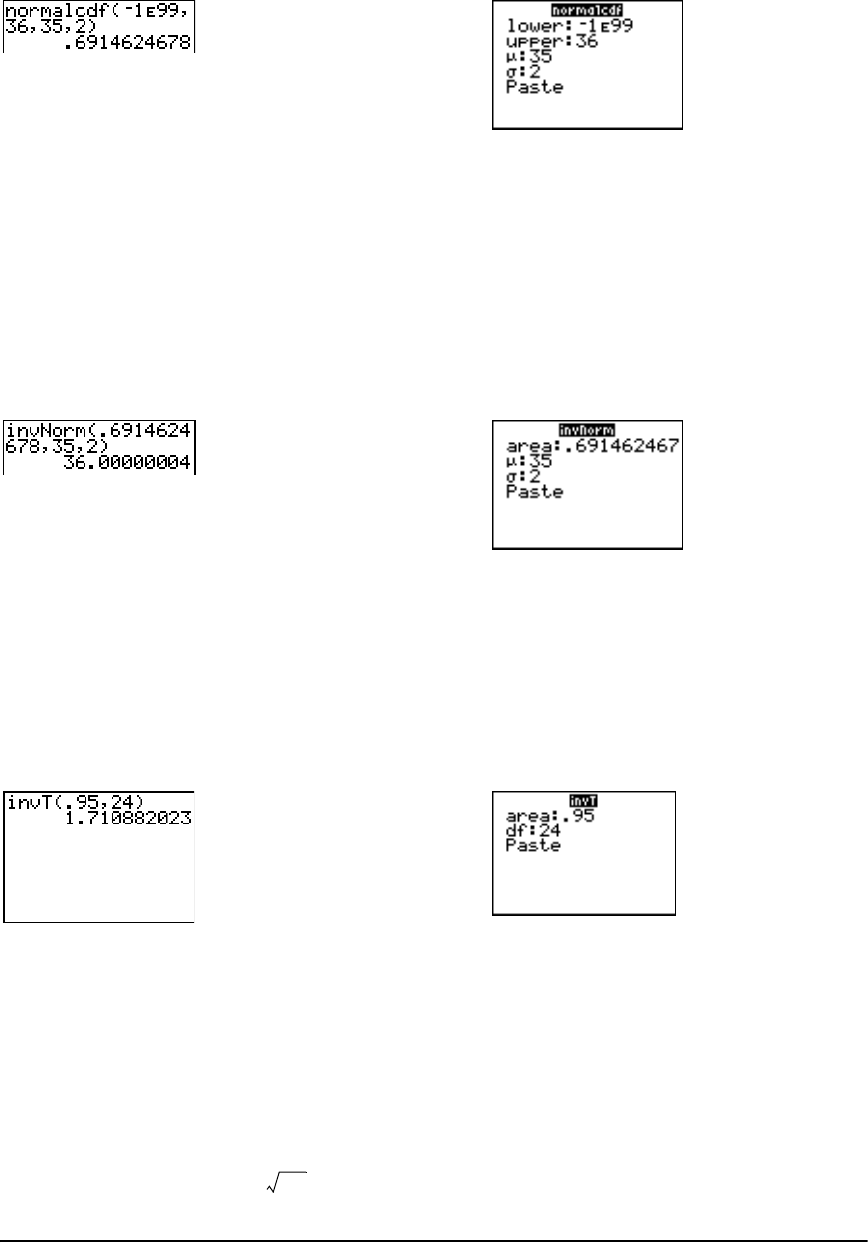
Chapter 13: Inferential Statistics and Distributions 243
normalcdf(lowerbound,upperbound[,m,s])
invNorm(
invNorm( computes the inverse cumulative normal distribution function for a given area under the
normal distribution curve specified by mean m and standard deviation s. It calculates the x value
associated with an area to the left of the x value. 0 area 1 must be true. The defaults are m=0 and
s=1.
invNorm(area[,m,s])
invT(
invT( computes the inverse cumulative Student-t probability function specified by Degree of
Freedom, df for a given Area under the curve.
invT(area,df)
f
x() Γdf 1+()/2[]
Γdf 2⁄()
---------------------------------= 1x2/df+()
df 1+()/2–
πdf
-------------------------------------------------
tpdf(
tpdf( computes the probability density function (pdf) for the Student-t distribution at a specified x
value. df (degrees of freedom) must be > 0. To plot the Student-t distribution, paste tpdf( to the Y=
editor. The probability density function (pdf) is:

Chapter 13: Inferential Statistics and Distributions 244
tpdf(x,df)
Note: For this example,
Xmin = L4.5
Xmax = 4.5
Ymin = 0
Ymax = .4
tcdf(
tcdf( computes the Student-t distribution probability between lowerbound and upperbound for the
specified df (degrees of freedom), which must be > 0.
tcdf(lowerbound,upperbound,df)
c2pdf(
fx() 1
Γdf 2⁄()
-------------------- 1/2()
df/2xdf 21–⁄ex/2–x0≥,=
c2pdf( computes the probability density function (pdf) for the c2 (chi-square) distribution at a
specified x value. df (degrees of freedom) must be an integer > 0. To plot the c2 distribution, paste
c2pdf( to the Y= editor. The probability density function (pdf) is:
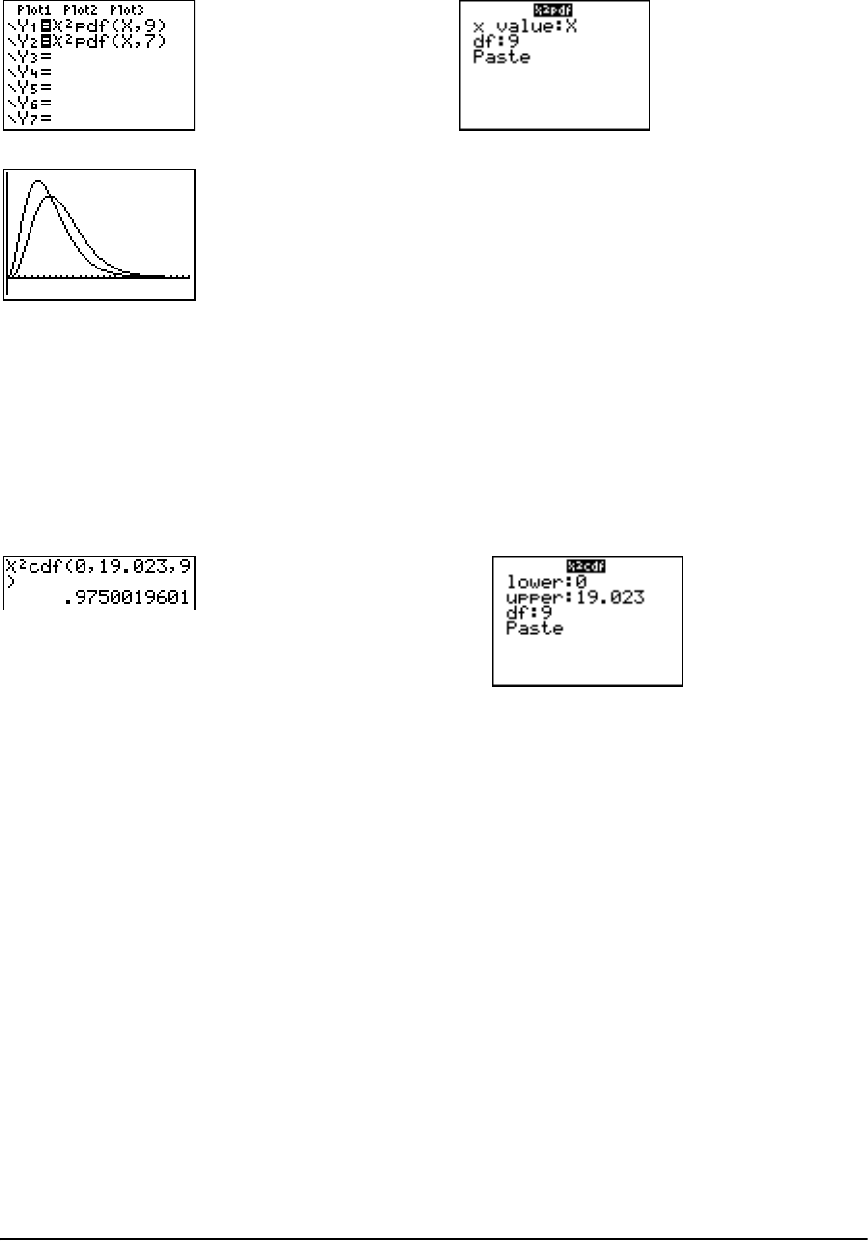
Chapter 13: Inferential Statistics and Distributions 245
c2pdf(x,df)
Note: For this example,
Xmin = 0
Xmax = 30
Ymin = L.02
Ymax = .132
c2cdf(
c2cdf( computes the c2 (chi-square) distribution probability between lowerbound and upperbound for
the specified df (degrees of freedom), which must be an integer > 0.
c2cdf(lowerbound,upperbound,df)
fx() Γnd+()/2[]
Γn/2()Γd/2()
----------------------------------n
d
---
⎝⎠
⎛⎞
n/2
xn/2 1–1nx/d+()
nd+()/2–x0≥,=
Fpdf(
Üpdf( computes the probability density function (pdf) for the Ü distribution at a specified x value.
numerator df (degrees of freedom) and denominator df must be integers > 0. To plot the Ü distribution,
paste Üpdf( to the Y= editor. The probability density function (pdf) is:
where n = numerator degrees of freedom
d = denominator degrees of freedom
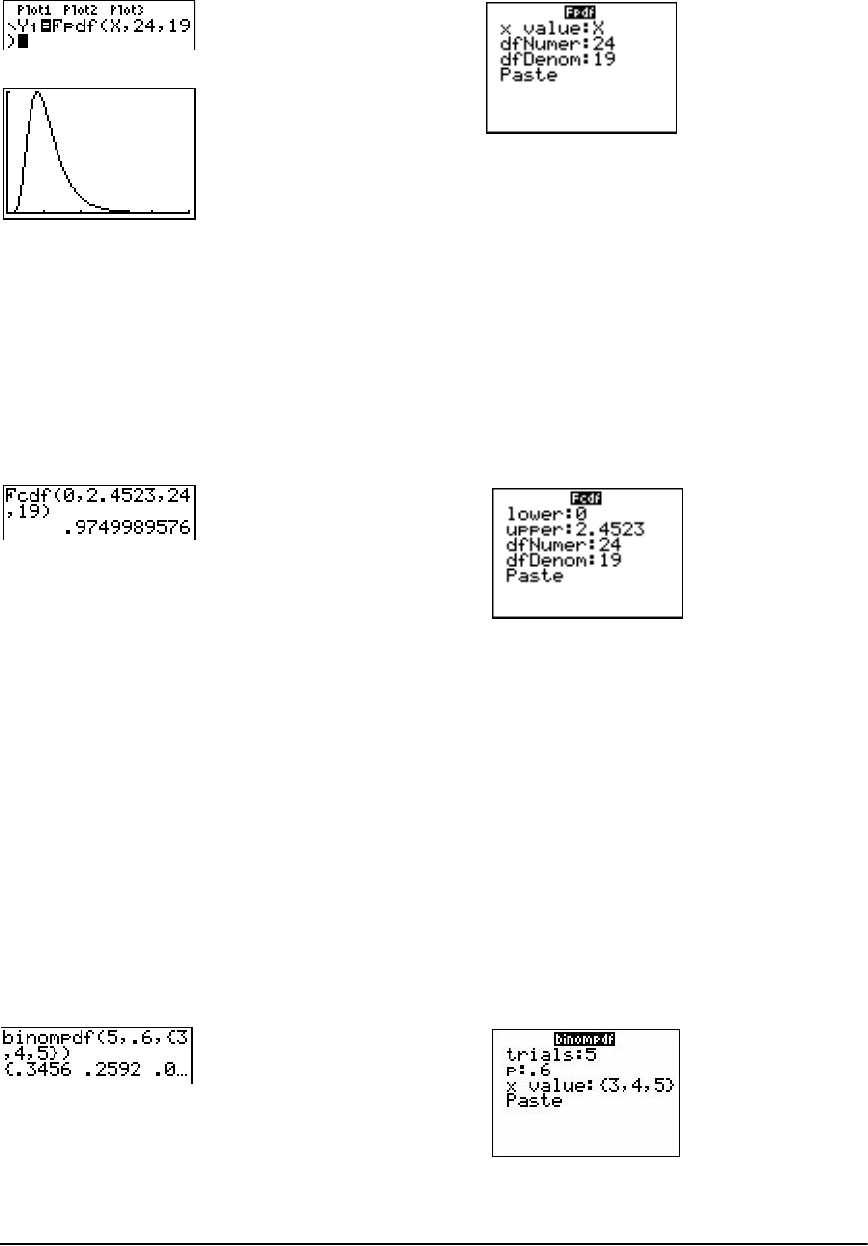
Chapter 13: Inferential Statistics and Distributions 246
Üpdf(x,numerator df,denominator df)
Note: For this example,
Xmin = 0
Xmax = 5
Ymin = 0
Ymax = 1
Fcdf(
Ücdf( computes the Ü distribution probability between lowerbound and upperbound for the specified
numerator df (degrees of freedom) and denominator df. numerator df and denominator df must be integers
> 0.
Ücdf(lowerbound,upperbound,numerator df,denominator df)
fx() n
x
⎝⎠
⎛⎞
px1p–()
nx–x, 0,1,...,n==
binompdf
binompdf( computes a probability at x for the discrete binomial distribution with the specified
numtrials and probability of success (p) on each trial. x can be an integer or a list of integers. 0p1
must be true. numtrials must be an integer > 0. If you do not specify x, a list of probabilities from 0 to
numtrials is returned. The probability density function (pdf) is:
where n = numtrials
binompdf(numtrials,p[,x])
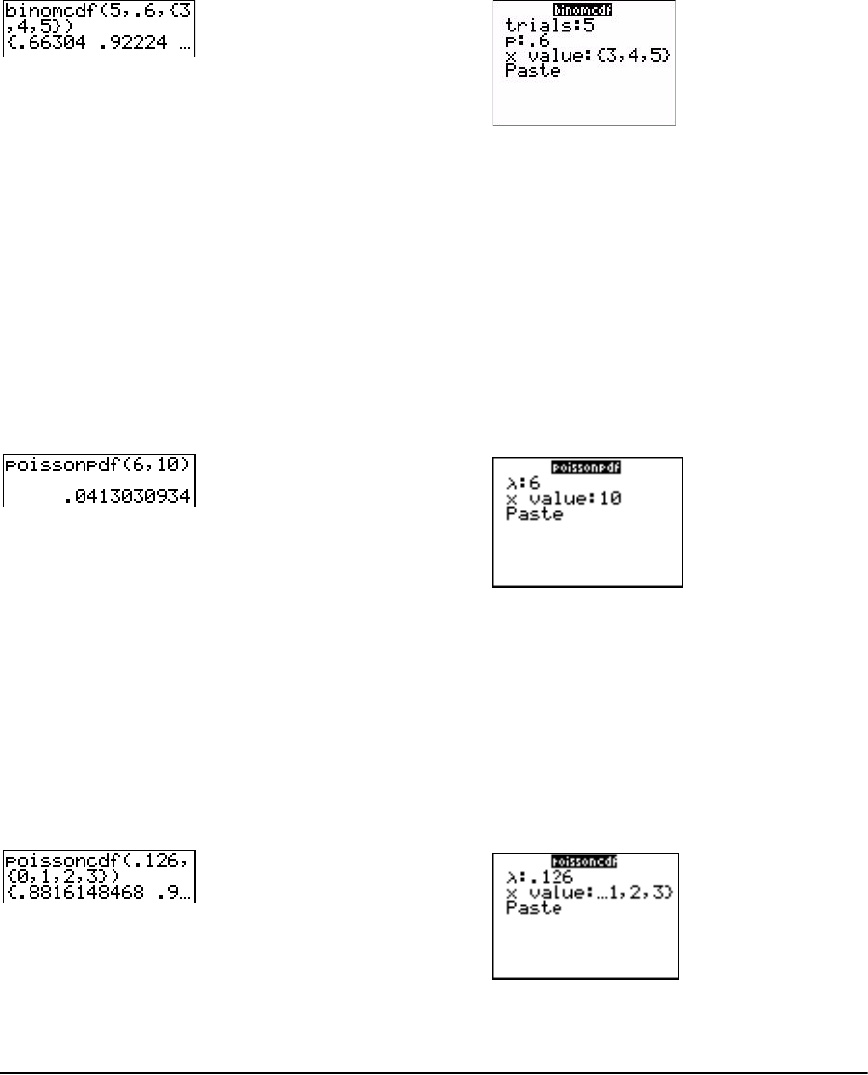
Chapter 13: Inferential Statistics and Distributions 247
binomcdf(
binomcdf( computes a cumulative probability at x for the discrete binomial distribution with the
specified numtrials and probability of success (p) on each trial. x can be a real number or a list of
real numbers. 0p1 must be true. numtrials must be an integer > 0. If you do not specify x, a list of
cumulative probabilities is returned.
binomcdf(numtrials,p[,x])
fx() eμ–μxx!⁄x, 0,1,2,...==
poissonpdf(
poissonpdf( computes a probability at x for the discrete Poisson distribution with the specified
mean m, which must be a real number > 0. x can be an integer or a list of integers. The probability
density function (pdf) is:
poissonpdf(m,x)
poissoncdf(
poissoncdf( computes a cumulative probability at x for the discrete Poisson distribution with the
specified mean m, which must be a real number > 0. x can be a real number or a list of real
numbers.
poissoncdf(m,x)
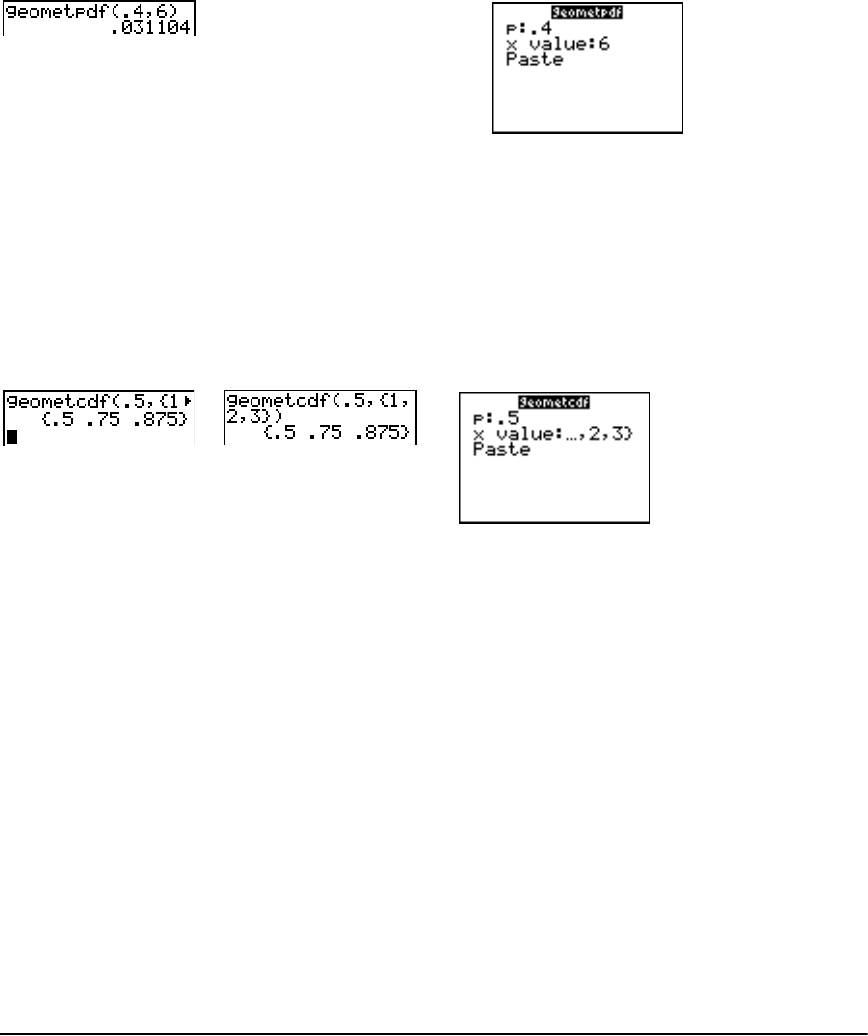
fx() p1p–()
x1– x, 1,2,...==
Chapter 13: Inferential Statistics and Distributions 248
geometpdf(
geometpdf( computes a probability at x, the number of the trial on which the first success occurs,
for the discrete geometric distribution with the specified probability of success p. 0p1 must be
true. x can be an integer or a list of integers. The probability density function (pdf) is:
geometpdf(p,x)
geometcdf(
geometcdf( computes a cumulative probability at x, the number of the trial on which the first
success occurs, for the discrete geometric distribution with the specified probability of success p.
0p1 must be true. x can be a real number or a list of real numbers.
geometcdf(p,x)
MathPrint™
Classic
Distribution Shading
DISTR DRAW Menu
To display the DISTR DRAW menu, press y = ~. DISTR DRAW instructions draw various
types of density functions, shade the area specified by lowerbound and upperbound, and display the
computed area value.
Selecting an item from the DIST DRAW menu opens a wizard for the input of syntax for that item.
Some of the arguments are optional. If an argument is not optional, the cursor will not move on to
the next argument until a value is entered.
If you access any of these functions through CATALOG, the command or function will paste and
you will be required to fill in the arguments.
To clear the drawings, select 1:ClrDraw from the DRAW menu (Chapter 8).
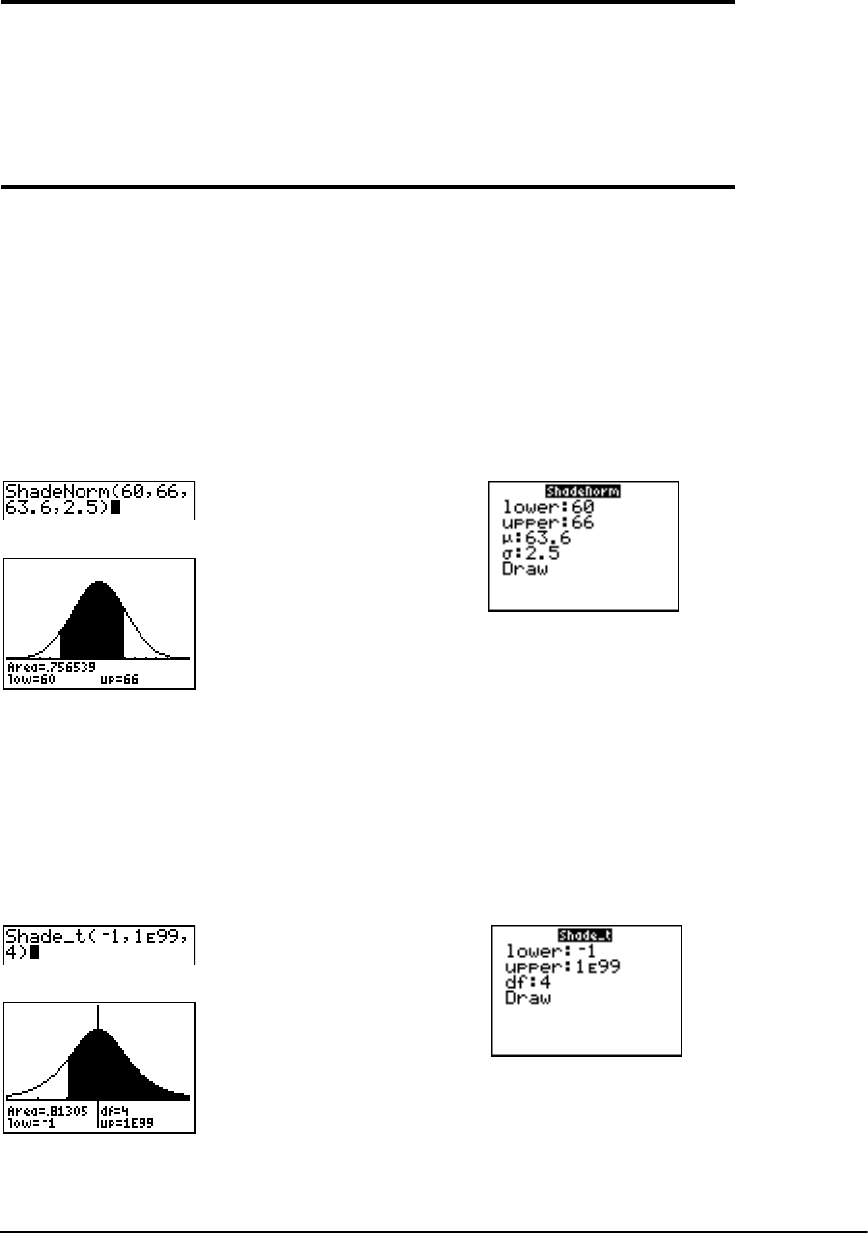
Chapter 13: Inferential Statistics and Distributions 249
Note: Before you execute a DISTR DRAW instruction, you must set the window variables so that the
desired distribution fits the screen.
DISTR DRAW
1: ShadeNorm( Shades normal distribution.
2: Shade_t( Shades Student-t distribution.
3: Shadec2(Shades c2 distribution.
4: ShadeÜ(Shades Üdistribution.
Note: L1â99 and 1â99 specify infinity. If you want to view the area left of upperbound, for example,
specify lowerbound=L1â99.
ShadeNorm(
ShadeNorm( draws the normal density function specified by mean m and standard deviation s and
shades the area between lowerbound and upperbound. The defaults are m=0 and s=1.
ShadeNorm(lowerbound,upperbound[,m,s])
Classic
Note: For this example,
Xmin = 55
Xmax = 72
Ymin = L.05
Ymax = .2
Shade_t(
Shade_t( draws the density function for the Student-t distribution specified by df (degrees of
freedom) and shades the area between lowerbound and upperbound.
Shade_t(lowerbound,upperbound,df)
Classic
Note: For this example,
Xmin = L3
Xmax = 3
Ymin = L.15
Ymax = .5
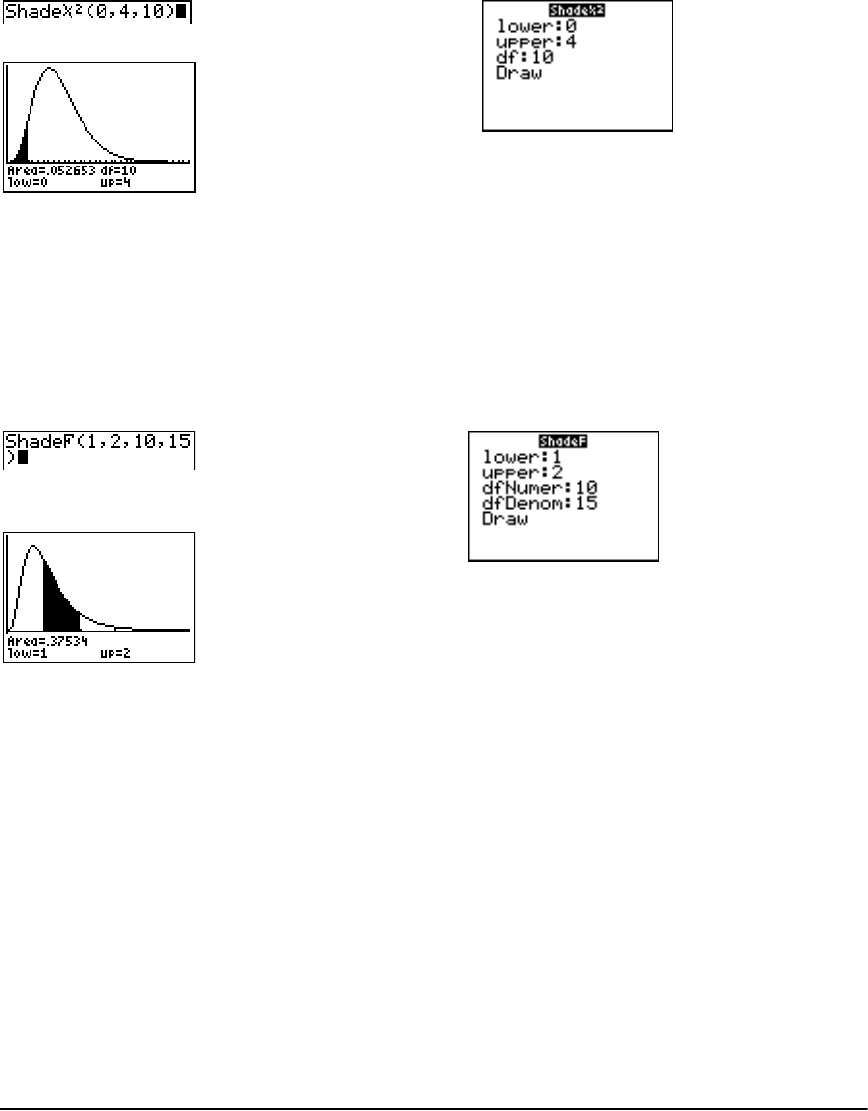
Chapter 13: Inferential Statistics and Distributions 250
Shadec2(
Shadec2( draws the density function for the c2 (chi-square) distribution specified by df (degrees of
freedom) and shades the area between lowerbound and upperbound.
Shadec2(lowerbound,upperbound,df)
Classic
Note: For this example,
Xmin = 0
Xmax = 35
Ymin = L.025
Ymax = .1
ShadeF(
ShadeÜ( draws the density function for the Ü distribution specified by numerator df (degrees of
freedom) and denominator df and shades the area between lowerbound and upperbound.
ShadeÜ(lowerbound,upperbound,numerator df,denominator df)
Classic
Note: For this example,
Xmin = 0
Xmax = 5
Ymin = L.25
Ymax = .9

Chapter 14: Applications 251
Chapter 14:
Applications
The Applications Menu
The TI-84 Plus comes with several applications already installed and listed on the APPLICATIONS
menu. These applications include the following:
Finance
Topics in Algebra 1
Science Tools
Catalog Help 1.1
CellSheet™
Conic Graphing
Inequality Graphing
Transformation Graphing
Vernier EasyData™
DataMate
Polynomial Root Finder and Simultaneous Equation Solver
StudyCards™
LearningCheck™
Except for the Finance application, you can add and remove applications as space permits. The
Finance application is built into the TI-84 Plus code and cannot be deleted.
Many other applications in addition to the ones mentioned above, including language localization
applications, are included on your TI-84 Plus. Press ŒÎ to see the complete list of applications
that came with your calculator.
You can download additional TI-84 Plus software applications from education.ti.com that allow you
to customize your calculator’s functionality even further. The calculator reserves 1.54 M of space
within ROM memory specifically for applications.
Guidebooks for applications are on the Texas Instruments Web site at: education.ti.com/guides.
Steps for Running the Finance Application
Follow these basic steps when using the Finance application.
1. Press Œ Í to select the Finance application.
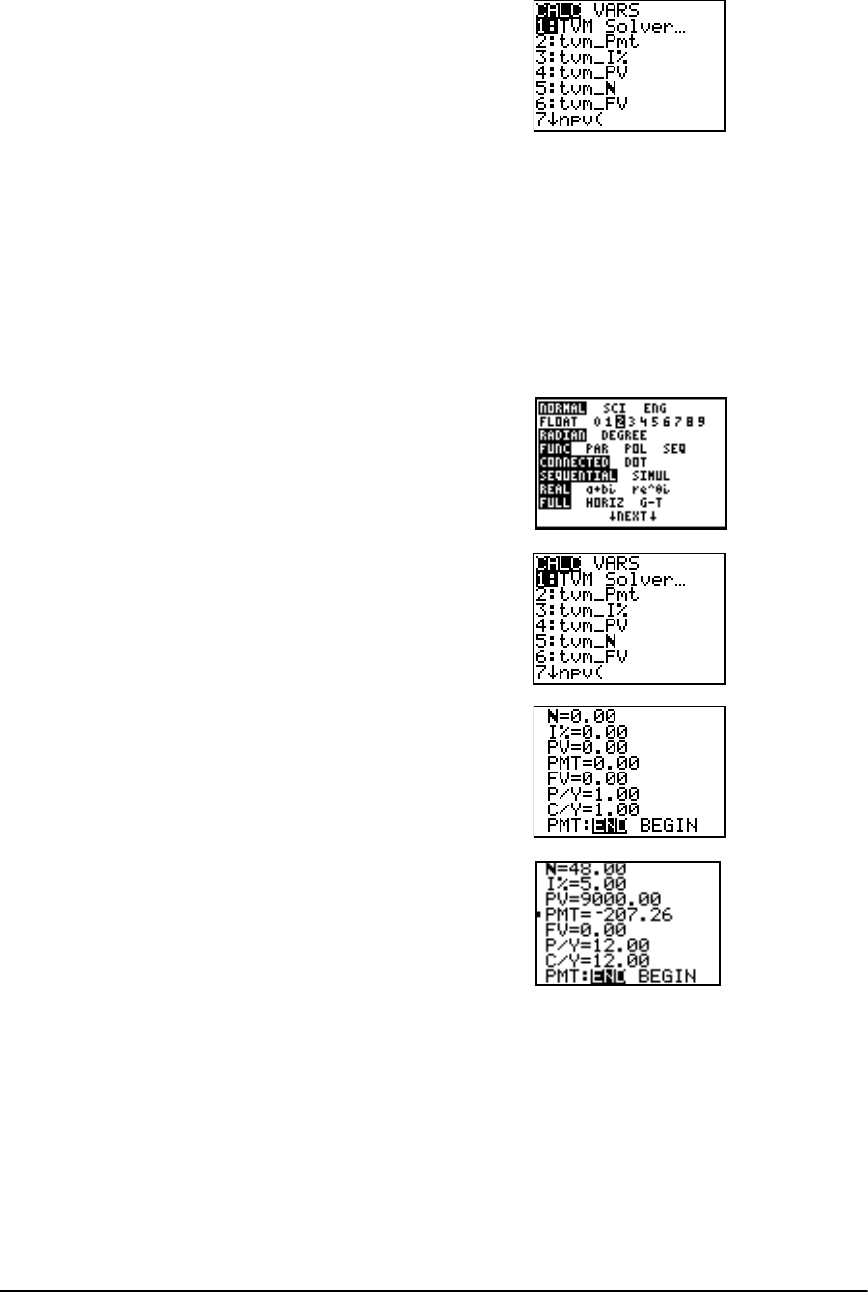
Chapter 14: Applications 252
Getting Started: Financing a Car
Getting Started is a fast-paced introduction. Read the chapter for details.
You have found a car you would like to buy. You can afford payments of 250 per month for four
years. The car costs 9,000. Your bank offers an interest rate of 5%. What will your payments be?
Can you afford it?
2. Select from list of functions.
1. Press z † ~ ~ ~ Í to set the fixed-decimal
mode setting to 2.
2. Press Œ Í to select 1:Finance from the
APPLICATIONS menu.
3. Press Í to select 1:TVM Solver from the
CALC VARS menu. The TVM Solver is displayed.
4. Enter the data:
N (number of payments)= 48
I% (interest rate)=5
PV (present value)=9000
FV (future value)=0
P/Y (payments per year)=12
C/Y (compounding periods per year)=12
5. Select PMT:END, which indicates that payments are
due at the end of each period.
6. Move the cursor to PMT and press ƒ \. Can
you afford the payment?

Chapter 14: Applications 253
Getting Started: Computing Compound Interest
At what annual interest rate, compounded monthly, will 1,250 accumulate to 2,000 in 7 years?
Note: Because there are no payments when you solve compound interest problems, PMT must be
set to 0 and P/Y must be set to 1.
1. Press Œ Í to select 1:Finance from the
APPLICATIONS menu.
2. Press Í to select 1:TVM Solver from the CALC
VARS menu. The TVM Solver is displayed.
3. Enter the data:
N=7
PV=M1250
PMT=0
FV=2000
P/Y=1
C/Y=12
4. Move the curstor to æ and press ƒ \.
YYou need to look for an interest rate of 6.73% to grow
1250 to 2000 in 7 years.
Using the TVM Solver
Using the TVM Solver
The TVM Solver displays the time-value-of-money (TVM) variables. Given four variable values,
the TVM Solver solves for the fifth variable.
The FINANCE VARS menu section describes the five TVM variables (Ú, æ, PV, PMT, and FV) and
P/Y and C/Y.
PMT: END BEGIN in the TVM Solver corresponds to the FINANCE CALC menu items Pmt_End
(payment at the end of each period) and Pmt_Bgn (payment at the beginning of each period).
To solve for an unknown TVM variable, follow these steps.
1. Press Œ Í Í to display the TVM Solver. The screen below shows the default
values with the fixed-decimal mode set to two decimal places.

Chapter 14: Applications 254
2. Enter the known values for four TVM variables.
Note: Enter cash inflows as positive numbers and cash outflows as negative numbers.
3. Enter a value for P/Y, which automatically enters the same value for C/Y; if P/Y ƒ C/Y, enter a
unique value for C/Y.
4. Select END or BEGIN to specify the payment method.
5. Place the cursor on the TVM variable for which you want to solve.
6. Press ƒ \. The answer is computed, displayed in the TVM Solver, and stored to the
appropriate TVM variable. An indicator square in the left column designates the solution
variable.
Using the Financial Functions
Entering Cash Inflows and Cash Outflows
When using the TI-84 Plus financial functions, you must enter cash inflows (cash received) as
positive numbers and cash outflows (cash paid) as negative numbers. The TI-84 Plus follows this
convention when computing and displaying answers.
FINANCE CALC Menu
To display the FINANCE CALC menu, press ÎŒ Í.
CALC VARS
1: TVM Solver... Displays the TVM Solver.
2: tvm_Pmt Computes the amount of each payment.
3: tvm_¾
¾¾¾æ Computes the interest rate per year.
4: tvm_PV Computes the present value.
5: tvm_ò
òòòÚ Computes the number of payment periods.
6: tvm_FV Computes the future value.
7: npv( Computes the net present value.
Chapter 14: Applications 255
Use these functions to set up and perform financial calculations on the home screen.
TVM Solver
TVM Solver displays the TVM Solver.
Calculating Time Value of Money (TVM)
Calculating Time Value of Money
Use time-value-of-money (TVM) functions (menu items 2 through 6) to analyze financial
instruments such as annuities, loans, mortgages, leases, and savings.
Each TVM function takes zero to six arguments, which must be real numbers. The values that you
specify as arguments for TVM functions are not stored to the TVM variables.
Note: To store a value to a TVM variable, use the TVM Solver or use ¿ and any TVM variable
on the FINANCE VARS menu.
If you enter less than six arguments, the TI-84 Plus substitutes a previously stored TVM variable
value for each unspecified argument.
If you enter any arguments with a TVM function, you must place the argument or arguments in
parentheses.
8: irr( Computes the internal rate of return.
9: bal( Computes the amortization sched. balance.
0: GPrn( Computes the amort. sched. princ. sum.
A: GInt( Computes the amort. sched. interest sum.
B: 4Nom( Computes the nominal interest rate.
C: 4Eff( Computes the effective interest rate.
D: dbd( Calculates the days between two dates.
E: Pmt_End Selects ordinary annuity (end of period).
F: Pmt_Bgn Selects annuity due (beginning of period).
CALC VARS
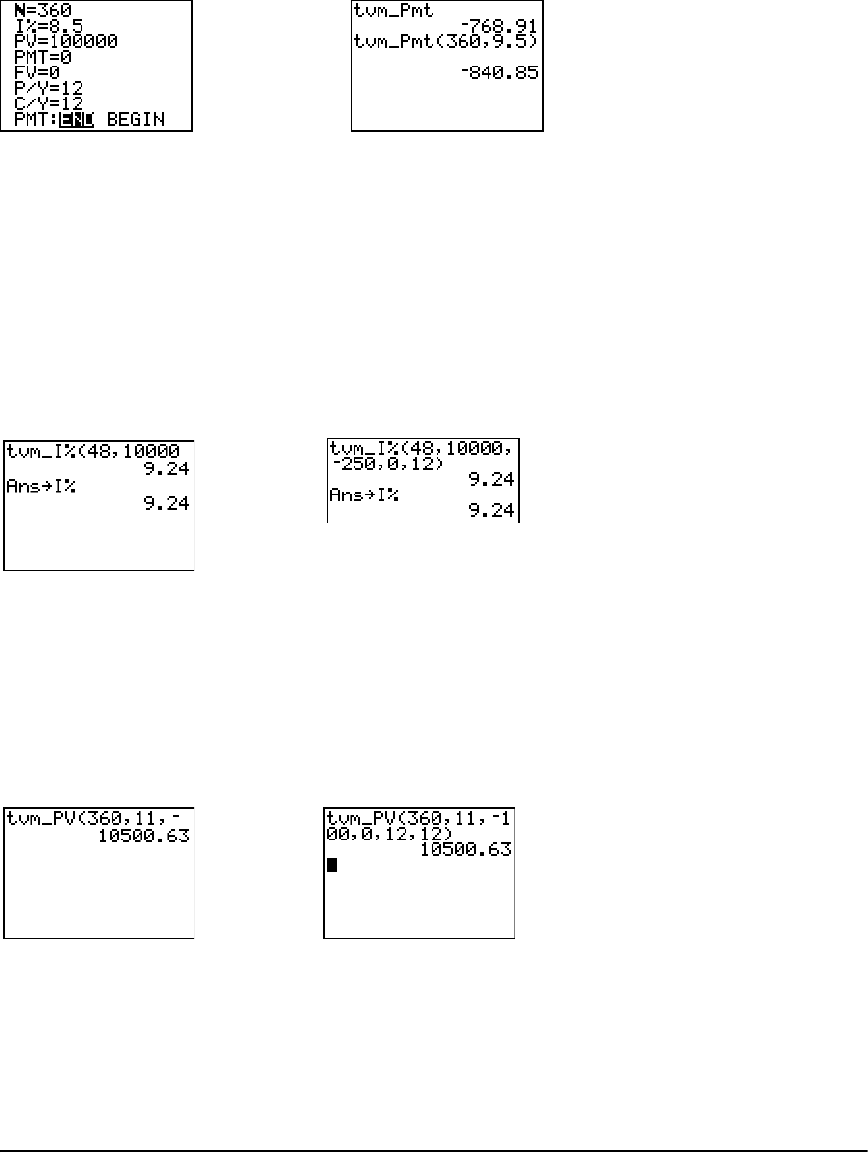
Chapter 14: Applications 256
tvm_Pmt
tvm_Pmt computes the amount of each payment.
tvm_Pmt[(òÚ,¾æ,PV,FV,P/Y,C/Y)]
Note: In the example above, the values are stored to the TVM variables in the TVM Solver. The
payment (tvm_Pmt) is computed on the home screen using the values in the TVM Solver. Next,
the interest rate is changed to 9.5 to illustrate the effect on the payment amount.
tvm_I%
tvm_æ computes the annual interest rate.
tvm_¾æ [(Ú,PV,PMT,FV,P/Y,C/Y)]
tvm_PV
tvm_PV computes the present value.
tvm_PV[(Ú,¾æ,PMT,FV,P/Y,C/Y)]
tvm_N
tvm_Ú computes the number of payment periods.
MathPrint™
Classic
MathPrint™
Classic
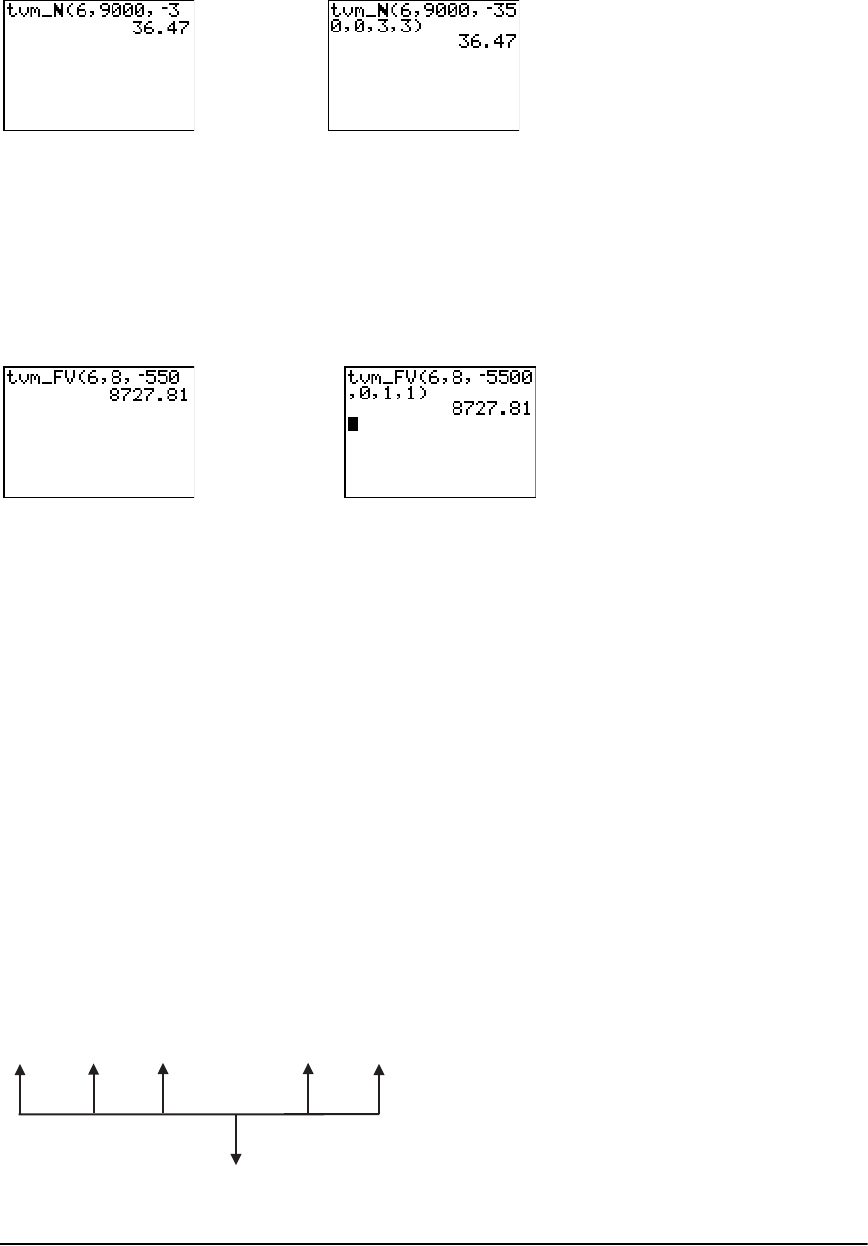
2000 4000 40002000 2000
-3000
Chapter 14: Applications 257
tvm_Ú[(æ¾,PV,PMT,FV,P/Y,C/Y)]
tvm_FV
tvm_FV computes the future value.
tvm_FV[(Ú,¾æ,PV,PMT,P/Y,C/Y)]
Calculating Cash Flows
Calculating a Cash Flow
Use the cash flow functions (menu items 7 and 8) to analyze the value of money over equal time
periods. You can enter unequal cash flows, which can be cash inflows or outflows. The syntax
descriptions for npv( and irr( use these arguments.
•interest rate is the rate by which to discount the cash flows (the cost of money) over one period.
•CF0 is the initial cash flow at time 0; it must be a real number.
•CFList is a list of cash flow amounts after the initial cash flow CF0.
•CFFreq is a list in which each element specifies the frequency of occurrence for a grouped
(consecutive) cash flow amount, which is the corresponding element of CFList. The default is 1;
if you enter values, they must be positive integers < 10,000.
For example, express this uneven cash flow in lists.
MathPrint™
Classic
MathPrint™
Classic
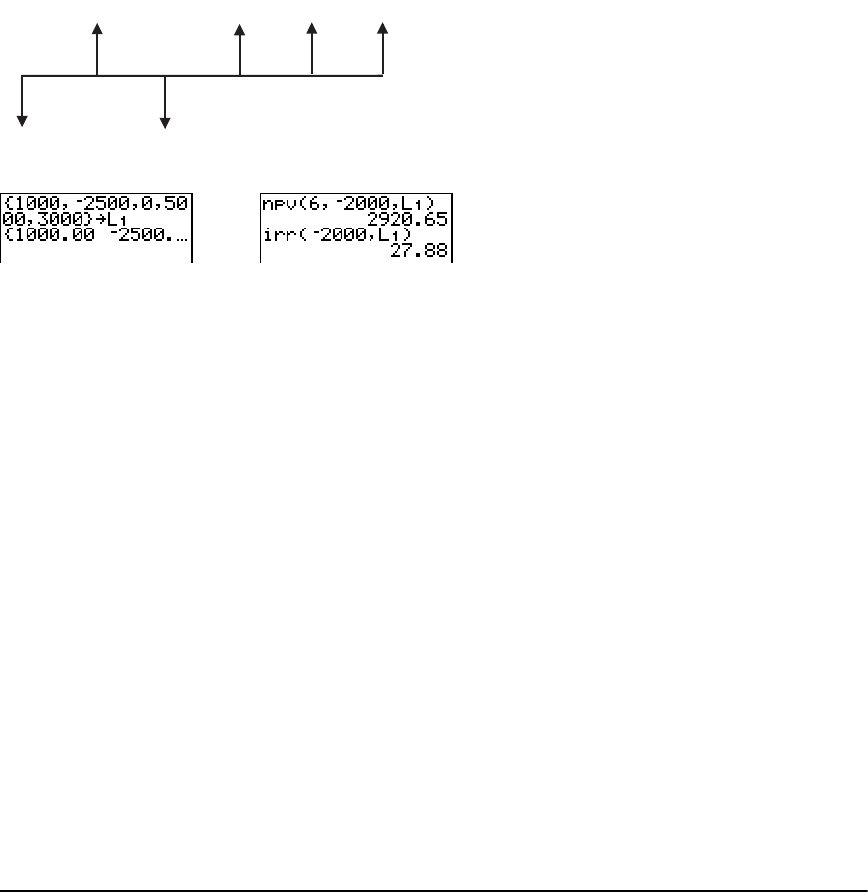
1000
-2000 -2500
050003000
Chapter 14: Applications 258
CF0 = 2000
CFList = {2000,L3000,4000}
CFFreq = {2,1,2}
npv(, irr(
npv( (net present value) is the sum of the present values for the cash inflows and outflows. A
positive result for npv indicates a profitable investment.
npv(interest rate,CF0,CFList[,CFFreq])
irr( (internal rate of return) is the interest rate at which the net present value of the cash flows is
equal to zero.
irr(CF0,CFList[,CFFreq])
Calculating Amortization
Calculating an Amortization Schedule
Use the amortization functions (menu items 9, 0, and A) to calculate balance, sum of principal, and
sum of interest for an amortization schedule.
bal(
bal( computes the balance for an amortization schedule using stored values for æ, PV, and PMT.
npmt is the number of the payment at which you want to calculate a balance. It must be a positive
integer < 10,000. roundvalue specifies the internal precision the calculator uses to calculate the
balance; if you do not specify roundvalue, then the TI-84 Plus uses the current Float/Fix decimal-
mode setting.

Chapter 14: Applications 259
bal(npmt[,roundvalue])
GPrn(, GInt(
GPrn( computes the sum of the principal during a specified period for an amortization schedule using
stored values for ¾æ, PV, and PMT. pmt1 is the starting payment. pmt2 is the ending payment in the
range. pmt1 and pmt2 must be positive integers < 10,000. roundvalue specifies the internal precision
the calculator uses to calculate the principal; if you do not specify roundvalue, the TI-84 Plus uses the
current Float/Fix decimal-mode setting.
Note: You must enter values for æ, PV, PMT, and before computing the principal.
GPrn(pmt1,pmt2[,roundvalue])
GInt( computes the sum of the interest during a specified period for an amortization schedule using
stored values for ¾æ, PV, and PMT. pmt1 is the starting payment. pmt2 is the ending payment in the
range. pmt1 and pmt2 must be positive integers < 10,000. roundvalue specifies the internal precision
the calculator uses to calculate the interest; if you do not specify roundvalue, the TI-84 Plus uses the
current Float/Fix decimal-mode setting.
GInt(pmt1,pmt2[,roundvalue])
Amortization Example: Calculating an Outstanding Loan Balance
You want to buy a home with a 30-year mortgage at 8 percent APR. Monthly payments are 800.
Calculate the outstanding loan balance after each payment and display the results in a graph and
in the table.
1. Press z. Press † ~ ~ ~ Í to set the
fixed-decimal mode setting to 2. Press † † ~ Í to
select Par graphing mode.
2. Press Œ Í Í to display the TVM Solver.
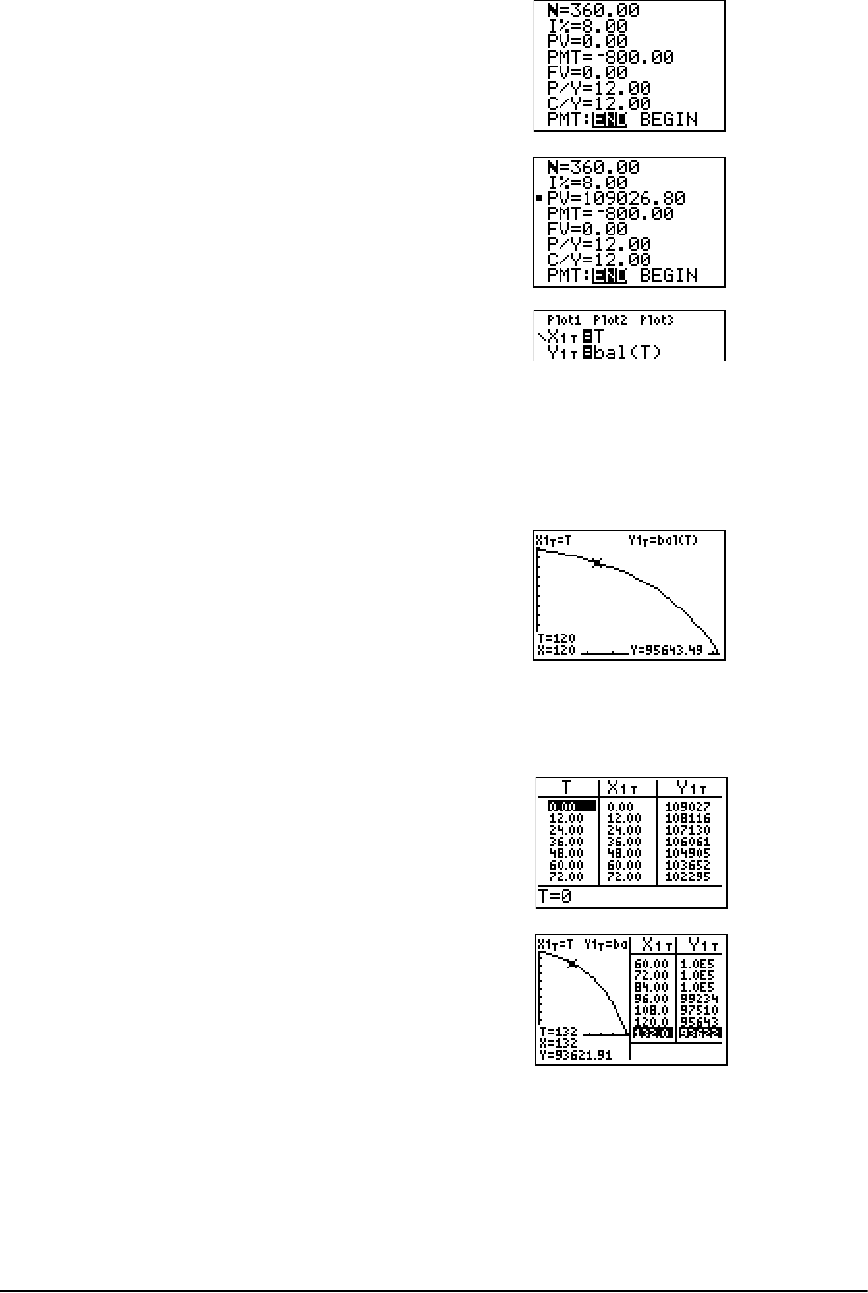
Chapter 14: Applications 260
3. Press 360 to enter number of payments. Press † 8 to
enter the interest rate. Press † † Ì 800 to enter the
payment amount. Press † 0 to enter the future value
of the mortgage. Press † 12 to enter the payments per
year, which also sets the compounding periods per
year to 12. Press † † Í to select PMT:END.
4. Move the cursor to the PV prompt and then press ƒ
\ to solve for the present value.
5. Press o to display the parametric Y= editor. Turn off
all stat plots. Press „ to define X1T as T. Press †
Œ Í 9 „ ¤ to define Y1T as bal(T).
6. Press p to display the window variables. Enter the
values below.
Tmin=0 Xmin=0 Ymin=0
Tmax=360 Xmax=360 Ymax=125000
Tstep=12 Xscl=50 Yscl=10000
7. Press r to draw the graph and activate the trace
cursor. Press ~ and | to explore the graph of the
outstanding balance over time. Press a number and
then press Í to view the balance at a specific
time T.
8. Press y - and enter the values below.
TblStart=0
@Tbl=12
9. Press y 0 to display the table of outstanding
balances (Y1T).
10. Press z and select G-T split-screen mode, so that
the graph and table are displayed simultaneously.
Press r to display X1T (time) and Y1T (balance) in
the table.

Chapter 14: Applications 261
Calculating Interest Conversion
Calculating an Interest Conversion
Use the interest conversion functions (menu items B and C) to convert interest rates from an
annual effective rate to a nominal rate (4Nom( ) or from a nominal rate to an annual effective rate
(4Eff( ).
4Nom(
4Nom( computes the nominal interest rate. effective rate and compounding periods must be real
numbers. compounding periods must be >0.
4Nom(effective rate,compounding periods)
4Eff(
4Eff( computes the effective interest rate. nominal rate and compounding periods must be real numbers.
compounding periods must be >0.
4Eff(nominal rate,compounding periods)
Finding Days between Dates/Defining Payment Method
dbd(
Use the date function dbd( (menu item D) to calculate the number of days between two dates using
the actual-day-count method. date1 and date2 can be numbers or lists of numbers within the range
of the dates on the standard calendar.
Note: Dates must be between the years 1950 through 2049.
dbd(date1,date2)
You can enter date1 and date2 in either of two formats.
• MM.DDYY (United States)
• DDMM.YY (Europe)
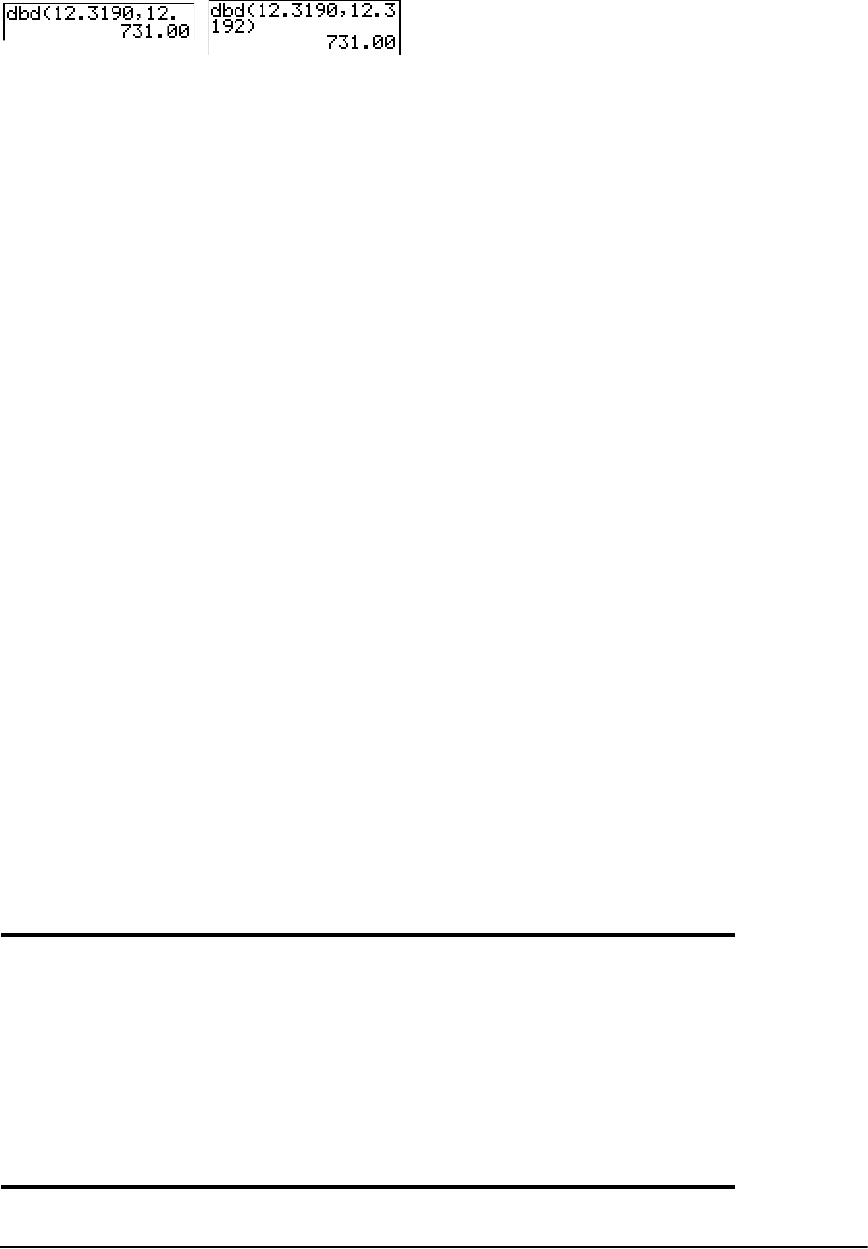
Chapter 14: Applications 262
The decimal placement differentiates the date formats.
Defining the Payment Method
Pmt_End and Pmt_Bgn (menu items E and F) specify a transaction as an ordinary annuity or an
annuity due. When you execute either command, the TVM Solver is updated.
Pmt_End
Pmt_End (payment end) specifies an ordinary annuity, where payments occur at the end of each
payment period. Most loans are in this category. Pmt_End is the default.
Pmt_End
On the TVM Solver’s PMT:END BEGIN line, select END to set PMT to ordinary annuity.
Pmt_Bgn
Pmt_Bgn (payment beginning) specifies an annuity due, where payments occur at the beginning of
each payment period. Most leases are in this category.
Pmt_Bgn
On the TVM Solver’s PMT:END BEGIN line, select BEGIN to set PMT to annuity due.
Using the TVM Variables
FINANCE VARS Menu
To display the FINANCE VARS menu, press Œ Í ~. You can use TVM variables in TVM
functions and store values to them on the home screen.
MathPrint™
Classic
CALC VARS
1: ÚTotal number of payment periods
2: æAnnual interest rate
3: PV Present value
4: PMT Payment amount
5: FV Future value
6: P/Y Number of payment periods per year

Chapter 14: Applications 263
N, I%, PV, PMT, FV
Ú, æ, PV, PMT, and FV are the five TVM variables. They represent the elements of common
financial transactions, as described in the table above. æ is an annual interest rate that is
converted to a per-period rate based on the values of P/Y and C/Y.
P/Y and C/Y
P/Y is the number of payment periods per year in a financial transaction.
C/Y is the number of compounding periods per year in the same transaction.
When you store a value to P/Y, the value for C/Y automatically changes to the same value. To
store a unique value to C/Y, you must store the value to C/Y after you have stored a value to P/Y.
The EasyData™ Application
The Vernier EasyData™ application by Vernier Software & Technology allows you to view and
analyze real-world data when the TI-84 Plus is connected to data collection devices such as Texas
Instruments CBR 2é, CBL 2é, Vernier LabProê, Vernier USB sensors, Vernier Go!éMotion, or
Vernier Motion Detector Unit. The TI-84 Plus comes with the EasyData™ App already installed.
Note: The application will only work with Vernier auto-ID sensors when using CBL 2é and
Vernier LabProê.
The EasyData™ App will autolaunch on your TI-84 Plus if you plug in a USB sensor such as the
CBR 2é or Vernier USB Temperature sensor.
Steps for Running the EasyData™ App
Follow these basic steps when using the EasyData™ App.
7: C/Y Number of compounding periods/year
CALC VARS

Chapter 14: Applications 264
Starting the EasyData™ App
1. Attach your data collection device to your TI-84 Plus.
Make sure the cables are firmly connected.
2. If the EasyData™ App has not auto-launched, press
Œ and the } or † to select the EasyData™ App.
3. Press Í. The EasyData™ information screen is
displayed for about three seconds followed by the main
screen.
Quitting the EasyData™ App
1. To quit the EasyData™ App, select Quit (press s).
The Ready to quit? screen is displayed, which indicates that the collected data has been
transferred to lists L1 through L4 on the TI-84 Plus.
2. Press OK (press s) to quit.
EasyData™ Settings
Changing EasyData™ settings
The EasyData™ App displays the most commonly used settings before data collection begins.
To change a predefined setting:
1. From the main screen in the EasyData™ App, choose Setup and select 2: Time Graph. The
current settings are displayed on the calculator.
Note: If using a motion detector, settings for 3: Distance Match and 4: Ball Bounce in the Setup
menu are preset and cannot be changed.
2. Select Next (press q) to move to the setting you want to change. Press ‘ to clear a
setting.
3. Repeat to cycle through the available options. When the option is correct, select Next to move
to the next option.
4. To change a setting, enter 1 or 2 digits, and then select Next (press q).
5. When all the settings are correct, select OK (press s) to return to the main menu.
6. Select Start (press q) to begin collecting data.
Restoring the EasyData™ App to the default settings
The default settings are appropriate for a wide variety of sampling situations. If you are unsure of
the best settings, begin with the default settings, and then adjust the settings for your specific
activity.
To restore the default settings in the EasyData™ App while a data collection device is connected
to the TI-84 Plus, choose File and select 1:New.

Chapter 14: Applications 265
Starting and Stopping Data Collection
Starting Data Collection
To start sampling, select Start (press q). Sampling will automatically stop when the number of
samples set in the Time Graph Settings menu is reached. The TI-84 Plus will then display a graph
of the sampled data.
Stopping Data Collection
To stop sampling before it automatically stops, select Stop (press and hold q) at any time
during the sampling process. When sampling stops, a graph of the sampled data is displayed.
Saving Collected Data
Collected data is automatically transferred to the TI-84 Plus and stored in lists L1 through L4 when
data collection is complete. When you exit the EasyData™ App, a prompt reminds you of the lists
in which time, distance, velocity, and acceleration are stored.
This manual describes basic operation for the EasyData 2 application. For more information about
the EasyData 2 App, visit www.vernier.com.
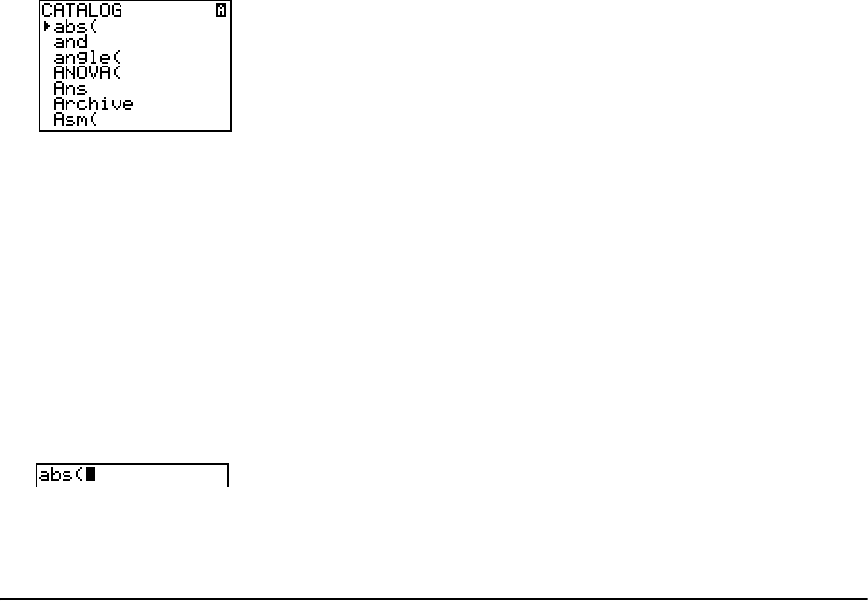
Chapter 15: CATALOG, Strings, Hyperbolic Functions 266
Chapter 15:
CATALOG, Strings, Hyperbolic Functions
Browsing the TI-84 Plus CATALOG
What Is the CATALOG?
The CATALOG is an alphabetical list of all functions and instructions on the TI-84 Plus. You also
can access each CATALOG item from a menu or the keyboard, except:
• The six string functions
• The six hyperbolic functions
•The
solve( instruction without the equation solver editor (Chapter 2)
• The inferential stat functions without the inferential stat editors (Chapter 13)
Note: The only CATALOG programming commands you can execute from the home screen are
GetCalc(, Get(, and Send(.
Selecting an Item from the CATALOG
To select a CATALOG item, follow these steps.
1. Press y N to display the CATALOG.
The 4 in the first column is the selection cursor.
2. Press † or } to scroll the CATALOG until the selection cursor points to the item you want.
• To jump to the first item beginning with a particular letter, press that letter; alpha-lock is
on.
• Items that begin with a number are in alphabetical order according to the first letter after
the number. For example, 2-PropZTest( is among the items that begin with the letter P.
• Functions that appear as symbols, such as +, L1, <, and ‡(, follow the last item that begins
with Z. To jump to the first symbol, !, press [q].
3. Press Í to paste the item to the current screen.

Chapter 15: CATALOG, Strings, Hyperbolic Functions 267
Note:
• From the top of the CATALOG menu, press } to move to the bottom. From the bottom, press
†to move to the top.
• When your TI-84 Plus is in MathPrint™ mode, many functions will paste the MathPrint™
template on the home screen. For example, abs( pastes the absolute value template on the
home screen instead of abs(.
Entering and Using Strings
What Is a String?
A string is a sequence of characters that you enclose within quotation marks. On the TI-84 Plus, a
string has two primary applications.
• It defines text to be displayed in a program.
• It accepts input from the keyboard in a program.
Characters are the units that you combine to form a string.
• Each number, letter, and space counts as one character.
• Each instruction or function name, such as sin( or cos(, counts as one character; the TI-84
Plus interprets each instruction or function name as one character.
Entering a String
To enter a string on a blank line on the home screen or in a program, follow these steps.
1. Press ƒ [ã] to indicate the beginning of the string.
2. Enter the characters that comprise the string.
• Use any combination of numbers, letters, function names, or instruction names to create
the string.
• To enter a blank space, press ƒ O.
• To enter several alpha characters in a row, press y 7 to activate alpha-lock.
3. Press ƒ [ã] to indicate the end of the string.
ãstringã
4. Press Í. On the home screen, the string is displayed on the next line without quotations. An
ellipsis (...) indicates that the string continues beyond the screen. To scroll to see the entire string,
press ~ and |.
MathPrint™
Classic

Chapter 15: CATALOG, Strings, Hyperbolic Functions 268
Note: A string must be enclosed in quotation marks. The quotation marks do not count as string
characters.
Storing Strings to String Variables
String Variables
The TI-84 Plus has 10 variables to which you can store strings. You can use string variables with
string functions and instructions.
To display the VARS STRING menu, follow these steps.
1. Press to display the VARS menu. Move the cursor to 7:String.
2. Press Í to display the STRING secondary menu.
Storing a String to a String Variable
To store a string to a string variable, follow these steps.
1. Press ƒ [ã], enter the string, and press ƒ [ã].
2. Press ¿.
3. Press 7 to display the VARS STRING menu.
4. Select the string variable (from Str1 to Str9, or Str0) to which you want to store the string.

Chapter 15: CATALOG, Strings, Hyperbolic Functions 269
The string variable is pasted to the current cursor location, next to the store symbol (!).
5. Press Í to store the string to the string variable. On the home screen, the stored string is
displayed on the next line without quotation marks.
Displaying the Contents of a String Variable
To display the contents of a string variable on the home screen, select the string variable from the
VARS STRING menu, and then press Í. The string is displayed.
String Functions and Instructions in the CATALOG
Displaying String Functions and Instructions in the CATALOG
String functions and instructions are available only from the CATALOG. The table below lists the
string functions and instructions in the order in which they appear among the other CATALOG
menu items. The ellipses in the table indicate the presence of additional CATALOG items.
CATALOG
...
Equ4String( Converts an equation to a string.
...
expr( Converts a string to an expression.
...
inString( Returns a character’s place number.
...
length( Returns a string’s character length.
...
String4Equ( Converts a string to an equation.
sub( Returns a string subset as a string.
...
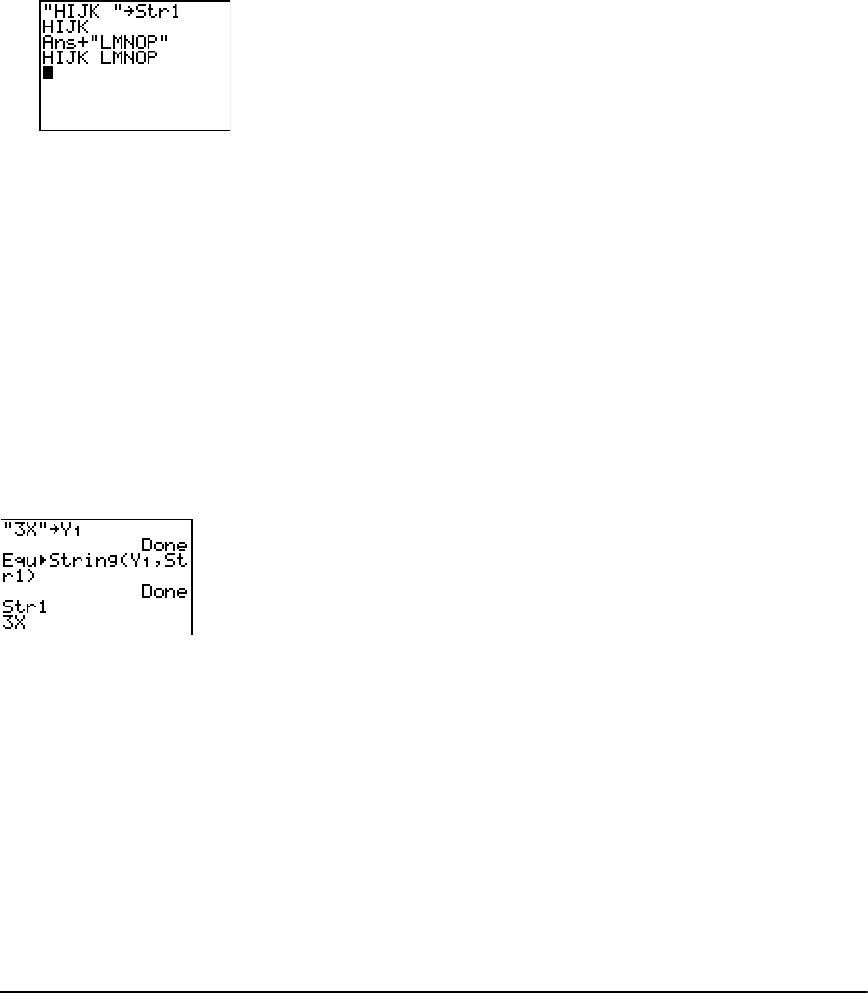
Chapter 15: CATALOG, Strings, Hyperbolic Functions 270
Concatenation
To concatenate two or more strings, follow these steps.
1. Enter string1, which can be a string or string name.
2. Press Ã.
3. Enter string2, which can be a string or string name. If necessary, press à and enter string3, and
so on.
string1+string2+string3...
4. Press Í to display the strings as a single string.
Selecting a String Function from the CATALOG
To select a string function or instruction and paste it to the current screen, follow the steps for
selecting an item from the CATALOG.
Equ4String(
Equ4String( converts an equation to a string. The equation must be store in a VARS Y-VARS
variable. Yn contains the equation. Strn (from Str1 to Str9, or Str0) is the string variable to which
you want the equation to be stored.
Equ4String(Yn,Strn)
expr(
expr( converts the character string contained in string to an expression and executes it. string can
be a string or a string variable.
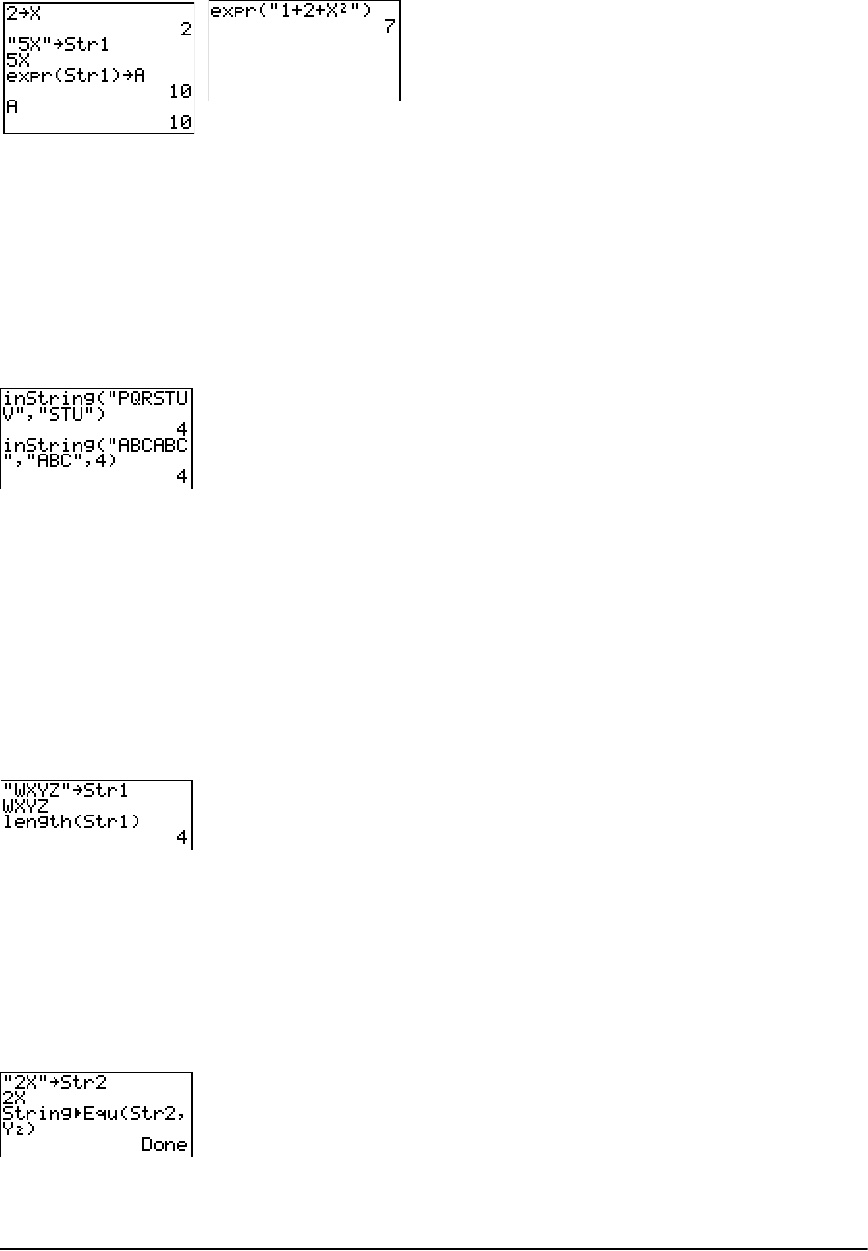
Chapter 15: CATALOG, Strings, Hyperbolic Functions 271
expr(string)
inString(
inString( returns the character position in string of the first character of substring. string can be a
string or a string variable. start is an optional character position at which to start the search; the
default is 1.
inString(string,substring[,start])
Note: If string does not contain substring, or start is greater than the length of string, inString( returns 0.
length(
length( returns the number of characters in string. string can be a string or string variable.
Note: An instruction or function name, such as sin( or cos(, counts as one character.
length(string)
String4Equ(
String4Equ( converts string into an equation and stores the equation to Yn. string can be a string or
string variable. String4Equ( is the inverse of Equ4String(.
String4Equ(string,Yn)
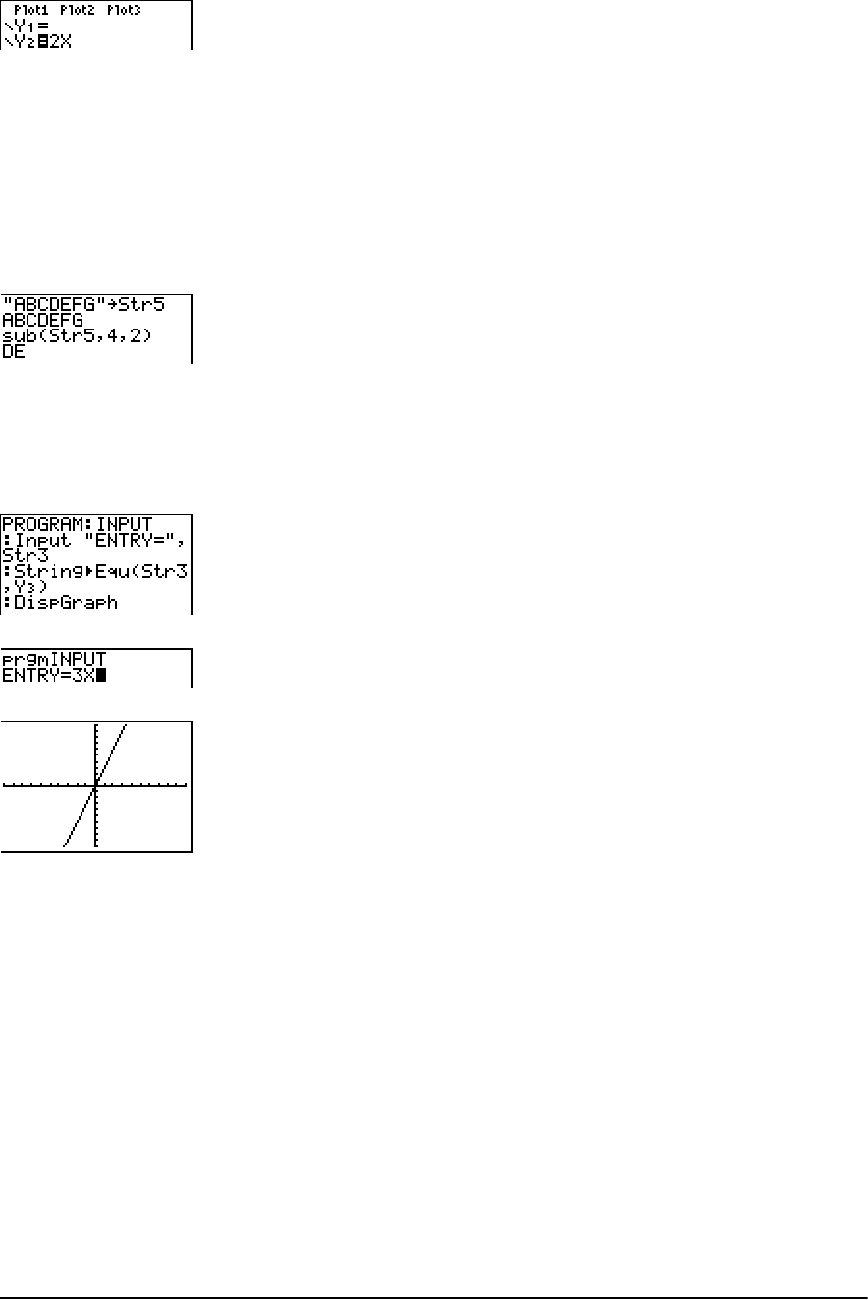
Chapter 15: CATALOG, Strings, Hyperbolic Functions 272
sub(
sub( returns a string that is a subset of an existing string. string can be a string or a string variable.
begin is the position number of the first character of the subset. length is the number of characters in
the subset.
sub(string,begin,length)
Entering a Function to Graph during Program Execution
In a program, you can enter a function to graph during program execution using these commands.
Note: When you execute this program, enter a function to store to Y3 at the ENTRY= prompt.
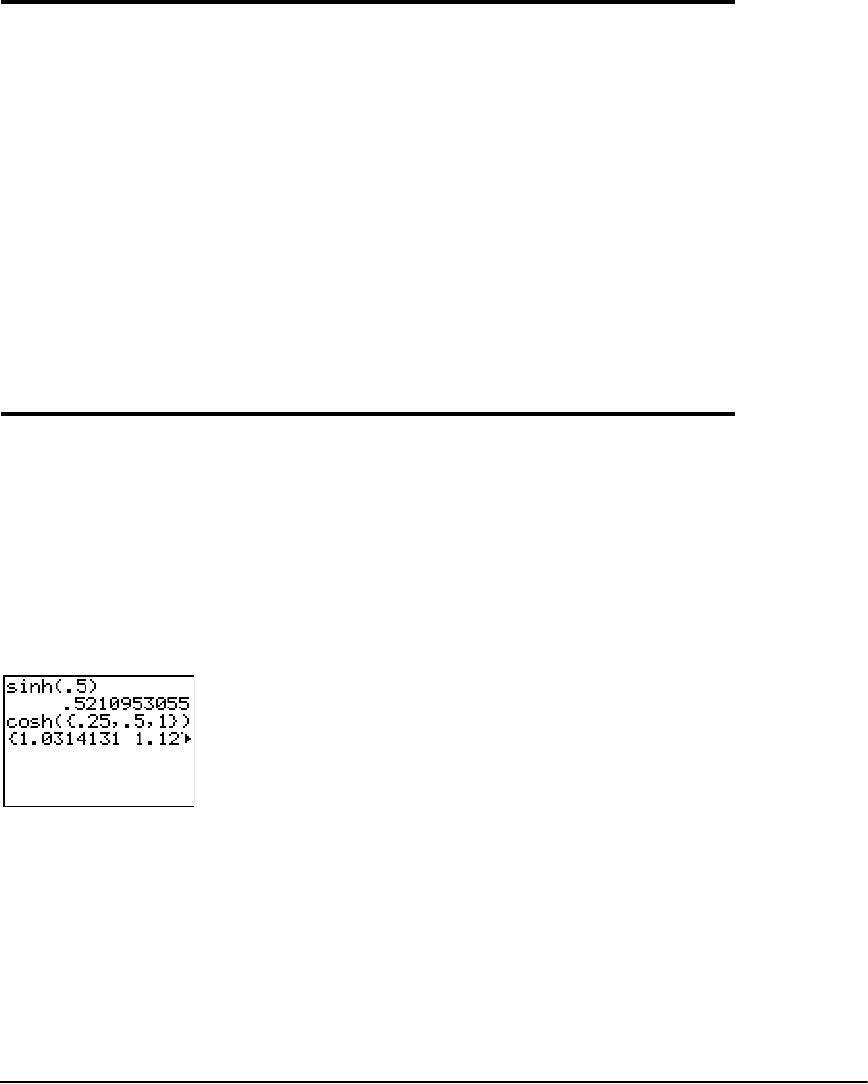
Chapter 15: CATALOG, Strings, Hyperbolic Functions 273
Hyperbolic Functions in the CATALOG
Hyperbolic Functions
The hyperbolic functions are available only from the CATALOG. The table below lists the
hyperbolic functions in the order in which they appear among the other CATALOG menu items. The
ellipses in the table indicate the presence of additional CATALOG items.
sinh(, cosh(, tanh(
sinh(, cosh(, and tanh( are the hyperbolic functions. Each is valid for real numbers, expressions,
and lists.
sinh(value)
cosh(value)
tanh(value)
sinh-1(, cosh-1(, tanh-1(
sinh-1( is the hyperbolic arcsine function. cosh-1( is the hyperbolic arccosine function. tanh-1( is the
hyperbolic arctangent function. Each is valid for real numbers, expressions, and lists.
CATALOG
...
cosh( Hyperbolic cosine
cosh-1(Hyperbolic arccosine
...
sinh( Hyperbolic sine
sinh-1(Hyperbolic arcsine
...
tanh( Hyperbolic tangent
tanh-1(Hyperbolic arctangent
...

Chapter 15: CATALOG, Strings, Hyperbolic Functions 274
sinh-1(value)
cosh-1(value)
tanh-1(value)
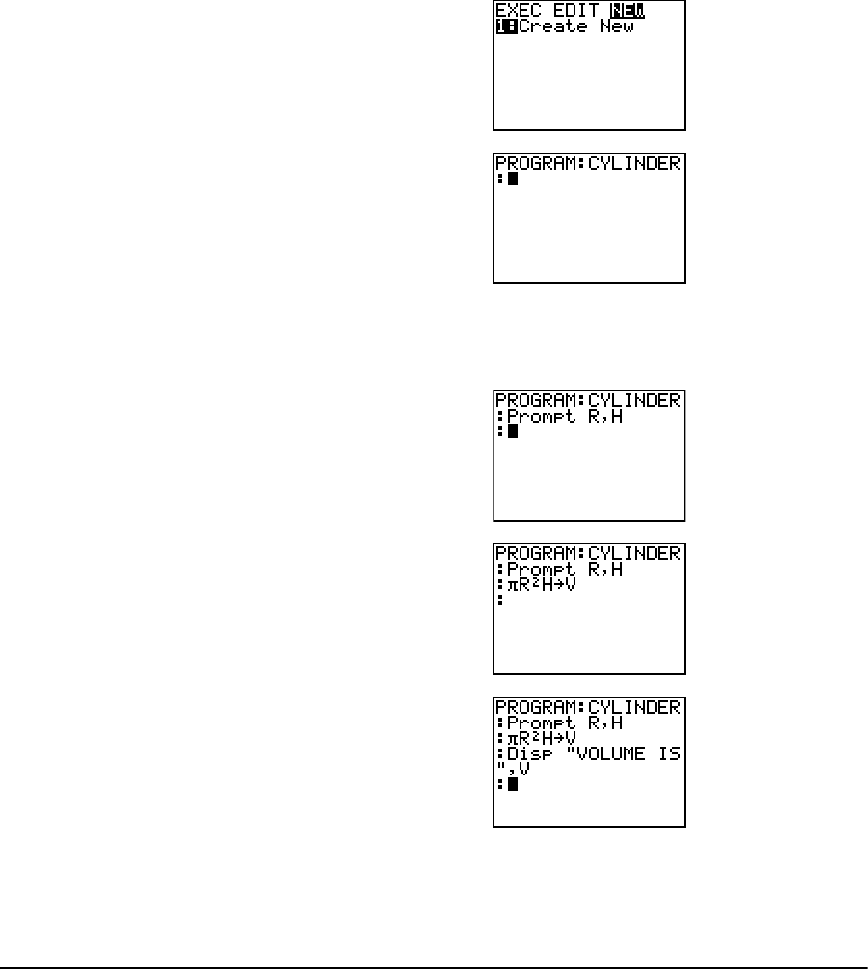
Chapter 16: Programming 275
Chapter 16:
Programming
Getting Started: Volume of a Cylinder
Getting Started is a fast-paced introduction. Read the chapter for details.
A program is a set of commands that the TI-84 Plus executes sequentially, as if you had entered
them from the keyboard. Create a program that prompts for the radius R and the height H of a
cylinder and then computes its volume.
1. Press ~ ~ to display the PRGM NEW menu.
2. Press Í to select 1:Create New. The Name=
prompt is displayed, and alpha-lock is on. Press C
Y L I N D E R, and then press Í to name the
program CYLINDER.
You are now in the program editor. The colon ( : )
in the first column of the second line indicates the
beginning of a command line.
3. Press ~ 2 to select 2:Prompt from the
PRGM I/O menu. Prompt is copied to the command
line. Press ƒ R ¢ ƒ H to enter the
variable names for radius and height. Press
Í.
4. Press y B ƒ R ¡ ƒ H ¿ ƒ V
Í to enter the expression pR2H and store it to
the variable V.
5. Press ~ 3 to select 3:Disp from the
PRGM I/O menu. Disp is pasted to the command
line. Press y 7 [ã] V O L U M E O I S [ã]
ƒ ¢ ƒ V Í to set up the program to
display the text VOLUME IS on one line and the
calculated value of V on the next.
6. Press y 5 to display the home screen.

Chapter 16: Programming 276
Creating and Deleting Programs
What Is a Program?
A program is a set of one or more command lines. Each line contains one or more instructions.
When you execute a program, the TI-84 Plus performs each instruction on each command line in
the same order in which you entered them. The number and size of programs that the TI-84 Plus
can store is limited only by available memory.
Operating Systems versions and programming
• Programs created with OS 2.43 and earlier should run correctly but may give unexpected
results when you run them using OS 2.53MP and higher. You should test programs created
with earlier OS versions to make sure you get the desired results.
• Programs can run in Classic or MathPrint™ mode.
• Shortcut menus are available wherever the MATH menu can be accessed.
• MathPrint™ templates are not available for programs. All input and output is in Classic format.
• You can use fractions in programs, but you should test the program to make sure that you get
the desired results.
• The spacing of the display may be slightly different in MathPrint™ mode than in Classic mode.
If you prefer the spacing in Classic mode, set the mode using a command in your program.
Screen shots for the examples in this chapter were taken in Classic mode.
• Stat Wizards are available only for syntax help for functions in the DISTR DISTR menu and the
seq( function (sequence) in the LIST OPS menu. Run the Catalog Help application for more
syntax help when programming.
7. Press to display the PRGM EXEC menu. The
items on this menu are the names of stored
programs.
8. Press Í to paste prgmCYLINDER to the current
cursor location. (If CYLINDER is not item 1 on your
PRGM EXEC menu, move the cursor to CYLINDER
before you press Í.)
9. Press Í to execute the program. Enter 1.5 for
the radius, and then press Í. Enter 3 for the
height, and then press Í. The text VOLUME IS,
the value of V, and Done are displayed.
Repeat steps 7 through 9 and enter different
values for R and H.
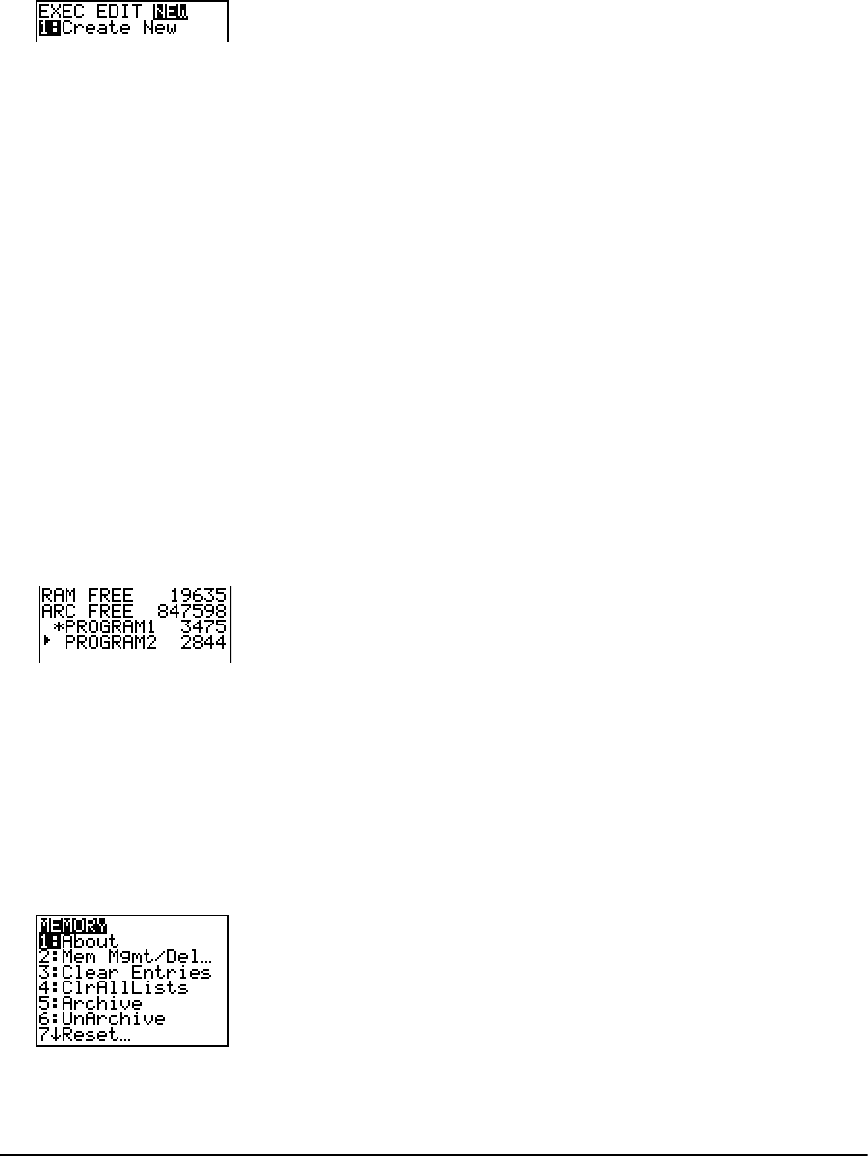
Chapter 16: Programming 277
Creating a New Program
To create a new program, follow these steps.
1. Press | to display the PRGM NEW menu.
2. Press Í to select 1:Create New. The Name= prompt is displayed, and alpha-lock is on.
3. Press a letter from A to Z or q to enter the first character of the new program name.
Note: A program name can be one to eight characters long. The first character must be a letter
from A to Z or q. The second through eighth characters can be letters, numbers, or q.
4. Enter zero to seven letters, numbers, or q to complete the new program name.
5. Press Í. The program editor is displayed.
6. Enter one or more program commands.
7. Press y 5 to leave the program editor and return to the home screen.
Managing Memory and Deleting a Program
To check whether adequate memory is available for a program you want to enter:
1. Press y L to display the MEMORY menu.
2. Select 2:Mem Mgmt/Del to display the MEMORY MANAGEMENT/DELETE menu (Chapter 18).
3. Select 7:Prgm to display the PRGM editor.
The TI-84 Plus expresses memory quantities in bytes.
You can increase available memory in one of two ways. You can delete one or more programs or
you can archive some programs.
To increase available memory by deleting a specific program:
1. Press y L and then select 2:Mem Mgmt/Del from the MEMORY menu.
2. Select 7:Prgm to display the PRGM editor (Chapter 18).

Chapter 16: Programming 278
3. Press } and † to move the selection cursor (4) next to the program you want to delete, and
then press {. The program is deleted from memory.
Note: You will receive a message asking you to confirm this delete action. Select 2:yes to
continue.
To leave the PRGM editor screen without deleting anything, press y 5, which displays the
home screen.
To increase available memory by archiving a program:
1. Press y L and then select 2:Mem Mgmt/Del from the MEMORY menu.
2. Select 2:Mem Mgmt/Del to display the MEM MGMT/DEL menu.
3. Select 7:Prgm... to display the PRGM menu.
4. Press Í to archive the program. An asterisk will appear to the left of the program to
indicate it is an archived program.
To unarchive a program in this screen, put the cursor next to the archived program and press
Í. The asterisk will disappear.
Note: Archive programs cannot be edited or executed. In order to edit or execute an archived
program, you must first unarchive it.
Entering Command Lines and Executing Programs
Entering a Program Command Line
You can enter on a command line any instruction or expression that you could execute from the
home screen. In the program editor, each new command line begins with a colon. To enter more
than one instruction or expression on a single command line, separate each with a colon.
Note: A command line can be longer than the screen is wide.
While in the program editor, you can display and select from menus. You can return to the program
editor from a menu in either of two ways.
• Select a menu item, which pastes the item to the current command line.
— or —
• Press ‘.
When you complete a command line, press Í. The cursor moves to the next command line.

Chapter 16: Programming 279
Programs can access variables, lists, matrices, and strings saved in memory. If a program stores a
new value to a variable, list, matrix, or string, the program changes the value in memory during
execution.
You can call another program as a subroutine.
Executing a Program
To execute a program, begin on a blank line on the home screen and follow these steps.
1. Press to display the PRGM EXEC menu.
2. Select a program name from the PRGM EXEC menu. prgmname is pasted to the home screen
(for example, prgmCYLINDER).
3. Press Í to execute the program. While the program is executing, the busy indicator is on.
Last Answer (Ans) is updated during program execution. Last Entry is not updated as each
command is executed (Chapter 1).
The TI-84 Plus checks for errors during program execution. It does not check for errors as you
enter a program.
Breaking a Program
To stop program execution, press É. The ERR:BREAK menu is displayed.
• To return to the home screen, select 1:Quit.
• To go where the interruption occurred, select 2:Goto.
Editing Programs
Editing a Program
To edit a stored program, follow these steps.
1. Press ~ to display the PRGM EDIT menu.
2. Select a program name from the PRGM EDIT menu. Up to the first seven lines of the program
are displayed.
Note: The program editor does not display a $ to indicate that a program continues beyond the
screen.
3. Edit the program command lines.
• Move the cursor to the appropriate location, and then delete, overwrite, or insert.
• Press ‘ to clear all program commands on the command line (the leading colon
remains), and then enter a new program command.

Chapter 16: Programming 280
Note: To move the cursor to the beginning of a command line, press y |; to move to the end,
press y ~. To scroll the cursor down seven command lines, press ƒ †. To scroll the cursor
up seven command lines, press ƒ }.
Inserting and Deleting Command Lines
To insert a new command line anywhere in the program, place the cursor where you want the new
line, press y 6, and then press Í. A colon indicates a new line.
To delete a command line, place the cursor on the line, press ‘ to clear all instructions and
expressions on the line, and then press { to delete the command line, including the colon.
Copying and Renaming Programs
Copying and Renaming a Program
To copy all command lines from one program into a new program, follow steps 1 through 5 for
Creating a New Program, and then follow these steps.
1. Press y K. Rcl is displayed on the bottom line of the program editor in the new program
(Chapter 1).
2. Press | to display the PRGM EXEC menu.
3. Select a name from the menu. prgmname is pasted to the bottom line of the program editor.
4. Press Í. All command lines from the selected program are copied into the new program.
Copying programs has at least two convenient applications.
• You can create a template for groups of instructions that you use frequently.
• You can rename a program by copying its contents into a new program.
Note: You also can copy all the command lines from one existing program to another existing
program using RCL.
Scrolling the PRGM EXEC and PRGM EDIT Menus
The TI-84 Plus sorts PRGM EXEC and PRGM EDIT menu items automatically into alphanumerical
order. Each menu only labels the first 10 items using 1 through 9, then 0.
To jump to the first program name that begins with a particular alpha character or q, press ƒ
[letter from A to Z or q].
Note: From the top of either the PRGM EXEC or PRGM EDIT menu, press } to move to the bottom.
From the bottom, press † to move to the top. To scroll the cursor down the menu seven items,
press ƒ †. To scroll the cursor up the menu seven items, press ƒ }.

Chapter 16: Programming 281
PRGM CTL (Control) Instructions
PRGM CTL Menu
To display the PRGM CTL (program control) menu, press from the program editor only.
These menu items direct the flow of an executing program. They make it easy to repeat or skip a
group of commands during program execution. When you select an item from the menu, the name
is pasted to the cursor location on a command line in the program.
To return to the program editor without selecting an item, press ‘.
Controlling Program Flow
Program control instructions tell the TI-84 Plus which command to execute next in a program. If,
While, and Repeat check a defined condition to determine which command to execute next.
Conditions frequently use relational or Boolean tests (Chapter 2), as in:
CTL I/O EXEC
1: If Creates a conditional test.
2: Then Executes commands when If is true.
3: Else Executes commands when If is false.
4: For( Creates an incrementing loop.
5: While Creates a conditional loop.
6: Repeat Creates a conditional loop.
7: End Signifies the end of a block.
8: Pause Pauses program execution.
9: Lbl Defines a label.
0: Goto Goes to a label.
A: IS>( Increments and skips if greater than.
B: DS<( Decrements and skips if less than.
C: Menu( Defines menu items and branches.
D: prgm Executes a program as a subroutine.
E: Return Returns from a subroutine.
F: Stop Stops execution.
G: DelVar Deletes a variable from within program.
H: GraphStyle( Designates the graph style to be drawn.
I: OpenLib( No longer used.
J: ExecLib( No longer used.
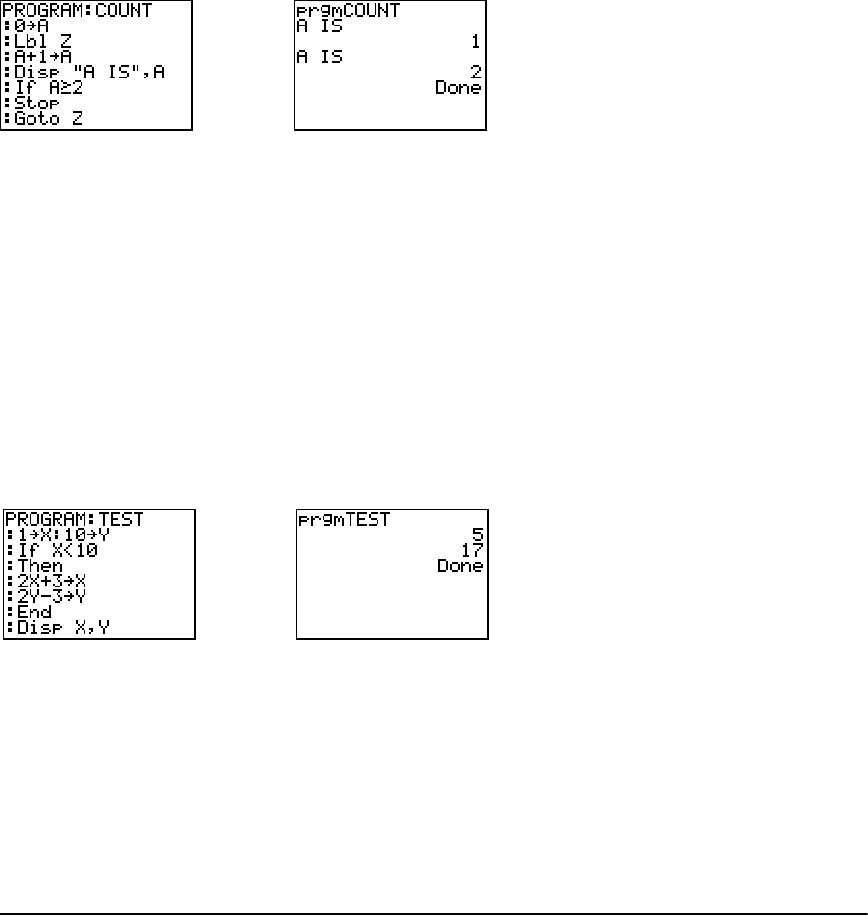
Chapter 16: Programming 282
If A<7:A+1!A
or
If N=1 and M=1:Goto Z
If
Use If for testing and branching. If condition is false (zero), then the command immediately following If
is skipped. If condition is true (nonzero), then the next command is executed. If instructions can be
nested.
:If condition
:command (if true)
:command
Program Output
If-Then
Then following an If executes a group of commands if condition is true (nonzero). End identifies the
end of the group of commands.
:If condition
:Then
:command (if true)
:command (if true)
:End
:command
Program Output
If-Then-Else
Else following If-Then executes a group of commands if condition is false (zero). End identifies the end
of the group of commands.
:If condition
:Then
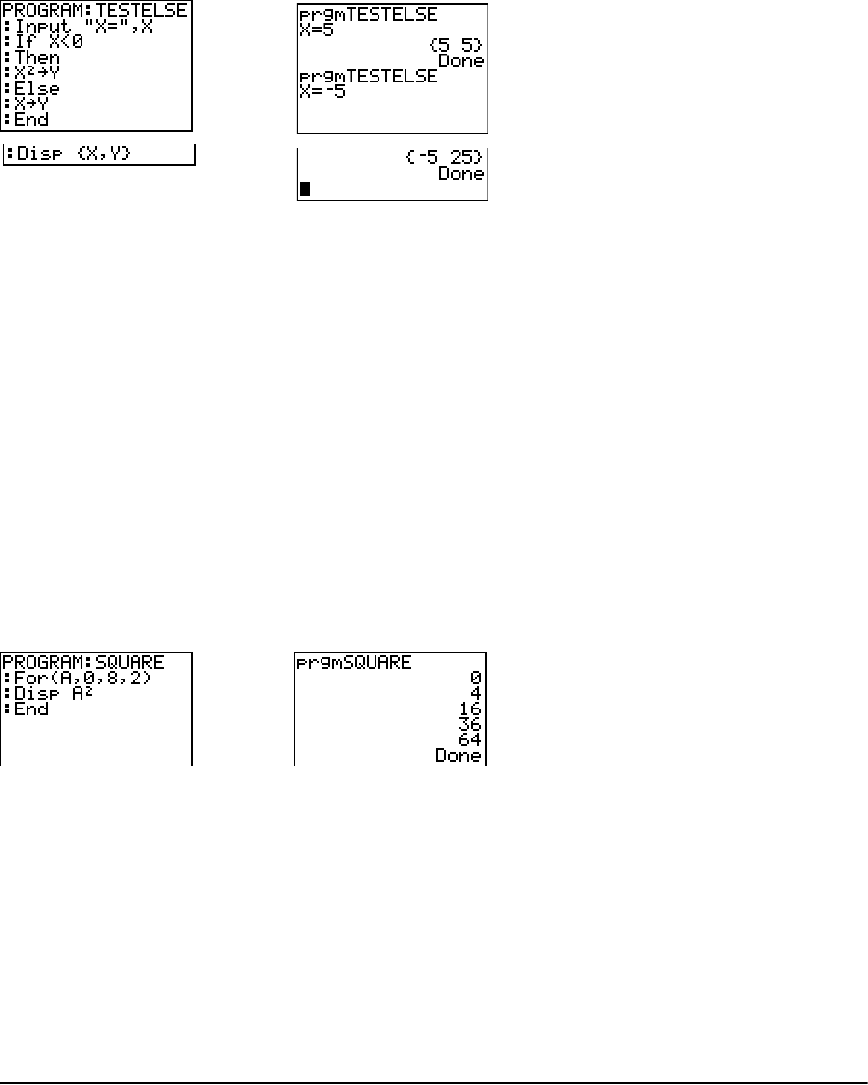
Chapter 16: Programming 283
:command (if true)
:command (if true)
:Else
:command (if false)
:command (if false)
:End
:command
Program Output
Note: In OS 2.53MP and higher, the program name displays again when you press Í to repeat
the program.
For(
For( loops and increments. It increments variable from begin to end by increment. increment is optional
(default is 1) and can be negative (end<begin). end is a maximum or minimum value not to be
exceeded. End identifies the end of the loop. For( loops can be nested.
:For(variable,begin,end[,increment])
:command (while end not exceeded)
:command (while end not exceeded)
:End
:command
Program Output
While
While performs a group of commands while condition is true. condition is frequently a relational test
(Chapter 2). condition is tested when While is encountered. If condition is true (nonzero), the program
executes a group of commands. End signifies the end of the group. When condition is false (zero), the
program executes each command following End. While instructions can be nested.
:While condition
:command (while condition is true)
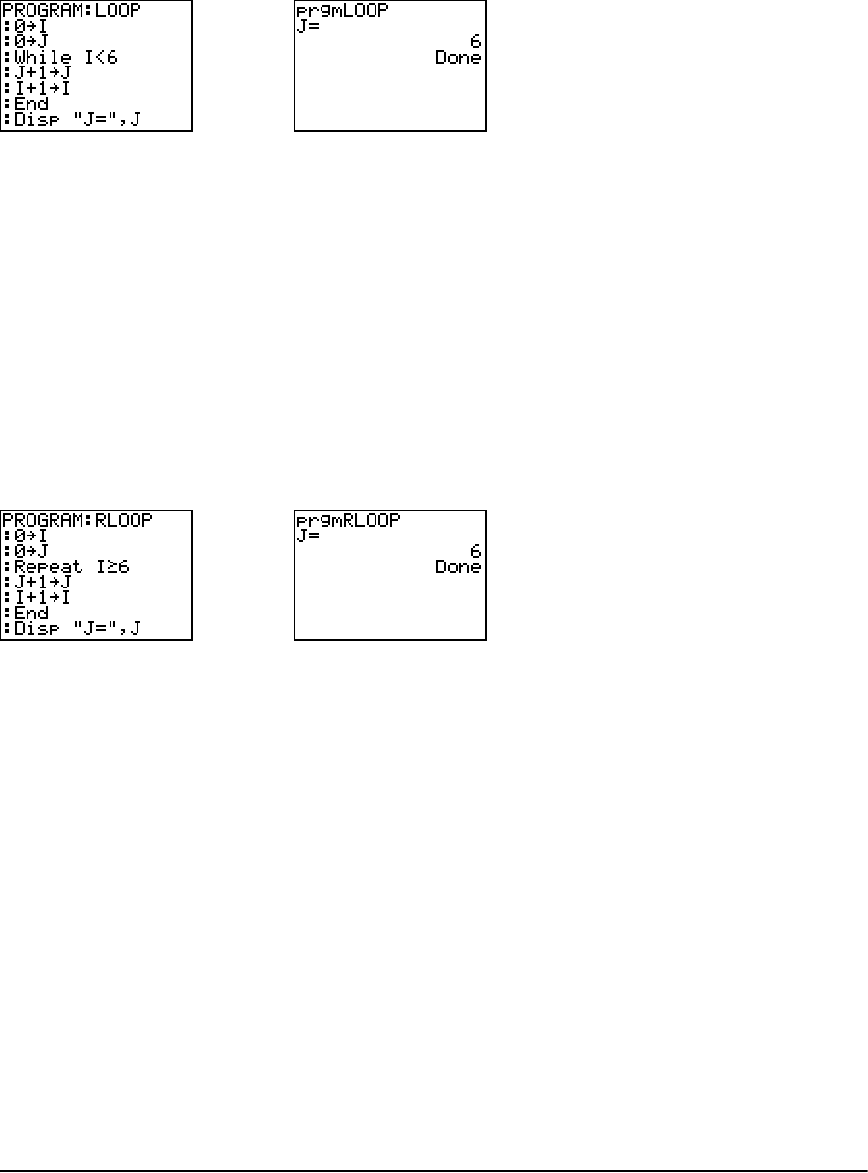
Chapter 16: Programming 284
:command (while condition is true)
:End
:command
Program Output
Repeat
Repeat repeats a group of commands until condition is true (nonzero). It is similar to While, but condition
is tested when End is encountered; therefore, the group of commands is always executed at least
once. Repeat instructions can be nested.
:Repeat condition
:command (until condition is true)
:command (until condition is true)
:End
:command
Program Output
End
End identifies the end of a group of commands. You must include an End instruction at the end of
each For(, While, or Repeat loop. Also, you must paste an End instruction at the end of each If-Then
group and each If-Then-Else group.
Pause
Pause suspends execution of the program so that you can see answers or graphs. During the
pause, the pause indicator is on in the top-right corner. Press Í to resume execution.
•Pause without a value temporarily pauses the program. If the DispGraph or Disp instruction has
been executed, the appropriate screen is displayed.
•Pause with value displays value on the current home screen. value can be scrolled.
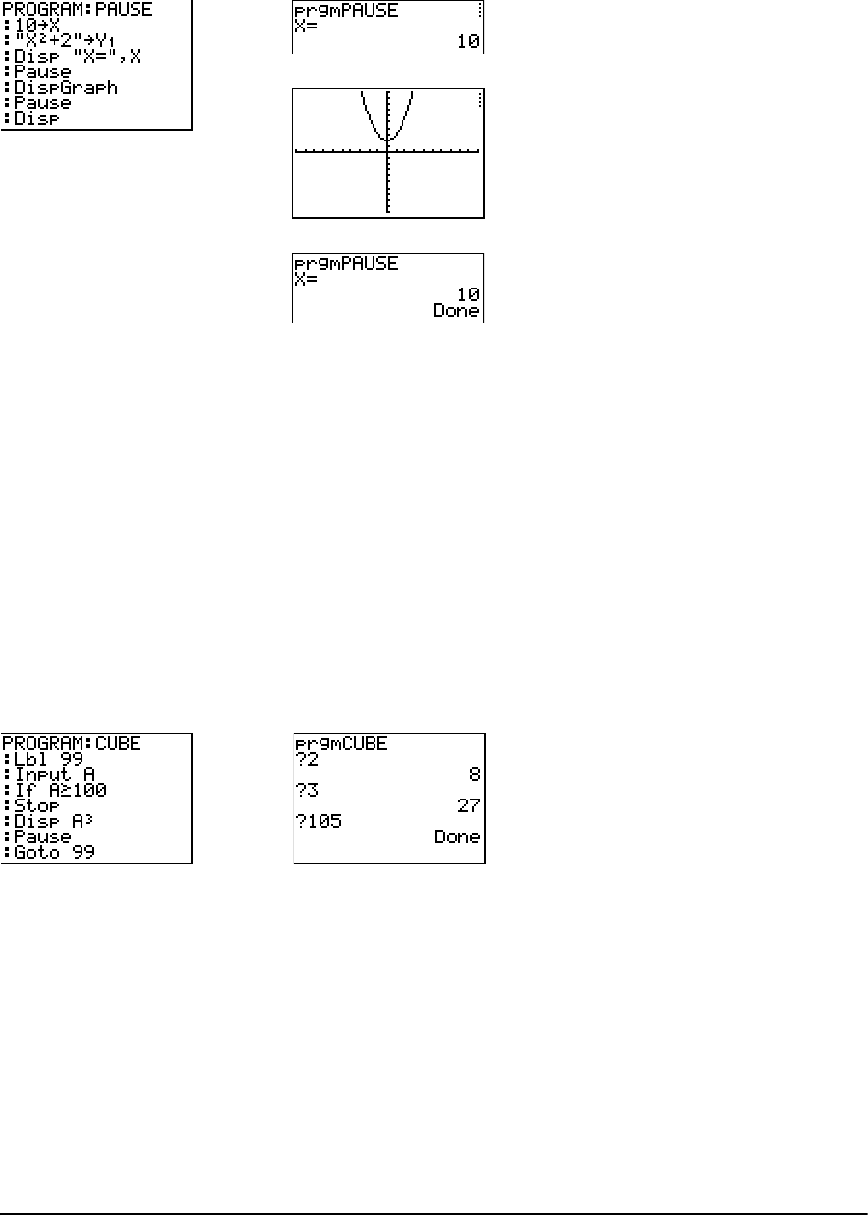
Chapter 16: Programming 285
Pause [value]
Program Output
Lbl, Goto
Lbl (label) and Goto (go to) are used together for branching.
Lbl specifies the label for a command. label can be one or two characters (A through Z, 0 through
99, or q).
Lbl label
Goto causes the program to branch to label when Goto is encountered.
Goto label
Program Output

Chapter 16: Programming 286
IS>(
IS>( (increment and skip) adds 1 to variable. If the answer is > value (which can be an expression),
the next command is skipped; if the answer is { value, the next command is executed. variable cannot
be a system variable.
:IS>(variable,value)
:command (if answer value)
:command (if answer > value)
Program Output
Note: IS>( is not a looping instruction.
DS<(
DS<( (decrement and skip) subtracts 1 from variable. If the answer is < value (which can be an
expression), the next command is skipped; if the answer is | value, the next command is executed.
variable cannot be a system variable.
:DS<(variable,value)
:command (if answer ‚ value)
:command (if answer < value)
Program Output
Note: DS<( is not a looping instruction.
Menu(
Menu( sets up branching within a program. If Menu( is encountered during program execution, the
menu screen is displayed with the specified menu items, the pause indicator is on, and execution
pauses until you select a menu item.
The menu title is enclosed in quotation marks ( " ). Up to seven pairs of menu items follow. Each
pair comprises a text item (also enclosed in quotation marks) to be displayed as a menu selection,
and a label item to which to branch if you select the corresponding menu selection.
Menu("title","text1",label1,"text2",label2, . . .)
Program Output
Chapter 16: Programming 287
The program above pauses until you select 1 or 2. If you select 2, for example, the menu
disappears and the program continues execution at Lbl B.
prgm
Use prgm to execute other programs as subroutines. When you select prgm, it is pasted to the
cursor location. Enter characters to spell a program name. Using prgm is equivalent to selecting
existing programs from the PRGM EXEC menu; however, it allows you to enter the name of a
program that you have not yet created.
prgmname
Note: You cannot directly enter the subroutine name when using RCL. You must paste the name
from the PRGM EXEC menu.
Return
Return quits the subroutine and returns execution to the calling program, even if encountered
within nested loops. Any loops are ended. An implied Return exists at the end of any program that
is called as a subroutine. Within the main program, Return stops execution and returns to the
home screen.
Stop
Stop stops execution of a program and returns to the home screen. Stop is optional at the end of a
program.
DelVar
DelVar deletes from memory the contents of variable.
DelVar variable

Chapter 16: Programming 288
GraphStyle(
GraphStyle( designates the style of the graph to be drawn. function# is the number of the Y= function
name in the current graphing mode. graphstyle is a number from 1 to 7 that corresponds to the
graph style, as shown below.
GraphStyle(function#,graphstyle)
For example, GraphStyle(1,5) in Func mode sets the graph style for Y1 to ë (path; 5).
Not all graph styles are available in all graphing modes. For a detailed description of each graph
style, see the Graph Styles table in Chapter 3.
PRGM I/O (Input/Output) Instructions
PRGM I/O Menu
To display the PRGM I/O (program input/output) menu, press ~ from within the program
editor only.
These instructions control input to and output from a program during execution. They allow you to
enter values and display answers during program execution.
To return to the program editor without selecting an item, press ‘.
1 = ç (line)
2 = è (thick)
3 = é (shade above)
4 = ê (shade below)
5 = ë (path)
6 = ì (animate)
7 = í (dot)
CTL I/O EXEC
1: Input Enters a value or uses the cursor.
2: Prompt Prompts for entry of variable values.
3: Disp Displays text, value, or the home screen.
4: DispGraph Displays the current graph.
5: DispTable Displays the current table.
6: Output( Displays text at a specified position.
7: getKey Checks the keyboard for a keystroke.
8: ClrHome Clears the display.
9: ClrTable Clears the current table.
0: GetCalc( Gets a variable from another TI-84 Plus.
A: Get( Gets a variable from CBL 2™ or CBR™.
B: Send( Sends a variable to CBL 2 or CBR.
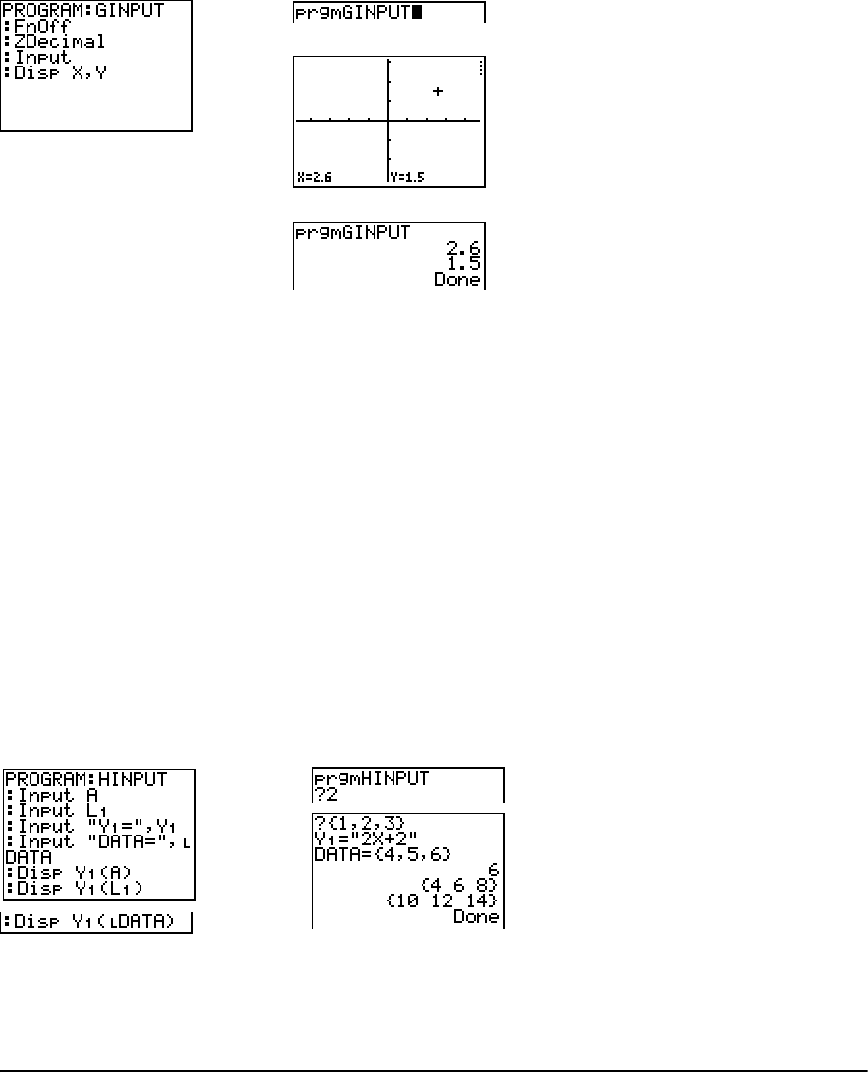
Chapter 16: Programming 289
Displaying a Graph with Input
Input without a variable displays the current graph. You can move the free-moving cursor, which
updates X and Y (and R and q for PolarGC format). The pause indicator is on. Press Í to
resume program execution.
Input
Program Output
Storing a Variable Value with Input
Input with variable displays a ? (question mark) prompt during execution. variable may be a real
number, complex number, list, matrix, string, or Y= function. During program execution, enter a
value, which can be an expression, and then press Í. The value is evaluated and stored to
variable, and the program resumes execution.
Input [variable]
You can display text or the contents of Strn (a string variable) of up to 16 characters as a prompt.
During program execution, enter a value after the prompt and then press Í. The value is
stored to variable, and the program resumes execution.
Input ["text",variable]
Input [Strn,variable]
Program Output
Chapter 16: Programming 290
Note: When a program prompts for input of lists and Yn functions during execution, you must
include the braces ( { } ) around the list elements and quotation marks ( " ) around the
expressions.
Prompt
During program execution, Prompt displays each variable, one at a time, followed by =?. At each
prompt, enter a value or expression for each variable, and then press Í. The values are stored,
and the program resumes execution.
Prompt variableA[,variableB,...,variable n]
Program Output
Note: Y= functions are not valid with Prompt.
Displaying the Home Screen
Disp (display) without a value displays the home screen. To view the home screen during program
execution, follow the Disp instruction with a Pause instruction.
Disp
Displaying Values and Messages
Disp with one or more values displays the value of each.
Disp [valueA,valueB,valueC,...,value n]
• If value is a variable, the current value is displayed.
• If value is an expression, it is evaluated and the result is displayed on the right side of the next
line.
• If value is text within quotation marks, it is displayed on the left side of the current display line. !
is not valid as text.
If Pause is encountered after Disp, the program halts temporarily so you can examine the screen.
To resume execution, press Í.
Program Output
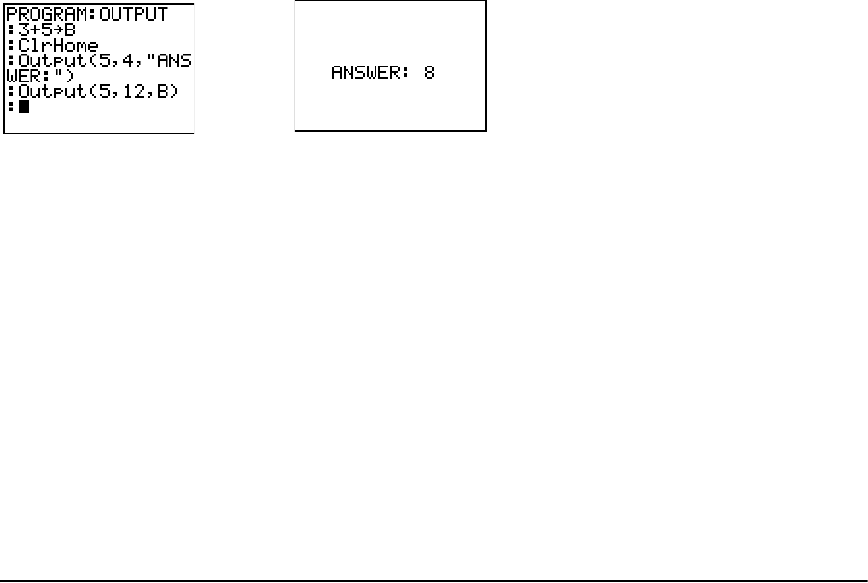
Chapter 16: Programming 291
Note: If a matrix or list is too large to display in its entirety, ellipses (...) are displayed in the last
column, but the matrix or list cannot be scrolled. To scroll, use Pause value.
DispGraph
DispGraph (display graph) displays the current graph. If Pause is encountered after DispGraph, the
program halts temporarily so you can examine the screen. Press Í to resume execution.
DispTable
DispTable (display table) displays the current table. The program halts temporarily so you can
examine the screen. Press Í to resume execution.
Output(
Output( displays text or value on the current home screen beginning at row (1 through 8) and column
(1 through 16), overwriting any existing characters.
Note: You may want to precede Output( with ClrHome.
Expressions are evaluated and values are displayed according to the current mode settings.
Matrices are displayed in entry format and wrap to the next line. ! is not valid as text.
Output(row,column,"text")
Output(row,column,value)
Program Output
For Output( on a Horiz split screen, the maximum value for row is 4.
Chapter 16: Programming 292
getKey
getKey returns a number corresponding to the last key pressed, according to the key code diagram
below. If no key has been pressed, getKey returns 0. Use getKey inside loops to transfer control,
for example, when creating video games.
Note: You can press É at any time during execution to break the program.
TI-84 Plus Key Code Diagram
ClrHome, ClrTable
ClrHome (clear home screen) clears the home screen during program execution.
ClrTable (clear table) clears the values in the table during program execution.
GetCalc(
GetCalc( gets the contents of variable on another TI-84 Plus and stores it to variable on the receiving
TI-84 Plus. variable can be a real or complex number, list element, list name, matrix element, matrix
name, string, Y= variable, graph database, or picture.
Program Output
Note: , Œ, , and Í were pressed
during program execution.

Chapter 16: Programming 293
GetCalc(variable[,portflag])
By default, the TI-84 Plus uses the USB port if it is connected. If the USB cable is not connected, it
uses the I/O port. If you want to specify either the USB or I/O port, use the following portflag
numbers:
portflag=0 use USB port if connected;
portflag=1 use USB port;
portflag=2 use I/O port
Note: GetCalc( does not work between TI.82 and TI-83 Plus or a TI.82 and TI-84 Plus calculators.
Get(, Send(
Get( gets data from the CBL 2™ or CBR™ and stores it to variable on the receiving TI-84 Plus.
variable can be a real number, list element, list name, matrix element, matrix name, string,
Y= variable, graph database, or picture.
Get(variable)
Note: If you transfer a program that references the Get( command to the TI-84 Plus from a TI.82,
the TI-84 Plus will interpret it as the Get( described above. Use GetCalc( to get data from another
TI-84 Plus.
Send( sends the contents of variable to the CBL 2™ or CBR™. You cannot use it to send to another
TI-84 Plus. variable can be a real number, list element, list name, matrix element, matrix name,
string, Y= variable, graph database, or picture. variable can be a list of elements.
Send(variable)
Note: This program gets sound data and time in
seconds from CBL 2™.
Note: You can access Get(, Send(, and GetCalc( from the CATALOG to execute them from the
home screen (Chapter 15).
Calling Other Programs as Subroutines
Calling a Program from Another Program
On the TI-84 Plus, any stored program can be called from another program as a subroutine. Enter
the name of the program to use as a subroutine on a line by itself.
You can enter a program name on a command line in either of two ways.
• Press | to display the PRGM EXEC menu and select the name of the program prgmname
is pasted to the current cursor location on a command line.
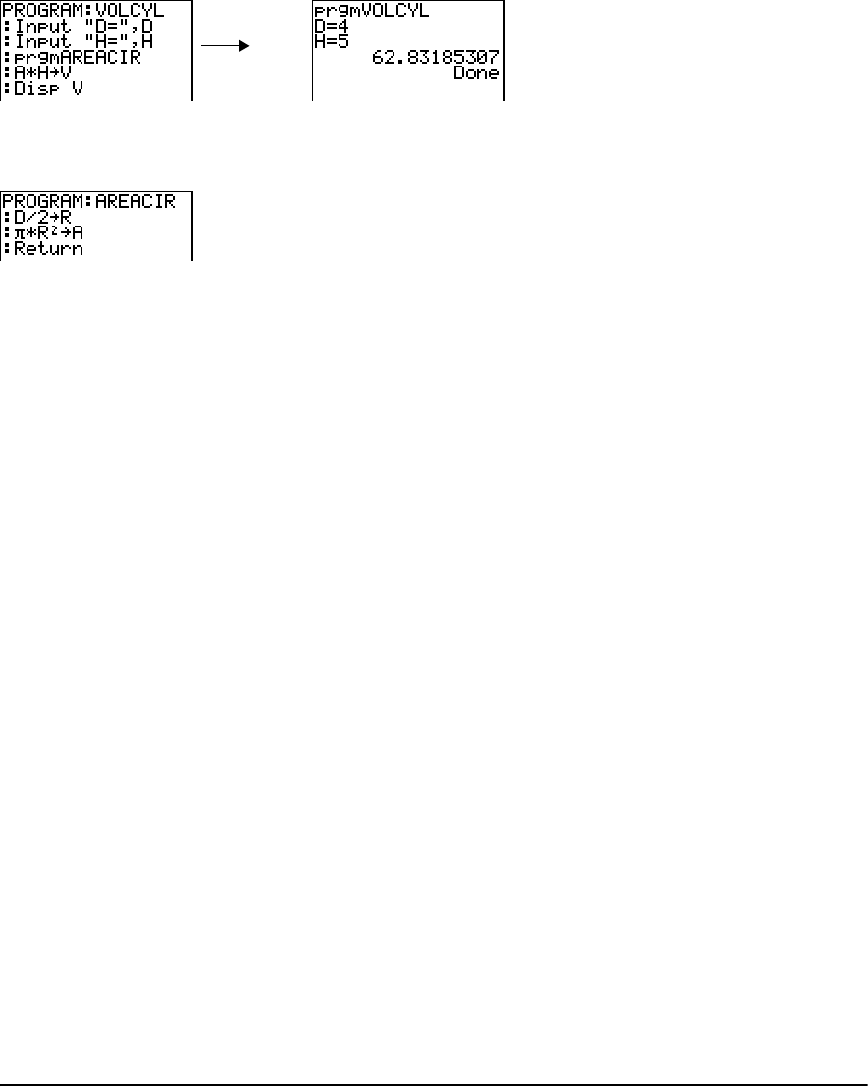
Chapter 16: Programming 294
•Select
prgm from the PRGM CTL menu, and then enter the program name.
prgmname
When prgmname is encountered during execution, the next command that the program executes is
the first command in the second program. It returns to the subsequent command in the first
program when it encounters either Return or the implied Return at the end of the second program.
Subroutine ( '
Notes about Calling Programs
Variables are global.
label used with Goto and Lbl is local to the program where it is located. label in one program is not
recognized by another program. You cannot use Goto to branch to a label in another program.
Return exits a subroutine and returns to the calling program, even if it is encountered within nested
loops.
Running an Assembly Language Program
You can run programs written for the TI-84 Plus in assembly language. Typically, assembly
language programs run much faster and provide greater control than the keystroke programs that
you write with the built-in program editor.
Note: Because an assembly language program has greater control over the calculator, if your
assembly language program has error(s), it may cause your calculator to reset and lose all data,
programs, and applications stored in memory.
When you download an assembly language program, it is stored among the other programs as a
PRGM menu item. You can:
• Transmit it using the TI-84 Plus communication link (Chapter 19).
• Delete it using the MEM MGMT DEL screen (Chapter 18).
To run an assembly Program, the syntax is: Asm(assemblyprgmname)
Program Output

Chapter 16: Programming 295
If you write an assembly language program, use the two instructions below from the CATALOG to
identify and compile the program.
To compile an assembly program that you have written:
1. Follow the steps for writing a program (16-4) but be sure to include AsmPrgm as the first line of
your program.
2. From the home screen, press y N and then select AsmComp( to paste it to the screen.
3. Press to display the PRGM EXEC menu.
4. Select the program you want to compile. It will be pasted to the home screen.
5. Press ¢ and then select prgm from the CATALOG.
6. Key in the name you have chosen for the output program.
Note: This name must be unique — not a copy of an existing program name.
7. Press ¤ to complete the sequence.
The sequence of the arguments should be as follows:
AsmComp(prgmASM1, prgmASM2)
8. Press Í to compile your program and generate the output program.
Instructions Comments
AsmComp(prgmASM1,
prgmASM2)
Compiles an assembly language program written in
ASCII and stores the hex version
AsmPrgm Identifies an assembly language program; must be
entered as the first line of an assembly language
program

Chapter 17: Activities 296
Chapter 17:
Activities
The Quadratic Formula
Note: This example uses MathPrint™ mode for real answers and Classic mode for non-real
(complex) results. You can also use the Polynomial Root Finder/Simultaneous Equation Solver
application to solve these types of problems with a quick set-up. This application comes preloaded
on your TI-84 Plus and can be downloaded from education.ti.com.
Use the quadratic formula to solve the quadratic equations 2x2 N 11x + 14 = 0 and
2x2 N 6x + 5 = 0.
Graphing the Functions
Before you begin, look at the graphs of the functions to see the approximate locations of the
solutions.
1. Press o to display the Y= editor.
2. Press 2 „ ¡ ¹ 11 „ Ã 14 for
Y1, and then press Í.
3. Press 2 „ ¡ ¹ 6 „ Ã 5 for Y2.
4. Press q and select 4:ZDecimal. The
graph of the functions displays.
You can see that the graph of the first
function, 2x2 N 11x + 14 = 0, crosses the
x-axis, so it has a real solution. The graph of
the second function does not cross the
x-axis, so it has a complex solution.
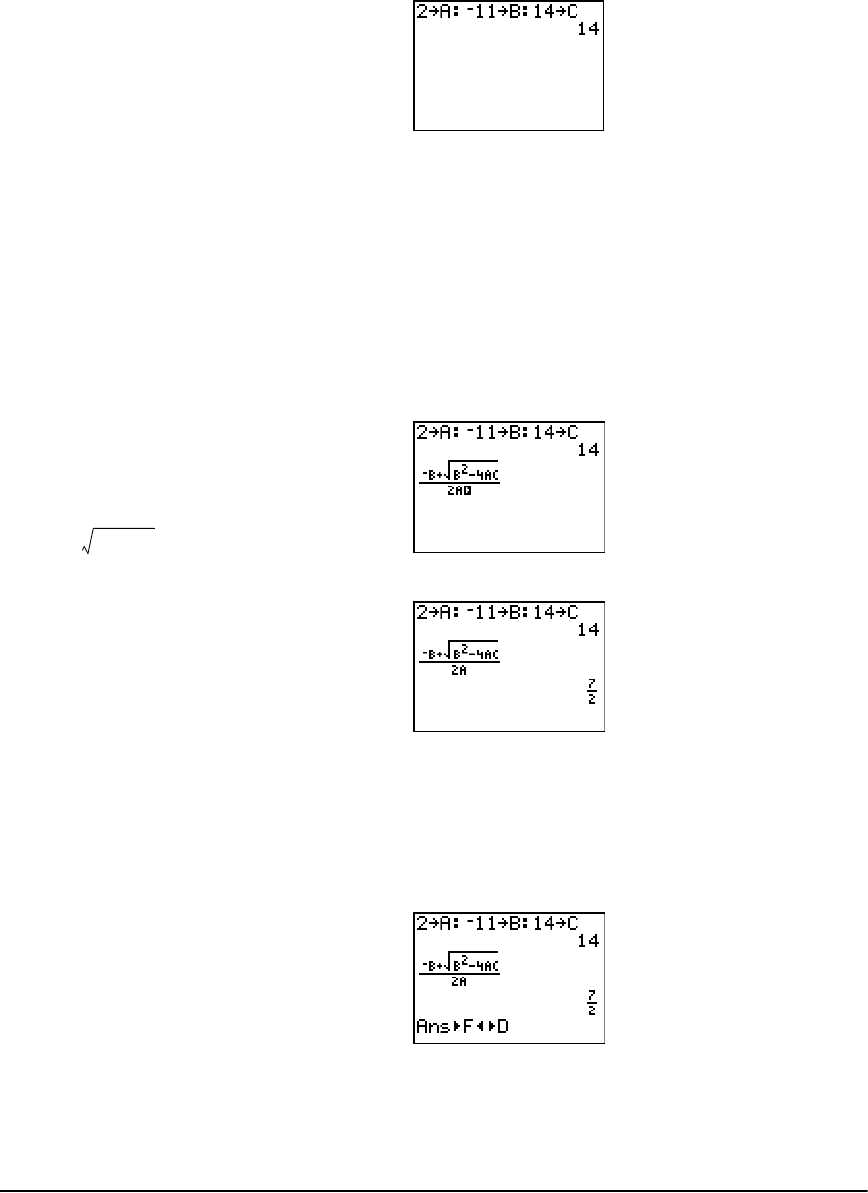
Chapter 17: Activities 297
Entering a Calculation
Begin with the equation 2x2 N 11x + 14 = 0.
Converting to a Decimal
You can show the solution as a decimal.
1. Press 2 ¿ ƒ A to store the
coefficient of the x2 term.
2. Press ƒ [:]. The colon allows you to
enter more than one instruction on a line.
3. Press Ì 11 ¿ ƒ B to store the
coefficient of the X term. Press ƒ [:]
to enter a new instruction on the same
line. Press 14 ¿ ƒ C to store the
constant.
4. Press Í to store the values to the
variables A, B, and C.
The last value you stored is shown on
the right side of the display. The cursor
moves to the next line, ready for your
next entry.
5. Press ƒ ^ 1 Ì ƒ B Ã y C
ƒ B ¡ ¹ 4 ƒ A ƒ C ~ ~ 2
ƒ A to enter the expression for one
of the solutions for the quadratic formula,
6. Press Í to find one solution for the
equation 2x2 N 11x + 14 = 0.
The answer is shown on the right side of
the display. The cursor moves to the next
line, ready for you to enter the next
expression.
1. Press ƒ ^ 4 to select 4F3 4D from
the FRAC shortcut menu.
b–b24ac–±
2a
--------------------------------------
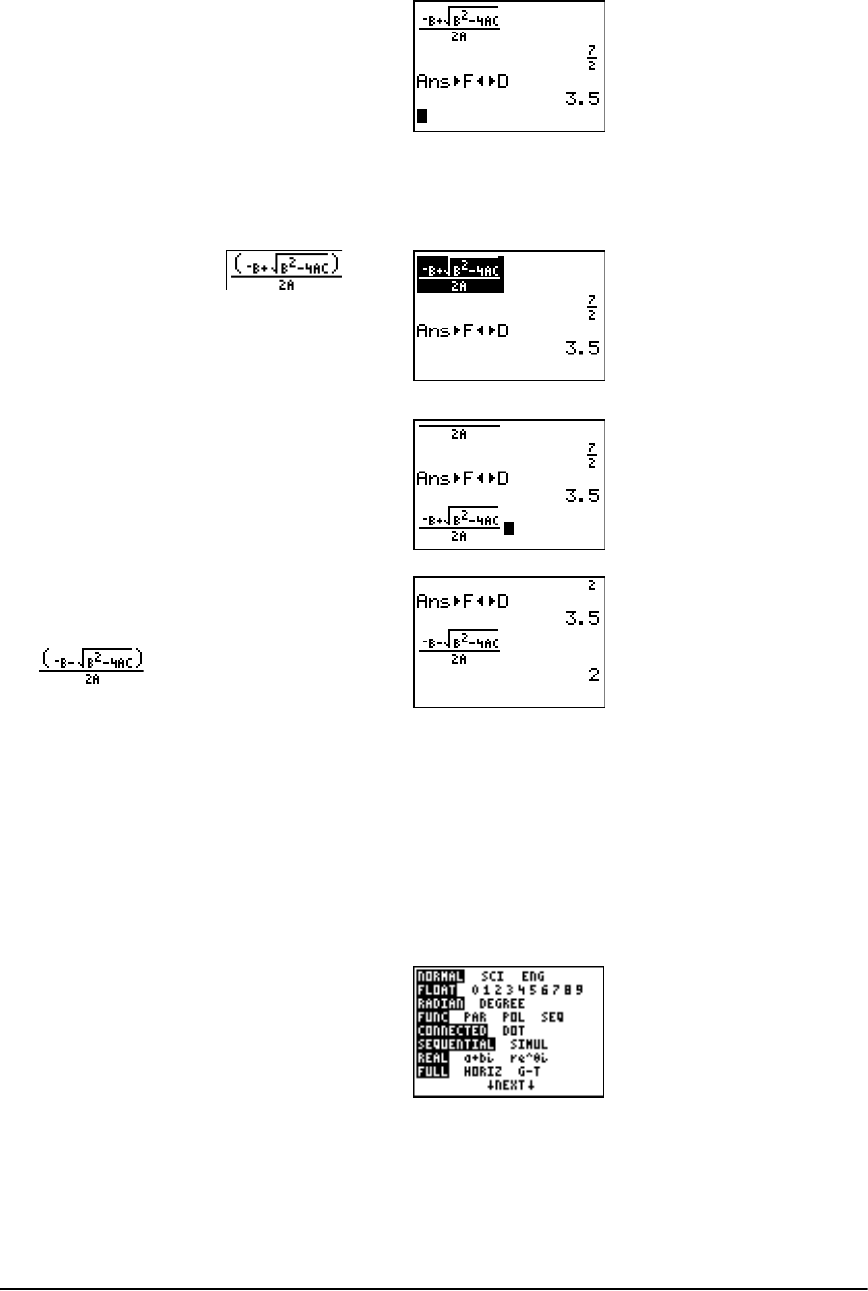
Chapter 17: Activities 298
To save keystrokes, you can scroll up to find an expression you entered, copy it, and then edit it for
a new calculation.
Displaying Complex Results
Now solve the equation 2x2 N 6x + 5 = 0. When you set a+bi complex number mode, the TI-84
Plus displays complex results.
2. Press Í to convert the result to a
decimal.
3. Press } to highlight and
then press Í to paste it to the entry
line.
4. Press | until the cursor is on the + sign
in the formula. Press ¹ to edit the
quadratic-formula expression to become
.
5. Press Í to find the other solution for
the quadratic equation
2x2 N 11x + 14 = 0.
1. Press z † † † † † † (6 times),
and then press ~ to highlight a+bi. Press
Í to select a+bi complex-number
mode.
2. Press y 5 to return to the home
screen, and then press ‘ to clear it.
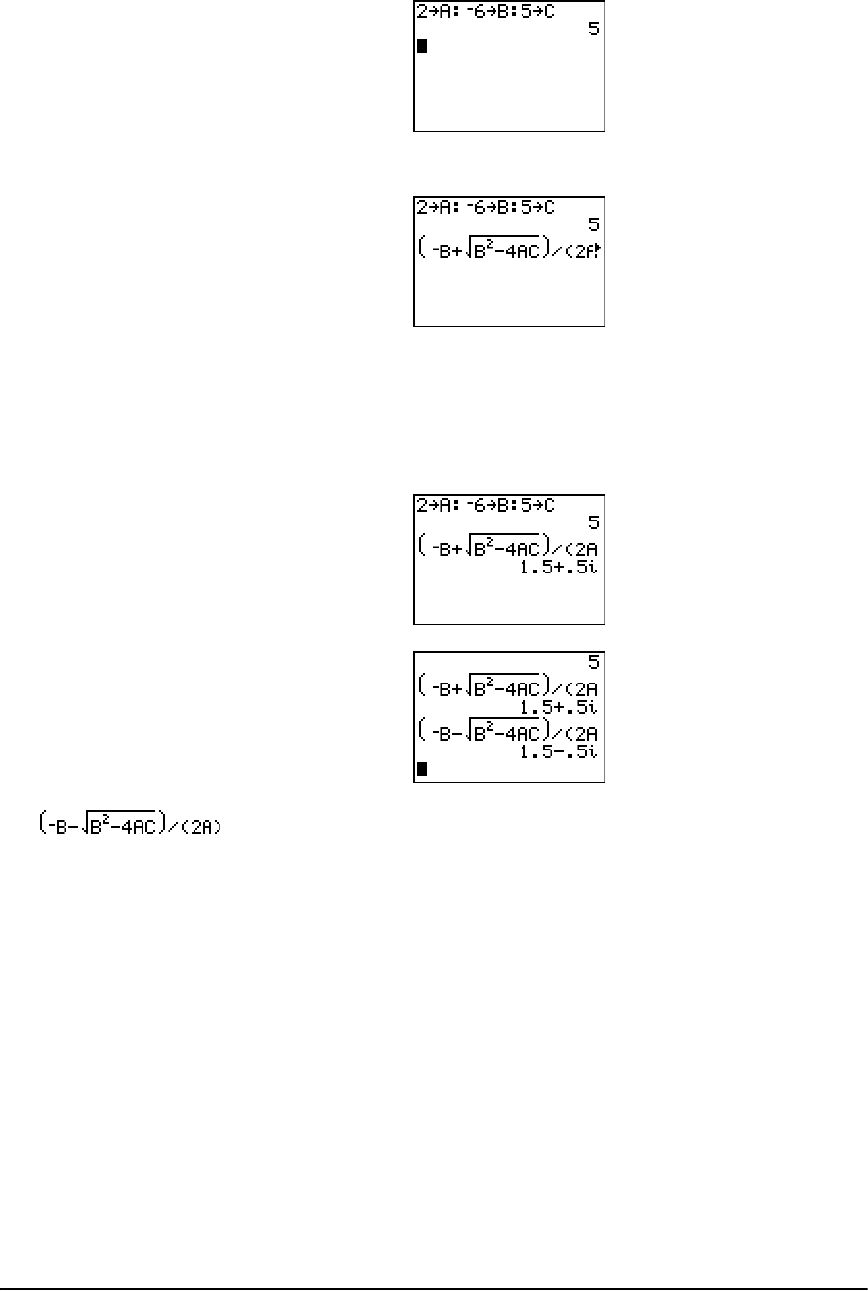
Chapter 17: Activities 299
Box with Lid
Defining a Function
Take a 20 cm × 25 cm. sheet of paper and cut X × X squares from two corners. Cut X × 12½ cm
rectangles from the other two corners as shown in the diagram below. Fold the paper into a box
with a lid. What value of X would give your box the maximum volume V? Use the table and graphs
to determine the solution.
3. Press 2 ¿ ƒ A ƒ [:] Ì 6
¿ ƒ B ƒ [:] 5 ¿ ƒ C
Í.
The coefficient of the x2 term, the
coefficient of the X term, and the
constant for the new equation are stored
to A, B, and C, respectively.
4. Enter the quadratic formula using Classic
entry: £ Ì ƒ B Ã y C ƒ B
¡ ¹ 4 ƒ A ƒ C ~ ¤ ¥ £ 2
ƒ A ¤.
Because the solution is a complex
number, you have to enter the formula
using the division operation instead of
using the n/d shortcut template. Complex
numbers are not valid in the n/d template
in input or output and will cause
Error: Data Type to display.
5. Press Í to find one solution for the
equation 2x2 N 6x + 5 = 0.
6. Press } to highlight the quadratic-
formula expression, and then press
Í to paste it to the entry line.
7. Press | until the cursor is on the + sign
in the formula. Press ¹ to edit the
quadratic-formula expression to become
.
8. Press Í to find the other solution for
the quadratic equation: 2x2 N 6x + 5 = 0.
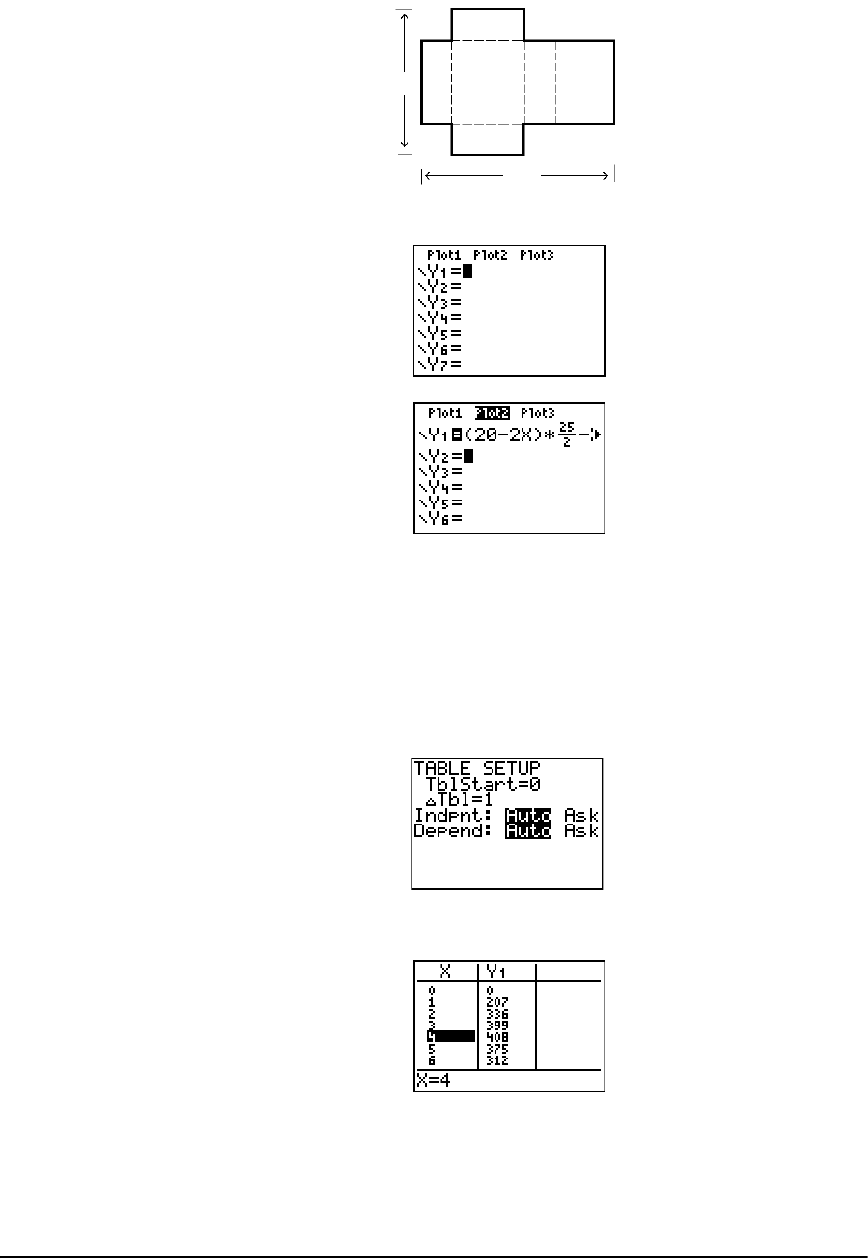
Begin by defining a function that describes
the volume of the box.
From the diagram:
2X + A = 20
2X + 2B = 25
V = A…B…X
Substituting:
V = (20 N 2X) (25à2 N X) X
X
A
XBXB
20
25
1. Press o to display the Y= editor, which
is where you define functions for tables
and graphing.
2. Press £ 20 ¹ 2 „ ¤ £ 25 t
^ 1 2 ~ ¹ „ ¤ „ Í to
define the volume function as Y1 in terms
of X.
Chapter 17: Activities 300
Defining a Table of Values
The table feature of the TI-84 Plus displays numeric information about a function. You can use a
table of values from the function you just defined to estimate an answer to the problem.
„ lets you enter X quickly, without
having to press ƒ. The highlighted =
sign indicates that Y1 is selected.
1. Press y - to display the TABLE
SETUP menu.
2. Press Í to accept TblStart=0.
3. Press 1 Í to define the table
increment @Tbl=1. Leave Indpnt: Auto
and Depend: Auto so that the table will be
generated automatically.
4. Press y 0 to display the table.
Notice that the maximum value for Y1
(box’s volume) occurs when X is about 4,
between 3 and 5.
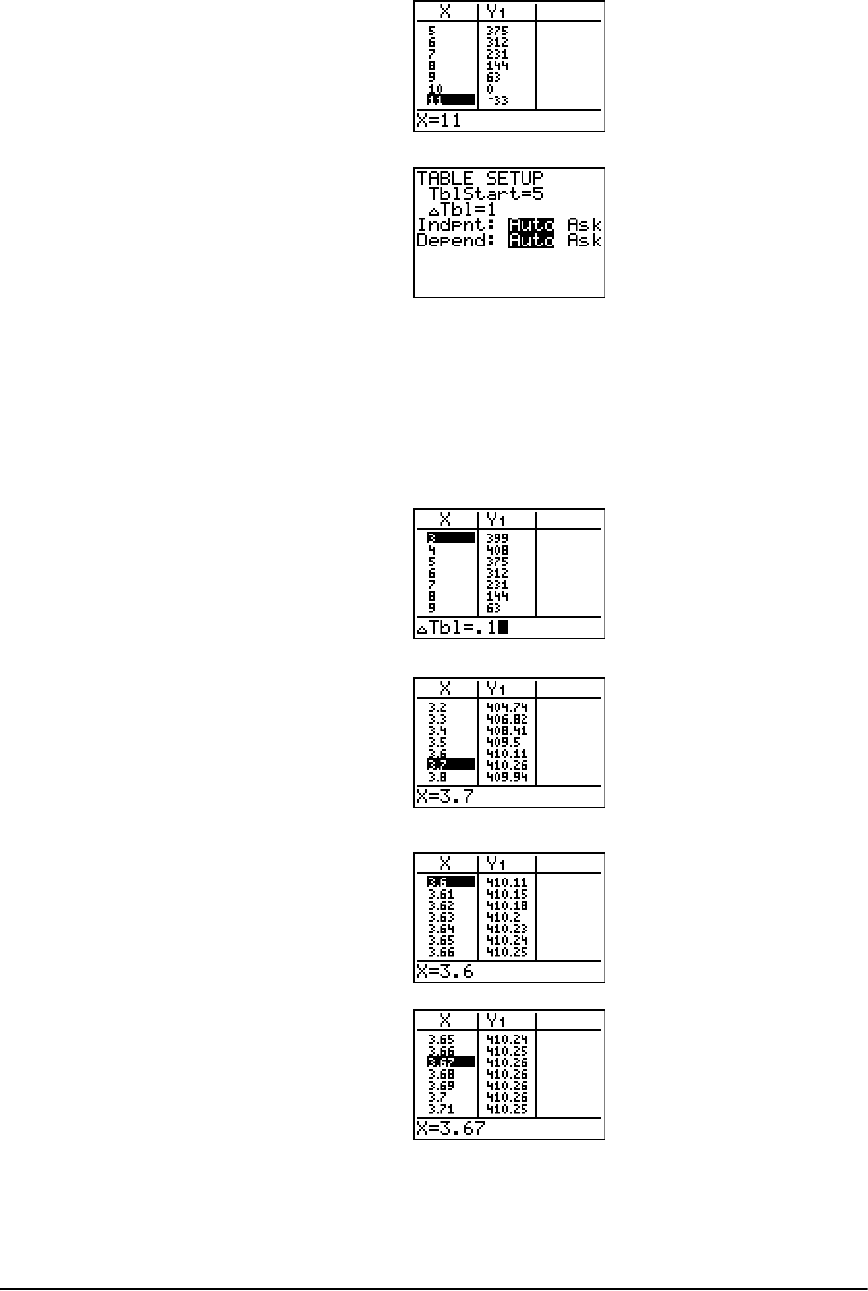
Chapter 17: Activities 301
Zooming In on the Table
You can adjust the way a table is displayed to get more information about a defined function. With
smaller values for @Tbl, you can zoom in on the table. You can change the values on the TBLSET
screen by pressing y - or by pressing à on the TABLE screen
5. Press and hold † to scroll the table until
a negative result for Y1 is displayed.
Notice that the maximum length of X for
this problem occurs where the sign of Y1
(box’s volume) changes from positive to
negative, between 10 and 11.
6. Press y -.
Notice that TblStart has changed to 5 to
reflect the first line of the table as it was
last displayed. (In step 5, the first value
of X displayed in the table is 5.)
1. Press y 0.
2. Press } to move the cursor to highlight
3.
3. Press Ã. The @Tbl displays on the entry
line.
4. Enter Ë 1 Í. The table updates,
showing the changes in X in increments
of 0.1.
Notice that the maximum value for Y1 in
this table view is 410.26, which occurs at
X=3.7. Therefore, the maximum occurs
where 3.6<X<3.8.
5. With X=3.6 highlighted, press Ã Ë 01
Í to set @Tbl=0.01.
6. Press † and } to scroll the table.
Four equivalent maximum values are
shown, 410.26 at X=3.67, 3.68, 3.69, and
3.70.
Chapter 17: Activities 302
Setting the Viewing Window
You also can use the graphing features of the TI-84 Plus to find the maximum value of a previously
defined function. When the graph is activated, the viewing window defines the displayed portion of
the coordinate plane. The values of the window variables determine the size of the viewing
window.
7. Press † or } to move the cursor to 3.67.
Press ~ to move the cursor into the Y1
column.
The value of Y1 at X=3.67 is displayed on
the bottom line in full precision as
410.261226.
8. Press † to display the other maximum.
The value of Y1 at X=3.68 in full precision
is 410.264064, at X=3.69 is 410.262318 and
at X=3.7 is 410.256.
The maximum volume of the box would
occur at 3.68 if you could measure and
cut the paper at .01-centimeter
increments.
1. Press p to display the window
editor, where you can view and edit the
values of the window variables.
The standard window variables define
the viewing window as shown. Xmin,
Xmax, Ymin, and Ymax define the
boundaries of the display. Xscl and Yscl
define the distance between tick marks
on the X and Y axes. Xres controls
resolution.
2. Press 0 Í to define Xmin.
3. Press 20 ¥ 2 to define Xmax using an
expression.
Note: For this example, the division sign
is used for the calculation. However, you
can use n/d entry format where fraction
output can be experienced, depending
on mode settings.
Chapter 17: Activities 303
Displaying and Tracing the Graph
Now that you have defined the function to be graphed and the window in which to graph it, you can
display and explore the graph. You can trace along a function using the TRACE feature.
4. Press Í. The expression is
evaluated, and 10 is stored in Xmax.
Press Í to accept Xscl as 1.
5. Press 0 Í 500 Í 100 Í 1
Í to define the remaining window
variables.
1. Press s to graph the selected
function in the viewing window.
The graph of Y1=(20N2X)(25à2NX)X is
displayed.
2. Press ~ to activate the free-moving
graph cursor.
The X and Y coordinate values for the
position of the graph cursor are
displayed on the bottom line.
3. Press |, ~, }, and † to move the free-
moving cursor to the apparent maximum
of the function.
As you move the cursor, the X and Y
coordinate values are updated
continually.
4. Press r. The trace cursor is
displayed on the Y1 function.
The function that you are tracing is
displayed in the top-left corner.
5. Press | and ~ to trace along Y1, one X
dot at a time, evaluating Y1 at each X.
You also can enter your estimate for the
maximum value of X.
6. Press 3 Ë 8. When you press a number
key while in TRACE, the X= prompt is
displayed in the bottom-left corner.
Chapter 17: Activities 304
Zooming In on the Graph
To help identify maximums, minimums, roots, and intersections of functions, you can magnify the
viewing window at a specific location using the ZOOM instructions.
7. Press Í.
The trace cursor jumps to the point on
the Y1 function evaluated at X=3.8.
8. Press | and ~ until you are on the
maximum Y value.
This is the maximum of Y1(X) for the X
pixel values. The actual, precise
maximum may lie between pixel values.
1. Press q to display the ZOOM menu.
This menu is a typical TI-84 Plus menu.
To select an item, you can either press
the number or letter next to the item, or
you can press † until the item number or
letter is highlighted, and then press
Í.
2. Press 2 to select 2:Zoom In.
The graph is displayed again. The cursor
has changed to indicate that you are
using a ZOOM instruction.
3. With the cursor near the maximum value
of the function, press Í.
The new viewing window is displayed.
Both XmaxNXmin and YmaxNYmin have
been adjusted by factors of 4, the default
values for the zoom factors.
4. Press | and ~ to search for the
maximum value.
5. Press p to display the new window
settings.
Note: To return to the previous graph,
press q ~ 1:ZPrevious.
Chapter 17: Activities 305
Finding the Calculated Maximum
You can use a CALCULATE menu operation to calculate a local maximum of a function. To do this,
pick a point to the left of where you think the maximum is on the graph. This is called the left
bound. Next, pick a point to the right of the maximum. This is called the right bound. Finally, guess
the maximum by moving the cursor to a point between the left and right bounds. With this
information, the maximum can be calculated by the methods programmed in the TI-84 Plus.
1. Press y / to display the
CALCULATE menu. Press 4 to select
4:maximum.
The graph is displayed again with a
Left Bound? prompt.
2. Press | to trace along the curve to a
point to the left of the maximum, and
then press Í.
A 4 at the top of the screen indicates the
selected bound.
A Right Bound? prompt is displayed.
3. Press ~ to trace along the curve to a
point to the right of the maximum, and
then press Í.
A 3 at the top of the screen indicates the
selected bound.
A Guess? prompt is displayed.
4. Press | to trace to a point near the
maximum, and then press Í.
Or, press 3 Ë 8, and then press Í to
enter a guess for the maximum.
When you press a number key in TRACE,
the X= prompt is displayed in the bottom-
left corner.
Notice how the values for the calculated
maximum compare with the maximums
found with the free-moving cursor, the
trace cursor, and the table.
Note: In steps 2 and 3 above, you can
enter values directly for Left Bound and
Right Bound, in the same way as
described in step 4.

Chapter 17: Activities 306
Comparing Test Results Using Box Plots
Problem
An experiment found a significant difference between boys and girls pertaining to their ability to
identify objects held in their left hands, which are controlled by the right side of their brains, versus
their right hands, which are controlled by the left side of their brains. The TI Graphics team
conducted a similar test for adult men and women.
The test involved 30 small objects, which participants were not allowed to see. First, they held 15
of the objects one by one in their left hands and guessed what they were. Then they held the other
15 objects one by one in their right hands and guessed what they were. Use box plots to compare
visually the correct-guess data from this table.
Each row in the table represents the results observed for one subject. Note that 10 women and 12
men were tested.
Procedure
1. Press … 5 to select 5:SetUpEditor. Enter list names WLEFT, WRGHT, MLEFT, and MRGHT,
separated by commas. Press Í. The stat list editor now contains only these four lists.
(See Chapter 11: Lists for detailed instructions for using the SetUpEditor.)
2. Press … 1 to select 1:Edit.
3. Enter into WLEFT the number of correct guesses each woman made using her left hand
(Women Left). Press ~ to move to WRGHT and enter the number of correct guesses each
woman made using her right hand (Women Right).
4. Likewise, enter each man’s correct guesses in MLEFT (Men Left) and MRGHT (Men Right).
Correct Guesses
Women
Left
Women
Right
Men
Left
Men
Right
84712
9186
12 8 7 12
11 12 5 12
10 11 7 7
811811
12 13 11 12
7124 8
9111012
11 12 14 11
13 9
59
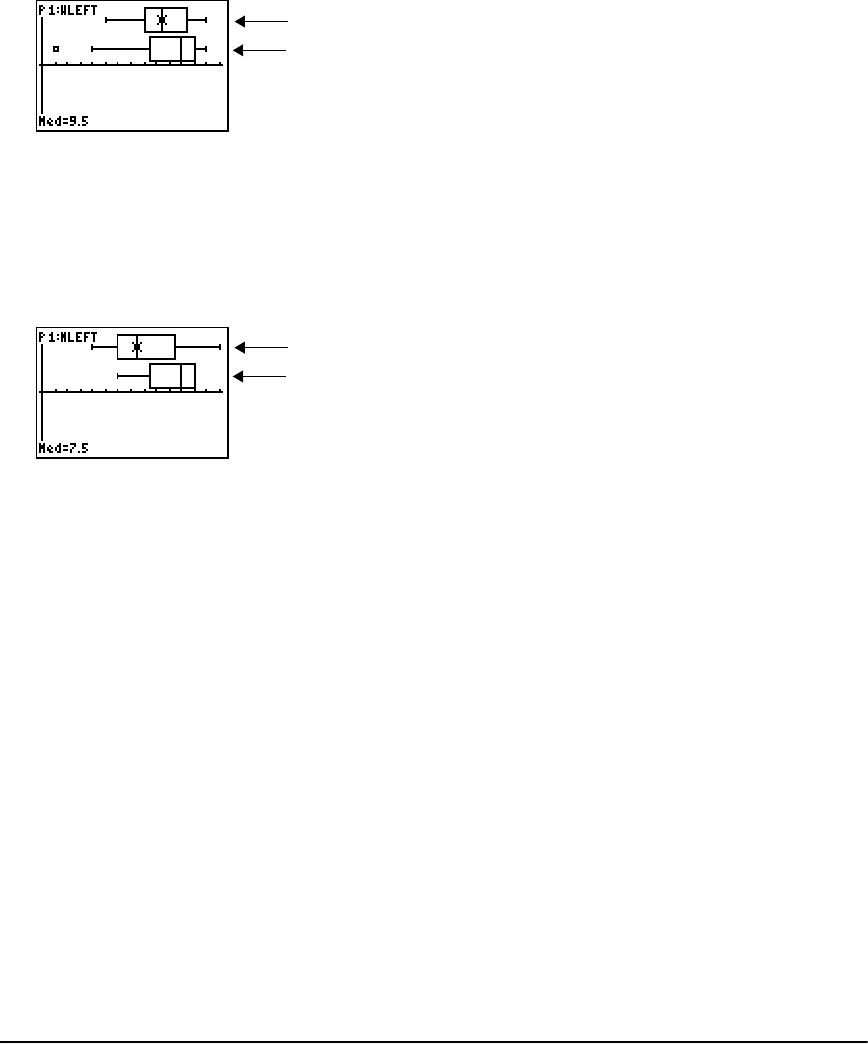
Chapter 17: Activities 307
5. Press y ,. Select 1:Plot1. Turn on plot 1; define it as a modified box plot Õ that uses
Xlist as WLEFT. Move the cursor to the top line and select Plot2. Turn on plot 2; define it as a
modified box plot that uses Xlist as WRGHT. (See Chapter 12: Statistics for detailed information
on using Stat Plots.)
6. Press o. Turn off all functions.
7. Press p. Set Xscl=1 and Yscl=0. Press q 9 to select 9:ZoomStat. This adjusts the
viewing window and displays the box plots for the women’s results.
8. Press r.
Women’s left-hand data
Women’s right-hand data
Use | and ~ to examine minX, Q1, Med, Q3, and maxX for each plot. Notice the outlier to the
women’s right-hand data. What is the median for the left hand? For the right hand? With which
hand were the women more accurate guessers, according to the box plots?
9. Examine the men’s results. Redefine plot 1 to use MLEFT, redefine plot 2 to use MRGHT. Press
r.
Men’s left-hand data
Men’s right-hand data
Press | and ~ to examine minX, Q1, Med, Q3, and maxX for each plot. What difference do
you see between the plots?
10. Compare the left-hand results. Redefine plot 1 to use WLEFT, redefine plot 2 to use MLEFT,
and then press r to examine minX, Q1, Med, Q3, and maxX for each plot. Who were the
better left-hand guessers, men or women?
11. Compare the right-hand results. Define plot 1 to use WRGHT, define plot 2 to use MRGHT, and
then press r to examine minX, Q1, Med, Q3, and maxX for each plot. Who were the better
right-hand guessers?
In the original experiment boys did not guess as well with right hands, while girls guessed
equally well with either hand. This is not what our box plots show for adults. Do you think that
this is because adults have learned to adapt or because our sample was not large enough?

Chapter 17: Activities 308
Graphing Piecewise Functions
Problem
The fine for speeding on a road with a speed limit of 45 kilometers per hour (kph) is 50; plus 5 for
each kph from 46 to 55 kph; plus 10 for each kph from 56 to 65 kph; plus 20 for each kph from 66
kph and above. Graph the piecewise function that describes the cost of the ticket.
The fine (Y) as a function of kilometers per hour (X) is:
,
which simplifies to:
Procedure
1. Press z. Select Func and Classic.
2. Press o. Turn off all functions and stat plots. Enter the Y= function to describe the fine. Use
the TEST menu operations to define the piecewise function. Set the graph style for Y1 to
í (dot).
3. Press p and set Xmin=L2, Xscl=10, Ymin=L5, Yscl=10 and @X=1. Ignore Xmax and Ymax;
they are set in step 4.

Chapter 17: Activities 309
4. Press y 5 to return to the home screen. Store 5 to @Y. @X and @Y are on the
VARS Window X/Y secondary menu. @X and @Y specify the horizontal and vertical distance
between the centers of adjacent pixels. Integer values for @X and @Y produce nice values for
tracing.
5. Press r to plot the function. At what speed does the ticket exceed 250?
Graphing Inequalities
Problem
Graph the inequality 0.4x3 N 3x + 5 < 0.2x + 4. Use the TEST menu operations to explore the values
of X where the inequality is true and where it is false.
Note: You can also investigate graphing inequalities using the Inequality Graphing application.
The application is pre-loaded on your TI-84 Plus and can be downloaded from education.ti.com.
Procedure
1. Press z. Select Dot, Simul, and the default settings. Setting Dot mode changes all graph
style icons to í (dot) in the Y= editor.
2. Press o. Turn off all functions and stat plots. Enter the left side of the inequality as Y4 and the
right side as Y5.
3. Enter the statement of the inequality as Y6. This function evaluates to 1 if true or 0 if false.
Note: You can use the YVARS shortcut menu to paste Y4 and Y5 in the Y= editor.
4. Press q 6 to graph the inequality in the standard window.
Chapter 17: Activities 310
5. Press r † † to move to Y6. Then press | and ~ to trace the inequality, observing the
value of Y.
When you trace, you can see that Y=1 indicates that Y4<Y5 is true and that Y=0 indicates that
Y4<Y5 is false.
6. Press o. Turn off Y4, Y5, and Y6. Enter equations to graph only the inequality.
7. Press r.
Notice that the values of Y7 and Y8 are zero where the inequality is false. You only see the
intervals of the graph where Y4<Y5 because intervals that are false are multiplied by 0
(Y6†Y4 and Y6†Y5)
Solving a System of Nonlinear Equations
Problem
Using a graph, solve the equation x3N2x=2cos(x). Stated another way, solve the system of two
equations and two unknowns: y = x3N2x and y = 2cos(x). Use ZOOM factors to control the decimal
places displayed on the graph and use y / 5:intersect to find an approximate solution.
Procedure
1. Press z. Select the default mode settings. Press o. Turn off all functions and stat plots.
Enter the functions.

Chapter 17: Activities 311
2. Press q 4 to select 4:ZDecimal. The display shows that two solutions may exist (points
where the two functions appear to intersect).
3. Press q ~ 4 to select 4:SetFactors from the ZOOM MEMORY menu. Set XFact=10 and
YFact=10.
4. Press q 2 to select 2:Zoom In. Use |, ~, }, and † to move the free-moving cursor onto
the apparent intersection of the functions on the right side of the display. As you move the
cursor, notice that the X and Y values have one decimal place.
5. Press Í to zoom in. Move the cursor over the intersection. As you move the cursor, notice
that now the X and Y values have two decimal places.
6. Press Í to zoom in again. Move the free-moving cursor onto a point exactly on the
intersection. Notice the number of decimal places.
7. Press y / 5 to select 5:intersect. Press Í to select the first curve and Í to select
the second curve. To guess, move the trace cursor near the intersection. Press Í. What
are the coordinates of the intersection point?
8. Press q 4 to select 4:ZDecimal to redisplay the original graph.
9. Press q. Select 2:Zoom In and repeat steps 4 through 8 to explore the apparent function
intersection on the left side of the display.
Using a Program to Create the Sierpinski Triangle
Setting up the Program
This program creates a drawing of a famous fractal, the Sierpinski Triangle, and stores the
drawing to a picture. To begin, press ~ ~ 1. Name the program SIERPINS, and then press
Í. The program editor is displayed.
Note: After you run this program, press y . † † † Í to turn on the axes in the graph
screen.
Program
PROGRAM:SIERPINS
:FnOff :ClrDraw
:PlotsOff
:AxesOff
:0!Xmin:1!Xmax
:0!Ymin:1!Ymax
Set viewing window.
:rand!X:rand!Y
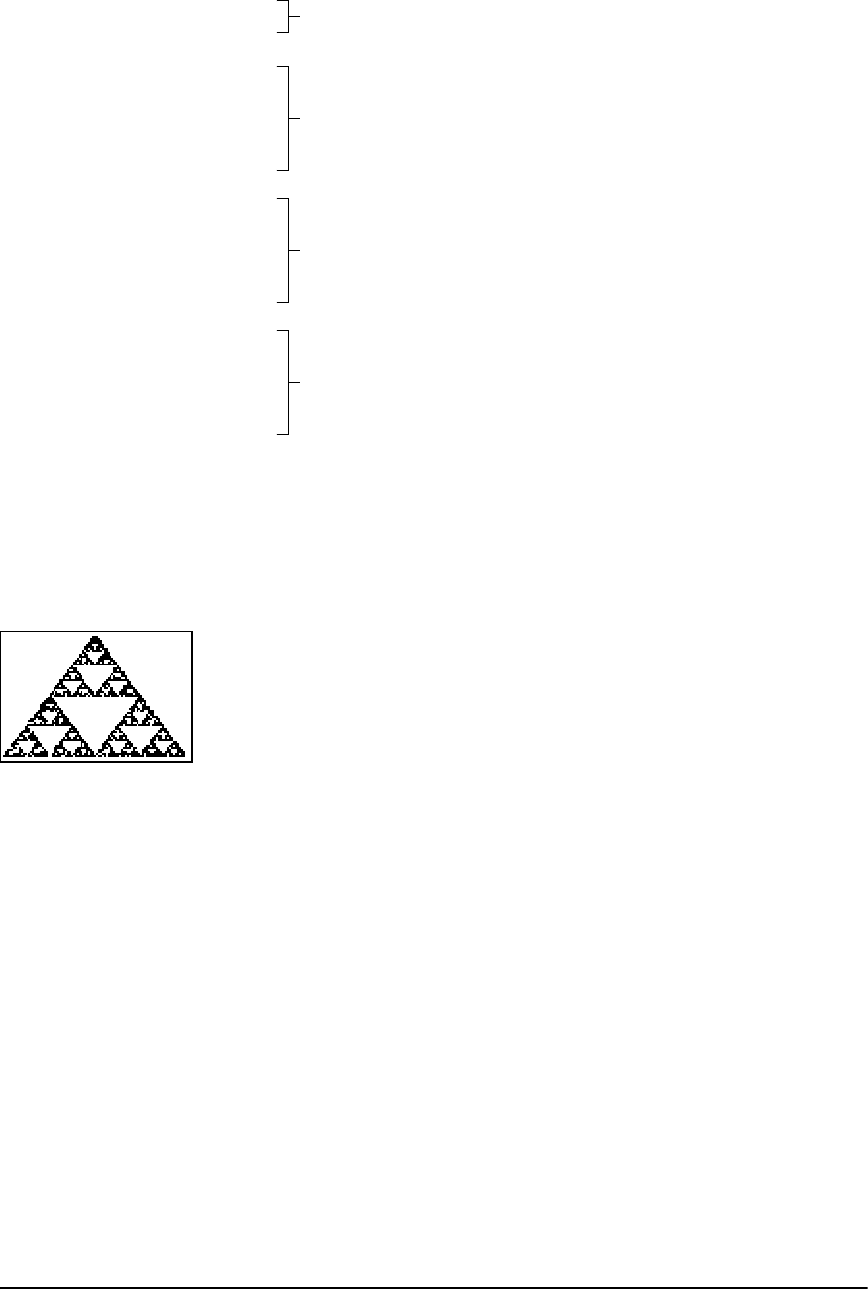
Chapter 17: Activities 312
After you execute the program above, you can recall and display the picture with the instruction
RecallPic 6.
Graphing Cobweb Attractors
Problem
Using Web format, you can identify points with attracting and repelling behavior in sequence
graphing.
Procedure
1. Press z. Select Seq and the default mode settings. Press y .. Select Web format
and the default format settings.
2. Press o. Clear all functions and turn off all stat plots. Enter the sequence that corresponds to
the expression Y = K X(1NX).
u(n)=Ku(nN1)(1Nu(nN1))
u(nMin)=.01
:For(K,1,3000)
:rand!N
Beginning of For group.
:If N1à3
:Then
:.5X!X
:.5Y!Y
:End
If/Then group
:If 1à3 <N and N2à3
:Then
:.5(.5+X)!X
:.5(1+Y)!Y
:End
If/Then group.
:If 2à3<N
:Then
:.5(1+X)!X
:.5Y!Y
:End
If/Then group.
:Pt-On(X,Y)
:End
:StorePic 6
Draw point.
End of For group.
Store picture.
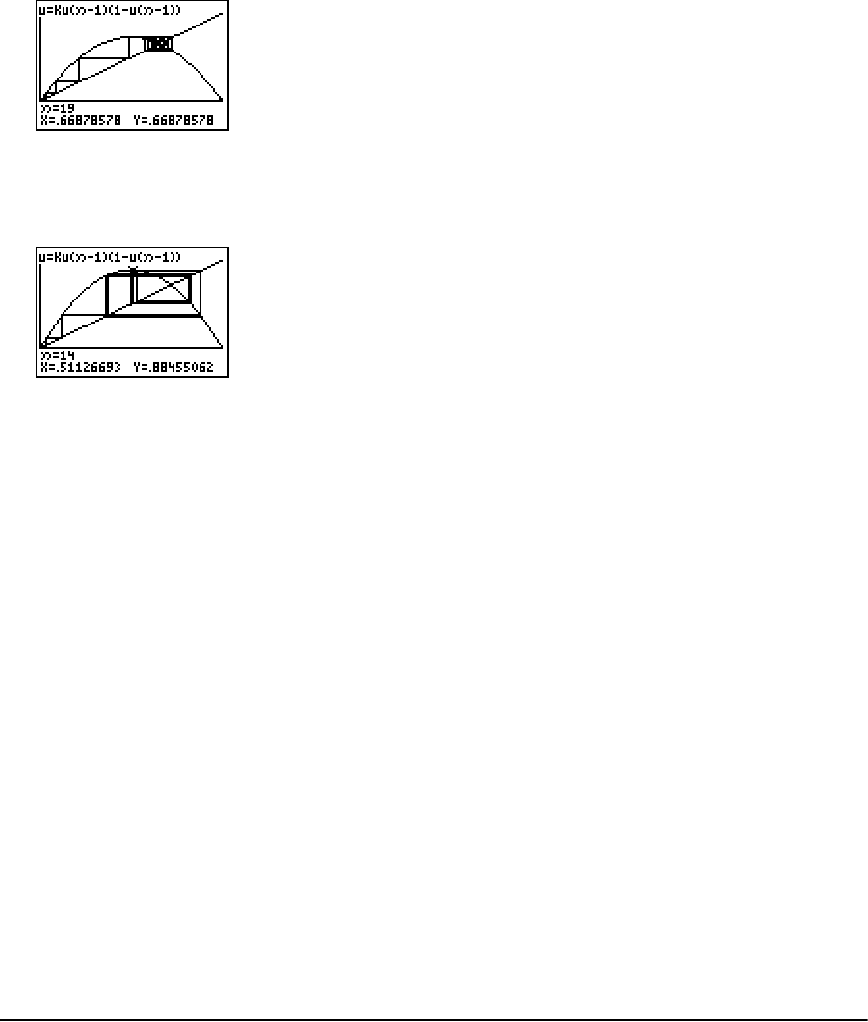
Chapter 17: Activities 313
3. Press y 5 to return to the home screen, and then store 2.9 to K.
4. Press p. Set the window variables.
5. Press r to display the graph, and then press ~ to trace the cobweb. This is a cobweb
with one attractor.
6. Change K to 3.44 and trace the graph to show a cobweb with two attractors.
7. Change K to 3.54 and trace the graph to show a cobweb with four attractors.
Using a Program to Guess the Coefficients
Setting Up the Program
This program graphs the function A sin(BX) with random integer coefficients between 1 and 10.
Try to guess the coefficients and graph your guess as C sin(DX). The program continues until your
guess is correct.
Note: This program changes the graph window and graph styles. After you run the program, you
can change individual settings as needed or you can press y L 7 2 2 to return to default
settings.
Programs typically do not restore your settings in MODE, Y=, WINDOW and other locations that
were used by the program. This is dependent on who created the program.
Program
nMin=0
nMax=10
PlotStart=1
PlotStep=1
Xmin=0
Xmax=1
Xscl=1
Ymin=M.26
Ymax=1.1
Yscl=1
PROGRAM:GUESS
:PlotsOff :Func
:FnOff :Radian
:ClrHome
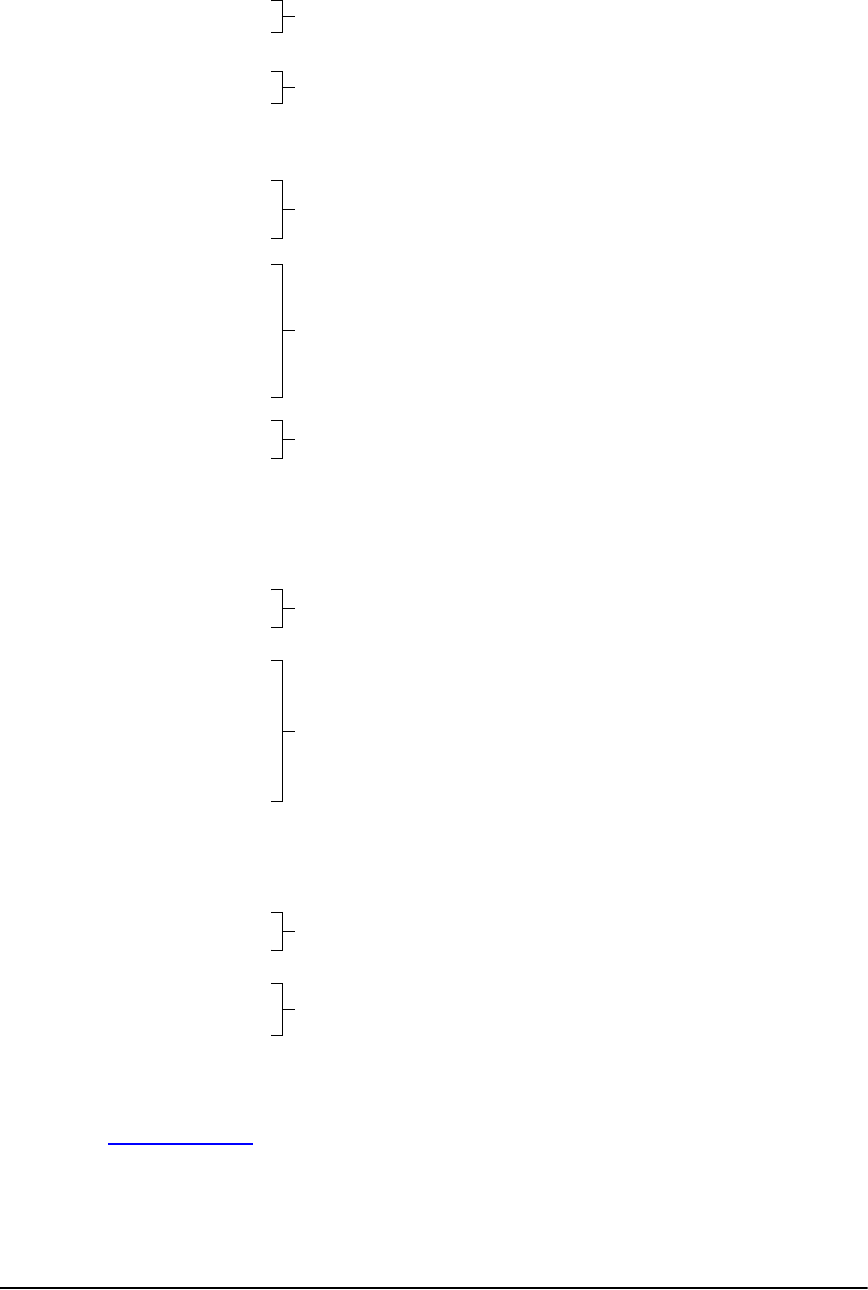
Chapter 17: Activities 314
Note: The Guess My Coefficients App is an educational game that challenges you to enter the
correct coeffiecients for graphs of linear, quadratic and absolute value functions. This app is
available at education.ti.com.
:"Asin(BX)"!Y1
:"Csin(DX)"!Y2
Define equations.
:GraphStyle(1,1)
:GraphStyle(2,5)
Set line and path graph styles.
:FnOff 2
:randInt(1,10)!A
:randInt(1,10)!B
:0!C:0!D
Initialize coefficients.
:L2p!Xmin
:2p!Xmax
:pà2!Xscl
:L10!Ymin
:10!Ymax
:1!Yscl
Set viewing window.
:DispGraph
:Pause
Display graph.
:FnOn 2
:Lbl Z
:Prompt C,D Prompt for guess.
:DispGraph
:Pause
Display graph.
:If C=A
:Text(1,1,"C IS OK")
:If CƒA
:Text(1,1,"C IS
WRONG")
:If D=B
:Text(1,50,"D IS OK")
:If DƒB
:Text(1,50,"D IS
WRONG")
Display results.
:DispGraph
:Pause
Display graph.
:If C=A and D=B
:Stop
:Goto Z
Quit if guesses are correct.

Chapter 17: Activities 315
Graphing the Unit Circle and Trigonometric Curves
Problem
Using parametric graphing mode, graph the unit circle and the sine curve to show the relationship
between them.
Any function that can be plotted in Func mode can be plotted in Par mode by defining the X
component as T and the Y component as F(T).
Procedure
1. Press z. Select Par, Simul, and the default settings.
2. Press p. Set the viewing window.
3. Press o. Turn off all functions and stat plots. Enter the expressions to define the unit circle
centered on (0,0).
4. Enter the expressions to define the sine curve.
5. Press r. As the graph is plotting, you may press Í to pause and Í again to
resume graphing as you watch the sine function “unwrap” from the unit circle.
Note:
• You can generalize the unwrapping. Replace sin(T) in Y2T with any other trig function to
unwrap that function.
Tmin=0
Tmax=2p
Tstep=.1
Xmin=L2
Xmax=7.4
Xscl=pà2
Ymin=L3
Ymax=3
Yscl=1

Chapter 17: Activities 316
• You can graph the functions again by turning the functions off and then turning them back on
on the Y= editor or by using the FuncOFF and FuncON commands on the home screen.
Finding the Area between Curves
Problem
Find the area of the region bounded by:
Procedure
1. Press z. Select the default mode settings.
2. Press p. Set the viewing window.
3. Press o. Turn off all functions and stat plots. Enter the upper and lower functions.
Y1=300Xà(X2+625)
Y2=3cos(.1X)
4. Press y / 5 to select 5:Intersect. The graph is displayed. Select a first curve, second
curve, and guess for the intersection toward the left side of the display. The solution is
displayed, and the value of X at the intersection, which is the lower limit of the integral, is
stored in Ans and X.
5. Press y 5 to go to the home screen. Press y < 7 and use Shade( to see the area
graphically.
Shade(Y2,Y1,Ans,75)
6. Press y 5 to return to the home screen. Enter the expression to evaluate the integral for
the shaded region.
fnInt(Y1NY2,X,Ans,75)
The area is 325.839962.
f(x)
g(x)
x
=
=
=
300x / (x2 + 625)
3cos(.1x)
75
Xmin=0
Xmax=100
Xscl=10
Ymin=L5
Ymax=10
Yscl=1
Xres=1

Chapter 17: Activities 317
Using Parametric Equations: Ferris Wheel Problem
Problem
Using two pairs of parametric equations, determine when two objects in motion are closest to each
other in the same plane.
A ferris wheel has a diameter (d) of 20 meters and is rotating counterclockwise at a rate (s) of one
revolution every 12 seconds. The parametric equations below describe the location of a ferris
wheel passenger at time T, where a is the angle of rotation, (0,0) is the bottom center of the ferris
wheel, and (10,10) is the passenger’s location at the rightmost point, when T=0.
A person standing on the ground throws a ball to the ferris wheel passenger. The thrower’s arm is at
the same height as the bottom of the ferris wheel, but 25 meters (b) to the right of the ferris wheel’s
lowest point (25,0). The person throws the ball with velocity (v0) of 22 meters per second at an angle
(q) of 66¡ from the horizontal. The parametric equations below describe the location of the ball at
time T.
Procedure
1. Press z. Select Par, Simul, and the default settings. Simul (simultaneous) mode simulates
the two objects in motion over time.
2. Press p. Set the viewing window.
3. Press o. Turn off all functions and stat plots. Enter the expressions to define the path of the
ferris wheel and the path of the ball. Set the graph style for X2T to ë (path).
Note: Try setting the graph styles to ë X1T and ì X2T, which simulates a chair on the ferris
wheel and the ball flying through the air when you press s.
X(T) = r cos a
Y(T) = r + r sin a
where a = 2pTs and r = dà2
X(T) = b N Tv0 cosq
Y(T) = Tv0 sinq N (gà2) T2
where g = 9.8 m/sec2
Tmin=0
Tmax=12
Tstep=.1
Xmin=L13
Xmax=34
Xscl=10
Ymin=0
Ymax=31
Yscl=10
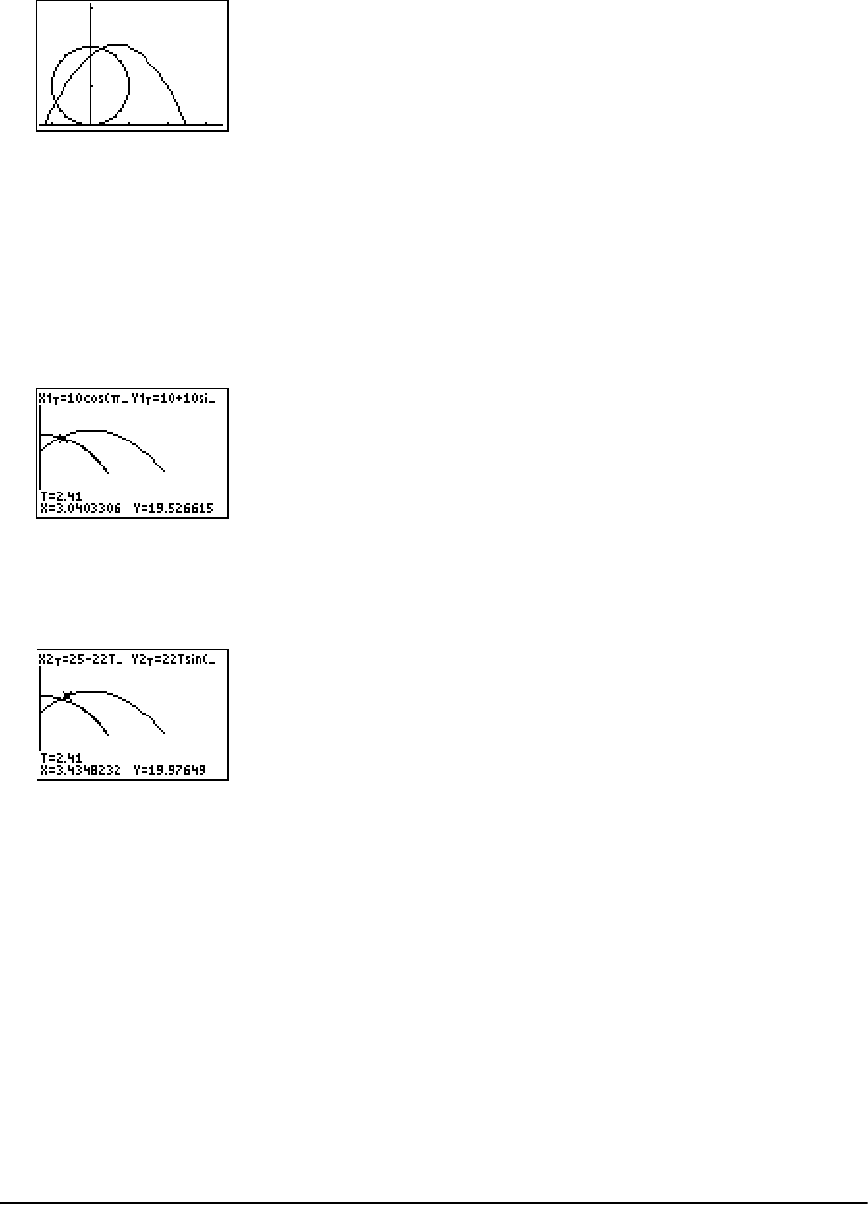
Chapter 17: Activities 318
4. Press s to graph the equations. Watch closely as they are plotted. Notice that the ball
and the ferris wheel passenger appear to be closest where the paths cross in the top-right
quadrant of the ferris wheel.
5. Press p. Change the viewing window to concentrate on this portion of the graph.
6. Press r. After the graph is plotted, press ~ to move near the point on the ferris wheel
where the paths cross. Notice the values of X, Y, and T.
7. Press † to move to the path of the ball. Notice the values of X and Y (T is unchanged). Notice
where the cursor is located. This is the position of the ball when the ferris wheel passenger
passes the intersection. Did the ball or the passenger reach the intersection first?
You can use r to, in effect, take snapshots in time and explore the relative behavior of
two objects in motion.
Tmin=1
Tmax=3
Tstep=.03
Xmin=0
Xmax=23.5
Xscl=10
Ymin=10
Ymax=25.5
Yscl=10

Chapter 17: Activities 319
Demonstrating the Fundamental Theorem of Calculus
Problem 1
Using the functions fnInt( and nDeriv( from the FUNC shortcut menu or the MATH menu to graph
functions defined by integrals and derivatives demonstrates graphically that:
and that
Procedure 1
1. Press z. Select the default settings.
2. Press p. Set the viewing window.
3. Press o. Turn off all functions and stat plots. Enter the numerical integral of 1àT from 1 to X
and the function ln(X). Set the graph style for Y1 to ç (line) and Y2 to ë (path).
4. Press r. Press |, }, ~, and † to compare the values of Y1 and Y2.
5. Press o. Turn off Y1 and Y2, and then enter the numerical derivative of the integral of 1àX
and the function 1àX. Set the graph style for Y3 to ç (line) and Y4 to è (thick).
Xmin=.01
Xmax=10
Xscl=1
Ymin=L1.5
Ymax=2.5
Yscl=1
Xres=3

Chapter 17: Activities 320
6. Press r. Again, use the cursor keys to compare the values of the two graphed functions,
Y3 and Y4.
y
t2
t
d
2
–
x
∫
=
Problem 2
Explore the functions defined by
, t2td
0
x
∫, and t2td
2
x
∫
Procedure 2
1. Press o. Turn off all functions and stat plots. Use a list to define these three functions
simultaneously. Store the function in Y5.
2. Press q 6 to select 6:ZStandard. The graphs are displayed as each calculation of the
integral and derivative occurs at the pixel point, which may take some time.
3. Press r. Notice that the functions appear identical, only shifted vertically by a constant.
4. Press o. Enter the numerical derivative of Y5 in Y6.
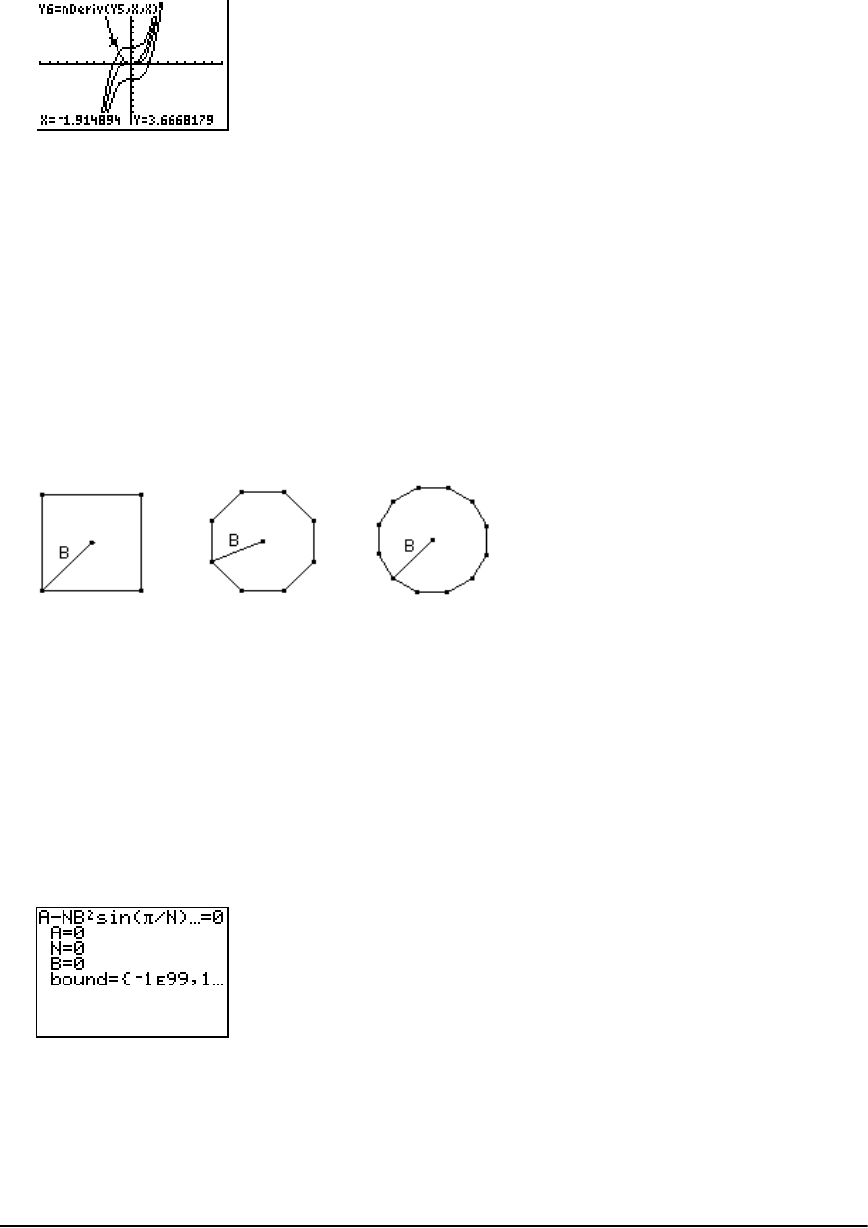
Chapter 17: Activities 321
5. Press r. Notice that although the three graphs defined by Y5 are different, they share the
same derivative.
N = 4 sides N = 8 sides N = 12 sides
Computing Areas of Regular N-Sided Polygons
Problem
Use the equation solver to store a formula for the area of a regular N-sided polygon, and then
solve for each variable, given the other variables. Explore the fact that the limiting case is the area
of a circle, pr2.
Consider the formula A = NB2 sin(pàN) cos(pàN) for the area of a regular polygon with N sides of
equal length and B distance from the center to a vertex.
Procedure
1. Press t B to select B:Solver from the MATH menu. Either the equation editor or the
interactive solver editor is displayed. If the interactive solver editor is displayed, press } to
display the equation editor.
2. Enter the formula as 0=ANNB2sin(p / N)cos(p / N), and then press Í. The interactive solver
editor is displayed.
3. Enter N=4 and B=6 to find the area (A) of a square with a distance (B) from center to vertex of
6 centimeters.
4. Press } } to move the cursor onto A, and then press ă \. The solution for A is
displayed on the interactive solver editor.

Chapter 17: Activities 322
5. Now solve for B for a given area with various number of sides. Enter A=200 and N=6. To find
the distance B, move the cursor onto B, and then press ƒ \.
6. Enter N=8. To find the distance B, move the cursor onto B, and then press ƒ \. Find
B for N=9, and then for N=10.
Find the area given B=6, and N=10, 100, 150, 1000, and 10000. Compare your results with p62 (the
area of a circle with radius 6), which is approximately 113.097.
7. Enter B=6. To find the area A, move the cursor onto A, and then press ƒ \. Find A for
N=10, then N=100, then N=150, then N=1000, and finally N=10000. Notice that as N gets large,
the area A approaches pB2.
Now graph the equation to see visually how the area changes as the number of sides gets large.
8. Press z. Select the default mode settings.
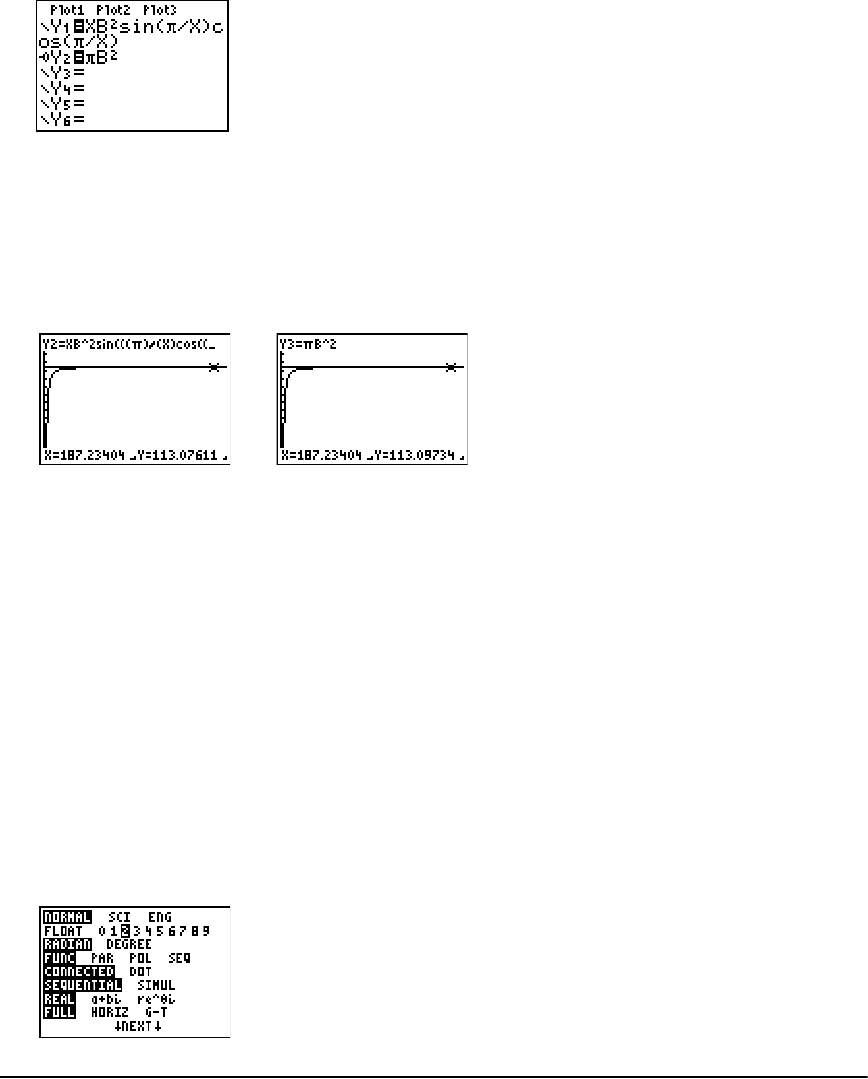
Chapter 17: Activities 323
9. Press p. Set the viewing window.
10. Press o. Turn off all functions and stat plots. Enter the equation for the area. Use X in place
of N. Set the graph styles as shown.
11. Press r. After the graph is plotted, press 100 Í to trace to X=100. Press 150 Í.
Press 188 Í. Notice that as X increases, the value of Y converges to p62, which is
approximately 113.097. Y2=pB2 (the area of the circle) is a horizontal asymptote to Y1. The
area of an N-sided regular polygon, with r as the distance from the center to a vertex,
approaches the area of a circle with radius r (pr2) as N gets large.
Computing and Graphing Mortgage Payments
Problem
You are a loan officer at a mortgage company, and you recently closed on a 30-year home
mortgage at 8 percent interest with monthly payments of 800. The new home owners want to know
how much will be applied to the interest and how much will be applied to the principal when they
make the 240th payment 20 years from now.
Procedure
1. Press z and set the fixed-decimal mode to 2 decimal places. Set the other mode settings
to the defaults.
Xmin=0
Xmax=200
Xscl=10
Ymin=0
Ymax=150
Yscl=10
Xres=1
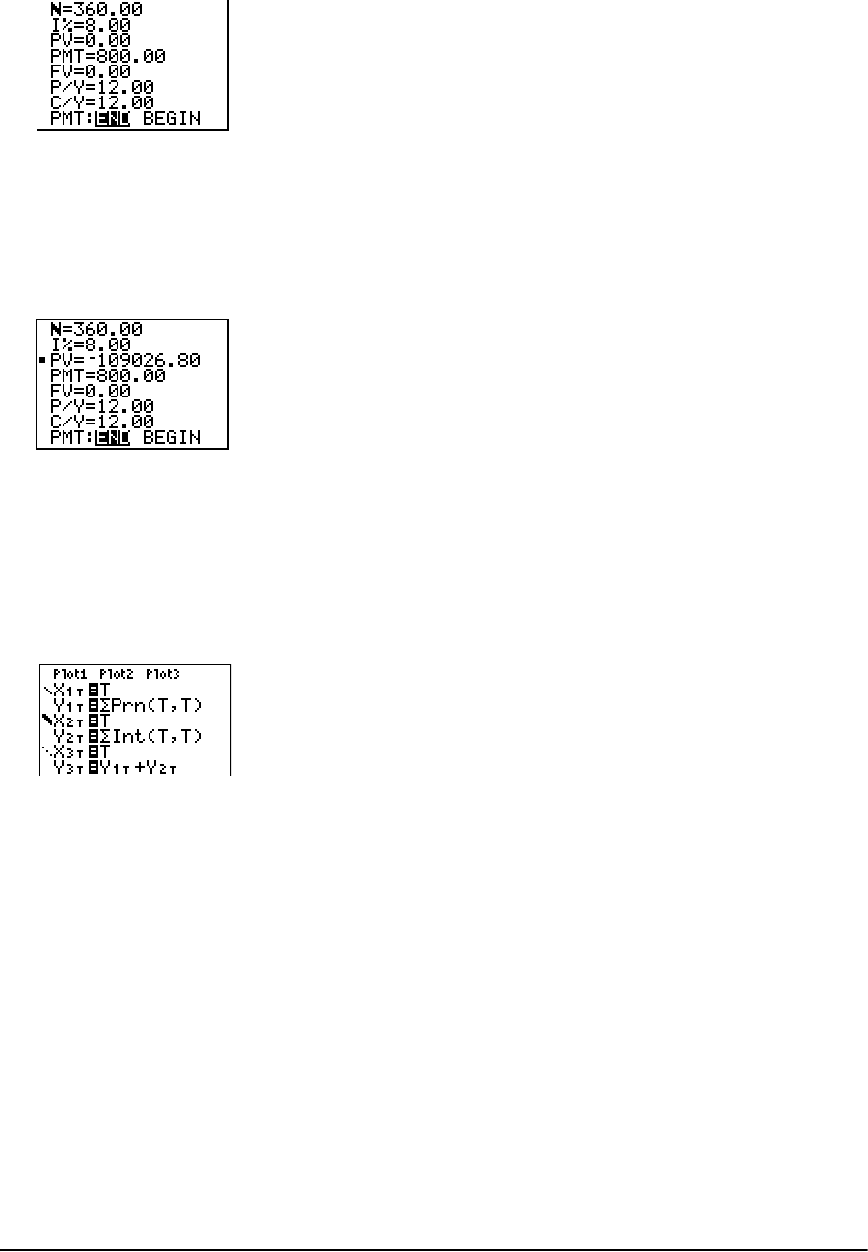
Chapter 17: Activities 324
2. Press Œ Í Í to display the TVM Solver. Enter these values.
Note: Enter a positive number (800) to show PMT as a cash inflow. Payment values will be
displayed as positive numbers on the graph. Enter 0 for FV, since the future value of a loan is 0
once it is paid in full. Enter PMT: END, since payment is due at the end of a period.
3. Move the cursor onto the PV= prompt, and then press ƒ \. The present value, or
mortgage amount, of the house is displayed at the PV= prompt.
Now compare the graph of the amount of interest with the graph of the amount of principal for each
payment.
4. Press z. Set Par and Simul.
5. Press o. Turn off all functions and stat plots. Enter these equations and set the graph styles
as shown.
Note: GPrn( and GInt( are located on the FINANCE menu (APPS 1:FINANCE).
6. Press p. Set these window variables.
Note: To increase the graph speed, change Tstep to 24.
7. Press r. After the graph is drawn, press 240 Í to move the trace cursor to T=240,
which is equivalent to 20 years of payments.
Tmin=1
Tmax=360
Tstep=12
Xmin=0
Xmax=360
Xscl=10
Ymin=0
Ymax=1000
Yscl=100
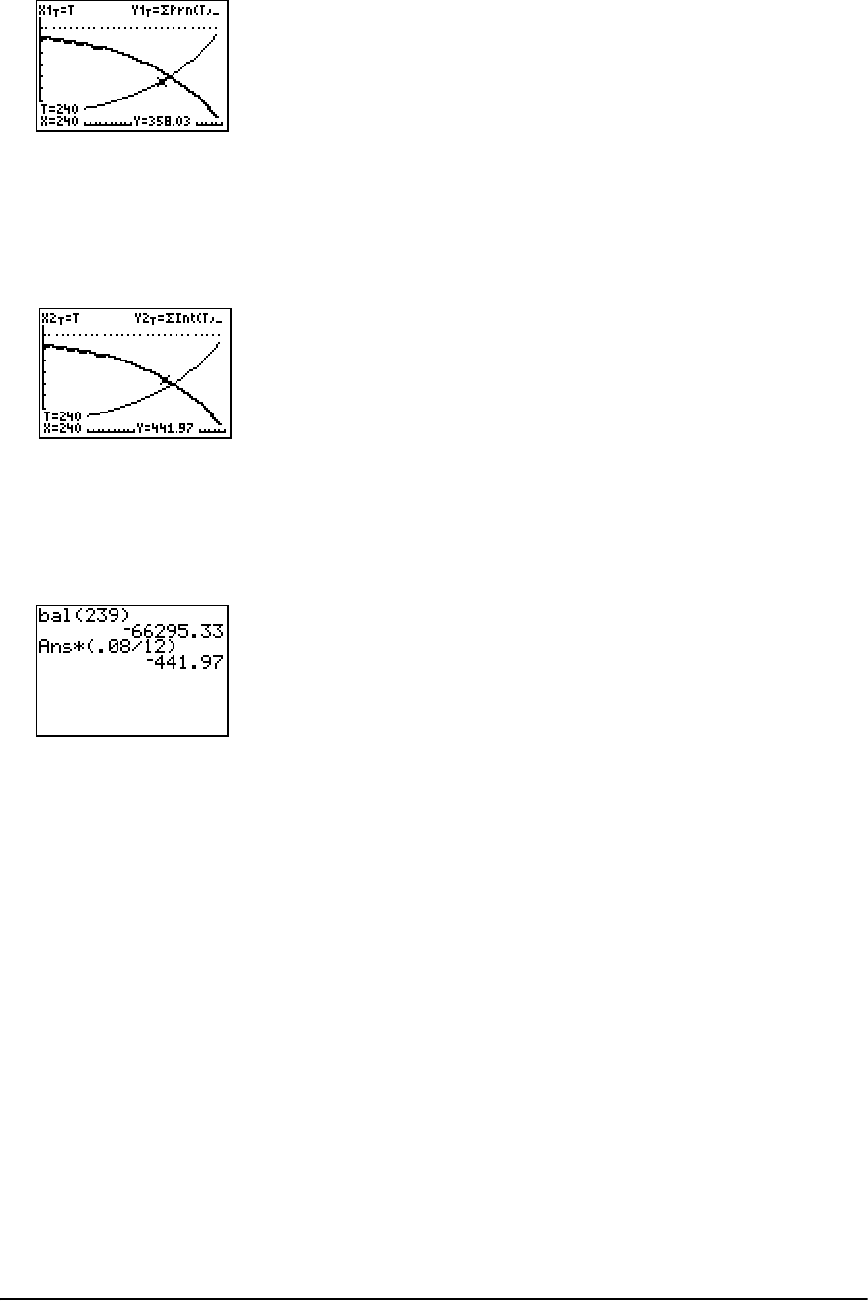
Chapter 17: Activities 325
The graph shows that for the 240th payment (X=240), 358.03 of the 800 payment is applied to
principal (Y=358.03).
Note: The sum of the payments (Y3T=Y1T+Y2T) is always 800.
8. Press † to move the cursor onto the function for interest defined by X2T and Y2T. Enter 240.
The graph shows that for the 240th payment (X=240), 441.97 of the 800 payment is interest
(Y=441.97).
9. Press y 5 Œ Í 9 to paste 9:bal( to the home screen. Check the figures from the
graph.
At which monthly payment will the principal allocation surpass the interest allocation?
Chapter 18: Memory and Variable Management 326
Chapter 18:
Memory and Variable Management
RAM FREE displays the
amount of available RAM.
ARC FREE displays the
amount of available Archive.
Checking Available Memory
MEMORY Menu
At any time you can check available memory or manage existing memory by selecting items from
the MEMORY menu. To access this menu, press y L.
To check memory availability, first press y L and then select 2:Mem Mgmt/Del.
Available RAM, Archive, and App Slots
The TI-84 Plus / TI-84 Plus Silver Edition has Archive, RAM, and Application (App) slot memory for
you to use and manage. The available RAM stores computations, lists, variables, and data. The
available Archive lets you store programs, Apps, groups, and other variables. The App slots are
actually individual sectors of Flash ROM where Apps are stored.
MEMORY
1: About... Displays information about the graphing
calculator including current OS version number.
2: Mem Mgmt/Del... Reports memory availability and variable usage.
3: Clear Entries Clears ENTRY (last-entry storage).
4: ClrAllLists Clears all lists in memory.
5: Archive... Archives a selected variable.
6: UnArchive... UnArchives a selected variable.
7: Reset... Displays the RAM, ARCHIVE, and ALL menus
8: Group... Displays GROUP and UNGROUP menus.
Graphing
calculator
Available RAM Available
Archive
App
Slots
TI-84 Plus 24 Kilobytes 491 Kilobytes 30
TI-84 Plus Silver
Edition
24 Kilobytes 1.5 Megabytes 94

Chapter 18: Memory and Variable Management 327
Note: Some Apps take up several App slots.
Displays the type of
graphing calculator. Displays the Product
ID. Each Flash-based
graphing calculator has
a unique product ID,
which you may need if
you contact technical
support. You can also
use this 14 digit ID to
register your calculator
at education.ti.com, or
identify your calculator
in the event that it is
lost or stolen.
Displays the OS
version. As new
software upgrades
become available,
you can
electronically
upgrade your unit.
Displaying the About Screen
About displays information about the TI-84 Plus Operating System (OS) Version, Product Number,
Product Identification (ID), and Flash Application (App) Certificate Revision Number. To display
the About screen, press y L and then select 1:About.
Displaying the MEMORY MANAGEMENT/DELETE Menu
Mem Mgmt/Del displays the MEMORY MANAGEMENT/DELETE menu. The two lines at the top report
the total amount of available RAM (RAM FREE) and Archive (ARC FREE) memory. By selecting
menu items on this screen, you can see the amount of memory each variable type is using. This
information can help you determine if you need to delete variables from memory to make room for
new data, such as programs or Apps.
To check memory usage, follow these steps.
Press y L to display the MEMORY menu.
Note: The # and $ in the top or bottom of
the left column indicate that you can scroll
up or down to view more variable types.
2. Select 2:Mem Mgmt/Del to display the MEMORY MANAGEMENT/DELETE menu. The TI-84 Plus
expresses memory quantities in bytes.

Chapter 18: Memory and Variable Management 328
3. Select variable types from the list to display memory usage.
Notes: Real, List, Y-Vars, and Prgm variable types never reset to zero, even after memory is
cleared.
Apps are independent applications which are stored in Flash ROM. AppVars is a variable
holder used to store variables created by Apps. You cannot edit or change variables in
AppVars unless you do so through the application which created them.
To leave the MEMORY MANAGEMENT/DELETE menu, press either y 5 or ‘. Both options
display the home screen.

Chapter 18: Memory and Variable Management 329
Deleting Items from Memory
Deleting an Item
To increase available memory by deleting the contents of any variable (real or complex number,
list, matrix, Y= variable, program, Apps, AppVars, picture, graph database, or string), follow these
steps.
1. Press y L to display the MEMORY menu.
2. Select 2:Mem Mgmt/Del to display the MEMORY MANAGEMENT/DELETE menu.
3. Select the type of data you want to delete, or select 1:All for a list of all variables of all types. A
screen is displayed listing each variable of the type you selected and the number of bytes
each variable is using.
For example, if you select 4:List, the LIST editor screen is displayed.
4. Press } and † to move the selection cursor (4) next to the item you want to delete, and then
press {. The variable is deleted from memory. You can delete individual variables one by
one from this screen. No warning will be given to verify the deletion.
Note: If you are deleting programs or Apps, you will receive a message asking you to confirm
this delete action. Select 2:Yes to continue.
To leave any variable screen without deleting anything, press y 5, which displays the
home screen.
You cannot delete some system variables, such as the last-answer variable Ans and the
statistical variable RegEQ.
Clearing Entries and List Elements
Clear Entries
Clear Entries clears the contents of the ENTRY (last entry on home screen) storage area. To clear
the ENTRY storage area, follow these steps.
1. Press y L to display the MEMORY menu.
2. Select 3:Clear Entries to paste the instruction to the home screen.
3. Press Í to clear the ENTRY storage area.
To cancel Clear Entries, press ‘.
Chapter 18: Memory and Variable Management 330
Note: If you select 3:Clear Entries from within a program, the Clear Entries instruction is pasted to
the program editor, and the Entry (last entry) is cleared when the program is executed.
ClrAllLists
ClrAllLists sets the dimension of each list in RAM to 0.
To clear all elements from all lists, follow these steps.
1. Press y L to display the MEMORY menu.
2. Select 4:ClrAllLists to paste the instruction to the home screen.
3. Press Í to set the dimension of each list in memory to 0.
To cancel ClrAllLists, press ‘.
ClrAllLists does not delete list names from memory, from the LIST NAMES menu, or from the stat
list editor.
Note: If you select 4:ClrAllLists from within a program, the ClrAllLists instruction is pasted to the
program editor. The lists are cleared when the program is executed.
Archiving and UnArchiving Variables
Archiving and UnArchiving Variables
Archiving lets you store data, programs, or other variables to the user data archive (ARC) where
they cannot be edited or deleted inadvertently. Archiving also allows you to free up RAM for
variables that may require additional memory.
Archived variables cannot be edited or executed. They can only be seen and unarchived. For
example, if you archive list L1, you will see that L1 exists in memory but if you select it and paste
the name L1 to the home screen, you won’t be able to see its contents or edit it.
Note: Not all variables may be archived. Not all archived variables may be unarchived. For
example, system variables including r, t, x, y, and q cannot be archived. Apps and Groups always
exist in Flash ROM so there is no need to archive them. Groups cannot be unarchived. However,
you can ungroup or delete them.
Variable Type
Names
Archive?
(yes/no)
UnArchive?
(yes/no)
Real numbers A, B, ... , Zyes yes
Complex
numbers
A, B, ... , Zyes yes
Matrices [A], [B], [C], ... , [J] yes yes

Chapter 18: Memory and Variable Management 331
Archiving and unarchiving can be done in two ways:
•Use the 5:Archive or 6:UnArchive commands from the MEMORY menu or CATALOG.
• Use a Memory Management editor screen.
Before archiving or unarchiving variables, particularly those with a large byte size (such as large
programs) use the MEMORY menu to:
• Find the size of the variable.
• See if there is enough free space.
Lists L1, L2, L3, L4, L5, L6,
and user-defined names
yes yes
Programs yes yes
Functions Y1, Y2, . . . , Y9, Y0 no not
applicable
Parametric
equations
X1T and Y1T, ... , X6T
and Y6T
no not
applicable
Polar functions r1, r2, r3, r4, r5, r6 no not
applicable
Sequence
functions
u, v, wno not
applicable
Stat plots Plot1, Plot2, Plot3 no not
applicable
Graph databases GDB1, GDB2,... yes yes
Graph pictures Pic1, Pic2, ... , Pic9,
Pic0
yes yes
Strings Str1, Str2, . . . Str9, Str0 yes yes
Tables TblStart, @Tbl,
TblInput
no not
applicable
Apps Applications see Note
above
no
AppVars Application variables yes yes
Groups see Note
above
no
Variables with
reserved names
minX, maxX, RegEQ,
and others
no not
applicable
System variables Xmin, Xmax, and others no not
applicable
For: Sizes must be such that:
Archive Archive free size > variable size
Variable Type
Names
Archive?
(yes/no)
UnArchive?
(yes/no)
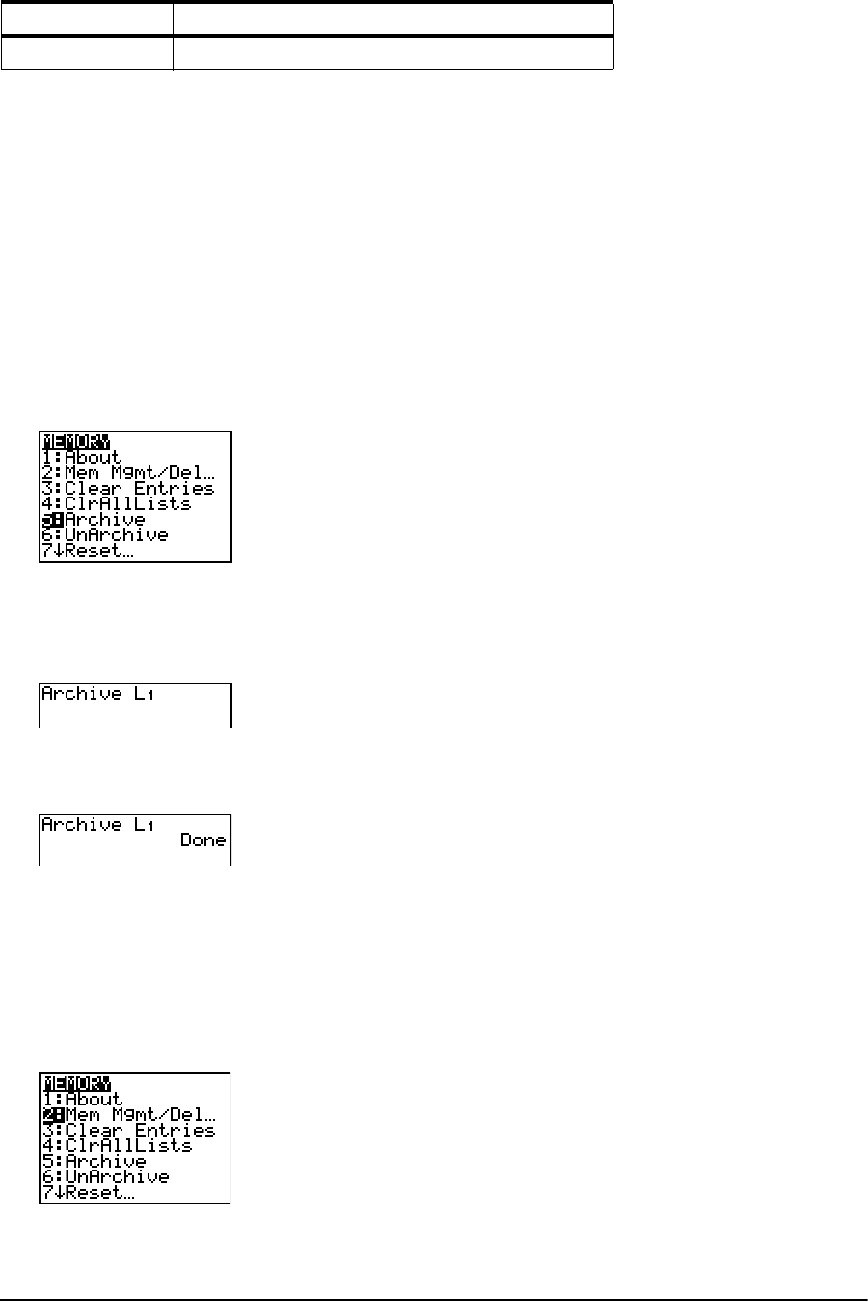
Chapter 18: Memory and Variable Management 332
Note: If there is not enough space, unarchive or delete variables as necessary. Be aware that
when you unarchive a variable, not all the memory associated with that variable in user data
archive will be released since the system keeps track of where the variable has been and where it
is now in RAM.
Even if there appears to be enough free space, you may see a Garbage Collection message when
you attempt to archive a variable. Depending on the usability of empty blocks in the user data
archive, you may need to unarchive existing variables to create more free space.
To archive or unarchive a list variable (L1) using the Archive/UnArchive options from the MEMORY
menu:
1. Press y L to display the MEMORY menu.
2. Select 5:Archive or 6:UnArchive to place the command in the Home screen.
3. Press y d to place the L1 variable in the Home screen.
4. Press Í to complete the archive process.
Note: An asterisk will be displayed to the left of the Archived variable name to indicate it is
archived.
To archive or unarchive a list variable (L1) using a Memory Management editor:
1. Press y L to display the MEMORY menu.
2. Select 2:Mem Mgmt/Del to display the MEMORY MANAGEMENT/DELETE menu.
UnArchive RAM free size > variable size
For: Sizes must be such that:
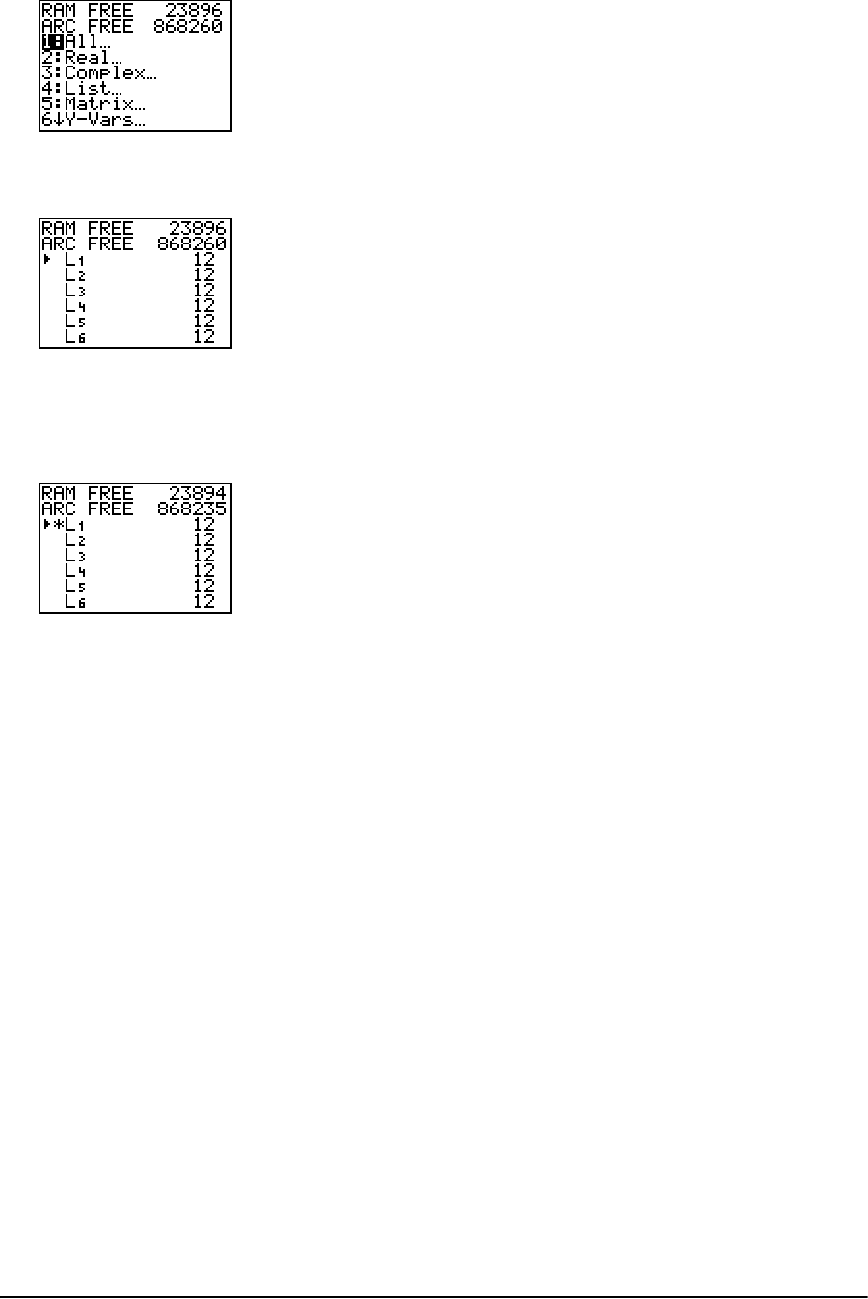
Chapter 18: Memory and Variable Management 333
3. Select 4:List to display the LIST menu.
4. Press Í to archive L1. An asterisk will appear to the left of L1 to indicate it is an archived
variable. To unarchive a variable in this screen, put the cursor next to the archived variable
and press Í. The asterisk will disappear.
5. Press y 5 to leave the LIST menu.
Note: You can access an archived variable for the purpose of linking, deleting, or unarchiving it,
but you cannot edit it.
Resetting the TI-84 Plus
RAM ARCHIVE ALL Menu
Reset displays the RAM ARCHIVE ALL menu. This menu gives you the option of resetting all
memory (including default settings) or resetting selected portions of memory while preserving
other data stored in memory, such as programs and Y= functions. For instance, you can choose to
reset all of RAM or just restore the default settings. Be aware that if you choose to reset RAM, all
data and programs in RAM will be erased. For archive memory, you can reset variables (Vars),
applications (Apps), or both of these. Be aware that if you choose to reset Vars, all data and
programs in archive memory will be erased. If you choose to reset Apps, all applications in archive
memory will be erased.
When you reset defaults on the TI-84 Plus, all defaults in RAM are restored to the factory settings.
Stored data and programs are not changed.
These are some examples of TI-84 Plus defaults that are restored by resetting the defaults.
• Mode settings such as Normal (notation); Func (graphing); Real (numbers); and Full (screen)

Chapter 18: Memory and Variable Management 334
•Y= functions off
• Window variable values such as Xmin=L10, Xmax=10, Xscl=1, Yscl=1, and Xres=1
•STAT PLOTS off
• Format settings such as CoordOn (graphing coordinates on); AxesOn; and ExprOn (expression
on)
•rand seed value to 0
Displaying the RAM ARCHIVE ALL Menu
To display the RAM ARCHIVE ALL menu on the TI-84 Plus, follow these steps.
1. Press y L to display the MEMORY menu.
2. Select 7:Reset to display the RAM ARCHIVE ALL menu.
Resetting RAM Memory
Resetting all RAM restores RAM system variables to factory settings and deletes all nonsystem
variables and all programs. Resetting RAM defaults restores all system variables to default
settings without deleting variables and programs in RAM. Resetting all RAM or resetting defaults
does not affect variables and applications in user data archive.
Note: Before you reset all RAM memory, consider restoring sufficient available memory by deleting
only selected data.
To reset all RAM memory or RAM defaults on the TI-84 Plus, follow these steps.
1. From the RAM ARCHIVE ALL menu, select 1:All RAM to display the RESET RAM menu or
2:Defaults to display the RESET DEFAULTS menu.
2. If you are resetting RAM, read the message below the RESET RAM menu.
• To cancel the reset and return to the HOME screen, press Í.
• To erase RAM memory or reset defaults, select 2:Reset. Depending on your choice, the
message RAM cleared or Defaults set is displayed on the home screen.

Chapter 18: Memory and Variable Management 335
Resetting Archive Memory
When resetting archive memory on the TI-84 Plus, you can choose to delete from user data
archive all variables, all applications, or both variables and applications.
To reset all or part of user data archive memory, follow these steps.
1. From the RAM ARCHIVE ALL menu, press ~ to display the ARCHIVE menu.
2. Select one of the following:
1:Vars to display the RESET ARC VARS menu.
2:Apps to display the RESET ARC APPS menu.
3:Both to display the RESET ARC BOTH menu.
3. Read the message below the menu.
• To cancel the reset and return to the HOME screen, press Í.
• To continue with the reset, select 2:Reset. A message indicating the type of archive
memory cleared will be displayed on the HOME screen.

Chapter 18: Memory and Variable Management 336
Resetting All Memory
When resetting all memory on the TI-84 Plus, RAM and user data archive memory is restored to
factory settings. All nonsystem variables, applications, and programs are deleted. All system
variables are reset to default settings.
Before you reset all memory, consider restoring sufficient available memory by deleting only
selected data.
To reset all memory on the TI-84 Plus, follow these steps.
1. From the RAM ARCHIVE ALL menu, press ~ ~ to display the ALL menu.
2. Select 1:All Memory to display the RESET MEMORY menu.
3. Read the message below the RESET MEMORY menu.
• To cancel the reset and return to the HOME screen, press Í.
• To continue with the reset, select 2:Reset. The message MEM cleared is displayed on the
HOME screen.
When you clear memory, the contrast sometimes changes. If the screen is faded or blank, adjust
the contrast by pressing y } or †.
Grouping and Ungrouping Variables
Grouping Variables
Grouping allows you to make a copy of two or more variables residing in RAM and then store them
as a group in user data archive. The variables in RAM are not erased. The variables must exist in
RAM before they can be grouped. In other words, archived data cannot be included in a group.
Once grouped, the variables can be deleted from RAM to open memory. When the variables are
needed later, they can be ungrouped for use.
To create a group of variables:
1. Press y L to display the MEMORY menu.
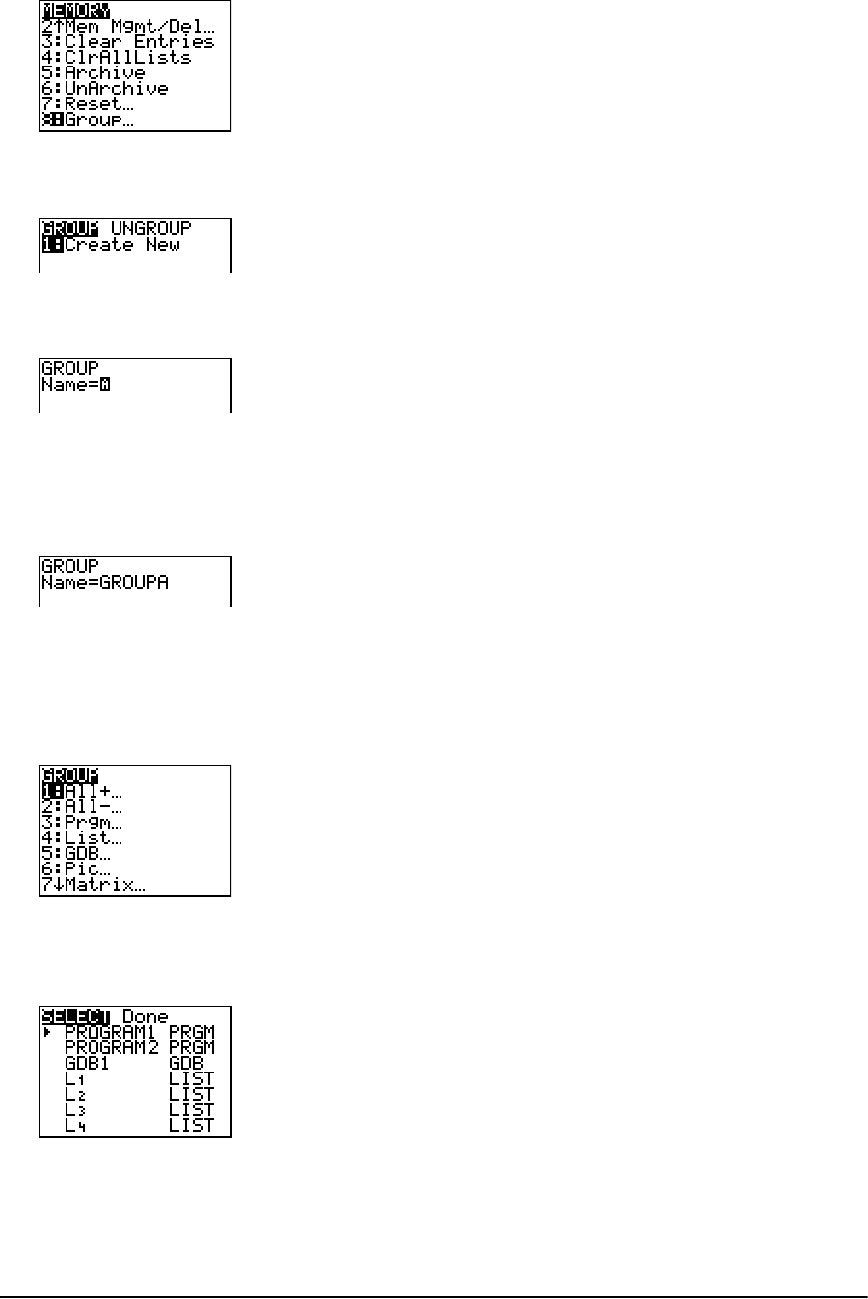
Chapter 18: Memory and Variable Management 337
2. Select 8:Group to display GROUP UNGROUP menu.
3. Press Í to display the GROUP menu.
4. Enter a name for the new group and press Í.
Note: A group name can be one to eight characters long. The first character must be a letter
from A to Z or q. The second through eighth characters can be letters, numbers, or q.
5. Select the type of data you want to group. You can select 1:All+ which shows all variables of
all types available and selected. You can also select 2:All- which shows all variables of all
types available but not selected. A screen is displayed listing each variable of the type you
selected.
For example, suppose some variables have been created in RAM, and selecting 2:All-
displays the following screen.
6. Press } and † to move the selection cursor (4) next to the first item you want to copy into a
group, and then press Í. A small square will remain to the left of all variables selected for
grouping.
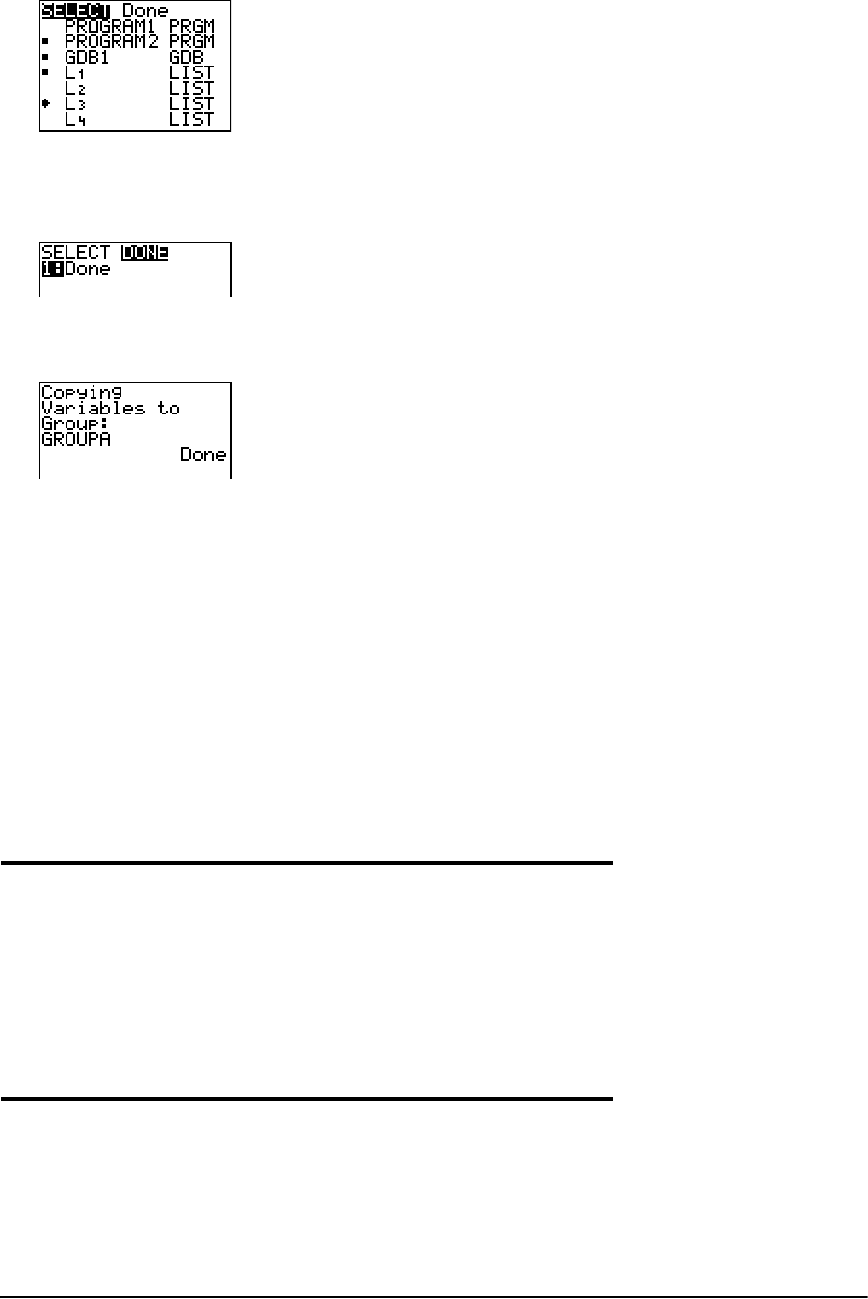
Chapter 18: Memory and Variable Management 338
Repeat the selection process until all variables for the new group are selected and then press
~ to display the DONE menu.
7. Press Í to complete the grouping process.
Note: You can only group variables in RAM. You cannot group some system variables, such as the
last-answer variable Ans and the statistical variable RegEQ.
Ungrouping Variables
Ungrouping allows you to make a copy of variables in a group stored in user data archive and
place them ungrouped in RAM.
DuplicateName Menu
During the ungrouping action, if a duplicate variable name is detected in RAM, the DUPLICATE
NAME menu is displayed.
Notes about Menu Items:
• When you select 1:Rename, the Name= prompt is displayed, and alpha-lock is on. Enter a new
variable name, and then press Í. Ungrouping resumes.
DuplicateName
1: Rename Prompts to rename receiving variable.
2: Overwrite Overwrites data in receiving duplicate variable.
3: Overwrite All Overwrites data in all receiving duplicate
variables.
4: Omit Skips ungrouping of sending variable.
5: Quit Stops ungrouping at duplicate variable.
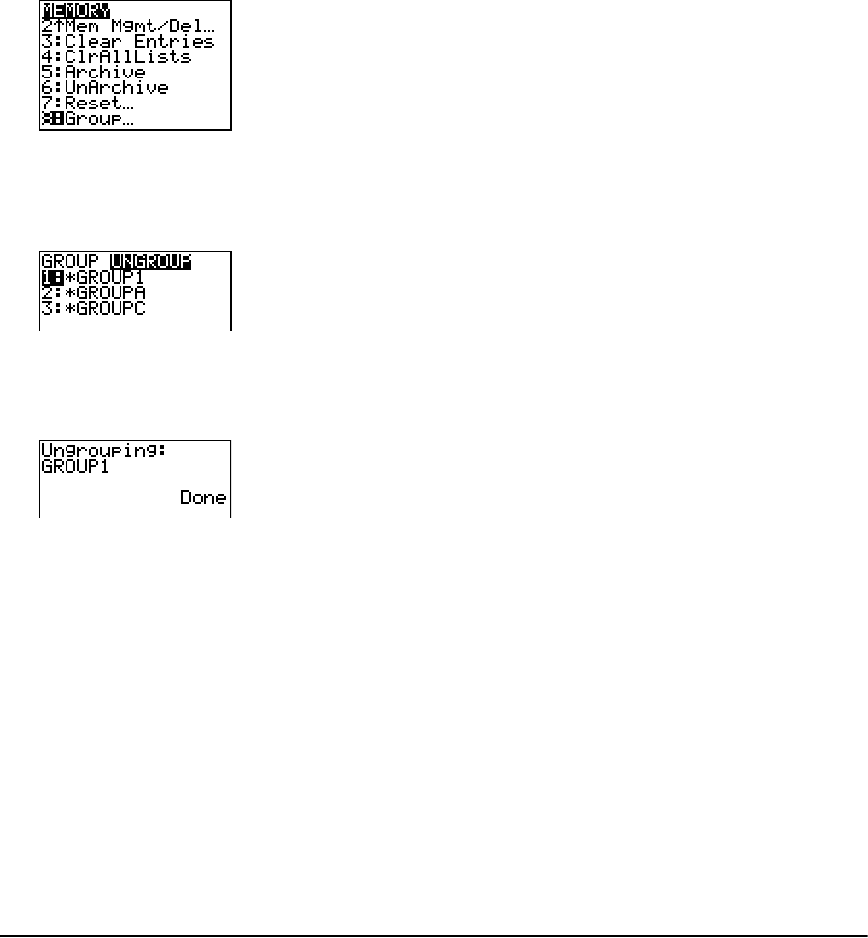
Chapter 18: Memory and Variable Management 339
• When you select 2:Overwrite, the unit overwrites the data of the duplicate variable name found
in RAM. Ungrouping resumes.
• When you select 3: Overwrite All, the unit overwrites the data of all duplicate variable names
found in RAM. Ungrouping resumes.
• When you select 4:Omit, the unit does not ungroup the variable in conflict with the duplicated
variable name found in RAM. Ungrouping resumes with the next item.
• When you select 5:Quit, ungrouping stops, and no further changes are made.
To ungroup a group of variables:
1. Press y L to display the MEMORY menu.
2. Select 8:Group to display the GROUP UNGROUP menu.
3. Press ~ to display the UNGROUP menu.
4. Press } and † to move the selection cursor (4) next to the group variable you want to
ungroup, and then press Í.
The ungroup action is completed.
Note: Ungrouping does not remove the group from user data archive. You must delete the group in
user data archive to remove it.
Garbage Collection
Garbage Collection Message
If you use the user data archive extensively, you may see a Garbage Collect? message. This
occurs if you try to archive a variable when there is not enough free contiguous archive memory.
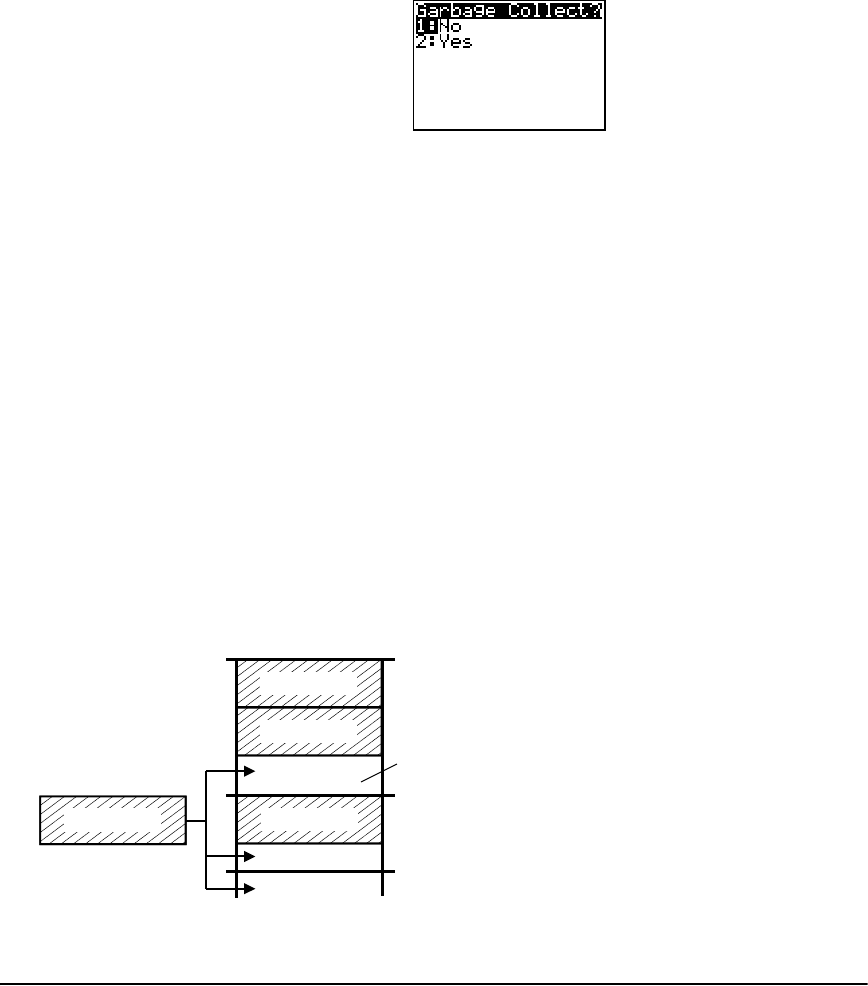
Chapter 18: Memory and Variable Management 340
The Garbage Collect? message lets you know an archive will take longer than usual. It also alerts
you that the archive will fail if there is not enough memory.
The message can also alert you when a program is caught in a loop that repetitively fills the user
data archive. Select No to cancel the garbage collection process, and then find and correct the
errors in your program.
When YES is selected, the TI-84 Plus will attempt to rearrange the archived variables to make
additional room.
Responding to the Garbage Collection Message
Note: The process message Defragmenting... is displayed whenever an application marked for
deletion is encountered. Garbage collection may take up to 20 minutes, depending on how much
of archive memory has been used to store variables.
After garbage collection, depending on how much additional space is freed, the variable may or
may not be archived. If not, you can unarchive some variables and try again.
variable B
variable C
variable A
variable D
Depending on its size,
variable D is stored in
one of these locations.
Sector 1
Sector 3
Sector 2
Empty
block
Why Is Garbage Collection Necessary?
The user data archive is divided into sectors. When you first begin archiving, variables are stored
consecutively in sector 1. This continues to the end of the sector.
An archived variable is stored in a continuous block within a single sector. Unlike an application
stored in user data archive, an archived variable cannot cross a sector boundary. If there is not
enough space left in the sector, the next variable is stored at the beginning of the next sector.
Typically, this leaves an empty block at the end of the previous sector.
• To cancel, select 1:No.
• If you select 1:No, the message
ERR:ARCHIVE FULL will be displayed.
• To continue archiving, select 2:Yes.
• If you select 2:Yes, the process message
Garbage Collecting... or Defragmenting...
will be displayed.
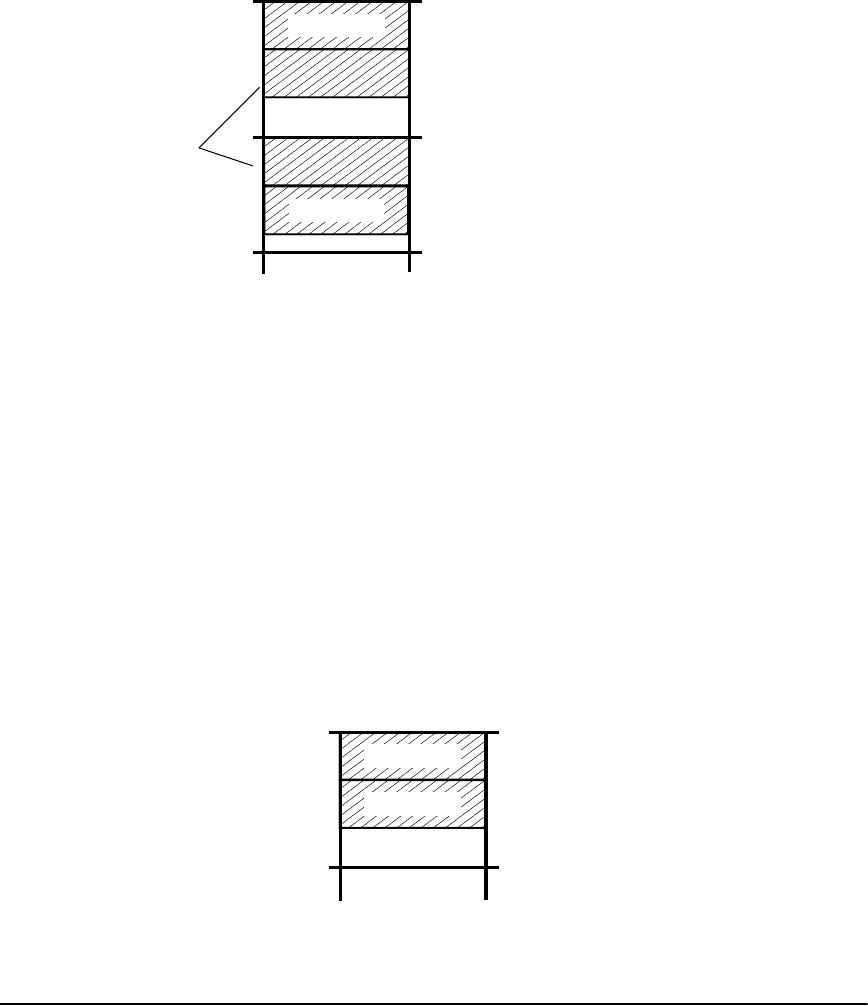
Chapter 18: Memory and Variable Management 341
Each variable that you archive is stored in the first empty block large enough to hold it.
This process continues to the end of the last sector. Depending on the size of individual variables,
the empty blocks may account for a significant amount of space. Garbage collection occurs when
the variable you are archiving is larger than any empty block.
How Unarchiving a Variable Affects the Process
When you unarchive a variable, it is copied to RAM but it is not actually deleted from user data
archive memory. Unarchived variables are “marked for deletion,” meaning they will be deleted
during the next garbage collection.
If the MEMORY Screen Shows Enough Free Space
Even if the MEMORY screen shows enough free space to archive a variable or store an application,
you may still get a Garbage Collect? message or an ERR: ARCHIVE FULL message.
When you unarchive a variable, the Archive free amount increases immediately, but the space is
not actually available until after the next garbage collection.
If the Archive free amount shows enough available space for your variable, there probably will be
enough space to archive it after garbage collection (depending on the usability of any empty
blocks).
The Garbage Collection Process
The garbage collection process:
variable A
variable D
After you unarchive
variables B and C,
they continue to take
up space.
Sector 1
Sector 2
Sector 3
• Deletes unarchived variables
from the user data archive.
• Rearranges the remaining
variables into consecutive
blocks.
variable A
variable D
Sector 1
Sector 2

Chapter 18: Memory and Variable Management 342
Note: Power loss during garbage collection may cause all memory (RAM and Archive) to be
deleted.
Using the GarbageCollect Command
You can reduce the number of automatic garbage collections by periodically optimizing memory.
This is done by using the GarbageCollect command.
To use the GarbageCollect command, follow these steps.
1. From the HOME screen, press y N to display the CATALOG.
2. Press † or } to scroll the CATALOG until the selection cursor points to the GarbageCollect
command or press G to skip to the commands starting with the letter G.
3. Press Í to paste the command to the HOME screen.
4. Press Í to display the Garbage Collect? message.
5. Select 2:Yes to begin garbage collection.

Chapter 18: Memory and Variable Management 343
ERR:ARCHIVE FULL Message
An ERR:ARCHIVE FULL message may be displayed:
• When there is insufficient space to archive a variable within a continuous block and within a
single sector.
• When there is insufficient space to store an application within a continuous block of memory.
When the message is displayed, it will indicate the largest single space of memory available for
storing a variable and an application.
To resolve the problem, use the GarbageCollect command to optimize memory. If memory is still
insufficient, you must delete variables or applications to increase space.
Even if the MEMORY screen shows enough
free space to archive a variable or store an
application, you may still get an ERR:
ARCHIVE FULL message.
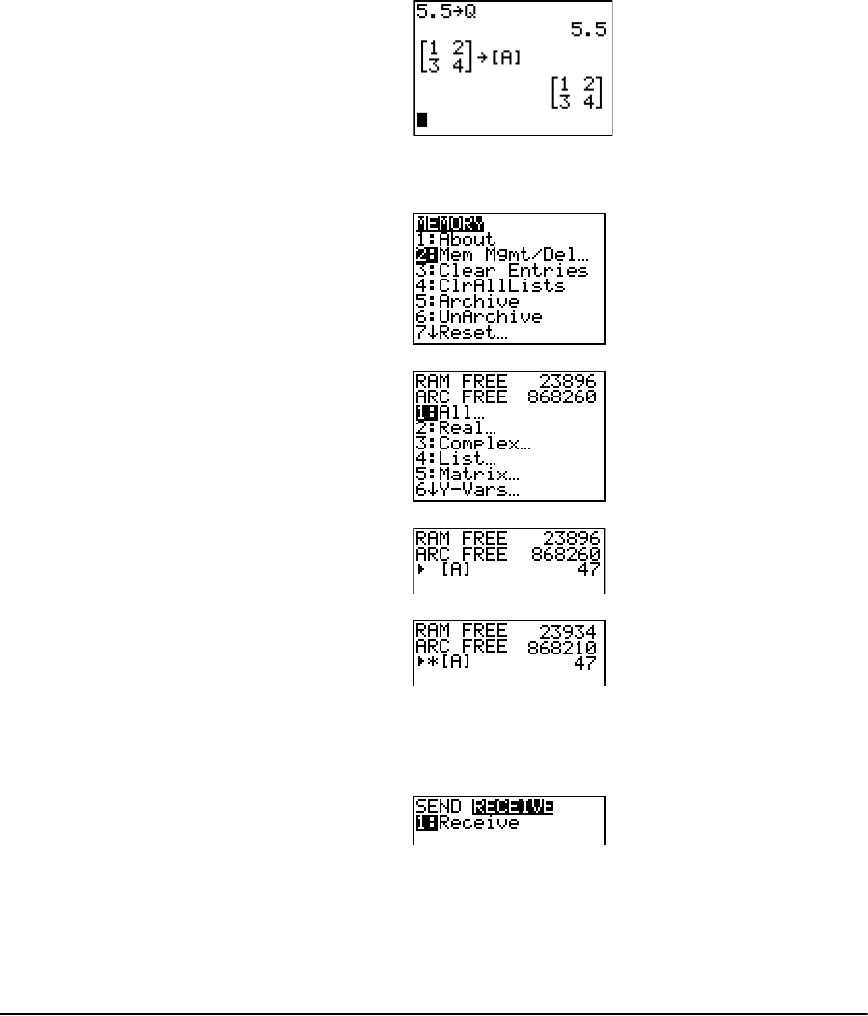
Chapter 19: Communication Link 344
Chapter 19:
Communication Link
Getting Started: Sending Variables
Getting Started is a fast-paced introduction. Read the chapter for details.
Create and store a variable and a matrix, and then transfer them to another TI-84 Plus.
1. On the home screen of the sending unit,
press 5 Ë 5 ¿ ƒ Q. Press Í
to store 5.5 to Q.
2. Press t ` † † Í to display
the 2x2 matrix template. Press 1 ~ 2 ~ 3
~ 4 ~ to enter the values. Press ¿
y > 1 Í to store the matrix to
[A].
3. On the sending unit, press y L to
display the MEMORY menu.
4. On the sending unit, press 2 to select
2:Mem Mgmt/Del. The MEMORY
MANAGEMENT menu is displayed.
5. On the sending unit, press 5 to select
5:Matrix. The MATRIX editor screen is
displayed.
6. On the sending unit, press Í to
archive [A]. An asterisk (ä) will appear,
signifying that [A] is now archived.
7. Connect the graphing calculators with
the USB unit-to-unit cable. Push both
ends in firmly.
8. On the receiving unit, press y 8 ~
to display the RECEIVE menu. Press 1 to
select 1:Receive. The message Waiting...
is displayed and the busy indicator is on.

Chapter 19: Communication Link 345
TI-84 Plus LINK
This chapter describes how to communicate with compatible TI units. The TI-84 Plus has a USB
port to connect and communicate with another TI-84 series calculator. A USB unit-to-unit cable is
included with the TI-84 Plus.
The TI-84 Plus also has an I/O port using a I/O unit-to-unit cable to communicate with:
You can send items from a calculator with an older OS to a calculator with OS 2.53MP and higher.
However, you may receive a version error if you send items from a calculator with OS 2.53MP or
higher to a calculator with an older OS. Transferring files between calculators works best if both
calculators have the latest operating system software installed. For example, if you send a list that
contains fractions (OS 2.53MP and higher) to a calculator with OS 2.43, a version error displays
because OS 2.43 does not support fractions.
9. On the sending unit, press y 8 to
display the SEND menu.
10. Press 2 to select 2:AllN. The AllN SELECT
screen is displayed.
11. Press † until the selection cursor ( 4 ) is
next to [A] MATRX. Press Í.
12. Press † until the selection cursor is next
to Q REAL. Press Í. A square dot
next to [A] and Q indicates that each is
selected to send.
13. On the sending unit, press ~ to display
the TRANSMIT menu.
14. On the sending unit, press 1 to select
1:Transmit and begin transmission. The
receiving unit displays the message
Receiving....When the items are
transmitted, both units display the name
and type of each transmitted variable.
• TI-83 Plus Silver Edition
• TI-83 Plus
•TI-83
•TI-82
•TI-73
• CBL 2™ or a CBR™
Chapter 19: Communication Link 346
Connecting Two Graphing Calculators with a USB Unit-to-Unit Cable or an I/O Unit-to-Unit
Cable
USB Unit-to-Unit Cable
I/O Unit-to-Unit Cable
TI-84 Plus to a TI-83 Plus using I/O Unit-to-Unit Cable
Linking to the CBL/CBR System
The CBL 2™ system and the CBR™ system are optional accessories that also connect to a TI-84
Plus with the I/O unit-to-unit cable. With a CBL 2™ system or CBR™ system and a TI-84 Plus, you
can collect and analyze real-world data.
Linking to a Computer
With TI Connect™ software and the USB computer cable that is included with your TI-84 Plus, you
can link the graphing calculator to a personal computer.
The TI-84 Plus USB link port is located at the
top right edge of the graphing calculator.
1. Firmly insert either end of the USB
unit-to-unit cable into the USB port.
2. Insert the other end of the cable into the
other graphing calculator’s USB port.
The TI-84 Plus I/O link port is located at the
top left edge of the graphing calculator.
1. Firmly insert either end of the I/O
unit-to-unit cable into the port.
2. Insert the other end of the cable into the
other graphing calculator’s I/O port.
The TI-84 Plus I/O link port is located at the
top left edge of the graphing calculator. The
TI-83 Plus I/O link port is located at the
bottom edge of the graphing calculator.
1. Firmly insert either end of the I/O
unit-to-unit cable into the port.
2. Insert the other end of the cable into the
other graphing calculator’s I/O port.
Chapter 19: Communication Link 347
Selecting Items to Send
LINK SEND Menu
To display the LINK SEND menu, press y 8.
When you select an item on the LINK SEND menu, the corresponding SELECT screen is displayed.
Note: Each SELECT screen, except All+…, is initially displayed with nothing pre-selected. All+… is
displayed with everything pre-selected.
To select items to send:
1. Press y 8 on the sending unit to display the LINK SEND menu.
SEND RECEIVE
1: All+... Displays all items as selected, including RAM
and Flash applications.
2: AllN... Displays all items as deselected.
3: Prgm... Displays all program names.
4: List... Displays all list names.
5: Lists to
TI82...
Displays list names L1 through L6.
6: GDB... Displays all graph databases.
7: Pic... Displays all picture data types.
8: Matrix... Displays all matrix data types.
9: Real... Displays all real variables.
0: Complex... Displays all complex variables.
A: Y-Vars... Displays all Y= variables.
B: String... Displays all string variables.
C: Apps... Displays all software applications.
D: AppVars... Displays all software application variables.
E: Group... Displays all grouped variables.
F: SendId Sends the Calculator ID number immediately.
(You do not need to select SEND.)
G: SendOS Sends operating system updates to another
TI-84 Plus Silver Edition or TI-84 Plus. You can
not send the operating system to the TI-83 Plus
product family.
H: Back Up... Selects all RAM and mode settings (no Flash
applications or archived items) for backup to
another TI-84 Plus, TI-84 Plus Silver Edition,
TI-83 Plus Silver Edition, or to a TI-83 Plus.

Chapter 19: Communication Link 348
2. Select the menu item that describes the data type to send. The corresponding SELECT screen
is displayed.
3. Press } and † to move the selection cursor ( 4 ) to an item you want to select or deselect.
4. Press Í to select or deselect the item. Selected names are marked with a 0.
Note: An asterisk (ä) to the left of an item indicates the item is archived.
5. Repeat steps 3 and 4 to select or deselect additional items.
Sending the Selected Items
After you have selected items to send on the sending unit and set the receiving unit to receive,
follow these steps to transmit the items. To set the receiving unit, see Receiving Items.
1. Press ~ on the sending unit to display the TRANSMIT menu.
2. Confirm that Waiting... is displayed on the receiving unit, which indicates it is set to receive.
3. Press Í to select 1:Transmit. The name and type of each item are displayed line-by-line
on the sending unit as the item is queued for transmission, and then on the receiving unit as
each item is accepted.
Note: Items sent from the RAM of the sending unit are transmitted to the RAM of the receiving
unit. Items sent from user data archive (flash) of the sending unit are transmitted to user data
archive (flash) of the receiving unit.
After all selected items have been transmitted, the message Done is displayed on both calculators.
Press } and † to scroll through the names.
Sending to a TI-84 Plus Silver Edition or TI-84 Plus
You can transfer variables (all types), programs, and Flash applications to another TI-84 Plus
Silver Edition or TI-84 Plus. You can also backup the RAM memory of one unit to another.
Note: Keep in mind that the TI-84 Plus has less Flash memory than the TI-84 Plus Silver Edition.

Chapter 19: Communication Link 349
• Variables stored in RAM on the sending TI-84 Plus Silver Edition will be sent to the RAM of the
receiving TI-84 Plus Silver Edition or TI-84 Plus.
• Variables and applications stored in the user data archive of the sending TI-84 Plus Silver
Edition will be sent to the user data archive of the receiving TI-84 Plus Silver Edition or TI-84
Plus.
After sending or receiving data, you can repeat the same transmission to additional TI-84 Plus
Silver Edition or TI-84 Plus units—from either the sending unit or the receiving unit—without
having to reselect data to send. The current items remain selected. However, you cannot repeat
transmission if you selected All+ or All..
To send data to an additional TI-84 Plus Silver Edition or a TI-84 Plus:
1. Use a USB unit-to-unit cable to link two units together.
2. On the sending unit press y 8 and select a data type and items to SEND.
3. Press ~ on the sending unit to display the TRANSMIT menu.
4. On the other unit, press y 8 ~ to display the RECEIVE menu.
5. Press Í on the receiving unit.
6. Press Í on the sending unit. A copy of the selected item(s) is sent to the receiving unit.
7. Disconnect the link cable only from the receiving unit and connect it to another unit.
8. Press y 8 on the sending unit.
9. Select only the data type. For example, if the unit just sent a list, select 4:LIST.
Note: The item(s) you want to send are pre-selected from the last transmission. Do not select
or deselect any items. If you select or deselect an item, all selections or deselections from the
last transmission are cleared.
10. Press ~ on the sending unit to display the TRANSMIT menu.
11. On the new receiving unit, press y 8 ~ to display the RECEIVE menu.
12. Press Í on the receiving unit.
13. Press Í on the sending unit. A copy of the selected item(s) is sent to the receiving unit.
14. Repeat steps 7 through 13 until the items are sent to all additional units.
Sending to a TI-83 Plus or TI-83 Plus Silver Edition
You can send all variables from a TI-84 Plus to a TI-83 Plus or TI-83 Plus Silver Edition except
Flash applications with new features, or programs with new features in them.
If archived variables on the TI-84 Plus are variable types recognized and used on the TI-83 Plus or
TI-83 Plus Silver Edition, you can send these variables to the TI-83 Plus or TI-83 Plus Silver
Edition. They will be automatically sent to the RAM of the TI-83 Plus or TI-83 Plus Silver Edition
during the transfer process. It will send to archive if the item is from archive.
To send data to a TI-83 Plus or TI-83 Plus Silver Edition:
1. Use an I/O unit-to-unit cable to link the two units together.
2. Set the TI-83 Plus or TI-83 Plus Silver Edition to receive.

Chapter 19: Communication Link 350
3. Press y 8 on the sending TI-84 Plus to display the LINK SEND menu.
4. Select the menu of the items you want to transmit.
5. Press ~ on the sending TI-84 Plus to display the LINK TRANSMIT menu.
6. Confirm that the receiving unit is set to receive.
7. Press Í on the sending TI-84 Plus to select 1:Transmit and begin transmitting.
Receiving Items
LINK RECEIVE Menu
To display the LINK RECEIVE menu, press y 8 ~.
Receiving Unit
When you select 1:Receive from the LINK RECEIVE menu on the receiving unit, the message
Waiting... and the busy indicator are displayed. The receiving unit is ready to receive transmitted
items. To exit the receive mode without receiving items, press É, and then select 1:Quit from the
Error in Xmit menu.
When transmission is complete, the unit exits the receive mode. You can select 1:Receive again to
receive more items. The receiving unit then displays a list of items received. Press y 5 to exit
the receive mode.
DuplicateName Menu
During transmission, if a variable name is duplicated, the DuplicateName menu is displayed on the
receiving unit.
When you select 1:Rename, the Name= prompt is displayed, and alpha-lock is on. Enter a new
variable name, and then press Í. Transmission resumes.
When you select 2:Overwrite, the sending unit’s data overwrites the existing data stored on the
receiving unit. Transmission resumes.
SEND RECEIVE
1: Receive Sets unit to receive data transmission.
DuplicateName
1: Rename Prompts to rename receiving variable.
2: Overwrite Overwrites data in receiving variable.
3: Omit Skips transmission of sending variable.
4: Quit Stops transmission at duplicate variable.

Chapter 19: Communication Link 351
When you select 3:Omit, the sending unit does not send the data in the duplicated variable name.
Transmission resumes with the next item.
When you select 4:Quit, transmission stops, and the receiving unit exits receive mode.
Receiving from a TI-84 Plus Silver Edition or TI-84 Plus
The TI-84 Plus Silver Edition and the TI-84 Plus are totally compatible. Keep in mind, however that
the TI-84 Plus has less Flash memory than a TI-84 Plus Silver Edition.
You cannot send memory backups between the TI-84 Plus product family and the TI-83 Plus
product family.
Receiving from a TI-83 Plus Silver Edition or TI-83 Plus
The TI-84 Plus product family and the TI-83 Plus product family are compatible with a few
exceptions.
Receiving from a TI-83
You can transfer all variables and programs from a TI-83 to a TI-84 Plus if they fit in the RAM of
the TI-84 Plus. The RAM of the TI-84 Plus is slightly less than the RAM of the TI-83.
Backing Up RAM Memory
Warning: H:Back Up overwrites the RAM memory and mode settings in the receiving unit. All
information in the RAM memory of the receiving unit is lost.
Note: Archived items on the receiving unit are not overwritten.
You can backup the contents of RAM memory and mode settings (no Flash applications or
archived items) to another TI-84 Plus Silver Edition. You can also backup RAM memory and mode
settings to a TI-84 Plus. The backup calculator must also have OS 2.55MP installed.
To perform a RAM memory backup:
1. Use a USB unit-to-unit cable to link two TI-84 Plus units, or a TI-84 Plus and a TI-84 Plus
Silver Edition together.
2. On the sending unit press y 8 and select H:Back Up. The MEMORYBACKUP screen
displays.
3. On the receiving unit, press y 8 ~ to display the RECEIVE menu.
4. Press Í on the receiving unit.

Chapter 19: Communication Link 352
5. Press Í on the sending unit. A WARNING — Backup message displays on the receiving
unit.
6. Press Í on the receiving unit to continue the backup.
— or —
Press 2:Quit on the receiving unit to cancel the backup and return to the LINK SEND menu
Note: If a transmission error is returned during a backup, the receiving unit is reset.
Memory Backup Complete
When the backup is complete, both the sending graphing calculator and receiving graphing
calculator display a confirmation screen.
Error Conditions
A transmission error occurs after one or two seconds if:
• A cable is not attached to the sending unit.
• A cable is not attached to the receiving unit.
Note: If the cable is attached, push it in firmly and try again.
• The receiving unit is not set to receive transmission.
• You attempt a backup between a TI-73, TI-82, TI-83, TI-83 Plus, or TI-83 Plus Silver Edition.
• You attempt a data transfer from a TI-84 Plus to a TI-83 Plus, TI-83 Plus Silver Edition, TI-83,
TI-82, or TI-73 with variables or features not recognized by the TI-83 Plus, TI-83 Plus Silver
Edition, TI-83, TI-82, or TI-73.
New variable types and features not recognized by the TI-83, TI-83 Plus, TI-82, or TI-73
include applications, application variables, grouped variables, new variable types, or programs
with new features in them such as Archive, UnArchive, SendID, SendOS, Asm(, AsmComp(,
AsmPrgm, checkTmr(, ClockOff, ClockOn, dayOfWk(, getDate, getDtFmt, getDtStr(, getTime,
getTmFmt, getTmStr, isClockOn, randIntNoRep(, setDate(, setDtFmt(, setTime(, setTmFmt(,
startTmr, summation(, timeCnv and fractions.
• You attempt a data transfer from a TI-84 Plus to a TI-82 with data other than real lists L1
through L6 or without using menu item 5:Lists to TI82.
• You attempt a data transfer from a TI-84 Plus to a TI-73 with data other than real numbers,
pics, real lists L1 through L6 or named lists with q as part of the name.
Although a transmission error does not occur, these two conditions may prevent successful
transmission.
• You try to use Get( with a graphing calculator instead of a CBL 2™ system or CBR™ system.
• You try to use GetCalc( with a TI-83 instead of a TI-84 Plus or TI-84 Plus Silver Edition.

Chapter 19: Communication Link 353
Insufficient Memory in Receiving Unit
• During transmission, if the receiving unit does not have sufficient memory to receive an item,
the Memory Full menu is displayed on the receiving unit.
• To skip this item for the current transmission, select 1:Omit. Transmission resumes with the
next item.
• To cancel the transmission and exit receive mode, select 2:Quit.

Appendix A: Functions and Instructions 354
Appendix A:
Functions and Instructions
Functions return a value, list, or matrix. You can use functions in an expression. Instructions initiate
an action. Some functions and instructions have arguments. Optional arguments and accompanying
commas are enclosed in brackets ( [ ] ). For details about an item, including argument descriptions
and restrictions, turn to the page listed on the right side of the table.
From the CATALOG, you can paste any function or instruction to the home screen or to a command
line in the program editor. However, some functions and instructions are not valid on the home
screen. The items in this table appear in the same order as they appear in the CATALOG.
† indicates either keystrokes that are valid in the program editor only or ones that paste certain
instructions when you are in the program editor. Some keystrokes display menus that are available
only in the program editor. Others paste mode, format, or table-set instructions only when you are
in the program editor.
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item
abs(value)Returns the absolute value of a real number, expression,
list, or matrix.
NUM
1:abs(
abs(complex value)Returns the magnitude of a complex number or list.
CPX
5:abs(
valueA and valueB Returns 1 if both valueA and valueB are ƒ 0. valueA and
valueB can be real numbers, expressions, or lists.
y :
LOGIC
1:and
angle(value)Returns the polar angle of a complex number or list of
complex numbers.
CPX
4:angle(
ANOVA(list1,list2
[,list3,...,list20])
Performs a one-way analysis of variance for comparing the
means of two to 20 populations.
…
TESTS
H:ANOVA(
Ans Returns the last answer. y Z
Archive Moves the specified variables from RAM to the user data
archive memory.
y L
5:Archive
Asm(assemblyprgmname)Executes an assembly language program. y N
Asm(
AsmComp(prgmASM1,
prgmASM2)
Compiles an assembly language program written in ASCII
and stores the hex version.
y N
AsmComp(
AsmPrgm Must be used as the first line of an assembly language
program.
y N
AsmPrgm
augment(matrixA,
matrixB)
Returns a matrix, which is matrixB appended to matrixA as
new columns.
y >
MATH
7:augment(

Appendix A: Functions and Instructions 355
augment(listA,listB)Returns a list, which is listB concatenated to the end of
listA.
y 9
OPS
9:augment(
AUTO Answer Displays answers in a similar format as the input. z
Answers: AUTO
AxesOff Turns off the graph axes. † y .
AxesOff
AxesOn Turns on the graph axes. † y .
AxesOn
a+biSets the mode to rectangular complex number mode
(a+bi).
† z
a+bi
bal(npmt[,roundvalue])Computes the balance at npmt for an amortization
schedule using stored values for PV, æ, and PMT and
rounds the computation to roundvalue.
Π1:Finance
CALC
9:bal(
binomcdf(numtrials,p
[,x])
Computes a cumulative probability at x for the discrete
binomial distribution with the specified numtrials and
probability p of success on each trial.
y =
DISTR
B:binomcdf(
binompdf(numtrials,p
[,x])
Computes a probability at x for the discrete binomial
distribution with the specified numtrials and probability p of
success on each trial.
y =
DISTR
A:binompdf(
checkTmr(starttime) Returns the number of seconds since you used startTmr
to start the timer. The starttime is the value displayed by
startTmr.
y N
checkTmr(
c2cdf(lowerbound,
upperbound,df)
Computes the c2 distribution probability between
lowerbound and upperbound for the specified degrees of
freedom df.
y =
DISTR
8:c2cdf(
c2pdf(x,df)Computes the probability density function (pdf) for the c2
distribution at a specified x value for the specified degrees
of freedom df.
y =
DISTR
7:c2pdf(
c2LTest(observedmatrix,
expectedmatrix
[,drawflag])
Performs a chi-square test. drawflag=1 draws results;
drawflag=0 calculates results.
† …
TESTS
C:c2LTest(
c2GOF-Test(observedlist,
expectedlist,df)
Performs a test to confirm that sample data is from a
population that conforms to a specified distribution.
† …
TESTS
D:c2GOFLTest(
Circle(X,Y,radius)Draws a circle with center (X,Y) and radius.y <
DRAW
9:Circle(
CLASSIC Displays inputs and outputs on a single line, such as
1/2+3/4.
z
CLASSIC
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 356
Clear Entries Clears the contents of the Last Entry storage area. y L
MEMORY
3:Clear Entries
ClockOff Turns off the clock display in the mode screen. y N
ClockOff
ClockOn Turns on the clock display in the mode screen. y N
ClockOn
ClrAllLists Sets to 0 the dimension of all lists in memory. y L
MEMORY
4:ClrAllLists
ClrDraw Clears all drawn elements from a graph or drawing. y <
DRAW
1:ClrDraw
ClrHome Clears the home screen. †
I/O
8:ClrHome
ClrList listname1
[,listname2, ...,
listname n]
Sets to 0 the dimension of one or more listnames.…
EDIT
4:ClrList
ClrTable Clears all values from the table. †
I/O
9:ClrTable
conj(value)Returns the complex conjugate of a complex number or list
of complex numbers.
CPX
1:conj(
Connected Sets connected plotting mode; resets all Y= editor graph-
style settings to ç .
† z
Connected
CoordOff Turns off cursor coordinate value display. † y .
CoordOff
CoordOn Turns on cursor coordinate value display. † y .
CoordOn
cos(value)Returns cosine of a real number, expression, or list. ™
cosL1(value)Returns arccosine of a real number, expression, or list. y @
cosh(value)Returns hyperbolic cosine of a real number, expression, or
list.
y N
cosh(
coshL1 (value)Returns hyperbolic arccosine of a real number,
expression, or list.
y N
coshL1(
CubicReg [Xlistname,
Ylistname,freqlist,
regequ]
Fits a cubic regression model to Xlistname and Ylistname
with frequency freqlist, and stores the regression equation
to regequ.
…
CALC
6:CubicReg
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 357
cumSum(list)Returns a list of the cumulative sums of the elements in
list, starting with the first element.
y 9
OPS
6:cumSum(
cumSum(matrix)Returns a matrix of the cumulative sums of matrix
elements. Each element in the returned matrix is a
cumulative sum of a matrix column from top to bottom.
y >
MATH
0:cumSum(
dayOfWk(year,month,
day)
Returns an integer from 1 to 7, with each integer
representing a day of the week. Use dayOfWk( to
determine on which day of the week a particular date
would occur. The year must be 4 digits; month and day can
be 1 or 2 digit.
y N
dayOfWk(
1:Sunday
2:Monday
3:Tuesday...
dbd(date1,date2)Calculates the number of days between date1 and date2
using the actual-day-count method.
Π1:Finance
CALC
D:dbd(
DEC Answers Displays answers as integers or decimal numbers. z
Answers: DEC
value4Dec Displays a real or complex number, expression, list, or
matrix in decimal format.
MATH
2:4Dec
Degree Sets degree angle mode. † z
Degree
DelVar variable Deletes from memory the contents of variable.†
CTL
G:DelVar
DependAsk Sets table to ask for dependent-variable values. † y -
Depend: Ask
DependAuto Sets table to generate dependent-variable values
automatically.
† y -
Depend: Auto
det(matrix)Returns determinant of matrix.y >
MATH
1:det(
DiagnosticOff Sets diagnostics-off mode; r, r2, and R2 are not displayed
as regression model results.
y N
DiagnosticOff
DiagnosticOn Sets diagnostics-on mode; r, r2, and R2 are displayed as
regression model results.
y N
DiagnosticOn
dim(listname)Returns the dimension of listname.y 9
OPS
3:dim(
dim(matrixname)Returns the dimension of matrixname as a list. y >
MATH
3:dim(
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 358
length!dim(listname)Assigns a new dimension (length) to a new or existing
listname.
y 9
OPS
3:dim(
{rows,columns}!
dim(matrixname)
Assigns new dimensions to a new or existing matrixname.y >
MATH
3:dim(
Disp Displays the home screen. †
I/O
3:Disp
Disp [valueA,valueB,
valueC,...,value n]
Displays each value. †
I/O
3:Disp
DispGraph Displays the graph. †
I/O
4:DispGraph
DispTable Displays the table. †
I/O
5:DispTable
value4DMS Displays value in DMS format. y ;
ANGLE
4:4DMS
Dot Sets dot plotting mode; resets all Y= editor graph-style
settings to í .
† z
Dot
DrawF expression Draws expression (in terms of X) on the graph. y <
DRAW
6:DrawF
DrawInv expression Draws the inverse of expression by plotting X values on the
y-axis and Y values on the x-axis.
y <
DRAW
8:DrawInv
:DS<(variable,value)
:commandA
:commands
Decrements variable by 1; skips commandA if variable <
value.
†
CTL
B:DS<(
eReturns e.y [e]
e^(power)Returns e raised to power.y J
e^(list)Returns a list of e raised to a list of powers. y J
Exponent:
valueâexponent
Returns value times 10 to the exponent.y D
Exponent:
listâexponent
Returns list elements times 10 to the exponent.y D
Exponent:
matrixâexponent
Returns matrix elements times 10 to the exponent.y D
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 359
4Eff(nominal rate,
compounding periods)
Computes the effective interest rate. Π1:Finance
CALC
C:4Eff(
Else
See If:Then:Else
End Identifies end of For(, If-Then-Else, Repeat, or While
loop.
†
CTL
7:End
Eng Sets engineering display mode. † z
Eng
Equ4String(Y= var,Strn)Converts the contents of a Y= var to a string and stores it in
Strn.
y N
Equ4String(
expr(string)Converts string to an expression and executes it. y N
expr(
ExpReg [Xlistname,
Ylistname,freqlist,regequ]
Fits an exponential regression model to Xlistname and
Ylistname with frequency freqlist, and stores the regression
equation to regequ.
…
CALC
0:ExpReg
ExprOff Turns off the expression display during TRACE.† y .
ExprOff
ExprOn Turns on the expression display during TRACE.† y .
ExprOn
Ücdf(lowerbound,
upperbound,
numerator df,
denominator df)
Computes the Û distribution probability between
lowerbound and upperbound for the specified numerator df
(degrees of freedom) and denominator df.
y =
DISTR
0:Ücdf(
4 F 3 4 DConverts an answer from a fraction to a decimal or from a
decimal to a fraction.
t ^
4: 4 F 3 4 D
or
NUM
8: 4 F 3 4 D
Fill(value,matrixname)Stores value to each element in matrixname.y >
MATH
4:Fill(
Fill(value,listname)Stores value to each element in listname.y 9
OPS
4:Fill(
Fix # Sets fixed-decimal mode for # of decimal places. † z
0123456789
(select one)
Float Sets floating decimal mode. † z
Float
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 360
fMax(expression,
variable,lower,upper
[,tolerance])
Returns the value of variable where the local maximum of
expression occurs, between lower and upper, with specified
tolerance.
MATH
7:fMax(
fMin(expression,variable,
lower,upper[,tolerance])
Returns the value of variable where the local minimum of
expression occurs, between lower and upper, with specified
tolerance.
MATH
6:fMin(
fnInt(expression,variable,
lower,upper[,tolerance])
Returns the function integral of expression with respect to
variable, between lower and upper, with specified tolerance.
MATH
9:fnInt(
FnOff [function#,
function#,...,function n]
Deselects all Y= functions or specified Y= functions.
Y-VARS
4:On/Off
2:FnOff
FnOn [function#,
function#,...,function n]
Selects all Y= functions or specified Y= functions.
Y-VARS
4:On/Off
1:FnOn
:For(variable,begin,end
[,increment])
:commands
:End
:commands
Executes commands through End, incrementing variable
from begin by increment until variable>end.
†
CTL
4:For(
fPart(value)Returns the fractional part or parts of a real or complex
number, expression, list, or matrix.
NUM
4:fPart(
Üpdf(x,numerator df,
denominator df)
Computes the Û distribution probability between
lowerbound and upperbound for the specified numerator df
(degrees of freedom) and denominator df.
y =
DISTR
9:Üpdf(
FRAC Answers Displays answers as fractions, if possible. z
Answers: FRAC
value4Frac Displays a real or complex number, expression, list, or
matrix as a fraction simplified to its simplest terms.
MATH
1:4Frac
Full Sets full screen mode. † z
Full
Func Sets function graphing mode. † z
Func
GarbageCollect Displays the garbage collection menu to allow cleanup of
unused archive memory.
y N
GarbageCollect
gcd(valueA,valueB)Returns the greatest common divisor of valueA and valueB,
which can be real numbers or lists.
NUM
9:gcd(
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item
Appendix A: Functions and Instructions 361
geometcdf(p,x)Computes a cumulative probability at x, the number of the
trial on which the first success occurs, for the discrete
geometric distribution with the specified probability of
success p.
y =
DISTR
F:geometcdf(
geometpdf(p,x)Computes a probability at x, the number of the trial on which
the first success occurs, for the discrete geometric
distribution with the specified probability of success p.
y =
DISTR
E:geometpdf(
Get(variable)Gets data from the CBL 2™ or CBR™ System and stores it
in variable.
†
I/O
A:Get(
GetCalc(variable
[,portflag])
Gets contents of variable on another TI-84 Plus and stores it
to variable on the receiving TI-84 Plus. By default, the TI-84
Plus uses the USB port if it is connected. If the USB cable
is not connected, it uses the I/O port.
portflag=0 use USB port if connected;
portflag=1 use USB port;
portflag=2 use I/O port.
†
I/O
0:GetCalc(
getDate Returns a list giving the date according to the current value
of the clock. The list is in {year,month,day} format.
y N
getDate
getDtFmt Returns an integer representing the date format that is
currently set on the device.
1 = M/D/Y
2 = D/M/Y
3 = Y/M/D
y N
getDtFmt
getDtStr(integer) Returns a string of the current date in the format specified
by integer, where:
1 = M/D/Y
2 = D/M/Y
3 = Y/M/D
y N
getDtStr(
getTime Returns a list giving the time according to the current value
of the clock. The list is in {hour,minute,second} format. The
time is returned in the 24 hour format.
y N
getTime
getTmFmt Returns an integer representing the clock time format that
is currently set on the device.
12 = 12 hour format
24 = 24 hour format
y N
getTmFmt
getTmStr(integer) Returns a string of the current clock time in the format
specified by integer, where:
12 = 12 hour format
24 = 24 hour format
y N
getTmStr(
getKey Returns the key code for the current keystroke, or 0, if no
key is pressed.
†
I/O
7:getKey
Goto label Transfers control to label.†
CTL
0:Goto
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 362
GraphStyle(function#,
graphstyle#)
Sets a graphstyle for function#.†
CTL
H:GraphStyle(
GridOff Turns off grid format. † y .
GridOff
GridOn Turns on grid format. † y .
GridOn
G-T Sets graph-table vertical split-screen mode. † z
G-T
Horiz Sets horizontal split-screen mode. † z
Horiz
Horizontal y Draws a horizontal line at y.y <
DRAW
3:Horizontal
iReturns a complex number. y V
identity(dimension)Returns the identity matrix of dimension rows x dimension
columns.
y >
MATH
5:identity(
:If condition
:commandA
:commands
If condition = 0 (false), skips commandA.†
CTL
1:If
:If condition
:Then
:commands
:End
:commands
Executes commands from Then to End if condition = 1
(true).
†
CTL
2:Then
:If condition
:Then
:commands
:Else
:commands
:End
:commands
Executes commands from Then to Else if condition = 1
(true); from Else to End if condition = 0 (false).
†
CTL
3:Else
imag(value)Returns the imaginary (nonreal) part of a complex number
or list of complex numbers.
CPX
3:imag(
IndpntAsk Sets table to ask for independent-variable values. † y -
Indpnt: Ask
IndpntAuto Sets table to generate independent-variable values
automatically.
† y -
Indpnt: Auto
Input Displays graph. †
I/O
1:Input
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 363
Input [variable]
Input ["text",variable]
Prompts for value to store to variable.†
I/O
1:Input
Input [Strn,variable] Displays Strn and stores entered value to variable.†
I/O
1:Input
inString(string,substring
[,start])
Returns the character position in string of the first
character of substring beginning at start.
y N
inString(
int(value)Returns the largest integer a real or complex number,
expression, list, or matrix.
NUM
5:int(
GInt(pmt1,pmt2
[,roundvalue])
Computes the sum, rounded to roundvalue, of the interest
amount between pmt1 and pmt2 for an amortization
schedule.
Π1:Finance
CALC
A:GInt(
invNorm(area[,m,s])Computes the inverse cumulative normal distribution
function for a given area under the normal distribution
curve specified by m and s.
y =
DISTR
3:invNorm(
invT(area,df)Computes the inverse cumulative student-t probability
function specified by degree of freedom, df for a given area
under the curve.
y =
DISTR
4:invT(
iPart(value)Returns the integer part of a real or complex number,
expression, list, or matrix.
NUM
3:iPart(
irr(CF0,CFList[,CFFreq])Returns the interest rate at which the net present value of
the cash flow is equal to zero.
Π1:Finance
CALC
8:irr(
isClockOn Identifies if clock is ON or OFF. Returns 1 if the clock is
ON. Returns 0 if the clock is OFF.
y N
isClockOn
:IS>(variable,value)
:commandA
:commands
Increments variable by 1; skips commandA if variable>value. †
CTL
A:IS>(
Ùlistname Identifies the next one to five characters as a user-created
list name.
y 9
OPS
B:Ù
LabelOff Turns off axes labels. † y .
LabelOff
LabelOn Turns on axes labels. † y .
LabelOn
Lbl label Creates a label of one or two characters. †
CTL
9:Lbl
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 364
lcm(valueA,valueB)Returns the least common multiple of valueA and valueB,
which can be real numbers or lists.
NUM
8:lcm(
length(string)Returns the number of characters in string.y N
length(
Line(X1,Y1,X2,Y2)Draws a line from (X1,Y1) to (X2,Y2). y <
DRAW
2:Line(
Line(X1,Y1,X2,Y2,0) Erases a line from (X1,Y1) to (X2,Y2). y <
DRAW
2:Line(
LinReg(a+bx) [Xlistname,
Ylistname,freqlist,
regequ]
Fits a linear regression model to Xlistname and Ylistname
with frequency freqlist, and stores the regression equation
to regequ.
…
CALC
8:LinReg(a+bx)
LinReg(ax+b) [Xlistname,
Ylistname,freqlist,
regequ]
Fits a linear regression model to Xlistname and Ylistname
with frequency freqlist, and stores the regression equation
to regequ.
…
CALC
4:LinReg(ax+b)
LinRegTInt [Xlistname,
Ylistname,freqlist,
confidence level, regequ]
Performs a linear regression and computes the t
confidence interval for the slope coefficient b.
† …
TESTS
G:LinRegTInt
LinRegTTest [Xlistname,
Ylistname,freqlist,
alternative,regequ]
Performs a linear regression and a t-test. alternative=L1 is
<; alternative=0 is ƒ; alternative=1 is >.
† …
TESTS
F:LinRegTTest
@List(list)Returns a list containing the differences between
consecutive elements in list.
y 9
OPS
7:@List(
List 4 matr(listname1,...,
listname n,matrixname)
Fills matrixname column by column with the elements from
each specified listname.
y 9
OPS
0:List 4 matr(
ln(value)Returns the natural logarithm of a real or complex number,
expression, or list.
μ
LnReg [Xlistname,
Ylistname,freqlist,
regequ]
Fits a logarithmic regression model to Xlistname and
Ylistname with frequency freqlist, and stores the regression
equation to regequ.
…
CALC
9:LnReg
log(value)Returns logarithm of a real or complex number,
expression, or list.
«
logBASE(value, base)Returns the logarithm of a specifed value determined from
a specified base: logBASE(value, base).
A: logBASE
Logistic [Xlistname,
Ylistname,freqlist,
regequ]
Fits a logistic regression model to Xlistname and Ylistname
with frequency freqlist, and stores the regression equation
to regequ.
…
CALC
B:Logistic
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 365
Manual-Fit equname Fits a linear equation to a scatter plot. …
CALC
D:Manual-Fit
MATHPRINT Displays most entries and answers the way they are
displayed in textbooks, such as .
z
MATHPRINT
Matr4list(matrix,
listnameA,...,listname n)
Fills each listname with elements from each column in
matrix.
y 9
OPS
A:Matr4list(
Matr4list(matrix,
column#,listname)
Fills a listname with elements from a specified column# in
matrix.
y 9
OPS
A:Matr4list(
max(valueA,valueB)Returns the larger of valueA and valueB.
NUM
7:max(
max(list)Returns largest real or complex element in list. y 9
MATH
2:max(
max(listA,listB)Returns a real or complex list of the larger of each pair of
elements in listA and listB.
y 9
MATH
2:max(
max(value,list)Returns a real or complex list of the larger of value or each
list element.
y 9
MATH
2:max(
mean(list[,freqlist])Returns the mean of list with frequency freqlist.y 9
MATH
3:mean(
median(list[,freqlist])Returns the median of list with frequency freqlist.y 9
MATH
4:median(
Med-Med [Xlistname,
Ylistname,freqlist,
regequ]
Fits a median-median model to Xlistname and Ylistname
with frequency freqlist, and stores the regression equation
to regequ.
…
CALC
3:Med-Med
Menu("title","text1",
label1[,...,"text7",label7])
Generates a menu of up to seven items during program
execution.
†
CTL
C:Menu(
min(valueA,valueB)Returns smaller of valueA and valueB.
NUM
6:min(
min(list)Returns smallest real or complex element in list. y 9
MATH
1:min(
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 366
min(listA,listB)Returns real or complex list of the smaller of each pair of
elements in listA and listB.
y 9
MATH
1:min(
min(value,list)Returns a real or complex list of the smaller of value or
each list element.
y 9
MATH
1:min(
valueA nCr valueB Returns the number of combinations of valueA taken valueB
at a time.
PRB
3:nCr
value nCr list Returns a list of the combinations of value taken each
element in list at a time.
PRB
3:nCr
list nCr value Returns a list of the combinations of each element in list
taken value at a time.
PRB
3:nCr
listA nCr listB Returns a list of the combinations of each element in listA
taken each element in listB at a time.
PRB
3:nCr
n/d Displays results as a simple fraction. t ^
1: n/d
or
NUM
D: n/d
nDeriv(expression,
variable,value[,H])
Returns approximate numerical derivative of expression
with respect to variable at value, with specified H.
MATH
8:nDeriv(
4 n/d 3 4 Un/d Converts the results from a fraction to mixed number or
from a mixed number to a fraction, if applicable.
t ^
3: 4 n/d 3 4 Un/d
or
NUM
A: 4 n/d 3 4 Un/d
4Nom(effective rate,
compounding periods)
Computes the nominal interest rate. Π1:Finance
CALC
B:4Nom(
Normal Sets normal display mode. † z
Normal
normalcdf(lowerbound,
upperbound[,m,s])
Computes the normal distribution probability between
lowerbound and upperbound for the specified m and s.
y =
DISTR
2:normalcdf(
normalpdf(x[,m,s])Computes the probability density function for the normal
distribution at a specified x value for the specified m and s.
y =
DISTR
1:normalpdf(
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 367
not(value)Returns 0 if value is ƒ 0. value can be a real number,
expression, or list.
y :
LOGIC
4:not(
valueA nPr valueB Returns the number of permutations of valueA taken valueB
at a time.
PRB
2:nPr
value nPr list Returns a list of the permutations of value taken each
element in list at a time.
PRB
2:nPr
list nPr value Returns a list of the permutations of each element in list
taken value at a time.
PRB
2:nPr
listA nPr listB Returns a list of the permutations of each element in listA
taken each element in listB at a time.
PRB
2:nPr
npv(interest rate,CF0,
CFList[,CFFreq])
Computes the sum of the present values for cash inflows
and outflows.
Π1:Finance
CALC
7:npv(
valueA or valueB Returns 1 if valueA or valueB is ƒ 0. valueA and valueB can
be real numbers, expressions, or lists.
y :
LOGIC
2:or
Output(row,column,
"text")
Displays text beginning at specified row and column. †
I/O
6:Output(
Output(row,column,
value)
Displays value beginning at specified row and column. †
I/O
6:Output(
Param Sets parametric graphing mode. † z
Par
Pause Suspends program execution until you press Í. †
CTL
8:Pause
Pause [value] Displays value; suspends program execution until you press
Í.
†
CTL
8:Pause
Plot#(type,Xlistname,
Ylistname,mark)
Defines Plot# (1, 2, or 3) of type Scatter or xyLine for
Xlistname and Ylistname using mark.
† y ,
STAT PLOTS
1:Plot1-
2:Plot2-
3:Plot3-
Plot#(type,Xlistname,
freqlist)
Defines Plot# (1, 2, or 3) of type Histogram or Boxplot for
Xlistname with frequency freqlist.
† y ,
STAT PLOTS
1:Plot1-
2:Plot2-
3:Plot3-
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 368
Plot#(type,Xlistname,
freqlist,mark)
Defines Plot# (1, 2, or 3) of type ModBoxplot for Xlistname
with frequency freqlist using mark.
† y ,
STAT PLOTS
1:Plot1-
2:Plot2-
3:Plot3-
Plot#(type,datalistname,
data axis,mark)
Defines Plot# (1, 2, or 3) of type NormProbPlot for
datalistname on data axis using mark. data axis can be X or Y.
† y ,
STAT PLOTS
1:Plot1-
2:Plot2-
3:Plot3-
PlotsOff [1,2,3] Deselects all stat plots or one or more specified stat plots
(1, 2, or 3).
y ,
STAT PLOTS
4:PlotsOff
PlotsOn [1,2,3] Selects all stat plots or one or more specified stat plots (1,
2, or 3).
y ,
STAT PLOTS
5:PlotsOn
Pmt_Bgn Specifies an annuity due, where payments occur at the
beginning of each payment period.
Π1:Finance
CALC
F:Pmt_Bgn
Pmt_End Specifies an ordinary annuity, where payments occur at
the end of each payment period.
Π1:Finance
CALC
E:Pmt_End
poissoncdf(m,x)Computes a cumulative probability at x for the discrete
Poisson distribution with specified mean m.
y =
DISTR
D:poissoncdf(
poissonpdf(m,x)Computes a probability at x for the discrete Poisson
distribution with the specified mean m.
y =
DISTR
C:poissonpdf(
Polar Sets polar graphing mode. † z
Pol
complex value 4Polar Displays complex value in polar format.
CPX
7:4Polar
PolarGC Sets polar graphing coordinates format. † y .
PolarGC
prgmname Executes the program name. †
CTRL
D:prgm
GPrn(pmt1,pmt2
[,roundvalue])
Computes the sum, rounded to roundvalue, of the principal
amount between pmt1 and pmt2 for an amortization
schedule.
Π1:Finance
CALC
0:GPrn(
prod(list[,start,end])Returns product of list elements between start and end. y 9
MATH
6:prod(
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 369
Prompt variableA
[,variableB,...,variable n]
Prompts for value for variableA, then variableB, and so on. †
I/O
2:Prompt
1-PropZInt(x,n
[,confidence level])
Computes a one-proportion z confidence interval. † …
TESTS
A:1-PropZInt(
2-PropZInt(x1,n1,x2,n2
[,confidence level])
Computes a two-proportion z confidence interval. † …
TESTS
B:2-PropZInt(
1-PropZTest(p0,x,n
[,alternative,drawflag])
Computes a one-proportion z test. alternative=L1 is <;
alternative=0 is ƒ; alternative=1 is >. drawflag=1 draws
results; drawflag=0 calculates results.
† …
TESTS
5:1-PropZTest(
2-PropZTest(x1,n1,x2,n2
[,alternative,drawflag])
Computes a two-proportion z test. alternative=L1 is <;
alternative=0 is ƒ; alternative=1 is >. drawflag=1 draws
results; drawflag=0 calculates results.
† …
TESTS
6:2-PropZTest(
Pt-Change(x,y)Reverses a point at (x,y). y <
POINTS
3:Pt-Change(
Pt-Off(x,y[,mark])Erases a point at (x,y) using mark.y <
POINTS
2:Pt-Off(
Pt-On(x,y[,mark])Draws a point at (x,y) using mark.y <
POINTS
1:Pt-On(
PwrReg [Xlistname,
Ylistname,freqlist,
regequ]
Fits a power regression model to Xlistname and Ylistname
with frequency freqlist, and stores the regression equation
to regequ.
…
CALC
A:PwrReg
Pxl-Change(row,column)Reverses pixel at (row,column); 0 row 62 and
0 column 94.
y <
POINTS
6:Pxl-Change(
Pxl-Off(row,column)Erases pixel at (row,column); 0 row 62 and
0 column 94.
y <
POINTS
5:Pxl-Off(
Pxl-On(row,column)Draws pixel at (row,column); 0 row 62 and
0 column 94.
y <
POINTS
4:Pxl-On(
pxl-Test(row,column)Returns 1 if pixel (row, column) is on, 0 if it is off;
0 row 62 and 0 column 94.
y <
POINTS
7:pxl-Test(
P4Rx(r,q)Returns X, given polar coordinates r and q or a list of polar
coordinates.
y ;
ANGLE
7:P4Rx(
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 370
P4Ry(r,q)Returns Y, given polar coordinates r and q or a list of polar
coordinates.
y ;
ANGLE
8:P4Ry(
QuadReg [Xlistname,
Ylistname,freqlist,
regequ]
Fits a quadratic regression model to Xlistname and
Ylistname with frequency freqlist, and stores the regression
equation to regequ.
…
CALC
5:QuadReg
QuartReg [Xlistname,
Ylistname,freqlist,
regequ]
Fits a quartic regression model to Xlistname and Ylistname
with frequency freqlist, and stores the regression equation
to regequ.
…
CALC
7:QuartReg
Radian Sets radian angle mode. † z
Radian
rand[(numtrials)] Returns a random number between 0 and 1 for a specified
number of trials numtrials.
PRB
1:rand
randBin(numtrials,prob
[,numsimulations])
Generates and displays a random real number from a
specified Binomial distribution.
PRB
7:randBin(
randInt( lower,upper
[,numtrials])
Generates and displays a random integer within a range
specified by lower and upper integer bounds for a specified
number of trials numtrials.
PRB
5:randInt(
randIntNoRep(lowerint,
upperint)
Returns a random ordered list of integers from a lower
integer to an upper integer which may include the lower
integer and upper integer.
PRB
8:randIntNoRep(
randM(rows,columns)Returns a random matrix of rows (1-99) × columns (1-99). y >
MATH
6:randM(
randNorm(m,s
[,numtrials])
Generates and displays a random real number from a
specified Normal distribution specified by m and s for a
specified number of trials numtrials.
PRB
6:randNorm(
re^qiSets the mode to polar complex number mode (re^qi). † z
re^qi
Real Sets mode to display complex results only when you enter
complex numbers.
† z
Real
real(value)Returns the real part of a complex number or list of
complex numbers.
CPX
2:real(
RecallGDB nRestores all settings stored in the graph database variable
GDBn.
y <
STO
4:RecallGDB
RecallPic nDisplays the graph and adds the picture stored in Picn.y <
STO
2:RecallPic
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 371
complex value 4Rect Displays complex value or list in rectangular format.
CPX
6:4Rect
RectGC Sets rectangular graphing coordinates format. † y .
RectGC
ref(matrix)Returns the row-echelon form of a matrix.y >
MATH
A:ref(
remainder(dividend,
divisor)
Reports the remainder as a whole number from a division
of two whole numbers where the divisor is not zero.
NUM
0:remainder(
remainder(list, divisor)Reports the remainder as a whole number from a division
of two lists where the divisor is not zero.
NUM
0:remainder(
remainder(dividend, list)Reports the remainder as a whole number from a division
of two whole numbers where the divisor is a list.
NUM
0:remainder(
remainder(list, list)Reports the remainder as a whole number from a division
of two lists.
NUM
0:remainder(
:Repeat condition
:commands
:End
:commands
Executes commands until condition is true. †
CTL
6:Repeat
Return Returns to the calling program. †
CTL
E:Return
round(value[,#decimals])Returns a number, expression, list, or matrix rounded to
#decimals ( 9).
NUM
2:round(
ärow(value,matrix,row)Returns a matrix with row of matrix multiplied by value and
stored in row.
y >
MATH
E:ärow(
row+(matrix,rowA,rowB)Returns a matrix with rowA of matrix added to rowB and
stored in rowB.
y >
MATH
D:row+(
ärow+(value,matrix,
rowA,rowB)
Returns a matrix with rowA of matrix multiplied by value,
added to rowB, and stored in rowB.
y >
MATH
F:ärow+(
rowSwap(matrix,rowA,
rowB)
Returns a matrix with rowA of matrix swapped with rowB.y >
MATH
C:rowSwap(
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 372
rref(matrix)Returns the reduced row-echelon form of a matrix.y >
MATH
B:rref(
R4Pr(x,y)Returns R, given rectangular coordinates x and y or a list
of rectangular coordinates.
y ;
ANGLE
5:R4Pr(
R4Pq(x,y)Returns q, given rectangular coordinates x and y or a list of
rectangular coordinates.
y ;
ANGLE
6:R4Pq(
2-SampÜTest [listname1,
listname2,freqlist1,
freqlist2,alternative,
drawflag]
(Data list input)
Performs a two-sample Û test. alternative=L1 is <;
alternative=0 is ƒ; alternative=1 is >. drawflag=1 draws
results; drawflag=0 calculates results.
† …
TESTS
E:2-SampÜTest
2-SampÜTest Sx1,n1,
Sx2,n2[,alternative,
drawflag]
(Summary stats input)
Performs a two-sample Û test. alternative=L1 is <;
alternative=0 is ƒ; alternative=1 is >. drawflag=1 draws
results; drawflag=0 calculates results.
† …
TESTS
E:2-SampÜTest
2-SampTInt [listname1,
listname2,
freqlist1,freqlist2,
confidence level,pooled]
(Data list input)
Computes a two-sample t confidence interval. pooled=1
pools variances; pooled=0 does not pool variances.
† …
TESTS
0:2-SampTInt
2-SampTInt v1,Sx1,n1,
v2,Sx2,n2
[,confidence level,pooled]
(Summary stats input)
Computes a two-sample t confidence interval. pooled=1
pools variances; pooled=0 does not pool variances.
† …
TESTS
0:2-SampTInt
2-SampTTest [listname1,
listname2,freqlist1,
freqlist2,alternative,
pooled,drawflag]
(Data list input)
Computes a two-sample t test. alternative=L1 is <;
alternative=0 is ƒ; alternative=1 is >. pooled=1 pools
variances; pooled=0 does not pool variances. drawflag=1
draws results; drawflag=0 calculates results.
† …
TESTS
4:2-SampTTest
2-SampTTest v1,Sx1,n1,
v2,Sx2,n2[,alternative,
pooled,drawflag]
(Summary stats input)
Computes a two-sample t test. alternative=L1 is <;
alternative=0 is ƒ; alternative=1 is >. pooled=1 pools
variances; pooled=0 does not pool variances. drawflag=1
draws results; drawflag=0 calculates results.
† …
TESTS
4:2-SampTTest
2-SampZInt(s1,s2
[,listname1,listname2,
freqlist1,freqlist2,
confidence level])
(Data list input)
Computes a two-sample z confidence interval. † …
TESTS
9:2-SampZInt(
2-SampZInt(s1,s2,
v1,n1,v2,n2
[,confidence level])
(Summary stats input)
Computes a two-sample z confidence interval. † …
TESTS
9:2-SampZInt(
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 373
2-SampZTest(s1,s2
[,listname1,listname2,
freqlist1,freqlist2,
alternative,drawflag])
(Data list input)
Computes a two-sample z test. alternative=L1 is <;
alternative=0 is ƒ; alternative=1 is >. drawflag=1 draws
results; drawflag=0 calculates results.
† …
TESTS
3:2-SampZTest(
2-SampZTest(s1,s2,
v1,n1,v2,n2
[,alternative,drawflag])
(Summary stats input)
Computes a two-sample z test. alternative=L1 is <;
alternative=0 is ƒ; alternative=1 is >. drawflag=1 draws
results; drawflag=0 calculates results.
† …
TESTS
3:2-SampZTest(
Sci Sets scientific notation display mode. † z
Sci
Select(Xlistname,
Ylistname)
Selects one or more specific data points from a scatter plot
or xyLine plot (only), and then store•s the selected data
points to two new lists, Xlistname and Ylistname.
y 9
OPS
8:Select(
Send(variable)Sends contents of variable to the CBL 2™ or CBR™
System.
†
I/O
B:Send(
seq(expression,variable,
begin,end[,increment])
Returns list created by evaluating expression with regard to
variable, from begin to end by increment.
y 9
OPS
5:seq(
Seq Sets sequence graphing mode. † z
Seq
Sequential Sets mode to graph functions sequentially. † z
Sequential
setDate(year,month,day) Sets the date using a year, month, day format. The year
must be 4 digits; month and day can be 1 or 2 digit.
y N
setDate(
setDtFmt(integer) Sets the date format.
1 = M/D/Y
2 = D/M/Y
3 = Y/M/D
y N
setDtFmt(
setTime(hour,minute,
second)
Sets the time using an hour, minute, second format. The
hour must be in 24 hour format, in which 13 = 1 p.m.
y N
setTime(
setTmFmt(integer) Sets the time format.
12 = 12 hour format
24 = 24 hour format
y N
setTmFmt(
SetUpEditor Removes all list names from the stat list editor, and then
restores list names L1 through L6 to columns 1 through 6.
…
EDIT
5:SetUpEditor
SetUpEditor listname1
[,listname2,...,
listname20]
Removes all list names from the stat list editor, then sets it
up to display one or more listnames in the specified order,
starting with column 1.
…
EDIT
5:SetUpEditor
Shade(lowerfunc,
upperfunc[,Xleft,Xright,
pattern,patres])
Draws lowerfunc and upperfunc in terms of X on the current
graph and uses pattern and patres to shade the area
bounded by lowerfunc, upperfunc, Xleft, and Xright.
y <
DRAW
7:Shade(
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 374
Shadec2(lowerbound,
upperbound,df)
Draws the density function for the c2 distribution specified
by degrees of freedom df and shades the area between
lowerbound and upperbound.
y =
DRAW
3:Shadec2(
ShadeÜ(lowerbound,
upperbound,
numerator df,
denominator df)
Draws the density function for the Û distribution specified
by numerator df and denominator df and shades the area
between lowerbound and upperbound.
y =
DRAW
4:ShadeÜ(
ShadeNorm(lowerbound,
upperbound[,m,s])
Draws the normal density function specified by m and s
and shades the area between lowerbound and upperbound.
y =
DRAW
1:ShadeNorm(
Shade_t(lowerbound,
upperbound,df)
Draws the density function for the Student-t distribution
specified by degrees of freedom df, and shades the area
between lowerbound and upperbound.
y =
DRAW
2:Shade_t(
Simul Sets mode to graph functions simultaneously. † z
Simul
sin(value)Returns the sine of a real number, expression, or list. ˜
sinL1(value)Returns the arcsine of a real number, expression, or list. y ?
sinh(value)Returns the hyperbolic sine of a real number, expression,
or list.
y N
sinh(
sinhL1 (value)Returns the hyperbolic arcsine of a real number,
expression, or list.
y N
sinhL1(
SinReg [iterations,
Xlistname,Ylistname,
period,regequ]
Attempts iterations times to fit a sinusoidal regression model
to Xlistname and Ylistname using a period guess, and stores
the regression equation to regequ.
…
CALC
C:SinReg
solve(expression,
variable,guess,
{lower,upper})
Solves expression for variable, given an initial guess and
lower and upper bounds within which the solution is sought.
†
MATH
0:solve(
SortA(listname)Sorts elements of listname in ascending order. y 9
OPS
1:SortA(
SortA(keylistname,
dependlist1[,dependlist2,
...,dependlist n])
Sorts elements of keylistname in ascending order, then
sorts each dependlist as a dependent list.
y 9
OPS
1:SortA(
SortD(listname)Sorts elements of listname in descending order. y 9
OPS
2:SortD(
SortD(keylistname,dependl
ist1[,dependlist2,
..., dependlist n])
Sorts elements of keylistname in descending order, then
sorts each dependlist as a dependent list.
y 9
OPS
2:SortD(
startTmr Starts the clock timer. Store or note the displayed value,
and use it as the argument for checkTmr( ) to check the
elapsed time.
y N
startTmr
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 375
STATWIZARD OFF Disables wizard syntax help for statistical
commands, distributions, and seq(.
y N
STATWIZARD
OFF
STATWIZARD ON Enables wizard syntax help for statistical commands,
distributions, and seq(.
y N
STATWIZARD ON(
stdDev(list[,freqlist])Returns the standard deviation of the elements in list with
frequency freqlist.
y 9
MATH
7:stdDev(
Stop Ends program execution; returns to home screen. †
CTL
F:Stop
Store: value!variable Stores value in variable.¿
StoreGDB nStores current graph in database GDBn.y <
STO
3:StoreGDB
StorePic nStores current picture in picture Picn.y <
STO
1:StorePic
String4Equ(string,Y= var)Converts string into an equation and stores it in Y= var.y N
String4Equ(
sub(string,begin,length)Returns a string that is a subset of another string, from
begin to length.
y N
sub(
sum(list[,start,end])Returns the sum of elements of list from start to end.y 9
MATH
5:sum(
summation G(expression
[,start,end])
Displays the MathPrint™ summation entry template and
returns the sum of elements of list from start to end, where
start <= end.
NUM
0: summation G(
tan(value)Returns the tangent of a real number, expression, or list. š
tanL1(value)Returns the arctangent of a real number, expression, or
list.
y A
Tangent(expression,
value)
Draws a line tangent to expression at X=value.y <
DRAW
5:Tangent(
tanh(value)Returns hyperbolic tangent of a real number, expression, or
list.
y N
tanh(
tanhL1(value)Returns the hyperbolic arctangent of a real number,
expression, or list.
y N
tanhL1(
tcdf(lowerbound,
upperbound,df)
Computes the Student-t distribution probability between
lowerbound and upperbound for the specified degrees of
freedom df.
y =
DISTR
6:tcdf(
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 376
Text(row,column,text1,
text2,...,text n)
Writes text on graph beginning at pixel (row,column), where
0 row 57 and 0 column 94.
y <
DRAW
0:Text(
Then
See If:Then
Time Sets sequence graphs to plot with respect to time. † y .
Time
timeCnv(seconds)Converts seconds to units of time that can be more easily
understood for evaluation. The list is in
{days,hours,minutes,seconds} format.
y N
timeCnv
TInterval [listname,
freqlist,confidence level]
(Data list input)
Computes a t confidence interval. † …
TESTS
8:TInterval
TInterval v,Sx,n
[,confidence level]
(Summary stats input)
Computes a t confidence interval. † …
TESTS
8:TInterval
tpdf(x,df)Computes the probability density function (pdf) for the
Student-t distribution at a specified x value with specified
degrees of freedom df.
y =
DISTR
5:tpdf(
Trace Displays the graph and enters TRACE mode. r
T-Test m0[,listname,
freqlist,alternative,
drawflag]
(Data list input)
Performs a t test with frequency freqlist. alternative=L1 is <;
alternative=0 is ƒ; alternative=1 is >. drawflag=1 draws
results; drawflag=0 calculates results.
† …
TESTS
2:T-Test
T-Test m0, v,Sx,n
[,alternative,drawflag]
(Summary stats input)
Performs a t test with frequency freqlist. alternative=L1 is < ;
alternative=0 is ă; alternative=1 is >. drawflag=1 draws
results; drawflag=0 calculates results.
† …
TESTS
2:T-Test
tvm_FV[(Ú,æ,PV,PMT,
P/Y,C/Y)]
Computes the future value. Π1:Finance
CALC
6:tvm_FV
tvm_æ[(Ú,PV,PMT,FV,
P/Y,C/Y)]
Computes the annual interest rate. Π1:Finance
CALC
3:tvm_æ
tvm_Ú[(æ,PV,PMT,FV,
P/Y,C/Y)]
Computes the number of payment periods. Π1:Finance
CALC
5:tvm_Ú
tvm_Pmt[(Ú,æ,PV,FV,
P/Y,C/Y)]
Computes the amount of each payment. Π1:Finance
CALC
2:tvm_Pmt
tvm_PV[(Ú,æ,PMT,FV,
P/Y,C/Y)]
Computes the present value. Π1:Finance
CALC
4:tvm_PV
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 377
UnArchive Moves the specified variables from the user data archive
memory to RAM.
To archive variables, use Archive.
y L
6:UnArchive
Un/d Displays results as a mixed number, if applicable.
NUM
C: Un/d
uvAxes Sets sequence graphs to plot u(n) on the x-axis and v(n)
on the y-axis.
† y .
uv
uwAxes Sets sequence graphs to plot u(n) on the x-axis and w(n)
on the y-axis.
† y .
uw
1-Var Stats [Xlistname,
freqlist]
Performs one-variable analysis on the data in Xlistname
with frequency freqlist.
…
CALC
1:1-Var Stats
2-Var Stats [Xlistname,
Ylistname,freqlist]
Performs two-variable analysis on the data in Xlistname
and Ylistname with frequency freqlist.
…
CALC
2:2-Var Stats
variance(list[,freqlist])Returns the variance of the elements in list with frequency
freqlist.
y 9
MATH
8:variance(
Vertical x Draws a vertical line at x.y <
DRAW
4:Vertical
vwAxes Sets sequence graphs to plot v(n) on the x-axis and w(n)
on the y-axis.
† y .
vw
Web Sets sequence graphs to trace as webs. † y .
Web
:While condition
:commands
:End
:command
Executes commands while condition is true. †
CTL
5:While
valueA xor valueB Returns 1 if only valueA or valueB = 0. valueA and valueB
can be real numbers, expressions, or lists.
y :
LOGIC
3:xor
ZBox Displays a graph, lets you draw a box that defines a new
viewing window, and updates the window.
† q
ZOOM
1:ZBox
ZDecimal Adjusts the viewing window so that @X=0.1 and @Y=0.1,
and displays the graph screen with the origin centered on
the screen.
† q
ZOOM
4:ZDecimal
ZFrac 1/2 Sets the window variables so that you can trace in
increments of , if possible. Sets @X and @Y to .
q
ZOOM
B:ZFrac1/2
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 378
ZFrac 1/3 Sets the window variables so that you can trace in
increments of , if possible. Sets @X and @Y to .
q
ZOOM
C:ZFrac1/3
ZFrac 1/4 Sets the window variables so that you can trace in
increments of , if possible. Sets @X and @Y to .
q
ZOOM
D:ZFrac1/4
ZFrac 1/5 Sets the window variables so that you can trace in
increments of , if possible. Sets @X and @Y to .
q
ZOOM
E:ZFrac1/5
ZFrac 1/8 Sets the window variables so that you can trace in
increments of , if possible. Sets @X and @Y to .
q
ZOOM
F:ZFrac1/8
ZFrac 1/10 Sets the window variables so that you can trace in
increments of , if possible. Sets @X and @Y to .
q
ZOOM
G:ZFrac1/10
ZInteger Redefines the viewing window using these dimensions:
@X=1 Xscl=10
@Y=1 Yscl=10
† q
ZOOM
8:ZInteger
ZInterval s[,listname,
freqlist,confidence level]
(Data list input)
Computes a z confidence interval. † …
TESTS
7:ZInterval
ZInterval s,v,n
[,confidence level]
(Summary stats input)
Computes a z confidence interval. † …
TESTS
7:ZInterval
Zoom In Magnifies the part of the graph that surrounds the cursor
location.
† q
ZOOM
2:Zoom In
Zoom Out Displays a greater portion of the graph, centered on the
cursor location.
† q
ZOOM
3:Zoom Out
ZoomFit Recalculates Ymin and Ymax to include the minimum and
maximum Y values, between Xmin and Xmax, of the
selected functions and replots the functions.
† q
ZOOM
0:ZoomFit
ZoomRcl Graphs the selected functions in a user-defined viewing
window.
† q
MEMORY
3:ZoomRcl
ZoomStat Redefines the viewing window so that all statistical data
points are displayed.
† q
ZOOM
9:ZoomStat
ZoomSto Immediately stores the current viewing window. † q
MEMORY
2:ZoomSto
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 379
ZPrevious Replots the graph using the window variables of the graph
that was displayed before you executed the last ZOOM
instruction.
† q
MEMORY
1:ZPrevious
ZQuadrant1 Displays the portion of the graph that is in quadrant 1. q
ZOOM
A:ZQuadrant1
ZSquare Adjusts the X or Y window settings so that each pixel
represents an equal width and height in the coordinate
system, and updates the viewing window.
† q
ZOOM
5:ZSquare
ZStandard Replots the functions immediately, updating the window
variables to the default values.
† q
ZOOM
6:ZStandard
Z-Test(m0,s[,listname,
freqlist,alternative,
drawflag])
(Data list input)
Performs a z test with frequency freqlist. alternative=L1 is <;
alternative=0 is ƒ; alternative=1 is >. drawflag=1 draws
results; drawflag=0 calculates results.
† …
TESTS
1:Z-Test(
Z-Test(m0,s,v,n
[,alternative,drawflag])
(Summary stats input)
Performs a z test. alternative=L1 is <; alternative=0 is ƒ;
alternative=1 is >. drawflag=1 draws results; drawflag=0
calculates results.
† …
TESTS
1:Z-Test(
ZTrig Replots the functions immediately, updating the window
variables to preset values for plotting trig functions.
† q
ZOOM
7:ZTrig
Factorial: value!Returns factorial of value.
PRB
4:!
Factorial: list!Returns factorial of list elements.
PRB
4:!
Degrees notation: value¡Interprets value as degrees; designates degrees in DMS
format.
y ;
ANGLE
1:¡
Radian: anglerInterprets angle as radians. y ;
ANGLE
3:r
Transpose: matrixTReturns a matrix in which each element (row, column) is
swapped with the corresponding element (column, row) of
matrix.
y >
MATH
2:T
xthrootx‡value Returns xthroot of value.
MATH
5:x‡
xthrootx‡list Returns xthroot of list elements.
MATH
5:x‡
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 380
listx‡value Returns list roots of value.
MATH
5:x‡
listAx‡listB Returns listA roots of listB.
MATH
5:x‡
Cube: value3Returns the cube of a real or complex number, expression,
list, or square matrix.
MATH
3:3
Cube root: 3‡(value)Returns the cube root of a real or complex number,
expression, or list.
MATH
4:3‡(
Equal: valueA=valueB Returns 1 if valueA = valueB. Returns 0 if valueA ƒ valueB.
valueA and valueB can be real or complex numbers,
expressions, lists, or matrices.
y :
TEST
1:=
Not equal:
valueAƒvalueB
Returns 1 if valueA ƒ valueB. Returns 0 if valueA = valueB.
valueA and valueB can be real or complex numbers,
expressions, lists, or matrices.
y :
TEST
2:ƒ
Less than:
valueA<valueB
Returns 1 if valueA < valueB. Returns 0 if valueA ‚ valueB.
valueA and valueB can be real or complex numbers,
expressions, or lists.
y :
TEST
5:<
Greater than:
valueA>valueB
Returns 1 if valueA > valueB. Returns 0 if valueA valueB.
valueA and valueB can be real or complex numbers,
expressions, or lists.
y :
TEST
3:>
Less than or equal:
valueAvalueB
Returns 1 if valueA valueB. Returns 0 if valueA > valueB.
valueA and valueB can be real or complex numbers,
expressions, or lists.
y :
TEST
6:
Greater than or equal:
valueA‚valueB
Returns 1 if valueA ‚ valueB. Returns 0 if valueA < valueB.
valueA and valueB can be real or complex numbers,
expressions, or lists.
y :
TEST
4:‚
Inverse: valueL1Returns 1 divided by a real or complex number or
expression.
—
Inverse: listL1Returns 1 divided by list elements. —
Inverse: matrixL1Returns matrix inverted. —
Square: value2Returns value multiplied by itself. value can be a real or
complex number or expression.
¡
Square: list2Returns list elements squared. ¡
Square: matrix2Returns matrix multiplied by itself. ¡
Powers: value^power Returns value raised to power. value can be a real or
complex number or expression.
›
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 381
Powers: list^power Returns list elements raised to power. ›
Powers: value^list Returns value raised to list elements. ›
Powers: matrix^power Returns matrix elements raised to power. ›
Negation: Lvalue Returns the negative of a real or complex number,
expression, list, or matrix.
Ì
Power of ten: 10^(value)Returns 10 raised to the value power. value can be a real or
complex number or expression.
y G
Power of ten: 10^(list)Returns a list of 10 raised to the list power. y G
Square root: ‡(value)Returns square root of a real or complex number,
expression, or list.
y C
Multiplication:
valueAävalueB
Returns valueA times valueB. ¯
Multiplication:
valueälist
Returns value times each list element. ¯
Multiplication:
listävalue
Returns each list element times value. ¯
Multiplication:
listAälistB
Returns listA elements times listB elements. ¯
Multiplication:
valueämatrix
Returns value times matrix elements. ¯
Multiplication:
matrixAämatrixB
Returns matrixA times matrixB. ¯
Division: valueAàvalueB Returns valueA divided by valueB.¥
Division: listàvalue Returns list elements divided by value. ¥
Division: valueàlist Returns value divided by list elements. ¥
Division: listAàlistB Returns listA elements divided by listB elements. ¥
Addition: valueA+valueB Returns valueA plus valueB. Ã
Addition: list+value Returns list in which value is added to each list element. Ã
Addition: listA+listB Returns listA elements plus listB elements. Ã
Addition:
matrixA+matrixB
Returns matrixA elements plus matrixB elements. Ã
Concatenation:
string1+string2
Concatenates two or more strings. Ã
Subtraction:
valueANvalueB
Subtracts valueB from valueA.¹
Subtraction:
valueNlist
Subtracts list elements from value.¹
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix A: Functions and Instructions 382
Subtraction:
listNvalue
Subtracts value from list elements. ¹
Subtraction:
listANlistB
Subtracts listB elements from listA elements. ¹
Subtraction:
matrixANmatrixB
Subtracts matrixB elements from matrixA elements. ¹
Minutes
notation:degrees¡minutes's
econds"
Interprets minutes angle measurement as minutes. y ;
ANGLE
2:'
Seconds notation:
degrees¡minutes'seconds"
Interprets seconds angle measurement as seconds. ƒ [ã]
F
unction or
Instruction/Arguments
Result
Key or
Keys/Menu or
Screen/Item

Appendix B: Reference Information 383
Appendix B:
Reference Information
Variables
User Variables
The TI-84 Plus uses the variables listed below in various ways. Some variables are restricted to
specific data types.
The variables A through Z and q are defined as real or complex numbers. You may store to them.
The TI-84 Plus can update X, Y, R, q, and T during graphing, so you may want to avoid using these
variables to store nongraphing data.
The variables (list names) L1 through L6 are restricted to lists; you cannot store another type of
data to them.
The variables (matrix names) [A] through [J] are restricted to matrices; you cannot store another
type of data to them.
The variables Pic1 through Pic9 and Pic0 are restricted to pictures; you cannot store another type
of data to them.
The variables GDB1 through GDB9 and GDB0 are restricted to graph databases; you cannot store
another type of data to them.
The variables Str1 through Str9 and Str0 are restricted to strings; you cannot store another type of
data to them.
Except for system variables, you can store any string of characters, functions, instructions, or
variables to the functions Yn, (1 through 9, and 0), XnT/YnT (1 through 6), rn (1 through 6), u(n), v(n),
and w(n) directly or through the Y= editor. The validity of the string is determined when the function is
evaluated.
Archive Variables
You can store data, programs or any variable from RAM to user data archive memory where they
cannot be edited or deleted inadvertently. Archiving also allows you to free up RAM for variables that
may require additional memory. The names of archived variables are preceded by an asterisk (*)
indicating they are in user data archive.
System Variables
The variables below must be real numbers. You may store to them. Since the TI-84 Plus can
update some of them, as the result of a ZOOM, for example, you may want to avoid using these
variables to store nongraphing data.
•Xmin, Xmax, Xscl, @X, XFact, Tstep, PlotStart, nMin, and other window variables.

Jc
1ae bxi
–
+
------------------------yi
–
⎝⎠
⎜⎟
⎛⎞
2
i1=
N
∑
=
Jasin bxic+()dy
i
–+[]
2
i1=
N
∑
=
Appendix B: Reference Information 384
•ZXmin, ZXmax, ZXscl, ZTstep, ZPlotStart, Zu(nMin), and other ZOOM variables.
The variables below are reserved for use by the TI-84 Plus. You cannot store to them.
n, v, Sx, sx, minX, maxX, Gy, Gy2, Gxy, a, b, c, RegEQ, x1, x2, y1, z, t, F, c2, Ç, v1, Sx1, n1, lower,
upper, r2, R2 and other statistical variables.
Statistics Formulas
This section contains statistics formulas for the Logistic and SinReg regressions, ANOVA,
2-SampÜTest, and 2-SampTTest.
Logistic
The logistic regression algorithm applies nonlinear recursive least-squares techniques to optimize
the following cost function:
which is the sum of the squares of the residual errors,
This technique attempts to estimate the constants a, b, and c recursively to make J as small as
possible.
SinReg
The sine regression algorithm applies nonlinear recursive least-squares techniques to optimize the
following cost function:
which is the sum of the squares of the residual errors,
This technique attempts to recursively estimate the constants a, b, c, and d to make J as small as
possible.
where: x
y
N
=
=
=
the independent variable list
the dependent variable list
the dimension of the lists
where: x
y
N
=
=
=
the independent variable list
the dependent variable list
the dimension of the lists
Appendix B: Reference Information 385
ANOVA(
The ANOVA Ü statistic is:
Ü = FactorMS
ErrorMS
--------------------------
FactorMS FactorSS
Factordf
------------------------=
ErrorMS ErrorSS
Errordf
---------------------=
FactorSS nixix–()
2
i1=
I
∑
=
ErrorSS ni1–()Sxi2
i1=
I
∑
=
Factordf I 1– numeratordf for ==
The mean squares (MS) that make up Ü are:
The sum of squares (SS) that make up the mean squares are:
The degrees of freedom df that make up the mean squares are:
Ü
Errordf ni1–()
i1=
I
∑denominatordf for == Ü
I
xi
Sxi
ni
x
2-SampFTest
Below is the definition for the 2-SampÜTest.
where: =
=
=
=
=
number of populations
the mean of each list
the standard deviation of each list
the length of each list
the mean of all lists
Sx1, Sx2=Sample standard deviations having
and degrees of freedom df,
respectively.
Ü
=Û-statistic =
n11–
n21–
Sx1
Sx2
---------
⎝⎠
⎛⎞
2

pf
F
α
∫xn
11n21–,–,()dx=
pf
0
F
∫xn
11n21–,–,()dx=
p
2
---fxn
11n21–,–,()xd
0
Lbnd
∫fxn
11n21–,–,()xd
Ubnd
∞
∫
==
tx1x2
–
S
----------------=
SSx12
n1
-----------Sx22
n2
-----------+=
df
Sx12
n1
-----------Sx22
n2
-----------+
⎝⎠
⎜⎟
⎛⎞
2
1
n11–
-------------- Sx12
n1
-----------
⎝⎠
⎜⎟
⎛⎞
21
n21–
-------------- Sx22
n2
-----------
⎝⎠
⎜⎟
⎛⎞
2
+
----------------------------------------------------------------------------=
Appendix B: Reference Information 386
2-SampÜTest for the alternative hypothesis .
2-SampÜTest for the alternative hypothesis .
2-SampÜTest for the alternative hypothesis s1 ƒ s2. Limits must satisfy the following:
where: [Lbnd,Ubnd] = lower and upper limits
The Ü-statistic is used as the bound producing the smallest integral. The remaining bound is
selected to achieve the preceding integral’s equality relationship.
2-SampTTest
The following is the definition for the 2-SampTTest. The two-sample t statistic with degrees of
freedom df is:
where the computation of S and df are dependent on whether the variances are pooled. If the
variances are not pooled:
df(x, , )=Ûpdf( ) with degrees of freedom df, ,
and
p = reported p value
n11– n21– n11–
n21–
σ1σ2
>
σ1σ2
<

Sxp
n11–()Sx12n21–()Sx22
+
df
--------------------------------------------------------------------=
S1
n1
----- 1
n2
----- Sxp
+=
df n1n22–+=
ie
yx1+()ln×()
[]1–=
i–FV PV÷()
1N÷()
1–=
Appendix B: Reference Information 387
otherwise:
and Sxp is the pooled variance.
Financial Formulas
This section contains financial formulas for computing time value of money, amortization, cash
flow, interest-rate conversions, and days between dates.
Time Value of Money
where: PMT = 0
where
:
PMT
y
x
C/Y
P/Y
I%
ƒ
=
=
=
=
=
0
C/Y ÷ P/Y
(.01 × I%) ÷ C/Y
compounding periods per year
payment periods per year
interest rate per year
0PV PMT Gi
11i+()
N–
–
i
------------------------------ FV 1i+()
N–
×+×+=
I%100CY e
yx1+()ln×()
1–[]×⁄×=
Gi1ik×+=
N
PMT GiFV i×–×
PMT GiPV i×+×
----------------------------------------------
⎝⎠
⎛⎞
ln
1i+()ln
----------------------------------------------------------=
N–PV FV+()PMT÷=
PMT –i
Gi
----- PV PV FV+
1i+()
N1–
----------------------------+×=
PMT –PV FV+()N÷=
PV PMT Gi
×
i
------------------------ FV–1
1i+()
N
-------------------PMT Gi
×
i
------------------------–×=
PV –FV PMT N×+()=
FV PMT Gi
×
i
------------------------ 1 i+()
N
–PV PMT Gi
×
i
------------------------+
⎝⎠
⎛⎞
×=
Appendix B: Reference Information 388
The iteration used to compute i:
where: i ƒ 0
where: i = 0
where: i ƒ 0
where: i = 0
where: i ƒ 0
where: i = 0
where: x=i
y=P/Y ÷ C/Y
where: k=0 for end-of-period payments
k=1 for beginning-of-period payments

FV –PV PMT N×+()=
ImRND RND12 –i bal m 1–()×()[]=
bal m() bal m 1–()Im
–RND PMT()+=
⎩
⎨
⎧
bal( ) bal pmt2()=
ΣPrn( ) bal pmt2()bal pmt1()–=
ΣInt( ) pmt2pmt1–1+()RND PMT()×ΣPrn( )–=
npv( ) CF0CFj1i+()
-Sj1– 11i+()
-nj
–()
i
-----------------------------------
j1=
N
∑
+=
Appendix B: Reference Information 389
where: i ƒ 0
where: i = 0
Amortization
If computing bal(), pmt2 = npmt
Let bal(0) = RND(PV)
Iterate from m = 1 to pmt2
then:
Balance, principal, and interest are dependent on the values of PMT, PV, æ, and pmt1 and pmt2.
Cash Flow
where: Sj
ni
i1=
j
∑j1≥
0j0=
⎩
⎪
⎪
⎨
⎪
⎪
⎧
=
Net present value is dependent on the values of the initial cash flow (CF0), subsequent cash flows
(CFj), frequency of each cash flow (nj), and the specified interest rate (i).
irr() = 100 × i, where i satisfies npv() = 0
where: RND = round the display to the number of decimal
places selected
RND12 = round to 12 decimal places

Appendix B: Reference Information 390
Internal rate of return is dependent on the values of the initial cash flow (CF0) and subsequent
cash flows (CFj).
i = I% ÷ 100
Interest Rate Conversions
100 (eCP x 1+()ln×1)–×
.01 × Nom ÷ CP
100 CP [×× e1CP÷x1+()ln×1]–
Days between Dates
With the dbd( function, you can enter or compute a date within the range Jan. 1, 1950, through
Dec. 31, 2049.
Actual/actual day-count method (assumes actual number of days per month and actual number
of days per year):
dbd( (days between dates) = Number of Days II - Number of Days I
4Eff =
where: x=
4Nom =
where: x=.01 × Eff
Eff =effective rate
CP =compounding periods
Nom =nominal rate
Number of Days I = (Y1-YB) × 365
+ (number of days MB to M1)
+DT1
+
Number of Days II = (Y2-YB) × 365
+ (number of days MB to M2)
+DT2
+
Y1YB–()
4
------------------------
Y2YB–()
4
------------------------

Appendix B: Reference Information 391
Important Things You Need to Know About Your TI-84 Plus
TI-84 Plus Results
There may be a number of reasons that your TI-84 Plus is not displaying the expected results;
however, the most common solutions involve order of operations or mode settings. Your calculator
uses an Equation Operating System™ (EOS™) which evaluates the functions in an expression in
the following order:
1. Functions that precede the argument, such as square root, sin(, or log(
2. Functions that are entered after the argument, such as exponents, factorial, r, ¡, and
conversions
3. Powers and roots, such as 2^5, or 5*square root(32)
4. Permutations (nPr) and combinations (nCr)
5. Multiplication, implied multiplication, and division
6. Addition and subtraction
7. Relational functions, such as > or <
8. Logic operator and
9. Logic operators or and xor
Remember that EOS™ evaluates from left to right and calculations within parentheses are
evaluated first. You should use parentheses where the rules of algebra may not be clear. In OS
2.53 MP, parentheses may be pasted in an expression to indicate how the input is interpreted.
If you are using trigonometric functions or performing polar and rectangular conversions, the
unexpected results may be caused by an angle mode setting. The Radian and Degree angle mode
settings control how the TI-84 Plus interprets angle values.
To change the angle mode settings, follow these steps:
1. Press z to display the Mode settings.
2. Select Degree or Radian.
3. Press Í to save the angle mode setting.
where: M1
DT1
Y1
M2
DT2
Y2
MB
DB
YB
=
=
=
=
=
=
=
=
=
month of first date
day of first date
year of first date
month of second date
day of second date
year of second date
base month (January)
base day (1)
base year (first year after leap year)
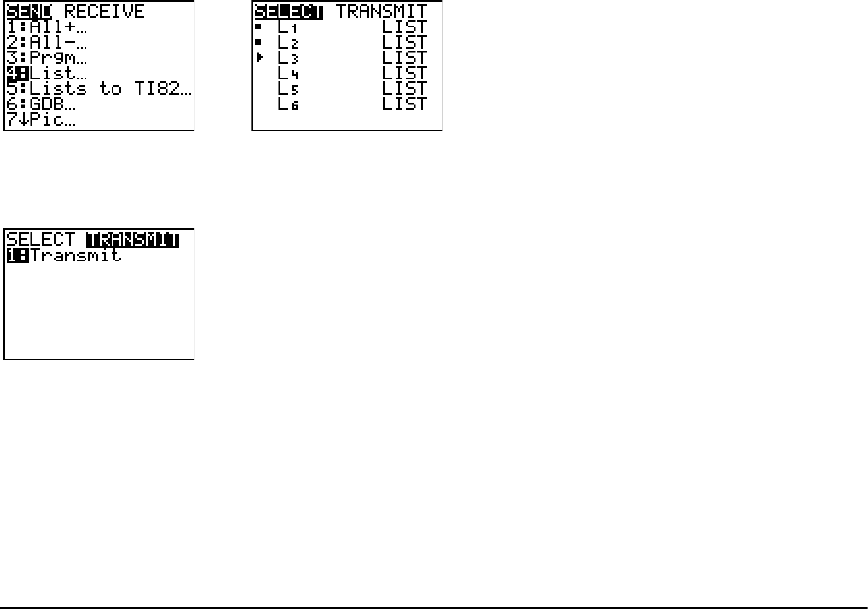
Appendix B: Reference Information 392
ERR:DIM MISMATCH Error
Your TI-84 Plus displays the ERR:DIM MISMATCH error if you are trying to perform an operation
that references one or more lists or matrices whose dimensions do not match. For example,
multiplying L1*L2, where L1={1,2,3,4,5} and L2={1,2} produces an ERR:DIM MISMATCH error
because the number of elements in L1 and L2 do not match.
ERR:INVALID DIM Error
The ERR:INVALID DIM error message may occur if you are trying to graph a function that does not
involve the stat plot features. The error can be corrected by turning off the stat plots. To turn the
stat plots off, press y , and then select 4:PlotsOff.
Link-Receive L1 (or any file) to Restore Message
Your TI-84 Plus displays the Link-Receive L1 (or any file) to Restore message if it has been disabled
for testing, and not re-enabled. To restore your calculator to full functionality after testing, link to
another TI-84 Plus and transfer any file to the disabled calculator, or use TI Connect™ software to
download a file from your computer to your TI-84 Plus.
To transfer a file from another TI-84 Plus:
1. On the receiving unit, press y 8 and then select RECEIVE.
2. On the sending calculator, Press y 8.
3. Select a file to send by selecting a category, and then selecting a file to send.
4. Select TRANSMIT to send the file.
Contrast Feature
If the contrast setting is too dark (set to 9) or too dim (set to 0) the unit may appear as if it is
malfunctioning or turned off. To adjust the contrast, press and release y, and then press and hold
} or †.

Appendix B: Reference Information 393
TI-84 Plus Identification Code
Your graphing calculator has a unique identification (ID) code that you should record and keep.
You can use this 14 digit ID to register your calculator at education.ti.com or identify your
calculator in the event that it is lost or stolen. A valid ID includes numbers 0 through 9 and the
letters A through F.
You can view the calculator’s Operating System, Product Number, ID, and Certificate Revision
Number from the About screen. To display the About screen, press y L and then select
1:About.
Your unique product ID code: _____________________________
Backups
Your TI-84 Plus is similar to a computer, in that it stores files and Apps that are important to you. It
is always a good idea to back up your graphing calculator device files and Apps using the
TI Connect™ software and a USB computer cable. You can find the specific procedures for
backing up your calculator’s device files and Apps in the TI Connect™ Help file.
Apps
TI-84 Plus Software Applications (Apps) is software that you can add to your calculator in the
same way you would add software to your computer. Apps let you customize your calculator for
peak performance in specific areas of study. You can find apps for the TI-84 Plus at
education.ti.com.
TI-Cares KnowledgeBase
The TI-Cares KnowledgeBase provides 24-hour access through the Web to find answers to
frequently asked questions. The TI-Cares KnowledgeBase searches its repository of known
solutions and presents you with the solutions that are most likely to solve your problem. You can
search the TI-Cares KnowledgeBase at education.ti.com/support.

Appendix B: Reference Information 394
Error Conditions
When the TI-84 Plus detects an error, it returns an error message as a menu title, such as
ERR:SYNTAX or ERR:DOMAIN. This table contains each error type, possible causes, and
suggestions for correction. The error types listed in this table are each preceded by ERR: on your
graphing calculator display. For example, you will see ERR:ARCHIVED as a menu title when your
graphing calculator detects an ARCHIVED error type.
Error Type Possible Causes and Suggested Remedies
ARCHIVED You have attempted to use, edit, or delete an archived variable. For example,
the expression dim(L1) produces an error if L1 is archived.
ARCHIVE FULL You have attempted to archive a variable and there is not enough space in
archive to receive it.
ARGUMENT A function or instruction does not have the correct number of arguments. See
Appendix A for function and instruction syntax.
Appendix A displays the arguments and punctuation needed to execute the
function or instruction. For example, stdDev(list[,freqlist]) is a function of the
TI-84 Plus. The arguments are shown in italics. The arguments in brackets are
optional and you need not type them. You must also be sure to separate
multiple arguments with a comma (,). For example, stdDev(list[,freqlist]) might
be entered as stdDev(L1) or stdDev(L1,L2) since the frequency list or freqlist is
optional.
BAD ADDRESS You have attempted to send or receive an application and an error (e.g.
electrical interference) has occurred in the transmission.
BAD GUESS • In a CALC operation, you specified a Guess that is not between Left Bound
and Right Bound.
• For the solve( function or the equation solver, you specified a guess that is not
between lower and upper.
• Your guess and several points around it are undefined.
Examine a graph of the function. If the equation has a solution, change the
bounds and/or the initial guess.
BOUND • In a CALC operation or with Select(, you defined
Left Bound > Right Bound.
•In
fMin(, fMax(, solve(, or the equation solver, you entered lower ‚ upper.
BREAK You pressed the É key to break execution of a program, to halt a DRAW
instruction, or to stop evaluation of an expression.
DATA TYPE You entered a value or variable that is the wrong data type.
• For a function (including implied multiplication) or an instruction, you entered
an argument that is an invalid data type, such as a complex number where a
real number is required. See Appendix A and the appropriate chapter.
• In an editor, you entered a type that is not allowed, such as a matrix entered
as an element in the stat list editor. See the appropriate chapter.
• You attempted to store an incorrect data type, such as a matrix, to a list.
DIM MISMATCH Your calculator displays the ERR:DIM MISMATCH error if you are trying to
perform an operation that references one or more lists or matrices whose
dimensions do not match. For example, multiplying L1*L2, where
L1={1,2,3,4,5} and L2={1,2} produces an ERR:DIM MISMATCH error because
the number of elements in L1 and L2 do not match.

Appendix B: Reference Information 395
DIVIDE BY 0 • You attempted to divide by zero. This error is not returned during graphing.
The TI-84 Plus allows for undefined values on a graph.
• You attempted a linear regression with a vertical line.
DOMAIN • You specified an argument to a function or instruction outside the valid range.
This error is not returned during graphing. The TI-84 Plus allows for undefined
values on a graph. See Appendix A.
• You attempted a logarithmic or power regression with a LX or an exponential
or power regression with a LY.
• You attempted to compute GPrn( or GInt( with pmt2 < pmt1.
DUPLICATE You attempted to create a duplicate group name.
Duplicate Name A variable you attempted to transmit cannot be transmitted because a variable
with that name already exists in the receiving unit.
EXPIRED You have attempted to run an application with a limited trial period which has
expired.
Error in Xmit • The TI-84 Plus was unable to transmit an item. Check to see that the cable is
firmly connected to both units and that the receiving unit is in receive mode.
• You pressed É to break during transmission.
• You attempted to perform a backup from a TI.82 to a TI-84 Plus.
• You attempted to transfer data (other than L1 through L6) from a TI-84 Plus to
a TI.82.
• You attempted to transfer L1 through L6 from a TI-84 Plus to a TI.82 without
using 5:Lists to TI82 on the LINK SEND menu.
ID NOT FOUND This error occurs when the SendID command is executed but the proper
graphing calculator ID cannot be found.
ILLEGAL NEST • You attempted to use an invalid function in an argument to a function, such as
seq( within expression for seq(.
INCREMENT • The increment in seq( is 0 or has the wrong sign. This error is not returned
during graphing. The TI-84 Plus allows for undefined values on a graph.
• The increment in a For( loop is 0.
INVALID • You attempted to reference a variable or use a function where it is not valid.
For example, Yn cannot reference Y, Xmin, @X, or TblStart.
• You attempted to reference a variable or function that was transferred from the
TI.82 and is not valid for the TI-84 Plus For example, you may have
transferred UnN1 to the TI-84 Plus from the TI.82 and then tried to reference
it.
•In
Seq mode, you attempted to graph a phase plot without defining both
equations of the phase plot.
•In
Seq mode, you attempted to graph a recursive sequence without having
input the correct number of initial conditions.
•In
Seq mode, you attempted to reference terms other than (nN1) or (nN2).
• You attempted to designate a graph style that is invalid within the current
graph mode.
• You attempted to use Select( without having selected (turned on) at least one
xyLine or scatter plot.
Error Type Possible Causes and Suggested Remedies

Appendix B: Reference Information 396
INVALID DIM • The ERR:INVALID DIM error message may occur if you are trying to graph a
function that does not involve the stat plot features. The error can be corrected
by turning off the stat plots. To turn the stat plots off, press y , and
then select 4:PlotsOff.
• You specified a list dimension as something other than an integer between 1
and 999.
• You specified a matrix dimension as something other than an integer between
1 and 99.
• You attempted to invert a matrix that is not square.
ITERATIONS • The solve( function or the equation solver has exceeded the maximum
number of permitted iterations. Examine a graph of the function. If the
equation has a solution, change the bounds, or the initial guess, or both.
•irr( has exceeded the maximum number of permitted iterations.
• When computing æ, the maximum number of iterations was exceeded.
LABEL The label in the Goto instruction is not defined with a Lbl instruction in the
program.
LINK L1 (or any other
file) to Restore
The calculator has been disabled for testing. To restore full functionality, use
TI Connect™ software to download a file to your calculator from your
computer, or transfer any file to your calculator from another TI-84 Plus. (See
the instructions under Important Things to Know about your TI-84 Plus, earlier
in this chapter.)
MEMORY Memory is insufficient to perform the instruction or function. You must delete
items from memory before executing the instruction or function.
Recursive problems return this error; for example, graphing the equation
Y1=Y1.
Branching out of an If/Then, For(, While, or Repeat loop with a Goto also can
return this error because the End statement that terminates the loop is never
reached.
MemoryFull • You are unable to transmit an item because the receiving unit’s available
memory is insufficient. You may skip the item or exit receive mode.
• During a memory backup, the receiving unit’s available memory is insufficient
to receive all items in the sending unit’s memory. A message indicates the
number of bytes the sending unit must delete to do the memory backup.
Delete items and try again.
MODE You attempted to store to a window variable in another graphing mode or to
perform an instruction while in the wrong mode; for example, DrawInv in a
graphing mode other than Func.
NO SIGN CHNG • The solve( function or the equation solver did not detect a sign change.
• You attempted to compute æ when FV, (Ú…PMT), and PV are all ‚ 0, or
when FV, (Ú…PMT), and PV are all _ 0.
• You attempted to compute irr( when neither CFList nor CFO is > 0, or when
neither CFList nor CFO is < 0.
NONREAL ANS In Real mode, the result of a calculation yielded a complex result. This error is
not returned during graphing. The TI-84 Plus allows for undefined values on a
graph.
OVERFLOW You attempted to enter, or you have calculated, a number that is beyond the
range of the graphing calculator. This error is not returned during graphing.
The TI-84 Plus allows for undefined values on a graph.
Error Type Possible Causes and Suggested Remedies

Appendix B: Reference Information 397
RESERVED You attempted to use a system variable inappropriately. See Appendix A.
SINGULAR MAT • A singular matrix (determinant = 0) is not valid as the argument for L1.
• The SinReg instruction or a polynomial regression generated a singular
matrix (determinant = 0) because it could not find a solution, or a solution
does not exist.
This error is not returned during graphing. The TI-84 Plus allows for undefined
values on a graph.
SINGULARITY expression in the solve( function or the equation solver contains a singularity
(a point at which the function is not defined). Examine a graph of the function.
If the equation has a solution, change the bounds or the initial guess or both.
STAT You attempted a stat calculation with lists that are not appropriate.
• Statistical analyses must have at least two data points.
•Med-Med must have at least three points in each partition.
• When you use a frequency list, its elements must be ‚ 0.
•(
Xmax N Xmin) à Xscl must be‚ 47 for a histogram.
STAT PLOT You attempted to display a graph when a stat plot that uses an undefined list is
turned on.
SYNTAX The command contains a syntax error. Look for misplaced functions,
arguments, parentheses, or commas. Appendix A displays the arguments and
punctuation needed to execute the function or instruction.
For example, stdDev(list[,freqlist]) is a function of the TI-84 Plus. The
arguments are shown in italics. The arguments in brackets are optional and
you need not type them. You must also be sure to separate multiple
arguments with a comma (,). For example stdDev(list[,freqlist]) might be
entered as stdDev(L1) or stdDev(L1,L2) since the frequency list or freqlist is
optional.
TOL NOT MET You requested a tolerance to which the algorithm cannot return an accurate
result.
UNDEFINED You referenced a variable that is not currently defined. For example, you
referenced a stat variable when there is no current calculation because a list
has been edited, or you referenced a variable when the variable is not valid for
the current calculation, such as a after Med-Med.
VALIDATION Electrical interference caused a link to fail or this graphing calculator is not
authorized to run the application.
VARIABLE You have tried to archive a variable that cannot be archived or you have tried
to unarchive an application or group.
Examples of variables that cannot be archived include:
• Real numbers LRESID, R, T, X, Y, Theta, Statistic variables under Vars,
STATISTICS menu, Yvars, and the AppIdList.
VERSION You have attempted to receive an incompatible variable version from another
graphing calculator.
Error Type Possible Causes and Suggested Remedies

Appendix B: Reference Information 398
Accuracy Information
Computational Accuracy
To maximize accuracy, the TI-84 Plus carries more digits internally than it displays. Values are
stored in memory using up to 14 digits with a two-digit exponent.
• You can store a value in the window variables using up to 10 digits (12 for Xscl, Yscl, Tstep,
and qstep).
• Displayed values are rounded as specified by the mode setting with a maximum of 10 digits
and a two-digit exponent.
•RegEQ displays up to 14 digits in Float mode. Using a fixed-decimal setting other than Float
causes RegEQ results to be rounded and stored with the specified number of decimal places.
Xmin is the center of the leftmost pixel, Xmax is the center of the next-to-the-rightmost pixel. (The
rightmost pixel is reserved for the busy indicator.) @X is the distance between the centers of two
adjacent pixels.
•In
Full screen mode, @X is calculated as (Xmax N Xmin) à 94. In G-T split-screen mode, @X is
calculated as (Xmax N Xmin) à 46.
• If you enter a value for @X from the home screen or a program in Full screen mode, Xmax is
calculated as Xmin + @X É… 94. In G-T split-screen mode, Xmax is calculated as
Xmin + @X É… 46.
Ymin is the center of the next-to-the-bottom pixel; Ymax is the center of the top pixel. @Y is the
distance between the centers of two adjacent pixels.
•In
Full screen mode, @Y is calculated as (Ymax N Ymin) à 62. In Horiz split-screen mode, @Y is
calculated as (Ymax N Ymin) à 30. In G-T split-screen mode, @Y is calculated as
(Ymax N Ymin) à 50.
• If you enter a value for @Y from the home screen or a program in Full screen mode, Ymax is
calculated as Ymin + @Y É… 62. In Horiz split-screen mode, Ymax is calculated as
Ymin + @Y … 30. In G-T split-screen mode, Ymax is calculated as Ymin + @Y É … 50.
WINDOW RANGE A problem exists with the window variables.
• You defined Xmax Xmin or Ymax Ymin.
• You defined qmax qmin and qstep > 0 (or vice versa).
• You attempted to define Tstep=0.
• You defined Tmax Tmin and Tstep > 0 (or vice versa).
• Window variables are too small or too large to graph correctly. You may have
attempted to zoom in or zoom out to a point that exceeds the TI-84 Plus’s
numerical range.
ZOOM • A point or a line, instead of a box, is defined in ZBox.
•A ZOOM operation returned a math error.
Error Type Possible Causes and Suggested Remedies

Appendix B: Reference Information 399
Cursor coordinates are displayed as eight-character numbers (which may include a negative sign,
decimal point, and exponent) when Float mode is selected. X and Y are updated with a maximum
accuracy of eight digits.
minimum and maximum on the CALCULATE menu are calculated with a tolerance of 1âL5; ‰f(x)dx is
calculated at 1âL3. Therefore, the result displayed may not be accurate to all eight displayed digits.
For most functions, at least five accurate digits exist. For fMin(, fMax(, and fnInt( on the MATH
menu and solve( in the CATALOG, the tolerance can be specified.
Function Limits
Function Range of Input Values
sin x, cos x, tan x
sinL1 x, cosL1 xL1 x 1
ln x, log x10L100 < x < 10100
exL10100 < x 230.25850929940
10xL10100 < x< 100
sinh x, cosh x|x| 230.25850929940
tanh x|x| < 10100
sinhL1 x|x| < 5 × 1099
coshL1 x1 x < 5 × 1099
tanhL1 xL1 < x < 1
‡x (real mode) 0 x < 10100
‡x (complex mode) |x| < 10100
x!L.5 _x 69, where x is a multiple of .5
Function Results
Function Range of Result
sinL1 x, tanL1 xL90¡ to 90¡or Lp à 2 to p à 2 (radians)
cosL1 x0¡ to 180¡ or 0 to p (radians)
0 |x| < 1012 (radian or degree)

Appendix C: Service and Warranty Information 400
Appendix C:
Service and Warranty Information
Texas Instruments Support and Service
For general information
For product (hardware) service
Customers in the U.S., Canada, Mexico, Puerto Rico and Virgin Islands: Always contact Texas
Instruments Customer Support before returning a product for service.
All other customers: Refer to the leaflet enclosed with this product (hardware) or contact your local
Texas Instruments retailer/distributor.
Battery Information
When to Replace the Batteries
The TI-84 Plus uses five batteries: four AAA alkaline batteries and one button cell backup battery.
The backup battery provides auxiliary power to retain memory while you replace the AAA
batteries.
When the battery voltage level drops below a usable level, the TI-84 Plus:
Home Page: education.ti.com
KnowledgeBase and
e-mail inquiries:
education.ti.com/support
Phone: (800) TI-CARES / (800) 842-2737
For U.S., Canada, Mexico, Puerto Rico, and
Virgin Islands only
International
information:
education.ti.com/international
Displays this message when
you turn on the unit.
Displays this message when you attempt
to download an application.
Message A Message B

Appendix C: Service and Warranty Information 401
After Message A is first displayed, you can expect the batteries to function for about one or two
weeks, depending on usage. (This one-week to two-week period is based on tests with alkaline
batteries; the performance of other types of batteries may vary.)
If Message B is displayed, you must replace the batteries immediately to successfully download an
application.
Effects of Replacing the Batteries
Do not remove both types of batteries (AAA and backup) at the same time. Do not allow the
batteries to lose power completely. If you follow these guidelines and the steps for replacing
batteries, you can replace either type of battery without losing any information in memory.
Battery Precautions
Take these precautions when replacing batteries.
• Do not leave batteries within reach of children
• Do not mix new and used batteries. Do not mix brands (or types within brands) of batteries.
• Do not mix rechargeable and nonrechargeable batteries.
• Install batteries according to polarity (+ and N) diagrams.
• Do not place nonrechargeable batteries in a battery recharger.
• Properly dispose of used batteries immediately. Do not leave them within the reach of
children.
• Do not incinerate or dismantle batteries.
Disposing of used batteries safely and properly
Do not mutilate, puncture, or dispose of batteries in fire. The batteries can burst or explode,
releasing hazardous chemicals. Discard used batteries according to local regulations.
Replacing the Batteries
To replace the batteries, follow these steps.
1. Turn off the graphing calculator. Replace the slide cover over the keyboard to avoid
inadvertently turning on the graphing calculator. Turn the back of the unit toward you.
2. Hold the graphing calculator upright, push downward on the latch on the top of the battery
cover, and then pull the cover toward you.
Note: To avoid loss of information stored in memory, you must turn off the graphing calculator.
Do not remove the AAA batteries and thebackup battery simultaneously.
3. Replace all four AAA alkaline batteries simultaneously. Or, replace the backup battery.
• To replace the AAA alkaline batteries, remove all four discharged AAA batteries and install
new ones according to the polarity (+ and N) diagram in the battery compartment.

Appendix C: Service and Warranty Information 402
• To replace thebackup battery, remove the screw from the backup battery cover, and then
remove the cover. Install the new battery, + side up. Replace the cover and secure it with
the screw.
4. Replace the battery compartment cover. Turn the graphing calculator on and adjust the
display contrast, if necessary, by pressing y } or †.
In Case of Difficulty
Handling a Difficulty
To handle a difficulty, follow these steps.
1. If you cannot see anything on the screen, you may need to adjust the graphing calculator
contrast.
To darken the screen, press and release y, and then press and hold } until the display is
sufficiently dark.
To lighten the screen, press and release y, and then press and hold † until the display is
sufficiently light.
2. If an error menu is displayed, follow these steps:
• Note the error type (ERR:error type).
•Select 2:GOTO, if it is available. The previous screen is displayed with the cursor at or near
the error location.
• Determine the error.
• Correct the expression.
Refer to the Error Conditions table for details about specific errors, if necessary.
3. If the busy indicator (dotted line) is displayed, a graph or program has been paused; the TI-84
Plus is waiting for input. Press Í to continue or press É to break.
4. If a checkerboard cursor ( # ) is displayed, then either you have entered the maximum number
of characters in a prompt, or memory is full. If memory is full:
• Press y L 2 to display the MEMORY MANAGEMENT / DELETE menu.
• Select the type of data you want to delete, or select 1:All for a list of all variables of all
types. A screen is displayed listing each variable of the type you selected and the number
of bytes each variable is using.
• Press } and † to move the selection cursor (4) next to the item you want to delete, and
then press {.

Appendix C: Service and Warranty Information 403
5. If the graphing calculator does not seem to work at all, be sure the alkaline batteries are fresh
and that they are installed properly.
6. If the TI-84 Plus does not function even though you are sure that the batteries are fresh, you
can try manually resetting it.
• Remove all of the AAA batteries from the graphing calculator.
• Press and hold the É key for ten seconds.
• Replace the batteries.
• Turn on the unit.
When you reset your graphing calculator, the contrast sometimes changes. If the screen is
faded or blank, adjust the contrast by pressing y and releasing } or †.
7. If the above solutions do not work you can reset all of the memory. The RAM, user data
archive memory, and system variables are restored to factory settings when you reset all
memory. All nonsystem variables, applications (Apps), and programs are deleted.
• Press y L to display the MEMORY menu.
•Select 7:Reset to display the RAM ARCHIVE ALL menu.
• Press ~ ~ to display the ALL menu.
•Select 1:All Memory to display the RESET MEMORY menu.
• To continue with the reset, select 2:Reset. The message Mem cleared is displayed on the
home screen.

404
Index
Symbols
!dim( (assign dimension) 169
(- (degrees notation) 379
(- (negation) 30, 37, 381
(– (subtraction) 36, 381
(! (factorial) 379
(! Store 20, 375
(!dim( (assign dimension) 155, 358
(# (not equal to) 380
($( (square root) 36, 381
(%, (, + (pixel mark) 132, 210
(& (plot type, histogram) 209
(' (minutes notation) 60, 382
(( ) (parentheses) 29
() (plot type, normal probability) 210
()Int( (sum of interest) 363
()Prn( (sum of principal) 368
(* (multiplication) 36, 381
(* (plot type, modified box) 209
(*f(x)dx operation on a graph 90
(*row( 160, 371
(*row+( 371
(+ (addition) 36, 381
(+ (concatenation) 270, 381
(+ (pixel mark) 132, 210
(+ (plot type, box) 209
(/ (division) 36, 381
(/ (inverse) 380
(: (colon) 278
(< (less than) 62, 380
(= (equal-to relational test) 62, 380
(> (greater than) 62, 380
([ ] (matrix indicator) 148
(^ (power) 36, 380, 381
({ (less than or equal to) 380
(| (greater than or equal to) 62, 380
(² (square) 36, 380
(³ (cube) 39, 380
(³$( (cube root) 39, 380
(“ ” (string indicator) 267
(4Dec (to decimal conversion) 39, 357
(4DMS (to degrees/minutes/seconds) 61, 358
(4Eff( (to effective interest rate) 261
(4Frac (to fraction) 39, 360
(4Nom( (to nominal interest rate) 261, 366
(4Polar (to polar) 56, 368
(4Rect (to rectangular) 56, 371
(χ²pdf( (chi-square pdf) 244
(χ²-Test (chi-square test) 233, 234, 245
(ΔTbl (table step variable) 116
(ΔX window variable 74
(ΔY window variable 74
(Fcdf( 245
(Fpdf( 245
/ (inverse) 37
{ } (list indicator) 163
Numerics
10^( (power of ten) 381
1-PropZInt (one-proportion z confidence interval)
232, 369
1-PropZTest (one-proportion z test) 227, 369
1-Var Stats (one-variable statistics) 200, 377
2-PropZInt (two-proportion z confidence interval)
232, 369
2-PropZTest (two-proportion z test) 228, 369
2-SampFTest (two-sample F-Test) 235, 372
2-SampTInt (two-sample t confidence interval) 231,
372
2-SampTTest (two-sample t test) 226, 373
2-SampZInt (two-sample z confidence interval) 230,
372
2-SampZTest (two-sample z test) 225, 372
2-Var Stats (two-variable statistics) 200, 377
A
a+bi (rectangular complex mode) 17, 50, 355
about 326
above graph style 71
abs( (absolute value) 46, 55, 152, 354
accuracy information
computational and graphing 398
function limits and results 399
graphing 78
addition (+) 36, 381
alpha cursor 8
alpha-lock 14
alternative hypothesis 219
amortization
)Int( (sum of interest) 363
)Prn( (sum of principal) 368
bal( (amortization balance) 258, 355
calculating schedules 258
formula 389
and (Boolean operator) 63, 354
ANGLE menu 59
angle modes 16
angle( 55, 354
animate graph style 71
ANOVA( (one-way variance analysis) 238, 354, 385
Ans (last answer) 24, 329, 354
APD (Automatic Power Down) 3
applications See examples, applications 36
Apps 20, 328
AppVars 20, 328
arccosine (cos/( ) 36
Archive 21, 330, 354
archive full error 343, 394
garbage collection 340
memory error 340
archived variables 383
arcsine (sin/( ) 36
arctangent (tan/( ) 36
Asm( 294, 354
AsmComp( 294, 354
AsmPrgm( 294, 354
assembly language programs 294
augment( 157, 173, 354
Automatic Power Down (APD) 3

405
automatic regression equation 196
automatic residual list (RESID) 195
axes format, sequence graphing 107
axes, displaying (AxesOn, AxesOff) 75, 355
AxesOff 75, 355
AxesOn 75, 355
B
backing up calculator memory 348, 351
bal( (amortization balance) 258, 355
batteries 4, 400
below graph style 71
binomcdf( 247, 355
binompdf( 246, 355
block 340
Boolean logic 63
box pixel mark (%) 132, 210
Boxplot plot type (+) 209
busy indicator 8
C
C/Y (compounding-periods-per-year variable) 253,
263
χ²cdf( (chi-square cdf) 355
χ²pdf( (chi-square pdf) 355
χ²-Test (chi-square test) 355
CALCULATE menu 87
Calculate output option 218, 220
cash flow
calculating 257
formula 389
irr( (internal rate of return) 258, 363
npv( (net present value) 258, 367
CATALOG 266
CBL 2™ 293, 346, 361
CBR™ 293, 346, 361
check memory 326
checkTmr( (check timer) 355
Chi 234
chi-square cdf (c²cdf( ) 245, 355
chi-square goodness of fit test 234
chi-square pdf (c²pdf( ) 244, 355
chi-square test (c²-Test) 233, 234, 355
Circle( (draw circle) 128, 355
Clear Entries 326, 356
clearing
all lists (ClrAllLists) 326, 356
drawing (ClrDraw) 123, 356
entries (Clear Entries) 326, 356
home screen (ClrHome) 292, 356
list (ClrList) 194, 356
table (ClrTable) 292, 356
Clock 9
Clock Off 11
Clock On 10
ClockOff, turn clock off 356
ClockOn, turn clock on 356
ClrAllLists (clear all lists) 326, 356
ClrDraw (clear drawing) 123, 356
ClrHome (clear home screen) 292, 356
ClrList (clear list) 194, 356
ClrTable (clear table) 292, 356
coefficients of determination (r2, R2) 196
colon separator (:) 278
combinations (nCr) 57, 366
compiling an assembly program 294, 354
complex
modes (a+bi, re^qi) 17, 50, 355, 370
numbers 17, 50, 370
compounding-periods-per-year variable (C/Y) 253,
263
concatenation (+) 270, 381
confidence intervals 36, 220
conj( (conjugate) 54, 356
Connected (plotting mode) 17, 356
connecting two calculators 346, 349
contrast (display) 4
convergence, sequence graphing 110
conversions
4Dec (to decimal) 39, 357
4DMS (to degrees/minutes/ seconds) 61, 358
4Eff (to effective interest rate) 261
4F3 4D 50
4Frac (to fraction conversion) 39, 360
4n/d3 4Un/d 49
4Nom (to nominal interest rate conversion) 261,
366
4Polar (to polar conversion) 56, 368
4Rect (to rectangular conversion) 56, 371
Equ4String( (equation-to-string conversion) 270,
359
List4matr( (list-to-matrix conversion) 158, 173,
364
Matr4list( (matrix-to-list conversion) 157, 174, 365
P4Rx(, P4Ry( (polar-to-rectangular conversion) 61,
369
R4Pr(, R4Pq( (rectangular-to-polar conversion) 372
R4Pr(, R4Pθ( (rectangular-to-polar conversion) 61
String4Equ( (string-to-equation conversion) 271,
375
convert time, timeCnv( ) 376
CoordOff 75, 356
CoordOn 75, 356
correlation coefficient (r) 196
cos( (cosine) 36, 356
cos/( (arccosine) 36, 356
cosh( (hyperbolic cosine) 273, 356
cosh/( (hyperbolic arccosine) 273, 356
cosine (cos( ) 36
cosine (cos( ) 356
cross pixel mark (+) 132, 210
cube (³) 39, 380
cube root (³$( ) 39
cube root (³$( ) 380
cubic regression (CubicReg) 201, 356
CubicReg (cubic regression) 201, 356
cumSum( (cumulative sum) 158, 170, 357
cumulative sum (cumSum( ) 158, 170
cumulative sum (cumSum( ) 357
cursors 8, 14

406
D
Data input option 218, 219
dayOfWk( (day of week) 357
days between dates (dbd( ) 261
days between dates (dbd( ) 357, 390
dbd( (days between dates) 261, 357, 390
decimal mode (float or fixed) 16
decrement and skip (DS<( ) 286
decrement and skip (DS<( ) 358
definite integral 40, 89, 96
defragmenting 340
Degree angle mode 16, 60, 357
degrees notation (-) 60, 379
delete variable contents (DelVar) 287, 357
deleting items from memory 329
DependAsk 116, 118, 357
DependAuto 116, 118, 357
derivative See numerical derivative 36
det( (determinant) 155, 357
determinant (det( ) 155
determinant (det( ) 357
DiagnosticOff 196, 357
DiagnosticOn 196, 357
diagnostics display mode(r, r2, R2) 196
differentiation 42, 89, 96, 101
dim( (dimension) 155, 169, 357
dimensioning a list or matrix 155, 169, 357
Disp (display) 290, 358
DispGraph (display graph) 291, 358
display contrast 4
display cursors 8
Displaying the Clock Settings 9
DispTable (display table) 291, 358
DISTR (distributions menu) 241
DISTR DRAW (distributions drawing menu) 248
distribution functions
binomcdf( 247, 355
binompdf( 246, 355
χ²cdf( 355
χ²pdf( 355
Fcdf( 244, 375
Fpdf( 243, 376
geometcdf( 248, 361
geometpdf( 248, 361
invNorm( 243, 363
normalcdf( 242, 366
normalpdf( 242, 366
poissoncdf( 247, 368
poissonpdf( 247, 368
distribution shading instructions
Shade_t( 249, 374
Shadeχ²( 250, 374
ShadeF( 250, 374
ShadeNorm( 249, 374
division (/) 36, 381
ΔList( 171, 364
DMS (degrees/minutes/seconds entry notation) 60,
382
Dot (plotting mode) 17, 358
dot graph style 71
dot pixel mark (() 132, 210
dr/dq operation on a graph 101
DRAW menu 122
Draw output option 218, 220
DRAW POINTS menu 131
DRAW STO (draw store menu) 134
DrawF (draw a function) 127, 358
drawing on a graph
circles (Circle( ) 128
functions and inverses (DrawF, DrawInv) 127
line segments (Line( ) 124
lines (Horizontal, Line(, Vertical) 125
points (Pt-Change, Pt-Off, Pt-On) 131
tangents (Tangent) 126
text (Text) 129
using Pen 130
DrawInv (draw inverse) 127, 358
DS<( (decrement and skip) 286, 358
DuplicateName menu 350
dx/dt operation on a graph 89, 96
dy/dx operation on a graph 89, 96, 101
E
E (exponent) 12, 15, 358
e^( (exponential) 37, 358
edit keys table 13
Else 282
End 283, 359
Eng (engineering notation mode) 15, 359
ENTRY (last entry key) 22
entry cursor 8
EOS (Equation Operating System) 29
eqn (equation variable) 42
Equ4String( (equation-to-string conversion) 270, 359
equal-to relational test (=) 62, 380
Equation Operating System (EOS) 29
Equation Solver 42
equations with multiple roots 44
errors
diagnosing and correcting 33
messages 394
examples—applications
area between curves 316
areas of regular n-sided polygons 321
box plots 306
box with lid 299
defining a 299
defining a table of values 300
setting the viewing window 302
tracing the graph 303
zooming in on the graph 304
zooming in on the table 301
cobweb attractors 312
fundamental theorem of calculus 319
guess the coefficients 313
inequalities 309
mortgage payments 323
parametric equations, ferris wheel problem 317
piecewise functions 308
quadratic formula

407
converting to a fraction 297
displaying complex results 298
entering a calculation 297
Sierpinski triangle 311
solving a system of nonlinear equations 310
unit circle and trig curves 315
examples—Getting Started
coin flip 35
compound interest 253
drawing a tangent line 121
financing a car 252
forest and trees 102
generating a sequence 161
mean height of a population 215
path of a ball 91
pendulum lengths and periods 178
polar rose 97
roots of a function 115
sending variables 344
solving a system of linear equations 144
unit circle 137
volume of a cylinder 275
examples—miscellaneous
calculating outstanding loan balances 259
convergence 110
daylight hours in Alaska 204
predator-prey model 111
examplesóGetting Started
graphing a circle 65
exponential regression (ExpReg) 202, 359
expr( (string-to-expression conversion) 270, 359
ExpReg (exponential regression) 202, 359
expression 11
converting from string (expr( ) 270
converting from string (expr( ) 359
turning on and off (ExprOn 76, 359
ExprOff (expression off) 76, 359
ExprOn (expression on) 76, 359
F
Faceplates 8
factorial (!) 379
family of curves 77
Fill( 156, 359
FINANCE CALC menu 254
FINANCE VARS menu 262
financial functions
amortization schedules 258
cash flows 257
days between dates 261
interest rate conversions 261
payment method 262
time value of money (TVM) 255
Fix (fixed-decimal mode) 16, 359
fixed-decimal mode (Fix) 16, 359
Float (floating-decimal mode) 16, 359
floating-decimal mode (Float) 16, 359
fMax( (function maximum) 360
fMin( (function minimum) 40, 360
fnInt( (function integral) 41, 360
FnOff (function off) 70, 360
FnOn (function on) 70, 360
For( 283, 360
format settings 74, 107
formulas
amortization 389
ANOVA 385
cash flow 389
days between dates 390
interest rate conversions 390
logistic regression 384
sine regression 384
time value of money 387
two-sample F-Test 385
two-sample t test 386
fPart( (fractional part) 47, 154, 360
fractions
n/d 18, 50
Un/d 18, 50
free-moving cursor 78
frequency 199
Full (full-screen mode) 17, 360
full-screen mode (Full) 17, 360
Func (function graphing mode) 16, 360
function graphing
accuracy 78
CALC (calculate menu) 87
defining and displaying 66
defining in the Y= editor 68
defining on the home screen, in a program 68
deselecting 69
displaying 66, 73, 76
ΔX and ΔY window variables 74
evaluating 69
family of curves 77
format settings 74
free-moving cursor 78
graph styles 71
maximum of (fMax( ) 40
maximum of (fMax( ) 360
minimum of (fMin( ) 360
modes 16, 67, 360
moving the cursor to a value 79
overlaying functions on a graph 77
panning 80
pausing or stopping a graph 76
Quick Zoom 80
selecting 69, 70, 360
shading 72
Smart Graph 76
tracing 78
viewing window 73
window variables 73
Y= editor 68
ZOOM MEMORY menu 85
ZOOM menu 80
function integral (fnInt( ) 41
function integral (fnInt( ) 360
function, definition of 12
functions and instructions table 354
future value 253, 257

408
FV (future-value variable) 253, 263
G
garbage collecting 339
GarbageCollect 341, 360
gcd( (greatest common divisor) 48, 360
GDB (graph database) 135
geometcdf( 248, 361
geometpdf( 248, 361
Get( (get data from CBL 2™ or CBR™) 293, 361
GetCalc( (get data from TI-84 Plus) 292, 361
getDate, get current date 361
getDtFmt, get date format 361
getDtStr( (get date string) 361
getKey 292, 361
getTime, get current time 361
Getting Started See examples, Getting Started 36
getTmFmt, get time format 361
getTmStr( (get time string) 361
Goto 285, 361
graph database (GDB) 135
graph style
above 71
animate 71
below 71
dot 71
line 71
path 71
shade above 71
shade below 71
thick 71
graph styles 71
graphing modes 16
graphing-order modes 17
GraphStyle( 288, 362
graph-table split-screen mode (G-T) 17, 140, 362
greater than (>) 62, 380
greater than or equal to (|) 62, 380
greatest common divisor (gcd( ) 48
greatest common divisor (gcd( ) 360
greatest integer (int( ) 47, 154
greatest integer (int( ) 363
GridOff 75, 362
GridOn 75, 362
grouping 336
G-T (graph-table split-screen mode) 17, 140, 362
H
Histogram plot type (&) 209
home screen 5
scrolling 5, 22
Horiz (horizontal split-screen mode) 17, 139, 362
Horizontal (draw line) 125, 362
hyperbolic functions 273
hypothesis tests 223
I
i (complex number constant) 52
I% (annual interest rate variable) 253, 263
identity( 156, 362
If instructions
If 282, 362
If-Then 282, 362
If-Then-Else 282, 362
imag( (imaginary part) 55, 362
imaginary part (imag( ) 55
imaginary part (imag( ) 362
implied multiplication 29
increment and skip (IS>( ) 286
increment and skip (IS>( ) 363
independent variable 116, 118, 362
IndpntAsk 116, 118, 362
IndpntAuto 116, 118, 362
inferential stat editors 218
inferential statistics
alternative hypotheses 219
bypassing editors 220
calculating test results (Calculate) 220
confidence interval calculations 220
data input or stats input 219
entering argument values 219
graphing test results (Draw) 220
input descriptions table 239
pooled option 220
STAT TESTS menu 221
test and interval output variables 240
inferential statistics See stat tests 36
Input 289, 362
insert cursor 8
Installing New Faceplates 9
Installing new faceplates 9
inString( (in string) 271, 363
instruction, definition of 13
int( (greatest integer) 47, 154, 363
integer part (iPart( ) 47, 154
integer part (iPart( ) 363
integral See numerical integral 36
interest rate conversions
4Eff( (compute effective interest rate) 261
4Nom( (compute nominal interest rate) 261
calculating 261
formula 390
internal rate of return (irr( ) 258
internal rate of return (irr( ) 363
intersect operation on a graph 89
inverse (/) 37, 380
inverse cumulative normal distribution (invNorm( )
243
inverse cumulative normal distribution (invNorm( )
363
inverse trig functions 36
invNorm( (inverse cumulative normal distribution)
243, 363
invT (inverse Student T distribution) 243
iPart( (integer part) 47, 154, 363
irr( (internal rate of return) 258, 363
IS>( (increment and skip) 286, 363
isClockOn, is clock on 363

409
K
keyboard
layout 1
math operations 36
key-code diagram 292
L
L (user-created list name symbol) 174
LabelOff 76, 363
LabelOn 76, 363
labels
graph 76, 363
program 285, 363
Last Entry 22
Lbl (label) 285, 363
lcm( (least common multiple) 48, 364
least common multiple (lcm( ) 48
least common multiple (lcm( ) 364
length( of string 271, 364
less than (<) 62, 380
less than or equal to ({) 62, 380
line graph style 71
line segments, drawing 124
Line( (draw line) 125, 364
lines, drawing 125
LINK RECEIVE menu 350
LINK SEND menu 347
linking
receiving items 350
to a CBL 2™ or CBR™ 346
to a PC or Macintosh 346
to a TI-84 Plus Silver Edition or TI-84 Plus 351
transmitting items 344
two TI-84 Plus units 348
Link-Receive L1 (or any file) to Restore message 392
LinReg(a+bx) (linear regression) 202, 364
LinReg(ax+b) (linear regression) 201, 364
LinRegTTest (linear regression t test) 236, 364
LinReqTInt (confidence interval for slope) 237
LIST MATH menu 175
LIST NAMES menu 164
LIST OPS menu 168
List4matr( (lists-to-matrix conversion) 158, 173, 364
lists
accessing an element 164
attaching formulas 165, 166, 188
clearing all elements 187
copying 163
creating 162, 186
deleting from memory 164, 329
detaching formulas 166, 190
dimension 163
entering list names 165, 185
indicator ({ }) 163
naming lists 162
storing and displaying 163
using to graph a family of curves 77, 164
using with math operations 36, 167
ln( 37, 364
LnReg (logarithmic regression) 202, 364
log( 37, 364
Logistic (regression) 203, 364
logistic regression formula 384
M
Manual Linear Fit 198, 205
marked for deletion 340
MATH CPX (complex menu) 54
MATH menu 38
MATH NUM (number menu) 45
math operations 36
MATH PRB (probability menu) 56
Matr4list( (matrix-to-list conversion) 157, 174, 365
matrices
accessing elements 150
copying 150
defined 145
deleting from memory 146
dimensions 146, 155, 156
displaying a matrix 149
displaying matrix elements 146
editing matrix elements 147
indicator ([ ]) 148
math functions 151
matrix math functions (det(, T, dim(, Fill(,
identity(, randM(, augment(, Matr4list(,
List4matr(, cumSum( ) 154
quick matrix 143
relational operations 153
row operations (ref(, rref(, rowSwap(, row+(,
*row(, *row+( ) 158
selecting 145
viewing 146
MATRX EDIT menu 145
MATRX MATH menu 154
max( (maximum) 48, 175, 365
maximum of a function (fMax( ) 40
maximum of a function (fMax( ) 360
maximum operation on a graph 88
mean( 175, 365
Med(Med (median-median) 200
median( 175, 365
Med-Med (median-median) 365
Mem Mgmt/Del menu 327
memory
backing up 351
checking available 326
clearing all list elements from 330
clearing entries from 329
deleting items from 329
error 341
insufficient during transmission 353
resetting defaults 334
resetting memory 334
MEMORY menu 326
Menu( (define menu) 286, 365
menus 25, 26
defining (Menu( ) 286
defining (Menu( ) 365
scrolling 26

410
shortcut 1, 6
min( (minimum) 48, 175, 365
minimum of a function (fMin( ) 40
minimum of a function (fMin( ) 360
minimum operation on a graph 88
minutes notation (') 60, 382
ModBoxplot plot type (*) 209
mode
Answers 18
Classic 5, 18
MathPrint 5, 18
mode settings 14
a+bi (complex rectangular) 17, 50, 355
Connected (plotting) 17, 356
Degree (angle) 16, 61, 357
Dot (plotting) 17, 358
Eng (notation) 15, 359
Fix (decimal) 16, 359
Float (decimal) 16, 359
Full (screen) 17, 360
Func (graphing) 16, 360
G-T (screen) 17, 362
Horiz (screen) 17, 362
Normal (notation) 15, 366
Par/Param (graphing) 16, 367
Pol/Polar (graphing) 16, 368
Radian (angle) 16, 61, 370
re^qi (complex polar) 370
re^θi (complex polar) 17, 50
Real 17, 370
Sci (notation) 15, 373
Seq (graphing) 16, 373
Sequential (graphing order) 17, 373
Simul (graphing order) 17, 374
modified box plot type (*) 209
multiple entries on a line 12
multiplication (*) 36, 381
multiplicative inverse 37
N
N (number of payment periods variable) 253, 263
n/d 18, 50
nCr (number of combinations) 57, 366
nDeriv( (numerical derivative) 40, 366
negation (-) 30, 37, 381
nonrecursive sequences 105
normal distribution probability (normalcdf( ) 242,
366
Normal notation mode 15, 366
normal probability plot type ()) 210
normalcdf( (normal distribution probability) 242
normalpdf( (probability density function) 242, 366
NormProbPlot plot type ()) 210
not equal to (#) 62, 380
not( (Boolean operator) 63, 367
nPr (permutations) 57, 367
npv( (net present value) 258, 367
numerical derivative 40, 89, 96, 101
numerical integral 40, 90
O
Omit 338, 351
one-proportion z confidence interval (1-PropZInt)
232, 369
one-proportion z test (1-PropZTest) 227, 369
one-sample t confidence interval (TInterval) 229, 376
one-variable statistics (1-Var Stats) 200, 377
or (Boolean) operator 63, 367
order of evaluating equations 29
Output( 142, 291, 367
Overwrite 338, 350
Overwrite All 338
P
P/Y (number-of-payment-periods-per-year variable)
253, 263
P4Rx(, P4Ry( (polar-to-rectangular conversions) 61,
369
panning 80
Par/Param (parametric graphing mode) 16, 367
parametric equations 94
parametric graphing
CALC (calculate operations on a graph) 96
defining and editing 94
free-moving cursor 95
graph format 94
graph styles 93
moving the cursor to a value 96
selecting and deselecting 94
setting parametric mode 93
tracing 96
window variables 94
Y= editor 93
zoom operations 96
parentheses 29
path graph style 71
Pause 284, 367
pausing a graph 76
Pen 130
permutations (nPr) 57, 367
phase plots 111
Pic (pictures) 134
pictures (Pic) 134
pixels in Horiz/G-T modes 133, 141
Plot1( 210, 367
Plot2( 210, 367
Plot3( 210, 367
PlotsOff 212, 368
PlotsOn 212, 368
plotting modes 17
plotting stat data 208
PMT (payment amount variable) 253, 263
Pmt_Bgn (payment beginning variable) 262, 368
Pmt_End (payment end variable) 262, 368
poissoncdf( 247, 368
poissonpdf( 247, 368
Pol/Polar (polar graphing mode) 16, 98, 368
polar equations 98
polar form, complex numbers 52
polar graphing

411
CALC (calculate operations on a graph) 101
defining and displaying 98
equations 98
free-moving cursor 100
graph format 99
graph styles 98
mode (Pol/Polar) 16, 98, 368
moving the cursor to a value 100
selecting and deselecting 98
tracing 100
window variables 99
Y= editor 98
ZOOM operations 101
PolarGC (polar graphing coordinates) 75, 368
pooled option 218, 220
power (^) 36, 380, 381
power of ten (10^( ) 37
power of ten (10^( ) 381
present value 253, 256
previous entry (Last Entry) 22
prgm (program name) 287, 368
PRGM CTL (program control menu) 281
PRGM EDIT menu 280
PRGM EXEC menu 280
PRGM NEW menu 277
probability 56
probability density function (normalpdf( ) 242
probability density function (normalpdf( ) 366
prod( (product) 176, 368
programming
copying and renaming 280
creating new 277
defined 276
deleting 277
deleting command lines 280
editing 279
entering command lines 278
executing 279
inserting command lines 280
instructions 281
name (prgm) 287, 368
renaming 280
running assembly language program 294
stopping 279
subroutines 293
Prompt 290, 369
Pt-Change( 132, 369
Pt-Off( 132, 369
Pt-On( 131, 369
PV (present value variable) 253, 263
p-value 240
PwrReg (power regression) 203, 369
Pxl-Change( 133, 369
Pxl-Off( 133, 369
Pxl-On( 133, 369
pxl-Test( 133, 369
Q
QuadReg (quadratic regression) 201, 370
QuartReg (quartic regression) 202, 370
Quick Zoom 80
Quit 338, 351
R
r (correlation coefficient) 196
R (radian notation) 61, 379
r2, R2 (coefficients of determination) 196
R4Pr(, R4Pq( (rectangular-to-polar conversions) 372
R4Pr(, R4Pθ( (rectangular-to-polar conversions) 61
Radian angle mode 16, 61, 370
radian notation (R) 61, 379
RAM ARCHIVE ALL menu 333
rand (random number) 57, 370
randBin( (random binomial) 59, 370
randInt( (random integer) 58, 370
randIntNoRep( 59
randM( (random matrix) 157, 370
randNorm( (random Normal) 58, 370
random seed 57
RCL (recall) 21
re^qi (polar complex mode) 370
re^θi (polar complex mode) 17, 50
Real mode 17, 370
real( (real part) 54, 370
RecallGDB 136, 370
RecallPic 135, 370
rectangular form, complex numbers 52
RectGC (rectangular graphing coordinates) 75, 371
recursive sequences 105
re-enabling a disabled calculator 392
ref( (row-echelon form) 159, 371
RegEQ (regression equation variable) 196, 329
regression model
automatic regression equation 196
automatic residual list feature 195
diagnostics display mode 196
models 200
relational operations 62, 153
remainder( 49
Removing a Faceplate 9
Repeat 284, 371
RESET MEMORY menu 336
resetting
all memory 336
archive memory 335
defaults 334
memory 334
RAM memory 334
residual list (RESID) 195
Return 287, 371
root (x$) 40, 379
root of a function 88
round( 47, 152, 371
row+( 371
rowSwap( 159, 371
rref( (reduced-row-echelon form) 159, 372
S
Sci (scientific notation mode) 15, 373
scientific notation 12

412
screen modes 17
second cursor (2nd) 8
second key (2nd) 2
seconds DMS notation (”) 60
sector 340
Select( 171, 373
selecting
data points from a plot 172
functions from the home screen or a program 70
functions in the Y= editor 70
stat plots from the Y= editor 70
Send( (send to CBL 2™ or CBR™) 293, 373
SendID 347
sending See transmitting 36
SendSW 347
Seq (sequence graphing mode) 16, 373
seq( (sequence) 170, 373
sequence graphing
axes format 107
CALC (calculate menu) 108
evaluating 109
free-moving cursor 107
graph format 107
graph styles 104
moving the cursor to a value 108
nonrecursive sequences 105
recursive sequences 105
selecting and deselecting 104
TI-84 Plus versus TI-82 table 114
tracing 108
web plots 109
window variables 106
Y= editor 103
ZOOM (zoom menu) 108
Sequential (graphing order mode) 17, 373
setDate( (set date) 373
setDtFmt( (set date format) 373
setTime( (set time) 373
setting
display contrast 4
graph styles 71
graph styles from a program 72
modes 15
modes from a program 15
split-screen modes 138
split-screen modes from a program 142
tables from a program 116
setTmFmt( (set time format) 373
SetUpEditor 194, 373
shade above graph style 71
shade below graph style 71
Shade( 128, 373
Shade_t( 249, 374
Shadeχ²( 250, 374
ShadeF( 250, 374
ShadeNorm( 249, 374
shading graph areas 72, 128
Simul (simultaneous graphing order mode) 17, 374
sin( (sine) 36, 374
sin/( (arcsine) 36, 374
sine (sin( ) 36
sine (sin( ) 374
sinh( (hyperbolic sine) 273, 374
sinh/( (hyperbolic arcsine) 273, 374
SinReg (sinusoidal regression) 203, 374
Smart Graph 76
solve( 44, 374
Solver 42
solving for variables in the equation solver 43
SortA( (sort ascending) 168, 194, 374
SortD( (sort descending) 168, 194, 374
split-screen modes
G-T (graph-table) mode 140
Horiz (horizontal) mode 139
setting 138, 142
split-screen values 130, 133, 141
square (²) 36, 380
square root ($( ) 36
square root ($( ) 381
startTmr, start timer 374
STAT CALC
Stat Wizards 198
STAT CALC menu 198
STAT EDIT menu 193
stat list editor
attaching formulas to list names 188
clearing elements from lists 187
creating list names 186
detaching formulas from list names 190
displaying 184
edit-elements context 192
editing elements of formula-generated lists 190
editing list elements 187
entering list names 185
enter-names context 193
formula-generated list names 189
removing lists 186
restoring list names L1–L6 186
switching contexts 190
view-elements context 192
view-names context 193
STAT PLOTS menu 210
stat tests and confidence intervals
1-PropZInt (one-proportion z confidence
interval) 232
1-PropZTest (one-proportion z test) 227
2-PropZInt (two-proportion z confidence
interval) 232
2-PropZTest (two-proportion z test) 228
2-SampFTest (two-sample F-Test) 235
2-SampTInt (two-sample t confidence interval)
231
2-SampTTest (two-sample t test) 226
2-SampZInt (two-sample z confidence interval)
230
2-SampZTest (two-sample z test) 225
ANOVA( (one-way analysis of variance) 236
χ²-Test (chi-square test) 233, 234
χ²-Test (chi-square test) 233, 234
LinRegTTest (linear regression t test) 236
TInterval (one-sample t confidence interval) 229
T-Test (one-sample t test) 224

413
ZInterval (one-sample z confidence interval) 229
Z-Test (one-sample z test) 223
STAT TESTS menu 221
STAT WIZARDS 1, 198, 199
statistical distribution functions See distribution
functions 36
statistical plotting 208
Boxplot (regular box plot) 209
defining 210
from a program 212
Histogram 209
ModBoxplot (modified box plot) 209
NormProbPlot (normal probability plot) 210
tracing 212
turning on/off stat plots 70, 212
viewing window 212
xyLine 208
statistical variables table 206
Stats input option 218, 219
stdDev( (standard deviation) 176, 375
Stop 287, 375
Store (!) 20, 375
StoreGDB 135, 375
StorePic 134, 375
storing
graph databases (GDBs) 135
graph pictures 134
variable values 20
String4Equ( (string-to-equation conversions) 271, 375
strings
concatenation (+) 270, 381
converting 270
defined 267
displaying contents 269
entering 267
functions in CATALOG 269
indicator (”) 267
length (length( ) 271
length (length( ) 364
storing 268
variables 268
student-t distribution
probability (tcdf( ) 244
probability (tcdf( ) 375
student-t distribution
probability density function (tpdf( ) 243
probability density function (tpdf( ) 376
sub( (substring) 272, 375
subroutines 287
subtraction (–) 36, 381
sum( (summation) 176, 375
system variables 383
T
T (transpose matrix) 155, 379
TABLE SETUP screen 116
tables
description 118
variables 116, 117
tan( (tangent) 36, 375
tan/( (arctangent) 36, 375
tangent (tan( ) 36
tangent (tan( ) 375
tangent lines, drawing 126
Tangent( (draw line) 126, 375
tanh( (hyperbolic tangent) 273, 375
tanh/( (hyperbolic arctangent) 273, 375
TblStart (table start variable) 116
tcdf( (student-t distribution probability) 244, 375
TEST (relational menu) 62
TEST LOGIC (Boolean menu) 63
Text(
instruction 129, 142, 376
placing on a graph 129, 142
Then 282, 362
thick graph style 71
TI Connect™ 346
TI-84 Plus
key code diagram 292
keyboard 1
Time axes format 107, 376
time value of money (TVM)
C/Y variable (number of compounding periods
per year) 263
calculating 255
formulas 387
FV variable (future value) 263
I% variable (annual interest rate) 263
N variable (number of payment periods) 263
P/Y variable (number of payment periods per
year) 263
PMT variable (payment amount) 263
PV variable (present value) 263
TVM Solver 253
tvm_FV (future value) 257, 376
tvm_I% (interest rate) 376
tvm_I% (interest rate) 256
tvm_N (# payment periods) 256, 376
tvm_Pmt (payment amount) 256, 376
tvm_PV (present value) 256, 376
variables 262
timeCnv( ), convert time 376
TInterval (one-sample t confidence interval) 376
TInterval (one-sample t confidence interval) 229
tpdf( (student-t distribution probability density
function) 243, 376
TRACE
cursor 79
entering numbers during 79, 96, 100, 108
expression display 76, 79
Trace instruction in a program 80, 376
transmitting
error conditions 352
from a TI-83 351
from a TI-83 Plus Silver Edition or TI-83 Plus 351
from a TI-84 Plus Silver Edition or TI-84 Plus 351
stopping 348
to a TI-84 Plus Silver Edition or TI-84 Plus 348
transpose matrix (T) 155, 379
trigonometric functions 36
T-Test (one-sample t test) 224, 376

414
turn clock off, ClockOff 356
turn clock on, ClockOn 356
turning on and off
axes 75
calculator 3
coordinates 75
expressions 76
functions 70
grid 75
labels 76
points 131
stat plots 70, 212
tvm_FV (future value) 257, 376
tvm_I% (interest rate) 376
tvm_I% (interest rate) 256
tvm_N (# payment periods) 256, 376
tvm_Pmt (payment amount) 256, 376
tvm_PV (present value) 256, 376
two-proportion z confidence interval (2-PropZInt)
232, 369
two-proportion z test (2-PropZTest) 228, 369
two-sample F-Test formula 385
two-sample t test formula 386
two-variable statistics (2-Var Stats) 200, 377
U
u sequence function 103
Un/d 18, 50
UnArchive 21, 330, 377
ungrouping 336
user variables 383
uv/uvAxes (axes format) 107, 377
uw/uwAxes (axes format) 107, 377
V
v sequence function 103
value operation on a graph 87
variables
complex 19
displaying and storing values 21
equation solver 43
graph databases 19
graph pictures 19
independent/dependent 118
list 19, 162
matrix 19, 145
real 19
recalling values 21
solver editor 43
statistical 206
string 268
test and interval output 240
types 19
user and system 20, 383
VARS and Y-VARS menus 27
variance of a list (variance( ) 176
variance of a list (variance( ) 377
variance( (variance of a list) 176, 377
VARS menu
GDB 27
Picture 27
Statistics 27
String 27
Table 27
Window 27
Zoom 27
Vertical (draw line) 125, 377
viewing window 73
vw/uvAxes (axes format) 107, 377
W
w sequence function 103
Web (axes format) 107, 377
web plots 109
While 283, 377
window variables
function graphing 73
parametric graphing 95
polar graphing 99
X
x$ (root) 379
XFact zoom factor 86
x-intercept of a root 88
xor (Boolean) exclusive or operator 63, 377
xth root (x$) 40
xyLine (() plot type 208
Y
Y= editor
function graphing 68
parametric graphing 93
polar graphing 98
sequence graphing 103
YFact zoom factor 86
Y-VARS menu
Function 28
On/Off 28
Parametric 28
Polar 28
Z
ZBox 81, 377
ZDecimal 82, 377
zero operation on a graph 88
ZInteger 83, 378
ZInterval (one-sample z confidence interval) 229, 378
zoom 80, 81, 82, 83, 85, 86
cursor 81
factors 86
function graphing 80
parametric graphing 96
polar graphing 101
sequence graphing 108
Zoom In (zoom in) 82, 378
ZOOM MEMORY menu 85
ZOOM menu 80
Zoom Out (zoom out) 82, 378
ZoomFit (zoom to fit function) 83, 378
