Andrea Hendricks Study Guide For
User Manual: Pdf
Open the PDF directly: View PDF ![]() .
.
Page Count: 18

Study Guide for the Final Exam
The Final Exam is a comprehensive, departmental exam. It will consist of 40 multiple
choice questions. Please use this guide in conjunction with the Midterm Study Guide.
Section 10.1 Roots and Radicals
1. Evaluate the nth root of a number.
The nth root of the number is the number that must be raised to the nth power to get back
to the original number.
if n
nabb a==
Some examples: 35
4
81 9, 8 2, 625 5, 32 2=−=− = =
2. Determine if the root of a number is rational, irrational or not a real number.
If the index (value of n) is even and a is negative, then na is not a real number.
Examples: 4
4, 100, 16−− −
If the radicand (value of a) is a perfect power of the index, then na is a rational number.
Examples: 3449
25, 27, 81, 64
If the radicand is not a perfect power of the index and the root is a real number, then na
is irrational.
Examples: 34
5, 12, 8
3. Use your calculator to find roots.
Keystrokes on calculator:
2nd, 2
x
, 625, ), Enter
MATH, 4, 216, ), Enter
4, MATH, 5, 343, Enter
(The 4 represents the index. If the index is greater
than 3, you must type this first before you select the
root key.)

4. Apply the inverse properties of roots.
()
, if is defined.
n
nn
aa a=
Examples:
()
()
()
2
2
3
3
55
11 (provided 10)
88
xx x
=
+=+ +≥
−=−
Section 10.2 Rational Exponents
1. Evaluate exponential expressions with fractional exponents.
(
)
1/ /
m
nmn
nn
x
xxx==
Examples:
1/2
25 25 5−=−=− (The negative sign is not connected to the base of the ½ power.)
()
1/2
16 16−=− not a real number
()
()
33
3/4 4
81 81 3 27===
()
()
55
5/4 4
16 16 2 32===
()
2/3
2
2/3 2
3
1111
8824
8
−== ==
2. Use the properties of exponents to simplify exponential expressions.
mn mn
aa a
+
⋅=
(
)
n
mmn
aa= ( )
mmm
ab a b=
( 0)
mm
m
aa
b
bb
⎛⎞=≠
⎜⎟
⎝⎠ ( 0)
m
mn
n
aaa
a
−
=
≠
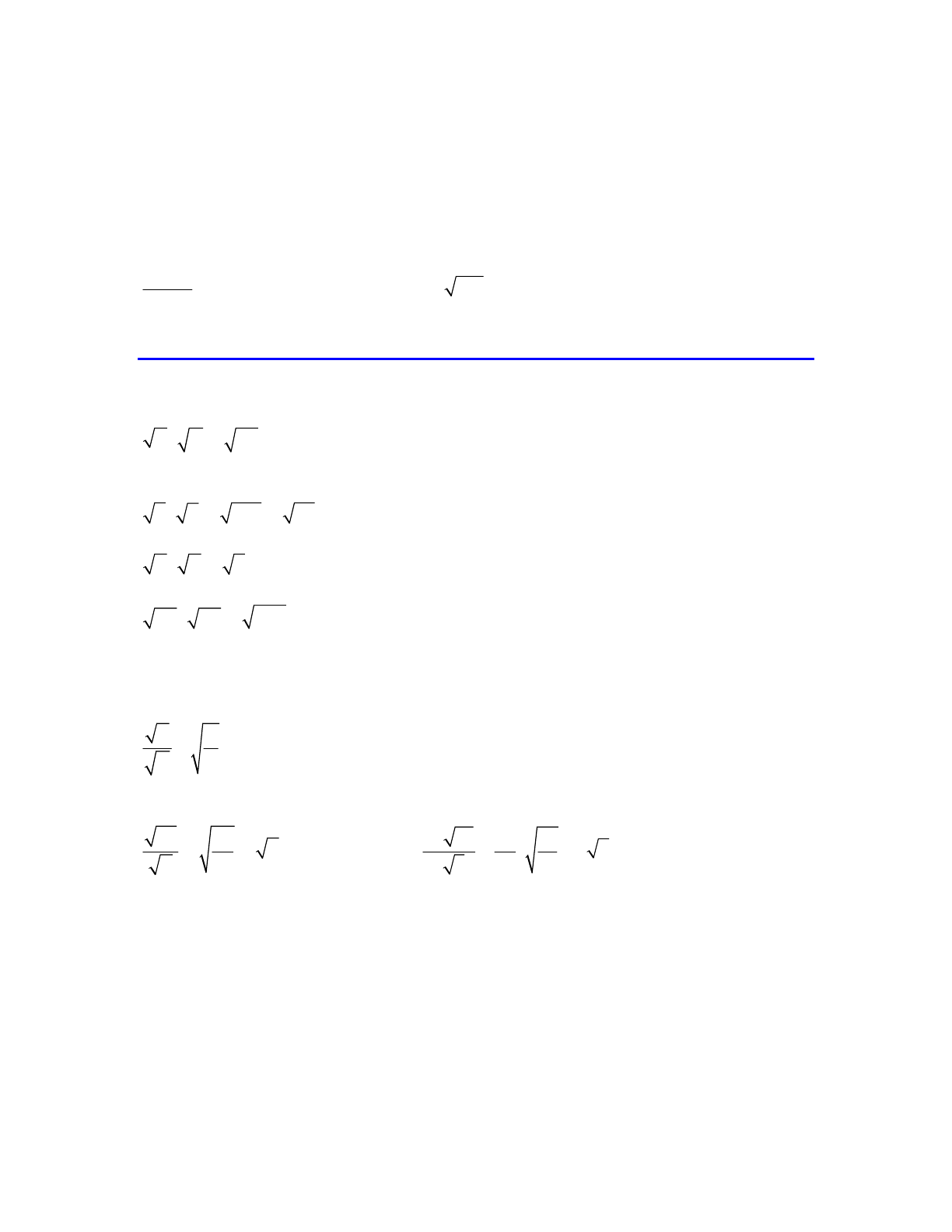
Examples:
4/5 1/5 5/5 1
99 9 99===i
() ()
1/4 1/ 4
81/48 2
16 16 2
x
xx==
()
9/4
9/4 7/4 2/4 1/2
7/4
100 100 100 100 100 10
100
−
=====
Section 10.3 Simplifying Radicals
1. Use the product rule to multiply radicals.
nnn
x
yxy⋅=
Examples:
35 35 15⋅=⋅=
33 3
42 82⋅==
2
33 9 3
x
xxx⋅= =
2. Use the quotient rule to divide radicals.
n
n
n
x
x
y
y=
Examples:
18 18 93
2
2===
20 10 20 10 52
45
45 =⋅ =
3. Use the product rule to simplify radicals.
Remove any factors that are perfect powers of the index from the radicand. Rewrite the
radicand as a product of this perfect power and the remaining factor, if possible. Apply
the product rule to simplify the result.
22 2
22 2
2
2
(3) (5)
925
16
4
ab c
b
b
b
b
+=
+=
+=
=
=
Examples:
120 3044230 30=⋅=⋅ =
33 333
8840 5 5 52=⋅=⋅=
44 2599318 2 2 2xxxx
x
xx=⋅ = =
4. Use the Pythagorean Theorem to find the length of a missing side of a right triangle.
Example: Find the value of b if a = 3 and c = 5.
5. Find the distance between two points.
()()
22
12 12
dxx yy=−+−
Example: Find the exact distance between the points (6, -16) and (-20, -2).
()()
()( )
()( )
22
12 12
22
22
22
6(20) 16(2)
620 162
(26) ( 14)
676 196
872
dxx yy
d
d
d
d
d
=−+−
=−− +−−−
=+ +−+
=+−
=+
=

Section 10.4 Adding/Subtracting Radicals
1. Identify like radical terms.
Like radicals have the same index and same radicand.
Examples: 32 and 52 are like radicals but 3
32 and 52 are not like radicals since
their roots are different.
2. Add/subtract radicals.
To add like radicals, combine the coefficients of the radicals and keep the radical part
unchanged. Express radicals in simplest radical form before adding.
Examples:
()
66 6 61116261+= + =+ =
32 52 (3 5)2 82+=+ =
145 5 45 5 (41)5 35−= − =− =
320 245 3 5 2 5 3()5 2()5934265 65 125+=⋅+⋅= + =+=
48 5 6 16 3 5 6 4 3 5 6−=⋅−=− Cannot be combined
Section 10.5 Multiplying/Dividing Radicals
1. Multiply radicals.
To multiply radical expressions, use properties and rules that you have previously
learned.
• Product Rule for Radicals nn n
ab ab
⋅
=⋅ (Any radicals that have the same root
(index) can be multiplied. The root stays the same and the radicands are
multiplied.)
• Distributive Property: ( )ab c ab ac
+
=+
• Multiply two binomials by distributing (FOIL).

Examples:
222
36 18 92 9 232
x
xx xx x⋅= =⋅= ⋅=
()()
56 56 25656536536 31+−=−+−=−=−
2. Divide radicals – really just know how to reduce fractions with radicals.
Reduce any radicals prior to reducing the fraction.
4324162442442
12
44444
++⋅+
===+=+
Section 10.6 Solving Radical Equations
1. Solve a radical equation. (Remember to check!)
The square root expression must be isolated to one side of the equation. Square both
sides of the equation. Solve the resulting equation and check your answers.
33 3 3
3
4( 2 4) 8 4 4 2 4 4−= − =−
()()()
2
410 41041016410410100168101026810+=+ +=+++=++=+
32
10 54 10 9 6
55
10 3 6
5
(10 3 6 )
5
10 3 6
5
yyy yy
yy
yyy
y
yy
y
y
++⋅⋅
=
+
=
+
=
+
=

1)
Check:
7+2 3
93
33 True
So, 7 is the solution to the equation.x
=
=
=
=
2)
So, there is no solution to this equation.
()
()
22
2143
214434 (Subtract 4 from both sides to isolate radical.)
21 1
21 1 (Square both sides to remove the radical.)
211 (Result of squaring)
20
x
x
x
x
x
x
++ =
++− =−
+=−
+=−
+=
= (Subtract 1 from both sides.)
0 (Divide both sides by 2.)x=
Check:
2(0) 1 4 3
01 4 3
143
14 3
53 False, so 0 is not a solution to the equation.x
++ =
++ =
+=
+=
==
()
()
22
23
23 (Radical is on a side by itself, so square both sides.)
29 (Result of squaring)
2292 (Subtract 2 from both sides.)
7
x
x
x
x
x
+=
+=
+=
+−=−
=
()
()
22
2
2
21 1
21 1
21 21
04
0(4)
0 or 4
xx
xx
x
xx
x
x
xx
x
x
+=−
+=−
+= − +
=−
=−
==
3)
Check:
0
2(0) 1 0 1
01 1
11
1 1 False, so 0 is not a solution.
4
2(4) 1 4 1
81 3
93
3 3 True, so 4 is a solution to the equation.
x
x
x
x
=
+=−
+=−
=−
=− =
=
+=−
+=
=
==
The solution set to this equation is {4}.
Section 10.7 Complex Numbers
1. Know the definition of i and 2
i.
2
1
1
i
i
=−
=−
2. Write non-real numbers in complex form.
kik−=
Examples:
16 16 1 16 1 4i−= ⋅−= ⋅−= 991913i
−
=⋅−=⋅−=
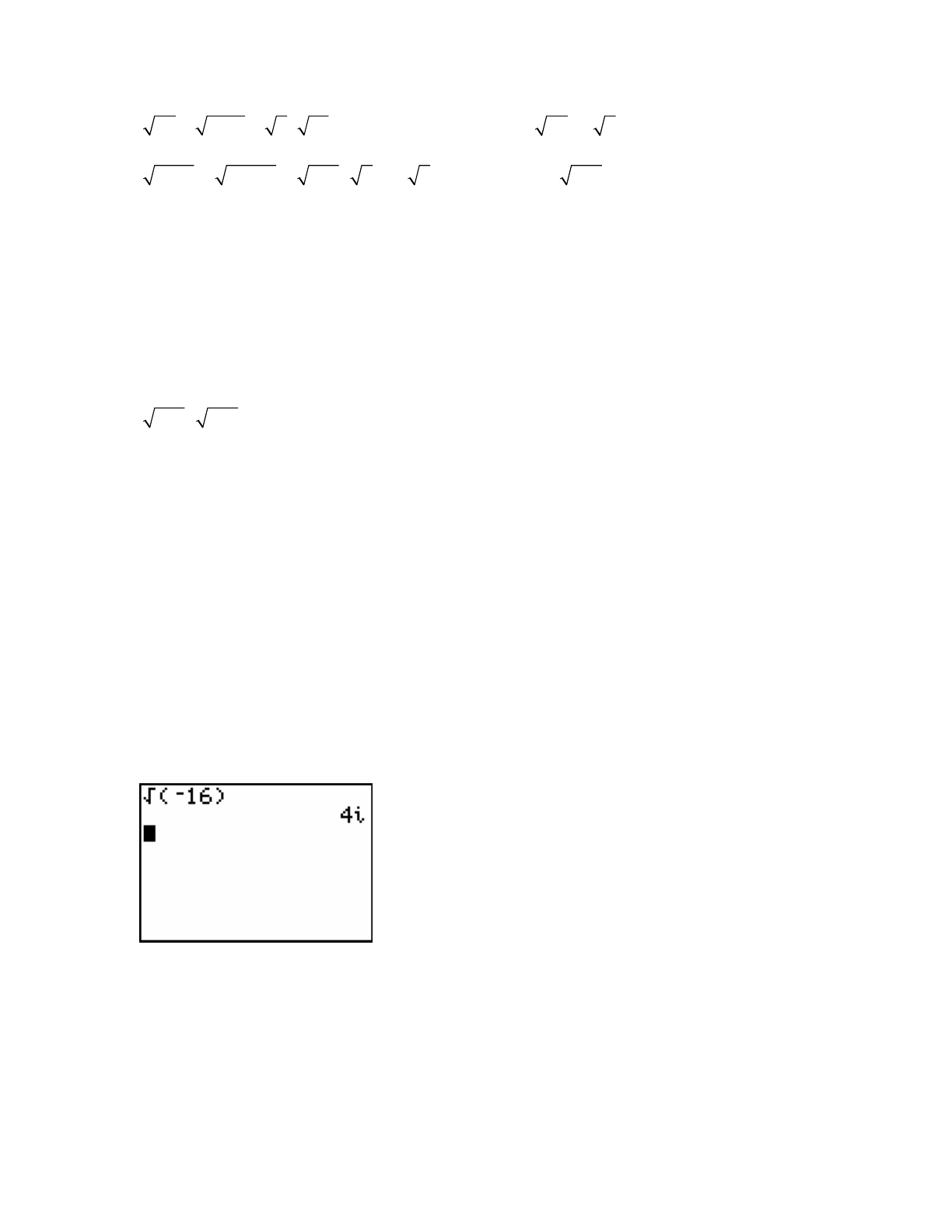
441412i−= ⋅−= ⋅−= 77i−=
175 25 7 25 7 5 7i−=−⋅=−⋅= 5 36 5 6i
−
−=−
3. Perform operations with complex numbers.
Add/Subtract Complex Numbers:
(-2 + 10i) + (5 – 5i) = -2 + 10i + 5 – 5i = -2 + 5 + 10i – 5i = 3 + 5i
(7 + 3i) – (2 – i) = (7 + 3i) –1(2 – i) = 7 + 3i – 2 + i = 7 – 2 + 3i + i = 5 + 4i
Multiply Complex Numbers:
2
25 64 5 8 40 40( 1) 40ii i−⋅−=⋅= = −=−
2
4 8 32 32( 1) 32ii i⋅= = −=−
.
4. Use the calculator to check.
To write numbers as complex numbers, change mode to a + bi.
You can also perform operations with complex numbers on your calculator. To enter the
complex number i, press 2nd and decimal point.
Here are some examples. These problems come from examples worked above by hand.
2
3( 7 4)
21 12
21 12( 1)
21 12
12 21
ii
ii
i
i
i
−+
−+
−+−
−−
−−
2
(3 7 )(9 4 )
27 12 63 28
27 51 28( 1)
27 51 28
55 51
ii
iii
i
i
i
+−
−+−
+−−
++
+
2
2
(6 8 )
(6 8 )(6 8 )
36 48 48 64
36 96 64( 1)
36 96 64
28 96
i
ii
iii
i
i
i
+
++
+++
++−
+−
−+

Section 11.1 Square Root Property
1. Solve an equation using the Square Root Property.
The Square Root Property states that if
2
or
xk
x
kx k
=
==−
Examples:
281
81 or 81
9 9
x
xx
xx
=
==−
==−
216
16 or 16
4 4
x
xx
x
ixi
=−
=− =−−
==−
()
2
45
45 or 4 5
4 5 4 5
x
xx
xx
+=
+= +=−
=− + =− −

Section 11.2 Completing the Square
1. Find the number that completes the square for a given binomial of the form 2
x
bx+.
To complete the square means to find the number that must be added to a binomial to
make it a perfect square trinomial. If the binomial is of the form 2
x
bx
+
, then the
number that completes the square is
2
2
b
⎛⎞
⎜⎟
⎝⎠
; that is, half of the coefficient of x, squared.
Example: Find the number that completes the square of 222
x
x+.
The number that completes the square is
()
2
2
22 11 121
2
⎛⎞
==
⎜⎟
⎝⎠ .
2. Solve a quadratic equation by completing the square.
This method is really not the method of choice. I recommend only using it if the equation
has a coefficient of 1 on the squared term and the coefficient of x is even.
Example:
2
2
2
2
850
8 5
85
(4)11
4 11 or 4 11
4 11 or 4 1
16
1
61
xx
xx
xx
x
xx
xx
−+=
−=−
−=−
−=
−= −=−
=+ =−
++
Section 11.3 Quadratic Formula
1. Solve a quadratic equation using the quadratic formula.
If a quadratic equation is of the form 20 ( 0)ax bx c a
+
+= ≠ , then the solutions to the
equation are
24
2
bb ac
xa
−± −
=.

Example:
2
2
2
15
1
3( 5) 4
3154
0
, ,
()()4()()
2( )
15 225 48
6
15 27
4
4
3
5
15 15
3
3
4
6
3
3
xx
xx
xx
x
a
x
cb
x
−=
−=
=
−
−
=−
±−
=
±+
=
±
=
−
=−
−
=
−
−
2. Find the discriminant and know what this number tells you about the solutions to the
equation.
The discriminant is the number in the radical of the quadratic formula, that is, 24bac−.
24bac− Conclusion
positive and perfect square two different rational solutions;
equation is factorable
positive and not a perfect square two different irrational solutions
zero one rational solution
Negative two different non-real complex solutions
Example: Find the discriminant of 2
4510xx
−
−= and determine the types of solutions.
The discriminant is
()
2
2454(4)(1)251641bac−=−− −=+=. Since this is a positive
number that is not a perfect square, the equation has two irrational solutions.
3. Use your calculator to check your solutions and to find approximations of irrational
solutions.
Please see my notes that are posted in MML Study Notes on this topic. These notes
are very detailed.
Section 11.4 Equations Quadratic in Form
1. Solve a rational equation.
To solve a rational equation, clear the fractions by multiplying both sides by the LCD.
Solve the resulting equation. Exclude any solutions that make the denominator zero.
Example:
2
22
2
2
412
10
412
1(0)
4120
(6)(2)0
60 or 20
6 2
xx
xx
xx
xx
xx
xx
xx
−− =
⎛⎞
−− =
⎜⎟
⎝⎠
−−=
−+=
−= +=
==−
The solution set is {-2, 6}.
2. Solve a square root equation.
This is a review of section 10.6. Please see these notes for an example.
3. Solve a higher degree factorable equation.
A higher degree equation has a degree greater than 2. Start solving this equation by
writing it in standard form and then factoring.
Example:
()()
42
22
22
22
340
410
40 or 10
4 or 1
2 1
xx
xx
xx
xx
x
xi
−−=
−+=
−= +=
==−
=± =± − =±
The solution set is {-2, 2, i, -i}

Section 11.5 Applications
1. Solve applications using the Pythagorean Theorem.
Example: Find the lengths of the sides of a right triangle in which the longer leg is one
inch more than the shorter leg and the hypotenuse is two inches more than the shorter leg.
Let x = length of the shorter leg
x + 1 = length of the longer leg
x + 2 = length of the hypotenuse
()( )
()()
22
2
22 2
22
2
12
21 4 4
221 44
230
310
3 or 1
xx x
xx x x x
xx xx
xx
xx
x
x
++ =+
+++=++
++=++
−−=
−+=
==−
The lengths of the sides of the right triangle are 3, 4, and 5 inches.
2. Solve an application involving area.
Example: Find the length and width of a rectangle whose area is 27 square feet and
whose length is 6 feet less than the width.
Let w = width
w-6 = length
2
(6)27
6270
(9)(3)0
9 or 3
ww
ww
ww
ww
−=
−−=
−+=
==−
The width is 9 feet and the length is 9 – 6 = 3 feet.
3. Solve an application given a model.
Example: The height of a ball thrown from the ground can be given by 2
16 32htt=− + ,
where t is the number of seconds after the ball is thrown. Find the time that the ball
reaches a height of 16 feet.

Divide both sides by the GCF of -16.
The ball will reach a height of 16 feet in 1 second after it is thrown.
Section 11.6 Graphing Quadratic Equations
1. Graph a parabola by identifying the vertex and two other points.
If an equation is of the form 2
()yaxh k=−+, the vertex of the form is (h, k). Find two
additional points – one on each side of the vertex to get the graph.
Example: Graph the equation 2
2( 3) 8yx=+−.
• The vertex of the parabola is (-3, -8).
• Since a = 2, the parabola opens up.
• Find two additional points. You can do this by hand or on the calculator.
By hand: Let x = -5 and x = -1 (a value to the left of -3 and to the right of -3)
x = -5: 22
2( 5 3) 8 2( 2) 8 2(4) 8 8 8 0y=−+ −=− −= −=−= (-5, 0)
x = -1: 22
2( 1 3) 8 2(2) 8 2(4) 8 8 8 0y=−+ −= −= −=−= (-1, 0)
By the calculator:
2
2
2
16 32 16
16 32 16 0
210
(1)(1)0
1
tt
tt
tt
tt
t
−+=
−+−=
−+=
−−=
=
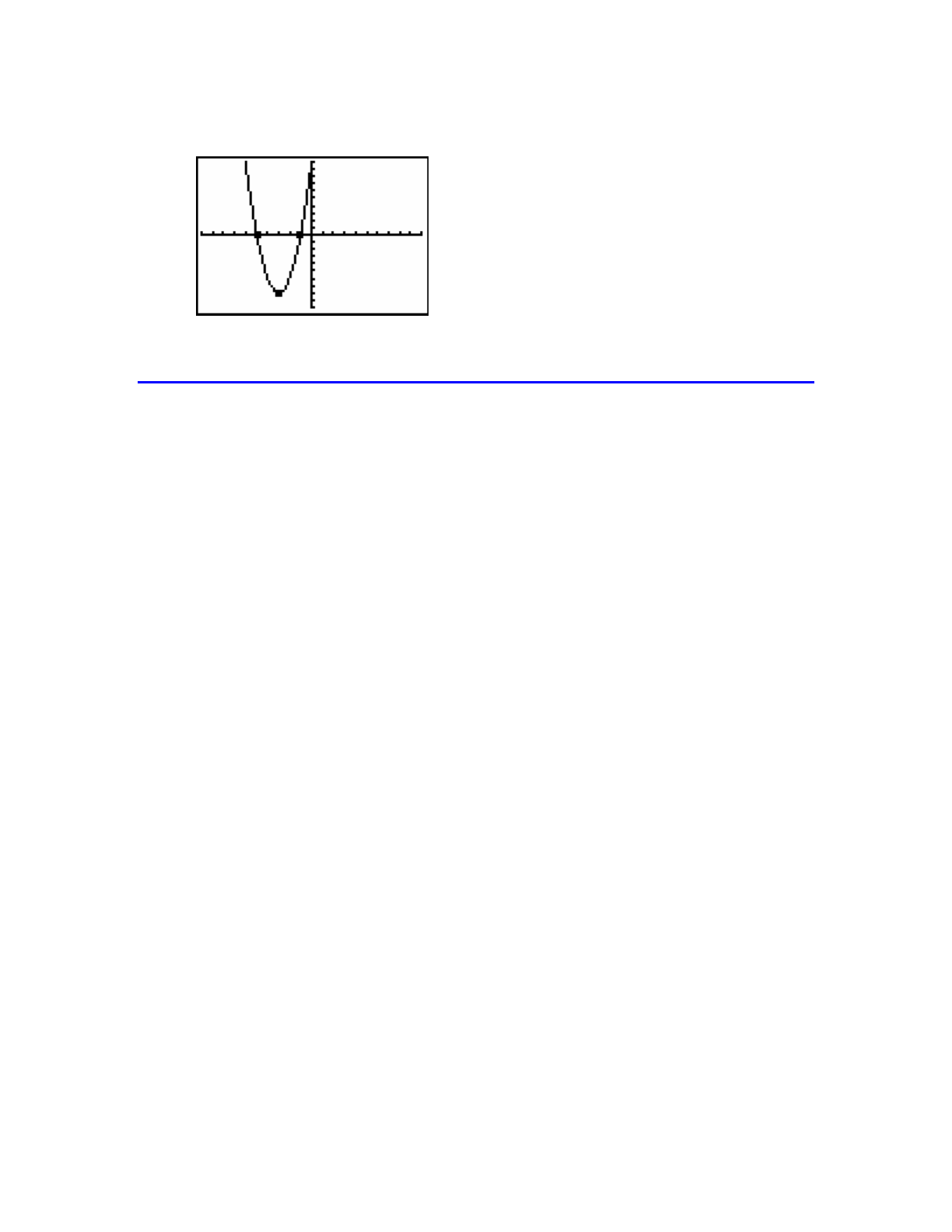
• Plot the three points and draw the parabola.
Section 11.8 Nonlinear Inequalities
1. Solve a quadratic inequality.
Example: Solve 260xx−−>.
Solution:
Find solutions to the associated equation.
Plot the solutions on the number line.
<-------|--------------------|-------------->
-2 3
Test points from the regions on the number line:
2
2
2
3: ( 3) ( 3) 6 0 6 0 True
0: (0) (0) 6 0 6 0 False
4: (4) (4) 6 0 6 0 True
x
x
x
=− − − − − > ⇒ >
=−−>⇒−>
=−−>⇒>
Shade the regions that test true and put the correct symbol on the endpoints.
The solution is <--------)-------------------(-------------->
-2 3
The interval for the solution is (,2)(3,)−∞ − ∪ ∞ .
260
(3)(2)0
3 or 2
xx
xx
xx
−−=
−+=
==−

2. Solve a polynomial inequality.
Example: Solve ( 5)( 1)( 3) 0xxx−+−≤.
Solution: The solutions to the equation are 5, 1, 3xx x
=
=− = .
Plot these numbers on the number line and test points from each of the regions formed.
<-----------|-----------------------|----------|------------------->
-1 3 5
2: ( 2 5)( 2 1)( 2 3) 0 ( 7)( 1)( 5) 0 35 0 True
0: (0 5)(0 1)(0 3) 0 ( 5)(1)( 3) 0 15 0 False
4: (4 5)(4 1)(4 3) 0 ( 1)(5)(1) 0 5 0 True
6: (6 5)(6 1)(6 3) 0 (1)(7)(3) 0 21 0 False
x
x
x
x
=− − − − + − − ≤ ⇒ − − − ≤ ⇒− ≤
=−+−≤⇒−−≤⇒≤
=−+−≤⇒− ≤⇒−≤
=−+−≤⇒ ≤⇒≤
Shade the regions that tested true and include the appropriate symbol on the endpoints.
<-----------]----------------------[-----------]------------------->
-1 3 5
Solution: ( , 1] [3,5]−∞ − ∪
Section 9.2 Absolute Value Equations and Inequalities
1. Solve an absolute value equation.
Isolate the absolute value expression to one side of the equation and then use the
following property to solve it.
|x| = k
X = k or x = -k (if k is positive)
X = k (if k = 0)
No solution if k is negative
Examples:
|x + 2| = 5
x + 2 = 5 or x + 2 = -5
x = 3 or x = -7
Solution set: {-7, 3}
|1 – 2x| + 4 = 3
|1 – 2x| = -1 (isolate abs. value)
No solution

2. Solve an absolute value inequality.
Apply the properties used to solve quadratic and higher degree polynomial inequalities.
Find the solutions to the associated equation, plot the points on the number line, and then
test a point from each region.
Examples:
|2x + 1| > 5
Solution: |2x + 1| = 5
2x + 1 = 5 or 2x + 1 = -5
2x = 4 2x = -6
x = 2 x = -3
<----------|-----------------|---------------->
-3 2
Test points:
X = -4: |2(-4) + 1| > 5
|-7| > 5
7 > 5 True
X = 0: |2(0) + 1| > 5
|1| > 5
1 > 5 False
X = 3: |2(3) + 1| > 5
7 > 5 True
Solution:
<----------)-----------------(---------------->
-3 2
Interval: (-∞, -3) union (2, ∞)