BIGSTICK Manual

BIGSTICK_Manual

User Manual: Pdf

Open the PDF directly: View PDF .
Page Count: 100

BIGSTICK: A ﬂexible conﬁguration-interaction

shell-model code 1

Calvin W. Johnson2, W. Erich Ormand3, Kenneth S. McElvain4, and Hongzhang Shan5

December 4, 2017

1UCRL number: LLNL-SM-739926

2Department of Physics, San Diego State University, 5500 Campanile Drive, San

Diego CA 92182-1233

3Lawrence Livermore National Laboratory, P.O. Box 808, L-414, Livermore, CA

94551

4Department of Physics, University of California, Berkeley 366 Leconte Hall MC

7300, Berkeley, CA 94720

5Computational Research Division, Lawrence Berkeley Laboratory, Berkeley, CA,

94720

Abstract

We present BIGSTICK, a ﬂexible conﬁguration-interaction open-source shell-

model code for the many-fermion problem. Written mostly in Fortran 90 with

some later extensions, BIGSTICK utilizes a factorized on-the-ﬂy algorithm for

computing many-body matrix elements, and has both MPI (distributed mem-

ory) and OpenMP (shared memory) parallelization, and can run on platforms

ranging from laptops to the largest parallel supercomputers. It uses a ﬂexible

yet eﬃcient many-body truncation scheme, and reads input ﬁles in multiple for-

mats, allowing one to tackle both phenomenological (major valence shell space)

and ab initio (the so-called no-core shell model) calculations. BIGSTICK can

generate energy spectra, static and transition one-body densities, and expecta-

tion values of scalar operators. Using the built-in Lanczos algorithm one can

compute transition probability distributions and decompose wave functions into

components deﬁned by group theory.

This manual provides a general guide to compiling and running BIGSTICK,

which comes with numerous sample input ﬁles, as well as some of the basic

theory underlying the code. The code also comes with an incomplete “inside

guide” which provides more details into the inner workings.

This code is distributed under the MIT Open Source License. The source

code and sample inputs are found at github.com/cwjsdsu/BigstickPublick.

Contents

1 Introduction 4

1.1 Expectations of users . . . . . . . . . . . . . . . . . . . . . . . . . 5

1.2 How to cite and copyright notices/licenses . . . . . . . . . . . . . 5

1.2.1 LAPACK copyright notice . . . . . . . . . . . . . . . . . . 6

1.3 Reporting bugs and other issues . . . . . . . . . . . . . . . . . . . 7

1.4 A brief history of BIGSTICK, and acknowledgements . . . . . . . 8

2 How we solve the many-body problem 9

2.1 Matrix formulation of the Schr¨odinger equation . . . . . . . . . . 10

2.2 Representation of the basis . . . . . . . . . . . . . . . . . . . . . 12

2.2.1 Factorization of the basis . . . . . . . . . . . . . . . . . . 14

2.3 The Lanczos algorithm and computational cost . . . . . . . . . . 17

2.4 Representation of the Hamiltonian . . . . . . . . . . . . . . . . . 18

2.5 An incomplete survey of other codes . . . . . . . . . . . . . . . . 19

3 Getting started with BIGSTICK 22

3.1 What can BIGSTICK do?....................... 22

3.2 Downloading and compiling the code . . . . . . . . . . . . . . . . 23

3.3 Requiredinputﬁles.......................... 24

3.4 Runningthecode........................... 24

3.5 Somesampleruns .......................... 29

3.6 Typicalruntimes........................... 29

4 Using BIGSTICK, in detail 30

4.1 Overview of input ﬁles . . . . . . . . . . . . . . . . . . . . . . . . 30

4.2 Deﬁning the model space . . . . . . . . . . . . . . . . . . . . . . 31

4.2.1 Particle-hole conjugation . . . . . . . . . . . . . . . . . . 35

4.2.2 Truncation of the many-body space . . . . . . . . . . . . 36

4.2.3 Advanced truncation options . . . . . . . . . . . . . . . . 38

4.2.4 How to handle ‘diﬀerent’ proton-neutron spaces . . . . . . 39

4.3 Interactionﬁles............................ 40

4.3.1 Scaling and autoscaling . . . . . . . . . . . . . . . . . . . 41

4.3.2 Proton-neutron and other isospin-breaking formats . . . . 42

4.3.3 MFDn formatinput...................... 45

4.3.4 Three-body forces . . . . . . . . . . . . . . . . . . . . . . 46

4.4 Primary runtime options . . . . . . . . . . . . . . . . . . . . . . . 47

4.4.1 Autoinput........................... 47

4.4.2 Standard or normal runs . . . . . . . . . . . . . . . . . . . 47

4.4.3 One-body density matrices and occupations . . . . . . . . 48

4.4.4 Other primary options . . . . . . . . . . . . . . . . . . . . 49

4.5 Diagonalization options . . . . . . . . . . . . . . . . . . . . . . . 50

4.5.1 Convergence ......................... 52

4.6 Secondary runtime options . . . . . . . . . . . . . . . . . . . . . . 53

4.6.1 Expectation value . . . . . . . . . . . . . . . . . . . . . . 54

4.6.2 Applying a one-body transition operator . . . . . . . . . . 55

4.6.3 Applying a two-body body scalar operator . . . . . . . . . 56

4.6.4 Generating strength function distributions . . . . . . . . . 56

4.6.5 Overlap or dot product of wave functions . . . . . . . . . 57

4.7 Outputﬁles.............................. 58

4.7.1 Secondary ﬁles . . . . . . . . . . . . . . . . . . . . . . . . 59

4.7.2 Diagnosticﬁles ........................ 59

4.8 Memoryusage ............................ 59

5 Applications 61

5.1 One-body density matrices . . . . . . . . . . . . . . . . . . . . . 61

5.1.1 Symmetries of density matrix elements . . . . . . . . . . . 63

5.1.2 Particle occupations from densities . . . . . . . . . . . . . 63

5.1.3 Strengths from density matrix elements . . . . . . . . . . 63

5.1.4 Sample case: spin-ﬂip . . . . . . . . . . . . . . . . . . . . 65

5.1.5 Charge-changing transitions . . . . . . . . . . . . . . . . . 66

5.1.6 Sample case: 19F....................... 67

5.2 Strength function option . . . . . . . . . . . . . . . . . . . . . . . 67

5.2.1 Decomposition . . . . . . . . . . . . . . . . . . . . . . . . 67

5.2.2 Transition strength function distributions: the basics . . . 70

5.2.3 Transitions with good angular momentum . . . . . . . . . 72

5.2.4 Gamow-Teller with strength function option . . . . . . . 74

6 A peek behind the curtain 77

6.1 Anormalrun............................. 77

6.2 Explicit representation of the basis . . . . . . . . . . . . . . . . . 78

6.3 Explicit representation of the Hamiltonian . . . . . . . . . . . . . 80

7 Lanczos algorithm 81

7.1 Standard Lanczos algorithm . . . . . . . . . . . . . . . . . . . . . 81

7.2 Thick-restart Lanczos . . . . . . . . . . . . . . . . . . . . . . . . 83

7.3 Can I restart standard Lanczos? . . . . . . . . . . . . . . . . . . 85

8 Parallel computing and timing 86

8.1 MPI .................................. 87

8.1.1 Fragments........................... 87

8.1.2 Opbundles and optypes . . . . . . . . . . . . . . . . . . . 88

8.1.3 Modeling ........................... 89

8.2 OpenMP................................ 89

8.3 Timing................................. 90

8.3.1 Modetimes.......................... 90

8.3.2 Timing for parallel runs . . . . . . . . . . . . . . . . . . . 91

A Matrix elements and operators 92

A.1 Reduced matrix elements . . . . . . . . . . . . . . . . . . . . . . 92

A.2 The Hamiltonian and other operators in second quantization . . 93

A.3 Symmetries of matrix elements . . . . . . . . . . . . . . . . . . . 94

B Highlighted references 95

Chapter 1

Introduction

There are many approaches to the quantum many-body problem. BIGSTICK is

a conﬁguration-interaction many-fermion code, written in Fortran 90. It solves

for low-lying eigenvalues of the Hamiltonian of a many fermion system; it does

this by creating a basis of many-body states of Slater determinants (actually, the

occupation representation of Slater determinants). The Slater determinants are

antisymmetrized products of single-particle states with good angular momen-

tum, typically derived from some shell-model-like potential; hence we call this

a shell-model basis. The Hamiltonian is assumed to be rotationally invariant

and to conserve parity, and is limited to two- and, optionally, three-body forces.

Otherwise no assumptions are made about the form of the single-particle states

or of the Hamiltonian.

The capabilities of BIGSTICK will be detailed below, but in addition to calcu-

lating the energy spectra and occupation-space wavefunctions, it can compute

particle occupations, expectation values of operators, and static and transition

densities and strengths. Most of the applications to date have been in low-

energy nuclear physics, but in principle any many-fermion system with two

ﬁxed ‘species’ and rotational symmetry can be addressed by BIGSTICK, such

as the electronic structure of atoms and cold fermionic gases in a spherically

symmetric trap; although we have yet to publish papers, we have carried out

demonstration calculations for such systems, with ‘spin-up’ and ‘spin-down’ re-

placing ‘proton’ and ‘neutron.’ We apologize to any atomic physicist who will

have to translate our terminology.

In this next chapter we review the basic many-body problem. Chapter 2

outlines the conﬁguration-interaction method and discusses in broad strokes

the principles of the algorithms in BIGSTICK. Chapter 3 gives an introduction

to how to compile and run BIGSTICK, while Chapter 4 goes into running the

code more detail. If you are interested in running BIGSTICK immediately,

go directly to Chapter 3.

In this manual we do not give substantial information on the inner workings

of the code. With the distribution you will ﬁnd an as-yet incomplete Inside

Guide which provide many details. In addition, the code itself is heavily com-

mented. While internal information in BIGSTICK is highly compressed through

factorization, a technique outlined in Chapter 2, it is possible to get out explicit

representations of the many-body basis states and the many-body Hamiltonian

matrix; see Chapter 6. Chapter 7 discusses our use of the Lanczos algorithm.

Finally, parallel capabilities of the code is discussed in Chapter 8.

1.1 Expectations of users

Who do we expect to use BIGSTICK, and how do we expect them to use it?

We designed BIGSTICK to be run on a variety of platforms, from laptops to

leadership-class supercomputers. We also imagined, and tried to design, BIGSTICK

for a spectrum of users, with various expectations of them.

A crucial point for any and all users: BIGSTICK requires at least two

kinds of input ﬁles to run, a description of the single-particle space and a

ﬁle of interaction matrix elements. While we supply with the distribution a

number of example input ﬁles. it is important for both novice and routine users

to understand that such examples are just the beginning and not the sum of

nuclear physics. In general it is up to the user to provide interaction

ﬁles. We can use the .int interaction ﬁles usable by NuShell/NuShellX as

well as the interaction ﬁles used by MFDn.

It is also equally important to not ask BIGSTICK to be smarter than you are.

While BIGSTICK employs many error traps to avoid or at least ﬂag the most

common mistakes, the principle of “garbage in, garbage out” still applies.

While this manual provides a fairly comprehensive introduction to running

BIGSTICK, it is not a detailed tutorial in conﬁguration-interaction methods, the

atomic or nuclear shell models, or to basic nuclear physics. We expect the reader

to, above all, be comfortable with non-relativistic quantum mechanics (i.e., to

fully understand the Schr¨odinger equation and with Dirac’s bra-ket notation),

and to be ﬂuent of the ideas and terminology of the shell model, especially the

nuclear shell model, and to understand the basic principles of conﬁguration-

interaction methods. We review the latter in the opening of Chapter 2, so that

is a good place to start to check your level of comfort. We suggest additional

references in Appendix B.

1.2 How to cite and copyright notices/licenses

If you successfully use BIGSTICK in your research, please use the following cita-

tions:

•C. W. Johnson, W. E. Ormand, and P. G. Krastev, Comp. Phys. Comm.

184, 2761-2774 (2013). (You can also ﬁnd this article at arXiv:1303.0905.)

•C. W. Johnson,W. E. Ormand, K. S. McElvain, and H. Z. Shan, UCRL number

LLNL-SM-739926, arXiv:XXXXX (this report)

The ﬁrst paper, Johnson et al. [2013], in particular discusses the underlying

factorized on-the-ﬂy algorithm. This documents focuses instead on how to run

BIGSTICK.

This code is distributed under the MIT Open Source License:

State University Research Foundation.

Permission is hereby granted, free of charge, to any person obtaining a copy

of this software and associated documentation ﬁles (the ”Software”), to deal in

the Software without restriction, including without limitation the rights to use,

copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the

Software, and to permit persons to whom the Software is furnished to do so,

subject to the following conditions:

The above copyright notice and this permission notice shall be included in

all copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED ”AS IS”, WITHOUT WARRANTY OF

ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO

THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTIC-

ULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE

AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM,

DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CON-

TRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CON-

NECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS

IN THE SOFTWARE.

1.2.1 LAPACK copyright notice

We use LAPACK subroutines in our code. The following are the LAPACK

reserved.

served.

Additional copyrights may follow

Redistribution and use in source and binary forms, with or without modiﬁ-

cation, are permitted provided that the following conditions are met:

- Redistributions of source code must retain the above copyright notice, this list

of conditions and the following disclaimer.

- Redistributions in binary form must reproduce the above copyright notice,

this list of conditions and the following disclaimer listed in this license in the

documentation and/or other materials provided with the distribution.

- Neither the name of the copyright holders nor the names of its contributors

may be used to endorse or promote products derived from this software without

speciﬁc prior written permission.

The copyright holders provide no reassurances that the source code provided

does not infringe any patent, copyright, or any other intellectual property rights

of third parties. The copyright holders disclaim any liability to any recipient

for claims brought against recipient by any third party for infringement of that

parties intellectual property rights.

THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS

AND CONTRIBUTORS ”AS IS” AND ANY EXPRESS OR IMPLIED WAR-

RANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WAR-

RANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR

PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT

OWNER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT,

INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES

(INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTI-

TUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR

BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THE-

ORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR

TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY

WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF

THE POSSIBILITY OF SUCH DAMAGE.

1.3 Reporting bugs and other issues

If you run into trouble, ﬁrst read this manual. Most issues are caused by mistakes

in setting up input ﬁles, in particular inconsistencies between the single-particle

space deﬁned and the interaction ﬁle(s). Second, please read the output carefully:

we have striven to write detailed error traps and often BIGSTICK will notify the

user of problems. Try running the sample cases and make sure they run to

correct completion and that you understand the inputs.

If, having exhausted all the resources presented here, you still have a prob-

lem, you may send your issue to Calvin Johnson, cjohnson@mail.sdsu.edu.

In particular send a copy of the entire output written to screen, which often

contains important clues, the input ﬁles, and all output ﬁles with the extensions

.res,.log and .bigstick. Although we hope to be able to help, we cannot

guarantee it.

As discussed elsewhere, BIGSTICK is developed for Linux and Linux-like envi-

ronments such as Mac OS X. We have made no attempt to adapt to a Windows

environment. Although it has a user-friendly menu-driven interface, it still as-

sumes a reasonable facility with many-body physics and in particular low-energy

nuclear physics.

Development of BIGSTICK is ongoing. We hope to release future versions of

the code as additional major capabilities come on line.

1.4 A brief history of BIGSTICK, and acknowl-

edgements

In 1997, when two of us (Ormand and Johnson) were both at Louisiana State

University, we decided to write our own many-fermion conﬁguration-interactionI

code christened REDSTICK, English for Baton Rouge. Over the next decade

REDSTICK evolved and improved. Most important were the addition of three-

body forces and parallelization. As it approached the ten-year mark, we noticed

certain limitations, particularly in the set-up, and starting in 2007 we began

developing new algorithms.

By this time, Ormand had moved to Lawrence Livermore National Labora-

tory and Johnson had left for San Diego State University. Working ﬁrst with

a student (Hai Ah Nam) and later a postdoc (Plamen Krastev) at San Diego

State University, we carefully studied bottlenecks in parallelization in the ap-

plication of the Hamiltonian. These studies led us to break up the application

of the Hamiltonian by basis sectors, which had two useful outcomes. First,

we rewrote our central application routines using simple arrays rather than the

derived types used in REDSTICK; this gave a speed-up of nearly a factor of 2.

Second, applying the Hamiltonian by quantum numbers allowed a more trans-

parent factorization of the Hamiltonian and better parallelization.

With these improvements and dramatic speed-ups, we had an entirely new

code, BIGSTICK.

Starting around 2014, through the good graces of Wick Haxton we teamed up

with UC Berkeley and Lawrence Berkeley Laboratory, and especially Haxton’s

graduate student Ken McElvain. Ken’s background in the computer industry

proved invaluable, and he was able to tweak the existing code into fantastic per-

formance, especially with regards to parallelism. Hongzhang Shan of Lawerence

Berkeley wrote an improved algorithm for using OpenMP in matvec operations.

In addition to the help of Hai Ah Nam and Plamen Krastev, we would also

like to thank Esmond Ng, Chao Yang, and Sam Williams, of Lawrence Berkeley

National Laboratory, James Vary and Pieter Maris of Iowa State University,

and many other colleagues who have provided helpful discussions, suggestions,

feedback and insight over the years. Jordan Fox helped ﬁnd some bugs in this

most recent version, and Stephanie Lauber helped ﬁnd typos and confusing

statements in this manual.

Over the years our primary research funding has come through the U.S.

Department of Energy, which has directly and often indirectly supported the

development of BIGSTICK. We are deeply grateful for this support. Support

for this project came primarily from the U.S. Department of Energy, in the

form of grants Grant DE-FG02-96ER40985, DE-FG52-03NA00082, DE-FG02-

03ER41272, as well as Louisiana State University, Lawrence Livermore National

Laboratory, San Diego State University, University of California, Berkeley, and

Lawrence Berkeley National Laboratory.

Chapter 2

How we solve the

many-body problem

In this chapter we discuss the principles of conﬁguration-interaction (CI) many-

body calculations [Shavitt, 1998, Brussard and Glaudemans, 1977, Brown and

Wildenthal, 1988, Caurier et al., 2005, Cook, 1998, Jensen, 2017, Weiss, 1961,

L¨owdin, 1955, Sherrill and Schaefer, 1999], including some diﬀerent classes of

CI codes, and give an overview of its application in BIGSTICK. Conﬁguration-

interaction is sometimes called the interacting shell model, as (a) one typically

builds the many-body basis from spherical shell-model single particle states and

(b) to distinguish from the non-interacting shell model, sometimes also called

the independent particle model.

The key points here are:

•We represent the many-body Schr¨odinger equation as a matrix eigenvalue

problem, typically with very large basis dimensions. BIGSTICK can com-

pute problems with dimensions up to ∼107on a laptop, up to ∼108on

a desktop machine, and up to ∼1010 on parallel supercomputers.

•The large-basis-dimension eigenvalue problem has two computational bar-

riers. The ﬁrst is how to solve the eigenvalue problem itself, especially

given that we almost never need all of the eigenvalues. The second is,

despite the fact the matrix is typically very sparse, the amount of data

required is still huge.

•We address the ﬁrst problem by using the Lanczos algorithm, which eﬃ-

ciently yields the low-lying eigenpairs.

•We address the second by not explicitly storing all the non-zero matrix

elements, but instead invoking a on-the-ﬂy algorithm. This on-the-ﬂy algo-

rithm, ﬁrst implemented in the Strasbourg group’s code ANTOINE [Caurier

and Nowacki, 1999], exploits the fact that the interaction only acts on two-

or three- particles at a time. The on-the-ﬂy algorithm can be thought of

as partially looping over spectator particles.

•The on-the-ﬂy algorithm explicitly depends upon the existence of two

species of particles, for example protons and neutrons, or in the case of

atoms, spin-up and spin-down electrons, so that both the many-body basis

and the action of the Hamiltonian can be factorized into two components.

This factorization is guided by additive/multiplicative quantum numbers,

such as M, the z-component of angular momentum, and parity. This fac-

torization eﬃciently and losslessly “compresses” information; we outline

the basic concepts below.

•In order to implement many-body truncations, we have an additional ad-

ditive pseudo-quantum number, which we call W. This allows a general,

though not inﬁnitely ﬂexible, ability to truncate the basis. We discuss

these truncations below, but include for example n-particle, n-hole trun-

cations and the Nmax truncation typical of the no-core shell model.

With these eﬃciencies we can run both “phenomenological” and ab initio

or no-core shell model calculations, on machines ranging from laptops to super-

computers. Although we do not discuss it in depth in this document, we rely

heavily upon both factorization and use of quantum numbers in parallelization.

2.1 Matrix formulation of the Schr¨odinger equa-

tion

The basic goal is to solve the non-relativistic many-body Schr¨odinger equation

for Aidentical fermions of mass M,





i=1 −∇2

2M+X

i<j

V(~ri−~rj)

Ψ(~r1, ~r2, . . . , ~rA) = EΨ(~r1, ~r2, . . . , ~rA),(2.1)

which we often will write using the more compact Dirac bra-ket notation

H|Ψi=E|Ψi.(2.2)

Already even Eq. (2.1) is simpliﬁed, as it leaves out explicit spin degrees of

freedom, and the potential here is purely local and two-body. BIGSTICK can

handle nonlocal interactions without blinking. BIGSTICK can also use three-

body forces, although the latter ups computational demands by nearly two

orders of magnitude, and in the current release the three-body forces are not

optimized.

The basic idea of conﬁguration interaction is to expand the wavefunction in

some convenient many-body basis {|αi}:

|Ψi=X

cα|αi(2.3)

Then, if the basis states are orthonormal, hα|βi=δα,β , the Schr¨odinger equation

becomes a matrix eigenvalue equation

Hα,βcβ=Ecα.(2.4)

Because we typically deal with many-fermion systems, the wavefunction |Ψi

is completely antisymmetric under interchange of any two particles,

Ψ(~r1, ~r2, . . . , ~ri, . . . , ~rj, . . .) = −Ψ(~r1, ~r2, . . . , ~rj. . . , ~ri, . . .).(2.5)

(One can use conﬁguration-interaction methods for many-boson systems, but

then the basis states would be totally symmetric, and a completely separate

code would be required.) A useful many-body basis are therefore Slater deter-

minants, which are antisymmetrized products of single-particle wavefunctions.

(As we will note several times in this manual, it is often important to distin-

guish between single-particle states and many-body states, as well as between,

for example, two-body matrix elements and many-body matrix elements.)

We do not explicitly use Slater determinants but rather the occupation rep-

resentation of Slater determinants using fermion creation and annihilation oper-

ators, also known as second quantization. We assume the reader is comfortable

with Slater determinants and the algebra of fermion operators, and therefore

give only a terse exposition in order to be clear about our terminology.

Suppose we have a set of Nssingle-particle states, φi(~r) where idescribes

each unique state by its quantum numbers. BIGSTICK assumes single-particle

states with rotational symmetry, and the available quantum numbers are n,

l,j, and m. Here lis the orbital angular momentum, jis the total angular

momentum, and mis the zcomponent of total angular momentum. nis the

‘radial’ quantum number; it distinguishes diﬀerent states with the same angular

momentum quantum numbers but a diﬀerent radial wavefunction. It plays no

other internal role in BIGSTICK, though it is relevant to calculating the value

of matrix element input into the code. BIGSTICK can use single-particle states

with arbitrary radial components, as long as they orthonormal; it is up to the

user to keep track of what radial wavefunction is being assumed. In many cases,

for example in so-called no-core shell model (NCSM) calculations, one uses a

harmonic oscillator basis, but that is by no means mandatory. In the same way,

lreally only gives the parity of each single-particle state.

Once a single-particle basis is deﬁned, second quantization allows us to deﬁne

many-body states. Starting with a fermion vacuum state |0i, the operator ˆa†

creates the single fermion state φi. Then the many-body state

ˆa†

i1ˆa†

i2ˆa†

i3. . . |0i(2.6)

is the occupation representation of the Slater determinant of the single particle

states φi1, φi2, . . .. For succinctness we will refer to such many-body states as

‘Slater determinants’ even when we mean the occupation representation.

Using a one-body operator such as the kinetic energy ˆ

Tcan be written using

second quantization:

T=X

Tij ˆa†

iˆaj,(2.7)

where Tij =hi|ˆ

T|ji=Rφ∗

iˆ

T φjis the one-body matrix element of the operator;

the actual value is determined through the integral sketched above. Two-body

operators, e.g. interactions between two particles, can be similarly represented,

though with two annihilation operators followed by two creation operators. It

is useful to note that all BIGSTICK and similar CI codes read in are numerical

values of the matrix elements. This means the actual form of the single-particle

wavefunctions is hidden (although BIGSTICK, like nearly all other nuclear CI

codes, requires single-particle states to have good angular momentum).

The many-body matrix elements are thus exercises in fermion second quan-

tization algebra: Hαβ =hα|ˆ

H|βiwhere the basis states |αi,|βiand the Hamil-

tonian operator ˆ

Hare all expressed using creation and annihilation operators,

given exactly in Appendix A.2.

2.2 Representation of the basis

The occupation representation is a natural one for the computer as a single

particle state can either be occupied or unoccupied, represented by a 1 or a 0.

Thus the state

ˆa†

2ˆa†

4ˆa†

5ˆa†

8|0i

can be represented by the bit string

01011001

as the single particle states 2,4, 5 and 8 are occupied and the rest unoccupied. Of

course, consistency in ordering is important as one has to pay careful attention

to phases.

In the 1970s Whitehead and collaborators used bit manipulation for fast

calculation of matrix elements in the occupation scheme [Whitehead et al., 1977].

The basic idea is simple: consider a creation operator, say ˆa†

4, applied to some

Slater determinant represented by a bit string. If the 4th bit is 0, then the

action of applying ˆa†

4is to create a 1 in its place:

ˆa†

3|110001i=|110101i,

while if it is already occupied, then the state vanishes in a puﬀ of digital smoke:

ˆa†

3|100101i= 0.

Similarly an annihilation operator such as ˆa2will destroy a state if the second

bit is empty

ˆa2|100111i= 0,

but will replace a 1 bit with a 0,

ˆa2|110101i=−|100101i.

The minus sign arises, of course, from fermion anticommutation relations. In

this way one can almost trivially ﬁnd the action of, say, a two-body operator on

a state:

ˆa†

3ˆa†

5ˆa4ˆa1|1101011i=−ˆa†

3ˆa†

5|0100011i=−|01101011i.

Then one can search through the basis to ﬁnd out what state |01101011iis.

In general we work with Hamiltonians which are rotationally invariant. This

means one can ﬁnd eigenstates of the Hamiltonian which are also simultaneous

eigenstates of total angular momentum ˆ

J2=ˆ

x+ˆ

Jy,2+ˆ

zand of (by conven-

tion) ˆ

Jz, that is,

H|Ψi=E|Ψi;

J2|Ψi= ¯h2J(J+ 1)|Ψi;

Jz|Ψi= ¯hM |Ψi.

We say such states ‘have good angular momentum.’ It is important to note that

Egenerally depends upon J, that is, except for special cases (usually involving

additional symmetries) states with diﬀerent Jare not degenerate, for a given

value of Jthe value of Edoes not depend upon M. In practical terms, what this

means is that the Hamiltonian is block-diagonal in J; it is also block-diagonal

in M, but the blocks for the same Jbut diﬀerent Mhave the exact same

eigenvalues.

Of course, whether or not the Hamiltonian is explicitly block diagonal de-

pends upon the choice of basis. We call these diﬀerent choices basis ‘schemes.’

BIGSTICK, like most nuclear CI codes, constructs its many-body basis states

using single-particle states which also have good angular momentum, i.e., have

eigenvalues j(j+ 1) and mfor ˆ

J2and ˆ

Jz, respectively. (Here and hereafter we

set ¯h= 1.) The addition of total angular momentum is nontrivial, requiring

Clebsch-Gordan coeﬃcient, but as ˆ

Jzis the generator of an Abelian subgroup,

any product of single-particle states each with good mihas good total M=

m1+m2+. . ..

What this means is it is both possible and easy to construct individual Slater

determinants which have good M(i.e., are eigenstates of ˆ

Jz). These will almost

never be states also of good J. But because ˆ

Hcommutes with both ˆ

Jzand

J2, if we take all states of a given Mand diagonalize ˆ

H, the eigenstates will be

guaranteed to also have good J(barring ‘accidental’ degeneracies that rarely

occur). Taking states of ﬁxed Mis called an M-scheme basis. It is the simplest

shell-model basis.

But the M-scheme isn’t the only choice. As mentioned above, one can also

make the many-body Hamiltonian matrix explicitly diagonal in Jas well as

M. This is a J-scheme basis. Such bases are signiﬁcantly smaller in dimension,

typically an order of magnitude smaller than the M-scheme. Of course, there

are obvious costs. Almost always a state with good Jmust ultimately be a

superposition of M-scheme Slater determinants. This means both the J-scheme

basis states, and the many-body matrix elements in this basis, are more costly

to calculate.

(Historically, in chemical and atomic physics one used conﬁguration state

functions with good angular momentum, which we would call the J-scheme.

The use of simple Slater determinants in chemical and atomic physics seems

to have been introduced by Knowles and Handy [1984] apparently unaware of

Whitehead’s innovation.)

One can go even further. Many nuclei exhibit strong rotational bands, which

can be reproduced using the group SU(3). If the nuclear Hamiltonian commuted

with the Casimir operators of SU(3), or nearly so, then the Hamiltonian would

be block diagonal in the irreps of SU(3), or nearly so, and SU(3) would be

dynamical symmetry. One can imagine other group structures as well.

Because of this, some groups use group-theoretical bases, also called symmetry-

adapted bases, such as a SU(3)-scheme basis [Draayer et al., 2012], based upon

calculations which suggest that nuclear wavefunction are dominated by a few

group irreps. The SU (3)-scheme is just like the Jonly more so: the basis is more

compact, but the basis states and the many-body matrix elements even more

complicated to derive. On the other hand, the SU (3)-scheme makes the origin

of rotational motion more transparent and potentially oﬀers a more compact

representation and understanding of the wavefunctions. Each of these schemes

oﬀer advantages and disadvantages.

2.2.1 Use of quantum numbers: factorization of the basis

One of the advantages of the M-scheme is that despite the fact it is the least

compact of basis schemes, it can be represented very eﬃciently with factoriza-

tion. Factorization is an idea used throughout BIGSTICK, and is most easily

illustrated in the basis.

We work in the M-scheme, which means every many-body basis state has

the same deﬁnite value of M. If we have an even number of particles, Mis an

integer, while for odd numbers it will be a half-integer (1/2,3/2,−5/2, etc.).

Internally BIGSTICK doubles these so they can be represented by even or odd

integers, respectively.

Each basis state, however, is a simple tensor product of a proton Slater de-

terminant and a neutron Slater determinant. Because the mquantum numbers

are additive, we have the total M=Mp+Mn, the sum of proton and neutron

M-values.

Absent other constraints, every proton Slater determinant with Mpnot only

can but must be combined with every neutron Slater determinant with Mn=

M−Mp; this, in part, guarantees that rotational invariance is respected and

that the ﬁnal eigenstates will have good total J. This in turn leads to a shortcut.

Consider the case of the 27Al nucleus, using the sd valence space. This

assumes ﬁve valence protons and six valence neutrons above a frozen 16O core.

The total dimension of the many-body space is 80,115, but this is constructed

using only 792 ﬁve-proton states and 923 six-neutron states.

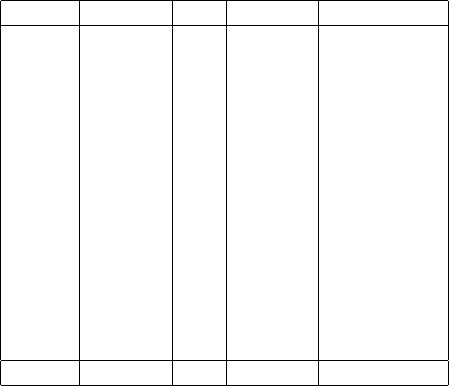
Table 2.1: Decomposition of the M-scheme basis for 5 protons and 6 neutrons

in the sd valence space (27Al), with total M=Mp+Mn+ 1/2. Here “pSD”

= proton Slater determinant and “nSD” = neutron Slater determinant, while

“combined” refers to the combined proton+neutron many-body basis states.

The subset of the basis labeled by ﬁxed Mp(and thus ﬁxed Mn) we label a

’sector’ of the basis.

Mp# pSDs Mn# nSDs # combined

+13/2 3 -6 9 27

+11/2 11 -5 21 231

+9/2 28 -4 47 1316

+7/2 51 -3 76 3876

+5/2 80 -2 109 8720

+3/2 104 -1 128 13,312

+1/2 119 0 142 16,898

-1/2 119 +1 128 15,232

-3/2 104 +2 109 11,336

-5/2 80 +3 76 6080

-7/2 51 +4 47 2444

-9/2 28 +5 21 588

-11/2 11 +6 9 99

-13/2 3 +7 1 3

Total 792 923 80,115

The reader will note that 792 ×923 = 731016 80115. Indeed, not every

ﬁve-proton state can be combined with every six-neutron state. The restric-

tion is due to conserving certain additive quantum numbers, and this restric-

tion turns out to limit usefully the nonzero matrix elements of the many-body

Hamiltonian, which we will discuss more in the next section.

For our example, we chose total M= +1/2 (though we could have chosen

a diﬀerent half-integer value). This basis requires that Mp+Mn=M; and for

some given Mp,every proton Slater determinant with that Mpcombines with

every neutron Slater determinant with Mn=M−Mp. This is illustrated in

Table 2.1, which shows how the many-body basis is constructed from 792 proton

Slater determinants and 923 neutron Slater determinants. Note we are “miss-

ing” a neutron Slater determinant; the lone Mn=−7 state has no matching

(or ‘conjugate’) proton Slater determinants.

As a point of terminology, we divide up the basis (and thus any wavefunction

vectors) into sectors, each of which is labeled by Mp, and any additional quan-

tum numbers such as parity Πp; that is, all the basis states constructed with

the same Mp(Πp, etc.) belong to the same basis ‘sector’ and have contiguous

indices. Basis sectors are also useful for grouping operations of the Hamiltonian,

as described below, and can be the basis for distributing vectors across many

processors, although because sectors are of diﬀerent sizes this creates nontrivial

issues for load balancing.

While we can represent the 80,115 basis states of 27Al in the sd with 792

proton Slater determinants and 923 neutron Slater determinants, the storage is

even more impressive for large systems. For example, in the pf shell, 60Zn, with

10 valence protons and 10 valence neutrons, has for M= 0 a basis dimension of

2.3 billion. But these are represented by ∼185,000 proton Slater determinants

and the same number of neutron Slater determinants. (In principle with self-

conjugate systems N=Zsystems one could gain further savings by keeping

only one set of Slater determinants. Because that is a small number of nuclides,

we chose not to do so.) The savings are not as dramatic for no-core shell model

calculations with Nmax truncation. For example, 12C in a basis or Nmax = 10

has a basis dimension of 7.8 billion, constructed from 1.8 million each proton

and neutron Slater determinants. The reason for the lessened eﬃciency is the

many-body truncation.

We note that factorization not only provides dramatic lossless compression

of data, it also accelerates the set up of data. In the set up phase of any CI

code, one of the major tasks is searching through long series of bitstrings and,

when one uses quantum numbers to organize the data, sorting. Factorization

improves this by reducing the length of lists to be searched and sorted. Our

second level of factorization further reduces those lists, making searches and

sorts even faster.

While factorization of the Hamiltonian was, to the best of our knowledge,

pioneered by Caurier and Nowacki [1999] in the code ANTOINE and adopted as

well by EICODE [Toivanen, 2006], NuShell/NuShellX [Brown and Rae, 2014],

and KSHELL [Shimizu, 2013] (and possibly others we are unaware of), BIGSTICK

has uniquely implemented a second level of factorization. Because most users

never see this level, we direct those interested to our paper for more details.

BIGSTICK does provide some information about this. In normal runs, as well

as in modeling runs, you will see

.... Building basis ...

Information about basis:

there are 27 sectors 1

there are 27 sectors 2

38760 SDs for species 1

184722 SDs for species 2

Total basis = 501113392

.... Basis built ...

The above example is for 56Fe in the pf shell with M= 0. The sectors are

the subsets of the proton and neutron Slater determinants (‘SDs’) with ﬁxed

quantum number M, parity, and optionally W. Here ‘species 1’ refers to protons

and ‘species 2’ refers to neutrons.

2.3 The Lanczos algorithm and computational

cost

With bit manipulation allowing one to quickly calculate matrix elements, one

could address much larger spaces, spaces so large they were not amenable

to complete diagonalization, e.g., through the Householder algorithm [Parlett,

1980, Press et al., 1992]. But in nuclear structure conﬁguration-interaction one

almost never wants all the eigensolutions; instead one typically just wants the

low-lying states. Thus Whitehead et al. [1977] introduced another innovation:

use of the Lanczos algorithm to ﬁnd the extremal eigenstates.

The Lanczos algorithm is a subspecies of Arnoldi algorithms. We describe

the Lanczos algorithm in Chapter 7, but the key idea is that, starting from

an initial vector often called the pivot, one iteratively constructs a sequence of

orthonormal basis vectors that form a Krylov subspace, as well as the elements

of the Hamiltonian in that subspace. The genius of Arnoldi/Lanczos algorithms

is that they use the matrix to be diagonalized to construct the basis vectors; by

applying the Hamiltonian matrix to a given basis vector one constructs, after

orthogonalization, the next basis vector. One can show via the classical theory

of moments that the extremal eigenvalues of the Hamiltonian in the Krylov

subspace quickly converge to those of the full space. Although it depends upon

the model space, the Hamiltonian, and the choice of pivot (starting vector to

kick oﬀ the Lanczos iterations), one can often reach a converged ground state

energy in as few as twenty Lanczos iterations, and the lowest ﬁve states in as

few as 100 iterations.

Now let us think about the computational cost of carrying out CI, both

in terms of operations (time) and memory (storage). Before doing so let us

highlight a key point. Most often in discussing CI one cites the basis dimen-

sion. But, as we will argue below, the real measure of the computational cost is

the number of nonzero matrix elements. Now, for any given scheme, the num-

ber of nonzero matrix elements scales with the basis dimension. However, for

diﬀerent schemes the proportionality is diﬀerent: J-scheme is denser than M-

scheme; furthermore, even within the same basis scheme, diﬀerent truncations

have diﬀerent densities, e.g., the NCSM is much denser than ‘phenomenological’

calculations. Therefore, for absolute comparison of the computational cost of a

problem, the number of nonzero matrix elements is a much better measure than

basis dimension.

That said, let us look at the computational cost of matvec:

wα=X

Hα,βvβ.

Let the dimension of the vector space be N. If the many-body matrix His

a fully dense (but real, symmetric) matrix, the above matvec requires N2

operations as well as storage of N2many-body matrix elements. However, His

almost never fully dense. This can be most easily understood in the M-scheme,

where the fundamental occupation-space basis states can be represented as raw

bit strings. A two-body interaction can at most shift two bits. Therefore if

two basis states |αiand |βidiﬀer by more than two bits, the matrix element

between them must be zero. A typical ‘sparsity’ of M-scheme Hamiltonians is

2×10−6, that is, only two out of every million many-body matrix elements is

nonzero. (Three-body forces, naturally, lead to denser matrices, roughly two

orders of magnitude denser.)

If one has a basis dimension of a million, then there are roughly a million

nonzero matrix elements; because one needs not only the value of the matrix

element but some index to local it in the matrix, in single precision this requires

roughly 8 megabytes of memory. When one goes up to a basis dimension of one

billion, however, this number goes up by (103)2to 8 terabytes! Reading 8 Tb

of data even from fast solid state disks is a very slow proposition. If one stores

the matrix elements in core memory across many processors, as the code MFDn

does, this requires a minimum of many hundreds if not thousands of processors.

2.4 Representation of the Hamiltonian

As discussed above, M-scheme conﬁguration-interaction calculations require a

many-body vector space of very large dimensions, and the many-body Hamil-

tonian matrix, while very sparse, still in large cases nonetheless the nonzero

matrix elements end requiring a huge amount of data.

If you were to examine closely, say, the bit representation of the basis states,

or the nonzero matrix elements, you’d ﬁnd something confounding: quite a lot of

data is repeated, over and over. The same proton bit strings (which we generally

call proton Slater determinants, although technically they are representations of

said determinants) are repeated many times, sometimes many millions of times

or more, and the same for the neutron bit strings (neutron Slater determinants).

In the same way, the same values appear, thousands and millions of times, in the

non-zero many-body matrix elements, though with both positive and negative

values.

This redundancy can not only be understood, it can be turned to our ad-

vantage through factorization, both of the basis and of matvec operations.

The idea is similar to the factorization of the basis. Any two-body Hamil-

tonian can be split into forces that act only on protons, forces that act only

on neutrons, and interactions between protons and neutrons. Consider forces

acting only on protons; in a factorized basis, the neutrons are spectators. If

we write our basis states as a simple tensor product between a proton ‘Slater

determinant’ |ipiand and a neutron Slater determinant, |jni, so that the basis

state |αi=|ipi|jnithe pure proton Hamiltonian matrix element is

hα|ˆ

Hpp|α0i=hip|ˆ

Hpp|i0

piδjn,j0

n.(2.8)

We therefore only have to store the proton matrix element hip|ˆ

Hpp|i0

pi, and can

trivially loop over the neutron Slater determinants. You can see how you could

get dozens, hundreds, or thousands of matrix elements with the same value,

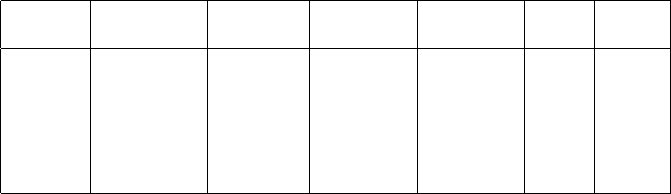
Table 2.2: Number of one- and two-body ‘jumps’ and storage requirements for

representative atomic nuclei in diﬀerent model spaces (described in Appendix

B). For storage of nonzero matrix elements (penultimate column) we assume

each many-body matrix element is stored by a 4-byte real number and its lo-

cation encoded by a single 4-byte integer. Storage of a single jump (initial and

ﬁnal Slater determinants for a species, and matrix element and phase) requires

13 bytes. All storage (ﬁnal two columns) are in gigabytes (GB).

Nuclide space basis # 1-body # 2-body Store Store

dim jumps jumps m.e.s jumps

28Si sd 9.4×1044.8×1047.6×1030.2 0.002

52Fe pf 1.1×1084.0×1068.5×106700 0.16

56Ni pf 1.1×1091.5×1074.0×1079800 0.6

4He Nmax = 22 9 ×1075.3×1084.7×1099300 69

12CNmax = 8 6 ×1086×1083×1095200 45

13CNmax = 6 3.8×1077×1073×108210 4.3

just with diﬀerent jn. Furthermore, because the neutron Slater determinants

are frozen, the quantum numbers cannot change, which severely restricts the

action of the proton-only Hamiltonian. The matrix elements hip|ˆ

Hpp|i0

piare

called jumps and we only need to store them (and know of the neutron indices

jnover which to loop).

For proton-neutron interactions the action is more complicated but the same

basic ideas hold: one stores separate proton jumps and neutron jumps and

reconstructs the value of the matrix element. Table 2.2 shows the storage for

nonzero matrix elements and of jumps needed for a number of representative

nuclei, in both phenomenological and NCSM calculations. You can see there

are at least two orders of magnitude diﬀerence. Thus, for example, 52Fe, which

would require 700 Gb of storage for just the nonzero matrix elements, only needs

less than a Gb for storage in factorization (in this particular case, storage of

the Lanczos vectors is much higher burden) and thus can be run on an ordinary

desktop computer.

The price one pays, of course, is the factorized reconstruct-on-the-ﬂy algo-

rithm is much more complicated.

2.5 An incomplete survey of other codes

While this manual is about BIGSTICK, it is appropriate to put it in the context of

other (nuclear) conﬁguration-interaction codes. One can broadly classify them

by (a) basis scheme, (b) representation and storage of many-body matrix el-

ements, (c) rank of interactions (i.e., two-body only or two- and three-body

forces), (d) parallelism, if any, and ﬁnally (e) general area of applicability, e.g.,

primarily to phenomenological spaces, which usually means a frozen core, and

interactions, or to ab initio no-core shell model calculations. Please keep in

mind that most of these codes are unpublished or have only partial informa-

tion published, and that many of the details have been gleaned from private

conversations; information on some codes, such as the powerful Japanese code

MSHELL, do not seem to be available. We apologize for any accidental misrep-

resentations. All of these codes have powerful capabilities and have made and

are making signiﬁcant contributions to many-body physics.

Among the very earliest codes was the Oak Ridge-Rochester code from the

1950s and 1960s, which fully diagonalized the Hamiltonian after computing

the many-body J-scheme matrix elements via coeﬃcients of fractional parent-

age. It was succeeded by the Whitehead (Glasgow) code and its descendents,

which used bit manipulation to compute the many-body matrix elements in the

M-scheme, and solved for low-lying eigenstates using the Lanczos algorithm,

ANTOINE [Caurier and Nowacki, 1999], MFDn [Sternberg et al., 2008], and KSHELL

[Shimizu, 2013] are also M-scheme codes. Examples of J-scheme codes in nu-

clear physics include OXBASH [Brown et al., 1985] and its successors NuShell

and NuShellX [Brown and Rae, 2014], NATHAN [Caurier et al., 1999], and EICODE

[Toivanen, 2006]. There have also been attempts to use group theory to con-

struct so-called symmetry-guided bases. The main eﬀort is in SU(3) [Draayer

et al., 2012]. Although this approach is very promising, only time will tell for

sure if the advantages gained by group theory will outweigh the technical diﬃcul-

ties needed to implement, for although the bases are small, they are signiﬁcantly

denser, and furthermore the group theory is very challenging.

Regarding access to the many-body Hamiltonian matrix element, the Oak

Ridge-Rochester and Whitehead codes stored matrix elements on disk, as do

OXBASH and NuShell. The very successful code MFDn [Sternberg et al., 2008],

used primarily but not exclusively for no-core shell model calculations, stores the

many-body Hamiltonian matrix elements in RAM, much faster to access than

storing on disk, but for all but the most modest of problems requires distribution

across hundreds or thousands of nodes on a parallel computer spread across

many MPI processes.

Factorization methods, pioneered in ANTOINE [Caurier and Nowacki, 1999],

have been used in several other major CI codes: NATHAN[Caurier et al., 1999],

EICODE [Toivanen, 2006], NuShellX [Brown and Rae, 2014], KSHELL [Shimizu,

2013], and our own unpublished codes REDSTICK (so named because it was orig-

inated at Louisiana State University, located in Baton Rouge), and of course

BIGSTICK. Factorization has also been used in nuclear structure physics as a

gateway to approximation schemes [Andreozzi and Porrino, 2001, Papenbrock

and Dean, 2003, Papenbrock et al., 2004, Papenbrock and Dean, 2005]. The

codes most widely used by people beyond their authors have been OXBASH and its

successor NuShell/NuShellX, and ANTOINE. Because of their wide use, and be-

cause one of us (Ormand) heavily used OXBASH, the default formats for our input

.sps and .int ﬁles are heavily modeled upon the OXBASH/NuShell/NuShellX

formats.

Like BIGSTICK,MFDn has been parallelized with both MPI and OpenMP and

has carried out some of the largest supercomputer runs in the ﬁeld. NuShellX

has only OpenMP parallelization. The parallelization of other codes is unknown.

In closing, we note that besides conﬁguration-interaction there are many

other approaches to the many-body problem, such as the coupled cluster method,

the Green’s function Monte Carlo method, the in-medium similarity renormal-

ization group, density functional methods, and so on, each with their own ad-

vantages and disadvantages. There are also methods closely related to conﬁgu-

ration interaction, such as the ‘Monte Carlo shell model,’ the ‘shell-model Monte

Carlo,’ generator-coordinate codes, and the importance truncation shell model.

The main weakness of conﬁguration interaction is that it is not size extensive,

which means unlinked diagrams must be cancelled and thus the dimensionality

of the problem grows exponentially with particle number and/or single-particle

basis. The advantages of CI is: it is fully microscopic; its connection to the

many-body Schr¨odinger equation (2.1) is pedagogically transparent; it gener-

ates excited states as easily as it does the ground state; it can handle even and

odd numbers of particle equally well and works well far from closed shells; and

ﬁnally places no restriction on the form of either the single-particle basis or on

the interaction (i.e., local and nonlocal forces are handled equally well, because

the occupation space basis is intrinsically nonlocal to begin with).

Chapter 3

Getting started with

BIGSTICK

BIGSTICK is a conﬁguration-interaction many-fermion code, written in Fortran

90. It solves for low-lying eigenvalues of the Hamiltonian of a many fermion

system. The Hamiltonian is assumed to be rotationally invariant and to con-

serve parity, and is limited to two-body (and three-body, in progress) forces.

Otherwise few assumptions are made.

BIGSTICK allows for two species of fermions, such as protons and neutrons.

BIGSTICK is ﬂexible, able to work with ”no-core” systems and phenomenolog-

ical valence systems alike, and can compute the electronic structure of single

atoms or cold fermionic gases (in which cases the two species are interpreted as

”spin-up” and ”spin-down”). BIGSTICK has a ﬂexible many-body truncation

scheme that covers many common truncations. For nuclei it can assume isospin

symmetry or break isospin conservation. Interaction matrix elements must be

pre-computed by a third-party program and stored as a ﬁle, but BIGSTICK

accepts a variety of matrix element formats.

3.1 What can BIGSTICK do?

BIGSTICK can:

•compute the ground state energies and low-lying excitation spectra, in-

cluding angular momentum and, if relevant, isospin, of many-body sys-

tems with a rotationally invariant Hamiltonian; wave functions are also

generated;

•compute expectation values of scalar one- and two-body operators;

•compute one-body densities, including transition densities, among the low-

lying levels, which allows one to calculate transition rates, life times, mo-

ments, etc.;

•compute transition strength probabilities or strength functions for one-

body transition operators, useful when one needs to model transitions to

many excited states;

•use the strength function capability to decompose the wave function by

the eigenvalues of an operator, such as the Casimir of some group.

Along with this, one can ask, what are BIGSTICK’s limitations? This largely

depends upon the computer used and the many-body system. In low-energy

nuclear structure physics, which is the main focus of our research, one can eas-

ily run on a laptop any nuclide in the phenomenological sd space, and on a

workstation reach most nuclides in the phenomenological pf space. Although

dimensionality is not the most important determination of computational bur-

den, one can generally run cases of dimension up to a few million or even tens of

millions, if one is patient, on a laptop, a few hundred million on a workstation,

and a few billion on a parallel supercomputer.

As always, of course, much of the limitations depend upon the user. Al-

though we provide a few example input ﬁles, it is generally up to the user

to provide ﬁles for the model space, the interaction, and codes to postprocess

density matrices into transitions. (We do provide some tools for this.)

3.2 Downloading and compiling the code

BIGSTICK was developed for UNIX/Linux/MacOSX systems. We made no eﬀort

to adapt it to running under Microsoft Windows.

To get BIGSTICK, download it from GitHub:

git clone https://www.github.com/cwjsdsu/BigstickPublick/

Your distribution includes a makeﬁle. We have developed BIGSTICK to com-

pile and run successfully with Intel’s ifort compiler and GNU gfortran. You may

need to edit the makeﬁle to put in the correct compiler and/or if you wish to use

for example LAPACK libraries. We have written the code to require minimal

special compile ﬂags.

For example,

PROMPT> make serial

makes a serial version of the code with the Intel ifort compiler by default. Several

other options are:

PROMPT> make openmp →an OpenMP parallel version using ifort

PROMPT> make gfortran →a serial version using gfortran

PROMPT> make gfortran-openmp →an OpenMP version using gfortran

and so on. To see all the options encoded into the makeﬁle,

PROMPT> make help

Each of these generates an executable with the nonstandard extension .x,

chosen to make deletion easy: bigstick.x, bigstick-openmp.x, bigstick-

-mpi.x, and bigstick-mp-omp.x. There are options for compiler on a number

of supercomputers. Please keep in mind, however, that compilers and compile

ﬂags on supercomputers are a Red Queen’s Race, and it is up to the user to

tune the makeﬁle for any given conﬁguration.

Libraries. In routine operations, BIGSTICK uses the Lanczos algorithm to

reduce the Hamiltonian matrix to a truncated tridiagonal matrix whose eigen-

values approximate the extremal eigenvalues of the full matrix. This requires an

eigensolver for the tridiagonal. For modest cases, one can also choose to fully di-

agonalize the Hamiltonian, using a Householder algorithm. (In practice we ﬁnd

this can be done quickly for basis dimensions up to a few thousand, and with

patience can be done up to a basis dimension ∼104.) For both cases we use the

LAPACK routine DSYEV, which solves the real-valued, double-precision symmet-

ric eigenvalue problem. The actual matrix elements are given in single-precision,

but we found when the density of eigenvalues is high, double-precision gives us

better values for observables, including angular momentum Jand isospin T.

Although in principle one could link to a library containing DSYEV, in practice

this is highly platform dependent. Also, except for special cases where one is

fully diagonalizing very large matrices and are impatient, the call to DSYEV is

a tiny fraction of the time. Hence we supply an unmodiﬁed copy of DSYEV and

required LAPACK routines, and there is no need to call any libraries.

3.3 Required input ﬁles

In order to solve the many-body Schr¨odinger equation, BIGSTICK requires at

least two inputs:

(a) A description of the single-particle space, usually through a ﬁle with exten-

sion .sps (although if one is running a no-core shell model calculation, there is

an option to generate this automatically); and

(b) A ﬁle containing the matrix elements of the interaction, in the form of

single-particle energies and two-body matrix elements (and, optionally, three-

body matrix elements).

We supply several example cases for both inputs, including some commonly

used spaces and interactions. But in general it is the user’s duty to supply

these input ﬁles and, importantly, to make sure they are consistent with each

other, i.e., to make sure the ordering of single-particle orbits in the .sps ﬁle

is consistent with those in the interaction ﬁle. We describe the ﬁle formats in

detail in Chapter 4

3.4 Running the code

BIGSTICK has a simple interactive input. It can also be run by pipelining the

input into the code.

To run:

PROMPT>bigstick.x

(we recommend you keep the source code, the executable, and the input

data ﬁles in separate directories, and make sure the executable is in your path).

We use the nonstandard extension .x to denote executables.

First up is a preamble, with the version number, information on parallel

processes, and a reminder for citations:

BIGSTICK: a CI shell-model code

Version 7.8.1 Aug 2017

by C. W. Johnson, W. E. Ormand,

K. S. McElvain, and H.Z. Shan

For reference please cite:

C. W. Johnson, W. E. Ormand, and P. G. Krastev

Comp. Phys. Comm. 184, 2761-2774 (2013)

[also found in arXiv:1303.0905]

This code distributed under Open Source License GPL.v2

Running on NERSC_HOST: none

scratch_dir (*.wfn,...): .

Number of MPI processors = 1

NUM_THREADS = 1

Next and most important is the main menu:

**************************************

* *

* OPTIONS (choose 1) *

* (i) Input automatically read from "autoinput.bigstick" file *

* (note: autoinput.bigstick file created with each nonauto run) *

* (n) Compute spectrum (default); (ns) to suppress eigenvector write up *

* (d) Densities: Compute spectrum + all one-body densities *

* (dx) Densities: Compute one-body densities from previous run *

* (x) eXpectation value of an operator (from previous wfn) *

* (?) Print out all options *

* *

**************************************

Enter choice

The most common choice is “n”for a normal run.

To facilitate batch runs or multiple runs with similar inputs, each time BIG-

STICK runs it creates a ﬁle autoinput.bigstick. This ﬁle can be edited;

choosing “i” from the initial menu will direct BIGSTICK to read all subsequent

commands from that ﬁle.

Next up:

Enter output name (enter "none" if none)

If you want your results stored to ﬁles, enter something like Si28run1.

The code will then create the following ﬁles:

Si28run1.res : text ﬁle of eigenenergies and timing information.

Si28run1.wfn: a binary ﬁle (not human readable) ﬁle of the wavefunctions for

post-processing or for other runs, e.g. “x” expectation values, etc.

Si28run1.log: a logﬁle of the run, useful for tracking the exact conditions

under which the run happened, as well as diagnosing problems.

Other ﬁles generated but not need by most users:

Si28run1.lcoef : text ﬁle of Lanczos coeﬃcients;

timinginfo.bigstick and timingdata.bigstick: ﬁles on internal timing;

distodata.bigstick: a ﬁle contain information on distribution of work across

MPI processes;

and others used primarily by the authors for diagonsing behavior.

If you enter “none,” the .bigstick ﬁles will be created but no results ﬁle

(.res) and no wavefunction ﬁle (.wfn).

Enter file with s.p. orbit information (.sps)

(Enter "auto" to autofill s.p. orbit info )

This provides information about the single-particle space. A typical answer

might be sd, which tells BIGSTICK to open the ﬁle sd.sps, and read in informa-

tion about the sd valence space. (Please be aware that in most cases one does

not enter the extension, such as .sps or .int.) The auto option can only be

used for “no-core” nuclear shell-model calculations.

Enter # of protons, neutrons

These are the valence protons and neutrons. So, for example, if one wants to

compute 24Mg, which has 12 protons and 12 neutrons, but the sd single-particle

space assumes a closed 16O core, so one has 4 valence protons and 4 valence

neutrons. For other kinds of fermions, see the appendix.

Enter 2 x Jz of system

BIGSTICK is a “M-scheme” code, meaning the many-body basis states have ﬁxed

total M=Jz(as opposed to J-scheme codes such as NuShell which the basis

has ﬁxed total J). You must enter an integer which is twice the desired value

of M. If there are an even number of particles, this is usually 0. For an odd

number of nucleons, you must enter an odd integer, typically ±1. Because the

Hamiltonian is rotationally invariant, the results should not change for a value

±M. One can choose a non-minimal Mif, for example, you are interested in

high-spin states.

Enter parity +/- :

In addition to ﬁxed M,BIGSTICK has ﬁxed parity. BIGSTICK automatically

determines if more than one kind of parity is allowed and asks for the parity.

The sd space, for example, has only positive parity states, and so this input is

automatically skipped.

If you would like to compute both parities, enter ‘0’. (At the current time,

this is necessary if you want to compute parity-changing transitions, as for any

transition calculations BIGSTICK must work in the same basis.)

Would you like to truncate ? (y/n)

In some cases it is possible to truncate the many-body space, discussed in

detail in section 4.2.2.

BIGSTICK will then generate the basis; in most cases this takes only a fraction

of a second. BIGSTICK will print out some information about the basis, which

you can generally ignore.

The next item is to read in the matrix elements of the Hamiltonian.

Enter interaction file name (.int)

(Enter END to stop )

You can enter in a number of interaction ﬁles. The format for the interaction

ﬁles will be discussed below.

Enter scaling for spes, A,B,X ( (A/B)^X ) for TBMEs

(If B or X = 0, then scale by A )

After the interactions ﬁles have been read in, BIGSTICK sets up the jump arrays

for reconstructing the matrix elements on the ﬂy. After that, the eigensolver

menu comes up:

/ ------------------------------------------------------------------------\

| |

| DIAGONALIZATION OPTIONS (choose one) |

| |

| (ex) Exact and full diagonalization (use for small dimensions only) |

| |

| (ld) Lanczos with default convergence (STANDARD) |

| (lf) Lanczos with fixed (user-chosen) iterations |

| (lc) Lanczos with user-defined convergence |

| |

| (td) Thick-restart Lanczos with default convergence |

| (tf) Thick-restart Lanczos with fixed iterations |

| (tc) Thick-restart Lanczos with user-defined convergence |

| (tx) Thick-restart Lanczos targeting states near specified energy |

| |

| (sk) Skip Lanczos (only used for timing set up) |

| |

\ ------------------------------------------------------------------------/

As noted, the standard choice is ‘ld’ for default Lanczos. Other options are

discussed later.

Enter nkeep, max # iterations for lanczos

(nkeep = # of states printed out )

Except for very small cases, BIGSTICK does not ﬁnd all the eigenvalues. In-

stead it uses the Lanczos algorithm (introduced by Whitehead et al to nuclear

physics) to ﬁnd the low-lying eigenstates. The variable nkeep is the number of

targeted eigenpairs; typical values are 5-10. One can either set a ﬁxed number

of iterations, typically 100-300, or set a maximal number of iterations and allow

BIGSTICK to stop sooner using a test for convergence (discussed in detail below).

BIGSTICK will then carry out the Lanczos iterations, printing out interme-

diate eigenvalues. The ﬁnal result, which if a output ﬁle name was chose is also

written to the .res ﬁle, looks like

State E Ex J T

1 -149.77950 0.00000 0.000 0.000

2 -147.78011 1.99939 2.000 0.000

3 -144.92743 4.85207 4.000 0.000

4 -144.11148 5.66801 0.000 0.000

5 -142.72124 7.05826 3.000 0.000

This is fairly self-explanatory. Eis the absolute energy, Ex the excitation energy

relative to the ﬁrst state, and Jand Tare the total angular momentum and

isospin, respectively. Even though only Mis ﬁxed, because the Hamiltonian

commutes with ˆ

J2the ﬁnal states will have good J. Lack of good Jmost likely

signals lack of convergence, or states degenerate in energy but with diﬀerent

J). Lack of good Jcan also signal an error in the input ﬁle (speciﬁcally, a

disallowed Jfor a particular set of orbits; we have written error traps to catch

such a problem), or, lastly and only infrequently, a bug in the code itself.

If the input matrix elements respect isospin, then Tshould also be a good

quantum number. BIGSTICK allows one to read in isospin-breaking matrix ele-

ments, discussed in more detail in section 4.3.2.

BIGSTICK can also compute one-body density matrix elements at the end of

a run; choose option din the initial menu. The format and conventions for the

density matrices are in section 4.4.3.

The wavefunctions are saved to a .wfn ﬁle, unless you choose option ns

in the initial menu. BIGSTICK can then post-process the ﬁles, for example

computing the expectation value of a scalar (Hamiltonian-like) operator, section

4.6.1; compute overlap between wavefunctions from two diﬀerent runs, section ;

or apply a non-scalar transition operator to a wavefunction and then compute

the strength distribution of that transition, sections 4.6.2, 5.2.2, and 5.2.3.

Nuclide space dim # ops min. store run time

24Mg sd 28,503 8.6M 34 Mb 5 s

48Cr pf 2 M 1.5 B 6 Gb 15 min

51Mn pf 44M 41B 160 Gb 9 hr

56Fe pf 500M 0.9 T 3.6 Tb 6 d

60Zn pf 2.3B 5T 20 Tb 35 d

12CNmax 6 32M 41 B 160 Gb 7 hr

6Li Nmax 12 49M 180 B 700 Gb 30 hr

12CNmax 8 594M 1.2T 5 Tb 8 d

16ONmax 8 1B 2 T 8 Tb 14 d

10BNmax 10 1.7B 5 T 20 Tb 35 d

6Li Nmax 16 800M 7T 27 Tb 46 d

Table 3.1: ‘Typical’ run times for various nuclides, running in serial for 150

Lanczos iterations. Here ‘min. store’ is an estimate of the minimal storage

required for nonzero matrix elements.

3.5 Some sample runs

In the directory SampleRuns that should be found in your distribution, you will

ﬁnd various examples of runs, along with sample outputs to check the code is

working correctly.

3.6 Typical run times

In this section we survey ‘typical’ run times for calculations using BIGSTICK. Of

course, these depend upon the clock-speed of your chip as well as the compiler,

as well as how much parallelism you are exploiting. As we show below, BIGSTICK

does scale well in parallel mode.

Table 3.1 gives, for a variety of nuclides, the dimensionality of the space, the

number of operations (which is approximately though not exactly the number

of nonzero matrix elements), the minimal storage which would be required to

store the nonzero matrix elements, and ﬁnally an approximate run time, as-

suming 150 Lanczos iterations on a serial machine. The actual time may vary

a lot, depending on clock speed and how eﬃciently the operations are actually

processed. Parallelism, of course, can speed up the wall clock times considerably.

Empirically, one ﬁnds that the number of nonzero matrix element (here,

operations) generally scales like (dim)1.25 for two-body interactions, and ≈

(dim)1.5for three-body forces.

Chapter 4

Using BIGSTICK, in detail

BIGSTICK has two basic modes. It can calculate many-body spectra and wave

functions, and it can process those wave functions in several ways. In order to

generate the low-lying spectrum and wave functions, you need to, ﬁrst, deﬁne

the model space, and second, provide an interaction.

4.1 Overview of input ﬁles

BIGSTICK uses three classes of externally generated ﬁles. Mandatory are: ﬁles

which deﬁne the single-particle space, and ﬁles for interaction matrix elements.

Optionally, BIGSTICK can also use ﬁles for one-body transition matrix elements.

Here we brieﬂy summarize those ﬁles, and in later sections give more details.

Files which deﬁne the single-particle space have the extension either .sps or

.sp. When prompted, the user only supplies the name, not the extension, i.e.,

if the ﬁle is sd.sps only enter sd.BIGSTICK will automatically search for both

sd.sps and, if not found, then sd.sp. These ﬁles can assume isospin symmetry

or separate proton-neutron orbits, but at this time, BIGSTICK requires that the

proton and neutron single-particle spaces initially be the same. BIGSTICK can

however truncate the proton and neutron spaces diﬀerently.

If the user is carrying out a ‘no-core shell-model’ calculation where the single-

particle orbits are assumed to occur in a default order, BIGSTICK has an ‘auto’

option for deﬁning the single-particle space and no input ﬁle is required.

BIGSTICK accepts two classes of ﬁles for interaction matrix elements. The

default format is derived from OXBASH/NuShell. It can be in isospin-conserving

format or in explicit proton-neutron format. Be aware that the latter has two

possibilities for normalization of the proton-neutron states. These ﬁles are used

primarily though not exclusively for phenomenological spaces and interactions.

All ﬁles with this format must end in the extension .int, and as with the single-

particle ﬁles, one enters only the name, i.e., if the ﬁle is usda.int one enters

in only usda. If the ﬁle is in isospin-conserving format, you only need to enter

the name of the ﬁle. If the ﬁle is in proton-neutron format, you must ﬁrst tell

BIGSTICK the normalization convention, see section 4.3.2. These ﬁles have broad

options for scaling the magnitudes of matrix elements, see section 4.3.1.

BIGSTICK also accepts ﬁles in a format readable by the MFDn code. Here one

must enter in the full name of the ﬁle, even if it has the extension .int, so that

if the ﬁle is TBME.int you enter TBME.int not TBME; this signals to BIGSTICK

to expect the MFDn format. Go to section 4.3.3 for more details.

Finally, BIGSTICK can apply a one-body operator to a wave function in order

to generate a transition strength function. These have extension .opme. These

are deﬁned in section 4.6.2, with advanced instruction and examples in sections

5.2.2 and 5.2.3.

While we supply sample ﬁles of these various formats, in general it is the

responsibility of the user to generate or obtain input ﬁles.

All other ﬁles BIGSTICK needs, such as wave function ﬁles with extension

.wfn, must been generated by a run of BIGSTICK itself.

4.2 Deﬁning the model space

A many-body model space is deﬁned by a single-particle space, the valence Zand

N, a total Mvalue, a total parity (if applicable), and, optionally, truncations on

that model space. Note that if you are carrying out what we call a secondary

option, which starts from an existing wave function as stored in a .wfn ﬁle,

BIGSTICK will automatically read from that ﬁle the information on the basis.

You only need to deﬁne the model space when carrying out a ‘primary’ option.

The single-particle space is deﬁned one or two ways. Either read in a ﬁle

deﬁning the single-particle space, or, for so-called no-core shell model calcula-

tions, automatically generate the basis in a pre-deﬁned form, using the autoﬁll

or ‘auto’ option.

For consistency, we generally refer to orbits as single-particle spaces labeled

by angular momentum jbut not jz, while states are labled by both jand jz.

Our default format for deﬁning the single-particle space are derived from the

format for OXBASH/NuShell/NuShellX ﬁles. A typical ﬁle is the sd.sps ﬁle:

! sd-shell

iso

0.0 2.0 1.5 2

0.0 2.0 2.5 2

1.0 0.0 0.5 2

There is no particular formatting (spacing) to this ﬁle. Any header lines starting

with ! or # are skipped over. The ﬁrst non-header line denotes about the isospin

symmetry or lack thereof. iso denotes the single-particle space for both species

is the same; one can still read in isospin breaking interactions. The second line

(3 in the example above) is the number of single-particle orbits. The quantum

numbers for the single-particle orbits as listed are: n, l, j, w; the ﬁrst three

numbers are real or integers, jis a real number. nis the radial quantum

number, which play no role in BIGSTICK except to distinguish between diﬀerent

states. lis the orbit angular momentum and jis the total angular momentum;

for the case of nucleons j=l±1/2. In BIGSTICK the most important quantum

number is j;lis used internally only to derive the parity of each state.

While for most applications jis a half-integer, i.e., 0.5, 1.5, 2.5, etc., it can

also be integer. In that case l=jand one should intepret ‘protons’ and ‘neu-

trons’ as ‘spin-up’ and ‘spin-down.’ One can compute the electronic structure

of isolated atoms, for example.

While nand lare not internally signiﬁcant for BIGSTICK, they aid the human-

readability of the .sps ﬁles; in addition, they can be invaluable as input to other

code computing desired matrix elements.

BIGSTICK automatically unpacks each orbit to arrive at the 2j+ 1 single-

particle states with diﬀerent jz.

The last ‘quantum number,’ w, is the weight factor, used for many-body

truncations, described in Section 4.2.2. It must be a nonnegative integer.

BIGSTICK can handle any set of single-particle orbits; the only requirement

is that each one have a unique set of n, l, j. (Although nand lare written above

as real numbers, for historical reasons, they must have integer values. jcan

take either half-integer values or integer values with l=j; this latter we refer

to as LS-coupling and is discussed in detail later on. All the j-values in a .sps

ﬁle must be consistent, that is, all half-integer or all integer.)

For example, one could have a set of l= 0, j = 1/2 states:

iso

0 0 0.5 0

1 0 0.5 0

2 0 0.5 0

3 0 0.5 0

As of the current version of BIGSTICK, one cannot deﬁne completely inde-

pendent proton and neutron spaces. One can however specify two variations.

One can have pns instead of iso, which originally signalled to BIGSTICK to

anticipate isospin-breaking interactions. This option is nearly obsolete. A more

useful option is wpn, where protons and neutrons can have diﬀerent weights:

wpn

3 3

0.0 2.0 1.5 3

0.0 2.0 2.5 2

1.0 0.0 0.5 2

0.0 2.0 1.5 3

0.0 2.0 2.5 2

1.0 0.0 0.5 3

While the proton and neutron orbits can have diﬀerent weights, at this time the

sets of quantum numbers must be the same and they must be listed in the same

order. In the example above, we have proton 0d3/2, 0d5/2, and 1s1/2, and then

the same for neutrons. Only the wvalues can be diﬀerent.

The ordering of the single particle orbits is important and must be consistent

with the input interaction ﬁles. If one uses our default-format interaction ﬁles,

one must supply a .sps ﬁle.

It is possible to set environmental variables so that BIGSTICK automatically

searches for .sps ﬁles in a diﬀerent directory:

You can set a path to a standard repository of .sps/.sp files

by using the environmental variable BIG_SPS_DIR.

Just do :

export BIG_SPS_DIR = (directory name)

export BIG_SPS_DIR=/Users/myname/sps_repo

Currently BIG_SPS_DIR is not set

While we recommend the default format, we also allow for NuShell/NuShellX-

compatible .sp ﬁles, which have a similar format. Like our default format, they

also come in isospin-symmetric and proton-neutron format. An annotated ex-

ample of the former is

! fp.sp

t ! isospin-symmetric

40 20 ! A, Z of core

4 ! number of orbits

1 4 ! number of species, orbits per species

1 1 3 7 ! index, n, l, 2 x j

2213

3135

4211

As with the default format, BIGSTICK will skip over any header lines starting

with ! or #. The next line, t, denotes isospin symmetry. (Note that, however,

because BIGSTICK requires the proton and neutron spaces to be the same, one

does not need this option, and independent of the form of the single-particle

space ﬁle one can read in interaction matrix elements in either isospin-conserving

or -breaking format.) The next line, 40 20 are the Aand Zof the core; these

are not actually needed but are inherited.

The third non-header line, here 4denotes the number of indexed orbits.

The fourth non-header line, 1 4, tells us there is just one ‘kind’ of particle

with 4 orbits. The next four lines are the orbits themselves, with the orbital

index, radial quantum number n, orbital angular momentum l, and twice the

total angular momentum j. Here ndistinguishes between diﬀerent orbits which

otherwise have the same land j. In this example, nstarts at 1, while in our

other example nstarts at 0. This makes no diﬀerence for BIGSTICK’s workings.

This can be contrasted with the pn option for the same space, which has

separate indices for protons and neutrons.

! fppn.sp

40 20

244

1137

2213

3135

4211

5137

6213

7135

8211

The main diﬀerentce are in the third and fourth lines. There are a total of 8

orbits labeled, among two kinds or ‘species’ of particles, each with 4 orbits. The

ﬁrst 4 orbits are attributed to protons and the the next 4 to neutrons. While

BIGSTICK accepts both formats, in practical terms it does not make a diﬀerence.

At this time BIGSTICK does not allow for fully independent proton and neutron

spaces, and the ordering of proton and neutron orbits must be the same. (We

hope to install the capability for more ﬂexible spaces in the future.)

Notice that the NuShell-compatible .sp format does not include the weight-

ing number w, which is assumed to be zero. Hence no many-body truncations

are possible with these ﬁles.

If, instead, one uses an MFDn-formatted interaction ﬁle, one can use the

autoﬁll option for deﬁning the single-particle states, by entering auto in place

of the name of the .sps ﬁle:

Enter file with s.p. orbit information (.sps)

(Enter "auto" to autofill s.p. orbit info )

auto

Enter maximum principle quantum number N

(starting with 0s = 0, 0p = 1, 1s0d = 2, etc. )

The autoﬁll option creates a set of single-particle orbits assuming a harmonic

oscillator, in the following order: 0s1/2,0p1/2,0p3/2,1s1/2,0d3/2,0d5/2, etc., that

is, for given N, in order of increasing j, up to the maximal value N. It also

associates a value wequal to the principal quantum number of that orbit, e.g.,

2n+l, so that Nabove is the maximal principal quantum number. So, for

example, if one choose the principle quantum number N= 5 this includes up

to the 2p-1f-0hshells, which will looks like

iso

0.0 0.0 0.5 0

0.0 1.0 0.5 1

0.0 1.0 1.5 1

1.0 0.0 0.5 2

0.0 2.0 1.5 2

0.0 2.0 2.5 2

...

1.0 3.0 3.5 5

0.0 5.0 4.5 5

0.0 5.0 5.5 5

4.2.1 Particle-hole conjugation

BIGSTICK constructs the many-body basis states by listing the occupied particle

states. Because the available single-particle space is ﬁnite, one can alternately

list the unoccupied hole states. Such a representation can be advantageous if

the single-particle space is more than half-ﬁlled, which only happens in phe-

nomenological spaces: while the dimension of the Lanczos basis is unchanged,

because of our jump technology the matrix elements can take much more space

and memory. To understand this, , consider diagonal matrix elements, hα|ˆ

V|αi

which are a sum over occupied states:

hα|ˆ

V|αi=X

a,b∈α

V(ab, ab).

The number of terms in the sum is quadratic in the number of ‘particles’ in the

system. Switching to holes can dramatically decrease the terms in this sum: if

one has 12 single-particle states, for example, having two holes rather than ten

particles makes a diﬀerence of a factor of 25! The overall scaling is not so simple,

of course, for oﬀ-diagonal matrix elements (quickly: matrix elements of the form

PbV(ab, cb), a 6=c, that is, between two states which diﬀer only by one particle,

go linearly in the number of particles, while those V(ab, cd), a 6=c, b 6=d, that

is, between two states which diﬀer by two particles, are independent of the

number of particles), in large model spaces one can see a big diﬀerence. In

particular cases with a large excess of neutrons, so that we have a small number

of protons but nearly ﬁll the neutron space, can lead to enormous slow downs,

as well as requiring many more jumps. Here transformation from particles to

holes make for much greater eﬃciency. In order to obtain the same spectra and

observables (density matrices), the matrix elements must be transformed via a

Pandya transformation.

How to invoke particle-hole conjugation: When you are asked to enter the

number of particles, you are told the maximum number of particles:

Enter # of valence protons (max 12 ), neutrons (max 12)

Simply enter the number of holes as a negative number, i.e.,

-2 -5

BIGSTICK will automatically carry out the Pandya transformation:

2 proton holes = 10 protons

5 neutron holes = 7 neutrons

You can conjugate protons, or neutrons, or both. If you enter the maximum

number of particles in a space, BIGSTICK will automatically regard it as zero

holes. Calculation of density matrices works correctly with particle-hole conju-

gation.

When written to ﬁle, hole numbers are also written as negative integers as

a ﬂag, and when post-processing, BIGSTICK will correctly interpret them.

We ﬁnd there is little signiﬁcant performance diﬀerence in spaces with up

to about 20 single particle states, i.e. the pf shell, but beyond 20 the timing

diﬀerence can become quite dramatic.

4.2.2 Truncation of the many-body space

Given a deﬁned single-particle space, the basis states have ﬁxed total Mand

ﬁxed parity. If we allow all such states, we have a full conﬁguration many-body

space. Sometimes, motivated either by physics or computational tractability,

one wants to further truncate this many-body space. BIGSTICK allows a ﬂexible

scheme for truncating the many-body space which encompasses many, though

not all, truncations schemes. We truncate the many-body space based upon sin-

gle particle occupations. One could truncate based upon many-body quantum

numbers, such as from non-Abelian groups (e.g., SU(2) for the J-scheme, or the

symmetry-adapted SU(3) scheme), but that is beyond the scope our algorithms.

Each single-particle orbit is assigned a weight factor w. This is read in from

the .sps ﬁle or if the autoﬁll option is used, is equal to the harmonic oscillator

principal quantum number. wmust be a nonnegative integer. If all orbits have

the same wthen no truncation is possible and BIGSTICK does not query about

truncations.

wis treated as an addititive quantum number: each basis state has a total

Wwhich is the sum of the individual ws of the occupied states. Because wis

assigned to an orbit, it does not violate angular momentum or parity, and the

total Wis the same for all many-body basis states that are members of the same

conﬁguration, e.g., (0d5/2)2(1s1/2)1(0d3/2)1. Typically one assigns the same w

to equivalent proton and neutron orbits (in principle one could assign diﬀerent

ws, which would break isospin, but we haven’t explored this in depth).

Given the basis parameters, the single-particle orbits and their assigned ws

and the number of protons and neutrons, BIGSTICK computes the minimum and

maximum total Wpossible. The diﬀerence between these two is the maximal

excitation:

Would you like to truncate ? (y/n)

Max excite = 20

Max excite you allow

The user chooses any integer between 0 and “Max excite.” BIGSTICK then

creates all states with total Wup to this excitation.

This scheme encompasses two major trunction schemes. The ﬁrst kind of

truncation is called a particle-hole truncation in nuclear physics, or sometimes

Inert core

Excluded

Limited valence

All valence

single particle states

Figure 4.1: Segregation of single-particle space. ’Inert core’ has all states ﬁlled.

‘Excluded’ disallows any occupied states. ‘All valence’ can have states up to the

number of valence particles ﬁlled, while ‘Limited valence’ can only have fewer

states ﬁlled (e.g. one, two, three...). See text for discussion. Figure taken from

Johnson et al. [2013].

n-particle, n-hole; in atomic physics (and occasionally in nuclear physics), one

uses the notation ‘singles,’ ‘doubles,’ ‘triples,’ etc. To understand this truncation

scheme, begin by considering a space of single-particle states, illustrated in

Figure 4.1. Any single-particle space can be partitioned into four parts. In the

ﬁrst part, labeled ‘inert core’, the states are all ﬁlled and remain ﬁlled. In the

fourth and ﬁnal part, labeled ‘excluded,’ no particles are allowed. Both the core

and excluded parts of the single-particle space need not be considered explicitly,

only implicitly. In some cases there is no core.

More important are the second and third sections, labeled ‘all valence’ and

‘limited valence’, respectively. The total number of particles in these combined

sections is ﬁxed at Nv, and this is the valence or active space.

The diﬀerence between the ‘limited valence’ and the ‘all valence’ spaces is

that only some maximal number Nl< Nvof particles are allowed in the ’limited

valence’ space. So, for example, suppose we have four valence particles, but only

allow at most two particles into the ’limited valence’ space. In this case the ‘all

valence’ might contain four, three, or two particles, while the ’limited valence’

space might have zero, one, or two particles. In more standard language, Nl= 1

is called ‘one-particle, one-hole’ or ‘singles’, while Nl= 2 is called ‘two-particle,

two-hole’ or ’doubles’, and so on. There are no other restrictions aside from

global restrictions on quantum numbers such as parity and M.

The second truncation is commonly used in no-core shell model calculations,

where center-of-mass considerations weigh heavily. For all but the lightest sys-

tems, one must work in the laboratory frame, that is, the wavefunction is a

function of laboratory coordinates, Ψ = Ψ(r1, r2, r3, . . .). It is only the relative

degrees of freedom that are relevant, however, so ideally one would like to be

able to factorize this into relative and center-of-mass motion:

Ψ(r1, r2, r3, . . .) = Ψrel(~r1−~r2, ~r1−~r3, . . .)×ΨCM(~

RCM) (4.1)

(note that we have only sketched this factorization). In a harmonic oscillator

basis and with a translationally invariant interaction, one can achieve this fac-

torization exactly, if the many-body basis is truncated as follows [Palumbo,

1967, Palumbo and Prosperi, 1968, Gloeckner and Lawson, 1974]:

•In the non-interacting harmonic oscillator, each single-particle state has

an energy ei= ¯hΩ(Ni+ 3/2). Here Niis the principal quantum number, which

is 0 for the 0sshell, 1 for the 0pshell, 2 for the 1s-0dshell, and so on. The

frequency Ω of the harmonic oscillator is a parameter but its numerical value

plays no role in the basis truncation.

•We can then assign to each many-body state a non-interacting energy

ENI =Piei, the sum of the individual non-interacting energies of each particle.

There will be some minimum Emin and all subsequent non-interacting energies

will come in steps of ¯hΩ–in fact for states of the same parity, in steps of 2¯hΩ.

•Now choose some Nmax, and allow only states with non-interacting energy

ENI ≤Emin +Nmax¯hΩ. In practice, restricting states to the same parity means

that the ‘normal’ parity will have ENI =Emin,Emin + 2¯hΩ, Emin + 4¯hΩ, . . .,

Emin +Nmax¯hΩ, while ‘abnormal’ parity will have EN I =Emin + ¯hΩ, Emin +

3¯hΩ, . . .,Emin +Nmax¯hΩ.

This is sometimes called the Nmax truncation, the N¯hΩ truncation, or simply

the energy truncation. It is more complicated than the previous ‘particle-hole’

truncation. We identify with each principal quantum number Nia major shell;

for a 4¯hΩ we can excite four particles each up one shell, one particle up four

shells, two particles each up two shells, one particle up one shell and another

up three shells, and so on. While complicated, such a truncation allows us to

guarantee the center-of-mass wavefunction is a simple Gaussian.

More generally, one can adjust the truncation scheme further, based upon

skillful choice of single-particle ws. The assigned ws need not be contiguous;

the only requirement is that they be nonnegative.

4.2.3 Advanced truncation options

All truncation is based upon the wweight factors. In most applications, both

protons and neutron orbits have the same weights, and one typically truncates

equally. A more general truncation scheme is possible.

First, as discussed in section 4.2, it is possible for proton and neutron orbits

to have diﬀerent values of w, if the .sps ﬁle has the ‘wpn’ format:

wpn

3 3

0.0 2.0 1.5 3

0.0 2.0 2.5 2

1.0 0.0 0.5 2

0.0 2.0 1.5 3

0.0 2.0 2.5 2

1.0 0.0 0.5 3

The dimensions of the proton and neutron orbits must be the same, as the order

of all the quantum numbers besides w.

Second, when asked for the truncation,

Would you like to truncate ? (y/n/?=more information)

choosing ‘p’ allows diﬀerent truncation on protons and neutrons:

Max excite for sum, protons, neutrons?

(must be less than or equal to 8 4 4, respectively )

That is, the maximum values of Wp+Wn,Wp, and Wn, respectively. If you do

not choose this option, then the limits are the same for all three.

4.2.4 How to handle ‘diﬀerent’ proton-neutron spaces

As of the current version, BIGSTICK cannot handle diﬀerent proton-neutron

spaces. You can, however trick it into behaving that way, with a small cost.

Both involve deft usage of the truncation and, in many cases, of particle-hole

truncation.

Let’s consider two toy cases. First, suppose the proton and neutron spaces

are entirely separate. For example, let’s suppose valence protons occupy only

the 0f7/2space and valence neutrons only the 1p3/2. The .sps ﬁle can look like:

iso

0.0 3.0 3.5 0

1.0 1.0 1.5 1

By choosing a Max excite of zero, you will assure no particles are excited

out of the 0f7/2into the 1p3/2. (It is your responsiblity to set up the correct

interaction ﬁle. You do not have to include cross-shell matrix elements if they

are not needed; however if they are included, they will induce an eﬀective single-

particle energy so choose wisely.)

A slightly more complex case: suppose you want protons active in 0f7/2,

1p3/2and 1p3/2, and neutrons in 1p3/2, 1p3/2, and 0f5/2. Set up the .sps ﬁle

wpn

4 4

0.0 3.0 3.5 0

1.0 1.0 1.5 0

1.0 1.0 0.5 0

0.0 3.0 2.5 1

0.0 3.0 3.5 0

1.0 1.0 1.5 1

1.0 1.0 0.5 1

0.0 3.0 2.5 1

It is required that the proton and neutron orbits be the same, though the weight

factors wis the last column can diﬀer. Again, choosing Max excite of zero will

keep the protons and neutrons in their respective valence spaces. If the valence

spaces are signiﬁcantly diﬀerent, we strongly recommend utilizing particle-hole

conjugation for the neutrons.

One can make the truncations even more complex, for example allow a few

protons to be excited but no neutrons, by careful usage of the options provided.

4.3 Interaction ﬁles

After the model space is deﬁned, BIGSTICK needs interaction matrix elements.

All matrix elements are deﬁned in the one-, two-, or possibly three-body-space.

BIGSTICK’s job is to embed these matrix elements into a many-body space and

solve the eigenvalue problem. (Because three-body interaction ﬁles are highly

specialized, we do not discuss their format.)

The default format for two-body interaction ﬁle is derived from OXBASH/NuShell

and always ends in the extension .int. When entering the name of the ﬁle, only

enter the name, not the extension, i.e., usdb not usdb.int; otherwise BIGSTICK

will misinterpret the ﬁle.

! Brown-Richter USDB interaction

63 2.1117 -3.9257 -3.2079

2 2 2 2 1 0 -1.3796

2 2 2 1 1 0 3.4987

2 2 1 1 1 0 1.6647

2 2 1 3 1 0 0.0272

2 2 3 3 1 0 -0.5344

2 1 2 1 1 0 -6.0099

2 1 1 1 1 0 0.1922

2 1 1 3 1 0 1.6231

2 1 3 3 1 0 2.0226

1 1 1 1 1 0 -1.6582

1 1 1 3 1 0 -0.8493

1 1 3 3 1 0 0.1574

...

There is no speciﬁc spacing for this ﬁle. BIGSTICK will skip any header lines

starting with ! or #. The ﬁrst line is

Ntbme spe(1) spe(2) spe(3) ...

where Ntbme is the number of two-body matrix elements (TBMEs) in the

rest of the ﬁle, and spe(i) is the single-particle energy of the ith orbit. Only 10

single particle energies are on each line.

The rest of the ﬁle are the two-body matrix elements. This is deﬁned as

VJT (ab, cd) = hab;J T |V|cd;JT i,(4.2)

where a, b, c, d label orbits, as ordered in the .sps ﬁle or as created by the

autoﬁll option; Jand Tare the total angular momentum and total isospin of

the two-body states |ab;JT i, which are normalized. This follows the convention

of Brussaard and Glaudemans. Each matrix element is read in as

a b c d J T VJT (ab, cd)

For input purposes, the order of a, b, c, d is not important (as long as one

has the correct phase), nor is the ordering of the TBMEs themselves. When

reading in the ﬁle, BIGSTICK automatically stores the matrix element according

to internal protocols, appropriately taking care of any relevant phases.

Matrix elements that are zero can be left out, as long as Ntbme correctly

gives the number of TBMEs in the ﬁle. More than one ﬁle can be read in; enter

end to tell BIGSTICK you are ﬁnished reading in ﬁles.

4.3.1 Scaling and autoscaling

Empirical studies with phenomenological interactions have found best agree-

ment with experiment if one scales the two-body matrix elements with mass

number A. (There is some justiﬁcation based upon the scaling of harmonic

oscillator wave functions with A). A standard scaling factor is

Aref

Ax

(4.3)

where Aref is the reference mass number (typically Aof the frozen core +2, as it

is ﬁt to the interaction of two particles above the frozen core), Ais the mass of

the desired nucleus, and xis an exponent, typically around 1/3. To accomodate

this scaling, when reading in the default format, BIGSTICK requests

Enter scaling for spes, A,B,X ( (A/B)^X ) for TBMEs

(If B or X = 0, then scale by A )

Typically the single particle energies are unscaled, but we allow for it. A typical

entry, for example for the USDA/B interactions [Brown and Richter, 2006],

would be

1 18 24 0.3

Here the single particle energies are unscaled, the core has mass number 16 and

hence the reference mass is 18, the target mass in this case has mass number

24, and the exponent is 0.3. Whoever provides the interaction has to provide

the exponent. If unsure, just enter

1, 1, 1, 1

Many ﬁles used with NuShell have autoscaling. For example, for the USDA/B

ﬁle, the ﬁrst lines are

! 1=d3/2 2=d5/2 3=s1/2

! the first line has the three single-particle energies

! the - sign tells oxbash that the tbme have a mass dependence of the form

! [18/(16+n)]^0.3 where n is the number of valence particles

-63 1.9798 -3.9436 -3.0612 16.0000 18.0000 0.30000

A negative integer for the number of two-body matrix elements (here, -63)

initiates autoscaling. The next three numbers are the single-particle energies,

and the next numbers are Acore, the reference mass, and the exponent. If

BIGSTICK encounters a negative integer for the number of two-body matrix

elements, it autoscale the two-body matrix elements as described above. To

turn oﬀ autoscaling, change -63 to 63.

Keep in mind that not all interactions will be scaled. Ab initio interactions

are almost never scaled, and ‘phenomenological’ interactions depend on how

they were derived and ﬁt. See your interaction provider for more information.

4.3.2 Proton-neutron and other isospin-breaking formats

Often one needs to break isospin. There are three modiﬁcations of the default

format which break isospin. In addition, ab initio inputs in the MFDn format,

described in section 4.3.3, also generally break isospin.

The most robust format, which we recommend, is the explicit proton-neutron

formalism. Here one has separate labels for proton and neutron orbits; however,

at this time the proton and neutron orbits must have the same quantum

numbers and be listed in the same order. For example, one might label

the proton orbits 1 = 0d3/2, 2 = 0d5/2, and 3 = 1s1/2. Then the neutron orbits

must be 4 = 0d3/2, 5 = 0d5/2, and 6 = 1s1/2.

While BIGSTICK generally allows for arbitrary order, for the proton-neutron

matrix elements the proton labels must be in the ﬁrst and third columns and

neutron labels in the second and fourth columns, that is, for VJ(ab, cd), aand

cmust be proton labels and b, d must be neutron labels. With twice as many

deﬁned orbits, one must also provide separate proton and neutron single particle

energies. As an example, here is part of the ﬁle of the p-shell Cohen-Kurath

matrix elements with good isospin:

! ORDER IS: 1 = 1P1/2 2 = 1P3/2

15 2.419 1.129

1 1 1 1 0 1 0.2440000

1 1 1 1 1 0 -4.2921500

2 1 1 1 1 0 1.2047000

2 1 2 1 1 0 -6.5627000

2 1 2 1 1 1 0.7344000

2 1 2 1 2 0 -4.0579000

2 1 2 1 2 1 -1.1443000

2 2 1 1 0 1 -5.0526000

and here is an excerpt in proton-neutron formalism

34 2.4190 1.1290 2.4190 1.1290

1 3 1 3 0 1 0.24400

1 1 1 1 0 1 0.24400

3 3 3 3 0 1 0.24400

1 3 1 3 1 1 -4.29215

1 3 1 4 1 1 -0.85185

1 3 2 3 1 1 0.85185

1 3 2 4 0 1 -5.05260

1 1 2 2 0 1 -5.05260

3 3 4 4 0 1 -5.05260

1 3 2 4 1 1 1.76980

1 4 1 4 1 1 -2.91415

1 2 1 2 1 1 0.73440

3 4 3 4 1 1 0.73440

In no case are headers required, but they do help as a check for the deﬁnition of

the orbits. BIGSTICK automatically checks that angular momentum and parity

selections are not violated. In the explicit proton neutron format Tis given in

the sixth column but not actually used.

There is one more question of convention one must deal with: the normal-

ization of the two-body states in the deﬁnition of matrix elements. All formats

assume two-proton and two-neutron states are normalized, and states with good

isospin are normalized. Files set up for NuShellX, however, have unnormalized

proton-neutron states.

BIGSTICK can read in default-format proton-neutron interactions with ei-

ther normalized (‘xpn’ or explicit proton-neutron) or unnormalized (‘upn’ or

unnormalized proton-neutron) conventions. In both cases the ﬁles also include

proton-proton and neutron-neutron matrix elements, with normalized states.

The relationship between the two is

Vxpn

J(aπbν, cπdν) = 2

p(1 + δab)(1 + δcd)Vupn

J(aπbν, cπdν) (4.4)

Here we have marked the orbits a, c as proton and b, d as neutron, but the

Kronecker-δs refer only to the quantum numbers n, l, j. For example, in the sd

shell, with the labels mentioned above,

Vxpn

J(16,25) = √2Vupn

J(16,25)

because proton orbit 1 (0d3/2) and neutron orbit 6 (1s1/2)are diﬀerent, but

proton orbit 2 and neutron orbit 5 are both d5/2

Unfortunately it is up the user to know whether or not the ﬁle uses normal-

ized or unnormalized proton-neutron states. If the ﬁle was originally produced

for use with NuShellX, it is almost certainly the latter.

(This arises out of the conversion of normalized isospin wave function to

normalized proton-neutron wave functions and the result matrix elements. One

ﬁnds

Vpn

J(ab, cd) = p(1 + δab)(1 + δcd)

2Viso

J,T =0(ab, cd) + Viso

J,T =1(ab, cd),(4.5)

but the unnormalized convention yields the simpler

Vupn

J(ab, cd) = Viso

J,T =0(ab, cd) + Viso

J,T =1(ab, cd).(4.6)

While our preference is for the former, given the prominence of the latter through

NuShellX we include it as an option.)

In order to read in proton-neutron matrix elements in the default format,

you must ﬁrst tell BIGSTICK to expect it.

For xpn/upn formats, you MUST specify the format.

In this format proton and neutron orbits are sequential and do not overlap,

E.g., proton orbits are 1,2,3 and neutron orbits are 4,5,6.

FOR NOW despite the distinct numbering the proton and neutron orbits

must encompass the same space.

NOTE: upn format is typical for TBME files distributed with NuShell;

xpn/upn files must have the name XXX.int, but enter XXX when requested.

As with default-format isospin-conserving ﬁles, the ﬁle name must be xxxx.int,

but the user enters in just ‘xxxx’.

Also as with default-format isospin-conserving ﬁles, after entering the name

of the ﬁle, the user is prompted for scaling. For maximal ﬂexibility, there are two

layers of possible scaling. The ﬁrst is the standard phenomenological scaling:

Enter global scaling for spes, A,B,X ( (A/B)^X ) for TBMEs

(If B or X = 0, then scale by A )

1 18. 24. 0.3

These scalings are applied to all single particle energies and to all two-body

matrix elements. In addition, one can enter in separate scaling factors for pro-

tons single-particle energies, neutron single-particle energies, proton-proton two-

body matrix elements, neutron-neutron two-body matrix elements, and ﬁnally

proton-neutron two-body matrix elements:

Enter individual scaling for: proton spes, neutron spes, pp TBMEs, nn TBMEs, p

n TBMES

(If not sure, just enter 1 1 1 1 1 )

There are two alternate formats for isospin-breaking ﬁles which build upon

the default format. These involve reading in separate ﬁles for proton-proton,

neutron-neutron, and proton-neutron, or for isoscalar, isovector, and isotensor

components. There are some tricky issues of deﬁnition, however. Thus we do not

actively support these alternative formats, instead recommending the explicit

proton-neutron format, whether normalized or unnormalized

One can mix all of these diﬀerent formats. You can read in an isospin-

conserving ﬁle, a proton-neutron format ﬁle, and so on, in any order. To stop

reading in interaction ﬁles, enter ‘end’ at the prompt.

4.3.3 MFDn format input

Another major conﬁguration-interaction code is MFDn (Many-Fermion-Dynamics,

nuclear version) out of Iowa State University [Sternberg et al., 2008]. While

within MFDn there are several variations on conventions, we describe here the

most common conventions.

Unlike the default format, to read in an MFDn-format ﬁle, you must enter

the entire name, including any extensions. This signals to BIGSTICK to prepare

to read in an an MFDn-format ﬁle. BIGSTICK will treat a ﬁle TBME.int very

diﬀerently if you answer ‘TBME’ versus ‘TBME.int’ for the ﬁle name. MFDn-format

ﬁles are almost always for ab initio or so-called no-core shell model calculations,

and almost always assume a harmonic oscillator basis.

The input ﬁle ﬁrst line is

nTBME (other stuﬀ which are not needed)

where nTBME is the number of TBMEs in the ﬁle. For example

2056271 13 14 20.0000 2.0000

The only number BIGSTICK requires is the ﬁrst one. The fourth number, 20.000,

is ¯hΩ in MeV, but not all codes generate this information.

The MFDn format does not include explicit single-particle energies. Subsquent

lines are of the form

a b c d J T Trel Hrel Vcoul V

or, more commonly,

a b c d J T Trel Hrel Vcoul Vpn Vpp Vnn

Here all matrix elements are of the form hab;JT |V|cd;JT i, that is the ma-

trix element between normalized two-body states with a,b,c,d labels of single

particle orbits, J(and, optionally, T) are total angular momentum and isospin

of the coupled two-body states. The isospin Tis not really used.

Now for the matrix element. Trel is the relative kinetic energy, that is

Trel =X

i<j

(~pi−~pj)2

2M,(4.7)

These matrix elements are computed in a harmonic oscillator basis for ¯hΩ =

1MeV , and A= 2, and thus must be rescaled correctly for the A-body system,

that is, must be multiplied by 2¯hΩ/A.

Now to the ﬁnal matrix elements. The actual Hamiltonian one wants is

H=ˆ

Trel +ˆ

Vrel +βc.m.(ˆ

Hcm −3

2¯hΩ).(4.8)

Here ˆ

Hcm is the center-of-mass Hamiltonian, used to push up spurious states via

the Palumbo-Lawson-Glocke method [Palumbo, 1967, Palumbo and Prosperi,

1968, Gloeckner and Lawson, 1974]:

Hcm =P2

2AmN

2AmNΩ2R2

cm.(4.9)

where mNis the nucleon mass and

Rcm =1

~ri,~

Pcm =¯h

∇i.(4.10)

These have the correct commutation relation, that is, [ ~

Rcm,~

Pcm] = i¯h, so that

Pcm is the conjugate momentum to ~

Rcm.

It is useful to separate ˆ

Hcm into one- and two-body parts:

Hcm =1

2AmNX

i+1

2AmNΩ2X

2AmNX

i6=j

~pi·~pj+1

2AmNΩ2X

i6=j

~ri·~rj(4.11)

The ﬁrst two terms are the single particle energies, with values ¯hΩ(N+ 3/2)/A,

with Nthe principal quantum number, and the second two terms is ˆ

Hrel ×¯hΩ/A.

BIGSTICK automatically accounts for all the factors, as long as you provide the

correct ¯hΩ as shown below:

When you select an MFDn-format ﬁle, you will be prompted for the following:

For MFD-formatted input choose one of the following :

(I) No isospin breaking

(P) Explicit proton-neutron formalism

Almost always you should select option ‘p’.

In order to use an ab initio ﬁle, you need to enter in the value of ¯hΩ for

both the kinetic energy term and the center-of-mass Hamiltonian to push up

spurious states:

Enter oscillator frequency (in MeV) and center-of-mass strength

You should know the frequency at which the ﬁle was created. The second term

is βc.m.. Typical values of βc.m. are 1-10.

4.3.4 Three-body forces

While BIGSTICK has a validated capability for three-body forces, it is not op-

timized for large calculations; the main issue is storage of the large number of

matrix elements. If you have the capability to generate three-body forces, please

to generate three-body forces for users.

In your distribution three-body forces are likely disabled. They can be

re-enabled by setting the logical ﬂag threebodycheck = .true. in module

flags3body in the ﬁle bmodules 3body.f90. If this ﬂag is enabled, BIGSTICK

will query if you want to use three-body forces:

Do you want 3-body forces (y/n) ?

If you answer ‘n,’ BIGSTICK will proceed with just 2-body forces. If you answer

‘y,’ BIGSTICK will ask for the name of the ﬁle. Actually using three-body forces

is complicated and beyond the scope of this current manual.

You can, however, use two-body forces in three-body mode (the matrix ele-

ments are multiplied internally by ( ˆ

N−2)/(A−1) to turn them into genuine

three-body forces), by answering ‘none’ to the question of the name of the ﬁle

of three-body forces. Most users will not be interested in this.

4.4 Primary runtime options

Here we outline the major run time options, although some issues are discussed

in more detail elsewhere. The main menu can be divided into two categories,

primary and secondary. We discuss secondary options, which require results

of a previous run, in section 4.6. In most primary runs one solves the matrix

eigenvalue problem, which invokes the diagonalization options menu, discussed

in section 4.5.

4.4.1 Autoinput

* (i) Input automatically read from "autoinput.bigstick" file *

* (note: autoinput.bigstick file created with each nonauto run) *

Each time BIGSTICK runs, it writes the user’s responses to a ﬁle autoinput.bigstick.

This ﬁle can be edited or used as the basis of a batch ﬁle. The autoinput option,

‘i,’ will read in the autoinput.bigstick instead of taking responses from the

user.

4.4.2 Standard or normal runs

* (n) Compute spectrum (default); (ns) to suppress eigenvector write up *

The normal run, ‘n,’ will generate the low-lying eigenspectrum and wave func-

tions. This is the most common option. Two variations on it are ns which will

compute the eigenspectrum and the Jand Tvalues, but not write the wave-

functions to a ﬁle, and ne, which will only compute eigenenergies. These latter

options can save on time and ﬁle storage, but in most cases are not necessary.

4.4.3 One-body density matrices and occupations

One of the most important options for BIGSTICK is to generate the one-body

density matrices, deﬁned as

ρfi

K(a†b) = [K]−1hJf||(a†b)K||Jii(4.12)

where we use the choice of reduced matrix elements from Edmonds [1996],

hJf||OK||Jii= [Jf](JfMf, KM|JiMi)−1hJfMf|OKM|JiMii(4.13)

The advantage of this deﬁnition of the density matrix is that the reduced matrix

element of a general, non-scalar one-body operator is just the density matrix ×

the reduced matrix elements of that operator, that is

hΨf, Jf|| ˆ

OK||Ψi, Jii=X

ab ha|| ˆ

OK||biρfi

K(a†b) (4.14)

where a, b are labels for single-particle orbits, and ha|| ˆ

OK||biare the reduced

one-body matrix matrix elements for the operator ˆ

Owith angular momentum

BIGSTICK has a number of options to generate density matrices.

* (d) Densities: Compute spectrum + all one-body densities *

* (dx[m]) Densities: Compute one-body densities from previous run (.wfn) *

* optional m enables mathematica output *

The density matrix option ‘d’ runs just like the normal option, except at the

end of the run it generates the one-body density matrices, which we describe

more fully in section . If the interaction ﬁle has good isospin, then the one-body

density matrices will be coupled up to good isospin. If the interaction ﬁle breaks

isospin, the density matrices will be in proton-neutron format. If you use an

interaction with good isospin but want the density matrices in proton-neutron

format, use the option ‘dp.’

Two variations are the option ‘dx,’ which reads in a previously computed

wave function ﬁle and from it computes the one-body density matrices, and

‘dxm’, which does the same but generates the density matrices in a format read-

able by Mathematica. Technically these options are secondary.

* (p) Compute spectrum + single-particle occupations; (ps) to suppress wfn*

* (occ) single-particle occupations (from previous wfn) *

A restricted version of the one-body densities are the single-particle occupations.

In principle given the former one can compute the latter, as described in section

5.1.2, but for convenience we give an option to do this directly. Option ‘p’ does

this as in the normal option, but also writes the single-particle occupations to

the .res ﬁle. Option ’ps’ does the same but does not write the wave functions

to a ﬁle on disk. Finally, the secondary option ‘occ’ reads in an existing wave

function ﬁle and generates the single-particle occupations.

Single particle state quantum numbers

ORBIT : 1 2 3

N : 0 0 1

J : 3 5 1

L : 2 2 0

State E Ex J T

1 -62.78960 0.00000 2.500 1.500

p occ: 0.136 1.590 0.275

n_occ: 0.353 4.299 0.347

A detailed discussion of using one-body density matrices to get transition

probabilities can be found in Chapter 5.1.

4.4.4 Other primary options

* (m) print information for Modeling parallel distribution *

The modeling option ‘m’ is useful for seeing if enough nodes and memory can be

allocated for a large parallel run. See also section 8.1.3. No interaction ﬁles are

read in and no diagonalization is carried out.

There are a couple ofadditional options most users are unlikely to use but

which we mention nontheless.

* (f) Self-consistent mean-field approximation (prepare pivot) *

* (c) Compute traces *

The ‘f’ or self-consistent mean-ﬁeld option is an attempt to quickly get an

good starting pivot for the ground state. Essentially what it does is replace the

full Hamiltonian by a one-body approximation. On each iteration, BIGSTICK

computes the one-body density matrices and generates an eﬀective, in general

non-scalar one-body potential by coupling the two-body force to those one-body

densities . This process is much faster than applying the full two-body inter-

action. It is inspired by but not the same as the Hartree-Fock approximation,

which assumes a single Slater determinant.

The resulting approximate states are written to a .wfn ﬁle, which can be

read back in as a pivot using the option ‘np.’ In our experiments this pivot

speeds up convergence to the ground state but not excited states. More work

especially on multishell systems have yet to be done. We have not fully tested

this option in parallel.

BIGSTICK can also compute the trace of the Hamiltonian and the trace of

the Hamiltonian squared, using the option ‘c.’ Speciﬁcally, it computes the

centroid, which is the trace divided by the dimension, and the width, which is

the square root of the variance.

for dimension 28503, centroid = -43.544457, width = 11.298695

(saved to file trace.bigstick )

As shown above, the results are written to the ﬁle trace.bigstick. We caution

users that in particular computing the width can be time consuming. We have

not fully tested this option in parallel.

4.5 Diagonalization options

After the interactions ﬁles have been read in, BIGSTICK sets up the jump arrays

for reconstructing the matrix elements on the ﬂy. After that, the eigensolver

menu comes up:

/ ------------------------------------------------------------------------\

| |

| DIAGONALIZATION OPTIONS (choose one) |

| |

| (ex) Exact and full diagonalization (use for small dimensions only) |

| |

| (ld) Lanczos with default convergence (STANDARD) |

| (lf) Lanczos with fixed (user-chosen) iterations |

| (lc) Lanczos with user-defined convergence |

| |

| (td) Thick-restart Lanczos with default convergence |

| (tf) Thick-restart Lanczos with fixed iterations |

| (tc) Thick-restart Lanczos with user-defined convergence |

| (tx) Thick-restart Lanczos targeting states near specified energy |

| |

| (sk) Skip Lanczos (only used for timing set up) |

| |

\ ------------------------------------------------------------------------/

The full diagonalization option, ‘ex,’ creates the entire Hamiltonian matrix,

stores it in memory, and solves it using the Householder algorithm as imple-

mented in the LAPACK routine DSYEV. As such, it should not be used except

for relatively small dimensions. On workstations one can solve up to ∼103in a

few or tens of minutes. We have solved up to ∼104, but that can take hours. In

principle MPI versions of Householder exist, but we have not installed one, as

one seldom has need for all eigensolutions of a very large matrix. (If you do not

need wave functions or the angular momenta, choosing option ‘ne’ will speed

this up dramatically, as DSYEV will run faster if one wants only eigenvalues.)

Under this option you can choose how many low-lying states, or all of them

if you wish, to keep. These get written to ﬁle.

The primary eigensolver is the Lanczos algorithm, described in Chapter 7.

Most of the time you will use option ‘ld’, the default Lanczos choice. Here you

get asked

Enter nkeep, max # iterations for lanczos

(nkeep = # of states printed out )

BIGSTICK will run until the standard convergence criterion, see section 4.5.1, is

satisﬁed, or until the maximum number of iterations is exceeded. The latter

must be speciﬁed to reserve memory for the Lanczos vectors. Although the

Lanczos and related Arnoldi algorithms are among the most studied in applied

mathematics, there is no simple, robust rule for the number of iterations needed.

For phenomenological spaces, the ground state will often converge in under 50

iterations, the ﬁrst 5 states in 100 to 150 iterations, and so on. For no-core shell

model calculations, the time to convergence is usualy longer.

The default convergence check is discussed in the next section, 4.5.1. If you

want a ﬁxed number of iterations without checking convergence, choose ‘lf.’ If

you want ﬁner control over convergence, choose ‘lc,’ discussed in 4.5.1.

The Lanczos vectors are stored in memory. For large-dimension cases, es-

pecially on a laptop or desktop, one can run out of memory just storing these

vectors. Alternately, if one needs a large number of converged states, after

a number of iterations reorthogonalization actually starts to take more time

than matvec. A robust alternative is the thick-restart Lanczos algorithm [Wu

and Simon, 2000], which requires fewer vectors stored in memory but requires

more iterations. While standard Lanczos ﬁnds the lowest Nkeep eigensolutions

with Niter iterations, thick-restart has three numbers: Nkeep < Nthick < Niter.

As described more fully in section 7.2, after Niter iterations the approximate

Hamiltonian is diagonalized, and Nthick of these eigenvectors are kept for restart-

ing. This process is repeated until convergence or until a maximum number of

restarts has been exhausted.

Enter # of states to keep, number of iterations before restarting

5 50

Enter max # of restarts

As with standard Lanczos, the values chosen usually come with experience. We

ﬁnd we usually want Nthick >∼3×Nkeep, and we take Niter as large as practical.

Speciﬁcally, BIGSTICK chooses

Nthick = max(3Nkeep, Nkeep + 5),

as long as this is not larger than Niter.

If you want a ﬁxed number of iterations, choose ‘tf’, and you will be

prompted for Nkeep,Niter, and then Nthick:

Enter # of states to keep, # of iterations before thick-restart

5 50

Enter # of vectors to keep after thick-restart

(Typical value would be 20 )

( Must be between 5 and 50 )

If you want to control the convergence, choose ‘tc’ and you will be prompted

for convergence choices much as for standard Lanczos.

Finally, ‘tx’ is an experimental mode attempting to ﬁnd highly excited

states. It modiﬁes thick-restart by choosing eigenpairs in the vincinity of a

selected absolute energy. In our experience the convergence is not very good,

but it does yield an eigenvector with very strong overlaps with the true eigen-

vectors in the vicinity of the target energy.

Option ‘sk’ is only for testing timing of set-up to this point.

4.5.1 Convergence

As BIGSTICK iterates, it checks for convergence. Every ten iterations it prints

to screen the current Nkeep lowest eigenvalues and the convergence criterion:

1 -135.86073

2 -133.92904

3 -131.25354

4 -131.02439

5 -129.53058

80 iterations

(energy convergence 0.70356 > criterion 0.00100)

1 -135.86073

2 -133.92904

3 -131.25354

4 -131.02439

5 -129.53059

90 iterations

(energy convergence 0.30353 > criterion 0.00100)

As far as we can tell from the literature, there is no robustly ideal convergence

criterion for general Lanczos. Our default convergence is on energy: BIGSTICK

takes the sum of the absolute value of the diﬀerences in energy between the

current iteration and one previous, not only for the Nkeep lowest energies but

also for the next 5, and divides by the square root of Nkeep + 5, that is,

δconv ≡PNkeep +5

i=1 Enew

i−Eold

i

pNkeep + 5 (4.15)

The reason for testing additional eigenvalues is to avoid the problem of

plunging eigenvalues, well known to occur in Lanzos Whitehead et al. [1977]; it

happens when by accident a low-lying state has a tiny overlap with the pivot or

initial vector. We divided not by the number of energies compared but by the

square root, because for a large number of energies one outlier could get washed

out by many small deviations. For our purposes this has worked well enough,

but it is not rigorously tuned.

If you want a diﬀerent criterion, choose ‘lc’ on the diagonalization menu.

One then gets a series of questions with which to tune the convergence, including

comparing eigenvectors rather than eigenvalues:

Enter nkeep, max # iterations for lanczos

5 150

Enter how many ADDITIONAL states for convergence test

( Default= 5 ; you may choose 0 )

Enter one of the following choices for convergence control :

(0) Average difference in energies between one iteration and the last;

(1) Max difference in energies between one iteration and the last;

(2) Average difference in wavefunctions between one iteration and the last;

(3) Min difference in wavefunctions between one iteration and the last;

Enter desired tolerance

(default tol = 0.100E-04 )

Similar options are available for thick-restart Lanczos.

4.6 Secondary runtime options

Once BIGSTICK has generated wave function, it can further process the wave

functions in secondary options. We discuss those options in detail here. Some

of these were already mentioned in section 4.4. All of these options will ask for

the name of a previously generated .wfn ﬁle.

Enter input name of .wfn file

You do not have to read in a .sps or similar ﬁle to deﬁne the model space; from

the information in the .wfn ﬁle, BIGSTICK reconstucts the basis. Depending

upon the option, you may be asked to enter names of appropriate ﬁles, such as

interaction ﬁles.

We list these in the order they are presented in the menu, but the most

important and commonly used option are ‘x,’ expectation value of a scalar

operator (section 4.6.1), ‘o,’ apply a one-body non-scalar transition operator

(section 4.6.2 and Chapter 5), and ‘s,’ the strength function option (section 5.2

and Chapter 5).

* (np) Compute spectrum starting from prior pivot *

Option ‘np’ allows you to choose a pivot, or initial starting vector, from a

previously generated wave function. This might be useful, for example, if you

wanted to try to get states of a particular quantum number such as J, although

we do not currently have the capability to enforce this condition, and even if it is

an exact quantum number numerical noise will allow states with other quantum

numbers to creep in. Alternately, you can generate a guess of the ground state

by the self-consistent mean-ﬁeld option ‘f.’ Our experiments suggest this latter

does lead to faster convergence of the ground state, but not excited states.

A related and more widely useful option is the strength function option ‘s’

discussed below and in section .

* (dx[m]) Densities: Compute one-body densities from previous run (.wfn) *

* optional m enables mathematica output

Options ‘dx’ and ‘dxm’ read in a previously generated wave function and compute

the one-body density matrices. The latter provides a Mathematica-friendly ﬁle

format. More details about one-body density matrices are found in section 5.1.

* (occ) single-particle occupations (from previous wfn) *

This option computes the single-particle occupations from a previously gener-

ated wave function ﬁle.

4.6.1 Expectation value

* (x) eXpectation value of a scalar Hamiltonian (from previous wfn) *

The option ‘x’ allows you to compute the expectation value of a operator, which

may have one-, two- (and in principle, three-) body components. It must be an

angular momentum scalar and thus is treated as a Hamiltonian, and is read in

exactly as Hamiltonians, along with standard requests for scaling information.

The results are written both to screen and, if an output name is given, to the

.res ﬁle.

STATE E J T^2 <H > (norm)

1 -92.7790 -0.0000 0.0000 499.287061 1.00000

2 -91.1196 2.0000 0.0000 488.826115 1.00000

3 -88.4779 2.0000 0.0000 509.922118 1.00000

4 -87.9781 4.0000 0.0000 452.853182 1.00000

The reason the norm of the vector is given is that after applying a one-body

transition operator, as described in the next section (4.6.2), the wave function

vector may no longer be normalized.

4.6.2 Applying a one-body transition operator

One of BIGSTICK’s important capabilities is to take a set of previously generated

wave functions and apply a non-scalar one-body operator to them:

* (o) Apply a one-body (transition) operator to previous wfn and write out*

* (oo) Apply a one-body (transition) operator with enforced orthogonality *

* (that is, forced resulting pivot to be orthogonal to starting pivot *

* to eliminate transition strength to original state) *

If you choose this option, you will be asked for the name of the input .wfn ﬁle as

well as the name of an output .wfn ﬁle. Then you will be asked for a ﬁle with

the reduced matrix elements of the operator, which must have the extension

.opme:

Enter name of .opme file

Here is an annotated example .opme ﬁle:

! header: Gamow-Teller-like

iso ! assumes isospin

3 ! # of single particle orbits

1 0 2 1.5 ! index, n, l, j of orbits

2 0 2 2.5

3 1 0 0.5

1 1 ! J, T of transition

1 1 -2.68328 ! a, b < a ||| O ||| b >

1 2 5.36656

2 1 -5.36656

2 2 5.01996

3 3 4.24264

The only formatting is the the ﬁrst non-header line, here iso, must be ﬂush

against the left. The ﬁle must contain the single-particle orbits, and BIGSTICK

checks against the orbits used to build the wave function. After the list of

orbits, the Jand Tof the operator come, and then the the non-zero reduced

matrix elements. Here, assuming isospin is a good quantum number, we have

doubly-reduced matrix elements. Although there is a symmetry ha||| ˆ

O|||bi=

(−1)ja−jbhb||| ˆ

O|||ai, at this time BIGSTICK requires both elements.

Many transition operators do not preserve isospin. Therefore BIGSTICK can

read in operators in an explicit proton-neutron symmetry:

! M1 matrix elements in the sd shell

pns

1 0 2 1.5

2 0 2 2.5

3 1 0 0.5

1 2

1 1 0.1568000 1.4481392 ! a b proton m.e. neutron m.e.

1 2 3.4710987 -2.8962784

2 1 -3.4710987 2.8962784

2 2 6.7871771 -2.7092204

3 3 3.3425579 -2.2897091

The code pns in the ﬁrst non-header line signals that the matrix elements are

in proton-neutron formalism, with the same list of orbital quantum numbers for

protons and neutrons. The 2 in the 5th line also signals that one is breaking

isospin. Thus in the list of reduced (in Jonly) matrix elements, the columns

are for protons and neutrons, respectively.

BIGSTICK will read in all the wave functions |Ψiifrom the initial wave func-

tion ﬁle, and write ˆ

O|Ψiiin the ﬁnal wave function ﬁle. These wave functions

will generally not be normalized and will not have good angular momentum or

isospin. More on this elsewhere.

Currently, both the initial and ﬁnal wave functions must be in the same

basis. Thus, there are no explicit charge-changing transitions. To handle charge-

changing transitions, one must use an interaction with good isospin and exploit

isospin rotation, described in section 5.1.5. For transitions which change parity,

one must use a basis with both parities, option 0in the parity-selection menu.

Because transition operators are not in general unitary, the result wave func-

tion vectors are not normalized. This information is important, as it tells us

about total transition strengths, also known as the non-energy-weighted sum

rule.

4.6.3 Applying a two-body body scalar operator

* (a) Apply a scalar Hamiltonian to a previous wfn and write out *

Option ‘a’ works very similar to option ‘o:’ one reads in a previously-generated

ﬁle of wave functions, applies an operator to each wave function, and writes the

results to another ﬁle. The diﬀerence is here the operator must be a one-plus-

two-body scalar operator, that is, like a Hamiltonian. The ﬁles are read in the

same as a Hamiltonian, along with scaling, and so on.

4.6.4 Generating strength function distributions

One of the most powerful and most useful capabilities is ‘s,’ the strength func-

tion distribution option. We give an overview here, with many more details of

application in section 5.2.

Like all secondary options, the strength function option starts by prompting

the user for a previously generated .wfn ﬁle. The user is then prompted for

a Hamiltonian or Hamiltonian-like interaction ﬁle or ﬁles. Next the user must

enter the number of iterations for Lanczos:

Fixed iterations ONLY:

Enter nkeep, # iterations for lanczos

(nkeep = # of states printed out )

The only way to make this option work is through standard Lanczos. The num-

ber of results to keep and the number of iteration depends upon the application;

see section 5.2. Finally, the user must choose from the input ﬁle the pivot or

starting vector, a key decision:

There are 5 wavefunctions

5 states

STATE E J <H >

1 -92.7790 -0.0000 0.0000

2 -91.1196 2.0000 0.0000

3 -88.4779 2.0000 0.0000

4 -87.9781 4.0000 0.0000

5 -87.4348 3.0000 0.0000

Which do you want as pivot?

What happens next is that Lanczos runs normally, produces eigenvalues and

eigenvectors and writes them to ﬁle. It also additionally computes the overlap

of the pivot with each of the eigenstates, that is, |hf|pivoti|2:

Energy Strength

______ ________

17.30356 0.00007

49.98777 0.00123

110.94935 0.00956

184.33815 0.01945

249.75355 0.01641

301.54676 0.08014

383.34766 0.05833

428.29023 0.14090

498.95403 0.04282

534.87775 0.17398

588.87306 0.45712

______ ________

This is the strength function or strength distribution. If the starting vector has

a norm diﬀerent from one, this is noted

0.99999999895896363 = total input strength

and this is included in the strengths. The usefulness of this capability cannot

be overestimated, and is discussed in depth in section 5.2.

4.6.5 Overlap or dot product of wave functions

* (v) Overlap of initial states with final states *

The output eigenstates are written as vectors. Although most users are unlikely

to need to use this, using the ‘v’ option BIGSTICK can compute the dot product

between two such wave functions, including from diﬀerent ﬁles. From the ﬁrst

ﬁle, you must choose a speciﬁc state:

Which do you want as initial state?

A second ﬁle is then opened (you can reopen the ﬁrst ﬁle), and the intial state

is dotted against each of them. The results are written to the ﬁle overlap.dat:

Initial state = 1

state E J T <i|f> |<i|f>|^2

1 -87.10445 -0.0 0.0 0.99885 0.99771

2 -85.60214 2.0 0.0 -0.00000 0.00000

3 -82.98830 2.0 0.0 0.00000 0.00000

4 -82.73201 4.0 0.0 0.00000 0.00000

5 -82.03407 3.0 0.0 -0.00000 0.00000

6 -81.22187 4.0 0.0 -0.00000 0.00000

7 -79.76617 -0.0 0.0 -0.02326 0.00054

We found this option useful in validating other capabilities, such as the strength

function capability.

4.7 Output ﬁles

BIGSTICK generates a number of output ﬁles. These fall into two broad cat-

egories. The most important output ﬁles have a name supplied by the user,

e.g., mg24 followed by an extension, e.g. .res or .wfn. Other ﬁles, which are

not needed by most casual users, have the same standard name upon each run,

ending in .bigstick.

Results. The most important ﬁle are the results ﬁles, which have an exten-

sion .res. When you initiate BIGSTICK, after the main menu choice, BIGSTICK

almost always asks you for the name of the output ﬁles:

Enter output name (enter "none" if none)

If you enter “none” then several ﬁles are suppressed, in particular the results

ﬁle.

The results ﬁle generally contains the output spectrum, e.g.

State E Ex J T

1 -41.39657 0.00000 0.000 0.000

2 -39.58581 1.81077 2.000 0.000

3 -37.08646 4.31012 4.000 0.000

4 -34.46430 6.93227 0.000 0.000

5 -33.56871 7.82786 2.000 -0.000

It also may contain one-body density matrices, or the results of strength function

runs.

Wave functions. The .wfn ﬁle contains wave function information, stored

in binary (or “unformatted.”) In addition to containing the wave function vec-

tors, it has a header which contains enough information the basis can be recre-

ated.

Autoinput. On each run BIGSTICK generates a ﬁle autoinput.bigstick.

This saves the various input when run from the terminal. This is useful if one

is making small tweaks to run, or to use as the basis for input directives. To

use the autoinput ﬁle directly from terminal, choose ‘i’ at the opening menu.

Log ﬁle. The .log ﬁle summarizes information about the run, such as the

date, time, BIGSTICK version number, dimensions, parallelization (number of

MPI processes and OpenMP threads), internal ﬂag settings, and so on. While

not needed by the casual user, they are useful to document the exact conditions

under which a particular result ran and for debugging. If no output name is

speciﬁed, this ﬁle is named logfile.bigstick.

4.7.1 Secondary ﬁles

BIGSTICK generates some intermediate ﬁles which are not needed for ordinary

runs but in some cases can be useful. The most useful of these are the .lcoef

ﬁles, which in an ordinary Lanczos run contains the Lanczos coeﬃcients αi, βi.

If no output name is speciﬁed, this ﬁle is called lanczosvec.lcoef.

4.7.2 Diagnostic ﬁles

BIGSTICK also generates a number of diagnostic ﬁles, primarily for development,

tuning, and debugging.

timingdata.bigstick contains the time spent in diﬀerent matvec modes

(SPE, PP, etc) on each MPI process.

distrodata.bigstick contains the type and size of jumps stored on each

MPI process.

4.8 Memory usage

The motivation for BIGSTICK’s on-the-ﬂy algorithm is to save memory over

storing the nonzero many-body matrix elements. Despite this, BIGSTICK can

still be quite memory-hungry. The main sinks of memory are: the Lanczos

vectors themselves, the jumps factorizing the many-body matrix elements, and

the uncoupled two-body matrix elements. Which dominates depends upon the

system. For example, in large phenomenological calculations, the main memory

usage is from Lanczos vectors. In no-core shell model calculations, it is typically

the jumps, except for very light systems (A= 3,4) where for large spaces the

uncoupled matrix elements actually dominate.

BIGSTICK gives a report on memory usage. It also has some default caps on

memory and will halt if these are violated. The default caps can be changed by

the user.

Both in normal runs and in modeling runs, BIGSTICK produces a report:

RAM for 2 lanczos vector fragments (max) : 3923.728 Mb

RAM for jumps in storage (total) : 2353.914 Mb

Max RAM for local storage of jumps : 177.069 Mb

RAM for uncoupled two-body matrix elements : 0.017 Mb

The RAM report above is for the initial and ﬁnal Lanczos vectors in matvec. In

order to reorthogonalize, BIGSTICK also stores all Lanczos vectors. When run

in MPI, these Lanczos vectors are distributed across many MPI processes:

Enter max number of Lanczos iterations

150

Assuming max memory per node to store Lanczos vectors 16.00000 Gb

Storage of Lanczos vectors distributed up across 128 nodes

Memory per node = 10.74658 Gb

The default memory caps can all be found in the module flagger in the ﬁle

bmodules flags.f90. The most important ones are

real :: maxjumpmemory_default = 16.0 ! in Gb

real :: maxlanczosstorage1 = 16.000 ! in Gb

These can be changed, though of course BIGSTICK must be recompiled.

Chapter 5

Applications

In this chapter we discuss in more detail applications of BIGSTICK, speciﬁcally

one-body density matrices and one-body transition strengths.

5.1 One-body density matrices

BIGSTICK can be directed to compute the reduced one-body density matrices,

ρfi

K(ab)≡1

p(2K+ 1) DΨfhˆca†⊗˜cbiKΨiE(5.1)

where we use reduced matrix elements as deﬁned in Appendix A.1. We use this

particular deﬁnition because the reduced matrix element of a generic one-body

operator is the sum of products of the density matrix elements and the reduced

matrix elements, namely,

hΨf|| ˆ

OK||Ψii=X

ρfi

K(ab)ha|| ˆ

OK||bi.(5.2)

It’s important to note that ha|| ˆ

OK||biare matrix elements between single-

particle states, while the density matrices are matrix elements between many-

body states. While some many-body codes compute the many-body matrix ele-

ments for speciﬁc operators, such as E2, M1, and so on, we chose for BIGSTICK to

produce one-body density matrices, allowing the user to compute the transition

matrix elements for any one-body operator.

For systems with good isospin one can also deﬁne “doubly-reduced” matrix

elements, that is, reduced in both angular momentum and isospin:

ρfi

K,T (ab)≡1

p(2K+ 1)(2T+ 1) hΨf|||hˆca†⊗˜cbiK,T |||Ψii(5.3)

When you choose the density matrix option, BIGSTICK will write to the .res

ﬁle (but not to screen) the density matrices, e.g.:

Initial state # 2 E = -85.60214 2xJ, 2xT = 4 0

Final state # 1 E = -87.10445 2xJ, 2xT = 0 0

Jt = 2, Tt = 0 1

1 1 -0.01957 0.00000

1 2 0.18184 0.00000

1 3 0.09721 0.00000

2 1 -0.18184 0.00000

2 2 -0.35744 0.00000

2 3 -0.26323 0.00000

3 1 -0.09721 0.00000

3 2 -0.26323 0.00000

The ﬁrst two lines are the labels and energies of the initial and ﬁnal wave-

functions; Jt and Tt are the angular momentum and isospin of the one-body

operator, and, for example,

1 3 0.09721 0.00000

1 is the label of the ﬁrst single-particle orbit, 3 the label of the second (as deﬁned

by the input .sps ﬁle), and the two real numbers are the T= 0,1 one-body

density matrix elements, that is,

Ψ2hˆa†

1⊗˜a3iJ=2,T =0

Ψ1= 0.09721

while that for T= 1 is, here, zero.

BIGSTICK has two options for densities. The option dwill compute one-

body densities with good isospin, where the output looks like (this example is

23Ne in the sd shell with the USDB interaction):

Initial state # 1 E = -62.78960 2xJ, 2xT = 5 3

Final state # 1 E = -62.78960 2xJ, 2xT = 5 3

Jt = 0, Tt = 0 1

1 1 0.84730 0.28105

2 2 8.32846 2.85633

3 3 1.52286 0.13245

Alternately, there is the option dp which puts the density matrix elements into

explicit proton-neutron form.

Initial state # 1 E = -62.78960 2xJ, 2xT = 5 3

Final state # 1 E = -62.78960 2xJ, 2xT = 5 3

Jt = 0, proton neutron

1 1 0.16625 0.43288

2 2 1.58968 4.29943

3 3 0.47558 0.60124

5.1.1 Symmetries of density matrix elements

A useful symmetry relation is

ρif

K,T (ba) = (−1)ja−jb+Ji−Jf+Ti−Tfρfi

K,T (ab).(5.4)

5.1.2 Particle occupations from densities

Particle occupations are the average number of particles in single-particle orbit

for a given wave function. Although there is an option, ‘p,’ to compute the orbit

occupation, you can also extract this information from the diagonal one-body

density matrices. The total number of particles in orbit ais

n(a) = [ja]

[Ji]ρii

K=0(a†a) (5.5)

If your densities are in proton-neutron format, you can extract the proton and

neutron occupations separately. If you have your densities in isospin formalism,

you can extract the total number of protons and neutrons in an orbit

nπ(a) + nν(a) = [ja][1/2]

[Ji][Ti]ρii

K=0,T =0(a†a) (5.6)

To separately extract proton and neutron occupation one must take careful

account of the Clebsch-Gordan coeﬃcients. One must have f=i, so that

Jf=Ji=J0and Tf=Ti=T0, as well as considering only a=b. Furthermore,

the answer depends upon Tz= (Z−N)/2 (using the notation [x] = √2x+ 1)

nπ(a) = 1

2[ja]

[J0] [T0]

2 ρii

K=0,T =0(a†a) + Tz√3

pT0(T0+ 1)ρii

K,T =1(a†a)!,(5.7)

nν(a) = 1

2[ja]

[J0] [T0]

2 ρii

K=0,T =0(a†a)−Tz√3

pT0(T0+ 1)ρii

K,T =1(a†a)!.(5.8)

5.1.3 Strengths from density matrix elements

Given some transition operator ˆ

OKcarrying deﬁnite angular momentum K, the

transition strength between an initial and ﬁnal state is just the square of the

matrix element:

hJfMf|ˆ

OKM |JiMii

This is the matrix element that goes into Fermi’s golden rule for decay and

transition rates.

But in most experimental situations we cannot pick out speciﬁc values of

Mi,f (unless we are doing an experiment with polarization). The ﬁnal result

must then average over initial states and sum over ﬁnal states, that is,

2Ji+ 1 X

MiX

MfhJfMf|ˆ

OKM |JiMii

.(5.9)

In most cases there is also implicitly a sum over M. (If not, the ﬁnal result

will be diﬀerent.) Now we can use the Wigner-Eckart theorem to rewrite the

average/sum as:

2Ji+ 1 X

MfX

MiX

M|(JiMi, KM|JfMf)|2(Jf|| ˆ

OK||Ji)

.(5.10)

Now we can use the the selection rule Mf=Mi+Mfto eliminate the sum over

Mfand the orthogonality of the Clebsch-Gordan coeﬃcients to sum over Mi

and MX

MiX

M|(JiMi, KM|JfMi+Mf)|2= 1 (5.11)

Thus we get the result in terms of reduced matrix elements,

(2Ji+ 1) X

MiX

MfX

M(JfMf|ˆ

OKM |JiMi)

(2Ji+ 1) (Jf|| ˆ

OK||Ji)

,(5.12)

As one often calls 1

2Ji+ 1 (Jf|| ˆ

OK||Ji)

,(5.13)

the B-value, written B(O) (for example, B(GT ) for Gamow-Teller, B(E2) for

electric quadrupole, etc.), this says the strength for an operator is B(O).

In the BIGSTICK code and most other shell-model codes, we compute tran-

sition strengths using transition density matrix elements: the doubly reduced

transition matrix element for a one-body operator ˆ

OK,T of angular momentum

rank Kand isospin rank Tis

hΨf||| ˆ

OK,T |||Ψii=X

ρfi

K,T (ab)ha||| ˆ

OK,T |||bi.(5.14)

Although the default output is doubly-reduced matrix elements, the deﬁ-

nition of B-values do not sum or average over ‘orientations’ in isospin space,

because Tz= (Z−N)/2 is ﬁxed. Hence we have to account for that by un-

doing the Wigner-Eckart reduction in isospin, so that, for non-charge changing

transitions (e.g., γ-transitions),

B(O:i→f) = 1

2Ji+ 1 (Ψf:Jf|| ˆ

OJ||ΨiJi)

2Ji+ 1 (Ψf:JfTf||| ˆ

OJ,T |||ΨiJiTi)

×|(TiTz, T 0|TfTz)|2

2Tf+ 1 .(5.15)

Note the last line uses the result of Eq. (5.14).

5.1.4 Sample case: spin-ﬂip

Let’s consider a couple of simple cases, both in the sd shell with the USDB

interaction [Brown and Richter, 2006]. Let’s consider the spin-ﬂip operator

~σ = 2~

S, which has the following doubly-reduced matrix elements:

One-body matrix element value

h0d3/2|||~σ|||0d3/2i-2.19089

h0d3/2|||~σ|||0d5/2i4.38178

h0d5/2|||~σ|||0d3/2i-4.38178

h0d5/2|||~σ|||0d5/2i4.09878

h1s1/2|||~σ|||1s1/2i3.46410

The nuclide 19F, which has only one valence proton and two valence neutrons,

has, with appropriate scaling of the matrix elements, the low-lying spectrum:

State E Ex J T

1 -23.86096 0.00000 0.500 0.500

2 -23.78367 0.07729 2.500 0.500

3 -22.09059 1.77037 1.500 0.500

4 -21.26237 2.59858 4.500 0.500

5 -19.25724 4.60371 6.500 0.500

The density matrix from the second state (J= 5/2) to the third (J= 3/2)

state is, up to some overall phases,

Initial state # 2 E = -23.78367 2xJ, 2xT = 5 1

Final state # 3 E = -22.09059 2xJ, 2xT = 3 1

Jt = 1, Tt = 0 1

1 1 -0.08640 -0.01635

1 2 0.44978 -0.36112

1 3 0.01255 -0.09014

2 1 -0.16826 0.08815

2 2 -0.00280 -0.35352

3 1 -0.03483 0.07521

3 3 0.28978 -0.20874

Because the vector of Pauli matrices ~σ carries one unit of angular momentum

and no isospin, we only use the (Tt= 0) set of matrix elements (column second

from the right ). BIGSTICK also generates the transition matrix elements for Jt

=2, 3, and 4, not shown. Applying (5.15), we get a B(σ: 2 →3)=1.2609

A second case is 20Ne. The ground state is at -40.4723 MeV, which the ﬁrst

J= 1, T = 0 state, state #25, is at -27.8364 MeV (or 12.636 MeV excitation

energy). The density matrix is

Initial state # 1 E = -40.47233 2xJ, 2xT = 0 0

Final state # 25 E = -27.83635 2xJ, 2xT = 2 0

Jt = 1, Tt = 0 1

1 1 0.00069 0.00000

1 2 0.14575 0.00000

1 3 -0.10567 0.00000

2 1 0.18722 0.00000

2 2 -0.04822 0.00000

3 1 -0.02309 0.00000

3 3 0.28308 0.00000

and B(σ: 1 →25) = 0.3597.

5.1.5 Charge-changing transitions

Charge-changing transition such as Gamow-Teller are a little more subtle. If

we have isospin-conserving interactions, so that our initial and ﬁnal states have

good isospin, we can use isospin rotation so that we don’t have to change basis.

If we want to have a transition

ZXN→A

Z±1YN∓1,

that is, from some initial Tz,i = (Z−N)/2 to some ﬁnal Tz,f = (Z−N)/2±1,

we must work in the basis with the smaller Tz; then both initial and ﬁnal states

will be somewhere in the spectrum. What we want to calculate is

hΨf:Jf, TfTz,f || ˆ

O||Ψi:Ji, TiTz,ii

but what we can actually calculate with BIGSTICK is

hΨf:Jf, TfTz|| ˆ

O||Ψi:Ji, TiTzi

Fortunately this can be accomplished with only a small modiﬁcation of the

above procedure:

B(O:i→f) = 1

2Ji+ 1 (Ψf:Jf|| ˆ

OJ||ΨiJi)

2Ji+ 1 (Ψf:JfTf||| ˆ

OJ,T |||ΨiJiTi)

×|(TiTz,i, T ±1|TfTz,f )|2

2Tf+ 1 ,(5.16)

where the diﬀerence between Eq. (5.15) and (5.16) is in the isospin Clebsch-

Gordan. There is, however, one more subtle point in treating the isospin rais-

ing/lowering operator, τ±. If one treats τas a rank-1 spherical tensor in isospin

space, one can show that

τ±=1

√2τ1,±1.(5.17)

Therefore, formally, in the above calculations, we are actually using 2−1/2τ1,0

in our calculation, and then rotating to a charge-changing transition.

It’s always good to have a way to check calculations, and in the case of

Gamow-Teller it’s the Ikeda sum rule, which says

B(~στ+:i→f)−B(~στ−:i→f) = 3(N−Z) (5.18)

independent of the initial state i. Here the isospin raising operator τ+changes a

neutron into a proton and hence is the operator for β−decay, while the isospin

lowering operator τ−changes a proton into a neutron and hence is the operator

for β+decay. This assume our convention that protons are isospin ‘up’ and

neutrons isospin ‘down;’ many authors have opposite conventions.

5.1.6 Sample case: 19F

Let’s calculate the Gamow-Teller B-value. The matrix elements for Gamow-

Teller are the same as for ~σ as shown above except multiplied by p3/2. Then

using the Tt= 1 one-body density matrix elements, we get B(GT: 2 →3) =

1.3990.

For 20Ne, there is at J= 1, T = 1 state at -29.3066 MeV (or 11.166 MeV

excitation energy, state #15); the density matrix is

Initial state # 1 E = -40.47233 2xJ, 2xT = 0 0

Final state # 15 E = -29.30659 2xJ, 2xT = 2 2

Jt = 1, Tt = 0 1

1 1 0.00000 0.05163

1 2 0.00000 0.09951

1 3 0.00000 -0.03397

2 1 0.00000 0.18236

2 2 0.00000 0.32717

3 1 0.00000 -0.03311

3 3 0.00000 -0.08363

Here B(GT) = 0.1654, for either β+ or β−.

5.2 Strength function option

One important capability of BIGSTICK is using the Lanczos algorithm to eﬃ-

ciently compute transition strength function distributions and to decompose a

wavefunction using a scalar operator, or option ‘s’ in the main menu.

5.2.1 Decomposition

We’ll start with decomposition of a wavefunction using a scalar operator [John-

son, 2015], because operationally it is the most straightfoward. Suppose you

have a wavefunction, |Ψi, which you have previously computed using BIGSTICK

and have stored in a .wfn ﬁle; further suppose you have some operator ˆ

Owhich

is an angular momentum scalar, which in turn means its matrix elements can be

stored in a ﬁle just like a Hamiltonian. This operator ˆ

Oin turn has eigenpairs,

O|Φωi=ω|Φωi.(5.19)

We can always expand |Ψiinto the eigenstates of ˆ

|Ψi=X

cω|Φωi(5.20)

and the fraction of the wavefunction |Ψilabeled by ωis simply

|hΦω|Ψi|2=|cω|2.

This is particularly useful when ˆ

Ois the Casimir of some group or subgroup,

such as total orbital angular momentum ˆ

L2or total spin ˆ

S2. In that case we

say we decompose the wavefunction |Ψiinto its L- or S- components.

BIGSTICK can carry out this decomposition easily. What you need is, ﬁrst,

a previously computed wavefunction in some .wfn ﬁle, and a ﬁle or ﬁles which

contain the matrix elements of the decomposing operator.

To do this:

1. From the initial menu choose the option ‘s’:

* (s) Strength function (using starting pivot ) *

Enter choice

Note: the pivot is the starting vector; here it is the wavefunction you wish

to decompose. BIGSTICK can only decompose one wavefunction at a time.

2. Enter name of ﬁle containing the wavefunction to be decomposed (i.e.,

the pivot):

Compute strength function distribution using previous wfn

Enter input name of .wfn file

mg24

Here the choice of the wavefunction ﬁle is mg24.wfn; you do not include the

extension. At this point, BIGSTICK reads in some information from the .wfn

ﬁle:

testing magic number 31415926 31415926

dimbasischeck= 28503

Valence Z, N = 4 4

Single particle space :

N L 2xJ

023

025

101

Total # of orbits = 3

2 x Jz = 0

The ‘magic number’ is a test of internal consistency to make sure, ﬁrst,

BIGSTICK is correctly reading the ﬁle (in particular if the binary ﬁle was created

on a diﬀerent platform) and also between diﬀerent versions of BIGSTICK if the

information protocol has changed.

From this information BIGSTICK reconstructs the basis and checks the di-

mensions agree. It then asks for the output ﬁle:

Enter output name (enter "none" if none)

After this, BIGSTICK will make the standard inquiries for the Hamiltonian.

When decomposing a wavefunction, the ‘Hamiltonian’ is actually an angular

momentum scalar which is a Casimir of the group or sub-group; for example, it

could be ˆ

S2or ˆ

L2. Such ﬁles are in in the same format as any interaction ﬁle.

While we provide a sample operator, it is up to the user to generate these ﬁles.

After the interaction ﬁle(s) have been read in, you must enter in the number

of iterations and number of states to keep (BIGSTICK automatically chooses a

ﬁxed-iteration run for Lanczos):

Enter nkeep, # iterations for lanczos

(nkeep = # of states printed out )

Exactly how many iterations to to choose requires some knowledge of the group,

or, speciﬁcally, knowledge of the eigenvalues of the Casimir, and, in many cases,

a few trials. Remember that the irreps of the group are labled by the eigenvalues

of the Casimir, which means the eigenvalues are highly degenerate. The number

of iterations needed should be no greater than the number of distinct eigenvalues.

So, for example, if one has 8 nucleons and is decomposing via spin, the values

of Scan be 0,1,2,3,or 4. Therefore the number of iterations should be no

more than 4 (because one wants a total dimension of 5). Often one can use

fewer iterations. If you use too many iterations, you will get duplication of

eigenvalues or, worse, unconverged duplicate eigenvalues.

Finally, BIGSTICK will print out a list of the starting states in the pivot ﬁle,

and their energies and Jand Tvalues, and ask you to choose a pivot:

There are 5 wavefunctions

5 states

STATE E J <H >

1 -92.7790 -0.0000 0.0000

2 -91.1196 2.0000 0.0000

3 -88.4779 2.0000 0.0000

4 -87.9781 4.0000 0.0000

5 -87.4348 3.0000 0.0000

Which do you want as pivot?

Hence if you want to decompose the J= 3 state, enter 5.

Immediately after reading in the pivot, BIGSTICK will print out the norm of

the input pivot (that generally does play a role in this kind of decomposition,

but will in transition strength functions):

0.999999998379788 = total input strength

Often the norm or total input strength is far diﬀerent from 1.

After carrying out the speciﬁed Lanczos iterations, the result will look some-

thing like this, depending on how many iterations:

Energy Strength

______ ________

0.00000 0.63545

2.00000 0.33880

6.00000 0.02515

12.00000 0.00059

20.00000 0.00000

______ ________

The ‘energies’ on the left are the eigenvalues of the operator you are using to

decompose the wavefunction, here ˆ

S2. Hence the J= 3 state (or state 5 in

the above example), is 63.5%S= 0, 33.9%S= 1, and so on. These results are

written to the standard .res ﬁle.

5.2.2 Transition strength function distributions: the ba-

sics

Often we want the transition function between two states, that is hΨf|ˆ

O|Ψii

where ˆ

Ois some one-body transition operator, for example the E2 or M1 tran-

sition operator. (As always, we assume the reader is familiar with these con-

cepts.) If one only wants one or two transitions, one can compute those using

the one-body density matrices, which we describe above in 5.1.3.

But sometimes we want many transitions to many ﬁnal (or ‘daughter’) states

from a single initial (‘parent’) state, for example if we want to proﬁle ‘giant’

resonances. We can do this using BIGSTICK in three to four steps. The ﬁrst

step is to generate and write to ﬁle an initial wavefunction.

The second step is to apply a one-body operator, ˆ

O. The matrix elements

of the one-body operator must be stored in ﬁle with extension .opme, with the

format deﬁned in the next section. To apply a one-body operator, choose option

‘o’ at the opening menu:

* (o) Apply a one-body (transition) operator to previous wfn....

BIGSTICK will then ask for the name of the input .wfn ﬁle and an output name,

required here. After reconstructing the basis from the information in the input

.wfn ﬁle, it will ask:

Enter name of .opme file

The matrix elements of the one-body operator are read in from a ﬁle with

extension .opme (‘operator matrix element’). While we distribute some sample

.opme ﬁles with BIGSTICK, in general it is up to the user to generate such ﬁles.

The format of such ﬁles are

iso ! indicating good isospin

3 ! # of single-particle orbits

1 0 2 1.5 ! index of orbit, n, l, and j

2 0 2 2.5

3 1 0 0.5

1 0 ! J and T of operator

1 1 -2.19089 ! a, b < a ||| O ||| b >

1 2 4.38178

2 1 -4.38178

2 2 4.09878

3 3 3.46410

BIGSTICK ﬁrst checks the list and order of single-particle orbits agrees with that

of the read-in wavefunction. BIGSTICK will then read in the matrix elements of

the one-body operator and apply it to each wavefunction stored in the input

.wfn ﬁle and write them to a new output .wfn ﬁle.

The ﬁnal step is to run BIGSTICK again, this time with the strength function

option ‘s,’ using the wavefunction generated in the second step as input. This

time, when BIGSTICK asks for the interaction ﬁle name, you should use the

same ﬁle(s) to generate the initial state, because you are diagonalizing the

Hamiltonian.

As with decomposition, BIGSTICK will now carry out a ﬁxed number of

iterations and print out the transition strength. Because it includes the norm

of the input pivot, these strengths can be greater than 1.

An important question is that of convergence. As you probably know, in the

Lanczos algorithm the extremal eigenpairs converge ﬁrst, with interior eigenpairs

converging later. This is true as well for the strengths described above: the

extremal strengths will converge quickly to strengths (and eigenenergies) of

extremal levels, but interior strengths will often not be converged; instead they

will be some sort of ‘local average’ of strengths.

What looks like a bug is actually a feature. In practice one often doesn’t need

each and every strength to be fully converged. Instead we only need integrals

over the strengths to be converged, and this does happen. While we can only

refer the reader to Caurier et al. [2005] and references therein, we can state that

the moments of the distributions of strengths do converge. In fact, if one carries

out NLanczos iterations, one has ∼2Nmoments of the distribution correctly.

Hence often only thirty or ﬁfty iterations suﬃce.

As an example, consider 20Ne in the sd shell with the USDB interaction. If

we apply the σoperator, with the matrix elements given above, and then apply

the strength function option s, the output will look something like:

0.38353481218057317 = total strength

35 iterations

Energy Strength

______ ________

-40.47233 0.00000

-38.72564 0.00000

-36.29706 0.00000

-33.77148 0.00000

-32.88892 0.00000

-30.18655 0.00000

-27.83635 0.11991

-25.73419 0.00003

-25.49045 0.17314

-24.73655 0.01326

-22.86589 0.00027

-22.24522 0.01542

Notices the strength at -27.836 MeV (which is the J;T= 1; 0 state) is 0.11991;

using the Clesbsch-Gordan coeﬃcients gives a factor of 3, or a total strength of

0.3597, which agrees with our previous result.

There is a small bug in this lovely ointment: it assumes we have treated

angular momentum (and isospin) correctly, a topic we now turn to.

5.2.3 Transition strength functions with good angular mo-

mentum

In the prior subsection we glided over questions of angular momentum, which

we treat more carefully here. An important question is correct calculation of

the B-values, as deﬁned in Eq. (5.13) above, which assume an average over

ﬁnal states and a sum over ﬁnal states. But what we computed in the previous

section was

|hΨf|ˆ

O|Ψii|2

where the states have ﬁxed Mand ﬁxed Tz, because, as currently written, both

initial and ﬁnal wavefunctions must be in the same basis. (We plan at a later

date to write a separate tool which will allow one to apply and operator from a

wavefunction in one basis to a wavefunction in a diﬀerent basis.) If you want the

applied operator to change parity, then both parities must be included in the

basis (option 0 when entering parity in the initial calculation of wavefunctions).

To extract the B-value, one has to invoke the Wigner-Eckart theorem:

B(O:i→f) = 1

2Ji+ 1 (Ψf:Jf|| ˆ

OJ||ΨiJi)

2Jf+ 1

(2Ji+ 1) 

hΨf:JfM|ˆ

OJ0|Ψi:JiMi

(JiM, J0|JfM)

.(5.21)

If one has Ji= 0 (which can only happen if M= 0), then the B-value is

straightforward to calculate:

B(O:i→f) = (2J+ 1)|hΨf:J0|ˆ

OJ0|Ψi: 00i|2.

It’s more complicated with Ji6= 0; in that case the triangle rule, |Ji−J| ≤ Jf≤

Ji+Jis in eﬀect, and in fact the state produced by BIGSTICK,

OK|Ψi:Jii

will be an admixture of states of diﬀerent Jf. Thus one needs an additional

step, of projecting out states of good angular momentum after applying the

transition operator but before carrying out the strength function option via

Lanczos. Fortunately we already know how to do this via decomposition as

discussed in 5.2.1.

Therefore, to properly carry out calculation of strength functions, you will

need (a) ﬁles for the interaction, (b) a ﬁle for the one-body transition operator,

and (c) ﬁles with matrix elements of ˆ

J2and, separately, T2(you only need

the latter if your transition operator has isospin rank 1). Then carry out the

following steps:

(1) With your interaction use option (n) or similar option, generate a .wfn

ﬁle containing an initial state;

(2) Use option (o) to apply the one-body operator (note this will be applied

to every wavefunction in the ﬁle);

(3) If your initial state has Ji6= 0, you will need to ﬁlter out a state of good

Jffor every possible Jf; in fact what you will do will be to decompose the state

from step (2) into its components Jf. Here you use option (s). If there are N

possible values of Jfyou only need to do N−1 iterations.

If your transition operator has T= 1 and your initial Ti6= 0, you will need

to further decompose into possible Tfstates.

(4) Finally, use option (s) again, but this time with the original interaction,

to get the strength function distribution. You will have to apply the Wigner-

Eckart theorem as in Eq. (5.21), but now that step (3) guarantees a deﬁnite

value of Jf(and, if needed, Tf), you can carry this out.

You will have to repeat for each possible ﬁnal value of Jf.

Here is an example using 19F: if we choose the J= 5/2 state (state #2) as

the pivot and apply ~σ, and then use the strength function option with ˆ

J2,

1.3726179231928042 = total strength

3 iterations

Energy Strength

______ ________

3.75000 1.13861

8.75000 0.05630

15.75000 0.17771

______ ________

This means 83% of the pivot has J= 3/2 and only 4.08% has J= 5/2. Next

we run the strength function again on the second state using the original (usdb)

interaction:

1.0000000433422094 = total strength

35 iterations

Energy Strength

______ ________

-23.86096 0.00000

-23.78367 0.00000

-22.09059 0.66440

-21.26237 0.00000

-19.25723 0.00000

Note that the wavefunction is normalized when it is read in. (By the way,

the zeroes show up because although there is no strength to them, or very

little, roundoﬀ error allows them to grow during Lanczos. This is the same

phenomenon which forces us to orthogonalize new Lanczos vectors against old

ones.) We have to multiply 0.66440 ×1.13861 = 0.756 to get the ‘raw’ strength,

which here is |hJfM|~σ|JiMi|2, then we have to follow Eq. (5.21):

0.756 ×2(3/2) + 1

2(5/2) + 1 ×1

|(5/2 1/2,1 0|3/2 1/2)|2= 0.756 ×4

6×1

2/5= 1.260

which agrees with our previous result! Note that you have to do each step with

care; if don’t scale the two-body matrix elements, you will get diﬀerent results.

5.2.4 Gamow-Teller with strength function option

Charge-changing transitions such as Gamow-Teller are a straightforward gen-

eralization but require even more care. Here one transitions from a state with

some initial Tz,i to some ﬁnal Tz,f =Tz,i ±1. Because, as of the time of this

writing, BIGSTICK requires the same initial and ﬁnal basis, we have to choose

Tz,0= min (abs(Tz,i),abs(Tz,f )) and invoke isospin rotation. Typically you will

have to ﬁlter both Jand T. The B-value is given by

B(O:i→f) = 1

2Ji+ 1 hΨf:Jf, TfTz,f || ˆ

OJ||Ψi:Ji, TiTz,ii

2Jf+ 1

(2Ji+ 1) 

hΨf:JfM, TfTz,0|ˆ

O1 0,1 0|Ψi:JiM, TiTz,0i

(JiM, J0|JfM)

(5.22)

×

(TiTz,i,1±1|TfTz,f )

(TiTz,0,1 0|TfTz,0)

where the last line uses the isospin Wigner-Eckart theorem to transform from

the isospin frame the calculation is carried out in, to the physically desired

isospin frame.

We use BIGSTICK’s strength function option sto compute the matrix element

|hΨf:JfM, TfTz,0|ˆ

O1 0,1 0|Ψi:JiM, TiTz,0i|2. This is slightly involved. We

give now a detailed example, again with 19F. After applying the Gamow-Teller

operator, we ﬁlter out ﬁrst with ˆ

J2, using the second state as the pivot:

0.72792934307990387 = total strength

3 iterations

Energy Strength

______ ________

3.75000 0.61870

8.75000 0.01998

15.75000 0.08925

______ ________

and then we ﬁlter this with ˆ

T2(applied to the ﬁrst state, that is, the one with

J= 3/2

0.99999997896552772 = total strength

3 iterations

Energy Strength

______ ________

0.75000 0.77481

1.10978 0.00000

3.75000 0.22519

______ ________

and then ﬁnally applying the strength function with the usdb interaction:

1.0000000877719881 = total strength

35 iterations

Energy Strength

______ ________

-23.86096 0.00000

-23.78367 0.00000

-22.09059 0.87875

-21.26237 0.00000

-19.25722 0.00000

Thus in this example the ‘raw’ transition strength is that for the J;T=

5/2; 1/2→3/2; 1/2 which is

0.61870 ×0.77481 ×0.87875 = 0.42125.

This now has to be converted to a Gamow-Teller B-value by Eq. (5.22):

B(GT ) = 2·3

2+ 1

2·5

2+ 1 ×0.42125

5

2,1 0|3

2

2×1

2−1

2,1 1|1

2

1

2+1

2,1 0|1

2

A good exercise is to compute low-lying transitions two ways, ﬁrst with

density matrices, and then via the strength function option, to conﬁrm they

agree with each other. For Gamow-Teller, one can and should verify results by

using the Ikeda sum rule.

One can also use other operators for projection, for example, using center-

of-mass to project out nonspurious states in no-core shell model calculations.

We plan to later allow two-body transition operators, but as of version 7.8.1

these options have not yet been installed.

Chapter 6

A peek behind the curtain

Although this manual details how to use BIGSTICK, it only outlines the algo-

rithms and program. The distribution includes an Inside Guide which, while

incomplete, contains many more details on the code, and the source code itself is

heavily commented. Even so, it is a complex program, with more than seventy

Fortran ﬁles and on the order of 70,000 lines. Several ﬁles are for specialized

applications most users will not care about, as well as for features slated for

obsolescence.

There are ways to get BIGSTICK to present more information about its inner

workings, as well as ways to extert more control over the algorithm. A number

of logical ﬂags turn behaviors on and oﬀ. The most important ﬂags, and some

default settings, are found in bmodules flags.f90. Some additional ﬂags for

output are in the module io in bmodules main.f90, and other ﬂags can be

found elsewhere. To detail all the possibilities would expand this already long

manual by a signiﬁcant amount.

In this chapter we outline the major steps BIGSTICK takes in carrying out

a ‘normal’ run, as well as telling the curious user how to print out an explicit

representation of the basis and of the many-body Hamiltonian matrix.

6.1 A normal run

Here are the steps BIGSTICK carries out in a ‘normal’ run, that is, setting up a

many-body Hamiltonian and ﬁnding the low-lying extremal eigensolutions.

•BIGSTICK sets up the basis.

•BIGSTICK counts up the number of jumps (data needed for constructing

the Hamiltonian on-the-ﬂy).

•BIGSTICK gathers the interaction data.

•If running in parallel, BIGSTICK computes the distribution

•BIGSTICK generates the data needed (on a speciﬁc MPI process if running

in parallel), speciﬁcally the jumps and the decoupled matrix elements.

•BIGSTICK sets up storage for the Lanczos vectors.

•BIGSTICK begins Lanczos iterations.

•Upon completion of Lanczos, BIGSTICK constructs the low-lying eigenvec-

tors. It resets the jumps and computes angular momentum and isospin

as expectation values. Eigenvalues and eigenvectors are written to ﬁle. If

density matrices requested, BIGSTICK resets jumps for one-body operators

and computes.

•Upon ﬁnishing, BIGSTICK reports on timing and closes down.

6.2 Explicit representation of the basis

Through factorization and other tricks, BIGSTICK only implicitly stores the basis

and the Hamiltonian. In actual operations, BIGSTICK stores information on

pieces of Slater determinants, which we call “haikus.” Haikus are organized by

quantum numbers, as are the action of single-fermion creation and annihilation

operators on the haikus. These latter we called “hops” and from them we

construct jumps, and from jumps we construct many-body matrix elements,

and so on. Once the hops are created the haikus are not needed, and once the

jumps are constructed the hops are not needed.

It can be useful, however, to have explicit representations of both the basis

and of the many-body Hamiltonian. In standard runs, the ﬁnal eigenvectors

are written to ﬁle with extension .wfn. These ﬁles are unformatted to save

space. Furthermore the detailed basis information is not saved; instead any

basis BIGSTICK is constructed in a standard order, and when reading a .wfn ﬁle

BIGSTICK swiftly reconstructs the basis.

From the main menu, however, the option ‘t’ will write out both the basis

and the eigenvectors in explicit, human-readable form, to a ﬁle with extension

.trwfn (originally written as an input to Petr Navratil’s density code TRDENS).

Here is an annotated example output from the p-shell, using the Cohen-

Kurath interaction. First is a header describing the nucleus:

4 ! valence Z

4 ! valence N

ckpot ! name of INTERACTION FILE

19.45492 ! HW (approx) 12

1 ! # of majors shells

12 1 ! total p+n s.p.s, # shells core

0 ! Nmax (excitations)

51 ! # of many-body configurations = basis dimension

1 ! parity, +

0 ! 2 x Jz

5 ! # of eigenstates kept

Next is a list of the eigenenergies, and numerical J and T values; the latter are

written as real numbers. Reading across we have E,J, and T.

-71.04467 3.6173283E-06 -4.1723251E-07

-66.39703 2.000000 -3.8743019E-07

-58.59552 1.000001 -4.4703484E-07

-57.57795 3.6235542E-06 -4.1723251E-07

-57.54143 4.000000 -2.9802322E-07

Then comes a list of the single particle state quantum numbers. Reading across

we have label, n(number of radial nodes), l, 2 ×j, 2 ×jz, and 2 ×tz:

1011-11

2013-11

3013-31

401111

501311

601331

7 0 1 1 -1 -1

8 0 1 3 -1 -1

9 0 1 3 -3 -1

10 0 1 1 1 -1

11 0 1 3 1 -1

12 0 1 3 3 -1

So single-particle state 1 is a 0p1/2with jz=−1/2 and is a proton, single-

particle state 2 is 0p3/2with jz=−1/2 and is a proton, etc.

Finally we have a listing of the 51 many-body basis states and their ampli-

tudes for the ﬁrst ﬁve eigenstates:

1 2 3 5 8 10 11 12

0.1989746094 0.1647298932 -0.0000000709 -0.0788139924 -0.1036236882

1 2 3 5 7 10 11 12

0.0805789307 0.0938614532 0.0855044648 -0.1246829554 -0.0399925224

1 2 3 4 8 10 11 12

-0.0805789307 -0.0938614309 0.0855044946 0.1246829703 0.0399925113

1 2 3 4 7 10 11 12

-0.0582427122 -0.0433882587 0.0000000068 0.0952372476 0.0186970048

1 2 3 6 7 8 11 12

0.0825415403 -0.0342168659 -0.0919694155 -0.0390651748 0.1794791222

1 2 3 6 7 8 10 12

0.0697834268 -0.0333072022 0.0155492499 -0.1079809889 0.1385308802

1 2 3 6 9 10 11 12

-0.1513192952 0.0582505427 -0.0000000329 0.0562667921 -0.3108672500

2 3 4 5 7 8 11 12

0.0560085103 -0.0361775197 -0.0000000029 -0.0111581217 0.1036224812

...

So the ﬁrst many-body basis states has occupied single particle states 1,2,3,5

(protons) and 8,10, 11, and 12 (neutrons). The ﬁve real numbers following are

the amplitudes for this basis state for the ﬁve eigenstates whose eigenenergies

are given above. You can see an example of factorization: the basis states 1 and

2 have the same proton occupancies loop over neutron occupancies; while basis

states 3 and 4 have the same proton occupancies (but diﬀerent from basis states

1 and 2) and loops over the same neutron occupancies as basis states 1 and 2.

By adding up the jzvalues, the proton “Slater determinants” have Mp=−2

and the neutron Slater determinants have Mn= +2. The next basis states,

number 5 through 7, have Mp=−Mn=−1. In this way BIGSTICK builds up

the basis. As shown in the example, in constructing the basis via factorization,

the innermost loop is over neutron Slater determinants while the outer is over

protons.

We recommend against using this option on a regular basis, because writing

this information to a ﬁle is slow, and BIGSTICK does not have postprocessing

options for this format. Nonetheless it can be useful for understanding what is

going on, and could be a basis for a user’s own post-processing code.

6.3 Explicit representation of the Hamiltonian

The many-body Hamiltonian can also be explicitly generated. If from the Lanc-

zos menu you choose ‘ex’ for exact or full diagonalization, the entire Hamiltonian

is created and explicitly stored and solve using the LAPACK routine DSYEV. This

occurs in the routine exactdiag p in the ﬁle blanczos main.f90. If the basis

dimension is less than 100, BIGSTICK will automatically write out the Hamilto-

nian matrix elements to a ﬁle ham.dat. This occurs around line 1246; the user

can edit this part of the code to control the dimension cutoﬀ for writing out

(in general we do not encourage writing out for large dimensions) as well as the

format.

Chapter 7

Lanczos algorithm

Today the most common way to ﬁnd all the eigenpairs of a Hermitian (here,

real and symmetric) matrix is ﬁrst reduce the matrix to tridiagonal form via a

sequence of unitary transformations, the Householder algorithm[Parlett, 1980,

Press et al., 1992], and then solve the resulting tridiagonal matrix via QL de-

composition with implicit shifts (or so we’ve been told). But for the very large

dimensions of standard CI calculations, one neither can extract all eigenpairs

nor does one want to: beyond a certain point one expects intruder many-body

states to enter and eventually dominate, rendering our calculated states lack-

ing physical meaning. (For the novice: an intruder state is a state outside the

designated model space. There is no simple way, at least for the non-expert, to

determine where we expect intruders to dominate.)

Instead we turn to the Lanczos and related algorithms [Parlett, 1980, Press

et al., 1992, Whitehead et al., 1977]. Lanczos is part of a family of so-called

Arnoldi algorithms, which iteratively construct a new orthonormal basis, the

Krylov subspace. In this new basis the Hamiltonian is tridiagonal, but unlike

the Householder algorithm, one does not need to fully carry out the transfor-

mation. The Lanczos algorithm is simple, beautiful, and powerful, though like

all algorithms it is not without its own limitations.

7.1 Standard Lanczos algorithm

The Lanczos algorithm is exceedingly straightforward. We will summarize it

here, though we will not explicate it in detail. Starting from some initial vector

|v1i, called the pivot, one iteratively generates a sequence of orthonormal vectors

{|vii, i = 1, k},hvi|vji=δij :

H|v1i=α1|v1i+β1|v2i

H|v2i=β1|v1i+α2|v2i+β2|v3i

H|v3i=β2|v2i+α3|v3i+β3|v4i

. . .

H|vii=βi−1|vi−1i+αi|vii+βi|vi+1i

. . .

H|vki=βk−1|vk−1i+αk|vki

(7.1)

Each iteration generates a new Lanczos vector. If we stop at the k−1th iter-

ation, we have kLanczos vectors and a k-dimension Krylov subspace. Using

orthonormality of the vectors, one can show that in this basis, the Hamiltonian

is tridiagonal:

Hi,i =hvi|ˆ

H|vii=αi,(7.2)

Hi,i+1 =Hi+1,i =hvi|ˆ

H|vi+1i=βi.(7.3)

and all other matrix elements are zero.

The speciﬁc steps for creating the next Lanczos vectors are straightforward:

(1) |wii=ˆ

H|viiInitial matvec on vector i;

(2) αi=hvi|wiidot product to get αi;

(3) |wii←|wii − αi|viiorthogonalize against initial vector i;

(4) If i > 1|wii←|wii−βi−1|vi−1iorthogonalize against prior vector i-1;

(5) βi=phwi|wiiﬁnd norm to get βi;

(6) |vi+1i=β−1

i|wiiNormalize to get i+1th Lanczos vector.

If we had perfect arithmetic, this would be suﬃcient: the new Lanczos vector

|vi+1iwould be guaranteed to be orthogonal to all previous vectors. But we

don’t have perfect arithmetic, and due to round-oﬀ noise, small components of

prior Lanczos vectors will creep in and eventuall grow exponentially.

This requires us to enforce orthogonality against all prior Lanczos vectors:

(4)(alt.) For j = 1 to i-1 : |wii←|wii−|vjihvj|wii

If one does not reorthogonalize, eventualy one gets ‘ghost eigenvalues’, or

repetitions of the same eigenvalues. It is this need for reorthogonalization that

keeps Lanczos from supplanting Householder as the go-to algorithm for full

tridiagonalization of Hermitian matrices.

There has been much discussion and experimentation around partial re-

orthogonalization, but no one clearly successful recipe. BIGSTICK fully reorthog-

onalizes against all prior vectors; in most cases (a few hundred iterations) re-

orthogonalization work does not overwhelm matvec work.

You might notice that if one extended the for loop in our alternate step

(4), we would already get step (3). Because of ﬁnite arithmetic, order matters.

We ﬁnd better results if we ﬁrst compute αiand then orthogonalize against all

other vectors, rather than as a last step.

It is possible for a user to experiment with these ﬁne tweaks in BIGSTICK. The

Lanczos iterations are found in subroutine lanczos p in ﬁle blanczoslib1.f90.

One can estimate the workload from reorthogonalization. Again, let Nbe

the dimension of the vector space. Each projection requires a dot product and

a subtraction, or about 2Noperations. For kLanczos vectors, one has k−1

iterations. For the jth iteration one orthogonalizes against jvectors or 2Nj

operations; thus for k−1 iterations one has 2N

Obviously with full reorthogonalization full Lanczos transformation to tridi-

agonal form becomes expensive; hence the dominance of the Householder algo-

rithm for complete diagonalization.

7.2 Thick-restart Lanczos

Sometimes there is insuﬃcient storage for the number of Lanczos vectors re-

quired for convergence. An alternative is the thick-restart Lanczos[Wu and

Simon, 2000]. In standard Lanczos there are essentially two dimensions, Nkeep,

the number of converged states desired, and Niter, the number of iterations

(typically kabove). But one must store Niter + 1 Lanczos vector, which can be

prohibitive. For thick-restart Lanczos, there is an additional dimension Nthick,

with Nkeep < Nthick < Niter, and is the dimension of the Krylov subspace when

restarting. In otherwords, one iterative creates a subspace of dimension Niter +1,

but then truncates down to dimension Nthick, and then adds additional vectors

back up to a subspace of dimension Niter + 1, truncate back down, and repeat

until convergence. The advantage is that Niter, and the consequent number of

vectors stored, is much smaller than would be needed for standard Lanczos.

Thick-restart Lanczos follows this basic outline:

1. Start with some initial Lanczos pivot vector |v1ias usual.

2. Carry out kLanczos iterations so that you have k+ 1 Lanczos vectors

|vii, i = 1, k + 1, and a truncated k+ 1 ×k+ 1 Hamiltonian matrix Tk+1.

3. Diagonalize the k×ksubmatrix Tk.

4. From the eigenpairs of step (3), choose the Nthick lowest states. These

will form the “new” Lanczos eigenvectors. In addition, keep |vk+1iand

use this as the restarting vector for Lanczos.

5. Now restart Lanczos, but instead of starting with |v1i, start with |vk+1i

which is our new |vNthick+1i.

6. Iterate until you have again k+ 1 Lanczos vectors and an truncated k+

1×k+ 1 Hamiltonian matrix Tk+1. This new matrix will no longer be

tridiagonal, but it will have a simple form, given below.

Now let’s describe this in more detail. Suppose we have carried out kLanczos

iterations, so that we have a total of k+1 vectors |vii, including the pivot. Then

the transformed Hamiltonian, which is the Hamiltonian in the basis {|vii}, looks

Tk+1 =







α1β10 0 . . . 0

β1α2β20. . . 0

0β2α3β3. . . 0

0 0 . . . αk−1βk−10

0 0 . . . βk−1αkβk

0 0 . . . 0βkαk+1







(7.4)

Suppose, however, we only diagonalize Tk, that is, stopping at the kth column

and row, with Lbeing the k×kunitary matrix of eigenvectors, that is,

j=1 Tkij Ljµ =Liµ ˜

Eµ,(7.5)

for µ= 1, k. Here ˜

Eµare the approximate eigenenergies. If we apply the unitary

transform Lto the ﬁrst kvectors, that is, introducing

|v0

µi=

i=1 |viiLi,µ, µ = 1, k (7.6)

and |v0

k+1i=|vk+1ithe transformed matrix, which is the Hamiltonian the basis

{|v0

ii}, now becomes







E10 0 0 . . . βkLk1

0˜

E20 0 . . . βkLk2

0 0 ˜

E30. . . βkLk3

0 0 . . . ˜

Ek−10βkLk,k−1

0 0 . . . 0˜

EkβkLkk

βkLk1βkLk2. . . βkLk,k−1βkLkk αk+1







(7.7)

The key to thick-restart Lanczos is to judiciously truncate this. If you want,

as is the usual case, to get the lowest Nkeep states, truncate to some Nthick (with

Nkeep < Nthick < k) vectors, that is, to

|v0

1i,|v0

2i,|v0

3i, . . . |v0

Nthick i

plus the last Lanczos vector, |vk+1i, then the truncated Hamiltonian looks like







E10 0 0 . . . βkLk1

0˜

E20 0 . . . βkLk2

0 0 ˜

E30. . . βkLk3

0 0 . . . ˜

ENthick−10βkLkNthick−1

0 0 . . . 0˜

ENthick βkLkNthick

βkLk1βkLk2. . . βkLk,Nthick −1βkLkNthick αk+1







(7.8)

Now declare |vk+1ito be the new |v0

Nthick+1iand start the Lanczos iterations

on it:

H|v0

Nthick+1i= (7.9)

βkLk1|v0

1i+βkLk2|v0

2i+. . . +αNthick+1|v0

Nthick+1i+βNthick+1|v0

Nthick+2i

This ﬁrst step is not a tridiagonal relation; furthermore , although our new

|v0

Nthick+1iis the same as our old |vk+1i, and our new αNthick+1 is the same as

the old αk+1, the new vector |v0

Nthick+2iis not the same as |vk+1iwould have

been had we continued the previous iteration, although the former contains the

latter as a component, because the iteration step is diﬀerent.

Now one continues iterations Nthick + 2, Nthick + 3, . . . , k + 1. Then one diag-

onalizes the approximate Tkagain,although it is no longer a pure tridiagonal,

and in fact looks like:







E10 0 0 . . . βkLk10. . .

0˜

E20 0 . . . βkLk20. . .

0 0 ˜

E30. . . βkLk30. . .

....

0 0 . . . ˜

ENthick−10βkLkNthick−10. . .

0 0 . . . 0˜

ENthick βkLkNthick 0

βkLk1βkLk2. . . βkLk,Nthick −1βkLkNthick αNthick+1 βNthick+1

0 0 . . . 0 0 βNthick+1 αNthick+2

....







and restarts as above, repeating under convergence.

This thick-restart algorithm requires more matvec multiplications than stan-

dard Lanczos, because information is thrown away at each restart, but the stor-

age and reorthogonalization of Lanczos vectors can be greatly reduced. There is

no recommended value of Nthick or k, but one should take kas large as practical,

and “typical” values of Nthick ≈3Nkeep or so.

Although the usual application to thick restart is to ﬁnd low-lying states, it

is conceivable to choose a slice of excited energy and to converge excited states.

This will be investigated.

7.3 Can I restart standard Lanczos?

The standard Lanzos algorithm is an iterative algorithm. In principle, if you

found the desired eigenpairs had not converged under the chosen number of

iterations, you could pick up and restart. To do this you would need the Lanczos

vectors created so far and the Lanczos coeﬃcients.

Although in prior version BIGSTICK wrote the Lanczos vectors to disk, in

its current version stores all Lanczos vectors in RAM. In MPI parallelization

the Lanczos vectors are stored across multiple processes. Therefore right now

the restart option has been turned oﬀ. It is possible in future versions we may

restore it, although it is not a high priority.

Chapter 8

Parallel computing and

timing

BIGSTICK can run many non-trivial problems on modest desktop or even lap-

top computers. Because problems grow exponentially, however, single-processor

calculations quickly reach limits. To overcome these limits we invoke parallel

processing.

Although many parts of the set up portion of the code have been paral-

lelized, by far the most time-consuming part of the code is the matrix-vector

multiplication, followed by reorthogonalization, and it is these two portions it

is most important to parallelize.

For very large calculations, one needs to distribute both matvec operations

(work load balance) and data (memory load balance). Operations are paral-

lelized using both MPI (distributed memory) and OpenMP (shared memory)

while data can only be distributed with MPI.

When BIGSTICK starts, it tells you how many MPI processes and how many

OpenMP threads per process it is using:

Number of MPI processors = 512

NUM_THREADS = 8

This information is also written to the .log ﬁle. BIGSTICK does not have any

special requirements for setting up parallel runs, although to run in parallel one

must use an executable compiled with parallel options, i.e. bigstick-mpi.x

compiled with make mpi,bigstick-opemp.x compiled with make openmp, or

the hybrid bigstick-omp-mpi.x compiled with make openmp-mpi. Any user

who wishes to use the parallel capability should already have some idea about

submitting parallel jobs. For example, to set up the number of OpenMP threads

on a desktop machine you typically

PROMPT>export OMP_NUM_THREADS=8

and to submit an MPI job you may do

PROMPT>mpirun -n 512 bigstick-mpi.x

Of course, the details will depend upon the local environment. Unfortunately, in

our experience supercomputers do not have a uniform job submission protocol.

8.1 MPI

To carry out a Lanczos iteration, which includes a matvec followed by reorthog-

onalization, one needs the following data:

•an initial vector;

•an ﬁnal vector;

•jump information used for on-the-ﬂy construction of the many-body matrix

elements; and

•the uncoupled two- (or, optionally, three-) body matrix used in construction

of the many-body matrix elements;

•previously computed Lanczos vectors (used for calculation of the Lanczos

coeﬃcients, for reorthogonalization and, ultimately, construction of the ﬁnal

eigenvectors which represent wavefunctions).

In large calculations some or all of these may need to be distributed via MPI.

To compute the distribution eﬃciently, BIGSTICK goes throught the setup in

two stages. First, it calculates the number of operations in each matvec, that

is, in

vﬁnal

i=X

Hij vinitial

j,(8.1)

each update

vﬁnal

i←vﬁnal

i+Hij vinitial

j.(8.2)

Because of factorization, BIGSTICK does not have to actually generate every

operation. BIGSTICK then generates the distribution, and each MPI process

creates locally the data it needs.

BIGSTICK attemps to distribute the operations across MPI processes as

evenly as possible. The operations are constructed from jumps, but the ra-

tio of operations to jumps is not ﬁxed. We ﬁnd it helpful to think of matvec

operations as represented by the area of a rectangle, and the sides of the rectan-

gle representing the jumps. If the rectangle is nearly square, the reconstruction

is eﬃcient, but if one has a long, thin rectangle in either dimension, one requires

considerably more storage of jumps relative to the number of operations. Oc-

casionally, an equitable distribution of operations will, on some small subset of

MPI processes, so many jumps they cannot be stored. In that case, BIGSTICK

will distribute those jumps over multiple MPI processes; this of course leads to

a load imbalance, but is necessary so as not to exhaust memory.

8.1.1 Fragments

If the basis dimension is so large both initial and ﬁnal vectors cannot be con-

tained in core memory, they must be broken into fragments. When running in

MPI, or in modeling mode, BIGSTICK will ask for this automatically:

Enter desired limit on fragment size for breaking Lanczos vectors

(Largest un-splittable block = 16602236 )

( Default = 200000000 )

( Enter 0 to use default )

Somewhat counterintuitively, BIGSTICK achieves best eﬃciency when the frag-

ments are as large as possible. The reason for this is that the factorization

principle behind BIGSTICK works most eﬃciently when combining large conju-

gate data.

Fragments are generally combinations of contiguous sectors (a portion of

the vector which is labeled by the proton quantum numbers), although, because

the lengths of sectors can vary signiﬁcantly, in some cases a fragment can be

comprised of a single sector. In the most extreme cases BIGSTICK will seek to

divide a sector into two new ‘sectors,’ although there are limitations to how

ﬁnely this can be done. Otherwise BIGSTICK attempts to make the fragments

as similar in size as practical.

If you run BIGSTICK in MPI mode, it will ask for the fragment size. The

fragment size is approximately the length of the initial and ﬁnal vectors stored

on a given MPI process (because of the way the code chunks data, BIGSTICK

actually allows for a small overrun). Choosing a value of 0 will select the default

value, currently around 200 million, which is actually on the small size. Because

Lanczos vectors are stored in single precision, this requires roughly 1.6 Gb of

RAM for the initial and ﬁnal vector fragments. On many machines you can

choose this to be larger.

Matvec operations are now deﬁned from an initial fragment (of a Lanczos

vector) to a ﬁnal fragment (of a Lanczos vector). This work will generally be

spread across mulitple MPI processes; hence one needs nproc (the number of

MPI processes) ≥nfragments2(the number of fragments). In fact, BIGSTICK

will complain if nproc <2×nfragments2.

8.1.2 Opbundles and optypes

The operations are organized by a derived type (Fortran’s designation for a

bundle of data, very much like a struct in C) called opbundles, or bundles of

operations. Opbundles are the ‘natural’ way to divide up work in BIGSTICK. Op-

bundles orchestrate the application of matvec operations, and BIGSTICK provide

information about opbundles. Most users will not need this information.

Each opbundle has an associated ‘optype,’ which classiﬁes the physical origin

of the matrix elements being reconstructed. For example, the ‘PP’ optype is for

interactions betwen two protons, with neutrons as spectators. There are also

NN and PN optypes, and for three-body forces, PPP, NNN, PNN, and PPN.

Finally there has been an optype SPE for single-particle energies and related

single-particle potentials. However this has been absorbed into PP, PN, and

NN optypes. We do this by multiplying any one-body term by ( ˆ

N−1)/(A−1),

with ˆ

Nthe number operator and Athe (valence) mass number. In the same

way, if one runs with three-body forces, any two-body forces are subsumed into

three-body by multiplying the two-body operators by ( ˆ

N−2)(A−2).

Optypes signal diﬀerent operations and invoke diﬀerent methods of recon-

structing the matrix elements. PP optypes use proton ‘two-body jumps’ and

loop over spectator neutron Slater determinants, NN optypes use neutron two-

body jumps and loop over spectator proton Slater determinants, and PN op-

types use both proton one-body jumps and neutron one-body jumps. Not only

do these invoke diﬀerent subroutines, the time per operation is diﬀerent for

diﬀerent optype, because the loops are diﬀerent, and may be diﬀerent on diﬀer-

ent machines. This information in turn is used to calculation the distribution

of work. Information on the timing of these operations is found in the ﬁle

timinginfo.bigstick. In many cases, by carrying out a short run to establish

the time per operation, written to timinginfo.bigstick, and then running the

desired run using this information, can lead to signiﬁcantly greater eﬃciency.

Unfortunately, the time per operation is not as ﬁxed for an optype as we

originally hope, and detailed investigations show a great deal of ﬂuctuations.

We are still investigating this issue and attempt to arrive at better weighting

and distribution algorithms.

8.1.3 Modeling

One menu option BIGSTICK oﬀers is modeling, or choice ‘m’ on the main menu.

This will run mostly like a normal run, with the following diﬀerences:

•No interaction ﬁle information will be requested (although if three-body

forces are enables, it will ask if you want to model the use of three-body

forces);

•Prompt for mandatory information on fragments;

•Prompt for mandatory information on the number of MPI processes; in-

formation on the number of OpenMP threads is not needed;

•Prompt for the number of Lanczos vectors.

You can model a run using a diﬀerent number of MPI processes than the

modelled number.

The modeling option will calculate the distribution of work and data. This

is useful because you can ﬁnd out if the number of MPI processes requested is

insuﬃcient, or if BIGSTICK can ﬁnd a distribution solution at all. (In some rare

cases the algorithm currently fails.)

8.2 OpenMP

BIGSTICK uses OpenMP where it can, in particular in matvec. Unfortunately

due to the nature of the problem, there are limitations to the speedup form

OMP. Because the matrix elements are very sparse, one tends to lose locality.

Modern computers have at least three levels of storage: disk storage, RAM

storage, and cache storage. These three kinds of memory are increasingly close

to the CPU and thus are increasingly faster; they are also increasing smaller in

size. When data is fetched from disk or even from RAM, the CPU also fetches

nearby data and leaves it in the cache. If the program needs that cached data

next, it is handily nearby and thus faster to be accessed. Because of the highly

nonlocal nature of the data, however, BIGSTICK has trouble reaching maximum

eﬃciency. While we continue to work on this issue, by the very nature of the

sparse matrix this is diﬃcult. Some of the work we have carried out is described

in Shan et al. [2015, 2017].

8.3 Timing

In order to improve eﬃciency, BIGSTICK contains a number of built-in vari-

ables and routines for tracking and reporting timing. When running in serial,

BIGSTICK uses the FORTRAN routines date and time or cpu time. Unfortu-

nately these do not provide very accurate timing, on the order of 0.01 second,

so some information is not accurate. When running in MPI, BIGSTICK uses

BMPI Wtime, which is much more accurate.

BIGSTICK will give an estimate of the time to run,

Approximate time per iterations estimated : 2112 sec, or 35.2 min

but keep in mind this is a rough estimate. This uses information in timinginfo.bigstick

which contains timing from previous runs. If you previously ran a similar prob-

lem, this estimate is likely reliable, but if the problem changes, or if you are

using the default assumption, when timinginfo.bigstick does not exist, then

the results may vary.

8.3.1 Mode times

The main timing in BIGSTICK is to measure the amount of time the code spends

in various modes of operation, i.e., in generating the basis, computing jumps,

matvec (matrix-vector multiplication), reorthognalization, and so on. At the

end of a run, BIGSTICK prints out the culmulative time. These times are written

to the terminal as well as the .res results ﬁle. The output looks something like

this:

Total time to run : 58.7889999998733

Time to compute basis : 3.999999724328518E-003

Time to count up jumps : 1.099999994039536E-002

Time to decouple matrix elements : 1.999999862164259E-003

Time to compute jumps : 1.899999985471368E-002

Time to compute lanczos : 42.0250000003725

Time total in H mat-vec multiply : 30.9959999998100

Time to apply sp energies : 4.599999962374568E-002

Time in pn : 13.1739999908023

Time in pn(back) : 8.17700000526384

Time in 2-body (pp) : 2.46199999982491

Time in 2-body (pp)(back) : 2.45600000442937

Time in 2-body (nn) : 4.66199999954551

Time in reorthogonalization : 10.8760000029579

Time to compute J^2, T^2 : 9.499999973922968E-002

Time in applyobs : 0.950999999884516

Time spent diagonalizing. : 7.299999939277768E-002

8.3.2 Timing for parallel runs

In addition to timing various modes during a run, BIGSTICK provides timing data

useful for load balancing MPI parallel runs. As discussed elsewhere, BIGSTICK

attempts to distribute work across MPI processes by counting up the number of

operations and distributing the work. Operations are managed by opbundles,

and each opbundle is associated with a particular Hamiltonian mode: proton-

proton (PP), neutron-neutron (NN), proton-neutron (PN), and so on. Therefore

BIGSTICK tracks the time spent on each MPI process, on each Hamiltonian mode

on each MPI process, and ﬁnally on each opbundle.

Appendix A

Matrix elements and

operators

A.1 Reduced matrix elements

The Wigner-Eckart theorem states that a matrix element which depends upon

Jzis proportional to a Clebsch-Gordan coeﬃcient, that is,

hJfMf|ˆ

OKM |JiMii= [Jf]−1(JiMi, KM|JfMf)(Jf|| ˆ

OK||Ji) (A.1)

= (−1)Jf−MfJfK Ji

−MfMKMi(Jf|| ˆ

OK||Ji)

where (Jf|| ˆ

OK||Ji) is the reduced matrix element, which encapuslates the funda-

mental matrix element independent of orientation, and which in 5.1.3 is related

to a sum over all orientations.

Eq. (A.1) can also be thought of as the deﬁnition of the reduced matrix

element (and the Wigner-Eckart theorem a statement that this deﬁnition is

consistent using any set of Ms). Note that it is possible to have a variant deﬁni-

tion with diﬀerent pre-factors, that is, the phase and factors like p2Jf+ 1 are

conventions. Only the Clebsch-Gordan coeﬃcients are dictated by the theorem.

The choices of (A.1), taken from Edmonds [1996] are the most widely used ones.

The Wigner-Eckart theorem applies not just to angular momentum but any

SU(2) algebra; hence one can reduce in isospin as well, and a doubly-reduced

matrix element follows naturally:

hJfMf;TfMT f |ˆ

OKM;T MT|JiMi;TiMT ii= (A.2)

(JiMi, KM|JfMf)

[Jf]

(TiMT i, T MT|TfMT f )

[Tf](Jf, TF|| ˆ

OK,T ||Ji, Ti).

A.2 The Hamiltonian and other operators in sec-

ond quantization

Here we carefully deﬁne our operators in second quantization, that is, using

fermion creation and annihilation operators and coupled up to good angular

momentum. To denote generic operators ˆα, ˆ

βcoupled up to good total angular

momentum Jand total z-component M, we use the notation

(ˆα×ˆ

β)JM =X

mα,mβ

(jαmα, jβmβ|JM )ˆαjαmαˆ

βjβmβ,(A.3)

where (jαmα, jβmβ|JM ) is a Clebsch-Gordan coeﬃcient (here and throughout

we use the conventions of Edmonds [1996]).

Hence we can deﬁne the general fermion pair creation operator

A†

JM (ab) = (ˆa†×ˆ

b†)JM (A.4)

with two particles in orbits aand b. We also introduce the time-reverse of

A†

JM (ab), the pair annihilation operator,

AJM (cd) = −(˜c×˜

d)JM (A.5)

Here we use the standard convention ˜cmc= (−1)jc+mcˆc−mc, where mcis the

z-component of angular momentum. An alternate notation is

AJM (cd) = ˆ

A†

JM (cd)†

= (−1)J+M˜

AJ,−M(cd) (A.6)

With this we can write down a standard form for any one- plus two-body

Hamiltonian or Hamiltonian-like operator, which are angular momentum scalars.

To simplify we use

H=X

eab ˆnab

abcd

ζabζcd X

VJ(ab, cd)X

A†

JM (ab)ˆ

AJM (cd),(A.7)

where ˆnab =Pmˆa†

mˆ

bmand ζab =√1 + δab. Here VJ(ab, cd) = hab;J|ˆ

V|cd;Ji

is the matrix element of the purely two-body part of ˆ

Hbetween normalized

two-body states with good angular momentum J; because it is a scalar it is in-

dependent of the z-component M. To make our results as broadly interpretable

as possible, we also write this as

eab[ja]ˆa†×˜

b0,0

abcd

ζabζcd X

VJ(ab, cd) [J]ˆ

A†

J(ab)×˜

AJ(cd)0,0(A.8)

where we use the notatation [x] = √2x+ 1, which some authors write as ˆx;

we use the former to avoid getting confused with operators which always are

denoted by either ˆaor ˜a.

Finally we also can introduce one-body transition operators with good an-

gular momentum rank Kand z-component of angular momentum M,

FK,M =X

Fab

[K]ˆa†×˜

bK,M (A.9)

Here Fab =ha|| ˆ

FK||biis the reduced one-body matrix element.

A.3 Symmetries of matrix elements

Two-body matrix elements satisfy the following symmetries:

VJ(ab, cd) = −(−1)ja+jb+JVJ(ba, cd) (A.10)

=−(−1)jc+jd+JVJ(ab, dc) = (−1)ja+jb+jc+jdVJ(ba, dc).

Including isospin,

VJT (ab, cd) = −(−1)ja+jb+J+1+TVJT (ba, cd) (A.11)

=−(−1)jc+jd+J+1+TVJT (ab, dc)=(−1)ja+jb+jc+jdVJT (ba, dc).

Because we assume real-valued matrix elements, VJT (ab, cd) = VJT (cd, ab). Al-

though internally BIGSTICK has a speciﬁed order for storing matrix elements,

the code can read in matrix elements in any order and with the indices a, b, c, d

in any order.

Non-scalar spherical tensors should satisfy [Edmonds, 1996]:

ˆ

FKM †

= (−1)Mˆ

FK,−M.(A.12)

For non-charge-changing transitions, Eq. (A.12) implies Fab = (−1)ja−jbF∗

ba.

Appendix B

Highlighted references

There are a number of books and review articles on the conﬁguration-interaction

shell model. We focus on those in nuclear physics. One of the best, but nowa-

days diﬃcult to get, is Brussard and Glaudemans [1977]. Some other useful

references, in historical order, are [De-Shalit and Talmi, 2013], Towner [1977],

Lawson and Lawson [1980] (thorough, but be aware his phase conventions diﬀer

from most others), Talmi [1993], Heyde [1994], Suhonen [2007], and others. A

particular useful review article touching on many of the ideas here Caurier et al.

[2005]; the review article Brown and Wildenthal [1988] is older but has useful

information on applications of the shell model. The no-core shell model and

other ab initio methods are a rapidly evolving ﬁeld, but good overviews of the

topic are Navr´atil et al. [2000] and Barrett et al. [2013].

For angular momentum coupling a widely used reference is the slim volume

by Edmonds [1996]. If you can’t ﬁnd what you need in Edmonds, you can

almost certainly ﬁnd it in Varshalovich et al. [1988]. Sadly, neither are good

pedagogical introductions to the topic of angular momentum algebra.

Bibliography

F. Andreozzi and A. Porrino. J. Phys. G: Nucl. Part. Phys, 27:845, 2001.

B. R. Barrett, P. Navr´atil, and J. P. Vary. Ab initio no core shell model. Progress

in Particle and Nuclear Physics, 69:131–181, 2013.

B. Brown, A. Etchegoyen, and W. Rae. Computer code OXBASH: the Oxford

University-Buenos Aires-MSU shell model code. Michigan State University

Cyclotron Laboratory Report No. 524, 1985.

B. A. Brown and W. D. M. Rae. The Shell-Model Code NuShellX@MSU.

Nuclear Data Sheets, 120:115–118, 2014.

B. A. Brown and W. A. Richter. New “usd” hamiltonians for the sd shell. Phys.

Rev. C, 74:034315, Sep 2006.

B. A. Brown and B. H. Wildenthal. Status of the nuclear shell model. Annual

Review of Nuclear and Particle Science, 38:29–66, 1988.

P. Brussard and P. Glaudemans. Shell-model applications in nuclear spec-

troscopy. North-Holland Publishing Company, Amsterdam, 1977.

E. Caurier and F. Nowacki. Present status of shell model techniques. Acta

Physica Polonica B, 30:705–714, 1999.

E. Caurier, G. Mart´ınez-Pinedo, F. Nowacki, A. Poves, J. Retamosa, and A. P.

Zuker. Full 0¯hω shell model calculation of the binding energies of the 1f7/2

nuclei. Phys. Rev. C, 59:2033–2039, Apr 1999.

E. Caurier, G. Martinez-Pinedo, F. Nowacki, A. Poves, and A. P. Zuker. The

shell model as a uniﬁed view of nuclear structure. Reviews of Modern Physics,

77:427–488, 2005.

D. B. Cook. Handbook of computational quantum chemistry. Oxford University

Press, 1998.

A. De-Shalit and I. Talmi. Nuclear shell theory, volume 14. Academic Press,

2013.

J. Draayer, T. Dytrych, K. Launey, and D. Langr. Symmetry-adapted no-

core shell model applications for light nuclei with qcd-inspired interactions.

Progress in Particle and Nuclear Physics, 67(2):516–520, 2012.

A. R. Edmonds. Angular momentum in quantum mechanics. Princeton Univer-

sity Press, 1996.

D. Gloeckner and R. Lawson. Spurious center-of-mass motion. Physics Letters

B, 53(4):313–318, 1974.

K. L. Heyde. The nuclear shell model. Springer, 1994.

F. Jensen. Introduction to computational chemistry. John Wiley & Sons, 2017.

C. W. Johnson. Spin-orbit decomposition of ab initio nuclear wave functions.

Phys. Rev. C, 91:034313, Mar 2015.

C. W. Johnson, W. E. Ormand, and P. G. Krastev. Factorization in large-scale

many-body calculations. Computer Physics Communications, 184:2761–2774,

2013.

P. Knowles and N. Handy. A new determinant-based full conﬁguration interac-

tion method. Chemical physics letters, 111(4-5):315–321, 1984.

R. Lawson and R. Lawson. Theory of the nuclear shell model. Clarendon Press

Oxford, 1980.

P.-O. L¨owdin. Quantum theory of many-particle systems. i. physical interpre-

tations by means of density matrices, natural spin-orbitals, and convergence

problems in the method of conﬁgurational interaction. Phys. Rev., 97:1474–

1489, Mar 1955.

P. Navr´atil, J. Vary, and B. Barrett. Large-basis ab initio no-core shell model

and its application to 12 c. Physical Review C, 62(5):054311, 2000.

F. Palumbo. Intrinsic motion and translational invariance in shell-model calcu-

lations. Nuclear Physics A, 99(1):100–112, 1967.

F. Palumbo and D. Prosperi. Eﬀects of translational invariance violation in

particle-hole calculations. application to 208pb. Nuclear Physics A, 115(2):

296–308, 1968.

T. Papenbrock and D. J. Dean. Factorization of shell-model ground states.

Phys. Rev. C, 67:051303, May 2003.

T. Papenbrock and D. J. Dean. Density matrix renormalization group and

wavefunction factorization for nuclei. Journal of Physics G: Nuclear and

Particle Physics, 31(8):S1377, 2005.

T. Papenbrock, A. Juodagalvis, and D. J. Dean. Solution of large scale nuclear

structure problems by wave function factorization. Phys. Rev. C, 69:024312,

Feb 2004.

B. N. Parlett. The symmetric eigenvalue problem, volume 7. SIAM, 1980.

W. H. Press, B. Flannery, S. Teukolsky, and W. Vetterling. Numerical recipes

in fortran. Cambridge university press, 1992.

H. Shan, S. Williams, C. Johnson, K. McElvain, and W. E. Ormand. Parallel im-

plementation and performance optimization of the conﬁguration-interaction

method. In Proceedings of the International Conference for High Performance

Computing, Networking, Storage and Analysis, page 9. ACM, 2015.

H. Shan, S. Williams, C. Johnson, and K. McElvain. A locality-based

threading algorithm for the conﬁguration-interaction method. 2017. URL

http://escholarship.org/uc/item/9sf515zf.

I. Shavitt. The history and evolution of conﬁguration interaction. Molecular

Physics, 94:3–17, 1998.

C. D. Sherrill and H. F. Schaefer. The conﬁguration interaction method: Ad-

vances in highly correlated approaches. Advances in quantum chemistry, 34:

143–269, 1999.

N. Shimizu. Nuclear shell-model code for massive parallel computation,” kshell”.

arXiv preprint arXiv:1310.5431, 2013.

P. Sternberg, E. Ng, C. Yang, P. Maris, J. Vary, M. Sosonkina, and H. V. Le.

Accelerating conﬁguration interaction calculations for nuclear structure. The

Proceedings of the 2008 ACM/IEEE Conference on Supercomputing, 2008.

J. Suhonen. From Nucleons to Nucleus: Concepts of Microscopic Nuclear The-

ory. Springer Science & Business Media, 2007.

I. Talmi. Simple models of complex nuclei. CRC Press, 1993.

J. Toivanen. Eﬃcient matrix-vector products for large-scale nuclear shell-model

calculations. arXiv preprint arXiv:nucl-th/0610028, 2006.

I. S. Towner. A shell model description of light nuclei. Clarendon Press Oxford,

1977.

D. A. Varshalovich, A. N. Moskalev, and V. K. Khersonskii. Quantum theory

of angular momentum. World scientiﬁc, 1988.

A. W. Weiss. Conﬁguration interaction in simple atomic systems. Phys. Rev.,

122:1826–1836, Jun 1961.

R. R. Whitehead, A. Watt, B. J. Cole, and I. Morrison. Computational methods

for shell model calculations. Advances in Nuclear Physics, 9:123–176, 1977.

K. Wu and H. Simon. Thick-restart lanczos method for large symmetric eigen-

value problems. SIAM Journal on Matrix Analysis and Applications, 22(2):

602–616, 2000.

BIGSTICK Manual

BIGSTICK_Manual

Navigation menu

Versions of this User Manual:

Views

Navigation