Bay Pass Manual 2.1

User Manual: Pdf

Open the PDF directly: View PDF .
Page Count: 40

Overview
Before you start
Running BayPass
Miscellaneous R functions
Worked Examples
- Cattle allele count data
- Littorina Pool–Seq read count data
Credits
Copyright
Contact
Bibliography
Appendix Comparisons of the computational efficiency of the different version of BayPass

December 9, 2015

BayPass version 2.1

User Manual

BayPass code c

INRA

This document c

Mathieu Gautier 2015

Contents

1 Overview 4

2 Before you start 4

2.1 How to get BayPass?...................... 4

2.2 How to compile BayPass?.................... 5

2.3 Input ﬁle format ......................... 6

2.3.1 The genotyping data ﬁle [always required] ......... 6

2.3.2 The pool (haploid) size ﬁle [only required for Pool–Seq data] 8

2.3.3 The covariate data ﬁle [required for the covariate modes] . . 8

2.3.4 The covariance matrix ﬁle [optional, required for the AUX

covariate mode] ....................... 9

3 Running BayPass 9

3.1 Overview of the diﬀerent models available in BayPass .... 9

3.1.1 The core model ...................... 10

3.1.2 The standard covariate model and extensions ..... 11

3.1.3 The auxiliary covariate model .............. 12

3.2 Detailed overview of all the options ............... 15

3.3 Format of the output ﬁles .................... 21

4 Miscellaneous R functions 24

4.1 The R function simulate.baypass() ................ 25

4.1.1 Description ........................ 25

4.1.2 Usage ........................... 25

4.1.3 Arguments (in alphabetic order) ............. 25

4.1.4 Values ........................... 27

4.1.5 Examples ......................... 29

4.2 The R function fmd.dist() .................... 29

4.2.1 Description ........................ 29

4.2.2 Usage ........................... 29

4.2.3 Arguments ......................... 29

4.2.4 Values ........................... 30

4.2.5 Example .......................... 30

4.3 The R function geno2YN() .................... 30

4.3.1 Description ........................ 30

4.3.2 Usage ........................... 30

4.3.3 Arguments ......................... 30

4.3.4 Values ........................... 30

4.3.5 Example .......................... 31

5 Worked Examples 31

5.1 Cattle allele count data ...................... 31

5.1.1 Analysis under the core model mode: MCMC is run

under the core model ................... 31

5.1.2 Analysis under the IS covariate mode: MCMC is run

under the core model ................... 33

5.1.3 Analysis under the MCMC covariate mode: MCMC is

run under the STD model ................ 34

5.1.4 Analysis under the AUX covariate mode: MCMC is

run under the AUX model ................ 35

5.2 Littorina Pool–Seq read count data ............... 36

6 Credits 36

7 Copyright 37

8 Contact 37

Bibliography 38

Appendix A Comparisons of the computational eﬃciency of the

diﬀerent version of BayPass 40

1 Overview

The package BayPass is a population genomics software which is primarily

aimed at identifying genetic markers subjected to selection and/or associated

to population-speciﬁc covariates (e.g., environmental variables, quantitative

or categorical phenotypic characteristics). The underlying models explicitly

account for (and may estimate) the covariance structure among the popula-

tion allele frequencies that originates from the shared history of the popula-

tions under study. Note that, apart from standard population genetics stud-

ies, BayPass is generic enough to be also suited to the analyses of data from

other kinds of experiments in which the allele frequency covariance structure

is simpler (e.g., experimental evolution). The genetic data typically consists

of allele (when derived from individual genotype calls) or read (when derived

from Pool–Seq experiments) counts at several markers (for now, BayPass is

restricted to the analysis of bi–allelic markers) in several populations. Note

that BayPass can handle missing data (no count available in one or several

populations) which might be helpful in some contexts.

The core BayPass model is based on the Bayenv model which was

proposed by Coop et al. (2010) and G¨

unther and Coop (2013). However,

as detailed in Gautier (2015), in addition to a complete and independant

reprogramming of the core Markov Chain Monte Carlo (MCMC) algorithm,

BayPass allows to monitor most of the parameters and the priors of the

original models and to introduce various extensions (via e.g., the optional

addition of hyper–parameters, the modeling of spatial dependency among

consecutive markers).

BayPass is written in Fortran90. The source code and compilation in-

structions for various platforms (OS X, Windows, Linux) are available. The

executable reads data ﬁle(s) supplied by the user, and a number of options

can be passed through the command line. Some R functions are also provided

in the package to facilitate interpretation of the resulting outputs.

This document provides information about how to format the data ﬁle,

how to specify the user-deﬁned parameters, and how to interpret the results.

2 Before you start

2.1 How to get BayPass?

Download the archive from http://www1.montpellier.inra.fr/CBGP/software/

baypass/, and extract it from a terminal:

tar -zxvf baypass_2.1.tar.gz

2.2 How to compile BayPass?

The source ﬁles are to be found in the src subdirectory. BayPass is coded

in Fortran90 and can therefore be compiled for any system supporting a For-

tran90 compiler using the provided Makefile. This Makefile is designed

to work with either the free compiler gfortran1or the commercial ifort

intelrFortran compiler2. As a consequence, using another Fortran90 com-

piler requires modifying the Makefile accordingly. Note also that BayPass

uses OpenMP (http://openmp.org/wp/) to implement multithreading, which

allows parallel calculation on computer systems that have multiple CPUs or

CPUs with multiple cores. Users thus have to make sure that the correspond-

ing libraries are installed (which is usually the case, at Linux OS or following

compiler installation previously described1). The following instructions run

within the src subdirectory allows to compile the code and to produce a

binary:

•using the gfortran free compiler (the command should automatically

produce an executable called g_baypass):

make clean all FC=gfortran

•using the ifort intelrFortran compiler (the command should auto-

matically produce an executable called i_baypass):

make clean all FC=ifort

From my (limited) experience, I would recommend using the ifort intelr

Fortran compiler instead of gfortran. Indeed, although gfortran options

could probably be better adapted to further improve the speed of the exe-

cutable (any feedback about this is welcome), using the options considered

in the Makeﬁle, the ifort executable is more than two times faster than the

gfortran one as illustrated in the comparison below3. An example compar-

ison of the computational performances of the diﬀerent version and binaries

of the program is illustrated in Table 1.

1If not already installed in your system, binaries are available at https://gcc.gnu.

org/wiki/GFortranBinaries and easy to install for most Windows, Mac and Linux OS

versions (many thanks to Andrew Beckerman for pointing this webpage to me!)

2Intel proposes a free personal non-commercial unsupported version that is es-

sentially identical to the commercial version: https://software.intel.com/en-us/

qualify-for-free-software/academicresearcher

3I however noticed that the ifort executable might sometimes crash in an unpre-

dictable way when reading the command line arguments (for a reason that remains very

obscure to me and that I am trying to ﬁgure out!)

Under Linux (or MacOS), before the ﬁrst use, make sure to give appropriate execution

rights to the program. For instance you may run:

chmod +x baypass

In the following, it is assumed that the program was made executable and

accessible in your path. For instance, under Linux, this may be achieved by

copying the executable in a directory declared in the path (e.g., /usr/local/bin)

or by adding the program to the $PATH system variable (using the export

command)

2.3 Input ﬁle format

Depending on the type of analyses, diﬀerent data ﬁles might be required by

the program. The following examples of the diﬀerent input ﬁles are available

in the examples directory:

•geno.bta14: this ﬁle contains allele count data for 18 French cattle

breeds at 1,394 SNPs mapping to the BTA14 bovine chromosome (see

Gautier (2015) for details).

•bta.pc1: this ﬁle contains the SMS (Synthetic Morpholy Score) for the

18 French cattle breeds (see Gautier (2015) for details).

•omega.bta: this ﬁle contains the matrix Ωfor the 18 French cat-

tle breeds (b

Ωbpas

BTA) as estimated under the core model from the whole

genome SNP data (see Gautier (2015) for details).

•lsa.geno: this ﬁle contains read count data (Pool–Seq data) for 12

populations from the Littorina saxatilis marine snail (Westram et al.,

2014) at 2,500 SNPs randomly chosen among the ones analysed in Gau-

tier (2015) (but including the ca. 150 outlier SNPs identiﬁed).

•lsa.poolsize: this ﬁle contains the haploid pool sizes of the 12 Litto-

rina saxatilis populations.

•lsa.ecotype: this ﬁle contains the code for the ecotype of the 12

Littorina saxatilis populations (−1 for the ”crab” habitat and 1 for the

”wave” habitat).

2.3.1 The genotyping data ﬁle [always required]

The genotyping data ﬁles contain allele or read count (for PoolSeq experi-

ment) data for each of the nsnp markers assayed in each of the npops popula-

tions sampled. The genotyping data ﬁle is simply organised as a matrix with

nsnp rows and 2 ∗npop columns. The row ﬁeld separator is a space. More

precisely, each row corresponds to one marker and the number of columns is

twice the number of populations because each pair of numbers corresponds to

each allele (or read counts for PoolSeq experiment) counts in one population4.

As a schematic example, the genotyping data input ﬁle for allele count

data should read as follows:

--- file begins here ---

81 19 86 14 2 98 8 92 32 68 23 77

89 11 81 19 9 91 1 99 27 73 27 73

89 11 91 9 0 0 15 85 77 23 80 20

[...97 more lines...]

--- file ends here ---

In this example, there are 6 populations and 100 SNP markers. At the ﬁrst

SNP, in the ﬁrst population, there are 81 copies of the ﬁrst allele, and 19

copies of the second allele. In the second population, there are 86 copies of

the ﬁrst allele, and 14 copies of the second allele, etc. Note that both alleles

in the third SNP in the third population have 0 copie. This marker will be

treated as a missing data in the corresponding population. The ﬁle named

geno.bta14 in the example directory provides a more realistic example.

Similarly, as a schematic example, the genotyping data input ﬁle for allele

count data should read as follows:

--- file begins here ---

71 8 115 0 61 36 51 39 10 91 69 58

82 0 91 0 84 14 24 57 28 80 18 80

93 28 112 30 0 0 0 113 33 68 0 106

[...97 more lines...]

--- file ends here ---

In this example, there are also 6 populations and 100 SNP markers. At

the ﬁrst SNP, in the ﬁrst population, there are 71 reads of the ﬁrst allele, and

8 reads of the second allele. In the second population, there are 115 reads

of the ﬁrst allele, and 0 read of the second allele, etc. Note that both alleles

in the third SNP in the third population have 0 copie. This marker will be

treated as a missing data in the corresponding population. The ﬁle named

lsa.geno in the example directory provides a more realistic example.

4For now, BayPass is restricted to bi–allelic marker

For Pool–Seq data to be analyzed properly (i.e. not like allele count data), it is

necessary to provide a ﬁle with the (haploid) size of each pool (see 2.3.2).

2.3.2 The pool (haploid) size ﬁle [only required for Pool–Seq data]

For Pool–Seq experiment, the haploid size (twice the number of pooled in-

dividuals for diploid species) of each population should be provided. As a

schematic example, the pool (haploid) size ﬁle should read as follows:

--- file begins here ---

60 75 100 90 80 50

--- file ends here ---

In this example, there are 6 populations with respective haploid sample

sizes of 60 (ﬁrst population), 75 (second population), 100 (third population),

90 (fourth population), 80 (ﬁfth population) and 50 (sixth population). The

order of the populations in the pool size ﬁle must be the same as in the allele

count (and the covariate) data ﬁle(s). The ﬁle named lsa.poolsize in the

example directory provides a more realistic example.

2.3.3 The covariate data ﬁle [required for the covariate modes]

The values of the covariates (e.g., environmental data, phenotypic traits, etc.)

for the diﬀerent populations should be provided in a ﬁle with the format

exempliﬁed in the following:

--- file begins here ---

150 1500 800 300 200 2500

181.5 172.6 152.3 191.8 154.2 166.8

1 1 0 0 1 1

0.1 0.8 -1.15 1.6 0.02 -0.5

--- file ends here ---

In this example, there are 6 populations (columns) and 4 covariates (row).

The ﬁrst covariate might be viewed as a typical environmental covariate, like

altitude in meters (the ﬁrst population is living at ca. 150m above the sea

level, the second at ca. 1,500m, and so on), the second as a quantitative traits

like average population sizes in cm (individuals from the ﬁrst population are

181.5 cm height on average, individuals from the second population 172.6

cm, and so on), the third covariate as a typical binary trait like presence (1,

for the ﬁrst, second, ﬁfth and sixth populations) or absence (0, for the thrid

and fourth populations) and the last might be viewed as a synthetic variable

like the ﬁrst principal components of a PCA. The order of the populations

(columns) in the covariate data ﬁle must be the same as in the allele count

(and the pool size) data ﬁle(s).

The ﬁles named bta.pc1 and lsa.ecotype in the example directory pro-

vide alternative real-life examples.

Note that in most cases, it is (strongly) recommended to scale each covariate (so that

ˆµ= 0 and c

σ2= 1 for each covariable). The scalecov option allows to perform this

step automatically prior to analysis, if needed.

2.3.4 The covariance matrix ﬁle [optional, required for the AUX co-

variate mode]

For some applications (see below), it might be interesting (e.g., to parallelize

some analyses) or required (when using the AUX covariate mode) to provide

the population covariance matrix Ω. As a schematic example, the covariance

matrix ﬁle reads as follows:

--- file begins here ---

0.098053 0.019595 0.032433 -0.029601 -0.024190 -0.029247

0.019595 0.160147 0.018942 -0.027348 -0.039733 -0.039010

0.032433 0.018942 0.149962 -0.054973 -0.058700 -0.057288

-0.029601 0.027348 0.054973 0.187511 0.221914 0.165862

-0.024190 0.039733 0.058700 0.221914 0.562666 0.260231

-0.029247 0.039010 0.057288 0.165862 0.260231 0.219761

--- file ends here ---

In this example, there are 6 populations. Hence, the population covari-

ance matrix is a 6×6 squared symmetric matrix. The order of the populations

(columns and rows) in the matrix Ω should be the same as the columns in

the allele count (and the pool size and the covariate) data ﬁle(s). Note that

this ﬁle is produced in the appropriate format by the program when running

BayPass under the core model (see 3.3).

The ﬁle named omega.bta provides a real-life example.

3 Running BayPass

3.1 Overview of the diﬀerent models available in Bay-

Pass

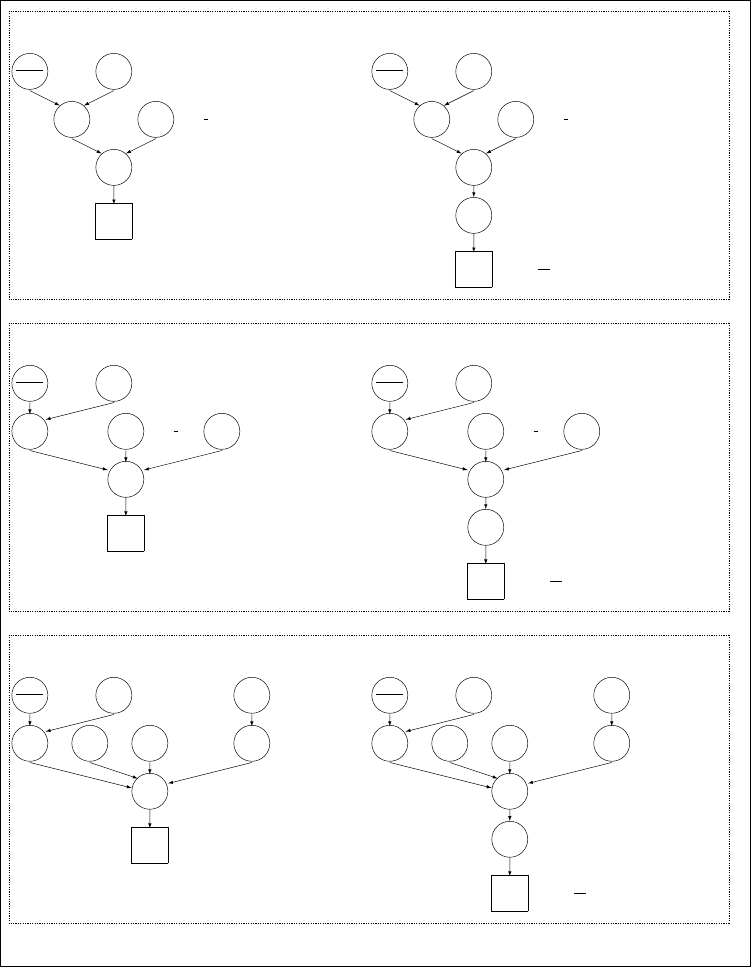
Directed Acyclic Graphs (DAG) of the diﬀerent family of models are repre-

sented in Figure 1(see Gautier (2015) for details). Brieﬂy, three types of

(closely related) models might be investigated using BayPass, considering

either Allele count data (left panel in Figure 1) or Read count data (right

panel in Figure 1) as obtained from Pool–Seq experiments.

3.1.1 The core model

The core model depicted in Figure 1A might be viewed as a generalisation

of the model proposed by Nicholson et al. (2002) and was ﬁrst proposed by

Coop et al. (2010). This model is the one considered by BayPass when no

covariate data ﬁle is provided and is actually nested in the others models.

The main parameter of interest is the (scaled) covariance matrix of pop-

ulation allele frequencies Ωresulting from their (possibly unknown and com-

plex) shared history. Conversely, one might rely on this matrix for demo-

graphic inference. For instance, Ωmight easily be converted (e.g., using

the cov2cor() function in R stats package) into a correlation matrix Σfur-

ther interpreted as a similarity matrix. From this latter matrix, one may

deﬁne a distance (dissimilarity) matrix (e.g., dij = 1− | ρij |where dij is

the distance between populations iand jand ρij is the element ij of Σ) to

perform hierarchical clustering5and summarise the history of the popula-

tion as a bifurcating phylogenetic tree (without gene ﬂow). A more complex

demographic inference based on an interpretation the matrix Ω(although

estimated in a less accurate way) in terms of tree with migration has been

recently proposed by Pickrell and Pritchard (2012).

The core model allows to perform genome scan for diﬀerentiation (covariate-

free) using the XtX statistics as introduced by G¨

unther and Coop (2013)

which is computed by default in BayPass. The main advantage of this

approach stems is to explicitly account for the covariance structure in pop-

ulation allele frequencies (via estimating Ω) resulting from the demographic

history of the populations. To identify outlier loci (based on the XtX statis-

tics), the R function simulate.baypass() provided in the utils directory

of the package (see 4) allows to simulate data under the inference model (e.g.,

using posterior estimates of Ω and any other hyperparameters) which might

further be analysed to calibrate the neutral XtX distribution (Gautier, 2015).

5For an interesting discussion and examples in R, see http://research.

stowers-institute.org/mcm/efg/R/Visualization/cor-cluster/index.htm

In the current implementation of BayPass, the prior distribution for Ωis an Inverse-

Wishart: Ω∼W−1

J(ρIJ, ρ) (where J is the number of populations). By default ρ= 1

(rather than ρ=Jas in Bayenv) which was found as the most reliable value (Gautier,

2015). Similarly, the hyperparameters aπand bπof the prior βdistribution for the

overall (across population) SNP allele frequencies are estimated by default. However,

they might be ﬁxed to aπ=bπ= 1 (as in e.g., Bayenv) using fixpibetapar option

or to any other values using further the betapiprior option (3.2).

3.1.2 The standard covariate model and extensions

The standard covariate model is represented in Figure 1B and is the one

considered by default in BayPasswhen a covariate data ﬁle is provided us-

ing efile option (3.2). This model allows to evaluate to which extent the

population covariable(s) kis (linearly) associated to each marker i(which

are assumed independant given Ω) by the introduction of the regression co-

eﬃcients βik (for convenience the indices kfor covariables are dropped in

Figure 1B).

In the current implementation of BayPass, the prior distribution for the βik’s is

Uniform: βik ∼Unif (βmin, βmax). By default, βmin =−0.3 and βmax = 0.3 but

these values might be changed by the user with the minbeta and maxbeta options

respectively (3.2). Note that in Bayenv (Coop et al., 2010), βmin =−0.1 and βmax =

0.1.

The estimation of the βik regression coeﬃcients for each SNP imay be

performed using two diﬀerent approaches (Gautier, 2015):

•Using an importance sampling estimator (IS) which is the default op-

tion and also allows the computation of Bayes Factor to the compare on

an individual SNP (and covariable) basis the two alternative models,

namely the model with association (βik 6= 0) against the null model

(βik = 0). Bayes Factor (BFis) and βik IS algorithm are inspired from

Coop et al. (2010) and are described in details elsewhere (Gautier,

2015). Note that the IS estimation procedure is based on a numerical

integration that requires the deﬁnition of a grid covering the whole sup-

port of the βik prior distribution. In BayPass, the grid consists in nβ

(by default nβ= 201) equidistant points from βmin to βmax (including

the boundaries) leading to a lag between two successive values equal to

βmax−βmin

nβ−1(i.e., 0.003 with default values). Other values for nβmight be

supplied by the user with the nbetagrid option (3.2).

•Using an MCMC algorithm (activated via the covmcmc option). In

this case, the user should provide the matrix Ω(e.g., using posterior

estimates available from a previous analysis) and it is recommended to

consider only one covariable at a time (particularly if some covariables

are correlated).

3.1.3 The auxiliary covariate model

The auxiliary covariate model, represented in Figure 1C and activated with

the auxmodel option, is an extension of the previous model (Figure 1B) in-

volving the introduction of a Bayesian (binary) auxiliary variable δik for each

regression coeﬃcient βik (Gautier, 2015). In a similar population genetics

context, this modelling was also proposed by Riebler et al. (2008) to identify

markers subjected to selection in genome-wide scan of adaptive diﬀerentia-

tion based on a F–model.

Here, the auxiliary variable actually indicates whether a speciﬁc SNP ican

be regarded as associated to a given covariable k(δik = 1) or not (δik = 1).

By looking at the posterior distribution of each auxiliary variable, it is then

straightforward to derive a Bayes Factor (BFmc) to compare both models

while dealing with multiple testing issues (Gautier, 2015). In addition, the

introduction of a Bayesian auxiliary variable makes it easier to account for

spatial dependency among markers. In BayPass, the general form of the δik

prior distribution is indeed that of an 1D Ising model with a parametrization

analogous to the one proposed in a similar context by Duforet-Frebourg et al.

(2014): π(δk)∝Ps1(1 −P)s0eηbis , where δkis the vector of the nsnp auxil-

iary variables for covariable k,s1and s0are the number of SNPs associated

(i.e. with δik = 0) and not associated (i.e. with δik = 0) to the covariable6,

and ηcorresponds to the number of pairs of consecutive markers (neighbors)

that are in the same state at the auxiliary variable7(i.e., δi,k =δi+1,k). The

parameter Pbroadly corresponds to the prior proportion of SNP associated

to the covariable. In the BayPass auxiliary model, Pis assumed a priori

beta distributed: P∼β(aP, bP). By default, aP= 0.02 and bP= 1.98 (this

values might be changed by the user with the auxPbetaprior option) which

amounts to consider that only a small fraction of the SNPs ( aP

aP+bP=1%) are

a priori expected to be associated to the covariable while allowing some un-

certainty on this key parameter (e.g., the prior probability of P >10% being

equal to 0.028 with these parameters). The parameter bis, called the in-

verse temperature in the Ising (and Potts) model literature, determines the

level of spatial homogeneity of the auxiliary variables between neighbors. In

6s1=

nsnp

i=1

δik = 1 and s0=

nsnp

i=1

δik = 0

7η=P

i∼j

1δik=δjk

BayPass, bis = 0 by default implying that auxiliary variables are indepen-

dent (no spatial dependency). Note that bis = 0 amounts to assume the

δik follows a Bernoulli distribution with parameter P. Conversely, bis >0

leads to assume that the δik with similar values tend to cluster according

to the underlying SNP positions (the higher the bis, the higher the level of

spatial homogeneity). In biological terms, SNP associated to a given covari-

able might be expected to cluster due to Linkage Disequilibrium with the

underlying (possibly not genotyped) causal variant(s). In practice, bis = 1 is

commonly used and a value of bis ≤1 is recommended.

In technical terms, the overall parametrisation of the Ising prior assumes no external

ﬁeld and no weight (as in the so-called compound Ising model) between the neigh-

boring auxiliary variables. In the current implementation of the BayPass auxiliary

covariate model (when bis >0), the information about the distances between SNPs

is therefore not accounted for. Only the relative position of markers are considered.

For the applications where this modeling might be relevant (whole genome scan), this

corresponds to assuming a relative homogeneity in marker spacing as measured by

genetic (rather than physical) distances (which might be unavailable, in practice).

A) Basic Model (without covariate)

A.1) Allele count data

aπ

aπ+bπ

∼U(0; 1) aπ+bπ∼Exp(1)

Ω−1∼WJ1

ρIJ, ρ

πi∼β(aπ;bπ)

α?

∼NJπi1J;πi(1 −πi)Ω

yij , nij yij ∼Bin min(1,max(0, α?

ij )); nij 

A.2) Read count data (Pool–Seq)

aπ

aπ+bπ

∼U(0; 1) aπ+bπ∼Exp(1)

Ω−1∼WJ1

ρIJ, ρ

πi∼β(aπ;bπ)

α?

∼NJπi1J;πi(1 −πi)Ω

yij ∼Bin min(1,max(0, α?

ij )); nj

rij , cij rij ∼Bin yij

nj, cij 

B) Standard covariate model (STD)

B.1) Allele count data

aπ

aπ+bπ

∼U (0; 1) aπ+bπ∼Exp(1)

πi∼β(aπ;bπ)Ω−1∼WJ1

ρIJ, ρβi∼Uβmin;βmax

α?

∼NJπi1J+βiZj;πi(1 −πi)Ω

yij , nij yij ∼Bin min(1,max(0, α?

ij )); nij 

B.2) Read count data (Pool–Seq)

aπ

aπ+bπ

∼U (0; 1) aπ+bπ∼Exp(1)

πi∼β(aπ;bπ)Ω−1∼WJ1

ρIJ, ρβi∼Uβmin;βmax

α?

∼NJπi1J+βiZj;πi(1 −πi)Ω

yij ∼Bin min(1,max(0, α?

ij )); nj

rij , cij rij ∼Bin yij

nj, cij 

C) Auxiliary variable covariate model (AUX)

C.1) Allele count data

aπ

aπ+bπaπ+bπ

πiΩ−1βi∼Uβmin;βmaxδ∼Ising bis;P

P∼βap;bp

α?

∼NJπi1J+δiβiZj;πi(1 −πi)Ω

yij , nij yij ∼Bin min(1,max(0, α?

ij )); nij 

C.2) Read count data (Pool–Seq)

aπ

aπ+bπaπ+bπ

πiΩ−1βi∼Uβmin;βmaxδ∼Ising bis;P

P∼βap;bp

α?

∼NJπi1J+δiβiZj;πi(1 −πi)Ω

yij ∼Bin min(1,max(0, α?

ij )); nj

rij , cij rij ∼Bin yij

nj, cij 

Figure 1: Directed Acyclic Graphs of the diﬀerent hierarchical Bayesian models available

in BayPass (see 3.1). For each model, optional (hyper–)parameters are displayed in

orange.

3.2 Detailed overview of all the options

BayPass is a command-line executable. The ASCII hyphen-minus (”-”) is

used to specify options. As speciﬁed below, some options take integer or ﬂoat

values and some options do not. Here is an example call of the program:

baypass -npop 12 -gfile data.geno -efile env.data -outprefix ana1

The full list of the options accepted by BayPass are printed out using the com-

mand: baypass -help as follows:

Version 2.1

Usage: BayPass [options]

Options:

I) General Options:

-help Display the help page

-npop INT Number of populations (always required)

-gfile CHAR Name of the Genotyping Data File (always required)

-efile CHAR Name of the covariate file: activate covariate mode (def="")

-scalecov CHAR Scale covariates (def="")

-poolsizefile CHAR Name of the Pool Size file => activate PoolSeq mode (def="")

-outprefix CHAR Prefix used for the output files (def="")

II) Modeling Options:

-omegafile CHAR Name of the omega matrix file => inactivate estim. of omega (def="")

-rho INT Rho parameter of the Wishart prior on omega (def=1)

-setpibetapar Inactivate estimation of the Pi beta priors parameters

-betapiprior FLOAT2 Pi Beta prior parameters (if -setpibetapar) (def=1.0 1.0)

-minbeta FLOAT Lower beta coef. for the grid (def=-0.3)

-maxbeta FLOAT Upper beta coef. for the grid (def= 0.3)

I.1) IS covariate mode (default covariate mode):

-nbetagrid INT Number of grid points (IS covariate mode) (def=201)

I.2) MCMC covariate mode:

-covmcmc Activate mcmc covariate mode (desactivate estim. of omega)

-auxmodel Activate Auxiliary variable mode to estimate BF

-isingbeta FLOAT Beta (so-called inverse temperature) of the Ising model (def=0.0)

-auxPbetaprior FLOAT2 auxiliary P Beta prior parameters (def=0.02 1.98)

III) MCMC Options:

-nthreads INT Number of threads (def=1)

-nval INT Number of post-burnin and thinned samples to generate (def=1000)

-thin INT Size of the thinning (record one every thin post-burnin sample) (def=25)

-burnin INT Burn-in length (def=5000)

-npilot INT Number of pilot runs (to adjust proposal distributions) (def=20)

-pilotlength INT Pilot run length (def=1000)

-accinf FLOAT Lower target acceptance rate bound (def=0.25)

-accsup FLOAT Upper target acceptance rate bound (def=0.40)

-adjrate FLOAT Adjustement factor (def=1.25)

-d0pi FLOAT Initial delta for the pi all. freq. proposal (def=0.5)

-upalphaalt Alternative update of the pij

-d0pij FLOAT Initial delta for the pij all. freq. proposal (alt. update) (def=0.05)

-d0yij INT Initial delta for the yij all. count (PoolSeq mode) (def=1)

-seed INT Random Number Generator seed (def=5001)

In this menu, each option is followed by the kind of argument (if any)

required (e.g., INT for integer, FLOAT for real, FLOAT2 for a pair of real

number space separated), a brief description of its function, and the default

value.

In the following, we detailed all the options of BayPass:

-help

This option prints out the help menu (see above). Note that this option

is dominating all the other options, i.e. if -help is used in conjunction

with any other option of the program, the help menu is displayed. No

argument is required for this option.

-npop

This option (mandatory) gives the number of population considered

in the data set (half the number of column in the genotype data ﬁle).

The required argument must be an integer (INT). (e.g., -npop 12 if 12

populations are studied).

-gfile

This option (mandatory) gives the name of the genotyping input ﬁle.

See 2.3.1 for a description of the corresponding input ﬁle format. The

required argument must be character chain (name of the input ﬁle)

without space (e.g., -gfile data.geno if the input ﬁle is named ”data.geno”).

-efile

This option gives the name of the covariate input ﬁle. See 2.3.3 for a

description of the corresponding input ﬁle format. The required argu-

ment must be character chain (name of the input ﬁle) without space

(e.g., -gfile data.env if the input ﬁle is named ”data.env”).

-scalecov

This option allows to perform scaling of each covariable in the covariate

input ﬁle (See 2.3.3). No argument is required for this option. If

activated, an output ﬁle named ”covariate.std” containing the scaled

covariables is produced.

-poolsizefile

This option gives the name of the input ﬁle containing the haploid sam-

ple size of each population. See 2.3.2 for a description of the correspond-

ing input ﬁle format. The required argument must be character chain

(name of the input ﬁle) with no space (e.g., -poolsizefile data.poolsize

if the input ﬁle is named ”data.poolsize”). Note that this option auto-

matically activates the Pool–Seq mode, i.e., the PoolSeq version of the

diﬀerent models are considered (as represented in Figures 1A2, B2 and

C2).

-outprefix

This option allows to add a preﬁx to all the output ﬁles. The required

argument must be a character chain without space. For instance, if

using -outprefix ana1, the name of all the output ﬁles will begin by

”ana1_”. By default, no preﬁx is added.

-omegafile

This option gives the name of the input ﬁle for the population co-

variance matrix (Ωin 3.1.1 and Figure 1). See 2.3.4 for a descrip-

tion of the corresponding input ﬁle format. The required argument

must be character chain (name of the input ﬁle) with no space (e.g.,

-omegafile matrix.dat if the input ﬁle is named matrix.dat). This

option inactivates the estimation of Ωand is mandatory in the co-

variate models involving estimation of the regression coeﬃcients via

MCMC i.e. the standard model (see 3.1.2) with the -covmcmc option

and the auxiliary variable model (see 3.1.3).

-rho

This option allows to specify the value of ρfor the Inverse-Wishart

prior of Ω(see Figure 1and 3.1.1). The required argument must be a

positive integer. By default, -rho 1 (i.e., ρ= 1).

-setpibetapar

This option allows to inactivate estimation of the two (hyper–)parameters

aπand bπof the prior βdistribution for the overall (across population)

SNP allele frequencies (see Figure 1and 3.1.1) (and set them to the val-

ues speciﬁed with the -betapiprior option). No argument is required

for this option.

-betapiprior

This option allows to specify the values of the two (hyper–)parameters

aπand bπ(respectively) of the prior βdistribution for the overall

(across population) SNP allele frequencies (see Figure 1and 3.1.1).

The required argument must be two positive real numbers. By default

-betapiprior 1.0 1.0 (i.e., aπ=bπ= 1).

-minbeta

This option allows to specify the lower bound of the Uniform prior

distribution on the regression coeﬃcients (see Figure 1and 3.1.2). The

required argument must be a real number (lower than maxbeta deﬁned

below). By default -minbeta -0.3 (i.e., βmin =−0.3).

-maxbeta

This option allows to specify the upper bound of the Uniform prior

distribution on the regression coeﬃcients (see Figure 1and 3.1.2). The

required argument must be a real number (greater than minbeta de-

ﬁned above). By default -maxbeta 0.3 (i.e., βmax = 0.3).

-nthreads

This option gives the number of threads to be used for parallel compu-

tations. By default, -nthreads 1 (i.e., a single core is used hence no

parallelization).

-nval

This option gives the number of post–burn–in (and thinned MCMC)

samples recorded from the posterior distributions of the parameters of

interest. The required argument must be a positive integer. By de-

fault, -nval 1000 (i.e., 1,000 post burn-in and thinned samples are

generated). Note that with default values, the total number of itera-

tions of the MCMC sampler run after the burn-in period is equal to

25,000 (since by default, the thinning rate is equal to 25 , see thin

option)

-thin

This option gives the size of the thinning (i.e., the number of iterations

between any two records from the MCMC). The required argument

must be a positive integer. By default, -thin 25 (i.e., the size of the

thinning is 25).

-burnin

This option gives the length of the burn-in period (i.e., the number

of iterations before the ﬁrst record from the MCMC). The required

argument must be a positive integer. By default, -burnin 5000 (i.e.,

5,000 iterations are run during the burn–in period).

-npilot

This option gives the number of pilot runs (i.e., the number of runs

used to adjust the parameters of the MCMC proposal distributions of

parameters updated through a Metropolis-Hastings algorithm). The

targeted acceptance rates are deﬁned with the accinf and accsup op-

tions (by default, these are set to 0.25 and 0.40 respectively). The

required argument must be a positive integer. By default, -npilot 20

(i.e., 20 pilot runs are performed).

-pilotlength

This option gives the number of iterations of each pilot run (see npilot

option above). The required argument must be a positive integer. By

default, -pilotlength 1000 (i.e., each pilot run consist of 1,000 iter-

ations).

-accinf

This option gives the lower bound of the targeted acceptance rates to

adjust the parameters of the MCMC proposal distributions of parame-

ters updated through a Metropolis-Hastings algorithm, during the pilot

runs. For instance, in the case of a uniform proposal distribution of the

form Unif(x−δ, x +δ) (where xrepresents the current value of the pa-

rameter of interest and δspeciﬁes the size of the support), if acceptance

rates are below this lower bound after a pilot run, then δis increased

(e.g., multiplied by a factor deﬁned with the adjrate parameter and

set to 1.25 by default). The required argument must be a positive

real number (<1 and lower than accsup deﬁned below). By default,

-accinf 0.25 (i.e., acceptance rates should be at least equal to 25%).

-accsup

This option gives the upper bound of the targeted acceptance rates

to adjust the parameters of the MCMC proposal distributions of pa-

rameters updated through a Metropolis-Hastings algorithm, during the

pilot runs. For instance, in the case of a uniform proposal distribution

of the form Unif(x−δ, x +δ) (where xrepresents the current value

of the parameter of interest and δspeciﬁes the size of the support), if

acceptance rates are above this upper bound after a pilot run, then δis

decreased (e.g., divided by a factor deﬁned with the adjrate parameter

and set to 1.25 by default). The required argument must be a positive

real number (≤1 and greater than accinf deﬁned above). By default,

-accinf 0.40 (i.e., acceptance rates should be less than 40%).

-adjrate

This option gives the factor used to adjust the parameters of the MCMC

proposal distributions of parameters updated through a Metropolis-

Hastings algorithm, during the pilot runs. For instance, in the case of

a uniform proposal distribution of the form Unif(x−δ, x +δ) (where x

represents the current value of the parameter of interest and δspeciﬁes

the size of the support), if acceptance rates are below (respectively

above) the lower (respectively upper) bound of the targeted regions (as

deﬁned above with the accinf and accsup options) after a pilot run,

then δis multiplied (respectively, divided) by this factor. The required

argument must be a real number >1. By default, -adjrate 1.25.

-d0pi

This option gives the initial value of the δπ, which is half the window

width from which proposal values of the overall SNP allele frequencies

πi(see Figure 1) are drawn uniformly around the current value pij in the

Metroplis–Hastings update. The value of δπis eventually adjusted for

each locus during the pilot runs (see options -npilot,-pilotlength,

-accinf,-accsup and -adjrate). The required argument must be a

positive real number. By default, -d0pi 0.5 (i.e., δp= 0.5).

-upalphaalt

This option activates an alternative Metropolis–Hastings algorithm for

the population SNP allele frequencies αij (see Figure 1). By default,

the proposal is the same as the one described by Coop et al. (2010)

(Appendix A). Brieﬂy, denoting αi. as the vector of allele frequencies

for SNP iin each population, the vector α?cdt

ievaluated in a given

Metropolis–Hastings update is sampled from the following multivariate

Gaussian distribution: α?cdt

i∼MNV (α?

i,Γσ2

i) where Γis obtained

by a Choleski decomposition of the matrix Ω(i.e., Ω=tΓΓ ). The al-

ternative proposal activated with the -upalphaalt option is deﬁned on

a SNP by population basis and is a uniform distribution centred on the

current values of the parameters (i.e., α?cdt

ij ∼Unif(α?ij −λα

ij , α?

ij −λα

ij )).

The algorithm is slower than the default one but may perform better,

in particular when sample sizes are heterogeneous across samples. No

argument is required for this option.

-d0pij

This option gives the initial value of the δαused in the proposal distri-

bution of the population SNP allele frequencies αij in the Metroplis–

Hastings updates. Following the notations used above (see -upalphaalt

option), δα=σ2

ifor the default algorithm and δα=λα

ij for the alter-

native algorithm. The value of δαis eventually adjusted for each locus

(and population, in the case of the alternative algorithm) during the pi-

lot runs (see options -npilot,-pilotlength,-accinf,-accsup and

-adjrate). The required argument must be a positive real number.

By default, -d0pij 0.05 (i.e., σ2

i= 0.05 for the default algorithm and

λα

ij = 0.05 for the alternative algorithm).

-d0yij

This option gives, in the Pool–Seq mode, the initial value of the δy

used in the proposal distribution of the population SNP allele count

Yij in the Metroplis–Hastings updates. The value of δyis eventually

adjusted for each locus and each population during the pilot runs (see

options -npilot,-pilotlength,-accinf,-accsup and -adjrate).

The required argument must be a positive integer number lower than

the haploid pool sizes. By default, -d0yij 1 (i.e., δy= 1).

-seed

This option gives the initial seed of the (pseudo-) Random Number

Generator. The required argument must be a positive integer number.

By default, -seed 5001.

3.3 Format of the output ﬁles

While running, BayPass printed on the console several information regard-

ing the execution of the analysis (these might be redirected in a log ﬁle using

the > log.file unix syntax). At the end of the analysis BayPass produces

several output ﬁles which might varied according to the options considered

(see 3.2). The name of these diﬀerent output ﬁles might be preceded by a

preﬁx as deﬁned with the outprefix options (see 3.2).

In the following, we detailed all the output ﬁles that may be generated

by BayPass:

•(outprefix_)summary_pij.out (default mode; e.g., for allele count

data) or (outprefix_)summary_yij_pij.out (Pool–Seq mode; e.g., for

read count data)

These ﬁles contain for each locus (MRK column) within each popula-

tion (POP column), the mean (M_P column) and the standard deviation

(SD_P column) of the posterior distribution of the α?

ij parameter (see

Figure 1) that is closely related to the frequency of the reference allele

αij = 1 ∧(0 ∨α?

ij ) except that its support is on the real line (hence pos-

sible values <0 or >1). It also contains the posterior mean (M_Pstd

column) and the standard deviation (SD_Pstd column) of the standard-

ized allele frequency αstd (αstd =Γ−1α?). The ﬁnal adjusted values

of the δα’s, the parameters of the MCMC proposal distributions for

the SNP allele frequencies (see -upalphaalt option) are also reported

in these ﬁles (DELTA_P column) together with the post-burn–in ﬁnal

acceptance rates (ACC_P column). Note that in the default Metropolis–

Hastings algorithm, the α?

ij are updated for each SNP as a vector of

allele frequencies across all populations. Hence, the δαand the accep-

tance rates have same values across all the populations for a given SNP.

In the Pool–Seq mode (i.e., in the (outprefix_)summary_yij_pij.out

ﬁle), the columns M_Y,SD_Y,DELTA_Y and ACC_Y similarly report the

posterior mean, the posterior standard-deviation, the δYof the corre-

sponding proposal distributions and the post-burn–in ﬁnal acceptance

rates for allele counts of each SNP within each population.

•(outprefix_)summary_pi_xtx.out

This ﬁle contains for each locus (MRK column), the mean (M_P column)

and the standard deviation (SD_P column) of the posterior distribution

of the (across populations) frequency πiof the SNP reference allele (see

Figure 1). The ﬁnal adjusted values of the δπ’s, the parameters of the

MCMC proposal distributions are also reported in these ﬁles (DELTA_P

column) together with the post-burn–in ﬁnal acceptance rates (ACC_P

column). In addition, this ﬁles contains for each SNP, the posterior

mean (M_XtX column) and standard deviation (SD_XtX column) of the

XtX statistics introduced by G¨

unther and Coop (2013) to identify out-

lier loci in genome–scan of adaptive diﬀerentiation (see 3.1.1).

•(outprefix_)summary_lda_omega.out and (outprefix_)mat_omega.out

The (outprefix_)summary_lda_omega.out ﬁle contains the posterior

means and posterior standard deviations of each element of the npop ×

npop scaled population allele frequencies covariance matrix Ω(M_omega_ij

and SD_omega_ij columns respectively) as described in Figure 1(see

also 3.1.1), and its inverse Λ=Ω−1(M_lambda_ij and SD_lambda_ij

columns respectively).

The (outprefix_)mat_omega.out ﬁle contains the posterior means of

the elements of Ωin a matrix format. Note that this ﬁle is in the

format required by the -omegafile option of BayPass.

•(outprefix_)summary_beta_params.out (generated with the -estpibetapar

option)

This ﬁle contains the posterior mean (Mean column) and standard de-

viation (SD column) of the two parameters (aπand bπ) of the Beta

prior distribution assumed for the (across populations) frequencies of

the SNP reference allele (see Figure 1).

•(outprefix_)summary_betai_reg.out

This ﬁle is only produced in the Bayenv–like mode, i.e. the stan-

dard covariate mode (see Figure 1B and 3.1.2) where the estimation

of the Bayes Factor (column BF(dB)) in dB units (i.e., 10 ×log10(BF))

measuring the support of the association of each SNP with each popula-

tion covariable and the corresponding regression coeﬃcients βi(column

Beta_is) are done via an Importance Sampling algorithm (Coop et al.,

2010). In addition, the ﬁle also contains the empirical Bayesian P–value

(eBPis) in the log10 scale i.e. eBPis = −log10(1 −2|0.5−Φ(cµβ/cσβ)|)

(where Φ(x) represents the cumulative distribution function for the

standard normal distribution) and thus allowing to evaluate the sup-

port in favour of a non-null regression coeﬃcient (e.g., eBPis >3).

This ﬁle contains for each covariable and each SNP, the posterior mean

and standard deviation of the Pearson correlation coeﬃcient (columns

M_Pearson and SD_Pearson respectively) between the scaled allele fre-

quencies f

α?

i=α?

−πi

√π(1−πi)(1..J)

and the given covariable after rotation

of both vectors by Γ−1(see G¨

unther and Coop, 2013) where Γis ob-

tained by a Choleski decomposition of the matrix Ω(i.e., Ω=tΓΓ).

•(outprefix_)summary_betai.out (generated with the -covmcmc op-

tion)

This ﬁle is produced in place of the (outprefix_)summary_betai_reg.out

described above when the -covmcmc option is activated (see 3.1.2).

Under the standard model (default), the ﬁle contains for each SNP,

the posterior mean cµβ(M_Beta column) and standard deviation cσβ

(SD_Beta column) of the regression coeﬃcient βitogether with the

adjusted δβparameter (DeltaB column) of the proposal distribution

and the post-burn–in acceptance rate (AccRateB column). In addition,

the ﬁle also contains an approximated Bayesian P–value in the log10

scale (eBPmc) measured as eBPmc = −log10(1 −2|0.5−Φ(cµβ/cσβ)|)

(where Φ(x) represents the cumulative distribution function for the

standard normal distribution) and thus allowing to evaluate the support

in favour of a non-null regression coeﬃcient (e.g., eBPmc >3).

Under the model with auxiliary variables (-auxmodel option, see 3.1.3),

the ﬁle contains for each SNP, the posterior mean (M_Beta column)

and standard deviation (SD_Beta column) of the regression coeﬃcient

βi, the posterior mean of the auxiliary variable (M_Delta column) and

the estimate of the Bayes Factor (column BF(dB)) in dB units (i.e.,

10 ×log10(BF)) for comparison of models with (βi6= 0) and without

(βi= 0) correlation with the given covariable.

•(outprefix_)summary_Pdelta.out (covariate model with auxiliary vari-

able, i.e. -auxmodel option, see 3.1.3)

This ﬁle contains the posterior mean (M_P column) and standard de-

viation (SD_P column) of the parameter P(see Figure 1C and 3.1.3)

corresponding to the overall proportion of SNP associated to the cor-

responding covariable.

•(outprefix_)covariate.std (generated by the scalecov option)

This ﬁle contains the scaled covariables.

•(outprefix_)DIC.out

This ﬁles contains the average deviance (bar(D) column), the eﬀective

number of parameters of the models (pD column) and the Deviance

Information Criterion (DIC column) as deﬁned in Spiegelhalter et al.

(2002) and that might be relevant for model comparison purposes. In

addition, the logarithm of the pseudo-marginal likelihood of the model

is also provided (LPML column).

4 Miscellaneous R functions

The baypass_utils.R ﬁle in the utils directory contains three R functions

(R Core Team, 2015) (simulate.baypass();fmd.dist() and geno2YN())

that may be helpful to interpret some of the results obtained with BayPass.

To use this functions, one may simply need to source the corresponding

ﬁles and ensure that the packages mvtnorm (Genz et al., 2015) and geigen

(Hasselman, 2015) have been installed. In addition, although not required by

theses functions, the packages corrplot (Wei, 2013) and ape (Paradis et al.,

2004) might proved useful for the visualisation of the Ωmatrix (see 5).

4.1 The R function simulate.baypass()

4.1.1 Description

The R function simulate.baypass() allows to simulate either allele or read

count data under the core inference model (Figure 1A) and possibly under the

STD covariate model (Figure 1B). It produces several objects and output ﬁles

in a format directly appropriate for analyses with BayPass and Bayenv28.

In practice, this function is useful to generate POD for calibration of the XtX

diﬀerentiation measure (or any other measures). More broadly, because the

Ωmatrix capture the demographic history of the populations, this function

might also be viewed as an eﬃcient simulator of population genetics data.

4.1.2 Usage

simulate.baypass(omega.mat,nsnp=1000,beta.coef=NA,beta.pi=c(1,1),

pop.trait=0,sample.size=100,pi.maf=0.05,suffix="sim",

remove.fixed.loci=FALSE,coverage=NA)

4.1.3 Arguments (in alphabetic order)

•beta.pi (def=c(1,1))

A two elements vector giving the parameters aπand bπrespectively, for

the Beta distribution of the πi(”ancestral”) allele frequencies.

•beta.coef (def=NA; required for simulation under the STD covariate

model)

A vector giving the values of the regression coeﬃcients (βiin Figure 1)

for the simulated associated SNPs (the number of the simulated asso-

ciated SNPs is equal to the dimension of the vector).

•coverage (def=NA; required to activate simulation of read count data)

8For analyses with Bayenv2, make sure ﬁxed loci have been removed, i.e.,

remove.fixed.loci=TRUE

Either a single value or a matrix giving the total read counts. In the

latter case, the vector of total read counts for each simulated SNP

are sampled with replacement from the row of the matrix. It is thus

mandatory that the number of columns of the matrix equals the number

of populations, but no restriction are set for the number of rows. For

instance, if the matrix has only one row, all the SNPs will have the

same read counts within a given population.

•omega.mat (always required)

A positive deﬁnite and symmetric matrix of rank npop corresponding

to the covariance matrix of population allele frequencies (Ωin Figure 1)

•nsnp (def=1000)

A single number giving the number of (neutral) SNPs to simulate.

•pi.maf (def=0.05)

A single value giving the MAF threshold on the simulated πi(”an-

cestral”) allele frequencies. In the simulation procedure, the pii’s are

sampled from the Beta distribution with parameters as speciﬁed in

the beta.pi argument. For a given SNP i, if pii<pi.maf (resp.

pii>1−pi.maf) then piiis set equal to pi.maf (resp. 1−pi.maf).

Setting pi.maf= 0 inactivates MAF ﬁltering.

•pop.trait (def=0; required for simulation under the STD covariate

model)

A vector of length npop giving each population-speciﬁc covariable val-

ues (ordering of the population is assumed to be the same as in the

omega.mat matrix). By default all values are set to 0 (meaning the

associated SNPs behave neutrally irrespective of their values at the

regression coeﬃcients).

•remove.fixed.loci (def=FALSE)

A logical indicating wether or not ﬁxed loci (in the observed simulated

data) should be discarded.

•sample.size (def=100)

If simulating allele count data, either a single value or a matrix giving

the total allele counts (twice the number of genotyped individuals in

diploid species). In the latter case, the vector of total allele counts

for each simulated SNP are sampled with replacement from the row of

the matrix. It is thus mandatory that the number of columns of the

matrix equals the number of populations, but no restriction are set for

the number of rows. For instance, if the matrix has only one row, all

the SNPs will have the same allele counts within a given population.

If simulating read count data, either a single value or a vector of length

npop giving the pool haploid sample sizes for each population.

•suffix (def=”sim”)

A character string giving the suﬃx of the output ﬁles generated by the

function.

4.1.4 Values

The function produces an object which is a list with the following compo-

nents:

•omega.sim

A matrix corresponding to the one used for simulation and declared

with the omega.mat argument

•alpha.sim

A matrix with dimension nsnp rows and npop columns giving the sim-

ulated (unbounded) allele frequencies for each simulated SNP within

each population (i.e., α?

ij in Figure 1).

•pi.sim

A vector of length nsnp giving the simulated πi”ancestral” allele fre-

quencies for each simulated SNP.

•N.sim

A matrix with dimension nsnp rows and npop columns giving the total

allele counts for each simulated SNP within each population.

•Y.sim

A matrix with dimension nsnp rows and npop columns giving the al-

lele counts for the reference allele for each simulated SNP within each

population.

•N.pool (read count data only)

A matrix with dimension nsnp rows and npop columns giving the total

read counts for each simulated SNP within each population.

•Y.pool (read count data only)

A matrix with dimension nsnp rows and npop columns giving the read

counts for the reference allele for each simulated SNP within each pop-

ulation.

•betacoef.sim (simulation under the STD covariate model only)

A vector of length nsnp giving the regression coeﬃcients of each SNP

used to simulate the data.

In addition, the following output ﬁles are printed out (the extension

.suffix is as deﬁned in the suffix argument):

•G.suffix

The allele count data ﬁle in BayPass format (see 2.3).

•Gpool.suffix (when simulating read count data)

The read count data ﬁle in BayPass format (see 2.3).

•bayenv_freq.suffix

The allele count data ﬁle in Bayenv2 format (see 8).

•bayenv_freq_pool.suffix (when simulating read count data)

The read count data ﬁle in Bayenv2 format (see 8).

•alpha.suffix

The simulated (unbounded) allele frequencies (nsnp rows and npop

columns) for each simulated SNP within each population (i.e., α?

ij in

Figure 1)

•pi.suffix

The simulated πi”ancestral” allele frequencies for each simulated SNP.

•betacoef.suffix (when simulating under the STD covariate model)

The regression coeﬃcients of each SNP used to simulate the data.

•pheno.suffix (when simulating under the STD covariate model)

The covariate data ﬁle in BayPass format (see 2.3).

•poolsize.suffix (when simulating read count data)

The haploid pool size data ﬁle in BayPass format (see 2.3).

4.1.5 Examples

#source the baypass R functions (check PATH)

source("utils/baypass_utils.R")

#load the bovine covariance matrix

om.bta <- as.matrix(read.table("examples/omega.bta"))

#simulate allele count data for 1000 SNPs

simu.res <- simulate.baypass(omega.mat=om.bta)

#simulate allele count data for 1000 neutral SNPs and

#100 associated SNPs with varying regression coefficients

simu.res <- simulate.baypass(omega.mat=om.bta,beta.coef=runif(100,-0.2,0.2),

pop.trait=rnorm(18))

#simulate read count data for 1000 SNPs

simu.res <- simulate.baypass(omega.mat=om.bta,coverage=50)

4.2 The R function fmd.dist()

4.2.1 Description

This function computes the metric proposed by (F¨

orstner and Moonen, 2003)

to evaluate the distance between two covariance matrices (FMD distance).

4.2.2 Usage

fmd.dist(mat1,mat2)

4.2.3 Arguments

•mat1 and mat2

Two positive-deﬁnite (symmetric) matrices

4.2.4 Values

The function returns a numeric corresponding to the FMD distance between

the two matrices.

4.2.5 Example

#source the baypass R functions (check PATH)

source("utils/baypass_utils.R")

#load the bovine covariance matrix

om.bta <- as.matrix(read.table("examples/omega.bta"))

#create a dummy diagonal covariance matrix

#this might be obtained from a star-shaped phylogeny with

#branch length (Fst) equal to 0.1

star.bta<-diag(0.1,nrow(om.bta))

#compute the fmd.dist between the two matrices

fmd.dist(om.bta,star.bta)

4.3 The R function geno2YN()

4.3.1 Description

This function reads the allele (or read) count data ﬁle in the BayPass format

and extract both the counts for the reference allele and total counts.

4.3.2 Usage

geno2YN(genofile)

4.3.3 Arguments

•genofile

A character string giving the name of the allele (or read) count data

ﬁle in the BayPass format.

4.3.4 Values

The function returns two matrices:

•genofile

A character string giving the name of the allele (or read) count data

ﬁle in the BayPass format.

The function produces an object which is a list containing the two follow-

ing matrices:

•YY

A matrix with nsnp rows and npop columns containing allele or read

counts for the reference allele.

•NN

A matrix with nsnp rows and npop columns containing the total allele

or read counts.

4.3.5 Example

#source the baypass R functions (check PATH)

source("utils/baypass_utils.R")

#load the bovine BTA 14 data

counts.obj <- geno2YN("examples/geno.bta14")

5 Worked Examples

For illustration purposes, diﬀerent types of analyses of the example ﬁles

(see 2.3) are detailed step by step. Users might try to reproduce the cor-

responding examples using the ﬁles included in the example directory.

5.1 Cattle allele count data

5.1.1 Analysis under the core model mode: MCMC is run under

the core model

The following command allows to analyse the data under the core model (this

should take ca. 4 min with the i_baypass executable and ca. 7 min with

the g_baypass executable):

baypass -npop 18 -gfile geno.bta14 -outprefix anacore

To visualize the results, one may open an R session and proceed as follows:

require(corrplot) ; require(ape)

#source the baypass R functions (check PATH)

source("utils/baypass_utils.R")

#upload estimate of omega

omega=as.matrix(read.table("anacore_mat_omega.out"))

pop.names=c("AUB","TAR","MON","GAS","BLO","MAN","MAR","LMS","ABO",

"VOS","CHA","PRP","HOL","JER","NOR","BRU","SAL","BPN")

dimnames(omega)=list(pop.names,pop.names)

#Compute and visualize the correlation matrix

cor.mat=cov2cor(omega)

corrplot(cor.mat,method="color",mar=c(2,1,2,2)+0.1,

main=expression("Correlation map based on"~hat(Omega)))

#Visualize the correlation matrix as hierarchical clustering tree

bta14.tree=as.phylo(hclust(as.dist(1-cor.mat**2)))

plot(bta14.tree,type="p",

main=expression("Hier. clust. tree based on"~hat(Omega)~"("*d[ij]*"=1-"*rho[ij]*")"))

#Compare the estimate of omega based on the whole genome

#and based on the BTA14 SNPs

wg.omega <- as.matrix(read.table("examples/omega.bta")) #check the PATH

plot(wg.omega,omega) ; abline(a=0,b=1)

fmd.dist(wg.omega,omega)

#Estimates of the XtX differentiation measures

anacore.snp.res=read.table("anacore_summary_pi_xtx.out",h=T)

plot(anacore.snp.res$M_XtX)

One may further wish to calibrate the XtX estimates using a POD sample.

For instance, to produce a (small) POD sample with 1,000 SNPs (continuing

the R example above) using the simulate.baypass() function (see 4):

#get estimates (post. mean) of both the a_pi and b_pi parameters of

#the Pi Beta distribution

pi.beta.coef=read.table("anacore_summary_beta_params.out",h=T)$Mean

#upload the original data to obtain total allele count

bta14.data<-geno2YN("geno.bta14")

#Create the POD

simu.bta<-simulate.baypass(omega.mat=omega,nsnp=1000,sample.size=bta14.data$NN,

beta.pi=pi.beta.coef,pi.maf=0,suffix="btapods")

Then, one may analyse the newly created POD (data ﬁle named ”G.btapods”

in the example) giving another preﬁx for the output ﬁles:

baypass -npop 18 -gfile G.btapods -outprefix anapod

Continuing the above example in R, calibration of the XtX and visuali-

sation of the results might be carried out as follows:

#######################################################

#Sanity Check: Compare POD and original data estimates

#######################################################

#get estimate of omega from the POD analysis

pod.omega=as.matrix(read.table("anapod_mat_omega.out"))

plot(pod.omega,omega) ; abline(a=0,b=1)

fmd.dist(pod.omega,omega)

#get estimates (post. mean) of both the a_pi and b_pi parameters of

#the Pi Beta distribution from the POD analysis

pod.pi.beta.coef=read.table("anapod_summary_beta_params.out",h=T)$Mean

plot(pod.pi.beta.coef,pi.beta.coef) ; abline(a=0,b=1)

#######################################################

#XtX calibration

#######################################################

#get the pod XtX

pod.xtx=read.table("anapod_summary_pi_xtx.out",h=T)$M_XtX

#compute the 1% threshold

pod.thresh=quantile(pod.xtx,probs=0.99)

#add the thresh to the actual XtX plot

plot(anacore.snp.res$M_XtX)

abline(h=pod.thresh,lty=2)

5.1.2 Analysis under the IS covariate mode: MCMC is run under

the core model

This analysis allows to perform association study (under the STD covariate

model) by estimating for each SNP the Bayes Factor, the empirical Bayesian

P-value (and the underlying regression coeﬃcient) using an Importance Sam-

pling algorithm (Gautier, 2015). As a consequence, the MCMC samples of

the parameters of interest are obtained by running the core model as above

(5.1.1). Hence, if covariables are available, one may rather used this mode as

a default mode. The example below corresponds to an association analysis

with the SMS covariable measured on the 18 French cattle breeds (Gautier,

2015).

baypass -npop 18 -gfile geno.bta14 -efile bta.pc1 -outprefix anacovis

Providing the same seed and the same options have been used, one may

verify that exactly the same estimates for Ω(e.g., ﬁles anacovis_mat_omega.out

and anacore_mat_omega.out) and other parameters in common are obtained

than under the previous analysis (5.1.1). Continuing the above example in

R, one may plot the Importance Sampling estimates of the Bayes Factor,

the empirical Bayesian P-value and the underlying regression coeﬃcient as

follows:

covis.snp.res=read.table("anacovis_summary_betai_reg.out",h=T)

graphics.off()

layout(matrix(1:3,3,1))

plot(covis.snp.res$BF.dB.,xlab="SNP",ylab="BFis (in dB)")

plot(covis.snp.res$eBPis,xlab="SNP",ylab="eBPis")

plot(covis.snp.res$Beta_is,xlab="SNP",ylab=expression(beta~"coefficient"))

Recall that in the example only a subset of SNPs mapping to BTA14 are

considered. To improve precision in this example, one may rather provide

the program with a more accurate estimate of the matrix Ωas obtained from

the original study on the complete data sets (with 40 times as many SNPs):

baypass -npop 18 -gfile geno.bta14 -efile bta.pc1 \

-omegafile omega.bta -outprefix anacovis2

The resulting Importance Sampling estimates of the Bayes Factor, the

empirical Bayesian P-value and the underlying regression coeﬃcient 9might

be plotted as follows:

covis2.snp.res=read.table("anacovis2_summary_betai_reg.out",h=T)

graphics.off()

layout(matrix(1:3,3,1))

plot(covis2.snp.res$BF.dB.,xlab="SNP",ylab="BFis (in dB)")

plot(covis2.snp.res$eBPis,xlab="SNP",ylab="eBPis")

plot(covis2.snp.res$Beta_is,xlab="SNP",ylab=expression(beta~"coefficient"))

5.1.3 Analysis under the MCMC covariate mode: MCMC is run

under the STD model

This analysis allows to perform association study under the STD covariate

model by estimating the empirical Bayesian P-value and the underlying re-

gression coeﬃcient using parameters values sampled from MCMC run under

the STD model (Gautier, 2015). Although one may also estimate Ωunder

the STD model, this option has been inactivated in BayPass. As a conse-

quence, an estimate of Ω(e.g., as obtained by a ﬁrst analysis under the core

model of IS covariate mode) must be provided. The example below corre-

sponds to an association analysis with the SMS covariable measured on the

18 French cattle breeds (Gautier, 2015).

baypass -npop 18 -gfile geno.bta14 -efile bta.pc1 \

-covmcmc -omegafile omega.bta -outprefix anacovmcmc

The resulting estimates of the empirical Bayesian P-values, the underly-

ing regression coeﬃcients (posterior mean) and the corrected XtX might be

plotted as follows:

covmcmc.snp.res=read.table("anacovmcmc_summary_betai.out",h=T)

covmcmc.snp.xtx=read.table("anacovmcmc_summary_pi_xtx.out",h=T)$M_XtX

graphics.off()

layout(matrix(1:3,3,1))

plot(covmcmc.snp.res$eBPmc,xlab="SNP",ylab="eBPmc")

plot(covmcmc.snp.res$M_Beta,xlab="SNP",ylab=expression(beta~"coefficient"))

plot(covmcmc.snp.xtx,xlab="SNP",ylab="XtX corrected for SMS")

9Note that one may carry out a calibration of these diﬀerent measures (as detailed for

the XtX in 5.1.1) by analysing a POD together with the covariables:

baypass -npop 18 -gfile G.pods -efile bta.pc1 -omegafile omega.bta -outprefix podcovis

5.1.4 Analysis under the AUX covariate mode: MCMC is run

under the AUX model

This analysis allows to perform association study under the AUX covariate

model by estimating the Bayes Factor (and the underlying regression coef-

ﬁcient) using parameters values sampled from MCMC run under the AUX

model (Gautier, 2015). Although one may also estimate Ωunder the AUX

model, this option has been inactivated in BayPass. As a consequence, an

estimate of Ω(e.g., as obtained by a ﬁrst analysis under the core model of

IS covariate mode) must be provided. The example below corresponds to

an association analysis with the SMS covariable measured on the 18 French

cattle breeds (Gautier, 2015).

baypass -npop 18 -gfile geno.bta14 -efile bta.pc1 \

-auxmodel -omegafile omega.bta -outprefix anacovaux

The resulting estimates of the Bayes Factor, the underlying regression

coeﬃcients (posterior mean) and the corrected XtX might be plotted as fol-

lows:

covaux.snp.res=read.table("anacovaux_summary_betai.out",h=T)

covaux.snp.xtx=read.table("anacovaux_summary_pi_xtx.out",h=T)$M_XtX

graphics.off()

layout(matrix(1:3,3,1))

plot(covaux.snp.res$BF.dB.,xlab="SNP",ylab="BFmc (in dB)")

plot(covaux.snp.res$M_Beta,xlab="SNP",ylab=expression(beta~"coefficient"))

plot(covaux.snp.xtx,xlab="SNP",ylab="XtX corrected for SMS")

One may further introduce spatial dependency among the SNPs by setting

bis = 1 in the Ising prior (Figure 1C) to reﬁne the associated region:

baypass -npop 18 -gfile geno.bta14 -efile bta.pc1 -auxmodel \

-isingbeta 1.0 -omegafile omega.bta -outprefix anacovauxisb1

The resulting estimates of the posterior mean of the each auxiliary vari-

able δiunder both models (AUX model with no SNP spatial dependency

and AUX model Bayes Factor, the underlying regression coeﬃcients (poste-

rior mean) and the corrected XtX might be plotted as follows:

covauxisb1.snp.res=read.table("anacovauxisb1_summary_betai.out",h=T)

graphics.off()

layout(matrix(1:2,2,1))

plot(covaux.snp.res$M_Delta,xlab="SNP",ylab=expression(delta[i]),main="AUX model")

plot(covauxisb1.snp.res$M_Delta,xlab="SNP",ylab=expression(delta[i]),

main="AUX model with isb=1")

5.2 Littorina Pool–Seq read count data

The Littorina Pool–Seq data may be analysed in a similar fashion as the

cattle data above except that one needs to specify the (haploid pool) size ﬁle

using the -poolsizefile option to activate the Pool–Seq mode. Because

the haploid pool sizes are relatively large (= 100) in the example, one may

also increase the initial δof the yij proposal distribution (as a rule of thumbs,

one may set it to a ﬁfth of the minimum pool size). Here is an example of

command to run BayPass under the IS covariate mode (MCMC run under

the core model):

i_baypass -npop 12 -gfile lsa.geno -efile lsa.ecotype \

-poolsizefile lsa.poolsize -d0yij 20 -outprefix lsacovis

6 Credits

BayPass makes use of several functions and subroutines that were previously

developed by other authors. These include:

•the Fortran code for the multiple streams MT19937 Mersenne–Twister

(parallel) Random Number Generator was adapted from the subrou-

tines available in the mt_stream_f90-1.11.tar.gz program written by

Ken-Ichi Ishikawa and available under the New BSD License10 at http:

//theo.phys.sci.hiroshima-u.ac.jp/~ishikawa/PRNG/mt_stream_

f90-1.11/).

•Various functions and subroutines for random number generations that

were adapted from the Alan Miller Fortran module random.f90 avail-

able at: http://jblevins.org/mirror/amiller/ available under the

GNU GPL license.

•the Wishart sampler utilities derived from the fortran wishart library

written by John Burkhardt and available at http://people.sc.fsu.

edu/~%20jburkardt/f_src/wishart/wishart.html under the GNU

GPL license.

•the kracken(3f) Fortran module developped by John S. Urban to

parse command line arguments (available at http://home.comcast.

net/~urbanjost/LIBRARY/libCLI/arguments/krackenhelp.html) un-

der the GNU GPL license.

10http://theo.phys.sci.hiroshima-u.ac.jp/~ishikawa/PRNG/mt_stream_f90-1.

11/LICENSE

I also wish to thank Renaud Vitalis for providing the L

EXtemplate for

this manual and Andrew Beckerman for reporting bugs and advices that

helped to improve the program.

7 Copyright

BayPass is a free software under the GPL- and BSD-compatible CeCILL-B

licence (see http://www.cecill.info/licences/Licence_CeCILL-B_V1-en.

html), and c

INRA.

8 Contact

If you have any question, please feel free to contact me. However, I strongly

recommend you read carefully this manual ﬁrst.

Bibliography

Coop, G., D. Witonsky, A. D. Rienzo, and J. K. Pritchard, 2010 Using en-

vironmental correlations to identify loci underlying local adaptation. Ge-

netics 185: 1411–1423.

Duforet-Frebourg, N., E. Bazin, and M. G. B. Blum, 2014 Genome scans for

detecting footprints of local adaptation using a bayesian factor model. Mol

Biol Evol 31: 2483–2495.

F¨

orstner, W., and B. Moonen, 2003 A metric for covariance matrices. In

Geodesy-The Challenge of the 3rd Millennium. Springer Berlin Heidelberg,

299–309.

Gautier, M., 2015 Genome-wide scan for adaptive divergence and association

with population-speciﬁc covariates. Genetics 201: 1555–1579.

Genz, A., F. Bretz, T. Miwa, X. Mi, F. Leisch, et al., 2015 mvtnorm: Multi-

variate Normal and t Distributions. R package version 1.0-3.

G¨

unther, T., and G. Coop, 2013 Robust identiﬁcation of local adaptation

from allele frequencies. Genetics 195: 205–220.

Hasselman, B., 2015 geigen: Calculate Generalized Eigenvalues of a Matrix

Pair. R package 1.5.

Nicholson, G., A. V. Smith, F. Jonsson, O. Gustafsson, K. Stefansson,

et al., 2002 Assessing population diﬀerentiation and isolation from single-

nucleotide polymorphism data. J Roy Stat Soc B 64: 695–715.

Paradis, E., J. Claude, and K. Strimmer, 2004 Ape: Analyses of phylogenetics

and evolution in r language. Bioinformatics 20: 289–290.

Pickrell, J. K., and J. K. Pritchard, 2012 Inference of population splits

and mixtures from genome-wide allele frequency data. PLoS Genet 8:

e1002967.

R Core Team, 2015 R: A Language and Environment for Statistical Comput-

ing. R Foundation for Statistical Computing, Vienna, Austria.

Riebler, A., L. Held, and W. Stephan, 2008 Bayesian variable selection for

detecting adaptive genomic diﬀerences among populations. Genetics 178:

1817–1829.

Spiegelhalter, D. J., N. G. Best, B. P. Carlin, and A. v. d. Linde, 2002

Bayesian measures of model complexity and ﬁt. Journal of the Royal

Statistical Society. Series B (Statistical Methodology) 64: 583–639.

Wei, T., 2013 corrplot: Visualization of a correlation matrix. R package

version 0.73.

Westram, A. M., J. Galindo, M. A. Rosenblad, J. W. Grahame, M. Panova,

et al., 2014 Do the same genes underlie parallel phenotypic divergence in

diﬀerent littorina saxatilis populations? Mol Ecol 23: 4603–4616.

Appendix A Comparisons of the computational

eﬃciency of the diﬀerent ver-

sion of BayPass

For illustration purposes, Table 1gives computational times obtained when

running the same example (Pool–Seq) analysis for the Littorina read count

example data set (12 pools, 2,500 SNPs) considered in paragraph 5.2. The

multi-threaded version (baypass 2.0) is compared to the initial non-parallel

version (baypass 1.01) with the same options as in paragraph 5.2 (except

for the number of threads). For both versions, both a gfortran and ifort

compiled binaries were considered. All comparisons were done under the

same standard computer running under Linux Debian 7.1.

Version nthreads gfortran binary ifort binary

BayPass 1.01 1 38 min 59 s 12 min 11 s

BayPass 2.0 1 (default) 39 min 48 s 14 min 54 s

BayPass 2.0 4 (-nthreads 4) 11 min 34 s 5 min 40 s

Table 1: Comparisons of the computational eﬃciency of diﬀerent version of BayPass for

the analysis of the Littorina Pool–Seq read count example data set (12 pools, 2,500 SNPs)

considered in paragraph 5.2.

Note that when running on a single core (and for very short runs as

well, not shown), as expected, the baypass 1.01 is slightly more eﬃcient

computationally than the baypass 2.0. Also, the ifort binaries always

outperform the gfortran binaries.

Bay Pass Manual 2.1

Navigation menu

Versions of this User Manual:

Views

Navigation